Задачник по физике. Издание пятое - Чертов А.Г., Воробьев А.А.

Author: Чертов А.Г. Воробьев А.А.

Tags: физика задачи по физике

ISBN: 5-06-001183-6

Year: 1988

Similar

Задачник по физике. Издание шестое

Задачник по физике

Задачник по физике.

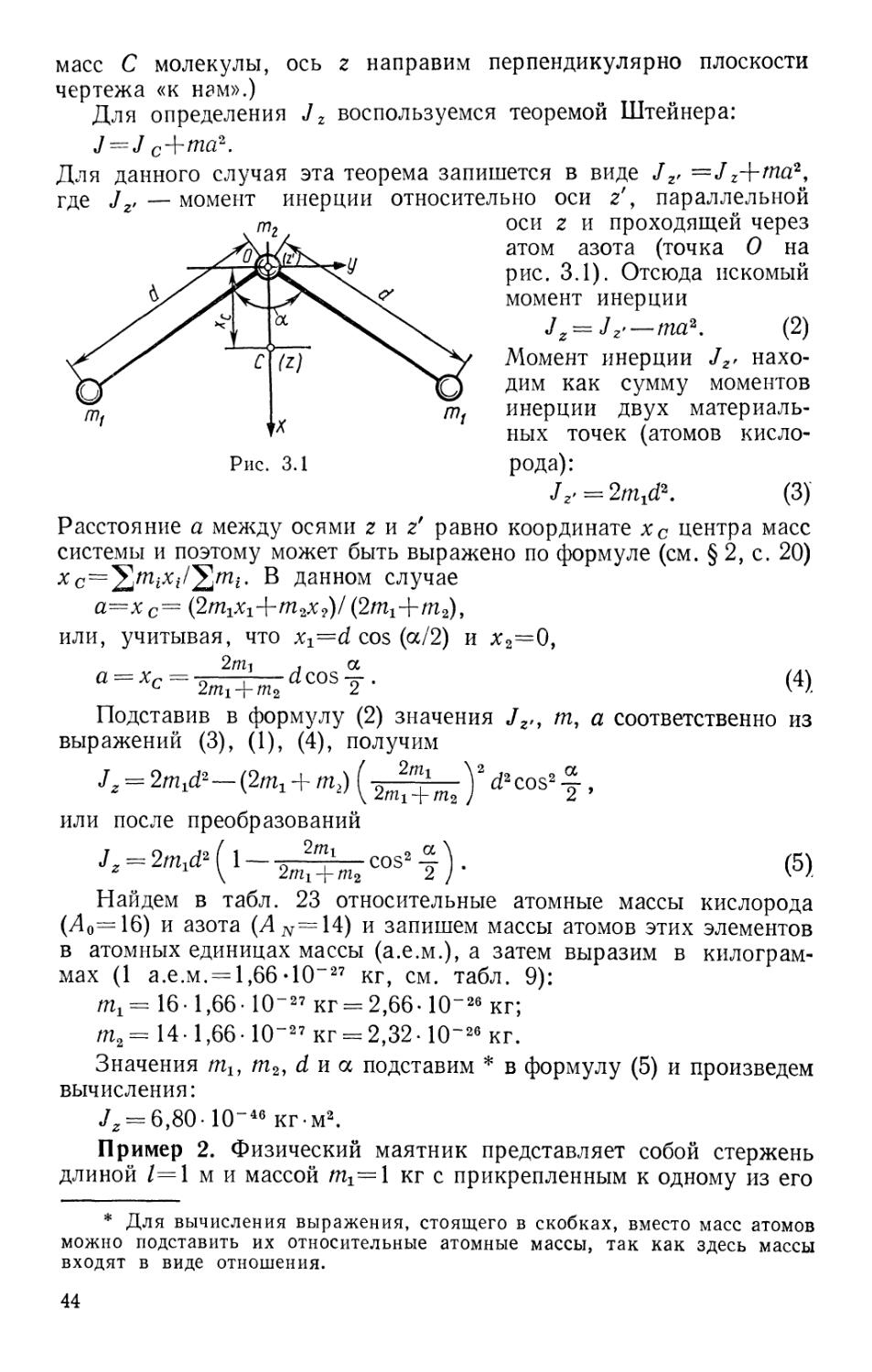
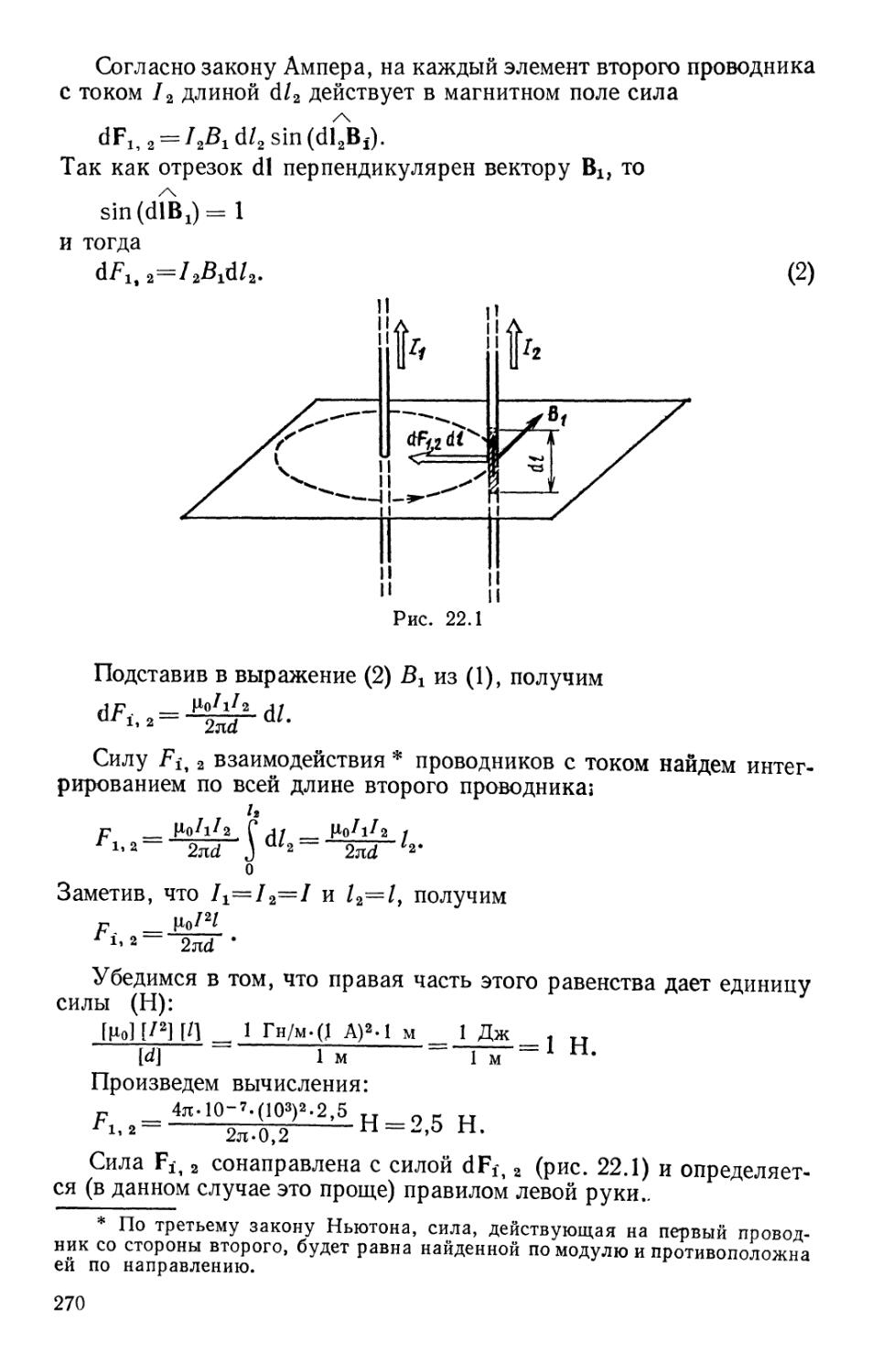
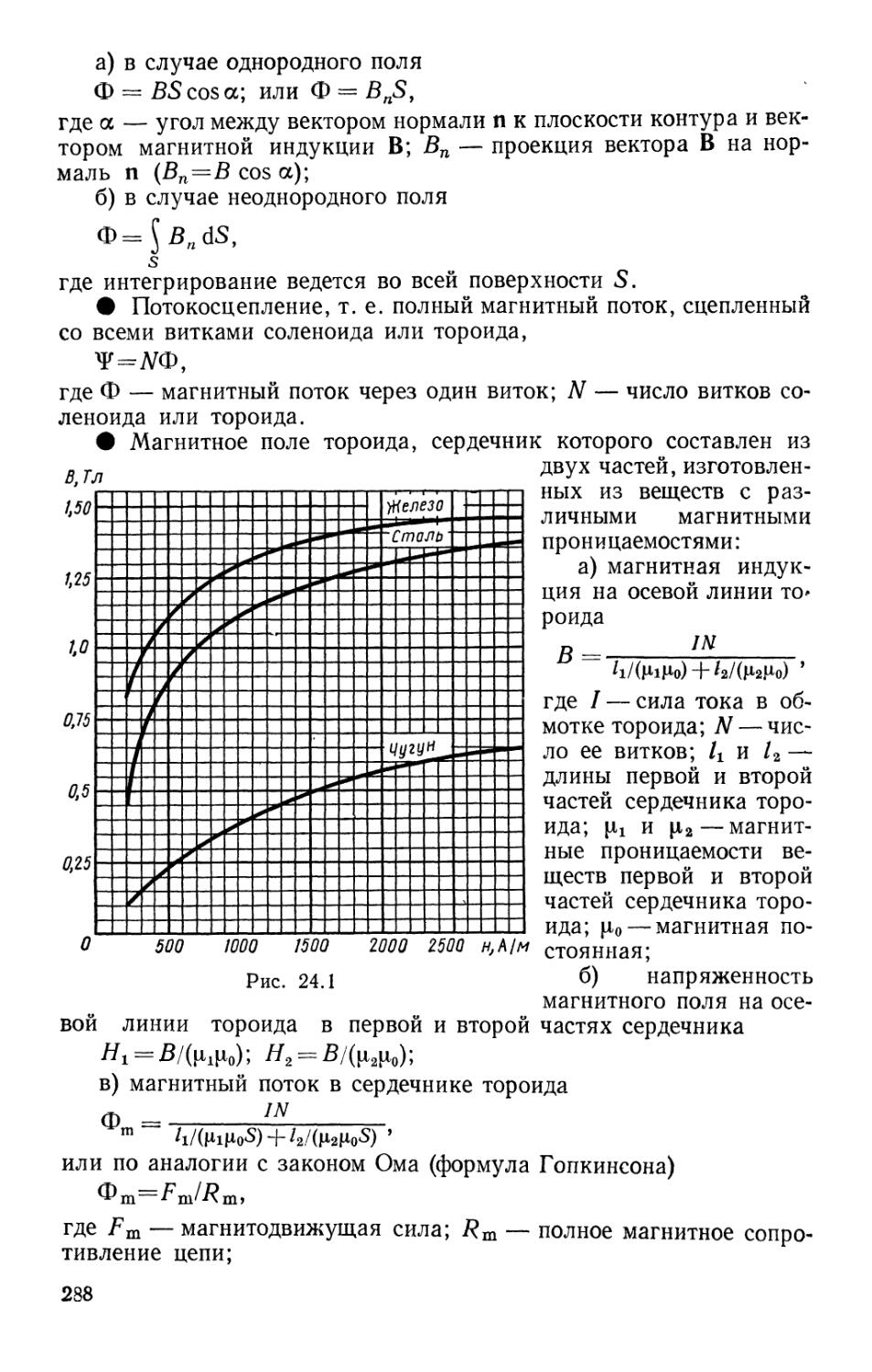
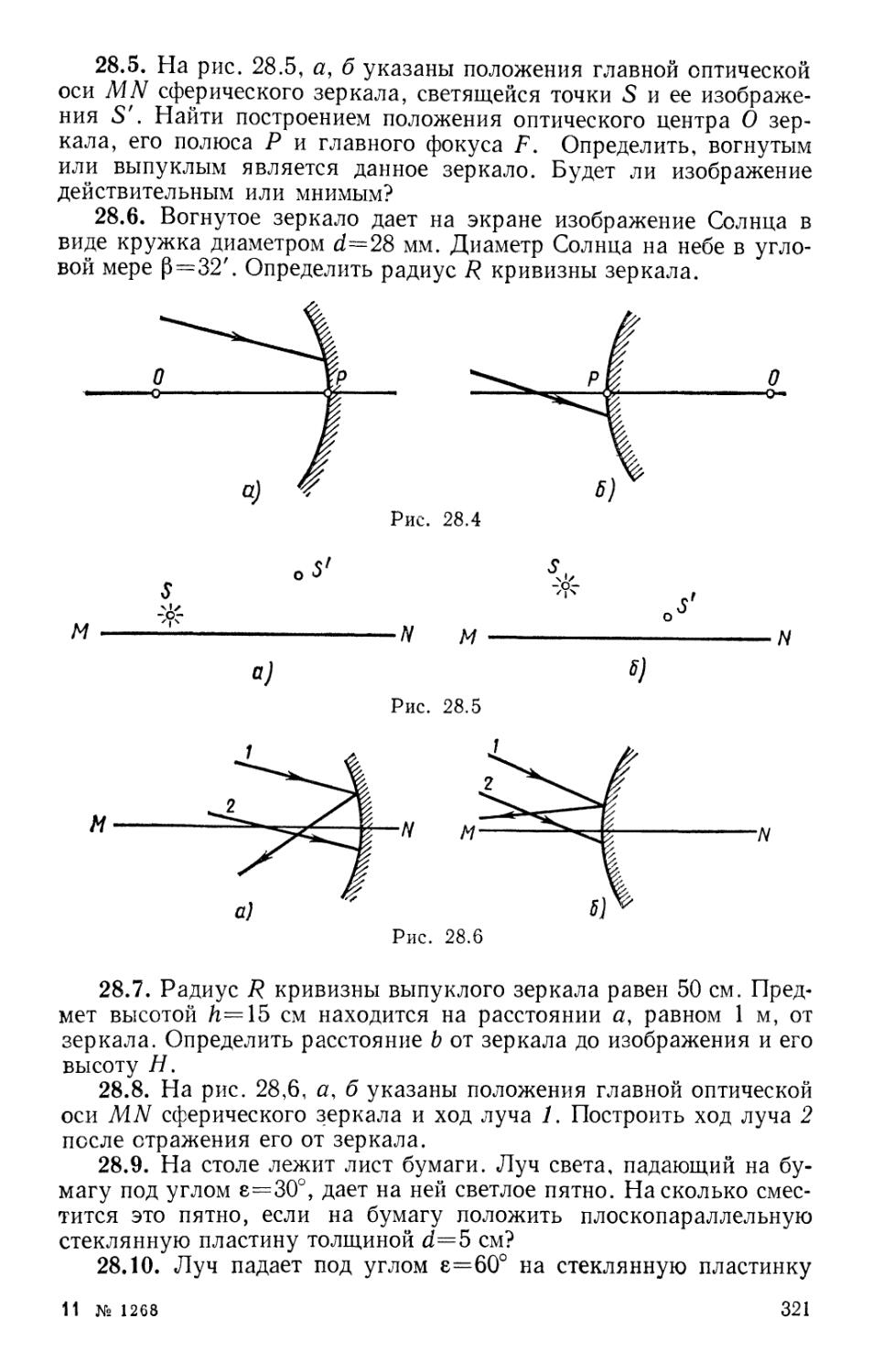
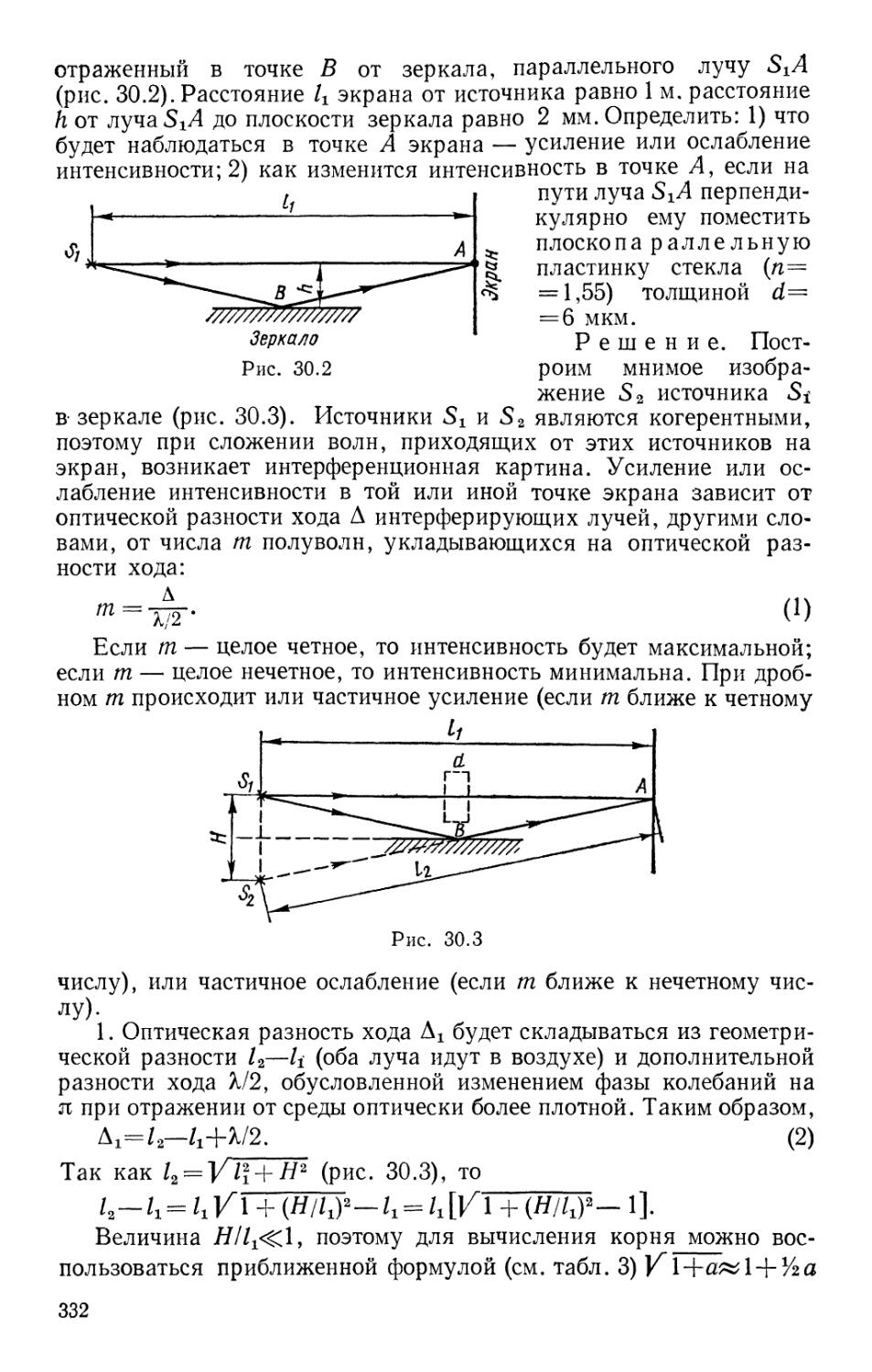
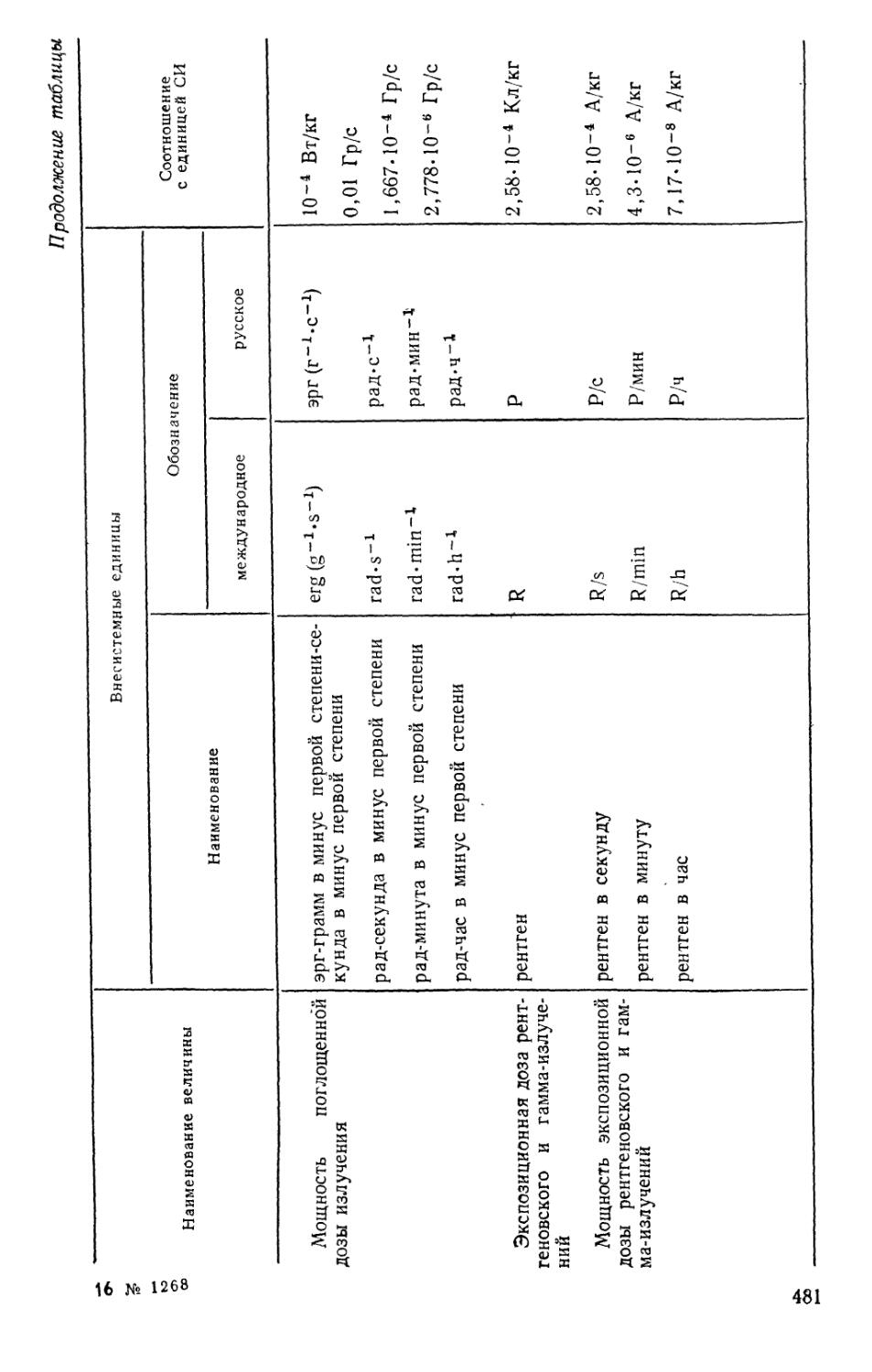
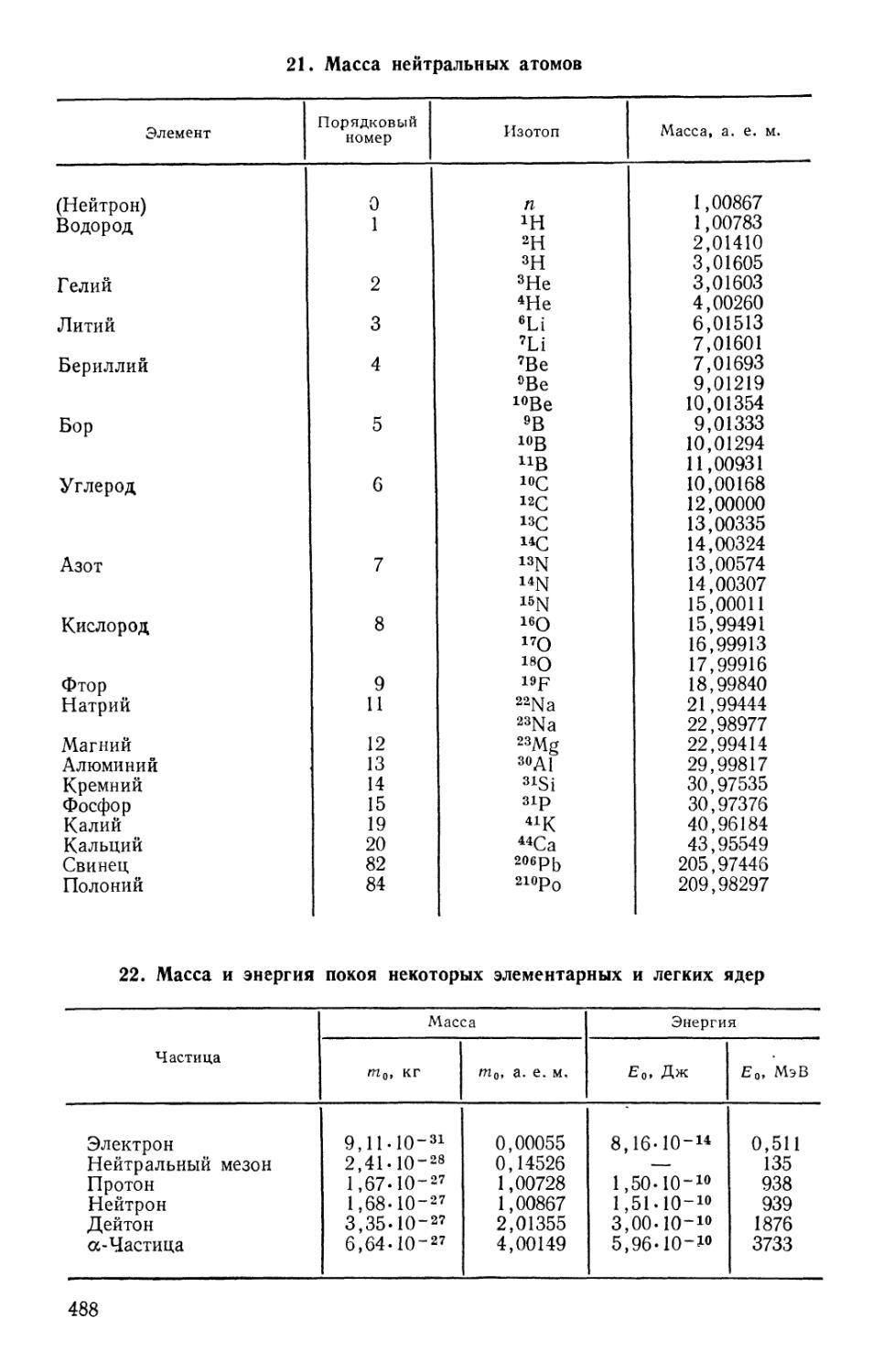
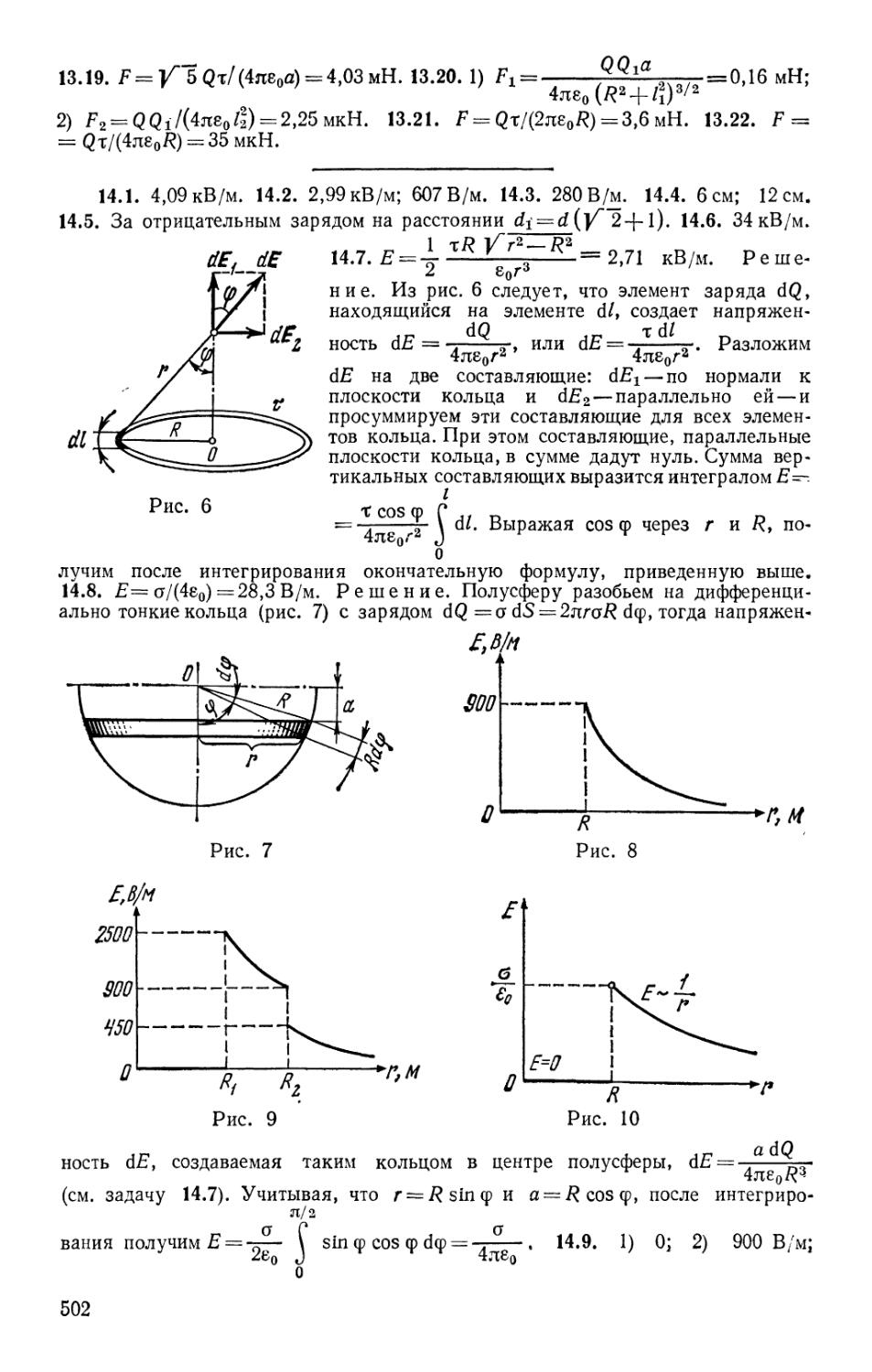
Text

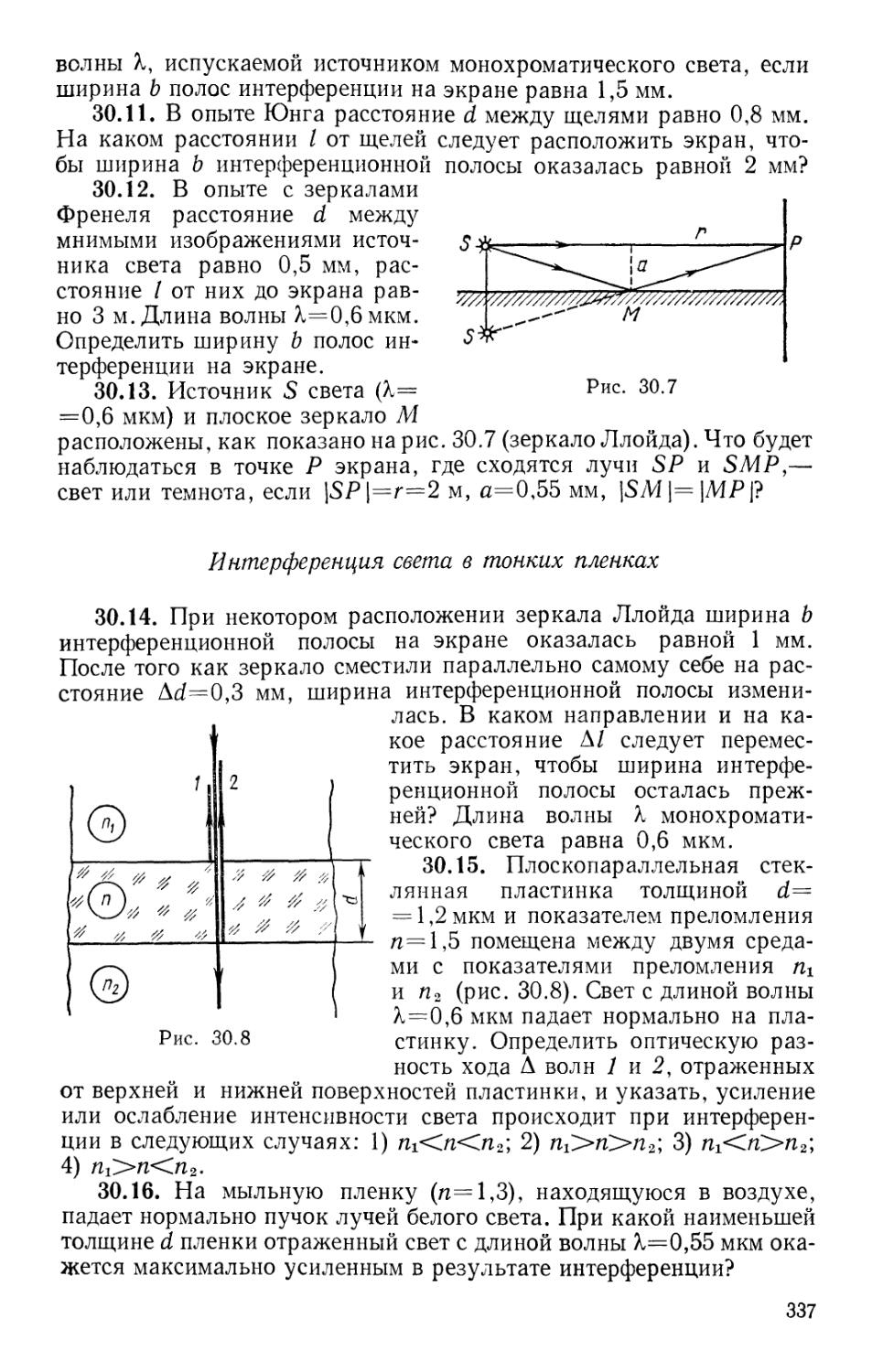
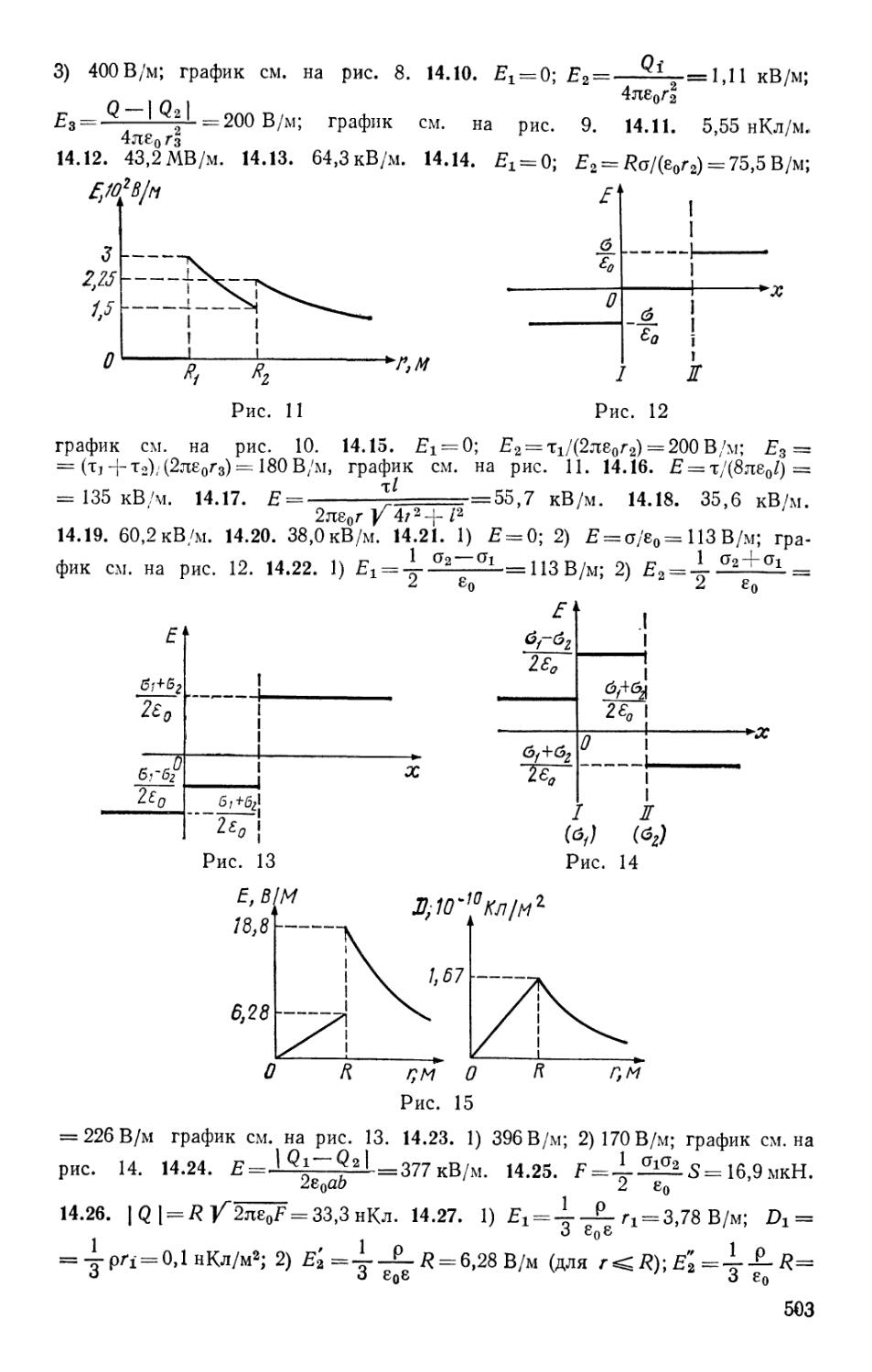
АХ ЧЕРТОВ
А.А.ВОРОББЕВ
ЗАДАЧНИК
ПО
ФИЗИКЕ
ИЗДАНИЕ ПЯТОЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено
Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия
для студентов высших технических
учебных заведений
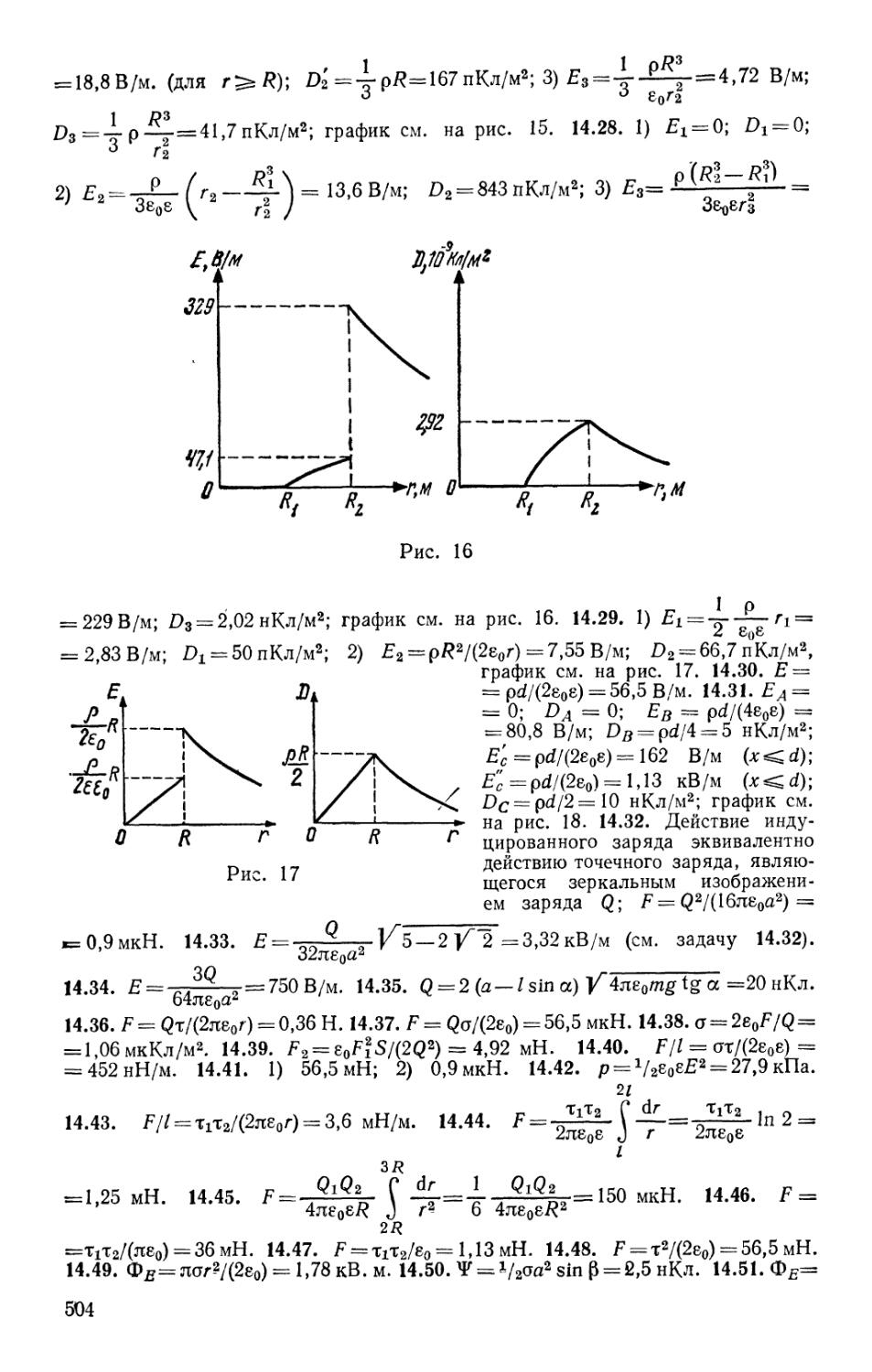
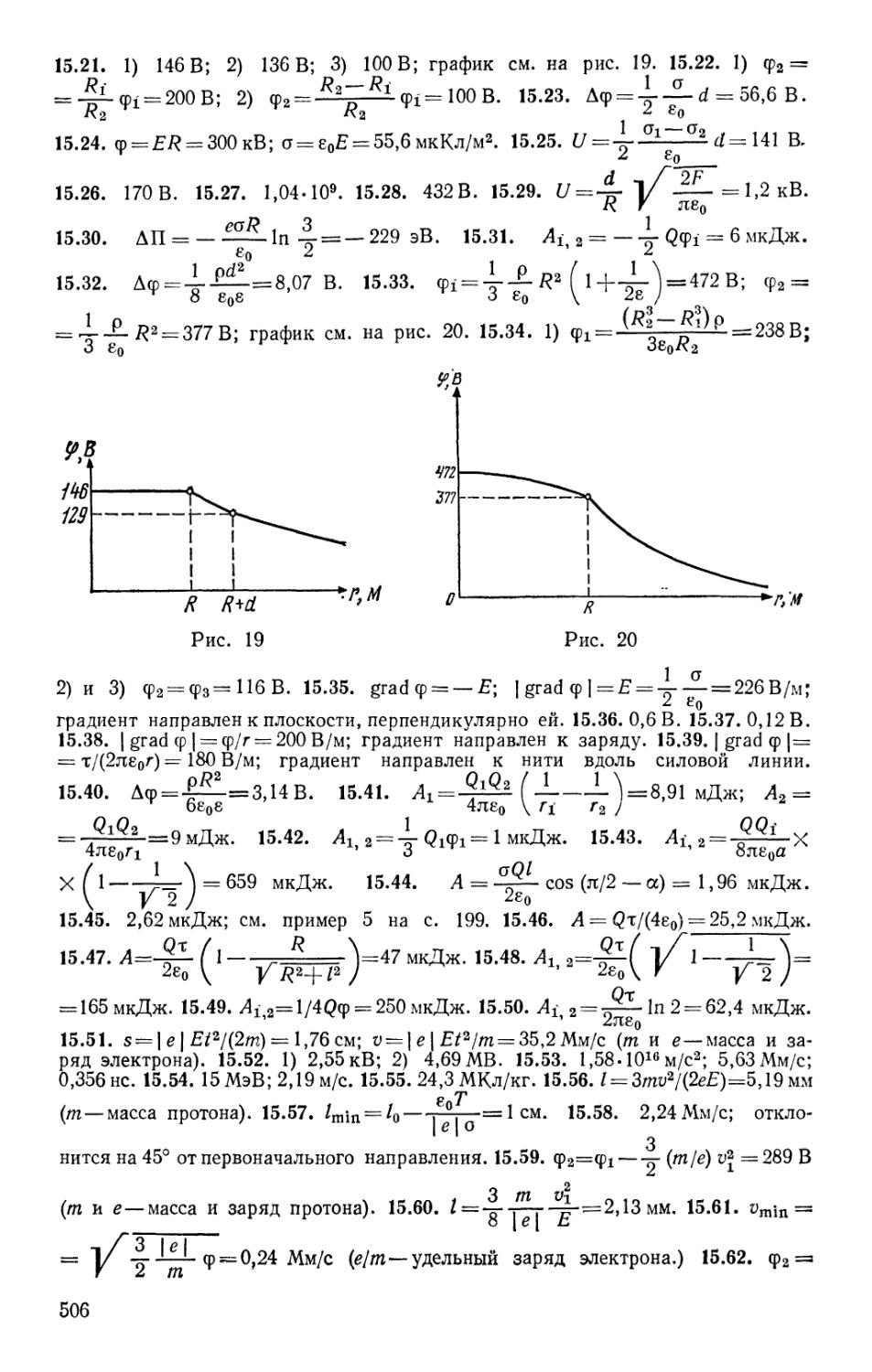
МОСКВА «ВЫСШАЯ ШКОЛА» 1988

ББК 22.31
4 50
УДК 530.1@76)
Рецензент — кафедра общей физики
Московского института электронного машиностроения
(зав. кафедрой— проф. А. Н. Губкин)
Чертов А. Г., Воробьев А. А.
Ч 50 Задачник по физике: Учеб. пособие для студентов вту-
втузов.— 5-е изд., перераб. и доп.— М.: Высш. шк., 1988.—
527 с: ил.
ISBN 5—06—001I83—6.
Задачник составлен в соответствии с действующей программой по курсу фи-
физики для втузов. В каждый раздел включено достаточное количество задач, труд-
трудность которых возрастает с увеличением порядкового номера. В начале каждого
параграфа приводятся основные законы и формулы, даются примеры решения ти-
типовых задач. В 5-м издании D-е — 1981 г.) учтены новые ГОСТы на терминоло-
терминологию, обозначения и единицы, включены новые задачи.
1704000000 D309000000)--213 ББК 22.31
001@1)—88 54—88 530 л
ISBN 5-06—001183—6
) Издательство «Высшая школа», 1981
) Издательство «Высшая школа», 1988,
с изменениями

ОГЛАВЛЕНИЕ
Предисловие 5
Глава 1. Физические основы механики 6
§ 1. Кинематика 6
§ 2. Динамика материальной точки и тела, движущихся посту-
поступательно 19
§ 3. Динамика вращательного движения твердого тела вокруг не-
неподвижной оси 41
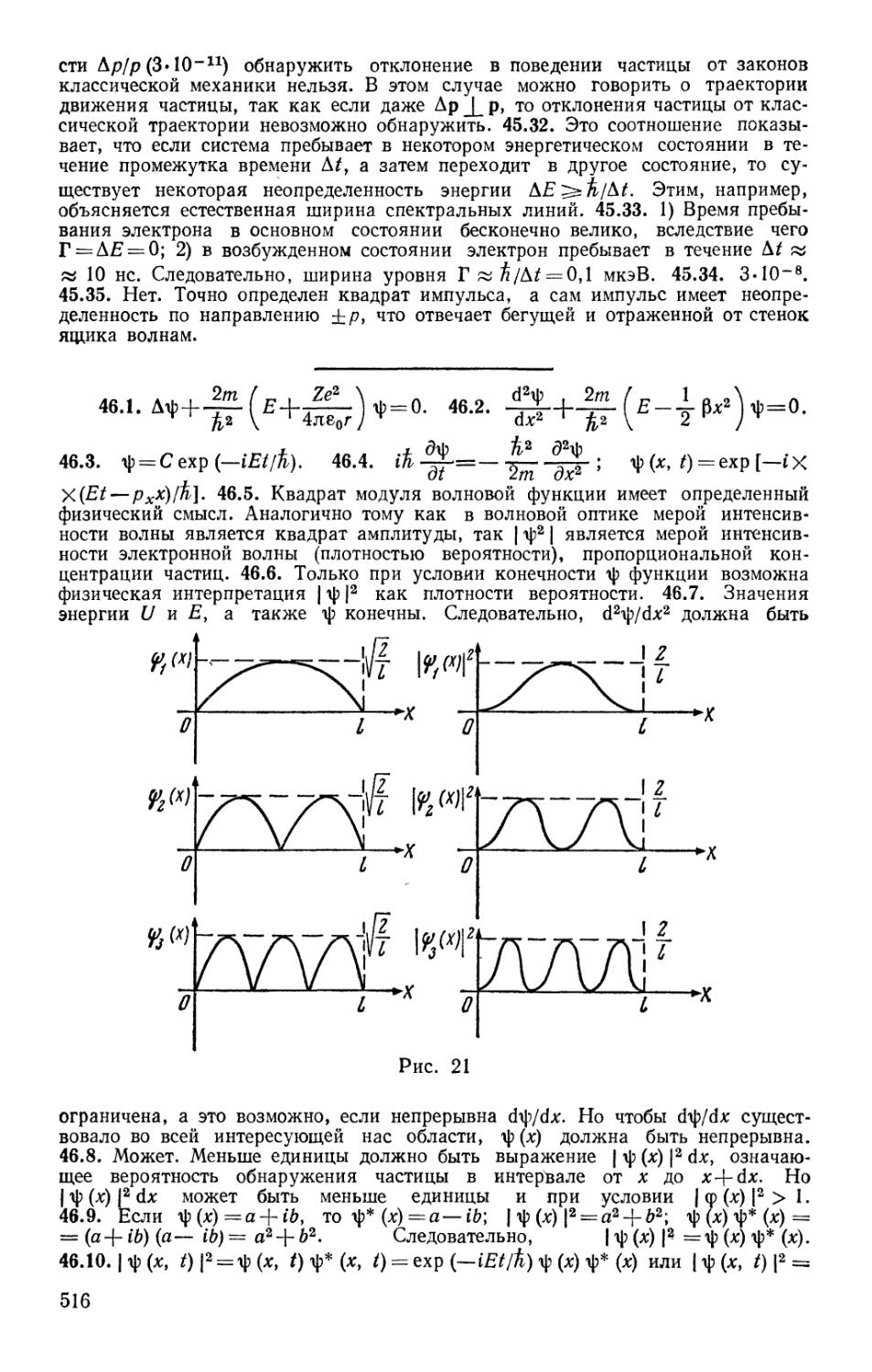
§ 4. Силы в механике 60
§ 5. Релятивистская механика 74
§ 6. Механические колебания 83
§ 7. Волны в упругой среде. Акустика 99
Глава 2. Молекулярная физика и термодинамика 113
§ 8. Молекулярное строение вещества. Законы идеальных газов 113
§ 9. Молекулярно-кинетическая теория газов 121
§ 10. Элементы статистической физики 127
§11. Физические основы термодинамики 140
§ 12. Реальные газы. Жидкости 156
Глава 3. Электростатика 170
§ 13. Закон Кулона. Взаимодействие заряженных тел 170
§ 14. Напряженность электрического поля. Электрическое сме-
смещение 177
§ 15. Потенциал. Энергия системы электрических зарядов. Работа
по перемещению заряда в поле 194
§ 16. Электрический диполь. Свойства диэлектриков 212
§ 17. Электрическая емкость. Конденсаторы 225
§ 18. Энергия заряженного проводника. Энергия электрического
поля 231
Глава 4. Постоянный электрический ток 237
§ 19. Основные законы постоянного тока 237
§ 20. Ток в металлах, жидкостях и газах 247
Глава 5. Электромагнетизм 256
§21. Магнитное поле постоянного тока 256
§ 22. Сила, действующая на проводник с током в магнитном поле 268
§ 23. Сила, действующая на заряд, движущийся в магнитном поле 279
§ 24. Закон полного тока. Магнитный поток. Магнитные цепи 287
§ 25. Работа по перемещению проводника с током в магнитном
поле. Электромагнитная индукция. Индуктивность .... 294
§ 26. Энергия магнитного поля 305
§ 27. Магнитные свойства вещества 310
Глава 6. Оптика 317
§ 28. Геометрическая оптика 317
§ 29. Фотометрия 326
§ 30. Интерференция света 330
§31. Дифракция света 340
§ 32. Поляризация света 348
§ 33. Оптика движущихся тел » . 355

Глава 7 Квантово-оптические явления Физика атома ...... 360
§ 34 Законы теплового излучения 360
§ 35 Фотоэлектрический эффект 364
§ 36. Давление света Фотоны 367
§ 37. Эффект Комптона 370
§ 38. Атом водорода по теории Бора 373
§ 39. Рентгеновское излучение 376
Глава 8. Физика атомного ядра и элементарных частиц 380
§ 40. Строение атомных ядер 380
§ 41. Радиоактивность 385
§ 42. Элементы дозиметрии ионизирующих излучений 389
§ 43. Дефект массы и энергия связи атомных ядер 394
§ 44. Ядерные реакции 397
Глава 9. Элементы квантовой механики . , . . , 403
§ 45. Волновые свойства микрочастиц 403
§ 46. Простейшие случаи движения микрочастиц 410
§ 47. Строение атома 422
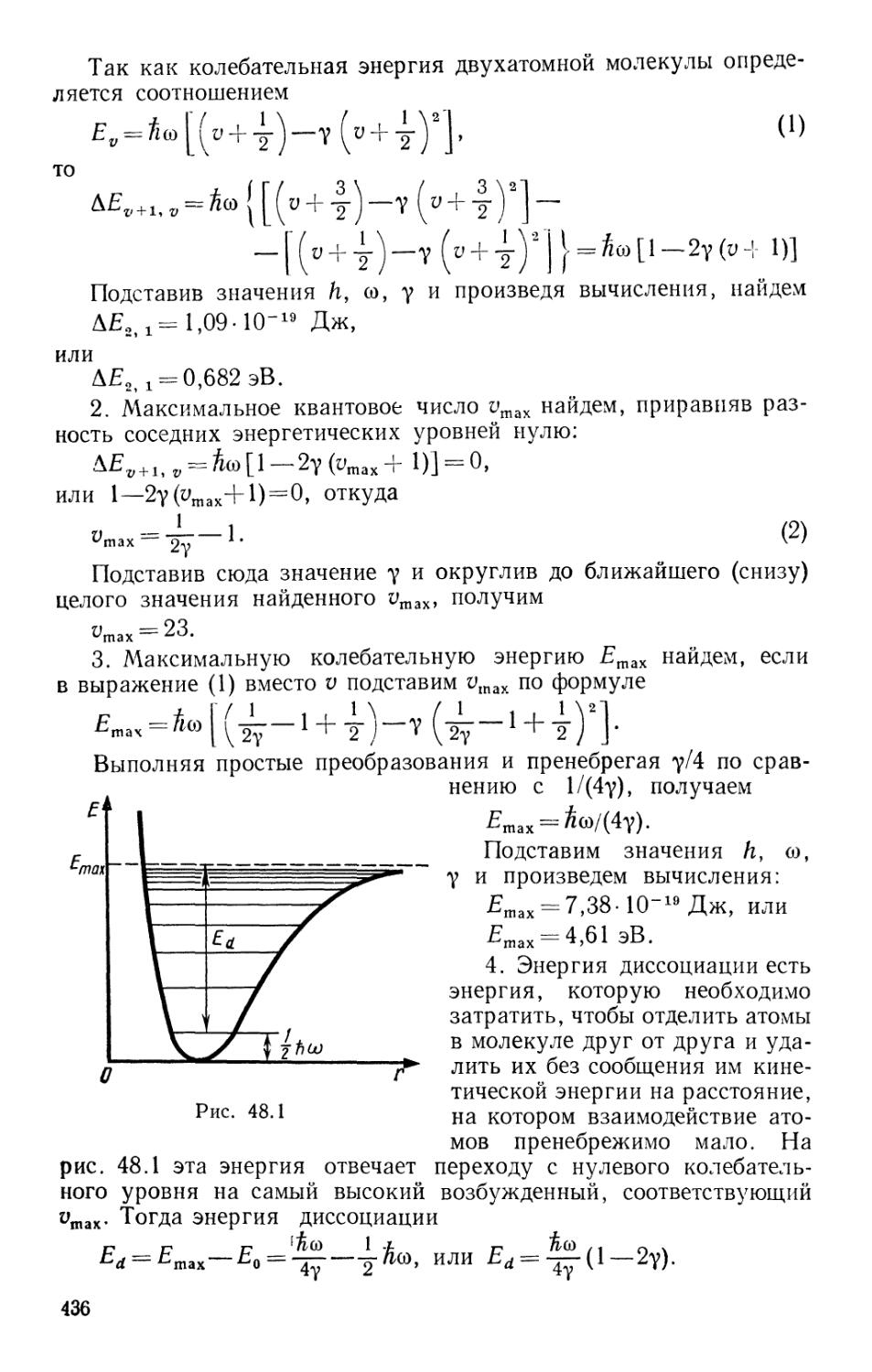
§ 48. Спектры молекул 434
Глава 10. Физика твердого тела , . . 441
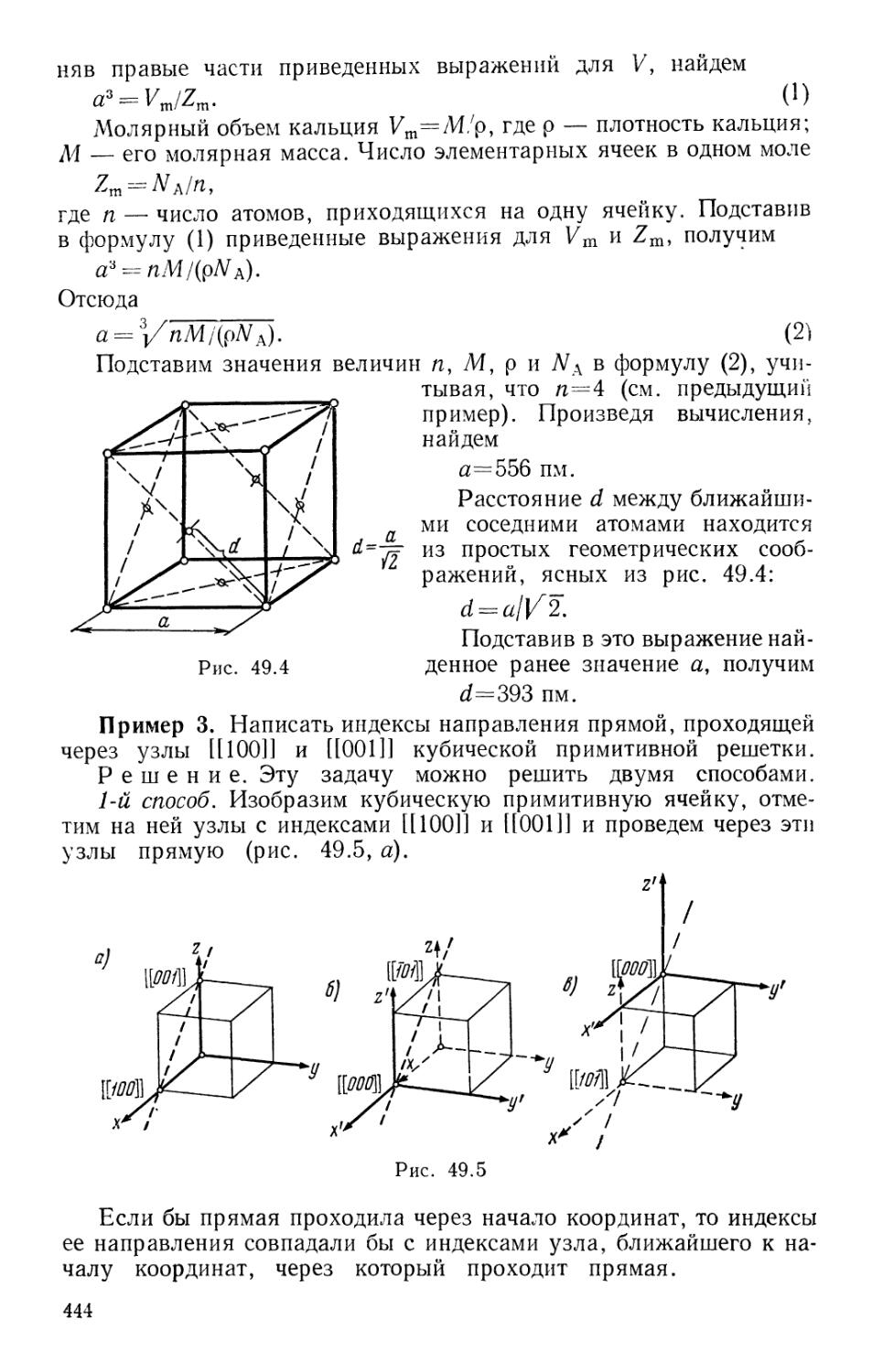
§ 49. Элементы кристаллографии 441
§ 50. Тепловые свойства 449
§51. Электрические и магнитные свойства твердых тел .... 461
Приложения 470
I. О приближенных вычислениях 470
II. Некоторые сведения по математике 471
III. Некоторые сведения о единицах физических величин 473
IV. Таблицы физических величин 477
Ответы . . . 482

ПРЕДИСЛОВИЕ
Пятое издание «Задачника по физике» переработано и в настоя-
настоящем виде соответствует программе курса физики для высших техни-
технических учебных заведений.
Задачи систематизированы по разделам программы. По некото-
некоторым, наиболее трудным задачам в ответах даны указания к решениям
или приведены расчетные формулы. Как и в предыдущем издании,
ответы даны с точностью до трех значащих цифр. С таким же числом
значащих цифр выражены величины в условиях задач, а также в спра-
справочных таблицах. Значащие цифры — нули, стоящие в конце чисел,—
в целях упрощения записи опущены.
В отличие от четвертого издания (М., Высшая школа, 1981) в дан-
данном издании внесен ряд изменений. Из гл. 10 задачи по диэлектрикам
перенесены в гл. 3, задачи по магнитным свойствам вещества — в гл. 5.
Подверглась некоторой переработке и пополнена новыми задачами
гл. 2 «Молекулярная физика и термодинамика». Значительно обновлен
также набор задач по физике атомного ядра.
В связи с переработкой задачника несколько изменилась нумера-
нумерация задач.
Авторы выражают благодарность преподавателям кафедры общей
физики Московского института электронного машиностроения (зав.
кафедрой — проф. А. Н. Губкин). Их ценные советы были использо-
использованы авторами при подготовке задачника к новому изданию.
Авторы

ГЛАВА 1
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
§ 1. КИНЕМАТИКА
Основные формулы
# Положение материальной точки в пространстве задается ра-
радиусом-вектором г:
r=ix+jy+kz,
где i, j, k — единичные векторы направлений (орты); х,у,г — коор-
координаты точки.
Кинематические уравнения движения в координатной форме:
*=М0; у=Ш; г=/.@.
где t — время.
• Средняя скорость
где Аг — перемещение материальной точки за интервал времени
At.
Средняя путевая * скорость
As
где As — путь, пройденный точкой за интервал времени А/.
Мгновенная скорость
dx du dz
где vx = -T7-; Vy^fa* Vz=z~&F— ПР°^КДИИ скорости v на оси
координат.
Модуль скорости
• Ускорение
dv
где а =-^-; а =-^-: аУ =-?*-— проекции ускорения а на
х dt у at г at
оси координат.
* См. об этом термине, например, в кн.: Детлаф Л. Л. и др. Курс фи-
физики. М., 1973. Т. I. С. 17.

Модуль ускорения
У X 1 у 1^ 2*
При криволинейном движении ускорение можно представить как
сумму нормальной ап и тангенциальной ат
составляющих (рис. 1.1): ^^-——
Модули этих ускорений: ап а
a»=i' а*=ж> «=v^+*. Рис-1Л
где R — радиус кривизны в данной точке траектории.
• Кинематическое уравнение равномерного движения мате-
материальной точки вдоль оси х
где х0 — начальная координата; t — время. При равномерном дви-
движении
v= const и а=0.
• Кинематическое уравнение равнопеременного движения (а=*
в= const) вдоль оси х
x=xo+vot+at2/2,
где v0 — начальная скорость; t — время.
Скорость точки при равнопеременном движении
v=vo+at.
0 Положение твердого тела (при заданной оси вращения) опре-
определяется углом поворота (или угловым перемещением) ср.
Кинематическое уравнение вращательного движения
ф=/@-
О Средняя угловая скорость
где Аф — изменение угла поворота за интервал времени At.
Мгновенная угловая скорость *
Угловое ускорение *
dco
"dT-
Кинематическое уравнение равномерного вращения
где ф0 — начальное угловое перемещение; / — время.
При равномерном вращении
и 8=0.
* Угловая скорость и угловое ускорение являются аксиальными век-
векторами, их направления совпадают с осью вращения.

Частота вращения
n=N/t9 или п=1/Т,
где N — число оборотов, совершаемых телом за время t\ T — период
вращения (время одного полного оборота).
О Кинематическое уравнение равнопеременного вращения
(е=const)
где со о — начальная угловая скорость; t — время.
Угловая скорость тела при равнопеременном вращении
• Связь между линейными и угловыми величинами, характери-
характеризующими вращение материальной точки, выражается следующими
формулами:
путь, пройденный точкой по дуге окружности радиусом R,
s—yR (ф — угол поворота тела);
скорость точки линейная
ускорение точки:
тангенциальное
ax = sR\ aT = [eR];
нормальное
an = @2R; an=—co2R.
Примеры решения задач
Пример 1. Кинематическое уравнение движения материальной
точки по прямой (ось л:) имеет вид x=A+Bt+Ct3, где А=4 м, В=
=2 м/с, С=—0,5 м/с2. Для момента времени U=2 с определить:
1) координату Xi точки, 2) мгновенную скорость vlt 3) мгновенное
ускорение а±.
Решение. 1. Координату точки, для которой известно кине-
кинематическое уравнение движения, найдем, подставив в уравнение
движения вместо t заданное значение времени U:
Xl = A + Bt1 + Ct\.
Подставим в это выражение значения Л, J5, С, U и произведем вы-
вычисления:
^=D+2-2—0,5 -23) м=4 м.
2. Мгновенную скорость в произвольный момент времени найдем,
продифференцировав координату х по времени: v = -? = B + 3Ct2.
Тогда в заданный момент времени t± мгновенная скорость
v1=B+3Ctl
Подставим сюда значения В, С, U и произведем вычисления:
?>!=—4 м/с.
8

Знак минус указывает на то, что в момент времени tx=2 с точка дви-
движется в отрицательном направлении координатной оси.
3. Мгновенное ускорение в произвольный момент времени най-
найдем, взяв вторую производную от координаты х по времени:
a = -g^-==-^-==6CY. Мгновенное ускорение в заданный момент вре-
времени U равно
Подставим значения С, t± и произведем вычисления:
^=(—6-0,5-2) м/с—6 м/с.
Знак минус указывает на то, что направление вектора ускорения
совпадает с отрицательным направлением координатной оси, при-
причем в условиях данной задачи это имеет место для любого момента
времени.
Пример 2. Кинематическое уравнение движения материальной
точки по прямой (ось х) имеет вид x=A-\-Bt-\-Ct2, где А=5 м, В=
=4 м/с, С——1 м/с2. 1. Построить график зависимости координаты
х и пути s от времени. 2. Определить среднюю скорость <vx> за ин-
интервал времени от tx=l с до t2=6 с. 3. Найти среднюю путевую ско-
скорость <и> за тот же интервал времени.
Решение. 1. Для построения графика зависимости коорди-
координаты точки от времени найдем характерные значения координаты —
начальное и максимальное и моменты времени, соответствующие ука-
указанным координатам и координате, равной нулю.
Начальная координата соответствует моменту t=0. Ее значение
равно
xo = x\t=o = A=^5 м.
Максимального значения координата достигает в тот момент,
когда точка начинает двигаться обратно (скорость меняет знак).
Этот момент времени найдем, приравняв нулю первую производную
от координаты по времени: v = — = В + 2Ct = 0, откуда
t=—B/2C=2 с.
Максимальная координата
хты = ^// = 2 = 9 М.
Момент времени t, когда координата л:=0, найдем из выражения
x=A+Bt+Ct2=0.
Решим полученное квадратное уравнение относительно /:
, _— в±
1
1 — 2С '
Подставим значения Л, В, С и произведем вычисления:
*=B±3) с.
Таким образом, получаем два значения времени: t'=5 с и f==
*=—1 с. Второе значение времени отбрасываем, так как оно не удов-
удовлетворяет условию задачи (^0)

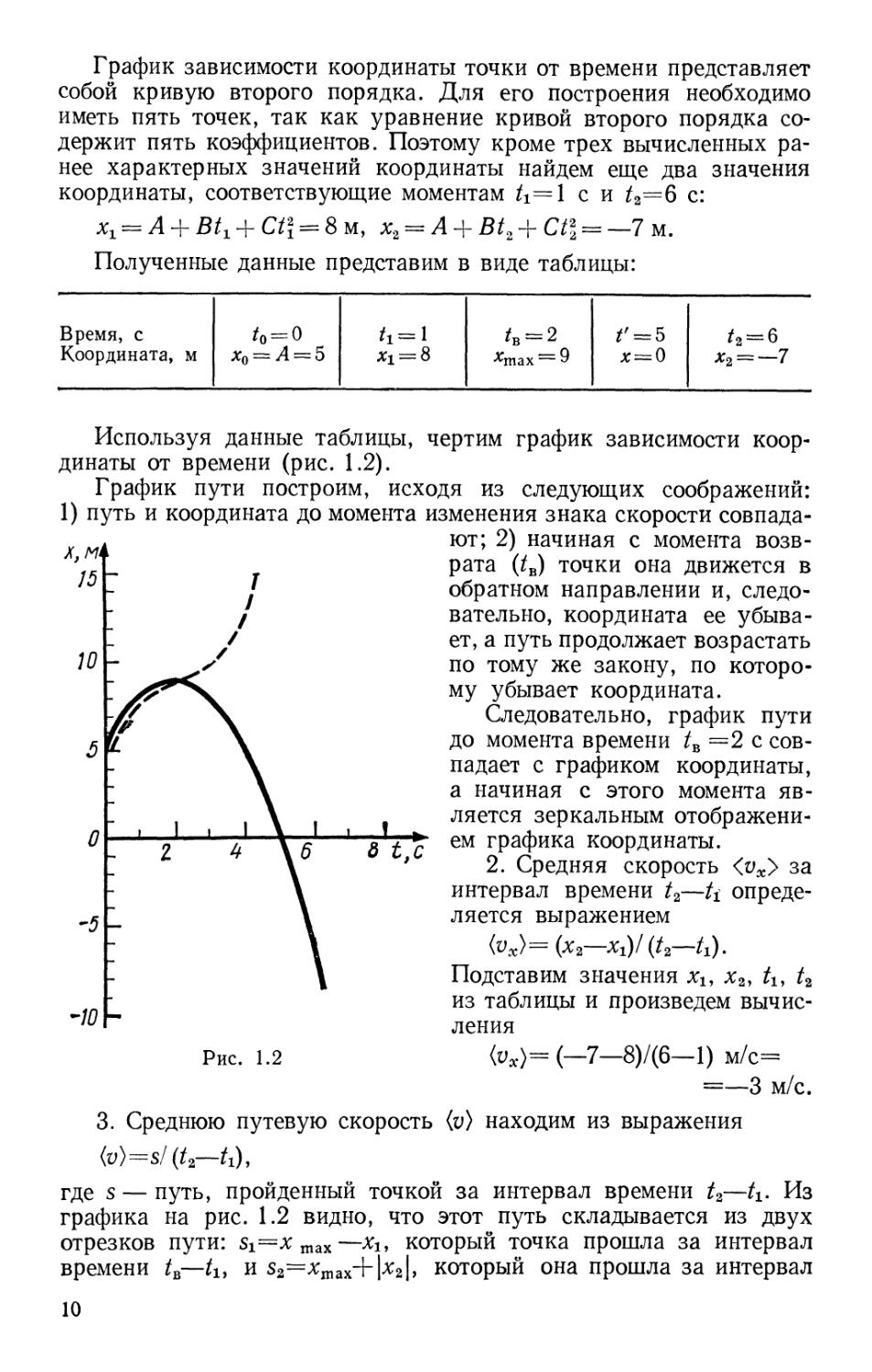
График зависимости координаты точки от времени представляет
собой кривую второго порядка. Для его построения необходимо
иметь пять точек, так как уравнение кривой второго порядка со-
содержит пять коэффициентов. Поэтому кроме трех вычисленных ра-
ранее характерных значений координаты найдем еще два значения
координаты, соответствующие моментам ^=1 с и ^2=6 с:
хг = А + Btx + Ct\ = 8 м, х2 = А + Bt2 -f Ct\ = —7 м.
Полученные данные представим в виде таблицы:
Время, с
Координата, м
о
х0 = А = 5
х2 = -7
Используя данные таблицы, чертим график зависимости коор-
координаты от времени (рис. 1.2).
График пути построим, исходя из следующих соображений:
1) путь и координата до момента изменения знака скорости совпада-
совпадают; 2) начиная с момента возв-
возврата (/в) точки она движется в
обратном направлении и, следо-
следовательно, координата ее убыва-
убывает, а путь продолжает возрастать
по тому же закону, по которо-
которому убывает координата.
Следовательно, график пути
до момента времени /в =2 с сов-
совпадает с графиком координаты,
а начиная с этого момента яв-
является зеркальным отображени-
отображением графика координаты.
2. Средняя скорость <vx> за
интервал времени /2—1± опреде-
определяется выражением
Wx/™ V^2 X\)l \t2 ty) .
Подставим значения хг, х2у tly t2
из таблицы и произведем вычис-
вычисления
Рис. 1.2 (vx)=(—7—8)/F—1) м/с=
=—3 м/с.
3. Среднюю путевую скорость (v) находим из выражения
где s — путь, пройденный точкой за интервал времени t2—U. Из
графика на рис. 1.2 видно, что этот путь складывается из двух
отрезков пути: S!=x max—хи который точка прошла за интервал
времени tB—tu и s2=xmax+\x2\, который она прошла за интервал
10

t2—tB. Таким образом, путь
s^s^s^ (хтах—х1) + (хтах + | х21) = 2хтах + | х2 \—xt.
Подставим в это выражение значения *i,"|*2|, #max и произведем вы-
вычисления :
(s>=B-9+7—8) м=17 м.
Тогда искомая средняя путевая скорость
<и>=17/F—1) м=3,4 м.
Заметим, что средняя путевая скорость всегда положительна.
Пример 3. Автомобиль движется по закруглению шоссе, имею-
имеющему радиус кривизны R=50 м. Уравнение * движения автомобиля
t(f)=A+Bt+CP, где А = 10 м, 5=10 м/с, С=—0,5 м/с2. Найти:
1) скорость v автомобиля, его тангенциальное ат, нормальное ап и
полное а ускорения в момент времени ^=5 с; 2) длину пути s и мо-
модуль перемещения |Дг| автомобиля за интервал времени т=10 с,
отсчитанный с момента начала движения.
Решение. 1. Зная уравнение движения, найдем скорость,
взяв первую производную от координаты по времени:
v = -~ = /J + 2Ct. Подставим в это выражение значения 5, С, t и
произведем вычисления:
v—Ъ м/с.
Тангенциальное ускорение найдем, взяв первую производную от
скорости по времени: а% = -jt- = 2C. Подставив значение С, получим
ах = — 1 м/с2.
Нормальное ускорение определяется по формуле an=v2/R.
Подставим сюда найденное значение скорости и заданное значение
радиуса кривизны траектории и произведем вычисления:
ап=0,5 м/с2.
Полное ускорение, как это видно из рис. 1.1, является геомет-
рической суммой ускорений ат иап: а=ат+ап. Модуль ускорения
а = V а\ + а2п. Подставив в это выражение найденные значения ах
и ап, получим
а=1,12м/са.
2. Чтобы определить путь s, пройденный автомобилем, заметим,
что в случае движения в одном направлении (как это имеет место
в условиях данной задачи) длина пути s равна изменению криволи-
криволинейной координаты 1> т. е.
s=g(T)_g(O), или s=A+Bx+Cx2—A=Bx+Cx\
Подставим в полученное выражение значения 5, С, т и произведем
вычисления:
s=50 м.
* В заданном уравнении движения 5 означает криволинейную коорди-
координату, отсчитанную от некоторой начальной точки на окружности.
11

Модуль перемещения, как это видно из рис. 1.3, равен
I Ar |=2/? sin (а/2),
где а — угол между радиусами-векторами, определяющими началь-
начальное 1@) и конечное |(т) положения автомашины на траектории.
Этот угол (в радианах) находим как отношение длины пути s к ра-
радиусу кривизны R траектории, т. е. а—
=s/R. Таким образом,
Подставим сюда значения R, s и
произведем вычисления:
|Дг| = 47,9 м.
Пример 4. Маховик, вращавшийся с
постоянной частотой по=1О с, при
Рис. 1.3 торможении начал вращаться равноза-
медленно. Когда торможение прекрати-
прекратилось, вращение маховика снова стало равномерным, но уже с час-
частотой п=6 с. Определить угловое ускорение 8 маховика и про-
продолжительность t торможения, если за время равнозамедленного
движения маховик сделал N=50 оборотов.
Решение. Угловое ускорение маховика связано с начальной
со0 и конечной со угловыми скоростями соотношением со2—со2,—
=2еф, откуда 8= (со2—со?)/Bф). Но так как <p=2ji#, со=2яя, то
^ СО*'—СОо 3l\fl —По)
8 2ф = N '
Подставив значения я, я, я0, Af и вычислив, получим
8-3,14 (б2—102)/50 Рад/с2=—4,02 рад/с2.
Знак минус указывает на то, что маховик вращался замедленно.
Определим продолжительность торможения, используя форму-
формулу, связывающую угол поворота ф со средней угловой скоростью
(со) вращения и временем /: ф=(со)/. По условиям задачи, угловая
скорость линейно зависит от времени и поэтому можно написать
(со)= (соо+со)/2, тогда
Ф=(со0+со)//2=я (no+n)t,
откуда
, Ф 2N
п(щ + ) гго + п
Подставив числовые значения и произведя вычисления, получим
2.50 _fi2.
'-"То+6^ '
Задачи
Прямолинейное движение
1.1. Две прямые дороги пересекаются под углом а=60°. От пере-
перекрестка по ним удаляются машины: одна со скоростью 1^=60 км/ч,
другая со скоростью и2=80 км/ч. Определить скорости v' и v", с ко-
12

торыми одна машина удаляется от другой. Перекресток машины
прошли одновременно.
1.2. Точка двигалась в течение /х= 15 с со скоростью t;x=5 м/с,
в течение t2=l0 с со скоростью v2=8 м/с и в течение ts=6 с со ско-
скоростью ^з^О м/с. Определить среднюю путевую скорость (v) точки.
1.3. Три четверти своего пути автомобиль прошел со скоростью
?>1=60 км/ч, остальную часть пути — со скоростью t^^SO км/ч. Ка-
Какова средняя путевая скорость (v) автомобиля?
1.4. Первую половину пути тело двигалось со скоростью vx~
=2 м/с, вторую — со скоростью г/2—8 м/с. Определить среднюю
путевую скорость (v).
1.5. Тело прошло первую половину пути за время U=2 с, вто-
вторую — за время t2=8 с. Определить среднюю путевую скорость
(v) тела, если длина пути s=20 м.
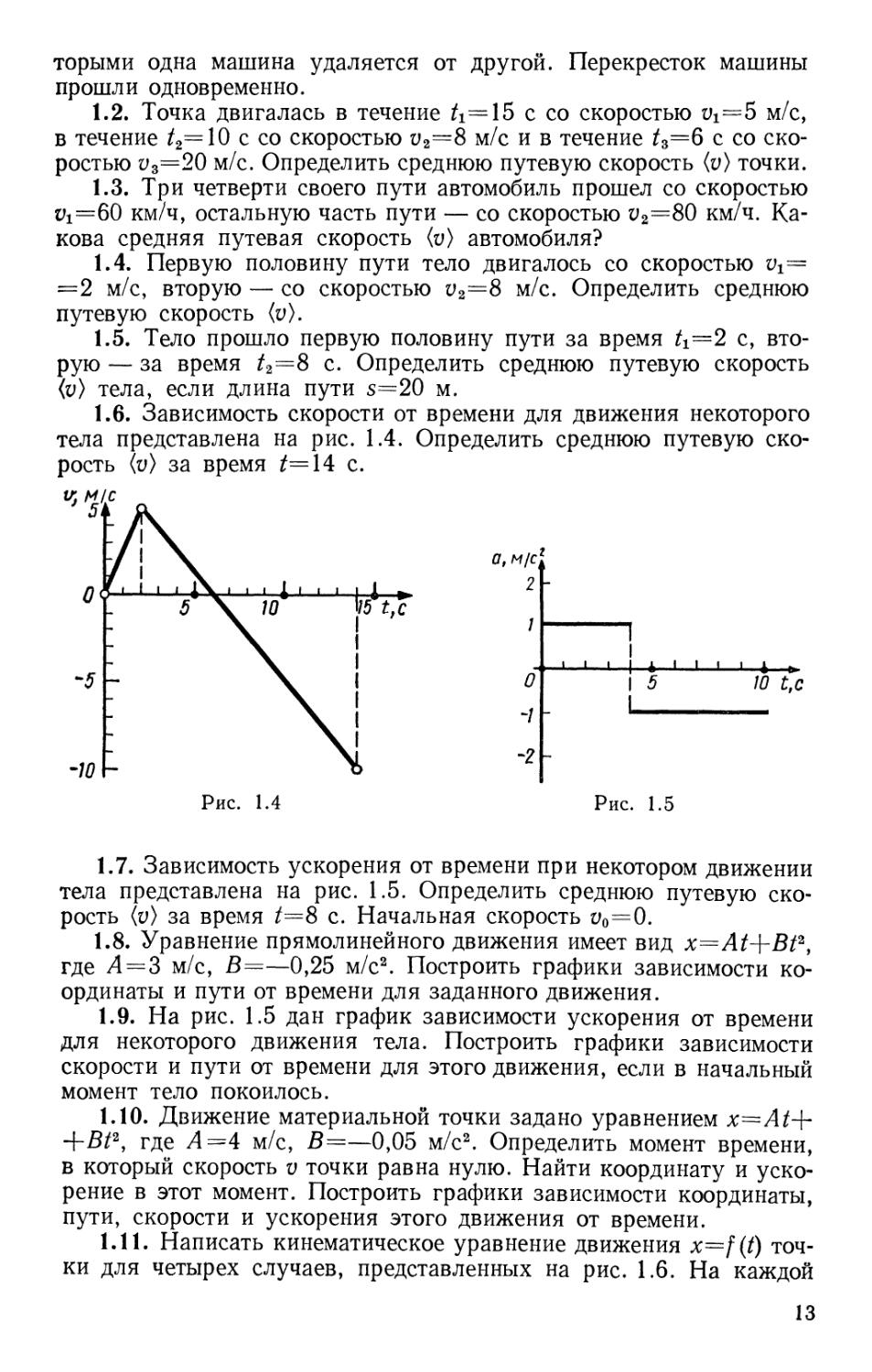
1.6. Зависимость скорости от времени для движения некоторого
тела представлена на рис. 1.4. Определить среднюю путевую ско-
скорость (v) за время ^=14 с.
о, м/с
2
-10 h
0
-2
I I I I X I I I
I 5
Ю t,c
Рис. 1.4
Рис. 1.5
1.7. Зависимость ускорения от времени при некотором движении
тела представлена на рис. 1.5. Определить среднюю путевую ско-
скорость (v) за время ^=8 с. Начальная скорость vo=O.
1.8. Уравнение прямолинейного движения имеет вид x=At-{-Bt2t
где А=3 м/с, В=—0,25 м/с2. Построить графики зависимости ко-
координаты и пути от времени для заданного движения.
1.9. На рис. 1.5 дан график зависимости ускорения от времени
для некоторого движения тела. Построить графики зависимости
скорости и пути от времени для этого движения, если в начальный
момент тело покоилось.
1.10. Движение материальной точки задано уравнением x=At-\-
-\-Bt2, где А =4 м/с, В=—0,05 м/с2. Определить момент времени,
в который скорость v точки равна нулю. Найти координату и уско-
ускорение в этот момент. Построить графики зависимости координаты,
пути, скорости и ускорения этого движения от времени.
1.11. Написать кинематическое уравнение движения x=f(t) точ-
точки для четырех случаев, представленных на рис. 1.6. На каждой
13

позиции рисунка — а, б, в, г — изображена координатная ось Ох,
указаны начальные положение х0 и скорость v0 материальной точки
Л, а также ее ускорение а.
1.12. Прожектор О (рис. 1.7) установлен на расстоянии /=100 м
от стены АВ и бросает светлое пятно на эту стену. Прожектор вра-
вращается вокруг вертикальной оси, делая один оборот за время Т=
=20 с. Найти: 1) уравнение движения светлого пятна по стене в те-
течение первой четверти оборота; 2) скорость v, с которой светлое пят-
пятно движется по стене, в момент времени t—2 с. За начало отсчета
принять момент, когда направление луча совпадает с ОС.
А
с в
у///////////////////////////////.
ко
' \ 1
\ /
W
Рис. 1.6
Рис. 1.7
1.13. Рядом с поездом на одной линии с передними буферами паро-
паровоза стоит человек. В тот момент, когда поезд начал двигаться с ус-
ускорением а=0,1 м/с2, человек начал идти в том же направлении со
скоростью 0=1,5 м/с. Через какое время t поезд догонит человека?
Определить скорость v± поезда в этот момент и путь, пройденный за
это время человеком.
1.14. Из одного и того же места начали равноускоренно двигаться
в одном направлении две точки, причем вторая начала свое движе-
движение через 2 с после первой. Первая точка двигалась с начальной
скоростью Ui=l м/с и ускорением #i=2 м/с2, вторая — с начальной
скоростью и2=Ю м/с и ускорением а2=1 м/с2. Через сколько вре-
времени и на каком расстоянии от исходного положения вторая точка
догонит первую?
1.15. Движения двух материальных точек выражаются уравне-
уравнениями:
x1=A1+B1t+C1P9 x2=A2+B2t+C2t\
где Аг=20 м, А2=2 м, В2=В±=2 м/с, d=—4 м/с2, С2-0,5 м/с2.
В какой момент времени t скорости этих точек будут одинаковы-
одинаковыми? Определить скорости v± и v2 и ускорения а± и а2 точек в этот мо-
момент:
1.16. Две материальные точки движутся согласно уравнениям:
Xl=A1t+B1t2+C1t\ x2=A2t+B2t2+C2t\
где Аг=4 м/с, Вг=8 м/с2, d=—16 м/с3, А2=2 м/с, В2=—4 м/с2,
Ся=1 м/с3.
14

В какой момент времени t ускорения этих точек будут одинаковы?
Найти скорости v± и v2 точек в этот момент.
1.17. С какой высоты Н упало тело, если последний метр своего
пути оно прошло за время ?=0,1 с?
1.18. Камень падает с высоты Л=1200 м. Какой путь s пройдет
камень за последнюю секунду своего падения?
1.19. Камень брошен вертикально вверх с начальной скоростью
ио=2О м/с. По истечении какого времени камень будет находиться на
высоте Л=15м? Найти скорость v камня на этой высоте. Сопротивле-
Сопротивлением воздуха пренебречь. Принять g*= 10 м/с2.
1.20. Вертикально вверх с начальной скоростью уо=2О м/с бро-
брошен камень. Через т=1 с после этого брошен вертикально вверх
другой камень с такой же скоростью. На какой высоте h встретятся
камни?
1.21. Тело, брошенное вертикально вверх, находилось на одной и
той же высоте /i—8,6 м два раза с интервалом At=3 с. Пренебрегая
сопротивлением воздуха, вычислить начальную скорость брошенно-
брошенного тела.
1.22. С балкона бросили мячик вертикально вверх с начальной
скоростью ^0=5 м/с. Через t=2 с мячик упал на землю. Определить
высоту балкона над землей и скорость мячика в момент удара о зем-
землю.
1.23. Тело брошено с балкона вертикально вверх со скоростью
ио^Ю м/с. Высота балкона над поверхностью земли Л=12,5 м.
Написать уравнение движения и определить среднюю путевую ско-
скорость (v) с момента бросания до момента падения на землю.
1.24. Движение точки по прямой задано уравнением x^At+Bt2,
где А =2 м/с, В=—0,5 м/с2. Определить среднюю путевую скорость
{и) движения точки в интервале времени от tt=l с до t2=3 с.
1.25. Точка движется по прямой согласно уравнению x=At-\-Bt3,
где А =6 м/с, В=—0,125 м/с3. Определить среднюю путевую ско-
скорость (v) точки в интервале времени от U—2 с до /2—6 с.
Криволинейное движение
1.26. Материальная точка движется по плоскости согласно урав-
уравнению r(t) = iAts+]Bt2. Написать зависимости: 1) v(/); 2) а(^).
1.27. Движение материальной точки задано уравнением r(t)=
=Л (i cos (dt+j sin Ш), где Л=0,5 м, со=5 рад/с. Начертить траек-
траекторию точки. Определить модуль скорости |v| и модуль нормального
ускорения |ап|.
1.28. Движение материальной точки задано уравнением г(/)~
=i(A+Bt*)+}Ct, где А = 10 м, В=—5 м/с2, С=10 м/с. Начертить
траекторию точки. Найти выражения v(/) и a.(t). Для момента
времени t=l с вычислить: 1) модуль скорости |v
ния |а|; 3) модуль тангенциального ускорения
; 2) модуль ускоре-
ат|; 4) модуль нор-
нормального ускорения |ад|.
1.29. Точка движется по кривой с постоянным тангенциальным
ускорением ат=0,5 м/с2. Определить полное ускорение а точки на
15

участке кривой с радиусом кривизны R=3 м, если точка движется
на этом участке со скоростью v=2 м/с.
1.30. Точка движется по окружности радиусом R=4 м. Началь-
Начальная скорость v0 точки равна 3 м/с, тангенциальное ускорение ат =
= 1 м/с2. Для момента времени t==2 с определить: 1) длину пути s,
пройденного точкой; 2) модуль перемещения |Лг|; 3) среднюю путе-
путевую скорость (v)\ 4) модуль вектора средней скорости |(v)|.
1.31. По окружности радиусом R=5 м равномерно движется
материальная точка со скоростью v=5 м/с. Построить графики зави-
зависимости длины пути s и модуля перемещения |Дг| от времени t.
В момент времени, принятый за начальный (/=0), s@) и |Дг@)|
считать равными нулю.
1.32. За время t=6 с точка прошла путь, равный половине длины
окружности радиусом R=0,8 м. Определить среднюю путевую ско-
скорость (v) за это время и модуль вектора средней скорости |(v)|.
1.33. Движение точки по окружности радиусом R=4 м задано
уравнением * t=A+Bt+CP, где Л = 10 м, В=—2 м/с, С=1 м/с2.
Найти тангенциальное ах> нормальное ап и полное а ускорения
точки в момент времени ?=2с.
1.34. По дуге окружности радиусом # = 10 м движется точка.
В некоторый момент времени нормальное ускорение точки ап=
=4,9 м/с2; в этот момент векторы полного и нормального ускорений
образуют угол ф=60°. Найти скорость v и тангенциальное ускоре-
ускорение ах точки.
1.35. Точка движется по окружности радиусом R=2 м согласно
уравнению * l=At3, где Л=2 м/с3. В какой момент времени t нор-
нормальное ускорение ап точки будет равно тангенциальному а%?
Определить полное ускорение а в этот момент.
1.36. Движение точки по кривой задано уравнениями х~АгР и
y=A2t, где Аг=1 м/с3, А2=2 м/с. Найти уравнение траектории точ-
точки, ее скорость v и полное ускорение а в момент времени /=0,8 с.
1.37. Точка А движется равномерно со скоростью v по окружно-
окружности радиусом R. Начальное положение точки и направление движе-
движения указаны на рис. 1.8. Написать кинематическое уравнение дви-
движения проекции точки А на направление оси х.
1.38. Точка движется равномерно со скоростью v по окружности
радиусом R и в момент времени, принятый за начальный (/=0),
занимает положение, указанное на рис. 1.8. Написать кинематиче-
кинематические уравнения движения точки: 1) в декартовой системе координат,
расположив оси так, как это указано на рисунке; 2), в полярной
системе координат (ось х считать полярной осью).
1.39. Написать для четырех случаев, представленных на рис. 1.9:
1) кинематические уравнения движения x=f±(t) и #=/а@; 2) урав-
уравнение траектории у=ц>(х). На каждой позиции рисунка — а, б, в,
г — изображены координатные оси, указаны начальное положение
точки Л, ее начальная скорость v0 и ускорение g.
1.40. С вышки бросили камень в горизонтальном направлении.
* См. сноску на с. 11.
16

Через промежуток времени t=2 с камень упал на землю на расстоя-
расстоянии s=40 м от основания вышки. Определить начальную v0 и конеч-
конечную v скорости камня.
1.41. Тело, брошенное с башни в горизонтальном направлении
со скоростью и=20 м/с, упало на землю на расстоянии s (от основания
башни), вдвое большем высоты h башни. Найти высоту башни.
a)
h]
0
/
s
Рис. 1.8
Рис. 1.9
1.42. Пистолетная пуля пробила два вертикально закрепленных
листа бумаги, расстояние I между которыми равно 30 м. Пробоина
во втором листе оказалась на /i=10cm ниже, чем в первом. Опреде-
Определить скорость v пули, если к первому листу она подлетела, двигаясь
горизонтально. Сопротивлением воздуха пренебречь.
1.43. Самолет, летевший на высоте h=2940 м со скоростью v=
=360 км/ч, сбросил бомбу. За какое время t до прохождения над
целью и на каком расстоянии s от нее должен самолет сбросить бом-
бомбу, чтобы попасть в цель? Сопротивлением воздуха пренебречь.
1.44. Тело брошено под некоторым углом а к горизонту. Найти
этот угол, если горизонтальная дальность s полета тела в четыре
раза больше максимальной высоты Н траектории.
1.45. Миномет установлен под углом а=60° к горизонту на крыше
здания, высота которого /г=40 м. Начальная скорость v0 мины
равна 50 м/с. Требуется: 1) написать кинематические уравнения
движения и уравнения траектории и начертить эту траекторию с
соблюдением масштаба; 2) определить время т полета мины, мак-
максимальную высоту Н ее подъема, горизонтальную дальность s по-
полета, скорость v в момент падения мины на землю. Сопротивлением
воздуха пренебречь.
Указание. Начало координат поместить на поверхности земли так, чтобы
оно находилось на одной вертикали с минометом и чтобы вектор скорости v
лежал в плоскости хОу.
1.46. Снаряд, выпущенвшн, да 01
зонту, дважды был на однв* и той!
под углом a^SCP к хори-
шшдее Н: спустя время /^
17

= 10 с и ?2=50 с после выстрела. Определить начальную скорость
v0 и высоту h.
1.47. Пуля пущена с начальной скоростью уо=2ОО м/с под углом
а=60° к горизонту. Определить максимальную высоту Н подъема,
дальность s полета и радиус R кривизны траектории пули в ее наи-
наивысшей точке. Сопротивлением воздуха пренебречь.
1.48. Камень брошен с вышки в горизонтальном направлении
с начальной скоростью vo=3O м/с. Определить скорость v, танген-
тангенциальное ах и нормальное о^ ускорения камня в конце второй секун-
секунды после начала движения.
1.49. Тело брошено под углом а=30° к горизонту. Найти
тангенциальное ах и нормальное ап ускорения в начальный момент
движения.
Вращение тела вокруг неподвижной оси
1.50. Определить линейную скорость v и центростремительное
ускорение ац точек, лежащих на земной поверхности: 1) на эквато-
экваторе; 2) на широте Москвы (ф=56°).
1.51. Линейная скорость vx точек на окружности вращающегося
диска равна 3 м/с. Точки, расположенные на Д/? = 10 см ближе к оси,
имеют линейную скорость v2=2 м/с. Определить частоту вращения
п диска.
1.52. Два бумажных диска насажены на общую горизонтальную
ось так, что плоскости их параллельны и отстоят на d=30 см друг от
друга. Диски вращаются с частотой /г=25 с. Пуля, летевшая па-
параллельно оси на расстоянии г= 12 см от нее, пробила оба диска.
Пробоины в дисках смещены друг относительно друга на расстоя-
расстояние s=5 см, считая по дуге окружности. Найти среднюю путевую
скорость (v) пули в промежутке между дисками и оценить создавае-
создаваемое силой тяжести смещение пробоин в вертикальном направлении.
Сопротивление воздуха не учитывать.
1.53. На цилиндр, который может вращаться около горизонталь-
горизонтальной оси, намотана нить. К концу нити привязали грузик и предоста-
предоставили ему возможность опускаться. Двигаясь равноускоренно, гру-
грузик за время t=3 с опустился на ft=l,5 м. Определить угловое уско-
ускорение е цилиндра, если его радиус г=4 см.
1.54. Диск радиусом г=10 см, находившийся в состоянии покоя,
начал вращаться с постоянным угловым ускорением 8=0,5 рад/с2.
Найти тангенциальное ах, нормальное ап и полное а ускорения точек
на окружности диска в конце второй секунды после начала враще-
вращения.
1.55. Диск радиусом г=20 см вращается согласно уравнению <р=
=A+Bt+Ctz, где Л=3 рад, В=—1 рад/с, С=0,1 рад/с3. Опреде-
Определить тангенциальное аХ1 нормальное ап и полное а ускорения точек
на окружности диска для момента времени ?=10 с.
1.56. Маховик начал вращаться равноускоренно и за промежу-
промежуток времени А?=10 с достиг частоты вращения п=300 мин. Опре-
18

делить угловое ускорение 8 маховика и число N оборотов, которое
он сделал за это время.
1.57. Велосипедное колесо вращается с частотой п=Ъ с. Под
действием сил трения оно остановилось через интервал времени
Д/=1 мин. Определить угловое ускорение е и число iV оборотов, ко-
которое сделает колесо за это время.
1.58. Колесо автомашины вращается равноускоренно. Сделав
N=50 полных оборотов, оно изменило частоту вращения от пг=
=4 с до /22=6 с. Определить угловое ускорение 8 колеса.
1.59. Диск вращается с угловым ускорением 8=—2 рад/с2. Сколь-
Сколько оборотов N сделает диск при изменении частоты вращения от
#1=240 мин ~1 до п2=90 мин "9 Найти время А/, в течение кото-
которого это произойдет.
1.60. Винт аэросаней вращается с частотой я=360 мин. Ско-
Скорость v поступательного движения аэросаней равна 54 км/ч. С какой
скоростью и движется один из концов винта, если радиус R винта
равен 1 м?
1.61. На токарном станке протачивается вал диаметром d=
=60 мм. Продольная подача h резца равна 0,5 мм за один оборот.
Какова скорость v резания, если за интервал времени Д/=1 мин
протачивается участок вала длиной 1=12 см?
§ 2. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ТЕЛА,
ДВИЖУЩИХСЯ ПОСТУПАТЕЛЬНО
Основные формулы
• Уравнение движения материальной точки (второй закон Нью-
Ньютона):
в векторной форме
N N
"dJr = SFi» или ma^^F,.,
N
где 2 F/— геометрическая сумма сил, действующих на мате-
i - 1
риальную точку; т — масса; а — ускорение; p=mv — импульс;
N — число сил, действующих на точку;
в координатной форме (скалярной)
та* = Ирх;> may = HFyi> rnaz = ^Fzi,
или
m
где под знаком суммы стоят проекции сил F^ на соответствующие
оси координат.
О Сила упругости *
Р by
УПР ПЛ9
* Силы упругости и гравитационного взаимодействия более подробно
рассмотрены в § 4.
19

где k — коэффициент упругости (жесткость в случае пружины);
х — абсолютная деформация.
• Сила гравитационного взаимодействия *
где G — гравитационная постоянная; тх и т2 — массы взаимодей-
взаимодействующих тел, рассматриваемые как материальные точки; г — рас-
расстояние между ними.
• Сила трения скольжения
где / — коэффициент трения скольжения; N — сила нормального
давления.
• Координаты центра масс системы материальных точек
где шг — масса i-й материальной точки; xt, y^ti — ее координаты.
Ф Закон сохранения импульса
N N
2 Pi = const, или 2 miv/ = const,
i = 1 1 = 1
где N — число материальных точек (или тел), входящих в систему.
• Работа, совершаемая постоянной силой,
AA = FArf или AA=FAr cos a,
где а — угол между направлениями векторов силы F и перемеще-
перемещения Аг.
• Работа, совершаемая переменной силой,
^F(r) cos a dr,
L
где интегрирование ведется вдоль траектории, обозначаемой L.
О Средняя мощность за интервал времени Д?
• Мгновенная мощность
N =—гг-9 или N = Fv cos a,
где dA — работа, совершаемая за промежуток времени cU.
Ф Кинетическая энергия материальной точки (или тела), дви-
движущейся поступательно,
T=mv2/2, или Т=р2/{2т).
• Потенциальная энергия тела и сила, действующая на тело
в данной точке поля, связаны соотношением
F —
где i, j, k — единичные векторы (орты). В частном случае, когда
* См. сноску на с* 19.
20

поле сил обладает сферической симметрией (как, например, грави-
гравитационное),
• Потенциальная энергия упругодеформированного тела (сжа-
(сжатой или растянутой пружины)
^*2
— ТГ"'
• Потенциальная энергия гравитационного взаимодействия
двух материальных точек (или тел) массами тх и /л2, находящихся
на расстоянии г друг от друга,
т-г р тп1пг2
г
• Потенциальная энергия тела, находящегося в однородном
поле силы тяжести,
U=mgh,
где h — высота тела над уровнем, принятым за нулевой для отсчета
потенциальной энергии. Эта формула справедлива при условии
h<<:R, где R — радиус Земли.
О Закон сохранения энергии в механике выполняется в замкну-
замкнутой системе, в которой действуют только консервативные силы, и
записывается в виде
T-\-U=const.
• Применяя законы сохранения энергии и импульса к прямому
центральному удару шаров, получаем формулу скорости абсолютно
неупругих шаров после удара
u=(miO1-\-m2v2)/ (fni-\-tn2)
и формулы скорости абсолютно упругих шаров после удара:
^i (^i •— /Иг) + 2m2v2
где Шх и т2 — массы шаров; иг и v2 — их скорости до удара.
Примеры решения задач
Пример 1. К концам однородного стержня приложены две про-
противоположно направленные силы: ^=40 Н и F2—\00 H (рис. 2.1, а).
/у
F, Г
Рис. 2.1
Определить силу натяжения Т стержня в поперечном сечении, кото-
которое делит стержень на две части в отношении 1 : 2.
21

Решение. Если бы силы F± и F2 были равны между собой, то
сила натяжения в любом сечении стержня была бы одинаковой и
равной силам, приложенным к концам стержня. Стержень в этом
случае находился бы в покое. Но так как сумма сил, действующих
на стержень, отлична от нуля, то стержень будет двигаться с уско-
ускорением, величина и направление которого определяются по второму
закону Ньютона: а= (F1+F2)/m, где т — масса стержня. Так как
обе силы действуют вдоль прямой, то геометрическую сумму можно
заменить алгебраической:
а=(Л-/?1)/т. A)
При ускоренном движении стержня силы натяжения в разных
сечениях различны. Для определения этих сил применим следую-
следующий прием: разделим стержень на две части в интересующем нас
сечении и отбросим одну из них, например левую. Действие левой
части на правую заменим силой натяжения Т (рис. 2.1, б). В ре-
результате действия разности сил F2—Т оставшаяся правая часть
стержня массой ггц должна двигаться с ускорением а= (F2—ТIт±,
равным по величине и направлению прежнему ускорению, выражае-
выражаемому формулой A). Так как стержень однородный, то т±=т13 и,
следовательно,
а т/3 ' W
Приравнивая правые части равенства A) и B) и выражая из
полученного равенства си-
силу натяжения Т, находим
T=F2-(F2-F1)/3.
Подставив значения F2 и
Fu получим
Г=80 Н.
Пример 2. В лифте на
пружинных весах находит-
находится тело массой т=10 кг
(рис. 2.2, а). Лифт движет-
движется с ускорением а=2 м/с2.
Определить показания ве-
весов в двух случаях, когда
ускорение лифта направле-
направлено: 1) вертикально вверх, 2) вертикально вниз.
Решение. Определить показания весов — это значит найти
вес тела G, т. е. силу, с которой тело действует на пружину. Но
эта сила, по третьему закону Ньютона, равна по модулю и противо-
противоположна по направлению силе упругости N (силе реакции опоры),
с которой пружина через посредство прикрепленной к ней чашки
весов действует на тело, т. е.
G=—ЛГ, или G=N. A)
Рис. 2.2
22

Следовательно, задача определения показания весов сводится
к нахождению реакции опоры N.
Задачу можно решать как в инерциальной, так и неинерциаль-
ной системе отсчета.
Решение в инерциальной системе отсчета. На тело действуют
две силы: сила тяжести Р и сила N.
Направим ось z вертикально вверх и спроецируем на нее все
силы, действующие на тело. Индекс z у проекции сил опустим, так
как проекции и сами силы совпадают по величине. Направление
сил учтем знаком плюс или минус. Напишем уравнение движения:
N—P=ma,
откуда
N=P+ma=m(g+a). B)
Из равенств A) и B) следует
G=m(g+a).
При вычислении показания весов следует учесть знак ускорения:
1) ускорение направлено вертикально вверх (а>0), тогда
Gi=10(9,81+2)H=118 H;
2) ускорение направлено вертикально вниз (а<0), тогда
G2=10(9,81— 2) Н-78 Н.
Отметим, что ни модуль, ни направление скорости лифта не влия-
влияют на показания весов. Существенны лишь величина и направление
ускорения.
Решение в неинерциальной системе отсчета, т. е. в системе, дви-
движущейся ускоренно вместе с лифтом. В этой системе отсчета законы
Ньютона не выполняются. Однако если к телу в соответствии с прин-
принципом Даламбера дополнительно к действующим на него силам при-
приложить силу инерции
F;=— ma,
где а — ускорение системы отсчета, то с учетом этой силы законы
Ньютона будут справедливы.
В этом случае на тело будут действовать три силы: сила тяжести
Р, сила упругости N и сила инерции F* (рис. 2.2, б). Под действием
этих сил тело в данной неинерциальной системе отсчета покоится.
Это значит, что вместо уравнений динамики (законов Ньютона) мож-
можно воспользоваться законами статики. Если тело под действием
системы сходящихся сил покоится, то геометрическая сумма этих
сил равна нулю. В данном случае это приводит к равенству
P+N+Fi=0.
Спроецируем все силы на ось z и напишем соответствующее ра-
равенство для проекций этих сил (индекс z опустим):
N—Р—та=0,
откуда сила реакции опоры
N=P+ma=m(g+a). C)
Из равенств A) и C) следует
G=m{g+a),
23

mg
Ffkvr
а)
иуст
что совпадает с результатом, полученным при решении в инерциаль-
ной системе отсчета.
Пример 3. При падении тела с большой высоты его скорость
flyCT при установившемся движении достигает 80 м/с. Определить
время т, в течение которого начиная от момента начала падения
скорость становится равной Va vyCT.
Силу сопротивления воздуха при-
принять пропорциональной скорости
тела.
Решение. На падающее те-
тело действуют две силы (рис. 2.3, а):
сила тяжести mg и сила сопротив-
сопротивления воздуха Fc.
Сила сопротивления воздуха
по условиям задачи пропорцио-
пропорциональна скорости тела и противо-
противоположна ей по направлению:
Fc = -?v, A)
где k — коэффициент пропорциональности, зависящий от раз-
размеров, формы тела и от свойств окружающей среды.
Напишем уравнение движения тела в соответствии со вторым
законом Ньютона в векторной форме: m—- = mg—Fc.
Заменив Fc согласно A), получим
m-TT- = mg—kv. B)
Спроецируем все векторные величины на вертикально направлен-
направленную ось и напишем уравнение B) для проекций:
dv у
Рис. 2.3
После разделения переменных получим
dv _ dt
mg — kv m
Выполним интегрирование, учитывая, что при изменении времени
от нуля до т (искомое время) скорость возрастает от нуля до
lU fycx (Рис. 2.3, б):
dv
mg—kv
In (mg—kv)
Густ
x
m
Подставим пределы интегрирования в левую часть равенства:
mg
m
и найдем из полученного выражения искомое время:
T=flnffigJ* ¦ C)
Входящий сюда коэффициент пропорциональности k определим
из следующих соображений. При установившемся движении (ско-
24

рость постоянна) алгебраическая сумма проекций (на ось у) сил,
действующих на тело, равна нулю, т. е. mg — kvycT =0, откуда
k=tng/vyCT. Подставим найденное значение k в формулу C):
mvyCT mg
"* * 111-
т8 1 trig g
После сокращений и упрощений получим
Проверка размерности в данном случае не обязательна, так
как результат очевиден. Подставив в эту формулу значения иуст,
g, In 2 и произведя вычисления, получим
т=5,66 с.
Пример 4. Шар массой т=0,3 кг, двигаясь со скоростью
и=10 м/с, упруго ударяется о гладкую неподвижную стенку так,
что скорость его направлена под углом а=30° к нормали. Опреде-
Определить импульс р, получаемый стенкой.
Решение. Сначала проанализируем условие задачи. Стен-
Стенка неподвижна, поэтому система отсчета, связанная с ней, будет
инерциальной. Удар о стенку уп-
упругий; следовательно, можно вос-
воспользоваться законом сохранения ме-
механической энергии. Из него, учи-
учитывая, что масса стенки много боль-
больше массы шара, следует равенство
модулей скоростей шара |v| до и |и|
после удара.
Покажем, что угол а' отражения ^—-?Х
шара от стенки равен углу а паде- !^^ ]и
ния шара. Спроецируем векторы v и u y
и на координатные оси Ох и Оу (рис. Рис. 2.4
2.4). Так как стенка гладкая, то пу=
= Vy. Учитывая, кроме того, что |u|= |v|, получим их — — vx, а от-
отсюда следует равенство углов падения и отражения (а'=а).
Для определения импульса, полученного стенкой, воспользу-
воспользуемся законом сохранения импульса. Для нашего случая этот за-
закон можно записать в виде
где pi и р[ — импульсы шара до и после удара (|pi|= |рЦ).
Отсюда импульс, полученный стенкой,
P=Pi — Pi-
Из рис. 2.5 видно, что вектор р сонаправлен с осью Ох и его
модуль р= |р 1=2/7! cos а. Подставив сюда выражение импульса
p1=mv1 получим
cos a.
25

Произведем вычисления:
- кг- м/с = 5,20 кг-м/с.
Рис- 2-5
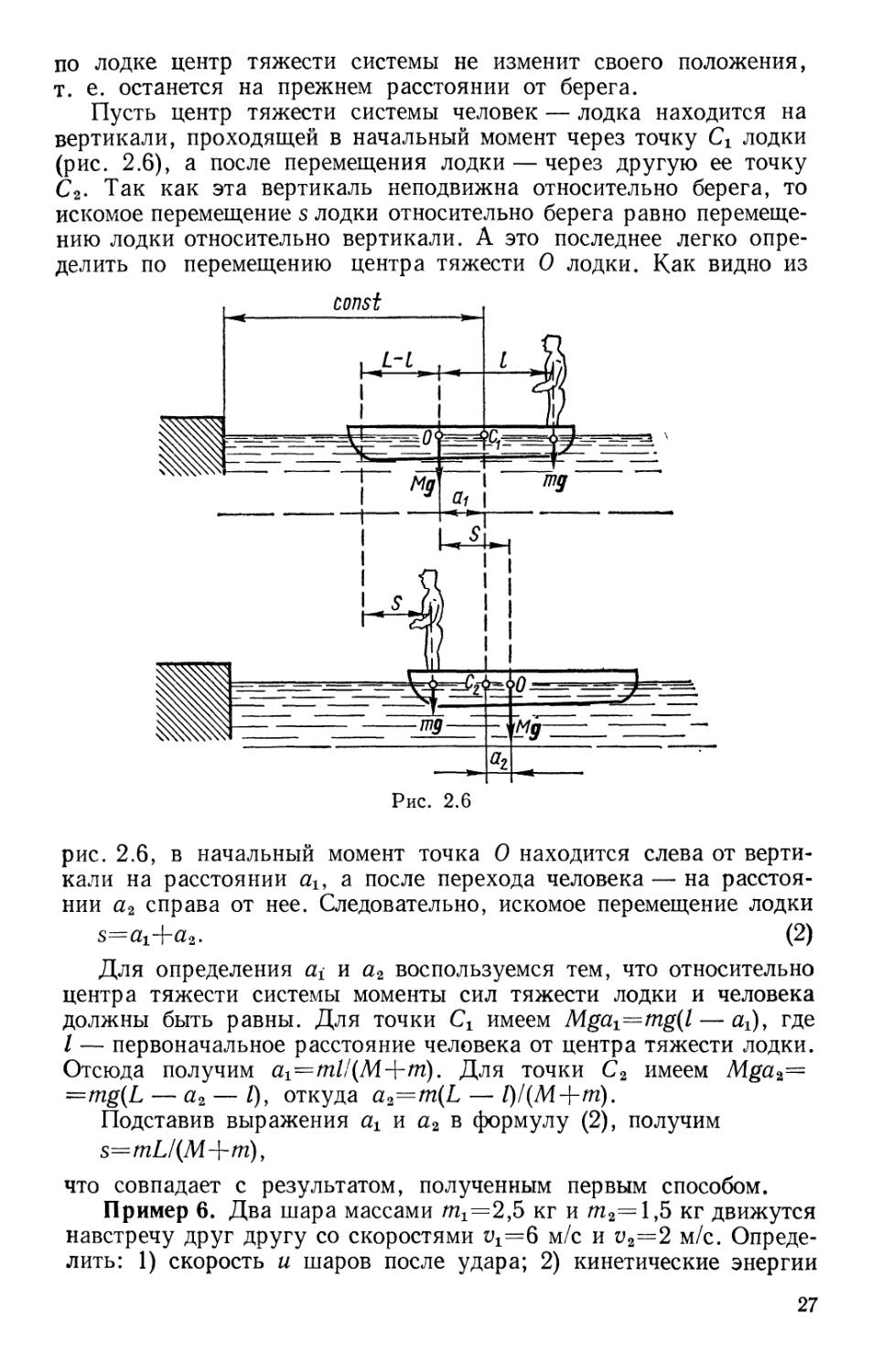
Пример 5. На спокойной воде пруда стоит лодка длиной L и
массой М перпендикулярно берегу, обращенная к нему носом. На
корме стоит человек массой т. На какое расстояние s приблизится
лодка к берегу, если человек перей-
перейдет с кормы на нос лодки? Трением о
воду и воздух пренебречь.
Решение. 1-й способ. Для
простоты решения будем считать, что
человек идет по лодке с постоянной
скоростью. Лодка в этом случае так-
также будет двигаться равномерно. По-
этому перемещение лодки относитель-
относительно берега определим по формуле
s=vt, A)
где v — скорость лодки относительно берега; t — время движения
человека и лодки. Направление перемещения человека примем
за положительное.
Скорость v лодки найдем, пользуясь законом сохранения им-
импульса * (количества движения). Так как, по условию задачи,
система человек — лодка в начальный момент была относительно
берега в покое, то по закону сохранения импульса получим Mv—
— ти=0, где и — скорость человека относительно берега; знак
минус указывает на то, что скорости человека и лодки по направ-
направлению противоположны. Отсюда v=mulM.
Время t движения лодки равно времени перемещения человека
по лодке, т. е. t=s1/u=(L — s)/u, где sx — перемещение человека
относительно берега.
Подставив полученные выражения v и t в формулу A), найдем
ти L-s . m (L ,
Ь ~ М и - М ^ S)'
откуда
s=mL/(m+M).
Заметим, что предположение о равномерности движения чело-
человека не является обязательным. В приведенном ниже более общем
способе решения задачи такое предположение не используется.
2-й способ. Согласно следствию из закона сохранения импуль-
импульса, внутренние силы системы тел не могут изменить положение
центра тяжести ** системы. Применяя это следствие к системе
человек — лодка, можно считать, что при перемещении человека
* В данном случае систему человек — лодка можно считать замкнутой,
так как векторная сумма внешних сил, действующих на отдельные тела
системы, равна нулю.
** Точнее было бы говорить о центре масс (центре инерции системы).
Но в том случае, когда система твердых тел находится в однородном поле
силы тяжести, центр масс и центр тяжести совпадают.
26

по лодке центр тяжести системы не изменит своего положения,
т. е. останется на прежнем расстоянии от берега.
Пусть центр тяжести системы человек — лодка находится на
вертикали, проходящей в начальный момент через точку Сх лодки
(рис. 2.6), а после перемещения лодки — через другую ее точку
С2. Так как эта вертикаль неподвижна относительно берега, то
искомое перемещение s лодки относительно берега равно перемеще-
перемещению лодки относительно вертикали. А это последнее легко опре-
определить по перемещению центра тяжести О лодки. Как видно из
const
Рис. 2.6
рис. 2.6, в начальный момент точка О находится слева от верти-
вертикали на расстоянии а1у а после перехода человека — на расстоя-
расстоянии а2 справа от нее. Следовательно, искомое перемещение лодки
B)
Для определения а± и а2 воспользуемся тем, что относительно
центра тяжести системы моменты сил тяжести лодки и человека
должны быть равны. Для точки Сг имеем Mga1=mg(l— ai), где
/ — первоначальное расстояние человека от центра тяжести лодки.
Отсюда получим а1=т1/(М-{-т). Для точки С2 имеем Mga%=
=mg(L— аг — /), откуда a2=m(L — 1)/(М-\-т).
Подставив выражения ах и а2 в формулу B), получим
s=mL/(M+m)y
что совпадает с результатом, полученным первым способом.
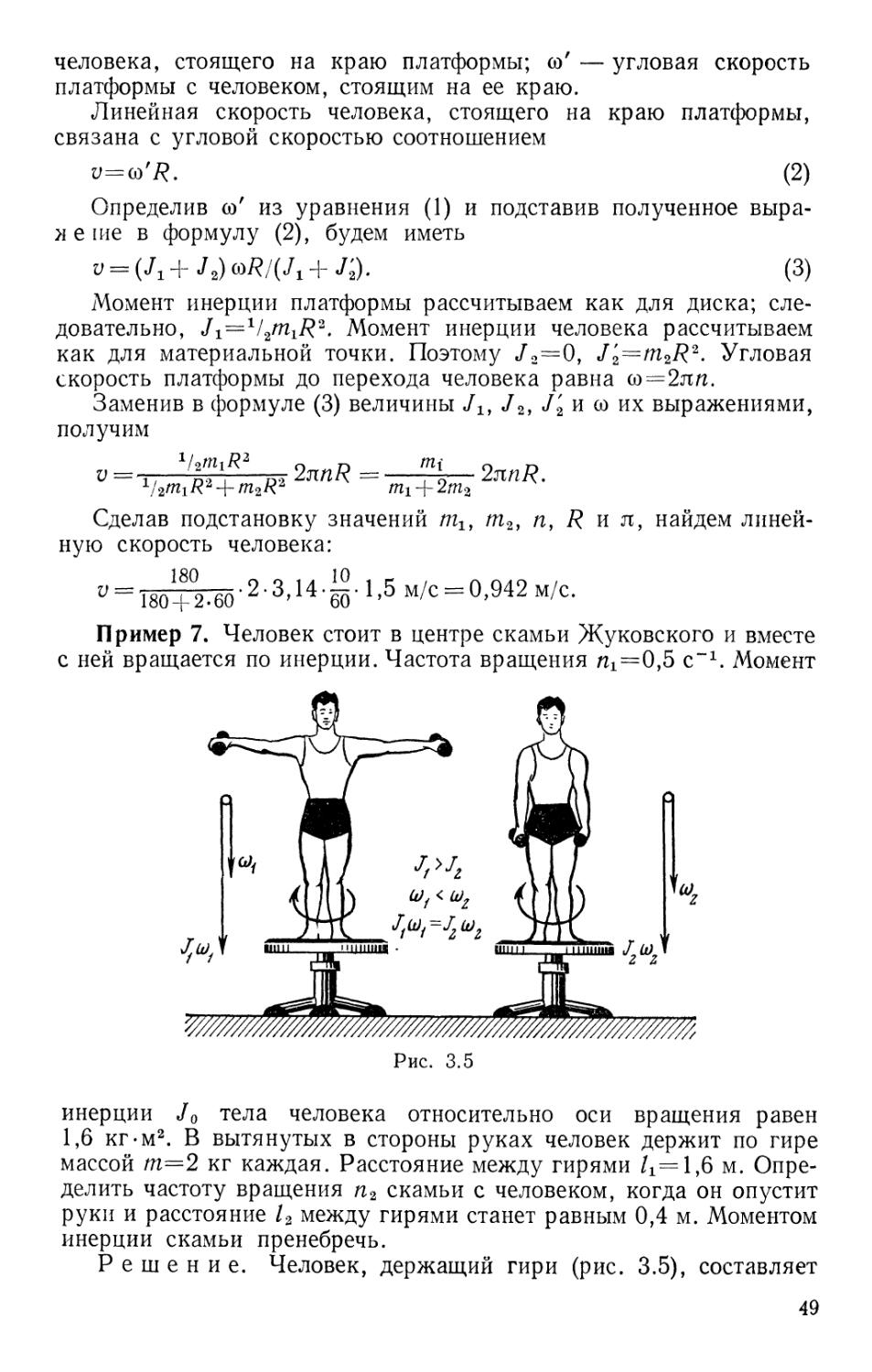
Пример 6. Два шара массами т1=2,Ъ кг и т2=1,5 кг движутся
навстречу друг другу со скоростями 1>1=6 м/с и v2=2 м/с. Опреде-
Определить: 1) скорость и шаров после удара; 2) кинетические энергии
27

шаров Ti до и Т2 после удара; 3) долю кинетической энергии w
шаров, превратившейся во внутреннюю энергию. Удар считать
прямым, неупругим.
Решение. 1. Неупругие шары не. восстанавливают после
удара своей первоначальной формы. Следовательно, не возникают
силы, отталкивающие шары друг от друга, и шары после удара бу-
будут двигаться совместно с одной и той же скоростью и. Определим
эту скорость по закону сохранения импульса. Так как шары дви-
движутся по одной прямой, то этот закон можно записать в скалярной
форме:
m1v1+m2v2==(m1+m2)uf
откуда
u=(m1v1+m2v2)/(m1Jrm2).
Направление скорости первого шара примем за положительное,,
тогда при вычислении скорость второго шара, который движется
навстречу первому, следует взять со знаком минус:
и=B,5-6—1,5 -2)/B,5+1,5) м/с=3 м/с.
2. Кинетические энергии шаров до и после удара определим
по формулам
Тг = mxv\l2 + m2v22/2; T2 = (щ + т2) и*/2.
Произведя вычисления по этим формулам, получим
7\=B,5 -6V2+1,5 -22/2) Дж-48 Дж;
Т2=B,5+1,5)-32/2 Дж=18 Дж.
3. Сравнение кинетических энергий шаров до и после удара
показывает, что в результате неупругого удара шаров произошла
уменьшение их кинетической энергии, за счет чего увеличилась
их внутренняя энергия. Долю кинетической энергии шаров, по-
пошедшей на увеличение их внутренней энергии, определим из со-
соотношения
ш= G\ — Т2IТг\ ау=0,62.
Пример 7. Шар массой тъ движущийся горизонтально с неко-
некоторой скоростью 1>х, столкнулся с неподвижным шаром массой т2.
Шары абсолютно упругие, удар прямой. Какую долю w своей ки-
кинетической энергии первый шар передал второму?
Решение. Доля энергии, переданной первым шаром вто-
второму, выразится соотношением
Т2 _ т2и\ _ т2 ( и2
где Тг — кинетическая энергия первого шара до удара; и2 и Т2—
скорость и кинетическая энергия второго шара после удара.
Как видно из выражения A), для определения w надо найти и2.
Воспользуемся тем, что при ударе абсолютно упругих тел одновре-
одновременно выполняются два закона сохранения: импульса и механиче-
механической энергии.
По закону сохранения импульса, учитывая, что второй шар до
удара покоился, имеем m1v1=m1u1-\-m2u2. По закону сохранения
28

2 2
энергии в механике, _g^L — m^11 _j- m^2 щ Решая совместно два по-
последних уравнения, найдем
Подставив это выражение и2 в равенство A), получим
__ т2 Г 2mii>i 12
^""% [ui(mi + /n2) J "~~
Из этого соотношения видно, что доля переданной энергии зави-
зависит только от масс сталкивающихся шаров. Доля передаваемой
энергии не изменится, если шары поменяются местами.
Пример 8. Молот массой т!=200 кг падает на поковку, масса
т% которой вместе с наковальней равна 2500 кг. Скорость v± мо-
молота в момент удара равна 2 м/с. Найти: 1) кинетическую энергию
Tt молота в момент удара; 2) энергию Т2, переданную фундаменту;
3) энергию 71, затраченную на деформацию поковки; 4) коэффициент
полезного действия г\ (КПД) удара молота о поковку. Удар молота
о поковку рассматривать как неупругий.
Решение. 1. Кинетическую энергию молота в момент удара
найдем по формуле T1=m1vl/2. Подставив значения тг и vx и про-
произведя вычисления, получим
7W00 Дж.
2. Чтобы определить энергию, переданную фундаменту, предва-
предварительно найдем скорость системы молот — поковка (с наковаль-
наковальней) непосредственно после удара. Для этого применим закон
сохранения импульса, который в случае неупругого удара двух
тел выражается формулой
т1г;1+таиа= (гп^+т^и, A)
где v2 — скорость поковки (вместе с наковальней) перед ударом; а —
скорость молота и поковки (вместе с наковальней) непосредственно
после удара. Так как поковка с наковальней до удара находи-
находилась в состоянии покоя, то v2=0. При неупругом ударе деформация
не восстанавливается, вследствие чего молот и поковка (с нако-
наковальней) движутся как одно целое, т. е. с одинаковой скоростью и.
Из формулы A) найдем эту скорость:
и= mi v±. B)
m1~\-m2 г \ }
В результате сопротивления фундамента скорость и быстро
гасится, а кинетическая энергия, которой обладает система молот —
поковка (с наковальней), передается фундаменту. Эту энергию
находим по формуле T2=^mi~tm2>u2-
2 2
Заменим скорость и ее выражением B): т = miVl ¦ или
т 2(т! + т2)'
учитывая, что Тг=гп10\12, запишем
29

Подставив в уравнение C) значения т^ т2 и Т± и произведя
вычисления, получим
Г2=29,6 Дж.
3. Молот до удара обладал энергией 7Y, Т2 — энергия, передан-
переданная фундаменту. Следовательно, на деформацию поковки исполь-
использовалась энергия
Т^Тг — 72.
Подставив в это выражение значения Т± и T2i получим
7=370 Дж.
4. Назначение молота — путем ударов о поковку, находящуюся
на наковальне, вызвать деформацию поковки; следовательно, энер-
энергию Т следует считать полезной. КПД удара молота о поковку
равен отношению энергии Т, затраченной на деформацию поковки^
ко всей затраченной энергии Т±\
n = T/Ti9 или я = (Tt — Т2IТ±.
Подставив в последнее выражение Т2 по формуле C), получим
yi=m2/(m1+ma).
После подстановки значений гп2 и пг1 найдем
П=92,6 %-
(См. примечание в конце примера 9.)
Пример 9. Боек (ударная часть) свайного молота массой m,i=*
=500 кг падает на сваю массой /п2= 100 кг со скоростью 1^=4 м/с.
Определить: 1) кинетическую энергию Т± бойка в момент удара;
2) энергию 7*2, затраченную на углубление сваи в грунт; 3) кинети-
кинетическую энергию Т, перешедшую во внутреннюю энергию системы;
4) КПД г\ удара бойка о сваю. Удар бойка о сваю рассматривать
как неупругий.
Решение. 1. Кинетическую энергию бойка в момент удара
о сваю находим по формуле T1=m1vl/2. Подставив значения пц
и v-l и произведя вычисления, получим
Г1-E00-42)/2 Дж-4000 Дж-4 кДж.
2. Чтобы определить энергию, затраченную на углубление
сваи, предварительно найдем скорость системы боек — свая не-
непосредственно после удара. Для этого применим закон сохранения
импульса, который в случае неупругого удара выражается формулой
tn1v1+mzv2= (mi+tn2) и, A)
где v2 — скорость сваи перед ударом; и — скорость бойка и сваи
непосредственно после удара. Свая перед ударом находилась в
состоянии покоя, поэтому v2=Q. Так как удар неупругий, то боек
и свая после удара движутся как одно целое, т. е. с одинаковой
скоростью и. Из формулы A) найдем эту скорость:
30

В результате сопротивления грунта скорость бойка и сваи после
удара быстро гасится, а кинетическая энергия, которой обладает
система боек — свая, затрачивается на углубление сваи в грунт.
Эту энергию находим по формуле Т2 = {<mi~*~™2>u . Заменим ско-
2 2
рость и ее выражением B): Т2 = о, mil[1—г, или, учитывая, что
Ту-=т{и\12, запишем
Подставив в формулу C) значения т*, т2 и Т* и произведя
вычисления, получим
7W500/E00+100)].4-Ю3 Дж=3,33.103 Дж=3,33 кДж.
3. Боек до удара обладал энергией 7\; Т2— энергия, затра-
затраченная на углубление сваи в грунт. Следовательно, во внутреннюю
энергию, связанную с неупругой деформацией сваи, превратилась
энергия
Т=Тг — Т2.
Подставив в это выражение значения 7\ и Т2, найдем
Г-0,67 кДж.
4. Свайный молот служит для забивки сваи в грунт; следова-
следовательно, энергию Т2 следует считать полезной. КПД удара бойка
о сваю выразится как отношение энергии Т29 затраченной на уг-
углубление сваи в грунт, ко всей затраченной энергии Тг:
Ч = Т21Тг.
Подставив в последнее выражение Т2 по формуле C), получим
Подставим значения пг1 и т2 и произведем вычисления:
Г|=83,3%.
Примечание к примерам 8 и 9. Оба примера решались одинаково с единст-
единственной разницей, что при ударе бойка молота о поковку полезной считалась
энергия Г, затраченная на деформацию поковки, а при ударе бойка свайного
молота о сваю — энергия Т2» затраченная на углубление сваи в грунт.
Задачи
Второй закон Ньютона
2.1. На гладком столе лежит брусок массой т=4 кг. К бруску
привязан шнур, ко второму концу которого приложена сила F=
= 10 Н, направленная параллельно поверхности стола. Найти уско-
ускорение а бруска.
2.2. На столе стоит тележка массой тх=4 кг. К тележке привя-
привязан один конец шнура, перекинутого через блок. С каким ускоре-
ускорением а будет двигаться тележка, если к другому концу шнура при-
привязать гирю массой т2=1 кг?
31

2.3. К пружинным весам подвешен блок. Через блок перекинут
шнур, к концам которого привязали грузы массами т1 = 1,5 кг
и т2=3 кг. Каково будет показание весов во время движения гру-
грузов? Массой блока и шнура пренебречь.
2.4. Два бруска массами т1=\ кг и тг=\ кг, соединенные шну-
шнуром, лежат на столе. С каким ускорением а будут двигаться бруски,
если к одному из них приложить силу F=10 H, направленную го-
горизонтально? Какова будет сила натяжения Т шнура, соединяющего
бруски, если силу 10 Н приложить к первому бруску? ко второму
бруску? Трением пренебречь.
2.5. На гладком столе лежит брусок массой т=4 кг. К бруску
привязаны два шнура, перекинутые через неподвижные блоки,
прикрепленные к противоположным краям стола. К концам шнуров
подвешены гири, массы которых т1=1 кг и т2=2 кг. Найти ускоре-
ускорение а, с которым движется брусок, и силу натяжения Т каждого
из шнуров. Массой блоков и трением пренебречь.
2.6. Наклонная плоскость, образующая угол а=25° с плоскостью
горизонта, имеет длину 1=2 м. Тело, двигаясь равноускоренно, со-
соскользнуло с этой плоскости за время t=2 с. Определить коэффи-
коэффициент трения / тела о плоскость.
2.7. Материальная точка массой т=2 кг движется под действием
некоторой силы F согласно уравнению x=A+Bt+Ct2+Dt3, где
С=1 м/с2, D=—0,2 м/с3. Найти значения этой силы в моменты
времени U=2 с и /2=5 с. В какой момент времени сила равна нулю?
2.8. Молот массой т=\ т падает с высоты h=2 м на наковальню.
Длительность удара /=0,01 с. Определить среднее значение силы
<^> удара.
2.9. Шайба, пущенная по поверхности льда с начальной ско-
скоростью i>0=20 м/с, остановилась через /=40 с. Найти коэффициент
трения / шайбы о лед.
2.10. Материальная точка массой т=\ кг, двигаясь равномерно,
описывает четверть окружности радиусом г= 1,2 м в течение времени
t=2 с. Найти изменение Ар импульса точки.
2.11. Тело массой т=Ъ кг брошено под углом а=30° к горизонту
с начальной скоростью уо=2О м/с. Пренебрегая сопротивлением воз-
воздуха, найти: 1) импульс силы F, действующей на тело, за время его
полета; 2) изменение Ар импульса тела за время полета.
2.12. Шарик массой т=100 г упал с высоты /i=2,5 м на горизон-
горизонтальную плиту, масса которой много больше массы шарика, и отско-
отскочил от нее вверх. Считая удар абсолютно упругим, определить им-
импульс р, полученный плитой.
2.13. Шарик массой т=300 г ударился о стену и отскочил от
нее. Определить импульс plf полученный стеной, если в последний
момент перед ударом шарик имел скорость vo= 10 м/с, направленную
под углом а=30° к поверхности стены. Удар считать абсолютно
упругим.
2.14. Тело массой т=0,2 кг соскальзывает без трения по желобу
высотой h=2 м. Начальная скорость v0 шарика равна нулю. Найти
32

изменение Ар импульса шарика и импульс ру полученный желобом
при движении тела.
2.15. Ракета массой т=1 т, запущенная с поверхности Земли
вертикально вверх, поднимается с ускорением a=2g. Скорость v
струи газов, вырывающихся из сопла, равна 1200 м/с. Найти рас-
расход Qm горючего.
2.16. Космический корабль имеет массу т=3,5 т. При маневри-
маневрировании из его двигателей вырывается струя газов со скоростью
у=800 м/с; расход горючего Qm=0,2 кг/с. Найти реактивную силу
R двигателей и ускорение а, которое она сообщает кораблю.
2.17. Вертолет массой т=3,5 т с ротором, диаметр d которого ра-
равен 18 м, «висит» в воздухе. С какой скоростью v ротор отбрасывает
вертикально вниз струю воздуха? Диаметр струи считать равным
диаметру ротора.
2.18. Брусок массой т2=5 кг может свободно скользить по гори-
горизонтальной поверхности без трения. На нем находится другой бру-
брусок массой тх=\ кг. Коэффициент трения соприкасающихся поверх-
поверхностей брусков /=0,3. Определить максимальное значение силы
^тах> приложенной к нижнему бруску, при которой начнется со-
соскальзывание верхнего бруска.
2.19. На горизонтальной поверхности находится брусок массой
т1==2 кг. Коэффициент трения Д бруска о поверхность равен 0,2. На
бруске находится другой брусок массой т2=8 кг. Коэффициент тре-
трения /2 верхнего бруска о нижний равен 0,3. К верхнему бруску
приложена сила F. Определить: 1) значение силы Flf при котором
начнется совместное скольжение брусков по поверхности; 2) значе-
значение силы F2, при котором верхний брусок начнет проскальзывать
относительно нижнего.
2.20. Ракета, масса которой М=6 т, поднимается вертикально
вверх. Двигатель ракеты развивает силу тяги ,Р=500 кН. Опреде-
Определить ускорение а ракеты и силу натяжения Т троса, свободно сви-
свисающего с ракеты, на расстоянии, равном V4 его длины от точки
прикрепления троса. Масса m троса
равна 10 кг. Силой сопротивления воз-
воздуха пренебречь.
2.21. На плоской горизонтальной
поверхности находится обруч, масса
которого ничтожно мала. К внутрен-
внутренней части обруча прикреплен груз _______
малых размеров, как это показано на ^^^^^
рис. 2.7. Угол а=30°. С каким уско- Рис. 2.7
рением а необходимо двигать плос-
плоскость в направлении, указанном на рисунке, чтобы обруч с грузом
не изменил своего положения относительно плоскости? Скольже-
Скольжение обруча по плоскости отсутствует.
2.22. Самолет летит в горизонтальном направлении с ускорением
«=20 м/с2. Какова перегрузка пассажира, находящегося в самолете?
(Перегрузкой называется отношение силы F, действующей на пас-
пассажира, к силе тяжести Р.)
2 № 1268 33

2.23. Автоцистерна с керосином движется с ускорением а—
=0,7 м/с2. Под каким углом ср к плоскости горизонта расположен
уровень керосина в цистерне?
2.24. Бак в тендере паровоза имеет длину 1=4 м. Какова раз-
разность А/ уровней воды у переднего и заднего концов бака при дви-
движении поезда с ускорением а=0,5 м/с2?
2.25. Неподвижная труба с площадью
S поперечного сечения, равной 10 см2,
изогнута под углом ф=90° и прикреп-
прикреплена к стене (рис. 2.8). По трубе течет
вода, объемный расход Qv которой 50 л/с.
Найти давление р струи воды, вызван-
вызванной изгибом трубы.
______________ 2.26. Струя воды ударяется о непод-
'//////////////////////////////////, вижную плоскость, поставленную под
Рис 2.8 углом ф=60° к направлению движения
струи. Скорость v струи равна 20 м/с,
площадь S ее поперечного сечения равна 5 см2. Определить силу F
давления струи на плоскость.
2.27*. Катер массой т=2 т с двигателем мощностью N=50 кВт
развивает максимальную скорость vmax =25 м/с. Определить время
t, в течение которого катер после выключения двигателя потеряет
половину своей скорости. Принять, что сила сопротивления движе-
движению катера изменяется пропорционально квадрату скорости.
2.28*. Снаряд массой т=\0 кг выпущен из зенитного орудия
вертикально вверх со скоростью уо=8ОО м/с. Считая силу сопротив-
сопротивления воздуха пропорциональной скорости, определить время t
подъема снаряда до высшей точки. Коэффициент сопротивления k=
-0,25 кг/с.
2.29*. С вертолета, неподвижно висящего на некоторой высоте
над поверхностью Земли, сброшен груз массой т=100 кг. Считая,
что сила сопротивления воздуха изменяется пропорционально ско-
скорости, определить, через какой промежуток времени А^ ускорение
а груза будет равно половине ускорения свободного падения. Ко-
Коэффициент сопротивления k=\0 кг/с.
2.30*. Моторная лодка массой т=400 кг начинает двигаться по
озеру. Сила тяги F мотора равна 0,2 кН. Считая силу сопротивления
Fc пропорциональной скорости, определить скорость v лодки через
Д^=20 с после начала ее движения. Коэффициент сопротивления
fe=20 кг/с.
2.31. Катер массой т=2 т трогается с места и в течение времени
т=10 с развивает при движении по спокойной воде скорость v=
=4 м/с. Определить силу тяги F мотора, считая ее постоянной. При-
Принять силу сопротивления Fc движению пропорциональной скорости;
коэффициент сопротивления &=100 кг/с.
2.32. Начальная скорость v0 пули равна 800 м/с. При движении
* Перед решением задач 2.27—2.30 следует предварительно разобрать
пример 3 из § 2.
34

в воздухе за время ?=0,8 с ее скорость уменьшилась до и=200 м/с.
Масса т пули равна 10 г. Считая силу сопротивления воздуха про-
пропорциональной квадрату скорости, определить коэффициент со-
сопротивления k. Действием силы тяжести пренебречь.
2.33. Парашютист, масса которого т=80 кг, совершает затяжной
прыжок. Считая, что сила сопротивления воздуха пропорциональна
скорости, определить, через какой промежуток времени А/ скорость
движения парашютиста будет равна 0,9 от скорости установившегося
движения. Коэффициент сопротивления &=10 кг/с. Начальная
скорость парашютиста равна нулю.
Закон сохранения импульса
2.34. Шар массой т^Ю кг, движущийся со скоростью v1-=
=4 м/с, сталкивается с шаром массой /п2=4 кг, скорость v2 которого
равна 12 м/с. Считая удар прямым, неупругим, найти скорость и
шаров после удара в двух случаях: 1) малый шар нагоняет большой
шар, движущийся в том же направлении; 2) шары движутся навстре-
навстречу друг другу.
2.35. В лодке массой т1=240 кг стоит человек массой т2=60 кг.
Лодка плывет со скоростью v±=2 м/с. Человек прыгает с лодки в го-
горизонтальном направлении со скоростью v=4 м/с (относительно лод-
лодки). Найти скорость и движения лодки после прыжка человека
в двух случаях: 1) человек прыгает вперед по движению лодки и
2) в сторону, противоположную движению лодки.
2.36. На полу стоит тележка в виде длинной доски, снабженной
легкими колесами. На одном конце доски стоит человек. Масса чело-
человека М=60 кг, масса доски т=20 кг. С какой скоростью и (отно-
(относительно пола) будет двигаться тележка, если человек пойдет вдоль
доски со скоростью (относительно доски) v=\ м/с? Массой колес
пренебречь. Трение во втулках не учитывать.
2.37. В предыдущей задаче найти, на какое расстояние d: 1) пере-
передвинется тележка, если человек перейдет на другой конец доски;
2) переместится человек относительно пола; 3) переместится центр
масс системы тележка — человек относительно доски и относитель-
относительно пола. Длина / доски равна 2 м.
2.38. На железнодорожной платформе установлено орудие.
Масса платформы с орудием М=15 т. Орудие стреляет вверх под
углом ер=60° к горизонту в направлении пути. С какой скоростью
i>i покатится платформа вследствие отдачи, если масса снаряда т=
=20 кг и он вылетает со скоростью и2=600 м/с?
2.39. Снаряд массой т—10 кг обладал скоростью и=200 м/с
в верхней точке траектории. В этой точке он разорвался на две части.
Меньшая массой т1=3 кг получила скорость Wi=400 м/с в прежнем
направлении. Найти скорость и2 второй, большей части после раз-
разрыва.
2.40. В предыдущей задаче найти, с какой скоростью и2 и под
каким углом ср2 к горизонту полетит большая часть снаряда, если
меньшая полетела вперед под углом ф1=60о к горизонту.
2* 35

2.41. Два конькобежца массами т1=80 кг и т2=50 кг, держась
за концы длинного натянутого шнура, неподвижно стоят на льду
один против другого. Один из них начинает укорачивать шнур, вы-
выбирая его со скоростью v=\ м/с. С какими скоростями иг и и2 будут
двигаться по льду конькобежцы? Трением пренебречь.
Динамика материальной точки,
движущейся по окруоюности
2.42. Диск радиусом R=A0 см вращается вокруг вертикальной
оси. На краю диска лежит кубик. Принимая коэффициент трения
/=0,4, найти частоту п вращения, при которой кубик соскользнет
с диска.
2.43. Акробат на мотоцикле описывает «мертвую петлю» радиусом
г=4 м. С какой наименьшей скоростью vm[n должен проезжать ак-
акробат верхнюю точку петли, чтобы не сорваться?
2.44. К шнуру подвешена гиря. Гирю отвели в сторону так, что
шнур принял горизонтальное положение, и отпустили. Как велика
сила натяжения Т шнура в момент, когда гиря проходит положение
равновесия? Какой угол ср с вертикалью составляет шнур в момент,
когда сила натяжения шнура равна силе тяжести гири?
2.45. Самолет описывает петлю Нестерова радиусом i?=200 м.
Во сколько раз сила F, с которой летчик давит на сиденье в нижней
точке, больше силы тяжести Р летчика, если скорость самолета v==
= 100 м/с?
2.46. Грузик, привязанный к шнуру длиной /=50 см, описывает
окружность в горизонтальной плоскости. Какой угол ср образует
шнур с вертикалью, если частота вращения п=\ с?
2.47. Грузик, привязанный к нити длиной 1=1 м, описывает
окружность в горизонтальной плоскости. Определить период Т
обращения, если нить отклонена на угол ср=60° от вертикали.
2.48. При насадке маховика на ось центр тяжести оказался на
расстоянии г=0,1 мм от оси вращения. В каких пределах меняется
сила F давления оси на подшипники, если частота вращения махо-
маховика лг= 10 с? Масса m маховика равна 100 кг.
2.49. Мотоцикл едет по внутренней поверхности вертикального
цилиндра радиусом /? = 11,2 м. Центр тяжести мотоцикла с челове-
человеком расположен на расстоянии /=0,8 м от поверхности цилиндра.
Коэффициент трения / покрышек о поверхность цилиндра равен
0,6. С какой минимальной скоростью vmin должен ехать мотоцик-
мотоциклист? Каков будет при этом угол ср наклона его к плоскости гори-
горизонта?
2.50. Автомобиль массой т=5 т движется со скоростью v=
= 10 м/с по выпуклому мосту. Определить силу F давления автомо-
автомобиля на мост в его верхней части, если радиус R кривизны моста
равен 50 м.
2.51. Сосуд с жидкостью вращается с частотой я=2 с вокруг
вертикальной оси. Поверхность жидкости имеет вид воронки. Чему
3G

равен угол ф наклона поверхности жидкости в точках, лежащих на
расстоянии г=5 см от оси?
2.52. Автомобиль идет по закруглению шоссе, радиус R кривизны
которого равен 200 м. Коэффициент трения / колес о покрытие доро-
дороги равен 0,1 (гололед). При какой скорости v автомобиля начнется
его занос?
2.53. Какую наибольшую скорость i>max может развить велосипе-
велосипедист, проезжая закругление радиусом jR=50 m, если коэффициент
трения скольжения / между шинами и асфальтом равен 0,3? Каков
угол ф отклонения велосипеда от вертикали, когда велосипедист дви-
движется по закруглению?
2.54. Самолет массой т=-2,5 т летит со скоростью ^=400 км/ч.
Он совершает в горизонтальной плоскости вираж (вираж — полет
самолета по дуге окружности с некоторым углом крена). Радиус R
траектории самолета равен 500 м. Найти поперечный угол ф накло-
наклона самолета и подъемную силу F крыльев во время полета.
2.55. Вал вращается с частотой /г=2400 мин. К валу перпенди-
перпендикулярно его длине прикреплен стержень очень малой массы, несу-
несущий на концах грузы массой т=1 кг каждый, находящиеся на рас-
расстоянии г=0,2 м от оси вала. Найти: 1) силу F, растягивающую стер-
стержень при вращении вала; 2) момент М силы, которая действовала бы
на вал, если бы стержень был наклонен под углом ф=89° к оси вала.
2.56. Тонкое однородное медное кольцо радиусом jR = 10 см вра-
вращается относительно оси, проходящей через центр кольца, с угловой
скоростью со = 10 рад/с. Определить нормальное напряжение а, воз-
возникающее в кольце в двух случаях: 1) когда ось вращения перпен-
перпендикулярна плоскости кольца и 2) когда лежит в плоскости кольца.
Деформацией кольца при вращении пренебречь.
Работа и энергия
2.57. Под действием постоянной силы F вагонетка прошла путь
s=5 м и приобрела скорость v=2 м/с. Определить работу А силы,
если масса т вагонетки равна 400 кг и коэффициент трения /=0,01.
2.58. Вычислить работу Л, совершаемую при равноускоренном
подъеме груза массой т=100 кг на высоту А=4 м за время t=2 с.
2.59. Найти работу Л подъема груза по наклонной плоскости
длиной 1=2 м, если масса т груза равна 100 кг, угол наклона ф=
=30°, коэффициент трения /=0,1 и груз движется с ускорением
а=1 м/с2.
2.60. Вычислить работу Л, совершаемую на пути s= 12 м равно-
равномерно возрастающей силой, если в начале пути сила Fi=10 H, в кон-
конце пути F2=46 Н.
2.61. Под действием постоянной силы .Г=400 Н, направленной
вертикально вверх, груз массой т=20 кг был поднят на высоту
Л=15 м. Какой потенциальной энергией П будет обладать поднятый
груз? Какую работу А совершит сила F?
2.62. Тело массой т=\ кг, брошенное с вышки в горизонталь-
горизонтальном направлении со скоростью i\>—20 м/с, через t=3 с упало на зем-
37

лю. Определить кинетическую энергию 7, которую имело тело в мо-
момент удара о землю. Сопротивлением воздуха пренебречь.
2.63. Камень брошен вверх под углом ф=60° к плоскости гори-
горизонта. Кинетическая энергия То камня в начальный момент времени
равна 20 Дж. Определить кинетическую Т и потенциальную П энер-
энергии камня в высшей точке его траектории. Сопротивлением воздуха
пренебречь.
2.64. Насос выбрасывает струю воды диаметром d—2 см со ско-
скоростью и=20 м/с. Найти мощность N, необходимую для выбрасы-
выбрасывания воды.
2.65. Какова мощность N воздушного потока сечением S—
=0,55 м2 при скорости воздуха и=20 м/с и нормальных усло-
условиях?
2.66. Вертолет массой ш=3 т висит в воздухе. Определить мощ-
мощность А/", развиваемую мотором вертолета в этом положении, при
двух значениях диаметра d ротора: 1) 18 м; 2) 8 м. При расчете при-
принять, что ротор отбрасывает вниз цилиндрическую струю воздуха
диаметром, равным диаметру ротора.
2.67. Материальная точка массой ш=2 кг двигалась под дей-
действием некоторой силы, направленной вдоль оси Ох согласно урав-
уравнению x=A+Bt+Ct2+Dt3, где В=—2 м/с, С=1 м/с2, D=—0,2 м/с3.
Найти мощность N, развиваемую силой в момент времени t±=2 с и
^2-5 с.
2.68. С какой наименьшей высоты h должен начать скатываться
акробат на велосипеде (не работая ногами), чтобы проехать по
дорожке, имеющей форму «мертвой петли» радиусом R=4 м,
и не оторваться от дорожки в верхней точке петли? Трением прене-
пренебречь.
2.69. Камешек скользит с наивысшей точки купола, имеющего
форму полусферы. Какую дугу а опишет камешек, прежде чем ото-
оторвется от поверхности купола? Трением пренебречь.
2.70. Мотоциклист едет по горизонтальной дороге. Какую наи-
наименьшую скорость v он должен развить, чтобы, выключив мотор,
проехать по треку, имеющему форму «мертвой петли» радиусом
R=4 м? Трением и сопротивлением воздуха пренебречь.
2.71. При выстреле из орудия снаряд массой mt=l0 кг получает
кинетическую энергию 7\=1,8 МДж. Определить кинетическую
энергию Т2 ствола орудия вследствие отдачи, если масса пг2 ствола
орудия равна 600 кг.
2.72. Ядро атома распадается на два осколка массами пг1=
= 1,6»10~25кг и т2=2,4«10~25 кг. Определить кинетическую энер-
энергию Т2 второго осколка, если энергия Т± первого осколка равна
18 нДж.
2.73. Конькобежец, стоя на льду, бросил вперед гирю массой
тг~Ъ кг и вследствие отдачи покатился назад со скоростью v2=
= 1 м/с. Масса конькобежца т2=60 кг. Определить работу Л, совер-
совершенную конькобежцем при бросании гири.
2.74. Молекула распадается на два атома. Масса одного из ато-
атомов в п=3 раза больше, чем другого. Пренебрегая начальной кине-
38

тической энергий и импульсом молекулы, определить кинетические
энергии 7\ и Т2 атомов, если их суммарная кинетическая энергия
Т=0,032 нДж.
2.75. На рельсах стоит платформа, на которой закреплено орудие
без противооткатного устройства так, что ствол его расположен
в горизонтальном положении. Из орудия производят выстрел вдоль
железнодорожного пути. Масса тх снаряда равна 10 кг, и его ско-
скорость Ux=l км/с. На какое расстояние /
откатится платформа после выстрела,
если коэффициент сопротивления /=
-0,002?
2.76. Пуля массой т=10 г, летев-
шая со скоростью и=600 м/с, попала в
баллистический маятник (рис. 2.9) мас-
массой М=о кг и застряла в нем. На ка-
какую высоту А, откачнувшись после уда- Рис<
ра, поднялся маятник?
2.77. В баллистический маятник массой М=5 кг попала пу-
пуля массой т= 10 г и застряла в нем. Найти скорость v пули, если
маятник, отклонившись после удара, поднялся на высоту
А=10 см.
2.78. Два груза массами т1=10 кг и т2=15 кг подвешены на ни-
нитях длиной 1=2 м так, что грузы соприкасаются между собой.
Меньший груз был отклонен на угол ф=60° и выпущен. Определить
высоту А, на которую поднимутся оба груза после удара. Удар
грузов считать неупругим.
2.79. Два неупругих шара массами т1=2 кг и т2=3 кг движутся
со скоростями соответственно v1=8 м/с и и2=4 м/с. Определить
увеличение AU внутренней энергии шаров при их столкновении
в двух случаях: 1) меньший шар нагоняет больший; 2) шары дви-
движутся навстречу друг другу.
2.80. Шар массой т±, летящий со скоростью vx=5 м/с, ударяет не-
неподвижный шар массой т2. Удар прямой, неупругий. Определить
скорость и шаров после удара, а также долю w кинетической энер-
энергии летящего шара, израсходованной на увеличение внутренней
энергии этих шаров. Рассмотреть два случая: 1) т1=2 кг, т2=8 кг;
2) /72! = 8 КГ, Ш2 = 2 КГ.
2.81. Шар массой т1=2 кг налетает на покоящийся шар массой
/722=8 кг. Импульс р! движущегося шара равен 10 кг-м/с. Удар
шаров прямой, упругий. Определить непосредственно после удара:
1) импульсы р[ первого шара и р'2 второго шара; 2) изменение крг
импульса первого шара; 3) кинетические энергии Т[ первого шара и
Т2 второго шара; 4) изменение АТг кинетической энергии первого
шара; 5) долю w кинетической энергии, переданной первым шаром
второму.
2.82. Шар массой тг=6 кг налетает на другой покоящийся шар
массой т2=4 кг. Импульс pi первого шара равен 5 кг-м/с. Удар
шаров прямой, неупругий. Определить непосредственно после уда-
удара: 1) импульсы рх первого шара и р'2 второго шара; 2) изменение
39

A/?i импульса первого шара; 3) кинетические энергии Т[ первого
шара и Т2 второго шара; 4) изменение AT1* кинетической энергии
первого шара; 5) долю w1 кинетической энергии, переданной первым
шаром второму и долю w2 кинетической энергии, оставшейся у пер-
первого шара; 6) изменение Л?/ внутренней энергии шаров; 7) долю w
кинетической энергии первого шара, перешедшей во внутреннюю
энергию шаров.
2.83. Молот массой m1=S кг ударяет небольшой кусок железа,
лежащий на наковальне. Масса т2 наковальни равна 100 кг. Мас-
Массой куска железа пренебречь. Удар неупругий. Определить КПД ц
удара молота при данных условиях.
2.84. Боек свайного молота массой тх=500 кг падает с некоторой
высоты на сваю массой /л2=100 кг. Найти КПД ц удара бойка,
считая удар неупругим. Изменением потенциальной энергии сваи
при углублении ее пренебречь.
2.85. Молотком, масса которого тг=\ кг, забивают в стену гвоздь
массой т2=75 г. Определить КПД г| удара молотка при данных
условиях.
2.86. Шар массой т!=200 г, движущийся со скоростью vx=
= 10 м/с, ударяет неподвижный шар массой т2=800 г. Удар пря-
прямой, абсолютно упругий. Каковы будут скорости иг и и2 шаров после
удара?
2.87. Шар массой т=1,8 кг сталкивается с покоящимся шаром
большей массы М. В результате прямого упругого удара шар по-
потерял w=0,36 своей кинетической энергии Т±. Определить массу
большего шара.
2.88. Из двух соударяющихся абсолютно упругих шаров боль-
больший шар покоится. В результате прямого удара меньший шар по-
потерял &>=3/4 своей кинетической энергии 7\. Определить отношение
k=M/m масс шаров.
2.89. Определить максимальную часть w кинетической энергии
Т1у которую может передать частица массой т1=2Л0~22 г, сталки-
сталкиваясь упруго с частицей массой т2=6Л0~22 г, которая до столкно-
столкновения покоилась.
2.90. Частица массой т1=\0~2Ъ кг обладает импульсом рг =
=5 -10~20 кг-м/с. Определить, какой максимальный импульс р2
может передать эта частица, сталкиваясь упруго с частицей массой
т2=4-10~25 кг, которая до соударения покоилась.
2.91. На покоящийся шар налетает со скоростью v±=2 м/с дру-
другой шар одинаковой с ним массы. В результате столкновения этот
шар изменил направление движения на угол а=30°. Определить:
1) скорости и± и и2 шаров после удара; 2) угол р между вектором
скорости второго шара и первоначальным направлением движения
первого шара. Удар считать упругим.
2.92. Частица массой mi=10~24 г имеет кинетическую энергию
7\=9 нДж. В результате упругого столкновения с покоящейся
частицей массой /п2=4-10"4 г она сообщает ей кинетическую энер-
энергию Т2=5 нДж. Определить угол а, на который отклонится частица
от своего первоначального направления.
40

§ 3. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Основные формулы
9 Момент силы F, действующей на тело, относительно оси
вращения
где Т7! — проекция силы F на плоскость, перпендикулярную оси
вращения; / — плечо силы F (кратчайшее расстояние от оси враще-
вращения до линии действия силы).
• Момент инерции относительно оси вращения:
а) материальной точки
J=mr2,
где т — масса точки; г — расстояние ее от оси вращения;
б) дискретного твердого тела
п
J = 2
где Amj — масса 1-го элемента тела; rt — расстояние этого элемента
от оси вращения; п — число элементов тела;
в) сплошного твердого тела
Если тело однородно, т. е. его плотность р одинакова по всему
объему, то
и / =
где V — объем тела.
• Моменты инерции некоторых тел правильной геометрической
формы:
Тело
Ось, относительно которой опре-
определяется момент инерции
Формула
момента
инерции
Однородный тонкий стержень
массой т и длиной /
Тонкое кольцо, обруч, труба
радиусом R и массой т, махо-
маховик "радиусом R и массой т,
распределенной по ободу
Круглый однородный диск
(цилиндр) радиусом R и мас-
массой т
Однородный шар массой т
и радиусом R
Проходит через центр тяже-
тяжести стержня перпендикулярно
стержню
Проходит через конец стерж-
стержня перпендикулярно стержню
Проходит через центр перпен-
перпендикулярно плоскости основания
Проходит через центр диска
перпендикулярно плоскости ос-
основания
Проходит через центр шара
41

• Теорема Штейнера* Момент инерции тела относительно про-
произвольной оси
где Л — момент инерции этого тела относительно оси, проходящей
через центр тяжести тела параллельно заданной оси; а — расстоя-
расстояние между осями; т — масса тела.
• Момент импульса вращающегося тела относительно оси
L~J(d.
• Закон сохранения момента импульса
п
2 L? = const,
i = 1
где Lt — момент импульса /-го тела, входящего в состав системы.
Закон сохранения момента импульса для двух взаимодействую-
взаимодействующих тел
где Л, J<l, e>i и оJ — моменты инерции и угловые скорости тел до
взаимодействия: J[, /2, coi и со2 — те же величины после взаимодей-
взаимодействия.
Закон сохранения момента импульса для одного тела, момент
инерции которого меняется,
где Л и J2 — начальный и конечный моменты инерции; coi и со2 —-
начальная и конечная угловые скорости тела.
Ф Основное уравнение динамики вращательного движения
твердого тела относительно неподвижной оси
М (К = (!(/©),
где М — момент силы, действующей на тело в течение времени d?;
J — момент инерции тела; ш — угловая скорость; J& — момент
импульса.
Если момент силы и момент инерции постоянны, то это уравнение
записывается в виде
МЛ/= 7 Лео.
В случае постоянного момента инерции основное уравнение
динамики вращательного движения принимает вид
М = Уе,
где 8 — угловое ускорение.
• Работа постоянного момента силы Мг действующего на
вращающееся тело,
где ф — угол поворота тела.
# Мгновенная мощность, развиваемая при вращении тела?
• Кинетическая энергия вращающегося тела
Т=1/2/оJ.
42

• Кинетическая энергия тела, катящегося по плоскости без
скольжения,
где 1/2ти2 — кинетическая энергия поступательного движения
тела; v — скорость центра инерции тела; x/2JoJ — кинетическая
энергия вращательного движения тела вокруг оси, проходящей
через центр инерции.
• Работа, совершаемая при вращении тела, и изменение кине-
кинетической энергии его связаны соотношением
Л = 72Ло22—VJ4.
• Величины, характеризующие динамику вращательного дви-
движения, и формулы, описывающие это движение, аналогичны соот-
соответствующим величинам и формулам поступательного движения.
Эта аналогия раскрывается следующей таблицей:
Поступательное движение
Вращательное движение
Основной закон динамики
M = mv2 — mv1; MM = /со2 — /соь
= ma M = Je
Закон сохранения
импульса момента импульса
п п
2 mtVi — const 2 Ji®i = const
=l t=l
Работа и мощность
A = Fs; Л = Мф;
N = Fv N = Ma>
Кинетическая энергия
T=y2mv* Г^Уз/со2
Примеры решения задач
Пример 1. Вычислить момент инерции Jz молекулы NO2 отно-
относительно оси z, проходящей через центр масс молекулы перпен-
перпендикулярно плоскости, содержащей ядра атомов. Межъядерное рас-
расстояние d этой молекулы равно 0,118 нм, валентный угол а=140°.
Решение. Молекулу NO2 можно рассматривать как систему,
состоящую из трех материальных точек общей массой
m=2m1+m2i A)
где тг — масса атома кислорода; т2 — масса атома азота.
Расположим молекулу относительно координатных осей так,
как это указано на рис. 3.1 (начало координат совместим с центром
43

масс С молекулы, ось z направим перпендикулярно плоскости
чертежа «к нам».)
Для определения Jz воспользуемся теоремой Штейнера:
J = J c-\-ma%.
Для данного случая эта теорема запишется в виде J'г, =Jz+rna2,
где jzt—момент инерции относительно оси г', параллельной
оси г и проходящей через
атом азота (точка О на
рис. 3.1). Отсюда искомый
момент инерции
JZ=JZ—та2. B)
Момент инерции Jz, нахо-
находим как сумму моментов
инерции двух материаль-
материальных точек (атомов кисло-
кислорода):
j О гп Аъ (fX\
J г' — 1Шга . \О)
Расстояние а между осями г и z' равно координате хс центра масс
системы и поэтому может быть выражено по формуле (см. § 2, с. 20)
*c=2m^2mz- В данном случае
а=хс= Bm1x1+m2x?)/ Bm1+m2)i
или, учитывая, что x±=d cos (a/2) и х2~0,
2tn-\ 1 ос
а = хГ = -к—; d cos -7T • D)
L 2mi-\-m2 2 v ^
Подставив в формулу B) значения Jz4 m, а соответственно из
выражений C), A), D), получим
2/щ ^
/п.
т<
Рис. 3.1
J2 =
2 — Bт1 + т2)
или после преобразований
-та — 2 ;• E)
Найдем в табл. 23 относительные атомные массы кислорода
(Ло=16) и азота (AN=l4) и запишем массы атомов этих элементов
в атомных единицах массы (а.е.м.), а затем выразим в килограм-
килограммах A а.е.м. = 1,66-Ю7 кг, см. табл. 9):
m1=-16-1,66-10~27 кг-2,66-10~26 кг;
т2=141,6610-27кг-2,32.10-26кг.
Значения mu m2, d и а подставим * в формулу E) и произведем
вычисления:
Пример 2. Физический маятник представляет собой стержень
длиной /=1 ми массой т1=\ кг с прикрепленным к одному из его
* Для вычисления выражения, стоящего в скобках, вместо масс атомов
можно подставить их относительные атомные массы, так как здесь массы
входят в виде отношения.
44

концов диском массой m2=0,5 т1. Определить момент инерции Jz
такого маятника относительно оси Ог, проходящей через точку О
на стержне перпендикулярно плоскости чертежа (рис. 3.2).
Решение. Общий момент инерции ма-
маятника равен сумме моментов инерции стерж-
стержня Jzl и диска Jхг:
JZ=JZ1+JZ2. A)
Формулы, по которым вычисляются момен-
моменты инерции стержня J± и диска /2 относитель-
относительно осей, проходящих через их центры масс,
даны в табл. на с. 41. Чтобы определить мо-
моменты инерции Jzi и /z2, надо воспользо-
воспользоваться теоремой Штейнера:
B)
Выразим момент инерции стержня сог-
согласно формуле B):
>
С)
0
1
У
Расстояние а± между осью Ог и параллель- Рис. 3.2
ной ей осью, проходящей через центр масс С*
стержня, как следует из рис. 3.2, равно V2Z — 1/31:=1/qI- С
том этого запишем
Кг = Vi2^a + ^i (VeO2 = V9^i/2 = 0,11 lm^2.
Момент инерции диска в соответствии с формулой B) равен
где R — радиус диска; R=1/J. Расстояние а2 между осью Ог и
параллельной ей осью, проходящей через центр масс диска, равно
(рис. 3.2) 2/3l+1/J=11/l2l. С учетом этого запишем
h% = Va^2 (V402 + ^2 (u/12/J = 0,0312m2/2 + 0,840m2/2 = 0,871m2/2.
Подставив полученные выражения Jzl и Jz2 в формулу A), най-
найдем
или, учитывая, что m2=0,5/n1,
Произведя вычисления, получим значение момента инерции
физического маятника относительно оси Ог:
Ы кг-м2=0,547 кг-м2.
Пример 3. Вал в виде сплошного цилиндра массой т1=10 кг
насажен на горизонтальную ось. На цилиндр намотан шнур, к сво-
свободному концу которого подвешена гиря массой т2=2 кг (рис. 3.3).
С каким ускорением а будет опускаться гиря, если ее предоставить
самой себе?
Решение. Линейное ускорение а гири равно тангенциально-
тангенциальному ускорению точек вала, лежащих на его цилиндрической поверх-
45

ности, и связано с угловым ускорением 8 вала соотношением
а=гг, A)
где г — радиус вала.
Угловое ускорение вала выражается основным уравнением ди-
динамики вращающегося тела:
г=ММ9 B)
где М — вращающий момент, действующий на вал; J — момент
инерции вала. Рассматриваем вал как однородный цилиндр. Тогда
его момент инерции относительно геометрической
оси равен
Вращающий момент М, действующий на вал,
равен произведению силы натяжения Т шнура на
радиус вала: М=Тг.
Силу натяжения шнура найдем из следующих
соображений. На гирю действуют две силы: сила
тяжести m2g, направленная вниз, и сила натяже-
натяжения Т шнура, направленная вверх. Равнодейст-
Равнодействующая этих сил вызывает равноускоренное дви-
движение гири. По второму закону Ньютона, m2g —
— T=m2ay откуда T=m2(g — а). Таким образом,
вращающий момент M=m2(g — а)г.
Подставив в формулу B) полученные выражения Ми/, найдем
угловое ускорение вала:
m2(g—a) r __2m2 (g—a)
^12Ш\Т^ TU\T
Для определения линейного ускорения гири подставим это
выражение е в формулу A). Получим а= m2^f"~~ » откуда
Пример 4. Через блок в виде диска, имеющий массу т=80 г,
перекинута тонкая гибкая нить, к концам которой подвешены грузы
массами mi =100 г и т2=200 г (рис. 3.4). С каким ускорением бу-
будут двигаться грузы, если их предоставить самим себе? Трением
пренебречь.
Решение. Применим к решению задачи основные законы
поступательного и вращательного движения. На каждый из движу-
движущихся грузов действуют две силы: сила тяжести mg, направленная
вниз, и сила Т натяжения нити, направленная вверх.
Так как вектор ускорения а груза тг направлен вверх, то 7\>
>т^. Равнодействующая этих сил вызывает равноускоренное дви-
движение и, по второму закону Ньютона, равна 7\ — m1g=m1a, от-
откуда
T1=m1g+m1a. A)
46

T'\ r _ mr a
1 l)l 2 г
т/
Вектор ускорения а груза т2 направлен вниз; следовательно,
T2<tn2g. Запишем формулу второго закона для этого груза:
tn2g — T2=m2a, откуда
T2=m2g — m2a. B)
Согласно основному закону динамики вращательного движе-
движения, вращающий момент М> приложенный к диску, равен произ-
произведению момента инерции / диска на его угло-
угловое ускорение г:
M=Je. C)
Определим вращающий момент. Силы натяже-
натяжения нитей действуют не только на грузы, но и на
диск. По третьему закону Ньютона, силы Т[ и Т2,
приложенные к ободу диска, равны соответственно
силам Tf и Т2, но по направлению им противопо-
противоположны. При движении грузов диск ускоренно
вращается по часовой стрелке; следовательно,
Т2>Т[. Вращающий момент, приложенный к дис-
диску, равен произведению разности этих сил на
плечо, равное радиусу диска, т. е. М^(Т2— Т[)г.
Момент инерции диска J=mr2/2, угловое ускоре-
ускорение связано с линейным ускорением грузов соот- Рис. 3.4
ношением г=а/г. Подставив в формулу C) выраже-
выражения М, J и 8, получим
откуда
Так как Т'г=Тг и Т2=Т2, то можно заменить силы Т[ и Т'2 вы-
выражениями по формулам A) и B), тогда
m
m2g—m2a—m-ig—m1a = -^-a, или
{m2—m1)g = [m2+ tn1 + -^
откуда
Ttl2 — /72f
Отношение масс в правой части формулы D) есть величина
безразмерная. Поэтому значения масс тх, т2 и т можно выразить
в граммах, как они даны в условии задачи. После подстановки
получим
О 27 9'81 М/С2 = 2'8
О = O,2+o7l+O,O4
Пример 5. Маховик в виде диска массой т=50 кг и радиусом
г=20 см был раскручен до частоты вращения ^1=480 мин и за-
затем предоставлен самому себе. Вследствие трения маховик остано-
остановился. Найти момент М сил трения, считая его постоянным для
47

двух случаев: 1) маховик остановился через ^=50 с; 2) маховик
до полной остановки сделал N=200 оборотов.
Решение. 1. По второму закону динамики вращательного
движения, изменение момента импульса вращающегося тела равна
произведению момента силы, действующего на тело, на время дей-
действия этого момента:
где / — момент инерции маховика; cof и со2 — начальная и конеч-
конечная угловые скорости. Так как ы2=0 и At=t, то Mt——/соь от-
откуда
М= —Jcojt. A)
Момент инерции диска относительно его геометрической оси
равен J=1/2mr2. Подставив это выражение в формулу A), найдем
М= —mr2(o1/Bt). B)
Выразив угловую скорость (Of через частоту вращения щ и
произведя вычисления по формуле B), найдем
М= —1 Н-м.
2. В условии задачи дано число оборотов, сделанных махови-
маховиком до остановки, т. е. его угловое перемещение. Поэтому приме-
применим формулу, выражающую связь работы с изменением кинетиче-
кинетической энергии:
A = J(ol/2—J<dl/2,
или, учтя, что «2=0,
Л = — /©f/2. C)
Работа при вращательном движении определяется по формуле
А=Мц). Подставив выражения работы и момента инерции диска
в формулу C), получим
Отсюда момент силы трения
Угол поворота <р=2я#=2 -3,14 -200 рад=1256 рад. Произведя
вычисления по формуле D), получим
Л1 = —1 Н-м.
Знак минус показывает, что момент силы трения оказывает
тормозящее действие.
Пример 6. Платформа в виде диска радиусом /? = 1,5 м и массой
ш1=180 кг вращается по инерции около вертикальной оси с часто-
частотой /г=10 мин. В центре платформы стоит человек массой /и2==
=60 кг. Какую линейную скорость относительно пола помещения
будет иметь человек, если он перейдет на край платформы?
Решение. По закону сохранения момента импульса,
(Л+ /2)<D = (/i+ /;)©', A)
где Jt — момент инерции платформы; /2 — момент инерции че-
человека, стоящего в центре платформы; со — угловая скорость
платформы с человеком, стоящим в ее центре; /2 — момент инерции
48

человека, стоящего на краю платформы; со' — угловая скорость
платформы с человеком, стоящим на ее краю.
Линейная скорость человека, стоящего на краю платформы,
связана с угловой скоростью соотношением
v=a'R. B)
Определив со' из уравнения A) и подставив полученное выра-
л е ше в формулу B), будем иметь
t; = (J1+J2)G)#/(J1+/;). C)
Момент инерции платформы рассчитываем как для диска; сле-
следовательно, J1=1l2m1R2. Момент инерции человека рассчитываем
как для материальной точки. Поэтому J2=0, J2=m2R2. Угловая
скорость платформы до перехода человека равна (о=2пп.
Заменив в формуле C) величины /ь J2) J'2 и ® их выражениями,
получим
1/R2 гщ
^2nnR=-
• 2nnR.
Сделав подстановку значений ти т2, пу R и я, найдем линей-
линейную скорость человека:
180 о о 1/1 10 1 к / л ало ,
P = -18Q , о 60 * 60' ' М/С = 0,942 М/С.
Пример 7. Человек стоит в центре скамьи Жуковского и вместе
с ней вращается по инерции. Частота вращения /Zi=0,5 с. Момент
Рис. 3.5
инерции /0 тела человека относительно оси вращения равен
1,6 кг-м2. В вытянутых в стороны руках человек держит по гире
массой т=2 кг каждая. Расстояние между гирями /х= 1,6 м. Опре-
Определить частоту вращения п2 скамьи с человеком, когда он опустит
руки и расстояние /2 между гирями станет равным 0,4 м. Моментом
инерции скамьи пренебречь.
Решение. Человек, держащий гири (рис. 3.5), составляет
49

вместе со скамьей замкнутую механическую систему *, поэтому
момент импульса /со этой системы должен иметь постоянное значе-
значение. Следовательно, для данного случая
где Ji и со! — момент инерции тела человека и угловая скорость
скамьи и человека с вытянутыми руками; J2 и со2 — момент инер-
инерции тела человека и угловая скорость скамьи и человека с опу-
опущенными руками. Отсюда
(O2=(J1/J2)(Oi.
Выразив в этом уравнении угловые скорости Of и со2 через частоты
вращения п± и п2(ы =2пп) и сократив на 2я, получим
n2=(Ji/J2)rii. A)
Момент инерции системы, рассматриваемой в данной задаче,
равен сумме момента инерции тела человека Jo и момента инерции
гирь в руках человека. Так как размер гирь много меньше рас-
расстояния их от оси вращения, то момент инерции гирь можно опре-
определить по формуле момента инерции материальной точки: J=mr2.
Следовательно **,
J1=J0+2rn(l1/2)*; J2=J0+2tn(l2/2)\
где т — масса каждой из гирь; /* и /2 — первоначальное и конеч-
ное расстояние между гирями. Подставив
выражения ^и J2 в уравнение A), полу-
получим
2m(t1/2)*
n W
Выполнив вычисления по формуле B),
найдем
п2=1,18 с-1.
Пример 8. Стержень длиной /=1,5 м и
массой М = 10 кг может вращаться вокруг
Рис. 3.6 неподвижной оси, проходящей через верх-
верхний конец стержня (рис. 3.6). В середину
стержня ударяет пуля массой т=10 г, летящая в горизонтальном
направлении со скоростью 1>0=500 м/с, и застревает в стержне.
На какой угол ф отклонится стержень после удара?
Решение. Удар пули следует рассматривать как неупругий:
после удара и нуля, и соответствующая точка стержня будут дви-
двигаться с одинаковыми скоростями.
Рассмотрим подробнее явления, происходящие при ударе. Сна-
Сначала пуля, ударившись о стержень, за ничтожно малый промежу-
* Предполагается, что моменты всех внешних сил (сил тяжести и сил
реакции), действующих на эту систему по отношению к оси вращения, яв-
являются уравновешенными. Трением пренебречь.
** В действительности с изменением положения рук человека (без гирь)
изменяется момент инерции его тела относительно оси вращения, однако
ввиду сложности учета этого изменения будем считать момент инерции J$
тела человека постоянным.
50

ток времени приводит его в движение с угловой скоростью со и
сообщает ему кинетическую энергию
7=/со2/2, A)
где J — момент инерции стержня относительно оси вращения.
Затем стержень поворачивается на искомый угол ф, причем
центр масс его поднимается на высоту h=(l/2) A — cos ф). В от-
отклоненном положении стержень будет обладать потенциальной
энергией
U=Mg{l/2)(l — собф). B)
Потенциальная энерги получена за счет кинетической энергии
и равна ей по закону сохранения энергии. Приравняв правые части
равенств A) и B), получим
Mg(L2) A — cos ф)-УоJ/2.
Отсюда
cos ф=1 — J
Подставив в эту формулу выражение для момента инерции стержня
J=M12!3, получим
созф-1 — /co2/Cg). C)
Чтобы из выражения C) найти ф, необходимо предварительно
определить значение о. В момент удара на пулю и на стержень
действуют силы тяжести, линии действия которых проходят через
ось вращения и направлены вертикально вниз. Моменты этих сил
относительно оси вращения равны нулю. Поэтому при ударе пули
о стержень будет справедлив закон сохранения момента импульса.
В начальный момент удара угловая скорость стержня соо=0,
поэтому его момент импульса L01=Jco0=0. Пуля коснулась стержня
и начала углубляться в стержень, сообщая ему угловое ускорение
и участвуя во вращении стержня около оси. Начальный момент
импульса пули L02=mv0r, где г — расстояние точки попадания от
оси вращения. В конечный момент удара стержень имел угловую
скорость со, а пуля — линейную скорость и, равную линейной
скорости точек стержня, находящихся на расстоянии г от оси вра-
вращения. Так как и=сог, то конечный момент импульса пули L2=
2
Применив закон сохранения импульса, можем написать
L01+LQ2=L1+L2f или
откуда
где J=Mt2J3— момент инерции системы стержень — пуля.
Если учесть, что в D) mr2<^J=Ml2/3, а также что г=//2, то
после несложных преобразований получим
2Ml ' \Pl
51

Подставив числовые значения величин в E), найдем
m=32°io!iT рад^0>5 рад*
По C) получим
cos Ф=1—1,5@,5J/C -9,81)=0,987.
Следовательно, ф=9°20\
Задачи
Момент инерции
3.1. Определить момент инерции J материальной точки массой
ш=0,3 кг относительно оси, отстоящей от точки на г=20 см.
3.2. Два маленьких шарика массой т=10 г каждый скреплены
тонким невесомым стержнем длиной /=20 см. Определить момент
инерции J системы относительно оси, перпендикулярной стержню
и проходящей через центр масс.
3.3. Два шара массами тя 2т (т=10 г) закреплены на тонком
невесомом стержне длиной /=40 см так, как это указано на
рис. 3.7, а, б. Определить моменты инерции J системы относитель-
относительно оси, перпендикулярной стержню и проходящей через его конец
в этих двух случаях. Размерами шаров пренебречь.
ч
l /77
\2т
#
Рис. 3.7
Рис. 3.8
3.4. Три маленьких шарика массой т=10 г каждый располо-
расположены в вершинах равностороннего треугольника со стороной а~
=20 см и скреплены между собой. Определить момент инерции J
системы относительно оси: 1) перпендикулярной плоскости треу-
треугольника и проходящей через центр описанной окружности; 2) ле-
лежащей в плоскости треугольника и проходящей через центр описан-
описанной окружности и одну из вершин треугольника. Массой стержней,
соединяющих шары, пренебречь.
3.5. Определить моменты инерции Jx, Jy, Jz трехатомных мо-
молекул типа АВ2 относительно осей х, у, г (рис. 3.8), проходящих
через центр инерции С молекулы (ось г перпендикулярна плоско-
плоскости ху). Межъядерное расстояние А В обозначено d, валентный угол а.
Вычисления выполнить для следующих молекул: 1) H2O(d=
=0,097 нм, а=104°30'); 2) SO2 (d=0,145 нм, а=124°).
3.6. Определить момент инерции / тонкого однородного стержня
длиной /=30 см и массой т=100 г относительно оси, перпендику-
52

лярной стержню и проходящей через: 1) его конец; 2) его середину;
3) точку, отстоящую от конца стержня на 1/3 его длины.
3.7. Определить момент инерции / тонкого однородного стержня
длиной /=60 см и массой т=\00 г относительно оси, перпендику-
перпендикулярной ему и проходящей через точку стержня, удаленную на
а=20 см от одного из его концов.
3.8. Вычислить момент инерции / проволочного прямоугольни-
прямоугольника со сторонами а=\2 см и 6 = 16 см относительно оси, лежащей
в плоскости прямоугольника и проходящей через середины малых
сторон. Масса равномерно распределена по длине проволоки с ли-
линейной плотностью т=0,1 кг/м.
3.9. Два однородных тонких стержня: АВ длиной /х=40 см
и массой т1=900 г и CD длиной /2=40 см и массой т2=400 г скреп-
скреплены под прямым углом (рис. 3.9). Определить момент инерции J
системы стержней относительно оси ОО\ проходящей через конец
стержня АВ параллельно стержню CD.
—-Я:—0' 0—
б]
Рис. 3.9
Рис. ЗЛО
3.10. Решить предыдущую задачу для случая, когда ось OOf
проходит через точку А перпендикулярно плоскости чертежа.
3.11. Определить момент инерции / проволочного равносто-
равностороннего треугольника со стороной а=10 см относительно: 1) оси,
лежащей в плоскости треугольника и проходящей через его
вершину параллельно стороне, противоположной этой вершине
(рис. 3.10, а); 2) оси, совпадающей с одной из сторон треугольника
(рис. 3.10, б). Масса т треугольника равна 12 г и равномерно рас-
распределена по длине проволоки.
3.12. На концах тонкого однородного стержня длиной / и мас-
массой Ът прикреплены маленькие шарики массами т и 2т. Опреде-
Определить момент инерции J такой системы относительно оси, перпенди-
перпендикулярной стержню и проходящей через точку О, лежащую на оси
стержня. Вычисления выполнить для случаев а, б, в, г, д, изобра-
изображенных на рис. 3.11. При расчетах принять 1=1 м, т=0,1 кг.
Шарики рассматривать как материальные точки.
3.13. Найти момент инерции J тонкого однородного кольца
радиусом R=20 см и массой т=100 г относительно оси, лежащей
в плоскости кольца и проходящей через его центр.
53

3.14. Определить момент инерции / кольца массой т=50 г
и радиусом # = 10 см относительно оси, касательной к кольцу.
3.15. Диаметр диска d=20 см, масса т-800 г. Определить
момент инерции J диска относительно оси, проходящей через се-
середину одного из радиусов перпендикулярно плоскости диска.
d
Рис. 3.12
3.16. В однородном диске массой т=\ кг и радиусом г=30 см
вырезано круглое отверстие диаметром d~2Q см, центр которого
находится на расстоянии /=15 см от оси диска (рис. 3.12). Найти
момент инерции J полученного тела относительно оси, проходя-
проходящей перпендикулярно плоскости диска через его центр.
3.17. Найти момент инерции J плоской однородной прямоуголь-
прямоугольной пластины массой т=800 г относительно оси, совпадающей с
одной из ее сторон, если длина а другой стороны равна 40 см.
3.18. Определить момент инерции J тонкой плоской пластины
со сторонами а=10 см и Ь=20 см относительно оси, проходящей
через центр масс пластины параллельно
большей стороне. Масса пластины равно-
равномерно распределена по ее площади с по-
поверхностной плотностью ст= 1,2 кг/м2.
Основное уравнение динамики
вращательного движения
3.19. Тонкий однородный стержень дли-
длиной 1=1 м может свободно вращаться во-
вокруг горизонтальной оси, проходящей че-
через точку О на стержне (рис. 3.13). Стер-
Стержень отклонили от вертикали на угол а и
отпустили. Определить для начального мо-
момента времени угловое 8 и тангенциальное
ах ускорения точки В на стержне. Вычис-
Вычисления произвести для следующих случаев:
1) а=о, b=2/3l, a=n/2] 2) а=1/3, Ь=1,
а=п/3; 3) а=//4, 6=//2, а=2/3я.
3.20. Однородный диск радиусом jR = 10 см может свободно вра-
вращаться вокруг горизонтальной оси, перпендикулярной плоскости
54

диска и проходящей через точку О на нем (рис. 3.14). Диск откло-
отклонили на угол ос и отпустили. Определить для начального момента
времени угловое 8 и тангенциальное ах ускорения точки 5, находя-
находящейся на диске. Вычисления выполнить для следующих случаев:
1) a=R, Ь=#/2, а=я/2; 2) а=Д/2, b=R, а=я/6; 3) а=?/8#, Ь=
=2/3#, а-2/3я.
3.21. Тонкий однородный стержень длиной /=50 см и массой
т=400 г вращается с угловым ускорением 8—3 рад/с2 около оси,
проходящей перпендикулярно стержню через его середину. Опре-
Определить вращающий момент М.
3.22. На горизонтальную ось насажены маховик и легкий шкив
радиусом R=5 см. На шкив намотан шнур, к которому привязан
груз массой т=0,4 кг. Опускаясь равноускоренно, груз прошел
путь s=l,8 м за время /=3 с. Определить момент инерции </ махо-
маховика. Массу шкива считать пренебрежимо малой.
3.23. Вал массой т=100 кг и радиусом R=5 см вращался с ча-
частотой п=8 с". К цилиндрической поверхности вала прижали
тормозную колодку с силой F=40 H, под действием которой вал
остановился через /=10 с. Определить коэффициент трения /.
Рис. 3.14
Рис. 3.15
3.24. На цилиндр намотана тонкая гибкая нерастяжимая лента,
массой которой по сравнению с массой цилиндра можно пренебречь.
Свободный конец ленты прикрепили к кронштейну и предоставили
цилиндру опускаться под действием силы тяжести. Определить
линейное ускорение а оси цилиндра, если цилиндр: 1) сплошной;
2) полый тонкостенный.
3.25. Через блок, имеющий форму диска, перекинут шнур.
К концам шнура привязали грузики массой mx=100 г и та=110 г.
С каким ускорением а будут двигаться грузики, если масса т блока
равна 400 г? Трение при вращении блока ничтожно мало.
3.26. Два тела массами /пх=0,25 кг и /п2=0,15 кг связаны тон-
тонкой нитью, переброшенной через блок (рис. 3.15). Блок укреплен
на краю горизонтального стола, по поверхности которого сколь-
скользит тело массой тг. С каким ускорениехМ а движутся тела и каковы
силы Ti и Т2 натяжения нити по обе стороны от блока? Коэффи-
Коэффициент трения / тела о поверхность стола равен 0,2. Масса т блока
равна 0,1 кг и ее можно считать равномерно распределенной по
55

ободу. Массой нити и трением в подшипниках оси блока прене-
пренебречь.
3.27. Через неподвижный блок массой т=0,2 кг перекинут
шнур, к концам которого подвесили грузы массами т1=0,3 кг и
/п2=о,5 кг. Определить силы натяжения Т1 и Т2 шнура по обе сто-
стороны блока во время движения грузов, если масса блока равномер-
равномерно распределена по ободу.
3.28. Шар массой т=10 кг и радиусом R=20 см вращается во-
вокруг оси, проходящей через его центр. Уравнение вращения шара
имеет вид y=A+Bt2+Cts, где B=4 рад/с2, С= —1 рад/с3. Найти
закон изменения момента сил, действующих на шар. Определить
момент сил М в момент времени t=2 с.
Закон сохранения момента импульса
3.29. Однородный тонкий стержень массой тг=0,2 кг и длиной
1=\ м может свободно вращаться вокруг горизонтальной оси z,
проходящей через точку О (рис. 3.16). В точку А на стержне попада-
попадает пластилиновый шарик, летящий горизонтально (перпендику-
(перпендикулярно оси г) со скоростью и=10 м/с и прилипает к стержню. Масса
О -1-
а
V
Рис. 3.16
Рис. 3.17
т2 шарика равна 10 г. Определить угловую скорость со стержня
и линейную скорость и нижнего конца стержня в начальный мо-
момент времени. Вычисления выполнить для следующих значений
расстояния между точками Л и О: 1) //2; 2) 1/3; 3) //4.
3.30. Однородный диск массой mi=0,2 кг и радиусом R=20 см
может свободно вращаться вокруг горизонтальной оси z, перпен-
перпендикулярной плоскости диска и проходящей через точку С (рис. 3.17).
В точку А на образующей диска попадает пластилиновый шарик,
летящий горизонтально (перпендикулярно оси г) со скоростью v=
= 10 м/с, и прилипает к его поверхности. Масса т2 шарика равна
10 г. Определить угловую скорость со диска и линейную скорость
и точки О на диске в начальный момент времени. Вычисления выпол-
выполнить для следующих значений а и Ъ\ 1) a=b^=R; 2) a=R/2, b=R;
3) a=2R/3y b=R/2; 4) a=#/3, b=2R/3.
56

3.31. Человек стоит на скамье Жуковского и ловит рукой мяч
массой т=0,4 кг, летящий в горизонтальном направлении со ско-
скоростью i>=20 м/с. Траектория мяча проходит на расстоянии г=
=0,8 м от вертикальной оси вращения скамьи. С какой угловой
скоростью со начнет вращаться скахмья Жуковского с человеком,
поймавшим мяч, если суммарный момент инерции / человека и
скамьи равен 6 кг *м2?
3.32. Маховик, имеющий вид диска радиусом R=40 см и массой
mi=48 кг, может вращаться вокруг горизонтальной оси. К его
цилиндрической поверхности прикреплен
конец нерастяжимой нити, к другому кон-
концу которой подвешен груз массой т2=
=0,2 кг (рис. 3.18). Груз был приподнят
и затем опущен. Упав свободно с высоты
h=2 м, груз натянул нить и благодаря
этому привел маховик во вращение. Какую
угловую скорость со груз сообщил при этом
маховику?
3.33. На краю горизонтальной платфор-
платформы, имеющей форму диска радиусом R=2m,
стоит человек массой пг1=80 кг. Масса т2
платформы равна 240 кг. Платформа мо-
может вращаться вокруг вертикальной оси, Рис. 3.18
проходящей через ее центр. Пренебрегая
трением, найти, с какой угловой скоростью со будет вращаться
платформа, если человек будет идти вдоль ее края со скоростью
v=2 м/с относительно платформы.
3.34. Платформа, имеющая форму диска, может вращаться око-
около вертикальной оси. На краю платформы стоит человек массой
т1=&0 кг. На какой угол ф повернется платформа, если человек
пойдет вдоль края платформы и, обойдя его, вернется в исходную
точку на платформе? Масса т2 платформы равна 240 кг. Момент
инерции J человека рассчитывать как для материальной точки.
3.35. Платформа в виде диска радиусом R = l м вращается по
инерции с частотой azi=6mhh~1. На краю платформы стоит человек,
масса т которого равна 80 кг. С какой частотой п будет вращаться
платформа, если человек перейдет в ее центр? Момент инерции /
платформы равен 120 кг -м2. Момент инерции человека рассчитывать
как для материальной точки.
3.36. В центре скамьи Жуковского стоит человек и держит в
руках стержень длиной /=2,4 м и массой т=8 кг, расположенный
вертикально по оси вращения скамейки. Скамья с человеком вра-
вращается с частотой /Zi=l с. С какой частотой п2 будет вращаться
скамья с человеком, если он повернет стержень в горизонтальное
положение? Суммарный момент инерции / человека и скамьи равен
6 кг-м2.
3.37. Человек стоит на скамье Жуковского и держит в руках
стержень, расположенный вертикально вдоль оси вращения ска-
скамейки. Стержень служит осью вращения колеса, расположенного
57

на верхнем конце стержня. Скамья неподвижна, колесо вращается
с частотой п=10 с. Радиус R колеса равен 20 см, его масса т~
=3 кг. Определить частоту вращения п2 скамьи, если человек
повернет стержень на угол 180°? Суммарный момент инерции J
человека и скамьи равен 6 кг-м2. Массу колеса можно считать рав-
равномерно распределенной по ободу.
Работа и энергия
3.38. Шарик массой т=№0 г, привязанный к концу нити длиной
h=l м, вращается, опираясь на горизонтальную плоскость, с ча-
частотой /гх= 1 с. Нить укорачивается и шарик приближается к оси
вращения до расстояния /2=0,5 м. С какой частотой п2 будет при
этом вращаться шарик? Какую работу А совершит внешняя сила,
укорачивая нить? Трением шарика о плоскость пренебречь.
3.39. Маховик вращается по закону, выражаемому уравнением
y=A+Bt+Ct\ где А=2 рад, В=32 рад/с, С—4 рад/с2. Найти
среднюю мощность (N), развиваемую силами, действующими на
маховик при его вращении, до остановки, если его момент инерции
/=100 кг-м2.
3.40. Маховик вращается по закону, выражаемому уравнением
q>=A+Bt+Ct2, где А=2 рад, В=\6 рад/с, С=— 2 рад/с2. Момент
инерции J маховика равен 50 кг «м2. Найти законы, по которым
меняются вращающий момент М и мощность N. Чему равна мощ-
мощность в момент времени t=3 с?
3.41. Якорь мотора вращается с частотой п=1500 мин. Опре-
Определить вращающий момент М, если мотор развивает мощность
iV=500 Вт.
3.42. Со шкива диаметром d=0,48 м через ремень передается
мощность N=9 кВт. Шкив вращается с частотой п=240 мин~х.
Сила натяжения TV ведущей ветви ремня в два раза больше силы
натяжения Т2 ведомой ветви. Найти силы натяжения обеих ветвей
ремня.
3.43. Для определения мощности мотора на его шкив диаметром
d=20 см накинули ленту. К одному концу ленты прикреплен дина-
динамометр, к другому подвесили груз Р. Найти мощность N мотора,
если мотор вращается с частотой n=24 с, масса m груза равна
1 кг и показание динамометра F=2b H.
3.44. Маховик в виде диска массой пг=80 кг и радиусом R=30 см
находится в состоянии покоя. Какую работу А± нужно совершить,
чтобы сообщить маховику частоту п=10 с? Какую работу Л2
пришлось бы совершить, если бы при той же массе диск имел мень-
меньшую толщину, но вдвое больший радиус?
3.45. Кинетическая энергия Т вращающегося маховика равна
1 кДж. Под действием постоянного тормозящего момента маховик
начал вращаться равнозамедленно и, сделав iV=80 оборотов, оста-
остановился. Определить момент М силы торможения.
3.46. Маховик, момент инерции J которого равен 40 кг -м2, начал
58

вращаться равноускоренно из состояния покоя под действием мо-
момента силы М=20 Н*м. Вращение продолжалось в течение t=
= 10 с. Определить кинетическую энергию Г, приобретенную ма-
маховиком.
3.47. Пуля массой т=10 г летит со скоростью i>=800 м/с, вра-
вращаясь около продольной оси с частотой я=3000 с. Принимая
пулю за цилиндрик диаметром d=8 мм, определить полную кине-
кинетическую энергию Т пули.
3.48. Сплошной цилиндр массой т=4 кг катится без скольжения
по горизонтальной поверхности. Линейная скорость v оси цилиндра
равна 1 м/с. Определить полную кинетическую энергию Г цилин-
цилиндра.
3.49. Обруч и сплошной цилиндр, имеющие одинаковую массу
т=2 кг, катятся без скольжения с одинаковой скоростью ^=5 м/с.
Найти кинетические энергии 7\ и Т2 этих тел.
3.50. Шар катится без скольжения по горизонтальной поверх-
поверхности. Полная кинетическая энергия Т шара равна 14 Дж. Опреде-
Определить кинетическую энергию Тг поступательного и Т2 вращательно-
вращательного движения шара.
3.51. Определить линейную скорость v центра шара, скатившего-
скатившегося без скольжения с наклонной плоскости высотой h=\ м.
3.52. Сколько времени t будет скатываться без скольжения обруч
с наклонной плоскости длиной 1=2 м и высотой h=\0 см?
3.53. Тонкий прямой стержень длиной 1=1 м прикреплен к гори-
горизонтальной оси, проходящей через его конец. Стержень отклонили
на угол ф=60° от положения равновесия и отпустили. Определить
линейную скорость v нижнего конца стержня в момент прохожде-
прохождения через положение равновесия.
3.54. Однородный тонкий стержень длиной 1=1 м может свобод-
свободно вращаться вокруг горизонтальной оси г, проходящей через точку
О на стержне. Стержень отклонили от положения равновесия на
угол а и отпустили (см. рис. 3.13). Определить угловую скорость со
стержня и линейную скорость v точки В на стержне в момент про-
прохождения им положения равновесия. Вычисления выполнить для
следующих случаев: 1) а=0, b=l/2, а=п/3; 2) а=1/3, 6=2//3,
а=я/2; 3) а=//4, &=/, а=2я/3.
3.55. Карандаш длиной /=15 см, поставленный вертикально,
падает на стол. Какую угловую со и линейную v скорости будет
иметь в конце падения: 1) середина карандаша? 2) верхний его ко-
конец? Считать, что трение настолько велико, что нижний конец
карандаша не проскальзывает.
3.56. Однородный диск радиусом 7^=20 см может свободно вра-
вращаться вокруг горизонтальной оси г, перпендикулярной плоскости
диска и проходящей через точку О (см. рис. 3.14). Определить угло-
угловую со и линейную v скорости точки В на диске в момент прохожде-
прохождения им положения равновесия. Вычисления выполнить для следую-
следующих случаев: 1) a=b=Ry а=я/2; 2) a=R/2y b=0, a=n/3\ 3) а=
2#/3 b=2R/3, а=5л/6; 4) a=R/3, b=R, a2/3
59

§ 4. СИЛЫ В МЕХАНИКЕ
Основные формулы
© Закон всемирного тяготения
F^GmitnJr2,
где F — сила взаимного притяжения двух материальных точек;
тг и т2 — их массы; г — расстояние между точками; G — гравита-
гравитационная постоянная.
В написанной форме закон всемирного тяготения можно приме-
применять и к взаимодействию шаров, масса которых распределена сфери-
сферически-симметрично. В этом случае г есть расстояние между центра-
центрами масс шаров.
О Напряженность гравитационного поля
g=F/m,
где F — сила тяготения, действующая на материальную точку
массы т, помещенную в некоторую точку поля.
® Напряженность гравитационного поля, создаваемого плане-
планетой, массу М которой можно считать распределенной сферически-
симметрично,
где г — расстояние от центра планеты до интересующей нас точки
поля, находящейся вне планеты.
Ф Ускорение свободного падения на высоте h над поверхно-
поверхностью Земли
?ft(l+/i//?J'
где R — радиус Земли; g — ускорение свободного падения на по-
поверхности Земли.
Если h<^R, то
• Потенциальная энергия гравитационного взаимодействия
двух материальных точек массами т1 и т2 (шаров с массой, распре-
распределенной сферически симметрично), находящихся на расстоянии
г друг от друга,
П=—Gmxmjr.
(Потенциальная энергия бесконечно удаленных друг от друга ма-
материальных точек принята равной нулю.)
9 Потенциал гравитационного поля
где П — потенциальная энергия материальной точки массой /л,
помещенной в данную точку поля.
• Потенциал гравитационного поля, создаваемого планетой,
массу М которой можно считать распределенной сферически-сим-
сферически-симметрично,
60

где г — расстояние от центра планеты до интересующей нас точки
поля, находящейся вне планеты.
9 Законы Кеплера.
1. Планеты движутся по эллипсам, в одном из фокусов которых
находится Солнце.
2. Радиус-вектор планеты в равные времена описывает одинако-
одинаковые площади.
3. Квадраты периодов обращения любых двух планет относятся
как кубы больших полуосей их орбит:
Г2/ТП2 /у3//у3
Законы Кеплера справедливы также для движения спутников
вокруг планеты.
© Относительная деформация при продольном растяжении или
сжатии тела
е=л-/Л
где 8 — относительное удлинение (сжатие); х — абсолютное удли-
удлинение (рис. 4.1); / — начальная длина тела.
Относительная деформация при сдвиге определяется из формулы
tg y
где tg 7 — относительный сдвиг; As — абсолютный сдвиг параллель-
параллельных слоев тела относительно друг друга (рис. 4.2); h — расстояние
между слоями; 7 — угол сдвига. (Для малых углов
tgy=y=As/h.)
© Напряжение нормальное
где
— упругая сила, перпендикулярная попереч-
F
Рис. 4.1
Рис. 4.2
ному сечению тела; S — площадь этого сечения.
Напряжение тангенциальное
где Fynv — упругая сила, действующая вдоль слоя тела; S —
площадь этого слоя.
® Закон Гука для продольного растяжения или сжатия
Fynp = — kx, или а = гЕ,
где k — коэффициент упругости (в случае пружины — жесткость);
Е — модуль Юнга.
61

Закон Гука для сдвига
As = -??-, или x = Gyi
где G — модуль поперечной упругости (модуль сдвига).
• Момент, закручивающий на угол ср однородный круглый стер-
стержень,
где С — постоянная кручения.
• Работа, совершаемая при деформации тела,
A=kx*/2.
• Потенциальная энергия растянутого или сжатого стержня
П = -|-, или U = -^-V, или П = -|-У,
где V — объем тела.
Примеры решения задач
Пример 1. Определить вторую космическую скорость v2 ракеты,
запущенной с поверхности Земли.
Примечание. Второй космической (или параболической) скоростью v$
называется минимальная скорость, которую нужно сообщить телу, чтобы
оно удалилось с поверхности Земли в бесконечность (при этом сопротивление
воздуха в расчет не принимается и предполагается, что на тело действует
только поле тяготения Земли),
Решение. При удалении тела массой т в бесконечность его
потенциальная энергия возрастает за счет убыли кинетической энер-
энергии и в бесконечности достигает максимального значения, равного
нулю. Согласно определению второй космической скорости, кине-
кинетическая энергия в бесконечности также равна нулю. Таким обра-
образом, в бесконечности Т^—0 и Пм —0. В соответствии с законом
сохранения энергии в механике
Ф , ТТ Т- . ГТ mV2 П тМ Л
Т + П = Т +П, или —~ G—гг- = 0,
где М — масса Земли. Отсюда находим v2 = \^2GM/R. Преобразу-
Преобразуем эту формулу, умножив и разделив подкоренное выражение
на R:v2=VBGM/R*)R.
Так как GM/R2=g (где g — ускорение свободного падения у
поверхности Земли), то
Подставив в эту формулу значения g и R и произведя вычисле-
вычисления, получим
1>2=П,2 км/с.
Пример 2. Ракета установлена на поверхности Земли для за-
запуска в вертикальном направлении. При какой минимальной ско-
скорости vif сообщенной ракете при запуске, она удалится от поверх-
62

ности на расстояние, равное радиусу Земли (#=6,37 -106м)? Сила-
Силами, кроме силы гравитационного взаимодействия ракеты и Земли,
пренебречь.
Решение. Чтобы определить минимальную скорость vx ра-
ракеты, надо найти ее минимальную кинетическую энергию 7\. Для
этого воспользуемся законом сохранения механической энергии.
Этот закон выполняется для замкнутой системы тел, в которой дей-
действуют только консервативные силы.
Систему ракета — Земля можно считать замкнутой. Единствен-
Единственная сила, действующая на систему,— сила гравитационного взаи-
взаимодействия, являющаяся консервативной.
В качестве системы отсчета выберем инерциальную систему от-
отсчета, так как только в такой системе справедливы законы динами-
динамики и, в частности, законы сохранения. Известно, что система отсчета,
связанная с центром масс замкнутой системы тел, является инерци-
альной. В рассматриваемом случае центр масс системы ракета —
Земля будет практически совпадать с центром Земли, так как масса
М Земли много больше массы т ракеты. Следовательно, систему
отсчета, связанную с центром Земли, можно считать практически
инерциальной. Согласно закону сохранения механической энергии,
запишем
П+П^^+П,, A)
где Тг и Пх — кинетическая и потенциальная энергия системы раке-
ракета — Земля в начальном состоянии (на поверхности Земли); Т2 и
П2 — те же величины в конечном состоянии (на расстоянии, равном
радиусу Земли).
В выбранной системе отсчета кинетическая энергия Земли равна
нулю. Поэтому 7\ есть просто начальная кинетическая энергия
ракеты: Т1=1/2 шо\. Потенциальная энергия системы в начальном
состоянии * 11!=—GmM/R. По мере удаления ракеты от поверхно-
поверхности Земли ее потенциальная энергия будет возрастать, а кинетиче-
кинетическая — убывать. В конечном состоянии кинетическая энергия Т2
станет равной нулю, а потенциальная энергия П2 достигнет макси-
максимального значения: П2=—Gm\i/BR).
Подставив значения Т1у Пъ Г2 и П2 в выражение A), получим
2 "*V1 ^ R ~~ " 2R >
откуда после сокращения на т найдем
v1 Vgm]r.
Заметив, что GM/R2=g (g — ускорение свободного падения у по-
поверхности Земли), перепишем эту формулу в виде
что совпадает с выражением для первой космической скорости
(см. пример 1). Подставив числовые значения величин и произведя
* Потенциальная энергия гравитационного взаимодействия тел, беско-
бесконечно удаленных друг от друга, принимается равной нулю.
63

вычисления, получим
^=7,9 -103 м/с.
Пример 3. Найти выражение для потенциальной энергии П гра-
гравитационного взаимодействия Земли и тела массой т, находящегося
на расстоянии г от центра Земли за пределами ее поверхности. По-
Построить график П(г).
Решение. Потенциальная энергия в поле консервативных
сил (гравитационные силы консервативны) связана с силой следую-
следующим соотношением:
дП . . дП . f ОТ
где i, j, k — единичные векторы осей координат (орты);
ОТ <Ш <Ш
1~' "Л""' ~7э частные производные потенциальной энергии по соот-
соответствующим координатам. В случае, когда поле сил обладает сфе-
сферической симметрией, это выражение упрощается. Если ось х
совместить с радиусом-вектором г, направленным по радиусу сферы,
то —- и -— обращаются в нуль и тогда F = —i -^--. Так как ве-
ду дг ох
кторы г и i совпадают (рис. 4.3) и П зави-
зависит только от г, то
Запишем в векторной форме закон все-
7 л мирного тяготения:
Рис. 4.3 F= G mM -L
F = _ G -L B)
где G — гравитационная постоянная; М — масса Земли.
Сравнивая выражения A) и B), найдем —-=G^-, откуда
dr.
Взяв от этого равенства неопределенный интеграл, получим
где С — постоянная интегрирования.
Полученное выражение показывает, что потенциальная энергия
может быть определена лишь с точностью до некоторой произволь-
произвольной постоянной.
1. Если принять потенциальную энергию бесконечно удаленных
друг от друга тел равной нулю, то постоянная С обращается в нуль.
В этом случае запишем
U(r)=—GmM/r.
64

Соответствующая зависимость П(г) изображается графиком,
представленным на рис. 4.4.
2. Если же принять потенциальную энергию равной нулю на
поверхности Земли, то П(г) = — G—-5-+C = 0, C^
и тогда
Но так как r=R-{-h, где h — высота тела над поверхностью Земли,
то
~ тМ
)==G^—G
Если h<^lR, то
-Л.
, или, так как g =
Пример 4. В гравитационном поле Земли тело массой т переме-
перемещается из точки 1 в точку 2 (рис. 4.5). Определить скорость v2
тела в точке 2, если в точке 1 его скорость vi = VgR = 7,9 км/с.
Ускорение свободного падения
g считать известным.
Решение. Система те-
тело — Земля является замкнутой,
в которой действует консерва-
Рис. 4.4
Рис. 4.5
тивная сила — сила гравитационного взаимодействия. Поэтому
можно воспользоваться законом сохранения механической энергии
(инерциальную систему отсчета свяжем с центром масс системы).
Тогда можно записать
?i = ?2, ИЛИ Гх + П^Та + Па,
где Ть Пх и 7%, П2 — соответственно кинетические и потенциальные
энергии в начальном / и конечном 2 состояниях. Заметим, что центр
масс системы тело — Земля практически совпадает с центром масс
Земли (т<М), и поэтому кинетическая энергия Земли в начальном
и конечном состояниях равна нулю. Тогда
м 1
mv\
2
mv2
Mm
F1
№ 1263
,65

Подставив эти выражения в A), получим
mvl p Mm mv\ p Mm
~ 3R ~~~~2 2R '
Заменив GM=gR2 и произведя сокращения, найдем v\=i
, .
+1/3gR, откуда y2=]/t)? + ^.
Так как vl=gR (по условию задачи), то
Произведя вычисления, получим
^2= Г 4'7'9 км/с = 9>12км/с-
Пример 5. Вычислить работу Л12 сил гравитационного поля
Земли при перемещении тела массой т=10 кг из точки / в точку 2
(рис. 4.5). Радиус /? земли и ускорение g свободного падения вблизи
поверхности Земли считать известными.
Решение. Для решения задачи воспользуемся соотношением
между работой А и изменением АП потенциальной энергии. Так как
силы системы — гравитационные — относятся к силам консерва-
консервативным, то работа сил поля совершается за счет убыли потенциаль-
потенциальной энергии, т. е.
А12=—ЛП^Пх-П,, A)
где Пх и П2 — потенциальные энергии системы тело — Земля соот-
соответственно в начальном и конечном ее состояниях.
Условимся, что потенциальная энергия взаимодействия тела и
Земли равна нулю, когда тело находится на бесконечно большом
расстоянии от Земли, тогда на расстоянии г потенциальная энергия
выразится равенством П = — G—-y где М — масса Земли.
Для расстояний rx=3R и r2=2R, заданных в условиях задачи
(рис. 4.5), получим два выражения потенциальной энергии:
n1=—GmM/CR); U2=—GmM/BR).
Подставив эти выражения иг и П2 в формулу A), получим
Заметив, что G-^- = g, преобразуем последнее выражение к
виду
A12 = 1/emgR.
Подставив значения m, g, R в это выражение и произведя вы-
вычисления, найдем
Л12 = 7в-10-9,8Ь6,37.10е ДЖ = 1,04-108 Дж= 104 МДж.
Пример 6. Верхний конец стального стержня длиной / = 5мс
площадью поперечного сечения S = 4 см2 закреплен неподвижно,
к нижнему подвешен груз массой т = 2-103 кг. Определить: 1) нор-
нормальное напряжение а материала стержня; 2) абсолютное х и отно-
66

сительное 8 удлинения стержня; 3) потенциальную энергию П
растянутого стержня.
Решение. 1. Нормальное напряжение материала растяну-
растянутого стержня выражается формулой o=F/S, где F — сила, дейст-
действующая вдоль оси стержня. В данном случае F равна силе тяжести
rag и поэтому можем записать
a=mg!S.
Сделав вычисления, найдем
(Т=49 МПа.
2. Абсолютное удлинение выражается формулой
x=Fl/(ES),
где Е — модуль Юнга.
Подставив значения величин F, /, S и Е в эту формулу (значе-
(значение Е взять из табл. 11) и произведя вычисления, получим
x = Fl/(ES) = mg//(?S)-2.103.9,81.5/B00.109.4.14-4) м =
= 1,23-10m=1,23mm.
Относительное удлинение стержня
8-х//-2,46-10-4.
3. Потенциальная энергия растянутого стержня П = (ecx/2)F,
где V — объем тела, равный SI. Поэтому
n = (ea/2)SZ.
Выполнив вычисления по этой формуле, получим
11 = 12,1 Дж.
Пример 7. Из пружинного пистолета был произведен выстрел
вертикально вверх. Определить высоту /г, на которую поднимается
пуля массой т = 20 г, если пружина жесткостью k = 196 Н/м была
сжата перед выстрелом на х = 10 см. Массой пружины пренебречь.
Решение. Система пуля — Земля (вместе с пистолетом) яв-
является замкнутой системой, в которой действуют консервативные
силы — силы упругости и силы тяготения. Поэтому для решения
задачи можно применить закон сохранения энергии в механике.
Согласно этому закону, полная механическая энергия Et системы
в начальном состоянии (в данном случае перед выстрелом) равна
полной энергии Е2 в конечном состоянии (когда пуля поднялась
на высоту /i), т. е.
?х = ?2, ИЛИ Тх + П^Га+Па, A)
где 7\ и Т2 — кинетические энергии системы в начальном и конеч-
конечном состояниях; Иг и П2 — потенциальные энергии в тех же состоя-
состояниях.
Так как кинетические энергии пули в начальном и конечном со-
состояниях равны нулю, то равенство A) примет вид
ПХ=П2. B)
Если потенциальную энергию в поле тяготения Земли на ее по-
поверхность принять равной нулю, то энергия системы в начальном
состоянии равна потенциальной энергии сжатой пружины, т. е.
3* 67

U1=kx2/21 а в конечном состоянии — потенциальной энергии пули
на высоте А, т. е. H2=mgh.
Подставив приведенные выражения Пх и П2 в формулу B),
найдем
kx2
2 -'"*"' "- 2mg'
Произведя вычисления по последней формуле, получим
h=5 м.
Задачи
Силы тяготения. Гравитационное поле
4.1. Центры масс двух одинаковых однородных шаров находятся
на расстоянии г = 1 м друг от друга. Масса т каждого шара равна
1 кг. Определить силу F гравитационного взаимодействия шаров.
4.2. Как велика сила F взаимного притяжения двух космических
кораблей массой т = Ют каждый, если они сблизятся до расстояния
г = 100 м?
4.3. Определить силу F взаимного притяжения двух соприка-
соприкасающихся железных шаров диаметром d = 20 см каждый.
4.4. На какой высоте h над поверхностью Земли напряженность
gh гравитационного поля равна 1 Н/кг? Радиус R Земли считать
известным.
4.5. Ракета, пущенная вертикально вверх, поднялась на высоту
/г=3200 км и начала падать. Какой путь s пройдет ракета за первую
секунду своего падения?
4.6. Радиус R планеты Марс равен 3,4 Мм, ее масса М = 6,4Х
Х1023 кг. Определить напряженность g гравитационного поля на
поверхности Марса.
4.7. Радиус Земли в п=3,66 раза больше радиуса Луны; средняя
плотность Земли в /г =1,66 раза больше средней плотности Луны.
Определить ускорение свободного падения gn на поверхности Луны,
если на поверхности Земли ускорение свободного падения g считать
известным.
4.8. Радиус R малой планеты равен 250 км, средняя плотность
р=3 г/см3. Определить ускорение свободного падения g на поверх-
поверхности планеты.
4.9. Масса Земли в п=81,6 раза больше массы Луны. Расстояние
/ между центрами масс Земли и Луны равно 60,3/? (R — радиус
Земли). На каком расстоянии г (в единицах R) от центра Земли на-
находится точка, в которой суммарная напряженность гравитацион-
гравитационного поля Земли и Луны равна нулю?
4.10. Искусственный спутник обращается вокруг Земли по ок-
окружности на высоте /i=3,6 Мм. Определить линейную скорость v
спутника. Радиус R Земли и ускорение свободного падения g на
поверхности Земли считать известными.
4.11. Период Т вращения искусственного спутника Земли равен
68

2 ч. Считая орбиту спутника круговой, найти, на какой высоте h
над поверхностью Земли движется спутник.
4.12. Стационарный искусственный спутник движется по окруж-
окружности в плоскости земного экватора, оставаясь все время над одним
и тем же пунктом земной поверхности. Определить угловую ско-
скорость со спутника и радиус R его орбиты.
4.13. Планета Нептун в ?=30 раз дальше от Солнца, чем Земля.
Определить период Т обращения (в годах) Нептуна вокруг Солнца.
4.14. Луна движется вокруг Земли со скоростью t^x= 1,02 км/с.
Среднее расстояние / Луны от Земли равно 60,3 R (R — радиус
Земли). Определить по этим данным, с какой скоростью v2 должен
двигаться искусственный спутник, вращающийся вокруг Земли на
незначительной высоте над ее поверхностью.
4.15. Зная среднюю скорость v± движения Земли вокруг Солнца
C0 км/с), определить, с какой средней скоростью v2 движется малая
планета, радиус орбиты которой в /г=4 раза больше радиуса орбиты
Земли.
4.16. Советская космическая ракета, ставшая первой искусствен-
искусственной планетой, обращается вокруг Солнца по эллипсу. Наименьшее
расстояние rmin ракеты от Солнца равно 0,97, наибольшее расстоя-
расстояние rmax равно 1,31 а. е. (среднего расстояния Земли от Солнца).
Определить период Т вращения (в годах) искусственной планеты.
4.17. Космическая ракета движется вокруг Солнца по орбите,
почти совпадающей с орбитой Земли. При включении тормозного
устройства ракета быстро теряет скорость и начинает падать на
Солнце (рис. 4.6). Определить время /, в течение которого будет
падать ракета.
Указание. Принять, что, падая на Солнце, ракета движется по эллипсу,
большая ось которого очень мало отличается от радиуса орбиты Земли,
а эксцентриситет — от единицы. Период обращения по эллипсу не зависит
от эксцентриситета.
4.18. Ракета, запущенная с Земли на Марс, летит, двигаясь во-
вокруг Солнца по эллиптической орбите (рис. 4.7). Среднее расстоя-
расстояние г планеты Марс от Солнца равно 1,5 а. е. В течение какого вре-
времени t будет лететь ракета до встречи с Марсом?

4.19. Искусственный спутник движется вокруг Земли по эллипсу
с эксцентриситетом 8=0,5. Во сколько раз линейная скорость спут-
спутника в перигее (ближайшая к центру Земли точка орбиты спутника)
больше, чем в апогее (наиболее удаленная точка орбиты)?
Указание. Применить закон сохранения момента импульса.
4.20. Комета движется вокруг Солнца по эллипсу с эксцентриси-
эксцентриситетом 8=0,6. Во сколько раз линейная скорость кометы в ближайшей
к Солнцу точке орбиты больше, чем в наиболее удаленной?
4.21. Ближайший спутник Марса находится на расстоянии г=
=9,4 Мм от центра планеты и движется вокруг нее со скоростью
^=2,1 км/с. Определить массу М Марса.
4.22. Определить массу М Земли по среднему расстоянию г от
центра Луны до центра Земли и периоду Т обращения Луны вокруг
Земли (Гиг считать известными).
4.23. Один из спутников планеты Сатурн находится приблизи-
приблизительно на таком же расстоянии г от планеты, как Луна от Земли,
но период Т его обращения вокруг планеты почти в /г= 10 раз мень-
меньше, чем у Луны. Определить отношение масс Сатурна и Земли.
4.24. Найти зависимость ускорения свободного падения g от
расстояния г, отсчитанного от центра планеты, плотность р которой
можно считать для всех точек одинаковой. Построить график зави-
зависимости g (г). Радиус R планеты считать известным.
4.25. Тело массой т—\ кг находится на поверхности Земли.
Определить изменение АР силы тяжести для двух случаев: 1) при
подъеме тела на высоту ft=5 км; 2) при опускании тела в шахту
на глубину h=b км. Землю считать однородным шаром радиусом
/?=6,37 Мм и плотностью р=5,5 г/см3.
4.26. Определить работу Л, которую совершат силы гравитаци-
гравитационного поля Земли, если тело массой т=1 кг упадет на поверхность
Земли: 1) с высоты Я, равной радиусу Земли; 2) из бесконечности.
Радиус R Земли и ускорение свободного падения g на ее поверхности
считать известными.
4.27. На какую высоту h над поверхностью Земли поднимется
ракета, пущенная вертикально вверх, если начальная скорость v
ракеты равна первой космической скорости?
4.28. Определить значения потенциала ср гравитационного поля
на поверхностях Земли и Солнца.
4.29. Вычислить значения первой (круговой) и второй (параболи-
(параболической) космических скоростей вблизи поверхности Луны.
4.30. Найти первую и вторую космические скорости вблизи
поверхности Солнца.
4.31. Радиус R малой планеты равен 100 км, средняя плотность
р вещества планеты равна 3 г/см 3. Определить параболическую ско-
скорость v2 у поверхности этой планеты.
4.32. Какова будет скорость v ракеты на высоте, равной радиусу
Земли, если ракета пущена с Земли с начальной скоростью vo =
= 10 км/с? Сопротивление воздуха не учитывать. Радиус R Земли
70

и ускорение свободного падения g на ее поверхности считать извест-
известными.
4.33. Ракета пущена с Земли с начальной скоростью vo=lb км/с.
К какому пределу будет стремиться скорость ракеты, если расстоя-
расстояние ракеты от Земли бесконечно увеличивается? Сопротивление
воздуха и притяжение других небесных тел, кроме Земли, не учи-
учитывать.
4.34. Метеорит падает на Солнце с очень большого расстояния,
которое практически можно считать бесконечно большим. Начальная
скорость метеорита пренебрежимо мала. Какую скорость v будет
иметь метеорит в момент, когда его расстояние от Солнца равно
среднему расстоянию Земли от Солнца?
4.35. Комета огибает Солнце, двигаясь по орбите, которую мож-
можно считать параболической. С какой скоростью v движется комета,
когда она проходит через перигей (ближайшую к Солнцу точку
своей орбиты), если расстояние г кометы от Солнца в этот момент
равно 50 Гм?
4.36. На высоте /i=2,6 Мм над поверхностью Земли космической
ракете была сообщена скорость у=10 км/с, направленная перпенди-
перпендикулярно линии, соединяющей центр Земли с ракетой. По какой
орбите относительно Земли будет двигаться ракета? Определить
вид конического сечения.
Силы упругости. .Механическое напряжение.
Прочность
4.37. К проволоке диаметром d=2 мм подвешен груз массой
т=1 кг. Определить напряжение а, возникшее в проволоке.
4.38. Верхний конец свинцовой проволоки диаметром d=2 см
и длиной /=60 м закреплен неподвижно. К нижнему концу подве-
подвешен груз массой т=100 кг. Найти напряжение а материала: 1) у
нижнего конца; 2) на середине длины; 3) у верхнего конца прово-
проволоки.
4.39. Какой наибольший груз может выдержать стальная прово-
проволока диаметром d=l мм, не выходя за предел упругости аупр =
=294 МПа? Какую долю первоначальной длины составляет удлине-
удлинение проволоки при этом грузе?
4.40. Свинцовая проволока подвешена в вертикальном положе-
положении за верхний конец. Какую наибольшую длину / может иметь
проволока, не обрываясь под действием силы тяжести? Предел проч-
прочности апр свинца равен 12,3 МПа.
4.41. Гиря массой т=\0 кг, привязанная к проволоке, враща-
вращается с частотой п=2 с вокруг вертикальной оси, проходящей через
конец проволоки, скользя при этом без трения по горизонтальной
поверхности. Длина / проволоки равна 1,2 м, площадь 5 ее попереч-
поперечного сечения равна 2 мм2. Найти напряжение а металла проволоки.
Массой ее пренебречь.
4.42. Однородный стержень длиной /=1,2 м, площадью попереч-
поперечного сечения S=2 см2 и массой т=10 кг вращается с частотой п~=
71

=2 с вокруг вертикальной оси, проходящей через конец стержня,
скользя при этом без трения по горизонтальной поверхности. Найти
наибольшее напряжение атах материала стержня при данной час-
частоте вращения.
Модуль упругости. Жесткость
4.43. К вертикальной проволоке длиной 1=5 м и площадью
поперечного сечения S=2 мм2 подвешен груз массой т=Ь,\ кг.
В результате проволока удлинилась на х=0,6 мм. Найти модуль
Юнга Е материала проволоки.
4.44. К стальному стержню длиной /=3 м и диаметром d=2 см
подвешен груз массой т=2,5-103 кг. Определить напряжение о в
стержне, относительное г и абсолютное х удлинения стержня.
4.45. Проволока длиной 1=2 м и диаметром d=\ мм натянута
практически горизонтально. Когда к середине проволоки подвесили
груз массой т=\ кг, проволока растянулась настолько, что точка
подвеса опустилась на /i=4 см. Определить модуль Юнга Е мате-
материала проволоки.
4.46. Две пружины жесткостью &!=(),3 кН/м и &2=0,8 кН/м
соединены последовательно. Определить абсолютную деформацию
хг первой пружины, если вторая деформирована на л:2=1,5 см.
V////////////////.
Рис. 4.8
Рис. 4.9
4.47. Определить жесткость k системы двух пружин при после-
последовательном и параллельном их соединении (рис. 4.8). Жесткость
пружин kx=2 кН/м и k2=6 кН/м.
4.48. Нижнее основание железной тумбы, имеющей форму ци-
цилиндра диаметром d=20 см и высотой h=20 см, закреплено непод-
неподвижно. На верхнее основание тумбы действует сила F=20 кН
(рис. 4.9). Найти: 1) тангенциальное напряжение т в материале тум-
тумбы; 2) относительную деформацию у (угол сдвига); 3) смещение
Ал: верхнего основания тумбы.
4.49. Тонкий стержень одним концом закреплен, к другому кон-
концу приложен момент силы М = 1 кН-м. Определить угол ф закручи-
закручивания стержня, если постоянная кручения С=120 кН-м/рад.
72

4.50. Тонкая однородная металлическая лента закреплена верх-
верхним концом. К нижнему концу приложен момент силы М = \ мН-м.
Угол ср закручивания ленты равен 10°. Определить постоянную кру-
кручения С.
Работа упругой силы.
Энергия деформированного тела
4.51. Какую работу А нужно совершить, чтобы растянуть на
х=\ мм стальной стержень длиной /=1 ми площадью S поперечно-
поперечного сечения, равной 1 см2?
4.52. Для сжатия пружины на лгх= 1 см нужно приложить силу
^=10 Н. Какую работу А нужно совершить, чтобы сжать пружину
на х2= 10 см, если сила пропорциональна сжатию?
4.53. Пружина жесткостью &=10 кН/м сжата силой /7=200 Н.
Определить работу А внешней силы, дополнительно сжимающей
эту пружину еще на х=\ см.
4.54. Пружина жесткостью k=\ кН/м была сжата на xt=i см.
Какую нужно совершить работу А, чтобы сжатие пружины увели-
увеличить до х2:=18 см?
4.55. Гиря, положенная на верхний конец спиральной пружины,
поставленной на подставке, сжимает ее на х=2 мм. На сколько со-
сожмет пружину та же гиря, упавшая на конец пружины с высотой
ft=5 см?
4.56. Пуля массой т1=\0 г вылетает со скоростью и=300 м/с
из дула автоматического пистолета, масса т2 затвора которого рав-
равна 200 г. Затвор пистолета прижимается к стволу пружиной жест-
жесткостью k=25 кН/м. На какое расстояние I отойдет затвор после вы-
выстрела? Считать пистолет жестко закрепленным.
4.57. Две пружины с жесткостями /^=0,3 кН/м и ^2=0,5 кН/м
скреплены последовательно и растянуты так, что абсолютная дефор-
деформация х2 второй пружины равна 3 см. Вычислить работу А растяже-
растяжения пружин.
4.58. Пружина жесткостью ^=100 кН/м была растянута на
#!=4 см. Уменьшая приложенную силу, пружине дают возможность
вернуться в первоначальное состояние (нерастянутое). Затем сжима-
сжимают пружину на х2=6 см. Определить работу А, совершенную при
этом внешней силой.
4.59. Стальной стержень массой /тг=3,9 кг растянут на 8=0,001
своей первоначальной длины. Найти потенциальную энергию П
растянутого стержня.
4.60. Стержень из стали длиной 1=2 м и площадью поперечного
сечения S=2 см2 растягивается некоторой силой, причем удлинение
х равно 0,4 см. Вычислить потенциальную энергию П растянутого
стержня и объемную плотность w энергии.
4.61. Стальной стержень длиной 1=2 м и площадью поперечного
сечения S=2 см2 растягивается силой F=IO кН. Найти потенци-
потенциальную энергию П растянутого стержня и объемную плотность w
энергии.
73

4.62. Две пружины, жесткости которых kx=\ кН/м и k2~3 кН/м,
скреплены параллельно. Определить потенциальную энергию П
данной системы при абсолютной деформации х=5 см.
4.63. С какой скоростью v вылетит из пружинного пистолета
шарик массой т=10 г, если пружина была сжата на х=5 см. Жест-
Жесткость k пружины равна 200 Н/'м?
4.64. В пружинном ружье пружина сжата на jcx=20 см. При
взводе ее сжали еще на л:2=30 см. С какой скоростью v вылетит из
ружья стрела массой т=Ь0 г, если жесткость k пружины равна
120 Н/м?
4.65. Вагон массой m=12 t двигался со ско-
скоростью v=l м/с. Налетев на пружинный буфер, он
остановился, сжав пружину буфера на л:= 10 см.
Найти жесткость k пружины.
4.66. Стальной стержень растянут так, что напря-
напряжение в материале стержня а=300МПа. Найти объ-
объемную плотность w потенциальной энергии растяну-
растянутого стержня.
4.67. Стержень из стали имеет длину /=2 м и
площадь поперечного сечения 5 = 10 мм2. Верхний
конец стержня закреплен неподвижно, к нижнему
прикреплен упор. На стержень надет просверленный
посередине груз массой т=10 кг (рис. 4.10). Груз
падает с высоты h=lO см и задерживается упором.
Найти: 1) удлинение х стержня при ударе груза; 2) нормальное
напряжение о, возникающее при этом в материале стержня.
§ 5. РЕЛЯТИВИСТСКАЯ МЕХАНИКА
Основные формулы
В специальной теории относительности рассматриваются только
инерциальные системы отсчета. Во всех задачах считается, что оси
у, у' и г, г' сонаправлены, а относительная скорость v0 системы ко-
координат К' относительно системы К нап-
направлена вдоль общей оси хх' (рис. 5.1).
Ф Релятивистское (лоренцево) сок-
сокращение длины стержня
Рис. 4.10
о
о'
®
где /0 — длина стержня в системе коор-
Рис. 5.1 динат /(', относительно которой стержень
покоится (собственная длина). Стержень
параллелен оси х'\ I — длина стержня, измеренная в системе /С,
относительно которой он движется со скоростью v\ с — скорость
распространения электромагнитного излучения.
Ф Релятивистское замедление хода часов
74

где Л/0 — интервал времени между двумя событиями, происходя-
происходящими в одной точке системы /(', измеренный по часам этой системы
(собственное время движущихся часов); Д? — интервал времени
между двумя событиями, измеренный по часам системы /С.
• Релятивистское сложение скооостей
1 -х-щу' [el '
где v' — относительная скорость (скорость тела относительно си-
системы К')\ v0 — переносная скорость (скорость системы К' относи-
относительно /С); v — абсолютная скорость (скорость тела относительно
системы К).
В теории относительности абсолютной скоростью называется
скорость тела в системе координат, условно принятой за непод-
неподвижную.
@ Релятивистская масса
ТПс\ 1Т1п
т = —— ¦, или т = -7==-,
У 1 — (с> гJ У 1 — Р2
где т0 — масса покоя; C — скорость частицы, выраженная в долях
скорости света ($=vc).
® Релятивистский импульс
или р =
© Полная энергия релятивистской частицы
?=mc2=moc2+7\
где Т — кинетическая энергия частицы; т0с2=Е0— ее энергия
покоя. Частица называется релятивистской, если скорость частицы
сравнима со скоростью света, и классической, если v^c.
® Связь полной энергии с импульсом релятивистской частицы
Е2—р2с2=т20с*.
• Связь кинетической энергии с импульсом релятивистской
частицы
Примеры решения задач
Пример 1. Космический корабль движется со скоростью v—
?=0,9 с по направлению к центру Земли. Какое расстояние / прой-
пройдет этот корабль в системе отсчета, связанной с Землей (/С-система),
за интервал времени Л^о= 1 с, отсчитанный по часам, находя-
находящимся в космическом корабле (К'-система)? Суточным вращением
Земли и ее орбитальным движением вокруг Солнца пренебречь.
Решение. Расстояние /, которое пройдет космический ко-
корабль в системе отсчета, связанной с Землей (/С-система), определим
по формуле
A)
75

где At — интервал времени, отсчитанный в /(-системе отсчета.
Этот интервал времени связан с интервалом времени, отсчитан-
отсчитанным в /('-системе, соотношением At —
выражение А/ в формулу A), получим
Подставив
1/" 1 — (и/сJ '
После вычислений найдем
/=619 Мм.
Пример 2. В лабораторной системе отсчета (/(-система) движется
стержень со скоростью и=0,8 с. По измерениям, произведенным в
/(-системе, его длина / оказалась равной 10 м, а угол ф, который он
составляет с осью х, оказался равным 30°. Определить собственную
длину /0 стержня в /('-системе, связанной со стержнем, и угол ф0,
который он составляет с осью х' (рис. 5.2).
5)
Рис. 5.2
Решение. Пусть в К'-системе стержень лежит в плоскости
х'О'у'. Из рис. 5.2, а следует, что собственная длина /0 стержня и
угол фо, который он составляет с осью х\ выразятся равенствами
/" A)
В /(-системе те же величины окажутся равными (рис. 5.2, б)
l = V(&x)*+(Ay)\ tgy = &y/&x. B)
Заметим, что при переходе от системы /(' к К размеры стержня в
направлении оси у не изменятся, а в направлении оси х претерпят
релятивистское (лоренцево) сокращение, т. е.
Ьу = ку'9 Ax = Ax'VT^J\ C)
С учетом последних соотношений собственная длина стержня
выразится равенством
/0=
или
Заменив в этом выражении Ау на / sin ф (рис. 5.2, б), получим
76

Подставив значения величин /, р, <р в это выражение и произведя
вычисления, найдем
/,-15,3 м.
Для определения угла ф0 воспользуемся соотношениями A),
B) и C):
tgq>0 = A#/(A*) V\— Р2, или tg Фо = tg ф]Л1—р^?
откуда
Подставив значения ф и |3 в это выражение и произведя вычисле-
вычисления, получим
Фо = 19,Г.
Пример 3. Кинетическая энергия Т электрона равна 1 МэВ.
Определить скорость электрона.
Решение. Релятивистская формула кинетической энергии
Выполнив относительно C преобразования, найдем скорость час-
частицы, выраженную в долях скорости света ($=v/c):
где Ео — энергия покоя электрона (см. табл. 22).
Вычисления по этой формуле можно производить в любых еди-
единицах энергии, так как наименования единиц в правой части формул
сократятся и в результате подсчета будет получено отвлеченное
число.
Подставив числовые значения Ео и Т в мегаэлектрон-вольтах,
получим
[3-0,941.
Так как v=p?, то
и = 2,82-108м/с.
Чтобы определить, является ли частица с кинетической энергией
Т релятивистской или классической, достаточно сравнить кинети-
кинетическую энергию частицы с ее энергией покоя.
Если 77?0<1, частицу можно считать классической. В этом
случае релятивистская формула A) переходит в классическую:
Р=К2ВД, или v =
Пример 4. Определить релятивистский импульс р и кинетическую
энергию Т электрона, движущегося со скоростью ^=0,9 с (где
с — скорость света в вакууме).
Решение. Релятивистский импульс
V 1 —ра A)
77

После вычисления по формуле A) получим
р-5,6-10-22 кг-м/с.
В релятивистской механике кинетическая энергия 7 частицы
определяется как разность между полной энергией Е и энергией
покоя Ео этой частицы, т. е.
Т=Е—Ео.
Так как Е=тс2 и E0=tn0c2, то, учитывая зависимость массы от
скорости, получим
т0с2 9
-mQc ,
или окончательно
Сделав вычисления, найдем
7=106 фДж.
Во внесистемных единицах энергия покоя электрона т0с2—
=0,51 МэВ. Подставив это значение в формулу B), получим
7=0,66 МэВ.
Пример 5. Релятивистская частица с кинетической энергией
Т=т0с2 (т0 — масса покоя частицы) испытывает неупругое столк-
столкновение с такой же покоящейся (в лабораторной системе отсчета)
частицей. При этом образуется составная частица. Определить:
1) релятивистскую массу m движущейся частицы; 2) релятивистскую
массу т! и массу покоя mQ составной частицы; 3) ее кинетическую
энергию 7".
Решение. 1. Релятивистскую массу т движущейся частицы
до столкновения найдем из выражения для кинетической энергии
релятивистской частицы Т=(т—то)с2. Так как Т=т0с2, то т==
=2т0.
2. Для того чтобы найти релятивистскую массу составной части-
частицы, воспользуемся тем, что суммарная релятивистская масса частиц
сохраняется *: m+mQ=m\ где т-тт0 — суммарная релятивистская
масса частиц до столкновения; т! — релятивистская масса состав-
составной частицы. Так как т=2т0) то
т' = Зт0.
Массу покоя т'о составной частицы найдем из соотношения
т'= г т'° г. A)
Скорость v' составной частицы (она совпадает со скоростью
Vс центра масс в лабораторной системе отсчета) можно найти из
закона сохранения импульса р=р', где р — импульс релятивистской
частицы до столкновения; р' — импульс составной релятивистской
* Этот закон см., например, в кн.: Савельев И. В. Курс общей физики.
М., 1977. Т. I, §70.
78

частицы. Выразим р через кинетическую энергию Т:
Так как Т=Еь=гп0с2, то
р = A/с) VBm0c2+m0c2) m0c2 = m0cV 3.
Релятивистский импульс p'=mfv'. Учитывая, что m'=3m0,
закон сохранения импульса можно записать в виде moc]/3=3mot>',
откуда
Подставив выражения и' и т' в формулу A), найдем массу покоя
составной частицы:
—A V 3J, или mo =
3. Кинетическую энергию 7" составной релятивистской частицы
найдем как разность полной энергии т'с1 и энергии покоя т'0с2
составной частицы:
Т' = {т' — то) с2.
Подставив выражения т' и mi, получим
Г = (Зт0 —} 6т0) с- = C —К 6) т0с2 - 0,55т0с°-.
Задачи
Релятивистское изменение длин
и интервалов времени
5.1. Предположим, что мы можем измерить длину стержня с точ-
точностью А/=0,1 мкм. При какой относительной скорости и двух
инерциальных систем отсчета можно было бы обнаружить реляти-
релятивистское сокращение длины стержня, собственная длина /0 которого
равна 1 м?
5.2. Двое часов после синхронизации были помещены в системы
координат /С и /С', движущиеся друг относительно друга. При
какой скорости и их относительного движения возможно обнару-
обнаружить релятивистское замедление хода часов, если собственная дли-
длительность т0 измеряемого промежутка времени составляет 1 с?
Измерение времени производится с точностью Дт=10 пс.
5.3. На космическом корабле-спутнике находятся часы, синхро-
синхронизированные до полета с земными. Скорость v0 спутника составля-
составляет 7,9 км/с. На сколько отстанут часы на спутнике по измерениям
земного наблюдателя по своим часам за время то=О,5 года?
5.4. Фотонная ракета движется относительно Земли со скоро-
скоростью v=0fi с. Во сколько раз замедлится ход времени в ракете с
точки зрения земного наблюдателя?
5.5. В системе К' покоится стержень, собственная длина /0 кото-
которого равна 1 м. Стержень расположен так, что составляет угол
Фо=45° с осью л'\ Определить длину /стержня и угол ф в системе /С,
если скорость v0 системы К' относительно К равна 0,8 с.
79

5.6. В системе К находится квадрат, сторона которого параллель-
параллельна оси х'. Определить угол ф между его диагоналями в системе /С,
если система К' движется относительно К со скоростью и=0,95 с.
5.7. В лабораторной системе отсчета (/(-система) пи-мезон с мо-
момента рождения до момента распада пролетел расстояние /=75 м.
Скорость v пи-мезона равна 0,995 с. Определить собственное время
жизни т0 мезона.
5.8. Собственное время жизни т0 мю-мезона равно 2 мкс. От точки
рождения до точки распада в лабораторной системе отсчета мю-ме-
зон пролетел расстояние /=6 км. С какой скоростью v (в долях ско-
скорости света) двигался мезон?
Релятивистское слооюение скоростей
5.9. Показать, что формула сложения скоростей релятивистских
частиц переходит в соответствующую формулу классической меха-
механики при v<^c.
5.10. Две релятивистские частицы движутся в лабораторной си-
системе отсчета со скоростями 1^=0,6 с и У2=О,9 с вдоль одной прямой.
Определить их относительную скорость u2i в двух случаях: 1) ча-
частицы движутся водном направлении; 2) частицы движутся в проти-
противоположных направлениях.
5.11. В лабораторной системе отсчета удаляются друг от друга
две частицы с одинаковыми по модулю скоростями. Их относитель-
относительная скорость и в той же системе отсчета равна 0,5 с. Определить
скорости частиц.
5.12. Ион, вылетев из ускорителя, испустил фотон в направлении
своего движения. Определить скорость фотона относительно уско-
ускорителя, если скорость v иона относительно ускорителя равна 0,8 с.
5.13. Ускоритель сообщил радиоактивному ядру скорость vx=
=0,4 с. В момент вылета из ускорителя ядро выбросило в направ-
направлении своего движения C-частицу со скоростью и2=0,75 с относи-
относительно ускорителя. Найти скорость u2i частицы относительно ядра.
5.14. Два ускорителя выбрасывают навстречу друг другу части-
частицы со скоростями |^|=0,9 с. Определить относительную скорость u2i
сближения частиц в системе отсчета, движущейся вместе с одной
из частиц.
Релятивистская масса
и релятивистский импульс
5.15. Частица движется со скоростью v=0,5 с. Во сколько раз
релятивистская масса частицы больше массы покоя?
5.16. С какой скоростью v движется частица, если ее релятивист-
релятивистская масса в три раза больше массы покоя?
5.17. Отношение заряда движущегося электрона к его массе,
определенное из опыта, равно 0,88-1011 Кл/кг. Определить реляти-
релятивистскую массу т электрона и его скорость v.
80

5.18. На сколько процентов релятивистская масса частицы боль-
больше массы покоя при скорости и=30 Мм/с?
5.19. Показать, что выражение релятивистского импульса пере-
переходит в соответствующее выражение импульса в классической ме-
механике при v<^c.
5.20. Электрон движется со скоростью v=0fi с. Определить реля-
релятивистский импульс р электрона.
5.21. Импульс р релятивистской частицы равен тос (т0 — масса
покоя). Определить скорость v частицы (в долях скорости света).
5.22. В лабораторной системе отсчета одна из двух одинаковых
частиц покоится, другая движется со скоростью v=0,8 с по направ-
направлению к покоящейся частице. Определить: 1) релятивистскую массу
движущейся частицы в лабораторной системе отсчета; 2) скорость
частиц в системе отсчета, связанной с центром инерции системы;
3) релятивистскую массу частиц в системе отсчета, связанной с
центром инерции.
5.23. В лабораторной системе отсчета находятся две частицы.
Одна частица с массой покоя т0 движется со скоростью и=0,6 с,
другая с массой покоя 2т0 покоится. Определить скорость Vс
центра масс системы частиц.
Взаимосвязь массы и энергии *
5.24. Полная энергия тела возросла на &Е=\ Дж. На сколько
при этом изменится масса тела?
5.25. Определить, на сколько должна увеличиться полная энер-
энергия тела, чтобы его релятивистская масса возросла на Ат=\ г?
5.26. Вычислить энергию покоя: 1) электрона; 2) протона; 3) сс-
частицы. Ответ выразить в джоулях и мегаэлектрон-вольтах.
5.27. Известно, что объем воды в океане равен 1,37 -109 км3. Оп-
Определить, на сколько возрастет масса воды в океане, если темпера-
температура воды повысится на At=\ °C. Плотность р воды в океане при-
принять равной 1,03 • 103 кг/м3.
5.28. Солнечная постоянная С (плотность потока энергии элект-
электромагнитного излучения Солнца на расстоянии, равном среднему
расстоянию от Земли до Солнца) равна 1,4 кВт/м2. 1. Определить
массу, которую теряет Солнце в течение одного года. 2. На сколько
изменится масса воды в океане за один год, если предположить, что
поглощается 50 % падающей на поверхность океана энергии излу-
излучения? При расчетах принять площадь S поверхности океана равной
3,6-108 км2.
Кинетическая энергия релятивистской частицы
5.29. Кинетическая энергия Т электрона равна 10 МэВ. Во
сколько раз его релятивистская масса больше массы покоя? Сделать
такой же подсчет для протона.
* Задачи на эту тему, в условиях которых речь идет о ядерных превра-
превращениях, помещены в § 43.
81

5.30. Во сколько раз релятивистская масса протона больше реля-
релятивистской массы электрона, если обе частицы имеют одинаковую
кинетическую энергию 7= 1 ГэВ?
5.31. Электрон летит со скоростью v=0,8 с. Определить кинети-
кинетическую энергию 7 электрона (в мегаэлектрон-вольтах).
5.32. При какой скорости v кинетическая энергия любой частицы
вещества равна ее энергии покоя?
5.33. Определить скорость v электрона, если его кинетическая
энергия равна: 1) 7=4 МэВ; 2) 7=1 кэВ.
5.34. Найти скорость v протона, если его кинетическая энергия
равна: 1) 7=1 МэВ; 2) 7=1 ГэВ.
5.35. Показать, что релятивистское выражение кинетической
энергии Т=(пг—то)с2 при г<Сс переходит в соответствующее выра-
выражение классической механики.
5.36. Какая относительная ошибка будет допущена при вычисле-
вычислении кинетической энергии релятивистской частицы, если вместо
релятивистского выражения Т=(т—т^с2 воспользоваться класси-
классическим T=1/2m0v2? Вычисления выполнить для двух случаев: 1) и=
=0,2 с; 2) и=0,8 с.
5.37. Две релятивистские частицы движутся навстречу друг
другу с одинаковыми (в лабораторной системе отсчета) кинетичес-
кинетическими энергиями, равными их энергии покоя. Определить: 1) ско-
скорости частиц в лабораторной системе отсчета; 2) относительную ско-
скорость сближения частиц (в единицах с)\ 3) кинетическую энергию
(в единицах т0с2) одной из частиц в системе отсчета, связанной с
другой частицей.
Связь энергии релятивистской частицы
с ее импульсом
5.38. Показать, что выражение релятивистского импульса через
кинетическую энергию p=(l/c)]/rBE0JrT) 7 при v<^c переходит
в соответствующее выражение классической механики.
5.39. Определить импульс р частицы (в единицах тос), если ее
кинетическая энергия равна энергии покоя.
5.40. Определить кинетическую энергию 7 релятивистской час-
частицы (в единицах т0с2), если ее импульс р=тос.
5.41. Кинетическая энергия релятивистской частицы равна ее
энергии покоя. Во сколько раз возрастет импульс частицы, если
ее кинетическая энергия увеличится в п=4 раза?
5.42. Импульс р релятивистской частицы равен тос. Под дейст-
действием внешней силы импульс частицы увеличился в два раза. Во
сколько раз возрастет при этом энергия частицы: 1) кинетическая?
2) полная?
5.43. При неупругом столкновении частицы, обладающей импуль-
импульсом р=тос, и такой же покоящейся частицы образуется составная
частица. Определить: 1) скорость v частицы (в единицах с) до столк-
столкновения; 2) релятивистскую массу составной частицы (в единицах
/п0); 3 скорость составной частицы; 4) массу покоя составной части-
82

цы (в единицах т0); 5) кинетическую энергию частицы до столкнове-
столкновения и кинетическую энергию составной частицы (в единицах т0с2).
5.44. Частица с кинетической энергией Т=т0с2 налетает на дру-
другую такую же частицу, которая в лабораторной системе отсчета по-
покоится. Найти суммарную кинетическую энергию Т частиц в си-
системе отсчета, связанной с центром инерции системы частиц.
§ 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Основные формулы
® Уравнение гармонических колебаний
х=А cos(co/-bcp),
где х — смещение колеблющейся точки от положения равновесия;
/ — время; Л, со, ер — соответственно амплитуда, угловая частота,
начальная фаза колебаний; (tof-fcp) — фаза колебаний в момент t.
® Угловая частота колебаний
или co = 2jt/7i,
где v и Т — частота и период колебаний.
@ Скорость точки, совершающей гармонические колебания,
v = x = — Асо sin (со/ + ф).
@ Ускорение при гармоническом колебании
а = х = — Лео2 cos (со/ + ср).
© Амплитуда А результирующего колебания, полученного при
сложении двух колебаний с одинаковыми частотами, происходящих
по одной прямой, определяется по формуле
А* = А1 + А1 + 2А1А2соз(цJ — ф1),
где Аг и А2 — амплитуды составляющих колебаний; фх и ср2 —
их начальные фазы.
9 Начальная фаза ф результирующего колебания может быть
найдена из формулы
^^ Аг cos ф1 + ^2 cosep2*
• Частота биений, возникающих при сложении двух колебаний,
происходящих по одной прямой с различными, но близкими по зна-
значению частотами v± и v2,
^Vj V2
• Уравнение траектории точки, участвующей в двух взаимно
перпендикулярных колебаниях с амплитудами Ах и Л2 и начальны-
начальными фазами ф1 и ф2,
х2 . у2 2ху , \ • о /
-^Г + ^Т—Л^СОЭ (ф, —ф1) = Sin2 (ф2 —
83

Если начальные фазы ср* и ср2 составляющих колебаний одинако-
одинаковы, то уравнение траектории принимает вид
у = /J? х, ИЛИ у = — -д- X,
т. е. точка движется по прямой.
В том случае, если разность фаз Дср=ф2—фх=я/2, уравнение
принимает вид
х2 г/2
т. е. точка движется по эллипсу.
@ Дифференциальное уравнение гармонических колебаний ма-
материальной точки
тх = — kx, или х + оJл: —О,
где т — масса точки; k — коэффициент квазиупругой силы (k—
)
© Полная энергия материальной точки, совершающей гармони-
гармонические колебания:,
@ Период колебаний тела, подвешенного на пружине (пружин-
(пружинный маятник),
где т — масса тела; k — жесткость пружины.
Формула справедлива для упругих колебаний в пределах, в ко-
которых выполняется закон Гука (при малой массе пружины в срав-
сравнении с массой тела).
Период колебаний математического маятника
где / — длина маятника; g — ускорение свободного падения.
Период колебаний физического маятника
Т = 2я VTjg = 2я VJ/(mga),
где J — момент инерции колеблющегося тела относительно оси
колебаний; а — расстояние центра масс маятника от оси колебаний;
L=J/(ma)— приведенная длина физического маятника.
Приведенные формулы являются точными для случая бесконеч-
бесконечно малых амплитуд. При конечных амплитудах эти формулы дают
лишь приближенные результаты. При амплитудах не более ^3°
ошибка в значении периода не превышает 1 %.
Период крутильных колебаний тела, подвешенного на упругой
нити,
где / — момент инерции тела относительно оси, совпадающей с
упругой нитью; k — жесткость упругой нити, равная отношению
упругого момента, возникающего при закручивании нити, к углу,
на который нить закручивается.
84

• Дифференциальное уравнение затухающих колебаний
т'х =— kx—гх, или х + 28х + и>1х = 0,
где г — коэффициент сопротивления; б — коэффициент затухания:
6=/7Bт); оH — собственная угловая частота колебаний *
9 Уравнение затухающих колебаний
х=А (t) cos(co/+cp),
где A (/) — амплитуда затухающих колебаний в момент /; со — их
угловая частота.
© Угловая частота затухающих колебаний
= |/со§ — б2.
Зависимость амплитуды затухающих колебаний от времени
Л(*) = Лое«,
где Ло — амплитуда колебаний в момент /=0.
@ Логарифмический декремент колебаний
где A(t) и A (t-\-T) — амплитуды двух последовательных колеба-
колебаний, отстоящих по времени друг от друга на период.
@ Дифференциальное уравнение вынужденных колебаний
тх =— kx—rx+ F0coscx)t, или
х + 2&х + (OqA: = /о cos со/,
где Fo cos wt — внешняя периодическая сила, действующая на
колеблющуюся материальную точку и вызывающая вынужденные
колебания; Fo — ее амплитудное значение; fo=Fo/m.
® Амплитуда вынужденных колебаний
А -
Резонансная частота и резонансная амплитуда
«рез = К 0)ё —Z04 И Лрез =
Примеры решения задач
Пример 1. Точка совершает колебания по закону x(t) =
=А cos(co/+(p), где А=2 см. Определить начальную фазу ср, если
х@)=—]/3 см и л@)<0. Построить векторную диаграмму для мо-
момента ^=0.
Решение. Воспользуемся уравнением движения и выразим
смещение в момент /=0 через начальную фазу: х@)=Л cos ср.
* В приведенных ранее формулах гармонических колебаний та же
величина обозначалась просто со (без индекса 0).
85

Отсюда найдем начальную фазу:
х@)
Ф = arccos —j~-
Подставим в это выражение заданные значения х@) и А: ср =
— arccos(—1/3/2). Значению аргумента (—У3'2) удовлетворяют
два значения угла:
Ф!=5я/6 и ф2=7л/6.
Для того чтобы решить, какое из этих значений угла ф удовлет-
удовлетворяет еще и условию х@)<0, найдем сначала x(t):
x(t) = — о)А sin (со/+ ф).
Подставив в это выражение значение t=0 и поочередно значения
начальных фаз ЦI=5п/6 и ф2=7я/6, найдем
^@) = — г12А<ь и Jc2@)-V2v4co.
Так как всегда Л>0 и со>0, то условию х @)<0 удовлетворяет толь-
только первое значение начальной фазы.
Таким образом, искомая начальная
фаза ф=5я/6.
По найденному значению ф постро-
построим векторную диаграмму (рис. 6.1).
Пример 2. Материальная точка
массой т=5 г совершает гармоничес-
гармонические колебания с частотой v=0,5 Гц.
Амплитуда колебаний А=3 см. Оп-
Определить: 1) скорость v точки в мо-
момент времени, когда смещение х=
= 1,5 см; 2) максимальную силу
Fmax, действующую на точку; 3) пол-
Рис. 6.1 ную энергию Е колеблющейся точ-
точки.
Решение. 1. Уравнение гармонического колебания имеет
вид
х=А cos(a>H-(p), A)
а формулу скорости получим, взяв первую производную по времени
от смещения:
v = x = dx/dt = — Лео sin (co^ + ф). B)
Чтобы выразить скорость через смещение, надо исключить из
формул A) и B) время. Для этого возведем оба уравнения в квад-
квадрат, разделим первое на Л2, второе на Л2со2 и сложим:
х2 , и2 _ t х2 , v2 __ t
А2 ~Г Л2со2 - !' ИЛП "Л2"+4яЧ2Л2 ~ 1ф
Решив последнее уравнение относительно v, найдем
v = ± 2nv VrA2—x2.
Выполнив вычисления по этой формуле, получим
v-±8,2 см/с.
86

Знак плюс соответствует случаю, когда направление скорости
совпадает с положительным направлением оси х, знак минус — ког-
когда направление скорости совпадает с отрицательным направлением
оси х.
Смещение при гармоническом колебании кроме уравнения A)
может быть определено также уравнением
х=А sin (со/+ф).
Повторив с этим уравнением такое же решение, получим тот же
ответ.
2. Силу действующую на точку, найдем по второму закону Нью-
Ньютона:
F=ma, C)
где а — ускорение точки, которое получим, взяв производную по
времени от скорости:
a = x = dv/dt =— Лео2 cos (со/ + ф), или
а = —4jx2vM cos (со/ -f ф).
Подставив выражение ускорения в формулу C), получИхМ
F=—4n2v2mA cos (со/+ф).
Отсюда максимальное значение силы
Подставив в это уравнение значения величин jt, v, m и Af
найдем
3. Полная энергия колеблющейся точки есть сумма кинетической
и потенциальной энергий, вычисленных для любого момента вре-
времени.
Проще всего вычислить полную энергию в момент, когда кинети-
кинетическая энергия достигает максимального значения. В этот момент
потенциальная энергия равна нулю. Поэтому полная энергия Е
колеблющейся точки равна максимальной кинетической энергии
* max-
E = Tmaii = 1/2mv*nax. D)
Максимальную скорость определим из формулы B), положив
cos (со/+ф) = 1: umax =2nvA. Подставив выражение скорости в фор-
формулу D), найдем
E=2n2mv2A2.
Подставив значения величин в эту формулу и произведя вычис-
вычисления, получим
?-2.C,14J.5.10-3-@,5J.C.10-2JДж-22,Ь10-вДж,
или ?=22,1 мкДж.
Пример 3. На концах тонкого стержня длиной /=1 ми массой
^з=400 г укреплены шарики малых размеров массами т1=200 г и
/и2=300г. Стержень колеблется около горизонтальной оси, перпен-
87

дикулярной стержню и проходящей через его середину (точка О на
рис. 6.2). Определить период Т колебаний, совершаемых стержнем.
Решение. Период колебаний физического маятника, каким
является стержень с шариками, определяется соотношением
где / — момент инерции маятника относительно оси колебаний;
m — его масса; 1С — расстояние от центра масс ма-
MfA^ ятника до оси.
Момент инерции данного маятника равен сумме
моментов инерции шариков Д и /2 и стержня /3:
J=J1+J2+J9. B)
Принимая шарики за материальные точки, вы-
выразим моменты их инерции: J1=m1(l/2J\ J2-=m2(l/2J.
Так как ось проходит через середину стержня, то
его момент инерции относительно этой оси J3=
=:1l12m3l2. Подставив полученные выражения Jly /2 и
J3 в формулу B), найдем общий момент инерции фи-
физического маятника:
J=m1 (//2J+m2 (//2J+V12m3/2-
=1/12Z2Cm1+3m2+m3).
Произведя вычисления по этой формуле, найдем
/=0,158 кг-м2.
Масса маятника состоит из масс шариков и массы
стержня:
m=m1+m2+m3=0,9 кг.
Расстояние 1С центра масс маятника от оси колебаний найдем,
исходя из следующих соображений. Если ось х направить вдоль
стержня и начало координат совместить с точкой О, то искомое рас-
расстояние / равно координате центра масс маятника, т. е.
/77,
X
Рис. 6.2
I r — Xr — -
(— 1/2) + т2 A/2) + т3
-т3
ИЛИ
(m2 — m1)l (m2— i
2m
Подставив значения величин ml9 m2, m, l и произведя вычисле-
вычисления, найдем
/с=5,55 см.
Произведя расчеты по формуле A), получим период колебаний
физического маятника:
Т = 2-3,14КО, 158/@,9-9,81. 5,55- 10)с= 11,2 с.
Пример 4. Физический маятник представляет собой стержень
длиной 1=1 м и массой Зш1 с прикрепленным к одному из его концов
обручем диаметром d=V2/ и массой т1. Горизонтальная ось Oz
88

маятника проходит через середину стержня перпендикулярно ему
(рис. 6.3). Определить период Т колебаний такого маятника.
Решение. Период колебаний физического маятника опреде-
определяется по формуле
Т — 2я У J/(mglc), A)
где J — момент инерции маятника относительно оси колебаний;
m — его масса; /с — расстояние от центра
масс маятника до оси колебаний.
Момент инерции маятника равен сумме мо-
моментов инерции стержня J1 и обруча /2:
J=J1 + J2. (*)
Момент инерции стержня относительно оси,
перпендикулярной стержню и проходящей
через его центр масс, определяется по форму-
формуле J1=1/12fnl2. В данном случае m=3m1 и
Момент инерции обруча найдем, восполь-
воспользовавшись теоремой Штейнера J = J0 \-ma2y
где J — момент инерции относительно про-
произвольной оси; У о — момент инерции отно-
относительно оси, проходящей через центр масс
параллельно заданной оси; а — расстояние
между указанными осями. Применив эту фор-
формулу к обручу,получим
J2=m1(l/AJ+m1Cl/4J=48m1l2. Рис. б.З
Подставив выражения Л и /2 в форму-
формулу B), найдем момент инерции маятника относительно оси вра-
вращения:
Расстояние 1С от оси маятника до его центра масс равно
_2jm''xi _Sm1-Q
ИЛИ
1 —3/ /
1с— /и1
Подставив в формулу A) выражения /, 1С и массы маятника
?J1=^m1), найдем период его колебаний:
Т =
После вычисления по этой формуле получим
Т=2,17 с
Пример 5. Складываются два колебания одинакового направле-
направления, выражаемых уравнениями х1=А1 cos со (t+Xj); x2=
=-Л2со5 со(/+т2), где Лх=1 см, Л2—2 см, x1=1U с, T2=V2 с, со —
=я с~г. 1. Определить начальные фазы фх и ф2 составляющих коле-
89

баний. 2. Найти амплитуду А и начальную фазу ф результирующего
колебания. Написать уравнение результирующего колебания.
Решение. 1. Уравнение гармонического колебания имеет
вид
х=А cos (<*>/+ф). A)
Преобразуем уравнения, заданные в условии задачи, к такому
же виду:
Х\=Аг cos(co/+(ot1), x2=A2 cos((o/+cot2). B)
Из сравнения выражений B) с равенством A) находим начальные
фазы первого и второго колебаний:
Ф1=о)т1=я/6 рад и ф2=сот2=я/'2 рад.
2. Для определения амплитуды А результирую-
результирующего колебания удобно воспользоваться векторной
диаграммой, представленной на рис. 6.4. Согласно
теореме косинусов, получим
А = VА\ + А22+2А1А1 cos Аф, C)
где Аф — разность фаз составляющих колебаний.
Так как Аф=ф2—фь то, подставляя найденные
значения ф2 и фь получим Аф=я/3 рад.
Подставим значения Аг, А2 и Аф в формулу
Рис 6 4 C) и произведем вычисления:
Л=2,65 см.
Тангенс начальной фазы ф результирующего колебания опреде-
определим непосредственно из рис. 6.4: tg ф = Ах ^" (р^Ад2 s'" ^, отку-
да начальная фаза
ф — arete
Ла cos
cos^>
± cos ф1 + ^2 cos ф2*
Подставим значения А1у А2, ф1? ф2 и произведем вычисления:
Ф - arctg EIV3) - 70,9° = 0,394я рад.
Так как угловые частоты складываемых колебаний одинаковы,
то результирующее колебание будет иметь ту же частоту со. Это
позволяет написать уравнение результирующего колебания в виде
х=А соз((о/+ф), где А=2,65 см, со=я с, ф=0,394 п рад.
Пример 6. Материальная точка участвует одновременно в двух
взаимно перпендикулярных гармонических колебаниях, уравне-
уравнения которых
х = Агсо^Ыу A)
y = A2cos^i, B)
где Лх=1 см, А2=2 см, со=я с. Найти уравнение траектории точ-
точки. Построить траекторию с соблюдением масштаба и указать
направление движения точки.
Решение. Чтобы найти уравнение траектории точки, ис-
исключим время t из заданных уравнений A) и B). Для этого восполь-
90

зуемся формулой cos (а/2) = ^A/2) A + cosa). В данном случае
a = o)t, поэтому
Так как согласно формуле A) cos cot=x/Aly то уравнение траекто-
траектории
У х/А1). C)
Полученное выражение представляет собой уравнение параболы,
ось которой совпадает с осью Ох. Из уравнений A) и B) следует,
что смещение точки по осям координат ограничено и заключено в
пределах от —1 до +1 см по оси Ох и от —2 до +2 см по оси Оу.
Для построения траектории найдем по уравнению C) значения
у, соответствующие ряду значений х, удовлетворяющих условию
\х\ ^ 1 см, и составим таблицу:
X,
У,
см
см
—1
0
—0
±0
,75
,707
—о,
±1
5
0
±1
,41
+0
±1
,5
,73
+ 1
±2
В
Начертив координатные оси и выбрав масштаб, нанесем на пло-
плоскость хОу найденные точки. Соединив их плавной кривой, получим
траекторию точки, совершающей колеба-
колебания в соответствии с уравнениями движе-
движения A) и B) (рис. 6.5).
Для того чтобы указать направление
движения точки, проследим за тем, как из-
изменяется ее положение с течением времени.
В начальный момент t~=0 координаты точ-
точки равны л:@) = 1 см и у@)=2 см. В по-
последующий момент времени, например при
t1=l с, координаты точек изменятся и ста-
станут равными х A)=—1 см, y(t)=O. Зная
положения точек в начальный и последую-
последующий (близкий) моменты времени, можно
указать направление движения точки по
траектории. На рис. 6.5 это направление
движения указано стрелкой (от точки А к
началу координат). После того как в мо-
момент t2 = 2 с колеблющаяся точка достиг-
достигнет точки Z), она будет двигаться в обратном направлении.
Задачи
Кинематика гармонических колебаний
6.1. Уравнение колебаний точки имеет вид х=А cos со (/+т),
где (д=тх с, т=0,2 с. Определить период Т и начальную фазу ф
колебаний.
91

6.2. Определить период Т, частоту v и начальную фазу ср коле-
колебаний, заданных уравнением х=А sin со (t+т), где (о =2,5я с,
т=0,4 с.
6.3. Точка совершает колебания по закону х=А cos((D^+(p),
где А =4 см. Определить начальную фазу ср, если: 1) х@)=2 см и
*@)<0;2) ?@)=— 2|/2"см и х @)< 0; 3) х@)=2 см и х@)>0; 4)
х@) =—2|^3см и #@)>0. Построить векторную диаграмму для
момента t=0.
6.4. Точка совершает колебания по закону х=А sin(a>H-<p),
где Л =4 см. Определить начальную фазу ср, если: 1) #@)=2 см и
х@)<0; 2) *(О)=21/3" см и ic@)>0; 3) x@)=— 2]/2 см и л?@)<0;
4) я@) =—2]/3 см и #@)>0. Построить векторную диаграмму для
момента /=0.
6.5. Точка совершает колебания по закону х=А cos(co/+9),
где А=2 см; со=я с; ф=я/4 рад. Построить графики зависимости
от времени: 1) смещения x(f)\ 2) скорости x{t)\ 3) ускорения x(t).
6.6. Точка совершает колебания с амплитудой А=4 см и перио-
периодом Т=2 с. Написать уравнение этих колебаний, считая, что в
момент /=0 смещения я@)=0 и х@)<0. Определить фазу (со^+ф)
для двух моментов времени: 1) когда смещение х=1 см и х>0;
2) когда скорость х=—6 см/с и л:<0.
6.7. Точка равномерно движется по окружности против часовой
стрелки с периодом Т=& с. Диаметр d окружности равен 20 см.
Написать уравнение движения проекции точки на ось х, проходя-
проходящую через центр окружности, если в момент времени, принятый за
начальный, проекция на ось х равна нулю. Найти смещение х,
скорость х и ускорение х проекции точки в момент t=\ с.
6.8. Определить максимальные значения скорости хтах и уско-
ускорения хтах точки, совершающей гармонические колебания с ампли-
амплитудой А=3 см и угловой частотой оо=я/2 с.
6.9. Точка совершает колебания по закону х=А cos со/, где Л =
=5 см; (о=2 с1. Определить ускорение \х\ точки в момент времени,
когда ее скорость х=8 см/с.
6.10. Точка совершает гармонические колебания. Наибольшее
смещение хтах точки равно 10 см, наибольшая скорость хтах=
=20 см/с. Найти угловую частоту о колебаний и максимальное уско-
ускорение хтгх точки.
6.11. Максимальная скорость хтах точки, совершающей гармо-
гармонические колебания, равна Юсм/с, максимальное ускорение хтах=
= 100 см/с2. Найти угловую частоту © колебаний, их период Т
и амплитуду А. Написать уравнение колебаний, приняв началь-
начальную фазу равной нулю.
6.12. Точка совершает колебания по закону x=Asin(dt. В не-
некоторый момент времени смещение хх точки оказалось равным
92

5 см. Когда фаза колебаний увеличилась вдвое, смещение х2 стало
равным 8 см. Найти амплитуду А колебаний.
6.13. Колебания точки происходят по закону х= A cos (со/+ф)«
В некоторый момент времени смещение х точки равно 5 см, ее скорость
jt'=2Q см/с и ускорение х——80 см/с2. Найти амплитуду Л, угло-
угловую частоту со, период Т колебаний и фазу (со/+ф) в рассматри-
рассматриваемый момент времени.
Сложение колебаний
6.14. Два одинаково направленных гармонических колебания
одного периода с амплитудами Аг=\0 см и Л2=6 см складыва-
складываются в одно колебание с амплитудой А=14 см. Найти раз-
разность фаз Аф складываемых колебаний.
6.15. Два гармонических колебания, направленных по одной
прямой и имеющих одинаковые амплитуды и периоды, складывают-
складываются в одно колебание той же амплитуды. Найти разность фаз Аср
складываемых колебаний.
6.16. Определить амплитуду А и начальную фазу ср результи-
результирующего колебания, возникающего при сложении двух колебаний
одинаковых направления и периода: х1=А1 sin со/ и х2=А2 sinco (/+
+т), где А1=А2=1 см; co=jx c^; т=0,5 с. Найти уравнение резуль-
результирующего колебания.
6.17. Точка участвует в двух одинаково направленных колеба-
колебаниях: х1=А1 sin со/ и х2=А2 cos со/, где Аг=\ см; А2=2 см; со =
= 1 с^1. Определить амплитуду А результирующего колебания,
его частоту v и начальную фазу ср. Найти уравнение этого движе-
движения.
6.18. Складываются два гармонических колебания одного на-
направления с одинаковыми периодами T1=T2=li5 с и амплитудами
А1=А2=2 см. Начальные фазы колебаний cpi=Jt/2 и ф2=я/3. Опре-
Определить амплитуду А и начальную фазу ф результирующего колеба-
колебания. Найти его уравнение и построить с соблюдением масштаба
векторную диаграмму сложения амплитуд.
6.19. Складываются три гармонических колебания одного на-
направления с одинаковыми периодами Тг=Т2=Т3=2 с и амплиту-
амплитудами Л1=Л2=Л3=3 см. Начальные фазы колебаний cpi=O, ф2=
=я/3, ф3=2я/3. Построить векторную диаграмму сложения ампли-
амплитуд. Определить из чертежа амплитуду А и начальную фазу ф ре-
результирующего колебания. Найти его уравнение.
6.20. Складываются два гармонических колебания одинаковой
частоты и одинакового направления: x1=A1cos((ot-{-(p1) и х2=
=А2 со$(со/+ф2). Начертить векторную диаграмму для момента
времени t=0. Определить аналитически амплитуду А и начальную
фазу ф результирующего колебания. Отложить А и ер на векторной
диаграмме. Найти уравнение результирующего колебания (в три-
тригонометрической форме через косинус). Задачу решить для двух
случаев: 1) Аг = 1 см, ф1=я/3; Л2=2 см, ф2=5я/6; 2) А1=\ см,
<Pi=2jt/3; Л2=1 см, ф2=7я/6.
93

6.21. Два камертона звучат одновременно. Частоты v± и v2 их
колебаний соответственно равны 440 и 440,5 Гц. Определить период
Т биений.
6.22. Складываются два взаимно перпендикулярных колебания,
выражаемых уравнениями х=Аг sin со/ и #=Л2 cos со(/+т), где
Аг=2 см, А 2=1 см, <о=л с, т=0,5 с. Найти уравнение траектории
и построить ее, показав направление движения точки.
6.23. Точка совершает одновременно два гармонических колеба-
колебания, происходящих по взаимно перпендикулярным направлениям
и выражаемых уравнениями х=А± cos со/ и у=А2 cos со (/+т),
где Аг=4: см, Л2=8 см, со=яс~1, т=1 с. Найти уравнение траекто-
траектории точки и построить график ее движения.
6.24. Точка совершает одновременно два гармонических колеба-
колебания одинаковой частоты, происходящих по взаимно перпендикуляр-
перпендикулярным направлениям и выражаемых уравнениями: 1) л;=Л cos со/ и
у=А cos со/; 2) х=А cos со/ и у=Аг cos со/; 3) х=А cos со/ и у~
=А cos(co/+(pi); 4) х=А2 cos со/ и у=А cos(co/-f(p2); 5) х=Аг cosco/
и у=Аг sin со/; 6) х=Л cos со/ и ^/=Лг sin со/; 7) х=Л2 sin со/ и
у=Лх sin со/; 8) х=А2 sin со/ и у=А sin (со/-Ьф2).
Найти чдля восьми случаев) уравнение траектории точки, пост-
построить ее с соблюдением масштаба и указать направление движения.
Принять: А = 2 см, Аг=3 см, Л2=1 см; фх=л/2, (р2=л.
6.25. Точка участвует одновременно в двух взаимно перпенди-
перпендикулярных колебаниях, выражаемых уравнениями х=Аг cos со/ и
у=А2 sin со/, где Ах=2 см, Л2=1 см. Найти уравнение траектории
точки и построить ее, указав направление движения.
6.26. Точка одновременно совершает два гармонических колеба-
колебания, происходящих по взаимно перпендикулярным направлениям
и выражаемых уравнениями х=Аг sin со/ и у=А2 cos со/, где Аг =
=0,5 см; А2=2 см. Найти уравнение траектории точки и построить
ее, указав направление движения.
6.27. Движение точки задано уравнениями х=Аг sin со/ и у~
=А2sin со (/+т), где Аг=10 см, А2=5 см, со=2 с, т=я/4 с. Найти
уравнение траектории и скорости точки в момент времени /=0,5 с.
6.28. Материальная точка участвует одновременно в двух вза-
взаимно перпендикулярных колебаниях, выражаемых уравнениями
jc^^xcosco/ и у=—Л2соз2со/, где Аг=2 см, Л2=1 см. Найти
уравнение тректории и построить ее.
6.29. Точка участвует одновременно в двух гармонических коле-
колебаниях, происходящих по взаимно перпендикулярным направлени-
направлениям и описываемых уравнениями: 1) х=А sin со/ и у=А cos 2co/;
2) х=А cos со/ и у=А sin 2со/; 3) х=А cos 2со/ и y=At cos со/;
4) х=Аг sin со/ и ^=Л cos со/.
Найти уравнение траектории точки, построить ее с соблюдением
масштаба и указать направление движения. Принять: Л =2 см;
Лх=3 см.
6.30. Точка участвует одновременно в двух взаимно перпенди-
перпендикулярных колебаниях, выражаемых уравненияхми х=Аг cos со/ и
94

y=A2 sin 0,5(o/, где Аг=2 см, А2=3 см. Найти уравнение траекто-
траектории точки и построить ее, указав направление движения.
6.31. Смещение светящейся точки на экране осциллографа явля-
является результатом сложения двух взаимно перпендикулярных коле-
колебаний, которые описываются уравнениями: 1) х=А sin Зсо/ и у=
=А sin 2со/; 2) х=А sin Зсо/ и у=А cos 2со/; 3) х=А sin Зсо/ и
у=А cos со/.
Применяя графический метод сложения и соблюдая масштаб,
построить траекторию светящейся точки на экране. Принять А =
—4 см.
Динамика гармонических колебаний. Маятники
6.32. Материальная точка массой т=50 г совершает колебания,
уравнение которых имеет видл;=Л cos со/, где Л = 10 см, со=5 с.
Найти силу F, действующую на точку, в двух случаях: 1) в момент,
когда фаза со/=л/3; 2) в положении наибольшего смещения точ-
точки.
6.33. Колебания материальной точки массой т=0,\ г происхо-
происходят согласно уравнениюх=А cos со/, где А=Ъ см; со=20 с. Опре-
Определить максимальные значения возвращающей силы Fma% и кинети-
кинетической энергии Ттах.
6.34. Найти возвращающую силу F в момент /=1 си полную
энергию Е материальной точки, совершающей колебания по закону
х=А cos со/, где А = 20 см; со=2я/3 с. Масса т материальной
точки равна 10 г.
6.35. Колебания материальной точки происходят согласно урав-
уравнению х=A cos со/, где А=8 см, со=я/6 с. В момент, когда возвра-
возвращающая сила F в первый раз достигла значения —5 мН, потенци-
потенциальная энергия П точки стала равной 100 мкДж. Найти этот момент
времени / и соответствующую ему фазу со/.
6.36. Грузик массой т=250 г, подвешенный к пружине, колеб-
колеблется по вертикали с периодом Т—\ с. Определить жесткость k
пружины.
6.37. К спиральной пружине подвесили грузик, в результате
чего пружина растянулась на х=9 см. Каков будет период Т коле-
колебаний грузика, если его немного оттянуть вниз и затем отпустить?
6.38. Гиря, подвешенная к пружине, колеблется по вертикали с
амплитудой А =4 см. Определить полную энергию Е колебаний
гири, если жесткость k пружины равна 1 кН/м.
6.39. Найти отношение длин двух математических маятников,
если отношение периодов их колебаний равно 1,5.
6.40. Математический маятник длиной 1=1 м установлен в лиф-
лифте. Лифт поднимается с ускорением а=2,5 м/с2. Определить период
Т колебаний маятника.
6.41. На концах тонкого стержня длиной /=30 см укреплены оди-
одинаковые грузики по одному на каждом конце. Стержень с грузиками
колеблется около горизонтальной оси, проходящей через точку,
удаленную на d=10 см от одного из концов стержня. Определить
95

приведенную длину L и период Т колебаний такого физического ма-
маятника. Массой стержня пренебречь.
6.42. На стержне длиной /=30 см укреплены два одинаковых
грузика: один — в середине стержня, другой — на одном из его
концов. Стержень с грузиком колеблется около горизонтальной оси,
проходящей через свободный конец стержня. Определить приведен-
приведенную длину L и период Т колебаний такой системы. Массой стержня
пренебречь.
6.43. Система из трех грузов, соединенных стержнями длиной
/=30 см (рис. 6.6), колеблется относительно горизонтальной оси,
проходящей через точку О перпендикулярно плоскости чертежа.
Найти период Т колебаний системы. Массами стержней пренебречь,
грузы рассматривать как материальные точки.
6.44. Тонкий обруч, повешенный на гвоздь, вбитый горизон-
горизонтально в стену, колеблется в плоскости, параллельной стене. Ра-
Радиус R обруча равен 30 см. Вычислить период Т колебаний обруча.
\0
I О
w
m
Рис. 6.6
Рис. 6.7
6.45. Однородный диск радиусом /? = 30 см колеблется около го-
горизонтальной оси, проходящей через одну из образующих цилинд-
цилиндрической поверхности диска. Каков период Т его колебаний?
6.46. Диск радиусом R=24 см колеблется около горизонтальной
оси, проходящей через середину одного из радиусов перпендику-
перпендикулярно плоскости диска. Определить приведенную длину L и период
Т колебаний такого маятника.
6.47. Из тонкого однородного диска радиусом 7^ = 20 см вырезана
часть, имеющая вид круга радиусом г= 10 см, так, как это показа-
показано на рис. 6.7. Оставшаяся часть диска колеблется относительно
горизонтальной оси О, совпадающей с одной из образующих ци-
цилиндрической поверхности диска. Найти период Т колебаний тако-
такого маятника.
6.48. Математический маятник длиной /х=40 см и физический
маятник в виде тонкого прямого стержня длиной /2=60 см син-
синхронно колеблются около одной и той же горизонтальной оси.
Определить расстояние а центра масс стержня от оси колебаний.
96

6.49. Физический маятник в виде тонкого прямого стержня дли-
длиной /=120 см колеблется около горизонтальной оси, проходящей
перпендикулярно стержню через точку, удаленную на некоторое
расстояние а от центра масс стержня. При каком значении а период
Т колебаний имеет наименьшее значение?
6.50. Физический маятник представляет собой тонкий однород-
однородный стержень массой m с укрепленным на нем маленьким шариком
массой т. Маятник совершает колебания около горизонтальной
оси, проходящей через точку О на стержне. Определить период Т
гармонических колебаний маятника для случаев а, б, <?, г, изобра-
изображенных на рис. 6.8. Длина / стержня равна 1 м. Шарик рассматри-
рассматривать как материальную точку.
—
0
\m
a) 5}
Рис.
J_
•A
S)
6.8
CM
/77
г)
о) б) 6)
Рис. 6.9
6.51. Физический маятник представляет собой тонкий однород-
однородный стержень массой m с укрепленными на нем двумя маленькими
шариками массами m и 2т. Маятник совершает колебания около
горизонтальной оси, проходящей через точку О на стержне. Опре-
Определить частоту v гармонических колебаний маятника для случаев
я, б, е, г, изображенных на рис. 6.9. Длина / стержня равна 1 м.
Шарики рассматривать как материальные точки.
6.52. Тело массой т=4 кг, закрепленное на горизонтальной оси,
совершало колебания с периодом 7i=0,8 с. Когда на эту ось был
насажен диск так, что его ось совпала с осью колебаний тела, пери-
период Г2 колебаний стал равным 1,2 с. Радиус R диска равен 20 см,
масса его равна массе тела. Найти момент инерции / тела относи-
относительно оси колебаний.
6.53. Ареометр массой /л=50 г, имеющий трубку диаметром d=
= 1 см, плавает в воде. Ареометр немного погрузили в воду и затем
предоставили самому себе, в результате чего он стал совершать
гармонические колебания. Найти период Т этих колебаний.
6.54. В открытую с обоих концов U-образную трубку с площа-
площадью поперечного сечения S=0,4 см2 быстро вливают ртуть массой
пг=200 г. Определить период Т колебаний ртути в трубке.
6.55. Набухшее бревно, сечение которого постоянно по всей
длине, погрузилось вертикально в воду так, что над водой находит-
находится лишь малая (по сравнению с длиной) его часть. Период Т коле-
колебаний бревна равен 5 с. Определить длину / бревна.
4 № 1268
97

Затухающие колебания
6.56. Амплитуда затухающих колебаний маятника за время U —
=5 мин уменьшилась в два раза. За какое время t2> считая от на-
начального момента, амплитуда уменьшится в восемь раз?
6.57. За время /=8 мин амплитуда затухающих колебаний маят-
маятника уменьшилась в три раза. Определить коэффициент затухания 6.
6.58. Амплитуда колебаний маятника длиной /=1 м за время
/=10 мин уменьшилась в два раза. Определить логарифмический
декремент колебаний 9.
6.59. Логарифмический декремент колебаний 9 маятника равен
0,003. Определить число N полных колебаний, которые должен сде-
сделать маятник, чтобы амплитуда уменьшилась в два раза.
6.60. Гиря массой т=500 г подвешена к спиральной пружине
жесткостью fe=20 Н/м и совершает упругие колебания в некоторой
среде. Логарифмический декремент колебаний 9=0,004. Опреде-
Определить число N полных колебаний, которые должна совершить гиря,
чтобы амплитуда колебаний уменьшилась в п=2 раза. За какое вре-
время t произойдет это уменьшение?
6.61. Тело массой т=5 г совершает затухающие колебания.
В течение времени /=50 с тело потеряло 60 % своей энергии. Опре-
Определить коэффициент сопротивления Ь.
6.62. Определить период Т затухающих колебаний, если период
То собственных колебаний системы равен 1 с и логарифмический
декремент колебаний 9=0,628.
6.63. Найти число N полных колебаний системы, в течение кото-
которых энергия системы уменьшилась в
п=2 раза. Логарифмический декре-
декремент колебаний 9=0,01.
6.64. Тело массой т=1 кг нахо-
находится в вязкой среде с коэффициентом
сопротивления 6=0,05 кг/с. С по-
помощью двух одинаковых пружин
жесткостью ?=50 Н/м каждое тело
удерживается в положении равнове-
равновесия, пружины при этом не деформиро-
деформированы (рис. 6.10). Тело сместили от
положения равновесия и отпустили. Определить: 1) коэффициент
затухания б; 2) частоту v колебаний; 3) логарифмический декре-
декремент колебаний 9; 4) число N колебаний, по прошествии которых
амплитуда уменьшится в е раз.
Вынужденные колебания. Резонанс
6.65. Под действием силы тяжести электродвигателя консольная
балка, на которой он установлен, прогнулась на/г=1 мм. При какой
частоте вращения п якоря электродвигателя может возникнуть
опасность резонанса?
6.66. Вагон массой m=80 t имеет четыре рессоры. Жесткость k
Рис. 6.10
98

пружин каждой рессоры равна 500 кН/м. При какой скорости v
вагон начнет сильно раскачиваться вследствие толчков на стыках
рельс, если длина / рельса равна 12,8 м?
6.67. Колебательная система совершает затухающие колебания
с частотой v=1000 Гц. Определить частоту v0 собственных колеба-
колебаний, если резонансная частота vpe3=998 Гц.
6.68. Определить, на сколько резонансная частота отличается
от частоты vo=l кГц собственных колебаний системы, характери-
характеризуемой коэффициентом затухания 6=400 с"*1.
6.69. Определить логарифмический декремент колебаний 0 коле-
колебательной системы, для которой резонанс наблюдается при частоте,
меньшей собственной частоты v0=10 кГц на Av=2 Гц.
6.70. Период То собственных колебаний пружинного маятника
равен 0,55 с. В вязкой среде период Т того же маятника стал рав-
равным 0,56 с. Определить резонансную частоту vpe3 колебаний.
6.71. Пружинный маятник (жесткость k пружины равна 10 Н/м,
масса пг груза равна 100 г) совершает вынужденные колебания в
вязкой среде с коэффициентом сопротивления г=2 • 10~2 кг/с. Опре-
Определить коэффициент затухания б и резонансную амплитуду Лрез,
если амплитудное значение вынуждающей силы F0=l0 мН.
6.72. Тело совершает вынужденные колебания в среде с коэффи-
коэффициентом сопротивления г=\ г/с. Считая затухание малым, опреде-
определить амплитудное значение вынуждающей силы, если резонансная
амплитуда Лрез=0,5 см и частота v0 собственных колебаний равна
10 Гц.
6.73. Амплитуды вынужденных гармонических колебаний при
частоте vx=400 Гц и v2=600 Гц равны между собой. Определить ре-
резонансную частоту vpe3. Затуханием пренебречь.
6.74. К спиральной пружине жесткостью й=10 Н/м подвесили
грузик массой т=10 г и погрузили всю систему в вязкую среду.
Приняв коэффициент сопротивления Ь равным 0,1 кг/с, определить:
1) частоту v0 собственных колебаний; 2) резонансную частоту vpe3;
3) резонансную амплитуду Лрез, если вынуждающая сила изменя-
изменяется по гармоническому закону и ее амплитудное значение Fo~
= 0,02 Н; 4) отношение резонансной амплитуды к статическому сме-
смещению под действием силы Fo.
6.75. Во сколько раз амплитуда вынужденных колебаний будет
меньше резонансной амплитуды, если частота изменения вынуж-
вынуждающей силы будет больше резонансной частоты: 1) на 10 %? 2) в два
раза? Коэффициент затухания б в обоих случаях принять равным
0,1 соо (оH — угловая частота собственных колебаний).
§ 7. ВОЛНЫ В УПРУГОЙ СРЕДЕ. АКУСТИКА
Основные формулы
О Уравнение плоской волны
l(x, t) = A cos (o(t—x/v), или t(x, t)=Acos (со/—kx) ,
где I (x, t) — смещение точек среды с координатой х в момент вре-
4* 99

мени /; оз — угловая частота; v — скорость распространения коле-
колебаний в среде (фазовая скорость); k — волновое число; k=2n/K;
X — длина волны.
• Длина волны связана с периодом Т колебаний и частотой
v соотношениями
%=vT и X=v/v.
• Разность фаз колебаний двух точек среды, расстояние между
которыми (разность хода) равно Ах,
Дф=Bл;М,)Дл;,
где X — длина волны.
• Уравнение стоячей волны
g(jc, t) = A cos со — -cos со/, или ?(лг, t) = A cos йл:-cos со/.
• Фазовая скорость продольных волн в упругой среде:
в твердых телах v = VE/p9
где Е — модуль Юнга; р — плотность вещества;
в газах v = VyRT/M, или v = ]/~yp/p,
где у — показатель адиабаты {y=cplcv — отношение удельных теп-
лоемкостей газа при постоянных давлении и объеме); R — моляр-
молярная газовая постоянная; Т—термодинамическая температура; М—
молярная масса; р — давление газа.
• Акустический эффект Доплера
где v — частота звука, воспринимаемого движущимся прибором
(или ухом); v — скорость звука в среде; unv — скорость прибора
относительно среды; иист — скорость источника звука относительно
среды; v0 — частота звука, испускаемого источником.
Ф Амплитуда звукового давления
pQ=2nvpvA,
где v — частота звука; А — амплитуда колебаний частиц среды;
v — скорость звука в среде; р — ее плотность.
Ф Средняя объемная плотность энергии звукового поля
где |о — амплитуда скорости частиц среды; со — угловая частота
звуковых волн.
• Энергия звукового поля, заключенного в некотором объеме Vy
W=(w)V.
• Поток звуковой энергии
где W — энергия, переносимая через данную поверхность за вре-
время /.
• Интенсивность звука (плотность потока звуковой энергии)
/
100

• Интенсивность звука связана со средней объемной плотно-
плотностью энергии звукового поля соотношением
I=(w)v,
где v — скорость звука в среде.
• Связь мощности N точечного изотропного источника звука
с интенсивностью звука
I=N/Dnr2),
где г — расстояние от источника звука до точки звукового поля,
в которой определяется интенсивность.
• Удельное акустическое сопротивление среды
Zs = pv.
Ф Акустическое сопротивление
z^zs/s,
где S — площадь сечения участка акустического поля (например,
площадь поперечного сечения трубы при распространении в ней
звука).
• Уровень интенсивности звука (уровень звуковой мощности)
(ДБ)
LP=10 1g (///„),
где /0 — условная интенсивность, соответствующая нулевому уров-
уровню интенсивности Aо=1 пВт/м2).
Крибые дробней громкости ^
500 W00
Частота, Гц
Рис. 7.1
5000 10000
• Уровень громкости звука LN в общем случае является слож-
сложной функцией уровня интенсивности и частоты звука и определя-
определяется по кривым уровня громкости (рис. 7.1). На графике по гори-
горизонтальной оси отложены логарифмы частот звука (сами частоты
101

указаны под соответствующими им логарифмами).На вертикальной
оси отложены уровни интенсивности звука в децибелах. Уровни
громкости звука отложены по вертикальной оси, соответствующей
эталонной частоте v = 1000 Гц. Для этой частоты уровень громкости,
выраженный в децибелах, равен уровню интенсивности в децибе-
децибелах. Уровень громкости звуков других частот определяется по
кривым громкости, приведенным на графике. Каждая кривая соот-
соответствует определенному уровню громкости.
Примеры решения задач
Пример 1. Поперечная волна распространяется вдоль упругого
шнура со скоростью f = 15 м/с. Период Т колебаний точек шнура
равен 1,2 с^ амплитуда А=2 см. Определить: 1) длину волны к;
2) фазу ф колебаний, смещение ?, скорость | и ускорение | точки,
отстоящей на расстоянии х=45 м от источника волн в момент /=
=4 с; 3) разность фаз Дер колебаний двух точек, лежащих на луче
и отстоящих от источника волн на расстояниях #1=20 м и л:2=30 м.
Решение. 1. Длина волны равна расстоянию, которое волна
проходит за один период, и может быть найдена из соотношения
k=vT.
Подставив значения величин v и Г, получим
Х=\8 м.
2. Запишем уравнение волны:
Ъ=А cos co(^—x/v), A)
где ? — смещение колеблющейся точки; х — расстояние точки от
источника волн; v — скорость распространения волн.
Фаза колебаний точки с координатой х в момент времени t
определяется выражением, стоящим в уравнении волны под знаком
косинуса:
ф=а> *—- , или ф =_-*_-.
v ] ' Y — Т
где учтено, что о=2л/Т.
Произведя вычисления по последней формуле, получим
Ф=5,24 рад, или ф-300°.
Смещение точки определим, подставив в уравнение A) значения
амплитуды А и фазы ф:
1=\ см.
Скорость % точки находим, взяв первую производную от смеще-
смещения по времени:
Подставив значения величин я, Л, Т и ф и произведя вычисле-
вычисления, получим
1 = 9 см/с.
102

Ускорение есть первая производная от скорости по времени,
поэтому
Произведя вычисления по этой формуле, найдем
'|=27,4 см/с2.
3. Разность фаз Аф колебаний двух точек волны связана с рас-
расстоянием Ах между этими точками соотношением
Аф=Bя/Х) Ах=Bп1Ц(х2—хх).
Подставив значения величин Я, х± и х2 и вычислив, получим
Аф = 3,49 рад, или Лф = 200°.
Пример 2. На расстоянии /=4 м от источника плоской волны
частотой v=440 Гц перпендикулярно ее лучу расположена стена.
Определить расстояния от источ- источник Стена
ника волн до точек, в которых тлоских вали \
будут первые три узла и три пуч- м '
ности стоячей волны, возникшей в fe
результате сложения бегущей и от- 0 —Е| Л»
раженной от стены волн. Скорость Ц
v волны считать равной 440 м/с. ^i {
Решение. Выберем систе- н И
му координат так, чтобы ось х
была направлена вдоль луча бегу- ис* *
щей волны и начало О координат
совпадало с точкой, находящейся на источнике MN плоской волны
(рис. 7.2). С учетом этого уравнение бегущей волны запишется в
виде
1г=А cos (со/—kx). A)
Поскольку в точку с координатой х волна возвратится, пройдя
дважды расстояние /—х, и при отражении от стены, как среды более
плотной, изменит фазу на я, то уравнение отраженной волны может
быть записано в виде
12 = A cos {со/—k [х+2 A-х)] + я}.
После очевидных упрощений получим
ga=—Л cos Ш—kB1—х)]. B)
Сложив уравнения A) и B), найдем уравнение стоячей волны:
l=li+l2=A cos (со/—kx)—A cos [со/—kBl—х)].
Воспользовавшись формулой разности косинусов, найдем
l=—2A sink A-х) sin (со/—kl).
Так как выражение A sin k(l—х) не зависит от времени, то, взятое
по модулю, оно может рассматриваться как амплитуда стоячей
волны:
Лст = 12А sin k (I—х) |.
Зная выражение амплитуды, можем найти координаты узлов
и пучностей.
103

Узлы возникнут в тех точках, где амплитуда стоячей волны рав-
равна нулю: | 2А sin k(l—л:)]=0. Это равенство выполняется для точек,
координаты хп которых удовлетворяют условию
Щ—хп)=пя(п=0, 1, 2, ...). C)
Но k=2n/h, или, так как X=v/v,
k=2nv/v. D)
Подставив это выражение k в C), получим
2nv (I—xn)=nnv,
откуда координаты узлов
xn = l—nv/Bv).
Подставив сюда значения /, и, v и п=0, 1, 2, найдем координаты
первых трех узлов:
лго=4 м, jcx=3,61 м, а:2=3,23 м.
Пучности возникнут в тех точках, где амплитуда стоячей волны
максимальна: 2Asink(l—х')=2А. Это равенство выполняется для
точек, координаты х'п которых удовлетворяют условию k(l—х'п) =
= Bл+1)(я/2) (я=0, 1, 2, 3, ...). Выразив здесь k по D), получим
откуда координаты пучностей
*; = /—Bn+l)i;/Dv).
Подставив сюда значения /, v, v и п=0, 1, 2, найдем координа-
координапучностей:
3,42 м, х2
ты первых трех
4-3,81 м,
3,04 м.
Мсточник
! плоских болн
Стена
Границы максимальных смещений точек среды в зависимости
от их координат изображены на рис. 7.3. Здесь же отмечены коор-
координаты х0, #i, х2, ... узлов и
координаты Xq, х'1у х'2, ... пуч-
пучностей стоячей волны.
Пример 3. Источник зву-
звука частотой v=18 кГц приб-
приближается к неподвижно уста-
установленному резонатору, на-
настроенному на акустическую
волну длиной Я=1,7 см. С ка-
какой скоростью должен дви-
двигаться источник звука, чтобы возбуждаемые им звуковые волны
вызвали колебания резонатора? Температура Т воздуха равна 290 К.
Решение. Согласно принципу Доплера, частота v звука,
воспринимаемая прибором (резонатором), зависит от скорости нист
источника звука и скорости «пр прибора. Эта зависимость выража-
выражается формулой
V =
Рис. 7.3
где v — скорость звука в данной среде; v0 — частота звуковых волн,
излучаемых источником.
104

Учитывая, что резонатор остается неподвижным («пр =0), из
формулы A) получим v =—-—v0, откуда
т V—иисг
uliCT = v(l—vQ/v). B)
В этом выражении неизвестны значения скорости v звука и час-
частоты V.
Скорость звука в газах зависит от природы газа и температуры
и определяется по формуле
v=VyRT/M. C)
Чтобы волны, приходящие к резонатору, вызвали его колеба-
колебания, частота v воспринимаемых резонатором волн должна совпадать
с собственной частотой vpe3 резонатора, т. е.
V = Vpe3 = uApe3, D)
где vpe3 — длина волны собственных колебаний резонатора.
Подставив выражения v и v из равенства C) и D) в формулу B),
получим
ИЛИ
t/yRT
a«cr== У Ad V°
Чрез*
Взяв значения 7 = 1,4, М=0,029 кг/моль, а также значения R, Г,
v0, Ярез и подставив их в последнюю формулу, после вычислений
получим
1гист = 36 м/с.
Пример 4. Уровень громкости LN звука двух тонов с частотами
Vj.^50 Гц и v2=400 Гц одинаков и равен 10 дБ. Определить уровень
интенсивности LP и интенсивность / звука этих тонов.
Решение. Искомые в задаче уровни интенсивности, соот-
соответствующие частотам Vi=50 Гц и v2=400 Гц, определим, пользу-
пользуясь графиком на рис. 7.1. Вторая кривая снизу является кривой
уровня громкости, равного 10 дБ. Из точек на горизонтальной оси,
соответствующих частотам vx и v2, восстанавливаем ординаты до
кривой уровня громкости в 10 дБ. Значения этих ординат укажут
искомые уровни интенсивности: LP1=60 дБ для частоты V!=50 Гц
и LP2=20 дБ для частоты v2=400 Гц.
Зная уровни интенсивностей LP1 и LP2, определим соответствую-
соответствующие им интенсивности 1г и /2 по формуле
LP= 10 lg(///„),
где / — интенсивность данного звука; /0 — интенсивность, соот-
соответствующая нулевому уровню интенсивности (/0=1 пВт/м2).
Из приведенной формулы получим
lg/=O,l?p + lg/o.
Подставив сюда значения LP и /0 и учтя, что 1 пВт/м2=
= 10~12Вт/м2, найдем для \х=50 Гц и V2=400 Гц соответственно
lg/, = 0,1 • 60 + lg Ю-12 = 6—12 = —6; 1Х = Ю-6 Вт/м2
105

и
lg/2 = 0,1.20 + lgl0-12 = 2—12 = —10; /2 = 10~10 Вт/м2.
Эти значения /х и /2 можно получить и по графику, пользуясь
шкалой интенсивности звука (на рис. 7.1 правая шкала).
Сопоставим полученные результаты: интенсивность первого тона
в 104 раз больше интенсивности второго тона; уровень интенсивно-
интенсивности первого тона на 40 дБ больше уровня интенсивности второго
тона; уровень громкости обоих тонов одинаков и равен 10 дБ.
Задачи
Уравнение плоской волны
7.1. Задано уравнение плоской волны ?(лг, /)=/1cos(g)/—kx),
где Л =0,5 см, (о=628с",&=2 м. Определить: 1) частоту колеба-
колебаний v и длину волны X; 2) фазовую скорость v; 3) максимальные зна-
значения скорости |тах и ускорения 1тах колебаний частиц среды.
7.2. Показать, что выражение ?(лг, /) = Л cos (со/—kx) удовлет-
d*t I d*t
воряет волновому уравнению -^-т = — -щ- при условии, что
(o=kv.
7.3. Плоская звуковая волна возбуждается источником колеба-
колебаний частоты v=200 Гц. Амплитуда А колебаний источника равна
4 мм. Написать уравнение колебаний источника ?@, /), если в на-
начальный момент смещение точек источника максимально. Найти
смещение I (x, /) точек среды, находящихся на расстоянии лг=100 см
от источника, в момент /=0,1 с. Скорость v звуковой волны при-
принять равной 300 м/с. Затуханием пренебречь.
7.4. Звуковые колебания, имеющие частоту v=0,5 кГц и ам-
амплитуду А=0,25 мм, распространяются в упругой среде. Длина
волны i=70 см. Найти: 1) скорость v распространения волн; 2) мак-
максимальную скорость |тах частиц среды.
7.5. Плоская звуковая волна имеет период Т=3 мс, амплитуду
А=0,2 мм и длину волны Я=1,2 м. Для точек среды, удаленных
от источника колебаний на расстояние х=2 м, найти: 1) смещение
?>(х, t) в момент /=7 мс; 2) скорость 1 и ускорение | для того же
момента времени. Начальную фазу колебаний принять равной
нулю.
7.6. От источника колебаний распространяется волна вдоль
прямой линии. Амплитуда А колебаний равна 10 см. Как велико
смещение точки, удаленной от источника на х=3/4 Л, в момент, когда
от начала колебаний прошло время /=0,9 Т>
7.7. Волна с периодом 7= 1,2 с и амплитудой колебаний Л=2 см
распространяется со скоростью и=15 м/с. Чему равно смещение
?(х, /) точки, находящейся на расстоянии л:=45 м от источника
волн, в тот момент, когда от начала колебаний источника прошло
время /=4 с?
106

7.8. Две точки находятся на расстоянии кх=50 см друг от друга
на прямой, вдоль которой распространяется волна со скоростью
v=50 м/с. Период Т колебаний равен 0,05 с. Найти разность фаз
Дф колебаний в этих точках.
7.9. Определить разность фаз Дф колебаний источника волн,
находящегося в упругой среде, и точки этой среды, отстоящей на
лг=2 м от источника. Частота v колебаний равна 5 Гц; волны рас-
распространяются со скоростью v=40 м/с.
7.10. Волна распространяется в упругой среде со скоростью
и=100 м/с. Наименьшее расстояние Ах между точками среды, фазы
колебаний которых противоположны, равно 1 м. Определить час-
частоту v колебаний.
7.11. Определить скорость v распространения волны в упругой
среде, если разность фаз Дф колебаний двух точек среды, отстоящих
друг от друга на Дл;=10 см, равна я/3. Частота v колебаний равна
25 Гц.
Скорость звука *
7.12. Найти скорость v распространения продольных упругих
колебаний в следующих металлах: 1) алюминии; 2) меди; 3) воль-
вольфраме.
7.13. Определить максимальное и минимальное значения длины
% звуковых волн, воспринимаемых человеческим ухом, соответст-
соответствующие граничным частотам Vi=16 Гц и v2=20 кГц. Скорость
звука принять равной 340 м/с.
7.14. Определить скорость v звука в азоте при температуре Г—
=300 К.
7.15. Найти скорость v звука в воздухе при температурах 7\ —
-290 К и Г2=350 К.
7.16. Наблюдатель, находящийся на расстоянии /=800 м от ис-
источника звука, слышит звук, пришедший по воздуху, на Д?=1,78 с
позднее, чем звук, пришедший по воде. Найти скорость v звука в
воде, если температура Т воздуха равна 350 К.
7.17. Скорость v звука в некотором газе при нормальных усло-
условиях равна 308 м/с. Плотность р газа равна 1,78 кг/м3. Определить
отношение cpicv для данного газа.
7.18. Найти отношение скоростей vjv2 звука в водороде и угле-
углекислом газе при одинаковой температуре газов.
7.19. Температура Т воздуха у поверхности Земли равна 300 К;
при увеличении высоты она понижается на АТ=7 мК на каждый
метр высоты. За какое время звук, распространяясь, достигнет вы-
высоты h=8 км?
* В задачах, где в условии не указана скорость звука и не заданы вели-
величины, по которым ее можно вычислить, значение скорости следует брать
из табл. 16.
107

Суперпозиция волн
7.20. Имеются два источника, совершающие колебания в одина-
одинаковой фазе и возбуждающие в окружающей среде плоские волны
одинаковой частоты и амплитуды {Аг=А2=1 мм). Найти амплитуду
А колебаний точки среды, отстоящей от одного источника колеба-
колебаний на расстоянии ^=3,5 м и от другого — на *2=5,4 м. Направ-
Направления колебаний в рассматриваемой точке совпадают. Длина волны
Л=0,6 м.
7.21. Стоячая волна образуется при наложении бегущей волны
и волны, отраженной от границы раздела сред, перпендикулярной
направлению распространения волны. Найти положения (расстоя-
(расстояния от границы раздела сред) узлов и пучностей стоячей волны,
если отражение происходит: 1) от среды менее плотной; 2) от среды
более плотной. Скорость v распространения звуковых колебаний
равна 340 м/с и частота v=3,4 кГц.
7.22. Определить длину X бегущей волны, если в стоячей волне
расстояние / между: 1) первой и седьмой пучностями равно 15 см;
2) первым и четвертым узлом равно 15 см.
7.23. В трубе длиной /=1,2 м находится воздух при температуре
Т^ЗОО К. Определить минимальную частоту vmin возможных коле-
колебаний воздушного столба в двух случаях: 1) труба открыта; 2) труба
закрыта.
7.24. Широкая трубка, закрытая снизу и расположенная верти-
вертикально, наполнена до краев водой. Над верхним отверстием трубки
помещен звучащий камертон, частота v колебаний которого равна
440 Гц. Через кран, находящийся внизу, воду медленно выпускают.
Когда уровень воды в трубке понижается на АЯ=19,5 см, звук
камертона усиливается. Определить скорость v звука в условиях
опыта.
'У////////////////////////////////////////
У/77/////////А
Рис. 7.4
7.25. Один из способов измерения скорости звука состоит в сле-
следующем. В широкой трубке А может перемещаться поршень В.
Перед открытым концом трубки Л, соединенным с помощью рези-
резиновой трубки с ухом наблюдателя, расположен звучащий камертон
К (рис. 7.4.). Отодвигая поршень В от конца трубки Л, наблюдатель
108

с
в
а
1
А
отмечает ряд следующих друг за другом увеличений и уменьшений
громкости звука. Найти скорость v звука в воздухе, если при часто-
частоте колебаний v=440 Гц двум последовательным усилениям интен-
интенсивности звука соответствует расстояние А/ между положениями
поршня, равное 0,375 м.
7.26. На рис. 7.5 изображен прибор, служащий для определения
скорости звука в твердых телах и газах. В латунном стержне Л,
зажатом посередине, возбуж-
возбуждаются колебания. При опре-
определенном положении легкого
кружочка Б, закрепленного
на конце стержня, пробковый
порошок, находящийся в
трубке С, расположится в ви- Рис. 7.5
де небольших кучек на рав-
равных расстояниях. Найти скорость v звука в латуни, если расстоя-
расстояние а между кучками оказалось равным 8,5 см. Длина стержня
/=0,8 м.
7.27. Стальной стержень длиной /=1 м, закрепленный посереди-
посередине, натирают суконкой, посыпанной канифолью. Определить часто-
частоту v возникающих при этом собственных продольных колебаний
стержня. Скорость v продольных волн в стали вычислить.
Эффект Доплера *
7.28. Поезд проходит мимо станции со скоростью и=40 м/с.
Частота v0 тона гудка электровоза равна 300 Гц. Определить кажу-
кажущуюся частоту v тона для человека, стоящего на платформе, в двух
случаях: 1) поезд приближается; 2) поезд удаляется.
7.29. Мимо неподвижного электровоза, гудок которого дает
сигнал частотой vo=3OO Гц, проезжает поезд со скоростью и=
=40 м/с. Какова кажущаяся частота v тона для пассажира, когда
поезд приближается к электровозу? когда удаляется от него?
7.30. Мимо железнодорожной платформы проходит электропо-
электропоезд. Наблюдатель, стоящий на платформе, слышит звук сирены
поезда. Когда поезд приближается, кажущаяся частота звука vx =
= 1100 Гц; когда удаляется, кажущаяся частота v2=900 Гц. Найти
скорость и электровоза и частоту v0 звука, издаваемого сиреной.
7.31. Когда поезд проходит мимо неподвижного наблюдателя,
высота тона звукового сигнала меняется скачком. Определить отно-
относительное изменение частоты Av/v, если скорость и поезда равна
54 км/ч.
7.32. Резонатор и источник звука частотой vo=8 кГц расположе-
расположены на одной прямой. Резонатор настроен на длину волны v=4,2 см
и установлен неподвижно. Источник звука может перемещаться
по направляющим вдоль прямой. С какой скоростью айв каком
См. сноску на с. 107
109

направлении должен двигаться источник звука, чтобы возбуждае-
возбуждаемые им звуковые волны вызвали колебания резонатора?
7.33. Поезд движется со скоростью и=120 км/ч. Он дает свисток
длительностью то=5 с. Какова будет кажущаяся продолжитель-
продолжительность т свистка для неподвижного наблюдателя, если: 1) поезд
приближается к нему; 2) удаляется? Принять скорость звука рав-
равной 348 м/с.
7.34. Скорый поезд приближается к стоящему на путях электро-
электропоезду со скоростью ^=72 км/ч. Электропоезд подает звуковой
сигнал частотой vo=O,6 кГц. Определить кажущуюся частоту v
звукового сигнала, воспринимаемого машинистом скорого поезда.
7.35. На шоссе сближаются две автомашины со скоростями
«!=30 м/с и и2=20 м/с. Первая из них подает звуковой сигнал час-
частотой vx=600 Гц. Найти кажущуюся частоту v2 звука, восприни-
воспринимаемого водителем второй автомашины, в двух случаях: 1) до встре-
встречи; 2) после встречи. Изменится ли ответ (если изменится, то как)
в случае подачи сигнала второй машиной?
7.36. Узкий пучок ультразвуковых волн частотой vo=5O кГц
направлен от неподвижного локатора к приближающейся подводной
лодке. Определить скорость и подводной лодки, если частота v^
биений (разность частот колебаний источника и сигнала, отраженно-
отраженного от лодки) равна 250 Гц. Скорость v ультразвука в морской воде
принять равной 1,5 км/с.
Энергия звуковых волн *
7.37. По цилиндрической трубе диаметром d=20 см и длиной
1=5 м, заполненной сухим воздухом, распространяется звуковая
волна средней за период интенсивностью /=50 мВт/м2. Найти
энергию W звукового поля, заключенного в трубе.
7.38. Интенсивность звука 1 = 1 Вт/м2. Определить среднюю объ-
объемную плотность <w> энергии звуковой волны, если звук распро-
распространяется в сухом воздухе при нормальных условиях.
7.39. Мощность N изотропного точечного источника звуковых
волн равна 10 Вт. Какова средняя объемная плотность <до> энер-
энергии на расстоянии г= 10 м от источника волн? Температуру Т
воздуха принять равной 250 К.
7.40. Найти мощность N точечного изотропного источника звука,
если на расстоянии г=25 м от него интенсивность / звука равна
20 мВт/м2. Какова средняя объемная плотность <^> энергии на
этом расстоянии?
Звуковое давление. Акустическое сопротивление *
7.41. Определить удельное акустическое сопротивление Zs воз-
воздуха при нормальных условиях.
* См. сноску на с. 107
ПО

7.42. Определить удельное акустическое сопротивление Zs
воды при температуре /=15 °С.
7.43. Какова максимальная скорость |шах колебательного дви-
движения частиц кислорода, через который проходят звуковые волны,
если амплитуда звукового давления /?0=0,2 Па, температура Т
кислорода равна 300 К и давление р=100 кПа?
7.44. Определить акустическое сопротивление Za воздуха в тру-
трубе диаметром d=20 см при температуре Г=300 К и давлении р —
=200 кПа.
7.45. Звук частотой v=400 Гц распространяется в азоте при тем-
температуре Т=290 К и давлении /7=104 кПа. Амплитуда звукового
давления /70=0,5 Па. Определить амплитуду А колебаний частиц
азота.
7.46. Определить амплитуду р0 звукового давления, если ампли-
амплитуда А колебаний частиц воздуха равна 1 мкм. Частота звука v =
-600 Гц.
7.47. На расстоянии г= 100 м от точечного изотропного источни-
источника звука амплитуда звукового давления /?0=0,2 Па. Определить
мощность Р источника, если удельное акустическое сопротивление
Zs воздуха равно 420 Па-с/м. Поглощение звука в воздухе не учи-
учитывать .
7.48. Источник звука небольших линейных размеров имеет мощ-
мощность Р=\ Вт. Найти амплитуду звукового давления /?0 на расстоя-
расстоянии г=100 м от источника звука, считая его изотропным. Затуха-
Затуханием звука пренебречь.
7.49. В сухом воздухе при нормальных условиях интенсивность
/ звука равна 10 пВт/м2. Определить удельное акустическое сопро-
сопротивление Zs воздуха при данных условиях и амплитуду р0 звуково-
звукового давления.
7.50. Найти интенсивности 1г и /2 звука, соответствующие амп-
амплитудам звукового давления /7Oi=7OO мкПа и /?02—40 мкПа.
Уровень интенсивности и уровень громкости
звука
7.51. Определить уровень интенсивности LP звука, если его
интенсивность равна: 1) 100 пВт/м2; 2) 10 мВт/м2.
7.52. На расстоянии гх=24 м от точечного изотропного источни-
источника звука уровень его интенсивности LP=32 дБ. Найти уровень
интенсивности LP звука этого источника на расстоянии г2 = 16 м.
7.53. Звуковая волна прошла через перегородку, вследствие
чего уровень интенсивности LP звука уменьшился на 30 дБ. Во
сколько раз уменьшилась интенсивность / звука?
7.54. Уровень интенсивности LP шума мотора равен 60 дБ.
Каков будет уровень интенсивности, если одновременно будут ра-
работать: 1 ) два таких мотора; 2) десять таких моторов?
7.55. Три тона, частоты которых равны соответственно vt==
—50 Гц, v2=200 Гц и v3=l кГц, имеют одинаковый уровень интен-
интенсивности LP=40 дБ. Определить уровни громкости LN этих тонов.
111

7.56. Звук частотой v=l кГц имеет уровень интенсивности
LP=50 дБ. Пользуясь графиком на рис. 7.1, найти уровни интен-
интенсивности равногромких с ним звуков с частотами: vx=l кГц, v2=
-5 кГц, v3-2 кГц, v4=300 Гц, v5-50 Гц.
7.57. Уровень громкости тона частотой v=30 Гц сначала был
LN1=l0 фон, а затем повысился до LiY2=80 фон. Во сколько раз
увеличилась интенсивность тона?
7.58. Пользуясь графиком уровней на рис. 7.1, найти уровень
громкости LN звука, если частота v звука равна 2 кГц и амплитуда
звукового давления /?0=0,1 Па. Условия, при которых находится
воздух, нормальные.
7.59. Для звука частотой v=2 кГц найти интенсивность /, уро-
уровень интенсивности LP и уровень громкости LN, соответствующие:
а) порогу слышимости; б) порогу болевого ощущения. При решении
задачи пользоваться графиком на рис. 7.1.
7.60. Мощность Р точечного изотропного источника звука равна
100 мкВт. Найти уровень громкости LN при частоте v=500 Гц на
расстоянии г= 10 м от источника звука.
7.61. На расстоянии г= 100 м от точечного изотропного источни-
источника звука уровень громкости LN при частоте v=500 Гц равен 20 дБ.
Определить мощность Р источника звука.

ГЛАВА 2
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
§ 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ВЕЩЕСТВА»
ЗАКОНЫ ИДЕАЛЬНЫХ ГАЗОВ
Основные формулы
© Количество вещества * тела (система)
где N — число структурных элементов (молекул, атомов, ионов и
т. п.), составляющих тело (систему); NA — постоянная Авогадро:
jVA=6,02-1023 моль.
© Молярная масса вещества
M=m/vy
где т — масса однородного тела (системы); v — количество вещест-
вещества этого тела.
© Относительная молекулярная масса вещества
где rti — число атомов /-го химического элемента, входящего в
состав молекулы данного вещества; Ar,t — относительная атомная
масса этого элемента. Относительные атомные массы приводятся
в таблице Д. И. Менделеева.
О Связь молярной массы М с относительной молекулярной
массой Мг вещества
M=Mrk,
где /г=10~3 кг/моль.
© Молярная масса смеси газов
CMiW2,,
i ' i = 1
где nil — масса i-vo компонента смеси; v^ — количество вещества
/-го компонента смеси; k — число компонентов смеси.
® Массовая доля ** i-го компонента смеси газов
wi=mi/m,
где ть — масса /-го компонента смеси; т — масса смеси.
* Количество вещества — число структурных элементов (молекул, ато-
атомов, ионов и т. п.), содержащихся в системе или теле. Количество вещества
выражается в молях. Моль равен количеству вещества системы, содержащей
столько же структурных элементов, сколько содержится атомов в углероде-12
массой 0,012 кг.
** Массовой долей компонента в смеси называется безразмерная величи-
величина, равная отношению массы компонента к массе смеси.
113

Ф Уравнение состояния идеальных газов (уравнение Клапей-
Клапейрона — Менделеева)
p %, или pV^,
где т — масса газа; М — его молярная масса; R — молярная га-
газовая постоянная; Т — термодинамическая температура; v — коли-
количество вещества.
® Закон Дальтона
P = Pi + p2+ • •• +pfe,
где р — давление смеси газов; pt — парциальное давление /-го
компонента смеси; k — число компонентов смеси.
Примеры решения задач
Пример 1. Определить молярную массу М углекислого газа
СО2.
Решение. Молярную массу данного вещества можно опре-
определить по формуле
M=Mrky A)
где Мг — относительная молекулярная масса вещества; &=
= 10~3 кг/моль.
Относительную молекулярную массу найдем из соотношения
Мг = 2Мг,/. B)
i
где nt — число атомов /-го химического элемента, входящих в моле-
молекулу данного вещества; Ar,t — относительная атомная масса /-го
химического элемента.
В нашем случае для углекислого газа формула B) примет вид
Мг = псАпС + поАг,о, C)
где яс=1 (число атомов углерода в молекуле углекислого газа);
до=2 (число атомов кислорода в той же формуле); АГщ с и АГуО —-
относительные атомные массы углерода и кислорода.
По таблице Д. И. Менделеева найдем
Лг.с=12, Лг,о=16.
После подстановки в формулу C) значений /гс, по, AKt c и АгО
получим
МГ=1 -12+2-16=44.
Подставив это значение относительной молекулярной массы, а
также значение k в формулу A), найдем молярную массу углекис-
углекислого газа:
М = 44.10~3 кг/моль = 4,4• 10~2 кг/моль.
Пример 2. Найти молярную массу М смеси кислорода массой
/Их=25 г и азота массой т2=75 г.
Решение. Молярная масса смеси Мсм есть отношение массы
смеси гасм к количеству вещества смеси vCM, т. е.
MCM-mCM/vCM. A)
114

Масса смеси равна сумме масс компонентов смеси mCM=
Количество вещества смеси равно сумме количеств вещества компо-
компонентов.
Подставив в формулу A) выражения тсм и vcM, получим
Применив способ, использованный в примере 1, найдем моляр-
молярные массы Мг кислорода и М2 азота:
Afi=32-10-3 кг/моль, 7И2=28-10 кг/моль.
Подставим значения величин во B) и произведем вычисления:
25-10~3 + 75- Ю-3 , __
М™ -~ 25-10~3/C2. Ю-3) + 75-10-3/B8.10) КГ'М0ЛЬ ~
= 28,9-10~3 кг/моль.
Пример 3. Определить: 1) число N молекул воды, занимающей
при температуре t=4 °C объем V= 1 мм3; 2) массу т1 молекулы воды;
3) диаметр d молекулы воды, считая, что молекулы имеют форму
шариков, соприкасающихся друг с другом.
Решение. 1. Число N молекул, содержащихся в теле неко-
некоторой массы т, равно произведению постоянной Авогадро NA на
количество вещества v: N=NAv. Так как v=m/M, где М — моляр-
молярная масса, то N=(m/M)NA. Выразив в этой формуле массу как про-
произведение плотности р на объем У, получим
N = (9V/M)NA. A)
Все величины, кроме молярной массы воды, входящие в A),
известны: р = 1-103 кг/м (см. табл. 9), V=l мм3=1*10"9 м3, NA=
=6,02-1023 моль (см. табл. 24).
Зная химическую формулу воды (Н2О), найдем молярную массу
воды (см. пример 1):
Af=Mr?=B-l + l-16)-10-3 кг/моль=18-10 кг/моль.
Подставим значения величин в A) и произведем вычисления:
JV-[M03-b 10"9/A8.10-3)].6,02-1023 молекул =
= 3,34-1019 молекул.
2. Массу одной молекулы воды найдем делением ее молярной
массы на постоянную Авогадро: m1=M/NA. Произведя вычисления
по этой формуле, получим
Щ= 6,02-КЯ3 кг-2,99-10-26 кг.
3. Будем считать, что молекулы плотно прилегают друг к другу,
тогда на каждую молекулу диаметром d приходится объем (куби-
(кубическая ячейка) Уг=й3. Отсюда
d=Vy[- A)
Объем Vi найдем, разделив молярный объем Vm вещества на
число молекул в моле, т. е. на постоянную Авогадро NA: Ух=
=Vm/NA. Молярный объем равен отношению молярной массы^к плот-
плотности вещества, т. е. Vm=M/p. Поэтому можем записать, что V±=
=M/(pNA). Подставив полученное выражение Уг в формулу A),
115

получим
d=3/M/(pNA). B)
Проверим, дает ли правая часть выражения B) единицу длины:
Г/Л — ( \Щ \1/з __ I кг/моль \ 1/з _
*- ¦* ~~ \ [р] [NA] ) ~~ 1 (кг/м3) • A/моль) J ~~ М*
Теперь подставим значения величин в формулу B) и произведем
вычисления:
d = 3,11 • 10~10 м = 311 пм.
Пример 4. В баллоне обемом V=10 л находится гелий под давле-
давлением /?х= 1 МПа при температуре Т^ЗОО К. После того как из
баллона был израсходован гелий массой т=10 г, температура в
баллоне понизилась до Г2=290 К. Определить давление /?2 гелия,
оставшегося в баллоне.
Решение. Для решения задачи воспользуемся уравнением
Клапейрона — Менделеева, применив его дважды к начальному и
конечному состояниям газа. Для начального состояния уравнение
имеет вид
PlV=(nh/M)RTlt A)
а для конечного состояния —
p2V=(mJM)RT2, B)
где т1 и т2 — массы гелия в начальном и конечном состояниях.
Выразим массы т1 и т2 гелия из уравнений A) и B):
m2^Mp2V/(RT2). D)
Вычитая из C) равенство D), получим
МргУ Мр2У
¦*\ 1 1 А ¦* 2
Отсюда найдем искомое давление:
_ rt2 (мР1у \^I± _ULBli_ <ъ
p* ~ му V RTi m)~- тг pl м v ' w
Проверим, дает ли правая часть формулы E) единицу давления.
Для этого выразим все величины, входящие в нее, в соответствую-
соответствующих единицах. Единица, в которой выражается первое слагаемое,
не вызывает сомнений, так как отношение TJTX — величина без-
безразмерная. Проверим, в каких единицах выражается второе сла-
слагаемое:
\пг] [R] [Т2] _ кг [Дж/(К-моль)]-К __ кг-Дж-К-моль __
[М] [У] кг/моль м5 ~~ кг-м3-К-моль
Убедившись в том, что правая часть полученной расчетной фор-
формулы дает единицу искомой величины — давления, можем подста-
подставить в E) значения всех величин и произвести вычисления.
В формуле E) все величины, кроме молярной массы М гелия,
известны. Найдем ее (см. пример 1). Для гелия как одноатомного
116

газа относительная молекулярная масса равна его относительной
атомной массе Аг.
Из таблицы Д. И. Менделеева найдем Аг=4. Следовательно,
молярная масса гелия
М = Аг-10~3 кг/моль = 4-10~3 кг/моль.
Подставив значения величин в E), получим
290 Ш6 10-Ю-3 8,ЗЬ 290 о Q ал 1П- о осл „
Рг ^зоо*10 —4.10-з - 10.10-а Па ^ 3,64-105 Па = 364 Па.
Задачи
Молекулярное строение вещества
8.1. Определить относительную молекулярную массу Мг:
1) воды; 2) углекислого газа СО2; 3) поваренной соли NaCl.
8.2. Найти молярную массу М серной кислоты H2SO4.
8.3. Определить массу т1 молекулы: 1) углекислого газа; 2) по-
поваренной соли.
8.4. В сосуде вместимостью V=2 л находится кислород, количе-
количество вещества v которого равно 0,2 моль. Определить плотность р
газа,
8.5. Определить количество вещества v и число N молекул азота
массой /п=0,2 кг.
8.6. В баллоне вместимостью V=3 л находится кислород массой
т=4 г. Определить количество вещества v и число N молекул газа.
8.7. Кислород при нормальных условиях заполняет сосуд вмес-
вместимостью V= 11,2 л. Определить количество вещества v газа и его
массу т.
8.8. Определить количество вещества v водорода, заполняю-
заполняющего сосуд вместимостью V=3 л, если плотность газа р=6,65х
х 10~3 кг/моль.
8.9. Колба вместимостью V=0,5 л содержит газ при нормаль-
нормальных условиях. Определить число TV молекул газа, находящихся в
колбе.
8.10. Сколько атомов содержится в газах массой 1 г каждый:
1) гелии, 2) углероде, 3) фторе, 4) полонии?
8.11. В сосуде вместимостью V=5 л находится однородный газ
количеством вещества v=0,2 моль. Определить, какой это газ,
если его плотность р= 1,12 кг/м3.
8.12. Одна треть молекул азота массой т=10 г распалась на
атомы. Определить полное число N частиц, находящихся в газе.
8.13. Рассматривая молекулы жидкости как шарики, соприка-
соприкасающиеся друг с другом, оценить порядок размера диаметра моле-
молекулы сероуглерода CS2. При тех же предположениях оценить поря-
порядок размера диаметра атомов ртути. Плотности жидкостей считать
известными.
8.14. Определить среднее расстояние </> между центрами моле-
молекул водяных паров при нормальных условиях и сравнить его с диа-
диаметром d самих молекул (d=0,311 нм).
117

8.15. В сосуде вместимостью 1/= 1,12 л находится азот при нор-
нормальных условиях. Часть молекул газа при нагревании до некото-
некоторой температуры оказалась диссоциированной на атомы. Степень
дисооциации а=0,3. Определить количество вещества: 1) v — азота
до нагревания; 2) vM0JI—молекулярного азота после нагревания;
3) vaT — атомарного азота после нагревания: 4) vn0JI — всего азота
после нагревания.
Примечание. Степенью диссоциации называют отношение числа молекул,
распавшихся на атомы, к общему числу молекул газа. Степень диссоциации
показывает, какая часть молекул распалась на атомы.
Уравнение газового состояния
8.16. В цилиндр длиной /=1,6 м, заполненный воздухом при
нормальном атмосферном давлении рОу начали медленно вдвигать
поршень площадью 5=200 см2. Определить силу F, которая будет
действовать на поршень, если его остановить на расстоянии 1г=
= 10 см от дна цилиндра.
8.17. Колба вместимостью V=300 см2, закрытая пробкой с краном,
содержит разреженный воздух. Для измерения давления в колбе
горлышко колбы погрузили в воду на незначительную глубину и
открыли кран, в результате чего в колбу вошла вода массой т—
=292 г. Определить первоначальное давление р в колбе, если атмо-
атмосферное давление /70=100 кПа.
8.18. В U-образный манометр налита ртуть. Открытое колено
манометра соединено с окружающим пространством при нормальном
атмосферном давлении /?0, и ртуть в открытом колене стоит выше,
чем в закрытом, на A/i=10 см. При этом свободная от ртути часть
трубки закрытого колена имеет длину /=20 см. Когда открытое
колено присоединили к баллону с воздухом, разность уровней ртути
увеличилась и достигла значения A/it=26 см. Найти давление р
воздуха в баллоне.
Рис. 8.1
8.19. Манометр в виде стеклянной U-образной трубки с внутрен-
внутренним диаметром d=5 мм (рис. 8.1, а) наполнен ртутью так, что остав-
оставшийся в закрытом колене трубки воздух занимает при нормальном
атмосферном давлении объем Ух=10 мм3. При этом разность уров-
уровней A/ii ртути в обоих коленах трубки равна 10 см. При соединении
118

открытого конца трубки с большим сосудом (рис. 8.1, б) разность
ДЛ2 уровней ртути уменьшилась до 1 см. Определить давление р
в сосуде.
8.20. В баллоне содержится газ при температуре ^=100 СС.
До какой температуры /2 нужно нагреть газ, чтобы его давление
увеличилось в два раза?
8.21. При нагревании идеального газа на ДГ=1 К при постоян-
постоянном давлении объем его увеличился на 1/350 первоначального объе-
объема. Найти начальную температуру Т газа.
8.22. Полый шар вместимостью У=10 см3, заполненный воздухом
при температуре 7\=573 К, соединили трубкой с чашкой, заполнен-
заполненной ртутью. Определить массу m ртути, вошедшей в шар при осты-
остывании воздуха в нем до температуры Tz=2§3 К. Изменением вмес-
вместимости шара пренебречь.
8.23. Оболочка воздушного шара вместимостью У=800 м3 цели-
целиком заполнена водородом при температуре Т1=273 К. На сколько
изменится подъемная сила шара при повышении температуры до
Т2=293 К? Считать вместимость V оболочки неизменной и внешнее
давление нормальным. В нижней части оболочки имеется отверстие,
через которое водород может выходить в окружающее пространство.
8.24. В оболочке сферического аэростата находится газ объемом
У=1500 м3, заполняющий оболочку лишь частично. На сколько
изменится подъемная сила аэростата, если газ в аэростате нагреть
от То=273 К до Т=293 К? Давления газа в оболочке и окружающе-
окружающего воздуха постоянны и равны нормальному атмосферному давле-
давлению.
Рис. 8.2
Рис. 8.3
8.25. Газовый термометр состоит из шара с припаянной к нему
горизонтальной стеклянной трубкой. Капелька ртути, помещен-
помещенная в трубку, отделяет объем шара от внешнего пространства
(рис. 8.2). Площадь 5 поперечного сечения трубки равна 0,1 см2.
При температуре Тг=273 К капелька находилась на расстоянии
/i=30 см от поверхности шара, при температуре Т2=278 К —
на расстоянии /2=50 см. Найти вместимость V шара.
8.26. В большой сосуд с водой был опрокинут цилиндрический
сосуд (рис. 8.3). Уровни воды внутри и вне цилиндрического сосуда
находятся на одинаковой высоте. Расстояние / от уровня воды до
дна опрокинутого сосуда равно 40 см. На какую высоту Ah подни-
119

мется вода в цилиндрическом сосуде при понижении температуры
от 7\=310 К до Т2=273 К? Атмосферное давление нормальное.
8.27. Баллон вместимостью У=12 л содержит углекислый газ.
Давление р газа равно 1 МПа, температура Г=300 К. Определить
массу т газа в баллоне.
8.28. Какой объем V занимает идеальный газ, содержащий коли-
количество вещества v = l кмоль при давлении р=1 МПа и температуре
Г=400 К?
8.29. Котел вместимостью V=2 м3 содержит перегретый водяной
пар массой т=Ю кг при температуре Т=500 К. Определить давле-
давление р пара в котле.
8.30. Баллон вместимостью 1/=20 л содержит углекислый газ
массой т=500 г под давлением р= 1,3 МПа. Определить темпера-
температуру Т газа.
8.31. Газ при температуре 7=309 К и давлении /7=0,7 МПа
имеет плотность р = 12 кг/м3. Определить относительную молеку-
молекулярную массу Мг газа.
8.32. Определить плотность р насыщенного водяного пара в воз-
воздухе при температуре Г=300 К. Давление р насыщенного водяного
пара при этой температуре равно 3,55 кПа.
8.33. Оболочка воздушного шара имеет вместимость У=1600 м3.
Найти подъемную силу F водорода, наполняющего оболочку, на
высоте, где давление /7=60 кПа и температура Т=280 К. При подъе-
подъеме шара водород может выходить через отверстие в нижней части
шара.
8.34. В баллоне вместимостью V=2b л находится водород при
температуре Г=290 К. После того как часть водорода израсходова-
израсходовали, давление в баллоне понизилось на А/7=0,4 МПа. Определить
массу m израсходованного водорода.
8.35. Оболочка аэростата вместимостью F=1600 м3, находяще-
находящегося на поверхности Земли, на &=7/8 наполнена водородом при
давлении /?х= 100 кПа и температуре 7\=290 К. Аэростат подняли
на некоторую высоту, где давление /?2=80 кПа и температура Т2—
=280 К. Определить массу Am водорода, вышедшего из оболочки
при его подъеме.
Смеси газов
8.36. Какой объем V занимает смесь газов — азота массой пг1=
= 1 кг и гелия массой /тг2= 1 кг — при нормальных условиях?
8.37. В баллонах вместимостью Vi=20 л и К2=44 л содержится
газ. Давление в первом баллоне /?i=2,4 МПа, во втором — р2—
= 1,6 МПа. Определить общее давление р и парциальные р[ и р'2
после соединения баллонов, если температура газа осталась преж-
прежней.
8.38. В сосуде вместимостью V=0,01 м3 содержится смесь
газов — азота массой ш1=7 г и водорода массой та=1 г — при
температуре 7=280 К. Определить давление р смеси газов.
120

8.39. Найти плотность р газовой смеси водорода и кислорода,
если их массовые доли wx и ш2 равны соответственно 1/9 и 8/9. Дав-
Давление р смеси равно 100 кПа, температура Г=300 К.
8.40. Газовая смесь, состоящая из кислорода и азота, находится
в баллоне под давлением /7=1 МПа. Определить парциальные дав-
давления рх кислорода и р2 азота, если массовая доля w1 кислорода в
смеси равна 0,2.
8.41. Сухой воздух состоит в основном из кислорода и азота.
Если пренебречь остальными составными частями воздуха, то мож-
можно считать, что массовые доли кислорода и азота соответственно
^=0,232, ^2=0,768. Определить относительную молекулярную
массу Мг воздуха.
8.42. Баллон вместимостью l/^ЗО л содержит смесь водорода
и гелия при температуре 7=300 К и давлении /7=828 кПа. Масса
т смеси равна 24 г. Определить массу т1 водорода и массу т2
гелия.
8.43. В сосуде вместимостью У= 15 л находится смесь азота и
водорода при температуре /=23 °С и давлении /7=200 кПа. Опреде-
Определить массы смеси и ее компонентов, если массовая доля w± азота в
смеси равна 0,7.
8.44. Баллон вместимостью 1/=5 л содержит смесь гелия и
водорода при давлении /7=600 кПа. Масса т смеси равна 4 г, мас-
массовая доля w-l гелия равна 0,6. Определить температуру Т смеси.
8.45. В сосуде находится смесь кислорода и водорода. Масса m
смеси равна 3,6 г. Массовая доля w± кислорода составляет 0,6.
Определить количество вещества v смеси, vx и v2 каждого газа в
отдельности.
§ 9. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
Основные формулы
9 Концентрация частиц (молекул, атомов и т. п.) однородной
системы
n=N/V,
где V — объем системы.
Ф Основное уравнение кинетической теории газов
где /7 — давление газа; (еп> — средняя кинетическая энергия
поступательного движения молекулы.
• Средняя кинетическая энергия:
приходящаяся на одну степень свободы молекулы
* Здесь и далее кинетическая энергия молекул и других частиц обозна-
обозначается е.
121

приходящаяся на все степени свободы молекулы (полная энергия
молекулы)
? — ~2~ #•* >
поступательного движения молекулы
е„=8/2*7\
где & — постоянная Больцмана; Т — термодинамическая темпера-
температура; i — число степеней свободы молекулы;
вращательного движения молекулы
г -1~3кТ
• Зависимость давления газа от концентрации молекул и тем-
температуры
p=nkT.
• Скорость молекул:
средняя квадратичная
1, или <1;КВ>
средняя арифметическая
т1), или
наиболее вероятная
1, или 1>в =
где т! — масса одной молекулы.
Примеры решения задач
Пример 1. В баллоне вместимостью У=6,9 л находится азот
массой /п=2,3 г. При нагревании часть молекул диссоциировали
на атомы. Коэффициент диссоциации* а=0,2. Определить: 1) об-
общее число N± молекул и концентрацию пг молекул азота до нагрева-
нагревания; 2) концентрацию п2 молекул и п3 атомов азота после нагрева-
нагревания.
Решение. По определению, концентрация частиц газа есть
отношение числа частиц к вместимости сосуда, занимаемого газом:
n=N/V. A)
1. Число Nx молекул газа до нагревания найдем из соотношения
где v — количество вещества азота; N& — постоянная Авогадро;
М — молярная масса азота; Мг — относительная молекулярная
масса азота; /е= 10~ кг/моль (см. пример 1 на с. 114).
Подставив значения величин в B), получим
9 о 1П-3
i^i =-/0.3.23 -6,02.1023 молекул-4,94-1023 молекул.
* См. примечание к задаче 8.15.
122

Концентрацию nt найдем, подставив значения величин в A):
Ni 4,94- 1023 _3 7 1С 1А25 3
Пг=-у = 6,9.10-3 М 3-7,16-102аМ-3.
2. Концентрацию после нагревания найдем из соотношения
где N — число молекул, не распавшихся на атомы.
После подстановки значений величин в C) получим
4 94-1
П2= ' 6 9. io-з "'"' М"а = 5,73-10*» М-
Концентрация атомов после нагревания азота
Лз=^у2- D)
Число 2 в формуле D) выражает тот факт, что каждая молекула
после распада дает два атома.
Подставим в D) значения величин и произведем вычисления:
п3^2>4^;11^33'0'2м-3^0,286-1026 м-3 = 2,86.1025 м3.
Пример 2. В колбе вместимостью V=0,b л находится кислород
при нормальных условиях. Определить среднюю энергию (Wn)
поступательного движения всех молекул, содержащихся в колбе.
Решение. Средняя энергия (Wn) поступательного движе-
движения всех молекул может быть выражена соотношением
где (еп) — средняя энергия поступательного движения одной моле-
молекулы; N — число всех молекул, содержащихся в колбе.
Как известно,
<еп> = 3/2?7\ B)
где k — постоянная Больцмана; Т — термодинамическая темпера-
температура.
Число молекул, содержащихся в колбе, найдем по формуле
Af = vAfA, C)
где v — количество вещества кислорода; NA — постоянная Аво-
гадро.
Количество вещества v найдем из таких соображений: известно,
что при нормальных условиях молярный объем Vm равен 22,4 X
Х10~3 м3/моль. Так как, по условию задачи, кислород в колбе
находится при нормальных условиях, то количество вещества кис-
кислорода в колбе выражается соотношением
v = WKm. D)
Подставив выражение v по D) в C), получим
N = VNA/Vm. E)
С учетом B) и E) выражение A) энергии поступательного движе-
движения молекул примет вид
F)
123

Проверим, дает ли правая часть расчетной формулы единицу
энергии (джоуль). Для этого вместо символов величин подставим
единицы, в которых эти величины выражаются:
XW/ 1 __(Дж/К)-К-м3'Моль-1__Дж-К-м3'Моль__ ^
L^n-1~ м3/моль ~~ м3-К-моль —АЖ-
Подставив значения величин в F) и произведя вычисления, най-
найдем
лу/ 3.1,38-10-23.273.0,5.10-3.6,02.1023 п -- п и
Wn = —¦ 2-22,4.10-3 ¦ Дж-75,9 Дж.
Пример 3. Найти среднюю кинетическую энергию одной моле-
молекулы аммиака NH3 при температуре t=27 °C и среднюю энергию
вращательного движения этой молекулы при той же температуре.
Решение. Средняя полная энергия молекулы определяется
по формуле
4*7\ A)
где i — число степеней свободы молекулы; k — постоянная Больц-
мана; Т — термодинамическая температура газа: T=t+T0, где
Го-273 К.
Число степеней свободы i четырехатомной молекулы, какой явля-
является молекула аммиака, равно 6.
Подставим значения величин в A):
<8>-6/2.1,38-10-23B7 + 273) Дж-1,242-100 Дж.
Средняя энергия вращательного движения молекулы определя-
определяется по формуле
<евр>=-^-*7\ B)
где число 3 означает число степеней свободы поступательного дви-
движения.
Подставим в B) значения величин и вычислим:
<?вР> = ^- 1,38-10-23 B7 +273) Дж = 6,21-10-21 Дж.
Заметим, что энергию вращательного движения молекул ам-
аммиака можно было получить иначе, разделив полную энергию (е) на
две равные части. Дело в том, что у трех (и более) атомных молекул
число степеней свободы, приходящихся на поступательное и враща-
вращательное движение, одинаково (по 3), поэтому энергии поступатель-
поступательного и вращательного движений одинаковы. В данном случае
Задачи
Концентрация молекул
9.1. В сосуде вместимостью V=12 л находится газ, число N
молекул которого равно 1,44 -1018. Определить концентрацию п
молекул газа.
124

9.2. Определить вместимость V сосуда, в котором находится газ,
если концентрация молекул ^г= 1,25 -1026 м~3, а общее их число
Л^2,5-1023.
9.3. В сосуде вместимостью F=20 л находится газ количеством
вещества v = l,5 кмоль. Определить концентрацию п молекул в
сосуде.
9.4. Идеальный газ находится при нормальных условиях в за-
закрытом сосуде. Определить концентрацию п молекул газа.
9.5. В сосуде вместимостью V=5 л находится кислород, кон-
концентрация п молекул которого равна 9,41 • 1023 м~3. Определить
массу т газа.
9.6. В баллоне вместимостью V=5 л находится азот массой т=
= 17,5 г. Определить концентрацию п молекул азота в баллоне.
9.7. Определить количество вещества v водорода, заполняющего
сосуд вместимостью V=3 л, если концентрация п молекул газа в
сосуде равна 2 • 1018 м~3.
9.8. В двух одинаковых по вместимости сосудах находятся раз»
ные газы: в первом — водород, во втором — кислород. Найти от-
отношение njn* концентраций газов, если массы газов одинаковы.
9.9. Газ массой т=58,5 г находится в сосуде вместимостью V=
=5 л. Концентрация п молекул газа равна 2,2 «1026 м~3. Какой это
газ?
9.10. В баллоне вместимостью V=2 л находится кислород мас-
массой т=1,17 г. Концентрация п молекул в сосуде равна 1,1 -1025 м~3.
Определить по этим данным постоянную Авогадро NA.
9.11. В баллоне находится кислород при нормальных условиях.
При нагревании до некоторой температуры часть молекул оказа-
оказалась диссоциированной на атомы. Степень диссоциации ос=0,4.
Определить концентрации частиц: 1) п^ — до нагревания газа;
2) я2 — молекулярного кислорода после нагревания; 3) п3 — ато-
атомарного кислорода после нагревания.
Основное уравнение кинетической теории
газов. Энергия молекул
9.12. Определить концентрацию п молекул идеального газа
при температуре 7=300 К и давлении р = 1 мПа.
9.13. Определить давление/? идеального газа при двух значени-
значениях температуры газа: 1) 7=3 К; 2) 7=1 кК. Принять концентра-
концентрацию ft молекул газа равной »1019 см.
9.14. Сколько молекул газа содержится в баллоне вместимостью
V=30 л при температуре 7=300 К и давлении /?=5 МПа?
9.15. Определить количество вещества v и концентрацию п
молекул газа, содержащегося в колбе вместимостью У=240 см3
при температуре 7=290 К и давлении /?=50 кПа.
9.16. В колбе вместимостью У= 100 см3 содержится некоторый
газ при температуре 7=300 К. На сколько понизится давление р
газа в колбе, если вследствие утечки из колбы выйдет 7V=1O20 мо-
молекул?
125

9.17. В колбе вместимостью У=240 см3 находится газ при тем-
температуре 7=290 К и давлении р=50 кПа. Определить количество
вещества v газа и число N его молекул.
9.18. Давление р газа равно 1 мПа, концентрация п его молекул
равна 1010см~3. Определить: 1) температуру 7 газа; 2) среднюю ки-
кинетическую энергию <еп> поступательного движения молекул газа.
9.19. Определить среднюю кинетическую энергию <еп> поступа-
поступательного движения и среднее значение <е> полной кинетической
энергии молекулы водяного пара при температуре 7=600 К. Най-
Найти также кинетическую энергию W поступательного движения всех
молекул пара, содержащего количество вещества v=l кмоль.
9.20. Определить среднее значение <е> полной кинетической
энергии одной молекулы гелия, кислорода и водяного пара при
температуре 7=400 К.
9.21. Определить кинетическую энергию <бх>, приходящуюся
в среднем на одну степень свободы молекулы азота, при температуре
7=1 кК, а также среднюю кинетическую энергию <еп> поступатель-
поступательного движения, <8вр> вращательного движения и среднее значение
полной кинетической энергии <е> молекулы.
9.22. Определить число N молекул ртути, содержащихся в
воздухе объемом V=l м3 в помещении, зараженном ртутью, при
температуре /=20 °С, если давление р насыщенного пара ртути
при этой температуре равно 0,13 Па.
9.23. Для получения высокого вакуума в стеклянном сосуде
необходимо прогревать его при откачке с целью удалить адсорби-
адсорбированные газы. Определить, на сколько повысится давление в сфе-
сферическом сосуде радиусом /? = 10 см, если все адсорбированные мо-
молекулы перейдут со стенок в сосуд. Слой молекул на стенках считать
мономолекулярным, сечение а одной молекулы равно 105 см2.
Температура 7, при которой производится откачка, равна 600 К.
9.24. Определить температуру 7 водорода, при которой средняя
кинетическая энергия <еп> поступательного движения молекул до-
достаточна для их расщепления на атомы, если молярная энергия
диссоциации водорода Wm=419 кДж/моль.
Примечание. Молярной энергией диссоциации называется энергия, за-
затрачиваемая на диссоциацию всех молекул газа количеством вещества v=
= 1 моль.
Скорости молекул
9.25. Найти среднюю квадратичную <fKB>, среднюю арифмети-
арифметическую <v> и наиболее вероятную vB скорости молекул водорода.
Вычисления выполнить для трех значений температуры: 1) 7=20 К;
2) 7=300 К; 3) 7=5 кК.
9.26. При какой температуре 7 средняя квадратичная скорость
атомов гелия станет равной второй космической скорости v2=
= 11,2 км/с?
9.27. При какой температуре 7 молекулы кислорода имеют такую
же среднюю квадратичную скорость <икв>, как молекулы водорода
при температуре 7х=100 К?
126

9.28. Колба вместимостью V=4: л содержит некоторый газ массой
rn^Ofi г под давлением р=200 кПа. Определить среднюю квадра-
квадратичную скорость <укв> молекул газа.
9.29. Смесь гелия и аргона находится при температуре Т= 1,2 кК.
Определить среднюю квадратичную скорость <укв> и среднюю кине-
кинетическую энергию атомов гелия и аргона.
9.30. Взвешенные в воздухе мельчайшие пылинки движутся так,
как если бы они были очень крупными молекулами. Определить
среднюю квадратичную скорость <икв> пылинки массой т=10~10 г,
если температура Т воздуха равна 300 К.
9.31. Во сколько раз средняя квадратичная скорость <укв> моле-
молекул кислорода больше средней квадратичной скорости пылинки
массой т=10~8 г, находящейся среди молекул кислорода?
9.32. Определить среднюю арифметическую скорость <и> молекул
газа, если их средняя квадратичная скорость <fKB>=:l км/с.
9.33. Определить наиболее вероятную скорость vB молекул водо-
водорода при температуре Г=400 К.
§ 10. ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Основные формулы
Ф Распределение Больцмана (распределение частиц в силовом
поле)
n = noe~u«kT\
где п — концентрация частиц; U — их потенциальная энергия;
п0 — концентрация частиц в точках поля, где U=0\ k — постоян-
постоянная Больцмана; Т — термодинамическая температура; е — основа-
основание натуральных логарифмов.
О Барометрическая формула (распределение давления в одно-
однородном поле силы тяжести)
где р — давление газа; m — масса частицы; М — молярная масса;
z — координата (высота) точки по отношению к уровню, принятому
за нулевой; р0 — давление на этом уровне; g — ускорение свобод-
свободного падения; R—молярная газовая постоянная.
9 Вероятность того, что физическая величина х, характери-
характеризующая молекулу, лежит в интервале значений от х до Jt+cLv,
определяется по формуле
dW(x)=f(x)dx\
где f(x)—функция распределения молекул по значениям данной
физической величины х (плотность вероятности).
• Количество молекул, для которых физическая величина х,
характеризующая их, заключена в интервале значений от х до
x+dx,
* Приведенная формула выражает также долю молекул, для которых
физическая величина х заключена в интервале от х до х-\-dx.
127

О Распределение Максвелла (распределение молекул по ско-
скоростям) выражается двумя соотношениями:
а) число молекул, скорости которых заключены в пределах от
v до v-\-dv,
dN (v) = Nf (v) dv = 4nN {^^ Y/2 e-™V<2*7V dvy
где f(v) — функция распределения молекул по модулям скоростей,
выражающая отношение вероятности того, что скорость молекулы
лежит в интервале от v до a+du, к величине этого интервала, а
также долю числа молекул, скорости которых лежат в указанном
интервале; N — общее число молекул; т — масса молекулы;
б) число молекул, относительные скорости которых заключены
в пределах от и до u+du,
dN (и) = Nf (и) du = -i=-Ne-»2 иЧи,
У п
где u=v/vB — относительная скорость, равная отношению скорости
v к наивероятнейшей скорости vB (о скоростях молекулы см. §9);
f(u) — функция распределения по относительным скоростям.
• Распределение молекул по импульсам. Число молекул, им-
импульсы которых заключены в пределах от р до p+dpy
dN (p) = Nf (p) dp = 4яЛ^ (^if K/2 e-*/<2«*n P2 dPi
где /(/?) — функция распределения по импульсам.
Ф Распределение молекул по энергиям. Число молекул, энер-
энергии которых заключены в интервале от е до e+de,
где /(е) — функция распределения по энергиям.
• Среднее значение * физической величины х в общем случае
/ (х) dx '
а в том случае, если функция распределения нормирована на еди-
единицу,
<х> = J xf (x) dx,
где f{x)—функция распределения, а интегрирование ведется по
всей совокупности изменений величины х.
Например, среднее значение скорости молекулы (т. е. средняя
арифметическая скорость) <и> = ]vf (v) dv\ средняя квадратичная
о
00
скорость <»кв>=<и2>1/2, где <и2> = j v2f (v) dv\ средняя кинетическая
о
энергия поступательного движения молекулы <е> = \ е/ (е) ds.
о
* Интегралы для вычисления средних значений приведены в табл. 2.
128

• Среднее число соударений, испытываемых одной молекулой
газа в единицу времени,
d2 n<v>,
где d — эффективный диаметр молекулы; п — концентрация моле-
молекул; (о)— средняя арифметическая скорость молекул.
9 Средняя длина свободного пробега молекул газа
~~ V l
V lnd2n '
® Импульс (количество движения), переносимый молекулами
из одного слоя газа в другой через элемент поверхности,
где ц — динамическая вязкость газа; ~—градиент (поперечный)
скорости течения его слоев; AS — площадь элемента поверхности;
At — время переноса.
@ Динамическая вязкость
где р — плотность газа (жидкости); (v) — средняя скорость хаоти-
хаотического движения его молекул; (/) — их средняя длина свободного
пробега.
@ Закон Ньютона
г ~ dt ' ч dzao>
где р — сила внутреннего трения между движущимися слоями газа.
© Закон Фурье
где AQ — теплота, прошедшая посредством теплопроводности через
сечение площадью 5 за время At; X — теплопроводность; -^—
градиент температуры.
® Теплопроводность (коэффициент теплопроводности) газа
Л = 7зСуР<1>></>, ИЛИ Я = 1/6ЙП<У></>,
где cv — удельная теплоемкость газа при постоянном объеме; р —
плотность газа; (v) — средняя арифметическая скорость его молеку-
молекулы; {/) — средняя длина свободного пробега молекул.
® Закон Фика
где Am — масса газа, перенесенная в результате диффузии через
поверхность площадью S за время At; D — диффузия (коэффициент
диффузии); ~ — градиент концентрации молекул; т1 —^ масса од-
одной молекулы.
в Диффузия (коэффициент диффузии)
5 № 1268 129

Примеры решения задач
Пример 1. Пылинки массой т=\0~18 г взвешены в воздухе.
Определить толщину слоя воздуха, в пределах которого концентра-
концентрация пылинок различается не более чем на 1 %. Температура Т
воздуха во всем объеме одинакова и равна 300 К.
Решение. При равновесном распределении пылинок кон-
концентрация их зависит только от координаты z по оси, направленной
вертикально. В этом случае к распределению пылинок можно при-
применить формулу Больцмана
n = noe-u^kTK A)
Так как в однородном поле силы тяжести U=mgz, то
n = nQe-m^kTK B)
По условию задачи, изменение An концентрации с высотой мало
по сравнению с п(Д/г/7г=0,01), поэтому без существенной погреш-
погрешности изменение концентрации An можно заменить дифференциа-
дифференциалом dn.
Дифференцируя выражение B) по г, получим
Так как noe-mgz/{kT)=n, то
Отсюда находим интересующее нас изменение координаты:
mg n
Знак минус показывает, что положительным изменениям координа-
координаты (dz>0) соответствует уменьшение относительной концентрации
(dn<0). Знак минус опустим (в данном случае он несуществен) и
заменим дифференциалы dz и dn конечными приращениями Az и
An:
mg n
Подставим в эту формулу значения величин An/n=0fily k—
= 1,38-103 Дж/К, Т=300 К, т=10~21 кг, g=9,81 м/с2 и, произведя
вычисления, найдем
Az = 4,23 мм.
Как видно из полученного результата, концентрация даже таких
маленьких пылинок (т=108 г) очень быстро изменяется с высотой.
Пример 2. В сосуде содержится газ, количество вещества v
которого равно 1,2 моль, Рассматривая этот газ как идеальный,
определить число AN молекул, скорости v которых меньше 0,001
наиболее вероятной скорости ив.
Решение. Для решения задачи удобно воспользоваться рас-
распределением молекул по относительным скоростям и (u=v/vB).
Число dN (и) молекул, относительные скорости и которых заключе-
130

ны в пределах от и до duf определяется формулой
dtf(a)=-^Le-ttVdM, A)
У л
где N — полное число молекул.
По условию задачи, максимальная скорость интересующих нас
молекул t;max=0,001 vB, откуда amax=umax/i>B=0,001. Для таких
значений и выражение A) можно существенно упростить. В самом
деле, для и<^1 имеем е~^1 — и2. Пренебрегая значением и2=
= @,001J= 10~6 по сравнению с единицей, выражение A) запишем
в виде
лм
dN(u)^-^=rU2du. B)
У л
Интегрируя это выражение по и в пределах от 0 до r/max, получим
и
max
AN =¦-;=- \ U2du=--F^ -^ тах, ИЛИ ДЛ^=—pzr-ttSiax. C)
у л J У я ^ 1° ЗУ л
Выразив в C) число молекул N через количество вещества и
постоянную Авогадро, найдем расчетную формулу:
4ex. D)
Подставим в D) значения величин v, Л^А и произведем вычисле-
вычисления:
4'1'2:6;0,2'1023 (Ю-3K молекул -5,44 • 1014 молекул.
О* 111
Пример 3. Зная функцию f(p) распределения молекул по импуль-
импульсам, определить среднее значение квадрата импульса (р2).
Решение. Среднее значение квадрата импульса (р2) можно
определить по общему правилу вычисления среднего:
lfi A)
6 о
Функция распределения молекул по импульсам имеет вид
Эта функция распределения уже нормирована на единицу, т. е.
со
\f(p)dp=l. С учетом нормировки формулу A) перепишем иначе:
о
^ C)
о
Подставим выражение f(p) по уравнению B) в формулу C) и выне-
вынесем величины, не зависящие от р, за знак интеграла:
5* 131

Этот интеграл можно свести к табличному (см. табл. 2]
\ x*e~ax2dx = -5- V яа/2, положив а=к-
о
В нашем случае это даст
После упрощений и сокращений найдем
Пример 4. Средняя длина свободного пробега (/> молекулы угле-
углекислого газа при нормальных условиях равна 40 нм. Определить
среднюю арифметическую скорость <и> молекул и число z соударе-
соударений, которые испытывает молекула в 1 с.
Решение. Средняя арифметическая скорость молекул опре-
определяется по формуле
где М — молярная масса вещества.
Подставив числовые значения, получим
м/с.
Среднее число (z) соударений молекулы в 1 с определяется отно-
отношением средней скорости (v) молекулы к средней длине ее свобод-
свободного пробега (/):
Подставив в эту формулу значения (и)=362 м/с, </>=40 нм=
=4 • 10~8 м, получим
<2> = 9,05-10° с.
Пример 5. Два тонкостенных коаксиальных цилиндра длиной
/= 10 см могут свободно вращаться вокруг их общей оси z. Радиус R
большого цилиндра равен 5 см. Между цилиндрами имеется зазор
размером d=2 мм. Оба цилиндра находятся в воздухе при нормаль-
нормальных условиях. Внутренний цилиндр приводят во вращение с посто-
постоянной частотой П!=20 с. Внешний цилиндр заторможен. Опреде-
Определить, через какой промежуток времени с момента освобождения
внешнего цилиндра он приобретет частоту вращения п2=1 с.
При расчетах изменением относительной скорости цилиндров пре-
пренебречь. Масса т внешнего цилиндра равна 100 г.
Решение. При вращении внутреннего цилиндра слой воз-
воздуха увлекается им и начинает участвовать во вращательном движе-
движении. Вблизи поверхности этого цилиндра слой воздуха приобретает
со временем практически такую же линейную скорость, как и ско-
скорость точек на поверхности цилиндра, т. е. v=2nn1 (R—d). Так как
d<tiR, то приближенно можно считать
v^2nn1R. A)
Вследствие внутреннего трения момент импульса передается
соседним слоям газа и в конечном счете внешнему цилиндру. За
132

интервал времени At внешний цилиндр приобретает момент импуль-
импульса L=pR, где р — импульс, полученный за At внешним цилинд-
цилиндром. Отсюда
р=Ш. B)
С другой стороны,
P-^SM, C)
dv
где г| — динамическая вязкость; -^ — градиент скорости; 5 —
площадь поверхности цилиндра (S = 2nRl).
Приравняв правые части выражений B) и C) и выразив из полу-
полученного равенства искомый интервал А/, получим
dz
Найдем входящие в эту формулу величины L, -~ uS. Момент
импульса L=J(?>2, где J — момент инерции цилиндра (J=mR2);
т — его масса; со2 — угловая скорость внешнего цилиндра (со2=
). С учетом этого запишем
Градиент скорости -~? = -j = ^ . Площадь цилиндра равна S =
Подставив в D) выражения L, -^-, S, получим
r\vl
Заменив здесь v no A), найдем
E)
Динамическая вязкость воздуха г| = 17,2 мкПа-с=1,72« 10~5Па-с
(см. табл. 14).
Подставив в E) значения входящих в нее величин и произведя
вычисления, получим
1 2-3,14.1,72-10--.5- Ю-2-10-10-2.20 С 'D C#
Пример 6. Барометр в кабине летящего самолета все время по-
показывает одинаковое давление р=79 кПа, благодаря чему летчик
считает высоту /ix полета неизменной. Однако температура воздуха
за бортом самолета изменилась с /=5 °С до t=\ °C. Какую ошибку
Ah в определении высоты допустил летчик? Давление р0 у поверх-
поверхности Земли считать нормальным.
Решение. Для решения задачи воспользуемся барометри-
барометрической формулой
133

Барометр может показывать неизменное давление р при раз-
различных температурах 7\ и Т2 за бортом только в том случае, если
самолет находится не на высоте h (которую летчик считает неизмен-
неизменной), а на некоторой другой высоте /i2.
Запишем барометрическую формулу для этих двух случаев:
Найдем отношение pjp и обе части полученного равенства про-
прологарифмируем:
1П РО _ M§hl . 1n PO -_ М^2
р~~ ЯТг ' % ~ ОТ2 •
Из полученных соотношений выразим высоты А2 и hx и найдем
их разность:
AAeA1_ftl=s?i^(TI_T1). A)
Проверим, дает ли правая часть равенства A) единицу длины:
[R] [Т]_\\ Дж/(моль./р]-К 1 Дж 1
[М] [g] A кг/моль).(м/с2) 1 Н
Подставим в A) значения величин (давления в отношении pjp
можно выразить в килопаскалях, это не повлияет на окончательный
результат):
А/ 8,31-In A01/79) /f r-s oo с
Aft= 29.10-3.9,8 A—5) м^—28,5 м.
Знак«—»означает, чтоh2<Ch1 и, следовательно, самолет снизился
на 28,5 м по сравнению с предполагаемой высотой.
Задачи
Распределение Больцмана
ЮЛ. Пылинки, взвешенные в воздухе, имеют массу т=10~18 г.
Во сколько раз уменьшится их концентрация п при увеличении
высоты на А/г= 10 м? Температура воздуха Г=300 К.
10.2. Одинаковые частицы массой ш=Ю~12 г каждая распреде-
распределены в однородном гравитационном поле напряженностью G=
=0,2 мкН/кг. Определить отношение njn^ концентраций частиц,
находящихся на эквипотенциальных уровнях, отстоящих друг от
друга на Аг=10 м. Температура Т во всех слоях считается одинако-
одинаковой и равной 290 К.
10.3. Масса m каждой из пылинок, взвешенных в воздухе, рав-
равна 1 аг. Отношение концентрации пг пылинок на высоте h±=l м к
концентрации п0 их на высоте ho=O равно 0,787. Температура воз-
воздуха Т=300 К. Найти по этим данным значение постоянной Аво-
гадро NA.
10.4. Определить силу F, действующую на частицу, находящую-
находящуюся во внешнем однородном поле силы тяжести, если отношение пг1пъ
134

концентраций частиц на двух уровнях, отстоящих друг от друга
на Дг=1 м, равно е. Температуру Т считать везде одинаковой и
равной 300 К.
10.5. На сколько уменьшится атмосферное давление /?= 100 кПа
при подъеме наблюдателя над поверхностью Земли на высоту h=
= 100 м? Считать, что температура Т воздуха равна 290 К и не из-
изменяется с высотой.
10.6. На какой высоте h над поверхностью Земли атмосферное
давление вдвое меньше, чем на ее поверхности? Считать, что темпе-
температура Т воздуха равна 290 К и не изменяется с высотой.
10.7. Барометр в кабине летящего вертолета показывает давле-
давление /7=90 кПа. На какой высоте h летит вертолет, если на взлетной
площадке барометр показывал давление /?0=Ю0 кПа? Считать, что
температура Т воздуха равна 290 К и не изменяется с высотой.
10.8. Найти изменение высоты Д/г, соответствующее изменению
давления на А/?= 100 Па, в двух случаях: 1) вблизи поверхности
Земли, где температура 7\=290 К, давление /^=100 кПа; 2) на
некоторой высоте, где температура Т2=220 К, давление /?2=25 кПа.
10.9. Барометр в кабине летящего самолета все время показыва-
показывает одинаковое давление /?=80 кПа, благодаря чему летчик считает
высоту h полета неизменной. Однако температура воздуха измени-
изменилась на ДГ=1 К. Какую ошибку Д/г в определении высоты допустил
летчик? Считать, что температура не зависит от высоты и что у по-
поверхности Земли давление /?0=100 кПа.
10.10. Ротор центрифуги вращается с угловой скоростью со.
Используя функцию распределения Больцмана, установить распре-
распределение концентрации п частиц массой ш, находящихся в роторе
центрифуги, как функцию расстояния г от оси вращения.
10.11. В центрифуге с ротором радиусом а, равным 0,5 м, при
температуре Т—300 К находится в газообразном состоянии вещест-
вещество с относительной молекулярной массой Мг=103. Определить от-
отношение njno концентраций молекул у стенок ротора и в центре
его, если ротор вращается с частотой п=30 с.
10.12. Ротор центрифуги, заполненный радоном, вращается с
частотой /г=50с. Радиус а ротора равен 0,5 м. Определить давле-
давление р газа на стенки ротора, если в его центре давление р0 равно
нормальному атмосферному. Температуру Т по всему объему счи-
считать одинаковой и равной 300 К.
10.13. В центрифуге находится некоторый газ при температуре
Т=271 К. Ротор центрифуги радиусом а=0,4 м вращается с угловой
скоростью со=500 рад/с. Определить относительную молекулярную
массу Мг таза, если давление р у стенки ротора в 2,1 раза больше
давления р0 в его центре.
10.14. Ротор ультрацентрифуги радиусом я=0,2 м заполнен ато-
атомарным хлором при температуре Т=3 кК. Хлор состоит из двух
изотопов: 37С1 и 35С1. Доля w1 атомов изотопа 3?С1 составляет 0,25.
Определить доли w[ и w\ атомов того и другого изотопов вблизи
стенок ротора, если ротору сообщить угловую скорость вращения
<о, равную 104 рад/с.
135

Распределение молекул по скоростям
и импульсам
10.15. Зная функцию распределения молекул по скоростям, вы-
вывести формулу наиболее вероятной скорости vB.
10.16. Используя функцию распределения молекул по скоростям,
получить функцию, выражающую распределение молекул по отно-
относительным скоростям и (u=v/vB).
10.17. Какова вероятность W того, что данная молекула идеаль-
идеального газа имеет скорость, отличную от 1/2?>в не более чем на
1 %?
10.18. Найти вероятность W того, что данная молекула идеаль-
идеального газа имеет скорость, отличную от 2vB не более чем на 1 %.
10.19. Зная функцию распределения молекул по скоростям,
вывести формулу, определяющую долю w молекул, скорости v
которых много меньше наиболее вероятной скорости vB.
10.20. Определить относительное число w молекул идеального
газа, скорости которых заключены в пределах от нуля до одной
сотой наиболее вероятной скорости vB.
10.21. Зная функцию распределения молекул по скоростям, оп-
определить среднюю арифметическую скорость (v) молекул.
10.22. По функции распределения молекул по скоростям опре-
определить среднюю квадратичную скорость (vKB).
10.23. Определить, какая из двух средних величин, (l/v) или.
l>'(v), больше, и найти их отношение k.
10.24. Распределение молекул по скоростям в молекулярных
пучках при эффузионном истечении * отличается от максвелловско-
го и имеет вид f(v)&v=Cv^-'mv2l{2kT)v^&u. Определить из условия
нормировки коэффициент С.
10.25. Зная функцию распределения молекул по скоростям в
т2
некотором молекулярном пучке /(и)=оРт2е~ш2/B|гГI;8) найти вы-
выражения для: 1) наиболее вероятной скорости vB; 2) средней ариф-
арифметической скорости (v).
10.26. Водород находится при нормальных условиях и занимает
объем V=l см3. Определить число N молекул в этом объеме, обла-
обладающих скоростями, меньшими некоторого значения атах=1 м/с.
10.27. Вывести формулу наиболее вероятного импульса рв моле-
молекул идеального газа.
10.28. Найти число N молекул идеального газа, которые имеют
импульс, значение которого точно равно наиболее вероятному
значению рв.
10.29. Вывести формулу, определяющую среднее значение ком-
компонента импульса (рх) молекул идеального газа.
10.30. На сколько процентов изменится наиболее вероятное
* Эффузионным называется истечение газов через отверстия, малые по
сравнению с длиной свободного пробега молекулы.
136

значение рв импульса молекул идеального газа при изменении тем-
температуры на один процент?
10.31. Найти выражение для импульса молекул идеального газа,
энергии которых равны наиболее вероятному значению энергии.
Распределение молекул по кинетическим
энергиям
10.32. Найти выражение средней кинетической энергии (8П>
поступательного движения молекул. Функцию распределения моле-
молекул по энергиям считать известной.
10.33. Преобразовать формулу распределения молекул по энер-
энергиям в формулу, выражающую распределение молекул по относи-
относительным энергиям со(со=8п/(8п>), где еп — кинетическая энергия;
(еп) — средняя кинетическая энергия поступательного движения
молекул.
10.34. Определить долю w молекул идеального газа, энергии
которых отличаются от средней энергии (еп) поступательного движе-
движения молекул при той же температуре не более чем на 1 %.
10.35. Вывести формулу, определяющую долю w молекул, энер-
энергия 8 которых много меньше kT. Функцию распределения молекул
по энергиям считать известной.
10.36. Определить долю w молекул, энергия которых заключена
в пределах от гг=0 до e2=0,0lkT.
10.37. Число молекул, энергия которых заключена в пределах
от нуля до некоторого значения 8, составляет 0,1 % от общего числа
молекул. Определить величину г в долях kT.
10.38. Считая функцию распределения молекул по энергиям
известной, вывести формулу, определяющую долю w молекул, энер-
энергия 8 которых много больше энергии теплового движения молекул.
10.39. Число молекул, энергия которых выше некоторого зна-
значения 8Х, составляет 0,1 от общего числа молекул. Определить вели-
величину 8Х в долях kT, считая, что E^>kT.
Указание. Получающееся трансцендентное уравнение решить графически,
10.40. Используя функцию распределения молекул по энергиям,
определить наиболее вероятное значение энергии ев.
10.41. Преобразовать функцию /(e)de распределения молекул
по кинетическим энергиям в функцию/(G)d9 распределения молекул
по относительным кинетическим энергиям (где 9=е/ев; sB — наибо-
наиболее вероятное значение кинетической энергии молекул).
10.42. Найти относительное число w молекул идеального газа,
кинетические энергии которых отличаются от наиболее вероятного
значения гв энергии не более чем на 1 %.
10.43. Определить относительное число w молекул идеального
газа, кинетические энергии которых заключены в пределах от нуля
До значения, равного 0,01 ев (ев — наиболее вероятное значение
кинетической энергии молекул).
137

10.44. Найти выражение для кинетической энергии молекул
идеального газа, импульсы которых имеют наиболее вероятное
значение рв.
10.45. Во сколько раз изменится значение максимума функции
/(&) распределения молекул идеального газа по энергиям, если тем-
температура 7 газа увеличится в два раза? Решение пояснить графи-
графиком.
10.46. Определить, во сколько раз средняя кинетическая энергия
<еп) поступательного движения молекул идеального газа отлича-
отличается от наиболее вероятного значения еп кинетической энергии по-
поступательного движения при той же температуре.
Длина свободного пробега и число
столкновений молекул
10.47. Найти среднюю длину свободного пробега (/> молекул
водорода при давлении /?=0,1 Па и температуре Т= 100 К.
10.48. При каком давлении р средняя длина свободного пробега
(/) молекул азота равна 1 м, если температура 7 газа равна 300 К?
10.49. Баллон вместимостью V=10 л содержит водород массой
т=1 г. Определить среднюю длину свободного пробега (/) моле-
молекул.
10.50. Можно ли считать вакуум с давлением /7=100 мкПа высо-
высоким, если он создан в колбе диаметром d=20 см, содержащей азот,
при температуре 7=280 К?
10.51. Определить плотность р разреженного водорода, если
средняя длина свободного пробега (/> молекул равна 1 см.
10.52. Найти среднее число (г) столкновений, испытываемых з
течение t=\ с молекулой кислорода при нормальных условиях.
10.53. Найти число N всех соударений, которые происходят в
течение t=l с между всеми молекулами водорода, занимающего
при нормальных условиях объем V=l мм3.
10.54. В газоразрядной трубке находится неон при температуре
7=300 К и давлении р=1 Па. Найти число N атомов неона, уда-
ударяющихся за время At—I с о катод, имеющий форму диска площа-
площадью S = l см2.
10.55. Найти среднюю продолжительность (т) свободного про-
пробега молекул кислорода при температуре 7=250 К и давлении
р=Ш Па.
10.56. Найти зависимость средней длины свободного пробега
(/) молекул идеального газа от давления р при следующих процес-
процессах: 1) изохорном; 2) изотермическом. Изобразить эти зависимости
на графиках.
10.57. Найти зависимость средней длины свободного пробега
(/) молекул идеального газа от температуры 7 при следующих
процессах: 1) изохорном; 2) изобарном. Изобразить эти зависимости
на графиках.
10.58. Найти зависимость среднего числа столкновений (г) моле-
молекулы идеального газа в 1 с от давления р при следующих процес-
138

сах: 1) изохорном; 2) изотермическом. Изобразить эти зависимости
на графиках.
10.59. Найти зависимость среднего числа столкновений (z) моле-
молекулы идеального газа в 1 с от температуры Т при следующих про-
процессах: 1) изохорном; 2) изобарном. Изобразить эти зависимости
на графиках.
Деления переноса: диффузия, вязкость,
теплопроводность
10.60. Средняя длина свободного пробега (/) атомов гелия при
нормальных условиях равна 180 нм. Определить диффузию D
гелия.
10.61. Диффузия D кислорода при температуре ^=0 °С равна
0,19 см2/с. Определить среднюю длину свободного пробега (/) моле-
молекул кислорода.
10.62. Вычислить диффузию D азота: 1) при нормальных услови-
условиях; 2) при давлении /7= 100 Па и температуре 7=300 К.
10.63. Определить, во сколько раз отличается диффузия Dt га-
газообразного водорода от диффузии D2 газообразного кислорода,
если оба газа находятся при одинаковых условиях.
10.64. Определить зависимость диффузии D от температуры Т
при следующих процессах: 1) изобарном; 2) изохорном.
10.65. Определить зависимость диффузии D от давления р при
следующих процессах: 1) изотермическом; 2) изохорном.
10.66. Вычислить динамическую вязкость г| кислорода при нор-
нормальных условиях.
10.67. Найти среднюю длину свободного пробега (/) молекул
азота при условии, что его динамическая вязкость т] = 17 мкПа-с.
10.68. Найти динамическую вязкость ц гелия при нормальных
условиях, если диффузия D при тех же условиях равна 1,06Х
Х10 м2/с.
10.69 Определить зависимость динамической вязкости г| от тем-
температуры Т при следующих процессах: 1) изобарном; 2) изохорном.
Изобразить эти зависимости на графиках.
10.70. Определить зависимость динамической вязкости г\ от дав-
давления р при следующих процессах: 1) изотермическом; 2) изохор-
изохорном. Изобразить эти зависимости на графиках.
10.71. Цилиндр радиусом R1=\0 см и длиной /=30 см располо-
расположен внутри цилиндра радиусом 7?2= 10,5 см так, что оси обоих
цилиндров совпадают. Малый цилиндр неподвижен, большой вра-
вращается относительно геометрической оси с частотой /2=15 с. Дина-
Динамическая вязкость г| газа, в котором находятся цилиндры, равна
8,5 мкПа-с. Определить: 1) касательную силу Fx, действующую на
поверхность внутреннего цилиндра площадью S = l м2; 2) вращаю-
вращающий момент М, действующий на этот цилиндр.
10.72. Два горизонтальных диска радиусами R=20 см располо-
расположены друг над другом так, что оси их совпадают. Расстояние d
между плоскостями дисков равно 0,5 см. Верхний диск неподвижен,
139

нижний вращается относительно геометрической оси с частотой
п=10с~1. Найти вращающий момент М, действующий на верхний
диск. Динамическая вязкость х\ воздуха, в котором находятся диски,
равна 17,2 мкПа-с.
10.73. В ультраразреженном азоте, находящемся под давлени-
давлением р=\ мПа и при температуре Т=300 К, движутся друг относи-
относительно друга две параллельные пластины со скоростью и=1 м/с.
Расстояние между пластинами не изменяется и много меньше сред-
средней длины свободного пробега молекул. Определить силу F внут-
внутреннего трения, действующую на поверхность пластин площадью
S=l м2.
10.74. Вычислить теплопроводность X гелия при нормальных ус-
условиях.
10.75. В приближенной теории явлений переноса получается со-
соотношение X/r\=cv- Более строгая теория приводит к значению
<к/к) = Ксу, где К — безразмерный коэффициент, равный (9у—
—5)/4(у—показатель адиабаты). Найти значения /С, вычисленные
по приведенной формуле и по экспериментальным данным, приве-
приведенным в табл. 12, для следующих газов: 1) аргона; 2) водорода;
3) кислорода; 4) паров воды.
10.76. При нормальных условиях динамическая вязкость ц
воздуха равна 17,2 мкПас. Найти для тех же условий теплопровод-
теплопроводность А, воздуха. Значение К вычислить по формуле, приведенной
в задаче 10.75.
10.77. Найти зависимость теплопроводности к от температуры
Т при следующих процессах: 1) изобарном; 2) изохорном. Изобра-
Изобразить эти зависимости на графиках.
10.78. Найти зависимость теплопроводности X от давления р
при следующих процессах: 1) изотермическом; 2) изохорном. Изо-
Изобразить эти зависимости на графиках.
10.79. Пространство между двумя большими параллельными
пластинами, расстояние d между которыми равно 5 мм, заполнено
гелием. Температура 7\ одной пластины поддерживается равной
290 К, другой — 72=310 К. Вычислить плотность теплового потока
\q\. Расчеты выполнить для двух случаев, когда давление р гелия
равно: 1) 0,1 МПа; 2) 1 МПа.
§ 11. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
Основные формулы
9 Связь между молярной (Ст) и удельной (с) теплоемкостями
газа
где М—молярная масса газа.
® Молярные теплоемкости * при постоянном объеме и постоян-
* Здесь и далее в целях упрощения записи в индексах обозначений
молярной теплоемкости при постоянном давлении и постоянном объеме
букву «т» будем опускать.
140

ном давлении соответственно равны
где i — число степеней свободы; R — молярная газовая постоян-
постоянная.
Ф Удельные теплоемкости при постоянном объеме и постоянном
давлении соответственно равны
с _± . с !?-.
ф Уравнение Майера
С р—Cy=R.
ф Показатель адиабаты
ср Ср 1 + 2
Y = -?, или т = с7, или Y = —•
® Внутренняя энергия идеального газа
U=N(e), или U=vCvT,
где (е) — средняя кинетическая энергия молекулы; N — число
молекул газа; v — количество вещества.
@ Работа, связанная с изменением объема газа, в общем случае
вычисляется по формуле
v8
V
где Vx — начальный объем газа; V2 — его конечный объем.
Работа газа:
а) при изобарном процессе (p=const)
б) при изотермическом процессе (Theorist)
в) при адиабатном процессе
А=жСу(Т1-Т1), или ^=^-1-^11-^) J,
где 7\ — начальная температура газа; Т2 — его конечная темпера-
температура.
Ф Уравнение Пуассона (уравнение газового состояния при адиа-
адиабатном процессе)
р Vy=const.
Ф Связь между начальным и конечным значениями параметров
состояний газа при адиабатном процессе:
? = (Yi.\ Za (ZlV Z± (!i
pi \v2) > ъ \vj ' rx"V pi
Первое начало термодинамики в общем случае записывается
в виде
141

где Q — количество теплоты, сообщенное газу; A U — изменение
его внутренней энергии; А — работа, совершаемая газом против
внешних сил.
Первое начало термодинамики:
а) при изобарном процессе
б) при изохорном процессе (А=0)
Q = AU = %CVAT;
в) при изотермическом процессе (Д(/=0)
г) при адиабатном процессе (Q=0)
А= — AU = — %rCvAT.
М V
• Термический коэффициент полезного действия (КПД) цикла
в общем случае
¦I- Qt >
где Qi—количество теплоты, полученное рабочим телом (газом)
от нагревателя; Q2—количество теплоты, переданное рабочим
телом охладителю.
КПД цикла Карно
ц = 4l Ч2 , или г] = г т 2 ,
где Тг — температура нагревателя; Т2 — температура охладителя.
• Изменение энтропии
в
А
где Л и В — пределы интегрирования, соответствующие начально-
начальному и конечному состояниям системы. Так как процесс равновесный!
то интегрирование проводится по любому пути.
• Формула Больцмана
S=k In W,
где S — энтропия системы; W — термодинамическая вероятность
ее состояния; k — постоянная Больцмана.
Примеры решения задач
Пример 1. Вычислить удельные теплоемкости неона и водорода
при постоянных объеме (cv) и давлении (ср), принимая эти газы за
идеальные.
142

Решение. Удельные теплоемкости идеальных газов выра-
выражаются формулами
с -
СР~
с 11. B)
СР~ 2 М • W
Для неона (одноатомный газ) /i=3, Afi=20-10~3 кг/моль.
Подставив в формулы A) и B) значения ilt Mx и R и произведя
вычисления, найдем:
cVi = 624 Дж/(кг./С); cPi= 1,04 кДж/(кг./С).
Для водорода (двухатомный газ) ?2=5, М2=2-10~3 кг/моль.
Вычисление по формулам A) и B) дает следующие значения
удельных теплоемкостей водорода:
?^=10,4 кДж/(кг./С); сл=14,6 кДж/(кг-К).
Пример 2. Вычислить удельные теплоемкости cF и ср смеси
неона и водорода. Массовые доли газов соответственно равны тг=
=0,8 и ^2=0,2. Значения удельных теплоемкостей газов взять из
примера 1.
Решение. Удельную теплоемкость смеси при постоянном
объеме cv найдем из следующих рассуждений. Теплоту, необходи-
необходимую для нагревания смеси на ДТ, выразим двумя соотношениями:
(З-СуК+т^ДГ, A)
где cv — удельная теплоемкость смеси; тх — масса неона; т2 —
масса водорода, и
Q = {сугпъ + cvm2) Д7\ B)
где с ух и Су 2 — удельные теплоемкости неона и водорода соответст-
соответственно.
Приравняв правые части выражений A) и B) и разделив обе
части полученного равенства на Д7\ найдем
cv{т± + т2) -Сугпъ + cvm2,
откуда
v~ vi m + m v
Отношения w1=m1/(m1Jrm2) и w^—mj (m1-\-m2) выражают мас-
массовые доли соответственно неона и водорода. С учетом этих обозна-
обозначений последняя формула примет вид
Подставив в эту формулу числовые значения величин, найдем
cv=2,58 кДж/(кг-К).
Рассуждая таким же образом, получим формулу для вычисления
удельной теплоемкости смеси при постоянном давлении:
cp-=cpw1+cpw2.
Произведя вычисления по этой формуле, найдем
cv==3J3 кДж/(кг-К).
143

Пример 3. Определить количество теплоты, поглощаемой водоро-
водородом массой т=0,2 кг при нагревании его от температуры ^=0 °С
до температуры ^2= 100 °С при постоянном давлении. Найти также
изменение внутренней энергии газа и совершаемую им работу.
Решение. Количество теплоты Q, поглощаемое газом при
изобарном нагревании, определяется по формуле
Q=mcpAT, A)
где т — масса нагреваемого газа; ср — его удельная теплоемкость
при постоянном давлении; AT — изменение температуры газа.
Как известно, ср = l "I -п- . Подставив это выражение ср в
формулу A), получим
Произведя вычисления по этой формуле, найдем
Q=291 кДж.
Внутренняя энергия выражается формулой U = ^^RT, сле-
следовательно, изменение внутренней энергии
После подстановки в эту формулу числовых значений величин и
вычислений получим
AU=208 кДж.
Работу расширения газа определим по формуле, выражающей
первое начало термодинамики: Q=AU-\-A,
откуда
A=Q—AU.
Подставив значения Q и At/, найдем
А =83 кДж.
Пример 4. Кислород занимает объем
Уг=\ м3 и находится под давлением рг==
=200 кПа. Газ нагрели сначала при по-
постоянном давлении до объема V2=3 м2, а
затем при постоянном объеме до давления
р2=500 кПа. Построить график процесса
и найти: 1) изменение Д(/ внутренней энер-
энергии газа; 2) совершенную им работу А; 3) количество теплоты Q,
переданное газу.
Решение. Построим график процесса (рис. 11.1). На графике
точками 1,2,3 обозначены состояния газа, характеризуемые пара-
параметрами (/?ь Vu 7\), (/?!, У2, Г2), (р2, 1/2, Т3).
1. Изменение внутренней энергии газа при переходе его из со-
состояния 1 в состояние 3 выражается формулой
AU=cvmAT,
где cY — удельная теплоемкость газа при постоянном объеме; m —
масса газа; AT — разность температур, соответствующих конечному
144

3и начальному /состояниям, т. е. АТ=Т3—7\.Так как Су — -^--— ;
где М — молярная масса газа, то
А?/ = -^Т7" R (Т3 — 7\). A)
Температуры 7\ и Г3 выразим из уравнения Менделеева — Кла-
Клапейрона lpV = ^rRT):
т = AlpiVj_ . т = Мр2У2
1 mR ' 3 /пД
С учетом этого равенство A) перепишем в виде
Подставим сюда значения величин (учтем, что для кислорода,
как двухатомного газа, /=5) и произведем вычисления:
А (У-3,25 МДж.
2. Полная работа, совершаемая газом, равна А=А1+А2, где
Аг — работа на участке 1—2\ А2 — работа на участке 2—3.
На участке 1—2 давление постоянно (/?=const). Работа в этом
случае выражается формулой A1=p1AV=p1(V2—Vx). На участке
2—3 объем газа не изменяется и, следовательно, работа газа на
этом участке равна нулю (Л2=0). Таким образом,
A=A1=p1(V2—V1).
Подставив в эту формулу значения физических величин, произ-
произведем вычисления:
А-=0,4 МДж
3. Согласно первому началу термодинамики, количество теплоты
Q, переданное газу, равно сумме ра-
работы А, совершенной газом, и изме-
изменению AU внутренней энергии:
Q=A+AU, или Q=3,65 МДж.
Пример 5. Идеальный двухатом-
двухатомный газ, содержащий количество ве-
вещества v=l моль, находится под дав-
давлением р1 = 250 кПа и занимает объем
Уг=\0 л. Сначала газ изохорно на-
нагревают до температуры Т2=400 К.
Далее, изотермически расширяя, до-
доводят его до первоначального давле-
давления. После этого путем изобарного
сжатия возвращают газ в начальное
состояние. Определить термический КПД г) цикла.
Решение. Для наглядности построим сначала график цикла,
который состоит из изохоры, изотермы и изобары. В координатах
р, V этот цикл имеет вид, представленный на рис. 11.2. Характерные
точки цикла обозначим /, 2, 3.
о
Рис. 11.2
14
145

Термический КПД любого цикла определяется выражением
a=(Qi—Q*VQu или -п=1—Q2/Q1, A)
где Qx — количество теплоты, полученное газом за цикл от нагре-
нагревателя; Q2 — количество теплоты, отданное газом за цикл охлади-
охладителю.
Заметим, что разность количеств теплоты Qx—Q2 равна работе
Л, совершаемой газом за цикл. Эта работа на графике в координа-
координатах /?, V (рис. 11.2) изображается площадью цикла (площадь цикла
заштрихована).
Рабочее вещество (газ) получает количество теплоты Qi на
двух участках: Qt_2 на участке 1—2 (изохорный процесс) и Q2_3
на участке 2—3 (изотермический процесс). Таким образом,
Qi = Qi-2 + Q2-3.
Количество теплоты, полученное газом при изохорном процессе,
равно
Qi-2 = Clrv(ra-T1),
где Cv — молярная теплоемкость газа при постоянном объеме;
v — количество вещества. Температуру Тг начального состояния
газа найдем, воспользовавшись уравнением Клапейрона — Менде-
Менделеева:
ri=/>iVi/(v/?).
Подставив числовые значения и произведя вычисления, получим
Количество теплоты, полученное газом при изотермическом про-
процессе, равно
где V2 — объем, занимаемый газом при температуре Т2 и давлении
рх (точка 3 на графике).
На участке 3—1 газ отдает количество теплоты Q2, равное
Q2-Qs-i = Cpv(T2—T1)f
где Ср — молярная теплоемкость газа при изобарном процессе.
Подставим найденные значения Qx и Q2 в формулу A):
^ - vCv (T2-T1) + ^RT2 In (Vz/Уг) '
В полученном выражении заменим отношение объемов VJVu со-
согласно закону Гей-Люссака, отношением температур (V2/V1=
= Т2/Т1) и выразим Cv и Ср через число степеней свободы молекулы
[Cv=iR/2, Cp=(i+2)R/2]. Тогда после сокращения на v и R/2
получим
.._ 1 (i + 2)(T2-T1)
1 t(^
Подставив значения i, Tly Т2 и R и произведя вычисления, най-
найдем
«=!_ E + 2) D00-300) =
Ч L 5D00 —300L-2-400InD00/300)
!4б
_41о/о

Пример 6. В цилиндре под поршнем находится водород массой
т=0,02 кг при температуре Тг=300 К. Водород начал расширяться
адиабатно, увеличив свой объем в пять раз, а затем был сжат изо-
изотермически, причем объем газа уменьшился в пять раз. Найти тем-
температуру Т2 в конце адиабатного расширения и работу А, совершен-
совершенную газом. Изобразить процесс графически.
Решение. Температуры и объемы газа, совершающего адиа-
адиабатный процесс, связаны между собой соотношением
где у — показатель адиабаты (для водорода как двухатомного газа
Y=l,4).
Отсюда получаем выражение для конечной температуры Т2:
Подставляя числовые значения заданных величин, находим
'4
l V'4 V
Прологарифмируем обе части полученного выражения:
lg Г2 = lg 300 + 0,4 (lg 1 — Ig 5) -2,477 + 0,4 (—0,699) =
= 2,477—0,280 = 2,197.
Зная lg T2, по таблицам антилогарифмов находим искомое зна-
значение Т2:
Т2=157 К.
Работа А г газа при адиабатном расширении определяется по
формуле
Подставив сюда числовые значения величин, после вычисления
получим
Л,= 2°1ff3 -|-8>31 C00—157) Дж-29,8.103 Дж = 29,8 кДж.
Работа А 2 газа при изотермическом сжатии выражается форму-
формулой
A 2=RT2(m/M)\n(V2/V1).
Произведя вычисления по этой формуле, найдем
А2=— 21 кДж.
Знак минус показывает, что при сжатии газа работа совершена
внешними силами.
Общая работа, совершенная газом при рассмотренных процессах,
А=А1+А2=29,8 кДж+(—21 кДж)=8,8 кДж.
График процесса приведен на рис. 11.3.
Пример 7. Нагреватель тепловой машины, работающей по обра-
обратимому циклу Карно, имеет температуру ^=200 °С. Определить
температуру Т2 охладителя, если при получении от нагревателя
147

количества теплоты Qt-=1 Дж машина совершает работу Л =0,4 Дж?
Потери на трение и теплоотдачу не учитывать.
Решение. Температуру охладителя найдем, использовав
выражение для термического КПД ма-
Р\ 1 шины, работающей по циклу Кар но,
П = G\—Т2IТ1. Отсюда
Га=Г1A-т1). A)
Термический КПД тепловой машины
выражает отношение количества тепло-
теплоты, которое превращено в механичес-
механическою работу Л, к количеству теплоты Qu
которое получено рабочим телом тепло-
{ Vg T Е°й машины из внешней среды (от нагре-
нагревателя), т. е. v[ = A/Q1. Подставив это
Рис- И-3 выражение в формулу A), найдем
r2=T1(l-^/Q1). B)
Учтя, что 7\=473 К, после вычисления по формуле B) получим
Т2=284 К.
Пример 8. Найти изменение AS энтропии при нагревании воды
массой гп= 100 г от температуры ^=0 °С до температуры t2= 100 °С и
последующем превращении воды в пар той же температуры.
Решение. Найдем отдельно изменение энтропии AS' при
нагревании воды и изменение энтропии AS" при превращении ее в
пар. Полное изменение энтропии выразится суммой AS' и AS".
Как известно, изменение энтропии выражается общей формулой
AS=S2-S1=f^- A)
о
При бесконечно малом изменении dT температуры нагреваемого
тела затрачивается количество теплоты dQ=mcdT, где m — масса
тела; с — его удельная теплоемкость. Подставив выражение dQ
в равенство A), найдем формулу для вычисления изменения энтро-
энтропии при нагревании воды:
Вынесем за знак интеграла постоянные величины и произведем
интегрирование, тогда получим
AS'=mclnGy7\).
После вычислений найдем
AS' = 132 Дж/К.
При вычислении по формуле A) изменения энтропии во время
превращения воды в пар той же температуры постоянная температу-
148

pa T выносится за знак интеграла. Вычислив интеграл, найдем
2
B =
1
где Q — количество теплоты, переданное при превращении нагре-
нагретой воды в пар той же температуры.
Подставив в равенство B) выражение количества теплоты Q=
=Xm, где Я — удельная теплота парообразования, получим
AS" = ^. C)
Произведя вычисления по формуле C), найдем
AS"=605 Дж/К.
Полное изменение энтропии при нагревании воды и последую-
последующем превращении ее в пар
AS = AS'+AS"=737 Дж/К.
Пример 9. Определить изменение AS энтропии при изотермиче-
изотермическом расширении кислорода массой гп=\0 г от объема 1/х=25 л до
объема У2= 100 л.
Решение. Так как процесс изотермический, то в общем вы-
2
ражении энтропии AS = S2—5Х = \ -^- температуру выносят за
1
знак интеграла. Выполнив это, получим
Q = -P-. A)
Количество теплоты Q, полученное газом, найдем по первому
началу термодинамики: Q=AU+A. Для изотермического процесса
&U=0, следовательно,
Q=A, B)
а работа А для этого процесса определяется по формуле
A = (m/M)RTln(V2/V1). C)
С учетом B) и C) равенство A) примет вид
AS = (m/M) R In (VVVx). D)
Подставив в D) числовые значения и произведя вычисления, по-
получим
AS = A0.10-3/C2-10-3))-8,31 1пA0(Ы0-3/B5-10-3)) Дж/К=
-3,60 Дж/К.
Задачи
Теплоемкость идеального газа
11.1. Вычислить удельные теплоемкости cv и ср газов: \) гелия;
2) водорода; 3) углекислого газа.
11.2. Разность удельных теплоемкостей ср—cv некоторого двух-
149

атомного газа равна 260 Дж/(кг»К). Найти молярную массу М газа
и его удельные теплоемкости cv и ср.
11.3. Каковы удельные теплоемкости cv и ср смеси газов, содер-
содержащей кислород массой т1=Ю г и азот массой /п2=20 г?
11.4. Определить удельную теплоемкость cv смеси газов, содер-
содержащей l/i=5 л водорода и К2=3 л гелия. Газы находятся при оди-
одинаковых условиях.
11.5. Определить удельную теплоемкость ср смеси кислорода и
азота, если количество вещества * vx первого компонента равно
2 моль, а количество вещества v2 второго равно 4 моль.
11.6. В баллоне находятся аргон и азот. Определить удельную
теплоемкость cv смеси этих газов, если массовые доли * аргона
{wx) и азота (w2) одинаковы и равны ^=0,5.
11.7. Смесь газов состоит из хлора и криптона, взятых при оди-
одинаковых условиях и в равных объемах. Определить удельную тепло-
теплоемкость ср смеси.
11.8. Определить удельную теплоемкость cv смеси ксенона и
кислорода, если количества вещества * газов в смеси одинаковы и
равны v.
11.9. Найти показатель адиабаты у для смеси газов, содер-
содержащей гелий массой т1= 10 г и водород массой т2=4 г.
11.10. Смесь газов состоит из аргона и азота, взятых при оди-
одинаковых условиях и в одинаковых объемах. Определить показатель
адиабаты у такой смеси.
11.11. Найти показатель адиабаты у смеси водорода и неона,
если массовые доли * обоих газов в смеси одинаковы и равны w=0,5.
11.12. Найти показатель адиабаты у смеси газов, содержащей
кислород и аргон, если количества вещества * того и другого газа
в смеси одинаковы и равны v.
11.13. Степень диссоциации ** а газообразного водорода равна
0,6. Найти удельную теплоемкость cv такого частично диссоцииро-
диссоциировавшего водорода.
11.14. Определить показатель адиабаты у частично диссоцииро-
диссоциировавшего газообразного азота, степень диссоциации а которого рав-
равна 0,4.
11.15. Определить степень диссоциации а газообразного хлора,
если показатель адиабаты 7 такого частично диссоциировавшего
газа равен 1,55.
11.16. На нагревание кислорода массой т=160 г на АТ=12 К
было затрачено количество теплоты Q=l,76 кДж. Как протекал
процесс: при постоянном объеме или постоянном давлении?
11.17. При адиабатном сжатии газа его объем уменьшился в
/г=10 раз, а давление увеличилось в fe=21,4 раза. Определить
отношение CpICv теплоемкостей газов.
* См. сноску на с. ИЗ.
** См. задачу 9.11.
150

Работа расширения газа
11.18. Водород массой т=\ г был нагрет на ДТ=10 К при по-
постоянном давлении. Определить работу А расширения газа.
11.19. Газ, занимавший объем Vi=12 л под давлением рг=
= 100 кПа, был изобарно нагрет от температуры 7\=300 К до Г2=
=400 К. Определить работу А расширения газа.
11.20. Какая работа А совершается при изотермическом расши-
расширении водорода массой /п=5 г, взятого при температуре 7=290 К,
если объем газа увеличивается в три раза?
11.21. При адиабатном сжатии кислорода массой т=1 кг совер-
совершена работа А = 100 кДж. Определить конечную температуру Т2
таза, если до сжатия кислород находился при температуре Тг=
=300 К.
11.22. Определить работу А адиабатного расширения водорода
массой /п=4 г, если температура газа понизилась на ДТ=10 К.
11.23. Азот массой т=2 г, имевший температуру 7\=300 К,
был адиабатно сжат так, что его объем уменьшился в я=10 раз.
Определить конечную температуру Т2 газа и работу А сжатия.
11.24. Кислород, занимавший объем l/i=l л под давлением рг=
= 1,2 МПа, адиабатно расширился до объема У2=10 л. Определить
работу А расширения газа.
Первое начало термодинамики
11.25. Азот массой т=Ъ кг, нагретый на ДГ=150 К, сохранил
неизменный объем V. Найти: 1) количество теплоты Q, сообщенное
газу; 2) изменение AU внутренней энергии; 3) совершенную газом
работу А.
11.26. Водород занимает объем Vi=10 м3 при давлении р±=
= 100 кПа. Газ нагрели при постоянном объеме до давления /?2=
=300 кПа. Определить: 1) изменение At/ внутренней энергии газа;
2) работу Л, совершенную газом; 3) количество теплоты Q, сооб-
сообщенное газу.
11.27. При изохорном нагревании кислорода объемом F=50 л
давление газа изменилось на Др=0,5 МПа. Найти количество теп-
теплоты Q, сообщенное газу.
11.28. Баллон вместимостью У=20 л содержит водород при тем-
температуре Т=300 К под давлением р=0,4 МПа. Каковы будут тем-
температура Тг и давление ри если газу сообщить количество теплоты
Q=6 кДж?
11.29. Кислород при неизменном давлении р=80 кПа нагрева-
нагревается. Его объем увеличивается от Ух=1 м3 до У2=3 м3. Определить:
1) изменение AU внутренней энергии кислорода; 2) работу Л, совер-
совершенную им при расширении; 3) количество теплоты Q, сообщенное
газу.
11.30. Азот нагревался при постоянном давлении, причем ему
было сообщено количество теплоты Q=21 кДж. Определить работу
151

Л, которую совершил при этом газ, и изменение AU его внутренней
энергии.
11.31. Кислород массой га=2 кг занимает объем Ух=1 м3 и на-
находится под давлением /^=0,2 МПа. Газ был нагрет сначала при
постоянном давлении до объема Уа^З м3, а затем при постоянном
объеме до давления ps=0,5 МПа. Найти: 1) изменение внутренней
энергии At/ газа; 2) совершенную им работу Л; 3) количество теп-
теплоты Q, переданное газу. Построить график процесса.
11.32. Гелий массой т=1 г был нагрет на Д7=100 К при посто-
постоянном давлении р. Определить: 1) количество теплоты Q, передан-
переданное газу; 2) работу Л расширения; 3) приращение AU внутренней
энергии газа.
11.33. Какая доля w± количества теплоты Qb подводимого к иде-
идеальному газу при изобарном процессе, расходуется на увеличение
At/ внутренней энергии газа и какая доля w% — на работу Л рас-
расширения? Рассмотреть три случая, если газ: 1) одноатомный; 2) двух-
двухатомный; 3) трехатомный.
11.34. Водяной пар расширяется при постоянном давлении. Оп-
Определить работу Л расширения, если пару передано количество теп-
теплоты Q=4 кДж.
11.35. Азот массой /п=200 г расширяется изотермически при
температуре 7=280 К, причем объем газа увеличивается в два ра-
раза. Найти: 1) изменение AU внутренней энергии газа; 2) совершен-
совершенную при расширении газа работу Л; 3) количество теплоты Q, полу-
полученное газом.
11.36. В цилиндре под поршнем находится азот массой т=0,6 кг,
занимающий объем Vi=l,2 м3 при температуре 7=560 К. В резуль-
результате подвода теплоты газ расширился и занял объем У2=4,2 м3,
причем температура осталась неизменной. Найти: 1) изменение
At/ внутренней энергии газа; 2) совершенную им работу Л; 3) коли-
количество теплоты Q, сообщенное газу.
11.37. Водород массой т=10 г нагрели на Д 7=200 К, причем
газу было передано количество теплоты Q=40 кДж. Найти измене-
изменение Д?/ внутренней энергии газа и совершенную им работу Л.
11.38. При изотермическом расширении водорода массой т—
= 1 г, имевшего температуру 7=280 К, объем газа увеличился в
три раза. Определить работу Л расширения газа и полученное газом
количество теплоты Q.
11.39. Азот, занимавший объем V^x= 10 л под давлением /?х=
=0,2 МПа, изотермически расширился до объема 1/2=28 л. Опре-
Определить работу Л расширения газа и количество теплоты Q, полу-
полученное газом.
11.40. При изотермическом расширении кислорода, содержав-
содержавшего количество вещества v = l моль и имевшего температуру 7=
=300 К, газу было передано количество теплоты Q=2 кДж. Во
сколько раз увеличился объем газа?
11.41. Какое количество теплоты Q выделится, если азот массой
т=1 г, взятый при температуре 7=280 К под давлением/?х=
=0,1 МПа, изотермически сжать до давления pa^l МПа?
152

11.42. Расширяясь, водород совершил работу А=6 кДж. Опре-
Определить количество теплоты Q, подведенное к газу, если процесс про-
протекал: 1) изобарно; 2) изотермически.
11.43. Автомобильная шина накачена до давления /?i=220 кПа
при температуре Тх=290 К. Во время движения она нагрелась до
температуры Т2=330 К и лопнула. Считая процесс, происходящий
после повреждения шины, адиабатным, определить изменение тем-
температуры AT вышедшего из нее воздуха. Внешнее давление р0
воздуха равно 100 кПа.
11.44. При адиабатном расширении кислорода с начальной тем-
температурой 7\=320 К внутренняя энергия уменьшилась на А[/=
=8,4 кДж, а его объем увеличился в п=\0 раз. Определить массу
т кислорода.
11.45. Водород при нормальных условиях имел объем Vi=
= 100 м3. Найти изменение AU внутренней энергии газа при его
адиабатном расширении до объема 1^2= 150 м3.
11.46. В цилиндре под поршнем находится водород массой т=
=0,02 кг при температуре 7\=300 К. Водород сначала расширился
адиабатно, увеличив свой объем в пять раз, а затем был сжат изо-
изотермически, причем объем газа уменьшился в пять раз. Найти тем-
температуру Т2 в конце адиабатного расширения и полную работу Л,
совершенную газом. Изобразить процесс графически.
11.47. При адиабатном сжатии кислорода массой /л=20 г
его внутренняя энергия увеличилась на AU=8 кДж и темпе-
температура повысилась до Т2:=900 К. Найти: 1) повышение темпе-
температуры АГ; 2) конечное давление газа /?2, если начальное давление
рг=200 кПа.
11.48. Воздух, занимавший объем Vi=10 л при давлении рг=
= 100 кПа, был адиабатно сжат до объема V2=l л. Под каким дав-
давлением р2 находится воздух после сжатия?
11.49. Горючая смесь в двигателе дизеля воспламеняется при
температуре Т2= 1,1 кК. Начальная температура смеси 7\=350 К.
Во сколько раз нужно уменьшить объем смеси при сжатии, чтобы
она воспламенилась? Сжатие считать адиабатным. Показатель адиа-
адиабаты у для смеси принять равным 1,4.
11.50. Углекислый газ СО2 массой т=400 г был нагрет на А7=
=50 К при постоянном давлении. Определить изменение At/ внут-
внутренней энергии газа, количество теплоты Q, полученное газом,
и совершенную им работу А.
11.51. Кислород массой га=800 г, охлажденный от температуры
fi=100°C до температуры /2=20 °С, сохранил неизменным объем
V. Определить: 1) количество теплоты Q, полученное газом; 2) из-
изменение AU внутренней энергии и 3) совершенную газом работу
А.
11.52. Давление азота объемом V=3 л при нагревании увеличи-
увеличилось на Ар=1 МПа. Определить количество теплоты Q, полученное
газом, если объем газа остался неизменным.
153

Круговые процессы. Термический КПД.
Цикл Карно
11.53. В результате кругового процесса газ совершил работу
А = 1 Дж и передал охладителю количество теплоты Q2=4,2 Дж.
Определить термический КПД rj цикла.
11.54. Совершая замкнутый процесс, газ получил от нагревателя
количество теплоты Qi=4 кДж. Определить работу А газа при
протекании цикла, если его термический КПД г|=0,1.
11.55. Идеальный двухатомный газ, содержащий количество
вещества v = l моль, совершает цикл, состоящий из двух изохор и
двух изобар. Наименьший объем Vmin=10 л, наибольший Fmax=
=20 л, наименьшее давление рт-т=
=246 кПа, наибольшее ртах=4\0 кПа.
Построить график цикла. Определить
температуру Т газа для характерных
точек цикла и его термический КПД г\.
11.56. Идеальный двухатомный газ,
содержащий количество вещества v = l
кмоль, совершает замкнутый цикл, гра-
фик которого изображен на рис. 11.4.
Определить: 1) количество теплоты Qu
полученное от нагревателя; 2) количест-
количество теплоты Q2, переданное охладителю;
3) работу Л, совершаемую газом за цикл; 4) термический КПД ц
цикла.
11.57. Идеальный двухатомный газ, содержащий количество
вещества v=l моль и находящийся под давлением /?i=0,l МПа
при температуре Ti=300 К, нагревают при постоянном объеме до
давления /?2=0,2 МПа. После этого газ изотермически расширился
до начального давления и затем изобарно был сжат до начального
объема Vi. Построить график цикла. Определить температуру 7*
газа для характерных точек цикла и его термический КПД ц.
11.58. Одноатомный газ, содержащий количество вещества v=
=0,1 кмоль, под давлением /?i=100 кПа занимал объем Vi=5 м3.
Газ сжимался изобарно до объема V2=l м3, затем сжимался адиа-
батно и расширялся при постоянной температуре до начальных объе-
объема и давления. Построить график процесса. Найти: 1) температуры
7\, Та, объемы 1/2, V3 и давление /?3, соответствующее характерным
точкам цикла; 2) количество теплоты Qi, полученное газом от нагре-
нагревателя; 3) количество теплоты Q2> переданное газом охладителю;
4) работу Л, совершенную газом за весь цикл; 5) термический КПД
т] цикла.
11.59. Идеальный многоатомный газ совершает цикл, состоящий
из двух изохор и двух изобар, причем наибольшее давление газа
в два раза больше наименьшего, а наибольший объем в четыре раза
больше наименьшего. Определить термический КПД г\ цикла.
11.60. Идеальный газ, совершающий цикл Кар но, 2/3 количества
теплоты Qi, полученного от нагревателя, отдает охладителю. Тем-
154

пература Т2 охладителя равна 280 К. Определить температуру Тг
нагревателя.
11.61. Идеальный газ совершает цикл Кар но. Температура Т2
охладителя равна 290 К. Во сколько раз увеличится КПД цикла,
если температура нагревателя повысится от Ti=400 К до Т1=
=600 К?
11.62. Идеальный газ совершает цикл Карно. Температура Т1
нагревателя в три раза выше температуры Т2 охладителя. Нагрева-
Нагреватель передал газу количество теплоты Qi=42 кДж. Какую работу
А совершил газ?
11.63. Идеальный газ совершает цикл Карно. Температура Tf
нагревателя равна 470 К, температура Т2 охладителя равна 280 К.
При изотермическом расширении газ совершает работу А = 100 Дж.
Определить термический КПД ц цикла, а также количество теплоты
Q2, которое газ отдает охладителю при изотермическом сжатии.
11.64. Идеальный газ совершает цикл Карно. Температура Т±
нагревателя в четыре раза выше температуры Т2 охладителя. Какую
долю w количества теплоты, получаемого за один цикл от нагрева-
нагревателя, газ отдает охладителю?
11.65. Идеальный газ, совершающий цикл Карно, получив от
нагревателя количество теплоты Qx=4,2 кДж, совершил работу
А=590 Дж. Найти термический КПД г| этого цикла. Во сколько
раз температура Тг нагревателя больше температуры Т2 охлади-
охладителя?
11.66. Идеальный газ совершает цикл Карно. Работа А± изотер-
изотермического расширения газа равна 5 Дж. Определить работу А2
изотермического сжатия, если терми-
термический КПД т) цикла равен 0,2.
11.67. Наименьший объем Vi газа,
совершающего цикл Карно, равен
153 л. Определить наибольший объем
F3, если объем V2 в конце изотерми-
изотермического расширения и объем 1/4 в
конце изотермического сжатия равны
соответственно 600 и 189 л. ° ч vz v
11.68. Идеальный двухатомный Рис. 11.5
газ совершает цикл Карно, график
которого изображен на рис. 11.5. Объемы газа в состояниях
В и С соответственно Ki=12 л и V2=16 л. Найти термический КПД
tj цикла.
Энтропия
11.69. Смешали воду массой mi=5 кг при температуре 7\=
—280 К с водой массой т2=8 кг при температуре Г2=350 К. Найти:
1) температуру 0 смеси; 2) изменение AS энтропии, происходящее
при смешивании.
11.70. В результате изохорного нагревания водорода массой
tfi=l г давление р газа увеличилось в два раза. Определить изме-
изменение AS энтропии газа.
155

11.71. Найти изменение AS энтропии при изобарном расшире-
расширении азота массой т=4 г от объема V1=5 л до объема V2=9 л.
11.72. Кусок льда массой т=200 г, взятый при температуре
tt=—10 °С, был нагрет до температуры t2=0 °C и расплавлен, после
чего образовавшаяся вода была нагрета до температуры /=10 °С.
Определить изменение AS энтропии в ходе указанных процессов.
11.73. Лед массой ш1=2 кг при температуре ^=0 °С был превра-
превращен в воду той же температуры с помощью пара, имеющего темпера-
температуру ^2= 100 °С. Определить массу т2 израсходованного пара. Ка-
Каково изменение AS энтропии системы лед—пар?
11.74. Кислород массой т=2 кг увеличил свой объем в п=5 раз
один раз изотермически, другой — адиабатно. Найти изменения
энтропии в каждом из указанных процессов.
11.75. Водород массой т=100 г был изобар но нагрет так, что
объем его увеличился в п=3 раза, затем водород был изохорно ох-
охлажден так, что давление его уменьшилось в п=3 раза. Найти
изменение AS энтропии в ходе указанных процессов.
§ 12. РЕАЛЬНЫЕ ГАЗЫ. ЖИДКОСТИ
Основные формулы
@ Уравнение Ван-дер-Ваальса для одного моля газа
для произвольного количества вещества v газа
где а и Ъ — постоянные Ван-дер-Ваальса (рассчитанные на один
моль газа); V — объем, занимаемый газом; Vm — молярный объем;
р — давление газа на стенки сосуда.
Внутреннее давление, обусловленное силами взаимодействия
молекул,
, а , 9 а
Р =77Г > или Р = v T7F •
v m
9 Связь критических параметров — объема, давления и темпе-
температуры газа — с постоянными а и Ъ Ван-дер-Ваальса:
Внутренняя энергия реального газа
где Cv — молярная теплоемкость газа при постоянном объеме.
Ф Поверхностное натяжение
o=F/l,
15G

где F— сила поверхностного натяжения, действующая на контур
/, ограничивающий поверхность жидкости, или
АЕ
_
_
AS
где А? — изменение свободной энергии поверхностной пленки
жидкости, связанное с изменением площади AS поверхности этой
пленки.
® Формула Лапласа в общем случае записывается в виде
где р — давление, создаваемое изогнутой поверхностью жидкости;
а — поверхностное натяжение; R± и R2 — радиусы кривизны двух
взаимно перпендикулярных сечений поверхности жидкости, а в
случае сферической поверхности
p=2o/R.
@ Высота подъема жидкости в капиллярной трубке
и _ 2сг cos ^
где 6 — краевой угол; R — радиус канала трубки; р — плотность
жидкости; g — ускорение свободного падения.
Ф Высота подъема жидкости
между двумя близкими и парал-
параллельными плоскостями
2а cos 6
h=-
9§d
где d — расстояние между плос-
плоскостями.
Ф Расход жидкости в трубке
тока (рис. 12.1):
а) объемный расход Qv=vS;
б) массовый расход Qm=pvS,
где S — площадь поперечного се-
сечения трубки тока; v — скорость жидкости; р — ее плотность.
в Уравнение неразрывности струи
У////////////////////////////////, У///////////////.
Рис, 12.1
где Si и S2 — площади поперечного сечения трубки тока в двух
местах; vt и v2 — соответствующие скорости течений.
@ Уравнение Бернулли для идеальной несжимаемой жидкости
в общем случае
где рх и /72 — статические давления жидкости в двух сечениях труб-
трубки тока; v± и v2 — скорости жидкости в этих сечениях; р^/2 и
ри|/2 — динамические давления жидкости в этих же сечениях; /zL
и h2 — высоты их над некоторым уровнем (рис. 12,1); pg/zL и pg/ь —
гидростатические давления.
157

Уравнение Бернулли в случае, когда оба сечения находятся на
одной высоте (/ii=/i2),
• Скорость течения жидкости из малого отверстия в открытом
широком сосуде
где h — глубина, на которой находится отверстие относительно
уровня жидкости в сосуде.
О Формула Пуазейля. Объем жидкости (газа), протекающей за
время t через длинную трубку,
V Ыц
где г — радиус трубки; / — ее длина; Ар — разность давлений на
концах трубки; г) — динамическая вязкость (коэффициент внут-
внутреннего трения) жидкости.
• Число Рейнольдса для потока жидкости в длинных трубках
где (v) — средняя по сечению скорость течения жидкости; d —-
диаметр трубки, и для движения шарика в жидкости
где v — скорость шарика; d — его диаметр.
Число Рейнольдса Re есть функция скорости v тела, линейной
величины /, определяющей размеры тела, плотности р и динамиче-
динамической вязкости т] жидкости, т. е.
Re = /(p, т], /, v).
При малых значениях чисел Рейнольдса, меньших некоторого
критического значения ReKP, движение жидкости является лами-
ламинарным. При значениях Re^>ReKP движение жидкости переходит
в турбулентное.
Критическое число Рейнольдса для движения шарика в жидкос-
жидкости ReKp=0,5; для потока жидкости в длинных трубках ReKP=
-2300.
• Формула Стокса. Сила сопротивления F, действующая со
стороны потока жидкости на медленно движущийся в ней шарик,
где г — радиус шарика; v — его скорость.
Формула справедлива для скоростей, при которых число Рей-
Рейнольдса много меньше единицы (Re<Cl).
Примеры решения задач
Пример 1. В баллоне вместимостью V—8 л находится кислород
массой т=0,3 кг при температуре Т=300 К. Найти, какую часть
вместимости сосуда составляет собственный объем молекул газа.
158

Определить отношение внутреннего давления р' к давлению р газа
на стенки сосуда.
Решение. Для получения ответа на первый вопрос задачи
необходимо найти отношение
k=V'IV9 A)
где V — собственный объем молекул.
Собственный объем молекул найдем, воспользовавшись постоян-
постоянной Ь Ван-дер-Ваальса, равной учетверенному объему молекул,
содержащихся в одном моле реального газа. В уравнении Ван-дер-
Ваальса
(p+v*a/V*)(V—vb)=vRT B)
поправка vb означает учетверенный объем молекул всего газа, т. е.
vb=4V'. Отсюда
V'=v&/4, или V'=nib/DM),
где v=m/M — количество вещества; М — молярная масса.
Подставив полученное значение V в выражение A), найдем
После вычисления по этой формуле получим
Следовательно, собственный объем молекул составляет 0,91%
от объема сосуда.
Для ответа на второй вопрос задачи надо найти отношение
ki=p'lp. C)
Как следует из уравнения B),
p'=v2a/V2, или p'=(m/MJa/V2, D)
где а — постоянная Ван-дер-Ваальса для одного моля газа.
После вычисления по формуле D) найдем
// = 179 кПа.
Давление /?, производимое газом на стенки сосуда, найдем из
уравнения B):
__ vRT 2_a__
Р— v — vb v V2 '
После вычисления по этой формуле получим
о ч
V>U О О1 ОЛЛ
32. Ю-3'*' WUU / 0,3 у 136-Ю-3
З.Ю-З-^-.ЗЛ/.Ю- V32.10-; (8.10-V
= 2,84-106 Па = 2,84 МПа.
Подставив в выражение C) значения р' и р и произведя вычисле-
вычисления, найдем
Следовательно, давление газа, обусловленное силами притяже-
притяжения молекул, составляет 6,3 % давления газа на стенки сосуда.
Пример 2. Углекислый газ, содержащий количество вещества
v=l моль, находится в критическом состоянии. При изобарном
159

нагревании газа его объем V увеличился в k=2 раза. Определить
изменение АГ температуры газа, если его критическая температу-
температура 7V--304 К.
Решение. Для решения задачи удобно воспользоваться
уравнением Ван-дер-Ваальса в приведенной форме, т. е. в такой
форме, когда давление р, молярный объем Vm и температура Т
реального газа с соответствующими критическими параметрами
представлены в виде следующих отношений:
Из этих равенств получим:
Подставив сюда выражения /?кр, Ушкр и Ткр через постоянные
Ван-дер-Ваальса а и Ь, найдем:
Полученные выражения /?, Vm и Т подставим в обычное уравне-
уравнение Ван-дер-Ваальса:
о/ /-, i-v 8а
3to 4 /?T
После сокращения на а/B7Ь) и в правой части на R получим
(я+3/оз2)Cо)— 1)=8т. A)
Это и есть уравнение Ван-дер-Ваальса в приведенной ф о р-
м е. Оно не содержит никаких параметров, характеризующих ин-
индивидуальные свойства газа, и поэтому является универсальным.
Теперь ответим на вопрос задачи. Так как давление остается
постоянным (p—pKV), то я = 1; молярный объем газа согласно усло-
условию увеличился в два раза, т. е. Vm=2VmKV\ следовательно, о>=2.
Из уравнения A) выразим приведенную температуру т:
т= 1 /8 (л Ч- З/оJ) C@—1).
Подставив сюда значения л и (о и произведя вычисления, най-
найдем
т-35/32.
Температура Г, как отмечалось, связана с приведенной темпера-
температурой т и критической Ткр соотношением T=xTKV. Произведя вы-
вычисления по этой формуле, получим
7-332 К.
Пример 3. В цилиндре под поршнем находится хлор массой
т=20 г. Определить изменение AU внутренней энергии хлора при
изотермическом расширении его от 1/х=200 см3 до У2=500 см3.
Решение. Внутренняя энергия U реального (ван-дер-ва-
альсового) газа определяется выражением
U=v(CvT-a/Vm). A)
Выразив в равенстве A) молярный объем l7m через объем V и
160

количество вещества v(Vm=V/v) и учтя, что v=m/M, получим
II - т [ С Т та\ <
Изменение At/ внутренней энергии в результате изотермическо-
изотермического расширения найдем как разность двух значений внутренней энер-
энергии при объемах V2 и Vx:
\П U U m2a{V2 — Vi) г>ч
ьи = и2—и1= M2ViV2 . C)
Подставив значения величин в формулу C) и произведя вычис-
вычисления, получим
Отметим, что для идеального газа такое изменение внутренней
энергии соответствовало бы нагреванию на 26,3 К.
Пример 4. Найти добавочное давление р внутри мыльного пузы-
пузыря диаметром d=\0 см. Определить также работу Л, которую нужно
совершить, чтобы выдуть этот пузырь.
Решение. Пленка мыльного пузыря имеет две сферические
поверхности — внешнюю и внутреннюю. Обе поверхности оказы-
оказывают давление на воздух, заключенный внутри пузыря. Так как
толщина пленки чрезвычайно мала, то диаметры обеих поверхнос-
поверхностей практически одинаковы. Поэтому добавочное давление /? =
=2-2о/г, где г — радиус пузыря. Так как r=dl2y то
/?=8cr/d.
Подставив в эту формулу значения а=40-10~3 Н/м (см. табл. 15)
и d=0,l м и произведя вычисления, найдем
р=3,2 Па.
Работа, которую нужно совершить, чтобы, растягивая пленку,
увеличить ее поверхность на Д5, выражается формулой
A = oAS, или A=a(S—S0).
В данном случае S — общая площадь двух сферических поверх-
поверхностей пленки мыльного пузыря; So — общая площадь двух по-
поверхностей плоской пленки, затягивающей отверстие трубки до
выдувания пузыря. Пренебрегая So, получим
Сделав подстановку значений величин, получим
А-2,5 мДж.
Пример 5. Определить изменение свободной энергии А? поверх-
поверхности мыльного пузыря при изотермическом увеличении его объема
от Vx-lOcM3 до V2=2V1.
Решение. Свободная энергия Е поверхности жидкости
пропорциональна площади S этой поверхности: E=gS, где а — по-
поверхностное натяжение.
У мыльного пузыря имеются две поверхности — внешняя и
внутренняя, площади которых практически равны из-за малой тол-
толщины мыльной пленки. Поэтому свободная энергия поверхности
6 № 1268 161

(внешней и внутренней вместе) мыльного пузыря
E=2oS. A)
Так как, по условию задачи, процесс изотермический, то по-
поверхностное натяжение, являющееся для данной жидкости функ-
функцией только температуры, остается постоянным. Следовательно,
по формуле A) изменение свободной энергии
A?=2crAS, B)
где AS — изменение поверхности пузыря (одной — внутренней или
внешней).
Считая, что мыльный пузырь имеет форму сферы, найдем изме-
изменение площади поверхности:
AS = 4nrl—Anr2lf C)
где г± и г2 — радиусы сфер, соответствующие начальному Vx и
конечному V2 объемам: riz==:[-^-) > Г2 = 1я ) • Теперь фор-
формула C) примет вид
Учитывая, что 1^2=21^, получим после вынесения общего члена
ЦЛ \2/3
г-*- за
D)
Подставим выражение AS в формулу B):
После вычисления по формуле D) получим
Л?=106 мкДж.
Пример 6. Вода подается в фонтан из большого цилиндрическо-
цилиндрического бака (рис. 12.2) и бьет из отверстия II—II со скоростью v2—
= 12 м/с. Диаметр D бака равен 2 м,
диаметр d сечения II—II равен 2 см.
Найти: 1) скорость vt понижения во-
воды в баке; 2) давление ри под кото-
которым вода подается в фонтан; 3) вы-
высоту hx уровня воды в баке и высоту
h2 струи, выходящей из фонтана.
Решение. 1. Проведем сечение
I—I в баке на уровне сечения II—II
фонтана. Так как площадь Sx сече-
сечения I—I много больше площади S2
сечения II—II, то высоту h± уровня
воды в баке можно считать для мало-
малого промежутка времени постоянной, а поток — установившимся.
Для установившегося потока справедливо условие неразрывности
струи: v1St=v2S2, откуда
u1=y2S2/Si, или vx=-v2{dlDY. A)
Рис. 12.2
162

Подставив в равенство A) значения заданных величин и
ведя вычисления, найдем
^=0,0012 м/с.
С такой же скоростью будет понижаться уровень в баке. Как
видно, эта скорость очень мала по сравнению со скоростью струи.
2. Давление ри под которым вода подается в фонтан, найдем
по уравнению Бернулли. В случае горизонтальной трубки тока
оно имеет вид
p1 + px%2 = p2 + pvl/2. B)
Учтя, что /?2=0 (под давлением подразумевается избыточное над
атмосферным давление), из уравнения B) получим
Р! = ри?/2—pvl/2. C)
Так как v1<^v2, то из равенства C) следует
рх = pv*/2.
После вычислений, произведенных по этой формуле, найдем
/?i=72 кПа.
3. Высоту /ix уровня воды в баке найдем из соотношения р±=^
=ftipg, откуда
hi=pj(pg).
Произведя вычисления по этой формуле, найдем
ft!=7,35 м.
Зная скорость и2, с которой вода выбрасывается фонтаном, най-
найдем высоту /i2, на которую она будет выброшена:
7,35 м.
Подчеркнем, что высота уровня воды в баке равна высоте, на
которую поднимается фонтан воды (по правилу сообщающихся сосу-
сосудов). Это замечание справедливо, если пренебречь сопротивлением
воздуха.
Пример 7. В сосуде с глицерином падает свинцовый шарик. Оп-
Определить максимальное значение диаметра шарика, при котором
движение слоев глицерина, вызванное падением шарика, является
еще ламинарным. Движение считать установившимся.
Решение. Если в вязкой жидкости движется тело, то вместе
с ним, как одно целое, движется и прилипший к телу слой жидкос-
жидкости. Этот слой вследствие внутреннего трения увлекает за собой и
соседние слои. Возникающее при этом движение жидкости является
ламинарным или турбулентным в зависимости от размеров и формы
тела и его скорости. Характер движения зависит также от свойств
жидкости и определяется безразмерным числом Рейнольдса.
Если тело, движущееся в жидкости, имеет форму шара диаметром
d, то число Рейнольдса определяется по формуле
Re=pvd'r\, A)
а критическое значение этого числа ReKp=0,5.
Скорость v выразим, исходя из следующих соображений. На
6* 163

свинцовый шарик, падающий д глицерине, действуют три силы;
1) сила тяжести шарика
где рсв — плотность свинца; V — объем шарика;
2) выталкивающая сила, определяемая по закону Архимеда,
^выт^Ргл^^'/бЛРрл,^3,
где ргл — плотность глицерина;
3) сила внутреннего трения, определяемая по формуле Стокса,
FTV = 6nr\rv = 3n\\dv.
При установившемся движении шарика в жидкости (u=const)
сила тяжести шарика уравновешивается суммой выталкивающей
силы и силы внутреннего трения, т. е.
Ve^pceg-d3 = Venpi^grf3 + 3n\\dv,
откуда
r> — (Рев —Prn)g ji /r>\
Решая совместно уравнения A) и B) относительно d, найдем
Ргл (рев — Ргл) g '
Максимальное значение диаметра dmax, при котором движение
остается еще ламинарным, соответствует критическому значению
числа Рейнольдса ReKp. Поэтому
Ргл (Рсв — Ргл) ё
Подставив сюда значения величин ц (см. табл. 14), ReKP, pCB,
Ргл и S и произведя вычисления, получим
dmax = 5>29 MM.
Задачи
Уравнение Ван-дер-Ваальса
12.1. В сосуде вместимостью У= 10 л находится азот массой т=
=0,25 кг. Определить: 1) внутреннее давление р' газа: 2) собствен-
собственный объем V молекул.
12.2. Определить давление /?, которое будет производить кисло-
кислород, содержащий количество вещества v=l моль, если он занимает
объем V=0,5 л при температуре Т=300 К. Сравнить полученный
результат с давлением, вычисленным по уравнению Менделеева —
Клапейрона.
12.3. В сосуде вместимостью У=0,3 л находится углекислый
газ, содержащий количество вещества v = l моль при температуре
7=300 К. Определить давление р газа: 1) по уравнению Менделее-
Менделеева — Клапейрона; 2) по уравнению Ван-дер-Ваальса.
12.4. Криптон, содержащий количество вещества v = l моль, на-
находится при температуре 7=300 К. Определить относительную
погрешность г=Ар/р, которая будет допущена при вычислении
164

давления, если вместо уравнения1 Ван-дер-Ваальса воспользоваться
уравнением Менделеева — Клапейрона. Вычисления выполнить
для двух значений объема: 1) V=2 л; 2) У=0,2 л.
12.5. Внутреннюю полость толстостенного стального баллона
наполовину заполнили водой при комнатной температуре. После
этого баллон герметически закупорили и нагрели до температуры
Т=650 К. Определить давление р водяного пара в баллоне при этой
температуре.
12.6. Давление р кислорода равно 7 МПа, его плотность р =
= 100 кг/м3. Найти температуру Т кислорода.
12.7. Определить давление р водяного пара массой т=1 кг,
взятого при температуре Г=380 К и объеме V: 1) 1000 л; 2) 10 л;
3) 2 л.
Критическое состояние
12.8. Вычислить постоянные а и Ъ в уравнении Ван-дер-Ваальса
для азота, если известны критические температуры Гкр=126 К и
давление /?кр=3,39 МПа.
12.9. Вычислить критические температуру Ткр и давление /?кр:
1) кислорода; 2) воды.
12.10. Критическая температура Гкр аргона равна 151 К и кри-
критическое давление /?кр=4,86 МПа. Определить по этим данным кри-
критический молярный объем Уткр аргона.
12.11. Жидким пентаном C5Hi2, плотность р которого равка
626 кг/м3, частично заполняют прочную кварцевую колбу и запаи-
запаивают ее так, что над пентаном остаются только насыщающие пары.
Определить, какую часть 8 внутреннего объема колбы должен за-
занимать пентан, чтобы можно было наблюдать при нагревании пере-
переход вещества через критическую точку . Постоянная Ь Ван-дер-
Ваальса равна 14,5-10~5 м3/моль.
12.12. Определить наибольший объем Утах, который может зани-
занимать вода, содержащая количество вещества v = l моль.
12.13. Определить плотность р водяных паров в критическом со-
состоянии.
12.14. Определить наибольшее давление /?тах насыщающих водя-
водяных паров.
12.15. Во сколько раз концентрация якр молекул азота в крити-
критическом состоянии больше концентрации п0 молекул при нормальных
условиях?
12.16. Найти критический объем Укр веществ: 1) кислорода мас-
массой /л=0,5 г; 2) воды массой т=1 г.
12.17 *. Газ, содержащий количество вещества v = l моль, нахо-
находится при критической температуре и занимает объем 1/, в п=3 раза
превышающий критический объем 1/кр. Во сколько раз давление
Р газа в этом состоянии меньше критического давления /?кр?
* В задачах 12.17—12.20 при решении удобнее использовать уравнение
Ван-дер-Ваальса в приведенной форме (см. пример 2).
165

12.18.* При какой температуре Т находится окисид<азота, если
ее объем V и давление р в к=3 раза превышают соответствующие
критические значения VKV и /?кр? Критическая температура Гкр
оксида азота равна 180 К.
12.19.* Газ находится в критическом состоянии. Как и во сколько
раз его давление р будет отличаться от критического ркр при одно-
одновременном увеличении температуры Т и объема V газа в k=2 раза?
12.20*. Газ находится в критическом состоянии. Во сколько раз
возрастет давление р газа, если его температуру Т изохорно увели-
увеличить в k=2 раза?
Внутренняя энергия
12.21. Определить внутреннюю энергию U азота, содержащего
количество вещества v = l моль, при критической температуре
Гк^ 126 К. Вычисления выполнить для четырех значений объемов
V: 1J0 л; 2) 2 л; 3) 0,2 л; 4) VKV.
12.22. Кислород, содержащий количество вещества v=l моль,
находится при температуре Т=350 К. Найти относительную по-
погрешность е в вычислении внутренней энергии газа, если газ рас-
рассматривать как идеальный. Расчеты выполнить для двух значений
объема V: 1) 2 л; 2) 0,2 л.
12.23. Найти внутреннюю энергию U углекислого газа массой
т=132 г при нормальном давлении р0 и температуре 7=300 К в
двух случаях, когда газ рассматривают: 1) как идеальный; 2) как
реальный.
12.24. Кислород массой т=8 г занимает объем V=20 см3 при
температуре Г=300 К. Определить внутреннюю энергию U кисло-
кислорода.
12.25. Определить изменение Д(/ внутренней энергии неона,
содержащего количество вещества v = l моль, при изотермическом
расширении его объема от V^l л до К2=2 л.
12.26. Объем углекислого газа массой т=0,1 кг увеличился от
Fx^lO3 л до V2=W л. Найти работу А внутренних сил взаимодей-
взаимодействия молекул при этом расширении газа.
12.27. В сосуде вместимостью Vi=l л содержится т—10 г азота.
Определить изменение ДТ температуры азота, если он расширяется
в пустоту до объема V2=10 л.
12.28. Газообразный хлор массой т=7,1 г находится в сосуде
вместимостью Vi=0,l л. Какое количество теплоты Q необходимо
подвести к хлору, чтобы при расширении его в пустоту до объема
Vz=l л температура газа осталась неизменной?
Поверхностное натяжение. Капиллярные явления
12.29. Масса т 100 капель спирта, вытекающего из капилляра,
равна 0,71 г. Определить поверхностное натяжение а спирта, если
диаметр d шейки капли в момент отрыва равен 1 мм.
* См. сноску на с. 165.
166

12.30. Трубка имеет диаметр d±^0,2 см. На нижнем конце трубки
повисла капля воды, имеющая в момент отрыва вид шарика. Найти
диаметр d2 этой капли.
12.31. Какую работу А нужно совершить, чтобы, выдувая мыль-
мыльный пузырь, увеличить его диаметр от d1=l см до d2=ll см? Счи-
Считать процесс изотермическим.
12.32. Две капли ртути радиусом г=\ мм каждая слились в одну
большую каплю. Какая энергия Е выделится при этом слиянии?
Считать процесс изотермическим.
12.33. Воздушный пузырек диаметром d=2 мкм находится в воде
у самой ее поверхности. Определить плотность р воздуха в пузырь-
пузырьке, если воздух над поверхностью воды находится при нормальных
условиях.
12.34. На сколько давление р воздуха внутри мыльного пузыря
больше атмосферного давления р0, если диаметр пузыря d=5 мм?
12.35. Определить силу F, прижимающую друг к другу две стек-
стеклянные пластинки размерами 10X 10 см, расположенные параллель-
параллельно друг другу, если расстояние / между пластинками равно 22 мкм,
а пространство между ними заполнено водой. Считать мениск вогну-
вогнутым с диаметром d, равным расстоянию между пластинками.
12.36. Покровное стеклышко для микроскопа имеет вид круга
диаметром d= 16 мм. На него нанесли воду массой т=0,1 г и нало-
наложили другое такое же стеклышко; в результате оба стеклышка слип-
слиплись. С какой силой Fy перпендикулярной поверхностям стеклы-
стеклышек, надо растягивать их, чтобы разъединить? Считать, что вода
полностью смачивает стекло и поэтому меньший радиус г кривизны
боковой поверхности водяного слоя равен половине расстояния d
между стеклышками.
12.37. Глицерин поднялся в капиллярной трубке на высоту Л=
=20 мм. Определить поверхностное натяжение а глицерина, если
диаметр d канала трубки равен 1 мм.
12.38. Диаметр d канала стеклянной трубки чашечного ртутного
барометра равен 5 мм. Какую поправку Ар нужно вводить в отсчеты
по этому барометру, чтобы получить верное значение атмосферного
давления?
12.39. Разность АЛ уровней жидкости в коленах U-образной
трубки равна 23 мм. Диаметры dx и d2 каналов в коленах трубки
равны соответственно 2 и 0,4 мм. Плотность р жидкости равна
0,8 г/см3. Определить поверхностное натяжение а жидкости.
12.40. В жидкость нижними концами опущены две вертикальные
капиллярные трубки с внутренними диаметрами ^=0,05 см и
d2=0,l см. Разность АЛ уровней жидкости в трубках равна 11,6 мм.
Плотность р жидкости равна 0,8 г/см3. Найти поверхностное натя-
натяжение g жидкости.
12.41. В воду опущена на очень малую глубину стеклянная труб-
трубка с диаметром d внутреннего канала, равным 1 мм. Найти массу
т вошедшей в трубку воды.
12.42. Капиллярная трубка диаметром d=0,5 мм наполнена во-
водой. На нижнем конце трубки вода повисла в виде капли. Эту каплю
1G7

можно принять за часть сферьь радиуса г=3 мм. Найти высоту h
столбика воды в трубке.
12.43. Широкое колено U-образного ртутного манометра имеет
диаметр dx=4 см, узкое d2=0,25 см. Разность A/i уровней ртути в
обоих коленах равна 200 мм. Найти давление р> которое показывает
манометр, приняв во внимание поправку на капиллярность.
12.44. На какую высоту h поднимается вода между двумя па-
параллельными друг другу стеклянными пластинками, если расстоя-
расстояние d между ними равно 0,2 мм?
Гидродинамика
12.45. Вода течет в горизонтально расположенной трубе пере-
переменного сечения. Скорость v1 воды в широкой части трубы равна
20 см/с. Определить скорость v2 в узкой части трубы, диаметр d2
которой в 1,5 раза меньше диаметра йг широкой части.
12.46. В широкой части горизонтально расположенной трубы
нефть течет со скоростью vx=2 м/с. Определить скорость v2 нефти в
узкой части трубы, если разность Ар давлений в широкой и узкой
частях ее равна 6,65 кПа.
12.47. В горизонтально расположенной трубе с площадью Sx
поперечного сечения, равной 20 см2, течет жидкость. В одном месте
труба имеет сужение, в котором площадь S2 сечения равна 12 см2.
Разность ДА уровней в двух манометрических трубках, установлен-
установленных в широкой и узкой частях трубы, равна 8 см. Определить объем-
объемный расход Qv жидкости.
12.48. Горизонтальный цилиндр насоса имеет диаметр d±—
=20 см. В нем движется со скоростью v±= 1 м/с поршень, выталкивая
воду через отверстие диаметром d2=2 см. С какой скоростью v2
будет вытекать вода из отверстия? Каково будет избыточное давле-
давление р воды в цилиндре?
12.49. К поршню спринцовки, расположенной горизонтально,
приложена сила F=15 H. Определить скорость v истечения воды
из наконечника спринцовки, если площадь S поршня равна 12 см2.
12.50. Давление р ветра на стену равно 200 Па. Определить ско-
скорость v ветра, если он дует перпендикулярно стене. Плотность р
воздуха равна 1,29 кг/м3.
12.51. Струя воды диаметром d=2 см, движущаяся со скоростью
v=\0 м/с, ударяется о неподвижную плоскую поверхность, постав-
поставленную перпендикулярно струе. Найти силу F давления струи на
поверхность, считая, что после удара о поверхность скорость частиц
воды равна нулю.
12.52. Бак высотой А=1,5 мм наполнен до краев водой. На рас-
расстоянии d= 1 м от верхнего края бака образовалось отверстие малого
диаметра. На каком расстоянии / от бака падает на пол струя, вы-
вытекающая из отверстия?
12.53. Струя воды с площадью Sx поперечного сечения, равной
4 см2, вытекает в горизонтальном направлении из брандспойта,
168

Рис. 12.3
расположенного на высоте #=«2<м над поверхностью Земли, и па-
падает на эту поверхность на расстоянии 1=8 м (рис. 12.3). Пренебре-
Пренебрегая сопротивлением воздуха движению воды, найти избыточное дав-
давление р воды в рукаве, если пло-
площадь S2 поперечного сечения рука-
рукава равна 50 см2?
12.54. Бак высотой Н=2 м до
краев заполнен жидкостью. На
какой высоте h должно быть про-
проделано отверстие в стенке бака,
чтобы место падения струи, выте-
вытекающей из отверстия, было на максимальном от бака расстоя-
расстоянии?
12.55. Вода течет по круглой гладкой трубе диаметром d=5 см
со средней по сечению скоростью (и)=10 см/с. Определить число
Рейнольдса Re для потока жидкости в трубе и указать характер те-
течения жидкости.
12.56. По трубе течет машинное масло. Максимальная скорость
t>max, при которой движение масла в этой трубе остается еще лами-
ламинарным, равна 3,2 см/с. При какой скорости v движение глицерина
в той же трубе переходит из ламинарного в турбулентное?
12.57. В трубе с внутренним диаметром d=3 см течет вода. Оп-
Определить максимальный массовый расход Qmmax воды при лами-
ламинарном течении.
12.58. Медный шарик диаметром d= 1 см падает с постоянной ско-
скоростью в касторовом масле. Является ли движение масла, вызванное
падением в нем шарика, ламинарным? Критическое значение числа
Рейнольдса ReKP=0,5.
12.59. Латунный шарик диаметром d=0,5 мм падает в глице-
глицерине. Определить: 1) скорость v установившегося движения шарика;
2) является ли при этой скорости обтекание шарика ламинарным?
12.60. При движении шарика радиусом ^=2,4 мм в касторовом
масле ламинарное обтекание наблюдается при скорости vx шарика,
не превышающей 10 см/с. При какой минимальной скорости v2
шарика радиусом г2=1 мм в глицерине обтекание станет турбулент-
турбулентным?

ГЛАВА iS
ЭЛЕКТРОСТАТИКА
§ 13. ЗАКОН КУЛОНА. ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ТЕЛ
Основные формулы
• Закон Кулона
где F — сила взаимодействия двух точечных зарядов Qt и Q2;
г — расстояние между зарядами; г — диэлектрическая проницае-
проницаемость среды; ?0 — электрическая постоянная:
8п == —* ^—гкк" Ф/М =^ О.оО • 1 U Ф/М.
0 4я-9-10° ' '
О Закон сохранения заряда
п
2 Q,- = const,
п
где 2Q/—алгебраическая сумма зарядов, входящих в изолиро-
I-1
ванную систему; п — число зарядов.
Примеры решения задач
Пример 1. Три одинаковых положительных заряда Q1=Q2=:
=Q8=1 нКл расположены по вершинам равностороннего треуголь-
q ника (рис. 13.1). Какой отрица-
{? тельный заряд Q4 нужно поместить
в центре треугольника, чтобы си-
сила притяжения с его стороны урав-
уравновесила силы взаимного отталки-
отталкивания зарядов, находящихся в вер-
вершинах?
Решение. Все три заряда,
расположенных по вершинам тре-
треугольника, находятся в одина-
одинаковых условиях. Поэтому для ре-
решения задачи достаточно выяснить,
какой заряд следует поместить в
центре треугольника, чтобы один
из трех зарядов, например Qu находился в равновесии.
В соответствии с принципом суперпозиции на заряд действует
каждый заряд независимо от остальных. Поэтому заряд Qx будет
/ I \
Рис. 13.1
170

находиться в равновесии, если векторная сумма действующих на
него сил равна нулю:
F2+F3+F4-F+F4-0, A)
где F2, F3, F4 — силы, с которыми соответственно действуют на
заряд Qx заряды Q2, Q3 и Q4; F — равнодействующая сил F2 и F3.
Так как силы F и F4 направлены по одной прямой, то векторное
равенство A) можно заменить скалярной суммой:
F—F4 = 0, или F4 = /\
Выразив в последнем равенстве F через F2 и F3 и учитывая, что
F3—F2y получим
jF4 Faj2( + c)
Применяя закон Кулона и имея в виду, что Qz=zQ3:=Qii найдем
= 1 Я у2A + cosa)> B)
л0 гг\ 0 er
откуда
Из геометрических построений в равностороннем треугольнике
следует, что
^ = ^F==2^ = 7T; cos a = cos 60° =4-
С учетом этого формула B) примет вид
Подставив сюда значение Qlt получим
Q4=0,58 нКл.
Отметим, что равновесие системы зарядов будет неустойчивым.
Пример 2. Два заряда 9Q и —Q закреплены на расстоянии /=
=50 см друг от друга. Третий заряд Qx может перемещаться только
вдоль прямой, проходящей через заряды. Определить положение
заряда Qu при котором он будет находиться в равновесии. При
каком знаке заряда равновесие будет устойчивым *?
Решение. Заряд Qx будет находиться в равновесии в том
случае, если векторная сумма сил, действующих на него, будет рав-
равна нулю. Это значит, что на заряд Qx должны действовать две силы,
равные по модулю и противоположные по направлению. Рассмот-
Рассмотрим, на каком из трех участков /, //, /// (рис. 13.2) может быть
выполнено это условие. Для определенности будем считать, что
заряд Qx — положительный **.
На участке / (рис. 13.2, а) на заряд Qx действуют две противо-
противоположно направленные силы: Fx и F2. Сила Fb действующая со сто-
* Равновесие называется устойчивым, если при малом смещении заряда
от положения равновесия возникают силы, возвращающие его в положение
равновесия.
** Рекомендуется читателю самостоятельно выполнить решение задачи
для отрицательного заряда.
171

роны заряда 9Q, в любой точке этого участка будет больше, чем
сила F2, действующая со стороны заряда —Q, так как больший (по
модулю) заряд 9Q всегда находится ближе к заряду Q1? чем меньший
заряд —Q. Поэтому равновесие на этом участке невозможно.
На участке // (рис. 13.2, б) обе силы ?л и F2 направлены в одну
сторону — к заряду —Q. Следовательно, и на втором участке равно-
равновесие невозможно.
1 + х
Рис. 13.2
На участке /// (рис. 13.2, в) силы Fx и F2 направлены в противо-
противоположные стороны, так же как и на участке /, но в отличие от него
меньший (по модулю) заряд (—Q) всегда находится ближе к заряду
Qly чем больший заряд (9Q). Это значит, что можно найти такую
точку на прямой, где силы ?г и F2 будут одинаковы по модулю, т. е.
IFxIH-F.I. A)
Пусть расстояние от меньшего заряда до заряда Q1 равно дс,
тогда расстояние от большего заряда будет 1+х. Выражая в равен-
равенстве A) fi и F2 в соответствии с законом Кулона, получим
9QQi QQi
Сокращая на QQi и извлекая из обеих частей равенства квадрат-
квадратный корень, найдем 1+х=±:Зх, откуда
Х!=+1/2 и *2=—//4.
Корень х2 не удовлетворяет физическому условию задачи (в
этой точке силы Fx и F2 хотя и равны по модулю, но направлены в
одну сторону).
Определим знак заряда, при котором равновесие будет устойчи-
устойчивым. Рассмотрим смещение заряда Qx в двух случаях: 1) заряд поло-
положителен; 2) заряд отрицателен.
1. Если заряд Qi положителен, то при смещении его влево обе
силы Т7! и F2 возрастают, но Ft возрастает медленнее (заряд 9Q
всегда находится дальше, чем —Q). Следовательно, F2 (по модулю)
172

больше, чем Fu и на заряд Qt будет действовать результирующая
сила, направленная также влево. Под действием этой силы заряд
Qx удаляется от положения равновесия. То же происходит и при
смещении заряда Qx вправо. Сила F2 убывает быстрее, чем /^.Век-
/^.Векторная сумма сил в этом случае направлена вправо. Заряд под дей-
действием этой силы также будет перемещаться вправо, т. е. удаляться
от положения равновесия. Таким образом, в случае положительно-
положительного заряда равновесие является неустойчивым.
2. Если заряд Qx отрицателен, то его смещение влево вызовет
увеличение сил F2 и Fu но сила F± возрастает медленнее, чем F2,
т.е. l^sl^lFil. Результирующая сила будет направлена вправо.
Под действием этой силы заряд Qx возвращается к положению рав-
равновесия. При смещении Qx вправо сила F2 убывает быстрее, чем
Fi, т. е. IFil^/^l, результирующая сила направлена влево и заряд
Qx опять будет возвращаться к положению равновесия. При отри-
отрицательном заряде равновесие является устойчивым. Величина само-
самого заряда Qi несущественна.
Отметим, что в электростатике устойчивое равновесие возможно
только при определенных ограничениях. В нашем примере заряд
Qx может перемещаться только вдоль прямой, проходящей через
заряды Q и —9Q. Если это ограничение снять, то устойчивого равно-
равновесия не будет. В системе зарядов, на-
находящихся под действием одних только иг ]\aj dF{
электростатических сил, устойчивое рав-
равновесие невозможно (теорема Ирншоу).
Пример 3. Тонкий стержень длиной
/=30 см (рис. 13.3) несет равномерно
распределенный по длине заряд с ли-
линейной плотностью т=1 мкКл/м. На рас-
расстоянии го=20 см от стержня находится
заряд Qi= 10 нКл, равноудаленный от
концов стержня. Определить силу F
взаимодействия точечного заряда с за-
заряженным стержнем.
Решение. Закон Кулона позво- Рис. 13.3
ляет вычислить силу взаимодействия то-
точечных зарядов. По условию задачи, один из зарядов не явля-
является точечным, а представляет собой заряд, равномерно распре-
распределенный по длине стержня. Однако если выделить на стержне диф-
дифференциально малый участок длиной d/, то находящийся на нем
заряд dQ=xd/ можно рассматривать как точечный и тогда по за-
закону Кулона * сила взаимодействия между зарядами Qx и dQ:
d
а4ле0 г* ' V>
где г — расстояние от выделенного элемента до заряда Qx.
Из чертежа (рис. 13.3) следует, что г = г° и d/ = а , где
r vr ' J cos a cos a '
* Здесь и далее, если в условии задачи не указана среда, имеется в виду,
что заряды находятся в вакууме (е=1).
173

Го —расстояние от заряда Qt до стержня. Подставив эти выражения
г и d/ в формулу A), получим
dF = j$?-da. B)
Следует иметь в виду, что dF — вектор, поэтому, прежде чем
интегрировать, разложим его на две составляющие: dF3, перпенди-
перпендикулярную стержню, и dF2, параллельную ему.
Из рис. 13.3 видно, что dF1=dF cos a, dF2=dF sin а. Подстав-
Подставляя значение dF из выражения B) в эти формулы, найдем:
1Г^ Qitcosa
da; dF2 = —A da.
2 4л8/-
00 00
Интегрируя эти выражения в пределах от —р до +Р, получим
„ Г Qit cos a i Qit Г л Q\X . . , + r
f = \ ^1 da = -r-^— \ cos a da ^-r^— sina J=?
1 J 4яе0г0 4ле0г0 J 4яе0г0 • l-Э
J
В силу симметрии расположения заряда Qx относительно стерж-
стержня интегрирования второго выражения дает нуль:
sinada^|
Таким образом, сила, действующая на заряд Ql9
in p. C)
//2 /
Из рис. 13.3 следует, что sinP = = Под-
ставив это выражение sin p в формулу C), получим
Произведем вычисления по формуле D):
г. 10.10-9.Ы0-6 0,3 „ - . 1А 4U АЕГ
f - 2.3,14-8,85.10-12.0,2 /Щ2ЗДР ' 0>
Задачи
Взаимодействие точечных зарядов
13.1. Определить силу взаимодействия двух точечных зарядов
Qi=Q2==l Кл, находящихся в вакууме на расстоянии г=1 м друг
от друга.
174

13.2. Два шарика массой т=0,1 г каждый подвешены в одной
точке на нитях длиной /=20 см каждая. Получив одинаковый заряд,
шарики разошлись так, что нити образовали между собой угол а=
=60°. Найти заряд каждого шарика.
13.3. Два одинаковых заряженных шарика подвешены в одной
точке на нитях одинаковой длины. При этом нити разошлись на
угол а. Шарики погружаются в масло плотностью ро^=8 -102 кг/м3.
Определить диэлектрическую проницаемость е масла, если угол
расхождения нитей при погружении шариков в масло остается не-
неизменным. Плотность материала шариков р = 1,6 • 103 кг/м3.
13.4. Даны два шарика массой т=\ г каждый. Какой заряд Q
нужно сообщить каждому шарику, чтобы сила взаимного отталки-
отталкивания зарядов уравновесила силу взаимного притяжения шариков
по закону тяготения Ньютона? Рассматривать шарики как матери-
материальные точки.
13.5. В элементарной теории атома водорода принимают, что
электрон обращается вокруг ядра по круговой орбите. Определить
скорость v электрона, если радиус орбиты г=53 пм, а также частоту
п вращения электрона.
13.6. Расстояние между двумя точечными зарядами Qx= 1 мкКл
и Q2=—Qi равно 10 см. Определить силу F, действующую на то-
точечный заряд Q=0,l мкКл, удаленный на гг=6 см от первого и на
г2=8 см от второго зарядов.
13.7. В вершинах правильного шестиугольника со стороной
а=10 см расположены точечные заряды Q, 2Q, 3Q, 4Q, 5Q, 6Q (Q=
=0,1 мкКл). Найти силу F, действующую на точечный заряд Q,
лежащий в плоскости шестиугольника и равноудаленный от его
вершин.
13.8. Два одинаковых проводящих заряженных шара находятся
на расстоянии г=60см. Сила отталкивания Ft шаров равна 70мкН.
После того как шары привели в соприкосновение и удалили друг
от друга на прежнее расстояние, сила отталкивания возросла и ста-
стала равной F2=\60 мкН. Вычислить заряды Q± и Q2, которые были
на шарах до их соприкосновения. Диаметр шаров считать много
меньшим расстояния между ними.
13.9. Два одинаковых проводящих заряженных шара находятся
на расстоянии г=30 см. Сила притяжения F± шаров равна 90 мкН.
После того как шары были приведены в соприкосновение и удалены
друг от друга на прежнее расстояние, они стали отталкиваться с
силой /г2=160 мкН. Определить заряды Qi и Q2, которые были на
шарах до их соприкосновения. Диаметр шаров считать много мень-
меньшим расстояния между ними.
13.10. Два положительных точечных заряда Q и 4Q закреплены
на расстоянии /=60 см друг от друга. Определить, в какой точке
на прямой, проходящей через заряды, следует поместить третий
заряд Qi так, чтобы он находился в равновесии. Указать, какой
знак должен иметь этот заряд для того, чтобы равновесие было ус-
устойчивым, если перемещения заряда возможны только вдоль пря-
прямой, проходящей через закрепленные заряды.
175

13Л1. Расстояние / между свободными зарядами Qx= 180 нКл
и Q2=720 нКл равно 60 см. Определить точку на прямой, проходя-
проходящей через заряды, в которой нужно поместить третий заряд Q3 так,
чтобы система зарядов находилась в равновесии. Определить ве-
величину и знак заряда. Устойчивое или неустойчивое будет рав-
равновесие?
13.12. Три одинаковых заряда Q=l нКл каждый расположены
по вершинам равностороннего треугольника. Какой отрицательный
заряд Qx нужно поместить в центре треугольника, чтобы его притя-
притяжение уравновесило силы взаимного отталкивания зарядов? Будет
ли это равновесие устойчивым?
13.13. В вершинах квадрата находятся одинаковые заряды Q—
=0,3 нКл каждый. Какой отрицательный заряд Qx нужно помес-
поместить в центре квадрата, чтобы сила взаимного отталкивания поло-
положительных зарядов была уравновешена силой притяжения отрица-
отрицательного заряда?
Взаимодействие точечного заряда
с зарядом, равномерно распределенным
13.14. Тонкий стержень длиной /=10 см равномерно заряжен.
Линейная плотность т заряда равна 1 мкКл/м. На продолжении оси
стержня на расстоянии а=20 см от ближайшего его конца находится
точечный заряд Q= 100 нКл. Определить силу F взаимодействия
заряженного стержня и точечного заряда.
13.15. Тонкий длинный стержень равномерно заряжен с линей-
линейной плотностью т заряда, равной 10 мкКл/м. На продолжении оси
стержня на расстоянии а=20 см от его конца находится точечный
заряд Q= 10 нКл. Определить силу F взаимодействия заряженного
стержня и точечного заряда.
13.16. Тонкий очень длинный стержень равномерно заряжен с
линейной плотностью т заряда, равной 10 мкКл/м. На перпендику-
перпендикуляре к оси стержня, восставленном из конца его, находится точеч-
точечный заряд Q= 10 нКл. Расстояние а заряда от конца стержня равно
20 см. Найти силу F взаимодействия заряженного стержня и точеч-
точечного заряда.
13.17. Тонкая нить длиной /=20 см равномерно заряжена с ли-
линейной плотностью т=10 нКл/м. На расстоянии а=10 см от нити,
против ее середины, находится точечный заряд Q=l нКл. Вычис-
Вычислить силу F, действующую на этот заряд со стороны заряженной
нити.
13.18. Тонкий длинный стержень равномерно заряжен с линей-
линейной плотностью т=10 мкКл/м. Какова сила F, действующая на то-
точечный заряд Q= 10 нКл, находящийся на расстоянии а=20 см от
стержня, вблизи его середины?
13.19. Тонкая бесконечная нить согнута под углом 90°. Нить
несет заряд, равномерно распределенный с линейной плотностью
т=1 мкКл/м. Определить силу F, действующую на точечный заряд
176

Q=O,1 мкКл, расположенный на* продолжении одной из сторон и
удаленный от вершины угла на а=50 см.
13.20. Тонкое кольцо радиусом /? = 10 см несет равномерно рас-
распределенный заряд Q=0,1 мкКл. На перпендикуляре к плоскости
кольца, восставленном из его середины,' находится точечный заряд
Qt = 10 нКл. Определить силу F, действующую на точечный заряд
Q со стороны заряженного кольца, если он удален от центра кольца
на: 1) /х=20 см; 2) /2=2 м.
13.21. Тонкое полукольцо радиусом R=IO см несет равномерно
распределенный заряд с линейной плотностью т=1 мкКл/м.
В центре кривизны полукольца находится заряд Q=20 нКл. Опре-
Определить силу F взаимодействия точечного заряда и заряженного
полукольца.
13.22. По тонкому кольцу радиусом /? = 10 см равномерно рас-
распределен заряд с линейной плотностью т=1 нКл/м. В центре кольца
находится заряд Q=0,4 мкКл. Определить силу F, растягивающую
кольцо. Взаимодействием зарядов кольца пренебречь.
§ 14. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ
Основные формулы
• Напряженность электрического поля
E=F/Q,
где F — сила, действующая на точечный положительный заряд Q,
помещенный в данную точку поля.
® Сила, действующая на точечный заряд Q, помещенный
в электрическое поле,
F=QE.
Ф Поток вектора напряженности Е электрического поля:
а) через произвольную поверхность S, помещенную в неодно-
неоднородное поле,
ФЕ = J ?cosadS, или OE=^EndS,
Е S
где a — угол между вектором напряженности Е и нормалью п к
элементу поверхности; AS — площадь элемента поверхности; Еп —
проекция вектора напряженности на нормаль;
б) через плоскую поверхность, помещенную в однородное элект-
электрическое поле,
Ф/7— ES cos a.
• Поток вектора напряженности Е через замкнутую поверх-
поверхность
s
где интегрирование ведется по всей поверхности,
177

• Теорема Остроградского — Гаусса. Поток вектора напряжен-
напряженности Е через любую замкнутую поверхность, охватывающую заря-
заряды Qx, Q2, . . ., Qn,
п
где2С/—алгебраическая сумма зарядов, заключенных внутри
замкнутой поверхности; п — число зарядов.
• Напряженность электрического поля, создаваемого точеч-
точечным зарядом Q на расстоянии г от заряда,
? = _!—?-
4ле0 е/-2 •
• Напряженность электрического поля, создаваемого металли-
металлической сферой радиусом R, несущей заряд Q, на расстоянии г
от центра сферы:
а) внутри сферы {r<LR)
?-0;
б) на поверхности сферы {r~R)
f^JL-2-.
4ле0 е#2 '
в) вне сферы {r>R)
?==r I Q т
4ле0 е/2 "
• Принцип суперпозиции (наложения) электрических полей,
согласно которому напряженность Е результирующего поля, создан-
созданного двумя (и более) точечными зарядами, равна векторной (геомет-
(геометрической) сумме напряженностей складываемых полей:
В случае двух электрических полей с напряженностями Ег и
Е2 модуль вектора напряженности
Е = VE\ + Е\ + 2ЕхЕг cos a,
где а — угол между векторами Ef и Е2.
• Напряженность поля, создаваемого бесконечно длинной рав-
равномерно заряженной нитью (или цилиндром) на расстоянии г от
ее оси,
Е== 1 2т
4ле0 ег1
где т — линейная плотность заряда.
Линейная плотность заряда есть величина, равная отношению
заряда, распределенного по нити, к длине нити (цилиндра):
т__Д0
17$

ф Напряженность поля, создаваемого бесконечной равномерно
заряженной плоскостью,
?-1-2-
где о— поверхностная плотность заряда.
Поверхностная плотность заряда есть величина, равная отно-
отношению заряда, распределенного по поверхности, к площади этой
поверхности:
Ф Напряженность поля, создаваемого двумя параллельными
бесконечными равномерно и разноименно заряженными плоскостя-
плоскостями, с одинаковой по модулю поверхностной плотностью а заряда
(поле плоского конденсатора)
F — —
Приведенная формула справедлива для вычисления напряжен-
напряженности поля между пластинами плоского конденсатора (в средней
части его) только в том случае, если расстояние между пластинами
много меньше линейных размеров пластин конденсатора.
ф Электрическое смещение D связано с напряженностью Е
электрического поля соотношением
Это соотношение справедливо только для изотропных диэлект-
диэлектриков.
ф Поток вектора электрического смещения выражается анало-
аналогично потоку вектора напряженности электрического поля:
а) в случае однородного поля поток сквозь плоскую поверхность
A^F^DAS cos a;
б) в случае неоднородного поля и произвольной поверхности
где Dn — проекция вектора D на направление нормали к элементу
поверхности, площадь которой равна dS.
Ф Теорема Остроградского — Гаусса. Поток вектора электри-
электрического смещения сквозь любую замкнутую поверхность, охваты-
охватывающую заряды Qb Q2, . . ., Qn,
2/
i= 1
где п — число зарядов (со своим знаком), заключенных внутри
замкнутой поверхности.
Ф Циркуляция вектора напряженности электрического поля
есть величина, численно равная работе по перемещению единичного
точечного положительного заряда вдоль замкнутого контура. Цир-
Циркуляция выражается интегралом по замкнутому контуру $?jd/,
179

Где el — проекция вектора напряженности Е в данной точке кон-
контура на направление касательной к контуру в той же точке.
В случае электростатического поля циркуляция вектора напря-
напряженности равна нулю:
(f
i
Примеры решения задач
Пример 1. Электрическое поле создано двумя точечными заря-
зарядами: Qi = 30 нКл и Q2=—Ю нКл. Расстояние d между зарядами
равно 20 см. Определить напряженность электрического поля в
точке, находящейся на расстоянии
Гх= 15 см от первого и на расстоя-
расстоянии л-2= Ю см от второго зарядов.
Решение. Согласно принципу
суперпозиции электрических полей,
каждый заряд создает поле незави-
независимо от присутствия в пространстве
других зарядов. Поэтому напряжен-
напряженность Е электрического поля в иско-
искомой точке может быть найдена как
векторная сумма напряженностей Ег и Е2 полей, создаваемых каж-
каждым зарядом в отдельности: E=Ei+E2.
Напряженности электрического поля, создаваемого в вакууме *
первым и вторым зарядами, соответственно равны
4Л8ОГ1 ' 4я80/*|
Вектор Ei (рис. 14.1) направлен по силовой линии от заряда
Qb так как заряд Qi>0; вектор Е2 направлен также по силовой
линии, но к заряду Q2, так как Q2<0.
Модуль вектора Е найдем по теореме косинусов:
14.1
+ Е\ + 2Ег cos a, B)
где угол а может быть найден из треугольника со сторонами гь г2
и d:
2г,г2
В данном случае во избежание громоздких записей вычислим
отдельно значение cos а. По этой формуле найдем
cos a = 0,25.
Подставляя выражения ?х и Е2 по формулам A) в равенство B)
и вынося общий множитель 1/Dяе0) за знак корня, получаем
?
4ле0
т\
* См. сноску на с. 173.
180

Подставив значения величий «., e0, Qx, Q2, r±, r2 и а в последнюю
формулу и произведя вычисления, найдем
Р n lft9i/C0.10-9J AQ.10-)» дC0-10-У
? — уш j/ A5-Ю-2L" A0.10-2L i"ZA5-10-2)
A5-
= 1,67- 104В/м = 16,7 кВ/м.
-10-2J
Пример 2. Электрическое поле создано двумя параллельными
бесконечными заряженными плоскостями с поверхностными плот-
плотностями заряда ах=0,4 мкКл/м2 и а2=0,1 мкКл/м2. Определить
напряженность электрического поля, созданного этими заряженны-
заряженными плоскостями.
Решение. Согласно принципу суперпозиции, поля, созда-
создаваемые каждой заряженной плоскостью в отдельности, накладыва-
накладываются друг на друга, причем каждая заряженная плоскость создает
электрическое поле независимо от при-
присутствия другой заряженной плоско-
сти (рис. 14.2).
Напряженности однородных элек-
электрических полей, создаваемых первой
и второй плоскостями, соответствен-
соответственно равны:
F __ * ai . F 1 а2
-2"
JL
Рис. 14.2
Плоскости делят все пространство
натри области: /. // и ///. Как вид-
видно из рисунка, в первой и третьей
областях электрические силовые линии обоих полей направлены в
одну сторону и, следовательно, напряженности суммарных полей
?(п и ?шп в первой и третьей областях равны между собой и рав-
равны сумме напряженностей полей, создаваемых первой и второй
плоскостями: Е{1)=Етх)=Е1-\-Е%, или
?41) >_ FUI1) __ ^
2 е0
Во второй области (между плоскостями) электрические силовые
линии полей направлены в противоположные стороны и, следова-
следовательно, напряженность поля ЕШ) равна разности напряженностей
полей, создаваемых первой и второй плоскостями: Е{П)=\Е1—?2|,
или
?Ш) ___1 I gi"~q2 t
2 80
Подставив данные и произведя вычисления, получим
?(i) = ?(ш) = 28,3 кВ/м; ?(ш = 17 кВ/м.
Картина распределения силовых линий суммарного поля пред-
представлена на рис. 14.3.
Пример 3. На пластинах плоского воздушного конденсатора
находится заряд Q= 10 нКл. Площадь 5 каждой пластины конден-
181

сатора равна 100 см2. Определить силу F, с которой притягиваются
пластины. Поле между пластинами считать однородным.
Решение. Заряд Q одной пластины находится в поле, соз-
созданном зарядом другой пластины конденсатора. Следовательно, на
первый заряд действует сила (рис. 14.4)
f=?iQ, A)
где Ег — напряженность поля, создаваемого зарядом одной пласти-
пластины. Но Ег — у— — о~с> где а — поверхностная плотность заряда
пластины.
+
+
F
+
+
<
+
Рис. 14.3 Рис. 14.4
Формула A) с учетом выражения для Е± примет вид
Подставив значения величин Q, е0 и S в эту формулу и произведя
вычисления, получим
F-565 мкН.
Пример 4. Электрическое поле создано бесконечной плоскостью,
заряженной с поверхностной плотностью G=400 нКл/м2, и бесконеч-
бесконечной прямой нитью, заряженной с линейной плотностью т=
= 100 нКл/м. На расстоянии г=10 см от нити находится точечный
заряд Q= 10 нКл. Определить силу, действующую на заряд, ее
направление, если заряд и нить лежат в одной плоскости, параллель-
параллельной заряженной плоскости.
Решение. Сила, действующая на заряд, помещенный в поле,
F=EQ, A)
где Е — напряженность поля в точке, в которой находится заряд Q.
Определим напряженность Е поля, создаваемого, по условию
задачи, бесконечной заряженной плоскостью и бесконечной заря-
заряженной нитью. Поле, создаваемое бесконечной заряженной плоско-
плоскостью, однородно, и его напряженность в любой точке
Е -±-2-
г~ 2 80 •
B)
Поле, создаваемое бесконечной заряженной линией, неоднород-
неоднородно. Его напряженность зависит от расстояния и определяется по
182

формуле
т
Согласно принципу суперпозиции электрических полей, напря-
напряженность поля в точке, где находится заряд Q, равна векторной
сумме напряженностей Ех и Е2 (рис. 14.5): E^Ej+Ea. Так как
векторы Ei и Е2 взаимно пер-
перпендикулярны, то ег ?"""/?[?
Подставляя выражения Ei
и Е2 по формулам B) и C) в
это равенство, получим
или
1 _а\2
Te0J -^
1 ,/_о , т2 Рис. 14.5
Теперь найдем силу У7, действующую на заряд, подставив вы-
выражение Е в формулу A):
Подставив значения величин Q, е0, с, т, я и г в формулу D)
и сделав вычисления, найдем
f=289 мкН.
Направление силы /\ действующей на положительный заряд
Q, совпадает с направлением вектора напряженности Е поля.
Направление же вектора Е задается углом а к заряженной пло-
плоскости. Из рис. 14.5 следует, что
tga = —-=znr— , откуда а= zrctg пг —.
Подставив значения величин я, г, а и т в это выражение и
вычислив, получим
а = 51°34\
Пример 5. Точечный заряд Q=25 нКл находится в поле, соз-
созданном прямым бесконечным цилиндром радиусом R = \ см, рав-
равномерно заряженным с поверхностной плотностью о=2 мкКл/м2.
Определить силу, действующую на заряд, помещенный от оси
Цилиндра на расстоянии г= 10 см.
Решение. Сила, действующая на заряд Q, находящийся
в поле,
F=QE, A)
где Е — напряженность поля в точке, в которой находится за-
Ряд Q.
183

Как известно, напряженность поля бесконечно длинного рав-
равномерно заряженного цилиндра
?=т/Bяе0г), B)
где т — линейная плотность заряда.
Выразим линейную плотность т через поверхностную плот-
плотность а. Для этого выделим элемент цилиндра длиной / и выразим
находящийся на нем заряд Qx двумя способами:
Q1=cS = o-2nRl и Q1=tl.
Приравняв правые части этих равенств, получим %l=2nRlo. После
сокращения на / найдем r=2nRo. С учетом этого формула B) при-
примет вид E=Ro/(eor). Подставив это выражение Е в формулу A),
найдем искомую силу:
F=QoR/(e0r). C)
Так как R и г входят в формулу в виде отношения, то они могут
быть выражены в любых, но только одинаковых единицах.
Выполнив вычисления по формуле C), найдем
/? = 25-10-92. Ю-10/(8,85- Ю-12-10-10~2) Н =
Направление силы F совпадает с направлением вектора напря-
напряженности Е, а последний в силу симметрии (цилиндр бесконечно
длинный) направлен перпендикулярно цилиндру.
Пример 6. Электрическое поле создано тонкой бесконечно
длинной нитью, равномерно заряженной с линейной плотностью
т=30 нКл/м. На расстоянии а==20 см от нити находится плоская
круглая площадка радиусом г=\ см. Определить поток вектора
напряженности через эту площадку, если плоскость ее составляет
угол |3=ЗО° с линией напряженности, проходящей через середину
площадки.
Решение. Поле, создаваемое бесконечно равномерно заря-
заряженной нитью, является неоднородным. Поток вектора напряжен-
напряженности в этом случае выражается интегралом
<D?=$?ndS, (I)
S
где Еп — проекция вектора Е на нормаль п к поверхности площад-
площадки dS. Интегрирование выполняется по всей поверхности площад-
площадки, которую пронизывают линии напряженности.
Проекция Еп вектора напряженности равна, как видно из
рис. 14.6,
Еп=Е cos a,
где а — угол между направлением вектора и нормалью п.
С учетом этого формула A) примет вид
s
Так как размеры поверхности площадки малы по сравнению
с расстоянием до нити (г<С#), то электрическое поле в пределах
184

площадки можно считать практически однородным. Следователь-
Следовательно, вектор напряженности Е очень мало меняется по модулю и на-
направлению в пределах площадки, что позволяет заменить под
знаком интеграла значения Е и cos a j
их средними значениями (Е) и (cos a)
и вынести их за знак интеграла:
Ф?= $ <?><cosa>dS =
s
= <?><cosa>
Выполняя интегрирование и за-
заменяя (Е) и (cos a) их приближен-
приближенными значениями ЕА и cos ал, вы-
вычисленными для средней точки пло-
площадки, получим
ФЕ — ЕА cos a 4 S = яг2 ЕА cos ал.
B)
Напряженность Ел вычисляется по формуле Ел = 2ле а*
рис. 14.6 следует cosc/M=cosfy—P) = sin|3.
С учетом выражения Ел и cos осл равенство B) примет вид
ф — Sill О, ИЛИ Of=t; Sin!
Рис. 14.6
2ле0а
Подставив в последнюю формулу данные и произведя вычис-
вычисления, найдем
Фя=424 мВ-м.
Пример 7. Две концентрические проводящие сферы радиуса-
радиусами Rx=6 см и i?2= 10 см несут соответственно заряды Qx= 1 нКл
и Q2= —0,5 нКл. Найти напряженность
Е поля в точках, отстоящих от центра
сфер на расстояниях гх = 5 см, г2=9 см
иг3=15см. Построить график Е(г).
Решение. Заметим, что точки,
в которых требуется найти напряжен-
напряженности электрического поля, лежат в трех
областях (рис. 14.7): область / (r</?i),
область // (J?i<r2<i?2), область ///
^е.
ш
Рис. 14 7 1. Для определения напряженности
Ег в области / проведем сферическую
поверхность Sx радиусом гг и воспользуемся теоремой Остроград-
Остроградского — Гаусса. Так как внутри области / зарядов нет, то сог-
согласно указанной теореме получим равенство
A)
185

где Еп — нормальная составляющая напряженности электрического
поля.
Из соображений симметрии нормальная составляющая Еп долж-
должна быть равна самой напряженности и постоянна для всех точек
сферы, т. е. Еп=Е1=const. Поэтому ее можно вынести за знак
интеграла. Равенство A) примет вид
f
Si
Так как площадь сферы не равна нулю, то
?i=0,
т. е. напряженность поля во всех точках, удовлетворяющих усло-
условию /y<7?i, будет равна нулю.
2. В области II сферическую поверхность проведем радиу-
радиусом г2. Так как внутри этой поверхности находится заряд Qu то
для нее, согласно теореме Остроградского — Гаусса, можно за-
записать равенство
ndS = Q1/e0. B)
Так как ?ln=?12=const, то из условий симметрии следует
Е (р dS = Q1/e0, или ES2 = Qje0,
откуда
E2=Qi/(eQS2).
Подставив сюда выражение площади сферы, получим
О' 2/ • \<Э)
3. В области /// сферическую поверхность проведем радиу-
радиусом г3. Эта поверхность охватывает суммарный заряд Qi+Q2.
Следовательно, для нее уравнение, записанное на основе теоремы
Остроградского — Гаусса, будет иметь вид
>->з
Отсюда, использовав положения, примененные в первых двух
случаях, найдем
Е3 = (Q1-\-Q2)/(Am0rl). D)
Убедимся в том, что правые части равенств C) и D) дают единицу
напряженности электрического поля:
[О] 1 Кл 1 Кл
[ео][г2] 1Ф/м-1м2 1Ф-1м
Выразим все величины в единицах СИ (Qi= 10~9 Кл, Q2=—0,5х
Х1О~9 Кл, Гх—0,09 м, г2=15 м, 1/Dяго)=9-1О9 м/Ф) и произведем
вычисления:
Е2 = 9- Ю9-ппш2 В/м— 1,11 - Ю3 В/м= 1,11 кВ/м;
?3 = 9-10* ° ~@°;^21()9 В/м = 200 В/м,
186

4. Построим график Е (г). В области I (r^Ri) напряженность
?=0. В области // (Ri^r<iR2) напряженность Е2(г) изменяется по
закону 1/г2. В точке r=Rx напряженность ?2(/?i)=Qi/DJte0/?f)=
=2500 В/м.В точке r=R2 (r стремится к R2 слева) E2(R2) =
Q1/(ine0Rl)=900B/M. В области /// {r>R2) E3(r) изменяется по за-
закону 1/г2, причем в точке r=R2 (r стремится к R2 справа)
Es(Rz) = (Qi — IQsl)/Dneo/?l) = 450
В/м. Таким образом, функция Е(г) Е,В/М1
в точках г = Rt и r=R2 терпит 2500
разрыв. График зависимости Е(г)
представлен на рис. 14.8
Задачи
900
Напряженность поля точечных 450
зарядов
й R г
14.1. Определить напряжен- f 2
ность? электрического поля, созда- Рис- 14*8
ваемого точечным зарядом Q=
= 10 нКл на расстоянии г—10 см от него. Диэлектрик — масло.
14.2. Расстояние d между двумя точечными зарядами Qi—+8 нКл
и Q<l=—5,3 нКл равно 40 см. Вычислить напряженность Е поля в
точке, лежащей посередине между зарядами. Чему равна напря-
напряженность, если второй заряд будет положительным?
14.3. Электрическое поле создано двумя точечными зарядами
Qi= 10 нКл и Q2=—20 нКл, находящимися на расстоянии d=20 см
друг от друга. Определить напряженность Е поля в точке, удален-
удаленной от первого заряда на гх=30 см и от второго на г2=50 см.
14.4. Расстояние d между двумя точечными положительными за-
зарядами Qi=9Q и Q2=Q равно 8 см. На каком расстоянии г от перво-
первого заряда находится точка, в которой напряженность Е поля заря-
зарядов равна нулю? Где находилась бы эта точка, если бы второй заряд
был отрицательным?
14.5. Два точечных заряда Qt=2Q и Q2=—Q находятся на рас-
расстоянии d друг от друга. Найти положение точки на прямой, про-
проходящей через эти заряды, напряженность Е поля в которой равна
нулю.
14.6. Электрическое поле создано двумя точечными зарядами
Qi=40 нКл и Q2=—10 нКл, находящимися на расстоянии d^=10 см
друг от друга. Определить напряженность Е поля в точке, удален-
удаленной от первого заряда на гх= 12 см и от второго на г2=6 см.
Напряженность поля заряда, распределенного по кольцу и сфере
14.7. Тонкое кольцо радиусом R=8 см несет заряд, равномерно
распределенный с линейной плотностью т=10 нКл/м. Какова на-
напряженность Е электрического поля в точке, равноудаленной от
всех точек кольца на расстояние г= 10 см?
187

14.8. Полусфера несет заряд, равномерно распределенный с по-
поверхностной плотностью а=1 нКл/м2. Найти напряженность Е
электрического поля в геометрическом центре полусферы.
14.9. На металлической сфере радиусом # = 10 см находится
заряд Q=l нКл. Определить напряженность Е электрического поля
в следующих точках: 1) на расстоянии гг=8 см от центра сферы;
2) на ее поверхности; 3) на расстоянии г2= 15 см от центра сферы.
Построить график зависимости Е от г.
14.10. Две концентрические металлические заряженные сферы
радиусами R±=6 см и R2=l0 см несут соответственно заряды Qi =
= 1 нКл и Q2=—0,5 нКл. Найти напряженности Е поля в точках,
отстоящих от центра сфер на расстояниях гг=5 см, га=9 см, г3=
= 15 см. Построить график зависимости Е(г).
Напряженность поля заряженной линии
14.11. Очень длинная тонкая прямая проволока несет заряд,
равномерно распределенный по всей ее длине. Вычислить линейную
плотность т заряда, если напряженность Е поля на расстоянии а=
=0,5 м от проволоки против ее середины равна 200 В/м.
14.12. Расстояние d между двумя длинными тонкими проволо-
проволоками, расположенными параллельно друг другу, равно 16 см. Про-
Проволоки равномерно заряжены разноименными зарядами с линейной
плотностью |т|=150 мкКл/м. Какова напряженность Е поля в точ-
точке, удаленной на г= 10 см как от первой, так и от второй проволоки?
14.13. Прямой металлический стержень диаметром d=5 см и
длиной 1=4 м несет равномерно распределенный по его поверхности
заряд Q=500 нКл. Определить напряженность Е поля в точке,
находящейся против середины стержня на расстоянии а=\ см от
его поверхности.
14.14. Бесконечно длинная тонкостенная металлическая трубка
радиусом R=2 см несет равномерно распределенный по поверхно-
поверхности заряд (а=1 нКл/м2). Определить напряженность Е поля в точ-
точках, отстоящих от оси трубки на расстояниях гх= 1 см, г2=3 см.
Построить график зависимости Е(г).
14.15. Две длинные тонкостенные коаксиальные трубки радиуса-
радиусами /?i=2 см и #2=4 см несут заряды, равномерно распределенные
по длине с линейными плотностями Tj=l нКл/м и т2=—0,5 нКл/м.
Пространство между трубками заполнено эбонитом. Определить
напряженность Е поля в точках, находящихся на расстояниях гг =
= 1 см, г2=3 см, г3=5 см от оси трубок. Построить график зависимо-
зависимости Е от г.
14.16. На отрезке тонкого прямого проводника длиной /=10 см
равномерно распределен заряд с линейной плотностью т=3 мкКл/м.
Вычислить напряженность Е, создаваемую этим зарядом в точке,
расположенной на оси проводника и удаленной от ближайшего кон-
конца отрезка на расстояние, равное длине этого отрезка.
14.17. Тонкий стержень длиной /=12 см заряжен с линейной
плотностью т=200 нКл/м. Найти напряженность Е электрического
188

поля в точке, находящейся на расстоянии г=5 см от стержня против
его середины.
14.18. Тонкий стержень длиной /=10 см заряжен с линейной
плотностью т=400 нКл/м. Найти напряженность Е электрического
поля в точке, расположенной на перпендикуляре к стержню, про-
проведенном через один из его концов, на расстоянии г=8 см от этого
конца.
14.19. Электрическое поле создано зарядом тонкого равномерно
заряженного стержня, изогнутого по трем сторонам квадрата (рис.
14.9.). Длина а стороны квадрата равна 20 см. Линейная плотность
т зарядов равна 500 нКл/м. Вычислить напряженность Е поля в
точке А.
-44
Рис. 14.9 Рис. 14.10
14.20. Два прямых тонких стержня длиной /г= 12 см и /2=16 см
каждый заряжены с линейной плотностью т=400 нКл/м. Стержни
образуют прямой угол. Найти напряженность Е поля в точке А
(рис. 14.10).
Напряженность поля заряженной плоскости
14.21. Электрическое поле создано двумя бесконечными парал-
параллельными пластинами, несущими одинаковый равномерно распре-
распределенный по площади заряд @=1 нКл/м2). Определить напряжен-
напряженность Е поля: 1) между пластинами; 2) вне пластин. Построить
график изменения напряженности вдоль линии, перпендикулярной
пластинам.
14.22. Электрическое поле создано двумя бесконечными парал-
параллельными пластинами, несущими равномерно распределенный по
площади заряд с поверхностными плотностями ог=1 нКл/м2 и о2—
=3 нКл/м2. Определить напряженность Е поля: 1) между пластина-
пластинами; 2) вне пластин. Построить график изменения напряженности
вдоль линии, перпендикулярной пластинам.
14.23. Электрическое поле создано двумя бесконечными парал-
параллельными пластинами, несущими равномерно распределенный по
площади заряд с поверхностными плотностями о±=2 нКл/м2 и
<т2=—5 нКл/м2. Определить напряженность Е поля: 1) между
пластинами; 2) вне пластин. Построить график изменения напря-
напряженности вдоль линии, перпендикулярной пластинам.
14.24. Две прямоугольные одинаковые параллельные пластины,
Длины сторон которых а=10 см и 6 = 15 см, расположены на малом
189

(по сравнению с линейными размерами пластин) расстоянии друг
от друга. На одной из пластин равномерно распределен заряд Qx—
=50 нКл, на другой — заряд Q2= 150 нКл. Определить напряжен-
напряженность Е электрического поля между пластинами.
14.25. Две бесконечные параллельные пластины равномерно за-
заряжены с поверхностной плотностью ах=10 нКл/м2 и а2=
=—30 нКл/м2. Определить силу взаимодействия между пластина-
пластинами, приходящуюся на площадь 5, равную 1 м2.
14.26. Две круглые параллельные пластины радиусом R = IO см
находятся на малом (по сравнению с радиусом) расстоянии друг от
друга. Пластинам сообщили одинаковые по модулю, но противо-
противоположные по знаку заряды |QX |== IQa 1==Q- Определить этот заряд
Q, если пластины притягиваются с силой F=2 мН. Считать, что
заряды распределяются по пластинам равномерно.
Напряженность поля заряда, распределенного по объему
14.27. Эбонитовый сплошной шар радиусом R=5 см несет заряд,
равномерно распределенный с объемной плотностью р= 10 нКл/м3.
Определить напряженность Е и смещение D электрического поля
в точках: 1) на расстоянии ri=3 см от центра сферы; 2) на поверхно-
поверхности сферы; 3) на расстоянии г2=10 см от центра сферы. Построить
графики зависимостей Е(г) и D(r).
14.28. Полый стеклянный шар несет равномерно распределенный
по объему з^ряд. Его.объемная плотность р=100 нКл/м3. Внутрен-
Внутренний радиус Ri шара равен 5 см, наружный — /?а=10 см. Вычислить
напряженность Е и смещение D электрического поля в точках, от*
стоящих от центра сферы на расстоянии: 1) гг=3 см; 2) г2=6 см;
3)г3=12см. Построить графики зависимо-
зависимостей E(r) uD (г).
14.29. Длинный парафиновый цилиндр
радиусом R=2 см несет заряд, равномер-
равномерно распределенный по объему с объемной
плотностью р= 10 нКл/м3. Определить на-
напряженность Е и смещение D электричес-
электрического поля в точках, находящихся от оси
цилиндра на расстоянии: 1) гг=\ см; 2) г2—
=3 см. Обе точки равноудалены от концов
цилиндра. Построить графики зависимо-
зависимостей Е (г) и D (г).
14.30. Большая плоская пластина толщиной d=l см несет заряд,
равномерно распределенный по объему с объемной плотностью
р= 100 нКл/м3. Найти напряженность Е электрического поля:
вблизи центральной части пластины вне ее, на малом расстоянии от
поверхности.
14.31. Лист стекла толщиной d=2 см равномерно заряжен с объ-
объемной плотностью р=1 мкКл/м3. Определить напряженность Е и
смещение D электрического поля в точках Л, В, С (рис. 14.11).
Построить график зависимости Е(х) (ось х координат перпендику-
перпендикулярна поверхности листа стекла).
190
Рис. 14.11

Метод зеркальных изображений
14.32. На некотором расстоянии а=5 см от бесконечной проводя-
проводящей плоскости находится точечный заряд Q=l нКл. Определить
силу F, действующую на заряд со стороны индуцированного им за-
заряда на плоскости.
14.33. На расстоянии а=\0 см от бесконечной проводящей плос-
плоскости находится точечный заряд Q=20 нКл. Вычислить напряжен-
напряженность Е электрического поля в точке, удаленной от плоскости на
расстояние а и от заряда Q на расстояние 2а.
14.34. Точечный заряд Q=40 нКл находится на расстоянии а=
=30 см от бесконечной проводящей плоскости. Какова напряжен-
напряженность Е электрического поля в точке А (рис. 14.12)?
•гт
///////////////////////77/
i
Рис. 14.12
Рис. 14.13
14.35. Большая металлическая пластина расположена в верти-
вертикальной плоскости и соединена с землей (рис. 14.13). На расстоянии
а=10 см от пластины находится неподвижная точка, к которой на
нити длиной /= 12 см подвешен маленький шарик массой т=0,1 г.
При сообщении шарику заряда Q он притянулся к пластине, в ре-
результате чего нить отклонилась от вертикали на угол а=30°. Най-
Найти заряд Q шарика.
Сила, действующая на заряд в электрическом поле
14.36. Тонкая нить несет равномерно распределенный по длине
заряд с линейной плотностью х=2 мкКл/м. Вблизи средней части
нити на расстоянии /-=1 см, малом по сравнению с ее длиной, нахо-
находится точечный заряд Q=0,l мкКл. Определить силу F, действую-
действующую на заряд.
191

14.37. Большая металлическая пластина несет равномерно рас-
распределенный по поверхности заряд (а=10 нКл/м2). На малом рас-
расстоянии от пластины находится точечный заряд Q= 100 нКл. Найти
силу F, действующую на заряд.
14.38. Точечный заряд Q=l мкКл находится вблизи большой
равномерно заряженной пластины против ее середины. Вычислить
поверхностную плотность а заряда пластины, если на точечный заряд
действует сила F=60 мН.
14.39. Между пластинами плоского конденсатора находится то-
точечный заряд Q=30 нКл. Поле конденсатора действует на заряд с
силой F±=l0 мН. Определить силу F2 взаимного притяжения плас-
пластин, если площадь S каждой пластины равна 100 см2.
14.40. Параллельно бесконечной пластине, несущей заряд, рав-
равномерно распределенный по площади с поверхностной плотностью
g=2Q нКл/м2, расположена тонкая нить с равномерно распределен-
распределенным по длине зарядом (т=0,4 нКл/м). Определить силу /, дейст-
действующую на отрезок нити длиной 1=1 м.
14.41. Две одинаковые круглые пластины площадью по S= 100 см2
каждая расположены параллельно друг другу. Заряд Qx одной пла-
пластины равен +100 нКл, другой Q2=—100 нКл. Определить силу F
взаимного притяжения пластин в двух случаях, когда расстояние
между ними: 1) гг=2 см; 2) г2=10 м.
14.42. Плоский конденсатор состоит из двух пластин, разделен-
разделенных стеклом. Какое давление р производят пластины на стекло перед
пробоем, если напряженность Е электрического поля перед пробоем
равна 30 МВ/м?
14.43. Две параллельные, бесконечно длинные прямые нити
несут заряд, равномерно распределенный по длине с линейными
плотностями T!=0,l мкКл/м и т2=0,2 мкКл/м. Определить силу F
взаимодействия, приходящуюся на отрезок нити длиной 1 м. Рас-
Расстояние г между нитями равно 10 см.
14.44. Прямая, бесконечная, тонкая нить несет равномерно рас-
распределенный по длине заряд (t^l мкКл/м). В плоскости, содержа-
содержащей нить, перпендикулярно нити находится тонкий стержень дли-
длиной /. Ближайший к нити конец стержня находится на расстоянии
/ от нее. Определить силу F, действующую на стержень, если он
заряжен с линейной плотностью т2=0,1 мкКл/м.
14.45. Металлический шар имеет заряд Qx=0,l мкКл. На рас-
расстоянии, равном радиусу шара, от его поверхности находится конец
нити, вытянутой вдоль силовой линии. Нить несет равномерно рас-
распределенный но длине заряд Q2=10 нКл. Длина нити равна радиусу
шара. Определить силу F, действующую на нить, если радиус R
шара равен 10 см.
14.46. Соосно с бесконечной прямой равномерно заряженной
линией (^=0,5 мкКл/м) расположено полукольцо с равномерно
распределенным зарядом (т2=20 нКл/м). Определить силу F взаимо-
взаимодействия нити с полукольцом.
14.47. Бесконечная прямая нить несет равномерно распреде-
распределенный заряд с линейной плотностью Тх=1 мкКл/м. Соосно с ни-
192

тью расположено тонкое кольцо, заряженное равномерно с линей-
линейной плотностью т2=10 нКл/м. Определить силу F, растягивающую
кольцо. Взаимодействием между отдельными элементами кольца
пренебречь.
14.48. Две бесконечно длинные равномерно заряженные тонкие
нити (т1=т2=т=1 мкКл/м) скрещены под прямым углом друг к дру-
другу. Определить силу F их взаимодействия.
Поток напряженности и поток электрического смещения
14.49. Бесконечная плоскость несет заряд, равномерно распре-
распределенный с поверхностной плотностью о=\ мкКл/м2. На некотором
расстоянии от плоскости параллельно ей расположен круг радиусом
г=\0 см. Вычислить поток ФЕ вектора напряженности через этот
круг.
14.50. Плоская квадратная пластина со стороной длиной а,
равной 10 см, находится на некотором расстоянии от бесконечной
равномерно заряженной (о=1 мкКл/м2) плоскости. Плоскость пла-
пластины составляет угол C=30° с линиями поля. Найти поток Чг эле-
электрического смещения через эту пластину.
14.51. В центре сферы радиусом R=20 см находится точечный
заряд Q= 10 нКл. Определить поток ФЕ вектора напряженности
через часть сферической поверхности площадью S = 20 см2.
14.52. В вершине конуса с телесным углом со=0,5 ср находится
точечный заряд Q=30 нКл. Вычислить поток W электрического
смещения через площадку, ограниченную линией пересечения по-
поверхности конуса с любой другой поверхностью.
14.53. Прямоугольная плоская площадка со сторонами, длины
а и Ь которых равны 3 и 2 см соответственно, находится на рассто-
расстоянии R = \ м от точечного заряда Q=l мкКл. Площадка ориентиро-
ориентирована так, что линии напряженности составляют }<гол ос=30° с ее
поверхностью. Найти поток ФЕ вектора напряженности через
площадку.
14.54. Электрическое поле создано точечным зарядом
Q=0,1 мкКл. Определить поток W электрического смещения че-
через круглую площадку радиусом R=30 см. Заряд равноудален от
краев площадки и находится на расстоянии а=40 см от ее цент-
центра.
14.55. Заряд Q=l мкКл равноудален от краев круглой пло-
площадки на расстоянии г=20 см. Радиус R площадки равен 12 см.
Определить среднее значение напряженности (Е) в пределах пло-
площадки.
14.56. Электрическое поле создано бесконечной прямой равно-
равномерно заряженной линией (т=0,3 мкКл/м). Определить поток Т
электрического смещения через прямоугольную площадку, две
большие стороны которой параллельны заряженной линии и оди-
одинаково удалены от нее на расстояние г=20 см. Стороны площадки
имеют размеры а=20 см, Ь=40 см.
7 лъ 1268 193

§ 15. ПОТЕНЦИАЛ. ЭНЕРГИЯ СИСТЕМЫ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ.
РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА В ПОЛЕ
Основные формулы
• Потенциал электрического поля есть величина, равная отно-
отношению потенциальной энергии точечного положительного заряда,
помещенную в данную точку поля, к этому заряду:
q>=II/Q,
или потенциал электрического поля есть величина, равная отноше-
отношению работы сил поля по перемещению точечного положительного
заряда из данной точки поля в бесконечность к этому заряду:
Ф-Л/Q.
Потенциал электрического поля в бесконечности условно при-
принят равным нулю.
Отметим, что при перемещении заряда в электрическом поле
работа Лп# с внешних сил равна по модулю работе АСг п сил поля
и противоположна ей по знаку:
• Потенциал электрического поля, создаваемый точечным за-
зарядом Q на расстоянии г от заряда,
• Потенциал электрического поля, создаваемого металличе-
металлической, несущей заряд Q сферой радиусом R, на расстоянии г от центра
сферы:
внутри сферы (г < R) <р = ^^ ;
на поверхности сферы (г = §
вне сферы (г > R)
Во всех приведенных для потенциала заряженной сферы форму-
формулах е есть диэлектрическая проницаемость однородного безгранич-
безграничного диэлектрика, окружающего сферу.
• Потенциал электрического поля, созданного системой п
точечных зарядов, в данной точке в соответствии с принципом су-
суперпозиции электрических полей равен алгебраической сумме
потенциалов <рь ср2, . . ., <рп, создаваемых отдельными точечными
зарядами Qb Q2, . . ., Qn:
• Энергия W взаимодействия системы точечных зарядов Qu
Q2, . . ., Qn определяется работой, которую эта система зарядов
может совершить при удалении их относительно друг друга в бес-
194

конечность, и выражается формулой
где фг — потенциал поля, создаваемого всеми п—1 зарядами
(за исключением /-го) в точке, где расположен заряд Qt.
9 Потенциал связан с напряженностью электрического поля
соотношением
Е= —grad ф.
В случае электрического поля, обладающего сферической сим-
симметрией, эта связь выражается формулой
_dcp г
с~ dr 7>
или в скалярной форме
р_ <*ф
^~ dr '
а в случае однородного поля, т. е. поля, напряженность которого
в каждой точке его одинакова как по модулю, так и по направле-
направлению,
где Ф1 и ф2 — потенциалы точек двух эквипотенциальных поверх-
поверхностей; d — расстояние между этими поверхностями вдоль электри-
электрической силовой линии.
• Работа, совершаемая электрическим полем при перемещении
точечного заряда Q из одной точки поля, имеющей потенциал фь
в другую, имеющую потенциал ф2,
А = Q (фх — ф2), или А = Q J Еь d/,
L
где Еi — проекция вектора напряженности Е на направление
перемещения; d/ — перемещение.
В случае однородного поля последняя формула принимает вид
A=QEl cos a,
где I — перемещение; а — угол между направлениями вектора Е
и перемещения 1.
Примеры решения задач
Пример 1. Положительные заряды Q!=3 мкКл и Q2—20 нКл
находятся в вакууме на расстоянии Гг=1у5 м друг от друга. Опре-
Определить работу Л', которую надо совершить, чтобы сблизить заряды
до расстояния г2=\ м.
Решение. Положим, что первый заряд Qx остается неподвиж-
неподвижным, а второй Q2 под действием внешних сил перемещается в поле,
созданном зарядом Qb приближаясь к нему с расстояния гх=1,5 м
до г2=1 м.
7* 195

Работа А' внешней силы по перемещению заряда Q из одной
точки поля с потенциалом q^ в другую, потенциал которой ф2, равна
по модулю и противоположна по знаку работе А сил поля по пере-
перемещению заряда между теми же точками:
А'^—А.
Работа А сил поля по перемещению заряда A^Q^ — ср2).
Тогда работа А' внешних сил может быть записана в виде
А'== -Q(9i — Фа)=<2(фа — <Pi). A)
Потенциалы точек начала и конца пути выразятся формулами
^2 4Я80Г2 '
Подставляя выражения ф* и ф2 в формулу A) и учитывая, что
для данного случая переносимый заряд Q=Q2, получим
Fl&^ 2 ___,
Если учесть, что 1/Dя80)=9«109 м/Ф, то после подстановки зна-
значений величин в формулу B) и вычисления найдем
_4' = 180 мкДж.
Пример 2. Найти работу А поля по перемещению заряда Q —
= 10 нКл из точки 1 в точку 2 (рис. 15.1), находящиеся между двумя
__,*• разноименно заряженными с поверх-
поверхностной плотностью а=0,4 мкКл/м2
бесконечными параллельными плос-
плоски. -^ _. * костями, расстояние / между которы-
-- ^^ — ми равно 3 см.
~6 Решение. Возможны два спо-
Рис. 15.1 соба решения задачи.
1-й способ. Работу сил поля по пе-
перемещению заряда Q из точки 1 поля с потенциалом фх в точку 2
поля с потенциалом ф2 найдем по формуле
Для определения потенциалов в точках 1 и 2 проведем через эти
точки эквипотенциальные поверхности I и II. Эти поверхности
будут плоскостями, так как поле между двумя равномерно заряжен-
заряженными бесконечными параллельными плоскостями однородно. Для
такого поля справедливо соотношение
<Pi — Ч>2=Е1, B)
где Е — напряженность поля; /—расстояние между эквипотен-
эквипотенциальными поверхностями.
Напряженность поля между параллельными бесконечными раз-
разноименно заряженными плоскостями Е=о/е0. Подставив это выра-
выражение Е в формулу B) и затем выражение ф* — ф2 в формулу A),
получим
-4=Q(a/e0)/.
2-й способ. Так как поле однородно, то сила, действующая на
заряд Q, при его перемещении постоянна. Поэтому работу переме-
196

щения заряда из точки 1 в точку 2 можно подсчитать по формуле
A=FArcosa, C)
где F — сила, действующая на заряд; Дг — модуль перемещения
заряда Q из точки / в точку 2; а — угол между направлениями пе-
перемещения и силы. Но F = QE = Q^-. Подставив это выражение F
в равенство C), а также заметив, что Ar cos a=/, получим
A=Q(o/e0)L D)
Таким образом, оба решения приводят к одному и тому же ре-
результату.
Подставив в выражение D) значение величин Q, a, s0 и /, найдем
/1 = 13,6 мкДж.
Пример 3. По тонкой нити, изогнутой по дуге окружности ра-
радиусом R, равномерно распределен заряд с линейной плотностью
т=10 нКл/м. Определить на- А
пряженность Е и потенциал ^J
ср электрического поля, соз-
создаваемого таким распределен-
распределенным зарядом в точке О, сов-
совпадающей с центром кривизны
дуги. Длина / нити составля-
составляет 1/3 длины окружности и
равна 15 см.
Решение. Выберем оси
координат так, чтобы начало
координат совпадало с цент-
центром кривизны дуги, а ось у
была симметрично расположе-
расположена относительно концов дуги
(рис. 15.2). На нити выделим элемент длины d/. Заряд dQ=xd/, на-
находящийся на выделенном участке, можно считать точечным.
Определим напряженность электрического поля в точке О. Для
этого найдем сначала напряженность dE поля, создаваемого заря-
зарядом dQ:
id/ i
Рис. 15.2
dE-
4Л8ОГ2
где г — радиус-вектор, направленный от элемента d/ к точке, напря-
напряженность в которой вычисляется. Выразим вектор dE через проек-
проекции dEx и dEy на оси координат:
где i и j — единичные векторы направлений (орты).
Напряженность Е найдем интегрированием:
I I I
Интегрирование ведется вдоль дуги длины /. В силу симметрии ин-
197

теграл ^ d?* равен нулю. Тогда
где АЕу s= d? cos •& — 41^[2 cos ft. Так как r=R=const и d/=#du, то
Подставим найденное выражение d?^ в A) и, приняв во внимание
симметричное расположение дуги относительно оси Оу, пределы
интегрирования возьмем от 0 до я/3, а результат удвоим:
я/3
j
Подставив указанные пределы и выразив R через длину дуги
=2nR), получим
Из этой формулы видно, что вектор Е совпадает с положительным
направлением оси Оу. Подставив значение т и / в последнюю фор-
формулу и сделав вычисления, найдем
?-2,18 кВ/м.
Определим потенциал электрического поля в точке О. Найдем
сначала потенциал dcp, создаваемый точечным зарядом dQ в точке О:
Заменим г на R и произведем интегрирование!
9 = rE_fd/ * .
О
Так как l=2nR/3, то
Ф=т/Fе0).
Произведя вычисления по этой формуле, получим
Ф=188 В.
Пример 4. Электрическое поле создано длинным цилиндром
радиусом R — 1 см, равномерно заряженным с линейной плотностью
т=20 нКл/м. Определить разность потенциалов двух точек этого
поля, находящихся на расстояниях #1=0,5 см v #2=2 см от поверх-
поверхности цилиндра, в средней его части.
Решение. Для определения разности потенциалов восполь-
воспользуемся соотношением между напряженностью поля и изменением
потенциала Е= —grad ф. Для поля с осевой симметрией, каким
является поле цилиндра, это соотношение можно записать в виде
Е = — -j2., или dф = — ЕАг.
198

Интегрируя последнее выражение, найдем разность потенциа-
потенциалов двух точек, отстоящих на г± и г2 от оси цилиндра:
Ф2—<Pi = —$?dr. A)
Г!
Так как цилиндр длинный и точки взяты вблизи его средней
части, то для выражения напряженности поля можно воспользо-
воспользоваться формулой ?=9 * Подставив это выражение Е в равен-
равенство A), получим
С dr % л Го
А = -2^1п7? илн
Так как величины г2 и г± входят в формулу в виде отношения,
то их можно выразить в любых, но только одинаковых единицах:
r1=R+a1=lf5 см; r2=R-\-a2~3 см.
Подставив значения величин т, е0, гг и г2 в формулу B) и вы-
вычислив, найдем
ф1_ф2^250 В.
Пример 5. Электрическое поле создано тонким стержнем, не-
несущим равномерно распределенный по длине заряд т=0,1 мкКл/м.
Определить потенциал ср поля в точке, удаленной от концов стержня
на расстояние, равное длине стержня.
Решение. Заряд, находящийся на стержне, нельзя считать
точечным, поэтому непосредственно применить для вычисления по-
потенциала формулу
* = A)
справедливую только для точечных зарядов, нельзя. Но если раз-
разбить стержень на элементарные отрезки d/, то заряд тс1/, находя-
находящийся на каждом из них, можно рассматривать как точечный и то-
тогда формула A) будет справедлива. Применив эту формулу, полу-
получим
где г — расстояние точки, в которой определяется потенциал, до
элемента стержня.
Из рис. 15.3 следует, что dl = — . Подставив это выражение
cos ос
d/ в формулу B), найдем
Интегрируя полученное выражение в пределах от а? до а2,
получим потенциал, создаваемый всем зарядом, распределенным
199

'на стержне:
— Г Tda — т Г
^ j 4ле0 cos а ~~ 4ле0 J
cos a"
В силу симметрии расположения точки А относительно концой
А к dip
стержня имеем
a 2 ax
и поэтому
cos a
_da_
cos a*
J
0
Следовательно,
a,
2т С da
4л?
0 j cos a'
о
Так как
Г da
Рис. 15.3
J cos a °
(см. табл. 2), то
Ф = ~л In tg ( — -
Y 4л8л ъ\ 2
Подставляя пределы интегрирования, получим
__ 2т
^ ~~ 4Л8О
Сделав вычисления по этой формуле, найдем
Ф-990 В.
Пример 6. Электрон со скоростью и= 1,83-106 м/с влетел в одно-
однородное электрическое поле в направлении, противоположном век-
вектору напряженности поля. Какую разность потенциалов U должен
пройти электрон, чтобы обладать энергией ?^ = 13,6 эВ *? (Обла-
(Обладая такой энергией, электрон при столкновении с атомом водорода
может ионизировать его. Энергия 13,6 эВ называется энергией
ионизации водорода.)
Решение. Электрон должен пройти такую разность потен-
потенциалов (/, чтобы приобретенная при этом энергия W в сумме с ки-
кинетической энергией 7, которой обладал электрон перед вхожде-
вхождением в поле, составила энергию, равную энергии ионизации Et,
гу, ?ь VL77 | Т1—— р1 ТЭТТ~Л~ ~ 2L Л ТТ/7 . 7 Г _. -П ^^
Выразив в этой формуле W=eU иТ=у,
полу-
получим
eU + ^ = Е(. Отсюда
2е
* Электрон-вольт (эВ) — энергия, которую приобретает частица, имею-
имеющая заряд, равный заряду электрона, прошедшая разность потенциалов
1 В. Эта внесистемная единица энергии в настоящее время допущена к при-
применению в физике.
200

Произведем вычисления в единицах СИ:
(/-4,15 В.
Пример 7. Определить начальную скорость v0 сближения про-
протонов, находящихся на достаточно большом расстоянии друг от
друга, если минимальное расстояние гтш, на которое они могут
сблизиться, равно 10~п см.
Решение. Между двумя протонами действуют силы оттал-
отталкивания, вследствие чего движение протонов будет замедленным.
Поэтому задачу можно решить как в инерциальной системе коор-
координат (связанной с центром масс двух протонов), так и в неинер-
циальной (связанной с одним из ускоренно движущихся протонов).
Во втором случае законы Ньютона не имеют места. Применение же
принципа Даламбера затруднительно из-за того, что ускорение
системы будет переменным. Поэтому удобно рассмотреть задачу
в инерциальной системе отсчета.
Поместим начало координат в центр масс двух протонов. По-
Поскольку мы имеем дело с одинаковыми частицами, то центр масс
будет находиться в точке, делящей пополам отрезок, соединяющий
частицы. Относительно центра масс частицы будут иметь в любой
момент времени одинаковые по модулю скорости. Когда частицы
находятся на достаточно большом расстоянии друг от друга, ско-
скорость vx каждой частицы равна половине v0, т. е. v1=v0/2.
Для решения задачи применим закон сохранения энергии, со-
согласно которому полная механическая энергия Е изолированной
системы постоянна, т. е.
E=T+Uy
где Т — сумма кинетических энергий обоих протонов относительно
центра масс; П — потенциальная энергия системы зарядов.
Выразим потенциальную энергию в начальный Пх и конечный
П2 моменты движения.
В начальный момент, согласно условию задачи, протоны нахо-
находились на большом расстоянии, поэтому потенциальной энергией
можно пренебречь (Пх^О). Следовательно, для начального момента
полная энергия будет равна кинетической энергии Тг протонов,
т. е.
Е = Тг. A)
В конечный момент, когда протоны максимально сблизятся,
скорость и кинетическая энергия равны нулю, а полная энергия
будет равна потенциальной энергии П2, т. е.
E=U2. B)
Приравняв правые части равенств A) и B), получим
Тг=Пг. C)
Кинетическая энергия равна сумме кинетических энергий про-
протонов:
т mv\ mv\ _ 2 tnvl (A,
201

Потенциальная энергия системы двух зарядов Qi и Q2, находя-
щихся в вакууме, определяется по формуле П = ~^ , где г—рас-
г—расстояние между зарядами. Воспользовавшись этой формулой,
получим
С учетом равенств D) и E) формула C) примет вид
mvl
0ТКУАа vo = elV лготгтп.
Выполнив вычисления по полученной формуле, найдем
i>0=2,35 Мм/с.
Пример 8. Электрон без начальной скорости прошел разность
потенциалов Uo= 10 кВ и влетел в пространство между пластинами
плоского конденсатора, заряженного до разности потенциалов
i/i = 100 В, по линии АВ, параллельной пластинам (рис. 15.4).
Расстояние d между пласти-
I 1г у нами равно 2 см. Длина U
!"* *1| пластин конденсатора в нап-
яЦ равлении полета электрона
ёЩЩ равна 20 см. Определить рас-
| стояние ВС на экране Р, от-
стоящем от конденсатора на
/2=1м.
Решение. Движение
Рис. 15.4 электрона внутри конденсато-
конденсатора складывается из двух дви-
движений: 1) по инерции вдоль линии АВ с постоянной скоростью v0,
приобретенной под действием разности потенциалов Uo, которую
электрон прошел до конденсатора; 2) равномерно ускоренного дви-
движения в вертикальном направлении к положительно заряженной
пластине под действием постоянной силы поля конденсатора. По
выходе из конденсатора электрон будет двигаться равномерно со
скоростью и, которую он имел в точке М в момент вылета из кон-
конденсатора.
Из рис. 15.4 видно, что искомое расстояние \BC\=h1+h2, где
hi — расстояние, на которое сместится электрон в вертикальном
направлении во время движения в конденсаторе; /i2 — расстояние
между точкой D на экране, в которую электрон попал бы, двигаясь
по выходе из конденсатора по направлению начальной скорости vOi
и точкой С, в которую электрон попадет в действительности.
Выразим отдельно hi и /i2.
Пользуясь формулой длины пути равномерно ускоренного
движения, найдем
/i!-a/2/2, A)
где а — ускорение, полученное электроном под действием поля
конденсатора; t — время полета электрона внутри конденсатора.
202

По второму закону Ньютона a=F/m, где F — сила, с которой
поле действует на электрон; т — его масса. В свою очередь, F=
==eE=eU1/d, где е — заряд электрона; [Д — разность потенциалов
между пластинами конденсатора; d — расстояние между ними.
Время полета электрона внутри конденсатора найдем из фор-
формулы пути равномерного движения I1=vot, откуда
t=l1/v0,
где 1г — длина конденсатора в направлении полета электрона.
Выражение скорости v0 найдем из условия равенства работы, совер-
совершенной полем при перемещении электрона, и приобретенной им
кинетической энергии: mvl/2=eU0. Отсюда
хJ = 2eU /m, B)
Подставляя в формулу A) последовательно значения a, F, t
и v\ из соответствующих выражений, получим
Длину отрезка А2 найдем из подобия треугольников MDС и век-
векторного:
Л2=—' C)
где v± — скорость электрона в вертикальном направлении в точке
М\ U — расстояние от конденсатора до экрана.
Скорость Vi найдем по формуле vx=at, которая с учетом выра-
выражений для a, F и t примет вид
1 dmv0 '
Подставив выражение vx в формулу C),плучим А2 =^г г[2, или,
заменив vl по формуле C), найдем
~ 2dU0'
Окончательно для искомого расстояния \ВС\ будем иметь
| ВС I — А 4- А — ^У* 4- и^1* — kVi ( ^ ! /
Подставив значения величин Uu UOt d, 1г и 12 в последнее выра-
выражение и произведя вычисления, получим
| ВС |-5,5 см.
Задачи
Потенциальная энергия и потенциал
поля точечных зарядов
15.1. Точечный заряд Q=\0 нКл, находясь в некоторой точке
поля, обладает потенциальной энергией 11 = 10 мкДж. Найти по-
потенциал ф ЭТОЙ ТОЧКИ ПОЛЯ.
203

г
/1
i Л
* 1
Рис.
15.5
В
Рис. 15.6
15.2. При перемещении заряда Q=20 нКл между двумя точ-
точками поля внешними силами была совершена работа А=4 мкДж.
Определить работу Ах сил поля и разность Аср потенциалов этих
точек поля.
15.3. Электрическое поле создано точечным положительным
зарядом Qi=6 нКл. Положительный заряд Q2 переносится из точки
А этого поля в точку В (рис. 15.5). Каково изменение потенциаль-
потенциальной энергии АП, приходящееся на единицу переносимого заряда,
если /^=20 см и г2=50 см?
С
8
15.4. Электрическое поле создано точечным зарядом Qi=50 нКл.
Не пользуясь понятием потенциала, вычислить работу А внешних
сил по перемещению точечного заряда Q2= —2 нКл из точки С
в точку В (рис. 15.6), если Г!=10 см, г2=20 см. Определить также
изменение АП потенциальной энергии системы зарядов.
15.5. Поле создано точечным зарядом Q=l нКл. Определить
потенциал ф поля в точке, удаленной от заряда на расстояние
г=20 см.
15.6. Определить потенциал ср электрического поля в точке,
удаленной от зарядов Qt= —0,2 мкКл и Q2=0,5 мкКл соответствен-
соответственно на Гх=15 см и Г2=25 см. Определить также минимальное и мак-
максимальное расстояния между зарядами, при которых возможно
решение.
15.7. Заряды Qx= 1 мкКл и Q2= —1 мкКл находятся на рас-
расстоянии d=lO см. Определить напряженность Е и потенциал (р
поля в точке, удаленной на расстояние г= 10 см от первого заряда
и лежащей на линии, проходящей через первый заряд перпенди-
перпендикулярно направлению от Qx к Q2.
15.8. Вычислить потенциальную энергию П системы двух то-
точечных зарядов Qx= 100 нКл и Q2= 10 нКл, находящихся на рас-
расстоянии d=lO см друг от друга.
15.9. Найти потенциальную энергию П системы трех точечных
зарядов Qx=10 нКл, Q2=20 нКл и Q3= —30 нКл, расположенных
в вершинах равностороннего треугольника со стороной длиной
а=10 см.
15.10. Какова потенциальная энергия П системы четырех оди-
одинаковых точечных зарядов Q= 10 нКл, расположенных в верши-
вершинах квадрата со стороной длиной а=10 см?
15.11. Определить потенциальную энергию П системы четырех
точечных зарядов, расположенных в вершинах квадрата со сторо-
стороной длиной а=10 см. Заряды одинаковы по модулю Q= 10 нКл,
204

но два из них отрицательны. Рассмотреть два возможных случая
расположения зарядов.
15.12. Поле создано двумя точечными зарядами +2Q и —Q,
находящимися на расстоянии яМ12 см друг от друга. Определить
геометрическое место точек на
плоскости, для которых потенциал
равен нулю (написать уравнение
линии нулевого потенциала).
15.13. Система состоит из трех
зарядов — двух одинаковых по
величине Qi=|Q2|=l мкКл и
противоположных по знаку и за- ^у ~
ряда Q=20 нКл, расположенного ;Н
в точке 1 посередине между дву-
двумя другими зарядами системы Рис' 15>7
(рис. 15.7). Определить изменение
потенциальной энергии АП системы при переносе заряда Q из точ-
точки 1 в точку 2. Эти точки удалены от отрицательного заряда Q2
на расстояние а^0,2 м.
Потенциал поля линейно распределенных зарядов
15.14. По тонкому кольцу радиусом R = \0 см равномерно рас-
распределен заряд с линейной плотностью т=10 нКл/м. Определить
потенциал ср в точке, лежащей на оси кольца, на расстоянии а=5 см
от центра.
15.15. На отрезке тонкого прямого проводника равномерно рас-
распределен заряд с линейной плотностью т—10 нКл/м. Вычислить
потенциал ф, создаваемый этим зарядом в точке, расположенной
на оси проводника и удаленной от ближайшего конца отрезка на
расстояние, равное длине этого отрезка.
15.16. Тонкий стержень длиной /=10 см несет равномерно
распределенный заряд Q=l нКл. Определить потенциал ср электри-
электрического поля в точке, лежащей на оси стержня на расстоянии а—
— 20 см от ближайшего его конца.
15.17. Тонкие стержни образуют квадрат со стороной длиной а.
Стержни заряжены с линейной плотностью т=1,33 нКл/м. Найти
потенциал ф в центре квадрата.
15.18. Бесконечно длинная тонкая прямая нить несет равно-
равномерно распределенный по длине нити заряд с линейной плотно-
плотностью т=0,01 мкКл/м. Определить разность потенциалов Аф двух
точек поля, удаленных от нити на гг=2 см и г2=4 см.
Потенциал поля зарядов,
распределенных по поверхности
15.19. Тонкая круглая пластина несет равномерно распреде-
распределенный по плоскости заряд Q=l нКл. Радиус R пластины равен
5 см. Определить потенциал ф электрического поля в двух точках:
205

1) в центре пластины; 2) в точке, лежащей на оси, перпендикуляр-
перпендикулярной плоскости пластины и отстоящей от центра пластины на а—
=5 см.
15.20. Имеются две концентрические металлические сферы ра-
радиусами i?i=3 см и #2=6 см. Пространство между сферами запол-
заполнено парафином. Заряд Qi внутренней сферы равен —1 нКл, внеш-
внешний Q2= 2 нКл. Найти потенциал ср электрического поля на рас-
расстоянии: 1) Гх=1 см; 2) г2=Ъ см; 3) г3=9 см от центра сфер.
15.21. Металлический шар радиусом #=5 см несет заряд Q—
= 1 нКл. Шар окружен слоем эбонита толщиной d=2 см. Вычис-
Вычислить потенциал ср электрического поля на расстоянии: 1) ^=3 см;
2) г2=6 см; 3) rs=9 см от центра шара. Построить график зависи-
зависимости ср(г).
15.22. Металлический шар радиусом /?х= 10 см заряжен до по-
потенциала фх=300 В. Определить потенциал ср2 этого шара в двух
случаях: 1) после того, как его окружат сферической проводящей
оболочкой радиусом #2= 15 см и на короткое время соединят с ней
проводником; 2) если его окружить сферической проводящей за-
заземленной оболочкой радиусом #2=15 см?
15.23. Заряд распределен равномерно по бесконечной плоскости
с поверхностной плотностью в=Ю нКл/м2. Определить разность
потенциалов Дер двух точек поля, одна из которых находится на
плоскости, а другая удалена от плоскости на расстояние d~
= 10 см.
15.24. Определить потенциал ср, до которого можно зарядить
уединенный металлический шар радиусом # = 10 см, если напря-
напряженность Е поля, при которой происходит пробой воздуха, равна
3 МВ/м. Найти также максимальную поверхностную плотность а
электрических зарядов перед пробоем.
15.25. Две бесконечные параллельные плоскости находятся на
расстоянии d=0,5 см друг от друга. На плоскостях равномерно
распределены заряды с поверхностными плотностями ах=0,2мкКл/м2
и о2= —0,3 мкКл/м2. Определить разность потенциалов U между
плоскостями.
15.26. Две бесконечные параллельные плоскости находятся на
расстоянии d=l см друг от друга. Плоскости несут равномерно рас-
распределенные по поверхностям заряды с плотностями 0^=0,2 мкКл/м2
и сг2=0,5 мкКл/м2. Найти разность потенциалов U пластин.
15.27. Металлический шарик диаметром d=2 см заряжен от-
отрицательно до потенциала ср=150 В. Сколько электронов находится
на поверхности шарика?
15.28. Сто одинаковых капель ртути, заряженных до потенци-
потенциала ср=20 В, сливаются в одну большую каплю. Каков потенциал
ер* образовавшейся капли?
15.29. Две круглые металлические пластины радиусом # = 10 см
каждая, заряженные разноименно, расположены одна против дру-
другой параллельно друг другу и притягиваются с силой F=2 мН.
Расстояние d между пластинами равно 1 см. Определить разность
потенциалов U между пластинами.
206

15.30. Электрическое поле создано бесконечно длинным равно-
равномерно заряженным (сг=О, 1 мкКл/м2) цилиндром радиусом R=5 см.
Определить изменение АП потенциальной энергии однозарядного
j j положительного иона при перемещении его
из точки / в точку 2 (рис. 15.8).
? 15.31. Электрическое поле создано отри-
отрицательно заряженным металлическим шаром.
Рис. 15.8
2
-о
2/?
Рис. 15.9
Определить работу Aft 2 внешних сил по перемещению заряда
Q=40 нКл из точки 1 с .потенциалом фх= —300 В в точку 2
(рис. 15.9).
Потенциал поля зарядов, распределенных по объему
15.32. Плоская стеклянная пластинка толщиной d=2 см заря-
заряжена равномерно с объемной плотностью р = 10 мкКл/м3. Найти
разность потенциалов Аф между точкой, лежащей на поверхности
пластины, и точкой, находящейся внутри пластины в ее середине.
Считать, что размеры пластины велики по сравнению с ее толщиной.
15.33. Сплошной парафиновый шар радиусом R = W см равно-
равномерно заряжен с объемной плотностью р = 1 мкКл/м3. Определить
потенциал ф электрического поля в центре шара и на его по-
поверхности. Построить график зависимости ф(г).
15.34. Эбонитовый толстостенный полый шар несет равномерно
распределенный по объему заряд с плотностью р=2 мкКл/м3. Внут-
Внутренний радиус i?i шара равен 3 см, наружный R2=6 см. Определить
потенциал ф шара в следующих точках: 1) на наружной поверхности
шара; 2) на внутренней поверхности шара; 3) в центре шара.
Градиент потенциала и его связь с напряженностью поля
15.35. Бесконечная плоскость равномерно заряжена с поверх-
поверхностной плотностью сг=4 нКл/м2. Определить значение и направле-
направление градиента потенциала электрического поля, созданного этой
плоскостью.
15.36. Напряженность Е однородного электрического поля в не-
некоторой точке равна 600 В/м. Вычислить разность потенциалов U
между этой точкой и другой, лежащей на прямой, составляющей
207

угол а=60° с направлением вектора напряженности. Расстояние
Дг между точками равно 2 мм.
15.37. Напряженность Е однородного электрического поля равна
120 В/м. Определить разность потенциалов U между этой точкой
и другой, лежащей на той же силовой линии и отстоящей от первой
на Дг=1 мм.
15.38. Электрическое поле создано положительным точечным
зарядом. Потенциал ср поля в точке, удаленной от заряда на г =
= 12 см, равен 24 В. Определить значение и направление градиента
потенциала в этой точке.
15.39. Бесконечная тонкая прямая нить несет равномерно рас-
распределенный по длине нити заряд с плотностью т=1 нКл/м. Каков
градиент потенциала в точке, удаленной на расстояние г= 10 см
от нити? Указать направление градиента потенциала.
15.40. Сплошной шар из диэлектрика (8=3) радиусом /? = 10 см
заряжен с объемной плотностью р=50 нКл/м3. Напряженность
электрического поля внутри и на поверхности такого шара выража-
выражается формулой Е = т^— г, где г — расстояние от центра шара до
точки, в которой вычисляется напряженность поля. Вычислить
разность потенциалов Дер между центром шара и точками, лежащими
на его поверхности.
Работа по перемещению зарядов в поле
15.41. Точечные заряды Qi=l мкКл и Q2=0A мкКл находятся
на расстоянии гх= 10 см друг от друга. Какую работу А совершат
силы поля, если второй заряд, отталкиваясь от первого, удалится
от него на расстояние: 1)
а >^< а -л | t ° ^| г2=10 м; 2) г3=оо?
U 1 I 15.42. Электрическое поле
iyl (+v- б создано двумя одинаковыми
4 ^ положительными точечными
Рис 15.10 зарядами Q. Найти работу
А1у2 сил поля по перемеще-
перемещению заряда Qi= 10 нКл из точки / с потенциалом фх=300 В в точ-
точку 2 (рис. 15.10).
15.43. Определить работу Аи 2 по перемещению заряда Qx =
=50 нКл из точки / в точку 2 (рис. 15.11) в поле, созданном двумя
точечными зарядами, модуль \Q\ которых равен 1 мкКл и а=0,1 м.
15.44. Электрическое поле создано бесконечной равномерно за-
заряженной плоскостью с поверхностной плотностью заряда о=
=2 мкКл/м2. В этом поле вдоль прямой, составляющей угол а=60
с плоскостью, из точки 1 в точку 2, расстояние I между которыми
равно 20 см (рис. 15.12), перемещается точечный электрический
заряд Q= 10 нКл. Определить работу А сил поля по перемещению
заряда.
15.45. На отрезке прямого провода равномерно распределен
заряд с линейной плотностью т=1 мкКл/м. Определить работу А
208

сил поля по перемещению заряда Q=l нКл из точки В в точку С
(рис. 15.13).
15.46. Тонкий стержень согнут в полукольцо. Стержень заряжен
2
©~
Рис. 15.il
Рис. 15.12
с линейной плотностью т=133 нКл/м. Какую работу А надо совер-
совершить, чтобы перенести заряд Q=6J нКл из центра полукольца
в бесконечность?
Г DO
Рис. 15.14
Рис. 15.15
15.47. Тонкий стержень согнут в кольцо радиусом R = 10 см.
Он заряжен с линейной плотностью т=300 нКл/м. Какую работу
А надо совершить, чтобы перенести за-
заряд Q=5 нКл из центра кольца в точку,
расположенную на оси кольца на рас-
расстоянии /=20 см от центра его?
15.48. Электрическое поле создано
равномерно распределенным по кольцу
зарядом (т=1 мкКл/м). Определить ра-
работу Alt 2 сил поля по перемещению за-
заряда B=^10нКл из точки 1 (в центре
кольца) в точку 2, находящуюся на пер-
перпендикуляре к плоскости кольца (рис.
15.14).
15.49. Определить работу Л1ч 2 сил
поля по перемещению заряда Q=l мкКл
из точки 1 в точку 2 поля, созданного заряженным проводящим
шаром (рис. 15.15). Потенциал ф шара равен 1 кВ.
209
2а
i
i
Рис. 15.16

15.50. Бесконечная прямая нить несет равномерно распределен-
распределенный заряд (т=0,1 мкКл/м). Определить работу Аг^ 2 сил поля по
перемещению заряда Q=50 нКл из точки 1 в точку 2 (рис. 15.16).
Движение заряженных частиц в электрическом поле
15.51. Электрон находится в однородном электрическом поле
напряженностью ?=200 кВ/м. Какой путь пройдет электрон за
время ?=1 не, если его начальная скорость была равна нулю? Ка-
Какой скоростью будет обладать электрон в конце этого интервала
времени?
15.52. Какая ускоряющая разность потенциалов U требуется
для того, чтобы сообщить скорость и=30Мм/с: 1) электрону; 2) про-
протону?
15.53. Разность потенциалов U между катодом и анодом элект-
электронной лампы равна 90 В, расстояние г=1 мм. С каким ускорением
а движется электрон от катода к аноду? Какова скорость v электро-
электрона в момент удара об анод? За какое время / электрон пролетает
расстояние от катода до анода? Поле считать однородным.
15.54. Пылинка массой т=1 пг, несущая на себе пять электро-
электронов, прошла в вакууме ускоряющую разность потенциалов U=
=ЗМВ. Какова кинетическая энергия Т пылинки? Какую скорость
v приобрела пылинка?
15.55. Заряженная частица, пройдя ускоряющую разность по-
потенциалов t/=600 кВ, приобрела скорость v=5,4 Мм/с. Определить
удельный заряд частицы (отношение заряда в массе).
15.56. Протон, начальная скорость v которого равна 100 км/с,
влетел в однородное электрическое поле (?=300 В/см) так, что
вектор скорости совпал с направлением линий напряженности.
Какой путь / должен пройти протон в направлении линий поля,
чтобы его скорость удвоилась?
15.57. Бесконечная плоскость заряжена отрицательно с поверх-
поверхностной плотностью а=35,4 нКл/м2. По направлению силовой
линии поля, созданного плоскостью, летит электрон. Определить
минимальное расстояние /min, на которое может подойти к плокости
электрон, если на расстоянии /0=5 см он имел кинетическую энер-
энергию Г=80 эВ.
15.58. Электрон, летевший горизонтально со скоростью и=
= 1,6 Мм/с, влетел в однородное электрическое поле с напряжен-
напряженностью ?=90 В/см, направленное вертикально вверх. Какова будет
по модулю и направлению скорость v электрона через 1 не?
15.59. Вдоль силовой линии однородного электрического поля
движется протон. В точке поля с потенциалом фх протон имел ско-
скорость ^=0,1 Мм/с. Определить потенциал ф2 точки поля, в которой
скорость протона возрастает в п=2 раза. Отношение заряда про-
протона к его массе е/т=96 МКл/кг.
15.60. В однородное электрическое поле напряженностью Е=
= 1 кВ/м влетает вдоль силовой линии электрон со скоростью
210

и0—1 Мм/с. Определить расстояние /, пройденное электроном до
точки, в которой его скорость vx будет равна половине начальной.
15.61. Какой минимальной скоростью vmln должен обладать про-
протон, чтобы он мог достигнуть поверхности заряженного до потен-
потенциала ср=400 В металлического шара (рис. 15.17)?
15.62. Электрон движется вдоль силовой линий однородного
электрического поля. В некоторой точке поля с потенциалом cpi=
= 100 В электрон имел скорость i>i=6 Мм/с. Определить потенциал
ф2 точки поля, в которой скорость v2 электрона будет равна 0,5^.
15.63. Из точки 1 на поверхности бесконечно длинного отрица-
отрицательно заряженного цилиндра (т=20 нКл/м) вылетает электрон
(vo=O). Определить кинетическую энергию Т электрона в точке 2,
находящейся на расстоянии 97? от
поверхности цилиндра, где R —
его радиус (рис. 15.18).
15.64. Электрон с начальной
скоростью i>0=3 Мм/с влетел в
1
!
/?
/
2
Л
Рис. 15.17
Рис. 15.18
однородное электрическое поле напряженностью ?=150 В/м.
Вектор начальной скорости перпендикулярен линиям напряженно-
напряженности электрического поля. Найти: 1) силу F, действующую на элек-
электрон; 2) ускорение а, приобретаемое электроном; 2) скорость v
электрона через /=0,1 мкс.
15.65. Электрон влетел в пространство между пластинами
плоского конденсатора со скоростью f = 10 Мм/с, направленной
параллельно пластинам. На сколько приблизится электрон к поло-
положительно заряженной пластине за время движения внутри конден-
конденсатора (поле считать однородным), если расстояние d между пласти-
пластинами равно 16 мм, разность потенциалов (/=30 В и длина I пластин
равна 6 см?
15.66. Электрон влетел в плоский конденсатор, имея скорость
и=10 Мм/с, направленную параллельно пластинам. В момент
вылета из конденсатора направление скорости электрона составляло
угол а=35° с первоначальным направлением скорости. Определить
разность потенциалов U между пластинами (поле считать одно-
однородным), если длина / пластин равна 10 см и расстояние d между
ними равно 2 см.
15.67. Электрон влетел в плоский конденсатор, находясь на
одинаковом расстоянии от каждой пластины и имея скорость v=
— 10 Мм/с, направленную параллельно пластинам, расстояние d
211

между которыми равно 2 см. Длина / каждой пластины равна 10 см.
Какую наименьшую разность потенциалов U нужно приложить к
пластинам, чтобы электрон не вылетел из конденсатора?
15.68*. Протон сближается с а-частицей. Скорость vt протона
в лабораторной системе отсчета на достаточно большом удалении
от а-частицы равна 300 км/с, а скорость v2 а-частицы можно принять
равной нулю. Определить минимальное расстояние rmin, на кото-
которое подойдет протон к а-частице, и скорости иг и и2 обеих частиц
в этот момент. Заряд а-частицы равен двум элементарным поло-
положительным зарядам, а массу т1 ее можно считать в четыре раза
большей, чем масса т2 протона.
15.69. Положительно заряженная частица, заряд которой равен
элементарному заряду е, прошла ускоряющую разность потенциа-
потенциалов U=60 кВ и летит на ядро атома лития, заряд которого равен
трем элементарным зарядам. На какое наименьшее расстояние rmin
частица может приблизиться к ядру? Начальное расстояние ча-
частицы от ядра можно считать практически бесконечно большим, а
массу частицы — пренебрежимо малой по сравнению с массой
ядра.
15.70.* Два электрона, находящиеся на большом расстоянии
друг от друга, сближаются с относительной начальной скоростью
у= 10 Мм/с. Определить минимальное расстояние rmin, на которое
они могут подойти друг к другу.
15.71.* Две одноименные заряженные частицы с зарядами Qt
и Q2 сближаются с большого расстояния. Векторы скоростей v,
и v2 частиц лежат на одной прямой. Определить минимальное рас-
расстояние rmin, на которое могут подойти друг к другу частицы, если
их массы соответственно равны тг и т2. Рассмотреть два случая:
1) т1=т2 и 2) т2^>т1.
15.72.* Отношение масс двух заряженных частиц равно k=
=m1/m2. Частицы находятся на расстоянии г0 друг от друга. Какой
кинетической энергией Тг будет обладать частица массой ш1у если
она под действием силы взаимодействия со второй частицей удалится
от нее на расстояние г^>г0. Рассмотреть три случая: 1) k=l; 2) k=0;
3) fe->oo. Заряды частиц принять равными Qi и Q2. Начальными
скоростями частиц пренебречь.
§ 16. ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬ.
СВОЙСТВА ДИЭЛЕКТРИКОВ
Основные формулы
Ф Диполь есть система двух точечных электрических зарядов,
равных по размеру и противоположных по знаку, расстояние / ме-
между которыми значительно меньше расстояния г от центра диполя
до точек наблюдения.
Вектор 1, проведенный от отрицательного заряда диполя к его
положительному заряду, называется плечом диполя.
* Задачи 15.68; 15.70—15.72 следует решать в движущейся инерциаль-
ной системе координат, начало отсчета которой находится в центре масс
обеих частиц.
212

Произведение заряда \Q | диполя на его плечо 1 называется элект-
электрическим моментом диполя:
Р=К2|1-
• Напряженность поля диполя
р
? = •
+3cos2a,
" 4Л8О8/-3 '
где р — электрический момент диполя; г — модуль радиуса-век-
радиуса-вектора, проведенного от центра диполя к точке, напряженность поля
в которой нас интересует; а — угол д
между радиусом-вектором г и плечом 1
диполя (рис. 16.1).
Напряженность поля диполя в точ- /»у
ке, лежащей на оси диполя (а=0),
2л?0ег3
и в точке, лежащей на перпендикуляре
к плечу диполя, восставленном из его
середины (а=п/2)у
р
Е =
Рис. 16.1
Ф
4Л8О8Г3 *
Потенциал поля диполя
= , р„ 9 cos ос.
Потенциал поля диполя в точке, лежащей на оси диполя (а=0),
ф
и в точке, лежащей на перпендикуляре к плечу диполя, восстав-
восставленном из его середины (ос=л/2),
® Механический момент, действующий на диполь с электри-
электрическим моментом р, помещенный в однородное электрическое поле
с напряженностью Е,
М=[рЕ], или М=рЕ sin a,
где а — угол между направлениями векторов р и Е.
В неоднородном электрическом поле кроме механического мо-
момента (пары сил) на диполь действует еще некоторая сила. В случае
поля, обладающего симметрией относительно оси х, сила выражается
соотношением
-v r дх
дЕ
где -^ частная
производная напряженности поля, характе-
характеризующая степень неоднородности поля в направлении оси х.
При а>я/2 сила Fx положительна. Это значит, что под дейст-
действием ее диполь втягивается в область сильного поля.
213

Поляризованность (при однородной поляризации)
t=l
где pi — электрический момент отдельной A-й) молекулы (или
атома); N — число молекул, содержащихся в объеме ДУ.
• Связь поляризованности с напряженностью Е среднего ма-
макроскопического поля в диэлектрике
где и — диэлектрическая восприимчивость; е0 — электриче-
электрическая постоянная.
• Связь диэлектрической проницаемости 8 с диэлектрической
восприимчивостью
е=1+х.
• Напряженность Е среднего макроскопического поля в ди-
диэлектрике связана с напряженностью Ео внешнего поля соотноше-
соотношениями
Е=Е0/& и ?=?о — Р/еб.
• Напряженность Елок локального поля для неполярных жидко-
жидкостей и кристаллов кубической сингонии выражается формулами
и ^ §8"
^^-г-з"-^" и ^лок —-§8" °*
• Индуцированный электрический момент молекулы
где а — поляризуемость молекулы (а^+аа, где ае — электронная
поляризуемость; аа — атомная поляризуемость).
• Связь диэлектрической восприимчивости с поляризуемостью
молекулы
х 1
х+з""з"ап>
где п — концентрация молекул.
• Уравнение Клаузиуса — Мосотти
8—1 1 Me—1 1 „
- 3 аП' ИЛИ р 8 + 2 — 3 А'
где М — молярная масса вещества; р — плотность вещества.
• Формула Лоренц-Лорентца
п2— 1 1 м п2—1 1 АТ
-^ру-уа./г, или ~т?+2~'~~'з"а' А'
где п — показатель преломления диэлектрика; ае — электронная
поляризуемость атома или молекулы.
214

Ориентационная поляризуемость молекулы
где р — электрический момент молекулы; k — постоянная Больц-
мана; Т — термодинамическая температура.
• Формула Дебая — Ланжевена
е—1
е + 2:
1
.PI
Me—I 1 ,
или -iq^yla-
Примеры решения задач
Пример 1. Диполь с электрическим моментом р=2 нКл-м
находится в однородном электрическом поле напряженностью
?=30 кВ/м. Вектор р составляет угол ао=6О° с направлением си-
силовых линий поля. Определить произведенную внешними силами
работу А поворота диполя на угол C=30°.
Рис. 16.2
Решение. Из исходного положения (рис. 16.2, а) диполь
можно повернуть на угол р=30°=я/6 двумя способами: или по
часовой стрелке до угла ос^осо — р=л/3 — л/6^=л/6 (рис. 16.2, б),
или против часовой стрелки до угла а2=а0-{-$=п/3+л/6=п/2
(рис. 16.2, в).
В первом случае диполь будет повертываться под действием
сил поля. Следовательно, работа внешних сил при этом отрицатель-
отрицательна. Во втором случае поворот может быть произведен только под
действием внешних сил, и, следовательно, работа внешних сил при
этом положительна.
Работу, совершаемую при повороте диполя, можно вычислить
двумя способами: 1) непосредственно интегрированием выражения
элементарной работы; 2) с помощью соотношения между работой
и изменением потенциальной энергии диполя в электрическом поле.
1-й способ. Элементарная работа при повороте диполя на угол а
dA=Mda=pE sin ada,
а полная работа при повороте на угол от а0 до а
A)
215
А = ^ рЕ sin ada ==рЕ J sin a da.
Произведя интегрирование, получим
А = —рЕ (cos a — cos ao)=pE (cos a0 — cos a).

Работа внешних сил при повороте диполя по часовой стрелке
Аг—рЕ (cos а0 — cos а^— —21,9 мкДж,
против часовой стрелки
А2=рЕ (cos а0 — cos а2)=30 мкДж.
2-й способ. Работа А внешних сил связана с изменением потен-
потенциальной энергии АП соотношением
где Пх и П2— потенциальные энергии системы соответственно в
начальном и конечном состояниях. Так как потенциальная энергия
диполя в электрическом поле выражается формулой П= —рЕ cos a,
то
А=рЕ (cos а0 — cos а), B)
что совпадает с формулой A), полученной первым способом.
Пример 2. Три точечных заряда Qu Q2 и Q3 образуют электри-
электрически нейтральную систему, причем Q1=Q2==10 нКл. Заряды рас-
расположены в вершинах равностороннего треугольника. Определить
максимальные значения напряженности Етах и потенциала сртах поля,
создаваемого этой системой зарядов, на расстоянии г=1 м от центра
треугольника, длина а стороны которого равна 10 см.
А
и
-J
Рис. 16.3
Рис. 16.4
Решение. Нейтральную систему, состоящую из трех то-
точечных зарядов, можно представить в виде диполя. Действительно,
«центр тяжести» зарядов Qx и Q2 лежит на середине отрезка прямой,
соединяющей эти заряды (рис. 16.3). В этой точке можно считать
сосредоточенным заряд Q = Qi+Qz=2Q1. А так как система зарядов
нейтральная (Qi+Q2+Q3=0), то
Q8=—(Qi+Q2)=—Q.
Так как расстояние / между зарядами Q3 и —Q, равными по
значению, много меньше г A<^.г) (рис. 16.4), то систему этих двух
зарядов можно считать диполем с электрическим моментом
P=|Q|1,
где 1 — плечо диполя, равное по модулю а|^3/2 (см. рис. 16.3).
Так как |Q|=2Qb то электрический момент такого точечного
216

диполя
Тот же результат можно получить другим способом. Систему из
трех зарядов представим как два диполя с электрическими момен-
моментами pi и р2 (рис. 16.5), равными по
модулю: pi=|pi|=Oifl; /?2= |p2HQ2a.
Электрический момент р системы заря-
зарядов найдем как векторную сумму рг и р2,
т. е. p=pi+p2. Как это следует из рис.
16.5, имеем p=2pt cos(p/2). Так как
pi=Qia и р=я/3, то
р = 2Q±a V3/2 - Q^ j/,
что совпадает с найденным ранее зна-
значением.
Напряженность Е и потенциал ср поля диполя выражаются
формулами
Е - -г-^—г К" И 3cos2a;
4л?Н
ш — , р 9 cos a,
где а — угол между векторами риг (см. рис. 16.1).
Напряженность и потенциал будут иметь максимальные значе-
значения при а=0; следовательно,
р _ 2р р
Так как p^QxaVS, to
F - 2Qia 1/3 ¦ ш - Ql^ КЗ
Вычисления дают следующие значения:
^тах = 3,12 В/м; фтах = 1,56 В.
Пример 3. В атоме иода, находящемся на расстоянии г=1 нм
от альфа-частицы, индуцирован электрический момент р = 1,5х
Х10~32 Кл-м. Определить поляризуемость а атома иода.
Решение. По определению поляризуемости, она может
быть выражена по формуле
где р — индуцированный электрический момент атома; ?лок —
напряженность локального поля, в котором этот атом находится.
В данном случае таким полем является поле, созданное а-части-
цей. Напряженность этого поля определяется выражением
Подставив выражение Елок из равенства B) в формулу A), найдем
а=2пг2р/\е\.
217

Произведя вычисления по этой формуле, получим
Пример 4. Криптон находится под давлением р=Ю ЛШа при
температуре Т=200 К. Определить: 1) диэлектрическую проницае-
проницаемость 8 криптона; 2) его поляризованность Р, если напряженность
Ео внешнего электрического поля равна 1 МВ/м. Поляризуемость
а криптона равна 4,5«10~29 м3.
Решение. 1. Для определения диэлектрической проницае-
проницаемости криптона воспользуемся уравнением Клаузиуса — Мосотти,
записанным в виде
8—1 __ 1
где п — концентрация атомов криптона. Выразим из этой формулы
диэлектрическую проницаемость:
8 =yz
Так как концентрация молекул (атомов) связана с давлением и
температурой соотношением n=p/(kT)y то
1 ар в
1 ~3 кТ
Выразив все величины, входящие в эту формулу, в единицах СИ
5П00Д/КТ200К)
и произведя вычисления, получим
е-1,17.
2. По определению, поляризованность
Р
где рг — электрический дипольный момент, индуцированный в
i-м атоме; N — число атомов в объеме AF. В однородном электри-
электрическом поле все рг совпадают по модулю и направлению, поэтому
геометрическую сумму можно заменить на арифметическую. Обо-
Обозначив |ргН/?, получим
Отношение числа iV атомов к объему АV есть концентрация п ато-
атомов. Тогда
Р=пр.
Так как электрический дипольный момент атома пропорционален
напряженности ЕЛ0К локального поля {р=о^г0Елок)у то поляри-
поляризованность
Выразив Елок через напряженность Ео внешнего поля
лок = —т~о ?<> ) и я через давление р и температуру T(n=pIkT)i
218

получим
Г ""(8 + 2) ?Г °'
Подставим числовые значения и произведем вычисления (при
этом воспользуемся значением 8=1,17 найденным в п. 1 данного
примера):
Р= 1,60-10 Кл/м2=1,60 мкКл/м2.
Пример 5. Жидкий бензол имеет плотность р=899 кг/м3 и по-
показатель преломления п=1,50. Определить: 1) электронную поля-
поляризуемость ае молекул бензола; 2) диэлектрическую проницаемость
8 паров бензола при нормальных условиях.
Решение, 1. Для определения электронной поляризуемости
воспользуемся формулой Лоренц-Лорентца:
р я»+ 2
откуда
В полученное выражение входит молярная масса М бензола. Най-
Найдем ее. Так как химическая формула бензола СбН6, то относитель-
относительная молекулярная массаМг=6-12+6«1=78. Следовательно, моляр-
молярная масса М=78'10~3 кг/моль.
Подставим в формулу A) числовые значения физических вели-
величин и произведем вычисления:
, 3.78.Ю-з [A,50I-1] 27-10-^
е~~ 899-6,02-1023 [A,50J + 2] >^' 1U
2. Диэлектрическую проницаемость паров бензола найдем, вос-
воспользовавшись уравнением Клаузиуса — Мосотти:
8—1 1 /оч
где п — концентрация молекул бензола.
Заметим, что молекулы бензола неполярны и поэтому обладают
только двумя типами поляризации: электронной и атомной,— при-
причем атомная поляризация мала и ею можно пренебречь, считая
а^осе. Кроме того, при нормальных условиях 8 мало отличается
от единицы и приближенно можно считать е+2^3. Учитывая эти
соображения, формулу B) можно упростить:
е—1
откуда
е=1-{-аеп.
При нормальных условиях концентрация п молекул известна
и равна числу Лошмидта (ял=2,69-1019 см~3). Выразим концентра-
концентрацию молекул бензола в СИ (лг=2,69-1025 м~3) и произведем вычис-
вычисления:
е = 1 + 1,27 • Ю-28 • 2,69 • 102§ = 1,00342.
219

л
Задачи
Напряженность и потенциал поля диполя.
Электрический момент диполя
16.1. Вычислить электрический момент р диполя, если его заряд
Q= 10 нКл, плечо /=0,5 см.
16.2. Расстояние / между зарядами Q=±3,2 нКл диполя равно
12 см. Найти напряженность Е и потенциал <р поля, созданного дипо-
диполем в точке, удаленной на г=
=8 см как от первого, так и от
второго заряда.
16.3. Диполь с электрическим
моментом р=0у 12 нКл -м образо-
образован двумя точечными зарядами
т | - > ©—?--— Q=z±=l нКл. Найти напряжен-
0> о\ ность Е и потенциал ср электри-
^"^ ~р *"• ческого поля в точках А и В
Рис. 16.6 (рис. 16.6), находящихся на рас-
расстоянии г=8см от центра диполя.
16.4. Определить напряженность Е и потенциал ф поля, создан-
созданного диполем в точках А и В (рис. 16.6). Его электрический момент
р = \ пКл 'М, а расстояние г от точек Л и В до центра диполя равно
10 см.
16.5. Определить напряженность Е и потенциал ср поля, созда-
создаваемого диполем с электрическим моментом p=i пКл »м на расстоя-
расстоянии г =10 см от центра диполя, в направлении, составляющем угол
а=60° с вектором электрического момента.
16.6. Диполь с электрическим моментом /7=1 пКл «м равномерно
вращается с частотой п== 103 с относительно оси, проходящей через
центр диполя и перпендикулярной его плечу. Вывести закон измене-
изменения потенциала как функцию времени в некоторой точке, отстоящей
от центра диполя на г=1 см и лежащей в плоскости вращения дипо-
диполя. Принять, что в начальный момент времени потенциал ф0 интере-
интересующей нас точки равен нулю. Построить график зависимости ф(/).
16.7. Диполь с электрическим моментом р=1 пКл -м равномерно
вращается с угловой скоростью со= 104 рад/с относительно оси, пер-
перпендикулярной плечу диполя и проходящей через его центр. Опре-
Определить среднюю потенциальную энергию (П) заряда Q=l нКл, на-
находящегося на расстоянии г=2 см от центра диполя и лежащего
в плоскости вращения, за время, равное: 1) полупериоду (от ^=0
до t2=T/2); 2) в течение времени ф>Т. В начальный момент считать
П=0.
16.8. Два диполя с электрическими моментами рх=1 пКл»м и
р2—4 пКл «м находятся на расстоянии г=2 см друг от друга. Найти
силу их взаимодействия, если оси диполей лежат на одной прямой.
16.9. Два диполя с электрическими моментами рг=20 пКл-м и
р2~50 пКл'М находятся на расстоянии г= 10 см друг от друга, так
220

Рис. 16.7
что их оси лежат на одной прямой. Вычислить взаимную потенци-
потенциальную энергию диполей, соответствующую их устойчивому равно-
равновесию.
Диполь в электрическом поле
16.10. Диполь с электрическим моментом р= 100 пКл «м прикреп-
прикреплен к упругой нити (рис. 16.7). Когда в пространстве, где находится
диполь, было создано электрическое поле напряженностью ?=
=3 кВ/м перпендикулярно плечу
диполя и нити, диполь повернулся
на угол а=30°. Определить посто-
постоянную кручения * С нити.
16.11. В условиях предыдущей
задачи диполь под действием поля
поворачивается на малый угол.
Определить постоянную кручения
С нити.
16.12. Диполь с электрическим
моментом /7=20 нКл»м находится
в однородном электрическом по-
поле напряженностью ?=50 кВ/м.
Вектор электрического момента
составляет угол а=60° с линиями
поля. Какова потенциальная энергия П диполя?
Указание. За нулевую потенциальную энергию принять энергию, соот-
соответствующую такому расположению диполя, когда вектор электрического
момента диполя перпендикулярен линиям поля.
16.13. Диполь с электрическим моментом /7=100 пКл *м свободно
устанавливается в однородном электрическом поле напряженностью
?=150 кВ/м. Вычислить работу Л, необходимую для того, чтобы
повернуть диполь на угол а=180°.
16.14. Диполь с электрическим моментом /7=100 пКл *м свобод-
свободно установился в однородном электрическом поле напряженностью
?=10 кВ/м, Определить изменение потенциальной энергии АП ди-
диполя при повороте его на угол а=60°.
16.15. Перпендикулярно плечу диполя с электрическим момен-
моментом /7=12 пКл *м возбуждено однородное электрическое поле напря-
напряженностью ?=300 кВ/м. Под действием сил поля диполь начинает
поворачиваться относительно оси, проходящей через его центр.
Найти угловую скорость со диполя в момент прохождения им поло-
положения равновесия. Момент инерции J диполя относительно оси,
перпендикулярной плечу и проходящей через его центр, равен
2-10-9 кг-м2.
16.16. Диполь с электрическим моментом /7=100 пКл-м свобод-
свободно установился в однородном электрическом поле напряженностью
* Постоянной кручения называют величину, равную моменту силы,
который вызывает закручивание нити на 1 рад.
221

?=9 МВ/м. Диполь повернули на малый угол и предоставили само-
самому себе. Определить частоту v собственных колебаний диполя
в электрическом поле. Момент инерции / диполя относительно оси,
проходящей через центр диполя, равен 4-10~12 кг-м2.
16.17. Диполь с электрическим моментом р=200 пКл -м находит-
находится в неоднородном электрическом поле. Степень неоднородности
поля характеризуется величиной -j- = 1 МВ/м2, взятой в направле-
направлении оси диполя. Вычислить силу F, действующую на диполь в этом
направлении.
16.18. Диполь с электрическим моментом р=^5 пКл-м свободно
установился в поле точечного заряда Q= 100 нКл на расстоянии
г=10 см от него. Определить для этой точки величину |d?/dr|, ха-
характеризующую степень неоднородности поля в направлении сило-
силовой линии, и силу F, действующую на диполь.
16.19. Диполь с электрическим моментом /7=4 Кпл-м свободно
установился в поле, созданном бесконечной прямой нитью, заря-
заряженной с линейной плотностью т=500 нКл/м на расстоянии г=
= 10 см от нее. Определить в этой точке величину |d?Vdr|, характе-
характеризующую степень неоднородности поля в направлении силовой
линии, и силу F, действующую на диполь.
Поляризация диэлектриков
16.20. Указать, какими типами поляризации (электронной — е,
атомной — а, ориентационной — о) обладают следующие атомы и
молекулы: 1) Н; 2) Не; 3) О2; 4) НС1; 5) Н2О; 6) СО; 7) СО2; 8) СН3;
9) СС14.
16.21. Молекула HF обладает электрическим моментом р=
=6,4 -10~30 Кл-м. Межъядерное расстояние d=92 пм. Найти заряд
Q такого диполя и объяснить, почему найденное значение Q суще-
существенно отличается от значения элементарного заряда \е\.
16.22. Расстояние d между пластинами плоского конденсатора
равно 2 мм, разность потенциалов [/=1,8 кВ. Диэлектрик — стек-
стекло. Определить диэлектрическую восприимчивость х стекла и по-
поверхностную плотность а' поляризационных (связанных) зарядов
на поверхности стекла.
16.23. Металлический шар радиусом .R=5cm окружен равномер-
равномерно слоем фарфора толщиной d=2 см. Определить поверхностные
плотности о[ и а'2 связанных зарядов соответственно на внутренней
и внешней поверхностях диэлектрика. Заряд Q шара равен 10 нКл.
16.24. Эбонитовая плоскопараллельная пластина помещена в од-
однородное электрическое поле напряженностью Ео=2 МВ/м. Грани
пластины перпендикулярны линиям напряженности. Определить
поверхностную плотность а' связанных зарядов на гранях пластины.
Электрическое поле в диэлектрике
16.25. Пространство между пластинами плоского конденсатора
заполнено диэлектриком, молекулы которого можно рассматривать
как жесткие диполи с электрическим моментом jam=2«10"^° Кл-м.
222

Концентрация п диполей равна 1026 м. Определить напряженность
Е среднего макроскопического поля в таком диэлектрике, если при
отсутствии диэлектрика напряженность Ео поля между пластинами
конденсатора была равна 100 МВ/м. Дезориентирующим действием
теплового движения молекул пренебречь.
16.26. В электрическое поле напряженностью Ео=1 МВ/м внесли
пластину диэлектрика (8=3). Определить напряженность ?лок ло-
локального поля, действующего на отдельную молекулу в диэлектри-
диэлектрике, полагая, что внутреннее поле является полем Лоренца.
16.27. Во сколько раз напряженность Елок локального поля
в кристалле кубической сингонии больше напряженности Е среднего
макроскопического поля? Диэлектрическая проницаемость е кри-
кристалла равна 2,5.
16.28. При какой максимальной диэлектрической проницаемости
8 погрешность при замене напряженности Елок локального поля
напряженностью Ео внешнего поля не превысит 1%?
16.29. Определить относительную погрешность, которая будет
допущена, если вместо напряженности Елок локального поля брать
напряженность Е среднего макроскопического поля в диэлектрике.
Расчеты выполнить для двух случаев: 1) е= 1,003; 2) е=2.
Поляризованность диэлектрика
16.30. При какой поляризованности Р диэлектрика (е=5) на-
напряженность Елок локального поля равна 10 МВ/м?
16.31. Определить, при какой напряженности Е среднего макро-
макроскопического поля в диэлектрике (е=3) поляризованность Р достиг-
достигнет значения, равного 200 мкКл/м2.
16.32. Определить поляризованность Р стекла, помещенного во
внешнее электрическое поле напряженностью Е0=Ъ МВ/м.
16.33. Диэлектрик поместили в электрическое поле напряжен-
напряженностью Ео=2О кВ/м. Чему равна поляризованность Р диэлектрика,
если напряженность Е среднего макроскопического поля в диэлект-
диэлектрике оказалась равной 4 кВ/м?
16.34. Во внешнем электрическом поле напряженностью Ео —
=40МВ/м поляризованность Р жидкого азота оказалась равной
109 мкКл/м2. Определить: 1) диэлектрическую проницаемость г жид-
жидкого азота; 2) индуцированный электрический момент р одной моле-
молекулы. Плотность р жидкого азота принять равной 804 кг/м3.
Электронная и атомная поляризации
16.35. Связь поляризуемости а с диэлектрической восприим-
восприимчивостью к для неполярных жидкостей и кристаллов кубической
сингонии задается выражением %/(х+3)=ад/3, где п — концентра-
концентрация молекул. При каком наибольшем значении х погрешность в вы-
вычислении а не будет превышать 1 %, если воспользоваться прибли-
приближенной формулой хжап?
223

16.36. При каком наибольшем значении произведения an форму-
формула Клаузиуса — Мосотти (е—1)/(е+2)=ая/3 может быть заменена
более простой е=1+ая при условии, что погрешность в вычислении
е не превысит 1%?
16.37. Определить поляризуемость а молекул азота, если ди-
диэлектрическая проницаемость г жидкого азота равна 1,445 и его
плотность р=804 кг/м3.
16.38. Поляризуемость а молекулы водорода можно принять
равной 1,0 «10~29 м3. Определить диэлектрическую восприимчивость
к водорода для двух состояний: 1) газообразного при нормальных
условиях; 2) жидкого, плотность р которого равна 70,8 кг/м3.
16.39. Диэлектрическая восприимчивость к газообразного арго-
аргона при нормальных условиях равна 5,54 «Ю. Определить диэлект-
диэлектрические проницаемости г1 и е2 жидкого (рх= 1,40 г/см3) и твердого
(р2=1,65 г/см3) аргона.
16.40. Система состоит из двух одинаковых по значению и проти-
противоположных по знаку зарядов |Q|=0,l нКл, связанных квазиупру-
квазиупругими силами. Коэффициент k упругости системы зарядов равен
1 мН/м. Определить поляризуемость а системы.
16.41. Вычислить поляризуемость а атома водорода и диэлект-
диэлектрическую проницаемость е атомарного водорода при нормальных
условиях. Радиус г электронной орбиты принять равным 53 пм.
16.42. Атом водорода находится в однородном электрическом
поле напряженностью Я=100 кВ/м. Определить электрический мо-
момент р и плечо I индуцированного диполя. Радиус г электронной
орбиты равен 53 пм.
16.43. Диэлектрическая проницаемость е аргона при нормальных
условиях равна 1,00055. Определить поляризуемость а атома арго-
аргона.
16.44. Атом ксенона (поляризуемость а=5,2-10~29 м3) находится
на расстоянии г=1 нм от протона. Определить индуцированный
в атоме ксенона электрический момент р.
16.45. Какой максимальный электрический момент /?тах будет
индуцирован у атома неона, находящегося на расстоянии г=1 нм
от молекулы воды? Электрический момент р молекулы воды равен
6,2 -10~30 Кл*м. Поляризуемость а атома неона равна 4,7 «Ю0 м3.
16.46. Криптон при нормальных условиях находится в однород-
однородном электрическом поле напряженностью Е=2 МВ/м. Определить
объемную плотность энергии w поляризованного криптона, если
поляризуемость а атома криптона равна 4,5 • 10~29 м3.
16.47. Определить поляризуемость а атомов углерода в алмазе.
Диэлектрическая проницаемость 8 алмаза равна 5,6, плотность р =
=3,5-103 кг/м3.
16.48. Показатель преломления п газообразного кислорода при
нормальных условиях равен 1,000272. Определить электронную
поляризуемость ае молекулы кислорода.
16.49. Показатель преломления п газообразного хлора при нор-
нормальных условиях равен 1,000768. Определить диэлектрическую
224

проницаемость е жидкого хлора, плотность р которого равна 1,56х
XlO3 кг/м3.
16.50. При нормальных условиях показатель преломления п уг-
углекислого газа СО2 равен 1,000450. Определить диэлектрическую
проницаемость е жидкого СО2, если его плотность р = 1,19 X
XIО3 кг/м3.
16.51. Показатель преломления п жидкого сероуглерода CS2
равен 1,62. Определить электронную поляризуемость ае молекул
сероуглерода, зная его плотность.
16.52. Поляризуемость а атома аргона равна 2,03хЮ~29 м3.
Определить диэлектрическую проницаемость 8 и показатель пре-
преломления п жидкого аргона, плотность р которого равна 1,44><
XlO3 кг/м3.
16.53. Определить показатель преломления п± жидкого кислоро-
кислорода, если показатель преломления п2 газообразного кислорода при
нормальных условиях равен 1,000272. Плотность р± жидкого кисло-
кислорода равна 1,19 X 103 кг/м3.
Ориентационная поляризация
16.54. Вычислить ориентационную поляризуемость аор молекул
воды при температуре /—27 °С, если электрический момент р моле-
молекулы воды равен 6,1 «Ю0 Кл »м.
16.55. Зная, что показатель преломления п водяных паров при
нормальных условиях равен 1,000252 и что молекула воды обладает
электрическим моментом /?=6,Ы0~30 Кл-м, определить, какую
долю от общей поляризуемости (электронной и ориентационной)
составляет электронная поляризуемость молекулы.
16.56. Электрический момент р молекул диэлектрика равен
5 • 10~30 Кл-м. Диэлектрик (8=2) помещен в электрическое поле
напряженностью ?лок=100 МВ/м. Определить температуру Т, при
которой среднее значение проекции (рЕ) электрического момента на
направление вектора Елок будет равно Мг/?.
16.57. Диэлектрик, молекулы которого обладают электрическим
моментом р=5«Ю0 Кл-м, находится при температуре Т=300 К
в электрическом поле напряженностью ?лок=100 МВ/м. Определить,
во сколько раз число молекул, ориентированных «по полю»
(ОФГ), больше числа молекул, ориентированных «против поля»
^0о). Угол -8" образован векторами р и Елок.
§ 17. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ. КОНДЕНСАТОРЫ
Основные формулы
Ф Электрическая емкость уединенного проводника или конден-
конденсатора
C—AQ/Аф,
где AQ — заряд, сообщенный проводнику (конденсатору); Аф —
изменение потенциала, вызванное этим зарядом.
8 № 1268 225

# Электрическая емкость уединенной проводящей сферы радиу-
радиусом R, находящейся в бесконечной среде с диэлектрической прони-
проницаемостью 8,
Если сфера полая и заполнена диэлектриком, то электроемкость
ее от этого не изменяется.
• Электрическая емкость плоского конденсатора
где S — площадь пластин (каждой пластины); d — расстояние
между ними; е — диэлектрическая проницаемость диэлектрика, за-
заполняющего пространство между пластинами.
Электрическая емкость плоского конденсатора, заполненного п
слоями диэлектриком толщиной dt каждый с диэлектрическими про-
ницаемостями et (слоистый конденсатор),
• Электрическая емкость сферического конденсатора (две кон-
концентрические сферы радиусами Ri и R2, пространство между кото-
которыми заполнено диэлектриком с диэлектрической проницаемостью
)
• Электрическая емкость цилиндрического конденсатора (два
коаксиальных цилиндра длиной / и радиусами Ri и R2y пространство
между которыми заполнено диэлектриком с диэлектрической про-
проницаемостью е)
с "~ In (/?2//?i)#
• Электрическая емкость С последовательно соединенных кон-
конденсаторов:
в общем случае 7^ = 7^ + т^" + • • • + т~ i
где п — число конденсаторов;
с с
в случае двух конденсаторов С = 1 * ;
в случае п одинаковых конденсаторов с электроемкостью Сг каж-
каждый
• Электрическая емкость параллельно соединенных конденса-
конденсаторов:
в общем случае C=Ci+C2+...+Cn;
в случае двух конденсаторов С—Ci+C2;
в случае л одинаковых конденсаторов с электроемкостью С± каж-
каждый C=nCi,
226

Примеры решения задач
Пример 1. Определить электрическую емкость С плоского кон-
конденсатора с двумя слоями диэлектриков: фарфора толщиной d1—
—2 мм и эбонита толщиной d2— 1,5 мм, если площадь S пластин рав-
равна 100 см2.
Решение. Емкость конденсатора, по определению, C=Q/U,
где Q — заряд на пластинах конденсатора; U — разность потен-
потенциалов пластин. Заменив в этом равенстве общую разность потен-
потенциалов U конденсатора суммой Ut+U2 напряжений на слоях ди-
диэлектриков, получим
C=Q/(U1+Ui). A)
Приняв во внимание, что Q = gS, U1 = E1d1~ — d< и U2 =
e08l
—— d2, равенство A) можно переписать в виде
е0?2
Dл , D .
~\ «2
е0?1 ?0е2
где а — поверхностная плотность заряда на пластинах; Е1 и Е2 —
напряженности поля в первом и втором слоях диэлектрика соответ-
соответственно; D — электрическое смещение поля в диэлектриках.
Умножив числитель и знаменатель равенства B) на е0 и учтя, что
D=cr, окончательно получим
Сделав вычисления по последней формуле, найдем
885.10-1М00.10-* _ ф ф
1,5.10-3/3
Пример 2. Два плоских конденсатора одинаковой электроемко-
электроемкости С1=С2=С соединены в батарею последовательно и подключены
к источнику тока с электродвижущей силой $. Как изменится раз-
разность потенциалов ?/* на пластинах первого конденсатора, если
пространство между пластинами второго конденсатора, не отключая
источника тока, заполнить диэлектриком с диэлектрической прони-
проницаемостью 8=7?
Решение. До заполнения второго конденсатора диэлектри-
диэлектриком разность потенциалов на пластинах обоих конденсаторов была
одинакова: U1=U2=SI2.После заполнения электроемкость второго
конденсатора возросла в г раз:
Электроемкость первого не изменилась, т. е. С[=С.
Так как источник тока не отключался, то общая разность потен-
потенциалов на батарее конденсаторов осталась прежней, она лишь пере-
перераспределилась между конденсаторами. На первом конденсаторе
U'^Q/Ci^Q/C, A)
где Q — заряд на пластинах конденсатора. Поскольку при последо-
последовательном соединении конденсаторов заряд на каждой пластине и
8* 227

После подстановки значения г получим
^/^=1,75.
Следовательно, разность потенциалов на пластинах первого
конденсатора после заполнения второго конденсатора диэлектриком
возросла в 1,75 раза.
Задачи
Электрическая емкость проводящей сферы
17.1. Найти электроемкость С уединенного металлического шара
радиусом /? = 1 см.
17.2. Определить электроемкость С металлической сферы радиу-
радиусом R=2 см, погруженной в воду.
17.3. Определить электроемкость С Земли, принимая ее за шар
радиусом /?=6400 км.
17.4. Два металлических шара радиусами jRi=2 cm и /?2=6 см
соединены проводником, емкостью которого можно пренебречь.
Шарам сообщен заряд Q=l нКл. Найти поверхностную плотность
о зарядов на шарах.
17.5. Шар радиусом i?i=6 см заряжен до потенциала cpi=300 В,
а шар радиусом R2=^ см — до потенциала ф2=500 В. Определить
потенциал ср шаров после того, как их соединили металлическим
проводником. Емкостью соединительного проводника пренебречь.
Электрическая емкость плоского конденсатора
17.6. Определить электроемкость С плоского слюдяного конден-
конденсатора, площадь S пластин которого равна 100 см2, а расстояние
между ними равно 0,1 мм.
17.7. Между пластинами плоского конденсатора, заряженного до
разности потенциалов ?/=600В, находятся два слоя диэлектриков:
стекла толщиной dx=7 мм и эбонита толщиной ^2=3 мм. Площадь
S каждой пластины конденсатора равна 200 см2. Найти: 1) электро-
228
1 -J- О
Подставив это выражение заряда в формулу A), найдем
Чтобы найти, как изменилась разность потенциалов на пласти-
пластинах первого конденсатора, вычислим отношение:

емкость С конденсатора; 2) смещение D, напряженность Е поля и
падение потенциала Дер в каждом слое.
17.8. Расстояние d между пластинами плоского конденсатора
равно 1,33 м, площадь S пластин равна 20 см2. В пространстве меж-
между пластинами конденсатора находятся два слоя диэлектриков:
слюды толщиной d1=0J мм и эбонита толщиной d2—0,3 мм. Опре-
Определить электроемкость С конденсатора.
17.9. На пластинах плоского конденсатора равномерно распре-
распределен заряд с поверхностной плотностью сг—0,2 мкКл/м2. Расстоя-
Расстояние d между пластинами равно 1 мм. На сколько изменится раз-
разность потенциалов на его обкладках при увеличении расстояния d
между пластинами до 3 мм?
17.10. В плоский конденсатор вдвинули плитку парафина тол-
толщиной d=\ см, которая вплотную прилегает к его пластинам. На
сколько нужно увеличить расстояние между пластинами, чтобы
получить прежнюю емкость?
17.11. Электроемкость С плоского конденсатора равна 1,5 мкФ.
Расстояние d между пластинами равно 5 мм. Какова будет электро-
электроемкость С конденсатора, если на нижнюю пластину положить лист
эбонита толщиной d1=3 мм?
17.12. Между пластинами плоского конденсатора находится
плотно прилегающая стеклянная пластинка. Конденсатор заряжен
до разности потенциалов f/x = 100 В. Какова будет разность потен-
потенциалов U2, если вытащить стеклянную пластинку из конденсатора?
Электрическая емкость сферического конденсатора
17.13. Две концентрические металлические сферы радиусами
Rx=2 см и /?2=2,1 см образуют сферический конденсатор. Опреде-
Определить его электроемкость С, если пространство между сферами за-
заполнено парафином.
17.14. Конденсатор состоит из двух концентрических сфер. Ра-
Радиус Rt внутренней сферы равен 10 см, внешней R2=l0t2 см. Про-
Промежуток между сферами заполнен парафином. Внутренней сфере
сообщен заряд Q=5 мкКл. Определить разность потенциалов U
между сферами.
Соединения конденсаторов
17.15. К воздушному конденсатору, заряженному до разности
потенциалов [/=600 В и отключенному от источника напряжения,
присоединили параллельно второй незаряженный конденсатор
таких же размеров и формы, но с диэлектриком (фарфор). Опреде-
Определить диэлектрическую проницаемость 8 фарфора, если после при-
присоединения второго конденсатора разность потенциалов уменьши-
уменьшилась до t/i=100 В.
17.16. Два конденсатора электроемкостями Ci=3 мкФ и С2=
^6 мкФ соединены между собой и присоединены к батарее с ЭДС.
?120 В. Определить заряды Qi и Q2 конденсаторов и разности
229

потенциалов Ui и U2 между их обкладками, если конденсаторы со-
соединены: 1) параллельно; 2) последовательно.
17.17. Конденсатор электроемкостью Ci=0,2 мкФ был заряжен
до разности потенциалов U1=32Q В. После того как его соединили
параллельно со вторым конденсатором, заряженным до разности
потенциалов ?/2=450 В, напряжение U на нем изменилось до 400 В.
Вычислить емкость С2 второго конденсатора.
17.18. Конденсатор электроемкостью Ci=0,6 мкФ был заряжен
до разности потенциалов U1=300 В и соединен со вторым конден-
конденсатором электроемкостью С2=0,4 мкФ, заряженным до разности
потенциалов U2—150 В. Найти заряд AQ, перетекший с пластин
первого конденсатора на второй.
17.19. Три одинаковых плоских конденсатора соединены после-
последовательно. Электроемкость С такой батареи конденсаторов равна
89 пФ. Площадь S каждой пластины равна 100 см2. Диэлектрик —
стекло. Какова толщина d стекла?
17.20. Конденсаторы соединены так, как это показано на
рис. 17.1. Электроемкости конденсаторов: Cf=0,2 мкФ, Cz=
=0,1 мкФ, Сз=0,ЗмкФ, С4=0,4 мкФ. Определить электроемкость
С батареи конденсаторов.
Рис. 17.1
Рис. 17.2
Рис. 17.3
17.21. Конденсаторы электроемкостями Ci=0,2 мкФ, С2~
=0,6 мкФ, С3=0,3 мкФ, С4=0,5 мкФ соединены так, как это ука-
указано на рис. 17.2. Разность потенциалов U между точками А я В
равна 320 В. Определить разность потенциалов Ut и заряд Qt на
пластинах каждого конденсатора (/=1, 2, 3, 4).
Рис. 17.4
В
Рис. 17.5
Рис. 17.6
17.22. Конденсаторы электроемкостями Ci=10 нФ, С2=
=40 нФ, С3=2 нФ и С4=30 нФ соединены так, как это показано
на рис. 17.3. Определить электроемкость С соединения конденсато-
конденсаторов.
17.23. Конденсаторы электроемкостями d=2 мкФ, С2=2 мкФ,
Сз—3 мкФ^ С*=1 мкФ соединены так, как указано на рис. 17.4.
230

Разность потенциалов на обкладках четвертого конденсатора ?/4=
= 100 В. Найти заряды и разности потенциалов на обкладках каж-
каждого конденсатора, а также общий заряд и разность потенциалов
батареи конденсаторов.
17.24. Определить электроемкость схемы, представленной на
рис. 17.5, где Ci=l пФ, С2=2 пФ, С3=2 пФ, С4=4 пФ, С5=3 пФ.
17.25. Пять различных конденсаторов соединены согласно схе-
схеме, приведенной на рис. 17.6. Определить электроемкость С4, при
которой электроемкость всего соединения не зависит от величины
электроемкости С5. Принять С±=8 пФ, С2=12 пФ, С3=6 пФ.
§ 18. ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА,
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Основные формулы
# Энергия заряженного проводника выражается через заряд
Q, потенциал ф и электрическую емкость С проводника следующими
соотношениями:
Энергия заряженного конденсатора
где С — электрическая емкость конденсатора; U — разность по-
потенциалов на его пластинах.
• Объемная плотность энергии (энергия электрического поля,
приходящаяся на единицу объема)
где Е — напряженность электрического поля в среде с диэлектри-
диэлектрической проницаемостью е; D — электрическое смещение.
Примеры решения задач
Пример 1. Конденсатор электроемкостью Сх=3 мкФ был заря-
заряжен до разности потенциалов ?/i=40 В. После отключения от источ-
источника тока конденсатор был соединен параллельно с другим незаря-
незаряженным конденсатором электроемкостью С2=5 мкФ. Определить
энергию AW, израсходованную на образование искры в момент
присоединения второго конденсатора.
Решение. Энергия, израсходованная на образование искры,
равна
AW=W1—W2i A)
где Wt — энергия, которой обладал первый конденсатор до присо-
присоединения к нему второго конденсатора; W2 — энергия, которую
имеет батарея, составленная из первого и второго конденсаторов.
Подставив в равенство A) формулу энергии заряженного конденса-
231

тора W=CU2/2 и приняв во внимание, что общая электроемкость
параллельно соединенных конденсаторов равна сумме электроем-
электроемкостей отдельных конденсаторов, получим
2
где Ci и С2 — электроемкости первого и второго конденсаторов;
Ux — разность потенциалов, до которой был заряжен первый кон-
конденсатор; U2 — разность потенциалов на зажимах батареи конден-
конденсаторов.
Учитывая, что заряд после присоединения второго конденсатора
остался прежним, выразим разность потенциалов U2 следующим
образом: Uo = „ > п = п г, * . Подставив это выражение U2
в формулу B), получим
AW =Д^1
2 2 (С, +С2J •
После простых преобразований найдем
2 c1+c2Ul'
Выполнив вычисления по этой формуле, получим
А №=1,5 мДж.
Пример 2. Плоский воздушный конденсатор с площадью 5 пла-
пластины, равной 500 см2, подключен к источнику тока, ЭДС ?
которого равна 300 В. Определить работу А внешних сил по раз-
движению пластин от расстояния ^х= 1 см до d2=3 см в двух слу-
случаях: 1) пластины перед раздвижением отключаются от источника
тока; 2) пластины в процессе раздвижения остаются подключенны-
подключенными к нему.
Решение. 1-й случай. Систему двух заряженных и отклю-
отключенных от источника тока пластин можно рассматривать как изоли-
изолированную систему, по отношению к которой справедлив закон со-
сохранения энергии. В этом случае работа внешних сил равна измене-
изменению энергии системы:
A=bW = W2—Wl9 A)
где W2 — энергия поля конденсатора в конечном состоянии (пласти-
(пластины находятся на расстоянии d2); Wx — энергия поля в начальном
состоянии (пластины находятся на расстоянии d,).
Энергию в данном случае удобно выразить через заряд Q на
пластинах, так как заряд пластин, отключенных от источника при
их раздвижении, не изменяется. Подставив в равенство A) выраже-
выражения DF2=Q2/BC2) и W1=Q2/BC1)y получим
Л_С2 Q2 или л_ Q2
Выразив в этой формуле заряд через ЭДС <§ источника тока
и начальную электроемкость Ci(Q=C±S)y найдем
232

Подставляя в формулу B) выражения электроемкостей (С1 =
=&0S/di и C2=z&oS/d2) плоского конденсатора, получим
л
После сокращения на e0S формула примет вид
A^^f-^-dJ. C)
Произведя вычисления по формуле C), найдем
= 3,98-10~6 Дж = 3,98 мкДж.
2-й случай. Пластины остаются подключенными к источнику тока
и система двух пластин уже не является изолированной (заряд
с пластин при их раздвижении перемещается к клеммам батареи).
Поэтому воспользоваться законом сохранения энергии в этом слу-
случае нельзя.
Заметим, что при раздвижении пластин конденсатора: а) раз-
разность их потенциалов остается неизменной (U=S); б) емкость бу-
будет уменьшаться ( С = ео-^Л. Будут уменьшаться также заряд на
пластинах (Q=CU) и напряженность электрического поля (?" =
= U/d). Так как величины Е и Q, необходимые для определения ра-
работы, изменяются, то работу следует вычислять путем интегриро-
интегрирования.
Напишем выражение для элементарной работы:
dA=QE1dxy D)
где Ех — напряженность поля, создаваемого зарядом одной пласти-
пластины.
Выразим напряженность поля Е± и заряд Q через расстояние х
между пластинами:
Е=тЕ=
*т1* и <г=с<?' или Q=?o4<?-
Подставив эти выражения Ег и Q в равенство D), получим
Проинтегрировав это равенство в пределах от dx до d2, найдем
выражение искомой работы:
d2
dx 1 с о
После упрощений последняя формула примет вид
Сделав вычисления по полученной формуле, найдем
А = 1,33 мкДж.
233

Пример 3. Плоский конденсатор заряжен до разности потенциа-
потенциалов 0=1 кВ. Расстояние d между пластинами равно 1 см. Диэлект-
Диэлектрик — стекло. Определить объемную плотность энергии поля кон-
конденсатора.
Решение. Объемная плотность энергии поля конденсатора
w=W/V, A)
где W — энергия поля конденсатора; V — объем, занимаемый по-
полем, т. е. объем пространства, заключенного между пластинами
конденсатора.
Энергия поля конденсатора определяется по формуле
B)
где U — разность потенциалов, до которой заряжены пластины
конденсатора; С — его электроемкость. Но C=ee0S/d, V=Sd.
Подставив выражение С в формулу B) и затем выражения W и V
в формулу A), получим
w=ee0U2/Bd2).
Подставив значения величин в последнюю формулу и вычислив,
найдем
i?>—0,309 Дж/м3.
Пример 4. Металлический шар радиусом i?=3 см несет заряд
Q=20 нКл. Шар окружен слоем парафина толщиной d=2 см. Опре-
Определить энергию W электрического поля, заключенного в слое ди-
диэлектрика.
Решение. Так как поле, созданное заряженным шаром, яв-
является неоднородным, то энергия поля в слое диэлектрика распре-
распределена неравномерно. Однако объемная
плотность энергии будет одинакова во
всех точках, отстоящих на равных рас-
расстояниях от центра сферы, так как поле
заряженного шара обладает сферической
симметрией.
Выразим энергию в элементарном сфе-
сферическом слое диэлектрика объемом dV:
dW=wdV,
Рис. 18.1 где w -г объемная плотность энергии (рис.
18.1).
Полная энергия выразится интегралом
R + d
W^^wdV^in ^ wr2dr§ A)
R
где г — радиус элементарного сферического слоя; dr — его толщи-
толщина. Объемная плотность энергии определяется по формуле ш=
УЕ Е — напряженность поля. В нашем случае
234

Подставив это выражение плотности в формулу A) и вынеся за
знак интеграла постоянные величины, получим
R + d
w== Q2 Г <*r _ Q2 ( i i \_ Q2d
8ле0е J г2 8яео8 \ R R + d
R
Произведя вычисления по этой формуле, найдем
W=12 мкДж.
Задачи
Энергия плоского конденсатора
18.1. Конденсатору, электроемкость С которого равна 10 пФ,
сообщен заряд Q=l пКл. Определить энергию W конденсатора.
18.2. Расстояние d между пластинами плоского конденсатора
равно 2 см, разность потенциалов U=6 кВ. Заряд Q каждой пласти-
пластины равен 10 нКл. Вычислить энергию W поля конденсатора и силу
F взаимного притяжения пластин.
18.3. Какое количество теплоты Q выделится при разряде плоско-
плоского конденсатора, если разность потенциалов U между пластинами
равна 15 кВ, расстояние d=\ мм, диэлектрик — слюда и площадь
S каждой пластины равна 300 см2?
18.4. Сила F притяжения между пластинами плоского воздушно-
воздушного конденсатора равна 50 мН. Площадь S каждой пластины равна
200 см2. Найти плотность энергии w поля конденсатора.
18.5. Плоский воздушный конденсатор состоит из двух круглых
пластин радиусом г= 10 см каждая. Расстояние dx между пластинами
равно 1 см. Конденсатор зарядили до разности потенциалов ?/=
= 1,2 кВ и отключили от источника тока. Какую работу А нужно
совершить, чтобы, удаляя пластины друг от друга, увеличить рас-
расстояние между ними до d2=3,5 см?
18.6. Плоский воздушный конденсатор электроемкостью С=
= 1,11 нФ заряжен до разности потенциалов ?/=300 В. После от-
отключения от источника тока расстояние между пластинами конден-
конденсатора было увеличено в пять раз. Определить: 1) разность потен-
потенциалов U на обкладках конденсатора после их раздвижения; 2) ра-
работу А внешних сил по раздвижению пластин.
18.7. Конденсатор электроемкостью Сх=666 пФ зарядили до
разности потенциалов ?/=1,5 кВ и отключили от источника тока.
Затем к конденсатору присоединили параллельно второй, незаря-
незаряженный конденсатор электроемкостью С2=444 пФ. Определить
энергию, израсходованную на образование искры, проскочившей
при соединении конденсаторов.
18.8. Конденсаторы электроемкостями Сг=\ мкФ, С2=2 мкФ,
С3=3 мкФ включены в цепь с напряжением ?/=1,1 кВ. Определить
энергию каждого конденсатора в случаях: 1) последовательного
их включения; 2) параллельного включения.
18.9. Электроемкость С плоского конденсатора равна 111 пФ.
235

Диэлектрик — фарфор. Конденсатор зарядили до разности потен-
потенциалов [/=600 В и отключили от источника напряжения. Какую
работу А нужно совершить, чтобы вынуть диэлектрик из конденса-
конденсатора? Трение пренебрежимо мало.
18.10. Пространство между пластинами плоского конденсатора
заполнено диэлектриком (фарфор), объем V которого равен 100 см3.
Поверхностная плотность заряда а на пластинах конденсатора рав-
равна 8,85 нКл/м2. Вычислить работу Л, которую необходимо совер-
совершить для того, чтобы удалить диэлектрик из конденсатора. Трени-
Трением диэлектрика о пластины конденсатора пренебречь.
18.11. Пластину из эбонита толщиной d=2 мм и площадью S=*
= 300 см2 поместили в однородное электрическое поле напряжен-
напряженностью Е=1 кВ/м, расположив так, что силовые линии перпендику-
перпендикулярны ее плоской поверхности. Найти: 1) плотность а связанных
зарядов на поверхности пластин; 2) энергию W электрического поля,
сосредоточенную в пластине.
18.12. Пластину предыдущей задачи переместили из поля в об-
область пространства, где внешнее поле отсутствует. Пренебрегая
уменьшением поля в диэлектрике с течением времени, определить
энергию W электрического поля в пластине.
Энергия поля заряженной сферы
18.13. Найти энергию W уединенной сферы радиусом R=4 см,
заряженной до потенциала ф=500 В.
18.14. Вычислить энергию W электростатического поля метал-
металлического шара, которому сообщен заряд Q= 100 нКл, если диаметр
d шара равен 20 см.
18.15. Уединенная металлическая сфера электроемкостью С=
= 10 пФ заряжена до потенциала ф=3 кВ. Определить энергию W
поля, заключенного в сферическом слое, ограниченном сферой и
концентрической с ней сферической поверхностью, радиус которой
в три раза больше радиуса сферы.
18.16. Электрическое поле создано заряженной (Q=0,l мкКл)
сферой радиусом /? = 10 см. Какова энергия W поля, заключенная
в объеме, ограниченном сферой и концентрической с ней сферической
поверхностью, радиус которой в два раза больше радиуса сферы?
18.17. Уединенный металлический шар радиусом Ri=6 см несет
заряд Q. Концентрическая этому шару поверхность делит простран-
пространство на две части (внутренняя конечная и внешняя бесконечная),
так что энергии электрического поля обеих частей одинаковы. Опре-
Определить радиус R2 этой сферической поверхности.
18.18. Сплошной парафиновый шар радиусом R = 10 см заряжен
равномерно по объему с объемной плотностью р= 10 нКл/м3. Опре-
Определить энергию Wx электрического поля, сосредоточенную в самом
шаре, и энергию W2 вне его.
18.19. Эбонитовый шар равномерно заряжен по объему. Во
сколько раз энергия электрического поля вне шара превосходит
энергию поля, сосредоточенную в шаре?

ГЛАВА 4
постоянный электрический ток
§ 19. ОСНОВНЫЕ ЗАКОНЫ ПОСТОЯННОГО ТОКА
Основные формулы
О Сила постоянного тока
I=Q/t,
где Q — количество электричества, прошедшее через поперечное
сечение проводника за время /.
9 Плотность электрического тока есть векторная величина,
равная отношению силы тока к площади S поперечного сечения про-
проводника:
где к — единичный вектор, по направлению совпадающий с на-
направлением движения положительных носителей заряда.
О Сопротивление однородного проводника
где р — удельное сопротивление вещества проводника; / — его
длина.
• Проводимость G проводника и удельная проводимость у
вещества
G=l/#, y=l/p.
• Зависимость удельного сопротивления от температуры
где р и ро — удельные сопротивления соответственно при /и О °С;
t — температура (по шкале Цельсия); а — температурный коэ4х|ш-
циент сопротивления.
О Сопротивление соединения проводников:
п
последовательного R = 2 /?,-;
i= 1
параллельного -^- = V -^
i
Здесь Ri — сопротивление /-го проводника; п — число провод-
проводников.
• Закон Ома:
для неоднородного участка цепи /=^— ^ =~5~'>
237

т (Pfs— (Do U
для однородного участка цепи / = Y1 Y2 = —;
для замкнутой цепи (фх=ф2) I=?/R.
Здесь (ф!—ф2) — разность потенциалов на концах участка цепи;
<?i2 — ЭДС источников тока, входящих в участок; U — напряжение
на участке цепи; R— сопротивление цепи (участка цепи); <§ —
ЭДС всех источников тока цепи.
• Правила Кирхгофа. Первое правило: алгебраическая сумма
сил токов, сходящихся в узле, равна нулю, т. е.
где п — число токов, сходящихся в узле.
Второе правило: в замкнутом контуре алгебраическая сумма на-
напряжений на всех участках контура равна алгебраической сумме
электродвижущих сил, т. е.
Где /. — сила тока на i-м участке; Rt — активное сопротивление
на i-u участке; Si — ЭДС источников тока на /-м участке; п —
число участков, содержащих активное сопротивление; k — число
участков, содержащих источники тока.
• Работа, совершаемая электростатическим полем и сторонни-
сторонними силами в участке цепи постоянного тока за время t,
• Мощность тока
P = IU.
• Закон Джоуля — Ленца
где Q — количество теплоты, выделяющееся в участке цепи за
время t.
Закон Джоуля — Ленца справедлив при условии, что участок
цепи неподвижен и в нем не совершаются химические превращения.
Примеры решения задач
Пример 1. Определить заряд Q, прошедший по проводу с сопро-
сопротивлением R=3 Ом при равномерном нарастании напряжения на
концах провода от Uo=2 В до t/=4 В в течение t=20 с.
Решение. Так как сила тока в проводе изменяется, то вос-
воспользоваться для подсчета заряда формулой Q=It нельзя. Поэтому
возьмем дифференциал заряда dQ=/d^ и проинтегрируем:
Q = )Mt. A)
О

Выразив силу тока по закону Ома, получим
B)
Напряжение U в данном случае переменное. В силу равномерно-
равномерности нарастания оно может быть выражено формулой
U=U0+ktt C)
где k — коэффициент пропорциональности. Подставив это выраже-
выражение U в формулу B), найдем
Проинтегрировав, получим
,D)
Рис. 19.1
В
Значение коэффициента пропорциональности k найдем из фор-
формулы C), если заметим, что при / = 20 с (/ = 4 В:
?=({/_ j/o)/f=0,1 В/с.
Подставив значения величин в формулу D), найдем
Q=20 Кл.
Пример 2. Потенциометр с сопротивлением /? = 100 Ом подклю-
подключен к источнику тока, ЭДС<? которого равна 150 В и внутреннее со-
сопротивление г=50 Ом (рис. 19.1). Опре-
Определить показание вольтметра с 'сопро-
'сопротивлением /?в=500 Ом, соединенного
проводником с одной из клемм потен-
потенциометра и подвижным контактом с се-
серединой обмотки потенциометра. Како-
Какова разность потенциалов между теми же
точками потенциометра при отключен-
отключенном вольтметре?
Решение. Показание U± вольт-
вольтметра, подключенного к точкам А и В (рис. 19.1), определяется по
формуле
?/i=/i#i, A)
где 1Х — сила тока в неразветвленной части цепи; Rx — сопротивле-
сопротивление параллельно соединенных вольтметра и половины потенциомет-
потенциометра.
Силу тока /f найдем по закону Ома для всей цепиз
h=S/(R+r)y B)
где R — сопротивление внешней цепи.
Внешнее сопротивление R есть сумма двух сопротивлений:
R=R/2+Rt. C)
239

Сопротивление Rx параллельного соединения может быть най-
найдено по формуле —=^ — -\- —р , откуда
Подставив в эту формулу числовые значения величин и произве-
произведя вычисления, найдем
/?!=45,5 Ом.
Подставив в выражение B) правую часть равенства C), опреде-
определим силу тока:
/ <§ 1 м д
Если подставить значения 1г и R± в формулу A), то найдем пока-
показание вольтметра:
(Л=46,9 В.
Разность потенциалов между точками А и В при отключенном
вольтметре равна произведению силы тока /2 на половину сопро-
сопротивления потенциометра, т. е. ?/2=
= /а(#/2), или
Рис. 19.2
Подставив сюда значения величин^,
R и г, получим
?/а=50 В.
Пример 3. Источники тока с элек-
тродвижущими силами ?х и $2 включены
в цепь, как показано на рис. 19.2. Оп-
Определить силы токов, текущих в сопротивлениях R2 и R3, если
tfi=10 В и <?2=4 В, aR1=RA=2OM и R2=R3=4 Ом. Сопротивле-
Сопротивлениями источников тока пренебречь.
Решение. Силы токов в разветвленной цепи определяют с
помощью законов Кирхгофа. Чтобы найти четыре значения силы
токов, следует составить четыре уравнения.
Указание, Перед составлением уравнений по закону Кирхгофа необхо-
необходимо, во-первых, выбрать произвольно направления токов, текущих через
сопротивления, указав их стрелками на чертеже, и, во-вторых, выбрать на-
направление обхода контуров (последнее только для составления уравнений по
второму закону Кирхгофа).
Выберем направления токов, как они показаны на рис. 19.2,
и условимся обходить контуры по часовой стрелке.
Рассматриваемая в задаче схема имеет два узла: А и В. Но состав-
составлять уравнение по первому закону Кирхгофа следует только для
одного узла, так как уравнение, составленное для второго узла,
будет следствием первого уравнения.
При составлении уравнений по первому закону Кирхгофа необ-
необходимо соблюдать правило знаков: ток, подходящий к узлу, входит
в уравнение со знаком плюс; ток, отходящий от узла,— со знаком
минус.
240

По первому закону Кирхгофа для узла В имеем
Недостающие три уравнения получим по второму закону Кирх-
Кирхгофа. Число независимых уравнений, которые могут быть составле-
составлены по второму закону Кирхгофа, также меньше числа контуров
(в нашем случае контуров шесть, а независимых уравнений три).
Чтобы найти необходимое число независимых уравнений, следует
придерживаться правила: выбирать контуры таким образом, чтобы
в каждый новый контур входила хотя бы одна ветвь, не участвовав-
участвовавшая ни в одном из ранее использованных контуров.
При составлении уравнений по второму закону Кирхгофа необ-
необходимо соблюдать следующее правило знаков:
а) если ток по направлению совпадает с выбранным направлени-
направлением обхода контуров, то соответствующее произведение IR входит
в уравнение со знаком плюс, в противном случае произведение IR
входит в уравнение со знаком минус,
б) если ЭДС повышает потенциал в направлении обхода контура,
т, е. если при обходе контура приходится идти от минуса к плюсу
внутри источника, то соответствующая ЭДС входит в уравнение
со знаком плюс, в противном случае — со знаком минус.
По второму закону Кирхгофа имеем соответственно для контуров
ЛЯхВЯаЛ, АЯгВЯъА, AR3BR,A:
I\Rl /2Ao=<Di <Q 27 A)
IiRi—I,R,=?i, B)
/3Я3 + /4Я4 = 0. C)
Подставив в равенства A)—C) значения сопротивлений и
ЭДС, получим систему уравнений:
27,-4/3 = 10,
4/3 + 2/4 = 0.
Поскольку нужно найти только два тока, то удобно воспользо-
воспользоваться методом определителей (детерминантов). С этой целью пере-
перепишем уравнения еще раз в следующем виде:
2/1-4/2
21х + 0—4/3 + 0=10,
Искомые значения токов найдем из выражений
/8 = Д/,/Д и /3 = Л/з/Л,
где Д — определитель системы уравнений; Д/2 и Д/,—определи-
Д/,—определители, полученные заменой соответствующих столбцов определителя
Д столбцами, составленными из свободных членов четырех выше-
241

приведенных уравнений. Находим;
А =
*/.=
1
2
2
0
1
2
2
0
1
—4
0
0
0
6
10
0
1
0
—4
4
1
0
—4
4
—1
о
о
2
1
О
о
2
= 96;
= 0; А/,=
1
—4
О
О
О
6
10
О
— 1
О
О
2
= —96.
Отсюда получаем
/ П / 1 Л
1 2 — ^» * 3 — к Л#
Знак минус у значения силы тока /3 свидетельствует о том, что
при произвольном выборе направлений токов, указанных на рисун-
рисунке, направление тока /3 было
указано противоположно истин-
истинному. На самом деле ток /3 те-
течет от узла В к узлу А.
Пример 4. Сила тока в про-
проводнике сопротивлением R =
=20 Ом нарастает в течение вре-
времени At=2 с по линейному за-
за7 2
Рис. 19.3
кону ОТ /0 = 0 ДО /тах^б А (рИС.
19.3). Определить количество
теплоты Qb выделившееся в этом
проводнике за первую секунду, и Q2 — за вторую, а также найти
отношение этих количеств теплоты QJQt.
Решение. Закон Джоуля — Ленца Q=I2Rt применим в слу-
случае постоянного тока (/=const). Если же сила тока в проводнике
изменяется, то указанный закон справедлив для бесконечно малого
промежутка времени и записывается в виде
dQ=PRdt. A)
Здесь сила тока / является некоторой функцией времени. В на-
нашем случае
I=kty B)
где k — коэффициент пропорциональности, равный отношению
приращения силы тока к интервалу времени, за который произошло
это приращение:
k=AIIAt.
С учетом равенства B) формула A) примет вид
dQ=k2Rt2dt. C)
Для определения количества теплоты, выделившегося за конеч-
конечный промежуток времени At, выражение C) следует проинтегриро-
проинтегрировать в пределах от t± до t2i
и
1 1.0 Г» /23 ЛЗУ
242

При определении количества теплоты, выделившегося за первую
секунду, пределы интегрирования /i=0, t2=l с и, следовательно,
Qx-60 Дж,
а за вторую секунду — пределы интегрирования tx=l c} 12=2 с и
тогда
Q2=420 Дж.
Следовательно,
т. е. за вторую секунду выделится теплоты в 7 раз больше, чем за
первую секунду.
Задачи
Закон Ома для участка цепи
19.1. Сила тока в проводнике равномерно нарастает от /о=0 до
/=3 А в течение времени ?=10 с. Определить заряд Q, прошедший
в проводнике.
19.2. Определить плотность тока / в железном проводнике дли-
длиной /=10 м, если провод находится под напряжением ?/=6 В.
19.3. Напряжение U на шинах электростанции равно 6,6 кВ.
Потребитель находится на расстоянии /=10 км. Определить пло-
площадь S сечения медного провода, который следует взять для уст-
устройства двухпроводной линии передачи, если сила тока / в линии
равна 20 А и потери напряжения в проводах не должны превышать
3 %.
19.4. Вычислить сопротивление R графитового проводника, из-
изготовленного в виде прямого кругового усеченного конуса высотой
/г=20 см и радиусами оснований гх= 12 мм и г2=8 мм. Температура
/ проводника равна 20 °С.
19.5. На одном конце цилиндрического медного проводника со-
сопротивлением Ro~lO Ом (при 0 °С) поддерживается температура
/i=20 °С, на другом t2=
=400 °С. Найти сопротив-
сопротивление jR проводника, счи-
считая градиент температуры
вдоль его оси постоянным, у
19.6. Проволочный куб й\
составлен из проводников.
Сопротивление Ri каждого
проводника, составляюще-
составляющего ребро куба, равно 1 Ом. Вычислить сопротивление R этого ку-
куба, если он включен в электрическую цепь, как показано на рис.
19.4. а.
19.7. То же (см. задачу 19.6), если куб включен в цепь, как пока-
показано на рис. 19.4, б.
19.8. То же (см. задачу 19.6), если куб включен в цепь, как по-
показано на рис. 19.4, в,
243
/
/
У
/
/
/
/
/
/
/
Б)
Рис. 19.4

19.9. Катушка и амперметр соединены последовательно и присо-
присоединены к источнику тока. К зажимам катушки присоединен вольт-
вольтметр сопротивлением i?B=l кОм. Показания амперметра /=0,5 А,
вольтметра ?/=100 В. Определить сопротивление R катушки.
Сколько процентов от точного значения сопротивления катушки
составит погрешность, если не учитывать сопротивления вольтмет-
вольтметра?
19.10. Зашунтированный амперметр измеряет токи силой до / =
= 10 А. Какую наибольшую силу тока может измерить этот ампер-
амперметр без шунта, если сопротивле-
сопротивление Ra амперметра равно 0,02 Ом
и сопротивление Rm шунта равно
5 мОм?
19.11. Какая из схем, изобра-
изображенных на рис. 19.5, ау б, более
пригодна для измерения больших
сопротивлений и какая — для
измерения малых сопротивлений?
Вычислить погрешность, допус-
допускаемую при измерении с помощью этих схем сопротивлений Rx =
= 1 кОм и R2=l0 Ом. Принять сопротивления вольтметра RB и
амперметра /?а соответственно равными 5 кОм и 2 Ом.
Закон Ома для всей цепи
19.12. Внутреннее сопротивление г батареи аккумуляторов рав-
равно 3 Ом. Сколько процентов от точного значения ЭДС составляет
погрешность, если, измеряя разность потенциалов на зажимах ба-
батареи вольтметром с сопротивлением iRB=200 Ом, принять ее рав-
равной ЭДС?
19.13. К источнику тока с ЭДС <? = 1,5 В присоединили катуш-
катушку с сопротивлением /?=0,1 Ом. Амперметр показал силу тока, рав-
равную /i=0,5 А. Когда к источнику тока присоединили последова-
последовательно еще один источник тока с такой же ЭДС, то сила тока /
в той же катушке оказалась равной 0,4 А. Определить внутренние
сопротивления г1 и г2 первого и второго источников тока.
19.14. Две группы из трех последовательно соединенных элемен-
элементов соединены параллельно. ЭДС $ каждого элемента равна 1,2 В,
внутреннее сопротивлениег=0,2 Ом. Полученная батарея замкнута
на внешнее сопротивление /? = 1,5 Ом. Найти силу тока / во внеш-
внешней цепи.
19.15. Имеется N одинаковых гальванических элементов
с ЭДС $ и внутренним сопротивлением гг каждый. Из этих элемен-
элементов требуется собрать батарею, состоящую из нескольких параллель-
параллельно соединенных групп, содержащих по п последовательно соединен-
соединенных элементов. При таком значении п сила тока / во внешней цепи,
имеющей сопротивление R, будет максимальной? Чему будет равно
внутреннее сопротивление Rt батареи при этом значении я?
244

в)
19.16. Даны 12 элементов с ЭДС <?=1,5 В и внутреннем сопро-
сопротивлением г=0,4 Ом. Как нужно соединить эти элементы, чтобы
получить от собранной из них батареи наибольшую силу тока во
внешней цепи, имеющей сопротивление - s
/?=0,3 Ом? Определить максимальную | ч
силу тока /тах.
19.17. Два одинаковых источника то- А \ \В А
ка с ЭДС<?=1,2 В и внутренним сопро-
сопротивлением г=0,4 Ом соединены, как
показано на рис. 19.6, а, б. Определить
силу тока / в цепи и разность потенциа- а)
лов U между точками Л и В в первом и Рис. 19.6
втором случаях.
19.18. Два элемента (^i=l,2 В, гх=0,1 Ом; <?2=0,9 В, г2=
— 0,3 Ом) соединены одноименными полюсами. Сопротивление R
соединительных проводов равно 0,2 Ом. Определить силу тока /
в цепи.
Правила Кирхгофа
19.19. Две батареи аккумуляторов (<^i= 10 В, гх = 1 Ом; ?2=
=8 В, г2=2 Ом) и реостат (R=6 Ом) соединены, как показано на
рис. 19.7. Найти силу тока в батареях и реостате.
19.20. Два источника тока (Si= 8В, ^=2 Ом; <?2=6 В, г2=
= 1,5 Ом) и реостат (/? = 10Ом) соединены, как показано на рис. 19.8.
Вычислить силу тока /, текущего через реостат.
^Нг
Рис. 19.7
Рис. 19..
19.21. Определить силу тока /3 в резисторе сопротивлением R3
(рис. 19.9) и напряжение U3 на концах резистора, если <^i=4 В,
<^2=3 В, R1=2Om, R2=6 Ом, /?3= 1 Ом. Внутренними сопротивле-
сопротивлениями источников тока пренебречь.
19.22. Три батареи с ЭДС ^=12 В,^2-5В и ? = 10 В и одина-
одинаковыми внутренними сопротивлениями г, равными 1 Ом, соединены
между собой одноименными полюсами. Сопротивление соединитель-
соединительных проводов ничтожно мало. Определрггь силы токов /, идущих че-
через каждую батарею.
19.23. Три источника токае ЭДС^=11 В,<?2=4 В к?3=6 В и
три реостата с сопротивлениями Rt=5 Ом, /?2= 10 Ом и ^3=2 Ом
соединены, как показано на рис. 19.10. Определить силы токов /
245

в реостатах. Внутреннее сопротивление источника тока пренебрежи-
пренебрежимо мало.
19.24. Три сопротивления R^S Ом, R2= 1 Ом и /?3=3 Ом, а так-
также источник тока с ЭДС<?1=1,4 В соединены, как показано на
Рис. 19.9
Рис. 19.10
Рис. 19.11
рис. 19.11. Определить ЭДС^? источника тока, который надо под-
подключить в цепь между точками Л и В, чтобы в сопротивлении R9
шел ток силой /=1 А в направлении, указанном стрелкой. Сопротив-
Сопротивлением источника тока пренебречь.
Работа и мощность тока
19.25. Лампочка и реостат, соединенные последовательно, при-
присоединены к источнику тока. Напряжение U на зажимах лампочки
равно 40 В, сопротивление R реостата равно 10 Ом. Внешняя цепь
потребляет мощность Р=120 Вт. Найти силу тока / в цепи.
19.26. ЭДС батареи аккумуляторов <8=\2 В, сила тока / ко-
короткого замыкания равна 5 А. Какую наибольшую мощность Ршах
можно получить во внешней цепи, соединенной с такой батареей?
19.27. К батарее аккумуляторов, ЭДС S которой равна 2 В
и внутреннее сопротивление г=0,5 Ом, присоединен проводник.
Определить: 1) сопротивление R проводника, при котором мощность,
выделяемая в нем, максимальна; 2) мощность Р, которая при этом
выделяется в проводнике.
19.28. ЭДС $ батареи равна 20 В. Сопротивление R внешней
цепи равно 2 Ом, сила тока /=4 А. Найти КПД батареи. При ка-
каком значении внешнего сопротивления R КПД будет равен 99%?
19.29. К зажимам батареи аккумуляторов присоединен нагрева-
нагреватель. ЭДС ? батареи равна 24 В, внутреннее сопротивление г=
= 1 Ом. Нагреватель, включенный в цепь, потребляет мощность
Р=80 Вт. Вычислить силу тока / в цепи и КПД т] нагревателя.
19.30. Обмотка электрического кипятильника имеет две секции.
Если включена только первая секция, то вода закипает через tx=
= 15 мин, если только вторая, то через ?2=30 мин. Через сколько
минут закипит вода, если обе секции включить последовательно?
параллельно?
19.31. При силе тока /*=3 А во внешней цепи батареи аккумуля-
аккумуляторов выделяется мощность Р!=18 Вт, при силе тока /2=1 А — со-
246

ответственно Р2=ЮВт. Определить ЭДС ? и внутреннее сопро-
сопротивление г батареи.
19.32. Сила тока в проводнике сопротивлением г= 100 Ом равно-
равномерно нарастает от /0=0 до 1т^=10 А в течение времени т=30 с.
Определить количество теплоты Q, выделившееся за это время в про-
проводнике.
19.33. Сила тока в проводнике сопротивлением R = 12 Ом равно-
равномерно убывает от /0=5 А до /=0 в течение времени ?=10 с. Какое
количество теплоты Q выделяется в этом проводнике за указанный
промежуток времени?
19.34. По проводнику сопротивлением R=3 Ом течет ток, сила
которого возрастает. Количество теплоты Q, выделившееся в про-
проводнике за время т=8 с, равно 200 Дж. Определить количество
электричества q, протекшее за это время по проводнику. В момент
времени, принятый за начальный, сила тока в проводнике равна
нулю.
19.35. Сила тока в проводнике сопротивлением R = 15 Ом равно-
равномерно возрастает от /0=0 до некоторого максимального значения
в течение времени т—5 с. За это время в проводнике выделилось
количество теплоты Q=10 кДж. Найти среднюю силу тока (/}
в проводнике за этот промежуток времени.
19.36. Сила тока в проводнике равномерно увеличивается от /0=
—0 до некоторого максимального значения в течение времени т=
=.10 с. За это время в проводнике выделилось количество теплоты
Q=l кДж. Определить скорость нарастания тока в проводнике,
если сопротивление R его равно 3 Ом.
§ 20. ТОК В МЕТАЛЛАХ, ЖИДКОСТЯХ И ГАЗАХ
Основные формулы
• Плотность тока j, средняя скорость (v) упорядоченного дви-
движения носителей заряда и их концентрация п связаны соотношением
где е — элементарный заряд.
О Закон Ома в дифференциальной форме
J=VE,
где у — удельная проводимость проводника; Е — напряженность
электрического поля.
• Закон Джоуля — Ленца в дифференциальной форме
w=yE\
где w — объемная плотность тепловой мощности.
• Удельная электрическая проводимость
где е и т — заряд и масса электрона; п — концентрация электро-
электронов; (/) — средняя длина их свободного пробега; и — средняя ско-
скорость хаотического движения электронов.
247

• Закон Видемана — Франца
у ег
где \ — теплопроводность.
• Термоэлектродвижущая сила, возникающая в термопаре,
с? = ссG\-7\2),
где а — удельная термо-ЭДС; G\—Т2) — разность температур
спаев термопары.
• Законы электролиза Фарадея. Первый закон
m=kQ,
где m — масса вещества, выделившегося на электроде при прохож-
прохождении через электролит электрического заряда Q; k — электрохими-
электрохимический эквивалент вещества.
Второй закон
k=Ml(FZ)y
где F — постоянная Фарадея (F=96,5 кКл/моль); М — молярная
масса ионов данного вещества; Z — валентность ионов.
Объединенный закон
1 М п \ М т,
где / — сила тока, проходящего через электролит; / — время, в те-
течение которого шел ток.
• Подвижность ионов
где (v) — средняя скорость упорядоченного движения ионов; Е —
напряженность электрического поля.
• Закон Ома в дифференциальной форме для электролитов и
газов при самостоятельном разряде в области, далекой от насыще-
насыщения,
} = Qn(b+ + b_)Et
где Q — заряд иона; п — концентрация ионов; Ь+ и Ь_ — подвиж-
подвижности соответственно положительных и отрицательных ионов.
• Плотность тока насыщения
где п0 — число пар ионов, создаваемых ионизатором в единице
объема в единицу времени; d — расстояние между электродами
[no=N/(Vt)y где Af — число пар ионов, создаваемых ионизатором
за время / в пространстве между электродами; V — объем этого
пространства].
Примеры решения задач
Пример 1. По железному проводнику, диаметр d сечения которо-
которого равен 0,6 мм, течет ток 16 А. Определить среднюю скорость
(v) направленного движения электронов, считая, что концентрация
п свободных электронов равна концентрации п' атомов проводника.
248

Решение. Средняя скорость направленного (упорядочен-
(упорядоченного) движения электронов определяется по формуле
iv)=l/t, A)
где t — время, в течение которого все свободные электроны, нахо-
находящиеся в отрезке проводника между сечениями / и /7, пройдя че-
через сечение // (рис. 20.1), пе-
перенесут заряд Q=eN и создадут
ток
/=4=?. B)
где е — элементарный заряд; / Е
N— число электронов в отрезке Рис. 20.1
проводника; / — его длина.
Число свободных электронов в отрезке проводника объемом V
можно выразить следующим образом:
N=nV=nlS, C)
где S — площадь сечения.
По условию задачи, п=п'. Следовательно,
()
где Л/"а — постоянная Авогадро; Vm — молярный объем металла;
М — молярная масса металла; р — его плотность.
Подставив последовательно выражения п из формулы D) в ра-
равенство C) и N из формулы C) в равенство B), получим
. _ NAplSe
Mt '
Отсюда найдем
IMt
l
Подставив выражение / в формулу A), сократив на t и выразив
площадь S сечения проводника через диаметр d, найдем среднюю
скорость направленного движения электронов:
41М /кч
Произведем по этой формуле вычисления:
4» 16.56» Ю-3
3,14-@,6-10-3J-6,02.1023-98.10-9-1,60- Ю-19 м/с "
= 4,20-10 м/с = 4,20 мм/с.
Пример 2. В цепь источника постоянного тока с ЭДС с?=6 В
включен резистор сопротивлением /?=80 Ом. Определить: 1) плот-
плотность тока в соединительных проводах площадью поперечного сече-
сечения S=2 мм2; 2) число N электронов, проходящих через сечение
проводов за время t=\ с. Сопротивлением источника тока и соеди-
соединительных проводов пренебречь.
249

Решение. L Плотность тока по определению есть отношение
силы тока / к площади поперечного сечения провода:
/W/S. A)
Силу тока в этой формуле выразим по закону Ома;
7=таТ7Г И"
где R — сопротивление резистора; Ri — сопротивление соедини-
соединительных проводов; гг — внутреннее сопротивление источника тока.
Пренебрегая сопротивлениями Rx и rt из B), получим
Подставив это выражение силы тока в A), найдем
Произведя вычисления по этой формуле, получим
/ = 80.2610-6 А/м2 = 3,75 • 10* А/м2.
2. Число электронов, проходящих за время t через поперечное
сечение, найдем, разделив заряд Q, протекающий за это время че-
через сечение, на элементарный заряд:
N=Q/e,
или с учетом того, что Q=Itn I=S/Rt
/V Re •
Подставим сюда числовые значения величин и вычислим (эле-
(элементарный заряд возьмем из табл. 24: е=1,60*10~:19 Кл):
п 1
iV =8(M 6q,10-jl9 электронов = 4,69-1017 электронов.
Пример 3. Пространство между пластинами плоского конденса-
конденсатора имеет объем У=375 см3 и заполнено водородом, который ча-
частично ионизирован. Площадь пластин конденсатора S=250 см2.
При каком напряжении U между пластинами конденсатора сила
тока /, протекающего через конденсатор, достигнет значения 2 мкА,
если концентрация п ионов обоих знаков в газе равна 5,3«Ю7 см?
Принять подвижность ионов 6+=5,4-10~4 м2/(В-с), Ь_=7,4х
Х10м2/(В.с).
Решение. Напряжение U на пластинах конденсатора свя-
связано с напряженностью Е электрического поля между пластинами и
расстоянием d между ними соотношением
U=Ed. A)
Напряженность поля может быть найдена из выражения плот-
плотности тока
где Q — заряд иона.
Отсюда
? = __?__ =
250

Расстояние d между пластинами, входящее в- формулу A), най-
найдем из соотношения
d=V/S.
Подставив выражения Е и d в A), получим
1У
Проверим, дает ли правая часть полученной расчетной формулы
единицу напряжения:
[/] [V] 1 А-1 м3 __
[Q] [п] [Ь] [S2] ~~ 1Кл.1м[1 м2/(с-В)] м* "^
_ 1 А-1 м6-! с»1 В _ 1 Кл-1 В « R
~~ 1 Кл-1 м6 " 1 Кл ""
Подставим в формулу B) значения величин и произведем вычис-
вычисления:
,j 2-10-g-375-10-6 R — 110R
U ~~ l,6-10-19-5,3-1013E,4+7,4).10-4B50.10-4J"* 1U '
Пример 4. Определить скорость и (мкм/ч), с которой растет
слой никеля на плоской поверхности металла при электролизе, если
плотность тока /, протекающего через электролит, равна 30 А/м.
Никель считать двухвалентным.
Решение. Для решения задачи воспользуемся объединенным
законом Фарадея
т = т-^-Н. A)
Будем считать, что электролитическое осаждение никеля идет рав-
равномерно по всей поверхности металла. Тогда массу т выделившего-
выделившегося за время t никеля можно выразить через плотность р, площадь
S поверхности металла и толщину h слоя никеля:
m—pSh. B)
Силу тока / выразим через плотность тока и площадь поверхности
металла:
I=jS. C)
Подставив в формулу A) выражения для массы B) и силы тока
C), получим
1 М
pfi^-pr-j-jt. D)
При неизменной плотности тока нарастание слоя никеля будет про-
происходить с постоянной скоростью и, определяемой отношением тол-
толщины слоя, наращенного за некоторый интервал времени, к этому
интервалу (u=h/t). Тогда из формулы D) следует
251

Убедимся в том, что правая часть равенства дает единицу скоро-
скорости:
[М] [/] __ 1 кг/моль-1 А/м2 __ 1 А-1 м __ 1 А*1 м _ *
[Л[р] "" 1 Кл/моль-1 кг/м3 1 Кл ~" 1 А/с ~~ М/С'
При этом было учтено, что валентность Z величина неименованная
(безразмерная).
Выпишем значения величин, выразив их в единицах СИ: F=
=9,65-104 Кл/моль (см. табл.24), М=58,7-10 кг/моль (см. Пе-
Периодическую систему элементов Д. И. Менделеева на внутренней
стороне обложки), Z=2, /=30 А/м2, р=8,8 -103 кг/м3 (см. табл. 9).
Подставим числовые значения и произведем вычисления:
58,7-Ю-3.30 , л л, 1A__q о пл
и= 9>65.104.2.8,8.1Q3 м/с= 1,04-10 9 м/с = 3,74 мкм/ч.
Задачи
Ток в металлах
20.1. Сила тока / в металлическом проводнике равна 0,8 А, се-
сечение 5 проводника 4 мм2. Принимая, что в каждом кубическом
сантиметре металла содержится /г=2,5-1022 свободных электронов,
определить среднюю скорость (v) их упорядоченного движения.
20.2. Определить среднюю скорость (v) упорядоченного движения
электронов в медном проводнике при силе тока /=10 А и сечении 5
проводника, равном 1 мм2. Принять, что на каждый атом меди при-
приходится два электрона проводимости.
20.3. Плотность тока / в алюминиевом проводе равна 1 А/мм2.
Найти среднюю скорость (v) упорядоченного движения электронов,
предполагая, что число свободных электронов в 1 см3 алюминия
равно числу атомов.
20.4. Плотность тока / в медном проводнике равна 3 А/мм2. Най-
Найти напряженность Е электрического поля в проводнике.
20.5. В медном проводнике длиной /=2 м и площадью S попереч-
поперечного сечения, равной 0,4 мм2, идет ток. При этом ежесекундно вы-
выделяется количество теплоты Q=0,35 Дж. Сколько электронов N
проходит за 1 с через поперечное сечение этого проводника?
20.6. В медном проводнике объемом 1/=6 см3 при прохождении
по нему постоянного тока за время t=l мин выделилось количество
теплоты Q=216 Дж. Вычислить напряженность Е электрического
поля в проводнике.
Классическая теория электропроводности металлов
20.7. Металлический проводник движется с ускорением а=
= 100 м/с2. Используя модель свободных электронов, определить
напряженность Е электрического поля в проводнике.
20.8. Медный диск радиусом R=0,5 м равномерно вращается
(со = 104 рад/с) относительно оси, перпендикулярной плоскости
252

.диска и проходящей через его центр. Определить разность потен-
потенциала U между центром диска и его крайними точками.
20.9. Металлический стержень движется вдоль своей оси со ско-
скоростью и=200 м/с. Определить заряд Q, который протечет через
гальванометр, подключаемый к концам стержня, при резком его
торможении, если длина / стержня равна 10 м, а сопротивление
R всей цепи (включая цепь гальванометра) равно 10 мОм.
20.10. Удельная проводимость у металла равна 10 МСм/м. Вы-
Вычислить среднюю длину (/) свободного пробега электронов в метал-
металле, если концентрация п свободных электронов равна 1028 м~3.
Среднюю скорость и хаотического движения электронов принять
равной 1 Мм/с.
20.11. Исходя из модели свободных электронов, определить чис-
число z соударений, которые испытывает электрон за время /=1 с,
находясь в металле, если концентрация п свободных электронов
равна 1029 м~3. Удельную проводимость у металла принять равной
10 МСм/м.
20.12. Исходя из классической теории электропроводности ме-
металлов, определить среднюю кинетическую энергию (е) электронов
в металле, если отношение Х/у теплопроводности к удельной прово-
проводимости равно 6,7-10~6 В2/К.
20.13. Определить объемную плотность тепловой мощности w
в металлическом проводнике, если плотность тока / = 10 А/мм2.
-Напряженность Е электрического поля в проводнике равна 1 мВ/м.
20.14. Термопара медь — константан с сопротивлением Rx=
=5 Ом присоединена к гальванометру, сопротивление R2 которого
равно 100 Ом. Один спай термопары погружен в тающий лед, дру-
другой — в горячую жидкость. Сила тока / в цепи равна 37 мкА. По-
Постоянная термопары &=43 мкВ/К. Определить температуру t жид-
жидкости.
20.15. Сила тока / в цепи, состоящей из термопары с сопротивле-
сопротивлением /?i=4 Ом и гальванометра с сопротивлением R3=80 Ом, равна
26 мкА при разности температур At спаев, равной 50 °С. Определить
постоянную k термопары.
Ток в жидкостях
20.16. При силе тока /=5 А за время /=10 мин в электролитиче-
электролитической ванне выделилось /п=1,02 г двухвалентного металла. Опреде-
Определить его относительную атомную массу Аг.
20.17. Две электролитические ванны соединены последовательно.
В первой ванне выделилось mx=3,9 г цинка, во второй за то же
время га2=2,24 г железа. Цинк двухвалентен. Определить валент-
валентность железа.
20.18. Электролитическая ванна с раствором медного купороса
присоединена к батарее аккумуляторов с ЭДС <?=4 В и внутрен-
внутренним соцротивленим г=0,1 Ом. Определить массу т меди, выделив-
выделившейся при электролизе за время /=10 мин, если ЭДС поляриза-
253

ции <?п= 1,5 В и сопротивление R раствора равно 0,5 Ом. Медь двух-
двухвалентна.
20.19. Определить толщину h слоя меди, выделившейся за время
t=5 ч при электролизе медного купороса, если плотность тока /=
^80 А/м2.
20.20. Сила тока, проходящего через электролитическую ванну
с раствором медного купороса, равномерно возрастает в течение
времени Д/=20 с от /0=0 до 1=2 А. Найти массу т меди, выделив-
выделившейся за это время на катоде ванны.
20.21. В электролитической ванне через раствор прошел заряд
Q=193 кКл. При этом на катоде выделился металл количеством ве-
вещества v=l моль. Определить валентность Z металла.
20.22. Определить количество вещества v и число атомов N двух-
двухвалентного металла, отложившегося на катоде электролитической
ванны, если через раствор в течение времени t=5 мин шел ток силой
1=2 А.
20.23. Сколько атомов двухвалентного металла выделится на
1 см2 поверхности электрода за время t=5 мин при плотности тока
/=10 А/м2?
Ток в газах
20.24. Энергия ионизации атома водорода ?^=2,18 «Ю"*8 Дж.
Определить потенциал ионизации Ut водорода.
20.25. Какой наименьшей скоростью vm{n должен обладать элект-
электрон, чтобы ионизировать атом азота, если потенциал ионизации
Цг азота равен 14,5 В?
20.26. Какова должна быть температура Т атомарного водорода,
чтобы средняя кинетическая энергия поступательного движения
атомов была достаточна для ионизации путем соударений? Потен-
Потенциал ионизации Ut атомарного водорода равен 13,6 В..
20.27. Посередине между электродами ионизационной камеры
пролетела а-частица, двигаясь параллельно электродам, и образо-
образовала на своем пути цепочку ионов. Спустя какое время после проле-
пролета а-частицы ионы дойдут до электродов, если расстояние d между
электродами равно 4 см, разность потенциалов 1/=5 кВ и подвиж-
подвижность ионов обоих знаков в среднем Ъ=2 см2/(В -с)?
20.28. Азот ионизируется рентгеновским излучением. Опреде-
Определить проводимость G азота, если в каждом кубическом сантиметре
газа находится в условиях равновесия по=1Ог пар ионов. Подвиж-
Подвижность положительных ионов 6+ = 1,27 см2/(В-с) и отрицательных
Ь_ = 1,81 см2/(В.с).
20.29. Воздух между плоскими электродами ионизационной ка-
камеры ионизируется рентгеновским излучением. Сила тока /, теку-
текущего через камеру, равна 1,2 мкА. Площадь S каждого электрода
равна 300 см2, расстояние между ними d=2 см, разность потенциа-
потенциалов {/=100 В. Найти концентрацию п пар ионов между пластина-
пластинами, если ток далек от насыщения. Подвижность положительных
254

ионов Ь+ = 1,4 см2/(Вс)и отрицательных Ь_ —1,9 см2/(В-с). Заряд
каждого иона равен элементарному заряду.
20.30. Объем V газа, заключенного между электродами иониза-
ионизационной камеры, равен 0,5 л. Газ ионизируется рентгеновским из-
излучением. Сила тока насыщения /нас^ нА. Сколько пар ионов
образуется в 1 с в 1 см3 газа? Заряд каждого иона равен элементар-
элементарному заряду.
20.31. Найти силу тока насыщения между пластинами конденса-
конденсатора, если под действием ионизатора в каждом кубическом санти-
сантиметре пространства между пластинами конденсатора ежесекундно
образуется n0=108 пар ионов, каждый из которых несет один элемен-
элементарный заряд. Расстояние d между пластинами конденсатора равно
1 см, площадь S пластины равна 100 см2.
20.32. В ионизационной камере, расстояние d между плоскими
электродами которой равно 5 см, проходит ток насыщения плот-
плотностью /=16 мкА/м2. Определить число п пар ионов, образующихся
в каждом кубическом сантиметре пространства камеры в 1 с.

ГЛАВА 5
ЭЛЕКТРОМАГНЕТИЗМ
§ 21. МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА
Основные формулы
Закон Био — Савара — Лапласа
где dB —магнитная индукция поля, создаваемого элементом про-
проводника с током; \i — магнитная проницаемость; \х0 — магнитная
постоянная (juio=4jt-10~7 Гн/м); dl — вектор, равный по модулю
длине d/ проводника и совпадающий по направлению с током (эле-
(элемент проводника); / — сила тока; г — радиус-вектор, проведенный
от середины элемента проводника к точке, магнитная индукция
в которой определяется.
Модуль вектора dB выражается формулой
где а — угол между векторами dl и г.
• Магнитная индукция В связана с напряженностью Н маг-
магнитного поля (в случае однородной, изотропной среды) соотноше-
соотношением
или в вакууме
Во—И'оН.
• Магнитная индукция в центре кругового проводника с током
где R — радиус кривизны проводника.
• Магнитная индукция поля, создаваемого бесконечно длин-
длинным прямым проводником с током,
где г — расстояние от оси проводника.
Магнитная индукция поля, создаваемого отрезком проводника,
В = ^ 77 (cos ф1 ~ cos ф2)'
256

Обозначения ясны из рис. 21.1, а. Вектор индукции В перпенди-
перпендикулярен плоскости чертежа, направлен к нам и поэтому изображен
точкой.
При симметричном расположении концов проводника относи-
относительно точки, в которой определяется магнитная индукция
(рис. 21.1, б), —cos qJ=cos фх=^
=cos ф и, следовательно,
2л rQ Y
# Магнитная индукция поля,
создаваемого соленоидом в сред-
средней его части (или тороида на его
оси),
II
11
II
ч
-г°ув
1
1
/
1
1
п
Чу
УУ а)
Рис.
II
I
21.1
i
i
[У
*\
/
/
—^/
г
/
/
/
1
1
" ь)
где п — число витков, приходящих-
приходящихся на единицу длины соленоида;
/ — сила тока в одном витке.
О Принцип суперпозиции маг-
магнитных полей: магнитная индук-
индукция В результирующего поля равна векторной сумме магнитных
индукций Вь В2, ..., ВЛ складываемых полей, т. е.
в=|в,.
В частном случае наложения двух полей
а модуль магнитной продукции
В - УВ\ + ВЦ- 2ВХВ2 cos a,
где а — угол между векторами Вх и В2.
Примеры решения задач
Пример 1. Два параллельных бесконечно длинных провода, по
которым текут в одном направлении токи /=60 А, расположены на
В
Рис. 21.2
метрически, т. е.
ме косинусов:
расстоянии d= 10 см друг от друга.
Определить магнитную индукцию В
в точке, отстоящей от одного про-
проводника на расстоянии /^=5 см и от
другого — на расстоянии г2=12 см.
Решение. Для нахождения
магнитной индукции в указанной точ-
точке А (рис. 21.2) определим направле-
направления векторов индукций Вх и В2 по-
1 лей, создаваемых каждым проводни-
проводником в отдельности, и сложим их гео-
1 = В!+В2. Модуль индукции найдем по теоре-
В = УВ* + В\ +
cos a.
A)
1268
257

Значения индукций ?* и В2 выражаются соответственно через
силу тока / и расстояния г± и г2 от провода до точки, индукцию
в которой мы вычисляем: Bt = -|~т » Вл — -к?г~ • Подставляя В± и
В2 в формулу A) и вынося J~j- за знак корня, получим
-cos a.
Убедимся в том, что правая часть этого равенства дает единицу
магнитной индукции (Тл):
jn0/ _ 1 Гн/м-l А _ 1 Гн-A АJ __ 1 Дж __ 1 Н
[r2]1^ TU 1 А-A мJ ~~ 1 А-A мJ ~* 1 А-1 м
_, т
1 А-A мJ
Здесь мы воспользовались определяющей формулой для маг-
магнитной индукции (S=Mmax Ipn). Откуда следует, что
1 т __ 1 Н-1 м _ 1 Н
1Л 1 А-A мJ~" 1 А*1 м •
Вычисляем cos а. Заметим, что a—ADAC. Поэтому по теореме
косинусов запишем й^=г\+г\—2Ay2cos а, где d — расстояние
между проводами. Отсюда
Подставив данные, вычислим значение косинуса:
cos a=0,576.
Подставив в формулу B) значения ^0, U >*i> ^2 и cos p, найдем
мкТл.
Пример 2. По двум длинным прямолинейным проводам, находя-
находящимся на расстоянии г=5 см друг от друга в воздухе, текут токи
/=10 А каждый. Опреде-
Определить магнитную индукцию
В поля, создаваемого то-
^ Yl,J ками в точке, лежащей по-
посередине между проводами,
для случаев: 1) провода
параллельны, токи текут в
одном направлении (рис.
21.3, а); 2) провода парал-
параллельны, токи текут в про-
противоположных направле-
направлениях (рис. 21.3, б); 3) про-
провода перпендикулярны, на-
направление токов указано
на рис. 21.3, #.
индукция магнитного поля
где Bi — индукция поля,
Рис. 21.3
Решение.
равна векторной
Результирующая
сумме: B=Bi+B
/ В
р р у j у ,
создаваемого током /*; В2 — индукция поля, создаваемого током
/
258

Если Вх и В2 направлены по одной прямой, то векторная сумма
может быть заменена алгебраической суммойi
B=B,+B2. A)
При этом слагаемые Вх и В2 должны быть взяты с соответствую-
соответствующими знаками.
В данной задаче во всех трех случаях модули индукций Вг и В2
одинаковы, так как точки выбраны на равных расстояниях от про-
проводов, по которым текут равные токи. Вычислим эти индукции по
формуле
В=\хо1/Bлг). B)
Подставив значения величин в формулу B), найдем модули В±
и В2:
Вх=В2=80 мкТл.
1-й случай. Векторы Bf и В2 направлены по одной прямой
(рис. 21.3, а); следовательно, результирующая индукция В опреде-
определяется по формуле A). Приняв направление вверх положительным,
вниз — отрицательным, запишем: Bt=—80 мкТл, /?2=80 мкТл.
Подставив в формулу A) эти значения В± и Л2, получим
2-й случай. Векторы Вх и В2 направлены по одной прямой в одну
сторону (рис. 21.3, б). Поэтому можем за-
записать
В1==В2=_80 мкТл.
Подставив в формулу A) значения Bxn B2i
получим
В=В1+В2=—160 мкТл.
3-й случай. Векторы индукций магнит-
магнитных полей, создаваемых токами в точке,
лежащей посередине между проводами,
взаимно перпендикулярны (рис. 21.3, в).
Результирующая индукция по модулю и
направлению является диагональю квадра-
квадрата, построенного на векторах Вх и В2. По
теореме Пифагора найдем
Подставив в формулу C) значения Вг и
В2 и вычислив, получим Рис. 21.4
5=113 мкТл.
Пример 3. Определить магнитную индукцию В поля, создаваемо-
создаваемого отрезком бесконечно длинного прямого провода, в точке, равно-
равноудаленной от концов отрезка и находящейся на расстоянии го=
=20 см от середины его (рис. 21.4). Сила тока /, текущего по про-
проводу, равна 30 А, длина I отрезка равна 60 см.
Решение. Для определения магнитной индукции поля, соз-
создаваемого отрезком провода, воспользуемся законом Био — Сава-
9*
259

pa — Лапласа:
dfi=Jd/ A)
4jtr2
Прежде чем интегрировать выражение A), преобразуем его так,
чтобы можно было интегрировать по углу а. Выразим длину
элемента d/ проводника через da. Согласно рис. 21.4, запишем
dl rda . Подставим это выражение d/ в формулу A):
sin ос
R — Цр/sin a-r da __ jh0/da
4яг2 sin a 4лт
Ho r — величина переменная, зависящая от a и равная г =
Подставив г в предыдущую формулу, найдем
sin os
Чтобы определить магнитную индукцию поля, создаваемого от-
отрезком проводника, проинтегрируем выражение B) в пределах от
ах до а2:
j
4яг
sinada==J!±L f sinada, или
Заметим, что при симметричном расположении точки А относитель-
относительно отрезка провода cos a2=—cosaj. С учетом этого формула C)
примет вид
1/2 I
Из рис. 21.4 следует cosaf = лГ =-= - =—• • Подставив
К/2/4 + г? К 42 + ^
выражение cos af в формулу D), получим
2яг0
Подставим числовые значения в формулу E) и произведем вы-
вычисления:
Пример 4. Длинный провод с током /=50 А изогнут под углом
а=2п/3. Определить магнитную индукцию В в точке А (рис. 21.5).
Расстояние d=b см.
Решение. Изогнутый провод можно рассматривать как два
длинных провода, концы которых соединены в точке О. В соответ-
соответствии с принципом суперпозиции магнитных полей магнитная ин-
индукция В в точке А будет равна геометрической сумме магнитных
индукций Вг и В2 полей, создаваемых отрезками длинных прово-
260

дов У и 2, т. е. B = Bi+B2. Магнитная индукция В2 равна нулю.
Это следует из закона Био — Савара — Лапласа, согласно которому
в точках, лежащих на оси проводника, dB=O([dlr]=O).
Магнитную индукцию Вг найдем, воспользовавшись формулой
C), полученной в примере 3:
аг— cosa2),
где г0 — кратчайшее расстояние от проводника 1 до точки А
(рис. 21.6).
=>/
Рис. 21.5
Рис. 21.6
В нашем случае а*-^) (проводник длинный), а2=а=
=2я/3 (cos a2=cos Bjc/3))=—У2. Расстояние ro=d sin (я—a)=
=d sm(n/3)=d]/rS/2. Тогда магнитная индукция
Так как В=В!(Ва=0), то
~~ 4nd
Вектор В сонаправлен с вектором Вх и определяется правилом
правого винта. На рис. 21.6 это направление отмечено значком X
(перпендикулярно плоскости чертежа от нас).
Проверка единиц аналогична выполненной в примере 1.
Произведем вычисления:
п /.4л>10-7.50
4Я-5-10-2
= 3,46-
= 34,6 мкТл.
Пример 5. По тонкому проводящему кольцу радиусом R = \0 см
течет ток 7—80 А. Найти магнитную индукцию В в точке Л, равно-
равноудаленной от всех точек кольца на расстояние г=20 см.
Решение. Для решения задачи воспользуемся законом
Био — Савара — Лапласа:
ли _ Цо / [dlr]
aD ~~ 4я г3 '
где dB — магнитная индукция поля, создаваемого элементом тока
/dl в точке, определяемой радиусом-вектором г.
261

Выделим на кольце элемент dl и от него в точку А проведем ра-
радиус-вектор г (рис. 21.7). Вектор dB направим в соответствии с пра-
правилом буравчика.
Согласно принципу суперпозиции магнитных полей, магнитная
в к индукция В в точке А опре-
I деляется интегралом
I
где интегрирование ведется
по всем элементам dl кольца.
Разложим вектор dB на
две составляющие: dB^ —
перпендикулярную плоскости
кольца и dB(| — параллель-
параллельную плоскости кольца, т. е.
dB = dBx + dBn. Тогда
В = $dB+ JdB.
L
Заметив,
L
что
> = 0 из
Рис. 21.7
соображений симметрии и что
векторы dBj_ от различных
элементов dl сонаправлены, заменим векторное суммирование (ин-
(интегрирование) скалярным:
где dB±=dB cos E и dB = -^—^ (поскольку dl перпендикулярен
г и, следовательно, sina=l). Таким образом,
А1__ jAp/ COS |
чим
После сокращения на 2я и замены cos р на R/r (рис. 21.7) полу-
Выразим все величины в единицах СИ, произведем вычисления!
410780@1J
или В-=62,8 мкТл.
Вектор В направлен по оси кольца (пунктирная стрелка на
рис. 21.7) в соответствии с правилом буравчика.
Пример 6. Бесконечно длинный проводник изогнут так, как это
изображено на рис. 21.8. Радиус дуги окружности #=10 см. Опре-
Определить магнитную индукцию В поля, создаваемого в токе О током
7=80 А, текущим по этому проводнику.
262

Решение. Магнитную индукцию В в точке О найдем, ис-
используя принцип суперпозиции магнитных полей В=2В/# В на-
нашем случае проводник можно разбить на три части (рис. 21.9)з
два прямолинейных проводника (У и 3), одним концом уходящие в
бесконечность, и дугу полуокружности B) радиуса R. Тогда
В = Bf+ B<2+ Bg,
где Вь В 2 и В3 — магнитные индукции поля в точке О, создавае-
создаваемые током, текущим соответственно на первом, втором и третьем
участках проводника.
Рис. 21.8
i
Рис. 21.9
Так как точка О лежит на оси проводника 1, то В±=0 и тогда
В=В2+В3.
Учитывая, что векторы В2 и В3 направлены в соответствии с пра-
правилом буравчика перпендикулярно плоскости чертежа от нас, гео-
геометрическое суммирование можно заменить алгебраическим:
Магнитную индукцию поля В2 можно найти, используя выраже-
выражение для магнитной индукции в центре кругового проводника с то-
током /:
Так как магнитная индукция В2 создается в точке О половиной
такого кругового проводника с током, то, учитывая равный вклад
в магнитную индукцию от каждой половинки проводника, можно
написать
R - М
Магнитную индукцию В3 найдем, используя формулу C) при-
примера 3:
В = Ji^L (cos af—cos aj.
4jtr0 v
В нашем случае rQ=R}
Тогда
cos ax=0), а2->я (cos a2=—1).
263

Используя найденные выражения для В2 и 53, получим
B — R -1-Я fXp/ . \xqI
ИЛИ
Произведем вычисления:
? = 3,ЗЫ0-4 Тл = 331 мкТл.
Задачи
Связь между напряженностью и индукцией
магнитного поля в вакууме
21.1. Напряженность Н магнитного поля равна 79,6 кА/м. Опре-
Определить магнитную индукцию Во этого поля в вакууме.
21.2. Магнитная индукция В поля в вакууме равна ЮмТл. Най-
Найти напряженность Н магнитного поля.
21.3. Вычислить напряженность Н магнитного поля, если его
индукция в вакууме Во=0,05 Тл.
Поле кругового тока и соленоида
21.4. Найти магнитную индукцию в центре тонкого кольца, по
которому идет ток /=10 А. Радиус г кольца равен 5 см.
21.5. По обмотке очень короткой катушки радиусом г =16 см
течет ток /=5 А. Сколько витков N проволоки намотано на катуш-
катушку, если напряженность Н магнитного поля
в ее центре равна 800 А/м?
21.6. Напряженность Н магнитного поля в
центре кругового витка радиусом г=8 см равна
30 А/м. Определить напряженность Я*.
21.7. При какой силе тока /, текущего по
тонкому проводящему кольцу радиусом /?=0,2 м,
магнитная индукция В в точке, равноудаленной
от всех точек кольца на расстояние г=0,3 м,
станет равной 20 мкТл?
21.8. По проводнику в виде тонкого кольца
радиусом R = \0 см течет ток. Чему равна сила
тока /, если магнитная индукция В поля в точ-
точке А (рис. 21.10) равна 1 мкТл? Угол р=10°.
21.9. Катушка длиной /=20 см содержит
N=100 витков. По обмотке катушки идет ток
7=5 А. Диаметр d катушки равен 20 см. Определить магнитную ин-
индукцию В в точке, лежащей на оси катушки на расстоянии а=
е= 10 см от ее конца.
21.10. Длинный прямой соленоид из проволоки диаметром d=
—0,5 мм намотан так, что витки плотно прилегают друг к другу.
264
I
Рис. 21.10

Рис. 21.11
Какова напряженность Я магнитного поля внутри соленоида при
силе тока /=4 А? Толщиной изоляции пренебречь.
21.11. Обмотка катушки диаметром d=\0 см состоит из плотно
прилегающих друг к другу витков тонкой проволоки. Определить
минимальную длину /min катушки, при которой магнитная индукция
в середине ее отличается от магнитной индукции бесконечного соле-
соленоида, содержащего такое же количество витков на единицу длины,
не более чем на 0,5 %. Сила тока, протекающего по обмотке, в обо-
обоих случаях одинакова.
21.12. Обмотка соленоида выполнена тонким проводом с плотно
прилегающими друг к другу витками. Длина / катушки равна 1 м,
ее диаметр d=2 см. По обмотке идет ток.
Вычислить размеры участка на осевой
линии, в пределах которого магнитная
индукция может быть вычислена по фор-
формуле бесконечного соленоида с погреш-
погрешностью, не превышающей 0,1 %.
21.13. Тонкая лента шириной /=
=40 см свернута в трубку радиусом
/?=30 см. По ленте течет равномерно
распределенный по ее ширине ток /=200 А (рис. 21.11). Опреде-
Определить магнитную индукцию В на оси трубки в двух точках: 1) в сред-
средней точке; 2) в точке, совпадающей с концом трубки.
Поле прямого тока
21.14. По прямому бесконечно длинному проводнику течет ток
/=50 А. Определить магнитную индукцию В в точке, удаленной
на расстояние г=5 см от проводника.
21.15. Два длинных параллельных провода находятся на расстоя-
расстоянии г=5 см один от другого. По проводам текут в противоположных
направлениях одинаковые токи /=10 А каждый. Найти напряжен-
напряженность Я магнитного поля в точке, находящейся на расстоянии
/-1=2 см от одного и г2=3 см от другого провода.
21.16. Расстояние d между двумя длинными параллельными про-
проводами равно 5 см. По проводам в одном направлении текут оди-
одинаковые токи /=30 А каждый. Найти напряженность Я магнитного
поля в точке, находящейся на расстоянии гх=4 см от одного и г2=
=3 см от другого провода.
21.17. По двум бесконечно длинным прямым параллельным про-
проводам текут токи /х=50 А и /2=100 А в противоположных направ-
направлениях. Расстояние d между проводами равно 20 см. Определить
магнитную индукцию В в точке, удаленной на /4=25 см от первого
и на г2=40 см от второго провода.
21.18. По двум бесконечно длинным прямым параллельным про-
проводам текут токи /i=20 А и /2=30 А в одном направлении. Расстоя-
Расстояние d между проводами равно 10 см. Вычислить магнитную индук-
индукцию В в точке, удаленной от обоих проводов на одинаковое расстоя-
расстояние г=10 см.
265

21.19. Два бесконечно длинных прямых провода скрещены под
прямым углом (рис. 21.12). По проводам текут токи /х=80 А и
/2=60 А. Расстояние d между проводами равно 10 см. Определить
магнитную индукцию В в точке А, одинаково удаленной от обоих
проводников.
Рис. 21.12
Рис. 21.13
21.20. По двум бесконечно длинным прямым проводам, скрещен»
ным под прямым углом, текут токи /х=30 А и /2=40 А. Расстояние
d между проводами равно 20 см. Определить магнитную индукцию
В в точке С (рис. 21.12), одинаково удаленной от обоих проводов
на расстояние, равное d.
21.21. Бесконечно длинный прямой провод согнут под прямым
углом. По проводнику течет ток /=20 А. Какова магнитная индук-
II ция В в точке А (рис. 21.13), если г=5 см?
21.22. По бесконечно длинному пря-
прямому проводу, изогнутому так, как это
показано на рис. 21.14, течет ток /=100 А.
Определить магнитную индукцию В в точ-
точке О, если г=10см.
21.23. Бесконечно длинный прямой про-
провод согнут под прямым углом. По проводу
течет ток / = 100 А. Вычислить магнитную
индукцию В в точках, лежащих на бис-
биссектрисе угла и удаленных от вершины угла на а=10 см.
21.24. По бесконечно длинному прямому проводу, согнутому
под углом а=120°, течет ток /=50 А. Найти магнитную индукцию
В в точках, лежащих на биссектрисе угла и удаленных от вершины
его на расстояние а—Ъ см.
21.25. По контуру в виде равностороннего треугольника идет
ток /=40 А. Длина а стороны треугольника равна 30 см. Определить
магнитную индукцию В в точке пересечения высот.
21.26. По контуру в виде квадрата идет ток /=50 А. Длина а
стороны квадрата равна 20 см. Определить магнитную индукцию
В в точке пересечения диагоналей.
Рис. 21.14
266

21.27. По тонкому проводу, изогнутому в виде прямоугольника,
течет ток 7=60 А. Длины сторон прямоугольника равны а=30 см
и Ь=40 см. Определить магнитную индукцию В в точке пересечения
диагоналей.
21.28. Тонкий провод изогнут в виде правильного шестиуголь-
шестиугольника. Длина d стороны шестиугольника равна 10 см. Определить
магнитную индукцию В в центре шестиугольника, если по проводу
течет ток /=25 А.
21.29. По проводу, согнутому в виде правильного шестиугольни-
шестиугольника с длиной а стороны, равной 20 см, течет ток /=100 А. Найти
напряженность Н магнитного поля в центре шестиугольника. Для
сравнения определить напряженность Но поля в центре кругового
провода, совпадающего с окружностью, описанной около данного
шестиугольника.
I
S)
г)
В)
Рис. 21.15
с)
21.30. По тонкому проволочному кольцу течет ток. Не изменяя
силы тока в проводнике, ему придали форму квадрата. Во сколько
раз изменилась магнитная индукция в центре контура?
21.31. Бесконечно длинный тонкий проводник с током /=50 А
имеет изгиб (плоскую петлю) радиусом i? = 10 см. Определить в точ-
точке О магнитную индукцию В поля, создаваемого этим током, в слу-
случаях а—е, изображенных на рис. 21.15.
21.32. По плоскому контуру из тонкого провода течет ток /=
==100 А. Определить магнитную индукцию В поля, создаваемого
этим током в точке О, в случаях а—е, изображенных на рис. 21.16.
Радиус R изогнутой части контура равен 20 см.
Поле движущегося заряда
21.33. Электрон в невозбужденном атоме водорода движется во-
вокруг ядра по окружности радиусом г=53 пм. Вычислить силу экви-
эквивалентного кругового тока / и напряженность Н поля в центре
окружности.
267

21.34. Определить максимальную магнитную индукцию J3max
поля, создаваемого электроном, движущимся прямолинейно со ско-
скоростью 1>=10 Мм/с, в точке, отстоящей от траектории на рас-
расстоянии d—\ нм.
Рис. 21.16
21.35. На расстоянии г= 10 нм от траектории прямолинейно
движущегося электрона максимальное значение магнитной индук-
индукции Дпах^бО мкТл. Определить скорость v электрона.
§ 22. СИЛА, ДЕЙСТВУЮЩАЯ НА ПРОВОДНИК С ТОКОМ
В МАГНИТНОМ ПОЛЕ
Основные формулы
# Закон Ампера. Сила, действующая на проводник с током
в магнитном поле,
F=[1B]/,
где / — сила тока; 1 — вектор, равный по модулю длине / провод-
проводника и совпадающий по направлению с током; В — магнитная
индукция поля.
Модуль вектора F определяется выражением
F=BIl sin a,
где а — угол между векторами 1 и В.
# Сила взаимодействия двух прямых бесконечно длинных па-
параллельных проводников с токами /х и /2, находящихся на расстоя-
расстоянии d друг от друга, рассчитанная на отрезок проводника длиной /,
268

выражается формулой
Г " 2л d *'
• Магнитный момент контура с током
где S — вектор, равный по модулю площади S, охватываемой кон-
контуром, и совпадающий по направлению с нормалью к его плоскости.
• Механический момент, действующий на контур с током, по-
помещенный в однородное магнитное поле,
М=[рпВ].
Модуль механического момента
М=ртВ sin a,
где а — угол между векторами рт и В.
• Потенциальная (механическая) энергия контура с током
в магнитном поле
• Сила, действующая на контур с током в магнитном поле (из-
(изменяющемся вдоль оси х),
п дВ
где -^-—изменение магнитной индукции вдоль оси Ох, рассчи-
рассчитанное на единицу длины; a — угол между векторами рт и В.
Примеры решения задач
Пример 1. По двум параллельным прямым проводам длиной
/=2,5 м каждый, находящимся на расстоянии d=20 см друг от дру-
друга, текут одинаковые токи 1=1 кА. Вычислить силу F взаимодей-
взаимодействия токов.
Решение. Взаимодействие двух проводников, по которым
текут токи, осуществляется через магнитное поле. Каждый ток соз-
создает магнитное поле, которое действует на другой проводник. Пред-
Предположим, что оба тока (обозначим их /г и /2) текут в одном направ-
направлении.
Вычислим силу Fx,2, с которой магнитное поле, созданное током
/i, действует на проводник с током /2. Для этого проведем магнит-
магнитную силовую линию так (штриховая линия на рис. 22.1), чтобы она
касалась проводника с током /2. По касательной к силовой линии
проведем вектор магнитной индукции Bj.. Модуль магнитной индук-
индукции Вх определяется соотношением *
я^-^Ш- (!)
* Длинный проводник (t^>d) можно приближенно рассматривать как бес-
бесконечно длинный.
269

Согласно закону Ампера, на каждый элемент второго проводника
с током /2 длиной d/2 действует в магнитном поле сила
1,a a12(C1)
Так как отрезок dl перпендикулярен вектору В1г то
sin(dlB1)=l
и тогда
B)
Рис. 22.1
Подставив в выражение B) Вг из A), получим
Силу Fff 2 взаимодействия * проводников с током найдем интег-
интегрированием по всей длине второго проводника;
h
Г fXp/l/2 Г А1 JhIllA.1
112 2ttd J 2 2я^ 2
Заметив, что /1=/а=/ и /г^/, получим
Убедимся в том, что правая часть этого равенства дает единицу
силы (Н):
Ы V2] \П _ 1 Гн/м-A А)«>1 м _ 1 Дж . „
[dj 1м ~~ 1 м ~ А П'
1м
Произведем вычисления:
Сила Fif a сонаправлена с силой dFf, 2 (рис. 22.1) и определяет-
определяется (в данном случае это проще) правилом левой руки..
* По третьему закону Ньютона, сила, действующая на первый провод-
проводник со стороны второго, будет равна найденной по модулю и противоположна
ей по направлению.
270

yi
— х 5
'4
Пример 2, Провод в виде тонкого полукольца радиусом R —
е=10 см находится в однородном магнитном поле (В=50 мТл). По
проводу течет ток /=10 А. Найти силу F, действующую на провод,
если плоскость полукольца перпендикулярна линиям магнитной
индукции, а подводя-
подводящие провода находятся
вне поля.
Решение. Распо-
Расположим провод в плоско-
плоскости чертежа перпенди-
перпендикулярно линиям маг-
магнитной индукции (рис.
22.2) и выделим на нем
малый элемент dl с то-
током. На этот элемент
тока /d/ будет действо- Рис. 22.2
вать по закону Ампера
сила dF=/[dlB]. Направление этой силы можно определить по
правилу векторного произведения или по правилу левой руки.
Используя симметрию, выберем координатные оси так, как это
изображено на рис. 22.2. Силу dF представим в виде
dF=ldFx+]dFy,
где i и j — единичные векторы (орты); dFx и dFy — проекции векто-
вектора dF на координатные оси Ох и Оу.
Силу F, действующую на весь провод, найдем интегрированиемз
= SdF = i J dFx+ l
где символ L указывает на то, что интегрирование ведется па всей
длине провода L.
Из соображений симметрии первый интеграл равен нулю
dFx = О V Тогда
A)
Из рис. 22.2 следует, что
dFy=dF cos a,
где dF — модуль вектора dF(dF=/5d/ sin(dlB)). Так как вектор
dl перпендикулярен вектору В vsin vdlBy = 1) у то dF=IBdl. Вы-
Выразив длину дуги dl через радиус R и угол а, получим
Тогда
dFy=IBR cosadoc.
271

Введем dFy под интеграл соотношения A) и проинтегрируем в пре-
пределах от — я/2 до +п/2 (как это следует из рис. 22.2):
+ Я/2
F=}IBR J cosada = 2j/?/?.
-я/2
Из полученного выражения видно, что сила F сонаправлена с по-
положительным направлением оси Оу (единичным вектором j).
Найдем модуль силы F:
Убедимся в том, что правая часть этого равенства дает единицу
силы (Н):
= l А-1 Тл-1 м=1 A- t^Zp-l м=1 Н.
Произведем вычисления:
F=2-10-50.10-8-0,l Н=0,1 Н.
Пример 3. На проволочный виток радиусом г= 10 см, помещен-
помещенный между полюсами магнита, действует максимальный механиче-
механический момент Мтах=6,5 мкН. Сила тока / в витке равна 2А. Опреде-
Определить магнитную индукцию В поля между полюсами магнита. Дей-
Действием магнитного поля Земли пренебречь.
Решение. Индукцию В магнитного поля можно определить
из выражения механического момента, действующего на виток с то-
током в магнитном поле,
М=РтВ sin a. A)
Если учесть, что максимальное значение механический момент
принимает при а=п/2 (sin a= 1), а также что рт=18, то формула A)
примет вид
Отсюда, учитывая, что S=nr2t находим
B = MmaJ(nr4). 12)
Произведя вычисления по формуле B), найдем
?=104 мкТл.
Пример 4. Квадратная рамка со стороной длиной а=2 см, содер-
содержащая N=100 витков тонкого провода, подвешена на упругой нити,
постоянная кручения С которой равна 10 мкН-м/град. Плоскость
рамки совпадает с направлением линии индукции внешнего магнит-
магнитного поля. Определить индукцию внешнего магнитного поля, если
при пропускании по рамке тока 1=1 А она повернулась на угол
а=60°.
Решение. Индукция В внешнего поля может быть найдена
из условия равновесия рамки в поле. Рамка будет находиться в рав-
равновесии, если сумма механических моментов, действующих на нее,
будет равна нулю:
2М=0. (I)
272

В данном случае на рамку действуют два момента (рис. 22.3):
Mi — момент сил, с которым внешнее магнитное поле действует на
рамку с током, и М2 — момент упругих сил, возникающих при за-
закручивании нити, на которой рамка подвешена. Следовательно,
формула A) может быть переписана в
виде
Мх+М2=0.
Выразив Мг и М2 в этом равенстве
через величины, от которых зависят мо-
моменты сил, получим
ртВ sin а—Сф=0. B)
Знак минус перед моментом М2 ста-
ставится потому, что этот момент противо-
противоположен по направлению моменту Мг.
Если учесть, что pm=ISN=Ia2N,
где / — сила тока в рамке; S=a2 —
площадь рамки; N — число ее bhtkoBj
равенство B) перепишем в виде
NIa2B sin а—Сф = 0, откуда
Я - Сф п\
и~~ NIa2 sin a ' 1 '
Из рис. 22.3 видно, что а=п/2—ф, значит, sin a=cos ф. С учетом
этого равенство C) примет вид
В— Сф D)
П~ NIa2 cos ф * **'
Значение постоянной кручения С, рассчитанной на градус (а не
радиан, как это следовало бы выразить в СИ), запишем в виде
C=10-10~6 Н-м/град,
так как значение угла ф также дано в градусах.
Подставим данные в формулу D) и произведем вычисления;
Пример 5. Плоский квадратный контур со стороной длиной а—
= 10 см, по которому течет ток /= 100 А, свободно установился в од-
однородном магнитном поле индукцией В=\ Тл. Определить работу
Л, совершаемую внешними силами при повороте контура относи-
относительно оси, проходящей через середину его противоположных сто-
сторон, на угол: 1) фх=90°; 2) ф2=3°. При повороте контура сила тока
в нем поддерживается неизменной.
Решение. На контур с током в магнитном поле действует
механический момент
М=ртВ sin ф. A)
По условию задачи, в начальном положении контур свободно
установился в магнитном поле. При этом момент сил равен нулю
273

{М=0), а значит ф=0, т. е. векторы pm и В совпадают по направле-
направлению.
Если внешние силы выведут контур из положения равновесия, то
возникший момент сил, определяемый формулой A), будет стремить-
стремиться возвратить контур в исходное положение. Против этого момента и
будет совершаться работа внешними силами. Так как момент сил
переменный (зависит от угла ф поворота), то для подсчета работы
применим формулу работы в дифференциальной форме
<L4=Afd(p. B)
Подставив сюда выражение М по формуле A) и учтя, что рт=
~IS=Ia2, где / — сила тока в контуре, S=a2 — площадь контура,
получим
dA=IBa2 sin <p dq).
Взяв интеграл от этого выражения, найдем работу при повороте
на конечный угол:
ф
A=IBa2 J sincpdcp. C)
о
1. Работа при повороте на угол ф3;=90с*
Я/2
Аг = IBa2 \ sin ф d9 = IBa21— cos <р |?/2 = 1Ва*. D)
о
Убедимся в том, что правая часть этого равенства дает единицу
работы (Дж):
[/][В][а2] = 1 А-1 Тл-A мJ=1 Н-1 м = 1 Дж.
После вычисления по формуле D) найдем
Лх=1 Дж.
2. Работа при повороте на угол фз^З0. В этом случае, учитывая,
что угол ф2 мал, заменим в выражении C) sin ф на ф:
Фз
А2 == IBa2 f q> dq> = y IBa2q>l E)
о
Выразим угол ф2 в радианах (см. табл. 9)i
ф2==3°-3-1,75-10-2 рад=0,0525 рад.
После подстановки значений /, В} а и q>2 в формулу E) получим
А2= 1,37 мДж.
Задачи
Сила Ампера
22.1. Прямой провод, по которому течет ток 1=1 кА, расположен
в однородном магнитном поле перпендикулярно линиям индукции.
С какой силой F действует поле на отрезок провода длиной /=1 Mj
если магнитная индукция В равна 1 Тл?
274

22.2. Прямой провод длиной /= 10 см, по которому течет ток
/—20 А, находится в однородном магнитном поле с индукцией В=^
=0,01 Тл. Найти угол а между направлениями вектора В и TOKaf
если на провод действует сила ?=10 мН.
22.3. Квадратная проволочная рамка расположена в одной плос-
плоскости с длинным прямым проводом так, что две ее стороны парал-
параллельны проводу. По рамке и проводу текут одинаковые токи /=?
= 1 кА. Определить силу F, действующую на рамку, если ближайшая
К проводу сторона рамки находится на расстоянии, равном ее длине.
22.4. Тонкий провод в виде дуги, составляющей треть кольца
радиусом 7? = 15 см, находится в однородном магнитном поле (В=*
=20 мТл). По проводу течет ток /=30 А. Плоскость, в которой ле-
лежит дуга, перпендикулярна линиям магнитной индукции, и подво-
подводящие провода находятся вне поля. Определить силу F, действую-
действующую на провод.
22.5. По тонкому проводу в виде кольца радиусом R=20 см течет
ток /=100 А. Перпендикулярно плоскости кольца возбуждено
однородное магнитное поле с индукцией В=20 мТл. Найти силу FM
растягивающую кольцо.
22.6. Двухпроводная линия состоит из длинных параллельных
прямых проводов, находящихся на расстоянии й=4мм друг от дру-
друга. По проводам текут одинаковые токи /=50 А. Определить силу
взаимодействия токов, приходящуюся на единицу длины провода.
22.7. Шины генератора представляют собой две параллельные
медные полосы длиной 1=2 м каждая, отстоящие друг от друга на
расстоянии d=20 см. Определить силу F взаимного отталкивания
шин в случае короткого замыкания, когда по ним течет ток /=*
= 10 кА.
22.8. По двум параллельным проводам длиной 1=1 м каждый те-
текут одинаковые токи. Расстояние d между проводами равно 1 см.
Токи взаимодействуют с силой F=l мН. Найти силу тока / в про-
проводах.
22.9. По трем параллельным прямым проводам, находящимся на
одинаковом расстоянии а=10 см друг от друга, текут одинаковые
токи /=100 А. В двух проводах направления токов совпадают.
Вычислить силу F, действующую на отрезок длиной 1=1 м каждого
провода.
22.10. По двум тонким проводам, изогнутым в виде кольца радиу-
радиусом R = 10 см, текут одинаковые токи /= 10 А в каждом. Найти силу
F взаимодействия этих колец, если плоскости, в которых лежат
кольца, параллельны, а расстояние d между центрами колец равно
1 мм.
22.11. По двум одинаковым квадратным плоским контурам со
стороной а=20 см текут токи /=10 А в каждом. Определить силу
F взаимодействия контуров, если расстояние d между соответствен-
соответственными сторонами контуров равно 2 мм.

Магнитный момент
22.12. По витку радиусом г=5 см течет ток /=10 А. Определить
магнитный момент рт кругового тока.
22.13. Очень короткая катушка содержит N=1000 витков тонко-
тонкого провода. Катушка имеет квадратное сечение со стороной длиной
а=10 см. Найти магнитный момент рт катушки при силе тока /=
= 1 А.
22.14. Магнитный момент рт витка равен 0,2 Дж/Тл. Определить
силу тока / в витке, если его диаметр d= 10 см.
22.15. Напряженность Я магнитного поля в центре кругового
витка равна 200 А/м. Магнитный момент рт витка равен 1 А-м2.
Вычислить силу тока / в витке и радиус R витка.
22.16. По кольцу радиусом R течет ток. На оси кольца на расстоя-
расстоянии d= 1 м от его плоскости магнитная индукция В—10 нТл. Опреде-
Определить магнитный момент рт кольца с током. Считать R много мень-
меньшим d.
22.17. Электрон в невозбужденном атоме водорода движется во-
вокруг ядра по окружности радиусом г=53 пм. Вычислить магнитный
момент рт эквивалентного кругового тока и механический момент
М, действующий на круговой ток, если атом помещен в магнитное
поле, линии индукции которого параллельны плоскости орбиты
электрона. Магнитная индукция В поля равна 0,1 Тл.
22.18. Электрон в атоме водорода движется вокруг ядра по кру-
круговой орбите некоторого радиуса. Найти отношение магнитного мо-
момента рт эквивалентного кругового тока к моменту импульса L ор-
орбитального движения электрона. Заряд электрона и его массу счи-
считать известными. Указать направления векторов рт и L.
22.19. По тонкому стержню длиной /=20 см равномерно распреде-
распределен заряд Q=240 нКл. Стержень приведен во вращение с постоянной
угловой скоростью со = 10 рад/с относительно оси, перпендикуляр-
перпендикулярной стержню и проходящей через его середину. Определить: 1) маг-
магнитный момент /?т, обусловленный вращением заряженного стерж-
стержня; 2) отношение магнитного момента к моменту импульса (pm/L)y
если стержень имеет массу т=12 г.
22.20. Тонкое кольцо радиусом R = l0 см несет заряд Q= 10 нКл.
Кольцо равномерно вращается с частотой п=Ю с относительно
оси, перпендикулярной плоскости кольца и проходящей через ее
центр. Найти: 1) магнитный момент рт кругового тока, создаваемого
кольцом; 2) отношение магнитного момента к моменту импульса
(pm/L)y если масса т кольца равна 10 г.
22.21. То же, что и в предыдущей задаче, но относительно оси,
совпадающей с одним из диаметров кольца.
22.22. Диск радиусом jR = 10 см несет равномерно распределен-
распределенный по поверхности заряд Q=0,2 мкКл. Диск равномерно вращается
с частотой я=20 с относительно оси, перпендикулярной плоско-
плоскости диска и проходящей через его центр. Определить: 1) магнитный
момент рт кругового тока, создаваемого диском; 2) отношение маг-
276

нитного момента к моменту импульса {pJL)y если масса т диска
равна 100 г.
22.23. Тонкостенная металлическая сфера радиусом /?=10 см не-
несет равномерно распределенный по ее поверхности заряд Q=3 мКл.
Сфера равномерно вращается с угловой скоростью со = 10 рад/с от-
относительно оси, проходящей через центр сферы. Найти: 1) магнит-
магнитный момент рт кругового тока, создаваемый вращением сферы;
2) отношение магнитного момента к моменту импульса (pm/L), если
масса т сферы равна 100 г.
22.24. Сплошной шар радиусом R = 10 см несет заряд Q=200 нКл,
равномерно распределенный по объему. Шар вращается относитель-
относительно оси, проходящей через центр шара, с угловой скоростью со =
= 10 рад/с. Определить: 1) магнитный момент рт кругового тока,
обусловленного вращением шара; 2) отношение магнитного момента
к моменту импульса (pJL), если масса т шара равна 10 кг.
Контур в магнитном поле
22.25. Проволочный виток радиусом R—Ъ см находится в одно-
однородном магнитном поле напряженностью #=2 кА/м. Плоскость
витка образует угол а=60° с направлением поля. По витку течет
ток /=4 А. Найти механический момент М, действующий на виток.
22.26. Виток диаметром d=20 см может вращаться около верти-
вертикальной оси, совпадающей с одним из диаметров витка. Виток уста-
установили в плоскости магнитного меридиана и пустили по нему ток
/= 10 А. Найти механический момент Му который нужно приложить
к витку, чтобы удержать его в начальном положении *.
22.27. Рамка гальванометра длиной а=4 см и шириной Ь=
= 1,5 см, содержащая N=200 витков тонкой проволоки, находится
в магнитном поле с индукцией ?=0,1 Тл. Плоскость рамки парал-
параллельна линиям индукции. Найти: 1) механический момент М, дей-
действующий на рамку, когда по витку течет ток /= 1 мА; 2) магнитный
момент рт рамки при этом токе.
22.28. Короткая катушка площадью S поперечного сечения, рав-
равной 150 см2, содержит А/=200 витков провода, по которому течет
ток /=4 А. Катушка помещена в однородное магнитное поле напря-
напряженностью Н=8 кА/м. Определить магнитный момент рт катушки,
а также вращающий момент М, действующий на нее со стороны
поля, если ось катушки составляет угол а=60° с линиями индукции.
22.29. Рамка гальванометра, содержащая N=200 витков тонкого
провода, подвешена на упругой нити. Площадь 5 рамки равна 1 см2.
Нормаль к плоскости рамки перпендикулярна линиям магнитной
индукции (В=5 мТл). Когда через гальванометр был пропущен ток
1=2 мкА, то рамка повернулась на угол а=30°. Найти постоянную
кручения С нити.
22.30. По квадратной рамке из тонкой проволоки массой /п=2 г
пропущен ток /=6 А. Рамка свободно подвешена за середину одной
из сторон на неупругой нити. Определить период Т малых колеба-
* Горизонтальную составляющую ВГ магнитной индукции поля Земли
принять равной 20 мкТл.
277

ний такой рамки в однородном магнитном поле с индукцией В=*
6=2 мТл. Затуханием колебаний пренебречь.
22.31. Тонкий провод в виде кольца массой т=3 г свободно под-
подвешен на неупругой нити в однородном магнитном поле. По кольцу
течет ток 1=2 А. Период Т малых крутильных колебаний относи-
относительно вертикальной оси равен 1,2 с. Найти магнитную индукцию
В> поля.
22.32. На оси контура с током, магнитный момент которого рт
равен 10 мА»м2, находится другой такой же контур. Вектор магнит-
магнитного момента второго контура перпендикулярен оси. Вычислить
механический момент М, действующий на второй контур. Расстоя-
Расстояние d между контурами равно 50 см. Размеры контуров малы по
сравнению с расстоянием между ними.
22.33. Магнитное поле создано кольцевым проводником радиусом
/^=20 см, по которому течет ток /=100 А. На оси кольца располо-
расположено другое кольцо малых размеров с магнитным моментом /?т=
= 10 мА'М2. Плоскости колец параллельны, а расстояние d между
центрами равно 1 см. Найти силу, действующую на малое кольцо.
Магнитный диполь
22.34. Магнитное поле создано бесконечно длинным проводником
с током 7=100 А. На расстоянии а=10 см от проводника находится
точечный диполь, вектор магнитного момента {рт=1 мА-м2) кото-
которого лежит в одной плоскости с проводником и перпендикулярен
ему. Определить силу F, действующую на магнитный диполь.
22.35. Определить степень неоднородности магнитного поля
(dB/cbt), если максимальная сила -Fmax» действующая на точечный
магнитный диполь, равна 1 мН. Магнитный момент рт точечного
диполя равен 2 мА«м2.
22.36. Проволочный виток радиусом R=20 см расположен в пло-
плоскости магнитного меридиана. В центре витка установлен компас.
Какой ток / течет по витку, если магнитная стрелка компаса откло-
отклонена на угол а=9° от плоскости магнитного меридиана *?
22.37. Определить число N витков катушки тангенс-гальвано-
тангенс-гальванометра, при котором сила тока, текущего по обмотке, численно равна
тангенсу угла отклонения магнитной стрелки, помещенной в центре
обмотки? Радиус г катушки равен 25 см. Ось катушки перпендику-
перпендикулярна плоскости магнитного меридиана *.
22.38. Длинный прямой соленоид, содержащий п=Ъ витков на
каждый сантиметр длины, расположен перпендикулярно плоскости
магнитного меридиана*. Внутри соленоида, в его средней части,
находится магнитная стрелка, установившаяся в магнитном поле
Земли. Когда по соленоиду пустили ток, стрелка отклонилась на
угол а=60°. Найти силу тока /.
22.39. Короткий прямой магнит расположен перпендикулярно
плоскости магнитного меридиана. На оси магнита на расстоянии
* См. сноску к задаче 22.26.
278

г=50 см от его середины (которое много больше длины магнита)
находится магнитная стрелка. Вычислить магнитный момент рт
магнита, если стрелка отклонена на угол а=6° от плоскости магнит-
магнитного меридиана *.
22.40. Конденсатор электроемкостью С=50 мкФ заряжается от
источника тока, ЭДС ? которой равна 80 В, и с помощью особого
переключателя полностью разряжается 100 раз в секунду через об-
обмотку тангенс-гальванометра, расположенного в плоскости магнит-
магнитного меридиана *. На какой угол а отклонится магнитная стрелка,
находящаяся в центре тангенс-гальванометра, если его обмотка
имеет iV= 10 витков радиусом г=25 см?
22.41. Магнитная стрелка, помещенная в центре кругового про-
провода радиусом jR = 10 см, образует угол а=20° с вертикальной пло-
плоскостью, в которой находится провод. Когда по проводу пустили
ток /=ЗА, то стрелка повернулась в таком направлении, что угол
а увеличился. Определить угол поворота стрелки.
§ 23. СИЛА, ДЕЙСТВУЮЩАЯ НА ЗАРЯД, ДВИЖУЩИЙСЯ
В МАГНИТНОМ ПОЛЕ
Основные формулы
9 Сила F, действующая на заряд Q, движущийся со скоростью v
в магнитном поле с индукцией В (сила Лоренца), выражается фор-
формулой
F=Q[vB] или F=\Q\vB sin a,
где а — угол, образованный вектором скорости v движущейся ча-
частицы и вектором В индукции магнитного поля.
Примеры решения задач
Пример 1. Электрон, пройдя ускоряющую разность потенциа-
потенциалов 0=400 В, попал в однородное магнитное поле с индукцией
В=1,5 мТл. Определить: 1) радиус R кривизны траектории; 2) ча-
частоту п вращения электрона в магнитном поле. Вектор скорости
электрона перпендикулярен линиям индукции.
Решение. 1. Радиус кривизны траектории электрона опре-
определим, исходя из следующих соображений: на движущийся в маг-
магнитном поле электрон действует сила Лоренца F. (Действием силы
тяжести можно пренебречь.) Вектор силы Лоренца перпендикуля-
перпендикулярен вектору скорости и, следовательно, по второму закону Ньютона,
сообщает электрону нормальное ускорение ап: F=man. Подставив
сюда выражения F и ап, получим
\e\vB sina=mv2/R, A)
где e,v,m — заряд, скорость, масса электрона; В — индукция маг-
магнитного поля; R — радиус кривизны траектории; а — угол между
направлениями векторов скорости v и индукции В (в нашем случае
vj_B и а=90°, sina=l).
* См. сноску на с. 277,
279

Из формулы A) найдем
Входящий в выражение B) импульс то выразим через кинетиче-
кинетическую энергию Т электрона:
C)
Но кинетическая энергия электрона, прошедшего ускоряющую
разность потенциалов (/, определяется равенством Т= \e\U. Под-
ставив это выражение Т в формулу C), получим mv = ]/r2m\e\ ?/.
Тогда выражение B) для радиуса кривизны приобретает вид
Убедимся в том, что правая часть этого равенства дает единицу
длины (м):
[т]1/2[Е/]1/2 __ О кгI/2>A ВI/2 Г 1 кг-1 В 1i/2 =
[В][е]1/г ~~ \ Тл-A КлI'2 L0 Тл)М Кл] "~
Г 1 кг-1 В-A АJ»A мJ 1i/2 г 1 кг-1 Дж>A мJ ]!/«_
~ [ A НJ-1 А-1 с J L lH.lc2 J
Г 1 кг-I м3 li/2
= [ l'H.l с2 J ==1М'
После вычисления по формуле D) найдем
/?=45 мм.
2. Для определения частоты вращения воспользуемся формулой,
связывающей частоту со скоростью и радиусом кривизны траекто-
траектории,
V
П =
2nR '
Подставив jR из выражения B) в эту формулу, получим
2л m
Произведя вычисления, найдем
п-4,20-107 с.
Пример 2. Электрон, имея скорость v=2 Мм/с, влетел в однород-
однородное магнитное поле с индукцией В=30 мТл под углом а=30° к на-
направлению линий индукции. Определить радиус R и шаг h винтовой
линии, по которой будет двигаться электрон.
Решение. Известно, что на заряженную частицу, влетевшую
в магнитное поле, действует сила Лоренца, перпендикулярная векто-
векторам магнитной индукции В и скорости v частицы:
F=QvB sin a, A)
где Q — заряд частицы.
В случае, если частицей является электрон, формулу A) можно
записать з виде
F= \e\vB sin a.
280

Так как вектор силы Лоренца перпендикулярен вектору скоро-
скорости, то модуль скорости не будет изменяться под действием этой
силы. Но при постоянной скорости, как это следует из формулы
A), останется постоянным и значение силы Лоренца. Из механики
известно, что постоянная си-
сила, перпендикулярная скоро-
скорости, вызывает движение по
окружности. Следовательно,
электрон, влетевший в маг-
магнитное поле, будет двигаться
по окружности в плоскости,
перпендикулярной линиям
индукции, со скоростью, рав-
равной поперечной составляю-
составляющей vt скорости (рис. 23.1);
одновременно он будет дви-
двигаться и вдоль поля со ско-
скоростью v ||:
Рис. 23.1
i>fl=ucosa.
В результате одновременного участия в движениях по окружно-
окружности и по прямой электрон будет двигаться по винтовой линии.
Радиус окружности, по которой движется электрон, найдем сле-
следующим образом. Сила Лоренца F сообщает электрону нормальное
ускорение ап. По второму закону Ньютона, F=many r&eF=\e\v1B
и an=v2L/R. Тогда
откуда после сокращения на vz находим радиус винтовой линии:
/?==-
mv,
или R =
mv sin a
| ejB ' "*"х XN - \e\B '
Подставив значений величин m, vy e, В и a и произведя вычисле-
вычисления, получим
Я-0,19 мм.
Шаг винтовой линии равен пути, пройденному электроном вдоль
поля со скоростью ихза время, которое понадобится электрону для
того, чтобы совершить один оборот,
Л = 0Н7\ B)
где T=2nR/vJu— период вращения электрона. Подставив это выра-
выражение для Т в формулу B), найдем
2nRv,. 2nRv cos a
h = !L или h = : = 2nRctga.
v^_ v sin a b
Подставив в эту формулу значения величин я, R и а и вычислив,
получим
/1-2,06 мм.
Пример 3. Электрон движется в однородном магнитном поле
с индукцией В=0,03 Тл по окружности радиусом г=10 см. Опреде-
Определить скорость v электрона.
281

Решение. Движение электрона по окружности в однородном
магнитном поле совершается под действием силы Лоренца (см. при-
примеры 1 и 2). Поэтому можно написать
' =\e\Bv, .A)
mw
г
откуда найдем импульс электрона:
pz=mv=\e\Br9 B)
Релятивистский импульс выражается формулой
Выполнив преобразования, получим следующую формулу для
определения скорости частицы:
C)
В данном случае р= \e\Br. Следовательно,
В = | е \ Вг/(тос) щ
V\+(\e\Br/(mQc))* '
В числитель и знаменатель формулы D) входит выражение
\е\Вг(гпос). Вычислим его отдельно:
\е\Вг/(т0с)=1,76.
Подставив найденное значение отношения \е\Вг[(тос) в формулу
D), получим
Р = 0,871, или и = ф = 2,6Ы08 м/с.
Электрон, обладающий такой скоростью, является релятивист-
релятивистским (см. § 5).
Пример 4. Альфа-частица прошла ускоряющую разность потен-
потенциалов ?/=104 В и влетела в скрещенные под прямым углом элект-
электрическое (?=10 кВ/м) и магнитное F=0,1 Тл) поля. Найти отно-
отношение заряда альфа-частицы к ее массе, если, двигаясь перпендику-
перпендикулярно обоим полям, частица не испытывает отклонений от прямо-
прямолинейной траектории.
Решение. Для того чтобы найти отношение заряда Q альфа-
частицы к ее массе т, воспользуемся связью между работой сил
электрического поля и изменением кинетической энергии частиц;
QU=mv*/2,
откуда
Qlm=v4{2U). A)
Скорость v альфа-частицы найдем из следующих соображений.
В скрещенных электрическом и магнитном полях на движущуюся
заряженную частицу действуют две силы:
а) сила Лоренца F^QIvB], направленная перпендикулярно
скорости v и вектору магнитной индукции В;
б) кулоновская сила FK=QE, сонаправленная с вектором на-
напряженности Е электростатического поля (Q>0).
Сделаем рисунок с изображением координатных осей и вектор-
282

ных величин. Направим вектор магнитной индукции В вдоль оси
Oz (рис. 23.2), скорость v — в положительном направлении оси
Ох, тогда Рл и FK будут направлены так, как это указано на ри-
рисунке.
Альфа-частица не будет испытывать отклонения, если геометри-
геометрическая сумма сил Рл+Fk будет равна нулю. В проекции на ось
Рис. 23.2
Оу получим следующее равенство (при этом учтено, что вектор ско-
скорости v перпендикулярен вектору магнитной индукции В и
sin(vB) =
QE —
откуда
v = Е/В.
Подставив это выражение скорости в формулу A), получим
Q/m=E2/BUB2).
Убедимся в том, что правая часть равенства дает единицу отно-
отношения заряда к массе (Кл/кг):
[Е2] _ A В/мJ __ A В-АJ _ 1 Дж-Кл 1 Кл-м
[U] [ВЦ
1 В-A ТлJ 1 В-A НJ
Произведем вычисления:
Q
A Н-сJ — 1
= 1 Кл/кг.
т ~ 2.104@,1J
Кл/кг = 4,8Ы07 Кл/кг = 48,1 МКл/кг.
Задачи
Сила Лоренца
23.1. Определить силу Лоренца F, действующую на электрон,
влетевший со скоростью v=4 Мм/с в однородное магнитное поле
под углом а=30° к линиям индукции. Магнитная индукция В поля
равна 0,2 Тл.
23.2. Вычислить радиус R дуги окружности, которую описывает
протон в магнитном поле с индукцией 5=15 мТл, если скорость
v протона равна 2 Мм/с.
23.3. Двукратно ионизированный атом гелия (а-частица) дви-
движется в однородном магнитном поле напряженностью #=100 кА/м
по окружности радиусом /^ = 10 см. Найти скорость v а-частицы.
283

23.4. Ион, несущий один элементарный заряд, движется в одно-
однородном магнитном поле с индукцией 6=0,015 Тл по окружности
радиусом R —10 см. Определить импульс р иона.
23.5. Частица, несущая один элементарный заряд, влетела в од-
однородное магнитное поле с индукцией В=0,5 Тл. Определить момент
импульса L, которым обладала частица при движении в магнитном
поле, если ее траектория представляла дугу окружности радиусом
#=0,2 см.
23.6. Электрон движется в магнитном поле с индукцией Б=
=0,02 Тл по окружности радиусом R=l см. Определить кинетиче-
кинетическую энергию Т электрона (в джоулях и электрон-вольтах).
23.7. Заряженная частица влетела перпендикулярно линиям ин-
индукции в однородное магнитное поле, созданное в среде. В результа-
результате взаимодействия с веществом частица, находясь в поле, потеряла
половину своей первоначальной энергии. Во сколько раз будут от-
отличаться радиусы кривизны R траектории начала и конца пути?
23.8. Заряженная частица, двигаясь в магнитном поле по дуге
окружности радиусом i?x=2 см, прошла через свинцовую пластину,
расположенную на пути частицы. Вследствие потери энергии части-
частицей радиус кривизны траектории изменился и стал равным R2=l см.
Определить относительное изменение энергии частицы.
23.9. Протон, прошедший ускоряющую разность потенциалов
G=600 В, влетел в однородное магнитное поле с индукцией В=
=0,3 Тл и начал двигаться по окружности. Вычислить ее радиус R.
23.10. Заряженная частица, обладающая скоростью и=2-106 м/с,
влетела в однородное магнитное поле с индукцией В=0,52 Тл. Най-
Найти отношение Q/m заряда частицы к ее массе, если частица в поле
описала дугу окружности радиусом R=4 см. По этому отношению
определить, какая это частица.
23.11. Заряженная частица, прошедшая ускоряющую разность
потенциалов U=2 кВ, движется в однородном магнитном поле с ин-
индукцией Б=15,1 мТл по окружности радиусом R = l см. Определить
отношение \e\ltn заряда частицы к ее массе и скорость v частицы.
23.12. Заряженная частица с энергией Т=\ кэВ движется в одно-
однородном магнитном поле по окружности радиусом R = l мм. Найти
силу 7\ действующую на частицу со стороны поля.
23.13. Электрон движется в однородном магнитном поле с индук-
индукцией В=0,1 Тл перпендикулярно линиям индукции. Определить
силу F, действующую на электрон со стороны поля, если радиус R
кривизны траектории равен 0,5 см.
23.14. Электрон движется в однородном магнитном поле напря-
напряженностью #=4 кА/м со скоростью и=10 Мм/с. Вектор скорости
направлен перпендикулярно линиям напряженности. Найти силу
F, с которой поле действует на электрон, и радиус R окружности,
по которой он движется.
23.15. Протон с кинетической энергией Т=1 МэВ влетел водно-
родное магнитное пале перпендикулярно линиям индукции (В=
= 1 Тл). Какова должна быть минимальная протяженность / поля
в направлении, по которому летел протон, когда он находился вне
284

•поля*, чтобы оно изменило направление движения протона на проти-
противоположное?
23.16. Электрон движется по окружности в однородном магнит-
магнитном поле напряженностью #=10 кА/м. Вычислить период Т враще-
вращения электрона.
23.17. Определить частоту п вращения электрона по круговой
орбите в магнитном поле, индукция В которого равна 0,2 Тл.
23.18. Электрон в однородном магнитном поле с индукцией В=
=0,1 Тл движется по окружности. Найти силу / эквивалентного
кругового тока, создаваемого движением электрона.
23.19. Электрон, влетев в однородное магнитное поле с индук-
индукцией В=0,2 Тл, стал двигаться по окружности радиусом R=5 см.
Определить магнитный момент рт эквивалентного кругового тока.
23.20. Два однозарядных иона, пройдя одинаковую ускоряющую
разность потенциалов, влетели в однородное магнитное поле пер-
перпендикулярно линиям индукции. Один ион, масса т1 которого равна
12 а. е. м. *, описал дугу окружности радиусом i?i=4 см. Опреде-
Определить массу т2 другого иона, который описал дугу окружности радиу-
радиусом ^2^6 см.
23.21. Два иона, имеющие одинаковый заряд, но различные мас-
массы, влетели в однородное магнитное поле. Первый ион начал дви-
двигаться по окружности радиусом jRx=5 см, второй ион — по окруж-
окружности радиусом jR2^2,5 см. Найти отношение т1/т2 масс ионов,
если они прошли одинаковую ускоряющую разность потенциалов.
23.22. В однородном магнитном поле с индукцией В=100 мкТл
движется электрон по винтовой линии. Определить скорость v
электрона, если шаг h винтовой линии равен 20 см, а радиус R—
=5 см.-
23.23. Электрон движется в однородном магнитном поле с индук-
индукцией В=9 мТл по винтовой линии, радиус R которой равен 1 см и
шаг /г=7,8 см. Определить период Т обращения электрона и его
скорость v.
23.24. В однородном магнитном поле с индукцией В=2 Тл дви-
движется протон. Траектория его движения представляет собой винто-
винтовую линию с радиусом R = 10 см и шагом h=60 см. Определить кине-
кинетическую энергию Т протона.
23.25. Электрон влетает в однородное магнитное поле напря-
напряженностью #=16 кА/м со скоростью v=8 Мм/с. Вектор скорости
составляет угол а=60° с направлением линий индукции. Определить
радиус R и шаг h винтовой линии, по которой будет двигаться
электрон в магнитном поле. Определить также шаг винтовой линии
для электрона, летящего под малым углом к линиям индукции.
23.26. Определить энергию 8, которую приобретает протон, сде-
сделав N=40 оборотов в магнитном поле циклотрона, если максималь-
максимальное значение Gтах переменной разности потенциалов между дуанта-
ми равно 60 кВ. Определить также относительное увеличение кпг/пц
* А. е. м.— обозначение атомной единицы массы.
285

массы протона в сравнении с массой покоя, а также скорость v про-
протона.
23.27. Вычислить скорость v и кинетическую энергию Т а-частиц*
выходящих из циклотрона, если, подходя к выходному окну, ионы
движутся по окружности радиусом R=50 см. Индукция В магнит-
магнитного поля циклотрона равна 1,7 Тл.
23.28. Индукция В магнитного поля циклотрона равна 1 Тл.
Какова частота v ускоряющего поля между дуантами, если в цикло-
циклотроне ускоряются дейтоны?
23.29. В циклотроне требуется ускорять ионы гелия (Не++).
Частота v переменной разности потенциалов, приложенной к ду ан-
антам, равна 10 МГц. Какова должна быть индукция В магнитного
поля, чтобы период Т обращения ионов совпадал с периодом измене-
изменения разности потенциалов?
23.30. Определить число N оборотов, которые должен сделать
протон в магнитном поле циклотрона, чтобы приобрести кинетиче-
кинетическую энергию Т—10 МэВ, если при каждом обороте протон проходит
между дуантами разность потенциалов [/=30 кВ.
23.31. Электрон движется по окружности в однородном магнит-
магнитном поле со скоростью v=0,8 с (с — скорость света в вакууме). Маг-
Магнитная индукция В поля равна 0,01 Тл. Определить радиус окруж-
окружности в двух случаях: 1) не учитывая увеличение массы со скоростью;
2) учитывая это увеличение.
23.32. Электрон движется в магнитном поле по окружности ра-
радиусом R=2 см. Магнитная индукция В поля равна 0,1 Тл. Опреде-
Определить кинетическую энергию Т электрона *.
23.33. Электрон, влетевший в камеру Вильсона, оставил след
в виде дуги окружности радиусом R = l0 см. Камера находится
в однородном магнитном поле с индукцией 5=10 Тл. Определить
кинетическую энергию Т электрона *.
23.34. Кинетическая энергия Т а-частицы равна 500 МэВ. Части-
Частица движется в однородном магнитном поле по окружности радиусом
#=80 см. Определить магнитную индукцию В поля *.
23.35. Электрон, имеющий кинетическую энергию 7=1,5 МэВ,
движется в однородном магнитном поле по окружности. Магнитная
индукция В поля равна 0,02 Тл. Определить период т обращения *.
Движение заряженных частиц в совместных
магнитном и электрическом полях
23.36. Перпендикулярно магнитному полю с индукцией В—
=0,1 Тл возбуждено электрическое поле напряженностью Е—
= 100 кВ/м. Перпендикулярно обоим полям движется, не отклоняясь
от прямолинейной траектории, заряженная частица. Вычислить
скорость v частицы.
23.37. Заряженная частица, двигаясь перпендикулярно скрещен-
скрещенным под прямым углом электрическому (?=400 кВ/м) и магнитному
* При решении задач 23.32—23.35 учесть изменение массы частицы от
ее скорости.
286

(В=0,25 Тл) полям, не испытывает отклонения при определенной
скорости v. Определить эту скорость и возможные отклонения Аи
от нее, если значения электрического и магнитного полей могут быть
обеспечены с точностью, не превышающей 0,2 %.
23.38. Протон, пройдя ускоряющую разность потенциалов t/=
*=800 В, влетает в однородные, скрещенные под прямым углом маг-
магнитное (В=50 мТл) и электрическое поля. Определить напряжен-
напряженность Е электрического поля, если протон движется в скрещенных
полях прямолинейно.
23.39. Заряженная частица движется по окружности радиусом
R = l см в однородном магнитном поле с индукцией В=0,1 Тл. Па-
Параллельно магнитному полю возбуждено электрическое поле напря-
напряженностью ?=100 В/м. Вычислить промежуток времени Af, в те-
течение которого должно действовать электрическое поле, для того
чтобы кинетическая энергия частицы возросла вдвое.
23.40. Протон влетает со скоростью у=100 км/с в область про-
пространства, где имеются электрическое (?"=210 В/м) и магнитное
(В=3,3 мТл) поля. Напряженность Е электрического поля и маг-
магнитная индукция В совпадают по направлению. Определить ускоре-
ускорение протона для начального момента движения в поле, если направ-
направление вектора его скорости v: 1) совпадает с общим направлением
векторов Е и В; 2) перпендикулярно этому направлению.
§ 24. ЗАКОН ПОЛНОГО ТОКА. МАГНИТНЫЙ ПОТОК.
МАГНИТНЫЕ ЦЕПИ
Основные формулы
• Циркуляция вектора магнитной индукции В вдоль замкну-
замкнутого контура
где Вь — проекция вектора магнитной индукции на направление
элементарного перемещения d/ вдоль контура L. Циркуляция век-
вектора напряженности Н вдоль замкнутого контура
Закон полного тока (для магнитного поля в вакууме)
п
где {л0 — магнитная постоянная; 2 // — алгебраическая сумма
i = i
токов, охватываемых контуром; п — число токов.
Закон полного тока (для произвольной среды)
Магнитный поток Ф через плоский контур площадью Si
287

а) в случае однородного поля
Ф = fiScosa; или Ф = BnS,
где a — угол между вектором нормали п к плоскости контура и век-
вектором магнитной индукции В; Вп — проекция вектора В на нор-
нормаль п (Вп=В cos a);
б) в случае неоднородного поля
S
где интегрирование ведется во всей поверхности 5.
• Потокосцепление, т. е. полный магнитный поток, сцепленный
со всеми витками соленоида или тороида,
В,Тл
где Ф — магнитный поток через один виток; N — число витков со-
соленоида или тороида.
• Магнитное поле тороида, сердечник которого составлен из
двух частей, изготовлен-
изготовленных из веществ с раз-
различными магнитными
проницаемостями:
а) магнитная индук-
индукция на осевой линии то*
роида
Bш
1,50
1,25
Ю
0,75
0,5
0,25
/
1
f
/
J
1
/
/
/
f
f
J
-
/
0*
0*
g^
00х
m
0*
0*
0*
'Cmofii
0*
Чугу
0*
0*
!)
С!
¦i
m
m
m
500
WOO 1500
Рис. 24.1
2000 2500
где / — сила тока в об-
обмотке тороида; N — чис-
число ее витков; 1Х и /2 —
длины первой и второй
частей сердечника торо-
тороида; |Лх и (л2—магнит-
(л2—магнитные проницаемости ве-
веществ первой и второй
частей сердечника торо-
тороида; jUL0 — магнитная по-
н,А/м стоянная;
б) напряженность
магнитного поля на осе-
вой линии тороида в первой и второй частях сердечника
Я
в) магнитный поток в сердечнике тороида
Ф =¦
IN
или по аналогии с законом Ома (формула Гопкинсона)
где Fm — магнитодвижущая сила; Rm — полное магнитное сопро-
сопротивление цепи;
288

г) магнитное сопротивление участка цепи
• Магнитная проницаемость (л ферромагнетика связана с маг-
магнитной индукцией В поля в нем и напряженностью Н намагничи-
намагничивающего поля соотношением
Ф Связь между магнитной индукцией В поля в ферромагнетике
и напряженностью Н намагничивающего поля выражается графи-
графически (рис. 24.1).
Примеры решения задач
Пример 1. В одной плоскости с бесконечно длинным прямым
проводом, по которому течет ток /=50 А, расположена прямоуголь-
прямоугольная рамка так, что две большие стороны ее длиной /=65 см парал-
параллельны проводу, а расстояние от провода до ближайшей из этих
сторон равно ее ширине. Каков магнитный поток Ф, пронизываю-
пронизывающий рамку?
Решение. Магнитный поток Ф через поверхность площадью
5 определяется выражением
Ф = J Bn dS.
s
В нашем случае вектор магнитной индукции В перпендикулярен
плоскости рамки. Поэтому для всех точек рамки Вп=В. Магнитная
индукция В, создаваемая бесконечно
длинным прямым проводником с током, ]I х * х
определяется формулой * dx
1
~ — 2ш >
где х — расстояние от провода до точки,
в которой определяется jB.
Для вычисления магнитного потока
заметим, что так как В зависит от х и
элементарный поток Ф будет также за-
зависеть от х9 то
6O=B(x)dS.
Разобьем площадь рамки на узкие
элементарные площадки длиной /, шири-
шириной dx и площадью dS=^ldx (рис. 24.2).
В пределах этой площадки магнитную
индукцию можно считать постоянной, так как все части площад-
площадки равноудалены (на расстояние х) от провода.
С учетом сделанных замечаний элементарный магнитный поток
можно записать в виде
г}Ф — ^° / (\у
2пх
X Х
J
X
X
X |
а
X
X
X
и х
И х
Рис.
i
1
х
dS = idx
а
24.2
X
X
X
10 № 1268
289

Проинтегрировав полученное выражение в пределах от Xi—a до
2—2а, найдем
2а 2а
х
а
Подставив пределы, получим
Убедимся в том, что правая часть полученного равенства дает
единицу магнитного потока (Вб):
[щ1 [/] [/1 = 1 Гн/м-1 А-1 м=1 Вб.
Произведя вычисления по формуле A), найдем
Ф=4,5 мкВб.
Пример 2. Определить индукцию В и напряженность Я магнит-
магнитного поля на оси тороида без сердечника, по обмотке которого, со-
содержащей N=200 витков, идет ток 1=5 А. Внешний диаметр dt
тороида равен 30 см, внутренний d2~20 см.
Решение. Для определения напряженности магнитного поля
внутри тороида вычислим циркуляцию вектора Н вдоль линии маг-
магнитной индукции поля: &Н&1.
Из условия симметрии следует, что линии магнитной индукции
тороида представляют собой окружности и что во всех точках этой
линии напряженности одинаковы. Поэтому в выражении циркуля-
циркуляции напряженность Н можно вынести за знак интеграла, а интегри-
интегрирование проводить в пределах от нуля до 2 пгу где г — радиус ок-
окружности, совпадающей с линией индукции, вдоль которой вычис-
вычисляется циркуляция, т. е.
2 яг
5
О
С другой стороны, в соответствии с законом полного тока цир-
циркуляция вектора напряженности магнитного поля равна сумме то-
токов, охватываемых контуром, вдоль которого вычисляется цирку-
циркуляция:
L
Приравняв правые части равенств A) и B), получим
2пгН = 2 //. гC)
Линия, проходящая вдоль тороида, охватывает число токов,
равное числу витков тороида. Сила тока во всех витках одинакова.
Поэтому формула C) примет вид 2nrH^NI} откуда
290

Для средней линии тороида г=У2 (/?i+/?2) = J4 (di+d2). Подставив
это выражение г в формулу D), найдем
Н= 2Ш . E)
jt (и\ -4- wo) \ /
Магнитная индукция Во в вакууме связана с напряженностью
поля соотношением B0=\i0H. Следовательно,
( + «
Подставив значения величин в выражения E) и F)* получим:
Я-1,37 кА/м, 50=1,6 мТл.
Пример. 3. Чугунное кольцо имеет воздушный зазор длиной
/о=5 мм. Длина / средней линии кольца равна 1 м. Сколько витков N
содержит обмотка на кольце, если при силе тока /=4 А индукция В
магнитного поля в воздушном зазоре равна 0,5 Тл? Рассеянием маг-
магнитного потока в воздушном зазоре можно пренебречь. Явление
гистерезиса не учитывать.
Решение. Пренебрегая рассеянием магнитного потока, мы
можем принять, что индукция поля в воздушном зазоре равна ин-
индукции поля в чугуне. На основании закона полного тока запишем
o
По графику (см. рис. 24.1) находим, что при В=0,5 Тл напря-
напряженность Н магнитного поля в чугуне равна 1,2 кА/м. Так как
для воздуха [г=1, то напряженность поля в воздушном зазоре
#0=5/^0=0,4 МА/м.
Искомое число витков
N=(Hl+H0l0)/I=8QQ.
Задачи
Закон полного тока
24.1. По соленоиду длиной /-=1 м без сердечника, имеющему N=
= 103 витков (рис. 24.2), течет ток /=20 А. Определить циркуляцию
вектора магнитной индукции вдоль контура, изображенного на
рис. 24.3, а, б,
_1НЕЗ§
а)
Рис. 24.3
Рис. 24.4
10*
291

24.2. Вычислить циркуляцию вектора индукции вдоль конту-
контура, охватывающего токи 1г= 10 А, /2= 15 А, текущие в одном направ-
направлении, и ток /3=20 А, текущий в противоположном направлении.
24.3. По сечению проводника равномерно распределен ток плот-
плотностью /=2 МА/м2. Найти циркуляцию вектора напряженности
вдоль окружности радиусом /?=5 мм, проходящей внутри провод-
проводника и ориентированной так, что ее плоскость составляет угол <х=
= 30° с вектором плотности тока.
24.4. Диаметр D тороида без сердечника по средней линии равен
30 см. В сечении тороид имеет круг радиусом г=5 см. По обмотке
тороида, содержащей N=2000 витков, течет ток /=5 А (рис. 24.4).
Пользуясь законом полного тока, определить максимальное и мини-
минимальное значение магнитной индукции В в тороиде.
Магнитный поток
24.5. Найти магнитный поток Ф, создаваемый соленоидом сече-
сечением S= 10 см2, если он имеет п= 10 витков на каждый санти-
сантиметр его длины при силе тока /=20 А.
24.6. Плоский контур, площадь S которого равна 25 см2, нахо-
находится в однородном магнитном поле с индукцией В=0,04 Тл. Оп-
Определить магнитный поток Ф, пронизывающий контур, если плос-
плоскость его составляет угол C=30° с линиями индукции.
24.7. При двукратном обводе магнитного полюса вокруг провод-
проводника с током /=100 А была совершена работа Л = 1 мДж. Найти
магнитный поток Ф, создаваемый полюсом.
24.8. Соленоид длиной /=1 ми сечением S = 16cm2 содержит N=
= 2000 витков. Вычислить потокосцеп-
ление Ч при силе тока / в обмотке
10 А.
24.9. Плоская квадратная рамка со
стороной а=20 см лежит в одной плос-
плоскости с бесконечно длинным прямым
проводом, по которому течет ток /=
= 100 А. Рамка расположена так, что
ближайшая к проводу сторона парал-
параллельна ему и находится на расстоя-
расстоянии /=10 см от провода. Определить
магнитный поток Ф, пронизывающий
рамку.
24.10. Определить, во сколько раз
отличаются магнитные потоки, прони-
пронизывающие рамку при двух ее положениях относительно прямого
проводника с током, представленных на рис. 24.5.
24.11. Квадратная рамка со стороной длиной а=20 см расположе-
расположена в одной плоскости с прямым бесконечно длинным проводом с то-
током. Расстояние / от провода до середины рамки равно 1 м. Вычис-
Вычислить относительную погрешность, которая будет допущена при рас-
расчете магнитного потока, пронизывающего рамку, если поле в пре-
]
1
(
а
I
а
5а
I
а
Рис. 24.5
292

делах рамки считать однородным, а магнитную индукцию — равной
значению ее в центре рамки.
24.12. Тороид квадратного сечения содержит N=1000 витков.
Наружный диаметр D тороида равен 40 см, внутренний d=20 см.
Найти магнитный поток Ф в тороиде, если сила тока /, протекаю-
протекающего по обмотке, равна 10 А.
Указание. Учесть, что магнитное поле тороида неоднородно.
Магнитная индукция в ферромагнетике
24.13. Железный сердечник находится в однородном магнитном
поле напряженностью Н=\ кА/м. Определить индукцию В магнит-
магнитного поля в сердечнике и магнитную проницаемость \х железа *.
24.14. На железное кольцо намотано в один слой N=500 витков
провода. Средний диаметр d кольца равен 25 см. Определить маг-
магнитную индукцию В в железе и магнитную проницаемость \i желе-
железа *, если сила тока / в обмотке: 1) 0,5 А; 2) 2,5 А.
24.15. Замкнутый соленоид (тороид) со стальным сердечником *
имеет п=10 витков на каждый сантиметр длины. По соленоиду те-
течет ток 1=2 А. Вычислить магнитный поток Ф в сердечнике, если
его сечение S=i см2.
24.16. Определить магнитодвижущую силу Fm, необходимую для
получения магнитного потока Ф=0,3 мВб в железном * сердечнике
замкнутого соленоида (тороида). Длина I средней линии сердечника
равна 120 см, площадь сечения 5=2,5 см2.
24.17. Соленоид намотан на чугунное * кольцо сечением S=5 см2.
При силе тока / = 1 А магнитный поток Ф=250 мкВб. Определить
число п витков соленоида, приходящихся на отрезок длиной 1 см
средней линии кольца.
Магнитные цепи
24.18. Электромагнит изготовлен в виде тороида. Сердечник то-
тороида со средним диаметром d=51 см имеет вакуумный зазор дли-
длиной /0=2 мм. Обмотка тороида равномерно распределена по всей
его длине. Во сколько раз уменьшится индукция магнитного поля в
зазоре, если, не изменяя силы тока в обмотке, зазор увеличить в
п=3 раза? Рассеянием магнитного поля вблизи зазора пренебречь.
Магнитную проницаемость \х сердечника считать постоянной и при-
принять равной 800.
24.19. Определить магнитодвижущую силу Fm, необходимую для
создания магнитного поля индукцией В=1,4 Тл в электромагните
с железным * сердечником длиной /=90 см и воздушным промежут-
промежутком длиной /0=5 мм. Рассеянием магнитного потока в воздушном
промежутке пренебречь.
* Для определения магнитной проницаемости воспользоваться графиком
(см. рис. 24.1). Явление гистерезиса не учитывать.
293

24.20. В железном * сердечнике соленоида индукция 5=1,3 Тл.
Железный сердечник заменили стальным. Определить, во сколько
раз следует изменить силу тока в обмотке соленоида, чтобы индук-
индукция в сердечнике осталась неизменной.
24.21. Стальной * сердечник тороида, длина / которого по сред-
средней линии равна 1 м, имеет вакуумный зазор длиной /0=4 мм. Об-
Обмотка содержит п=8 витков на 1 см. При какой силе тока / индукция
В в зазоре будет равна 1 Тл?
24.22. Обмотка тороида, имеющего стальной * сердечник с уз-
узким вакуумным зазором, содержит N=1000 витков. По обмотке те-
течет ток /=1 А. При какой длине /<> вакуумного зазора индукция В
магнитного поля в нем будет равна 0,5 Тл? Длина I тороида по сред-
средней линии равна 1 мо
24.23. Определить магнитодвижущую силу, при которой в уз-
узком вакуумном зазоре длиной /0=3,6 мм тороида с железным * сер-
сердечником, магнитная индукция В равна 1,4 Тл. Длина / тороида по
средней линии равна 0,8 м.
24.24. Длина I чугунного * тороида по средней линии равна 1,2 м,
сечение S=20 см2. По обмотке тороида течет ток, создающий в уз-
узком вакуумном зазоре магнитный поток Ф=0,5 мВб. Длина /0
зазора равна 8 мм. Какова должна быть длина зазора, чтобы маг-
магнитный поток в нем при той же силе тока увеличился в два раза?
§ 25. РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМ
В МАГНИТНОМ ПОЛЕ.
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ИНДУКТИВНОСТЬ,
Основные формулы
• Работа по перемещению замкнутого контура с током в маг-
магнитном поле
Л-/АФ,
где АФ — изменение магнитного потока, пронизывающего поверх-
поверхность, ограниченную контуром; / — сила гока в контуре.
• Основной закон электромагнитной индукции (закон Фара-
дея — Максвелла)
ф'-~ dt — dt '
где S( — электродвижущая сила индукции; N — число витков кон-
контура; Ч — потокосцепление.
Частные случаи применения основного закона электромагнитной
индукции:
а) разность потенциалов U на концах проводника длиной 1г
движущегося со скоростью v в однородном магнитном поле,
U=Blvsma,
где а — угол между направлениями векторов скорости v и магнит-
магнитной индукции В;
• См. сноску на с. 293.
294

б) электродвижущая сила индукции <?,-, возникающая в рамке,
содержащей -/V витков, площадью S, при вращении рамки с угловой
скоростью со в однородном магнитном поле с индукцией В
где tot — мгновенное значение угла между вектором В и вектором
нормали п к плоскости рамки.
• Количество электричества Q, протекающего в контуре.
где R — сопротивление контура; А? — изменение потокосцепле-
ния.
• Электродвижущая сила самоиндукции <?,, возникающая в
замкнутом контуре при изменении силы тока в немг
?i = — L-gp ИЛИ <^>.> = _/,_,
где L — индуктивность контура.
• Потокосцепление контура
Y=L/,
где L — индуктивность контура.
• Индуктивность соленоида (тороида)
L=\io\in2V.
Во всех случаях вычисления индуктивности соленоида (тороида)
с сердечником по приведенной формуле для определения магнит-
магнитной проницаемости следует пользоваться графиком зависимости В
от Н (см. рис. 24.1), а затем формулой
• Мгновенное значение силы тока / в цепи, обладающей актив-
активным сопротивлением R и индуктивностью Li
а) после замыкания цепи
/ = -1A— e-<*/L>'),
где ? — ЭДС источника тока; t — время, прошедшее после замы-
замыкания цепи;
б) после размыкания цепи
где /0 — сила тока в цепи при /=0; t — время, прошедшее с момен-
момента размыкания цепи.
Примеры решения задач
Пример 1. Виток, по которому течет ток 1=20 А, свободно уста-
установится в однородном магнитном поле ?=16 мТл. Диаметр d витка
равен 10 см. Какую работу нужно совершать, чтобы медленно по-
повернуть виток на угол а=я/2 относительно оси, совпадающей с диа-
диаметром?
Решение. При медленном повороте контура в магнитном поле
индукционными токами можно пренебречь и считать ток в контуре
295

неизменным. Работа сил поля в этом случае определяется выраже-
выражением
гдеФх и Ф2 — магнитные потоки, пронизывающие контур в началь-
начальном и конечном положениях.
Работа внешних сил будет равна модулю работе сил поля и про-
противоположна ей по знаку, т. е.
Так как в начальном положении контур установился свободно (по-
(положение устойчивого равновесия), то момент внешних сил, действу-
действующий на контур, равен
нулю. В этом положении
вектор магнитного мо-
момента рт контура сона-
правлен с вектором В
(рис. 25.1, а) и магнит-
магнитный поток Фх максима-
максимален (а=0, cos a = l),
т. е. Ot=BS (где S —
площадь контура). В ко-
конечном положении (рис,
5
Ю
Рис. 25.1
25.1, б) вектор рт пер-
пендикулярен вектору В
(а=я/2, cos a=0) и маг-
магнитный поток Ф2=0. Перепишем выражение A) с учетом сделан-
сделанных замечаний:
Так как площадь контура S—nd2/4, то работа
Убедимся в том, что правая часть равенства дает единицу работы
СДж):
1 а 1 ^ if, IA-H-m2
1А-м
¦=1Н.м=1Дж.
Произведем вычисления:
Л О, 1т: <-»л <л i/4 — q /(
Пример 2. В однородном магнитном поле с индукцией В=0,1 Тл
равномерно вращается рамка, содержащая N=1000 витков, с часто-
частотой п= 10 с~х. Площадь 5 рамки равна 150 см2. Определить мгновен-
мгновенное значение ЭДС $h соответствующее углу поворота рамки 30°.
Решение. Мгновенное значение ЭДС индукции <§t определя-
определяется основным уравнением электромагнитной индукции Фарадея —
Максвелла:
tf, —dV/d*. A)
Потокосцепление ?=Л^Ф, где N — число витков, пронизывае-
пронизываемых магнитным потоком Ф. Подставив выражение ? в формулу A),
296

получим
*/ = -*¦!?- <2>
При вращении рамки магнитный поток Ф, пронизывающий рам-
рамку в момент времени t, изменяется по закону (&=BS cos со t, где В —
магнитная индукция; S — площадь рамки; со — угловая частота.
Подставив в формулу B) выражение Ф и продифференцировав по
времени, найдем мгновенное значение ЭДС индукции:
g — NBSaslnat. C)
Угловая частота со связана с частотой п вращения соотношением
@=2 пп. Подставив выражение со в формулу C) и заменив cot на
угол а, получим
?i = 2nnNBSsin<i>t. D)
Убедимся в том, что правая часть полученного равенства дает
единицу ЭДС (В). Учтя, что 2 я, N и sin cat — величины безразмер-
безразмерные и неименованные, получим
Произведя вычисления по формуле D), найдем
«?,. = 47,13.
Пример. 3 По соленоиду течет ток 1=2 А. Магнитный поток Ф,
пронизывающий поперечное сечение соленоида, равен 4 мкВб. Оп-
Определить индуктивность L соленоида, если он имеет N=800 витков.
Решение. Индуктивность L соленоида связана с потокосцеп-
лением Ч соотношением 4f=L/, откуда L=yP/I. Заменив здесь по-
токосцепление W его выражением через магнитный поток Ф и число
витков N соленоида (XP=ON), получим
L=Q)NII. A)
Произведя вычисления по формуле A), получим
L = 1,6 мГн.
Пример 4. При скорости изменения силы тока Д//А/ в соле-
соленоиде, равной 50 А/с, на его концах возникает ЭДС самоиндук-
самоиндукции tfj—0,08 В. Определить индуктивность L соленоида.
Решение. Индуктивность соленоида связана с ЭДС само-
самоиндукции и скоростью изменения силы тока в его обмотке соотноше-
соотношением *
р _ Д? _ A(L7)
Вынося постоянную величину L за знак приращения, получим
Опустив знак минус в этом равенстве (направление ЭДС в данном
случае несущественно) и выразив интересующую нас величину —
индуктивность, получим
Сравните с предыдущим примером.
297

Д//Д* *
Сделав вычисления по этой формуле, найдем
L = l,6 мГн.
Пример 5. Обмотка соленоида состоит из одного слоя плотно
прилегающих друг к другу витков медного провода диаметром
d=0,2 мм. Диаметр D соленоида равен 5 см. По соленоиду течет ток
1 = 1 А. Определить количество электричества Q, протекающее
через обмотку, если концы ее замкнуть накоротко. Толщиной изо-
изоляции пренебречь.
Решение. Возможны два способа решения. 1-й способ. Ко-
Количество электричества dQ, которое протекает по проводнику за
время dt при силе тока /, определяется равенством
dQ=/d/. A)
Полное количество электричества, протекающее через проводник
t
за время t, будет Q=\}Idt. Сила тока в данном случае убывает
о
экспоненциально со временем и выражается формулой
Внося выражение силы тока / под знак интеграла и интегрируя от
О до оо (при /-XX)/-^0), получим
ОС 00 СО
Q = 5 IQe-WL)t d/ = /0 J e-<*/L>' d* == /0 ( —-|-Л e-<*/L>' I .
0 0 ^ ' 0
Подставим пределы интегрирования и определим количество
электричества, протекающее через обмотку:
Q=I0(—L/R) @—l)=/0L/?. B)
2-й способ. Подставив в формулу A) вместо силы тока / выраже-
выражение ее через ЭДС индукции <?z- и сопротивление R соленоида, т. е.
I=?t/R, найдем dQ = -^-d*.
Но S{ связана со скоростью изменения потокосцепления Т по
закону Фарадея — Максвелла: <§ ~—dWldt, тогда
dQ=—dV/R.
Интегрируя, получаем
q=_Dt1_Y1)//?. C)
Потокосцепление "V пропорционально силе тока в соленоиде.
Следовательно, Х?±=ЫО\ ^г2==0, так как W2 соответствует тому мо-
моменту, когда ток в цепи обратится в нуль. Подставив выражения ?|
и ?2 в формулу C), получим Q=YxAR, или
Q=IoL/R,
что совпадает с формулой B).
Для определения заряда, протекающего через обмотку соленои-
соленоида, следует найти индуктивность L соленоида и сопротивление R
обмотки соленоида, которые выражаются формулами
298

™. n 1 _ V
где |i0 — магнитная постоянная; N — число витков; 1± — длина
соленоида; Sx — площадь сечения соленоида; р — удельное сопро-
сопротивление провода; / — длина провода; 5 — площадь сечения про-
провода; d — диаметр провода; dx — диаметр соленоида.
Подставив найденные выражения L и R в формулу B), получим
^ г L
OI jkP/ ()
У "У° R - 4/г4р/ Ш У°' W
Заметим, что длина провода / может быть выражена через диа-
диаметр dx соленоида соотношением l=ndiN, где N — число витков,
тогда формуле D) можно придать вид
п_ [i0N*nd\nd2 j nppNdtd* f
* IGlipndtN ° 16p/i °"
Но IJN есть диаметр провода, так как витки плотно прилегают
друг к другу. Следовательно,
У° "" 16р aai/°* ^Dj
Произведя вычисления по формуле E), получим
Q-363 мкКл.
Задачи
Работа по перемещению проводника * е магнитном поле
25.1. В однородном магнитном поле с индукцией 6=0,01 Тл
находится прямой провод длиной /=8 см, расположенный перпен-
перпендикулярно линиям индукции. По проводу течет ток 1=2 А. Под
действием сил поля провод переместился на расстояние s=5 см.
Найти работу А сил поля.
25.2. Плоский контур, площадь 5 которого равна 300 см2, на-
находится в однородном магнитном поле с индукцией В=0,01 Тл.
Плоскость контура перпендикулярна линиям индукции. В контуре
поддерживается неизменный ток / = 10 А. Определить работу А
внешних сил по перемещению контура с током в область пространст-
пространства, магнитное поле в которой отсутствует.
25.3. По проводу, согнутому в виде квадрата со стороной дли-
длиной а=10 см, течет ток 1=20 А, сила которого поддерживается не-
неизменной. Плоскость квадрата составляет угол а=20° с линиями
индукции однородного магнитного поля F=0,1 Тл). Вычислить
работу Л, которую необходимо совершить для того, чтобы удалить
провод за пределы поля.
25.4. По кольцу, сделанному из тонкого гибкого провода радиу-
радиусом jR = 10 см, течет ток /=100 А. Перпендикулярно плоскости коль-
кольца возбуждено магнитное поле с индукцией В=0,1 Тл, по направле-
направлению совпадающей с индукцией Вх собственного магнитного поля
* Перемещение проводника или контура с током в магнитном поле счи-
считать настолько медленным, что возникающими индукционными токами можно
пренебречь.
299

кольца. Определить работу А внешних сил, которые, действуя на
провод, деформировали его и придали ему форму квадрата. Сила
тока при этом поддерживалась неизменной. Работой против упру-
упругих сил пренебречь.
25.5A). Виток, по которому течет ток 1=20 А, свободно устано-
установился в однородном магнитном поле с индукцией В=0,016 Тл. Диа-
Диаметр d витка равен 10 см. Определить работу Л, которую нужно
совершить, чтобы повернуть виток на угол а=п/2 относительно
оси, совпадающей с диаметром. То же, если угол а=2 я.
25.5B). Квадратная рамка со стороной а=10 см, по которой
течет ток /=200 А, свободно установилась в однородном магнитном
поле (В=0,2 Тл). Определить работу, которую необходимо совер-
совершить при повороте рамки вокруг оси, лежащей в плоскости рамки и
перпендикулярной линиям магнитной индукции, на угол Ь=2 п/3.
Электродвижущая сила индукции
25.6. Магнитный поток Ф=40 мВб пронизывает замкнутый
контур. Определить среднее значение ЭДС индукции (Si), возни-
возникающей в контуре, если магнитный поток изменится до нуля за
время Д/=2 мс.
25.7. Прямой провод длиной /=40 см движется в однородном
магнитном поле со скоростью и=5 м/с перпендикулярно линиям
индукции. Разность потенциалов U между концами провода равна
0,6 В. Вычислить индукцию В магнитного поля.
25.8. В однородном магнитном поле с индукцией В=1 Тл нахо-
находится прямой провод длиной /=20 см, концы которого замкнуты вне
поля. Сопротивление R всей цепи равно 0,1 Ом. Найти силу F,
которую нужно приложить к проводу, чтобы перемещать его пер-
перпендикулярно линиям индукции со скоростью у—2,5 м/с.
25.9. Прямой провод длиной /=10 см помещен в однородном маг-
магнитном поле с индукцией В=\ Тл. Концы его замкнуты гибким про-
проводом, находящимся вне поля. Сопротивление R всей цепи равно
0,4 Ом. Какая мощность Р потребуется для того, чтобы двигать про-
провод перпендикулярно линиям индукции со скоростью и=20 м/с?
25.10. К источнику тока с ЭДС<?=0,5 В и ничтожно малым внут-
внутренним сопротивлением присоединены два металлических стержня,
расположенные горизонтально и параллельно друг другу. Рас-
Расстояние / между стержнями равно 20 см. Стержни находятся в
однородном магнитном поле, направленном вертикально. Магнит-
Магнитная индукция В= 1,5 Тл. По стержням под действием сил поля сколь-
скользит со скоростью v=\ м/с прямолинейный провод сопротивлением
/?=0,02 Ом. Сопротивление стержней пренебрежимо мало. Опреде-
Определить: 1) ЭДС индукции «§У, 2) силу F, действующую на провод со
стороны поля; 3) силу тока / в цепи; 4) мощность Ръ расходуемую
на движение провода; 5) мощность Р2, расходуемую на нагревание
провода; 6) мощность Р3, отдаваемую в цепь источника тока.
25.11. В однородном магнитном поле с индукцией В=0,4 Тл в
плоскости, перпендикулярной линиям индукции поля, вращается
300

стержень длиной /= 10 см. Ось вращения проходит через один из
концов стержня. Определить разность потенциалов U на концах
стержня при частоте вращения /г= 16 с.
25.12. Рамка площадью S=200 см2 равномерно вращается с
частотой п=\0 с относительно оси, лежащей в плоскости рамки и
перпендикулярно линиям индукции однородного магнитного поля
(В=0,2 Тл). Каково среднее значение ЭДС индукции (?t) за время,
в течение которого магнитный поток, пронизывающий рамку, из-
изменится от нуля до максимального значения?
25.13. В однородном магнитном поле с индукцией В=0,35 Тл
равномерно с частотой п=480 мин вращается рамка, содержащая
JV=500 витков площадью S=50 см2. Ось вращения лежит в плос-
плоскости рамки и перпендикулярна линиям индукции. Определить
максимальную ЭДС индукции ^ах, возникающую в рамке.
25.14. Рамка площадью S = 100 см2 содержит Л^= 103 витков
провода сопротивлением i?i= 12 Ом. К концам обмотки подключено
внешнее сопротивление R2=20 Ом. Рамка равномерно вращается в
однородном магнитном поле (В=0,1 Тл) с частотой л=8 с. Оп-
Определить максимальную мощность Ртах переменного тока в цепи.
25.15. Магнитная индукция В поля между полюсами двухполюс-
двухполюсного генератора равна 0,8 Тл. Ротор имеет N=100 витков площадью
S=400 см2. Определить частоту п вращения якоря, если максималь-
максимальное значение ЭДС индукции <?~200 В.
25.16. Короткая катушка, содержащая N=1000 витков, рав-
равномерно вращается в однородном магнитном поле с индукцией
В=0,04 Тл с угловой скоростью со=5 рад/с относительно оси, совпа-
совпадающей с диаметром катушки и перпендикулярной линиям индук-
индукции поля. Определить мгновенное значение ЭДС индукции $( для
тех моментов времени, когда плоскость катушки составляет угол
а=60р с линиями индукции поля. Площадь S катушки равна
100 см2.
Количество электричества, протекающее
в контуре при изменении магнитного потока *
25.17. Проволочный виток радиусом r=i см, имеющий сопротив-
сопротивление #=0,01 Ом, находится в однородном магнитном поле с ин-
индукцией В=0,04 Тл. Плоскость рамки составляет угол а=30с с
линиями индукции поля. Какое количество электричества Q проте-
протечет по витку, если магнитное поле исчезнет?
25.18. Проволочное кольцо радиусом /*—10 см лежит на столе.
Какое количество электричества Q протечет по кольцу, если его
повернуть с одной стороны на другую? Сопротивление R кольца
равно 1 Ом. Вертикальная составляющая индукции В магнитного
поля Земли равна 50 мкТл.
25.19. В проволочное кольцо, присоединенное к баллистическому
гальванометру, вставили прямой магнит. По цепи протекло коли-
* При решении задач этого раздела собственный магнитный поток кон-
контуров можно не учитывать.
301

чество электричества Q= 10 мкКл. Определить магнитный поток Ф,
пересеченный кольцом, если сопротивление R цепи гальванометра
равно 30 Ом.
25.20. Между полюсами электромагнита помещена катушка, сое-
соединенная с баллистическим гальванометром. Ось катушки парал-
параллельна линиям индукции. Катушка сопротивлением Ri=4 Ом име-
имеет N=15 витков площадью 5=2 см2. Сопротивление R2 гальвано-
гальванометра равно 46 Ом. Когда ток в обмотке электромагнита выключи-
выключили, по цепи гальванометра протекло количество электричества Q—
=90 мкКл. Вычислить магнитную индукцию В поля электромаг-
электромагнита.
25.21. Рамка из провода сопротивлением R=0fil Ом равномер-
равномерно вращается в однородном магнитном поле с индукцией 5=0,05 Тл.
Ось вращения лежит в плоскости рамки и перпендикулярна линиям
индукции. Площадь 5 рамки равна 100 см2. Найти, какое количест-
количество электричества Q протечет через рамку за время поворота ее на
угол а=30° в следующих трех случаях: 1) от ао=О до 0^=30°; 2) от
«1 ДО а2=60°; 3) от а3=90°.
25.22. Тонкий медный провод массой т=1 г согнут в виде квад-
квадрата, и концы его замкнуты. Квадрат помещен в однородное маг-
магнитное поле (В=0,1 Тл) так, что плоскость его перпендикулярна
линиям индукции поля. Определить количество электричества Q,
которое протечет по проводнику, если квадрат, потянув за противо-
противоположные вершины, вытянуть в линию.
25.23. На расстоянии а=1 м от длинного прямого провода с то-
током /=кА находится кольцо радиусом г=1 см. Кольцо расположе-
расположено так, что поток, пронизывающий его, максимален. Определить
количество электричества Q, которое протечет по кольцу, когда
ток в проводнике будет выключен. Сопротивление R кольца 10 Ом.
Указание. Поле в пределах кольца считать однородным.
25.24. По длинному прямому проводу течет ток. Вблизи провода
расположена квадратная рамка из тонкого провода сопротивле-
сопротивлением R=0,02 Ом. Провод лежит в плоскости рамки и параллелен
двум ее сторонам, расстояния до которых от провода соответствен-
соответственно равны ax=10 см, а2=20 см. Найти силу тока / в проводе, если
при его включении через рамку протекло количество электричест-
электричества Q=693 мкКл.
Самоиндукция и взаимоиндукция
25.25. По катушке индуктивностью L=0,03 мГн течет ток /=
=0,6 А. При размыкании цепи сила тока изменяется практически до
нуля за время At=l20 мкс. Определить среднюю ЭДС самоиндук-
самоиндукции (^/), возникающую в контуре.
25.26. С помощью реостата равномерно увеличивают силу тока
в катушке на А/=0,1 А в 1 с. Индуктивность L катушки равна
0,01 Гн. Найти среднее значение ЭДС самоиндукции (<?;).
25.27. Индуктивность L катушки равна 2 мГн. Ток частотой v—
;=50 Гц, протекающий по катушке, изменяется по синусоидаль-
302

ному закону. Определить среднюю ЭДС самоиндукции (Si), воз-
возникающую за интервал времени Д?, в течение которого ток в катуш-
катушке изменяется от минимального до максимального значения. Ампли-
Амплитудное значение силы тока /0=Ю А.
25.28. Катушка сопротивлением 7?i=O,5 Ом с индуктивностью
L=4: мГн соединена параллельно с проводом сопротивлением
j^2=2,5 Ом, по которому течет постоянный
ток / = 1 А. Определить количество электри-
электричества Q, которое будет индуцировано в ка-
катушке при размыкании цепи ключом К (рис.
25.2).
25.29. На картонный каркас длиной /=
—50 см и площадью S сечения, равной 4 см2,
намотан в один слой провод диаметром d=
= 0,2 мм так, что витки плотно прилегают
друг к другу (толщиной изоляции пренеб-
пренебречь). Вычислить индуктивность L получившегося соленоида.
25.30. Индуктивность L соленоида длиной 1=1 м, намотанного в
один слой на немагнитный каркас, равна 1,6 мГн. Площадь 5 сече-
сечения соленоида равна 20 см2. Определить число п витков на каждом
сантиметре длины соленоида.
25.31. Сколько витков проволоки диаметром d=0,4 мм с изоля-
изоляцией ничтожной толщины нужно намотать на картонный цилиндр
диаметром D =2 см, чтобы получить однослойную катушку с индук-
индуктивностью L—\ мГн? Витки вплотную прилегают друг к другу.
25.32. Катушка, намотанная на немагнитный цилиндрический
каркас, имеет N1=750 витков и индуктивность 1^=25 мГн. Чтобы
увеличить индуктивность катушки до L2=36 мГн, обмотку с катуш-
катушки сняли и заменили обмоткой из более тонкой проволоки с таким
расчетом, чтобы длина катушки осталась прежней. Определить чис-
число N2 витков катушки после перемотки.
25.33. Определить индуктивность L двухпроводной линии на
участке длиной 1=1 км. Радиус R провода равен 1 мм, расстояние d
между осевыми линиями равно 0,4 м.
Указание. Учесть только внутренний магнитный поток, т. е4 поток,
пронизывающий контур, ограниченный проводами,
25.34. Соленоид индуктивностью L=4 мГн содержит Л/"=600
витков. Определить магнитный поток Ф, если сила тока /, протекаю-
протекающего по обмотке, равна 12 А.
25.35. Индуктивность L катушки без сердечника равна 0,02 Гн.
Какое потокосцепление ? создается, когда по обмотке течет ток 1=^
-5 А?
25.36. Длинный прямой соленоид, намотанный на немагнитный
каркас, имеет N=1000 витков и индуктивность L=3 мГн. Какой
магнитный поток Ф и какое потокосцепление W создает соленоид
при силе тока / = 1 А?
25.37. Соленоид, площадь 5 сечения которого равна 5 см2, со-
йержит N=1200 витков. Индукция В магнитного поля внутри соле-
303

ноида при силе тока 1=2 А равна 0,01 Тл. Определить индуктивность
L соленоида.
25.38. Соленоид содержит N=1000 витков. Площадь S сечения
сердечника равна 10 см2. По обмотке течет ток, создающий поле с
индукцией В=1,5 Тл. Найти среднюю ЭДС индукции ($()9 возни-
возникающей в соленоиде, если ток уменьшится до нуля за время
/=500 мкс.
25.39. Обмотка соленоида с железным сердечником содержит
N=500 витков. Длина / сердечника равна 50 см. Как и во сколько
раз изменится индуктивность L соленоида, если сила тока, протека-
протекающего по обмотке, возрастет от /х=0,1 А до 12=1 А (см. рис. 24.1).
25.40. Две катушки расположены на небольшом расстоянии од-
одна от другой. Когда сила тока в первой катушке изменяется с быст-
быстротой: -д^- = 5А/с, во второй катушке возникает ЭДС индук-
индукции <§\=0,1 В. Определить коэффициент М взаимной индукции ка-
катушек.
25.41. Обмотка тороида с немагнитным сердечником имеет Ыг=
=251 виток. Средний диаметр (D) тороида равен 8 см, диаметр d
витков равен 2 см. На тороид намотана вторичная обмотка, имею-
имеющая N2=100 витков. При замыкании первичной обмочи в ней в
течение /=1 мс устанавливается сила тока /=3 А. Найти среднюю
ЭДС индукции (<§(), возникающей на вторичной обмотке.
Экстратоки замыкания и размыкания
25.42. В цепи шел ток /0=50 А. Источник тока можно отключить
от цепи, не разрывая ее. Определить силу тока / в этой цепи че-
через /=0,01 с после отключения ее от источника тока. Сопротивле-
Сопротивление R цепи равно 20 Ом, ее индуктивность /.=0,1 Гн.
25.43. Источник тока замкнули на катушку с сопротивлением
R = 10 Ом и индуктивностью L=l Гн. Через сколько времени сила
тока замыкания достигнет 0,9 предельного значения?
25.44. Цепь состоит из катушки индуктивностью L~\ Гн и со-
сопротивлением /? = 10 Ом. Источник тока можно отключать, не раз-
разрывая цепи. Определить время /, по истечении которого сила тока
уменьшится до 0,001 первоначального значения.
25.45. К источнику тока с внутренним сопротивлением 7?^=2 Ом
подключают катушку индуктивностью L=0,5 Гн и сопротивлением
/?=8Ом. Найти время /, в течение которого ток в катушке, нарас-
нарастая, достигнет значения, отличающегося от максимального
на 1 %.
25.46. В цепи (см. рис. 25.1) Яг=5 Ом, /?2=95 Ом, L=0,34 Гн,
<?=38 В. Внутреннее сопротивление г источника тока пренебрежи-
пренебрежимо мало. Определить силу тока / в резисторе сопротивлением jR2 в
следующих трех случаях: 1) до размыкания цепи ключом /С; 2) в
момент размыкания (/i=0); 3) через /2=0,01 с после размыкания.
304

Бетатрон
25.47. Средняя скорость изменения магнитного потока
в бетатроне, рассчитанном на энергию 7=60 МэВ, составляет
50 Вб/с. Определить: 1) число N оборотов электрона на орбите за
время ускоренного движения; 2) путь /, пройденный электроном,
если радиус г орбиты равен 20 см.
25.48. В бетатроне скорость изменения магнитной индукции
— ^ = 60 Тл/с. Определить: 1) напряженность Е вихревого
электрического поля на орбите электрона, если ее радиус г=0,5 м;
2) силу F, действующую на электрон.
25.49. Электрон в бетатроне движется по орбите радиусом
г=0,4 м и приобретает за один оборот кинетическую энергию
Т=20 эВ. Вычислить скорость изменения магнитной индукции
A(В>*1Аг, считая эту скорость в течение интересующего нас про-
промежутка времени постоянной.
§ 26. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
Основные формулы
Ф Энергия W магнитного поля, создаваемого током в замкнутом
контуре индуктивностью L, определяется формулой
где / — сила тока в контуре.
• Объемная (пространственная) плотность энергии однородного
магнитного поля (например, поля длинного соленоида)
__
2
9 Формула Томсона. Период собственных колебаний в контуре
без активного сопротивления
где L — индуктивность контура; С — его электроемкость.
• Связь длины электромагнитной волны с периодом Т и час-
частотой v колебаний
К=сТ или h=c/v,
где с — скорость электромагнитных волн в вакууме (с=3*108 м/с).
Ф Скорость электромагнитных волн в среде
где е — диэлектрическая проницаемость; \i — магнитная проницае-
проницаемость среды.
* (В) есть среднее значение магнитной индукции в пределах круга,
очерченного орбитой электрона.
305

Примеры решения задач
Пример 1. На стержень из немагнитного материала длиной
Z=50 см намотан в один слой провод так, что на каждый сантиметр
длины стержня приходится 20 витков. Определить энергию W маг-
магнитного поля внутри соленоида, если сила тока / в обмотке равна
0,5 А. Площадь S сечения стержня равна 2 см2.
Решение. Энергия магнитного поля соленоида с индуктив-
индуктивностью L, по обмотке которого течет ток /, выражается формулой
W=V2LI\ A)
Индуктивность соленоида в случае немагнитного сердечника за-
зависит только от числа витков на единицу длины и от объема V сер-
сердечника: L=\xQn2V, где (х0 — магнитная постоянная. Подставив вы-
выражение индуктивности L в формулу A), получим W=Y2\xQn2VI2.
Учтя, что V=lSt запишем
W=V2\i0n2I2SL B)
Сделав вычисления по формуле B), найдем
117=126 мкДж.
Пример 2. По обмотке длинного соленоида со стальным сердеч-
сердечником течет ток 1=2А. Определить объемную плотность w энергии
магнитного поля в сердечнике, если число п витков на каждом сан-
сантиметре длины соленоида равно 7 см.
Решение. Объемная плотность энергии магнитного поля оп-
определяется по формуле
w=BH/B |x0). A)
Напряженность Н магнитного поля найдем по формуле Н=п1.
Подставив сюда значения п(п=7 см=700 м) и /, найдем
Я=1400 А/м.
Магнитную индукцию В определим по графику (см. рис. 24.1)
зависимости В от Н. Находим, что напряженности #=1400 А/м со-
соответствует магнитная индукция В=1,2 Тл.
Произведя вычисление по формуле A), найдем объемную плот-
плотность энергии:
w=840 Дж/м3.
Пример 3. На железный сердечник длиной /=20 см малого се-
сечения (d<C/) намотано N=200 витков. Определить магнитную прони-
проницаемость |jl железа при силе тока /=0,4 А.
Решение. Магнитная проницаемость \i связана с магнитной
индукцией В и напряженностью Н магнитного поля соотношением
B=\xo\iH. A)
Эта формула не выражает линейной зависимости В от Я, так как
|i является функцией Н. Поэтому для определения магнитной прони-
проницаемости обычно пользуются графиком зависимости В(Н) (см. рис.
24.1). Из формулы A) выразим магнитную проницаемость:
|л=Я/(|г,Я). B)
306

Напряженность # магнитного поля вычислим по формуле (ка-
(катушку с малым сечением можно принять за соленоид) #=я/, где
п — число витков, приходящихся на отрезок катушки длиной 1 м.
Выразив в этой формуле п через число N витков катушки и ее дли-
длину /, получим
H=(Nlt) 1.
Подставив сюда значения N, I и / и произведя вычисления, най-
найдем
#=400 А/и.
По графику находим, что напряженности #=400 А/м соответст-
соответствует магнитная индукция 5=1,05 Тл. Подставив найденные значе-
значения В и #, а также значение {х0 в формулу B), вычислим магнитную
проницаемость:
(i=2,09-103.
Пример 4. Колебательный контур, состоящий из воздушного кон-
конденсатора с двумя пластинами площадью 5= 100 см2 каждая и
катушки с индуктивностью L= 1 мкГн, резонирует на волну длиной
Я=10 м. Определить расстояние d между пластинами конденсатора.
Решение. Расстояние между пластинами конденсатора мож-
можно найти из формулы электроемкости плоского конденсатора С—
=eoeS/d, где г — диэлектрическая проницаемость среды, заполняю-
заполняющей конденсатор, откуда
d=eozS С. A)
Из формулы Томсона, определяющей период колебаний в элек-
электрическом контуре: Т = 2л ]/LC, находим электроемкость
C=7?/Dji2L). B)
Неизвестный в условии задачи период колебаний можно опреде-
определить, зная длину волны Я, на которую резонирует контур. Из соот-
соотношения Х=сТ имеем
Подставив выражения периода Т в формулу B), а затем электро-
электроемкости С в формулу A), получим
а-с
Произведя вычисления, найдем
d=3,14 мм.
Пример 5. Колебательный контур состоит из катушки с индук-
индуктивностью L= 1,2 мГн и конденсатора переменной электроемкости от
Сх=12 пФ до С2=80 пФ. Определить диапазон длин электромаг-
электромагнитных волн, которые могут вызывать резонанс в этом контуре.
Активное сопротивление контура принять равным нулю.
Решение. Длина X электромагнитной волны, которая может
вызвать резонанс в колебательном контуре, связана с периодом Т
307

колебаний контура соотношением
Х^сТ. A)
Период колебаний, в свою очередь, связан с индуктивностью L
катушки и электроемкостью С конденсатора колебательного конту-
контура соотношением (формула Томсона) T=2nYLC, Следовательно,
Х= 2те VLC. B)
Согласно условию задачи, индуктивность контура неизменна,
а электроемкость контура может изменяться в пределах от Сг до С2.
Этим значениям электроемкости соответствуют длины волн Хг и К2,
определяющие диапазон длин волн, которые могут вызвать резо-
резонанс. После вычислений по формуле B) получим:
Хх=226 м; Х2=
Задачи
Энергия магнитного поля соленоида и тороида
26.1. По обмотке соленоида индуктивностью L=0,2 Гн течет ток
/=10 А. Определить энергию W магнитного поля соленоида.
26.2. Индуктивность L катушки (без сердечника) равна 0,1 мГн.
При какой силе тока / энергия W магнитного поля равна 100 мкДж?
26.3. Соленоид содержит ЛА = 1000 витков. Сила тока / в его об-
обмотке равна 1 А, магнитный поток Ф через поперечное сечение соле-
соленоида равен 0,1 мВб. Вычислить энергию W магнитного поля.
26.4. На железное кольцо намотано в один слой iV=200 витков.
Определить энергию W магнитного поля, если при токе 1=2,5 А
магнитный поток Ф в железе равен 0,5 мВб.
26.5. По обмотке тороида течет ток силой /=0,6 А. Витки провода
диаметром d=0,4 мм плотно прилегают друг к другу (толщиной изо-
изоляции пренебречь). Найти энергию W магнитного поля в стальном
сердечнике тороида, если площадь S сечения его равна 4 см2, диа-
диаметр D средней линии равен 30 см *.
Объемная плотность энергии
26.6. При индукции В поля, равной 1 Тл, плотность энергии
w магнитного поля в железе равна 200 Дж/м3. Определить магнит-
магнитную проницаемость \i железа в этих условиях *.
26.7. Определить объемную плотность энергии w магнитного поля
в стальном сердечнике, если индукция В магнитного поля равна
0,5 Тл*.
26.8. Индукция магнитного поля тороида со стальным сердечни-
сердечником возросла от B1=0t5 Тл до В2—1 Тл. Найти, во сколько раз из-
изменилась объемная плотность энергии w магнитного поля *.
26.9. Вычислить плотность энергии w магнитного поля в желез-
железном сердечнике замкнутого соленоида, если напряженность Н на-
намагничивающего поля равна 1,2 кА/м *.
* Для определения магнитной проницаемости следует воспользоваться
графиком на рис. 24.1. Явление гистерезиса не учитывать.
308

26.10. Напряженность магнитного поля тороида со стальным
сердечником возросла от #х=200 А/м до #2=800 А/м. Определить,
во сколько раз изменилась объемная плотность энергии w магнит-
магнитного поля *.
26.11. При некоторой силе тока / плотность энергии w магнит-
магнитного поля соленоида (без сердечника) равна 0 2 Дж/м3. Во сколько
раз увеличится плотность энергии поля при той же силе тока, если
соленоид будет иметь железный сердечник?
26.12. Найти плотность энергии w магнитного поля в железном
сердечнике соленоида, если напряженность Н намагничивающего
поля равна 1,6 к А/м*.
26.13. Обмотка тороида с немагнитным сердечником имеет п=
= 10 витков на каждый сантиметр длины. Определить плотность
энергии w поля, если по обмотке течет ток /=16 А.
26.14. Обмотка тороида содержит п=10 витков на каждый сан-
сантиметр длины. Сердечник немагнитный. При какой силе тока /
в обмотке плотность энергии w магнитного поля равна 1 Дж/м3?
26.15. Катушка индуктивностью L = l мГн и воздушный конден-
конденсатор, состоящий из двух круглых пластин диаметром D=20 см
каждая, соединены параллельно. Расстояние d между пластинами
равно 1 см. Определить период Т колебаний.
26.16. Конденсатор электроемкостью С=500 пФ соединен па-
параллельно с катушкой длиной /=40 см и площадью S сечения, рав-
равной 5 см2. Катушка содержит N=1000 витков. Сердечник немагнит-
немагнитный. Найти период Т колебаний.
26.17. Колебательный контур состоит из катушки индуктив-
индуктивностью L=20 мкГн и конденсатора электроемкостью С'=80 нФ.
Величина емкости может отклоняться от указанного значения на
2 %. Вычислить, в каких пределах может изменяться длина волны,
на которую резонирует контур.
26.18. Колебательный контур имеет индуктивность L=1,6 мГн,
электроемкость С=0,04 мкФ и максимальное напряжение Umax на
зажимах, равное 200 В. Определить максимальную силу тока /тах
в контуре. Сопротивление контура ничтожно мало.
26.19. Колебательный контур содержит конденсатор электро-
электроемкостью С=8 пФ и катушку индуктивностью L=0,5 мГн. Каково
максимальное напряжение t/max на обкладках конденсатора, если
максимальная сила тока /щах^О мА?
26.20. Катушка (без сердечника) длиной /=50 см и площадью Si
сечения, равной 3 см2, имеет JV=1000 витков и соединена параллель-
параллельно с конденсатором. Конденсатор состоит из двух пластин площадью
«S2=75 см2 каждая. Расстояние d между пластинами равно 5 мм.
Диэлектрик — воздух. Определить период Т колебаний контура.
26.21. Колебательный контур состоит из параллельно соединен-
соединенных конденсатора электроемкостью С=1 мкФ и катушки индуктив-
индуктивностью L = l мГн. Сопротивление контура ничтожно мало. Найти
частоту v колебаний.
См. сноску на с. 308.
309

26.22. Индуктивность L колебательного контура равна 0,5 мГн.
Какова должна быть электроемкость С контура, чтобы он резони-
резонировал на длину волны ^=300 м?
26.23. На какую длину волны К будет резонировать контур, сос-
состоящий из катушки индуктивностью L=4 мкГн и конденсатора
электроемкостью С=1,11 нФ?
26.24. Для демонстрации опытов Герца с преломлением электро-
электромагнитных волн иногда берут большую призму, изготовленную из
парафина. Определить показатель преломления парафина, если его
диэлектрическая проницаемость 8=2 и магнитная проницаемость
26.25. Два параллельных провода, погруженных в глицерин,
индуктивно соединены с генератором электромагнитных колебаний
частотой v=420 МГц. Расстояние / между пучностями стоячих волн
на проводах равно 7 см. Найти диэлектрическую проницаемость в
глицерина. Магнитную проницаемость \i принять равной единице.
§ 27. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
Основные формулы
# Намагниченность J — величина, равная отношению магнит-
магнитного момента малого объема AF вещества к этому объему:
N
I
где jmM/ — магнитный момент отдельной (i-й) молекулы; N — число
молекул в объеме AF.
• Намагниченность J в изотропном магнетике пропорциональ-
пропорциональна напряженности магнитного поля Н:
где % — магнитная восприимчивость (безразмерна).
• Удельная магнитная восприимчивость %уд связана с магнит-
магнитной восприимчивостью х соотношением
где р — плотность вещества.
• Молярная магнитная восприимчивость Хт связана с магнит-
магнитной восприимчивостью х соотношением
Am p Л*
• Магнетон Бора |iB — элементарный магнитный момент —
определяется формулой
где е — элементарный заряд; те — масса электрона.
310

• Магнитная индукция В, напряженность Н и намагничен-
намагниченность J в изотропном магнетике связаны соотношением
где ji0 — магнитная постоянная.
О Намагниченность изотропного парамагнетика (по Ланжеве-
ну)
J = n\iHL(a),
где п — концентрация молекул; \iu — магнитный момент отдельной
молекулы; L(a)—функция Ланжевена.
О Функция Ланжевена
где а=рыВ/(кТ).
Приближенное значение функции Ланжевена можно предста-
представить в виде знакопеременного ряда
ь()аа' + 4аЪ
При а<1 (цм5<&Г) L(a)&y3 и намагниченность
* ШВ> или ' = #
Магнитная восприимчивость парамагнитных веществ при
Примеры решения задач
Пример 1. Определить магнитную восприимчивость % и молярную
восприимчивость Хш висмута, если удельная магнитная восприим-
восприимчивость xyjx=—1,3 -10~9 м3/кг.
Решение. Магнитная восприимчивость % определяется со-
соотношением
где / — намагниченность, Н — напряженность магнитного поля.
Намагниченность /, в свою очередь, определяется следующей
формулой:
где 2цМ|. — суммарный магнитный момент всех молекул в объеме
V (магнетик предполагается однородным).
Соответственно
где v — количество вещества (число молей данного вещества), и
где m — масса вещества.
311

1. Для определения удельной магнитной восприимчивости най-
найдем отношение
откуда
Х = РХуд>
где р — плотность.
Убедимся, в том, что правая часть равенства, так же как и %%—
величина безразмерная (неименованная):
Произведем вычисления, выписав из табл. 9 плотность висмута
(р-9,8-103 кг/м3):
Х = 9,8-108-(—1,3.10-9)«—1,3.10-5.
2. Для определения молярной магнитной восприимчивости най-
найдем отношение
Xm/Худ = Лп/^уд = ГП/V = М,
где М — молярная масса.
Тогда
Убедимся в том, что правая часть этого равенства дает единицу
молярной магнитной восприимчиво-
восприимчивости (м3/моль):
[М] [Худ]— 1 кг/моль-1 м3/кг =
= 1 М3/МОЛЬ.
Найдем сначала относительную
молекулярную массу висмута: Мг=
=209. Так как относительная молеку-
молекулярная масса численно равна моляр-
молярной массе М, выраженной в г/моль,
то М=209 г/моль=0,209 кг/моль,
что соответствует выражению моляр-
молярной массы в СИ.
Произведем вычисления:
%т = 0,209- (-1,3- Ю-9) »
« — 2,7-10-10м3/моль.
Пример 2. Определим частоту со^
ларморовой прецессии электронной
орбиты в атоме, находящемся в одно-
однородном магнитном поле (В=1 Тл).
Решение. Пусть электрон движется со скоростью v по кру-
круговой орбите радиусом г в направлении, указанном стрелкой на
рис. 27.1. Момент импульса 3? г орбитального движения электрона в
соответствии с правилом винта направлен перпендикулярно плос-
плоскости орбиты так, как это отмечено на рисунке.
Рис. 27.1
312

Орбитальный магнитный момент сМг будет противонаправлен
вектору 3?г. Под действием внешнего магнитного поля (В), возбуж-
возбужденного вдоль оси Oz, на электронную орбиту будет действовать
момент силы М=[в^В], направление которого перпендикулярно
плоскости, содержащей векторы оМг и В. Под действием этого мо-
момента вектор 3?t получит приращение d^^Md/в направлении,
совпадающем с М, в результате чего плоскость, содержащая век-
векторы оМ\ и В, повернется на угол dcp. Из рис. 27.1 видно, что
Тогда угловая скорость прецессии (ларморова частота)
L dt ~
L dt ~ Xt sin Ь At '
Так как dJ^i^oddt, a M=o?i В sinu, то
Sin # dt ^f fl
n -
1
Воспользовавшись гиромагнитным отношением
получим
Убедимся в том, что правая часть равенства дает единицу угло-
угловой скорости (с):
[е] [В] __ 1 Кл-1 Тл _ 1 Кл-1 Н __ 1 Н-с _ 1 кг-м-с
[т] 1кг кг-1А-м 1кг-м 1 кг-с2«м
Произведем вычисления:
ГА 1 Ь6'10~19 i ! _ О О. 1Л10 г-1
__ ^
ГА .
°^-"Т 9,1-Ю-31
Пример 3. Молекула N0 имеет магнитный момент ©#у=1,8 (ив.
Определить удельную парамагнитную восприимчивость %уд газо-
газообразного оксида азота при нормальных условиях.
Решение. По теории Ланжевена, магнитная восприимчи-
восприимчивость парамагнитного вещества определяется выражением
A)
где \х0 — магнитная постоянная (\хо=^ я-10~7 Гн/м); п — концент-
концентрация молекул (число молекул в единице объема); qSj — магнит-
магнитный момент атома; k — постоянная Больцмана; Т — термодинами-
термодинамическая температура.
Удельная магнитная восприимчивость %уд связана с магнит-
магнитной восприимчивостью х соотношением
Заменив в этом выражении % согласно A), получим
313

ЛЬ п
Худ = Но •
р #
Заметим, что концентрацию молекул и плотность газа можно вы-
выразить следующим образом:
n = NA/Vm и p = M/Vm,
где NA — постоянная Авогадро; М — молярная масса; Vm — мо-
молярный объем.
Тогда n/p=NA/M и
_ XAcs*
Худ — ^0 3kTM .
Убедимся в том, что правая часть равенства дает единицу удельной
магнитной восприимчивости (м3/кг):
Ы [#а] \Л)\ 1 Гн/м-1 моль-М А2-м4 1 Гн-1 А2-м3
, , *¦ " j = ___________________________ = . = 1 м3/кт
[к] [Т] [М] 1 Дж/К-1 К-1 кг/моль 1 Дж-кг /л '
Произведем вычисления (учтем, что 1 [1в=9,27«10~24 А*м?
и М=30-10~3 кг/моль):
, 1п. 6,02.1023.A,8-9,27-Ю-24J м3 . о 1Л , ,,
ХУД=4^10 U 3.1,38.10-2з.273.30.10-з 1J - 6,2> 10^М3/КГ.
Задачи
Намагниченность. Магнитная восприимчивость
27.1. Определить намагниченность «/ тела при насыщении, если
магнитный момент каждого атома равен магнетону Бора \iB и
концентрация атомов 6 *1028 м.
27.2. Магнитная восприимчивость % марганца равна 1,21 «10.
Вычислить намагниченность /, удельную намагниченность /уд
и молярную намагниченность Jm марганца в магнитном поле на-
напряженностью #=100 кА/м. Плотность марганца считать извест-
известной.
27.3. Найти магнитную восприимчивость % AgBr, если его мо-
молярная магнитная восприимчивость %т~7,5*10~X0 м3/моль.
27.4. Определить магнитную восприимчивость % и молярную
магнитную восприимчивость %т платины, если удельная магнит-
магнитная восприимчивость Худ=1,30-10"9 м3/кг.
27.5. Магнитная восприимчивость % алюминия равна 2,1 «10~^.
Определить его удельную магнитную Худ и молярную Хт воспри-
восприимчивости.
27.6. Висмутовый шарик радиусом R=l см помещен в однород-
однородное магнитное поле (-30=0,5 Тл). Определить магнитный момент pmi
приобретенный шариком, если магнитная восприимчивость % вис-
висмута равна —1,5-10~4.
27.7. Напряженность Н магнитного поля в меди равна 1 МА/м.
Определить намагниченность / меди и магнитную индукцию Bi
если известно, что удельная магнитная восприимчивость Худ^
*=—1,1-Ю"» м3/кг.
314

Диа- и парамагнетизм
27.8. Определить частоту a)L ларморовой прецессии электрон»
ной орбиты в атоме, находящемся в магнитном поле Земли (В =
^=50 мкТл).
27.9. Атом водорода находится в магнитном поле с индукцией
5=1 Тл. Вычислить магнитный момент fiM, обусловленный прецес-
прецессией электронной орбиты. Принять, что среднее значение квадрата
расстояния (г2) электрона от ядра равно 2/зг1{г1 — радиус первой
боровской орбиты).
27.10. Молярная магнитная восприимчивость %т оксида хро-
хрома Сг2О3 равна 5,8 «10~8 м3/моль. Определить магнитный мо-
момент \iM молекулы С12О3 (в магнетонах Бора), если температура
7=300 К.
27.11. Удельная парамагнитная восприимчивость %уд трехок-
сида ванадия (V2O3) при t=l7 °C равна 1,89-10~2 м3/кг. Определить
магнитный момент |ям (в магнетонах Бора), приходящийся на
молекулу V2O3, если плотность р трехоксида ванадия равна
4,87-103 кг/м3.
27.12. Молекула кислорода имеет магнитный момент (iM=2,8 fiB
(где \iE—магнетон Бора). Определить намагниченность J газо-
газообразного кислорода при нормальных условиях в слабом магнит-
магнитном поле (Во^Ю мТл) и в очень сильном поле.
27.13. Определить, при каком наибольшем значении магнитной
индукции В уже следует пользоваться не приближенным выра-
выражением функции Ланжевена Ь(а)жа/3, а точным, чтобы погреш-
погрешность вычислений не превышала 1 %. Для расчетов принять маг-
магнитный момент молекул равным магнетону Бора. Температура
Т=300 К.
27.14. Определить наибольшее значение величины а, при кото-
котором погрешность, вызванная заменой точного выражения функции
Ланжевена приближенным L(a)^a/3, не превышает 1 %.
27.15. Определить температуру Т, при которой вероятность того,
что данная молекула имеет отрицательную проекцию магнитного
момента на направление внешнего магнитного поля, будет равна
10~3. Магнитный момент молекулы считать равным одному магне-
магнетону Бора, а магнитную индукцию В поля — равной 8 Тл.
27.16. Определить, во сколько раз число молекул, имеющих по-
положительные проекции магнитного момента на направление векто-
вектора магнитной индукции внешнего поля (В=1 Тл), больше числа мо-
молекул, имеющих отрицательную проекцию, в двух случаях: 1)
7\=300 К; 2) Г2=1 К. Магнитный момент молекулы принять рав-
равным магнетону Бора.
27.17. При температуре 7\=300 К и магнитной индукции
-Bi—0,5, Тл была достигнута определенная намагниченность J па-
парамагнетика. Определить магнитную индукцию В2у при которой
сохранится та же намагниченность, если температуру повысить до
Г2-450 К.
315

Ферромагнетизм
27.18. Кусок стали внесли в магнитное поле напряженностью
#=1600 А/м. Определить намагниченность J стали.
Указание, Необходимо воспользоваться графиком на рис. 24.1
(с. 288).
27.19. Прямоугольный ферромагнитный брусок объемом V= 10см3
приобрел в магнитном поле напряженностью //=800 А/м магнит-
магнитный момент рт=0,8 А'М2. Определить магнитную проницаемость
|i ферромагнетика.
27.20. Вычислить среднее число (л) магнетонов Бора, приходя-
приходящихся на один атом железа, если при насыщении намагниченность
железа равна 1,84 МА/м.
27.21. На один атом железа в незаполненной 3 d-оболочке при-
приходится четыре неспаренных электрона. Определить теоретическое
значение намагниченности /нас железа при насыщении.

ГЛАВА 6
ОПТИКА
§ 28. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
Основные формулы
О Фокусное расстояние сферического зеркала
/=#/2,
где R — радиус кривизны зеркала.
Оптическая сила сферического зеркала
Ф = 1//.
Формула сферического зеркала
1-1 + 1
где а и Ь — расстояния от полюса зеркала соответственно до пред-
предмета и изображения.
Если изображение предмета мнимое, то величина Ь берется со
знаком минус.
Если фокус сферического зеркала мнимый (зеркало выпуклое),
то величина / берется со знаком минус.
• Закон преломления света
21у
sin Go
где г1 — угол падения; г2 — угол преломления; пг\=пг1гы — отно-
относительный показатель преломления второй среды относительно пер-
первой; fti и я2 — абсолютные показатели
преломления соответственно первой и
второй сред.
Нижние индексы в обозначениях уг-
углов указывают, в какой среде (первой
или второй) идет луч. Если луч перехо-
переходит из второй среды в первую, падая
на поверхность раздела под углом е2—
—eg, то по принципу обратимости све-
световых лучей угол преломления е^ будет Рис- 28>1
равен углу ех (рис. 28.1).
• Предельный угол полного отражения при переходе света из
среды более оптически плотной в среду менее оптически плотную
enp = arcsin(Ai2/n1) (n2 < п^.
317

Оптическая сила тонкой линзы
где / — фокусное расстояние линзы; пл — абсолютный показатель
преломления вещества линзы; /гср — абсолютный показатель пре-
преломления окружающей среды (одинаковой с обеих сторон линзы).
В приведенной формуле радиусы выпуклых поверхностей (Rx и
R2) берутся со знаком плюс, вогнутых — со знаком минус.
• Оптическая сила двух тонких сложенных вплотную линз
• Формула тонкой линзы
1-1 + 1
где а — расстояние от оптического центра линзы до предмета; Ь —
расстояние от оптического центра линзы до изображения.
Если фокус мнимый (линза рассеивающая), то величина / отри-
отрицательна.
Если изображение мнимое, то величина Ь отрицательна.
О Угловое увеличение лупы
V=Dlf,
где D — расстояние наилучшего зрения (D=25 см).
• Угловое увеличение телескопа
где /об и /ок — фокусные расстояния соответственно объектива и
окуляра.
Расстояние от объектива до окуляра телескопа
L = /об + /ок-
Эти формулы можно применять только в том случае, если в теле-
телескоп наблюдают весьма удаленные предметы.
О Угловое увеличение микроскопа
r = 6D/(/o6//OK)'s
где б — расстояние между задним фокусом объектива и передним
фокусом окуляра.
Расстояние от объектива до окуляра микроскопа
Примеры решения задач
Пример 1. На стеклянную призму о преломляющим углом
8=50° падает под углом 8=30° луч света. Определить угол откло-
отклонения а луча призмой^ если показатель преломления п стекла
равен 1,56.
Решение. Данную задачу целесообразно решать не в общем
виде, как принято, а пооперационно, производя все промежуточ-
промежуточные вычисления. В этом случае мы несколько проигрываем в точ-
точности расчетов, но выигрываем в наглядности и простоте вычисле-
318

ний. Из рис. 28.2 видно, что угол отклонения
tf^T+Y'» A)
а углы 7 и 7' просто выражаются через углы е*, е2, г[, е2, которые
последовательно и будем вычислять:
1) из закона преломления
sin e^sm е2 имеем
" ' = 18,7°;
2) из рис. 28.2, следует, что
угол падения е2 на вторую грань
призмы равен
Рис. 28.2
Угол 8 2 меньше предельного
(S2npea=arcsin(l/tt)=39,9°), по-
поэтому на второй грани луч преломится и выйдет из призмы;
3) так как sin e2/sin ei=l//z, то ei=arcsin (n sin е2)=54,Г.
Теперь найдем углы у и/:
у = г1—ej= 11,3° и
По формуле A) находим
a=v+Y'=34,l°.
Пример 2. Оптическая сис-
система представляет собой тон-
тонкую плосковыпуклую стек-
стеклянную линзу, выпуклая по-
поверхность которой посереб-
посеребрена. Определить главное фо-
фокусное расстояние / такой
системы, если радиус кривиз-
кривизны R сферической поверхно-
поверхности линзы равен 60 см.
Решение. Пусть на
линзу падает параксиальный
луч KL, параллельный глав-
главной оптической оси MN лин-
линзы (рис. 28.3). Так как луч
KL перпендикулярен плоской
поверхности линзы, то он
проходит ее без преломления.
На сферическую посеребренную поверхность луч падает в точке L
под углом 8f и отражается от нее под углом 8i=8!. Отраженный
луч падает на границу плоской поверхности линзы под углом 2 ее
и по выходе из линзы пересекает главную оптическую ось в точке
F, образуя с осью угол е2. Длина полученного при этом отрезка FP
и равна искомому фокусному расстоянию рассматриваемой оптичес-
оптической системы.
319

Если учесть, что в силу параксиальности луча KL углы ех и е2
малы, а их синусы и тангенсы практически равны самим углам, вы-
выраженным в радианах, то из рис. 28.3 следует
Входящее в формулу A) отношение е^ба углов найдем, пользуясь
законом преломления света, который в нашем случае записывается
в виде 2 е1/е2= 1/я, откуда
ei/e2=l/B n).
Подставив это отношение углов в формулу A), найдем
f=R/Bn).
Такой же результат можно получить и из формальных соображе-
соображений. Так как луч KL последовательно проходит линзу, отражает-
отражается от вогнутого зеркала и еще раз проходит линзу, то данную оп-
оптическую систему можно рассматривать как центрированную сис-
систему, состоящую из сложенных вплотную двух плосковыпуклых
линз и сферического зеркала. Фокусное расстояние оптической
системы может быть найдено по формуле
где Ф — оптическая сила системы.
Как известно, оптическая сила системы равна алгебраической
сумме оптических сил отдельных компонентов системы. В нашем слу-
случае
= (п-1)± + ?+(п-1)± = Щ-. т. е.
что совпадает с результатом, выраженным формулой B).
Задачи
Отражение и преломление света
28.1. Два плоских прямоугольных зеркала образуют двугранный
угол ф = 179°. На расстоянии /=10 см от линии соприкосновения
зеркал и на одинаковом расстоянии от каждого зеркала находится
точечный источник света. Определить расстояние d между мнимыми
изображениями источника в зеркалах.
28.2. На сферическое зеркало падает луч света. Найти построе-
построением ход луча после отражения в двух случаях: а) от вогнутого
зеркала (рис. 28.4, а); б) от выпуклого зеркала (рис. 28.4, б). На
рисунке: Р — полюс зеркала; О — оптический центр.
28.3. Вогнутое сферическое зеркало дает на экране изображение
предмета, увеличенное в Г=4 раза. Расстояние а от предмета до
зеркала равно 25 см. Определить радиус R кривизны зеркала.
28.4. Фокусное расстояние / вогнутого зеркала равна 15 см.
Зеркало дает действительное изображение предмета, уменьшенное
в три раза. Определить расстояние а от предмета до зеркала.
320

28.5. На рис. 28.5, а, б указаны положения главной оптической
оси MN сферического зеркала, светящейся точки S и ее изображе-
изображения S'. Найти построением положения оптического центра О зер-
зеркала, его полюса Р и главного фокуса F. Определить, вогнутым
или выпуклым является данное зеркало. Будет ли изображение
действительным или мнимым?
28.6. Вогнутое зеркало дает на экране изображение Солнца в
виде кружка диаметром d=28 мм. Диаметр Солнца на небе в угло-
угловой мере р=32'. Определить радиус R кривизны зеркала.
О
-о-
V 5)
Рис. 28.4
М
-N И
•N
Рис. 28.5
N И
Рис. 28.6
28.7. Радиус R кривизны выпуклого зеркала равен 50 см. Пред-
Предмет высотой /г= 15 см находится на расстоянии а, равном 1 м, от
зеркала. Определить расстояние Ь от зеркала до изображения и его
высоту Н.
28.8. На рис. 28,6, а, б указаны положения главной оптической
оси MN сферического зеркала и ход луча 1. Построить ход луча 2
после отражения его от зеркала.
28.9. На столе лежит лист бумаги. Луч света, падающий на бу-
бумагу под углом ?=30°, дает на ней светлое пятно. Насколько смес-
сместится это пятно, если на бумагу положить плоскопараллельную
стеклянную пластину толщиной d=5 см?
28.10. Луч падает под углом е=60° на стеклянную пластинку
11 № 1268
321

толщиной d=30 мм. Определить боковое смещение Дл: луча после
выхода из пластинки.
28.11. Пучок параллельных лучей падает на толстую стеклян-
стеклянную пластину под углом 8=60°, и преломляясь переходит в стек-
стекло. Ширина а пучка в воздухе равна 10 см. Определить ширину Ъ
пучка в стекле.
28.12. Луч света переходит из среды с показателем преломления
щ в среду с показателем преломления п2. Показать, что если угол
между отраженным и преломленным лучами равен я/2, то выпол-
выполняется условие tg&1=njrii (ei — угол падения).
28.13. Луч света падает на грань призмы с показателем прелом-
преломления п под малым углом. Показать, что если преломляющий угол
9 призмы мал, то угол отклонения а лучей не зависит от угла паде-
падения и равен 9 (п — 1).
28.14. На стеклянную призму с преломляющим углом 9=60Q
падает луч света. Определить показатель преломления п стекла|
если при симметричном ходе луча в призме угол отклонения а=40°.
28.15. Преломляющий угол 9 стеклянной призмы равен 30°.
Луч света падает на грань призмы перпендикулярно ее поверхнос-
поверхности и выходит в воздух из другой грани, отклоняясь на угол o=20Q
от первоначального направления. Определить показатель прелом-
преломления п стекла.
28.16. Луч света падает на грань стеклянной призмы перпенди-
перпендикулярно ее поверхности и выходит из противоположной грани^
отклонившись на угол а=25° от первоначального направления.
Определить преломляющий угол 9 призмы.
28.17* На грань стеклянной призмы с преломляющим углом 9=;
=60° падает луч света под углом гх==4:5о. Найти угол преломления
8g луча при выходе из призмы и угол отклонения а луча от перво-
первоначального направления.
28.18. Преломляющий угол 9 призмы равен 60°. Угол наимень-
наименьшего отклонения луча от первоначального направления а=30°.
Определить показатель преломления п стекла, из которого изготов-
изготовлена призма.
28.19. Преломляющий угол 9 призмы, имеющей форму острого
клина, равен 2°. Определить угол наименьшего отклонения crmin
луча при прохождении через призму, если показатель преломления
п стекла призмы равен 1,6.
Оптические системы
28.20. На тонкую линзу падает луч света. Найти построением
ход луча после преломления его линзойз а) собирающей (рис. 28.7,
а)\ б) рассеивающей (рис. 28,7 б). На рисунке: О — оптический центр
линзы; F — главный фокус.
28.21. На рис. 28.8, а, б^ указаны положения главной оптичес-
оптической оси MN линзы и ход луча I. Построить * ход луча 2 после пре-
преломления его линзой.
* Считатц что среды по обе стороны линзы одинаковы.
322

28.22. Найти построением положение светящейся точки, если
известен ход лучей после преломления их в линзах: а) собираю-
собирающей (рис. 28.9, а)\ б) рассеивающей (рис. 28.9, б). На рисунке: О —
оптический центр линзы; F — ее главный фокус.
„U й U
Рис. 28.7
N И
Рис. 28.8
28.23. На рис. 28.10, а, б указаны положения главной оптичес-
оптической оси MN тонкой линзы, светящейся точки S и ее изображения
S'. Найти построением * положения оптического центра О линзы и
ее фокусов F. Указать, собирающей или рассеивающей будет дан-
данная линза. Будет ли изображение действительным или мнимым?
¦N
к
Рис. 28.9
S
#
¦М
-N
а) °5' В)
Рис. 28.10
28.24. Линза, расположенная на оптической скамье между лам-
лампочкой и экраном, дает на экране резко увеличенное изображение
лампочки. Когда лампочку передвинули Д/=40 см ближе к экрану,
на нем появилось резко уменьшенное изображение лампочки. Оп-
Определить фокусное расстояние / линзы, если расстояние / от лампоч-
лампочки до экрана равно 80 см.
28.25. Каково наименьшее возможное расстояние I между пред-
предметом и его действительным изображением, создаваемым собираю-
собирающей линзой с главным фокусным расстоянием /=12 см?
См4 сноску на с. 322,
323

28.26. Человек движется вдоль главной оптической оси объекти-
объектива фотоаппарата со скоростью v=5 м/с. С какой скоростью и необ-
необходимо перемещать матовое стекло фотоаппарата, чтобы изображе-
изображение человека на нем все время оставалось резким. Главное фокус-
фокусное расстояние / объектива равно 20 см. Вычисления выполнить
для случая, когда человек находился на расстоянии а=10 м от фо-
фотоаппарата.
28.27. Из стекла требуется изготовить плосковыпуклую линзу,
оптическая сила Ф которой равна 5 дптр. Определить радиус R
кривизны "выпуклой поверхности линзы.
28.28. Двояковыпуклая линза имеет одинаковые радиусы кри-
кривизны поверхностей. При каком радиусе кривизны R поверхностей
линзы главное фокусное расстояние / ее будет равно 20 см?
28.29. Отношение k радиусов кривизны поверхностей линзы
равно 2, При каком радиусе кривизны R выпуклой поверхности оп-
оптическая сила Ф линзы равна 10 дптр?
28.30. Определить радиус R кривизны выпуклой поверхности
линзы, если при отношении k радиусов кривизны поверхностей
линзы, равном 3, ее оптическая силаФ=—8 дптр.
28.31. Из двух часовых стекол с одинаковыми радиусами R
кривизны, равными 0,5 м, склеена двуяковогнутая «воздушная»
линза. Какой оптической силой Ф будет обладать такая линза в
воде?
28.32. Линза изготовлена из стекла, показатель преломления
которого для красных лучей пк=1,50, для фиолетовых Пф=1,52.
Радиусы кривизны R обеих поверхностей линзы одинаковы и равны
1 м. Определить расстояние А/ между фокусами линзы для красных
и фиолетовых лучей.
28.33. Определить главное фокусное расстояние / плосковыпук-
плосковыпуклой линзы, диаметр d которой равен 10 см. Толщина h в центре лин-
линзы равна 1 см, толщину у краев можно принять равной нулю.
28.34. Определить оптическую силу Ф мениска *, если радиусы
кривизны Rx и R2 его выпуклой и вогнутой поверхностей равны
соответственно 1 м и 40 см,
28.35. Главное фокусное расстояние / собирающей линзы в воз-
воздухе равно 10 см. Определить, чему оно равно: 1) в воде; 2) в корич-
коричном масле,
28.36. У линзы, находящейся в воздухе, фокусное расстояние
ft=5 см, а погруженной в раствор сахара /а^Зб см. Определить по-
показатель преломления п раствора.
28.37. Тонкая линза, помещенная в воздухе, обладает оптической
силой Фх=5 дптр, а в некоторой жидкости Ф2=—0,48 дптр. Оп-
Определить показатель преломления п2 жидкости, если показатель
преломления п± стекла, из которого изготовлена линза, равен 1,52.
28.38. Доказать, что оптическая силаФ системы двух сложенных
* Мениском называют линзу, ограниченную двумя сферическими поверх-
поверхностями, имеющими одинаковое направление кривизны.
324

вплотную тонких линз равна сумме оптических сил ФхиФ2 каждой
из этих линз.
28.39. В вогнутое сферическое зеркало радиусом R=20 см на-
налит тонким слоем глицерин. Определить главное фокусное расстоя-
расстояние / такой системы.
28.40. Плосковыпуклая линза имеет оптическую силу Oi=4
дптр. Выпуклую поверхность линзы посеребрили. Найти оптичес-
оптическую силу Ф2 такого сферического зеркала.
28.41. Поверх выпуклого сферического зеркала радиусом кри-
кривизны R=20 см налили тонкий слой воды. Определить главное фо-
фокусное расстояние / такой системы.
28.42. Человек без очков читает книгу, располагая ее перед собой
на расстоянии а=\2,Ь см. Какой оптической силы Ф очки следует
ему носить?
28.43. Пределы аккомодации глаза близорукого человека без
очков лежат между ^=16 см и а2=80 см. В очках он хорошо видит
удаленные предметы. На каком минимальном расстоянии d он может
держать книгу при чтении в очках?
28.44. Лупа, представляющая собой двояковыпуклую линзу,
изготовлена из стекла с показателем преломления n=lfi. Радиусы
кривизны R поверхностей линзы одинаковы и равны 12 см. Опреде-
Определить увеличение Г лупы.
28.45. Лупа дает увеличение Г=2. Вплотную к ней приложили
собирательную линзу с оптической силой Oi=20 дптр. Какое уве-
увеличение Г2 будет давать такая составная лупа?
28.46. Оптическая сила Ф объектива телескопа равна 0,5 дптр.
Окуляр действует как лупа, дающая увеличение Г^Ю. Какое
увеличение Г2 дает телескоп?
28.47. При окуляре с фокусным расстоянием /=50 мм телескоп
дает угловое увеличение 1^=60. Какое угловое увеличение Г2
даст один объектив, если убрать окуляр и рассматривать действи-
действительное изображение, созданное объективом, невооруженным гла-
глазом с расстояния наилучшего зрения?
28.48. Фокусное расстояние Д объектива телескопа равно 1 м.
В телескоп рассматривали здание, находящееся на расстоянии а=\
км. В каком направлении и на сколько нужно передвинуть окуляр,
чтобы получить резкое изображение в двух случаях: 1) если после
здания будут рассматривать Луну; 2) если вместо Луны будут рас-
рассматривать близкие предметы, находящиеся на расстоянии а^=^
= 100 м?
28.49. Телескоп наведен на Солнце. Фокусное расстояние Д
объектива телескопа равно 3 м. Окуляр с фокусным расстоянием
/2=50 мм проецирует действительное изображение Солнца, создан-
созданное объективом, на экран, расположенный на расстоянии Ь=60 см
от окуляра. Плоскость экрана перпендикулярна оптической оси
телескопа. Определить линейный диаметр d изображения Солнца на
экране, если диаметр Солнца на небе виден невооруженным глазом
под углом а=32'.
28.50. Фокусное расстояние Д объектива микроскопа равно 8 мм,
325

окуляра /2=4 см. Предмет находится на Аа=0у5 мм дальше от объек-
объектива, чем главный фокус. Определить увеличение Г микроскопа.
28.51. Фокусное расстояние ft объектива микроскопа равно 1 см,
окуляра /2=2 см. Расстояние от объектива до окуляра L=23 см.
Какое увеличение Г дает микроскоп? На каком расстоянии а от
объектива находится предмет?
28.52. Расстояние S между фокусами объектива и окуляра внут-
внутри микроскопа равно 16 см. Фокусное расстояние /i объектива рав-
равно 1 мм. С каким фокусным расстоянием /2 следует взять окуляр,
чтобы получить увеличение Г=500?
§ 29. ФОТОМЕТРИЯ
Основные формулы
• Световой поток Ф^, испускаемый изотропным * точечным ис-
источником света в пределах телесного угла со, в вершине которого
находится источник, выражается формулой
где / — сила света источника; со—2яA — cosft); -& — угол между
осью конуса и его образующей.
• Полный световой поток, испускаемый изотропным точечным
источником света,
Ф0=4 л/.
• Освещенность поверхности определяется соотношением
где S — площадь поверхности, по которой равномерно распределя-
распределяется падающий на нее световой поток Ф^.
Освещенность, создаваемая изотропным точечным источником
света,
E
где г — расстояние от поверхности до источника света; 8 — угол
падения лучей.
• Сила света любого элемента поверхности косинусного излуча-
излучателя
/:=/0cos(p,
где ф — угол между нормалью к элементу поверхности и направ-
направлением наблюдения; /0 — сила света элемента поверхности по на-
направлению нормали к этому элементу.
• Яркость светящейся поверхности
где / — сила света в направлении наблюдения; ст — площадь про-
проекции светящейся поверхности на плоскость, перпендикулярную
этому направлению.
• Источник называется изотропным, если сила света источника одина*
кова во всех направлениях.
326

• Светимость определяется соотношением
Mv=<bv/S,
где Фу — световой поток, испускаемый поверхностью; S — пло-
площадь этой поверхности.
Светимость косинусных излучателей
Примечание. В соответствии с ГОСТ 26148—84 световые величины обо-
обозначаются теми же буквами, что и соответствующие им энергетические вели-
величины излучений. Отличаются обозначения только индексами: е — для энер-
энергетических величин и v — для световых. Но в обозначениях световых величин
индекс v разрешается опускать в тех случаях, когда это не может привести
к недоразумениям (например, энергетическая яркость—Lei яркость —
Lv или L),
Примеры решения задач
Пример 1. Прожектор ближнего освещения дает пучок света в
виде усеченного конуса с углом раствора 2Ф=40°. Световой поток
Ф прожектора равен 80 клм. Допуская, что световой поток распре-
распределен внутри конуса равномерно, определить силу света / прожек-
прожектора.
Решение. Сила света / изотропного источника равна отно-
отношению светового потока Ф к телесному углу со, в пределах которо-
которого распространяется световой поток, т. е.
/=Ф/со. A)
Выразим телесный угол через угол раствора. Из рис. 29.1 сле-
следует, что элементарный телесный угол do—2 Jtsin-Э- dft. Телесный
угол, соответствующий углу
раствора 2Ф
интегралом:
#0
конуса, выразится
или
о = 2я A — соз $0) = 4л sin2 (fl/2).
Подставив выражение со в
формулу A), получим
¦*
4л sin2 @/2) #
Произведя вычисления по
формуле B), найдем Рис. 29.1
/-211 ккд.
Пример 2. Люминесцентная цилиндрическая лампа диаметром
d—2,5 см и длиной /=40 см создает на расстоянии г=5 м в направ-
направлении, перпендикулярном оси лампы, освещенность Ev=2 лк. При-
Принимая лампу за косинусный излучатель, определить! 1) силу
света / в данном направлении; 2) яркость L; 3) светимость М лампы.
Решение. 1. Больший из двух размеров лампы — длина —
в 12 раз меньше расстояния, на котором измерена освещенность.
327

Следовательно, для вычисления силы света в данном направлении
можно принять лампу за точечный источник и применить формулу
Е=1/г2, откуда 1=Ег\
Подставив значения величин в эту формулу и произведя вычис-
вычисления, получим
/=25 кд.
2. Для вычисления яркости применим формулу
L=I/o9 ,
где а — площадь проекции протяженного источника света на плос-
плоскость, перпендикулярную направлению наблюдения.
В случае цилиндрической люминесцентной лампы проекция име-
имеет форму прямоугольника длиной / и шириной d. Следовательно,
Произведя вычисления по этой формуле, найдем
L=2,5 ккд/м2.
3. Так как люминесцентную лампу можно считать косинусным
излучателем, то ее светимость
M=nL=7,9 клк.
Задачи *
Световой поток и сила света
29.1. Определить силу света / точечного источника, полный све-
световой поток Ф которого равен 1 лм.
29.2. Лампочка, потребляющая мощность Р=75 Вт, создает на
расстоянии г—3 м при нормальном падении лучей освещенность
?=8 лк. Определить удельную мощность р лампочки (в ваттах на
канделу) и световую отдачу ц лампочки (в люменах на ватт).
29.3. В вершине кругового конуса находится точечный источник
света, посылающий внутри конуса световой поток Ф=76 лм. Сила
света / источника равна 120 кд. Определить телесный угол со и
угол раствора 2 -& конуса.
29.4. Какую силу тока / покажет гальванометр, присоединен-
присоединенный к селеновому фотоэлементу, если на расстоянии г=75 см от
него поместить лампочку, полный световой поток Фо которой ра-
равен 1,2 клм? Площадь рабочей поверхности фотоэлемента равна
10 см2, чувствительность /—300 мкА/лм.
Освещенность
29.5. Лампочка силой света 7=80 кд находится на расстоянии
а=2 м от собирательной линзы с диаметром d=l2 см и главным
фокусным расстоянием /=40 см. Линза дает на экране, располо-
* При решении задач по фотометрии электрические лампочки принимать
за изотропные точечные источники света.
328

женном на расстоянии 6=30 см от линзы, круглое светлое пятно.
Найти освещенность Е экрана на месте этого пятна. Поглощением
света в линзе пренебречь.
29.6. При печатании фотоснимка негатив освещался в течение
^=3 с лампочкой силой света /х=15 кд с расстояния ^=50 см.
Определить время t2, в течение которого нужно освещать негатив
лампочкой силой света /2=60 кд с расстояния г2=2 м, чтобы полу-
получить отпечаток с такой же степенью почернения, как и в первом
случае?
29.7. На высоте /г=3 м над землей и на расстоянии г=4 м от сте-
стены висит лампа силой света /=100 кд. Определить освещенность Е±
стены и Е2 горизонтальной поверхности земли у линии их пересе-
пересечения.
29.8. На мачте высотой /i=8 м висит лампа силой света /=1 ккд.
Принимая лампу за точечный источник света, определить, на ка-
каком расстоянии / от основания мачты освещенность Е поверхности
земли равна 1 лк.
29.9. Над центром круглой площадки висит лампа. Освещенность
Ег в центре площадки равна 40 лк, Е2 на краю площадки равна 5 лк.
Под каким углом г падают лучи на край площадки?
29.10. Над центром круглого стола радиусом г=80 см на высоте
ft=60 см висит лампа силой света /=100 кд. Определить: 1) осве-
освещенность Ег в центре стола; 2) освещенность Е2 на краю стола; 3)
световой поток Ф, падающий на стол; 4) среднюю освещенность
(Е) стола.
29.11. На какой высоте h над центром круглого стола радиу-
радиусом г=\ м нужно повесить лампочку, чтобы освещенность на краю
стола была максимальной?
Яркость и светимость
29.12. Отверстие в корпусе фонаря закрыто плоским молочным
стеклом размером 10x15 см. Сила света / фонаря в направлении,
составляющем угол ф=60° с нормалью, равна 15 кд. Определить
яркость L стекла.
29.13. Вычислить и сравнить между собой силы света раскален-
раскаленного металлического шарика яркостью Ьг=3 Мкд/м2 и шарового
светильника яркостью L2=5 ккд/м2, если их диаметры &х и d2 со-
соответственно равны 2 мм и 20 см.
29.14. Светильник из молочного стекла имеет форму шара диа-
диаметром d=20 см. Сила света / шара равна 80 кд. Определить пол-
полный световой поток Ф, светимость М и яркость L светильника.
29.15. Солнце, находясь вблизи зенита, создает на горизонталь-
горизонтальной поверхности освещенность ?=0,1 Млк. Диаметр Солнца виден
под углом а=32\ Определить видимую яркость L Солнца.
29.16. Длина / раскаленной добела металлической нити равна 30
см, диаметр d=0,2 мм. Сила света / нити в перпендикулярном ей
направлении равна 24 кд. Определить яркость L нити.
329

29.17. Яркость L светящегося куба одинакова во всех направле-
направлениях и равна 5 ккд/м2. Ребро а куба равно 20 см. В каком направ-
направлении сила света / куба максимальна? Определить максимальную
силу света /тах куба.
29.18. Светящийся конус имеет одинаковую во всех направле-
направлениях яркость 5=2 ккд/м2. Основание конуса не светится. Диаметр
d основания равен 20 см, высота /г= 15 см. Определить силу света /
конуса в направлениях: 1) вдоль оси; 2) перпендикулярном оси.
29.19. На высоте h= 1 м над горизонтальной плоскостью парал-
параллельно ей расположен небольшой светящийся диск. Сила света /о
диска в направлении его оси равна 100 кд. Принимая диск за то-
точечный источник с косинусным распределением силы света, найти
освещенность Е горизонтальной плоскости в точке Л, удаленной
на расстояние г=3 и от точки, расположенной под центром диска.
29.20. На какой высоте h над горизонтальной плоскостью (см.
предыдущую задачу) нужно поместить светящийся диск, чтобы осве-
освещенность в точке А была максимальной?
29.21. Определить освещенность Я, светимость М и яркость L
киноэкрана, равномерно рассеивающего свет во всех направлениях,
если световой поток Ф, падающий на экран из объектива киноаппа-
киноаппарата (без киноленты), равен 1,75 клм. Размер экрана 5X3,6 м, ко-
коэффициент отражения р=0,75.
29.22. На какой высоте h нужно повесить лампочку силой све-
света 7=10 кд над листом матовой белой бумаги, чтобы яркость L бу-
бумаги была равна 1 кд/м2, если коэффициент отражения р бумаги
равен 0,8?
29.23. Освещенность Е поверхности, покрытой слоем сажи, рав-
равна 150 лк, яркость L одинакова во всех направлениях и равна
1 кд/м2. Определить коэффициент отражения р сажи.
§ 30. ИНТЕРФЕРЕНЦИЯ СВЕТА
Основные формулы
• Скорость света в среде
v=c/n,
где с — скорость света в вакууме; п — абсолютный показатель
преломления среды.
• Оптическая длина пути световой волны
L=nl,
где ; — геометрическая длина пути световой волны в среде с пока-
показателем преломления п.
3. Оптическая разность хода двух световых волн
A=Lx—L2.
• Оптическая разность хода световых волн, отраженных от
верхней и нижней поверхностей тонкой плоскопараллельной плас-
330

тинки или пленки, находящейся в воздухе (рис. 30.1, а),
Д = 2d Vn2 — sin2 8! + Я/2, или Д = 2d/zcose; +V2,
где d — толщина пластинки (пленки); ef— угол падения; е'2—•
угол преломления.
Второе слагаемое в этих формулах учитывает изменение опти-
оптической длины пути световой волны на Х/2 при отражении ее от сре-
среды оптически более плотной.
В проходящем свете (рис. 30.1, б) отражение световой волны
происходит от среды оптически менее плотной и дополнительной
разности хода световых лучей не возникает.
Рис. 30.1
• Связь разности фаз Дер колебаний с оптической разностью хо-
хода волн
• Условие максимумов интенсивности света при интерферен-
интерференции
Д=±*А, (fe=0, 1, 2, 3, . . .).
• Условие максимумов интенсивности света при интерферен-
интерференции
А=±B k+l) (M2).
• Радиусы светлых колец Ньютона в отраженном свете (или
темных в проходящем)
где k — номер кольца (/5=1, 2, 3, . . .); R — радиус кривизны по-
поверхности линзы* соприкосающейся с плоскопараллельной стек-
стеклянной пластинкой.
Радиусы темных колец в отраженном свете (или светлых в про-
проходящем)
Примеры решения задач
Пример 1. В точку А экрана от источника St монохроматическо-
монохроматического света длиной волны А,=0,5мкм приходит два луча: непосредствен-
непосредственно от источника луч StЛ, перпендикулярный экрану, и луч 5ХВЛ,
331

/77777//////////////
Зеркало
Рис. 30.2
отраженный в точке В от зеркала, параллельного лучу SXA
(рис. 30.2). Расстояние 1г экрана от источника равно 1 м. расстояние
h от луча5И до плоскости зеркала равно 2 мм. Определить: 1) что
будет наблюдаться в точке А экрана — усиление или ослабление
интенсивности; 2) как изменится интенсивность в точке Л, если на
пути луча SXA перпенди-
перпендикулярно ему поместить
плоскопа раллельную
пластинку стекла (п=
= 1,55) толщиной d=
= 6 мкм.
Решение. Пост-
Построим мнимое изобра-
изображение S2 источника Si
в зеркале (рис. 30.3). Источники St и S2 являются когерентными,
поэтому при сложении волн, приходящих от этих источников на
экран, возникает интерференционная картина. Усиление или ос-
ослабление интенсивности в той или иной точке экрана зависит от
оптической разности хода А интерферирующих лучей, другими сло-
словами, от числа т полуволн, укладывающихся на оптической раз-
разности хода:
т = ~. A)
Если т — целое четное, то интенсивность будет максимальной;
если т — целое нечетное, то интенсивность минимальна. При дроб-
дробном т происходит или частичное усиление (если т ближе к четному
Рис. 30.3
числу), или частичное ослабление (если т ближе к нечетному чис-
числу).
1. Оптическая разность хода А2 будет складываться из геометри-
геометрической разности U—h (оба луча идут в воздухе) и дополнительной
разности хода Я/2, обусловленной изменением фазы колебаний на
п при отражении от среды оптически более плотной. Таким образом,
B)
Так как 12 = V l\ +H2 (рис. 30.3), то
Величина Я//Х<с1, поэтому для вычисления корня можно вос-
воспользоваться приближенной формулой (см. табл. V
332

при a<Cl. Применив ее, получим
1J
Подставив полученное выражение /2—k в формулу B), найдем
Дх =T?f- + у- Зная Дь по Ф°РмУле 0) найдем тх:
п» НЧ&Ц + т __№ хЛ
Так как H=2h, то окончательно получим
/,2
4A , 4
После вычисления найдем
/тг!=33.
Так как на разности хода укладывается нечетное число длин
полуволн, то в точке А наблюдается минимум интенсивности.
2. Стеклянная пластина толщиной d, поставленная на пути луча
S±A (рис. 30.3), изменит оптическую длину пути. Теперь оптическая
длина пути L будет складываться из геометрической длины пути
lx—d и оптической длины пути nd луча в самой пластине, т. е.
Оптическая разность хода лучей
Д2=/2_^+Я/2=/2—IU+ (n—l)d]-\-k/2,
или
A^A.— in— I) d.
Пользуясь формулой A), найдем
д2 __ Al^(n^i)d _^ о d(n-l)
Произведя вычисления, получим
та=19,8.
Число длин полуволн оказалось дробным. Так как 19,8 ближе к
целому четному числу 20, чем к целому нечетному числу 19, то в
точке А будет частичное усиле-
усиление.
Пример 2. На толстую стек-
стеклянную пластинку, покрытую
очень тонкой пленкой, показа-
показатель преломления п2 вещества
которой равен 1,4, падает нор-
нормально параллельный пучок
монохроматического света (А,=
=0,6 мкм). Отраженный свет пз>пг
максимально ослаблен вследст- Стенлянная пластинна \
вие интерференции. Определить рис зо.4
толщину d пленки.
Р е ш е н и е. Из световой волны, падающей на пленку, выделим
узкий пучок SA. Ход этого пучка в случае, когда угол падения
333

ФО, показан на рис. 30.4. В точках А и В падающий пучок частич-
частично отражается и частично преломляется. Отраженные пучки света
AS± и BCS2 падают на собирающую линзу L, пересекаются в ее
фокусе F и интерферируют между собой.
Так как показатель преломления воздуха (/2i=1,00029) меньше
показателя преломления вещества пленки (п2= 1,4), который, в
свою очередь, меньше показателя преломления стекла (п3^=\,5),
то в обоих случаях отражение происходит от среды оптически более
плотной, чем та среда, в которой идет падающая волна. Поэтому
фаза колебания пучка света AS± при отражении в точке А изменя-
изменяется на я рад и точно так же на я рад изменяется фаза колебаний
пучка света BCS2 при отражении в точке В. Следовательно, резуль-
результат интерференции этих пучков света при пересечении в фокусе F
линзы будет такой же, как если бы никакого изменения фазы коле-
колебаний ни у того, ни у другого пучка не было.
Как известно, условие максимального ослабления света при
интерференции в тонких пленках состоит в том, что оптическая раз-
разность хода А интерферирующих волн должна быть равна нечетному
числу полуволн: А= Bfe-+-l) (^/2).
Как видно из рис. 30.4, оптическая разность хода
Следовательно, условие минимума интенсивность света примет
вид
{\АВ\+ВС\)п2— \AD\nl=Bk+l) {112).
Если угол падения гг будет уменьшаться, стремясь к нулю, то AD-*
~^0 и |ЛВ|+|ВС|->24, где d — толщина пленки. В пределе при
гг=0 будем иметь
откуда искомая толщина пленки
d== Тп •
Полагая k=0, 1, 2, 3, . . ., получим ряд возможных значений
толщины пленки:
йо==1^ = О,11мкм; ^ = -1^ = 340 = 0,33 мкм и т.д.
Пример 3. На стеклянный клин нормально к его грани падает
монохроматический свет с длиной волны Я=0,6 мкм. В возникшей
при этом интерференционной картине на отрезке длиной 1=1 см
наблюдается 10 полос. Определить преломляющий угол 0 клина.
Решение. Параллельный пучок света, падая нормально к
грани клина, отражается как от верхней, так и от нижней грани.
Эти пучки когерентны, и поэтому наблюдается устойчивая картина
интерференции. Так как интерференционные полосы наблюдаются
при малых углах клина, то отраженные пучки света 1 и 2 (рис. 30.5)
будут практически параллельны.
334

Темные полосы видны на тех участках клина, для которых раз-
разность хода кратна нечетному числу половины длины волны:
Д=B6+1) (Х/2), где k=0, 1, 2, .... A)
Разность хода Д двух волн складывается из разности оптических
длин путей этих волн Bdncose'2) и половины длины волны (V2).
Рис. 30.5
Величина к/2 представляет собой добавочную разность хода, воз-
возникающую при отражении волны от оптически более плотной среды.
Подставляя в формулу A) значение разности хода Д, получим
2dkn cos e; + к/2 = Bft + 1) (к/2), B)
где п — коэффициент преломления стекла (я=1,5); dk — толщина
клина в том месте, где наблюдается темная полоса, соответствую-
соответствующая номеру k\ е'2— угол преломления.
Согласно условию, угол падения равен нулю, следовательно, и
угол преломления г2 равен нулю, a cos 8o==l. Раскрыв скобки в
правой части равенства B), после упрощения получим
2dkn=kk. C)
Пусть произвольной темной полосе номера к соответствует опре-
определенная толщина клина в этом месте dk9 а темной полосе номера
?+10 соответствует толщина клина dk+10. Согласно условию за-
задачи, 10 полос укладываются на отрезке длиной 1=1 см. Тогда ис-
искомый угол (рис. 30.5) будет равен
O = (dh+lo—dk)/l, D)
где из-за малости преломляющего угла sin Эя^0 (угол 6 выражен
в радианах).
Вычислив dk и dk+10 из формулы C), подставив их в формулу D)
и произведя преобразования, найдем
9-5 X/ (nl).
После вычисления получим
Выразим 0 в градусах. Для этого воспользуемся соотношением
й ( б 6) 1
у
между радианом и секундой (см. табл. 6): 1 рад=2,06М06
9 = 2. Ю-4.2,06*. 105 = 41,2*,
т.е.
335

или в соответствии с общим правилом перевода из радиан в градусы
Искомый угол равен 41,2".
Задачи
Интерференция волн от двух когерентных источников
30.1. Сколько длин волн монохроматического света с частотой
колебаний v=5-1014 Гц уложится на пути длиной /=1,2 мм: 1) в
вакууме; 2) в стекле?
30.2. Определить длину 1г отрезка, на котором укладывается
столько же длин волн в вакууме, сколько их укладывается на отрез-
отрезке /а^Змм в воде.
30.3. Какой длины 1г путь пройдет фронт волны монохромати-
монохроматического света в вакууме за то же время, за какое он проходит путь
длиной 12=\ м в воде?
30.4. На пути световой волны, идущей в воздухе, поставили стек-
стеклянную пластинку толщиной /i=l мм. На сколько изменится оп-
оптическая длина пути, если волна падает на пластинку: 1) нормаль-
нормально; 2) под углом 8=30°?
30.5. На пути монохроматического света с длиной волны Х=
=0,6 мкм находится плоскопараллельная стеклянная пластина
толщиной d=0,l мм. Свет падает на
пластину нормально. На какой угол
Ф следует повернуть пластину, чтобы
L
2см
\
оптическая длина пути L изменилась
Х/2
j * » I y^^ ^ на К/27
30.6. Два параллельных пучка све-
световых волн I и II падают на стек-
Рис 30.6 лянную призму с преломляющим уг-
углом 9=30° и после преломления вы-
выходят из нее (рис. 30.6). Найти оптическую разность хода А
световых волн после преломления их призмой.
30.7. Оптическая разность хода А двух интерферирующих волн
монохроматического света равна О,ЗХ. Определить разность фаз
Аф.
30.8. Найти все длины волн видимого света (от 0,76 до 0,38 мкм),
которые будут: 1) максимально усилены; 2) максимально ослаблены
при оптической разности хода А интерферирующих волн, равной
1,8 мкм.
30.9. Расстояние d между двумя когерентными источниками све-
света (Л,=0,5 мкм) равно 0,1 мм. Расстояние Ъ между интерференцион-
интерференционными полосами на экране в средней части интерференционной кар-
картины равно 1 см. Определить расстояние / от источников до экрана.
30.10. Расстояние d между двумя щелями в опыте Юнга равно
1мм, расстояние /отщелей до экрана равно 3 м. Определить длину
336

волны X, испускаемой источником монохроматического света, если
ширина Ъ полос интерференции на экране равна 1,5 мм.
30.11. В опыте Юнга расстояние d между щелями равно 0,8 мм.
На каком расстоянии / от щелей следует расположить экран, что-
чтобы ширина Ъ интерференционной полосы оказалась равной 2 мм?
30.12. В опыте с зеркалами
Френеля расстояние d между
мнимыми изображениями источ-
источника света равно 0,5 мм, рас-
расстояние / от них до экрана рав-
равно 3 м. Длина волны Я=0,6 мкм.
Определить ширину Ъ полос ин-
интерференции на экране.
30.13. Источник S света (Я== Рис. 30.7
==0,6 мкм) и плоское зеркало М
расположены, как показано на рис. 30.7 (зеркало Ллойда). Что будет
наблюдаться в точке Р экрана, где сходятся лучи SP и SMP,—
свет или темнота, если \SP\=r=2 м, а=0,55 мм, |SA1 |=|Л1Р|?
Интерференция света в тонких пленках
30.14. При некотором расположении зеркала Ллойда ширина Ь
интерференционной полосы на экране оказалась равной 1 мм.
После того как зеркало сместили параллельно самому себе на рас-
расстояние Ad=0,3 мм, ширина интерференционной полосы измени-
изменилась. В каком направлении и на ка-
какое расстояние А/ следует перемес-
переместить экран, чтобы ширина интерфе-
интерференционной полосы осталась преж-
прежней? Длина волны X монохромати-
монохроматического света равна 0,6 мкм.
30.15. Плоскопараллельная стек-
стеклянная пластинка толщиной d=
= 1,2 мкм и показателем преломления
п=1,5 помещена между двумя среда-
средами с показателями преломления пх
и п2 (рис. 30.8). Свет с длиной волны
Я=0,6 мкм падает нормально на пла-
пластинку. Определить оптическую раз-
разность хода А волн / и 2, отраженных
от верхней и нижней поверхностей пластинки, и указать, усиление
или ослабление интенсивности света происходит при интерферен-
интерференции в следующих случаях: 1) п1<п<п2; 2) п1>п>п2\ 3) ni</On2;
4) П!>/г</г2.
30.16. На мыльную пленку (я=1,3), находящуюся в воздухе,
падает нормально пучок лучей белого света. При какой наименьшей
толщине d пленки отраженный свет с длиной волны Я=0,55 мкм ока-
окажется максимально усиленным в результате интерференции?
Рис. 30.8
337

30.17. Пучок монохроматических (Х=0,6 мкм) световых волн
падает под углом е^ЗО0 на находящуюся в воздухе мыльную плен-
пленку (/г=1,3). При какой наименьшей толщине d пленки отраженные
световые волны будут максимально ослаблены интерференцией?
максимально усилены?
30.18. На тонкий стеклянный клин (п=1,55) падает нормально
монохроматический свет. Двугранный угол а между поверхностя-
поверхностями клина равен 2'. Определить длину световой волны Я, если рас-
расстояние Ь между смежными интерференционными максимумами в
отраженном свете равно 0,3 мм.
30.19. Поверхности стеклянного клина образуют между собой
угол 9=0,2'. На клин нормально к его поверхности падает пучок
лучей монохроматического света с длиной волны Х=0,55 мкм. Оп-
Определить ширину Ъ интерференционной полосы.
30.20. На тонкий стеклянный клин в направлении нормали к
его поверхности падает монохроматический свет (^=600 нм). Оп-
Определить угол 0 между поверхностями клина, если расстояние b
между смежными интерференционными минимумами в отраженном
свете равно 4 мм.
30.21. Между двумя плоскопараллельными стеклянными плас-
пластинками положили очень тонкую проволочку, расположенную
параллельно линии соприкосновения пластинок и находящуюся
на расстоянии 1=75 мм от нее. В отраженном свете (Я=0,5 мкм) на
верхней пластинке видны интерференционные полосы. Определить
диаметр d поперечного сечения проволочки, если на протяжении
а=30 мм насчитывается /тг=16 светлых полос.
30.22. Две плоскопараллельные стеклянные пластинки прило-
приложены одна к другой так, что между ними образовался воздушный
клин с углом Э, равным 30". На одну из пластинок падает нормально
монохроматический свет (А,=0,6 мкм). На каких расстояниях U и /2
от линии соприкосновения пластинок будут наблюдаться в отражен-
отраженном свете первая и вторая светлые полосы (интерференционные мак-
максимумы)?
30.23. Две плоскопараллельные стеклянные пластинки образуют
клин с углом 0=30". Пространство между пластинками заполнено
глицерином. На клин нормально к его поверхности падает пучок
монохроматического света с длиной волны ^=500 нм. В отражен-
отраженном свете наблюдается интерференционная картина. Какое число
N темных интерференционных полос приходится на 1 см длины
клина?
30.24. Расстояние Дг^ между вторым и первым темным кольца-
кольцами Ньютона в отраженном свете равно 1 мм. Определить расстоя-
расстояние Дг10л9 между десятым и девятым кольцами.
30.25. Плосковыпуклая линза выпуклой стороной лежит на
стеклянной пластинке. Определить толщину d слоя воздуха там,
где в отраженном свете (^=0,6 мкм) видно первое светлое кольцо
Ньютона.
30.26. Диаметр d2 второго светлого кольца Ньютона при наблю-
наблюдении в отраженном свете (А,=0?6 мкм) равен 132 мм. Определить
338

оптическую силу D плосковыпуклой линзы, взятой для опыта.
30.27. Плосковыпуклая линза с оптической силой Ф^2 дптр
выпуклой стороной лежит на стеклянной пластинке. Радиус г4
четвертого темного кольца Ньютона в проходящем свете равен
0,7 мм. Определить длину световой волны.
30.28. Диаметры dt и dk двух светлых колец Ньютона соответст-
соответственно равны 4,0 и 4,8 мм. Порядковые номера колец не определя-
определялись, но известно, что между двумя измеренными кольцами располо-
расположено три светлых кольца. Кольца наблюдались в отраженном свете
(Я=500 нм). Найти радиус кривизны плосковыпуклой линзы, взя-
взятой для опыта.
30.29. Между стеклянной пластинкой и лежащей на ней плоско-
плосковыпуклой стеклянной линзой налита жидкость, показатель прелом-
преломления которой меньше показателя преломления стекла. Радиус г8
восьмого темного кольца Ньютона при наблюдении в отраженном
свете G^=700 нм) равен 2 мм. Радиус R кривизны выпуклой поверх-
поверхности линзы равен 1 м. Найти показатель преломления п жидкости.
30.30. На установке для наблюдения колец Ньютона был из-
измерен в отраженном свете радиус третьего темного кольца (k=3).
Когда пространство между плоскопараллельной пластиной и лин-
линзой заполнили жидкостью, то тот же радиус стало иметь кольцо с
номером, на единицу большим. Определить показатель преломле-
преломления п жидкости.
30.31. В установке для наблюдения колец Ньютона свет с дли-
длиной волны Х=0,5 мкм падает нормально на плосковыпуклую линзу
с радиусом кривизны Яг=1 м, положенную выпуклой стороной на
вогнутую поверхность плосковогнутой линзы с радиусом кривизны
jR2=2 м. Определить радиус г3 третьего темного кольца Ньютона,
наблюдаемого в отраженном свете.
30.32. Кольца Ньютона наблюдаются с помощью двух одинако-
одинаковых плосковыпуклых линз радиусом R кривизны равным 1м, сло-
сложенных вплотную выпуклыми поверхностями (плоские поверхности
линз параллельны). Определить радиус г2 второго светлого кольца,
наблюдаемого в отраженном свете (Х=660 нм) при нормальном па-
падении света на поверхность верхней линзы.
Интерференционные приборы
30.33. На экране наблюдается интерференционная картина от
двух когерентных источников света с длиной волны ^=480 нм. Когда
на пути одного из пучков поместили тонкую пластинку из плавле-
плавленого кварца с показателем преломления п=1,46, то интерференци-
интерференционная картина сместилась на /тг=69 полос. Определить толщину d
кварцевой пластинки.
30.34. В оба пучка света интерферометра Жамена были помеще-
помещены цилиндрические трубки длиной /=10 см, закрытые с обоих кон-
концов плоскопараллельными прозрачными пластинками; воздух из
трубок был откачан. При этом наблюдалась интерференционная
картина в виде светлых и темных полос. В одну из трубок был впу-
339

щен водород, после чего интерференционная картина сместилась на
т=23,7 полосы. Найти показатель преломления п водорода. Дли-
Длина волны К света равна 590 нм.
30.35. В интерферометре Жамена две одинаковые трубки дли-
длиной /=15 см были заполнены воздухом. Показатель преломления
rii воздуха равен 1,000292. Когда в одной из трубок воздух заменили
ацетиленом, то интерференционная картина сместилась на т=80
полос. Определить показатель преломления п2 ацетилена, если в
интерферометре использовался источник монохроматического света
с длиной волны А,=0,590 мкм.
30.36. Определить перемещение зеркала в интерферометре Май-
кельсона, если интерференционная картина сместилась на т=
= 100 полос. Опыт проводился со светом с длиной волны А,=546 нм.
30.37. Для измерения показателя преломления аргона в одно
из плеч интерферометра Майкельсона поместили пустую стеклян-
стеклянную трубку длиной /= 12 см с плоскопараллельными торцовыми по-
поверхностями. При заполнении трубки аргоном (при нормальных
условиях) интерференционная картина сместилась на т—106 полос.
Определить показатель преломления п аргона, если длина волны к
света равна 639 нм.
30.38. В интерферометре Майкельсона на пути одного из интерфе-
интерферирующих пучков света (А,=590 нм) поместили закрытую с обеих
сторон стеклянную трубку длиной /=10 см, откачанную до высокого
вакуума. При заполнении трубки хлористым водородом произошло
смещение интерференционной картины. Когда хлористый водород
был заменен бромистым водородом, смещение интерференционной
картины возросло на Дт=42 полосы. Определить разность An
показателей преломления бромистого и хлористого водорода.
§ 31. ДИФРАКЦИЯ СВЕТА
Основные формулы
• Радиус k-ii зоны Френеля:
для сферической волны
ah
где а — расстояние диафрагмы с круглым отверстием от точечного
источника света; Ь — расстояние диафрагмы от экрана, на котором
ведется наблюдение дифракционной картины; k — номер зоны Фре-
Френеля; а — длина волны;
для плоской волны
• Дифракция света на одной щели при нормальном падении
лучей. Условие минимумов интенсивности света
• t о у л» , у л * 1 О Q
340

где а — ширина щели; ф — угол дифракции; k — номер минимума;
А, — длина волны.
Условие максимумов интенсивности света
)^, k=l, 2, 3, ...,
где ср' — приближенное значение угла дифракции.
• Дифракция света на дифракционной решетке при нормальном
падении лучей. Условие главных максимумов интенсивности
dsmy=±kX, k=0, 1, 2, 3, . . .,
где d — период (постоянная) решетки; k — номер главного макси-
максимума; ср — угол между нормалью к поверхности решетки и нап-
направлением дифрагированных волн.
• Разрешающая сила дифракционной решетки
где ДА, —наименьшая разность длин волн двух соседних спектраль-
спектральных линий (к и М-ДА,), при которой эти линии могут быть видны
раздельно в спектре, полученном посредством данной решетки;
N — число штрихов решетки; k — порядковый номер дифракцион-
дифракционного максимума.
9 Угловая дисперсия дифракционной решетки
п __ 6ф k
UV~ ~бГ~ dcoscp'
линейная дисперсия дифракционной решетки
*>.-¦&•
Для малых углов дифракции
где / — главное фокусное расстояние линзы, собирающей на экра-
экране дифрагирующие волны.
Ф Разрешающая сила объектива телескопа
Р ~~ 1,22V
где р — наименьшее угловое расстояние между двумя светлыми
точками, при котором изображения этих точек в фокальной плос-
плоскости объектива могут быть видны раздельно; D — диаметр объек-
объектива; А,— длина волны.
• Формула Вульфа — Брэгга
2 d sin b=k%,
Где d — расстояние между атомными плоскостями кристалла;
•& — угол скольжения (угол между направлением пучка параллель-
параллельных лучей, падающих на кристалл, и гранью кристалла), опре-
определяющий направление, в котором имеет место зеркальное отраже-
отражение лучей (дифракционный максимум).
341

Примеры решения задач
Пример 1. На диафрагму с круглым отверстием радиусом г= 1 мм
падает нормально параллельный пучок света длиной волны
^=0,05 мкм. На пути лучей, прошедших через отверстие, помещают
экран. Определить максимальное расстояние bmax от центра от-
отверстия до экрана, при котором в центре дифракционной картины
еще будет наблюдаться темное пят-
пятно.
Решение. Расстояние, при
котором будет видно темное пят-
пятно, определяется числом зон Фре-
Френеля, укладывающихся в отвер-
отверстии. Если число зон четное, то в
центре дифракционной картины бу-
будет темное пятно.
Число зон Френеля, помещаю-
помещающихся в отверстии, убывает по
мере удаления экрана от отверстия. Наименьшее четное число зон
равно двум. Следовательно, максимальное расстояние, при котором
еще будет наблюдаться темное пятно в центре экрана, определяется
условием, согласно которому в отверстии должны поместиться
две зоны Френеля.
Из рис. 31.1 следует, что расстояние от точки наблюдения О
на экране до края отверстия на 2 (К/2) больше, чем расстояние R0=t
По теореме Пифагора получим
AV-6* =
Рис. 31.1
Учтя, что Я<с&тах и ЧТ0 членом, содержащим Я2, можно пренеб-
пренебречь, последнее равенство перепишем в виде
r2 = 2Mmax, откуда bmax = r*/Bl).
Произведя вычисления по последней формуле, найдем
Пример 2. На щель шириной а=0,1 мм нормально падает
параллельный пучок света от монохроматического источника
(>о=О,6 мкм). Определить ширину / центрального максимума в
дифракционной картине, проецируемой с помощью линзы, нахо-
находящейся непосредственно за щелью, на экран, отстоящий от лин-
линзы на расстоянии L=\ м.
Решение. Центральный максимум интенсивности света за-
занимает область между ближайшими от него справа и слева миниму-
минимумами интенсивности. Поэтому ширину центрального максимума
интенсивности примем равной расстоянию между этими двумя
минимумами интенсивности (рис. 31.2).
Минимумы интенсивности света при дифракции от одной щели
наблюдаются под углами срг определяемыми условием
342

Щель
a sin ф=±&Х, A)
где k — порядок минимума; в нашем случае равен единице.
Расстояние между двумя минимумами на экране определим не-
непосредственно по чертежу: /=2L tg ср. Заметив, что при малых уг-
углах tg фя^ sin ф, перепишем эту
формулу в виде
l=2L sincp. B)
Выразим sin ф из формулы A)
и подставим его в равенство B):
l=2Lkk/a. C)
Произведя вычисления по фор-
формуле C), получим
/=1,2 см.
Пример 3. На дифракционную
решетку нормально к ее поверх-
поверхности падает параллельный пучок
света с длиной волны Х=^0,5 мкм.
Помещенная вблизи решетки лин-
линза проецирует дифракционную
картину на плоский экран, удаленный от линзы на L=\ м. Расстоя-
Расстояние I между двумя максимумами интенсивности первого порядка,
наблюдаемыми на экране, равно 20,2 см (рис. 31.3). Определить:
1) постоянную d дифракционной решетки; 2) число п штрихов на
1 см; 3) число максимумов, которое при этом дает дифракционная
решетка; 4) максимальный угол фтах отклонения лучей, соот-
соответствующих последнему дифракционному максимуму.
Решение 1. Постоянная d дифракционной решетки, длина
волны X и угол ф отклоне-
Рис. 31.2
и
Дифракционная
решетка
ния лучей, соответствую-
соответствующий &-му дифракционному
максимуму, связаны соот-
соотношением
dsin (p=kki A)
где k — порядок спектра,
или в случае монохрома-
монохроматического света порядок
максимума.
В данном случае fe=l,
sin ф:=tg ф (ввиду того, что
//2<I), tg cp=(//2)L (следу-
(следует из рис. 31.3). С учетом последних трех равенств соотношение
A) примет вид
ш/////////////////////.
ж I у
////п//У/// чшниишшш,
Экран
Рис. 31.3
откуда постоянная решетки
d=2 Lkll.
343

Подставляя данные, получим
d=4,95 мкм.
2. Число штрихов на 1 см найдем из формулы
л=Ш.
После подстановки числовых значений получим
п=2,02.103 см.
3. Для определения числа максимумов, даваемых дифракцион-
дифракционной решеткой, вычислим сначала максимальное значение 6тах,
исходя из того, что максимальный угол отклонения лучей решеткой
не может превышать 90°.
Из формулы A) запишем
Подставляя сюда значения величин, получим
Ь —Q Q
Число k обязательно должно быть целым. В то же время оно не
может принять значение, равное 10, так как при этом значении
sin ф должен быть больше единицы, что невозможно. Следователь-
Следовательно, ?max=9.
Определим общее число максимумов дифракционной картины,
полученной посредством дифракционной решетки. Влево' и вправо
от центрального максимума будет наблюдаться по одинаковому
числу максимумов, равному &тах, т. е. всего 2&тах. Если учесть
также центральный нулевой максимум, получим общее число мак-
максимумов
tf = 2ftmax+l.
Подставляя значение &тах, найдем
#=2.9+1 = 19.
4. Для определения максимального угла отклонения лучей,
соответствующего последнему дифракционному максимуму, выра-
выразим из соотношения B) синус этого угла:
Отсюда
Фтах = arcsin (km2iXX/d).
Подставив сюда значения величин X, d, &max и произведя вычис-
вычисления, получим
Фтах = 65,4°.
Задачи
Зоны Френеля
31.1. Зная формулу радиуса k-n зоны Френеля для сферической
волны (pk = У'аЬкЩа + Ь)), вывести соответствующую формулу
для плоской волны.
344

31.2. Вычислить радиус р5 пятой зоны Френеля для плоского
волнового фронта (к=0,5 мкм), если построение делается для точки
наблюдения, находящейся на расстоянии b=l мот фронта волны.
31.3. Радиус р4 четвертой зоны Френеля для плоского волнового
фронта равен 3 мм. Определить радиус р6 шестой зоны Френеля.
31.4. На диафрагму с круглым отверстием диаметром d=A мм
падает нормально параллельный пучок лучей монохроматического
света (А,=0,5 мкм). Точка наблюдения находится на оси отверстия
на расстоянии Ь=\ м от него. Сколько зон Френеля укладывается в
отверстии? Темное или светлое пятно получится в центре дифрак-
дифракционной картины, если в месте наблюдений поместить экран?
31.5. Плоская световая волна (^=0,5 мкм) падает нормально на
диафрагму с круглым отверстием диаметром d=l см. На каком рас-
расстоянии b от отверстия должна находиться точка наблюдения, что-
чтобы отверстие открывало: 1) одну зону Френеля? 2) две зоны Френеля?
31.6. Плоская световая волна падает нормально на диафрагму с
круглым отверстием. В результате дифракции в некоторых точках
оси отверстия, находящихся на расстояниях Ьг, от его центра, наблю-
наблюдаются максимумы интенсивности. 1. Получить вид функции Ь^=
=/(г, X, /г), где г — радиус отверстия; Я, — длина волны; п — чис-
число зон Френеля, открываемых для данной точки оси отверстием.
2. Сделать то же самое для
точек оси отверстия, в кото-
которых наблюдаются минимумы
интенсивности.
31.7. Плоская световая
волна (^=0,7 мкм) падает нор-
нормально на диафрагму с круг-
круглым отверстием радиусом г=
= 1,4 мм. Определить рас-
расстояния bl9 Ь2, Ь3 ОТ диафраг- Рис. 31.4
мы до трех наиболее удален-
удаленных от нее точек, в которых наблюдаются минимумы интенсив-
интенсивности .
31.8. Точечный источник S света(к=0,5мкм), плоская диафрагма
с круглым отверстием радиусом г=\ мм и экран расположены, как
это указано на рис. 31.4 (а=1 м). Определить расстояние Ь от экра-
экрана до диафрагмы, при котором отверстие открывало бы для точки Р
три зоны Френеля.
31.9. Как изменится интенсивность в точке Р (см. задачу 31.8),
если убрать диафрагму?
Дифракция на щели. Дифракционная решетка
31.10. На щель шириной а=0,05 мм падает нормально монохро-
монохроматический свет (А,=0,6 мкм). Определить угол ф между первоначаль-
первоначальным направлением пучка света и направлением на четвертую тем-
темную дифракционную полосу.
345

31.11. На узкую щель падает нормально монохроматический
свет. Угол ф отклонения пучков света, соответствующих второй
светлой дифракционной полосе, равен 1°. Скольким длинам волн
падающего света равна ширина щели?
31.12. На щель шириной а=0,1 мм падает нормально монохрома-
монохроматический свет (^=0,5 мкм). За щелью помещена собирающая лин-
линза, в фокальной плоскости которой находится экран. Что будет на-
наблюдаться на экране, если угол ф дифракции равен: 1) 17'; 2) 43'.
31.13. Сколько штрихов на каждый миллиметр содержит диф-
дифракционная решетка, если при наблюдении в монохроматическом
свете (Х=0,6 мкм) максимум пятого порядка отклонен на угол ф=
-18°?
31.14. На дифракционную решетку, содержащую п=100 штри-
штрихов на 1 мм, падает нормально монохроматический свет. Зритель-
Зрительная труба спектрометра наведена на максимум третьего порядка.
Чтобы навести трубу на другой максимум того же порядка, ее
нужно повернуть на угол Аф=20°. Определить длину волны X
света.
31.15. Дифракционная решетка освещена нормально падающим
монохроматическим светом. В дифракционной картине максимум
второго порядка отлонен на угол ф^Н0. На какой угол ф2 откло-
отклонен максимум третьего порядка?
31.16. Дифракционная решетка содержит п=200 штрихов на
1 мм. На решетку падает нормально монохроматический свет
(А,=0,6 мкм). Максимум какого наибольшего порядка дает эта
решетка?
31.17. На дифракционную решетку, содержащую п=400 штри-
штрихов на 1 мм, падает нормально монохроматический свет (Х=0,6мкм).
Найти общее число дифракционных максимумов, которые дает эта
решетка. Определить угол ф дифракции, соответствующий послед-
последнему максимуму.
31.18. При освещении дифракционной решетки белым светом
спектры второго и третьего порядков отчасти перекрывают друг
друга. На какую длину волны в спектре второго порядка наклады-
накладывается фиолетовая граница (Х=0,4 мкм) спектра третьего порядка?
31.19. На дифракционную решетку, содержащую п=500 штри-
штрихов на 1 мм, падает в направлении нормали к ее поверхности белый
свет. Спектр проецируется помещенной вблизи решетки линзой на
экран. Определить ширину Ь спектра первого порядка на экране,
если расстояние L линзы до экрана равно 3 м. Границы видимости
спектра А,кр=780 нм, А,ф=400 нм.
31.20. На дифракционную решетку с периодом d=\0 мкм под
углом а=30° падает монохроматический свет с длиной волны
1=600 нм. Определить угол ср дифракции, соответствующий вто-
второму главному максимуму.
31.21. Дифракционная картина получена с помощью дифрак-
дифракционной решетки длиной 1= 1,5 см и периодом d=5 мкм. Определить,
в спектре какого наименьшего порядка этой картины получатся
раздельные изображения двух спектральных линий с разностью
346

длин волн АЛ,=О,1 нм, если линии лежат в крайней красной части
спектра (^«760 нм).
31.22. Какой наименьшей разрешающей силой R должна обла-
обладать дифракционная решетка, чтобы с ее помощью можно было раз-
разрешить две спектральные линии калия (^=578 нм и Х2=580 нм)?
Какое наименьшее число N штрихов должна иметь эта решетка,
чтобы разрешение было возможно в спектре второго порядка?
31.23. С помощью дифракционной решетки с периодом d=20 мкм
требуется разрешить дублет натрия (^=589,0 нм и А,2=589,6 нм)
в спектре второго порядка. При какой наименьшей длине / решетки
это возможно?
31.24. Угловая дисперсия 1)ф дифракционной решетки для излу-
излучения некоторой длины волны (при малых углах дифракции) сос-
составляет 5 мин/нм. Определить разрешающую силу R этой решетки
для излучения той же длины волны, если длина / решетки равна
2 см.
31.25. Определить угловую дисперсию ?>ф дифракционной решет-
решетки для угла дифракции ср=30° и длины волны Х=600 нм. Ответ вы-
выразить в единицах СИ и в минутах на нанометр.
31.26. На дифракционную решетку, содержащую п=500 штри-
штрихов на 1 мм, падает нормально монохроматический свет с длиной
волны ^=700 нм. За решеткой помещена собирающая линза с глав-
главным фокусным расстоянием /—50 см. В фокальной плоскости линзы
расположен экран. Определить линейную дисперсию Dt такой сис-
системы для максимума третьего порядка. Ответ выразить в милли-
миллиметрах на нанометр.
31.27. Нормально поверхности дифракционной решетки падает
пучок света. За решеткой помещена собирающая линза с оптичес-
оптической силой Ф=1 дптр. В фокальной плоскости линзы расположен
экран. Определить число п штрихов на 1 мм этой решетки, если
при малых углах дифракции линейная дисперсия Dt = \ мм/нм.
31.28. На дифракционную решетку нормально ее поверхности
падает монохроматический свет (^=650 нм). За решеткой находится
линза, в фокальной плоскости которой расположен экран. На экра-
экране наблюдается дифракционная картина под углом дифракции ф=
=30°. При каком главном фокусном расстоянии / линзы линейная
дисперсия Di=0,5 мм/нм?
Дифракция на кристаллической решетке
31.29. На грань кристалла каменной соли падает параллельный
пучок рентгеновского излучения (^=147 пм). Определить расстоя-
расстояние d между атомными плоскостями кристалла, если дифракционный
максимум второго порядка наблюдается, когда излучение падает
под углом -&=31°30' к поверхности кристалла.
31.30. Какова длина волны X монохроматического рентгеновского
излучения, падающего на кристалл кальцита, если дифракционный
максимум первого порядка наблюдается, когда угол •& между на-
направлением падающего излучения и гранью кристалла равен 3°?
347

Расстояние d между атомными плоскостями кристалла принять рав-
равным 0,3 нм.
31.31. Параллельный пучок рентгеновского излучения падает
на грань кристалла. Под углом й=65° к плоскости грани наблю-
наблюдается максимум первого порядка. Расстояние d между атомными
плоскостями кристалла 280 пм. Определить длину волны X рентге-
рентгеновского излучения.
Разрешающая сила объектива телескопа
31.32. Диаметр D объектива телескопа равен 8 см. Каково на-
наименьшее угловое расстояние [3 между двумя звездами, дифракцион-
дифракционные изображения которых в фокальной плоскости объектива по-
получаются раздельными? При малой освещенности глаз человека
наиболее чувствителен к свету с длиной волны Х=0,5 мкм.
31.33. На шпиле высотного здания укреплены одна под другой
две красные лампы (^=640 нм). Расстояние d между лампами 20 см.
Здание рассматривают ночью в телескоп с расстояния г= 15 км.
Определить наименьший диаметр Dmm объектива, при котором в
его фокальнбй плоскости получатся раздельные дифракционные
изображения.
§ 32. ПОЛЯРИЗАЦИЯ СВЕТА
Основные формулы
# Закон Брюстера
где ев — угол падения, при котором отраженная световая волна
полностью поляризована; n2i — относительный показатель прелом-
преломления.
О Закон Малюса
1=1о cos2a,
где / — интенсивность плоскополяризованного света, прошедшего
через анализатор; /0 — интенсивность плоскополяризованного све-
света, падающего на анализатор; а — угол между направлением колеба-
колебаний светового вектора волны, падающей на анализатор, и плоско-
плоскостью пропускания анализатора.
Ф Степень поляризации света
Р = тах 'кип
¦'max~r-'min
гДе Лпах и /min — максимальная и минимальная интенсивности
частично поляризованного света, пропускаемого анализатором.
О Угол поворота ср плоскости поляризации оптически актив-
активными веществами определяется соотношениями:
а) в твердых телах cp^ad, где а — постоянная вращения; d —
длина пути, пройденного светом в оптически активном веществе;
348

б) в чистых жидкостях q>=[a]pd, где [а] — удельное вращение;
р — плотность жидкости;
в) в растворах y=[a]Cd, где С — массовая концентрация опти-
оптически активного вещества в растворе.
Примеры решения задач
Пример 1. Пучок естественного света падает на полированную
поверхность стеклянной пластины, погруженной в жидкость. Отра-
Отраженный от пластины пучок света составляет угол ср=97° с падаю-
падающим пучком (рис. 32.1). Определить
показатель преломления п жидкости,
если отраженный свет полностью по-
поляризован.
Решение. Согласно закону
Брюстера, свет, отраженный от ди-
диэлектрика, полностью поляризован в
том случае, если тангенс угла паде-
падения
tge1B = n21,
где /г2i — относительный показатель
преломления второй среды (стекла)
относительно первой (жидкости).
Относительный показатель преломления равен отношению аб-
абсолютных показателей преломления этих сред. Следовательно2
Согласно условию задачи, отраженный луч повернут на угол ср от-
относительно падающего луча. Так как угол падения равен углу отра-
отражения, то 81в=ф/2 и, следовательно, tg(q>/2)=n2/nlt откуда
П1 tg(q>72)-
Сделав подстановку числовых значений, получим
Пример 2. Два николя Л/i и N2 расположены так, что угол а
между их плоскостями пропускания равен 60°. Определить: 1) во
сколько раз уменьшится интенсивность света при прохождении че-
через один николь (A/"i); 2) во сколько раз уменьшится интенсивность
света при прохождении через оба николя? При прохождении каждо-
каждого из николей потери на отражение и поглощение света составляют
5 %.
Решение 1. Пучок естественного света, падая на грань ни-
николя Nx (рис. 32.2), расщепляется вследствие двойного лучепрелом-
лучепреломления на два пучка: обыкновенный и необыкновенный. Оба пучка
одинаковы по интенсивности и полностью поляризованы. Плоскость
колебаний для необыкновенного пучка лежит в плоскости чертежа
(плоскость главного сечения). Плоскость колебаний для обыкновен-
349

ного пучка перпендикулярна плоскости чертежа. Обыкновенный
пучок (о) вследствие полного отражения от границы АВ отбрасы-
отбрасывается на зачерненную поверхность призмы и поглощается ею.
Необыкновенный пучок (е) проходит через николь. При этом интен-
интенсивность света уменьшается вследствие поглощения в веществе ни-
николя.
Естестденный, <
С/ет А ,,„„„„,,, ffj Iq [П]2 COS2 ОС
Рис. 32.2
Таким образом, интенсивность света, прошедшего через николь
где k = 0,05— относительная потеря интенсивности света в николе;
/0 — интенсивность естественного света, падающего на николь Nlt
Относительное уменьшение интенсивности света получим, разде-
разделив интенсивность /0 естественного света на интенсивность 1г по-
поляризованного света:
h
Подставив числовые значения, найдем
h/1^2,10.
Таким образом, интенсивность света при прохождении через
николь Ni уменьшается в 2,10 раза.
2. Пучок плоскополяризованного света интенсивности 1% падает
на николь Af 2 и также расщепляется на обыкновенный и необыкновен-
необыкновенный. Обыкновенный пучок полностью поглощается в николе, а ин-
интенсивность необыкновенного пучка света, вышедшего из николя,
определяется законом Малюса (без учета поглощения в этом николе):
/2=/i cos2 a,
где а — угол между плоскостью колебаний в поляризованном
пучке и плоскостью пропускания николя N2.
Учитывая потери интенсивности во втором николе, получим
I^I^l—k) cos2 a.
Искомое уменьшение интенсивности при прохождении света че-
через оба николя найдем, разделив интенсивность /0 естественного
света на интенсивность /2 света, прошедшего систему из двух нико-
лей:
/о_^ /о
/2 /i(l — k) cos2a'
350

Заменив /0//i его выражением по формуле A), получим
/о_ 2
/2 A — &J cos2a*
Подставив данные, произведем вычисления;
^ = 8,86.
Таким образом, после прохождения света через два николя интен-
интенсивность его уменьшится в 8,86 раза.
Пример 3. Пучок частично-поляризованного света рассматри-
рассматривается через николь. Первоначально николь установлен так, что его
плоскость пропускания параллельна плоскости колебаний линейно-
поляризованного света. При повороте николя на угол ф=60° интен-
интенсивность пропускаемого им света уменьшилась в k=2 раза. Опреде-
Определить отношение I Jin интенсивностей естественного и линейно-поля-
линейно-поляризованного света, составляющих данный частично-поляризован-
ный свет, а также степень поляризации Р пучка света.
Решение. Отношение интенсивности Ie естественного света к
интенсивности /п поляризованного света найдем из следующих сооб-
соображений. При первоначальном положении николя он полностью
пропустит линейно-поляризованный свет и половину интенсивности
естественного света. Общая интенсивность пропущенного при этом
света
Il = fn + l/Jt.
При втором положении николя интенсивность пропущенного по-
поляризованного света определится по закону Малюса, а интенсив-
интенсивность пропущенного естественного света, как и в первом случае,
будет равна половине интенсивности естественного света, падающего
на николь. Общая интенсивность во втором случае
В соответствии с условием задачи Ii=kl2y или
In + 1/2Ie = k(Incos*q> + i/2Ie).
Подставив сюда значение угла <р, k и произведя вычисления, по-
получим
/е//п=1, или /в = /П1
т. е. интенсивности естественного и поляризованного света в задан-
заданном пучке равны между собой.
Степень поляризации частично-поляризованного света определя-
определяется соотношением
Р = (Лпах— Anln)/(Anax + Anin)> 0)
гДе Апах и /min — соответственно максимальная и минимальная ин-
интенсивности света, пропущенного через николь.
Максимальная интенсивность 1тлх=11=1п+У2 1е> или5 учи-
учитывая, что /е=/п*
351

Минимальная интенсивность соответствует положению николя,
при котором плоскость пропускания его перпендикулярна плоско-
плоскости колебаний линейно-поляризованного света. При таком положе-
положении николя поляризованный свет будет полностью погашен и через
николь пройдет только половина интенсивности естественного
света. Общая интенсивность выразится равенством
-'min /2^e==z /г'п»
Подставив найденные выражения /гаах и /min в формулу A),
получим
Следовательно, степень поляризации пучка света
Р=1/2.
Пример 4. Пластинка кварца толщиной dx=l мм, вырезанная
перпендикулярно оптической оси кристалла, поворачивает пло-
плоскость поляризации монохроматического света определенной длины
волны на угол q)i=20°. Определить: 1) какова должна быть толщина
d2 кварцевой пластинки, помещенной между двумя «параллельными»
николями, чтобы свет был полностью погашен; 2) какой длины I труб-
трубку с раствором сахара массовой концентрацией С=0,4 кг/л надо
поместить между николями для получения того же эффекта? Удель-
Удельное вращение [а] раствора сахара равно 0,665 град/(м-кг-м~3).
Решение. 1. Угол поворота плоскости поляризации кварце-
кварцевой пластинкой определяется соотношением q=ad.
Пользуясь этой формулой, выразим искомую толщину d2 пла-
пластинки:
^2=ф2/а, A)
где ф2 — угол поворота плоскости поляризации, при котором свет
будет полностью погашен (ф2=90°).
Постоянную вращения а для кварца найдем также из формулы
q=ad, подставив в нее заданные в условии задачи значения dx и <px:
Подставив это выражение а в формулу A), получим
d2= (<p2/<Pi)di.
Произведя вычисления по этой формуле, найдем толщину пла-
пластинки:
d2=4,5 мм.
2. Длину трубки с сахарным раствором найдем из соотношения
cp2==[a]Cld, выражающего угол поворота плоскости поляризации рас-
раствором сахара, где d — толщина раствора сахара (принимается рав-
равной длине I трубки). Отсюда получим
/=<р2/([а]С).
Подставив сюда значения q>2, [a], С=0,4 кг/л=400 кг/м3 и произ-
произведя вычисления, найдем
/-3,8 дм.
352

Задачи
Закон Брюстера. Закон Малюса
32.1. Пучок света, идущий в воздухе, падает на поверхность
жидкости под углом 81=54°. Определить угол преломления е'2 пуч-
пучка, если отраженный пучок полностью поляризован.
32.2. На какой угловой высоте ф над горизонтом должно нахо-
находиться Солнце, чтобы солнечный свет, отраженный от поверхности
воды, был полностью поляризован?
32.3. Пучок естественного света, идущий в воде, отражается от
грани алмаза, погруженного в воду. При каком угле падения гв
отраженный свет полностью поляризован?
32.4. Угол Брюстера ев при падении света из воздуха на кристалл
каменной соли равен 57°. Определить скорость света в этом кристал-
кристалле.
32.5. Предельный угол г[ полного отражения пучка света на гра-
границе жидкости с воздухом равен 43°. Определить угол Брюстера ев
для падения луча из воздуха на поверхность этой жидкости.
32.6. Пучок естественного света падает на стеклянную (п=1,6)
призму (рис. 32.3). Определить двугранный угол 9 призмы, если
отраженный пучок максимально поляризован.
///
Рис. 32.3
Рис. 32.4
32.7. Алмазная призма находится в некоторой среде с показа-
показателем преломления пх. Пучок естественного света падает на призму
так, как это показано на рис. 32.4. Определить показатель прелом-
преломления пх среды, если отраженный пучок максимально поляризован;
32.8. Параллельный пучок естественного света падает на сфери-
сферическую каплю воды. Найти угол ф между отраженным и падающим
пучками в точке А (рис. 32.5).
32.9. Пучок естественного света падает на стеклянный шар
(я=1,54). Найти угол у между преломленным и падающим пучками
в точке А (рис. 32.6).
32.10. Пучок естественного света падает на стеклянный шар,
находящийся в воде. Найти угол ф между отраженным и падающим
пучками в точке А (рис. 32.7). Показатель преломления п стекла
принять равным 1,58.
12
1268
353

32.11. Анализатор в k=2 раза уменьшает интенсивность света,
приходящего к нему от поляризатора. Определить угол а между
плоскостями пропускания поляризатора и анализатора. Потерями
интенсивности света в анализаторе пренебречь.
Рис. 32.5
Рис. 32.6
32.12. Угол а между плоскостями пропускания поляризатора
и анализатора равен 45°. Во сколько раз уменьшится интенсивность
света, выходящего из анализатора, если угол увеличить до 60°?
32.13. Во сколько раз ослабляется интенсивность света, прохо-
проходящего через два николя, плоскости
пропускания которых образуют угол
а=30°, если в каждом из николей в
отдельности теряется 10 % интенсив-
интенсивности падающего на него света?
32.14. В фотометре одновременно
рассматривают две половины поля
зрения: в одной видна эталонная све-
светящаяся поверхность с яркостью Lt=
=5 ккд/м2, в другой — испытуемая
поверхность, свет от которой прохо-
проходит через два николя. Граница меж-
между обеими половинами поля зрения
исчезает, если второй николь повер-
повернуть относительно первого на угол
а =45°. Найти яркость L2 испытуемой поверхности, если извест-
известно, что в каждом из николей интенсивность падающего на него све-
света уменьшается на 8 %.
Степень поляризации света
32.15. В частично-поляризованном свете амплитуда светового
вектора, соответствующая максимальной интенсивности света, в
п=2 раза больше амплитуды, соответствующей минимальной ин-
интенсивности. Определить степень поляризации Р света.
32.16. Степень поляризации Р частично-поляризованного света
354
Рис. 32.7

равна 0,5. Во сколько раз отличается максимальная интенсивность
света, пропускаемого через анализатор, от минимальной?
32.17. На пути частично-поляризованного света, степень поля-
поляризации Р которого равна 0,6, поставили анализатор так, что интен-
интенсивность света, прошедшего через него, стала максимальной. Во
сколько раз уменьшится интенсивность света, если плоскость
пропускания анализатора повернуть на угол а=30°?
32.18. На николь падает пучок частично-поляризованного света.
При некотором положении николя интенсивность света, прошедшего
через него, стала минимальной. Когда плоскость пропускания нико-
николя повернули на угол C=45°, интенсивность света возросла в k=
= 1,5 раза» Определить степень поляризации Р света.
Вращение плоскости поляризации
32.19. Пластинку кварца толщиной dx=2 мм, вырезанную перпен-
перпендикулярно оптической оси, поместили между параллельными нико-
лями, в результате чего плоскость поляризации света повернулась
на угол ф^53°. Определить толщину &ъ пластинки, при которой
данный монохроматический свет не проходит через анализатор.
32.20. Никотин (чистая жидкость), содержащийся в стеклянной
трубке длиной d=8 см, поворачивает плоскость поляризации жел-
желтого света натрия на угол ср=137°. Плотность никотина р= 1,01 X
Х103 кг/м3. Определить удельное вращение [а] никотина.
32.21. Раствор глюкозы с массовой концентрацией Сх=280 кг/м3,
содержащийся в стеклянной трубке, поворачивает плоскость поляри-
поляризации монохроматического света, проходящего через этот раствор,
на угол ф!=32°. Определить массовую концентрацию С2 глюкозы в
другом растворе, налитом в трубку такой же длины, если он пово-
поворачивает плоскость поляризации на угол 92=24°.
32.22. Угол ф поворота плоскости поляризации желтого света
натрия при прохождении через трубку с раствором сахара равен 40°.
Длина трубки d= 15 см. Удельное вращение [а] сахара равно 1,17Х
К10~2 рад«м3/(м«кг). Определить плотность р раствора.
§ 33. ОПТИКА ДВИЖУЩИХСЯ ТЕЛ
Основные формулы
• Эффект Доплера в релятивистском случае
где v — частота электромагнитного излучения, воспринимаемого
наблюдателем; v0 — собственная частота электромагнитного излуче-
излучения, испускаемого неподвижным источником; $=v/c — скорость ис-
источника электромагнитного излучения относительно наблюдателя;
с—скорость распространения электромагнитного излучения в ва-
вакууме; •& — угол между вектором v и направлением наблюдения,
измеренный в системе отсчета, связанной с наблюдателем.
12* 355

При движении источника вдоль прямой, соединяющей наблюда-
наблюдателя и источник, возможны два случая:
а) источник удаляется от наблюдателя (й=0)
б) источник приближается к наблюдателю (Ф=я)
• Эффект Доплера в нерелятивистском случае
Av v Q
- = Tcos0,
где Av — изменение частоты (Av=v—v0).
# Эффект Вавилова — Черенкова. При движении заряжен-
заряженной частицы в некоторой среде со скоростью и, больше фазовой
скорости света в данной среде, возникает излучение света. Свет
этот распространяется по направлениям, составляющим острый угол
•& с траекторией частицы, тГе. вдоль образующих конуса, ось кото-
которого совпадает с направлением скорости частицы. Угол -& определя-
определяется из соотношения
cos §=v/(nc), или cosd=l/(pn),
где п — показатель преломления среды, в котором движется заря-
заряженная частица.
Примеры решения задач
Пример 1. Источник монохроматического света с длиной волны
Х0=600 нм движется по направлению к наблюдателю со скоростью
у=0,1 с (с — скорость распространения электромагнитных волн).
Определить длину волны к излучения, которую зарегистрирует
спектральный прибор наблюдателя.
Решение. В системе отсчета, связанной с наблюдателем,
спектральный прибор зарегистрирует электромагнитное излучение
частоты
v = v0Ku^/(l + pcosd), A)
где v0 — собственная частота монохроматического излучения источ-
источника; §=vlc\ Ь— угол между вектором v и направлением наблюде-
наблюдения, измеренный в системе отсчета, связанной с наблюдателем.
Выразим частоты v и v0 через длины волн % и Яо: v=c/X и vo=
=с/Х0. Заметив, что в нашем случае {}=Jt(cosd=—1), перепишем
формулу A) с учетом последних соотношений:
JL —J_J^IEll
откуда
(Р)(Р)
Подставим значения р(р=^/с=О,1) и К в полученное выражение
и произведем вычисления:
к=Ы2 нм.
356

Пример 2. Каким минимальным импульсом pmin (в единицах
МэВ/с) должен обладать электрон, чтобы эффект Вавилова —
Черенкова можно было наблюдать в воде?
Решение. Эффект Вавилова— Черенкова состоит в излуче-
излучении света, возникающем при движении в веществе заряженных
частиц со скоростью и, превышающей скорость распространения
световых волн (фазовую скорость) в этой среде. Так как фазовая
скорость света v^=c/n (с — скорость распространения электромаг-
электромагнитного излучения в вакууме; п — показатель преломления среды),
то условием возникновения эффекта Вавилова — Черенкова явля-
является
у>иф, или v>cln.
Обычно это условие записывают иначе, учитывая, что $=v/c:
ря>1. A)
Поскольку черенковское излучение1наблюдается для релятивист-
релятивистских частиц, то запишем сначала выражение для релятивистского
импульса:
— Р2> или р = тоф1У1— р2,
где учтено, что v=$c.
Минимальному импульсу соответствует минимальное значение
Pmin, которое находим из условия A):
РтШ=1/Л.
Тогда минимальное значение импульса
Pmin^riwlVJF-i. B)
Вычисления выполним во внесистемных единицах — МэВ/с (с —¦
скорость распространения электромагнитного излучения). Для этого
поступим следующим образом. Известно, что т0с2=0,511 МэВ, от-
отсюда запишем т0с=0,511 МэВ/с. Подставив в B) п=1,33 и най-
найденное значение тос, произведем вычисления:
/^„=0,583 МэВ/с.
Задачи
Эффект Доплера
33.1. При какой предельной скорости v (в долях скорости
света) источника можно вместо релятивистской формулы v=
= voj/ A—P)/(l +P) для эффекта Доплера пользоваться прибли-
приближенным выражением v«vo(l—Р), если погрешность в определении
частоты не должна превышать 1 %?
33.2. Для определения угловой скорости вращения солнечного
диска измеряли относительный сдвиг ДАЛ спектральных линий от
восточного и западного краев Солнца. Он оказался равным
1,5-10"§. Определить угловую скорость ш вращения солнечного
диска. Радиус R Солнца считать известным.
33.3. Космический корабль удаляется от Земли со скоростью v==
— 10 км/с. Частота v0 электромагнитных волн, излучаемых антенной
357

корабля, равна 30 МГц. Определить доллеровское смещение Av
частоты, воспринимаемой приемником.
33.4. При изучении спектра излучения некоторой туманности
линия излучения водорода (Ха=656,3 нм) оказалась смещенной на
А^=2,5 нм в область с большей длиной волны (красное смещение).
Найти скорость v движения туманности относительно Земли и ука-
указать, удаляется она от Земли или приближается к ней.
33.5. Определить обусловленное эффектом Доплера уширение
АИ спектральных линий излучения атомарного водорода, находя-
находящегося при температуре Г=300 К.
33.6. В результате эффекта Доплера происходит уширение ли-
линий ^-излучения ядер. Оценить уширение Av/v линий 7-излучения
ядер кобальта, находящихся при температуре: 1) комнатной (Г=
=-290 К); 2) ядерного взрыва (Г=10 МК).
33.7. Два космических корабля движутся вдоль одной прямой.
Скорости vx и v2 их в некоторой инерциальной системе отсчета соот-
соответственно 12 и 8 км/с. Определить частоту v сигнала электромаг-
электромагнитных волн, воспринимаемых вторым космическим кораблем, если
антенна первого корабля излучает электромагнитные волны ча-
частотой vo=l МГц. Рассмотреть следующие случаи: 1) космические
корабли движутся навстречу друг другу; 2) космические корабли
удаляются друг от друга в противоположных направлениях; 3) пер-
первый космический корабль нагоняет второй; 4) первый космический
корабль удаляется от второго, движущегося в том же направлении.
33.8. Монохроматический свет с длиной волны ^=600 нм падает
на быстро вращающиеся в противоположных направлениях зеркала
(опыт А. А. Белопольского). После N=\Q отражений от зеркал пу-
пучок света попадает в спектрограф. Определить изменение ДА, длины
волны света, падающего на зеркала нормально их поверхности. Ли-
Линейная скорость v зеркал равна 0,67 км/с. Рассмотреть два случая,
когда свет отражается от зеркал: 1) движущихся навстречу одно дру-
другому; 2) удаляющихся одно от другого.
33.9. Плоское зеркало удаляется от наблюдателя со скоростью v
вдоль нормали к плоскости зеркала. На зеркало посылается пучок
света длиной волны Я0=500 нм. Определить длину волны X света,
отраженного от зеркала, движущегося со скоростью: 1) 0,2с (с —
скорость в вакууме); 2) 9 км/с.
33.10. Приемник радиолокатора регистрирует частоты биений
между частотой сигнала, посылаемого передатчиком, и частотой сиг-
сигнала, отраженного от движущегося объекта. Определить скорость v
приближающейся по направлению к локатору ракеты, если он рабо-
работает на частоту vo=6OO МГц и частота v* биений равна 4 кГц.
33.11. Рассказывают, что известный физик Роберт Вуд, проехав
однажды на автомашине на красный свет светофора, был остановлен
блюстителем порядка. Роберт Вуд, сославшись на эффект Доплера,
уверял, что он ехал достаточно быстро и красный свет светофора для
него изменился на зеленый. Оценить скорость и, с которой должна
была бы двигаться автомашина, чтобы красный сигнал светофора
(А,!=650 нм) воспринимался как зеленый (Х2—550 нм).
358

Источник
радиоизлучения v
Наблюдатель
Рис. 33.1
33.12» Длины волн излучения релятивистских атомов, движу-
движущихся по направлению к наблюдателю,оказались в два раза меньше,
чем соответствующие длины волн нерелятивистских атомов. Опре-
Определить скорость v (в долях ско-
скорости света) релятивистских ато-
атомов.
33.13. Наиболее короткая
длина волны Кг в спектре излу-
излучения водорода равна 410 нм.
С какой скоростью v должно уда-
удаляться от нас скопление атомов
водорода, чтобы их излучение
оказалось вследствие эффекта
Доплера за пределами видимой
части спектра. Граница видимой
части спектра соответствует дли-
длине волны Х2=760 нм.
33.14. На некотором расстоянии I от наблюдателя (рис. 33.1)
прямолинейно со скоростью 0=0,6 с движется источник радиоизлу-
радиоизлучения, собственная частота v0 которого равна 4 ГГц. В каких пре-
пределах изменяется частота v сигнала, воспринимаемого наблюдате-
наблюдателем, если наблюдение ведется в течение всего времени движения ис-
источника из положения 1 в положение 2? Углы указаны в системе
отсчета, связанной с наблюдателем.
Эффект Вавилова—Черепкова
33.15. Какой наименьшей скоростью v должен обладать электрон,
чтобы в среде с показателем преломления п= 1,60 возникло черенков-
ское излучение?
33.16. При какой скорости v электронов (в долях скорости света)
черенковское излучение происходит в среде с показателем преломле-
преломления п=1,80 под углом -&=20° к направлению их движения?
33.17. Найти наименьшую ускоряющую разность потенциалов
f/min, которую должен пройти электрон, чтобы в среде с показа-
показателем преломления п=1,50 возникло черенковское излучение.
33.18. Известно, что быстрые частицы, входящие в состав кос-
космического излучения, могут вызывать эффект Вавилова — Черенко-
ва в воздухе (п~ 1,00029). Считая, что такими частицами являются
электроны, определить их минимальную кинетическую энергию.
33.19. Электрон с кинетической энергией Т=0,51 МэВ движется
в воде. Определить угол Ф, составляемый черенковским излучением
с направлением движения электрона.
33.20. Импульс релятивистского электрона равен mQc. При каком
минимальном показателе преломления nmin среды уже можно наб-
наблюдать эффект Вавилова — Черенкова?
33.21. Мю- и пи-мезоны имеют одинаковые импульсы р=
= 100 МэВ/с. В каких пределах должен быть заключен показатель
преломления п среды, чтобы для ji-мезонов черенковское излучение
наблюдалось, а для я-мезонов — нет.

ГЛАВА 7
КВАНТОВООПТИЧЕСКИЕ ЯВЛЕНИЯ.
ФИЗИКА АТОМА
§ 34. ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
Основные формулы
# Закон Стефана — Больцмана
Ме=оТ\
где Ме — энергетическая светимость черного тела; Т — термоди-
термодинамическая температура; а — постоянная Стефана — Больцмана
[а=5,67-10"8 Вт/(м2.К4I.
О Энергетическая светимость серого тела
Ме=гаТ\
где е — коэффициент теплового излучения (степень черноты) серого
тела.
• Закон смещения Вина
где %т — длина волны, на которую приходится максимум энергии
излучения; b — постоянная закона смещения Вина (Ь=2,90Х
Х10~3 м-К).
• Формула Планка
где М^ т, ММ} т — спектральные плотности энергетической свети-
светимости черного тела; К — длина волны; со — круговая частота; с—
скорость света в вакууме; k — постоянная Больцмана; Т — термо-
термодинамическая температура; h — постоянная Планка; %=Ш Bя) —
постоянная Планка, деленная на 2я *.
# Зависимость максимальной спектральной плотности энерге-
энергетической светимости от температуры
где С —постоянная [С=1,30-10-* Вт/(м3-К5I.
* Первоначально постоянной Планка называлась величина /i=6,63X
X 10~34 Дж'С. Позднее постоянной Планка стали называть также величину
л=й/Bя)=1,05'10"-34 Дж'С. При дальнейшем изложении в данном пособии
все больше будет отдаваться предпочтение величине %.
360

Примеры решения задач
Пример 1. Исследование спектра излучения Солнца показы-
показывает, что максимум спектральной плотности энергетической све-
светимости соответствует длине волны Я=500нм. Принимая Солнце за
черное тело, определить: 1) энергетическую светимость М^ Солнца;
2) поток энергии Фе, излучаемый Солнцем; 3) массу т электромаг-
электромагнитных волн (всех длин), излучаемых Солнцем за 1 с.
Решение. 1. Энергетическая светимость Ме черного тела
выражается формулой Стефана — Больцмана
Мв=оТ*. A)
Температура излучающей поверхности может быть определена
из закона смещения Вина: hm=b/T. Выразив отсюда температуру Т
и подставив ее в формулу A), получим
Me=G(b%m)*. B)
Произведя вычисления по формуле B), найдем
Ме-64 МВт/м2.
2. Поток энергии Фе, излучаемый Солнцем, равен произведению
энергетической светимости Солнца на площадь S его поверхности:
<Pe=MeS, или
е, C)
где г — радиус Солнца.
Подставив в формулу C) значения я, г и Ме и произведя вычис-
вычисления, получим
Фе=3,9-10ав Вт.
3. Массу электромагнитных волн (всех длин), излучаемых Солн-
Солнцем за время /=1 с, определим, применив закон пропорциональ-
пропорциональности массы и энергии Е=пгс2. Энергия электромагнитных волн,
излучаемых за время t, равна произведению потока энергии Ф (мощ-
(мощности излучения) на время: E=Ot. Следовательно,Фе=тс2, откуда
т=Фе/с2.
Произведя вычисления по этой формуле, найдем
т=4,3-109 кг.
Пример 2. Длина волны Ят, на которую приходится максимум
энергии в спектре излучения черного тела, равна 0,58 мкм. Опре-
Определить максимальную спектральную плотность энергетической
светимости (M%t 7)max, рассчитанную на интервал длин волн Д^=
= 1 нм, вблизи'im.
Решение. Максимальная спектральная плотность энергети-
энергетической светимости пропорциональна пятой степени температуры
Кельвина и выражается формулой
(Мь.Т)тп = СТ1. A)
Температуру Т выразим из закона смещения Вина hm=b/T,
откуда T=b/km.
361

Подставив полученное выражение температуры в формулу
A), найдем
В табл. 24 значение С дано в единицах СИ, в которых единичный
интервал длин волн Д^=1 м. По условию же задачи требуется вы-
вычислить спектральную плотность энергетической светимости, рас-
рассчитанную на интервал длин волн 1 нм, поэтому выпишем значение С
в единицах СИ и пересчитаем его на заданный интервал длин волн:
С= 1,3010-5 Вт/(м3-К5) = 1,30-10-5 Вт/(м2.м-К5) =
-1,30-10~14 Вт/(м2.нм-К5).
Вычисление по формуле B) дает
(>Ъ Лтах-40,6 КВТДМ-НМ).
Задачи
Закон Стефана—Больцмана
34.1. Определить температуру Т, при которой энергетическая
светимость Ме черного тела равна 10 кВт/м2 .
34.2. Поток энергии Фе, излучаемый из смотрового окошка
плавильной печи, равен 34 Вт. Определить температуру Т печи,
если площадь отверстия 5=6 см2.
34.3. Определить энергию IF, излучаемую за время t~\ мин
из смотрового окошка площадью S=8 см2 плавильной печи, если ее
температура Т=1,2 кК.
34.4. Температура Т верхних слоев звезды Сириус равна 10 кК,
Определить поток энергии Фе, излучаемый с поверхности площадью
5=1 км2 этой звезды.
34.5. Определить относительное увеличение А Ме/Ме энергетиче-
энергетической светимости черного тела при увеличении его температуры на
1%.
34.6. Во сколько раз надо увеличить термодинамическую тем-
температуру черного тела, чтобы его энергетическая светимость Ме
возросла в два раза?
34.7. Принимая, что Солнце излучает как черное тело, вычислить
его энергетическую светимость Ме и температуру Т его поверхности.
Солнечный диск виден с Земли под углом -Э=32. Солнечная постоян-
постоянная * С=1,4 кДж/(м2-с).
34.8. Определить установившуюся температуру Т зачерненной
металлической пластинки, расположенной перпендикулярно солнеч-
солнечным лучам вне земной атмосферы на среднем расстоянии от Земли до
Солнца. Значение солнечной постоянной приведено в предыдущей
задаче.
* Солнечной постоянной называется величина, равная поверхностной
плотности потока энергии излучения Солнца вне земной атмосферы на сред-
среднем расстоянии от Земли до Солнца.
362

34.9. Принимая коэффициент теплового излучения 8 угля при
температуре Г=600 К равным 0,8, определить: 1) энергетическую
светимость Ме угля; 2) энергию W, излучаемую с поверхности
угля с площадью S=5 см2 за время /=10 мин.
34.10. С поверхности сажи площадью S—2 см2 при температуре
Т=400 К за время t=5 мин излучается энергия W—83 Дж, Опреде-
Определить коэффициент теплового излучения е сажи.
34.11. Муфельная печь потребляет мощность Р=1 кВт. Темпе-
Температура Т ее внутренней поверхности при открытом отверстии пло-
площадью S=25 см2 равна 1,2 кК. Считая, что отверстие печи излучает
как черное тело, определить, какая часть w мощности рассеивается
стенками.
34.12. Можно условно принять, что Земля излучает как серое
тело, находящееся при температуре Г=280 К. Определить коэффи-
коэффициент теплового излучения 8 Земли, если энергетическая светимость
Ме ее поверхности равна 325 кДж/(м2-ч).
34.13. Мощность Р излучения шара радиусом R = 10 см при неко-
некоторой постоянной температуре Т равна 1 кВт. Найти эту темпера-
температуру, считая шар серым телом с коэффициентом теплового излучения
8-0,25.
Закон Вина. Формула Планка
34.14. На какую длину волны Хт приходится максимум спект-
спектральной плотности энергетической светимости (И^, г)тах черного
тела при температуре t=0 °C?
34.15. Температура верхних слоев Солнца равна 5,3 кК. Считая
Солнце черным телом, определить длину волны А,т, которой соответ-
соответствует максимальная спектральная плотность энергетической све-
светимости {M%f r)max Солнца.
34.16. Определить температуру Т черного тела, при которой
максимум спектральной плотности энергетической светимости
(Мя, r)max приходится на красную границу видимого спектра
(^=750 нм); на фиолетовую (^2=380 нм).
34.17. Максимум спектральной плотности энергетической све-
светимости (Мх r)max яркой звезды Арктур приходится на длину волны
Ят=580 нм. Принимая, что звезда излучает как черное тело, опре-
определить температуру Т поверхности звезды.
34.18. Вследствие изменения температуры черного тела макси-
максимум спектральной плотности (М^ г)тах сместился с Хх—2,4 мкм
на Х2=0,8 мкм. Как и во сколько раз изменились энергетическая
светимость Ме тела и максимальная спектральная плотность энерге-
энергетической светимости?
34.19. При увеличении термодинамической температуры Т чер-
черного тела в два раза длина волны ^т, на которую приходится макси-
максимум спектральной плотности энергетической светимости (М^ r)max,
уменьшилась на ДХ=400 нм. Определить начальную и конечную
температуры Тх и Г2.
363

34.20. Эталон единицы силы света — кандела — представляет
собой полный (излучающий волны всех длин) излучатель, поверх-
поверхность которого площадью 5=0,5305 мм2 имеет температуру t зат-
затвердевания платины, равную 1063 °С. Определить мощность Р
излучателя.
34.21. Максимальная спектральная плотность энергетической
светимости (Mit r)max черного тела равна 4,16 «1011 (Вт/м2)/м. На
какую длину волны Ят она приходится?
34.22. Температура Т черного тела равна 2 кК. Определить:
1) спектральную плотность энергетической светимости (М^ т) для
длины волны 1=600 нм; 2) энергетическую светимость Ме в интер-
интервале длин волн от Ях=590 нм до Х,2=610 нм. Принять, что средняя
спектральная плотность энергетической светимости тела в этом ин-
интервале равна значению, найденному для длины волны Х=600 нм.
§ 35. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
Основные формулы
О Формула Эйнштейна:
а) в общем случае
е = Ь = Л + Тшах, или А(о-Л + Ттах,
где e=hv=fl(i)—энергия фотона, падающего на поверхность метал-
металла; А — работа выхода электрона из металла; Ттах — максималь-
максимальная кинетическая энергия фотоэлектрона;
б) в случае, если энергия фотона много больше работы выхода
4)
ftv = Tmax, или Ao) = Tmax.
Максимальная кинетическая энергия фотоэлектрона в двух слу-
случаях (нерелятивистском и релятивистском) выражается различными
формулами:
а) если фотоэффект вызван фотоном, имеющим незначительную
энергию (ftv=feco=5 кэВ), то
¦* max ~ /г^о^тах»
где т0 — масса покоя электрона;
б) если фотоэффект вызван фотоном, обладающим большой энер-
энергией (/iv=^(o^>5 кэВ), то
Ттах = (т—т,)с\ или Гтах = mQc2( yjir^ ~~
где ^=vmaji/c; m — масса релятивистского электрона.
О Красная граница фотоэффекта
или %0 = 2nhc/A; yQ = A/h или
где Ко — максимальная длина волны излучений (v0 и coq — мини-
минимальные соответственно частота и круговая частота), при которых
еще возможен фотоэффект.
364

Примеры решения задач
Пример 1. Определить максимальную скорость итах фотоэлект-
фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым
излучением с длиной волны ^=0,155 мкм; 2) у-излучением с длиной
волны Я2=2,47 пм.
Решение. Максимальную скорость фотоэлектронов опреде-
определим из уравнения Эйнштейна для фотоэффекта:
е = Л + Гтах. A)
Энергия фотона вычисляется по формуле E=hc/X, работа выхода
А указана в табл. 20 для серебра A=4J эВ.
Кинетическая энергия фотоэлектрона в зависимости от того, ка-
какая скорость ему сообщается, может быть выражена или по класси-
классической формуле
Т = Чмр\ B)
или по релятивистской
Т= (tn—m,)c\ C)
Скорость фотоэлектрона зависит от энергии фотона, вызывающе-
вызывающего фотоэффект: если энергия фотона е много меньше энергии покоя
электрона ЕОу то может быть применена формула B); если же е
сравнима по размеру с Ео, то вычисление по формуле B) приводит к
грубой ошибке, в этом случае кинетическую энергию фотоэлектрона
необходимо выражать по формуле C).
1. В формулу энергии фотона г=Нс1'к подставим значения вели-
величин ft, си 1 и, произведя вычисления, для ультрафиолетового излу-
излучения получим
8!= 1,28 аДж=8 эВ.
Это значение энергии фотона много меньше энергии покоя элек-
электрона @,51 МэВ). Следовательно, для данного случая максимальная
кинетическая энергия фотоэлектрона в формуле A) может быть вы-
выражена по классической формуле B) е1=Л+1/2т0^ах, откуда
tW = V2 (г1 —АIщ. D)
Выпишем величины, входящие в формулу D): 8x^1,28-10~18 Дж
(вычислено выше); Л—4,7 эВ=4,7 -1,6-Ю9 Дж=0,75-10~18 Дж;
то=9,1МО-31 кг (см. табл. 24).
Подставив числовые значения в формулу D), найдем максималь-
максимальную скорость:
ишах= 1,08 Мм/с.
2. Вычислим теперь энергию фотона у-излучения:
е2 = /к?А2 = 8,04 фДж = 0,502 МэВ.
Работа выхода электрона (А=4,7 эВ) пренебрежимо мала по
сравнению с энергией ^-фотона, поэтому можно принять, что макси-
максимальная кинетическая энергия электрона равна энергии фотона:
7\паХ = е2- 0,502 МэВ.
365

Так как в данном случае кинетическая энергия электрона сравни-
сравнима с его энергией покоя, то для вычисления скорости электрона
следует взять релятивистскую формулу кинетической энергии
T=F.J> l —]\ где Е0=т0с2. Выполнив преобразования,
найдем
Сделав вычисления, получим
р-0,755.
Следовательно, максимальная скорость фотоэлектронов, вырывае-
вырываемых 7-излучением,
ятах = Ф = 226 Мм/с.
Пример 2. Определить красную границу Хо фотоэффекта для
цезия, если при облучении его поверхности фиолетовым светом
длиной волны Я=400 нм максимальная скорость итах фотоэлектро-
фотоэлектронов равна 0,65 Мм/с.
Решение. При облучении светом, длина волны Хо которого
соответствует красной границе фотоэффекта, скорость, а следова-
следовательно, и кинетическая энергия фотоэлектронов равны нулю.
Поэтому уравнение Эйнштейна для фотоэффекта г=А+Т в случае
красной границы запишется в виде
г=Л, или hc/X0=A.
Отсюда
()
Работу выхода для цезия определим с помощью уравнения Эйн-
Эйнштейна:
л rp he mv2
A-*-T = T~ — • B)
Выпишем числовые значения величин, выразив их в СИ* h=
=6,62-10~34 Дж.с;с=3.108 м/с;Я=400 нм=4.10"^м; т=9 11х
ХЮ~31 кг; и-6,5.105 м/с.
Подставив эти значения величин в формулу B) и вычислив, полу-
получим
А = 3,05- Ю-19 Дж = 0,305 аДж.
Для определения красной границы фотоэффекта подставим
значения Л, h и с в формулу A) и вычислим:
Яо=651 нм.
Задачи
35.1. Определить работу выхода А электронов из натрия, если
красная граница фотоэффекта А,о=500 нм.
35.2. Будет ли наблюдаться фотоэффект, если на поверхность
серебра направить ультрафиолетовое излучение с длиной волны Х=
=300 нм?
366

35.3. Какая доля энергии фотона израсходована на работу вы-
вырывания фотоэлектрона, если красная граница фотоэффекта Хо=
=307 нм и максимальная кинетическая энергия 7тах фотоэлектрона
равна 1 эВ?
35.4. На поверхность лития падает монохроматический свет (А,=
=310 нм). Чтобы прекратить эмиссию электронов, нужно приложить
задерживающую разность потенциалов U не менее 1,7 В. Определить
работу выхода А.
35.5. Для прекращения фотоэффекта, вызванного облучением
ультрафиолетовым светом платиновой пластинки, нужно прило-
приложить задерживающую разность потенциалов U1=3J В. Если пла-
платиновую пластинку заменить другой пластинкой, то задерживающую
разность потенциалов придется увеличить до 6 В. Определить ра-
работу А выхода электронов с поверхности этой пластинки.
35.6. На цинковую пластинку падает монохроматический свет
с длиной волны Х=220 нм. Определить максимальную скорость
vmax фотоэлектронов.
35.7. Определить длину волны X ультрафиолетового излучения,
падающего на поверхность некоторого металла, при максимальной
скорости фотоэлектронов, равной 10 Мм/с. Работой выхода элект-
электронов из металла пренебречь,
35.8. Определить максимальную скорость vmaji фотоэлектронов,
вылетающих из металла под действием 7-излучения с длиной волны
Я=0,3 нм.
35.9. Определить максимальную скорость игаах фотоэлектронов,
вылетающих из металла при облучении у-фотонами с энергией е=
= 1,53 МэВ.
35.10. Максимальная скорость vmaK фотоэлектронов, вылетаю-
вылетающих из металла при облучении его у-фотонами, равна 291 Мм/с.
Определить энергию е -у-фотонов.
§ 36. ДАВЛЕНИЕ СВЕТА. ФОТОНЫ
Основные формулы
• Давление, производимое светом при нормальном падении,
р = ^A +р), или p = w(l+p),
где Е€ — облученность поверхности; с — скорость электромагнит-
электромагнитного излучения в вакууме; w — объемная плотность энергии излу-
излучения; р — коэффициент отражения.
• Энергия фотона
e=hv=hc/h, или е=^со,
где h — постоянная Планка; h=h/ Bл); v — частота света; о
круговая частота; к — длина волны.
• Масса и импульс фотона выражаются соответственно форму-
формулами
г h h
367

Примеры решения задач
Пример 1. Пучок монохроматического света с длиной волны К=
^663 нм падает нормально на зеркальную плоскую поверхность.
Поток энергии Фе=0,6 Вт. Определить силу F давления, испытывае-
испытываемую этой поверхностью, а также число N фотонов, падающих на нее
за время t=5 с.
Решение. Сила светового давления на поверхность равна
произведению светового давления р на площадь S поверхности:
F=pS. A)
Световое давление может быть найдено по формуле
р=Ееф+1)/с. B)
Подставляя выражение B)"давления света в формулу A), получим
F = ^(P+1). C)
Так как произведение облученности Е€ на площадь S поверх-
поверхности равно потоку Ф энергии излучения, падающего на поверх-
поверхность, то соотношение C) можно записать в виде
После подстановки значений Фе и с с учетом, что р=1 (поверх-
(поверхность зеркальная), получим
F=4 нН.
Число N фотонов, падающих за время А/ на поверхность, опре-
определяется по формуле
где AW— энергия излучения, получаемая поверхностью за время
At.
Выразив в этой формуле энергию фотона через длину волны (е=
=hc/k), получим
N=O>№t/(hc).
Подставив в этой формуле числовые значения величин, найдем
iV = Ю19 фотонов.
Пример 2. Параллельный пучок света длиной волны А-=500 нм
падает нормально на зачерненную поверхность, производя давление
р=\0 мкПа. Определить: 1) концентрацию п фотонов в пучке; 2)
число пг фотонов, падающих на поверхность площадью 1 м2 за вре-
время 1 с.
Решение. 1. Концентрация п фотонов в пучке может быть
найдена, как частное от деления объемной плотности энергии w на
энергию е одного фотона:
n=w/e. A)
Из формулы p=w(l+p), определяющей давление света, где р—
коэффициент отражения, найдем
w=p/(р+1). B)
368

Подставив выражение %ля w из уравнения B) в формулу A),
получим
Энергия фотона зависит от частоты v, а следовательно, и от длины
световой волны Я:
D)
Подставив выражение для энергии фотона в формулу C), опре-
определим искомую концентрацию фотонов:
"=<
Коэффициент отражения р для зачерненной поверхности прини-
принимаем равным нулю.
Подставив числовые значения в формулу E), получим
п-2,52-1013 м.
2. Число пг фотонов, падающих на поверхность площадью 1 м2
за время 1 с, найдем из соотношения nx~NI (St), где N — число фо-
фотонов, падающих за время / на поверхность площадью S. Но N=
=ncSt, следовательно,
ncSt
Подставив сюда значения п и с, получим
Ях-7,56-1021 м-2.с-\
Задачи
36.1. Определить давление р солнечного излучения на зачернен-
зачерненную пластинку, расположенную перпендикулярно солнечным лу-
лучам и находящуюся вне земной атмосферы на среднем расстоянии
от Земли до Солнца (см. сноску к задаче 34.7).
36.2. Определить поверхностную плотность / потока энергии
излучения, падающего на зеркальную поверхность, если световое
давление р при перпендикулярном падении лучей равно 10 мкПа.
36.3. Поток энергии Фе, излучаемый электрической лампой, ра-
равен 600 Вт. На расстоянии г= 1 м от лампы перпендикулярно падаю-
падающим лучам расположено круглое плоское зеркальце диаметром
d=2 см. Принимая, что излучение лампы одинаково во всех направ-
направлениях и что зеркальце полностью отражает падающий на него
свет, определить силу F светового давления на зеркальце.
36.4. На зеркальце с идеально отражающей поверхностью пло-
площадью S=l,5 см2 падает нормально свет от электрической дуги.
Определить импульс р, полученный зеркальцем, если поверхност-
поверхностная плотность потока излучения ср, падающего на зеркальце, равна
0,1 МВт/м2. Продолжительность облучения ?=1 с.
36.5. Спутник в форме шара движется вокруг Земли на такой
высоте, что поглощением солнечного света в атмосфере можно пре-
пренебречь. Диаметр спутника d=40 м. Зная солнечную постоянную
369

(см. задачу 34.7) и принимая, что поверхность спутника полностью
отражает свет, определить силу давления F солнечного света на
спутник.
36.6. Определить энергию е, массу т и импульс р фотона, кото-
которому соответствует длина волны А=380 нм (фиолетовая граница
видимого спектра).
36.7. Определить длину волны Я, массу т и импульс р фотона с
энергией е=1 МэВ. Сравнить массу этого фотона с массой покояще-
покоящегося электрона.
36.8. Определить длину волны А, фотона, импульс которого ра-
равен импульсу электрона, обладающего скоростью и=10 Мм/с.
36.9. Определить длину волны X фотона, масса которого равна
массе покоя: 1) электрона; 2) протона.
36.10. Давление р монохроматического света (^=600 нм) на чер-
черную поверхность, расположенную перпендикулярно падающим лу-
лучам, равно 0,1 мкПа. Определить число N фотонов, падающих за
время t=\ с на поверхность площадью S=l см2.
36.11. Монохроматическое излучение с длиной волны ^=500 нм
падает нормально на плоскую зеркальную поверхность и давит на
нее с силой /г= 10 нН. Определить число Nx фотонов, ежесекундно
падающих на эту поверхность.
36.12. Параллельный пучок монохроматического света (А—
=662 нм) падает на зачерненную поверхность и производит на нее
давление р=0,3 мкПа. Определить концентрацию п фотонов в све-
световом пучке.
§ 37. ЭФФЕКТ КОМПТОНА
Основные формулы
# Изменение длины волны ДА, фотона при рассеянии его на элек-
электроне на угол 6
Ab = V—%=-.— A— cos 9), или ДА-2 —sin2 4-,
тс х п тс 2 '
где т — масса электрона отдачи; X и Х'с — длины волн.
• Комптоновская длина волны
(При рассеянии фотона на электроне Ас=2,436 пм.)
Примеры решения задач
Пример 1. В результате эффекта Комптона фотон при соударе-
соударении с электроном был рассеян на угол 0=90°. Энергия г' рассеянного
фотона равна 0,4 МэВ. Определить энергию г фотона до рассеяния.
Решение. Для определения первичного фотона воспользу-
воспользуемся формулой Комптона в виде
370

Формулу A) преобразуем следующим образом: 1) выразим длины
волн к' и А, через энергии е'ие соответствующих фотонов, восполь-
воспользовавшись соотношением e=2nfic/X; 2) умножим числитель и зна-
знаменатель правой части формулы на с. Тогда получим
2л^с 2nfic 2nfic n . J
—т = —о-2 sin2-о- •
e e me2 2
Сократив на 2л%с, выразим из этой формулы искомую энергию:
fc — me2-8'.2 sin2 F/2) ""?0-28' — sin2 F/2) ' W
где Е0=тс2 — энергия покоя электрона.
Вычисления по формуле B) удобнее вести во внесистемных еди-
единицах. Взяв из табл. 22 значение энергии покоя электрона в мега-
электрон-вольтах и подставив числовые данные, получим
е-1,85 МэВ.
Пример 2. Фотон с энергией 8=0,75 МэВ рассеялся на свобод-
свободном электроне под углом 9—60°. Принимая, что кинетическая энер-
энергия и импульс электрона до соударения с фотоном были пренебре-
пренебрежимо малы, определить: 1) энергию г' рассеянного фотона; 2)
кинетическую энергию Т электрона отдачи; 3) направление его
движения.
Решение. 1. Энергию рассеянного фотона найдем, восполь-
воспользовавшись формулой Комптона:
Я'—Я = — A —cosB).
me v ;
Выразив длины волн А/ и К через энергии е' и г соответствующих
фотонов, получим
2rikc 2ntic 2rik n Оч
'—-, = A —COS0).
е' 8 me v ;
Разделим обе части этого равенства на 2nlic: = ~~c(f . От-
8 8 тс
сюда, обозначив для краткости энергию покоя электрона тс2 через
/?<>, найдем
8 ^ 0)
Подставив числовые значения величин, получим
е'=0,43 МэВ.
2. Кинетическая энергия электрона отдачи, как это следует из
закона сохранения энергии, равна разности между энергией 8 па-
падающего фотона и энергией е' рассеянного фотона:
Т=г—е'=0,32 МэВ.
3. Направление движения электрона отдачи найдем, применив
закон сохранения импульса, согласно которому импульс падающего
фотона р равен векторной сумме импульсов рассеянного фотона р' и
электрона отдачи mv:
371

Векторная диаграмма импульсов изображена на рис. 37.1. Все
векторы проведены из точки О, где находился электрон в момент
соударения с фотоном. Угол <р определяет направление движения
электрона отдачи.
Из треугольника OCD находим
t — 1CD I — 1СЛ | sin 9
g(p~ \OD\ ~~ \OA\ — | С A | cose '
или
j p' sin e sin e
p—p cos e pip —cos 0
Так как р=г/с и р'=е7с, то
tgq> = ,sin9 a. B)
Преобразуем формулу B) так, чтобы угол <р выражался непо-
непосредственно через величины е и 0, за-
заданные в условии задачи. Из формулы
A) следует
~3=i-(l_ cos0)+ 1. C)
Заменим в формуле B) соотношение е/е'
по формуле C):
fgtp- sin9_
Учитывая, что sin 0=2 sin @/2) cos@/2)
и 1—cos 0=2 sin2 @/2), после соответствующих преобразований
получим
fa.n-Ctgffl/Z) D)
После вычисления по формуле D) найдем tg9=O,7Ol, откуда
35°
Задачи
37.1. Рентгеновское излучение длиной волны Я=55,8 пм рассеи-
рассеивается плиткой графита (комптон-эффект). Определить длину волны
А/ света, рассеянного под углом 0=60° к направлению падающего
пучка света.
37.2. Определить максимальное изменение длины волны при
комптоновском рассеянии: 1) на свободных электронах; 2) на сво-
свободных протонах.
37.3. Определить угол 0 рассеяния фотона, испытавшего соуда-
соударение со свободным электроном, если изменение длины волны ДА,
при рассеянии равно 3,62 пм. .
37.4. Фотон с энергией 8=0,4 мэВ рассеялся под углом 0=90°
на свободном электроне. Определить энергию г' рассеянного фотона
и кинетическую энергию Т электрона отдачи.
372

37.5. Определить импульс р электрона отдачи при эффекте Комп-
тона, если фотон с энергией, равной энергии покоя электрона, был
рассеян на угол 8=180°.
37.6. Какая доля энергии фотона при эффекте Комптона прихо-
приходится на электрон отдачи, если фотон претерпел рассеяние на угол
6^=180°? Энергия е фотона до рассеяния равна 0,255 МэВ.
37.7. Фотон с энергией 8=0,25 МэВ рассеялся на свободном
электроне. Энергия е' рассеянного фотона равна 0,2МэВ. Опреде-
Определить угол рассеяния 6.
37.8. Угол рассеяния 9 фотона равен 90°. Угол отдачи <р элек-
электрона равен 30°. Определить энергию е падающего фотона.
37.9. Фотон (Х= 1 пм) рассеялся на свободном электроне под уг-
углом 0=90° Какую долю своей энергии фотон передал электрону?
37.10. Длина волны А, фотона равна комптоновской длине Хс
электрона. Определить энергию 8 и импульс р фотона.
37.11. Энергия е падающего фотона равна энергии покоя элек-
электрона. Определить долю w1 энергии падающего фотона, которую
сохранит рассеянный фотон, и долю w2 этой энергии, полученную
электроном отдачи, если угол рассеяния 8 равен: 1) 60°; 2) 90°; 3) 180°.
§ 38. АТОМ ВОДОРОДА ПО ТЕОРИИ БОРА
Основные формулы
• Момент импульса электрона на стационарных орбитах *
L = mvr = rik (л=1, 2, 3, ...),
где т — масса электрона; г — радиус орбиты; v — скорость элект-
электрона на орбите; п — главное квантовое число; % — постоянная
Планка.
• Энергия электрона, находящегося на /г-й орбите,
Е г=- те*
где 80 — электрическая постоянная.
• Сериальная формула, определяющая длину волны А, или ча-
частоту v света, излучаемого или поглощаемого атомом водорода при
переходе из одного стационарного состояния в другое,
где R' и R — постоянная Ридберга (i?' = l,097*107 м; R=cR'~
^3,290 *1015 с); nt и п2 — целые числа; пг — номер серии спект-
спектральных линий (пг=1 — серия Лаймана, /2i=2 — серия Бальмера,
* Бор исходил из предположения, что электроны обращаются по круго-
круговым орбитам. Зоммерфельд дополнил теорию Бора введением эллиптических
орбит. Современная физика отказалась от представления об электронных
орбитах. Вместо орбит введено понятие об энергетических уровнях атома.
При этом номера уровней совпадают с номерами боровских орбит. Однако
.в целях наглядности иногда пользуются термином «орбита». Подробнее
см. § 47.
373

П1=3 — серия Пашена и т. д.). Для данной серии n2=tti+l, nx+
+2, Пг+3 И Т. Д.
• Энергия фотона, испускаемого атомом водорода при переходе
из одного стационарного состояния в другое,
где Et — энергия ионизации * водорода: Ei=2nfiR = l3,6 эВ.
Примеры решения задач
Пример 1. Вычислить радиус первой орбиты атома водорода (бо-
ровский радиус) и скорость электрона на этой орбите.
Решение. Согласно теории Бора, радиус г электронной ор-
орбиты и скорость v электрона на ней связаны равенством mvr=nfi.
Так как в задаче требуется определить величины, относящиеся к
первой орбите, то главное квантовое число п=\ и указанное выше
равенство примет вид
mvr = fi. A)
Для определения двух неизвестных величин г и v необходимо
еще одно уравнение. В качестве второго уравнения воспользуемся
уравнением движения электрона. Согласно теории Бора, электрон
вращается вокруг ядра. При этом сила взаимодействия между
электрическими зарядами ядра и электрона сообщает электрону
центростремительное ускорение. На основании второго закона Нью-
Ньютона можем записать
г ~~ 4jte0 r2
(е и т — заряд и масса электрона), или
--hit- <2>
Совместное решение равенств A) и B) относительно г дает
Подставив сюда значения %, е, т и произведя вычисления, най-
найдем боровский радиус:
ri-a-5,29-10-11 м.
Из равенства A) получим выражение скорости электрона на
первой орбите:
v = 'h/(mr).
Произведя вычисления по этой формуле, найдем
0=2,18 Мм/с.
* Энергия ионизации, выраженная в электрон-вольтах, равна потенци-
потенциалу ионизации, выраженному в вольтах. Потенциалом ионизации называется
ускоряющая разность потенциалов, которую должен пройти бомбардирую-
бомбардирующий электрон, чтобы приобрести энергию, достаточную для ионизации атома.
374

Пример 2. Определить энергию 8 фотона, соответствующего вто-
второй линии в первой инфракрасной серии (серии Пашена) атома
водорода.
Решение. Энергия 8 фотона, излучаемого атомом водорода
при переходе электрона с ^
одной орбиты на другую, ^*^ ""-¦-С^
Излучение, соотбетстбу-
ющее спектральной ли-
серии Пашена
где Et — энергия иониза-
ионизации атома водорода; п1=
= 1,2,3,...— номер орбиты,
на которую переходит
электрон (рис. 38.1); п2=
+l +2 +
Рис. 38.1
номер орбиты, с которой
переходит электрон; т —
номер спектральной линии
в данной серии. Для серии Пашена #1=3; для второй линии этой
серии т=2, п2=п1+т= 3+2=5.
Подставив числовые значения, найдем энергию фотона:
8=0,97 эВ.
Задачи
38.1. Вычислить радиусы г2 и г3 второй и третьей орбит
в атоме водорода.
38.2. Определить скорость v электрона на второй орбите атома
водорода.
38.3. Определить частоту обращения электрона на второй орбите
атома водорода.
38.4. Определить потенциальную П, кинетическую Т и полную
Е энергии электрона, находящегося на первой орбите атома водоро-
водорода.
38.5. Определить длину волны Я, соответствующую третьей
спектральной линии в серии Бальмера.
38.6. Найти наибольшую Ятах и наименьшую A,min длины волн в
первой инфракрасной серии спектра водорода (серии Пашена).
38.7. Вычислить энергию 8 фотона, испускаемого при переходе
электрона в атоме водорода с третьего энергетического уровня на
первый.
38.8. Определить наименьшую 8mln и наибольшую етах энергии
фотона в ультрафиолетовой серии спектра водорода (серии Лаймана).
38.9. Атомарный водород, возбужденный светом определенной
длины волны, при переходе в основное состояние испускает только
три спектральные линии. Определить длины волн этих линий и ука-
указать, каким сериям они принадлежат.
38.10. Фотон с энергией 8=16,5 эВ выбил электрон из невозбуж-
375

денного атома водорода. Какую скорость v будет иметь электрон вда-
вдали от ядра атома?
38.11. Вычислить длину волны X, которую испускает ион гелия
Не+ при переходе со второго энергетического уровня на первый.
Сделать такой же подсчет для иона лития Li+ + .
38.12. Найти энергию Et и потенциал Ut ионизации ионов Не+
и Li+ + .
38.13. Вычислить частоты Д и /2 вращения электрона в атоме во-
водорода на второй и третьей орбитах. Сравнить эти частоты с частотой
v излучения при переходе электрона с третьей на вторую орбиту.
38.14. Атом водорода в основном состоянии поглотил квант света
с длиной волны Х= 121,5 нм. Определить радиус г электронной орби-
орбиты возбужденного атома водорода.
38.15. Определить первый потенциал Ux возбуждения атома водо-
водорода.
§ 39. РЕНТГЕНОВСКОЕ ИЗЛУЧЕНИЕ
Основные формулы
• Коротковолновая граница Ят1п сплошного рентгеновского
спектра
. __ 2nfic
Amln — | е | и f
где е — заряд электрона; U — разность потенциалов, приложенная
к рентгеновской трубке; % — постоянная Планка.
• Закон Мозли:
а) в общем случае
<o=CR(Z—o)\
где со — частота линий рентгеновского спектра; Z — атомный но-
номер элемента, излучающего этот спектр; R — постоянная Рид-
берга (#=2,07-1016 с); а — постоянная экранирования; С —
постоянная;
б) для /Са-линий (сг=1, С=3/4)
0)Ka = 3/4jR(Z_1J или _L_3/4jR'(Z__1J>
где R' — штрихованная постоянная Ридберга (/?' = 1,1(Ы07 м);
1/А,— (о/ Bпс) — волновое число *.
• Энергия фотона /Са-линии рентгеновского излучения
где Et — энергия ионизации атома водорода.
* Волновое число v= lA, не следует путать с циклическим волновым чис-
числом k=2n/'k.
376

Примеры решения задач
Пример 1. Определить длину волны к%а и энергию г^а фотона
Ка-линии рентгеновского спектра, излучаемого вольфрамом при
бомбардировке его быстрыми электронами.
Решение. При бомбардировке вольфрама быстрыми элект-
электронами возникает рентгеновское излучение, имеющее линейчатый
спектр. Быстрые электроны, проникая внутрь электронной оболоч-
оболочки атома, выбивают электроны, принадлежащие электронным слоям.
ха-
характеристическое
излучение ка-линии.
Рис. 39.1
Ближайший к ядру электронный слой (/(-слой) содержит два элект-
электрона. Если один из этих электронов оказывается выбитым за пре-
пределы атома, то на освободившееся место переходит электрон из
вышележащих слоев (L, M, N). При этом возникает соответствую-
соответствующая линия /(-серии. При переходе электрона с L-слоя на /(-слой из-
излучается наиболее интенсивная /(а-линия рентгеновского спектра
(рис. 39.1).
Длина волны этой линии определяется по закону Мозли:
откуда
Kol 3R'(Z—IJ'
Подставив сюда значения Z (для вольфрама Z=74) и R\ найдем
^ = 2,28-lO1 м = 22,8 пм.
Зная длину волны, определим энергию фотона по формуле
Подставив в эту формулу значения %у с, ККа и произведя вы-
вычисления, найдем
е^ = 54,4 кэВ.
377

Заметим, что энергию фотона а-линии /(-серии рентгеновского
излучения можно определить также непосредственно по формуле
о
eKa = -j- E{(Z—IJ, приведенной в начале параграфа.
Пример 2. Определить напряжение U, под которым работает
рентгеновская трубка, если коротковолновая граница ^min в спектре
тормозного рентгеновского излучения оказалась равной 15,5 пм.
Решение. Тормозное рентгеновское излучение возникает
за счет энергии, теряемой электроном при торможении. В рентгенов-
рентгеновской трубке электрон приобретает кинетическую энергию Т, кото-
которая связана с ускоряющей разностью потенциалов U соотношением
T=\e\U, A)
где е — заряд электрона.
В соответствии с законом сохранения энергии энергия фотона
не может превысить кинетической энергии электрона (Йсо<Г).
Максимальная энергия фотона в этом случае определяется равенст-
равенством
й<*тах = т = \е\и. B)
Так как максимальная угловая частота сотах связана с минимальной
длиной волны Xmin соотношением
то из выражений A) и B) находим
тг 2nkc
u=J7lu-
Произведем вычисления:
U~- 1,60.10-*М,55.Ю-" Ь~/^'1и В = 79,8кВ.
Задачи
39.1. Определить скорость v электронов, падающих на антикатод
рентгеновской трубки, если минимальная длина волны кт1л в сплош-
сплошном спектре рентгеновского излучения равна 1 нм.
39.2. Определить коротковолновую границу ^min сплошного
спектра рентгеновского излучения, если рентгеновская трубка ра-
работает под напряжением [/=30 кВ.
39.3. Вычислить наибольшую длину волны А,тах в /(-серии ха-
характеристического рентгеновского спектра скандия.
39.4. При исследовании линейчатого рентгеновского спектра
некоторого элемента было найдено, что длина волны К линии Ка
равна 76 пм. Какой это элемент?
39.5. Какую наименьшую разность потенциалов ?/min нужно
приложить к рентгеновской трубке, антикатод которой покрыт
ванадием (Z=23), чтобы в спектре рентгеновского излучения появи-
появились все линии /(-серии ванадия? Граница /(-серии ванадия А,=226 пм.
39.6. Определить энергию г фотона, соответствующего линии
Ка в характеристическом спектре марганца (Z=25).
378

39.7. В атоме вольфрама электрон перешел с М-слоя на L-слой.
Принимая постоянную экранирования а равной 5,5, определить
длину волны X испущенного фотона.
39.8. Рентгеновская трубка работает под напряжением [/= 1 MB.
Определить наименьшую длину волны A,min рентгеновского излуче-
излучения.
39.9. Вычислить длину волны X и энергию 8 фотона, принадле-
принадлежащего /Са-линии в спектре характеристического рентгеновского
излучения платины.
39.10. При каком наименьшем напряжении Um{n на рентгенов-
рентгеновской трубке начинают появляться линии серии Ко. меди?

ГЛАВА 8
ФИЗИКА АТОМНОГО ЯДРА
И ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
§ 40. СТРОЕНИЕ АТОМНЫХ ЯДЕР
Основные формулы
• Ядро обозначается тем же символом, что и нейтральный
атом: ?Х,
где X — символ химического элемента; Z — зарядовое число (атом-
(атомный номер; число протонов в ядре); А—массовое число (число
нуклонов в ядре). Число N нейтронов в ядре равно разности А—Z.
ф Радиус ядра определяется соотношением
где г0 — коэффициент пропорциональности, который можно счи-
считать для всех ядер постоянным и равным 1,4-10~" м.
Примеры решения задач
Пример 1. Водород обогащен дейтерием. Определить массовые
доли wt протия и w2 дейтерия, если относительная атомная масса
Аг такого водорода оказалась равной 1,122.
Решение. Массовые доли wx протия и w2 дейтерия можно
выразить соотношениями
Wi=mJ (m1+m2); w2=m2l (т^т^, где т1 и т2— массы соот-
соответственно протия и дейтерия в смеси.
Выразим из этих равенств массы тх и т2
и подставим их в знаменатель формулы, определяющей молярную
массу М смеси (см. § 8):
%я
где Мг и М2 — молярные массы компонентов смеси.
После такой подстановки и простых преобразований получим
Так как молярные массы протия и дейтерия пропорциональны их
относительным атомным массам, то равенство A) можно переписать
в виде
380

где Аг1 и Лг2 — относительные атомные массы соответственно протия
и дейтерия.
Заметим далее, что сумма массовых долей всех компонентов
должна быть равна единице, т. е.
Wx+W 2=1. C)
Решив совместно равенства B) и C), найдем
_ ЛпАг2— АгАп . . .v
В табл. 21 найдем: Лг1= 1,00783, Лг2=2,01410.
Подставив числовые значения величин в D) и E), получим
о;^ 0,796 и а;2=0,204.
Пример 2. Определить отношение сечений gJo2 ядер висмута
и алюминия JJA1.
Решение. Будем рассматривать ядро как шар радиусом г.
Тогда площадь его поперечного сечения (сечения ядра) может быть
найдена по формуле
о=пг2.
Радиус ядра зависит от числа нуклонов в ядре (массового числа А)
и определяется соотношением
г г Л 1/3
где г0 — коэффициент пропорциональности, практически одинако-
одинаковый для всех ядер. Тогда
о = пг20А2/\
Используя это выражение, найдем сечения а± и а2 ядер висмута
и алюминия с массовыми числами Ах и Л2:
a1 = nr\A\z и о2 = пг20А%3.
Отношение сечений найдем разделив ах на ст2:
Сделав подстановку числовых значений (Лх=209 и А 2=27),
получим
0^/G2=3,91.
Пример 3. Ядро нептуния 29з^р захватило электрон из /(-обо-
/(-оболочки атома (/(-захват) и испустило а-частицу. Ядро какого эле-
элемента получилось в результате этих превращений?
Решение. При /(-захвате из ближайшей к ядру электрон-
электронной оболочки (/(-оболочки) атома электрон захватывается ядром. В
результате этого протон в ядре превращается в нейтрон *. Общее
число нуклонов в ядре не изменяется, а зарядовое число уменьшится
на единицу. Поэтому промежуточное ядро будет иметь зарядовое
число 93—1 =92; массовое число останется прежним — 234. Цо
* При /(-захвате из ядра выбрасывается нейтрино, однако для реше-
решения данной задачи это существенной роли не играет.
381

таблице Д. И. Менделеева определяем, что промежуточным ядром
является изотоп урана 2Ц11.
Промежуточное ядро испустило а-частицу. Так как а-частица
(ядро атома изотопа гелия\Не) содержит два протона и два нейтрона,
то промежуточное ядро 2Ц1] при акте испускания а-частицы умень-
уменьшит зарядовое число на две единицы и массовое число на четыре
единицы. Таким образом, конечное ядро будет иметь Z=90 и Л =
=230, что соответствует изотопу тория ^Th.
Вопросы и задачи
Масса ядра
40.1. Зная постоянную Авогадро NA, определить массу /па
нейтрального атома углерода 12С и массу т, соответствующую угле-
углеродной единице массы. .
40.2. Чем отличаются массовое число от относительной массы
ядра?
40.3. Хлор представляет собой смесь двух изотопов с относитель-
относительными атомными массами Лг1=34,969 и Лг2=36,966. Вычислить от-
относительную атомную массу Лг хлора, если массовые доли w± и
w2 первого и второго изотопов соответственно равны 0,754 и 0,246.
40.4. Бор представляет собой смесь двух изотопов с относитель-
относительными атомными массами Лг1= 10,013 и Лг2= 11,009. Определить
массовые доли хюг и w2 первого и второго изотопов в естественном
боре. Относительная атомная масса Лг бора равна 10,811.
40.5. Какую часть массы нейтрального атома плутония состав-
составляет масса его электронной оболочки?
40.6. Определить массу ядра лития, если масса нейтрального
атома лития равна 7,01601 а. е. м.
Состав ядра. Размеры ядра
40.7. Укажите, сколько нуклонов, протонов, нейтронов содержат
следующие ядра: 1) *Не; 2) 105В; 3) ??Na; 4) JJFe; 5) ^Ag; 6) 293*U.
40.8. Напишите символические обозначения ядер изотопов водо-
водорода и назовите их.
40.9. Укажите, сколько существует изобар с массовым числом
Л=3. Напишите символические обозначения ядер.
40.10. Какие изотопы содержат два нейтрона? (Дать символичес-
символическую запись ядер.)
40.11. Определить атомные номера, массовые числа и химические
символы зеркальных ядер, которые получатся, если в ядрах |Не,
JBe, *дО протоны заменить нейтронами, а нейтроны — протонами.
Привести символическую запись получившихся ядер.
40.12. Определить диаметры следующих ядер: 1) ILi; 2) JJA1;
3) SJCu; 4) ToSn; 5) 218*Ро.
40.13. Определить концентрацию нуклонов в ядре.
382

40.14. Оценить, какую часть от объема атома кобальта состав-
составляет объем его ядра. Плотность р кобальта равна 4,5 -103 кг/м3.
40.15. Показать, что средняя плотность (р) ядерного вещества
одинакова для всех ядер. Оценить (по порядку величины) ее значе-
значение.
40.16. Используя соотношение Z—Л/2, которое справедливо
для многих легких ядер, определить среднюю объемную плотность
заряда ядра.
40.17. Два ядра ^В сблизились до расстояния, равного диаметру
ядра. Считая, что масса и заряд равномерно распределены по объе-
объему ядра, определить силу Р1 гравитационного притяжения, силу
F2 кулоновского отталкивания и отношение этих сил (FJF?).
Спин и магнитный момент ядра
40.18. Каково значение спина нуклона (в единицах ft)?
40.19. Что называется спином ядра? Из чего он складывается?
40.20. Какие значения может иметь спин ядра (в единицах %)?
40.21. Какие теоретически возможные значения спина (в едини-
единицах Ь) могут иметь следующие ядра: 1) |Н; 2) JH; 3) 32Не; 4) ?Не?
40.22. Какие значения может иметь спин (в единицах К) следую-
следующих ядер: 1) четно-четных; 2) четно-нечетных; 3) нечетно-четных;
4) нечетно-нечетных?
40.23. В первоначальной модели ядра предполагалось, что ядро
состоит из протонов и электронов. Показать, что это предположение
не оправдывается, например для ядра азота ^N (азотная катастро-
катастрофа). Спин ядра азота равен К, протона 1I2K и электрона Х1г%.
40.24. Спин дейтрона, находящегося в основном состоянии, ра-
равен %. Зная, что спиновое квантовое число протона равно 1/2, опре-
определить теоретически возможные значения спина нейтрона.
40.25. Что такое ядерный магнетон и как он выражается?
40.26. Каково соотношение между ядерным магнетоном и магне-
магнетоном Бора?
40.27. Как выражается магнитный момент ядра?
40.28. Чем обусловлено сверхтонкое расщепление спектральных
линий? В чем отличие сверхтонкого расщепления от тонкого?
Модели ядра
40.29. В чем сущность капельной модели ядра?
40.30. Какие явления объясняет капельная модель ядра?
40.31. В чем сущность оболочечной модели ядра?
40.32. Какие явления объясняет оболочечная модель ядра?
40.33. Могут ли электроны находиться в ядре? Ответ обосновать.
40.34. Какие ядра называются магическими? дважды магичес-
магическими?
383

Ядерные силы
40.35. К какому типу взаимодействия относятся ядерные силы?
40.36. В чем проявляется короткодействующий характер ядер-
ядерных сил?
40.37. Что такое зарядовая независимость?
40.38. В чем проявляется нецентральный характер ядерных сил?
40.39. Что означает свойство насыщения ядерных сил?
40.40. Что называется виртуальными частицами и какую роль
они играют в объяснении ядерных сил?
Превращение ядер
40.41. Ядро радия 2ggRa выбросило а-частицу (ядро атома гелия
^Не). Найти массовое число А и зарядовое число Z вновь образо-
образовавшегося ядра. По таблице Д. И. Менделеева определить, какому
элементу это ядро соответствует.
40.42. Ядро азота ^N захватило а-частицу и испустило протон.
Определить массовое число А и зарядовое число Z образовавше-
образовавшегося в результате этого процесса ядра. Указать, какому элементу
это ядро соответствует.
40.43. Ядро цинка HZn захватило электрон из /(-оболочки атома
(/(-захват). Указать, в ядро какого элемента превратилось ядро
цинка (написать химический символ элемента, массовое и зарядовое
число).
40.44. Ядро берилия ^Ве захватило электрон из /(-оболочки ато-
атома. Какое ядро образовалось в результате /С-захвата?
40.45. В ядре изотопа углерода г\С один из нейтронов превратил-
превратился в протон (Р~-распад). Какое ядро получилось в результате такого
превращения?
40.46. Два ядра гелия ЦНе) слились в одно ядро, и при этом был
выброшен протон. Укажите, ядро какого элемента образовалось в
результате такого превращения (приведите символическую запись
ядра).
40.47. В ядре изотопа кремния gSi один из протонов превратился
в нейтрон (Р+-распад). Какое ядро получилось в результате такого
превращения?
40.48. Ядро цинка ЦЪп захватило электрон из К-оболочки и
спустя некоторое время испустило позитрон. Какое ядро получилось
в результате таких превращений?
40.49. Ядро плутония 2д|Ри испытало шесть последовательных
а-распадов. Написать цепочку ядерных превращений с указанием
химических символов, массовых и зарядовых чисел промежуточ-
промежуточных ядер и конечного ядра.
40.50. Покоившееся ядро радона 22J!Rn выбросило а:частицу со
скоростью и= 16 Мм/с. В какое ядро превратилось ядро радона?
Какую скорость vx получило оно в результате отдачи?
384

§ 41. РАДИОАКТИВНОСТЬ
Основные формулы
9 Основной закон радиоактивного распада
где N — число нераспавшихся атомов в момент времени t\ No—
число нераспавшихся атомов в момент, принятый за начальный
(при t=0); е — основание натуральных логарифмов; А, — постоян-
постоянная радиоактивного распада.
• Период полураспада Г1/2 — промежуток времени, за который
число нераспавшихся атомов уменьшается в два раза. Период полу-
полураспада связан с постоянной распада соотношением
т _1п2 _ 0,693
1x12 - к ТГШ
• Число атомов, распавшихся за время /,
ДМ = No—N = No (I — е~х0-
Если промежуток времени Д/<с7\/2, то для определения числа
распавшихся атомов можно применять приближенную формулу
AN&KNAL
Среднее время жизни т радиоактивного ядра — промежуток
времени, за который число нераспавшихся ядер уменьшается в е
раз:
т=1Л,.
• Число атомов, содержащихся в радиоактивном изотопе,
где т — масса изотопа; М — его молярная масса; NA— постоян-
постоянная Авогадро.
• Активность А нуклида в радиоактивном источнике (актив-
(активность изотопа) есть величина, равная отношению числа dN ядер,
распавшихся в изотопе, к промежутку времени cU, за которое
произошел распад. Активность определяется по формуле
л—%-м.
или после замены N по основному закону радиоактивного распада
Активность изотопа в начальный момент времени (/=0)
А0=Ш0.
Активность изотопа изменяется со временем по тому же закону,
что и число нераспавшихся ядер:
А=Аое-м.
0 Массовая активность а радиоактивного источника есть вели-
13 х, 1268 385

чина, равная отношению его активности А к массе т этого источни-
источника, т. е.
а=А/т.
О Если имеется смесь ряда радиоактивных изотопов, образую-
образующихся один из другого, и если постоянная распада X первого члена
ряда много меньше постоянных всех остальных членов ряда, то в
смеси устанавливается состояние радиоактивного равновесия, при
котором активности всех членов ряда равны между собой:
Примеры решения задач
Пример 1. Определить начальную активность Ао радиоактив-
радиоактивного магния 27Mg массой т=0,2 мкг, а также активность А по исте-
истечении времени t=l ч. Предполагается, что все атомы изотопа ра-
радиоактивны.
Решение. Начальная активность изотопа
A0 = XN0, A)
где X — постоянная радиоактивного распада; iV0 — количество ато-
атомов изотопа в начальный момент (/—0).
In 2
Гхуа
вид
Если учесть, что Х=--~— у Л^о — ^^л» то формула A) примет
Ь2. B)
Выразим входящие в эту формулу величины в СИ и произведем
вычисления:
Л0=5,15-1012 Бк-5,15ТБк.
Активность изотопа уменьшается со временем по закону
А=Аое-м. C)
Заменив в формуле C) постоянную распада X ее выражением, по-
получим
А = Аое~1п2'*/Ту* =А0 (eln ^)~t/T^.
Так как еЫ2=2, то окончательно будем иметь
Сделав подстановку числовых значений, получим
Л-8,05-1010 Бк=80,5 ГБк .
Пример 2. При определении периода полураспада 7\/2 коротко-
живущего радиоактивного изотопа использован счетчик импульсов.
За время At= 1 мин в начале наблюдения (^0) было насчитано ^пг=
=250 импульсов, а по истечении времени ?=1 ч—Ап2=92 импуль-
импульса. Определить постоянную радиоактивного распада X и период
полураспада Г1/2 изотопа.
Решение. Число импульсов Ад, регистрируемых счетчиком
за время А^, пропорционально числу распавшихся атомов
386

Таким образом, при первом измерении
где N± — количество радиоактивных атомов к моменту начала от-
отсчета; k — коэффициент пропорциональности (постоянный для
данного прибора и данного расположения прибора относительно
радиоактивного изотопа).
При повторном измерении (предполагается, что расположение
приборов осталось прежним)
где N2 — количество радиоактивных атомов к моменту начала вто-
второго измерения.
Разделив соотношение A) на выражение B) и приняв во внима-
внимание, что по условию задачи At одинаково в обоих случаях, а также
что N± и Л^2 связаны между собой соотношением N2=Nie~lt, по-
получим
?г = е«, C)
где t — время, прошедшее от первого до второго измерения. Для вы-
вычислена
откуда
числения X выражение C) следует прологарифмировать: In j—-=^
t Дя2
Подставив числовые данные, получим постоянную радиоактив-
радиоактивного распада, а затем и период полураспада:
« __ 1 250 _!_ 1 _ь
~ In 2 0,693 Л ?ПО л -
Т\/2 = -пг- = -ly~ ч = 0,693 ч = 41,5 мин.
Задачи
Закон радиоактивного распада
41.1. Какова вероятность W того, что данный атом в изотопе ра-
радиоактивного йода 1311 распадается в течение ближайшей секунды?
41.2. Определить постоянные распада X изотопов радия 2J|Ra и
¦SSRa.
41.3. Постоянная распада X рубидия 89Rb равна 0,00077 с.
Определить его период полураспада 71/2.
41.4. Какая часть начального количества атомов распадется за
один год в радиоактивном изотопе тория 228Th?
41.5. Какая часть начального количества атомов радиоактивного
актиния 225Ас останется через 5 сут? через 15 сут?
41.6. За один год начальное количество радиоактивного изотопа
уменьшилось в три раза. Во сколько раз оно уменьшится за два года?
13* 387

41.7. За какое время t распадается V4 начального количества
ядер радиоактивного изотопа, если период его полураспада 7\/2 =
=24 ч?
41.8. За время /=8 сут распалось &=3/4 начального количества
ядер радиоактивного изотопа. Определить период полураспада 7\/2.
41.9. При распаде радиоактивного полония 210Ро в течение вре-
времени ?=1 ч образовался гелий 4Не, который при нормальных усло-
условиях занял объем V=89,5 см3. Определить период полураспада 7\/3
полония.
41.10. Период полураспада Г1/2 радиоактивного нуклида равен
1 ч. Определить среднюю продолжительность т жизни этого нуклида.
41.11. Какая часть начального количества радиоактивного нук-
нуклида распадается за время t, равное средней продолжительности
т жизни этого нуклида?
Активность. Радиоактивное равновесие
41.12. Определить число N атомов, распадающихся в радиоактив-
радиоактивном изотопе за время ?=10 с, если его активность А=0,1 МБк.
Считать активность постоянной в течение указанного времени.
41.13. Активность А препарата уменьшилась в /г=250 раз.
Скольким периодам полураспада 7\/2 равен протекший промежуток
времени ??
41.14. За время ?=1 сут активность изотопа уменьшилась от Лг=
= 118 ГБк до А2=7,4 ГБк. Определить период полураспада 7\/2
этого нуклида.
41.15. На сколько процентов снизится активность А изотопа
иридия 1921г за время ?=30 сут?
41.16. Определить промежуток времени т, в течение которого
активность А изотопа стронция 90Sr уменьшится в йх=10 раз? в
/?2=100 раз?
41.17. Счетчик Гейгера, установленный вблизи препарата ради-
радиоактивного изотопа серебра, регистрирует поток |3-частиц. При пер-
первом измерении поток Фх частиц был равен 87 с, а по истечении
времени t—\ сут поток Ф2 оказался равным 22 с. Определить
период полураспада Г1/2 изотопа.
41.18. Определить активность А фосфора 32Р массой т=\ мг.
41.19. Вычислить удельную активность а кобальта 60Со.
41.20. Найти отношение массовой активности ах стронция 90Sr
к массовой активности а2 радия 226Ra.
41.21. Найти массу тг урана 238U, имеющего такую же актив-
активность Л, как стронций 90Sr массой т2=1 мг.
41.22. Определить массу т2 радона 222Rn, находящегося в ради-
радиоактивном равновесии с радием 226Ra массой т1=1 г.
41.23. Уран 234U является продуктом распада наиболее распро-
распространенного изотопа урана 238U. Определить период полураспада
7\ , урана 234U, если его массовая доля w в естественном уране 238U
равна 6-10~^
388

41.24. Радиоактивный изотоп UNa излучает у-кванты энергией
е= 1,28 МэВ. Определить мощность Р гамма-излучения и энергию
W, излучаемую за время t=b мин изотопом натрия массой т=5 г.
Считать, что при каждом акте распада излучается один 7"Ф0Т0Н с
указанной энергией.
41.25. Точечный изотропный радиоактивный источник создает
на расстоянии г=\ м интенсивность / гамма-излучения, равную
1,6 мВт/м2. Принимая, что при каждом акте распада ядра излу-
излучается один ^-фотон с энергией 8=1,33 МэВ, определить активность
А источника.
41.26. Определить интенсивность / гамма-излучения на расстоя-
расстоянии г=5 см от точечного изотропного радиоактивного источника,
имеющего активность А = 148 ГБк. Считать, что при каждом акте
распада излучается в среднем п=1,8 ^-фотонов с энергией е=
=0,51 МэВ каждый.
§ 42. ЭЛЕМЕНТЫ ДОЗИМЕТРИИ ИОНИЗИРУЮЩИХ ИЗЛУЧЕНИЙ
Основные формулы
Закон ослабления узкого пучка моноэнергетических
чений при прохождении через поглощающее вещество:
а) ослабление плотности потока ионизирующих частиц или фото-
фотонов
где /0 — плотность потока частиц, падающих на поверхность ве-
вещества; J — плотность потока частиц после прохождения слоя ве-
вещества толщиной х; \i — линейный коэффициент ослабления
(рис. 42.1);
б) ослабление интенсивности излучений
/ = /ое"^,
где / — интенсивность у-излучений в веществе на глубине х\ /0 —
интенсивность у-излучений, падающих на поверхность вещества.
• Слоем половинного ослабления называется слой, толщина
#1/2 которого такова, что интенсивность проходящих через него
у-излучений уменьшается в два раза:
In 2 0,693
Доза излучения (поглощенная доза излучения)
где Д№ — энергия ионизирующего излучения, переданная элементу
облучаемого вещества; Am — масса этого элемента.
Доза излучения выражается в греях A Гр = 1 Дж/кг).
Мощность дозы излучения (мощность поглощенной дозы излуче-
излучения)
389

где At— время, в течение которого была поглощена элементом
облучения доза излучения AD.
Мощность дозы излучения выражается в греях в секунду (Гр/с).
# Экспозиционная доза фотонного излучения (экспозиционная
доза гамма- и рентгеновского излучения) есть величина, равная
отношению суммы электрических зарядов AQ всех ионов одного
знака, созданных электронами, освобожденными в облученном воз-
воздухе при условии полного использования ионизирующей способ-
способности электронов, к массе Am этого воздуха:
X=AQ/Am.
Единица экспозиционной дозы — кулон на килограмм (Кл/кг).
• Мощность экспозиционной дозы фотонного излучения X
есть величина, равная отношению экспозиционной дозы АХ фотон-
фотонного излучения к интервалу времени At, за которое получена эта
доза, т. е.
X = AX/At.
Мощность экспозиционной дозы выражается в амперах на кило-
килограмм (А/кг).
• Экспозиционная доза рентгеновского и у-излучения, падаю-
падающего на объект, экранированный защитным слоем толщиной х,
где Хо — экспозиционная доза при отсутствии защитного слоя.
• Экспозиционная доза 7~излУчения> падающего за время t
на объект, находящийся в воздухе на расстоянии R от точечного
390

источника,
где X — мощность экспозиционной дозы на расстоянии, равном
единице. Поглощением у-излучением в воздухе пренебрегаем.
Примеры решения задач
Пример 1. Вычислить толщину слоя половинного ослабления
Xt/2 параллельного пучка у-излучения для воды, если линейный ко-
коэффициент ослабления |i=0,047 см.
Решение. При прохождении 7-излучения через слой веще-
вещества происходит их поглощение за счет трех факторов: фотоэффек-
фотоэффекта, эффекта Комптона и образования пар (электрон — позитрон).
В результате действия этих трех факторов интенсивность 7-излу-
чения экспоненциально убывает в зависимости от толщины слоя:
/ = /ое-^. A)
Пройдя поглощающий слой толщиной, равной толщине слоя
половинного ослабления х1/2, пучок у-излучения будет иметь интен-
интенсивность 1=10/2. Подставив значения / и х в формулу A), получим
/0/2 =/0е~й*1/2, или после сокращения на /0
Прологарифмировав последнее выражение, получим искомое
значение толщины слоя половинного ослабления:
*1/2 = 1п2/ц. B)
Подставив в формулу B) значения \i и In 2, найдем х1/2
Х\/2 = 14,7 см.
Таким образом, слой воды толщиной в 14,7 см снижает интен-
интенсивность у-излучения в два раза.
Пример 2. Точечный радиоактивный источник 60Со находится
в центре свинцового сферического контейнера с толщиной стенок
х=\ см и наружным радиусом i?=20 см. Определить максимальную
активность Лтах источника, который можно хранить в контейнере,
если допустимая плотность потока /доп ^-фотонов при выходе из
контейнера равна 8-Ю6 с~1-м. Принять, что при каждом акте
распада ядра 60Со испускается п=2 у-фотона, средняя энергия ко-
которых (е>=1,25 МэВ.
Решение. Активность радиоактивного источника связана
с потоком излучения 7-ф°тонов соотношением Ф=Ап, где п —
число у-фотонов, испускаемых при одном акте распада, откуда
А=Ф/п. A)
Поток Ф, входящий в эту формулу, выразим через плотность
потока. Плотность потока на расстоянии R от точечного источника
излучений
. B)
391

После прохождения излучений через свинцовую стенку контей-
контейнера плотность потока уменьшится и выразится соотношением /а=
= J^-^X. Выразив отсюда Jx и подставив в формулу B), найдем
откуда
ф =
Подставив выражение Ф в A), получим
Если в полученной формуле принять /2~^Доп> то эта формула
будет выражать искомую максимальную активность источника,
который можно хранить в контейнере:
Amax = inR*Jmtte»*/n. C)
По графику на рис. 42.1 находим, что линейный коэффициент
ослабления \i для 7-ф°тонов с энергией е= 1,25 МэВ равен 0,64 см.
Выразим величины, входящие в формулу C), в единицах СИ и,
выполнив вычисления, получим
Л=3,8 МБк.
Пример 3. Космическое излучение на уровне моря на экваторе
образует в воздухе объемом У=1 см3 в среднем N=24: пары ионов
за время ^=10 с. Определить экспозиционную дозу X, получаемую
человеком за время t2=l год.
Решение. Экспозиционную дозу, получаемую человеком,
можно выразить по формуле
X=Xt2, A)
где X — мощность экспозиционной дозы излучения.
Мощность дозы X=Q/(mt1)t где Q — заряд ионов одного знака,
образуемых излучением за время t1 в воздухе массой т. Масса воз-
воздуха может быть найдена как произведение плотности р воздуха
на его объем V : m=pV. Заряд всех ионов одного знака найдем,
помножив элементарный заряд на число ионов: Q=\e\N.
Формула A) с учетом выражений X, т и Q примет вид
У У/ Q , \e\Nt2 ,9.
УЛ. = Л. Ic, :=z —-— 10 = ГГ2 . I Z)
2 mtx 2 рУ^1 v ;
Выразим величины, входящие в формулу B), в единицах СИ
и, выполнив вычисления, получим
X—9,41 мкКл/кг.
Задачи
Поглощение гамма-излучений *
42.1. Определить число N слоев половинного ослабления, умень-
уменьшающих интенсивность / узкого пучка ^-излучения в fe=100 раз.
* При решении задач 42.2—42.7 воспользоваться графиком, изображен-
изображенным на рис. 42.1.
392

42.2. Определить для бетона толщину слоя половинного ослаб-
ослабления Хх/2 узкого пучка 7-излучения с энергией фотонов 8=0,6 МэВ.
42.3. На какую глубину нужно погрузить в воду источник уз-
узкого пучка 7-излучения (энергия е гамма-фотонов равна 1,6 МэВ),
чтобы интенсивность / пучка, выходящего из воды, была уменьшена
в ?=1000 раз?
42.4. Интенсивность / узкого пучка 7-излучения после про-
прохождения через слой свинца толщиной #=4 см уменьшилась в k=
=8 раз. Определить энергию е гамма-фотонов и толщину хх/2 слоя
половинного ослабления.
42.5. Через свинец проходит узкий пучок 7-излучения. При
каком значении энергии 8 гамма-фотонов толщина хг/2 слоя поло-
половинного ослабления будет максимальной? Определить максималь-
максимальную толщину хтах слоя половинного ослабления для свинца.
42.6. Узкий пучок 7-излучения (энергия г гамма-фотонов равна
2,4 МэВ) проходит через бетонную плиту толщиной хг=1 м. Какой
толщины х2 плита из чугуна дает такое же ослабление данного пучка
7-излучения?
42.7. Чугунная плита уменьшает интенсивность / узкого пучка
у-излучения (энергия 8 гамма-фотонов равна 2,8 МэВ) в &=10 раз.
Во сколько раз уменьшит интенсивность этого пучка свинцовая
плита такой же толщины?
Элементы дозиметрии
42.8. Какая доля w всех молекул воздуха при нормальных усло-
условиях ионизируется рентгеновским излучением при экспозиционной
дозе Х=258 мкКл/кг?
42.9. Воздух при нормальных условиях облучается 7-излуче-
нием. Определить энергию W, поглощаемую воздухом массой т=5 г
при экспозиционной дозе излучения Х=258 мк Кл/кг.
42.10. Под действием космических лучей в воздухе объемом V=
— I см3 на уровне моря образуется в среднем N=120 пар ионов за
промежуток времени Д/= 1 мин. Определить экспозиционную дозу X
излучения, действию которого подвергается человек за время t=
= 1 сут.
42.11. Эффективная вместимость V ионизационной камеры кар-
карманного дозиметра равна 1 см3, электроемкость С=2 пФ. Камера
содержит воздух при нормальных условиях. Дозиметр был заряжен
до потенциала фх= 150 В. Под действием излучения потенциал
понизился до ф2= 110 В. Определить экспозиционную дозу X излу-
излучения.
42.12. Мощность X экспозиционной дозы, создаваемая удален-
удаленным источником 7-излучения с энергией фотонов 8=2 МэВ, равна
0,86 мкА/кг. Определить толщину х свинцового экрана, снижаю-
снижающего мощность экспозиционной дозы до уровня предельно допусти-
допустимой Х=0,86 нА/кг (см. рис. 42.1).
42.13. На расстоянии /=10 см от точечного источника 7-излуче-
393

ния мощность экспозиционной дозы Х=0,86 мкА/кг. На каком наи-
наименьшем расстоянии /min от источника экспозиционная доза излу-
излучения X за рабочий день продолжительностью /=6 ч не превысит
предельно допустимую 5,16 мкКл/кг? Поглощением Y-излучения в
воздухе пренебречь.
42.14. Мощность экспозиционной дозы X гамма-излучения на
расстоянии /4=40 см от точечного источника равна 4,30 мкА/кг.
Определить время /, в течение которого можно находиться на рас-
расстоянии г2=6 м от источника, если предельно допустимую экспози-
экспозиционную дозу X принять равной 5,16 мкКл/кг. Поглощением 7-излу-
чения в воздухе пренебречь.
§ 43. ДЕФЕКТ МАССЫ И ЭНЕРГИЯ СВЯЗИ
АТОМНЫХ ЯДЕР
Основные формулы
О Согласно релятивистской механике, масса покоя т устойчи-
устойчивой системы взаимосвязанных частиц меньше суммы масс покоя
пг1+т2+...+п1к тех же частиц, взятых в свободном состоянии.
Разность
Ат = (т1 + т2+ . .. + тк)— т A)
называется дефектом массы системы частиц.
Ф Энергия связи прямо пропорциональна дефекту массы систе-
системы частиц:
где с — скорость света в вакууме (с2=8,987 -1016 м2/с2=8,987х
ХЮ16 Дж/кг).
Если энергия выражена в мегаэлектрон-вольтах, а масса в атом-
атомных единицах, то
с2—931,4 МэВ/а. е. м.
# Дефект массы * Am атомного ядра есть разность между сум-
суммой масс свободных протонов и нейтронов и массой образовавшегося
из них ядра:
Am = (Zmp + Nmn) — тя,
где Z — зарядовое число (число протонов в ядре); тр и тп — массы
протона и нейтрона соответственно; тя — масса ядра.
Если учесть, что
mp + me=miu; N = (A—Z),
* Термин «дефект массы» иногда применяют в другом смысле, а именно:
дефектом массы А называют разность между относительной массой Аг дан-
данного изотопа и его массовым числом Л: Д=ЛГ—Л. Таким образом, дефект
массы А показывает отклонение относительной атомной массы от целочислен-
целочисленного значения. Эта величина прямого физического смысла не имеет, но ее
использование позволяет в ряде случаев значительно упростить вычисления.
В настоящем пособии всюду имеется в виду дефект массы Am, определяе-
определяемый общей формулой A).
394

то формулу дефекта массы ядра можно представить в виде
Am = Zmin + (А—Z)mn—ma,
где А—массовое число (число нуклонов в ядре).
• Удельная энергия связи (энергия связи на нуклон)
у д — Я ев/'
Примеры решения задач
Пример 1. Вычислить дефект массы Am и энергию связи Есв
ядра ^В.
Решение. Дефект массы ядра определим по формуле
Am^Zm +(A—Z)mn—ma. A)
iH
Вычисление дефекта массы выполним во внесистемных единицах
(а. е. м.). Для ядра ^В Z=5, Л = 11. Массы нейтральных атомов
водорода (JH) и бора (ЧВ)У а также нейтрона (я) найдем из табл. 21.
Подставим найденные массы в выражение A) и произведем вычис-
вычисления:
Am-[5-1,00783+(И—5). 1,00867—11,00931]а. е.м.,
или
Am = 0,08186 а. е. м.
Энергия связи ядра определяется соотношением
Есв = Атс\ B)
Энергию связи ядра также найдем во внесистемных единицах
(МэВ). Для этого дефект массы подставим в выражение B) в а. е. м.,
а коэффициент пропорциональности (с2) — в МэВ/ (а. е. м.), т. е.
?„ = 931-4-1,08186 МэВ = 76,24 МэВ,
и округлим полученный результат до трех значащих цифр:
?св-76,2 МэВ.
Пример 2. Определить удельную энергию связи ядра |Li.
Решение. Удельная энергия связи есть энергия связи ядра,
приходящаяся на один нуклон:
или
Подставим в эту формулу значения величин (см. табл. 21,22)
и произведем вычисления:
?уд = ^[3-1,00783 + G—3)-1,00867—7,01601] МэВ/нуклон =
=5,61 МэВ/нуклон.
Пример 3. Определить энергию Еу которую нужно затратить для
отрыва нейтрона от ядра gNa.
Решение. После отрыва нейтрона число нуклонов А в ядре
уменьшится на единицу, а число протонов Z останется неизменным;
395

получится ядро 22Na. Ядро 23Na можно рассматривать как устойчи-
устойчивую систему, образовавшуюся в результате захвата свободного
нейтрона ядром 22Na. Энергия отрыва нейтрона от ядра 23Na равна
энергии связи нейтрона с ядром 22Na (Е=ЕСВ).
Выразив энергию связи нейтрона через дефект массы системы, по-
получим
Е = ?св = с2 Am = с2 (m22Na + тп—М 23Na).
При подстановке числовых значений заменяем массы ядер масса-
массами нейтральных атомов. Так как число электронов в оболочках ато-
атомов 22Na и 23Na одинаково, то разность масс атомов 23Na и 22Na от
такой замены не изменится:
? = 931,4МэВ/а. е. м.- 0,01334 а. е.м.= 12,42 МэВ.
После округления
?=12,4 МэВ.
Задачи
43.1. Используя известные значения масс нейтральных атомов
JH, 2Н, 12.С и электрона, определить массы тр протона, md дейтона,
тя ядра 12.С.
43.2. Масса та альфа-частицы (ядро гелия SHe) равна 4,00150
а. е. м. Определить массу та нейтрального атома гелия.
43.3. Зная массу та нейтрального атома изотопа лития ?Li
(см. табл. 21), определить массы т1у т2 и т3 ионов лития: одноза-
однозарядного (JLi)+, двухзарядного (lLi) + + и трехзарядного (JLi) + + + .
43.4. Определить дефект массы Am и энергию связи Есв ядра
атома тяжелого водорода.
43.5. Определить энергию ?св, которая освободится при соедине-
соединении одного протона и двух нейтронов в атомное ядро.
43.6. Определить удельную энергию связи ?уд ядра 12,С.
43.7. Энергия связи Есв ядра, состоящего из двух протонов и
одного нейтрона, равна 7,72 МэВ. Определить массу та нейтрально-
нейтрального атома, имеющего это ядро.
43.8. Определить массу /ла нейтрального атома, если ядро этого
атома состоит из трех протонов и двух нейтронов и энергия связи
Есв ядра равна 26,3 МэВ.
43.9. Атомное ядро, поглотившее у-фотон (^=0,47 пм), пришло в
возбужденное состояние и распалось на отдельные нуклоны, разле-
разлетевшиеся в разные стороны. Суммарная кинетическая энергия Т
нуклонов равна 0,4 МэВ. Определить энергию связи Есв ядра.
43.10. Какую наименьшую энергию Е нужно затратить, чтобы
разделить на отдельные нуклоны ядра ^Li и ]Ве? Почему для ядра
бериллия эта энергия меньше, чем для ядра лития?
43.11. Определить энергию Е, которая выделится при образо-
образовании из протонов и нейтронов ядер гелия ?Не массой т~\ г.
43.12. Какую наименьшую энергию Е нужно затратить, чтобы
оторвать один нейтрон от ядра азота X^N?
396

43.13. Найти минимальную энергию ?, необходимую для уда-
удаления одного протона из ядра азота ^N.
43.14. Энергия связи ?св ядра кислорода 188О равна 139,8 МэВ,
ядра фтора 1д9? — 147,8 МэВ. Определить, какую минимальную
энергию Е нужно затратить, чтобы оторвать один протон от ядра
фтора.
43.15. Какую наименьшую энергию связи Е нужно затратить,
чтобы разделить ядро |Не на две одинаковые части?
43.16. Определить наименьшую энергию Е, необходимую для
разделения ядра углерода Х|С на три одинаковые части.
§ 44. ЯДЕРНЫЕ РЕАКЦИИ
Основные формулы
• Символическая запись ядерной реакции может быть дана или
в развернутом виде, например
или сокращенно
9Ве(р, aN Li.
При сокращенной записи порядковый номер атома не пишут, так
как он определяется химическим символом атома. В скобках на пер-
первом месте ставят обозначение бомбардирующей частицы, на втором—
частицы, вылетающей из составного ядра, и за скобками — химиче-
химической символ ядра-продукта.
Для обозначения частиц приняты следующие символы: р — про-
протон, п — нейтрон, d — дейтон, t — тритон, а — альфа-частица, у —
гамма-фотон.
• Законы сохранения:
а) числа нуклонов А1+А2=А3-\-АА]
б) заряда Z1+Z2=Z3+24;
в) релятивистской полной энергии Е1-\-Е2=Е3-{-Е^
г) импульса р1+р2=Рз+р4-
Если общее число ядер и частиц, образовавшихся в результате
реакции, больше двух, то запись соответственно дополняется.
# Энергия ядерной реакции
Q = с* [(тг + т2) — (т3 + т4)],
где тх и т2 — массы покоя ядра-мишени и бомбардирующей части-
частицы; m3+/n4 — сумма масс покоя ядер продуктов реакции.
Если m1+/n2>m3+m4, то энергия освобождается, энергетиче-
энергетический эффект положителен, реакция экзотермическая.
Если m1Jrm2<:m3+m^ то энергия поглощается, энергетический
эффект отрицателен, реакция эндотермическая.
Энергия ядерной реакции может быть записана также в виде
397

где Тх и Г2 — кинетические энергии соответственно ядра-мишени
и бомбардирующей частицы; 73иГ4 — кинетические энергии вы-
вылетающей частицы и ядра — продукта реакции.
При экзотермической реакции Тз+Г^Т^+ТУ, при эндотерми-
эндотермической реакции T3+Ti<T1+T2.
Примеры решения задач
Пример 1. Найти энергию реакции
если известно, что кинетические энергии протона Тн=5,45 МэВ,
ядра гелия 7^6=4 МэВ и что ядро гелия вылетело под углом 90° к
направлению движения протона. Ядро-мишень рЗе неподвижно.
Решение. Энергия реакции Q есть разность между суммой
кинетических энергий ядер-продуктов реакции и кинетической энер-
энергией налетающего ядра:
Q==TLi + Tue-TH. A)
В этом выражении неизвестна кинетическая энергия Ти лития.
Для ее определения воспользуемся законом сохранения импульса
рН = РНе+Ры. B)
Векторы рн и рне, по условию задачи, взаимно перпендикуляр-
перпендикулярны и, следовательно, вместе с вектором ры образуют прямоуголь-
прямоугольный треугольник. Поэтому
p2u = pL + p2h- C)
Выразим в этом равенстве импульсы ядер через их кинетические
энергии. Так как кинетические энергии ядер, по условию задачи,
много меньше энергий покоя этих ядер (см. табл. 21), то можно
воспользоваться классической формулой
р*=2 тТ. D)
Заменив в уравнении C) квадраты импульсов ядер их выражения-
выражениями D), после упрощения получим
откуда
т muelue + muTu ^з,58МэВ.
mLi
Подставив числовые значения в формулу A), найдем
Q = THe +Ты —Гн = 2,13МэВ.
Пример 2. Решить задачу предыдущего примера, считая, что
кинетические энергии и направления движения ядер неизвестны.
Решение. Применим закон сохранения релятивистской пол-
полной энергии
Еве + Ен = ЕНе + Еи. A)
398

Релятивистская полная энергия ядра равна сумме энергии покоя
и кинетической энергии:
Е=тс2+Т. B)
В формуле B) для упрощения записи масса покоя обозначена не
через т0, а через т.
Так как ядро-мишень 9Ве неподвижно, то на основании фор-
формулы B) уравнение A) примет вид
твеС2 + тнс2 + Гн - тнеС2 + ^не + mLlc2 + Ти. C)
Определим энергию реакции:
Q = THe+Tu — Tu-c2[(mBe + mu) — (mHe + mLi)]. D)
При числовом подсчете массы ядер заменим массами нейтральных
атомов. Легко убедиться, что такая замена не повлияет на результат
вычисления. В самом деле, так как масса т ядра равна разности
между массой та нейтрального атома и массой Zme электронов, об-
образующих электронную оболочку, то
Q = c2[(mBe + ^rne + mu—me) — (mHe—2me + mLi—3me)]. E)
Упростив уравнение E), найдем
Q = с2 [{тВе + тн) — (тНе + ти)\ F)
Подставив числовые значения коэффициента пропорциональ-
пропорциональности с2 (МэВ/а. е. м.) и масс нейтральных атомов (а. е. м.), получим
Q=2,13 МэВ,
что совпадает с результатом, полученным в примере 1.
Пример 3. Радиоактивное ядро магния 23Mg выбросило позитрон
и нейтрино. Определить энергию Q C+-распада ядра.
Решение. Реакцию р+-распада ядра магния можно записать
следующим образом:
Принимая, что ядро магния было неподвижным, и учитывая, что мас-
масса покоя нейтрино равна нулю, напишем уравнение энергетического
баланса. На основании закона сохранения релятивистской полной
энергии имеем
с2тщ - с2тш + Тш + c2me + Te + Tv. A)
Энергия распада
Q = TNa + Te + Tv = c2(mfAg— mNa — me). B)
Выразим массы ядер магния и натрия через массы соответствую-
соответствующих нейтральных атомов:
Q = с2 [(niMg — 12m е) — (mNa —\\me) — me].
Так как массы покоя электрона и позитрона одинаковы, то после
упрощений получим
Q = с2 (niMg—mNa — 2me).
Сделав подстановку, найдем
Q-3,05 МэВ.
399

Задачи
Законы сохранения в ядерных реакциях
44.1. Определить порядковый номер Z и массовое число А ча-
частицы, обозначенной буквой х, в символической записи ядерной
реакции:
JHe
44.2. То же, для реакции ЦА\ 4 х—> JH + iSMg.
44.3. Определить энергию Q ядерных реакций:
1) jBe+fH-^B + S/r, 4) ?Lj + iH —JBe + J/i;
2) 36Li + 2H-^4He + 4He; 5) 44Ca + \H — ЦК + Ще;
3) JLi + JHe^JB + J/i.
Освобождается или поглощается энергия в каждой из указанных
реакций?
44.4. Найти энергию Q ядерных реакций:
1) 3Н (р, у) 4Не; 2) 2Н (d, 7) 4Не; 3) 2Н (п, у) 3Н; 4) 19F (p, а) 16О.
44.5. При соударении ^-фотона с дейтоном последний может рас-
расщепиться на два нуклона. Написать уравнение ядерной реакции и
определить минимальную энергию 7"Фотона> способного вызывать
такое расщепление.
44.6. Определить энергию Q ядерной реакции 9Ве(/г, <уI0Ве,
если известно, что энергия связи Есв ядра 9Ве равна 58,16 МэВ, а
ядра 10Ве —64,98 МэВ.
44.7. Найти энергию Q ядерной реакции 14N (/г, /?I4С, если энер-
энергия связи ?св ядра 14N равна 104,66 МэВ, а ядра 14С — 105,29 МэВ.
44.8. Определить суммарную кинетическую энергию Т ядер,
образовавшихся в результате реакции 13С (d, а) ПВ, если кинети-
кинетическая энергия Гхдейтона равна 1,5 МэВ. Ядро-мишень 13С считать
неподвижным.
44.9. При ядерной реакции 9Ве(ос, п) 12С освобождается энергия
<2=5,70МэВ. Пренебрегая кинетическими энергиями ядер бериллия
и гелия и принимая их суммарный импульс равным нулю, опреде-
определить кинетические энергии 7\ и Т2 продуктов реакции.
44.10. Пренебрегая кинетическими энергиями ядер дейтерия и
принимая их суммарный импульс равным нулю, определить кинети-
кинетические энергии 7\ и Т2 и импульсы рг и р2 продуктов реакции
?Н + 2Н — 32He + Jn.
44.11. При реакции 6Li(d, p) 7Li освобождается энергия Q=
=5,028 МэВ. Определить массу m 6Li. Массы остальных атомов взять
из табл. 21.
44.12. При реакции 2Н (d, p) 3Н освобождается энергия Q=
=4,033 МэВ. Определить массу m атома 3Н. Массы остальных ато-
атомов взять из табл. 21.
44.13. При ядерной реакции 3Не (d, p) 4Не освобождается энер-
энергия Q=18,34 МэВ. Определить относительную атомную массу Ат
изотопа гелия 3Не. Массы остальных атомов взять из табл. 21.
400

Реакция деления
44.14. Определить кинетическую энергию Т и скорость v теп-
теплового нейтрона при температуре ^окружающей среды, равной 27 °С.
44.15. Найти отношение скорости их нейтрона после столкнове-
столкновения его с ядром углерода 12С к начальной скорости vx нейтрона.
Найти такое же отношение кинетических энергий нейтрона. Счи-
Считать ядро углерода до столкновения покоящимся; столкновение —
прямым, центральным, упругим.
44.16. Ядро урана 2|J!|U, захватив один нейтрон, разделилось на
два осколка, причем освободилось два нейтрона. Одним из осколков
оказалось ядро ксенона ^Хе. Определить порядковый номер Z и
массовое число А второго осколка.
44.17. При делении одного ядра урана-235 выделяется энергия
Q=200 МэВ. Какую долю энергии покоя ядра урана-235 составляет
выделившаяся энергия?
44.18. Определить энергию ?", которая освободится при делении
всех ядер, содержащихся в уране-235 массой пг=1 г.
44.19. Сколько ядер урана-235 должно делиться за время t=\ с,
чтобы тепловая мощность Р ядерного реактора была равной 1 Вт?
44.20. Определить массовый расход mt ядерного горючего 235G
в ядерном реакторе атомной электростанции. Тепловая мощность Р
электростанции равна 10 МВт. Принять энергию Q, выделяющуюся
при одном акте деления, равной 200 МэВ. КПД ц электростанции
составляет 20 %.
44.21. Найти электрическую мощность Р атомной электростан-
электростанции, расходующей 0,1 кг урана-235 в сутки, если КПД^ станции
равен 16 %.
Энергия радиоактивного распада ядер
44.22. Определить энергию Q альфа-распада ядра полония 2g$Po,
44.23. Покоившееся ядро полония 2?$Ро выбросило а-частицу с
кинетической энергией Т=5,3 МэВ. Определить кинетическую
энергию Т ядра отдачи и полную энергию Q, выделившуюся при а-
распаде.
44.24. Ядро углерода *JC выбросило отрицательно заряженную
Р-частицу и антинейтрино. Определить полную энергию Q бета-
распада ядра.
44.25. Неподвижное ядро кремния l\Si выбросило отрицательно
заряженную Р-частицу с кинетической энергией Т=0,5 МэВ. Пре-
Пренебрегая кинетической энергией ядра отдачи, определить кинети-
кинетическую энергию 7\ антинейтрино.
44.26. Определить энергию Q распада ядра углерода ^С, выбро-
выбросившего позитрон и нейтрино.
44.27. Ядро атома азота X?N выбросило позитрон. Кинетическая
энергия ТР позитрона равна 1 МэВ. Пренебрегая кинетической
энергией ядра отдачи, определить кинетическую энергию Tv нейт-
нейтрино, выброшенного вместе с позитроном.
401

Элементарные частицы
44.28. Свободный нейтрон радиоактивен. Выбрасывая электрон
и антинейтрино, он превращается в протон. Определить суммарную
кинетическую энергию Т всех частиц, возникающих в процессе
превращения нейтрона. Принять, что кинетическая энергия нейтро-
нейтрона равна нулю и что масса покоя антинейтрино пренебрежимо мала.
44.29. Фотон с энергией 8=3 МэВ в поле тяжелого ядра превра-
превратился в пару электрон — позитрон. Принимая, что кинетическая
энергия частиц одинакова, определить кинетическую энергию Т
каждой частицы.
44.30. Электрон и позитрон, имевшие одинаковые кинетические
энергии, равные 0,24 МэВ, при соударении превратились в два
одинаковых фотона. Определить энергию г фотона и соответствую-
соответствующую ему длину волны X.
44.31. Нейтральный я-мезон (я°), распадаясь, превращается в
два одинаковых 7-фотона. Определить энергию е фотона. Кинети-
Кинетической энергией и импульсом мезона пренебречь.

ГЛАВА 9
ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
§ 45. ВОЛНОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ
Основные формулы
• Формула де Бройля, выражающая связь длины волн с импуль-
импульсом р движущейся частицы, для двух случаев:
а) в классическом приближении (v<^c\ p=mQv)
%
б) в релятивистском случае (скорость v частицы сравнима со
скоростью с света в вакууме; p = mv = muvl\/"l—v2/c2)
л =— У 1—v2 с2.
mov
• Связь длины волны де Бройля с кинетической энергией Т
частицы:
а) в классическом приближении % = —jr. \
б) в релятивистском случае X = , "ьс , где Ео — энергия
покоя частицы (Е0==пг0с2).
Ф Фазовая скорость волн де Бройля
где со — круговая частота; k — волновое число (k=2n/X).
# Групповая скорость волн де Бройля
# Соотношения де Бройля:
E = fi(o; p = fik,
где Е — энергия движущейся частицы; р — импульс частицы; к —
волновой вектор; |к|=?=2л/Я; h — постоянная Планка (А=
=/i|Bjx) = 1,05-10-34 Дж-с).
# Соотношения неопределенностей:
а) для координаты и импульса частицы ApxAx^fh, где Арх —
неопределенность проекции импульса частицы на ось х\ Ах — неоп-
неопределенность ее координаты;
б) для энергии и времени AEAt^fi, где АЕ — неопределенность
энергии данного квантового состояния; Д? — время пребывания
системы в этом состоянии.
403

Примеры решения задач
Пример 1. Электрон, начальной скоростью которого можно
пренебречь, прошел ускоряющую разность потенциалов U. Найти
длину волны де Бройля К для двух случаев: 1) i/i=51 В; 2) ?/2=
=510 кВ.
Решение. Длина волны де Бройля к частицы зависит от ее
импульса р и определяется формулой
A)
Импульс частицы можно определить, если известна ее кинетичес-
кинетическая энергия Т. Связь импульса с кинетической энергией для не-
нерелятивистского (когда Т<^Е0) и для релятивистского (когда Тж
&Е0) случаев соответственно выражается формулами:
B)
T)T. C)
Формула A) с учетом соотношений B) и C) запишется соответ-
соответственно в нерелятивистском и релятивистском случаях:
D)
У 2m0T
% = 2Л E)
Сравним кинетические энергии электрона, прошедшего заданные
в условии задачи разности потенциалов f/x=51 В и ?/2=510 кВ, с
энергией покоя электрона и в зависимости от этого решим вопрос,
которую из формул D) и E) следует применить для вычисления
длины волны де Бройля.
Как известно, кинетическая энергия электрона, прошедшего ус-
ускоряющую разность потенциалов U>
T=\e\U.
В первом случае Тх= |e |t/!=51 эВ=0,51 • 10~4 МэВ, что много
меньше энергии покоя электрона ?0=m0?2=0,51 МэВ. Следователь-
Следовательно, можно применить формулу D).
Для упрощения расчетов заметим, что Т^Ю т0с2. Подставив
это выражение в формулу D), перепишем ее в виде
л _ 2лк _ Ю2 2л&
1 ~" j/~2m0-10-4m0c ~~ /Т ™оС '
Учтя, что -^~ есть комптоновская длина волны Яс, получим
Так как Яс=2,43-Ю2 м, то
404

Во втором случае кинетическая энергия Т2=\е \U2=5№ кэВ =
=0,51 МэВ, т. е. равна энергии покоя электрона. Следовательно,
необходимо применить релятивистскую формулу E).
Учтя, что 712=0,51 МэВ=т0с2, по формуле E) найдем
2пЯ
А2 =
—jr= , ИЛИ Л2 = -—= .
У Зт*с У3
Подставив значение %с в последнюю формулу и произведя вы-
вычисления, получим
Х2=1,4 пм.
Пример 2. На узкую щель шириной а==1 мкм направлен парал-
параллельный пучок электронов, имеющих скорость у=3,65 Мм/с. Учи-
Учитывая волновые свойства электронов, определить расстояние х
между двумя максимумами интенсивности первого порядка в диф-
дифракционной картине, полученной на экране, отстоящем на L=IO см
от щели.
Решение. Согласно гипотезе де Бройля, длина волны Я,
соответствующая частице массой
т, движущейся со скоростью v,
выражается формулой
Дифракционный максимум при
дифракции на одной щели наб-
наблюдается при условии
a sin ф= B^+1) (Я/2), B)
где k=0, 1, 2, 3, . . .— порядко-
порядковый номер максимумов; а — ши-
ширина щели.
Для максимумов первого поряд- Рис. 45.1
ка (k=l) угол ф заведомо мал, по-
поэтому sin ф=ф, и, следовательно, формула B) примет вид
аф=3/2Я, C)
а искомая величина х, как следует из рис. 45.1,
x=-2L tg ф=21ф, D)
так как tg ф=ф.
Подставив значение ф из соотношения C) в формулу D), получим
Подстановка в последнее равенство длины волны де Бройля по
формуле A) дает
—. (о)
amv x '
После вычисления по формуле E) получим
jc = 6 • 10~5м = 60мкм.
405

Пример 3. На грань кристалла никеля падает параллельный
пучок электронов. Кристалл поворачивают так, что угол скольже-
скольжения Ф изменяется. Когда этот угол делается равным 64°, наблюдается
максимальное отражение электронов, соответствующее дифракцион-
дифракционному максимуму первого порядка. Принимая расстояние d между
атомными плоскостями кристалла равным 200 пм, определить длину
волны де Бройля X электронов и их скорость v.
Решение. К расчету дифракции электронов от кристалли-
кристаллической решетки применяется то же уравнение Вульфа — Брэгга,
которое используется в случае рентгеновского излучения (см. § 31):
2dsin b=kk,
где d — расстояние между атомными плоскостями кристалла: 0 —
угол скольжения; k — порядковый номер дифракционного макси-
максимума; %— длина волны де Бройля. Очевидно, что
*,= B d sin b)/k.
Подставив в эту формулу значения величин и вычислив, получим
Х=360 пм.
Из формулы длины волны де Бройля X=2nh/ (то) выразим ско-
скорость электрона:
Подставив в эту формулу значения я, %, т (масса электрона),
К и произведя вычисления, найдем
v=2 Мм/с.
Пример 4. Кинетическая энергия Т электрона в атоме водорода
составляет величину порядка 10 эВ. Используя соотношение неопре-
неопределенностей, оценить минимальные линейные размеры атома.
Решение. Неопределенность координаты и импульса элект-
электрона связаны соотношением
АхАр^К, A)
где Ал: — неопределенность координаты электрона; Ар — неопреде-
неопределенность его импульса.
Из этого соотношения следует, что чем точнее определяется
положение частицы в пространстве, тем более неопределенным
становится импульс, а следовательно, и энергия частицы. Пусть атом
имеет линейные размеры /, тогда электрон атома будет находиться
где-то в пределах области с неопределенностью: Ах=1/2. Соотноше-
Соотношение неопределенностей A) можно записать в этом случае в виде
A/2) Ap^h, откуда
/>2&/(Д/?). B)
Физически разумная неопределенность импульса Ар, во всяком
случае, не должна превышать значения самого импульса /?, т. е.
Импульс р связан с кинетической энергией Т соотношением
= У2пгТ. Заменим Ар значением V 2тТ (такая замена не увели-
406

чит /). Переходя от неравенства B) к равенству, получим
Подставив числовые значения и произведя вычисления, найдем
/ш1п=124пм.
Пример 5. Используя соотношение неопределенностей энергии
и времени, определить естественную ширину ДА спектральной линии
излучения атома при переходе его из воз-
возбужденного состояния в основное. Сред-
Среднее время х жизни атома в возбужденном
состоянии принять равным 10~8 с, а дли-
длину волны А излучения — равной 600 нм.
Решение. При переходе атомов из
возбужденного состояния в основное су-
существует некоторый разброс (неопреде- ___^____
ленность) в энергии испускаемых фотонов. Е Энергия
Это связано с тем, что энергия возбужден- Рис. 45.2
ного состояния не является точно опре-
определенной, а имеет конечную ширину Г (рис, 45.2). Согласно со-
соотношению неопределенностей энергии и времени, ширина Г энер-
энергетического уровня возбужденного состояния связана со средним
временем т жизни атомов в этом состоянии соотношением
Тогда ширина энергетического уровня определяется выражением
Г — fil%.
Вследствие конечной ширины уровня энергии возбужденного состоя-
состояния энергия фотонов, испускаемых атомами, также имеет разброс,
равный ширине энергетического уровня, т. е. Де=Г. Тогда
Де-^/т. A)
Поскольку энергия е фотона связана с длиной волны А соотношением
то разбросу Де (Де<Се) энергии соответствует разброс ДА длин волн
(ДЖХ):
Де^ДХ B)
(знак минус опущен).
Входящий в это выражение конечный интервал длин волн ДХи
есть естественная ширина спектральной линии. Выразив ДА, из фор-
формулы B) и заменив Де согласно A), получим
Произведем вычисления:
407

Вопросы и задачи
Волны де Бройля
45Л. Определить длину волны де Бройля X, характеризующую
волновые свойства электрона, если его скорость v=l Мм/с. Сделать
такой же подсчет для протона.
45.2. Электрон движется со скоростью и=200Мм/с. Определить
длину волны де Бройля X, учитывая изменение массы элктрона в
зависимости от скорости.
45.3. Какую ускоряющую разность потенциалов U должен прой-
пройти электрон, чтобы длина волны де Бройля X была равна 0,1 нм?
45.4. Определить длину волны де Бройля X электрона, если его
кинетическая энергия Т=1 кэВ.
45.5. Найти длину волны де Бройля X протона, прошедшего
ускоряющую разность потенциалов U : 1) 1 кВ; 2) 1 MB.
45.6. Найти длину волны де Бройля X для электрона, движуще-
движущегося по круговой орбите атома водорода, находящегося в основном
состоянии.
45.7. Определить длину волны де Бройля X электрона, находя-
находящегося на второй орбите атома водорода.
45.8. С какой скоростью движется электрон, если длина волны де
Бройля X электрона равна его комптоновской длине волны Хс?
45.9. Определить длину волны де Бройля X электронов, бомбарди-
бомбардирующих антикатод рентгеновской трубки, если граница сплошного
рентгеновского спектра приходится на длину волны Х=3 нм.
45.10. Электрон движется по окружности радиусом г=0,5 см в
однородном магнитном поле с индукцией В=8 мТл. Определить
длину волны де Бройля X электрона.
45.11. На грань некоторого кристалла под углом а=60° к ее по-
поверхности падает параллельный пучок электронов, движущихся с
одинаковой скоростью. Определить скорость v электронов, если они
испытывают интерференционное отражение первого порядка. Рас-
Расстояние d между атомными плоскостями кристаллов равно 0,2 нм.
45.12. Параллельный пучок электронов, движущихся с одина-
одинаковой скоростью v=l Мм/с, падает нормально на диафрагму с длин-
длинной щелью шириной а=1 мкм. Проходя через щель, электроны
рассеиваются и образуют дифракционную картину на экране,
расположенном на расстоянии /=50 см от щели и параллельном
плоскости диафрагмы. Определить линейное расстояние х между
первыми дифракционными минимумами.
45.13. Узкий пучок электронов, прошедших ускоряющую раз-
разность потенциалов U==30 кВ, падает нормально на тонкий листок
золота, проходит через него и рассеивается. На фотопластинке,
расположенной за листком на расстоянии /==20 см от него, получена
дифракционная картина, состоящая из круглого центрального пят-
пятна и ряда концентрических окружностей. Радиус первой окружно-
окружности г=3,4 мм. Определить: 1) уголй отражения электронов от мик-
408

рокрметаллов золота, соответствующий первой окружности (угол
измеряется от поверхности кристалла); 2) длину волны де Бройля
К электронов; 3) постоянную а кристаллической решетки золота.
Фазовая и групповая скорости
45.14. Прибор зарегистрировал скорость распространения элект-
электромагнитного импульса. Какую скорость зарегистрировал прибор —
фазовую или групповую?
45.15. Можно ли измерить фазовую скорость?
45.16. Волновой «пакет» образован двумя плоскими монохрома-
монохроматическими волнами:
Ых, f)=cosA002f—Зх); ?a(jt, *)=cosA003 *—3,01 *).
Определить фазовые скорости vx и v2 каждой волны и групповую
скорость и волнового «пакета».
45.17. Известно, что фазовая скорость v=a>/k. Найти выражения
фазовой скорости волн де Бройля в нерелятивистском и релятивист-
релятивистском случаях.
45.18. Фазовая скорость волн де Бройля больше скорости света в
вакууме (в релятивистском случае). Не противоречит ли это посту-
постулатам теории относительности?
45.19. Зная общее выражение групповой скорости, найти группо-
групповую скорость и волн де Бройля в нерелятивистском и релятивистском
случаях.
45.20. Написать закон дисперсии (т. е. формулу, выражающую
зависимость фазовой скорости от длины волны) волн де Бройля в
нерелятивистском и релятивистском случаях.
45.21. Будут ли расплываться в вакууме волновые пакеты, обра-
образованные из волн: 1) электромагнитных; 2) де Бройля?
Соотношение неопределенностей
45.22. Определить неточность Ал: в определении координаты
электрона, движущегося в атоме водорода со скоростью и=1,5х
X 10е м/с, если допускаемая неточность Аи в определении скорости
составляет 10 % от ее величины. Сравнить полученную неточность
с диаметром d атома водорода, вычисленным по теории Бора для ос-
основного состояния, и указать, применимо ли понятие траектории в
данном случае.
45.23. Электрон с кинетической энергией 7=15 эВ находится в
металлической пылинке диаметром d=l мкм. Оценить относитель-
относительную неточность Аи, с которой может быть определена скорость элект-
электрона.
45.24. Во сколько раз дебройлевская длина волны X частицы
меньше неопределенности Ах ее координаты, которая соответ-
соответствует относительной неопределенности импульса в 1 %?
45.25. Предполагая, что неопределенность координаты движу-
движущейся частицы равна дебройлевской длине волны, определить отно-
относительную неточность Д/?'/? импульса этой частицы.
409

45.26. Используя соотношение неопределенностей
найти выражение, позволяющее оценить минимальную энергию Е
электрона, находящегося в одномерном потенциальном ящике ши-
шириной I.
45.27. Используя соотношение неопределенностей AxApx^fi, оце-
оценить низший энергетический уровень электрона в атоме водорода.
Принять линейные размеры атома /^0,1 нм.
45.28. Приняв, что минимальная энергия Е нуклона в ядре равна
10 МэВ, оценить, исходя из соотношения неопределенностей, линей-
линейные размеры ядра.
45.29. Показать, используя соотношение неопределенностей, что
в ядре не могут находиться электроны. Линейные размеры ядра
принять равными 5 фм.
45.30. Рассмотрим следующий мысленный эксперимент. Пусть
моноэнергетический пучок электронов (Т=10 эВ) падает на щель
шириной а. Можно считать, что если электрон прошел через щель,
то его координата известна с неточностью &х=а. Оценить получае-
получаемую при этом относительную неточность в определении импульса
lS.plр электрона в двух случаях: 1) а=\0 нм; 2) а=0,1 нм.
45.31. Пылинки массой т=10~12 г взвешены в воздухе и нахо-
находятся в тепловом равновесии. Можно ли установить, наблюдая за
движением пылинок, отклонение от законов классической механики?
Принять, что воздух находится при нормальных условиях, пылинки
имеют сферическую форму. Плотность вещества, из которого состоят
пылинки, равна 2 • 103 кг/м3.
45.32. Какой смысл вкладывается в соотношение неопределен-
неопределенностей AEAt^fh?
45.33. Используя соотношение неопределенности ЛЯД?>&, оце-
оценить ширину Г энергетического уровня в атоме водорода, находяще-
находящегося: 1) в основном состоянии; 2) в возбужденном состоянии (время
т жизни атома в возбужденном состоянии равно 10~8 с).
45.34. Оценить относительную ширину Лш/о) спектральной
линии, если известны время жизни атома в возбужденном состоянии
(т^10~8 с) и длина волны излучаемого фотона (?t=0,6 мкм).
45.35. В потенциальном бесконечно глубоком одномерном ящике
энергия Е электрона точно определена. Значит, точно определено и
значение квадрата импульса электрона (р2=2 тЕ). С другой стороны,
электрон заперт в ограниченной области с линейными размерами /.
Не противоречит ли это соотношению неопределенностей?
§ 46. ПРОСТЕЙШИЕ СЛУЧАИ ДВИЖЕНИЯ МИКРОЧАСТИЦ
Основные формулы
• Одномерное временное уравнение Шредингера
dt ~~~ 2т дх2 '
где / — мнимая единица (К^Т); т — масса частицы; ?(*, t)—
волновая функция, описывающая состояние частицы.
410

Волновая функция, описывающая одномерное движение свобод-
свободной частицы,
где А — амплитуда волны де Бройля; р — импульс частицы; Е —
энергия частицы.
Одномерное уравнение Шредингера для стационарных состоя-
состояний
где Е — полная энергия частицы; U (х) — потенциальная энергия;
у\)(х) — координатная (или амплитудная) часть волновой функции.
Для случая трех измерений я|з(л;, у, г) уравнение Шредингера
записывается в виде
или в операторной форме
g (?_t/)t[>=: О,
где А = -^2+ g^2 + gp-—оператор Лапласа.
При решении уравнения Шредингера следует иметь в виду стан-
стандартные условия, которым должна удовлетворять волновая функ-
функция: конечность (во всем пространстве), однозначность, непрерыв-
непрерывность самой "ф-функции и ее первой производной.
# Вероятность dU? обнаружить частицу в интервале от х до
x+dx (в одномерном случае) выражается формулой
где |я|) (х) |2 — плотность вероятности.
Вероятность W обнаружить частицу в интервале от хг до х2
находится интегрированием df в указанных пределах:
• Собственное значение энергии Еп частицы, находящейся
на п-м энергетическом уровне в бесконечно глубоком одномерном
прямоугольном потенциальном ящике, определяется формулой
Е —^-п^ (п — 1 9 Ч \
п — 2т/2 1"—1, ^, о, . . .).
где / — ширина потенциального ящика.
Соответствующая этой энергии собственная волновая функция
имеет вид
411

@ Коэффициент преломления п волн де Бройля на границе
низкого потенциального барьера бесконечной ширины * (рисо 46.1)
где Хх и К2— длины волн де Бройля в областях I и II (частица дви-
движется из области / во //); k±—k2—
соответствующие значения волновых
чисел.
® Коэффициенты отражения р и
пропускания т волн де Бройля через
низкий (?/<?) потенциальный барь-
барьер бесконечной ширины
Низкий барьер р =
Е-
j UM
Ж
¦и
Рис* 46Л где kx и k2 — волновые числа волн
де Бройля в областях I и II.
® Коэффициент прозрачности D прямоугольного потенциаль-
потенциального барьера конечной ширины
D « ехр [— j V2m (U—E) d\ ,
где U — высота потенциального барьера; Е — энергия частицы;
d — ширина барьера.
Примеры решения задач
Пример 1. Электрон находится в бесконечно глубоком одно-
одномерном прямоугольном потенциальном ящике шириной /. Вычис-
Вычислить вероятность того, что электрон, находящийся в возбужденном
состоянии (п=2), будет обнаружен в средней трети ящика.
Решение. Вероятность W обнаружить частицу в интервале
2 определяется равенством
52dx, A)
где Vpa(x) — нормированная собственная волновая функция, отве-
отвечающая данному состоянию.
Нормированная собственная волновая функция, описывающая
состояние электрона в потенциальном ящике, имеет вид
2 . пп
"Sin — X.
Возбужденному состоянию (/г=2) отвечает собственная функция
sin ^Ь*. B)
" Такой барьер называют также потенциальной ступенью, если при
перехоле из области / в область // потенциальная энергия частицы умень-
уменьшается.
412

Подставив ty2(x) в подынтегральное выражение формулы A)
и вынося постоянные величины за знак интеграла, получим
W=ZT
C)
Согласно условию задачи, лг1=1/3/ и х2=2/31 (рис. 46.2). Подста-
Подставим эти пределы интегрирования в формулу C), произведем замену
. 2 2л 1 / , 4л \ ^
sin2 —.*; = — ( 1— cos— я] и разобьем интеграл на два:
2//3
W=ZT
( 2//3
I Г
\1
2//3
//3
8я
1/3
л
3 4л
4л
8я
)
4л
з—slIb3"
//з
~Т \~3"~~л
Заметив, что sin -^- = sin 4 > a sm-^- = — sin-?, получим
117=0,195.
Пример 2. Моноэнергетический поток электронов (?=100эВ)
падает на низкий * прямоугольный потенциальный барьер беско-
бесконечной ширины (рис.
46.1). Определить высо-
высоту потенциального барь-
барьера U, если известно,
что 4 % падающих на
барьер электронов отра-
отражается.
Решение. Коэф-
Коэффициент отражения р от
низкого потенциального
бар ьер а выр ажаетс я
формулой
Ц>@)=0
Рис. 46.2
р = |;
где ki и &2 — волновые числа, отвечающие движению электронов
в областях lull (см. рис. 46.1).
В области / кинетическая энергия электрона равна Е и волновое
число
Поскольку координата электрона не определена, то импульс
электрона определяется точно и, следовательно, в данном случае
можно говорить о точном значении кинетической энергии.
* Прямоугольный потенциальный барьер называется низким, если энер-
энергия Е частицы больше высоты U потенциального барьера, в противном случае
барьер называется высоким.
413

В области // кинетическая энергия электрона равна Е—U
и волновое число
k2 = (l/h)V2m(E-U).
Коэффициент отражения может быть записан в виде *
Разделим числитель и знаменатель дроби на \г2тЕ:
Решая уравнение относительно ]/~l — U/E, получим
Возведя обе части равенства в квадрат, найдем высоту потенци-
потенциального барьера:
Подставив сюда значения величин и произведя вычисления,
найдем
17=55,6 эВ.
Пример 3. Электрон с энергией ?=4,9 эВ движется в положи-
положительном направлении оси х (рис. 46.3). Высота U потенциального
барьера равна 5эВ. При какой ши-
ширине d барьера вероятность W про-
прохождения электрона через него бу-
будет равна 0,2?
Решение. Вероятность W про-
прохождения частицы через потенциаль-
ный барьер по своему физическому
смыслу совпадает с коэффициентом
прозрачности D(W=D). Тогда веро-
вероятность того, что электрон пройдет
через прямоугольный потенциальный барьер, выразится соотно-
соотношением
W « ехр Г — | V'2m(U — E) d\ , A)
где m — масса электрона. Потенцируя это выражение, получим
* В случае низкого потенциального барьера kx и k2 действительны, а знак
модуля можно опустить.
414

Для удобства вычислений изменим знак у правой и левой части
этого равенства и найдем d:
d== fv\n(l/W)
2Y~2m(U — E)'
Входящие в эту формулу величины выразим в единицах СИ
и произведем вычисления:
Учитывая, что формула A) приближенная и вычисления носят оце-
оценочный характер, можно принять d«0,5 нм.
Вопросы и задачи
Уравнение Шредингера
46.1. Написать уравнение Шредингера для электрона, находя-
находящегося в водородоподобном атоме.
46.2. Написать уравнение Шредингера для линейного гармони-
гармонического осциллятора. Учесть, что сила, возвращающая частицу в по-
положение равновесия, /=—$х (где E — коэффициент пропорцио-
пропорциональности, х — смещение).
46.3. Временная часть уравнения Шредингера имеет вид
ih-^- = E4. Найти решение уравнения.
46.4. Написать уравнение Шредингера для свободного электро-
электрона, движущегося в положительном направлении оси X со ско-
скоростью v. Найти решение этого уравнения.
46.5. Почему при физической интерпретации волновой функции
говорят не о самой if-функции, а о квадрате ее модуля г|J?
46.6. Чем обусловлено требование конечности я|)-функции?
46.7. Уравнение Шредингера для стационарных состояний имеет
вид jf + tj(U—?)i|3 = 0. Обосновать, исходя из этого уравнения,
требования, предъявляемые к волновой функции,— ее непрерыв-
непрерывность и непрерывность первой производной от волновой функции.
46.8. Может ли |я|?(л;)|2 быть больше единицы?
46.9. Показать, что для ор-функции выполняется равенство
\ty(x)\2=ty(x)ty*(x), гдег|)*(л;) означает функцию, комплексно сопря-
сопряженную ty(x).
46.10. Доказать, что если г|?-функция циклически зависит от
времени т. е. "*Р (х, /) = ехр ( — -г Et ji|? (x) \, то плотность вероят-
вероятности есть функция только координаты.
Одномерный бесконечно глубокий потенциальный ящик
46.11. Электрон находится в бесконечно глубоком прямоуголь-
прямоугольном одномерном потенциальном ящике шириной / (рис. 46.4). Напи-
Написать уравнение Шредингера и его решение (в тригонометрической
форме) для области //@<х</).
415

0 I
46.12. Известна волновая функция, описывающая состояние
электрона в потенциальном ящике шириной /: ty(x)=C1 sin kx+
+С2 cos kx. Используя граничные условия гр(О)=О и г|з(/)=О, опре-
определить коэффициент С2 и возможные значения волнового вектора &,
;г/ )А при котором существуют нетривиальные
т\ \ решения.
1 46.13. Электрону в потенциальном ящи-
Ш ке шириной / отвечает волновое число k=
= пп/1 (л = 1, 2, 3, . . .). Используя связь
энергии Е электрона с волновым числом k,
г^оа получить выражение для собственных зна-
—>х чений энергии Еп.
46.14. Частица находится в потенциаль-
Рис. 46.4 ном ящике. Найти отношение разности
соседних энергетических уровней АЕп+1,п
к энергии Еп частицы в трех случаях: 1) п=3; 2) /i=10; 3) п -*оо.
Пояснить полученные результаты.
46.15. Электрон находится в потенциальном ящике шириной /=
=0,5 нм. Определить наименьшую разность АЕ энергетических
уровней электрона. Ответ выразить в электрон-вольтах.
46.16. Собственная функция, описывающая состояние частицы
в потенциальном ящике, имеет вид *ф„ (х) = С sin ^— х. Используя
условия нормировки, определить постоянную С.
46.17. Решение уравнения Шредингера для бесконечно глубо-
глубокого одномерного прямоугольного потенциального ящика можно
записать в виде ty(x)=C1elkx+C2e'~ikxJ где k = Vr2mE/h. Исполь-
Используя граничные условия и нормировку я|э-функции, определить:
1) коэффициенты Сг и С2; 2) собственные значения энергии Еп. Найти
выражение для собственной нормированной ар-функции.
46.18. Изобразить на графике вид первых трех собственных
функций tyn(x), описывающих состояние электрона в потенциальном
ящике шириной /, а также вид №?l(x)|2. Установить соответствие
между числом N узлов волновой функции (т. е. числом точек, где
волновая функция обращается в нуль в интервале 0<Сх<С1) и кван-
квантовым числом п. Функцию считать нормированной на единицу.
46.19. Частица в потенциальном ящике шириной / находится
в возбужденном состоянии (/г=2). Определить, в каких точках ин-
интервала @<Ос</) плотность вероятности №2(#)|2 нахождения час-
частицы максимальна и минимальна.
46.20. Электрон находится в потенциальном ящике шириной /.
В каких точках в интервале @<х</) плотность вероятности нахож-
нахождения электрона на первом и втором энергетических уровнях
одинакова? Вычислить плотность вероятности для этих точек. Ре-
Решение пояснить графически.
46.21. Частица в потенциальном ящике находится в основном
состоянии. Какова вероятность W нахождения частицы: 1) в сред-
средней трети ящика; 2) в крайней трети ящика?
416

46.22. В одномерном потенциальном ящике шириной / находит-
находится электрон. Вычислить вероятность W нахождения электрона на
первом энергетическом уровне в интервале 1/4, равноудаленном от
стенок ящика.
46.23. Частица в потенциальном ящике шириной / находится
в низшем возбужденном состоянии. Определить вероятность W
нахождения частицы в интервале 1/4, равноудаленном от стенок
ящика.
46.24. Вычислить отношение вероятностей WJW2 нахождения
электрона на первом и втором энергетических уровнях в интервале
1/4, равноудаленном от стенок одномерной потенциальной ямы
шириной /.
46.25. Показать, что собственные функции tyn(x) = 1/ ysin^-x
и ^т (х)= у Tsmirx> описываю1Дие состояние частицы в потен-
потенциальном ящике, удовлетворяют условию ортогональности, т. е.
( 1 при п^
п (Х) ^т (Х) &Х = Л л
46.26. Электрон находится в одномерном потенциальном ящике
шириной /. Определить среднее значение координаты <х> элек-
электрона @<Ос</).
46.27. Используя выражение энергии En=n2fi2n2/Bml2) части-
частицы, находящейся в потенциальном ящике, получить приближенное
выражение энергии: 1) гармонического осциллятора; 2) водородо-
подобного атома. Сравнить полученные результаты с истинными
значениями энергий.
Двух- и трехмерный потенциальный ящик
46.28. Считая, что нуклоны в ядре находятся в трехмерном
потенциальном ящике кубической нормы с линейными размерами
/=10 фм, оценить низший энергетический уровень нуклонов в ядре.
46.29. Определить из условия нормировки коэффициент С собст-
собственной 1|з-функции ^пхп2 (х, у) =Csm^~-x-sm^у, описывающей
состояние электрона в двухмерном бесконечно глубоком потенци-
потенциальном ящике со сторонами 1г и /2.
46.30. Электрон находится в основном состоянии в двухмерном
квадратном бесконечно глубоком потенциальном ящике со сторо-
стороной /. Определить вероятность W нахождения электрона в области,
ограниченной квадратом, который равноудален от стенок ящика
и площадь которого составляет V4 площади ящика.
46.31. Определить из условия нормировки коэффициент собст-
собственной гр-функции грЛ1/г Л (-V, у, z) = Csin^xsin^ysin^~z, опи-
*1 ^2 *3
1 2 3
сывающей состояние электрона в трехмерном потенциальном бес-
бесконечно глубоком ящике со сторонами /ь /2, /3.
14 № 1268 417

Низкий * потенциальный барьер бесконечной ширины
46.32. Написать уравнение Шредингера для электрона с энер-
энергией ?, движущегося в положительном направлении оси X для об-
областей I и II (см. рис. 46.1), если на границе этих областей имеется
низкий потенциальный барьер высотой U.
46.33. Написать решения уравнений Шредингера (см. предыду-
предыдущую задачу) для областей I и II. Какой смысл имеют коэффициенты
Аг и Вг для ipi(x) и А 2 и В2 для ^и(х)? Чему равен коэффициент В2?
46.34. Зная решение уравнений Шредингера для областей I и II
потенциального барьера ^l(x)=A1^x+B1e"?kiX9 tyn(x)=A2ekx,
определить из условий непрерывности гр-функций и их первых
производных на границе барьера отношение амплитуд вероятности
В11А1 и AJAX.
46.35. Зная отношение амплитуд вероятности -р = t1"~,2 для
волны, отраженной от барьера, и — =, , , для проходящей вол-
?Г
ны, найти выражение для коэффициента отражения р и коэффициен-
коэффициента прохождения т.
46.36. Считая выражение для коэффициента отражения р от
потенциального барьера и коэффициента прохождения т извест-
известными, показать, что р+т=1.
46.37. Электрон с энергией ?=25 эВ встречает на своем пути
потенциальный барьер высотой [/=9эВ (см. рис. 46.1). Определить
коэффициент преломления п волн де
Ж Бройля на границе барьера.
46.38. Определить коэффициент пре-
преломления п волн де Бройля для прото-
\тт нов на границе потенциальной ступени
(рис. 46.5). Кинетическая энергия про-
^х тонов равна 16 эВ, а высота U потенци-
потенциальной ступени равна 9 эВ.
Рис. 46.5 46.39. Электрон обладает энергией
?=10 эВ. Определить, во сколько раз
изменятся его скорость и, длина волны де Бройля X и фазовая
скорость при прохождении через потенциальный барьер (см. рис.
46.1) высотой 0=6 эВ.
46.40. Протон с энергией ?=1 МэВ изменил при прохождении
потенциального барьера дебройлевскую длину волны на 1 %.
Определить высоту U потенциального барьера.
46.41. На пути электрона с дебройлевской длиной волны
Ях=0,1 нм находится потенциальный барьер высотой /7—120 эВ.
Определить длину волны де Бройля к2 после прохождения
барьера.
46.42. Электрон с энергией ?=100 эВ попадает на потенциаль-
потенциальный барьер высотой (/=64 эВ. Определить вероятность W того, что
электрон отразится от барьера.
* См. сноску на с. 413.
418

46.43. Найти приближенное выражение коэффициента отраже-
отражения р от очень низкого потенциального барьера (U<^E).
46.44. Коэффициент отражения р протона от потенциального
барьера равен 2,5-10~5. Определить, какой процент составляет
высота U барьера от кинетической энергии Т падающих на барьер
протонов.
46.45. Вывести формулу, связывающую коэффициент преломле-
преломления п волн де Бройля на границе низкого потенциального барьера
и коэффициент отражения р от него.
46.46. Определить показатель преломления п волн де Бройля
при прохождении частицей потенциального барьера с коэффициен-
коэффициентом отражения р=0,5.
46.47. При каком отношении высоты U потенциального барьера
и энергии Е электрона, падающего на барьер, коэффициент отраже-
отражения р=0,5?
46.48. Электрон с энергией ?=10 эВ падает на потенциальный
барьер. Определить высоту U барьера, при которой показатель пре-
преломления п волн де Бройля и коэффициент отражения р численно
совпадают.
46.49. Кинетическая энергия Т электрона в два раза превышает
высоту U потенциального барьера. Определить коэффициент отра-
отражения р и коэффициент прохождения т электронов на границе
барьера.
46.50. Коэффициент прохождения х электронов через низкий
потенциальный барьер равен коэффициенту отражения р. Опреде-
Определить, во сколько раз кинетическая энергия Т электронов больше
высоты U потенциального барьера.
46.51. Вывести формулу, связывающую коэффициент прохож-
прохождения т электронов через потенциальный барьер и коэффициент
преломления п волн де Бройля.
46.52. Коэффициент прохождения т протонов через потенциаль-
потенциальный барьер равен 0,8. Определить показатель преломления п волн
де Бройля на границе барьера.
46.53. Электрон с кинетической энергией Т движется в положи-
положительном направлении оси X. Найти выражение для коэффициента
отражения р и коэффициента прохождения т на границе потенциаль-
потенциальной ступени высотой U (рис. 46.5).
46.54. Найти приближенное выражение для коэффициента про-
прохождения т через низкий потенциальный барьер при условии, что
кинетическая энергия Т частицы в области // (см. рис. 46.1) много
меньше высоты U потенциального барьера.
46.55. Вычислить коэффициент прохождения т электрона с энер-
энергией ?=100 эВ через потенциальный барьер высотой ?/=99, 75 эВ.
46.56. Показать на частном примере низкого потенциального
барьера сохранение полного числа частиц, т. е. что плотность по-
потока N электронов, падающих на барьер, равна сумме плотности
потока Np электронов, отраженных от барьера, и плотности потока
Nx электронов, прошедших через барьер.
14* 419

46.57. На низкий потенциальный барьер направлен моноэнерге-
моноэнергетический поток электронов с плотностью потока энергии Jx=
= 10Вт/м2. Определить плотность потока энергии /2 электронов,
прошедших барьер, если высота его (/=0,91 эВ и энергия Е электро-
электронов в падающем потоке равна 1 эВ.
46.58. Моноэнергетический поток электронов падает на низкий
потенциальный барьер (см. рис. 46.1). Коэффициент прохождения
т=0,9. Определить отношение JjJx плотности потока энергии вол-
волны, прошедшей барьер, к плотности потока энергии волны, падаю-
падающей на барьер.
48.59. На низкий потенциальный барьер падает моноэнергети-
моноэнергетический поток электронов. Концентрация п0 электронов в падающем
потоке равна 109 мм, а их энергия ?=100 эВ. Определить давле-
давление, которое испытывает барьер, если его высота G=9,7 эВ.
Высокий * потенциальный барьер бесконечной ширины
46.60. Написать уравнение Шредингера и найти его решение
для электрона, движущегося в положительном направлении оси х
для областей I и II (рис. 46.6), если на границе этих областей имеет-
имеется потенциальный барьер высотой U.
46.61. Для областей I к II высокого потенциального барьера
(см. рис. 46.5)г|)-функции имеют вид ^^А^^хЛ-В^-1^* Ht|)f/(#) =
= А 2е~ кх. Используя непрерывность
я))-функций и их первых производных
на границе барьера, найти отноше-
отношение амплитуд AJAX.
46.62. Написать выражение для
ij) и(х) в области // (рис. 46.6) высо-
Высокай. барьер кого потенциального барьера, если
Рис. 46.6 г|)-функция нормирована так, что
46.63. Амплитуда А2 волны в области // высокого потенциаль-
ного барьера (рис. 46.6) равна 2kll(k1 + ik) (kx = УИтЁ/Ь, k =
= ]/2m(U—E)j%). Установить выражение для плотности вероят-
вероятности нахождения частицы в области // (.00), если энергия части-
частицы равна Е, а высота потенциального барьера равна U.
46.64. Используя выражение для коэффициента отражения от
низкой ступени р== /TV , где kx и k2 — волновые числа, найти
I «1 -j- к2
выражение коэффициента отражения от высокой ступени (T<.U).
46.65. Показать, что имеет место полное отражение электронов
от высокого потенциального барьера, если коэффициент отражения
может быть записан в виде р =
r U(xh
*-
'1
¦и
* См. сноску на с. 413..
420

46.66. Определить плотность вероятности |ip/,@)|2 нахождения
электрона в области // высокого потенциального барьера в точке
х=0, если энергия электрона равна ?, высота потенциального барь-
барьера равна U и if-функция нормирована так, что А±=\.
Прямоугольный потенциальный барьер конечной ширины
46.67. Написать уравнения Шредингера для частицы с энер-
энергией ?, движущейся в положительном направлении оси X для об-
областей /, // и /// (см. рис. 46.3), если на границах этих областей
имеется прямоугольный потенциальный барьер высотой U и шири-
шириной d.
46.68. Написать решения уравнений Шредингера (см. предыду-
предыдущую задачу) для областей /, // и ///, пренебрегая волнами, отра-
отраженными от границ/—// и //—///, и найти коэффициент прозрач-
прозрачности D барьера.
46.69. Найти вероятность W прохождения электрона через пря-
прямоугольный потенциальный барьер при разности энергий U—?=
= 1 эВ, если ширина барьера: 1) d=0,l им; 2) d=0,5 нм.
46.70. Электрон проходит через прямоугольный потенциальный
барьер шириной d=0,5 нм. Высота U барьера больше энергии Е
электрона на 1 %. Вычислить коэффициент прозрачности D, если
энергия электрона: 1) ?=10 эВ; 2) ?=100 эВ.
46.71. Ширина d прямоугольного потенциального барьера равна
0,2 нм. Разность энергий U—?=1 эВ. Во сколько раз изменится
вероятность W прохождения электрона через барьер, если разность
энергий возрастет в я=10 раз?
46.72. Электрон с энергией ?=9 эВ движется в положительном
направлении оси X. При какой ширине d потенциального барьера
коэффициент прозрачности D=0,l, если высота U барьера равна
10 эВ? Изобразите на рисунке примерный вид волновой функция
(ее действительную часть) в пределах каждой из областей /, //, ///
(см. рис. 46.3).
46.73. При какой ширине d прямоугольного потенциального
барьера коэффициент прозрачности D для электронов равен 0,01?
Разность энергий U—?=10 эВ.
46.74. Электрон с энергией ? движется в положительном направ-
направлении оси X. При каком значении U—?, выраженном в электрон-
вольтах, коэффициент прозрачности D = 10~3, если ширина d барь-
барьера равна 0,1 нм?
46.75. Электрон с энергией ?=9 эВ движется в положительном
направлении оси X. Оценить вероятность W того, что электрон прой-
пройдет через потенциальный барьер, если его высота [/=10 эВ и ши-
ширина rf=0,l нм.
46.76. Прямоугольный потенциальный барьер имеет ширину
d=0,l нм. При какой разности энергий U—? вероятность W про-
прохождения электрона через барьер равна 0,99?
46.77. Ядро испускает ос-частицы с энергией ?=5МэВ. В гру-
грубом приближении можно считать, что а-частнцы проходят через
421

прямоугольный потенциальный барьер высотой U=\0 МэВ и шири-
шириной d=5 фм. Найти коэффициент прозрачности D барьера для
ос-частиц.
46.78. Протон и электрон прошли одинаковую ускоряющую раз-
разность потенциалов Дф=10 кВ. Во сколько раз отличаются коэффи-
коэффициенты прозрачности De для электрона и Dp для протона, если вы-
высота U барьера равна 20 кэВ и ширина d=0,l пм?
§ 47. СТРОЕНИЕ АТОМА
Основные формулы
• Уравнение Шредингера для стационарных состояний в сфе-
сферических координатах
1 д
гдегр=я|)(г, -&, ф) — волновая функция; Е — полная энергия части-
частицы; U — потенциальная энергия частицы (являющаяся функцией
координат).
• В атоме водорода (или водородоподобном ионе) потенциаль-
потенциальная энергия U (г) имеет вид
где Z — зарядовое число; е — элементарный заряд; е0 — электри-
электрическая постоянная.
• Собственное значение энергии Еп электрона в атоме водорода
где % — постоянная Планка, п — главное квантовое число (п—
= 1, 2, 3, . . .).
• Символическая запись я|з-функции, описывающей состояние
электрона в атоме водорода,
^п,1,т{г, й, ф),
где п, U га — квантовые числа: главное, орбитальное, магнитное.
Вероятность dW того, что электрон находится в области, огра-
ограниченной элементом объема dK, взятого в окрестности точки с коор-
координатами г, -&, ф,
где dV=r2sln -&d& dф dr (в сферических координатах).
В s-состоянии (/=0, т=0) волновая функция сферически-сим-
сферически-симметричная (т. е. не зависит от углов •& и ф).
Нормированные собственные я|)-функции, отвечающие s-состоя-
нию (основному) и 25-состоянию,
422

или в атомных единицах
WPHy^e-P и ф200(р)=_1=B-р)е-р/а,
где в качестве единицы длины принят боровский радиус
fl== JE°_^52,9 пм. При таком выборе единицы длины расстояние
от ядра р=г/а будет выражаться в безразмерных единицах длины,
называемых атомными единицами.
Вероятность dW найти электрон в атоме водорода, находящемся
в s-состоянии, в интервале (г, r+dr) одинакова по всем направлени-
направлениям и определяется формулой
9 Орбитальные момент импульса и магнитный момент элек-
электрона:
где / — орбитальное квантовое число, которое может при-
принимать значения 0, 1, 2, . . ., (п—1); \хв—магнетон Бора:
• Проекции орбитальных момента импульса и магнитного мо-
момента на направление внешнего магнитного поля (совпадающего
с осью Z):
О Гиромагнитное отношение для орбитальных магнитного и ме-
механического моментов
щ, z и-в __ 1 е
i %и z ~~ Y ~~ ~2 ~т~ '
Спин * и спиновый магнитный момент электрона:
где s — спиновое квантовое число (s=V2).
9 Проекции спиновых момента импульса и магнитного момента
на направление внешнего магнитного поля (совпадающего с осью Z):
%
где ms — спиновое магнитное квантовое число (ms=—1/42, +^2).
• Гиромагнитное отношение для спиновых магнитного и меха-
механического моментов
%
* Спином называется собственный момент импульса электрона и других
элементарных частиц. Спин не связан с перемещением частицы как целого
и имеет квантовую природу. Спин выражается в единицах постоянной План-
Планка %.
423

© Распределение электронов по состояниям в атоме записывает-
записывается с помощью спектроскопических символов:
Значение побочного кван-
квантового числа
Спектроскопический сим-
символ
0
s
1
Р
2
d
3
/
4
8
5
h
6
i
7
k
Электронная конфигурация записывается следующим образом:
число, стоящее слева перед спектроскопическим символом, означает
главное квантовое число я, а сам спектроскопический символ отве-
отвечает тому или иному значению орбитального квантового числа /
(например, обозначению 2р отвечает электрон с п=2 и /=1; 2/?2
означает, что таких электронов в атоме 2, и т. д.).
9 Принцип Паули. В атоме не может находиться два (и более)
электрона, характеризуемых одинаковым набором четырех кванто-
квантовых чисел: n, /, tnu ms.
Ф Полный момент импульса электрона
где / — внутреннее квантовое число (/=/+1/2, /—1/2).
• Полный орбитальный момент атома
где L — полное орбитальное квантовое число.
О Полный спиновый момент атома
где S — полное спиновое квантовое число.
Ф Полный момент импульса атома
где J — полное внутреннее квантовое число.
• Символическое обозначение состояния атома (спектральный
терм)
где 2S+1 —мультиплетность. Вместо полного орбитального кван-
квантового числа L пишут символ в соответствии с таблицей:
Значение
Символ
0
5
1
Р
2
D
3
F
4
G
5
Н
Пример. Терм 2Р3/2 расшифровывается следующим образом:
мультиплетность 2S+1 =2; следовательно, S = l/2, символу Р
соответствует L=l, а У=3/2.
• Магнитный момент атома
424

где g — множитель (или фактор) Ланде,
1
* l~r 2J(J+l)
• Проекция магнитного момента атома на направление внешне-
внешнего магнитного поля (совпадающего с осью Z)
где nij—полное магнитное квантовое число (my=/, J—1, ...
. . ., -J).
• Сила, действующая на атом в неоднородном магнитном поле,
где dB/dz — градиент магнитной индукции.
Ф Частота ларморовой прецессии
где т — масса электрона.
• Энергия атома в магнитном поле
Е = -р/9ЖВ.
• Величина расщепления спектральной линии при эффекте
Зеемана:
а) сложном (аномальном)
Асо = {trijg"—mjgr) сол,
где тГ,, m'j и g\ gr — магнитные квантовые числа и множители
Ланде соответствующих термов;
б) простом (нормальном)
А(о = 0, ±сол.
• Правила отбора для квантовых чисел S, L, / и mSf mLi ту.
AS 0 A 0
л = 0, ±1;
Д/ = 0, ±1; Amy-0, ±1.
Не осуществляются переходы /=0 ->У=0, а при J=0 — пере-
переходы rrij= 0 -> rrij= 0.
Примеры решения задач
Пример 1. Атом водорода находится в состоянии Is. Определить
вероятность W пребывания электрона в атоме внутри сферы ради-
радиусом г=0,1 а (где а — радиус первой боровской орбиты). Волновая
функция, описывающая это состояние, считается известной.
Решение. Вероятность обнаружить электрон в окрестности
точки с координатами г, •&, ф в объеме dV определяется равенством
W = \*n,tAr, Ь, cp)pdl/.
В ls-состоянии волновая функция if сферически симметрична,
т. е. зависит только от г, и поэтому
V, A)
423

где i|IOo(r) — собственная нормированная волновая функция, от*
вечающая основному состоянию: \|I00 (г) =¦ г— е~г/а.
у яа3
Благодаря сферической симметрии я|>функции вероятность обна-
обнаружить электрон на расстоянии г одинакова по всем направлениям.
Поэтому элемент объема dl/, отвечающий одинаковой плотности
вероятности, можно представить в виде объема сферического слоя
радиусом г и толщиной dr : dV=inr2dr.
С учетом выражений i|I00(r) и dV формула A) запишется в виде
1 -2 4
— Г /@ А. ТТ Г ~ П У —— f*~~ 2Г/й/'2 Н *¦
/ яаз а3
При вычислении вероятности удобно перейти к атомным едини-
единицам, приняв в качестве единицы длины радиус первой боровской
орбиты а. Если ввести безразмерную величину р=г/а, то
r2 = p2a2, dr = adp и dW = 4e-2*>p2 dp.
Вероятность найдем, интегрируя dW в пределах от г^О до г2=
=0,1 а (или от р!—0 до р2—0,1):
о, 1
W = 4 J p2e~2pdp.
о
Этот интеграл может быть точно вычислен интегрированием по
частям, однако при малых р (ртах~0>1) выражение е~2р можно раз-
разложить в ряд Маклорена:
и произвести приближенное вычисление.
Пренебрегая всеми членами степени выше первой, запишем
интеграл в виде
0,1 0,1 0,1
№ = 4 J A—2p)p2dp = 4 J p2dp—8 J p3dp.
0 0 0
Первый и второй интегралы дают соответственно результаты
Таким образом, искомая вероятность
1^=1,33-10-3—0,2-10~3=1,13-10-3.
Пример 2. Электрон в возбужденном атоме водорода находится
в 3 р-состоянии. Определить изменение магнитного момента, обус-
обусловленного орбитальным движением электрона, при переходе атома
в основное состояние.
Решение. Изменение A\it магнитного момента найдем как
разность магнитных моментов в конечном (основном) и начальном
(возбужденном) состояниях, т. е. Л(яг=[хг2—\in.
Магнитный момент орбитального движения электрона зависит
только от орбитального квантового числа И
426

Отсюда имеем: в основном состоянии 1=0 и fxZ2=0; в возбужден-
возбужденном (Зр) состоянии /=1 и \1ц=\1вУ 2. Следовательно, изменение маг-
магнитного момента
Знак минус показывает, что в данном случае магнитный момент
уменьшился. Подставив значение |лв=0,927 «Ю3 Дж/Тл, получим
A\it = —1,31 • 10~23 Дж/Тл.
Вопросы и задачи
Атом водорода
47.1. Уравнение Шредингера в сферической системе координат
для электрона, находящегося в водородоподобном атоме, имеет вид
l^/r2<5\j?\J_lj 1 д / . п д\р
Показать, что это уравнение разделяется на два, если волновую
функцию представить в виде произведения двух функций:
Ф(г, а, ^) = /?(г)Г(», Ф),
где 7? (г) — радиальная и7(9,ф) — угловая функции.
47.2. Уравнение для радиальной /?(г) функции, описывающей
состояние электрона в атоме водорода, имеет вид
где а, р и / — некоторые параметры. Используя подстановку % (г) =
=rR(r), преобразовать его к виду
47.3. Уравнение для радиальной функции %(г) может быть пре-
преобразовано к виду
где a=2mE/fi2; $=Ze2m/Dne0fiJ; I — целое число. Найти асимпто-
асимптотические решения уравнения при больших числах г. Указать, какие
решения с Е>0 или с ?<С0 приводят к связанным состояниям.
47.4. Найти по данным предыдущей задачи асимптотическое
решение уравнения при малых г.
Указание. Считать при малых / члены а и 2р/г малыми по сравнению
с /(/+1)/г2. Применить подстановку %(r)=zr^.
47.5. Найти решение уравнения для радиальной функции R(r),
описывающей основное состояние (/=0), и определить энергию элек-
электрона в этом состоянии. Исходное уравнение для радиальной функ-
427

ции может быть записано в виде
d*R , 2 6R
dr2 n r dr
где а=2тЕ/%2\ $=Ze2m/Dtt&01i2)\ I — орбитальное квантовое число.
Указание. Применить подстановку R (г) = е~^г.
47.6. Атом водорода находится в основном состоянии. Собствен-
Собственная волновая функция, описывающая состояние электрона в атоме,
имеет вид ty(r)=Ce-r/a, где С — некоторая постоянная. Найти из
условия нормировки постоянную С.
47.7. Собственная функция, описывающая основное состояние
электрона в атоме водорода, имеет вид ty(r)=Ce~r/a, где а=4яео/г2/
i(e2m) (боровский радиус). Определить расстояние г, на котором ве-
вероятность нахождения электрона максимальна.
47.8. Электрон в атоме водорода описывается в основном со-
состоянии волновой функцией ty(r) = Ce~r/a. Определить отношение
вероятностей о^/соа пребывания электрона в сферических слоях
толщиной Аг=0,01 а и радиусами гг=0,5а и r2=h5 а.
47.9. Атом водорода находится в основном состоянии. Вычис-
Вычислить: 1) вероятность сох того, что электрон находится внутри обла-
области, ограниченной сферой радиуса, равного боровскому радиусу а;
2) вероятность со2 того, что электрон находится вне этой области;
3) отношение вероятностей ayj^i- Волновую функцию считать
известной: \Ь100 (г) = г е~г/а,
У яа3
47.10. Зная, что нормированная собственная волновая функция,
описывающая основное состояние электрона в атоме водорода, имеет
вид яЬ(г) = г е~г/а, найти среднее расстояние <О> электрона
У ла3
от ядра.
47.11. Принято электронное облако (орбиталь) графически изоб-
изображать контуром, ограничивающим область, в которой вероятность
обнаружения электрона составляет 0,9. Вычислить в атомных еди-
единицах радиус орбитали для ls-состояния электрона в атоме водо-
водорода. Волновая функция, отвечающая этому состоянию, ipioo(p) —
=е~р/Кл;, где р — расстояние электрона от ядра, выраженное
в атомных единицах.
Указание. Получающееся трансцендентное уравнение решить графи-
графически.
47.12. Волновая функция, описывающая 2з-состояние электрона
в атоме водорода, имеет вид ^200 (р) = B—р)е~&2, где р —
расстояние электрона от ядра, выраженное в атомных единицах.
Определить: 1) расстояние р± от ядра, на которых вероятность об-
обнаружить электрон имеет максимум; 2) расстояния р2 от ядра, на
которых вероятность нахождения электрона равна нулю; 3) по-
построить графики зависимости |i|Joo(p)|2 от р и Р2№2оо(р)|2 от р.
428

47.13. Уравнение для угловой функции Y(§, ср) в сферической
системе координат может быть записано в виде
1 ) 1 д ( . „дУ\ , 1 dW \ .
где к — некоторая постоянная. Показать, что это уравнение можно
разделить на два, если угловую функцию представить в виде произ-
произведения двух функций: Y(b, ср)=в ({}) Ф (ф), где 0 ({» —функция,
зависящая только от угла &; Ф (ф) — то же, только от угла ф.
47.14. Угловая функция Ф (ф) удовлетворяет уравнению
-|—2-~-тФ = 0. Решить уравнение и указать значения параметра
пг, при которых уравнение имеет решение.
47.15. Зависящая от угла ф угловая функция имеет видФ(ф) =
—Ceim(p. Используя условие нормировки, определить постоянную С.
47.16. Изобразить графически угловое распределение плотности
вероятности нахождения электрона в атоме водорода, если угловая
функция Fj,m(ft, ф) имеет вид: 1) в s-состоянии (/=0) У"о, о= 1/V^"^;
2) в /^-состоянии (/=1) при трех значениях m: a) m=l, Flfl =
=КЗ/(8я) sin be1*; б) /n=0, Klf0=K3/Djt) cos ft; в) m=—I, rlt_\ =
=КЗ/(8я) sin -&e~i(p. Для построений воспользоваться полярной
системой координат.
47.17. Угловое распределение плотности вероятности нахожде-
нахождения электрона в атоме водорода определяется видом угловой функ-
функции У/, m(d, ф). Показать, что /7-подоболочка имеет сферически сим-
симметричное распределение плотности вероятности. Воспользоваться
данными предыдущей задачи.
Орбитальный момент импульса и магнитный момент электрона
47.18. Вычислить момент импульса S\ орбитального движения
электрона, находящегося в атоме: 1) в s-состоянии; 2) в/7-состоянии.
47.19. Определить возможные значения проекции момента им-
импульса J?*iz орбитального движения электрона в атоме на направле-
направление внешнего магнитного поля. Электрон находится в ^-состоянии.
47.20. Атом водорода, находившийся первоначально в основном
состоянии, поглотил квант света с энергией 8=10,2 эВ. Определить
изменение момента импульса AJ?'t орбитального движения электро-
электрона. В возбужденном атоме электрон находится в /^-состоянии.
47.21. Используя векторную модель атома, определить наимень-
наименьший угол а, который может образовать вектор 3?i момента импульса
орбитального движения электрона в атоме с направлением внешнего
магнитного поля. Электрон в атоме находится в d-состоянии,
47.22. Электрон в атоме находится в /-состоянии. Найти орби-
орбитальный момент импульса J?j электрона и максимальное значение
проекции момента импульса 2 \г тач на направление внешнего маг-
магнитного поля.
47.23. Момент импульса J27 г орбитального движения электрона
429

в атоме водорода равен 1,83 • 10~34 Дж*с. Определить магнитный
момент |ib обусловленный орбитальным движением электрона.
47.24. Вычислить полную энергию Е, орбитальный момент им-
импульса 3?х и магнитный момент )хх электрона, находящегося в 2/7-со-
стоянии в атоме водорода.
47.25. Может ли вектор магнитного момента \к\ орбитального
движения электрона установиться строго вдоль линий магнитной
индукции?
47.26. Определить возможные значения магнитного момента ць
обусловленного орбитальным движением электрона в возбужденном
атоме водорода, если энергия 8 возбуждения равна 12,09 эВ.
Спиновый момент импульса и магнитный момент электрона
47.27. Вычислить спиновый момент импульса^5 электрона и про-
проекцию 3?sz этого момента на направление внешнего магнитного поля.
47.28. Вычислить спиновый магнитный момент \is электрона
и проекцию магнитного момента \xsZ на направление внешнего поля.
47.29. Почему для обнаружения спина электрона в опытах
Штерна и Герлаха используют пучки атомов, принадлежащих
первой группе периодической системы, причем в основном со-
состоянии?
47.30. Атомы серебра, обладающие скоростью и=0,6 км/с, про-
пропускаются через узкую щель и направляются перпендикулярно
линиям индукции неоднородного магнитного поля (опыт Штерна
и Герлаха). В поле протяженностью 1=6 см пучок расщепляется
на два. Определить степень неоднородности dB/dz магнитного поля,
при которой расстояние Ь
между компонентами расщеп-
расщепленного пучка по выходе его
из поля равно 3 мм. Атомы
серебра находятся в основном
состоянии.
47.31. Узкий пучок ато-
атомарного водорода пропуска-
пропускается в опыте Штерна и Гер-
Герлаха через поперечное неод-
неоднородное (dB/dz—2 кТл/м)
магнитное поле протяжен-
протяженностью /=8 см. Скорость v атомов водорода равна 4 км/с. Опре-
Определить расстояние Ь между компонентами расщепленного пучка
атомов по выходе его из магнитного поля. Все атомы водорода
в пучке находятся в основном состоянии.
47.32. В опыте Штерна и Герлаха узкий пучок атомов цезия
(в основном состоянии) проходит через поперечное неоднородное
магнитное поле и попадает на экран Э (рис. 47.1). Какова должна
быть степень неоднородности dB/dz магнитного поля, чтобы расстоя-
расстояние Ь между компонентами расщепленного пучка на экране было
430
Рис. 47.1

равно 6 мм? Принять /1=/2=10см. Скорость атомов цезия равна
0,3 км/с.
47.33. Узкий пучок атомов рубидия (в основном состоянии) про-
пропускается через поперечное неоднородное магнитное поле протя-
протяженностью /i=10 см (рис. 47.1). На экране Э, отстоящем на расстоя-
расстоянии /2=20 см от магнита, наблюдается расщепление пучка на два.
Определить силу Fz, действующую на атомы рубидия, если расстоя-
расстояние Ь между компонентами пучка на экране равно 4 мм и скорость v
атомов равна 0,5 км/с.
47.34. Узкий пучок атомов серебра при прохождении неодно-
неоднородного (dB/dz=l кТл/м) магнитного поля протяженностью 1Х=
=4 см расщепился на два пучка. Экран для наблюдения удален от
границы магнитного поля на расстояние /2= 10 см (рис. 47.1). Опре-
Определить (в магнетонах Бора) проекции (ыл г магнитного момента
атома на направление вектора магнитной индукции, если расстоя-
расстояние Ь между компонентами расщепленного пучка на экране равно
2 мм и атомы серебра обладают скоростью у=0,5 км/с.
Застройка электронных оболочек
47.35. Какое максимальное число S-, р- и d-электронов может
находиться в электронных /С-, L- и М- слоях атома?
47.36. Используя принцип Паули, указать, какое максималь-
максимальное число iVraax электронов в атоме могут иметь одинаковыми сле-
следующие квантовые числа: 1) п, I, m, ms\ 2) /г, /, т\ 3) /г, /; 4) п.
47.37. Заполненный электронный слой характеризуется кванто-
квантовым числом я=3. Указать число N электронов в этом слое, которые
имеют одинаковые следующие квантовые числа: 1) т5= + 1/2;
2) т=—2; 3) ms=—l/2 и т=0; 4) т5= + 1/2 и 1=2.
47.38. Найти число N электронов в атомах, у которых в основ-
основном состоянии заполнены: 1) /С- и L-слои, Зя-оболочка и наполовину
3/7-оболочка; 2) /(-, L- и Af-слои и 4s-, 4p- и 4^-оболочки. Что это
за атомы?
47.39. Написать формулы электронного строения атомов: 1) бо-
бора; 2) углерода; 3) натрия.
Векторная модель атома. Спектральные термы
47.40. Как можно согласовать использование векторной модели
атома с соотношением неопределенностей для проекций момента им-
импульса?
47.41. Электрон в атоме водорода находится в /^-состоянии. Оп-
Определить возможные значения квантового числа / и возможные зна-
значения (в единицах ft) полного момента импульса J?y электрона. По-
Построить соответствующие векторные диаграммы.
47.42. В возбужденном атоме гелия один из электронов нахо-
находится в /7-состоянии, другой в d-состоянии. Найти возможные зна-
значения полного орбитального квантового числа L и соответствующего
431

ему момента импульса 3 L (в единицах Ь). Построить соответствую-
соответствующие векторные диаграммы.
47.43. Определить угол ср между орбитальными моментами им-
импульсов двух электронов, один из которых находится в d-состоянии,
другой — в /-состоянии, при следующих условиях: 1) полное орби-
орбитальное квантовое число L=3; 2) искомый угол — максимальный;
3) искомый угол — минимальный.
47.44. Система из трех электронов, орбитальные квантовые
числа /i, /2, h которых соответственно равны 1, 2, 3, находятся
в S-состоянии. Найти угол cpi, 2 между орбитальными моментами
импульса первых двух электронов.
47.45. Каковы возможные значения полного момента импульса
Sj электрона, находящегося в d-состоянии? Чему равны при этом
углы ф между спиновым моментом импульса и орбитальным?
47.46. Спиновый момент импульса двухэлектронной системы
определяется квантовым числом S=l. Найти угол ср между спино-
спиновыми моментами импульса обоих электронов.
47.47. Система, состоящая из двух электронов, находится в
состоянии с L=2. Определить возможные значения угла ср между
орбитальным моментом импульса /?-электрона и полным орбиталь-
орбитальным моментом импульса 3j системы.
47.48. Найти возможные значения угла между спиновым мо-
моментом импульса и полным моментом: 1) одноэлектронной системы,
состоящей из d-электрона; 2) двухэлектронной системы с J=2.
47.49. Определить возможные значения (в единицах ft) проекции
3'Sz спинового момента импульса электронной системы, находящей-
находящейся в состоянии Ю3, на направление полного момента.
47.50. Определить возможные значения квантового числа /
электронной системы, для которой: 1) S=2 и L=l; 2) S = l и L-=3.
Найти (в единицах %) возможные значения полного момента импуль-
импульса 3?j системы и построить соответствующие векторные диаграммы.
47.51. Определить возможные значения квантового числа У,
соответствующего полному моменту импульса 3?s электронной сис-
системы, у которой L=3, a S принимает следующие значения: 1) 3/2;
2) 2; 3) 5/2; 4) 4. Построить соответствующие векторные диаграммы.
47.52. Записать основные термы для следующих атомов: 1) Н;
2) Не; 3) Be; 4) Li; 5) В.
47.53. Перечислить возможные термы для следующих состояний
атомов: 1) 2S; 2) 2Р; 3) 4Р; 4) Ю.
47.54. Определить кратности вырождения следующих термов:
1) 2D3/2; 2) 3/V, 3) *F.
47.55. Объяснить на основе векторной модели атома наличие
двух систем термов (синглетных и триплетных) в атомах с двумя
валентными электронами.
47.56. Определить возможные мультиплетности BS+1) термов
следующих атомов: 1) Li; 2) Be; 3) В; 4) С; 5) N.
47.57. Выписать все возможные термы для комбинации р- и
d-электронов по типу связи Рассель — Саундерса. Дать их спект-
спектральные обозначения.
432

Магнитный момент атома. Атом в магнитном поле
47.58. Вычислить множитель Ланде g для атомов с одним
валентным электроном в состояниях 5 и Р.
47.59. Вычислить множитель Ланде g для атомов, находящихся
в синглетных состояниях.
47.60. Определить магнитный момент jli7 атома в состоянии Ю.
Ответ выразить в магнетонах Бора (jlib).
47.61. Вычислить магнитный момент \ij атома в состоянии 3Р2-
Ответ выразить в магнетонах Бора.
47.62. Атом находится в состоянии 2D3/2. Найти число возмож-
возможных проекций магнитного момента на направление внешнего поля
и вычислить (в магнетонах Бора) максимальную проекцию (x7zraax.
47.63. Вычислить в магнетонах Бора магнитный момент \ij атома
водорода в основном состоянии.
47.64. Атом находится в состоянии 1/7. Найти соответстующий
магнитный момент \ij и возможные значения его проекции \ijz на
направление внешнего хмагнитного поля.
47.65. Максимальная проекция |лл гтах магнитного момента
атома, находящегося в состоянии 2D, составляет четыре магнетона
Бора. Определить мультиплетность BS+1) соответствующего терма.
47.66. На сколько составляющих расщепляется в опыте Штерна
и Герлаха пучок атомов, находящихся в состояниях: 1) 2Р3/2\
2) Ю- 3) 5/ч.
47.67. Определить максимальные проекции ji7i zmax магнитных
моментов атомов ванадия (*F), марганца FS) и железа ED), если
известно, что пучки этих атомов при прохождении через сильно не-
неоднородное магнитное поле по методу Штерна и Герлаха расщепля-
расщепляются соответственно на 4, 6 и 9 составляющих. (В скобках указаны
состояния, в которых находятся атомы.)
47.68. Вычислить частоты сол ларморовой прецессии электрон-
электронных оболочек атомов: I) в магнитном поле Земли (В=5-Ю"Б Тл);
2) в поле, магнитная индукция В которого равна 50 Тл.
47.69. Найти угловую скорость со прецессии магнитных момен-
моментов атомов, помещенных в магнитном поле (В=ЮмТл) в случае,
когда атомы находятся в состояниях: I) 1Р\ 2) 2Р3/2-
47.70. Определить максимальную энергию f/rrax магнитного
взаимодействия атома, находящегося в состоянии Ю с магнитным
полем, индукция которого: 1) В=\ Тл; 2) В=50 Тл. Ответ выразить
в электрон-вольтах.
Эффект Зеемана
47.71. Какое магнитное поле в случае эффекта Зеемана следует
считать: 1) «слабым», 2) «сильным»?
47.72. Состояния атома характеризуются двумя спектральными
термами. Указать квантовые числа 5, L и возможные значения кван-
квантового числа J для состояний: 1) XS и гР; 2) Ю и 2/\ Изобразить для
433

этих состояний схему энергетических уровней при отсутствии маг-
магнитного поля.
47.73. Состояние атома характеризуется двумя спектральными
термами. Указать возможные значения квантового числа J для
состояний: 1) 2S и 2Р; 2) 3Р и 2D; 3) 3S и Ю. Изобразить для этих
состояний схему энергетических уровней с учетом спин-орбиталь-
спин-орбитального взаимодействия (естественного мультиплетного расщепления)
при отсутствии магнитного поля.
47.74. Определить возможные значения квантового числа т3
и изобразить на схеме расщепление энергетических уровней атома
в магнитном поле для состояний, определяемых спектральными
термами: 1) 2S; 2) 2Р3/2; 3) 2D5/2; 4) 1F.
47.75. Построить схему возможных энергетических переходов
в слабом магнитном поле между состояниями атома, определяемыми
следующими термами: 1) 2Р1/2 ->2S; 2) 2Р3/2 ->2S; 3) 2D3/2 -^2Р3/2.
47.76. Вычислить смещение Асо спектральных линий при слож-
сложном (аномальном) эффекте Зеемана в случае перехода атома из со-
состояния, определяемого термом 2Pi/2, в состояние — 2Si/2. В каче-
качестве единицы смещения принять нормальное (лоренцово) смещение
A /A)B
§ 48. СПЕКТРЫ МОЛЕКУЛ
Основные формулы
# Приведенная масса двухатомной молекулы
|л=/7г1т2/(т1+т2),
где т1 и т2 — массы атомов, входящих в состав молекулы.
# Собственная круговая частота осциллятора
где р — коэффициент квазиупругой силы.
9 Нулевая собственная волновая функция одномерного кван-
квантового гармонического осциллятора
где параметр а = V
• Энергия колебания гармонического осциллятора
где п — колебательное квантовое число (л=0, 1, 2, 3, . . .).
Для квантового числа п существует правило отбора, согласно
которому Дя=±1.
• Нулевая энергия
Энергия колебания ангармонического осциллятора
434

где v — колебательное квантовое число (и^О, 1, 2, ...)*» У — коэф-
коэффициент ангармоничности; Av — любое целое число. Для кванто-
квантового числа v нет правила отбора, поэтому Av может принимать лю-
любые целочисленные значения.
• Разность энергий двух соседних колебательных уровней
Максимальное значение квантового числа v
ах ~~~Щ 1#
Максимальная энергия колебательного движения
ax = *«>/DY).
Энергия диссоциации двухатомной молекулы
• Момент инерции двухатомной молекулы относительно оси,
проходящей через ее центр инерции перпендикулярно прямой,
соединяющей ядра атомов,
где [х — приведенная масса молекулы; d — межъядерное расстоя-
расстояние.
• Вращательная постоянная
Энергия вращательного движения двухатомной молекулы
где f-—вращательное квантовое число (^=0, 1, 2, . . .).
• Спектроскопическое волновое число
v=lM,,
где X — длина волны излучения.
О Энергия 8 фотона излучения связана с спектроскопическим
волновым числом v соотношением
где с — скорость распространения электромагнитного излучения.
Примеры решения задач
Пример 1. Собственная угловая частота со колебаний молекулы
НС1 равна 5,63 «1014 с", коэффициент ангармоничности 7^0,0201.
Определить: 1) энергию A?2i г (в электрон-вольтах) перехода моле-
молекулы с первого на второй колебательный энергетический уровень;
2) максимальное квантовое число fmax; 3) максимальную колебатель-
колебательную энергию Етах; 4) энергию диссоциации Ed.
Решение. 1. Энергию перехода AEv+it v между двумя со-
соседними уровнями найдем как разность двух значений колебатель-
колебательной энергии:
AEv+Uv = Ev+i-Ev.
435

Так как колебательная энергия двухатомной молекулы опреде-
определяется соотношением
то
Подставив значения Л, со, 7 и произведя вычисления, найдем
Л?2|1=1,09.10-19 Дж,
или
A?2il -0,682 эВ.
2. Максимальное квантовое число итах найдем, приравняв раз-
разность соседних энергетических уровней нулю:
или 1—27(^тах+1)=0, откуда
fmax = -27—!• ^
Подставив сюда значение -у и округлив до ближайшего (снизу)
целого значения найденного итах, получим
Umax = 23.
3. Максимальную колебательную энергию ?шах найдем, если
в выражение A) вместо v подставим итах по формуле
Выполняя простые преобразования и пренебрегая у/4 по срав-
сравнению с 1 /D^), получаем
у
Подставим значения ft, со,
у и произведем вычисления:
или
4. Энергия диссоциации есть
энергия, которую необходимо
затратить, чтобы отделить атомы
*^bu) B молекуле друг от друга и уда-
Т^ лить их без сообщения им кине-
кинетической энергии на расстояние,
Рис- 48>1 на котором взаимодействие ато-
атомов пренебрежимо мало. На
рис. 48.1 эта энергия отвечает переходу с нулевого колебатель-
колебательного уровня на самый высокий возбужденный, соответствующий
итах. Тогда энергия диссоциации
436

Заменив /1(o/Dy) на Еты, получим
?rf = ?max(l-2v).
Произведя вычисления, найдем
Пример 2. Для молекулы HF определить: 1) момент инерции J,
если межъядерное расстояние d=9\J пм; 2) вращательную посто-
постоянную В; 3) энергию, необходимую для возбуждения молекулы на
первый вращательный уровень.
Решение. 1. Если воспользоваться формулой приведенной
массы [I молекулы, то ее момент инерции можно выразить соотно-
соотношением
или J= mim2 d\
mfm
где тг и m2 — массы атомов водорода и фтора.
Приведенную массу молекулы удобно сначала выразить в а. е. м.
(относительные атомные массы химических элементов приведены
в табл. 30):
\i= ' 19-а. е. м =0,95 а. е.м.
Выразив приведенную массу в единицах СИ (|л=0,95 -1,67 *10~27 кг=
= 1,59-10"7 кг), найдем момент инерции молекулы HF:
2. Вращательная постоянная В с учетом выражения для
равна
Подставив значения h, \i, d и произведя вычисления, получим
? = 4,37.10~22 Дж или В = 2,7
3. Энергия, необходимая для возбуждения молекулы на первый
вращательный уровень, равна разности энергий молекулы на пер-
первом и нулевом вращательных уровнях.
Так как вращательная энергия двухатомной молекулы выража-
выражается соотношением Esu=Bf-(f>+\)y то разность энергий двух со-
соседних вращательных уровней
После упрощений получим
Положив здесь ^=0, найдем значение энергии, необходимое
для возбуждения молекулы с нулевого уровня на первый:
437

Задачи
Колебательный спектр двухатомной молекулы
48.1. Изобразить графически зависимость г|H(х) и |г|зо(л:)|2 для
нулевой собственной волновой функции осциллятора.
48.2. Используя условие нормировки, определить нормировоч-
нормировочный множитель Со нулевой собственной волновой функции осцил-
осциллятора.
48.3. Рассматривая молекулу как квантовый гармонический ос-
осциллятор, находящийся в основном состоянии (п=0), найти ампли-
амплитуду А классических колебаний, выразив ее через параметр ос.
48.4. Гармонический осциллятор находится в основном состоя-
состоянии (ai=0). Какова вероятность W обнаружения частицы в области
(—A<Lx<iA), где А — амплитуда классических колебаний?
48.5. Определить среднюю потенциальную энергию (U(х)) гар-
гармонического осциллятора, находящегося в основном состоянии,
выразив ее через нулевую энергию Ео.
48.6. Собственная круговая частота со колебаний молекулы во-
водорода равна 8,08 -1014 с. Найти амплитуду А классических коле-
колебаний молекулы.
48.7. Зная собственную круговую частоту со колебаний молеку-
молекулы СО (со=4,08 -1014 с), найти коэффициент Р квазиупругой силы.
48.8. Определить энергию ?ВОЗб возбуждения молекулы НС1
с нулевого колебательного энергетического уровня на первый, если
известны собственная круговая частота со=5,63«1014 с и коэффи-
коэффициент ангармоничности 7=0,0201.
48.9. Определить число N колебательных энергетических уров-
уровней, которое имеет молекула НВг, если коэффициент ангармонич-
ангармоничности 7=0,0208.
48.10. Во сколько раз отличаются максимальная и минимальная
(отличная от нуля) разности двух соседних энергетических уровней
для молекулы Н2G=0,0277)?
48.11. Определить максимальную колебательную энергию Етзх
молекулы О2, для которой известны собственная круговая частота
@=2,98 »1014 с и коэффициент ангармоничности 7==9>46-10~3.
48.12. Определить энергию диссоциации D (в электрон-вольтах)
молекулы СО, если ее собственная частота со^^Ов-1014 с и коэф-
коэффициент ангармоничности 7=:5,83-10~3. Изобразить на потенциаль-
потенциальной кривой схему колебательных энергетических уровней и отметить
на ней энергию диссоциации.
48.13. Найти коэффициент ангармоничности 7 молекулы N2,
если ее энергия диссоциации ?=9,80эВ и собственная круговая
частота со=4,45 «1014 с. На потенциальной кривой изобразить
схему энергетических уровней молекулы и отметить на ней энергию
диссоциации.
48.14. Молекула NO переходит из низшего возбужденного со-
состояния в основное. Определить длину волны X испущенного при
этом фотона, если собственная круговая частота ш=3,59-1014 с~г
438

и коэффициент ангармоничности 7=8,73-10 3. На потенциальной
кривой изобразить схему колебательных энергетических уровней
молекулы и отметить на ней соответствующий энергетический
переход.
Вращательный спектр двухатомной молекулы
48.15. Найти момент импульса J? двухатомной молекулы, со-
соответствующий низшему возбужденному состоянию.
48.16. Определить изменение A.S7 момента импульса двухатом-
двухатомной молекулы при переходе ее с первого вращательного уровня на
второй.
48.17. Определить угловую скорость со вращения молекулы S2,
находящейся на первом возбужденном вращательном уровне.
Межъядерное расстояние d= 189 пм.
48Л8. Вычислить вращательную постоянную В для молекулы
СО, если межъядерное расстояние d= 113 пм. Ответ выразить в мил-
лиэлектрон-вольтах.
48.19. Найти момент импульса g молекупы кислорода, враща-
вращательная энергия Е/и которой равна 2,16 мэВ.
48.20. Найти момент инерции / и межъядерное расстояние d мо-
молекулы СО, если интервалы АЕ между соседними линиями чисто
вращательного спектра испускания молекул СО равны 0,48 мэВ.
48.21. Определить для молекулы НС1 вращательные квантовые
числа ^ двух соседних уровней, разность энергий A?V + 1 /и кото-
которых равна 7,86 мэВ.
48.22. Для молекулы N2 найти: 1) момент инерции У, если межъ-
межъядерное расстояние ^=110пм; 2) вращательную постоянную В;
3) изменение |А?| энергии при переходе молекулы с третьего вра-
вращательного энергетического уровня на второй. Относительная атом-
атомная масса Л N = 14.
48.23. Для молекулы О2 найти: 1) приведенную массу м,; 2) межъ-
межъядерное расстояние d, если вращательная постоянная В=0,178 мэВ;
3) угловую скорость со вращения, если молекула находится на пер-
первом вращательном энергетическом уровне. Относительная атомная
масса Ло=16.
48.24. Для молекулы N0 найти: 1) момент инерции / молекулы,
если межъядерное расстояние d=H5 пм; 2) вращательную постоян-
постоянную В молекулы; 3) температуру 7\ при которой средняя кинетиче-
кинетическая энергия поступательного движения молекулы равна энергии,
необходимой для ее возбуждения на первый вращательный энерге-
энергетический уровень. Относительные атомные массы ЛN и Ао равны
соответственно 14 и 16.
48.25. Установить числовое соотношение между энергией г
излучения и спектроскопическим волновым числом v.
48.26. Найти расстояние d между ядрами молекулы СН, если
интервалы Av между соседними линиями чисто вращательного
спектра испускания данной молекулы равны 29 см.
439

48.27. Определить, на сколько изменится импульс молекул азо-
азота при испускании спектральной линии с длиной волны Л,= 1250 мкм,
которая принадлежит чисто вращательному спектру.
48.28. Длины волн ^ и Х2 двух соседних спектральных линий
в чисто вращательном спектре молекулы НС1 соответственно равны
117 и 156 мкм. Вычислить вращательную постоянную (см) для
молекулы НС1.
48.29. Будет ли монохроматическое электромагнитное излучение
с длиной волны Х=3 мкм возбуждать вращательные и колебатель-
колебательные уровни молекулы HF, находящейся в основном состоянии?
48.30. Определить кратность вырождения энергетического уров-
уровня двухатомной молекулы с вращательным квантовым числом ^.

ГЛАВА 10
ФИЗИКА ТВЕРДОГО ТЕЛА
§ 49. ЭЛЕМЕНТЫ КРИСТАЛЛОГРАФИИ
Основные формулы
Молярный объем кристалла
где М—молярная масса вещества; р — плотность кристалла.
Объем V элементарной ячейки в кристаллах:
а) при кубической сингонии V=ad;
б) при гексагональной сингонии V=]^3a2c/2. Здесь а и с — па-
параметры решетки.
Если для гексагональной решетки принять теоретическое значе-
значение
У т0 V
• Число Zm элементарных ячеек в одном моле кристалла
7 z=z V l\f ИЛИ Z z==z kN & Ifl
где k — число одинаковых атомов в химической формуле соедине-
соединения (например, в кристалле AgBr число одинаковых атомов Ag или
Вг в химической формуле соедине-
соединения равно единице); NA — постоян-
постоянная Авогадро; п — число одинаковых
атомов, приходящихся на элементар-
элементарную ячейку. На рис. 49.1 представ-
представлена структура NaCl; аналогичную
структуру имеют соединения КВг,
AgBr, MnO и др.
Число Z элементарных ячеек в
единице объема кристалла
Z = ZjVmi
или в общем случае
Z = p——; Рис. 49.1
для кристалла, состоящего из одинаковых атомов (k=l),
Параметр а кубической решетки
а =
441

Расстояние d между соседними атомами в кубической решетке:
а) в гранецентрированной d=alV2\
б) в объемно центрированной d=V3al2.
• Для обозначения узлов, направлений и плоскостей в решетке
вводятся специальные ин-
индексы.
Индексы узлов записы-
записывают в двойных квадрат-
квадратных скобках [[тпр]]. Для
отрицательных индексов
над буквой ставится знак
минус, например т (рис.
49.2).
• Индексы направле-
направлений записываются в оди-
одинарных квадратных скоб-
скобках [тпр]. Индекс направ-
х ления совпадает с индек-
Рис. 49.2 сом узла, через который
проходит прямая, если эта
прямая одновременно проходит и через начало координат [[000]]
(рис. 49.2).
Индексы направления задают не одну прямую в кристалле, а се-
семейство параллельных прямых. Изменение всех индексов на обрат-
обратные по знаку [тпр] означает то же самое направление в кристалле.
• Период идентичности вдоль прямой, заданной индексами
[тпр], в кубической решетке выражается соотношением
где а — параметр решетки.
• Угол ф между прямыми
шетке выражается формулой
i
/
>-
7
i>
Ш
/
/
/
/
/
/
г] и \т%п2р2] в кубической ре-
реф Индексы плоскости (индексы Миллера) записывают в круг-
круглых скобках (hkl). Изменение всех индексов на обратные (h~kl) от-
отвечает тому же семейству плоскостей.
Индексы Миллера связаны с минимальными отрезками, отсе-
отсекаемыми плоскостью на осях координат.
# Для нахождения отрезков следует взять обратные величины
индексов Миллера (Ш; \lk\ Ml) и привести их к наименьшему
целому, кратному каждому из полученных чисел. Полученные зна-
значения и есть наименьшие отрезки, отсекаемые плоскостью {hkl)
на осях координат.
Если известны отрезки, отсекаемые на осях координат, то ин-
индексы Миллера находятся аналогичным путем (см. пример 4).
Индексы Миллера пропорциональны направляющим косинусам
442

вектора нормали к данной плоскости. Поэтому индексы Миллера для
некоторого семейства плоскостей совпадают с индексами направ-
направлений нормали к этим плоскостям.
• Угол между плоскостями (/ii&i/i) и (h^kih) определяется из
формулы
а между прямой [тар] и плоскостью (hkl) — из формулы
hm-\- kn + In
cos(p=- — и
у/
у
у
У
у
у
у
у:
А
Л
-4-'
У
у
у
у
-р
у
у/
У
Примеры решения задач
Пример 1. Определить число п узлов, приходящихся на одну
элементарную ячейку в гранецентрированной кубической решетке.
Решение. Выделим элементарную ячейку в кубической ре-
решетке (рис. 49.3) и определим, скольким соседним элементарным
ячейкам принадлежит тот или
иной узел выделенной ячейки.
В этой ячейке имеются узлы
двух типов: А (находящиеся
в вершинах куба) и В (нахо-
(находящиеся на гранях куба в
точке пересечения диагона-
диагоналей).
Узел А принадлежит одно-
одновременно восьми элементар-
элементарным ячейкам. Следовательно,
в данную ячейку узел А вхо-
входит с долей 1/8. Узел В вхо-
входит одновременно только в две
ячейки и, следовательно, в Рис. 49.3
данную ячейку узел В входит
с долей 1/2. Если учесть, что число узлов типа А в ячейке равно
восьми, а число узлов типа В равно шести, т. е. числу граней, то
общее число узлов, приходящихся на одну элементарную ячей-
ячейку в гранецентрированной решетке,
п = A/8) - 8 + A/2) .6 = 1 + 3 = 4 узла.
Так как число узлов равно числу атомов, то в соответствующей
структуре на элементарную ячейку приходится четыре атома.
Пример 2. Определить параметр а решетки и расстояние d
между ближайшими соседними атомами кристалла кальция (решет-
(решетка гранецентрированная кубической сингонии). Плотность р кри-
кристалла кальция равна 1,55-103 кг/м3.
Решение. Параметр а кубической решетки связан с объемом
элементарной ячейки соотношением V=a3. С другой стороны, объем
элементарной ячейки равен отношению молярного объема к числу
элементарных ячеек в одном моле кристалла: V= Vm/Zm. Прирав-
443

няв правые части приведенных выражений для V, найдем
a^VjZm. A)
Молярный объем кальция Vm=Af/p, где р — плотность кальция;
М — его молярная масса. Число элементарных ячеек в одном моле
Zm = NA/n,
где п — число атомов, приходящихся на одну ячейку. Подставив
в формулу A) приведенные выражения для Vm и Zm, получим
Отсюда
а = \/nM/(pNA). B)
Подставим значения величин n, M, р и NA в формулу B), учи-
учитывая, что п=4 (см. предыдущий
пример). Произведя вычисления,
найдем
а=556 пм.
Расстояние d между ближайши-
ближайшими соседними атомами находится
&=lf из простых геометрических сооб-
соображений, ясных из рис. 49.4:
Рис. 49.4
Подставив в это выражение най-
найденное ранее значение а, получим
d-393 пм.
Пример 3. Написать индексы направления прямой, проходящей
через узлы [[100]] и [[001]] кубической примити&ной решетки.
Решение. Эту задачу можно решить двумя способами.
1-й способ. Изобразим кубическую примитивную ячейку, отме-
отметим на ней узлы с индексами [[100]] и [[001]] и проведем через эти
узлы прямую (рис. 49.5, а).
Рис. 49.5
Если бы прямая проходила через начало координат, то индексы
ее направления совпадали бы с индексами узла, ближайшего к на-
началу координат, через который проходит прямая.
444

Заданная прямая не проходит через начало координат. Но этого
можно достигнуть, перенеся начало координат в один из узлов, через
которые проходит прямая.
Если перенести начало координат в узел [[100]] (рис. 49.5, б)у
то узел, лежащий на той же прямой и ближайший к выбранному
началу координат, будет иметь индексы [[101]], а искомое направле-
направление в этом случае определится индексами [101].
Если же начало координат перенести в узел [[001]] (рис. 49.5, в),
то соответственно индексы искомого направления будут [101].
Итак, индексы искомого направления в кристалле [101] или [101].
2-й способ. Не всегда бывает легко определить, как изменятся
индексы узлов при переносе начала координат. Поэтому рассмотрим
аналитический метод решения.
Напишем в общем виде уравнение прямой, проходящей через две
точки в пространстве, с индексами узлов [[т^рг]] и [[г
X—ttl\ у—П\ 2 — Р\
A)
Величины, стоящие в знаменателе, пропорциональны направ-
направляющим косинусам прямой. Но так как эти величины целочислен-
ны, то они и будут являться индексами направления.
Подставив в знаменатель
выражения A) значения ин- *л
дексов узлов ml=lJ пг=0у
Pi = 0 И ftlz^O, A22 —0, /?2—1»
получим:
Рз_л= 1_0=1.
Таким образом, искомые
индексы направления [101].
Пример 4. Написать ин-
индексы Миллера для плоскос-
плоскости, содержащей узлы с ин-
индексами [[200]], [[0101] и
[[001]]. Решетка кубическая, примитивная.
Решение. Возможны два способа решения задачи.
1-й способ применим в тех случаях, когда узлы, принадлежащие
плоскости, лежат одновременно и на осях координат (т. е. известны
отрезки, отсекаемые плоскостью на осях координат).
В данном случае узлы, принадлежащие плоскости, лежат на
осях координат, и отрезки (в единицах постоянной решетки),
отсекаемые на осях координат этой плоскостью, соответственно
бУДУТ (рис. 49.6) 2, 1, 1.
В соответствии с общим правилом нахождения индексов Миллера
напишем обратные значения полученных чисел у; у; у и при-
приведем их к наименьшему целому кратному этих чисел. Для этого
Рис. 49.6
445

умножим числа на два. Полученная совокупность значений, заклю-
заключенная в круглые скобки, и есть искомые индексы Миллера A, 2, 2),
2-й способ (аналитический) особенно удобен тогда, когда извест-
известные узлы не лежат на осях координат. Этот способ является общим
и применим во всех случаях.
Известно, что индексы Миллера равны наименьшим целочислен-
целочисленным коэффициентам при переменных в уравнении плоскости. По-
Поэтому решение задачи по определению индексов Миллера сводится,
по существу, к отысканию уравнения плоскости.
Уравнение плоскости, проходящей через три точки с координа-
координатами [[mxiiiPi]], I[m2n2p2]]i [[m3n3p3]], дается определителем третьего
порядка
—rii г—
=0.
т3—т± п3—щ р3—}
В нашем случае: тг=2, fti=O, р±=0\ т2=0, п2=1, р2=0; т3=0,
п3=0, р3=0. Подставляя значения индексов узлов в определитель,
получим
х—2 у—0 2—0 х—2 у г
0_2 1—0 0 — 0 =0, или —2 1 0 =0.
0—2 0—0 1—0 —2 0 1
Разложим этот определитель по элементам первой строки:
(х-2)
1
0
0
1
—у
—2
—2
0
1
—2
—2
1
0
= 0.
Раскрывая определитель второго порядка, получим
(х—2) (+1) — г/ (—2) + 2 (+2) = 0, или x+2y + 2z = 2.
Выписав коэффициенты при х, yf z и заключив их в круглые скобки,
получим индексы Миллера
A,2,2).
Эти значения индексов, как и следовало ожидать, совпадают со
значениями, полученными первым способом.
Задачи
Элементарная ячейка. Параметры решетки
49.1. Сколько атомов приходится на одну элементарную ячейку:
1) примитивной решетки кубической сингонии; 2) объемно-центри-
объемно-центрированной решетки ромбической сингонии; 3) гранецентрированной
решетки кубической сингонии; 4) базоцентрированной решетки ром-
ромбической сингонии; 5) примитивной решетки гексагональной син-
сингонии; 6) гексагональной структуры с плотной упаковкой.
49.2. Определить число элементарных ячеек кристалла объемом
V—1 м3: 1) хлористого цезия (решетка объемно-центрированная
кубической сингонии); 2) меди (решетка гранецентрированная ку-
446

бической сингонии); 3) кобальта, имеющего гексагональную струк-
структуру с плотной упаковкой.
49.3. Найти плотность р кристалла неона (при 20 К), если из-
известно, что решетка гранецентрированная кубической сингонии.
Постоянная а решетки при той же температуре равна 0,452 нм.
49.4. Найти плотность р кристалла стронция, если известно, что
решетка гранецентрированная кубической сингонии, а расстояние d
между ближайшими соседними атомами равно 0,43 нм.
49.5. Определить относительную атомную массу Аг кристалла,
если известно, что расстояние d между ближайшими соседними ато-
атомами равно 0,304 нм. Решетка объемно-центрированная кубической
сингонии. Плотность р кристалла равна 534 кг/м3.
49.6. Найти постоянную а решетки и расстояние d между бли-
ближайшими соседними атомами кристалла: 1) алюминия (решетка гра-
гранецентрированная кубической сингонии); 2) вольфрама (решетка
объемно-центрированная кубической сингонии).
49.7. Используя метод упаковки шаров, найти отношение с/а
параметров в гексагональной решетке с плотнейшей упаковкой.
Указать причины отклонения этой величины в реальном кристалле
от вычисленного.
49.8. Определить постоянное а и с решетки кристалла магния,
который представляет собой гексагональную структуру с плотной
упаковкой. Плотность р кристаллического магния равна 1,74х
XIО3 кг/м3.
49.9. Вычислить постоянную а решетки кристалла бериллия,
который представляет собой гексагональную структуру с плотной
упаковкой. Параметр а решетки равен 0,359 нм. Плотность р кри-
кристалла бериллия равна 1,82 • 103 кг/м3.
49.10. Найти плотность р кристалла гелия (при температуре
Г—2 К), который представляет собой гексагональную структуру
с плотной упаковкой. По-
Постоянная а решетки, опре-
определенная при той же тем-
температуре, равна 0,357 нм.
Индексы узлов, направлений
и плоскостей
49.11. Определить ин-
индексы узлов, отмеченных
на рис. 49.7 буквами Л,
В, С, D.
49.12. Написать индек-
индексы направления прямой,
проходящей в кубической
Z
\
У\ У
УЛ У
у'
L
^У
^У
1
1
У
L
А
У
У^
У
/У
/^
^У
1
if
ч
У^\
9 У
Рис. 49.7
решетке через начало координат и узел с кристаллографическими
индексами, в двух случаях: 1) [[242]]; 2) [[112]].
49.13. Найти индексы направлений прямых Л Б, CD,
изображенных на рис. 49.8, а, б, в.
447

49.14. Написать индексы направления прямой, проходящей
через два узла с кристаллографическими индексами (в двух случа-
случаях): 1) [[123]] и [[321]]; 2) [[121]] и [[201]].
49.15. Вычислить период / идентичности вдоль прямой [111]
в решетке кристалла NaCl, если плотность р кристалла равна 2,17Х
X 103 кг/м3.
*)
А
у/
У.
б)
у
/
/
в/
/
у
/ у
Г
\
\
/
\
ч
4
¦у
Рис. 49.8
49.16. Вычислить угол ф между двумя направлениями в куби-
кубической решетке кристалла, которые заданы кристаллографическими
индексами [ПО] и [111].
49.17. Написать индексы Миллера для плоскостей в примитив-
примитивной кубической решетке, изображенных на рис. 49.9, а — е.
Рис. 49.9
49.18. Плоскость проходит через узлы [[100]], НОЮ]], [[001II
кубической решетки. Написать индексы Миллера для этой пло-
плоскости .
49.19. Система плоскостей в примитивной кубической решетке
задана индексами Миллера B21). Найти наименьшие отрезки, отсе-
отсекаемые плоскостью на осях координат, и изобразить эту плоскость
графически.
49.20. Направление нормали к некоторой плоскости в кубиче-
кубической решетке задано индексами [110]. Написать индексы Миллера
448

для этой плоскости и указать наименьшие отрезки, отсекаемые
плоскостью на осях.
49.21. Написать индексы Миллера для плоскостей, содержащих
узлы с кристаллографическими индексами, в двух случаях: 1) [[111]],
ПГ12]], [[101]]; 2) [[111]], [[010]], [[III]]. Найти отрезки, отсекаемые
этими плоскостями на осях координат.
49.22. Система плоскостей примитивной кубической решетки
задана индексами A11). Определить расстояние d между соседними
плоскостями, если параметр а решетки равен 0,3 нм.
49.23. Определить параметр а примитивной кубической решет-
решетки, если межплоскостное расстояние d для системы плоскостей, за-
заданных индексами Миллера B12) при рентгеноструктурном измере-
измерении, оказалось равным 0,12 нм.
49.24. Три системы плоскостей в примитивной кубической ре-
решетке заданы индексами Миллера: а) A11); б) A10); в) A00). Ука-
Указать, для какой системы межплоскостные расстояния d минимальны
и для какой системы — максимальны. Определить отношения меж-
межплоскостных расстояний dni : dlw : d100.
49.25. Вычислить угол <р между нормалями к плоскостям (в ку-
кубической решетке), заданных индексами Миллера A11) и A11).
49.26. Две плоскости в кубической решетке заданы индексами
Миллера @10) и @11). Определить угол q> между плоскостями.
49.27. В кубической решетке направление прямой задано индек-
индексами [011]. Определить угол ср между этой прямой и плоскостью
он).
49.28. Определить в кубической решетке угол ф между прямой
[111] и плоскостью A11).
49.29. Плоскость в кубической решетке задана индексами Мил-
Миллера @11), направление прямой — индексами [111]. Определить
угол ф между прямой и плоскостью.
§ 50. ТЕПЛОВЫЕ СВОЙСТВА
Основные формулы
• Молярная внутренняя энергия химически простых (состоя-
(состоящих из одинаковых атомов) твердых тел в классической теории теп-
теплоемкости выражается формулой
Um=3RT,
где R — молярная газовая постоянная; Т — термодинамическая
температура.
• Теплоемкость С системы (тела) при постоянном объеме опре-
определяется как производная от внутренней энергии U по температуре,
т. е.
C=dl//d7\
• Закон Дюлонга и Пти. Молярная теплоемкость Сш химиче-
химически простых твердых тел
Cm=3R.
15 № 1268 449

• Закон Неймана — Коппа. Молярная теплоемкость химиче-
химически сложных тел (состоящих из различных атомов)
Cm=n-3R,
где п — общее число частиц в химической формуле соединения.
Ф Среднее значение энергии (s> квантового осциллятора, при-
приходящейся на одну степень свободы, в квантовой теории Эйнштей-
Эйнштейна выражается формулой
<8> = 80 -)
expl - "
где 80 — нулевая энергия (e^V^co); % — постоянная Планка;
со — круговая частота колебаний осциллятора; k — постоянная
Больцмана; Т — термодинамическая температура.
• Молярная внутренняя энергия кристалла в квантовой теории
теплоемкости Эйнштейна определяется по формуле
ТТ 77 i QD ®Е
где Um0=s/2RQE— молярная нулевая энергия по Эйнштейну;
QE=~fl(?>/k— характеристическая температура Эйнштейна.
• Молярная теплоемкость кристалла в квантовой теории тепло-
теплоемкости Эйнштейна
При низких температурах
Cm = 3R(QE/T)exp(-QE/T).
• Частотный спектр колебаний в квантовой теории теплоемко-
теплоемкости Дебая задается функцией распределения частот g"(co). Число
dZ собственных частот тела* приходящихся на интервал частот от
со до co+dcD, определяется выражением
dZ=g"(co)dv.
Для трехмерного кристалла, содержащего N атомов^
где comax — максимальная частота^ ограничивающая спектр коле-
колебаний.
• Энергия U твердого тела связана с средней энергией <е>
квантового осциллятора и функцией распределения частот g"(co)
соотношением
=> S <8>g-(co)d(o.
о
Молярная внутренняя энергия кристалла по Дебаю
450

где ?/mo=9/8#0D — молярная нулевая энергия кристалла по Де-
баю; QD=h(umax/k — характеристическая температура Дебая.
• Молярная теплоемкость кристалла по Дебаю
Г Vr 1
Г — 1J? 19ГГ/А \з С x3dx 3 (QD/T)
Cm-3Rll2(T/0D) j expW-l-expCe^/T)-! '
L о J
Предельный закон Дебая. В области низких температур *
6) последняя формула принимает вид
с l
Ф Энергия 8 фонона ** связана с круговой частотой со колеба-
колебаний классической волны соотношением
8 = ^@.
• Квазиимпульс фонона
р = 2nh/l.
• Скорость фонона является групповой скоростью звуковых
волн в кристалле
При малых значениях энергии фонона дисперсией волн можно
пренебречь и тогда групповая и фазовая скорости совпадут:
u=v=E/p.
Скорости продольных (vt) и поперечных (vt) волн в кристалле
определяются по формулам
где Е и G — модули соответственно продольной и поперечной упру-
упругости.
Усредненное значение скорости звука v связано с vx и vt соотно-
соотношением
у3 ~~ v? + IV3 °
• Закон Фурье. Количество теплоты dQ, перенесенное через
поверхность площадью 5, перпендикулярную направлению тепло-
теплового потока, за время d/, равно
dQ=—X(dT/dx)Sdt9
где Я — теплопроводность; dT/dx — градиент температуры. Знак
минус в формуле показывает, что направление теплового потока
противоположно вектору градиента температуры.
• Теплопроводность Я, теплоемкость С, рассчитанная на еди-
единицу объема, скорость v звука (усредненное значение) и средняя
длина свободного пробега Л фононов связаны соотношением
* Считать для решения задач Т<0?), если T/QD<0,\.
** Фонон — квазичастица, являющаяся квантом поля колебаний кри-
кристаллической решетки.
15* 451

• Относительное изменение частоты, обусловленное эффектом
Доплера,
где v — скорость атома; с — скорость распространения электро-
электромагнитного излучения; -0 — угол между вектором v и направлением
наблюдения (от атома к наблюдателю).
Ф Энергия отдачи ядра при испускании гамма-фотона
Я-(?оJ/Bт^2),
где i^co — энергия гамма-фотона; тя — масса ядра.
• Естественная ширина спектральной линии
г=4/т,
где т — среднее время жизни ядра (атома) в возбужденном со-
состоянии.
• Сила /(#), возвращающая частицу в положение равновесия
при ангармонических колебаниях, определяется выражением
где р — коэффициент гармоничности, связанный с равновесным рас-
расстоянием г0 между атомами кристалла и модулем продольной упру-
упругости Е соотношением
у — коэффициент ангармоничности, характеризующий асимметрию
колебаний атомов в твердом теле. Для оценки по порядку величин
можно принять
• Коэффициент линейного расширения, по определению,
1 d/
a=TdT'
Теоретически он выражается через коэффициенты E и у формулой
yk ^ Ik
a=p-, или приближенно а = -^——г
где k — постоянная Больцмаиа.
Пример решения задач
Пример. Определить количество теплоты AQ, необходимое
для нагревания кристалла NaCl массой т=20 г на АГ=2 К, в двух
случаях, если нагревание происходит от температуры: 1) TX=QD;
2) 72=2 К. Характеристическую температуру Дебая 0D для NaCl
принять равной 320 К.
Решение. Количество теплоты AQ, подводимое для нагрева-
нагревания тела от температуры тх до т2, может быть вычислено по формуле
где С — теплоемкость тела (системы).
452

Теплоемкость тела связана с молярной теплоемкостью Ст соот-
соотношением С=(т/М)Ст, где т — масса тела; М — молярная масса.
Подставив это выражение С в формулу A), получим
ndT. B)
В общем случае Ст есть функция температуры, поэтому за знак
интеграла ее выносить нельзя. Однако в первом случае изменением
теплоемкости по сравнению с ее значением при температуре Тг мож-
можно пренебречь и считать ее на всем интервале температур AT посто-
постоянной и равной CmGi). Ввиду этого формула B) примет вид
Л<2=(™Ш)СтG\)Л7\ C)
Молярная теплоемкость Ст(Г1) в теории Дебая выражается фор-
формулой
f
L о е J
V7"! 1
С х^ dx С х^ dx
В первом случае при Т'1=8 интеграл \ ¦ х__, = \ х__,- — 0,225
о о
(см. табл. 2) и, следовательно,
Cm=2,87 R.
Подставляя это значение Ст в формулу C), получим
AQ=2,87 (тШ)# Д7\ D)
Произведя вычисление по формуле D), найдем
AQ=16,3 Дж.
Во втором случае (Т<с9 ) нахождение AQ облегчается тем, что
можно воспользоваться предельным законом Дебая, в согласии с
которым теплоемкость пропорциональна кубу абсолютной темпе-
температуры. В этом случае теплоемкость сильно изменяется в пределах
заданного интервала температур и ее нельзя выносить за знак ин-
интеграла в формуле B)
Используя выражение предельного закона Дебая Ст=
124 / Т \з
\-^)' получим
Выполним интегрирование:
R [(Т2+АТ)* Т\\
4
С учетом того, что Т2-\-АТ=2 Г2, выражение E) примет вид
m \*>Т* или АО Qtt4 m
[Ь1 или дУУя
453

Подставив в последнюю формулу значения величин я, т} М Rt T§
и 9D и произведя вычисления, найдем
Д()=1,22мДж.
Задачи
Классическая теория теплоемкости
50.1. Вычислить удельные теплоемкости с кристаллов алюминия
и меди по классической теории теплоемкости.
50.2. Пользуясь классической теорией, вычислить удельные
теплоемкости с кристаллов NaCl и СаС12.
50.3. Вычислить по классической теории теплоемкости теплоем-
теплоемкость С кристалла бромида алюминия А1Вг3 объемом V=l м3-. Плот-
Плотность р кристалла бромида алюминия равна 3,01 *103 кг/м3.
50.4. Определить изменение А(/ внутренней энергии кристалла
никеля при нагревании его от ?=0 °С до t2=200 °С. Масса т кри-
кристалла равна 20 г. Теплоемкость С вычислить.
50.5. Вывести формулу для средней энергии (г) классического
линейного гармонического осциллятора при тепловом равновесии.
Вычислить значение <е> при Т=300 К.
50.6. Определить энергию U и теплоемкость С системы, состоя-
состоящей из JV=1025 классических трехмерных независимых гармониче-
гармонических осцилляторов. Температура Т=300 К.
Указание, Использовать результат решения задачи 50.5.,
Теория теплоемкости Эйнштейна
50.7. Определить: 1) среднюю энергию (е> линейного одномер-
одномерного квантового осциллятора при температуре T=QE (9Б=200 К);
2) энергию U системы, состоящей из N=1025 квантовых трехмер-
трехмерных независимых осцилляторов, при температуре T=QE (QE=*
-300 К).
50.8. Найти частоту v колебаний атомов серебра по теории теп-
теплоемкости Эйнштейна, если характеристическая температура 9Е
серебра равна 165 К.
50.9. Во сколько раз изменится средняя энергия (е) квантового
осциллятора, приходящаяся на одну степень свободы, при повыше-
повышении температуры от Ti=6E/2 до Т2=8Е? Учесть нулевую энергию.
50.10. Определить отношение (е>/(ег> средней энергии кванто-
квантового осциллятора к средней энергии теплового движения молекул
идеального газа при температуре T=QE.
50.11. Используя квантовую теорию теплоемкости Эйнштейна*
вычислить изменение Af/m молярной внутренней энергии кристал-
кристалла при нагревании его на АТ=2 К от температуры T=QE/2.
50.12. Пользуясь теорией теплоемкости Эйнштейна, определить
изменение At/m молярной внутренней энергии кристалла при на-
нагревании его от нуля до Тг=0,1 вЕ. Характеристическую темпера-
ТУРУ ®е Эйнштейна принять для данного кристалла равной 300 К.
454

50.13. Определить относительную погрешность, которая будет
допущена, если при вычислении теплоемкости С вместо значения, да-
даваемого теорией Эйнштейна (при Т=вЕ), воспользоваться значе-
значением, даваемым законом Дюлонга и Пти.
50.14. Вычислить по теории Эйнштейна молярную нулевую
энергию Um0 кристалла цинка. Характеристическая температура
6# для цинка равна 230 К.
Теория теплоемкости Дебая
50.15. Рассматривая в дебаевском приближении твердое тело
как систему из продольных и поперечных стоячих волн, установить
функцию распределения частот g((o) для кристалла с трехмерной
кристаллической решеткой. При выводе принять, что число собст-
собственных колебаний Z ограничено и равно 3N (N — число атомов
в рассматриваемом объеме).
50.16. Зная функцию распределения частот g-(co)=: ——со2 для
^гпах
трехмерной кристаллической решетки, вывести формулу для энер-
энергии кристалла, содержащего число N (равное постоянной Авогадро)
атомов.
50.17. Используя формулу энергии трехмерного кристалла
получить выражение для молярной теплоемкости.
50.18. Молярная теплоемкость трехмерного кристалла
г ел/Т
Г
Найти предельное выражение молярной теплоемкости при низких
температурах (Д<Сб/)).
50.19. Вычислить по теории Дебая молярную нулевую энергию
Um о кристалла меди. Характеристическая температура 0D меди
равна 320 К.
50.20. Определить максимальную частоту (отах собственных
колебаний в кристалле золота по теории Дебая. Характеристиче-
Характеристическая температура 9D равна 180 К.
50.21. Вычислить максимальную частоту сотах Дебая, если из-
известно, что молярная теплоемкость Сш серебра при Т=20 К равна
1,7 Дж/(моль-К).
50.22. Найти отношение изменения AU внутренней энергии
кристалла при нагревании его от нуля до А=0,1 0D к нулевой энер-
энергии UQ. Считать Г<С0?)-
50.23. Пользуясь теорией теплоемкости Дебая, определить из-
изменение AUm молярной внутренней энергии кристалла при нагре-
нагревании его от нуля до 7=0,1 6^. Характеристическую температуру
455

QD Дебая принять для данного кристалла равной 300 К. Считать
e
50.24. Используя квантовую теорию теплоемкости Дебая, вы-
вычислить изменение Д(/т молярной внутренней энергии кристалла
при нагревании его на АГ=2 К от температуры T=QD/2.
50.25. При нагревании серебра массой т=10 г от 7\=10 К до
Т2=20 К было подведено AQ=0,71 Дж теплоты. Определить ха-
характеристическую температуру QD Дебая серебра. Считать Г<^0о.
50.26. Определить относительную погрешность, которая будет
допущена при вычислении теплоемкости кристалла, если вместо
значения, даваемого теорией Дебая (при T=QD)y воспользоваться
значением, даваемым законом Дюлонга и Пти.
50.27. Найти отношение 9^/9^ характеристических температур
Эйнштейна и Дебая.
Указание. Использовать выражения для нулевых энергий, вычисленных
по теориям Эйнштейна и Дебая.
50.28. Рассматривая в дебаевском приближении твердое тело как
систему из продольных и поперечных стоячих волн, установить функ-
функцию распределения частоту (со) для кристалла с двухмерной решет-
решеткой (т. е. кристалла, состоящего из невзаимодействующих слоев).
При выводе принять, что число собственных колебаний Z ограни-
ограничено и равно 3N (N — число атомов в рассматриваемом объеме).
50.29. Зная функцию распределения частот g-(co) = -g—со для
Wmax
кристалла с двухмерной решеткой, вывести формулу для внутрен-
внутренней энергии U кристалла, содержащего N (равное постоянной Аво-
гадро) атомов.
50.30. Получить выражение для молярной теплоемкости Ст,
используя формулу для молярной внутренней энергии кристалла
с двухмерной решеткой:
0
50.31. Молярная теплоемкость кристалла с двухмерной решеткой
выражается формулой
= ЗЯ Гб(Г/9 J °[Т х%Ах 2(9р/Г> "|
I 1 6 -—¦ I Г)/ II
Найти предельное выражение молярной теплоемкости кристалла
при низких температурах (T<t,QD).
50.32. Вычислить молярную внутреннюю энергию Um кристал-
кристаллов с двухмерной решеткой, если характеристическая температура
G^ Добая равна 350 К.
50.33. Рассматривая в дебаевском приближении твердое тело
как систему из продольных и поперечных стоячих волн, установить
функцию распределения частот gf(co) для кристалла с одномерной
решеткой (т. е. кристалла, атомы которого образуют цепи, не вза-
456

имодействующие друг с другом). При выводе принять, что число
собственных колебаний Z ограничено и равно 3N (N — число ато-
атомов в рассматриваемом объеме).
50.34. Зная функцию распределения частот g"(co)=3A/Y(omax для
кристалла с одномерной решеткой, вывести формулу для внутрен-
внутренней энергии кристалла, содержащего число N (равное постоянной
Авогадро) атомов.
50.35. Получить выражение для молярной теплоемкости, ис-
используя формулу для молярной внутренней энергии кристалла
с одномерной решеткой:
50.36. Молярная теплоемкость кристалла с одномерной решеткой
выражается формулой
Найти предельное выражение молярной теплоемкости кристалла
при низких температурах (r<c9D).
50.37. Вычислить молярную нулевую энергию f/max кристалла
с одномерной решеткой, если характеристическая температура 9^
Дебая равна 300 К.
Теплопроводность неметаллов. Фононы
50.38. Вода при температуре ^=0 °С покрыта слоем льда тол-
толщиной /г=50 см. Температура tt воздуха равна 30 °С. Определить
количество теплоты Q, переданное водой за время т=1 ч через по-
поверхность льда площадью S=l м2. Теплопроводность к льда равна
2,2Вт/(м-К).
50.39. Какая мощность N требуется для того, чтобы поддержи-
поддерживать температуру ^=100 °С в термостате, площадь S поверхности
которого равна 1,5 м2, толщина h изолирующего слоя равна 2 см
и внешняя температура ^=20 °С?
50.40. Найти энергию 8 фонона, соответствующего максималь-
максимальной частоте сотах Дебая, если характеристическая температура 9О
Дебая равна 250 К.
50.41 Определить квазиимпульс р фонона, соответствующего
частоте со=0,1 сотах. Усредненная скорость v звука в кристалле
равна 1380 м/с, характеристическая температура QD Дебая равна
100 К. Дисперсией звуковых волн в кристалле пренебречь.
50.42. Длина волны X фонона, соответствующего частоте о> =
=0,01 сотах, равна 52 нм. Пренебрегая дисперсией звуковых волн,
определить характеристическую температуру 9D Дебая, если усред-
усредненная скорость v звука в кристалле равна 4,8 км/с.
457

50.43. Вычислить усредненную скорость v фононов (скорость
звука) в серебре. Модули продольной Е и поперечной G упругости,
а также плотность р серебра считать известными.
50.44. Характеристическая температура QD Дебая для вольфра-
вольфрама равна 310 К. Определить длину волны А,фононов, соответствую-
соответствующих частоте v=0,l vmax. Усредненную скорость звука в вольфраме
вычислить. Дисперсией волн в кристалле пренебречь.
50.45. Период d решетки одномерного кристалла (кристалла,
атомы которого образуют цепи, не взаимодействующие друг с дру-
другом) равен 0,3 нм. Определить максимальную энергию етах фоно-
фононов, распространяющихся вдоль этой цепочки атомов. Усредненная
скорость v звука в кристалле равна 5 км/с.
50.46. Определить усредненную скорость v звука в кристалле,
характеристическая температура 0 которого равна 300 К. Меж-
Межатомное расстояние d в кристалле равно 0,25 нм.
50.47. Вычислить среднюю длину (/> свободного пробега фоно-
фононов в кварце SiO2 при некоторой температуре, если при той же тем-
температуре теплопроводность X—13 Вт/(м*К), молярная теплоемкость
С=44 Дж/(моль'К) и усредненная скорость v звука равна 5 км/с.
Плотность р кварца равна 2,65«Ю3 кг/м3.
50.48. Найти отношение средней длины </) свободного пробега
фононов к параметру d решетки при комнатной температуре в кри-
кристалле NaCl, если теплопроводность X при той же температуре равна
71 Вт/(м*К). Теплоемкость вычислить по закону Неймана — Коппа.
Относительные атомные массы: А^а=23, Лс1=35,5; плотность р
кристалла равна 2,17-103 кг/м3. Усредненную скорость v звука
принять равной 5 км/с.
50.49. Вычислить фононное давление р в свинце при температуре
Г=42,5 К. Характеристическая температура 0D Дебая свинца
равна 85 К.
50.50. Определить фононное давление р в меди при температуре
T=QD, если 9D=320 К.
Эффект Мёссбауэра
50.51. Исходя из законов сохранения энергии и импульса при
испускании фотона движущимся атомом, получить формулу допле-
ровского смещения До/со для нерелятивистского случая.
50.52. Вычислить энергию R, которую приобретает атом вследст-
вследствие отдачи, в трех случаях: 1) при излучении в видимой части спект-
спектра (Х=500 нм); 2) при рентгеновском излучении (Я=0,5 нм); 3) при
гамма-излучении (А,=5*10~3 нм). Массу та атома во всех случаях
считать одинаковой и равной 100 а. е. м.
50.53. Уширение спектральной линии излучения атома обуслов-
обусловлено эффектом Доплера и соотношением неопределенностей. Кроме
того, вследствие отдачи атома происходит смещение спектральной
линии. Оценить для атома водорода относительные изменения (АХ/Я)
длины волны излучения, обусловленные каждой из трех причин.
Среднюю скорость (v) теплового движения атома принять равной
458

3 км/с, время т жизни атома в возбужденном состоянии — 10 не,
энергию 8 излучения атома—10 эВ.
50.54. При испускании у-фотона свободным ядром происходит
смещение и уширение спектральной линии. Уширение обусловлено
эффектом Доплера и соотношением неопределенностей, а смещение —
явлением отдачи. Оценить для ядра ?7Fe относительные изменения
(Av/v) частоты излучения, обусловленные каждой из трех причин.
При расчетах принять среднюю скорость {v) ядра (обусловленную
тепловым движением) равной 300 м/с, время х жизни ядра в возбуж-
возбужденном состоянии — 100 не и энергию ev гамма-излучения равной
15 кэВ.
50.55. Найти энергию Д? возбуждения свободного покоившегося
ядра массы тя, которую оно приобретает в результате захвата гам-
гамма-фотона с энергией е.
50.56. Свободное ядро 40К испустило гамма-фотон с энергией
ev=30 кэВ. Определить относительное смещение ДАУА, спектральной
линии, обусловленное отдачей ядра.
50.57. Ядро 67Zn с энергией возбуждения АЕ=93 кэВ перешло
в основное состояние, испустив гамма-фотон. Найти относительное
изменение Asv/ev энергии гамма-фотона, возникающее вследствие
отдачи свободного ядра.
50.58. Энергия связи Есв атома, находящегося в узле кристал-
кристаллической решетки, составляет20 эВ. Масса та атома равна 80 а. е. м.
Определить минимальную энергию eY гамма-фотона, при испуска-
испускании которого атом вследствие отдачи может быть вырван из узла
решетки.
50.59. Энергия возбуждения Д? ядра 1911г равна 129 кэВ. При
какой скорости v сближения источника и поглотителя (содержащих
свободные ядра 1911г) можно вследствие эффекта Доплера скомпен-
скомпенсировать сдвиг полос поглощения и испускания, обусловленных
отдачей ядер?
50.60. Источник и поглотитель содержат свободные ядра 83Кг.
Энергия возбуждения Д? ядер равна 9,3 кэВ. Определить ско-
скорость v сближения источника и поглотителя, при которой будет
происходить резонансное поглощение гамма-фотона.
50.61. Источник и поглотитель содержат ядра mDy. Энергия
возбуждения АЕ ядер равна 26 кэВ, период полураспада Т1/2 —
=28 не. При какой минимальной скорости vmln сближения источ-
источника и поглотителя нарушается мёссбауэровское поглощение гам-
гамма-фотона?
50.62. При скорости v сближения источника и поглотителя (со-
(содержащих свободные ядра 153Ег), равной 10 мм/с, нарушается мёсс-
мёссбауэровское поглощение гамма-фотона с энергией ev=98 кэВ. Оце-
Оценить по этим данным среднее время х жизни возбужденных ядер 153Ег.
50.63. Источник гамма-фотонов расположен над детектором-по-
детектором-поглотителем на расстоянии 1=20 м. С какой скоростью v необходимо
перемещать вверх источник, чтобы в месте расположения детектора
было полностью скомпенсировано изменение энергии гамма-фотонов!
обусловленное их гравитационным взаимодействием с Землей?
459

Тепловое расширение твердых тел
50.64. Найти коэффициент объемного расширения р для анизо-
анизотропного кристалла, коэффициенты линейного расширения которо-
которого по трем взаимно перпендикулярным направлениям составляют
^=1,25-10-* К; а^МО-Ю^К-1; а8=1,5-10-* К.
50.65. Вычислить максимальную силу ?тах, возвращающую
атом твердого тела в положение равновесия, если коэффициент гар-
гармоничности р=50 Н/м, а коэффициент ангармоничности 7=500 ГПа.
50.66. Определить силу F (соответствующую максимальному
смещению), возвращающую атом в положение равновесия, если ам-
амплитуда тепловых колебаний составляет 5 % от среднего межатом-
межатомного расстояния при данной температуре. При расчетах принять:
коэффициент гармоничности Р=50 Н/м, коэффициент ангармонич-
ангармоничности 7=500 ГПа, среднее межатомное расстояние го=О,4 нм.
50.67. Каково максимальное изменение АПтах потенциальной
энергии атомов в кристаллической решетке твердого тела при гар-
гармонических колебаниях, если амплитуда тепловых колебаний со-
составляет 5 % от среднего межатомного расстояния? Среднее рас-
расстояние г0 между атомами принять равным 0,3 нм, модуль Юнга
?-100 ГПа.
50.68. Показать, что если смещение частиц в кристаллической
решетке твердого тела подчиняется закону Гука F(x) =—рх, то
тепловое расширение отсутствует.
50.69. Определить коэффициент гармоничности C в уравнении
колебаний частиц твердого тела, если равновесное расстояние г<>
между частицами равно 0,3 нм, модуль Юнга ?=200 ГПа.
50.70. Оценить термический коэффициент расширения а твер-
твердого тела, считая, что коэффициент ангармоничности у&$/B г0).
При оценке принять: модуль Юнга ?=100 ГПа, межатомное рас-
расстояние го=О,3 нм.
50.71. Вычислить коэффициент ангармоничности 7 Для железа,
если температурный коэффициент линейного расширения а—
= 1,2 -10~5 К, межатомное расстояние го=О,25 нм, модуль Юнга
?=200 ГПа.
50.72. Определить, на сколько процентов изменится межатом-
межатомное расстояние в твердом теле (при нагревании его до Т=400 К) по
сравнению с равновесным расстоянием го=О,3 нм, отвечающим ми-
минимуму потенциальной энергии. При расчетах принять 7=Р/Bг0),
модуль Юнга ?=10 ГПа.
50.73. Оценить термический коэффициент расширения а твер-
твердого тела, обусловленного фононным давлением (в области T<^QD).
При оценке принять: плотность р кристалла равной 104 кг/м3, мо-
модуль Юнга ?=100 ГПа, относительную атомную массу Лг=60-

§ 51. ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ СВОЙСТВА
ТВЕРДЫХ ТЕЛ
Основные формулы
Электроны в металле (по квантовой статистике)
Ф Распределение Ферми по энергиям для свободных электронов
в металле:
гг , А 1 , ч \ Bт 1/
при ТфО dn(e) = 2^
при Г = О dn(8)^^^K/28^d8 (при
где dn(e) — концентрация электронов, энергия которых заключена
в интервале значений от 8 до e+de; m и 8 — масса и энергия элек-
электрона; sf — уровень (или энергия) Ферми.
Ф Уровень Ферми в металле при Г—О
• Температура Ткр вырождения
Укр- km П *
Полупроводники
Ф Удельная проводимость собственных полупроводников
где е — заряд электрона; п — концентрация носителей заряда
(электронов и дырок); Ьп и Ьр — подвижности электронов и дырок.
Напряжение Un ца гранях образца при эффекте Холла
UH==RnBjlt
где jRh — постоянная Холла; В — индукция магнитного поля;
/ — ширина пластины; / — плотность тока.
# Постоянная Холла для полупроводников типа алмаза, крем-
кремния, германия и др., обладающих носителями заряда одного вида
(п или р),
1±
8 еп,'
где п — концентрация носителей заряда.
Магнитный резонанс
% Магнитный момент ядра *
V
где g — ядерный фактор Ланде (g-фактор); \iN — ядерный магне-
тон (\iN=eri/B тр))\ тр — масса протона; / — спиновое квантовое
число ядра (спин ядра).
* Магнитным моментом ядра называют также максимальное значение
проекции магнитного момента ядра на направление вектора магнитной
индукции внешнего поля, т.е. li=lizm2LX=giiMl.
461

• Связь магнитного момента ядра с моментом импульса
ядра
где у — гиромагнитное отношение (y=g\iN/h) и
• Проекция магнитного момента ядра на направление вектора
магнитной индукции внешнего поля
где mj — спиновое магнитное квантовое число ядра, mz=/, /—1, ...
. . ., -/.
• Круговая частота соо переменного магнитного поля, при ко-
которой происходит резонансное поглощение энергии,
ао=уВо,
где Во — магнитная индукция внешнего постоянного магнитного
поля.
Ф Отношение заселенностей энергетических уровней (в отсутст-
отсутствие высокочастотного поля)
!hz=eB
где Nt—заселенность энергетического уровня Ег; N2 — заселен-
заселенность энергетического уровня Е2) Е2>Е±,
Примеры решения задач
Пример 1. Кусок металла объема F=20 см3 находится при тем-
температуре Т=0. Определить число AN свободных электронов, им-
импульсы которых отличаются от максимального импульса /?тах не
более чем на 0,1 /?тах. Энергия Ферми 8^=5 эВ.
Решение. Для того чтобы установить распределение свобод-
свободных электронов в металле по импульсам, воспользуемся распределе-
распределением Ферми для свободных электронов при Г=0;
1 / 2пг \з/2 , ,
Так как dn(e) есть число электронов в единице объема, энергии
которых заключены в интервале значений от 8 до e+de (e<Cef),
то оно должно быть равно числу электронов dn (p) в единице объема,
заключенных в интервале значений импульса от р до p+dp, т. е.
dn(p) = dn(e). B)
При этом должно соблюдаться следующее условие. Данной энер-
энергии s соответствует определенный импульс р (&=р2/Bш)) и интерва-
интервалу энергии de отвечает соответствующий ему интервал импульсов
dpi de = -^dp J. Заметив, что г^2=р/Bт)^2у подставим в правую
часть равенства B) вместо dn(e) выражение A) с заменой ена р и
462

ds на dp в соответствии с полученными соотношениями, т. е.
з/2
После сокращений получим искомое распределение свободных элек-
электронов в металле по импульсам при Г=0:
Число электронов в единице объема, импульсы которых заключе-
заключены в интервале от /?тах —0,1 ртах до /?тах, найдем интегрированием
в соответствующих пределах:
Ртах 3
.. 0,271 Ртах
Учитывая, что максимальный импульс ртах и максимальная энер-
энергия е электронов в металле (при Т=0) связаны соотношением ртах=
s=2 mefi найдем искомое число AN свободных электронов в металле:
или ДЛГ =
Подставив значения величин л, т, 8/, % и V и произведя вычисле-
вычисления E эВ=-8-10~19 Дж), получим AAf = 2,9-1023 электронов.
Пример 2. Образец из германия n-типа в виде пластины длиной
L=10 см и шириной 1=6 мм помещен в однородное магнитное поле
(В=0,1 Тл) перпендикулярно
линиям магнитной индукции.
При напряжении G=250 В,
приложенном к концам пла-
пластины, возникает холловская
разность потенциалов Un=
=8,8 мВ. Определить: 1) по-
постоянную Холла Rh; 2) кон-
концентрацию пп носителей тока.
Удельную проводимость 7 гер-
германия принять равной 80См/м.
Решение. 1. При по-
помещении полупроводника в
магнитное поле (рис. 51.1)
носители тока (в полупровод-
полупроводнике я-типа это электроны), перемещающиеся под действием при-
приложенной к нему разности потенциалов ?/, будут отклоняться в по-
поперечном направлении. Это отклонение, вызванное силой Лоренца!
приведет к «накоплению» заряда на боковых поверхностях образца,
причем создаваемое в результате этого напряжение (Ун (холловская
разность потенциалов) действием своим будет уравновешивать си-
силу Лоренца. Холловская разность потенциалов определяется соот-
соотношением
Рис. 51.1
463

откуда постоянная Холла
Плотность тока / найдем, воспользовавшись законом Ома в диф-
дифференциальной форме:
где Е — напряженность поля в образце.
Считая поле в образце однородным, можно написать E=U/L
и тогда
Подставив плотность тока в выражение A), получим
Убедимся в том, что правая часть равенства B) дает единицу
постоянной Холла (м3/Кл):
[Ци]\Ц 1 В-1 м 1м
[Щ [Щ[у] [/]"" 1 Тл-1 в-1 См/м-1 м Тл-1 См~~
__ 1 А-1 м-1 м-1 В 1 Дж-1 м2 1 з/т/
ГнТа—= 1 н.1 кл М/Кл*
Выразим все величины в единицах СИ ((/н=8,8'10~3 В, L =
=0,1 м, В=0,\ Тл, ^7=250 В, у=80 См/м, /=6-10~3м) и произве-
произведем вычисления:
880^° = 7'33• 10~"
2. Концентрацию п носителей тока в полупроводнике одного
типа (в нашем случае я-типа) можно найти из соотношения
р Зя 1
где е — элементарный заряд. Отсюда
Зд
п
Произведя вычисления, получим
п=1023 электронов/м3.
Пример 3. Образец из вещества, содержащего эквивалентные
ядра (протоны), находится в однородном внешнем магнитном поле
(В=\ Тл). Определить: 1) относительную разность заселенностей
энергетических уровней при температуре 7=300 К; 2) частоту v0,
при которой будет происходить ядерный магнитный резонанс. Эк-
Экранирующим действием электронных оболочек и соседних ядер
пренебречь.
Решение. 1. В магнитном поле ядра приобретают дополни-
дополнительную энергию, определяемую соотношением
е=-рА A)
где \xz — проекция магнитного момента ядра на направление векто-
464

pa В (ось Oz). Проекция магнитного момента ядра выражается
формулой
где g — ядерный фактор Ланде; \iN— ядерный магнетон; mf —
спиновое магнитное квантовое число ядра.
Подставив это выражение в формулу A), получим
Спиновое магнитное квантовое число тг протона может прини-
принимать только два значения: mI=Jrl/2 и /тг7=—1/2. Значение тх~
= + 1/2 соответствует нижнему
энергетическому уровню:
1 " B)
Значение Шу=—1/2 соответству-
соответствует верхнему энергетическому
уровню (рис. 51.2):
В отсутствие магнитного по-
поля число ядер с противополож- Рис. 51.2
но направленными спинами оди-
одинаково и равно N/2 (N — общее ч pic л о ядер). В магнитном поле
происходит перераспределение ядер по энергетическим уровням.
На нижнем уровне с энергией Ех будет находиться больше ядер,
чем на верхнем с энергией Е2. Число ядер Nx (заселенность данного
уровня), находящихся на нижнем энергетическом уровне Е1у может
быть вычислено по формуле Больцмана:
at N p libTS AT N +—gixNB/(kT)
уу — Q—*-'i/\Ri) или iV = е *
Соответственно можно найти и число ядер N2, находящихся на
верхнем энергетическом уровне:
Л/ ^ -FHkT) \J N —?-ёИ7у?/(&П
Так как 1/2g\iJVB<^kT (это будет показано ниже), то можно восполь-
воспользоваться приближенными равенствами е~х^1—х и e*«l+#, если
(см. табл. 3). Тогда
и N9 ^-тг
Разность AN заселенности энергетических уровней найдем, вы-
вычитая из первого приближенного равенства второе:
Разделив AN на N, получим относительную разность заселенностей
энергетических уровней:
Л \Т 1
D)
465

Выразим все величины в единицах СИ: g"=5,58 (для протона),
[хЛГ=5,05.10-27 А-м2, 5=1 Тл, fe=l,38 -Ю3 Дж/К, Т=300 К.
Подставим эти значения в формулу D) и произведем вычисления:
AA^_ 5,58>5t05-10~27» 1 _я ш_6
Полученный результат оправдывает наше допущение, что 1
2. Под действием электромагнитного излучения, угловая частота
которого
щ = (Е1 — Е2)/%9 E)
будут происходить переходы между уровнями энергии Ег и Е21
причем электромагнитное излучение вызывает переходы Ег -+Е2
h?2->?iC равной вероятностью при условии одинаковой заселен-
заселенности энергетических уровней. Так как нижний уровень имеет
большую заселенность, чем верхний, то переходы с поглощением
электромагнитного излучения (Е1 -+Е2) будут происходить чаще,
чем с излучением (Е2 ->?i). Это и есть резонансное поглощение
электромагнитного излучения, обусловленное ядерным магнетиз-
магнетизмом (ЯМР).
Подставив в E) выражение для энергий Е± и Е2 согласно B)
и C) и заменив угловую частоту со0 на частоту v0(co0=2kv0), найдем
резонансную частоту v0 для внешнего магнитного поля В *:
Bf
Подставим в это выражение числовые значения физических
величин и произведем вычисления:
vo= 5,58-5,05.10"^. 1/B-3,14.1,05-Ю"»4) Гц = 4,27-107 Гц,
или
vo = 42,7 МГц.
Задачи
Электроны в металле. Распределение Ферми—Дирака
51.1. Определить концентрацию п свободных электронов в ме-
металле при температуре Т—0 К. Энергию Ферми 8 принять равной
1 эВ.
51.2. Определить отношение концентраций п1/п2 свободных
электронов при Т=0 в литии и цезии, если известно, что уровни
Ферми в этих металлах соответственно равны е/ !=4,72 эВ, г/ 2^
= 1,53 эВ.
51.3. Определить число свободных электронов, которое прихо-
приходится на один атом натрия при температуре 7=0 К. Уровень Ферми
Sy для натрия равен 3,12 эВ. Плотность р натрия равна 970 кг/м3.
* В реальных образцах магнитное поле В, действующее на ядро, отли-
отличается от внешнего постоянного поля Во на величину Вг поля, создаваемого
в месте нахождения ядра электронами и ядрами всех молекул образца, в том
числе и той, к которой принадлежит данное ядро. В условиях данной задачи
полем В± мы пренебрегаем.
466

51.4. Во сколько раз число свободных электронов, приходящих-
приходящихся на один атом металла при 7=0, больше в алюминии, чем в меди,
если уровни Ферми соответственно равны e/^UJsB, ef 2=
-7,0 эВ?
51.5. Определить вероятность того, что электрон в металле зай-
займет энергетическое состояние, находящееся в интервале Де=0,05 эВ
ниже уровня Ферми и выше уровня Ферми, для двух температур:
1) 7х=290 К; 2) 72=58 К.
51.6. Вычислить среднюю кинетическую энергию (е) электронов
в металле при температуре 7=0 К, если уровень Ферми zf=7 эВ.
51.7. Металл находится при температуре 7=0 К. Определить,
во сколько раз число электронов с кинетической энергией от &f/2
до Ef больше числа электронов с энергией от 0 до е/2.
51.8. Электроны в металле находятся при температуре 7=0 К.
Найти относительное число AN/N свободных электронов, кинети-
кинетическая энергия которых отличается от энергии Ферми не более чем
на 2 %.
51.9. Оценить температуру 7кр вырождения для калия, если при-
принять, что на каждый атом приходится по одному свободному элек-
электрону. Плотность р калия 860 кг/м3.
51.10. Определить отношение концентрации птах электронов
в металле (при 7=0 К), энергия которых отличается от максималь-
максимальной не более чем на Де, к концентрации пт{п электронов, энергии
которых не превышают значения е=Де; Де принять равным 0,018^.
51.11. Зная распределение dn(e) электронов в металле по энер-
энергиям, установить распределение dn(p) электронов по импульсам.
Найти частный случай распределения при 7=0 К.
51.12. По функции распределения dn (p) электронов в металле по
импульсам установить распределение dn(v) по скоростям: 1) при
любой температуре 7; 2) при 7=0 К.
51.13. Определить максимальную скорость итах электронов
в металле при 7=0 К, если уровень Ферми 8^=5 эВ.
51.14. Выразить среднюю скорость (v) электронов в металле
при 7=0 К через максимальную скорость vmax. Вычислить (и) для
металла, уровень Ферми ef которого при 7=0 К равен 6эВ.
51.15. Металл находится при температуре 7=0 К. Определить,
во сколько раз число электронов со скоростями от fmax/2 до i>max
больше числа электронов со скоростями от 0 до ^тах/2.
51.16. Выразить среднюю квадратичную скорость V (v2) электро-
электронов в металле при 7=0 К через максимальную скорость vmax элек-
электронов. Функцию распределения электронов по скоростям считать
известной.
51.17.' Зная распределение dn(v) электронов в металле по скоро-
скоростям, выразить A Iv) через максимальную скорость итах электронов
в металле. Металл находится при 7=0 К.
467

Полупроводники. Эффект Холла
51.18. Определить уровень Ферми 8у в собственном полупровод-
полупроводнике, если энергия A?o активации равна 0,1 эВ. За нулевой уровень
отсчета кинетической энергии электронов принять низший уровень
зоны проводимости.
51.19. Собственный полупроводник (германий) имеет при неко-
некоторой температуре удельное сопротивление р=0,48Ом»м. Опреде-
Определить концентрацию п носителей заряда, если подвижности Ьп и Ьр
электронов и дырок соответственно равны 0,36 и 0,16 м2/(В-с).
51.20. Удельная проводимость у кремния с примесями равна
112 См/м. Определить подвижность Ьр дырок и их концентрацию
Aip, если постоянная Холла ^н=3,66'10~4 м3/Кл. Принять, что
полупроводник обладает только дырочной проводимостью.
51.21. В германии часть атомов замещена атомами сурьмы.
Рассматривая дополнительный электрон примесного атома по моде-
модели Бора, оценить его энергию Е связи и радиус г орбиты. Диэлек-
Диэлектрическая проницаемость 8 германия равна 16.
51.22. Полупроводник в виде тонкой пластины шириной 1=1 см
и длиной L=10 см помещен в однородное магнитное поле с индук-
индукцией В=0,2 Тл. Вектор магнитной индукции перпендикулярен пло-
плоскости пластины. К концам пластины (по направлению L) прило-
приложено постоянное напряжение ?/=300 В. Определить холловскую
разность потенциалов Uw на гранях пластины, если постоянная
Холла 7?н=0,1 м3/Кл, удельное сопротивление р=0,5Ом-м.
51.23. Тонкая пластина из кремния шириной 1=2 см помещена
перпендикулярно линиям индукции однородного магнитного поля
(?=0,5 Тл). При плотности тока /=2 мкА/мм2, направленного вдоль
пластины, холловская разность потенциалов 1)ц оказалась равной
2,8 В. Определить концентрацию п носителей заряа.
Магнитный резонанс
51.24. Определить гиромагнитное отношение у для свободного
электрона.
51.25. Свободный электрон находится в постоянном магнитном
поле (Во=1 Тл). Определить частоту v0 переменного магнитного
поля, при которой происходит резонансное поглощение энергии
электроном (g-фактор для свободного электрона равен 2).
51.26. Определить отношение соэпр/^иик резонансной частоты
электронного парамагнитного резонанса к циклотронной частоте
(g-фактор равен 2,00232).
51.27. Стандартные спектрометры для наблюдения электронного
парамагнитного резонанса (ЭПР) имеют на одном из диапазонов
фиксированную частоту vo=9,9 ГГц. Определить магнитную индук-
индукцию поля ВОу при которой происходит резонансное поглощение
энергии радиочастотного поля свободным электроном (g-фактор
равен 2).
468

51.28. Определить гиромагнитное отношение у для свободного
протона.
51.29. Свободный протон находится в постоянном магнитном
поле {Во= 1 Тл). Определить частоту v0 переменного магнитного поля,
при которой происходит резонансное поглощение энергии протоном
(g-фактор равен 5,58).
51.30. В опытах по изучению магнитным резонансным методом
магнитных свойств атомов 25Mg в основном состоянии обнаружено
резонансное поглощение энергии при магнитной индукции Во поля,
равной 0,54 Тл, и частоте v0 переменного магнитного поля, равной
1,4 МГц. Определить ядерный g-фактор.
51.31. Методом магнитного резонанса определяют магнитный
момент нейтрона. Резонансное поглощение наблюдается при маг-
магнитной индукции Во поля, равной 0,682 Тл, и частоте v0 переменного
магнитного поля, равной 19,9 МГц. Вычислить ядерный g-фактор
и магнитный момент \in нейтрона. Известно, что направления спино-
спинового механического и магнитного моментов противоположны. Спин
нейтрона /=1/2.
51.32. Для молекулы HD, находящейся в основном состоянии,
ядерный магнитный резонанс наблюдался: 1) для протонов (/ = 1/2)
в постоянном магнитном поле (В0=94 мТл) при частоте v0 перемен-
переменного магнитного поля, равной 4 МГц; 2) для дейтонов (/ — 1) соот-
соответственно при 60=0,37 Тл и vo=2,42 МГц. Определить по этим
данным g-факторы и магнитные моменты \iv и \id протона и дейтона
(в единицах \iN).
51.33. При какой частоте v0 переменного магнитного поля будет
наблюдаться ЯМР ядер 19Р (/=1/2; jx=2,63ц, jv-), если магнитная
индукция Во постоянного поля равна 2,35 Тл?
51.34. Ядра Li (/=3/2 и g=2,18) находятся в однородном маг-
магнитном поле (В0=2 Тл). Температура Т окружающей среды равна
80 К. Найти отношение заселенностей каждого из возможных энер-
энергетических уровней к заселенности уровня с наименьшей энергией.

ПРИЛОЖЕНИЯ
I. О ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЯХ
Числовые значения величин, с которыми приходится иметь дело при
решении физических задач, являются большей частью приближенными.
К таким величинам относятся, в частности, многие константы, приводи-
приводимые в справочниках. Например, для нормального ускорения свободного па-
падения в справочниках дается значение 9,81 м/с, для отношения длины окруж-
окружности к диаметру — 3,14, для массы электрона — 9,1 *10~31 кг и т. п. При
более точном вычислении или измерении эти величины оказываются равными
?=9,80665 м/с2, зх=3,1416, me=9,106 «10~31 кг. Однако и эти значения, в свою
очередь, являются приближенными или в силу недостаточной точности
измерения, или в силу того, что получены путем округления еще более точ-
точных значений.
Очень часто неопытные лица при вычислениях добиваются получения
такой точности результатов, которая совершенно не оправдывается точ-
точностью использованных данных, Это приводит к бесполезной затрате труда
и времени.
Рассмотрим такой пример. Пусть требуется определить плотность р
вещества некоторого тела. При взвешивании тела на весах с точностью до
0,01 г определили массу тела: т=(9,38±0,01) г. Затем с точностью до 0,01 см3
был измерен объем тела: V=C,46=^0,01) см3.
Без критического подхода к вычислениям можно получить такой резуль-
результат:
т 9,38 г
Но так как числа 9,38 и 3,46 приближенные, то последние цифры в этих
числах сомнительны. Эти числа при измерении могли быть получены такими:
первое — 9,39 или 9,37, второе — 3,45 или 3,47. В самом деле, при взвеши-
взвешивании с указанной выше точностью могла быть допущена погрешность на
0,01 как в сторону увеличения массы, так и в сторону ее уменьшения. То же
самое в отношении объема.
Таким образом, плотность тела, если ее вычислять с точностью до пятого
десятичного знака, как это сделано выше, могла оказаться
Р = о \J v = 2>7QQ28 г/см3, или р = ъ 'Z , = 2,72174 г/см3.
г 3,47 см3 i * v з,45 см3 '
Сравнение всех трех результатов показывает, что они отличаются уже
вторыми десятичными знаками и что достоверным является лишь первый
десятичный знак, а второй — сомнительным. Цифры, выражающие осталь-
остальные десятичные знаки, являются совершенно случайными и способны лишь
ввести в заблуждение пользующегося вычисленными результатами. Следова-
Следовательно, работа по вычислению большинства знаков затрачена впустую.
Во избежание бесполезных затрат труда и времени принято вычислять
кроме достоверных знаков еще только один сомнительный.
В рассмотренном примере надо было вести вычисление до второго деся-
десятичного знака:
9,38 г о ~, , о
- = 2,71 г/см3.
г 3,46 см3
Приближенные вычисления следует вести с соблюдением следующих
правил,
470

1. При сложении и вычитании приближенных чисел окончательный
результат округляют так, чтобы он не имел значащих цифр * в тех разрядах,
которые отсутствуют хотя бы в одном из приближенных данных, Например,
при сложении чисел
4,462
.2,38
~*~ 1,17273
1,0262
9,04093
следует сумму округлить до сотых долей, т. е. принять ее равной 9,04.
2. При умножении следует округлять сомножители так, чтобы каждый
из них содержал столько значащих цифр, сколько их имеет сомножитель
с наименьшим числом таких цифр.
Например, вместо вычисления выражения
3,723-2,4-5,1846
следует вычислять выражение
3,7-2,4.5,2.
В окончательном результате необходимо оставлять такое же число зна-
значащих цифр, какое имеется в сомножителях, после их округления.
В промежуточных результатах следует сохранять на одну значащую
цифру больше. Такое же правило соблюдается и при делении приближенных
чисел.
3. При возведении в квадрат или в куб следует в степени брать столько
значащих цифр, сколько их имеется в основании степени. Например,
1,322 « 1,74.
При извлечении квадратного или кубического корня в результате нужно
брать столько значащих цифр, сколько их имеется в подкоренном выраже-
выражении. Например,
У ТЛтЛо-"8«1,08 • 1 о -4.
5. При вычислении сложных выражений следует применять указанные
правила в соответствии с видом производимых действий, Например,
C,2+ 17,062) V 3J
5,Ь2,007-Ю3
Сомножитель 5,1 имеет наименьшее число значащих цифр — две. По-
Поэтому результаты всех промежуточных вычислений должны округляться
до трех значащих цифр:
C,2+17,062)^377 _ 20,3-1,92 _ 39,0 _
5,1-2,007-Ю3 ~ 10,3-103 ~ 19,3-103 ~ '
После округления результата до двух значащих цифр получаем 3,8-10~3.
При вычислениях рекомендуем пользоваться счетной линейкой или
калькулятором.
II. НЕКОТОРЫЕ СВЕДЕНИЯ ПО МАТЕМАТИКЕ
1. Формулы алгебры и тригонометрии
— b ±Vb2 — 4ac __ р ,
Z* = a— ib
Z = р (cos ф + i sin ф) Z* = p (cos ф — i sin ф)
* Значащими цифрами называются все цифры, кроме нуля, а также и
нуль в двух случаях: 1) когда он стоит между значащими цифрами; 2) когда
он стоит в конце числа и когда известно, что единиц соответствующего раз-
разряда в данном числе не имеется.
471

sin (x-\-y) = sinx cos # + sin у cos x sin (x—y) = sinx cos y— sin г/ cos jc
cos (# + #) = cos л: cos t/— sin a: sin у cos (л:—у) = cos x cos у-{-sin xsiny
sin 2л: = 2 sin x cos r/ cos 2л; = cos2 л:—sin2 x
sin2A: = 1/2 A —cos 2x) cos2 л: = г/2A + cos 2л:)
sin ax sin 6л: = 1/2 cos (a—b)x— V2 cos (a -J- 6) л:
sin ал; cos frx = x/2 sin (a -f- 6) jc + V2 sin (a — b) x
2. Формулы дифференциального и интегрального исчислений
, / и \ du dv
j / ч л л d — V-. U-r-
d (uv) du . dv \ v j dA: dA:
sin
0
472
«e*
dx; dA:
d (e*)
"d]T = "w ' TI
d(ln*) 1 d(ax) r1
—i = — —\—- = ax In a
dx x ax
d (cos x) . d (sin л:)
~^-j '-—— sinA: —Ц—^ = cosa:
dA: dA:
d (ctcj a:) 1
dA: sin2 a: dA: cos2 x
Г 1 +1 , , 14 PdA- 1
\ a:^ dA:=—r-r xm + l (при m ^ 1) \ —==
Г dA: Г
\— = \nx \sinA:dA: = —cos a:
J x J
\ cos A:dA:=sin x
sin2 A:dx=YA:—-j-sin^ \ cos2A:dA: = -2-A:-|--T- sin 2л;
00 09
Г Г
у»е-^х = п\ j
о о
оо со
Г п -ах А —Л
=~ a-3
tli I » ~„9 , О ,/ —5/2
с —1~ 6
О
оо
О
:3 dA: я4

- ==0,225
Vя ~-
rt V ТС
\ х2е~ах26х=^-
3/2
= 1,18
3. Формулы для приближенных вычислений
Если а<С1, то в первом приближении можно принять:
Если угол а мал (а<5° или а<0,1 рад) и выражен в радианах, то в пер-
первом приближении можно принять:
sina = tga = a, cosa=l.
III. НЕКОТОРЫЕ СВЕДЕНИЯ О ЕДИНИЦАХ
ФИЗИЧЕСКИХ ВЕЛИЧИН
4. Единицы физических величин СИ, имеющие собственные наименования
Величина
Длина
Масса
Время
Плоский угол
Телесный угол
Сила, вес
Давление
Напряжение (механическое)
Модуль упругости
Работа, энергия
Мощность
Частота колебаний
Термодинамическая температура
Разность температур
Теплота, количество теплоты
Количество вещества
Электрический заряд
Сила тока
Потенциал электрического поля, электрическое
напряжение
Электрическая емкость
Электрическое сопротивление
Электрическая проводимость
Магнитная индукция
Магнитный поток
Индуктивность
Сила света
Световой поток
Освещенность
Поток излучения
Поглощенная доза излучения (доза излучения)
Активность изотопа
Единица
наименование
метр
килограмм
секунда
радиан
стерадиан
ньютон
паскаль
паскаль
паскаль
джоуль
ватт
герц
кельвин
кельвин
джоуль
моль
кулон
ампер
вольт
фарад
ом
сименс
тесла
вебер
генри
кандела
люмен
люкс
ватт
грэй
беккерель
обозначение
М
КГ
с
рад
ср
Н
Па
Па
Па
Дж
Вт
Гц
К
К
Дж
моль
Кл
А
В
Ф
Ом
См
Тл
Вб
Гн
кд
лм
лк
Вт
Гр
Бк
473

5. Множители и приставки для образования десятичных кратных
и дольных единиц и их наименований *
Множи-
Множитель
1018
1015
1012
109
106
103
Ю2
10*
Пристав-
Приставка
экса
пета
тер а
гига
мега
кило
гекто
дека
Обозначение
приставки
между-
международное
Е
Р
Т
G
М
к
h
da
русское
э
п
т
г
м
к
г
да
Множи-
Множитель
ю-1
ю-2
Ю-3
ю-6
ю-9
Ю-12
Ю-15
Ю-18
Пристав-
Приставка
деци
санти
МИЛЛИ
микро
нано
пико
фемто
атто
Обозначение
приставки
между-
международное
d
с
m
И<
п
F
а
русское
Д
С
м
мк
н
п
ф
а
Примечание. Приставки гекто, дека, деци и санти допускается применять
только в наименованиях кратных и дольных единиц, уже получивших широкое
распространение (гектар, декалитр, дециметр, сантиметр и др.).
При сложном наименовании производной единицы СИ приставку при-
присоединяют к наименованию первой единицы, входящей в произведение или
числитель дроби. Например, кПа-с/м, но не Па-кс/м.
В виде исключения из этого правила временно в обоснованных случаях,
т. е. в случаях, когда это нашло широкое распространение, допускается при-
присоединение приставки к наименованию единицы, входящей в знаменатель
дроби. Например, кВ/см, А/мм2, Бк/мл, кэВ/мкм.
Выбор десятичной кратной или дольной единицы от единицы СИ диктует-
диктуется прежде всего удобством ее применения. Из многообразия кратных и доль-
дольных единиц, которые могут быть образованы при помощи приставок, выби-
выбирают единицу, приводящую к числовым значениям величины, применяемым
на практике. В принципе кратные и дольные единицы выбирают таким об-
образом, чтобы числовые значения величины находились в диапазоне от 0,1
до 1000.
Для снижения вероятности ошибок при расчетах десятичные кратные
и дольные единицы рекомендуется подставлять только в конечный резуль-
результат, а в процессе вычислений все величины выражать в единицах СИ, заменяя
приставки степенями числа 10.
Кроме десятичных кратных и дольных единиц допущены к использова-
использованию кратные и дольные единицы времени, плоского угла и относительных
величин, не являющихся десятичными. Например, единицы времени (минута,
час, сутки), единицы плоского угла (градус, минута, секунда)*
* В соответствии с международным стандартом ИСО 31/0—74 десятич-
десятичные кратные и дольные единицы не являются единицами СИ.
474

6. Внесистемные единицы, допускаемые к применению наравне
с единицами СИ
Наименование
величины
Масса
Время !
Плоский угол
Объем, вмести-
вместимость
Длина
Оптическая сила
Площадь
Энергия
Полная мощ-
мощность
Реактивная мощ-
мощность
Единица
Наименование
тонна
атомная единица массы
минута
час
сутки
градус
минута
секунда
град2
литр3
астрономическая единица
световой год
парсек
диоптрия
гектар
электрон-вольт
вольт-ампер
вар
Обозначение
Т
а. е. м.
мин
ч
сут
о
г
и
град
л
а. е.
св. год
ПК
дптр
га
эВ
В.А
вар
Соотншоение
с единицей СИ *
103 КГ
1,66-Ю-27 кг
60 с
3600 с
86 400 с
1,74.10-2 рад
2,9Ы0-4 рад
4,85-Ю-6 рад
(л/200) рад
Ю-3 м3
1,50.1011 м
9,46-1015
3,08-1016м
1 м-»
104-m2
l,60.10-i9 Дж
1 Допускается также применять другие единицы, получившие широкое распростране-
распространение. Например, неделя, месяц, год, век, тысячелетие и т. п.
2 Допускается применять по-русски наименование «гон».
3 Не рекомендуется применять при точных измерениях. При возможности смешения
обозначения / с цифрой 1 допускается обозначение L.
Примечание. Единицы времени (минуту, час, сутки), плоского угла (градус,
минуту, секунду), астрономическую единицу, световой год, диоптрию и атом-
атомную единицу массы не допускается применять с приставками.
* Соотношения с единицей СИ даны приближенно с точностью до трех значащих цифр.
475

7. Соотношение между внесистемными единицами
и единицами СИ
Единицы пространства и времени. Единицы механических величин
Длина 1 ангстрем (А) = К)-10 м = 10~8см
Время 1 сут = 86400 с
1 год = 365,25 сут = 3,16.107 с
Плоский угол 1° = л/180 рад= 1,75-Ю-2 рад
1'=л/108.10-2рад=2,9Ы0-4 рад
1" = л/F48.10-3) рад =
= 4,85. Ю-6 рад
Объем, вместимость 1 л = 10-3м3=103 см3
Масса 1 т=103 кг
1 а.е. м. = 1,66-10-27 кг
Сила 1 кгс = 9,81 Н
Работа, энергия 1 кгс-м = 9,81 Дж
1 Вт-ч = 3,6.103 Дж
1 эВ = 1,60.10-19 Дж
Мощность 1 л. с. = 736 Вт
Давление 1 кгс/см2 = 9,81 -104 Па
1 мм рт. ст. = 133 Па
1 бар=105 Па
1 атм=1,0Ы05 Па
Напряжение (механическое) 1 кгс/мм2 = 9,8Ы06 Па
Частота вращения 1 об/с=1 с
1 об/мин =1/60 с-1
Волновое число 1 см~1=100 м-1
Единицы величин молекулярной физики и термодинамики
Концентрация частиц 1 см~3 = 106 м~3
Теплота (количество теплоты) 1 кал = 4,19 Дж
1 ккал = 4,19.103 Дж
Единицы электрических и магнитных величин
Электрический момент диполя 1 Д = 3,34.10-30 Кл*м
Удельное электрическое сопротив-
сопротивление 1 Ом«мм2/м= 10~6 Ом«м
Магнитная индукция 1 Гс=10~4 Тл
Магнитный поток 1 Мкс=10~8 Вб
103 А
Напряженность магнитного поля 1 Э = -^ = 79,6 А/м
Единицы световых величин и величин энергетической фотометрии
Освещенность 1 фот=104 лк
Единицы величин ионизирующих излучений
Доза излучения (поглощенная доза
излучения) 1 рад = 0,01 Гр
Мощность дозы излучения (мощ-
(мощность поглощенной дозы излуче- 1 рад/с = 0,01 Гр/с
ния) 1 рад/ч = 2,78.10-6 Гр/с
Экспозиционная доза рентгенов-
рентгеновского и гамма-излучений 1 Р = 2,58*10~4 Кл/кг
Мощность экспозиционной дозы
рентгеновского и гамма-излуче- 1 Р/мин = 4,30-10-6 А/кг
ний 1 Р/ч = 7,17.10-8 А/кг
Активность нуклида в радиоактив-
радиоактивном источнике (активность изо- 1 расп./с=1 Бк
топа) 1 Ки = 3,70.1010 Бк
Плотность потока ионизирующих
частиц 1 част./(ом2) = 1 с~1м~2
476

477

478

4Z9

480

16 № 1268
481

Перечень некоторых кратных и дольных единиц,
рекомендованных к применению ГОСТ 8.417—81
Наименование
величины
Длина
Площадь
Объем, вмести-
вместимость
Время
Частота периоди-
периодического процесса
Масса
Сила
Момент силы
Давление
Динамическая
вязкость
Кинематическая
вязкость
Механическое на-
напряжение
Энергия, работа
Мощность
Температура
Теплота (количе-
(количество теплоты)
Теплоемкость
Удельная тепло-
теплоемкость
Энтропия
Единица
Наименование
метр
квадратный метр
кубический метр
секунда
герц
килограмм
ньютон
ньютон-метр
паскаль
паскаль-секунда
квадратный метр
на секунду
ньютон на метр
джоуль
ватт
кельвин
джоуль
джоуль на кельвин
джоуль на кило-
грамм-кельвин
джоуль на кельвин
Обозначение
М
М2
м3>
с
Гц
кг
Н
Н.м
Па
Па»с
М2/О
Н/м
Дж
Вт
К
Дж
Дж/К
Дж/(кг-К)
Дж/К
Обозначения кратных и
дольных единиц, рекомен-
рекомендованных к применению
КМ, СМ, ММ, МКМ, НМ
км2, дм2 см2, мм2
дм3, см3, мм3
КС, МС, МКС, НС
ТГц, ГГц, МГц, кГц
Мг, г, мг, мкг
МН, кН, мН, мкН
МН»м, кН«м, мН»м,
мкМ-м
ГПа, МПа, кПа, гПа,
даПа, мПа,мкПа
МПа.с
ММ2/С
мН/м
ТДж, ГДж, МДж, кДж,
мДж
ГВт, МВт, кВт, мВт,
мкВт
МК, кК, мК, мкК
ТДж, ГДж, МДж, кДж,
мДж
кДж/К
кДжДкг.К)
кДж/К
482

Продолжение таблицы
Наименование
величины
Удельная тепло-
теплота фазового прев-
превращения
Количество веще-
вещества
Молярная масса
Молярный объем
Молярная кон-
концентрация
Внутренняя энер-
энергия
Сила тока
Электрический
заряд
Пространствен-
Пространственная плотность за-
заряда
Поверхностная
плотность заряда
Напряженность
электрического по-
поля
Электрическое
напряжение, элект-
электрический потен-
потенциал
Электрическое
смещение
Поток электри-
электрического смещения
Единица
Наименование
джоуль на кило-
килограмм
моль
килограмм на моль
кубический метр
на моль
моль на кубичес-
кубический метр
джоуль
ампер
кулон
кулон на кубиче-
кубический метр
кулон на квадрат-
квадратный метр
вольт на метр
вольт
кулон на квадрат-
квадратный метр
кулон
Обозначение
Дж/кг
МОЛЬ
кг/моль
м'3/моль
моль/м3
Дж
А
Кл
Кл/м3
Кл/м2
В/м
В
Кл/м2
Кл
Обозначения кратных и
дольных единиц, рекомен-
рекомендованных к применению
МДж/кг, кДж/кг
кмоль, ммоль, мкмоль
г/моль
ДМ3/МОЛЬ, СМ3/МОЛЬ
моль/дм3, моль/см3
ТДж, ГДж, кДж, мДж
кА, мА, мкА, нА, пА
кКл, мкКл, нКл, пКл
Кл/мм3, МКл/м3, Кл/см3,
кКл/м3, мКл/м3, мкКл/м3
МКл/м2, Кл/мм2, Кл/см2,
кКл/м2, мКл/м2, мкКл/м2
МВ/м, кВ/м, В/мм, В/см,
мВ/м, мкВ/м
MB, кВ, мВ, мкВ, нВ
Кл/см2, кКл/см2, мКл/м2,
мкКл/м2
МКл, кКл, мКл
16*
483

Продолжение единицы
Наименование
величины
Электрическая
емкость
Поляризован-
ность
Плотность элект-
электрического тока
Линейная плот-
плотность электрическо-
электрического тока
Н апр яженность
магнитного поля
Магнитная ин-
индукция
Индуктивность
Длина волны
Звуковое давле-
давление
Поток звуковой
энергии
Интенсивность
звука
Поглощенная до-
доза излучения
Активность нук-
нуклида в радиоактив-
радиоактивном источнике
Единица
Наименование
фарад
кулон на квадрат-
квадратный метр
ампер на квадрат-
квадратный метр
ампер на метр
ампер на метр
тесла
генри
метр
паскаль
ватт
ватт на квадрат-
квадратный метр
грей
беккерель
Обозначение
Ф
Кл/м2
А/м2
А/м
А/м
Тл
Гн
м
Па
Вт
Вт/м2
Гр
Бк
Обозначения кратных и
дольных единиц, рекомен-
рекомендованных к применению
мФ, мкФ, нФ, пФ
Кл/см2, кКл/м2, мКл/м2,
мкКл/м2
МА/м2, А/мм2, А/см2,
кА/м2
к А/м, А/мм, А/см
к А/м, А/мм, А/см
мТл, мкТл, нТл
мГн, мкГн, нГн, пГн
мм, мкм, нм, пм
мПа, мкПа
кВт, мВт, мкВт, пВт
мВт/м2, мкВт/м2, пВт/м2
ТГр,ГГр,МГр,кГр, мГр,
мкГр
ЭБк, ПБк, ТБк, ГБк,
МБк, кБк
484

IV. ТАБЛИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
8. Некоторые астрономические величины
Радиус Земли 6,37-106 м
Масса Земли 5,98-1024 кг
Радиус Солнца 6,95-108 м
Масса Солнца 1,98-1030 кг
Радиус Луны 1,74-106 м
Масса Луны 7,33-1022 кг
Расстояние от центра Земли до центра Солнца . . 1,49* 1011 м
То же, до центра Луны 3,84-108 м
Период обращения Луны вокруг Земли 27,3 сут = 2,36-106 с
9. Плотность р твердых тел и жидкостей (Мг/м3, или г/см3)
Твердые тела
Алюминий 2,70
Висмут 9,80
Вольфрам 19,3
Железо (чугун, сталь) 7,87
Золото 19,3
Каменная соль 2,20
Латунь 8,55
Марганец 7,40
Медь 8,93
Никель 8,80
Платина 21,4
Свинец 11,3
Серебро 10,5
Уран 18,7
Жидкости (при 15°С)
Вода (дистиллированная при 4 °С) 1,00
Глицерин 1,26
Керосин 0,8
Масло (оливковое, смазочное) 0,9
Масло касторовое 0,96
Ртуть 13,6
Сероуглерод U26
Спирт 0,8
Эфир 0,7
10. Плотность р газов при нормальных условиях (кг/м3)
Азот • 1,25
Аргон . 1J8
Водород 0,09
Воздух 1,29
Гелий 0,18
Кислород 1,43
11. Упругие постоянные твердых тел (округленные значения)
Вещество
Алюминий
Вольфрам
Железо (сталь)
Медь
Серебро
Модуль Юнга
Е, ГПа
69
380
200
98
74
Модуль сдвига
G, ГПа
24
140
76
44
27
485

12. Эффективный диаметр молекул, динамическая вязкость и теплопроводность
газов при нормальных условиях
Вещество
Азот
Аргон
Водород
Воздух
Гелий
Кислород
Пары воды
Эффективный
диаметр d, нм
0,38
0,35
0,28
—
0,22
0,36
Динамическая
вязкость х\, мкПа-с
16,6
21,5
8,66
17,2
—
19,8
8,32
Теплопроводность
Л, мВт/(м-К)
24,3
16,2
168
24,1
—
24,4
15,8
13. Критические параметры и поправки Ван-дер-Ваальса
Газ
Азот
Аргон
Водяной пар
Кислород
Неон
Углекислый газ
Хлор
Критическая
температура
Гкр' К
126
151
647
155
44,4
304
417
Критическое
давление
Ркр, МПа
3,39
4,86
22,1
5,08
2J2
7,38
7,71
Поправки Ван-дер-Ваальса
о,
Н-м*/моль2
0,135
0,134
0,545
0,136
0,209
0,361
0,650
ь.
10~6 М'/МОЛЬ
3,86
3,22
3,04
3,17
1,70
4,28
5,62
14. Динамическая вязкость г) жидкостей при 20 °С (мПа-с)
Вода ...,,.,,,•,,...,,«, 1,00
Глицерин .»•.......,. 1480
Масло касторовое .,.**.,, 987
Масло машинное . . * « , 100
Ртуть ,....,,.¦,.*¦ # .... 1,58
15. Поверхностное натяжение о* жидкостей при 20 °С (мН/м)
Вода .. ................ 73
Глицерин , л 62
Мыльная вода 40
Ртуть .,,..,.,,. ....... 5,0-10?
Спирт в * , * . . в * * 8 * * » , » , 4 22
486
16. Скорость звука с, м/с
Вода , , 1450
Воздух (сухой при нормальных условиях) л s 332

17. Диэлектрическая проницаемость 8
Вода ,, s ....... 81
Масло (трансформаторное) 2,2
Парафин 2,0
Слюда , . в 7,0
Стекло s . . » 7,0
Фарфор ..» 5,0
Эбонит .....t».*,,,.,..,.3,0
18. Удельное сопротивление р и температурный коэффициент а проводников
Вещество
Железо
Медь
Алюминий
Графит
р при 20 °С, нОм-м
98
17
26
3,9.10s
а, °С-1
6,2-10-3
4,2-10-3
3,6-10-3
—0,8-103
19. Показатели преломления п
Алмаз ...••..,,....,.... 2,42
Вода 1,33
Масло коричное , 1,60
Сероуглерод ' t 1,63
Стекло . . j , . * . f , e t , . 1,50
Примечание. Показатели преломления стекла зависят от сорта стекла
и длины волны проходящего через него излучения. Поэтому приведен-
приведенное здесь значение показателя преломления следует рассматривать как
условное и использовать его только в том случае, когда он не указан
в условии задачи.
20. Работа выхода электронов из металла
Металл
Калий
Литий
Натрий
Платина
Серебро
Цинк
А, эВ
2,2
2,3
2,5
6,3
4,7
4,0
А-10-19, Дж
3,5
3,7
4,0
10,1
7,5
6,4
487

21. Масса нейтральных атомов
Элемент
(Нейтрон)
Водород
Гелий
Литий
Бериллий
Бор
Углерод
Азот
Кислород
Фтор
Натрий
Магний
Алюминий
Кремний
Фосфор
Калий
Кальций
Свинец
Полоний
Порядковый
номер
0
1
2
3
4
5
6
7
8
9
И
12
13
14
15
19
20
82
84
Изотоп
п
iH
2Н
3Н
3Не
4Не
6Li
7Li
7Ве
°Ве
i°Be
9В
юв
ИВ
i°C
12С
1зс
i*C
13N
14N
15N
16Q
17Q
18Q
19р
22Na
23Na
23Mg
зоА1
31Si
3ip
41K
44Ca
206Rb
210po
Масса, а. е. м.
1,00867
1,00783
2,01410
3,01605
3,01603
4,00260
6,01513
7,01601
7,01693
9,01219
10,01354
9,01333
10,01294
11,00931
10,00168
12,00000
13,00335
14,00324
13,00574
14,00307
15,00011
15,99491
16,99913
17,99916
18,99840
21,99444
22,98977
22,99414
29,99817
30,97535
30,97376
40,96184
43,95549
205,97446
209,98297
22. Масса и энергия покоя некоторых элементарных и легких ядер
Частица
Электрон
Нейтральный мезон
Протон
Нейтрон
Дейтон
сс-Частица
9
2
1
1
3
6
т0,
,11-
,41-
,67-
,68-
,35-
,64.
Масса
кг
ю-31
Ю-28
Ю-27
Ю-27
Ю-27
Ю-27
т
о, а. е. м,
0,00055
0,14526
1,00728
1,00867
2,01355
4,00149
Энергия
Ео, Дж
8,16- Ю-14
—
1,50.10-1°
1,51.10-1°
3,00.10-ю
5,96.10-1°
Ео, МэВ
0,511
135
938
939
1876
3733
488

Изотоп
Актиний
Иод
Иридий
Кобальт
Магний
Радий
Радий
Радон
Стронций
Торий
Уран
Фосфор
Натрий
23. Период полураспада
Символ изотопа
225 д
89 АС
131т
53 1
192J
77 U
2jMg
219ря
88 Ка
226ря
88 ^а
IT**
229Th
9 0 iU
238тт
92 U
32р
15Г
»n.
)адиоактивных
Тип распада
а
Р-. y
Р-. y
Р-. y
Р-
а
а, y
а
Р~
а, V
а, у
Р-
V
изотопов
Период
полураспада
10 сут
8 сут
75 сут
5,3 года
10 мин
Ю-3 с
1,62.103 лет
3,8 сут
28 лет
7-103 лет
4,5-109 лет
14,3 сут
2,6 года
24. Основные физические постоянные (округленные с точностью
до трех значащих цифр)
Нормальное ускорение свободного падения . g = 9,81 м/с2
Гравитационная постоянная G = 6,67-10-u м3/(кг-с2)
Постоянная Авогадро Л/тА = 6,02« 102J моль
Молярная газовая постоянная /^ = 8,31 Дж/(К-моль)
Стандартный объем * Vm = 22,4«10-3 м3/моль
Постоянная Больцмана &=1,38-10-23 Дж/К
Постоянная Фарадея F = 9,65-104 Кл/моль
Элементарный заряд е= 1,60-10~19 Кл
Масса электрона тг = 9,1Ы01 кг
Удельный заряд электрона е/т~ 1,76- 10й Кл/кг
Скорость света в вакууме "* с = 3,00 ¦ 108 м/с
Постоянная Стефана — Больцмана .... а = 5,67«10~8 Вт/(м2«К4)
Постоянная закона смещения Вина .... C = 2,90-10~3 м«К
Постоянная Планка /г = 6,63-104 Дж«с
& = /1/Bя)=:1,05.10-34 Дж-с
Постоянная Ридберга R'^l.lOAO17 м-1
^ = 3,29.Ю15 с-1
Радиус первой боровской орбиты а = 5,29- Ю-11 м
Комптоновская длина волны электрона . . Хс —2,43-10~12 м
Магнетон Бора jlib = 9,27.10-24 Дж/Тл
Энергия ионизации атома водорода . . . Я/= 2,16» 10~18 Дж
Атомная единица массы 1 а. е. м. = 1,66-10-27 кг
Ядерный магнетон 1^=5,05-Ю-2.7 Дж/Тл
* Молярный объем идеального газа при нормальных условиях.
** Скорость света в вакууме, по данным измерений на 1973 г., равна
B99792,462± 0,018) км/с.

ОТВЕТЫ
1.1. у'= 122 км/ч; v" ==72,2 км/ч.
= 2fli02/(i'i + tf2) = 3>2 м/с. 1.5. <u>==s/(
1.8. Графики изображены на рис. 1.
1.2. 8,87 м/с. 1.3. 64 км ч. 1.4. <у> =
/1 + ^2) = 2 м/с. 1.6. 3,93 м/с. 1.7. 2 м/с.
1.9. Графики изображены на рис. 2.
Иг
15
Рис. 1
1.10. 40 с; 80 м; —0,1 м/с2; графики
+vot — at2j2. 1.12. 1) x=ltg^-t;2)v--
3 м/с; 45 м. 1.14. Встретятся дважды:
х
изображены на рис. 3. 1.11. а) * = *0 +
2; в) x = xo — vot — at2/2; г) х = — х0+
= 2jt/^ T cos2 ^Л= 48,0 м/с. 1.13. 30 с;
через 3,4 с на расстоянии 15 м и через
60
й,м/с2
'Путь
х\Ноордината.
80
но
80
Рис. 3
10,6 с на расстоянии 123 м. 1.15. 0:
= 1 м/с2. 1.16. 0,235 с; i>i = 5,l м/с; \
= 5,61 м, где s=l м. 1.18. 150 м. 1
490
; Vx — 2 м/с; v2~2 м/с; at = —8 м/с2; а2 ==
у2 = 0,286 м/с. 1.17. H = Bs + g/2J/(8g/2) =
.19. 1с; 10 м/с (при движении вверх); 3 с;

— 10 м/с (при падении). 1.20. 19,2 м. 1.21. 19,6 м/с. 1.22. 9,62 м; 14,6 м/с.
1.23. x=-h + VQt — gt2/2; 7,77 м/с. 1.24. 0,5 м/с. 1.25. 3 м/с. 1.26. 1) v = i3A/2 +
+ ]2Bt; 2) a=i 6At + ]2B. 1.27. 2,5 м/с; 12,5 м/с2. 1.28. 1) 14,1 м/с; 2) —10 м/с2;
3) 7,07 м/с2; 4) 7,07 м/с2. 1.29. 1,42 м/с2. 1.30. 1) 8 м; 2) 6,73 м; 3) 4 м/с;
4) 3,36 м/с. 1.31. Графики см. на рис. 4. 1.32. <и> = л/?/т = 0,837 м/с; |<v> | =
= 2Rjx = 0,267 м/с. 1.33. 2 м/с2; 1 м/с2; 2,24 м/с2. 1.34. 7 м/с; 8,5 м/с2.
1.35. 0,872 с; 14,8 м/с2. 1.36. ty3 — 8х = 0; 2,77 м/с; 4,8 м/с2. 1.37. *=#f sin(i;/#).
1.38. 1) y = Rt cos(v/R), x = Rtsin(v/R); 2) r = R, Ф=4г —-тг*. 1.39. Слу-
чай a: 1) # = f0^ # = — h — gt2/2; 2) y = — h—^y ; случай б; 1) x = v$t cosa,
o
—g/2/2; 2) t/ = — /г + xtga ^- > случай в: l)x =
2v0 cos2 a
= h — gt2j2; 2) y = h—^——L.; случай r: 1) * = s+0ofcosa,
2^
— gt2/2; 2) y = h — (x—s)tga S(x—sJ . 1.40. 20м/с; 28м/с.
2i>o cos2 a
1.41. /i = i;2/Bg) = 20,4 м. 1.42. v = l Vё!(Щ = 210 м/с. 1.43. 24,5 с; 2,45 км.
1.44. 45°. 1.45. 1) «/ = H^sina- ^-, д: = и0^ cos a; f/ = /i + ^tga-
g^ 2) 9 28C 136 m, 242m, 57,3 м/с. 1.46. vo^g j?1 + /a) =588 м/с;
2^2 ^ 2suia
2^coscc
/1 = ^^2 = 2,45 км. 1.47. Я = 1;о8т2а/B^) = 1,53 km; s = Buo sin a cos a)Ig =
= 3,53 km; ^ = (uS cos2a)/g= 1,02 км. 1.48. 3,58 м/с; 5,37 м/с2; 8,22 м/с2.
1.49. 4,9 м/с2; 8,55 м/с2. 1.50. v = Bn/T) R cos <p, ац = Dл2/Г2) R cos ф (Г —пе-
—период вращения Земли); 1) 463 м/с, 3,37 см/с2; 2) 259 м/с, 1,88 см/с2. 1.51. я =
=(у1 —у2)/Bя6) = 1,59с-1, где&=10см. 1.52. 113м/с; 35 мкм. 153. e = 2/i/(r/2) =
=8,33 рад/с2. 1.54. 5см/с2; 10см/с2; 11 см/с2. 1.55. 1,2 м/с2; 168 м/с2; ^168 м/с2.
1.56. е = 2яя/(Д0 = 3,14 рад/с2; N = 1/2n М = 2Ъ. 1.57. —0,523 рад/с2; 150.
1.58. е = я(я! —Mi)/#=1,26 рад/с2. 1.59. N = n{n\ — nf)/6 = 21,6; A/=
= 2я(п2 — ni)/e = 7,85 с. 1.60. « = уг4я2д2^2 + и2 = 40,6 м/с. 1.61. v = ndl/
ДЛ А/) = 0,754 м/с.
2.1. 2,5м/с2. 2.2. a = m2g/(m1 + m2) = l,96 м/с2. 2.3. F= 4mfm2 g = 39,2H.
2.4. 2м/с2;8Н; 2Н. 2.5. а = ^Г™1)^ = 1Л0 м/с2; Г1 = т1 (g + a) = ll,2 H;
— a) = 16,8H. 2.6. / = tga 2^ =0,35. 2.7. Fx = — 0,8H; F2 =
= —8Н; F = 0 при *= 1,67 с. 2.8. <F> = (m//) |/^/г = 626 кН. 2.9. 0,051.
2.10. 1.33 кг-М/С. 2.11. 100 Н-с; 100 кг-м/с. 2.12. 1,4 Н-с. 2.13. p1 = 2mvosina=
= ЗН-с. 2.14. 1,25 Н.с; —1,25 Н-с. 2.15. Qm = m (g + a)/v = 24,5 кг/с. 2.16. R =
==-QmV = -\60 H; fl = -Qfflt//m = -4,57 см/са. 2.17. 11 = 1"/^ =
a r яр
= 10,2 м/с, где р —плотность воздуха. 2.18. Fmax = /(mj + mo) g-= 17,7 Н,
2.19. Fi = /i(m1 + m2)gr=19,6 H; /72 = (f2 —/i) (m2/mi) (т1 + т2)§ = 39,2 H.
2.20. a = -/- Я = 73,5 мс2; T = L™ F = 625H. 2.21. fl=
L F = 625H. 2.21. fl= д
4 Л1 + т 1 — cos a
= 36,6 м/с2. 2.22. 2,27. 2.23. ^4°. 2.24. 20,4 см. 2.25. p= /Tpa2/^J =
= 3,5-10gH/m2 (p —плотность воды). 2.26. F = 2pSv2 sin ф = 346 H (p —плот-
—плотность воды). 2.27. t = mvm2X/N = 25 с. 2.28. t = ^- lnmg + feu°^44 5 с
2.29. A/ = (m/^) In 2 = 6,93 с 2.30. v = -j> (l _е"(А:/т)Л0 = 6,3 м/с. 2.31. F =
491

kv =1,03 кН. 2.32. к = Щ-^—- = 4,7.10-5 кг/м. 2.33. At =
_ . = 1,03 кН. 2.32. /г = ^
\ е-(Л/т)т t V0V
= (m/ife) In 10= 18,4 с. 2.34. 1) 6,3 м/с; 2) —0,57 м/с. 2.35. 1) 1 м/с; 2) 3 м/с.
2.36. 0,75 м/с. 2.37. 1) 1,5 м; 2) 0,5 м; 3) 1,5 м, 0. 2.38. 0,4 м/с. 2.39. и2 =
= 114 м/с. 2.40. и2 = 250м/с, ф2 = —36,6°. 2.41. ых = 0,385 м/с; м2 = —0,615 м/с.
2.42. 0,5 с. 2.43. uminL = 6,26 м/с. 2.44. 3mg; 70°30'. 2.45. В 6,1 раза.
2.46. (p = arocos j^j- = 60,2°. 2.47. 1,42 с. 2.48. F = m (g ± 4jt2/zV); Fmax =
= 1,02кН; Fmin = 942H. 2.49. t>mhl = Kg (#-/)// = 13 м/с; ф-arctg / = 31°.
2.50. 39kH. 2.51. cp = arctg Dп2я2г/^) = 38°50/. Указание. При равновесии жид-
кссти равнодействующая всех сил, действующих на частицу жидкости, нахо-
находящуюся на ее поверхности, направлена по нормали к поверхности. 2.52. v =
14 м/с. 2.53. 12,1 м/с; 16°42\ 2.54. cp = arctg -^-=58,2°; F =
= mg/cosq) = 66,2 кН. 2.55. 1) F = 4tt2n2mr= 12,7 кН; 2) M = 2Frcos(p =
— 86,5 Н-м. 2.56. a = p(D2R2; 1) ст = 8,9 кН/м2; 2) а = 8,9 кН/м2. 2.57. Л =
= fgms + mv2/2 = 996 Дж. 2.58. A = mh (g + 2h!t2) = 4,72 кДж. 2.59. 1,35 кДж.
2.60. 336 Дж. 2.61. 2,94 кДж, 6 кДж. 2.62. Т = (т/2) (^ + ^2/2) = 633 Дж.
2.63. 5 Дж; 15 Дж. 2.64. N = лр d2^3/8 = 1,26 кВт (р — плотность воды).
1 /^mspd
2.65. JV = 1/2p5f3 = 2,84 кВт (р —плотность воздуха). 2.66. N = -r у —?-;
1) 139 кВт; 2) 313 кВт. 2.67. 0,32 Вт; 56^т. 2.68. А = 5/?/2 =10 м. 2.69. а =
= arccos B/3) = 0,268я рад. 2.70. v=yr5gR=l4 м/с. 2.71. T2 = (m1/m2)T1=:
= 30кДж. 2.72., r2=(mi/7??2) 7^=1,2.10~8Дж=12нДж. Решение. Поза-
кону сохранения импульса, импульсы осколков после разрыва должны быть
равны: р1 = р2A). Выразим импульс через кинетическую энергию p = mv,
p2 = m2v2; T = mv2/2; 2mT — tn2v2. Из этих равенств найдем р=}^2тТ. Под-
Подставив в A), получим У~2тх7\ = У~2т2Т'2, откуда найдем Т2. 2.73. 390 Дж.
2.74. Т1 = пТ/(п + 1) = 24 пДж; Т2 = Т/(п + 1) = 8 пДж. 2.75. l = m\u\l{2fgm\)=
= 6,37 м. 2.76. h = m2v2/BgM) = 7,34 см. 2.77. и = M + m V^^^ 701 м/с.
2.78. Л = /A-со8Ф)(—^—^=16 см. 2.79. AU =
V i+2 У (! + 2)
J) 9,6 Дж; 2) 86,4 Дж. 2.80. u = m1v1/(m1 + rn2)\ w = m2/(m1 + m2); 1) м=1 м/с;
ш = 0,8; 2) и = 4м/с; ш = 0,2. 2.81. 1) pi = (mi — т2I{тг+т2) = — 6 кг-м/с,
= 16 кг-м/с; 2) Api = ^P2=16 кг-м/с; 3) Т[ = -^-х
= ^=16 Дж;
5) a, = i^li= J^%)t =0.64. 2.82. 1) й
= m2p1/(mi + ma) = 2 кг-м/с, 2) А^^ —ра = ~2 кг-м/с; 3) Т^=
=0,75 Дж, г;=о;т2Р21 ,2^0,5Дж; 4)
= 1,ЗЗДж; 5) ^ = 1г-= Т1» =0,24, и^ = -^= . jm ., -0,36;
ii (mi-\-m2r Ji (fn1 + mr
6) Д?/ = д—^1 - = 0,833 Дж; 7) W = AU/T1 = —^— = 0,4. 2.83. т| =
' 2m1(m1 + m2) J (mi + ma)
) = 0,952. 2.84. T] = m1/(m1 + ma) = 0,833. 2.85. r\ = ^L
2.86. —6 м/с, 4 м/с. 2.87. M = m (l + /T^SJVw^ 16,2 кг. 2.88.
492

493

3.47. 7 = (m/4) Bv +
2 = 50 Дж; Г2 =
м/с. 3.52.
) = 3,2\ кДж. 3.48. T = 3mv2/4 = 3 Дж. 3.49. Гх =
= 37,5 Дж._3.50. 7\=10 Дж; 7\, = 4 Дж. 3.51. р =
t 2l/Vh 404 353 /"
mi Д
= V~10/Gg/) = 3,74 м/с. 3.52. t 2l/Vgh 4,04 с. 353.
= 3,84 м/с. 3.54. 1) со =У 3g/Bl) = 3,83 рад/с, w= >/"
7/=542 рад/с у= |/"J7/3= 181 м/с; 3) со =
= yr3i7/=_5L42 рад/с, у= |/"J7/3= 1,81 м/с; 3) со = 6
9/-|/"^/7 532 / 355 1) 14 / 105 / 2)
7,5 Дж._3.50. \10 Дж; 7,
= 2l/Vgh = 4,04 с. 3.53. и= j/g/ A — cos ф)
2l 383 >/"з^= 1,92 м/с; 2) со =
7,10 рад/с,
'с, v=Vgl/3=\,8l м/с; 3) © = 6^/G0 = 7,10 рад/с,
м/с. 3.55. 1) 14 рад/с, 1,05 м/с; 2) 14 рад/с, 2,1 м/с (см.
1) со = 2/* g/C#) = 8,08 рад/с, v = 4 у" gR/3 = 3,23 м/с;
5,71 рад/с, v = 1/2V2gRj3 = 0t57l м/с; 3) со =
^ ПL рад/с> „= 4.
= 0,571 м/с; 3)
м/с; 4) оз =
=8,95 рад/с, и =
=2,39 м/с.
4.1. 66,7 пН. 4.2. 667_пН. 4.3. F = G (яр d2/6J= 1,78 мкН (р —плотность
железа). 4.4. Л = Л A/~?/?Л—0 = 13,6 Мм. 4.5. 2,18 м. 4.6. 3,7 Н/кг. 4.7. gjl =
= 1,61 м/с2. 4.8. ^ = 4/з^р/^ = 0,21 м/с2. 4.9. г = =- = 54,3 #.
1 + 1/У
R
Рис. 5
l + 1/Vn
4.10. 6,33 км/с. 4.11. 1,69 Мм. 4.12. 7,27-10~5 рад/с; 42,2 Мм. 4.13. 164 г.
4.14. 7,92 км/с. 4.15. 15 км/с. 4.16. 1,22
года. 4.17. 65 сут. 4.18. 255 сут.
4.19. Vl/v2 = (l+e)/(l — е) = 3, ^ — ско-
скорость спутника в перигее; v2 — в апогее.,
4.20. В четыре раза. 4.21. 6,2Ы023 кг.
4.22. 5,98-1024 кг. 4.23. 100. 4.24. g(г) =
при r^R; график зависимости g (r)
дан на рис. 5. 4.25. 1) АР = 8/3nGpmh =
= 15,4 мН; 2) ДР = 4/3я0рт/1 = 7,71 мН.
4.26. 1) A1 = 1/2mgR = 3\,2 МДж;
2) A2 = mgR = 62,4 МДж. 4.27. h = R.
4.28. ф = —62,6 МДж/кг; ф = —190 ГДж/кг. 4.29. 1,68 км/с; 2,37 км/с.
4.30. 436 км/с; 617 км/с. 4.31. 130 м/с. 4.32. v = Vv20— gR = 6,12 км/с,
4.33. v = Vvq — 2gR=\0 км/с. 4.34. v = V~2GM/R = 42,\ км/с. 4.35. 72,6 км;с.
4.36. Ракета будет двигаться по гиперболе. Указание. Перед решением задачи
рекомендуется познакомиться с примером 1 (с. 62). Сравнить заданную в усло-
условии задачи скорость и =10 км/с со скоростями круговой t»KP и параболической
vn на указанной высоте, предварительно вычислив их. Если окажется, что
у = икр, то ракета движется по окружности; если икр < v < vn, то ракета дви-
движется по эллипсу; если fKp = i'n, то ракета движется по параболе; если v > уп,
то траектория ракеты —гипербола. 4.37. a = 4mg/(jrd2) = 3,12 МПа. 4.38. 1) a =
2) a=-
3) (T=lS ()
8 = аупр/?= 1,47-10~3, 4.40. / = anp/(p^f) = 111 м (р —плотность свинца).
4.41. а = 4л2я2Ы/5 = 948 МПа. 4.42. Om.x=^ = i^^dr = ?=^ =
) = 78,5 МПа;
= 4,74 МПа. 4.43. Е = mgl/(Sx) = 208 ГПа. 4.44. a =
3,90.10-4; * = е/=1,2мм. 4.45. Е
4.47. k' = -t
= 1,5 кН/м; ^ =
= 8 кН/м#
494

495

496

7.22. 1) 5 см; 2) 10 см. 7.23. 1) 144 Гц; 2) 72 Гц. 7.24. 343 м/с. 7.25. 330 м/с.
7.26. »i = (//fl) 0 = 3,12 км/с. 7.27. 2,52 кГц. 7.28. 1) 341 Гц; 2) 268 Гц.
7.29. 366 Гц; 264 Гц. 7.30. 120 км/ч; 990 Гц. 7.31. 0,09. 7.32. 4,1 м/с; по на-
направлению к резонатору. 7.33. 1) 4,5 с; 2) 5,5 с. 7.34. 636 Гц. 7.35. 1) 699 Гц;
Д v
2) 517 Гц. Изменится: 1) 696 Гц; 2) 515 Гц. 7.36. и= g v = 3J4 м/с.
7.37. 23,7 мкДж. 7.38. 3,01 мДж/м3. 7.39. 0,251 Дж/°м3. 7.40. 157 Вт;
60,2 мкДж/м3. 7.41. 428 Па-с/м. 7.42. 1,39 МПа-с/м. 7.43. 0,472 мм/с.
7.44. 25,7 кПа-с/м3. 7.45. 475 нм. 7.46. 1,61 Па. 7.47. 5,98 Вт. 7.48. 82,5 мПа.
7.49. 430 Па-с/м; 93 мкПа. 7.50. 27,2 пВт/м2 и 1,87 пВт/м2. 7.51. 1) 20 дБ;
2) 100 дБ. 7.52. 35,5 дБ. 7.53. В 103 раз. 7.54. 1) 63 дБ; 2) 70 дБ. 7.55. Пер-
Первый тон не слышен; 20; 40. Указание. Воспользоваться графиком на с. 101.
7.56. 64 дБ; 50 дБ; 50 дБ; 56 дБ; 77 дБ. 7.57. В 100 раз. 7.58. 70.
7.59. а) 0,4 пВт/м2, 4 дБ, 0; б) 0,5 Вт/м2, 117 дБ. 120. 7.60. 50. 7.61. 40 мкВт.
8.1. 1) 18; 2) 44; 3) 58,4. 8.2. M = Mrk = 98 кг/моль (Мг — относительная
молекулярная масса; &=10~3 кг/моль). 8.3. m-i = MrkjN&\ 1) 7,31 »10~26 кг;
2) 9,70-10~26 кг. 8.4. р = Mrkv/V = 3,2 кг/м3 (Мг — относительная молекуляр-
молекулярная масса; &=10~3 кг/моль). 8.5. v = 7,14 моль; Л^ = 4,30« 1024 молекул.
8.6. 0,125 моль; 7,52-1021 молекул. 8.7. Известно, что молярный объем Vm
любого газа при нормальных условиях равен 22,4 л/моль. Поэтому n=V/Vm=
=-0,5 моль; m = Mv = Mrkv=16 г. 8.8. v = pV/M = 9,97-10 моль. 8.9. N =
= NруiVm = 1,34« 1022 молекул (Vm— молярный объем идеального газа при нор-
нормальных условиях; Ут=22,4.10 3 м3/моль). 8.10. 1) 1,50-1023 атомов; 2M,02х
XIО22 атомов; 3) 3,17-1022 атомов; 4) 2,87-1021 атомов. 8.11. Для определения вида
газа найдем его относительную молекулярную массу: Mr~pV/(kv)~28. Сле-
4 tn
довательно, данный газ — азот. 8.12. # = — —- N^=2,87-1020 частиц. 8.13. Пусть
о 1VI
жидкость заполняет куб. Число молекул в кубе N = (l/dK = V/d? A) (/ — длина
ребра куба, d — диаметр молекулы). Число молекул можно выразить также
формулой N=\Na—-J7- Np, = ~-r- Na B) (v —количество вещества жидкости
в кубе; т — масса; р — плотность; М — молярная масса жидкости). Приравняв
правые части A) и B) и выразив из полученного равенства диаметр d моле-
молекулы, найдем d= у M/(qNa); ^ = 0,464 нм; <i2 = 0,290 нм. 8.14. Диаметр
молекулы воды d= у M/(qNa) A) (см. задачу 8.13). Среднее расстояние между
з /—
центрами молекул </>= у V± (Vi —объем куба, приходящегося на одну моле-
молекулу). Искомое отношение: </>Д/= у Vmp/Al = 10,7. 8.15. v = V/Vm = 50 ммоль
(Vm — молярный объем); Ут=:22,4-10~3 м3/моль; vM0JI = v A — а) = 35 ммоль;
vaT = 2va = 30 ммоль; vn01 = 65 ммоль. 8.16. F = -r-pS = 32,3 кН. 8.17. р =
8.19. р = (Po-PgbhJVi =232 кШ 820 /а = ^1(/1 + Го)_Го = 473°С
^i+^(A/i2-A/n) Pl
(Г0 = 273°С). 8.21. 350 К. 8.22. m = pV Tl~T2 =66,5 г (р-плотность воды).
8.23. bF = (pO2-pol)gV T2~Tl =642 Н. 8.24. AF = pogF A^"Го) =1,39 кН
1 2 ^0
(Г0 = 273 К; ро —плотность воздуха при нормальных условиях). 8.25. V —
= —%f,—^-Тр—-—/х5=106 см3. 8.26. Давление воздуха р± в цилиндрическом
1 2— ^ 1
сосуде до понижения температуры, уравнивается атмосферным давлением р0:
Po = Pv @
497

После понижения температуры атмосферное давление уравнивается сум-
суммой двух давлений: р2 воздуха в сосуде и Ар, создаваемого столбом воды
высотой АЛ:
Ро = Р2 + Ар = Р2 + pgbh. B)
Приравняв правые части формул A) и B) и выразив р2, найдем
C)
Давление, объем'и температура воздуха в цилиндре связаны уравнением
газового состояния
P2V2 итти PiShj p2Sh2
-=——-=— , ИЛИ —¦=— = —=—»
¦«1 J 2 i 1 * 2
Сократив на S, получим Pihi/Ti = p2h2/T2.
Подставив сюда выражение р2 по C), а также учтя, что h2 = hi—АЛ,
после преобразования найдем
Решив это квадратное уравнение и отбросив второе значение АЛ, не имею-
имеющее физического смысла, получим АЛ = 4,5см. 8.27. m = MpV/(RT) ==0,212 кг.
8.28. V = v#77p = 3,32 м3. 8.29. p = mRTJ(MV)= 1,16 МПа. 8.30. Г =
= pMV/(mR) = 275 К. 8.31. Относительную молекулярную массу Мг найдем
из соотношения M = Mrk A) (где М — молярная масса); /г=10~3 кг/моль*
Из уравнения Клапейрона — Менделеева получим M = mRT/(pV) = pRT/p =
=44 кг/моль. Из A) найдем Mr = M/k = 4A. 8.32. р = <Мр/(ДГ)=2,56-10-2 кг/м3.
8.33. F = (M2 — Mi) ?^=10,9 кН. 8.34. т = МХдр = 8,3 г. 8.35. Am
~ (k%r—%r-) =6,16 кг (^ = 7/8). 8.36. V = (mi/M1 + m2/A2)
\^У/ Р
8.37. Pi=yPffir =0J6МПа; р2 = ^ру- = 1,12 МПа; p = pl + pi==l,88 МПа.
8.41. Mr — Mjk (М — молярная масса воздуха; k = 10~§ кг/моль); Мвозд =
8-42- ^=
1
?= 6,87 г; т1-=^1/тг = 4,81 г; т2= A — wx) = 2,06г.
8.44. Т = -; ]р- = 259 К. 8.45. п = 0,788 моль; V! = 67,5 ммоль:
v2 = 0,720 моль.
9.1. 1,2-1020 м-3. 9.2. 2 л. 9.3. л = уЛ?л/К = 4,52.1028 м~3. 9.4. л =»
= iV^/VOT = 2,69'1025 м~3 (где Ут —молярный объем газа при нормальных
условиях). 9.5. m = MnV/NA = 0,25 г. 9.6. n = mNA/(yMrk) = 7,52-102^ м-а
(^г=Ю-3 кг/моль). 9.7. v = nK/^ = 9,97.10-9 моль. 9.8. mln2 = Mr 2/Mr 1==
= 16. 9.9. Mr = mNA/(knV) = 32 (^ = 10~3 кг/моль). Следовательно, газ—
кислород. 9.10. Л^л = knVMr/m = 6,02-1023 моль. 9.11. n1 = NA/Vm = 2t69x
ХЮ25м~3; ло = я1A— а) = 1,6Ы025м~3; n3 = 2«ia = 2,15.1025 м~3. 9.12. 2,42х
ХЮ^7 м-а. 9.13. 414 Па; 138 кПа. 9.14. N = pV/(kT) = 3,62-102& молекул.
498

9.15. v = pl//(#r) = 4,98MMcm>; n = vNA/V =1,25-10™ м~*. 9.16. Лр = ~ kT =
= 4,14 кПа. 9.17. v = 4,97 ммоль; W = 2,99.1021 молекул. 9.18. 1) Г = 7,25кК'
2) <8п>=1,5.10-1<> Дж. 9.19. <8п>=1,24.10-20 Дж; <е> = 2,48-10-*> дж';
^^ 9.20. 8,28.10~21 Дж; 13,8х
ХЮ-21Дж; 16,6-Ю-21 Дж. 9.21. 6,9-Ю-21 Дж; 20,7-Ю-21 Дж; 13,8-10~21 Дж;
34,5-Ю-21 Дж. 9.22. 3,22.109. 9.23. Лр = 3?77(а/?) = 2,48 Па. 9.24. Г =
2 W
= -g---^1 = 33,6 кК. 9.25. 1) 500 м/с, 462 м/с, 407 м/с; 2) 1,94 км/с, 1,79 км/с,
1,58 км/с; 3) 7,90 км/с, 7,30 км/с, 6,48 км/с. 9.26. 20.1 кК. 9.27. 1,6 кК.
9.28. 2 км/с. 9.29. Гелий: 2,73 км/с и 2,48-Ю0 Дж; аргон: 864 м/с и
2,48.1О-2о ДЖ. 9.30. 352 мкм/с. 9.31. 1,37-107 раз. 9.32. 0,92 км/с.
9.33. 1.82 км/с.
10.1. В е23,6 раза. 10.2. 1,65. 10.3. 5,97-1023 моль. 10.4. 4,14-101 Н.
10.5. 1,18 кПа. 10.6. 5,88 км. 10.7. 885 м. 10.8. 1) 8,75 м; 2) 25,8 м. 10.9. 6,5 м.
10.10. n = nQem(d2r2^2kT^ (n0 — концентрация частиц на оси ротора). 10.11. 5,91.
10.12. 304 кПа. 10.13. 84 (криптон). 10.14. 28%; 72%. 10.15. vB = }/'2kT/m.
10.16. f(u)du = -^=:e-u2u2du. 10.17. 4,39-10~3. 10.18. 6,63-10~3. 10.19. w =
=тд[;)"'A)""-- "f- --«¦»-' <«¦• *>-
10.22. vKB = V<o2> = V3fzT/m. 10.23. ii/^- = i.= 1,27.
10.24. С-г|^, 10.25. vB = V3kT/m; <u> = 3/я^ГДв/л). 10.26. 6,0-109.
10.27. pb = V2mkf. 10.28. 0. 10.29. <рх> = Ут1гТ/Bп). 10,30. 0,5%
Я3/2Л/
10.31. p^VmkT. 10.32. <8П> = 3/2^Г. 10.33. d^(co) = -—Ц- e-3o)/2col/2dco.
BдI/2
10.34. 9,3.10-з# 10.35. w = ^f = 7,^^ 83^2. 10.36. 7,53.10~4.
10.37. 8=8,28-10-3^Г. 10.38. ш=^ = Д- f ^ V/2e-8o/(^r). 10.39. 8^8,1 ЛГ
10.40. EB = 1JokT. 10.41. /(9)d6 = —-—e~e/201/2 d9. 10.42. 4,84-10~3
BI/2
BлI/2
10.43. 2,67-10~4. 10.44. e = kT. 10.45. Уменьшится в два раза. 10.46. В три
раза. 10.47. 6,4 см. 10.48. 3,5 мПа. 10.49. 1,55 нм. 10.50. Можно, так как
длина свободного пробега (</> = 97 м) много больше диаметра d колбы.
10.51. 1,55 мг/м3. 10.52. 3,7-Ю9 с. 10.53. 1,57-Ю21. 10.54. 3,38-Ю18.
10.55. 288 нс. 10.56. 1) Не зависит; 2) <1>~1/р. 10.57. 1) Не зависит;
2) ф~Т. 10.58. 1) <г>~"|/>, 2) <г> - р. 10.59. 1) <2>-]/*Г; 2) <г> ~
— 1/1/"Г. 10.60. 7,23.10-5 м2/с. 10.61. 135 нм. 10^2. 1) 90-10-5 м2/с;
2) 0,061 м^с. 10.63. 7,1. 10.64. 1) D-lAr3; 2) Z) — Ут. 10.65. 1) D - 1/р;
2) О~Ур. 10.66. J8 мкПа-с. 10.67. 90 пм. 10.68. 19 мкПа-с. 10.69. 1) т] ~
— 1/"Г; 2) ti — V^T. 10.70. 1) Не зависит; 2) г\~Ур. 10.71. 1) 16,8 Н;
2K,17.10-4Н.м. 10.72. M=^V^4/^=0,58 мН-м. 10.73. F = I f-^LVp
о \л1Ц ]
= 0,89мкН. 10.74. 38,6 мВт/(м-К). 10.75. 1) 2,5, 2,41; 2) 1,90^ 1,86; 3) 1,90,
1,90; 4) 1,75, 1,38. 10.76. 23,4jviBt/(m.K). 10.77. 1)к~УТ; 2) Я—У"Г*
10.78. 1) Не зависит; 2) к~Ур. 10.79. 1) 196 Вт/м2; 2) 35 мВт/м2.
499

500

501.

13.19. F =
2) F2 =
2D
. 13.20.
QQict __
= 0,16 мН;
. 13.21. F = Qr/BmQR) =3,6мН. 13.22. F =
14.1. 4,09 kB/m. 14.2. 2,99 кВ/м; 607 В/м. 14.3. 280 В/м. 14.4. 6 см; 12 см.
14.5. За отрицательным зарядом на расстоянии rfj = rf(j/~ 2-f-l). 14.6. 34 кВ/м.
4 КУ з ==2>71 кВ/м- Реше-
1 тР
14.7. Е = 4г К з
ние. Из рис. 6 следует, что элемент заряда dQ,
находящийся на элементе d/, создает напряжен-
напряженность d? = -. о, или d?" = -r2—-. Разложим
4яе0г2 4ле0г2
d?" на две составляющие: d?i — по нормали к
плоскости кольца и d?2 — параллельно ей —и
просуммируем эти составляющие для всех элемен-
элементов кольца. При этом составляющие, параллельные
плоскости кольца, в сумме дадут нуль. Сумма вер-
вертикальных составляющих выразится интегралом Е~
I
\ d/. Выражая cos ф через г и R, по-
о
лучим после интегрирования окончательную формулу, приведенную выше,
14.8. Е== о7Dе0) =28,3 В/м. Решение. Полусферу разобьем на дифференци-
дифференциально тонкие кольца (рис. 7) с зарядом dQ = о dS = 2nroR dcp, тогда напряжен-
Рис. 6
SD0
Рис. 7
R
Рис. 8
Рис. 10
ность d?, создаваемая таким кольцом в центре полусферы, dE= ^^ „
(см. задачу 14.7). Учитывая, что r~Rsinq> и a = R cos ф, после интегрир
Я/2
вания получим Е = -%г \ shl Ф cos Ф d(P = ^" * 14t9f ^ 0; 2^ 900 В/
о
502

3) 400В/м; график см. на рис. 8. 14.10. Е1 = 0; Е2 = —-^Ц-=1,11 кВ/м;
?з= а = 200В/м; график см. на рис. 9. 14.11. 5,55 нКл/м.
14.12. 43,2 MB/м. 14.13. 64,3 кВ/м. 14.14. ?1==0; ?2 = Яа/(е0г2) = 75,5 В/м;
Рис. 11
7
Рис. 12
график см. на рис. 10. 14.15. ?i = 0; E2 =
14.15. ?i 0; ^а Т1/Bяеог2) 2ООВ/м; Е3 =
график см. на рис. 11. 14.16. ? = т/(8ле0/) =
= 135кВ/м. 14.17. Е = 11. =55,7 кВ/м. 14.18. 35,6 кВ/м.
2]/42+/2
14.19. 60,2 кВ/м. 14.20. 38,0кВ/м. 14.21. 1) ? = 0; 2) Е = а/ео = 113 В/м; гра-
график см. на рис. 12. 14.22. 1) ?i = y a2~~gl — 11Д R/**- * F--i- a2 + gi _
-=113 В/м; 2) ?, = .!.
-i 80
f
???_
6, +6
I
•
i
¦
IEO
2S0
Z7
Рис. 13
E,B/M
18,8'
6,28
I I
Рис. 14
Л?10^Кл/Мг
Л
Я
г,м
Рис. 15
= 226 В/м график см. на рис. 13. 14.23. 1) 396 В/м; 2) 170 В/м; график см. на
рис. 14. 14.24. Е=-
. 14.25. F = i-
2 80
?=16,9мкН.
14.26. |С1 = Л 1^2^80^ = 33,3 нКл. 14.27. 1) ^^i--^- Гг = 3,78 В/м; Dx =
:== ~^" p^"i:=: 0,1 Нх\л/м f 2j ?2 *== "TjT ¦*>== 6,28 В/м (для /" ^^ ^)* Еъ ==: ¦ ^-~ /ч—=
О О 8q8 3 8q
503

504

505

15.21. 1) 146 В; 2) 136 В; 3) 100 В; график см. на рис. 19. 15.22. 1) ф2 =
==J^(pi==200B; 2) Ф2 = - р Фг=100В. 15.23. Аф = —- — d = 56,6 В.
А2
15.24. ф = ?^ =
. 15.25. U = ~ в1~
15.26. 170В. 15.27. 1,04.10е. 15.28. 432В. 15.29. U = 4r l/ -^- = *>
1530 ДП ^l 4 229 В 1531 A С} 6
= 141 В.
кВ-
15.30.
е0
4 = — 229 эВ-
2
15.32. Дф^-L-^—=8,07 В. 15.33. Щ = -тг — ?
О EqS О Eq
= -т-—/^2 = 377 В; график см. на рис. 20. 15.34. 1) фх =
- = 238 В:
I
У?
Рис. 19
2) и 3) ф2 = фз=
. 15.35.
= — Е; Jgrad ф1 = ?" = 4--?- = 22бВ/м;
градиент направлен к плоскости, перпендикулярно ей. 15.36.0,6 В. 15.37.0,12 В.
15.38. | grad ф | = ф//- = 200 В/м; градиент направлен к заряду. 15.39. | grad ф |=
= т/Bяеог) — 180 В/м; градиент направлен к нити вдоль силовой линии.
15.40. Аф = ?^1=з,14В. 15.41. Аг= QlQa f- -
68О8 4Я8О \ fi Г2
X
15.42.
7=-] = 659 мкДж. 15.44. Л = •
э а = 1 QlVl= 1 мкДж. 15.43. А± а =
X
• cos (я/2 — а) = 1,96 мкДж.
15.45. 2,62 мкДж; см. пример 5 на с. 199. 15.46. Л = <2т/Dео) = 25,2мкДж.
Ох / к \ с
15.47. Л=-т^—( 1 ,- 1=47 мкДж. 15.48. Ал 2=-^
= 165мкДж. 15.49. Л112=1/4<2ф = 250мкДж. 15.50. А^ 2 = ^— In 2 = 62,4 мкДж.
15.51. s = |e|?72/Bm) = l,76cM; у = | е\ ?'/2/т = 35,2Мм/с (т° и е—масса и за-
заряд электрона). 15.52. 1) 2,55кВ; 2) 4,69MB. 15.53. 1,58-1016м/с2; 5,63Мм/с;
0,356 нс. 15.54. 15МэВ; 2,19 м/с. 15.55. 24,ЗМКл/кг. 15.56. / = 3ти2/Bе?)=5,19мм
(т—масса протона). 15.57. 1т\п = 10—гА—=1см. 15.58. 2,24 Мм/с; откло-
нится на 45° от первоначального направления. 15.59. ф2=ф1—к (т/ё) v\ ==289 В
(т и е — масса и заряд протона). 15.60. t =----^т —^=2,13 мм. 15.61. vm\n =
= 0?24 Мм/с (elm—удельный заряд электрона.) 15.62. ф2 ==
506

507

508

509

510

511

28.1. 3,5 мм. 28.3. 40 см. 28.4. 60 см. 28.6. 6 м. 28.7. —20 см; 3 см;
28.9. 1,1 см. 28.10. 15,4 мм. 28.11. 16,3 см. 28.14. 1,53. 28.15. 1,63.
28.16. 35°30'. 28.17. 53°38\ 28.18. 1,41. 28.19. 1°12\ 28.24. 15 см. 28.25. 48 см.
28.26. 2,08 мм/с. 28.27. 10 см. 28.28. 7,5 см. 28.30. 12,5 см. 28.31. —1,32 дптр.
28.32. 3,84 см. 28.33. 26 см. 28.34. —0,75 дптр. 28.35. 1) 39 см; 2) —80 см.
28.36. 1,4. 28.37. 1,6. 28.39. 8,1 см. 28.40. 24 дптр. 28.41. —8 см.
28.42. —4 дптр. 28.43. 20 см. 28.44. 2,5. 28.45. 7. 28.46. 80. 28.47. 12.
28.48. 1) К объективу на 1 мм; 2) от объектива на 9 мм. 28.49. 30,3 см.
28.50. 100. 28,51. 250, 10,5 мм. 28.52. 2 см.
29.1. 0,08 кд. 29.2. 1 Вт/кд; 12,1 лм/Вт. 29.3. со = О,633 ср; 2у = 52°.
29.4. 51 мкА. 29.5. 180 лк. 29.6. 12 с. 29.7. 3,2 лк; 2,4 лк. 29.8. 18,3 м.
29.9. 60°. 29.10. 1) 278 лк; 2) 60 лк; 3) 251 лм; 4) 125 лк. 29.11. 0,707 м.
Указание. По правилам дифференциального исчисления найти максимум функ-
функции ?(/i) = //*/(/z2 + г2K/2. 29.12. 2 ккд/м2. 29.13. 9,4 кд; 157 кд. 29.14. 2 клм;
Е
8 клк; 2,5 ккд/м2. 29.15. ? = —-——=1,5 Гкд/м2. 29.16. 400 кд/м2.
3Ttg (&/)
29.17. По диагонали куба; lmax = V3 ?а2 = 350 кд. 29.18. 1) 63 кд; 2) 30 кд.
29.19. Е—J0h2/{h2-irr2J= 1 лк. 29.20. 3 м. Указание. По правилам дифферен-
дифференциального исчисления найти максимум функции Е (h) = IQh2/{h2-\-r2J.
29.21. 97 лк; 73 лк; 23 кд/м2. 29.22. 1,6 м. 29.23. 0,98.
30.1. 2.103; 3-103. 30.2. 4 мм. 30.3. 1,33 мм. 30.4. Увеличится; 1) на
0,50 мм; 2) на 0,548 мм. 30.5. ф = У nX/2d (л— 1) = 30 мрад=1,72°. Указание.
При решении задачи угол поворота пластины считать малым. 30.6. 1,73 см.
30.7. 0,6я. 30.8. 1) 0,6 и 0,45 мкм; 2) 0,72; 0,51 и 0,4 мкм. 30.9. 2 м.
30.10. 500 мм. 30.11. / = *Й>/Х = 2,5 м. 30.12. 3,6 мм. 30.13. Темнота; геомет-
геометрическая разность хода лучей Дгеом = Л = 0,6 мкм. Оптическая разность хода
А = Агеом + Я/2. 30.14. Л/= 2 (Ad/X) Ь= 1 м; отодвинуть от источника на 1 м.
30.15. 1) 4,8 мкм; 2) 4,8 мкм; 3) 5,1 мкм; 4) 5,1 мкм; в первых двух случаях
усиление, в последних двух —ослабление. 30.16. 0,1 мкм. 30.17. 0,25 мкм;
0,125 мкм. 30.18. 541 нм. 30.19. Ь = А,/2лв) = 3,15мм. 3о.2О. 10,3". 30.21. 10 мкм.
30.22. 3,1 мм; 5,2 мм. 30.23. # = 2я9Д = 8,55 см-1. 30.24. 0,39 мм.
30.25. 0,15 мкм. 30.26. 1,25 дптр. 30.27. 490 нм. 30.28. 880 мм. 30.29. 1,4.
30.30. /i = (fe+l) ?=1,33.30.31. rk = VkR1R2K/(R2~R1) = 1,73 мм. 30.32. rk =
= >^BА?+1)/? (Л/4) = 0,704 мм. 30,33. й = тЩп— 1)=-72 мкм. 30.34. 1,00014.
30.35. na = /ii + mX//= 1,000607. 30.36. 27,3 мкм. 30.37. п = 1 + kX/Bl) = 1,000282.
30.38. An = AmK/Bl) = 0,000124.
31.2. 1,58 мм. 31.3. 3,69 мм. 31.4. 8 зон; темное пятно. 31.5. 1) 50 м;
2) 25 м. 31.6. 1) Ь = г21(пХ), /i=l, 3, 5, ...; 2) 6 = г2/(/гЛ), п = 2, 4, 6, ...
31.7. bi=l,4 м; Ь2 = 0,7 м; Ь3=-0,47 м. 31.8. b = ar2l(ak% — r2) = 2 м.
31.9. Уменьшится в 4 раза. 31.10. 2°45'. 31.11. 143. 31.12. 1) Первый дифрак-
дифракционный минимум; 2) дифракционный максимум, соответствующий k~2.
31.13. 103. 31.14. 580 нм. 31.15. 21°17'. 31.16. 8. 31.17. 8; 74°. 31.18. 0,6 мкм.
31.19. 66 см. 31.20. 9 = aresin(sina + mtyd) = 38,3°. 31.21. 3. 31.22. R = k/AX =
= 290; N = R/k. 31.23. / = М/(Ш) = 10 мм. 31.24. Я = ?ф/ = 2,9Ы04.
31.25. D<p =-(tgq))A = 9,62.105 рад/м = 3,31.. .7/нм. 31.26. 1 мм/нм.
31.27. 103 штрихов/мм. 31.28. f = D{k cos3 ф/sin ф = 21,1 см. 31.29. 0,28 нм.
31.30. 31 пм. 31.31. 506 пм. 31.32. 1,6". 31.33. 6 см.
32.1. 36°. 32.2. 37°. 32.3. 61°12'. 32.4. 194 Мм/с. 32.5. 55°45\ 32.6. 32°.
32.7. 1,52. 32.8. 106°. 32.9. 156°. 32.10. 100°. 32.11. 45°. 32.12. В 2 раза.
32.13. В 3,3 раза. 32.14. 23,6 ккд/м2. 32.15. 0,33. 32.16. В 3 раза. 32.17. В 1,23
раза. 32.18. 0,348. 32.19. 3,4 мм. 32.20. 169 град-см3/(дм-г). 32.21. 0,21 г/см3.
32.22. 0,4 г/см3.
512

513

мера: 656,3 нм. 38.10. 1 Мм/с. 38.11. 30,3 нм; 13,5 нм. 38.12. Гелий: 8,64 аДж =
= 54 эВ; 54 В; литий: 19,5 аДж= 122 эВ; 122 В. 38.13. 8,2.1014 с;
2,4-Ю1* с-1, 4,6.10й Гц. 38.14. 212 пм. 38.15. 10,2 В.
39.1. 21 Мм/с. 39.2. 41 пм. 39.3. 304 пм. 39.4. Ниобий B = 41).,
39.5. 5,5 кВ. 39.6. 5,9 кэВ. 39.7. 0,14 нм. 39.8. 1,24 пм. 39.9. 20,5 пм; 60,5 кВ.
39.10. 8,00 кВ.
40.1. 19,9-10~27 кг; 1,66. Ю^27 кг. 40.2. Массовое число-—число нуклонов
в ядре, поэтому оно всегда целое. Относительная масса ядра определяется
отношением массы ядра к x/i2 массы изотопа углерода 12С. Это число це-
целым быть не может. 40.3. 35,439. 40.4. 0,186; 0,814. 40.5. 2,16-10~4.
40.6. 1,01436 а.е.м. 40.7. 1) 3, 2, 1; 2) 10, 5, 5; 3) 23, 11, 12; 4) 54, 26, 28;
5) 104, 47, 57; 6) 238, 92, 146. 40.8. {Н — протон; ?Н—дейтон; ?Н —тритон.
40.9. Два; ?Н и 2Не. 40.10. ?Н; 2Не. 40.11. ^Н; jLi; }BN. 40.12. 1) 5,6 фм;
2) 8,4 фм; 3) 11,2 фм; 4) 14 фм; 5) 16,8 фм. 40.13. п = 3/Dлго) =
= 8,7-1047 нуклонов/м3. 40.14. З-Ю7. 40.15. <р> = Зт^яго) ~
« 1,4-1017 кг/м3. Указание. Массу ядра приближенно можно выразить как
произведение массового числа Л (числа нуклонов в ядре) на массу т^ одного
нуклона, которую можно принять равной атомной единице массы A а. е. м. =
= 1,66-Ю-27 кг.) 40.16. р = Зе/(8я/-о) = 6,96.1О24 Кл/м3 (е—элементарный за-
заряд). 40.17. F1== 5,05- Ю-25- Н; F2 = 735 H; F1/F2 = 6,87.10-28. 40.18. Спин
нуклона в единицах % равен 1/2. 40.19. Спином ядра называется собственный
момент импульса ядра. Он складывается из спинов нуклонов и их орбиталь-
орбитальных моментов импульса. Орбитальные моменты импульса нуклонов всегда це-
лочисленны. 40.20. Спин ядра может иметь значения 0, г/2, 1, 3/2 и т. д.
40.21. 1) 0, 1; 2) V* 3/2; 3) */2, 3/2; 4) 0, 1, 2. 40.22. 1) 0, 2) i/a, 3/2 и т. д.;
3) х/2> 3/2 и т. д.; 4) 0, 1, 2. 40.23. Если принять протон-электронную мо-
модель ядра, то в состав ядра азота \*Ы должны входить 14 протонов (они оп-
определяют массу ядра) и 7 электронов (они компенсируют заряд протонов до 7;
14 — 7 = 7). Всего в состав ядра должна входить 21 частица. Суммарный спин
нечетного числа частиц всегда будет полуцелочисленным (в единицах ^), тогда
как ядро азота имеет целочисленный спин, равный %. Это и доказывает несо-
несостоятельность протон-электронной модели ядра. 40.24. 1/2А. 40.25. ц,дг =
= е%/Bтр) (trip—масса протона). 40.26. \in/\ib = тв/тр~ 1/1836. 40.27. [ijv =
— Vzmzx—gV'Nl (g—ядерный фактор Ланде; \ijv-ядерный магнетон, /—спи-
/—спиновое квантовое число ядра). 40.28. Сверхтонкое расщепление обусловлено
взаимодействием магнитных моментов ядра и электронной оболочки атома.
Тонкое расщепление обусловлено взаимодействием полного спинового момента
импульса в атоме с полным орбитальным моментом импульса. 40.41. Л = 222;
Z = 86; |22Rn. 40.42. Л = 17; Z = 8; 17О. 40.43. JjljCu. 40,44. Образовалось ядро
лития ILL 40.45. J4N. 40.46. lU. 40.47. flAl. 40.48. J|NL 40.49. jJfPu—¦¦
234TT 230T, 226D 222Dtn 218D 214D, Ал -л 21бПл. OQ^ .
U —> go Th —>¦ §8 Ka —>- 86 Kn —*¦ 84 Po —>¦ 82 Pb. 40.50. 84 Po; 296 км/с»
¦ 92
41.1. Ю-6. 41.2. 700 c-1; 13,6 nc-«. 41.3. 15 мин. 41.4. 10~4. 41.5. 0,71;
0,36. 41.6. В 9 раз. 41.7. 10,5 ч. 41.8. 4 дня. 41.9. 138 сут. 41.10. 1,44 года.
41.11. 63,3%. 41.12. 106 атомов. 41.13. 8. 41.14. 6 ч. 41.15. На 24%.
41.16. 93 года; 186 лет. 41.17. 0,5 сут. 41.18. 10,5 ТБк. 41.19. 40,7 ТБк/г.
41.20. 145. 41.21. /n2 = miM27'2/(Mir1) = 425 кг (Mi и Tf^-молярная масса и
период полураспада 90Sr; М2 и Т2 — то же, для 238U). 41.22. 6,33 мкг.
41.23. 2,7.105 лет. 41.24. W = ln2 I?^L=70,6 кДж (М и Тт — молярная
Ш 1 1/2
масса и период полураспада ^2Na), 41.25. А = 4яг2//е == 94,4 ГБк. 41.26. / =
°6B/2
514

515

сти Др/рC»10"и) обнаружить отклонение в поведении частицы от законов
классической механики нельзя. В этом случае можно говорить о траектории
движения частицы, так как если даже Ар _[_ р, то отклонения частицы от клас-
классической траектории невозможно обнаружить. 45.32. Это соотношение показы-
показывает, что если система пребывает в некотором энергетическом состоянии в те-
течение промежутка времени Му а затем переходит в другое состояние, то су-
существует некоторая неопределенность энергии кЕ^К/Ы. Этим, например,
объясняется естественная ширина спектральных линий. 45.33. 1) Время пребы-
пребывания электрона в основном состоянии бесконечно велико, вследствие чего
Г = Д? = 0; 2) в возбужденном состоянии электрон пребывает в течение Л/ «
« 10 не. Следовательно, ширина уровня Г^Й/Д^ = 0,1 мкэВ. 45.34. 3'10~8.
45.35. Нет. Точно определен квадрат импульса, а сам импульс имеет неопре-
неопределенность по направлению ±р, что отвечает бегущей и отраженной от стенок
яшика волнам.
X(Et — Рхх)/М- 46.5. Квадрат модуля волновой функции имеет определенный
физический смысл. Аналогично тому как в волновой оптике мерой интенсив-
интенсивности волны является квадрат амплитуды, так | г|J | является мерой интенсив-
интенсивности электронной волны (плотностью вероятности), пропорциональной кон-
концентрации частиц. 46.6. Только при условии конечности я|? функции возможна
физическая интерпретация |г|)|2 как плотности вероятности. 46.7. Значения
энергии U и ?, а также ty конечны. Следовательно, d2ty/dx2 должна быть
ограничена, а это возможно, если непрерывна dif/d-*:. Но чтобы dty/dx сущест-
существовало во всей интересующей нас области, i|?(#) должна быть непрерывна.
46.8. Может. Меньше единицы должно быть выражение | -ф (л:) |2 dx, означаю-
означающее вероятность обнаружения частицы в интервале от х до x-\-dx. Но
Iib(;t)|2dA; может быть меньше единицы и при условии |ф(д:)|2>1.
46.9. Если y(x)=a + ib, то Ц>* (х) =а— ib; 11|> (*) \2 = a* + b2; *(*)**(*) =
= (a+ib)(a— ib)= a2 + b*. Следовательно, Ж*) I* =*(*) V (*)•
46.10. | г|? (x, t) |2 = if (x9 t) if* (*, t) = exp (—iEt/A) i|? (x) г|>* (х) или | if (*, /) |2 =
516

517

518

519

520

521

522

523

= Д?/(тяс) = 218 м/с. 50.60. у = Д?/(т„с) = 36 м/с. 50.61. v = \n2fic/(Tey) =
= 0,19 мм/с. 50.62. т = Лс/(уе7) = 0,2 не. 50.63. y = g//c = 65 мкм/с.
50.64. 3,40-10-5 К. 50.65. 1,25 нН. 50.66. Максимальная сила притяжения
0,8 нН, отталкивания 1,2 нН. 50.67. 3,4-10~21 Дж. 50.68. Среднее смещение
<л:> обращается в нуль при чисто гармонических колебаниях. 50.69. 60 Н/м.
50.70. 2,5-10 К. 50.71. 540 ГПа. 50.72. 1 %. 50.73. 3-10"! К.

ОБОЗНАЧЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН,
ПРИНЯТЫЕ В ЗАДАЧНИКЕ
Активность изотопа А
Активность изотопа удель-
удельная (массовая активность) а
Амплитуда А
Вектор Пойнтинга S
Вероятность W
Восприимчивость диэлектри-
диэлектрическая х
Восприимчивость магнитная %
Вращение плоскости поля-
поляризации удельное [а]
Время t
Время жизни среднее * т
Вязкость динамическая (ко-
(коэффициент внутреннего тре-
трения) ц
Граница фотоэффекта крас-
красная %q,
Давление р
Декремент колебаний лога-
логарифмический 9
Дефект массы Дт
Деформация относительная е
Деформация сдвига
Дисперсия линейная
Дисперсия угловая
Диффузия (коэффициент
диффузии) *
Длина волн
Длина волны комптоновская
Длина физического маятника
приведенная
Длина пути (путь)
Длина пути оптическая
Длина свободного пробега
средняя
Доза излучения (поглощен-
(поглощенная доза излучения) D
Доза излучения эквивалент-
эквивалентная D
Доза излучения экспозицион-
экспозиционная X
Емкость электрическая С
Жесткость (коэффициент
упругости) k
Заряд электрический (коли-
(количество электричества) Q
Заряд элементарный е
Импульс (количество движе-
движения) тела р
Импульс силы /
у
L
s
L
</>
eq
Индуктивность L
Индуктивность взаимная М
Индукция магнитная В
Интенсивность звука (сила
звука) /
Интенсивность ионизирую-
ионизирующего излучения /
Интенсивность света /
Количество вещества v
Количество теплоты (теплота) Q
Концентрация частиц (плот-
(плотность числа частиц) п
Коэффициент (степень) дис-
диссоциации а
Коэффициент ангармонично-
ангармоничности у
Коэффициент затухания б
Коэффициент ослабления ли-
линейный [л,
Коэффициент отражения р
Коэффициент поглощения
линейный а
Коэффициент полезного дей-
действия ц
Коэффициент пропускания т
Коэффициент сопротивления г
Коэффициент температурный
линейного расширения а
Коэффициент температурный
объемного расширения р
Коэффициент трения сколь-
скольжения f
Коэффициент упругости k
Коэффициент черноты ат
Магнетон Бора [гв
Масса m
Масса молярная М
Масса относительная атом-
атомная Аг
Масса относительная моле-
молекулярная Мг
Масса приведенная \i
Множитель (фактор) Ланде g
Модуль сдвига G
Модуль Юнга Е
Момент инерции J
Момент импульса (момент
количества движения) L
Момент импульса частицы
(механический момент) J?
525

Момент магнитный контура
с током
Момент магнитный частицы
Момент силы
Момент электрический ди-
диполя
Мощность
Мощность поглощенной дозы
излучения
Мощность эквивалентной до-
дозы излучения
Мощность экспозиционной
дозы излучения
Намагниченность
Напряжение механическое
касательное
Напряжение механическое
нормальное
Напряжение электрическое
Напряженность гравитацион-
гравитационного поля
Напряженность магнитного
поля
Напряженность электриче-
электрического поля
Натяжение поверхностное
(коэффициент поверхностно-
поверхностного натяжения)
Облученность (энергетиче-
(энергетическая освещенность)
Объем (вместимость)
Объем молярный
Освещенность
Отношение гиромагнитное
Перемещение
Период колебаний
Период полураспада
Плечо диполя
Плотность
Плотность оптическая
Плотность потока ионизи-
ионизирующих частиц
Плотность электрического
тока
Плотность электрического
заряда линейная
Плотность электрического
заряда объемная
Плотность электрического
заряда поверхностная
Плотность энергетической
светимости спектральная
Плотность энергии объемная
Подвижность ионов
Показатель адиабаты
Показатель преломления
абсолютный
Показатель преломления от-
относительный
Поляризованность
Поляризуемость молекулы
Рт
И- Им
М
Р
Р, N
D
X
J
X
а
и
G
Н
Е
а
Ее
V
У
Аг
Т
1
р
D
/
/
X
Р
а
rv, T>
а, г
W
b
У
п
р
а
Постоянная Авогадро
Постоянная Больцмана
Постоянные Ван-дер-Ваальса
Постоянная вращательная
Постоянная вращения пло-
плоскости поляризации
Постоянная газовая моляр-
молярная
Постоянная закона смеще-
смещения Вина
Постоянная гравитационная
Постоянная дифракционной
решетки
Постоянная магнитная
Посгоянная Планка
Постоянная радиоактивного
распада
Постоянная Ридберга
Постоянная Стефана —
Больцмана
Постоянная Фарадея
Постоянная электрическая
Потенциал электрический
Поток излучения спектраль-
спектральный
Поток магнитный
Поток напряженности
электрического поля
Потокосцепление
Поток световой
Поток тепловой
Поток электрического
смещения
Поток энергии излучения
Проводимость активная
электрическая
Проводимость удельная
электрическая
Проницаемость относитель-
относительная диэлектрическая
Проницаемость относитель-
относительная магнитная
Работа
Работа выхода
Радиус боровский
Разность хода оптическая
Разность фаз
Разность потенциалов
Расстояние фокусное
Расход массовый
Расход объемный
Светимость
Светимость энергетическая
Сила
Сила оптическая
Сила разрешающая
Сила света
Сила тока (ток)
Сила тяжести
Сила электродвижущая
Скорость угловая
k
a, b
а
а
R
b
G
d
h, t
К
R, R*
о
F
Ф
ф
фв
х?в
Ф
Ф
W
Ф
G
У
8
JX
^4
А
а
А
Дф
и
f
Qm
Qv
R
Re
F
Ф
R
J
I
P
?
CO
526

Смещение точек среды при
распространении в ней ко-
колебаний 5
Смещение электрическое D
Сопротивление активное
электрическое R
Сопротивление удельное
электрическое р
Сопротивление акустическое Za
Сопротивление акустическое
удельное Z$
Степень поляризации Р
Температура термодинамиче-
термодинамическая Т
Температура характеристи-
характеристическая 0
Температура Цельсия t
Теплоемкость молярная Ст
Теплоемкость при постоян-
постоянном давлении Ср
Теплоемкость при постоян-
постоянном объеме Су-
Теплоемкость системы С
Теплоемкость удельная с
Теплопроводность (коэффи-
(коэффициент теплопроводности) А,
Толщина слоя половинного
ослабления Х\^
Увеличение линейное р
Увеличение угловое Г
Угол краевой #
Угол отражения г'г
Угол падения е
Угол поворота (угловое пе-
перемещение) Ф
Угол преломления е^
Угол скольжения -в1
Угол телесный Q, со
Уровень громкости звука L^
Уровень звукового давления Lp
Уровень интенсивности звука Lp
Ускорение линейное а
Ускорение касательное (тан-
(тангенциальное) ах
Ускорение нормальное
(центростремительное) ап
Ускорение свободного паде-
падения g
Ускорение угловое 8
Функция волновая ?
Функция волновая (коорди-
(координатная) Я|)
Частота вращения п
Частота излучения v
Частота колебаний v
Частота ларморова (угловая) со/;
Частота угловая со
Число витков N
Число витков на единицу
длины п
Число волновое N
Число волновое спектроско-
спектроскопическое v
Число зарядовое (атомный
номер элемента) Z
Число Лошмидта щ
Число массовое А
Число степеней свободы i
Число нейтронов в ядре N
Число Рейнольдса Re
Число столкновений молеку-
молекулы в единицу времени (сред-
(среднее) <г>
Ширина интерференционной
полосы Ъ
Эквивалент электрический k
Энергия Е
Энергия внутренняя U
Энергия внутренняя моляр-
молярная Um
Энергия диссоциации D
Энергия звуковая W
Энергия излучения W
Энергия ионизации Е(
Энергия кинетическая Т
Энергия покоя Е§
Энергия полная Е
Энергия потенциальная П
Энергия связи Есв
Энергия частицы s
Энергия электромагнитная W
Энергия электромагнитная
удельная w
Энергия ядерной реакции Q
Энтропия S
Яркость энергетическая Ве

Учебное издание
Александр Георгиевич Чертов
Анатолий Александрович Воробьев
ЗАДАЧНИК ПО ФИЗИКЕ
Зав. редакцией Е. С. Гридасова. Редактор Л. С. Куликова. Мл. редакторы Н. П. Майкова.
Г. В. Вятоха. Художник К. П. Яриков. Художественный редактор В. И. Пономаренко.
Технический редактор Е. И. Герасимова. Корректор Г. И. Кострикова
ИБ № 6766
Изд. № ФМ-901. Сдгно в набор 24.06.87. Подп. в печать 05.02 88. Формат 60X907i«-
Бум. тип. № 2. Гарнитура литературная. Печать высокая. Объем 33 усл. печ. л. +0,13
усл. печ. л. форзац. 33,25 усл. кр.-отт. 32,08 уч.-изд. л. +0,21 уч.-изд. л. форзац.
Тираж 75 000 экз. Зак. № 1268. Цена 1 р. 40 к.
Издательство «Высшая школа», 101430, Москва, ГСП-4. Неглинная ул., д. 29/14.
Ордена Октябрьской Революции и ордена Трудового Красного Знамени МПО «Первая
Образцовая типография» имени А. А. Жданова Союзполиграфпрома при Государственном
комитете СССР по делам издательств, полиграфии и книжной торговли, 113054, Москва*
Валовая, 28