Основы машинной арифметики - Шайман А.М.

Author: Шайман А.М.

Tags: приборы, устройства, аппараты с механизмами передачи или с подвижными механизмами арифметика монография издательство ленинградского университета цифровые машины перевод чисел арифметические операции

Year: 1979

Similar

Арифметика цифровых машин

Вычислительные системы и синхронная арифметика

Помехоустойчивое кодирование числовой информации

Параллельные вычислительные системы

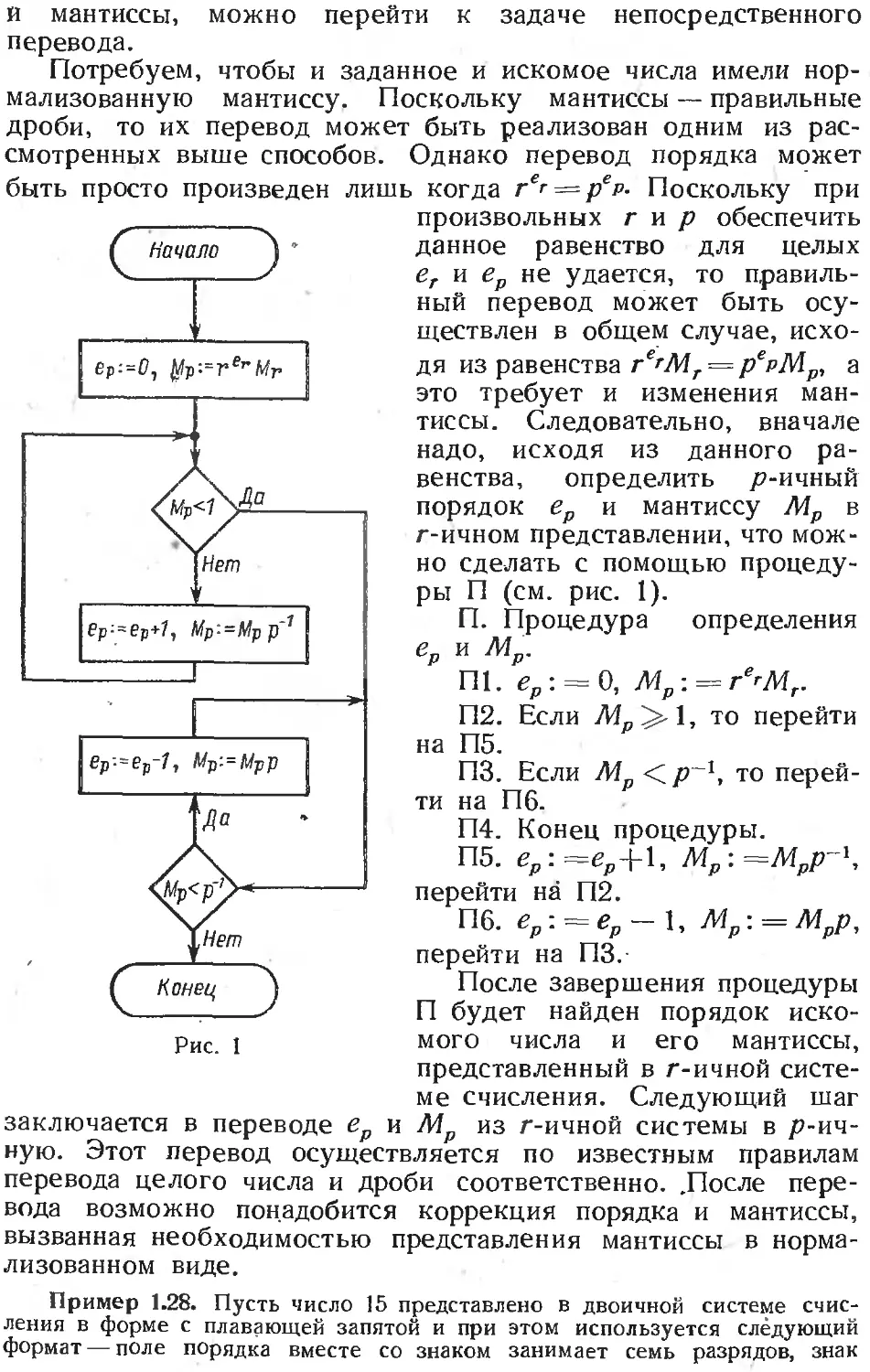
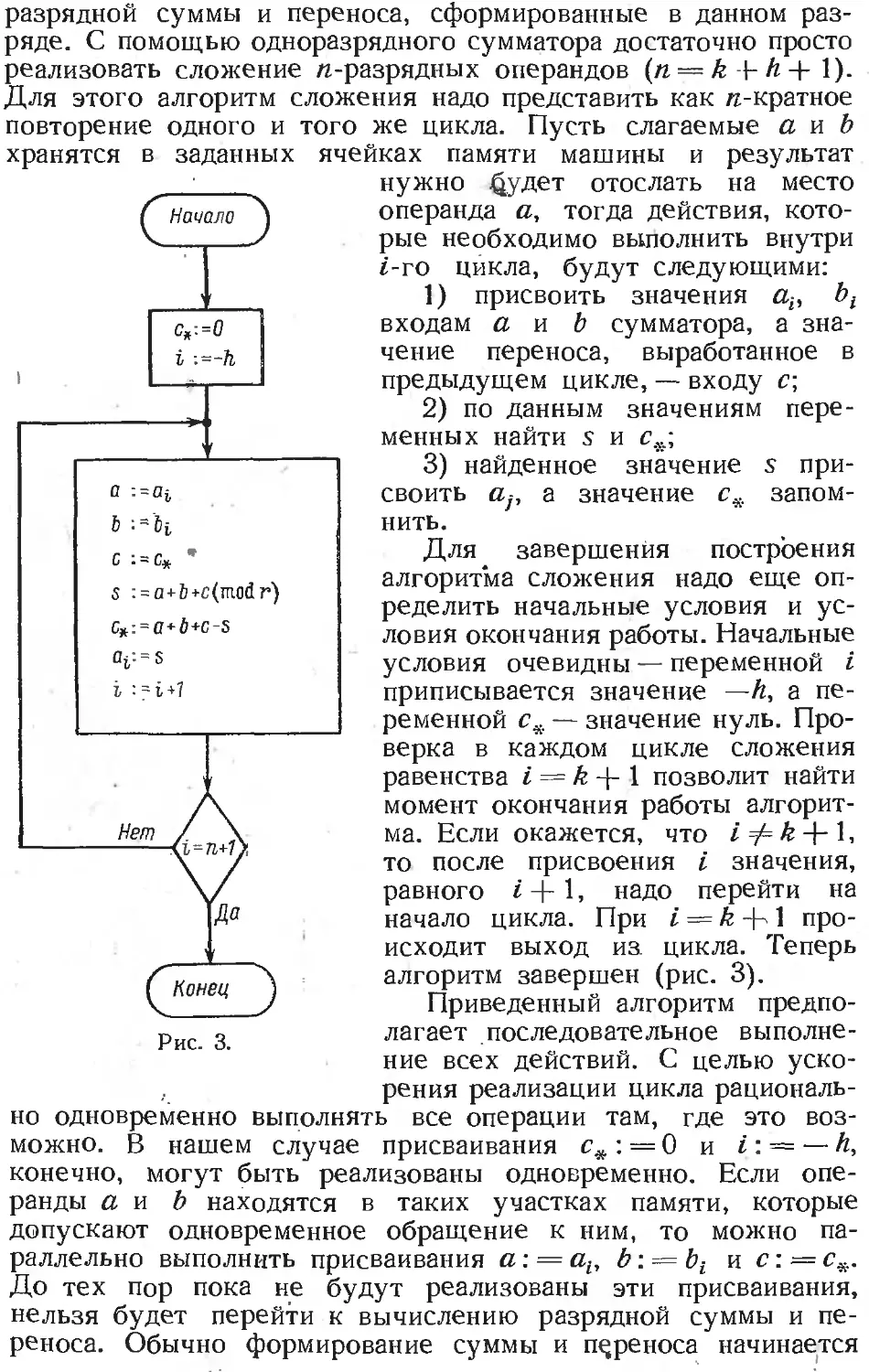
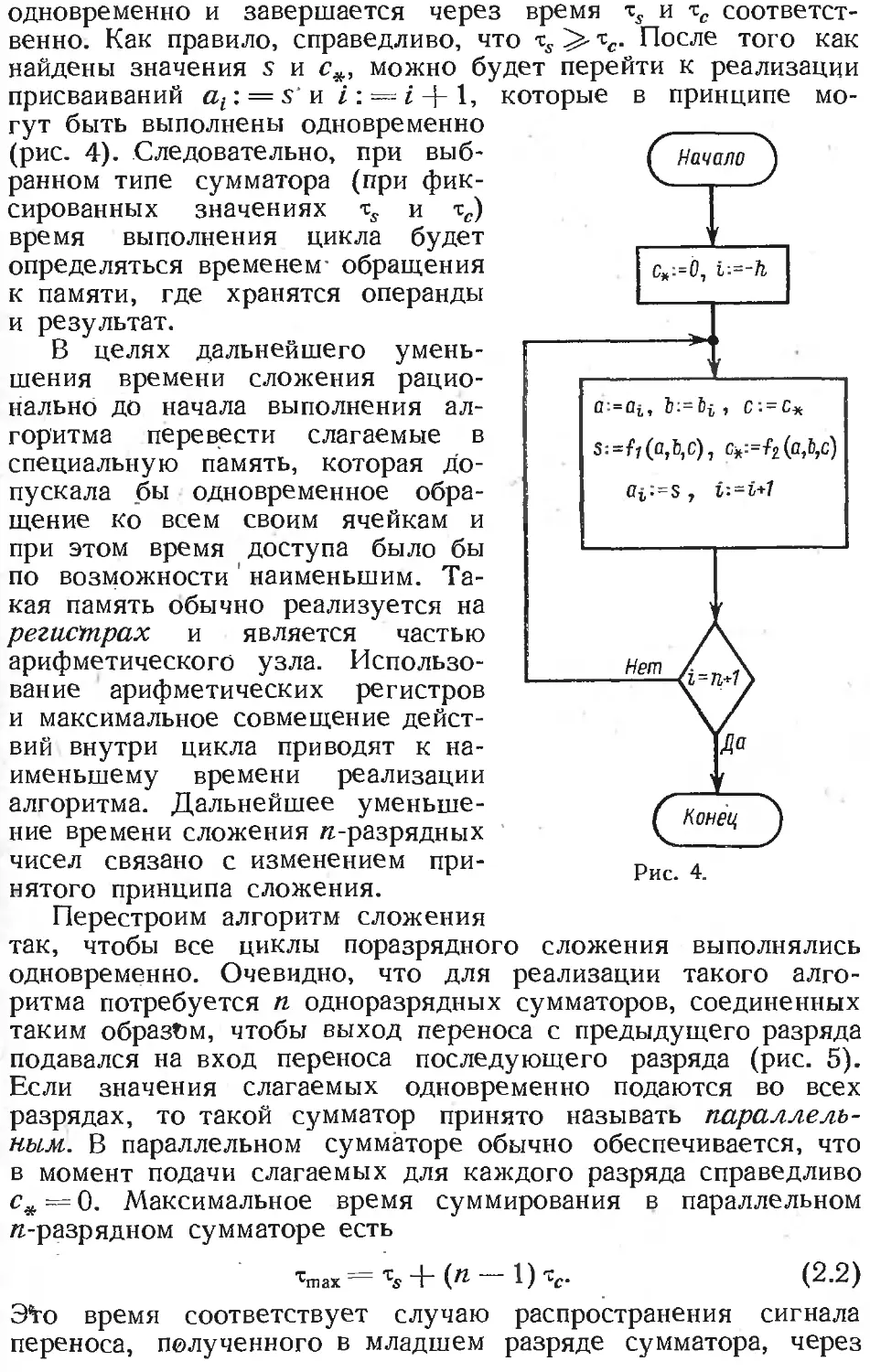
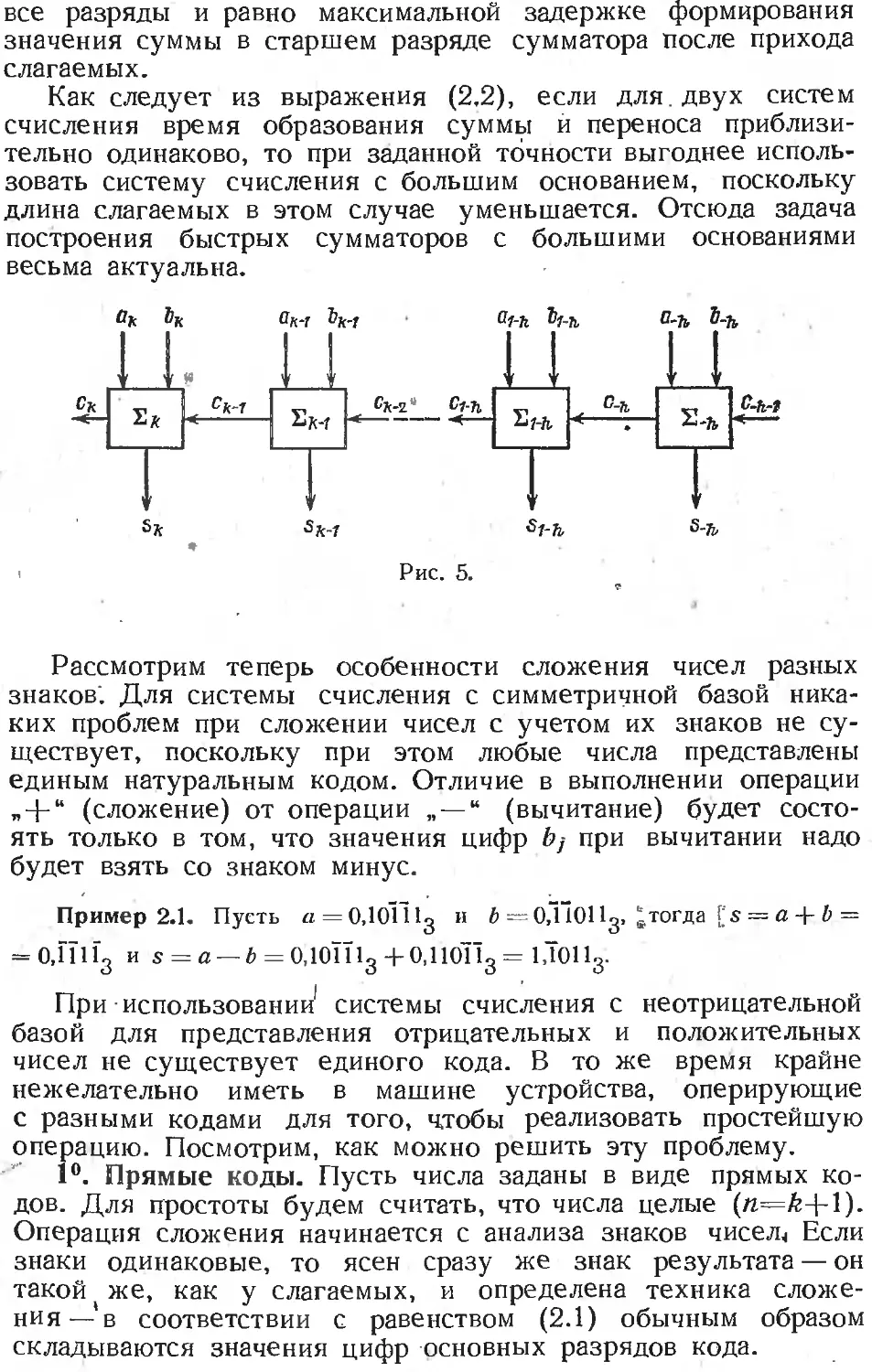
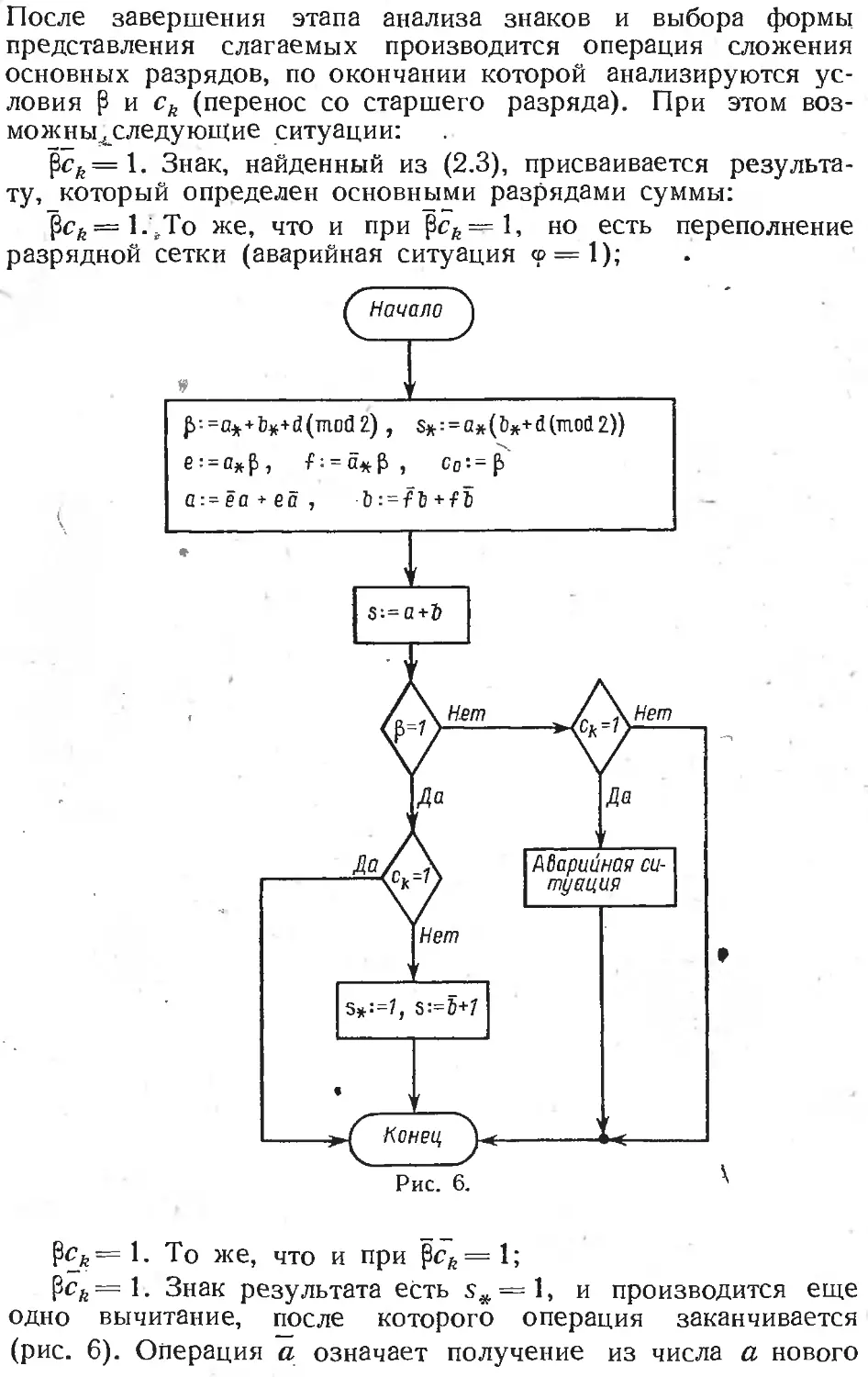
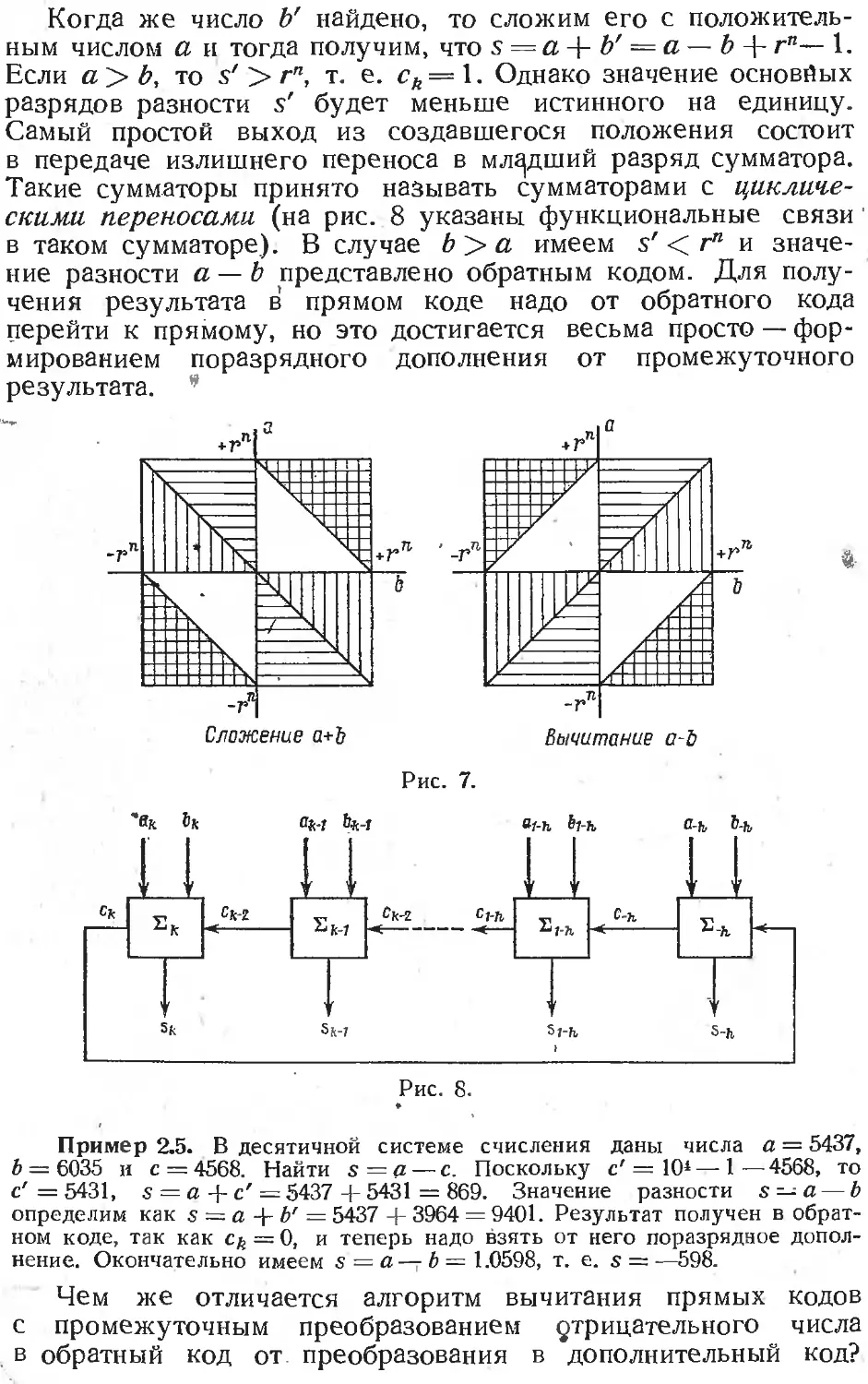
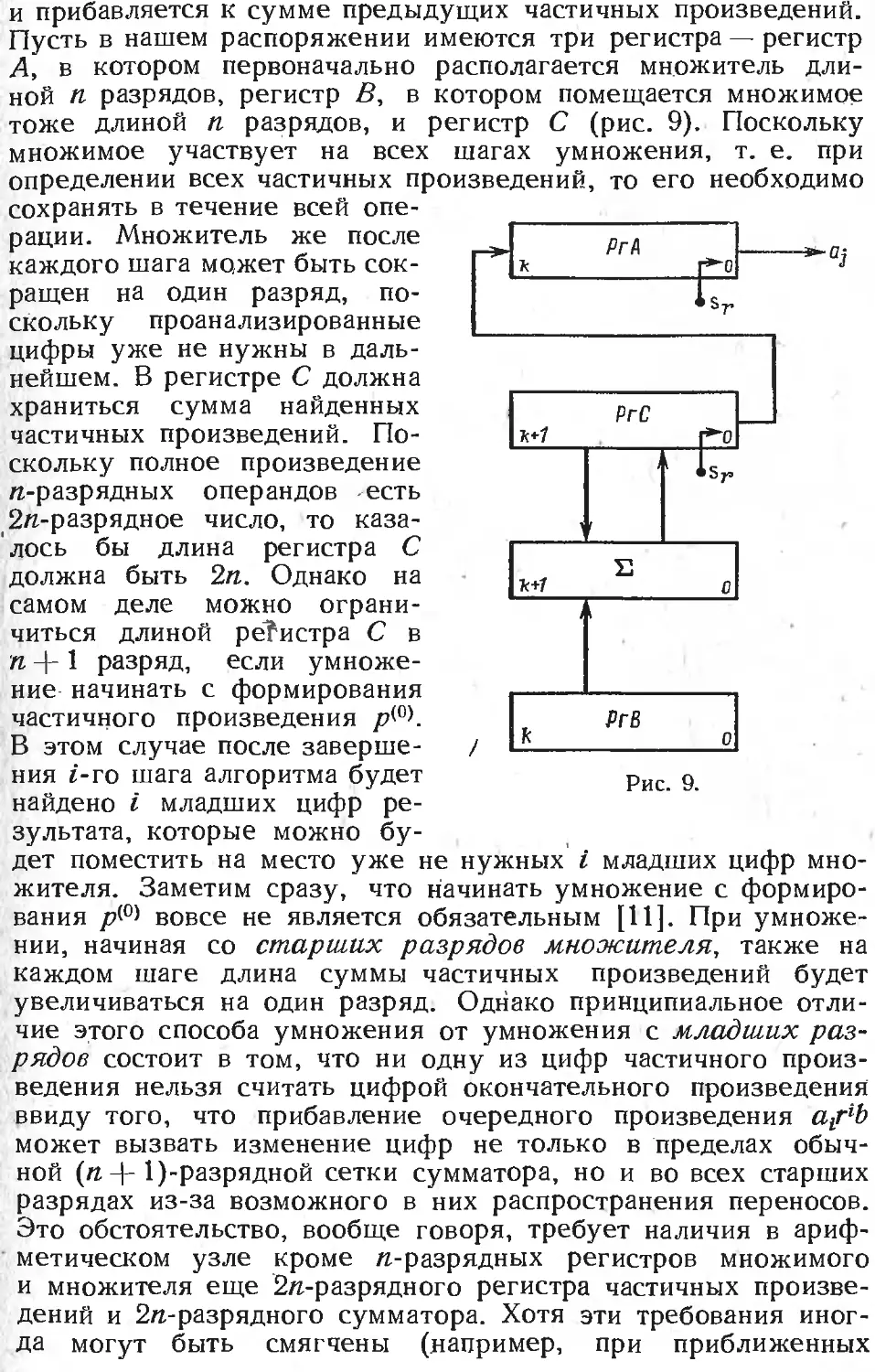
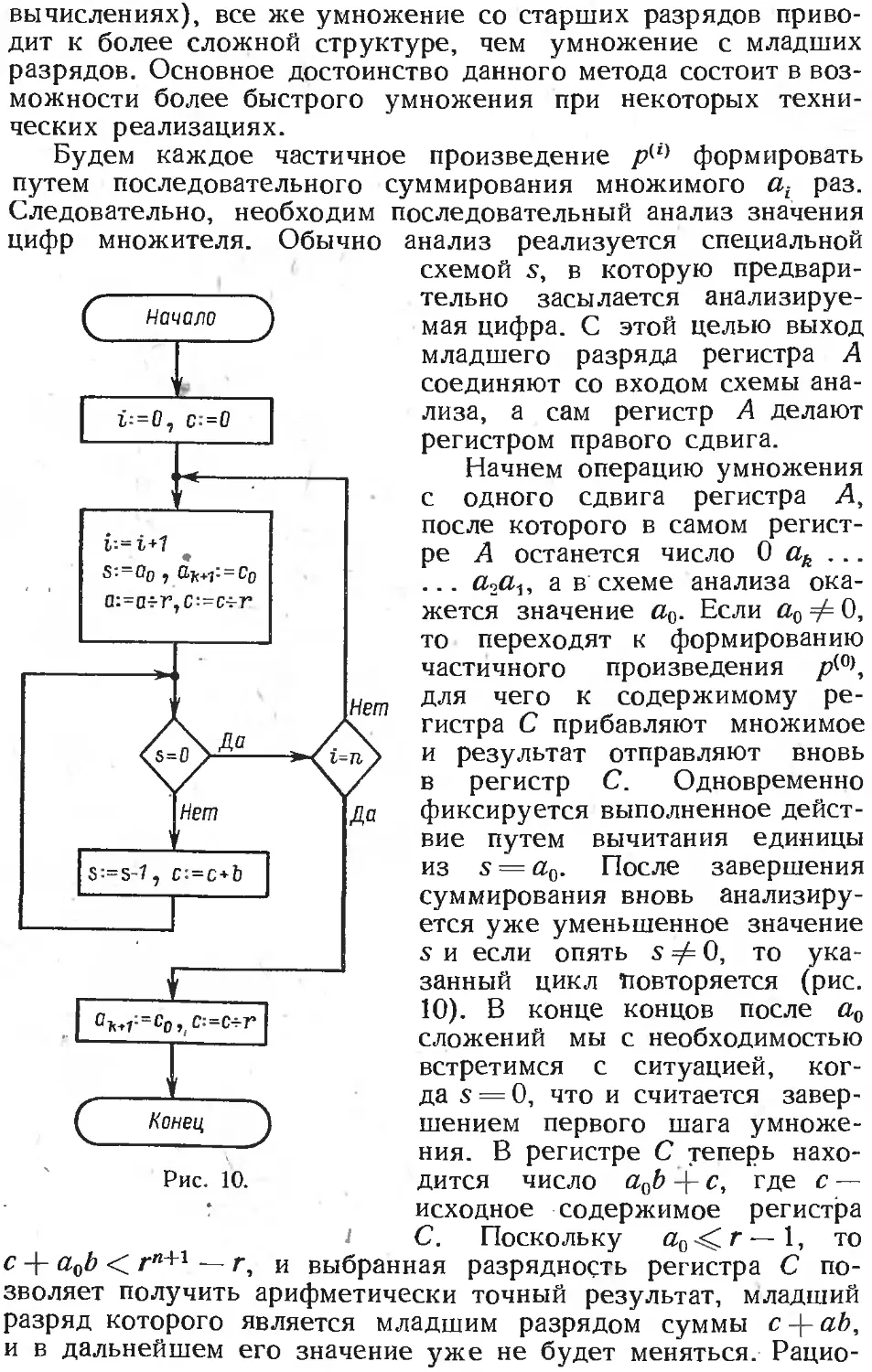
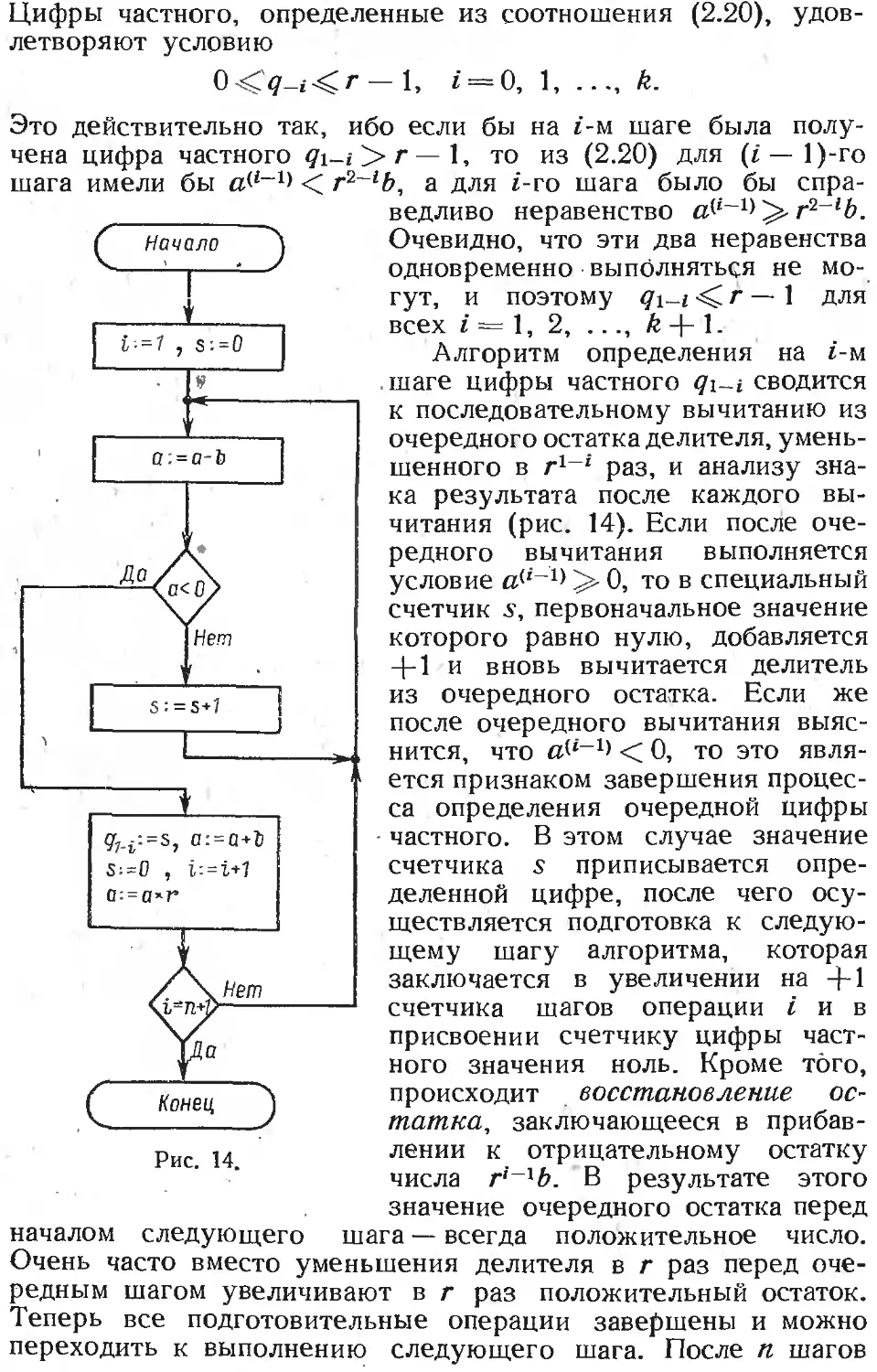
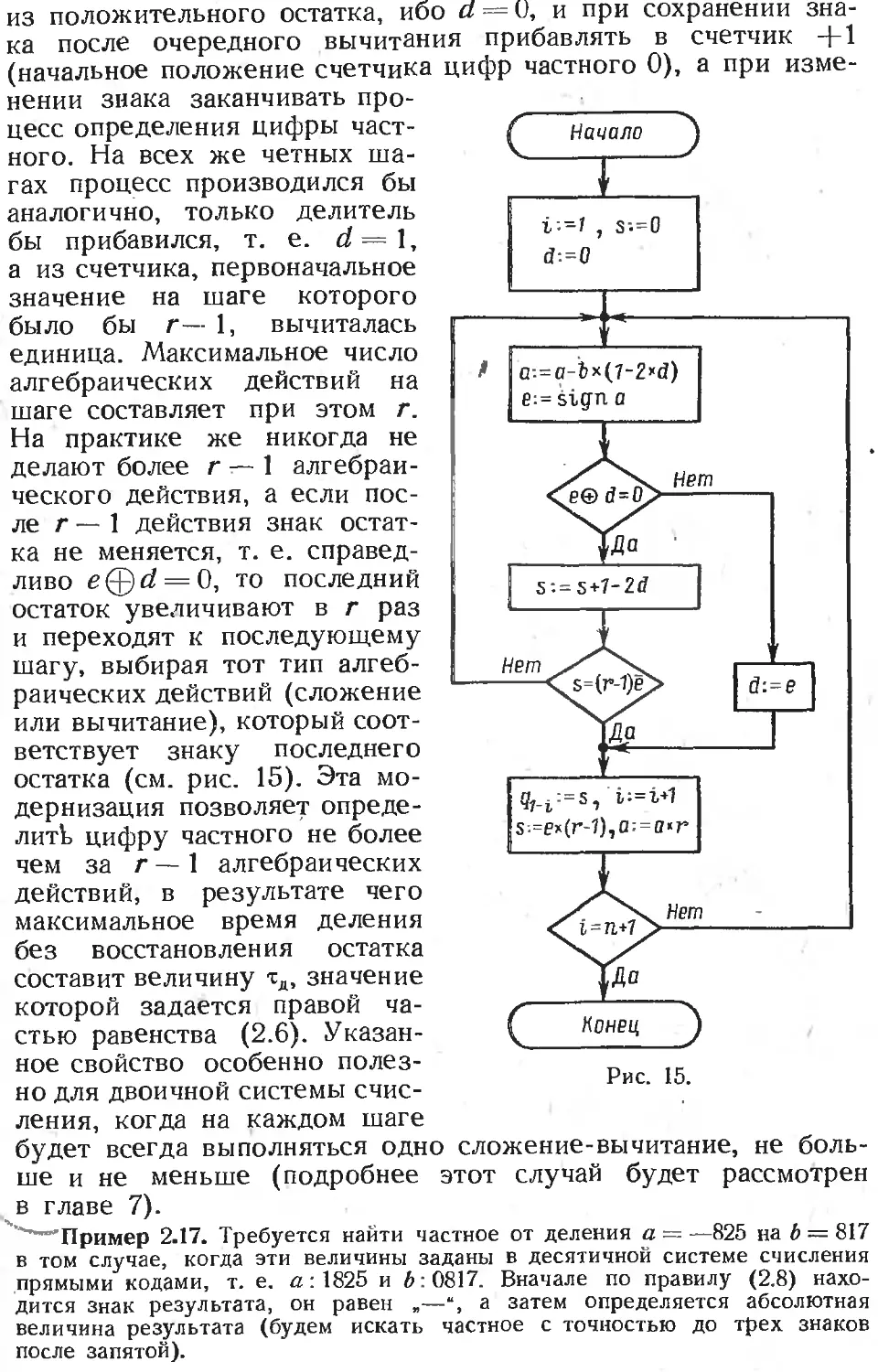
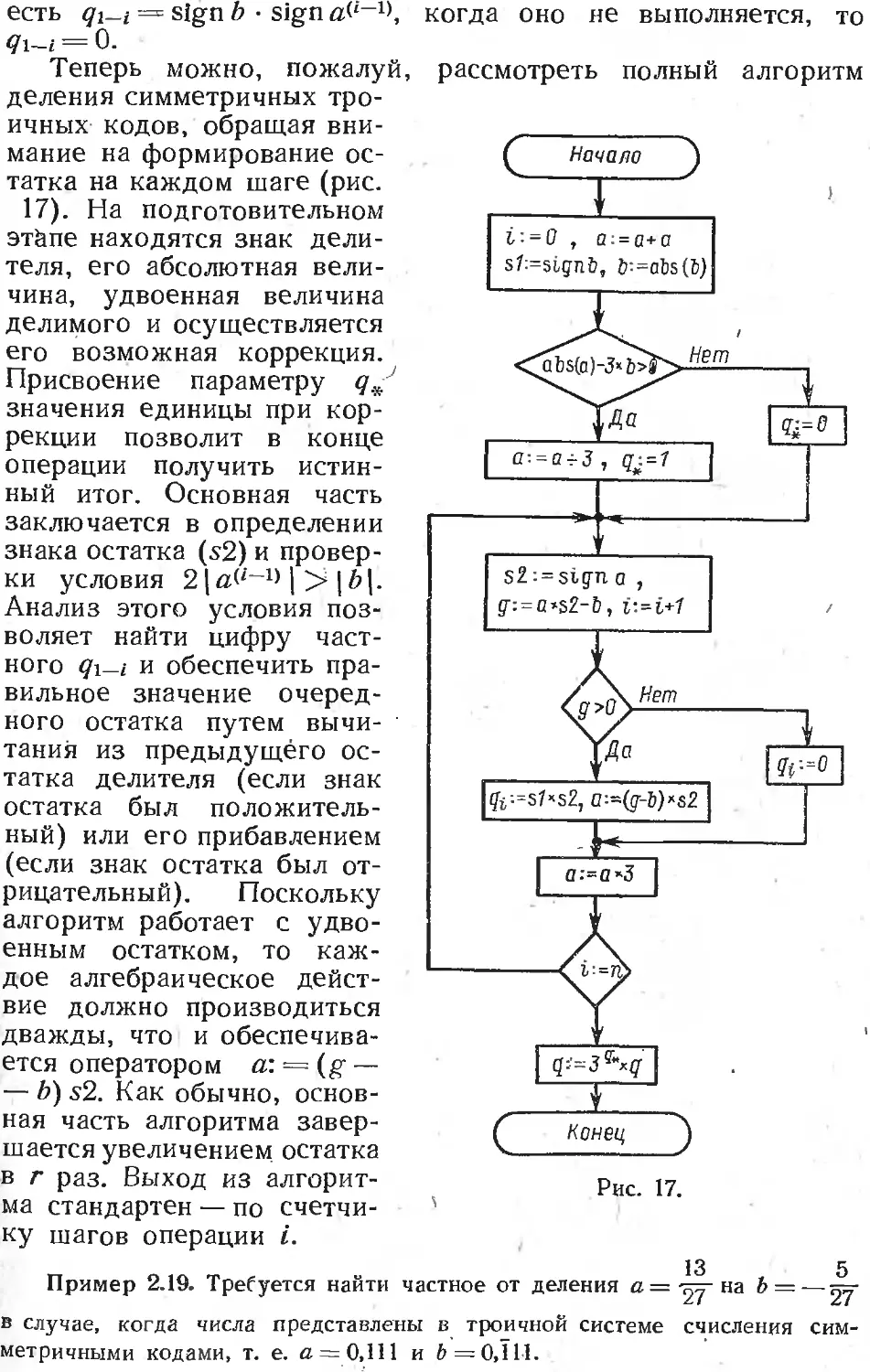
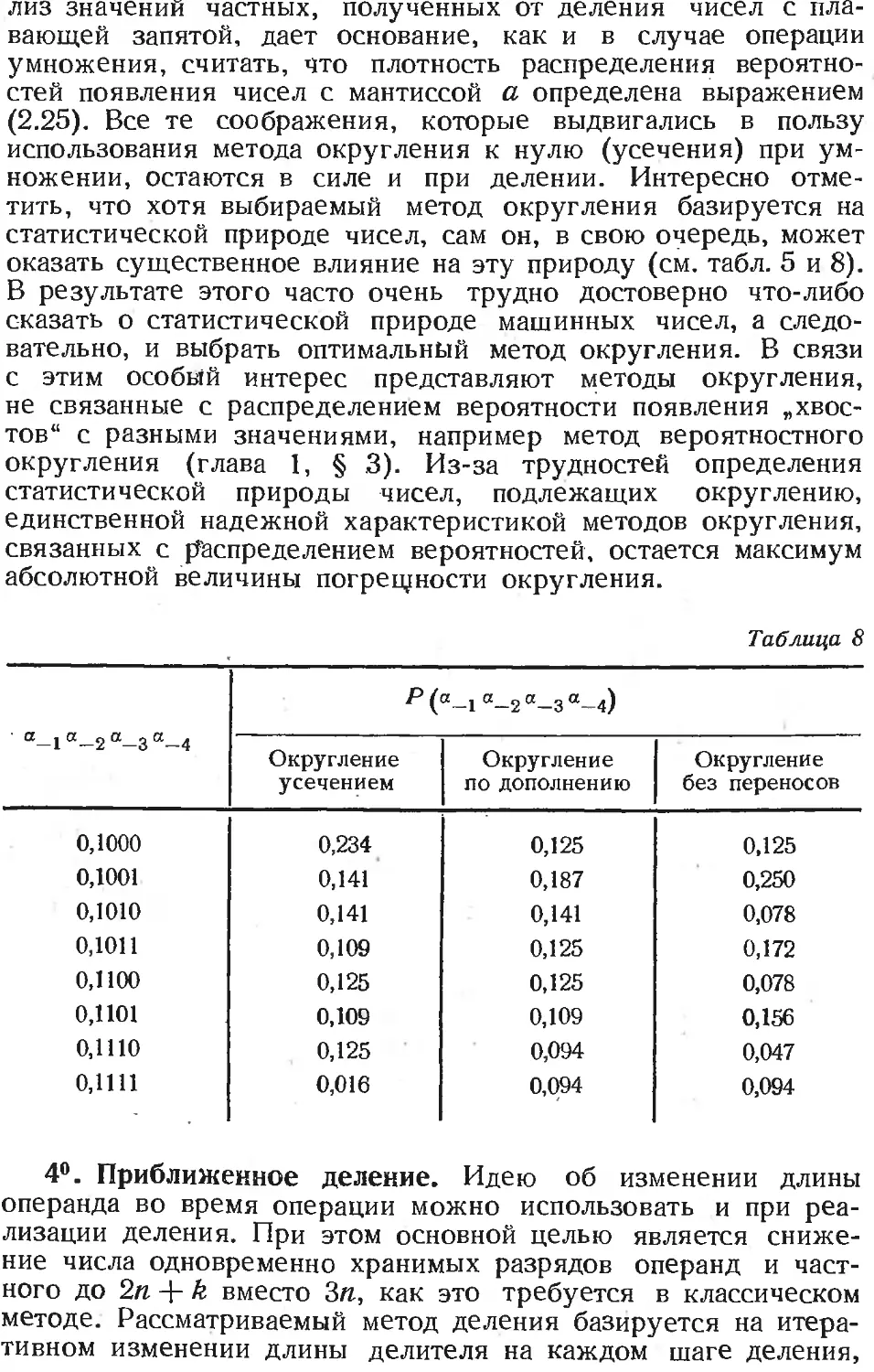
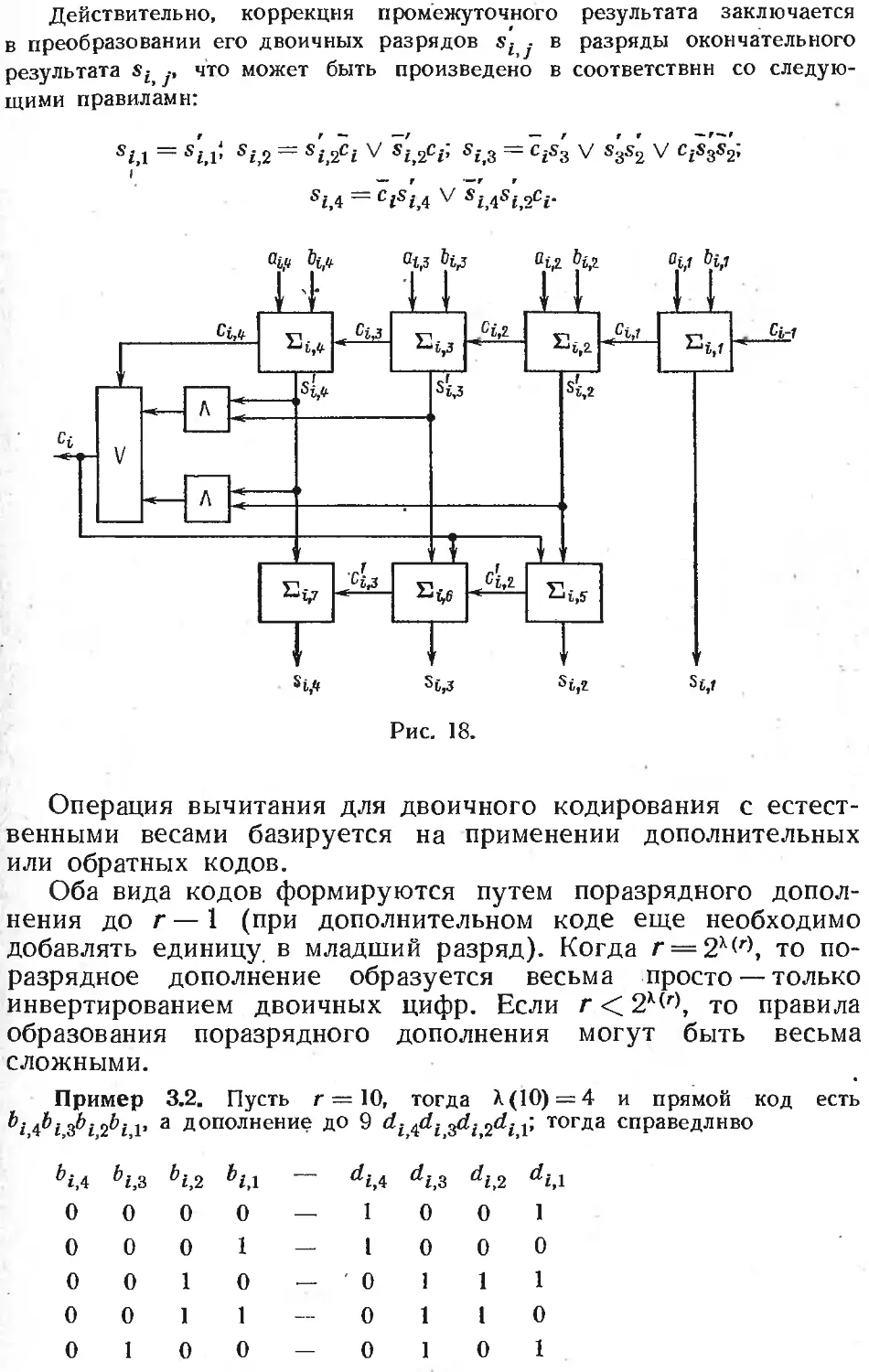
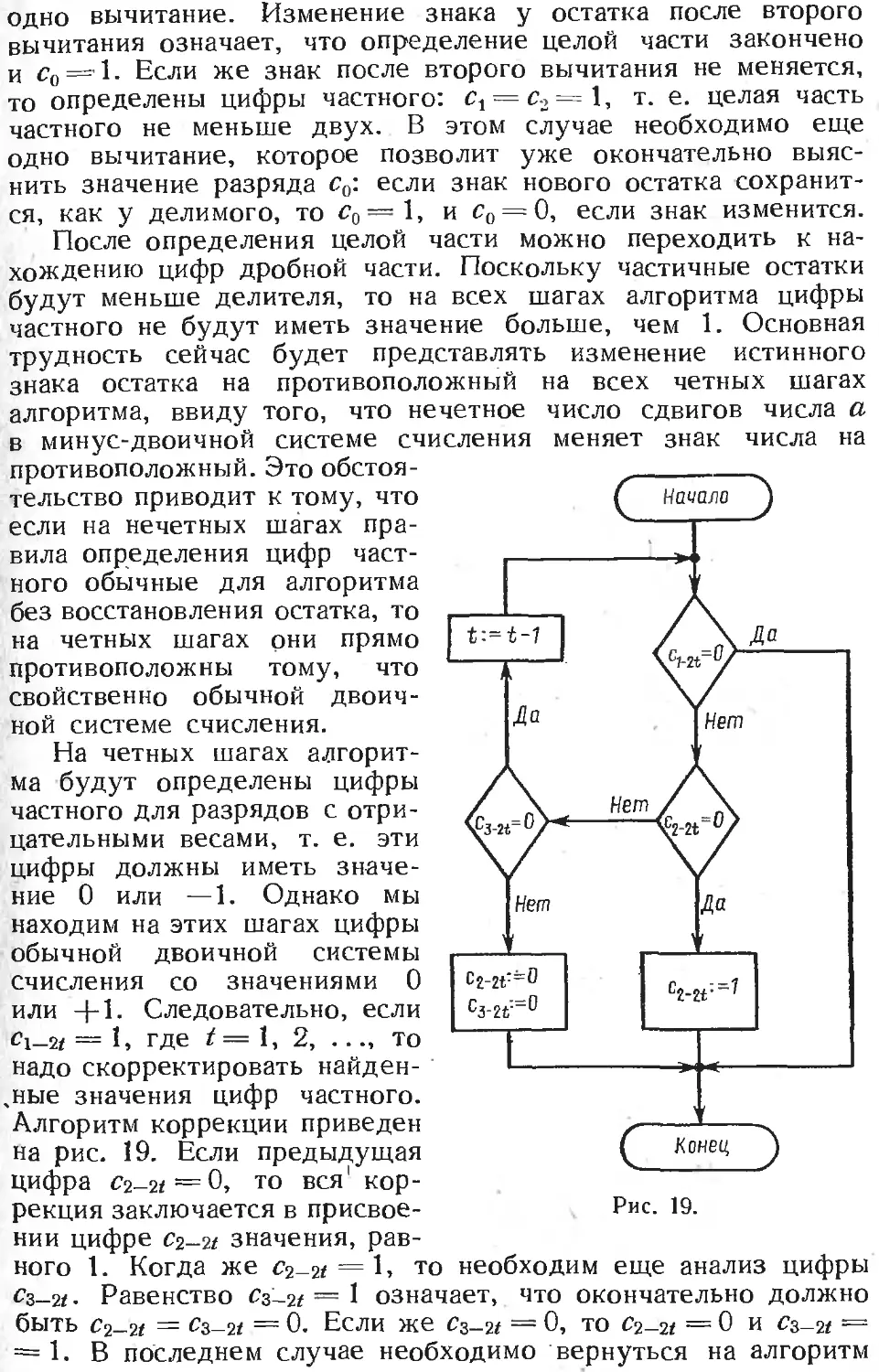
Text

ОГЛАВЛЕНИЕ
т
ПРЕДИСЛОВИЕ 3
ГЛАВА 1. Представление чисел в цифровой машине 6
§ 1. Основные понятия и определения । —
§ 2. Представление отрицательных чисел 11
§ 3. Формы представления чисел в машине 16
§ 4. Округление чисел 28
§ 5. Перевод чисел из одной системы счисления в другую 39
ГЛАВА 2. Особенности выполнения арифметических операций 52
§ 1. Алгебраическое сложение —
§ 2. Сложение чисел с плавающей и естественной запятой 66
§ 3. Методы умножения 71
§ 4. Методы деления 83
§ 5. Приближенные вычисления 98
ГЛАВА 3. Двоично-кодированные системы счисления 111
§ 1. Опенка экономичности представления
§ 2. Коды с естественными весами 113
§ 3. Коды с искусственными весами 120
§ 4. Невесомозначные коды 122
§ 5. Экономное представление двоично-кодированных чисел 124
ГЛАВА 4. Особые случаи систем счисления 128
§ 1. Двоичная система счисления с цифрами —1 и 1 —
§ 2. Система счисления с основанием —-2 140
§ 3. Система остаточных классов 153
§ 4. Знакологарифмическая система счисления 160
ГЛАВА 5. Методы ускоренного выполнения арифметических
операций 166
§ 1. Методы ускоренного сложения —
§ 2. Методы ускоренного умножения 188
§ 3. Методы ускоренного деления 198
ГЛАВА 6. Неосновные арифметические операции 219
§ 1. Возведение в квадрат 220
§ 2. Извлечение квадратного корня 228
§ 3. Методы вычисления элементарных функций 233
§ 4. ' Вычисление логарифма двоичных чисел методом линейно-
кусочной аппроксимации 237
§ 5. Таблично-итерационный метод извлечения квадратных
корней 243
§ 6. Вычисление элементарных функций по методу „цифра за
цифрой" 246
ГЛАВА 7. Обнаружение и исправление ошибок при реализа-
ции арифметических операций 255
§ 1. Метод дублирования 257
§ 2. Арифметические помехозащитные коды 258
§ 3. Алгоритмы арифметических операций при кодировании
операндов помехозащитными кодами 265
§ 4. Адаптивные алгоритмы 273
ГЛАВА 8. Реализация алгоритмов арифметических операций
на базе матричных структур 282
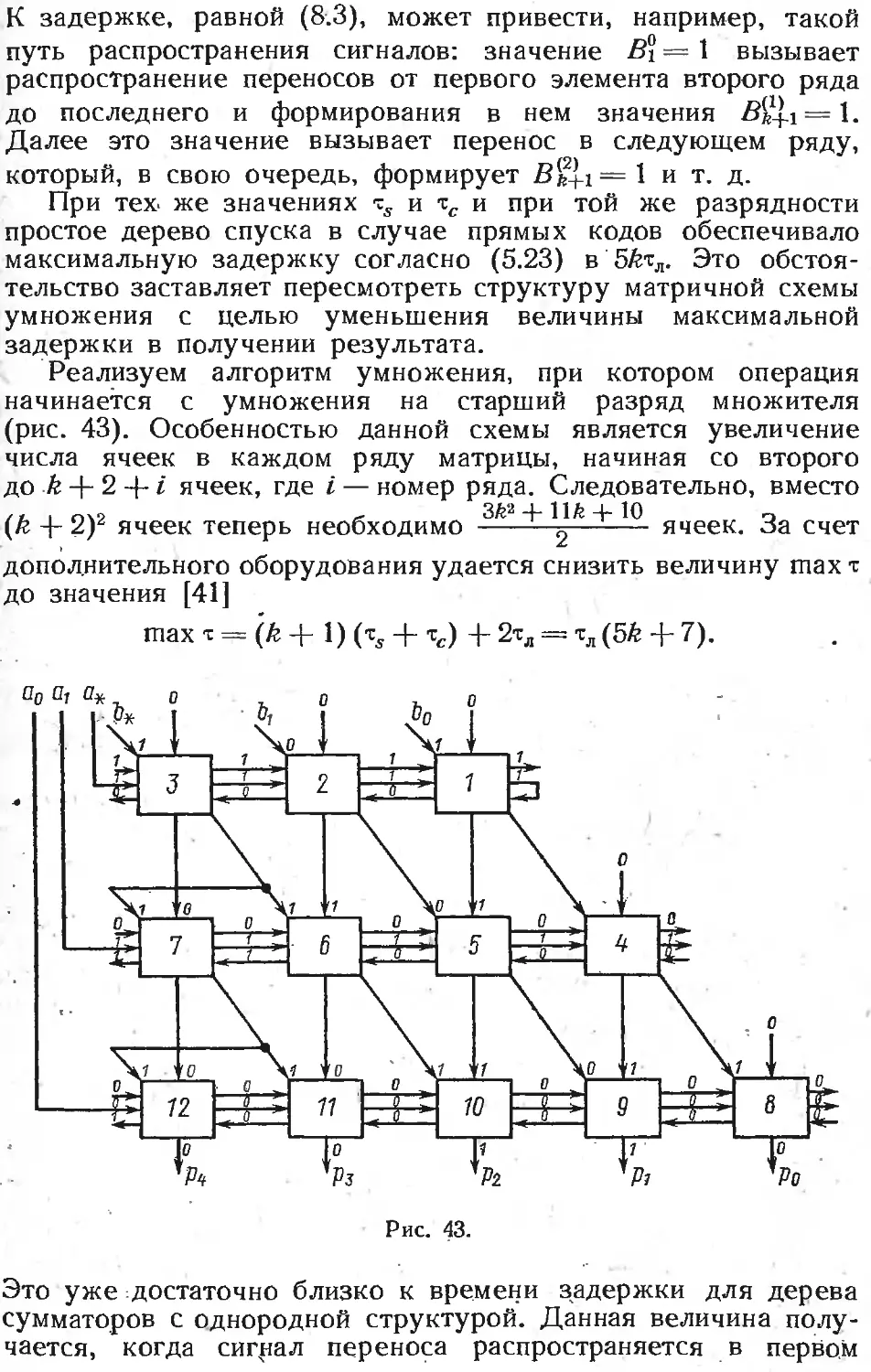
§ 1. Матричные схемы умножения 283
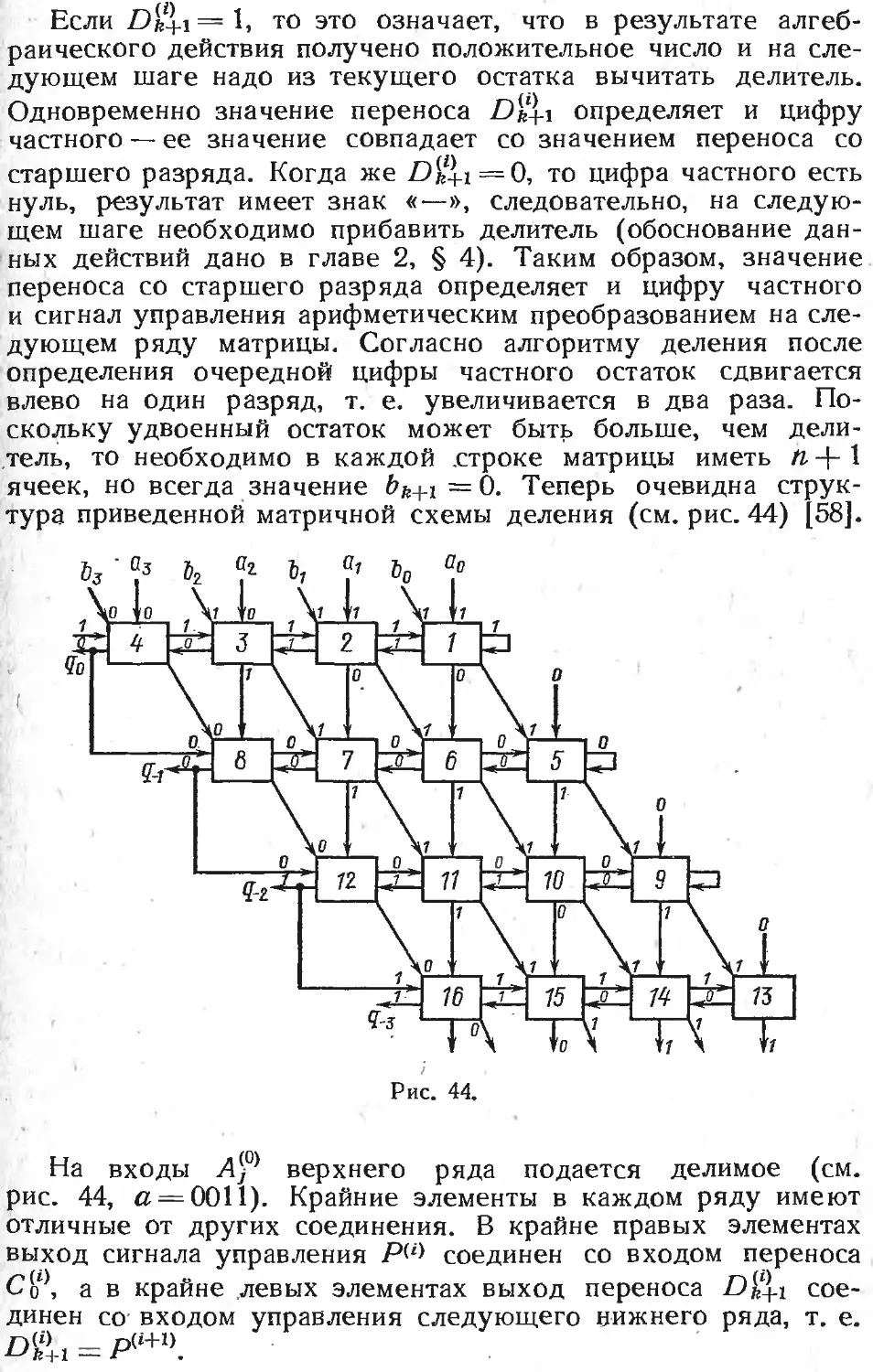
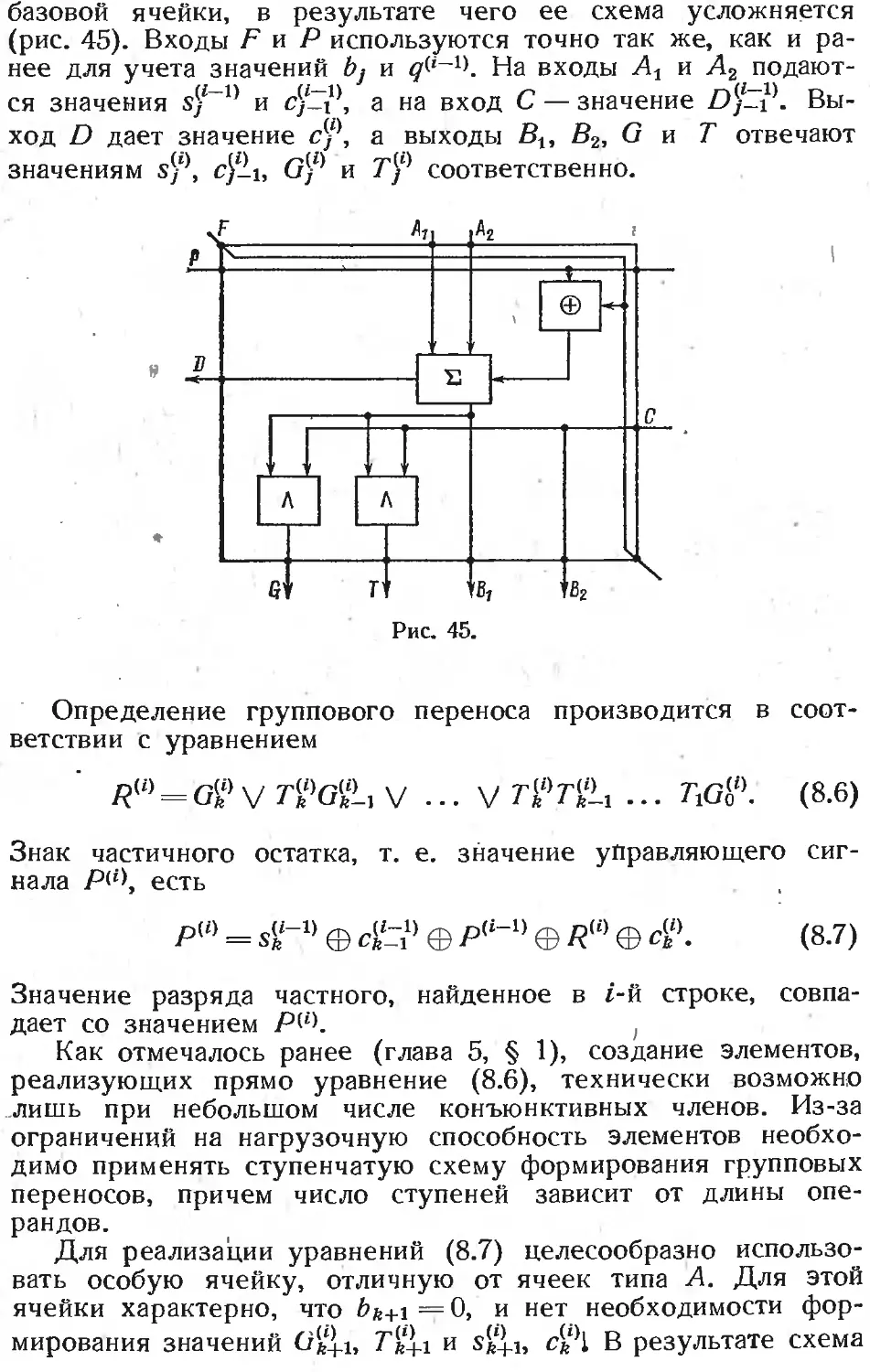
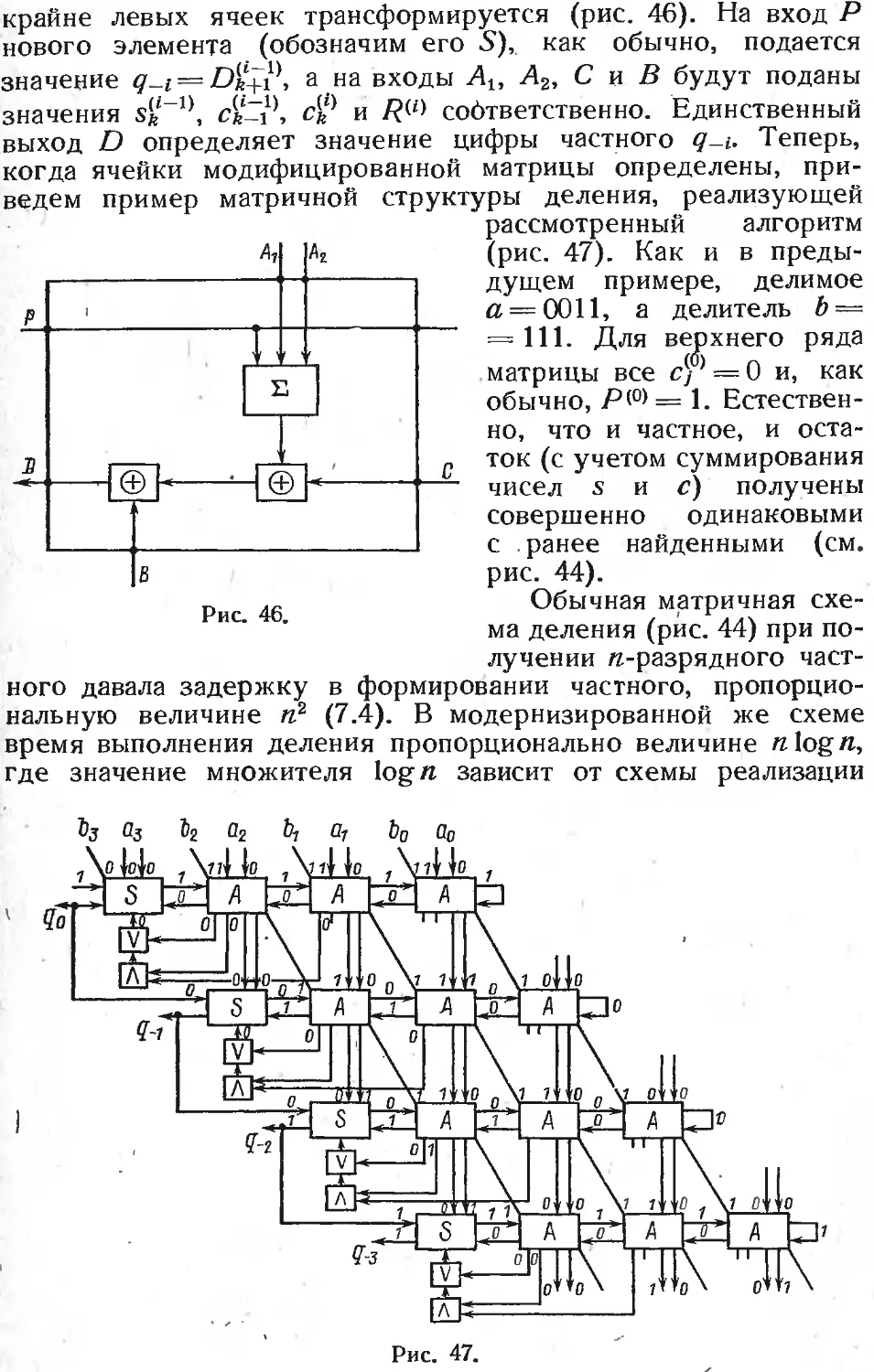
§ 2. Матричные схемы деления 288
§ 3. Комбинированные матричные схемы 294
§ 4. Матричная схема извлечения квадратного корня 298
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 302
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ 306
ПРЕДИСЛОВИЕ
Многие считают арифметику три-
виальной вещью, которой обучают
детей в школе и действия которой
выполняют машины, но, как мы уви-
дим, арифметика — это увлекатель-
ный предмет, имеющий много инте-
ресных аспектов.
Дональд Кнут
„Искусство программирования для
ЭВМ“. Т. 2
\
В этой книге изложены основы арифметики, реализуемой
в современных цифровых машинах. Машинная арифметика
совсем еще юная отрасль науки, которая стала стремитель-
но развиваться с середины нашего столетия в связи с нача-
лом массового изготовления электронных вычислительных
машин, способных с большой скоростью перерабатывать
разнообразную информацию. Определенную часть перераба-
тываемой информации составляют числа. Эти числа являются
объектами, над которыми выполняются арифметические дей-
ствия. Алгоритмы выполнения арифметических операций
в значительной степени зависят как от способа представления
чисел в машинах, так и от тех технических средств, которые
используются для построения машин. Большое разнообразие
технических средств, естественно, приводит к обилию раз-
личных схемных реализаций машинной арифметики. Мы не
будем заниматься анализом отдельных схемных решений,
а постараемся исследовать общие методы выполнения ариф-
метических операций в цифровых машинах, характерные для
той или иной системы счисления и формы представления
чисел в машине. Смещение интересов в область исследова-
ния структуры алгоритмов'арифметических операций позволит
более четко выделить основные принципиальные моменты
машинной арифметики и выявить пути ее дальнейшего
развития.
Изложение материала начинается с вопросов представле-
ния чисел в цифровых машинах, среди которых наибольшее
внимание уделено представлению чисел с учетом знаков, фор-
ме представления чисел, определению оптимальной системы
счисления для чисел с плавающей запятой, методам округ-
ления и методам перевода из одной системы счисления
в другую.
Далее для аддитивных позиционных систем счисления с це-
лым положительным основанием, которые в настоящее время
используются практически во всех проектах машин, рассмат-
риваются классически'е методы выполнения основных арифме-
тических операций алгебраического сложения, умножения
и деления.' Характеристики реализации классических методов,
такие, как точность полученных результатов, время выполне-
ния операций, требуемое оборудование, будут служить ориен-
тирами для оценки других методов, например методов уско-
ренного выполнения основных арифметических операций,
рассмотрению которых посвящена отдельная глава (глава 5).
Вопросы представления чисел в двоично-кодированных
системах счисления с целым основанием г>2 и выполнение
арифметических операций при таком представлении изложены
отдельн^) ввиду того, что они представляют интерес для
практической реализации машинной арифметики в системах
счисления с большими основаниями.
В книге выделены ещё четыре самостоятельных раздела,
посвященные машинной арифметике для непозиционных
и квазипозиционных систем счисления, выполнению арифме-
тических операций с обнаружением и исправлением ошибок,
реализации алгоритмов машинной арифметики на однородных
структурах и алгоритмам выполнения некоторых неосновных
операций, таких, как возведение в квадрат, извлечение квад-
ратного корня, вычисление логарифма и других элементарных
функций.
Материал, изложенный в этих разделах, не является тра-
диционным для машинной арифметики. Однако успехи в раз-
витии технологии изготовления машинных схем, дающие воз-
можность аппаратурной реализации все более сложной ариф-
метики, позволяют сегодня на вполне реальной основе
исследовать новые пути развития машинной арифметики,
приводящие к повышению эффективности и производитель-
ности машин.
С целью облегчения чтения материала в книге почти,
не дается детальный вывод, основных соотношений и формул,
а вместо этого приводится ссылка на соответствующую пуб-
ликацию. Этой же цели служит включение большого числа
примеров, позволяющих лучше понять материал, проверить
и закрепить полученные знания. Приводимые в книге схемы
не являются конструкторскими схемами узлов цифровых ма-
шин, они лишь отражают наиболее важные функциональные
связи, существующие при машинной реализации алгоритмов
арифметических операций.
Автор глубоко признателен Б. А. Бабояну и В. Б. Смоло-
ву за обстоятельное рецензирование и В. Д. Байкову, В. Г.
Горнштейну, В. В. Пикулину за многочисленные замечания
и беседы, которые способствовали улучшению изложения
материала и устранению ряда неточностей.
ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В ЦИФРОВОЙ МАШИНЕ
§ 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1°. Массивы г-значных элементов. Вычислительные ма-
шины реализуют различного рода процессы, связанные с пре-
образованием, передачей и хранением информации. В цифро-
вых машинах, а только они и будут рассматриваться в даль-
нейшем, информация представляется массивами дискретных
элементов. Элемент называется r-значным, если ему можно
присвоить каждое из г попарно различимых значений. Сово-
купность всех значений, присваиваемых г-значному элементу,
называется r-значным алфавитом. Если все значения равно-
правны и обладают единственным свойством — попарной раз-
личимостью, то такой алфавит принято называть абстракт-
ным.
Массив — это упорядоченная (пронумерованная) совокуп-
ность элементов. Массив, в котором значность всех элементов
одинакова, называется однородным. В зависимости от системы
нумерации элементов массивы могут быть одномерными или
многомерными. Одномерные массивы элементов называются
также словами.
Важной характеристикой слова является его длина, под
которой понимается число элементов, содержащихся в слове.
Так, слово а, состоящее из элементов ап, ап-л,..., аг, имеет
длину п. Слово длиной п изображается записью всех своих
элементов в п. позициях, которые можно перенумеровать
(например, слева направо) в возрастающем или убывающем
порядке последовательными числами. Отдельную позицию
в изображении слова принято называть разрядом слова, но-
мер позиции — номером разряда. Число разрядов в записи
слова называется разрядностью и совпадает с его длиной.
Значение, принимаемое массивом, определяется совокуп-
ностью значений, присвоенных элементам этого массива. Мас-
сив, содержащий п г-значных элементов, способен принимать
гп различных значений. Если массив содержит элементы раз-
личной значности (гг) и число элементов значности гг есть nh
а общее число элементов в массиве есть п = то мас-
сив будет принимать q различных значений и
= (1.1)
Пример 1.1. Пусть массив состоит из пяти элементов и знач-
ность элементов аааг есть -10, элементов ща2 есть 6, а значность элемента
а6 есть 24. Тогда этот массив, задающий текущее время суток в часах,
минутах и секундах, согласно (1.1) будет принимать q = 24-62-102 = 86 400
различных значений.
В цифровых машинах один и тот же массив может по-раз-
ному интерпретироваться в различных операционных устрой-
ствах машины. Так, например, одно и то же слово в устрой-
стве управления рассматривается как команда, в арифметиче-
ском устройстве — как число, а . в устройстве вывода — как
текстовая величина. В основу всякой интерпретации положена
интерпретация абстрактного алфавита, которая определяется
заданием операций, устанавливающих те или иные отношения
между значениями алфавита [4].
2°. Системы счисления. При числовой интерпретации аб-
страктное значение слова рассматривается как запись опреде-
ленного числа в некоторой системе счисления. Эту запись
в дальнейшем будем называть кодом числа. Системой счис-
ления называют совокупность приемов для наименования
и обозначения чисел. Элементы алфавита, который исполь-
зуется для записи чисел в некоторой системе счисления,
принято называть цифрами. Если алфавит имеет г различных
значений, то элемент а, рассматривается при числовой интер-
претации как г-ичная цифра. Каждой цифре at данного числа
однозначно сопоставляется ее количественный (числовой)
эквивалент — (1(а(). По тому, как зависит или не зависит
числовой эквивалент цифры от местоположения ее в записи
числа, системы счисления делятся на позиционные и непози-
ционные. В позиционных системах счисления эквивалент
цифры определяется ее-значением и местом (позицией) в за-
писи числа, а в непозиционной — только значением этой циф-
ры. Таким образом, в позиционной системе счисления одна
и та же цифра может означать различные числа в зависимо-
сти от того, в каком разряде она находится, а в непозицион-
ной каждая цифра всегда обозначает одно и то же число.
Хорошо известным примером непозиционной системы счисле-
ния (правда, с некоторыми оговорками) является римская
система, где, например, символ V всегда означает пять, вне
зависимости от места его появления в записи числа. В ка-
честве примера позиционной системы счисления можно ука-
зать общепринятую . десятичную систему. Принципиально
возможны и частично-позиционные системы счисления, в ко-
торых часть цифр имеет числовой эквивалент, зависящий
от позиции цифры в записи числа, а другая часть цифр всегда
имеет постоянный числовой эквивалент.
Система счисления называется однородной, если множест-
во допустимых цифр для всех разрядов одинаково. В про-
тивном случае система счисления называется смешанной.
С однородной системой счисления мы имеем дело в случае
обычной десятичной системы счисления, а со смешанной
столкнулись в примере 1.1.
Количественный эквивалент числа а, заданного в опре-
деленной системе счисления, является некоторой функцией
числовых эквивалентов всех его цифр, т. е#
d(a)=f\d(an)$..., d(aj}.
На практике в подавляющем большинстве случаев функция f
является функцией алгебраического сложения или умножения.
Пример 1.2. В десятичной системе счисления задано число а = 3,1,4159*
Количественные эквиваленты его цифр есть d («,) = 9-10“5, d (а2) — 5 X
Х10~4, rf(«3) = ЬКП3, d(«i) = 4-10“2, d(«5) = l-10-1 и d(«6) = 3-10°.
Количественный эквивалент числа а есть сумма количественных эквивален-
тов всех его цифр, т. е. d (а) = d («,) = 3,14159.
Пусть задан числовой эквивалент для некоторого разряда
числа (например, г0) и он отличен от нуля, т. е. известна
величина d (aiD) 0. Назовем весом j-ro разряда отношений
если значение «у постоянно при всех возможных aj =
Поскольку значение d(atc) считается заданным, то при из-
вестном значении <»у из отношения (1.2) легко найти числовой
эквивалент у\го разряда. Согласно определению (1.2) по край-
ней мере один разряд в любой системе счисления имеет вес,
равный единице. Если каждый разряд числа имеет вес, то
говорят, что система счисления, в которой представлено
данное число, имеет вес. В противном случае говорят о сис-
теме счисления, не имеющей веса.
Пусть запись числа в некоторой системе счисления имеет
вид
a: ak... a^a-i... а_л, (1.3)
причем ti = 1 и разряд с номером 0 имеет вес, равный
единице. Естественными называются такие веса разрядов,
которые удовлетворяют соотношениям:
• ыi = r-t при 7 = 1, 2, ...,
' t=0 г (1.4)
<B/=nLirr1 ПРИ /=“!> —2, •••>
где гг — значимость цифры в i-м разряде. Если вес какого-
либо из разрядов не удовлетворяет соотношению (1.4), то
говорят, что разряд имеет искусственный, вес. Для однород-
ных систем счисления с естественными весами имеем
— г«>у_1, 1 — h j <; k. (1.5)
Величина г называется основанием системы счисления. В од-
нородных системах счисления с естественными весами число-
вые эквиваленты цифр d{aj) выражаются на основании (1.5)
через величину г и значение цифры в у-м разряде, которое
в дальнейшем будем обозначать просто aj, следующим об-
разом:
d(aj)=a,jr}. (1.6)
Наибольшее распространение получили однородные адди-
тивные позиционные системы счисления с естественными
весами, т. е. системы, в которых количественный эквивалент
числа а, представленного в виде (1.3), однозначно определя-
ется через числовые эквиваленты цифры всех разрядов и ос-
нование системы счисления с учетом (1.6) по следующему
правилу:
d(a,)=-^=_hajri. (1.7)
В дальнейшем для упрощения записи везде количественный
эквивалент числа а будет обозначаться как а. Представление
чисел, удовлетворяющее соотношению (1.7), принято называть
натуральным кодом. Умножение числовых эквивалентов цифр
в натуральном коде на постоянный множитель р приводит
к умножению на р всех чисел, представленных в системе
счисления с основанием г.
, Обычно в качестве возможных значений цифр г-ичного
алфавита выбирают последовательность из г целых чисел,
включая нуль, и эту последовательность называют базой сис-
темы счисления. На' практике наибольшее распространение
получили разновидности натуральных кодов с целым положи-
тельным основанием г и неотрицательной базой, в которых
в качестве значений цифр используется последовательность
О, 1, ..., г—1. В этом случае числа, представленные конеч-
ным числом разрядов,' располагаются на числовой оси через
равные интервалы, начиная с нуля, и любое целое положи-
тельное число может быть точно представлено натуральным
кодом.
Действительно, как следует из (1.7), в рассматриваемом
случае наименьшее число есть нуль, а соседние числа, боль-
шие нуля, отличаются на единицу. Когда же дано целое поло-
жительное число а, то всегда можно найти такое k, что а —
= akrk-}-bk, где «й<г и bk<Zrk. Теперь представим bk в виде
bk = ak~irk~x -j- bk-i, причем опять ak_\ < г и bk-х < г*-1, тогда
а — akrk + -)- bk-x- Продолжая этот процесс, дойдем
до равенства b^ = axr^-b^. Обозначив Ь, = а0, получим
т. е. а можно представить натуральным кодом с основанием
г и записать в виде а: aka/,^x... а0.
При использовании слов конечной длины рациональные
числа в ряде случаев .не могут быть точно представлены. Од-
нако при заданной точности представления е всегда можно
найти такое конечное число (Л) разрядов дробной части, чтобы
оказалось справедливым неравенство | е | r~h.
При неотрицательной базе для количественных эквивален-
тов-чисел, представимых конечным числом разрядов, справед-
ливо неравенство
0<а<г*+’-г-Л. (1.8)
♦
Если все значения цифр неотрицательной базы системы
счисления с основанием г умножить на —1, то натуральный
код (1.7) будет давать представление отрицательных чисел
и нуля. При этом отрицательные числа располагаются на чис-
ловой оси симметрично относительно нуля с положительными
числами, отвечающими случаю неотрицательной базы.
Другим интересным способом выбора значений цифр явля-
ется использование алфавитов, в которых наряду с положи-
тельными цифрами имеются и отрицательные. Примерами
таких алфавитов могут служить симметричные относительно
нуля алфавиты, значения цифр которых при r = 2t-\- 1 состав-
ляют следующий ряд: — t, — / + 1, ..., —1, 0, 1, ..., t — 1, t
и в которых число положительных значений цифр равно числу
отрицательных {симметричная база). В этом случае на осно-
вании (1.7) для абсолютных величин чисел, заданных конеч-
ным числом ti = k h + 1 разрядов, имеет место неравенство
Наличие среди цифр симметричного алфавита нуля позво-
ляет натуральным кодом задать точное представление любого
целого числа в конечном виде.
Действительно, пусть а — произвольное целое число (й=0).
Всегда можно найти такие целые k, ak и bk, чтобы выполня-
лось равенство а = akrk -|- bk, причем для ak, справедливо, что
a k выбирается таким, чтобы выполнялось нера-
венство < r*+1. Число bk должно быть представ-
лено k разрядами симметричного кода, и поэтому на основа-
' r*-l
нии (1.9) для него справедлива следующая оценка: 2~•
Теперь представим bk в виде bk = ак-\Гк~г + bk-X, где опять
| a*-i I < I «л-11 г*"1 < I bk | < г* и | Ьк_х | < --- ^ \ тогда
а == akrk + a/j-ir*-1 + bk-\. Продолжая эту процедуру далее,
получим в конце концов, что а = акгк + ак-\Гк~х + -.. + atr-j-
Г ____________________ 1
причем | | <—g— = ^- Обозначим Ьх через а0, тогда
а = ^ij=oajr^ т- е- а представимо натуральным кодом.
Системы счисления со смешанной базой можно в принципе
допустить и при четном основании, но тогда возможно либо
применение симметричных алфавитов без нуля (например, при
г = 2 возможен алфавит —1, 1), либо алфавитов, у которых
число положительных значений цифр не равно числу отрица-
тельных (например, при г = 4 допустим алфавит —1, 0, 1, 2).
Системами счисления с симметричной и неотрицательной
базами и целым положительным основанием г конечно же не
исчерпываются все случаи построения аддитивных позицион-
ных систем счисления. В качестве основания системы счисле-
ния можно взять целое отрицательное число г, и тогда нату-
ральным кодом (1.7) будут представлены как положительные,
так и отрицательные числа. Если в качестве г выбрать комп-
лексные числа 21 или i — 1, то натуральный код (1.7) будет
задавать комплексные числа [12]. Однако дальнейшее иссле-
дование систем счисления носило бы несколько отвлеченный
характер, поскольку нам сейчас не ясно, что же определяет
выбор системы счисления для цифровой машины, какие
свойства систем при этом считаются главными, определяющи-
ми. Ответы на эти вопросы будут получены при рассмотрении
всех особенностей представления чисел в машине и реализиции
арифметических действий над ними. Именно этим мы и зай-
мемся в дальнейшем, причем основное внимание будет уде-
лено аддитивным позиционным системам счисления как наи-
более значимым с практической точки зрения, ибо подавляю-
щее число проектов цифровых машин базируется в настоящее
время на использовании этих систем.
- § 2. Представление отрицательных чисел
В повседневной практике одинаково широко пользуются
как отрицательными, так и положительными числами, поэтому
естественным является вопрос о необходимости представления
этих чисел в машине, работающей в какой-либо системе счис-
ления. Однако при использовании аддитивных позиционных
систем счисления с положительным основанием и неотрица-
тельной базой натуральным кодом возможно изображение
только положительных чисел и нуля. Если же выберем непо-
ложительную базу, то возможно представление отрицательных
чисел и нуля.
1°. Представление знака числа на уровне цифр. Возмож-
ность представлять положительные и отрицательные числа
единым натуральным кодом появляется при использовании
системы счисления с положительным основанием и симмет-
ричной базой, что возможно при нечетном основании. Заметим,
что при этом представляемые числа лежат в симметричном
относительно нуля диапазоне. Когда же основание системы
четно (и база имеет как положительные, так и отрицательные
значения), то натуральный код также дает представление от-
рицательных и положительных чисел, но при этом не удается
получить симметричный относительно нуля диапазон представ-
ляемых чисел.
Действительно, пусть г = 4 и база системы есть —1, 0, 1,
2; тогда если й = 0, k = 2, то натуральным кодом можно будет
изобразить нуль, положительные числа от 1 до 42 и отрица-
тельные от —1 До —21, т. е. диапазон представления отрица-
тельных чисел в два раза меньше, чем положительных.
Единый натуральный код для чисел обоих знаков сущест-
вует и при отрицательном основании системы счисления и не-
отрицательной базе, т. е. когда натуральный код определяется
равенством
а = 2/=~ла;(—f)1, а/б{0, 1, ..., г— 1}.
Однако для этого кода характерна еще большая диспропорция
диапазона положительных и отрицательных чисел. Так, если
г = —4, h = 0 и k = 2, то при неотрицательной базе натураль-
ным кодом можно изобразить число нуль, положительные
числа от 1 до 51 и отрицательные от —1 до —12.
Подводя итоги, можно сказать, что оптимальное представ-
ление чисел с разными знаками единым натуральным кодом
связано с использованием симметричной базы и положитель-
ного основания г>3. Такой код будет в дальнейшем назы-
ваться симметричным. Знак числа, представленного симмет-
ричным кодом, определяется знаком старшей значащей цифры
в изображении числа. В симметричном коде естественным
образом определяется и нуль — число без знака.
2°. Учет знаков на уровне слов. При неотрицательной
базе и положительном основании системы счисления не суще-
ствует единого натурального кода для положительных и отри-
цательных чисел. Это приводит к тому, что проблему пред-
ставления чисел со знаком приходится решать на уровне слов
при помощи специальных кодов.
2°.1. Прямой код. Один из кодов близок к конструкции,
используемой в обычной практике, когда число представляется
изображением его абсолютной величины с добавлением спе-
циального двоичного разряда — разряда алгебраического зна-
ка. Для представления чисел в машине такой способ приме-
няют довольно часто, но с одним отличием. Введение спе-
циальных знаков „+“ и „ — “ неоправданно расширило бы
алфавит, который соответствует выбранной системе счисления.
Чтобы избежать этого, принято в качестве знака исполь-
зовать цифру с нулевым значением и знака „-г-“ — цифру
со значением единица, поскольку при целом г >2 эти цифры
всегда присутствуют в допустимом алфавите. Знаковый разряд
обособлен от остальных разрядов числа (обозначим его как
а*) и помещается либо непосредственно перед изображением
абсолютной величины, как, например,
a: a*ak ... а0 ... а_й, (1-10)
либо после него. Величина числа, изображенного в виде
(1.10), есть
а = (1(1-11)
'х
Такое представление чисел со знаком принято называть пря-
мым кодом. Вообще говоря, прямой код есть отступление
от аддитивных позиционных систем счисления, поскольку раз-
ряду алгебраического знака не приписывается никакого веса
и истинное значение числа определяется умножением абсо-
лютной величины на величину, зависящую от значения зна-
кового разряда. Как мы увидим в дальнейшем, это обстоя-
тельство вызывает ряд трудностей при машинной реализации
действий над числами, представленными прямыми кодами.
При использовании прямых кодов в r-ичной системе счис-
ления можно представить 2г*+л+1 — 1 различных чисел. По-
теря одной комбинации вызвана неоднозначностью представ-
ления нуля, ибо допустимым изображением нуля является
не только код, где a^. = at=0, но также и код, где а*=1,
= 0, j = —h, ..., k, т. е. в качестве нуля можно использовать
и -ф0', и —0. В прямых кодах диапазон представления поло-
жительных и отрицательных чисел одинаков, и наибольшее
по абсолютной величине число, записанное в виде (1.10), есть
|а| = r*+i _ г-ь
2°.2. Дополнительный код. Рассмотрим еще один способ
представления отрицательных чисел в r-ичной системе счис-
ления с неотрицательной базой, также основанный на приме-
нении знакового разряда, значения цифр которого есть нуль
для положительных чисел и единица для отрицательных. Этот
способ базируется на том, что знаковому разряду приписы-
вается вес —г*+1. Пусть число а изображено в виде (1.10),
тогда его количественный эквивалент есть
. (1.12)
Когда а* = 0, то все числа либо положительные либо нуль
и максимальное положительное число есть а = г*+1 — i—h.
Если же а* = 1, то все числа отрицательные и наибольшая
абсолютная величина числа а есть |a| = rft+1, что соответст-
вует случаю ak = ... = = 0. Вообще же абсолютная ве-
личина отрицательных чисел есть |а( = гА+1— т. е.
она является дополнением количественного эквивалента, зада-
ваемого основными разрядами числа ak, ..а-h. до величины
г*+1. По этой причине код вида (1.12) называется дополни-
тельным.
Положительные числа в прямом и дополнительном кодах
имеют одно и то же изображение. Отрицательные числа по-
разному изображаются в этих кодах.
5 5
Пример 1.3. Даны числа a=+~g~ и 6 = — -g—. Требуется предста-
вить их в двоичной системе счисления прямым и дополнительным кодом.
В этом случае г = 2, k = —1 и h = 3, тогда апр: 0.101 (точкой отделяем
знаковый разряд) и «доп: 0.101, но 6пр; 1.101 и йдоп: 1.011.
В случае отрицательных чисел между цифрами основных
разрядов прямого кода aj и цифрами дополнительного кода а,
нетрудно установить простые соотношения. Приравняем абсо-
лютные величины одинаковых чисел, представленных прямым
и дополнительным кодами; тогда
, a7r7 = rk+1 - а}?. (1.13)
Представим г*+1 в виде
rft+I = S^_ft(r-l)ry + <ft- (1.14)
Подставляя (1.14) в (1.13), получим
2*==-й ар-1 = 2*=_й (г — 1 — a’j) г1 -{- г\
Приравнивая коэффициенты при одинаковых степенях г>, имеем
aj+a'j = г— 1, у = 1 — h, ..., k, (1-15)
a—h - J a_h = г.
Таким образом, если нам известно изображение отрица-
тельного числа в одном коде, то изображение его в другом
коде находится на основе соотношений (1.15).
Пример 1.4. В шестнадцатиричной системе счисления, цифры которой
имеют значение от 0 до 15 и изображаются символами 0, 1, ..., &, А, В, С ,
3701
D, Е, F соответственно, даио число а = —2—, представленное прямым
кодом при А = 0иА=3, т. е. апр: 1.2£75jg. Представить это число допол-
нительным кодом.
На основании (1.15) имеем а'_2 =16 — 5 = 11, а'_2 =15 — 7 = 8, <а'_х =
= 15 — 14 = 1, °() — 15 — 2 = 13. Отсюда адоп : l.£18B|g.
Формула (1.15) свидетельствует о том, что преобразование
цифр прямого кода в дополнительный может быть произве-
дено как поразрядная операция. Единственной трудностью
этого преобразования является расширение алфавита для
младшей цифры, значение которой может быть г, что счи-
тается недопустимым. Для устранения этого недостатка обыч-
но производят преобразования, одинаковые для всех разря-
дов, — нахождение дополнения до г—1, а затем к преобра-
зованному числу прибавляют единицу младшего разряда (г-й).
Добавление этой единицы в некоторых случаях будет занимать
столько же времени, сколько сложение полноразрядных чи-
сел, что часто рассматривается как чрезмерная трата времени.
Иногда при технической реализации удается избежать спе-
циального добавления единицы в младший разряд, совмещая
его с выполнением арифметических действий над дополни-
тельными кодами. Однако наилучшее решение этой проблемы
состоит в ее ликвидации, т. е..применении таких кодов, в ко-
торых необходимость выполнения сложения при формировании
дополнительного кода отпадает.
Формирование поразрядных дополнений до г— 1 обычно
производится без привлечения арифметических действий, ис-
пользуя только логические операции. Например, если г = 2,
то а, = а}-, т. е. цифры дополнительного кода отрицательного
числа образуются простой инверсией цифр прямого кода. Для
завершения формирования дополнительного кода к числу
с инверсированными цифрами надо еще добавить единицу
в младший разряд. В машинах параллельного действия прос-
тота формирования дополнительного кода имеет решающее
значение, в то время как для машин последовательного дей-
ствия сложность образования дополнений не играет главной
роли ввиду незначительности аппаратурных затрат на реали-
зацию дополнений и циклического характера обработки чисел.
2°.3. Обратный код. Рассмотрим теперь коды для пред-
ставления отрицательных чисел, взаимное преобразование
которых в прямые коды не требует привлечения арифмети-
ческих действий.
Пусть знаковый разряд числа имеет вес — (г*+’ — г~й),
а не —1*+1, как это было в дополнительном коде; тогда ко-
личественный эквивалент числа а, заданного в виде (1.10)
в позиционной системе счисления с основанием г, будет опре-
деляться как
а = - (rft+1 - r~h}a* + (1.16)
Такие коды принято называть обратными. Положительные
числа в обратном коде имеют такое же изображение, как
и в прямом и дополнительном кодах. Наибольшая величина
положительного числа вновь есть r*+’ —r~h. Отрицательных
чисел теперь будет меньше ввиду неоднозначности представ-
ления нуля. Действительно, код, соответствующий а* = 1
и aj = r—1, / = —/г, ..., k, имеет численный эквиваленте,
так же как и код а* = а,- = 0. Связь между значениями цифр
прямого кода а, и цифр обратного кода а, выводится так же,
как и для дополнительного кода, и имеет вид
«; + «/ = г— 1, /= — h, k. ‘ (1.17)
Отсюда взаимное преобразование прямого и обратного кодов
осуществляется как поразрядная операция взятия дополнения
до г — 1 от заданных цифр. Это свойство является преиму-
ществом обратного кода перед дополнительным, поскольку
позволяет в общем случае реализовать формирование кода
отрицательного числа и быстрее и проще.
Пример 1.5. В шестнадцатиричной системе счисления задано отрица-
тельное число at 1.1/7500Э1в прямым кодом. Найти обратный и дополнитель-
ный коды этого числа.
В соответствии с соотношением (1.17) находим поразрядное дополнение
основных разрядов числа а, тем самым определяем обратный код этого
числа Ообр: 1 .E6AFFF. Для получения дополнительного кода надо к об-
ратному коду добавить единицу в младший разряд и тогда адоп.: 1.Е0В000.
§ 3. Формы представления чисел в машине
В предыдущем параграфе были исследованы особенности
представления положительных и отрицательных чисел в ма-
шине. При этом предполагалось, что запятая, разделяющая
целую и дробную части, расположена в изображении числа
естественным образом, т. е. там, где это требуется при обыч-
ной записи числа. Однако для представления чисел в цифрот
вой машине более удобным оказываются другие специальные
формы указания положения запятой в слове. Рассмотрению
вопросов, связанных с указанием положения запятой при
изображении чисел, и посвящен этот параграф. Естественно,
речь пойдет о системах счисления с естественными весами,
поскольку понятие запятой как указателя разделения целой
и дробной частей в общем случае справедливо для систем
счисления, в которых значение всех разрядов, стоящих правее
разряда с единичным весом, меньше единицы.
Формой представления чисел в машине назовем свод пра-
вил, позволяющих установить взаимное соответствие между
записью числа и его количественным эквивалентом. При огра-
ниченной длине машинных слов множество чисел, которые
можно представить в машине (будем .их называть в дальней-
шем машинными числами), конечное. Если произвольное
вещественное число а' таково, что ar = aeD, где D — мно-
жество количественных эквивалентов машинных чисел, то
говорят, что такое число точно представляется в машине при
заданной форме представления чисел. Если же а'фа^О, то
произвольное вещественное число а' может быть представлено
в машине приближенно, либо вообще не может быть пред-
ставлено. При приближенном представлении вещественное
число а' заменяется некоторым числом а, принадлежащим
множеству машинных чисел.
Сравнение различных форм представления чисел в цифро-
вой машине будем производить на основе оценки диапазона
и точности представления чисел. Обычно в качестве харак-
теристики диапазона представления чисел рассматривают ве-
личину
T> = logr-^, (1.18)
^mln
где amax и amin — соответственно самое большое и самое малое
по абсолютной величине из машинных чисел, причем amln=£
¥=0 [44].
Точность представления будем оценивать значением вели-
чин
дс= । а(2)_«(1)| (1-19)
и
которые назовем абсолютной, и относительной разностью
Мишиных чисел соответственно. Здесь а(2) и — значения
двух.последовательных машинных чисел, таких, что
и |а(2>|>।ат|.
С параметрами Дс и ес тесно связаны величины абсолютной
и относительной ошибок приближения реального числа а!
машинным числом а, которые обозначим как Л и е соответст-
венно и . '
Д = |а'-а], (1.21)
а
(1-22)
Заметим, что величины Диев отличие от Дс и ес зависят от
выбранного способа приближения реальных чисел машинными.
Приближение считается хорошим, если для произвольного
вещественного числа а' справедливо [13]
Д-
и приемлемым, если
При хорошем приближении числа, большие по абсолютной
величине числа а^ах + вообще не могут быть представ-
лены в машине. Если такие числа появятся в машине при
выполнении арифметических операций, то возникшая ситуация
расценивается как аварийная. Обычно эту аварийную ситуацию
называют переполнением разрядной сетки. Числа, меньшие
. „ 1
по абсолютной величине, чем amin —- но не равные нулю,
будут представлены в машине как нуль. Число, отличное от
нуля, но представленное в машине как нуль, принято назы-
вать машинным нулем. Хотя само появление машинного нуля
не расценивается как аварийная ситуация, но оно может при-
вести к ней впоследствии, например, при делении на машин-
ный нуль. Иногда числа, которые являются машинными ну-
лями, отмечаются специальными признаками.
1°. Естественная запятая. Наиболее распространенная в по-
вседневной практике форма представления чисел есть после-
довательность цифр, разделенная запятой на целую и дробную
части. Если число отрицательное, то данная последователь-
ность добавляется знаком „ — “, стоящим обычно непосредст-
венно перед старшей цифрой целой части. Числа, представлен-
ные в такой форме, будем называть числами с естественной
запятой. При представлении чисел в форме с естественной
запятой обязательно требуется для каждого числа указание
о положении его запятой в одном из разрядов кода.
Диапазон представления чисел в форме с естественной
запятой согласно (1.8) и (1.18) будет при п = k h-\- \ харак-
теризоваться величиной
‘v = 2n-\- logr(l — r~n). (1.23)
Абсолютная разность машинных чисел равна r~h и тогда
г-«<Лг<1.
Разброс значений относительной разности машинных чисел
лежит в диапазоне
(rn - I)-1 О^г-1.
Основные недостаки представления чисел в форме с есте-
ственной запятой связаны с невозможностью оперирования
с очень большими или очень малыми по абсолютной величине
числами. Поэтому,.несмотря на привычность чисел с естествен-
ной запятой, эта форма представления получила значительное
распространение лишь в калькуляторах, где естественность
положения запятой имеет большое значение. В универсальных
машинах затраты, связанные с хранением указания положения
запятой и реализацией ари метических операции с числами
в указанной форме, рассматриваются как чрезмерные, а диа-
пазон и точность представления чисел считаются неудовлет-
ворительными, поэтому в них получили распространение две
другие формы представления: с фиксированной и плавающей
запятой.
2°. Фиксированная запятая. Необходимость в указании
положения запятой полностью отпадает, если место запятой
в разрядной сетке машины заранее фиксировано раз и навсег-
да. Такая форма представления чисел называется представле-
нием с фиксированной запятой. Реализация алгоритмов ариф-
метических операций над числами, представленными в ука-
занной форме, оказывается значительно более быстрой и про-
стой, чем при естественной запятой. Однако, как и ранее, при
выполнении ’ некоторых действий могут получиться резуль-
таты, которые невозможно представить в форме с фиксиро-
ванной запятой ввиду переполнения разрядной сетки целой
части.
Пусть фиксирована запятая перед (й-}-1)-м разрядом чис-
ла (разряды пронумерованы от 1 до п справа налево); тогда
для ненулевых машинных чисел справедливо неравенство
1). (1.24)
Как следует из (1.18) и (1.24), диапазон представляемых
чисел уменьшается, и теперь
v = п + logr (1 — г~п). (1.25)
Абсолютная разность машинных чисел постоянна для всего
диапазона машинных чисел, и ее значение равно r~h. Вели-
чина же параметра ес согласно условия (1.21) зависит от а<’>,
и с учетом (1.8) имеем
(/«-IF’C^l. (1.26)
При выполнении арифметических действий над числами
с фиксированной запятой возможно получение результатов,
выпадающих из заданного диапазона (1.24), что приводит
к аварийной ситуации. Фиксация запятой перед старшим раз-
рядом числа (п = h) позволяет все числа сделать правильны-
ми дробями, и, следовательно, их перемножение никогда не
дает переполнения разрядной сетки. Эта особенность объяс-
няет причину, почему на практике принято иметь именно
такое положение запятой, но и это представление не избав-
ляет от переполнения разрядной сетки при сложении и деле-
нии чисел. Переполнения разрядной сетки можно в большин-
стве случаев избежать, если предварительно провести мас-
штабирование представляемых чисел. Процесс масштабиро-
вания заключается в умножении всех величин, участвующих
в решении задачи, на масштаоные коэффициенты, подооран-
ные таким образом, чтобы избавиться от переполнения раз-
рядной сетки в процессе решения задачи. При выборе коэф-
фициентов надо помнить, что правильный результат алгебраи-
ческого сложения возможен лишь для одинаковых масштабных
коэффициентов; а операции умножения и деления формируют
новые масштабные коэффициенты у результатов. ' Ввиду того,
что машина обычно не имеет сведений о масштабных коэф-
фициентах, всю работу по выравниванию масштабов вынужден
сделать программист при составлении программы. Кроме того,
поскольку трудно заранее определить весь диапазон чисел,
которые могут появляться при решении задачи, часто возни-
кает необходимость менять масштабные коэффициенты по ходу
вычислений* Все это не только значительно усложняет про-
цесс программирования, но .и приводит к усложнению самой
программы.
Хотя для малых чисел вероятность переполнения при их
сложении не велика, мы все же вынуждены стремиться к ис-
пользованию чисел, величины которых близки к верхнему
пределу в *(1.24), с тем, чтобы согласно (1.26) обеспечить
высокую точность вычислений.
3°. Плавающая запятая. Для устранения указанных не-
достатков представления чисел с фиксированной запятой при-
меняют представление чисел в форме с плавающей запятой.
Идея, лежащая в основе представления чисел в форме с пла-
вающей запятой, базируется на том факте, что для .любого
числа а, представленного в системе счисления с основанием
г, можно записать
а = геМ, (1.27)
где е — целое, число (положительное, отрицательное или
нуль), называемое порядком, a М ~ значение числа со зна-
ком, представленного в форме с запятой, фиксированной
перед старшим разрядом, называемое мантиссой. Запись
числа с плавающей запятой можно понимать как одновремен-
ную запись самого масштабируемого числа, так и. запись
связанного с этим числом масштабного коэффициента. В том
случае, когда старшая цифра мантиссы отлична от нуля, чис-
ло М называется нормализованным. Следовательно, для
s-разрядной мантиссы нормализованного числа справедливо
следующее выражение:
г-1 <|7И|< 1 -t~s. (1.28)
Пример 1.6. Десятичное число 3,14 в случае фиксации запятой перед
старшим разрядом мантиссы может иметь любой вид: 0,314-10’, 0,0314-102.
0,00314-103, но лишь одна запись, а именно 0,314-10’, является нормализо-
ванным числом, а остальные ненормализованные.
Указание положения запятой осуществляется заданием
порядка числа в выражении (1.27). Порядок записывается
в специально отведенных разрядах слова {поле порядка)
в виде целых чисел со знаком или только положительных
чисел. В первом случае порядок числа лежит в диапазоне
—{гр — 1) С гр — 1, где р — число основных разрядов
в поле порядка. Во втором случае порядок числа определя-
ется по формуле е — ес — е0, где ес — значение положитель-
ного числа, заданного р разрядами r-ичной системы счисле-
ния, а е0 — константа одна и та же для всех машинных чи-
сел. Величина порядка е определяет, на сколько разрядов
нужно перенести запятую, первоначально расположенную
перед старшим разрядом мантиссы1, для того, чтобы получить
истинное число. Знак порядка показывает направление пере-
носа запятой — при плюсе вправо, при минусе влево.
Пример 1.7. Даны числа а = 0,1975-104 и 6 = —0,26-10~3, представлен-
ные в форме с плавающей запятой. Требуется представить их в форме
с естественной запятой. Получим, руководствуясь приведенными правила-
ми: а = 1975, b = —0,00026.
Поскольку масштабные коэффициенты при представлении
чисел в форме с плавающей запятой вводятся в явном виде
вместе с числами, все операции над масштабами (порядками)
могут выполняться в машине автоматически и беспокоиться
б преобразовании масштабов не приходится. Однако, как
и при фиксированной запятой, . здесь возможно переполнение
разрядной сетки, которое выражается в том, что результат
какой-либо операции имеет порядок больше допустимого.
Обычно эта ситуация рассматривается как аварийная. Конеч-
но, при выполнении операций возможно получение чисел,
имеющих порядок меньше допустимого и нормализованную
мантиссу. Эти числа рассматриваются как машинные нули,
так же как и числа, имеющие нулевую мантиссу и допусти-
мый порядок. Обычно принято\ машинные нули изображать
нулевой мантиссой и специальным порядком, отличным от
порядков ненулевых машинных чисел. Такое изображение
принято и при исходной записи нуля, т. е. представление
нуля не удовлетворяет форме (1.27).
Пусть из п + 2 разрядов,, изображающих число в форме
с плавающей запятой, один двоичный разряд изображает
знак (о^.) мантиссы, другой — знак порядка, а остальные п
разрядов r-ичной системы счисления распределяются между
s разрядами мантиссы (поле мантиссы) и разрядами порядка
р = п — s; тогда
а = (1 — 2о*) CL-tr~l.
Значение порядка меняется от emin до етах, следовательно,
для нормализованных чисел допустимый диапазон представ-
ления абсолютных величин машинных чисел есть
| а I Гетах (1 — Г~s). (1.29)
Отсюда диапазон представляемых чисел характеризуется ве-
личиной
® ^max “1“ 1 ^min Н“ О О*
(1.30)
Даже при малых значениях р диапазон представления чисел
в форме с плавающей запятой значительно больше, чем для
других форм.
Пример 1.8. Пусть г = 16 и для изображения чисел задано восемь
разрядов шестнадцатиричной системы счисления. В случае представления
чисел в форме с плавающей запятой из восьми разрядов шесть отводятся
под изображение мантиссы, а два •— под изображение знака мантиссы (один
двоичный разряд) и порядок. Будем считать, что при этом етах = 27—1,
a ^min = 0, тогда согласно (1.30) имеем, пренебрегая членом logle (1—2—24),
что v — 128. Е£ли бы при том же числе разрядов мы использовали форму
с естественной запятой, то получили бы согласно (1.23), что v — 16, а при
фиксированной запятой согласно (1.25) v = 8.
При представлении чисел в форме с плавающей запятой
последовательными машинными числами являются числа вида
геМ и re(M + r~s), отсюда с учетом (1.19) Дс = ге~5, й усло-
вия „хорошего" и „приемлемого*1 приближения запишутся
как (см. [13]) A<^2~1re~-S и L^re~s соответственно. Кроме
того, согласно (1.20) параметр ес в этом случае есть
e.c = r~sM~1. (1.31)
Учитывая, что для нормализованных чисел справедливо нера-
венство (1.28), получим (rs — I)-1 г1--5. Следовательно,
точность представления чисел с нормализованной мантиссой
при данном г зависит только от числа разрядов -мантиссы,
и чем их больше, тем меньше погрешность представления.
Когда числа ненормализованы, величина мантиссы может
быть весьма близка к /—s и тогда точность представления резко
падает (в наихудшем случае ес=1). Окончательный выбор
формы представления мантиссы нужно сделать после анализа
точности представления результатов арифметических операций.
При заданном основании системы счисления г и длине
машинного слова п количество различных чисел, с которыми
может оперировать машина, а их число есть q — гп, так или
иначе определяет точность представления чисел. Пусть вели-
чина q зафиксирована, тогда встает вопрос о выборе оптималь-
ного основания и об оптимальном распределении разрядов
слова между полем порядка и полем, мантиссы. Рассмотрим
эти вопросы подробнее.
3°.1. Выбор основания при постоянной длине слова. Пусть
слова в форме с плавающей запятой изображаются двоичным
разрядом знака мантиссы и п разрядами r-ичной системы счис-
ления. Зафиксируем значение п. Будем теперь считать, что
мантисса — это нормализованная дробь в г0-ичной системе
счисления и г0 > г. Это действительно справедливо, если s
разрядов мантиссы разбить на группы из X разрядов в каждой
и значение группы из цифр r-ичной системы счисления рас-
сматривать как цифру г0-ичной системы; тогда величина числа
а есть а = ге0Мй, причем
г-х-^7И0<1. (1.32)
Имеет смысл рассмотреть только случай г0 = гх, ибо если
г0 < гх, то возможности г0-ичного представления используются
не полностью, например, при той же разрядности существенно
снижается диапазон представляемых чисел [46].
При сохранении размеров полей порядка и мантиссы пере-
ход от r-ичной системы счисления к гх-ичной увеличивает
диапазон представляемых чисел, но одновременно снижает их
точность представления (1.31), поскольку теперь для норма-
лизованной мантиссы справедливо (1.32). Потребуем сейчас,
чтобы диапазон представления чисел при переходе от г-ичной
системы счисления к г0-ичной сохранился. Этого, очевидно,
можно достичь, уменьшив число разрядов в поле порядка
до р0 и соответственно увеличив их в поле мантиссы до s0.
Отсюда, учитывая (1.32), получим
rX<?<nln-x < | а | rXemax Q _
Пусть emin = 0, a emax=r^ — 1; тогда диапазон представляемых
чисел согласно (1.30) есть
v (го) = * rP° + log, (1 — r~s”). (1.33)
Если же ту же самую запись трактовать как число, представ-
ленное в r-ичной системе счисленця, то
v(r) = rp+ logr(l — r~s). (1-34)
Из условия v(r) = v(r0) с учетом равенств (1.33) и (1.34)
получим, что
Ро=Р —log,X. (1.35)
Поскольку нас интересует решение уравнения (1.35) в целых
числах, то следует принимать во внимание лишь значение
X = г₽, где р — целое число. I
Рассмотрим, как меняется величина ес при переходе к г-ич-
ной системе счисления. Из (1.31) имеем при г0 = гх с учетом
(1.32) гс , но поскольку s0 = п — р logf X, то
£ ГХ~JOg X
с ' Г •
Таким образом, переход к гх-ичной системе счисления вы-
зывает увеличение максимума рассматриваемой величины
в гх— logrx-1 раз. Рассмотрим неравенство X — logrX^l или
rx-1 i>X. При к > 1 для всех г > 2 справедливо, что А"1 > Х.Это
означает, что для всех г > 3 переход к системе счисления
с основанием гх при условии сохранения диапазона представ-
ляемых чисел не рационален с точки зрения обеспечения
наибольшей точности представления.
В случае г = 2 для всех Х>2 справедливо, что 2х~1>Х, а
при X == 2 имеем 2 — log22 = l, т. е. четвертичная, система
счисления равноценна двоичной относительно точности пред-
ставления чисел.
Помимо относительной разности машинных чисел для
оценки погрешности приближения чисел имеет слысл оценить
величину математического ожидания случайной величины ес,
тогда с учетом (1.31) получим

где k — число различных значений мантиссы М, а р(М^ —
вероятность их появления. Установлено [53], что для мантисс
чисёл с плавающей запятой плотность распределения вероят-
ностей определяется как 7И-1 In-1 г, тогда
Когда осуществляется переход от r-ичной системы счисления
к гх-ичной, то значение ег(гх) определяется из равенства
(1.37)
Найдем экстремум функции р = ес (г)1&с (г1), учитывая, что
Sq s + logr X. Оказывается, что максимум функции р = Х2(г —
— l)/(rx— 1) достигается при X таких, что
Х = 2(1 — r-x) In-1 г.
(1.38)
Как это следует из (1.38), при г >2 имеем 1—r_x<lnr
и наибольшее значение функции р достигается при X = 1, т. е.
оптимальное значение базы есть г. Когда же г = 2, наиболь-
шее значение функции р, отвечающее целым X, достигается
при Х = 2. Это означает, что. четверичная система счисления
превосходит двоичную в отношении средней точности пред-
ставления чисел. Однако надо иметь в виду, что в случае
двоичной системы счисления старший разряд мантиссы всегда
равен единице, ибо имеем дело только с нормализованными
мантиссами, а поэтому он может быть опущен. Это равно-
сильно увеличению разрядности двоичной мантиссы на еди-
ницу, но тогда согласно (1.37) и (1.36) имеем
ес(2) _ 2-1 2 In 2 2
ес(4) ' In 2 • 3 • 2“'s~1 3 ’
т. е. двоичная система теперь имеет явные преимущества
перед четверичной. При опускании старшего бита для норма-
лизованных мантисс значение максимума относительной по-
грешности также уменьшается по сравнению с четверичной.
Таким образом, можно сделать вывод, что при сохранении
размеров полей порядка и мантиссы переход от r-ичной сис-
темы счисления в гх-ичной не может обеспечить повышения
исходной точности вычислений, если диапазон представляе-
мых чисел в обеих системах счисления одинаков, либо при
одинаковой верхней границе точности представления не мо-
жет обеспечить расширение диапазона представления чисел.
Этот вывод справедлив, если мантисса числа в гх-ичной системе
счисления удовлетворяет неравенству (1.32). Если же мантисса
близка по абсолютной величине к г~г, то переход к гх-ичным
системам счисления при этом условии является вполне оправ-
данным .как в отношении расширения диапазона представляе-
мых чисел, так и в отношении повышения точности представ-
ления заданных чисел. Окончательный вывод относительно
выбора основания системы счисления при фиксированном фор-
мате машинных чисел следует сделать после детального об-
суждения особенностей реализации арифметических операций
над числами с плавающей запятой в r-ичной и гх-ичной си-
стемах счисления.
3°.2. Выбор основания при переменной длине слова. По-
дойдем к выбору основания системы счисления с другой сто-
роны. Мы не будем требовать, чтобы числа в г0-ичной сис-
теме счисления (г0 > г) обязательно имели длину п г-ичных
разрядов. Наше основное требование будет теперь состоять
в равенстве диапазона представляемых чисел для различных
систем счисления г и г0 и в равенстве максимума относитель-
ной погрешности. Это означает, что на основании (1.30)
и (1.31) должны выполняться равенства
<?max - <?mln + 1 + logr (1 - Г~") = <ах - <in + 1 + logjl-Г,*)
И
rx~s —
Пусть ешах = гр — 1, = Го° — 1 И <?min = <?mln = 0, тогда дан-
ные равенства эквивалентны соответственно равенствам
Ро =Р logro г, s0 = (s — 1) logro г 4-1, (1.39)
причем, как обычно, считаем, что logr(l—г--5)^!.
Сделаем. предположение о том, что сложность элемента,
моделирующего цифру в r-ичной системе, счисления, прямо
пропорциональна г, т. е. числу устойчивых состояний, в кото-
рых может находиться данный элемент. Сразу же заметим,
что далеко не для всех физических реализаций элементов
это предположение оправдывается. Однако, если это предпо-
ложение все же справедливо, то общее количество оборудо-
вания, необходимое для представления «-разрядного числа
(п = s 4- р) элементами с г устойчивыми состояниями, оказы-
вается пропорциональным величине R(r) = nr.
Для оценки затрат количества оборудования при исполь-
зовании системы счисления с основанием г принято [11] рас-
сматривать отношение
/(г)=^. (1.40)
т. е. отношение количества оборудования, необходимого для
представления одного числа из множества q в системе с осно-
ванием г, к количеству оборудования, необходимому для
представления одного числа в двоичной системе счисле-
ния при одинаковой точности и диапазоне представления..
Пусть г = 2 и г0 = г, тогда отношение (1.40) с учетом (1.31)
примет вид
* f(r\ _ г + s —1 + log2r 4
' ' ' 2 loggг P-г s
Обычно на практике s + р log2 г — 1 и тогда
АП—
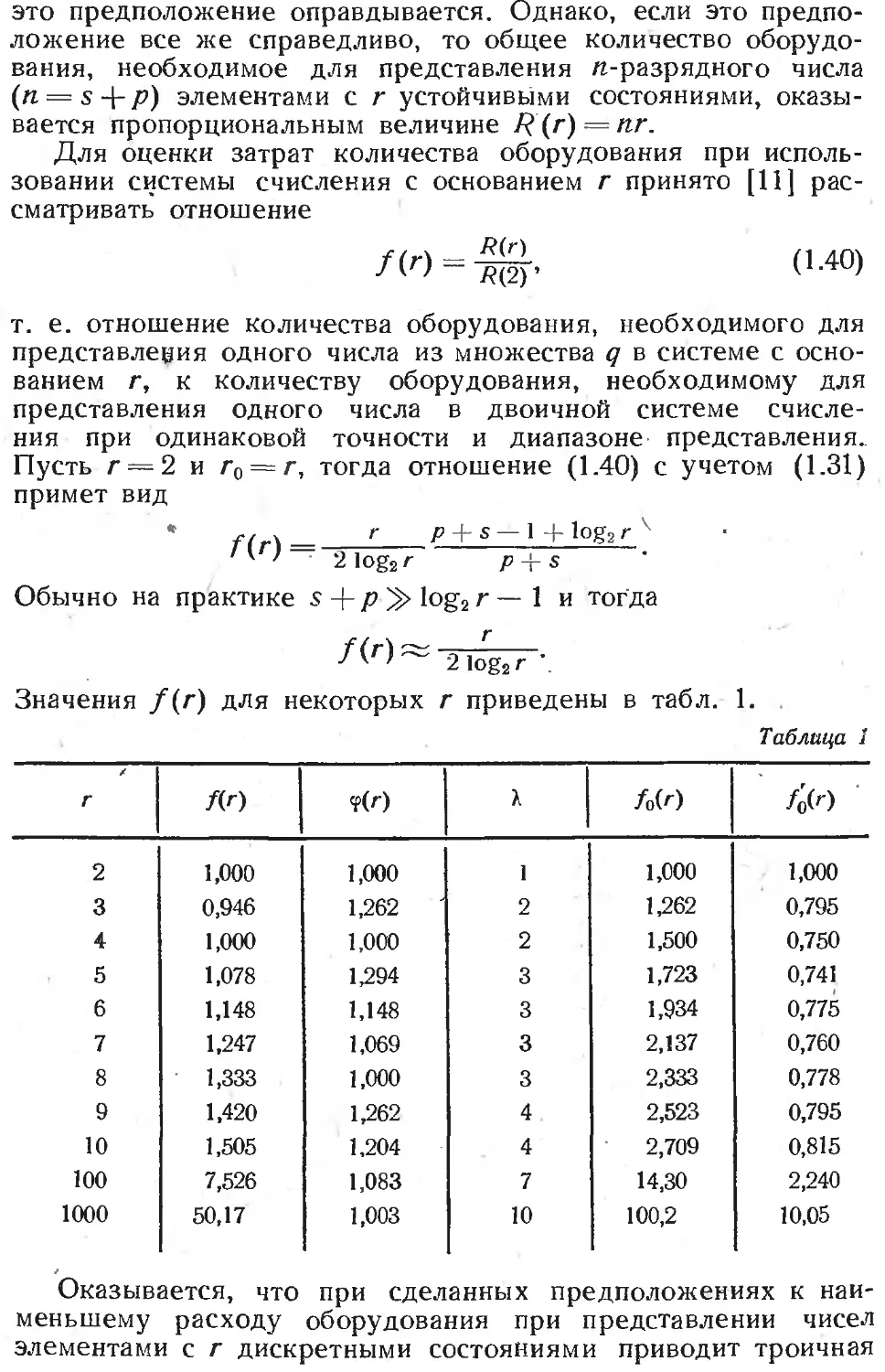
Значения f(r) для некоторых г приведены в табл. 1.
Таблица 1
X Г /(О ?(г) X /о(г) А') '
2 1,000 1,000 1 1,000 1,000
3 0,946 1,262 2 1,262 0,795
4 1,000 1,000 2 1,500 0,750
5 1,078 1,294 3 1,723 0,741
6 1,148 1,148 3 1,934 0,775
7 1,247 1,069 3 2,137 0,760
8 • 1,333 1,000 3 2,333 0,778
9 1,420 1,262 4 2,523 0,795
10 1,505 1,204 4 2,709 0,815
100 7,526 1,083 7 14,30 2,240
1000 50,17 1,003 10 100,2 10,05
Оказывается, что при сделанных предположениях к наи-
меньшему расходу оборудования при представлении чисел
элементами с г дискретными состояниями приводит троичная
система счисления. Несколько худшие результаты дают двоич-
ная и четверичная системы счисления, а десятичная система
более чем в 1,5 раза увеличивает количество оборудования
по сравнению с двоичной. Полученные оценки главным обра-
зом характеризуют количество оборудования в арифметичес-
ком узле (АУ) и некоторых видах запоминающих устройств.
Оценка логических и управляющих схем не может быть про-
изведена на основе столь простых соотношений.
Реальная экономичность той или иной системы счисления
может быть достоверно оценена лишь применительно к конк-
ретной физической реализации элементов. Так, если исполь-
зуются такие элементы, как биакс и индуктивный параметрон,
оборудование двузначного и трехзначного элементов одина-
ково. Это обусловлено тем, что при г = 2 возможности данных
элементов используются не полностью. В этих случаях приме-
нение троичной системы счисления вместо двоичной дает
экономию количества оборудования на 37%. Такая же экономия
характерна для запоминающих устройств с использованием
магнитной поверхности, многослойных ферритовых пластин,
электромагнитных линий задержки или двух сердечников на
на один разряд [4].
До настоящего времени создание многопозиционных циф-
ровых и запоминающих устройств, обладающих большим
быстродействием, достаточно высоким уровнем надежности
и экономичностью, на основе которых могли бы строиться
машины универсального назначения, встречает значительные
трудности, и поэтому в цифровых машинах не применялось
непосредственное изображение цифр с числом дискретных
состояний больше трех.
3°.3. Представление чисел с переменным полем мантиссы.
Для данного основания системы счисления г при изображении
чисел в форме с плавающей запятой поле мантиссы и поле
порядка имеют величину, одинаковую для всех машинных чи-
сел. В то же время очевидно, что при небольшой величине
порядка рязряды используются не полностью и имеется опре-
деленное число „пустых“ разрядов. Было бы разумным при-
соединить их к полю мантиссы с тем, чтобы повысить точность
вычислений. Сделать это достаточно просто.
Пусть, как и ранее, все слова имеют фиксированную длину
п +1 разрядов, из которых один двоичный разряд отводят
под знак мантиссы. Из п r-ичных разрядов выделяют поле
длиной в т разрядов.
Это поле носит название индикатора, и оно определяет,
как надо разделить п — т разрядов между порядком и ман-
тиссой. Само разделение производится следующим образом.
Поле индикатора G рассматривается как изображение целого
числа в г-ичной системе счисления. Пусть величина этого чис-
ла есть q. Число разрядов порядка р есть некоторая функция
от q, например, p = q^~ с, где с -^константа [61]. В этом слу-
чае число разрядов мантиссы есть
s = n — m — q — с.
(1-41)
Положим гт — 1 4- с = //, тогда коэффициент перекрытия
диапазона v точно такой, каким он был бы, если бы из п
разрядов р' отводились постоянно под порядок, a s'=n—p' —
под мантиссу. Однако относительная точность представления
падает, поскольку из (1.41) следует, что теперь s — n — т —
— Р' < • Следовательно, при максимальном порядке мы те-
ряем точность вычислений, и эта потеря весьма ощутима —
верхний предел для увеличен в г?-1 раз. При q< гт — 1 4-с
точность повышается, при q = гт — 1 — т сравнивается с преж-
ней и становится наибольшей при q = 0, когда s = п — т —
— c^>sr. Это уже намного лучше, чем при постоянных полях
порядка и мантиссы.
Представление чисел в форме с плавающей запятой при
переменной длине полей порядка и мантиссы существенно
повышает точность вычислений на цифровой машине, когда
мы имеем дело не с очень большими или не с очень малыми
числами и лежащими приблизительно в одном диапазоне.
§ 4. Округление чисел
Для обеспечения наибольшей точности вычислений надо
стремиться к тому, чтобы все представляемые числа имели
хорошее или по крайней мере приемлемое приближение. Ре-
шением проблемы удовлетворительного приближения чисел
до ввода их в машину занимается пользователь, но как только
числа оказываются внутри машины и подвергаются обработке,
машина сама должна уметь осуществлять хорошее или прием-
лемое приближение. Весьма часто проблема приближения
числа а' возникает при получении внутри машины чисел раз-
рядностью, большей, чем это допустимо. В этом случае число
округляют, т. е. заменяют его машинным числом а заданной
разрядности. Округление (обозначим его знаком □) называ-
ется оптимальным, если для любого машинного числа а
справедливо \Ja = a: Пусть «(1) и а<2) — два последовательных
машинных числа, тогда при оптимальном округлении вещест-
венное число а’ такое, что а(1) < а' < а(2), заменяется либо
числом аР\ либо числом а(2). Если Qa' <. а', то говорят об
округлении по недостатку, когда то говорят об
округлении по избытку. Округление называется симметрич-
ным, если □«'= —□(— а'). Рассмотрим три вида симметрич-
ного округления [55]:
округление в направлении к нулю — когда вещественное
число округляется до ближайшего к нулю машинного числа;
округление в направлении от нуля — когда округление
производится до машинного числа, лежащего дальше от нуля,
чем вещественное число а'\
округление по дополнению — когда округление произво-
дится до ближайшего машинного числа. Если же вещественное
число а' находится точно посередине между двумя машин-
ными числами, то округление производится по специальным
правилам.
В качестве параметров, по которым будут сравниваться
методы округления, используются максимальная величина
модуля погрешности, т. е. гпахД, где Д определена из (1.21),
математическое ожидание погрешности округления Д
и дисперсия погрешности округления D.
При конечном числе т округляемых чисел математическое
ожидание определится как
д^^Д^ДО,
где Д, —значение погрешности округления, а р (Дг)— вероят-
ность появления этого значения.
Дисперсия погрешности округления задается равенством
D = - Д)2Р(Д;) = ДГР (дг) - Д2.
В случае округления (п 4- /)-разрядных чисел до «-разрядных
значение погрешности округления представим в виде
Дг = 0 а,- г — 1,
где ₽ — целое число, a t — разрядность отсекаемой части числа
(его „хвоста"). Для двоичной системы счисления имеем [23]
Д = 2Р 2уС1А (а7)2Ч
где а (ау) — вероятность появления единицы в у-м разряде
числа Д. Тогда выражение для дисперсии примет вид
D = У^р^-Ъ + 2 2 ^p^W+i - Д2.
Значение А(айа;) есть вероятность появления единицы в двух!
любых разрядах мантиссы числа Д;. Следовательно, для того
чтобы определить важнейшие характеристики дискретного
случайного числа Дг-, надо знать корреляционную матрицу ве-
роятностей
^(аЛ) =
Pt (ai) Pi (а1аг) - • • Pi (“1“/)
Pi («г) • • • Pi (а2а<)
Pi (“/)
При составлении данной матрицы учитывались очевидные
соотношения =А(“/) и А(а;ал) = А(ала;)-
Будем считать, что числа в машине представлены в форме
с запятой, фиксированной перед старшим разрядом, т. е. а:
a~i . . . Пусть в результате каких-либо действий над
машинными числами внутри машины сформировалось число а',
имеющее длину п > //.''Оставим пока в стороне вопрос, какие
именно действия могут привести к такой ситуации, а займемся
решением вопроса, каким методом лучше всего округлить это
число до машинного числа, т. е. уменьшить длину слова а'
до h разрядов. -
Очевидно, что самый простой способ округления состоит
в отбрасывании лишних разрядов слова а', т. е. всех разря-
дов с номерами a-*_i, a_*_2, ..., a-h-t- Величина абсолют-
ной погрешности приближения тогда есть
Д = |h JI •
Заметим, что для прямых кодов данный способ округления
есть реализация метода округления к нулю.
Пусть основание системы счисления нечетно и база сим-
метрична, тогда согласно (1.9) имеем
шах Д = 2~lr~h (1 — (1.42)
а сама погрешность может иметь как положительный, так
и отрицательный знак, поскольку она является значением от-
секаемого «хвоста". Будем считать, что любое значение «хвос-
та" от 0 до ±2~1r~h (1—r-z) равновероятно, следовательно,
вероятность появления погрешности Дг есть /?(Д£) = г~* для
всех Такое предположение кажется естественным’
до тех пор, пока не установлена природа появления в машине
чисел с разрядностью больше допустимой. При равновероятном
появлении всех значений „хвоста" математическое ожидание
погрешности округления есть Д = 0для симметричной базы,
поскольку число положительных и отрицательных значений,
равных по абсолютной величине, в этом случае одинаково.
Отсюда значение дисперсии определится как
D = - г~2г). (1.43)
Рассмотрим теперь данный метод, когда числа заданы пря-
мыми кодами. На основании (1.8) очевидно, что
шах Д = r~h (1 — г~1), (1 -44)
т. е. максимальная величина модуля погрешности выросла
в два раза по сравнению с симметричными кодами. Если счи-
тать, что появление чисел с абсолютной величиной а, но раз-
ных знаков равновероятно и по-прежнему равновероятны все
значения хвоста “ чисел одного знака, то и в рассматриваемом
случае математическое ожидание погрешности есть Д = 0.
Однако дисперсия увеличится довольно значительно по срав-
нению с симметричным кодом и составит
D = З-1 r-2ft(l — 1,5/~' + 0,5г-и). (1.45)
На практике обычно приходится считаться с тем, что ве-
роятность появления чисел разного знака при выполнении
определенной программы не одинакова, и поэтому имеет смысл
рассмотреть данный метод еще Хля случая округления абсо-
лютных величин (фактически чисел одного знака). Естествен-
но, что значение max Д при этом остается точно таким же, как
(1.44), но математическое ожидание уже будет отлично от
нуля и определится как
д’ = 2-'r-ft(l - r-z). (1.46)
Неравенство Д=£0 означает, что при действиях с числами одного
знака погрешность округления носит систематический характер
и происходит накопление ошибок. Дисперсия случайной вели-
чины Дг не меняет своего значения (1.45) в случае работы
с числами одного знака. Накопление систематических ошибок
заставляет обратиться к исследованию других методов округ-
ления, которые проведем для прямых кодов.
1°. Округление от нуля. Реализация 'данного метода тре-
бует учета двух факторов. Во-первых, необходимо знать,
имеет ли „хвост** , значение нуль или нет. Если отсекаемая
часть имеет ненулевое значение, то она игнорируется, зато
к абсолютной величине оставшейся части добавляется единица
в младший разряд и, следовательно, тогда
П® = i=—hGif* Ч- Г *)- j
Это добавление может вызвать распространение переносов
через все разряды числа, что требует в общем случае исполь-
зования операции сложения для реализации данного метода
округления. Помимо дополнительных временных затрат это
может привести также к переполнению разрядной сетки целой
части. Несмотря на заметное усложнение реализации данного
метода по сравнению с методом округления к нулю за счет
включения операции сложения и анализа отсекаемой части на
нуль, никаких выгод мы от него не получаем, поскольку ос-
новные характеристики в рассматриваемом случае точно такие
же, как и при округлении к нулю. Таким образом, данный
метод не дает никаких преимуществ по сравнению с округ-
лением к нулю. '
2°. Округление по недостатку. Реализация данного метода
существенным образом базируется на результате анализа знака
округляемого числа. Если а' > 0, то округление заключается
в простом отбрасывании „хвоста". Если же а' < 0, то помимо
отбрасывания „хвоста" к абсолютной величине оставшейся
части добавляется единица в младший разряд, если только
„хвост" имеет ненулевое значение. Таким образом, реализация
данного метода еще более усложнена по сравнению с методом
округления от нуля за счет анализа знака числа а'. Однако
это усложнение не снижает значения максимума модуля пог-
решности (1.42). Более того, даже в случае равновероятного
появления чисел положительного и отрицательного знака
математическое ожидание погрешности округления имеет не-
нулевое значение, определенное из равенства (1.46). Ради
справедливости надо отметить, что дисперсия случайной вели-
чины Дг будет точно такой, как. при симметричных кодах
(1.43).
Если рассматривать округление только чисел одного знака,
то при а' > 0 данный способ совпадает с округлением к нулю,
а при а' < 0 — с округлением от нуля. Отсюда ясно, что дан-
ный способ ре может конкурировать со способом округления
к нулю.
3°. Округление по избытку. Этот способ во всем подобен
предыдущему, с тем лишь отличием, что добавление в млад-
ший разряд сохраняемой части числа а' производится, когда
а' > 0 и „хвост" имеет ненулевое значение. При а'<0 „хвост"
просто отбрасывается. Следовательно, при «/>0 данный способ
совпадает с округлением от нуля, а при а' < 0 —’ с округле-
нием к нулю. Характеристики данного способа точно такие,
как у предыдущего, за исключением знака величины Д, кото-
рый меняется на противоположный. '
4°. Округление по дополнению. Данный способ является
объединением способов округления к нулю и от нуля. Реали-
зация способа связана с коррекцией сохраняемой части числа
а', производимой по результатам анализа значения старшей
цифры отсекаемой части d-h-i- Округленное число □«' будет
иметь значение
□а' = ± (27=-л aJrJ + 0 -47)
где
1 при
0 при aLh~i < г/2.
Когда 7 = 0, происходит округленна к нулю, в -противном
случае — от нуля. Значение максимума погрешности при чет-
ном г есть
max Д = 2-1 r~h.
а для нечетного г (
max Д = 2~l r~h(l + r~l) — г-11-*.
В случае равновероятного появления чисел разных знаков
и равномерного распределения вероятностей появления раз-
личных значений „хвоста“ числа а' математическое ожидание
погрешности округления равно нулю. Однако при округлении
чисел одного знака значение Д отлично от нуля. Так, напри-
мер, если «'>0, то при четном г имеем
Д = — 2-1 г-*-*, (1.48)
а при нечетном г
д = 2-! г-- г1-').
Следовательно, при округлении, чисел одного знака данный
способ даст систематические ошибки округления, которые осо-
бенно заметны при нечетном основании системы счисления г.
Дисперсия случайной величины Д, при округлении равно-
вероятных чисел разных знаков равна при четном г
£>=12~’ г-2Л(1 +2r-2Z).
Когда округляем числа одного знака, дисперсия определяется
выражением (1.43) вне зависимости от того, четно или нечет-
но г. Таким образом, в отношении значений параметров max Д
и D метод округления по дополнению лучше метода округле-
ния к нулю для несимметричной базы и достаточно близок
к характеристикам этого метода для симметричной базы. Един-
ственным его недостатком является наличие систематических
ошибок при округлении чисел одного знака. Это вызвано тем
обстоятельством, что округление особенно неточно произво-
дится, когда значение отсекаемой части в точности равно
половине единицы младшего сохраняемого разряда. В целях
устранения данного недостатка произведем некоторые усо-
вершенствования в методе округления по дополнению.
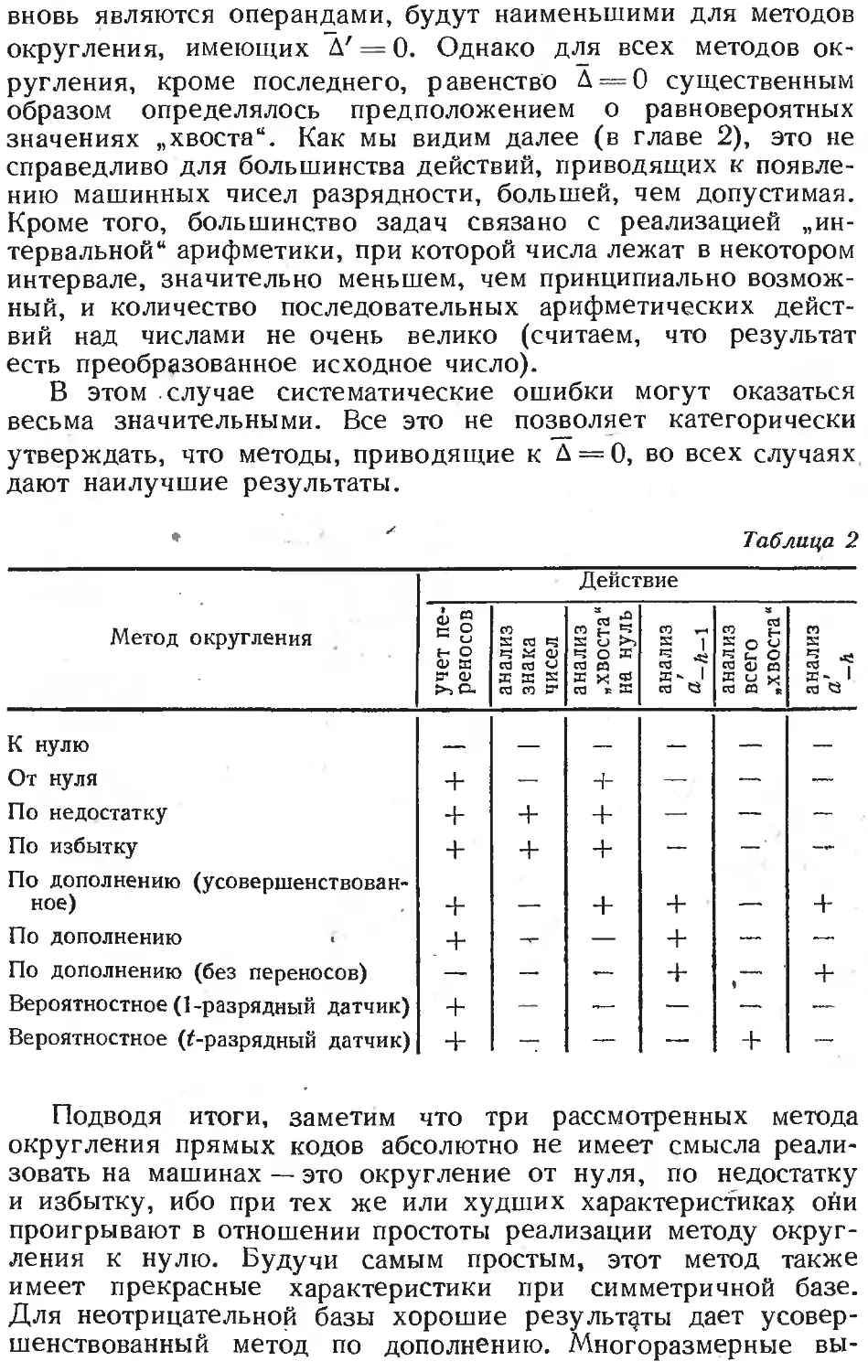
5°. Усовершенствованное округление по дополнению.
Пусть решение о коррекции сохраняемой части числа а' при-
нимается на основе анализа значения всех разрядов отсекае-
мой части, а не только старшего разряда, как ранее. Обоз-
начим значение отсекаемой части числа а' как а*, и пусть
1 + (—1) J, т. е. для четного имеем <р = 0,
иначе <р=1, тогда для четного г параметр -у в выражении
(1-47) определяется по следующим правилам:
1, если а' > 2-1 r~h,
<р, если а* = 2-1 r~h,
0,’ если а* < 2-1r-ft.
При нечетном г правила определения 7олее просты
1, если а' > 2-1 r~h,
О, если а' < 2-1г~й.
Данный способ округления при нечетном г снижает значе-
ние тахД до величины 2~'— r-z), а при четном г эта
величина остается прежней: 2-1/—h. Главное его достоинство —
это сведение к нулю систематических— ошибок, ибо как при
четном, так и при нечетном г теперь Д = 0. Для четного г
это равенство получено в предположении, что вероятность
появления четного или нечетного значения цифры младшего
разряда сохраняемой части одинакова, т. е. значения «= 0
и <р = 1 равновероятны. Таким образом, усовершенствованный
метод дает теперь хорошее округление (Д = 0) в случае чисел
одного знака как для четных, так и нечетных систем счисле-
ния. Надо отметить, что в отличие от симметричных кодов
этого удалось достичь за счет усложнения правила округле-
ния, что приводит к определенным дополнительным времен-
ным и материальным затратам.
В случае четных значений г правила формирования значе-
ния параметра 7 могут быть упрощены. Здесь достаточно
знать значение не всей отсекаемой части, а только старшей
отсекаемой цифры и значение параметра ф, который может
быть либо единицей либо нулем. Когда все разряды отсекае-
мой части, кроме старшего равны нулю,.ф = 1, а в противном
случае ф = 1. Теперь мо&но утверждать, что
1, если a-h-\ > 2-1 г или = 2-1 гф,
<Р, если = 2-1 гф,
0, если а_/г-1 < 2-1 г.
(1-49)
Действительно, как это следует .из (1.49), для определения
добавки в младший разряд не надо считать значение отсе-
каемой части числа а', достаточно лишь проанализировать
значение старшей цифры отсекаемой части и параметра ф.
Пример 1.9. Пусть г = 2 и параметры округляемых чисел таковы: п =
= 3, h = —1 и требуется их округлить до целых чисел: й = 0 и t = 1. При
обычном округлении по дополнению чисел +0,5, +1,5, ±2,5, ..., +3,5 мы
получим числа +1, +2, +3, +4 соответственно. Если же используем усо-
вершенствованный метод округления по дополнению, то получим для исход-
ных чисел следующие результаты: +0, ±2, +2, +4. В первом случае знак
погрешности округления чисел одного знака сохраняется, а во втором — ме-
няется. Следовательно, более правильное округление достигается при ис-
пользовании метода усовершенствованного дополнения.
6°. Округление без распространения переносов. Добавле-
ние единицы в младший разряд может вызвать распростране-
ние переносов при коррекции оставшейся части числа а', и их
учет требует, чтобы коррекция выполнялась как сложение
двух чисел. Затраты на это дополнительное сложение зачастую
рассматриваются как чрезмерная плата за округление, и по-
этому задача отыскания метода округления без распростра-
нения переносов весьма актуальна. Заметим, что перенос из
младшего разряда может выйти только в том случае, когда
a,-h — г — 1. Очевидно, если при a_h = г—1 отменить воз-
можную коррекцию, то распространения переносов не будет.
Будем формировать параметр -у в соответствии со следую-
щими правилами при четном г.
<р, если > 2-1 г,
I = ]
О, если d-h-x < 2-1 г.
Когда положительные и отрицательные числа равновероятны,
математическое ожидание погрешности есть нуль, но для
чисел одного знака нетрудно найти при равновероятной чет-
ной-нечетной цифре что
д=4-1г-Л(1 _ 2г-<).
Математическое ожидание будет равно нулю теперь только
в том случае, если г = 2 и /=1, т. е. в случае двоичной сис-
темы счисления, когда длина отсекаемой части есть один
разряд. Оказывается, что только в этом, очень важном с прак-
тической точки зрения случае округЛение происходит пра-
вильно, без накопления систематических ошибок. Само округ-
ление производится очень просто — лишний разряд отбрасыва-
ется и если а_/г=0, то этому разряду приписывается значение
a_h-\, в противном случае он остается без изменений. Следо-
вательно, округление заключается в логическом сложении
младшего разряда сохраняемой части и сформированного по-
правочного коэффициента <р. Дисперсия случайной величины
в данном методе округления определится как
D = 8-1 r-2ft(l - l,5r~z + r~2').
Отсутствие распространения переносов при округлении
делает данный способ особенно перспективным в тех случаях,
когда от машины требуется повышенное быстродействие,
правда, максимальная величина погрешности округления сос-
тавит — Н).
7°. Вероятностное округление. До сих пор решение о кор-
рекции сохраняемой части округляемого1 числа а' мы прини-
мали на основе анализа значений некоторых разрядов этого
числа, причем данный анализ базировался на детерминирован-
ных правилах, т. е. правилах, не допускающих получения
случайного, вероятностного решения. В то же время методы
округления, основанные на вероятностных процессах, весьма
очевидны, и их стоило бы рассмотреть.
Пусть округление заключается в том, что „хвост" округ-
ляемого числа отбрасывается, а оставшаяся часть корректи-
руется обычным путем — добавлением единицы в младший
разряд. Однако выработка этой коррекции будет теперь про-
изводиться по случайному закону с некоторой вероятностью
р0. Будем считать, что эта вероятность не зависит от значения
отбрасываемой части, т. е. постоянна. Тогда
Д'== — Pgr~h..
Отсюда
тахеД =^г-Л.
Математическое ожидание случайной величины Дг есть
\ - Por~hY
Считая, что значения отбрасываемой части распределены рав;
номерно для положительных и отрицательных чисел, т. е.
р (Д,) = 2-1 получим, что Д=0. Для чисел же одного знака,
например а' > 0, имеем
д==-г-л(ро-4-+4-г-0- >
Когда вероятность р0 = 2-1 (1 — г~*), Д = 0. Если вероятность
добавления единицы в младший., разряд не зависит от длины
„хвоста" и равна просто 2-1, то имеем Д = — 2-1 r~h~4. Сле-
довательно, значение Д в точности совпадает с величиной Д
для метода округления по дополнению в случае чисел одного
знака при четном г (см. (1.48)), т. е. за устранение анализа
старшей цифры „хвоста" пришлось заплатить удвоением вели-
чины тахД. Зайетим, что для ликвидации систематических
ошибок надо сделать pQ зависимым от длины „хвоста", однако
значение его никак не сказывается на величине р0.
Сейчас рассмотрим метод округления, в котором значение
вероятности коррекции р0 будет зависеть от значения отсекае-
мой части [6].
Пусть в машине имеется генератор /-разрядных случайных
чисел с квазиравномерным распределителем в интервале 0 -ь
1—г~1. Для округления числа а', имеющего „хвост" дли-
ной t разрядов, вначале сравним значение „хвоста" (а*) со
случайным числом 2~hR. Будем считать, что .
( 1 при R < as2ft,
[ 0 при R'^a^2.h.
При этом вероятность «коррекции оказывается равной 2Лаж.
Значение максимума модуля погрешности составит величину
ft(l — г~1). Величина математического ожидания в данном
случае с учетом р0 = 2~k^ltj==ia-h-j r~h~] составит
А = Si=ip(Az) («1 - <) = 0.
Следовательно, математическое ожидание равно нулю вне
зависимости от длины отбрасываемого „хвоста" и, что главное,
вне реального распределения значений этого „хвоста", т. е.
независимо от значений р(Д,). Недостатком данного, метода
является необходимость сравнения случайного числа R с от-
брасываемой частью числа а', что при больших значениях t
равносильно операции алгебраического сложения /-разряд-
ных чисел.
Произведем обзор рассмотренных методов округления. За
исключением метода округления к нулю все остальные тре-
буют выполнения тех или иных действий для своей реализа-
ции в цифровой машине. Среди этих действий учет распрост-
ранения переносов и анализ всех разрядов отсекаемой части
числа представляются наиболее сложными. В табл. 2 приве-
дены все действия, которые необходимы для реализации конк-
ретного метода округления. Знаком „ + “ отмечена необходи-
мость данного действия, а знаком „ — “—его отсутствие. Как
видно, самым простым образом реализуется округление к нулю,
когда не требуется ни дополнительных затрат' времени, ни
оборудования.
При ответе на вопрос, какой метод округления приводит
к более точным вычислениям, надо учитывать, что на практике
для нас иногда важнее всего гарантированная точность, на-
пример, при выполнении деления с помощью умножения или
вычисления элементарных функций с помощью умножения
и деления, а иногда и результатов многоразмерной задачи
без накопления систематических ошибок. Гарантированная
точность будет определяться величиной тахД, которая близка
к половине единицы младшего разряда машинного числа
только для трех методов округления по дополнению, а во
всех других случаях близка к единице.
Систематические ошибки при достаточно длительных вы-
числениях, когда получаемые, результаты округляются, а затем
вновь являются операндами, будут наименьшими для методов
округления, имеющих = 0. Однако для всех методов ок-
ругления, кроме последнего, равенство Д = 0 существенным
образом определялось предположением о равновероятных
значениях „хвоста". Как мы видим далее (в главе 2), это не
справедливо для большинства действий, приводящих к появле-
нию машинных чисел разрядности, большей, чем допустимая.
Кроме того, большинство задач связано с реализацией „ин-
тервальной" арифметики, при которой числа лежат в некотором
интервале, значительно меньшем, чем принципиально возмож-
ный, и количество последовательных арифметических дейст-
вий над числами не очень велико (считаем, что результат
есть преобразованное исходное число).
В этом случае систематические ошибки могут оказаться
весьма значительными. Все это не позволяет категорически
утверждать, что методы, приводящие к Д = 0, во всех случаях
дают наилучшие результаты.
Таблица 2
Метод округления Действие
учет пе- реносов анализ знака чисел и « £ s о ьз о К Л И я к « Л * К анализ a-h-\ анализ : всего яхвоста“| анализ а’ Л -Л 1
К нулю — — — — — —
От нуля + — + — — —
По недостатку + + + — — —
По избытку + + + — —
По дополнению (усовершенствован- ное) + — + + —~ +
По дополнению + -г- — + — —
По дополнению (без переносов) — — — + +
Вероятностное (1-разрядный датчик) + — — — — —
Вероятностное (^-разрядный датчик) + — — — + —
Подводя итоги, заметим что три рассмотренных метода
округления прямых кодов абсолютно не имеет смысла реали-
зовать на машинах — это округление от нуля, по недостатку
и избытку, ибо при тех же или худших характеристиках они
проигрывают в отношении простоты реализации методу округ-
ления к нулю. Будучи самым простым, этот метод также
имеет прекрасные характеристики при симметричной базе.
Для неотрицательной базы хорошие результаты дает усовер-
шенствованный метод по дополнению. Многоразмерные вы-
числения могут быть выполнены с минимальными система-
тическ1ули ошибками при использовании метода вероятност-
ного округления с /-разрядным датчиком случайных чисел.
Наконец, когда округление требуется произвести в наикрат-
чайшее время, при положительной базе к лучшим результатам
приводит метод округления по дополнению без распростра-
нения переносов. По-видимому, было бы целесообразно
реализовать в машине два-три метода округления с возмож-
ностью выбора наилучшего для текущего задания.
§ 5. ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ
В ДРУГУЮ
Будем считать, что число а дано или найдено, если
известна его запись в некоторой системе счисления R. Пере-
водом числа из системы счисления R в систему счисления Р
называется задача изображения заданного числа в системе
счисления Р. Необходимость перевода чисел возникает всякий
раз, когда в машине используется система счисления, отлич-
ная от той, в которой заданы исходные данные. Естественно,
наиболее важной является задача перевода из обычной обще-
принятой десятичной системы счисления в ту систему счис-
ления, в которой работает машина, и обратно. Реализация
перевода связана с выполнением ряда арифметических и логи-
ческих действий с заданными числами и поэтому требует
определенных затрат оборудования и времени. В большинстве
случаев процент действий, связанных с переводами, очень
невелик по сравнению с полным объемом операций, необходи-
мых для решения поставленной задачи. Это дает основание
выбирать систему счисления для цифровой машины, игнори-
руя проблему перевода и руководствуясь при этом другими
соображениями (например, быстродействием и экономичностью
реализации системы команд машины). Однако для некоторых
типов цифровых машин, например настольных калькуляторов
и бухгалтерских машин, для которых характерна поопера-
ционная обработка больших массивов чисел, выбор системы
счисления, исходя из требования наибольшей простоты пря-
.мого и обратного перевода ее с десятичной системой, явля-
ется обязательным условием.
Важным моментом реализации перевода чисел из одной
системы счисления в другую является вопрос о том, в какой
системе счисления должны быть выполнены все необходимые
для перевода действия. Обычно эти действия реализуются
в той же системе счисления, в которой работает машина. При
этом появляется возможность осуществить достаточно просто
перевод путем выполнения специальной программы (микро-
программы) перевода или реализовать его аппаратурными
средствами. В дальнейшем, если специально не оговорено,
будем считать, что перевод осуществляется во „внутренней*
системе счисления, т. е. в той системе, в которой работает
процессор машины.
1°. Перевод чисел с естественной запятой. Для произ-
вольных систем счисления алгоритмы перевода весьма разно-
образны, поэтому в целях конкретности в этой главе ограни-
чиваемся случаем натурального кода и представлением чисел
в форме с естественной запятой, т. е. когда заданное число
а и переведенное число b представлены в виде (1.3), а их
количественные эквиваленты определены соотношением (1.7).
Систему счисления с основанием г будем считать „внутрен-
ней*, а с основанием р —„внешней*. Тогда проблема перево-
да сведется к решению двух задач:
для числа а, заданного в р-ичной системе счисления,
найти его изображение в r-ичной системе счисления,
для числа' а, заданного в r-ичной системе счисления,
найти его изображение в р-ичной системе счисления.
Задача 1. Пусть в машине определены в r-ичной системе
счисления такие операции, как алгебраическое сложение,
умножение й деление; тогда имеется простая возможность
осуществить перевод числа а, заданного в р-ичной системе
счисления в г-ичную.
Для этого достаточно значения всех цифр а} и число р
заменить их представлениями в r-ичной системе счисления
и провести все требуемые по формуле (1.7) операции в этой
же системе счисления. Если полином (1.7) вычислять по схе-
ме Горнера, то для реализации перевода потребуется 1-J-&+A
умножений и сложений, причем умножение всегда произво-
дится на константу р в r-ичном изображении. Несмотря на
кажущуюся простоту реализация данного метода наталкива-
ется на ряд трудностей. Одна из них связана с тем, чтб
числовые эквиваленты цифр Оу и величина р не всегда мо-
гут быть точно изображены в системе счисления с осно-
ванием г. Так, в системе счисления с целым положительным
основанием и .положительным алфавитом нельзя изобразить
отрицательные числа, а в системе счисления, алфавит которой
не содержит нуля (например, двоичная система с алфавитом
-Н, —1), нельзя точно изобразить нуль и четные числа. Дру-
гой неприятный момент связан с тем, что не всегда дробь
может быть точно записана в виде конечной r-ичной дроби,
и тогда невозможно осуществить точный перевод, т. е. такой
перевод, при котором достигается равенство а = Ь. Однако
в ряде случаев эти трудности удается преодолеть достаточно
просто. Рассмотрим эти случаи подробно.
1°.1. Пусть p = r® (Р — целое положительное) и обе сис-
темы счисления имеют либо симметричные, либо неотрица-
тельные базы. В этом случае цифра р-ичной системы счисле-
ния может быть точно представлена конечным числом т
разрядов г-ичной системы счисления (см. § 1), т. е. a,j =
= 2Х=о btjr1. Если т = р — 1, то число различных значений, ко-
торые может принимать сумма в правой части, есть г₽, т. е.
р. Следовательно, каждая цифра р-ичной системы счисления
может быть представлена группой из р разрядов г-ичной
системы счисления, и тогда можно записать:
а = akpk + ... + aGp° 4- ... + a_hp~h = bp_i,k г?<*+1)-1 4* ...
... -|-+ • • • 4*bp—i,or₽-14~ ... 4*bofi4- ...
... + 4- ... + bo,_hr-w = 2ВДГ V = b.
Следовательно, перевод осуществляется простой заменой цифр
р-ичной системы счисления их г-ичным изображением.
Пример 1.10. В шестнадцатиричной системе счисления задано число
а = ABCD, Требуется перевести его в обычную двоичную систему
счисления.
Поскольку р = 24, то перевод осуществим следующим образом: а —
= (1010) (1011) (1100) (1101), (0001) (1110). Отсюда Ь= 1010 1011 1100 1101,
0001 п2.
Пример 1.11. В девятиричной системе счисления с симметричной ба-
зой, положительные цифры которой изображаются арабскими цифрами,
а отрицательные арабскими цифрами с чертой сверху, дано число а =
= 3241,02g. Требуется его перевести в троичную систему счисления
с симметричной базой —1, 0, 1. Поскольку р = З2, то а = 3241,02д =
= (ТО) (fl) (ТТ) (ОТ), (00) (17), отсюда b ="01 ТПо!,0011g.
1°.2. Пусть р₽= г(₽ — целое положительное) и базы обеих
систем счисления либо симметричны, либо неотрицательны.
В этом случае перевод очень прост. В качестве цифры Ьй
искомого числа b выбирается совокупность разрядов ар-\ ... а0
заданного числа а, а в качестве цифры bh берется
совокупность ... ар,.. В качестве группы, соответст-
вующей цифре Ь-\ искомого представления, берутся разряды
а-!, ... а-p, а в качестве цифры b-i, группа
d-i-pfi-j) ... a—pi. Если самая левая или самая правая группы
разрядов исходного представления окажутся не полными, то
они дополняются соответственно слева или справа необходи-
мым числом нулей. Перевод осуществляется простой заменой
каждой группы соответствующей цифрой в г-ичной системе
счисления.
I Пример 1.12. Двоичное число а~ 110110111,01011требуется перевести
в шестнадцатиричную систему счисления с неотрицательной базой.
Здесь р = 2 и г = 24. Поскольку а = 1 (1011)(0111),(0101)- 11g, то Ъ =
= (0001) (1011) (0111), (0101) (П00)16; b = 1В7,9£>16.
Пример 1.13. Из троичной системы счисления с симметричной базой
перевести в девятири^ную систему счисления также с симметричной ба-
зой число а = 11001,11011g, тогда а = 1 (10) (01)^(Н) (01) 1g. Отсюда 6 =
= (01) (10) (01), (11) (01) (10)3 = 13Т,213д.
1°.3. Пусть р = г и база р-ичной системы неотрицательна
а г-ичной системы симметрична. В этом случае р = 2t + 1 и t
цифр системы счисления с основанием р совпадают с t циф-
рами г-ичной системы счисления. Остальные цифры в задан-
ной системе счисления представляются суммой двух цифр
г-ичной системы счисления. Отсюда ясен алгоритм перевода —
вначале- запись цифр р-ичной системы счисления через цифры
г-ичной системы, а затем выполнение действия сложения
в системе счисления с симметричной базой.
Пример 1.14. Дано число в троичной системе счисления с неотрица-
тельной базой а = 211,12g. Требуется перевести его в троичную систему
счисления с симметричной базой. Перевод осуществим следующим образом:
а = (1. + 1)-32 Ч- 1-31 + 1-3» + 1.-3-1 + (1 + 1)-3—2 = 1- 33— 1-31— 1-30-
- 1-3“* — 1-3~2. Отсюда b = 1011,11g.
1°.4. Пусть р — г и база р-ичной (внешней) системы счис-
ления симметрична, а г-ичной (внутренней) неотрицательна.
В этом случае каждая отрицательная цифра ау- заданной за-
писи заменяется разностью 0 — ар, а затем производится
вычитание в системе счисления с неотрицательной базой.
Пример 1.15. Число а = 1ГЬ111,Г1д, заданное в троичной системе счис-
ления с симметричной базой, перевести в троичную систему счисления
с неотрицательной базой. Так как а=1-35—1-34—1-32—1-31-J-1-30 —
^-l-З'1— 1-3~2 = 1-31 4-2-33+ 1.З^ + г-З! + ЬЗ^+г-З-2, то 6=12120,12g.
1°.5. Пусть р += г₽ (Р — целое число) и базы обеих систем
счисления неотрицательны. Рассмотрим вначале два частных
случая.
А. Положим в выражении (1.3) Л = 0, т. е. исходные чис-
ла есть целые. Как мы знаем, произвольное положительное
целое число может быть точно изображено в позиционной
системе счисления с основанием р и неотрицательной базой.
Следовательно, целые числа принципиально можно перевести
точно. Техника перевода также известна — значения всех
цифр и значение р изображаются через значения цифр сис-
темы счисления г, а затем подставляются в соотношение
(1.7), отвечающее заданному числу. Выполняя необходимые
действия умножения и сложения в г-ичной системе счисле-
ния, получаем результат в виде полинома по степеням г.
Коэффициенты при степенях г1 и есть искомые цифры.
Пример 1.16. Перевести число а = 1979 из десятичной системы счис-
ления в шестнадцатиричную. Поскольку а = 1 • 103 + 9-102 + 7-101 +9-10°,
то b= 1-Л3 + 9-Л2 + 7-Л + 9 = 3£816 + 38416 + 4616 + 916 и b = 7BBj6-
В. Положим теперь k=— 1, т. е. выражением (1.3) дана
запись правильной /2-ичной дроби. Действуя как и раньше,
попытаемся найти точное изображение заданной дроби в г-ич-
ной системе счисления в виде полинома отрицательных сте-
пеней г, имеющего конечное число членов. Это удастся
сделать, если дробь р~1 может быть точно представлена
в виде конечной г-ичной дроби. В пробивном случае точный
перевод невозможен и встает вопрос о допустимой точности
перевода, а следовательно, о длине слова в г-ичной системе
счисления.
Определить необходимую разрядность можно исходя из
требования равноточности представления заданной дроби
во внешней и внутренней системах счисления [13]. В случае
„хорошего** приближения для чисел с естественной запятой
абсолютная величина погрешности представления не превос-
ходит 2“1р-й. Естественно потребовать, чтобы погрешность
представления этой же дроби в r-ичной системе счисления
не превышала величины 2-1г_/ и была близкой к 2_1р-й, т. е.
p~h = г~*, откуда
t^hAogrP. (1.50)
После перевода дроби р~1 в г-ичную систему счисления
перевод дроби а может быть осуществлен по схеме, приня-
той для перевода целых чисел (только вместо степеней р1
будет степень (Р'1)')- Однако, поскольку перевод величины
р-1 произведен приблизительно и число умножений при пе-
реводе велико, то может накопиться значительная погреш-
ность. Более точной оказывается следующая процедура пе-
ревода Т.
Т 1. Умножим заданную дробь на ph.
Т 2. Переведем полученное целое число в г-ичную систе-
му счисления.
Т 3. Разделим полученное число на рк.
Т 4. Полученный результат округлим методом дополнений
до t верных знаков.
Пример 1.17. Дано р = 2, г = 10 и а = 0,101012- Найти изображение
этой дроби в десятичной системе счисления. Из соотношения (1.50) уста-
навливаем, что достаточно ограничиться двумя десятичными знаками. Вна-
чале заменяем дробь целым числом а' = 10101g, затем находим его деся-
тичное представление Ь' = 21 jq, b' = 1 -24 + 1 -22 4- 1 -2°. Теперь делим полу-
ченный результат на 25 = 32, округляя частное до двух верных цифр после
запятой: 21/32 = 0,66, т. е. b = 0,66|д.
Когда в г-ичную систему счисления переводится число,
имеющее целую и дробную части, то один из возможных
путей перевода состоит в раздельном переводе целой и дроб-
ной частей и сложении полученных результатов. Однако
можно использовать также процедуру Т, описанную выше.
Пример 1.18. Перевести число а = 4;62 из десятичной системы счис-
ления (р = 10) в двоичную (г = 2). Для данного случая h = 2, тогда соглас-
но (1.50) 1к6,6, следовательно, выбираем t — 1. Умножаем число 4,62
на 102. Переводим целое число 462 в двоичную систему счисления а' =
= 462jq = 100-(1010)24-110-10104-10 и b'= 1110011 10g. Затем разделим полу-
ченный результат на 102 = IIOOIOO^ с точностью до 7-го знака после запя-
той; получаем частное q = 100,1001111 и остаток, равный 100100. ^Поскольку
остаток больше половины делителя, то к полученному результату добавляем
2—1. Окончательно получаем Ь = 100,1 OlOOOOg.
. Пример 1.19. Перевести число а = 100,101^ из двоичной системы (р — 2)
счисления в десятичную (г = 10). Для данного случая h = 3, тогда выбираем
t = 3. Умножаем а на г7. Переводим целое число ЮОЮЮООО^ в десятичную
систему счисления 1 -2® + 1 -2е + 1 -24 + 1 =592. Полученный результат делим
на 2* = 128 и оставляем три знака после запятой: b = 592: 128 = 4,625, т. е.
Ь = 4,62510.
1°.6. Пусть p = r± 1. В том случае, когда основания сис-
тем счисления отличаются друг от друга на единицу, т. е.
когда p = r+ 1, перевод может быть упрощен по сравнению
с классической схемой 1°.5. Это объясняется тем, что резуль-
тат умножения целого числа a=2*=o#z-p‘ на число р ± 1
может быть представлен как число b = где bh 0
ik2*определяется по.рекуррентным формулам [21]
i Ci+1 “1“ [^Z ± ^f]p> Co == 0-
Здесь считается, что для целых чисел аир справедливо
соотношение а~ [а]рр + {а}р, т. е. {а}р — наименьший неотри-
цательный вычет по основанию р. Замена операции умножения
поразрядной операцией алгебраического сложения открывает
путь к простой аппаратурной реализации перевода в „сосед-
ние“ системы счисления.
Пример 1.20. Число а = 2345g, заданное в девятиричной системе счис-
ления, перевести в десятичную систему счисления. Так как а = ((2-9 4- 3) X
X 9 + 4)-9 + 5, то на первом шаге имеем Cj = 2 + [3 — 2] до = 2. В качестве
с0 на каждом шаге берется очередная цифра исходного числа, при z = 1
выбираем c0 = zzft_j. Соответствующие значения будут &j = 2 и &0= 1. На
вторбм шаге с0 = 4 и ct = 1 + [4— 1]10 = 1, с2 = 2 + [1 — 2J10 = 1, значения-
ми b0, bi и Ь2 будут соответственно: Ьо = {4—1}|д = 3, br = {1—2) до = 9,
b2 = {1—0)iq= 1. На третьем шаге вычисляется значение 193-9+5, т. е.
здесь с0 = 5, zzq = 3, = 9 и a., = 1, но тогда сг = 3, Ci = 8 и с3 = 1 и Ьо =
= {5-2}10 = 2; />1 = {3-9)10 = 4; Ь2•= {8- 1} 10 = 7 и Ь3 = {1 0) 10 =
= 1. Перевод закончен и b= 1742] д.
1°.7. Пусть р =/= г и одна из систем имеет неотрицательную
базу, а другая — симметричную. Перевод в таких системах
счислейия может быть реализован как перевод через проме-
жуточную систему счисления по известным правилам.
Допустим, число задано в р-ичной системе счисления
с неотрицательной базой, а его требуется перевести в систе-
му счисления с основанием г и симметричной базой. Такой
перевод осуществляется поэтапно. На первом этапе произво-
дится перевод в систему счисления с основанием г, но с не-
отрицательной базой по правилам, указанным в п. 1°.5. Затем
в соответствии с правилами 1°.3 реализуется перевод также
в r-ичную систему счисления, но с симметричной базой.
Рассмотрим теперь случай, когда задано число в /2-ичной
системе счисления с симметричной базой, а надо его пере-
вести в r-ичную систему и с положительной базой. Тогда на
первом этапе выполняется перевод в /2-ичную систему, но
с положительной базой по правилу 1°.4, а уже на втором
этапе осуществляется перевод из р-ичной системы в г-ичную
(правило 1°.5).
Пример 1.21. В пятиричной системе счисления с симметричной базой
задано число а = 210,12g, надо перевести его в четверичную систему счис-
ления с неотрицательной'базой.
1-й этап: а = 2-52 4- 1-5 4-0-5<> 4-(0—1)-5-1 + (0 — 2)-5“2 = 2-52 4-
+ 0-51 + 4-5° + 3-5“1 4- 3-5~2. Отсюда а' = 204,33g.
2-й этап: имеем р = 5, г = 4, h = 2, тогда t х 2,35, выбираем t = 3.
Умножаем число а' на 52. Переводя по известным правилам целое число
а" = 20433g в четверичную систему счисления, получим а" = 2(1-414-
4- 1-4°)* 4- (1 -41 4- 0.40) - (1-41 4-1.40)24-3(1.41 4-|1-40) 4-3= 1-45-|-1.4*4-
4-1-43 4- 1-42 4- 2-41 -|-0-4°. Поскольку а" = Ь', то 6' = 1111204. Теперь
полученный результат разделим на 52, т. е. на целое число с =|1214> с точ-
ностью до третьего знака. Получим частное q =312,232. Остаток равен 2.
Остаток меньше половины делителя и поэтому окончательный итог есть
b = 312,232^ Заметим, что количественный эквивалент заданного числа есть
а = 54,72, а переведенного Ь = 54,718.=
Задача 2. Дано число а, представленное во внутренней
г-ичной системе счисления. Найти его изображение во внеш-
ней р-ичной системе счисления. Вновь будем считать, что обе
системы позиционные с положительными основаниями и имеют
либо неотрицательную, либо симметричную базу. Действия,
необходимые для перевода, выполняются во внутренней сис-
теме счисления.
В случаях р = ге и ре = г перевод осуществляется по пра-
вилам 1°.2 и 1°.1 задачи 1 соответственно. Если же р~г
и одна система счисления имеет симметричную базу, а дру-
гая — неотрицательную, то правила перевода такие же, как
1°.3 и 1°.4 задачи 1.
Пусть теперь р =/= г* (е — целое число) и базы обеих сис-
тем неотрицательны. Поскольку для перевода произвольного
числа достаточно перевести отдельно его целую и дробную
части, то рассмотрим эти случаи отдельно.
1°.8. Пусть дано целое число а в системе счисления, с ос-
нованием г, и требуется перевести его в систему счисления
с основанием р. Количественный эквивалент заданного в виде
(1.3) числа а определен выражением (1.7). Поскольку а —
целое, то оно может ыть точно изображено в /2-ичной сис-
теме счисления конечным числом разрядов слова b и
a = b^=^objpi. (1.51)
Наша задача — определить цифру Ь} для каждого разряда.
Разделим обе части равенства (1.51) на р и приравняем между
собой полученные целые и дробные части результата: '

Отсюда значение младшей искомой цифры есть
т. е. является остатком от деления а на р. Обозначим целое
число | как и применим к нему описанную процедуру
для определения следующей искомой цифры. Полагая с№=а,
выполним перевод из г-ичной системы в р-ичную в соответст-
вии с рекуррентными соотношениями
, ( 1
bi = P\---г,
'• р ’ (1.52)
Г aW 1
г«(/+1) = _е_ 1, 2, ...
L р J
Признаком окончания процесса служит равенство «w+1) = 0.
Пример 1.22. Перевести десятичное число 'а = 1978 в шестнадцатирич-
ную систему счисления.
Применяя (1.52) и выполняя действия в десятичной системе счисления,
получаем
. а(0) = 1978= 123.16 + 10; Ьо = А;
а(1) = 123 = 7-16 + 11; bt = B;
а(2) = 7 < 16, Ь2 = 7,
следовательно, b = 7£Mjg.
Полученный результат точно такой же, как и при выпол-
нении аналогичного задания в примере 1.16. Принципиальная
разница решения примеров 1.16 и 1.22 состоит в средствах,
исйользуемых для достижения цели. Перевод в примере 1.16
базируется на использовании действий сложения и умножения
в шестнадцатиричной системе счисления, в примере 1.22 —на
использовании операции деления в десятичной системе счис-
ления. Реализация же этих действий в указанных системах
счисления обычно существенно отличается по времени и по
требуемым средствам.
1°.9. Пусть теперь А=—1, т. е. записью (1.3) задана пра-
вильная дробь в г-ичной системе счисления, надо найти ее
представление в р-ичной системе счисления в виде b =
= b-\b_2 .... Мы ранее говорили о том, что точный перевод
возможен не для всех дробей, следовательно, вначале необ-
ходимо определить наименьшее число разрядов, при котором
сохранится введенная точность представления числа a 2~xr~h.
Исходя из равноточное™ представлений, получим, что число
разрядов переведенной дроби должно удовлетворять нера-
венству
t>h\ogpr. (1.53)
Искомые значения цифр b-j могут быть определены из ре-
куррентных соотношений,
&-J-1 =
д-О-Ы) = {а№р\, 7 = 0, 1, 2, ...
Здесь, как и ранее, а(°) = а. Процесс будет продолжаться,
пока не определятся t разрядов искомого числа, т. е. 1.
Если окажется, что > 2-1, то погрешность результата
будет больше 2~1p~t. Добавление числа р~( к полученному
результату позволит устранить данный недостаток, но надо
иметь в виду, что данное сложение придется выполнить
в /7-ичной (внешней) системе счисления, в то время как ум-
ножение выполнялось во внутренней системе счисления. Один
из возможных путей выхода из этого положения состоит
в начальном добавлении числа 2~1Р“< к заданному числу а,
тогда
6Z<°) — {а + 2~lp~t], b0 = [а + 2~ 1р~*],
где b0 =OV1, есть целая часть искомого числа. Далее выпол-
няется обычная процедура.
Пример 1.23. Десятичную дробь а = 0,21 перевести в двоичную систе-
му счисления. Здесь г — 10, р = 2, h = 2, тогда
t = 2 log210 ss 6,6,
выбираем t = 7. Определяем целую и дробную части числа а = 0,21 +
+ 2~8, получаем Ьо = 0 и й; 0,2139;
2а(0) = 0,4278, = 0; 2а(,) = 0,8556, Ь_2 = 0;
2Д2) = 1,7112, &_3 = 1; 2а(3) = 1,4224, b_4 = 1;
2а(4) = 0,8448, Ь_5 = 0; 2а(5) = 1,6896, Ь_ъ = 1;
2а^ = 1,3792; b_7 = 1, следовательно, b = O.OOHOl^-
Количественный эквивалент переведенного числа b = 0,2109.
Для переводапроизвольного числаможно перевести от-
дельно целую и дробную части по известным правилам. В тех
случаях, когда желательно единообразие действий, необходи-
мых для перевода, заданное число вначале либо делят на ре
(е— целое положительноё число) так, чтобы ар~е < 1, либо
умножают на р*, где t определено из (1.53), и округляют
ар* до ближайшего целого числа. Далее полученную дробь
или целое число переводят в /2-ичную систему счисления.
Для сохранения количественного эквивалента найденный ре-
зультат (число в р-ичной системе счисления) надо умножить
или разделить соответственно на ре или р*. Фактически для
этого надо перенести запятую на е разрядов вправо в первом
случае и отделить запятой i цифр справа во втором случае.
Пример 1.24. В десятичной системе счисления задано число а = 4,62»
перевести его в двоичную систему счисления. Из соотношения (1.53) нахо-
дим, что £ > 2 log2 10 ss 6,6. Выбираем t = 7, умножаем 4,62 на 21 и округ-
ляем результат, получим 591 и переводим это число в двоичную систему
счисления:
- ат =295-2+ 1, b0= 1; а(1) = 147-2 + 1, bx = 1;
Д2> = 73‘2 + 1, 62=1;. а(3) = 36-2 + 1, &3=1;
а(4) = 18-2, = 0; a(S)=9-2, b& = 0;
a(6) = 4-2+1, &6=1; a(7)=2-2, />, = 0;
a(8) = 2, bs = 0; a(9) = 1, b9 = 1.
Получим b' = 1001001 Illg и окончательно b = 100,1001111^- Количественный
эквивалент этого числа есть b = 4,617.
С целью сокращения количества действий, необходимых
для перевода из г-ичной системы в р-ичную, можно вначале
осуществить перевод в ре-ичную систему счисления, а затем
из ре- в р-ичную, чТо, как мы видели, выполняется достаточ-
но просто.
Пример 1.25. Из десятичной системы в двоичную требуется перевести
число а = 4,62. Переведем заданное число вначале в шестнадцатиричную
систему счисления. Имеем t >21ogi610K 1,66. Выбираем t = 2. Умножаем
4,62 на 162 и округляем полученный результат, получим 1183. Далее пере-
водим это число в шестнадцатиричную систему счисления: а^°' = 73-16 +
+ 15, b0 = F, aw = 4-16 + 9, bx = 9, а(2) = 4 < 16; b2 = 4.
Итак, />'=49Г16 и 6 = 4,9/716. Теперь достаточно записать каждую по-
лученную шестнадцатиричную цифру ее двоичным изображением, тогда
b = 100,10011111g. Количественный эквивалент переведенного числа Ь =
= 4,621. Для реализации перевода в этом случае понадобилось всего два
деления вместо 9, когда перевод осуществлялся без посредника (пример
1.24).
Перевод через посредника производится также, когда
РЧ=Г и одна система имеет неотрицательную базу, а другая
симметричную. Выбор посредника производится точно так же,
как и при решении задачи 1.
Пример 1.26. Число а = 321,012^, заданное в четверичной системе счис-
ления, перевести в троичную систему с симметричной базой. В качестве
посредника выступает троичная система счисления с неотрицательной ба-
зой. Здесь г = 4, р = 3, h = 3, t 3 log3 4. Выбираем t = 4. Умножим а =
= 321,012^ на З4 = 81 = 11014 и округлим полученный результат до ближай-
шего целого числа. Получим а* = 102010Ц. Осуществляем перевод:
а(0) = 1200114-3 4- 2, Ьо = 2; а(1) = 1000Ц-3 4-2, Ьг = 2;
а(2) = 22234-3, £>2 = 0; а™ = 3214-3, Ь3 = 0;
д(4) = 1034-3, £>4 = 0; а(5) = 124.3 4- 1, £>5=1;
а(6) = 2-3, £>6 = 0; а(7) = 2 < 3, £>7 = 2.
Тогда b' = 20100022g и b = 2010,0022g. Теперь осуществляем перевод из си-
стемы посредника в троичную систему счисления с отрицательной базой:
Ь = 2010,0022g = 1 ГОЮ,0101g. Количественный эквивалент исходного числа
а — 57,0938, а переведенного числа b = 57,0937.
1°.10. В случае перевода целых чисел в „соседние" систе-
мы счисления операцию деления на г + 1, как и в случае
умножения, можно свести к операциям > над разрядами [21].
Действительно, если в г-ичной системе счисления задано
число а, то [<z]r+i = ^=2i=o = bf1 и {a}r+i = c0, где bh 1 =
= 0, 1, ...,£, и с0 определяются по рекуррентным формулам
bt = g+i + [at Т G+i]r+i, Q = (аг + O+i}r±i, ck+i = 0. (1.54)
Пример 1.27. Число a = 2345g перевести из девятиричной системы
счисления в восьмиричную. На первом шаге Oq = 5, = 4, а2 = 3 и а3 = 2.
В соответствии с (1.54) имеем с4 = 0, Ь3 = 0, с3 = 2, Ь2 = 2, е2 = 5, bt = 6,
Cj = 1, £>о=1, с0 = 6. На втором шаге Оо=1, «1 = 6. и а2 = 2. Отсюда
с3 = 0, £>2 = 0, с2 — 2, £>, = 3, Cj = 0, £>о = 0, с0 = 1. На третьем шаге = 0,
flj = 3 и с2 = 0, £>j = 0, Cj = 3, £>0 = 3, с0 = 3. *На четвертом шаге а0 = 3
и Со = 3. Окончательно а = 2345g = 3316g.
2°. Перевод чисел с плавающей запятой. Перевод чисел,
представленных в форме с плавающей запятой, является бо-
лее сложным, чем в случае представления чисел в форме
с естественной запятой. Действительно, пусть нам задано
в г-ичной системе счисления число а с плавающей запятой,
т. е. а = + гег Мг, и надо перевести его в /2-ичную систему
счисления, когда оно будет изображено словом b и Ь —
= + рерМр. Во-первых, надо определить формат представле-
ния чисел в /2-ичной системе счисления, т. е. определить
в новой системе разрядность поля порядка и поля мантиссы.
Выберем разрядность поля порядка из условия равенства
диапазона представляемых чисел в г-ичной и р-ичной системах
счисления. Определение разрядности мантиссы порядка про-
изведем, приравняв величины максимума относительной ошиб-
ки приближения (е). Когда установлена разрядность порядка
й мантиссы, можно перейти к задаче непосредственного
перевода.
Потребуем, чтобы и заданное и искомое числа имели нор-
мализованную мантиссу. Поскольку мантиссы — правильные
дроби, то их перевод может быть реализован одним из рас-
смотренных выше способов. Однако перевод порядка может
быть просто произведен лишь когда гег = рер- Поскольку при
произвольных г и р обеспечить
данное равенство для целых
ег и ер не удается, то правиль-
ный перевод может быть осу-
ществлен в общем случае, исхо-
дя из равенства ге'Мг = рерМ.р, а
это требует и изменения ман-
тиссы. Следовательно, вначале
надо, исходя из данного ра-
венства, определить р-ичный
порядок ер и мантиссу Мр в
г-ичном представлении, что мож-
но сделать с помощью процеду-
ры П (см. рис. 1).
П. Процедура определения
ер и Мр.
П1. ер: = 0, Мр-. = гегМг.
П2. Если то перейти
на П5.
ПЗ. Если Мр < р~\ то перей-
ти на П6.
П4. Конец процедуры.
П5. ер: =ер+1, Мр : =Мрр~1,
перейти на П2.
П6. ер: = ер - 1, Мр: = Мрр,
перейти на ПЗ.
После завершения процедуры
П будет найден порядок иско-
мого числа и его мантиссы,
представленный в г-ичной систе-
ме счисления. Следующий шаг
заключается в переводе ер и Мр из г-ичной системы в р-ич-
ную. Этот перевод осуществляется по известным правилам
перевода целого числа и дроби соответственно. .После пере-
вода возможно понадобится коррекция порядка и мантиссы,
вызванная необходимостью представления мантиссы в норма-
лизованном виде.
Пример 1.28. Пусть число 15 представлено в двоичной системе счис-
ления в форме с плавающей запятой и при этом используется следующий
формат — поле порядка вместе со знаком занимает семь разрядов, знак
мантиссы — один разряд и абсолютная величина мантиссы — 24 разряда,
т. е. всего 32 разряда. Требуется перевести это число в десятичную систе-
му счисления.
Вначале определим необходимый формат представляемых чисел в деся-
тичной системе и найдем длину полей порядка и мантиссы. Пусть в двоич-
ной системе счисления етах=27—1, a emin = 0, тогда, учитывая, что для
десятичной системы имеем етах=10гР — 1 и erain = 0, из равенства диапа-
зонов получим, что 10еР + logjo (1 — 10“SP) = 27 -f- log2 (1—2J) или ер =
= 7-logi02 » 2,1. Выбираем ер = 3. Теперь из равенства верхних границ
относительной погрешности находим, что sp = (24—1) logic 2 + 1 ~ 7,9.
Окончательно выбираем sp — 8.
Для осуществления перевода надо определить вначале порядок и ман-
тиссу десятичного числа, выраженные в дйоичной системе счисления. Сде-
лаем это с помощью процедуры П, тогда:
1. ё?ю: =0, Л4Ю: =2^0,11112= 15 = 11112.
2. Поскольку Л4ю=15>1, то е10 :• = е10 + 1, /Ию : = 15-10 1 = 1,5 —
= 1,12-
- 3. Опять Afto = 1,5 > 1 и вновь et0 : = 1 + 1, AJt0: = 1,5-10 1, получим
#10 — 2 и /И10 = 0,0010011001100110011001Ю9, и поскольку Л410 > 10-1 выпол-
нено, то осуществляется выход из процедуры П.
Когда найдены значения е10 и A4t0 для десятичной системы счисления,
можно перейти непосредственно к переводу, который выполним в два эта-
па. На первом этапе осуществим перевод £10 и М10 в десятичную систему
счисления, имеем ei0 = 102 = 2. Перевод же мантиссы выполним по пра-
вилу 1°.9 (см. пример 1.23) и найдем, что Л410 = 0,14999999. Окончательно
получим, что ею = 2 и Л410 = 0,14999999. Количественный эквивалент этого
числа есть b = 102-0,14999999 = 14,999999.
Как видно из этого примера, перевод чисел, представлен-
ных. в форме с плавающей запятой, оказывается существенно
более сложным, чем перевод чисел с естественной запятой.
Как упростить такой перевод? Очевидный путь таков: числа
с плавающей запятой будем рассматривать как компактную
запиеъ чисел с естественной запятой. Отсюда ясна идея пере-
вода. Вначале переведем число с плавающей запятой в число
с естественной запятой. Сделать это очень просто — надо
„только" сдвинуть мантиссу на е разрядов влево или вправо,
сохранив при этом все разряды. Затем по обычным правилам
произвести перевод числа, имеющего целую и дробную части.
При очень больших или очень малых значениях е у нас бу-
дут получаться „длинные" числа, и возможность реализации
данного метода будет связана со способностью машины рабо-
тать с числами большой длины. Если цифровая машина не
позволяет этого сделать, то имеет смысл этот быстрый алго-
ритм перевода применять при —поскольку тогда
получившиеся слова будут двойной длины, а большинство
машин могут выполнять логические и арифметические опе-
рации с числами двойной длины.
ГЛАВА 2
ОСОБЕННОСТИ ВЫПОЛНЕНИЯ
АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
В этой главе мы' рассмотрим особенности выполнения
арифметических операций в цифровой машине для различных
форм представления чисел в аддитивной позиционной системе
счисления с целым положительным основанием. Нашей зада-
чей является исследование основных принципиальных момен-
тов реализации каждой арифметической операции в цифровой
машине. Здесь не будут затронуты „тонкие" вопросы выпол-
нения операций, такие, как методы ускорения выполнения
операций, экономичные схемы реализации, адаптивные (при-
спосабливающиеся) алгоритмы машинных операций и т. д. Об
этих .вопросах речь пойдет в следующих главах. Сейчас же
для нас важно выяснить самые существенные моменты ма-
шинной реализации арифметических действий. Рассмотрение
начнем с представления чисел в форме с фиксированной
запятой, считая, что числа заданы в позиционной системе
счисления с естественными весами. В этом случае все допус-
тимые числа являются полиномами по степеням г-основания
системы счисления, следовательно, все арифметические дейст-
вия выполняются по правилам алгебраического сложения,
умножения и деления полиномов.
§ 1. АЛГЕБРАИЧЕСКОЕ СЛОЖЕНИЕ
Для позиционной системы счисления простейшей арифме-
тической операцией является сложение, которое заключается
в последовательном определении цифр суммы s7- двух сла-
гаемых а и Ь, каждое из которых задано в виде (1.3). Сло-
жение начинается с определения цифры суммы в младшем
разряде (у =— h). Поскольку для значений цифр слагаемых
справедливо, что — 1 и bj^,r — 1 при неотрицательной
базе и |gy{г- 2 и 2 • при симметричной базе, то
весьма вероятно, что + (или \as + bj|> —). По-
требуем, чтобы алфавит цифр результата был точно такой
же, ка,к и у слагаемых, тогда должно выполняться равенство
-|- bj= Cj-r + Sj,
причем для неотрицательной базы справедливо
( 0, если а, + bj < г — 1,
( 1, если dj -ф bj ^ г.
Переменная называется переносом из разряда с jномером у.
Так как при сложении полиномов суммируются все члены
с одинаковыми степенями, то окончательно приходим к сле-
дующей формуле для определения цифр суммы:
aj + bj + ci~i—.Cjr A-Sj. (2.1)
При сделанных ограничениях на значения цифр слагаемых
и результата, как это следует из выражения (2.1), имеем, что
1, У = — h, ..., k.
Будем считать, что для суммы установлена та же длина
слова, что и для слагаемых, тогда правильное представление
значений суммы будет существовать только в тех случаях,
когда ck === 0. В случае ck = 1 происходит переполнение рпз-
рядной- сетки. Из выражения (2.1) следует еще одна крайне
неприятная при практической
реализации особенность сложе-
ния в позиционных системах
счисления с неизбыточным ил-
фивитом (т. е. с алфавитом,
имеющим точно г различных
значений цифр). Эта особенность
заключается в принципиальной
зависимости значения старшей
цифры суммы от значения всех
предыдущих разрядов слагаемых.
Формирование r-ичной цифры
суммы и переноса из значений
цифр слагаемых и переноса
с предыдущего разряда обычно
производится в машине с по-
мощью специальной схемы, на-
VS
Рис. 2.
зываемой однорпзрядным сумматором с основанием г (рис.2).
На входы d и b подаются значения выбранного разряда сла-
гаемых, на вход с — значение переноса с предыдущего раз-
ряда. На выходах .х и с* получаются соответственно значения
разрядной суммы и переноса, сформированные в данном раз-
ряде. С помощью одноразрядного сумматора достаточно просто
реализовать сложение /г-разрядных операндов (д = k 4- h + 1).
Для этого алгоритм сложения надо представить как п-кратное
повторение одного и того же цикла. Пусть слагаемые а и b
ячейках памяти машины и результат
хранятся в заданных
нужно фудет отослать на место
операнда а, тогда действия, кото-
рые необходимо выполнить внутри
Z-ro цикла, будут следующими:
1) присвоить значения ait bt
входам а и b сумматора, а зна-
чение переноса, выработанное в
предыдущем цикле, — входу с;
2) по данным значениям пере-
менных найти s и с,.;,
3) найденное значение s при-
своить ау-, а значение запом-
нить.
Для завершенйя построения
алгоритма сложения надо еще оп-
ределить начальные условия и ус-
ловия окончания работы. Начальные
условия очевидны — переменной I
приписывается значение —h, а пе-
ременной — значение нуль. Про-
верка в каждом цикле сложения
равенства i = k 4-1 позволит найти
момент окончания работы алгорит-
ма. Если окажется, что i=/=k-\-\,
то после присвоения I значения,
равного Z-j- 1, надо перейти на
начало цикла. При i = k -Е1 про-
исходит выход из цикла. Теперь
алгоритм завершен (рис. 3).
Приведенный алгоритм предпо-
лагает последовательное выполне-
ние всех действий. С целью уско-
рения реализации цикла рациональ-
но одновременно выполнять все операции там, где это воз-
можно. В нашем случае присваивания : = О и I: = — h,
конечно, могут быть реализованы одновременно. Если опе-
ранды а и b находятся в таких участках памяти, которые
допускают одновременное обращение к ним, то можно па-
раллельно выполнить присваивания а: = at, b: = bt и с: =
До тех пор пока не будут реализованы эти присваивания,
нельзя будет перейти к вычислению разрядной суммы и пе-
реноса. Обычно формирование суммы и переноса начинается
которые в принципе мо-
Рис. 4.
одновременно и завершается через время и соответст-
венно. Как правило, справедливо, что тс. После того как
найдены значения s и с*, можно будет перейти к реализации
присваиваний at: = s' и i: = i + 1,
гут быть выполнены одновременно
(рис. 4). Следовательно, при выб-
ранном типе сумматора (при фик-
сированных значениях и тс)
время выполнения цикла будет
определяться временем- обращения
к памяти, где хранятся операнды
и результат.
В целях дальнейшего умень-
шения времени сложения рацио-
нально до начала выполнения ал-
горитма перевести слагаемые в
специальную память, которая до-
пускала бы одновременное обра-
щение ко всем своим ячейкам и
при этом время доступа было бы
по возможности ' наименьшим. Та-
кая память обычно реализуется на
регистрах и является частью
арифметического узла. Использо-
вание арифметических регистров
и максимальное совмещение дейст-
вий внутри цикла приводят к на-
именьшему времени реализации
алгоритма. Дальнейшее уменьше-
ние времени сложения «-разрядных
чисел связано с изменением при-
нятого принципа сложения.
Перестроим алгоритм сложения
так, чтобы все циклы поразрядного сложения выполнялись
одновременно. Очевидно, что для реализации такого алго-
ритма потребуется п одноразрядных сумматоров, соединенных
таким образам, чтобы выход переноса с предыдущего разряда
подавался на вход переноса последующего разряда (рис. 5).
Если значения слагаемых одновременно подаются во всех
разрядах, то такой сумматор принято называть параллель-
ным. В параллельном сумматоре обычно обеспечивается, что
в момент подачи слагаемых для каждого разряда справедливо
с* == 0. Максимальное время суммирования в параллельном
«-разрядном сумматоре есть
ттах = ^ + (« — 1)V (2.2)
3to время соответствует случаю распространения сигнала
переноса, полученного в младшем разряде сумматора, через
все разряды и равно максимальной задержке формирования
значения суммы в старшем разряде сумматора после прихода
слагаемых.
Как следует из выражения (2.2), если для. двух систем
счисления время образования суммы и переноса приблизи-
тельно одинаково, то при заданной точности выгоднее исполь-
зовать систему счисления с большим основанием, поскольку
длина слагаемых в этом случае уменьшается. Отсюда задача
построения быстрых сумматоров с большими основаниями
весьма актуальна.
Рис. 5.
Рассмотрим теперь особенности сложения чисел разных
знаков'. Для системы счисления с симметричной базой ника-
ких проблем при сложении чисел с учетом их знаков не су-
ществует, поскольку при этом любые числа представлены
единым натуральным кодом. Отличие в выполнении операции
„ + “ (сложение) от операции „ — “ (вычитание) будет состо-
ять только в том, что значения цифр bj при вычитании надо
будет взять со знаком минус.
Пример 2.1. Пусть а = 0,10111д и b = 0,11011g, “ тогда [s = а + b =
= 0,1"Т11'3 и s = a — 6 = O.lOlllg -ЬO.UOllg = IJOII3.
При использовании1 системы счисления с неотрицательной
базой для представления отрицательных и положительных
чисел не существует единого кода. В то же время крайне
нежелательно иметь в машине устройства, оперирующие
с разными кодами для того, чтобы реализовать простейшую
операцию. Посмотрим, как можно решить эту проблему.
1°. Прямые коды. Пусть числа заданы в виде прямых ко-
дов. Для простоты будем считать, что числа целые (/г=£-|-1).
Операция сложения начинается с анализа знаков чисел< Если
знаки одинаковые, то ясен сразу же знак результата — он
такой же, как у слагаемых, и определена техника сложе-
ния — в соответствии с равенством (2.1) обычным образом
складываются значения цифр основных разрядов кода.
Пример 2.2. Пусть исходные величины представлены целыми десятич-
ными числами а = 1075, Ь = 4936, с = —4751 и d = —5299. Тогда а + Ь =
= + (1075 + 4936) = +6011, с + d = — (4751 + 5299) = —1.0050. В последнем
случае произошло переполнение. Точкой здесь и далее знаковый разряд
отделяется от основных разрядов.
Когда знаки слагаемых разные, то фактически вместо сло-
жения надо выполнять операцию вычитания. Заранее, не зная
значений слагаемых, знак результата в этом случае опреде-
лить нельзя. Для реализации операции вычитания а — b от-
рицательное число (—Ь) м<сжно вначале заменить на его
дополнение до г", а затем выполнить операцию сложения
двух положительных чисел, т. е. s' = £Z-|-(rn—b). Заметим,
что истинное значение разности s = а — Ь меньше s' на вели-
чину гп. Если л>&, то s' > гп, и, следовательно, истинное'
значение разности, имеющее знак плюс, будет определяться
основными разрядами суммы s'. Значение переноса из стар-
шего разряда при этом надо игнорировать.
Пример 2.3. Пусть в десятичной системе счисления при k = 3, h = 0
заданы числа: а = 5627 и b = —4533; тогда s' = а + гп — b = 5627 + (104 —
— 4533) = 1.1094. Перенос со старшего разряда игнорируется и окончатель-
но имеем s = а + b = 1094.
В случае а<_Ь имеем s'= гп — (Ь — а) < гп, т. е. значение
s' является дополнительным кодом разности а — Ь. Следова-
тельно, для получения истинного значения разности надо от
дополнительного кода перейти к прямому. Как отмечалось
в § 1 главы 1, эта операция в общем случае реализуется как
алгебраическое сложение. В итоге разность с отрицательным
знаком будет определяться за два прохода.
Пример 2.4. В десятичной системе счисления при п = 4 заданы числа
а = 5627 и 6 = —6228, тогда s' = 5627 + (104 — 6228) = 0,9399.
Полученный результат представлен в дополнительном коде и поэтому
необходимо второе действие 0 + (10* — 9399) = 601. Окончательный итог:
$ = а + Z> = —601. ,
Рассмотренный алгоритм легко обобщается и на случай
операции вычитания. Действительно, пусть cfe {0,1} определяет
характер заданной операции: d = 0 при сложении, d=] при
вычитании, а а* и Ь* — знаки слагаемых. Тогда вначале опре-
делим знак машинной операции ₽ в соответствии с правилом:
₽ = <7* ф Ь* ф d,
где ф — знак .суммирования по модулю 2. Далее определяет-
ся знак результата
** = (6* ® (2.3)
и условия представления слагаемых дополнениями е = 1 для
а и /= 1 для Ь’.
е = а* (Ь* ф d) = аД
f= а* (#* ®d)= а$. ,
После завершения этапа анализа знаков и выбора формы,
представления слагаемых производится операция сложения
основных разрядов, по окончании которой анализируются ус-
ловия ₽ и ck (перенос со старшего разряда). При этом воз-
можны,следующие ситуации:
§сй=1. Знак, найденный из (2.3), присваивается результа-
ту, который определен основными разрядами суммы:
₽сй=1.\То же, что и при ₽cft=l, но есть переполнение
разрядной сетки (аварийная ситуация <р = 1);
₽£*= 1. То же, что и при рсй= 1;
$ck = 1. Знак результата есть = 1, и производится еще
одно вычитание, после которого операция заканчивается
(рис. 6). Операция а означает получение из числа а нового
числа путем замены всех цифр в й на их дополнение до
г — 1.
Применение при вычитании дополнительных кодов приво-
дит к тому, . что сумматоры должны работать с операндами
фиксированной длины. Это вызвано тем, что при формирова-
нии дополнительного кода после образования поразрядных
дополнений всех цифр к новому числу еще необходимо при-
бавить единицу в младший разряд. Это достаточно просто
сделать, если считать, что c_*=l, когда ₽ = 1, т. е. совмес-
тить прибавление этой единицы с последующим суммирова-
нием. Таким образом, в сумматоре особыми становятся два
разряда — старший, значение которого определяет характер
дальнейших действий в машине, и младший, в который при
работе с дополнительными кодами необходимо добавлять
единицу. Фиксация длины обрабатываемых слов приводит
к определенному замедлению выполнения алгебраического
сложения чисел, представленных в прямых кодах, когда они
в действительности имеют малую разрядность, и не позволяет
в одном сумматоре складывать сразу несколько коротких
$йсел.
Реализация алгебраического сложения прямых кодов зна-
чительно усложнена по сравнению с тем, как выполняется
эта же операция в симметричных кодах. Это усложнение
связано с введением анализа знаков и характерных признаков
после первого сложения. Кроме того, сама операция будет
производиться значительно дольше. Действительно, считая,
что все целые «-разрядные числа («= k Д1) из диапазона
— (г"—1), г"—1 равновероятны, получим, что в 2/3 случаев
допустимых чисел (недопустимыми считаются такие числа,
сумма абсолютных величин которых больше г" [11]) необхо-
димо применение дополнительного кода. Второе суммирование
и второе применение дополнительного кода необходимо в 1/3
всех случаев (рис. 7). Следовательно, среднее время сложения
в параллельном сумматоре составит
— 2 1 4
ТСЛ = + -у Тд -f- -у (Тд TS) = — тЕ 4- Тд,
где Тд —- время образования поразрядных дополнений, а тЕ —
время сложения «-разрядных операндов. Максимальное время
суммирования будет 2 (тЕ + тд). Для симметричных же кодов
время суммирования постоянно и составляет тЕ.
Реализация вычитания через промежуточный переход
к дополнительным кодам не является единственной. Можно
отрицательное число заменить его дополнением до гп— 1, т. е.
вместо числа — b использовать число Ь', такое, что Ь' =
= гп—1—Ь. Заметим, что получить Ь' из числа — b весьма
простд — надо лишь сформировать дополнение до г—1 всех
основных разрядов числа Ь.
Когда же число Ь' найдено, то сложим его с положитель-
ным числом а и тогда получим, что s = а-\- Ь' = а — b + гп— 1.
Если а>£, то s' > гп, т. е. сй=1. Однако значение основйых
разрядов разности s' будет меньше истинного на единицу.
Самый простой выход из создавшегося положения состоит
в передаче излишнего переноса в младший разряд сумматора.
Такие сумматоры принято называть сумматорами с цикличе-
скими. переносами (на рис. 8 указаны функциональные связи
в таком сумматоре). В случае 6 > а имеем s' < г" и значе-
ние разности а — Ь представлено обратным кодом. Для полу-
чения результата в прямом коде надо от обратного кода
перейти к прямому, но это достигается весьма просто — фор-
мированием поразрядного дополнения от промежуточного
результата. *
-И -г"
Сложение а+Ъ Вычитание о-Ь
Рис. 7.
«•
Пример 2.5. В десятичной системе счисления даны числа а = 5437,
6 = 6035 и с = 4568 Найти s=a — с. Поскольку с' = 101—1 —4568, то
с'=5431, s = а + с' = 5437 + 5431 = 869. Значение разности s — а — b
определим как s = а + Ь' = 5437 + 3964 = 9401. Результат получен в обрат-
ном коде, так как сй = 0, и теперь надо взять от него поразрядное допол-
нение. Окончательно имеем s = a—6= 1.0598, т. е. s = —598.
Чем же отличается алгоритм вычитания прямых кодов
с промежуточным преобразованием 2тРии.ательного числа
в обратный код от. преобразования в дополнительный код?
Первый этар — анализ знаков у них одинаков. Если выпол-
няется действительно вычитание, то отрицательное число за-
меняется его поразрядным дополнением и этот этап для двух
форм кодирования также совпадает. После сложения двух
чисел производится анализ признаков, который для случая
сумматоров с циклическими переносами будет следующим:
фсй=1. Знак, определенный из (2.3), присваивается ре-
зультату, абсолютная величина которого задается основными
разрядами сумматора;
рсй=1. То же, что и при == 1, перенос из старшего
в младший разряд разрешен;
рсА=1. То же, что и при рсй=1, но распространение пе-
реноса из старшего разряда в младший блокируется;
рсй=1. Знак результата есть $# = 1. Производится форми-
рование поразрядного дополнения от полученного результата.
Основное отличие этого алгоритма от предыдущего состоит
в том, что достаточно выполнить лишь одно алгебраическое
сложение для получения окончательного результата, хотя
в наихудшем случае вновь необходимо дважды формировать
поразрядное дополнение. Отсюда максимальное время сумми-
рования в сумматоре с циклическим переносом есть
шах тсл = ?s 4- 2тд,
а среднее время сложения в параллельном сумматоре соста-
вит
— .2.1 .
тсл = + -3" S. + “з" тд = + S-
Учитывая, что для некоторых систем счисления формиро-
вание тд поразрядного дополнения весьма мало (например,
для двоичной системы счисления формирование дополнения —
это просто выбор одного из двух парафазных выходов с ре-
гистра, т. е. значения at либо at), переход к промежуточному
кодированию отрицательных чисел обратными кодами дает
существенное увеличение быстродействия в параллельных
машинах по сравнению с переходом к дополнительному коду.
2°. Дополнительные коды. Будем считать, что числа с уче-
том ' знаков задаются в форме дополнительных кодов. Для
этих кодов характерно, что знаковый разряд имеет вес—гп и,
следовательно, не отличается так резко от основных разря-
дов, как в прямых кодах. Это позволяет единым образом
обрабатывать в сумматоре все разряды кода и избежать этап
анализа знаков операнд, правда, при этом надо изменить вид
дополнительного кода. Причина, по которой необходима мо-
дификация ранее используемой форумы дополнительного кода,
становится ясной из рассмотрения следующего примера.
Пример 2.6. Пусть а: 0.5627 и Ь: 0.4555 есть дополнительные коды чи-
сел, представленных в десятичной системе счисления при k = 3, h = 0,
тогда s = а + b — 0.5627 + 0.4555 = 1.0182. Однако этот результат, если он
рассматривается как дополнительный код, отвечает числу s =—9818. Прав-
да, то что единица в знаковом разряде означает переполнение разрядной
сетки, а ие знак „—“, можно было бы установить, проанализировав знаки
слагаемых (они положительные) и результата, но обычно такая процедура
считается сложной.
Для того, чтобы результат переполнения отличался от
обычной формы дополнительного кода, часто используют
модифицированный дополнительный код [11,20]. В модифи-
цированном коде двоичный знаковый разряд а* заменяется
двоичным числом а,а*, причем справедливо а'* = а*. Таким
образом, старшие две цифры модифицированного кода явля-
ются знаком* числа, и если он положителен, то они равны
нулю, а если знак отрицателен, то цифры есть единицы. Зна-
ковые разряды слагаемых совместно с признаком переполне-
ния сумматора основных разрядов ck обрабатываются по пра-
вилам двоичной арифметики. Двухразрядная сумма опре-
делит значение знаковых разрядов результата:
2s; + = 2«; + аЛ + 2&; + Ь’Л + ck (mod 4). (2.4)
Отсюда при сложении положительных чисел, если ck = 0 (пере-
полнения в основном сумматоре нет), имеем s'S! = s.x. = 0, т. е.
знак результата положительный. Когда же переполнение
в основном сумматоре есть, то s^ = 0 и s,= l. При сложении
двух отрицательных чисел, с учетом, что основные разряды
слагаемых определяют дополнения до г" от абсолютных ве-
личин этих чисел, т. е. а' = rn — \а \, b' = rn — \b\, получим
s' = а' + Ь' = гп + [г" — (| а | ф- | b |).
Пусть \а| + | Ь] < гп, тогда s' = гп и, следовательно, ck = 1.
Отсюда из (2.4) следует, что s; = st=l, т. е. знак резуль-
тата отрицательный. Значение же основных разрядов есть
s = rn— |а[ — [&[, т. е. сразу получен верный результат.
Когда же | а | -j- [ b ] > гп, то переноса в знаковом разряде нет
(сй = 0) и s;=l, £* = 0. Эта комбинация отмечает наличие
переполнения разрядной сетки осн овного сумматора при сло-
жении двух отрицательных чисел.
Пример2.7. Пусть а — —5627, Ъ =—1243 и d — —6785 представлены
в десятичной системе счисления при k = 3 и h = 0 дополнительными мо-
дифицированными кодами, т. е. «: 11.4373, Ь: 11.8757 и d: 11.3215. Тогда
s = а + b = 11.4373 + 11.77.57 = 111.3130; старший знаковый разряд игнори-
руется и окончательно имеем s: 11.3130. Сложим а и d, s=a + d =
= 11.4373 + 11.3215= 110.7588. Старший знаковый разряд игнорируется
и тогда s = а + d = —12412, т. е. имеем случай переполнения разрядной
сетки.
Для чисел разныхзнаковпереполнение разрядной сетки
отсутствует. Будем для определенности считать, что а^О
и Ь < 0. Тогда суммирование дополнительных кодов а и b
определяет величину
s = а + (1м — \'Ь |) == гп + (а — | Ь |).
Если а^-\Ь\, то гп, следовательно, s' = s» = 0 и знак
числа есть „ + Значение же основных разрядов равно раз-
ности а — \Ь{. В случае а<С\Ь\ перенос в знаковые разряды
отсутствует, поэтому $' = .$4 = 1, знак результата есть „ —
В основных же разрядах находится значение г'1 — ( | b | —-а),
следовательно, результат есть дополнительный код разности
| — а, что и должно быть на самом деле.
Пример ,2.8. Пусть а = 5627, Ь = —1224 и d = —6858 представлены
в десятичной системе счисления при k — 3 и h = 0 модифицированными
дополнительными кодами, тогда s = а + Ь = 00.5627 + 11.8776 = 100.4403
и s = а + b = 4403. В то же время s = а 4- d = 00.5627 4- 11.3142 = 11.8769
и s = а + d = —1231.
-. Таким образом, после одного сложения результат опреде-
ляется окончательно и представлен в том же виде, что и сла-
гаемые. Наличие переполнения разрядной сетки (<р = 1) легко
устанавливается из анализа двух знаковых разрядов резуль-
тата s* и s* в соответствии с уравнением
<р = V •
Вычитание в модифицированном дополнительном коде сво-
дится к. сложению с предварительным изменением знака
у вычитаемого, т. е. базируется на соотношении а — b =
— а + (-—।Ь). Добавление единицы в младший разряд, необ-
ходимое при изменении знака у дополнительного кода, про-
изводится, как и раньше, при выполнении сложения, следо-
вательно, необходимо затратить время лишь на формирование
поразрядных дополнений кода числа Ь, а это время есть тд.
Отсюда максимальное время сложения чисел в дополнитель?
ных кодах есть шахтсл = т2 4- тд, а среднее, считая, что
операции сложения .и вычитания равновероятны, есть
^сл == 4~ 2 1^д,
что значительно меньше, чем при использовании прямых
кодов.
Структура алгоритма алгебраического сложения в моди-
фицированном коде оказывается существенно проще, чем при
использовании прямых кодов (особенно в случае применения
сумматоров без циклического переноса), за счет отсутствия
анализа знака и характерных признаков после завершения
первого сложения.
3°. Обратные коды. Будем для представления чисел ис-
пользовать модифицированные обратные коды, которые фор-
мируются из обычных обратных кодов путем замены знаково-
го разряда на двоичное число a'ja*, причем а'* = а*.
Знаковые разряды а' и а* совместно с переносом из стар-
шего разряда r-ичных сумматоров (сй) обрабатываются по
правилам двоичной арифметики. Однако перенос со старшего
знакового разряда не игнорируется (как в случае модифици-
рованных дополнительных кодов), а направляется в младший
r-ичный разряд сумматора.
Рассмотрим теперь особенности сложения обратных кодов.
Пусть й>0*и й>0, тогда, если а-}-Ь<гп, то оба знаковых
разряда результата равны нулю, а основные разряды его оп-
ределяют значение суммы а -ф Ь. В случае а -ф & > г" проис-
ходит передача переноса из старшего основного в младший
знаковый разряд. В окончательном результате этому соот-
ветствует комбинация знаковых разрядов 01.
Пример 2.9. Пусть числа а = 5627, b = 1238 и с = 4553 представлены
в десятичной системе счисления при k = 3 и Л = О модифицированными
обратными кодами s = а + Ь = 00.5627 4- 00.1238 = 00.6865, т. е. s = 6865
и s = а + с — 00.5627 4- 00.4553 = 01.0180. Окончательный итог: s = 10180,
что соответствует случаю переполнения разрядной сетки, так как п = 4.
Пусть теперь оба числа имеют отрицательные знаки, т. е.
оба знаковых разряда у каждого из слагаемых есть единица.
В этом случае всегда присутствует циклический перенос,
и, следовательно, значение основных разрядов определится
следующим образом:
s = г" - i;- I а]\ +/«,-[1 - IM+1!= Г.+ [Г" - 1 - (I а | -ф \Ь |)].
Когда гп—1 \а| -ф \ b |, обязательно происходит передача
переноса в младший разряд, в результате чего окончательная
комбинация знаковых разрядов есть 11, что соответствует
знаку Значение же основных разрядов есть г"—1 —
— (]а|-ф\&(), что отвечает обратному коду числа — (а -ф Ь).
В случае же, когда г"—1 < | а] -ф1 Ь\, переноса в знаковый
разряд не происходит, и комбинация 10 в знаковых разрядах
фиксирует переполнение разрядной сетки.
Пример 2.10. Числа а = —4276, Ь = —2345 и с = —6891 представлены
модифицированными обратными кодами в десятичной системе счисления
при п = 4 и h = 0. Тогда s = а 4- Ь = 11.5723 4- 11.7654 = 111.3377; s = 6621
и s = а 4- с = 11.5723 4- 11.3108 = 110.8831. Окончательно имеем а 4- с =
= —11167. В последнем случае фиксируется переполнение разрядной сетки.
Когд^ числа имеют разные знаки, переполнение разрядной
сетки принципиально невозможно. Значение основных разря-
дов будет следующим: если b < 0, то
s = a±b = rn~ 1-фа — [ & |.
Если справедливо неравенство а > | 61,то обязательно про-
исходит передача переноса из основных разрядов в знаковые,
и поскольку первоначальное значение знаковых разрядов
сумматора было 11, то это вызовет и циклический иеренос.
Следовательно, окончательное значение основных разрядов
есть а — | b |, а знаковых — 00, что отвечает обратному коду
положительного числа а — | b |. Когда же то ни цик-
лического переноса, ни переноса из основных разрядов
в знаковые не происходит, и, следовательно, результат окон-
чательно имеет знак „ — “ (комбинация знаковых разрядов 11),
а значение основных разрядов есть г"—l-f-a—-т. е.
соответствует коду отрицательного числа а —1'&). Интересно,
что случай а — \Ь\ расценивается при этом как итог с отри-
цательным знаком —0. Как мы уже видели, это является
одной из двух допустимых форм представления нуля в об-
ратных кодах.
Пример 2.11. Числа а — 5627, Ь = —4375, с = —6591 и d = —5627 пред-
ставлены модифицированными обратными кодами. в десятичной системе
счисления при п = 4 и Л = 0. Тогда а + 6 = 00.5627 + 11.5624 = 100.1251 =
= 00.1252; й + с = 00.5627 + 11.3408= 11.9035, т. е. $ = —964; й + ^ =
= 00.5627+ 11.4372= 11.9999, т. е. $=—0.
Очевидно, что когда одно из слагаемых есть 4-0, т. е. зна-
чения всех цифр числа есть 0, никаких необычных ситуаций
при сложении не возникает. Однако при использовании —0,
когда значение знаковых разрядов есть единица, а всех основ-
ных г— 1, утверждение становится не очевидным. Итак, пусть
а = —0, тогда если b > 0, значение основных разрядов есть
—0|+"& = rtl — 1 4- Ь,
следовательно, происходит передача переноса >из основных
разрядов в знаковые, а учитывая, что их значение есть И,
это, в свою очередь, вызовет циклический перенос. Тогда
значения основных разрядов окончательно есть Ь, а знако-
вых — 00, т. е. —0 4- b = Ь. Теперь пусть b < 0 и а — —0,
тогда поскольку оба слагаемых имеют единицы в знаковых
разрядах, то обязательно будет циклический перенос; и, сле-
довательно, значения основных разрядов есть
г»-14-г«-1_&4-1.
Поскольку гп — 1 >-1 b |, то перенос в знаковые разряды проис-
ходит, устанавливая их окончательные значения как it, а в ос-
новных разрядах представлена величина г”—1 —1&|, т. е.
обратный код числа —Ь, т. е. —0 — j b | = — | b I.
Операция вычитания в обратных кодах легко реализуется
через операцию сложения с операндом обратного знака, т. е.
а — Ь = а-\-(—Ь). Изменение знака достигается простым по-
разрядным дополнением этого операнда, которое, как обычно,
реализуется за время тд. тсюда максимальное время сло-
жения чисел, заданных обратными кодами, в параллельном
сумматоре составит, как и для дополнительных кодов, max тсл =
— + тд, а среднее (при равновероятных сложениях и вы-
, 1 г,
питаниях) тсл = -g-Тд. В целом же и по аппаратурным за-
тратам, и по времени реализации, и по структуре алгоритма
алгебраическое сложение обратных кодов эквивалентно сло-
жению дополнительных кодов.
Таким образом, для систем счисления с неотрицательной
базой, какие бы коды ни использовались для представления
отрицательных чисел, приходится решать определенные проб-
лемы при выполнении алгебраического сложения. Все эти
проблемы отпадают, как только мы выбираем системы счис-
ления с симметричной базой. В этом случае логика алгоритма
сложения проста и время сложения составляет при использо-
вании параллельного сумматора всего лишь Единственно,
о чем можно сожалеть при выборе симметричного кода, это
свойственная всем неизбыточным позиционным системам счис-
ления зависимость времени от числа разрядов слагаемых.
В главе 5 будут исследованы методы устранения подобной
зависимости.
§ 2. СЛОЖЕНИЕ ЧИСЕЛ С ПЛАВАЮЩЕЙ
И ЕСТЕСТВЕННОЙ ЗАПЯТОЙ
Рассмотрим особенности алгебраического сложения чисел,
представленных в форме с плавающей запятой (1.27). Естест-
венно, что результат сложения двух чисел а и b также дол-
жен быть числом с = гесМс с плавающей запятой, для кото-
рого в случае нормализованных мантисс должны выполняться
неравенства <?mIn ес етах и r~x < \МС | 1 — r~s, причем
мы вправе ожидать, что для слагаемых и результата должно
выполняться равенство
re-M^re»Mb = recMc. (2.5)
Путь к определению порядка и мантиссы результата ста-
новится очевидным, если учесть, что
+ltre»Mb = ге° (Ма + Мь), (2.6)
где /И* = геь~еаМь. Из равенства (2.6) следует, что в качестве
порядка результата можно взять порядок одного из операн-
дов, а в качестве мантиссы результата — сумму мантиссы
этого операнда'и преобразованной мантиссы , второго операнда.
1°. Выравнивание порядков. Согласно (2.6) для реализа-
ции сложения чисел с плавающей запятой надо перед сумми-
рованием вначале выровнять порядки. Э.та операция будет
заключаться в определении слагаемого, оставляемого ез из-
менений, и в преобразовании мантиссы второго слагаемого.
Преобразованная мантисса должна быть правильной дробью
с тем, чтобы ничем не отличаться при сложении от обычных
(непреобразованных) мантисс. Это означает, что разность Де =
= еь — еа должна быть меньше нуля. Если при анализе по-
рядков будет установлено, что Де > 0, то это приведет к по-
следующей трансформации мантиссы числа а, число же b
останется неизменным. Следовательно, анализ знака разности
Де определяет число, мантисса которого подлежит преобразо-
ванию. /
Преобразование мантиссы заключается в ее умножении' на
число вида г₽, где р — целое отрицательное. Умножение нату-
рального кода (1.7) числа а, заданного в аддитивной позици-
онной системе счисления, на г>0 приводит к тому, что вес
каждого разряда числа а увеличится в г раз. Это означает,
что в качестве цифры р; результата будет фигурировать циф-*
ра числа а,. за исключением р_и, которая будет иметь
значение нуль. Следовательно, можно сказать, что число га
образовалось в результате сдвига всех разрядов числа а на
одну позицию влево и увеличения длины записи на один раз-
ряд. Точно так же можно найти результат умножения на г-1,
только сдвиг разрядов числа а надо произвести в противопо-
ложном направлении — вправо. Для умножения числа а на г₽,
где р — целое число, требуется произвести р сдвигов числа а
вправо или влево в зависимости от знака р.
Техническая реализация операций сдвига на цифровых ма-
шинах может быть просто осуществлена, если регистр, хра-
нящий число а, допускает возможность передачи значений
из любого данного разряда в соседний с ним, т. е. будет ре-
гистром сдвига. Однако конечная длина регистров заставляет
решить вопрос, что делать с цифрами, вышедшими за пре-
делы их разрядной сетки. Эти цифры либо могут терять-
ся, либо при циклическом сдвиге направляться вновь в этот
же регистр в противоположный крайний разряд.
В процессе преобразования мантиссы ее величина умень-
шается- в г раз при каждом сдвиге. Ввиду конечной длины
разрядной сетки мантисс слагаемых (s разрядов) не имеет
смысла сдвигать мантиссу более чем на s 4~ 1 разряд (при
г > 2 можнр ограничиться сдвигом на s разрядов), ибо при
большем числе сдвигов величина мантиссы будет меньше, чем
и, следовательно, она даже с учетом возможного округ-
ления будет всегда представлена машинным нулем. Когда
Де >s 4-1, результат может быть получен уже на этапе ана-
лиза порядков — это большее число, возможно только с изме-
ненным знаком, если оно вычиталось. В случае Де-<$4-1
сдвиг мантиссы вправо происходит. Судьба разрядов преобра-
зованной мантиссы, вышедших за разрядную сетку, зависит
от принятого метода округления. Например, для симметрич-
ных кодов они просто теряются. При других ситуациях они
могут сохраняться частично или полностью.
Освободившиеся при сдвиге разряды, если мантиссы име-
ют положительный знак или заданы симметричным кодом,
заполняются нулями. Знаковый разряд при использовании
прямых, дополнительных или обратных кодов в сдвигах
не участвует. Это обстоятельство заставит в случае примене-
ния дополнительных и обратных кодов при отрицательном
знаке мантиссы освободившиеся разряды заполнять не нуля-
ми, а значениями г—1,
2°. Алгебраическое сложение мантисс. После завершения
этапа выравнивания порядков определен первоначальный по-
рядок результата и преобразована мантисса меньшего числа.
В случае использования дополнительных кодов для реализа-
ции операции вычитания прямых кодов имеет смысл всегда
вычитать меньшее число из большего, что позволит операцию
вычитания выполнить за один проход. Естественно, что если
большее число имело знак „ —то этот знак сразу припи-
сывается результату, а знаки слагаемых меняются. Хотя дан-
ный прием и позволяет в среднем существенно ускорить
выполнение операции сложения, он все же не может пол-
ностью избавить от необходимости двух проходов сложения
в случае равенства порядков операндов и отрицательного
Знака у результата их сложения-вычитания.
После приведения отрицательного слагаемого к заданному
коду (если это необходимо) и выравнивания порядков можно
приступить непосредственно к суммированию мантисс. Однако
мы должны помнить о наличии „хвоста" у преобразованной
мантиссы и, если только не использовался метод округления
к нулю (отбрасывание „хвоста"), решить его судьбу. В .прин-
ципе возможны два решения:
отбросить „хвост", округлить преобразованную мантиссу
и совместить округление со сложением' мантисс,
сложите мантиссы с учетом „хвоста" и уже потом решать
вопрос о необходимости округления.
Отложим вопрос о выборе конкретного решения до выяс-
нения особенностей результата сложения двух мантисс.
3°. Нормализация результата. После завершения алгеб-
раического сложения мантисса результата удовлетворяет не-
равенству 0 С] Мс\ <2. В то же время для случая нормали-
зованных чисел следует обеспечить неравенство г~1 -С (Мс | <
< 1. Отсюда переполнение разрядной сетки мантиссы, когда
| Мс[ > 1 расценивается не как аварийная ситуация, а как
признак необходимости нормализации вправо результата. Эта
нормализация состоит в уменьшении мантиссы в г раз (сдвиг
разряда переполнения и мантиссы вправо на один разряд)
и в увеличении порядка результата на 1. Сдвиг мантиссы
с одновременным изменением порядка, при котором величина
числа остается неизменной, принято называть модифициро-
ванным сдвигом. При нормализации вправо два момента зас-
луживают особого внимания. Один связан с увеличением
порядка, что может вызвать переполнение порядка (если
еа = ешах), которое должно расцениваться как аварийная си-
туация. Другой момент касается представления сдвинутой
мантиссы. Поскольку после сдвига вправо (s + l)-fl разряд
может иметь ненулевое значение, то необходимо после нор-
мализации вправо произвести округление. Необходимость
данного округления совсем не зависит от того, округлялась
ли преобразованная мантисса. Если мы будем использовать
методы округления, основанные на добавлении единицы
в младший разряд, то нам придется ;выполнить еще одно
сложение. В случае двоичной системы счисления это сложе-
ние вновь может привести к переполнению и необходимости
повторной нормализации вправо. Все это заставляет самым
внимательным образом отнестись к 'выбору метода округле-
ния на данном этапе. Для обеспечения наибольшей скорости
при сложении следует остановиться на методах округления,
не требующих учета распространения переносов.
Пусть теперь мантисса по абсолютной величине меньше,
чем г-1, тогда необходима нормализация влево. Эта опера-
ция может быть реализована как левый модифицированный
сдвиг, который необходимо повторять до тех пор, пока пре-
образованная мантисса по абсолютной величине будет не мень-
ше, чем г-1. Однако возможны такие ситуации, когда резуль-
тат алгебраического сложения мантисс есть нуль, тогда
указанный процесс окажется бесконечным, поэтому обычно
число сдвигов влево ограничивают числом разрядов сумма-
тора. В случае, если после предельного числа сдвигов ман-
тисса оказывается ненормализованной,, то результат представ-
. ляют машинным нулем. К подобному итогу обычно приходят
и в случае, когда в результате модифицированного сдвига
влево порядок окажется меньше допустимого, но МС=£.О, т.е.
абсолютная величина результата будет меньше, чем мини-
мально возможное машинное число, поэтому она и заменяет-
ся машинным нулем. По-видимому, более разумным было бы
эту ситуацию отмечать как особую, а решение вопроса и за-
мену числа с машинным нулем сделать альтернативной.
При сдвиге влево разряды, вышедшие за разрядную сет-
ку, теряются, освободившиеся же разряды в случае симмет-
ричных, прямых и дополнительных кодов заполняются нуля-
ми, а в случае обратных кодов заполняются значениями г—1.
Нормализация влево заканчивается, когда мантисса результата
Мс станет после очередного сдвига не мейее чем г-1. Анали-
зируя только старший разряд мантиссы, всегда можно ответить
на вопрос, нуждается ли мантисса в дальнейшей формализации
или нет. Для симметричных и прямых кодов оказывается до-
статочным сравнить значение этого разряда с нулем, а для
дополнительных и обратных кодов при отрицательной мантис-
се модифицированный сдвиг влево оказывается необходимым,
если значение старшего разряда есть г—1. Единственным
исключением из данного правила является случай равенства
мантиссы, представленной в дополнительном коде, числу
r~s, когда код мантиссы есть 11.(г—1) ... (г—1). Тогда
значение г — 1 в последнем разряде не является признаком
нормализации. Поэтому для дополнительных кодов число
допустимых сдвигов влево при отрицательной мантиссе дос-
таточно ограничить s— 1.
* Если округления до или в процессе сложения не произ-
водится („хвост" преобразованной мантиссы сохранен), то
после окончания нормализации влево имеет смысл округлить
результат. Возможное при этом переполнение мантиссы уст-
раняется применением нормализации вправо.
Наше естественное желание состоит в такой реализации
сложения чисел с плавающей запятой, которая могла бы быть
осуществлена как можно быстрее и как можно точнее. Наи-
большей точности мы достигнем, если будем складывать
(2s + 1)-разрядные операнды (учет точного значения сдви-
гаемой мантиссы) и после возможных нормализаций вправо
или влево округлим результат до s-разрядного. Однако боль-
шая длина слагаемых и длительная нормализация влево (до
2 s шагов) существенно увеличивают время выполнения опе-
рации и усложняют схему сумматора. Наименьшее время
реализации сложения будет достигнуто при совмещении ок-
ругления со сложением s-разрядных мантисс и выполнении
повторного округления методами без учета распространения
переносов. Если основное округление проводим методом усо-
вершенствованного округления по дополнению, а повторное
округление методом логического преобразования значения
младшего разряда результата, (см. главу 1, § 3), то макси-
мальная суммарная погрешность составит величину
шах Д = r~s -----~у~) = г ~S
Если в процессе выравнивания порядков окажется, что
„хвост" преобразуемой мантиссы отличен от нуля, или при
переполнении мантисс младший разряд результата имел не-
нулевое значение, то результат оказывается приближенным
и равенство (2.5) нарушается. Поскольку степень преобразо-
вания мантиссы зависит от величины большего числа, то оче-
видно, что результат сложения нескольких чисел может за-
висеть от порядка суммирования, т. е. в общем случае ассо-
циативный закон при сложении чисел с плавающей запятой
не выполняется.
4и. Слежение чисел с естественной запятой. Сложение
чисел с естественной запятой во многом зависит от способа
задания положения запятой в разрядной сетке. Иногда числа
с естественной запятой внутри машины представляются чис-
лом с плавающей запятой, и тогда надо только внести кор-
рективы в соответствующие этапы процесса сложения, учиты-
вающие специфику чисел с естественной запятой.
На первом этапе выравниваются целые части слагаемых,
при этом число с меньшей целой частью удлиняется на &р
разрядов, где р — разница числа разрядов целой части сла-
гаемых. Для реализации сложения „длинное" число надо ок-
руглить до заданного формата. После сложения возможно,
что понадобится нормализация результата вправо, в резуль-
тате которой целая часть увеличится на разряд. Нормализа-
ция влево для чисел с естественной запятой производится
при необходимости не более чем на р — 1 разрядов, где р —
число разрядов целой части слагаемых перед сложением, по-
скольку по крайней мере один разряд для изображения целой
части всегда необходим.
В зависимости от способа представления информации
о местонахождении запятой в разрядной сетке чисел детали-
ровка алгоритмов выравнивания целых частей и нормализации
вправо или влево может оказаться весьма сложной и своеоб-
разной [27].
§ 3. МЕТОДЫ УМНОЖЕНИЯ
В этом параграфе рассматриваются основные идеи и осо-
бенности методов умножения чисел, представленных в адди-
тивных позиционных системах счисления. Здесь, как и ранее
при исследовании методов сложения, не будут затронуты
„тонкие" вопросы: такие, как методы ускорения умножения,
методы приближенного умножения, методы умножения с уд-
военной точностью, умножение помехозащитных кодов ит.д.,
6 которых речь пойдет ниже.
1°1. Умножение положительных чисел. Рассмотрение нач-
нем со случая целых чисел, когда « = Будем счи-
тать, что если знак чисел учитывается на уровне слов, то
сомножители есть положительные числа. Тогда величина
произведения чисел а и b есть .
Р = 5£=о 2;=о afijri+i,
и для его определения достаточно просуммировать все час-
тичные произведения вида р1} = ар'^^Ьу1, каждое из ко-
торых образовано умножением г’-го разряда множителя на пол-
ное множимое. Умножение же на значение г-го разряда сво-
дится к двум умножениям множимого — на цифру г-го разряда
множителя (az) и на ее вес г1. Как выполняется .умножение
на г», мы уже знаем — оно реализуется сдвигом соответствую-
щего числа на i разрядов влево. Остается только рассмотреть
особенности умножения множимого на цифру множителя.
Казалось бы естественным выполнить это умножение обычным
способом, как это принято делать,’ пользуясь таблицами умно-
жения и сложения. Таблица сложения в машинах технически
реализована в сумматорах, а таблицу умножения пришлось
бы конструировать дополнительно, например как некоторую
постоянную память. Даже для малых оснований системы счис-
ления эти таблицы достаточно сложны. При обычном счете
мы определяем частичное произведение, последовательно обра-
щаясь к таблице умножения. Для последовательных машин
этот принцип может быть полностью повторен, и тогда нам
потребуется* всего одна технически реализованная таблица
умножения.
Иначе обстоит дело, когда мы хотим параллельно выпол-
нить умножение множимого на цифру множителя. Здесь по-
требуется одновременное обращение сразу к п = k -ф 1 табли-
цам умножения. Кроме того, результаты, полученные для
каждого разряда, надо еще просуммировать с учетом весов.
При больших п табличная реализация умножения приводит
к значительным затратам оборудования. Исключение состав-
ляют двоичная система счисления и троичная с цифрами 1, О,
1, имеющие исключительно простые таблицы умножения:
0X0 = 0
1X0 = 0
г = 2
0X1 = 0
1X1 = 1
Тх“=1
1хо=о
Тх1 = Г
г = 3
ох“=о
0X0 = 0
0X1=0
1 х1=1
1 хо = о
1X1 = 1
В этих случаях произведение множителя на множимое обра-
зуется без применения таблиц суммирования и если а£ = 0,
то //6 = 0, если аг=\, то р^==г1Ь, и когда at—— 1 (для
троичной системы счисления), то р& — —г‘Ь, т. е. множимое
с учетом веса берется с отрицательным знаком.
Поскольку табличный метод для других систем счисления
для параллельных машин приводит к значительным затратам
оборудования, то умножение множимого на цифру множителя
производят как последовательное суммирование множимого
столько раз, сколько единиц содержит цифра at. В этом слу-
чае умножение в целом реализуется как последовательное
суммирование и сдвиги чисел. Отсюда определяются и техни-
ческие средства реализации умножения — регистры сдвига,
сумматор и схема управления.
Рассмотрим подробнее алгоритм умножения, базирующийся
на методе последовательного суммирования, когда произведе-
ние определяется последовательно за п = k 1 шагов, на каж-
дом из которых формируется частичное произведение р^1\
и прибавляется к сумме предыдущих частичных произведении.
Пусть в нашем распоряжении имеются три регистра — регистр
А, в котором первоначально располагается множитель дли-
ной п разрядов, регистр В, в котором помещается множимое
тоже длиной п разрядов, и регистр С (рис. 9). Поскольку
множимое участвует на всех шагах умножения, т. е. при
определении всех частичных произведений, то его необходимо
сохранять в течение всей опе-
рации. Множитель же после
каждого шага может быть сок-
ращен на один разряд, по-
скольку проанализированные
цифры уже не нужны в даль-
нейшем. В регистре С должна
храниться сумма найденных
частичных произведений. По-
скольку полное произведение
«-разрядных операндов есть
2«-разрядное число, то каза-
лось бы длина регистра С
должна быть 2«. Однако на
самом деле можно ограни-
читься длиной регистра С в
«4-1 разряд, если умноже-
ние начинать с формирования
частичного произведения рт.
В этом случае после заверше-
ния г-го шага алгоритма будет
найдено I младших цифр ре-
зультата, которые можно бу-
дет поместить на место уже не
нужных i младших цифр мно-
жителя. Заметим сразу, что начинать умножение с формиро-
вания рт вовсе не является обязательным [11]. При умноже-
нии, начиная со старших разрядов множителя, также на
каждом шаге длина суммы частичных произведений будет
увеличиваться на один разряд. Однако принципиальное отли-
чие этого способа умножения от умножения с младших раз-
рядов состоит в том, что ни одну из цифр частичного произ-
ведения нельзя считать цифрой окончательного произведения
ввиду того, что прибавление очередного произведения а^’Ь
может вызвать изменение цифр не только в пределах обыч-
ной (« 4- 1)-разрядной сетки сумматора, но и во всех старших
разрядах из-за возможного в них распространения переносов.
Это обстоятельство, вообще говоря, требует наличия в ариф-
метическом узле кроме «-разрядных регистров множимого
и множителя еще 2«-разрядного регистра частичных произве-
дений и 2«-разрядного сумматора. Хотя эти требования иног-
да могут быть смягчены (например, при приближенных
множителя.
Начало
1: = 0, С’.=о
S'-Og , а>^+1- — Сд
a:=a+r,c:=c±r
Да
Нет
вычислениях), все же умножение со старших разрядов приво-
дит к более сложной структуре, чем умножение с младших
разрядов. Основное достоинство данного метода состоит в воз-
можности более быстрого умножения при некоторых техни-
ческих реализациях.
Будем каждое частичное произведение /?(f) формировать
путем последовательного суммирования множимого at раз.
Следовательно, необходим последовательный анализ значения
анализ реализуется специальной
схемой х, в которую предвари-
тельно засылается анализируе-
мая цифра. С этой целью выход
младшего разряда регистра А
соединяют со входом схемы ана-
лиза, а сам регистр А делают
регистром правого сдвига.
Начнем операцию умножения
с одного сдвига регистра А,
после которого в самом регист-
ре А останется число 0 ak ...
... а в схеме анализа ока-
жется значение а0. Если а0 =Д О,
то переходят к формированию
частичного произведения //°>,
для чего к содержимому ре-
гистра С прибавляют множимое
и результат отправляют вновь
в регистр С. Одновременно
фиксируется выполненное дейст-
вие путем вычитания единицы
из х = а0. После завершения
суммирования вновь анализиру-
ется уже уменьшенное значение
х и если опять s =£0, то ука-
занный цикл Повторяется (рис.
10). В конце концов после а0
сложений мы с необходимостью
встретимся с ситуацией, ког-
да s = 0, что и считается завер-
шением первого шага умноже-
ния. В регистре С теперь нахо-
дится число а0Ь + с, где с —
исходное содержимое регистра
С. Поскольку а0<;г—1, то
с + aQb < r"+1 — г, и выбранная разрядность регистра С по-
зволяет получить арифметически точный результат, младший
разряд которого является младшим разрядом суммы с -|- ab,
и в дальнейшем его значение уже не будет меняться. Рацио-
Нет
Да
S’-=S-1, c-. = c + b
а^г=св, С:=С^Г
Рис. 10.
нально переслать его в старший разряд регистра А, который
сейчас свободен. Это сделать очень просто—достаточно сое-
динить выход с младшего разряда регистра С с входом стар-
шего разряда регистра А и регистр С сделать регистром пра-
вого сдвига (см. рис. 9). Если теперь после обнаружения
условия s = 0 сделать сдвиг регистра С, то в регистре А ока-
жется младший разряд результата, а в регистре С — старшие
п разрядов частичного произведения а0Ь, которые еще будут
участвовать в формировании результата. На этом полностью
заканчивается шаг умножения, и можно переходить к анализу
цифры ах. Обычно совмещают по времени сдвиг регистров А
и С, кроме начального (если с = 0, то совмещают и началь-
ный сдвиг). /
' Остальные шаги реализуются точно так же, и после завер-
шения п-го шага произведение определено полностью, причем
старшие п разрядов произведения хранятся в регистре С,
а младшие — в регистре А, множимое сохранилось в регистре В.
Максимальное время умножения для данного алгоритма дости-
гается, когда at = r— 1, г = 0, ..., k, и оно есть
max = п [(г — 1)тЕ 4-Tsh], (2.6)
где Tsh — время сдвига на один разряд, а — время сложения
«-разрядных операндов. Для симметричных кодов справедливо
max хр = п (r~1-ф- Tsh у. (2.7)
Сравнение соотношений (2.6) и (2.7) показывает, что переход
к симметричным кодам при том же основании системы счис-
ления дает ускорение выполнения умножения почти в два раза.
2°. Умножение чисел с учетом их знаков. Рассмотрим
сейчас особенности умножения чисел, которые могут быть
как положительными, так и отрицательными. Для симметрич-
ных кодов проблемы учета знаков сомножителей не сущест-
вует, поскольку знак цифры множителя полностью определяет
характер действия (сложение или вычитание), которое необ-
ходимо при выполнении очередного шага. Знак результата
есть знак старшей значащей цифры суммы частичных произ-
ведений. В случае использования прямых кодов для представ-
ления сомножителей знак результата р* также определяется
весьма просто, а именно в соответствии с правилом t
P* = a*®b*, (2.8)
где а* и Ь* — знаки сомножителей. Абсолютная величина ре-
зультата есть произведение абсолютных величин сомножи-
телей.
Неприятности начинаются, когда операнды представляются
дополнительными или обратными кодами. Если сомножители
а и b заданы дополнительными кодами, то величина произве-
дения должна удовлетворять равенству
Р = (—+ SLo «ггг) (—+ S/=o bfj) =
= “ rk+1 (tt* 2 /=о bfi +
+ b* SL0 «£г0 + а*Ь*г™+\ (2.9)
Первое слагаемое в правой части выражения (2.9) определяет
результат, когда сомножители расположены в первой четверти
плоскости {а, Ь), т. е„ оба они положительны. Второе и третье
слагаемые представляют коррекцию, необходимую, если точ-
ка («, Ь) лежит во второй, третьей и четвертой четвертях
(а, Ь), когда по крайней мере один из сомножителей отрица-
телен. Реализация возможного вычитания основана, как обыч-
но, на прибавлении дополнительного кода отрицательного
числа.
Прибавление дополнительного кода множимого (когда =
= 1) не вызывает никаких принципиальных трудностей, чего
нельзя сказать о прибавлении дополнительного кода множи-
теля при Ь* = \. Действительно, при наличии трех регистров
номинальной разрядности (см. рис. 9) в структуре арифмети-
ческого узла множитель в процессе выполнения операции
теряется и, следовательно, его необходимое добавление потре-
бует либо дополнительных временных затрат (повторное обра-
щение к памяти для вызова множителя), либо введения чет-
вертого регистра в АУ для дублирования множителя.
Конечно, можно было бы отрицательный множитель пред-
варительно поместить в регистр частичных произведений до
начала собственно умножения, но тогда потребовалось бы
увеличить вдвое длину этого регистра. Отсюда ясно, что реа-
лизация коррекции произведения прямым способом потребует
дополнительных аппаратурных или временных затрат по срав-
нению с реализацией умножения, когда точка (а, Ь) лежит
в первом квадранте.
Возможным выходом из создавшегося положения является
замена операндов, заданных дополнительными кодами, до на-
чала операции умножения их прямыми кодами. Естественно,
что при этом после завершения операции, если результат
окажется отрицательным числом, то его надо будет вновь
перевести в дополнительный код. Считая, что появление чи-
сел отрицательного и положительного знаков равновероятно,
найдем что в среднем на каждую операцию умножения необ-
ходимо иметь
обращений кода одного вида в другой. Заметим, что при
многих реализациях операции умножения обращение сомно-
,жителей может быть выполнено не полно — только как фор-
мирование поразрядных дополнений. Добавление 1 в младший
разряд обращаемых кодов, необходимое для получения допол-
нения, тогда производится при анализе цифр множителя и при
формировании частичных произведений путем сложения мно-
жимого с учетом с0=1. Обращение кода результата должно
производиться в половине всех случаев, и здесь уже без пря-
мого добавления единицы в младший разряд 2/г-разрядного
числа не обойтись.
Пример 2.12. Пусть величины а = —457 и b = 824 представлены допол-
нительными кодами в десятичной системе счисления при п = 3, т.- е. b : 1543
и 6:0824. Найдем значение произведения p = ab. Вначале переведем допол-
нительный код числа а в прямой, тогда а': 1457. Затем найдем произведе-
ние р = а'Ь = —376568. Наконец, результат, полученный в виде прямого
кода, переводим в дополнительный, и тогда окончательно р: 1623432.
До сих пор мы пытались осуществить, коррекцию явно,
т. е. вначале найти значение произведения 2л=о S;=o
а уже потом уточнить этот результат, если это необходимо.
Попробуем теперь реализовать ’ коррекцию неявно. С этой
целью представим операнды в виде
а = -(г - 1) г*+! 4- (г - 1 - «J r*+i + «Л (2.10)
Заметим, что в равенстве (2.10) отрицательный член не зави-
сит от значения разрядов числа. Значение г — 1 — есть не
что иное, как а*, т. е. дополнение значения знака операнда
до г—1.“[Будем считать, что а =— (г — 1) rk+1 + а’, и тогда
p = ab = a'b' + (г— I)2 г2*+2 — (г — 1)гй+! (а'+ Ь'). (2.11)
Произведение p = ab также представим в виде р = р’ — (г —
— 1)г2*+2. Нашей задачей является определение значения р',
т. е. всех разрядов произведения, из которых один (знаковый)
будет представлен в виде дополнения до г — 1, а остальные —
прямыми значениями. Из равенства (2.11) имеем
р' = а'Ь' — (г — 1) rk+l (а' + Ь’) (mod 22ft+3), (2.12)
или, заменяя вычитание сложением дополнительных кодов,
получим
р' = а’Ь' + (г — 1) г*+! (a^rk+l + + 1) + г
+ (г - 1) + SLo V1’ + 1), (2.13)
где xt — r— 1 —xt. Таким образом, произведение чисел а и Ь,
представленных дополнительными кодами, есть сумм,а трех
Оо^* О;Ь)( ОдЬ), .. О/Ьм. . .
а'хъ'=- ак^к °i<bz ДхЬ* б*Ьц 5#ЬК.; zi-c*b7 04? °*ь0 У' X акЪц
(Г-1)гмЬ’= (r-7)i* (г-1)Ък (г-1)Ък-г... (r-ffo (т-7)(5^7)
(г-1)гма’= 1г-1)ак (r-1)aR.j... (г-7)с, (г-1)(а0
слагаемых (рис. 11). Попробуем так преобразовать эту сумму,
чтобы число слагаемых, зависящих от значений операндов,
уменьшилось. С этой целью рассмотрим ксумму + (г —
— 1) bL. С учетом xt = г— 1 ~xL 'получим ditbl 4- (г — 1)=
= (г—I)2 — a*bh Аналогично b^at-\- (г— l)at =
= (г — I)2 — Ь^. Кроме того, справедливо aji* 4- (г — 1) X
X (а* + Ь*) = (г — I)2 + d*b*. Используя данные равенства,
преобразуем выражение (2.13) к ,виду
р' = (Г2 _ 3) г2*+2 + 2г*+1 4- 2Lo 2Lo 4-
+ as6sr2ft+2 + rk+l SLo («i + b’i} rl (mod 22*+3).
r2#2 r2^1 r2t __ .r**2 rM r1 r0
G — G# Gfc ... G-j Gq
Ъ - b# b* ... b7 b0
ОдЬ7 а$Ъ0
Gifio
I _ ’
P = P* Р2кЧ Pzx • P/;*2 Pfc+7 Pft • • pj Po
Рис. 11.
/
Здесь di = r — 1 — b*di и bi = r — 1 — d^bt. Величину pr можно
представить как сумму двух слагаемых:
р' = с -\-db (mod 22ft+3),
где с = {г2 — 3) г2й+2 4- 2rft+1 — константа для заданной системы
счисления, a db — член, зависящий от значений сомножителей
(рис. 12). Значение константы с' = (г2 — 3) r2ft+2 может быть
в некоторых случаях учтено весьма простым образом. Напри-
мер, при г=2 в произведении db надо добавить единицу
к элементу d*b* и единицу к двум элементам (Z*-|-2)-ro столб-
ца. Кроме того, в этом случае d't — b*db bi — d^bt и 1 @ d^b^. =
= d^b^, следовательно и массив становится более однородным
(рис. 13).
p2V7 ггк. ... г™ p . . . r' r°
о' = a* a* . . a, a0
ь' = b* h . . b, bB
a'tfi Gob* • • Otfit °ofy)
a-, alby-i О;ЬВ
c*ob = .
с' . . . osb2 a*bt Oybo
Ъ'к ь1-^р^ь\ b'0*1
р' = P# Ргм Pit. • • Pk*2 Pfc+7 Pt. Pl Po
Рис. 12.
g2i<*2 22* *2^*2 2К 2^ 2°
o' = b' = % b* a* bk • 0/ b. 0° bo
c+ob= . a7b# ЬцОо+1 aibk °obj; - Oobj ofbo Goty)
°tb* °#b>< Ojfbj-; . . аЛ. o^bj йкЬ7 a#bff*l ° A
p' = P* P2k+/ P2U - • Pw Pk • • Pr Po
Рис. 13.
Пример 2.13. Пусть величины а = —457 и b = —825 заданы в десятич-
ной системе счисления при п = 3 в виде дополнительных кодов, т. е. а: 1543
и 5:1175. Найти произведение этих чисел. Поскольку «* = 6*=1, то
= a-i и Ь\ = bv Учитывая, что 6 = 2 и г = 10, получим с' = 7002-103.
Произведение ab будем находить по алгоритму, основанному на методе
последовательного суммирования строк матрицы:
1-й шаг 0.0000 —начальное состояние суммы частичных произведений
+0.6525 — значение 1-й строки матрицы ab
0.6525—сумма частичных произведений 1-го шага;
2-й шаг 0'.0652—результат 1-го сдвига суммы частичных произведе-
ний, р0 = 5—цифра результата
+0.5700 — значение 2-й строки матрицы ab
0.6352—сумма частичных произведений 2-го шага;
3-й шаг 0.0635—результат 2-го сдвига регистра В, рх = 2 — цифра
результата
+0.4875—значение 3-й строки матрицы ab
0.5510—сумма частичных произведений 3-го шага;
4-й шаг 0.0551—-результат 3-го сдвига регистра В, р.г = 0—-цифра
результата
+0.1824 — значение 4-й строки матрицы аЪ\
коррекция 0.2375 — сумма частичных произведений 4-го шага
+0.7002 — константа
0.9377 — значение старших разрядов результата.
Поскольку р* = 9, то р* = 0, и окончательно р = ab = 377025.
Пример 2.14. Пусть величины а = 457 и b = —825 заданы в десятич-
ной системе счисления при п = 3 в виде дополнительных кодов, т. е. а: 0457
и b: 1175; найти их произведение.
Поскольку а* = О, то = r—-1 и at — at из-за того, что b* = 1. Зна-
чение корректирующей константы есть с' = 7002-103, так как k = 2 и г —
= 10. Значение произведения будем находить по тому же алгоритму, что
и в примере 2.13, тогда:
1-й шаг OjOOOO—начальное значение'суммы частичных произведений
+0.3225 — значение первой строки матрицы аЬ
0.3225 — сумма частичных произведений 1-го шага;
2-й шаг 0.032^ — сдвиг вправо суммы частичных произведений, р0 = 5
+0.4875 — значение 2-й строки матрицы ab
0.5197 — сумма частичных произведений 2-го шага;
• 3-й шаг 0.0519 — сдвиг вправо суммы частичных произведений, рх—1
+0.5700 — значение третьей строки матрицы ab
0.6219 — сумма частичных произведений 3-го шага;
4-й шаг 0.0621 — сдвиг вправо суммы частичных произведений, р.2 = 9
+0.0999 — значение четвертой строки матрицы ab
и.1620— сумма частичных произведений 4-го шага;
коррекция +0.7002 — корректирующая константа с*
0.8622 — значение старших разрядов произведения.
Поскольку р = 8, то »* = !, и окончательно р 11622975, т. е. р =
= —377025.
Для некоторых систем счисления (например, двоичной) шаг,
связанный с добавлением корректирующей константы, может
быть устранен за счет специфического формирования строк
матрицы ab. Однако это не меняет главного — умножение до-
полнительных кодов, каким бы способом оно ни производи-
лось, всегда заметно' сложнее, чем умножение прямых кодов,
когда матрица ab состоит из меньшего числа членов: (й-|-1)2
вместо (k 4- 2)2 и, кроме того, все элементы матрицы обра-
зуются по одному закону. В матрице же дополнительных
кодов один ряд и одна диагональ составлены из элементов,
отличных по своей природе от остальных, что является опре-
деленным недостатком.
Использование обратных кодов при умножении еще в боль-
шей степени усложняет алгоритм. Действительно, теперь для
числа а справедливо, что а = —a* (rA+1 — 1) + и, сле-
довательно,
p = ab = SLoS;=oafijri+] + «Л (rfe+1 — I)2 —
- (rfc+1 - 1) (a# 2;=o bfi + b* £Lo af'). (2.14)
По сравнению с (2.9) для обратных кодов (2.14) характерно
еще большее число дополнительных сложений помимо есте-
ственной операции перемножения основных разрядов. Посколь-
ку преобразование из обратного кода в прямой и наоборот
делается весьма просто — как поразрядная операция дополне-
ния, то имеет ^смысл заменить умножение обратных кодов
умножением прямых кодов, с необходимыми преобразования-
ми в начале и конце операции.
Пример 2.15. Пусть величины а = 457 и 6 = —525 заданы в десятич-
ной системе счисления при п = 3 обратными кодами, т. е. а: 0457 и b : 1474;
надо найти их произведение в заданной форме кодирования.
Вначале переводим отрицательные сомножители в прямой код, тогда
Ь': 1525. Затем по правилу (2.8) находим знак результата, получим /?*=!,
а затем перемножим основные разряды, тогда найдем, что р : 1239925. По-
скольку этот результат представлен прямым кодом, то надо его перевести
в обратный код. Проделав эту поразрядную операцию, окончательно найдем,
что р : 1760074 или р = —239925,
3°. Умножение чисел с плавающей запятой. Для умноже-
ния чисел, представленных в форме с плавающей запятой,
достаточно сложить порядки чисел и перемножить мантиссы,
являющиеся числами с фиксированной запятой, а затем скор-
ректировать полученный результат, если это необходимо. При
сложении порядков может оказаться, что суммарный порядок
меньше допустимого, и тогда результат представляется ма-
шинным нулем, либо суммарный порядок больше, чем на еди-
ницу, превышает допустимый и тогда возникшая ситуация
должна оцениваться как аварийная. Однако в последнем слу-
чае полученный результат рассматривается как предваритель-
ный. Для окончательного решения надо оценить произведение
мантисс Ма и Мь. Поскольку г~1 < | Ма | < 1 и г~1 <3 Mb | < 1,
то г-2 | МаЬ | < 1. Когда \ Mab | < 1, то требуется произвести
сдвиг мантиссы результата влево, одновременно уменьшив
порядок результата на единицу. Это уменьшение порядка
может ликвидировать первоначальное превышение его допу-
стимой величины, либо привести к тому, что окончательный
порядок станет меньше допустимого и тогда результат ока-
жется машинным нулем. После нормализации мантиссу обычно
округляют до п разрядов, т. е. до разрядности мантиссы со-
множителей (подробнее об этом будет сказано в § 5).
4°. Влияние основания системы счисления на время реа-
лизации умножения. Какая система счисления наиболее
выгодна при машинной реализации умножения? Для ответа
на этот вопрос рассмотрим функцию
/0(г) = -^±, (2.15)
tp (Го)
где г и г0 — основания сравниваемых систем счисления,
a tp (г) — среднее время выполнения операции умножения
в г-ичной системе счисления.
При равновероятном появлении цифр множителя значение
тр(г) для симметричных кодов есть
# (r) = п + Tsh)- (2.16).
Здесь все обозначения такие же, как и в выражении (2.7)
Когда используются несимметричные коды, то значение т (г)
определится как правая часть равенства (2.7). Будем считать,
что точность вычислений определяется количеством допусти-
мых чисел, различных по абсолютной величине. При длине
слов в п разрядов число таких чисел есть гп. Пусть две си-
стемы счисления обеспечивают одинаковую точность, т. е.
г" = Го°. Тогда для несимметричных кодов на основании (2.7)
имеем из (2.15)
1 (г—1) т,(г) 4-2т.
<217’
Здесь мы считаем, что время сдвига на один разряд 'tsh не
зависит от выбора системы счисления. Будем считать, что
г0 < г. Обычно (г — 1) (г) 2tsh и ts (г) = /тз (г0), тогда при
г0 = 2 можно считать, что
<2Л8>
Значения функции f0(r), определенные из (2.18) при t = \,
даны в табл. 1 (см. главу 1, § 3).
Для симметричных систем счисления найдем, подставляя
выражение (2.16) в формулу (2.15), что при г0 = 3 прибли-
женное значение функции /0 (г) может быть задано равенством
/0(г)= я0-,2" °-. (2.19)
Как в случае симметричных кодов, так и в случае несиммет-
ричных кодов функция /0 (г) монотонно возрастает с ростом г.
Это означает, что при использовании двоичной системы счис-
ления и троичной системы счисления с цифрами 1, 0, 1 сред-
нее время .умножения окажется наименьшим. Конечно, функция
f0 (г), определенная из (2.^18) и (2.19), дает лишь очень при-
ближенную оценку. Точное значение функции /0(г) для слу-
чая несимметричных кодов можно было бы получить из вы-
ражения (2.17), но, к сожалению, входящие в него величины
тЕ (г) и т£ (г0) в сильной стейени зависят от особенностей тех-
нической реализации параллельного суммирования в конкрет-
ной машине. Поэтому, говоря об оценках, задаваемых функ-
цией /0 (г), мы на самом деле говорим о тенденциях, прису-
щих данному методу умножения. Интересно, что троичная
система счисления с симметричной базой позволяет в среднем
почти в два раза быстрее реализовать умножение, чем при
использовании двоичной системы счисления.
Для сумматоров последовательного принципа действия ве-
личина т£ (г) может быть определена как тЕ (г) = (га + 1) тЕ (г),
где га — число разрядов слагаемых, а тЕ (г) — время цикла сум-
мирования одного разряд^. Пусть опять тЕ (г) = /тЕ (г0), тогда,
пренебрегая ts11 в (2.17), получим следующую оценочную
функцию для несимметричных кодов:
/о'(г) = (г- 1И log-2 г.
Если для г = 5 добьемся, чтобы t было меньше 1,33, то пяти-
ричная система счисления будет более эффективной при дан-
ном способе умножения, чем двоичная.
§ 4. МЕТОДЫ ДЕЛЕНИЯ
1°. Деление прямых кодов. Рассмотрение особенностей
операции деления начнем для чисел с запятой, фиксированной
в старшем разряде. Будем считать, что и делимое и делитель
представлены прямыми кодами, тогда знак результата опре-
деляется точно так же, как и при умножении (2.8), а основ-
ные разряды частного определены только значением основных
разрядов делимого а и делителя Ь. Пусть делитель нормали-
зован, т. е.
— 1.
Частное от деления а на b определим последовательно за
n = k-\-\ шагов, причем на каждом шаге I выбираем макси-
мальное q\-i (1 <11 k + 1), при котором
aw = a(i-v - q^r'-p > 0. (2.20)
-i
Здесь ra(i) — частичный остаток после i-го шага деления и га(0) =
= а. Частное от деления га на & есть
q = ^=oq~tr-1,
причем
о г — г1-".
Цифры частного, определенные из соотношения (2.20), удов-
летворяют условию
Г-1,
Рис. 14.
MO-
для'
г = 0, 1, ..., k.
Это действительно так, ибо если бы на г-м шаге была полу-
чена цифра частного 1, то из (2.20) для (г—1)-го
шага имели бы гг<г-1> < r2~lb, а для г-го шага было бы спра-
ведливо неравенство г2~1Ь.
Очевидно, что эти два неравенства
одновременно выполняться не
гут, и поэтому qi-i г — 1
всех i = 1, 2, ..., А 1.
Алгоритм определения на г-м
.шаге цифры частного qi-t сводится
к последовательному вычитанию из
очередного остатка делителя, умень-
шенного в г1-1’ раз, и анализу зна-
ка результата после каждого вы-
читания (рис. 14). Если после оче-
редного вычитания выполняется
условие гг(,-1) 0, то в специальный
счетчик 5, первоначальное значение
которого равно нулю, добавляется
4-1 и вновь вычитается делитель
из очередного остатка. Если же
после очередного вычитания выяс-
нится, что гг^-1> < 0, то это явля-
ется признаком завершения процес-
са определения очередной цифры
- частного. В этом случае значение
счетчика s приписывается опре-
деленной цифре, после чего осу-
ществляется подготовка к следую-
щему шагу алгоритма, которая
заключается в увеличении на 4~1
счетчика шагов операции г и в
присвоении счетчику цифры част-
ного значения ноль. Кроме того,
происходит восстановление ос-
татка, заключающееся в прибав-
лении к отрицательному остатку
числа г'~хЬ. В результате этого
значение очередного остатка перед
шага — всегда положительное число.
началом следующего
Очень часто вместо уменьшения делителя в г раз перед оче-
редным шагом увеличивают в г раз положительный остаток.
Теперь все подготовительные операции завершены и можно
переходить к выполнению следующего шага. После п шагов
алгоритм деления завершается определением всех п цифр
частного. Заметим, что для определения одной цифры в наи-
худшем случае надо будет выполнить г операций вычитания
и одну операцию сложения (для восстановления остатка).
В наилучшем же случае достаточно двух действий — вычита-
ния и сложения.
Пример 2.16. Требуется найти частное отделения величины а = 223
на b.— TZI, которые заданы в десятичной системе счисления прямыми ко-
дами, т. е. а : 0223 и b : QTZI.
1-й шаг 0.223 — с№ — значение делимого, исходное значение 5=0 —0.723 — делитель —0.500 — < 0, поэтому остаток восстанавливается 4-0.723 — делитель 0.223 — восстановленный остаток, окончательно qQ = 0;
2-й шаг 2.230 — остаток исходное значение 5=0 — 0.723 — делитель 1.507 — текущее значение >0, s = 1 — 0.723 — делитель 0.784 — текущее значение >0, s = 2 — 0.723 — делитель 0.061 —текущее значение > 0, s = 3 —0.723 — 0.662 — текущее значение < 0, окончательно д_г =3 4-0.723 — делитель 0.061 — восстановленный остаток;
3-й шаг 0.610-—остаток увеличен в 10 раз, 5 = 0 —0.723 -— делитель —0.113 — текущее значение < 0, окончательно д_2 — 0 4-0.723 — делитель 0.610 — восстановленный остаток;
4-й шаг 6.100 — остаток увеличен в 10 раз, 5 = 0 • —0.723 — делитель 5.377 — а(3) > 0 и s = 1 — 0.723 — делитель 4.654 —а(3) >0, s = 2 — 0.723 — делитель 3.931 — а(3) > 0, 5 = 3 — 0.723 — делитель 2.208 —а(3) >0, s =,4 — 0.723 — делитель 1.485 —а(3) > 0, 5 = 5 — 0.723 — делитель 0.762 — а(3) >0, s = 6 — 0.723 — делитель 0.039 —а(3) > 0, s = 7 — 0.723 — делитель — 0.684 — > 0, окончательно q__3 = 7 4-0.723 — делитель 0.039 — восстановленный остаток.
Если ограничиться тремя знаками после запятой, то получим q — 0,307.
Достаточно просто построить алгоритм деления без вос-
станоеления остатка, с целью уменьшения числа действий,
необходимых для определения цифр частного. 'Действительно,
ведь восстановление производится уже после того, как ста-
новится ясно, что цифра частного определена (очередной
остаток стал отрицательным) и само • восстановление нужно
только для того, чтобы обеспечить стереотипную процедуру
определения цифры частного на последующем шаге. Встает
вопрос, а что произойдет, если мы не будем восстанавливать
отрицательный остаток, а прямо используем его на следую-
щем шаге деления? Вполне очевидно, что этот остаток мы
можем рассматривать как результат вычитания на (Z-f- 1)-м
шаге деления из „правильного" остатка (т. е. восстановленно-
го на 4-м шаг^) r-кратного делителя, ибо на (г-|-1)-м шаге
делитель в г раз уменьшен по сравнению с величиной дели-
теля на 4-м шаге. В этом случае (когда остаток отрицателен)
для определения цифры частного надо прибавить делитель
и проанализировать знак суммы. Как только сумма станет
положительной, надо закончить 4-й шаг. Покажем, что такая
процедура приведет точно к такому же результату, что и про-
цедура деления с восстановлением остатка.
, Пусть на t-м шаге мы восстановили остаток, тогда после
завершения шага aW = — + Ьг1-1, где —— отрица-
тельный остаток, полученный на 4-м шаге. Если на следующем
(4'ф-1)-м шаге найдена цифра частного q~t, то остаток после
завершения (4 ф- 1)-го шага есть
сФ+1) = а(б — q_ir^~ib = brx~l — аб-v — q^r^b. (2.21)
Когда же применяется- метод деления без восстановления
остатка, то на (i ф-1 )-м шаге мы у раз добавляем к отрица-
тельному остатку величину bi—в результате чего получаем
aV+v = ybr-i — 44<г-!). (2.22)
Будем считать, что цифра частного, которая найдена., при этом
шаге, есть q'_t = г — у, тогда, если эта цифра истинная, то,
подставляя y = r — q'_. в равенство (2.22), мы должны полу-
чить правую часть равенства (2.21), что и есть на самом деле.
Цифру = q_. можно получить, если в счетчике s форми-
рования цифр частного при отрицательном знаке остатка, когда
e = signa = 1 (рис. 15), предварительно занести значение г—1,
а затем при каждом добавлении, не вызывающем изменение
знака очередного остатка, вычитать единицу.
Если строго придерживаться рассмотренного метода без
восстановления остатка, то на всех нечетных шагах алгоритма
следовало бы вычитать делитель (с соответствующим весом)
Рис. 15.
из положительного остатка, ибо с! 0, и при сохранении зна-
ка после очередного вычитания прибавлять в счетчик +1
(начальное положение счетчика цифр частного 0), а при изме-
нении знака заканчивать про-
цесс определения цифры част-
ного. На всех же четных ша-
гах процесс производился бы
аналогично, только делитель
бы прибавился, т. е. d = \,
а из счетчика, первоначальное
значение на шаге которого
было бы г— 1, вычиталась
единица. Максимальное число
алгебраических действий на
шаге составляет при этом г.
На практике же никогда не
делают более г — 1 алгебраи-
ческого действия, а если пос-
ле г — 1 действия знак остат-
ка не меняется, т. е. справед-
ливо e@rf = 0, то последний
остаток увеличивают в г раз
и переходят к последующему
шагу, выбирая тот тип алгеб-
раических действий (сложение
или вычитание), который соот-
ветствует знаку последнего
остатка (см. рис. 15). Эта мо-
дернизация позволяет опреде-
литЬ цифру частного не более
чем за г—1 алгебраических
действий, в результате чего
максимальное время деления
без восстановления остатка
составит величину тд, значение
которой задается правой ча-
стью равенства (2.6). Указан-
ное свойство особенно полез-
но для двоичной системы счис-
ления, когда на каждом шаге
будет всегда выполняться одно
ше и не меньше (подробнее этот случай будет рассмотрен
в главе 7).
"''“’’Пример 2.17. Требуется найти частное от деления а = —825 на Ь = 817
в том случае, когда эти величины заданы в десятичной системе счисления
прямыми кодами, т. е. а: 1825 и 6:0817. Вначале по правилу (2.8) нахо-
дится знак результата, он равен „—“, а затем определяется абсолютная
величина результата (будем искать частное с точностью до трех знаков
после запятой).
сложение-вычитание, не боль-
1-й шаг 0.825 — делимое, начальное значение 5=0
—0.817 — делитель
0.008—-текущее значёние остатка, з = 1
—0.817 — делитель
—0.809 — < 0, окончательно q0 = 1,-
2-й шаг —8.090 — остаток z/1) начальное значение 5 = 9
+0.817 — делитель '
—7.273 —zz(1) < 0, s = 8
+0-817 — делитель
' —6.456 —а(1> < 0, s = 7
+0.817 — делитель
—5.639 —z/1» < 0, s = 6
+0.817 — делитель
—4.822 —а(1> <0, s = 5
+0.817 — делитель (
—4.605 — <0, s = 4
+0.817 — делитель
—3.188 —а{1> < 0, s = 3
+0.817 — делитель
—2.371—<0, s = 2
+0.817—делитель
—1.^54 —а(1> < 0, s = 1
+0.817 — делйтель
— 737 — z/1» <0, 5 = 0, шаг закончен q_r = 0;
3-й шаг —7.370 — остаток < 0, начальное значение 5=9
к +0.817 — делитель
—6.553 - а(2> < 0, s = 8
+0-817 — дели тел ь
—5.736 —а(2) <0, 5=7
+0.817 — делитель
—4.919 — а™ <0, s = 6
+0-817 — делитель
—4.102 — zz<2> <0, 5 = 5
+0-817 — делитель
'—3.285 —а<2> < 0, s = 4
- +0.817 — делитель
-2.468 —а(2) < 0, s = 3
+0.817 — делитель
—1.651 — а(2) < 0, s = 2
+0.817 — делитель
—0.834 —о(2> < 0, s = 1
+0.817 — делитель
' —0.017 — z^2) <0, 5 = 0, шаг закончен #_2 = 0;
4-й шаг —0.170 — остаток z/3). < 0, начальное значение 5=9
+0.817 — делитель
0.647 — остаток а№ > 0, шаг закончен q_3 — 9.
Три знака после запятой определены, и окончательно q = —1,009.
Определенным недостатком алгоритма деления без восста-
новления остатка является анализ знака остатка после опре-
деления полного частного и его коррекция в случае отрица-
тельного знака. Коррекция заключается в добавлении дели-
теля. Для двоичной системы счисления вместо знака остатка
достаточно проанализировать значение младшей цифры част-
ного qn [43] и если #п = 0, то коррекция необходима.
Для получения большей точности при делении «-разряд-
ных операнд обычно получают (« + 1)-разрядное частное,
а затем округляют его до п
разрядов (подробнее об этом
сказано в § 5).
Логическая структура алго-
ритма деления во многом похо-
дка на структуру алгоритма ум-
ножения, что позволяет в зна-
чительной степени использовать
при делении оборудование, тре-
буемое для реализации умноже-
ния. Так, если структура ум-
ножения соответствовала схеме
рис. 9, то алгоритм деления
удобно реализовать на схеме,
соответствующей рис. 16.
Делимое находится в регист-
ре С, а делитель — в регистре
В. Связи между сумматором,
регистрами В и С точно такие
же, как и при умножении. В от-
личие от умножения измени-
лось направление сдвига в регистрах С и А. В последний по-
следовательно поступают из специального счетчика сформи-
ровавшиеся цифры частного. Это вынуждает либо применять
регистры двустороннего сдвига, либо реализовать сдвиги
влево через сдвиги вправо и логические операции. В маши-
нах последовательного действия решение этой проблемы обыч-
но не вызывает затруднения. Например, вместо сдвига влево
регистра С можно просто блокировать 1-й сдвиг вправо
в первом цикле сложения-вычитания.
2°. Деление симметричных кодов. Рассмотрим особеннос-
ти деления симметричных кодов, когда основание системы
счисления г нечетно и г^-3. Каждая цифра принадлежит мно-
жеству — г~1, — г~3, ..., —1, 0, 1, ..., > Г . Сле-
довательно, максимум абсолютной величины операндов (бу-
дем рассматривать только правильные дроби) есть -1- (1 —r~s).
Поскольку делитель нормализован, то его абсолютная величина
не может быть меньше, чем —г1^), что соответствует
г_______________________________________________]
случаю, когда 6_i = 1 и 6_2 = ... = Ь~х —------. Отсюда
абсолютная величина частного удовлетворяет неравенству
(2.23)
Хотя диапазон изменения абсолютных величин частного почти
такой же, как и при делении прямых кодов, разрядность це-
лой части частного должна быть увеличена на единицу. Это
действительно так, ибо согласно (1.8) при k = 0 диапазон
допустимых значений чисел с одноразрядной целой частью
меньше, чем правая часть неравенства (2.23).
Определенные трудности при делении симметричных кодов
вызывает то обстоятельство, что цифры частного могут быть
разных знаков. Это приводит к тому, что для определения
цифры частного приходится анализировать не только знак
очередного остатка, но и его величину, что, как правило,
является достаточно сложной процедурой [5].
Значительно более простым получается алгоритм деления
симметричных кодов, если частное получать в два этапа. На
первом этапе определяется знак результата, а затем по обыч-
ным правилам* деления прямых кодов ищется частное от де-
ления абсолютных величин делимого и делителя. Результат
представляется в системе счисления с основанием г, но с не-
отрицательной базой, т. е. диапазон цифр частного есть ОС
С qt С г — 1. При этом все действия производятся в симмет-
ричной системе счисления.
На втором этапе найденное частное приводится к виду,
соответствующему симметричному коду, и одновременно ему
присваивается знак результата.
Пример 2.18. Даны величины а =16 и Ь = —47, представленные сим-
метричными кодами в пятеричной системе счисления, т. е. а =121 и b =
= 212. Надо найти частное от деления а на b с точностью до четырех
знаков дробной части.
1-й этап. Определяется знак результата, он будет „—“, и находится
абсолютная величина делителя — это Ь' = 212. Далее выполняется деление
по правилам деления прямых кодов:
1-й шаг _ 0.121—делимое, начальное значение 5=0
0.212 — делитель
0.Г1 Г—остаток а®* < 0, окончательно <7о = О;
2-й шаг । 1.110—остаток < 0, начальное значение s = 4
0.212 —• делитель
, Т.122 — а*1) <0, s = 3
0.2 Г2— делитель
0.221"— aw < 0, s =2
0.212 — делитель
0.Т21— a<’> < 0, s = 1
0.212 — делитель
0.122 — > 0, окончательно q_x = 1;
3-й шаг —-U.220 — с№ > 0, начальное значение s —О
0.212 — делитель
_ 1.015—я(2) > 0, s = I
0.212 — делитель
_ 1.211 — Д(2) > 0, s = 2
0.212 — делитель
_ ОЛОТ—«(2) >0, 5 = 3
0.212 — делитель
0.102 — < 0, окончательно q_2 = 3;
4-й Hiar _j_ "1.020—«(3) < 0, начальное значение s = 4
0-212 — делитель
+ 1.212 — «(3) <0, s = 3
0.212 — делитель
+ 0.Т1Т —«(3) < 0, 5 = 2
0.212 — делитель
0.101 —с№ > 0, окончательно q_^ = 2';
5-й шаг___ 1.010— > 0, начальное значение 5 = 0
0.2Т2 — делитель
__ 1.222 —«(4) >0, s = I
0.212 — делитель
"0121 — «(4) >0, 5 = 2
— \
0.212 — делитель
0.021 —< 0, окончательно q__4 = 2.
Итак, частное, полученное на 1-м этапе, есть q = 0,1322g.
2-й этап. Полученное на первом этапе частное затем приводится к фор-
ме симметричного кода. С этой целью с помощью сумматора симметрич-
ного кода (а именно такой сумматор реализовал алгебраическое, сложение
на первом этапе) находится сумма слагаемых, на которые разбивается най-
денное ранее частное. В нашем случае такое сложение позволит найти
окончательное значение частного q 0,2222g.
Приведенный алгоритм деления симметричных кодов прак-
тически является алгоритмом деления прямых кодов без вос-
становления остатка с некоторой дополнительной частью
в начале и в конце операции. Его достоинством является
упрощенный анализ остатков (анализируется только их знак),
а очевидным недостатком — недостаточное быстродействие.
Усложняя анализ остатка, можно при определенных условиях
добиться прямого вычисления цифр частного в симметричном
коде [5]. В зависимости от глубины анализа можно получить
различную скорость реализации алгоритма.
Рассмотрим один из возможных алгоритмов деления сим-
метричных троичных кодов, т. е. кодов с цифрами 1, 0, 1.
Пусть делимое а и делитель b задают правильные л-разряд-
ные дроби и пусть делитель нормализован, т. е. b-i 0. Бу-
дем считать, что если знак числа а положительный, то
sign a =1, а если отрицательный, то sign a =—1, тогда a-.b =
= sign a sign b]a |: | b |. Определим вначале условия выбора
возможных значений цифр частного.
Отношение |а|: | b | запишем в виде |а[:|6| = ^* +
+ 7 = §"* + где q* — целая часть отношения, q —
дробная. Согласно (1.8) наибольшее значение дробной части
есть шах^ = -^-(1—3~т). Если при проверке будет установ-
лено, что справедливо неравенство
;|Д' < —(1 — 3~т)
то это будет означать равенство нулю целой части, т. е. q* =
= 0. На практике достаточно проверить отношение 2|а(> | Ь\.
Если в качестве а используется делимое, а затем частичные
остатки то значение q* есть значение цифры частного
qi-i, определяемой на /-м шаге деления. Покажем теперь,
что в нашем ^случае целая часть отношения | a^i} |: | b | может
быть сделана не больше, чем единица. Это окажется дей-
ствительно так, если для всех а№ будет справедливо нера-
венство , ’
|а(О| , 1
-±^1 + _£_(i _ з-т). (2.24)
Правая часть неравенства (2.24) есть наибольшее значение
троичного кода при одноразрядной целой части и /«-разряд-
ной дробной. Легко установить, что если неравенство (2.24)
выполняется для /=1, то оно будет выполняться и для всех
г = 2, 3, ..., п. Действительно, если |а| — |&|<;Ц-!(1— 3~т),
т. е. |a(D| = 3||a|-16|| <-f-|6|(l -3-), то -^-<ф X
X (1—3~m). С другой стороны, очевидно, что правая часть
этого неравенства меньше, .чем правая часть неравенства
(2.24).. Таким образом, если будет установлено, что 21 а [ >
> 31 b |, то это свидетельствует о необходимости уменьшения
а в три раза. Это новое значение а не может быть по вели-
чине больше, чем -^-(1 — 31-п), и, следовательно, даже при
min| 6[ — -§-(1 Н-З1-") неравенство (2.24) выполняется. Отсю-
да правила определения очередной цифры частного следую-
щие: проверяется соотношение 2|а[>3|й| и, если необхо-
димо, уменьшается делимое, затем анализируется неравенство
2|а</-1> | > |6| и, если оно выполняется, то цифра частного
есть qi-i = sign b • sign «('-n,
q\~i = 0.
Теперь можно, пожалуй,
деления симметричных тро-
ичных кодов, обращая вни-
мание на формирование ос-
татка на каждом шаге (рис.
17). На подготовительном
этйпе находятся знак дели-
теля, его абсолютная вели-
чина, удвоенная величина
делимого и осуществляется
его возможная коррекция.
Присвоение параметру q*J
значения единицы при кор-
рекции позволит в конце
операции получить истин-
ный итог. Основная часть
заключается в определении
знака остатка (s2) и провер-
ки условия 21 | > | b |.
Анализ этого условия поз-
воляет найти цифру част-
ного q\-i и обеспечить пра-
вильное значение очеред-
ного остатка путем вычи-
тания из предыдущего ос-
татка делителя (если знак
остатка был положитель-
ный) или его прибавлением
(если знак остатка был от-
рицательный). Поскольку
алгоритм работает с удво-
енным остатком, то каж-
дое алгебраическое дейст-
вие должно производиться
дважды, что и обеспечива-
ется оператором <г. = (g —
— ft) s2. Как обычно, основ-
ная часть алгоритма завер-
шается увеличением остатка
в г раз. Выход из алгорит-
ма стандартен — по счетчи-
ку шагов операции i.
когда оно не выполняется, то
рассмотреть полный алгоритм
Рис. 17.
13 5
Пример 2.19. Требуется найти частное от деления а = на Ъ = —
в случае, когда числа представлены в троичной системе счисления сим-
метричными кодами, т. е. « = 0,111 и b = 0,111.
Подготовительный этап. Находим знак и модуль делителя — si = —1
и | b | = ОДН, удваиваем делимое «' = 1,001 и проверяем условие 2 | а | >
>3|6|. При данных значениях чисел это условие выполнено, поэтому
окончательно q* = 1, = ОДОЙ, b = 0,111, si — 1-
Основная часть. Каждый шаг включает проверку условия 2 | | >
> ] b | и формирование цифры частного и остатка •
1-й шаг ОДООТ —«<0)s2 (s2=l)
•—0,1110 — делитель
0.011Т — g > 0, поэтому q$ = —1
—0.1 НО — делитель
0.001 Т— £ — 6;
2-й шаг 0.0.110 — a^s2 (s2 = —1)
—0.11 ГО — делитель
0.0010 — g < 0, поэтому 9_j = 0;
3-й шаг 0.1100 — c№s2 (s2 = —1)
—0.1710 — делитель
0.1,110— g > 0, поэтому q_2 = 1
—0.1710 — делитель
0.0110 — g — b;
4-й шаг 0.1100 — a^s2 (s2 =—1)
—0.1170 — делитель
0.0010 — g > 0, поэтому <?_3 = 1
—ОДНО — делитель
0.0110— g — b\
5-й шаг 0.1100 — c№s2 (s2=1)
—ОД НО — делитель
ОДНО—g > 0, поэтому <?_4 =— 1
—0.1110 — делитель
0.0110 —£ —
6-й шаг 0.1100 — «<5,s2 (s2 = 1)
—ОД 110 — делитель
0.0010 — g > 0, поэтому q_s — —1
—0.1 ПО — делитель
0.0110 — g > 0
0.1100-«(6).
Найденное значение частного есть q — 1,01111g, его еще надо скоррек-
тировать, потому что q* = 1. Окончательно будем иметь q— 10,1111g. Чис-
ленное значение найденного частного есть q ~ —2,605.
За счет определенного усложнения алгоритма можно, до-
биться увеличения скорости его реализации, например, введя
анализ значений остатка на ноль, рационально прекратить
операцию, когда встречаемся с ситуацией а(/“1) = 0[5].
3°.' Деление дополнительных кодов. Будем искать частное
от деления двух дополнительных кодов в виде прямого кода.
Знак результата определяется из соотношения (2.8), а абсо-
лютную величину найдем по алгоритму деления без восста-
новления остатка (см. рис. 15), для которого форма пред-
ставления операндов не играет существенной роли. Если
.результат будет иметь знак минус, то прямой код частного
переводится в дополнительный.
Пример 2.20. В десятичной системе счисления дополнительными кода-
ми заданы числа а: 0727 и 6:1149. Требуется найтй частное от деления а
на 6 с точностью до трех цифр после запятой. Вначале из соотношения
(2.8) определяем знак результата <7* = 0ф1 = 1. Поскольку знаки операнд
разные, то 1-й шаг начинается с их сложения. Заметим, что, разрядность
сумматора есть п 4- 1, поэтому Ь : 19149.
1-й шаг 0.0727 — с№ > 0—-делимое, начальное значение s = 0 4-1.9149-— делитель 1.9876 — <0, шаг закончен, q0 = 0;
2-й шаг 1.8760 — <0, поэтому начальное значение s = 9
—1.9149 — делитель
1.9611 — < 0, отсюда s = 8
—1.9149 — делитель <
0.0462 — а№ >_(), шаг закончен, q_x =8;
3-й шаг 0.4620 — с№ >0, начальное значение s = 0
4-1.9149 — дел итель
0.3769 — с№ > 0, отсюда s = 1
4-1.9149 — дел итель
0.2918 — а№ > 0, отсюда s = 2
4-1.9149 — делитель
0.2067 — с№ > 0, отсюда s = 3 v
4-1.9149 — делитель
0.1216 — >0, отсюда s = 4
4-1-9149 — делитель
0.0365 — с№ > 0, отсюда s = 5
4-1.9149 — делитель
1.9514 — с№ < 0, шаг закончен q_% = 5;
4-й шаг 1.5140 — < 0, начальное значение s = 9 —1.9149 — делитель 1.5991 — с№ < 0, отсюда s = 8 —1.9149 — делитель- 1.6842 — < 0, отсюда s = 7 —1.9149 — делитель 1.7693 — < 0, отсюда s = 6
—1.9149 — делитель
1.8544 — < 0, отсюда s = 5
• —1.9149'—делитель
1.9395'—а^л> < 0, отсюда s = 4
—1.9149 — делитель
0.0246 —- > 0, шаг закончен, q_s = 4.
Таким образом, абсолютная величина частного найдена: q = 0,854. По-
скольку знак результата „—“, то результат переводится в дополнительный
код и окончательно q : 19146.
Для деления дополнительных кодов можно, как и при ум-
ножении, после определения знака результата отрицательные
операнды перевести в прямые коды, а дальше выполнить деле-
ние в прямых кодах. Напомним, что для положительных ‘чисел
прямой и дополнительный коды совпадают. Если знак резуль-
тата «—», то после определения частного его надо вновь пере-
вести в дополнительный код. Считая, что числа с разными
знаками равновероятны, получим, что в среднем в одном деле-
нии требуется 1,5 обращения кода операндов или результата,
т. е. точно столько же, как и при умножении.
При использовании обратных кодов для представления
отрицательных чисел структура алгоритма деления точно та-
кая же, как и в случае дополнительных кодов. Естественно,
что при этом надо учитывать все особенности выполнения
алгебраического сложения обратных кодов и сдвига их влево.
Принимая во внимание простоту обращения прямых и обрат-
ных кодов, по-видимому, имеет смысл выполнять деление об-
ратных кодов посредством предварительного преобразования
отрицательных чисел в прямые коды. -
4°. Деление чисел с плавающей запятой. При делении чи-
сел, представленных в форме с плавающей запятой, требуется
выполнить три этапа. Первый заключается в определении по-
рядка частного, что производится как вычитание порядка де-
лителя из порядка делимого. На втором этапе определяется
частное от деления нормализованных мантисс, представленных
с учетом знака. На третьем этапе найденные порядок и ман-
тисса частного, если это необходимо, приводятся в соответ-
ствие, требуемое представлением чисел в форме с плавающей
запятой.
При выполнении первого этапа порядок частного может
оказаться больше допустимого и тогда произойдет переполне-
ние разрядной сетки, которое расценивается как аварийная си-
туация. Возможна также ситуация, когда порядок частного
будет меньше допустимого, и тогда следует эту ситуацию за-
помнить до третьего этапа.
В результате завершения второго этапа, который реализу-
ется в соответствии с одним из выше описанных методов, полу-
чится частное q, такое, что
Поскольку мантисса должна быть по абсолютной величине
меньше единицы, то при >1, т. е. когда целая часть не ноль
(<7о=т^=О)л необходимо полученное частное уменьшить в г раз,
что достигается сдвигом мантиссы вправо на один разряд и од-
новременным увеличением предварительного порядка на еди-
ницу. Эта коррекция и составляет содержание третьего этапа.
Именно после коррекции становится окончательно ясно, будет
ли переполнение разрядной сетки или нет и окажется ли по-
рядок частного меньше допустимого предела. Если на послед-
ний вопрос будет получен положительный ответ, то результат
деления представляется машинным нулем.
Рассмотрение особенностей выполнения основных арифме-
тических операций — алгебраического сложения, умножения
и деления — при использовании различных кодов показывает,
что несомненным преимуществом при реализации самых рас-
пространенных действий — алгебраического сложения и умно-
жения— обладает симметричный код. При использовании дан-
ного кода удается достигнуть значительного увеличения быст-
родействия машины, сокращения оборудования и весьма суще-
ственного упрощения структуры"* алгоритмов указанных дей-
ствий. Единственным недостатком симметричного кода являет-
ся определенная усложненность алгоритмов деления. Однако
весьма заметное число машин не имеет прямой реализации
операции деления, а, кроме того, в мощных машинах часто
используются итерационные схемы деления, базирующиеся на
применении умножения. В этих методах полностью исключают-
ся анализ частичных остатков и пошаговое определение цифр
частного, что собственно и приводит к усложнению структуры
алгоритмов деления. Данное обстоятельство позволяет сделать
вывод, что в большинстве случаев замечательные свойства
симметричного кода будут не сильно скомпрометированы за-
труднениями в выполнении деления.
Наиболее существенным препятствием к широкому исполь-
зованию симметричного кода является в настоящее время от-
сутствие экономичных быстродействующих и надежных элемен-
тов, имеющих более двух устойчивых состояний, способных
эффективно конкурировать с двоичными элементами.
Для несимметричных кодов трудно указать какую-либо
форму, имеющую очевидные преимущества перед другой. При
сложении выгодно использовать дополнительные и обратные
коды, в то время как для умножения и деления более рацио-
нальным оказывается применение прямых кодов. Существен-
ные трудности в реализации умножения и деления дополни-
тельных и обратных кодов, по-видимому, делают нерациональ-
ными их использование при г>2. В то же время для двоичной
системы счисления имеет смысл применять как прямые, так
и дополнительные, коды в зависимости от ориентации цифровой
машины, ввиду того, что трудности в реализации алгоритмов
«длинных» операций могут быть преодолены сравнительно
просто.
В этой главе мы в самых общих чертах познакомились с ме-
тодами выполнения арифметических операций на цифровых
машинах. Естественно, что многие важные вопросы, такие, как
ускорение выполнения операций, методы экономической и на-
дежной реализации, не были здесь затронуты, хотя их решение
и будет во многом определять выбор того или иного алгорит-
ма выполнения арифметических операций. Эти вопросы будут
темой нашего дальнейшего исследования. Однако влияние
формы представления чисел на структуру алгоритмов выясне-
но здесь было достаточно полно, и в дальнейшем нет нужды
в дополнительных уточнениях.
§ 5. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
Операции умножения и деления рассматривались в предпо-
ложении, что операнды являются «-разрядными числами. При
этом мы предполагали, что произведение должно быть ариф-
метически точным, т. е. быть 2«-разрядным числом, а частное
определяется с погрешностью, меньшей чем единица младшего
разряда п-раз'рядного результата. Но весьма часто формат
представления данных (:в том числе и результатов) задается
постоянным, и, кроме того, допустимой является погрешность
вычислений, не превосходящая некоторого предела, который
может быть и существенно большим, чем единица младшего
разряда «-разрядного результата. При указанных требованиях
к точности вычислений имеет смысл пересмотреть классические
алгоритмы умножения и деления в плане их более экономичной
и быстрой реализации.
1°. Округление произведения. Наиболее распространенный
способ формирования «-разрядного приближенного произведе-
ния двух чисел а и b (будем для простоты считать их целыми
«-разрядными числами) состоит, в округлении арифметически
точного результата, наиример, одним из тех методов, которые
рассматривались в § 3 главы 1. Тогда приближение р' есть
pr = ab + у* — S"=o PS1,
где г — основание системы счисления; ргС {0, 1, ..., г—1} —
цифра произведения и у — значение поправочного коэффициен-
та (у=0,1). Различные стратегии формирования поправочных
коэффициентов (методы округления) могут быть использова-
ны. Например, пусть
_ 1 1 при /?„-! > хо;
1 I 0 при pn-i < Хо.
Параметр ХоС {0, 1, ..., г—1} называют порогом округления.
Погрешность .округления, которая есть Д'=ab—p', удовлетворя-
ет в этом случае неравенству
— (г — Хо) г”-1 < Д' < Xor«-i — 1.
Если переписать это неравенство в терминах единицы младше-
го разряда «-разрядного результата, то оно примет следующий
вид:
. . — (1 —
Таблица 3
Пределы, в которых лежит
погрешность округления,
точно такие, как если бы
мы округляли случайное
2«-разрядное число до
«-разрядного. Однако две
другие характеристики —
математическое ожидание
ошибки округления Д' и
дисперсия случайной вели-
чины — будут теперь ины-
ми. Это связано с .тем, что
при умножении нельзя счи-
тать равномерно распреде-
ленными все значения от-
брасываемой части округ-
ляемых слов— их „хвоста".
Действительно, достаточно
очевидно, что произведение
«-разрядных операндов не
может принимать всех зна-
чений, отвечающих 2«граз-
рядному случайному числу.
Кроме того, часть получен-
ных значений совпадает (ибо
ab = Ьа). Отсюда ясна тен-
денция к неравномерной
вероятности получения всех
значений „хвоста" чисел,
являющихся произведени-
ем двух случайных «-раз-
рядных чисел. Особенно
сильно эта тенденция про-
является при перемноже-
нии чисел, представленных
в форме с плавающей за-
пятой, ввиду дополнитель-
ного преобразования ман-
тиссы из-за ее возможной
нормализации.
Пример 2.21. Двоичные чис-
ла заданы в форме с плавающей
запятой при длине мантиссы в че-
тыре разряда и имеют одинако-
вые порядки. Будем считать, что
в исходном состоянии появление
чисел с произвольной нормали-
зованной мантиссой равновероят-
1
но, т. е. р (а) = -g-. Перемножим каждое произвольное число а с каждым
допустимым числом, т. е. составим таблицу умножения (см. табл. 3). Пос-
ле нормализации мантиссы результатов окажется, что вероятности появле-
ния „хвоста” со значениями от нуля до 2'-4 (1 — 2-4) будут не равными
(см. табл. 4). Округлим теперь значение мантиссы до четырех разрядов.
В зависимости от способа округления вероятность появления мантисс со
значением от 0,5 до 1 — 2—4 будет различной (см. табл. 5).
Как видно ив приведенного примера, даже однократное
преобразование чисел, имеющих равные вероятности появле-
ния, приводит к тому, что равновероятность распределения ре-
зультатов нарушается. Можно ожидать, что дальнейшее- пре-
образование чисел приведет к еще большей диспропорции
в значениях вероятности появления чисел с различными ман-
тиссами. В свою очередь, это скажется и на значениях вероят-
ности появления «хвостав» разной величины. Было бы крайне
интересным найти закон распределения вероятностей появления
чисел с различными мантиссами, являющимися результатами
операции умножения, определив тем самым статистическую
природу чисед, подлежащих округлению. Ранее (глава I, § 3)
мы говорили о том, что случайное число задано в статистиче-
ском смысле, если известна в общем случае его корреляцион-
ная матрица.
В рассмотренном примере корреляционная матрица получи-
лась следующей:
0,3125 0,1563 0,0938 0,0469
0,4219 0,1563 0,0469
0,3438 0,0469 ’
0,1563
Pt =
Таблица 4
“-5 “-6 “—7 “-8 a-7a-s) “-г“-R — О —О 1 о Л“_6 “_6“_7“_8)
0000 0,281 1000 0,078
0001 0,016 1001 0,016
0010 0,094 1010 0,063 ,
ООН 0,031 1011 0,000
0100 0,109 1100 0,125
0101 0,031' 1101 0,000
оно 0,094 1110 0,000
0111 0,031 1111 0,031
Таблица 5
а а а а —1 —2 “3 —4
Округление усечением Округление по дополнению Округление без переносов
1000 0,172 0,141 0,109
1001 0,141 0,141 0,203
1010 0,125 0,141 0,078
1011 0,125 0,172 0,172
1100 0,125 0,109 0,109
1101 0,125 0,078 0,141
1110 0,078 0,109 0,047
1111 0,109 0,109 0,141
в то время как предположение о равной вероятности появ-
ления любых значений „хвоста“ приводит к корреляционной
матрице вида
0,5 0,25 0,25 0,25
(^ау) == 0,5 0,25 0,25 0,5 0,25. 0,5
Анализ природы чисел, получающихся в результате умно-
жения, приводит к мысли, что плотность распределения
вероятности появления чисел с мантиссой а будет не равно-
мерной, она будет определяться как (см. [53])
р (а) = —г—> Г~1 < а < 1,
е ' ' а In г’
(2.25)
т. е. чем больше значение „хвоста", тем меньше вероятность
его появления. При этих условиях кажется особенно перспек-
тивным метод округления к нулю, ибо в этом случае мате-
матическое ожидание будет существенно меньше, чем в слу-
чае равномерной плотности вероятности, поскольку наиболь-
ший вклад в среднее значение случайной .-величины при равной
вероятности вносит наибольшее значениё „хвоста".
2°. Приближенное умножение. Для получения'приближен-
ного произведения весьма эффективными оказываются методы
умножения с итеративным изменением длины одного операнда.
Будем использовать, например, следующий алгоритм умно-
жения [30]:
на Z-м шаге умножения 1 г « — k— 1 частичное произ-
ведение определяется как
р™ = bn+x_jrn-i + т„_А_гг«-й-г),
а если п — k^i<^.n, то
р(0 = airl~lb,
окончательно
Р = 2^1=1 р >
где k — параметр алгоритма k £ {0, 1, ..., п}, а поправочный
коэффициент '[n-h-t определяется на первых п — k—\ шагах
умножения по правилу
fl при bn_k-iК
7„_й_г = |0 при bn_k i<K
у — порог поправки и Х£{0, 1, ..., г}.
Принципиальное отличие данного метода от классического
состоит в том, что частичные произведения имеют на первых
i шагах умножения (1 — k— 1) переменную длину.
Эта длина составляет k + i ф- 1 разряд, что позволяет иметь
для реализации' алгоритма умножения как минимум 2n-\-k
разрядов памяти для операндов и частичных произведений,
а не 3«, как это требовалось ранее. Распределение памяти
после окончания операции следующее: «-разрядный сохранив-
шийся операнд (в нашем случае множимое) и («+ ^-раз-
рядный результат. Полученный результат приближенный и по-
грешность в его определении есть Ьр = ab—р:
Др StT1 {rb+i~n 2"=Г1 ь^ - T„_U.
Граничные значения функции Др,_ (определяющие предел
погрешности приближенного умножения, в значительной сте-
пени зависят от выбора порога X. При X = 0 и X = г величина
поправки на первых шагах алгоритма фиксирована вне зави-
симости от значений разрядов множимого, т. е. yz= 1 и yz = 0
соответственно для всех — k—1. Естественно, что
это обстоятельство упрощает логику алгоритмов, однако при-
водит к значительной погрешности при Х = 0 до
шах | Др| = г"-*-1 (г — 1) (« — k— 1),
а при X =г до
/ 1 _ „1+Й—п \
шах | Др ] = г”-*-1 (г — ])(« — k— 1 '
г—1
При этом вся погрешность смещается в область одного знака
[30] („ — “ при Х = 0 и „ + “ при Х = г).
Когда справедливо — 2, что возможно для всех
г ^>4, то погрешность может лежать как в области положи-
тельных Др, так и отрицательных Др значений, причем сумма
Д^ 1Д^ I не зависит от X, а выбор этого порога влияет толь-
ко на перераспределение величин Др и | Д^Г ] в общей сумме.
Наибольшие значения Др и |Д^| есть соответственно [30]
шах Др = rn~k~l (к - 1) I п - k - 1 - г_х---к
шах | Д^| = г11-11-1 [(« — k — 1) (г — X — 1) Ц- .
+ 7^т(1-г1+й-")]. (2.26)
Причем эти выражения справедливы, когда 0<СХ^г— 2
и 2 X г соответственно. Когда X то доля Др и | Д^ |
в сумме примерно равна и пределы, в которых лежит погреш-
ность, наименьшие.
Случаи Х=1 и Х = г —1 особые в том смысле, что
— погрешность в области положительных значений — меньше,
чем величина Д^“ из (2.26), а
Ail и ь 1 г.— 1 Г п — k + а ..
max IД1U-1 = Г т+т I 2 +
Ьт?£гг(1-г^") + а(Г“1
r2+fi-n \1
Г+1 Д
— модуль погрешности в области отрицательных значений —•
I —1 1— (—п”-*
меньше, чем. величина [Др [ из (2.26), здесь а —--.
Однако только для двоичной системы счисления одновре-
менно удается использовать эти замечательные свойства
порога поправки, ибо тогда Х = г—1 = 1. Для троичной си-
стемы ^числения порог поправки Х=1 или Х = 2 также при-
водит к хорошим результатам, хотя погрешность и оказы-
вается неравномерно распределенной в области положительных
и отрицательных значений.
риближенный результат имеет разрядность п + k, и если
нам надо его округлить до п разрядов, то суммарная погреш-
нрсть есть А* = Д'.+ Др и
— (шах | Д71 + г" — V"-1) < А* < шах Др + ^г"-1 — г"-*.
Приемлемым может считаться результат, отличающийся от
истинного не более чем на единицу младшего разряда, т. е.
должно выполняться

(2.27)
Из этого условия можно определить параметр k, который
задает число дополнительных (свыше 2«) разрядов, необхо-
димых для реализации умножения с заданной точностью. Ес-
тественно, что "пороги поправки при этом должны выбираться
такими, чтобы отклонение от точного результата было наи-
меньшим. В табл. 6 приведены наибольшие значения п, при
которых неравенство (2.27) еще выполняется при фиксиро-
ванных значениях параметра k. Эти максимальные значения
длин операндов найдены для систем счисления, представ-
ляющих практический интерес (г = 2, 3, 4, 8, 10, 16).
Таблица 6
Г k
0 ' 1 2 3 4 5
2 10 12 25 f 50 99 196
3 2 7 20 57 168 —
4 4 9 34 129 — —
8 3 12 88 — — —
10 3 13 127 — — —
16 3 19 295 —
Как видно из таблицы, число дополнительных разрядов, ко-
торые необходимо добавить к памяти из 2п разрядов, оказы-
вается На практике весьма малым. Так, для двоичной системы
счисления это всего 2—-.4 разряда при длине операнд в 25—99
разрядов.
Выбор поправочных коэффициентов может быть произведен
также и на основании анализа - цифр множителя, а также
только в зависимости от нечетности или четности номера ша-
га умножения, но значение максимума модуля погрешности
оказывается более высоким, чем у рассмотренной стратегии.
3°. Округление частного. Частное от деления двух чисел,
представленных в форме с плавающей запятой при длине
Таблица 7\
пп'о 0,100010 0,100110 0,101010 0,101110 0,110011 0,110111 0,111011 0,100000
ош'о . 0,100100 0,101001 0,101101 0,110010 0,110110 0,111011 0,100000 0,100010
0,1101 0,100111 0,101100 0,110001 0,110110 0,111011 0,100000 0,100010 0,100100
001 го 0,101010 0,110000 0,110101 0,111010 0,100000 0,100010 0,100101 0,101000
0,1011 0,101110 0,110100 0,111010 0,100000 0,100010 0,100101 0,101000 0,101011’
0101-0 0,110011 0,111001 0,100000 0,100011 0,100110 0,101001 0,101100 0,110000
• Ю01‘0 0,111000 0,100000 0,100011 0,100111 0,101010 0,101110 0,101110 0,110101
0001'0 0,100000 0,100100 0,101000 0,101100 0,110000 0,110100 0,111000 0,111100
<3 0,1000 0,1001 0,1010 0,1011 0,1100 0,1101 0,1110 0,1111
мантиссы в п. разрядов,
обычно вычисляется с точ-
ностью до п + 1 или п + 2
разрядов нормализованной
мантиссы. Затем для повы-
шения точности этот ре-
зультат округляется до п.
разрядов. Для выбора пра-
вильного метода округле-
ния надо знать статисти-
ческую природу значений
частного. Можно ожидать,
что разные значения част-
ного будут иметь неоди-
наковую вероятность появ-
ления ввиду нормализации
результатов и невозможно-
сти получения некоторых
значений при делении «-раз-
рядных чисел.
Пример 2.22. Даны числа,
представленные двоичными кода-
ми в форме с плавающей запятой
при длине мантиссы в четыре
разряда и имеющие одинаковые
порядки. Пусть все числа с раз-
личными мантиссами равноверо-
ятны. Разделим каждое число а
с фиксированной мантиссой на
каждое допустимое число Ь. По-
лученные результаты после нор-
мализации сведены в табл. 7.
Как видно из этой таблицы, ве-
роятность появления „хвоста“ со
значением 0 есть 0,391, со значе-
нием 2~6 есть 0,156, со значением
2-2—6 есть 0,281 и со значением
3-2-6 есть 0,172. После округле-
ния результатов методом усече-
ния, дополнения и нераспростра-
нения переносов получим, что
вероятности появления мантисс
не одинаковы и зависят от мето-
да округления (табл. 8).
Данное обстоятельство
приводит к тому, что при
повторном делении «-раз-
рядных чисел вероятности
появления „хвостов" с раз-
ными значениями будут су-
щественно отличаться. Ана-
лиз значении частных, полученных от деления чисел с пла-
вающей запятой, дает основание, как и в случае операции
умножения, считать, что плотность распределения вероятно-
стей появления чисел с мантиссой а определена выражением
(2.25). Все те соображения, которые выдвигались в пользу
использования метода округления к нулю (усечения) при ум-
ножении, остаются в силе и при делении. Интересно отме-
тить, что хотя выбираемый метод округления базируется на
статистической природе чисел, сам он, в свою очередь, может
оказать существенное влияние на эту природу (см. табл. 5 и 8).
В результате этого часто очень трудно достоверно что-либо
сказать о статистической природе машинных чисел, а следо-
вательно, и выбрать оптимальный метод округления. В связи
с этим особый интерес представляют методы округления,
не связанные с распределением вероятности появления „хвос-
тов" с разными значениями, например метод вероятностного
округления (глава 1, § 3). Из-за трудностей определения
статистической природы чисел, подлежащих округлению,
единственной надежной характеристикой методов округления,
связанных с распределением вероятностей, остается максимум
абсолютной величины погрещности округления.
Таблица 8
' “_1«_234 Р(“-1 а_2а_3а_4)
Округление усечением Округление по дополнению Округление без переносов
0,1000 0,234 0,125 0,125
0,1001 0,141 0,187 0,250
0,1010 0,141 0,141 0,078
0,1011 0,109 0,125 0,172
0,1100 0,125 0,125 0,078
0,1101 0,109 0,109 0,156
0,1110 0,125 0,094 0,047
0,1111 0,016 0,094 0,094
4°. Приближенное деление. Идею об изменении длины
операнда во время операции можно использовать и при реа-
лизации деления. При этом основной целью является сниже-
ние числа одновременно хранимых разрядов операнд и част-
ного до 2« + k вместо 3«, как это требуется в классическом
методе. Рассматриваемый метод деления базируется на итера-
тивном изменении длины делителя на каждом шаге деления,
начиная с (А + 2)-го. Как обычно, на каждом г-м шаге опре-
деляется цифра частного q\-i. Алгоритм приближенного де-
ления числа а на число b тогда может иметь следующий
вид [17]:
на г-м шаге деления 1 <7 k ф- 1 выбираем максимальное
qi-t, при котором
#(0 = «('-!> — qY_L г1-1 b 0;]
а если k ф- 2 -< i п, то выбираем максимальное qi-t, при
котором
«(О = «(/-!> - г1-1 ( 2^г_й + Т/ л-1 г'-*-1) > 0.
Положим частное q = 2"=i Qi-i rl~l- Здесь «(^ — частичные
остатки и с№ = а — делимое. Данный алгоритм имеет не-
сколько особенностей. Так, цифра частного, определенная на
Z-м шаге (Z>- k + 2), может быть по величине больше, чем
г —1, т. е. в принципе возможно переполнение цифр частно-
го. Однако исследования показывают, что переполнение воз-
можно только в одном разряде, причем значения цифр, сле-
дующие за разрядом переполнения, есть нуль. Сама же циф-
ра переполнения, если она не последняя, равна в точности г.
Это дает возможность прервать деление, как только произо-
шло переполнение, а цифру в разряде переполнения и во всех
последующих разрядах заменить на г — 1. Переполнение
никогда не возникает на Z-м шаге, если все ранее определен-
ные цифры равны г — 1, поэтому оно не может вызвать пере-
полнение разрядной сетки. Погрешность частного, найденного
в соответствии с приведенным алгоритмом, есть
А = aw 6-i + b^Lk+2 qi-i (ц-ь-г - 2/=Г\^-1);'
и она во многом зависит от стратегии выбора поправочных
коэффициентов на шагах алгоритма k + 2 I п. Посколь-
ку в процессе операции меняется значение делителя (6), то
было бы естественным поправочные коэффициенты определять
на основе анализа отбрасываемых разрядов делителя. Пусть
Ъ определены как
7/-л-1=
1 при
О при
bt-k-i X,
6j-*-i < X.
(2.28)
При крайних значениях порога поправки X, т. е. когда Х = 0
и X = г, коэффициенты не зависят от цифр делителя и по-
стоянны, как и при умножении (уг = 0 при Х = г и '[г = 1 при
X = 0). Можно выбрать и другие стратегии формирования
коэффициентов yz, в. которых отсутствует зависимость от зна-
чений операндов и частного, например, на первых k + 1 ша-
гах коэффициента у равны нулю, а начиная с (A-j-2)-ro
шага на четных шагах можно брать 7=1, а на нечетных —
7 = 0 [22].
Рассмотрим более подробно вопрос о величине погрешно-
сти, когда коэффициенты определены из (2.28). Если функция
Д лежит в области положительных значений, то ее наиболь-
шее значение находится при = (г — 1) 7г-й-1. Когда же
погрешность лежит в области отрицательных значений, то
наибольшее значение ее модуля достигается при Qxi =
= (г—1) (1 — 7/_й_1). ЛСроме того, очевидно, что условием
наибольших значений функции Д является также равенство
6 = г«-1+2?Г1й-16/г'-х.
Следовательно,
- 6-1 (г -1) 2ХГ1 (1 - Ъ) г-1-* 6//-1 < д <
< (1 + Г-* 7„_ft_t) Г1-" + 6-1 (г — 1) X
X Ж"1 V-'-* № ~ (2.29)
В случае, если Х=0, т. е. 7г=1 для всех — k— 1,
то неравенство (2.29) принимает вид
0< Д < (1 + г-й) r’-« + ri-*-« (г — 1) (п — k - 1),
т. е. вся погрешность лежит в одной области и довольно зна-
чительна.
Когда 7г = 0 (X = г), то справедливо
1 4- г~к V"-*-l h-
(2.30)
Пусть справедливо 2<Д<;г, тогда левая часть неравенства
(2.29) будет иметь точно такой вйд, как и левая часть нера-
венства (2.30), но 6; должно удовлетворять условию 6г<Д —
— 1. Предположим, что для параметра k справедливо нера-
венство
, 1 X—1 ( ' о 1— rt + k-n \
* > 1о£г \ri-k-2--------------------J,
тогда наибольшее значение функции <р есть (см. [28])
1 +r~*(X —l)(n —fe —1)
Было бы естественным считать, что погрешность не долж-
на по абсолютной величине превосходить г1~п (единицы млад-
шего разряда результата), т. е.
[ДКг1,-".
Выберем X = г, тогда это условие будет выполнено, если па-
раметр k окажется больше определенного значения, а именно
k > logr[(r— 1)(« — k— 1) — 2].- (2.31)
В табл. 9 приведены предельные значения п., при которых
еще справедливо неравенство (2.31) при фиксированных зна-
чениях параметра k для наиболее интересных с практической
точки зрения основаниях систем счисления г — 2, 3, 4, 8, 10, 16.
Таблица 9
2
3
4
8
10
16
3
2
1
1
1
1
5
4
3
3
3
3
2 3 4 5
8 13 22 39
8 18 46 128
8 25 90 347
12 76 247 —
14 115 — —
20 273 — —
6 7
72 137
0 1
Как видно из таблицы, для реальных значений п. число до-
полнительных разрядов не столь уж велико, хотя и несколько
большее, чем при умножении. Это объясняется тем, что при
делении помимо погрешности, связанной с итеративным изме-
нением операнда, имеется еще и погрешность метода — вели-
чина остатка от деления которую мы взяли максимально
возможной. Если оценивать только погрешность, вносимую
изменением делителя, то окажется, что, как и при итератив-
ном умножении, она наименьшая, когда Х== 1 для области
отрицательных значений и когда X = г — 1 для области поло-
жительных значений. Следовательно, только двоичная система
счисления приводит к минимальной погрешности в обеих об-
ластях. Заметим, что и простое игнорирование части разрядов
делителя, а именно в случае X = г и когда все поправочные
коэффициенты у,- равны нулю, также приводит к тому, что
двоичная система счисления более приспособлена к реализа-
ции данного алгоритма деления, чем другие. Действительно,
как это следует из табл. 9, при том же количестве оборудо-
вания, которое выразим в числе двоичных разрядов п, число
дополнительных двоичных разрядов оказывается меньшим
для г = 2 по сравнению с г = 4, 8 или 16.
Часто с целью уменьшения величины погрешности вычи-
сляют не п цифр частного, а п + 1 и получившийся резуль-
тат округляют обычным образом до «-разрядного. Сочетая
метод округления частного с итеративным изменением дели-
теля, при оптимальных значениях X можно добиться, чтобы
истинный результат отличался от полученного не более чем
на единицу младшего разряда при числе дополнительных
разрядов таком же, как это требуется при умножении (см.
табл._ 6).
Прмимо уменьшения требуемого количества оборудования
алгоритмы приближенного умножения и деления отличаются
повышенным быстродействием ввиду того, что на большин-
стве шагов алгоритма используются неполноразрядные опе-
ранды, а алгебраическое сложение обычно зависит от числа
разрядов операндов.
ГЛАВА 3
ДВОИЧНО-КОДИРОВАННЫЕ СИСТЕМЫ
СЧИСЛЕНИЯ
Ввиду того, что в настоящее время наиболее освоенным
является двоичный алфавит, имеет смысл рассмотреть вопрос
о представлении цифр некоторой системы счисления с нату-
ральным основанием г > 2 группой двоичных цифр. Систему
счисления,- в которой все цифры изображаются группой цифр
двоичного алфавита, будем называть двоишо-кодированной
r-ичной системой счисления.
§ 1. ОЦЕНКА ЭКОНОМИЧНОСТИ ПРЕДСТАВЛЕНИЯ
Обозначим через А (г) минимальное число двоичных раз-
рядов, необходимых для представления каждой цифры систе-
мы счисления с основанием г. Очевидно, что
А (г) = [Jog2 г] + 5,
(О при г = 2₽,
8 (1 при гу^2₽, р= 1, 2, ... .
Когда r = 2n(r), то каждой комбинации из А (г) двоичных цифр
ставится в соответствие одна из цифр r-ичной системы счис-
ления. В этом случае число различных способов кодирования,
т, е. выбора однозначного соответствия между каждой из г
цифр и определенной двоичной последовательности из А (г)
цифр, оказывается равным
А22х$ = 2Х(г)!
При г < 2Х<Г> имеется 2Х(г) —г „свободных" двоичных ком-
бинаций. Это приводит к сокращению числа различных спо-
собов кодирования до
Л2Х(О = <ЗЛ)
Например, пусть г = 10, тогда А(10)=4 и Д]б = 2,9-1010,
т. е. кодирование десятичных цифр можно осуществить при-
близительно одним из 29 миллиардов способов. Естественно,
что при наложении некоторых требований, которым должны
удовлетворять двоично-кодированные системы счисления, чис-
ло этих способов сильно уменьшится.
Оценим количество оборудования, необходимое для изо-
бражения одного числа, представленного в двоично-коДиро-
ванной системе счисления. Будем считать, как и ранее (гла-
ва 1, § 2), что точность вычислений характеризуется количе-
ством «> различных чисел одного знака, с которыми оперирует
машина. Тогда число основных разрядов, необходимое для
изображения абсолютной величины одного числа в г-ичной
системе счисления, есть п — logr u> + ar, 0<Саг< 1. Количество
же двоичных цифр, требуемых для каждого числа, есть соот-
ветственно Х(г)/г. Рассмотрим функцию '
/ v = * (г) (logr м + «г)
' loga и + а2 ’
которая показывает, во сколько раз количество двухпозицион-
ных элементов, необходимых при использовании систем счис-
ления с основанием г, больше числа элементов, необходимых
для двоичной системы счисления. Значения функции <р (г) для
ряда аргументов приведены в табл. 1, причем эти значе-
ния даны в предположении logrw>ar, когда можно считать
[11], что
cp .(r)^A(r)/log, г. (3.2)
Как следует из (3.2), при г = 2?, р —целое положительное,
функция <р(г) = 1, а в остальных случаях имеем <р(г)>1.
Отсюда следует, что наиболее экономичными являются систе-
мы счисления с основаниями 2, 4, 8, 16 и т. д. К наихудшим
результатам приводит пятиричная система счисления. Если
г <6, то справедливо неравенство /(г)<С<р(г), свидетельст-
вующее о том, что не имеет смысла моделировать систему
счисления с основанием г цифрами двоичного алфавита. С дру-
гой стороны, для систем счисления с г 7 замена каждой
цифры группой из А (г) двоичных разрядов оказывается более
экономичной, чем использование элементов с г устойчивыми
состояниями. Заметим, что поскольку lim<p(r) = l, то системы
счисления с большими основаниями (например, г = 100 или
г = 1000) оказываются весьма экономичными. Десятичная си-
стема оказывается при двоичном кодировании более эконо-
мичной, чем при прямом представлении 10-значными элемен-
тами, но все же требует при заданных условиях на 20% боль-
ше оборудования, чем двоичная система счисления.1
§ 2. КОДЫ С ЕСТЕСТВЕННЫМИ ВЕСАМИ
При заданной системе счисления с основанием г -соответ-
ствие между цифрами этой системы счисления и двоичными
последовательностями длины А (г) можно установить весьма
многими способами. Однако поскольку эти коды базируются
на двоичном алфавите, то рационально из возможных видов
двоично-кодированных кодов выбрать такие, которые бы наи-
более полно могли использовать все преимущества техниче-
ских достижений двоичной системы счисления, особенно когда
это касается реализации арифметических операций. Кроме
того, очень важными являются также вопросы, связанные с пря-
мым и обратным переводом выбранных видов двоично-коди-
рованных кодов в десятичную ц двоичную системы счисления.
Учитывая вышесказанное, мы будем определять вид двоич-
ного кодирования при предъявлении некоторых требований
к выбираемому коду.
Первым требованием пусть будет весомозначность всех
X двоичных разрядов кода r-ичной цифры Ь-кЬх—i ... Ьг, т. е.
потребуем, чтобы было справедливо равенство
= (3.3)
где at — значение цифры г-го разряда числа, представленного
в r-ичной системе счисления, a Ьщ — двоичная цифра и g7 —
вес /-й цифры, !<;/<;А.
Ранее были исследованы особенности выполнения арифме-
тических операций для аддитивной позиционной системы счис-
ления с естественными весами. Будем считать, что цифры at
представляются также в аддитивной позиционной системе счис-
ления с основанием 2, тогда g7- = 2/-1.
Заметим, что коды с естественными весами обладают свой-
ством однозначности представления, т. е. каждой цифре
г-ичной системы счисления может быть сопоставлена лишь
одна из 2Х(Г) двоичных последовательностей из А (г) цифр [20].
Коды с естественными весами, для которых г = 2х<г\ особенно
просты. Действительно, в этом случае базой г-ичной системы
счисления является полное множество двоичных чисел раз-
рядностью А (г), и каждая цифра базы определена из (3.3).
Отсюда действия над цифрами г-ичной системы счисления
на самом деле являются действиями над А (г)-разрядными
двоичными числами. В частности, одноразрядный сумматор
с основанием г оказывается не чем иным, как А (г)-разрядным
параллельным двоичным сумматором. Цифры суммы двух чи-
сел в г-ичной системе счисления будут вычетами по модулю
2Х(Н от суммы двух А (г)-разрядных двоичных чисел. Перенос
со старшего двоичного сумматора определяет признак пере-
полнения сумматора с основанием г.
В случае, когда г <2Х(Г), база системы счисления меньше,
чем полное множество двоичных последовательностей, и толь-
ко те из них, которые удовлетворяют соотношению (3.3),
допустимы, остальные же считаются запрещенными. В этом
случае попытка использовать X (г)-разрядный параллельный
двоичный сумматор для получения суммы двух цифр г-ичной
системы счисления обеспечит правильный результат только
тогда, когда значение суммы окажется меньше г. Остальные
же возможные значения суммы двух двоичных чисел (их чис-
ло есть г—1) будут представлены в виде, недопустимом для
выбранного типа двоичного кодирования. Следовательно, если
сумма больше г—1, то необходима коррекция полученного
результата. Оказывается, что в случае кодов с естествен-
ными весами эта коррекция достаточно проста — к получен-
ному результату добавляется величина 2Х<Г>— г. После кор-
рекции цифра суммы есть вычет по модулю г (как это
и требуется для r-ичной системы счисления), а признаком
переполнения с сумматора служит, как и ранее, перенос со
старшего двоичного сумматора, причем неважно, когда он
произошел до или после коррекции.
Наиболее существенным моментом при г < 2Х<Г) является
фиксация необходимости проведения коррекции, т. е. опреде-
ление условия
-ф Ci—\ г, (3.4)
где a-L и bL— цифры Z-ro разряда слагаемых г-ичной системы
счисления, a ct-i — перенос из предыдущего разряда. Пусть
Г=1, если выполнено неравенство (3.4), и Г=0в противном
случае. Значение Т есть значение некоторой переключатель-
ной функции, определяемой значениями двоичных разрядов
промежуточного результата и переноса со старшего двоичного
сумматора. Поскольку Т = 1 всегда, когда выполнено нера-
венство (3.4), то можно считать, что перенос с данного Z-ro
разряда (с;) есть с; = Tt.
Пример 3.1. Пусть цифры десятичной системы счисления кодируются
двоичным кодом с естественными весами, т. е. удовлетворяют соотношению
(3.3) при X == 4 и g — 2. Для построения десятичного сумматора потребует-
ся четыре двоичных сумматора и схема коррекции промежуточного резуль-
тата (рис. 18). Условие коррекции этого результата, а следовательно, и по-
явления переноса с г-го десятичного сумматора, задается следующей пере-
ключательной функцией:
ci = ci,4 v v sb)-
Если Ci= 1, то для получения кода правильного результата к промежуточ-
ному итогу прибавляется число 24—10 = 6. Сама коррекция осуществляется
с помощью дополнительных сумматоров (сумматоры — ^1,7 изобра-
жены на рис. 18). Заметим, что возможности этих сумматоров используются
далеко не полностью, и поэтому в случае построения комбинационных
сумматоров имеются определенные предпосылки для экономии оборудова-
ния схемы, если требования применения однотипных элементов не являются
превалирующими.
Действительно, коррекция промежуточного результата заключается
в преобразовании его двоичных разрядов s; у- в разряды окончательного
результата s; у-, что может быть произведено в соответствии со следую-
щими правилами:
Si,l = si,P Si,2 ~ si,2cl V sl,2ci’ Si,3 = cis3 V S3S2 V cis3s2:
si,4 = clsi,4 V Si,4Sf,2ci‘
Операция вычитания для двоичного кодирования с естест-
венными весами базируется на применении дополнительных
или обратных кодов.
Оба вида кодов формируются путем поразрядного допол-
нения до г — 1 (при дополнительном коде еще необходимо
добавлять единицу в младший разряд). Когда r = 2x<r)j то по-
разрядное дополнение образуется весьма просто — только
инвертированием двоичных цифр. Если г < 2Х<Г\ то правила
образования поразрядного дополнения могут быть весьма
сложными.
Пример 3.2. Пусть г — 10, тогда А. (10) = 4 и прямой код есть
bt Ф'1 Ф'12Ь1 р а дополнение до 9 idi idi 2di р тогда справедливо
’i,4 bi,3 bl,2 bi,l ^i,4 ^1,3 di,2 di,l
0 0 0 0 — 1 0 0 1
0 0 0 1 - 1 0 0 0
0 0 1 0 — ' 0 1 1 1
0 0 1 1 0 1 1 0
0 1 0 0 - 0 1 0 1
0X10 1 — 0 100
0 110 — 0011
0 111 — 0010
1 0 0 0 — 0 0 0 1
10 0 1 — о о о о
= rfi,2 = bi,2'
^i,3 = 2^i,3 v ^i,2^i,3’ ^г‘,4 = ^i,A,3^i,2-
Выполнение вычитания как сложения прямого кода поло-
жительного числа и дополнительного кода отрицательного
числа позволяет специфику вычитания свести лишь к добав-
лению +1 в младший разряд сумматора. Другой возможный
путь выполнения вычитания — это получение поразрядных ин-
версий отрицательных чисел до 2Х<Г)— 1 для обратных кодов
или до 2Х<Г) для дополнительных кодов с последующей кор-
рекцией результата, но данный путь связан с существенным
усложнением логики операции в зависимости от знаков сла-
гаемых и полученного промежуточного результата.
Выполнение операций умножения и деления в двоично-
кодированных системах счисления осуществляется так, как это
было описано в главе 2. Единственным замечанием, которое
следовало бы сделать, является то, что счетчик, с помощью
которого анализируется цифра множителя или формируются
цифры частного, является в этом случае чисто двоичным счет-
чиком, считающим как в сторону увеличения, так и в сторону
уменьшения своего значения. Стоит отметить, что если мы
работали с двоичной системой счисления и длина операнд
составляла пк(г) разрядов, то для определения произведения
двух чисел нам понадобилось бы в наихудшем случае «Х(г)
сложений и столько же сдвигов. Когда же мы умножаем
«-разрядные операнды в r-ичной системе счисления, каждая
цифра которой кодируется X (г)-двоичными разрядами, то
в наихудшем случае нужно будет произвести п(г—1) сло-
жений и п сдвигов, причем 2Х<Г)-1 < г 2Х<Г). Подобного типа
оценка справедлива и для операции деления.
Рассмотрим теперь особенности перевода двоично-кодиро-
ванных г-ичных систем счисления в системы счисления, наи-
более интересные с практической точки зрения. С общими
положениями операций перевода мы уже знакомились в гла-
ве 1 и здесь нет ничего нового по сравнению с известными
результатами. Однако для г < 2Х(Г) можно найти пути построе-
ния алгоритмов перевода, реализация которых может быть
произведена весьма экономично и быстро.
Перевод из r-ичной системы счисления в двоично-кодиро-
ванную и обратно делается простым кодированием и декоди-
рованием каждой цифры в отдельности, т. е. выполняется как
поразрядная операция. При кодировании нам надо определить
двоичную последовательность из Х(г) цифр для каждой из г
возможных цифр, а процесс декодирования будет заключаться
в определении цифры по виду заданной двоичной последова-
тельности.
Часто приходится осуществлять также перевод из двоично-
кодированной системы счисления в двоичную и обратно. Рас-
смотрим для простоты только случай правильных дробей,
когда для а = 0, a_i, ..., справедливо а = ^Li а_1Г~1.
Для перевода числа а в двоичную систему счисления преоб-
разуем это выражение к виду
где
Значение d-t можно рассматривать как “цифру" 2х<г)-ичной сис-
темы счисления, хотя на самом деле это многоразрядное чис-
ло. Получить эту „цифру" достаточно просто, если в машине
/ 2x<r) У
имеются константы, значение которых есть c_f = l—— I , за-
данные в двоичной системе счисления. Тогда надо двоично-
кодированные цифры r-ичной системы умножить на эти кон-
станты. Окончательное значение числа а в двоичной системе
счисления получим, когда сложим все „цифры" a^t с учетом
их весов в 2Х(г)-ичной системе счисления.
Пример 3.3. Число 0,453, заданное в двоично-десятичной системе счис-
ления с весами 8421, перевести в двоичную систему счисления. Здесь X = 4
, 16 162 163
и будем считать, что константы с—1 = • jq » с_2 = jq> ' с_3 — [рз заданы
с восемью знаками после запятой. Тогда с—1 = 1,10011001, с_2 = 10,10010000,
с_3 = 100,00011001. Значения a_j = 0100, д_2 — 0101 иа_3 = 0011, следо-
вательно, <z_j = 110,011001, д_2 = 1100,1101, а_3 = 1100,01001011. Теперь
просто найти а, для этого надо сложить a_j-2—4, а_2-2~8 и а__3-2~12
и в результате получим а = 0,01110011110101 <?. Численный эквивалент этого
двоичного числа есть а х 0,452.
Перевод из двоичной системы счисления в двоично-коди-
рованную также осуществляется достаточно просто. Будем
считать, что числа есть правильные двоичные дроби, т. е.
« = Sz-ia-i2-z.
Умножим это двоичное число на г. Далее представим
произведение а на двоичный код числа г в виде суммы двух
слагаемых, одно из которых представляет целую часть произ-
ведения «г, а другое — дробную, тогда
а = г~1 2z-i + г-1
Сумма в первом слагаемом есть старшая цифра в двоично-
кодированной системе счисления. Повторяя указанную проце-
дуру над оставшейся частью, определим последующие цифры
числа а в двоично-кодированной r-ичной системе счисления.
Пример 3.4. Дано число а = 0,0111001 HlOlOlg. Надо найти двоично-
десятичное представление этого числа.
Умножим число а на г = 1010g и после деления на 10 этого произве-
дения получим а = (1002) • 10-1 + (0,1000011001001g) Ю-1. Теперь умножаем
и делим второй член на 10 и вновь выделяем целую часть произведения,тог-
да а = (1002) • 10-1 +(1012)-10~2 + (0,0011111011012)-10-2. Умножаем и де-
лим на 10 третий член этой суммы а = (1002) 10"1 + Ю-1 + (1012) • 10“2+
+ (10)2 -10-3 + (0,01110100002)-10~3. Если мы теперь остановимся на трех
двоично-десятичных цифрах и пренебрежем четвертым членом этой суммы,
то получим а = 0,452.
Перевод целых чисел из двоичной системы счисления
в двоично-кодированную г-ичную систему счисления базиру-
ется (см. главу 1) на использовании операции деления в дво-
ичной системе счисления для последовательного определения
цифр r-ичной системы. При аппаратурной реализации алго-
ритма перевода крайне нежелательно применение такой слож-
ной операции, как деление, ибо сама операция перевода
не должна быть существенно сложнее, чем арифметические
операции умножения и деления.
Рассмотрим методы перевода из двоичной системы счисле-
ния в двоично-кодированную г-ичную систему счисления
и обратно, основанные на использовании простых арифмети-
ческих операций.
Пусть число а задано в двоично-кодированной системе
счиёления с естественными весами, тогда
а = Ъ^^Ь^\
Обозначим через citj константы вида г'2-'"1, тогда
Следовательно, если в нашем распоряжении есть двоичные
коды этих констант, то перевод из двоично-кодированной
г-ичной системы счисления в двоичную производится весьма
просто — образуются частичные произведения вида btj-Cij,
где bt,jС {0,1}, которые затем суммируются, причем можно
одновременно складывать все частичные произведения.
Пример 3.5. В двоично-десятичной системе счисления задано число 39,
т. е. а = (0011)2 (1001)2- Требуется найти двоичный код этого числа.
Коэффициенты с(- . в этом случае будут следующими: с01=1, с0 2 =
= 2 = Ю2, с0>3 ='4 = 1002, с04 = 8 = 10009, с,,, = 10 = 10102> ’ с12 = 20 =
= 101002, с13 = 40 = 1010009, С14 = 80 = 10100002- Тогда а = 0-10100002 +
+о • 101000., + 1 • 101002 + Г10102+ Ы0002 + 0-1002 + 0-102+ 1 = 1001112
Для перевода из двоичной системы счисления в двоично-
кодированную r-ичную систему надо найти значения Ьщ по
заданному двоичному числу а. Вначале находите^ необходи-
мое число разрядов'в r-ичной системе счисления, тем самым
фиксируется используемый набор констант вида Cij. Затем
из числа а вычитается наибольшая константа, т. е. c*,x; если
разность отрицательна, то 6*>х=0, в противном случае 6*,х=1.
На следующем шаге остаток сравнивается со следующей
константой и вновь значение ^*,x-i определится по зна-
ку результата сравнения по тем же правилам. Процедура
повторяется до тех пор, пока не найдутся все Ьщ. Следова-
тельно, алгоритм перевода будет следующим:
на ?-м шаге находится
Q^Q^ + d -2^-0^,
bt = sign Qt,
искомый код есть a=btb2 ... бцй+i)- Здесь b1 = bk,\', b2 =
= bk,x-\, ', b\ — bkx, ...; йх(л-н) = bo,i и c1 = C/9x; с2 = слл-ь
...; cx = q,i; ...; Cx(*+D = Am- Кроме того, Qt-1 = a-, b0=l.
Пример 3.6. Задано число a = 100111g- Требуется найти его представ-
ление в двоично-десятичной системе счисления с естественными весами.
В нашем случае Х(10) = 4 и а = 39, следовательно, k=l и Х(10)-2 = 8,
т. е. из набора констант выберем только константы с0 4 — с0 4 и Cj j — Cj 4, их
двоичные коды приведены в примере 3.5. Последовательно за восемь ша-
гов найдем искомые коэффициенты:
1-й шаг + + 100111 — Qo
1010000 — Cl,
2-й шаг — 101001 — Ql, bl = 4 = 0
"Г + 101000 — c2;
3-й шаг — 00001 - Q2, ^2 “ 3 ~ 0
-г + 10100 — C3,
4-й шаг 1 + 10011 — Q3’ bz = b4 2 = 1
1 — 1010 — Cl,
5-й шаг + 1001 - Qi. bt=blx = \
1 — 1000 —
6-н шаг 4- + 001 — Q&’ ^5 ~ ^0 4 ” 1
-—• 100-
7-й шаг — 11 — Qe> ь§ = ьо 3,= 0
г + 10 — c7;
8-й шаг + + 1 — 1 — Q7, bq =-- 2 " 0 c8;
0 — Qe» ^8 “
Окончательно а = (0011)2(1001)2-
Перевод из двоичной системы счисления в двоично-коди-
рованную r-ичную систему счисления с естественными весами
данным методом фактически является алгоритмом „деления"
с получением Х(г) (k + 1)-разрядного частного. Спецификой
данного алгоритма деления является изменение „делителя"
на каждом шаге умножения. Даже без всяких усовершенст-
вований данный алгоритм реализуется практически за то же
время, что и алгоритм деления без восстановления остатка.
Важным свойством данного способа перевода является исполь-
зование одних и тех же констант для прямого и обратного
преобразований, что облегчает аппаратурную реализацию дан-
ного метода.
§ 3. КОДЫ С ИСКУССТВЕННЫМИ ВЕСАМИ
Коды с естественными весами оказываются единственными
кодами, удовлетворяющими требованию однозначности. Иног-
да считают возможным отказаться от этого требования с тем,
чтобы попытаться устранить недостатки,, присущие кодам
с естественными весами при г < 2Х(Г), которые связаны с труд-
ностью полуиения поразрядных дополнений до г — 1 и услож-
ненной логикой сложения (необходимостью коррекции неко-
торых результатов).
Будем считать, что весомозначные коды удовлетворяют
требованию единственности, т. е. каждой из разрешенных
двоичных комбинаций из Х(г) двоичных цифр сопоставляется
одна цифра r-ичной системы счисления. Однако для этих ко-
дов в отличие от однозначных кодов допустимо, что число
разрешенных двоичных комбинаций больше г. Это означает,
что некоторые коды имеют одинаковое численное значение,
соответствующее некоторой цифре r-ичной системы счисления.
Следовательно, несколько последовательностей из Х(г) двоич-
ных цифр могут отвечать одной цифре г-ичной системы
счисления.
Вначале рассмотрим вопрос о требовании простоты фор-
мирования поразрядных дополнений.
Наиболее просто формирование поразрядного дополнения
до г — 1 реализуется простой инверсией двоичных цифр сло-
ва. Естественно, что этим свойством могут обладать только
системы счисления с четными основаниями. Если веса двоич-
ных разрядов положительные, то очевидно, что цифра г—1
должна кодироваться последовательностью, состоящей из Х(г)
единиц, т. е. сумма всех весов должна быть г — 1. Если коды
удовлетворяют требованиям весомозначности, единственности
и инверсии, то число допустимых видов резко сокращается
по сравнению с (3.1). Так, например, если г = 10,, то сущест-
вует всего лишь четыре двоично-десятичных кода, удовлет-
воряющих указанным требованиям, — это коды с весами 5211,
4311, 4221, 3321 [20].
Весьма часто коды, удовлетворяющие требованиям просто-
ты образования дополнения, заметно усложняют правила сум-
мирования в одном разряде. Для упрощения »этих правил
можно использовать коды r-ичных цифр не только с поло-
жительными, но и отрицательными весами. В этом случае
можно добиться, чтобы код обладал свойствами однозначно-
сти и инверсимости, что невозможно при положительных ве-
сах. Так, например, двоично-десятичный код с весами 84 —
— 2—1, обладая свойством поразрядной инверсимости, в то
же время является однозначным, т. е. каждой цифре г-ичной
системы счисления соответствует одна и только одна двоич-
ная последовательность из четырех двоичных цифр.
Приведенные требования к кодам не всегда являются
единственными и превалирующими. Так, для некоторых фи-
зических реализаций очень большое значение имеет посто-
янство числа единиц в выбранных двоичных комбинациях для
всех цифр г-ичной системы счисления, так как при этом обес-
печивается наиболее надежный режим работы элементов. Если
хранение единицы связано с расходом энергии по сравнению
с хранением нуля, то имеет смысл строить коды с минималь-
ным числом единиц. .Тогда веса надо выбирать, исходя из
этого требования, и при этом надо помнить, что X. (г) выби-
рается по возможности минимальным, т. е. < г.
Например, двоично-десятичный код 8421 имеет в изображении
цифр от нуля до трех единиц, а в среднем 1,5 единицы на
цифру. Код с положительными весами 7421 — уже от нуля
до двух единиц на цифру, а в среднем 1,4 единицы на циф-
ру. Для обеспечения постоянного числа единиц на, цифру
необходимо, чтобы выполнялось условие
r<CtoW, (3.5)
где — число сочетаний из п по k.
Для двоично-десятичных кодов неравенство (3.5) удовлет-
воряется, если Хо (10) = 5 и k равно либо двум, либо трем —
коды „два из пяти" и „три из пяти". Интересно, что посколь-
ку при этом в точности выполняется равенство С* =10, то
эти коды обладают определенными свойствами помехозащит-
ное™, ибо появление лишней или- потеря одной единицы
в коде легко может быть обнаружено.
1 Веса могут выбираться также, исходя из требований прос-
тоты и быстродействия реализации не простых операций типа
сложения, а таких сложных операций, как умножение и деле-
ние. Так, например, двоично-десятичный код 5421 позволяет,
используя технику двоичного сдвига влево и вправо, доволь-
но просто умножать на цифру от нуля до пяти включительно,
ибо умножение на пять реализуется как сдвиг множимого
на один десятичный разряд влево, а затем полученное число
сдвигается на один двоичный разряд вправо. Умножение на
четыре и два реализуется как сдвиг на один или два разряда.'
При допущении определенной избыточности в кодировании
можно получить и другие интересные свойства этих кодов,
с некоторыми из которых мы познакомимся дальше. Особенно
широкие возможности появляются, если алфавит цифр г-ичной
системы счисления включает не только положительные значе-
ния (только этот случай и рассматривается в этом параграфе),
но и отрицательные.
§ 4. НЕВЕСОМОЗНАЧНЫЕ КОДЫ)
С цельЮвобеспечения простоты реализации алгебраического
сложения при г < 2Х<Г) двоичное кодирование цифр г-ичной
системы счисления можно осуществить и с помощью, невесо-
мозначных кодов, среди которых наибольшее распростране-
ние получили коды с избытком. Значение каждой цифры
г-ичной системы счисления при представлении кодом с из-
бытком можно определить как
at = bij gj + c = at тЬ с, (3.6)
где, как и в выражении (3.3), btj — значения двоичных цифр,
a gj — их веса. Число с есть одна и та же константа для
всех цифр, причем 2Х<Г) — г. Выбор константы с может
быть обусловлен рядом требований. Потребуем, например;
чтобы код обладал свойством инверсимости, т. е. дополнение
до г — 1 образовывалось бы простой инверсией двоичных
цифр. Как и обычно, мы требуем, чтобы множество допол-
нительных кодов совпадало со множеством прямых кодов.
Следовательно, для любой цифры должно выполняться
соотношение
at + = 2Х<Г> — 1
и
2Х<Г> = г + 2с.
Отсюда
с = 2М0-1 _ г2-1. (3.7)
Посмотрим, каковы теперь особенности алгебраического
сложения, когда константа определена из соотношения (3.7),
а цифры слагаемых определены из равенства (3.6). Сумма
двух слагаемых at и bt есть at + bt + 2Х^ — г, где 0 < at,
< г — 1. Пусть эта сумма меньше 2Х<Г) (т. е. не было пере-
носа со старшего двоичного сумматора), что отвечает случаю
a’t + b'i < г. Тогда результат получается с избытком 2с вместо
с и, следовательно, из промежуточного результата надо вы-
честь константу с. Если же at + &i + 2x<r> — г ^>2ХЙР или a't +
+ то для получения правильного кода суммы, имею-
щего численное значение tZi+^i + c —г, к полученному ре-
зультату надо прибавить с. Таким образом, при использова-
нии данного кода всегда происходит коррекция промежуточ-
ного результата, полученного путём двоичного сложения цифр
слагаемых. Если окажется, что найденная двоичная сумма
меньше 2х<г), т. е. нет переноса с последнего двоичного сум-
матора, то из промежуточного результата вычитается констан-
та с. Когда промежуточный результат больше 2Х(Г), то к нему
добавляется константа с.
.. Код с избытком, удовлетворяющий требованию инверси-
мости, приводит к весьма простой структуре алгебраического
сложения и1 образования поразрядных дополнений до г — 1,
но в то же время он всегда требует коррекции, что, вообще
говоря, в среднем увеличивает время реализации операций.
Пример 3.7.^ Рассмотрим случай кодирования десятичных цифр г = 10
и X. (г) = 4; тогда значение с, удовлетворяющее соотношению (3.7), есть
с = 3.
Выберем естественные веса для gt, т. е. 8421, получившийся код носит
название „8421 с избытком три", для него характерны следующие соот-
ветствия двоичных последовательностей и десятичных цифр: 0 — ООП; 1 —
0100; 2 — 0101; 3—ОНО; 4 — 0111; 5 — 1000; 6—1001; 7—1010; 8 — 1011;
9—1100. Сложим в этом коде числа а = 395 и 6 = 478. Будем действовать
последовательно, и тогда 1-й шаг есть 1000 + 0110= 1110. Переноса со
старшего разряда нет (ct- 4 = 0), и, следовательно, из промежуточного ре-
зультата вычитается константа 3. Это вычитание реализуется как сложение
константы 1101 с промежуточным итогом и с игнорированием переноса
со старшего разряда, тогда 1110+ 1101 = 1011, т. е. младшая цифра резуль-
тата есть 8.
Для определения 2-й цифры результата надо сложить 1100 и 1010, по-
лучим 1.0110 (с04 = 1). Теперь добавляем константу ООП (+3), получим
1.1001. Отсюда вторая цифра результата есть 6 и появился перенос в 3-й
разряд. Находим последнюю цифру 0110 + 0111 +0001 = 1110 и, произ-
ведя необходимую коррекцию (+1101 с игнорированием переноса), полу-
чим 0.1011. Окончательно имеем s = 1011 1001 1011, т. е. а + b = 868.
Код с избытком с = 2Х<Г)-1 — г2-1 и естественными весами
обладает еще рядом полезных свойств. Например, цифры
r-ичной системы счисления, значения di которых больше
г2-1, отличаются тем, что в старшем разряде двоичной пос-
ледовательности всегда присутствует единица, ибо в этом
случае
а{ = a't + с > г2-> + 2Х<Г>-1 — Г2-1 > 2W-1.
Это свойство полезно при выполнении округления, когда
только по значению одного разряда определяется необхо-
димость округления. Это же свойство полезно и при реали-
зации ускоренного умножения, о котором речь пойдет ниже.
Выбор константы избытка можно произвести, исходя из
иных требований, нежели инверсимость кодов. Например, если
в избираемом коде необходимо строить счетчик по модулю, г,
то рационально использовать код с .естественными весами
и избытком с =2Х<Г) — г. В этом случае переполнение К (^-раз-
рядного двоичного счетчика происходит всякий раз, когда
количественный эквивалент его содержимого есть г. При
отсутствии переполнения содержимое счетчика есть цифра
r-ичной системы сч'исления, которая увеличивается на +1
при подаче на счетчик +1.
Наиболее часто отказ от требования весомозначности связан
с построением двоично-кодированных систем счисления, об-
ладающих свойством обнаружения и исправления ошибок,
возникающих при передаче цифр между устройствами цифро-
вой машины и при обработке их в арифметическом блоке.
Следует заметить, что и при требовании помехоустойчивости
всегда приходится иметь в виду, насколько просто рекомен-
дуемые коды реализуют операцию алгебраического сложения
и насколько полно их применение позволяет использовать
технические,достижения,-, полученные для двоичного алфави-
та. О невесомозначных кодах, обладающих свойством поме-
хоустойчивости, речь еще пойдет ниже. По-видимому, можно
обнаружить невесомозначные коды, ориентированные на прос-
тую и быструю реализацию машинной арифметики, если от-
казаться от ориентации на классические способы выполнения
арифметических операций. В этом плане особенно перспек-
тивными кажутся методы табличной арифметики, т. е. прямой
реализации действий сложения, умножения и деления.
г
§ 5. ЭКОНОМНОЕ ПРЕДСТАВЛЕНИЕ ДВОИЧНО-
КОДИРОВАННЫХ ЧИСЕЛ
Кодирование цифр г-ичной системы счисления Х(г) двоич-
ными разрядами приводит при г.^213 к нерациональному ис-
пользованию памяти машины. Количественная оценка увели-
чения требуемого объема памяти при представлении чисел
в смешанной системе счисления вместо чисто двоичной за-
дается выражением (3.2). Для большинства систем счисления
это увеличение весьма значительное. Так, например, широко
применяемое на практике представление десятичных чисел
в двоично-десятичном коде' требует на 20% большего объема
памяти, чем двоичное представление тех же чисел. Было
чрезвычайно важно найти такой способ кодирования г-ичных
чисел, который по затратам памяти не очень бы отличался
от двоичного кодирования. Определенные указания к нахож-
дению эффективной формы кодирования дает анализ выраже-
ния (3.2), из которого следует, что с ростом основания сис-
темы счисления функция <р (г) стремится к единице, т. е.
рациональное использование памяти для двоично-кодирован-
ных чисел связано с применением больших значений г. Осо-
бенно интересны случаи г = го, где р — целое положительное
число, а г0 — основание заданной системы счисления, когда
„цифра" в системе счисления г есть двоичный код группы
из р разрядов числа в системе счисления с основанием г0.
Поскольку обычно вся арифметика рассчитана на представ-
ление чисел именно в г0-ичной системе счисления, то прихо-
дится от такого способа кодирования отказаться, ибо из дво-
ичного кода группы разрядов трудно получить коды цифр
г0-ичной системы счисления.
Рассмотрим сейчас другой способ кодировки, который, од-
нако, использует главную идею предыдущего способа — о ко-
дировании не отдельных цифр г0-ичной системы счисления,
а сразу целой группы разрядов. Рассмотрение проведем на
примере десятичной системы счисления.
Пусть для кодирования десятичных цифр применяется
двоично-десятичный код с естественными весами (код 8421).
Обозначим соответствующие двоичные разряды кода деся-
тичной цифры как &4, b3, b2, bt. Все цифры можно разбить
на две группы: „малые" (меньше 8) и „большие" (8, 9). Для
„малых" цифр характерно, что &4 = 0, а для „больших" &4=1.
Рассмотрим комбинацию из двух десятичных цифр а-.а^а^
и b: bj)sb2bi. При этом мы встретимся с одной из четырех
ситуаций:
1°. а464=1, т. е. обе цифры „малые". В этом случае кро-
ме индикатора достаточно знать только значение шести дво-
ичных разрядов (a3a2axb3b2bi) для того, чтобы определить
значение десятичных цифр. Вероятность появления такой
ситуации составляет 0,64.
2°. а4&4=1, т. е. старшая цифра „большая", а младшая —
„малая". Теперь достаточно только четырех двоичных разря-
дов для представления кода этих цифр—одного разряда ах
для. „большой" цифры и трех (b3b2bi)— для „малой". Такая
ситуация будет встречаться в 0,16 всех случаев.
3°. а4&4=1. Эта ситуация появляется, когда старшая циф-
ра „малая", а младшая — „большая". Здесь также достаточно
четырех разрядов для определения значений десятичных цифр
(а^ам^)^. Вероятность появления этой ситуации такая же, как
и предыдущей.
4°. а4&4 = 1, т. е. обе цифры „большие" и требуется всего
два двоичных разряда для их определения (a^bt). Вероятность
появления данной ситуации всего 0,04.
Анализ возможных ситуаций подсказывает идею оптималь-
ного кодирования группы из двух десятичных цифр — код
группы должен состоять из двух полей — индикатора, опре-
деляющего характер двух цифр, и. поля значащих разрядов.
Для поля индикатора надо не более двух двоичных разрядов,
а поле значащих разрядов имеет переменную длину от двух
до шести разрядов. Математическое ожидание случайной ве-
личины длины кода двух десятичных цифр оказывается в этом
случае равным 7,2. Хотя в принципе в последовательности
двоичных разрядов можно выделить коды переменной длины,
анализируя поле .индикатора, крайне неудобно организовать
хранение кодов переменной длины с произвольным доступом
к одному коду. В связи с этим необходимо придумать способ
формирования кода двух десятичных цифр постоянной длины.
Основным моментом при конструировании искомых кодов
должна быть простота взаимного преобразования между
этим кодом и двумя двоично-десятичными цифрами
и Ь^3Ь2Ь2, поскольку арифметические действия выполняются
именно над двоично-десятичными кодами. Естественно, что
прямое и обратное преобразование должно осуществляться
без привлечения арифметических действий.
Пусть длина искомого кода зафиксирована семью, двоич-
ными разрядами. Пусть поле индикатора имеет переменную
длину [48]. ’Старший разряд искомого кода (е7) всегда опре-
деляет значение индикатора. Если еч = 0, то все остальные
разряды задают две „малые" десятичные цифры. Если же
еч = 1, то два следующих разряда рассматриваются как поле
нового индикатора при <?6 = <?5=1, обе цифры „большие".
Ситуация <?6<?5 = 1 соответствует тому, что старшая десятичная
цифра „малая",Ца младшая — „большая". При е6е5=1, наобо-
рот, „большой" является старшая цифра. Разряды <?4 и ег
всегда отводятся для младших двоичных разрядов старшей
и младшей десятичных цифр соответственно. Разряды ея, е2
отводятся для изображения разрядов а3а2 и при ебе6 = 1 так-
же и разрядов Ь3Ь2. Отсюда уравнения прямого преобразования
для данного способа кодирования имеют следующий вид:
е7 == а4 V’&4. ee = a.iv^41 e5r=^va2,
= ах, е3'= Ь3 ^2=}Ь2 V Ь^,^ = bt.
Обратное преобразование осуществляется в соответствии со
следующими уравнениями:
^4 ^7^6» ^3 == ^7^6 V ^7^5 ^3» ^2 === V ^7^5^2» ^1 == ^4»
bt = <?7<?6, Ь3 = е7е3 v <%> b2 = <?,<?.> v bt = et.
Кодирование группы из двух десятичных цифр единым
кодом позволило сократить один двоичный разряд на группу
(7 разрядов вместо 8). Более высокий эффект может быть
получен при кодировании группы из трех десятичных разря-
дов, когда удается построить код длиной в 10 двоичных раз-
рядов вместо обычных. 12. Таким образом, при кодировании
группы из трех десятичных цифр достигнута экономия памяти
машины на 20%.
Для машин последовательного принципа действия требо-
вание постоянной длины кода чисел может быть снято. Это
позволит еще лучше использовать память, поскольку при
постоянной длине мы вынуждены применять коды наиболь-
шей длины. Кроме того, в этом случае можно предложить
и способы эффективного кодирования отдельных десятичных
цифр. Рассмотрим код 8421. Пусть цифрам 2—7 соответст-
вуют трехразрядные коды (efg) 010, 011, 100, 101, ПО и 111.
Характерной особенностью кодов является выполнение усло-
вия у = е\//=1- Цифры 0 и 1, 8, 9 закодируем четырех-
разрядными кодами (efgh) следующим образом: 0000, 0010, 0001
и ООП. Для всех кодов этой группы справедливо у = 0. При
указанном способе кодирования средняя длина кода оказы-
вается равной 3,4 разряда вместо обычных 4. Достаточно
просто перейти от обычного двоично-десятичного кодирования
(а: a4a3a2«i) к указанному коду (efgh.)-.
е = а3, f = as, g = аи hw = а4, = а^3а2.
Если формируется код переменной длины — код {efgh), то
три его разряда полностью совпадают с исходным кодом. Чет-
вертый разряд (А) формируется только в том случае, если
десятичная цифра „большая* (8, 9) или очень „малая" (0, 1).
Формирование кода постоянной длины очевидно — три разряда
просто повторяются, а значение разряда а4=1 только тогда,
когда h—\. Анализ двух старших разрядов (ef) позволяет
определить длину кода — при у = е \J f = 1 длина кода состав-
ляет три разряда, а при у = 0 — четыре. В заключение отме-
тим, что использование одноразрядного кода переменной дли-
ны позволяет в среднем сэкономить около 17% памяти, ма-
шины, требуемой для хранения десятичных чисел при обычном
двоично-десятичном кодировании.
ГЛАВА 4
ОСОБЫЕ СЛУЧАИ СИСТЕМ СЧИСЛЕНИЯ
Ранее достаточно подробно были рассмотрены вопросы
выполнения арифметических операций для чисел, представ-
ленных в аддитивных позиционные системах счисления. При
этом мы считали, что основание системы счисления есть це-
лое положительное число, а база системы счисления обяза-
тельно содержит нуль. Имеет смысл рассмотреть некоторые
другие системы счисления в поисках путей существенного
упрощения алгоритмов арифметических операций, либо уско-
рения их выполнения.
Объектами исследования будут аддитивные позиционные
системы счисления с целым отрицательным основанием и с
целым положительным четным основанием, но при использо-
вании симметричной базы без нуля, а также два случая не-
позиционных систем счисления — система остаточных классов
и знакологарифмическая система счисления. В качестве ис-
следуемой позиционной системы счисления выберем двоич-
ную как наиболее важную для сегодняшнего дня с практи-
ческой точки зрения. Базируясь в значительной степени на
технике реализации алгоритмов в обычной двоичной системе
счисления, мы постараемся выяснить, какими особенностями
обладают алгоритмы арифметических операций для двоичной
системы счисления с базой без нуля и двоичной системы
счисления с положительной базой и основанием, равным —2.
§ 1. ДВОИЧНАЯЕСИСТЕМА СЧИСЛЕНИЯ
С ЦИФРАМИ^— 1 И 1
Пусть база двоичной системы счисления состоит из цифр
— 1 и 1. Цифру —1 в дальнейшем будем изображать как 1.
Первая трудность, с которой мы сталкиваемся при исполь-
зовании этой системы счисления, состоит в невозможности
точного представления конечным числом разрядов целых
четных чисел, включая нуль, когда применяется форма пред-
ставления чисел с естественной запятой и количественный
эквивалент чисел вычисляется подформуле (1.7). Однако дан-
ное обстоятельство не должно приводить нас в смятение,
ибо и раньше мы сталкивались с невозможностью точного
представления всех вещественных чисел при конечной длине
машинных слов. Просто в нашем случае четные числа ока-
зываются не принадлежащими множеству машинных слов
и, следовательно, должны быть представлены приближенно.
При желании мы можем рассматривать изображение числа
а в виде (1.3) как его некоторое символическое представле-
ние, например, такое, при котором количественный эквива-
лент числа а определяется как
а = 2^-Аа(2‘-2-*, (4.1)
где а: £ {1, 1) для всех — йПри фиксированной
длине дробной части чисел значение аддитивной добавки
будет всегда постоянным. Символическое представление ука-
занного вида позволяет конечным числом двоичных разрядов
с алфавитом 1, 1 изобразить любое ,целое число [11].
Пример 4.1. Число нуль ^согласно равенству (4.1) должно представ-
ляться как = 1 и с; = 1 для всех —h < i < k— 1, т. е. если а = 0, то
а = 11Т ... 1, Г ... 1. Если k i 3, a h = 1, то с = 11П,Т. Число 8 при этих
условиях изобразится как а =1111,1. s
Особенностями двоичной системы счисления с цифрами
1, 1 является представление единым кодом как положитель-
ных, так и отрицательных чисел. Естественно, что из-за ад-
дитивной добавки положительных чисел будёт меньше на
одно число, чем отрицательных, но это не играет сущест-
венной роли. Заметим, что ближайшие два числа будут от-
стоять друг от друга на величину 21-й, а не на 2“й, как этб
было при обычной двоичной системе счисления. Всего при
п = k + 1 + h можно изобразить 2" чисел: 2П-1 отрицательных,
2Л~1 — 1 положительных и нуль вместо 2"— 1 числа в двоич-
ной системе с цифрами 0, 1, ибо в последней число нуль
представляется неоднозначно (+0, —0).
1°. Перевод из двоичной системы счисления с цифрами
0, 1 в систему с цифрами 1, 1 и обратно. Пусть нам задано
число в двоичной системе счисления с цифрами 0, 1 и тре-
буется перевести его в двоичную систему счисления с циф-
рами 1, 1. Для осуществления перевода вначале к исходному
числу приписывается справа еще один разряд, значение ко-
торого есть 1. Затем в исходном изображении выделяем
конструкции, состоящие из последовательности нулей и еди-
ниц справа, т. е. конструкции вида 00_____01. Выделенные
конструкции преобразуем к виду 111 ... 11, т. е. самый стар-
ший нулевой разряд заменяется на 1, а остальные разряды,
включая 1 в младшем разряде конструкции, заменяются на 1.
Основанием для такой реорганизации выделенных конструк-
ций являются равенства
2т _ (2» — 1) = 2m — Sti 21-1 = 2m + StiT-2'-^ 1.
Пример 4.2. Дано число а = 10001 >10101 g- Требуется перевести его
в двоичную систему счисления с цифрами 1, 1.
Вначале приписываем к исходному числу справа разряд со значением 1,
тогда а' = 10001,101011g- Далее выделяем в этой записи конструкции вида
0 ... 01 а' = 10001,101011g- Теперь реорганизуем выделенные конструкции
по приведенным правилам; тогда получим с = 11111,111111g. Численнцй
эквивалент полученного числа в соответствии с (4.1) есть 17,65625, т. е.
точно такой, какой имеет исходное число.
Добавлением единицы справа к исходной записи реали-
зуется учет аддитивной поправки. Однако надо иметь в виду,
что при практической реализации значение этой поправки
одно и то же для всех чисел (ввиду постоянства разрядной
сетки чисел), поэтому, если в исходной записи дробная часть
числа имеет меньше, чем h—1, значащих цифр, то ее надо
заполнить нулями до h — 1 разрядов и уже в й-й разряд
записать 1. Фиксация длины разрядной сетки заставляет так-
же в исходной записи выписывать необходимое число нулей
до перевода и учитывать эти нули при переводе.
Пример 4.3. Дано число 2,5, представленное в двоичной системе счис-
ления. Требуется представить его в двоичной системе счисления с цифра-
ми 1,1 в форме с естественной запятой при k = 3 и h — 3. Вначале под-
готовим запись числа а = 10,1g для выделения специфических конструк-
ций, учитывая, что аддитивная добавка есть в нашем случае Т3, тогда
а = 0010,10g. Теперь дополним число а справа разрядом со значением 1
и выделим специфические конструкции: а' = 001 0,1 01g, а затем по обыч-
ным правилам преобразуем выделенные конструкции: а = 1111,111g. Полу-
ченное число имеет численный эквивалент 2,5.
Представление отрицательных чисел в системе счисления
с цифрами 1, 1 по известному изображению их в двоичной
системе с цифрами'.0, 1 в случае использования прямых ко-
дов производится также достаточно просто. Вначале реорга-
низуется запись абсолютной величины числа а путем Дописы-
вания слева и справа необходимого числа нулей. Затем в этом
изображении все 1 заменяются на 1, а потом к полученному
изображению дописывается 1 справа (аддитивная добавка).
Далее выделяются конструкции вида'0 ... 01 и 0 ... 01, если
они есть. Конструкции 0 ... 0Г преобразуются к виду И ... 11,
а правила преобразования конструкций вида 0 ... 01 прежние.
Пример 4.4. Дано число —2,5; представленное прямым кодом в двоич-
ной системе счисления, т. е. а = —10,1g. Найти запись этого числа в сис-
теме счисления с цифрами 1, 1 при &=3 и h = 3.
Вначале подготавливаем для перевода абсолютную величину числа а,
получим а' = 0010,10. Затем в этой записи заменяем все 1 на 1 и припи-
сываем 1 справа: а" = OOW.fOlg. Остается заменить выделенные конструкции
по приведенным правилам и тогда получим а = Till,111g. Численный экви-
валент полученного числа есть —2,5, считая, что он определяется из соот-
ношения (4.1).
Будем теперь считать, что исходные числа заданы в обыч-
ной двоичной системе счисления дополнительными кодами
в форме с естественной запятой.'Наша задача состоит в оты-
скании их изображения в двоичной системе счисления с циф-
рами 1, 1. Положим, как обычно, что целая часть исходного
числа содержит k + 1 разряд, а дробная — h. Для осуществ-
ления перевода чисел е>0 расширим вначале нулями (если
это необходимо) целую часть до k 4- 1 разряда, а дробную —
до h— 1 разряда. Припишем слева еще один разряд со зна-
чением 1, в результате чего количественный эквивалент но-
вого числа станет равным а' = 2*+14- а. Затем все нули
в изображении нового числа а' заменим на 1, что равносиль-
но вычитанию из числа а' числа Ь, имеющего значение Ь —
= 2Й+1 — а — 21-ft. В результате получим новое гчисло а", та-
кое, что а" = а' — b = 1a-\- 21-ft. Это действительно так, ибо
если в изображении числа а!' все нули заменить на 1, то по-
лученный результат будет точно таким, как если бы к числу
а' добавили такое число Ь, что а' 4- b = 2ft+2 — 21-ft или Ь =
= 2ft+1 — 21-ft — а. Для завершения перевода сдвинем число
е" на один разряд вправо, т. е. уменьшшм его значение в два
раза. Окончательно получим некоторое число с, такое, что
с = = а 4- 2~ft. Именно такой количественный эквивалент
имеет исходное число.
Пример 4.5. Задано число а = 10001,10101g. Надо найти его изображе-
ние в системе счисления с цифрами 1 и 1, если й = 6 и- k — 5. Вначале
дописываем слева необходимые нули и еще один разряд со значением 1,
получим а' — 1010001,10101g. На следующем шаге заменяем все нули в изо-
бражении а' на 1: а" = 1111111,lllTlg. Наконец, на 3-м шаге сдвигаем а"
вправо на разряд и окончательно получим а = 111111,111111g. Количествен-
ный эквивалент этого числа есть согласно (4.1) 17,65625 (сравним это с при-
мером 4.2).
Поскольку дополнительные и прямые коды положительных
чисел совпадают, то рассмотренный алгоритм может быть
применен и для перевода прямых кодов.
Рассмотрим теперь случай, когда число а, заданное допол-
нительным кодом, имеет отрицательный знак, т. е. его
количественный эквивалент определен как . а = — 2ft+1 +
+ 2/=-л®г2' = — 26+1+«*, где at — значение основных разря-
дов дополнительного кода. При записи числа а дополнитель-
ным кодом будем считать, что целая часть исходного числа
имеет столько же разрядов, сколько и искомого. Тогда для
перевода числа а в двоичную систему счисления с цифрами
1, 1, вначале расширим исходную запись нулями справа до А—1
разрядов, если это необходимо, и знаковый разряд заменим
на ноль. В результате этих действий получим новое число,
такое, что а' = а*. Затем все нули в числе а', включая зна-
ковый разряд, заменим ?на 1. Получившееся число есть а" и
а" = — 2Л+> + «* — (2*+J — е* — 21-*) = 2 (—2/г+1 + а*) +
„ +21-ft = 2e-|-21-ft.
Теперь найденное число 'а" сдвинем на один разряд вправо
и получим окончательно число (обозначим его Ь), представ-
ленное в двоичной системе счисления с цифрами 1,1 и имею-
щее значение, равное е + 2~й. Согласно (4.1) это есть изоб-
ражение чис^а, количественный эквивалент которого есть а.
Пример 4.6. В двоичной системе счисления с цифрами 0, 1 дополни-
тельным кодом задано число —2,5 в форме с естественной запятой при
k = 3 и h = 3, т. е. а = 11101,12- Надо найти изображение этого числа
в системе счисления с цифрами 1, 1. Вначале трансформируем исходную
запись, заменяя знаковый разряд на 0 и дополняя справа запись нулями
до h—1 разрядов дробной части: а' = 01101,10g- Затем все нули в записи
этого числа заменим на 1, получим а" = 11111,11g. Далее уменьшим в два
раза число а" и окончательно найдем, что искомое число b есть b =
= 1111,ll^- Согласно (4.1) количественный эквивалент этого числа есть
—2,5. Сравним этот пример с примером 4.4, где для нахождения изобра-
жения числа —2,5, заданного прямым кодом, использовался другой алго-
ритм.
Итак, перевод чисел, заданных в двоичной системе -Счис-
ления с цифрами 0,.1, в двоичную систему с цифрами 1,1 осу-
ществляется достаточно просто путем выполнения логических
преобразований над исходной записью в соответствии с одним
из' двух рассмотренных алгоритмов. Обратный перевод, т. е.
перевод чисел, изображенных в двоичной системе счисления
с цифрами 1,1, в обычную двоичную систему с положитель-
ной базой, может быть реализован путем выполнения логи-
ческих преобразований, отвечающих прямому переводу, в об-
ратном порядке.
Пример 4/7. В двоичной система счисления с цифрами 1, 1 задано чис-
ло —2,5 в форме с естественной запятой при k = Z и h = 3. Требуется
найти изображение этого числа в обычной двоичной системе счисления
дополнительным кодом. Итак, исходная запись есть = 111 Tgl 112‘ Будем
считать, что прямой перевод осуществлялся по алгоритму 2, тогда вначале
сдвинем влево исходную запись, получим число 6 = Т1 lll.llg- Затем все 1
заменим на нули, тогда Ь" = 01101,10g. Теперь, поскольку исходное число
имело знак „—“, знаковому разряду припишем значение 1, окончательно
получим а =11101,12- Количественный эквивалент получившегося числа а
есть —2,5 и оно представлено дополнительным кодом в двоичной системе
счисления. Сопоставим обратный перевод с прямым (пример 4.6).
2°. Сложение-вычитание. Пусть операнды заданы в дво-
ичной системе счисления с цифрами 1,1 и требуется найти
их сумму. Будем считать, что количественный эквивалент
слагаемых определен соотношением (4.1). Следовательно, если
мы найдем сумму двух слагаемых, то согласно (4.1) она бу-
дет увеличена по сравнению с ее реальным значением на 2-й.
Отсюда ясна необходимость коррекции результата сложения.
При определении разрядной суммы и переноса надо иметь
в виду, что слагаемые имеют только ненулевые значения,
а перенос может иметь значение как +1, так и —1. Если
считать, что для значений поразрядной суммы и переноса
допустимы значения 1,0,1, то таблица сложения в двоичной
системе счисления с цифрами 1, 1 примет вид табл. 10.
Таблица 10
ai bi ci—1 Si Ci bi ct-i Si Ci ai bi С{_г Si Cl
1 1 . 0 0 т 1 1 f т 1 1 7 1 I 0
1 1 0 0 0 1 1 Г т 0 1 1 1 1 0
1 Т 0 0 0 1 Г I г 0 1 Т 1 1 0
1 1 0 0 1 1 1 т 1 0 1 1 1 1 1
Характерной особенностью сложения является то, что значе-
ние разрядной суммы'отлично от нуля только в том случае,
если в предыдущем разряде был выработан перенос. Если же
в предыдущем разряде переноса не было ^выработано, то раз-
рядная сумма обязательно есть нуль. Легко заметить, что
необходимая коррекция может быть произведена как при-
своение переносу в младший разряд сумматора значения 1.
Пример 4.8. Найти сумму двух чисел а и Ь, представленных в двоич-
ной системе счисления с цифрами 1, 1 в форме с естественной запятой
при k = 3 и h = 3, если а = 2 и b = -0,75. Имеем а = 1111,111 и Ъ =
= 1111,1112- Сложим эти числа по правилам табл. 10. Учитывая, что с0=1,
получим а + b = 0010,101.
Результат сложения представлен в двоичной системе счисления с циф-
рами 1, 0, 1, поэтому необходимо еще перевести его в систему счисления
с цифрами 1, 1. Сделаем этот перевод в соответствии с ранее рассмотрен-
ным алгоритмом — выделим вначале в изображении исходного числа кон-
струкции вида 0 ... 01 и 0 ... 01, а затем заменим их на конструкции
11 ... 11 и 11 ... 11. Например, если а + Ь = 0010, lOTg, то после перевода
получим а -J- b = 1111,111g, что в соответствии (4.1) отвечает числу 1,25,
как и следовало ожидать (см. пример 4.7).
Для ускорения операции сложения следует избавиться от
этапа перевода, т. е. сразу получать результат в окончатель-
ном виде. Очевидно, для этого следует изменить таблицу
сложения таким образом, чтобы исключить получение нуле-
вых значений разрядной суммы. Попробуем это сделать. Как
обычно, сложение начинается с младших разрядов (с0=1),
и поэтому надо уметь найти начало выделяемых конструкций
01 или 01 и значение sz = l или sz=l заменить на противо-
положное. Сделать это можно, ибо признаком начала комби-
нации есть значение st =/= 0 и одновременно ct = 0. После из-
менения знака st надо это значение запомнить для того, что-
бы определить правильные значения последующих разрядов.
Если же S, =f= р и С[ 0, то правила сложения остаются преж-
ними и запоминать значения поразрядных сумм не надо. Сле-
довательно, если cz_i = l, то правила сложения будут такими,
как показано в табл. 11 (1-я секция).
Таблица 11
1 I lq Ip tT 1 1 Ъ S; cz at 7 7 ёг с* 7 е* 7 в4 St Cl at
IT То Г Г о Т Го 1 I Т о I То Т 1 Г о Т Г1 о 1 0 1
Г1 То 1 0 1 Г1 о 1 1 0 1 Т 1 о Т Г о Т Т1 1 о I о Т
1Т Го 1 0 1 I Т о 1 1 0 1 1 Го Г Т о Т 1110 1 01
1 1 Го Го Т 110 1 Г 1 0 1 1 оТ 1 1 0 1110 1 1 0
Если В Z-M разряде окажется сг~1 = 0, тс в следующем
разряде надо будет либо повторить значение sz (при cz = 0,
когда az = sz), либо изменить у него знак на противополож-
ный (при сг^=0, когда Si= — az). При этом, когда cz = 0, зна-
чение sz опять запоминается (az = sz), а когда cz^=l, то az = 0
(2-я и 3-я секции табл. 11). Ситуация ci=/=\ и cz_i = 0 сви-
детельствует о том, что в /-м разряде находится левая гра-
ница выделенных конструкций. Наконец, остается рассмотреть
еще случай, когда cz-i = 1 (4-я секция табл. 11). В этом слу-
чае, если cz=l, то аг = 0, и Правила определения значения sz
прежние. Когда же ct = 0, то прежние значения sf меняют
знак на противоположный, и, кроме того, az = sz. Теперь мож-
но написать равенства для определения на i-м шаге значений
поразрядной суммы (sz), переноса (cz) и заготовки для значе-
ния поразрядной суммы следующего разряда (az). Если обо-
di “F
значить ъ = получим
$г = az&z (cz_i — az_,),
> V с~Ъ(1-сЬ+-1- ), (4.2)
ai = sz(i — cLi).
Заметим, что однопроходовое суммирование чисел, представ-
ленных в двоичной системе счисления с цифрами 1,1, не ме-
няет условия выработки переноса из данного разряда I, кото-
рые существуют при двухэтапном сложении (см. табл. 10).
Вне зависимости от того, как получен результат, его надо
еще проанализировать для выполнения возможной коррекции.
Это связано с тем, что наличие переноса из старшего разряда
сумматора еще не означает переполнения сумматора. Только
в том случае, если знаки переноса со старшего разряда сум-
матора и значение суммы в этом разряде совпадают, перепол-
нение реально существует. Когда же знаки этих величин раз-
ные, то переполнения фактически нет и для коррекции ре-
зультата надо отбросить значение переноса, а знак старшего
разряда суммы изменить на противоположный.
Пример 4.9. Найти сумму двух величин а = 4 и b = 8,5, которые зада-
ны в двоичной системе счисления с цифрами 1, 1 в форме с естественной
запятой при k = 3 и h = 3. Действуя по правилам (4.2), получим что s =
= а + £ = llll.lllg + 1111,1 llg = 1Л lll.lfig- Поскольку знаки переноса
и старшего разряда суммы не совпадают, то необходима коррекция суммы,
и после ее выполнения получим окончательно s = 1111,1 llg-
Для осуществления операции вычитания чисел, представ-
ленных в двоичной системе счисления с цифрами 1,1, надо
вначале у вычитаемого числа поменять знаки во всех разря-
дах на противоположные, а затем сложить это число с дру-
гим операндом. Будем считать, что количественный эквива-
•лент числа определен соотношением (4.1), тогда после
инверсии знака у всех разрядов числа b и сложения его
с числом а получим новое число s, численное значение
которого меньше истинной величины а — & на 2~й, поэтому,
как и при сложении, необходимо значение переноса в млад-
ший разряд сумматора сделать ненулевым, а именно с0 = 1.
Пример 4.10. Даны числа <2 = 3,25 и b = 12,75, представленные в двоич-
ной системе счисления с цифрами 1, 1 и в форме с естественной запятой
при k — 3 и h = 3, т. е. а= lllljllg и Ь= 1111,11 Надо найти разность
s = a — b. Вначале инвертируем знаки во всех разрядах числа Ь, тогда
/>'= Tlll.lllg. Затем сложим а и Ь' по правилам (4.2) с учетом с0 = 1, по-
лучим 5 = Ш1Лп2- Численный эквивалент результата согласно (4.1) есть
с — а — b = —9,5.
Основное достоинство сложения чисел в двоичной системе
счисления состоит в однопроходовом выполнении операции
и отсутствии анализа знаков операндов. В то же время здесь
усложнены определение переполнения сумматора, операции
сдвига чисел и округления.
Хотя технически циклический сдвиг осуществляется точно
так же, как и в случае обычной системы счисления, реализа-
ция нециклического сдвига имеет свои особенности. При
сдвиге вправо старший разряд инвертируется, затем все чис-
ло сдвигается вправо на t разрядов. Разряды, вышедшие за
разрядную сетку, теряются, а освободившиеся слева разряды
заполняются новым (инвертированным) значением старшей
цифры исходного числа. После завершения сдвига значение
старшего разряда вновь инвертируется.
Пример 4.1 Г. Число а— 11111,111g сдвинуть натри разряда вправо
сохранив положение запятойЯЗначале получаем а’ = 11111,111g, затем а" =
= пп1,ТП2 и, наконец, окончательно а"’ = 11111,111 2- Полученное значе-
ние а’" есть 2 (исходное а = 16).
Сдвиг влево должен быть произведен с учетом возможной
свертки разрядов, выходящих за разрядную сетку. С этой
целью анализируется очередной разряд, вышедший за разряд-
ную сетку; если он'совпадает со старшим из оставшихся раз-
рядов, то никаких изменений не производится, если же он
имеет противоположный знак, то старший разряд инвертиру-
ется. Освобождающиеся справа разряды должны быть запол-
нены цифрами 1. Действительно, при сдвиге влево на t раз-
рядов из равенства (4.1) получим а! = 2*е = 2* 2ь=-л«,2г—2<-й.
Если на место освободившихся слева разрядов записать t цифр
1, то значение а" станет равным а' (2f — 1) 2~h, т. е. а!' =
= 2l-a — 2-h.
Пример 4.12. Число а =11111,111g сдвинуть влево на три разряда.
После 1-го сдвига имеем а' = ПШП.ПТд, следовательно, в пределах п
разрядов число должно иметь вид а" = 11111,111 g. Действуя подобным об-
разом и далее, получим окончательно а" = 111 11,Illg- Численный эквива-
лент числа а" есть, таким образом, 16, а численный эквивалент исходного
числа был 2.
Округление в двоичной системе счисления с цифрами 1,1
связано не только с уменьшением разрядности округляемых
чисел, но и с изменением величины аддитивном поправки.
Само округление заключается либо в простом отбрасывании
„хвоста" округляемых чисел, либо в отбрасывании „хвоста",
но с изменением оставшейся части. Первый способ округления
аналогичен округлению методом усечения в обычной двоич-
ной системе счисления, но приводит к лучшему математиче-
скому ожиданию погрешности округления ввиду симметрич-
ности значений „хвоста" для чисел одного знака. Метод
округления, аналогичный округлению по дополнению в дво-
ичной системе, заключается в анализе старшей цифры „хвоста".
Если значение этой цифры есть 1, то значение оставшейся
части числа не меняется, в противном случае к ней добавля-
ется единица в младший разряд. В том случае, когда значение
этого разряда было единица, коррекция при округлении
выливается в обычное сложение. Примеры округления неко-
торых чисел в двоичной системе с цифрами 1, 1 методами
усечения и по дополнению приведены в табл. 12.
Таблица 12
Число Код исходного числа х Код числа, округленного усечением Код числа, округленного по дополнению
0 и,in 171^0 17д =0
0,25 17 ш 1Т,Т=о ил=о
0,50 1Г.Т1Т 17Г=о П,1=1
0,75 Пдн 17д=о 11,1=1
1 17, ПТ 17,1=1 1Тд=1
1,25 1Т,1Т1 17,1=1 ii,i==i
1,5 1ТДП 17,1=1 11,7=2
1,75 1Т.1П 1Г,1=1 11,Т=2
Хотя выполнение сложения в двоичной системе счисления
и встречает определенные трудности, все же ради справедли-
вости следует сказать, что эти затруднения преодолеваются
весьма просто и в целом операция сложения оказывается
близкой к этой же операции в обычной системе счисления
при использовании дополнительных кодов.
3°. Умножение. Умножение чисел, представленных в дво-
ичной системе .счисления с цифрами 1,1 и удовлетво-
ряющих соотношению (4.1), не вызывает принципиальных
трудностей, но следует иметь в виду, что полученный ре-
зультат p = ab будем иметь величину р — ab + 2~й (а +
+ b) -f- 2-2*. Приведение его к принятой для ' операндов
форме потребует дополнительных действий, что скажется
на усложнении алгоритма умножения и увеличении времени
его реализации. В то же время не видно .никаких особых
преимуществ выполнения операции умножения, когда оба
операнда заданы в системе счисления с цифрами 1 и 1. Одна-
ко совсем иначе обстоит дело, когда запись в системе с циф-
рами 1, Г используется в качестве промежуточного представ-
ления. В главе 2 мы видели, что выполнение умножения
в дополнительных и обратных кодах весьма усложнено по
сравнению с умножением в прямых кодах. Эти усложнения
кажутся иногда настолько серьезными, что предпочитают до-
полнительные коды переводить в прямые и в них выполнять
операцию, а затем вновь переходить к дополнительным ко-
дам. В плане облегчения выполнения операции умножения
в дополнительных и обратных кодах имеет смысл рассмотреть
варианты с предварительным преобразованием множителя
в Систему счисления с цифрами 1, 1, что осуществляется дос-
таточно просто. При этом фактически вычисленное значение
произведения окажется ab -\-2~h Ь, но вычитание числа 2~hb
из произведения осуществить весьма просто, если вспомнить,
что реализация умножения всегда производится как операция
ab 4- с, где с обязательно должно быть меньше г", если а и
b — целые «-разрядные числа, представленные в системе счис-
ления с основанием г. Отсюда достаточно перед началом опе-
рации в регистр частичных произведений (см. рис. 9) помес-
тить величину — Ь. Обычное выполнение операции приведет
к автоматическому вычитанию величины 2~hb из произведе-
ния, т. е. обеспечит получение правильного результата. При
новом представлении множителя процесс умножения обычен
и на каждом, шаге производится либо прибавление множимого
к сумме частичных произведений (когда цифра множителя
+ 1), либо его вычитание (цифра множителя —1). Результат
получается сразу же в дополнительном коде.
3 5
Пример 4.13. Даны величины а = — -g- и b = -g-, представленные
в двоичной системе счисления модифицированными двоичными кодами,
т. е. а =11.101 и Ь = 00.101. Найти их произведение р = ab с помощью
промежуточного представления множителя в системе счисления с цифрами
1, Т. Вначале представим множитель в системе с цифрами 1, 1. Действуя
по обычным правилам, найдем, что а = Т.11Т12-
1-й шаг 1.011 — начальное значение суммы частичных произведений
, (загрузка Ь) 2о
0.101 — множимое b
0.000—
2-й шаг 0.000 — учет веса цифры множителя а_3, р_7 =0
0.101 — множимое Ь',
toil -S2;
3-й шаг . 1.101 + 0.101
0.010
4-й шаг 0.001
“Г 0.101
0.110
5-й шаг 0.011
0.101
л_2, Р_6 = 1
b
«-Р P-5 =0
b
a*, P_4 = 0
b
— учет веса
— множимое
-Ь:
— учет веса
— множимое
-24;
— учет веса
— множимое
1.110 — — старшие разряды произведения.
Окончательно имеем р= 1.110001. Согласно (1.12) количественный эк-
15
вивалент числа р есть —"gj"-
Таким образом, преобразование множителя, представлен-
ного дополнительным кодом, в систему счисления с цифрами
1, 1 позволяет умножение дополнительных кодов произвести
точно так же, как умножение прямых кодов, т. е. устраняют-
ся все трудности умножения дополнительных кодов. Важно
отметить, что результат сразу же получается в исходной
форме, а преобразование множителя может быть произведено
в процессе анализа его цифр, т. е. нет необходимости пред-
варительно осуществлять преобразование, достаточно множи-
тель проинтерпретировать в двоичной системе с цифрами 1,1.
4°. Деление. Прямая реализация операции деления чисел,
представленных в двоичной системе счисления с цифрами 1,1,
вряд ли имеет смысл, ибо частное от деления числа а на
а 1 2 h
число b будет иметь значение с = — которое при ма-
й-1- 2
лых а и b может быть весьма далеким от истинной величины
а/b. Наиболее рациональным кажется применение рассматри-
ваемой системы счисления для изображения частного от де-
ления чисел, представленных в обычной двоичной системе
счисления прямыми, дополнительными или обратными кодами.
В этом случае цифра ч'астного на каждом шаге деления есть
1 (если уменьшаемое имеет знак „ + “) либо 1 (если оно имеет
знак „ — “). Перевод частного из системы счисления с цифра-
ми 1,1 в исходную производится по известным правилам.
, 13 9
Пример 4.14. Величины а = —ц?- и Ъ = — -jg- представлены в двоич-
ной системе счисления дополнительными кодами в форме с фиксированной
запятой, т. е. а = 0.1101 и b — 1.0111. Требуется найти их отношение. Вна-
чале находится знак 1-го уменьшаемого, он должен совпадать со знаком
результата. В нашем случае этот знак есть „—“ и поэтому первое умень-
шаемое будет 1.0011. Следовательно, с0 = 1. Далее находим остальные раз-
ряды' частного:
1-й шаг _1.10011 — 1-е уменьшаемое, с0 = 1
1.10111—делитель b
1.11100 — 1-й остаток;
2-й шаг 1.11000 — 2-е уменьшаемое, с-1 ~ *
1.10111 — делитель b
0.00001—2-й остаток;
3-й шаг . 0.00010 — 3-е уменьшаемое, ‘“1.10111—делитель b 1.11001—3-й остаток; г_2 = 1
4-й шаг _ 1.10010 — 4-е уменьшаемое, 1.10111—делитель Ь 1.11011—4-й остаток; с—з 1
5-й шаг _ 1.10110 — 5-е уменьшаемое, 1.10111 — делитель Ь 1.11111—5-й остаток; С-4 '
6-й шаг .1.11110 — 6-е уменьшаемое, *1.10111—делитель b 0.00111—6-й остаток; с_5 = Т
7-й шаг 0.01110 — 7-е уменьшаемое, С-6 = Ь
Окончательно имеем с = 1.111111. После преобразования этого числа
в дополнительный код двоичной системы счисления получим с =—O.lOOOOl^
* 29
Количественный эквивалент этого числа есть —1 , или —1,4591.
Промежуточное представление частного в системе счисле-
ния с цифрами 1, Т имеет ряд преимуществ. Во-первых, циф-
ра частного определяется знаком уменьшаемого, а не остатка,
как обычно. Во-вторых, результат сразу получен в дополни-
тельном коде, который представлен в системе счисления
с цифрами 1,1, что не требует дополнительных действий, как
в случае прямой реализации деления дополнительных кодов.
Таким образом, исследование особенностей двоичной сис-
темы счисления с цифрами 1, 1 показывает, что наиболее
рационально использовать эту систему как промежуточную
при выполнении операций умножения и деления в дополни-
тельных или обратных кодах. В то же время возможна и пря-
мая реализация арифметических действий в системе с цифрами
1, 1, которая, однако, оказывается заметно сложнее, особенно
при сложных операциях, таких, как умножение и деление.
§ 2. СИСТЕМА СЧИСЛЕНИЯ С ОСНОВАНИЕМ -2
Рассмотрим систему счисления, имеющую положительную
базу 0, 1 и основание системы счисления, равное —2. Для
числа а, представленного в этой системе счисления, количе-
ственный эквивалент, когда используется форма с естествен-
ной запятой, определяется по формуле
а = 2?=-й«г(-2)г, ^ = 0,1. (4.3)
{Важной особенностью этой системы счисления является пред-
ставление положительных и отрицательных чисел единым на-
туральным кодом. Знак числа определяется четностью или
нечетностью старшей значащей цифры в его изображении.
При заданном значении п = k-[- \ h абсолютная величина
числа а не может быть больше, чем
шах | а | = З-1 • 2~h [2"+1 + 8 («) - 2], (4.4)
где 8 (л) =---g--- для целого х. Наибольшее же значение
абсолютной величины числа противоположного знака (обозна-
чим его как л) определится при подстановке п = п — 1 в (4.4).
Тогда, учитывая, что 8 (« — 1) = 1 — 8 («), получим
шах§|а| = 3-1-2-Л [2П — 8 («) — 1].ч (4.5)
Из сравнения выражений (4.4) и (4.5) следует, что диапа-
зон представления положительных и отрицательных чисел при
фиксированной длине машинных слов отличается приблизи-
тельно в два раза. Это означает, что если мы потребуем,
чтобы диапазон представления чисел разного знака был оди-
наков, то тем самым около 1/3 всех возможных значений кода
будут считаться запрещенными. В частности, если данную
систему счисления применять для кодирования цифр г-ичной
системы счисления с симметричной базой, то в каждом раз-
ряде r-ичной системы счисления будет 30%-ная информаци-
онная избыточность.
1°. Перевод из двоичной системы счисления в систему
с основанием —2 и обратно. Пусть исходное число b = bn ...
... bGb-y ... b-h задано в двоичной системе счисления, и надо
его перевести в минус-двоичную систему счисления, т. е. по
слову b найти слово a = ak ... «0«_i ... Начнем с пере-
вода положительных чисел. Рассмотрим исходную запись как
уже готовый результат перевода, т. е. будем считать, что
а — Ьп ... ... b-h. Согласно (4.3) количественный экви-
валент числа в минус-двоичной системе счисления можно
представить как разность сумм количественных эквивалентов
разрядов с четными {а') и нечетными («") номерами, т. е.
а = а’ — а!'. Следовательно, когда в качестве а рассматривается
исходное слово Ь, то имеем а = Ь' — Ь", но количественный
эквивалент исходного слова был b = b' -\-Ь". Поскольку коли-
чественные эквиваленты исходного и переведенного чисел
должны быть равны, то к значению а = Ь' — Ь" надо добавить
еще величину 2Ь", т. е. удвоенное значение суммы количе-
ственных эквивалентов всех нечетных разрядов, и это дейст-
вие произвести в минус-двоичной системе счисления. Теперь
можно сформулировать алгоритм перевода П.
П1. Из исходного слова b формируем новое слово Ь', у ко-
торого разряды с нечетными номерами совпадают с исходным,
а разряды с четными номерами имеют значение 0.
П2. Слово b сдвигаем на один разряд влево, результат
есть новое слово Ь".
ПЗ. В минус-двоичной системе счисления складываем числа
b и Ь". Результат сложения есть искомое число а.
Пример 4.15. Число 11,125 задано в двоичной системе счисления, т. е.
b = 1011,0019. Требуется найти его представление в минус-двоичной системе
счисления. Вначале формируем вектор, у которого все разряды с четным
номером есть 0, а с нечетным совпадают с значениями нечетных разрядов
числа Ь, тогда получим Ь' = 1010,001. Затем сдвинем полученное слово
на один разряд влево: Ь” = 10100,010. Сложим два числа Ь' и Ь", получим
а= 11111,011. Проверим правильность перевода, для чего подсчитаем коли-
чественный эцривалент числа а по формуле (4.3): а = 1 (—2)4 + 1 (—2)3 +
+ 1 (—2)2 + 1 (—2)1 + 1 (—2)0 + 0 (—2)-1 + 1 (—2)“2 + 1 (—2)~3 = 1М25.
Так же просто осуществляется перевод, когда отрицатель-
ное исходное число задано прямым кодом. В этом случае по
исходной записи надо сформировать вектор, в котором все
разряды с нечетными номерами есть нули, а- разряды с чет-
ными номерами повторяют значения разрядов исходной записи.
Затем, как и ранее, надо сложить по правилам минус-двоич-
ной арифметики это число, сдвинутое влево на один разряд
с исходным.
В том случае, когда' отрицательные числа представляются
дополнительными кодами, алгоритм перевода является комби-
нацией алгоритмов перевода положительных и отрицательных
чисел. Это обстоятельство связано с тем, что количественный
эквивалент числа в этом случае есть сумма положительного
и отрицательного чисел, ибо — + __hbj2>. Исходной
записью числа b является его полное изображение вместе
со знаковым разрядом Ь*. Отсюда перевод основных разрядов
дополнительного кода осуществляется по правилу перевода
положительных чисел, а знакового — по правилу перевода от-
рицательных чисел, представленных прямыми кодами.
• Пример 4.16. Дано число b = 1.00П9. Требуется осуществить его пере-
вод в минус-двоичную систему счисления.
Вначале в исходном представлении числа b выделяют знаковый и ос-
новные разряды, в результате чего формируются два слова: Ь' = 10000
и Ь" = 00011. Далее переводим отдельно эти числа по правилам перевода
отрицательных и положительных чисел соответственно, тогда найдем два
числа а' = 110000 и а" = 00011. Для получения искомого числа а надо сло-
жить числа а' и а". Выполнив операцию сложения, определим о =110111.
Действительно, согласно (4.3) количественный эквивалент числа а есть —13.
Пока еще не был рассмотрен вопрос о необходимой раз;
рядности слов в минус-двоичной системе счисления. Если
считать, что в исходном представлении числа имеют п основ-
ных разрядов и один знаковый, то, принимая во внимание
верхние оценки для значений чисел в минус-двоичной системе
счисления (4.4) и (4.5 , найдем, что необходимая разрядность
р минус-двоичной системе счисления есть п + 2. -
Приведенный алгоритм перевода базировался на использо-
вании действий в минус-двоичной арифметике. Если же до-
пустимы лишь действия в обычной двоичной арифметике, то
приходится менять алгоритм перевода [10]. Количественный
эквивалент переведенного числа, который определен из (4.3),
представим в виде разности двух двоичных чисел, т. е. а =
= a*—v, где (1 — (1 — «Л_2) ... (1 — й1)«о(1—
— a-i) ... a-h и V. 101 ... 101 .. .0. В слове v значение всех
разрядов с нечетными номерами есть 1, ас четными — 0.
Вектор же а* отличается от искомого вектора а противопо-
ложными значениями нечетных разрядов. Следовательно, если
удастся найти слово а*, то искомое слово а легко найти по
правилу а = а*ф‘П. В свою очередь, числом* можно просто
определить, если в двоичной системе счисления сложить b
и V, ибо а* = & + v, поскольку для исходного (&) и искомого
слова (а) должно выполняться равенство Ь = а. Число а, ка-
ким бы ни было исходное число Ь, всегда будет положитель-
ным, ибо если число имеет знак минус ,то |&|<C2n, a v всегда
больше 2", поскольку число разрядов в целой части а больше
на 1 (в общем случае), чем у исходного числа b (с учетом
разряда знака).
Пример 4.17. Число —13, представленное в двоичной системе счисле-
ния дополнительным кодом, записать в минус-двоичной системе счисления.
Имеем />=1.0011, и тогда £>=101010, следовательно, а* 5= b + v =—13 +
+ 42 = 29, т. е. о* = 011101. Наконец, из равенства а = а* §5 v находим, что
0=110111.
Перевод из минус-двоичной системы в двоичную особенно
прост, когда он реализуется в двоичной системе счисления.
Действительно, достаточно исходное слово а: ак ... «0«_1 • • -
... представить в виде двух слов а': а^ак-1 ... а00 ...
и а": 0ак-10 ... 0«_i ... 0, а затем из двоичного числа а'
вычесть двоичное число для того чтобы получить искомое
число Ь. При этом очевидно, что справедливо равенство а =
= а' — а" = Ь.
Требование о выполнении действий в минус-двоичной сис-
теме заставляет изменить алгоритм перевода, вернувшись
к идеям, изложенным в начале этого раздела. Рассмотрим
исходное положительное число а как уже готовый результат
перевода его в двоичную систему счисления. Очевидно, что
тогда Ь = а' а", в то время как а = а' — а". Поскольку ко-
личественные эквиваленты ^сходного и переведенного числа
должны быть равны, то из а необходимо вычесть 2а,", т. е.
удвоенное значение суммы всех нечетных разрядов. Получен-
ный результат есть искомое число Ь.
Пример 4.18. Число 19 задано в минус-двоичной системе счисления.
Требуется найти его изображение в двоичной системе. Из исходного числа
а= 10111 выделяются вначале нечетные разряды а’ =00010, затем сдвигаем
это слово на один разряд влево, получаем а" = 1W. далее осуществляем
вычитание слова а!' из исходного слова а, результат есть искомое слово,
b = 10011, представленное в двоичной системе счисления.
Если исходное слово а имеет значение меньше нуля, то
для получения прямого кода надо из него вычесть в Минус-
двоичной системе счисления удвоенное значение четных раз-
рядов. Для того- чтобы получить дополнительный код, надо
из исходного числа вычесть удвоенное значение всех нечет-
ных разрядов, кроме самого старшего, определяющего знак.
Г» Пример 4.19. Число —21 задано в минус-двоичной системе счисления,
т. е. а = 111111. Требуется найти его изображение дополнительным кодом
в двоичной системе. Формируем слово а' из всех неч'етных разрядов, кроме
старшего: а' = 001010, сдвигаем это слово на разряд влево: а” = 010100.
Вычитаем это слово из исходного, получаем b = 1.01011. Количественный
эквивалент слова b есть —21.
*
2°. Алгебраическое сложение в минус-двоичной системе
счисления. Сложение в минус-двоичной системе счисления
имеет свои особенности, которые не были раскрыты в при-
мерах 4.15 — 4.19. Эта специфика обусловлена тем, что веса
соседних разрядов имеют разные знаки. Следовательно, пере-
нос, сформированный в предыдущем разряде, при поступлении
в данный разряд должен вызвать не добавление единицы
к разрядной сумме, а вычитание ее. Но оказывается, что этим
не исчерпываются все особенности сложения в минус-двоич-
ной системе счисления. Для их выяснения более детально
рассмотрим таблицу сложения (табл. 13) в одном разряде.
Таблица 13
at bi ci-l Si С/
0 0 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 . 1 0 1 0 0 0 0 —1 —1 —1 —1 +1 +1 +1 +1 0 1 1 0 1 0 0 1 1 0 0 1 0 0 0 —1 +1 0 0 0 0 —1 —1 —1
При отсутствии переноса из предыдущего разряда никаких
проблем в формировании значения поразрядной суммы и пе-
реноса нет (первые четыре строки таблицы). Не появляются
они и в тех случаях, когда перенос присутствует и хотя бы
одно из слагаемых отлично от нуля. Однако если оба слагае-
мых равны нулю', а перенос присутствует, т. е. значение сум-
мы есть —1, мы сталкиваемся с трудной ситуацией изображе-
ния цифры со знаком, противоположным знаку данного разряда.
Поскольку прямо сделать это никак нельзя, то приходится
разрядному значению суммы приписать величину 1, а значе-
нию переноса величину +1. Ввиду противоположности знака
весов соседних разрядов добавление по единице в два сосед-
них разряда равносильно вычитанию единицы из младшего.
Последние четыре строки таблицы определяют значение по-
разрядной суммы и переноса в том случае, когда знак посту-
пающего переноса совпадает со знаком разряда. Как видно
из таблицы, правила сложения в минус-двоичной системе
счисления оказались существенно более сложными, чем
в двоичной системе. Теперь приходится определять значение
переноса двух типов: переноса —1 (<?Г) и +1 (ct). Если
в обычной двоичной системе счисления уравнения для опре-
деления поразрядной суммы st и переноса Q имели вид
si = apid-i V apid-i V а&с^ V
ct = afii \/ aft-х V (4.6)
то в минус-двоичной системе они следующие:
sl = ai Ф ф (ctl V 0-1),
ct = ajbfT-i, » (4.7)
cT = afifF-i V («г V К) ct-i.
Техническая реализация уравнений (4.7) требует лишь не-
много больше оборудования, чем реализация уравнений (4.6),
и легко может быть выполнена за время задержки сигнала
на трех логических ступенях.
Мы уже упоминали о том, что добавление по 1 в два со-
седних разряда числа в минус-двоичной системе счисления
равносильно вычитанию 1 из младшего разряда. Это обстоя-
тельство позволяет перенос со значением —1 в i-й разряд
заменить на два переноса в i-й и (i + 1)-й разряды с одина-
ковыми значениями -|-1. В этом случае специфика сложения
в минус-двоичной системе счисления сводится к формированию
в каждом разряде двух переносов ct и dit а также участию
этих значений в формировании разрядных сумм [35, 63]. По-
разрядные суммы и переносы будут определены по табл. 14.
Первые 12 строк табл. 14 являются повторением табл. 13
с учетом изображения переноса со значением ct = — 1 в виде
c.==rfi== 1.
Последние четыре строки учитывают возможные переносы
di-2 в Z-м разряде, когда перенос с предыдущего разряда ра-
вен нулю (ct-_i = 0). Уравнения алгебры логики, определяю-
щие поразрядную сумму st и переносы ct и db будут следую-
щими:
V afi^i^di-2 V ajbfit^di-i V
V «fM-i^i-2 V aibfit-xdi-2 V atbfit-idi-z V
V aibiCi^dt-2 V «Дсг--1£Л-_2, (4.8)
ct = «zM-idt-2 V aft-idi-2 V aiCt-idi-2 V
. V afii-yd^ V bfifh_2 V bfi-xdi-2 V M-idj-2,
di = afii V V «A-г V M-i v Mi-2 V O-i^i-2.
Хотя система уравнений (4.8) может быть реализована за то
же время, что и система (4.7), первая требует больше обору-
дования, чем последняя.
Для выполнения операции вычитания числа b из числа а
в минус-двоичной системе счисления можно вначале изменить
знак числа b на противоположный, а затем сложить число а
с преобразованным числом Ь. К решению проблемы изменения
знака числа b на противоположный подойдем точно так же,
как мы это делали при переводе, т. е. рассмотрим исходную
запись числа b как уже готовый результат. Ясно, что все
разряды, отличные от нуля, при такой интерпретации имеют
противоположный знак. Поэтому для сохранения количествен-
ного эквивалента к исходному числу b надо прибавить его
удвоенное значение. Результатом сложения и будет исходное
число с противоположным знаком.
Пример 4.20. Дано число —7,75, представленное в минус-двоичной си-
стеме счисления, т. е. а = 1000,01. Требуется в этой же системе найти чис-
ло 7,75. Вначале удваиваем исходное число: а’ = 10000,1, а затем, склады-
ваем это число с исходным, получаем —а = 11000,11. Согласно (4.3) коли-
чественный эквивалент результата есть 7,75.
При выбранном способе изменения знака операнда на про-
тивоположный операция вычитания в минус-двоичной системе
счисления выполняется за два прохода, что является опреде-
ленным недостатком. Положительным моментом следует счи-
тать полное отсутствие анализа знаков операндов (для выбора
реального типа операции и кода операндов) и результата,
а также отсутствие специальной роли у младшего разряда сум-
матора, что позволяет достаточно легко суммировать операн-
ды переменной длины.
Изменить знак операнда можно и без привлечения опера-
ции сложения, если вначале из исходного слова а сформиро-
вать вспомогательное слово а', цифры которого определятся
по правилу [63]
<7/+1 = «,(1 — а’,), —и «1Л = 0. (4.9)
Когда слово а' найдено, то цифры числа —а, которые мы
обозначим как аь будут сформированы в соответствии с урав-
нением
в( = «гф«;. (4.Ю)
С учетом (4.10) уравнение (4.9) можно переписать в виде
al+i =
(4.Н)
Соотношение (4.10) позволяет сформировать число —а по ис-
ходному числу а и числу а' с помощью поразрядной логической
операции сравнения, что может быть выполнено достаточно
быстро. Однако само формирование числа а' займет времени
немного меньше, чем сложение «-разрядных операндов ввиду
итеративной зависимости значений разрядов слова а’.
Для определения переполнения сумматора, работающего
с «-разрядными операндами, надо проанализировать значения
ck и dk. Если окажется, что ck = dk = 0, то переполнения нет.
Когда ck = dk==i, это означает, что результат больше, чем
максимально допустимая величина (4.4). При этом знак ре-
зультата совпадает со знаком старшего разряда слагаемых.
В случае ск = 1 и dk — 0 также фиксируется переполнение,
но теперь результат имеет знак, противоположный знаку
старшего разряда слагаемых, и он больше, чем величина
тах|«|, определенная из (4.5). Заметим, что сочетания сЛ = 0,
dk = 1 никогда быть не может, потому что при этом абсо-
лютная величина результата была бы не меньше, чем 2fc+2 —
—max | а* |, а даже сумма самых больших допустимых чисел не
превзойдеФ по абсолютной величине значения 2 max | а | + 2~Л.
Легко показать, что
2n+1-ft > 2 max | а | + тах[| а* | + 2-л.
При реализации арифметических операций важным момен-
том является вопрос о способе округления в системе счисле-
ния с основанием —2. Пусть исходное число есть «-разряд-
ное, и его надо округлить до m-разрядов, и п = k \ И,
а т = k + 1 + h'. Проанализируем отсекаемую часть. Если
абсолютная величина отсекаемой части не меньше 2-1-л', что
возможно, когда a-w-\ = 1, то в разряд добавляется едини-
ца,знак которой совпадает со знаком величины отсекаемой час-
ти, а, следовательно, противоположен знаку разряда с номером
h'. Если же абсолютная величина остатка меньше 2-1~л', то
никакого уточнения величины сохраняемых разрядов не произ-
водится. Для определения величины отсекаемой части, строго
говоря, надо проанализировать значения всех разрядов. Однако
имеет смысл упростить этот анализ, рассматривая значение
лишь двух старших разрядов отсекаемой части. В этом случае
величина и знак переноса в младший разряд будут определены
из табл. 15. Сокращенный анализ лишь в случае, когда =
= ± 1 и «-2-л' = 0, может нарушить выбранный принцип
округления, да и то, если старший из оставшихся непроана-
лизированными значащих разрядов имеет знак, противополож-
ный знаку «-I-*-. В остальных же случаях сокращенный ана-
лиз дает такой же результат, что и полный, т. е. приводит
к погрешности меньшей, чем 2~1-л'.
Таблица 15
й-1-Л' й-2-Л' Значение переноса
0 0 0
0 +1 0
0 —1 ' 0
+1 0 + 1
+1 —1 0
—1 0 —1
-1 +1 0
минус-двоичной системе
3°. Умножение. Умножение в
счисления выполняется точно так ж.е, как умножение прямых
положительных чисел в обычной двоичной системе счисления.
Вначале находятся частичные произведения = —2)1Ь, где
b — множимое, а «г —цифры множителя. Если «,=£0, то час-
тичное произведение р№ есть просто множимое в Ь, сдвину-
тое на i разрядов влево. Здесь только надо учитывать, что
сдвиг влево числа а в минус-двоичной системе счисления не
только увеличивает его величину вдвое, но и меняет знак
на противоположный. Полное произведение есть сумма всех
частичных произведений. Поскольку знаки операндов опреде-
лены весом старшей значащей цифры, то произведение полу-
чается сразу с правильным знаком. В отличие от обычной
двоичной системы счисления произведение «-разрядных опе-
рандов (n = k-\- 1 +А) может иметь не 2п разрядов, а согласно
(4.4) 2п + 3, что обусловлено спецификой представления чи-
сел в минус-двоичной системе счисления.
Пример 4.21. В минус-двоичной системе счисления заданы целые числа
о = 1101_2 и b = Ю1_2. Требуется найти их произведение. Поскольку ни-
какого анализа знака операнд или их преобразования не требуется, то сра-
зу можно приступить к собственно умножению чисел а и Ь.
1-й шаг 0.000 — начальное значение суммы частичных произведений (СЧП) 0.101 — а^Ь
+
0.101 — сумма частичных произведений l-ro шага; СЧПр
2-й шаг . 0.010 — г-ЕсчПь р0 = 1
0.000 — а^Ь
0.010 —СЧП2;
3-й шаг , 0.001 — 2—1 .СЧПо, А = 0
+ 0.101 — а%Ь
11.010 — СЧП3;
4-й шаг , 1.101—2-1-СЧП3, р2 = 0
0.101 —а?Ь .
olio — счп4. 7
Умножение закончено и р = 110001—2- Согласно (4.3) численный экви-
валент числа р есть —15, что и должно быть.
За счет отсутствия этапа формирования знака результата
алгоритм умножения в минус-двоичной системе счисления
оказывается даже проще, чем в обычной двоичной системе
счисления при использовании прямых кодов, когда умножение
реализуется наиболее легко.
4°. Деление. Операция деления является наиболее сложной
операцией в минус-двоичной системе счисления ввиду необ-
ходимости формирования цифр частного разного знака на чет-
ных и нечет-Ных шагах алгоритма. В целях упрощения алго-
ритма процесс деления можно было бы разбить на два этапа.
На первом этапе ищется частное в обычной двоичной системе
счисления с помощью алгоритма деления без Восстановления
остатка. Затем, на втором этапе, полученное частное перево-
дится в минус-двоичную систему счисления. Перевод из дво-
ичной системы счисления в минус-двоичную можно осуще-
ствлять итеративно, по мере получения цифр частного, и тог-
да второй этап оказывается излишним. Именно такой алгоритм
мы исследуем более детально.
Будем считать, что операнды являются целыми числами,
представленными в' минус-двоичной системе счисления в фор-
ме с естественной запятой, т. е. n = k-\-\. Пусть делитель
нормализован, т. е. bk = \. До начала' собственно деления
нормализуем также делимое а, т. е. увеличим его в (—2)у
раз, где j — число нулей у делимого до первой значащей
цифры.
Наибольшее значение нормализованного числа определяется
соотношением (4.4), а наименьшее значение нормализованного
числа есть
min |«| = 2"-1 — max |«|, (4.12)
где max |«| задано соотношением (4.5). Учитывая, (4.4) и (4.12),
найдем, что абсолютная величина частного от деления нор-
мализованных чисел, представленных в минус-двоичной сис-
теме счисления, удовлетворяет неравенству
0 2"+1~2 + 6(») <4
\ 2п-1 ! + 5 (п)
Отсюда следует, что определение целой части частного долж-
но иметь свою специфику, которая заключается в том, что
если результат первого вычитания делителя из делимого со-
храняет исходный знак делимого, то следует провести еще
одно вычитание. Изменение знака у остатка после второго
вычитания означает, что определение целой части закончено
и с0==1. Если же знак после второго вычитания не меняется,
то определены цифры частного: Ci = c>=l, т. е. целая часть
частного не меньше двух. В этом случае необходимо еще
одно вычитание, которое позволит уже окончательно выяс-
нить значение разряда с0: если знак нового остатка сохранит-
ся, как у делимого, тог0=1, и со = О, если знак изменится.
После определения целой части можно переходить к на-
хождению цифр дробной части. Поскольку частичные остатки
будут меньше делителя, то на всех шагах алгоритма цифры
частного не будут иметь значение больше, чем 1. Основная
трудность сейчас будет представлять изменение истинного
знака остатка на противоположный на всех четных шагах
алгоритма, ввиду того, что нечетное число сдвигов числа а
в минус-двоичнои системе счисления меняет знак числа на
противоположный. Это обстоя-
тельство приводит к тому, что
если на нечетных шагах пра-
вила определения цифр част-
ного обычные для алгоритма
без восстановления остатка, то
на четных шагах они прямо
противоположны тому, что
свойственно обычной двоич-
ной системе счисления.
На четных шагах алгорит-
ма будут определены цифры
частного для разрядов с отри-
цательными весами, т. е. эти
цифры должны иметь значе-
ние 0 или —1. Однако мы
находим на этих шагах цифры
обычной двоичной системы
счисления со значениями О
или 4-1. Следовательно, если
Ci-2/ — 1, где /= 1, 2, ..., то
надо скорректировать найден-
ные значения цифр частного.
Алгоритм коррекции приведен
на рис. 19. Если предыдущая
цифра c2-2z=0, то вся' кор-
рекция заключается в присвое-
Рис. 19.
нии цифре с2-2/ значения, рав-
ного 1. Когда же с2_2< = 1, то необходим еще анализ цифры
Сз-2/- Равенство с3_2< = 1 означает, что окончательно должно
быть с2_2< = с3_2< = 0. Если же с3_2/ = 0, то с2_2< = 0 и <?3_2< =
= 1. В последнем случае необходимо вернуться на алгоритм
коррекции, но теперь уже для значения с3_2/==1. Нетрудно
показать, чте если Ci_2/ = 1, то возможная коррекция после-
дующих цифр частного не может затронуть цифры частного
старше, чем С1-2/. Это обстоятельство приводит к тому, что
в процессе итеративного перевода цифра частного может кор-
ректироваться не более двух раз за все время реализации
алгоритма.
После определения дробной части полученное частное
сдвигается вправо на j разрядов с тем, чтобы учесть знак
и реальную величину делимого, который предварительно был
нормализован. Как обычно, при делении введение анализа
значения частичных остатков на нуль позволит значительно
ускорить выполнение алгоритма за счет его прерывания при
нулевом остатке.
Пример 4.22. Найти частное от деления величины а = —4 на b = 1,
которые представлены в минус-двоичной системе счисления, т. е. а = 100
и b = 1001.
БудекСсчитать делитель нормализованным, тогда нормализация делимого
будет заключаться в сдвиге его влево на один разряд, тогда а' = 1000. Зна-
чение j = 1 запомним и перейдем к реализации алгоритма деления.
1-й шаг . *0.1000 — «<°><0 — делимое
0.1010 — b — делитель
1.0010 — 26
0.0011_д(°) < 0, поэтому продолжим вычитание
+ 0Л001 — b
1.0010 — 26
1.1010 — а(0) > 0, следовательно, с0 = 1;
2-й шаг , 11.0100 — < 0, начальное значение с, = 1
+ 0.100Г— 6
1.0010 — 26
0.1111—< 0, c_j = 0 ввиду специфики четных шагов,
поскольку с_j = 0, коррекции частного нет;
3-й шаг , 1.1110 — < 0, начальное значение с_2 = 1
+ 0.1001—6
• 0.0111 —с№ > 0, следовательно, с_2= 0;
4-й шаг 0.1110 — аФ <0, начальное значение с_3 = 0
+ 0.1001 —6
1.0010 — 26
0.0001 —< 0, окончательно с_3 = 1, коррекция резуль-
тата дает с_2 = 1;
5-й шаг , 0.0010 — < 0, начальное значение с . = 0
+ 0.1001—6
1.0010 — 26
1.0101 —> 0, окончательно с_4 = 0;
6-й шаг , 11.1010 — < 0, начальное значение с_ч =0
+ 0.1001—6
1.0010----26
00.1101 —я® < 0, окончательное значение с_5 = 0;
7-й шаг , 11.1010 — 4^6) > 0, начальное значение c_fi = 1
+ 0.1001—6
0.0011 —< 0, окончательно с_6 = 1.
Отсюда полученное^ частное есть с' — 1,011001. С учетом начальной норма-
лизации делимого это значение надо сдвинуть вправо на разряд (ибо 7=1)
и тогда окончательно с = 0,1011001. Количественный эквивалент найденного
числа есть с = —0,5703, в то время как частное от деления а на b есть
—4 : 7 =-0,5714.
В минус-двоичной системе счисления изящно и просто вы-
полняются операции сложения и умножения, а реализация
операций вычитания и деления вызывает определенные труд-
ности. Правда, трудности в реализации операции деления не
кажутся уж столь грозным препятствием, к применению дан-
ной системы счисления, хотя бы по той причине, что простота
и быстрота выполнения операции умножения позволяют эф-
фективно использовать итерационные схемы деления, бази-
рующиеся на умножении. Кроме того, и прямая реализация
алгоритма деления в минус-двоичной системе счисления не вы-
глядит столь уже невыполнимой [63].
§ 3. СИСТЕМА ОСТАТОЧНЫХ КЛАССОВ
1°. Представление чисел в системе остаточных классов.
Возьмем натуральный ряд чисел от 0 до I и некоторое целое
положительное'число р. Для целого числа «, такого, что
0<Cft<^, найдем устаток а от деления его на р, т. е.
Если t <Zp, то справедливо а = а, т. е. система остатков от
чисел ft(Z) при делении их на число р (иначе система вычетов
от чисел ft(Z) по модулю р) совпадает с самими числами.
Иначе обстоит дело, когда t > р. В этом случае все мно-
жество чисел ft(Z> разбивается на р непересекающихся классов
эквивалентности, в каждый из которых с номером k входят
все числа ft(Z), удовлетворяющие соотношению
= ft(Z) (mod/?).
где < р — минимальное по величине целое положительное
число, входящее в &-й класс эквивалентности и являющееся
его представителем. Классы эквивалентности принято называть
остаточными классами. Если мы теперь рассмотрим систему
вычетов от чисел ft(Z) по модулю р, то по значению a<z) в об-
щем случае не удается сказать, какому именно числу ft(Z) соот-
ветствует этот вычет. Для однозначного определения числа
ft(,) надо проанализировать системы вычетов от этого числа
еще по нескольким модулям р;. Число этих модулей зависит
от соотношения между величиной t и значениями Pj
При использовании нескольких модулей каждому
числу aW будет отвечать некоторая последовательность
а(/)=(аР, 4°, 4°), (4.13)
где а.Й* = aiL} (motipj).
Число различных (несовпадающих) последовательностей ай)
есть наименьшее общее кратное всех модулей pj, которое
обозначим как т. Это действительно так, ибо число ай) = т
дает последовательность ай) = (0, 0, ..0), т. е. точно такую,
как и число «й) = о. Если справедливо сравнен'ие a = b (mod р,),
то также справедливо и сравнение а = b + xpj (mod/),), где
х—целое число. Тогда, поскольку tn = ypj, то для ай) = у
+ хт, где у < т, мы получим точно такую же последова-
тельность ай), как и для числа а(/) = у. Следовательно, число
различных последовательностей есть т. Отсюда т = П”=1/?,,
если только все числа Pj взаимно-простые.
Для однозначного представления всех чисел ай)(0<Сай)^
t) последовательностью из п вычетов по модулям ри ..
рп необходимо, чтобы выполнялось неравенство t < т. Пред-
ставление числа -ай) последовательностью ай) = (<ф£), ..., а„£))
можно рассматривать как представление его п цифрами, при-
надлежащими п различным системам счисления с основаниями
А, ...,рп. Пусть А<Рг< ••• <Рп, тогда алфавит, приме-
няемый для изображения цифр в системе счисления с осно-
ванием pj, может быть усечением алфавита системы исчисле-
ния с основанием р [1].
Пример 4.23. Пусть t = 9. Выберем для представления чисел натураль-
ного ряда 0, 1, .... 9 два взаимно-простых значения рг = 2 и р2 = 5. Тогда
т = 2-5 — 10. Поскольку т > t, то все заданные числа могут быть заданы
последовательностями ай) = (ай), ай^. Действительно, 0 — (0,0); 1—(1.1);
2 — (0,2); 3 — (1,3); 4 — (0,4); 5 —(1,0); 6 —(0,1); 7 —(1,2); 8 —(0,3); 9 —
При решении вопроса о представлении чисел с учетом
знаков будем считать, что диапазон положительных и отри-
цательных чисел одинаков, тогда последовательностями выче-
тов по модулям ри ..., рп требуется изобразить 2^+1 чисел
и должно выполняться неравенство
Знак числа в системе остаточных классов может быть за-
дан несколькими способами. Например, в качестве. pt взять
число 2 и считать, что все положительные числа и нуль
имеют a*£) = 0, отрицательные а}£)=1, В этом случае знак
числа выделен явно (это значение а)£>), однако возникают
-серьезные трудности при выполнении арифметических опера-
ций. Конечно, пока не рассмотрены особенности выполнения
арифметических операций в системе остаточных классов это
утверждение бездоказательно. Однако некоторые общие сооб-
ражения относительно простоты выполнения этих операций
могут повлиять на выбор формы представления отрицательных
чисел.
Пусть дано некоторое число в системе остаточных
классов. Потребуем, чтобы 6<г> = ф- (—а(/)) = 0, т. е. =
= (0, 0, ..., 0). Очевидно, этого можно добиться, если в ка-
честве —с№ взять положительное число т — а^, т. е. допол-
нение числа до т. Фактически в этом способе представ-
ления отрицательных чисел реализуется идея дополнительных
кодов для аддитивной однородной позиционной системы счис-
ления.
В качестве положительных чисел можно взять числа нату-
г, гп 1
рального ряда, лежащие на отрезке 1, -у , а в качестве от-
рицательных— на отрезке |-у ф- 1, т—1]. Если т четно
. т т
(/?1 = 2), то числа -у и-----у представляются одинаково,
и обычно в этом случае договариваются о несимметричности
диапазона представления положительных и отрицательных
чисел, считая, что положительные числа находятся на отрезке
[, т 1 г т . ,
1, -у|» а отрицательные, как и ранее, — на отрезке -уф-1,
т — 1].
Пример 4.24. Пусть рх = 2, р2 — 3, р3 = 5. Требуется представить числа
а = 14 и b — —11. Поскольку т = 2-3-5 = 30, то диапазоном представления
положительных чисел есть 1-^14, а отрицательных —15 1, следова-
тельно, поставленная задача корректна. Число Ь представим в виде допол-
нения | Ь | до т и тогда получим а = (0, 2, 4) и b = (1,1, 4).
2°. Реализация арифметических операций. Алгебраиче-
ское сложение и умножение чисел, представленных в системе
остаточных классов, реализуются достаточно просто. Они ба-
зируются на известном свойстве сравнений: если ft = «(mod/?)
и b р (modр), где а, р <р, то а + Ь = а ф- р (mod/?) и ай =
sap (mod/?). Это становится очевидным, если учесть, что
« = аф-й/? и b = $ -\- tp, где k и t — целые неотрицательные
числа. Тогда а ± b = (k ± t)p ф- (a + Р) и ab = ар ф- р (йр ф-
ф- to. ф- ktp), т. е. а + b = а + р (mod/?) и ab = ар (mod/?). От-
сюда для сложения чисел и «<2>, представленных в форме
(4.13), достаточно просуммировать вычеты а^ и а^2) по моду-
лю Vj.
Пример 4.25. Числа = 2 и = 3 заданы в системе остаточных
классов с рх = 2 и р2 = 5; найти их сумму. Имеем д(1) _ 2) и = (1, 3);
тогда s = _[_ я(2) = (ц Q) (см. пример 4.23).
Изменение знака числа можно реализовать путем вычита-
ния заданного числа из нуля.
Пример 4.26. В системе остаточных классов с ft = 2, р2 =₽ 3 и Рз — 5
задано число а — И, т. е. а~ (1,1,4). Требуется найти изображение числа
со значением —11. Пусть искомое число есть Ь, тогда Ь = —а = (О, О, О) —
— (1, 1,4) = (—1,-1,—4) = (1,2,1).
При сложении двух чисел может оказаться, что их сумма
выйдет из допустимого. диапазона. Однако обнаружить это
„переполнение" будет очень трудно.
Пример 4.27. Сложить два числа = (0, 2, 4) и с№ = (1,0,3) в сис-
теме остаточных классов с рх = 2, р2 = 3 и р3 = 5. Производя сложение,
получим s = (1, 2, 2). Число з в соответствии с правилами изо-
бражения отрицательных чисел трактуется как величина —13, в то время
как истинная сумма должна иметь значение 17.
Главная беда не в том, что результат неверен, а в том,
что отсутствуют какие-либо простые способы определения вы-
хода результата из допустимого диапазона. При использовании
аддитивных позиционных систем счисления признак перепол-
нения разрядной сетки всегда определяется достаточно просто
и позволяет легко обнаружить аварийную ситуацию. Пред-
ставление чцрел системой вычетов по модулям Pj сильно за-
трудняет определение аварийных ситуаций, связанных с выхо-
дом результатов из области допустимых значений. Конечно,
обнаружить такие ситуации можно, если произвести тщатель-
ный анализ операндов и результата. Например, отрицательное
значение суммы двух положительных чисел может служить
признаком выхода из допустимого диапазона, но произвести
такой анализ не просто.
Операция умножения также реализуется как поразрядная
операция, в которой производится перемножение цифр опе-
рандов. Эта операция дает правильный результат, если про-
изведение не выходит из допустимого диапазона положитель-
ных или отрицательных значений.'
Пример 4.28. В системе остаточных классов с р, = 2, р2 = 3 и р3 = 5
найти произведение чисел с = 6 и 6 = 2, с = —3 и d = 5, а и d. В соответ-
ствии с приведенными правилами найдем, что р^ = ab = (0,0, 1)-(0, 2, 2) =
= (0, 0, 2); р<2> = cd = (1,0,2) - (1, 2,0) = (1,0,0); р(3) = ad = (0, 0, 1)-(1,2,0) =
= (0, 0, 0). Значение полученных произведений есть р^ = 12, pW = —15,
Р^ = 0. Последний результат неверен, ибо значение произведения вышло
за пределы диапазона, допустимого для положительных чисел.
Так же как и при сложении, нет простого способа обнару-
жения переполнения области допустимых значений. Отсюда
для того чтобы осуществить реализацию данных операций,
надо либо строить весьма сложные системы обнаружения вы-
хода результата из заданных областей, либо следить за вели-
чиной операндов с тем, чтобы при сложении не допускать
чисел одинакового знака больших, чем —, а при умножении:
I / т „
у Однако и в том и в другом случае возможность вы-
полнения последовательных вычислении значительной длины
выглядит весьма проблематичной.
Конечно, проблема расширения диапазона машинных чисел
в результате выполнения арифметических операций сущест-
вует и для аддитивных позиционных систем счисления, но там
положение спасают очень простой способ обнаружения пере-
полнения и коррекция порядка, когда числа представлены
в форме с плавающей запятой и все действия фактически
выполняются с дробями. Большое значение имеет также воз-
можность округления „длинных" чисел, позволяющая приво-
дить полученные числа к формату машинных чисел. В системе
остаточных классов мы вынуждены всегда проводить точные
вычисления, с целыми числами и не имеется возможности
округлять результаты. Отсутствие удобного и быстрого спо-
соба сравнения двух чисел или определения знака числа еще
в большей степени затрудняет выполнение арифметических
операций, особенно такой важной операции, как деление.
В настоящее время имеется слишком много нерешенных во-
просов для того, чтобы представление чисел в системе вычетов
по совокупности модулей pj могло серьезно конкурировать
с аддитивной позиционной системой счисления. Означает ли
это, что у данной системы счисления нет никаких достоинств?
Вовсе нет.
Достоинство этой системы состоит в независимости обра-
зования цифры /?7-ичной системы счисления от других цифр
й, как следствие, возможности их параллельной независимой
обработки при таких операциях, как сложение и умножение.
Если при сложении с помощью /?7--значных сумматоров, реа-
лизованных на базе двоичных сумматоров, и не удастся пре-
высить наилучшие достижения для позиционных систем счис-
лейия (максимальное время задержки в получении суммы есть
время пяти задержек на одной логической ступени вне зави-
симости от длины операндов), то количество оборудования,
которое при этом потребуется, оказывается существенно мень-
ше. Это естественно, поскольку зависимость между разрядами
при суммировании распространяется только в пределах огра-
ниченной длины, зависящей от значения р}-. Для умножения
можно получить скорость реализации более высокую, чем для
позиционной системы счисления, если только результат не
выйдет из заданной области. Другим достоинством указанной
системы счисления является малая значность оснований pj,
что делает практически достижимой в некоторых случаях
табличную реализацию операций сложения и умножения, и это,
в свою очередь, может обеспечить повышение быстродействия
машины.
Что касается перспектив представления чисел в системе
остаточных классов, то в той или иной форме оно уже
существует в большинстве больших машин, правда как
вспомогательная форма. Речь идет о контроле по модулю при
передаче и обработке слов. С этим применением данной сис-
темы счисления мы познакомимся дальше. При контроле по
модулю используются все достоинства этой системы счисле-
ния,'причем главное внимание уделяется выбору такого зна-
чения модуля, которое позволило бы найти вычеты по модулю
р достаточно простым образом.
3°. Перевод из позиционной системы счисления в систе-
му остаточных классов и обратно. Пусть число а задано
в аддитивной позиционной системе счисления с основанием г,
и требуется перевести его в систему остаточных классов.
Один из алгоритмов перевода является очевидным. Число а
делится последовательно на Pj, каждое из которых представ-
лено в r-ичной позиционной системе счисления. Деление про-
исходит по правилам r-ичной арифметики. Найденные значе-
ния остатков а7- представляются также в r-ичной системе
счисления. В некоторых случаях вычеты по модулю Pj удается
получить и без деления (см. главу 7). В этом случае алгоритм
перевода сильно упрощается.
Другой алгоритм перевода базируется на выполнении необ-
ходимых действий в системе остаточных классов. При этом
каждой цифре r-ичной системы счисления и значению г соот-
ветствует константа, представленная в системе остаточных
классов, т. е. «z==(ai°, <4°, ..., <4Z)), 0<C«z<Cr—1 и г = (a*,
<4 • - ««). Имея набор этих констант, легко вычислить по
схеме Горнера полином (1.7) при й = 0, задающий значение
числа а в r-ичной системе счисления, произведя все действия
умножения и сложения в системе остаточных классов.
Пример-4.29. Число а = 971 представлено в десятичной системе счис-
ления. Требуется найти его изображение в системе остаточных классов
с Л = 3,/>2 = 5, р3 = 7, =11. Поскольку zn=1155, то заданное число
не выходит из области допустимых чисел (считаем, что представляются
только положительные числа). По условию имеем а0 = (1,1,1, 1); аг =
= (1,2,0,7); «2 = (0, 4,2,9) и 10 = (1,0, 3,10). Для определения искомого
представления надо в системе остаточных классов вычислить следующий
полином:
Ь = ((0, 4,2, 9) (1,0,3, 10) + (1,2,0, 7)) (1,0,3,10) + (1,1,1, 1).
Выполним два умножения и сложения, найдем, что Ь — (2, 1,5,3). К такому
же результату придем, если будем последовательно определять вычеты
от числа а — 971 по модулям 3, 5, 7, 11.
Рассмотрим теперь перевод чисел, заданных в системе
остаточных классов, в позиционную систему счисления с ос-
нованием г. Исходное число «<Z) = (<41), ..., a^Z)) можно пред-
ставить как сумму п чисел Ь^, каждое из которых имеет только
один ненулевой вычет aJZ) в j-м разряде, т. е. ft(Z) = (a(iZ),
О, ..., 0) +- (0, <4°, .О) +- ... + (0,0, ..., а^). Число
представим как произведение на число, которое имеет
только один ненулевой вычет, занимающий /-й разряд и рав-
ный 1, тогда
«<Z> = 4°(1, 0, 0, , 0) + 4°(0, 1, ... ,0)+ ... +
+ 4° (0, 0, ... , 1). (4.14)
Векторам, имеющим один единичный вычет, соответствуют
определенные численные эквиваленты, которые заранее из-
вестны. Зная эти эквиваленты, легко найти численный экви-
валент числа а, просуммировав все члены в выражении (4.14).’
Полученное численное значение может быть увеличено по
сравнению с истинным на 1т, где I — целое число, и поэтому
результат следует скорректировать таким образом, чтобы
< т. Такую коррекцию достаточно просто сделать, опре-
деляя вычет по модулю т от полученного результата. Далее
найденный вычет обычным образом переводится в г-ичную
систему счисления. Переход к численному эквиваленту вовсе
не является обязательным. Можно значения 4° и численные
значения векторов с единственным единичным элементом сра-
зу же представить в r-ичной системе счисления. Тогда, про-
изводя действия, которые требует вычисление выражения
(4.14), в г-ичной системе счисления, мы сразу же получим
результат в г-ичной системе счисления. Для получения иско-
мого числа надо еще найти вычет от найденного числа по
модулю т.
Пример 4.30. В системе вычетов по модулю рг = 2, ps = 3, р3 = 5
и Рь = 1 задано число а = 93. Тогда я = (1,0, 3,2). Требуется перевести
это число в десятичную и двоичную системы счисления. В рассматриваемом
случае т = 210, at = 1, а2 = 0, ag = 3 и а4 = 4. Численный эквивалент век-
тора ₽1 = (1,0,0,0) есть 105, вектора р2= (0,1,0,0) — 70, вектора ₽3 =
= (0,0, 1,0)—126 и вектора {34 = (0,0, 0, 1) — 120. Тогда согласно (4.14)
получим
а* = 1-105 + 0-70 + 3-126 + 2-120 = 723.
Поскольку а* > т = 210, то еще надо найти вычет от а* по модулю 210.
Окончательно имеем а* = 93. Для перевода в двоичную систему счисления
вначале представим в этой системе значения всех и ₽;•
“I = 1, “г = 0, о3 = 11g» “<£ = и Pi = 1101001g.
₽2 = 10001102, ₽з= 11 111 102, pt= 1111000g.
Затем найдем согласно (4.14) число
а* = 1 (1101001) + 0(1000110) + 11 (1111110) + 10(1111000) = 1011010011.
Поскольку полученное число больше, чем т= 11010010g, то еще находится
вычет от величины а* по модулю т и окончательно а* = 1011101g.
Имеются и другие алгоритмы перевода из системы оста-
точных классов в позиционную систему счисления, которые,
однако, являются столь же сложными, причем некоторые из
них базируются на использовании операции- деления в г-ичной
системе счисления.
§ 4. ЗНАКОЛОГАРИФМИЧЕСКАЯ СИСТЕМА СЧИСЛЕНИЯ
1°. Представление чисел в знакологарифмической системе
счисления. Пусть любое вещественное число а, представляется
в цифровой машине его знаком а* и двоичным логарифмом
его абсолютной величины Z, (ft), причем а*=.1, если а^.0,
и а* = 0, если а 0. Следовательно, если а = 0, то а* равно
нулю или единице. Величина L (а) определяется следующим
образом [65]:
£(«) = {
log2(I cft|-), если |«1>с-1,
0 , если [ а [ с~1,
где с — константа, роль которой сводится к тому, чтобы обес-
печить выполнение неравенства L (а) 0. Значение L(a) от-
лично от нуля, если ш> 1. Выбор константы с обеспечивает
выбор диапазона представляемых чисел. Управление значением
константы с открывает пути к выбору диапазона чисел, необ-
ходимому для решения текущей задачи.
Представление вещественных чисел знаковыми логарифма-
ми позволяет все вычисления производить не с вещественны-
ми числами, а с их представителями в знакологарифмической
системе счисления, которые мы обозначим как а и
а = (1 — 2ft.x.) L (а).

Связь между количествен-
ным эквивалентом числа а
и величиной а представлена
на рис. 20 при с = 8. За
исключением мертвой зоны
вблизи нуля, когда —с-1
<^ft<C^-1, логарифм есть
монотонная функция. Сле-
довательно, сравнение двух
чисел а и Ь, таких-, что
[ а | > с-1 и [ b J > с~1, легко
может быть осуществлено
простым вычитанием значе-
Рис. 20.
Связь между количественным
личинами а*
ний а и Ь.
эквивалентом числа а и ве-
и L (а) устанавливается следующим образом:
а = (1 — 2ft.x) c~1<2SLb\ (4.15)
Для выполнения действия в цифровой машине над вели-
чинами а надо величины а представить машинными числами.
Будем считать, что для представления значений а дано «-раз-
рядное двоичное слово. Это слово будет рассматриваться как
представление числа а в форме с естественной запятой, где
под дробную часть выделено h разрядов, а под целую, как
обычно, k -ф 1 = п. — h. Тогда
a:a*ak ...
и
а = (1 — 2а*) 2£=-л «Д'.
Сумма аг-2’ есть представление величины L (а) в двоич-
ной системе счисления, обозначим ее как S (а). Для повыше-
ния точности представления L (а) в цифровой машине значе-
ние S (а) получим как округление по дополнению величины
L (а), т. е.
S(a) = 2-/![L(a)2k + 2-1], (4.16)
где [а] есть целая часть числа а.
Диапазон вещественных чисел, отличных от нуля, которые
можно представить в знакологарифмической системе счисле-
ния при п = k -ф 1 -ф h, есть
с-122-Л < | а К с-1 22*+1~2~Л. (4.17)
При одной и той же разрядности чисел (л) и одинаковом
числе разрядов (/г), отводимых под мантиссу, и дробную часть
S (а) и (А-ф1) под порядок и целую часть S(a), диапазон
чисел, представленных в форме с плавающей запятой и в зна-
кологарифмической системе счисления, оказывается одинако-
вьш, если только с — 22 .В этом можно убедиться, сравнив
соответствующие части неравенств (1.29) и (4.17). Числа,
меньшие по абсолютной величине, чем с-122'Л, представляются
машинным нулем, а числа, большие по абсолютной величине
с~122*+1-2~Л, не могут быть представлены в машине, имеющей
разрядность п— Лф 1 -ф h. В этом случае, как обычно, можно
говорить о переполнении разряднрй сетки машины.
2°. Реализация арифметических операций. Пусть числа а
и b заданы в знакологарифмической системе счисления, т. е.
нам известны значения a*, b*, S (а) и 5 (Ь). Нашей задачей
является нахождение правил определения результата основных
арифметических действий, представленных в той же системе
счисления, т. е. в виде знакового разряда и п-разрядного
значения логарифма его абсолютной величины.
Так, например,, произведение р двух чисел должно опре-
делиться значением знакового разряда р* и значением S (р).
Количественный эквивалент числа р должен быть равен произ-
ведению ab, что согласно (4.15) равносильно равенству
(1 — 2р J = (1 - 2aJ (1 - 2feJ c-^a'>+L<b'>. (4.18)
Изфавенства (4.18) следует, что
Р* =-a*+ = «*©** (4.19)
и
, L(p) ==£ (а)+ £(&)-£ (с),
где £(c) = log2c. Поскольку £ (х) . представляется в машине
.значением S (х), то
S(p) = S(a) + S(b)-S(c), (4.20)
где S (с) определено соотношением (4.16). Значение S (с) яв-
ляется константой, и, следовательно, для получения произве-
дения двух чисел достаточно сложить значения S (а) и (S (Ь)
и вычесть из результата константу S (с). Время реализации
операции умножения в знакологарифмической системе счисле -
ния составит в общем случае 2тсл, хотя в принципе за счет
выбора константы с оно может быть существенно уменьшено
ввиду замены арифметической операции вычитания логическим
преобразованием суммы S (а) + S (Ь).
Значение S (р), вычисленное в соответствии с равенством
(4.20), может оказаться больше допустимого, т. е. S(p)>
>. 2*+’ — 2_ft, и тогда перенос со старшего разряда сумматора,
осуществляющего сложение значений S (х), зафиксирует пе-
реполнение разрядной сетки машины. Если же окажется, что
S(p)<0, то произведение а на Ь можно представить машин-
ным нулем.
При операции деления числа а на число b знак частного
q* определяется соотношением (4.19), а значение S(q) нахо-
дится из равенства
$(<?) = 5(a)-£(&) + $ (с). ' (4.21)
Следует отметить, что алгоритмы умножения и деления фак-
тически совпадают (с точностью до знака разности S(b) — S(c))
и их реализация чрезвычайно проста.
Пример 4.31. Найти произведение и частное чисел а = 8, b = —2—1,
представленных в знакологарифмической системе счисления при п — 8, с = 8
и h =>= 4. Согласно определению чисел в знакологарифмической системе
счисления имеем а* = 0, 6* = 1, S (а) = 110g и S (Ь) = 10. Равенства (4.19)
и (4.20) определяют соответственно значения знакового разряда р.г =
и S(p)=1012- Численный эквивалент полученного числа согласно (4.15)
есть —4, что и следовало ожидать. Для определения частного надо сосчи-
тать значение S (д) по формуле (4.21), что в нашем случае дает S (д) —
= Ш2, т. е. q = —16.
Для осуществления операции суммирования (вычитания)
чисел а и b преобразуем выражение s = а -ф b к виду
s = <z(l + ba~1). (4.22)
Как видно из (4.22), три операции должны быть выполнены
для вычисления значения s: деление b на а, вычисление функ-
ции 1 -\-ba~1, умножение полученного результата на а. Среди
этих операций пока новой для нас является операция вычис-
ления суммы 1 -|- bfa.
Будем считать, что S(a)^>S(b), тогда, очевидно, каким
бы ни был знак числа Ьа~1, знак суммы (s) или разности (</)
чисел а и b сразу известен ц он равен а*, т. е. s* = d... = tz*.
'Пусть знаки чисел а и b совпадают, тогда частное bar1 имеет
знак т. е. д* = 0. Нам надо сумму 1 + Ьа-1 представить
в знакологарифмической системе счисления, т. е. с-12Л(с) +
+ с-1= с-12Л(х\ откуда
£(%) = £ (с) + a (L(b) — £ (а)), (4.23)
где а (£ (fe) — £ (а)) = log2 (1 + 2Л(6)-Л(О)). Переходя к машин-
ному представлению значений £ (х), получим
S (х) = S (с) + a (S (b) — S (а)).
Для определения суммы надо еще найти модуль значения
произведения числа а на число х. Подставляя в равенство
(4.21) вместо S(b) выражение для S (х), найдем, что
S(s) = S(fz) + «(S(fe)-S(<z)). (4.24)
Если число b имело знак, противоположный знаку числа а,
то частное имеет знак „ — и вместо равенства (4.23) полу-
чим новое равенство
£(х) = £(с) + ₽(£ (b) — L (а)),
где р (£ (b) — £ (а)) = log2 (1 — 2Л(6>~Л(С>). Отсюда значение ве-
личины S (d) разности двух чисел а. и b есть
S(rf) = S(<z) + p(S(&)-S(<z)). (4.25)
В случае, когда S (а) < S (Ь), знак результата есть Ь*, т. е.
s* = dVr = b*. Машинное значение логарифма суммы s и раз-
ности d чисел а и b в этом случае также определяется урав-
нениями (4.24) и (4.25), только везде надо S (а) заменить на
S (ft), и наоборот.
Таким образом, для сложения чисел в знакологарифмиче-
ской системе выполняются следующие действия. Вначале на-
ходятся разность у величин S (а) и S (Ь) и сумма по модулю
2 знаков операндов (рис. 21). По знаку разности сразу же
определяется знак результата $* и формируется значение S (/),
которое равно либо S(a), либо S(b).
Далее в зависимости от совпадения или несовпадения зна-
ков чисел а и Ь величине S (х) присваивается либо значение
а (у), либо ₽ (у)- Наконец, машинное значение логарифма ре-
зультата S (г) определится как сумма S (х) и S (/). Будем
считать, что значения функций а (у) и р (у) для каждого у
хранятся в специальной таблице, находящейся в постоянном
запоминающем устройстве. Тогда для присвоения S (х) значе-
ния р (у) или а (у) надо обратиться к этой памяти по адресу
у. Поскольку у — это обычное машинное n-разрядное число,
то объем каждой таблицы для а (,у) и р (у) составляет 2" • п
бит.
Операция вычитания будет отличаться от суммирования
лишь предварительным изменением знака слагаемого b на про-
тивоположный, а в остальном алгоритм не отличается от сло-
жения,
т
Пример 4.32. Найти разность чисел а — 2 и b = 4, представленных
в знакологарифмической системе счисления при п = 8, с = 8 и й = 4. По-
скольку выполняется операция вычитания, то сразу же меняем знак числа b
на противоположный, получим а* = О, b* = 1, следовательно, z = а* А 6* =
= 1. Значения S (а) = lOOg и .S (Z>) = 101g» отсюда разность у = S (а) —
— S (Ь) < 0. Это приводит к тому, что s* = 1 и S (О = S (6) = lOly Знак
операндов различен (г — 1), поэтому надо S (х) присвоить значение ₽ (у) =
= log2(l—2-1) =—1. Теперь уже можно определить значение S (г): оно
равно сумме S (t) и S (х), т. е. S (г) = lOOg. Количественный эквивалент
результата согласно (4.15) есть —2, т. е. а — b = —2.
Время сложения операндов в знакологарифмической систе-
ме счисления, как видно из программы (рис. 21), состоит
в основном из 2т:сл, времени обращения к постоянной памяти
то6, а иногда и времени перевода из дополнительного кода
в прямой, если для вычитания используются дополнительные
коды, которое также равно тсл. Следовательно, в наихудшем
случае мы имеем
== Зтсл -|- Tog.
При использовании постоянной памяти такого же объема
и при прочем равном оборудовании для позиционной системы
счисления можно достичь следующих времен выполнения опе-
раций умножения и деления [65]:
’’•ум = Зтсл 4тоб,
. ^дел 6тсл -|- 8то6.
Табличное определение значений функций а(у) и 'Р(у) не
позволяет, применять знакологарифмическую систему счисле-
ния при больших значениях п. Выход из этого положения
Состоит в создании простых алгоритмов вычисления функций
О ± 2У), где у < 0. Решение этой задачи мы рассмотрим
в главе 6.
ГЛАВА 5
z
МЕТОДЫ УСКОРЕННОГО ВЫПОЛНЕНИЯ
АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
В этой главе будут рассмотрены методы, позволяющие
реализовать арифметические операции "значительно быстрее,
чем 'это было возможно при использовании традиционных
методов, о которых шла речь в главе 2. Ускорение выполне-
ния операций будет достигнуто за счет изменения структуры
соответствующих алгоритмов, а не за счет применения более
быстродействующих элементов. Здесь мы предполагаем, что
конструктор машины умеет грамотно воплощать методы в ма-
шинные схемы, т. е. умеет строить схемы с минимальными
путями пробега электрических сигналов, может избежать
влияния „паразитных" емкостей в схемах, не перегружает
элементы и т. д. Наше предположение не означает, что эти
вопросы второстепенные при создании быстродействующих
ЭВМ, наоборот, они имеют решающее значение хотя бы по-
тому, что чересчур много проектов оказались неудачными
именно из-за неразумных конструкторских и технологических
решений.
§ 1. МЕТОДЫ УСКОРЕННОГО СЛОЖЕНИЯ
В целях ускорения алгебраического сложения формирова-
ние поразрядных сумм во всех разрядах начинается одновре-
менно. Однако вследствие зависимости суммы в данном раз-
ряде не только от значений цифр слагаемых, но и от значе-
ний в общем случае всех младших цифр (через значение
переноса с предыдущего разряда) время завершения форми-
рования результата в параллельном сумматоре (определение
старшей цифры результата) может оказаться равным
= (П — 1)^ + ^, (5.1)
где Ту—задержка в получении цифры суммы в одноразряд-
ном сумматоре после подачи всех сигналов; хс — задержка
в получении цифры переноса. Если не предпринимать ника-
ких специальных мер, то цикл сложения должен иметь время,
приблизительно равное 1,2тт, чтобы обезопаситься от разного
рода случайностей. Рассмотрим способы, позволяющие умень-
шить время хт.
1°. Асинхронный сумматор. Общая задержка в получении
суммы, определенная соотношением (5.1), получается только
для определенных слагаемых. При других же значениях сла-
гаемых время сложения может быть уменьшено даже до зна-
чения (когда нет переносов). В среднем же максимальная
длина распространения переноса в сумматоре, работающем
в прямом или дополнительном коде для двоичной системы
счисления, удовлетворяет неравенству [45]
I < log2 п — 2-1
и для обратного кода
I < (log2n — 2-1) (1 +»-1).
Следовательно, в среднем максимальная величина задержки
в получении суммы есть
хт = 1ХС + Xs-
Поскольку средняя длина наибольшего распространения ока-
зывается существенно меньше п, то рационально строить та-
кие сумматоры, которые давали бы признак реального завер-
шения распространения переносов в сумматоре. Имея этот
признак, можно сразу же после его появления завершать опе-
рацию суммирования.
Рассмотрим случай двоичной системы счисления. Пусть
значение переменной Аг- = 1 служит признаком завершения
формирования переноса в д-м разряде. Иногда еще до того
как пришел перенос из предыдущего разряда, удается опре-
делить момент завершения формирования переноса в данном
разряде и сделать это довольно просто, если положить, что
h't = агЬг V afit.
Если одно из слагаемых имеет значение нуль, а второе —
единицу, то определение переменной hi в соответствии с. урав-
нением
. h"t = а-i (di V V hi-iCi-i (at V
также позволит в случае установить, что формирова-
ние переноса в данном разряде закончено. Отсюда ясно, что
переменная ht должна определяться как
Лг = аД V dibt V d-i (di V bi) V (аг V &г).
В качестве сигнала об окончании процесса распростране-
ния переносов в сумматоре выберем выполнение условия
и = 1, где
k
' и = /\hi.
1=0 •
Наибольший задержка в получении результата, как и ра-
нее, достигается при распространении переноса через все раз-
ряды сумматора, когда операнды d и b таковы, что
«oV 60 = 1, 1 < i < k,
но в среднем время сложения оказывается существенно мень-
шим, чем определенное из (5.1).
Например, при п = 64 максимальная длина распространения
переносов составит в среднем 5,5 разрядов,, в то время как
в худшем случае перенос может пройти через все разряды.
Следовательно, ориентация не на максимальное, а на реальное
время выполнения сложения дает значительный эффект в сни-
жении времени выполнения суммирования.
2°.'Сумматоры со сквозным переносом. Наиболее опасны
при суммировании ситуации, когда значения группы последо-
вательных разрядов суммы есть одни и те же и равны г—1.
В- этом случае сигнал переноса, пришедший в младший раз-
ряд группы, распространяется последовательно через всю
группу. Можно получать определенное ускорение операции
суммирования, если этот перенос направить по обходному пу-
ти, который должен быть значительно короче, чем последо-
вательное распространение его через группу разрядов.
Реализация данной идеи осуществляется следующим обра-
зом. Все п разрядов сумматора разбиваются на h[k групп, по
k разрядов в каждой. Внутри группы соединение сумматоров
обычное для параллельного сумматора с последовательным
переносом (рис. 22). Кроме того, для каждого Z-го разряда
группы J k, 0^j^.n/k—1) формируется функция
Tj_i, зависящая только от цифр слагаемых данного разряда
следующим образом:
11 при aJti + bj,i = г — 1,
(О при ajsi + bj^г — 1.
(5.2)
В том случае, когда ау-,г + Ь^ < г, функция 7у,г- определяет
условия передачи переноса через данный разряд, т. е. пере-
нос в разряд i + 1 произойдет только в том случае, когда
есть перенос из предыдущего разряда и 7},/=1. Легко найти
условия распространения переноса по обходному пути, для
этого необходимо, чтобы выполнялось равенство [56]
Тj,i А — А Л,* Л Cj-i = 1.
Рис. 22.
Пройдя по обходному пути, перенос направляется в конец
группы и является переносом с группы Cj. Если сигнал пере-
носа сформировался внутри группы (например, в разряде Z),
то он передается последовательно обычным образом (см.
рис. 22). Время распространения по обходному пути есть тс,
оно равно времени задержки прохождения сигнала через одну
логическую ступень. Максимальная задержка в получении
значения цифр оказывается равной
щах t = xs + (2k—V)xc-\-(n/k — 2)xc, (5.3)
l
что соответствует следующему пути распространения перено-
са: перенос сформировался в первом разряде первой группы,
затем распространился через нее последовательно, а потом
прошел через n/k — 2 обходных путей и, наконец, последова-
тельно распространился в последней группе от первого до
последнего разряда, но его не прошел.
При данных п, хс и хс существует значение k, приводящее
к минимальной величине шахт. Это значение найдем, если
сравним между собою величину выражения (5.3) при А=1,
1 / п^с
k = п/2 (крайние значения k) и при k = |/ (это значение
отвечает экстремуму функции шах т). Довольно часто на прак-
тике встречается случай 2тс = тс, и тогда оптимальное значе-
ние k есть k = У~гГ/2, если только п > 4. Отсюда
шах т = + 2тс — Г)- (5.4)
Чем больше величина п, тем более значительным окажется
выигрыш в быстродействии сумматора со сквозным переносом.
Например, если и = 64, то сумматор со сквозным переносом
имеет согласно (5.4) max т = ts-|- 14тс, в то время как сумма-
тор с последовательным переносом дает шах т = + 63тс.
Дополнительные затраты при реализации данного метода
обычно невелики, особенно при г = 2, когда = aj,i ф b^i.
Конечно, реальная техническая схема значительно отличается
от схемы рис. 22, поскольку надо учитывать и синхронизацию
сигналов, и особенности элементной базы, но идеи, лежащие
в основе данного метода, остаются неизменными.
3°. Сумматоры с блочным переносом. Пусть для каждого
разряда сумматора формируется значение функции Tt, опре-
деленное из (5.2). Кроме того, в каждом разряде будем фор-
мировать еще и значение функции G,, определяемое по сле-
дующему правилу:
Gf =
1 при at + bi г,
О при + bt < г, —h.
Равенство G, = 1 означает, что перенос из i-ro разряда сум-
матора равен единице вне зависимости от значения переноса
Ct-i с предыдущего разряда. Если известны величины 7), Gt
и G-i, то
Q — Gt V
Это соотношение можно рассматривать как рекуррентное,
и тогда
= Gi V Tfii^ V \/ ... ... 7\~hG~h V
. v Ti . Г_Лс_1_й. (5.5)
Для определения переноса ct достаточно знать значение всех
функций Tj и Gj, где —и значение переноса C-i-h,
приходящего в младший разряд сумматора. Если, только нам
удастся реализовать схемы совпадения и сборки на i + h 4-1
входов, то время формирования переноса ct окажется равным
времени формирования значений двух логических функций.
Действительно, вначале можно сформировать все необходимые
конъюнкции, а затем использовать их для формирования
дизъюнкций уравнения (5.5). Формирование переносов в соот-
ветствии с (5.5) во всех разрядах сумматора позволит обеспе-
чить одинаковую задержку в формировании переноса для
любого разряда, т. е. она оказывается независящей в отличие
от ранее рассмотренных сумматоров от числа предшествую-
щих разрядов. Однако достичь этого удалось за счет введе-
ния значительного дополнительного оборудования. Если логи-
ческие элементы, реализующие 'уравнения (5.5), не допускают
большого числа входов или требуется экономить оборудова-
ние, то имеет смысл все разряды сумматора разбить ria груп-
пы по k разрядов в каждой, как это делалось в сумматоре
со сквозным переносом. Для каждой группы (блока) j фор-
мируются функции Tj и Gj, где О7- определяет условия фор-
мирования переноса со старшего разряда группы только по
значению групповых слагаемых, а функция 7) определяет
условия передачи сигнала внешнего переноса через данную
группу разрядов. Значение переноса Gj из группы k разрядов
и значение функции Tj определены следующими уравнениями:
б?/ — Gj'k V Tjj,Gjj>~\ \J .. ..^TjfiGjt\,
Tj = Tj'k /\ Tj,k^ /\ .. ’л Л,2Дд. (5.6)
Полученные значения Gj, Tj рассматриваются как сигналы
отдельных „разрядов", которые, в свою очередь, вновь мож-
но объединить в блоки из k штук. При необходимости
(т. е. при большом числе разрядов) этот процесс повторяется,
и в результате получается пирамидальная схема распростра-
нения переносов. Поскольку формирование каждого блочного
переноса требует времени задержки в две логические сту-
пени, то время формирования окончательного переноса зави-
сит от числа ступеней в пирамиде и оказывается пропорцио-
нальным величине logftn. Однако количества дополнительного
оборудования для таких сумматоров требуется значительно
меньше, ибо для всех групп первого уровня нужно одно
и то же количество оборудования вне зависимости от того,
составлены они из старших или из младших разрядов. Такое
положение сохраняется и для группы следующих ступеней
пирамиды. Помимо „блочного" переноса Gj и „групповой"
функции Tj в каждой группе нужно еще сформировать зна-
чения Cj,i, 1, которые необходимы для получения
цифры суммы. Каждая из функций Cjti формируется в соот-
ветствии с уравнением (5.5), где c-i-a заменено на Q-i. По-
требуем дополнительно, чтобы время задержки для всех Gj^
было одинаковым, тогда схема
и разрядных переносов в группё
кой, как показано на
формирования группового
из k = 4 разрядов будет та-
рис. 23.
Рис. 23.
Напомним, что
Роль одновходовых схем совпадения и сборки лишь одна —
обеспечить одинаковую задержку сигналов поразрядных пе-
реносов, каким бы путем они ни образовывались. Это дает
гарантию, что через время, равное задержке на двух логиче-
ских ступенях, сформируются значения функций Gj и Tj и по-
ступят, если необходимо, значения разрядных переносов. Хотя
сумматоры с блочными переносами и требуют значительного
количества дополнительного по сравнению со схемой после-
довательного переноса оборудования (иногда [56] эти затраты
оцениваются более чем в 100%), но зато они позволяют резко
уменьшить максимальное время сложения — в принципе до
+ тс.
В случае двоичной системы счисления имеем Gt = atbi
и Tt — © bh что позволяет реализовать эти функции весьма
просто и за время Зтл, где тл — время задержки на одну логи-
ческую ступень. Групповые функции Gj, Tj, реализуемые
в соответствии с уравнениями (5.6), могут быть сформированы
через время 2тл и тл соответственно, после того, как будут
определены разрядные функции Gb Ть Если из двух группо-
вых функций Ог, G/+1 и Th Tt+i построить еще секционные
функции Gk, Tk, что займет еще время 2тл, то на базе функ-
ций G, Т трех уровней (разрядных, групповых и секционных)
за время 2тл удается сформировать переносы в секцию cf,
а уже по секционным переносам Cj, групповым и разрядным
значениям функций Gh Th Gj, h окончательно определить
в каждом разряде значение приходящего переноса ct-i. Сле-
довательно, при таком построении пирамиды переносов через
время 9тл = 4,5тс мы сможем в каждом разряде уточнить пред-
варительное значение суммы sl = al@bi, Q^i^k. Оказы-
вается, что при k = 55 данное формирование переносов в сум-
маторе обеспечивает высокое быстродействие при разумном
увеличении оборудования [37].
Мы рассмотрели несколько типов быстрых сумматоров,
получивших наибольшее распространение. В зависимости от
системы используемых логических элементов основные типы
сумматоров могут допускать различного рода модернизацию,
обеспечивающую еще большее быстродействие [56].
Отказ от использования традиционных способов кодирова-
ния чисел и методов организации процесса суммирования,
оказывается, открывает новые пути ускорения сложения,
к рассмотрению которых мы щ приступаем.
4°. Суммирование при избыточном кодировании. Одним
из наиболее действенных методов ускорения операции сумми-
рования является сокращение максимальных путей распрост-
ранения переносов за счет введения избыточности при пред-
ставлении цифр в r-ичной системе счисления. Очень важно
при этом добиться, чтобы распространение переносов не за-
висело от длины слагаемых.
4°.1. Знакоразрядные системы счисления. Пусть цифры
системы счисления с основанием г имеют значения: —а, 1 —
— а,..., —1,0, 1, ..., а—1, а, причем для а справедливо, что
г2-1 < а < г.
(5-7)
Здесь мы рассматриваем случай использования избыточного
алфавита, ибо согласно (5.7) в нем число допустимых цифр
больше, чем г. Значение разрядной суммы операндов а и Ь,
заданных в рассматриваемой системе, определяется уравнением
$i = Щ. + bi + сг_1 — rct,
где — значение переноса, выработанного в предыдущем
разряде. Значение же переноса ct определяется следующим
образом:
— 1 при at + bt —а,
G =
0 при | at + bt | < а,
1' при at + bt а.
Здесь принципиальным моментом является то, что значение
переноса с; определяется только значениями цифр /-го разряда
операндов и не зависит от значения переноса из предыдущего
разряда. Последний может лишь уточнить значение разряда
суммы, которая в результате этого может быть равна по аб-
солютной величине а, что допустимо. Таким образом, рас-
пространение переноса происходит на один разряд, и поэтому
время суммирования сокращается до величины шах тЕ = -ф tc.
Заметим, что поскольку, а — целое положительное число, то
согласно (5.7) лишь для двоичной системы счисления не удает-
ся указанным образом построить алфавит со знакопеременными
цифрами. Однако оказывается, что и для двоичной системы
счисления удается значительно сократить длину максималь-
ного пробега переноса [39, 42].
Рассмотрим следующий алгоритм суммирования знакораз-
рядных двоичных чисел а и р. На первом этапе производится
поразрядное суммирование операндов а, и Ь-.
-[- = 2с/ х£.
Значениями с* и s, могут быть 1,0, 1, но | ct | = 1, если | aL +
+ (табл. 16). На втором этапе к найденному значению
разрядной суммы s, прибавляется перенос Ct-i из предыдуще-
го разряда:
s'£ + c'i-i == 2с" + s"ir
Таблица 16
ai h ct s\ cki // ci и sl
1 1 1 0 i 1 1 0
1 0 1 I i 0 0 1
1 T 0 0 1 Г 0 0
0 1 i Г 0 i 0 1
0 0 0 0 0 0 0 0
0 T T 1 0 Г 0 Т
1 1 0 0 T i 0 0
1 0 T 1 T 0 0 Т <
Т Г 1 0 I 7 г 0
Здесь уже k"| = = 1, если | St + ct- Д>,2 'см. If табл. 16). На
третьем этапе складываются значения St и St + cLi = 2g" + S;. Ci-г.
Пусть это суммирование осуществляется точно так же, как
на втором этапе, т; е. хг^{Т, 0, 1] и |cf|= 1, если | s£ + cl | 2.
Докажем, что при этих условиях ct = 0. Действительно, а
=f= 0, если Si = d-i = ± 1. Пусть c£_i = 1, но тогда s£_i ==е£_2 =
= 1, а раз = 1, то обязательно должно быть c£-_i = 1. Это,
в свою очередь, приводит к тому, что St =/= 1 (см. табл. 16).
Точно так же оказывается, что Ct =1=—1, следовательно, с; =0
и тогда si=s£ = Ci-i. Таким образом, при сложении знакораз-
рядных двоичных операндов перенос может распространяться
не более чем на два разряда и, следовательно, максимальное
время суммирования операндов произвольной длины составит
max ts = Зт5, считая, что в каждом одноразрядном сумматоре
время формирования суммы \ больше, чем время формирова-
ния переноса тс.
• Для переносов ct и ct допустимыми значениями были 1,0, 1.
Можно считать, что при сложении используются два типа
переносов—„положительный" ct со значениями 0, 1 и „отри-
цательный" с, со значениями 0, 1. При наличии двух типов
переносов можно перестроить алгоритм суммирования следую-
щим образом [42]. Вначале находится сумма at, bt и „поло-
жительного" переноса из предыдущего разряда e£_i:
CLi Ч- bi — 2ct ~T 2c£ -|- Sj,
где для St допустимы значения 0,1 (табл. 17). Затем получен-
ное значение разрядной суммы s£- уточняется путем прибавле-
ния к ней „отрицательного" переноса из предыдущего разряда:
$£ = St ].
Таблица 17
ai~\-bi . ci-i С/ cl si
2 0 1 0 0
1 0 0 0 1
0 0 _ 0 0 0
— 1 0 0 У 1
—2 0 0 У 0
2 1 1 0 1
1 1 1 0 0
0 1 0 0 1
-1 1 0 0 0
—2 1 0 Т 1
Очевидно; что при таком сложении переноса быть не может.
Хотя данный алгоритм и не приводит к ускорению сложения,
ибо здесь перенос также распространяется на два разряда, но
при практической реализации он может привести к меньшим
затратам оборудования [24].
Для двоичной системы счисления можно добиться рас-
пространения переносов на один разряд, если один операнд
представить в знакоразрядной форме, а второй — в обычной
двоичной системе счисления. В этом случае на первом этапе
поразрядно суммируются операнды а и Ь:
ai + bi = ^C'i +
Пусть at(^ [1,Д, 1], а (0,1]. Интересно, что можно выбрать
значения с,- и st так, что d £ {0, 1}, a £ (О, 1]. На втором
этапе складываются значения Si и Cj-i:
Sj —
♦
Очевидно, что при этом никогда не будет переполнения
и ^{1,0,Т}.
Таким образом, использование знакоразрядного представ-
ления двоичных чисел позволяет сделать время суммирования
операндов не зависящим от операндов и довести его до 3tv
(когда оба операнда представлены в знакоразрядной форме)
и даже до 2ts (когда только один операнд представлен в зна-
коразрядной форме).
4°.2. Избыточное кодирование при неотрицательной базе.
Пусть теперь в нашем распоряжении имеется алфавит, зна-
чения цифр которого есть 0, 1, ..., г —1, ..., r-\-k, vufi k —
некоторое целое положительное число. Выберем k^r—4,
тогда количественный эквивалент целого положительного чис-
ла а, представленного в r-ичной системе счисления с избы-
точной базой, удовлетворяет следующим неравенствам:
(гп_ 1).
\ г— j \ /
(5-8)
А. Случай явного представления сохраняемого переноса.
Поскольку k^r— 1, то значение каждой цифры числа а мож-
но представить в виде
• at = di г + щ,
где и — 1. В этом случае можно каждую
цифру r-ичной системы счисления представлять парой цифр
a'i, dt обычного неизбыточного алфавита, причем цифра at
имеет смысл обычного разряда операнда а, а цифра сц —
смысл сохраняемого разрядного переноса. Для хранения раз-
рядных переносов требуется дополнительно п двоичных раз-
рядов на слово..
При сложении операндов а и Ь, представленных в такой
системе счисления, надо в каждом разряде сложить все вели-
чины с одинаковым весом. В г-м разряде такими величинами
будут значения данного разряда операндов гг£, bi и цифры
сохраняемых переносов предыдущего разряда аг_1 и bt-i,
а также значения переноса с (г'— 1)-го разряда с^. В резуль-
тате сложения этих величин мы должны получить полную
разрядную сумму sz = s£r4~s£ и значение переноса с данного
разряда Q. Принципиальным моментом вновь будет определе-
ние ct только по значениям цифр операндов и распростране-
ние переноса не более чем на разряд.
Будем считать, что в нашем распоряжении имеются обыч-
ные одноразрядные сумматоры r-ичной системы счисления
с тремя входами (два для цифр и один для переноса) и двумя
выходами (суммы и переноса из данного разряда). Тогда все
сложение в г’-м разряде можно осуществить в два этапа.
На'первом этапе по значениям гг£, bt и либо гг£_], либо 6/-1
определяются значения s£- и c-L по формула^
= a-i + b” + a'i-i (mod г),
rCi = CLi ф- bi ф- CLi—i — Si,
где 0 < ct 1 и 0 < < г - 1.
. На втором этапе ищутся значения Si и s£:
tt Q г
Si = s£ + bi-i ф- Ct-x (mod r),
(5.9)
(5.10)
r 0 • 7/
rSi = Si ф- bi-x + Ci-x — Si,
где 0<s£<^l и 0<Si<:r—1. Оценка слагаемых в уравне-
ниях (5.9) и (5.10) дает единственно возможное значение
k = \, ибо полная сумма должна быть не больше r-\-k.
Вполне очевидно, что если в уравнениях (5.9) и (5.10)
поменять местами bi и 6£_i, то мы придем к тому же резуль-
тату. Однако при этом единственно возможное значение k
будет г— 1. Заметим, что и тот и другой способы распреде-
ления аг, bi, at-! и bt-i по этапам суммирования приводят
к одинаковым аппаратурным затратам и к одному и тому же
времени выполнения операции. Однако согласно (5.8) диапа-
зон представляемых чисел оказывается различным. Поскольку
распространение переносов происходит лишь на один разряд,
то время сложения «-разрядных операндов не зависит от чис-
ла разрядов и будет равным 2^, где — время суммирования
в одноразрядном сумматоре с основанием г. При этом счи-
тается, что где тс — время формирования переноса
в этом же сумматоре.
Для упрощения сложения операндов а и b в r-ичной сис-
теме счисления с избыточной базой будем считать, что зна-
чение сохраняемого переноса в А-м разряде всегда есть нуль,
т. е. = bk = 0. Если в процессе суммирования окажется, что
Ss=l, то это будет служить признаком переполнения сум-
матора, так же как и условие ek=l. Поскольку, как это сле-
дует из уравнений (5.9) и (5.10), возможна ситуация, когда
cft = Sfe=l, то суммарное значение переноса с «-разрядного
сумматора может быть 0, г", 2г" или <?rn (п = k + 1), где ср =
= 0, 1, 2. Условие переполнения сумматора есть ©=^=0.
Представление отрицательных чисел в рассматриваемой сис-
теме счисления будет осуществляться дополнительными кода-
ми [34]. Для того чтобы диапазон представления отрицатель-
ных чисел оказался не меньше, чем положительных, прихо-
дится значение знакового разряда дополнительного кода числа а
(обозначим его а*) брать равным 0, 1,2. Тогда для равенства
диапазонов представления чисел отрицательного и положи-
тельного знаков надо было бы при а* = 2 согласно (1-12)
ввести ограничение на величину определяемую ос-
новными разрядами кода числа а. Для упрощения реализации
алгебраического сложения допустим, что при а* = 2 ограни-
чений на 2т=о а^1 нет. Это означает, что абсолютная величина
отрицательного числа а лежит в диапазоне от 1 до 2г" (когда
«г = 0 для всех г = 0, 1, ..., k).
При сложении операндов а и Ь, заданных дополнитель-
ными кодами, основные разряды суммы s определяются в соот-
ветствии с уравнениями (5.9) и (5.10). Значение знакового
разряда суммы с учетом его веса (—г") находится из следую-
щего уравнения:
$* = «* + &* — <?. (5.11)
Ситуация s* < 0 расценивается как превышение допустимого
диапазона для чисел положительного знака. Если же s* > 2,
то это означает, что результат выходит из диапазона, допус-
тимого для отрицательных чисел. В остальных случаях резуль-
тат оценивается как правильный.
Операция вычитания операнда b из операнда а реализуется
как сложение чисел а и (—Ь). Для изменения знака у чис-
ла b достаточно сформировать его дополнительный код. С этой
целью мы представим величину, определяемую основными
разрядами числа Ь, т. е. разрядами bt = i = O, 1, ..., k, в виде
суммы двух чисел b' = bkbk-\ ... &10 и b" = ... 6Д0.
Тогда количественный эквивалент числа можно представить
в следующем виде:
при п = k + 1
-b = - (-Vя + Ь' + Ь") = - (2 - b*) гп + (г« - 1 - Ь') +
+ (г«-1 -H + 2 = -(2-^)rB +
+ 2Lo — 1 — &/) + 2г=о (г — 1 — bt) + 2.
Величины, стоящие под знаком суммирования в правой части
этих равенств, есть не что иное, как значение чисел Ь' и Ь",
у которых все цифры заменены на их дополнение до г — 1.
Обозначим эти новые числа как D и F. Основные разряды
кода —b будут являться разрядами суммы чисел D, F и 2.
Последнее число можно трактовать как значение переносов
do и /о, равное 1, и тем самым осуществить сложение чисел
D, F и 2 за один переход. Остается еще определить значе-
ние знакового разряда кода числа —b из уравнения
= 2 — Ь* — ср. (5.12)
Заметим, что $*<^2, а если окажется, что s.x. < 0, то это
будет свидетельствовать о превышении допустимого диапазона
для положительных чисел. Ввиду договоренности о диапазоне
представления отрицательных чисел этот результат оказывает-
ся совершенно естественным.
Пример 5.1. В десятичной системе счисления, цифры которой имеют
значения 0, 1, .... 9. 10, И и изображаются двумя цифрами обычной деся-
тичной системы счисления, задано число а = 0. (0'3) (1'0) (1'1)(здесь
штрихи отделяют цифру сохраняемого переноса от собственно разрядной
цифры). Численный эквивалент числа а есть 411. Требуется найти код
числа —а.
Число а представим в виде суммы двух чисел а' = 110|д и а" = 301,
кроме того, а* = 0. Вначале формируем числа D и F путем замены цифр
чисел а' и а" на их дополнения до 9, получим D = 889 и F = 698. Затем
сложим эти числа с числом 2 и найдем, что s = D + ++ 2 = 889+698 + 2 =
= 1. (0'5) (0'8) (0'9) 10, т. е. <р= 1. Теперь в соответствии с уравнением (5.12)
найдем, что «* = 2 — 0 — 1 =1. Окончательно имеем s = l.(0'5)(0'8)(0'9)jg.
Количественный эквивалент этого числа согласно (1.12) есть —411.
После изменения знака у операнда происходит сложение
чисел а и — Ь. Поскольку операция изменения знака .числа
выполняется как обычное сложение, общее время выполнения
операции вычитания составит 4^, т. е. в два раза больше,
чем при сложении. ,
Представление цифр r-ичной системы счисления с избы-
точной базой парой цифр обычной r-ичной системы счисления
позволяет весьма значительно ускорить выполнение операции
суммирования. Однако расплатой за это служит удвоение
количества оборудования, требуемого для реализации сумма-
тора с последовательным распространением переносов, и уве-
личение разрядности операндов на п — 1 двоичных разрядов
для хранения переносов. Наиболее рациональным кажется
применение данного метода при г = 2\ когда одноразрядный
сумматор с основанием г есть просто параллельный /--разряд-
ный двоичный сумматор, а образование поразрядных допол-
нений производится как простая инверсия двоичных разрядов.
Б. Случай неявного представления сохраняемого перено-
са. Рассмотрим случай двоично-кодированных систем счисления
с основанием г, когда каждая г-ичная цифра изображается
группой из X двоичных разрядов. Значения цифр r-ичной си-
стемы счисления пусть будут 0, 1, ..., г—1, г, ..., r-^-k,
и пусть справедливо неравенство
г<2? — k-\.
Если знач£ние г таково, что г > 2х-1, то для представления
цифр в обычной и избыточной r-ичной системах счисления
требуется одно и то же число двоичных разрядов, т. е. избы-
точность системы счисления не приводит к увеличению тре-
буемого объема памяти.
Вновь процесс суммирования разобьем на два этапа. На
первом этапе по значению /-го разряда операндов а и b опре-
делим предварительное значение суммы s® и окончательное
значение переноса с данного разряда (с;) в соответствии
с уравнениями
s® = at + bt (mod г),
г ct = at + bL — s®. (5.13)
Поскольку справедливо равенство 2 (г -ф k) = rct + s*, то
0<q<2 + -^=^-. (5.14)
Задачейвторого этапасуммированияявляется выработка
окончательного значения разрядной суммы sz по известным
о
значениям St и Ci-i:
s£ = sz + Ci-! (mod r'),
(5.15)
Причем r' ^r + ^4-1, поскольку ДОЛЖНО быть, ЧТО Sf-^r+fe.
Последнее требование равносильно тому, что max c/_i = £-}- 1.
С учетом (5.14) данное равенство приводит к уравнению
k
г — S*
г —2 *
(5-16)
Решение уравнения (5.16) в целых числах для г>4 только
одно, а именно k=\. Для троичной и четверичной систем
счисления другим решением с учетом /г<Д—1 может быть
£ = 2. Поскольку k—\ приводит к наименьшей избыточности
базы систем счисления, то в дальнейшем будем всегда счи-
тать, что k = 1 для всех г > 2. При этом значение переноса,
выработанного в Z-м разряде, есть 0, 1, 2.
Реализация суммирования на первом и втором этапах имеет
свои особенности. На первом этапе используется г-ичный
сумматор, который отличается от обычного двоично-г-ичного
сумматора только формированием переноса со значением 2
и коррекцией промежуточного результата, соответствующей
этому случаю. В качестве сумматора второго этапа, если
только 2х ^г-т£ + 1, рационально взять Х-разрядный двоичный
сумматор. В этом сумматоре цепи формирования сигнала пе-
реноса и входа второго операнда для X 2 старших двоичных
сумматоров и схемы 'коррекции промежуточного результата
оказываются избыточными.
Можно ожидать, что время суммирования в одном разряде
будет равным 2ts, где — время формирования суммы в обыч-
ном двоично-г-ичном сумматоре. Однако в некоторых случаях
результат оказывается намного лучше.
/
Пример 5.2. Пусть г = 10, тогда X = 4 и k = 1. Условия формирования
переноса сг со значением 1 есть (рис. 24)
4° = ЧзсМ v V Si,2) = 1,
а условия формирования переноса со значением 2 есть
f(2) — г — 1
При = 1 коррекция промежуточного результата состоит в прибавлении
к нему числа 1109(6), а при с*-2) = 1 — числа 11009(12). Коррекцию проме-
жуточного результата, производимую на первом этапе суммирования, мож-
но по времени совместить с формированием окончательного значения суммы
S/. Это удается сделать потому, что всегда = 0, и поэтому число
слагаемых в сумматорах и 2й7 никогда не превышает трех. В резуль-
тате оказывается, что сумматор имеет практически такое же быстродейст-
вие, что и обычный десятичный сумматор, и в то же время требуемое
количество дополнительного оборудования весьма невелико (сравним со
схемой рис. 18). Если из сумматоров, изображенных на рис. 24, построить
«-разрядный параллельный десятичный сумматор, то его быстродействие
окажется точно таким же, как и быстродействие одноразрядного сумматора. '
Рис. 24.
Г'
Для представления отрицательных чисел будем использо-
вать дополнительные коды. Тогда операция сложения операн-
дов а и Ь, представленных в г-ичной системе счисления с из-
быточной базой, будет заключаться в определении основных
разрядов суммы в соответствии с уравнениями (5.13) и (5.15),
сложении знаковых разрядов операндов по правилам обычной
г-ичной арифметики и в определении значения знакового раз-
ряда суммы по значению переноса со старшего разряда сум-
матора ck в соответствии с уравнением (5.11).
Операция вычитания а — b реализуется как сложение чи-
сел а и — Ь. Правила формирования кода числа с противопо-
ложным знаком (дополнительного кода) оказываются весьма
своеобразными. Количественный эквивалент числа —b согласно
(1.12) определится как
-ь=- (-Vя + = (гп-1 ~
- 2" о*biri + 6*Г" “ Т=Т (г"_1 ~ 1) = 2--0 (r + k~ bi)ri +
+ /тгА-2.. (гЯ-1 - 1) + 2 - (-&;!! + 2) г». (5.17)
Первое слагаемое правой части равенств (5.17) есть число
(обозначим его Ь'), цифры которого являются дополнениями
цифр bt до г ф- k. Второе слагаемое есть константа с, изобра-
жаемая числом с одинаковыми цифрами (г — k — 2) во всех
п разрядах. Число 2 можно интерпретировать как <?о2)=1.
Отсюда ясен алгоритм формирования кода числа — Ь. Вначале
(£=1) определяются поразрядные дополнения числа b до
г + 1 и тем самым определяется число Ь'. Затем это число
складывается с константой с, т. е. числом, все цифры кото-
рого есть г — 3, ив младший разряд сумматора добавляется
перенос cffl = 1. Полученная сумма в основных разрядах дает
значение разрядов дополнительного кода. Значение знакового
разряда определится из уравнения (5.12).
Пример 5.3. В десятичной системе счисления с цифрами 0
задано число а = (3) (10) (9)jq. Требуется найти код числа —а.
Вначале формируем поразрядные дополнения от цифр числа а до И
и тем самым определяем число а’. Затем к этому числу добавим константу
с = 777 и одновременно в младший разряд еще прибавим число два, по-
лучаем s = «'4-c + 2=l. (5) (8) (И)|р- У полученной суммы ck = 1, поэто-
му согласно (5.20) имеем s* = 2 — 0— 1 — 1, т. е. код числа —а будет число
s = 1. (5) (8) (H)]Q- Количественный эквивалент полученного числа s есть
—409, как это и должно быть.
Определение сложности формирования поразрядных допол-
нений до г 1 в общем случае затруднительно. Однако, ког-
да г + £ = 2х — 1, т. е.
г = 2(2х-1 —1), (5.18)
мы имеем дело с „самодополняющимся" кодом, у которого
поразрядные дополнения образуются простой инверсией двоич-
ных разрядов, образующих цифру в г-ичной системе счисле-
ния. Если же условие (5.18) не выполняется, то правила об-
разования цифр дополнительного кода усложняются.
Пример 5.4. Пусть цифры десятичной системы счисления, принимаю-
щие значения 0, 1, ..., 10, 11, кодируются четырьмя двоичными символами
х4, х3, х2, х1( тогда уравнения формирования дополнений этих цифр до 11,
которые обозначим как у4, у3, у2> Уь будут следующими:
У4 = х4хз> у3 = х3, уз = х..; у, = xt.
Заметим, что эти уравнения заметно проще, чем в случае образования до-
полнений до 9 цифр обычной десятичной системы счисления (см. пример 3.2).
Рассмотренный метод определения кодачисла —а имеет
преимущество по сравнению со случаем представления цифр
г-ичной системы счисления с явным представлением сохраняе-
мого переноса: здесь надо формировать поразрядное допол-
нение лишь для одного числа, и сложение полученного до- '
полнения всегда осуществляется с константой.
Неявное представление сохраняемого переноса при исполь-
зовании двоично-г-ичных систем счисления с избыточной
базой открывает широкие возможности для реализации быст-
рого параллельного суммирования. Важно отметить, что в от-
личие от случая явного представления сохраняемого переноса
здесь не.требуется увеличения объема памяти для хранения
операндов, представленных в системах счисления с избыточ-
ной базой. Дополнительные аппаратурные затраты по сравне-
нию с обычной двоично-г-ичной системой счисления здесь
также значительно меньше. Время параллельного суммирова-
ния не зависит от длины операндов и может быть сделано
(по крайней мере для десятичной системы счисления) весьма
близким ко времени сложения в одном разряде неизбыточной
системы счисления с основанием г, если в процессе операции
не формируется дополнительный код.
5°. Конвейерное суммирование. Методы ускорения сло-
жения, рассмотренные выше, обеспечивали наименьшее время
суммирования при выполнении отдельной операции. При этом
нас совсем не интересовал вопрос, как часто в машине воз-
никает необходимость в выполнении операции сложения-вы-
читания. Вместе с тем вполне очевидно, что частота запросов
на суммирование может оказать существенное влияние на ор-
ганизацию этого процесса.'
Будем считать, что число операций суммирования настоль-
ко велико, что запросы на выполнение этой операции в тече-
ние какого-то времени идут сплошным потоком. Наша задача
сейчас состоит в том, чтобы обеспечить, движение очереди
запросов с наибольшей .допустимой скоростью, и при этом
у нас нет ограничений на время выполнения отдельной опе-
раций суммирования.
Такая специфика требований позволяет решать поставлен-
ную задачу путем новой организации суммирования, идея ко-
торой подсказывается самой природой параллельного сложения
чисел в сумматоре с последовательным распространением пе-
реносов (см. рис. 5). К моменту прихода в i-й разряд сумма-
тора переноса с (г — 1)-го разряда- значение суммы во всех
разрядах J, таких, что —h— 1, определено оконча-
тельно, а значения разрядов, таких, что i + 1 j k, будут
найдены в общем случае после того, как сформируется пере-
нос ct. Вполне очевидно, что, не дожидаясь полного завер-
шения суммирования, можно в младших разрядах обрабатывать
соответствующие разряды операндов следующей пары. При
этом надо, конечно, ооеспечить независимость оора отки раз-
личных пар. Добиться этого весьма просто путем запоминания
поразрядных переносов и синхронизации поступления слагае-
мых.
Действительно, пусть схема .одноразрядного сумматора
будет такой, как показано на рис. 25. В момент времени t
на входы обычного однораз- Ri
рядного сумматора поступают
значения операндов а!р (t) !------------------1
и и переноса из преды-. [ - у [
дущего разряда (I). Через Cji m | v | ; Си
время и тс будут сформиро- । ELTiAr*
ваны значения разрядной сум- I “ -----
мы и переноса. Затем в мо- [
мент времени t -ф где Ч > I __________________Д-i [
> (max ts, тс), поступает сигнал ] I
синхронизации Т, по которо- 1-------------------1
му осуществляется выдача
разрядной суммы а пе- r
ренос cL запоминается в ячей- Рис- 25‘
ке памяти М. Для формиро-
вания следующих разрядов суммы значения аР) (I), (0>
С/21 (t), (t) и cP (f) уже не нужны, и, следовательно, в мо-
мент времени t -ф в z-й разряд сумматора можно подавать
значения z-ro разряда второй пары операндов. В тот же са-
мый момент в (Z -ф 1)-м разряде начинается сложение (z-|-l)-x
разрядов первой пары операндов и переноса cP (t -ф /*), кото-
рый берется со схемы М предыдущего разряда [66].
Таким образом, если число заданий на сложение в потоке
заявок велико и в произвольный момент времени в младшем
разряде сумматора (z — —h) обрабатывается /-я заявка, то
в z-м сумматоре происходит сложение z-x разрядов операндов
заявки с номером у —z'+l. В этом случае обычный парал-
лельный сумматор с последовательным переносом (см. рис. 5),
составленный из одноразрядных сумматоров указанного типа
(см. рис. 25), работает точно так, как часовой или автомо-
бильный конвейер. Очевидно, что обратные и прямые коды
плохо приспособлены к конвейерной обработке ввиду того,
что обратные коды требуют учета циклического переноса
из старшего разряда в младший, а прямые коды дают резуль-
тат в ряде случаев за два прохода.
Конвейерное суммирование обеспечивает большое быстро-
действие (грубо можно считать^, что период синхронизации
есть 2tJ для сумматора с последовательным распространением
переносов только в том случае, когда частота заявок близка
к частоте синхронизации. Отдельная же операция будет 'реа-
лизована за время 2/гт4, где п — разрядность операндов. Если
для универсальных цифровых машин, даже работающих в ре-
жиме мультипрограммного исполнения, организовать конвейер
данных совсем не просто, то в ряде специальных применений,
таких, как цифровая фильтрация, анализ спектров, преобразо-
вание Фурье и др., это можно сделать сравнительно легко.
6°. Ускорение суммирования в двоично-кодированных
системах счисления. Одноразрядный сумматор в двоично-г-ич-
ной Системе счисления представляет собой обычный Х-разряд-
ный двоичный сумматор и схему коррекции промежуточного
результата (см. главу 3 § 2). Для ускорения суммирования
Х-разрядных двоичных чисел могут быть использованы методы
ускорения суммирования, рассмотренные выше. Что касается
ускорения реализации коррекции, то здесь многое зависит от
вида корректирующего числа для данной системы счисления.
С некоторыми идеями ускорения сложения в двоично-коди-
рованных системах счисления мы познакомимся на примере
двоично-десятичной системы счисления с естественными ве-
сами 8421.
В двоично-десятичной системе счисления с естественными
весами 842 (, процесс коррекции промежуточного двоичного
результата $г>4, хг,з, St,2 (см. рис. 18) заключался в прибавле-
нии к нему числа ОНО, если десятичный перенос сг=1. Сле-
довательно, полное время коррекции складывалось из времени
формирования десятичного переноса, которое составляло 2тл,
где тл — временная задержка на одну логическую ступень,
и времени суммирования в трехразрядном параллельном двоич-
ном сумматоре, которое в наихудшем случае ’ составляет 7тл.
Заметим, что сумматор коррекции значительно упрощен
по сравнению с обычным двоичным сумматором за счет от-
сутствия входа переноса в младший сумматор и входного сла-
гаемого в старшем сумматоре. Это обстоятельство дает осно-
вание попытаться получить значения разрядов окончательной
суммы s/j4, St,3, Stt2, St'i как значения соответствующих пере-
ключательных функций от переменных Х/д; здз; хг-,2; $z,i и сг.
Оказывается, что эти .уравнения не очень сложны, а именно
[36[:
57,4 — C1S1 9 V ^i,3 — CiSi,2 V V С/Х/(3,
1 , , (5.19)
Si,2 = CiSi,2 \/ CtSi,2", Si,\ — Si,i.
Реализация системы уравнений (5.19) потребует всего лишь
Зтл вместо 7тл, как было раньше. Кроме того, значительно
уменьшится количество оборудования, требуемое для осуще-
ствления коррекции.
Дальнейшее ускорение сложения получим, если значения
разрядных сумм sij будем определять только по значению
промежуточной суммы s'ij и переносу со старшего двричного
сумматора Cij. С этой целью в систему уравнений (5.19) под-
ставим выражение для определения десятичного переноса
и тогда получим
X/ S 1,4 $ 1,381,2',
Si,3 = G-,45z,2 V Si,3s'i,2 V (5.20)
-$z,2 ==: Ci,481,2 V V £/,4^/,4-$r,2i
Si.l = Si,i.
Система 'уравнений (5.20) лишь немного сложнее системы
(5.19), но зато значения Sij могут быть получены теперь все-
го лишь через Зтл после сформирования промежуточного ре-
зультата. Поскольку десятичный перенос формируется парал-
лельно с коррекцией, то теперь временная задержка коррек-
ции составит Зтл ^вместо 9тл, как это было в начальном
варианте. Идеи, лежащие в основе ускорения сложения двоич-
но-десятичного сложения, могут быть использованы и Для
других систем счисления.
7°. Табличные методы. Любой тип «-разрядного сумматора
призван реализовать таблицу сложения, включающую г2п раз-
личных сочетаний значений слагаемых. Результат может иметь
всего 2гп—1 значений. Поскольку каждой паре слагаемых
всегда отвечает вполне определенный результат, то реализа-
ция сложения (впрочем, как и любой другой арифметической
операции) может быть произведена как обращение к таблице
результатов по адресу, который задается парой слагаемых —
операндами а и Ь. Самая простая организация такой таблицы
состоит в построении матрицы с г" строками и столбцами, ко-
торые имеют г2" ячеек памяти на одно число, состоящее из
возможного переноса и «-разрядной суммы. При наличии
такой матрицы сложение двух «-разрядных чисел будет опре-
деляться временем обращения к одной ячейке памяти’ по ад-
ресу («, Ь). Если выполнить предварительную проверку соот-
ношения « > &, то можно больший операнд всегда подавать
на вход х матрицы, а меньший — на вход у. Это позволит
сократить число ячеек памяти с г2п до 2~1rn(rn-|-1). Таблич-
ные методы хотя и обеспечивают в принципе очень большое
быстродействие, требуют при больших значениях гп нереаль-
ного объема памяти. Однако при г"<С2с табличное сложение
является вполне реальным. При последовательно-параллельном
сложении, когда группы из k разрядов слагаемых обрабаты-
ваются последовательно, а внутри одной группы производится
суммирование сразу всех k разрядов, табличный метод сум-
мирования может дать особенно большой эффект, несмотря
на то, что в этом случае таблица сложения должна учитывать
возможный перенос в группу.
8°. Ускоренное суммирование чисел с плавающей запятой.
До сих пор мы рассматривали методы собственно суммирова-
ния «-разрядных' операндов, отвлекаясь от формы представ-
лений чисел в машине. В то же время собственно суммиро;
вание при использовании чисел с плавающей запятой составляет
только некоторую часть полного времени сложения, другую
значительную часть составляет время преобразования мантиссы
меньшего операнда и время возможной нормализации влево.
Если мантисса представлена в г-ичной системе счисления, то
переход к гх-ичной системе, где X — целое положительное
число, позволит в среднем существенно быстрее выполнить
операцию сложения за счет того, что в новой системе счис-
ления вероятность преобразования мантисс операндов и нор-
мализации результата заметно меньше, чем в исходной сис-
теме счисления [12]. Препятствием к безусловному переходу
сложения гх-ичных чисел вместо г-ичных является снижение
относительной точности представления, характерное для уве-
личения основания системы счисления при неизменном числе
г-ичных разрядов мантиссы (см. главу 1 § 2).
♦
§ 2. МЕТОДЬ! УСКОРЕННОГО УМНОЖЕНИЯ
В зависимости от количества дополнительного оборудова-
ния, вносимого в арифметическое устройство машин, методы
ускорения умножения делятся на логические и аппаратные.
I0.' Логические методы. Методы, при которых ускорение
умножения достигается лишь за счет усложнения схемы уп-
равления и количество дополнительного оборудования не за-
висит от разрядности операндов (применительно к параллель-
ным устройствам), называются логическими.
Наиболее мощным логическим методом для систем счис-
ления с основанием г > 2 и положительным алфавитом явля-
ется метод преобразования цифр множителя к симметричному
алфавиту. Это связано с тем обстоятельством, что при реали-
зации умножения методом последовательных суммирований
частичных произведений число операций сложения опреде-
ляется величиной где at — цифры множителя. При
переходе к симметричному алфавиту наибольшее значение at
снижается с г — 1 до г2-1 для четных систем счисления
г — 1 „
и —2— для нечетных систем счисления. Естественно, что при
переходе к симметричному алфавиту мы должны наряду со
сложением применять и вычитание. Необходимый переход
к симметричному алфавиту легко осуществить путем переко-
дирования цифр множителя ai в соответствии со следующим
правилом:
«г==(-1)р‘ [rpi + (-l)pi(az +Р/-0],
О при ai + pt-i <-2-,
1 при at +pt-i >-у,
(5.21)
О < Z < & + 1 и р-i = О.
Данный метод годится для всех г > 2. Заметим, что хотя
величина преобразованного множителя точно такая же, как
и исходного, его разрядность может быть увеличена до k + 2.
Если множитель есть двоичное число, то, рассматривая груп-
пы по t разрядов как цифры в 2<-ичной системе счисления,
мы можем использовать этот метод и для двоичной системы
счисления. Однако для двоичной системы обычно используют
иной метод, связанный с преобразованием множителя к пред-
ставлению, содержащему наименьшее число единиц. Целью
такого преобразования является, как обычно, уменьшение чис-
ла суммирований при формировании произведения. Само пре-
образование заключается в том, что суммирование по группе
из t последовательных единиц заменяется вычитанйем в начале
группы и сложением в конце, поскольку справедливо
Разряды преобразованного множителя аг, которые теперь
имеют значения —1, 0, 1, могут быть определены по значе-
нию двух соседних разрядов исходного множителя, например,
в соответствии с соотношением
аг = (1 — 2«z+i) (аг ф Рг-\), (5.22)
где
Pt = ai+rai V Pi-\ («z-н V «J-
Преобразованный множитель может иметь- длину на один раз-
ряд больше, чем исходный, ибо,хотя а^+г =^= «*+2 = 0, но со-
гласно (5.22) аь+1 = pk- Нетрудно установить, что aial+i = О
каким бы ни было Z = 0, 1, .... k. Это означает, что соседние
разряды в преобразованном множителе не могут быть оба
отличны от нуля, вследствие чего число суммирований при
умножении на преобразованный множитель не превышает 1 +
4- р + 1 j. Поскольку цифры нового множителя могут иметь
значение —1, 0, 1, то операция суммирования должна произ-
водиться с учетом знаков. Это обстоятельство не вызывает
никаких затруднений, ибо операция вычитания всегда реали-
зуется в цифровой машине. Теория показывает [11], что при
достаточно большом числе разрядов множителя среднее число
сложений-вычитаний, приходящееся на один разряд множите-
ля, равно З-1. Оказывается, что это наилучший результат,
которого можно достичь при использовании логических мето-
дов. Среди гэтих методов можно еще отметить метод группи-
ровки разрядов множителя.
В этом методе анализируется сразу группа разрядов мно-
жителя. Внутри группы множитель также преобразуется к ви-
ду, позволяющему представить значение, задаваемое группой
из X двоичных разрядов, наименьшим числом слагаемых вида
+2Л Правила, которые позволяют перейти к такому пред-
ставлению, могут быть такими же, как и (5.21). Помимо но-
вого представления разрядов выбранной группы надо опреде-
лить и еще значение группового переноса (аналогично (5.22)).
После сложения-вычитания всех кратных множимого, которые
выявились после преобразования внутри группы, множитель
сдвигается на X разрядов вправо и цикл анализа повторяется.
С увеличением количества разрядов в группе здесь также
можно достигнуть в среднем З-1 сложений-вычитаний, при-
ходящихся на одну цифру исходного множителя.
Если при анализе группы цифр множителя разрешено при-
менение кратных иного вида, нежели + 2Л то число действий
сложения-вычитания, приходящихся в среднем на одну цифру
множителя, может быть еще меньше, чем З"1 (например, 4~’
[16]).
2°. Аппаратные методы. Методы ускорения умножения,
при которых количество дополнительного оборудования зави-
сит от числа разрядов операндов (для параллельных устрой-
ств), называют аппаратными. В последовательных устройствах
аппаратные методы вызывают увеличение основного оборудо-
вания (увеличение общей разрядности регистров или услож-
нение схемы сумматора).
2°.1. Метод ускоренного сдвига. Наиболее простой аппа-
ратный метод заключается в построении дополнительных це-
пей сдвига на два разряда. Дело в том, что йреобразование
множителя, связанное с переходом к троичному алфавиту,
исключает последовательное' появление ненулевых разрядов
множителя1. Следовательно, если at есть -|-1 или —1, то at+i —
— О, а раз это так, то после алгебраического суммирования
частичного произведения а^Ь с предыдущим результатом
можно произвести сдвиг сразу на два разряда. При этом ока-
зывается, что в среднем на каждый разряд множителя при-
ходится 5/9 сдвига. Если принять, что время сдвига в па-
раллельном устройстве составляет половину времени сумми-
рования (что обычно оправдывается на практике), то среднее
время умножения оказывается равным [11] при п = £-|-1
/ 1 , 5 х 11
^ум — \ 3 * 9 ^с) 18
При отсутствии дополнительных цепей сдвига среднее время
умножения получилось бы равным (опять в предполо-
жении, что тЕ=2тс). t
2° .2. Метод кратных множимого. Для систем счисления
с основанием больше двух одним из наиболее сильных аппа-
ратных методов является метод кратных множимого. Посколь-
ку при умножении на цифру aL в r-ичной системе счисления
частичное произведение формируется как сумма at сложений,
то имеет смысл заранее подготовить все возможные произве-
дения xb, где х = 1, 2, ..., г — 1, и, проанализировав текущее
значение <zz, выбрать одну из г — 1 заготовок. В этом случае
максимальное число суммирований сократится до 1 вне зави-
симости от at, но при этом, конечно, значительные трудности
вызовет подготовка всех возможных кратных множимого,
число которых есть г—1. Существенное упрощение полу-
чается при комбинировании метода кратных с методом преоб-
разования множителя (5.21), когда приходится вместо г—1
кратного множимого формировать всего г/2 (при четном г)
и (г—1)/2 (при нечетном г) кратных.
При кодировании цифр r-ичной системы счисления Х(г)
двоичными цифрами метод кратных имеет дополнительные
'преимущества, ввиду того, что получение кратных вида Ь‘2]'
осуществляется простым сдвигом множимого на j разрядов
влево, поэтому количество дополнительного оборудования
здесь резко сокращается. Насколько эффективен такой метод,
можно судить по данным табл. 18, где указано количество
Таблица 18
0 1 2 3 4 5 6 7 8 9
— +1 +2 4-2, +1 4-4 4-4. 4-1 —4 -4,4-1 —2 —1
к 0 1 1 2- 1 2 1 2 1 1
сложений-вычитаний (v), необходимое для получения частич-
ного произведения произвольной десятичной цифры аг на мно-
жимое Ь, если используются кратные 7= +1, +2, +4 и двоич-
но-десятцчный код есть код с весами 8421 (код 8421). Ока-
зывается, что при этом для получения, частичного произведения
в среднем необходимо 1,2 сложений:вычитаний, а в наихуд-
шем случае требуется всего 2 действия алгебраического сло-
жения. В этом случае также несложен анализ цифр множи-
теля Действительно, признаком выбора кратного
+ 1 является выполнение условия <Zz,4«z,i = 1, а кратного —1 —
условия <Zz.4«z,i = l- Для кратных -j-2 и —2 условия ' будут
соответственно <Zf,3«i,2 = 1 и «гдащ = 1, а для кратных +4
и — 4 — ai,3fh,2 = 1 и аг-,зйг,2== 1. Добавление к этому набору еще
кратных -]-3 приведет к тому, что среднее число алгебраи-
ческих сложений станет равным 1, и лишь при az = 5 число
сложений есть 2. 1
2°.3. Метод параллельного суммирования частичных про-
изведений. Когда множимое и множитель расположены на
регистрах машины, нетрудно (особенно для двоичной системы
счисления) образовать сразу все частичные произведения.
Следовательно, при наличии дополнительных сумматоров мож-
но складывать сразу несколько частичных произведений,
а в предельном случае и все. В этом случае формирование
произведения можно себе представить как спуск по дереву
сумматоров qt слагаемых до их общей суммы. Время спуска
по дереву будет зависать от его организации и типа приме-
няемых сумматоров [51]. Рассмотрим случай двоичной системы
счисления. Массив частичных произведений может быть изо-
бражен в виде матрицы. Элементы, составляющие i-й столбец
матрицы, просуммируем с помощью / обычных трехвходовых
двоичных сумматоров. Значения переносов с этих сумматоров
должны быть слагаемыми для (г + 1)-го столбца. Это приведет
к тому, что появление слагаемых будет произведено с запаз-
дыванием по времени. Произведем распределение первичных
и запаздывающих слагаемых так, как это показано на рис. 26.
Для одноразрядных сумматоров время образования суммы
не меньше, чем время образования переноса тс,' поэтому
наибольшее время спуска по дереву данного вида есть
S = («—1)^ + ^). ' (5.23)
если только все конъюнкции вида afij поступают на дерево
спуска одновременно. Это время складывается из спуска по
самой длинной вертикали, а затем последовательного распрост-
ранения переноса через сумматоры нижнего, ряда вплоть до
самого левого.
Наибольший вклад в величину вносит время спуска
по вертикали. Отдельная вертикаль в исследуемом дереве
представляет собой последовательное соединение сумматоров
по модулю два. При этом если
число слагаемых есть т, то чис- V/ \/ \У V/
ло сумматоров есть О*- О*~ Ч*-
т — 1 + ъ \ / \ /
р =---?---’
i + (—ЧГ >4*“
где 8 =------, X /
а время спуска составит
^СП == PV
Если бы все т слагаемых по- рис 27
ступали бы на вертикаль дерева
в одно и то же время, то наи-
скорейший спуск осуществлялся деревом с троичным алфави-
том и полным множеством концевых узлов. Однако примерно
только половина слагаемых на каждой вертикали может быть
подана в одно время, остальные приходят с различным запаз-
дыванием. Это вынуждает иметь свободные узлы по одному
на сумматоре для каждой ступени, кроме последней. Тогда
дерево спуска по вертикали будет таким,, как показано на
рис. 27. Если такое дерево имеет j ступеней, то справедливо
неравенство
27 т 2/'+1 — 1.
Время спуска по этому дереву составит
^сп=А-
Указанная организация спуска по вертикали приводит к тому,
что дерево сумматоров трансформируется (рис. 28). Новое
дерево более „низкое", чем исходное, и естественно, что вре-
мя спуска уменьшается до величины
^ = 2h + («-2K], , (5.24)
если только для справедливо
1 <2Z,
что обычно выполняется на практике.
Таким образом, преобразование дерева спуска уменьшит
время спуска по нему в q раз:
, _ п — 1 t +1
q 2 Z(n-2)+1 *
Когда тс = тл, то q=l, ибо в данном случае оказывается, что
спуск по вертикали происходит за то же время, что и по диа-
г? , 1 3 п — 1
гонали. Если же t = —, то q = ---------—> т- е- ускорение
спуска происходит почти в 1,5 раза.
Рп Рп Рп Ря Рв Pi Ps Ps Ря- Pi Рг Pi
, Рис. 28.
Как следует из соотношения (5.24), время формирования
произведения деревом с измененной организацией оказывается
приблизительно равным сложению чисел разрядности 2п
в сумматоре с последовательным
распространением переноса [62].
Дальнейшее ускорение умно-
жения может быть связано с при-
менением в нижнем ряду дерева
спуска сумматора не с последо-
вательным распространением пе-
реноса, а какого-либо другого
типа из описанных ранее, кото-
рый приводит к уменьшению
времени сложения.
Задачей дерева спуска явля-
ется сведение п частичных про-
изведений к их сумме. Рассмот-
ренная структура дерева спуска
не единственная. Будем строить
дерево спуска из однотипных
параллельных сумматоров, каж-
дый из которых состоит из обыч-
ных двоичных сумматоров, не связанных друг с другом. Де-
рево построим следующим образом. Все п частичных произ-
ведений будем одновременно суммировать на j-^-j суммато-
pax. Полученные m = 2[-^~] слагаемые вновь одновременно
суммируем на сумматорах и объединяем выходы с этих
сумматоров в новый массив и т. д. Через X ступеней мы от
«слагаемых приходим к двум слагаемым — векторам $»и с
(рис. 29). Наибольшее число слагаемых, которое может быть
приведено таким деревом при X ступенях, определится из ре-
куррентного соотношения
Г Зп, , “I
«л = [ ], (5.25)
где я0 = 2. Если число слагаемых « больше, чем значение «л,
определенное из (5.25), то число ступеней в дереве спуска
должно быть увеличено. Для Х<; 15 оптимальное значение
числа слагаемых при заданном числе ступеней приведено
в табл. 19.
Таблица 19
К 1 2 3 4 5 6 '7 8 9 10 11 12 13 14 15
«Л 3 4 6 9 13 19 28 42 63 94 141 211 316 474 681
Время спуска по дереву приведенной структуры есть
Tcn = XV
Всего число параллельных сумматоров в дереве спуска есть
«— 2, правда, конечно, они не все одинаковой разрядности.
На рис. 30 представлена деталировка дерева спуска, изобра-
женного на рис. 29 в двоичных одноразрядных сумматорах.
Номера внутри этих сумматоров указывают их принадлеж-
ность к соответствующим параллельным сумматорам.
Частичные произведения
♦ I I
Е? I
с| si
33
Е2
1с
5
I , V
тй
I * Е«
Рис. 31.
^аВержт суммы |
Дерево спуска рассмотренной структуры формирует произ-
ведение, обрабатывая одновременно все п частичных произ-
ведений. При определенном компромиссе между стоимостью
оборудования и временем получения результата возможен
одновременный учет лишь
группы частичных произве-
дений. В этом случае полу-
ченная сумма наряду с но-
выми частичными произве-
дениями вновь подается
в дерево спуска для по-
следующих суммирований.
Итеративный процесс закан-
чивается, когда все частич-
ные произведения будут
учтены. Для уменьшения
времени, отводимого для
реализации одной итерации,
полученную сумму следует
направлять не на вход де-
рева спуска, а на самую
нижнюю допустимую сту-
пень (рис. 31). Пусть п =
= ия, где п — число частич-
ных произведений, v — чис-
ло итераций, и. — число
частичных произведений, обрабатываемых на одной итерации;
тогда полное время приведения п слагаемых к двум при ис-
пользовании дерева спуска типа рис. 31 составит
тсп == (к) -f- 2“у)
Если же использовать полное дерево время спуска, то =
= X(«)ts. Например, при п ==30, zz = 6 и v — 5 получим тсп =
= 13^ и 't*n = 8Ts. Заметим, что требуемое оборудование су-
щественно отличается для этих двух схем — при итерационном
спуске число сумматоров есть и, а при прямом п—2. В на-
шем случае эти величины есть 6 и 28 соответственно.
Чрезвычайно важным моментом при использовании деревьев
спуска рассмотренного вида является снижение числа слагае-
мых,. Поскольку слагаемыми являются частичные произведе-
ния, то рационально при использовании деревьев спуска мно-
житель вначале преобразовать к виду, содержащему наимень-
шее число ненулевых членов [37]. Например, преобразование
(5.22), обеспечивающее наличие в двух соседних разрядах
множителя не более одной ненулевой цифры, позволяет сни-
зить число входных слагаемых для дерева спуска с п до 1 +
[я 1
Тг,
2°.4. Быстрое умножение чисел большой разрядности.
Пусть в нашем распоряжении имеется умножитель, позволяю-
щий перемножать «/-разрядные числа в г-ичной системе счис-
ления, а нам требуется перемножить «-разрядные числа и п =
= km, где k > 1 и целое. Нас будет интересовать вопрос
о времени Т(п) умножения «-разрядных чисел, выраженных
в единицах времени перемножения /«-разрядных чисел.
Рассмотрим случай целых чисел и выберем вначале k = 2,
тогда сомножители а и b можно представить в виде а =
— гта' + а", где а' = 2S' a,m+irl и а!' = «ггг. Произве-
дение чисел а и b определится как p — ab = r‘ima'b' -}-гтУ,
X (a'V + a"b') -f- a"lf. Для того чтобы вычислить это произ-
ведение, надо произвести четыре умножения «/-разрядных
чисел, две операции сдвига и три операции сложения, следо-
вательно,
Т (2«z) = 4 Г («/) + ЗтЕ + 2тсд.
В то же время совершенно очевиден и другой алгоритм вы-
числения произведения ab
р = (/-2m _|_ гту а'1,' _|_ гт цу __ _|_ (rm _|_ 1)
Время вычисления произведения по этому алгоритму есть
Т (2т) = 3 Г («/) + 4тЕ + 4тсд.
Обычно Т (т) + 2тсд и второй алгоритм оказывается более
быстрым.
Приведенный пример показывает, что п|эи перемножении
/г-кратных чисел число умножений однократных чисел может
быть сделано пропорциональным не k2, как это кажется на
первый взгляд, а меньшей величине; Какова эта величина для
произвольного k? Оказывается, что [12]
Т (km) (2k — 1) Т (m) + cm,
где с — константа, учитывающая необходимость выполнения по-
мимо умножений еще и некоторого числа сложений и сдвигов.
Для «-разрядных чисел, представленных в двоичной сис-
теме счисления, существуют алгоритмы [12, 64], которые
позволяют вычислять 2«-разрядное произведение за время
меньшее, чем сп2^21о^п log2« шагов. Если при умноже-
нии двоичных чисел использовать быстрое преобразование
Фурье, то
Т(«) = сп log2«log2 log2«.
Эти алгоритмы оказываются значительно более быстрыми, не-
жели очевидный алгоритм умножения-, требующий для своей
реализации времени, пропорционального.величине «2.
§ 3. МЕТОДЫ УСКОРЕННОГО ДЕЛЕНИЯ
1°. Логические методы. Два метода ускоренного деления
уже рассматривались ранее — это метод деления без восста-
новления остатка и метод приближенного деления. Оба метода
можно отнести к логическим методам ускоренного деления.
Дополним логические методы еще одним способом, осно-
ванным на анализе цифр очередного остатка и делителя, кото-
рый будем считать нормализованным, т. е. bk О- Опять для
простоты будем считать, что операнды заданы в виде целых
чисел прямыми кодами.
Операция деления начинается с анализа величины очеред-
ного остатка. Если этот остаток очень мал — имеет р нулевых
старших разрядов, то это означает, что по крайней мере р
очередных цифр частного будут нулями. В этом случае для
определения цифр частного совершенно излишне производить
пробные вычитания делителя из остатка, а достаточно просто
сдвинуть остаток влево р раз, а частному принимать р оче-
редных цифр со значением нуль.
Когда же остаток очень близок к делителю (оба имеют
р одинаковых старших цифр), это означает, что р очередных
цифр частного одинаковы и имеют значение г—1. И в дан-
ном случае можно существенно ускорить деление, если вмес-
то р(г—1) вычитаний (по г—1 на каждую цифру частного,
считая, что выполняем деление без восстановления остатка)
и р сдвигов вначале осуществить вычитание делителя b из
остатка затем полу ценную разность с№—b сдвинуть
на р разрядов влево и, наконец, к полученному числу rp —
— b) добавить делитель. Приведенный алгоритм позволяет
уменьшить число действий алгебраического сложения на р X
Х(г—1) —2. Возможность подобного изменения алгоритма
деления базируется на том факте, что остаток после выпол-
нения р шагов обычного алгоритма деления при совпадении
р старших цифр остатка и делителя Ь определится как
аи+Р) = г (... (г (ГЙ(Л __ (Г _ 1) b) - (г — 1) b ...) - (г - 1) b =
= гра^ (гр~1 (гр~1 + гр~2 + ... + г + 1) =
= гр (й(>) -*) + &. (5.26)
Значение aV+p\ определенное из (5.26), совпадает с вели-
чиной остатка, полученного по видоизмененному алгоритму.
Данный метод особенно эффективен для двоичной системы
счисления, когда сравнение остатка и делителя производится
достаточно просто.
2°. Аппаратные методы. Многие идеи, лежащие в основе
методов ускоренного умножения, могут, быть использованы
и для ускорения выполнения операции деления, ь то же вре-
мя ряд методов реализации деления имеет много общего
с методами вычисления элементарных функций.
2°.1. Метод кратных. Для определения цифр частного мы
последовательно вычитаем делитель из остатка и следим за
знаком разности после каждого вычитания. Число последова-
тельных вычитаний позволяет найти искомую цифру частного.
Можно на первом пробном вычитании вычитать (складывать)
не сам делитель, а его ^-кратное значение, l<Z<r—1.
В этом случае процесс определения цифры частного будет
точно таким, как при ловле льва в пустыне, описанной в из-
вестной шутке. Первое пробное вычитание позволит ограни-
чить область, где находится искомая цифра, приблизительно
вдвое, если значение t выбрать приблизительно равным г/2.
Выбор одной из двух областей определит значение кратности
делителя и знак алгебраического сложения для следующей
пробы. С целью уменьшения дополнительного оборудования
при делении рационально использовать те же кратные, что
и при- умножении. Так, например, для десятичной системы
счисления к хорошим результатам приводит набор кратных
±4, ±2, +1. Этот же набор в случае деления позволяет сниг
зить максимальное число алгебраических действий при опре-
делении цифр частного до 4, а среднее — до 3, 4. В табл. 20
представлены значения кратности делителя и знак алгебраи-
ческого сложения для последовательных проб при определе-
нии у-й десятичной цифры частного. Здесь юу—знак анализи-
руемого остатка, a — знак следующего остатка. Значение
<о = 1 соответствует отрицательному знаку.
Таблица 20
Цифры част- ного Последовательность’проб
<°i = о 8 “i+l — 1 “f-f-i
0 —4, +2, 4-1 ' г 4-4, —2, —1 0
1 -Ч +2, +1 0 4-4, —2, —1- 1
2 —4, 4-2, —1 . г 4-4. —2, 4-1 0
3 -4, 4-2, -1 0 4-4, —2, +1 1
4 --4, —2, 4-1 г 4-4, 4-2, —1- 0
5 —4, —2, 4-1 0 4-4, 4-2, —I * 1
6 —4, —2, —2, 4-1 1 4-4, 4-2, 4-2, -1 0
7 —4, —2, —2, 4-1 0 4-4, 4-2, 4-2, —1 г
.8 —4, —2, —2, —1 1 4-4, 4-2, 4-2, 4-1 0
9 —4, —2, —2, —1 0 4-4, 4-2, 4-2, 4-1 1.
2°.2. Метод параллельных проб. При наличии известного’
дополнительного оборудования в арифметическом устройстве
можно уменьшить число последовательных действий в опре-
делении цифр частного за счет выполнения на каждом шаге
алгоритма одновременно нескольких вычитаний из остатка
делителя различной кратности. Совместный анализ результа-
тов нескольких проб позволит более определенно указать
область, в которой будет находиться цифра частного. Для
иллюстрации этого метода рассмотрим случай десятичной сис-
темы счисления и выбора кратных +4, + 2, +1. На первом
этапе выполним сразу две пробы (рассмотрим случай положи-
тельного остатка): вычтем учетверенный делитель из остатка
и параллельно найдем разность между остатком и удвоенным
делителем. Пусть знак первой разности есть ш}0 и второй
тогда возможны следующие ситуации: = 1, «РМ4 = 1
и = 1. Первый случай соответствует диапазону цифр част-
ного 0,1, второй — 2,3 и третий — 4 -г- 9. Найти окончательную
цифру частного для первых двух случаев достаточно просто:,
для этого надо на втором этапе взять результат второй пробы
И при = 1 добавить к нему, а при = 1 вычесть
из него делитель. Знак результата второго, этапа позволит,
окончательно уточнить цифру частного (табл. 21). Если же
Таблица 21
Цифры частного Последовательность частного
ч>1 = 0 <Oj — 1 «"/4-1
0 —2, +1 1 4-2, —1 0
"к 1 —2, +1 0, +2, -1 1
; 2 —2, —1 1 4-2, +1 0
; 3 —2, —1 0 +2, +1 1
1 4 —4,1 —2, +1 1. : +4, +2, ^1 0
; 5 —4, —2, +1 0 i +4, 4-2, -1 1
е —4, —2, —1 1 : 4-4, 4-2, 4-1 0
7 —4, —2, —1 0 : 4-4, 4-2, 4-1 1
8 —4, —4, —1 1 ; 4-4, 4-4, 4-1 0
; 9 —4, —4, —1 0 4-4, 4-4, 4-1 1
«>11>=^=1,: то в качестве результата' берется первая разность
и на втором этапе из нее вычитается опять учетверенный
и удвоенный делитель. Теперь сочетание знаков проб позво-
лит выделить следующие диапазоны цифр частного: —
— 1 — диапазон 4, 5; wiZ)<oj2) =1 — диапазон 6, 7 и, наконец,
mf' = 1 — диапазон 8,'9. Теперь уже просто определить окон-
чательные цифры частного на третьем этапе. Для этого надо
к итогу второго этапа, а это есть вторая разность при «>[2) = 1
и первая при <и[2)=1, добавить (при <u[2)o42) = 1) или вычесть
(при <42) = 1) делитель. Знак результата алгебраического сло-
жения на третьем этапе выберет окончательно цифру частного
для каждой возможной пары. Следовательно, при двух одно-
временных пробах на первом и на втором этапах определения
цифр частного число этапов сократилось до трех, а их сред-
нее число стало 2,6.
Увеличение числа проб, проводимых одновременно на каж-
дом шаге алгоритма, позволит еще больше сократить число
этапов в определении цифры частного, но, конечно, потребует
увеличения дополнительного оборудования для реализации
этих проб и анализа знаков результатов в этих пробах.
2°.3. Метод формирования знакоразрядного частного.
Предположим, что для цифр частного от деления чисел а и Ь,
представленных в r-ичной системе счисления с неотрицатель-
ной базой, допустимы значения 0, +1, +2, ..., ±1, причем
2-1 (г— l)<Z<r — 1. (5.27)
Когда 2t + 1 > г, для представления цифр частного исполь-
зуется избыточная симметричная база, которая приводит к не-
однозначному представлению чисел (см. § 1 настоящей главы).
Например, если г = 10 и t = 9, то число а = 802 в десятичной
системе с избыточной базой может быть представлено как
«.(О = 80210 и как а<2) = 99810- Как мы увидим, именно неод-
нозначность представления позволяет на каждом шаге деления
искать не единственно возможную цифру частного, а одну
из Допустимых, и этот поиск может быть реализован значи-
тельно быстрее, чем обычная процедура отыскания цифр част-
ного [11]. Мерой избыточности при представлении цифр част-
ного в симметричной базе служит отношение t/(r—1).
При использовании обычной процедуры определения цифр
частного методом последовательного вычитания из очередного
«(»-!) остатка делителя b выполнение неравенства
rb > ай-1)г«-1 (г _ 1) ь
свидетельствует о том, что цифры частного есть Ci-i — r—1.
Пусть теперь для представления цифр частного применяется
избыточная симметричная база, такая, что t = r—1, тогда
можно расширить пределы изменения остатка, при которых
цифры частного есть ci-i = r — 1, до следующих:
rb > ай-йг'-1 >(г — 2) Ь.
Когда (r-V)b> a(«-i)r'-i (г— 2) Ь, мы можем сознательно
увеличить значение с г — 2 до г— 1, получив правильный
результат за счет того, что дальнейшие цифры частного опре-
делят величину со знаком минус, которая компенсирует уве-
личение частного на i-ы шаге. Эти же соображения позволяют
записать следующую систему:
rb > ~^-{г — 2) #=> cy-i = г — 1
(г — 1) b > >- (г — 3) £=> cy-i = г— 2
2Ь > > 0=> ci-/ = 1
s
b > —b=~> Cy-i = О
0> >• —26=> Cy-i = —1
— (г —3) b > — (г — 1) b ~-> Cy-i = — (г — 2 )
— (г — 2) b > a(i~^ri~'1 —rb—> Cy—i = — (г — 1)
*
Как следует из этой системы, если величина тако-
ва, что
dp > aV-Vr1-1 (dy — V) b,
то в качестве цифры частного Cy-i можно выбрать либо зна-
чение dh либо dy—1, где dy = r— 1, г — 2, ..., 1, 0, —1, ..
— (г — 2). Расширение диапазона величины остатка, отвечаю-
щей данной цифре частного при известном делителе, позво,
ляет произвести сравненйе делителя и остатка более грубо
имея лишь приближенные значения делителя и остатка. Если
эти приближения таковы, что достаточно только взять не-
сколько старших разрядов нормализованного делителя и остат-
ка, то сравнение может быть произведено непосредственной
расшифровкой этих разрядов. Данная процедура может быть
реализована „табличным" методом без привлечения арифме-
тических операций, а следовательно, достаточно быстро.
Для определения следующей цифры частного необходимо
найти еще очередной остаток, а чтобы сделать это быстро,
желательно использовать метод вычитания кратных делителя:
Cy-ib. Поскольку при максимальной избыточности (^ = г—1)
набор кратных практически невозможно иметь в арифметиче-
ском устройстве (АУ), то приходится выбирать более разум-
ные значения t<r—1. Это, в свою очередь, будет сужать
диапазон изменения остатков, допускающих неоднозначный
выбор цифр частного, и потребует более детального анализа
усеченных остатков и делителя. Детальный анализ возникаю-
щих при этом ситуаций выполнен в работах [38, 57].
Заметим, что для полного завершения операции надо еще
перевести найденное частное в обычную г-'ичную систему
счисления с неизбыточным алфавитом положительных цифр.
(Способы подобного перевода были рассмотрены в §4 главы 1.)
Приведенные идеи могут дать значительное ускорение
и двоичного деления, если группы из р-двоичных разрядов
рассматривать как цифры в системе счисления с основанием 2Р.
Например, при р — 2 набор цифр может быть выбран следую-
щим: 0, +1, +2. Кратные делителя образуются весьма легко
(простым сдвигом), и получение остатка возможно всего лишь
за одно алгебраическое сложение. Расшифровка же лишь' не-
скольких старших разрядов остатка и частного позволяет за
один такт определить четверичную цифру частного.
Набор допустимых цифр частного может быть различен
для одной системы счисления. Например, соображения, касаю-
щиеся простоты выбора очередной цифры частного и, преоб-
разования его к обычной форме представления чисел, могут
привести к тому, что цифры частного будут не равноотстоя-
щими друг от друга и не обязательно целыми [11].
2°.4. Метод предварительного анализа. Предварительный
анализ значения остатка и делителя в начале каждого шага
деления позволяет значительно ускорить определение всех
цифр частного. Рассмотрим случай двоичной системы счисле-
ния. Будем на каждом шаге деления анализировать значения
трех старших разрядов очередного остатка и трех
разрядов нормализованного делителя bn =j= 1, bn-\ и Ьп_2. Когда
= ООО или 001, то вне зависимости От значений
&n-i и Ьп—2 имеем, что й-i = C-t = 0; а в первом случае
и c_j_z=O (табл. 22). Все действия на шаге деления тогда
будут сведены к сдвигу остатка ай-D влево на 3 :или 2 раз-
ряда соответственно. В случае, когда ап~1}а„-Р == 1, всегда
С1-г = 0. Однако, если а„ ^л-i = 1, то еще и c_t- =
= 0, если же = 1, то с_г=1. Следователь-
но, всегда необходимо остаток сдвинуть влево на раз-
ряд. Когда ясно значение цифры частного надо еще либо
прямо сдвинуть остаток еще раз влево, либо вначале вычесть
из 2а(г~1) делитель Ь, а затем уже разность увеличить в,два
раза.
При а-п = 1 выполнять вычитание делителя надо обяза-
тельно. Интересно, что только когда a^ZpanZ^bnbn-ibn-2 = 1,
цифра частного заранее неизвестна, она определится после
определения знака разности При отрицательном
знаке этой разности Ci_f = 0,, а в противоположном случае
Таблица 22
Значение трех остатков разряда Очевидные цифры частного
ап~1 ап~2 V1 cl-i = 0, bn_2 = 0 c-l c-l-i bn-l с1-1 = 0, V2=1 c—l c—l—i *„-1 = с1-1 О 44 II д О) 1 * .. - 1 11 « Ьп-1 cl-i = 1, b„ 9 = 1 ’ п~ 2 c—i c-l-t
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 — 0 0 — 0 0 — 0 0 —
0 1 0 0 — — 0 — — 0 0 — 0 0 —
0 1” 0 1 — 0 1 — 0 — — 0 — —
1 0 0 — — — 0 1 — 0 1 — 0 1 —
1 0 1 1 0 — — — — 0 1 — 0 1 —
1 1 0 1 — — 1 0 — — — — 0 1 —
1 1 1 1 — — 1 — —. 1 0 — —
сг_, = 1. Будем считать, что реализация вычитания не уничто-
жает остаток (он сохраняется), тогда, если = 0, то
«.(О = 2с('Х), а когда = 1, то aSi} — 2 — Ь).
Что же происходит при других ситуациях? Если X
X = 1, то Ci-i = 0 и c-i=l. Остаток а№ есть тогда
2 (2а(/) — Ь), и для реализации шага деления надо из удвоен-
ного остатка аУ-1) вычесть делитель и сдвинуть влево на один
разряд полученный результат. Точно такая же ситуация воз-
никает при ап^ап^Ра^-^ = 100 и = 01. Несколько
иначе обстоит дело, когда а1п~^ап-1\ = 101 и bn^bn-2 =
= 00, тогда cf-_j = l, c_f- = 0 и = 22 (а(£-1) — £>). Здесь
надо вначале определить разность — Ь, а затем сдвинуть
ее еще на два разряда влево. Наконец, когда ап~^а.п-Р = 1,
мы сталкиваемся с новой ситуацией, когда ci_t-=l, а значение
не определено. В этом случае = 2 — Ь).
Таким образом, все 32 возможных сочетания кода трех
старших разрядов остатка и делителя разбиваются на семь
различных групп, для каждой из которых характерна своя
специфика определения очередного остатка. Считая, что все
значения старших разрядов остатка и делителя равновероятны,
получим, что в среднем на одном шаге деления определяется
1,78 цифра частного и количество вычитаний чна каждом шаге
есть 0,56. Поскольку число цифр частного, определяемых
на 4-м шаге, различно, то число шагов может оказаться су-
щественно меньшим, чем п, п — разрядность операн-
дов.
3°. Итерационные методы, использующие умножение.
В тех случаях, когда умножение реализуется за очень малое
время, имеет смысл операцию деления выполнять как после-
довательность арифметических и логических действий, вклю-
чающих умножение. Обычно эта последовательность разби-
вается на повторяющиеся циклы (итерации). Каждая итерация
с номером у (у ='1, 2, ...) формирует некоторое приближе-
ние Pj к результату, в качестве которого обычно выступает
обратная величина делителя.
В отличие от итерационных методов деления, которые
мы рассматривали ранее, методы, использующие умножение,
на каждой итерации уточняют приближение, а не определяют
очередную цифру частного. Следовательно, теперь итерацион-
ный процесс закончится, как только будет достигнуто желаем
мое приближение. После завершения итерационного процесса
результат умножают на делимое и тем самым определяют
частное. Быстродействие итерационных методов деления, как
правило, оценивают через суммарное число умножений, тре-
буемых для выполнения операции деления. Это вызвано тем,
что среди всех операций, реализующих отдельную итерацию,
наибольшее время требуется для осуществления умножения.
Временем выполнения других операций обычно можно прене-
бречь.
3°.1. Метод оптимальной геометрической прогрессии.
Среди итерационных методов деления, базирующихся на ис-
пользовании умножения, наибольшее распространение получил
метод геометрической прогрессии, суть которого такова. При-
ближение Pj находится в соответствии с уравнением
р,=р,-^!.^
где
ej_^l-Pj^b. (5.28)
Значение Ро называется начальным приближением и опреде-
ляется каким-либо образом до начала итерационного процесса.
Погрешность в определении результата после у’-й итерации
есть
Д = - Pj = b~l£j = = b-1^, (5.29)
где
, £ = Т1й(/г+1). (5.30)
Каждая итерация реализуется за /у- + 1 умножений, lj — 1
из которых тратится для вычисления полинома P(ej_l) =
= Sz=oe;-i по схеме Горнера. При заданном общем числе
умножений т наиболее быстрая сходимость достигается, если
/г = 2 для всех 4=1, 2, .... В случае, когда т = 0, одно из
значений lt есть либо 2, либо 4. Метод геометрической про-
грессии с определенными указанным образом значениями Zf-
называется методом оптимальной геометрической прогрес-
сии (ОГП). Любое натуральное число т можно выразить
в виде
т = 3р + а, а£{—1, 0, 1} и р=1, 2, ...,
тогда для метода ОГП справедливо
L (т) — Зр-1 (3 + а).
На практике часто используется случай /г=1. Хотя при
этом.достигается худшая сходимость, чем в методе ОГП, но
зато каждая итерация оказывается наиболее простой. Частным
случаем метода геометрической прогрессии является метод
сведения- делителя к единице. По этому /методу делитель
и делимое последовательно умножаются на одни и те же
числа, что ы делитель стремился к единице, а делимое
к искомому частному, т. е.
а ах,х.> ... xi
(5.31)
b ЬХ]Х.2 ... Xj ''
причем
axtx2 ... Xj-^ab-1 при у—>со,
Ьхгх2 ... 1 при j.-Ъ со.
Основное достоинство данного метода состоит в принципиаль-
ной возможности одновременного умножения числителя и зна-
менателя дроби (5.31) на число xt [37].
3°.2. Метод наискорейшего вычисления полинома Р(е).
Вычисление полинома Р(е) — 2;=ое' по схеме Горнера не яв-
ляется оптимальным с точки зрения минимальности числа
требуемых умножений. Более рационально вычислять этот
полином по следующей схеме:
Р(е) = 1 + (е + е2 *) (1 + (е2 + е4) (1 + (е« + е«) (1 + (...)))).
(5.32)
В этом случае [14] за 4 умножений удается реали-
зовать итерацию, включающую вычисление полинома Р(е)
степени
т-Н—2
Z = (3-v)2 ^~-2,
где
2
f
Итерационный метод, основанный на вычислении полинома
Р (е) по схеме (5.32), обозначим как метод Ml. В случае,
когда т = 4, 5, 6, 7, значения L (т) будут соответственно
5, 7, 1Г и 15. При т>-8 справедливо, что наибольшее значе-
ние функции L (т) при заданном т определится как
'+7 7~»
£(т) = 5* ~7’-11 2 ,
m = 4Z + T, 1 = 2, 3, ..., у С {0, 1, 2, 3].
3°.3. Метод приближенного вычисления полинома Р(е).
Известно, что приближенные вычисления могут реализоваться
за значительно меньшее время, чем точные. Например, опе-
рация возведения в квадрат может быть выполнена за время
существенно меньшее, чем время сложения, если разрядность
операндов не велика (л<^8) и основание системы счисления
есть 2 (глава 6 § 1). Для уменьшения времени реализации
отдельной итерации попробуем значение полинома Р(е) вы-
числить приближенно. Особенности этого метода рассмотрим
на примере метода ОГП, когда Pj = Pj-i (1 + e;-i +e;-i)
и г = 2. Будем вычислять величину e2_i приближенн'о с неко-
торой погрешностью 8, тогда из (5.28) следует, что
= 1 - —(1 + е;-! + - 8) Ь =
= Д-8(1-е7_1). (5.33)
Для величины 8 справедлива оценка
х 181 < 2-2Л~9-1, (5.34)
где h — количество нулей до старшей значащей цифры в дво-
ичной записи чисел e7_i, a q— количество сохраняемых раз-
рядов у числа e7_i после старшей значащей цифры. Остальные
разряды просто отбрасываются. На основании (5.33) и (5.34)
имеем
I I < 1 +| 8111 -ey-j | < 2"2Л + 2^ +
Если h то |еу-| < 2-зл(2 4-2-л), т. е. число верных
знаков на каждой итерации почти утраивается. Когда же
то | еу. | < 2~2Л-в, т. е. число верных знаков стано-
вится равным удвоенному числу плюс еще не менее q знаков.
Приближенное вычисление е2~г может осуществиться умно-
жением коротких (q + 2)-разрядных операндов, либо при
небольших q значение e2_i может быть задано таблично. Учи-
тывая, что квадрат может быть вычислен весьма быстро
и просто (подробнее об этом см. в главе 6) йри небольших зна-
чениях q с помощью реализации переключательных, функций,
имеет смысл приближенное вычисление функции e7_i реализо-
вать схемным путем, когда можно пренебречь временем вы-
2
числения е7_1 по сравнению с умножением.
. 3°.4. Выбор начального приближения Ро. Для обеспече-
ния быстрой сходимости итерационных методов необходимо,
чтобы начальное приближение Ро было весьма -точным. В ма-
шинах большой производительности, где время выполнения
операций играет существенную роль, рационально хранить
в специальных таблицах либо само начальное приближение,
либо исходные данные для его вычисления. Причем для по-
вышения точности начального приближения таблица хранит
данные для каждого из 2й равных поддиапазонов, на которые
разбивается диапазон изменения делителя [2-1, 1 — 2~п] (в даль-
нейшем речь пойдет только о двоичном делении). Делитель
Ь, который считаем нормализованным, представим в виде b =
= d + Д, где
d = 2-1 + Sfi1 b^2~\ Д = Ь^2~1,
заметим, что 0^Д<2-*-1.
Начальное приближение к обратной величине будем искать
для каждого поддиапазона как значение соответствующего
аппроксимирующего полинома наилучшего приближения (по-
линома Чебышева для обратной величины) степени X. Можно
показать [14], что в этом случае, справедливо неравенство
[е0| = | l-P0M<2-ft(X+I)“2X-1. (5.35)
3(,.5. Оценка скорости сходимости итерационных методов.
Время реализации операции деления зависит в основном от
общего числа умножений. Точность же, с которой за т умно-
жений будет вычислена обратная величина, определяется кон-
кретной схемой применяемого итерационного процесса. Однако
каким бы ни был этот итерационный процесс, вначале за I
умножений будем определять начальное приближение Ро.
Случай I = 0 означает, что Ро формируется путем прямого
выбора из таблицы константы, соответствующей выбранному
поддиапазону. При т = I вычисление обратной величины
производится с помощью полиномов Чебышева, коэффициенты
которых хранятся в специальной таблице. Ситуация 1 = т — 1
расценивается как недопустимая, ибо для реализации отдель-
ной итерации необходимо по крайней мере два умножения.
После определения начального приближения - за т — 1 умно-
жений с помощью выбранного итерационного процесса нахо-
дится желаемое приближение к обратной величине делителя.
Для завершения операции необходимо еще одно умножение
обратной величины на делимое.
Учитывая (5.29) и (5.35), а также принимая во внимание,
что &>-2-1, находим, что точность приближения к обратной
величине делителя удовлетворяет неравенству
|е| 2“ 0+1 (5 36)
Здесь Лм {т — I) — максимум функции L (5.30), который мо-
жет быть достигнут при использовании итерационного метода
М Для фиксированного значения т — I. Задача состоит в том,
чтобы при заданных числе умножений т и числе анализируе-
мых разрядов делителя k найти такое Z, а следовательно,
и степень полинома Чебышева X, при котором величина
В (т, I) = (т — I) [k (X ф- 1) + 2Х 1] (5.37)
была бы наибольшей.
Известно, что полиномы с вещественными коэффициентами
степени Х^>5 могут быть сосчитаны за [-5"]+ 2 умножений,
а не за X, когда они считаются по схеме Горнера. При Х^З
для их вычисления надо X умножений, а для Х = 4 можно
обойтись тремя умножениями. Это обстоятельство мы всегда
будем иметь в виду, когда определяем степень полинома
Чебышева, который вычисляем за I умножений. Исследования
показывают [14], что когда заданное число умножений мало
(т 4), то наилучшая сходимость будет достигнута, если
обратная величина определяется с помощью полиномов'Чебы-
шева. Если же т — 5, 6, то более быструю сходимость обе-
спечивает метод ОГП и для m 7 явное преимущество имеет
метод Ml. Что касается метода приближенного вычисления
полиномов р (е), то при достаточно больших q этот метод
(обозначим его как М2) может обеспечить даже большую
сходимость, чем метод Ml. Однако надо учитывать, что за-
траты (времени или оборудования) сильно растут с увеличе-
нием q. Сравнение скорости сходимости рассмотренных мето-
дов можно произвести на основании табл. 23, в которой при-
ведены значения Во (т, I) — метод ОГП, Вг (т, I) — метод Ml
и В2 (т, I) — метод М2.
Рассмотренные итерационные схемы базировались на исполь-
зовании одного из трех методов: ОГП, Ml, М2. Естественно,
что можно строить итерационные процессы с применением
различных комбинаций этих методов, т. е. искать оптималь-
ные последовательности итераций. Приведенные значения
функции B^m^l) относились к наихудшему случаю, когда
начальное приближение ищется для первого из 2* поддиапа-
зона изменения делителя. Для большинства других поддиапа-
зонов сходимость итерационных процессов будет существенно
более быстрая. Это дает возможность строить итерационные
схемы, оптимальные для каждого поддиапазона или некоторой
части их, т. е. строить адаптивные относительно величины
делителя итерационные процессы. Очевидно, при этом в таб-
лице помимо коэффициентов для определения начального при-
ближения Ро должны храниться указания о природе итера-
ционного процесса. При однородном процессе достаточно ука-
зать число необходимых итераций.
3°.6. Реализация методов. Главным вопросом реализации
данных методов является объем таблицы, хранящей информа-
цию о данных для определения начального приближения /%,
хотя и погрешность реализации также не следует- выпускать
из вида.
Объем таблицы будет определяться не только числом под-
диапазонов (их 2й), но и точностью коэффициентов полинома
Чебышева, используемого в качестве начального приближения.
Оказывается, что наилучшая сходимость методов обеспечи-
вается, когда значение степени этих полиномов невелико. Так,
например, если для Хф>5 справедливо, что / = ф- 2, то
оптимальное значение I есть 3, т. е. X = 4.
Для того чтобы при вычислении полиномов погрешность
реализации не превосходила погрешность метода, определяе-
мую выражением (5.36), надо, чтобы длина ячеек, хранящих
коэффициенты, была не менее k (Xф-1) ф- 2Х-|-р, где р>1 —
целое положительное число. Объем таблицы в битах при этом
равен
Qx=2* (Хф- 1) \k (Х+ 1) +2Х + р].
Если в качестве начальных приближений использовать поли-
номы Чебышева степени ниже 4-й, например 0, 1 или 2-й, то
объем таблицы коэффициентов резко сократится соответст-
венно до (
Q0 = 2*(£ + p),
Q1 = 2^ (2£ + р + 2),
Q2 = (3-2*) (З^ + р + 4).
Как следует из соотношений (5.37) и (5.30) И табл. 23,
для методов ОГП (г= 1) и Ml (г = 2) справедливо неравенство
(т, 0) |й=Ао < Bi (т, 1)
Снижение значения k0 на 1 при I = 1 позволяет при лучшей
сходимости уменьшить объем таблицы коэффициентов до
Q, |л=л0-1 = 2* (2k + р). Объем таблицы будет во многом зави-
сеть от формы представления полинома Чебышева. Например,
полином первой степени может быть представлен в Фиде
Ро = a + — Д). Здесь достаточно хранить лишь коэф-
фициент d, ибо а — это адрес этого коэффициента в таблице,
т. е. значение старших (&ф-1)-го разряда делителя. Следова-
тельно, в этом случае объем таблицы будет равным Qt =
= 2/г+1 (k 4- 1 Еще большую экономию дает запись
в таблице алгоритма формирования необходимого коэффициен-
та из делителя, например, такого типа: коэффициент Р есть
сумма двух чисел — делителя, уменьшенного в два и восемь
раз, т. е. ₽ = Р2'1 ф- Ь2~\ '
Пример 5.5. Требуется, найти с помощью итерационных методов, ис-
пользующих умножение, обратную величину нормализованного делителя
с точностью до 2-56. Количество анализируемых разрядов делитёля есть
k = 5, а число сохраняемых старших значащих разрядов при приближенном
Таблица 23
в т
1 2 ' 3 4 5 6 7 8 9 10
В0(т, 0) 2.4+2 34+3 4.4+4 6.4+6 9.4+9 124+12 «18.4+18 27.4+27 364+36
В0(т, 1) — — 4.4+6 6.4+9 8.4+-12 124+18 18.4+27 24.4+36 36.4+54 54.4+81
В0(т, 2) — — — 64+10 9.4+15 12.4+20 18.4+30 27.4+45 36.4+60 54.4+90
В0(т, 3) — — — — 10.4+18 15.4+27 20.4+36 30.4+54 45.4+81 60.4+108
В0(т, 4) — — — — —• 19.4+22 18.4+33 24.4+44 304+66 54.4+77
В0(т, т) 2.4+3 3.4+5 54+9 6.4+11 8.4+15 10.4+19 124+23 144+27 16.4+31 18.4+35
В1(т, 0) — — — 5.4+5 7.4+7 11.4+11 15.4+15 25.4+25 35.4+35 55.4+55
Bi(m, 1) — — — — 104+15 14.4+21 22.4+33 30.4+45 504+75 70.4+107
Bj (т, 2) — — — — — 154+25 214+35 33.4+55 45.4+75 75.4+125
В1(т, 3) — — — — —. — 25.4+45 35.4+63 55.4+99 75.4+135
Bi(m, 4) — — — — — — 30.4+55 424+77 77.4+143
В2{т, 0) 2.4+2+? — 4.4+4+3? — 84+8+7? — 16.4+16+15? — 324+32+31?
В2(т, 1) — — 4.4+6+? — 8.4+12+3? — 16.4+24+7? — 32.4+48+15? —
В2(т, 2) — — 6.4+10+? — 12.4+20+3? — 244+40+7? — 48.4+80+15?
В2(Гп, 3) — — . — — 10.4+18+? — 20.4+36+3? — 40.4+72+7? —
В2(т, 4) — — — — — 12.4+22+? — 28.4+52+3? — 56.4+104+7?
вычислении величины e*._j есть 9 = 3. Пусть 1 = 0, т. е. начальное прибли-
жение есть константа для каждого подынтервала. В этом случае для полу-
чения желаемой точности требуется выполнить четыре обычные итерации
с общим числом умножений 8. Если использовать метод ОГП, то потре-
буется уже семь умножений. Методы Ml и М2 дают желаемую1 точность
уже при шести умножениях (заметим, что при этом метод Ml не требует
никакого дополнительного оборудования в отличие от метода М2). Нако-
нец, формируя начальное приближение с помощью полинома первой сте-
пени (Z = 1), можно желаемую точность получить за пять умножений, ис-
пользуя метод Ml. Храня для каждого из 2s = 32 поддиапазонов лишь
по одному коэффициенту разрядностью в 2 байта (т. е. р = 4), получим,
что полный объем таблицы составит лишь 64 байта.
Быстрая сходимость итерационного метода Ml и высокая
точность начального приближения, которое рационально брать
как аппроксимацию обратной величины полиномом Чебышева
первой степени, позволяют весьма быстро реализовать деле-
ние при вполне умеренном количестве дополнительного обо-
рудования..
4°. Определение частного с помощью степенных рядов.
Вычисление полинома Р(е) по схеме (5.32) позволяет за не-
сколько умножений сосчитать полином высокой степени. Это
подсказывает идеи определения частного путем разложения
обратной величины через степенные ряды. Здесь важно, чтобы
этот ряд мог быть сведен к полиному, все коэффициенты
которого есть единицы. Будем искать обратную величину как
вычисление ряда Тейлора следующего вида [33]:
b~' = а~г >Хо (1 - Ьа~У, (5.38)
причем считается, что делитель нормализован:
г-1 < b < 1 — г-я,
кроме того, а > 0, тогда область сходимости ряда к заданной
функции определена неравенством 0 < b < 2а. Введем обозна-
чение у=1—Ьа~А. Возьмем в качестве искомого значения
сумму конечного числа членов ряда (5.38), а именно р + 1.
Естественно, что результат при этом будет определен с по-
грешностью
,е = 1Г1 - a~l 2Lo у1 = - &~У+1. (5.39)
4°.1. Погрешность метода. Пусть пределы изменения де-
лителя есть ld,d-f-d0\, где r~1^d=l—d0, и значение а
лежит внутри пределов изменения делителя. Тогда согласно
(5.39) погрешность равна нулю, если а — Ь, и достигает наи-
большего значения по абсолютной величине на концах диапа-
зона. Выберем значение а, исходя из равенства абсолютных
значении погрешности, отвечающих концам интервала изме-
нения делителя, т. е. из условия
(1 - da-1 )P+1d~1 = (d + do)-1 |(d 4- d0) a-1 - lp+\ (5.40)
откуда
аопт = d + do (Ц- PVl +dod-! ). (5.41)
Подставляя это значение в одну из частей равенства (5.40),
получим
шах |е| = шахd'1 [1 + ddff1 (1 + + dod'1 )] Р (5.42)
Как следует из (5.42), чем меньше будет значение d0, т. е.
чем уже будет промежуток -изменения делителя, тем меньше
оказывается погрешность вычисления обратной-величины.
С целью уменьшения погрешности вычислений разобьем
весь диапазон изменения нормализованного делителя [г-1, 1)
на (г—l)/-*-1 равных промежутков (k — целое, положитель-
ное) и в качестве d0 возьмем d0 = r~k. Тогда для г-го под-
диапазона границами будут значения dt и dt 4- г~ь. Откуда
max | е | = г [1 г*-1 (1 Р+^ 1 4- г1-* )] р . (5.43)
Легко заметить, что выражение (5.43) принимает максималь-
ное значение, когда di = mind = r-1, т. е. делитель лежит
в первом поддиапазоне, и тогда
шах | е| = г [1 4- г”-1 (1 + 1 + )] Р • (5.44)
Величина тах|е| не может превзойти значение
So = r(l +2rk-1)~p~1. (5.45)
При определении обратной величины требуется т умно-
жений для вычисления полинома р(у) степени I (5.32) и до-
полнительно еще два умножения — одно для вычисления у =
=. 1—Ьа~х и второе для вычисления а^р(у). Значения коэф-
фициентов а-1 определены из (5.41). Однако рационально
выбрать такие значения а^1, которые позволили бы вычислить
значение хат1 без привлечения операции умножения. Напри-
мер, если ат1 есть некоторый ряд по степеням г, то умноже-
ние на аг1 реализуется как сложение нескольких чисел xrj,
которые образуются простым сдвигом числа х на j разрядов.
В дальнейшем будем предполагать, что коэффициенты аг1
таковы, что позволяют заменить умножение хат1 несколькими
сложениями, тогда вся процедура вычисления обратной вели-
чины займет I умножений. В этом случае для каждого под-
диапазона нужно хранить только информацию о разложении
числа ат1 по степеням г. Указанное разбиение на диапазоны
позволяет наиболее просто организовать доступ к информации
об аг1. Действительно, рассматривая k старших разрядов нор-
мализованного делителя как адрес некоторой ячейки памяти,
мы при конкретных значениях Ь-%, ..Ь-ь выберем одну
из (г—I)/"*-1 ячеек этой памяти, где должны храниться све-
дения о коэффициенте аг-1.
Поскольку операнды имеют разрядность п, то естественно
потребовать, чтобы максимум абсолютной величины погреш-
ности вычисления Ь~г не превышал единицы младшего разряда
обратной величины, т. е. должно выполняться неравенство
£0<^г1~п или с учетом (5.32) и (5.45)
Г m+v Т
Л<[(3-м)2 2 — 1J [£ — t-Ь logy (2 + г)1-*)], (5.46)
1 - (—1)т
где v определено как v =-------.
При заданной системе счисления с основанием г и числе k
анализируемых старших разрядов нормализованного делителя
неравенство (5.46) позволяет найти наибольшую длину опе-
рандов, при которой вычисленная в соответствии с изложен-
ным методом обратная величина делителя будет отличаться
от истинного не более чем на единицу младшего разряда.
Для двоичной системы счисления эти значения для
и приведены в табл. 24.
Таблица 24
& tn k
1 2 3 4 5 6 7 8 9 10
1 4 6 9 12 15 18 21 24 27 30
2 7 11 15 20 •25 30 35 40 45 50
3 И 16 22 28 35 42 49 56 63 70
4 17 25 34 44 55 66 77 88 99 110
5 23 34 47 61 75 90 105 120 135 150
6 36 53 72 93 115 138 161 184 — —
7 49 71 98 126 156 186 — — — —
8 74 108 149 191 — — — — — —
9 100 145 199 — — — -— — — —
10 151 220 — — — — — — — -
Интересно сравнить сходимость метода определения част-
ного с помощью степенных рядов и рассмотренных выше ите-
рационных методов. По затрате дополнительного оборудования
метод рядов сравним с итерационным методом при 1 = 0, т. е.
когда начальное приближение есть полином Чебышева^ нуле-
вой степени для каждого из поддиапазонов. Как видно цз
табл. 23 и 24, при одном и том же значении т > 1 метод
степенных рядов имеет существенно более быструю сходи-
мость, чем итерационные методы. Так, например, если k = 6,
то погрешность е0 = 2-64 достигается при четырех умножение
ях для метода степенных рядов и шести умножениях для ите-
рационного метода Ml.
4°.2. Реализация метода. Максимальное значение погреш-
ности (5.44) «достигается, когда делитель находится в первом
поддиапазоне • [г-1, + С ростом номера поддиапазона
максимум абсолютной величины погрешности снижается. По-
требуем сейчас, чтобы максимум абсолютной величины погреш-
ности для каждого из поддиапазонов также не превосходил
величины (5.45), т. е. для всех промежутков расширить пре-
делы допустимой, погрешности по сравнению с (5.43). Это
позволит выбирать в качестве коэффициентов ат1 такие вели-
чины, которые просто реализуются, т. е. имеют наименьшее
число членов при представлении их в виде суммы степеней г.
Другим полезным свойством данной ситуации является воз-
можность использования одного коэффициента для несколь-
ких подынтервалов, имеющих большой номер. Оба указанных
свойства позволяют снизить объем таблицы коэффициентов
Cf1 и уменьшить время реализации операции деления.
Представление дробной части величин аг1 в виде суммы
отрицательных степеней г в общем случае не может быть
сделано точным. Если для представления дробной части а^1
(целая часть ее всегда равна 1, ибо 1 < ат1 < 2) выделено
X разрядов, то
^7 1 ~ (^опт)< 4” А/»
причем О А/1 2-1г~\ В то же время чем меньше значе-
ние X, т^м более быстро и просто может быть найдено зна-
чение аг1 и тем меньше будет объем таблицы. Определяющим
фактором выбора значения X является максимальное значение
абсолютной величины погрешности Дг, при которой общая
погрешность в определении обратной величины делителя не
превосходит заданной величины. Было бы желательным этот
заданный уровень не очень превышать по сравнению со зна-
чением е0, определенным из (5.45). Например, по-видимому»
терпимой является верхняя граница для абсолютной величины
погрешности, имеющая значение
е* = г .
Погрешность в определении обратной величины не будет пре-
вышать заданное значение е*, если только справедливы нера-
венства [33]
I - 2г~Ч kd + Р+^1 +r-*dr')+ Г-*] 1 (5.47)
при Дг < 0 и
когда Дг > 0. Зная допустимые значения Дг, можно среди всех
возможных аг1 выбрать такие, которые имели бы наименьшее
число членов в представлении ат1 по степеням г.
Пример 5.6. Пусть задан нормализованный делитель, представленный
в двоичной системе счисления. Весь диапазон изменения делителя [~2~>
разделим на четыре поддиапазона (т. е. k — 3) с левыми границами dr =
15 3 7
= “2", d2 = “g-. d3 = и d4 = -g~. При вычислении обратной величины
делителя ограничимся пятой степенью в выражении (5.38), тогда оптималь-
ные значения будут следующими: = 1,78, = 1,455, Cjf1 = 1,23
и = 1,07. Весьма просто реализовать значения aj-1 = 1,75 = 2 — 2—2,
а^1 = 1,5 = 1 + 2-1, а^1 = 1 + 2—2 и а*1 = 1 + 2-4, при этом погрешность
представления будет следующей: Aj = —0,03, Д2 = 0,045, А3 = 0,02 и А4 =
= —0,007. Проверяем соотношения (5.48) и (5.47), из которых получаем
| Д( | < 0,03, Д2 < 0,053, Д3 < 0,063 и | Д4 | < 0,067. Отсюда находим, что вы-
бранные представления для а^1 допустимы. Более того, оказывается, что
в пределах заданной точности значение можно выбрать равным 1,125 =
= 1 + 2~3. Хотя это и не уменьшит числа сложений при умножении на
но зато потребует сдвига влево на три разряда, а не на четыре. По-
лученные значения а^1 допускают очень простое умножение вида а^1 х.
Для этого необходимо сделать два сдвига числа х (один влево на один раз-
ряд и один вправо на два разряда) и вычесть сдвинутые числа. При I = 2,
3, 4 надо сделать один сдвиг и одно сложение.
Сделанное нами расширение допустимых пределов погреш-
ности с е0 до е* не столь уж существенно повлияло на сте-
пень сходимости метода степенных рядов,. Разрешенные зна-
чения • и, при которых погрешность меньше, чем единица
младшего разряда обратной величины, определяются теперь
из неравенства

(k -Ц- log, 2)
вместо неравенства (5.46). Как видно, сходимость остается
практически прежней, а коэффициенты а^1 определяются зна-
чительно проще. с.
Недостатком данного метода деления, как и метода ите-
раций, является сложность получения остатка от деления, ко-
торый в этих методах прямо не определяется.
ГЛАВА б
НЕОСНОВНЫЕ АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ
Алгебраическое сложение, умножение и деление являются
основными арифметическими операциями цифровых машин.
Время реализации этих операций будет при, всех прочих рав-
ных условиях определять быстродействие машины. Конечно,
помимо основных операций в процессе прохождения программы
приходится выполнять, а иногда и довольно часто, другие
арифметические операции, такие, как вычисление квадратного
корня, вычисдение логарифмов, тригонометрических функций
и т. д. Как правило, неосновные арифметические операции
реализуются программным путем, т. е. как выполнение опре-
деленной программы, вычисляющей по заданному аргументу
ту или иную функцию. Подобные программы входят в состав
математического обеспечения машин и при необходимости
вычисления заданного арифметического действия достаточно
указать номер соответствующей программы в библиотеке стан-
дартных программ. Однако для того чтобы получить резуль-
тат, приходится выполнить несколько десятков машинных
операций, и поэтому время ожидания ответа оказывается во
много раз больше, чем время выполнения основных арифме-
тических операций.
С развитием технических средств вычислительной техники
и постоянным снижением их стоимости все более актуальным
становится вопрос о передаче части функций математического
обеспечения машин на аппаратные средства. В первую очередь
это касается сложных арифметических функций, которые в не-
которых типах вычислений встречаются весьма часто, а время
реализации их программным путем весьма велико. Несомнен-
ный интерес представляет исследование методов вычисления
сложных арифметических операций, таких, как перевод из од-
ной системы счисления в другую, извлечение квадратного
корня, вычисление элементарных функций, допускающих
аппаратурную реализацию этих методов за время, близкое
к времени выполнения операции деления.
Проблема аппаратурной реализации элементарных функций
вначале возникла при создании проблемно-ориентированных
вычислительных машин, таких, как машины для решения на-
вигационных задач и калькуляторы для выполнения научных
расчетов. Однако по мере развития технологии больших ин-
тегральных схем (БИС) эта проблема стала актуальной и для
универсальных машин в связи с созданием „твердого" мате-
матического обеспечения (МО), т. е, такого МО, которое реа-
лизовано не программным, а аппаратурным путем.
Алгоритмы неосновных арифметических операций в случае
аппаратурной реализации часто существенно отличаются от
алгоритмов программной реализации. Это связано с тем, что
при аппаратной реализации вполне очевидно стремление строить
алгоритмы на основе многократного сложения-вычитания
и сдвигов. Рассмотрение алгоритмов неосновных арифметиче-
ских операций начнем с операции возведения в квадрат.
§ 1. ВОЗВЕДЕНИЕ В КВАДРАТ
Возведение в квадрат относится к числу довольно распро-
страненных операций цифровых машин. На практике эта опе-
рация выполняется как обычное умножение. В то же время
можно ожидать, что прямая реализация операции возведения
в квадрат окажется более экономичной и более быстродей-
ствующей, чем умножение.
Пусть операнды представлены целыми положительными
числами. Когда операнды равны (случай возведения в квад-
рат), массив частичных произведений оказывается симметрич-
ным относительно диагонали, составленной из элементов ар.
Кроме этих элементов, образующих главную диагональ, осталь-
ные встречаются дважды (apj = ар-^, и, следовательно, час-
тичное произведение на г-м шаге алгоритма определится как
= ар (ар + 2 i = 0,1. (6.1)
Отсюда длина частичных произведений оказывается перемен-
ной и зависимой от номера шага алгоритма. Поскольку с уве-
личением номера шага длина обрабатываемых операндов умень-
шается, то имеется возможность реализации операции возве-
дения в квадрат .более экономичным и быстрым способом, чем
обычное умножение. Количественные оценки зависят от прак-
тического способа выполнения умножения. Рассмотрим не-
сколько примеров {31]. .
1°. Использование деревьев спуска. Пусть г = 2 и произ-
ведение формируется как' спуск частичных произведений по
дереву, составленному из двоичных сумматоров с тремя вхо-
дами и двумя выходами (рис. 26). Для построения такого
дерева требуется п? схем совпадения с двумя входами, п (п —
— 2) сумматоров с тремя входами и п сумматоров с двумя
входами. Максимальная задержка в получении результата
после одновременного поступления всех конъюнкций на дере-
во спуска определяется выражением (5.37).
Рис. 32.
При возведении в квадрат дерево спуска значительно упро-
щается (рис. 32). Для его построения требуется лишь n w 2 *
схем, совпадения на два входа, (п — 2) (-у-) трехвходовых
и п — 1 двухвходовых сумматоров [31]. Деревья спуска при
возведении в квадрат оказываются симметричными относи-
тельно п 2 1 -й вертикали, которая к тому же является самой
высокой. Очевидно, что максимальная задержка в получении
результата не будет превышать величины
Т = + (п — 2) тс + шах (д~| + 5. Ts) (я — 2) Тс),
где
На практике обычно выполняется соотношение
VC^.X 2тс.
Тогда спуск по самой высокой вертикали оказывается более
быстрым, чем распространение переноса по основанию дерева
до этой вертикали. Отсюда
т = Л + 2 (п — 1) V
(6.2)
Сравнивая (5.37) и (6.2), находим, что возведение в квадрат
реализуется быстрее, чем умножение, причем выигрыш во
времени может достичь одной трети максимального времени
формирования произведения (при ts = 2tc). На самом деле
верхняя граница времени задержки в получении результата
при квадрате (6.2) может быть снижена до
^ + («- *) V (6-3)
При заданной организации дерева спуска эта верхняя граница
зависит от порядка расположения входных переменных' на вер-
тикалях дерева, и существуют по крайней мере для некото-
рых п > 4 такие распределения переменных, которые приводят
к еще меньшей верхней границе, чем (6.3). В то же время
даже при самом неудачном распределении переменных нельзя
превысить для т величины, определенной из (6.2).
Заметим, что имеются еще определенные возможности
в уменьшении оборудования дерева спуска при возведении
в квадрат, ибо в этом дереве имеется р = (п — 1 + 8)/2 двух-
входовых сумматоров, каждый из которых суммирует две ве-
личины ak+i и a*aj>+i, но в этом случае s = ak+i ф =
= и p — akUk+x- Если считать, что реализация конъюнк-
ции акак+1 требует столько же оборудования, как и'конъюнкции
aka.k+i, то количество оборудования дерева спуска сокращается
на р двухвходовых сумматоров, но увеличивается на столько
схем совпадения. Имеются еще и другие возможности умень-
шения количества оборудования, но при этом нарушается
однородная структура дерева сумматоров.
Указанные усовершенствования позволяют еще уменьшить
время спуска. Например, если при квадрате двухвходовые сум-
маторы заменяются на схемы совпадения, то время спуска
уменьшается до величины
п— 1 — 6 I Z п\
7 = ---2—+ (/г —2)тс.
При модификации деревьев спуска, такой, какая была опи-
сана в главе 5 § 3, вычисление произведения и квадрата будет
производиться приблизительно за одно и то же время (хотя
квадрат всегда вычисляется быстрее). Основное же отличие
заключается в существенном уменьшении оборудования (более
чем в два раза) при реализации операции возведения в квадрат.
2°. Последовательное суммирование. Пусть теперь в на-
шем распоряжении имеется лишь один сумматор, тогда час-
тичные произведения могут быть просуммированы лишь после-
довательно. Время образования произведения при /г-разрядных
операндах составит величину при п = k -|- 1
где т0 — время сложения (п ф- 1)-разрядных чисел в г-ичной
системе счисления в параллельном сумматоре. Весьма часто
т0 есть линейная функция числа разрядов п и времени сложе-
ния в одном разряде ts, т. е.'
где -[ — постоянная величина и
При возведении в квадрат методом последовательного сум-
мирования существенное значение имеет метод формирования
частичных произведений вида (6.1). Например, для двоичной
системы счисления имеем
p<0=a^(^ + S^f+1ay2>),
а следовательно, длина частичного произведения будет умень-
шаться с ростом I, причем самая большая длина (при I = 0)
есть п ф-1. Отсюда
। т 2л=о (n ф- 1 — 0. (6.4)
Если а,-=1, 4 = 0, 1, ..., k, то
л 4~ 3
max т = ^tsti —g—•
Таким образом, по сравнению с умножением время реали-
зации возведения в квадрат уменьшилось в t раз, и
2п
< 1 ' п + 3"
В случае, когда г > 2, выигрыш оказывается еще более
ощутимым, если только удвоение части множимого может
быть произведено операцией сдвига. Если же этого не удастся
достичь, то время умножения равно времени возведения
в квадрат.
При использовании метода приближенного умножения,
когда в процессе операции меняется длина множимого, время
реализации определится как
Т = (п ф- 1) “Ь TTs а1 (Р Ф" 2 ф- I).
Заметим, что наибольшее сокращение времени приближенного
умножения по сравнению с точным достигается, когда а,=
= r—1 для всех i = 0, 1, ..., k—p и
шах Дт = (k ф-1 -p)(k— р).
Напомним, что итеративное умножение приводит к опре-
деленной погрешности в получении результата, но требует
для своей реализации меньшего оборудования (вместо памяти
в Зп разрядов в. арифметическом узле необходима память
лишь в 2п + р разрядов).
В случае равенства операндов (возведение в квадрат) этот
результат может быть существенно улучшен. Прямая реали-
зация этой операции в соответствии с уравнением (6.1) позво-
ляет достигнуть той же точности уже с памятью в п -]- р + 1
разрядов, а не с памятью в 2/i-f-p + 2 разрядов. Следователь-
но, точное значение квадрата получается при емкости памяти
арифметического устройства 2n + 1 разряд (не считая одного
разряда для хранения переноса при г > 2). Это является су-
щественным преимуществом данной операции перед умноже-
нием. В случае, когда удвоение числа производится простым
сдвигом и время сложения прямо пропорционально числу
разрядов в слове, задержка в получении результата опреде-
лится как
т — Г, [2д=л (п + 2 — i) + 2Ьо‘(Р + i)L
где 'Х = Р4г-]-
Выигрыш во времени при итеративном возведении в квад-
рат (на каждом шаге операнд уменьшается на один разряд,
а его место занимает очередной разряд результата) пр срав-
нению с прямым возведением в квадрат (6.4) составит величину
Ат = Vs Si=o а{ (п + 2 — р — 2t).
Если для всех i = 0, 1,' .... k, то
шах Ат = ps(X — 1) (п — р —гХ).
Таким образом, и при формировании результата с помощью
одного сумматора возведение в квадрат оказывается и более
быстродействующей, и более экономичной операцией. Послед-
нее свойство может оказаться весьма привлекательным для
некоторых типов минимашин.
3°. Табличные методы. При двоичном умножении каждый
результат есть 2п-разрядное число, и всего таких различных
чисел будет 2n-1 (2n—1). Значения операндов можно рассмат-
ривать как адреса для нахождения ответа в таблице резуль-
татов. Когда подобная таблица строится для возведения в квад*
рат, то число адресов уменьшается до 2л—1, хотя каждый
адрес соответствует, как и ранее, 2я-разрядному результату.
Отсюда табличная реализация возведения в квадрат несрав-
ненно экономичнее, чем умножение.
Значение каждого разряда произведения двоичных чисел
в принципе можно определить как значение определенной
переключательной функции. И тогда реализация табличных
методов сводится к определению 2п переключательных функ-
ций. Однако даже при небольшой разрядности практическая
реализация этих переключательных функций для умножения
чрезвычайно затруднительна. В то же время при возведении
в квадрат уменьшение числа переменных, участвующих в фор-
мировании переключательной функции для у-го разряда
(рис. 33), позволяет найти приемлемое решение, правда все-
таки при небольших n(n-<8).
о6а7 а5а7 а4а7 о3о7 а2с7
С5С2 @5^2 @3^2 П2
о?
аба3- °3°3 а4а3 а3
Q6Q4 Q5C4 Qif
йвК. as
ае_____________________________________________
Р12 Р77 Рю Рд Ре Р? Ре Рз ' Рд Рз Рг Pi
Рис. 33.
Итак, пусть результат есть р = а2= Т + К, где функция Т
есть 2п-разрядное число, образованное верхней строкой и край-
ней левой диагональю массива данных и элементом ak (рис. 33):
^ == 1, CtkClk—i, iZfeiZfe—2, • .CLjjCLq, . . ., U^CLq, 0, CLq.
Функция /C=S»^o1A'i2' есть двоичное представление суммы
оставшихся после формирования Т элементов массива частич-
ных произведений. Значение 7\, Z = 0, 1, ..., 2k -]- 1, есть
конъюнкция двух переменных, а значение Kt— нормальная
дизъюнктивная форма переключательной функции. Приведем
выражения для Kt при п — 6:
Ко = 0, Ki = 0, К2 — Къ = 0, /<4 = а2«7,
КЪ = V Л'е = «1«2«3 V V «7«з«4 V «2йЗа4>
К = V «2«за4 V V «i«2«3, К& = azai V «за4,
Aj = Кю = 0, Кц — 0.
Время формирования функций Tt и Kt равно времени за-
держки на одной и двух логических ступенях соответственно
(считаем, что инверсии переменных заданы). Таким образом,
время возведения в квадрат оказывается равным времени сло-
жения (2/г — 2)-разрядных операндов. Представление величины
р в виде двух слагаемых позволило использовать уже имею-
щиеся аппаратные средства (сумматор на 2п входов) для реа-
лизации возведения в квадрат и тем самым снизить дополни-
тельные затраты. При реализации переключательных функций
на однородных средах более эффективным оказывается иное
представление значения р в виде двух слагаемых, чем приве-
денное выше.
Пусть теперь р — а2 = s с, где sf ис;, i=0, 1, ..., 2п —
— 1, есть значение суммы по модулю два от всех переменных,
образующих г-й разряд произведения, и значение двоичного
переноса соответственно. Тогда для п = 6 имеем
s0 = «0, с0 = 0; Sj = 0, = 0; s2 = с2 = aiao,
s3 = «2ао, сз = 0; st, ct = s, с (a3a0, a2al, a2);
s5, c5 = s, с (а^а0, a3ai); s6, c6 = s, c (a5, a0, a^, d^a2y,
s7, cr= s, c (a5ait ata2, a3a2)', s&, c& = s,c (a5a2, ata3, at);
Sg = d$d3, = 0; s10 - d^d^, = <256/4; = 0, = 0,
где s, c (x, y, z) определяется из соотношений
s = x ф у ф z, с = ху v XZ V yz.
Формирование функции s и с производится за время задержки
на три и две логические ступени. Количество оборудования,
необходимое для реализации функций s и с, оказывается су-
щественно меньшим, чем функции р прямо. Так, если одно-
родная среда состоит из двоичных сумматоров, то при п = 6
необходимо всего пять сумматоров вместо 15 при использо-
вании дерева спуска.
4°. Реализация умножения через возведение в квадрат.
В подавляющем числе будущих цифровых машин, как и сей-
час, возведение в квадрат будет осуществляться через умно-
жение. Однако представляется возможной и прямая реализация
возведения в квадрат. В очень -мощных вычислительных сис-
темах, где скорость выполнения операций является решающим
фактором, имеет смысл наряду- с аппаратурой, реализующей
алгоритм умножения, включать аппаратуру, позволяющую
выполнять возведение в квадрат, хотя, может быть, и для
чисел меньшей разрядности. При этом может существенно
увеличиться скорость реализации сложных операций, например
деления, когда оно основано на,итерациях (глава 5, § 4).
Наиболее реально применение прямого возведения в квад-
рат в минимашинах, где сложные операции выполняются через
подпрограммы. В этом случае экономичная и быстрая реали-
зация возведения в квадрат позволяет достаточно просто вы-
числять произведение по формуле
^=(а + />)22-2 + (й-Ь)22-2. (6.5)
Возможны также и другие формулы вычисления произведения
ab, но они связаны с большим числом возведения в квадрат.
Вычисление по формуле (6.5) сталкивается с двумя затрудне-
ниями. Во-первых, необходимость втцснуть операнды х = (а +
+ Ь) 2~’ и у = (а — b) 2-1 в прокрустово ложе п-разрядной
сетки машины приводит к приближенному вычислению произ-
ведения, что иногда недопустимо. Во-вторых, деление на 2,
лишь для некоторых систем счисления осуществляемое сдви-
гом, приводит к существенному увеличению времени реали-
зации. Для двоичной системы счисления, наиболее интересной
с практической точки зрения, точное произведение может
быть вычислено следующим образом. Вначале определяется
младшая цифра суммы а -|- Ь, которая есть х0 = а0 ф Ьо. Заме-
тим, что значение этой цифры равно значению младшей циф-
ры разности а — Ь, ибо у0 = а0 ф Ьо ф 1 = а0 ф Ьо. Затем путем
сложения-вычитания и сдвига вправо формируются операнды
х' = х — х02-1 и у' = у— у02-1. При этом разряды, вышедшие
за разрядную сетку при сдвиге, теряются. Окончательный ре-
зультат вычисляется по формуле
р = х2 — у'2Ч- х0Ь.
Полученное значение р в точности равно ab. Таким образом,
умножение реализуется через два возведения в квадрат и от
трех до четырех сложений (четыре сложения необходимы,
когда один операнд четный, а другой нет).
5°. Возведение в квадрат дополнительных кодов. Ранее
неявно Предполагалось, что сомножители представлены в виде
прямых кодов. Когда же используются дополнительные коды,
т. е. сомножители имеют значение (1.4), то операция умно-
жения усложняется (см. главу 2, § 2). При возведении в квад-
рат результат всегда будет положительным, что позволяет
упростить алгоритм умножения одинаковых дополнительных
кодов.
Рассмотрим случай двоичной системы счисления, когда
р^а2 = (2Lo + а*22к+2 - a„2k+2 a-2l =
= (SLo «г2‘Т + a*22k+2 (1 - «*) - «*2*+2 Sfco1 at2l. (6.6)
В выражении (6.6) отрицательный ; член заменим суммой
—a^.22fe+2 + rz.y.2ft|2 (2/-1 aft1 + 1), тогда
р = ~a*ak2*^ + (2Lo а?)* + а*2^ (2U1 а? + 1). (6.7)
Поскольку квадрат дополнительных чисел есть положительное
число, то значение р, определенное из (6.7), надо взять по
модулю 22/г, следовательно,
Р = + а.^ (2U1 at2l + 1) (mod 22*).
Пример 6.1. Число 5 представлено в двоичной системе счисления до-
полнительным кодом при п = 3, т. е. « = 1.011. Найти квадрат числа а.
Вначале находим значение квадрата основных разрядов числа а, получим
а.' = 1001. Затем определяем произведение «д.24 (Q-Р-1 + 1), которое
есть а" = 10000. * Для определения «2 сложим а' и «", тогда окончательно
получим в2 = а' + а" = 11001, т. е. в2 = 25.
Предложенный способ не требует для своей реализации
операции вычитания и предварительного преобразования опе-
ранда. . Единственно, чем будет отличаться возведение в квад-
рат дополнительных кодов, — это увеличение числа частичных
произведений, отвечающее прямым кодам, еще на одно. В це-
лом, как и для прямых кодов, операция возведения в квадрат
оказывается при реализации более экономичной, чем умно-
жение. Роль операции возведения в квадрат значительно уси-
ливается при аппаратурной реализации элементарных функций.
§ 2. ИЗВЛЕЧЕНИЕ КВАДРАТНОГО КОРНЯ
При аппаратурной реализации операции извлечения квад-
ратного корня стараются по возможности максимально исполь-
зовать аппаратуру основных арифметических операций. Вполне
очевидными являются два пути решения рассматриваемой
задачи. Первый путь связан с разработкой микропрограммы
извлечения квадратного корня, базирующейся на использова-
нии основных арифметических операций. При этом удается
наиболее полно использовать базовую аппаратуру и сама мик-
ропрограмма является реализацией того или иного итерацион-
ного метода извлечения квадратного корня. Другой путь со-
стоит в создании алгоритма извлечения квадратного корня,
сходного по структуре с алгоритмами умножения и сложения.
Можно ожидать, что второй путь приведет к более быстрой
реализации, но, возможно, здесь потребуется создание само-
стоятельного блока.управления, дополнительного по сравне-
нию с аппаратурой основных операций.
Ниже будет рассмотрен алгоритм извлечения квадратного
корня, используюфий- известную закономерность — квадрат
целого числа есть сумма ряда последовательных нечетных
чисел. Этот алгоритм мы попытаемся реализовать как вариант
алгоритма деления. Будем считать, что операнды представлены
прямыми кодами в форме с запятой, фиксированной перед
старшим разрядом. Учет порядка операнда трудностей не вы-
зывает— если он четный, то порядок результата есть поло-
вина порядка операнда, если же он нечетен, то сам операнд
сдвигается вправо на один разряд (уменьшая в г раз), а его
порядок увеличивается на единицу. Порядок результата будет
половина нового порядка операнда.
Перед началом операции имеет смысл провести анализ
знака операнда и его величины на нуль. При нулевой вели-
чине результат известен сразу — это нуль. Если знак операн-
да отрицательный, то обычно ситуация рассматривается как
аварийная и операция не производится (АВОСТ). В остальных
случаях определение корня квадратного из мантиссы органи-
зуется следующим образом.
Весь процесс разбивается на ряд однотипных шагов, вы-
полняемых последовательно, и на каждом шаге находится
очередная цифра результата. Значение цифры определяет
результат вычитания из остатка (на первом шаге остаток —
это подкоренное число) специально сформированного числа.
По знаку разности выбирается дальнейший путь развития
алгоритма. Если разность оказалась положительной, то в спе-
циальный счетчик, где образуется очередная цифра, заносится
+1, и происходит формирование нового значения вычитаемого.
Затем управление вновь передается на вычитание из остатка
этого заново сформированного числа, и данный процесс про-
должается до тех пор, пока не будет получен отрицательный
знак разности. Тогда процесс нахождения цифры результата
заканчивается, восстанавливается остаток, сдвигается влево
на разряд, формируется новое вычитаемое и осуществляется
переход на следующий шаг алгоритма. Рассмотренный алго-
ритм весьма похож на обычный алгоритм деления, за тем
исключением, что в процессе операции все время меняется
„делитель
В случае двоичной системы счисления процесс формиро-
вания вычитаемого и определения очередной цифры резуль-
тата особенно просты, ибо они производят в соответствии
со следующим алгоритмом:
в качестве очередной цифры результата c~i (•!>< i п — 1)
выбираем максимальное при котором
4° = а<1~» - с^1-1 (2^ + 2~I-Z) > 0. (6.8)
Результат операции есть Алгоритм (6.8) пол-
ностью совпадает с алгоритмом деления (2.28), если принять
что „делитель“ есть с^2Гу Н-2-1 Этот „делитель“ об-
разуется весьма просто — берется уже. найденный на предыду-
щих i — 1 шагах алгоритма результат и. к нему приписываются
еще два младших разряда с учетом веса, зависящего от но-
мера шага (рис. 34). При обычной разрядности регистров
арифметического устройства и сумматора (рис. 35) результат
определится за п — 1 шаг, следовательно, его погрешность
не превысит 21-", что лишь в два раза больше погрешности
обычного деления. Время реализации операции извлечения
квадратного корня оказывается, приблизительно таким же, как
время выполнения операции деления с восстановлением остатка
для n-разрядных операндов.
Рис. 34.
Особенности формирования „делителя*1 при извлечении
квадратного корня позволяют ограничиться всего двумя ре-
гистрами арифметического узла (рис. 35) при технической
реализации операции вместо трех регистров при делении
(рис. 16). Само формирование „делителя*1 может быть легко
осуществлено путем записи очередной сформированной цифры
результата в регистр В под управлением счетчика шагов опе-
рации (на рис. 16 он не показан, хотя, конечно, существует
в схеме управления арифметическим узлом). Таким образом,
перед выполнением i-го шага алгоритма в регистре В будет
записано число 1 Завершение формирования „дели-
теля" (для чего к содержимому регистра В необходимо до-
бавить величину 2-1-') производится суммированием значения
регистра В с соответствующим выходом счетчика шагов опе-
рации.
57
Пример 6.2. Дано число а = 1 , представленное двоичным кодом
в форме с плавающей запятой, т._ е. а = 21-0,1111001g- Требуется найти
корень квадратный из а. Поскольку порядок нечетный, то вначале произ-
водится денормализация числа а, т. е. а = 22-0,0111 1001g, а затем перехо-
дим к реализации алгоритма извлечения квадратного корня из мантиссы.
1-й шаг + 0.01111001 1.11000000 Ъ, а<°> = а b = 0,01
10.00111001 -а(0) > 0, поэтому с_! = 1
2-й шаг + 0.01110010 1.01100000 ь, b = .0,101
1.11010010 -а™ < 0, отсюда С-2 — 0;
3-й шаг + 0.11100100 1.01110000 -а™ ь. b = 0,1001
10.01010100 > 0, поэтому с_3 = 1
4-й шаг + 0.10101000 1.01011000 -а™ ь, b = 0,10101
10.00000000 -а^ = 0, отсюда с_4 = 1.
Остаток после 4-го шага алгоритма есть нуль и поэтому, хотя счетчик
шагов операции еще не заполнен (т. е. операция не закончена), процесс
можно прервать, поскольку все последующие цифры результата будут
иметь нулевое значение. Окончательно получим, что с— а = 2-0,1011g, т. е.
11
с= 8 "
Основным недостатком данного алгоритма является необ-
ходимость восстановления остатка, что приводит к разному
числу действий алгебраического сложения на i-м шаге опе-
рации. Не говоря о том, что это заметно увеличивает время
выполнения операции, данный недостаток затрудняет построе-
ние однородных структур для реализации извлечения квад-
ратного корня. Было бы естественным использовать алгоритм
без восстановления остатка, который в случае двоичной сис-
темы при делении давал лишь одно действие на каждом шаге
операции. Однако алгоритм без восстановления остатка суще-
ственным образом базировался на постоянстве делителя на всех
шагах. При извлечении квадратного корня „делитель" же
меняется на каждом шаге. Положение оказывается не столь
уж безнадежным для двоичной системы счисления.
Заметим, что отрицательный остаток получается, если оче-
редная цифра результата имеет значение нуль. Это означает,
что „делитель" этого г-го шага больше делителя следующего
Рнс. 36.
шага на величину 22~г. Следовательно, после удвоения оче-
редного остатка результат получается меньше истинного на
2 1-z. Но иногда легко осуществить необходимую коррекцию —
для получения правильного, итога надо на следующем шаге
прибавить делитель + 2~1~z + 2“2~z. Этот модифи-
цированный делитель отлйчается от обычного только тем, что
он больше исходного на 2-1~z- Это увеличение реализуется
точно так же, как и прибавление величины 2~2-1 (рис. 36).
Пример 6.3.
Дано число а =
289
1024 ,
представленное двоичным кодом
в форме с плавающей запятой, т. е. а = 2 1 • 0,100100001. Найти У а . Пос-
ле необходимой денормализации мантиссы получим « = 0,0100100001:
1-й шаг , 0.0100100001 — «(0), «(0) = а
+ 1100000000 ------b, b = 0,01
10.0000100001 —> 0, поэтому c_j = 1;
2-й шаг , 0.0001000010 — «(1)
+ 1.0110000000 -------b, b = 0,101
1.0111000010 —с№ <0, отсюда с_2 = 0;
3-й шаг , 0.1110000100 — «(2)
+ 0.1011000000 — 6, Ь = 0,1011
1.1001000100 —< 0, следовательно, с_3 = 0;
4-й шаг , 1.0010001000 — я(3>
+ Д). 1001100000 — b, b = 0,10011
1.1011101000 — < 0, поэтому с_4 = 0;
5-й шаг , 1.0111010000 — «<4)
+ 0.1000110000 — b, b = 0,100011
10.0000000000 — аУ* = 0, отсюда с_5 = 1.
Поскольку остаток после 5-го Шага есть нуль, операция заканчивается,
и окончательно имеем с= У а — 2°-0,100012, т. е. с = 17/32.
Алгоритм извлечения квадратного корня, базирующийся
на методе „псевдоделения“, без восстановления остатка может
быть достаточно просто реализован на однородных матричных
структурах (см. главу 8). В случае двоичной системы счисле-
ния на каждом шаге алгоритма выполняется одно алгебраиче-
ское сложение, что позволяет довести быстродействие опера-
ции извлечения квадратного корня до быстродействия опе-
рации деления. Итеративное изменение длины „делителя" на
каждом шаге' алгоритма открывает дополнительные возмож-
ности повышения быстродействия данной операции особенно
для арифметических устройств последовательного действия
либо арифметических устройств с матричной структурой.
§ 3. МЕТОДЫ ВЫЧИСЛЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Можно ожидать, что при аппаратурной реализации не все
методы, которые ранее использовались для вычисления эле-
ментарных функций программным путем, окажутся в одина-
ковой степени приемлемыми. На выбор конкретного метода
будут влиять те цели, которых мы стремимся достичь при
аппаратурной реализации, и те технические средства, которы-
ми мы будем при этом располагать.
1°. Приближение функций полиномами. Широко извест-
ные методы вычисления элементарных функций f(x) с по-
мощью их разложения в ряды или путем их аппроксимации
полиномами наилучшего приближения основаны на вычисле-
нии полинома степени I от заданного аргумента х, имеющего
для данной функции постоянные коэффициенты [3, 8, 15]. Если
в вычислительной машине выделить область в быстрой памяти
для хранения этих коэффициентов (или указания как их фор-
мировать), то время вычисления элементарных функций будет
зависеть от того, как быстро мы сумеем сосчитать полином
Z-й степени. При использовании для вычисления полинома
схемы Горнера потребуется приблизительно I операций умно-
жения и I операций сложения. Для обеспечения большой точ-
ности1'требуется считать полиномы высокой степени, что при
применении схемы Горнера может привести к чрезмерной
задержке получения ответа. Выход может быть найден в вы-
числении полиномов по схемам, учитывающим конкретное
значение коэффициентов (12, 19]. Грубо говоря, можно всегда
снизить чисЛо умножений до
+ 2, а иногда (см. главу 5,
§ 3) и несравненно больше [14]. В результате может оказать-
ся, что вычисление элементарной функции с большой точ-
ностью будет произведено за несколько (четыре — шесть) умно-
жений (как это было с вычислением обратной величины). Для
повышения точности при использовании указанных методов^
промежуток изменения аргумента разбивают на несколько
поддиапазонов, но тогда приходится уже хранить сведения
о коэффициентах для каждого поддиапазона. Тенденция сни-
жения стоимости постоянной памяти и использование только
двух арифметических операций (умножения и сложения) де-
лают этот метод весьма перспективным для аппаратурной
реализации элементарных функций особенно в машинах уни-
версального назначения.
2°. Метод цепных дробей. Пусть функция f(x) представ-
лена в виде
f (х\ ~ С1° + С11Х + С12'у2 3~ • •
Соо + С01Х + Соз*2 + • • -
После ряда преобразований [3, 8] эта функция принимает вид
/(*) =
с10
с00 +
с10 +
Cso*
с20 + ;
С2(Х
т. е. представлена цепной дробью. Коэффициенты разложения
вычисляются по формуле cjk г
Cj—2,0 Cj-2, fell
Cjk Л S’
Cj-ifi cj—l, k+1
Вычисление различных функций с помощью цепных дробей
производится по одной и той же схеме [3, 9] и требует хра-
нения небольшего числа коэффициентов cjk. Однако использо-
вание операции деления и большое время вычислений, кото-
рое есть
х = Т (тум 4“ '’•дел 4" Т-сл)»
где 7 — число звеньев дроби, не дают возможности широко
использовать данный метод при аппаратурной реализации вы-
числения элементарных функций. Для вычислительных машин,
где время выполнения вычислений не является определяющим
(например, калькуляторы), этот метод вполне приемлем.
3°. Метод рациональных дробей. В этом методе функция
f (х) представляется как отношение двух полиномов, каждый
из которых имеет степень, существенно меньшую, чем при
вычислении этой функции методом приближения полиномами.
Время вычисления функций складывается из времени вычис-
ления полиномов и времени одного деления.
. 4°. Табличные /методы. Суть Табличных методов заклю-
чается в том, что для каждого из допустимых значений аргу-
мента х в специальных таблицах хранятся значения функции
f(x). Для получения значения f(x) по заданному аргументу
достаточно только обратиться к этим таблицам за выбором
ответа. В случае реализации таблицы в виде специальной по-
стоянной памяти цифровой машины время ответа будет чрез-
вычайно мало. Трудности, связанные с аппаратурной реализа-
цией данного метода, заключаются в чрезвычайно большом
объеме таблиц, если мы требуем высокую точность вычисле-
ния функций. Так, если аргумент представлен «-разрядной
двоичной дробью, то таблица результатов, заданных с той же
точностью, что и аргументы, должна иметь 2”-« бит, что со-
вершенно не реально. Однако получение значений функций
с небольшой точностью — вполне реальная вещь. Эта возмож-
ность стимулировала развитие таблично-алгоритмических ме-
тодов.
5°. Таблично-алгоритмические методы. В этих методах
процесс вычисления функции f(x) разбивается на два этапа.
На первом этапе по значению аргумента х из специальных
таблиц извлекается некоторая информация, позволяющая вы-
числить значение функции f(x). Характер этой информации
зависит от принятого метода вычисления функции f(x). На-
пример, если функция f (х) вычисляется с помощью линейно-
кусочной аппроксимации f (х) = ах + b на каждом из 2/г отрез-
ков, на которые разбивается диапазон изменения аргумента,
то в таблицах могут храниться либо значения коэффициентов
а и Ь, либо указания, как их можно сформировать (см. гла-
ву 6, § 4).
На втором этапе производится непосредственное вычисле-
ние функции /(х) по выбранному алгоритму. В зависимости
от этого алгоритма при вычислении/(х) могут использоваться
различные арифметические действия. При небольшой разряд-
ности аргумента таблично-алгоритмические методы, основан-
ные на разного рода аппроксимациях функции f (х) на выде-
ленном подынтервале, оказываются очень эффективными, и их
аппаратурная реализация не требует больших затрат обору-
дования и в то же время обеспечивает очень быстрое вычис-
ление элементарных функций f(x) [3, 18]. В тех случаях,
когда требуется получение результата с большой степенью
точности, на втором этапе реализуется не вычисление аппрок-
симирующих полиномов, а некоторый итерационный процесс.
6°. Итерационные методы. При вычислении функции f{x)
итерационными методами мы последовательно определяем числа
У.п = Т п = 1, 2, ..., (6.9)
каждое из которых есть некоторое приближение к искомому
значению у. Если последовательность чисел уп сходящаяся,
то формула (6.9) обеспечивает вычисление функции у =f (х)
с любой степенью точности при достаточно большом числе
шагов (числе п) [3, 8]. Итерационный процесс может быть
построен таким образом, чтобы на i-й итерации, т. е. когда
вычисляется значение у; по известному значению уг-i, опре-
делялись все цифры i-го приближения. Однако возможны
и такие процессы, когда на каждом шаге определяется одна,
но уже окончательная цифра результата. Такие методы полу-
чили название „цифры за цифрой".
Средства, привлекаемые для выполнения уг — <р (yi-i)., мо-
гут быть весьма разнообразными, но все-таки их можно раз-
бить на две группы: средства, использующие только простей-
шие арифметические операции (сдвиг, сложение), и средства,
использующие сложные арифметические операции (умноже-
ние, деление). В первом случае алгоритмы вычисления всех
элементарных функций организуются точно так же, как алго-
ритмы умножения и деления, и, следовательно, допускают
очень простую аппаратурную реализацию [2, 3, 18, 59, 67].
В случае использования сложных операций можно добиться
более быстрых вычислений (за счет уменьшения числа итера-
ций), если цифровая машина обеспечивает малое время ответа
при делении и особенно умножении. Среди итерационных
методов, развивающихся в последнее время, особенно следует
отметить один из методов „цифра за цифрой", позволяющий
свести вычисление всех элементарных функций к вычислению
базовых процедур, реализуемых на базе алгебраического сло-
жения и сдвигов.
Эффективность аппаратурной реализации итерационных ме-
тодов в ряде применений будет определяться скоростью
сходимости выбранного итерационного процесса. этой связи
несомненный интерес представляет построение оптимальных
итерационных процессов, позволяющих при заданных усло-
виях добиться наилучшей сходимости (пример такого метода
был дан в главе 5, § 3 при исследовании методов ускорен-
ного деления). Весьма быстрая сходимость обеспечивается,
если начальное приближение у0 задается с большой точностью,
что можно обеспечить построением специальных таблиц для
значений начальных приближений. В этом случае принято
говорить о таблично-итерационных методах вычисления эле-
ментарных функций.
Поскольку алгоритм вычисления значения yz не зависит
от номера итерации i, то аппаратурная реализация итерацион-
ных методов обычно не вызывает большой сложности. Для
более детального знакомства с методами аппаратурной реали-
зации элементарных функций мы ниже рассмотрим вычисле-
ния логарифма двойных чисел методом линейно-кусочной
аппроксимации, таблично-итерационный метод извлечения квад-
ратного корня и универсальный метод „цифра за цифрой".
§ 4. ВЫЧИСЛЕНИЕ! ЛОГАРИФМА ДВОИЧНЫХ ЧИСЕЛ
МЕТОДОМ ЛИНЕЙНО-КУСОЧНОЙ АППРОКСИМАЦИИ
Будем считать, что числа, с которыми оперирует цифровая
машина, заданы в двоичной системе счисления в форме с пла-
вающей запятой, т. е, а = 2рЛ1, где 2"1 | М | 1 — 2~” и 7И —
нормализованная //-разрядная дробь. Введем обозначение х =
= 21М | — 1, тогда 0 х 1 — 21-". Логарифм числа а по
основанию два при этих условиях определится как
Iog2 а = р{— 1 -ф log2 (1 -ф х):-~' (6.10)
Для вычисления функции log2 (1 -?с) разобьем вначале
интервал изменения переменной х на 2k одинаковых частей
(k — целое положительное число). Обозначим через значе-
ние левого конца /-го промежутка (/ = 1, 2, ..., 2ft), тогда
значение правого конца этого промежутка есть уг -ф 2~k. Оче-
видно, что значения "ц меняются от 0 до 1 —2~~k и х = тг + А,
где 0 A 2~k.
1°. Определение погрешности вычисления функции
log2 (!+•*)• Значение функции iog2(l-}-^c) для i-го проме-
жутка будем определять как величину
<рг (х) = агх + &, ’ (6.11)
ч
где аг и Р( — константы. Тогда погрешность вычисления лога-
рифма числа а есть S,-==log2(l -фх) — aLx — pf. Экстремальное
значение функции 8f внутри промежутка (уг, 77 + 2 fc) дости-
гается при
X = (аг In 2) 1 — 1,
и тогда 8/э) есть
8;э) = Й1 - + 1 (6.12)
Потребуем, чтобы значения функции 8Z на концах проме-
жутка совпадали, тогда должно выполняться равенство
log2 (1 + Ti) — «гТ/ ~ Pi = log2 (1 + Ъ + 2 fc) — af (ъ + 2 Л) — pz,
откуда
где
az = 2ftln(l+yz) (1п2)-\
yz=2-ft(i+Tzr1.
(6.13)
Выберем значение pz из условия равенства абсолютных ве-
личин погрешности на концах промежутка и в точке экстре-
мума, т. е. когда выполняется равенство
In (az In 2) + 1
Гп2
In (1 + Ti)
In 2
= М/ + -
откуда найдем, что
Pi = 4" [“z
1 . a; e ln2 I
ЙТ‘"ТН71-
(6.14)
Подставляя выражения для az и Pz —(6.13) и (6.14) — соответ-
ственно в (6.12), получим, что
31Э) = [zz - In (1 - zz)] 2-1 (In 2)-1,
(6.15)
где
г, = уГ1 In (1 + yz) - 1. (6.16)
Разложив в (6.16) функцию 1п(1 + уг) в ряд Тейлора, полу-
чим для гг следующее выражение:
zi=----2“yi+-3-yz--j-y/4- ... (6.17)
Из выражения (6.13) следует, что yz<:2 k, тогда согласно
(6.17) имеем
|гг|<4-уг<2-*-’.
(6.18)
В формуле (6.15) разложим в ряд функцию In (1 +£,) и тогда
g? —- ( 1___I Z% -I_— Z*_ А
1 4 In 2 \ 3 Zi ' 2 5 2 3 21 • •
Ряд в круглых скобках можно представить в виде суммы
двух рядов
д_^(' + ' '^4-...),
В = 1 — 2zz (— + -g-г? + — zi + -д’zt + ...
г
Заметим, что А < г?, поскольку |г£|<2-2:
~2 + ТПГ + ТТ + • • • + t(t+ 1) + • • ’ = 1 •
Для 2-го ряда справедливо, что В < 1 — гг, так как zt < 0:
_L+_L + _^+ +________!______+ = _L
3 r 3-5 ' 5-7 ' '' ’ ' (2n — l)(2n+l) 2 ’
Отсюда получим следующую оценку для -8?:
г2
8’<41Й(’-г< + ^-
Учитывая оценку (6.18) для гг, найдем, что »
8э<2-2-А+Г^+Г^. (6.19)
Как следует из неравенства (6.19), при достаточно больших
значениях параметра k можно достичь весьма высокой точ-
ности вычисления логарифма по основанию два. Так, напри-
мер, при #=10 применение рассмотренного метода дает точ-
ность вычисляемых логарифмов лучше, чем 2~24. Само вычис-
ление производится по формуле (6.11) и требует одного
умножения константы az на х и прибавления к полученному
результату константы рг.
Коэффициенты аг и рг составляют специальную таблицу
на 2/г адресов. В качестве отдельного адреса берется значение
Ъ, т. е. значение k старших разрядов мантиссы с номерами
т-2 т-з ... m-k-x - Отсюда ясна деталирбвка процесса вычис-
ления логарифма числа, представленного в форме с плавающей
запятой. Вначале выделяются разряды мантиссы аргумента:-
т-2 т-ъ ... m—k-i, которые рассматриваются как адрес в спе-
циальной таблице. По данному адресу из таблицы выбираются
коэффициенты а, и рг. Коэффициент а( умножается на удвоен-
ное значение мантиссы без единицы и складывается с коэф-
фициентом рг. К сумме, которая есть правильная дробь, при-
писывается целая часть, равная порядку, уменьшенному на
единицу.
2°. Реализация метода. Нашей задачей является построе-
ние алгоритма вычисления логарифма на основе использова-
ния только простых арифметических операций, без привлече-
ния таких операций, как умножение или деление. Очевидно,
что представление коэффициента аг суммой небольшого числа
слагаемых вида 2} позволит в нашем случае избежать умно-
жения, заменив его сложением ряда чисел вида 2Ах, каждое
из которых получается сдвигом числа х на j разрядов вправо
или влево в зависимости от знака J. Обозначим новое значе-
ние коэффициента как аг, тогда
а* = аг (1 + е£). (6.20)
Естественно, что замена значения а£ на а* приведет к сни-
жению точности вычисления логарифма. Будем сейчас счи-
тать, что в новых условиях погрешность вычислений по мо-
дулю не превосходит величины 80 для всех 2k интервалов.
Зйачение 80 будем стремиться выбирать достаточно близким
к верхней границе функции 8® (6.19).
Замена значения ah определенного из (6.13), на приво-
дит к нарушению условия равенства значений функции 8® на
концах i-ro промежутка, а следовательно, к нарушению усло-
вий выбора коэффициента р£. Будем теперь искать оптималь-
ное значение р£ из равенства абсолютных величин максимума
погрешности внутри промежутка и наибольшей погрешности
на концах этого промежутка, которую обозначим как 8£.
Когда at < а£, то
5г = апг + ₽г — log2(l +ъ). (6.21)
Приравняв это значение к значению 8f, найденному из (6.12)
при подстановке а£ = а£, получим
* 1 Г » 1 / аТ 1п 2 \1
₽г = _ [а* (1 _ Т/) _ — (in - 1)]. (6.22)
Подставляя в (6.21) значения 4 и рГ, определенные из (6.20)
и (6.22), найдем
8* = -2КТ lZi — ln U + + ег 0 + — In (1 -4- ег)]. (6.23)
При a-t > a-i имеем после выполнения подобных действий
Й - ф h (1 - т. - 2~*) - (<” , °‘"L22-« )1 (6 24)
и
8* = гЪГТ ^Zl — 1п (! + + ег (1 + Zi) (1 + уг) — In (1 + ег)]_
(6.25)
Таким образом, переход от оптимального значения аг (6.13)
к его некоторому приближению приводит к тому, что погреш-
ность вычисления функции log2 (1 +х) оказывается суммой
погрешности метода (6.15) и погрешности реализации этого
метода, зависящей от степени приближения а{ к az.
Из неравенства 18i 1 < 80, используя выражения (6.23)
и (6.25), можно определить допустимые значения отклонений
коэффициента 4 от его оптимального значения аг для каждого
г-го промежутка.
Пример 6.4. Пусть двоичное число а представлено в форме с плаваю-
щей запятой, тогда для вычисления log2 а надо согласно (6.10) определить
значение log2 (1 + х), где 0 < х < 1—21—п и п — разрядность мантиссы
числа а. Разобьем диапазон изменения х на восемь отрезков (/г = 3). Будем
считать, что погрешность’ для каждого поддиапазона не может превосхо-
дить по абсолютной величине 2“9, т. е. | 4| < 2~9 (см. (6.1'9)). Далее с уче-
том равенств (6.23) и (2.24) определяем допустимые пределы значения
коэффициента аг для каждого поддиапазона и затем выбираем значения
af-, которые имеют наименьшее число членов при его представлении в дво-
ичной системе счисления. В результате этого выбора найдем, что
4 = 1 + 2—2 + 2“3; а* = 1 + 2~2 + 2~4;
4 = 1 + 2~3 - 2“5; а* = 1; а* = 1 — 2~4; 4 = 1 “ 2“3;
4 = 1 - 2“2 + 2“4; 4 = 1 — 2~2.
Отсюда умножение' величины х на 4 потребует до двух сложений числа -х
и слагаемых, образованных путем сдвига числа х на 2 — 5 разрядов впра-
во. В среднем для получения значения log2 (1 + х) потребуется 2,4 алгеб-
раических сложения.
Таблица коэффициентов а* и pt будет содержать значения
Pi и описания для каждого поддиапазона разложения коэффи-
циента a-i по степеням 21, т. е. фактически указываются зна-
чение j и знак слагаемого 2Л Значение pz может быть пред-
ставлено приближенно, но таким образом, чтобы это прибли-
жение не увеличивало существенно погрешность вычисления
функции log2 (1 +х). Если отвести для представления коэф-
фициентов Pi (2Л + 5)-двоичных разрядов, то погрешность
приближения коэффициентов р*, определяемых выражениями
(6.22) и (6.24), не будет превышать 2~2*-6, что не скажется
заметным образом на общей точности вычислений, которая
будет определяться выражениями (6.23) и (6.25).
Объем таблицы коэффициентов может быть дополни-
тельно уменьшен, если значение выбирать из некоторого
допустимого диапазона. Такой диапазон при уже выбранных
значениях a't может быть найден из условия, что абсолютное
значение погрешностей' для данного подынтервала не превос-
ходит 80.
При < а. для значений рг должно выполняться неравенство
* , In (1 + 7/) * In (a* In 2)+1
— а«7» + -1П2 > ₽г > «/------ЙГ2-------
80, (6.26)
а при аг > аг — неравенство
8о = а* (ъ + £ *)
,п (1 + Ti + 2 *) * In (a* In 2)
+------Ь2------>₽/>“*--------ЙГ2----8°-
(6.27)
После того, как определены эти пределы, можно выбрать из
допустимых такое значение рг, которое имеет наименьшее
число членов при его представлении в двоичной системе счис-
ления, т. е. будет найден минимальный объем таблицы коэф-
фициентов.
Пример 6.5. Пусть двоичное число а представлено в форме с плаваю-
щей запятой. При вычислении функции log2a рассмотренным методом
разобьем весь диапазон изменения переменной х (6.10) на восемь равных
отрезков и для каждого из отрезков найдем значения коэффициентов
at-, обеспечивающих наименьшее число действий при выполнении операции
а^х (см. пример 6.4). Затем из неравенств (6.26) или (6.27) найдем значения
коэффициентов (Зг, приводящих к минимальному объему таблицы коэффи-
циентов при заданном значении 60 = 2-9. Эти оптимальные значения
таковы: = 0, ₽2 = 0,000001001, ₽3 = 0,000011001, ₽4 = 0,0001011, ₽5 =
= 0,000111011, р6 = 0,00100111, ₽7 = 0,001100101, р8 = 0,01. Учитывая, что все
значения есть правильные дроби, не превосходящие 2~\ обьем таблицы
коэффициентов составит 46 бит. Если бы мы отводили для изображения
коэффициентов 2й + 5 разрядов, то объем таблицы составил бы 80 бит.
Таким образом, вычисление логарифма по основанию два
от двоичных чисел, представленных в форме с плавающей
запятой, рассмотренным методом позволяет определить резуль-
тат за небольшое число сложений-вычитаний (примерно k),
и при этом обеспечивается погрешность вычислений, не пре-
восходящая по абсолютной величине значения 2~2k~3. Для
реализации метода необходимо иметь таблицу, имеющую 2*
строк, в каждой из которых хранится значение коэф ициен-
тов и указание о характере сложений и виде слагаемых.
При росте параметра k объем таблицы становится весьма
значительным, а при k=\ значение максимальной погреш-
ности оказывается чрезмерно большим. Поэтому при неболь-
ших значениях k использование данного метода (например,
в минимашинах) обеспечивает большую скорость вычисления
двоичного логарифма при умеренном объеме таблицы коэф-
фициентов.
§ 5. ТАБЛИЧНО-ИТЕРАЦИОННЫЙ МЕТОД ИЗВЛЕЧЕНИЯ
КВАДРАТНЫХ КОРНЕЙ
Будем считать для простоты, что подкоренное число а
есть правильная двоичная дробь. Результат извлечения квад-
ратного корня определим последовательно за т итераций.
На итерации с номером 7 = 1, 2, ... находится некоторое
приближение к у = ~\Га ,, и это приближение есть
be?.!- ...), (6.28)
где s,-i — малый параметр и
1 /. а \
е/ = 2 V pJJ'
(6.29)
1°. Выбор итерационной схемы. Начальное приближение
Ро считается заданным, и тогда для вычисления а методом
итераций остается только выбрать конечную степень полинома
в (6.28). Мы будем исследовать итерационные схемы с тремя
возможными степенями полинома Р(е), а именно
Р (е) = 1 — е7_1; Р(е) = 1 - - А е?_1;
и
Р(е) = 1 - е2_х (1 е.^).
Число действий, которые необходимы для вычисления при-
ближений Ру, оценивается для 1-го случая как одно умноже-
ние, для 2-го случая — как два умножения, один сдвиг и одно
вычитание и для 3-го случая — как три умножения, один
сдвиг и два сложения-вычитания. Формирование величины
1 — еу_! обычно не требует операции вычитанйя, ибо она яв-
ляется дополнительным кодом числа sy_i. Помимо Ру на каж-
дой итерации еще вычисляется значение еу-, на что требуется
еще один сдвиг, одно умножение и одно (Деление.
Из соотношений ( . 8) и ( .29 легко получить, что
= ej~i (1 — еу_!) 2 при .1 = 1 — схема I;
и
еу=
' -2^ +^(1 +2-%._1)
при 1 = 2 — схема II
е^[1+2-^(1+^]
при 1 = 3 — схема III,
где I — степень полинома Р(г).
После завершения у-й итерации значение абсолютной по-
грешности результата есть
А = УУ - Pj,
ИЛИ
[- --I
1—(1—2еу) 2 J.
_ 1
Используя разложение и ряд Тейлора функции (1 — 2еу) 2
получим, ограничиваясь тремя членами разложения,
еу(1 + Ае.).
Поскольку обычно начальное приближение, выбирается весьма
точно, значение е0 мало, и приближенно можно считать, что
е/ = е7-1
или
_ B(*+W
е, = ео
(6.30)
где J — число итераций.
. Для оценки эффективности трех схем итераций сравним
значение еу- при одинаковых временных затратах на итерацион-
ный процесс. Временные затраты будем оценивать числом
умножений, которое необходимо для получения результата.
Пусть общее число умножений при вычислении результата
по схеме I и схеме II одинаково, т. е. 2J = 3q, где j — число
итераций по схеме I, a q — по схеме II. Из соотношения (6.30)
получим, что
2/
Это означает, что итерационная схема II обеспечивает более
быструю сходимость, чем схема I. Следует учесть, что число
делений при использовании схемы II будет меньше, чем при
схеме’ I. При равном числе умножений итерационная схема III
дает ту же сходимость, что и схема I, но требует меньшего
числа делений.
Таким образом, к наилучшим результатам приводит ите-
рационная схема И, когда
Pj = Л-i С1 — s/-i — 4" е*-1) и &i ~ ео7-
2°. Выбор начального приближения. Хотя выбранная схе-
ма и обеспечивает быструю сходимость, все же для умень-
шения числа итераций желательно выбрать достаточно точное
начальное приближение Ре. Будем искать это приближение
в виде
Ро = аа + ₽,
где а и Р — постоянные коэффициенты, а а — подкоренное
число.
Разобьем интервал изменения переменной а на 2* одина-
ковых частей (k > 1 — целое число). Обозначим. через ъ зна-
чение левого конца г-го промежутка. Тогда значение правого
конца промежутка есть 7г4-.2~А. Значение аргумента а есть
а = ъ + гДе 1г = 2;=1«-/2-у и X = 2”=fc+i «-/2-7.
Погрешность вычисления а на ^"м промежутке есть
= — агХ —рг.
Наименьшее значение погрешности достигается в случае, когда
“i = (КЪ + — Уъ"),
Рг = 2-1 (^fi + УтГ + 2~2аГг),
и тогда
8/ = 2й-’ъ (/ъ + 2~k - У^) - 2-1 /ъ +
' + 2-*-3 (]Лг + 2~* - /ъ) -1-
Наибольшее значение функции 8г достигается при ?i = 2 *,
тогда, ограничиваясь пятью членами разложения функции
У1 + 2-ft~I в ряд Тейлора, найдем
Как следует из (6.31), даже при умеренных значениях пара-
метра k (например, & = 5) начальное приближение получается
достаточно точно (при Л = 5 точность есть ~2-15). Для до-
стижения точности 2~56 при использовании одной итерации,
выполняемой по схеме II, достаточно взять значение k = 7.
.3°. Реализация метода. Для определения начального при-
ближения Ро надо вначале из специальной таблицы выбрать
значения коэффициентов at и pz, а затем найти произведение
агХ' и прибавить к нему значение рг. После определения Ро
выполняется итерация по схеме II. В принципе можно умно-
жение на коэффициент а; исключить, если представить его
в виде ряда по степеням 2-', имеющего небольшое число чле-
нов. Условия выбора коэффициентов az и pz в этом случае
описаны в §4, где исследуется вопрос о вычислении двоич-
ного логарифма. Замена умножения примерно на сложений
позволяет вычислить корень за время, равное приблизительно
одному делению и трем умножениям. Дополнительного обо-
рудования при этом не требуется, кроме таблицы, хранящей
коэффициенты az, [3; или сведения о том, как их можно сфор-
мировать.
Таблично-итерационный метод извлечения квадратного кор-
ня одинаково хорошо пригоден и для минимашин, и для боль-
ших машин. Для минимашин можно ограничиться только эта-
пом I (определением Ро), ибо при k=6 точность определения
результата будет 2-17. В больших машинах выбор метода из-
влечения квадратного корня будет определяться тем, насколько
удачно в них решена задача реализации операции умножения.
Если умножение выполняется значительно дольше, чем сло-
жение, то имеет смысл применять итерационный метод, осно-
ванный на псевдоделении (см. § 2).
§ 6. ВЫЧИСЛЕНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
ПО МЕТОДУ „ЦИФРА ЗА ЦИФРОЙ"
1°. Обоснование метода „цифра за цифрой". Пусть веще-
ственные числа а и b заданы в позиционной системе счисле-
ния с основанием г правильными «-разрядными дробями. Будем
искать сумму двух чисел («=^=0) в виде
« + & = «П"Г01(1
где <7zC{0, 1, ..., г—1). Значение параметра £z может выби-
раться исходя из различных стратегий. Стратегии могут быть
следующими: все равны 1, значение £z может быть +1,
значение есть 0,1. Если нам удастся найти данное представ-
ление суммы двух чисел, т. е. определить значения qt и £z, то
легко потом найти и значение функции In (1 +« 1Ь). Действи-
тельно, тогда
1п (1 + a^b) = StJo1 qt In (1 + ^).
Когда в специальной памяти машины хранятся константы
In (1 + то процесс вычисления функции In (1 -1- a~lb}
сводится к простому суммированию 9г-кратных констант, вы-
бранных из заданного множества в соответствии со значе-
нием Вг.
При наличии константы указанного вида, задавая значения
qt и 1г, можно найти число
<р = (1+М-
Экспоненцируя это число, получим
ехр <р = ПГД1 (1 + ^г~‘)Ч (6.32)
Умножением обеих частей равенства (6.32) на величину а
легко получить значение ае^.
Пусть, теперь парой чисел а и b задается комплексное
число z^= а + ib = Re1*, где R2 = а2 ф- Ь2 и <р = arctg ba~l.
Будем вначале искать представление комплексного числа в виде
Re* = сПГДо1 (1 + (6.33)
где с — неизвестное пока вещественное число.
Логарифмируя выражение (6.33) и приравнивая мнимые
части, получим с учетом 1 ф- = R^t
или
arctg -^- = qt arctg
С учетом используемых стратегий выбора значений коэффи-
циентов окончательно имеем
arctg 4" = 2Гп arct& г“'- (6-34)
Из равенства действительных частей главного логарифма вы-
ражения (6.33) получим
Таким образом, если Mbiz найдем значения qt, 5г, то согласно
(6.34) при наличии констант вида arctg г~‘ легко вычисляется
функция arctg ba-1.
С другой стороны, если нам уже задано число ® в виде
(6.34), т. е, известны коэффициенты q^At, то, экспоненцируя
выражение (6.34), определяем выражение
z — cos <f> + i sin <p =.П"Г01 (—1 + ^,r — 1.
, \ pi+?r2i )
Когда число z найдено, то отношение Imz/Rez дает значение
функции tg ср.
В общем случае парой вещественных чисел задаем гипер-
комплексное число вида z = а-\- lb, где /£ {г, е, е\ [22]. Пред-
ставим гиперкомплексное число в форме
z = R (COS <р + / SIN ср) = Re\
ч
где 12 = т^{ — 1, 0, 1} и параметры R = |z|, <? = argz, COS<p
и SIN ср для /£ {/, е, е] заданы табл. 25.
Таблица 25
Параметр 1= i I = e I — e

7? J/ a2 + ft2 a sign a]/ a2 — №
<? arctg ba~1 ba~l ' arth ba~~l
, COS tp COS 1 ch <p
SIN <f> sin <p <? sh<p
Модуль числа z определен также соотношением |z|2 = zz =
= а2 — mb2, где z = a ~ lb — число, сопряженное с г. Будем
искать представление гиперкомплексных чисел в виде [22]
а + lb = сП?4+р (1 + 4 (6.35)
где 9г£{0, 1, ..., г — 1} при I = i, е. и С[0, 1, .... П при
1=е; р = 0 при 1 = 1, е. и р=1 при 1 = е и Вг£{—1, 1).
Логарифмируя выражение (6.35) и приравнивая мнимые части,
получаем
arg (а + lb) = arg (1 + /г~г). ’ (6.36)
Из равенства вещественных частей следует, что
Таким образом, если нам удастся найти представление гипер-
комплексного числа в виде (6.36), то затем значение функции
arg и при наличии констант arg(l Ir~l) вычисляется простым
суммированием выбранных 9г-кратных констант. В случае комп-
лексных чисел (1=1) вычисляется функция arctgfea-1, в слу-
чае двойных чисел (/= ё) происходит вычисление функции
arth ba~l и, наконец, в случае дуальных чисел (/=е) вычис-
ляется отношение bar*.
При обращении процесса (6.35) — (6.37) вначале по задан-
ному числу <f> находятся значения qh Вг из равенства
? = 1$=р+р V&i arg (1 + Ir~l),
а затем после экспоненцирования этого выражения получим
г== COS (f> +/SIN (f> = exp (Z(f>) =
= n?-p1+p
1 +/gjr~£ \gi
|1+/Е<г1 /
(6.38)
После того как определено гиперкомплексное число z, можно
определить функции tg ср и th (f> при 1=1 и 1=е соответст-
венно из соотношения Imz/Rez. При /=е величина Imz опре-
деляет число (f>.
Заметим, что хотя прямым методом вычисляются только
гиперкомплексные числа и функции ab~r, arctga~lb, arth ba.-1,
exp (f>, In (1 -\-а~гЬ), другие элементарные функции легко мо-
гут быть вычислены через „базовые" функции и арифметиче-
ские действия. Например, для вычисления функции У а2Ь2
надо после нахождения правой части равенства (6.33) умно-
( 1Л +Е-г-2£ V*
жить ее на величину П”=о I—— I , а затем в качест-
ве У а? + Ь2 взять реальную часть произведения.
2°. Реализация метода „цифра за цифрой". Метод „цифра
за цифрой" позволяет алгоритмы вычисления элементарных
функций представить в виде рекуррентных соотношений, весь-
ма похожих на рекуррентные соотношения, отвечающие опе-
рациям умножения и деления. Для реализации рекуррентных
соотношений надо иметь обычные операции алгебраического
сложения', сдвига и выбора, констант из памяти. Это позволяет
весьма просто осуществить аппаратурную реализацию метода
„цифра за цифрой" на базе простого арифметического узла.
Рассмотрим специфику этих рекуррентных соотношений.
Перепишем соотношение (6.36) в виде
Т - 2^Р1+р q& arg (1 + Ir~l) = 0, (6.39)
Задача состоит в отыскании таких значений q-t и tjj, при кото-
рых разрешимо равенство (6.39). Очевидно, что если известны
все qt и Вг вплоть до i = /0, то определить q4 можно вычита-
нием из © некоторого члена вида Qh arg (1 + /r~i},
т. е. применить итерационную схему, очень похожую на схему
деления, а точнее на итерационную схему извлечения квад-
ратного корня, когда „делитель" менялся на каждом шаге
итерации (см. § 2).
Пусть k — номер алгебраического сложения при определе-
нии цифры qh — нормализованный остаток, получаемый
в процессе вычисления qt и
У О = гЧт — [Sj=p+P Qh arg (1 + + ^arg (1 + Ir~l) ]),
тогда рекуррентные соотношения, определяющие qt и при-
мут вид v
=r‘arg(l+/г~‘), г = р, ..п.— 1+р,
ei = signK^, У^ = ?, Y(oi+1} = rY^.
Определение цифры qt производится -до тех пор, пока не
выполнится условие
| у | < Xw = rl arg (1 + Ir~l).
После n итераций псевдоделения определится псевдочастное
Q = QpQi+p Qn-i+p-
Найденное псевдочастное Q позволяет на этапе II вычис-
лить согласно (6.38) правую часть выражения
аП?4+р | 1 -у I^r-i ft (COS <? + / SIN ©) = аП?4+р (1 +
Обозначим через + IYl^r~l частное произведение, полу-
ченное на i-й итерации после k алгебраических сложений и
Х^ + lY^r-1 = alL^f (1 + (1 +Г^)\
+ IY^r~l = + lY^r-1] (1 + Дгг-9,
тогда
Г(0 v (О । t v(0
fe-н — г й -f- ft ,
X^+1 = X^-{-m\Y^r-^, i=p, n-l+p,
y^"-1+p) = 0, ^"-1+p) = a,
y<i-1) = r-1y« x^1} = Xg, i=p+ 1, ..., л-l +p. .
По окончании процесса псевдоумножения
е
Imz = Ла SIN ср =
Res = /<aCOScp = X^),
1 р
где K=Yl^p+p\ 1 +/£zr-zp. Таким образом, рассматриваемая
схема приводит к вычислению следующих функций:
умножение Кау при т = 0,
\
sin ср и cos <р при т = — 1 и а = №\
sh ср и ch ср при ттг = +1 и а = К~г.
Однако простота вычисления этих функций только кажущаяся.
Действительно, после этапа I, когда определены значения qt
и коэффициент еще не найден и поэтому до этапа II его надо
определить, непосредственное вычисление коэффициента К
даже при наличии операции умножения занимает много вре-
мени и поэтому вряд ли ’приемлемо. Выходом из положения
может быть вычисление функции tgcp и th ср, что не требует
знания значения К. Далее по обычным тригонометрическим
соотношениям находятся значения sin ср (sh ср), cos ср (ch ср).
Другой способ состоит в трансформации алгоритмов так, что-
бы можно было всегда использовать одно и то же значение
коэффициента К, т. е. использовать константу Л~’. Замена
всех значений qh входящих в выражение для К, на постоян-
ную величину позволяет получить желаемую константу и в то
же время лишь незначительно усложнить алгоритмы, введя
на этапе псевдоумножения несколько лишних шагов [2, 22].
Легко заметить, что из равенства (6.35) вытекает соотно-
шение
Jm {(а + 1Ь) П?~р1+р (1 - = 0. (6.40)
Попробуем найти значения qt и Вг, при которых равенство
(6.40) разрешимо. Пусть iY'k г~1 — остаток, получаемый
после выполнения k вычитаний на г-й итерации псевдоделе-
ния, и
Х$ + IY^r-1 = (а + lb) П1Г2Р (1 - Kjr~j)qi (1 - Дгг~‘)\
(6.41)
Х^ + IY^r~l= (Х% + lY^r-1) (1 - Л/~г).
Из соотношения (6.41) вытекают следующие рекуррентные
соотношения:
= -brnY^r-*, i=p, .... «-1+а '
Ytf' = b, Х(У = а,
Ytf+» = rY%, x^+1) = Xg, i=p, .... п-2+р,
Ег = sign sign Xq\
Вычисление цифры qt происходит до тех пор, пока не выпол-
нится условие
В результате выполнения псевдоделения определяется псевдо-
частное Q = Qrfi+p . . qn-i+p.
После того как определены значения qt и на этапе II,
можно вычислить выражение
arg (а + lb) = ^z arg (1 + lr~i). (6.42)
Выражение (6.42) вычислим, организовав процесс псевдоумно-*
жения. Пусть Y%) — частичное произведение, получившееся
после k алгебраических действий на i-й итерации, и
= г1 {2”z/+f q^ arg (1 + Ir~i) + klt arg (1 +
тогда
______ y(0 । c v(0
I Ze-|l — I k + ?Z^ k ,
X6) = Harg(l + i = p, n-\-Yp,
Y^+p) = 0, %(z-d = _ p + д > j + .
По окончании процесса .псевдоумножения получим arg(.« +
-YIb)=Y{q\ Заметим, что по окончании этапа I мы получили
K\z\ = Х^^^. Таким образом., новая схема (обратная по от-
ношению к предыдущей) приводит к вычислению следующих
функций:
деление Ьа~? при т — 0, <
К У'а2 + b2 , arctg Ьа~г при лг = — 1,
КУ~а? — b2 , arth Ьа~г при т = 1.
Как обычно, здесь наиболее трудная проблема состоит в вы-
числении коэффициента К, и поэтому вновь самое присталь-
ное внимание заслуживают алгоритмы, позволяющие исполь-
зовать постоянные значения К, не зависящие от' величины
чисел а и Ь. Если это так, то весьма просто определить
величины j/a3 b2 и J/а? — Ь2 путем деления на эту
константу.
3°. Особенности вычисления элементарных функций в слу-
чае представления аргумента в форме с плавающей запятой.
При вычислении элементарных функций в том случае, когда
аргументы заданы в форме с плавающей запятой, весь процесс
разбивается на три этапа — сведение аргумента к диапазонам,
допустимым для метода „цифра за цифрой", непосредственное
выполнение по рекуррентным соотношениям, определение ман-
тиссы и порядка результата. Для большинства функций поря-
док результата может быть непосредственно определен по зна-
чению порядка'операнда, и формирование мантиссы и порядка
может быть произведено независимо друг от друга.
Например, при вычислении корня квадратного (tZ) из числа
а = граМ, получаем pd = -^pa, если ра четное, и pd = (ра ф-
ф- 1), если ра нечетное. В последнем случае мантисса числа а
перед вычислением корня квадратного уменьшается в г раз.
Вычисление логарифма числа а = гр^М определяется соот-
ношением In а = In М ф- ра In г. При этом порядок и мантисса
результата сформируются в процессе умножения ра на In г
и затем сложения произведения с 1п«.
В зависимости от значений порядка аргумента экспонента
будет определена следующим, образом:
1 + « при ра< —(« — !),
е|о1 при и ра

' при а < 0, ра — (я — 1).
Для вычисления = Мсгрс необходимо осуществить
дение модуля а к диапазону [0, In г]
приве
| а | = t In г + R, 0 R < In г,
где t — целые. Тогда е>а1 — еУг1 = следовательно, Мс =
= еР и pc = t.'
Вычисление арктангенса числа а = гр^М определяется соот-
ношениями
; |а| при Ра < 1),
rPa arctg | а | При — (П— 1ХАг<0.
arctg а [ = -J- - arctg | а Г1 При 0 ^.ра^.П— Д
V при ра > п — l;i
sign (arctg a) = sign а.
При вычислении функций sin ср, cos ср и tg ср сначала проис-
1ит приведение аргумента а к диапазону |0, ,
« = + + ср, 0<ср<^-,
где I и k— целые и ££{0,1,2, 3}. Если рй<—(/г—1), то
sin а = tga = a, cos а = 1. Поскольку {sin а | — | sin ср| и |cosa| =
— {cosср|, то
I' sin ср I ,
---1- при четном £.
I COS ср | »
ltga|= , ,
COS ср ,
sjn т при нечетном /г,
1-1
sign (sin а) = (—1 )L 2 1 sign а,
[—1
sign (cos а) = (—1)L 2 . ,
sign (tg a) = (—1 )k sign a.
При вычислении прямых гиперболических функций [68]
умент приводится к диапазону [0, In г)
а = / In г + R, 0 R < In г,
sh а — [ch R + sh R — r-2/ (ch R — sh /?)],
cha = -j- [ch R + shR + r~™ (ch/? - sh /?)],
th a = sh «/ch a.
При вычислении функции arth а используется соотношение
arth (1 — Mar~pa) = arth T + In r,
T 2 — Mor Pa — M,
_p
2-Mar Pa + Ma
Большое значение для определения областей применимости
вычислений элементарных функций по методу „цифра за циф-
рой “ имеет оценка погрешности данного метода. Детальный
анализ показывает [2], что метод „цифра за цифрой“ обеспе-
чивает вычисление элементарных функций с весьма высокой
точностью.
ГЛАВА 7
ОБНАРУЖЕНИЕ И ИСПРАВЛЕНИЕ ОШИБОК ПРИ
РЕАЛИЗАЦИИ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
В процессе эксплуатации цифровых машин неизбежно воз-
никают отказы оборудования (устройств, блоков, элементов),
приводящие к выходу машин из строя. Хотя вероятность
безотказной работы в течение заданного промежутка времени
для современных машин достаточно высока, все же для по-
вышения надежности приходится принимать специальные меры,
направленные на устранение влияния отказов оборудования.
Эти меры обычно различны для различных устройств машины,
поскольку для каждого устройства наиболее вероятен какой-
либо определенный вид неисправностей.
Отказы принято делить на сбои *— отказ, приводящий к еди-
ничной ошибке в работе и самоустраняющийся при дальнейшем
функционировании оборудования, и внезапные отказы — отка-
зы, приводящие к постоянному выходу из строя оборудования.
Возможен и постепенный отказ оборудования, когда неис-
правность вначале проявляется в виде сбоев, частота появления
которых с течением времени увеличивается, а затем наступает
постоянный отказ.
Будем считать, что выбранные алгоритмы арифметических
операций оптимальным образом реализованы с технической
точки зрения, т. е. осуществлен оптимальный режим нагрузки
всех элементов, их питания, применена рациональная техно-
логия изготовления элементов и схем и т. п. Следовательно,
при заданной структуре алгоритма и системе элементов обе-
спечивается максимально достижимый уровень функциональной
надежности. Эти мероприятия, конечно, увеличивают вероят-
ность безотказной работы в течение заданного интервала вре-
мени, однако они не могут полностью устранить появление
отказов.
Для устранения влияния отказов на достоверность полу-
ченных результатов применяют избыточные методы, которые
принято делить на аппаратные, программные и аппаратно-
программные. Аппаратные методы основаны на введении опре-
деленного количества избыточного оборудования в машину,
которое используется только для устранения влияния отказов.
Программные методы достигают той же Цели без введения
дополнительного оборудования с помощью более сложной
организации выполняемой программы и применения специаль-
ных (например, диагностических) программ. Аппаратно-прог-
раммные методы используют и аппаратную и программную
избыточность и позволяют использовать наиболее сильные
стороны обоих методов.
При выполнении арифметических операций с обнаружением
и устранением ошибок наибольшую роль играют аппаратные
и аппаратно-программные методы. По способу использования
избыточного оборудования аппаратные и аппаратно-программ-
ные методы можно подразделить на статические и динами-
ческие.
Статические методы отличаются тем, что уменьшение влия-
ния отказов элементов какого-либо отдельного устройства
машины на работу этого устройства достигается за счет по-
стоянно включенного дополнительного оборудования. Среди
статических методов наиболее известны метод дублирования
и метод информационной избыточности.
Динамические методы основываются на том, что для устра-
нения неисправности внутри данного блока используется внеш-
нее оборудование. При этом важнейшими функциями внешнего
оборудования являются обнаружение ошибок в работе блока,
диагностирование отказов и переконфигурация системы либо
за счет включения резервного блока вместо неисправного,
либо за счет перестройки' логической структуры поврежден-
ного блока. В соответствии с этим среди динамических мето-
дов выделяют метод резервирования и метод адаптивных
структур.
Достоинство статических методов заключается в том, что
при их использовании коррекция ошибок происходит непо-
средственно в процессе получения результата без дополни-
тельных затрат времени. Постоянные ошибки и сбои одинаково
хорошо корректируются статическими методами, но эти ме-
тоды приводят к значительному расходу оборудования.
Дйнамические методы имеют следующие преимущества
перед статическими: сохранение работоспособности системы
вплоть до полного исчерпывания резервных компонент или
возможностей переконфигурации; возможность исправления
ошибок путем повторения действия на перестроенной струк-
туре; легкость обеспечения заданных параметров надежности
за счет выбора количества и типа резервных компонент;
использование малой интенсивности отказов резервных компо-
нент, находящихся в выключенном состоянии.
ри возникновении отказов применение динамических ме-
тодов связано с значительными дополнительными временными
затратами. Эти методы наиболее эффективны при корректи-
ровке постоянных отказов или часто' повторяющихся сбоев,
которые можно при определенной частоте считать"^ постоян-
ный отказ, и наиболее часто применяются в сочетании с прог-
раммными методами.
§ 1. МЕТОД ДУБЛИРОВАНИЯ
В простейшем случае метод дублирования состоит в замене
устройства совокупностью п идентичных устройств, выпол-
няющих одинаковые функции. При подаче одинаковых вход-
ных значений па все устройства одновременно путем сравне-
ния результатов можно определить правильность работы от-
дельного блока, если принять, что правильный. результат
соответствует совпадающим на большинстве устройств выход-
ным значениям. В этом методе оборудование увеличивается
в п раз. Однако, если отказы в устройстве приводят к несов-
падающим результатам, то эффективность данного метода
весьма высока- ибо для того чтобы система перестала давать
правильные результаты, надо чтобы число различных отказов
приближалось к п. В применении к арифметическим устрой-
ствам данный метод вряд ли стоит рекомендовать, ибо сам
по себе арифметический узел — это очень сложная схема
с большим количеством оборудования и достаточно дорого-
стоящая. Однако в системах, где требуется чрезвычайно высо-
кая достоверность результатов, метод двойного дублирования
оказывается весьма полезным для определения наличия оши-
бок в работе устройства, какой бы ни была природа их воз-
никновения. После обнаружения ошибки встает задача о лик-
видации ее последствий на ход выполняемой программы. Эта
задача в настоящее время решается методами, не связанными
с дублированием.
Для повышения надежности системы с дублированием
обычно сравнение сигналов с однотипных устройств произво-
дят не только на выходе, но и несколько раз внутри устройств.
Это позволяет обеспечить правильное функционирование при
выходе значительно большего числа элементов, чем при осу-
-ществлении одного сравнения. Блок, который осуществляет
сравнение, сам может иметь неисправность, поэтому часто
в методе дублирования используют идею многократных линий,
которая заключается в том, что любой сигнал в системе пере-
дается не по одному, а по я каналам, где п — число задубли-
рованных устройств. Как обычно, за правильный сигнал при-
нимается сигнал, передаваемый большинством каналов. Есте-
ственно, что число сравнивающих элементов с при этом
увеличивается в п раз.
§ 2. АРИФМЕТИЧЕСКИЕ ПОМЕХОЗАЩИТНЫЕ КОДЫ
Сложность современных цифровых машин приводит к необ-
ходимости применения эффективных средств обнаружения
и исправления ошибок, возникающих в результате появления
неисправностей оборудования. Рассмотренные в предыдущем
параграфе методы дублирования хотя и дают хорошие резуль-
таты в борьбе с отказами, но становятся чрезвычайно дорого-
стоящими при росте сложности систем. Кроме того, если на
вход системы с дублированием попадается искаженная инфор-
мация, то система вообще оказывается бессильной установить
факт такого вида неисправности. Очень важно для цифровых
машин всегда иметь уверенность, что данные, подлежащие
обработке, хранению и передаче, достоверны.
Оказывается, что ошибки в машинных словах (командах,
числах) могут быть весьма эффективно обнаружены, если при
кодировании этих слов применять метод информационной из-
быточности. Кратко суть этого метода состоит в следующем.
Пусть каждое слово представляется п разрядами в г-знач-
ном алфавите. Тогда число различных слов есть гп, но для
представления машинных слов выбирается из них лишь N <
< гп. Используемые слова назовем разрешенными кодами,
а оставшиеся rn — N—запрещенными. Поставим обязательным
условием правильного функционирования цифровой машины
принадлежность хранимых, передаваемых и обрабатываемых
машинных слов только разрешенным кодам. Тогда, анализируя
в процессе работы машины все слова, можно обнаружить в ее
работе ошибки, когда появляется запрещенный код. Подобный
анализ, однако, не сможет обнаружить такие ошибки, которые
приводят к появлению нового разрешенного кода, отличного
от истинного.
Для исправления обнаруженных ошибок необходимо до-
биться, чтобы разные ошибки не приводили к одним и тем
же запрещенным кодам. Очевидно, что построить код, кото-
рый бы исправлял всевозможные ошибки, практически невоз-
можно. К счастью, не все ошибки одинаково опасны для
конкретного устройства. Всегда можно выделить классы
ошибок, которые для данного устройства наиболее вероятны1
и, следовательно, наиболее’ опасны. Построить коды, позво-
ляющие обнаружить п исправить определенный класс оши-
бок, оказывается практически возможным делом. Пусть для
каждого разрешенного кода выделено L различных запре-
щенных кодов, отвечающих отдельным классам ошибок
в разрешенном коде. Тогда общее число ошибок, которое
можно исправить, есть LN. Очевидно, что сумма разрешен-
ных кодов и выделенных запрещенных кодов должна быть
не меньше числа допустимых кодов, поэтому
г”>Л(£+1). (7.1)
В этом случае, когда имеет место знак равенства в (7.1),
разрешенные коды называют кодами без потерь, или плот-
но-упакованными кодами.
Способность кодов к обнаружению и исправлению ошибок
связана с введением информационной избыточности, т. е.
с увеличением длины кодовых слов. Число дополнительных
разрядов зависит от корректирующих свойств кода (от зна-
чения L). Иногда разрешенные коды можно представить
в виде совершенно автономных частей, одна из которых есть
основное информационное сообщение, а вторая определяет
способность этого кода к исправлению и обнаружению оши-
бок. Такой код называется разделимым, или систематиче-
ским. Для систематических кодов характерна независимость
обработки основного и контрольного сообщений.
При выполнении арифметических операций машинные
слова рассматриваются как числа и судить о том, правильный
ли получен результат, можно только на основе анализа их
количественного эквивалента. Поэтому и понятие ошибки
при арифметических операциях определяется через числен-
ные величины, а не через число искаженных позиций в сло-
ве, как это делается при передаче информации |7]. Дейст-
вительно, появление при сложении чисел лишнего (ошибоч-
ного) переноса в г-м разряде, дающее изменение результата
на величину г1, может привести к тому, что изображение
полученного числа будет отличаться от изображения истин-
ной суммы во многих разрядах, хотя, конечно, по смыслу
произошла одиночная ошибка. В целях лучшего учета харак-
тера ошибок при арифметических вычислениях вводится
понятие арифметического расстояния q между парой чисел
а и Ь, которое определяется как арифметический вес w аб-
солютной величины их разности и
q(a, b) = (п(\а — Ь\).
Арифметическим весом числа а, т. е. w (а), называется
наименьшее число слагаемых в представлении количественного
эквивалента числа а в виде afj’ Оу — О, ±1, ±2, •••
±(r-l). Когда/вместо числа а получено число а', то
говорят о появлении ^-кратной ошибки, если арифметическое
расстояние между а и а' есть q.
Рассмотрим наиболее распространенные конструкции поме-
хозащитных арифметических кодов.
1°. Разделимые арифметические коды. Пусть разрешенный
код состоит из двух частей — основной и проверочной. Основ-
ная часть представляет собой исходное слово a-. ak ...
которое задает величину a = ^li=oalrl. Проверочная часть яв-
ляется словом Ь; Ьт ,,, Ьф0, Количественный эквивалент
этого числа определяется как вычет от числа а по моду-
лю р, т. е.
b = «(modP).
Здесь р — положительное целое число, b — наименьшее неот-
рицательное число, сравнимое с а по модулю р. Такой разде-
лимый код называется остаточным. Основная и проверочная
части этого кода могут обрабатываться независимо и одновре-
менно каждая по своим правилам.
Пусть над основными частями двух кодов выполняется
бинарная операция <р/ (операция может быть также и унар-
ной). Результат операции обозначим как 7? = <pz(a(,), а(2)). Пусть
й(1> и &(2) обозначают вычеты от чисел и по модулю р.
Если мы сумеем найти оператор фу, такой, что
#(2>) = A?(m6dP), (7.2)
то контроль вычисленцй можно ^удет реализовать как про-
верку соотношения сравнимости между вычетом по модулю р
от полученного в результате данного действия числа R и ре-
зультатом действия оператора фу над проверочными сообще-
ниями операндЪв.
Любое нарушение равенства (7.2) указывает на возникно-
вение ошибки. Однако довольно трудно сказать, где именно
произошла ошибка — в основной части или в проверочной.
Если главной целью контроля является только обнаружение
ошибки, То это обстоятельство не играет никакой роли. Дей-
ствительно, когда несравнение вызвано сбоем, то обнаружение
ошибки позволит зафиксировать его. Полученный результат
отменяется и рационально еще раз повторить операцию с ис-
ходными аргументами. Если же расхождение вызвано, постоян-
ным отказом, то оно будет подтверждено и при повторных
проходах операции, и факт обнаружения неисправности будет
установлен.
Появление ошибок, величина которых кратна модулю Р,
естественно, не будет обнаружено данной системой контроля.
Обычно выбирают значение модуля таковым, чтобы появление
ошибок, величина которых кратна модулю, было бы чрезвы-
чайно мало вероятно. В то же время выбранное значение р
не должно приводить к значительной избыточности.
В арифметическом устройстве наиболее важной и ответст-
венной частью является сумматор, поэтому в первую очередь
приходится заботиться о контроле работы именно этой схемы.
При сложении оператор фу определяется достаточно просто —
это сложение по модулю р. Следовательно, основное слово
и его проверочная часть могут одновременно складываться
(вычитаться), но соответственно по модулю rki и Р (здесь пред-
полагается, что используются прямые коды разрядностью к).
В случае, если арифметические ошибки разной .кратности
взаимно независимы, то наиболее вероятны однозначные ошиб-
ки. Обнаружение этих ошибок может быть произведено при
введении минимальной избыточности. Фактически достаточно
выбрать такое значение модуля р, чтобы удовлетворялось
соотношение
д.у'”1 -/= 0 (mod ₽), at = 0, 1.г — 1.
Для двоичной системы счисления значение р = 3 позволяет
обнаружить однозначные ошибки, какой бы длины ни была
основная часть слова. Сложение основного и проверочного
сообщений производится независимо, каждого в собственном
сумматоре, а затем результаты сравниваются. Выбранный спо-
соб контроля позволяет реализовать такие операции, как ал-
гебраическое сложение, простой и циклический сдвиг операн-
дов, очистка и заполнение сумматора. При попытке использо-
вать разделимый код для контроля поразрядных • операций,
таких, как логическое умножение, логическое сложение
и суммирование1 по модулю два, возникают трудности, кото-
рые, однако, удается преодолеть путем выражения логических
операций через комбинации ряда арифметических операций,
используя следующие соотношения [60]:
а(1) + а(2) = aW Л <т(2) + «(1> у ^(2),
й(1) ф = а!» 4- с№ - 2 («Ф Л а<2>). (7.3)
Соотношения (7.3) позволяют использовать одно и то же
устройство для контроля как арифметических, так и логиче-
ских операций, перечисленных выше.
Одна из попыток практической реализации двоичного про-
цессора с контролем операций дала следующие результаты.
При длине основного сообщения в 16 бит и значении р = 15
избыточность оборудования, связанная с обнаружением оши-
бок, составила около 50%. Введение контроля не замедлило
выполнение основных операций, поскольку собственно конт-
роль выполнялся во время реализации следующей операции,
на этапе дешифрации команды. Обнаружение ошибок приоста-
навливало действие новой операции [40]. .
Обнаружение ошибки не является самоцелью, главная за-
дача состоит в устранении ее влияния на достоверность резуль-
тата. В случае минимальной избыточности арифметического
кода анализ результата повторного использования арифмети-
ческих операций с теми же операциями позволит либо устра-
нить ошибки (при сбое), либо твердо установить факт повреж-
дения аппаратуры в целях ее дальнейшего ремонта либо замены.
В тех же случаях, когда допустима существенная информа-
ционная избыточность, рационально применять арифметические
коды с исправлением ошибок.
Для исправления ошибки помехозащитный код должен не
Только установить факт нарушения, но и определить точную
величину ошибки. При использовании кода рассмотренного
ранее типа это не удается сделать, ибо сравнение вычетов
не позволяет даже сказать, где точно произошла ошибка,
в основном сумматоре или в контрольном. Поэтому для рас-
ширения корректирующих способностей разделимого кода надо
модернизировать его конструкцию.
Пусть проверочное сообщение состоит теперь из двух вы-
четов от значения числа а по модулям р, и р2, т- е- прове-
рочное сообщение есть теперь Ьг и Ь-,:
Ьг = a (mod ₽t), b2 = а (mod ₽2).
В этом случае одновременно с основной частью обрабатывают-
ся независимо обе части проверочного сообщения. После окон-
чания операции формируется вычет от R по модулю и по
модулю, р,. Анализ значений ^(modpj, /?(modp2) и фДМУ, М2)),
^22)) позволяет теперь не только обнаружить ошибку,
но и указать ее точное местоположение. Например., пусть
^(modpj = фД&11), М2)), /? (mod) р2 ф; (&2П, Ь®)- Это означает,
что ошибка произошла в контрольном устройстве, работающем
по модулю р2. Точное определение местоположения ошибок
дает возможность исправить обнаруженные ошибки. Обычно
значения Pi Р2 ... Рр (контроль может происходить по р мо?
дулю) — это взаимно-простые числа [7].
2°. Неразделимые арифметические коды. Умножим чис-
ло а на некоторое целое положительное число В. Полученный
результат а' — аВ представим в г-ичной системе счисления
и будем его рассматривать как помехозащитный код чис-
ла а. Количественный эквивалент слова а' определится из ра-
венства
а' = SLo «И, 0 < а, < г — 1.
В (k + 1)-разрядном слове а! уже нельзя, как ранее, выде-
лить информационные и проверочные разряды, ибо код чис-
ла а' неразделимый. Это приводит к тому, что в арифмети-
ческом узле нельзя будет выделить независимо работающие
основную и проверочную схемы. Кроме того, алгоритмы ум-
ножения и деления должны быть построены с учетом того,
что при умножении результат надо будет дополнительно раз-
делить на В, а при делении частное умножить на В, ибо
ат = а^В, а<П = с№В и = а^а^В’; аВ»:а'Ю =
= а(1): «<2>. Все это заставляет крайне осмотрительно выбирать
значение константы В для неразделимого кода.
Обнаружение ошибок базируется на анализе вычета от ре-
зультата /? некоторой операции по модулю В. Если спра-
ведливо, что
R (mod В) Ф О,
то это говорит о том, что произошла ошибка при выполненци
арифметической операции. Как и ранее, появление ошибок,
величина которых кратна В, не будет замечено схемой контроля.
В случае' двоичной системы счисления для обнаружения
одиночной ошибки достаточно взять 5 = 3. Это приведет
к постоянной избыточности помехозащитного кода (£+1 вмес-
то k — 1 необходимых разрядов), которая не зависит от дли-
ны слова а. При двоично-кодированных системах счисления
эта избыточность может сказаться еще меньше — один допол-
нительный разряд. Например, код, кратный трем в случае
кодирования десятичных цифр двоичными разрядами, требует
пяти двоичных разрядов вместо четырех для обычного двоич-
но-десятичного кода.
Для произвольной системы счисления г при обнаружении
одиночных ошибок следует выбирать такое значение В, кото-
рое взаимно-просто с г и 5 > г. В частности, всегда можно
взять 5 = г+1. Общее число одиночных арифметических
ошибок составляет 2 (г — 1) (А + 1). Для того чтобы выделить
каждую одиночную ошибку, нужно найти такое значение В,
чтобы число классов вычетов взаимно-простых с модулем
было не менее числа одиночных ошибок и чтобы отдельная
одиночная ошибка соответствовала единственному из этих
классов. Если это удается сделать, то к'од вида аВ позволяет
при той же процедуре контроля не только обнаружить ошиб-
ку, но и исправить ее. Действительно, если первоначальный
анализ определил, что R (mod В) 0, то теперь для исправле-
ния обнаруженной ошибки надо знать, чему же именно равна
величина p = /?(mod5), ибо аВ j p = R, где р — величина
ошибки. Когда каждой ошибке соответствует свой класс вы-
четов, взаимно-простых с модулем, то для исправления ошиб-
ки необходимо определить этот класс и, найдя его, произвести
соответствующую коррекцию результата. Проще всего приба-
вить величину, равную величине ошибки с противоположным
знаком.
Избыточность, вносимая умножением числа а на коэффи-
циент В, достаточно велика, особенно при малой разрядности
числа а. Например, для двоичной системы счисления при раз-
рядности чисел, равной 13, избыточность составляет 7 двоич-
ных разрядов. Правда, при тех же семи избыточных разрядах
можно построить плотно упакованный код, где разрядность
числа а составляет 23 двоичных разряда. Главная беда состоит
не в значительном увеличении длины помехозащитных кодов
по сравнению с исходным, а в том, что возникают большие
Трудности при реализаций йрй метическихопераций й этих
кодах, в частности даже такой простой операции, как вычи-
тание.
3°. Комбинированные помехозащитные арифметические
коды. Рассмотренные выше коды являются частными случаями
комбинированных арифметических кодов, обнаруживающих
и корректирующих ошибки. Комбинированные коды образуют-
ся следующим образом. Вначале некоторое слово а, которое
интерпретируется как число, трансформируется в слово а',
которому отвечает число аВ, где В > 1 — целое положитель-
ное число. Затем из слова а' формируется проверочное сооб-
щение с, которое представляет собой вычет от аВ по моду-
лю р, т. е.
с = аВ (mod Р).
Полный код будет состоять из двух частей: а' и с. Раздели-
мые коды получаются из данной конструкции при В—\,
а неразделимые — при р = 0.
Для построения комбинированных кодов, исправляющих
одиночные ошибки, значение В рационально выбрать таким,
чтобы только путем анализа кода аВ можно было бы опре-
делить, произошла или нет ошибка. Для этого надо проанали-
зировать вычет от результата R по модулю В. Если окажет-
ся, что /?(mod5) = 0, то это расценивается как отсутствие
одиночной ошибки. Если же R (mod£?) 0, то ошибка прои-
зошла, и по значению p = R (mod Z?j можно определить, к ка-
кому классу она принадлежит. Исправление ошибок требует
их локализации внутри выбранного класса. Эту задачу можно
выполнить, анализируя вычеты по модулю р от значений R
при фиксированном значении /? = /?(mod5). Конечно, для
того чтобы построить коды с минимальной избыточностью,
нужно, чтобы при заданном В значение р удовлетворяло осо-
бым условиям [26].
В случае двоичной системы счисления комбинированный
код, исправляющий одиночные ошибки, можно построить сле-
дующим образом. Значение В выберем наименьшим, при ко-
тором можно обнаружить одиночные ошибки, т. е. В = 3.
Какой бы ни была величина числа а, код За всегда позволяет
обнаружить одиночную ошибку. Значение же модуля р зави-
сит от величины а. Так, например, если длина кода За в пре-
делах от 28 до 35 разрядов, то значение р есть 29, т. е. длина
проверочного сообщения составит пять разрядов. Для фикси-
рованного значения числа а увеличение коэффициента В вы-
зывает уменьшение длины проверочного сообщения. Кроме
того, есть возможность выбрать такое значение В, которое
при заданной величине чисел а обеспечивало бы наиболее
простую реализацию арифметических' операций.
Возможность варьирования значений В и р и разделение
помехозащитных свойств между основной аВ и проверочной
частью с слова делают комбинированные помехозащитные
арифметические коды весьма перспективными при реализации
вычислений с исправлением и обнаружением ошибок особенно
в вычислительной системе, имеющей различный характер наи-
более вероятных ошибок в различных ее устройствах.
§ 3. АЛГОРИТМЫ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ ПРИ
КОДИРОВАНИИ ОПЕРАНДОВ ПОМЕХОЗАЩИТНЫМИ КО-
ДАМИ
При выборе помехозащитного арифметического кода поми-
мо его корректирующих свойств необходимо принимать во
внимание все стороны реализации алгоритмов арифметических
операций. Особенно важно решение таких вопросов, как фор-
мирование дополнений для выполнения вычитания, учет пере-
полнения сумматора, коррекция промежуточного результата,
округление, умножение и деление на константу В при исполь-
зовании кодов вида аВ.
1°. Неразделимые помехозащитные коды. Будем считать,
что помехозащитный неразделимый код вида аВ для г-ичной
системы счисления представлен в двоичной системе счисления.
Тогда количественный эквивалент целого числа а' = аВ есть
a' = 2«=o«j2z, «/ = 0,1, 0С«'<Д(гт — 1),
где tn — длина числа а при представлении его в г-ичной сис-
теме счисления. Выберем значение константы В таковым,
чтобы выполнялось соотношение
В (гт — 1) = 2/;+1 — 1. (7.4)
Правая часть соотношения (7.4) есть нечетное число, следо-
вательно, это равенство может быть выполнено только при
четном г. Соотношение (7.4) является необходимым и'доста-
точным условием самодополняемоспш кодов аВ, представлен-
ных в двоичной системе счисления; т. е. в случаях, когда
дополнительный код числа а' образуется простым инверсиро-
ванием всех его двоичных разрядов (плюс, конечно, 1 в млад-
ший разряд). Другим важным свойством кодов, удовлетворяю-
щих соотношению (7.4), является простота определения суммы
двух таких кодов, превышающих значение B(rm — 1). Дей-
ствительно, если ck — 1 (перенос со старшего разряда сумма-
тора равен 1), то это является признаком того, что . |
+ Ва'^ ’> В (гт — 1). Это свойство позволяет избежать анализа
значений разрядов суммы для определения переполнения
в г-ичной системе счисления.
1°. 1. Реализация суммирования. Пусть соотношение (7.4)
выполнено при г = 2‘ и (В, 29 = 1. Последнее условие харак-
теризует коды, обнаруживающие одиночные ошйбки, и оно
выполнимо, если 5 = 2Z+1, где 1 = 1, 2... Полагая, что
&+1 — mt + /, получим из соотношения (7.4), что
I
2mt-\ (2f _ J)
4ml - 1
(7.5)
Наибольший интерес представляет определение минимальных
значений /, которые приводят к минимальной избыточности
помехозащитного кодирования. Поскольку 2Z — 1 и 2mZ — 1 —
нечетные числа, то при Z <Zmt решения равенства (7.5) в це-
лых числах” нет. Отсюда нижняя граница для значений 5,
удовлетворяющих (7.4), есть 5min = 2mt + 1 (Z = mt). Этот ре-
зультат в общем случае является разочаровывающим. Дейст-
вительно, удвоение разрядности слов при большом значении
т и t весьма неблагоприятно сказывается на общем количе-
стве оборудования, так же как и на быстродействии арифме-
тического узла. Отсюда применение кодов, удовлетворяющих
соотношению (7.4), целесообразно при малых значениях т
и Z, например, для помехозащитного кодирования цифр г-ич-
ной системы счисления, когда т = \.
В случае, когда г + 2Z, но четно, результаты носят такой
же характер, и опять наиболее благоприятная ситуация соот-
ветствует малым значениям т и г.
Пример 7.1. Пусть г = 10 и т=\, тогда Brain, удовлетворяющее
соотношению (7.4), есть 7. Следовательно, каждая цифра десятичной систе-
мы счисления будет теперь кодироваться 6-разрядным двоичным словом
следующим образом:
Лр d^ d± ci^ d% a J
0—0 00000
1—0 0 0 1 1 1
2—0 01110
3—0 10101
4—0 11100
fig fig fi^ fig fi fi|
5—1 000 1 1
6—101010
7-110001
8—1 1 1000
9—111111
Как следовало ожидать, дополнение каждой цифры в новом коде, „кратном
семи", образуется простоя инверсией кода исходной цифры, т. е. = Д/
для 1 < z < 6, а, —значение двоичных цифр дополнительного кода. Очень
просто определяется и условие превышения суммы двух цифр допустимых
значений. Это условие фиксируется значением переноса со старшего раз-
ряда сумматора, т. е. когда с6 = 1. Однако перенос со старшего разряда
уменьшает значение суммы на 64, а значение десятичного переноса должно
быть 70. Следовательно, необходима коррекция промежуточного результата.
Для экономии времени и оборудования данную коррекцию можно осуще-
:твить без привлечения арифметических действий путем реализации еле-
тующей системы переключательных функций:
5'1 = Sp
S3= 5з(С6 V Ss) V C6S3S2’
s5 = S5C6 V C6S3S2 V S5S2’
S2 —’ S2 Ф C6’
= S^g V SgCg (sg V Sg V ^4)» (7.6)
s6 “ S6 (c6 v ss v s i)-
Система уравнений (7.6) .не очень уж сильно усложнена ио сравнению
с „однократным" двоично-десятичным кодом 8421, а реализуется за такое
же 'время, как и система (5.20).
Неприятным моментом кодирования цифр помехозащитным
кодом является представление значения разрядного г-ичного
переноса в виде слова В, ибо оно тоже должно быть пред-
ставлено помехозащитным кодом. Это обстоятельство вынуж-
дает производить учет разрядных переносов как сложения
чисел, что вызывает замедление выполнения операции сложе-
ния. Некоторым утешением может служить возможность осу-
ществления на двух шагах сложения (перенос и цифра, их
сумма и цифра 2-го слагаемого) одной коррекции, хотя сама
коррекция при этом будет усложнена за счет учета еще од-
ного значения суммы, равного 2В (гт — 1) ф В = В (2гт — 1).
Отказ от свойства самодополняемости помехозащитных
кодов приводит к уменьшению информационной избыточности
за счет выбора минимального значения константы В. Однако
сложность уравнений формйрования разрядов дополнительного
кода может при этом существенно увеличиться. Нарушение
соотношения (7.4) может также привести к усложнению усло-
вий определения переполнения'сумматора для г-ичной систе-
мы счисления.
Пример 7.2. Пусть г = 10, k = 4 и В = 3, тогда соотношение (7.4) не
выполнено. В этом случае формирование дополнительного кода (а/) произ-
водится по значениям прямого кода (at) в соответствии с уравнениями
ZZj — ZZj, Un = ZZ3, ZZ[ —— ZZjZZg \/ ZZg = ZZg (ZZ^ V ZZ3).
При сложении двух кодов, „кратных трем", если сумма больше 27, необ-
ходимо произвести коррекцию промежуточного результата. Признаком
необходимой коррекции служит выполнение равенства
с = с5 v s4s4s3 = 1,
где S/ — значения разрядов промежуточного результата, а с5 — значение
переноса со старшего двоичного сумматора. Поскольку перенос с5 умень-
шает значение суммы на 23 = 32, а значение десятичного переноса есть 30,
то коррекция заключается в добавлении +2 к промежуточному результату.
В случае, когда коррекция осуществляется как логическое преобразование
кода промежуточного. результата, уравнения преобразования будут сле-
дующими;
7
Sj — Sp S9 = S9 ф c, s3 --- S3C6 V c (s3 ф s9),
, .... ’ (7’7)
— S4 (^c \/ ^3^2) V cs^s-jSg, Sg — Sg (^4 ^3)*
Как видно из (7.7), формирование дополнительных кодов
оказывается сложным делом, сравнимым по сложности с кор-
рекцией промежуточных результатов. Поэтому при больших
значениях т равенство (7.4) играет определяющую роль. К со-
жалению, это равенство справедливо для некоторых ограни-
ченных значений константы В.
Диапазон допустимых констант существенно можно рас-
ширить, если использовать помехозащитные коды вида аВ + с,
где В и с — целые положительные числа. Условием самодо-
полняемосТи кодов данного вида при представлении их двоич-
ными числами будет равенство
B(rm — 1) + 2с = 2*+‘ - 1. (7.8)
Уточнений значений В й с можно произвести на основании
учета дополнительных требований. Например, очень важно
исключить этап коррекции промежуточного результата сложе-
ния двух чисел r-ичной системы счисления, представленных
в коде аВс, с тем, чтобы суммирование производилось как
прямое сложение двоичных чисел. Этого удается достичь,
если значени'е переноса с последнего (старшего) двоичного
разряда сумматора будет равно r-ичному переносу (Вгт -|-
+ с), т. е.
-с = 2^+1. (7-9)
Равенства (7.8) и (7.9) выполняются одновременно, если толь-
ко с = В — 1. Единственным недостатком данного кода яв-
ляется’ необходимость коррекции суммы, когда ее значение
меньше, чем 2", поскольку ее значение будет х — 5я(,) + с
4- Вс№ + с = В (а*1’ а<2>) + 2с. Это противоречит принятой
форме кодирования, поэтому из результата надо при ck — О
еше вычесть константу с.
Пример 7.3. Пусть г = 10, tn = 1, В = 3, тогда с = В — 1 = 2 и исход-
ным помехозащитным кодом будет двоично-десятичный код вида За + 2:
0 — 0 0 0 1 0
1—00101
2—01000
3—0 10 11
4 — 0 1110
5—1 О О 0 [
6—10100
7—10111
8—11010
9—11101
Дополнительный код образуется простой инверсией двоичных разрядов
прямого кода. Коррекции результата при значениях суммы больше, чем
29, не требуется, ибо результат автоматически получается правильным
(например, 5 + 5 = 10001g + 10001g — 1.000109). Однако, когда сумма мень-
ше 30, необходима ее коррекция. Эта коррекция заключается в вычитании
двух из полученного промежуточного значения. Если-коррекцию осуще-
ствлять логическим путем, то уравнения преобразования примут следую-
щий вид:
6’1 s', s, = s' ф с5> S;j = s' (s' V c5) V CsSgZ,
, ~.......................... (7.10)
s4 = S4 (c5 v »3) v css>;, s5=(S; v v s-;).
Сложность системы корректирующих уравнений для кодов За и За 4- 2
в случае десятичной системы счисления практически одинакова (см. (7.10)
и (7.7)). Однако условия образования дополнительных кодов оказываются
существенно разными.
Реализация контроля в случае применения кодов вида
аВ + с оказывается более трудной ввиду того, что вначале
из числа надо вычесть константу с, а затем определить вычет
от разности по модулю В, т. е. разделить его на В. Если де-
ление произойдет нацело, то это будет означать, что резуль-
тат верный (йет одиночной ошибки). В противном случае
фиксируется ошибка в работе сумматора. Процесс вычитания
константы с может быть реализован без привлечения арифме-
тических действий, если длина кодов не очень велика.
1°.2. Реализация умножения и деления. Помимо простоты
образования дополнений заметную роль в алгоритмах умно-
жения и деления операндов, представленных помехозащитными
неразделимыми кодами, играет простота реализации деления
и умножения промежуточных результатов на константу В.
Необходимость в выполнении этих действий возникает потому,
что а^В-а^В = а^а^В2, а^В: а{-]В = а(1); а<2>.
Пусть £ = 2*41, тогда произведение а' = аВ получается
всего за одно сложение: а' = аЧ! 4- а, ибо произведение «2*
образуется путем приписывания к изображению числа a t ну-
лей справа, т. е. расширением его на t разрядов. Умножение
на В = 21 — 1 реализуется столь же просто, только вместо
сложения приходится использовать вычитание. Если при дан-
ном п допустим выбор значений 2*4 1 и 2*---1, то лучше
выбирать значение В == 2*—1, поскольку в данном случае
расширяется диапазон чисел, представимых помехозащитным
кодом. Поэтому в дальнейшем чаще использовать значение
В = 2* —1.
Пример 7.4. Пусть п — 6, В — 23.— I = 7 и а = 6. Тогда а’ --- аВ == 42
определится как результат вычитания из числа — HOOOOg числа а, т. е.
а' — 0.1100009 0.111001.) -|-0.000001,? = 1.1010109. Перенос из старшего раз-
ряда сумматора, как принято при вычитании, игнорируется и окончательно
«' =•- аВ — 101010g/ т. е. а’ — 42.
Пусть у = аВ и В~2'—1, тогда при делении числа у
на константу В надо найти значение «, удовлетворяющее ра-
венств^
а = 2*а — у, (7-11)
где у < а2‘. На первый взгляд решение уравнения (7.11)
затруднительно, но на самом деле оно достаточно простое.
Действительно, будем вычислять значение а итеративно, пор-
циями по t разрядов. Результат на первой итерации опреде-
лить просто, ибо младшие t разрядов числа а21 есть нули.
Найденные младшие t разрядов числа а являются операндом
на 2-й итерации, где из а21 вычитаются t следующих разря-
дов числа у и добавляется значение переноса, полученное
на 1-м шаге. Этот процесс продолжается до завершения всех
пЦ шагов итерационного процесса, причем всегда значения
t разрядов числа а, найденные на г-й итерации, будут опе-
рандом на (Z + 1)-итерации.
Пример 7.5. Даны целые числа а' — аВ = 101010g и В -= 1119 (В ~ 7).
Найти а.
Поскольку а = 6, a t 3, то число а найдем за две итерации. На 1-м
шаге из t младших разрядов числа а21, значение которых есть 00Q, вычи-
таются младшие разряды числа а' (заметим, что а' = 0101019), т. е. выпол-
няется действие 000+ 101 +001 = НО. Результат первого шага рассматри-
вается как операнд для 2-го шага, во время которого происходит сложение
ПО + 010 — 1.0Q0. Процесс определения а закончен и а = 0001109, т. е. а=+.
Таким образом, умножение и деление на константу В =
= 2‘ — 1 реализуется за одно вычитание, но если при умно-
жении используется параллельный сумматор по основанию 2п
(или 2й—1), то вычитание при делении выполняется как по-
следовательное определение результата по t цифр на каждом
шаге и здесь уже используется сумматор по основанию 2(
(или 2* ~ 1). Отметим еще одну особенность итеративного
процесса — результат, г-го шага является и операндом Для
(г + 1)-го шага и одновременно г-й порцией (можно сказать
г'-м байтом) в окончательном значении величины а.
Произведение «-разрядных операндов, полученное в виде
р’= рВ, не помещается в заданную длину помехозащитного
слова (в п разрядов), и поэтому необходимо произвести опе-
рацию округления младших разрядов произведения. Но обыч-
ное округление нарушит кодированный вид произведения
и поэтому приходится принимать особые меры. Самым есте-
ственным кажется найти значение младших разрядов, произ-
ведения (не кодированных), т. е. найти их из числа р, по их
значению произвести округление старших разрядов числа р,
а затем полученный результат вновь умножить на В. 1
Процесс округления при делении кодов вида' аВ проще,
ибо частное получается сразу в виде q — a:b. Этот резуль-
тат до умножения на константу В округляется обычным об-
разом.
1°.3. Особенности поразрядного помехозащитного коди-
рования в двоично-г-ичных системах счисления. При коди-
ровании цифр r-ичной системы счисления двоичными числами
всегда, если г =/= 2\ имеется определенная избыточность в пред-
ставлении цифр r-ичной системы. Эту избыточность можно
использовать при кодировании цифр r-ичной системы счисле-
ния неразделимым помехозащитным кодом вида аВ. В этом
случае легко удается избежать затруднений, связанных с ум-
ножением и делением на константу В, сделав эти операции
поразрядными. Это объясняется тем, что в данном случае
нет необходимости в делении произведения двух чисел атВ
и с№В на константу В, ибо достаточно просто разделить
на В множитель. Фактически это деление совмещается с ана-
лизом цифры множителя, который производится всегда (см.
главу 2). Так, например, на каждом шаге анализа вычитать
из цифры множителя не 1, как ранее, а число В. Реализация
деления методом последовательного вычитания делителя из
очередного остатка дает цифры частного в однократном виде
и их совсем нетрудно представить в 5-кратном виде.
Поскольку деление и умножение чисел на константу В
оказывается поразрядной операцией, то имеет смысл реали-
зовать эти операции как логическое преобразование 5-крат-,
ных цифр r-ичной системы счисления в однократные и обратно.
Пример 7.6. Пусть дана двоично-десятичная система счисления с циф-
рами, представленными в коде 8421 (X) и в,коде (К), кратном трем —
3(8421). В этом случае при умножении однократного кода на константу 3
надо выполнить преобразование X -» Y, а при делении трехкратного кода
на 3 — преобразование Y -> X, т. е. производятся следующие преобразо-
вания:
Xi-Xs х2 Xi у-о у4 у3 у3 у,
0 0 0 0 ---► 0 0 0 0 0
0 0 0 1 ----- 0 0 0 11
0 0 10 ----► 0 0 110
0 0 11 -- 0 10 0 1
0 10 0 -- 0 110 0
0 10 1 *-- 0 1111
,0110 -------- 10010
0 111 --- 10 10 1
10 0 0 --110 0 0
10 0 1 -----> 110 11
Соответствующие уравнения преобразований цифр из одного вида в дру-
гой будут следующими:
У1 = X]. у2 = х, ф х2, уд = х3 (х2 V Xi) V Х3*2*1.
Ут = хл v х3х2 V x3x2x,, у5 = х, V х3х2,
Л'1 = у„ х3 = у, Ф у3, х3 у4 (Уз V Уз), Х4 = у4у5.
Реализация уравнений достаточно проста и не требует большого времени
Естественно, что и проблема округления при поразрядном
кодировании кодом, „кратным 5“, решается несравненно про-
ще, чем при кодировании полных чисел. Однако поразрядное
помехозащитное кодирование треоуетзначительно большей
информационной избыточности, хотя при этом обеспечивает
значительно более высокий процент обнаруживаемых ошибок.
Иногда избыточность помехозащитного кодирования не столь
уж велика (как, например, в случае кода 3 (8421)), ибо эф-
фективно используется естественная избыточность двоично-
кодированных систем счисления с основанием г < 2х (см.гла-
ву 3).
2°. Разделимые помехозащитные коды. Затруднения, свя-
занные с реализацией арифметических операций в коде, крат-
ном В, даже если этот код самодополняющийся и требует
простой коррекции промежуточных результатов, особенно
сильно проявляются при попытке реализовать операции с уд-
военной точностью, хотя они довольно очевидны и при опе-
рациях с обычной точностью. Можно ожидать, что использо-
вание разделимых остаточных помехозащитных кодов снимет
хотя бы часть этих затруднений.
При использовании остаточных разделимых кодов обра-
ботка производится в двух процессорах —в процессоре для
операндов (основной процессор) и в процессоре для прове-
рочных сообщений (контрольный процессор). Обработка слов
в этих процессорах производится независимо. Это действи-
тельно так, когда используются сумматоры с циклическим
переносом (см. главу 2, § 1). Если же применяются сумма-
торы дополнительного кода, то при положительном итоге
операции вычитания перенос со старшего разряда сумматора
сп игнорируется и рассматривается только значение основных
разрядов. Уменьшение значения суммы на 2" требует соот-
ветствующей коррекции суммы в контрольном процессоре.
Сама коррекция заключается в уменьшении контрольной сум-
мы на величину 7 = 2"(mod₽). В. случае, когда p = 2z—1
и п == pt, где t и р — целые положительные числа, имеем,
что 7=1.
Зависимость работы основного и контрольного процессо-
ров приводит к мысли о возможной компенсации ошибок
и невозможности создания эффективной системы контроля.
К счастью, это не так, и компенсации не происходит. - Дей-
ствительно, пусть у=1 — „ложный*1 перенос, т. е. сигнал,
который возник в результате одиночной ошибки 2у и при
наличии условий распространения переноса 27' до старшего
разряда сумматора. Величина ошибки в сумматоре, которая
обусловлена пропажей переноса со старшего разряда и до-
бавлением величины 27, есть —2"2Л Изменение значения
суммы контрольного сумматора, вызванное появлением лож-
ного переноса 7 = 1, не может полностью скомпенсировать
значение ошибки, ибо по условию схема коррекции компен-
сирует величину —2", а ошибка 2' окажется обнаруженной.
При другой ситуации ошибка в' сумматоре величины —2У
запрещает появление переноса <?„, т. е. результат в основном
сумматоре отличается от истинного на величину 2" —2Л По-
скольку переноса со старшего разряда сумматора нет, а сле-
довательно, нет и коррекции контрольного процессора, то
в последнем будет значение, равное а(1) ф- «(2) (mod р); когда
же контрольное сообщение будет формироваться из основного
процессора, то оно окажется равным о(,) ф-«(2) — 2^ (mod р),
т. е. ошибка будет обнаружена.
Проблема корректировки проверочного сообщения при
определении чисел в основном процессоре хоть и остается,
но она намного проще решается для остаточных разделимых
кодов, чем для неразделимых.
Одним из важных моментов структуры основного сумма-
тора является способ вычисления остатков от кода результата
по модулю р. Результат в основном сумматоре представлен
в двоичном коде и если 2Z—1, то вычисление вычетов
по модулю р оказывается побайтовой операцией. С этой целью
код основного процессора (рассматриваем целые числа) раз-
бивается на байты по Z разрядов, а затем все байты склады-
ваются по модулю р. Эта процедура основана на том фгщте, что
аг^о-фтобг'- 1), (7.12)
ибо а2г = а (2Z — 1) ф- а.
Пусть основное сообщение есть a: akak-i ... и &ф-
ф-1 -= pt. Поскольку « = 2ь=ой!г2\ то на основании (7.12) имеем
a (mod р) = (Оо ф- at ф- ... at{p^) ф 2 (at J- at+i ф ...
... i)+i) + 2*”1 i ф- cpit-1 + ... ф- ctk) (mod 2г — 1).
(7.13)
Если k ф- 1 pt, то старшие разряды слова а дополняются
нулями, так чтобы было k ф-1 = pt, а затем производится
вычисление вычета по формуле (7.13).
Возможность побайтовой обработки кода основного про-
цессора при подсчете вычета по модулю 2Z — 1 позволяет
ускорить выполнение операции сложения, поскольку форми-
рование вычета можно осуществить по мере определения
младших цифр результата, не дожидаясь, когда он будет
найден во всех k ф-1 разрядах. Разделение кода на основную
и проверочную части позволяет в значительной степени рас-
параллелить процессы в основйом и контрольном процессо-
рах, упростить алгоритмы арифметических операций и умень-
шить время их реализации.
§ 4. АДАПТИВНЫЕ АЛГОРИТМЫ
Каждая исправная цифровая машина может быть детально
определена путем задания основных параметров, таких, как
список операций, объем оперативной, внешней и постоянной
памяти, время выполнения отдельных команд, величина до-
пустимой погрешности в определении результатов для каждой
из арифметических операций и т. д. Назовем эти параметры
нормальными. Неисправность в работе машины приводит
к тому, что ряд ее параметров ухудшается и отойдет от нор-
мальных значений. Иногда ухудшения будут настолько силь-
ными, что машина не сможет приемлемо функционировать.
Неисправность, приводящая к прекращению функционирова-
ния, может быть вызвана выходом одного лишь элемента
в большой системе. Эта ситуация кажется просто несуразной
и нелепой, поскольку в живой природе ’мы постоянно стал-
киваемся с примерами, когда даже при значительном повреж-
дении организма он сохраняет основные функциональные
возможности,, В значительной степени это свойство объяс-
няется высокой адаптивной способностью организма, т. е. его
приспособляемостью к выполнению заданных функций путем
перестройки и перераспределения обязанностей между раз-
личными частями организма. Идеи адаптивной перестройки
могут быть применены и к повышению функциональной на-
дежности цифровой машины. При этом можно попытаться
перестроить неисправную структуру таким образом, чтобы
поврежденный участок исключить из работы, а оставшуюся
часть аппаратуры перекомпоновать таким образом, чтобы
параметры перестроенной машины оказались не слишком да-
лекими от нормальных. Структуры, которые могут перестраи-
ваться в случае необходимости, назовем адаптивными, а ал-
горитмы, которые реализуются перестроенными структурами,
назовем адаптивными алгоритмами. Например, если память
разбита на страницы, то при выходе из строя одной страницы
она исключается из памяти, а оставшаяся часть функциони-
рует как новая память с тем же быстродействием, но мень-
шим числом страниц, которые могут быть при перестройке
вновь перенумерованы с тем, чтобы иметь, сквозную нуме-
рацию.
Зная заранее пределы максимальных отклонений парамет-
ров перестроенной машины от нормальных, можно оценить
целесообразность перестройки при том или ином типе повреж-
дений. Перестройка структуры наряду с ухудшением ряда
нормальных параметров может также привести к улучшению
других параметров. Например, при выходе из строя части
разрядов регистра арифметического устройства погрешность
вычислений увеличивается, но зато может увеличиться ско-
рость реализации арифметических операций по сравнению с ис-
ходной структурой. До тех пор пока ряд одновременных или
последовательных нарушений не выведет параметры пере-
строенной машины из допустимых пределов; ее функциони-
рование будет считаться допустимым. Адаптивные струк-
туры и алгоритмы могут реализоваться двумя основными
методами — Методом подмены иметодом перекомпоновки
аппаратуры.
1°. Метод подмены. Этот метод заключается в передаче
функций вышедшей из строя аппаратуры исправным блокам.
Естественно, что поскольку основные функции этих блоков
иные, то перестройка приведет к ухудшению параметров ма-
шины. Например, если вышел из строя блок умножения, то
эта операция может быть реализована в блоке сложения
путем последовательных сложений и сдвигов, но это приведет
к значительному увеличению времени умножения. В методе
подмены важную роль играют программы распределения за-
даний исправной аппаратуры для выполнения функций неис-
правного блока. Это особенно важно для машин с микропро-
граммным уцравлением, ибо в этом случае в Зависимости от
состояния аппаратуры можно формировать тот или иной набор
команд для машины. Например, если вышла из строя аппара-
тура, реализующая арифметические операции с удвоенной
точностью, то команды этих операций программируются как
процедуры, приводящие к желаемой точности, но базирую-
щиеся на использовании лишь команд обычного формата.
2°. Метод перекомпоновки аппаратуры. Данный метод
основан на передаче функций неисправной части блока той
части этого же блока, которая осталась неповрежденной.
Поскольку функции других блоков при этом не меняются, то
подобная перестройка производится за счет некоторого внут-
риструктурного резерва блоков, а точнее за счет изменения
его параметров. Рассмотрим метод перекомпоновки аппаратуры
более подробно на примере перестройки структуры арифме-
тического узла (АУ), которая довольно часто применяется
в машинах последовательного действия. Эта структура (рис. 37)
включает три регистра, два из которых (регистры А и В)
имеют разрядность n = k Jri 1, а один (регистр С) — разряд-
ность /г-|- 1 и одноразрядный сумматор. Связи между регист-
рами и сумматором, приведенные на рис. 37, отвечают опе-
рации умножения. Вее регистры являются регистрами од-
нонаправленного сдвига/ Входами сумматора служат выходы
регистров В и С, а его выход подан на вход регистра С.
Пусть в одном из регистров произошла неисправность,
в результате которой он полностью или частично перестал
функционировать. Если в арифметическом узле нет других
регистров, кроме указанных выше, т. е. нет резерва, то при-
ходится искать выход из положения путем перекомпоновки
оставшейся исправной аппаратуры [25]. Наиболее просто нахо-
дится выход при сложении. Здесь надо обеспечить помещение
операндов перед началом операции в исправные регистры
и результат отослать на местю. одного из операндов. .
А. Адаптивный алгоритм умножения. Рассмотрим те-
перь алгоритм умножения. В исправной машине реализуется
классический метод умножения, начиная с младшей цифры
множителя, расположенного в регистре А. Частичные произ-
ведения формируются методом последовательных суммирова-
ний множимого, находящегося в регистре В. Найденное (и-!
+ 1)-разрядное частичное произведение а(]Ь располагается
в регистре С. Младшая цифра этого произведения является
цифрой окончательного результата, и поэтому перед следую-
щим шагом умножения производится сдвиг вправо регистров
С и А с целью перевести эту цифру в освободившийся раз-
ряд регистра А. Далее цикл повторяется до тех пор, пока
будет сформировано полное 2/г-разрядное произведение, стар-
шие разряды которого будут расположены в регистре С,
а младшие — в регистре А (см. главу 2, § 6).
Рис. 37.
Предположим теперь, что в результате неисправностей
вышли из строя п — k разрядов какого-либо из трех регист-
ров АУ. Установить этот факт можно, например, с помощью
диагностических программ. Пусть в нашем распоряжении
имеются средства, которые позволят „вырезать11 испорченные
разряды регистра. В результате этой операции окажется, что
один из трех регистров АУ имеет не п, a k разрядов. Можно
попытаться реализовать классический метод умножения на
этой перестроенной структуре. Тогда оказывается, что погреш-
ность результата, определенная как
• Л =—(ab)* + ab,
где («А)* и ab есть результат, полученный на перестроенной
и исходной структуре соответственно, не зависит от того,
в каком регистре произошло повреждение, а определяется
только количеством разрядов, вышедших из строя. Макси-
мальная величина погрешности при этом оказывается весьма
значительной [30]:
max |Д | = (гп — 1) (rn~k — 1), (7.14)
где г — основание системы счисления и операнды рассматри-
ваются как целые числа. Максимальная погрешность дости-
гается при dt — bt~ г ~ 1, 0 — 1, т. е. когда ab =
= (ги —I)2. Как видно из выражения (7.14), если один из ре-
гистров целиком вышел из строя, то полученный результат
равен нулю. Это естественно, ибо классический алгоритм
умножения требует для своей реализации трех регистров
в арифметическом узле и не может быть реализован на двух
регистрах.
С другой стороны, известны алгоритмы умножения (см. гла-
ву 2, § 5), которые могут быть принципиально реализованы
на регистрах АУ общей памятью в 2/гДЛ разрядов. Логично
в случае повреждения части разрядов в каком-либо из ре-
гистров АУ так перекомпоновать два целых и один укоро-
ченный регистры, чтобы имелась возможность применять
алгоритмы приближенного умножения. С этой целью укоро-
ченный (поврежденный) регистр, каким бы он ни был в ис-
ходной структуре, всегда в перестроенной структуре будет
играть роль регистра А (множителя). В этом регистре раз-
местим k младших разрядов множителя а. Остальные п — k
его разрядов находятся в младших разрядах регистра С. Дру-
гой целый регистр используется в качестве регистра множи-
мого (регистр В). В результате подобной перестройки всегда
множимое и множитель перед началом операции представлены
неискаженными исходными величинами (рис. 38), а регистр С
(регистр частичных произведений) сокращается до n — k разря-
дов. Полученная перестроенная структура полностью отвечает
требованиям реализации приближенного умножения, который
мы и используем, как это было описано в главе 2, § 5. На-
помним, что главное отличие алгоритма приближенного умно-
жения от классического состоит в итеративном изменении
длины множимого в зависимости от номера шага умножения.
Максимум абсолютной величины погрешности зависит от стра-
тегий выбора поправочных коэффициентов, роль которых
состоит в уменьшении погрешности, вызванной изменением
величины множимого. Наиболее важные случаи рассмотрены
в главе 2, § 5. Так, например, если коррекция множимого
не производится, т. е. на первых п — k — 1 шагах отбрасы-
ваются „лишние" разряды множимого, то
шах | (г—\)(n — k—1). >(7-15)
Рис. 38.
Как видно из сравнения выражений (7.14) и (7.15), новая
перекомпондвка аппаратуры, оставшейся исправной, которая
позволяет реализовать алгоритм приближенного умножения,
приводит к значительно меньшей погрешности вычислений.
Важно отметить, что даже выход из строя целиком одного
регистра не выведет арифметический узел из строя, посколь-
ку данный алгоритм допускает реализацию и на двух регист-
рах АУ. Поскольку обычно на практике произведение /7-раз-,
рядных операндов представляется также /г-разрядным чис-
лом, то алгоритм приближенного умножения, используемый
в качестве адаптивного алгоритма, дает особенно большой
эффект. Действительно, в этом случае погрешность округле-
ния, абсолютная величина которой достигает 2-1/'", оказывается
обычно существенно более высокой, чем погрешность итера-
тивного умножения, задаваемая выражением (7.15).
Б. Адаптивный алгоритм деления. Для реализации алю-
ритма деления в машинах стараются использовать те же ап-
паратные средства, что и при умножении. Для последова-
тельного АУ функциональные связи при делении будут таки-
ми, как на рис. 39. В исходном положении делимое хранится
в регистре С, а делитель — в регистре В. Путем последова-
тельных вычитаний делителя вначале из делимого, а затем
из очередных остатков за п шагов определяются цифры част-
ного, начиная со старшей. Поскольку регистр А имеет только
сдвиг вправо, то для записи частного в нужном виде (стар-
шая цифра частного должна находиться в разряде с номе-
ром k) после записи очередной цифры частного производится
циклический сдвиг вправо на п— 1 разрядов1. Для реализации
этой перезаписи выход из регистра А соединен с входом,
а связь с регистром С, необходимая для умножения, нарушена.
Остальные связи сохранены точно- такими же, кйк и при ум-
ножении. Это получилось потому, что для последовательной
машины нет необходимости делать сдвиг влево очередного
остатка в регистре С, достаточно просто в первом такте вы-
читания использовать только младшую цифру делителя, а циф-
ры остатка включать в вычитание, начиная со второго такта,
т. е. „отложить"', ввод в действие остатка до 2-го такта алгеб-
раического сложения. Это и быстрее и проще, чем реализовать
сдвиг влево на регистрах, имеющих только сдвиг вправо.
Рис. 39.
Как и ранее, будем считать, что при выходе из строя час-
ти разрядов регистра АУ имеется возможность их исключать,
в результате чего этот регистр окажется укороченным до
k разрядов. Перестроим поврежденную структуру таким
образом, чтобы этот укороченный регистр всегда был регист-
ром частного (регистр А). Кроме того, выход регистра А
соединим со входом регистра С. Остальные же связи сохра-
ним неизменными (рис. 40).
Перестроенная структура приспособлена для реализации
алгоритма адаптивного деления, в качестве которого выберем
алгоритм приближенного деления (см. главу 2, § 5). Этот
алгоритм характерен тем, что на’первых k ф -1 шагах дели-
тель имеет нормальную длину в п разрядов. Цифры частного
поступают в регистр А. В конце (А+1)-го шага при записи
очередной цифры частного происходит сдвиг влево „длинного11
регистра, т. е. объединенного регистра, состоящего из ре-
гистров А и С, последовательно соединенных. Этот сдвиг
реализуется через n-Yk сдвигов вправо. В результате сдвига
после (&4~1)-го шага старшая цифра частного окажется
в младшем разряде регистра С. Очевидно, что для того что-
бы не испортить полученные цифры частного, теперь на каж-
дом шаге, начиная с (k ф- 2)-го, надо будет уменьшать длину
делителя на один разряд. После завершения действия п раз-
рядов результата находятся в регистре A (k младших разря-
дов) и в регистре С (п — k старших разрядов). Дополнитель-
ными сдвигами частное полностью переводится в регистр А.
Поскольку частное, найденное в соответствии с данным
алгоритмом, получено приближенно, то важно оценить вели-
чину его максимального отклонения от точной величины. Как
было показано в главе 2, если ограничиться простым отбра-
сыванием младших разрядов делителя, без коррекции остав-
шейся части, то при выполнении условий
гк> (г- 1) {n-k~ 1)-2 (7.16)
погрешность в определении частного не превышает по абсо-
лютной величине единицы младшего разряда частного, т. е.
не превосходит погрешности деления, выполняемого по цик-
лическому алгоритму. Таким образом, при выполнении уело-,
вия (7.16) перестройка структуры полностью компенсирует
выход из строя п — k разрядов какого-либо из регистров АУ.
Итак, адаптивные алгоритмы умножения и деления по-
зволяют получать результаты с погрешностью меньше, чем
единица младшего разряда при небольшом числе поврежден-
ных разрядов в произвольном регистре АУ последовательного
принципа действия. В случае дальнейшего выхода из строя
разрядов в этом же регистре, т. е. уменьшении параметра k,
погрешность становится значительной. Даже при полном вы-
ходе из строя одного регистра (k = 0) адаптивные алгоритмы
позволяют выполнить умножение и деление, при этом погреш-
ность не будет превышать величины порядка п единиц млад-
шего разряда, что в большинстве является вполне допусти-
мым.
Весьма заманчивой кажется идея подобной перекомпоновки
аппаратуры и при повреждениях в разных регистрах АУ.
Естественно, что перестройка в этом случае получится более
сложной, нежели при повреждениях в одном регистре, и по-
этому аппаратные средства, осуществляющие переконфигура-
цию АУ, окажутся существенно большими. Вообще следует
отметить, что ликвидация последствий выхода из строя эле-
ментов в разных регистрах АУ, несмотря на принципиальную
простоту, на практике оказывается чрезвычайно> сложным
делом.
По-видимому, идеи адаптивной перестройки структур при
повреждениях могут плодотворно использоваться в однород-
ных структурах, где достаточно просто обеспечить необходи-
мый резерв оборудования и существуют однотипные связи
между элементами.
В заключение хотелось бы отметить, что уже на совре-
менном этапе применение комплексных методов повышения
надежности позволяет строить цифровые машины,, способные
работать без выхода из строя в течение нескольких лет.
ГЛАВА 8
РЕАЛИЗАЦИЯ АЛГОРИТМОВ АРИФМЕТИЧЕСКИХ
ОПЕРАЦИЙ НА БАЗЕ МАТРИЧНЫХ СТРУКТУР
9
Выбор того или иного алгоритма выполнения арифметиче-
ской операции для конкретной машины всегда производится
с учетом той элементной базы, на основе которой строится
машина, и,технологии производства.' Долгое время многие
алгоритмы, обеспечивающие весьма высокое быстродействие
машины, не находили применения на практике ввиду значи-
тельной стоимости реализации или чрезвычайной громоздко-
сти и ненадежности технического воплощения. В последнее
время положение существенным образом изменилось, благо-
даря исключительным успехам в технологии изготовления
больших интегральных схем (БИС). Высокая надежность,
чрезвычайная компактность и низкая стоимость БИС стиму-
лируют разработку новых типов арифметических устройств,
универсальность и высокое быстродействие которых дости-
гается за счет существенного усложнения логической струк-
туры и увеличения объема оборудования. Желательно, чтобы
такие устройства имели однородную матричную структуру,
что обеспечивает возможность их простого наращивания
и высокую технологичность изготовления при массовом про-
изводстве. Внесение небольшой избыточности в однородные
схемы позволяет помимо основных функций на том же обо-
рудовании реализовать и некоторые дополнительные функции,
например, такие, как контроль выполнения арифметических
операций. Поэтому естественно потребовать, чтобы арифме-
тические устройства, реализованные на БИС, помимо чисто
арифметических функций осуществляли бы и другие необхо-
димые для машины функции, такие, как выполнение логиче-
ских операций, сортировка хранимой информации, процедуры
типа перевода или преобразования формата данных и т. д.
Матричные структуры, как правило, характерны для парал-
лельных арифметических устройств, имеющих высокую сте-
пень совмещения выполнения различного типа действий.
§ 1. МАТРИЧНЫЕ СХЕМЫ УМНОЖЕНИЯ
Операция умножения наиболее полно приспособлена к па-
раллельному выполнению. Действительно, формирование про-
изведения заключается в одновременном суммировании всех
п независимо найденных произведений цифр множителя на
полное множимое. Подобное приведение п слагаемых к сум-
ме, как мы видели ранее (глава 5, § 2), может быть осу-
ществлено с помощью деревьев спуска. Такое дерево может
быть построено из идентичных элементов (ячеек), одинаковым
образом соединенных (обычно за исключением некоторой
части элементов на границах). Нетрудно дерево спуска изо-
бразить в виде матрицы и получить матричную схему умно-
жения. Входными величинами для матричных схем умноже-
ния являются значения разрядов сомножителей, а выходны-
ми — значения разрядов произведения.
Одним из главных вопросов прстроения матричной схемы
умножения является выбор типового элемента дерева. В на-
.стоящее время известно несколько схем ячеек, которые
представляют собой полный двоичный сумматор с добавле-
нием некоторых логических схем. Выбор типа ячейки во
многом определяется видом представления операндов. На
практике для двоичной системы счисления наибольшее рас-
пространение получили прямые и дополнительные *коды,
имеющие разную специфику сложения.
Пусть операнды (множитель а и множимое &), заданные
дополнительными (k -f- 2)-разрядными двоичными кодами,
являются целыми числами, т. е.
а = -a*2*+1 + SLoар, b=- bp1 S/=o6у2Л
Будем искать произведение p = ab в виде (2k + 3)-разрядного
дополнительного кода, старший разряд которого является
знаковым, а остальные — основными разрядами произведения.
Произведение p = ab есть
р = 2to Л=о atbp+i + - 2ft+1 (а* 3)=0 bp +
+ b* 2L0«z29 = SLo afip+i -f- 22^+2 __a* — bj +
+ 2й+> [a* (Zj^bp + !) + &* (SLoap + 1)]. (8.1)
Сумма двух первых слагаемых правой части выражения (8.1)
определяет значение основных разрядов произведения, а пос-
ледний член наряду с возможным переносом в (2k 4- 3)-й
разряд от суммы двух первых членов определяет значение
знакового разряда произведения. Поскольку исходными ве-
личинами являются только сомножители, заданные дополни-
тельным кодом, то для построения матричной схемы умно-
жения надо выбрать такой элемент, который позволил бы
реализовать все необходимые действия, включая формирова-
ние инверсии (как этого требует равенство (8.1).
Рассмотрим следующую структуру ячейки (рис. 41). Здесь
ф — сумматор по модулю два, a J - полный двоичный сум-
матор. Значения сигналов на входах Р и Т определяют ре-
жим работы ячейки. Вход А соответствует значению суммы
частичных произведений в данном разряде, а .вход С — зна-
чению переноса от предыдущей справа ячейки; выход В —
значение выходного сигнала с ячейки, а выход D — значение
переноса с данной ячейки. Значения выходов В и D опреде-
ляются по входным значениям, А, С, Р, Т — в соответствии
со следующими уравнениями:
B = A®C®T(P®F),
D = ACV T(P®F)(AV С).
(8.2)
Рис. 41.
Из уравнений (8.2) следует, что когда Р = 0, то В = А ф С ф
ф TF, а при Р= 1 имеем В = ЛфСф7’/-'. Следовательно,
при Т = 1 в первом случае суммируется прямой код числа F,
а во втором—обратный. Отсюда ясно, что если на вход Т
подать цифру множителя а\, а на вход F — цифру множимого
bj, то внутри ячейки можно сформировать элемент частичного
произведения либо вида а^Ь,, либо вида afij [41].
Рассмотрим особенности организации матричной схемы ум-
ножения, состоящей из элементов, представленных на рис. 41,
в том случае, когда умножение начинается с младших раз-
рядов множителя (рис. 42). Схема состоит из (k + 2)2 одина-
ковых ячеек (в данном случае 6=1), которые образуют £ + 2
рядов по k + 2 столбцов в каждом. В принципе данйая схема
позволяет вычислить выражение p=ab-\-l, где I есть (&-По-
разрядное положительное число. Значения всех разрядов
числа I подаются на входы А верхнего ряда элементов мат-
рицы, который при I = 0 формирует частичное произведение
айЬ. Для данного ряда никаких особых условий нет, за исклю-
чением крайне левого элемента, особая роль которого связана
с необходимостью учета в общей сумме (8.2) члена вида
С2?=о^2‘+ 1). Выполнение условий P=l, F = a0 и А —
= Т=Ь* позволяет на данном элементе вычислять выражения
В — Ь* (а0 ф 1) ф с и D — aob*. Структура соединений ячеек
в рядах со 2-го по (k-\- 1)-й включительно будет одинаковой.
В этих рядах Pji} = 0 для всех a P*+i==l. Кроме
того, Т*;0 = at. В крайне левых элементах вход T^+i = b*,
а вход Ffi+i = at. Значения выхода переноса с этих элементов
подаются в нижний ряд на вход А, так что £)*+! = Бла-
годаря такому соединению в каждом из этих рядов сумми-
руется число af2z 2/=о с суммой всех предыду-
щих частичных произведений, следовательно, выходы В эле-
ментов (& + 1)-го ряда и перенос D^+i задают величину
+ b*2*+' (SLoaz2z + 1). Теперь для получе-
ния значений всех основных разрядов произведения к этой
сумме согласно (8.1) надо добавить еще число <zs2ft+1 X
X (2;=о&/2<-|-1). Это просто сделать, если к матрице доба-
вить еще один ряд, в котором Pjft+1)= 1 для всех k +
+ 1, и, кроме того, необходимо обеспечить Сой+1> = я* (рис. 42).
Все остальные соединения в этом ряду обычные.
Остается еще сформировать знаковый разряд произведения.
Согласно (8.1) это значение суммы по модулю два величин
—а* — Ь* и переноса с основных разрядов суммы. Заме-
тим, что aj)* — а*~ Ь* =—(a*VM. Значение переноса
с основных разрядов есть сумма и Легко уста-
новить, что 2)1+1 = b*ak ... а0, и если Z)*+i = l, то D*ft+1) = 0,
если только b =^= —2ft+I. Следовательно, D^i £>й:+1) =0 и по-
этому = V D{kk+1\ Отсюда
Ай+2= (й* V &*) Ф (^hi V
Реализация, уравнения может быть осуществлена с помощью
типового элемента, у которого Cfe+i1) = D(k+i V D(k+1\
= F^i1) = ^. P^i1)=l и = (см. рис. 42).
Приведенная матричная схема позволяет получить все воз-
можные произведения, как положительные, так и отрицатель-
ные. На рис. 42 приведены значения всех входов и выходов
ячеек матричной схемы умножения, соответствующих случаю
перемножения чисел а=1.102 и 6=1.1012. Как и следовало
ожидать, результат этого перемножения есть р = 0.01102.
Особенностью матричной схемы умножения является то,
что на входы Р, Т и F всех элементов сигналы поступают
в одно и то же время, поэтому задержка в получении резуль-
тата после поступления сомножителей будет определяться
только путями распространения сигналов, приходящих на вхо-
ды А и С. Формирование первого частичного произведения
Ро завершится через время 7тл, где тл — задержка на один
логический уровень. Общая сумма 7тл образуется из задержки
ио Зтл на сумматорах У, и ф элемента, изображенного на
рис. 41, и задержки тл на схеме совпадения. Элементы дру-
гого ряда могут внести дополнительную задержку либо Bts=
= Зтл (для выхода суммы В), либо в тс = 2тл (для выхода
переноса D). Отсюда наибольшая задержка в получении
произведения определится как
шах т = 7тл + тс (k + 1) + + (тя + тс) (k — 1) =
= ^(тл-|-2тс) + 7тл = 7тл(й+ 1).
(8.3)
К задержке, равной (8.3), может привести, например, такой
путь распространения сигналов: значение В®— 1 вызывает
распространение переносов от первого элемента второго ряда
до последнего и формирования в нем значения /$+1 = 1.
Далее это значение вызывает перенос в следующем ряду,
который, в свою очередь, формирует Вй+1=1 и т. д.
При тех. же значениях и и при той же разрядности
простое дерево спуска в случае прямых кодов обеспечивало
максимальную задержку согласно (5.23) в 5&тл. Это обстоя-
тельство заставляет пересмотреть структуру матричной схемы
умножения с целью уменьшения величины максимальной
задержки в получении результата.
Реализуем алгоритм умножения, при котором операция
начинается с умножения на старший разряд множителя
(рис. 43). Особенностью данной схемы является увеличение
числа ячеек в каждом ряду матрицы, начиная со второго
до k + 2 4- i ячеек, где i — номер ряда. Следовательно, вместо
Z Z. I Л\2 3/^ 4 11& + 10 q
(k 4 2) ячеек теперь необходимо -----2----- ячеек. За счет
дополнительного оборудования удается снизить величину шах т
до значения [41]
шах т == (k 4- 1) (ts 4- тс) 4 2тл = тл (5k 4 7).
Рис. 43.
Это уже достаточно близко к времени задержки для дерева
сумматоров с однородной структурой. Данная величина полу-
чается, когда сигнал переноса распространяется в первом
ряду справа налево до крайнего элемента, а затем вниз по
вертикалй до = 1.
Приведенные матричные схемы умножения рассчитаны на
использование дополнительных кодов. Они могут быть суще-
ственно упрощены в случае применения прямых кодов. В этом
случае упрощается сама ячейка, ибо случай прямых кодов
соответствует режиму Р& = 0 для всех ячеек и тогда схема
сложения по модулю два внутри ячейки, изображенной на
рис. 41, просто не нужна. Кроме того, уменьшается число
ячеек до (&-J-1)2 и упрощается схема соединений. Построе-
ние матричной схемы с диагональными переносами вместо
горизонтальных при числе ячеек (&+ I)2 дает время задержки
в получении результата,, равное значению, определенному
из (5.23). »
§ 2. МАТРИЧНЫЕ СХЕМЫ ДЕЛЕНИЯ
При построении матричных схем деления следует иметь
в виду, что процесс формирования частного является процес-
сом последовательного определения цифр частного. До тех
пор пока не завершится вычитание делителя из текущего
остатка, что реализуется элементами выбранного ряда, т. е.
до тех пор пока не определена старшая цифра разности, ни-
чего нельзя сказать о характере арифметического действия
на следующем шаге алгоритма. Отсюда управление каждой
строкой матрицы может бытй произведено лишь после завер-
шения формирования значений выходных сигналов в старшем
разряде ряда.
Матричные схемы деления желательно строить на основе
тех же элементов, которые используются для построения
матричных схем умножения. Ячейки, изображенные на рис. 41,
вполне подходят для этой цели, ибо позволяют реализовать
не только сложение, но и вычитание. В то же время в дан-
ном случае эта ячейка является избыточной, поскольку при
делении делитель обязательно присутствует в каждом ряду,
следовательно, Т<г) = 1 для всех i = 0, 1, ..., k. Этот упро-
щенный вариант базовой ячейки мы и будем использовать
для построения матричной схемы деления.
Рассмотрим реализацию деления прямых двоичных /г-раз-
рядных кодов (я==^4-1). Будем считать, что делитель. нор-
мализован, т. е. bk—\. Значение управляющего сигнала Р
для первого ряда матрицы (рис. 44) есть единица, ибо всегда
деление начинается с вычитания делителя из делимого. Этого
нельзя сказать о значении Р& для других рядов, ибо оно
будет определяться знаком результата алгебраического дей-
ствия в предыдущем ряду матриц. Знак результата легко
может быть найден по значению переноса со старшего
разряда данного ряда.
Если = 1, то это означает, что в результате алгеб-
раического действия получено положительное число и на сле-
дующем шаге надо из текущего остатка вычитать делитель.
Одновременно значение переноса определяет и цифру
частного — ее значение совпадает со значением переноса со
старшего разряда. Когда же Dk+i = O, то цифра частного есть
нуль, результат имеет знак «—», следовательно, на следую-
щем шаге необходимо прибавить делитель (обоснование дан-
ных действий дано в главе 2, § 4). Таким образом, значение
переноса со старшего разряда определяет и цифру частного
и сигнал управления арифметическим преобразованием на сле-
дующем ряду матрицы. Согласно алгоритму деления после
определения очередной цифры частного остаток сдвигается
влево на один разряд, т. е. увеличивается в два раза. По-
скольку удвоенный остаток может быть больше, чем дели-
.тель, то необходимо в каждой .строке матрицы иметь л + 1
ячеек, но всегда значение bk+i = 0. Теперь очевидна струк-
тура приведенной матричной схемы деления (см. рис. 44) [58].
Рис. 44.
На входы верхнего ряда подается делимое (см.
рис. 44, а = 0011). Крайние элементы в каждом ряду имеют
отличные от других соединения. В крайне правых элементах
выход сигнала управления P(Z) соединен со входом переноса
Со\ а в крайне .левых элементах выход переноса сое-
динен со- входом управления следующего нижнего ряда, т. е.
^+1=Р™
Число строк матрицы соответствует разрядности искомого
частного. Общее число элементов в матрице зависит не толь-
ко от разрядности частного, но и от длины делителя. Так,
если делитель имеет п разрядов, а частное т, то число эле-
ментов в матрице' есть При этом длина делимого
может быть до т + п разрядов, важно лишь, чтобы величина
делимого была меньше удвоенного значения делителя, по-
скольку под целую часть у частного отводится лишь один
разряд т. е. О 2. Помимо частного данная схема
позволяет также получить остаток, величина которого задает-
ся значениями для всех / = 0, 1, ..., k ф- 1.
Наибольшее время формирования частного определится как
шах т = т [тс (п -f- 1) -|- Зтл] = mt. (2k + 7), (8.4)
ибо здесь считаем, что тс = 2тл. Заметим, что задержка бу-
дет, как и при умножении, различной в зависимости от зна-
чений слагаемых на входах элементов. Наибольшее время
задержки составит 5тл и соответствует одновременному при-
ходу всех Входных сигналов, если при этом А =/= 1 и С=^=1.
Если А = С=1 или сигналы А и С приходят после управ-
ляющего сигналами Р& через время Зтл (т. е. когда завер-
шится формирование значения FQ)P), то время задержки
сигнала переноса есть 2тл. Большая задержка в формировании
переноса характерна только для .крайне правых элементов,
в остальных же случаях тс = 2тл. Максимальная задержка
в получении частного отвечает случаю пробега переноса по
всем рядам, от крайне правого до крайне левого’ элемента
в каждом ряду.
Сравнивая выражения (8.4) и (8.3), находим, что матрич-
ные схемы деления обладают значительно худшим быстро-
действием. Грубо оценивая, можно считать, что умножение
производится в раз быстрее, чем деление. Такое суще-
ственное отличие во времени выполнения деления делает
обоснованным вывод об использовании для получения част-
ного итерационных процессов, базирующихся на применении
операции умножения (см. главу 5, § 3).
Наибольший вклад в величину шах т при делении вносит
распространение переносов вдоль строк матрицы. С целью
уменьшения времени распространения переноса в строках
матрицы можно использовать какой-либо из способов уско-
рения сложения. При этом надо иметь в виду специфику
операций—при каждом сложении-вычитании одно из слагае-
мых постоянно, а именно делитель. Рассмотрим сейчас мат-
ричную схему деления, в которой для уменьшения времени
распространения -переносов вдоль строки матрицы применены
сразу два способа ускорения сложения — метод формирования
блочных переносов и метод» суммирования с сохранением
переносов [47]. Напомним, что сумматоры с сохранением пе-
реносов дают сумму (разность) слагаемых в виде двух чисел —
поразрядной суммы s и поразрядных переносов с. Будучи
сложенными в обычном сумматоре, эти два числа дадут ис-
тинное значение суммы или разности.
Трансформируем матрицу таким образом, чтобы каждая
строка являлась параллельным сумматором с сохранением пе-
реносов и, следовательно, в каждом ряду матрицы должны опре-
делиться числа s<Z) и cW>. Эти два числа будут найдены при сум-
мировании (или вычитании) делителя с числами s(z-1) и
Анализ двух чисел.s' и с1 должен позволить найти цифру част-
ного и значение управляющего сигнала для следующей стро-
ки: 7->(Z+I). Сложение с сохранением переносов займет время
= max(tJ., тс), и поэтому основным фактором, определяющим
задержку в получении частного, будет служить время опреде-
ления управляющего сигнала для следующего ряда. К сожале-
нию, эта операция не может быть произведена без полного
анализа чисел s<z> и с№. Поскольку в качестве управляющего
сигнала выступает значение переноса со старшего разряда, то
для уменьшения времени формирования управляющего сигнала
целесообразно использовать идеи определения блочного пере-
носа в «-разрядном сумматоре. Рассмотрим более детально
алгоритм деления целых чисел (n = k-\- 1) при использовании
сложения с сохранением переносов и метода блочного фор-
мирования переноса с последующего разряда. '
Для i-й строки матрицы, которые пронумерованы сверху
вниз, значение пары чисел s(Z) и dz) определится следующим
образом:
SW + 2c(z> = s<z-z) + 2c<z-D + (1 — 2Р«~Г>) Ь2~1,
где -1 и s(°> = «, с<°) = 0 и Р(°> = 1; причем
s? = © с'-'Д0 © P[i~r} © bp
= хГ V (Р™ © (s?-*> Vc^), (8.5)
4° = P(/-1), ^+1=0.
Кроме поразрядных значений суммы и переноса, определяе-
мых из уравнений (8.5), в каждой ячейке матрицы (обозначим
ячейки такого типа буквой А) надо еще сформировать вспо-
могательные функции Gj0 и для определения блочного
переноса (см. главу 5, § 1). Для двоичной системы счисления
уравнения, задающие значения этих функций, оказываются
достаточно простыми G;° = и Г}0 = sjl) V cj-j. Реали-
зация данных функций должна быть осуществлена внутри
базовой ячейки, в результате чего ее схема усложняется
(рис. 45). Входы F и Р используются точно так же, как и ра-
нее для учета значений Ь} и На входы At и Д2 подают-
ся значения и cfyz?, а на вход С — значение Вы-
ход D дает значение с^\ а выходы Ви В2, G и Т отвечают
значениям S;0, 4-i> GjZ) и У)0 соответственно.
Рис. 45.
Определение группового переноса производится в соот-
ветствии с уравнением
/?<z> = G£> V 71°G(ft% V ... ... (8.6)
Знак частичного остатка, т. е. значение управляющего сиг-
нала Р&>, есть
Р(0 = s^-iy © 4-,1» © Pil~l} © Я(0 © 4°. (8.7)
Значение разряда частного, найденное в i-й строке, совпа-
дает со значением Р^К ;
Как отмечалось ранее (глава 5, § 1), создание элементов,
реализующих прямо уравнение (8.6), технически возможно
..лишь при небольшом числе конъюнктивных членов. Из-за
ограничений на нагрузочную способность элементов необхо-
димо применять ступенчатую схему формирования групповых
переносов, причем число ступеней зависит от длины опе-
рандов.
Для реализации уравнений (8.7) целесообразно использо-
вать особую ячейку, отличную от ячеек типа Д. Для этой
ячейки характерно, что Ьь+у =0, и нет необходимости фор-
мирования значений G^+i, ТЧ+i и sl+i, 4°1 В результате схема
л?
крайне левых ячеек трансформируется (рис. 46). На вход Р
нового элемента (обозначим его S), как обычно, подается
значение q_i = Dk+i\ а на входы Az, С и В будут поданы
значения sV-1), Сь-i, и RW> содтветственно. Единственный
выход D определяет значение цифры частного q~i. Теперь,
когда ячейки модифицированной матрицы определены, при-
ведем пример матричной структуры деления, реализующей
рассмотренный алгоритм
(рис. 47). Как и в преды-
дущем примере, делимое
а = 0011, а делитель Ь =
~ =111. Для верхнего ряда
матрицы все cj =0 и, как
обычно, P(°)= 1. Естествен-
но, что и частное, и оста-
с ток (с учетом суммирования
— чисел х и с) получены
совершенно одинаковыми
с .ранее найденными (см.
рис. 44).
Обычная матричная схе-
ма деления (рис. 44) при по-
лучении «-разрядного част-
ного давала задержку в формировании частного, пропорцио-
нальную величине п2 (7.4). В модернизированной же схеме
время выполнения деления пропорционально величине «logл,
где значение множителя log л зависит от схемы реализации
Р
Е
Рис. 46.
Рис. 47.
блочного переноса, ибо основание логарифма будет опре-
деляться числом ступеней матрицы, формирующей блоч-
ный перенос для старшего разряда строки матрицы, т. е.
определяться в конечном счете нагрузочной < способно-
стью элементов, реализующих уравнение (8.6). Для не-
которых типов технических реализаций элементов было
произведено сравнение обычной и модифицированной схем
деления [47]. При этом считалось, что задержка элемента А
по выходу D составляет 5тл, а по выходам G и Г —7тл. За-
держка, вносимая элементом S, составит 9тл, а задержка
на одну ступень формирования блочного переноса есть 2тл.
Для данных условий оказалось, что при п = 16 модифициро-
ванная схема в 2,6 раза быстрее основной и лишь на 22%
дороже. При п — 32 выигрыш в быстродействии был уже
равен 5, хотя формирование значения производилось на
двух ступенях, а схема была дороже лишь на 25% основной
схемы. Относительно незначительное увеличение оборудова-
ния связано с тем, что блочный перенос формируется только
для старшего разряда. Если бы данный перенос формиро-
вался для ’всех разрядов, то при сохранении достигнутого
быстродействия пришлось бы значительно увеличить допол-
нительные аппаратурные затраты. Именно, комбинируя сум-
мирование с сохранением переносов с формированием- блоч-
ного переноса только для старшего разряда, удается при
умеренных затратах получить достаточно высокое быстродей-
ствие схемы деления. В случае одноступенчатого формирова-
ния блочного переноса наибольшая задержка в получении
частного определится как
т= 12(«+1)тл.
В то же время заметим, что усложнение схемы ячеек при
делении и зависимость времени определения результата от
разрядности частного оставляют определенные перспективы
для итерационных методов деления, особенно при большой
разрядности операндов и когда получение остатка не являет-
ся обязательным.
§ 3. КОМБИНИРОВАННЫЕ МАТРИЧНЫЕ СХЕМЫ
Несмотря на определенные различия структур матричного
умножения и деления, все же они имеют много общего. Так,
например, элемент, изображенный на рис. 41, может быть
использован в качестве базового элемента как матрицы умно-
жения, так и матрицы деления. Кроме того, можно попытать-
ся выбрать такие матричные схемы этих операций, которые
имели бы одинаковое соединение элементов и одинаковое
распространение сигналов по крайней мере в основной части
матрицы, как, например, схемы рис. 43 и рис. 44. Все это
говорит о том, что имеет смысл рассмотреть вопрос о пост-
роении комбинированных матричных схем с программируемым
режимом работы — либо эта матрица выполняет умножение,
либо деление. Программируемый выбор режима все же необ-
ходим, поскольку полностью сгладить различия в структурных
схемах этих операций не удается, и поэтому целесообразно
выбором режима построить нужную • структуру из массива
основных элементов. Рассмотрим один из возможных вариан-
тов построения комбинированной матричной схемы.
Комбинированная матричная схема предназначена для ум-
ножения и деления двоичных чисел, представленных прямыми
кодами. В качестве базового элемента матрицы выберем эле-
мент рис. 41, а умножение и деление будем выполнять по
схемам рис. 43 и 44. Беглое сравнение этих схем выявляет,
во-первых, определенную избыточность схемы умножения
по сравнению с делением и, во-вторых, управление сложе-
нием-вычитанием делителя производится в зависимости от зна-
чения цифры частного, найденной на предыдущей строке
матрицы. Следовательно, для обеспечения нужной организа-
ции матричной структуры помимо основных элементов необ-
ходимы и управляющие элементы, схема которых представ-
лена на рис. 48. Входы управляющего элемента (обозначим
Рис. 48.
его С) А, С, F, Р>, Т принимают точно такие же значения,
как и основного элемента (см. рис. 41). Отличие состоит
в том, что вход F не определяет значение цифры множителя-
делителя, а задает режим работы матрицы. При 7?=0 мат-
ричная структура реализует операцию умножения, а при
7?= 1 —деления. По сравнению с основным элементом управ-
ляющий элемент С имеет дополнительный выход Е, который
обеспечивает управление выходом делителя при осуществлении
операции деления. Уравнения, задающие значения Выходных
сигналов В и D, значительно проще, чем у основного эле-
мента:
В = А © Р © С,
D = AP\J РСу АС.
Выход Е имеет значение, равное единице, лишь когда DF =
= 1, т. е. когда при делении есть перенос с управляющего
элемента.
Комбинированную матричную схему построим следующим
образом: каждую строку матрицы деления, как обычно, по-
строим из п основных элементов и к ним добавим слева еще
один элемент, но теперь в отличие от схемы рис. 44 это бу-
дет управляющий элемент С (рис. 49). Выходы D всех эле-
ментов CW являются значениями цифр q-t. Если в строке
матрицы содержится п © 1 элемент, а число строк есть т,
то комбинированная схема позволяет разделить число, а =
= l на число b = Ь£.1+т с получением частного
д — д_,2~1. Особенностями режима „деления** является
условие для всех i = Q, т—1, а также соедине-
ние с управляющей шиной Р& выхода Е управляющего эле-
мента С предыдущей строки с номером I—1.
Рис. 49.
В режиме умножения элементы, формирующие частное,
позволяют получить все необходимые частичные произведе-
ния вида а^Ь. При этом, поскольку умножение производится
для прямых кодов, все РШ = 0, а значения цифр множителя
подаются на входы Т элемента С каждой строки матрицы.
Суммирование частичных произведений не может быть
осуществлено только элементами, используемыми при делении.
Необходимо еще добавить в каждую строку матрицы с номе-
ром i I — li дополнительных элементов (см. рис. 49), распо-
ложенных левее управляющих элементов С. Эти дополнитель-
ные элементы могут быть либо базовыми элементами матрицы,
либо некоторыми специализированными элементами, ибо, по
сути дела, они должны просуммировать значения входов
А и С (на рис. 49 в качестве дополнительных элементов взя-
ты базовые элементы). Таким образом, в режиме умножения
комбинированная матричная схема позволяет получить число
s = d/?-{-a, где а определено так же, как делимое при де-
лении.
Рассмотренная матричная схема обладает одной важной
особенностью — хотя значения всех разрядов операндов по-
даются на схему одновременно на все строки и столбцы мат-
рицы, окончательное значение выходов данного ряда будет
установлено только после того, как будут определены выход-
ные значения предыдущего ряда. В принципе после того как
сформированы значения выходных сигналов для данной стро-
ки, роль элементов сводится только к хранению информации,
а функции элемента, связанные с переработкой информации,
оказываются неиспользуемыми. Имеется возможность повысить
эффективность матричных схем за счет буферизации выходных
сигналов, т. е. их временного запоминания. В случае буфе-
ризации сигналов Р и В каждого основного элемента можно
после сформирования результата в отдельной строке запом-
нить его и затем передать к следующей строке, а основное
оборудование строки предоставить для реализации опреде-
ленного(шага следующей операции — умножения или деления.
Идеи о буферизации ряда сигналов позволяют построить
комбинированные матричные схемы с глубоким совмещением
операций умножения и деления на одном и том же обору-
довании.
Само запоминание обычно не требует очень больших ап-
паратурных затрат, но все же заметно усложняет схемы
ячеек матрицы, а раз это так, то естественно встает вопрос —
нельзя ли за счет дальнейшего усложнения элементов суще-
ственно расширить его функции. В качестве дополнительных
функций комбинированных матричных схем обычно выби-
раются функции по хранению, сортировке, ассоциативному
поиску данных, переводы их из одной системы счисления
в другую. Тенденция развития матричных схем, выполняю-
щих наряду с арифметическими и другие функции, обуслов-
лена тем, что, как показывает опыт последнего десятилетия,
за одну и ту же стоимость с течением времени можно сде-
лать все более сложный и „умный"1 элемент, обладающий все
большим числом разнообразных функций. С другой стороны,
широкое применение таких сложных элементов окажется оп-
равданным, если усложнение структуры не снизит быстродей-
ствия матричных схем при выполнении главных арифметиче-
ских операций — умножения и деления.
§ 4. МАТРИЧНАЯ СХЕМА ИЗВЛЕЧЕНИЯ
КВАДРАТНОГО КОРНЯ
Ранее мы видели (глава 6, § 2), что операцию извлечения
квадратного корня можно реализовать как своеобразную опе-
рацию деления, имеющую однородную структуру. Так же как
и при делении без восстановления остатка, на очередном
шаге либо происходит вычитание „делителя" из остатка
(Р(0 = 1), либо его сложение с отрицательным остатком (Р<1>=
— 0). В отЛичие от деления на каждом шаге алгоритма при-
ходится заново формировать „делитель", хотя в случае дво-
ичной системы счисления это формирование и происходит
весьма простым образом, если операция реализуется методом
восстановления остатка. При извлечении квадратного корня
методом без восстановления остатка величина „делителя"
оказывается* зависящей от знака алгебраического действия
на данном Z-м шаге. Как и при обычном делении, если q_i=
= 1, то на следующем шаге алгоритма „делитель" вычитает-
ся из очередного остатка, а при q-t = 0 — прибавляется. За-
висимость „делителя" от значения знака разности на преды-
дущем шаге легко учитывается следующим соотношением,
определяющим величину „делителя" на Z-м шаге алгоритма:
*(0 = S/=i9-^-F9i-^2-i + 2-1-i. ” (8.8)
Из выражения (8.8) следует, что как при сложении „делите-
ля" (когда q\- г = 0), так и при вычитании его, когда
_ /,(0 = _ 1 + q-j 2-J + qi-i 2-' + ьг-1-* + 2-1-* = -1 +
+ q-j^' + 2~‘ + 2-1~‘, два младших разряда „делителя"
всегда равны единице. Данное обстоятельство позволяет
упростить реализацию операции извлечения квадратного .корня
матричной структурой.
Для построения матричной схемы извлечения квадратного
корня' будем использовать такие же элементы, как и при
делении. Верхний ряд матрицы должен содержать всего два
элемента для прибавления к двум старшим разрядам искомо-
го числа величины 2-1 + 2-2, следовательно, P(0) = 0. Значе-
ние переноса со старшего разряда и есть значение старшей
цифры результата. Этот же сигнал является управляющим
сигналом для двух старших элементов 2-го ряда (напом-
ним, что для всех рядов младшие два разряда имеют Аг>=0).
Спецификой всех рядов, начиная со 2-го, является соедине-
ние входов F и Р для 3-го справа элемента, чем достигается
формирование нового „делителя" (рис. 50). Если требуется
вычислить /n-разрядный результат, то число элементов в мат-
т(т-4-5) , п
рице есть —------- — 1. При этом разрядность подкоренного
числа есть п = 2т. На рис. 50 приведена матричная схема
ст = 4и/г = 8, с помощью которой вычисляется корень
квадратный из числа Д = 0,1010. Полученный результат есть
9 = 0,75, в то время как истинное значение 9 = 0,7926.
Рис. 50
Рис. 51
Приведенная схема построена целиком на однородных
элементах (назовем их элементами типа D). С другой сторо-
ны, эта матричная структура имеет значительную
ность, поскольку три младших элемента в каждом
сути дела, являются двоичными полусумматорами,
и много проще по обо-
рудованию, и облада-
ют меньшей задерж-
кой в получении ре-
зультата, ибо перенос
формируется всего за
тл, а сумма за Зтл.
Имеет смысл при по-
строении матрицы ис-
пользовать наряду с
элементами типа D
также и специальные
элементы типа Е. Эти
элементы имеют столь-
ко же входов и выхо-
избыточ-
ряду, по
которые
дов, сколько и элемент типа D, и такое же о орудование
(полусумматор и полный сумматор), но структура соединений
внутри элемента типа Е другая (рис. 51). Каждый элемент
типа Е позволяет заменить три крайних левых элемента
в каждом ряду матрицы, начиная со 2-го. При использовании
одновременно элементов типа D и Е матричная схема для
извлечения квадратного корня трансформируется (рис. 52).
Рис. 52
Обе схемы (рис. 50 и рис. 52) при т рядах в матрице
определяют m-разрядный результат и при этом могут быть
использованы 2/п-разрядные подкоренные числа. Однако схе-
ма рис. 52 более экономична — она требует ——%----- элемен-
тов, т. е. на 2т — 1 элементов меньше, чем схема рис. 50.
Различаются эти схемы и по времени получения результата.
Максимальная задержка (тт) получения результата есть
время выхода переноса с крайнего левого элемента послед-
него тд-го ряда матрицы после поступления подкоренного
числа. Для первой матричной схемы рис. 50 выход переноса
с крайнего левого элемента г-й строки (Di+г) зависит от за-
держки поступления управляющего сигнала PW — q_i. К мо-
менту прихода этого сигнала в трех правых элементах г-го
ряда все выходные значения будут определены (ибо они не
зависят от Р(‘>). Следовательно, максимальная задержка сиг-
нала, вносимая i-м рядом, есть = 5тл-ф (г— 2)2хл. Первый
член этой суммы является вкладом 4-го слева элемента, для
которого справедливо = (P(i) © Дз0) (Дз0 V Сз°). Форми-
рование этого сигнала требует времени 5тл. Поскольку значе-
ние P(Z) поступает на все элементы ряда одновременно, то
для всех остальных элементов с номером j выражение для
переноса есть СуЦД;0 V ® К моменту прихода С;0
значения Л;г) и Р(,) ф F™ уже определены, поэтому задержка,
вносимая /-м элементом ряда, есть 2тл. Суммируя по всем
i > 2 и принимая во внимание, что т, = 4тд, получим [32]
тт = (^+ 1)2ТЛ.
Вторая матричная схема (см. рис. 52) дает несколько мень-
шее значение тш, а именно
= (w2 + 2/га — 1) тл,
ввиду того, что теперь т, = 2тл.
Сравнение матричных схем деления и извлечение квадрат-
ного корня показывает, что последние и Ьолее экономичны
и более быстродействующие. Действительно, если результат
вычисляется с точностью п двоичных разрядов, а длина опе-
рандов есть также п разрядов, то отношение числа элементов
матричной схемы деления (см. рис. 44) и извлечения квадрат-
ного корня (см. рис. 52) есть
/ — о я(" + 1)
1 п (п + 5) - 2'
Время деления для тех же схем оказывается в
4. _о ”2 + 2,5п
2 «2 + 2л — 1
раз больше, чем извлечения квадратного корня. Таким обра-
зом, матричная схема извлечения квадратного корня почти
в два раза более экономична и при этом снижает максималь-
ную задержку получения результата более чем в два раза.
Адаптивные структуры 274
Алгоритмы
— адаптивные 274, 277, 279
— арифметических операций . 52,
166
— возведения в квадрат 220
— вычисления логарифма 164,
237, 247
— вычитания 57, 133, 147, 165
— деления 83, 106, 139, 150, 162,
198, 278, 288, 296
— извлечения квадратного корня
228, 243, 298
— сложения 54, 114, 133, 144,
165, 163, 173, 177, 180.
— умножения 71, 101, 137, 149,
156, 162, 275, 283, 296
Алфавит
— абстрактный 6
— без нуля 11, 128
— избыточный 173
— неизбыточный 53
— симметричный 10, 173
Арифметическое расстояние 259
База
— системы счисления 9
— избыточная 173
— неотрицательная 9
— симметричная 10, 128
Вес
— арифметический 259
— естественный 8, 113
— искусственный 9, 120
— разрядов числа 8, 13, 16
Возведение в квадрат
— дополнительных кодов 227
— -методом последовательных-
суммирований 222
— методом спуска по дереву 220
— методом формирования пере-
ключательных функций 225
Выравнивание порядков 66
Вычисление полиномов 234
---по схеме Горнера 40
---с единичными коэффициен-
тами 207
Вычисление элементарных функций
233, 246
Деление
— без восстановления остатка 86
— в знакологарифмической систе-
ме счисления 162
— в минус-двоичной системе счи-
сления 150
— в системе счисления с цифра-
ми — 1,1 139
— дополнительных кодов 95
— на константу 269
— прямых кодов 83
— с восстановлением остатка 84
। — симметричных кодов 89
— с плавающей запятой 96
— ускоренное 198
Деревья спуска 192
Диапазон представления чисел 17,
18, 19, 21, 141, 161
Дисперсия погрешности округления
29
Длина слова 6
Дополнение, чисел 14
। — поразрядное 15, 59, 115
Единственность кодирования 120
Значность алфавита (элемента) 6
Инверсимость кода 120, 122
Итеративное изменение длины опе-
рандов 101, 107
Код числа
— без потерь (плотно-упакован-
иый) 259
— дополнительный 14, 57, 178,
182, 267
— запрещенный 258 ।
— модифицированный дополни-
тельный 62
— модифицированный обратный
64
— натуральный 9, 12
— неразделимый 262, 265
— обратный 15, 60
— остаточный 260
— помехозащитный 121, 262
— прямой 13
— разделимый 259
— разрешенный 258
— самодополняющийся 183, 265
— симметричный 12
Кодирование
— избыточное 173, 176
— экономичное группы разрядов
125
Количественный эквивалент числа 8,
9, 129, 162
Комбинированные помехозащитные
арифметические коды 264
Корреляционная матрица 29, 100
Коррекция результата 114, 123, 133,
151, 267
Мантисса числа 20
Математическое ожидание погреш-
ности округления 29
Матричные схемы
---- деления 288
----извлечения квадратного кор-
ня 298
----комбряяр'оваиные 294
----умножения 283
Массив элементов 6
— многомерный 6
— одномерный 6
— однородный 6
Масштабирование 19
Масштабные коэффициенты 20
Машинное число 16
Машинный нуль 18, 21
Методы повышения функциональ-
ной надежности машины
— адаптивных структур 256
— аппаратно-программные 256
— аппаратные 256
— динамические 256
— дублирования 256
— информационной избыточнос-
ти 256
— многократных линий 257
— перекомпоновки 275
— подмены 275
— программные 256
— статические 256
Начальное приближение 206, 245
Неоднозначное представление нуля
13, 16
Нормализованная запись числа 20
Нормализация чисел
----влево 69
---- вправо 68
Нормальные параметры машины 274
Номер разряда 6
Однозначность представления 113
Округление чисел
— без распространения переносов
35
— вероятностное 35
— в минус-двоичной системе счис-
ления 148
— в направлении к нулю 28
— в направлении от нуля 29, 31
— в системе счисления с цифра-
ми — 1,1 136
— оптимальное 28
— по дополнению 29, 32
— по избытку 28, 32
— по недостатку 28, 31
— по усовершенствованному до-
полнению 33
— при помехозащитном кодирова-
нии 270
— симметричное 28
Определение знака результата 57,
75
Основание системы счисления 9, 22,
25
Отказ оборудования
— внезапный 255
— постепенный 255
Перевод в другую систему счисле-
ния 39
— для двоично-кодированных чи-
сел 117
— для минус-двоичной системы
счисления 141
— для позиционных систем счи-
сления 40
— для системы остаточных клас-
сов 158
— для системы счисления с циф-
рами—1,1 129
-1- правильных дробей 42, 47
— приближенный 43, 47
— с естественной запятой 40
— с плавающей запятой 49
— точный 42
— целых чисел 42, 46
Перенос 53
—• групповой (блочный) 170, 291
— последовательный 55, 168
— сквозной 168
— сохраняемый 176
Переполнение разрядной сетки 18,
21, 31, 53, 58, 63, 81, 96
— сумматора 59, 136, 148, 267
Поля в записи чисел
— значащих разрядов 125
— индикатора 27, 125
— мантиссы 21, 23, 27, 49
— основных разрядов 14
— порядка 21, 23, 27, 49
Помехозащитность 121
Порог округления 98
— поправки 102, 107
Порядок числа 20
Плотность распределения вероятно-
стей 24, 101
Представление чисел
— в знакологарифмической систе-
ме счисления 160
— в минус-двоичной системе счи-
сления 140
— в позиционной системе счисле-
ния 7, 9
— в системе остаточных классов
153
— в системе счисления с цифра-
ми—1,1 129
— приближенное 17
— • символическое 129
Приемлемое приближение чисел 17,
22
Разряд алгебраическо.гю знака чис-
ла 13, 178
— слова 6
Разрядность слов 6
Регистр 55, 73
— сдвига 67
Сдвиг числа 67, 136
— модифицированный 69
— циклический 67
Система счисления 7 i
— аддитивная позиционная 9
— внешняя 40, 45
— внутренняя 40, 45
— двоично-кодированная 111
— знакологарифмическая 160
— знакоразрядная 173
— минус-двоичная 140
— непозициовная 7
— однородная 8
— остаточный классов 153
— позиционная 7
смешанная 8
— с цифрами—1,1 128
Средняя длина распространения пе-
реносов в 'сумматоре 167
Сумматор
— асинхронный 167
— одноразрядный 53
— параллельный 55
— с блочным переносом 170
— с сквозным переносом 168
— с сохраняемым переносом 177,
194
— с циклическим переносом 60
Суммирование
— в знакологарнфмической си-
стеме счисления 163
— в минус-двоичной системе счи-
1 сления 144
— в системе счисления с цифра-
ми—1,1 133
— двоично-кодированных чисел
114, 122, 186
— дополнительных кодов 61
— знакоразрядных чисел 174
— конвейерное 184
— обратных кодов 64
— прямых кодов 56
— с сохранением переносов 177,
180, 291
— чисел с естественной запятой 71
— чисел с плавающей запятой 66,
188
Таблично-алгоритмический метод
вычисления элементарных
функций
— логарифма двоичных чисел 237
— обратной величины 213
Таблично-итерационный метод из-
влечения квадратного корня
243
Табличные методы выполнения
арифметических операций
— возведения в квадрат 224
— суммирования 187
— умножения 72
Точность представления чисел 17,
40
Умножение
— в знакологарифмической систе-
ме счисления 162
— в минус-двоичной системе счи-
сления 149
— в позиционной системе счи-
сления 71
— в системе остаточных классов
156
— в системе счисления с цифра-
ми—1,1 137
— Длинных чисел 197
— на константу 269
— положительных чисел 71
— с младших разрядов множите-
ля 73
— со старших разрядов множи-
теля 73
— с плавающей запятой 81
— с учетом знаков 75
— ускоренное 188
— через возведение в квадрат
226
Форма представления чисел 16
— с естественной запятой 18
— с плавающей запятой 20
— с фиксированной запятой 19
Формирование вычетов по модулю
273
Хорошее приближение чисел 17, 22
Цифра 7
Частичное произведение 71, 192
Числовой эквивалент цифры 7
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Акушский И. Я., Юдицкий Д. И. Машинная арифметика в оста-
точных классах.— М., 1968.— 439 с.
2. Байков В. Д., Смолов В. Б. Аппаратурная реализация элементарных
функций в ЦВМ.— Л., 1975.— 96 с.
3; Благовещенский Ю. В., Тесл ер Г. С. Вычисление элементарных
функций на ЭВМ.— Киев, 1977.—207 с.
4. Брусенцов Н. П. Об использовании троичного кода и трехзначной
логики в цифровых машинах.— В кн.: Вычислительная техника и во-
просы кибернетики. Вып. 7. М., 1970, с. 3—34.
5. Брусенцов Н. П. Алгоритм деления для троичного кода с цифрами
—1, 0, 1.— В кн.: Вычислительная техника и вопросы кибернетики.
Вып. 10. Л., 1974, с. 39—44.
6. Гладкий В. С. Вероятностное округление чисел и аспекты его при-
менения в вычислительной математике и технике.— Кибернетика, 1975,
№ 6, с. 126—1130.
7. Дадаев Ю. Г. Арифметические коды, исправляющие ошибки.—М.,
1969,— 168 с.
8. Д е м и д о в и ч Б. П., Марон И. А. Основы вычислительной матема-
тики.— М., 1966.— 664 с.
9. Дор одн ицина А. А. Микропрограммирование элементарных функций,
представленных разложением в цепную дробь.— Кибернетика, 1966.
№ 6, с. 34—40.
10. З'азнова Н. Е. Перевод чисел из двоичной системы счисления в ми-
нус-двоичную н обратно.— Автоматика и вычислительная техника,
1975, № 4, с. 64—72.
11. Карцев М. А. Арифметика цифровых машин.— М., 1969.— 576 с.
12. Кнут Д. Искусство программирования для ЭВМ. Т. 2.— М., 1977.—
723 с.
13. Лавров С. С. Введение в . программирование.— М., 1973.— 352 с.
14. Л а д а т к о В. И. Ш а у м а н А. М. Итерационные схемы деления, ис-
пользующие умножение.— В кн.: Вычислительная техника и вопросы
• кибернетики. Вып. 13. М.,. 1977, с. 59—78.
15. Люстерник Л. А., Черноненкнс О. А., Ямпольский А. Р.
Математический анализ. Вычисление элементарных функций.— М.,
1963.— 247 с.
16. Мокринский А. М., Трофимов Н. Н. Два алгоритма ускоренного
умножения в ЦВМ.— Автоматика и телемеханика, 1969, № 1,
с. 114—120.
17. О вру цк ий А. И., Шауман А. М. Исследование алгоритмов прибли-
женного деления.— В кн.: Вычислительная техника и вопросы кибер-
нетики. Вып. 7. М., 1970, с. 65—87."
18. Оранский А. М. Аппаратные методы цифровой вычислительной тех-
ники.— Минск, 1977,—208 с.
19. Пан В. Е. Некоторые схемы для вычисления многочленов с веществен-
ными коэффициентами.— Докл. АН СССР, 1959, с. 127, № 2,
с. 261—269.
20. Поспелов Д. А. Арифметические основы вычислительных машин диск-
ретного действия.— М., 1970.— 308 с.
21. Рамиль Альварес X. Простые алгоритмы переводов р->р+1
и р->р—1. В кн.: Вычислительная техника и вопросы кибернетики.
Вып. 13. М„ 1976, с. 50—58.
22. Рувинский Б. И., Селютин С. А. Аппаратный метод вычисления
элементарных функций.— Электронная техника. Микроэлектроника.
Вып. 4 (58). М., 1975, с. 9—13.
23. Соренков Э. И., Т е л и г а А. И., Шатилов А. С. Точность вычис-
лительных устройств и алгоритмов.— М., 1976.— 200 с.
24. Тентиева С. М., Шаляпин В. В., Шумилов Л. А., Зайце-
ва Л. А. Об оптимальном кодировании в знакоразрядных суммато-
рах.— В кн.: Вычислительная техника. Вып. 6. Л., 1977, с. 82—91.
25. Чирков М. К., Шауман А. М. Основы функциональной структуры
вычислительных машин.— Л., 1974,—268 с.
26. Ш а у м а н А. М. Комбинированные помехозащитные арифметические
коды.— В кн.: Вычислительная техника и вопросы кибернетики.
Вып. 7. М„ 1970, с. 53—64.
27. Ш а у м а н А. М., Чирков М. К- Выполнение арифметических опера-
ций с автоматической расстановкой запятых.— В кн.: Вычислительная
техника и вопросы кибернетики. ВыЦ. 6. Л., 1971, с. 3—20.
28. Ш а у м а и А. М. К оценке адаптивности алгоритмов деления.— В кн.:
Вычислительная техника и вопросы кибернетики. Вып. 9. М., 1972,
с. 54—79.
29. Шауман А. М. Об одном классе алгоритмов приближенного деле-
ния.— В кн.: Вычислительная техника и вопросы кибернетики. Вып. 10.
Л., 1974, с. 44—49.
30. Ш а у м а н А. М. Исследования адаптивных алгоритмов умножения.—
В кн.: Вычислительная техника и вопросы кибернетики. Вып. 10. Л.,
1974, с. 22—38.
31. Шауман А. М. О машинной реализации возведения в квадрат.— В кн.:
Вычислительная техника и вопросы кибернетики. Вып. 12. Л., 1975,
с. 37—50.
32. Шауман А. М. Матричное извлечение квадратного корня.—В кн.: Вы-
числительная техника. Вып. 6. Л., 1977, с. 105—ПО.
33. Ш а у м а н А. М. Об одном методе быстрого деления.— В кн.: Вычисли-
тельная техниика и вопросы кибернетики. Вып. 14. Л., 1977, с. 3—11.
34. Ш а у м а н А. М. О суммировании с сохранением переносов для систем
счисления с положительной базой.— В кн.: Вычислительная техника
и вопросы кибернетики. Вып. 14. Л., 1977, с. 194—202.
35. A g г a w а 1 D. Р. Arithmetic algorithms in a negative base.— IEEE Trans.
Comput., 1975, C-24, N 10, p. 998—1000.
36. A g r a w a 1 D. P. Circuit adds BCD numbers faster with less hardware.—
Electronics, 1975, N 23, p. 120.
37. A n d e r s о n S. F. Earle J. G., С о 1 d s c h m i d t R. Ё., Po-
wers D. M. The IBM system 360 model 91. Floating point execution
unit.— фМ J. Res. a Develop., 1967, vol. 11, N 1, p. 34—53.
38. A t k i n s D. E. Higher-radix division using estimates of the divisor and
partical remainders.—IEEE Trans. Comput., 1968, C-17, N 10, p. 925—934.
39. Avizienis Д. Signed-digit number representations for fast parallel arith-
metic.—IRE Trans. Electr. Comput., 1961, EC-10, N 9, p. 389—400.
40. A v i z i e n i s A. Arithmetic algorithms for error-coded operands.— Dig.
Par. Int, Symp. Fault-Tolerant Comput. Newton, Mass., 1972, New York,
p. 25—29.
41. Bandyopadhayay S., Choudhuri A. K, An iterative array for mul-
tiplication of signed binary numbers.— IEEE Trans. Comput., 1972, C-21,
N 8, p. 921—922.
42. Bankowski Y. Addition in redandant representations.—Bull. Acad. Po
lonaise des Sciences, 1966, vol. 14, N 2, p. 183—186.
43. В a s u D. J a у a s h r i. On a simple part correction for nonrestoring divi-
sion.— IEEE Trans, on Comput., 1975, C-24, N 10, p. 1019—1020.
44. Brent R. P. On the precision attainable with various floating-point number
systems.— IEEE Trans. Comput., 1973,. C-22, N 6, p. 783—785.
45. В r i 11 e у Bruce E. Some new results on average case carry.— IEEE
Trans. Comput., 1973, C-22, N 5* p 459—463.
46. В г о w n W. S., R i c h a n P. L. The choice of base.— Commun. ACM, 1969,
vol. 12, N 10, p. 22—23.
47. Capp a M., Hamacher V. C. An augmented iterative array for high-
speed binary division.— IEEE Trans. Comput., 1973, C-22, N 2,
p. 172—175.
48. Chen-Tien - Chi, Ho Irving T. Storage-efficient representation of
decimal data.—Commun. ACM, 1975, vol. 18, N 1, p. 49—52.
49. D e v e r e 11 J. The design of cellular arrays for arithmetic. — Radio and
Electron. Eng., 1974, vol. 44, N 1, p. 21—26.
50. G i b s о n J. A., G i b b a r d R. W. Synthesis and comparision of two’s
complement parallel multipliers.— IEEE Trans. Comput., 1975, C-24,
N 10, p. 1020—1027.
51. H a b i b i A., Wi nt z P. A. Fast multipliers.— IEEE Trans. Comput., 1970,
C-19, N 2, p. 153—157.
52. H a I i n T. C., Flinn M. J. Pipelining of arithmetic functions.— IEEE
Trans. Comput., 1972, C-21, N 8, p. 808—816.
53. H a m m i n g R. W. On the distribution of numbers — The BELL System
Techn. J., 1970, vol. 49, N 8, p. 13—61. '
54. J a у a s h r i T., Basu D. Cellular arrays for multiplications of signed
binary numbers.— Radio a. Electronic Erig., 1974, vol. 44, N 1, p. 18—20.
55. J о h e J. M. Roundings in floating-point arithmetic.— IEEE Trans. Com-
put., 1973, C-22, N 6, p. 577—587.
56. Kinnement D. J., Steven G. B. Sequential state binary parallel
adder.— Proc. Jast. Electr. Eng., 1970, vol. 117, N 7, p. 1211—1213.
57. Krishnaumurthy E. V. A more efficient range-transformation algo-
rithm for signed digit division.— Int. J. Contr., 1970, vol. 12, N 12,
p. 73—79.
58. Majithia J. C. Non-restoring binary division using a cellular array.—
Electron. Lett., 1970, vol.’ 6, N 10, p. 303—304.
59. M e g g i t J. E. Psetldodivision and pseudomultiplication processes.
— IBM J. Res. a. Develop., 1962, vol. 6, N 2, p. 210—226.
60. M о nte i г о P, Ra о T. K. N. A residue checker for arithmetic and logical
operations.— Dig. Par. Int. Symp. Fault-Tolerant Comput. Newton Mass.,
New York, 1972, p. 8—13.
61. M о r r i s R. Tapered floating point new floating point representation.—
- IEEE Trans. Comput., 1971, C-20, N 12, p. 1578—1580.
62. Resaris Stylians D. A. 40-ns 17-bit by 17-bit array multiplier.—
IEEE Trans. Comput., 1971, C-20, N 4, p. 442—447.
63. SankarP. V., Chakrabarti S., Krishnaumurthy E. V. Arithmetic
algorithms in a negative base.— IEEE Trans. Comput., 1973, vol. C-22,
N 2, p.'120—125.
64. Schonhage A., Strassen V. Multiplikation grober Zahlen.—Comput.
Archiv f. electronisches Rechnen, 1971, Bd. 7, fasc. 3—4, S. 281—284.
65. Swartzlander E. E., Elexopouls A. G. The sign-logarithm num-
ber system.— IEEE Trans. Comput., 1975, C-24, N 12, p. 1238—1242.
66. T h о m p s о n P. M., Belanger A. Digital arithmetic units for a high
data rate.— Radio a. Electronic Eng., 1975, vol. 45, N 3, p. 116—120.
67. V о 1 d e r J. E. The CORDIC trigonometric computing technique.— IEEE
Trans. Electronic Comput., 1959, vol. 8, N 3, p. 330—334.
68. W a 11 h e n J. S. A unified algorithm for elementary functions.— AFLPS
Conf. Ros. Spring Joint Comput. Atlantic City, 1971, vol. 138, p. 235—252.
ЛЕНИНГРАДСКИЙ ОРДЕНА ЛЕНИНА
И ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ А. А. ЖДАНОВА
А. М. ШАУМАН
ОСНОВЫ
МАШИННОЙ
АРИФМЕТИКИ
Издательство Ленинградского университета
Ленинград 1979
Печатается по постановлению
Редакционно-издательского совета
Ленинградского университета
УДК 681.142
Шауман А. М. Основы машинной арифметики.— Л.: Изд-во
Ленингр. ун-та, 1979. 312 с. Ил.—52, табл. — 25, библиогр.—
68 назв.
В монографии изложены основы арифметики, реализуемой
в современных цифровых машинах. Исследуются вопросы пред-
ставления чисел с учетом знаков, формы представления чисел,
методы округления и перевода чисел из одних систем счисления
в другие, классические методы выполнения основных арифмети-
ческих действий и. приближенного умножения и деления, методы
аппаратурной реализации элементарных функций, выполнения
арифметических операций с обнаружением и исправлением
ошибок.
Рассчитана на специалистов в области вычислительной тех-
ники, математического обеспечения ЭВМ, а также на студентов
факультетов прикладной математики и технической кибернетики.
30592-136
Ш 076(02) —79 141 “ 79' 1702070000
© Издательство Ленинградского
университета, 1979 г;