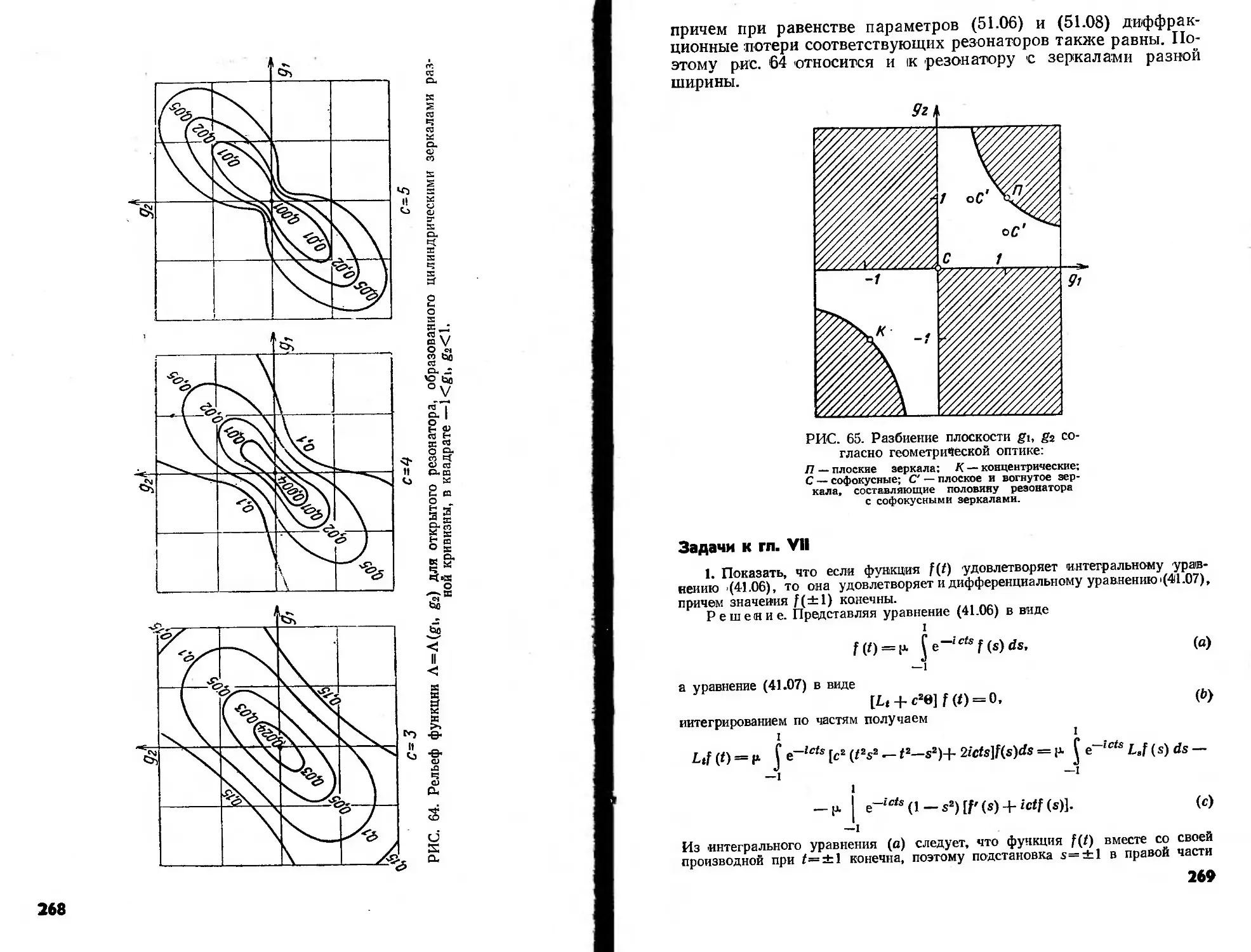
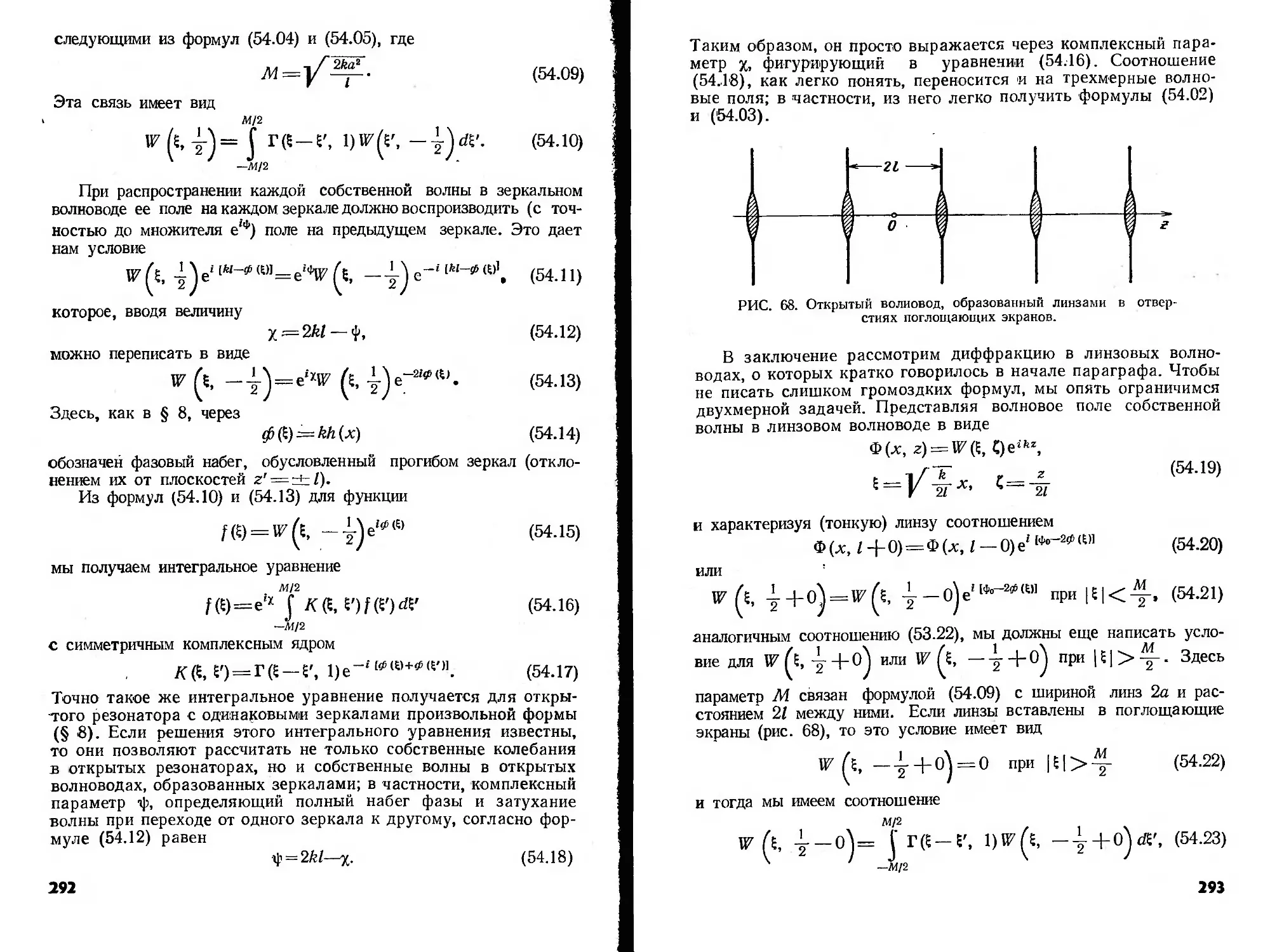
Text
Л. А. Вайнштейн
ОТКРЫТЫЕ
РЕЗОНАТОРЫ
и
ОТКРЫТЫЕ
ВОЛНОВОДЫ
Издательство
«Советское радио»
Москва 1966
УДК 621.372
Книга представляет собой монографию, посвящен-
ную теории «квазиоптических» устройств — открытых
резонаторов и открытых волноводов, которые все ши-
ре применяются в качестве колебательных систем и
линий передачи для миллиметровых, субмиллиметро-
вых и световых волн; основные свойства этих
устройств определяются диффракционными явлениями.
Книга предназначена для научных работников —
физиков и радиоинженеров, а также для студентов
старших курсов и аспирантов, специализирующихся по
физике и технике миллиметровых и более коротких
волн.
3-4-1
10-66
Предисловие
Как известно, в оптических квантовых генераторах в качестве
колебательной системы применяется открытый резонатор, в про-
стейшем случае состоящий из двух зеркал, расположенных друг
против друга. Это — первое, но далеко не последнее применение
открытых резонаторов, которые замечательны тем, что все их
размеры гораздо больше длины волны, а спектр их собственных
частот разрежен по сравнению со спектром частот замкнутых
резонансных объемов тех же размеров; вместе с тем, потери на
изучение некоторых собственных колебаний открытого резонато-
ра могут быть сделаны весьма малыми, так что эти колебания
имеют высокие добротности, часто превосходящие добротности
колебаний в закрытых резонаторах. По этим причинам открытые
резонаторы находят все более широкое применение в физике и
технике не только для световых волн, но и для миллиметровых
и субмиллиметровых волн. В некоторых случаях они могут ока-
заться полезными и для более длинных волн.
Эта книга посвящена теории открытых резонаторов, причем
«изложение в значительной степени основано на работах автора,
выполненных и опубликованных в 1962—1965 гг. Открытые вол-
новоды, образованные периодически расположенными линзами
или зеркалами, позволяют осуществлять передачу миллиметро-
вых и субмиллиметровых волн на большие расстояния. Теория
открытых волноводов, во многом аналогичная теории открытых
резонаторов, также приведена в этой книге, хотя ряд вопросов,
специфических для линий передачи (расчет допусков и стати-
стических характеристик), в книге не рассмотрен.
Цель книги — систематизировать основные результаты, полу-
ченные в теории открытых систем. Чтобы уменьшить число ссы-
лок в тексте, в конце книги (стр. 465) дан обзор литературы,
использованной при написании каждой главы. В конце каждой
главы помещены задачи (с решениями), дополняющие основной
текст и облегчающие его проработку.
Основные свойства открытых резонаторов и открытых волно-
водов определяются диффракционными явлениями. Поэтому
теория этих систем существенным образом опирается на мате-
1
магический аппарат теории диффракции, созданный ранее при-
менительно к задачам волновой оптики, теории распространения
радиоволн и радиотехники сантиметрового диапазона (т. е. тео-
рии антенн, волноводов и объемных резонаторов). По сравнению
с теорией обычных волноводов и объемных резонаторов в тео-
рии открытых систем длину волны можно считать малой по
сравнению со всеми характерными размерами (шириной зеркал,
расстоянием между ними и т. п.), что позволяет вводить ряд
аппроксимаций и, в частности, широко пользоваться геометриче-
ской оптикой (см. особенно гл. VII).
Главное содержание теории открытых систем составляет
исследование собственных колебаний в открытых резонаторах и
собственных волн в открытых волноводах, а также расчет воз-
буждения этих колебаний и волн внешними источниками. Такой
подход к открытым системам совершенно естествен, если рас-
сматривать их как развитие «закрытых» систем — резонаторов
и волноводов, применяемых в радиотехнике сантиметрового диа-
пазона. Он оправдывается лишь тогда, когда в открытой системе
имеются слабозатухающие колебания или волны; поэтому в тео-
рии диффракции и распространения волн этот подход до сих пор
почти не использовался.
Автор ‘приносит свою благодарность П. Л. Капице и В. А. Фоку
за интерес к этой работе и ее поддержку. Автор весьма при-
знателен В. П. Быкову и С. П. Капице за ценное обсуждение
многих вопросов, относящихся к открытым системам.
Глава I
Открытые резонаторы
с параллельными
плоскими зеркалами
§ 1. Основные свойства
открытых резонаторов
- Для электромагнитных волн сантиметрового диапазона в ка-
честве колебательных систем широко применяются объемные
резонаторы. Если в соответствии с изменением рабочей длины
волны пропорционально изменять все размеры объемного резо-
натора, то при переходе к более длинным волнам будут полу-
чаться все более громоздкие системы. Это в конце концов за-
ставляет переходить к обычным колебательным контурам,
состоящим из конденсаторов и катушек самоиндукции. При пе-
реходе к более коротким волнам объемные резонаторы стано-
вятся все более миниатюрными, и их добротность падает; поэто-
му эффективность объемных резонаторов в миллиметровом и
субмиллиметровом диапазонах тем ниже, чем короче длина
волны.
Переходя к более коротким волнам, можно, оставляя разме-
ры объемного резонатора постоянными, использовать колебания
с более высокими индексами (колебания высших типов), соб-
ственные частоты которых выше, чем у колебаний с небольшими
индексами, применяемых в сантиметровом диапазоне. Однако
по этому пути далеко продвинуться нельзя, так как спектр соб-
ственных частот замкнутых резонансных объемов при переходе
к более высоким частотам сгущается: число колебаний A7V, при-
ходящееся на интервал частот Дсо, равно
ДЛГ=т®2Д®,
2п2с3 ’
(1.01)
где V — объем резонатора, с — скорость света.
5
Эта асимптотическая формула (тем более точная, чем выше
круговая частота со) в физической литературе (см., например,
fl]) обычно называется формулой Рэлея — Джинса, она легко
выводится для объема V прямоугольной формы и для других
объемов правильной формы (сфера, круговой цилиндр). Для ре-
зонансных объемов произвольной формы вывод формулы (1.01)
вместе с поправочными членами дан Курантом [2], поэтому в ма-
тематической литературе ее обычно называют теоремой Куран-
та. В качестве сравнения приведем аналогичные формулы
для двухмерной области
ДМ = -^о>Дш (1.02)
(S — площадь области) и для одномерной области
о/
ДМ = ^-Д<о (1.03)
(L — длина области, которая является интервалом длины L).
В этих формулах учтен векторный характер электромагнитных
полей, т. е. наличие двух независимых поляризаций; для скаляр-
ных колебаний правые части этих формул должны быть умно-
жены на 72-
Как видно из формулы (1.03), сгущение спектра для одно-
мерных областей отсутствует; собственные частоты одномерной
резонансной системы (например, струны) образуют эквиди-
стантный спектр, т. е., проще говоря, арифметическую прогрес-
сию. Для двухмерных и особенно для трехмерных областей
спектр при переходе к более высоким частотам сгущается. Это
препятствует применению колебаний высших типов: так как
коэффициент затухания, вызванного джоулевыми потерями
в стенках резонатора, при их постоянной проводимости пропор-
ционален У со, то резонансные кривые резонатора фиксирован-
ных размеров при достаточно высоких частотах перекрываются
и его резонансные свойства сходят на нет. Как показывает фор-
мула (1.01), для высоких частот (таких, что длина волны мала
по сравнению со всеми размерами резонатора) спектр вообще не
зависит от формы резонатора, а определяется только его
объемом.
Эти общие соображения заставляют искать новые колеба-
тельные системы, к которым формула (1.01) была бы неприме-
нима и которые имели бы более разреженный спектр собствен-
ных частот, чем объемные резонаторы. Такие системы почти
одновременно предложили Прохоров [3] и Шавлов и Таунс [4]
в виде двух параллельных и одинаковых зеркал, расположенных
друг против друга.
Физическая аргументация в работе (3] (см. также (5] и [6])
была примерно следующей: между параллельными зеркалами
с точки зрения геометрической оптики могут существовать два
6
параллельных пучка лучей, преобразующихся один в другой при
отражении от зеркал. Такие пучки, несколько размывающиеся
(расходящиеся) вследствие диффракции, образуют собственные
колебания данной системы, которая оказывается эквивалентной
одномерной колебательной системе, рассмотренной выше (см.
формулу (1.03), в которой под L надо понимать расстояние меж-
ду зеркалами).
В работе [4] собственные колебания между зеркалами рас-
сматривались как возмущенные собственные колебания ци-
линдрического объемного резонатора, основания (торцы) кото-
рого совпадают с зеркалами. Каждое колебание в замкнутом
цилиндрическом объеме можно разложить на плоские волны и
представить в виде наложения пучков параллельных лучей; эти
пучки (при удалении боковой поверхности и переходе к двум
зеркалам в свободном пространстве) в результате диффракции
испытывают тем меньшее возмущение, чем меньше угол, кото-
рый они образуют с нормалью к зеркалам. Чем меньше этот
угол, тем должны быть меньше потери на излучение у данного
колебания, тем большую добротность имеет колебание. Разре-
жение спектра достигается вследствие того, что для большин-
ства колебаний этот угол недостаточно мал и эти колебания
«выходят из игры» из-за больших потерь на излучение.
Приведенные выше соображения являются лишь наводящи-
ми и не позволяют рассчитать основные характеристики данной
колебательной системы. Тем не менее эти соображения предвос-
хищают результаты, вытекающие из количественной теории (см.
ниже § 5—7), и показывают, что потери на излучение в подоб-
ных системах являются скорее полезными, чем вредными: хотя
все колебания в результате излучения приобретают дополнитель-
ное затухание, но это затухание для разных колебаний резко
различается — почти для всех колебаний оно велико и лишь для
сравнительно небольшого числа колебаний мало. Благодаря
излучению спектр собственных частот оказывается разрежен-
ным. Если бы потери в объемных резонаторах имели избира-
тельный характер, то они также приводили бы к разрежению
спектра; однако ни джоулевы потери, ни потери за счет малых
отверстий связи такой избирательностью не обладают.
Будем называть открытыми резонаторами такие системы, ко-
торые имеют достаточно добротные собственные колебания, при-
чем колебания в этих системах сопровождаются излучением
в свободное пространство. Рассмотренный выше пример открыто-
го резонатора из двух плоских зеркал поясняет принципиальную
важность излучения. Не во всех открытых системах могут суще-
ствовать слабозатухающие колебания: если в рассмотренном
примере зеркала непараллельны, то при некотором угле наклона
(ср. гл. II) потери на излучение у всех колебаний возрастут на-
столько, что резонансные свойства пропадут. В последнем отно-
шении открытые резонаторы радикально отличаются от закры-
7
тых, в которых резонансные свойства наблюдаются при любой
форме ограничивающей поверхности. Впрочем, надо иметь в ви-
ду, что при наличии потерь в стенках объемного резонатора и
в среде, его заполняющей, резонансные свойства также могут
пропасть, следовательно, излучение из открытого резонатора
действует так же, как другие виды потерь.
Добротные колебания в открытых системах могут реализо-
ваться благодаря одному из трех физических явлений: 1) отра-
жению от краев резонатора; 2) образованию каустических по-
верхностей; 3) полному внутреннему отражению.
Отражение от края существенно в открытых резонаторах,
образованных параллельными плоскими зеркалами (см. гл. I)
Как оказывается, эти резонаторы по принципу действия анало-
гичны открытым трубам в акустике или же отрезкам двухпро-
водной линии, применяемым в качестве колебательных систем
для метровых радиоволн. Различие состоит лишь в том, что
в открытых резонаторах расстояние между плоскими зеркалами
велико по сравнению с длиной волны и колебание формируется
в результате отражения волноводной волны при частоте, близ-
кой к критической частоте этой волны.
Образование каустических поверхностей обусловливает весь-
ма малое радиационное затухание ряда собственных колебаний
в открытых резонаторах со сферическими зеркалами (см. гл. IV).
Известно, что в результате отражения или преломления систе-
мы лучей часто возникают каустические поверхности (каусти-
ки), касающиеся отраженных или преломленных лучей и огра-
ничивающие эти лучи. В части пространства за каустикой, куда
лучи не проникают, волновое поле является слабым — оно бы-
стро (экспоненциально) убывает при удалении от каустики.
В резонаторе со сферическими зеркалами внешняя каустическая
поверхность, образующаяся у некоторых колебаний, защищает
их от излучения в стороны и приводит к пренебрежимо малым
радиационным потерям.
Полное внутреннее отражение проявляется в системах, где
оптически более плотная среда окружена средой менее плотной.
Так, например, в диэлектрическом стержне, окруженном пусто-
той, в результате полного внутреннего отражения могут распро-
страняться незатухающие монохроматические волны (см., на-
пример, [7], § 66), поэтому отрезок диэлектрического стержня,
помещенный между двумя плоскими зеркалами, является от-
крытым резонатором с высокой добротностью, равно как диэлек-
трический тор или шар. Подобные колебательные системы будут
рассмотрены в гл. IX.
Во многих системах мы имеем дело сразу с двумя или даже
тремя перечисленными выше явлениями (ср. гл. VII и IX), но
одно из них обычно является главным. Выделение главного фак-
тора, обеспечивающего малое затухание собственных колебаний,
не только позволяет составить наглядное представление о коле-
8
баниях в данной системе и качественно предугадать их свойства,
но также дает исходные положения для построения количествен-
ной теории и для создания открытых резонаторов с новыми
свойствами.
§ 2. Диффракции на открытом конце волновода
Как уже отмечалось в § 1, малость потерь на излучение
в открытых резонаторах с параллельными плоскими зеркалами
связана с тем, что собственные колебания в них имеют характер
волноводных волн между параллельными плоскостями при ча-
стоте, лишь слегка превышающей их критические частоты. Такие
волны, как показано в теории диффракции на открытом конце
волновода [8], приходя к краю резонатора, почти не излучают,
а с коэффициентом отражения, близким по абсолютной величи-
не к единице, отражаются обратно.
РИС. 1. Волновод с открытым концом.
Как будет видно из дальнейшего, это представление позво-
ляет построить количественную теорию открытых резонаторов
с плоскими зеркалами, которая, таким образом, неявно содер-
жится в теории диффракции на открытом конце волновода.
Рассмотрим диффракцию на конце плоского волновода
(рис. 1) с несколько иной точки зрения, чем это сделано в нашей
книге [8], но опираясь на математический аппарат, изложенный
в ней. Иной подход, более наглядный физически и более простой
математически, хотя и менее полный, будет изложен в § 3.
Беря зависимость от времени в видее-*0*, будет считать, что
волновое число k= связано с расстоянием 2а между пласти-
нами волновода соотношением
ka^(^-\rPy (2.01)
где q — большое целое число, а | р | < у.
9
Пусть к открытому концу волновода приходит волна HoQ
или ЁОд, поле которой не зависит от координаты х и частота ко-
торой в силу формулы (2.01) близка к ее критической частоте
(эти частоты равны при р = 0). Диффракционное поле этой вол-
ны выражается через функцию F(w), связанную с поверхност-
ной плотностью тока на верхней пластине у=а соотношением
f(z) = [ el'“2F (w) dw, (2.02)
с
где контур С в основном проходит по вещественной оси и оги-
бает точку W — —Wo, соответствующую приходящей волне, снизу.
Функция F(w) определяется из функциональных уравнений (см.
(8], гл. I).
fe’wZF(w)(Zw = 0 приз<0,
С (2.03)
[eiwZL (w) F (w) dw = 0 при z > 0,
c
где для волны Нм
— (— 1)? е2’”»], (2.04)
а для волны Ем
L(w) = ~[\ — (- 1)«е21^]. (2.05)
При условиях*
^-|w|*<l (2.06)
функции (2.04) и (2.05) можно заменить более простой (целой)
функцией
/о Е’2° \
L(w)=l — е v (2.07)
так как в экспоненте можно положить
v = —w2 = k — -J, (2.08)
а в множителе перед скобкой положить v — k.
* Смысл этих условий заключается в том, что мы рассматриваем волно-
вые поля, изменение которых в направлениях, параллельных зеркалам (пла-
стинам у=±а). является гораздо более медленным, чем изменение вдоль
нормали к зеркалам. Если рассматриваемые поля являются суперпозицией
плоских волн (или волноводных волн НВп и Еоп, каждая из которых есть
сумма двух плоских волн), то направления распространения этих плоских
волн должны образовывать с нормалями к зеркалам малые углы. Различ-
ная зависимость поля от тангенциальной и нормальной координат будет
использована в § 3 при переходе к параболическому уравнению, позволяю-
щему составить более маглядное представление о диффракции на открытом
конце волновода.
10
Функция (2.07) обращается в нуль при w=±w}, где
Sj= Г4* а+р)‘
(2.09)
Легко проверить, что Wj есть волновое число волны
или Eoq-2j в плоском волноводе [приближенно, при условиях (2.01)
и (2.06)]. При значениях /= 1, 2,... в формуле (2.09) получаются
распространяющиеся волны, при значениях J = — 1, —2,...—за-
тухающие волны (тогда Sj = i | s} | — i 4к (— j — р)), значение /—
= 0 соответствует приходящей волне Hoq или Е^, которая при
/?>-0 распространяется, а при /?<0 затухает.
Будем решать уравнения (2.03) с целой функцией (2.07), вводя
таким образом с самого начала в диффракционную задачу аппро-
ксимации, связанные с условиями (2.06). Функция (2.07) разби-
вается на множители
L(w) — L+ (w)L_ (w), L_(w) = L+(—w), (2.10)
где L+ (w) — функция, голоморфная в верхней полуплоскости
Imw>0, удовлетворяющая там условию L+(w)-»-l при |к>|—• оо
и определяемая формулами
, , . U(s,p) -\f 2а
L+(w) = e , s=y ~k~w’
= (2Л1>
—оо , 4
t — se
Функция U (s, р) детально изучена и табулирована в книге {8].
При решении уравнений (2.03) функции F(w) и f(z) получаются
в виде
7 ч (2-12)
' ' 2т (w + w„) L- (ш) ' ’
И
/ (г)^/7е—г + У Y (2.13)
где А есть амплитуда тока приходящей волны;
Ее. з — *
V (s0, p)+U (S,, р)
е J
(so + si) si
(2.14)
есть (при /=#0) коэффициент трансформации падающей волны
в волну с индексом /, а /?о,о — коэффициент отражения падаю*-
Щей волны по току.
Аналогичные формулы получаются в случае, когда падает
волна с индексом /=1, /=—1 и т. д., а не волна с индексом /=0.
11
Все эти формулы можно получить ([8], задача 6 к гл. I) из стро-
гих выражений, если в них считать а > 1, и
Х/=о, ±1,...).
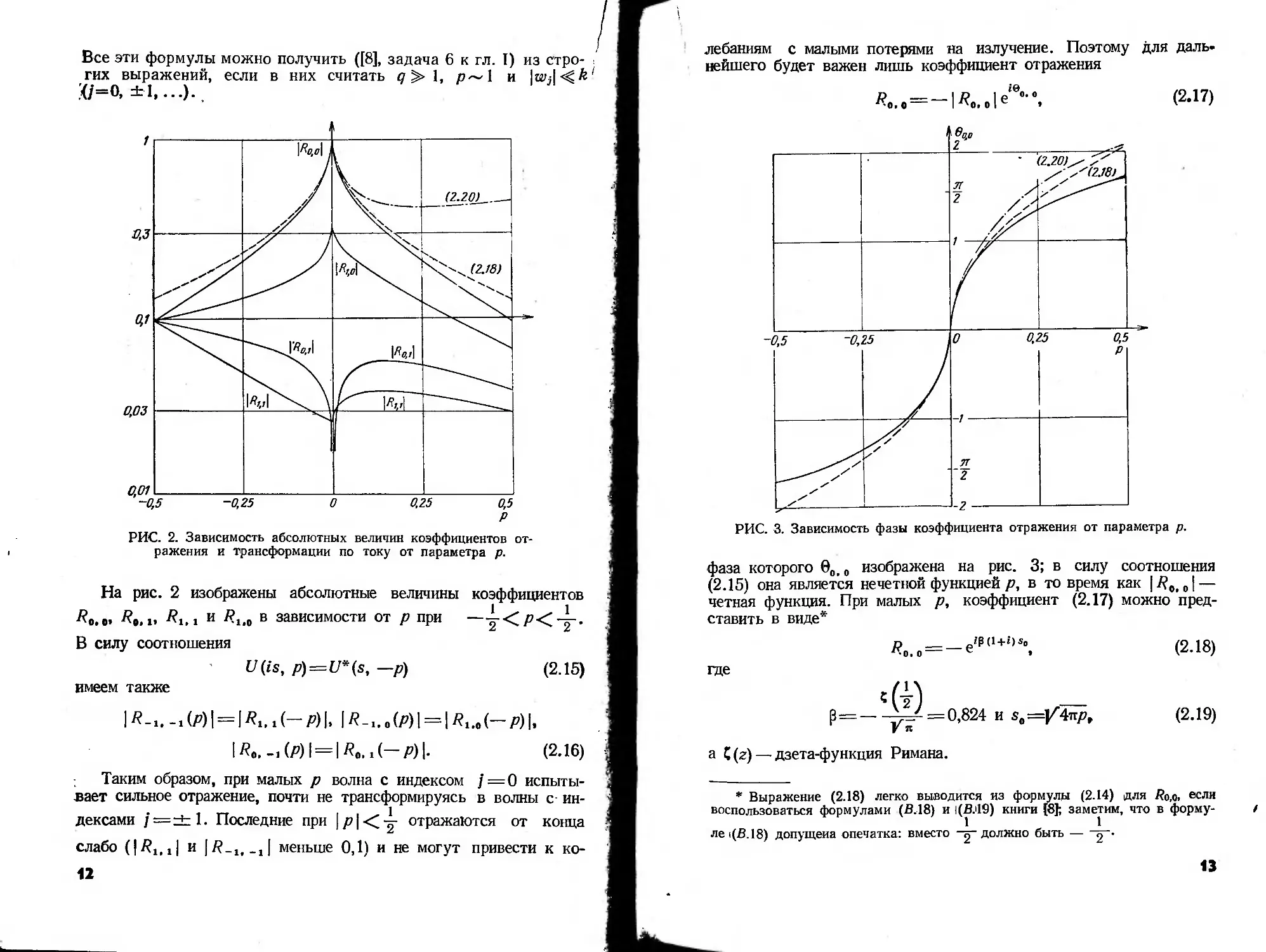
РИС. 2. Зависим ость абсолютных величин коэффициентов от-
ражения и трансформации по току от параметра р.
На рис. 2 изображены абсолютные величины коэффициентов
/?0,0, Яв, 1, Ri,t и /?ьо в зависимости от р при —
В силу соотношения
U (is, p) = U*(s, —р) (2.15)
имеем также
= |Я-1>о(/01 = |Я1.в(-/01.
\R0. -,(P)\ = \RO. А—/01- (2.16)
Таким образом, при малых р волна с индексом / = 0 испыты-
вает сильное отражение, почти не трансформируясь в волны с ин-
дексами /=±1. Последние при отражаются от конца
слабо (|/?i,i| и .J меньше 0,1) и не могут привести к ко-
12
лебаниям с малыми потерями на излучение. Поэтому для даль,
нейшего будет важен лишь коэффициент отражения
РИС. 3. Зависимость фазы коэффициента отражения от параметра р.
фаза которого 00,0 изображена на рис. 3; в силу соотношения
(2.15) она является нечетной функцией р, в то время как |/?0> J —
четная функция. При малых р, коэффициент (2.17) можно пред-
ставить в виде*
п __________i₽(l+i)s0
" 0. О С 1
(2.18)
где
0,824 и s0=J/’4ir/2t
(2.19)
a C(z) — дзета-функция Римана.
* Выражение (2.18) легко выводится из формулы (2.14) для /?о,о> если
воспользоваться формулами (В. 18) и I(ВЛЭ) книги [8]; заметим, что в форму- /
ле|(В.18) допущена опечатка: вместо -^должно быть — -g-.
13
На рис. 2 и 3 пунктиром нанесены функции |/?ОгО| и 0О1О, вы-
численные по приближенной формуле (2.18), которая, как мы
видим, дает графическую точность при | р | < 0,05 и качественно
применима вплоть до . | р | =& 0,5. Последнее обстоятельство вы- •
годно отличает формулу (2.18) от других формул, эквивалентных '
ей при малых s0, например от формулы
1+^-S.
R°-0 = ~ i₽(l+0 ' (2’20>
1 — 2 s«
На рис. 2 и 3 штрих-пунктиром даны функции |7?о,о| и 0о,о, вы-
численные по этой формуле: мы видим, что при конечных s0 она
непригодна, поэтому в дальнейшем будем пользоваться исклю-
чительно формулой (2.18).
Выше исследованы асимптотические закономерности, относя-
щиеся к отражению волн больших номеров вблизи их критиче-
ских частот (т. е. при ika > 1). Естественно поставить вопрос:
когда эти закономерности вступают в силу? Просмотр графиков,
приведенных в книге [8], показывает, что уже для волн Е03 и Н03
в плоском волноводе (ka -g-J асимптотические закономерности
качественно применимы; их точность быстро улучшается с ро-
стом ka, т. е. с увеличением номера волны.
Отметим, что на асимптотические закономерности не влияет
поведение тока вблизи острого края, различное для волн раз-
ных поляризаций — для волн HOq и EOq в плоском волноводе.
Кроме того, в полученном решении (2.13) отсутствует ток, зате-
кающий на внешнюю поверхность стенок [так как функция
(2.07) —целая]. Поэтому асимптотические закономерности спра-
ведливы для волноводов с фланцами или со стенками конечной
толщины (не обязательно металлическими, но обеспечивающи-
ми полное отражение, например, за счет интерференции в слоях).
В этом случае важно лишь, чтобы отражающие поверхности бы-
ли такие же, как у плоского волновода (рис. 1).
Результаты, полученные выше, имеют следующий физиче-
ский смысл. Как известно, волну, распространяющуюся в пло-
ском волноводе, можно представить в виде суммы двух плоских
волн, т. е. в виде двух пучков параллельных лучей. Если частота
волны близка к ее критической частоте, то эти лучи составляют
малый угол е0 с нормалью к стенкам волновода (рис. 4) и по-
этому благодаря диффракции легко поворачиваются на угол 2ео,
вследствие чего и образуется отраженная волна. Трансформация
в волны с другими индексами почти не происходит, поскольку
при такой трансформации лучи должны повернуться на гораздо
большие углы. Коэффициент отражения зависит не просто от
угла во, а от параметра So=eoy2ka, характеризующего диф-
14
L
фракционную размытость пучка лучей, отраженных от каждой
полубесконечной стенки, на расстоянии 2а от ее края, где нахо-
дится другая стенка, формирующая из повернутых лучей отра-
женную волну.
РИС. 4. К интерпретации формулы (2.18).
Эта физическая картина выявляется наиболее четко, если
диффракцию на открытом конце волновода исследовать методом
параболического уравнения. Это исследование мы проведем
в следующем параграфе.
§ 3. Параболическое уравнение
и диффракция на открытом
конце волновода
Параболическое уравнение впервые было предложено Леон-
товичем и Фоком [9, 10] для анализа распространения радио-
волн и затем неоднократно использовалось в теории диффрак-
ции для получения приближенных (асимптотических) решений
при условии, что длина волны мала по сравнению со всеми ха-
рактеристическими размерами. Поскольку открытые резонаторы
обычно удовлетворяют этому условию, метод параболического
уравнения находит широкое применение при построении их тео-
рии. В этом параграфе мы рассмотрим с помощью параболиче-
ского уравнения диффракцию на открытом конце плоского вол-
новода, отражающие поверхности которого определяются соот-
ношениями
0<Х<со, —оо<у<оо, z=±/, (3.01)
причем будем считать
kl > 1. (3.02)
Это — та же задача, которая рассмотрена в § 2, но обозна-
чения изменены в соответствии с принятыми в теории открытых
резонаторов (см. § 4 и дальше). Мы будем решать эту задачу
в предположениях, сделанных в § 2, т. е. примем, что к откры-
15
тому концу волновода приходит волна при частоте, близкой /]
к критической. / •
Будем искать решение Ф=Ф(х, г) волнового уравнения
£?+5 + *2ф = 0’ (3-°3¥ ’
удовлетворяющее условию Ф—О на зеркалах — полуплоскостях^
определяемых соотношениями (3.01), в виде
Ф = 1Г(х, z)eikz — (— 1)<(л, — z)e~ihz, (3.04)
так как Ф будет либо четной, либо нечетной функцией z (q —
целое число). Выделение множителей е±,Лг в формуле (3.04) обу-
словлено тем, что поле набегающей волны и вызванное им
диффракционное поле имеют характер (неоднородных) плоских
волн, слабо зависящих от координаты х, поэтому функция
1Г(х, z) будет по сравнению с этими множителями медленно ме-
няющейся. Требуя, чтобы каждое слагаемое в правой части
(3.04) удовлетворяло уравнению (3.03), для функции W полу-
чаем уравнение
dzW । d2W i dw n
в котором пренебрегаем членом сводя задачу к параболи-
ческому уравнению
— +2^=0. (3.06)
Здесь (ср. [11]) учтена поперечная диффузия комплексной вол-
новой амплитуды W (в направлении оси х) и отброшена про-
дольная диффузия (по оси z, составляющей малые углы с на-
правлением распространения волн в нашей задаче). Основанием
для такого пренебрежения является более слабая зависимость
W от z по сравнению с зависимостью от х; эти зависимости лег-
ко оценить, если перейти к безразмерным переменным. Мы сде-
лаем эти оценки в конце параграфа, сейчас же доведем до
конца решение задачи, пользуясь уравнением (3.06).
Параболическое уравнение (3.06) имеет функцию Грина, ко-
торая при z>zr равна
G(x — х', z — z')^\f 6 / ехр<[^~^- —4]» (3.07)
' ’ ' Т 2 л (z—г') г [ 2 (г—г') 4 J ' '
удовлетворяет предельному соотношению
lim G (х — х', z — г') = 8 (х — х') (3.08)
г-»г' +0
16
и равна нулю при z<z'. Легко также проверить, что при z^>zr
имеет место соотношение
J G (х— х', z — z')dx=l. (3.09)
—со
В правой части (3.08) стоит дельта-функция, удовлетворяющая
аналогичному соотношению
J 8(х— x')dx=l, (3.10)
х'—Лх
где Дх есть положительная величина, которая может быть взята
сколь угодно малой.
Функция W (х, г) определяет в формуле (3.04) амплитуду
волны, распространяющуюся в положительном направлении оси z
(временнбй множитель е~м, k = от нижнего зеркала z =
=— I. Такая волна при z = — / и х<0, очевидно, отсутствует,
поэтому
W (х, —1) = 0 при х<0. (3.11)
Кроме того, граничное условие Ф=0 приводит к соотношению
W (х, — 1) = el (х, /) при х > 0. (3.12)
Решение уравнения (3.06) с учетом условия (3.11) имеет вид
W (х, z) = J G (х — х', z-\-l)W(х', — Г) dx' при z> — I. (3.13)
о
Полагая z — l и пользуясь условием (3.12), получаем интегральное
уравнение
Г(х, —/) = ег(2Ы“^ jG(x —х', 21) W (х', — l)dx', (3.14)
б
которое легко преобразовать к виду
Iе <31б>
о
где
/(8) = Г(х, —/), (3.16)
4 х’ <ЗЛ7>
2—2547
17
а параметр p определяется формулой
(3.18)/
откуда
2чг/7=2^/ — тс?,
kl = тс
(3.19)
в соответствии с выражением (2.01). В дальнейшем будем считать
\р|<-i- или даже |р| < 1, тогда из условия (3.02) следует, что
q — большое целое число.
Если бы мы рассматривали не полубесконечный волновод,
а волновод, бесконечный в обе стороны, то в интегральном урав-
нении (3.15) были бы пределы —оо и оо. Уравнение с предела-
ми —оо и оо имеет решения
f(5) = conste } , Sj = J/r4ir(/4-/’), /=0, ± 1, =t2,..., (3.20)
причем для определенности будем считать, что при веществен-
ном р либо Sj=jsjl, либо Sj=i|s,|. Решения (3.20) приближенно
соответствуют волноводным волнам, распространяющимся или
затухающим между параллельными плоскостями z= ±1 и разла-
гающимся на плоские волны, волновые векторы (kx, ky, kz) ко-
торых удовлетворяют условиям
ky = 0, kz^±k.
(3.21)
Исследуем теперь (при р>0) диффракцию волны с индек-
сом / = 0 на открытом конце плоского волновода, образованного
параллельными полубесконечными зеркалами z=±l, х>0. Для
этого будем искать решение уравнения (3.15) в виде
f (?) = Д /е-‘^ + £ Яо. \, (3.22)
\ / /
где слагаемое Де~'5^ есть набегающая волна с индексом /=0,
а ряд охватывает все волны (3.20), распространяющиеся или за-
тухающие в положительном направлении оси х и возникающие
у конца волновода с амплитудами Д/?01Подставляя выражение
(3.22) в уравнение (3.15), получим уравнение для неизвестных ве-
личин /?0,
e~lsA — .e,s* = 0 пр» (3.23)
где
(3.24)
есть комплексный интеграл Френеля.
18
Чтобы из уравнения (3.23) получить грубую оценку коэффи-
циента Ro,о, положим 1=0 и пренебрежем всеми R0,j, кроме Ro,o>
тогда
Я». о
F(So) *
(3.25)
Если, кроме того, величины р и s малы, т. е. частота набегаю-
щей волны достаточно близка к ее критической частоте, то фор-
мула (3.25) переходит в формулу (2.20), причем величина [3 по-
лучается равной
₽ = -|==1,13,
У тс
(3.26)
и отличается от точного значения [3=0,824, полученного в § 2.
Интегральное уравнение (3.15) решается точно методом
Винера — Хопфа — Фока, для чего, пользуясь интегральным пре-
образованием Фурье, нужно перейти к функциональным уравне-
ниям. Они написаны и решены в § 2, причем для коэффициен-
тов R0,j получены формулы (2.14) и (2.18). Из этих формул сле-
дует, что при малых «о коэффициенты R0,j (/= ± 1, ±2,...)
пропорциональны so, поэтому если мы хотим, не пользуясь мето-
дом Винера — Хопфа — Фока, найти (хотя бы для малых значе-
ний s0) более точное выражение для ROiO, то должны учесть все
коэффициенты Ro,j.
Это можно сделать, преобразовывая функциональное уравне-
ние (3.23) в бесконечную систему линейных уравнений для
коэффициентов Ro,, и приближенно решая последнюю. Умножим
уравнение (3.23) на е~ ш проинтегрируем по 1 от 0 до оо. Вы-
числяя возникающий при этом интеграл с помощью формулы
Дирихле
получаем уравнение
е 2 F(s) — F(—s„) j у „ e
s-H.
s?—s*
1
— = °- (3.28)
2*
19
в котором полагаем $ = хЛ(/г = О, ±1, zt2,...). Пользуясь тожУ
дествами /
(3.29)
и
s? —®*
I -----
Пт £-------= _ iShp {Sh) _|_ F, {Sh)t (з 30)
s^h s-s»
где
/ c2 \
,'(-Г~т) /(’•'-T-)
(3-31>
приходим к искомой системе уравнений
+ R°-h [F'(So) “iShF (5h)1+
+ ^^.j -(^Z-£(S,) -0 (Л = о,±1,±=2,...). (3.32)
МЛ
Если в этой системе ограничиться только нулевым уравне-
нием и положить в нем 7?oj=0 (при /='±1, ±2,...), то для коэф-
фициента отражения получим формулу
П _________F (So) ' F ( so) /О QQ\
« — 2s0 [Р (s.) - is0F (s0)] ’
гораздо более точную, чем формула (3.25). При малых s0 вслед-
ствие соотношений
(3.34)
формула (3.33) принимает вид
= — (1 + 0,886i (1 4- i) s0 — 0,91i^ (3.35)
в то время как аналогичное разложение для формулы (2.18)
имеет вид
#0.0 = — [1 + 0,824/ (1 + i) s0 — 0,68/^ +...]. (3.36)
Таким образом, формула (3.33) дает значение [3=0,886, что го-
раздо ближе к точному значению (2.19), чем значение (3.26).
Заменяя в формуле (3.33) $0 на Sj, получаем выражение для
коэффициента отражения Rjj. При больших s3 можно считать
F(Sj) = l, F(-Sj)=0 (3.37)
и
(3.38)
в согласии с формулой (2.14); в последней при больших s3 нуж-
но полагать U (Sj, р) =0.
Заменяя в /-м уравнении (3.32) ряд одним членом, пропор-
циональным jRo.o, для коэффициента Ro,j (/=±1, ±2, ...) полу-
чаем приближенное выражение
п ______ 1 Г ? ( ®о) I n Т (Sj) F ($<>) 1
«о.з— r(s„)—tSjFfSj) L S3 + Se T««-o Sj—Se. J’
(3.39)
которое показывает, что при $о 1 коэффициент Ro,j пропор-
ционален So, что согласуется как с формулой (2.14), так и с фор-
мулой (3.35). Коэффициент Rh,j мы найдем, заменив $0 на sh.
При условиях
sh > 1, Sj > 1
(3.40)
получаем
(sj, -|- Sj) Sj
(3-41)
в согласии с формулой (2.14).
Несомненно, что выражения (3.33) и (3.39) можно уточнить,
считая их первым приближением и подставляя в уравнения
(3.32); так мы придем ко второму приближению для jRo,o и R0,j.
Мы не будем этого делать, поскольку формулы получаются
сложными — более сложными, чем точная формула (2.14); вме-
сте с тем, фактическое уточнение будет сравнительно незначи-
тельным. В гл. II будут рассмотрены задачи о диффракции на
открытом конце волновода, которые не могут быть решены мето-
дом Винера — Хопфа — Фока: для таких задач оказываются
полезными приближенные выражения, аналогичные формулам
(3.25) и (3.33).
Другим преимуществом подхода, использованного выше,
является его физическая наглядность: интегралы Френеля
в уравнении (3.23) и последующих формулах появляются пото-
му, что они определяют диффракцию плоской волны на полу-
21
плоскости. Пользуясь соотношениями (3.13), (3.16) и (3.28),
получаем для функции W выражение
где безразмерная координата Е определяется формулой (3.17),
а безразмерная координата С равна
C=i. . (3.43)
Полагая в выражении (3.42) С = 4- (z = l) и пользуясь условием
(3.12) и соотношением
F(s) +f(- s) = l,
(3.44)
приходим опять к уравнению (3.23).
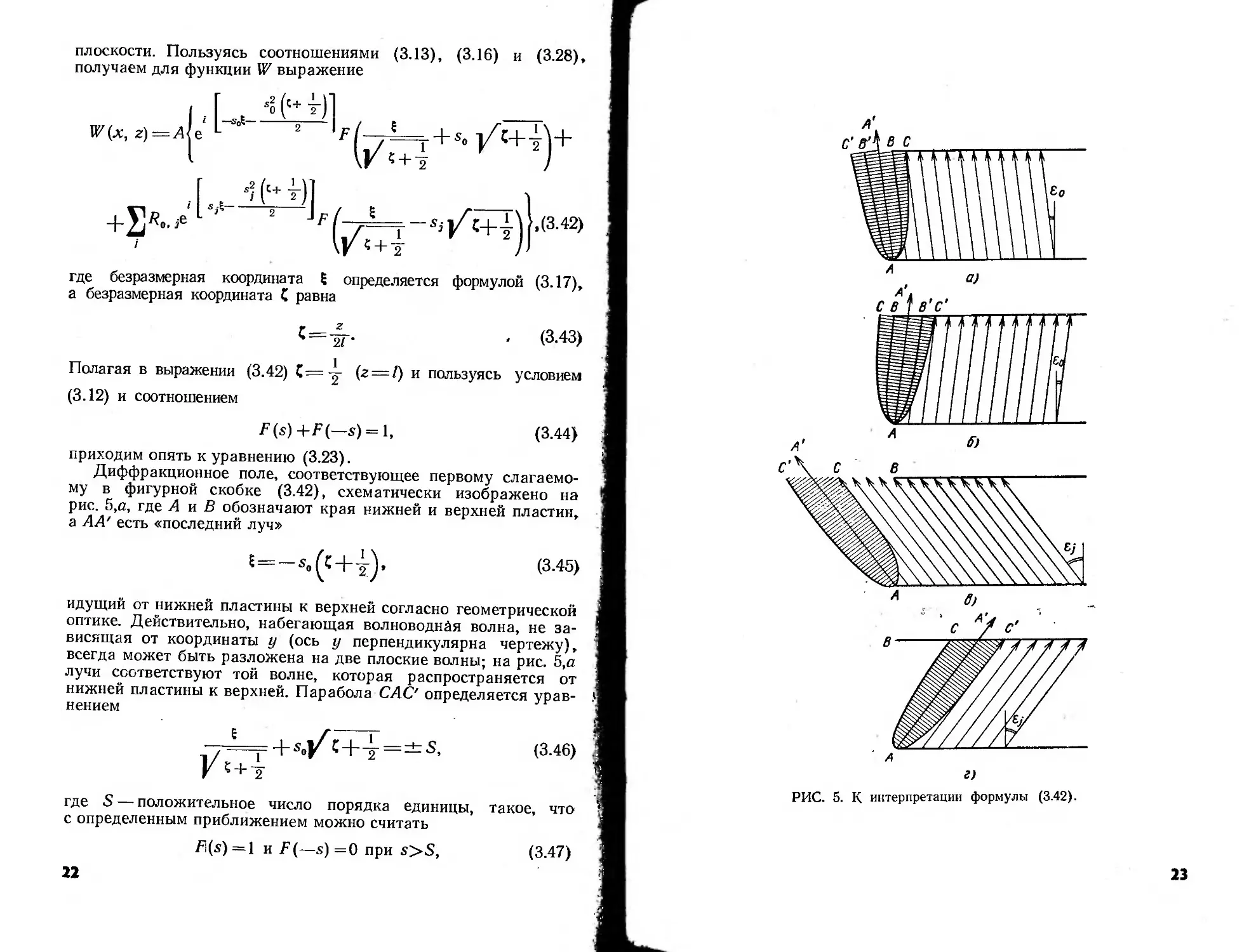
Диффракционное поле, соответствующее первому слагаемо-
му в фигурной скобке (3.42), схематически изображено на
рис. 5,о, где А и В обозначают края нижней и верхней пластин,
а АА' есть «последний луч»
— So(j + 2^»
(3.45)
идущий от нижней пластины к верхней согласно геометрической
оптике. Действительно, набегающая волноводнйя волна, не за-
висящая от координаты у (ось у перпендикулярна чертежу),
всегда может быть разложена на две плоские волны; на рис. 5,а
лучи соответствуют той волне, которая распространяется от
нижней пластины к верхней. Парабола САС' определяется урав-
нением
Е
(3.46)
где S — положительное число порядка единицы, такое, что
с определенным приближением можно считать
F(s) =4 и F(—s) =0 при s>S,
(3.47)
22
A'
™ЧВД формулы (3 42)
23
а парабола ВАВ', проходящая через край верхней пластины,—•
уравнением
(3.48)
При So<S (в частности, при < 1) парабола (3.48) лежит вну-
три параболы (3.46); последняя определяет ту область, где
диффракция имеет решающее значение, поскольку правее этой
области плоская волна практически не возмущена, а левее этой
области поле практически отсутствует. На рис. 5,6 аналогичные
области показаны для слагаемого в формуле (3.42), пропорцио-
нального /?о,О-
Если к открытому концу приходит волна с индексом /',
у которой 1, то область, ограниченная параболой САС'
с уравнением
5,
(3.49)
будет иметь вид, изображенный на рис. 5,в: в этом случае
в окрестности точки В имеется практически невозмущенное по-
ле плоской волны, которая, хотя и претерпевает диффракцию на
крае В, но в соответствии с формулой (3.38) почти не дает отра-
женной волноводной волны, распространяющейся от открытого
конца. Сильное отражение получается лишь при малых s0, когда
(как на рис. 5,а и 5,6) диффракционные области для падающей
и отраженной волн существенно перекрываются и край противо-
положной пластины находится внутри областей; в этом случае
легко происходит поворот лучей, о котором говорилось в кон-
це § 2, возникает (с амплитудой, близкой к амплитуде падаю-
щей волны) отраженная волна. Волны других номеров при этом
имеют малые амплитуды, что ясно как из закона сохранения
энергии, так и из рис. 5,а, где изображена диффракционная
область САС' для отраженной волны, у которой параметр
Sj = е3- ]/~2kl
(3.50)
велик; поле такой волны пропорционально коэффициенту /?0;3
в формуле (3.42). Энергетические соображения и рис. 5 спра-
ведливы только для распространяющихся волноводных волн
(е3 и Sj вещественные), но формулы (2.14) и (3.39) приводят
к тем же выводам для затухающих волноводных волн (е3- и S}
мнимые).
Сделанный в начале параграфа переход от эллиптического
уравнения (3.05) к более простому параболическому уравнению
(3.06) можно обосновать, если от переменных х и z перейти
к безразмерным переменным Е и £, через которые выражается,
24
как мы видели выше, диффракционное поле. В этих переменных
уравнение (3.05) принимает вид
дг№ .1 d‘W ! „. dW
“Г 2kl д’? 21 <3?
(3.51)
и перед отброшенным членом стоит малый коэффициент Бо-
лее полное обоснование можно получить, если рассмотреть точ-
ные решения диффракционных задач для полуплоскости и для
полубесконечного плоского волновода. Первое слагаемое в фи-
гурной скобке (3.42) соответствует точному диффракционному
полю, возникающему при падении плоской волны на полупло-
скость £>0, £=---g’, при условиях
ео < 1, kr > 1, (3.52)
где г — расстояние от края А, и при малых углах диффракции,
т. е. для таких точек наблюдения Р, для которых угол А'АР мал.
Интегральное уравнение (3.15) и функциональное уравнение
(3.23) дают правильные значения коэффициентов Rh,-j при ана-
логичных условиях
kt > 1 (3.53)
и
ел<< 1, Ej 1. (3.54)
При тех же условиях применима и формула (2.14). Если усло-
вие (3.53) выполняется, а условия (3.54) не выполняются, то
результатами этого и предыдущего параграфа пользоваться
нельзя, однако волны, не удовлетворяющие условиям (3.54),
практически не трансформируются друг в друга при диффрак-
ции на открытом конце и не отражаются, так как им соответ-
ствуют большие значения и Sj, и поэтому не представляют
интереса для теории открытых резонаторов.
Переход к параболическому уравнению (3.06), как раньше
переход к целой функции (2.07), эквивалентен обычному в физи-
ческой оптике расчету диффракции Френеля (ср. [11], а также
ниже конец § 4), основанному на принципе Гюйгенса — Френе-
ля и предположении о малых углах диффракции (последнее
предположение оправдывается тем, что переход от «света» к «те-
ни» происходит при малых углах, ср. рис. 5). Приближенное
рассмотрение диффракции на открытом конце не только упро-
щает все соотношения, но также делает их (при условиях, сфор-
мулированных выше) применимыми как к системе из двух
параллельных полуплоскостей (см. рис. 1), так и к любой паре
полубесконечных пластин, отражающие поверхности которых
(зеркала) определяются соотношениями (3.01). Последнее
обстоятельство имеет большое значение: если бы полученные
25
нами результаты относились только к бесконечно тонким полу-
плоскостям (т. е. к пластинам, толщина которых мала по
сравнению с длиной волны), то для достаточно коротких волн
(субмиллиметровых и световых) эти результаты имели бы чисто
академический интерес и не позволили бы рассчитать реальные
открытые резонаторы с зеркалами конечной толщины (см. § 4).
В этом параграфе мы исходили из скалярного волнового
уравнения (3.03). Связь функции Ф = Ф(х, z) с электромагнит-
ным полем можно установить, пользуясь электрическим векто-
ром Герца Пе, который определяет электромагнитное поле Е, Н
по формулам
Е = grad div IIе+ FIF, Н — — z^rotlF, (3.55)
где полагаем
Пе = ф, IIе = IIе =0 (3.56)
у ’ X Z 7
ИЛИ
Пе = ф, 1Г = 1Г=0. (3.57)
В первом случае полученные выше соотношения относятся к вол-
нам , во втором — к волнам Е{^ в плоском волноводе, причем
индекс 0 относится к координате у, индекс q — к координате z,
а значок <ж) показывает, что классификация волн производится
относительно оси х.
Если в формулу (3.16) ввести коэффициент пропорциональ-
ности, записав ее в виде
f (5) = e~i2npW (х, — I), (3.58)
то для волны поверхностная плотность тока на верхнем зер-
кале z — l будет иметь составляющие
/х=о, /,=/» (3.59)
а для волны £',Л) — составляющие
/х=Л /,=о. (3.60)
Граничное условие Ф = 0 на зеркалах приводит к граничным
условиям
Ex = Ey = Hz=0 (3.61)
для составляющих электромагнитного поля. Если функция Ф должна
йФ „
удовлетворять граничному условию = 0 на зеркалах, то вместо
выражения (3.04) достаточно взять выражение
Ф = 1Г(х, z)eift* + (— l^W(х, —z)e-iftz (3.62)
26
с той же функцией W. Выражение (3.62) может понадобиться, если
воспользоваться формулами
Е = /£гоШт, Н = grad div IF” + k2Hm, (3.63)
где Пт есть магнитный вектор Герца. Полагая
П' = Ф, П'п = Пт=0, (3.64)
получаем диффракционное поле волн — Е{^, а полагая
П^ = Ф, П” = П“=0 (3.65)
— диффракционное поле волн Е^ = . Двоякое обозначение
одной и той же волны объясняется тем, что, например, у волны
Н™ ПрИ частоте, близкой к критической, наиболее сильно выра-
жены составляющие Нх и Еу, поскольку эта волна разлагается
на две плоские волны, распространяющиеся под малым углом
к оси г.
Как мы видели, при условиях (3.53) и (3.54) волны различ-
ных поляризаций'ведут себя одинаково. Это «поляризационное
безразличие» диффракционного поля имеет место при достаточ-
но коротких волнах и при малых углах диффракции; мы с ним
будем неоднократно встречаться в дальнейшем.
§ 4. Двухмерный резонатор,
образованный плоскими зеркалами
На рис. 6 изображен резонатор, образованный двумя параллель-
ными зеркалами шириной 2о и бесконечной длины, отстоящими на
расстоянии 2/. Введем координаты х, у, г, как показано на рис. 6,
и рассмотрим в таком резонаторе двухмерные колебания, поле ко-
торых не зависит от у. В координатной системе х, у, г эти коле-
бания можно обозначить как и индекс <х> показы-
вает, что классификация основана на составляющих поля по оси х,
а не по оси г, как обычно (колебание можно также обозна-
чить как Е^ , ср. конец § 3).
Свойства колебаний без труда выводятся из соотношений,
полученных в § 2 и 3, так как данный резонатор есть отрезок
плоского волновода, открытый с обоих концов. Добротные соб-
ственные колебания происходят при частоте со = сЛ, определяе-
мой соотношением
« = + (4.01)
27
причем q есть большое целое число (практически </>3), ар —
малое слагаемое, которое получается комплексным (см. ниже).
Величина
s0 = j/4^P (4.02)
определяет волновое число волны, которая отражается от от-
крытого конца волновода
РИС. 6. Двухмерный открытый
резонатор с параллельными
плоскими зеркалами.
с коэффициентом отражения (2.18),
близким при So < 1 к минус едини-
це, и практически не трансформи-
руется в воляы других номеров
(рис. 2). В результате последова-
тельных отражений этой волны от
концов х=а и х=—а возникают
собственные функции. Если прене-
бречь слабой трансформацией дан-
ной волны в волны других номеров,
то эти собственные функции можно
представить в виде стоячих волн.
Поскольку система симметрична, то
собственные функции являются ли-
бо четными, либо нечетными функ-
циями безразмерной координаты
(3.17):
f (£) = cos s0£ при т = 1, 3,...,
f(£) = sins0$ при тге = 2, 4,...,
(4.03)
причем функция /(£) определяет
распределение тока на зеркалах
(см. конец § 3). Безразмерная ко-
ордината g при х=±а, на краях
зеркал, принимает значения £=±-£-,где
7И = |/ (4.04)
есть основной параметр рассматриваемой системы, который
обычно велик и лишь иногда (в миллиметровом диапазоне волн)
составляет несколько единиц. Вместо параметра М иногда поль-
зуются параметром
= (4-05)
который называют числом зон Френеля или просто числом Фре-
неля (см. [12] или [13], стр. 325). Легко показать, что N при-
ближенно равно числу зон Френеля, укладывающихся при а
на одном из зеркал, если их строить для точки, находящейся
28
в центре другого зеркала. Параметры М. и N связаны очевидным
соотношением
М = /8я1У,
(4.06)
причем большие значения М и N соответствуют диффракции
Френеля, а малые — диффракции Фраунгофера.
Комплексный параметр So, входящий в функции (4.03), на-
ходится следующим образом. Пользуясь формулой Эйлера, ко-
синусы и синусы можно представить в виде
при т — 1, 3,...,
при т — 2, 4,...
(4.07)
Первое слагаемое в квадратной скобке есть волна, приходящая
М
к открытому концу $ =------g-, второе слагаемое — отраженная
волна, которая согласно формуле (3.22) должна быть равна
'*>(*+ 4)
^о. ое V • Приравнивая /?0,0 коэффициенту, стоящему в фор-
муле (4.07), получаем характеристические уравнения
^.o = e“is”M И=1, 3,...),
/?o.o = -e-iSoM (^ = 2, 4,...),
которые согласно формуле (2.18) можно переписать в виде
еЧ(м+р+/₽»=(_ 1)»»= е/гал = 1, 2,...) (4.09)
с очевидным решением
s0 = /44---- ,р (т = 1, 2,...). (4.10)
Искомый комплексный параметр р, определяющий по формуле (4.01)
частоту колебаний, равен
лтг /Л 1 1 \
Р— 4 (Л4 4- ₽ + i₽)2
или подробнее
p=p'-ip"t (4.12)
, rtm2 Л4(Л1 + 2₽) „ пт* Р (Л1 + Р)
/’—4 [(Д4+₽)г + ₽г]г’ Р — 2 [(М + Р)2 +
Частота <о = <о'— iw" колебаний и комплексна. В
силу соотношения е~‘и/=е~г<°'*е-<°"/ величины р' и р" имеют сле-
дующий смысл: Д = 2я// есть дополнительный набег фазы за
19
время t==— вследствие того, что
точно критической частоте, а слегка
частота колебаний не равна
больше ее;
Л = 1 — е
(4.13)
есть относительное уменьшение энергии колебаний за то же
время т. Радиационная добротность этих колебаний (т. е. доб-
ротность, обусловленная только потерями на излучение) в силу
малости р' равна
Q-4F"- (4.14)
Формулы (4.10)—(4.12) являются приближенными. Они до-
статочно точны, если по формуле (4.11) получается |р|<0,05, и
дают грубое приближение вплоть до значений |р| ~0,5 (ср. § 2).
При больших значениях М
itm2 _____ ttfm2
~W’ Р ~'2лр
(4.15)
и мы получаем серию резонансов, схематически изображенную
на рис. 7. Ширина т-й резонансной кривой пропорциональ-
на т2, расстояние между соседними кривыми пропорционально
2т± 1; при т~М резонансные кривые начинают перекрываться,
вместе с тем, наши приближенные формулы становятся непри-
менимыми.
РИС. 7. Резонансная кривая открытого резонатора.
Полагая в формулах (4.10) —(4.12) ш = 0, получаем фор-
мальное решение уравнения (4.09), не имеющее физического
смысла: оно соответствует незатухающим колебаниям с крити-
ческой частотой, а такие колебания в открытых системах невоз-
можны.
30
От функций (4.03) нетрудно перейти к функции
—(с+ v)
W(x, Z) = f(t)e { (4.16)
где £ есть безразмерная координата (3.43), откуда
Ф(х, z) = 2e~tB/’f (E)cost^C при q нечетном, (4.17)
Ф(л, z) = 2ie~‘Kpf (^sinrajC при q четном.
Выражая электрический вектор Герца через функцию Ф согласно
формулам (3.56) и (3.57), легко получаются выражения для элек-
трического и магнитного полей колебаний и Е^ в данной
системе. Для колебаний в силу соотношений (3.17), (3.59),
(4.04) и (4.10) функции
fm (х) = cos — (т = 1, 3,...),
2\1 + ₽т)
fm (x)=sin —”mxi , . (zn = 2, 4,...)
характеризуют распределение поперечного тока на пластинах (со-
ставляющей jy поверхностной плотности тока). Интересно отме-
тить, что при М > 1 колебания в открытом и закрытом ре-
зонаторах тех же размеров имеют мало отличающиеся распре-
деления токов и полей; разница лишь в том, что в закрытом
резонаторе при х=±а ток спадает до нуля, а в открытом —до
малых значений порядка (ср. рис. 8 и 9). Спадание тока
у краев до малых значений — явление, характерное для откры-
тых резонаторов: благодаря ему потери на излучение становят-
ся минимальными (см. ниже).
Те же формулы применимы и к колебаниям Е^д, для которых
функции (4.18) дают распределение продольного тока, направлен-
ного по оси х. Таким образом, для данного резонатора характерно
поляризационное вырождение — колебания Е™ и имеют одну
и ту же частоту (4.01). При /И > 1 распределение тока колебания
в открытом резонаторе имеет узел вблизи каждого конца х=
=^za, в то время как в закрытом резонаторе у торцевых стенок
х = ±а расположены пучности тока. По этой причине в закрытом
Резонаторе есть колебание не существующее в открытом, но
собственные частоты других колебаний у закрытого и откры-
того резонаторов близки, если величина М достаточно велика.
31
Согласно формулам (4.01) и (4.15) радиационное затухание сво-
бодных колебаний определяется мнимой частью р, которая при
М > 1 пропорциональна , т. е. для небольших т достаточно
мала. Малость потерь на излучение можно понять так: составляю-
щие электромагнитного поля между зеркалами пропорциональны
либо /(?) (т. е. coss05 или sins0£), либо-^-^^^т. е.—sins05
или cos . Последняя функция всюду мала, так как | $0|<
<1 и kl > 1, что же касается f ($), то на краях зеркала, т. е.
при , как видно из формул (4.10) и (4.18), она умень-
шается до малых значений порядка . Так как у краев резона-
тора все составляющие электромагнитного поля малы, то и потери
на излучение тоже малы.
Полученное выше решение тем точнее, чем короче длина вол-
ны, т. е. чем больше параметр М. Действительно, при росте М
параметры $0 и р согласно формулам (4.10) и (4.11) уменьшают-
ся, вследствие чего применение формулы (2.18) и пренебреже-
ние волнами других номеров становится все более обоснован-
ным. Следует однако, иметь в виду, что это решение не является
асимптотическим в строгом смысле этого слова: в нем учтены
члены порядка в распределении тока (4.18) и опущены чле-
ны, обусловленные волнами других номеров и имеющие тот
же порядок или s0 [см. замечание после формулы (3.39)].
Более точное асимптотическое рассмотрение собственных ко-
лебаний в данной системе (при условии I > а, см. задачу 20)
естественно основывать на интегральном уравнении
М/2
/К*) Г
f(g) = ^——----- I е f(V)d!=', (4.19)
V 2п J
—М/2
аналогичном интегральному уравнению (3.15) и выводимом тем
же путем. Интегральное уравнение, эквивалентное уравнению
(4.19), впервые было получено в работе Фокса и Ли ([12] или
[13], стр. 325) с помощью принципа Гюйгенса—Френеля и квад-
ратичной аппроксимации фазовой функции (эта аппроксимация
законна при малых углах диффракции), что эквивалентно при-
менению параболического уравнения (3.06). Это интегральное
уравнение Фокс и Ли решали на электронной вычислительной
машине и с помощью метода итераций нашли две первые соб-
ственные функции (четную функцию с индексом т=1 и нечет-
32
ную с индексом т—2) и соответствующие им собственные зна-
чения р (или е'2”р), которые определяют введенные выше вели-
21
чины Л и А (Л — относительная убыль энергии за время т=у,
А— дополнительный сдвиг фазы за время т). Колебания с бо-
лее высокими индексами (т=3,4,...) в работе [12] не исследова-
ны и вряд ли могут быть рассмотрены в рамках примененного
там метода.
В нашей теории Л и Д определяются простыми формулами
Л — 4г.р" = 2я2тп2
Р(Л4 + Р)
[(М + ₽)г + ₽Т’
Л____О_____I___п*тг м (М + 2₽)
— 2 [(М + ₽)г + ₽2]г‘
(4.20)
Если сравнивать эти формулы с кривыми, приведенными в [12]
для т= 1 и 7п=2, то окажется, что в пределах графической точ-
ности они дают одно и то же (ср. [98]).
На рис. 8,а и б изображено распределение тока на пластинах
резонатора для колебаний ;п=1 и т=2 при тех значениях N,
для которых приведены соответствующие кривые в работе [12].
Сравнивая последние с полученными >нами кривыми (рис. 8),
видим, что они несколько отличаются друг от друга: кривые
Фокса и Ли—нерегулярные, волнистые, но в общем ход кривых
такой же, как у наших плавных кривых. Различие объясняется
тем1, что мы не учитываем волн других номеров (/=1, /=—1
и т. д.), возникающих, хотя и с малыми амплитудами, при отра-
жении волны от края. Для вычисления собственных частот эти
«тонкие детали» в распределении тока не существенны (см. за-
дачу 19), точно так же они не существенны при расчете джоуле-
вых и иных потерь, вызванных тем, что стенки открытого резо-
натора не являются идеально отражающими. Эти детали влияют
на ортогональность различных собственных функций: из интег-
рального уравнения (4.19) следует, что две различные собствен-
ные функции fm, (х), соответствующие одному и тому же
значению параметра М (в котором мы берем общее значение k.
скажем, для всех колебаний одной и той же серии, т. е. с фикси-
рованным индексом q, полагая «=-2^1, но разным значениям
р(рт=£= рт,), ортогональны; под ортогональностью мы понимаем
выполнение соотношения
J (x)dx—0 при т^=т'. (4.21)
~а
Для приближенных функций (4.18), имеющих индексы т одной
и той же четности, соотношение (4.21) выполняется лишь прибли-
3—2547 33
34
женно — с ошибкой порядка , обусловленной, очевидно, не-
сенными волнами других номеров. Можно показать, что если
\iecTO формулы (2.18) для коэффициента отражения использовать
Формулу (2.20), то для величины х0 в формулах (4.03) вместо (4.09)
получаем уравнения
(/n = 1, 3,...),
— «о ctg (т = 2, 4, ...).
В этом случае функции /(!•) удовлетворяют граничным
df,l — t М
+ р f 0 при £— 2 ,
df 1 — i t , М
-di----trf = ° пРие = -^Г
(4.22)
условиям
(4.23)
и
г.
РИС. 9. Стоячие волны
между параллельными
плоскими зеркалами.
являются строго ортогональными. Однако, как было показано
§2 (см. рис. 2 и 3), формула (2.20) по точности сильно усту-
пает формуле (2.18), поэтому мы не бу-
дем применять «насильственную ортого-
нализацию» функций (4.03)*.
Двухмерный открытый резонатор,
рассмотренный выше, является простей-
шей системой, позволяющей разобраться
в основных закономерностях и затем пе-
рейти к расчету трехмерных открытых
резонаторов (см. ниже § 5, 6 и начало
гл. V). В чистом виде двухмерные резо-
наторы могут быть осуществлены, если
вместо электромагнитных или звуковых
волн использовать волны на поверхно-
сти жидкости. В работе Быкова (14] мо-
делирование колебаний в двухмерных
открытых резонаторах осуществлялось
с помощью волн, возбуждаемых на по-
верхности ртути. На рис. 9 приведена
картина стоячих волн, устанавливаю-
Если искать решение уравнений (4.22) в виде
М ___~т
s0 ~2 2~ + °’
то для величины S получаем уравнение
₽(!+»’)
tg о = —-----g----so-
Заменяя в нем tgS на 8, возвращаемся к формуле (4.10). Такое применение
н гаедансных граничных условий носит довольно искусственный характер, но оно
, Уменьшает точности решения и вместе с тем облегчает решение ряда задач
м- § 6, 61 и 77, а также задачи 10 и 11 к гл. X).
3*
.35
щихся между параллельными зеркалами при резонансе: этот
рисунок сделан по фотографии, где отчетливо видны узлы
(темные линии) и пучности (светлые), обрывающиеся у откры-
тых 'концов резонатора. Узлы и пучности образуют систему па-
раллельных линий, характерную для стоячей волноводной волны
с фиксированным индексом q и иллюстрирующую возможность
пренебречь волнами с другими индексами q (см. выше).
§ 5. Открытый резонатор,
образованный прямоугольными зеркалами
'Пусть открытый резонатор образован параллельными пря-
моугольными зеркалами
—о<х<о, —b<i/<b, z=i±/. (5.01)
При анализе колебаний в этой системе будем исходить из ска-
лярного волнового уравнения
ДФ4-/г2Ф=0 1(5-02)
и граничного условия Ф=0 на зеркалах. Решение уравнения
(5.02) 'можно записать в виде
<£> = W(x,y, z)eihz — (— 1)еГ(х, у, —z)e~ihz. (5.03)
Для функции W получаем параболическое уравнение
d2W . d2W . dW n /c n..
dxt "Ь dy2 дг (о-04)
и граничные условия
W (х, у, —1) — 0 при |л-|>а или | у | >Ь,
Г(х, у, —l)^=ei{2k‘-I4)W(x,y, /) при |х|<а и (5.05)
Уравнение (5.04) допускает решение в виде
W=Wa(x,z)Wb(y,z), (5.06)
где функции Wa и Wb удовлетворяют уравнениям
дхг 1 дг ’
^_|_2t-b^-o (507>
ду2 dz — U
и граничным условиям:
Wa(x, —l) — Q при | х| ~>а,
Wb(y, — /) = 0 при \у\>Ь,
Wa(x, —0=е*2 PaWa(x, 0 при |х|<л,
Wb(y, —l)=t2*PbWb(y, I) при \у |<b.
36
Эти формулы показывают, что функция Wa(x, z) совпадает
с функцией W(х, z) двухмерной задачи, рассмотренной в § 4,
а функция Wb отличается от W(x, z) тем, что х заменен на у, а—
на Ь; кроме того, индекс т заменим для функции Wb на п. Соб-
ственная частота получаемого таким образом колебания вычис-
ляется по формуле
kl=^ (t + Z7)’ Р=^Ра-\~Рь, (5.09)
где
Ра = 4(Л4а + ? + *₽)2 ’ Рь = 4 (Мь + ₽ + i₽)2 И. « = 1 > 2, • • • ) (5.10)
И
Ма = У^-, = (5.11)
Пользуясь формулами (3.56) и (3.57), получаем колебания
Нм и £(x) = Н^ в резонаторе с прямоугольными зер-
калами. Нетрудно найти распределение электромагнитного поля
при таких .колебаниях. Распределение тока на зеркалах при не-
четных тип определяется функцией
а при четном т или п нужно заменить косинус на синус. На
рис. 10 схематически изображено распределение тока для колебаний
и между прямоугольными зеркалами [заметим, что ча-
стота колебания определяется формулой (5.09) и не зависит от его
поляризации].
В безразмерных координатах
мы имеем
W = fa(t)fb(ii)e 1 ’ (5.14)
и
Ф = Зе"-'"7’/а (£) fb (»]) cos vqC (нечетное q),
<]? = 2ie~“pfa(t)[b(7])sinnqC (четное q), (5.15)
где
fa ()=sm Д|в +1+(-g <m = 2. 4,...),
37
Таким образом, в рамках параболического уравнения (5.04)
переход от двухмерной задачи к трехмерной для прямоугольных
зеркал происходит без каких-либо затруднений.
§ 6. Открытый резонатор,
образованный круглыми зеркалами
В резонаторе, образованном параллельными круглыми зер-
калами, которые и цилиндрической системе координат г, <р, z
определяются уравнениями
0<ir<a, z=±l,
уравнение (5.04) принимает вид
1 д ( . 1 d*W । о., dW
—л- I г~т~Н—т -ТТ+2гк -5—=
г dr dr I 1 г2 д?* 1 dz
(6.01)
(6.02)
Используя граничные условия, нетрудно свести задачу к интег-
ральному уравнению [ср. ниже формулу (6.22) и следующие за
ней]. Однако с помощью дополнительных аппроксимаций можно
решить задачу в замкнутом виде.
38
По аналогии с формулой (5.14) будем искать решение урав-
нения (6.02) при 0<г<а и — l<z<l, т. е. внутри резонатора,
в виде
—-2^Л+ 2-j
W = f(r, <f>)e ' (6.03)
где
f(r, ?) = Jm(SoP)cosm<p (m = 0, 1, 2,...),
f (r, <p) = J„ (sop) sin tnq (m — 1, 2,...), (6.04)
причем
р = |/АгиС = -^- (6.05)
суть безразмерные координаты, Jm — функция Бесселя, s0=
— ]^4ър, а параметр р связан с частотой колебаний формулой
= (б.об)
где q — большое целое число.
При небольших m(m=0 или т—1) мы делаем предположе-
ние, что вблизи края, при г~а, функцию Jm(s0 р) можно заме-
нить асимптотическим выражением! Ханкеля
(sop) = |/ cos [ sop — (2т + 1) -J 1 ==
L 'г J
(6.07)
т. е. представить в виде двух радиальных волн, пропорциональных
e's°p и e-'s°p. Связывая эти волны, так же как в § 4, коэффициен-
том отражения (2.18), т. е. считая, что кривизна края и цилин-
дричность волны не влияют на коэффициент отражения, и вводя
обозначение
М = (6.08)
получаем
V2
(6‘09>
где утп есть n-й положительный корень уравнения
Jm(v)=0. (6.10)
Сделанное выше предположение оправдывается тем, что функ-
ции Бесселя J0(x) и Jt(x) в самом грубом приближении можно
при x«voi и x^vn заменить первым членом асимптотического
ряда Ханкеля.
___1
V 2п$ор
39
При больших т на коэффициент отражения от края г—а
влияет зависимость функции (6.04) от координаты <р. Однако
при этом формулы (6.09) не изменяются. Здесь дело обстоит так
же, как в резонаторе с прямоугольными зеркалами, где волна,
отражающаяся, например, от края х=а, зависит от координа-
ты у, но зависимость от х получается по формулам (5.16) такой
же, как и для двухмерных колебаний, не зависящих от у (§4).
Более подробно это утверждение можно обосновать так. Введем
функции Лт(х) и Пт(х)—амплитуду и фазу цилиндрической
волны — по формулам
(х) = — iAm (х) e/8m W, Jm (л) — Ат (х) sin (х), (6.11)
тогда
I ,Вт (so / 1 [йт (SoP)-Bm (so yjl
Jm(sj>)=^-Am(sop)e '• 2'|е I ;J-
— e V 'e 1 1 'Jl. (6.12)
Требуя, чтобы коэффициент при отраженной волне был равен
/?0,0, получим характеристическое уравнение
Учитывая соотношение
(6.14)
при x~vmn можем написать
(х)--"КП -ф* О т (Утпп) (% ^тп) (6.15)
и таким образом упростить правую часть (6.13). Левую часть (6.13)
следует заменить выражением
/₽(1+ПЯ'т (VBn)so
^0,0=----е !
(6.16)
поскольку фазовая зависимость бегущих волн вблизи края зеркал,
Л4 , ±«я' (»„„)sop
при р =s- -у, определяется функциями е
Преобразуем уравнение (6.13) к виду
е'(«+₽+>» _е2Ьт„й'т (vm„)
40
откуда опять* получаем формулы (6.09). Величины Л и А для ре-
зонатора с круглыми зеркалами равны
— vvmn[(Af + p2)1+₽lp,
А == 2т.р’ = 2v2mn цлГ+ТТ+Й5’ <6’18^
а функция (6.04) принимает вид
f (г, Т)=jm (— \ c°s . (6.19)'
' ' ’ т/ I / 14- А | sin m<f ' '
°(,+ ₽-ATj )
Связывая функцию Ф с электромагнитным полем по формулам:
(3.55)—(3.60), получаем колебания E{^nq h=0) и E^nq (jx=
= 0, jy — f) в резонаторе с круглыми зеркалами. При =
= 1, 2,... каждое колебание Е™п и Е^ обладает поворотным
вырождением — при замене cos на sin m<t получаются два но-
вых колебания, следовательно, формулы (6.09) при т=£0 отно-
сятся к четырем колебаниям.
В первом и втором столбцах рис. 11 схематически изображено
распределение тока на круглом зеркале для колебаний E(^qy
и El*t’y\ Путем комбинирования колебаний E™q и E(^q можно по-
лучить колебания с радиальными или азимутальными токами, об-
* Довольно громоздкий анализ, проведенный выше, можно сократить,
если воспользоваться импедансным граничным условием
df . 1 — i t Л м
^-+-|-f=0 при р=т, (а)
аналогичным первому условию (4.23) и соответствующим основному пред-
положению о том, что цилиндрические волны отражаются от края г=а так
же, как плоские волны — от края плоского волновода. Подставляя в это
граничное условие функции (6.04), приходим к характеристическому урав-
нению
решение которого ищем в виде
М
50 2 + о,
где величина б мала. В первом приближении она равна
откуда получаем формулу (6.09) для So.
Из результатов § 5 следует, что граничные условия (4.23) справедливы
и в том случае, когда поле зависит от всех координат, причем зависимость
°т х и у более слабая, чем от г. Поэтому условие (а) справедливо для ко-
лебаний с любой азимутальной зависимостью.
41
ладающие симметрией вращения (третий столбец рис. И). Более
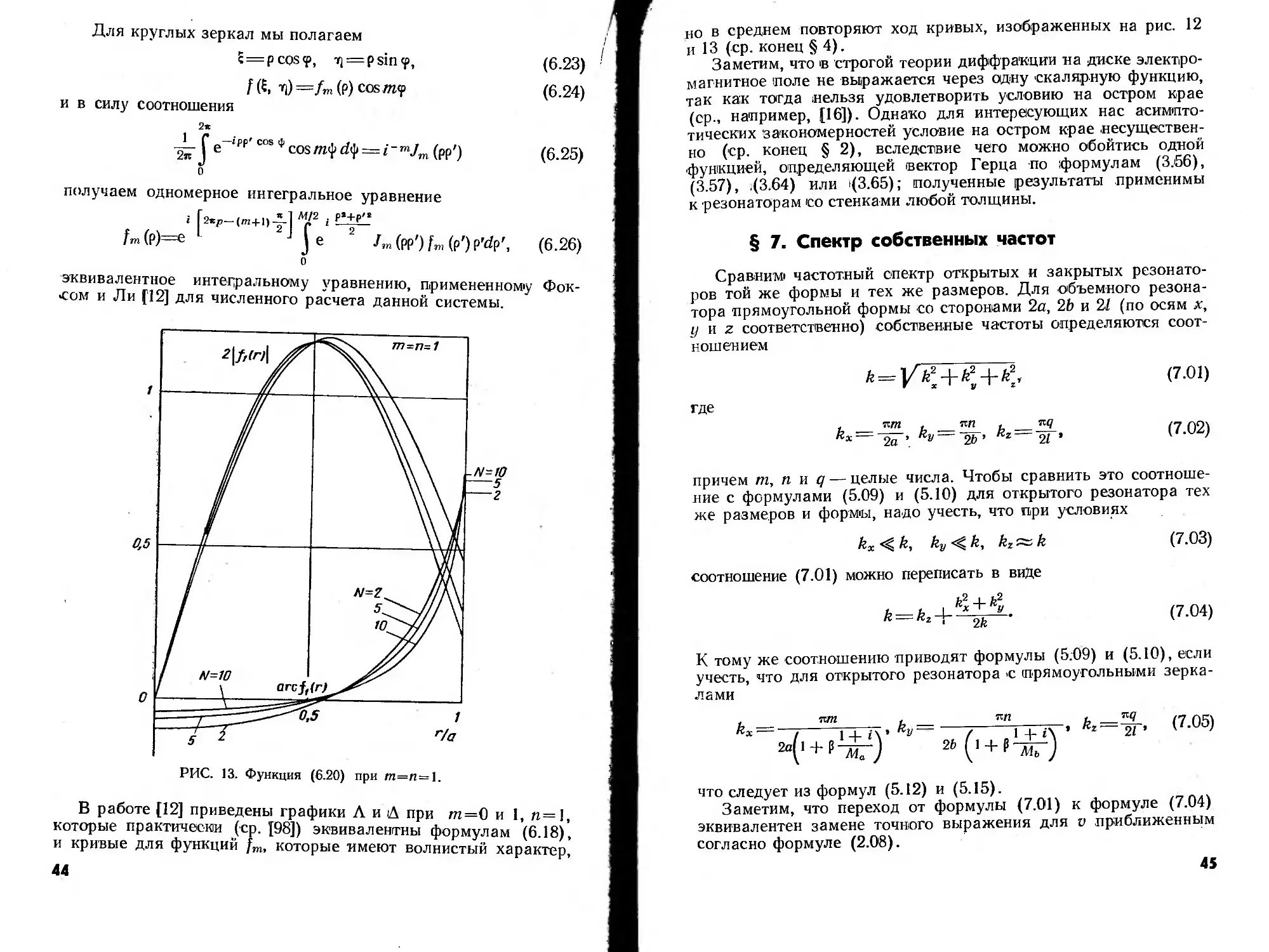
детально распределение тока показано на рис. 12 и 13, где нане-
сена абсолютная величина и фаза функции
(6.20)
при т=0, я = 1 (v0J = 2,405) и т = n=l (v„ = 3,832), причем
параметр
РИС.
на
11. Распределение тока
а—колебание /х = Л> («оРК б —колебание = Л>:
= J. cos ф; г —колебание еМ i = J sin ф:»—колебание Е^УУ,
1 т 1IQ v ид
круглом
зеркале при
• oiif = J°:
колебаниях Etta и Eliq:
е—колебание /:(*», I =
11<? *
, iy~ Ji cos ф; е— колебание
. /С = Л Sin ф; ж — колебание £(9 . /_ = Л: з —колебание Ety . С —
ид х па на*
42
связанный с М соотношением (4.06), принимает значения 2, 5
и 10. Вычисления производились с помощью таблиц (15].
Наше рассмотрение колебаний между плоскими зеркалами
круговой формы является приближенным, причем наряду с до-
пущениями, принятыми в § 4 и 5, сделаны дополнительные допу-
РИС. 12. Функция (6.20) при т=0, п=1.
щения. Поэтому интересно сравнить полученные результаты
с теми, которые следуют из более точного (асимптотического)
рассмотрения. Если открытый резонатор образован плоскими
зеркалами произвольной формы — одинаковыми, параллель-
ными и расположенными друг против друга, то для него можно
написать интегральное уравнение
I (2хр-
----(Jexpi- [(S-Vr + fTj—n')W, 4')<W.
(6.22)
обобщающее уравнение (4.19) и использующее безразмерные
переменные (5.13). Уравнение (6.22) нетрудно получить, исполь-
зуя трехмерную функцию Грина G(x—х', у—у\ z—z'), которая
строится по формулам (3.07) и (5.06) в виде
G(x—х', у—у', z—z') = G(x—х', z—z')G(y—у', z—г').
Интегрирование в этом уравнении производится по поверхности
зеркала.
43
Для круглых зеркал мы полагаем
£ = pcos<p, iq = psin<p, (6.23)
f (Е. *1) (Р) cos (6.24)
и в силу соотношения
J е—*рр' cos ф cos _mj^ (pp,j (6.25)
о
получаем одномерное интегральное уравнение
fm(p)=e J J е Jm (pp') fm (p') p'dp', (6.26)
о
эквивалентное интегральному уравнению, примененному Фок-
сом и Ли [12] для численного расчета данной системы.
В работе [12] приведены графики А и А при m=Q и 1, п=1,
которые практически (ср. [98]) эквивалентны формулам (6.18),
и кривые для функций fm, которые имеют волнистый характер,
44
но в среднем повторяют ход кривых, изображенных на рис. 12
и 13 (ср. конец § 4).
Заметим, что в строгой теории диффракции на диске электро-
магнитное поле не выражается через одну скалярную функцию,
так как тогда нельзя удовлетворить условию на остром крае
(ср., например, [16]). Однако для интересующих нас асимпто-
тических закономерностей условие на остром крае несуществен-
но (ср. конец § 2), вследствие чего можно обойтись одной
функцией, определяющей вектор Герца по формулам (3.56),
(3.57), .(3.64) или '(3.65); полученные результаты применимы
к резонаторам со стенками любой толщины.
§ 7. Спектр собственных частот
Сравним' частотный спектр открытых и закрытых резонато-
ров той же формы и тех же размеров. Для объемного резона-
тора прямоугольной формы со сторонами 2о, 2Ь и 2/ (по осям х,
у и z соответственно) собственные частоты определяются соот-
ношением
k = y k2x^-k2v + k2z, (7.01)
где
= = Аг = >, (7.02)
причем т, п и q — целые числа. Чтобы сравнить это соотноше-
ние с формулами (5.09) и (5.10) для открытого резонатора тех
же размеров и формы, надо учесть, что при условиях
kx <^.k, ky<^k, kz^k (7.03)
соотношение (7.01) можно переписать в виде
Ь2 1 il2
k = k2 + ^^- (7.04)
К тому же соотношению приводят формулы (5.09) и (5.10), если
учесть, что для открытого резонатора с прямоугольными зерка-
лами
f ТЪТП t г с"] /ЛС"\
Г+Т\ * ~ 7 1 4- i\ ’ kz—~2Г> (7.05)
что следует из формул (5.12) и (5.15).
Заметим, что переход от формулы (7.01) к формуле (7.04)
эквивалентен замене точного выражения для v приближенным
согласно формуле (2.08).
45
Частота колебаний в цилиндрическом объемном резона- /
торе с радиусом основания а и высотой 21 определяется соотно-'
шением j
k=^k2r + k2z, (7.06 j
где I
(7-07> .
При условии kr < k имеем -
fe2
A = + (7.08)
что согласуется с формулами (6.06) и (6.09) для открытого резо- ‘
натора с круглыми зеркалами, если положить
t >~‘.+ц. *=§- р-09»;
Следует отметить, что формулы (7.09) для открытого резонатора
справедливы для любой поляризации колебаний, в то время как 1
в формуле (7.07) для колебаний 77^ под v„,n нужно понимать <
корень уравнения
J'm(v) = 0. (7.10)
Заметим, что для закрытых резонаторов приведенные выше
формулы дают явное выражение для частоты, в то время как ,
для открытых резонаторов в выражение для k входят величины I
Ма, Мь и М, которые сами зависят от волнового числа k\ обыч- '
ко, однако, при вычислении М достаточно положить k = kz=~,
какие-либо уточнения приходится вводить только при неболь-
ших значениях индекса q.
РИС. 14. Частотный спектр открытых резонаторов.
Главное отличие закрытых резонаторов от открытых в том.
что при отсутствии потерь в стенках (зеркалах) собственные ча-
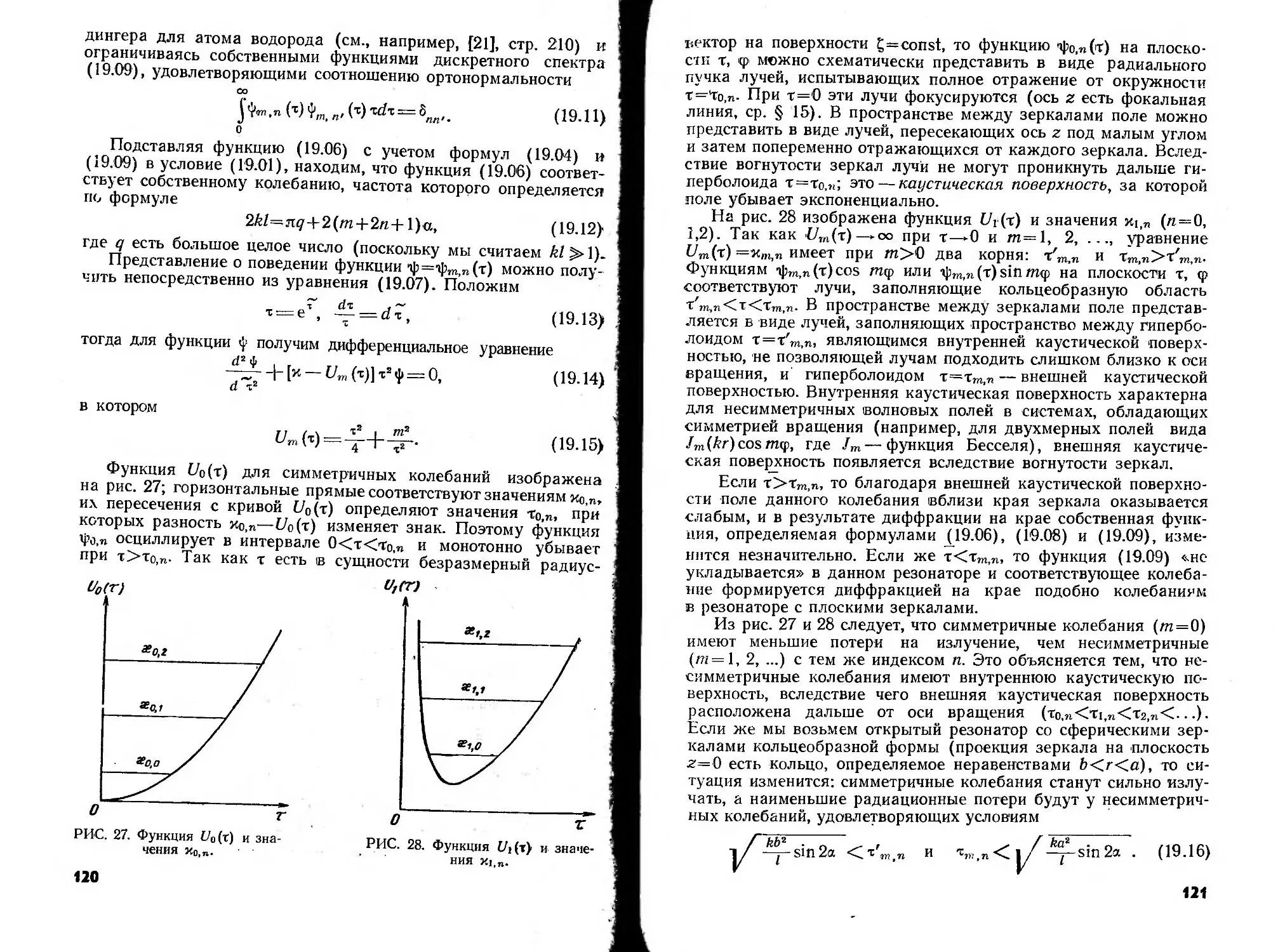
стоты закрытых резонаторов вещественны, а собственные часто-
ты открытых резонаторов комплексны, что приводит к разре-
жению спектра. Чтобы разобраться в этом вопросе, нанесем
комплексные собственные частоты <отП9 резонатора с квадрат-
ными или круглыми зеркалами в виде точек на плоскость ком-
плексного переменного со (рис. 14). Как следует из формул
46
,(5.09), (5.10), (6.06) и (6.09), эти точки лягут на полупрямые.
1 "сс!
Начинающиеся в точках сод= на вещественной оси и обра-
зующие с ней угол
<р = 2агс1ё-^р^Л. приЛ1>1, (7.11)
причем величину М нужно брать при (o=toQ.
। Из рис. 14 видно, что с увеличением индексов т и п радиа-
ционное затухание колебаний увеличивается — точки отходят
от вещественной оси [фактически затухание увеличивается бы-
стрее, так как формула (2.18) при конечных значениях |р| пре-
уменьшает потери на излучение; ср. рис. 2]. Более того, ордина-
ты точек по абсолютной величине растут гораздо быстрее, чем
разность абсцисс соседних точек. Так как резонансные кри-
вые, соответствующие двум соседним собственным частотам
<о_=<о —Ш И t'>+=t'J+— + » при
, , - а>"+ + <о"_
О) , ---OJ <L ---------------
+ - 9
(7.12)
перекрываются, то вблизи каждой частоты остается лишь
конечное число собственных частот, которые проявляются при
работе с открытым резонатором. Если остается одно колебание
с наименьшими индексами (/п=п=1 для прямоугольных и т =
=0, п=1 для круглых зеркал), то мы получаем практически
эквидистантный спектр без какого-либо сгущения, такой же, как
в идеальном случае одномерной резонансной системы (ср. § 1).
Для замкнутого резонатора ф = 0 и полупрямые на рис. 14
накладываются на ось абсцисс, вследствие чего и происходит
сгущение спектра.
Выше изложена теория собственных колебаний в открытых
резонаторах простейшего типа, на основе которой для каждого
колебания легко вычислить собственную частоту и радиацион-
ное затухание, а также распределение тока на стенках, позво-
ляющее рассчитать дополнительное затухание, вызванное джоу-
левыми потерями или частичной прозрачностью стенок. Нетруд-
но также построить распределение электрического и магнитного
полей в объеме резонатора.
Полученные формулы имеют простой вид, не представляют
каких-либо трудностей при расчетах и допускают наглядное
физическое толкование. Они являются приближенными, причем
точность их тем больше, чем больше радиационная доброт-
ность данного колебания.
Хотя термин «открытый резонатор» вошел в употребление
всего несколько лет назад, по существу открытые резонаторы
используются в физике и технике уже давно. Прежде всего, все
музыкальные инструменты и ряд акустических приборов (резо-
натор Гельмгольца, камертон и т. д.) представляют собой от-
крытые резонаторы, поскольку они обладают резонансными
47
свойствами и колеблясь излучают звуковые волны в окружаю-
щее пространство. В акустике наиболее полно развита теория
органных труб, представляющих собой отрезок круглой трубы,
с одного конца открытой, с другого закрытой; резонансные свой
ства органной трубы обусловлены тем, что основная (поршне
вая) волна, распространяющаяся в трубе, испытывает от от
крытого конца сильное отражение, если длина волны велика по
сравнению с радиусом трубы (ср. |[8], гл. III). В радиотехник^
для метровых волн применяются отрезки двухпроводных линий,
резонансные свойства которых опять-таки обусловлены сильный
отражением от концов линии (ср. [8], гл. гл. VI); антенные вибра-
торы также являются открытыми резонаторами (ср. [8], гл. IX).
Обычные объемные резонаторы никогда не являются полностью
изолированными (как это предполагают при их теоретическом
исследовании) и связаны либо с какими-то линиями передачи,
либо непосредственно со свободным пространством.
Перечисленные выше резонансные системы отличаются от
систем, рассмотренных в этой главе, тем, что излучение не из-
меняет качественно спектра их собственных частот (в том ча-
стотном диапазоне, где они фактически используются), и лишь
приводит к некоторому смещению частоты и небольшому допол-
нительному затуханию. Так, труба, закрытая с обоих концов,
имеет примерно такие же собственные частоты, как и открытая;
коаксиальный резонатор — такие же частоты, что и двухпровод-
ная линия или вибратор той же длины; полностью изолирован-
ный объемный резонатор есть первое приближение к реальному
резонатору с малыми элементами связи.
При исследовании открытых резонаторов в этой главе мы
применяли в основном те же методы (см. особенно § 4), что и
при расчете органных труб и отрезков двухпроводной линии.
Однако для достаточно коротких волн (малых по сравнению
•с характеристическими размерами открытого резонатора) излу-
чение, как видно из рис. 14, качественно изменяет спектр собст-
венных частот, радикально разрежая его. Это — отличительное
свойство открытых резонаторов, которым посвящена данная
книга.
Задачи к гл. I
1. Показать, что интегральное уравнение (3.15) эквивалентно функцио-
нальным уравнениям (2.03), в которых L(w) определяется формулой (2.07).
Решение. Представим функцию 1(|), определяющую ток на верхней
пластине, в виде
f(5) = J e'^G(s) ds,
с
где С — контур в плоскости комплексного переменного s. Поскольку на
геометрическом продолжении пластины /(£)=0, мы получаем уравнение
J eistG (s) ds — 0 при Е < 0. (0)
С
48
Подставляя интегральное представление для /(g) в левую и правую части
уравнения (3.15) и пользуясь тем, что >в силу уравнения (а)
-i Y оо . №-У)»
— Ге 2 dg' fe's*'G(s)ds =
У2п J J
О С
1 Н~т
е ' ' G (s) ds.
получаем второе функциональное уравнение
которое вместе с первым уравнением (а) переходит в систему (2.03), если
положить
_ / k , / 2а
2^z, s = JZ jtti, G(s) = f(a>).
2. Рассмотреть электромагнитные колебания в полуоткрытом двухмерном
резонаторе с плоскими идеально проводящими зеркалами (рис. 15,а) и свя-
зать их с колебаниями, исследованными в § 4.
'7777722/727772
’/222222222/272,
6)
РИС. 15. Модификации двухмерного резонатора
с плоскими зеркалами.
Решение. В системе, изображенной на рис. 15,а, возможны колебания
с нечетными индексами т и колебания с четными индексами т,
такие же, как в открытом резонаторе, изображенном на рис. 6. Поляриза-
ционное вырождение, характерное для открытого резонатора, при переходе
к полуоткрытому резонатору исчезает.
3. Рассмотреть двухмерные электромагнитные колебания в системе, изо-
браженной на рис. 15,6 и состоящей из плоского идеально проводящего
зеркала
—а<х<а, ~-оо<у<<х>, z—l
над бесконечной идеально (проводящей плоскостью z—0.
4—2547
49
Решение. В этой системе возможны колебания и с четными
индексами q, такие же, как в открытом резонаторе (рис. 6).
4. Исходя из уравнения (4.19), показать, что собственные функции двух-
мерного открытого резонатора, удовлетворяющие соотношению
f(!)=/(-?) при m=l, 3, .... (а)
являются решениями интегрального уравнения
, Z 2 Ч2*р~ г) Г ~~2~ I
fG)=y — е 1 \ е cos (&') f (S')
о
а собственные функции, удовлетворяющие соотношению
f(«)=-/(-£) при m=2, 4, .... (Ь)
— решениями интегрального уравнения
f ($)=]/ 4 е 4 ' ( е 2 sin(S5')f(£')dE'.
о
5. Пользуясь интегральным уравнением (4.19) нли интегральными урав-
нениями, выведенными в предыдущей задаче, и представляя собственные
функции в виде
00
f(E) = У Aj cos Sj5 (m=l, 3, ...)
/=—00
или
00
f(6)= Aj sin «Д (m=2, 4, . . .),
y=—oo
вывести функциональные уравнения для неизвестных постоянных Aj, ана-
логичные уравнениям (3.23), и перейти затем к бесконечной системе линей-
ных уравнений для Aj, аналогичной системе (3.32). Написать характеристи-
ческое уравнение, определяющее собственные частоты двухмерного открытого
резонатора.
Решение. Подставляя /(£) в уравнение (4.19), получим функциональное
уравнение (при — Л1/2 < £ < Л4/2)
которое в силу соотношения (3.44) можно переписать в виде
SI ist Г Г Л-1 , \ / Л4
AiV 3 ।F +F +s>)] ±
so
Умножим это уравнение на e'st + е [т. е. по существу на cos sE или
\ , Л1
I sins?, в зависимости от четности функции f (?)], проинтегрируем по ? от — -5- до
\ м
и воспользуемся соотношениями вида
м/2 is+s4^L
j е,(8+^НГ(? + а)</Е = цГр^у|е J2F^4 + “)“
—M/2
которые можно вывести так же, как формулу (3.27) или же (что проще)
интегрированием по частям. В результате получается уравнение
V Tj(s)Aj =0,
)
где
1 [ i(s+s5)^-
Z^s) = s-| ’sjC [F (—Sj) + F (—Л1 + sJ]—
м
-'(s+sp —
— e [F(sj) + F( — M — Sj)J —
c2 _cS
— e 2 1 2 [F(s)-F(-M + s)] +
s2__.si
, i : (s ., s >M I
+ e 2 3 2 [F(—s) —F(—Л4—s)]J±
1 Г ij-s+sp^-
i — s + Sj |e (— sj) 4- F (— Al + s,)J
M
1 {S~S>1 T
-e [FtoJ + Ff-Af-Sj)]-
s?—s* ..
1 . м
1 —л-—-s +Sj) -5-
— e 2 3 2 [F (— s) — F(-M — s)J +
s2_c2
+ e 2 3 2 [F(s)-F(-A1 + s)]|’
Полагая s=Sn(h=0, ±1, ±2, ...) и обозначая
Thj-Tj(Sh),
получаем искомую бесконечную систему уравнений для коэффициентов /П:
£тмЛ = 0 (Л = 0, +1, ±2, ...).
j
Условие существования нетривиального решения этой системы имеет вид
Det||Tftj||=0.
4*
S1
Это и есть характеристическое уравнение, определяющее собственные ча-
стоты двухмерного открытого резонатора, точнее, параметр р, входящий
в формулу (4.01) и определяющий величины
Sj= y47t(/ + p).
6. Заменить точное характеристическое уравнение, полученное в преды-
дущей задаче, приближенным уравнением
7оо=О.
Исследовать это уравнение, считая параметр М большим; сравнить резуль-
таты с формулами i(3.33) и (4.08).
Решение. Пользуясь формулой (3.30), из выражения для Tj(s) легко
получить выражение для матричного элемента Тц. Оно имеет вид
У” = 2s7 J
+ e~is>M [F (- s}) - F (Sj) - 2F (-Л4- Sj)]} ±
± {ls> (si) — F ( si) — F M + sj) -|- F ( M — sj)] —
F' (sj) F' ( Sj) -|- F' ( M -|- s j) Ц- F' (— Л1 — Sj)}.
Если в уравнении Г«)=0 пренебречь членами Е(—-M±so) и, кроме того,
отбросить члены F'(—M±.So) (последнее, строго говоря, незаконно, но иначе
уравнением 7оо=0 пользоваться нельзя), .то получается уравнение
cis0M +е-1*>м = ± [G (So) + G (— s0)], (а)
где
— . , 2s0 ]F' (s„) is„F (s.)]
P(So)= p (So)_F(_So) *
Если в уравнения (4.08) подставить выражение (3.33) для коэффициента
отражения Ro,о, то оно примет вид
e-isoM = ± _±_ или = ± 0 (So). (&)
Если функция G удовлетворяет соотношению
G (so) G (—so) = 1
]так будет в случае, когда Ro,о вычисляется по формуле (2.18) или (2.20)],
то наряду с уравнением (&) будет удовлетворяться уравнение
e~is0M = ± G So)
и уравнение (а).
7. Результаты, полученные в § 2 и 3, относились к полубесконечному
волноводу с идеально отражающими пластинами (коэффициент отражения
от пластины 7?=4). Обобщить формулы (2.14) и (2.18) на случай, когда
коэффициент отражения от пластин
Я = е-'2*Р, р = if",
зависит от частоты, «о не вависит от угла падения. Обобщить интегральное
уравнение (3.15).
Решение. Для пластин, отражающих неидеально, соотношение (3.12)
принимает вид
W (х, —l) = ei(26t-^~2K^W(x, I).
Если ввести величину р посредством соотношения
2тгр = 2Ы — nq — 2лр,
52
то интегральное уравнение (3.15) и вытекающие из него формулы (2.14) и
(2.18) останутся без изменений, только параметр р Qyjiet определяться по-
другому н в случае вещественной частоты .может быть комплексным.
8. Пользуясь результатами предыдущей задачи, обобщить формулы
(4.01), (5.09) и (6.06) для собственных частот открытых резонаторов на
случай неидеально отражающих зеркал. Рассмотреть отдельно следующие
возможности: a) R не зависит ни от частоты, ни от 'угла падения; б) R за-
висит от частоты, но не зависит от угла падения; в) R зависит как от ча-
стоты, так и от угла падения.
Решение. Собственные частоты определяются для зеркал с коэффициен-
том отражения е“'2пр формулой
kl= к Р^’
где комплексный параметр р принимает те же значения, что и для соб-
ственных колебаний между идеально отражающими зеркалами. В случае
а) эта формула дает явное выражение для частоты каждого колебания;
в случае б) она является уравнением относительно k или M=ck\ в случае
в) надо учесть, что согласно формуле (3.50) каждое колебание представляет
собой лучок лучей, падающих на зеркало под углом
1/2^.
V ~ЬГ'
поэтому комплексный параметр р надо взять соответствующим этому углу
падения.
9. Исходя из выражения
Ф (х, у, z) = ~ е' 1 [ег° । I _ (_ 1)e е.т I г + /j у
—00
X F(WX, Wy)dwxdwy,
где
v — yf k2 — w2 — wy ,
получить для открытого резонатора, образованного бесконечно тонкими
идеально отражающими зеркалами (5.01), строгие функциональные уравне-
ния, аналогичные уравнениям (2.03), а из лих — интегральное уравнение
(6.22); из последнего уравнения вывести соотношение (5.06).
Решение. Обозначая
k
L (wx, «»„) = — [1 — (— 1)« еМ’«],
получаем для неизвестной функции F(wx, wy) уравнения
00
J J F(wx, ши) dwx dwy = 0 прн | х | > а или | у | > Ь,
—оо (а)
00
j J e'iw*y+wv^ nWxt р (Их1 Wj/f ciwx dwy = 0 при | х | < а и 11/| <6.
—00
При wx<^k и Wy <£.k функция L(wx, wv) принимает вид
51
где
Ы="(4+/')’ J
х (
и функциональные уравнения >(а) становятся эквивалентными интегральному;
уравнению (6.22) (см. задачу 1).
Функцию L можно также представить в виде
/ w2 I ч , w2 I,
i (2пр ~ ] I (sxp.— У
L(wx, wy) = 1— е ' * ' е ' *
Р = Ра + Рь-
Подставляя это выражение в уравнения (а), мы видим, что они имеют
решение
F(wx, wy)=Fa(wx)Fb(wy),
где функция Fa (ш) есть решение уравнений
00
eiwx Fа (w)dw = 0 при | х | > о,
—00 ,
00 . ( шЧ \
С Г 1 12кРа------------Г 1
I etwX 1 — е V / Fn (w) dw = 0 при | х | < а,
—00
соответствующих двухмерным колебаниям резонатора, рассмотренного в § 4.
а функция Fb(w) удовлетворяет таким же уравнениям, в которых а за-
менено на Ь. Функция
f (*• У) = J Jei(“’xx+a'vi') р (wx, Wy) dWx dWi/
—00
также представляется в виде произведения
f(X, y)=fa(X)fll(y), (f>>
где согласно § 4
т.тх
I а (х) = cos - - г---—j-: f-. при т= 1, 3......
2й(1 + ₽^г)
г.тх
fa(x) = sin-----------г 7 ПРИ т~ 2. 4, . .
2»(l + f^r)
fb(y) = cos----- I 4. К п₽и «= 1. 3.................
1ь (у) = Sin-—---при п = 2, 4, . . .,
а(1 + ’!яг)
причем ра, рь, Ма и Мь определяются формулами (5.10) н (5.11).
Соотношение (Ь) по существу является более точным, чем формулы,
следующие за ним, и соответствует соотношению (5.06) при г=—!; справед-
ливость соотношения (5.06) при любых z вытекает из уравнения (5.04).
54
10. Рассмотреть собственные электромагнитные колебания в полуоткры-
том резонаторе с тремя стенками:
0<х<а, —b<y<b, z—±l (параллельные зеркала);
х=0, —b<y<b, —1<г<1 (боковая стенка).
Решение. В таком резонаторе существуют колебания EMm4q с не-
четными m и колебания Ewmnq с четными ш, такие же, как в открытом
резонаторе с прямоугольными зеркалами (5.01). Поляризационное вырож-
дение, характерное для последнего, в полуоткрытом резонаторе снимается
(ср. задачу 2).
11. Вычислить собственные частоты электромагнитных колебаний в от-
крытом резонаторе, получаемом из зеркал (5.01) и дополнительных стенок
х—±а, —b<y<b, ~~Kz<l
при условии kx-^.kz. Этот резонатор представляет собой отрезок прямо-
угольного волновода с сечением 2а X 21 и длиной 26, открытый с концов
У=±Ь.
Решение. Собственные частоты определяются формулой (7.04), в ко-
торой
k
Кг— 21
Они соответствуют колебаниям Е^пч и Вследствие условия kx^.k2
коэффициент отражения от открытого конца такой же, как в двухмерной за-
даче (§ 4); если это условие не выполняется, то kv будет зависеть еще от па-
раметра
12. Формула (2.18)
Я = -ег₽,,+'>», эо=)/у®о.
выведенная в § 2 и позволяющая дать простой расчет открытых резонаторов
с плоскими зеркалами, пригодна для волн Н$ 11 Ед0 ПРИ > 1 и «о < 1-
Используя результаты, полученные в гл. I книги [8], показать, что для волн
Мю> Нго, Е1п и Его коэффициент отражения вблизи критической частоты
можно представить в виде
R = — е‘ se=jZ-ytia0, (а)
и вычислить постоянные Р' И р" для этих волн.
Решение. Вблизи критической частоты получаем
я А
Wql — —2~ So для волн Hto И Ею I « ’
/7" (
~2 So для волн Нго и Его I « I
Из формул (5.04), (5.05), (6.03) и (6.07) книги [8] легко находим выраже-
ния для постоянных Р"; они получаются равными:
для волны Hoi
55
ДЛЯ волны Нв2
для волны Eoi
для волны Ео2
Постоянные |У определяются из формулы (9.09) и рис. 14 и 15 книги [8J.
Так как для волн Н01 и Eoi фаза коэффициента отражения равна
0 = 0,217-4к1о/ при fess
а для волн НЛ2 и £ог
0 = О,162-4шо1 прий^-у-.
то
для волн Л701 и Eet
для волн Нвг и Евг
₽’ = 0,217-2]Лг =0,77,
₽' = 0,162-2/аг = 0,81.
Эти соотношения выведены из строгой теории диффракции иа открытом
конце волновода и поэтому применимы только к волноводу, образованному
бесконечно тонкими пластинами. Для пластин, толщина которых сравнима
с длиной волны или больше ее, или для волновода с фланцем будут другие
постоянные 10' и Р". Эти постоянные зависят от q и при увеличении q стре-
мятся к пределу р=0,824.
13. Используя результаты предыдущей задачи, вычислить собственные
частоты колебаний и в двухмерном резонаторе с плоскими зерка-
лами |х|<а, г — + 1 при q—1 и q =2. Найти собственные функции.
Решение. Собственные функции определяются формулами (4.18), в ко-
торых Р(1 +<) надо заменить на Р'-Н'Р'' и положить
для колебаний и
для колебаний //*^2 и
Собственные частоты определяются формулами (4.01) и (4.11), в которых
нужно произвести те же замены. Для того чтобы параметр sc был мал и
можно было пользоваться формулой (а) задачи 12, необходимо выполнение
условий
Af > 1 или а^>1.
Таким образом, открытый резонатор для этих колебаний имеет совер-
шенно иной вид, чем для колебаний с индексами q ^>1. Поляризационное
вырождение в нем отсутствует, так как волны разных поляризаций отра-
жаются от открытого конца по-разному.
14. Используя результаты двух предыдущих задач, исследовать колебания
^tnnq и ^mnq в открытом резонаторе, образованном плоскими зеркалами (5.01)
прямоугольной формы.
Решение. Мы ищем функцию распределения тока в виде
J(x, y)=fa(x)fb(y),
а собственную частоту в виде (5.09). Величины ра, рь и функции fa (х), [ь(у)
56
легко получаются из формул для двухмерного открытого резонатора с плос-
кими зеркалами (задача 13), если учесть, что при колебаниях E$nt/ (E$nq )
к открытым концам х = + а приходит волна Е^(Н^). а к открытым концам
У = ± Ь — волна (£<*>).
В результате получаем:
fa = COS kxX при
fa = Sin kxX Шри
fi,='CosktJy при
fb=sin kyy При
т = 1,3, ...,
т=2,4, ...,
п = 1,3, ...,
л=2,4, ...,
где
, kv —
причем параметры Ма и Мь определяются формулами (5.11), а постоянные
р"а и Р"ь берутся из задачи 12 в зависимости от поляризации волны, при-
ходящей к концам х=±а и у='±Ь соответственно, т. е. в зависимости от
того, определяет функция f составляющую jx или jy плотности тока. Соб-
ственные частоты вычисляются <по формуле (7.04).
Эти формулы справедливы при больших значениях Ма и Мь, т. е. при
а b
больших отношениях и
15. Исследовать симметричные колебания E$q и H$q в открытом резо-
наторе, образованном круглыми зеркалами (6.01) при q — 1 и q = 2. Под сим-
метричным колебанием ',E$q (H^q) понимается такое колебание, у которого
магнитное (электрическое) поле имеет единственную составляющую (£,.),
не зависящую от азимута у (ср. рис. 11, ж, з). Использовать результаты за-
дачи 12.
Решение. Поскольку составляющие Ни Е^ удовлетворяют уравнению
fe2 — Ф = 0,
, 1
дгг + г дг
для плотности тока можно написать выражение
f = Jt (wor),
причем для* колебаний E^q имеем /Г = Л = 0,
ны полагать / = f, jr — 0. [Рассуждая, как в §
задачи 12, получаем
а для колебаний долж-
6, и пользуясь формулой (а)
w„ ——7—
а ( 1 -)
значения ф' и р" надо брать из решения задачи 12. Собственные частоты
определяются по формуле (6.06), где
Параметр М
(при q = 1) и М =
(при
q = 2) должен быть
большим, иначе нельзя пользоваться формулой (а) задачи 12.
57
16. В дополнение к формулам (3.55)—(3.65) исследовать возможность
использования составляющих П® и П"‘ в качестве потенциалов электромагнит-
ного поля. Написать .выражения, связывающие поля с .потенциалами, и пра-
ничные условия для последних.
Решение. Полагая
П* = Ф, П«==П*=0,
Л л У
получаем выра^^я для полей:
_ <ДФ с)ф
Ех ~ дхдг' Нх~ tk ду ’
()2ф оФ
~ ду dz' Hv ~ lk дх ’
д2Ф . *
£г = -^- + ^Ф, /7г = 0.
Эти поля удовлетворяют уравнениям Максвелла, если Ф есть решение волно-
дф
вого уравнения (5.02), и граничным условиям (3.61), если ~т— = 0 на зерка-
лах. Полагая П'"=Ф, п” =п- = о
и пользуясь формулами (3.63), получаем: Ex~lk ду н Пх~ дхдг'
Г -идф Е'~ 1к дх н д2ф пу~ дудг'
Ег = 0. д2Ф , Иг - дг2 +*2ф’
причем теперь на зеркалах должно быть Ф = 0.
17. Используя потенциалы, введенные в предыдущей задаче, рассмотреть
симметричные колебания Е^ и Hfyq между круглыми зеркалами (6.01) при
<7=1 и q = 2. Показать, что оии совпадают с колебаниями, исследованными
в задаче 15.
Решение. Для колебаний Eq^q функция П® = Ф не зависит от у, и от-
личные от цуля составляющие поля равны
<12Ф <?2ф , <)Ф
Ег=д^- Ех==~д^+кгф- Hf = lk~dT-
Такие же составляющие имеются у колебаний Поле колебаний Н^ (при
П™ = ф) имеет составляющие
<7ф й2Ф д2Ф
Е = — ik -з— , Hr = л—• Иг = + Ь?Ф,
V dr r dr dz dz2 '
такие же, что и поле колебаний Hq^ .
18. Используя потенциалы, введенные в задачах 16 и 17, исследовать ко-
лебания E%q и H%q между круглыми зеркалами (6.01) при <7^>1. Сравнить
эти колебания с колебаниями E^q и E^q, рассмотренными в § 6.
58
Ре шение. Для колебаний Е^п(/ полагаем
П® = П«(г, z) cos zny (m—Q. I, 2, . ..).
П® = П'(г, z)sinm<f {m—l, 2, ...)
и
r.qz
Пе = (wor) sin (q нечетное),
~qz
Пе = Jm (^„г) cos (q четное).
Для колебаний H$ng полагаем
П"! = П"‘ (г, z) sin ту {tn = 1, 2, . . .),
П” = Пт(г, z) cos my (m = 0, 1, 2, . . .),
причем
Jliyz
It" = Jm (Mof) cos -gj- {q нечетное),
r.qz
Пп> = Jm {w<>r) sin (q четное).
Колебаниям E^g соответствует (с точностью до постоянного множителя)
плотность тока
/г = — J'm (wor) COS ту,
m
(w°r>> sin/”?-
а колебаниям JJ^ng — плотность тока
. m
,r==w^rJm (wor)cos my.
jy = — J’m {wQr) sin my.
Мы рассматриваем первый вариант азимутальной зависимости (П® —
= П" cos ту. П™ = П™ sin ту); второй рассматривается аналогично. Пользуясь
тождествами
Jт — 1 (-Л-') = J*т (Л.') ~ Jт (л),
т
Jт+1 (л) = J т (Л") Jт (л)
и образуя сумму колебаний Е(^пд + получаем плотность тока
/г = Jm+1 (W) COS ту.
i4, = Jm+i{w<1r)sin ту,
а образуя разность получим
ir = — Jm-i (O’of)cos ту.
/<p = /nl-i(w(,r)sin ту.
59
Так как при <?^>1 коэффициент отражения по току не зависит от его
направления, то для суммарного колебания получаем <
w„ =
____Ут +1 ,п
—7 „ 1 +
а ₽ м )
а для разностного
w0 =
_____- l,n
c(1 + ₽ м J
Из этих формул следует, что суммарное колебание есть суперпозиция ко- 1
лебаний и а разностное —колебаний Е^_1>п9 и Д^,]
Действительно, для суммарного колебания декартовы составляющие плотности
тока определяются формулами
jx = Jm+1 (War) cos (m + 1) ?,
jy = (war) Sin (7П + 1) ?,
а для разностного колебания
jx = — Лп-i (w«r)cos (и— l)y.
jy = -1 ( W) sin (m — 1) </.
Эти результаты справедливы прн т = 1, 2, ... При т = 0 колебания Д^.
и Н1^ являются суперпозицией колебаний Д^ и Д|^? (см. задачу 17, § 6
и рис. 11). При q ~ 1 приходится учитывать влияние поляризации на коэффи-
циент отражения, что ведет к серьезным осложнениям.
19. Исходя из разложения функции f(£) по косинусам или синусам,
использованного в задаче 5, .выразить постоянные Л, (/ f 0) через Ло с по-
мощью коэффициентов /?о,ц фигурирующих в формулах (2.13) и (2.14).
Показать, что характеристические уравнения (4.08) остаются в силе и при
учете волн других номеров (/ ./-0) в выражении для f(g). Показать, что
при |s0| << 1 собственные функции могут быть представлены в виде
или
f (Е) = cos s0E + Safe (Е) (т—1, 3, ...) (а) I
f (Е) = sin s0E + Sofs (Е) (m = 2, 4, . ..), (6)4
где fc(g)—четная, a fs(g)—нечетная функции Оценить влияние распро-
страняющихся (/=1, 2,...) и затухающих (/=—1, —2,...) волн на функ-
цию f(g)
Решение. Представляя f(g) в виде
f (Е) = у Л + 4 <е'*Л +e-/Sj?)
Mo
или
f (6) А° )
МО
и рассуждая так же, как при анализе формул (4.07), получаем соотношение
i Uo+Sj) у-
Л3- = + Л0Л0,3е
которое при / = 0 эквивалентно характеристическим уравнениям (4.08), а при
/ = + 1, +2, .. . позволяет оценить влияние волн других номеров на функцию
«0
f (g). Из этого соотношения видно, что вклад затухающих волн (/ =— Г
— 2, ...) в середине резонатора мал (пропорционален ехр{—п(—j—р)Л4})'
М
и лишь на краях, при 5 == + сравним с вкладом распространяющихся волн...
При | se | <5 1 согласно формуле (В. 18) книги [8] имеем
U (so, р) = — i + In (у<2 so), «о = У4пр ,
откуда по формуле (2.14) получаем
— sor j.
где
1 f Зп
P1V exPf (SJ-
s j = У 4п/.
Отсюда получаем выражения (а) и (6), причем
fс (£) — tз cos Sj?, fs (B) — tJ sin Sj£, Л» 1,
MO MO
где
, M
tsi 2 при m = 1, 3, ....
= г”Ч-3е
. M
lsi T
tj = — imrje при m — 2, 4, .. .
Значения t, малы по абсолютной величине (хотя для распространяющихся
волн эти абсолютные величины не связаны с каким-либо большим или ма-
лым параметром задачи), поэтому функции /с(£) и fs(£) получаются не-
большими и после умножения на s0 вносят малую осциллирующую поправ-
ку к собственным функциям (ср. конец § 4).
Приведенные выше формулы не дают, разумеется, точного решения на-
шей задачи и являются лишь вторым приближением для собственных функ-
ций [если выражения (4.03) считать первым приближением]. В следующих,
приближениях наряду с трансформациями 0—>0 (отражением) и.
0 >/ надо учесть другие трансформации, например, /—>0, j—>/г,
0__„/__и т. д. Характеристическое уравнение в первом и втором прибли-
жениях получилось одним и тем же: это объясняется тем, что обычно по-
методу возмущений для вычисления собственных значений во втором при-
ближении требуется знание собственных функций лишь в первом прибли-
жении.
20. Пользуясь формулами (3.06)—(3.13), исследовать диффракционное
поле плоской волны
фо —
в верхнем полупространстве z>0 при условии, что вблизи плоскости z=0
расположен непрозрачный полубесконечный экран, который не пропускает
в верхнее полупространство ту часть падающей волны Ф°, которая соответ-
ствует значениям х<0 (этот экран может быть полуплоскостью г—0, х<0-
или иметь другой вид). Подставляя полученное решение в исходное урав-
нение (3.05), выяснить пределы его применимости. Произвести сравнение
с формулой (3.52) и с тем, что сказано после нее. Показать необходимость
условия 1^>а при выводе интегрального уравнения ,(4.19).
61
Решение. Представляя волновое поле при г>0 в виде
Ф=М(х, z)eiftI,
пользуясь формулой
00
W(x, z)= f G (x — x', z) w (x’, 0) dx’,
—CO
аналогичной формуле (3.13), и ставя начальные условия
W(x, 0)=0 при *<0,
1й(х, 0) ='1 при п>0,
получаем
U7 = F(t),
где F (т) есть интеграл Френеля (3.24).
Полученное решение точно удовлетворяет уравнению (3.06) и должно
приближенно удовлетворять уравнению (3.05). Мы имеем
<Ж tF'(t)
dz 2z
и
d2W_ t2F" (т) + ЗтГ (т)
dz2 4z2
f d2W
Слагаемое в уравнении (3.05) мало, если
d2Xff dW
dz2 2k dz’
Таким образом мы приходим к двум условиям:
X
kz > 1 и — < 1.
Первое условие показывает, что параболическое уравнение применимо
лишь на больших (по сравнению с длиной волны) расстояниях от апертуры
z—0 [или от отражающего зеркала; ср. второе условие (3.52)]. Второе усло-
вие требует малости угла диффракции. В задаче о двухмерном открытом
резонаторе параболическое уравнение и вытекающее из него интегральное
а
уравнение (4.19) справедливы лишь при условии 1, гарантирующем
малость углов диффракции при волновом взаимодействии зеркал. При ho-
строении приближенного решения этой задачи [формулы (4.03), (4.09) и
следующие] условие применимости другое — оно сводится к малости s0 и р,
причем условия ео 1 и ka 1>1 подразумеваются
Глава II
Допуски для открытых резонаторов
с плоскими зеркалами
§ 8. Интегральные уравнения
для произвольных зеркал
В гл. I были исследованы колебания в открытых резонато-
рах с параллельными плоскими зеркалами, одинаковыми и рас-
положенными точно друг против друга. Естественно возникает
вопрос: при каких отклонениях реальных резонаторов от
идеальных собственные колебания в них
будут мало отличаться от колебаний
в идеальных резонаторах, рассмотрен-
ных выше? Иначе говоря, каковы допус-
ки для открытых резонаторов с парал-
лельными плоскими зеркалами?
Поскольку нас интересуют лишь оцен-
ки допусков, ограничимся двухмерной
задачей, относящейся к допускам для
двухмерного открытого резонатора, рас-
смотренного в § 4. Здесь возможны сле-
дующие отклонения от идеальной формы:
I)1 перекос (наклон) зеркал;
2) параллельный сдвиг или неодина-
ковость зеркал, в силу чего края зеркал
не приходятся друг против друга;
3) прогиб зеркал (вогнутость или вы-
пуклость) .
В некоторых случаях надо учитывать.
РИС. 16. Двухмерный
открытый резонатор.
что зеркала не являются идеально отра-
жающими; однако это делается очень просто (см. задачи 7 и 8
к гл. I), поэтому ниже мы будем пользоваться простейшим
граничным условием Ф=0 на зеркалах.
67
Рассмотрим открытый резонатор, образованный двумя зер-
калами (рис. 16):
z = —/ + Л1(л), — «1<л<61,
z — l — h2(x), ~а2<х<Ь2, (8.01)
для чего введем безразмерные переменные
СНг (8.02)
и будем искать решение двухмерного волнового уравнения (3.03)
в виде
Ф = W, (S, С) eihz — (— iy>W2 (S, — С) е -ikz. (8.03)
Для функций W2 и W2 получается уравнение (3.51) или после
. пренебрежения членом, пропорциональным параболическое урав-
нение
lF + 2t'w=0> (8-04)
имеющее функцию Грина
r(E_S'. -I екр<[Л=^_^. (8.05)
которая удовлетворяет соотношениям (ср. § 3)
lim r(S —S', £ —C')=8(S —6'),
С-»С'+О
J T(S — S', С —C)dS'=l.
—оо
Введем обозначения
^1(i) = kh1(x), f/b2^)=khl(x),
тогда на зеркалах (8.01) безразмерная координата
значения
Г_____1 I Ф1& г— 1 <МЕ)
4 ~ 2 Г 2kl ’ 4 2 2Ы
(8.06)
(8.07)
С принимает
(8.08)
Если выполняются условия
А, < /, h2 < /, (8.09)
то значения Wx и W2 на зеркалах можно отождествить с их зна-
чениями при С = -<- 2.. Тогда справедливы соотношения
Р1
Г, (е, С) = { г Л - S', С+4) - 4) dV'
Л v J k J (8.10)
WZ2(S, jr^S-S', -C + 4)^ ^,4)^>
64
а граничные условия Ф = 0 на зеркалах принимают вид
r2 (е* ~ т) е‘** <ч=e<z w* (£’ т)е”^1 (Ъ
при — а1<8<Р„ (8.11)
Г2 (l, — у)ег<е*(t)=e,x W\ (е, у)e“^*U)
при — я2<Е<₽2,
где
ав=|Л^, (s = l, 2) (8.12)
и
7 = 2kl — itq. (8.13)
Для функций
fl(E)s=IFB ^Е, -|) е/<мЬ и f2(B)=1F2 0, -1) ег<М5’ (8.14)
получаем систему интегральных уравнений
₽.
fBO)=e,x J /СВ.(Е, E')f2(E')dE',
(8.15)
f WUCW
V
—«!
с ядрами
Кгг (Е, Е') = Г (Е —- Е', 1) е~‘ и*u,+^(V)],
Л21(Е, Е') = Г(Е — Е', 1)е-'^«>+л^'М. <8Л6>
Эта система выводится из соотношений (8.10) и (8.11), величина
% (точнее, е‘х) является собственным значением, определяющим
комплексные собственные частоты открытого резонатора по фор-
муле
2Н=л^+х- (8.17)
Ввиду того, что нужно дать лишь оценку допусков, мы будем
рассматривать каждое отклонение от идеальной формы в от-
дельности.
§ 9. Перекос зеркал
Если плоские одинаковые зеркала не параллельны, а обра-
зуют угол 2v, то без ограничения общности всегда можно подо-
брать систему координат х, z так, чтобы было (рис. 17)
at = аг = 6, -- Ь2 = а,
К (х) — Л2 (х) = х tg v
(9.01)
5—2547
65
и
РИС. 17. Перекос пло-
ских зеркал.
^(5) = ^. (?) = «?, (9-02)
где
a = /2^tgv = ^-v (9.03)
и
(9.04)
причем
2ka tg v = k [й, (а) — &i(—tz)]. (9.05)
В силу симметрии резонатора относитель-
но плоскости z = 0 мы имеем
К1г£, И=К21& V)=K(5, *'). (9.06)
где
к(!- Е')=йя‘р‘ т].
(9.07)
Вследствие этой симметрии функции Wt и №2 совпадают (ср.
гл. I) и система интегральных уравнений (8.15) сводится к одно-
му интегральному уравнению
М/2
f(E)=e,x j (9.08)
-Л1/2
для функции
f©=A(D=f2(6). (9.09)
Исследуем это интегральное уравнение. Напишем сначала
такое же интегральное уравнение, но в бесконечных пределах
f (Е)=eiX J К (5, V) f (?) dtr. (9.10)
—00
Образуя первую и вторую производные функции f(g) и интегри-
руя по частям, из уравнения (9.10) получаем такое же уравне-
ние для функции
f А? \
(9.Н)
Поэтому функции g(g) и f(g) могут отличаться только постоян-
ным множителем. Обозначая этот множитель через —s2,, т. е.
полагая
£(c) = _SJ(E),
(9.12)
66
для функции f (g) получаем дифференциальное уравнение
-g-+(^-4a$)f = 0, (9.13)
которое с помощью подстановки
(9-14)
где
s2
т=(4а)1'3, г,=^. (9.15)
приводится к дифференциальному уравнению Эйри
M=ta(0, (9.16)
подробно иследованному Фоком [17] (см. также [19], стр. 379
и следующие). Частное решение этого уравнения, убывающее
при t—±oo, можно представить в виде интеграла
П(О=^ + (9.17)
Подставляя функцию
Г(0=о(?(Н1)) (9-18)
в интегральное уравнение (9.10), после довольно громоздких
выкладок видим, что оно удовлетворяется, причем
г ИИ
ez‘z = e к2 6< (9.19)
При а=0 уравнение (9.10) превращается в уравнение (3.15)
с пределами —оо и оо; в этом случае
Х = 2яр, 55 = К4«(/4-/7) (/=0, =tl, ±2,...). (9.20)
При <хУ=0 мы полагаем
Х = -4+2^’ = (/ + />) (/ = 0, ±1,±2,...) (9.21)
и считаем по-прежнему р небольшим числом [скажем, IPKyl.
При а = 0 уравнение (9.13) принимает вид
g + = (9.22)
Оно допускает решения (3.20), имеющие характер бегущих
волн, а также решения
f=cossjg и /=sinSj|, (9.23)
67
5*
имеющие характер стоячих волн; Функция (9.18) имеет харак-
тер 'стоячей волны, поскольку при больших отрицательных t для
функции v(t) можно написать асимптотическое выражение
[4(-/)3/2+т]- <9-24>
Эта функция может быть разложена на сумму двух бегущих
волн, если воспользоваться формулой
Ч0=-(1>й“1,(‘>. (9.25)
где и а>2(0 суть решения уравнения (9.16), имеющие при
-—оо асимптотические выражения
1 <9-26>
щ2(/) = —1—е 1 J
'' (—<)1/4
и соответствующие бегущим волнам: функция u>i(y(|—£j)) дает
волну, бегущую в отрицательном направлении оси |, функция
®2(у(|—&))—в положительном. Обе эти функции экспонен-
циально возрастают при /—со и удовлетворяют интегральному
уравнению (9.10), если в последнем верхний предел взять слег-
ка комплексным — таким, чтобы интеграл стал сходящимся.
Эти функции определяют волны между двумя плоскими зер-
калами, образующими малый угол 2v, т. е. волны ;в секториаль-
ном рупоре с малым углом раствора 2v. Значения харак-
теризуют положение каустики для волны с индексом j на каж-
дом из зеркал [поскольку функция ц(у(£—£,)) определяет поле
и ток на зеркале]: при £<£,• эта волна является распространяю-
щейся при — затухающей. Как легко понять, в плоскости
х, z каустики являются окружностями, центр которых лежит
в точке, где геометрические продолжения зеркал пересекаются,
а радиус определяется значениями на зеркалах или на их
геометрических продолжениях.
Перейдем теперь к более сложному интегральному уравне-
нию
f(E)=eZ3t[K(E,V)f(^)dV, (9.27)
V
£
которое при |=—М/2 определяет диффракцию волн у левого
края х =—а данного резонатора (рис. 17).
По аналогии с формулой (3.22) будем искать решение инте-
грального уравнения (9.27) в виде
f (5) = A- [w, (у (« - ?.)) + У к; . ®2 (у (В - В,-))]. (9.28)
J
68
Подставляя это выражение в интегральное уравнение, получаем
соотношение
(Y (В - Во)) + S j (Y(5-Ej)) =
i
=e‘z[jK(e, £') (?'-£.)) d£' +
Г
/ г
при £<£<оо. (9.29)
Так как каждое слагаемое в выражении (9.28) есть решение
интегрального уравнения (9.10), то это соотношение можно пере-
писать в более простом, виде:
Г Г
J Я(иэ^(т(5'-ео))^'+£яо- jK(M')«UY(e'-^))^'==o
-оо / —оо
при £<£<оо. (9.30)
Мы получили функциональное уравнение, из которого можно
вычислить коэффициент отражения Д~о,о и коэффициенты
трансформации R^j (/=±1, ±2, ...). Если мыв соотношении
(9.30) пренебрежем всеми коэффициентами трансформации и
положим g=£, то получающаяся при этом формула
Т
J К(£. 5) «Мт (£ —£0))d£
/?;о=-ф--------------------- (931)
J К(£, £)«Мг (£ — £0)ИЕ
—00
аналогична формуле (3.25).
Более точное решение можно дать, преобразуя соотношение
(9.30) в бесконечную систему линейных уравнений для неизвест-
ных величин Raj. .Для этого умножим соотношение (9.30) на
^i'(y(€—&,))> где й=0, ±1, ±2, ..., и проинтегрируем по g от
£ ДО оо; получим систему
<«’+ S < № = 0 (й = 0, =t 1, ± 2,...), (9.32)
hO ‘ о, J hj , 1 \ z
1
в которой
<Т= J Wx(Y(£-M)^ J KG, ^)wg(T(£'-£3))d£' (s= 1, 2). (9.33)
Г —оо
69
Пользуясь интегральным представлением для функций w, и w2:
I гг(т + Ч
®,(f) = ^= ev ’ dx (s=l, 2), (9.34)
У ” J
г«
где Гх и Г2 —контуры интегрирования, изображенные на рис. 18,
изменяя порядок интегрирования и вводя новые переменные t и t'
получаем
по формулам
(9.35)
Здесь интеграл
(9.36)
(t + t'Y
2
a(t — Г) + Т^ — xt')^dtdt' (9.37)
выражается через интегралы Френеля (3.24): если ввести обозначе-
ние
то
G(f)=e 2 F(t),
(9.38)
. Зте
/7 =]/2я е 4
G(a — ух) — G (— а + чу)
2а — у(х + у)
(9.39)
До сих пор, переходя от уравнения (9.27) к системе (9.32),
мы не прибегали к каким-либо аппроксимациям. Для того что-
бы упростить вычисление интегралов (9.36), 'будем считать вели-
чины а и у, определяемые формулами (9.03) и (9.15), малыми
и заменим функции G(t) их первыми членами разложения:
311
G(0 = 4-(l-j/^-e 4/-4<j- (9.40)
Тогда получим
. it
(9.41)
70
4Т=(y (е - М) *My£ - ej) -
—Уе 4 Yk'i (Y(B—Sa)>«(y(I — *j)) — (Т(Ё — M) №'s(y(B—Ej))],
(9.42)
причем множитель, общий для всех величин мы опустили.
Решая систему уравнений (9.32) в первом приближении, по-
лучим! выражения
ЯП)
^о = -7^ (9.43)
Joo
и
*« = --(/=±1. ±2.-). (9.44)
аналогичные выражениям (3.33) и (3.39). В силу соотношения
w'i (/) w2(f)—Wi(t) w'2(t) ~—2i
формула (9.43) приводит к выражению
_ W1(O W +‘ХГ
R°-°- w2(/p е
где
<=------
Wi (t0 )w2 (f0 )
*о"=Т(5-Л),
причем выражение (9.46) справедливо лишь при]$71 1- Зна-
чение параметра р получается равным
p = i^- = 0,886; (9.49)
в соответствии с формулой (2.18) лучше брать точное значение
Р=0,824. (9.50)
Формула (9.31) при сделанных выше предположениях также
приводит к выражению (9.46), но значение р получается еще
более далеким от истинного, а именно (ср. формулу (3.26)]:
₽=-^= 1,13. (9.51)
у я
(9.45)
(9.46)
(9.47)
(9.48)
71
Аналогичным образом решается интегральное уравнение
1
f(e)=e'z:JWf(?H'. (9.52)
—оо
Решение имеет вид
f (6) = А+ |^(Y(6 ~ U)+£ ^iwr (Y(? - ^))1, (9.53)
i
причем для коэффициента отражения от открытого конца 6 = 6 по-
лучается выражение
+ w2(t+) i₽(l+i)sj
^0.0---- ..х, е
аналогичное (9.46); в этом выражении
+_____________________________у_____
S° а>, (/+) о>г (z+)
** = Y(T—te).
(9.54)
(9.55)
(9.56)
Теперь мы можем построить приближенное решение исход-
ного интегрального уравнения (9.08). Пренебрегая трансформа-
цией волны с индексом 0 в волны с другими индексами, ищем
собственную функцию в виде
КВ)=А1^(Т(|-Ы)+Л2и>2(т(1а-Ы) (9-57)
и связываем А, и Аг с коэффициентами отражения (9.46) и
(9.54) от каждого открытого конца, полагая
'o’=-y(4 + 9 и ~ (9-58)
Эта связь имеет вид
A2 = Ai/?o>o> ^1==^г^о,о> (9.59)
так что характеристическое уравнение, определяющее комплекс-
ные собственные частоты резонатора с перекошенными плоски-
ми зеркалами, имеет вид
<0^0=1. (9-60)
Выясним, при каких условиях оно переходит в характери-
стическое уравнение для параллельных зеркал, рассмотренное
в гл. I. Если выполняются условия
YW, 5О>4’ <9-61>
16у у£0
то из формул (9.26) получаем выражение
) = y^expi [4(Y*/'2-4^^ + t] <9'62)
72
и аналогичные выражения для w2(f^), Wj(t0) и &г(*о)- При этом
согласно формуле (9.15) имеем
*о==«о = / 4a$e = s0 (9.63)
и характеристическое откуда уравнение принимает вид (9.64)
s0 = / 1 п \ Al + ₽ + i₽ 11 2> (9.65)
что согласуется с формулой (4.10).
Пусть имеется колебание, которое при параллельных зерка-
лах характеризуется параметром «о- Для того чтобы это колеба-
ние было слабо возмущено наклоном зеркал, необходимо, чтобы
величина
б —2&ntgv=aM (9.66)
удовлетворяла условиям
S<±s02, (9.67)
вытекающим из условий (9.61). Обычно М > 1, поэтому все три
условия (9.67) накладывают почти одинаковые требования на
малость величины 6; при т= 1 наиболее существенно второе
условие (9.67), а при т—2, 3, ... — третье условие (9.67). Чем
больше индекс колебания т, тем больше и тем легче выпол-
няются условия (9.67). Таким образом, перекос сильнее всего
действует на колебание с индексом m= 1, имеющее наименьшие
диффракиионные потери. Физический смысл этого результата
очевиден: такое колебание представляется в виде системы лу-
чей, составляющих (по сравнению с другими колебаниями) наи-
меньшие углы с осью г и поэтому наиболее чувствительных к пе-
рекосу зеркал. Чем больше т, тем больше «перекос» лучей и
тем менее они чувствительны к перекосу зеркал. С другой сто-
роны, при увеличении М перекос лучей уменьшается, и поэтому
требования к параллельности зеркал становятся все более
жесткими.
Вместо трех условий (9.67) можно написать одно условие
где N — число Френеля, определяемое
(4.06), или условие
формулами
. .ml
(9.68)
(4.05) и
(9.69)
для угла перекоса. Все эти условия показывают, что в оптиче-
ском диапазоне очень трудно осуществить открытый резонатор
73
с параллельными плоскими зеркалами, к которому теория, раз-
витая в гл. I, была бы применима.
Данные выше оценки допусков согласуются с численными ре-
зультатами, полученными в работе Фокса и Ли [18]; в этой ра-
боте для трех значений величины (9.66), а именно для £—-^-=0,349;
3 = 1^- =0,174 и 5 = -^ = 0,0873, численно решалось интегральное
уравнение, эквивалентное уравнению (9.08), при 0,5<Af<20 и
т = 1 и 2*.
Заметим, что из второго условия (9.61) следует, что для лу-
чей, образующих собственное колебание, которое мало отли-
чается от собственного колебания в резонаторе с параллельны-
ми зеркалами, каустика должна быть мнимой, т. е. лежать
далеко от резонатора, на геометрическом продолжении зеркал.
В этом случае волна отражается от края, не дойдя до каустики,
причем согласно формулам (9.26) поле будет более интенсив-
ным в той части резонатора, где расстояние между зеркалами
меньше. Если же зеркала наклонены более сильно, то каустика
может образоваться внутри резонатора, причем поле за каусти-
кой (на рис. 17 правее каустики, там, где расстояние между
зеркалами такое, что волноводная волна распространяться не
может) будет значительно слабее, чем перед каустикой. Таким
образом, симметрия колебаний, характерная для параллельных
зеркал, при их перекосе может нарушаться по-разному: при вы-
полнении условий (9.67) — (9.69) поле будет более интенсивным
в узкой части резонатора, а при большем перекосе поле будет
гораздо более интенсивным в широкой части резонатора. При
сильных перекосах используется лишь часть площади зеркал и
* В литературе часто утверждают, что потери на излучение вследствие
перекоса зеркал можно учесть, если к величине Л, которой определяются по
формуле (4.20) _диффракциониые потери при параллельных зеркалах, приба-
вить величину Л=7зб2- Если потребовать, чтобы потери на перекос были
меньше диффракционных потерь ,(Л<Л), то мы приходим к условию
бпгВтдг
82 < ~лг~ пр" Л1 >1 (« )
которому удовлетворить легче, чем условию (9.68).
По существу, единственным серьезным обоснованием приведенного выше
простого выражения для Л и условия (а) является то обстоятельство, что
численные расчеты, проведенные в работе [18], привели (в ограниченном ин-
тервале изменения Af) к значениям Л того же порядка. Даже если бы усло-
вие (а) было правильным при сколь угодно больших Л1, оно относилось
только к потерям на излучение, а другие характеристики резонатора (часто-
та^распределение поля) не зависели от перекоса зеркал только при условии
В оптических квантовых генераторах всегда имеются диэлектрические
тела, благодаря которым требования к параллельности зеркал смягчаются
(см. ниже § 62).
74
отражение от края ослабевает. В результате радиационное за-
тухание всех колебаний увеличивается, поэтому при достаточно
сильных перекосах резонансные свойства могут вообще исчез-
нуть.
§10. Параллельный
сдвиг зеркал
Пусть параллельные зеркала различной ширины сдвинуты
относительно друг друга. Мы будем считать, что (см. рис. 19)
&i = a2=a, а и Ь^а,
причем условия
—а<х<а, z=±l,
определяют рабочую часть обоих зеркал, а отрезки
—а}<х<—а, z=—I,
а<х<_Ьч., z~l,
выходящие за пределы рабочей час-
ти, существенны лишь в том отно-
шении, что они влияют на коэффи-
циент отражения волноводной вол-
ны от открытых концов х=±а.
Также представляет интерес слу-
чай, когда, например, верхнее зер-
кало уже нижнего. Тогда нерабо-
чие отрезки будут лишь у 1нижнего
зеркала; этот случай исследуется
тем же способом (см. конец пара-
графа).
Чтобы разобраться, как отрезки
(10.03) влияют на отражение, ис-
следуем систему интегральных урав-
нений
(10.03)
г л
-а а Ьг
~а, -а а
РИС. 19. Параллельный
сдвиг плоских зеркал.
Д“'-4) F >М?-
где применительно к рис. 19 полагаем
(10.01)
(10.02)
(10.04)
(10.05)
7S
Прежде чем решать систему (10.04), рассмотрим предельные
случаи. При Е=0 имеем
Ш=ШЧ(Ю _ (10.06)
и система (10.04) сводится к уравнению (3.15). При £=оо не-
трудно исключить функцию fi(|), тогда получаем для функции
fs(£) интегральное уравнение
А (5) =*- е f2 (V)dl', (10.07)
(Г
которое легко преобразовать в уравнение вида (3.15) или же ре-
шать заново тем же способом, каким мы решали уравнение
(3.15). Отсюда получаем
Г^ = л( ) (S>0), (10.08)
где числа s, получаются в результате решения уравнения (10.07)
с пределами —оо и оо в виде
Sj=\T2^j + 2p) (j=Q, ±=1, +2, ...), (10.09)
а коэффициенты ROij удовлетворяют соотношению
----е^(-^-)=0 (10.10)
при ?>0
или_ системе линейных уравнений (3.32), в которых Sj заменены на
Y 2sj, вычисленные по формуле (10.09). Подставляя выражение
(10.08) в первое уравнение (10.04), получаем
fi (?)=А [е-г^ F(? + se) +£(- WRB,^ F(l- s,)]. (10.11)
/
Таким образом, если при 5 = 0 коэффициент отражения равен
Ro,o= — ew+i)s° ({J=0,824), (10.12)
то при 5 = 00 имеем
/?e.0 = -ez₽(1+°r^ , (10.13)
где малый параметр р связан с частотой соотношением
^=*(4 + ^)’ (Ю.14)
а
(10.15)
76
Результат (10.13) совершенно очевиден с физической точки зре-
ния: ^плоскопараллельный волновод с полубесконечной верхней
и бесконечной нижней пластинами эквивалентен обычному вол-
новоду удвоенной ширины (2/ надо заменить на 4/). Поэтому
в выражении (10.12) для коэффициента отражения нужно р за-
менить на 2р: таким путем всего проще получить формулу
(10.13).
Для того чтобы проследить, как при увеличении Е формула
(10.12) переходит в формулу (10.13), надо возвратиться к систе-
ме (10.04). Ища функцию f2(|) в виде (10.08), мы из первого
уравнения (10.04) опять получаем функцию /)(£) в виде (10.11);
подставляя это выражение во второе уравнение (10.04), получим
функциональное уравнение, определяющее неизвестные коэффи-
циенты
(10.16)
Из этого уравнения, как впрочем и из исходных уравнений
(10.04), видно, что при g < 1 сдвигом зеркал можно пренебречь
а при £ > 1 выступающее зеркало можно считать бесконечным и
пользоваться формулой (10.13). Из формулы (10.13) следует, что
при условиях
|ЛА(6г-п)>1 (10.17)
резонатор, изображенный на рис. 19, рассчитывается по форму-
лам § 4, в которых р надо заменить на р |/2. Если нерабочие
участки имеются лишь у нижнего зеркала, то при достаточной
их ширине [при условиях, аналогичных условиям (10.17)] мы
можем считать нижнее зеркало бесконечным (как на рис. 15,6)
и рассматривать верхнее зеркало вместе с его зеркальным изоб-
ражением, находящимся на расстоянии 4/ от него, как открытый
резонатор с одинаковыми зеркалами: это_опять сводится к при-
менению формул § 4 с заменой р на р]/2.
§ 11. Прогиб зеркал
Рассмотрим теперь влияние прогиба зеркал. Пусть одинако-
вые зеркала, расположенные друг против друга, будут не пло-
скими, а вогнутыми с радиусом кривизны г0. В гл. III будет по-
77
казано, что для такого открытого резонатора величина %, фигу-
рирующая в формулах (8.13) и (8.17), определяется выраже-
нием !
%=(2т—1)а+2лр (т=1, 2, ...), 611.01)
где первое слагаемое правой части, в котором
a = arcsin yZ—• (11.02)
» /*0
учитывает влияние кривизны зеркал на собственную частоту
колебаний, а второе слагаемое учитывает диффракцию на
краях. Точное вычисление второго слагаемого при произволь-
ных значениях а весьма затруднительно, однако при малых про-
гибах, т. е. при условии
(11.03)
F / О
величину р можно брать такой же, как для плоскопараллельных
зеркал, т. е. вычислять по формуле (4.11).
Влияние кривизны зеркал будет пренебрежимо мало, если
наряду с условием (11.03) будет выполняться условие
(2т—1 ).а < 2лр',
(11.04)
т. е. если поправка к частоте, вызванная кривизной, будет мала
по сравнению с поправкой на диффракцию. Пользуясь первой
формулой (4.15), это условие можно переписать в виде
. п2,п2
а *^2(2т — 1)2И2*
(11.05)
Таким образом, к прогибу зеркал (равно как и к перекосу, ср.
конец § 9) наиболее чувствительно колебание с наименьшим
индексом т=1, а колебания с большими индексами возмуща-
ются при прогибе в меньшей степени.
В результате прогиба зеркала могут стать не вогнутыми,
а выпуклыми; в этом случае, как можно показать (см. конец
§ 15 и задачу 7 к гл. III), радиус кривизны г0 в формулах
(11.01) — (11.03) нужно считать отрицательным, тогда при
|г0| >/ мы имеем
а = — i |а| = — (11.06)
г И о
Влияние прогиба будет мало, если наряду с условием (11.03)
выполняется условие
(2/п—1)|а|<2лр", (11.07)
заменяющее условие (11.04). Мнимость а физически означает
появление дополнительного затухания, обусловленного выпук-
лостью зеркал, а условие (11.07) есть условие малости этого за-
78
тухания по сравнению с затуханием, обусловленным диффрак-
цией на краях. Пользуясь второй формулой (4.15), мы можем
переписать условие (11.07) в виде
I |д| < ^2т\. ..
11 (2m—1)Л43
(11.08)
Эта формула показывает, что допустимая выпуклость зеркал меньше
яг
в раз допустимой вогнутости.
На основании результатов, полученных в этой главе, можно
сделать вывод, что допуски для плоских зеркал являются до-
вольно жесткими — тем более жесткими, чем короче длина вол-
ны. Как мы увидим в следующих главах, для открытых резо-
наторов с вогнутыми зеркалами дело обстоит иначе.
Задачи к гл. II
1. Показать, что уравнение (10.16) можно переписать в виде
e~'s^/(—«о. £. 6)+^ ^o.ie"Sjt 7 (sjF 5, £) = 0 при £>0,
i
где
“ 00 i (г
- 1 с т С * * т
I (S. 5. 6) = 1 — 2^ | е dy J е v ' dx.
2s—5—Y
Из этого уравнения нетрудно получить оценочную формулу для коэффициента
отражения
аналогичную формуле (3.25). Показать, что при Jsol'C 1 эта формула при-
нимает вид
1+^-,
.=-eiB(US°
и найти выражение для В (5) в виде отношения интегралов. Вычислить эти ин-
тегралы при 5 = оо и £ = 0. Объяснить причину расхождения формулы (6) при
5 = 0 с формулой, вытекающей из выражения (3.25).
Решение. Подставляя в уравнение (10.16) интегралы Френеля (3.23)
и производя замену переменных
Sj, t=x—y,
получаем выражение (о). Чтобы получить формулу (6), надо воспользовать-
ся разложением
/(з, 0, £) = /«+ Го« (Ы«1).
79
где
00 , »" со I и\2
— 1 с ~Т С ‘ I 2")
Л> = /(0, О, 6)=1 —-^rje dy J е v > dx,
° -г
00 T* 00 i HL
Г»=-Й'<0’ °’ ё)=2йг(2 f eix'd*+e 2 Je 2 dyj’,
-Г V
тогда функция В (5) в формуле (b) оказывается равной
В(5) = 2«9--
* о
Прн 5 = со мы имеем
2 _
B(o°) = T^(, + i)F2 =₽(1+/)У2
в согласии с формулами (3.26) и (10.13). При 5=0 вычисляем полагая
х = г cos <f, у = г sin у,
f (?) = cos2? — cos ? sin ? + Ц- sin2? = (3 + cos 2? — 2 sin 2?);
тогда
OO J oo . ОО n/2
j e 4 dу § e ' 2 ' dx = J d<f § e‘r'l^rdr = | Г(ч) '
6o oo b
Полагая затем
получаем
к/2 —I
f d<f C dz 3л
J J (1+2t)z2 + 6z + (l-2i)----tln(-0 = -2-.
o i
откуда
r 5 , 1 + K2 - i ~
Io=-g-. Го = e 4, B(0) = ₽(l+i),
где величина
отличается от величины (3.26). Это расхождение объясняется тем, что мы
рассматриваем функциональное уравнение (10.16), которое при 5= 0 отличается
от уравнения (3.23). При точном решения этих уравнений мы должны, ра-
зумеется, получить тождественные результаты, но приближенное их рас-
смотрение приводит к различным значениям р.
80
2. 1 Показать, что из системы интегральных уравнений (8.15) выводятся
интегральные уравнения
I ME) = e2i* Г К1(5,
I д,
i ₽»
fa(E)=e2Z* J К2(?, E')fa(E'W
1 — as
для функций Л(£) и fs(^) в отдельности, причем ядра этих интегральных
уравнений определяются следующим образом:
₽.
Ki(E. ЕЭ = J К>а(Е. Е")Ка1(Е". Е'ИЕ".
—“а
Ка(Е. Е') = J Км (6- E")Ki2(E", Е'ИЕ".
—“1
3. Написать интегральные уравнения для двухмерного резонатора из
двух цилиндрических зеркал с радиусами кривизны и н г2, а также для двух
одинаковых цилиндрических зеркал (в частности, Г1=Г2=Го), расположенных
симметрично относительно плоскости 2=0 м имеющих ось симметрии х=0.
При выводе уравнений полагать
X2 X2
а*(х) = 17Г’ а“(х) = -27Г-
Решение. Из формул (8.02) и (8.07) имеем
I I
(£)=—£'. <ME) = ~ Е2,
поэтому ядра в интегральных уравнениях (8.15) для данной системы име-
ют вид
1 Г/ 1 I \ / 1 I \ я 1
(£.£') = ехРi | (—тг/ + ТТЛ2 - - Т J ’
(Е. Е) =p^expz [(——) *2 + (т-7Г/'2-^-^-] =
= Ku (Е'. Е).
Для одинаковых зеркал функция
f(E) = h (Е) = Ь(Е)
удовлетворяет интегральному уравнению
f(E)=-----т=--- expt (^—— ) (Е2 + Е'2)-ЕЕ' f(E')dE'. (a)
у2я J L\zr°/ J
—М/2
где
причем 2а есть ширина зеркал по оси х.
4. Интегральное уравнение (а), полученное в задаче 3, для удобства
исследования часто заменяют таким же уравнением, но с бесконечными
6—2547. 81
пределами (—оо и оо): соответствующие собственные функции f(g) и соб-
ственные значения отличаются от тех, которые получаются при конечных
f М М\ '
пределах I---g” и ~2~ )’ тем> что в них не учтечы краевые эффекты
(диффракции на краях). Для неодинаковых зеркал пренебрежений крае-
выми эффектами вводится путем замены конечных пределов интегрирования
в уравнениях (8.15) бесконечными (—оо и оо).
Пользуясь результатами, полученными в задачах 2 и 3, показать, что
если пренебрегать краевыми эффектами, то резонатор с зеркалами различ-
ной кривизны (Г1 ф гг) будет эквивалентен резонатору с зеркалами одинако-
вой кривизны (радиус кривизны го), и установить связь между rh гг и го-
Решение. Полагая для краткости
2/
получаем
— i ' V- (Ь*-*-Vя) р
М (6Л') = -2Ге j exp i [g£”’- (S + £') S"] dS" =
-CO
причем при отрицательном ga нужно считать
l^gs = i У— gz-
Аналогично,
. 71
—J
При л=Г2=Го функции fi=f2=f удовлетворяют интегральному уравне-
нию
f(S) = e2,x J к0 (?, В')Г(П< (а)
—со
с ядром
. к
е~Г г 1 / 1 \ £₽' 1
(е> 5,)=ехр 1 h- (л° - 2+*'2) - 2KI •
где
Это уравнение получается в результате итерации уравнения (а) задачи 3
(с бесконечными пределами), т. а в результате подстановки интегрального
выражения для f(g) под знак интеграла.
Считая gi>0 и ga>0 и полагая
Л==Д= Ч_~ L
Kg« Kgs’ V go Vgl'
82
для функции f(5i)=fi(S) получаем интегральное уравнение (а), в котором
go = £ift- (*>
Такое же уравнение получается для функции
Радиус кривизны го эквивалентного симметричного резонатора опреде-
ляется соотношением (Ь), которое можно переписать в виде
21 f 7 21 \f 21 \
или
21
причем квадратный корень берется в арифметическом смысле (так, чтобы
При Г1=Г2 6ЫЛ0 go = gl=g2)-
При отрицательных gt и g2 по формуле (Ь) мы берем не go = Vgiga> а
go = — Vg^ga < 0.
Следонательно, радиус кривизны эквивалентного симметричного резона-
тора определяется выражением
Если же gi и g2 имеют разные знаки, то по формуле (Ь) величина go
получается мнимой, поэтому эквивалентного симметричного резонатора не
существует.
5. Обобщить интегральные уравнения (8.15) на трехмерные резонаторы,
поверхность зеркал которых определяется соотношениями
/+/ц(х, у) и z~l—h2(x, у).
Написать интегральное уравнение для симметричного резонатора, у кото-
рого
h^x, y) = h2(x, У)=2г+-2^->
где г0 и во — главные радиусы кривизны (в плоскостях хг и уг соответ-
ственно) .
Решение. Интегральные уравнения имеют вид
Л(Е, 7}) = e^ J J К12(Е. Tj, I', 4t)dW,
s„
fa (E> >)) = e'z J J K21 (g, ij, E', V) fi (E'. V) dW
Si
где интегрирование производится по поверхности первого (Si) и второго
(S2) зеркал, а ядра
К12(Е, у, S'. tf) = r(g — ?, 1)Г(1] —у, 1)е-Ч«М£.’1)+{М!;', ’)')!,
К21(Е, 1), S'. tf)=T(6 — 6', l)r(ij — tf, i)e—15’s«,’))+{6i(V.5v)]>
6*
83
где.
(Е. ч) = khx (х, у), ф2 (Е. »]) = kh2 (х, у).
1/ k лГ k
е= V 1гх’ ~2iy-
Для резонатора нз одинаковых
тральное уравнение
зеркал получаем (ср. задачу 3) инте-
р
f (Е- ч) = ”
4“ go (Е2 + Е'2) + 4 А° + ч'2) -
— ЕЕ' — ЧЧ' f (Е'. ч') dZ'd-ф,
(а)
где
21
go = 1----
Го
, . 2/
ho = 1 —-
So
6. Обобщить результаты задачи 4 на трехмерный случай, когда
(xcosipj — ysin^,)2 , (xsin $4 + g cos <pi)2
«1 (х, у) — 2ri 1 2fii
и
(х cos <f2 — у sin (х sin <f 2 4- у cos <f2)2
Ла(х, j/)= —’
где, например, rt — радиус кривизны первого зеркала в плоскости xtz(xi=
=xcos<pi—f/sin<pi). Выяснить, при каких условиях разнозеркальный резо-
натор эквивалентен (в пренебрежении краевыми эффектами) равновер-
кальному.
Решение. В трехмерной задаче без учета краевых эффектов функции
ft и f2 удовлетворяют интегральным уравнениям
ME. ч) = е2/х ЭД ч’ 4')fi(E'. чЭ^Е'^ч'.
—00
ME. ч) = е2‘х ЭДкг(Ь ч> Е'> ч')Ь(Е'< ч')йЕ'^ч'>
где
оо
Ki(E. ч. Е'. ЧЭ = J У ^12 (Е. ч> 6". 4")Ksi(E", ч". Е'. ч')^Е"^Ч".
—00
00
Кг(Е. ч. Е', Ч')= ЭД #21 (Е. Ч> Е". ч")К12(Е", Ч" Е'. ч') <*Е"<*ч"-
—ОО
Мы имеем
К12(Е. Ч» Е'> Ч') = ~2к ехР‘ ^4^Л,?г + В1^ + А£'2 +В2Ч'2) —
— (ЕЕ' + чч') + С\Еч + СгЕ'Ч'1 ’
84
Ksi (E. ч. E', V) = 2^exP1 [4~ + В^ + A€'“ + a) —
- (ЕЕ' + W) + С&-Ч + Cig'tf 1,
где
2/, 21
А, — 1 — — cos2?,-—- sin2?j = gj cos2?, + h3 sin2?,-,
' i si
21 21
Bj = 1 — —— sin2 <oj — — cos2?,- — gj sin2 ?,• + hj cos2 ?,-,
r, S,
„ f 21 21 \ , 1 , „ . „
Cj = —— — Jsin ?3 cos ?, = -и- (hj — g}) sin 2?„
\ ' i si J
причем
21 , 21
gj=i-—, hi=l-7r’ / = i;2.
'3 Oj
Вводя новые переменные x, у по формулам
Е" = х cos ?2 + у sin ?2, ij" = — х sin ?s + у cos ?а,
получаем
Ki(E. 1. Е'. Ч') = ^Н X
Xexр i А (е* + Е'2) + у В, rt2 + V2) + Cl (El + EV)] X
ОО
X { J exp i [АГ2 + В^'2 + 2C# V — (Е + £') Е" — (->}+ч') V'J <*EW =
—ОО
— i г 1 ( Во \ 1 / а \
=ехр' [2 И* ~2мг)«2 + е'2) + у (**- 2^) +^'2) +
< f ^*2 \ В 2 лДг С*2 I
Л 1++w + «г
и аналогичное выражение для Ка- При г, = гг = rt и ?, = ?г = 0 ядра Кз и
К а совпадают с ядром
Ко (г> е''ч>) = iT7|Xexp/ [т - i)(ea + £,2) +
+т(Л<>-wX+4'!)-2£K'“i
т. е. с ядром итерированного уравнения (а) задачи 5 (с бесконечными пре-
делами). Вводя вместо Е, т] и tf новые безразмерные координаты х, у и
х', у1 по формулам:
Е — х cos ? + у sin ?, Е' = х' cos ? + у’ sin ?,
У) — — х sin ? + у cos ?, т)' = — x'sin ? + у' cos ?,
где
hz — gz
(Ih — gi) Sin 2?, + 2gafe— Sin 2?2
tg2?=------------------------------
(fti — gi) cos 2?! + -g-^- cos 2?2
85
получим в новой системе координат для функции gi(x, y)=fi(H, т]) инте-
гральное уравнение с ядром
Li (х, у, х', у') =
----,--г- ехР»
4л V gzhz
[у a, (Xs + х' ») + 4 ₽1 (У* + «/'“)-
— fiXX' — 6ау'+ «1 (ху' + х'у) ,
где постоянные ai, рь у,, 61 и 6i определяются параметрами gj, h, и угла-
ми <pj. Если последняя постоянная
— g» . „,
*» = ’4^2 ' sin 2 (?»-?)
отлична от нуля, то ядра £i и Ко имеют существенно различный вид и ре-
шения соответствующих интегральных уравнений нельзя просто связать друг
с другом. Если же £1=0, то такую связь установить можно (так же, как
в задаче 4).
а)
РИС. 20. Открытые резонаторы, образованные
углублениями или выступами н бесконечных
параллельных плоскостях.
Таким образом, эквивалентность разнозеркальных и равнозеркальных
трехмерных резонаторов имеет место не всегда, а лишь тогда, когда е,=0.
Условие ei=0 может выполняться: 1) при <Pi=q>2. когда главные радиусы
кривизны обоих зеркал расположены в одних и тех же плоскостях (тогда
<t>=<pI=<p2); 2) при g2=ft2 (когда <р=<₽1) и gi=/ii (когда <р=<р2), т. е. в слу-
чае совпадения главных радиусов кривизны у одного из зеркал (одно зер-
кало — сферическое). Это условие необходимо, но не достаточно.
86
7. Пользуясь результатами § 8, составить интегральное уравнение для
двухмерного открытого резонатора, у которого
h (х) — h при |х| < а,
й (х) = О при |х| > а.
Такой резонатор изображен на рис. 20. Он представляет собой две беско-
нечные параллельные плоскости с канавкой (при й>0, рис. 20,а) или вы-
ступом (при й<0, рис. 20,6) шириной 2а. Составить интегральное уравнение,
позволяющее рассчитать отражение волн от волноводной ступеньки, пред-
ставляющей собой переход от волновода шириной 21 к волноводу шириной
2(1—h), как на рис. 20; привести это уравнение к функциональным уравне-
ниям, аналогичным уравнениям (2.03), и вывести выражение для коэффици-
ентов Ro.i-
Система, изображенная на рис. 20, отличается от обычных открытых
резонаторов тем, что излучение происходит не в свободное пространство,
а в пространство между плоскостями.
Решение. Интегральное уравнение для открытого резонатора имеет
вид
f (g) = e'z £ Г (£ — £', 1) е—1 +«fi (i/)1 f (?') dE'.
—ОО
где
$(Е) = йй при |Е| <~2"» Ф(И) = О при |е|>~2
и
/2йа2
—•
Для волноводной ступеньки, у которой
ф (Е) = kh. при 5 > О, ф (6) =- 0 при 5 < 0
интегральное уравнение имеет такой же вид. Если положить
f(E) = f+ (5) + Г- (6).
f+(E) = ° ПРИ Е<0> f~ (0 = 0 при Е>0,
то интегральное уравнение можно переписать в виде системы уравнений
ОО 0°
f+(g) = e, <z-2ft/,) J Г (£ — £', l)f+ (6')de’ + е‘ ftft> У Г (Е — Е'. \)f~(i')di'
—00 —со
при Е > О,
f-(£)=e/(z-feft> у г (е-S', i)f+(e')de'+e'x J г (6i)f-(6')rfe'
—СО —00
при Е < 0.
Представляя f+ и f~ в виде модифицированных интегралов Фурье
f + (Е) = J e,s* F+ (s) ds, f~ (E) = Je1’^ F- (s) ds,
c c
функции F+ и F~ подчиняем условиям
yeIs^ F+ (s) ds = 0 при E < 0 (a)
c
87
и
j'e1^ F~ (s) ds = 0 при 5 > 0,
c
в силу которых из системы уравнений может быть выведено тождество (ср»
задачу 1 к гл. I)
£е,г* [£+ (s) F+ (s) + е- «»•£- (s) F~ (s)] ds = 0,
c
справедливое при любых E; в нем
l (2»р+-£)
£+($)= 1—е ' 2кр+=t—2kh,
I
£-(s)=l—е ' 2т. р- —~L.
Из тождества получаем
£+ (s)
e-«ftF-(S) = -rr^F+ (s),
в результате чего первое уравнение системы принимает вид
^е1Л £(s)F+ (s) ds = 0 при Е>0, (&)
с
где
Г[у L+ (s)
£(«)— £_ js)-
Представляя функцию f+(6) в виде (3.22), для коэффициентов RB,j по-
лучаем (решая уравнения (а) и (&) методом факторизации; ср. § 2] следую-
щую формулу:
1_е«2я(р-—р+)
Rt.i = —« (<, .Л <-ехР I17 (s«> Р+) —и (So. F")+tt(Sj, Р+)—и (Sj, />-)], .
где ______
sj == У4л (/+/>+), 7 = 0, ± 1, +2, ...
8. Пользуясь формулой для коэффициента отражения RB,о, полученной
в задаче 7, и применяя формулы:
(7 (so. p+) = ln(/2 so)— i-^-+^j^So. ₽ = 0,824,
U(s„, р-)= 4- In (1-е12”р~) + In (1-J--44 +
\ S° J
ге'^ 1 1
+ [^rl/'o(p-)-—jso,
___гя e*2npn ____
V'B(p) = V2v.y —-=~, s7 = /4Kp-,
4J V n
n=l
пригодные при малых s0 и p+ и выведенные в приложении В к книге [8J, вы-
яснить, как влияет параметр р~ на коэффициент Ro,o и при каких условиях
l-Ro.ol =5= 1 (в этих формулах надо считать, что |/>~|^1/2, выделяя из р~
целую часть). Особое внимание обратить на поведение 7?о,о при р- -* р+,
88
р—>±1/2 и р~ —» 0. Воспользоваться таблицей дзета-функции Римана, приве-
денной в книге [20] (стр. 368 — 372). Считать р+ > 0.
Решение. При р~=р+ коэффициент отражения обращается в нуль.
Этот результат не является тривиальным, поскольку равенство р-=р+ мо-
жет реализоваться ие только при Л=0, но и три М=2лп, где л=±1, ±2.........
поскольку мы считаем |р~|^2'” При р_~р+ имеем
л(р~— р+) So —«0
К о, о Яа 2 , —
Sq s0 -f- s0
причем эта формула применима и при конечных значениях р+.
Бели параметр р~ не мал, так что |s0| <Clso~|, то, пренебрегая членами
порядка Sq, имеем
илн по формуле (2.19)
В g 2 =
отсюда при р~ = ± -g- получаем
(/2 - 1) ₽.
Ко.о = — eI₽a (1+,)s», ₽а = ₽ — ₽, = (2 — /2) ₽ = 0,483.
При |р-| 1 мы имеем
... sjf + so я «₽(1 + 0
U (so. р-) = In ------g-----s®
и
So— Sq
Ло,о = : -
So + Sq
(«)
Таким образом, Ро,о=1 при р_=0; при положительных р~ абсолютная вели-
чина Ro,о быстро спадает до нуля .в интервале 0<р~<р+, а при отрицатель-
ных р~ абсолютная величина Ro,о почти постоянна [ее уменьшение обусловле-
но членами, опущенными при выводе формулы (a)], Я' фаза быстро меняется.
9. Показать, что ®се результаты задач 7 и 8 остаются в силе, если нместо
выступов или углублений (как на рис. 20) параллельные плоскости г—±1
89
имеют импедансный участок, на котором граничное условие Ф=0 заменяется
условиями импедансного типа
дФ
-^-=— ikZ& при z = — I.
дФ
-^-=ikZ<I> при z = l.
где импеданс Z=—iX является чисто реактивным.
Решение. Реактивный импеданс стенок означает, что коэффициент от-
ражения от 'них (для волй, составляющих малые углы с осью z) равен
Z—\_iX+\
R~Z-\-\ IX —
в то время как при условии Ф=0 мы имели R=\. Коэффициент отраже-
ния (а) по абсолютной величине равен единице, поэтому его можно запи-
сать в виде
«=е~г*л,
Учитывая фазу коэффициента отражения, мы приходим к интегральным
уравнениям задачи 8 (ср. задачу 7 к гл. I).
Глава III
. Открытые резонаторы
с цилиндрическими зеркалами
§12. Эллиптическая система координат
и параболическое уравнение
В гл. I показано, что собственные колебания открытых резо-
наторов, образованных параллельными плоскими зеркалами,
имеют вид стоячих волноводных волн. Такие волны возникают
в результате того, что волноводная волна, распространяющаяся
между параллельными плоскостями при частоте, лишь немного
превышающей ее критическую частоту, почти полностью отра-
жается от края резонатора.
Оказывается (ср. гл. VII), что радиационное затухание от-
крытых резонаторов можно сделать очень малым (практически
равным нулю), если применять не плоские зеркала, а вогнутые
(по отношению к пространству между зеркалами). Этот резуль-
тат становится понятным, если рассматривать открытый резо-
натор с вогнутыми зер’калами как неоднородный волновод; по-
скольку расстояние между зеркалами максимально в центре и
уменьшается к краям, некоторые колебания могут оказаться
«запертыми» в центральной части резонатора. В этом случае
периферийная часть резонатора представляет собой 'волновод
в котором данная волна распространяться не может, т. е. волно-
водный ослабитель, благодаря которому поле у края и излуче-
ние, вызванное этим полек, оказываются весьма слабыми.
Приведенные выше качественные соображения положены
в основу количественной теории открытых резонаторов с цилин-
дрическими зеркалами, изложенной ниже. Наиболее простой вид
все соотношения приобретают, если рассматривать волновое
поле в эллиптической системе координат, соответствующей зер-
калам резонатора; при этом открывается еще одна сторона
91
явления — геометро-оптическая (образование каустик, см.
§ 13).
Введем в плоскости х, z эллиптические координаты g, g по
формулам
л = d ch С sin!;, z = dshCcos$, (12.01)
где
-оо<С<оо, —^<S<-J- (12.02)
и 2d есть расстояние между фокусами 'эллипсов g=const. Зада-
дим поверхности цилиндрических зеркал соотношениями
(рис. 21)
—Т<В<1, — оо<у<со, (12.03)
тогда при условии
sin2 5 << ch2 С (12.04)
РИС. 21. Открытый резонатор с вогнутыми зеркалами
в эллиптической системе координат.
эти зеркала будут иметь практически постоянный радиус кривизны
',= <*>• (12-05)
Расстояние между зеркалами по оси z будет равно 2/, где
/ = dshC, (12.06)
а ширина зеркал по оси х будет равна 2а, где a — d ch С sin Е. (12.07)
92
Исходя из геометрических величин \r0, I и а, можно (при
г0>1) подобрать параметры g, 4; и d эллиптической системы коор-
динат так, чтобы соответствующие цилиндры задавались усло-
виями (12.03). Для этого нужно положить
sinT=-^=, thC = |/ —. (12.08)
У Го/ У г0 she ' 1
и учесть условие (12.04). Софокусные (или, как еще говорят,
конфокальные) зеркала определяются условием г0=2/; для них
shC=l, ch £=/2, sinT=^-, d = l. (12.09)
Исследуем двухмерные колебания открытого резонатора,
изображенного на рис. 21. Будем исходить из волнового урав-
нения
Д|ф+£2ф=0, (12.10)
где k = -~- есть волновое число в свободном пространстве, соот-
ветствующее комплексной частоте данного собственного колеба-
ния. В эллиптических координатах функция Ф=Ф(£, £), не за-
висящая от у, должна удовлетворять уравнению
^+^- + Y2(ch4-sinse)® = 0 (12.11)
и граничному условию на зеркалах
Ф = 0 при — Г<Е<£? С = ±С (12.12)
Мы будем искать асимптотическое решение поставленной за-
дачи при больших значениях параметра
Y = (12.13)
sn ч
аппроксимируя волновое уравнение (12.11) параболическим
уравнением. При этом наряду с условием у>1 будем считать
выполненным условие
sin2T< 1, (12.14)
более сильное,, чем условие (12.04).
Ввиду симметрии системы по оси z функция Ф для каждого
собственного колебания должна быть либо четной, либо нечет-
ной функцией £. Поэтому мы ищем Ф' в виде
Ф = №(£, t)eZ1(shC— (— 1)<(?, — 0e“‘Tsh\ (12.15)
так что при q=l, 3... получим четную, а при q=Q, 4, ... — нечет-
ную функцию £. Требуя, чтобы каждое слагаемое в выражении
(12.15) удовлетворяло уравнению (12.11), получаем уравнение
+2ZYchC ^ + (iYshC-rsin25)r = 0 (12.16)
93
и делаем следующие аппроксимации: 1) вычеркиваем член
который по порядку величины в у раз меньше соседних членов;
2) заменяем, пользуясь условием (12.14), sin2 В на Е2. В результате
получается параболическое уравнение
+2tychc5+(I‘YshC-Y252)VF=0, (12.17)
которое подстановкой
и7=Йт'Г(г’0)’ (12Л8)
г =/!’2у5, 0=1^1= arcsin (th С)
О
приводится к виду
Мы получили уравнение, формально совпадающее с временным
уравнением Шредингера для линейного гармонического осцилля-
тора. Это уравнение нужно интегрировать с учетом условия
Ф (т, —а) = е?хФ(т:, а) при |*|«О, (12.20)
где введены обозначения
y — 2kl — та/ (12.21)
а=arcsin (th С) = arcsin 1/ —
F Г0
t —V2f ^-sin 2а-
(12.22)
Ha остающейся части поверхности £==—£ должно выполняться
условие
Ф(т, — а)=0 при |т|>тГ (12.23)
означающее, что здесь отсутствует волна, распространяющаяся
вверх.
Остановимся на физическом смысле сделанных пренебреже-
ний. Мы ищем решение в виде выражения (12.15), т. е. в виде
суперпозиции волн, распространяющихся под малыми углами
к оси z в направлениях, близких к направлениям ±£. Быстро
меняющиеся множители e±'1sh,: в формуле (12.15) определяют при
условии (12.14) главную часть комплексной фазы, связанной
с распространением в направлениях ±£, множители IF(g, ±£)
изменяются более медленно и определяют комплексную ампли-
туду соответствующей волны. Эта амплитуда определяется как
законами геометрической оптики (наклоном и расширением лу-
94
чевых трубок), так и диффракционными явлениями — попереч-
ной и продольной диффузией. Пренебрегая продольной диффу-
зией (ср. § 3), мы и получаем параболические уравнения (12.171
и (12.19).
Уравнение (12.19) имеет частные решения
—г(т+vV
Чг=е 1 ;фт(г), (12.24)
где функции
(«=0,1,2,...) (12.25)
' у ml
ортогональны и нормальны на бесконечном интервале (ср. [21])
J Фш(т)Фт,(т)<^ = Ътт„ (12.26)
образуя полную систему. Через Нгп (у) здесь обозначены полиномы
Эрмита:
//m(T)=(-l)me2 ^-е 2, (12.27)
//0(г)=1, Я1(г) = «, //2(т) = г“-1, Яз(т) = т»-3г.
Формула (12.24) дает решение интересующей ‘нас задачи при
достаточно больших значениях т (формально при т=оо), когда
можно пренебречь влиянием края, т. е. излучением из резона-
тора. Собственную частоту, соответствующую решению (12.24),
находим с помощью формул (12.20) и (12.21); получаем
2Л/=л<7+'(2т + 1)а, (12.28)
где большое целое число q есть число полуволновых осцилляций
функции Ф по оси z, а т+1 (т=0, 1,2,...) — число ее по-
луволновых осцилляций по оси X.
§13. Каустики
Функция (12.25) есть решение дифференциального уравнения
4)ф-=°’ (13°о
нормированное согласно формуле (12.26). Переписывая это урав-
нение в виде
^>+2Ц2^фт = О, (13.02)
где = 2 у/ т ~, видим, что при | т | < функция (т)
осциллирует, а при | т j > — затухает. Это соответствует ска-
95
занному в начале § 12: стоячая волна имеется в центральной ча-
сти резонатора; в периферийной части, при — т<Х— и
волноводная волна затухает, не распространяясь, и по-
этому подходит к краям! значительно^ ослабленной— в тем боль-
шей степени, чем больше разность т—тт- Таким образом, фор-
РИС. 22. Положение каустик для колебаний
с различными индексами tn.
мулы (12.24) и (12.28) приближенно соответствуют собственным
колебаниям открытого резонатора при условии, что разность
т—гт 'положительна и достаточно велика. Это условие может
выполняться лишь для конечного числа собственных колебаний
(скажем, для т=0, 1, ..., т), все остальные колебания этому
условию не удовлетворяют и подчиняются совершенно иным за-
кономерностям. На рис. 22 изображена парабола у, собственные
значения т+ ~ (т=4) и точки ±ть и i±ti.
Уравнение (13.02) можно также решить приближенно, с по-
мощью метода эталонных уравнений (см., например, (22] или
(19], стр. 303 и 386). Получаем
фт=лт (13.03)
I/ ъ* — t
F tn
где A m — нормирующий множитель; v(t)—функция Эйри
(см. § 9, а также [17] и [19]), осциллирующая при tf<0 и зату-
хающая при />0, а переменные t и т>0 связаны соотношениями
________________________________
2_(_/)3/г=Д_ J К.™ — ** при /<0л <
4^=4 Л
при />0,т >*т. (13.04)
96
В интервале 0<т<тт—Лт (Лт>0), где функция фт(т)
осциллирует, для нее и для ее производной можно написать при-
ближенные выражения {см. формулу (9.24)]
(13.05)
которые, как и сама формула (13.03), дают тем большую точ-
ность, чем больше т. Однако, ставя граничные условия при
т=0
фт = 0 (т — 1,3,...),
.4^ = 0 И = 0,2,...), (13.06)
получим точное значение —2 у т 4~ . Условия (13.06) вы-
текают из четности функций ф0 (-), (т),... и нечетности функций
Ф1 (т), Фз (т), • • • [ср- формулы (12.25) и (12.27)].
Интересно отметить, что функция v(t) впервые введена Эйри
при исследовании волнового поля вблизи каустики. Дальней-
шее применение функций Эйри в теории диффракции на выпук-
лых телах (см., например, [17] или [23]) связано с тем, что их
поверхность является каустикой для диффракционных лучей. Из
формулы (13.03) следует, что гиперболы g= ± —Lb открытом
Г ^Y
резонаторе, изображенном на рис. 21, являются каустиками;
поле между каустиками представляет собой совокупность пере-
секающихся лучей; за каустиками, куда лучи не проникают,
поле экспоненциально убывает.
Сказанное можно пояснить так. При т~тт формула (13.03)
принимает вид
K = Bmv ( \, Вт = Агп(У\^ , (13.07)
I / i * I \ T?n J
) )
где
(13.08)
есть радиус кривизны гиперболы ? = Em = -^==, а X — расстоя-
ние от нее, отсчитываемое по нормали. Формула (13.07) совпадает
с обычной формулой для поля вблизи каустики (см. [24]).
7—2547 97
Каустические поверхности должны появляться всякий раз,
когда волна в сужающемся волноводе испытывает полное отра-
жение. Пусть, например, плоскопараллельный волновод при
х>0 начинает постепенно сужаться (рис. 23). Если волна, при-
ходящая к сечению х=0 слева, не зависит от у, то ее можно
представить в виде суммы двух плоских волн, т. е. в виде двух
пучков параллельных лучей, переходящих друг в друга при от-
ражении от плоскостей z= ±i. При х>0 лучи уже непараллель-
ны и заполняют область левее некоторой линии С —• каустики,
касаясь ее; по этой причине каустика нормальна к стенке.
г и
< ///
; \\\ ।
РИС. 23. Образование каустики при сужении
волновода.
Ограничение поля каустиками приводит к тому, что колеба-
ния становятся нечувствительными к небольшому перекосу зер-
кал, сдвигу и другим малым возмущениям, сильно влияющим на
свойства открытых резонаторов с параллельными плоскими зер-
калами (гл. II). Если оставить в стороне концентрические зерка-
ла, по своим свойствам! подобные плоским (см. .ниже § 14), то
колебания с каустиками, сформированные одинаковыми вогну-
тыми зеркалами, чувствительны к малым деформациям откры-
того резонатора только в одном случае — для софокусных зеркал
(см. § 36).
§ 14. Интегральное уравнение
Назовем функцией Грина G(r, г', а—</) такое решение урав-
нения (12.19), которое удовлетворяет предельному соотношению
lira G (т, t’, а — а') == 8 (т — т') = V фт (т) (т'), (14.01)
а->а' 4-0
m=z0
где б(т—V) есть дельта-функция, разложение которой по функ-
циям в бесконечном интервале —оо<т<оо строится обыч-
98
ным способом. Из уравнения (12.19) получаем выражение для
функции Грина в виде ряда
оо — i + 4~)(а—а')
G(x,x', а — а')=^ е V ' К (х)ф^.(тг) (14.02)
т=0
при а > а'
или же «(см., например, [25], стр. 194) в явном виде
к
1 “ф"
г / , е 1 Г ,'2 +'t'2 2тт' I
G (т, х , а — а'): — — ехр —г- т—г—к--------------7V ‘
’ /4л sin (о—а') 4 [tg(o—а') sin (а— «') J
(14.03)
Эквивалентность выражений (14.02) и (14.03) можно доказать
из общих соображений (см. ниже задачи 1 и 3).
Интересующее нас решение уравнения (12.19) можно теперь
записать так:
Чг(т,а) = G(t, т', а-|-а) 1F (т',—a)dx'. (14.04)
-—т
Полагая а = а и используя условие (12.20), получаем для функции
Ч’ (т, — а) интегральное уравнение
Ф(т, —a)=e'z j* G(x,x’,2a)W(xr, — a)dx', (14.05)
—т
которое в приципе позволяет найти как функцию ’Г(т, —а),
определяющую ток на зеркалах при каждом собственном коле-
бании (см. § 17), так и комплексную частоту собственного коле-
бания, определяемую формулой
2feZ=«9+x- (14.06)
Для собственного значения е'х из уравнения (14.05) нетруд-
но получить стационарное выражение, в которое вместо неизве-
стной функции Чг(т, —а) естественно подставить (для колеба-
ний с каустикой) ее пра^лиженное выражение (12.24). В ре-
зультате получаем (ср. [26])
JJ G (т, т', 2а) фт (т)фт (V) d-.d-.'
e“'z = --------=----------------, (14.07)
откуда можно вычислить неизвестную величину х- Она может
быть представлена в виде
Х= (2иг+1)а+2лр (/n=0, 1, 2, ...), (14.08)
7* 99
где первое слагаемое дает поправку на кривизну, а второе —
поправку на диффракцию. Комплексный параметр р при увели-
чении т быстро убывает, по формуле (14.07) получается, что он
пропорционален е Г (мы отвлекаемся от предэкспоненциально-
го множителя, зависящего от т). На самом деле закон убыва-
ния р другой — более быстрый, по крайней мере для софокус-
ных зеркал. Это объясняется тем, что в результате диффракции
на крае функция гИ(т, —а) испытывает вблизи края сильное
возмущение, которое не учитывается формулой (14.07); мы вер-
немся к этому вопросу в гл. VII.
Интегральное уравнение (14.05) можно преобразовать к виду
1
f (0 = Р J exp i (е0-~*- - с, tt' \ f (f) dt', (14.09)
—1
где функция
Г(0 = ’Г(т,а), Z = 4- (14.10)
т
пропорциональна плотности тока на верхнем зеркале (§ 17), а
о 7И2'
c0 = c1cos2a, , ^=У (14.11)
Из интегрального уравнения (14.09) вытекает следующая связь
между свойствами сопряженных резонаторов. Назовем два резона-
тора сопряженными, если первый имеет параметр а, а второй—па-
Л тс
раметр а = “2---а< эти резонаторы отличаются лишь радиусами
л
кривизны г0 и г0, причем
Го
Так как интегральные уравнения для сопряженных резонато-
ров отличаются только знаком Со и собственные функции удов-
летворяют соотношению
f(-O = ±/(-f), (14.13)
то собственные функции и собственные значения сопряженных
резонаторов связаны следующим образом:
?(0=Г(0- (14.14)
где звездочкой обозначена комплексно-сопряженная величина.
Если собственные частоты резонатора согласно формулам
(14.06) и (14.08) вычисляются по формуле
2kl == ~q -J- (2m—l)a-J-2i7> (m=l,2,...), (14.15)
100
то для сопряженного резонатора имеем
(14.17)
(14.18)
2kl = r.q -j- (2т—1)а— 2тср*, (14.16)
где параметр р тот же. Резонатор с софокусными зеркалами
является самосопряженным: f (/) и р. для него вещест-
венны, а /?= — i|p|.
Полагая а=0, т. е. беря в качестве первого резонатора резо-
натор с плоскими зеркалами, мы можем воспользоваться ре-
зультатами гл. I и приближенно положить:
f (/) = cos —-—при m = 1,3,..
2('+’т)
' j (/) = sin —-—. при т — 2,4,...
и
₽=0’824-
Сопряженным ему будет резонатор с соосными цилиндрическими
зеркалами (r0 = l, собственные функции которого ком-
плексно сопряжены с функциями (14.17), а комплексная частота
определяется соотношением
2kl=r.^q-\-m----—2т.р* (т—1,2,...). (14.19)
Таким образом, соосные зеркала имеют те же диффракционные.
потери, что и плоские: каустика между такими зеркалами обра-
зоваться не может.
В общем случае координата х на зеркале связана с перемен-
ной т соотношением
x=V . * т, (14.20)
Г k Sin 2а ’ ' '
поэтому часть зеркала между каустиками, где в основном сосре-
доточены токи, при фиксированных значениях I и k имеет ми-
нимальную ширину на софокусных зеркал ах ^при а=-у^: в такой
системе диффракционные потери минимальны, однако она обла-
дает неустойчивостью (см. § 36).
Поле имеет наименьшую протяженность по оси х в плоско-
сти z—О, где
101
При а —- ~ каустики пропадают, но концентрация поля вблизи оси
Л
у усиливается, так как она при а = становится фокальной ли-
нией. Предельный случай а=-^- заслуживает отдельного рас- •
смотрения, которое будет проведено в следующем параграфе.
§15. Открытый резонатор
с соосными зеркалами
При Го=1 и а= у мы имеем открытый резонатор с соосными
(коаксиальными) зеркалами, когда в плоскости xz центры кри-
визны зеркал совпадают друг с другом и с началом координат, j
В такой системе согласно геометрической оптике может сущест-
вовать система радиальных лучей, проходящих через начало ко- j
ординат и отражающихся от зеркал обратно к началу коорди-
нат. В данном случае ось у является фокальной линией, в кото- i
рой по лучевым законам волновое поле бесконечно. Согласно
волновой оптике (ср. [27]) волновое поле на фокальной линии
конечно, хотя для достаточно коротких волн и велико.
Волновое поле при наличии фокальной линии нетрудно ис-
следовать с помощью параболического уравнения. Выводя ос- :
новные соотношения в § 12, мы считали, что у>'1; однако у —0 i
п
при а— у, поэтому можно опасаться, что формула (14.04) и
интегральные уравнения (14.05) и (14.09) к соосным зеркалам
не применимы. На самом деле оказывается, что при а— -^-пе-
ременные тио неудобны, но выведенное с их помощью урав-
нение (14.09) справедливо и при а= у. Это можно показать,
используя полярные координаты г, g, где радиус-вектор r=d sh £
между зеркалами изменяется в интервале —1<г<1. В пределе
d=0 мы полагаем
Ф = № (г, £) eiftr—(—1)9 №(—'',*) e-’ftr (15.01)
и получаем для функции W уравнение
1 д Г dW \ । dW । 1 d*W , ik ,,c„,
<15-02)
I
которое заменяем параболическим уравнением ,
+ 2^2 _|_ ikrW = 0. (15.03)
102
Соответствующая функция Грина равна
Г (г Е г' Е')— k exp t Г —~ ___— 1
Иг, — у 2я(г-г') ехр 1 L 2(г — г') 4J
при г>г' и гг'>0, (15.04)
t , „. if k . (krr' (E + E')2 ” 1
г(r,E,r ,E) у 2я(г—/) exp 1 L 2(r—r>) Гj
при r>r' и rr' <0;
она удовлетворяет предельному соотношению
lim —5') (15.05)
r-»r'+O И I
и обращается в нуль при r<fr'. Записывая решение уравнения
(15.03) в виде
I
№(г,Е)=/ J Г(г,Е, —/,Е')Г(—/,Е')^, (15.06)
мы опять получаем интегральное уравнение (14.09), в котором
а ==-£-, — с0=С1 = ~, М=^2М1г. (15.07)
Нетрудно видеть, что формулы (15.04) и (15.06) применимы
при /гг —0, если только k | г' | 1 или kl^> 1; они характеризуют
концентрацию поля вблизи фокальной линии r — Q. Волна, прошед-
шая через фокус, испытывает асимптотический „скачок фазы®
(ср. [27]), который получается из формул
при г<0,
оо
j Г(г,Е,-/,Е')йЕ'
—ОО
при г>0,
(15.08)
вытекающих из выражений (15.04).
Заметим, что интегральное уравнение (14.09) можно выве-
сти, рассматривая диффракционные поля в декартовой системе
координат (см. гл. II и ниже задачу 2). Таким путем в работе
[26] установлена связь между свойствами резонаторов с плоски-
ми и концентрическими зеркалами. Вместе с тем, интегральное
уравнение (14.09) можно написать для выпуклых (го<0) и ко-
л
роткофокусных (го<0 зеркал; резонаторы с такими зеркалами
л
будут сопряженными, если г0 и г0 удовлетворяют условию
103
(14.12). Для таких резонаторов параметры с0 и Ci в уравнении
(14.09) имеют вид
/, 21 \ М2 ka2
Со — Гв )' С1 4 - 2/ '
(15.09)
Следовательно, если написать
с0 —CiCos2a, (15.10)
то а будет комплексным: а = — i | а | при г0 < 0 иа=-^--|-<х ПРИ
л
г0 < I. В этом случае определением сопряженных зеркал будет
л
соотношение (14.12), а мнимые части у а и а выбираются так,
чтобы по формулам (14.15) и (14.16) получалось затухание (а не
нарастание) колебаний во времени.
Эти резонаторы малоинтересны, поскольку потери на излу-
чение у них велики. Впрочем, недавно было предложено (см.
статью {28]) использовать их в оптических квантовых генера-
торах, поскольку они имеют диффракционные потери, сравни-
мые с другими видами потерь и растущие с увеличением попе-
речных индексов тип,
из-за чего происходит дополнительное
разрежение спектра. Теоретиче-
ские результаты для таких резо-
наторов приведены в § 11 (см.
также задачу 7 к гл. III).
РИС. 24. Стоячие волны
между концентрически-
ми зеркалами.
РИС. 25. Стоячие волны
между (почти) софокус-
ными зеркалами.
На рис. 24 и 25, выполненных на основании фотографий Бы-
кова [14], схематически изображены колебания в открытом ре-
зонаторе с соосными (го=О и софокусными (г9=2/) зеркалами.
Несмотря на кажущееся подобие этих колебаний, они сущест-
венно отличаются тем, что между концентрическими зеркалами
не образуется каустик (как на рис. 25), а граница колебаний
104
определяется краем зеркала. Концентрация поля вблизи фо-
кальной линии —оси системы, характерная для соосных зеркал,
может найти различные применения.
§16. Цилиндрические зеркала
конечной длины
Пусть цилиндрические зеркала конечной длины 26 определя-
ются соотношениями
—5<В<5, — Ь<у<Ь, С— (16.01),
В координатах Ъ,у,1 волновое уравнение (12.10) имеет вид
+ d> (Ch-С -sin-8) ** + т (ch-С - sin-8) Ф=0.
(16.02)'
Полагая
Ф = W (5, у, С) е'т sh с — (— 1)ч W (В, у, — С) е~'т shC , (16.03);
мы приходим к уравнению
d*W , ,2/ . .. . d*W .
4" (ch 4“ 4"
+ 2iy ch С+ (iy sh С — у2 sin2 5) W= 0, (16.04)
которое заменяем параболическим уравнением
^ + rf2ch2C^ + 2/Ych^+
+ (iyshC —y2^2)IF = O,
пренебрегая (в дополнение к аппроксимациям § 12) членом
t2 dsW
s=«S2 —-и—в множителе при —7-5-.
2? дуг
Уравнение (16.05) имеет решение
1Р=1М,9ВД,
(16.05)
sin2 &&
(16.07)
(16.06)
где функция Wa удовлетворяет уравнению (12.17), a Wb есть ре-
шение уравнения
’ 4^+2^4^^°, Z = dshC,
дуг 1 dZ ’ ’
соответствующего двумерным колебаниям в резонаторе с пло-
скими зеркалами (см. § 4).
Граничное условие Ф=0 на зеркалах (16.01) приводит к со-
отношению ’
W(l,y, — Q = ei{2kl~^W^, у~1) при ]Е|<1 и |у|<6, (16.08)
наряду с которым должно удовлетворяться условие
’ W(^,y, — С) = 0 при |5|>6 или |р|>6. (16.09)
105
Эти условия будут удовлетворены, если в качестве Wa и Wb
взять решения указанных выше двухмерных задач.
Для частоты колебаний получаем выражение
2kl = ~q -j- (2т 1)а -\-2кра-\-2г.рь, (16.10)
где ра определяет поправку из-за диффракции на краях х—'±а
(§ 14), а величина
лп2 л л 1 f 2kb* , _ ,
4(Мь + ₽ + /₽)2 ’ V ~1 (« = 1,2,...) (16.11)
связана с диффракцией на краях у— ±Ь.
Если вместо граничного условия Ф=0 взять условие
^- = 0 при —?<$<£, —b<y<Zb, C = ztC, (16.12)
то, полагая
Ф = № (£,#,£) e'’TSht +(— 1)? W,!/,— C)e~ZTShC, (16.13)
получаем для W то же уравнение (16.05) и те же граничные усло-
вия (16.08) и (16.09). Действительно, при вычислениидля под-
становки в граничное условие (16.12) следует положить
= iychC (с, у, С) е‘т shC - (- 1)9 W (£, у,- sh <],
(16.14)
пренебрегая членами, в у раз меньшими. Таким образом, в слу-
чае граничного условия (16.12) величины W, Wa, Wt>, Ра и рь
остаются прежними, но функция Ф связана с W не формулой
(16.03), а формулой (16.13).
§ 17. Электромагнитные поля
между цилиндрическими зеркалами
Беря в качестве Ф составляющую электрического вектора
Герца (см. § 3) по оси у, обращающуюся в нуль на поверхности
зеркал, получаем электромагнитное поле:
Р — 1 6)2 Ф Н — ik дФ
h д&у * h a; •
+ H, = 0,
£7 1 Ф rj ik ^Ф /17 л 1 \
Л dV)y • h dl ' (17.01)
так как коэффициенты Ламе равны
й$ = h^ — h = d j/ch2C — sin26, hv— 1. (17.02)
106
Из решения (17.01) следует, что плотность поверхностного тока
на зеркалах имеет только составляющую по оси у. На верхнем
зеркале С —С эта составляющая равна
= — Л-Н =—• (17.03)
или приближенно
(17.04)
Из формул (12.20), (12.24) и (4.18) следует, что с точностью
до постоянного множителя функции /(£, у) можно представить,
в таком приближенном виде:
f («, у) = фт -1 СО cos — w i м при п = 1,3,..
»(' + »-!Ж7)
Z(!.y)=<'»-,(’)sta— *,”>1 при л=2,4...... <17.05)
2Ь(, + ’тг-)
где т =1,2,... Соответствующее колебание мы называем коле-
банием • На левой половине рис. 26 схематически изображе-
но распределение тока на зеркале для простейших колебаний £^1в
с каустиками. 5 = zt , за пределами которых поля и токи
имеют незначительную интенсивность.
Электромагнитное поле с другой поляризацией можно по-
строить по формулам:
__ ik дФ н __ 1 <?2Ф
h К ’ h didy ’
£, = 0, Я, = ^ + ЛгФ, (17.06)
Р ik дФ р. \ д2Ф
h di ’ h dtjdy ’
причем функция Ф должна удовлетворять граничному условию
(16.12). Плотность тока по оси £ (т. е. практически по оси х)
в этом случае определяется формулами(17.04) и(17.05), наряду
с ней имеется также малая составляющая по оси у, которой
можно пренебречь. Такое колебание естественно назвать коле-
S банием .
Учитывая приближенность решения, можно то же колебание
выразить через единственную составляющую электрического
вектора Герца (ср. § 22) и назвать его колебанием (или £^д)-
На правой половине рис. 26 изображены токи, соответствующие
107
к
простейшим колебаниям £^nq •' эти токи распределены так же, как
у колебаний , но направлены по оси 6.
В этой главе исследованы собственные колебания в резона-
торах с цилиндрическими зеркалами, причем основное внимание
уделено колебаниям, которые в направлении оси х ограничены
каустическими поверхностями g=const. В этом случае резонатор
излучает в основном через концевые плоскости у=±Ь, т. е.
вдоль образующих, а излучение поперек образующих, через пло-
скости х=±а, весьма мало. В следующей главе теми же мето-
дами будут исследованы колебания в открытом резонаторе со
сферическими зеркалами.
108
Задачи к гл. Ill
1, Проверить непосредственно, не прибегая к разложению (14.02), что
функция (14.03) есть функция Прина для уравнения (12.19), т. е. что она
при и>и' удовлетворяет этому уравнению и при о-» о' — начальному усло-
вию (ср. §3)
lim G (т, т', а — а') = 6 (т — т').
а-»а'+0
2. Показать, что интегральное уравнение (14.09) эквивалентно интеграль-
ному уравнению <(о) задач» 3 к гл. II. Обобщить уравнение (14.09) на случай
выпуклых зеркал.
Решение. Полагая в уравнении (а)
2t , 2t’
М ’ Е' — М
п учитывая, что
( 21 X М2
Со — Cl COS 2а = С, (1 — 2sin2 а) = Ct ( 1 — — 1, Cl = —7~i
\ г Q J “
приходим к уравнению ('14.09). Для выпуклых зеркал надо считать г0 отри-
цательным и параметр а мнимым (ср. § 11).
3. Показать, что функции^ (12.24) и (12.25) удовлетворяют интеграль-
ному уравнению (14.05) при т=оо.
Решение. Это следует из разложения (14.02), которое можно вывести
из разложения дельта-функции согласно формуле (14.01) и возможности
записать функцию Г.рина в виде (14.03) (ср. задачу 1).
4. Пользуясь формулами § 15, написать интегральные уравнения для
двухмерного открытого резонатора, образованного соосными цилиндрически-
ми зеркалами, которые определяются соотношениями:
г = -Г1, —Г<е<1.
г = Гг,
— е<Е<Е-
Рассмотреть также случай отрицательного rt, считая все время г2>—г(, г2>0
и /г|гт| 1.
Решение. При п>0 мы имеем согласно второй формуле (15.04)
r(rs, е, — Г1, £') = г(г!, е, — г2, е') =
iГ k . Г fer>r2 (Е + Е')г * 1
V 2л(Г1 + г2)ехрг L 2(п+г2) 4 J’
поэтому, полагая
получаем для функции
f(t) = w& -n) = W(&, r2)
интегральное уравнение (14.09), в котором
л М2
“ = ^2“’ —с0 = С1 = -^-’
у,.
Согласно формулам (15.07) такой разнозеркальный резонатор эквивалентен
равнозеркальнсму, у которого
2r,r2 _2_=_L+J_
г> + г2 ’ I ri rg
109
При ri<0 мы имеем согласно первой формуле (15.04)
Г (п, Е, |г,|, £9 = Г (— |г,|, £, - г„ Е') =
1/ k . Г/г |г,| г2 (Е — Е')2 “ 1,
~V 2л(г2-|г,|) еХР' L 2(г2-|г,]) 4]
С помощью той же подстановки получаем интегральное уравнение (14.09),
в котором
„о. „
Такой резонатор эквивалентен резонатору из двух одинаковых плоско-
параллельных зеркал (§ 4), у которого расстояние между зеркалами 21 н
их ширина 2а определяются следующим образом:
21 = r2 — |г,|. a =Vki| гг Е.
5. Используя результаты, полученные в задаче 6 к гл. II, рассчитать
(без учета краевых эффектов) собственные функции и собственные частоты
открытого резонатора, образованного двумя одинаковыми цилиндрическими
зеркалами с радиусом кривизны г, повернутыми относительно друг друга
(ось поворота совпадает с осью г) на 90°.
Решение. В задаче 6 к гл. II для нашего случая без ограничения
общности полагаем
л
fi = 0, f2 = ~2~> Г1 = П = г. Sj = s2 = oo,
тогда
? = 0, е, = 0.
Следовательно, необходимое условие эквивалентности данного резона-
тора и равнозеркального выполняется. Ядро Ki в силу соотношений
21
>ii — в% ~ g— 1 — = В| i, с, = сz - о
имеет вид
К.(Е, Ч. £'• Ч')=^р=ехр( ^^-4-)u2 + E'2) +
1 f 1 \ 1 11
+ “Г ~ 2i) *) - ~2 •
При g>0 данный резонатор, как нетрудно показать с помощью подстановки
е=4^=. ч=Им1.
V go
сводится к резонатору с одинаковыми зеркалами, у которых радиусы кри-
визны равны н
go = ht = Vg\
откуда
При g<0 данный резонатор к симметричному не сводится.
Собственные функции /)(£, т]) имеют вид (ср. задачу 3)
fi (Е. = (tx) Фп (ъ),
110
где
x3[ = /sin4a$,
ty = У 2 tg 2ai), sin а =
а собственные частоты определяются формулой
2£/=Л9+2(я1+п+1)а.
6. Вывести интегральное уравнение, аналогичное уравнению (14.09), для
резонатора с цилиндрическими зеркалами, коэффициент отражения от кото-
х
рых зависит от поперечной координаты t = — по закону
R = R(t)~ е~р (— оо < t < со).
Вычислить собственные функции и собственные частоты такого резонатора,
пользуясь результатом, полученным в задаче 3.
Решение. При учете коэффициента отражения от зеркал граничное
условие (12.20) принимает вид
Ф (т, _ а) = R (t) ф (т, а),
поэтому интегральное уравнение (14.09) изменяется следующим образом:
00
Г / 1г + 1'2 \ г
f(O = /?(/)p. I expt I Со—-------c.tt'J f(t')dt'.
Если ввести новую функцию
7(0 = гШ) = а°еГ’ /(0 = Г(<)е г
и обозначить
/ ka2
co = Co4-i I Со == Ci cos 2а, sina =
то это интегральное уравнение принимает вид
/Т г’(х-г) 7 /~«2 + Гг \~
f(t) = y С±е V ' J exp/fco—j—— с.И')7(/')Л'.
—00
Вводя комплексный параметр а по формуле
cos 2а = £?_ = cos 2а + _£
с, с.
и делая замеву переменных
< = =-, т = V2C, sin 2 a, f(t) = g(-c),
т
получим интегральное уравнение
оо
£ (т) = е'х j G (т, х', 2 a) g (т') dt.’,
—00
формально совпадающее с уравнением (14.05) при бесконечных пределах.
Согласно задаче 3 юно имеет собственные функции
5(т)=фт(т) (гп=О, 1, 2, ...)
111
и собственные значения
X=(2m+l) а.
7. Используя результаты задачи 6, исследовать собственные частоты от-
крытых резонаторов с зеркалами, близкими к плоским (|п|<^1). Выяснить,
как влияет малый прогиб зеркал (вогнутость или выпуклость) на собствен-
ные частоты и при каких условиях прогиб несуществен. Сравнить результаты
с оценками, приведенными в § 11. Считать параметр С| большим.
Решение. При малых значениях а связь между а и а принимает вид
~ i
а2 = а2 — .
2с,"
При а = 0 величина у равна
1__i ___ / 2ka2
2л/? = (2/п+1)—> Af=/4C1= у — >
причем комплексная величина р определяет поправку к частоте, обусловленную
диффракцией на „сглаженных* краях зеркала [определяемых функцией R (/)].
При | <х | <g мы имеем
~ 1 —« . . 1 —i , 1+ »'
а— (l-l-iCja2)— дд + 4 Ма2,
поэтому вогнутые зеркала уменьшают диффракционные по-
/ I \ 1
терн, а выпуклые (а2 = ^“'<0 I увеличивают их. При |а1^>д^
~ i i
а — а — ---= а — - гт *
4acj аЛР
откуда
1 = (2т + 1) а + 2л/л 2-р = — i ~ ,
причем здесь р определяет диффракционные потери при условии, что кри-
визна зеркал влияет сильнее, чем диффракции.
В § 11 мы считали, что кривизна зеркал несущественна, если
(2т + 1) а 2лр' при вещественном а,
(2т + 1) | « | <С 2лр" приа = — ij а |,
где комплексный параметр
p=p'—ip"
(о)
характеризует плоские зеркала. В данном случае
„ 2т + 1
2Я// = 2л/Х'= —(т = 0, 1,2,...)
и правильность условий (а) проверяется непосредственно.
8. Обобщить результаты задачи 6 иа случай, когда зеркала открытого
резонатора перекошены, так что согласно формулам (9.02), (9.03) и >(9 66)
имеем
а
Ф1 (5) = Фг (5) = <*Е = ~2 t-
112
Р е ш е Н'ие. Мы получаем интегральные уравнения
00
Г / /2 t 4- t' \
f (t) = R (0 p. \ exp i Г Co —2“ “ C1^ — 8 —2~J ? dt
—OO
и
7(f) = j/g e Z(Z- <) J exp/
—co
Делая подстановку:
d
t=S— So. t' = S'— So. So— ~ ’
2 (cj — Co)
s = =-, t = \Г 2c> sin 2 a, ](t) = g(t),
t
приходим к интегральному уравнению того же вида, что и в задаче &,.
а именно:
g (т) = e‘z j’ G (т, t', 2 а) g (•f) dt',
—00
причем
Поэтому собственные функции (от переменной т) остаются прежними, а соб-
ственные значения определяются формулами
у — {2т + 1) а (т — О, 1, 2. ... ),
аг
7. = (2т + 1) а —-----— .
4 (с, —с»)
9. Используя результаты предыдущей задачи, исследовать влияние ма-
лого перекоса на собственные частоты открытого резонатора с плоскими
зеркалами. Сравнить с тем, что получается при конечных значениях а.
Решение. При а=0 мы имеем
Ci—Со=
поэтому согласно задачам 7 и 8
i—i а2
X=(2«+l)-^--i
откуда видно, что перекос вносит дополнительное радиационное затухание,
(л \
О < -х I мы имеем
Л4г
с, — co = 2cisin2a — i, Ci=-4’
8—2547
113
й2 / 2i \
X — (2m + 1)“ — 2Af2sin2a + Af2sin2a J’
в этом случае влияние перекоса гораздо слабее: в основном перекос влияет иа
й2
частоту, а приращение радиационного затухания пропорционально
Для выпуклых и короткофокусных зеркал (см. конец § 15) влияние их
перекоса также слабое, поэтому плоскопараллельные зеркала с их чувстви-
тельностью к перекосу (§ 9) занимают особое положение.
Глава IV
Открытые резонаторы
со сферическими зеркалами
§ 18. Сфероидальная система
координат
В этой главе исследованы собственные колебания открытого
резонатора со сферическими зеркалами при произвольном от-
ношении радиуса кривизны зеркал к расстоянию между ними.
Поле колебаний рассматривается в криволинейной (сфероидаль-
ной) системе координат, соответствующей конфигурации зеркал,
причем задача приближенно сводится к интегрированию пара-
болического уравнения. Такой подход наиболее просто и на-
глядно дает нам асимптотическое решение рассматриваемой
диффракционной задачи при условии, что длина волны доста-
точно мала по сравнению с характерными размерами системы и
что система достаточно вытянута по оси z (параксиальное при-
ближение) .
Введем сфероидальные координаты р, <р, £, связанные с ци-
линдрическими координатами г, <р, z соотношениями
r=dchCsinp, z = dshCcosp (18.01)
и изменяющиеся в пределах
0<р<4Ь —сю<С<оо. (18.02)
При этом поверхность C==tconst есть сплюснутый эллипсоид-
для которого ось z—-ось вращения и расстояние между фокуса,
ми равно 2d, а поверхность р — const есть однополостный гипер-
болоид вращения, при С — zt оо асимптотически приближающийся
к конусу, образующие которого проходят через начало координат
и составляют угол р с осью z.
8*
115
Зададим отражающие поверхности зеркал с помощью соот-
ношений
0<р<р, 0
Если выполняется условие
sin2 р < ch2 С,
(18.03)
(18.04)
то радиус кривизны таких зеркал можно считать постоянным и
равным
, ch2?
r„ = d——
° sh?
(18.05)
так что соотношения (18.03) практически задают нам сфериче-
ские зеркала круговой формы (наряду с такими зеркалами мы
рассмотрим в § 20 также сферические зеркала прямоугольной
формы). Фазовые соотношения для сферических зеркал радиу-
са го и для сфероидальных зеркал (18.03) практически совпа-
дают при дополнительном условии
kd sin4 р ch С < 1, (18.06)
которое мы также будем считать выполненным.
Максимальное расстояние между зеркалами равно 21, где
/ = rfshZ, (18.07)
а диаметр зеркал равен 2а, где
a = dchCsinp. (18.08)
Если задать геометрические параметры r0, I и а, то при г0>/
всегда можно найти такие d, С и р, что открытый резонатор впи-
сывается в соответствующую сфероидальную систему координат,
позволяющую наиболее просто исследовать распределение поля
в резонаторе.
Коэффициенты Ламе в сфероидальной системе р, у, С равны
hp = hz = h — dyrch2C~sin2p , /i9 = dchCsinp, (18.09)
поэтому волновое уравнение (12.10) принимает вид
1___. дФ\ . /J_____________1 \д2Ф ।
sin р dp ^slnP др J~r(sin2p ch2? J ду2
+чет i (ch c (ch“ c ~sin! p) ф=°. (i8.io)
где параметр y=kd, a Ф есть скалярная функция, связь которой
с электромагнитным полем будет рассмотрена в § 23. Пока же
будем искать асимптотическое решение уравнения (18.10), удов-
летворяющее граничному условию Ф=0 на зеркалах (18.03),
в виде
Ф = W (р, <?, С) е'т sh с - (- 1)9 W (р, C)e-iT sh\ (18.11)
116
т. е. в виде двух волн, распространяющихся в направлениях
и переходящих друг в друга при замене Z, на —£ (с точностью
до множителя —(—1)«, где q есть целое число). Функция W
определяет комплексную амплитуду этих волн и удовлетворяет
уравнению
1___д_ / . дФ \ ______1_\ d2W
sin р dp ^Slfl Р др J • ^sin2 р ch2£ J ду2 т-
+стг4 (ch с^)+2Zych с -^+sh с - sin“ Р)W= 0>
(18.12)
которое мы будем приближенно решать при следующих условиях
Y > 1, sin2p < 1,
(18.13)
совместных с условием (18.06).
Первое условие (18.13) выполняется, коль скоро все размеры
открытого резонатора велики по сравнению с длиной волны (см.,
впрочем, § 22). Второе условие усиливает условие (18.04) и озна-
чает, что между зеркалами, при 0<р<р, ось С составляет с
осью z малые углы, причем множители e±,TSht в формуле (18.11)
соответствуют распространению по оси z со скоростью, близкой
к с. Первое условие (18.13) позволяет в уравнении (18.12) пре-
небречь членом —(ch поскольку он мал по сравне-
нию с членами, следующими за ним, а второе условие (18.13)
позволяет заменить в уравнении (18.12) sinp на р и пренебречь
членом — ch2?'~d^~‘ ® результате мы получаем параболическое
уравнение довольно простого вида:.
р dp др ) 1 р2 ду2 11 д; 1
+ (2iYshC — Y2p2)U7 = 0, (18.14)
в то время как уравнения (18.10) и (18.12) — эллиптические.
Делая подстановку
’Г (х,?,а),
Г Л (18.15)
т=)/2ур, О = j ThT== arc sin (th С),
о
преобразуем уравнение (18.14) к еще более простому виду
1 д / дФ\ . 1 д2Ф . . дФ г2 _ /10
---Н--------------г---+ — Ф = 0. (18.16)
т дт V дт J 1 т2 ду2 1 de 4 ' ’
117
Последнее уравнение формально совпадает с временным уравне- j
ннем Шредингера для изотропного двухмерного гармонического i
осциллятора. Оно позволяет рассмотреть собственные колебания :
между сферическими зеркалами круговой формы.
§ 19. Сферические зеркала
круговой формы
Для зеркал круговой формы функция V должна удовлетво-
рять соотношению
—a)=eZ(2W-'?)‘F(x,T,a) при 0<t<5, (19.01) ’
вытекающему из условия Ф=0 на зеркалах. Параметры т и « J
в соотношении (19.01) определяются формулами: '*
x = р = |/-^-sin2a .
а — arc sin (th С) =arc sin у — , (19.02) •
Г Го
sina — 1/”— , cosa= j/ 1-----— , sin2a = 2i / — ( 1---—) . j
' г <, Т ге ’ I/ г»\ r° / 1
На геометрическом продолжении нижнего зеркала должно вы- 1
подняться условие
W (т, у,— а) —0 при т>т, (19.03)
выражающее отсутствие волны, распространяющейся вверх и !
возбуждаемой токами на нижнем зеркале (которые согласно |
§ 23 пропорциональны Т(т, <р, —а) и на геометрическом продол-
жении зеркала отсутствуют).
Наличие двух граничных условий (19.01) и (19.03) связано
с диффракцией на краях зеркал, при т=т. Учет диффракции про- j
изводится сравнительно просто (см. § 21) только в случае пло- i
ских (а=0, г0 = со) и концентрических (а= у,го=1) зеркал, для -1
которых она имеет решающее значение, поскольку между та- j
кими зеркалами только благодаря влиянию краев могут суще- j
ствовать колебания с малыми потерями на излучение. Чтобы ।
рассчитать диффракционные явления в общем случае, прихо- 1
дится решать интегральное уравнение для плотности тока на 1
зеркалах (ср. гл. VII). Оказывается, однако, что для колебаний,
обладающих весьма малыми радиационными потерями в ре- |
зультате образования внешней каустической поверхности (см. 1
ниже), вычисление этих потерь не имеет большого практического !
значения, так как они заведомо перекрываются джоулевыми и 1
другими потерями. Поэтому мы сначала исследуем колебания j
в открытом резонаторе, не учитывая диффракции и условия .
118
(19.03), т. е. считая то = со, и лишь потом (в § 21) рассмотрим,
к чему приводит диффракции при конечных значениях т.
В силу симметрии задачи положим
'Г = 'I'm (т, a) cos ту (/п = 0,1,2,...),
Ф — 'Г,п (т, а) sin ту (т = 1,2,...). (19.04)
Функция Ч.;то удовлетворяет уравнению
— 4- (* -^4+ i f — - J—-4V1 ™ = 0, (19.05)
-С Ox V дт j 1 до 1 I 4 z2 J 4,1 ’ v 7
частное решение которого имеет вид
<Fm = e-b>(T), (19.06)
где х — постоянная, а ф есть решение обыкновенного дифферен-
циального уравнения
Id/ (/ф \ I / X® \ , ____________/\
----I 1+( х-----------7------2 )Ф = 0, (19.07)
1 di I dt ) 1 1 4 z J
имеющего конечное значение при т=0 и исчезающее при т—-оо.
Первое требование вытекает из того, что на оси z поле не долж-
но иметь особенностей, а второе — из того, что функция (19.06)
должна давать приближенное решение задачи при конечных,
хотя и больших значениях т. Действительно, мы решаем сейчас
задачу без учета условия (19.03), но если при т>т, где пара-
метр т достаточно велик, функция ф достаточно мала, то усло-
вие (19.03) по существу удовлетворяется приближенно, и в ре-
зультате его уточнения функция (19.06) испытает лишь малое
возмущение.
Можно показать, что уравнение (19.07) допускает решение,
удовлетворяющее поставленным выше требованиям, лишь при
x=xm<n = m-|-2ra-|-1 (// = 0,1,2,...). (19.08)
Это решение имеет вид
Ф = фт.п (т) = -----------е , (19.09)
2 2 Ул! (лг+л)!
где L*™’— полиномы Лагерра, определяемые соотношениями (ср. [21])
£(nm,(x)=:(— ех ^-(xm+rie~x),
L(om> (х) = 1, L[m) (х) = х - (т + 1),
L{^(x) = x2 — 2 (л/г-j—2) jv-|(m-ф-1) (m2). (19.10)
К этим соотношениям легче всего прийти, вводя новую пере-
менную х=-^-, преобразуя уравнение (19.07) в уравнение И] ре-
119
дингера для атома водорода (см., например, [21], стр. 210) и
ограничиваясь собственными функциями дискретного спектра
(19.09), удовлетворяющими соотношению ортонормальности
,n СО фт> (0 td-c = Ьпп,^ (19.11)
о
Подставляя функцию (19.06) с учетом формул (19.04) и
(19.09) в условие (19.01), находим, что функция (19.06) соответ-
ствует собственному колебанию, частота которого определяется
по формуле
26/=л?+2(/и+2га+1)а, (19.12}
где q есть большое целое число (поскольку мы считаем kl > 1).
Представление о поведении функции 'ф=ф7П>п(т) можно полу-
чить непосредственно из уравнения (19.07). Положим
т=е~, ~ = (19.13)
тогда для функции ф получим дифференциальное уравнение
-^ + [х-/7т(т)]т2ф = 0, (19.14)
d т2
в котором
t/mco=4+^f- <19л5>
Функция £7о("г) для симметричных колебаний изображена
на рис. 27; горизонтальные прямые соответствуют значениям хо.п,
их пересечения с кривой 170(т) определяют значения то,п. при
которых разность х0,п—/7о(т) изменяет знак. Поэтому функция
фо.п осциллирует в интервале О<т<то,п и монотонно убывает
при т>то,п. Так как т есть в сущности безразмерный радиус-
РИС. 27. Функция U0(r) и зна-
чения Хо.п-
РИС. 28. Функция и значе-
ния Х1,„.
120
вектор на поверхности £=const, то функцию фо.п('Т) на плоско-
сти т, ф можно схематически представить в виде радиального
пучка лучей, испытывающих полное отражение от окружности
т=То,п- При т=0 эти лучи фокусируются (ось z есть фокальная
линия, ср. § 15). В пространстве между зеркалами поле можно
представить в виде лучей, пересекающих ось z под малым углом
и затем попеременно отражающихся от каждого зеркала. Вслед-
ствие вогнутости зеркал лучи не могут проникнуть дальше ги-
перболоида т=то,п; это — каустическая поверхность, за которой
поле убывает экспоненциально.
На рис. 28 изображена функция (7г(т) и значения (п=0,
1,2). Так как [7т(т)—>оо при т—>0 и т=1, 2, ..., уравнение
£Лп(т) =х/п,п имеет при т>0 два корня: т'т,„ и хт,п>т'т,п.
Функциям фт,п(т)со5 пир или фт,?1 (т) sin «ф на ПЛОСКОСТИ Т, ф
соответствуют лучи, заполняющие кольцеобразную область
х'т,п<г<хт,п- В пространстве между зеркалами поле представ-
ляется в виде лучей, заполняющих пространство между гипербо-
лоидом т=т'т,п, являющимся внутренней каустической поверх-
ностью, не позволяющей лучам подходить слишком близко к оси
вращения, и гиперболоидом т=тт>Г! — внешней каустической
поверхностью. Внутренняя каустическая поверхность характерна
для несимметричных волновых полей в системах, обладающих
симметрией вращения (например, для двухмерных полей вида
Jm(kr) cos пир, где Jm—функция Бесселя), внешняя каустиче-
ская поверхность появляется вследствие вогнутости зеркал.
Если т>тт,п, то благодаря внешней каустической поверхно-
сти поле данного колебания вблизи края зеркала оказывается
слабым, и в результате диффракции на крае собственная функ-
ция, определяемая формулами (19.06), (1'9.08) и (19.09), изме-
нится незначительно. Если же х<тт,п, то функция (19.09) «.не
укладывается» в данном резонаторе и соответствующее колеба-
ние формируется диффракцией на крае подобно колебаниям
в резонаторе с плоскими зеркалами.
Из рис. 27 и 28 следует, что симметричные колебания (т=0)
имеют меньшие потери на излучение, чем несимметричные
(т = 1, 2, ...) с тем же индексом п. Это объясняется тем, что не-
симметричные колебания имеют внутреннюю каустическую по-
верхность, вследствие чего внешняя каустическая поверхность
расположена дальше от оси вращения (to,?i<Ti,,i<T2,?i<. ..).
Если же мы возьмем открытый резонатор со сферическими зер-
калами кольцеобразной формы (проекция зеркала на плоскость
2=0 есть кольцо, определяемое неравенствами 5<г<а), то си-
туация изменится: симметричные колебания станут сильно излу-
чать, а наименьшие радиационные потери будут у несимметрич-
ных колебаний, удовлетворяющих условиям
]//П^Г'8*п2а и 1 sin 2а . (19.16)
121
§ 20. Сферические зеркала
прямоугольной формы
Рассмотрим теперь сферические зеркала, проекция которых на
плоскость 2 = 0 является прямоугольником со сторонами 2а и 2Ь.
Поверхность таких зеркал определяется соотношениями
— a<<dchCsinpcos а,
— b < d ch С sin р sin у < b,
С = (20.01)
Обозначим через р максимальное значение координаты р на зер-
калах и будем считать, что выполняются условия (18.13). Вводя
„квазидекартовы* координаты
5=pcos<p, 7j = psin<p, (20.02)
мы можем переписать уравнение (18.14) в виде
-г 2q ch C + [2tу sh С — у2 (E2 + r,2)] W = 0,
считая W функцией Е, т; и С. Подстановки
IF = -I?- V (тх, т„, a),
ch С ' x* y'
tx=p/'2y«, S—V^yv;, a=arc sin (th C),
приводят к уравнению
а2Ф аФ _1±± ш _ n
da ' 4 ’
Л 1)
которое надо решать с учетом граничных условий
'F (*х, ху, — а) = е'(2*'~”?) W (тх, tv, а)
ПРИ | Тх | < Та И | Ту | < ть
и
л) = 0 при I тя | > та или |Ty|>Tb.
Через 2/ мы по-прежнему обозначаем расстояние между
лами по оси 2, через г0 — радиус кривизны зеркал, параметр а
определяется теми же формулами (19.02), а параметры та и т&
соответственно равны
ta= sin2a, ть=-^_^-sin2a . (20.08)
Уравнение (20.05) имеет решение
'F=(тх, о) Yь (ту, о), (20.09)
(20.03)
(20.04)
(20.05)
(20.06)
(20.07)
зерка-
122
где функции и Ч^ удовлетворяют уравнениям
д' Фа
1 да 4
'Га = 0,
, .дЪ
д^у до
С2
f-Wb = 0.
(20.10)
Условия (20.06) и (20.07) будут удовлетворены, если функции
Чг„ и Чг6 подчинить условиям:
'Га(хж, — а) = е‘х»Чга(<гзс,а) при |тх|<та,
^(Ъ>~ а) — ег,Сь Ч’ь (ty, а) при | ^ (< ть, (20.11)
и
^аК, —а) = 0 при I Тх|>та,
Ч'ь(га,-а) = 0 при |г,|>гь. (20.12)
Частота собственных колебаний определяется формулой
2kl=nq+%a+Xb- (20.13)
Функции Ч^а н Чгь соответствуют двухмерным собственным
колебаниям открытого резонатора с цилиндрическими зеркала-
ми (бесконечной длины и конечной ширины 2а и 2Ь, см. гл. III).
Если пренебречь диффракцией на краях, то будем иметь:
'Г<х = е V Ха = (2/га4-1)а,
-'(« + 4- у
Wb = e > ф^), Хь=(2«4-1)а, (20.14)
Ха+хь = 2(/га + /г4- 1)а, т, п=0, 1,2,...,
где
К» СО = (2л)1/4 е , (20.15)
причем Нт(г) есть полином Эрмита (см. § 12). Функции (20.15)
удовлетворяют дифференциальному уравнению (13.01) и соот-
ношению ортонормальности (12.26).
Колебание, определяемое формулами (20.09) и (20.14),
можно интерпретировать как совокупность лучей, заполняющих
область
(20.16)
123
границы которой являются каустическими поверхностями. Если
эта область целиком помещается между зеркалами, не выступая
за их края, то 'под влиянием краев собственные функции и соб-
ственные значения (20.14) испытывают лишь слабое возмуще-
ние, в противном случае возмущение является сильным.
Заметим, что
%.о('1)=Г2^Фо('1х),?о(''г/)- (20.17)
В общем случае функция фт,и(т)соз тер или фт.„(т)з1п т<р есть
линейная комбинация произведений Фт, (гж) <lin, , соответст-
вующих той же частоте (19.12). Дело в том, что собственные ча-
стоты, определяемые формулами (19.12), (20.13) и (20.14), при
т>0 или «>0 являются вырожденными, поэтому собственные
функции, не учитывающие влияния краев, можно выбирать по-
разному. Возмущающее действие краев ликвидирует произвол
в выборе невозмущенной системы функций и приводит к тому,
что для зеркал круговой формы следует пользоваться функция-
ми (19.09), а Для зеркал прямоугольной формы — функциями
(20.15).
Кроме диффракции на краях могут быть другие возмущаю-
щие факторы, снимающие вырождение и делающие однознач-
ным выбор собственных функций. Прежде всего, таким факто-
ром являются сферические аберрации, учитывающие непарак-
сиальность данной системы, а также незначительный астигма-
тизм системы. Мы вернемся к этому вопросу в гл. VI (см. так-
же задачу 3).
§ 21. Диффракционные
явления
Выше мы учитывали диффракцию лишь постольку, посколь-
ку поведение волнового поля при наличии каустических поверх-
ностей есть в сущности диффракционное явление. В открытых
резонаторах также важна диффракция на краях зеркал, а в слу-
чае концентрических зеркал (см. ниже § 22) — диффракция
в фокусе.
При учете диффракции на краях зеркал формулу (19.12)
следует переписать в виде
2kl=nq+2(m + 2n—1)а + 2лр
(m = 0, 1, 2, ...; и=1, 2, ...), (21.01)
а формулы (20.13) и (20.14) —в виде
2kl=nq+2(m+n—1)а+2лр
(т, п=1, 2, ...), (21.02)
124
где р=р'—ip" есть диффракционная поправка, зависящая от
индексов типи учитывающая влияние краев на частоту коле-
баний и их затухание во времени.
Влияние диффракции на колебания с каустическими поверх-
ностями можно понять так: невозмущенное поле у края сфери-
ческих зеркал круговой формы согласно формуле (19.09) про-
порционально е (мы отвлекаемся от предэкспоненциального
множителя, зависящего от т и п). Если рассчитать излучение
из резонатора, пользуясь выражением для невозмущенного поля'
(как это часто делают для получения приближенных оценок),
то комплексный параметр р будет, очевидно, пропорционален
е~следовательно, колебания с небольшими индексами тип
будут иметь весьма малые потери на излучение при умеренных
значениях т. Этот вывод подтверждается численными результа-
тами, полученными в гл. VII для софокусных зеркал (г0=2/),
однако оказывается, что р уменьшается быстрее, почти как
е-х*. Таким образом, диффракция на краях приводит к сниже-
нию радиационных потерь. При отсутствии каустических по-
верхностей диффракция на краях сама по себе обеспечивает
малые радиационные потери (см. гл. I), хотя и превышающие
потери при образовании каустик в открытых резонаторах тех
же размеров.
х2
Кривизна зеркал учитывается членом — ЧГТО в уравнении
t2+r2
(19.05) и членом ——— W в уравнении (20.05). Если параметр
t невелик, то этим членом можно пренебречь и влияние кривизны
будет несущественным, в частности каустики образоваться не мо-
гут; тогда диффракция на краях происходит так же, как на краях
плоских зеркал, рассмотренных в гл. I. Из формул (19.02) следует,
что малые т могут получиться при sin 2а « 0, a sin 2а обращает-
ся в нуль либо при -у- = оо, либо при -р-=1. Первый случай
соответствует плоским 'зеркалам, второй — концентрическим сфе-
рическим зеркалам.
Между распределением токов на плоских и концентрических
зеркалах существует простая связь (см. § 14 и [26]), которая
не распространяется на распределение поля между зеркалами.
Эту связь легко установить с помощью интегрального уравне-
ния для тока на зеркалах. Введем при о>сг/ функцию
G t' т',., 5-------а') = --:—----т; X
' х' У' х> > 4л sin (о—о')/х
[о 9 /о /О ‘
zx + zy+zx + zy 2 (тх z’x + Тц -/„)
tg(c — o') Sin (а — а')
(21.03)
125
удовлетворяющую уравнению (20.05) и предельному соотноше-
нию
lim G (тЖ) тц, т'х, т у, о о) — 8 (тх т ж) 8 (by т у). (21.04)
а->а'+0
Это — функция Грина для параболического уравнения (20.05)
(ср. § 14). Она позволяет написать для функции У при а>—а
выражение
'Г К, о) =f ('х. Х'х, *'и, ° + <*) 'Г (^'х, *'у, — а) dz'x dt'y,
s'
(21.05)
•автоматически удовлетворяющее уравнению (20.05) и условиям
(19.03) или (20.07); в качестве 5 взята область в плоскости хх,
xv, соответствующая поверхности зеркала (т. е. круг или прямо-
угольник). Граничные условия (19.01) или (20.06) приводят
к интегральному уравнению
‘5Г К, — а) = e‘z J j G (тя, ту, т'х, т'у, 2а) Ф (т'ж, т'у,— а) dt'x dt'y,
s
(21.06):
-определяющему собственные функции Ф(Тх, ху, —а), собствен- :
ные значения е*х и собственные частоты колебаний, определяе- 1
мые формулой
2kl=nq+^. (21.07)
Рассмотрим теперь два сопряженных резонатора (ср. § 14),
л
радиусы кривизны которых г0 и г0 удовлетворяют соотношению
^+4=4’ <21-08)
Го
в то время как размеры зеркал (а или а и Ь) и расстояние меж-
ду зеркалами 21 у них одинаковы. Из формул (19.02) следует,
л
что параметры а и а сопряженных резонаторов связаны соот-
ношениями
а = -£--а, tg2a =— tg2a, sin2a=sin2a, (21.09)
откуда
G К, т'х, т’у, 2а) = — G* (— тж, — Ту, т'х, т'у, 2а). (21.10)
Вследствие симметрии области S собственные функции удов-
летворяют соотношению
(^х, — a) = z±: Ф (— tx, — Ту, — а),
(21-11)
426
поэтому функция Ф* есть решение интегрального уравнения
Ф* К. ‘'г/. — а) = e~‘z* J jG К, ту, t'x, т'у, 2а) X
S
X Ф* «, *’у, - а) dT'x dz'y, (21Л 2)
А
которому должна удовлетворять функция Ф (%., ту, — а) для соп-
ряженного резонатора. Отсюда следует, что
е‘^=^е~^. (21.13}
Последнее соотношение вместе с формулой (21.01) позволяет най-
А
ти связь между х и Z для зеркал круговой формы в виде
X = (/та —2/г—l)?t — х* (т = 0,1,...; п=1,2,...). (21.14}
Для зеркал прямоугольной формы имеем
Х=(т~1-п—1)я — х* (т, п= 1,2,...). (21.15)
Диффракционные поправки в формулах (21.01) и (21.02) для со-
пряженных резонаторов связаны соотношением
р= — р*. (21.16}
Таким образом, резонатор с софокусными зеркалами (г0 = 2/,
а=-^-А является самосопряженным:- его собственные функции
Ф (тх, Ту, — а) — вещественные, а диффракционные поправки р —
— — i | р | — чисто мнимые.
Если исходить из плоских зеркал и постепенно увеличивать
их кривизну, оставляя размеры зеркал и расстояние между ни-
ми неизменными, то наиболее благоприятные условия для обра-
зования каустических поверхностей будут при Го=2/, в случае
софокусных зеркал. Это видно из формул (19.02) и (20.08), по-
скольку sin 2а достигает максимума при а— -j-; для софокусных
зеркал радиационное затухание колебаний с каустиками наи-
меньшее, так как поле у края резонатора оказывается наиболее
слабым (впрочем, следует иметь в виду неустойчивость резона-
тора с софокусными зеркалами, см. § 36).
При дальнейшем увеличении кривизны каустические поверх-
ности вблизи зеркал движутся к их краям, вследствие чего ра-
диационное затухание колебаний растет. Вместе с тем, усили-
вается концентрация поля вблизи центра резонатора; это видно
из того, что в плоскости z=0
r=y/"-^-ctga т. (21.17}
127
.и при увеличении а каустические поверхности движутся к оси z, .
охватывая все меньшую площадь. Наконец, при а = каусти- ’j
ческие поверхности пропадают, и в месте их сужения образует-
ся фокус. Дальнейшее увеличение кривизны нерационально, так
как мы приходим к резонаторам, которые сопряжены с резона-
торами, имеющими выпуклые зеркала (см. конец § 15), и по-
РИС. 29. Лучи между плоскими (а), софокусными (б, г) и концен-
трическими (в) зеркалами.
Если рассматривать открытые резонаторы с точки зрения
геометрической оптики, то для плоских зеркал можно построить
совокупность параллельных лучей (рис. 29,а), а для концентри-
ческих зеркал — совокупность радиальных лучей (рис. 29,в),
переходящих друг в друга при отражении и в какой-то мере со-
ответствующих волновым полям в резонаторах. Для софокусных
зеркал можно построить (рис. 29,6) параллельные лучи, которые
после одного отражения проходят через центр резонатора, а по-
сле второго отражения становятся опять параллельными. Одна-
ко такие лучи никакого отношения к собственным колебаниям
не имеют. Если колебание имеет внешнюю каустическую по-
верхность, то его можно представить (ср. § 19 и § 20) так, как
это показано на рис. 29,г, т. е. в виде лучей, попеременно от-
ражающихся от зеркал и при этом не доходящих до краев.
§ 22. Концентрические
сферические зеркала
Резонатор с концентрическими сферическими зеркалами яв-
ляется сопряженным по отношению к резонатору с параллель-
ными плоскими зеркалами той же формы, так что приведенные
в гл. I выражения для плотности тока на поверхности плоских
зеркал (прямоугольных и круглых) позволяют без труда найти
128
плотность тока на концентрических зеркалах. Диффракционная
поправка для концентрических зеркал круговой формы равна
2
П=________________
Р я(М + ₽-«₽)8 ’
М=^р = 0,824, (22.01)
где vmn есть n-й нуль функции Бесселя Jm. Для концентрических
зеркал прямоугольной формы
__ ТОЙ® ПП2
Р~~~~ 4(Mo + ₽-i₽)8’-4(Mb+₽-W‘
Л4а = |/^-,
(22.02)
Следует отметить, что в случае плоских и концентрических
зеркал переменные т, тж и гу неудобны; кроме того, для концен-
трических зеркал d = 0 и у = 0. Так как в § 18 мы считали
у > 1, то концентрические зеркала следует рассмотреть отдельно.
Введем сферические координаты R, р, <р такие, что угол р изменя-
ется в пределах 0 < р < , но зато радиус-вектор R принимает
как положительные, так и отрицательные значения; как мы уви-
дим ниже, такие координаты удобны при рассмотрении диффрак-
ции в фокусе.
Мы ищем решение волнового уравнения (12.10) в виде
Ф = W (р, ?, R) eikR — (— 1)« W (р, — R) e~ikR (22.03)
и получаем для IF уравнение
1 д (. гатг X , 1 d2W }____д / dW \
sin р др ? др у sin2 р д<р2 "• dR dR }
+ 2ikR (RW) = 0. (22.04)
Задавая поверхность зеркал соотношениями
0<р<(Г, 0<<р<2я, R = ±l (22.05)
и считая sin2 р< 1, можно в уравнении (22.04) заменить sinp на р.
Пренебрегая, кроме того, членом получаем парабо-
лическое уравнение
+ = (22.06)
р dp kг др J 1 р2 ду2 1 дк ' ' '
которое после перехода к координатам (20.02) принимает вид
-4^+^+2<М-^«Ю=О. (22.07)
9—2547
129
Функция Грина для этого уравнения имеет вид (ср. § 15) 1
г (Е, та, R, Е', 7]\ R') = -2п ехр ----------------J 3
при R > R', RR' > 0, (22.08) I
Г(Е т /? £' г' /?')______~ехр / ikRR' (6 + V)*+ (ч + ч,)8-1 I
1 («, •»!, а, 5 , 1Q , ) 2* (Я — R') ехр | 2 R — R' J 1
при R "> 0, /?' < 0, 1
причем £
lim r(UW,fl>|^M')«(’l-’l')- (22.09)1
Д-»Я'+0 Iк I >
Легко видеть, что при 1 и любых kR отброшенный член -1
д ( дг X 1
~dR\™~dRi Действительно мал по сравнению с остальными. я
Вместо формулы (21.05) теперь имеем 1
Г (И, R) — — l JJr(E,ij,/?,£', if,— Z) IF (£', ц', — l)dk'dri', Я
(22.10)1
где S есть область в плоскости £, тр соответствующая поверхно- 1
ста зеркала [круг для зеркала (22.05), прямоугольник]. Из вы- Я
ражения (22.10) нетрудно получить интегральное уравнение для 1
функции W(1-, т), —0- Оно сводится к уравнению для пло- я
ских зеркал; это подтверждает связь между резонаторами с кон- 'I
центрическими и плоскими зеркалами, сформулированную выше Я
(ср- § 14). 1
Вместе с тем, выражение (22.10) показывает, что поле кон- J
центрируется вблизи фокуса R — 0. Если, например, положить^
IF=1 на нижнем зеркале (22.05), то получим формулу ।
“р ь М J
^ = -TClfe 2 ^(VPP')P^P', v = (22.11)1
0 1
согласующуюся с классическим выражением для поля у фокуса 1
(ср. [29]). Асимптотический скачок фазы в фокусе вытекает из я
тождества 4
j f Г (Е, TJ, R, Е', V, — 0 ^Е' dr/ = ~, (22.12) $
—со
поскольку /?<0 до прохождения волны U7eiftR через фокус и R>
>0 после прохождения фокуса. Распределение поля собствен- «
ного колебания вблизи фокуса является более сложным, чем _(
вычисляемое по формуле (22.11), так как функция IF на зерка- J
ле имеет непостоянную амплитуду и фазу. I
130
§ 23. Электромагнитные поля.
Общие замечания
До сих пор мы решали скалярное волновое уравнение с гра-
ничным условием Ф=0 на зеркалах. Однако нас интересуют
электромагнитные колебания, поэтому нужно решать уравнения
Максвелла
rotH = — ikE, rotE = i£H (23.01)
вместе с вытекающими из них уравнениями
div Е = 0, div Н=0 (23.02)
и граничными условиями на идеально проводящих зеркалах
^ = ^ = ^ = 0. (23.03)
Учитывая, что мы ищем приближенное (асимптотическое)
решение, можно выразить электромагнитное поле линейно по-
ляризованных собственных колебаний через скалярную функ-
цию Ф следующим образом. Положим
E=rotrotlle, Н=—i&rotIF, (23.04)
тогда первое уравнение (23.01) и оба уравнения (23.02) удов-
летворяются. Если вектор Герца Пе удовлетворяет векторному
волновому уравнению
—rot ro*tlle+grad div IIе+Л2 Пе=0, (23.05)
то будет удовлетворяться и второе уравнение (23.01), причем
электрическое поле представится в виде
Е=grad div Пе+й2Пе. (23.06)
Положим теперь
П* = Ф или = Ф [(23.07)
и будем считать, что другие две составляющие вектора Герца
равны нулю. Тогда мы не можем точно удовлетворить уравнению
(23.05) и вместо этого требуем, чтобы, например, составляющая
П® удовлетворяла уравнению, которое получится, если прирав-
нять составляющие Е^, вычисляемые по формулам (23.04)
и (23.06). Вычислив Ег и Et по формулам (23.04) и (23.06),
нетрудно убедиться, что эти формулы дают практически эквива-
лентные результаты — несовпадающие члены в у раз меньше совпа-
дающих. Этим и обосновывается применение составляющих 1Ц и
П®в качестве потенциалов электромагнитного поля.
9»
131
Производя вычисления в системе координат g, т], g, опреде-'1
ленной формулами (18.01), (18.09) и (20.02), надо иметь в ви- !
ду, что она ортогональна лишь приблизительно, а именно лишь S
постольку, поскольку можно положить = Лр. Мы будем счи-
тать, что такой аппроксимацией пользоваться можно (полагая •
ft=dj/ch2£ — р2), тогда все коэффициенты Ламе координатной <
системы г), g равны h. Для функций (23.07) получаются урав- ’
нения
h4г Г4 4- (Л2п*) 1 [-L А (йШ ) 14-
[ h3 х ' J 1 ду | h ду ' £ 7 J 1
+4 [4- i nt=°- (23.08)
4144(лпч)1+л4Г44(лгПч) 1+ !
dl [ h v J 1 ду [ h3 dft v J 1
+4[44«]+й2Л2П^0>
отличные от уравнения (12.10). Однако если мы будем искать^
функции (23.07) в виде (18.11) и делать те же пренебрежения, 1
что и в § 18, то для функции W получим прежние параболиче- !
ские уравнения (18.14) и (20.03). Если к тому же П*=0и = (
= 0 на зеркалах, то поля (23.04) будут точно удовлетворять гра-i
ничным условиям (23.03). '
Для зеркал прямоугольной формы можно согласно § 20 поло- '<
жить
1^ = е“г,'"+п-1)офт_1(тзс)фп_1(ъ) (тЛ=1,2,...), (23.09)!
тогда по формулам (23.04) и (23.07) нетрудно вычислить электро-.j
магнитные поля колебаний, которые естественно назвать колеба-
ниями Д^ и Д^’ в открытом резонаторе со сферическими зер-;;
калами прямоугольной формы; частота этих колебаний определяет- ’
ся формулой (21.02).
Для зеркал круговой формы согласно § 19 полагаем ,1
Wm=e-f,m+2”-1,>w.„_1(T) (m = 0,1,2,...;п=1, 2,...) (23.10) •
и получаем колебания Д^* и Д^в в таком резонаторе, частота
которых вычисляется по формуле (21.01).
Поверхностная плотность тока на зеркалах имеет для колеба-
ний Д^’з единственную составляющую по оси £, а для колеба-
ний Д^’ —по оси »]. Эта составляющая на верхнем зеркале
равна
f = ——Чг (6, т, С) eihl=—^4- 'Г (;, 7],—Q е~! ,
2itchS ' 1 ’ 2лсЬ? ’ ‘
(23.11)
132
а на нижнем равна—(— 1)<г/. Распределение токов на поверхности
зеркал при колебаниях Е{х} и E{v) качественно то же, что и
* 1 mnq mnq
при одноименных колебаниях в резонаторе с плоскими зерка-
лами прямоугольной и круговой формы (рис. 10 и 11), но и при
этом токи ограничены не размерами зеркала, а размерами ка-
устической поверхности, за пределами которой токи незначи-
тельны.
Заметим, что при приближенном рассмотрении уравнений
Максвелла можно исходить также из магнитного вектора Герца
IT”, определяющего поля по формулам
Е=ik го*1Пт, Н = rot rot П™. (23.12)
Полагая
П^ФшП^Ф, (23.13)
мы опять приходим к уравнениям (23.08). Так как для выпол-
нения граничных условий (23.03) на зеркалах должно быть
^-(йФ) = 0, (23.14)
1
то с точностью до поправочных членов порядка у вместо выра-
жения (18.11) можно пользоваться выражением
Ф = W (р, <р, С) е‘7 sh с + (— 1)« W (р, С) е“'7 sh-c | (23.15)
с той же самой функцией W. Мы получим такие же колебания—
с теми же частотами и практически тем же распределением по-
лей и токов.
Выше изложена теория собственных колебаний в открытых
резонаторах со сферическими зеркалами. С теоретической и
практической точки зрения наиболее интересны колебания
с весьма малыми радиационными потерями. Эти колебания мож-
но представить в виде двух волн или двух лучевых потоков, рас-
пространяющихся навстречу друг другу и защищенных каусти-
ческими поверхностями от потерь на излучение в стороны. В
некоторых случаях эти лучевые потоки могут быть полыми вслед-
ствие образования внутренней каустической поверхности (§ 19).
Такие волны представляют интерес не только для открытых
резонаторов, но также для систем, осуществляющих передачу и
направленное излучение электромагнитной энергии.
Внешние каустические поверхности имеют наименьшие попе-
речные размеры в случае софокусных зеркал, когда радиус кри-
визны зеркал равен расстоянию между ними; такой резонатор
имеет наименьшее радиационное затухание. Однако применение
софокусных зеркал в ряде случаев (например, в квантовых ге-
нераторах света) нерационально вследствие слишком сильной
конкуренции колебаний с различными индексами и слишком ма-
133
лой радиальной протяженности колебаний с наименьшими поте-
рями на излучение; надо также иметь в виду чувствительность
резонатора с софокусными зеркалами к малым возмущениям
(см. § 36). Резонаторы с почти плоскими или почти концентри-
ческими зеркалами имеют большее радиационное затухание, но
зато спектр их более разрежен и распределение поля более рав-
номерно: для некоторых применений эти обстоятельства могут
быть решающими.
Задачи к гл. IV
1. Написать явное выражение для значений тт,п и определенных
графически на рис. 27 и 28.
Решение. Вычисляя положительные корни биквадратного уравнения
(т) =0
и учитывая формулы (19.08) и(19.15), получаем (/1=0, 1, 2, ...)
tm.n = [т + 2л 4- 1+ f(2n+ l)(2m-f-2n + 1)].
= lZ2 [m + 2л + 1 — Y(2л + 1)(2/п + 2л + 1)].
В частности, при т = 0 имеем
то,„ = 2/2п+1. t'o>n==0.
2. Свести уравнение ।(19.07) к дифференциальному уравнению второго
порядка без первой производной с помощью замены зависимой перемен-
ной— функции ф (а не независимой переменной т, как в формуле (19.13)
и следующих). Вычислить значения tln,n и т'т.п для нового уравнения.
Решение. Полагая
ф(т) = Ж,
j/V
для новой функции ф получим дифференциальное уравнение
^4 + [х-17т(г)]Т=О. («)
ат2
в котором функция
1
2 т2— ~4
Um (т) = “^'"4 ^2
отличается от функции (19.15) тем, что вместо тг в нее входит тг—Заме-
няя т на т2—--L в формулах для tm,„ и т'ГО1П задачи 1, получаем при
лг= 1, 2,. .. выражения, соответствующие новому дифференциальному уравне-
нию (а). При т = 0 мы имеем
то.„ = 1^/4 (2л + ОМ7! + 2 (2« + О-
t'o.n = ± i V/4 (2л + 1)!Т1 - 2 (2л + V
Если л>1 или /л > 1, то тт>„ и т'т.п, вычисленные по новым и старым фор-
134
мулам, мало отличаются; при конечных значениях тип оии несколько раз-
личны. Поскольку "^171,п и т т,п применяются для качественного анализа
функции ф(т), это отличие не ведет к каким-либо противоречиям.
3. Решить уравнение (18.10) методом разделения переменных, полагая
Ф = R (р ) Z (о) cos rnf (и = 0, 1, 2, . ..)
или
Ф = R ( р) Z (о) sin m<f
(m=1.2, ...).
где
Р
f dp р
₽ =
z/2
р ~ 2ер
tg9' = ep, sinp=-------
2 1+е2р
С
Г d?
а = I = arcsin (th?), th ? = sin а, ch?
о
Пренебрегая диффракцией на краях, вывести уравнение, обобщающее
уравнение (19.14). Показать, что при отказе от параксиальности собствен-
ные функции, найденные в § 20, ие существуют.
Решение. Для функций R и Z получаются уравнения
d2R
—™ + (Д’ sin2 р — у2 sin* р — тг) R — 0,
d р2
^+(-Rch2?+Y2ch«? + w2)Z = 0.
где К — постоянная разделения. При замене sin р иа р первое уравнение сво-
дится к уравнению (19.14) с вырожденными собственными значениями
(19.08), без этой замены вырождение отсутствует. В квазидекартовых коор-
динатах, подобных координатам >(20.02), переменные в уравнении (18.10); не
разделяются, поэтому решения вида (20.09) существуют только в паракси-
альном приближении; они отсутствуют, если взять точное уравнение (18.10),
не заменяя sin р иа р.
Вырождение собственных значений (19.08) тесно связано с возможностью
разделения переменных в двух различных координатных системах [см. фор-
мулу (20.17) и рассуждения, следующие за ней]. При отказе от параксиаль-
ное™ пропадает как вырождение, так и возможность разделения во второй
координатной системе (квазидекартовой).
4. Основываясь на формулах § 22, составить интегральное уравнение
для одинаковых концентрических зеркал круговой и прямоугольной формы
и написать выражения для собственных функций.
Решение. Обозначая
ЧЕ, i))=!F(g, ч, -/),
из граничного условия Ф=0 и выражения (22.10) получаем интегральное
уравнение
f (Е. >!) = - /ег J J г (Е, т). I. Е'. 7j', -1) f (£', v) dt'd-rf.
s
откуда для круговых зеркал, согласно гл. I. полагая
Е = р cos у, 7j — р sin у, 0 < р < р.
135
получим
/ VmnP \ cos /«?
Г — -’™!, 1—i\]sinwiip’
а для прямоугольных зеркал 1
—Т < Е < Е. i
имеем Ч
cos пот£ COS nn-Q
sin — / .1 — i \ sin — f 1 — i \ ч
£ (/ + ) 4 + ₽ -m~) j
5. Исследовать колебания между сферическим зеркалом (прямоуголь- <
ним или круглым) и бесконечной идеально проводящей плоскостью z=0,
перпендикулярной оси зеркала.
Решение. В такой системе возможны колебания £*/» и £(J2„ с четны- 1
гппц ттщ
ми индексами q— такие же, как и в симметричном резонаторе с двумя
одинаковыми зеркалами (§ 23).
6. Исследовать колебания между двумя сферическими зеркалами, коэф-
фициент отражения от которых изменяется по закону
/ х2 х2 \
1т2 х2 ]
R(tx. Ти) = е ' а ь' (— со<тж, ти<оо).
Для этого обобщить интегральное уравнение (21.06) и воспользоваться ре-
зультатом, полученным в задаче 3 к гл. III. Рассмотреть, что происходит при
Та = Tfc.
Решение. Рассуждая как в задаче 6 к гл. III, мы вместо интеграль-
ного уравнения (21.06) получаем
00
f (tx. Tv) == R (tx, ty) e‘z ££ G (tx, xv. т'х. x'v. 2a) f (t'x, t'v) dt'x dx'y.
—00
Полагая
__ i
_________ 2
f (tx. t„) = X (xx) Y (tv) VR (tx, Ту) = X (tx) Y (ty) e
и обозначая
„ „ 2i I /sin 2ao
COS 2an = cos 2a Д- —X sin 2a, т = I/
Tz r Sin 2a **
a
для функции
получаем интегральное уравнение
о»
X (г) = e‘Xa J G (т. т', 2aa) X (V) dx‘
где функция G(T, х', 2ао) определяется формулой (14.03). Собственные
функции этого уравнения определяются формулой (12.25)
Л’(т) = фга(г) (m=0. 1, 2, ...),
136
а собственные значения
Xo = (2m+ 1)«а-
Аналогичные результаты получаются для функции Y; при этом
Х = Ха + хь = (2т+ 1)ао + (2л + О'Ч-
Если to = ть, то ап = аь и собственные значения
X — 2 (т-(- п + 1) аа
вырождены. При наличии вырождения собственные функции f(tx, tv) инте-
грального уравнения также могут быть представлены в виде (ср. § 19).
f (тя, ту) = R (t) cos m<f (т == 0. 1. 2. . . .)
и
f (t«. tv) = R (т) sin ту (т=1. 2. . . .),
где г, <р — полярные координаты в плоскости хх, гу:
Tx=Tcosq>, ту=т sirup.
В качестве R(r) мы получаем
___________________________________________________
где функции фт,п определяются формулой (19.09).
7. Обобщить результаты задачи 6 на случай выпуклых (го<0) и корот-
кофокусных (г0<1) сферических зеркал.
Решение. Если мы во всех случаях определим величину а соотно-
шениями
sin а = у/ — . Im “ -С 0,
F го
то для выпуклых зеркал будем иметь
а для короткофокусных
тс
а = "2
Все соотношения, полученные в задаче 6, остаются в силе, причем мнимые
части а определяют затухание колебаний во времени, вызванные отрицатель-
ной или чрезмерной (|перефокусировка лучей) кривизной зеркал.
8. Собственные функции и собственные значения, полученные в § 19 и 20
(тс х
при Oc^a^-g-l, не учитывают
краевых эффектов (диффракции на краях зеркал). Найти в том же прибли-
жении собственные функции и собственные значения при го<0 и г0>1 (см.
задачу 7). Выяснить, при каких условиях краевые эффекты мало влияют иа
собственные частоты.
137
Решение. Если в задаче 6 положить тп=Ть = оо, то будем иметь ао =
=аь='а, и с учетом решения задачи 7 получим все требуемые соотношения.
Из выражений
’ж = у у sin 2а X, Ту = у -j- sin 2а у
следует, что т* и будут чисто мнимыми, поэтому собственные функции
4m (*х) Фп (ty) не локализованы вблизи начала координат.
Диффракционные поправки к частоте при условиях
Л4> 1. Л1О>1, Мь>1
я
"(см. формулы (22.01) и (22.02)] существенны только при а^О и , т. е.
для почти плоских и почти концентрических зеркал. Прн других значениях а
радиационное затухание, обусловленное кривизной зеркал, значительно больше
затухания, обусловленного диффракцией на краях (ср. задачу 7 к гл. III).
Глава V
Цилиндрические и бочкообразные
открытые резонаторы
§ 24. Цилиндрический
резонатор
В этой главе мы будем исследовать собственные колебания
цилиндрических и бочкообразных открытых резонаторов. Ци-
линдрическим открытым резонатором назовем отрезок трубы
кругового сечения, открытый с обоих концов; внутренняя по-
верхность этой трубы в цилиндрической системе координат г, ф,
z определяется соотношениями
г=а, 0<?<2к,
(24.01)
Добротные колебания в таких резонаторах обусловлены
сильным отражением волноводных волн от открытых концов ре-
зонатора подобно тому, как резонансные колебания открытых
труб в акустике обусловлены сильным отражением поршневой
волны. Если перейти от цилиндрической поверхности к бочко-
образной (т. е. сужающейся к концам), то в результате появ-
ления внешних каустических поверхностей излучение через от-
крытые концы может уменьшиться до весьма малых значений.
Будем искать решение скалярного волнового уравнения
(12.10) с граничным условием Ф = 0 на поверхности, определяе-
мой соотношениями (24.01), считая, что
kl > 1 и а > /, (24.02)
т. е. поверхность (24.01) имеет вид обруча.
139
Нетрудно показать (ср. [8], гл. III), что сформулированная
выше задача для бесконечно тонкой цилиндрической стенки
(24.01) сводится к функциональным уравнениям
etwz р (w)dw = 0 при | z | > I (24.03)
и
J F(w)dw = 0 при [z|</. (24.04)
—ОО
Входящая в эти уравнения функция F(w) позволяет вычислить
функцию Ф=Ф(1г, ф, z) во всем пространстве. Она связана со
скачком нормальной производной Ф при г—а соотношениями
^-(а + 0, z) — [а — 0, z) = — f (z) e±imp,
j (z) = j eiwZF(w)dw. (24.05)
—oo
При выводе уравнения (24.04) мы пользуемся условием излу-
чения и предполагаем, что собственные функции в нашей зада-
че имеют вид
Ф = фм (г, г) е±!т- (т=0, 1,2,...). (24.06)
Те же соотношения получаются при замене 屑т’> на cos дар или
sin дар. Функция <рт(иа) в уравнении (24.04) равна
<pm (va) = та F/^} (va) Jm (va), (24.07)
где
v = - \Fkz — w2 , Im v > 0. (24.08)
Вводя функции Am и Qm по формулам (6.11) так, что при
вещественных положительных х функция Ат (х) будет абсолют-
ной величиной функции (х), а Ц.Дх) —-ее фазой, мож-
но представить функцию (24.07) в виде
(va) = А2т (va) [ 1 - е^”*'™’]. (24.09)
Для колебаний с малыми потерями на излучение существенны
те значения w и v, которые удовлетворяют соотношениям (ср. § 2)
и
|ау|<£ (24.10)
v = k-^-t (24.11)
140
поэтому функцию Q,n(va) в формуле (24.09) можно представить
в виде
Qm (va) = (ka) - (24.12)
где
bm — a£l'm(ka), (24.13)
а в остальных множителях положить u = k.
В силу сделанных предположений частота колебаний удовлет-
воряет соотношению (ср. начало § 4)
где v°n есть /г-й положительный корень уравнения(х) = 0, для
которого справедливо равенство
= (24-15)
а -----, о------малая комплексная добавка, обусловленная диф-
&п ( утп)
фракцией на краях резонатора. Учитывая малость р, можно напи-
сать
£lm(ka) = n(n-\-р). (24.16)
Если ввести величину*
bm = aQ'm(v°mn), (24.17)
то функциональное уравнение (24.04) заменяется более простым
уравнением
Je?u,z£l — е ( F k ' J F(w)dw=0 при |’z| (24.18)
—-ОО
Согласно асимптотическим формулам Дебая для функций Бес-
селя и Ханкеля имеем:
£)т (х) = ]/хг — т2 — т arcsin 1-----------, (24.19)
* Величина Ьт зависит и от индекса п; ее можно было бы обозначить
через Ьтп, чего мы, однако, делать не будем. То же относится к величинам
ат, рт и другим, введенным ниже.
141
откуда
bm=ya*-a2m , (24.20)
где
= (24.21)
V
тп
При т <^ka можно положить Ьт=а. При х~т >1 формулы
(24.19) следует заменить формулами:
AnW=J^-,
У я д
Qm (л) = arc w (t), (24.22)
= м«2 (0 + ^(0!’
где u(t), v(t) и w(t) =ut (t) = u(t) +iv(t) функции Эйри (см.
§ 9 и книги [17] и [19]), а
t = (24.23)
V = (24'24)
Формулы (24.19) и (24.22) имеют общую область примени-
мости
1 < ц2, (24.25)
в которой
. (24.26)
Обозначим через t°n корни уравнения v(t)=O: t° =— 2,34;
<2= — 4,09; =— 5,52 (более полные данные см. [17], стр. 43
или [19], стр. 384). При т>1 и —корни v°n можно
представить в виде
< = («=1,2,...). (24.27)
Сами корни t°n уже при /г > 1 с удовлетворительной
вычисляются по простой асимптотической формуле
точностью
4<-О3'2=«(^^). (24.28)
142
Это свидетельствует о там, что асимптотические формулы
(24.19) применимы и вблизи корней (24.27). Следовательно,
величину Ьт в функциональном уравнении (24.18) всегда можно
вычислить по формуле (24.21).
Как показано в § 4, приближенное решение уравнений
(24.03) и (24.18) приводит к формулам
f (z) = cos ”дг (q = 1,3,...),
(24.29)
f (z)=sin ту (9 = 2,4,...),
где
м==у и P = 0,824. (24.30)
Параметр p в формуле (24.14) получается в виде
Р- 4(Л)Г; + эд. И=1.2.(24.31)
Если искать решение волнового уравнения при граничном
условии-^- — 0 на поверхности (24.01), то, вводя функции f(z)
и F(w) по формулам
Ф(а + 0,<р,г) —Ф(а —0, <p,z)=-^-f (z) e±ln\
(24.32)
f (z) = J eiwZ F (w) dw,
получаем для F(w) систему функциональных уравнений, а имен-
но уравнение (24.03) и уравнение
j* eiwZ-^- tym(va) F(w) dw = 0 при [z^l, (24.33)
—00
в котором
фт(оа) =nva (va)J'm(va). (24.34)
Рассуждая так же, как выше, и, в частности, полагая
где по-прежнему
ka — V -4________
(24.35)
Q'm(x) = y 1--5-
(24.36)
143
и v'mn есть n-й положительный корень уравнения /'т(х)=0, мы
легко преобразуем уравнение (24.33) в уравнение (24.18), при-
чем величина Ьт определяется формулой (24.20), в которой
Если обозначить через t'n корни уравнения v'(t)=O: t\ =
=—1,02; /'2=—3,25; /'з=—4,82, то при т > 1 и —t'n << g2 кор-
ни Vmn можно вычислять по формуле
V >пп“И1 р/ п. (24.38)
Для вычисления t'n имеется асимптотическая формула
-г"==[т-(й-^-)]2/3’ г)’ <24-39)
точность которой растет с увеличением п; она грубо применима
уже при п— 1.
В результате приближенного решения уравнений (24.03) и
(24.18) для функции f(z) опять получаются выражения (24.29),
а для параметра р в формуле (24.35)—выражение (24.31).
Следует иметь в виду, что функциональные уравнения (24.04)
и (24.33) написаны для цилиндрических резонаторов с беско-
нечно тонкой стенкой (24.01). Однако эти уравнения с помощью
ряда аппроксимаций [в частности, с помощью формулы (24.11)]
были преобразованы в уравнение (24.18); такие же уравнения
мы получили раньше для плоского волновода [второе уравне-
ние (2.03) с функцией (2.07)], они эквивалентны интегральному
уравнению (3.15); поэтому функциональные уравнения (24.04)
и (24.33) эквивалентны интегральному уравнению (4.19) и име-
ют такой же физический смысл и такие же пределы применимо-
сти. В частности, полученное решение справедливо для резона-
тора со стенкой любой толщины и даже с произвольной формой
внешней поверхности; важно лишь, чтобы внутренняя поверх-
ность резонатора определялась соотношениями (24.01).
§ 25. Внутренняя каустика
Исследуем теперь распределение волнового поля в объеме
резонатора, т. е. при г<а и \z\<l. Формулы (24.29) показывают,
что вдоль резонатора устанавливается стоячая волна, поэтому
функция Ф в объеме резонатора равна
® = CJm(gr)f(z)e±im’, (25.01)
где
£ = ~Г~- (25.02)
144
Под vmn мы понимаем v°mn или v'mn в зависимости от гранично-
го условия на поверхности г—а.
Функция Ли(£г) удовлетворяет уравнению
(г т) +(^2 - =0 <25-03)
или
4- (g2 Г2 — тг) Jm = 0, gr=е~. (25.04)
dr2
Полагая
/л та ,пг- Лг-.
ат=—=-— (25.05)
е "inn
и учитывая, что коэффициент при Jm в уравнении (25.04) поло-
жителен при г><т7П и отрицателен при г<ат, можно заключить,
что при г>ат функция Jm осциллирует, а при 0<г<ат — моно-
тонно возрастает (Jm=0 при г=0). Двухмерное волновое поле
Ф = Лп(^г)е±<т¥ (25.06)
можно наглядно представить в виде системы лучей, касающихся
окружности г — ат и отражающихся от окружности г—а^>ат
(рис. 30). Таким образом, поверхность г=ат есть внутренняя
каустика для этой системы лучей, а 6,п = р/Га2— осесть длина
луча между точкой касания и точкой отражения.
Данная интерпретация функции Ф непосредственно следует из
формул (6.11) и (24.19)*. Она объясняет, почему в уравнение
(24.18) и формулу (24.30) входит величина Ьт, которая лишь при
—0 совпадает с радиусом цилиндра а. Из формул (24.27) и
(24.38), которые можно переписать в виде одной формулы
Утп---Ш
(«=1,2,...; /п>1; — /п<р.2), (25.07)
где /п означает t° или 1'п, следует, что каустика может очень
близко подходить к отражающей поверхности г = а.
* Действительно, согласно этим формулам поле представляется в виде
суммы слагаемых, пропорциональных e±,AS, где
kS = ту ± em (kr).
Функция S удовлетворяет уравнению эйконала
/ dS у , 1 /д$\2
(gradS)2 = (-^j =1-
поэтому направление лучей определяется вектором grad S; последний опреде-
ляет семейство лучей, касающихся окружности г = ат-
•0—2547 145
Введем угол 6 ^0 < 6 < -g-y по формуле
cosfi = — или sinO=Q,7n(vmn),
тогда
am = ccos6, feTO = asin0
и формулы (24.14) и (24.35) можно переписать в виде
(25.08
(25.09
(25.10
ka — vmn4- sl^0
РИС. 30. Внутренняя каустика и лучи
в цилиндрическом резонаторе.
Геометрический смысл угла 6 ясен из рис. 30. Угол 6 ecu
угол скольжения лучей, отражающихся от поверхности г=с
------6 есть угол падения, равный углу отражения). Чем мень-
ше угол 6, тем ближе прижимаются лучи к поверхности г=а.
Формулы (24.15) и (24.19) приводят к соотношению
/n(tg6 —6)+^- = т (п=1,2,...), (25.11’
позволяющему получить для корней приближенные асимпто-
тические представления
{ 1 \
п ( tl-у- )
tg 6 — 6 = —v° = , (25.12)
° ГП ^ап COS 6 '
146
которые при 6 < 1 эквивалентны формулам (24.27) и (24.28), а при
б приводят к формуле
v°
тп
(25.13)
Для корней v'„in получаем аналогичное соотношение
/n(tge — (п=1,2,...), (25.14)
откуда
« (п~ v)
tge-6 = - m (25.15)
При б < 1 мы получаем формулу (24.38), в которой t'n вычисля-
ются по асимптотической формуле (24.39), а при б ~ имеем
+ n-----(25.16)
В соотношениях (25.11) и (25.14) zntg6 = gZ>m представляет
собой набег фазы на отрезке луча между точкой касания и точ-
кой отражения; rn.fi — набег фазы на том же отрезке, обусловлен-
ный множителем е*inVf, а слагаемые и определяются
скачком фазы при прохождении луча мимо каустики г~ат и при
отражении от поверхности г—а. Скачки фаз вместе с набегом
фазы 2т tg 6 должны отличаться от набега фазы 2/пб на величину
2-пп (п— 1,2,...) — в этом наглядный геометрический смысл соот-
ношений (25.11) и (25.14), приводящих к простым формулам
(25.12) и (25.15) для корней v#„n. Эти формулы можно перепи-
сать в виде
*8«-«=---------------, (25.17)
При больших т и умеренных п, когда угол 0 мал, соотношения
(25.17) приводят к формуле (25.07). В этом случае более точ-
ные результаты получаются, если под tn понимать точные зна-
чения корней уравнения v(t)=O или v'(t)=O, а не асимптоти-
ческие выражения (24.28) и (24.39).
При т=0 функция Ф обладает симметрией вращения, внут-
ренняя каустика отсутствует — точнее, переходит в фокальную
линию — и функция Jo(gr) соответствует радиальному пучку лу-
чей, отражающихся от поверхности г—а и фокусирующихся на
оси г=0; формулы (25.13) и (25.16) в грубом приближении
применимы уже при п>1. При небольших значениях т (т—1,
10*
147
т=2) образуется внутренняя каустика, радиус которой про-
порционален азимутальному индексу т. Выражения (25.13) и
(25.16) для корней vmn в этом случае применимы уже при не-
больших п (п=2, п=3).
При больших значениях т каустика находится на большом
расстоянии от точки г=0. Распределение поля выражается че-
рез функцию Эйри v(t) в соответствии с асимптотической фор-
мулой (ср. [17], стр. 56)
JTO(gr)=|/ р(А=1/ v(t), (25.18)
/ I/ Jtgr sin ’ у 5tgr sh 1] ' ' '
где
— (—^)3/2 =m(tge —5), cosS=-^- (при r>am),
2 ,3/2 / +i i i m , . . (25.19)
Г =/n(vi —thij), chi)=— (при r<am).
o gr
Из асимптотического выражения (9.24) следует, что формула
(25.18) при больших отрицательных t принимает вид
Лп (gr) = У я-grlins sin \т (tg< — *;) + -г]. (25.20)
соответствующий асимптотическим формулам Дебая (24.20).
При условии (ср. [17], стр. 31)
Н 15/2 < 1 (25.21)
формула (25.18) упрощается следующим образом:
Jm (gr) = , t = . (25.22)
|/ П р. г
Фиксируем большой индекс т и положим последовательно
n= 1, 2, ... Если индекс п не слишком велик, точнее, если при
t—tn условие (25.21) удовлетворяется, то формула (25.22) при-
годна практически всюду; ее можно также переписать в виде
Jm (gr) = , у = g(a~r) . (25.23)
Г П р Г*
Действительно, в этом случае формулы (25.22) и (25.23) при-
годны в области дт<г<а (0<г/<—tn), т. е. между каустикой
и стенкой, а также в части области г<_ат (//>—tn), приле-
гающей к каустике, где происходит спадание поля до весьма
малых значений. При gr £ 1 формулы (25.22) и (25.23) в отли-
чие от более общей формулы (25.18) неприменимы, но функция
Jm(gr) весьма мала.
Волновые поля, определяемые выражениями (25.06) и
(25.23), суть не что иное, как волны шепчущей галереи, кото-
148
рые бегут вдоль стенки г=а по азимуту, прижимаясь к стенке
тем ближе, чем больше индекс т и чем меньше индекс п. Эти
волны, равно как и волны, вычисляемые по более сложным фор-
мулам (25.18) и (25.20), в области ат<г<а представляются
в виде потока лучей, отражающихся от стенки под углом —6
[см. формулу (25.08) и следующие за ней] и касающихся каусти-
ки. Вблизи каустики лучевая трактовка недостаточна и надо
учитывать проникание поля внутрь каустики; необходимое уточ-
нение лучевой трактовки дают формулы (25.18), (25.22) и
(25.23).
Спектр собственных частот открытого цилиндрического ре-
зонатора более густой, чем, например, спектр открытого резо-
натора с плоскими зеркалами, имеющего те же размеры. Даже
в крайнем случае, когда резонансными свойствами обладают
только колебания с индексом <7=1, при /га>1 густота спектра
определяется по формуле (1.02), характерной для двухмерных
областей (S=na?). Поэтому такие резонаторы можно применять
лишь в сравнительно длинноволновых диапазонах, где сгущение
спектра, характеризуемое формулой (1.02), еще терпимо. Из вы-
веденных выше формул это сгущение получается так. При фик-
сированном значении q радиационное затухание согласно фор-
мулам (24.31) и (25.10) определяется параметром
М = л/ Д^-й, (25.24)
Г asm 8’ ' '
а также самим углом 6. Угол 6 зависит от индексов т и п, и в
общем случае sin 6 1, поэтому большинство колебаний имеет
примерно одинаковое затухание, слабо зависящее от индексов т
и п, что и обусловливает густоту спектра. Колебания с малыми
углами 6, соответствующие волнам шепчущей галереи, несколько
выделяются тем, что их затухание меньше, чем затухание
у большинства колебаний. Действительно, мнимая часть р" ком-
плексного параметра р=р'—ip" согласно формуле (24.31) при
Л1 > 1 равна
р" = ^ (25-25)
„ яр''
и потому величина , определяющая согласно выражению
(25.10) радиационное затухание колебаний, пропорциональна
Ksinfi, т. е. при малых 6 пропорциональна (—7„)|/4. Таким обра-
зом, радиационное затухание очень медленно увеличивается
с ростом индекса п, и спектр резонансных частот получается гу-
стым. Резонаторы, рассматриваемые ниже, имеют спектр гораз-
до более разреженный.
149
Выше было исследовано распределение поля в плоскости z=
=const внутри резонатора. У концов резонатора, при z~±Z,
поле, определяемое формулой (25.01), непрерывно переходит
в поле излучения. Собственные колебания формируются в ре-
зультате сильных отражений от концов, причем потери на излу-
чение оказываются малыми. Они существенно уменьшаются
(для некоторых колебаний), если цилиндрический резонатор су-
жается к концам, т. е. имеет форму бочки. С волноводной точки
зрения этот эффект объясняется тем, что волноводная волна не
может распространяться в суженных частях волновода, которые
играют роль волноводных ослабителей; благодаря им поле у кра-
ев оказывается слабым (ср. § 12). С оптической точки зрения
этот эффект объясняется тем, что образуются внешние каусти-
ки, защищающие собственное колебание от излучения из от-
крытых концов резонатора. К исследованию колебаний с внеш-
ними каустиками мы и переходим.
§ 26. Бочкообразный резонатор
в вытянутых сфероидальных координатах
Введем вместо цилиндрических координат г, <р, z сферо-
идальные координаты р,<р, С по формулам
r = dshpcos?, z—d ch р sin?, (26.01)
где
0<р<оо,
(26.02)
0< <f> < 2-п,
Поверхности р =const в этой координатной системе суть вытя-
нутые эллипсоиды вращения с расстоянием 2d между фокусами,
а поверхности ?=‘±iconst суть двухполостные гиперболоиды вра-
щения с теми же фокусами в точках z= ±d на оси z.
Зададим отражающую поверхность бочкообразного резона-
тора соотношениями
, Р = р, 0<<р<2тг, — ?<?<?, (26.03)
тогда (рис. 31)
a = dshp (26.04)
есть радиус бочки в ее среднем (наибольшем) сечении z=0
(радиус ее кривизны в плоскости z=.‘0), а
ch2 р
sh р
а
(26.05)
есть радиус ее кривизны в меридиональной плоскости ср = const
при z=0. Высота резонатора, отсчитываемая по оси z, равна
2Z, где
I = d ch р sin?.
(26.06).
150
Размеры и форма резонатора однозначно задаются тремя парамет-
рами d, р и С или же а, г0>а и I.
Коэффициенты Ламе в координатной системе р, SP, С равны
hf ~ =d j/ch2p— sin2 С — d )/sh2 p -|-cos2 C ,
\ sh p cos C, (26.07}
РИС. 31. Система координат вытянутого сфероида.
поэтому волновое уравнение (12.10) принимает вид
1 д ( . дФ \ . ( 1 , 1 \ д2 Ф .
sh р df V Р dp ^sh2p1- cos2?J д¥2 '
—X -X (cos С 4^+ V (sh2 Р + cos2 С) Ф — 0,
cos ? оЦ о? ) 1 1 ' г 1 '
(26.08)
где
y—kd.
(26.09)
Частные решения этого уравнения легко находятся методом раз-
деления переменных. Они имеют вид
Ф = /?(р)_£В^е±,’"ф (т = 0,1,2,...), (26.10)
у cos С
151
причем функции R и Z должны удовлетворять уравнениям:
-]- (у2 sh4p — К sh3 р— тг) R = 0,
dp
p,= jsKp-==lncthT-’ P = lncth-|- (26.11)
p
и
( m2 —-\
d2 7 I m 4 I
А^-4-l T’cos4+K--------_-—_)z=0, (26.12)
где К — постоянная разделения.
Можно показать (ср. § 12, 19 и 20), что выражение (26.10)
приближенно представляет собственные колебания, защищенные от
излучения из открытых концов С = внешними каустиками.
Для простоты предположим, что
sin2C< 1, (26.13)
тогда в уравнении (26.12) можно считать
cos2C=l—С2, —1—=1-J_C«, (26.14)
в результате чего оно принимает вид
= (26-15)
где
К + г3 — т2 + 4~
« =----- ~ , г=Г4(г + /П3-4-)11,4С. (26.16)
2|/т= + ^-т 4 /J
При
« = 9----Г (9=1,2,...), (26.17)
уравнение (26.15) имеет решение
2=ф9_.(т) (9=1,2,...), (26.18)
где функции ф0,ф2>... определяются формулой (12.25). Посто-
янная разделения /( получается равной
К = та — 4" — y2 + (29— 1)уЛпг------J-+Y2. (26.19)
152
Точками поворота ,в дифференциальном уравнении (26.15)
при условии (26.17) являются точки т=!±Тд-ь где
т9_1==2|/9-4 (26.20)
поэтому за пределами интервала — функция (26.18)
убывает экспоненциально с ростом |т|. Введем обозначение
—_1.)у/4С. (26.21)
При функция (26.18) в основном укладывается на зерка-
лах резонатора и образуются внешние каустики (двух-
полостные гиперболоиды), за пределами которых поле спадает по
экспоненциальному закону, и поэтому излучение через концевые
отверстия т=±т весьма мало. При каустика образо-
ваться не может, решение (26.18) неприменимо даже прибли-
женно, и колебание формируется лишь благодаря отражениям
от краев резонатора.
Рассмотрим теперь уравнение (26.11). Коэффициент при /? в
этом уравнении обращается в нуль при р=рот, где
sh2Pm=^r + /^-+^-. (26.22)
Такой же характер имеет уравнение (25.04), поэтому решения
обоих уравнений качественно ведут себя одинаково. Более того,
метод эталонных уравнений (ср. § 42) позволяет установить ко-
личественную связь между решениями обоих уравнений — при-
ближенно выразить функцию R через функцию Бесселя Jm. Мы
не будем приводить общих выражений и ограничимся случаем
1, когда сама функция Бесселя выражается через функцию
Эйри по формуле (25.18). Аналогичная формула для функции
R имеет вид
/?(р) = Р<(26.23)
где
Р (Р) = Г sh2 Р - К - (26.24)
и
-|-( — Z)3/2 = j /^(p)dp при p>pm,
Pm
(26.25)
4-*3/2 = j к— p (p)при p < p™-
t
153
Собственные частоты определяются соотношением ' j
р
(26.26$
Ртп
аналогичным формуле (25.17). Они получаются вещественными,.'
так как в формулах (26.17)— (26.19) не учтена диффракция на
краях (см. ниже § 29).
Сфероидальная поверхность р = рт есть внутренняя каустика
(ср. § 25); вблизи нее формулы (26.23) — (26.25) принимают вид
R(p) — Cv(t), t = [P'(Pm)]'l3(pm-P), (26.27)
где постоянная С равна
Вычислим собственную частоту колебаний, ограниченных тремя
каустиками (p = pm, t — и т = — tq-i)- Перепишем формулы
(26.19) и (26.24) в виде
К = /пг —V + Д/С, Д/С = (2//—1)Кт2 + у2,
(26.29)
Р (p) = ch2p (V - 5?) - М-
Считая слагаемое — Д7( в выражении для Р (р) малым, полагаем
____ г------------— (?—44
/P(P) = chpj/y2----------------Z — , (26.30)
chPK V2-^-
тогда интегралы легко вычисляются и соотношение (26.26) прини-
мает вид
/n(tg6-0)-^--l-jarctg-^^L =-|-(_Мз/2 , (26.31).
причем
ka = у sh р+ . (26.32)
Решение уравнения (26.31) целесообразно искать в виде
0 = 6 +ДО, (26.33)
где 0 определяется формулами (25.17), а
f 1 \
( 9 —-J- ) а
Л« = ,„,г.е (26.34)
1S4
есть малая добавка, причем
а — arctg - ?”tg6 — = arc sin (th p sin 6).
(26.35)
Поэтому выражение (26.32) для Частоты колебаний принимает
вид
( 1 >
ka = v ^„4- v ^д/- • (26.36)
Второе слагаемое в правой части, пропорциональное а, пред-
ставляет собой поправку к частоте, обусловленную бочкообраз-
ной формой резонатора.
Формула (26.21) при замене 6 на 6 принимает вид
* = (26.37)
или
Т^1/ sin 2а (26.38)
Г a sin 6 ’
где
sin а = th р sin 0, th р= ~ . (26.39)
Выражение (26.38) показывает, что при фиксированных размерах
резонатора (2а и 2/) и фиксированном положении внутренней кау-
стики (угол 6) минимальные потери на излучение будут при а =
=~4~, так как в этом случае т будет наибольшим. Однако в си-
стеме координат вытянутого сфероида должны выполняться нера-
венства:
thp< 1, sina<sin6, а<6, (26.40)
поэтому при малых углах 6, соответствующих волнам шепчущей
галереи, значение а=-^-, при котором радиационные потери ми-
нимальны, достигнуто быть не может. Таким образом, эта коор-
динатная система позволяет исследовать бочкообразные резонато-
ры, оптимальные только для колебаний, у которых 6 > .
Колебания, у которых имеют минимальные потери
при г0<а (см. ниже). Для рассмотрения бочкообразных резона-
торов, имеющих Го<п, мы воспользуемся системой координат
сплюснутого сфероида.
155
§ 27. Бочкообразный резонатор
в сплюснутых сфероидальных
координатах
Введем новые координаты р, <р, £, которые изменяются в тех
же пределах (26.02) и связаны с цилиндрическими координа-
тами г, ф, z так:
r = dchpcosC, z=c?shpsinC. (27.01]
Поверхности p=const в этой координатной системе суть сплюс-
нутые эллипсоиды вращения, а поверхности C=ztconst — одного>
лостные гиперболоиды вращения. Эти поверхности вырождаются
при р —0 и С = 0: поверхность р—0 есть диск радиуса d н«
плоскости z = 0, а поверхность С = 0 есть плоскость 2 = 0 без
этого диска.
РИС. 32. Система координат сплюснутого сфероида.
Задавая отражающую поверхность резонатора теми же соот-
ношениями (26.03), мы получим бочкообразный резонатор, изо-
браженный на рис. 32, причем
a = dchp (27.02)
есть максимальный радиус бочки (в сечении z = 0),
ch2 О
(27.03)
— радиус кривизны меридионального сечения бочки при z=0,
а
I = d sh р sin С
(27.04)
156
— «половина высоты бочки (по оси z).
Коэффициенты Ламе
Ар =/гс 1Лс112 р — cos2 С , /гф = d ch р cos С (27.05)
позволяют представить волновое уравнение в виде
_JL_Lfchp^_\+(____________
ch р dp Мр / * \ ch2 р cos2 ty dig2
4 (cosС + V <ch‘ Р - cos4) Ф = 0, (27.06)
где
у = Ы.
Это уравнение имеет частные решения
Ф = R (р) e±inKp, (27.07)
V cos t
где R и Z — решения уравнений:
+ (у2 ch4 р — К ch2 р + т2) R = 0,
d р2
р = J(j~ = arc sin (th р), thp = sinp (27.08)
о
и
/ ».-4\
jy. + l_Y-cos4+«----------(27.09)
Последнее уравнение в силу формул (26.13) и (26.14) мож-
но аппроксимировать уравнением (26.15), имеющим решения
(26.17) и (26.18). При этом
К-гг-«!+Т , . i v.I/4
х =--- —y2j С, (27.10)
так что
K = y2+W2-l + (2/7-l)j//n2-i-y2- (27.11)
При /п> 1 последнюю формулу можно переписать в виде
К = у2+/п2 + ДК, ДК = (2/7 —1)/т2 —у2 , (27.12)
157
а уравнение (27.08) решить асимптотически. Такое решение име-з!
ет вид (26.23), где
Р (р) = ch2 р + - К = sh2 р (у - - ДЛ, (27.13)
а рт — корень уравнения Р(р) = О; соотношения (26.25) и (26.26)
’остаются в силе, если под Р(р) понимать новую функцию (27.13).
Полагая
/p(p)=shp/r-^_A------------у , (27.14)
преобразуем соотношение (26.26) к виду
т (tg Г— Г) - (q - 1) arctg (- tn)3'2. (27.15)
V z J у m*— у2 °
причем
ta=TchF=~. (27.16)
Если решать уравнение (27.14) относительно 6 так же, как урав-
нение (26.31), то, обозначив
а = arctg —6 — arcsin (cth р sin 6), (27.17)
у тг— у2
придем к той же формуле (26.36) для собственных частот.
Параметр т в этом случае равен
т — [4 (т2 — Ya)]1/4 С = cth р cos а- (27.18)
Последнюю формулу легко преобразовать к виду (26.38). В си-
лу тождеств
sin а = cth р sin 6, cthp = l/ — (27.19)
параметр а определяется формулой
sin а — тЛsin б, (27.20)
* го
справедливой как при г0>а, так и при г0<^а. Радиус кривизны,
при котором а =-^- и радиационное затухание минимально (ср. § 26
и 29), равен
r0 = 2asin26.
(27.21)
158
§ 28. Бочкообразный резонатор
в сферических координатах
При г0=а поверхность бочкообразного резонатора есть часть
сферы. В этом случае удобно ввести сферические координаты
R, ф, £, связанные с цилиндрическими координатами г, ф, z фор-
мулами
r=i/? cos£, z=/?sint; (28.01)
и изменяющиеся в пределах
0< /?<"00,
(28.02)
Поверхность резонатора определим соотношениями
R=a, 0<¥<2т:, — Г<С<С.
Волновое уравнение имеет частные решения
Ф j S (kR) z (g) ±lm<t
У kR cos S
(рис. 33)
(28.03)
(28.04)
Функция Бесселя Js(kR) есть решение уравнений (25.03) и
(25.04), в которых надо заменить т на s, g на k и г на R. Функ-
ция Z удовлетворяет уравнению
(т2—"дА
s2-----Z=0 (28.05)
cos2 i ]
159
и может быть представлена в виде я
Z=/E^[C^-t^^^ + ^Qs-vztsinQJ. (28.O6J J
где P™_i/2 и Q™_l/2— решения присоединенного уравнения Лежан- I
дра, а С, и С2—постоянные. I
При условии (26.13) уравнение (28.05) можно заменить бо- .1
лее простым уравнением (26.15), в котором 1
s2 — m2+ Хц ;
х=- ^=г» •== |4 {т2 -|)1 (28.07) !
и Z определяется формулой (26.18). Тогда
Sa=zn2— 1-^(29— 1)|/т2 — у • (28.08) -
Собственные частоты определяются формулой
fto=vsri, (28.09)
где при граничном условии Ф=0 на поверхности (28.03)
vsn = v°„. J5(x) = 0 при x=v°n, (28.10)
а при граничном условии ~(/?Ф) = 0
vsn=v,sn, ^ [/jcJs(jc)] = O при x=v'sn- (28.11)
корни v'sn>l практически совпадают с корнями уравнения
J's(x)=0. При больших т и умеренных q(q<^.m) формула
(28.08) упрощается следующим образом:
s = zn-j-<7—(28.12)
Пользуясь соотношениями
s(tgO-0)=4(-Q3/2, vsn=-^= (28.13)
° cos 0
и ища 6 в виде (26.33), получаем
Де = («-?)^Н?Г- (28-14)
так что формула (28.09) приобретает вид
— vmn-|- sjn g • (28.15)
Последнее выражение согласуется с (26.36), так как по форму-
ле (27.20) мы имеем
а= в при г0 —а. (28.16)
160
При симметричных колебаниях (т=0) внешние каустики в ре-
зонаторе со сферической поверхностью (28.03) образоваться не
могут; это следует из того, что коэффициент при Z в уравнении
(28.05) при т = 0 всегда положителен, а также из того, что ве-
личина т согласно формуле (28.07) при т=0 получается мни-
мой. Для образования внешних каустик нужно, чтобы параметр
т = 2т £ (т^>1)
(28.17)
удовлетворял условию
T>X9_1 = 2jA-i (9=1,2,...) (28.18)
в соответствии с формулой (26.20). Поскольку мы считаем £<jl,
внешние каустики образуются лишь при больших значениях т.
Формулу (28.17) можно также переписать в виде
т= I/ ------COS6-
г а
(28.19)
При заданных значениях k, I и а наименьшее радиационное зату-
хание будет у колебаний с малыми углами 6 (ср. конец § 25), в то
время как колебания, у которых затухают сильнее.
В § 26—28 мы рассмотрели колебания в бочкообразных ре-
зонаторах, пренебрегая диффракцией на их краях. Заметим, что
исследование колебаний между цилиндрическими и сферически-
ми зеркалами (гл. III и IV) можно произвести таким же путем,
решая методом разделения переменных не параболическое урав-
нение, а исходное эллиптическое уравнение (12.11) или (18.10).
Более общие результаты будут получены в гл. VI (§ 37 и 38).
В следующем параграфе мы покажем, как в бочкообразных ре-
зонаторах учесть диффракцию на краях.
§ 29. Интегральное уравнение
для бочкообразных резонаторов
Собственные колебания в бочкообразных резонаторах можно
исследовать, составляя и решая интегральное уравнение для то-
ка на поверхности резонатора. Такой подход не только приво-
дит быстро к .ряду результатов, полученных выше в § 26—28
с помощью трех различных координатных систем, но в принци-
пе позволяет также рассчитать диффракционные поправки к соб-
ственным частотам и к распределениям токов и полей.
11—2547
161
Вернемся к цилиндрическому резонатору, для которого в §24.
были выведены функциональные уравнения (24.03) и (24.18).
Последнее уравнение можно представить в виде
Г eiwZ р — e2tS™( а) ' k J F(w)dw = 0 при |г|<7, (29.01)
—ОО
если не применять соотношения (24.16); функция Qm(x) при х>
>0 равна в зависимости от граничного условия
(х) = аге (х) + у
или
От (х) = аге (х) + -J (29.02)
и затем продолжается аналитически.
Вводя функцию
f(z) = j eiwZF(w)dw,
—00
удовлетворяющую условию
f(z)=O при |z|>/,
получаем для нее интегральное уравнение
(29.03)
(29.04)
f (г) = e2lSra(fca)
fe(z —z-)s
4bm
(29.05)
2/Й (fea)
в котором множитель е учитывает радиальный набег фазы
(см. § 25), а интеграл передает диффракцию волновой ампли-
туды на отрезке 2Ьт, т. е. на отрезке луча между его последо-
вательными отражениями от стенки(ср. § 12); величина Ьт опре-
деляется формулами (25.08) и (25.09).
Бочкообразный резонатор можно рассматривать как цилин-
дрический резонатор, слегка сужающийся к концам по закону
a(z) = a —2^- (2^^°)’ (29.06)
где a(z) —радиус резонатора в поперечном сечении г, а — ра-
диус при z = 0, го—радиус кривизны меридионального сечения
при 2=0. Интегральное уравнение для бочкообразного резона-
тора легко получить, заменяя в уравнении (29.05) величину а
на функцию a (2); эту замену достаточно сделать в функции
Qm(ka), величину Ьт при /2 < 2г0а можно считать постоянной.
Полагая
—v™n~T go' L )
т\*тп)
(29.07)
162
и
g6(2)=^WM2a=g^2aj (29.08)
получаем интегральное уравнение
f(z) = e\* 4 jexp/[^=^-20(z)]f(z')dz'. (29.09)
—i
Преобразуем это уравнение следующим образом. Введем
угол а по формулам
6т /~ ь~
sina = r^=, cosa=l/ 1 — — (29.10)
V аг0 Г По ’
И положим
т = j/" A-sin 2а z, t = ^^—s'm2a. • (29.11)
Для функции
f'(<c) = f(z)e^<2) (29.12)
получается интегральное уравнение
' (х~ ?
/“(г) = с . . С ехр 4- Г -^5-1 ГЬ') (29.13)
' ' ’ К 4тг sin 2а J Н 4 [ tg 2а Sin 2а J ' > ’
—т
совпадающее с интегральным уравнением (14.05) для открыто-
го резонатора с цилиндрическими зеркалами. Этому совпадению
не следует удивляться, так как в обоих случаях интегральное
уравнение описывает распространение волн в волноводе, сужа-
ющемся к концам, и диффракцию на открытых концах. При де-
тальном сопоставлении уравнений видно, что при переходе от
резонатора с цилиндрическими зеркалами к бочкообразному на-
до заменить расстояние между цилиндрическими зеркалами на
2Ьт, а радиус кривизны цилиндрических зеркал — на
г ____го
т~~ьгп — sin е
(29.14)
Величину гт можно назвать эффективным радиусом кривизны.
Выражение для т можно переписать в виде
(29.15)
где использовано соотношение (27.20), вытекающее из формул
(25.09) и (29.10). Формула (29.15) при Го=а переходит в фор-
мулу (28.19).
П
163
При т=оо уравнение (29.13) имеет собственные функции [ср.п
формулу (26.18)] j
/>М,-.(’) (9=1,2,...) (29.16)'
и собственные значения
%=!(29-1)а (9=1,2,...), (29.17).
собственные частоты вычисляются по формуле
г 1 \ ’
(? — у!»
to = vmn4-A_--------. (29.18)
Таким образом, мы снова пришли к формуле (26.36), выведенной'
ранее. Вследствие того, что параметр т конечен, возникает диф-'
фракция на краях и функция (29.16) испытывает возмущение (ма-,
лое при и большое при а собственные значения
(29.17) принимают вид *
z = (29—1)а + 2^, (29.19)
где р—комплексная поправка, обусловленная диффракцией. 1
Некоторые свойства этой поправки обсуждены в § 14.
Если фиксировать размеры резонатора (2а и 21) и, кроме I
того, задать ат, Ьт или 6, то, как уже говорилось в конце § 26, ]
наименьшее радиационное затухание колебаний с внешними ка- 1
устиками достигается при максимальном т, т. е. при а=^-, когда I
г0=-^. (29.20) 1
Если Ьт=а, то затухайте минимально при г0=2а, т. е. когда
диаметрально противоположные участки отражающей поверх- I
ности являются софокусными зеркалами. Соотношение (29.20) <
является в сущности обобщенным условием софокусности и мо- '
жет быть переписано в виде ,«
гт=2Ьт, (29.21)
где гт есть эффективный радиус кривизны, определяемый фор-
мулой (29.14). ,
Если выбрать Ьт < а и г0 < 2а в соответствии с условием
(29.20), то для других значений Ьт, удовлетворяющих условию
Ьт >К«го, (29.22)
мы будем получать по формулам (29.10) комплексный параметр
(см. конец § 15)
а = 4 - i Arch -^=, (29.23) •
< W о I
и многие колебания будут иметь большое радиационное затуха-
ние, в том числе колебания с небольшими индексами т << ka
164
и колебания, у которых п > т. За счет таких колебаний
произойдет .значительное разрежение спектра резонансных ча-
стот данной колебательной системы. Еще большее разрежение
можно получить, применяя открытый сектор бочкообразного ре-
зонатора, рассматриваемый ниже.
§ 30. Сектор бочкообразного
резонатора
Сектор бочкообразного резонатора можно получить из резо-
наторов, исследованных в § 26—28, добавлением меридиональ-
ных перегородок
0<р<р, ?=rt<p, —с<с<с
(30.01)
и удалением той части поверхности (26.СЗ), ютсргя лежит Еие
сектора — В результате мы нолучгем стрееок сужаю-
щегося к краям волновода, имекщего треугольное сечение (рис. 34).
При наличии меридиональных перегородок (30.01) бегущие
по азимуту волны (26.10) или (27.07) существовать не могут,
и колебания имеют вид стоячих
волн. В частности, выражение \
(27.07) следует заменить выра- у' \
жениями \
Ф = У? (р) J,cos ту (30.02) w=u> у' \
У cos $ г /
и и ----------9-о—
Ф = R (р) - Z-Q. sin /п?, (30.03) \
1/ cos ? -X
Р-Р X
где т уже не является целым чис- X. /
лом. Если на перегородках (30.01) /
должно выполняться граничное ус- X. /
ловие Ф = 0, то х. /
в формуле (30.02)
„ РИС. 34. Сектор бочкообразного
т—_ ... или цилиндрического резонатора.
2<р 2у 2у
в формуле (30.03) (30.04)
п 2п Зп
т= —, —, ,...
? v ?
При граничном условии —0
на перегородках (30.01)
165
в формуле (30.02)
п п 2л
т = 0, —,
в формуле (30.03) (30.05)
г. Зл 5л
т = —
2у 2и
Все формулы § 26—28, за исключением (26.10), (27.07) и
(28.04), остаются в силе, если т брать в соответствии с форму-
лами (30.04) и (30.05).
В цилиндрическом резонаторе согласно формулам (25.22) и
(25.23) существуют колебания, имеющие вид бегущих и стоя-
чих волн шепчущей галереи. Аналогичные формулы для бочко-
образного резонатора и его сектора получатся, если применить
формулу (26.27). Учитывая, что в вытянутых сфероидальных
координатах для таких колебаний можно приближенно считать
Т = йГГ ’ Р' ch ₽”<>’’ (зо.ое)
о II f/t
и, используя соотношение
Н. = cl ch pm (pm — p) = d (sh pm — sh p), (30.07)
справедливое вблизи каустики, можно переписать формулу (26.27)
в виде
R(p) — Cv(t), (30.08)
где
j kH ___f m \ 1/3 лсл
z = ~. ^=(-2- (30.09)
г* \ J
и Н есть расстояние от каустики, положительное для точек вну-
три каустики и отрицательное для точек вне каустики. Если ка-
устика находится вблизи стенки резонатора (рт^р), то форму-
ла (30.08) определяет волну шепчущей галереи и может быть
переписана в виде
/?(й = Со(^+у). (30.10)
Здесь
kh
У = (30.11)
Г
и h есть расстояние точки наблюдения от поверхности резона-
тора.
Для волн шепчущей галереи формулы (30.02) и (30.03) при-
нимают вид
Ф — Сп^п+^^.Д^созт? (30.12)
и
Ф = Су(/п-|-«/)ф9_1(т:)81пту, (30.13)
где функции 1 (т) определяются формулой (12.25).
166
Соотношения (30.09) — (30.13) справедливы и для бочкооб-
разных резонаторов, исследованных в § 27 с помощью сплюс-
нутых сфероидальных координат, и для соответствующих секто-
ров. Для резонаторов, исследованных в сферических координа-
тах (§ 28), формулы (30.12) и (30.13) легко выводятся, если
функцию Js(kR) заменить выражением (25.23).
Формулы (30.12) и (30.13) соответствуют колебаниям, поле ко-
торых ограничено тремя каустическими поверхностями (у — — tn,
т = и ч —— т9_,) и тремя стенками (р = р, ? = ? и =
= — <р); при этом внутренняя каустика z/ = — tn близка к стенке
р =р, так что угол 6 мал.
Сектор бочкообразного резонатора имеет примерно такой же
спектр резонансных частот, как и сам бочкообразный резона-
тор. Можно получить дополни-
тельное разрежение спектра,
если сектор бочкообразного резо-
натора сделать более открытым и
перейти к резонатору, поперечное
сечение которого изображено
на рис. 35. В таком открытом
секторе меридиональные перего-
родки имеют высоту h<a-, при
h <^.а колебания в открытом сек-
торе определяются формулами
(30.12) и (30.13), выведенными
выше для закрытого сектора,
если выполняется условие
^> —и (30.14)
в
которое в силу соотношения ka^m
можно переписать в виде
А>=£. (30.15)
РИС. 35. Открытый сектор.
Условия (30.14) и (30.15) означают, что внутренняя каусти-
ческая поверхность попадает на меридиональные перегородки;
в противном случае данное колебание сильно излучает через
меридиональные плоскости <р= ±<р и существенно отличается от
соответствующего колебания в закрытом секторе. За счет таких
колебаний, излучающих через меридиональные плоскости,
спектр резонансных частот дополнительно разрежается. Малым
радиационным затуханием обладают в открытом секторе (при
h<^a) лишь колебания, имеющие вид стоячих волн шепчущей
галереи и удовлетворяющие условию (30.14) или (30.15).
§ 31. Электромагнитные поля
Выше мы решали скалярное волновое уравнение (12.10).
К электромагнитным полям нетрудно перейти, полагая функцию
Ф равной составляющей электрического или магнитного вектор-
ного потенциала по оси £ (ср. § 23). Мы не будем, однако, при-
водить довольно громоздких общих формул и ограничимся двумя
частными случаями — цилиндрическим резонатором и бочкооб-
разным резонатором, рассмотренным в § 28.
Полагая Ф равной составляющей электрического вектора
Герца по оси z, получим электромагнитное поле в открытом ци-
линдрическом резонаторе с проводящей стенкой (24.01):
р _ д2Ф и _ ik дФ
Пт~дгдг. ’ Лг— г ,
Е Н (31.01)
г d<fdz' <₽— к дг ' '
Нг = 0.
V0
Если функцию Ф определить формулой (25.01) при g = -~p, то
получаются колебания Emnq в цилиндрическом резонаторе, соот-
ветствующие бегущим азимутальным волнам. Колебания Emnq
в виде стоячих азимутальных волн получаются из функции
Ф = CJm (gr) [ (z) cos (31.02)
или
Ф=CJm (gr) J (z) sin m<?. (31.03)
В секторе цилиндрического резонатора индекс m согласно фор-
мулам (30.04) принимает значения (m'=l, 2, ...),
2?
и формулы (31.01)—(31.03) определяют колебания Em,nq в секторе.
Токи, соответствующие этим колебаниям, являются продоль-
ными— направлены по оси г. Поверхностная плотность тока на
стенке цилиндрического резонатора для колебания Emnq с бе-
гущей азимутальной волной равна
b = f(z)e±;m*. (31.04)
Электромагнитное поле колебания Hmnq в цилиндрическом
резонаторе определяется формулами:
,, _ ik дФ _ д2Ф
Гг г d<f ’ drdz ’
£=-^,/7=^,
9 dr ’ ч> г d<fdz*
168
Ez=0, Hz~^ + №. (31.05)'
Здесь функцию Ф надо вычислять по формуле (25.01) для бегу-
щих и по формулам (31.02) и (31.03) для стоячих азимутальных
волн, причем В секторе цилиндрического резонатора
согласно формулам (30.05) мы имеем т — -^т' (т'—0, 1, 2, ...);
2¥
беря стоячие азимутальные волны с такими индексами т, мы по-
лучаем по формулам (31.05) электромагнитное поле колебания
Hm,nq в секторе.
Этим колебаниям соответствуют главным образом попереч-
ные токи — азимутальные на цилиндрической поверхности и
радиальные на меридиональных перегородках. Продольная со-
ставляющая тока гораздо меньше; ее отношение к поперечной
„ я
составляющей по порядку величины равно и ею можно пре-
небречь (ср. § 17). Главная составляющая поверхности плотно-
сти тока на стенке цилиндрического резонатора при колебании
Нmnq с бегущей азимутальной волной равна
y;=f(z)e±/'"'F. (31.06)
Собственные колебания, рассмотренные выше, являются либо
волнами, бегущими по азимуту, либо стоячими волнами, кото-
рые можно разложить на сумму двух бегущих волн. Азимуталь-
ная фазовая скорость бегущих волн равна
и =с—, (31.07)
? gam '
так что вблизи каустики вне каустики и внутри
каустики, где поле ослабевает, <с.
Колебания в бочкообразных резонаторах можно классифи-
цировать аналогичным образом. Оказывается, что структура по-
ля колебаний Envnq и Hmnq в бочкообразном резонаторе ана-
логична структуре поля одноименных колебаний в цилиндриче-
ском резонаторе; точнее, структура поля в поперечном сечении
у обоих резонаторов очень близка, но зависимость поля от про-
дольной координаты (z или £) различная, как это видно из фор-
мул (24.29) и (26.18).
Поясним сказанное на примере бочкообразного резонатора,
рассмотренного в § 28. Определим в сферической системе коор-
динат R, <р, £ (см. § 28) электромагнитное поле с помощью фор-
мул:
Е,= 0; Н,= (^-+4-)(«Ф),
= <3108>
169
С' _ г Т ____________ 1 / £)Л\\
Е1~~~ 7БГ? 7)^ ’ Hr'~R dRdt ^Ф)'
Оно удовлетворяет уравнениям Максвелла, если функция Ф, со-
впадающая с одним из потенциалов Дебая (см., например [7],
стр. 96 и 527), удовлетворяет волновому уравнению (12.10). Эту
функцию надо брать в виде (28.04). Так как на стенке (28.03)
согласно формулам (31.08) при больших т преобладают про-
дольные токи (направленные по оси £), то это колебание следу-
ет назвать колебанием Emnq. Его частота определяется форму-
лами (28.09) и (28.15) при =
Электромагнитное поле колебаний Нтпд в таком бочкооб-
разном резонаторе имеет составляющие:
/г)2 X
£«=(4г + Р)<ЛФ>- Н»=0'
<3109>
Ег = (ЯФ), Я,== ~.
' R dRdi С cos? ()<а
Частота этих колебаний вычисляется по формулам (28.09) и
(28.15) при vmn=v'mn- При больших т на стенке резонатора
возбуждаются главным образом азимутальные токи, так что эти
колебания аналогичны колебаниям Hmriq в цилиндрическом ре-
зонаторе.
Электромагнитные колебания Em,nq и Hm,nq в секторе такого
бочкообразного резонатора мы получаем, полагая
Ф = ^^R)Z(t.) cos m(p (31.10)
у kR cos ?
и
, Js (kR)Z(£\ .
Ф =—V sin my. (3l.ll)
J^Kcos?
Для колебаний E , нужно брать tn =-Е=т' в соответствии с фор-
мулой (30.05) а для колебаний Hm,nq считать т=-^=т’ в соот-
ветствии с формулой (30.04). Колебания, имеющие вид стоячих
волн шепчущей галереи, определяются выражениями (30.12)
и (30.13).
Из рассмотренных в данной главе открытых резонаторов —
цилиндрических и бочкообразных — наибольший интерес пред-
ставляет бочкообразный резонатор, а также открытый сектор
бочкообразного резонатора. Поле некоторых собственных коле-
баний в бочкообразном резонаторе представляет собой лучевой
поток, с трех сторон ограниченный каустическими поверхностя-
170
ми, а с четвертой — стенкой резонатора; такие колебания имеют
весьма малые потери на излучение.
Цилиндрические и бочкообразные резонаторы могут иметь
различные применения. В частности, колебания Hmnq в таких
резонаторах при больших пг и умеренных п и q должны эффек-
тивно возбуждаться электронами, совершающими круговое дви-
жение в магнитном поле, направленном по оси вращения.
Несколько иной вывод всех соотношений для цилиндриче-
ских резонаторов дан в книге [8] (задачи 2—4 к гл. II, 4—13
к гл. III и 4—8 к гл. IV).
Задачи к гл. V
1. Исследовать электромагнитные колебания в полуоткрытом цилиндри-
ческом резонаторе длиной /, который при z=0 имеет идеально отражающий
поршень, а ири г=1 — открытый конец.
Решение. В полуоткрытом резонаторе существуют колебания Emnq
с нечетными q и Нтпо с четными q, совпадающие с одноименными колеба-
ниями в открытом резонаторе длиной 2/ (см. § 31).
2. Преобразовать уравнение Бесселя (25.03) к уравнению второго по-
рядка без первой производной, переходя от функции Jm к функции
Установить положение внутренней каустики по уравнению для функции jm_\p (gr)-
Решение. Функция R (г) == /т_!у2 (gr) удовлетворяет дифференциальному
уравнению
в котором точка поворота, соответствующая внутренней каустике, располо-
жена при г=ат, где величина
1
тг— 4
Ощ —
8
несколько отличается от величины (25.05).
3. Б § 13 был применен метод приближенного интегрирования диффе-
ренциальных уравнений (метод эталонного уравнения с использованием
функций Эйри). Применить этот метод к уравнению (25.04) при m ^>1 и
показать, что полученное выражение для функции Jm (gr) при gr -»оо пере-
ходит в асимптотическую формулу Ханкеля
/m(gr) = J/ A.cos | gr —(2m-(- От-
решение. Мы получаем для функции /т, стремящейся к нулю при
gr-* оо, выражение
/"о" 4 Г ___t
-V 2 2 ~
п г g2r2 — т2
171
в котором
г ёг ~______
~ (—f)3/2 = j ]/g2r2 —>n2y = j j/" 1 — p dx
m/g m
ИЛН
m
gr
причем t -» оо при gr -* 0.
Эти формулы по существу совпадают с формулами (25.18) и (25.19). Если
тг
gr -» оо, то t -»—оо и Е -> -jj- соответственно; функцию v (t) можно заменить
.асимптотическим выражением (9.24), причем согласно первой формуле (25.19)
(— /)3/2 = gr_ т^,
и мы приходим к асимптотической формуле Ханкеля.
4. Применить метод эталонного уравнения (см. задачу 3) к дифференциаль-
ному уравнению для функции /т_1/2(Яг)> выведенному в задаче 2. Сравнить по-
лученное выражение с результатами задачи 3.
Решение. Получающиеся формулы отличаются от приведенных в реше-
нии задачи 3 тем, что т заменен иа 1/ т2 — — , в силу чего при gr -» со
г 4
асимптотическая формула Ханкеля получается в несколько искаженном виде.
Последнее обстоятельство приводит к тому, что обычно предпочитают поль-
зоваться формулами, выведенными в задаче 3, так как они имеют более
широкую область применимости, а именно пригодны, когда по крайней мере
одна из величин gr или т велика.
5. В литературе часто утверждают, что асимптотическая формула Ханке-
ля (см. задачу 3) применима три условиях gr^>l и gr т. Исходя из
формул (25.18) и (25.19), показать, что формула Ханкеля справедлива толь-
ко в том случае, если выполняется более сильное (при щ^>1) условие
gr> /и2.
Решение. Последнее условие следует из того, что
4 (-оз/2=яг j/
wz2
g*r*
m2
g*r‘ -
я /m2\
= gr-m -s+O^-).
6. Опираясь на результаты задачи 3, вывести формулы (24.19) и (24.22).
Решение. Для функции Ханкеля имеем формулу
где переменная t та же, что и для функции Jт, а функция =
определяется формулами (9.34) и (9.26). При больших отрицательных t мы
получаем формулы (24.19), а при —формулы (24.22).
172
7. В § 25 книги [8] для несимметричных электромагнитных волн Етп и
Н-тп в полубесконечном круглом волноводе (г—a, 0<z<oo) выведена систе-
ма функциональных уравнений
eiwzG (w)dw=0 при z<0, (а)
С
С Г imw _ 1
I e1MZ I F (w) + — G (w) dw = 0 при z < 0, (t>)
c
^imzvfm(va)F(w)dw = 0 . Приг>0, (c)
C
[eiwz f^y^G(w)+Jdw = 0 приг>0. (d)
C
Показать, что в результате аппроксимаций, примененных в § 24, мы полу-
чаем из этих функциональных уравнений те же окончательные уравнения,
какие были получены в § 24 из скалярного волнового уравнения, т. е. что
векторный характер электромагнитных волн в рассматриваемой задаче не
проявляется.
Решение. В силу условия (24.10) дополнительное слагаемое в квадрат-
т w т
ной скобке уравнения {Ь) мало — оно пропорционально , причем 1 и
£-<^1; если этим слагаемым пренебречь, то уравнения (Ь) и (с) совпадут с
уравнениями (24.03) и (24.04). Точно так же дополнительное слагаемое ® квад-
т w
ратной скобке уравнения (d) пропорционально , при пренебрежении им
уравнения (а) и (d) для функции G (w) эквивалентны уравнениям (24.03) и
(24.33).
8. Пользуясь формулами § 31, вывести 'Выражения для составляющих
электромагнитного поля колебаний Етпд и Hmnq, соответствующих волнам
шепчущей галереи в цилиндрическом резонаторе.
Решение Полагая в соответствии с формулой (25.22)
1
Ф = -р v (t) f (г) cos mtf,
для колебаний E,nnq будем иметь:
Ег — — —-— sin mf, Hr = iv (t) f (z) sin ma,
f' (г) n' (/).
Eip= — v(t)—^-sinmf. H^ = — i f (z) cos mf,
Ez — v (t) f (z) cos m<f, Hz = 0,
а для колебаний Hmnq-
V (t) f' (z)
E.r = — iv (0 f (z) sin my. Hr = — — ---jp cos my,
E^ — i ~~ f (2)cos = — v (0 sin my,
£z = 0, Hz =v (t)f(z) cos my.
В первом случае наибольшую величину имеют составляющие £г и Нг, во вто-
ром— составляющие Ег и Нг.
173
Глава VI
Геометрическая оптика
открытых резонаторов
§ 32. Лучевые потоки
в эллиптическом зеркале
Многие свойства открытых резонаторов, например образо-
вание каустик, ограничивающих поле некоторых собственных
колебаний, по существу являются следствием геометрической
оптики. Интересно проследить связь между геометрической опти-
кой и теорией открытых резонаторов. Для этого мы сначала рас-
смотрим двухмерные волновые поля, где эта связь обнаружи-
вается наиболее естественным образом. Простейшей задачей та-
кого 'рода является задача об эллиптических зеркалах, которую
мы рассмотрим в первую очередь, а затем обобщим результаты
на зеркала и каустики произвольной формы. В § 37 мы перей-
дем к исследованию трехмерных волновых полей.
Рассмотрим эллипс, изображенный на рис. 36; от эллипса
могут отражаться лучи света, лежащие в его плоскости (этот
эллипс будем ’называть зеркальным). После ряда отражений
луч света, первоначально совпадающий с отрезком АВ, покроет
какую-то часть площади внутри зеркального эллипса, а часть
этой площади останется не покрытой лучом. Исследуем свойства
таких лучевых потоков.
Построим на рис. 36 эллипс, софокусный с зеркальным и
касающийся луча АВ (назовем этот эллипс внутренним). По-
кажем, что луч света после отражения в точке В вновь коснет-
ся внутреннего эллипса. Для этого сделаем следующее построе-
ние: точки касания Si и S2 и точка отражения В соединяются
с фокусами эллипсов О] и О2. Треугольник SjC^B отражается
относительно стороны StB, в результате чего получаем тре-
угольник SiO'tB. Биссектриса угла О^Ог между радиусами-
174
векторами является нормалью к эллипсу, поэтому если обозна-
чить ZO(SiO2 через 2а', то Z.O2SXB= —a', a Z0/151B = -^-|~
+ а', откуда следует, что точка O't лежит на продолжении от-
резка SiO2. Точно так же доказывается, что при отражении тре-
угольника S2O2B относительно отрезка BS2 вершинй 0'2 «отра-
женного» треугольника S2O’2B лежит на продолжении отрез-
ка OiS2.
Покажем теперь, что треугольники О'\ВО2 и О\ВО'2 равны.
Действительно, стороны O/1O2 = O1S1+51O2 и OXO'2 — OXS2 +
+ O2S2 равны, так как сумма радиусов-векторов одного и того
же эллипса постоянна. Сторона О'\В равна сторо-
не ОХВ, так как является отражением последней; по той же при-
чине сторона ВО2 равна стороне В0'2. Из равенства треуголь-
ников следует, что
ZO'1BO2=ZO1BO'2.
Введем обозначения
ZOIBO2 = 2a, ZS1BO] = ₽1, ZS2BO2=p2.
Тогда
O'1BO2=2a + 2pI, ZOIBO/2 = 2a+2p2.
Из равенства последних углов следует, что Pi =‘Р2. Вспомнив,
что биссектриса угла ОХВО2 нормальна к зеркальному эллипсу,
приходим к выводу, что угол падения равен углу отражения,
т. е. что касательная BS2C к внутреннему эллипсу есть луч, воз-
никший при отражении луча Л51В от зеркального эллипса. Оче-
175
видно, что после всех последующих отражений луч будет каж-
дый раз касаться внутреннего эллипса. Таким образом, вну-
тренний эллипс является огибающей данного семейства лучей,
т. е. каустикой.
Сказанное выше относится к случаю, когда первоначальный
луч пересекает большую ось эллипса правее или левее обоих
фокусов. Если же первоначальный луч пересекает большую ось
эллипса между фокусами, то каустиками будут гиперболы, со-
фокусные зеркальному эллипсу, а лучи покроют площадь меж-
Л<,
РИС. 37. Зеркальный эллипс и гиперболические каустики.
ду ветвями гиперболы. Для того чтобы убедиться в этом, нужно
доказать, что луч, касательный к гиперболе, после отражения
от зеркального эллипса будет касаться той же гиперболы. На
рис. 37 первоначальный луч /1S1B касается гиперболы в точ-
ке Si, a BS2C есть касательная к другой ветви той же гипербо-
лы. Точка S'| является отражением точки S| относительно пря-
мой О1В, а точка S'2— отражением точки S2 относительно пря-
мой 02В. Треугольники5'1В52,и51В5/2равны,таккак5'1В=51В,
S'2B=S2B и SiS'2=S'iS2. Последнее равенство следует из того,
что S!S'2=O2Si + O2S2 и S')S2 = OiSi + OlS2, асогласно известно-
му свойству гиперболы
0|S2—O2S2 = 02S,—0^!.
Следовательно,
O1S2+O,S! = 02S| + O2S2.
Из равенства углов
ZS1BS'2=ZS'IBS2
следует равенство половинных углов
Z.OXBS\ = Z.O2BS2.
176
Так как радиусы-векторы OjB и О2В образуют одинаковый угол
с нормалью к зеркальному эллипсу в точке В, то это справед-
ливо и для прямых SiB и S2B, поэтому касательная BS2C явля-
ется отраженным лучом, если /ISiB — падающий луч.
В случае гиперболических каустик возможно некоторое ос-
ложнение. После касания с одной ветвью гиперболы луч света
может испытать не одно, а несколько отражений от зеркального
эллипса, прежде чем произойдет касание с другой ветвью ги-
перболы. Это означает, что после некоторых отражений не луч
касается гипербол, а его геометрическое продолжение вне пло-
щади, ограниченной эллипсом. Однако это не меняет существа
дела.
Легко видеть, что эти построения имеют непосредственное
отношение к открытым резонаторам. В случае гиперболических
каустик, .как мы убедились, луч света, распространяющийся вну-
три эллипса, не выходит из области, ограниченной двумя ветвя-
РИС. 38. Открытый резонатор, образованный отрезками
эллипса и гипербол.
ми гиперболы, поэтому некоторые части эллипса, например ду-
ги и R2N2P2, можно без ущерба удалить. Таким образом
получается открытый резонатор, в котором между двумя зер-
калами— отрезками эллипса — существует система лучей, огра-
ниченных каустиками. При переходе от геометрической оптики
к волновой оказывается, что волновое поле все же проникает
за каустики, поэтому зеркала нельзя обрывать у самой каусти-
ки, а нужно их продлить несколько дальше (например, верхнее
зеркало — до точек Qi и Q2) для того, чтобы радиационные по-
тери сделать достаточно малыми.
Эллиптические каустики реализуются в открытом резонато-
ре, образованном дугой зеркального эллипса, если ее ограни-
чить по концам зеркалами, изогнутыми по гиперболам, софо-
кусным зеркальному эллипсу, и простирающимися от зеркаль-
ного эллипса к внутреннему и несколько дальше. В таком
резонаторе образуется каустика в виде отрезка эллипса, софокус-
ного зеркальному (рис. 38). Эллиптические каустики аналогич-
12—2547 177
ны круговым каустикам в цилиндрическом резонаторе, а откры-
тый резонатор, показанный на рис. 38, — открытому сектору та-
кого резонатора (см. § 30).
Использованные выше геометрические (или геометро-опти-
ческие) свойства эллипса являются следствием известных теорем
геометрии (см., например, [30]). Мы дали подробный вывод этих
свойств, чтобы не отсылать читателя к литературе.
Наряду с рассмотренными выше лучевыми потоками, огра-
ниченными гиперболическими и эллиптическими каустиками,
в зеркальном эллипсе могут быть лучевые потоки особого ти-
па—расходящиеся из фокусов эллипса и после отражения от
эллипса опять сходящиеся к ним. Лучевые потоки особого типа
не имеют каустик и поэтому для теории открытых резонаторов
не представляют интереса.
Существенно, что кроме этих потоков никаких других нет:
в частности, отсутствуют лучевые потоки, локализованные вбли-
зи большой оси зеркального эллипса.
£ 33. «Квантовые» условия
Таким образом, согласно геометрической оптике любой эл-
липс или гипербола, софокусные зеркальному эллипсу, могут
быть каустиками. Однако фактически лишь некоторые из них,
удовлетворяющие определенным «квантовым» условиям, могут
быть каустиками. Эти условия определяют резонансные частоты
открытого резонатора; их можно было бы также назвать усло-
виями периодичности или условиями стационарности.
В силу двухмерности системы можно ожидать, что будет два
квантовых условия. Очевидно, что квантоваться будут величины,
которые являются инвариантами, т. е. не зависят от первона-
чального направления луча. Первое условие, почти очевидное,
состоит в том, что длина замкнутой каустики должна составлять
целое число длин волн, а длина каустики, опирающейся на отра-
жающие зеркала—целое число полуволн. Второе условие ме-
нее очевидно. Ниже мы докажем, что периметр фигуры
QSjBS2Q (рис. 36), состоящей из отрезка эллипса и двух .каса-
тельных, является константой, не зависящей от положения точ-
ки отражения на зеркальном эллипсе. Естественно поэтому счи-
тать, что этот периметр также должен составлять целое число
длин волн — в этом и заключается второе квантовое условие.
Первое условие применительно к эллиптической каустике
£=£п (рис. 36) приводит к формуле
2п
Y j j/ch2C0 —sin25 = (/n = l, 2, ...). (33.01)
о
178
Здесь 5 и С — эллиптические координаты, связанные с декартовыми
координатами лиг посредством соотношений (ср. § 42)
x=dch?sinE, z = dshCcosE, (33.02)
d — половина расстояния между фокусами, а параметр y — kd,
, <о 2л
где к=—==у—волновое число, соответствующее циклической
частоте ш или длине волны Л.
При выполнении первого условия второе условие эквивалент-
но тому, что целому числу длин волн равна разность между
суммарной длиной двух касательных S{B и BS2 и дугой эллип-
са SiPS2. Для вычисления этой разности определим разность фа-
зовых набегов kds^—kds2. Из формулы (33.02) следует, что
вдоль касательных фазовый набег равен
в то время как вдоль внутреннего эллипса £=£0 фазовый набег
равен
kds2 = Y ( /ch2C0 —sin2E dt,
причем производная вычисляется вдоль касательной SJ?
(рис. 36). Таким образом,
kdsx — kds2 = Y { ]/ (ch" С — sin2 ?) [ 1 + j —
— I/Eh40 —sin2? I <%. (33.03)
\ J I
Уравнение касательной к эллипсу, проходящей через точку go,
£о, в эллиптических координатах имеет вид
A ch С sin £ + В sh С cos ? == С
(/A = shCosin ?0, ^=chC0cos?0, C=shCochto). (33.04)
Дифференцирование no С приводит к равенству
(d? \_Bch ?ccs Е + 4 sh S sin ? /ЧЧ
d'C, j Bsh ? sin Е — Л ch 5 cos Е * ' ‘ °*
Это равенство легко преобразовать, пользуясь тождествами
В ch С cos Е A sh С sin ? = /(ch2 Со — sin2 ?0) (ch2£0 — sin2 ?j,
В sh C sin ? — Д ch C cos ? = / (ch2 Co — sin2 ?0) (ch2 C — ch2 Co).
(33.06)
12* 179
Для доказательства первого тождества возведем в квадрат обе
части уравнения (33.04):
A2 ch2 С sin2 5 4“ 2ЛД ch С sh С sin Е cos Е + В2 sh2 C cos2 E = C2.
Преобразуя это выражение очевидным образом, получаем
(Z?ch CcosE-|-.AshCsinE)2 = C2 — A2 sin2 £ + Z?2cos2E.
Подставляя в правую часть значения А, В и С и извлекая из
обеих частей квадратный корень, получим первое тождество
(33.06). Аналогично доказывается второе тождество.
Подставляя эти тождества в формулу (33.05), получим
ch2;, — sin2 £
ch2 5— ch2 ;0
Соответственно выражение (33.03) примет вид
kdSt —kds2=~i V ch2C — ch2C0dC
Такое же выражение получается для касательной BS%. Поэтому
разность между суммарной длиной касательных и длиной дуги
эллипса равна
__ Т _____________
Л (SJB + BS2 — S.PS.) = 2у j /ch2 С— ch2 Со <К,
^0
где С— С—уравнение зеркального эллипса. Второе квантовое усло-
вие имеет вид
Г
Y f Г ch2С-ch2Со Л=-Jп, (33.07)
Со
причем п—2, 4, ..., если отражение от зеркального эллипса про-
исходит без изменения фазы, и п=1, 3, ..., если отражение со-
провождается скачком фазы на л.
Если эллиптическая каустика реализуется не полностью,
а лишь частично, при igi<;g<g2 (см. рис. 38), то первое кванто-
вое условие (33.01) модифицируется следующим образом:
и
^0 —sin2E dt — im>
(33.08)
а второе квантовое условие (33.07) остается без изменений.
В случае гиперболических каустик первое квантовое условие
Г ____________
у j/ch2C —sin2E0dC = K/z (л=1, 2, ...) (33.09)
180
означает, что длина каустики, опирающейся на зеркала, состав-
ляет целое число полуволн. Второе квантовое условие
и _______________
Y J >/sin2 50 — sin2 Б tZ; = тгт (m = 0, 1, 2, ...) (33.10)
-ь>
эквивалентно тому, что на длине кривой PlSlBS2P2 (см. рис. 37)
укладывается целое число полуволн. Уравнения g=±g опреде-
ляют положение эллиптических зеркал, а уравнения |=±£0 —
положение гиперболических каустик.
Приведенные выше квантовые условия позволяют вычислить
как положение каустик (т. е. параметры g0 или go), так и часто-
ту колебания (т. е. у, k или о). Они аналогичны квантовым
условиям Бора в старой квантовой механике. В следующем па-
раграфе будет показано, что эти условия незначительно отли-
чаются от условий, полученных более строгим путем.
§ 34. Аналитический вывод
квантовых условий
При аналитическом рассмотрении волновых полей мы долж-
ны исходить из двухмерного волнового уравнения
д2Ф । д2ф
)-&2ф = 0
(34.01)
и граничного условия на зеркалах
Ф; 0 или ~ — 0.
dt,
(34.02)
Уравнение (34.01) в эллиптических координатах (33.02) при-
нимает вид (12.11) и допускает разделение переменных, т. е.
имеет частные решения
O=X(,g)Z(g).
•Функции X и Z суть решения обыкновенных дифференциальных
уравнений
®+Тг(х —sin2g)X = 0 (34.03)
IM
g_+r(ch2C-x)Z = 0. (34.04)
При 0<и<1 мы полагаем x=sin2g0 и коэффициент при X в урав-
нении (34.03) обращается в нуль в точке g=g0- При х>1 пола-
гаем x=chgo и соответственно коэффициент при Z в уравнении
(34.04) обращается в нуль в точке g=go- Как станет ясно из
дальнейшего, уравнения g=±g0 и g=go определяют форму и по-
ложение каустик.
181
Перейдем теперь к решению уравнения (34.03) при x=ch2go-
Так как мы предполагаем, что все размеры зеркального эллип-
са много больше длины волны, то в уравнение (34.03) входит
большой параметр у > 1, благодаря которому решение уравне-
ния сильно упрощается. Если искомое решение разложить
в ряд по величине, обратной этому параметру, и ограничиться
первым приближением, то оно примет следующий вид:
Е
Х = V 'ГГ f^exp[±ZY f/ch40-sin2Sdd. (34.05)
г/T2(ch2 sin2 £) L J J
* 0
Такое приближение называется полуклассическим или прибли-
жением WKB (§ 42).
Очевидно, решение (34.05) должно быть периодическим по g:
Х(|)=Х(|+2л),
что сразу же приводит к квантовому условию (33.01).
Для резонатора, изображенного на рис. 38, вместо условия
периодичности надо использовать граничные условия (34.02) на
зеркалах g=gi и g=g2, причем функцию X следует брать в виде
t
Х==у 2 ^nSt г -S'n R (УсЬЧо- sinaEcft|.
j/ у2 (ch2 Со — sin2 g) cos L .) J
В этом случае приходим к квантовому условию (33.08).
Решая аналогичным образом уравнение (34.04) при x=cli2»0
и £>&, получим
с
— sink f/ch4-ch2C0^ + y01. (34.06)
y2(ch2 ch2 У L J J
При C<40 решение имеет вид
Co
J ==^/6,exp Г-Tf [v'ch40-ch4dCl +
/ y2(ch2 5,— ch2 ?) | L J J
Co
+ C2exp[j (Vch40—ch2CrfC]|, (34.07)
c
где Co, Ci и C2 — постоянные. Вблизи точки g=go все эти реше-
ния неприменимы, поскольку там большой параметр у умно-
жается на малую величину ch2 £—ch2
Так как при уменьшении g решение не может экспоненциаль-
но возрастать, то С2 следует положить равным нулю. Таким об-
разом, при £>£о функция Z должна осциллировать, а при £<
<£0 — экспоненциально затухать. Уравнение определяет
каустику. Для того чтобы связать решения по обе стороны от
182
точки go, т. е. выбрать фазовую константу <р0 в выражении (34.06),
требуется провести более глубокий анализ.
Приближенное представление функции Z во всем интервале
(включая точку Q при больших значениях у имеет вид
(ср. § 13)
Z ~ Vy2(ch2 ?— ch2 Q V ’ (34.08)
где переменные t и g связаны соотношениями
с
(-03/2 = у j/ch2C-ch2C0 dt при g >g0.
(34.09)
| /2 = Y J /ch2:0 - ch2 С dt при С < g0,
с
a v(t) есть та функция Эйри, которая экспоненциально убывает
при i—>оо. При t—<—оо эта функция имеет асимптотическое вы-
ражение (9.24). Есть также вторая функция Эйри «(/), экспо-
ненциально возрастающая при t—-оо. Ее следует отбросить по
той же причине, по какой мы положили С2=0 в формуле (34.07).
При g>igo и при достаточном удалении от каустики, когда
— 1, формула (34.08) в силу выражения (9.24) принимает
вид
г=И 4 /ch4 -д'+ т]- <3410>
Таким образом, в выражении (34.06) константа = Для того
чтобы решение (34.10) удовлетворяло граничным условиям (34.02),
необходимо выполнение условия
Г
Y |Vch4—сЬгС0<К = у (л + т) (« = 0,1,2,...). (34.11)
6»
Условие (34.11) отличается от условия (33.07) тем, что в него
вместо п входит п+ у". Смысл обоих условий один и тот же, но
в условии (34.11) учтено то обстоятельство, что вблизи каустики
g=go геометрическая оптика, которой соответствует формула
(34.06), неприменима. Если же ограничиться рассмотрением лу-
чей при g>go, вдали от каустики, то в -соответствии с формулой
(9.24) нужно учесть, что фаза волнового поля, соответствующего
лучу, отходящему от каустики, отличается от фазы, которая вы-
числяется из геометрических соображений по фазе приходящего
183
луча, на слагаемое —• Это — так называемый скачок фазы на 1
каустике (см., например, (24]), он и приводит к замене п на I
в квантовом условии (34.11). <|
Пусть теперь x=sin2go. Рассмотрим сначала уравнение!
(34.04). Так как теперь коэффициент при Z нигде не обращается 1
в нуль, то полуклассическое приближение применимо во всей '1
области изменения £, следовательно, 1
у 2, --7^ C°S ГY ГКсЬгС — sin*£0 #1 • (34.12)1
У Y2 (ch2 s — sin2 $„) sin L J J fl
0 ’
Из граничных условий (34.02) на зеркалах £=±£ вытекает кван- J
товое условие (33.09). Ч
Для функции X (при x=sin2go) полуклассическое прибли- 1
жение >
X = т == cos Г у [ /sin2 — sin2 5 dgl (34.13) j
Л Y2 (sin2 g, — sin2 5) sin L J J 1
0 i
недостаточно, так как разность sin2g0—sin2g обращается в нуль j
при g=±go, т. е. на гиперболических каустиках. Наличие синуса 1
или косинуса определяется симметрией задачи, поскольку соб- 1
ственные функции должны быть либо четными, либо нечетными д
функциями g. С помощью функций Эйри для функции X полу-.]
чается при 0< g<|o следующее выражение: ;
Ь> 1
Х = 4/~77- 2 6 sin ГY (Vsin2 с0 —sin2? dz-f-J [, (34.14)
У Y (sin2 — sin2 5) I J 4 I
' £
которое согласуется с выражением (34.13) при условии
Y Ji/sin2B0 — sin2EdE = -^ + (fn = 0, 1, 2, ...), (34.15) 1
0 1
причем четным т соответствует в формуле (34.13) косинус, а не- I
четным т — синус. 1
Это условие отличается от квантового условия (33.10) тем, I
что вместо т стоит т+ у, что, как и раньше, связано со скачком 1
фазы на каустике, т. е. с неприменимостью геометрической опти- I
ки вблизи каустики.
Выведенные выше соотношения неприменимы при х^ 1
^т. е. при Со~О или Если точно х=1, то такое коле-
бание соответствует лучевым потокам особого типа (см. конец
184
§ 32), при х»1 реализуется переход от колебаний с эллиптиче-
скими каустиками к колебаниям с гиперболическими каустика-
ми. Для таких переходных колебаний выведенные формулы нуж-
даются в уточнении. Действительно, при £о~О каустический эл-
липс становится тонким, а при g0~ y верхние и нижние полови-
ны каустических гипербол сближаются, что приводит к необхо-
димости учитывать просачивание поля через узкий зазор между
каустиками, свободный от лучей; это значит, что, например,
в формуле (34.08) функцию v(t) необходимо заменить на ли-
нейную комбинацию функций u(t) и v(t). Однако переходные
колебания, равно как и лучевые потоки особого типа, не пред-
ставляют интереса для теории открытых резонаторов, поскольку
их поле заполняет эллипс целиком.
Если параметр .&> мал, что формулы (33.09) и (34.06) сво-
дятся к приближенным формулам, выведенным в § 12 и 13 для
цилиндрических зеркал. Действительно, в этом случае sin £ мож-
но заменить на £ и условие (34.15) принимает вид
U ________
(m + y) (/« = 0, 1, 2, ...) (34.16)
о
или
(34.17)
Делая аналогичные аппроксимации в условии (33.09), получим
или
у sh С — 4 Y^ зге sin (th С) = у п.
(34.18)
Если ввести обозначения
Z = dshC,
a = arcsin (th С) =arcsin |/" у
(34.19)
где
,sh2?
г„ = а —=
0 ch?
есть радиус кривизны зеркал в точке g=0, 2/— расстояние меж-
ду ними, и воспользоваться соотношением (34.17), то формула
(34.18) примет вид
2kl=nn+ (2m+l)a
в согласии с § 12.
(34.20)
185
Нужно заметить, что приведенные выше приближенные фор- ’]
мулы справедливы лишь для достаточно коротких волн. Это зна- I
чит, что квантовые числа тип должны быть велики — либо оба, 1
либо одно из них. Формула (34.20) применима при больших пи |
умеренных т.
Как отмечено в § 12, между квантовой механикой гармониче- I
ского осциллятора и волновой оптикой цилиндрических зеркал I
(при £о<1) существует глубокая аналогия. Формула (34.17)1
соответствует полуцелому квантованию энергии осциллятора, 1
в противоположность целочисленному квантованию, вытекающе- 1
му из формулы (33.10). i
§ 35. Зеркала и каустики
Для того чтобы из предыдущих параграфов сделать выводы '!
общего характера, докажем следующую теорему. Пусть на пло- ;
скости дана выпуклая замкнутая кривая (рис. 39). Из некоторой
точки А проведем две касательные к этой кривой. Рассмотрим
РИС. 39. Построение биэвольвенты.
геометрическое место точек А, для которых периметр фигуры Л
ASiSqS2A постоянен; эту кривую можно назвать биэвольвентой. .
Докажем, что касательные SiA и 32А составляют с нормалью В
к биэвольвенте в точке А равные углы. .
Пусть s — длина дуги исходной кривой, отсчитываемой от точ- 1
ки So по часовой стрелке, а х0 — периметр исходной кривой. Век- 1
торы tj и т2 — единичные векторы, направленные по касательным *1
в точках 5, и S2. Как видно из рис. 39, j
R = р, + г Л = р2 — Г2т2. (35.01) Ч
186
Кроме того, согласно условию теоремы
si + g + g + $0 — S2 = const, (35.02)
ds2 — dr2 = ds, 4- dr,.
Продифференцировав равенства (35.01), получаем
dR — dp! 4-nrfT! r1dr1 = dp2 — r2dr2 — r2dr2. (35.03)
Учитывая, что
dp, —т/s,, dp2 = x2ds2, (35.04)
получим
dR = t, (ds,4- dr,) 4- r/Tj = x2 (ds2 — dr2) — r2dz2. (35.05)
Проекции вектора dR на векторы x, и x2 соответственно равны
x1dR = dsl 4-dfj,
x2dR ~ ds2 — dr2, (35.06)
так как
x1dx1 = x!,dx2 = 0. (35.07)
Вследствие равенства (35.02) имеем
x1dR = x2dR, (35.08)
что и доказывает наше утверждение.
Справедлива также обратная теорема: если нормаль к некото-
рой кривой составляет в каждой ее точке равные углы с каса-
тельными к некоторой другой кривой S0S]S2, то периметр фигуры
Д525052Д постоянен независимо от положения точки Д. Действи-
тельно, если бы это было не так, то вместо равенства (35.02) мы
имели бы неравенство. Следовательно, проекции dR на х2 и х2
не были бы равны, т. е. не были бы равны углы касательных
с нормалью. Из этой обратной теоремы, в частности, следует по-
стоянство периметра фигуры QS2BS2Q на рис. 36.
Если биэвольвента представляет собой зеркало, то исходная
кривая является каустикой, т. е. огибающей семейства лучей, от-
ражающихся от биэвольвенты. Как мы уже видели в случае эл-
липтического зеркала, могут осуществиться не всякие каустики,
а лишь те, которые подчиняются квантовым условиям.
В случае зеркал произвольной формы также имеются кван-
товые условия. Первое квантовое условие состоит в том, что пе-
риметр замкнутой каустики должен равняться целому числу
волн, а периметр каустики, опирающейся на зеркала,—шелому
числу полуволн. Второе квантовое условие с учетом поправок,
полученных в § 34 и имеющих общий характер, должно заклю-
чаться в том, что в случае одной замкнутой каустики (рис. 39)
периметр фигуры ДЗ^^Д должен составлять целое число волн
187
минус четверть волны. Если же каустика состоит из двух ветве/
(как на рис. 37 и 40), то длина кривой PlStBS2P2 должна рав
няться нечетному числу четвертей волны.
Первое условие следует из того, что при достаточно коротки)
волнах, когда применима геометрическая оптика, фазовая ско-
РИС. 40. Построение зеркал по круговым
каустикам.
рость поля вдоль каустики равна с. Второе условие 'следует из
однозначности поля; при его формулировке предполагается, что
каустика имеет конечную кривизну (и радиус кривизны значи-
тельно превышает длину волны).
Из сказанного вытекает способ графического построения зер-
кал по заданным каустикам. Пусть, например, каустики заданы
в виде двух окружностей (рис. 40); на этом конкретном примере
мы покажем, как изменить способ построения в том случае, ког-
да луч испытывает более одного отражения от зеркал на пути
от одной каустики до другой.
Натянем гибкую нить по контуру OiSiBS2O2. Затем, поставив
карандаш в точку В и держа нить натянутой, вычерчиваем кри-
вую между точками и С2. Эти точки находятся на общих ка-
сательных к двум заданным окружностям. Небольшие отрезки
зеркала C[Di и C2D2 строятся иначе, а именно нить натягивается
188
на одну из окружностей. Например, для построения отрезка C\D\
нить должна быть натянута по контуру SQFPO,. Затем вычер-
чиваем отрезок C\DX при условии, что разность длин SQF и
FPO\ постоянна. В данном случае, когда каустиками являются
окружности, отрезок CiD{ оказывается прямолинейным.
При последнем построении использовано то обстоятельство,
что построенная кривая делит угол между нитями (или каса-
тельными). пополам. Доказательство этого аналогично доказа-
тельству теоремы, сформулированной выше.
Изложенный способ построения зеркал по данным каусти-
кам может быть использован при создании кинематических ме-
ханизмов для изготовления и полировки зеркал.
Таким образом, колебания в открытых резонаторах, ограни-
ченные каустиками, могут быть рассчитаны с помощью геоме-
трической оптики. Этот подход обладает наглядностью и позво-
ляет вычислить собственную частоту и распределение поля
для каждого колебания, но не дает диффракционных потерь
(см., впрочем, § 40).
§ 36. Открытый резонатор,
образованный зеркалами
разной кривизны
Гибкость и наглядность лучевой трактовки хорошо иллюстри-
руется на примере открытого резонатора, образованного двумя
зеркалами разной кривизны. Пусть его зеркала в эллиптической
системе координат (33.02) определяются соотношениями:
-¥<£<], с=-с,
-Г<е<1 с=с2, (36.oi>
где 5, и С2 — положительные величины. Можно показать, что-
при условии
5 < 1 (36.02)'
такой резонатор эквивалентен симметричному резонатору с зер-
калами, которые в некоторой другой эллиптической системе ко-
ординат определяются соотношениями
— $<;<?, С = (36.03)
С 'помощью геометрических рассуждений § 32 нетрудно по-
казать, что между зеркалами (36.01) могут существовать два по-
тока лучей, ограниченных гиперболическими каустиками g=-
= ±igoi(£о<€) и переходящих друг в друга при отражении. Кван-
товое условие (34.16) и (34.17) при этом остается без изменений,
а квантовое условие (33.09) в этом случае принимает вид
с.
Y j |/ch2C—sin250
—с.
189
причем при ?0 << 1 из него получается соотношение
Y (sh Cj -j- sh Q — у у[arcsin (th Q arcsin (th C2)] = тот.
Сравнивая его с соотношением (34.20), видим, что параметры
(34.19) эквивалентного симметричного резонатора определяют-
ся формулами
/ = ^-(shC1 + shQ,
i (36.04)
а — у [arcsin (th Q 4- arcsin (th Q].
Однако обычно зеркала задаются не соотношениями (36.01),
а своими радиусами кривизны и и г2 и расстоянием 21 между зер-
калами. По величинам гь г2 и 21 находим параметры g2 и
характеризующие зеркала в эллиптической системе координат
(если ее удастся подобрать); при этом надо учитывать, что в со-
ответствии с формулами (36.01) мы имеем
t\—d
ch2?t
sht, ’
г =dc^
2 sh ?г
2Z = d(shC14-shQ, (36.05)
.а также
ri = d (jiTsT “b sh ’ r2==^(sh«7”^sh^)’
•откуда
shC1ShC2 = ^-, О = i. (36.06)
Наряду с этим имеется тождество
(fj — 21) (гг 21) = d2 (-h sh?2+sh C, sh C2 — 2^ =d2 + 4Ю -.
из которого следует, что
‘г,='р4((7.+^,)^а) (36-07)
И
shC, + sh(;2=^- (36.08)
*90
Комбинируя соотношения (36.06) и (36.08), для shCj и sht2
получаем квадратное уравнение
X2-* %+^=0, '(36.09)
откуда
sh^i.a — d =t
/г 1
d2 D
(36.10)
Таким образом, формально по заданным величинам гь г2 и
21 всегда можно найти £2 и d. Фактически же это возможно
только тогда, когда по формулам (36.07) и (36.10) получаются
вещественные величины, т. е. когда
0<d2 < ID.
(36.11)
Если кривизна зеркал одинакова (Г1 = г2=го), то
d2=lD, D = r0—l (36.12)
и неравенства (36.11) удовлетворяются при г0>1 в соответствии
с § 12. При Г1=#Г2 дело обстоит сложнее: на рис. 41 изображена
РИС. 41. Величины d2 и ID для зеркал разной
кривизны.
зависимость величин d2 и ID от 21 при фиксированных значени-
ях Г! и г2>П- Отсюда следует, что в интервале
П<2/<г2 (36.13)
величина d2, вычисленная по формуле (36.07), получается отри-
цательной; то же будет при условии
Г1 + г2<2/, (36.14)
когда £><0. Интервалы, где величина d2 отрицательна, на рис. 41
заштрихованы. В этих интервалах невозможны колебания, кото-
рые представлялись бы системой лучей, ограниченных каусти-
ками. Действительно, при условии (36.14) можно подобрать та-
кую эллиптическую координатную систему, в которой зеркала
191
лежали бы вблизи большой оси эллипсов (см. задачу 1). По-
скольку внутри зеркального эллипса не может существовать си-
стема лучей, локализованных вблизи его большой оси (см. ко-
нец § 32), такие открытые резонаторы не имеют колебаний, ко-
торые допускали бы лучевую трактовку и имели малое
радиационное затухание. При условии (36.13) подобрать эллип-
тическую систему координат вообще нельзя, но отсутствие коле-
баний в виде лучевых потоков может быть доказано из других
соображений (см. задачу 9).
Отсутствие добротных колебаний, имеющих вид параксиаль-
ных лучевых потоков, при условиях (36.13) и (36.14) было впер-
вые обнаружено Бойдом и Когелышком [34]. Наиболее просто
и наглядно это доказывается (см. [34]) применением законов
геометрической оптики к параксиальным лучам в этой системе;
а именно, любой такой луч (за исключением центрального луча,
совпадающего с осью системы) после отражений все более уда-
ляется от оси.
Величина d2 положительна при условиях
Г! >2/, г2>2/, (36.15)
а также при условиях
Г1<2/, г2<2/, Г1+г2>2/. (36.16)
Легко видеть (ср. рис. 41), что при d2>0 неравенсто d2< ID
выполняется автоматически, поскольку формулу (36.07) можно
переписать в виде
d2 = /D-^^-, G>0, fe>0. (36.17)
При условиях (36.15) или (36.16) можно построить эллиптиче-
скую систему координат, соответствующую данным зеркалам, и
при условии (36.02) рассчитать открытый резонатор по форму-
лам, приведенным выше.
Полученные результаты позволяют критически оценить опти-
мальность открытых резонаторов с софокусными зеркалами, о ко-
торой говорилось в гл. III и IV. Действительно, при точном сов-
падении кривизны зеркал (п —г2=го) софокусные зеркала (2/=
= го) дают наименьшие диффракционные потери; однако, пы-
таясь достичь того же эффекта со слегка различными зеркалами
(п<т2), мы можем попасть в интервал (36.13), где диффрак-
ционные потери велики — гораздо больше, чем при условиях
(36.15) и (36.16), соответствующих несофокусным зеркалам. Та-
ким образом, использовать оптимальность софокусных зеркал
в полной мере не удается — используемые зеркала могут быть
близки к софокусным лишь настолько, насколько это позволяют
допуски. Нужно еще иметь в виду, что согласно законам
геометрической оптики поперечная протяженность области, за-
полненной лучами, оказывается значительной, если гь г2 и 2/
192
определяют точку, лежащую на рис. 41 вблизи заштрихованных
областей. Это значит, что не только в заштрихованных областях,
но и вблизи них нужно учитывать либо диффракционные эффек-
ты, либо непараксиальность лучей, либо то и другое.
Указанные трудности, возникающие при осуществлении ре-
зонатора с софокусными зеркалами, пропадают, если перейти
к резонатору, образованному вогнутым и плоским зеркалами.
В самом деле, при г2=о° мы будем иметь
d2=21 (и—21), D = oo. (36.18)
Следовательно, неравенства (36.11) выполняются, если г\>21
(21 в данном случае есть расстояние между плоскостью и во-
гнутым зеркалом). Этот результат является самоочевидным: во-
гнутое зеркало вместе со своим изображением в плоскости обра-
зует симметричный открытый резонатор, к которому применима
формула (36.12).
Полученные выше результаты относятся не только к цилин-
дрическим, но и к сферическим зеркалам, поскольку формулы
(36.05) справедливы и для сферических зеркал.
§ 37. Лучевые потоки
в трехосном эллипсоиде
В § 32—36 было показано, что двухмерные колебания в от-
крытых резонаторах, обладающие вследствие образования кау-
стик весьма малыми диффракционными потерями, подчиняются
законам геометрической оптики. Было показано также, что на
основании законов геометрической оптики можно получить ча-
стоты собственных колебаний и положение каустик, соответ-
ствующих собственным колебаниям. Для этого оказалось необ-
ходимым ввести так называемые квантовые условия, состоящие
в том, что вдоль некоторых замкнутых путей полный набег фазы
полагается кратным 2пп.
Такой расчет собственных частот с помощью геометрической
оптики вполне аналогичен квантованию орбит в старой кванто-
вой механике Бора, поэтому условия, определяющие собствен-
ные частоты и положение каустик, мы назвали квантовыми
условиями.
Геометрический подход обладает наглядностью и, кроме то-
го, позволяет легко отказаться от требования параксиальности
лучей, которое является обычным при волновом подходе. Ввиду
этого целесообразно распространить его на трехмерный случай,
что и сделано ниже.
Прежде всего, обобщая результаты § 32—34, мы рассмот-
рим лучевые потоки в трехосном эллипсоиде. Это рассмотрение
можно вести чисто геометрически, опираясь на геометрические
свойства поверхностей второго порядка (см. [31] и (49]), либо
13—2547 193
аналитически, решая скалярное волновое уравнение в эллипсои-
дальной системе координат методом разделения переменных.
Оба подхода в нужном нам приближении дают эквивалентные
результаты. Мы ограничимся аналитическим рассмотрением,
быть может, менее наглядным, но зато более простым, посколь-
ку доказательство всех необходимых нам свойств эллипсоидов
и гиперболоидов достаточно громоздко.
О сг Ьг a2 iS
РИС. 42. Эллипсоидальные координаты т], £
Пусть нас интересует волновое поле внутри эллипсоида,
определяемого уравнением
у2 , г/2
(37.01)
где а, Ь, с — главные полуоси эллипсоида, удовлетворяющие не-
равенствам
a>fe>c>0. (37.02)
Эллипсоидальная система координат, соответствующая взятому
эллипсоиду (37.01), определяется уравнением
jr2 0*2
а2—Ь2 — С2_ 1- (37.03)
Это уравнение при О=£, где
—оо<£<с2, (37.04)
определяет эллипсоиды [при |<0 эллипсоиды лежат вне эллип-
соида (37.01), при £>0 — внутри него], при &=т], где
с2<т1<Ь2, (37.05)
оно определяет однополостные гиперболоиды, а при •&=£, где
Ь2<£<а2, (37.06)
— двухполостные гиперболоиды (ср. рис. 42).
На рис. 43 изображен зеркальный эллипсоид g=0, а также
фокальный эллипс, определяемый уравнениями
г = 0, (37.07)
и фокальная гипербола, определяемая уравнениями
у2 £.2
^“^"2=1. * У=0- (37.08)
Полагая ^=с2, получаем часть плоскости z=0, заключенную
внутри фокального эллипса, а полагая т)=с2,— часть той же пло-
194
скости, лежащую вне эллипса. При т] = 62 мы получим часть пло-
скости «/ = 0, лежащую внутри фокальной гиперболы (эта часть
состоит из двух изолированных областей и содержит фокусы ги-
перболы), а при — остальную часть плоскости z/=0.
РИС. 43. Зеркальный эллипсоид, фокаль-
ные эллипс и гипербола.
Декартовы координаты х, у, z выражаются через эллипсо-
идальные координаты g, т], t, следующим образом:
л (Ь2 — а2)(с2 — а2)
(б2-?)(&2-ч)(*2-С)
У ~ (С* — Ь2)(а2 — Ь2)
_2 . (c2-S)(c2-4)(c2-Q
(а2 — с2) (Ь2 — с2)
(37.09)
Координаты Е, •»], С образуют ортогональную криволиней-
ную систему координат, связанных в пределах октанта (напри-
мер, при х>0, «/>0, г>0) с декартовыми координатами взаимно
однозначными соотношениями. Коэффициенты Ламе в эллипсои-
дальной системе координат Е, тд, С равны:
h 1
\ — 2 V D (t)
\=4 /(’1~”Й)~6)- <371°)
h -1,
С 2 Г D (S)
где
D (&) = (а2 — &) (Ьг — &) (с2 — &). (37.11)
13* 195
Поэтому скалярное волновое уравнение
ДФ-]-/ггФ = 0 (37.12)
принимает в эллипсоидальных координатах следующий вид:
4 (7] - С) -4 (С - 5) ^[/=^N)^j +
+4(5-ч)ГЩС)4[ГщР^]+^(5-ч)(5-С)(ч-С)Ф=о,
(37.13)
причем при написании уравнения (37.13) мы учли, что
D (5) > О, D (ч) < О, D (С) > 0. (37.14)
Использованные выше соотношения хорошо известны в ли-
тературе (см., например, [32] и [33]), однако обычно отрицатель-
ность D(x\) не учитывается и второй член в левой части (37.13)
записывается так же, как первый и третий, что приводит к мни-
мостям, маскирующим характер решений.
Введем новые переменные:
6
г== Г
о
. М (37.15)
J 2 Y— D (Й) ' '
са
С
.] 2КО(Й)
Поскольку 5 есть монотонная функция 6, то она допускает одно-
значное обращение и можно считать 5 функцией 5 и аналогично ч
функцией •>} и С функцией С. Переменные (37.15) позволяют пере-
писать волновое уравнение (37.13) в более компактном виде:
(П - 9 -(С - У ~ + (? - 7]) (5- ч) (5- С) (ч- С) Ф=0.
о?2 [От]2 й2
(37.16)
Это уравнение мы будем решать для области, заключенной
внутри эллипсоида (37.01), ставя на его поверхности граничное
условие
Ф = 0 при 5 = 0 (37.17)
или
-^ = 0 при 5 = 0. (37.18)
196
Скалярное волновое уравнение (37.16) и граничные условия
(37.17) и (37.18) позволяют в какой-то степени судить об элек-
тромагнитных колебаниях идеально отражающей эллипсоидаль-
ной полости. Более строгое решение этой задачи должно бази-
роваться на уравнениях Максвелла, которые, однако, не допус-
кают разделения переменных и поэтому ведут к довольно гро-
моздким выкладкам.
Уравнение (37.16) допускает разделение переменных, т. е.
имеет частные решения вида
Ф='Х(ё)У(т))ад. (37.19)
Функции X, Y, Z суть (решения уравнений:
— + k2p(k)X = O,
-^--k2p^)Y = 0, (37.20)
drf
— ~H2p(C)Z=0,
где через p(ft) обозначен полином второго порядка:
p(fl) =‘fl2+ia'fl+₽, (37.21)
а через аир — постоянные разделения. Этот полином можно
записать в виде
р (fl) =i(fl—fli) (fl—fl2). (37.22)
Уравнения (37.20) по существу совпадают с волновыми урав-
нениями Ламе (ср. {33], стр. 97). Принятая нами запись этих
уравнений существенно облегчает исследование асимптотиче-
ских (при k—>оо) свойств функций X, Y, Z—волновых функций
Ламе.
Функция Ф определяет собственное колебание внутри замк-
нутой идеально отражающей поверхности £=0 и поэтому являет-
ся — с точностью до постоянного множителя — вещественной, рав-
но как и функции X, Y, Z. Отсюда следует, что полином p(fl)
должен быть вещественным, т. е. корни fli и fl2 либо веществен-
ные, либо комплексно-сопряженные. Если fli и fl2—комплексно-
сопряженные, то полином p(fl) сохраняет знак и по крайней
мере одно из уравнений (37.20) имеет монотонное решение, не
удовлетворяющее всем условиям задачи (см. ниже). Поэтому
остается лишь одна возможность: считать fli и fl2 вещественны-
ми. Полагая fli<fl2, при fl2<c2 или fli>£2 получаем р(л)>° и
монотонную функцию Y, а при -fli<0 (или fl2>a2) функция X
(или Z) становится монотонной.
197
В результате оказывается, что все собственные колебания
трехосного эллипсоида принадлежат одному из четырех типов,
определяемых неравенствами (см. также рис. 44):
А. с2<-&1<д2<62.
В. c2<-&1<62<fl-2<a2-
С. ОС^С^СОгСб2.
D. OCtfiCc2, b2<&2<a?.
На рис. 44 функция X, Y или Z осциллирует в интервалах,
отмеченных волнистыми линиями.
Таким образом, собственные колебания в трехосном эллип-
соиде, как правило, имеют каустические поверхности (-&=-&! и
0=^2)» которые соответствуют точкам поворота в дифференци-
о с* а, а2 ьг аг
С -ИаМ-------frwwwf-----|^<ллааа4-
0 it с2 i2 Ь2 а2
в ivwwj—frwwwwvwl —|лллл|---------й
о а, с2 ь2 #2 а2
РИС. 44. Графическое изображение неравенств, определяющих
колебания четырех типов.
альных уравнениях (37.20). В некоторых частных случаях кау-
стические поверхности вырождаются в фокальные линии или
фокусы (см., например, § 39). Чем выше частота колебаний, т. е.
чем больше k, тем точнее можно трактовать волновые поля этих
колебаний как лучевые потоки, ограниченные каустическими по-
верхностями, и тем более четко выражены эти поверхности.
Асимптотические свойства функций X, У, Z будут рассмот-
рены в § 38, однако уже сейчас мы можем составить качествен-
ное 1представление о каждом из четырех типов колебаний. Для
колебаний А каустическими поверхностями, ограничивающими
лучевые потоки, являются два однополосных гиперболоида;
область, занятая лучами, имеет вид полого криволинейного ци-
линдра, вытянутого вдоль оси z (рис. 45). Колебаниям В соот-
198
ветствуют лучевые потоки, для которых каустическими поверх-
ностями будут двухполостный и однополостный гиперболоиды,
ограничивающие объем в виде криволинейной прямоугольной
РИС. 45. Колебание А.
призмы с плоскостями симметрии х=0, у=0 и z=0 (рис. 46).
Колебания С в качестве каустических поверхностей имеют
эллипсоид и однополостный гиперболоид; лучевые потоки запол-
РИС. 46. Колебание В.
199
няют тороидальную область (с сечением в виде криволинейного
прямоугольника), лежащую вблизи плоскости ху (рис. 47). На-
конец, для колебаний D каустическими поверхностями будут
г
РИС. 47. Колебание С.
эллипсоид и двухполостный гиперболоид, а лучи заполняют то-
роидальную область (также с прямоугольным сечением), рас-
положенную вблизи плоскости yz (рис. 48).
РИС. 48. Колебание D.
200
§ 38. Асимптотические формулы
для функций Ламе
и квантовые условия
Прежде чем переходить к выводу асимптотических формул
для функций Ламе, определяемых уравнениями (37.20), остано-
вимся на (точных) условиях, которым эти функции должны
удовлетворять на концах интервалов 0<g<c2, (37.05) и (37.06),.
в которых они определены.
Из граничных условий (37.17) и (37.18) следует, что
Х = 0 или — = 0 при Е = 0. (38.01)/
d~
Остальные граничные условия вытекают из того обстоятельства,
что по формулам (37.09) декартовы координаты однозначно
определяются координатами g, rj, £ лишь в пределах одного
октанта. На границах этого октанта функция Ф в соответствии
с симметрией задачи должна удовлетворять условиям:
Ф = 0 или при л=0,
ф=0 или при у = 0, (38.02)
Ф = 0 или =0 при 2 = 0.
Уравнения |=с2 и т] = с2 определяют (см. § 37) плоскость z=
= 0, поэтому из третьего условия (38.02) мы получаем гранич-
ные условия
Х = 0 или—= 0 при Е=с2, (38.03)
dl
F = 0 или ^=0 при 7] = с2. (38.04)
dt}
Уравнения т] = 62 и £=!62 определяют плоскость у—0, поэтому
из второго условия (38.02) имеем
У = 0 или ^ = 0 при -q-Ь2, (38.05)
d >]
Z = 0 или — = 0 при С=£2. (38.06)
Плоскость х=0 получается при £=а2, поэтому из первого усло-
вия (38.02) получаем
Z=0 или — = 0 при ? = аг. (38.07)
dK
201
Если функция X, Y или Z является монотонной, то условиям
на обоих концах соответствующего интервала удовлетворить
нельзя, и мы не получаем решения интересующей нас задачи.
Для осциллирующих функций X, Y, Z получаем три квантовых
условия, которые определяют как корни От и Ф2, так и волновое
число k, т. е. частоту колебания.
Для колебаний А мы имеем p(g)>0 во всем интервале
(37.04). Поэтому при достаточно больших k можно написать
для функции X полуклассическое приближение
Е ____
<38 08)
где введено обозначение
(38 09)
и использовано тождество
Т Е z_____. Е
J /p(e)dF= 1 j J/ j f v'P^d*. (зело)
fl о о
Из условий (38.03) вытекает квантовое условие
= (AJ
о
где — целое число. В дальнейшем через N Nz мы обозна-
чаем целые числа (1,2, 3, . . .). Они могут обращаться в нуль,
если это не приводит к бессмысленному соотношению; в частно-
сти, вводимые ниже „каустические11 квантовые числа, входящие в
комбинации N-]- -могут принимать значение W—0. При этом
нужно иметь в виду, что хотя бы одно из чисел , Nz должно
быть велико для того, чтобы была применима геометрическая оп-
тика (т. е. чтобы длина волны была мала по сравнению с харак-
теристическими размерами эллипсоида). Для открытых резонаторов
наиболее интересны колебания, у которых одно из чисел Л^, N
большое, а два остальных небольшие (ср. далее § 39).
При интегрировании второго уравнения (37.20) мы будем
считать, что корни От и лежат достаточно далеко от концов
интервала (37.0)5), вследствие чего условия (38.04) и (38.05)
можно заменить требованием, чтобы функция Y при т]<От и
т]>-&2 экспоненциально убывала. В интервале О1<т]<'&2 мы ре-
шаем второе уравнение (37.20) асимптотически и выражаем
202
функцию Y через функцию Эйри v(t) (ср. § 13) следующим
образом:
^Г) (38. П)
где переменные t, и т; связаны соотношением
ч
| (-/,)3'2 = AJ (38.12),
in
С равным правом можно написать
y=b^^Г)(38 ГЗ>
где
|(-/2)3/2=|J/P(&)d&, (38.14),
ч
а А и В — постоянные.
Поскольку при больших отрицательных t справедлива
асимптотическая формула (9.24), для совпадения выражений
(38.11) и (38.13) в середине интервала Oi <*п<<>2» вдали от точек
поворота и ik, нужно, чтобы выполнялось второе квантовое
условие
*JV7W»=2«(m4). (А,)
Третье квантовое условие выводится так же, как первое, и имеет
вид
а'
k^V"P^)d»=^Nv (AJ
Для колебаний В выражение (38.08) остается справедливым,
и первое квантовое условие
<?а
& [ = (BJ
о
совпадает с условием (А£). Во всем интервале 01<т]<&2 для
функции Y справедливо выражение (38.11), причем условия
(38.05) вместе с формулой (9.24) дают второе квантовое условие
^f/P(»)d&=K^4+iy (BJ
Sr
203
Аналогичным путем мы приходим к третьему квантовому
условию
о"
(bj
Очевидно, что для колебаний С квантовые условия имеют
вид:
»i
k J vW) d&=«+1), (ct)
0
ft.
k j кт =* K+4)’ (4)
С»
a1
^J/P(&)</& = ^, (Cc)
b>
а для колебаний D:
ft.
(Ц)
0
b* _____
= (D^)
c*
a*
k jjZP(&jd& = K^ + l). (DJ
ft.
Выведенные выше формулы нуждаются в уточнении, если
0] »с2 или 0-2~'fez, т. е. если мы имеем дело с переходными коле-
баниями (ср. § 34). Интересно отметить, что при а—>оо колеба-
ния В и D превращаются в двухмерные колебания, существую-
щие внутри зеркального эллипса, а колебания А и С исчезают.
Действительно, при а —оо интегралы, стоящие в левых частях
условий (Ас) и (Сс), стремятся к бесконечности, в то время как
правая часть постоянна; это значит, что отсутствуют двухмерные
колебания, соответствующие колебаниям А и С.
Из условия (Вс) видно, что &2-» оо при а—*оо, так как ин-
тервал интегрирования возрастает пропорционально а2, а подынтег-
ральное выражение (при конечных и &2) пропорционально —.
Поэтому условие (Вс) можно при а —оо записать в виде
+ (38.15)
204
Очевидно, что
и3 ,_____________ а3
<38.16)
откуда
^><Nl + l, (38.17)
Так как k не стремится к нулю, то стремится к единице при
я—оо и условия (В£) и (В^) принимают вид
k'\v4
о (00.1 о)
ь2 г_____________
Г (62 —Ч)(с2 —+
Для колебаний D из условия (Dc) также следует, что || -► 1
при а -» оо, а условия (D^) и (D^) упрощаются следующим обра-
зом:
». ______________
k f г (Ь2 — 5) (с2 — £) —21 Г^+т)’
о
Ь‘ ________________
k f V (h2 °'^5 d-ц = nN.
J V t^ — Tl)(c2 — T^ • 4
c'
Полагая
t — b2— (b2— c2)ch2u (О-Сы-С00).
T) = fe2 — (b2 — c2)sin2o f0O<y\
(38.19)
(38.20)
легко показать, что, отвлекаясь от различия в обозначениях,
условия (38.18) переходят в условия (33.10) и (34.15), а усло-
вия (38.19) —в условия (34.11) и (33.01). Таким образом, коле-
бания В при а—>-оо превращаются в колебания с гиперболиче;
скими каустиками, а колебания D-—в колебания с эллиптиче-
скими каустиками.
§ 39. Применение полученных результатов
к открытым резонаторам
До сих пор мы рассматривали колебания в замкнутой поло-
сти. К колебаниям ® открытых резонаторах можно перейти, беря
вместо всей отражающей поверхности g=0 ту ее часть (с неко-
205
торым запасом), от которой происходит отражение лучевых по-
токов, соответствующих данному колебанию. Такое колебание
будет слабо возмущено диффракцией на краях отражающей
площадки и будет иметь малые диффракционные потери. В том
же открытом резонаторе другие колебания эллипсоидальной
полости, лучевые потоки которых отражаются от отсутствующих
участков поверхности £=0, будут сильно искажены, и их
диффракционные потери будут большими. Так реализуется раз-
режение спектра собственных частот, характерное для открытых
резонаторов.
Форма зеркал, необходимых для поддержания тех или иных
колебаний, следует из рис. 44—48: зеркала должны охватывать
те интервалы значений т] и £ на поверхности £=0, которые на
рис. 44 отмечены волнистыми линиями.
В качестве примера рассмотрим открытый резонатор, обра-
зованный двумя одинаковыми сферическими зеркалами. Если
поперечные размеры зеркал малы по сравнению с расстоянием
2с, то эти зеркала можно аппроксимировать участками сплюс-
нутого эллипсоида вращения (а—‘Ь>с), что и сделано в гл. IV.
В этом случае малыми диффракционными потерями обладают
лишь колебания А, а именно те из них, у которых кольцеообраз-
ная площадка |==0, &1<т]<02 целиком укладывается на зерка-
ле. В параксиальном приближении (когда Ат и <)-2 близки к а2)
частота таких колебаний определяется формулой (19.12), кото-
рая теперь может быть переписана в виде
2йс=^4-2(^4-2^+ 1)«. (39.01)
Здесь > 1, и А'^ принимают значения 0, 1, 2, ...,
. с
а = arcsin — = arcsin
а
(39.02)
и
(39.03)
есть радиус кривизны сферических зеркал. Таким образом, в па-
раксиальном приближении имеет место вырождение: собственные
частоты зависят только от^ 2Nri~\- Nv а не от и в отдель-
ности; это вырождение снимается, если учесть непараксиальность
системы, дающей добавочные члены в правой части (39.01), или вос-
пользоваться квантовыми условиями (А^), (А^) и (А;) § 38.
Соотношение (39.01) нетрудно получить из формул § 38. Счи-
тая разности Ti = a2—th и т2=а2—в'г малыми (т. е. лучи — па-
206
ра1ксиальными), мы можем преобразовать интеграл, стоящий
в условии (At), следующим образом:
б о г
~ f г 1 — Г1 — == 2с — а, (39.04)
.) Ус2 — Й L 2 (а2 — »)] у а2 — с2
где параметр
a = arctg-F=^=== (39.05)
V а2 — с2
совпадает с тем, который введен выше по формуле (39.02). Таким
образом, условие (Ар принимает вид
2kc = nN -i-k а. (39.06)
у а2 — с2
Интеграл в условии (А^) преобразуется так:
&2 $2 —____________ ___________ _____
(= —L= f .
J v ' ’ У a2 — c2 J a2 — S a2 — c2 2
6, s.
(39.07)
поэтому оно записывается в виде
k = 2 (2^ + 1). (39.08)
В интеграле (Ар при a = b возникает неопределенность, кото-
рую мы раскрываем, считая сначала а >6:
у ’ Г а — с J у (а2 —в) (8 — Ь2) У а2 — с2
*« Ь2
(39.09)
и получаем
k = N.. (39.10)
У а2 — с2 с ’
Формулы (39.06), (39.08) и (39.10) приводят нас к формуле
(39.01), определяющей частоту колебаний А.
Колебания В между сферическими зеркалами существовать
не могут. Однако если между сферическими зеркалами вставле-
ны две плоскопараллельные пластины, наклоненные под углом
Брюстера к оси z (рис. 49), то можно показать, что открытый
резонатор становится астигматическим и благодаря этому в нем
возможны колебания В.
207
Действительно, система из зеркала и прилежащей к нему
пластины фокусирует лучи на разных расстояниях от зеркала
в зависимости от того, лежат ли эти лучи в плоскости симмет-
рии системы или в плоскости, ей перпендикулярной. Иначе го-
РИС. 49. Сферические зеркала с наклонными пла-
стинками.
воря, такая система эквивалентна одному зеркалу с разными
радиусами кривизны в двух взаимно перпендикулярных направ-
лениях. Разность главных радиусов кривизны эквивалентного
зеркала равна
Ar0 = r"0-r'0=d^|/n!+l (39.11)
(где d — толщина пластины, п — ее показатель преломления),
если пластина достаточно близка к зеркалу.
Два таких противостоящих друг другу эквивалентных зерка-
ла естественно аппроксимировать трехосным эллипсоидом, не-
много отличающимся от эллипсоида вращения, таким, что его
радиусы кривизны
Ь2 а2
(39.12)
(на концах его малой оси 2с) удовлетворяют соотношении»
(39.11).
В эллипсоиде вращения обе ветви фокальной гиперболы сов-
падают с осью вращения. Если эллипсоид немного отличается от
фигуры вращения, то эти ветви будут немного раздвинуты.
Кратчайшее расстояние между двумя ветвями гиперболы рав-
няется
s = 2Kc^fe3 = 2/cAr~ (39.13)
Для софокусных зеркал 2cs^=>r0 и, следовательно,
(39.14)
Рассмотрим случай, типичный для оптического диапазона:
го=1ОО см, d=0,3 см, п= 1,5. Тогда Лго=О,1 см и s~4 см.
В этом случае, несмотря на малую величину Дг0, обе ветви фо-
кальной гиперболы могут уже лежать вне зеркал или вне рабо-
чего пространства. Так как колебания А всегда охватывают
обе ветви фокальной гиперболы, то они также выйдут за преде-
2ое
лы рабочего пространства. Вследсгвие этого они будут в значи-
тельной степени искажены, и их добротность будет мала. Коле-
бания В лежат между ветвями фокальной гиперболы, они более
добротны и поэтому возбуждаться будут в первую очередь.
Волновое поле между сферическими зеркалами в основном
заключено между двумя однополостными гиперболоидами вра-
щения. Поэтому светлые пятна на зеркале будут заключены
между двумя концентрическими окружностями и иметь перио-
дичность по азимуту, соответствующему индексу
При наличии наклонных пластин часть зеркала, заполненная
светлыми пятнами, будет ограничена линиями пересечения одно-
полостного и двухполостного гиперболоидов с зеркалом. При
больших радиусах кривизны зеркал эти линии будут весьма
близки к эллипсу и гиперболе, имеющим общие фокусы. Таким
образом, астигматизм системы приводит к появлению колеба-
ний В.
Астигматизм может появляться в результате диффракции
на краях прямоугольных зеркал (§ 20), которая снимает вы-
рождение, характерное для параксиальной системы [формула
(39.01)], и определяет однозначно систему собственных функ-
ций.
Надо иметь в виду, что в реальных резонаторах вырожде-
ние собственных частот по формуле (39.01) и связанная с ним
неопределенность системы собственных функций снимаются под
влиянием совокупности возмущающих факторов, причем наряду
с перечисленными выше факторами (непараксиальность, пла-
стинки, диффракции) могут быть и другие, например, между
зеркалами может быть неоднородная среда, распределение по-
казателя преломления в которой не обладает симметрией вра-
щения.
Рассмотрим теперь колебания шепчущей галереи при некото-
рых упрощающих предположениях. Начнем с колебаний D в вы-
тянутом эллипсоиде вращения (Ь = с). Эти колебания ограниче-
ны эллипсоидом g='t>i и двухполостным гиперболоидом £=<12.
Будем полагать, что параметр -От мал, а параметр близок
к а2. Это означает, что каустический эллипсоид близок к зер-
кальному, а обе части двухполостного гиперболоида близки
к плоскости yz.
При этих предположениях условие (DJ приводит к равенству
4k ( _2?) (39 15)
з ьг — "и 2/ 1 МОв X f
или
8.=*’[5в(^+4)Г- <3916>
Из условия (D^) получаем
<3917>
14—2547 209
из условия (Ц)
£(а’-®г) = (2У; + 1)
(39.18)
Комбинируя формулы (39.16), (39.17) и (39.18), получим соот-
ношение, определяющее частоту колебаний
*»=N,+4t('v£+t)F+(Nc + I)^ <39Л9>
в котором
J3 соотношении (39.19) N— большое целое число, a
нимают значения 0, 1, 2, ... , причем второе и третье
в правой части (39.19) должны быть малы по сравнению с N.
Последнее
(39.20)
и 1\\ при-
лагаемые
условие позволяет переписать формулу (39.20) в виде
М\У/3
^=\2j *
(39.21)
после чего она согласуется с формулой (26.36), в которой вели-
чины а и |0 надо считать малыми и пользоваться формулами
(24.27), (24.28), (24.38) и (24.39).
Радиусы кривизны эллипсоида вблизи плоскости yz (рис. 31)
равны b и го, где
(39.22)
поэтому
В рассматриваемом случае г0>Ь, поскольку а>Ь.
Из соотношения (39.16) следует, что расстояние от зерка-
ла до каустического эллипсоида в плоскости yz равно
0, Ь I Зл । 1 \ I2/3 ZQO
51 — 2b— 2[2kb J] (39.24)
Из соотношения (39.18) следует, что минимальное расстояние «2
от плоскости yz до каустического двухполостного гиперболоида
равно
= |/(2^ + 1)^1- (39.25)
Переходя к колебаниям С, рассмотрим сплюснутый эллип-
соид вращения (а=Ь). В этом случае лучевой поток ограничен
двумя каустическими поверхностями: эллипсоидом ^=01 и одно-
полостным гиперболоидом т] = й,2, которые также являются тела-
ми вращения.
7Ю
Величину fti будем считать малой, что означает близость,
каустического эллипсоида к зеркальному. Величину будем
считать близкой к с2; это означает, что однополостный гипербо-
лоид пересекается с зеркальным эллипсоидом вблизи эквато-
риальной плоскости z=0. При этих предположениях квантовые
условия (Ц), (Ст) и (С^) приводят к соотношениям:
Ч гГ3п ( ы I 1 М2/3
л п2_
&2-сг = (2^+1)^^, (39.26)
, Г . »! — С2
2а2 2(а2—с2)]"-'ч’
частота колебаний определяется формулой
*=*<+^+4)Г+(*,+4)т.
в которой
(39.27)
(39.28)
Радиусы кривизны зеркального эллипсоида в плоскости ху
равны а и
г0-=С~, (39.29)
поэтому
(39.30)
Если учесть тождества (39.23) и (39.30), то соотношение
(39.27) по своему смыслу полностью совпадает с соотношением
(39.19), что еще раз подчеркивает родство обоих типов колеба-
ний шепчущей галереи. Однако в последнем случае г0<_а — этой
есть главное различие между колебаниями С и D.
Расстояние между зеркальным и каустическим эллипсоида-
ми, как и прежде, определяется формулой (39.24) с заменой b
на а, а расстояние от плоскости ху jyo линии пересечения одно-
полостного гиперболоида с зеркальным эллипсоидом опреде-
ляется формулой
«2 = /»2-г2=/ (2^4- 1)~/’
(39.31)
аналогичной формуле (39.25).
В заключение отметим, что общая эллипсоидальная система
координат, введенная в § 37, может быть применена для реше-
ния задач, рассмотренных в гл. Ill, IV и V. Однако мы предпоч-
ли в каждой главе вводить свою систему координат, наиболее
удобную для соответствующей задачи.
14*
211
§ 40. Возможности
геометрической оптики
Геометрическая оптика, дополненная квантовыми условиями,
позволяет рассчитывать открытые резонаторы, зеркала которых
могут быть аппроксимированы частью поверхности трехосного
эллипсоида (§ 39). На самом деле возможности геометрической
оптики гораздо шире — ее можно применять к открытым резо-
наторам гораздо более сложной формы, но при этом, естествен-
но, все соотношения значительно усложняются.
Ограничимся параксиальными пучками лучей, т. е. такими
пучками, все лучи которых образуют малые углы с некоторым
«центральным» лучом (причем последний может поворачивать-
ся и на большие углы, ср. рис. 50). Исследование собственных
РИС. '50. Отражение наклонного пучка от сферического
зеркала.
колебаний, которым соответствуют параксиальные пучки, всего
проще произвести, если ввести понятие эквивалентного эллип-
соида. В § 39 мы по существу ввели это понятие при анализе ко-
лебаний в открытом резонаторе, образованном сферическими
зеркалами с прозрачными пластинами (рис. 49).
Как известно, любая поверхность в каждой своей точке
характеризуется двумя главными радиусами кривизны. В даль-
нейшем мы будем считать поверхность вогнутой и главные ра-
диусы кривизны г'о и г"о положительными; они определяют по-
ложение главных центров кривизны, лежащих на нормали к по-
верхности на расстояниях г'о и г"0 от поверхности. Оптический
смысл главных центров кривизны, следующий: если в один из
центров поместить точечный источник света, то параксиальные ‘
лучи, лежащие в соответствующем главном сечении (в плоско-
сти, которая проходит через нормаль к поверхности и при пере-
сечении с поверхностью дает кривую, центр кривизны которой
совпадает с главным центром), после отражения от поверхности
соберутся в том же центре. В качестве примера можно привести
эллипсоид, главные радиусы кривизны которого в точке пересе-
чения его с меньшей осью определяются формулами (39.12).
212
Покажем, как ввести понятие эквивалентного эллипсоида
для параксиального пучка лучей, падающего на сферическое
зеркало под углом у (рис. 50). Обозначим через EAQBF цен-
тральный луч, О —центр сферического зеркала, ro=OQ— его
радиус кривизны. Вводя понятие эквивалентного эллипсоида,
мы отвлекаемся от того, что центральный луч после отражения
от зеркала изменяет свое направление, и считаем точки А и В
как бы совпадающими, если AQ — QB-, тогда зеркало будет пре-
образовывать данный параксиальный пучок лучей так же, как
эллипсоид преобразует пучок, падающий на него нормально
(при у=0). Главные радиусы кривизны г'о и г"о эквивалентного
эллипсоида, очевидно, определяются соотношениями (см.
рис. 5Q)
Р’o=AQ='QB,
r"0=EQ=QF, .(40.01)
где А и В— точечный источник и его изображение в пара-
ксиальных лучах, лежащих в плоскости чертежа, а Е и F — то-
чечный источник и его изображение в параксиальных лучах, ле-
жащих в плоскости, перпендикулярной чертежу и проходящей
через радиус OQ.
Чтобы найти положение точек Л и В на центральном луче,
повернем падающий и отраженный лучи на угол б вокруг оси,
проходящей через точку О и перпендикулярной чертежу; точ-
ка Q при этом перейдет в точку Р, а пересечение смещенного
луча АР и центрального луча AQ как раз даст искомую точку А
(рис. 50). Из соотношений
PQ = r0\ PQ=^ (40.02)
получаем
r'0=r0 cos у. (40.03)
Чтобы найти положение точек Е и F, повернем падающий и от-
раженный лучи вокруг оси EOF, перпендикулярной радиусу OQ;
очевидно, что при этом точки пересечения центрального луча
с осью EOF останутся на месте. Из рис. 50 видно, что
(40.04)
° cos у ' ’
С помощью эквивалентного эллипсоида нетрудно рассчитать
открытый резонатор, состоящий из четырех сферических зеркал,
расположенных в вершинах квадрата (рис. 51). Вместо пучка
лучей, распространяющегося по замкнутому пути 12341, рас-
смотрим пучок лучей в эквивалентном эллипсоиде, распростра-
няющийся вдоль его малой оси 2с. При этом мы должны малую
ось 2с эллипсоида взять равной стороне квадрата, а большую
213
и среднюю ось (2а и 2b) согласно формулам (39.12) определить
соотношениями
аг = /2сг„ 6г = у=сг„ (40.05)
где г0 — радиус кривизны сферических зеркал; в данном случае
cos у = . Кроме того, мы должны считать, что после двух от-
ражений в эллипсоиде пучок лучей не замыкается и что замыка-
ние происходит только после четырех отражений. Это приводит
к тому, что для колебаний В, которые представляют основной
интерес в данной системе, условие (В?) запишется следующим
образом:
2k J УР (») , (40.06)
о
а условия (В^) и (В,.) останутся без изменений (см. § 38).
Понятие эквивалентного эллипсоида может быть применено
также для расчета открытых волноводов, образованных перио-
дически расположенными вогнутыми зеркалами (гл. VIII).
Методы, основанные на геометрической оптике и на волно-
вых поправках к ней, пронизывают всю теорию открытых резо-
наторов и открытых волново-
дов. В гл. VIII и IX геометри-
ческая оптика будет широко
применяться к диэлектриче-
ским телам. В этой главе под
«геометрической оптикой от-
крытых резонаторов», мы по-
нимали геометрическую опти-
ку, дополненную квантовыми
условиями и учитывающую
скачок фазы на каустике, т. е. >
учитывающую те поправки
к полю вблизи каустической .
поверхности, которые опреде-
ляются волновой оптикой.
Применяя эту модификацию ,
геометрической оптики, мож-
но найти собственные частоты
РИС. 51. Четырехзеркальный от-
крытый резонатор.
колебаний с каустиками, положение каустик и распределение
волновых полей. Диффракционные поправки к волновым полям
и к собственным частотам (в частности, радиационное затуха-
ние колебаний) таким способом найти нельзя.
Нужно, однако, иметь в виду, что геометрическая оптика, при
всей своей неспособности учесть диффракционные явления, мо-
жет в ряде важных случаев привести к выводу о тождественно-
214
сти дифракционных эффектов в двух различных системах, если
лучевые потоки в этих системах одинаковы и если они ограниче-
ны в 'пространстве одинаковым образом. Это следует из того, что
волновые поправки к геометрической оптике имеют локальный
характер: таковы поправ-
ки к полю у каустики,
у фокуса, на границе све-
та и тени и т. д.
Иллюстрируем это об-
щее положение примера-
ми. В системе, изобра-
женной на рис. 52,а и
состоящей из бесконеч-
ных плоско-параллель-
ных зеркал и поглощаю-
щего экрана с отверсти-
ем, собственные колеба-
ния согласно геометриче-
ской оптике представля-
ют собой пучок парал-
лельных лучей, заполняющих отверстие в экране. Такой же пу-
чок лучей будет между конечными параллельными зеркалами,
форма и размеры которых соответствуют отверстию в экране
(рис. 52,6). Диффракционные свойства систем, изображенных
Черный
UH III Illi iimul
экран
Iiiiiiiiiiihhhii
б)
а)
РИС. 52. Эквивалентные системы с плоски-
ми зеркалами.
а)
/Линза \
\ Линза !
। черный
/
। экран Черный
SiiHiiijE
экран
\ Линза /
I
\
РИС. 53. Эквивалентные системы с зеркалами и линзами.
на рис. 52, также оказываются одинаковыми, по крайней мере
в параксиальном приближении; в частности, к системе на
рис. 52,а применимы все результаты, полученные в гл. I.
На рис. 53 изображены четыре системы, эквивалентность лу-
чевых потоков в которых приводит к тождественности их диф-
фракционных свойств: если половинки линз, укрепленные на
плоских зеркалах (рис. 53,6), создают такие же лучевые потоки,
как и зеркала (рис. 53,а, в), и если эти потоки ограничены
в продольных и поперечных направлениях одинаково, то эти
открытые резонаторы по всем своим свойствам одинаковы. На
рис. 53,а, б поперечное ограничение лучевых потоков осуществ-
215
ляется краями зеркал и линз, на рис. 53,в — краем отверстия
в поглощающем экране. Системы, изображенные на рис. 53,6
и а, также эквивалентны; последнее становится особенно
ясным, если учесть, что без изменения свойств системы, изобра-
женной на рис. 53,6, в плоскости ее зеркал (за их пределами)
можно поместить поглощающий экран.
\ Линза I I 1
\ I II
II I \
j ? ! Линза \
Sjiilllllllinijjg
I \ '
I Линза \ I I
itlHIIIIIIIIlii.
а} 6)
Рис. 54. Точно эквивалентные системы.
В системах, изображенных на рис. 53,6 и 54,а, лучевые по-
токи одинаковы, но ограничены по-разному: на рис. 53,6 край
зеркала совпадает с краем линзы, а на рис. 54,а плоские зерка-
ла бесконечны. Системы, изображенные на рис. 54,а, б, эквива-
лентны, причем эта эквивалентность имеет место не только
в рамках приближенной теории диффракции, которой мы поль-
зуемся на протяжении всей книги, но и при точном теоретиче-
ском рассмотрении.
t I2
<___________
а> 6)
РИС. 55. Системы, не вполне эквивалентные.
Асимметричные системы, изображенные на рис. 55 и состоя-
щие из зеркал разной кривизны, не являются вполне эквива-
лентными, поскольку на рис. 55,а диффракционное расплывание
пучка лучей происходит на пути 1—2, а на рис. 55,6 — на путях
216
0—*1—>„о и 0~>-2—-0, отличных от пути 1-^2. При переходе
к симметричным системам (см. рис. 53,а, в) эквивалентность
будет полной.
Задачи к гл. VI
1. Показать, что при условии (36.14) цилиндрические зеркала «вписыва-
ются» в эллиптическую систему координат таким образом, что они будут
лежать вблизи прямой, соединяющей фокусы.
Решение. Если зеркала лежат вблизи прямой, соединяющей фокусы,
то вместо формул (36.05) мы будем иметь
.sh2?! , sh2?2
r* — ch ?t 1 r2-dch?2’
21 = d (ch ?! + ch ?2),
а формулы (36.06), (36.07) и (36.08) заменяются следующими:
, ri +гг , ,
ch ch ^2 — » 5 — g “|“
4(21-г,) (21-г8)
(Г1 + г2 + 41)2 ’
ch ?! -f- ch ?2 — •
Отсюда видно, что условия
0 < d2 < IS.
гарантирующие вещественность и положительность ch и ch g2, выполняют-
ся. При условии |(36.'13) мы имеем сР<0. Следовательно, подобрать эллипти-
ческую систему координат таким способом также нельзя.
2. Пользуясь результатами § 14, составить интегральное уравнение для
открытого резонатора, определяемого формулами (36.01) и (36.02), н пока-
зать его эквивалентность симметричному открытому .резонатору, определяе-
мому формулами (36.03) и (36.04).
Решение. Полагая
Ф = Pi (t. о) е‘7 sh q — (— i)« (т. — о) е~‘т sh с ].
для функций и 'Р2 получаем уравнение (12.19), откуда
Ч?, (т< °) = ( G (т, т'. о -)- aj) Ф1 (т', — сц) d-d.
Ф2 (т, о) — j G (т. т', о -|- а2) ЧР2 (т',—а2) d-d,
—т
где
<4 = arcsin (th ?,), а2 = arcsin (th ?2), i:=='|/’2y£.
Ставя граничные условия при о = — а, и о = а2, получаем соотношения:
>₽! (т, — «1) = е‘ 2т sh С1—Ч?8 (т, «1) при | т | < т,
Ч'г (t. — “г) = е‘(2т Sh Са~’"г) Ч?1 (т. “г) при | т |< т?
^(т, —ai)=4f2(T, —cts)=O при |т|>т.
217
Если определить (и а по формулам (36.04) и положить
ф, (и, — 04) = ф (т, — а) е'7 sh Ч
Ф2 (т, — а2) = Ф (т, — а) eZT sh Ч
где ^(-г, —а) есть решение уравнения (14.05), то все соотношения удовле-
творятся. Таким образом, асимметричный резонатор (36.01) и (36.02) экви-
валентен симметричном у резонатору (36.03) и (36.04). Это — частный случай
эквивалентности, более сложный, чем в примерах § 40. Другой случай экви-
валентности рассмотрен в задаче 4 к гл. III.
3. Вычислить собственные частоты асимметричного резонатора, рассмот-
ренного в начале § 36 « задаче 2, при условиях
rj —оо, 0<г2<'2/,
пренебрегая диффракцией на краях зеркал. Сравнить с результатами § 12
и задачи 4 к гл. II.
Решение. Полагая в задаче 2
51 = 0, а1=0, а2 = arcsin 1/ —>
Г г2
получаем
“а ( 1 X
“ = ’2'. у = (/п4-у ) “г (т = °, 1, 2, . . .),
и собственные частоты будут определяться соотношением
/ 1 X
2kl = r.q 1 т + I “а.
где 2/ есть расстояиие между плоским (Г1 = оо) и вогнутым зеркалами. Если
это соотношение переписать в виде
4Л/=2л</+ (2/п+1)а2,
то оно по существу совпадает с формулой (12.28), так как 4/ есть расстоя-
ние между вогнутым зеркалом и его изображением в плоскости, а замена q
на 2q связана с тем, что мы рассматриваем поля, удовлетворяющие условию'
Ф=0 на плоскости.
Согласно задаче 4 к гл. II данный резонатор эквивалентен симметрич-
ному резонатору с тем же расстоянием 2/ между зеркалами и радиусом
кривизны г0, определяемым соотношением
go=l — = 1^§2 = 1 — 1 — sin2 а2 = cos а2.
Собственные частоты симметричного резонатора определяются формулой
2kl = nq -|- (т -|- 2а0,
где
go=cos2ao, 2ao=arccos §о=а2,
что согласуется с формулами, приведенными выше.
4. Сравнить собственные частоты асимметричного резонатора, рассмот-
ренного в начале § -36 и задаче 2, с теми, которые получаются согласно ре-
зультатам задачи 4 к гл. II. Краевыми эффектами пренебрегать, параметры
£1 и £2 считать произвольными.
Решение. Согласно задаче 2
X = 2а, 2а = ajа2,
218
где
at — arcsin (th £,), a2 = arcsin (th ?2),
а согласно задаче 4 к гл. II
Х = + 2“<”
причем при положительных gi и g2
go = COS 2ао = = р/ (1 — ^(1—^.
Обе формулы для у должны, очевидно, совпадать, т. е. должно быть а = а0.
Для доказательства того, что это действительно так, запишем
1 — sh?1Sh£2
COS 2а = COS a, cos а2 — Sin <4 sin а2 =-----•
Согласно формулам (36.05) и (36.06) имеем
. . г1гг rirz 1
ch2 ch2 ?2 = -g2-sh?1sh?2= -iyg-,
откуда по формуле (36.07) получаем
+ r2 — 4Z / Т 2/ \ / 2Г\
+Т^4Л|/( ’-йД'-гт)
или
где корень надо всегда понимать в арифметическом смысле, знак + брать
при условии (36.15), а знак — при условии (36.16). Мы видим, что cos 2а
совпадает с величиной go=icos2ao, определенной в задаче 4 к гл. II также
со знаком ±.
5. Вычислить с помощью геометрической оптики затухание колебаний
в открытых резонаторах с плоскими, цилиндрическими и сферическими зер-
калами (для параксиальных пучков), вызванное конечной проводимостью
зеркал (коэффициент отражения от зеркала по абсолютной величине меньше
единицы). Сравнить с результатом задачи 8 к гл. I.
Решение. В этих резонаторах поле представляется в виде двух встреч-
21
ных пучков лучей. Через промежуток времени т =• — каждый из этих пучков
из-за неполного отражения от зеркал (диффракционными потерями пренебре-
гаем) по амплитуде умножается на | /? |. Если обозначить коэффициент затуха-
ния колебаний через со" (поле в резонаторе пропорционально е_'в>,,<), то можно
получить
откуда легко находится ш". Если, как в задаче 8 к гл. I, положить
|Д|=е-2Кр",
то будем иметь
= 2k”l — 2пр",
что согласуется с результатом этой задачи, поскольку при наличии диффрак-
ционных потерь коэффициенты затухания складываются.
21»
6. Для немагнитных металлов коэффициент отражения при нормальном
падении волны
можно представить в виде
1 — i
Р__________-s. Р— О—0
1 — 1. =^е
1 +—j—Ы
где d — толщина скин-слоя, определяемая соотношением ,
Пользуясь формулой
| R 1 = е~М
и результатами предыдущей задачи, вычислить добротность открытых ре- j
зонаторов, обусловленную конечной проводимостью зеркал.
Решение. Добротность равна . j
_ fe =J_ j
Q ~ 2k" d * 1
7. Вычислить затухание, вызванное неидеальным отражением от стенки, 1
для колебаний Етпди Нтпд в цилиндрических и бочкообразных резонато- |
рах (гл. V). Представить добротность этих колебаний (для металлических I
стенок) в таком же виде, как это сделано в предыдущей задаче. Считать J
sin6> 1.
Решение. Затухание w."=ck" определяется соотношением j
e-2*"“sine=|
поскольку (см. рис. 30) 2а sin 0 есть путь, проходимый лучом между двумя 1
отражениями. Для колебаний Етпд коэффициент отражения определяется j
формулой 1
l—l/ lisinS ]
R = ' L =5: е~(1—г) kd sln е, 1
1 -|- 1/^sin 0
соответствующей волне, поляризованной перпендикулярно плоскости паде-
ния; поэтому добротность равна
220
Для колебаний Нmnq электрическое поле лежит в плоскости падения, по*
этому
i—1/—— ' n kd
„ V е sin 6 ( sine
К=-------7=------=5=е
1 + 1/± —
Г б sin 6
И
Л а .
Q=rsi
8, Показать, что интегральные уравнения
со
f.(9=e'* J К12 (?,?') А
—оо
Со
Щ5') = е‘х J К2> (S'. ?)fi(?)d£.
—со
исследованные в задачах 3 и 4 к гл. II (с несколько иной точки зрения),,
имеют при gig2>0 решения
'(«-K-fr'fZf*)
где f(T)) есть собственная функция эквивалентного симметричного резона-
тора, удовлетворяющая интегральному уравнению
f(4) = e'* J V) f (Y) rfV
—CO
[см. уравнение (а) задачи 3 к гл. II], в котором
g^=glg2
и знак go выбирается таким же, как у величин gi и g2.
Решение. Полагая
71
мы удовлетворяем обоим уравнениям.
9. В задаче 4 к гл. II было выведено уравнение
fl (У = е2,х J к, (5, £') f, (£') <*'
—со
для функции fi(|), характеризующей распределение тока 1и поля на первом
зеркале. Путем замены переменных (как в задаче 8) исследовать это уравне-
ние при условиях
gi<0, g2>0,
равнозначных условию (36.13). Найти собственные значения и собственные
функции. Интерпретировать полученные результаты.
Решение. Полагая
’-/Ь’
221
получаем интегральное уравнение
00
f (4) == e2'z J Ко (ч- Ч') f (ч') dtf,
—00
IB котором
. к
Ко (Ч- ч') = е ехр 1 [У go + т,,2) — ’И']’
причем
go = 2gtg2 — 1 < 0, | g9 | > 1.
Если ввести комплексный угол а по формуле
go=cos 2а,
то собственные значения этого интегрального уравнения будут определяться
формулой (ср. гл. III и IV)
2x=(2m+l)a (m=0, 1, 2, ...),
а собственные функции
f (ч) = Фт (i). t=V2sin 2а т).
Так как
1
“ = V (” —' Arch I St I)’
то собственные значения х будут комплексными '(затухание колебаний, выз-
ванное «расползанием» лучей из-за их дефокусировки), а величина т2 — чисто
мнимой (собственные функции не локализованы вблизи начала координат,
ср. задачу 8 к гл. IV).
Примененный выше метод, основанный на интегральных уравнениях с бес-
конечными пределами (благодаря чему диффракция на краях не учитывает-
ся), эквивалентен параксиальной геометрической оптике, дополненной кванто-
выми условиями. Это видно из того, что при существовании лучевых потоков,
ограниченных каустиками, оба метода приводят к одинаковым результатам
(см. задачи 3 и 4). Полученные выше результаты показывают, что при усло-
вии gig2<0 таких потоков быть не может.
10. Упростить квантовые условия для колебаний. В (§ 38), считая пучок
лучей параксиальным. Вывести формулу для собственных частот этих колеба-
ний, сравнить ее с формулой (12.28) для цилиндрических зеркал.
Решение. Полагая
Т1 = 62—©1, т2=о2—
и считая пучок параксиальным, т. е.
Т1 Ьг — с2, т2<^а2— с2,
•получаем [ср. формулы (39.04) и (39.05)] условие (В^) в виде
/11 12 \
k I 2с — - — а, — —,-а2 1 =
у рП>2 — с2 р'а2 — С2 /
где
а*= arctg = arcsln
“2=arcts =arcsin dr-
221
Квантовые условия (В^) и (В;) примут вид
k .... .
УЬ2 — с2
= 2^ +
1,
Частоты определяются соотношением
2kc = + (2^ + 1)О1+ (2Л’С + 1) <х2,
аналогичным формуле (12.28). В этом соотношении
/с -1/" с
—1 а2 = arcsin 1/ ~г~’
'о ’ г о
где радиусы кривизны г'й и r"D определяются формулой (39.12).
11. Вычислить (в пренебрежении диффракнией) собственные частоты ко-
лебаний В в четырехзеркальном открытом резонаторе (рис. 51).
Решение. Учитывая, что квантовое условие (Bt) для этого резонатора
имеет вид (40.06), и пользуясь результатами предыдущей задачи, получаем
выражение
2kc = + (2^ + 1) а, + (2N^ + 1) а2,
2с — сторона квадрата, г0—радиус кривизны сферических зеркал. .
12. Вычислить (в том же приближении, что и в задаче 11) собственные
частоты трехзеркального открытого резонатора, зеркала которого расположены
в вершинах равностороннего треугольника. Обобщить результат на случай
«-зеркального резонатора (зеркала в вершинах правильного п-угольника).
Решение. Для трехзеркального резонатора условие (40.06) перепишется
в виде
3 р _________
— k I УР(Ъ)М = тМ^
о
Лучевой поток после трех отражений оказывается перевернутым, поэтому индекс
будет целым только при = 0,2,.... а при AL = 1,3, . .. индекс —
полуцелый. Для n-зеркального резонатора это условие принимает вид
с»
/г j
о
поэтому частота определяется соотношением
2л
2kc = — + (2^ + 1) а, + (2ЛГ< + 1) а2,
223
Для четных п индекс будет всегда целым, а для нечетных п и — полуце-
лым (как выше для л = 3).
13. Составить интегральное уравнение для двухмерного открытого резона-
тора, изображенного на рис. 52,а. Показать, что оно тождественно уравнению
(4.19).
Решение. Представляя поле в виде (3.04), мы можем выразить функ-
цию W прн 0<г </ через ее значения на отверстии при —а<х<а, 2=0;
а
W (х, г) = у С (х — х', г) W (х', 0) dx’.
—а
Ставя граничное условие Ф = 0 на бесконечных зеркалах 2 = + Z, получаем
соотношение
а
U7 (х, — l) = ei2np W (х, I) = е‘2пр G (х — х', I) W (х'< 0) dx',
—а
справедливое при —оо<х<оо, причем
2лр=2&/—stq.
Отсюда можно найти
ОО
№(х, —z) = j G(x — х', — z + Z) W(x', — Ijdx*
—OO
(0 < z Z);
в силу соотношения
ОО
J G(x—х", — z~jl)G(x" — x', I) dx" = G(x—x’, — z + 2l),
—00
которое можно проверить непосредственно, пользуясь выражением (3.07), по-
лучаем
а
W (х, — г) = ег2пр у G (х— х', — г + 21) W (х*. 0) dx' (0 < г <Z).
—а
Полагая в этой формуле z—0, получаем интегральное уравнение, эквивалент-
ное (4-19). Смысл этой формулы заключается в том, что от зеркал z—±l вол-
на отражается без диффракции и после отражения продолжает испытывать
дпффракцию так же, как при свободном распространении.
14. Обобщить формулы (40.03) и (40.04) на случай, когда зеркало
(рис. 50) не сферическое, а имеет радиус кривизны rt в плоскости падения
(плоскости чертежа) и радиус кривизны г2 в перпендикулярной плоскости.
Выяснить, когда, при заданном угле падения у, эквивалентный эллипсоид
является эллипсоидом вращения.
Решение. Радиусы кривизны эквивалентного эллипсоида равны rt cos у
г2
(в плоскости падения) и eos (в перпендикулярной плоскости). Этот эллип-
соид является эллипсоидом вращения (сфероидом), если
Г2 2
— = cos2 7.
224
Глава VII
Диффракция
в открытых резонаторах
с софокусными зеркалами
§ 41. Дифференциальное уравнение
для софокусных цилиндрических зеркал
В то время как в открытых резонаторах с плоскими зеркала-
ми диффракция на краях зеркал определяет их основные свой-
ства и может быть учтена сравнительно простым образом
(см. гл. I), в открытых резонаторах с цилиндрическими и сфери-
ческими зеркалами (см. гл. III и IV), а также в бочкообразных
открытых резонаторах (гл. V) для полного расчета диффракции
необходимо решить соответствующее интегральное уравнение.
Эта трудность лишь отчасти компенсируется тем, что диффрак-
ция на краях слабо возмущает колебания с каустиками, а также
тем, что ряд качественных результатов можно получить, не ре-
шая интегрального уравнения. В частности, оказывается, что
в заданном диапазоне частот и при заданных размерах резона-
тора наименьшие диффракционные потери имеют колебания
в симметричном открытом резонаторе с софокусными зеркалами
(цилиндрическими или сферическими), радиус кривизны кото-
рых равен максимальному (расстоянию между ними. Для бочко-
образных резонаторов выводится аналогичное условие [см. фор-
мулы (27.21) и (29.20)].
В силу последнего свойства открытых резонаторов с софо-
кусными зеркалами (подтверждаемого прямым численным рас-
четом, см. § 51) исследование их диффракционных потерь при-
обретает особый интерес. В этой главе мы приближенно интегри-
руем дифференциальное уравнение, эквивалентное интегрально-
му уравнению для цилиндрических софокусных зеркал, и полу-
чаем явные выражения для диффракционных потерь в таких ре-
зонаторах.
15—2547
225
В гл. Ill исследованы собственные колебания открытого ре-
зонатора, образованного двумя одинаковыми цилиндрическими
зеркалами, расположенными друг против друга. Комплексная
частота aj=ck двухмерных колебаний в таком резонаторе опре-
деляется формулой
2/й/—ruy+y, (41.0!)
где 21— максимальное расстояние между зеркалами по оси z
(ср. рис. 21), q — большое целое число, а
z = (2m+l)a + 2^ (zn = O, 1,2, .. .), (41.02)
где
а = arcsin у — (41.03)
и г0 есть радиус кривизны зеркал.
Слагаемое (2т + 1)а в формуле (41.02) учитывает влияние
кривизны зеркал на частоту колебаний, а слагаемое 2лр — влия-
ние диффракции на краях зеркал. Комплексная величина р —
=р—ip определяет энергию, излученную за время т= — (бла-
-д!
годаря излучению энергия колебания пропорциональна е х, где
А=4лр") и дополнительный сдвиг фазы Д=2лр/ за то же вое-
мя т. Можно сказать, что А есть мера диффракционных потерь,
а А — мера диффракционного смещения частоты.
Заметим, что ранее мы определяли величину Л несколько иначе
[см. формулу (4.13)]. При Л < 1 оба определения совпадают, при
Л > 1 новое определение предпочтительнее.
Величина / (или, точнее, e'z) есть собственное значение интег-
рального уравнения (14.09), которое мы перепишем в виде
= 4) jexpz (41.04)
—i
где
„ ka2
Cl 21 ’
с0 = ct cos 2а = ct
(41.05)
а 2а есть ширина зеркал по оси х. Собственная функция )(/)дает
распределение тока на зеркалах при каждом колебании, причем
В § 16 показано, что если решить интегральное уравнение
(41.04), то можно рассчитать трехмерные колебания в резонато-
ре с цилиндрическими зеркалами конечной длины. В § 21 пока-
зано, что к тому же уравнению (41.04) сводится задача о собст-
венных колебаниях открытого резонатора со сферическими
226
зеркалами прямоугольной формы, а в § 29 такое же уравнение
выведено для бочкообразных открытых 'резонаторов. Это же
интегральное уравнение определяет собственные волны в откры-
том волноводе, образованном периодически расположенными
линзами или зеркалами прямоугольной формы (гл. VIII).
В дальнейшем для определенности будем говорить лишь об от-
крытых резонаторах с цилиндрическими зеркалами.
До сих пор интегральное уравнение (41.04) было решено (при-
ближенно) в явном виде лишь для резонаторов с плоскими зерка-
лами, у которых г0=оо и а = 0 (гл. I), а также для резонаторов
с коаксиальными или концентрическими зеркалами, у которых гв =
= 1 и а = у (см. § 14 и 21). Явное решение можно получить так-
же в случае софокусных зеркал, когда г0 = 2/, я —-г и инте-
гральное уравнение (41.04) принимает вид
—I
= (41.06)
Действительно, в работе Бойда и Гордона [35] (см. также [13],
стр. 363) показано, что 1собствённая функция /(/) удовлетворяет
дифференциальному уравнению
(1 - П -- 2/ g + с2 (0 - и f=°, (41.07)
в котором постоянная €) выбирается так, чтобы функция f(l)
при f=±l была конечной. В соответствии с работой [35] пара-
метр С] обозначается просто как с; так как дальше в этой глазе
скорость света встречаться не будет, то это обозначение не мо-
жет привести к недоразумениям.
Для собственного значения х в работе [35] получено выраже-
ние
i(2m+l)'~
17 4
•. =е
(41.08)
где А есть постоянная, входящая в асимптотическую формулу
f (0 = ^ cos \ct — (т-\- 1)^-1 при/ —ос, (41.09)
для функции f(t). Учитывая формулу (41.02) и полагая в ней а =
=у, можно переписать выражение (41.08) в виде
1/
V 2с НО
(41.10)
Функция f(t) при |/| <1 определяет магнитное поле на идеально
проводящем зеркале, а при |/|>1 —магнитное поле на геомет-
15*
227
рическом продолжении зеркала. Формула (41.10) показывает,
что радиационное затухание тем больше, чем больше постоян-
ная А, т. е. чем больше поле «выплескивается» за пределы зер-
кал.
Практический интерес представляют значения с порядка
единицы или большие. Малые значения с неинтересны, так как
при малых с резонансные свойства системы почти не проявля-
ются. Соотношения (41.07)—(41.10) можно применить для чис-
ленного расчета собственных функций и собственных значений,
если учесть, что уравнение (41.07) есть дифференциальное урав-
нение волновых функций вытянутого сфероида и что для этих
функций имеются таблицы (см., например, [36] и [37]). Однако
получаемые таким путем численные результаты имеют ограни-
ченный характер. В данной главе мы 'получим асимптотическое
решение уравнения (41.07), пользуясь методом эталонных урав-
нений и считая параметр с большим. Этот подход позволяет по-
лучить выражения для собственных значений в виде квадратур
и составить полное количественное представление о диффрак-
ционных явлениях в данной системе.
Следует заметить, что при т=0, 2, ... функция /(/) четная
и для нее уравнение (41.06) можно записать в виде
(41.И)
При ;т=1, 3, ..., для нечетных функций f(t), уравнение (41.06)
принимает вид
sin (ctt')f (t')dt'.
(41.12)
В § 47 будет рассмотрено интегральное уравнение, содержащее
уравнения (41.11) и (41.12) как частные случаи и позволяющие
вывести соотношения, которые обобщают соотношения (41.07) —
(41.10). Читатель, интересующийся выводом этих соотношений,
может обратиться к § 47 (см. также задачи 1 и 2).
Прежде чем решать уравнение (41.07), преобразуем ею
в уравнение, не содержащее первой производной. Полагая
но
Vt2 — 1
получаем для функции f(t) уравнение
___—] F—О
dt2 ‘ |/ 1 — t2 (1 — t2)2 J I ~ u-
(41.13)
(41.14)
228
Так как функция f(t) либо четная, либо нечетная, то достаточно
ее рассмотреть при 0<^<оо; она удовлетворяет граничным ус-
ловиям:
-— = 0 при t = Q и т = 0, 2, . . .-,
dt (41.15)
f = 0 при/ = 0 и/п= 1, 3,. ..
и
7=0 при f =1, (41.16)
поскольку функция f (/) при t= 1 конечна.
Уравнение (41.14) можно переписать в виде
^-Н2ПЛ0)Г=О, (41.17)
где
/t_(i + e)<» + 0 + ±
T{t, 0)=---------(ртл?-------- <41Л8)
Корни уравнения Т = 0 определяются формулами
(41.19)
причем
^ + ^=1 + 0. (41.20)
При t=l функция Т имеет полюс второго порядка, а при t—<x>
функция Т стремится к единице.
Поскольку параметр с можно считать большим (фактически,
как мы увидим, полученные результаты оказываются примени-
мыми при 1), к уравнению (41.17) естественно применить
метод эталонных уравнений. В § 42 мы дадим краткий обзор это-
го метода и исследуем дифференциальное уравнение, которое
будем употреблять как эталонное. Подготовив таким образом
почву, мы в § 43 приступим к приближенному решению уравне-
ния (41.17).
§ 42. Метод эталонных уравнений.
Исследование функции g[u, v]
В теории функций, определяемых линейным дифференциаль-
ным уравнением второго порядка
g + c27’(0f=0, (42.01)
229
часто возникает следующий вопрос: как найти асимптотическое
выражение для функции f(t)=f(t, с) (при с—оо), не зная
ее точного выражения, т. е. пользуясь только уравнением
(42.0i). Ответ на этот вопрос дает метод эталонных уравнений,
в котором'функция f(/) приближенно выражается через функ-
цию g(u), удовлетворяющую более _ простому (или лучше
изученному) дифференциальному уравнению
§ + Р(«)^=0, (42.02)
которое называется эталонным.
Функция Р(и), определяющая эталонное уравнение, выби-
рается так, чтобы качественный характер функций f(t) и g(u')
был одинаков. Не стремясь ни к общности, ни к строгости, мы
на частных примерах покажем, как производится выбор эталон-
ного уравнения (42.02) для задач, рассмотренных в этой кише,
и как находится (в первом приближении) асимптотическое вы-
ражение для функции f(t). Читатель, интересующийся обобще-
ниями и обоснованиями, отсылается к статьям {38] и [39] и книге
[40]. Заметим, что в книге [48] приведены таблицы специальных
функций, являющихся решениями простейших и наиболее часто
встречающихся эталонных уравнений; используемая ниже функ-
ция g(u, v) к числу этих функций не относится.
Если в рассматриваемом интервале значений t функция Т поло-
жительна и ограничена сверху и снизу (т. е. с2Т mtn > 1), то в
эталонном уравнении можно положить Р = 1. Если же функция Г
отрицательна и ограничена сверху и снизу (т. е. —с27'> 1), то
мы полагаем Р — —1. В обоих случаях функция g(u) имеет эле-
ментарный вид:
при Р = 1
g(u) =А cos и + В sin u=Ceiu+£)e-iu, (42.03)
а при Р=—1
g(u) =Achu+Bshu = Ceu+De~u, (42.04)
где А, В, С и D — постоянные. Искомая функция f(t) выражает-
ся через функцию g(u) следующим образом:
(42.05)
где
t ____
и = с С [/"Т (t) dt при Т (t) > 0,
, (42.06)
и = с J /— Т (/) dt при Т (0 < 0,
причем нижний предел произволен. Интегралы, стоящие
в (42.06), называются фазовыми интегралами для уравнения
(42.01): при 7,(/)>0 они дают фазу осциллирующих функций
(42.03), при T(t) <0 — аргумент монотонных функций (42.04).
230
В силу'соотношения
^=cjZ^T(F) = r/^ (42.07)
мы получаем
(42.08)
ИЛИ
f (0 = у4(«) - f (0. (42.09)
причем первое слагаемое в правых частях (42.08) и (42.09) по
порядку величины в с раз больше второго. Дифференцируя еще
раз, в силу уравнения (42.02) получим
Г (0 =-с*Т(М (f)-x(i/),f (/), (42.10)
где
х(/)=^)_^(/)> (42.11)
Таким образом, функция f(f), определяемая формулой
(42.05), удовлетворяет не исходному уравнению (42.01), а урав-
нению
g + + (42.12)
несколько отличающемуся от него. Однако при условии
c2T(t) >x(iZ) (42.13)
уравнения различаются мало и можно считать, что формула
(42.05) дает асимптотическое выражение для функции f(r),
определяемой уравнением (42.01).
Выражение (42.05) называется полуклассическим приближе-
нием для функции f(t), или приближением WKB (Вентцеля —
Крамерса — Бриллюена); оба названия берут свое начало из
квантовой механики. В теории волновых полей оно соответствует
геометрической оптике (при Р = 1). Мы его уже применяли
в § 34 [см. формулы (34.05), (34.06), (34.07) и т. д.].
Условие применимости выражения (42.05) имеет вид (42.13),
это условие нарушается, если в рассматриваемом интервале из-
менения t или достаточно близко к нему функция Т(/) имеет
нуль или полюс. Пусть, например,
Т (0 = К (t - при t t„, (42.14)
тогда
п IL-L-n-
4 4 Чб
’<0=^- Х(0=-<ьГадГ (4215)
и условие (42.13) нарушается, по крайней мере если п>—2.
Поэтому, если функция T(t) в рассматриваемом интервале
231
имеет нуль или полюс, то эталонное уравнение (42.02) должно
быть изменено так, чтобы функция Р(и) имела такой же нуль
или полюс.
Наиболее прост случай, когда в рассматриваемом интервале
функция T(t) меняет знак только в одной точке to, причем вбли-
зи этой точки ведет себя согласно формуле (42.14) при п — 1.
В этом случае мы полагаем
Р(и) =—и (42.16)
и уравнение (42.02) совпадает с уравнением Эйри (9.16), поэто-
му общее выражение для функции g(u) имеет вид
g(u) =C]Wi(u) + C2w2(u), (42.17)
где Сх и С2 — постоянные, a wt и w2 — функции Эйри, опреде-
ляемые интегралами (9.34) и имеющие асимптотические выра-
жения (9.26); последние можно предугадать, применяя к урав-
нению (9.34) формулу (42.05) и учитывая, что фазовые интег-
ралы для функции (42.16) имеют вид
и
§]/udu=-^- и312 прии>0,
Ро (42.18)
J |/ — и du = -j- (— п)3/2 при и < 0.
и
Однако при этом постоянные, входящие в формулу (42.03),
остаются неопределенными.
Искомая функция f(() выражается через функцию (42.17) по
формуле
f(0 = / (42.19)
формально совпадающей с формулой (42.05). Связь между пе-
ременными и и t устанавливается путем приравнивания фазовых
интегралов для исходного уравнения (42.01) и эталонного урав-
нения (42.02); в данном случае эта связь имеет вид (если
ЛЬО)
t
-|-(—и)3,2 = с у \Z~T(i)dt при />(,, и<^0,
I. ‘°_____ (42-20)
п3/2=с у V — T(t)dt при t < t0, « > 0,
t
причем
da_,/W)_]/W. ,499П
dt~~r —и — у Р(и)
232
Проверка того, что выражение (42.19) есть приближенное реше-
ние уравнения (42.01) [в духе уравнения (42.12)], производится
так же, как и выше. Если —«>1,то к функциям и w2 при-
менимы асимптотические выражения (9.26) и формула (42.19)
переходит в приближение WKB, соответствующее распростра-
няющимся волнам (Р=1).
Формула (42.19) применяется при исследовании волнового
поля вблизи каустики (ср. § 13, 25, 26, 34 и 38); при этом, чтобы
получить за каустикой поле, экспоненциально убывающее при
удалении от нее, надо в соответствии с формулой (9.25) поло-
жить
С1=—Сг, (42.22)
т. е. в качестве решения эталонного уравнения взять функцию
v(и), экспоненциально убывающую при и^оо. Тогда при
и—»—оо мы получаем распределение поля, соответствующее за-
конам геометрической оптики.
Интересующее нас уравнение (41.17) имеет более сложный
вид: в интервале 0^f<oo, которым допустимо ограничиться,
функция Т может иметь два корня и t2, определяемые форму-
лами (41.19); кроме того, она имеет полюс второго порядка при
f=l. Эталонное уравнение (42.02), передающее все эти свойства
уравнения (41.17), лишь немногим проще этого уравнения;
функцию Р в эталонном уравнении приходится брать в виде
Р (и) = Р (и, V) = 1 (1 + 1), (42.23)
причем точке и=0 соответствует точка /=1, а параметр -v выби-
рается так, чтобы корни Л и t2 соответствовали корням уравне-
ния Р=0.
В силу условия (41.16) нужное нам решение эталонного
уравнения обращается в нуль при и=О. Обозначим это решение
через g(u, v). Функцию g(u, v) можно представить в виде
где
g (и, v) == ]/ не
— / 1
2ф1 y-J-tv, 1; iu
(42.24)
Ф(а, с;л)=1-4-у у
а (а -|- 1) х2
rc(c+ I) 2Г
(42.25)
— конфлюентная гипергеометрическая функция. Она хорошо
изучена, ее дифференциальное уравнение после подстановки
(42.24) преобразуется в эталонное; для нее известен ряд
асимптотических формул (см. [41]). Нам понадобятся, однако,
более общие асимптотические формулы, подобные выведенным
в работах Фока [42] и Фока и Федорова [43] (см. так-
же [19]). Мы приведем здесь эти формулы, кратко наметив их
вывод.
233
Поведение функции g (и, v) определяется знаком функции (42.23).
Так как Р при |ц|-> оо, то при больших и функция g(u, v)
осциллирует. Для нее можно написать асимптотические фор-
мулы, пользуясь формулами (42.05) и (42.06) и находя постоян-
ные в выражениях (42.03) и (42.04) с помощью известных
асимптотических формул. При ы—оо можно написать (см. [41],
стр. 278 или [42], стр. 10—11)
Если использовать функцию
X(v)
еЬ(1~1п *>
(42.27)
введенную Фоком [44] (см. также [19], стр. 319), то
(42.26) можно переписать в виде
g(u, v) = j/‘1(14_е-2”-) cos[-f+ vln«4-
+ v(l —In v) — arcX(v) — y]-
формулу
(42.28)
Функция X(-v) стремится к единице при v—оо, при веществен-
ных v ее абсолютная величина равна
|X(v)|=K 1+е“2'\ (42.29)
чем мы и воспользовались при написании формулы (42.28).
При введем функцию
1
— 4- 2v
£1+ (Ы, v) = y ]/‘«a+4vtz+ 1—1 Arch Arch Л* »
z V 4v2 — 1 у 4v — 1
(42.30)
удовлетворяющую соотношениям
(42.31)
и
\ i 1 f f 1 2 I 4 2v —I— I
+ ’ 2 1 ~ ~ 74^—1 2 V4v2— 1 (42.32)
при и -> оо.
234
Вводя также функцию
O0(v)= vln2v — у (2v -{- 1) In (2v-|- 1) — у (2v — l)ln(2v— 1)-|-
H-arcX(v), (42.33)
можно написать для функции g(u, v) асимптотическую формулу
.—2itv
cos
(42:34)
переходящую в формулу (42.23) при и~-оо. Формула (42.34) в
отличие от формулы (42.28) пригодна при больших положительных и
1
И произвольных Vj>—.
Асимптотическая формула, пригодная при больших отрицатель-
ных и, выводится аналогично. Она имеет вид
/ я
cos I 2_ -j- 20 —
g = i
(42.35)
где функция
О_ (и, v) = ±/H2+ 4т«4- 1 + у Arch
1
г+2’
л 1. — и—2v
v Arch -г —
V 4v2— 1
(42.36)
удовлетворяет соотношениям
dQ-
ди
(42.37)
и
// 9
о_(ц, v) = —-н-— vln(—и) —V—vln-===
х у — 1
1 ln
2 111
(42.38)
при и—- — оо.
Корни уравнения Р = 0 суть
«, = —2v—|/4v2—1, u2 = —2v-|-j/4v2—1 (1/,1/j = 1). (42.39)
В интересующем нас случае v> i- они отрицательны, причем
Q+ (и2, V)=£)_ («„ v)=0. (42.40)
Поэтому в силу соотношений (42.31) и (42.37)
О+ (и, v) = J jZu24-4v«-|- 1 D_(u, v)= j/tz2 + 4vrz + l^.
Ua Ui
(42.41)
235
g =
Я
Интеграл для Q+ при ы>0 надо понимать в смысле главного
значения Коши. В дальнейшем неоднократно встречаются интег-
ралы такого типа; они всегда понимаются в этом смысле.
Формула (42.34) справедлива при «>0, а формула (42.35) —
при u<ui. В интервале функция g затухает, так как там
Р<0. Мерой этого затухания является фазовый интеграл
U1
j V—P(U, V) du = (2v - 1) -J. (42.42)
Если 0 < v < 4 • то формула (42.34) применима при и > 0, а
формула (42.35)—при п<0, но функции Q+, £1_ и Qo опреде-
ляются иначе:
1
— + 2v
К“!-Н™+1 - ± Arsh + ' Arsh ,
—+ 2v
Q- = 4/«2 + 4vu+ 14- 4 Arsh~^===- — VArsh ,
(42.43)
q0 = vln2v—4(l + 2v)ln(l+2v) + 4(l—2v)ln(l—2v) +
arc X (v).
В этом случае корни щ и и2 комплексно-сопряженные, и Р>0 при
всех вещественных и. Функции Q+ и Q_ можно представить
в виде
и и
v)=4 [J j/u«+4v« + 1 j /«2 + 4w+ 1 gj, (42.44)
«1
причем при u>0 мы получаем функцию Q+, а при u<0 — функ-
цию Q_. Интегрирование от щ и и2 до и производится по крат-
РИС. 56. Функция &o(v).
236
чайшим путям или путям, им эквивалентным, причем радикал
Уu[~l-4vu-j-l принимается равным единице при и=0 и далее
продолжается аналитически.
Функция fio(v), определенная формулами (42.33) и (42.43),
изображена на рис. 56. При т=0 она обращается в нуль; в даль-
нейшем (см. § 44) мы будем ее считать нечетной функцией V.
При v= у ее производная бесконечна. При v->oo функция Йо
стремится к нулю.
Нетрудно выписать асимптотические формулы для функции
g(u, -v) при v<0, но проще воспользоваться тем, что
g(u, v) =—ig(—и, —v) при v>0 (42.45)
в силу эталонного уравнения и формулы (42.24).
§ 43. Колебания с каустикой
Вернемся к дифференциальному уравнению (41.17). Харак-
тер функции f(t), которая определяется этим уравнением, зави-
сит от расположения корней и t2, определяемых формулой
(41.19), т. е. в конечном счете от постоянной 0, входящей в урав-
нения.
При малых положительных 0 корень 0, а /2 1 (мы ин-
тересуемся только положительными корнями и считаем с > 1). При
условии
О<0<1— | (43.01)
корни и лежат в интервале (0,1), а при условии
1-|<0<Ц-| (43.02)
они являются комплексно-сопряженными. На границах интер-
вала (43.02) корни совпадают:
= = —4 при 0=1 —
r .-i-г 2 (43-03)
= 1 + 7 при 0=1 + у
Наконец, при условии
0>1 — -j- (43.04)
мы имеем Z2>^i>l
В этом параграфе мы рассмотрим колебания, удовлетворяю-
щие условию (43.01). Соответствующая функция осцилли-
рует при и затухает при t~>t\. На языке геометриче-
ской оптики значение определяет положение каустики. Ко-
лебания без каустики, при условии (43.04), будут исследованы
237
в § 45. Переход от колебаний с каустикой к колебаниям без
каустики реализуется при условиях (43.02) и (43.03), он будет
исследован в § 44.
Беря при условии (43.01) в качестве эталонной функцию g(u, v)
. 1
при v > у, мы связываем переменные и и t, приравнивая фазовые
интегралы для уравнений (42.01) и (42.02):
/, t, ________________
£1_ (и, v) = с f jZFO) dt=с [ V(t\ -t2) (К -t2) (43.05)
7 t
а параметр v, пользуясь формулой (42.42), выбираем из условия
cJ=(2v-l)|, (43.06)
где
j = jV- Т (/, 6) dt = f V (t2 -1\) (f - Z2) y-^-, (43.07)
G t,
t. e. приравнивая фазовые интегралы (от корня до корня) для
обоих уравнений; так приводятся в соответствие корни функций
Р(и, v) и T(t). Таким образом, точкам t=0, Zb t2, 1, оо соответ-
ствуют точки и=и0, иь и2, 0, оо. Функция /(Z) будет при с > 1
определяться формулой
f(0 = /(43-08)
аналогичной формулам (42.05) и (42.19). Если при и-^и0
к функции g применить формулу (42.35), то граничные условия
(41.15) приводят к соотношению
= —Q0(v) (/71 = 0,1,2,...), (43.09)
где
I = j /(^ - П £ - (43-10)
о
Интегралы J и 7 легко выражаются через полные эллиптиче-
ские интегралы 1, 2 и 3-го рода. Представляя полные интегралы
3-го рода через полные и неполные интегралы 1-го и 2-го рода
(см. [15], стр. 223—231) и пользуясь также теоремами сложения
(,[15], стр. 13), получаем
cJ= — у + ct, (Е' — k2K') + К'Е (6, k) + (Е’ — К') F (б, k),
cl = ct2 (Е — k’2K) — KE(6,k) 4- EF (0, k),
238
где
Из формул (41.13), (42.24) и (43.08) имеем
(43.11)
(43.12)
При t > 1 связь между и п t устанавливается соотношением
о+ J /(^-ф(^-0 (43.13)
^2
При / —оо из формул (41.13), (42.34) и (43.08) следует асимпто-
тическое выражение (41.09), если учесть соотношение
lim [ J /(/а-ф(/’-ф -/]=-/, (43.14)
/а
которое выводится путем довольно громоздкого преобразования
эллиптических интегралов. Постоянная А оказывается равной
Д = /^(1+е“П
(43.15)
По формулам (41.10), (43.12) и (43.15) мы получаем р ——ip”
(ср. § 14), причем величина Л =4itp" (см. начало § 41) равна
A = ln(l + e~2wv). (43.16)
Формулы (43.06), (43.09) и (43.16) значительно упрощаются в
случае, когда каустика достаточно далека от края, так что модуль
xit, эллиптических интегралов (43.11) мал и они могут
*2 *
быть заменены приближенными выражениями
+ + (43.17)
Заменяя также Q0(v) нулем (так как v> 1), получаем
Л ==е~2“’—e-D<<,)c, (43.18)
где
D(O = 2—J(ln-| + 1) (43-19)
239
(43.20)
(43.21)
и
f 2w+ 1
1 с
При первом условии (43.03) мы имеем
v=l, 7=0,
Если обозначить через с+ корень уравнения
с'(/>Т7)=(т+т)т-П«^)- <43'22>
где
о0^)=-о,2507,
то при с—с* величина Л для колебания с индексом т равна
A + = ln(l-J-e~“) = 0,0423. (43.23)
При с < с* и А > Л+ нужно пользоваться формулами следую-
щего параграфа.
§ 44. Колебания переходного типа
При условиях (43.02) и (43.03)
0=1— (44.01)
и корни уравнения Т = 0 определяются формулами
/>1+=-*--'/^. + + (44.02)
В эталонном уравнении мы полагаем ,v=-j и связываем пере-
менные и и t соотношением
°* (“.’)=4 ИКа’-фг-ф р4т+
+J |/а2-ф(/2-ф тЛу]. (44.03)
240
в котором знак 4~ берется при £>1, знак — при /-<1. Функции
вычисляются по формуле (42.44), причем при 0 < v < — их явные
выражения даны в формуле (42.43), а при —•— <v<0 нужно
еще воспользоваться соотношениями
Q+ (и, v) = (— и, — v), CL (и, v) = О+ (— и, — v) (44.04)
Формулы (44.05) — (44.07) позволяют найти величину (43.16)
для колебания с индексом т при условии
с ^с<с+
(44.08)
где с* есть корень уравнения
(43.22), а ст — корень уравнения
с/(/1 + т)=('" + 7)т + °.(т)- <«09)
При с—ст мы имеем v=— -i- и Л==Л~, где
А- = 1п(14-е’) = 3,184. (44.10)
Таким образом, при изменении параметра с от с* до с радиацион-
ное затухание т-го колебания увеличивается почти в сто раз.
16—2547
241
Из формулы (44.06) следует, что для т-го колебания значения
v = 0 и Л=Л°, где
Л°=1п2 = 0,693, (44.11)
реализуются при значении с, равном
[<=("‘+4)т (41.12)
и лежащем (см. далее рис. 59 и 60) вблизи середины интервала
(с~, с*). Согласно элементарной теории, не учитывающей диф-
фракции на краях зеркал (см. § 13), каустика приходит к краю
при с == Im Ц- 1, причем при с < 2тп 1 колебание с индексом т
должно иметь заметное радиационное затухание. Полученные выше
соотношения подтверждают это; в частности, при с—с^^Ът -|-1
мы имеем Л = In 2, т. е. за время т энергия колебания вдвое
уменьшается за счет излучения.
§ 45. Колебания без каустики
При условии (43.04), когда с<ст, — -i- и корни (42.39)
положительны, переменные и и t связываются так:
О+ (и, v) = с J (Z2 — ф (t2 — приt
(45.01)
£l_(«.v)=cjV(^-H(^-Z2) при/<1.
Явные выражения для £1± легко получить из формул (42.30),
(42.36) и (44.04). Соотношение (43.06) заменяется следующим:
cJ= — (2v+l)-J, (45.02)
где
^2 G
|* y-T{t, 0)dt = J ]/аг-ф(/22-П (45.03) .
ti i.
Формулы (41.15), (42.34) и (42.45) приводят к соотношению
^=(/»+4) | + Qo(- V), (45.04)
242
где I определяется формулой (43.10). Формулы (43.14) —(43.16)
остаются в силе. Интегралы J и I представляются в виде
cJ^= Е + ci, (Е' - К') — Е'Е (<?, k) + (К' - Е') F (?, k),
cl = ct,E + ЕЕ (<?, k) — EF (<f>, k), (45.05)
где
k==tr
*2
_____К
0<«p<T,
поэтому при t, > tx 1 мы приближенно получаем
cJ=E — ct, (In Y — 1 Y
2 \ *2 J
cl = ~ ct2.
(45.06)
В этом предельном случае величина v — большая отрицательная
величина:
v=-^-(ln4/2-l),
(45.07)
и
Л = — 2м= (2т + 1) рп 112^+ '* — 1 ], (45.08)
поэтому при с < с~ радиационное затухание с уменьшением с
растет весьма медленно.
Полученные в данной работе соотношения позволяют также
вычислить собственные значения 0 = 0ТО (с) дифференциально-
го уравнения (41.07). В частности, при т—*оо формула (45.07)
приводит к выражению
(т+
0=(-^-|, (45.09)
которое согласуется с более сложной формулой, выведенной
Кармазиной (46].
Прежде чем> приступить к анализу численных результатов,
сделаем следующее замечание. В гл. I показано, что расчет от-
крытых резонаторов с плоскими зеркалами легко произвести,
если рассматривать пространство между зеркалами как волно-
вод и воспользоваться теорией диффракции на открытом конце
волновода. Можно было бы ожидать, что для резонаторов с со-
фокусными зеркалами также применим волноводный подход
(в духе теории волноводов с плавно меняющимся поперечным
16*
243
сечением, ср. (47]); тогда диффракционные потери определялись
бы коэффициентом отражения волноводной волны от открытого
конца нерегулярного волновода, а резонансная частота — поло-
жением критических поперечных сечений волновода. Получен-
ные выше формулы для диффракционных потерь не допускают
волноводной интерпретации, а резонансная частота из волновод-
ных соображений получается с ошибкой (ср. ниже § 55). Это
объясняется тем, что метод поперечных сечений, на котором
основана трактовка плавно меняющихся волноводов (см. [47]),
применим лишь при а < 1, в то время как для софокусных зер-
кал а= -^-ф Неприменимость этого метода при конечных а наи-
более ярко иллюстрирует случай концентрических зеркал, когда
а=-^-: между такими зеркалами каустики вообще образовать-
ся не могут (см. § 14 и 21), хотя поперечное сечение волновода
уменьшается при приближении к краям зеркал.
§ 46. Численные результаты
Для получения численных результатов общие формулы
с эллиптическими интегралами, например формулы (43.06),
(43.0'9) и (43.11) или (45.02), (45.04) и (45.05), слишком слож-
ны, в то время как простые формулы (43.18) и (45.08) примени-
мы лишь в предельных случаях, а формулы § 44 дают, вообще
говоря, не высокую точность (см. ниже рис. 58). Поэтому мы
используем также результаты точного решения дифференциаль-
ного уравнения (41.07). Пользуясь формулой^
А = 21п[1/Г^—--------1, Я(1)(с, 0=-Цг-’ (46.01)
I/ 2С С?(с- !)] А ’
выражениями
f т V
2т Т!)
0 =----------dlm при т = 0, 2, ...,
(46’02)
^0,т(С’ 0 =------3(ОТ-р1)! ---- ПРИ т= 3’ • ’ ’
и таблицами коэффициентов d°om и d\m ([36], стр. LIV и 16—28),
нетрудно вычислить Л при 0<с<5 и т = 0, 1, 2 и 3. С по-
мощью таблиц [37] для этих значений т можно дополнительно
вычислить Л в интервале 5<с<8, а также рассчитать Л во всем
интервале 0<с<8 для значений т<8. Результаты таких рас-
четов приведены на рис. 58 и 59 сплошными линиями.
На рис. 58 показана связь между кривыми, вычисленными по
точным формулам (46.01) и (46.02) и по различным приближен-
244
ным формулам, для т=2 и т=8. Кривая 1 вычислена по фор-
мулам (43.18) — (43.20); при /21 <1 она должна смыкаться с точ-
ной кривой; из рис. 58 видно, что точная кривая действительно
имеет тенденцию асимптотически приближаться к кривой 1. По-
этому точную кривую можно продолжить для О8 со сравни-
тельно небольшой погрешностью.
Кривая 2 на рис. 58 построена по уравнению (44.06), в кото-
ром задавалось значение vi — <v< — ) и с помощью правила
ложного положения вычислялось соответствующее значение с,
245
а по формуле (43.16) определялась величина Л. Мы видим, что
кривая 2 заметно отклоняется от точной кривой; причина этого
лежит не в приближенности метода эталонных уравнений, а в до-
полнительной аппроксимации (замене и /2 на £х), введенной
в § 44 и позволившей свести эллиптические интегралы к элемен-
тарной функции (44.07). В самом деле, крайние точки (с*, Л+) и
(с~, Л~), вычисляемые по формулам (43.22), (43.23) и (44.09),
(44.10) без такой аппроксимации (она не нужна, так как в этих
точках t1==t2 точно), ложатся на точную кривую. Центральная
точка (с"п, Л°), определяемая элементарными соотношениями (44.11)
и (44.12), также лежит на точной кривой. Эти три точки удобно
применять для приближенного построения кривых, дающих зави-
симость Л от с при других /п.
Кривая 3 построена по формуле
c=<4-A(v) (—(46.03)
где
/ 2с° \
A(v) = — Qc(v)-]-vHn —1 ) при v>0,
д(_ v) = — A(v).
Эта формула заменяет уравнение (44.06), по ней вычислять зави-
симость с от v гораздо проще, вместе с тем, она дает погреш-
ность того же порядка, что и само уравнение (44.06). Недостаток
формулы (46.03) в том, что она определяет крайние значения
+ - г , 1 \
ст и ст (при v=ct-y) с заметной погрешностью, так что
концы кривой 3 (в отличие от кривой 2) не лежат на точной
кривой.
При т =8 хорошую точность дает простая формула (45.08).
Пунктирная кривая, построенная на рис. 58 по этой формуле, при
с<8 практически совпадает с точной кривой (сплошной) и при
с>8 позволяет продолжить эту кривую. Вместе с тем, пунктир-
ная кривая проходит вблизи точки (с~, Л"), поэтому для построе-
ния кривых т = 7, 8 и 9 в интервале 0<с<15 (см. рис. 59)
достаточна формула (45.08) вместе со значениями с~, с° и с+.
Для кривых, соответствующих меньшим значениям т, наряду
с точными результатами и значениями с~ и с°т использовались
точки, построенные по формулам (43.18) — (43.20).
Рис. 59 является нашим основным результатом: 'на нем дана
зависимость радиационного затухания (точнее, десятичного ло-
гарифма Л) первых десяти собственных колебаний от с в интер-
вале 0<с<15. Сплошные кривые соответствуют точному реше-
246
нкю уравнений (41.06) и (41.07), пунктиром нанесены кривые,
построенные с помощью графической интерполяции и прибли-
женных формул (ср. рис. 58). Точность пунктирных кривых не-
велика, однако уточнение численных значений может привести
лишь к небольшому смещению этих кривых, едва заметному на
графике.
РИС. 59. Зависимость Л (в логарифмическом масштабе) от параметра с
для первых десяти колебаний.
247
Иногда удобнее пользоваться рис. 60, где по оси ординат от-
ложена сама величина Л. На рис. 60 кривые, дающие зависи-
мость Л от с, доведены до значения Л=А~=3,184. Большие зна-
чения Л малоинтересны, так как в режиме вынужденных коле-
баний соответствующие собственные колебания практически не
С
РИС. 60. Зависимость Л от с для первых десяти коле-
баний.
проявляются. Действительно, для резонаторов с цилиндрически-
ми софокусными зеркалами соотношения (41.01) и (41.02) мож-
но переписать в виде
2kl = к (q + -^+-1-)- i А. (46.04)
Если по оси абсцисс вместо частоты вынужденных колебаний от-
2kl
кладывать пропорциональную ей величину (где k веществен-
но), то расстояние между соседними резонансными частотами
будет равно половине, а ширина резонансной кривой будет равна
—, следовательно, при Л ~ (или, что то же, при А ~
резонансные кривые уже перекрываются.
Сказанное относится к двухмерным колебаниям между бес-
конечными цилиндрическими зеркалами. В открытом резонато-
ре с софокусными сферическими зеркалами квадратной формы
(ср. § 21) вместо формулы (46.04) надо писать
2^ = -* tA. (46.05)
248
В таком резонаторе соседние резонансные кривые начинают пе-
рекрываться при Если сферические зеркала имеют фор-
- му прямоугольника со сторонами 2а и 2Ь, то формула (46.05)
принимает вид
2kl = к + -+~+-j - i Л°+-Ль . (46.06)
где величины Ла и Ль относятся к цилиндрическим зеркалам, ши-
рина которых соответственно равна 2а и 2Ь.
Отметим, что в резонаторах с софокусными зеркалами резо-
нансные частоты вырождены — они зависят только от суммы
. т । т 4- п
или q-\---±—.
Для анализа колебаний с малым радиационным затуханием
часто применяют упрощенный подход, основанный на замене ин-
тегральных уравнений вида (41.04) и (41.06) такими же уравне-
ниями с бесконечными пределами (—оо, оо). Этот подход дает
правильные результаты для резонансных частот и для функций
f(t) на большей части зеркала, однако вблизи краев получается
значительная погрешность. Согласно упрощенному подходу (см.
С
§ 14) значения [(±1) пропорциональны е 2 (считаем параметре
достаточно большим и отвлекаемся от предэкспоненциальных мно-
жителей), если в середине зеркала f (t) 1. В таком случае мы
имели бы Л-~е-с, а на самом деле по формуле (43.18) Л^е-2'
и f1)^е“с.
Отсюда видно, что диффракция на краях, не учитываемая
при упрощенном подходе, приводит к сильному возмущению
функции f(t) вблизи краев. В результате этого возмущения пе-
реход от колебаний с каустикой к колебаниям без каустики, ко-
торый со1ласно § 13 должен иметь место при с=2ют+1, растя-
гивается на довольно значительный интервал с~т<с<с+т. При
фиксированном значении с колебания, у которых с-т>с, имеют
большие диффракционные потери и перекрывающиеся резонанс-
ные кривые, высокую добротность будут иметь лишь колебания,
у которых с+т<с. Значениям с=2/и+1 при разных т соответст-
вуют разные значения Л (см. рис. 58 и 59). В какой-то степени
роль величины сП1 = 2/д+1 играет величина с°т (см. конец § 44),
лежащая в центре переходного интервала.
Мы рассчитали диффракционные потери в открытых резона-
торах с софокусными зеркалами — цилиндрическими или пря-
моугольными сферическими. Развитый метод позволяет рассчи-
тать также диффракцию в открытых резонаторах, образованных
софокусными сферическими зеркалами круговой формы, что и
будет сделано ниже.
249
§ 47. Дифференциальное уравнение
для софокусных сферических зеркал
круговой формы
Если открытый резонатор образован двумя одинаковыми
сферическими зеркалами, расположенными в пустоте друг про-
тив друга, то плотность тока f(tx, ty) на этих зеркалах согласно
§ 21 должна удовлетворять интегральному уравнению
/ \lx, Ly) — 2п с /ч
х Яехр/
1 (^я/ х “I- tyt у)
f (I х» у) dt xdt у ,
(47.01)
получающемуся из уравнения (21.06) путем замены переменных
тх и Ту. Для зеркал круговой формы область интегрирования
есть единичный круг иа плоскости /ж, ty с центром в начале ко-
ординат, а параметры с0 и с1 равны соответственно
= c0 = c1cos2a = c1 Г1 — (47.02)
где го—радиус кривизны зеркал, 21— максимальное расстоя-
ние между ними, а — радиус зеркал (радиус их проекции на
плоскость симметрии резонатора), k— волновое число. Угол а,
лежащий в первом квадранте, определяется соотношением
(47.03)
1
sin а —
о
Комплексная величина % является собственным значением
интегрального уравнения (47.01) и определяет комплексную ча-
стоту соответствующего собственного колебания по формуле
2kl=nq+%,
где q — большое целое число.
Для сферических зеркал круговой формы решения
ния (47.01) имеют вид
(47.04) :
уравне- >•
Г
fttx, ty) =fn(t) cos мер
f(tx, tv) =fm(t) sin m<p
(m=0, 1, 2, ...),
(m=l, 2, ...),
(47.05)
где t, <p — полярные координаты в плоскости tx, ty. Благодаря
тождеству (6.25) для функции fm(t) можно написать интеграль-
ное уравнение
i lz_(m+i)Z.l 1
f,n(t) = cie L JJe Jm(c^')fm(f)Z'^'. (47.06)
0
250
Если ввести вместо 'функции Бесселя Jm функцию
/ i (*)= У^ЛДх)
т-- г
(47.07)
и искомую функцию fm (t) представить в виде
(47.08)
то новая функция f(t) будет удовлетворять интегральному урав-
нению
Л2с" 1
z-(m+l)yl *
J е / , (с,^)/(/')<//'.
J tn--—
(47.09)
Согласно § 21
X=2(m4-2n-b 1)а+2лр, (47.10)
где слагаемое 2(m+2n+l)a учитывает влияние кривизны зер-
кал на частоту колебания с азимутальным индексом т(т--
= 0, 1, 2, ...) и радиальным индексом n(n=0, 1, 2, ...), а слага-
емое 2лр — диффракцию на краях зеркал. Приближенные вы-
ражения [вместе с приближенными выражениями для функции
Ап(0] Для 2лр были получены в § 6 для плоских зеркал (гс=
= оо, а=0), для концентрических зеркал r0=l, а= у) их также
нетрудно вычислить (см. § 21), во всех других случаях мы огра-
ничились анализом собственных колебаний без учета диффрак-
ции на краях.
Исследуем диффракцию в случае софокусных зеркал, когда
г0 = 2/, а==-т-, со = 0; тогда интегральное уравнение (47.09)
принимает вид
f(0=J/4eL J / , (47.11)
0 т~ 2
причем вместо мы пишем просто с. Следует отметить, что при
т=± Ц- интегральное уравнение (47.11) формально переходит
в уравнения (41.11) и (41.12), которые сводятся к дифферен-
циальному уравнению. Как мы увидим ниже, более общее урав-
нение (47.11) при любом т также сводится к дифференциаль-
ному уравнению.
251
Ядро интегрального уравнения (47.11) определяется функ-
цией (47.07), которая удовлетворяет дифференциальному урав-
нению
m-А- [ т2~ 4 ]
(4712>
Введем оператор
(1 - И ~ 2Z А _ . (47.13)
(0 = (1 -П^-- 2/ 1^4--------— If (0- (47-14)
Пользуясь уравнением (47.12) и интегрируя по частям, из
интегрального уравнения (47.11) легко получить тождество
W(0=
о
/ , (ctf) Lt,f(t')dt' +
т ——-
1 dl
+ ----f(n-fm_±(^')^P]j- (47.15)
0 2
Потребуем, чтобы функция f (t) была регулярна при t = 1 и
исчезала как tm+1/2 при / — 0. Так как / i (л)'v xm+l/2 при л->0,
m ——
то подстановка i'=0 в тождестве (47.15) дает нуль, а подста-
новка/'=1 также дает нуль благодаря множителю (1 — t'2).
Отсюда видно, что функции Ltf (t) и f(t) удовлетворяют одному
и тому же интегральному уравнению (47.11) и, следовательно,
Ltf(/)=Kf(,/), (47.16)
где постоянная К не зависит от t, но может зависеть от пара-
метра с и индексов тип. Обозначая
7<=_С2 0> (47.17)
получаем для функции f(/) дифференциальное уравнение
(1-
2>d*f
> dt2
(47.18)
в котором постоянная 0 должна быть такова, чтобы функция
f(t) удовлетворяла сформулированным выше требованиям при
t=Q и /=1.
252
Определим функцию f(it) при t>l с помощью уравнений
(47.11) и (47.18). Так как
/ , (x) = cospc — (2/n4-l)-^-J при л-►оо, (47.19)
то из интегрального уравнения (47.11) следует (см. задачу 3),
что
f (0 = 4COS [rf - (тп+ 2«+ 4) <47-20>
где
А = у-^-е>- ЧП)- (47.21)
В силу формулы (47.10) последнее соотношение можно перепи-
сать в виде
е'2"=/¥/7Г>; (4?.22)
решение уравнения (47.18) позволяет найти р.
Подстановка
(47.23)
преобразует уравнение (47.18) к виду
^ + с!Г(/, 6)^=0, (47.24)
где
2 _L
та 1 т ~ 4 а2-^)«2-Ф«2-Ф
1 ™ 1— f* -t-c2(l— t2)2 c2t2(l —f2)- t2(t2— I)2
(47.25)
a t20 , t2 и t2 суть корни кубического уравнения
I m ) т — Т
/в_(1 + 0)/4 + ^-------- JZ2-------_--= о, (47.26)
удовлетворяющие соотношению
• (47-27)
При t 1 функцию Т (t, 0) можно заменить более простой
1
1 т2 ~ 4
Т (t, 0) = 0 + -----(47.28)
253
Полагая
t = |/2rf, «= 4 (св+~г) • (47.29)
вместо уравнения (47.24) получаем для функции ф(т), аппроксими-
рующей функцию f(t), более простое уравнение
, 1 \
~ ( т* — ~л~ \
45+^--т—^-Д=°’ <47-3°)
которое учитывает кривизну зеркал и образование каустик, но не
учитывает диффракцию на краях зеркал. На функцию ф(т) при
•с = 0 накладывается то же требование, что и на f(t) при /=0,
но условие )(!) —О заменяется условием ф (оо) —0. Полагая
ф(х) = ]/^ф(т), (47.31)
для функции ф(т) получаем дифференциальное уравнение (19.07),
которое в § 19 было выведено не только для софокусных зеркал
но и для любых Возможные значения
х согласно формуле (19.08) равны
и—т-\-2п-[-1 (т, п = 0, 1,2, ...); (47.32)
им соответствуют согласно формуле (19.09) функции
ф (х) =Ct™L™ (у)е~ \ (47.33)
где £*т)(л) — полиномы Лагерра, а С — постоянная.
В следующем параграфе мы произведем асимптотическое
интегрирование уравнения (47.30), а полным уравнением
(47.24) займемся в § 49.
§ 48. Асимптотическое интегрирование
уравнения (47.30)
Интегрируя дифференциальное уравнение (47.30) асимптоти-
чески, мы не будем стремиться к получению приближенного ре-
шения в виде одной формулы, подобной формуле (43.08), а сна-
чала получим два решения, пригодные при т->0 и при т—ос,
а затем подберем постоянные так, чтобы в промежуточной обла-
сти решения совпали.
254
Если наряду с заменой функции по формуле (47.31) заме-
нить т на т в соответствии с формулой (49.13), то мы придем
к уравнению (19.14), которое можно переписать в виде
j^4~(-ze2~—-Le4~—ю2)ф=0, (48.01)
где
т=ет, •t = lti'c. (48.02)
В уравнении (48.01) коэффициент при ф можно представить
в виде
_ _L = _ _L (Т2 _ (г2 _ (48 03)
причем
х2 = 2х — 2 ]/z2 —m2, z2 = 2х +2 ^и2 — т2,
(48.04)
xo+xf=4x. x2if=4ms;
-.2 2
при х > т корень т0 мал, а корень т, велик.
В качестве эталонного уравнения при малых т можно взять
уравнение
О+(е2“-дг2)^ = 0, (48.05)
которое сводится к уравнению Бесселя и имеет частное решение
g(u)=Jm(x), х=еи (48.06)
и общее решение
g (и) = Crf" (л) + СгН^ (х). (48.07)
Связь между переменными т и и устанавливается соотношением
(48.08)
или, переходя к переменным тих [см. формулы (48.02) и
(48.06)], соотношением
jj /(^_x2)(x2-x2) (48.09)
m
Поскольку нас интересует такое решение уравнения (48.01), ко-
торое остается конечным при т=0 (т=—оо), мы должны в ка-
255
честве функции g(u) взять частное решение (48.06), а не общее
решение (48.07). Тогда
4 ' — 172^
>(<)=£)/ <48-i0>
где В — постоянная.
При условиях
л>1, х — т^>\~2] (48.11)
для функции Бесселя справедлива асимптотическая формула
Дебая (ср. § 25), которую можно записать в виде
1
= .—.sin
2—т2
I ух2 —т2
т
причем
f
т
- . fix * -
— m2 —=)Лл2 — т2 — т arcsin
zn2
(48.13)
Поэтому при условиях (48.11) функцию (48.10) можно заменить
более простым выражением
Ф ('Е)==
Xsin [j/(x2-^)(^-T2)^+^-], (48.14)
то
которое, как и выражение (48.10), непригодно при т~Г1.
В качестве эталонного уравнения при т~Т1 мы возьмем
уравнение Эйри (см. § 42), но в силу условия ф(оо)=0 нужно
взять то его решение, которое исчезает при и—»оо,т. е. функцию
о(«), определяемую формулой (9.17) и имеющую асимптотиче-
ское выражение (9.24). Устанавливая между переменными т и
и связь:
4 (- ")3,2=
(48.15)
получаем асимптотическое решение уравнения (48.01) в виде
(48.16)
256
которое при н —— оо в силу выражения (9.24) принимает вид
ф('с)=
(48.17)
Формулы (48.14) и (48.17) согласуются в интервале % <;-с < т,
при условии
j/(^-г^-х2) ^ = (2/2 + 1) (48.18)
Интеграл, стоящий слева, вычисляется подстановкой
,____-_____ Л
c—Tj у/1 — /у2 sin2 <р, </2=1-g-, (48.19)
Ti
которая приводит к интегралам
Г____d' . п___________
J 1—<72sin2¥ 2jM — <72
О
•я
2
4 Г sin2у cos2<fdf _(,_<£__1/1 21 (48.20)
4 J 1— </2 sin2 у “I1 2 V 1 q J 2 •
о
Соотношение (48.18) принимает вид
то)2=2«+1,
(48.21)
следовательно,
(48.22)
в полном согласии с точной формулой (47.32).
Мы произвели асимптотическое интегрирование уравнения
(47.30), допускающего точное решение (47.32) и (47.33), главным
образом для подготовки к исследованию более сложного урав-
нения (47.24). Как уже отмечалось, больший положительный
корень Т] определяет положение внешней каустики, а меньший
положительный корень to — положение внутренней каустики
(отсутствующей при т=0). При небольших т(т~\ или /п=2)
внутренняя каустика выражена слабо, так как она близка к фо-
кальной линии т=0. Лишь при распределение полявблизи
внутренней каустики таково же, как вблизи внешней каустики.
Выше мы применили метод эталонных уравнений к диффе-
ренциальному уравнению (48.01), не имеющему явно выражен-
ного большого параметра, и получили точную формулу для соб-
17—2547
257
ственного значения х. Последнее обстоятельство является слу-
чайным (хотя оно бывает не так редко, ср. § 13); при ином при-
менении метода эталонного уравнения можно получить выра-
жение для и, справедливое лишь при х > 1 или при 1, т. е.
когда в уравнении (47.30) действительно имеется большой па-
раметр. Для собственных функций (47.33) асимптотические
формулы (48.10) и (48.16) могут дать достаточно точные ре-
зультаты лишь при больших п или т.
§ 49. Асимптотическое интегрирование
уравнения (47.24)
Для определенности предположим, что бикубическое уравне-
ние (47.26) имеет корни, удовлетворяющие неравенствам
O<tfo<tfi«2<l.
(49.01)
Корни t0 и соответствуют корням то и Ti (см. § 48), они опреде-
ляют положение внутренней и внешней каустик. Корень t2 бли-
зок к точке /=1, он учитывает диффракцию на краях зеркал.
При в качестве эталонного уравнения мы берем урав-
нение (47.12). Связав переменные х и t соотношением
= с (49.02)
^0
получим асимптотическое решение уравнения (47.24) в виде
(49.03)
это решение пригодно при с
жительных х и больших т \
^t<^tl. При больших поло-
можно не различать т2 и
тг
это решение принимает вид
Г(0
(49.04)
<0
как это следует из формул (47.07), (48.12) и (48.13).
2S8
В качестве эталонного уравнения при и возьмем
уравнение для функции g(u, v), использованное выше в
§ 42—46. Условия (49.01) соответствуют значениям параметра
сам параметр v определяется формулой
_____________________
С-Г) z(1_f8y ==(2v - (49.05)
I,
Переменные и и t связаны соотношением
Н _____________________
Q-(«, v)=c j/(^-ф(^ -О(^ -Н (49-06)
t
а связь между функциями fug такова:
F(0 = (и, V). (49.07)
При больших отрицательных и мы имеем
F(0= |/e^+1y^A-^sin [Q- («, v)+Q>(v)+^-],
(49.08)
где функцию Q_ надо заменить интегралом по формуле (49.06).
Выражения (49.04) и (49.08) согласуются при условии
с j V- ф (/* - t*) (t22 - ?) щ^рг=(2« + 1) -J--Q, (v)
*0
(и = 0, 1, 2, ...). (49.09)
В формулах (49.05) и (49.09) фигурируют эллиптические
интегралы, поэтому они мало пригодны для практических рас-
четов. Упростим эти формулы с помощью дальнейших аппрокси-
маций. Обычно корень to мал по сравнению с 0 и ’t2, поэтому
в формуле (49.05) полагаем ^0=0, после чего она принимает вид
cj=(2v—1)-^-, (49.10)
переходя в формулу (43.06). С формулой (49.09) дело обстоит
сложнее: поскольку в ней интегрирование производится от t0 до
нельзя просто положить /0=0, а надо считать, что
г. ____________________
С J V(t2 - t2o) (t- - п (f2 -
(49JI)
о
17'
259
Действительно, интегрируя дифференциальное
(47.12) методом эталонных уравнений и пользуясь
Эйри, получим (ср. § 42)
уравнение
уравнением
где
(49.12)
(49.13)
для того чтобы при больших отрицательных и, пользуясь фор-
мулой (9.24)/получить асимптотическое выражение (47.19), надо
считать, что
(49.14)
Соотношения (49.11) и (49.14) являются неточными, но их
можно применять, учитывая приближенность всего рассмотре-
ния. С помощью соотношения (49.11) формула (49.09) преобра-
зуется к виду
с1=х ~—Q,(v).
(49.15)
Последняя формула отличается от формулы (43.09) только тем,
что полуцелое квантовое число /п+у в этой формуле заменяет-
ся целым квантовым числом х, определяемым формулой (47.32).
Эта замена обусловлена асимптотическим скачком фазы в фо-
кальной линии tf=0 (ср. § 15). Так как интегралы J и I в форму-
лах (49.10) и (49.15) те же, что в § 43, то связывать в них корни
t\ и t2 с величиной 0 нужно формулами (41.19).
Переходя от первоначальных формул (49.05) и (49.09) к упро-
щенным формулам (49.10) и (49.15), мы в левых частях первона-
1
т2~~ 4
чальных формул отбрасываем члены порядка --------. При умерен-
ных значениях с эти члены могут влиять на результат, даже
если индекс т невелик (скажем, т=1 или zn = 2). Однако учет
260
отброшенных членов приводит к слишком громоздким соотноше-
ниям.
При t -► оо функция 7 (0 принимает вид
F(0 = - -+-^2" cos (“> v) - °о (v) ~ v]- (49.16)
где
t _______________
□+(«, v)=c [К (49.17)
Используя соотношение (43.14), а также формулы (47.23) и
(49.15), получаем асимптотическое выражение (47.20), в кото-
ром
-^(1+е-2’7 (49.18)
По формулам (47.23) и (49.07)
Н1) = рГ. (49.19)
поэтому величина р получается по формуле (47.22) чисто мни-
мой (р=—ip"). Мерой диффракционных (потерь является вели-
чина
Л = 4^" = 1п(14-е“2”’’), (49.20)
характеризующая затухание колебания за время прохождения
волны от одного зеркала к другому (см. § 41) и зависящая от
параметра с и индекса х.
Выше были выведены асимптотические формулы для коле-
баний с каустикой. Формулы для колебаний переходного типа
и для колебаний без каустики получаются из формул, выведен-
ных в § 44 и 45, также путем замены i/rt+Va на х. Надо только
иметь в виду, что вырождение собственных значений (комплекс-
ные частоты зависят от «главного» квантового числа х, а не от
чисел т и п в отдельности) характерно лишь для приближен-
ных формул (49.10) и (49.15). При более точном анализе (при
т2 — L
учете отброшенных членов порядка ------1—,см. выше) должна
с
выявиться «тонкая структура» спектра, а именно комплексная
частота, соответствующая значению х=2/—1 или х=2/ (/=
=2, 3, .. . ), должна расщепиться на / различных комплексных
частот. Впрочем, эти частоты различаются [в том приближении,
в каком справедливо уравнение (47.11)] только своими мнимыми
частями, т. е. коэффициентами затухания. Вещественные части
собственных частот определяются суммой q+ у—это свойство
характерно для софокусных зеркал (ср. § 46).
261
§ 50. Диффракционные потери
для софокусных зеркал
круговой формы
В § 46 приведены графики, дающие зависимость Л от с для
значений введенного там целочисленного индекса т от 0 до 9.
Если заменить тп+'А на величину х, определяемую формулой
(47.32), то в первом приближении мы получим, как показано
выше, радиационное затухание соответствующего колебания
в открытом резонаторе с софокусными зеркалами круговой фор-
мы. В частности, будем иметь:
Л =JA+ — 0,0423 при с = б£_1/2,
Л=Л0 = 0,693 прис=с' =хА (50.01)
Л = Л" =3,184 при с = с~_х/2,
где числа с* и с” определяются уравнениями (43.22) и (44.09).
Численные расчеты показывают, что числа с* и с” с хорошей
точностью удовлетворяют соотношению
^в=й’+г‘”'- (30-02)
Числа с°т удовлетворяют этому соотношению точно. Поэтому для
колебаний переходного типа зависимость Л от с нетрудно полу-
чить, производя в соответствии с формулой (50.02) интерполя-
цию по осп абсцисс между соседними кривыми на рис. 59 и 60.
Расчеты по формуле (43.18) показывают, что такую же интер-
поляцию можно провести и для колебаний с каустикой.
Кривые на рис. 61 построены путем указанной выше интер-
поляции, правильность которой для колебаний без каустики
проверялась при х=9 с помощью формулы
Л = 2х(1п-у-—1), (50.03)
выведенной в § 45. Наряду с рис. 61, где дана зависимость IgA
от с, мы приводим также рис. 62, где по оси ординат отложена
сама величина Л; при этом ограничиваемся значениями Л<А~,
поскольку при Л>А~ резонансные кривые соседних колебаний
перекрываются (см. § 46). Рис. 61 и 62 позволяют рассчитывать
комплексные собственные частоты по формуле
2£/+20-/А, (50.04)
причем результаты получаются менее точными, чем в § 46.
Назовем колебание с азимутальным индексом т и радиаль-
ным индексом п в резонаторе с софокусными зеркалами круго-
262
(вой формы просто колебанием тп. Кривые на рис. 61 и 62 по-
зволяют рассчитать радиационное затухание пяти симметричных
колебаний 00, 01, 02, 03 и 04, четырех колебаний с азимуталь-
ными индексами /д=1 ии=2ит. д.
РИС. 61. Зависимость Л (в логарифмическом масштабе) от параметра с
при различных значениях х.
Эти результаты интересно сравнить с кривыми, полученными
Фоксом и Ли 1[12] для колебаний 00, 10 и 20 совершенно иным
методом — путем численного решения интегрального уравнения,
263
эквивалентного уравнению (47.11). Оказывается, что кривая
для колебания 00 практически совпадает с нашей кривой х=1,
однако кривая для колебания 10 и особенно для колебания 20
заметно отходит от наших кривых х=2 и х=3. Отсюда можно
сделать вывод, что радиационное затухание пяти симметричных
РИС. 62. Зависимость Л от с при различных значениях и.
колебаний с графической точностью передается рис. 61 и 62,
а применительно к несимметричным колебаниям рис. 61 и 62
дают заметную погрешность, уменьшающуюся с ростом пара-
метра с и быстро увеличивающуюся с ростом индекса т. В сущ-
ности, отклонение точной кривой для колебания 20 от нашей
кривой х=3 есть проявление тонкой структуры спектра, о кото-
рой говорилось в конце § 49.
§ 51. Диффракция при произвольном
отношении радиуса кривизны зеркал
к расстоянию между ними
Выше были рассчитаны диффракционные потери для откры-
тых резонаторов с софокусными зеркалами, причем выведенные
формулы были пригодны не только в случае, когда эти потери
малы (как в гл. I), но и при конечных и больших значениях
Л=4лр". Расчет диффракционных эффектов был основан на
том, что интегральные уравнения в случае софокусных зеркал
сводятся к дифференциальным, которые в силу условия с >• 1
могут быть проинтегрированы приближенно с помощью метода
эталонных уравнений. При этом оказывается, что такой
264
асимптотический расчет дает правильные результаты уже пр»
с=1 (и даже при 0=172, см. рис. 58 и 59).
К сожалению, более общие интегральные уравнения (41.04)
и (47.06) нельзя свести к дифференциальным, вместе с тем,
в теории интегральных уравнений нет метода, который позволил
бы получить аналитическое решение этих уравнений при с^> 1.
Правда, в гл. I мы получили приближенное решение этих инте-
гральных уравнений, пригодное при Cq=Ci > 1, но это решение
было построено, скорее, на основании физических соображений,
исходя из представления об отражении волноводной волны от
края резонатора. Такое представление становится малопригод-
ным при увеличении кривизны зеркал; в частности, оказывается,
что для софокусных зеркал волноводная трактовка не дает
правильных количественных результатов (см. конец § 45).
Отсутствие наглядного физического понимания диффракцион-
ных явлений в открытых резонаторах с вогнутыми зеркалами
приводит к тому, что диффракционные поправки для таких резо-
наторов при произвольных соотношениях между радиусами кри-
визны зеркал и расстояниями между ними приходится находить,
решая интегральные уравнения численно, как правило, на элек-
тронных вычислительных машинах. Без расчетов на электрон-
ных вычислительных машинах иногда удается обойтись, пред-
ставляя неизвестную функцию, входящую в интегральное урав-
нение, в виде разложения по собственным функциям, не учиты-
вающим диффракции на краях, или по собственным функциям
для плоских зеркал, или по собственным функциям для софо-
кусных зеркал. Однако получаемые таким путем результаты
имеют довольно ограниченную область применимости и поэтому
не представляют, по крайней мере в настоящее время, самостоя-
тельного интереса.
Для полноты мы приведем несколько графиков, рассчитан-
ных на машине. Обозначим через %' и %" вещественную и мни-
мую части величины %, определяемой интегральным уравне-
нием (14.05) или (14.09):
Х=х'-*%", (51.01)
а через g— величину
g = cos2a=l —(51.02)
определяемую отношением расстояния 21 между зеркалами кг,—
радиусу их кривизны. На‘рис. 63,а изображена зависимость вели-
чины 1—е—2х”~2у" от g, а на рис. 63,6 — зависимость от g
при
с= -^-=«, (51.03)
где 2а есть ширина зеркал. При т. е. при —
265
мы записывали у в виде (14.08), тогда величина
(51.04)
определяет затухание колебаний вследствие диффракции на
краях, а величина
%'= (2т+ 1)«+2лр' (51.05)
РИС. 63. Зависимость 2х" и х' от величины g=l— — при с=л для откры-
ло
того резонатора, образованного одинаковыми цилиндрическими зеркалами.
определяет поправку к частоте, обусловленную кривизной зер-
кал (первое слагаемое) и диффракцией (второе слагаемое).
Если |g| >1, то 'величина « становится, комплексной и изменяет
не только вещественную, но и мнимую части у (см. конец § 15).
Как видно из рис. 63, у" есть четная, а у/— (2/п-|-1)-^-
нечетная функции g, в соответствии с общими выводами § 14;
в частности, четность %" как функции g обеспечивает равенство
диффракционных потерь для сопряженных резонаторов. При
|gi|>l колебания между зеркалами также возможны, но их ра-
266
диационное затухание больше, чем при |g|<l. Рис. 63 заимство-
ван из работы [18].
Рис. 64 дополняет результаты, полученные в § 36 с помощью
геометрической оптики. Пусть имеется открытый резонатор,
образованный цилиндрическими зеркалами с различными ра-
диусами кривизны rt и г2, но одинаковой ширины 2а. Такой ре-
зонатор можно характеризовать тремя параметрами:
. 21 ,21 ka2
и С=~2Г- (51-06>
На рис. 64 изображен рельеф величины
Л = 1 — е-2х" == 1 — е~2кр" (51.07)
на плоскости gi, g2 при трех значениях параметра с для основ-
ного колебания с наименьшим затуханием. Вытянутость линий
уровня Л=const вдоль прямой gi=g2 указывает на то, что
резонаторы с одинаковыми зеркалами имеют наименьшее ра-
диационное затухание, сжатие их в поперечном направлении
обусловлено тем, что второй и четвертый квадранты плоскости
gi, §2 соответствует колебаниям, которые нельзя рассматривать
как лучевые потоки, ограниченные каустиками (§ 36). Точка
£i=£2=0 соответствует одинаковым софокусным зеркалам,
имеющим наименьшие диффракционные потери, а рис. 64 пока-
зывает, какие диффракционные потери получаются при отступ-
лении от этой оптимальной системы.
На рис. 65 дано разбиение той же плоскости gi, g2 согласно
геометрической оптике (§ 36): незаштрихованная область
в первом квадранте определяется условиями (36.15), в третьем
квадранте — условиями (36.16), в этих областях лучевые потоки
ограничены каустиками и радиационное затухание мало;
второй и четвертый квадранты заштрихованы, они соответству-
ют условию gig2<0, т. е. условию (36.13) и аналогичному усло-
вию, в котором Г1 и г2 переменились местами. Заштрихованные
области в первом и третьем квадрантах соответствуют условию
(36.14), которое можно записать в виде gig2> 1; они определяют
резонаторы со сравнительно большим радиационным затуха-
нием; резонаторы с плоскими (g’i=^2=ll) и концентрическими
(gi=g2=—1) зеркалами лежат на границе заштрихованных в
незаштрихованных областей.
Симметрия функции A=A(gb g2) легко может быть доказа-
на из общих соображений. Можно также показать, что резона-
тор, образованный зеркалами различной ширины (2ai и 2а2),
также характеризуется тремя параметрами:
п — а' ( 1 _ А а _____ аг (1 \ г____ kataz /г, ло\
a, (J rj’ с-----2Г' <51-08>
267
РИС. 64. Рельеф функции A=A(g’i, gz) для открытого резонатора, образованного цилиндрическими зеркалами раз-
ной кривизны, в квадрате —l<gi, gz<l.
268
причем при равенстве параметров (51.06) и (51.08) диффрак-
ционные потери соответствующих резонаторов также равны. По-
этому рис. 64 относится и ik резонатору с зеркалами разной
ширины.
9г (1
РИС. 65. Разбиение плоскости gt, gj со-
гласно геометрической оптике:
П — плоские зеркала: К. — концентрические;
С — софокусные; С' — плоское и вогнутое зер-
кала. составляющие половину резонатора
с софокусными зеркалами.
Задачи к гл. VII
1. Показать, что если функция ((/) удовлетворяет интегральному урав-
нению (41.06), то она удовлетворяет и дифференциальному уравнению'(41.07),
причем значения f(±l) конечны.
Решемие. Представляя уравнение (41.06) в виде
1
f (О = Р J е~'cts f («) (a)
—1
а уравнение (41.07) в виде
[Lt + c20] f (/) = 0, (b>
интегрированием по частям получаем
1 I
Ltf (t) = p e~lcls [c2 (/2s2 — t2—s2)+ 2icts]f(s)ds = P J L,f (s) ds —
I
— P | e~‘rfs(l — s2) [f'(s) + ictf (s)J. (c)
—1
Из интегрального уравнения (а) следует, что функция f(t) вместе со своей
производной при /=±1 конечна, поэтому подстановка s=±l в правой части
26»
(с) дает нуль, и получается для Ltf (i) то же интегральное уравнение, что а
для f(t). Так как при данном собственном значении р, собственные функции
могут отличаться только постоянным множителем, то мы должны иметь
lJ(i)=Kf(t),
где К—постоянная (не зависит от t). Полагая К=—с1 20, приходим к диффе-
ренциальному уравнению (6), которому функция f(t) будет удовлетворять
при любых значениях t (как вещественных, так и комплексных).
2. Считая, что при |t|>l функция f(i) определяется интегральным урав-
нением (41.06), показать, что при t для функции f(i) справедливо асимп-
тотическое выражение (41.09), причем постоянная А определяется формулой
(41.08).
Решение. Записывая интегральное уравнение так, как это сделано
в предыдущей задаче [формула («)]. и интегрируя по частям, получаем со-
отношение
1 1
f(0 = 7f | e-,cfef(s)—С e~ictsf'(s)dS.
—1 —1
Повторное интегрирование по частям показывает, что при ct -»оэ интеграл
имеет порядок • Поэтому при t
—» оо получаем асимптотическое выраже-
ние
/и.
= 7Г [е-*=* f(l) - eici f (_ 1)].
Нумеруя колебания так, что при т=0, 2, ... функции f(t) четные, а при
гп=1, 3, ... нечетные, будем иметь
и асимптотическое выражение примет вид
f (О {е-»‘ + еМс'-(т+1«} = 4'cos
ci— (m + 1)-у-1.
где
2с г 1 X
А - 2i~^f (1) =
Отсюда и получается выражение (41.08).
3. Исходя из интегрального уравнения (47.11) и асимптотического выра-
жения (47.19), вывести формулы (47.20) и (47.21).
Решение. Запишем интегральное уравнение (47.11) в виде
f(O = H
(cis) f (s) ds
и обозначим
Интегрируя по частям, получаем
(х) dx.
I
tn
2
1
(cis) f (s) + j”
о
j ( (cis) f (s) ds
m------—
270
Л'= Hf(l) = ^ ~f(l)e
асимптотическое выражение для функции j , (х). В си-
га -
(47.19) можно написать
Г я 1
(х) = С 4- sin х — (2/ге + 1) ~г- при х -» со,
и при t -»со (ср. задачу 2) имеем
НО “4’7 I И). («)
« т- —
где
Ф-<«+!) vi
Остается найти
лу соотношения
7
1 * J
поскольку при дифференцировании / । мы должны получить j । . По-
т~Т • га--
стоянная С должна быть равна нулю, так как согласно уравнению (47.24)
функция f (t) при t -» со должна иметь вид
f (/) — В cos (ct — ₽),
где В и р — постоянные, а согласно формуле (47.23)
В
f (О = ~f~ cos (с< — ₽) ПРИ <_>со-
Поэтому формула (а) приводит к соотношению
, Л' Г я 1 А'
= sin ci —(2m-b 1) -4- =-^-cos
ci-(2/n + 3) -J-l-
Если ввести новую постоянную
А = А'е-1пп =
то асимптотическая формула для f (/) принимает вид
f(0 = 4cos
Таким образом, мы получили формулы (47.20) и (47.21).
4. Показать, что из интегрального уравнения (41.04) можно вывести тож-
дество
I 5=1
L»f(O = H Je^’LJ (s)ds + n I e'^-s> [Г (s)+ « («>/-CoS) f(s)],
—l s=—I
где
Ь« = -^2-—(<ц —Co)<2-
5. Исходя из интегрального уравнения (41.04), вывести асимптотическое
выражение для функции f(t) при t -*оо.
271
Решение. Записывая интегральное уравнение (41.04) в виде
f(t)^^ ^lK2~CltS)f(s)dS
и интегрируя по частям, получаем при f -» со
1е <*+1
/(0=77^° 2 [e_‘C,'f(’)-e‘C1,f(-l)]
или (ср. задачу 2)
A Г " 1
f(f) = —е 2 cos Icjf —(т+
где
Z=2/-M(l) = |/<V1f (1) е I
-(2т+1)-£-
6. В общем случае метод эталонного уравнения связывает функции f(f)
и g(u)—решения уравнений (42.01) и (42.02)—соотношением
НП = V Ю
где
Л _ 1/~Р(“Г du _т/с27’(0
du Г c2T(t)' dt V P(u) ‘
Показать, что функция f(i), вычисленная по формуле (а), удовлетворяет
уравнению вида (42.12). Вычислить и оценить функцию х(0-
du . d2u
Решение. Обозначая ~dp=u и т- д-» получаем
1
Г (0
и , 'г~ и
f" (0 = К dug" (и) + g’ (и) + -|-
21/а 2
2
и
и
/(0-^'(0 =
[3 / и \2 и 1
т(-) “S-J'W-
Таким образом, f(f) удовлетворяет уравнению (42.12), причем функция х(0
равна
х(0
и 3 / а А2
2а 4 \ й )
Она не содержит большого параметра с (он при образовании дробей— и —г—
а а
сокращается). Большие значения эта функция может принимать лишь вблизи
точек, где а = 0, или а = оо, или а = оо. Наличие этих точек в интересую-
щем нас интервале изменения t означает, что данное эталонное уравнение не-
применимо. В частности, если нули функций Г(<) и Р(а) не соответствуют
272
друг другу 17'(<о)=О. а в соответствующей точке Рф 0], то мы будем иметь
й=0 при t—to.
7. Как известно, конфлюентная гипергеометрическая функция (42.25) есть
решение^ уравнения
хё-+(с-х>27-од==0
(см., например, (41], стр. 248). Показать, что, полагая
. и
1 . •./- т
а = IV, с=1, х = ш, g—Viie у,
можно получить для функции g = g (и) уравнение
</2g . 1 ( 4-j 1 \
diF+T (j + и + a2 ) S = °.
8. Пользуясь интегральными уравнениями (8.15), показать, что любой от-
крытый резонатор с различными цилиндрическими зеркалами, обладающий
плоскостью симметрии х=0, характеризуется тремя безразмерными парамет-
рами (51.08), полностью определяющими его собственные частоты.
Решение. В соответствии с условиями задачи мы имеем
„ i/~ k -Г k
“1 = ₽1 = У ~2Га1’ “2 = ₽2 = У ~2Г °2
И
bl-2 I I
^^ = -277=77^
Полагая
ctj di 0-2 Uz
h (E) = F, (0. f2 (E') = -4- F2 (/').
У а1 у a2
приходим к интегральным уравнениям
1
Л(0=е'х JL(/, t’)F^t')dt’,
—1
1
F»(f)=e^ j L (f, t) Fi (t) dt,
—1
в которых ядро равно
-? Т
е Г 1 ( 9 1/ 2/ \ 9 п
L(t' г) = /2^ ехр ' LТ 0 - тг) + т (’ - тг) “2f -
Обозначая
18—2547
271
получаем /
-I /
е 4 fl 1.1 /
L(Z’ /,)=У^ eXP‘Cl 2’^+^g2Z “«'J’ /
поэтому собственные значения х зависят только от трех параметров g2 и с.
9. Пользуясь результатами, полученными в предыдущей задаче, пока-
зать, что Л как функция gi и g2 удовлетворяет соотношениям
Л (gi> gi) = Л (gi. gi), Л (gi, gi) = Л (— gi, — g2) = Л (— gt, — gi),
т. e. линии уровня A=const на плоскости g>, g2 должны быть кривыми, сим-
метричными относительно прямых gi—g2 и gi=—g2 (см. рис. 64).
Решение. При замене giJ? g2 функции Fx и F2 также меняются места-
ми (зеркала переставляются), но собственные значения остаются теми же.
При изменении знаков gi и g2 надо учесть, что функции Ft и F2 либо обе
четные, либо обе нечетные. В случае четности Ft и F2 они удовлетворяют
уравнениям
I
F1 (Г) = е'> J L (t, — Г) F2 (Г) df,
—I
1
Fi(t') = ^ ^L(t', -t)Fi(t)dt,
—I
а комплексно-сопряженные функции — уравнениям
I
F* (t) = у £* (t, — t’) F*2 (tr) dt' ,
—1
1
F* (/') = J L* (Г, — t) F*{ (0 dt,
—1
где
e 4
L‘(z’-z') = ^TexpZc
[—4" gj2—тg2t'2~~ttr ]
только множителем i отличается от ядра, соответствующего резонатору с па-
раметрами —gi, —g2. Для обоих резонаторов мнимая часть х. а также
Л=2х" одинаковы: они являются сопряженными в том смысле, в каком это
понятие употребляется для резонаторов с одинаковыми зеркалами (§ 14).
Глава VIII
Открытые волноводы
§ 52. Основные свойства открытых
волноводов
Для электромагнитных волн сантиметрового диапазона в ка-
честве линий передачи широко используются волноводы прямо-
угольного и кругового сечений. При переходе к более коротким
волнам применение волноводов связано с осложнениями, ана-
логичными тем, которые возникают при применении объемных
резонаторов (§ 1). Если поперечные размеры волновода под-
бирать так, чтобы по нему могла распространяться только одна ,
волна, то с укорочением длины волны трудности изготовления
волноводов и волноводных узлов растут, вместе с тем, коэффи-
циент затухания волны в волноводе увеличивается, а максималь-
ная мощность, которую можно передавать, уменьшается. Если
же использовать волноводы, поперечное сечение которых суще-
ственно больше длины волны, то электромагнитная энергия,
введенная в волновод, распределяется между многими волнами.
В самом деле, в каждом частотном интервале Лю появляется
ДД=^5шД<о (52.01)
новых распространяющихся волн (S — площадь поперечного
сечення волновода). Эта формула формально совпадает с фор-
мулой (1.02) и вытекает из следующих соображений: волна мо-
жет распространяться, если ее критическая частота меньше ра-
бочей частоты ю; поэтому при увеличении частоты на Дю число
распространяющихся волн увеличивается благодаря тем волнам,
критические частоты которых лежат в интервале Дю. Критиче-
ские частоты волновода являются, вместе с тем, резонансными
частотами двухмерной области — поперечного сечения волново-
да; к спектру этой области применима формула (1.02).
18*
275
Полнее число распространяющихся волн при увеличение ча-
сторы растет по асимптотическому закону
"=2^“,= ^- /(52.02)
пропорционально квадрату частоты. Поэтому при передаче ко-
ротких волн (скажем, миллиметровых) по волноводу, предназна-
ченному для сантиметрового диапазона, возбуждается много
волн. Если эти волны имеют примерно одинаковое затухание,
то к приемному концу волновода приходит сложное электромаг-
нитное поле, дальнейшее использование которого весьма затру-
днительно. Положение улучшается в том случае, когда различ-
ные волны в данном волноводе распространяются с существен-
но различными коэффициентами затухания; тогда в процессе
распространения происходит постепенное «самоочищение» элек-
тромагнитного поля от волн, испытывающих сильное затухание,
и на достаточно больших расстояниях остаются только слабо-
затухающие волны.
С таким явлением мы встречаемся в волноводе кругового се-
чения, где симметричные магнитные волны (Hoi, Н02, ...) на
достаточно высоких частотах имеют затухание, гораздо мень-
шее, чем затухание всех других волн. При использовании коль-
цевых и спиральных волноводов (см. ниже § 57) затухание волн
НОп остается малым, а затухание всех других волн резко увели-
чивается; в такой системе передача энергии производится волна-
ми НОп, число которых растет пропорционально частоте (см. за-
дачу !1), а не квадрату частоты, поэтому она применима при
более высоких частотах. Однако такая система становится прак-
тически неприменимой, если слабозатухающих волн НОп будет
слишком много.
В последние годы интенсивного исследовались линии переда-
чи, основанные на тех же принципах, что и открытые резонато-
ры. Эти линии используют оптические элементы — линзы или
зеркала, и подчиняются тем же закономерностям, что и откры-
тые резонаторы (см. ниже § 53—55). В частности, в открытых
резонаторах благодаря излучению происходит разрежение
спектра собственных частот, а в линиях из линз или зеркал
благодаря излучению разрежается спектр собственных волновых
чисел, т. е. лишь сравнительно небольшое число волн может при
данной частоте о распространяться с малым радиационным за-
туханием, а остальные волны сильно затухают вследствие излу-
чения в стороны.
Линии передачи, в которых распространение волн может
сопровождаться излучением в стороны, мы будем называть от-
крытыми волноводами. Термин «открытый волновод» весьма
подходит для передающих систем, в поперечном сечении кото-
рых поле не ограничено какими-либо непроницаемыми стенками
(как в обычном волноводе) и может излучаться в стороны. Вме-
276
сте с тем, этот термин подчеркивает связь, существующую меж-
ду такими системами и открытыми резонаторами,—связь, кото-
рая (как мы увидим ниже) порой переходит в тождественность
основных теоретических соотношений.
Открытые волноводы, образованные периодически располо-
женными линзами, были предложены Губо (см. [50]). Открытые
волноводы, образованные периодически расположенными зерка-
лами, предложены Каценеленбаумом [51] и Бондаренко и Та-
лановым (см. [52] и [53]). В этих работах уже была указана
связь между теорией открытых волноводов и теорией открытых
резонаторов; для систем такого типа мы рассмотрим эту связь
в § 53—55.
С точки зрения данного выше определения к числу открытых
волноводов нужно отнести спиральный и кольцевой волноводы,
а также обычные волноводы, стенки которых имеют щели или
обладают частичной прозрачностью. Диэлектрические волново-
ды, например диэлектрические стержни в свободном пространст-
ве, также являются открытыми волноводами. Свойства этих си-
стем мы рассмотрим в данной главе, не входя, однако, в детали.
Следует отметить, что вдоль диэлектрических волноводов мо-
гут распространяться волны, у которых радиационное затуха-
ние полностью отсутствует: при данной частоте может быть
конечное число таких волн, все другие волны при распростране-
нии затухают в результате излучения >(§ 56). >В других периоди-
ческих структурах также могут существовать незатухающие
волны, если период этих структур меньше половины длины вол-
ны в свободном пространстве, окружающем эти структуры
(§ 57). Наличие электромагнитных волн, затухание которых
точно равно нулю, является свойством, характерным для откры-
тых волноводов (гладких или с достаточно малым периодом);
в трехмерных открытых резонаторах, со 'всех сторон окружен-
ных пустотой, собственные колебания всегда- имеют некоторое
радиационное затухание (хотя и малое, ср. § 58).
Периодические структуры для электромагнитных волн в об-
щем случае можно определить как такое распределение
комплексной диэлектрической и магнитной проницаемостей
е(х, у, г) и р (х, у, z), которое по осн z имеет период L; следо-
вательно,
е(х, у, z+L) = е(х, у, z), ц(х, у, z+L)=p.(x, у, z). (52.03)
Эти проницаемости могут также зависеть от частоты. Открытые
периодические волноводы (линзовые, зеркальные, кольцевые и
другие), кроме того, должны удовлетворять условию
е = р. = 1 при г — ]/х2 у2 > г, (52.04)
т. е. за пределами цилиндра радиусом г, охватывающего ось
волновода, должна быть пустота.
При исследовании волн в периодических структурах большое
значение имеет обобщенная теорема Флокё, которой часто поль-
277
зуются, не формулируя ее явно. Насколько нам известно,
в математике достаточно общее и строгое доказательство этой
теоремы отсутствует, однако с физической точки зрения ее спра-
ведливость не вызывает сомнений. Эта теорема формулирует-
ся так: волновое поле каждой собственной волны, существую-
щей при данной частоте в бесконечной периодической
структуре с периодом L, удовлетворяет соотношению
Ф(х, у, г-|-£)=е'фФ(х, у, z), (52.05)
причем ф (или, точнее, е'ф) есть комплексный параметр, харак-
теризующий данную волну; та же волна, но распространяющая-
ся в противоположном направлении, удовлетворяет соотноше-
нию
Ф (х, у, z + L) = е“'фФ (х, у, z), (52.06)
в котором по сравнению с соотношением (52.05) вместо ф
стоит — ф.
В трехмерной периодической структуре волны определяются
двумя индексами (скажем, индексами тип). В двухмерной пе-
риодической структуре (когда отсутствует, например, зависи-
мость от координаты у) волны при данной частоте определяют-
ся одним индексом. В одномерной периодической структуре вол-
новое поле Ф=Ф(г) удовлетворяет дифференциальному урав-
нению
g-4-/^(zp = 0 (52.07)
с периодическим коэффициентом
p(z) =p(z+L). (52.08)
При данной частоте a — ck имеется два решения Ф+(г) и Ф_(г),
удовлетворяющие соотношениям
Ф+(г4-£)=ефФ+(г), Ф_ (z + Ь)=е~1фФ_ (z), (52.09)
причем общее решение уравнения (52.07) есть линейная ком-
бинация функций Ф+ и Ф_. Последняя формулировка (для одно-
мерной задачи) есть теорема Флокё в собственном смысле
этого слова: она доказывается в теории обыкновенных дифферен-
циальных уравнений, причем оказывается, что при некоторых
частотах (их можно назвать критическими) решения Ф+ и Ф_
являются линейно зависимыми, поэтому общее решение урав-
нения (52.07) имеет более сложный вид. В двухмерных и трех-
мерных задачах также могут быть критические частоты, при ко-
торых прямая и встречная волны, определяемые соотношениями
(52.05) и (52.06), становятся неразличимыми: это будет при
е,ф==±1. Если распространение волн вдоль периодической струк-
туры сопровождается затуханием (в результате комплексно-
сти виц. или излучения в стороны), то для волны, распростра-
278
няющейся в положительном направлении оси z, мы будем иметь
|е'^| <1, следовательно критические частоты отсутствуют.
Если определить волновое числю kz с помощью соотношения
kzL=^, (52.10)
то соотношение (52.05) можно записать в виде
Ф(х, у, z) — e'kzZ Ф(х, у, z), (52.11)
где Ф есть периодическая функция г, удовлетворяющая соотноше-
нию
Ф(х, у, г4-Л) = Ф(л, у, г); (52.12)
действительно
Ф(л, у, z-}-L)=e ‘*1<г+£)Ф(л, у, z-\-L) =
=е ‘kzZ Ф(л, у, г) —Ф(х, у, г). (52.13)
Разлагая функцию Ф в ряд Фурье
Ф(х, у, z)— Ф9(х, у)е L , (52.14)
q= — оо
по формуле (52.11) получаем Ф в виде
Ф(х,У, z) = f (52-15)
q= — оо
где
kzq = kz + ^. (52.16)
Ряд (52.15) обычно называется разложением по простран-
ственным гармоникам, а величины (52.16) —продольными вол-
новыми числами пространственных гармоник. Соотношения
(52.05) — (52.16) мы выписали для скалярного волнового по-
ля Ф; они справедливы и для электромагнитного поля в перио-
дической структуре (52.03), если под Ф понимать любую состав-
ляющую электрического или магнитного поля. Если периодичес-
кая структура является открытой и удовлетворяет условию
(52.04), а Ф есть декартова составляющая электромагнитного
поля, то при r>f функция Ф будет удовлетворять волновому
уравнению (12.10), а функции Ф9, входящие в разложение
(52.15), — уравнению
+(^-^)ф9=0. (52.17)
Поскольку в теории открытых волноводов рассматриваются
волны, которые в радиальном направлении расходятся (т. е.
27»
уходят во все стороны, а не приходят из бесконечности), то са-
мое общее решение уравнения (52.17) мы можем записать так:
ф,= £ (A^cosm? -(-В,™ sin ту)/7^’ {kT(jfy, (52.18)
т=0
здесь Ад,п и BQm — постоянные, а
= —. (52.19)
При г—оо функция Ф, превращается в цилиндрическую волну
(52.20)
где
00 гте
Е-Z (2m +1)
(Agm cos rn<?-\-BQm sin , (52.21)
tn— О
а Ф — в суперпозицию конических волн
Ф= £ Xe(?)|/’^-reZ(^r+ft-z’. (52.22)
q~ — оо
Зависимость цилиндрических и конических волн от коорди-
наты г определяется величиной (52.19), которая называется ра-
диальным волновым числом q-й пространственной гармоники.
Для того чтобы эти волны действительно расходились в ради-
альном направлении, квадратный корень в формуле (52.19)
нужно извлекать так, чтобы было
Re£rg>0. (52.23)
Поскольку волновое число k= -у-, соответствующее частоте воз-
буждения электромагнитного поля, является вещественным по-
ложительным и поскольку волна, распространяющаяся в по-
ложительном направлении оси г, в том же направлении и зату-
хает, т. е.
1птф>0 и Im&zg>0, (52.24)
то мнимая часть krg получается вполне определенной. В зависи-
мости от соотношения между k и kzq может быть
1тАгд>0 (52.25)
или же
1т£гд<0. (52.26)
В первом случае данная пространственная гармоника лока-
лизована вблизи открытого волновода, ее толе экспоненциаль-
но убывает при удалении от него. Во втором случае поле дан-
ной пространственной гармоники экспоненциально возрастает
280
в радиальном направлении. Физический смысл обоих случаев
будет рассмотрен ниже на примерах (см. § 56 и 57). Здесь мы
остановимся только на одном вопросе: при каких условиях
вдоль открытого волновода может распространяться незатухаю-
щая электромагнитная волна, у которой
1шф = 0, Im/sz=ImZjzg=o (52.27)
и поэтому согласно соотношениям (52.05) и (52.11) амплитуда
одинакова во всех периодах данной открытой структуры. Физи-
чески очевидно, что незатухающая волна может быть только
при отсутствии потерь в самой структуре, т. е. при
Irri£=Imp=0. (52.28)
Кроме того, должны отсутствовать потери на излучение в сто-
роны; так будет, если все радиальные волновые числа (52.19)
будут чисто мнимыми:
&rg = i|ferg|- (52.29)
Для выполнения последнего условия необходимо, чтобы все про-
дольные волновые числа (52.16) удовлетворяли неравенству
&2zg>fc2, (52.30)
которое выполняется при всех q=0, ±1, ±2, ..., если kz удов-
летворяет двойному неравенству
k<kz<-?- (52.31)
или
— ^<kz< — k. (52.32)
Физический смысл неравенства (52.30) очень прост: по-
скольку
(52.33)
есть фазовая скорость q-й пространственной гармоники по оси
z, условие (52.30) требует, чтобы все пространственные гармони-
ки данной волны были медленными, т. е. чтобы было |ug|<c.
Следует иметь в виду, что соотношением (52.05) комплекс-
ный параметр ф определяется не однозначно, а с точностью до
слагаемого 2nq, где q — целое число; поэтому соотношение
(52.10) определяет kz с точностью до слагаемого Без огра-
ничения общности можно для незатухающих волн считать
— «<ф<тг, —£-<*,<-£-» (52.34)
тогда условия (52.31) и (52.32) будут выполнены, если
kz>k или kz<—k, (52.35)
281
т. е. если нулевая пространственная гармоника с продольным
волновым числом kz, удовлетворяющим условиям (;52.34), являет-
ся медленной. Одновременное выполнение неравенств (52.34) и
(52.35) возможно только при условии
kL<_n, (52.36)
т. е. когда период структуры меньше половины длины волны
в свободном пространстве.
Если хотя бы одна пространственная гармоника данной вол-
ны является быстрой (|tzQ|~>с), то в разложениях (52.15) и
(52.22) ей соответствует расходящаяся волна, уносящая энер-
гию из открытого волновода и вызывающая затухание волны
в направлении! оси г.
§53. Параксиальные лучевые потоки
в открытых волноводах,
образованных линзами или зеркалами
На первом этапе изучения открытых волноводов применим
геометрическую оптику (см. гл. VI) к системе из периодически
расположенных одинаковых линз, изображенную на рис. 66.
В рамках параксиальной геометрической оптики линза однознач-
РИС. 66. Открытый волновод, образованный периодически распо-
ложенными линзами.
но характеризуется фокусным расстоянием F\ для тонких линз
(толщина которых мала по сравнению с F) мы имеем
(Ге-1) (/•. + »,)
где У£ — показатель преломления линзы, г, и г, — радиусы кри-
визны ее поверхностей. Сферическое зеркало с радиусом кривизны
гв имеет фокусное расстояние
(53.01)
р___
2 '
(53.02)
Если фокусные расстояния (53.01) и (53.02) равны, то в ре-
зультате преломления лучей линзой параксиальные лучевые
потоки преобразуются так же, как в результате их отражения
сферическим зеркалом: таким образом легко найти радиус кри-
визны
г0 = 2Е =
____2Г]Гг___
(ГГ-Щ^ + гг)
(53.03)
282
сферического зеркала, эквивалентного данной линзе. Мы отвле-
каемся здесь от того, что при отражении направление лучей из-
меняется (это несущественно, ср. § 40), а также от того, что
при преломлении интенсивность лучей ослабляется (это анало-
гично неполному отражению от зеркал и легко может быть учте-
но, см. конец параграфа).
Преобразованный лучевой поток, .пройдя расстояние 21 меж-
ду линзами, преломляется следующей линзой, и т. д. Если пер-
вую линзу заменить эквивалентным зеркалом, то зеркало, экви-
валентное следующей линзе, будет на расстоянии 2/ от первого
и вместе с первым может быть аппроксимировано эквивалент-
ным сфероидом (эллипсоидом вращения), полуоси которого
определяются формулами
c — l, a — b= yrj — \T2lF, (53.04)
где F — фокусное расстояние линзы. К лучевым потокам в та-
ком сфероиде можно применить все результаты, полученные
в гл. VI; единственным отличием будет отсутствие квантового
условия, связанного с граничным условием (38.01). Действи-
тельно, при повторном отражении от первого зеркала (в экви-
валентном эллипсоиде) само зеркало эквивалентно уже новой
линзе, поэтому граничного условия на зеркалах ставить .не на-
до. Это соответствует тому обстоятельству, что в открытых вол-
новодах частота волнового поля может быть произвольной —
она задается возбуждением, в то время как в открытых резо-
наторах частота собственных колебаний определяется параме-
трами резонатора.
В сфероиде, эквивалентном линзовому открытому волноводу
(рис. 66), согласно § 39 могут быть только колебания А, для
которых квантовое условие (А^), выведенное в § 38, опускается,
точнее, заменяется формулой
ф = А J/P(&)d&, (53.05)
о
определяющей .набег фазы ф при переходе лучевого потока от
зеркала к зеркалу, т. е. при продвижении его на расстояние
21— период открытого волновода. В параксиальном приближе-
нии в силу соотношения (39.04) эта формула принимает вид
Ф = 2kc — k —у1—-- — а, л — arcsin l/' —. (53.06)
УI (го — Z) v г0
Все остальные соотношения, характеризующие собственные вол-
ны в линзовом волноводе, например положение внутренней и
внешней каустик (определяемых параметрами tj и Тг), можно
получить из § 39. Проще, однако, воспользоваться формулами
§ 19, в котором только формула (19.12) для собственной часго-
283
ты оказывается неприменимой; вместо нее мы получаем выра-
жение для фазового набега
ф=2&/—2(т+2н+1)а (т, п=0, 1,2,...). (53.07)
' Данная волна передается вдоль линзовой линии практически
без радиационного затухания, если ее поперечная протяжен-
ность (определяемая радиусом внешней каустики) меньше по-
перечных размеров линзы. Если же поперечные размеры волны
больше и она не укладывается на линзе, то радиационное зату-
хание этой волны велико, и распределение электромагнитного
поля в ней определяется не геометрической оптикой, а диффрак-
цией на краях линзы.
РИС. 67. Открытый волновод, образованный периодически рас-
положенными зеркалами.
Оставляя исследование диффракционных явлений в открытых
волноводах до § 54, рассмотрим лучевые потоки в открытом вол-
новоде, образованном периодически расположенными одинако-
выми сферическими зеркалами (см. рис. 67; возможны и более
сложные зеркальные линии, см. [51] и [61]). Расчет такого волно-
вода по геометрической оптике производится примерно так же,
как расчет многозеркального открытого резонатора (рис. 51,
§ 40), только квантовое условие (40.06), обусловленное гранич-
ным условием на зеркалах, опускается. Радиусы кривизны экви-
валентного эллипсоида определяются формулами (40.03) и
(40.04), где го — радиус кривизны сферических зеркал, а у —
угол падения центрального луча (рис. 67). Что же касается ма-
лой оси 2с эквивалентного эллипсоида, то она, очевидно, долж-
на быть взята равной длине 2/ прямолинейного отрезка цен-
трального луча (между двумя последовательными отраже-
ниями).
Поскольку для зеркального открытого волновода эквива-
лентный эллипсоид сильно отличается от эллипсоида вращения,
в нем малым радиационным затуханием будут, вообще говоря,
обладать только колебания В (колебания А имеют большую по-
перечную протяженность, см. § 39). В параксиальном прибли-
жении набег фазы на пути 2/ между двумя зеркалами получает-
ся равным
<]> = 2kl — (2т -]— 1) <zx — (2« -f-1) аг (т, п = 0, 1, 2,...), (53.08)
284
где
sin а, = 1/ 4~=1Z —'—’
1 “ r't r ra cos у
(53.09)
(ср. задачу 10 к гл. VI).
В предыдущих главах мы не рассматривали во всех подроб-
ностях колебания между зеркалами, радиусы кривизны которых
в плоскостях xz и уг различны и равны соответственно /о и г''о-
Этот пробел легко восполнить: для интересующих нас колеба-
ний В в параксиальном приближении справедливы все формулы
§ 20 с тем лишь изменением, что безразмерные координаты тх
и Ту определяются по-другому, а именно на зеркалах нужно
положить
хд = у у sin 2а, х, ту=у sin 2аг у.
(53.10)
Если зеркала прямоугольные, т. е. их проекция на плоскость z=O
есть прямоугольник — а<Сх<С«, —Ь<^у<^Ь, то надо дополни-
тельно положить
та = )Z—у- sin 2а,, = sin2as« (53.11)
причем си и аг определяются формулами (53.09).
Из результатов § 20 также легко получить выражение (53.08)
для зеркального волновода и выяснить пределы его применимо-
сти, т. е. оценить, когда диффракционные поправки для данной
собственной волны малы.
Выше мы рассмотрели волны в открытых волноводах, опи-
раясь на результаты, полученные в предыдущих главах и от-
носящиеся к открытым резонаторам. Более непосредственное и
наглядное исследование этих волн можно произвести, исполь-
зуя метод параболического уравнения. Для линзового волново-
да (рис. 66) мы в интервале —/<г</ вводим сфероидальную
систему координат Р, <р, £ (§ 18) и ищем решение скалярного
волнового уравнения (12.10) в виде бегущей волны
Ф (х, y,z) = W (р, <f>, С)е‘т sh с (— I < z < /). (53.12)
Для функции W получается выражение (18.15), в котором можно
считать С, а и 1 связанными с цилиндрическими координатами г =
— Кл2+1/2 и 2 формулами:
shC = |, chC = rj!!+—.
. z -1/ 2fed (53.13)
a = arcsin —= , т — I/ -т——5 r.
Vd2 + 2s ’ r d2 + 22
285
Для величины yshC в экспоненте *(53.12) надо взять более точное
выражение, а именно:
TShC=to(14-l^J^), (53.14)
откуда
. — ikl
ф(х, у, —/-|-0)=—=-'Г(т, <р, —а)е
сп£
1 гы(1+Т7Й+р)
Ф(х, у, I — 0)=-U^(x, <р, а)е V (53.15)
ch?
здесь
. > 1<б?г + /г . I 1/ 2kd /со
спС = -—-----, а = arcsin-. —= , т=1/ , ,2 г. (53.16)
г? ’ г d2 + l2 '
Волновое поле в других интервалах значений z определяется
соотношением (см. § 52)
Ф(х, у, z + 2l) =еф Ф(х, у, г), (53.17)
где
ф=ф'+|/ф// (53.18;
есть в общем случае комплексный параметр, вещественная
часть которого ф' дает полный набег фазы бегущей волны на пе-
риоде 21, а мнимая часть ф"— ослабление поля на том же пе-
риоде.
В гл. IV для функции Т мы получили выражения (19.04),
(19.06), (19.08) и (19.09), не учитывающие диффракции на кра-
ях открытого резонатора (т. е. не учитывающие конечных разме-
ров зеркал). Применительно к открытым волноводам можно
поставить следующий вопрос: каким образом должно преобра-
зовываться волновое поле в плоскостях z=—I, z=l, z=3>l и т. д.
чтобы поддерживалось распространение волны, определяемой
формулами (53.12), (53.15) и (53.17)? Так как согласно форму-
ле (53.17)
Ф(л, у,/ + 0) = е,фФ(х, у, — Z-f-O), (53.19)
то искомый закон преобразования записывается следующим об-
разом:
Ф(л, у, /4-0) = Ф(х, у, I — 0)е v (53.20)
где фо есть скачок фазы при л=0, т. е. на оси 'волновода. Тогда
в силу формул (19.06) и (19.08) полный набег фазы равен
ф = 2kl +фо—2(m+2n + l)a, (53.21)
а ослабление отсутствует. Формула (53.21) отличается от при-
веденной выше формулы (53.07) наличием слагаемого фо, не
учтенного в формуле (53.07).
286
Тонкая линза с фокусным расстоянием F, расположенная
в плоскости z=l, преобразует (в пределах своего поперечного
сечения) волновое поле по закону
, {, kr‘\
I ’’° 2F I
Ф(Л, у,/ + О) = Ф(х, у, l — O)e v (53.22)
т. е. изменяет фазу поля на слагаемое, пропорциональное г2.
Закон (53.22) легче всего проверяется, если слева на плоскость
z=l падает плоская волна, фаза которой постоянна в плоскости
z=const; тогда после преломления в линзе волна приобретает
фазовый множитель
(kf z \
(53.23>
соответствующий '(в параксиальном приближении) сферической
волне, сходящейся к фокусу.
Сравнивая формулы (53.20) и (53.22), видим, что искомое
преобразование (53.20) может быть осуществлено тонкой лин-
зой с фокусным расстоянием
(53.24)
если пренебречь диффракцией на краях линзы, т. е. считать
линзу бесконечно широкой. Практически это означает, что ра-
диус линзы а должен быть больше радиуса внешней каустики
для волны с данными индексами тип. Переход от скалярного
волнового поля к электромагнитному производится с помощью
формул (23.07), (19.04) и (23.10): таким образом мы легко полу-
чаем электромагнитные волны в линзовом волноводе (без учета
диффракции на краях линз), которые по аналогии с колеба-
ниями и , рассмотренными в § 23, естественно назвать
волнами и E{lJ}.
тп тп
Поскольку в формулах (53.13) и (53.14) мы перешли к ци-
линдрическим координатам гиг, вместо формул /(23.07) можно
воспользоваться формулами (3.56) и (3.57), дающими более про-
стые выражения для полей в цилиндрической и декартовой си-
стемах координат.
Волны в зеркальном волноводе (рис. 67) анализируются та-
ким же образом: между каждыми двумя соседними зеркалами
вводится своя декартова система координат так, что ось г сов-
падает с центральным лучом, ось х лежит в плоскости падения
(плоскости чертежа), а ось у перпендикулярна к этой плоско-
сти. В силу астигматизма системы электромагнитные волны
в ней определяются (без учета диффракции на краях) не фор-
мулой (23.10), а формулой (23.09), которую надо применять
совместно с формулами (3.56), (3.57), (20.04) и (53.10). Эти
287
формулы определяют электромагнитные волны, которые естест-
венно назвать волнами Е^п и Е^п в зеркальном волноводе.
Отличие этих волн от одноименных в линзовом волноводе за-
ключается в том, что для зеркального волновода разделение
- переменных производится в декартовой системе координат, а не
в цилиндрической, как для линзового волновода. В этом от-
ношении зеркальный волновод аналогичен обычному прямо-
угольному волноводу, а линзовый — круглому. Аналогия между
зеркальным и прямоугольным волноводами будет более полной,
если сами зеркала имеют прямоугольную форму {см. выше пояс-
нения к формуле (53.11)]. В этом случае и при учете диффрак-
ции на краях переменные будут разделяться — будет справедли-
ва формула (20.09). Если же зеркала имеют круговую форму,
то при рассмотренная диффракции разделением переменных уже
воспользоваться нельзя, поэтому расчет диффракционных явле-
ний оказывается более сложным, чем в открытых резонаторах
с двумя зеркалами.
Вообще говоря, реальные линзы не только изменяют фазу
волнового поля в соответствии с соотношением (53.22), но и
ослабляют это поле — как вследствие поглощения волн в объеме
линзы, так и вследствие отражения от ее поверхностей. Это
ослабление проще всего учесть, считая параметр ф0 в формуле
(53.22) комплексным:
фо=ф,о+«фо" (53.25)
так что е“ф 0 характеризует ослабление поля при прохождении
через линзу В этом случае величина (53.21) также будет
комплексной, причем ф"=фо". Неполное отражение от зеркал
можно учесть путем введения в правую часть формулы (53.08)
слагаемого, аналогичного фо.
Диффракционные потери также приводят к тому, что пара-
метр ф, входящий в формулу (53.17), становится комплексным
(см. ниже § 54).
До сих пор мы исследовали волны в линзовых и зеркальных
волноводах, пренебрегая как аберрациями (т. е. считая лучевые
потоки параксиальными), так и диффракцией. Естественно за-
дать вопрос: как влияют неучтенные эффекты в случае, когда их
можно считать малыми, т. е. когда лучи составляют с централь-
ным лучом малые углы и каустические поверхности укладывают-
ся на линзах и зеркалах? Известно, например, что оптическое
изображение подобно объекту только в параксиальном прибли-
жении, а под влиянием аберраций (не говоря уже о диффрак-
ции) изображение оказывается размытым. Ёсли бы наш вывод
о существовании распространяющихся волн, поле которых при
переходе к следующему периоду открытого волновода умно-
жается на е'у основывался только на параксиальной геометри-
ческой оптике, то он был бы приближенным и, следовательно,
288
волна после прохождения достаточно большого числа периодов
могла бы сильно исказиться. Однако существование неискажаю-
щихся волн вытекает из фундаментальных соображений, а имен-
но из обобщенной теоремы Флокё (§ 52), а приближенные рас-
четы, проведенные выше, позволили вычислить основные харак-
теристики наиболее интересных волн, обладающих малым ра-
диационным затуханием. Более точные расчеты, учитывающие
диффракцию (см. § 54), лишь уточняют распределение поля
этих волн и позволяют найти их радиационное затухание; к та-
ким же малым поправкам приводит учет аберраций и других
возмущений.
Сказанное относится к идеальным открытым волноводам,
в которых линзы или зеркала тождественны и расположены
строго периодически. Возмущение волн, обусловленное наруше-
нием периодичности открытых волноводов, нуждается в особом
исследовании, которое должно использовать статистические
сообращения; это исследование, целью которого является оцен-
ка допусков в открытых волноводах, выходит за рамки данной
книги.
В строго периодической структуре учет малых эффектов,
опущенных при первоначальном исследовании волн, может при-
вести к немалым возмущениям только в том случае, когда волны
в первом приближении получились вырожденными, т. е. когда
две волны (или большее число волн) имеют одно и то же зна-
чение е"1’. Тогда система собственных волн, соответствующих
одному и тому же собственному значению е'*, является неод-
нозначной и любое сколь угодно малое возмущение может при-
вести к «перестройке» этой системы. В качестве примера можно
привести линзовый волновод, у которого согласно формуле
(53.21) имеется вырождение, так как ф зависит от т+2п, а не
от т и п в отдельности; как и в открытых резонаторах (см. осо-
бенно § 39), это вырождение может сниматься различными воз-
мущающими факторами по-разному.
§ 54. Диффракция
в открытых волноводах
В предыдущем параграфе мы рассматривали волны в откры-
тых волноводах без учета диффракции на краях линз и зеркал.
При этом оказалось, что в параксиальном геометро-оптическом
приближении задача об открытом- волноводе сводится к задаче
о двухзеркальном открытом резонаторе, зеркала которого суть
части эквивалентного эллипсоида; при этом в задаче о резонато-
ре не следует ставить граничного условия на зеркалах, вслед-
ствие чего aq заменяется на ф. Таким образом, из формулы
(19.12) легко получается формула (53.07) или, если учесть ска-
чок фазы фо, формула (53.21); аналогичные соображения позво-
19—2547 289
дяют сразу написать формулу (53.08) для зеркального волно-
вода.
Как уже отмечалось в § 40, эквивалентность двух систем
в рамках геометрической оптики ведет к тому, что диффракцион-
ные явления 'в обеих системах одинаковы. Если взять систему
линз, закрывающих круговые отверстия в периодически распо-
ложенных поглощающих плоскостях (рис. 68), то диффракции
в таком открытом волноводе будет происходить так же, как
в открытом резонаторе со сферическими зеркалами круговой
формы — при условии, что лучевые потоки (без учета диф-
фракции) одинаковы и что диаметр линз и зеркал совпадает.
Таким образом из формулы (21.01) для открытого резонатора
сразу можно получить формулу
ф —2&/-|-ф0 —2(те-|-2/г—1)а—2тт? (п=1, 2,...) (54.01)
для линзового волновода. Комплексный параметр р=р'— ip" тот
же, что и в теории открытых резонаторов; в частности, при
а=-^- мы имеем р' = 0, а величину Л —4~р" можно найти, поль-
зуясь результатами § 50.
При отсутствии поглощающих оправ диффракция в линзовом
волноводе происходит иначе, чем в открытом резонаторе. Физи-
ческая причина различия в том, что волновое поле, прошедшее
мимо зеркала открытого резонатора, выбывает из игры (так же,
как при падении на поглощающий экран), в то время как вол-
новое поле, не испытавшее преломления в линзе, переходит
в следующий период открытого волновода, изображенного на
рис. 66, и, как будет показано в § 55, уменьшает диффракцион-
ные потери тех собственных волн, поле которых ограничено кау-
стиками.
Формула (53.08) для зеркального волновода при учете диф-
фракции на краях зеркал принимает вид
ф=2Л/—(2т—l)ai—(2п—1)«2—2лр (т, п=1, 2, ...). (54.02)
Если зеркала имеют прямоугольную форму, т. е. их проекция на
плоскость, перпендикулярную центральному лучу, есть прямо-
угольник со сторонами 2а (в плоскости падения) и 2b (в перпен-
дикулярной плоскости), центр симметрии которого лежит на
центральном луче, то комплексный параметр р можно вычислить
по формуле
р=ра+рь, (54.03)
где параметр ратт же, что для открытого резонатора, образо-
ванного цилиндрическими зеркалами с радиусом кривизны г'д,
шириной 2а и расстоянием между зеркалами 21, а параметр рь
тот же, что для такого же резонатора с параметрами г"0, 2Ъ
,и 21.
Формулы (54.02) и (54.03) применимы и к волноводу, образо-
ванному плоскими зеркалами прямоугольной формы. В этом слу-
290
чае выражения для ра и рь надо брать из гл. I; с помощью фор-?
мул гл. I нетрудно найти распределение электромагнитных полей
для волн и Е{^п, распространяющихся в таком открытом
волноводе. Разрежение спектра, о котором говорилось в § 52, здесь
демонстрируется наиболее очевидно образом: рь^п2,
поэтому радиационное затухание волн быстро растет с увеличением
индексов тип.
Приведенные выше соображения достаточны для расчета
диффракционных явлений в открытых волноводах. Чтобы сде-
лать эквивалентность резонаторных и волноводных задач более
явной, выведем интегральное уравнение для собственных волн
в открытом волноводе, образованном зеркалами (рис. 67), и
покажем его тождественность интегральному уравнению для
собственных волн в открытом резонаторе. Для простоты мы
ограничимся двухмерной задачей, в которой поле не зависит
от координаты у', перпендикулярной плоскости рис. 67. Цеш
Я
тральный луч, обегающий зеркала, образует угол у—Y
с осью х', период структуры по оси х' равен 4/sin у, где 2/ —
длина прямолинейного отрезка центрального луча между зер-
калами. Поверхность нулевого зеркала пусть задается соотно-
шениями
----— —, —сю<#'<оо, z' = /cosy— (54.04)
cos у cos у ’ а * cos у ' '.
Исследуем распространение волны между двумя соседними
зеркалами, например между минус первым <и нулевым зеркала-
ми. Введем безразмерные координаты (ср. § 8)
Е — [(-к' +1 sin у) cos y — z' sin y],
C = [(л/ -f-1 sin y) sin y + z' cos y! (54.05)
и будем искать решение волнового уравнения (3.03) в виде
Ф=№(|, £)expife[(x'+/sin у) siny+2< cosy]. (54.06) -
Для функции W. мы получаем уравнение (3.51), которое заме-
няем параболическим уравнением (8.04), имеющим функцию
Грина (8.05). Функция Грина позволяет связать значения W
на соседних зеркалах; при условиях
/>asinY, (54.07)
эти зеркала определяются соотношениями
-4<е<4> t54-08)
19*
291:
следующими из формул (54.04) и (54.05), где
М = У (54.09)
Эта связь имеет вид
М/2
j г (*-«'» 1)№(е', -4)^'- <54-10)
—М/2
При распространении каждой собственной волны в зеркальном
волноводе ее поле на каждом зеркале должно воспроизводить (с точ-
ностью до множителя е'ф) поле на предыдущем зеркале. Это дает
нам условие
W ) е< {kl~* (0I=е'^ — 4) е"‘ lk‘^ U>’. (54.11)
которое, вводя величину
X = 2fc/~ ф, (54.12)
можно переписать в виде
W (*’ “ 4) = e'W (£> 4) е~2‘Ф а> • (54.13)
Здесь, как в § 8, через
$ty=kh(x) (54.14)
обозначен фазовый набег, обусловленный прогибом зеркал (откло-
нением их от плоскостей г' = ±/).
Из формул (54.10) и (54.13) для функции
= -4)e/s6(5) (54.15)
мы получаем интегральное уравнение
М/2
f(E)=e'z J K(£,V)f(V)dV (54.16)
—M/2
с симметричным комплексным ядром
tf(S, £') = Г(£ — £', 1)е“И*«>+«<*(И’. (54.17)
Точно такое же интегральное уравнение получается для откры-
того резонатора с одинаковыми зеркалами произвольной формы
(§ 8). Если решения этого интегрального уравнения известны,
то они позволяют рассчитать не только собственные колебания
в открытых резонаторах, но и собственные волны в открытых
волноводах, образованных зеркалами; в частности, комплексный
параметр ф, определяющий полный набег фазы и затухание
волны при переходе от одного зеркала к другому, согласно фор-
муле (54.12) равен
ф = 2kl—у.
(54.18)
292
Таким образом, он просто выражается через комплексный пара-
метр %, фигурирующий в уравнении (54.16). Соотношение
(54.18), как легко понять, переносится и на трехмерные волно-
вые поля; в частности, из него легко получить формулы (54.02)
и (54.03).
РИС. 68. Открытый волновод, образованный линзами в отвер-
стиях поглощающих экранов.
В заключение рассмотрим диффракцию в линзовых волно-
водах, о которых кратко говорилось в начале параграфа. Чтобы
не писать слишком громоздких формул, мы опять ограничимся
двухмерной задачей. Представляя волновое поле собственной
волны в линзовом волноводе в виде
Ф(х, z) = U7(E, C)eifez,
t i/T z (54.19)
£ Г 2/ X> 21
и характеризуя (тонкую) линзу соотношением
Ф (х, I + 0)=Ф (х, I — 0) е‘1фо-2* ° (54.20)
или ’
117 Л 1 4- оА = W (Е, ~ — o') е’1Фо~2*(ея при | Е | < 4L (54.21)
аналогичным соотношению (53.22), мы должны еще написать усло-
вие для W ^Е, у 4- о) или W ^Е, — I" 4“ о) при | Е | > у-. Здесь
параметр М связан формулой (54.09) с шириной линз 2а и рас-
стоянием 2/ между ними. Если линзы вставлены в поглощающие
экраны (рис. 68), то это условие имеет вид
Г^’~т+°)=О при i*i>4 <54-22)
и тогда мы имеем соотношение
М/2
W <Е, у — о)= j Г(Е —Е', W^E, _A-4-o)dE', (54.23)
—М/2
293
аналогичное (54.10). Пользуясь обобщенной теоремой Флокё
w т+°)&ihl=е'Фи7 0* —т+°) е‘ihl <54-24)
1 и соотношением (54.21), для функции
f(?) = r^, — 4+°)e'^U> (54.25)
мы опять получаем интегральное уравнение (54.16), в котором
%—2kl—ф+ф0. (54.26)
i
Таким образом, в этом случае расчет диффракции в линзо-
вом волноводе сводится к расчету диффракции в открытом ре-
зонаторе. Если же открытый волновод образован линзами, пе-
риодически расположенными в свободном пространстве
(рис. 66), то вместо условия (54.22) надо брать условие непре-
рывности поля
j + 0) = R7(^T-°) при1Н>4’ (54’27>
дополняющее условие (54.21), и аналогичное условие при С =
= ——0. Вместо соотношения (54.23) мы будем теперь иметь
W (Е’ — 4+°)d£'- (54.28)
—ОО
Если ввести новую функцию
<£(E) = $t>G)- 4о 2 при |е|< м " 2 • м (54.29)
при 2 *
то условия (54.21) и (54.27) можно записать в виде одного соот-
ношения
W (Е’ 4 + °) = Г (Е> 4 “ °) % (54.30)
которое вместе с соотношением (54.24) приводит к интегральному
уравнению
= JK(UW)d^ (54.31)
—оо
где
)(Е) = №0, —1+о)е,<иЧ х = 2^/-ф (54.32)
294
и
Л(«, Е') = Г(Е —Е', l)e“Ue6(6)+^(V)1. (54.33)
Основное отличие уравнения (54.31) от уравнения (54.16)
заключается в том, что пределы интегрирования в уравнении
(54.31) бесконечны*. Поэтому открытый волновод, образован-
РИС. 69. Открытые резонаторы, эквивалентные линзовому волново-
ду (рис. 66).
ный линзами в свободном пространстве, эквивалентен открыто-
му резонатору с 'бесконечными зеркалами, изображенными на
рис. 69,а; эти зеркала задаются соотношениями
z = r±z[Z— й(л)], kh(x) = gj(ty, (54.34)
причем при |х|>о функция h(x) обращается в нуль.
Более точная связь существует между линзовым волноводом
и открытым резонатором, изображенным на рис. 69,6; этот ре-
зонатор образован идеально отражающими плоскостями z=\±l,
к которым примыкают половинки линзы, тождественной линзам
в открытом волноводе. При практическом осуществлении такого
открытого резонатора бесконечные плоскости можно заменить
конечными, если вблизи краев расстояние между зеркалами
плавно увеличивать (рис. 69,в), осуществляя таким образом
согласование волноводных волн, распространяющихся между
плоскостями z—±l, со свободным пространством.
Методы решения интегрального уравнения (54.31) разрабо-
таны слабо, поэтому из этого уравнения трудно получить какие-
либо результаты. Исключение представляет случай, когда функ-
ция ф(^) является кусочно-постоянной, т. е. когда открытый
волновод образован не линзами, а прозрачными пластинками
конечных размеров (см. задачу 4). Поэтому в следующем па-
раграфе, вводя дополнительные аппроксимации, мы исследуем
собственные колебания в открытом резонаторе, изображенном
* Здесь надо иметь в виду замечания, сделанные в гл. I по поводу урав-
нений 1(3.15) и 1(4.19), а кроме того, учесть, что интеграл (54.31) будет схо-
диться лишь при слегка комплексных пределах (Е' = ±сое‘т, т>0; ср. § 9).
295
на рис. 69,а, и таким образом получим некоторые (в основном
качественные) сведения о диффракции в открытом волноводе,
образованном линзами без оправ (рис. 66), а также в резона-
торах, изображенных на рис. 69,6 и в.
§ 55. О диффракции на линзах
в свободном пространстве.
Метод приближенного
разделения переменных
Двухмерные собственные колебания в открытом резонаторе,
изображенном на рис. 69,а, мы исследуем, сочетая метод inane-
речных сечений |[47] и метод приближенного разделения перемен-
ных [54]. Будем искать приближенное решение двухмерного вол.
нового уравнения (3.03), удовлетворяющее граничному условию
на бесконечных зеркалах (54.34), в виде*
O=P(x)f(gz), (55.01)
где
g = g U) = 2[i — h(x)] ’ (55.02)
q — целое число, a
F{gz) — cos gz при нечетных q,
Fi(gz)=singz при четных q. (55.03)
Поскольку на зеркалах F=0, функция (55.01) точно удов-
летворяет граничному условию, однако волновому уравнению
(3.03) она удовлетворять не может [при любом выборе функции
Действительно, мы имеем
«+«+« = {^+[А.-г-_(^г=]р^ +
+(2S37+§₽)^'. (55-W)
где через F' обозначена производная функции F (gz) по всему
аргументу. Поэтому уравнение (3.03) может удовлетворяться лишь
,в среднем". Потребуем, чтобы функция (55.01) удовлетворяла
уравнению
I—л (*)
[ (~4~ + ^W==0, (55.05)
J \дх2 dzs )
-l+h(x)
* Согласно методу поперечных сечений [47] поле представляется в виде
суммы слагаемых (55.01), соответствующих различным значениям q; мы огра-
ничиваемся одним таким слагаемым.
296
тогда для функции Р (х) мы получаем дифференциальное уравнение
d‘P } dg dP . ( 1 /d£V____1 d2g
dx2 ' g dx dx ' j ® ' 2g2 ydx J 2g dx2
-t(^)‘['-aw]'}/’=o. f»»»
которое с помощью подстановки
P=VgQ (55.07)
сводится к более простому уравнению
^-+|/--«!-,р(ЙгУ(1 + =У)]С=0. (55.08)
Считая q^> 1, мы можем записать это уравнение в виде
g-+-g2 -1 £2 О] Q = 0. (55.09)
ИЛ I о \ил у 1
Полагая
h(x) = ~, (55.10)
"о
где г0 — радиус кривизны зеркал, и считая
h(x)^l, k^^-, (55.11)
получаем дифференциальное уравнение
д.+2ф_а-^(1+1.).)ф=0. (55.12)
Это уравнение аналогично уравнению (13.02) и может быть
к нему приведено. Решая его без учета диффракции на краях
(как в § 13), получаем соотношение
2kl = + (2т + 1) а, (55.13)
определяющее частоту колебаний. Параметр а здесь равен
(55.14)
или, учитывая первую формулу (12.22),
(55.15)
297
Сравнивая формулу (55.13) с формулой (12.28), мы видим,
- что развитый выше приближенный метод приводим к ошибке
в частоте колебаний, а также в распределении поля. Более точ-
ное рассмотрение, основанное на эллиптических координатах
(а не на декартовых, как выше), приводит к формуле (55.13),
в которой вместо величины (55.15) стоит просто а. Величины а
и « практически совпадают при а << 1, когда радиус кривизны
зеркал велик то сравнению с расстоянием между «ими, и 'поэто-
му эллиптические координаты мало отличаются от декартовых.
Впрочем, даже для софокусных зеркал разница между а и а
невелика, так как
a = = 0,785 иа = |/-^-=0,764. (55.16)
Для резонатора, изображенного на рис. 69,а, надо положить
‘«=-2^- "ри |х|<0, (6517>
й(л) = 0 при | х | > а,
причем для линзы г0 вычисляется по формуле (53.03). Диффе-
ренциальное уравнение (55.09) в этом случае при jx|<a будет
отличаться наличием еще одного постоянного члена в квадрат-
ной скобке, а при |х| >а будет иметь вид
S-+[*-(?-)’]«=°- (55.lt»
соответствующий распространению волны с номером q между
параллельными плоскостями. Если колебание ограничено кау-
стиками, расположенными при |х| <а, то при |х|>а ему соответ-
ствует затухающая волноводная волна, экспоненциально убы-
вающая при |х| —оо. Частота такого колебания без учета диф-
фракции (прих=±о) определяется соотношением
2^^+^=^4-(2т + 1)а, (55.19)
причем
k<^-. (55.20)
Учет диффракции при х=±а в рамках уравнения (55.09)
приводит к некоторому изменению частоты колебания, но ра-
диационное затухание при этом опять получается равным нулю.
Такие колебания могут излучать в пространство |х|>а между
параллельными плоскостями z—±l только вследствие транс-
формации данного колебания в волноводные волны с низшими
индексами (q—2, q—4 и т. д.), которые могут распространять-
ся при частоте данного колебания. Представляя волновое поле
в виде (55.01), этой трансформацией мы пренебрегли.
298
Из сказанного можно сделать следующий качественный вы-
вод: радиационное затухание 'колебаний с каустиками в откры-
том резонаторе (рис. 69,а) должно быть меньше, чем в таком
же резонаторе без параллельных плоскостей z=±l. Действи-
тельно, в обычном резонаторе излучение происходит 'благодаря
тому, что затухающая волноводная волна (подходит к краю,
а в резонаторе с плоскостями она должна еще трансформиро-
ваться в волны других номеров.
Если колебание в системе, изображенной на рис. 69,а, не
ограничено каустиками, то уравнение (55.18) для него опреде-
ляет волноводную волну, распространяющуюся между плоско-
стями z=±l и уносящую с собой энергию этого колебания. Та-
кое колебание будет затухающим, причем из физических сооб-
ражений ясно, что его радиационное затухание должно увели-
читься по сравнению с колебаниями в резонаторе без плоско-
стей z=±/. Действительно, в резонаторе без плоскостей волна
будет отражаться от краев зеркал х=±а, а в рассматриваемом
резонаторе (рис. 69,а) отражение происходит от неоднородности,
выраженной слабее. Если 'переход от вогнутых зеркал к плоским,
показанным на рис. 69,а, сгладить, то радиационное затухание
для колебаний без каустики должно возрасти (так как отраже-
ние от перехода уменьшится), а для колебаний с каустикой —
уменьшиться (так как трансформация волн станет более сла-
бой) .
Эти качественные соображения можно проверить и превра-
тить в количественные результаты, если решать задачу более
точно, а именно искать поле в виде суммы слагаемых вида
(55.01); при этом получаются системы обыкновенных диффе-
ренциальных уравнений (ср. [47]), которые можно решить на
электронных вычислительных машинах.
Метод, развитый выше, применительно к данной задаче при-
водит к результатам качественного характера, которые почти
очевидны сами по себе. Для других задач этот метод дает коли-
чественные результаты, которые трудно получить другими мето-
дами (ср. задачи 5 и 6, а также § 78).
Выше мы разобрали задачу о резонаторе, которая, как пока-
зано в конце § 54, эквивалентна задаче о линзовом волноводе
(рис. 66). Анализ задачи о резонаторе показал, что в открытом
волноводе, образованном линзами в свободном пространстве,
собственная волна с внешней каустикой имеет меньшее радиа-
ционное затухание, а собственная волна без внешней каустики—
большее радиационное затухание, чем в открытом волноводе,
в котором линзы снабжены поглощающими оправами (рис. 68).
Это свойство линз в свободном пространстве обусловлено влия-
нием лучей, не испытавших преломления линзой: они остают-
ся вблизи волновода и ослабляют диффракционные эффекты.
При наличии оправы преломленные лучи имеют резкую границу,
ведущую к более сильной диффракции.
299
§ 56. Диэлектрические
, волноводы
Электромагнитные волны в диэлектрических волноводах
(т. е. в диэлектрических стержнях и пластинках) довольно под-
робно рассмотрены в научной и учебной литературе( см., напри-
мер, книгу [7] и работы, указанные в ней). Диэлектрический
волновод может служить примером открытого волновода
(в смысле определения, данного в § 52), поскольку распростра-
нение электромагнитной волны в диэлектрике неизбежно связа-
но с просачиванием поля во внешнее пространство, а это проса-
чивание, вообще говоря, дает начало излучению в стороны.
Р
х=а
РИС. 70. Диэлектрическая пластинка.
Более того, диэлектрический волновод является простейшим
примером открытого волновода, поскольку он однороден по дли-
не (периодичность структуры отсутствует), и поэтому многие
свойства открытых волноводов в нем проявляются наиболее
простым и наглядным образом.
По ряду причин исследование электромагнитных волн в ди-
электрических волноводах ограничивалось почти исключительно
волнами, распространяющимися вдоль этих волноводов без ра-
диационного затухания. Это — волны, испытывающие на границе
диэлектрика с пустотой полное внутреннее отражение и поэтому
имеющие в шустоте поверхностный характер (поле экспонен-
циально затухает при.удалении от поверхности диэлектрика);
эти поверхностные волны всегда являются медленными — их фа-
зовая скорость вдоль оси диэлектрического волновода всегда
меньше с (ср. [7], гл. XI).
Ясно, что наряду с такими волнами вдоль диэлектрических
волноводов могут распространяться электромагнитные волны,
также главным образом локализованные в диэлектрике, но
отражающиеся от границы диэлектрик — пустота только частич-
но. Такие волны распространяются, испытывая затухание вслед-
ствие излучения электромагнитной энергии в стороны.
Рассмотрим волны в диэлектрической пластинке. Пусть ди-
электрическая пластина — а<х<а (рис. 70) имеет диэлектри-
ческую проницаемость е и магнитную проницаемость р; практи-
300
чески можно полагать р=1, сохранять р имеет смысл с точки
зрения симметрии формул [ср. ниже уравнения (56.08) и (56.11)].
Будем рассматривать двухмерные электрические волны, элек-
тромагнитные поля которых в (пластине определяются электри-
ческим вектором Герца Пе по формулам
Е — grad divПе+А2ерПе, Н =—ikErotHe, (56.01)
а вне пластины —в пустоте — по тем же формулам, но в них
надо положить е=р=1. Будем считать, что вектор Герца имеет
только продольную составляющую Псг, зависящую от коорди-
нагг х и г, но не зависящую от у. Поскольку вектор Герца дол-
жен удовлетворять уравнению
Д Пе 4~ Л2брПе = 0,.
(56.02)
то внутри пластинки для бегущей волны будем иметь (учитывая
симметрию системы относительно (плоскости х=0)
или
П® = В sin (kxx)
при | х К а, (56.03)
П® = В cos (kxx)
где В — постоянный коэффициент, a kx и kz связаны соотноше-
нием
Л*
(56.04)
Вне пластины, при |х|>а, зависимость от z должна быть
такой же (е , так как поля при х — rt а непрерывны), а зависи-
мость от х должна соответствовать волне, уходящей в стороны*.
Поэтому полагаем
n® = ^e'<fcj:X+V> при х>а, (56.05)
где А — постоянная, а
k\ = Уkz—k2z, Rek°x >0,
(56.06)
поскольку k°x и li^=kz должны удовлетворять соотношению
(k°xY + (l?y==k*. (56.07)
* Это — условие излучения, которое мы накладываем в соответствии
с постановкой задачи (см. выше). При анализе собственных колебаний в от-
крытых резонаторах также используется условие излучения (см. ниже § 58).
301
Требование непрерывности тангенциальных составляющих элек-
. тромагнитного поля приводит к характеристическим уравнениям
k°
tg (kxa)= —
k°
ctg (kxa) = ie (56.08)
в которых можно k° считать функцией kx, а именно
k0x = \Z~k2x—k2(^—l). (56.09)
Если исходить из магнитного вектора Герца П’п, определяю-
щего электромагнитное поле по формулам
Е = iky. rot Пт, Н = grad div Пт -f- ^ерЛ"1, (56.10)
и ограничиться составляющей II™, зависящей от х и z, то полу-
чаются характеристические уравнения для двухмерных магнитных волн
k°
k° (56.11)
ctg(^a) = /p.
отличающиеся от уравнений (56.08) только заменой е на р..
Будем считать показатель преломления 1. Уравнения
(56.08), как и уравнения (56.11), при частоте, удовлетворяющей
условию
— 1=™ (m = 0, 1, 2,...), (56.12)
имеют частное решение
£° = 0, kxa=™, (56.13)
причем при четных т это есть решение первого уравнения,
а при нечетных — второго.
Как известно (ср. [7] § 64), условие (56.12) определяет кри-
тическую частоту электрической и магнитной волн с индек-
сом т. При частоте выше критической данная волна распро-
страняется без радиационного затухания, поскольку поперечное
волновое число в пустоте
= i Уk\ — k2 = i | k°x | (56.14)
является чисто мнимым (медленная поверхностная волна). Если
частота ниже критической частоты, то данная волна также су-
ществует, но в виде быстрой волны, обладающей радиационным
302
затуханием. Это видно из того, что вблизи критической частоты-'
можно положить
М=™-Н» (56.15)
где 8— малая величина, тогда уравнения (56.08) принимают вид
k°
tg8 = -»6-^. (56.16)
При частоте выше критической в силу формулы (56.14) мы по-
лучаем 6>0, следовательно, волна распространяется без зату-
хания. При частоте немного ниже критической величина k°x
в силу неравенства (56.06) имеет положительную вещественную
часть, поэтому мнимая часть б отрицательна, а также
Im kx 0 и Im k°x < 0, (56.17)
в то время как из соотношения (56.04) мы имеем
1шЛ2>0. (56.18)
Формула (56.05) показывает, что поле данной волны по абсолют-,
ной величине убывает в направлении оси z и возрастает в направ-
—Im х
лении оси х (пропорционально е х ). Возрастание поля при
|х|—>оо на первый взгляд парадоксально и противоречит поло-
жению о локализации энергии вблизи волновода. Оно объяс-
няется физически следующим образом. Быстрая электромагнит-
ная волна, распространяющаяся в пластинке, создает во внеш-
нем пространстве плоскую волну (56.05), волновой вектор кото-
рой имеет составляющие k°x и k° =kz (см. рис. 70). Эта пло-
ская волна создается за счет энергии поля в пластинке, поэтому
распространение сопровождается затуханием в направлении
оси z. Электромагнитное поле в точке Р, лежащей при 2=0 и‘
х>а (рис. 70), создается благодаря излучению из пластины при
отрицательных значениях 2, где волна имеет большую ампли-
туду, чем при z=0, поэтому экспоненциальное возрастание поля
при |х|—>оо является прямым следствием его экспоненциального
возрастания при z——оо.
Выше были рассмотрены двухмерные волны в диэлектриче-
ской пластине. Электромагнитные волны в диэлектрическом
стержне (круговом цилиндре) радиусом а могут быть исследо-
ваны аналогичным образом. Будем выражать поле этих волн
в цилиндрической системе координат г, <p, z через продольные
составляющие электрического и магнитного векторов Герца, по-,
лагая
П® = AJm (krr) sin (m<f> 4- <p0) e‘ *z
при r<a (56.19)
П™ = BJm (kTr) cos (m? + <p0) e<ft**
303
П® = СН(^ (k°r) sin (m<p + <p0)e
при r > a, (56.20)
П™ = DH^ (k°rr) cos (my + <p0) e *г*
где
kr = |Л k^-k2*, knr = У kz — k\ (56.21)
Находя составляющие электромагнитного поля в виде суперпо-
зиции полей (56.01) и (56.10) и ставя граничные условия при
г=а, мы приходим 'к характеристическому уравнению (см., на-
пример, [7] § 66)
(е/т Лп)(и/т
(56.22)
определяющему kz как функцию k. В этом уравнении использованы
обозначения
kjfCIJул ’
(56.23)
При m = 0 это уравнение распадается на два:
е/о = Л> и Р/о=Л>. (56.24)
причем первое определяет симметричные электрические волны
(11^—0, Hz — 0), а второе — симметричные магнитные волны
(П®~0, Ez — 0). При т=1, 2,... это уравнение определяет не-
симметричные волны, имеющие все шесть составляющих элек-
тромагнитного поля. Одна из этих несимметричных волн (с ази-
мутальным индексом т=1) при ер>1 не имеет критической ча-
стоты, т. е. может распространяться без затухания при сколь
угодно низких частотах; она аналогична волнам (электрической
и магнитной) в диэлектрической пластине, у которых индекс
/п = 0 и поэтому критическая частота, определяемая соотноше-
нием (56.12), равна нулю.
Число волн, могущих распространяться без радиационного за-
тухания в диэлектрической пластинке толщиной 2а или в диэлек-
трическом стержне диаметром 2а, тем больше, чем больше пара-
метр kay/'ty.—1 [ср. формулу (56.12)]. Это значит, что с увеличе-
нием частоты диэлектрические волноводы ведут себя подобно
обычным волноводам (§ 52), а именно они способны поддержи-
вать распространение все большего числа волн.
304
Наряду с медленными волнами в диэлектрических стержнях
могут распространяться и быстрые волны. Из формулы (56.21)
видно, что (в соответствии со сказанным в § 52) быстрые вол-
ны возбуждают в окружающем пространстве коническую вол-
ну, экспоненциально возрастающую в радиальном направлении;
каждая волна, существующая при частоте ниже критической
в виде быстрой затухающей волны, при частоте выше критиче-
ской становится медленной (поверхностной) волной, затухание
которой при отсутствии потерь в диэлектрике равно нулю.
Как уже говорилось в § 52, обычные (металлические) волно-
воды становятся неприменимыми для достаточно коротких волн.
€ диэлектрическими волноводами дело обстоит иначе, поскольку
можно варьировать их показатель преломления В самом деле,
если показатель преломления диэлектрического волновода близок
к единице, то параметр ka )Zsp.— 1 для него может быть неболь-
шим даже при 1, и в нем может распространяться всего
одна волна или несколько волн. С конструктивной точки зрения
удобно брать диэлектрические стержни, окруженные другим
диэлектриком, показатель преломления которого немного
меньше.
При теоретическом рассмотрении диэлектрического волно-
вода (например, пластинки или стержня) с проницаемостями
е», pi, окруженного безграничной средой с проницаемостями ев,
р₽, все результаты, в частности характеристические уравнения
(56.08), (56.11), (56.22) и (56.24), остаются в силе, если поло-
жить
е = Т-’ Н = ? (56.25)
ее г**е
и заменить k на Л|Леере, т. е. положить
kx = = Vk4eV.e-k\ (56.26)
или
kr = ykh^-k*, k°r=Vk4eV.e-k\. (56.27)
В таких системах число распространяющихся волн определяется
величиной kaVeiPi — евр.е (или, практически, величиной/гар%-—ее ,
поскольку обычно рг = р.с=1).
В качестве диэлектрических волноводов для оптического
диапазона Снитцер (см. [62], а также [13], стр. 413) использовал
тонкие нити диаметром от 0,1 до 25 мкм, имевшие показатель
преломления [^8,= 1,49->1,75, в то время как оболочка имела
показатель преломления j/’ee—1,48-> 1,59 (8г>8е). В таких вол-
новодах удалось возбуждать отдельные волны, вводя пучок
света в нить, и наблюдать их излучение с другого конца.
Применяются также пучки таких нитей, помещенных в общую
20—2547 305
для всех нитей диэлектрическую среду с несколько меньшим по-
казателем преломления.
Следует отметить, что теорию электромагнитных волн в ди-
электрических волноводах можно строить иначе, а именно осно-
вываясь на геометрической оптике. Применительно к диэлектри-
ческой пластинке этот подход заключается в разложении поля
внутри пластинки, определяемого функциями (56.03), на две
плоские волны, к которым применяются законы отражения и
преломления (формула Снеллиуса и коэффициенты Френеля).
Таким путем получаются в точности те же результаты, что и при
волновой трактовке, т. е. характеристические уравнения (56.08)
и (56.1'1); это совпадение является вполне естественным, по-
скольку для плоских волн геометрическая оптика точно согла-
суется с волновой.
Применение геометрической оптики приводит к наглядности
и оказывается полезным при рассмотрении конкретных вопро-
сов (ср. задачи 10 и 11). В частности, на основании лучевых,
соображений легко прийти к выводу, что вдоль диэлектрическо-
го волновода, помещенного в оптически более плотную среду
(егРг<еец«), могут распространяться затухающие волны (быст-
рые по отношению к любой из сред), причем радиационное за-
тухание этих волн мало при условии kx К сожалению,
с помощью геометрической оптики не удается решить задачу
о волнах в диэлектрическом стержне прямоугольного сечения,
а также аналогичную задачу о собственных колебаниях диэлек-
трической призмы (ср. § 62).
§ 57. Открытые волноводы
других типов
Обычный волновод, например круглый, становится открытым
волноводом, если по его образующей прорезана бесконечно длин-
ная щель (или система таких параллельных щелей). Если щели
достаточно узкие, то в волноводе будут распространяться волны,
мало отличающиеся по своей скорости и по распределению поля
от волн в «закрытом» волноводе (без щелей). В силу того, что
все волны, распространяющиеся в волноводе, — быстрые, они
будут в результате излучения через щели затухать в продоль-
ном направлении * и нарастать в радиальном направлении
(ср. конец § 56).
* В желобковых волноводах с поперечным сечением, изображенным на
рис. 20 и 69,а, в направлении оси у (перпендикулярно чертежу) могут рас-
пространяться волны с весьма малым радиационным затуханием, поскольку
в узкой части поперечного сечения (при |х|>а) поле этих волн экспонен-
циально затухает. Омические потерн в таких волноводах меньше, чем в обыч-
ных волноводах тех же размеров, поскольку токи проводимости фактически
имеются лишь прн |*| (ср. [74], стр. 565—579). Вместе с тем, спектр
волновых чисел в таких волноводах будет разреженным.
306
Может возникнуть вопрос: как эволюционируют волновод-
ные волны, когда щель расширяется и открытый волновод путем
непрерывной деформации переходит в бесконечную по оси z лен-
ту (полосу) конечной ширины? Исследование показывает (см.
задачу 8), что вдоль ленты могут распространяться быстрые
волны, сильно затухающие в продольном направлении из-за
излучения в стороны; в волны такого типа и переходят волно-
водные волны при расширении щели.
При наличии узких продольных щелей в волноводе наи-
меньшим радиационным затуханием будут обладать электриче-
ские волны, которые возбуждают на стенках волновода только
продольные токи; 'магнитные волны, токи которых пересекают
щель, будут излучаться гораздо сильнее, их радиационное зату-
хание будет существенно больше. Если же по всей длине круг-
лого волновода прорезать поперечные (кольцевые) щели, то
наименьшее затухание будет у симметричных магнитных
волн НОп, токи которых не имеют продольной составляющей,
а все другие волны будут обладать сильным радиационным за-
туханием.
Круглый волновод, у которого стенка заменена периодически
расположенными кольцами, разделенными кольцевыми щелями,
часто называют просто кольцевым волноводом. Это — открытый
волновод, который (в отличие от волновода с продольными ще-
лями) является периодической структурой. Поскольку период
кольцевого волновода обычно мал по сравнению с длиной вол-
ны, все пространственные гармоники волн в таком волноводе,
за исключением одной (ее без ограничения общности в соответ-
ствии с формулами (52.16) и (52.34) можно считать нулевой),
являются медленными и локализуются вблизи колец и щелей
между ними. Нулевая же пространственная гармоника является
быстрой (—kz<k) и поэтому создает излучение в стороны.
Вместо кольцевого волновода часто применяют спиральный
волновод, который можно рассматривать либо как проводник,
намотанный по винтовой линии, либо как круглый волновод,
в стенке которого по винтовой линии прорезана бесконечно
длинная щель. Если винтовая линия составляет малый угол
с плоскостями z=const (т. е. если «угол намотки» спирали мал),
го в отношении быстрых (волноводных) волн спиральный вол-
новод обладает примерно теми же свойствами, что и кольцевой
волновод: он обеспечивает распространение волн НОп с малым
радиационным затуханием, вместе с тем, другие волны сильно
затухают. Омические потери волн НОп (в особенности волны Но1)
в кольцевом и спиральном волноводах также малы — того же
порядка, что и потери в сплошном круглом волноводе, благо-
даря чему эти волноводы могут быть попользованы в качестве
линий дальней связи.
У спирального волновода есть важное свойство, отличающее
его от кольцевого волновода: при малом угле намотки и при пе-
20* 307
риоде, малом по сравнению с длиной волны (а эти условия вы-
'полняются при использовании спиральных волноводов в линиях
связи), спиральный волновод поддерживает также распростра-
нение медленных (поверхностных) волн; теорию этих волн мож-
но, например, найти в гл. XIII книги [7]. Благодаря этому свой-
ству спираль широко применяется в качестве замедляющей си-
стемы в электронных приборах типа лампы с бегущей волной.
Возможность распространения незатухающих медленных волн
в такой системе связана с условием (52.36) и общими сообра-
жениями, высказанными в конце § 52.
При условии (52.36) медленные (поверхностные) волны мо-
гут распространяться и в других открытых периодических струк-
турах, например в гребенчатой структуре (см. [8], § 48—51).
Трехмерным аналогом этой структуры является ребристый стер-
жень (см., например, [7], § 70), также поддерживающий — при
определенных условиях — распространение поверхностных волн.
Несомненно, что диэлектрические периодические структуры (на-
пример, линзовый волновод, изображенный на рис. 66) также
могут поддерживать распространение «чистых» поверхностных
волн, радиационное затухание которых точно равно нулю, если
период этих структур достаточно мал по сравнению с длиной
волны. Действительно, в этом случае электрические свойства'
периодической структуры как бы усредняются, и она становится
эквивалентной однородному по оси z диэлектрическому волно-
воду. Напомним, что практически линзовые волноводы приме-
няются в других условиях, когда период структуры велик по
сравнению с длиной волны, и поэтому радиационное затухание
для них отлично от нуля, хотя и может быть сделано достаточ-
но малым.
Фактически все диэлектрики в какой-то степени поглощают
электромагнитную энергию, поэтому с практической точки зре-
ния различие между волноводами с нулевым и малым радиа-
ционным затуханием несущественно. Однако это различие важ-
но в теоретическом отношении, так как оно приводит к различ-
ной зависимости поля в поперечном сечении от радиальной ко-
ординаты г (при г—оо): волны без радиационного затухания —
это всегда медленные поверхностные волны (их поверхностный
характер сохраняется и при наличии потерь в диэлектрике),
а волны с радиационным затуханием экспоненциально возра-
стают при Г—оо.
Задачи к гл. VIII
1. Вывести формулу, аналогичную формуле (52.02), для кольцевого или
спирального волновода (§ 57), в котором могут распространяться только вол-
ны, близкие по своим свойствам к волнам Won в круглом волноводе того же
радиуса а.
Решение. Волна НОп является распространяющейся при условии
308
где суть корни уравнения Jl(y)=0; для этих корней использована асим-
птотическая формула (25.13). Пренебрегая слагаемым -у по сравнению с N,
для числа распространяющихся волн получаем искомую формулу
,, ka ыа 2а
N = ----=----= .
я пс К
2. Показать, что если функцию Ф, определяемую формулами (53.12) —
(53.15), представить в виде
Ф = V (г, <р, z) e<ftz,
то функция
ikzr2
V(r, <р, z) = W (₽, у. 5) ехр <2(d2 + ^)
[где W определяется формулами (18.15), (19.04), (19.06) и (19.09) и удовлет-
воряет параболическому уравнению (18.14)] удовлетворяет параболическому
уравнению в цилиндрических координатах
1_d_f dl£\ . Д
г dr dr )' г2
d2V п-с
-Ч—2- 4- 2lk
ду2 ‘
(«>
аналогичному (6.02).
Решение. По формулам '(53.13) мы получаем:
dV Г 1 dW rz dW ,ikr2 (d2 — z2) 1 ikzr2
~di~ "T 2(d2 + z2)’ W ]exp2(d2+z2)*
V (d2 + z2} 2
1 d / dV \ 1 Г 1 d I dW \ 'dW .
r dr у dr J d2 + z2 [ p dp dp J 1 ₽ dp '
/ \ 1 ikzr2
+ (bkz — +г2 ) W j exp 2(d® + z2) ’
1 d2V 1 d2W ikzr2
'T2'dp'“'7r d^rexp 2(d2 + z2) *
Подставляя эти слагаемые в левую часть уравнения (а) и пользуясь уравне-
нием (18.14), мы легко убеждаемся, что уравнение (а) удовлетворяется.
Этот результат показывает, что всю теорию открытых резонаторов с во-
гнутыми зеркалами (гл. III и IV), а также теорию открытых волноводов мож-
но построить, пользуясь параболическим уравнением в декартовых и цилинд-
рических координатах (как это сделано в гл. II). Соотношения здесь полу-
чаются более громоздкими, поскольку в этих координатных системах зеркала,
не совпадают с координатными поверхностями.
3. Показать, что система поглощающих экранов без линз (с одними от-
верстиями, ср. рис. 68) является открытым волноводом. Найти систему волн
в таком открытом волноводе с прямоугольны ми и круговыми отверстиями и
написать выражение для ф.
Решение. Из интегрального уравнения (54.16), в котором надо поло-
жить
К (?,$’) = Г (5-Г, 1), Х = 2яр,
следует эквивалентность системы отверстий и резонатора с плоскими зеркала-
ми. Таким образом, в данном волноводе могут распростран'яться собственные
волны Е(*\ и Е^п, структура поля которых такая же, как у каждой из двух
встречных волн, суперпозиция которых дает колебания E^q и E<£>q в от-
крытом резонаторе с плоскими зеркалами — прямоугольными или круглыми
30»
{гл. I). Величина ф для каждой из этих собственных волн определяется фор-
мулой
ф=2й/—2лр,
комплексный параметр р, зависящий от индексов тип, дается формулами
(5.09)—>(5.11) для прямоугольных отверстий и формулами (6.08) и (6.09) для
круговых отверстий.
4. Используя решения задач 7—9 к гл. II и связь между резонаторными
и волноводными задачами (§ 54 и 55), >найти систему собственных волн в от-
крытом волноводе, в котором вместо линз (как на рис. 66) поставлены тонкие
прозрачные пластинки, сдвигающие фазу нормально проходящей через них
волны на л (по сравнению с волной, распространяющейся в пустоте). Рассмот-
реть пластинки прямоугольной и круглой формы. Ослаблением волны при про-
хождении через плоскопараллельную пластинку пренебречь.
Решение. В резонаторной системе (такой, как на рис. 69,6, причем
вместо линзы — пластинка) коэффициент отражения волноводной волны при
частоте, близкой к критической, определяется формулой (2.18), в которую со-
гласно задаче 8 к гл. II надо вместо р подставить р2=0,483. Этот коэффициент
отражения определяет все свойства добротных колебаний, существующих в та-
ком открытом резонаторе между диэлектрическими пластинками и слабо за-
тухающих вследствие излучения в пространство между плоскостями z~±l.
Если диэлектрические пластинки имеют прямоугольную форму, то колебания
аналогичны колебаниям Е^щ и между прямоугольными зеркалами. Если
пластинки круглые, то колебания аналогичны колебаниям и между
круглыми зеркалами. Единственное отличие в том, что во все формулы вместо
$ надо подставлять ps.
Собственные волны в открытом волноводе, образованном прозрачными
пластинками, аналогичны волнам в волноводе, образованном отверстиями
в поглощающих экранах (задача 3), но при расчете надо во всех формулах р
заменять на р2.
5. Используя метод § 55, рассчитать собственные частоты двухмерных ко-
лебаний в двухмерном открытом резонаторе, зеркала которого состоят из
плоского участка шириной 2а и вогнутого участка с радиусом кривизны г0.
Такие зеркала определяются формулой
z=±{Z—Л(х)],
где
h (х) = 0 при — а < х < а;
(х— а)а
л (х) = —27— ПРИ х > °;
1г (— х) = й (х).
При .расчете ограничиться колебаниями, имеющими каустики, и пренебречь
диффракцией на краях вогнутых зеркал.
Решение. При |х|<а для функции Q(x) получается уравнение (55.18);
в силу симметрии задачи его решение мы пишем в виде
Q—cos (kxx)
«ли
Q = sin (kxx),
где
Прн х>а для функции Q получается уравнение (55.12), в котором надо за-
менить х на х—а. Вводя новую независимую переменную
,/"2Г^
т = у -j— а (х — а),
310
где а определяется формулами (55.14) и (55.15), и обозначая
2 Л п? \ 4/ ь2 2/ / 21
—= ’”• = ** I/ Т’
\ J а /га V /га
преобразуем уравнение для Q в уравнение (13.02). Решая это уравнение, как
в § 13, согласно формулам (13.05) будем иметь при х=а+0 и т=0
или
cos у
где
Требуя, чтобы Q и были непрерывны при х = а, получаем’характери-
стические уравнения
tg (kxa) =ctg <р
и
ctg(/w?)=— ctg <р.
При a=0, когда зеркала являются цилиндрическими (без плоских участков),
эти уравнения имеют решения
= (m + 1)-у- (т=0, 1, 2, ...),
откуда получаем
хт = 4^ + у),
и для собственных частот имеем соотношение (55.13), в котором для большей
точности, как уже отмечалось в § 55, вместо а нужно брать «.
В общем случае из характеристических уравнений вытекает соотношение
я
¥ + kxa - (т + 1) -g-,
физический смысл которого очень прост: так как переход от плоской часта
зеркал к вогнутой гладкий, то от этого перехода волноводная волна не от-
ражается и набег фазы на плоском участке складывается с набегом <р между
вогнутыми зеркалами. Из этого соотношения для неизвестной величины
X —— kxa
получается квадратное уравнение
X2 ( 1\ я
~ m т 2 I 2 ’
с2 \ J
в котором
311
При't -♦ 0 мы получаем решения, соответствующие цилиндрическим зеркалам,
~ ~ ( 1 \ п \
а при т -» со I точнее, при г I т + -у j I — решения
причем значению т — 0 соответствует косинусоида, остающаяся на плоском
участке зеркал почти постоянной ^cos kxa = cos = 0,707^.
В общем случае, решив уравнение (а), мы можем вычислить частоту ко-
лебаний с помощью соотношения
2/г/ = nq -j- X2,
которое можно также переписать в виде
2kl — nq +
По аналогии с формулой (55.13) можно заменить а на а; в результате такой
замены формула должна стать точнее.
Уравнение r=±tm определяет положение каустик (без учета их искрив-
ления). Если эти каустики с некоторым запасом «укладываются» на вогнутых
частях зеркал, то диффракцией на краях можно пренебречь.
6. Опираясь на результаты, полученные в задаче 5, вывести выражение
для собственных частот открытого резонатора, образованного двумя одинако-
выми зеркалами, имеющими форму корыт: каждое зеркало имеет вид цилиндра
длиной 2а (по оси х), к обоим концам которого примыкают две полусферы
с тем же радиусом кривизны гв. Ограничиться колебаниями, защищенными от
излучения со всех четырех сторон каустиками, и пренебречь днффракцией на
краях зеркал.
Решение. Используя мультипликативность функций W по осям х и у
[т. е. соотношения вида (5.06) и (16.06)], мы для собственной частоты трех-
мерных колебаний между «корытами» получаем соотношение
/ 2Х
2kl = nq 2 ( т -]- п -|- 1 — ——
а,
•где т и п принимают значения 0, 1, 2, ..Л' есть корень квадратного урав-
нения (а) задачи 5, а
•/ I
о. = arcsin I/ —'
Га
причем 2/ есть максимальное расстояние между зеркалами по оси z.
7. Рассмотреть слабозатухающне монохроматические волны, распространя-
ющиеся вдоль оси у между двумя параллельными зеркалами, имеющими по
оси х ширину 2а, а по оси у — бесконечную длину (как на рнс. 6); расстояние
между зеркалами по оси z равно 2/. Считать, что длина волны мала по срав-
нению с а, а ширина 2а существенно меньше 2Z.
Решение. В теории двухмерных колебаний открытого резонатора, изо-
браженного на рис. 6, вычислены собственные частоты <Цто«=с^тО5, опреде-
ляемые соотношением
2kmBql=n(q+2p).
312
Поле этих колебаний не зависит от координаты у, поэтому в волноводной за-
даче эти частоты являются критическими. Продольные волновые числа, ха-
рактеризующие распространение оо оси у, определяются формулой
/ги = ^~ks —
СО
где k = — соответствует частоте возбуждения. Поскольку kml)q является
комплексным, мы получаем при k^>P,ekmoq
1т&и >0,
т. е. волна затухает вследствие излучения.
Это утверждение можно обосновать следующим образом. Если Ф8 (х, г, ks}
есть (при k= ks) решение двухмерного волнового уравнения (3.03), удовлетво-
дФ
ряющее граничным условиям Ф=0 или &— — 0 на зеркалах, то
Ф= etk4y Ф„ (X, 2, ks), ky = + yrk2—l%
есть решение трехмерного волнового уравнения (12.10), удовлетворяющее тем
же граничным условиям. С помощью формул (3.55) и (3.56) мы получаем
электрические волны в данной волноводной системе, а с помощью формул
(3.63) и (3.65) — магнитные. Применением цилиндрических зеркал (гл. Ill)
радиационное затухание монохроматических волн, распространяющихся в от-
крытом волноводе, можно уменьшить.
В этой же системе возможна и незатухающая (чисто поперечная) волна,
соответствующая волне в двухпроводной линии.
8. В работах [55] .и [56] показано, что собственные двухмерные колебания
бесконечно длинной ленты шириной 2а происходят с комплексными частотами,
определяемыми соотношением
, « х„
k~ с ~~ а'
где при граничном условии Ф = 0 на ленте мы имеем
/ 1 \ я 31 Г —/ 1\1
Хп = [п+тН“2--------4~1п 2л^/4п1п+—I , (а)
<ЭФ
а при граничном условии = 0
/ 3 \ л 1 Г / 3 \ 1
х"=(л+т) “2—т,п [2"!
Обе формулы для х„ применимы при больших значениях индекса п.
Пользуясь этими результатами, найти продольные волновые числа элек-
трических и магнитных волн, распространяющихся вдоль ленты при заданной
хп
частоте возбуждения. Выяснить физический смысл волнового числа — в вол-
новодной задаче.
Решение. Комплексное волновое число kz, определяющее распростране-
ние волн вдоль ленты — по оси г, определяется выражением (ср. задачу 7)
причем для электрических волн хп надо брать по формуле (а), для магнит-
ных— по формуле (6). Волновое число
kr= —
г а
313
определяет комплексную критическую частоту ckr и, вместе с тем, распреде-
ление поля в поперечном сечении z=const; в частности, на больших расстоя-
ниях г от оси ленты поле пропорционально
e'(fer'’+*xz>
Vkrr
(ср. § 52).
9. Используя результаты задачи 5, вывести характеристическое уравнение
для колебаний без каустики, существующих в открытом резонаторе, изобра-
женном на рис. 69,а и рассмотренном в § 55. Дать качественное исследование
этого уравнения.
Решение. Полагая
_ /" 2fe — f 2/ f [ itq \
t = y —a-X, — &х = 1/ — "2/"b
мы сводим уравнение (55.12) к уравнению
rf2f) . т?, -4- т2 — т2
~ 4- --------<2=о.
dt2 * 4
причем при х—а решение этого уравнения должно удовлетворять условию
dQ . tm - 2ka2~
~d^^zt~2'Q при т = t = у —j—a. (a)
поскольку при x>a функция Q удовлетворяет уравнению (55.18) и должна
иметь вид уходящей волны
Q — Се 1 при х > а.
Представляя прн функцию Q в виде (ср. § 9, 13 и 42)
„ / — 4t \Ч4
Q=(—Г [c,w* +СгШ2 юь
\ тт -Г х т у
где
у(—03/2~ j у t?m+t2 — t2dt,
«з граничных условий (13.06) получаем соотношения
Ci^i (f0) + CiW2 (/<>) = 0 или Ctw'i (to) + C»w’2 (te) = 0, (b)
а из граничного условия (а) — соотношение
Ctot>'i (t) -}- C2wr2 (t) — i t [Citi’i (t) -p CtW2 (#)], (c)
где
о 1 p ___________
y (— <o)3/2 =2- J y/' t2m+-c2—t2 dt,
0
1/ J +Д2
у m
2 Ip -
"3 (- O3/2 = 2 J / < +^2 - X2 dt.
314
Комбинируя соотношения (b) и (с), получим характеристическое урав-
нение
W] (to) ___w'i (t) — i j/~— t wt (t)
W* (/o) (0 — i /—7 (t)
пли аналогичное ему, в котором функции wi,2(^o) заменены на w'lj2(/0).
При больших отрицательных t правая часть характеристического уравне-
ния велика, так как знаменатель мал в'силу второй формулы (9.26); поэтому
колебание обладает большим радиационным затуханием. При t=0, когда
тт=0 и каустика расположена точно на краю вогнутого зеркала, радиацион-
ное затухание равно нулю; это можно вывести как из характеристического
уравнения (правая часть которого по абсолютной величине равна единице прн
t=0), так и сразу из граничного условия (а).
Первый результат довольно естествен, поскольку коэффициент отражения
от сечения х—а при —t^> 1 должен иметь малую величину. Второй результат
связан с тем, что мы не учитываем появления волн других номеров.
10. Рассмотреть волны в плоскопараллельном зазоре —а<х<а между
двумя диэлектриками с проницаемостями е, р. Магнитное поле волн в этом
зазоре имеет единственную составляющую
Ну = cos (kxx) e‘kzZ или Ну = sin (kxx) ек*г •
Воспользоваться методом геометрической оптики (см. конец § 56) и форму-
лой для коэффициента отражения
е COS <f — ец — Sin2 <f
R =-----------,r ~ . kx = k cos <p, kz = k sin <p,
e cos <p + V ep.— sin2 у
считая «p^-g-H R —1. Обобщить результаты на случай, когда электри-
ческое поле имеет единственную составляющую Еу того же вида.
Решение. Прн у когда kx k, выражение для R можно пере-
писать в виде
j
/г У ер. — 1 k у ер. — I
ekx 6
1+Ту^Г
Рассуждая, как в § 4, получим для kx уравнение
откуда
era
/ 'е \
2а ( 1 + ]
\ kaV ер — 1J
e-2^«“=±R,
Ге
/га У ер — 1
(а)
(т= 1, 2,...)
k~x t тс2/»2 f, is
kz = k~ IF = k~ 8FF ЬУ^Т
Таким образом, мы получаем Re kz < k < &Уер и Im kz > 0. Если в этих со-
отношениях заменить е на р, то они будут относиться к другой поляризации
(с составляющей £„).
315
11. Пользуясь методом, примененным в предыдущей задаче, вычислить
продольное волновое число kz для электрических и магнитных волн в диэлек-
трической пластинке при частоте, немного меныпей критической частоты.
Решение. Коэффициент отражения по составляющей Ну равен
1
— COS¥-|/ ^-sin2<p
V cos <р + j/"sin2 ч
k°
(o)
где
kx = k]/' epCOS ff, kz = k V ep sin y; fe° =|/^fe* — fe2 (ep—1).
Вблизи критической частоты R~l, причем можно написать приближенное вы-
ражение
R = e к*.
Применяя уравнение (а) предыдущей задачи, мы придем к уравнению
(
Rx \__™П
1 + /efe^
пт
откуда в первом приближении получаем kx — , а во втором
Поскольку согласно условиям задачи
(тг/п\2 /nm\s п
fe2ep-^j <fe2, fe“>o,
то мы имеем быструю затухающую волну:
Re kz < k, Im kz > 0.
Выведенные формулы для kx и kz применимы и при частоте, немного боль-
шей критической, тогда fe® =i|fe°| и волна будет медленной незатухающей
Так как коэффициент отражения по составляющей Еу получается из форму-
лы (а) путем замены е на р и ц на е, то во всех последующих формулах
для волн другой поляризации нужно сделать эту же замену.
12. Показать, что при условиях
kT < kz feyер, ka^>\
характеристическое уравнение (56.22) упрощается, а именно в первом при-
ближении может быть заменено уравнением
т
i (fera)2’ №
Выяснить, каким граничным условиям на поверхности г=а соответствует это
уравнение и какова структура электромагнитного поля соответствующих волн.
316
Решение. При условиях задачи Кер. — 1, поэтому — боль-
шое мнимое число, а функция
р К'т(Х) 1 .-------
Fm = -адТ’ х = ka - 1
(К.™—функция Макдональда, ср. [7], § 61 и 66) мала. Пренебрегая ею и сла-
гаемыми
• 0 в правой части (56.22),
(«,.«)
получаем уравнение
f-_.
‘т (kra)2’
эквивалентное уравнение (а). Составляющим (56.19) электрического и магнит-
ного векторов Герца соответствуют (при заданных условиях) составляющие
полей
== J in BJ'm (^rr) J cos (ягу -j- уо) е >
^<р= ikTk]/r ер у- AJ'm(kTr) — (krr) J sin (my + y0) e'M .
Ставя граничные условия
£<P= Hv= 0 при г = a,
приходим к уравнениям для постоянных Я и В:
А ~^а 1т ~ Р^4г BI™ (kra>>= °’
р. AJ'm (krfi) — В Jтп(кгС1) — О,
условие совместности которых имеет вид (а); при этом
л=±У^в.
При знаке плюс мы имеем (ср. задачу 18 к гл. I)
-^-Нг=С/т+1 (kTr) cos (mtf + <p„) e'*'2 ,
£r = -y- 77?= — CJm+1 (kTr) sin (m<p + <f>o)e'fczZ •
а при знаке минус
•~77r = CJm_1(^Tr)cos(my + ?о)е'**г »
Вт = (ferr)sin (ягу + <р0)е 2 ’
317
где
С = ikrk^c[>. А-
Таким образом, структура поля локально близка к структуре плоской волны,
что можно было предвидеть из условий задачи. Радиальная зааисимость поля
определяется уравнениями
7m+l(^rC)=0 ИЛИ Jm_l(M)=0,
эквивалентными уравнению (а); таким образом,
, '’m + l.n , *m-I, п
яг =---------- или ят =---------1
где Vrn.n —Я-Й нуль функции
Глава IX
Открытые резонаторы
с диэлектрическими телами
§ 58. Электромагнитные колебания
диэлектрического шара
Прозрачные тела сами по себе, без каких-либо зеркал, яв-
ляются открытыми резонаторами, хотя с помощью зеркал их
резонансные свойства можно изменить в нужную сторону
(§ 60—62). В качестве примера рассмотрим однородный изо-
тропный шар радиусом а с проницаемостями виц, окруженный
пустотой (в=|л=1 при R>a).
Электрические колебания шара определяются функцией U,
через которую составляющие электромагнитного поля в сфери-
ческой системе координат R, О, выражаются следующим обра-
зом (ср. [7] § 20):
F _ l d*U
R dRd$ •
Е -- 1 d4J
? R sin © dRd>f ’
^=0,
г, _ ike dU
8 R sin fi d<f *
и _ ike dU
R ~d$'
(58.01)
Сама функция U должна удовлетворять уравнению
R* [sin» <)» <Sln& сф)"^sin28 df J + k °- (58.02)
Начнем с рассмотрения симметричных колебаний, для кото-
рых функция U(R, О) не зависит от <р. Поскольку при /?—»оо
исследуемые нами колебания имеют вид расходящихся сфери-
ческих волн, мы представляем вне шара в виде
U = Bh{" (kR) Рп (cos &) (/? > а). (58.03)
319
Внутри шара поле должно быть конечным при R—0, по-
этому полагаем
U = Ajn (k Рп (cos &) (R < а). (58.04)
В этих формулах А и В — постоянные, Рп (cos &) — полином Ле-
жандра, а функции ]п и А(п*'2) связаны с функциями Бесселя и
Ханкеля соотношениями:
(х) = J Дх).
"+ 2 (58.05)
,(л), , (X).
г 2 п+ Т 2 ”+ т
Заметим, что наши обозначения несколько отличаются от общепри-
нятых: в ряде работ через ]п и Л(|,2) обозначены функции, в наших
i
обозначениях равные ~ и х ; однако для дальнейшего удобно
ввести обозначения (58.05).
Легко видеть, что функции (58.03) и (58.04) удовлетворяют
уравнению (58.02) при R>a (где е=р.= 1) и при R<a соответ-
ственно, поэтому поле (58.01) удовлетворяет уравнениям Мак-
свелла. Ставя граничные условия при R—a, получаем характе-
ристическое уравнение
8 h^\ka)* ‘
определяющее собственные частоты электрических колебаний
в шаре (штрихом обозначены производные по всему аргументу),
и соотношение между постоянными А и В
в=г А (58 07
Такие же соотношения (58.06) и (58.07) получаются для не-
симметричных электрических волн, они определяются формула-
ми (58.03) и (58.04), в которых надо PK(cosO) заменить на
Р{™} (cos &) cos ту или P(nm) (cos &) sin my,
где m=l, 2, ..., n, a Pl™}—присоединенные функции Лежандра.
Эти колебания обозначаются символом Етпд, симметричные ко-
лебания— символом ЕОпд.
Рассмотрим корни уравнения (58.06) при 1 и|/ер.;>1,
когда лучи внутри шара могут испытывать полное отражение
от его границы. В результате просачивания энергии в окружаю-
320
щее пространство собственные колебания, соответствующие та-
ким лучам, затухают. Очевидно, наименьшим радиационным
затуханием, будут обладать колебания, имеющие характер волн
шепчущей галереи, для которых угол падения лучей на границу
шара близок к у. Для таких колебаний функции jn и j'n мож-
но заменить асимптотическими выражениями:
/n(A:l/'efia) = 17'vo(/), j'n(ky^a)= — (58.08)
1 , / l'V
п + у—Ауера
t —--------------= , v = ’ <58-09>
пригодными при k n-j-y > а функции //n и .//^'—асимпто-
тическими выражениями Дебая, пригодными при ka < п
А.
(см. задачу 1). Уравнение (58.06) примет тогда вид
(t) /" g ОТ
^(0 =У vvsh4(1-ie (58.10)
где
л + "2 / 1\
(Тthl!)- (58.11)
Считая параметр v большим, можно представить t в виде /°-|-
4~Д/П9, где есть q-ii корень уравнения
о(0 = 0 0/=1, 2,...; /°<0), (58.12)
а
1 4- ie~2Tnq
Ыпд = , (58.13)
причем
Тn<7 = f«+4-1) fArchlZsp. — 1/1-—— 1------—р—•
1 nq \ ' 2 J \ Г f ер./1 qf ер.*е
Отсюда
п + у — *(«”+ Л*па)
k-nq== ’
У ера
и радиационная добротность равна
(58.14)
(55.15)
21—2547
321
Она возрастает с увеличением индекса п и убывает с увеличе-
нием индекса q.
Как уже отмечалось, формулы (58.06) — (58.15) относятся
к электрическим колебаниям £mng. Если в этих формулах заме-
нить е на .pi и ц на е, то получим формулы для магнитных коле-
баний Hmnq.
Заметим, что резонансные свойства сферических частиц про-
являются при рассеянии электромагнитных волн на них (см., на-
пример, [57]). В работе f'58] (см. также |[13], стр. 408) была осу-
ществлена генерация света в кристалле шарообразной формы;
возбуждались колебания Emnq—волны шепчущей галереи, причем
(2/Ц-1!)-кратное вырождение собственных значений (58.14) при-
водило к одновременной генерации многих колебаний. Однако
преимущественное возбуждение колебаний с небольшими q свя-
зано не с формулой (58.15), дающей чрезвычайно большую до-
бротность, а с тем, что для них согласно известному критерию
Релея (см., например, [59]) шероховатость границы сказывается
меньше.
Остановимся на некоторых принципиальных вопросах. Так как
функция А(и1}(х) имеет асимптотическое выражение
I Гх-(п+1)Л1
A(J,(x) = e 1 J при х—со, (58.16)
то составляющие электромагнитного поля, вычисленные по форму-
лам (58.01) и (58.03), при R —*оо пропорциональны (если учесть
временной множитель е )
pik (R—ct)
---- (58.17)
Так как для собственных колебаний
k=k'—ik", k">Q, (58.18)
то амплитуда поля при R—^oo определяется функцией
т. е. экспоненциально возрастает при удалении от шара.
Это возрастание является неизбежным следствием экспонен-
циального затухания поля при оо. Действительно, посколь-
ку при R—^oo поле каждого собственного колебания имеет со-
гласно формуле (58.17) характер сферической волны, уходящей
на бесконечность со скоростью света, то, например, при t=Q
поле на большом расстоянии R обусловлено волной, излученной
шаром при , когда амплитуда колебаний в нем была
гораздо больше, чем при t=0, в силу чего это поле экспонен-
циально велико.
Высказанные соображения являются весьма общими и позво-
ляют утверждать, что экспоненциальное возрастание поля соб-
322
ственных колебаний при R'—><x> согласно формулам (58.18) и
(58.19) имеет место для всех открытых резонаторов (трехмер-
ных), в частности для тех, которые были исследованы в пред-
шествующих главах. Это важное обстоятельство не было отме-
чено ранее при теоретическом исследовании открытых резона-
торов потому, что мы ограничивались рассмотрением поля в са-
мих резонаторах.
Связь затухания колебаний во времени со сферической вол-
ной (58.17) является, так сказать, двухсторонней: не только за-
тухание вызывает экспоненциальное нарастание этой волны при
возрастании R, но и сама сферическая волна является причиной
затухания колебаний во времени, поскольку на ее создание тре-
буется определенная мощность. Можно утверждать, что в любом
открытом резонаторе поле собственного колебания, непрерывно
продолжаясь все дальше и дальше от резонатора, в конце кон-
цов на достаточно больших расстояниях формирует сфериче-
скую волну, которая уносит энергию и поэтому вызывает зату-
хание колебаний во времени.
Изучим более подробно процесс формирования сферической
волны при рассмотренных выше собственных колебаниях ди=
электрического шара. С точки зрения геометрической оптики
этим колебаниям соответствуют лучевые потоки, испытывающие
на поверхности R—a полное внутреннее отражение, поэтому
можно было бы ожидать, что радиационное затухание будет
равно нулю. Однако это затухание оказалось отличным от нуля
(хотя для оптических частот оно весьма мало), и сферическая
волна также имеет амплитуду, отличную от нуля. Этот резуль-
тат с волновой точки зрения можно интерпретировать так: лучи,
претерпевающие полное внутреннее отражение, соответствуют
волне, скользящей вдоль поверхности раздела с фазовой ско-
ростью «о<с; поэтому при удалении от поверхности в сторону
пустоты поле экспоненциально убывает. Если поверхность пло-
ская, то экспоненциально убывающее поле всюду имеет ско-
рость и0; если же поверхность сферическая (i/?=o), то при R>a
фазовая скорость равна
D
n = (58.20)
поэтому при
R = (58.21)
фазовая скорость будет равна с, а при больших R будем иметь
п>с. На поверхности (58.21) и начинается формирование сфе-
рической волны, уходящей в бесконечность; так как в слое
с
а —
ил
(58.22)
21*
323
поле экспоненциально убывает, то как радиационное затухание,
так и амплитуда сферической волны оказываются экспонен-
циально малыми.
§ 59 Внешние электромагнитные колебания
идеально проводящего
и импедансного шара
Полагая в уравнении (58.06) E=ioo, получаем характеристи-
ческое уравнение
h™'(ka) = O, (59.01)
определяющее комплексные собственные часготы внешних элек-
трических колебаний Emnq идеально проводящего шара. Для
магнитных колебаний Hmnq идеально проводящего шара харак-
теристическое уравнение имеет вид
h("(ka) = 0. (59.02)
На рис. 71 точками нанесены значения ka, полученные из
этих уравнений при л.=>1, 2 и 3. Эти точки лежат вблизи полу-
окружности радиусом п, причем при данном п имеется п+1
(для электрических колебаний) или п (для магнитных колеба-
ний) различных значений ka', каждому из них соответствует
2п+1 колебаний Emnq или Hmnq, отличающихся зависимостью
от О и ф (см. § 58).
РИС. 71. Собственные частоты внешних колебаний идеально прово-
дящей сферы (на комплексной плоскости ka).
324
Рис. 71 показывает, что радиационное затухание внешних
колебаний идеально проводящего шара довольно велико: наи-
меньшим затуханием обладают электрические колебания с ин-
дексом п='1, с возрастанием п затухание растет. Интересно
отметить, что при возбуждении шара с помощью источников,
лежащих на его поверхности, частотная характеристика имеет
только один резонансный максимум, соответствующий электри-
ческому колебанию с индексом п=1 (см. ([60]), а другие соб-
ственные колебания не проявляются, видимо, потому, что их ра-
диационное затухание значительно, а частоты близки друг
к другу (ср. § 7).
В дополнение к рис. 71 нетрудно вывести формулы для кор-
ней уравнений (59.01) и (59.02), справедливые при ka^n. Вос-
пользуемся асимптотическими формулами
(ka) —— i)Zvw(T), h^' (ka) — (59.03)
в которых w(t) = w1(t)— функция Эйри (ср. § 9 и 24), а
_LX 1/3
1 1П+ 2 1 .
ka = п -j-----v-s, v = I —g— I (59.04)
Эти формулы аналогичны формулам (58.08) и (58.09). Поль-
зуясь ими, мы можем заменить уравнение (59.01) уравнением
к/(т)=0, (59.05)
а уравнение (59.02) примет вид
wi(t) =0. (59.06)
Корни уравнений (59.05) и (59.06) нетрудно найти, пользуясь
тождеством (см. [17], стр. 29 или [19], стр. 380)
W (te “П = 2е' % (/); (59.07)
поэтому корни уравнения (59.05) определяются формулой
_ •4тс
т',=Г,е ‘3 (9=1, 2, ...), (59.08)
а корни уравнения (59.06) — формулой
~i —
? е 3 (9=1,2,...), (59.09)
где t'q — корни уравнения и'(0=0, a t°q — корни уравнения
1»(/)=0, рассмотренные в § 24. Так как эти корни отрицательны,
то числа (59.08) и (59.09) имеют вид
(59.10)
325
Подставляя в выражение (59.04) вместо т значения и , мы
можем вычислить собственные частоты волн Етт) и HKnq\ надо
только иметь в виду, что это выражение применимо при не слиш-
ком больших т (а именно, при |т| < №).
Рассмотрим в заключение импедансный шар, на поверхности
которого ставятся граничные условия
= —Z^, E^ZH* (при /? = а). (59.11)
Характеристическое уравнение для электрических колебаний такого
шара получается из уравнения (58.06), если в нем положить
Оно имеет вид
Z—y ~ и Imfc I/spa= оо.
h^’(ka) _
h^(ka) ~
(59.12)
(59.13)
и по>сле применения формул (59.03) и (59.04) принимает вид
^'(т)— gw(r) =0, (59.14)
где
g=ivZ. (59.15)
Характеристическое уравнение (59.14) при g—О переходит
в уравнение (59.05), а при g = oo—в уравнение (59.06). При
конечных значениях параметра g корни уравнения (59.14) обыч-
но лежат вблизи прямой агст= -у- между корнями тд и т°7,
мы их обозначим через ть тг, ... Кроме того, при |g| > 1
уравнение (59.14) может иметь особый корень то, приближенно
равный
r0=g2=—v2Z2 (59.16)
и при условии
Z= — iX, Х>0, (59.17)
дающий нам слабозатухающие собственные колебания, обу-
словленные поверхностной волной, локализованной при R~a.
Частота этих колебаний определяется соотношением
ka = (n + ~^(\-~X^, (59.18)
которое вследствие условий
|т0| < v2, Х<1, (59.19)
необходимых для применения формул (59.03) и (59.04), можно
переписать в виде
1
п + ~2~
ka = —=• (59.20)
/1 + Xs '
326
Последняя формула применима и при конечных значениях Л'
(см. задачу 3).
Радиационное затухание поверхностных колебаний оказы-
вается экспоненциально малым (см. задачу 2), как у колебаний
шепчущей галереи, рассмотренных в § 58. Таким образом, за-
медление электромагнитных волн импедансной поверхностью
может приводить к появлению поверхностных колебаний с ма-
лым радиационным затуханием. Это физическое явление можно
было бы причислить к числу основных явлений, обеспечиваю-
щих добротные колебания в открытых резонаторах (§ 1), если
бы не его близкое родство с полным внутренним отражением.
Очень часто для фактического создания импедансной поверх-
ности на металл наносят диэлектрический слой, полное внутрен-
нее отражение в котором и создает нужное замедление.
§ 60. Двухмерные электромагнитные колебания
прямоугольной призмы
Исследование электромагнитных колебаний в диэлектриче-
ских телах более сложной формы, чем шар, связано с рядом
математических трудностей. Поэтому мы ограничимся рас-
смотрением двухмерных электромагнитных колебаний (не зави-
РИС. 72. Диэлектрическая призма:
а — в свободном пространстве; б — между бесконечными плоскими зеркалами
z=±l; в — между плоскими зеркалами, совпадающими с гранями призмы.
сящих от у) в прямоугольных призмах, имеющих поперечное
сечение со сторонами 2а и 21 (рис. 72) и бесконечную длину (по
оси у).
Начнем с собственных колебаний призмы в свободном прост-
ранстве (рис. 72,а) и будем их рассматривать в приближении гео-
метрической оптики, пренебрегая диффракцией на ребрах призмы.
Эти колебания можно получить, пользуясь потенциалами П* и
П™ (см. § 56), однако более удобно в качестве потенциалов ис-
327
пользовать составляющие Hv или Ev, удовлетворяющие внутри
призмы, при ——l<^z<^l, двухмерному волновому
уравнению
д2Ну д2Ну
дх2 'г дг2
д2Е„ д2Еу
дх2 * дг2
k2e\»Ey == О
(60.01)
и позволяющие вычислить остальные составляющие
нитного поля по формулам:
Р _____ 1 д/7у .1_____________________1 дЕу
х' ike дг 2 х~~ ifep. дг 2
Р ____________ I дЕу
2 ike дх ’ г iky. дх ‘
электромаг-
(60.02)
Вне призмы в формулах (60.01) и (60.02) надо положить
е=р,= 1. Из всех этих формул видно, чтв двухмерные колеба-
ния в призме либо имеют только составляющие Ех, Ez, Ну, либо
составляющие Еу, Нх, Hz. Как мы увидим ниже, колебания этих
двух типов, отличающихся своей поляризацией, имеют различ-
ные собственные частоты.
Для колебаний первого типа положим внутри призмы
Hy=Afx(kxx)fz(kzz), (60.03)
где А — постоянная, функции fx(t) и fz(t) —тригонометрические
функции cos/ или sin/, выбранные в произвольной комбинации,
a kx и kz в силу уравнения (60.01) удовлетворяют соотношению
= (60.04)
Величины kx и kz, а следовательно, и собственные частоты
ы—ck можно определить, раскладывая (по формулам Эйлера
для cost и sin/) поле (60.04) на четыре плоские волны и поль-
зуясь выражениями для коэффициентов отражения Френеля.
Быстрее ведет к цели чисто аналитический подход: прене-
брегая диффракцией, вблизи каждой грани мы пишем выраже-
ние для Ну в виде уходящей плоской волны, например при х>а,
—l<z<l полагаем
Hy = AoekxXfz(kzz), (60.05)
где
k°x =k2 — k2 = ** —г^Г~1) • (60.06)
Требование непрерывности Ez и Ну при х = а приводит к соот-
ношениям
,.о о
Afх (kxa) = Аае Ц-kxAf'х(kxa) = ik°x А,е ха (60.07)
328
и к характеристическому уравнению
<о
•£, (60.08)
эквивалентному уравнениям (56.08). Из граничных условий на
грани г=1 получается аналогичное характеристическое урав-
нение
Г«(М) kz
ft (kzi) kt'
в котором
k°t=j/ °- (60.10)
Если потерь в диэлектрике нет и если выполняется условие
®р,>2, (60.11)
то в призме возможны колебания, для которых
k°x — i\k°x\, k°t = i\k°\, (60.12)
и kx, kz и k получаются вещественными благодаря тому, что
парциальные плоские волны, -на которые может быть разложено
поле в диэлектрической призме, испытывают полное внутреннее
отражение на всех гранях призмы. Разумеется, этот результат
не является точным, а связан с применением геометрической
оптики (ср. § 58); поэтому можно лишь утверждать, что радиа-
ционное затухание таких колебаний уменьшается с ростом ka
и kl. Другие колебания затухают во времени вследствие проса-
чивания энергии через грани.
Систему уравнений (60.08) и (60.09) в общем случае можно
решить только численными методами, однако в частных случаях
ее удается решить приближенно и получить простые аналитиче-
ские формулы; в дальнейшем мы будем считать еу.>1.
Рассмотрим прежде всего колебания, у которых
kx <^kz (60.13)
k2
Тогда, с точностью до членов порядка мы можем положить
kz
k°t=k, (60.14)
и система (60.08) и (60.09) принимает вид
= — ф- (еГ — 1) (60.15)
fx(kxa) kx Г р. г ’
и
VAkzl) = • -1/Т. (60. 16)
f z (kzl) V р.
329
Полагая
’^/=^- + 8, (60.17)
где нечетные q соответствуют функции f2(/) = cos/, а четные q—
функции fz(t) = sin/, получаем соотношение
ctg 8, (60.18)
откуда
8= — i Arcth Jz —==—i Arth -у-* (60.19)
Поскольку правая часть уравнения (60.15) согласно условию
(60.13) велика, мы будем искать kxa в виде
кха = ^--\-Ът, (60.20)
где нечетные т опять соответствуют функции fx(/)=cos/, а чет-
ные— функции /x(/)=sinZ. Малая величина 6т равна
о
m~qa V
е(ер.~ 1)’
(60.21)
при написании последней формулы мы пренебрегли слагае-
мым 6 в правой части (60.17). Частота колебаний определяется
соотношением
k +8+^S-. (60.22)
z 4Л4*
где
М* = у- (60.23)
Колебания, у которых
kz^kx^= k p^sp-, (60.24)
исследуются совершенно аналогично. Их частота определяется
формулой
k /e}W=^-|-84-^-£-, (60.25)
где
Л42 = |/ (60.26)
В обеих формулах (60.22) и (60.25) фигурирует величина
(60.19), определяющая радиационное затухание колебаний, обу-
330
словленное тем, что при почти нормальном падении на грань
коэффициент отражения плоской волны равен
(60.27)
Если вместо Ну взять составляющую Еу и для нее написать
выражение
£v^Afx(kxx)fz(kzz), (60.28)
то мы придем к характеристическим уравнениям
f'x (kxa) = k°x (60.29)
fx (kxa) и kx
И
ffz (M) _ • ^z /СЛ
fz (kzi) ~ k2 ’ (60.30)
отличающимся от уравнений (60.08) и (60.09) заменой е на ц.
Формулы (60.22) и (60.25) остаются в силе, если 6 определить
из соотношения
ctg3 = jj/-^. (60.31)
а именно положить
8 = -J- — i Ar th (60.32)
Иное определение 6 обусловлено тем, что при замене е на р и
р. на е величина (60.27) меняет знак.
От призмы в свободном пространстве перейдем к призме,
зажатой между двумя бесконечными идеально проводящими
зеркалами z=±l (рис. 72,6). В этой системе формулы (60.03)
и (60.28) дают точное выражение для поля в призме, причем kz
нужно брать в виде
Л2 = f-, (60.33)
a kx определять из уравнений (60.08) и (60.29). Таким путем
для системы, изображенной на рис. 72,6, получается точное ре-
шение; в приближении геометрической оптики оно применимо
к системе, изображенной на рис. 72,в, где зеркала покрывают
только грани z=±Z, —а<х<а. Если же зеркала определяются
соотношениями
— а<^л<а, —<х><^У <C°°j z==±l, (60.34)
331
причем ширина зеркал 2а больше ширины граней 2а, то при усло-
вии
(60.35)
где
<6О-36>
необходимо учитывать отражение волноводной волны, затухаю-
щей или распространяющейся между зеркалами (60.34), от
краев х=±а (ср. гл. I). Характеристические уравнения, кото-
рые получаются при учете диффракции на краях зеркал, слож-
нее уравнений (60.08) и (60.29) и количественное их исследова-
ние затруднительно; по этой причине мы их здесь не приводим
(см., впрочем, задачу 9). Укажем только, что учет диффракции
на краях приводит к тому, что незатухающие колебания, кото-
рым соответствуют чисто мнимые значения k°x, вследствие излу-
чения из плоскостей х=>±а приобретают радиационное затуха-
2i а
ние, пропорциональное е , а затухающие колебания, кото-
рым соответствуют распространяющиеся волноводные волны,
могут уменьшить свое радиационное затухание из-за отражения
от краев х = ±а. Кроме того, объемы а<х<а и —а<х<—а при-
обретают резонансные свойства, и колебания в них взаимодей-
ствуют с колебаниями в диэлектрике.
Хотя качественные выводы, сделанные выше, очевидны и без
вычислений, при количественном исследовании диэлектрических
тел между конечными плоскими зеркалами приходится пользо-
ваться формулами (2.14) и (2.18), которые выведены в гл. I.
В связи с этим возникает вопрос: при каких расстояниях между
диэлектриком и краем зеркала можно пользоваться этими фор-
мулами? Ясно, что, например, при й=а край зеркала (60.34)
совпадает с ребром диэлектрической призмы, так что диффрак-
ция между краями зеркал происходит совершенно иначе, чем
при отсутствии диэлектрика; поэтому для применимости формул
гл. I требуется, чтобы разность а—а была положительна и до-
статочно велика. Из формул § 3 видно, что если координата
(3.17) принимает большие положительные значения, такие, что
интегралы Френеля, входящие в уравнение (3.23), практически
равны нулю, то это значит, что соответствующий отрезок волно-
вода формирует отраженное поле так же, как полубесконечный
волновод. В частности, для двухмерного открытого резонатора
(§ 4) можно пользоваться коэффициентами отражения от конца
полубесконечного волновода лишь при условии Л4> 1, выпол-
нение которого требовалось в гл. I из других соображений. Для
диэлектрической призмы, расположенной между зеркалами
(60.34), соответствующее условие имеет вид
Л4> 1, (60.37)
332
Л7 = у 2k(al -а)-. (60.38)
Существенно новые явления возникают, если диэлектриче-
ская призма расположена между плоскими зеркалами так, что
между каждым зеркалом и гранью призмы имеется значитель-
ный зазор. Перейдем к исследованию таких открытых резонато-
ров, ограничиваясь по-прежнему двухмерными задачами.
§ 61. Прямоугольная призма
между плоскими зеркалами
Рассмотрим открытый резонатор, изображенный на рис. 73:
диэлектрическая призма —а<х<_а, —1<г<1 находится между
зеркалами z=±l бесконечной длины, причем зазор I—I между
призмой и зеркалами будем считать
гораздо больше длины волны.
Если вернуться к собственным
колебаниям призмы, помещенной
в свободном пространстве (§ 60), и
рассмотреть, как на зги колебания
влияют зеркала z=±T, то окажет-
ся, что колебания, определяемые
условием (60.24), и колебания, за-
пертые внутри призмы в результате
полного отражения от всех граней,
зеркалами практически не возму-
щаются, поэтому их исследование
в более сложной системе, изобра-
138
женной на рис. 73, не представляет _________________________
интереса. Однако колебания, опре-
деляемые формулами (60.13)— РИС. 73. Диэлектрическая
(60.23), существенно изменяются пРнзма ме^а™оскпмн зер’
при наличии зеркал хотя бы пото-
му, что зеркала возвращают назад
к диэлектрику волну, выходящую из граней z=±l и обусловли-
вающую слагаемое 6 в формулах (60.17) и (60.22).
По этой причине мы в данной системе (рис. 73) ограничимся
рассмотрением колебаний, удовлетворяющих условию (60.13).
Чтобы максимально упростить вывод основных соотношений,
прежде всего выведем граничные условия, позволяющие огра-
ничиться рассмотрением поля при —а<х<а. Из формул (60.02)
и (60.05) видно, что в диэлектрике эти граничные условия
имеют вид
dJ^- = iek° Ну
ОХ х
при х=а — 0, —l<^z<l, (61.01)
333
причем в силу формулы (60.14) эти граничные условия можно
переписать при выполнении соотношений (60.13) следующим
образом:
дНу=..
дх
dEv
дх
ke j/'ey. — \НУ
kp. — \EV
при Л —« —О, —/<z<Z. (61.02)
В зазоре Z<z<Z между диэлектриком и зеркалом происходят
те же диффракционные явления, что и между двумя плоскими
зеркалами в двухмерном резонаторе (§ 4), в частности происхо-
дит излучение из открытых концов х—±а*. Волноводные вол-
ны, возникающие в этом зазоре вследствие отражения от пло-
скостей z=l и z=l, отражаются от конца х=а в соответствии
с первым граничным условием (4.23), которое в данном случае
можно переписать в виде
дНу
дх
дЕу
дх
при х=а —0, Z<z<Z; (61.03)
поэтому здесь в отличие от (61.02) мы имеем одинаковые усло-
вия для Ну и Еу. Вместо расстояния 21 между зеркалами сюда
входит 2 (Z—/) —расстояние между гранью z=l и ее изображе-
нием в бесконечном зеркале z = Z (ср. задачу 7).
Для расчета собственных колебаний рассмотрим сначала
отражение сложной волны, распространяющейся в волноводе,
образованном бесконечными параллельными зеркалами z—±l,
между которыми расположена (при х>0, —l<z<l, 1<1) полу-
бесконечная диэлектрическая пластина; отражение происходит
от сечения х=0, где пластина кончается. Если электромагнитное
поле имеет составляющие Ех, Ez и Ну, то согласно § 60 мы будем
иметь:
/7, = fz(^)(e /?е'Лх) + ...
Ez — fz (kzz)(e —Re )-[-...
при л>0, —l<z<l
(61.04)
* Строго говоря, излучение происходит не в открытое пространство,
а в волновод, образованный плоскостями z=±Z; представлением об излуче-
нии в открытое пространство можно пользоваться, если на продолжении
горизонтальных граней диэлектрика при z=±Z и |х|>а находятся погло-
щающие экраны.
334
Hy = A cos [k\ {I -- z)] (e ik^x+Re^) +...
Ez^ A cos (F- z)] (e^-fle*’*) +...
при x>0, /<z</,
(61.05)
где многоточием обозначены волны других номеров, возникаю-
щие при отражении.
Ставя граничные условия при z=7, мы приходим к соотно-
шениям
fz(kj) = A cos [k°z (Г— I)], ^-f'z(kzl)=k°z Дsin[6° (Т—1)]. (61.06)
В силу условия (60.13) можно положить
__ k2 п k2
kz = ky^-—^, k°z=k-^, (61.07)
2k V ер. г
причем вне тригонометрических функций просто считать kz —
= k j/ер. и k° = k. Поэтому из соотношений (61.06) мы получаем
уравнение
-щВг’/Р» к" (Г-01- <61.08)
При переходе к грани х= — а правые части формул (61.01) и
(61.02) меняют знак. Для нашей задачи можно написать граничное
условие:
Hy = — Y (z) Ez при х=0,
У (z) = У, = . — при —l<z<ZR (31.09)
у — 1
y(z) —У2 = ф(1 +01/при /<|г|<7.
Вследствие малости -у- мы получаем /?s=—1. Более точное значе-
ние коэффициента отражения /? можно найти методом возмущений,
если учесть ортогональность волн в волноводе ([7], § 79). Обоз-
начая
H'y = fz(kzz), E\=.^fz(kzz) при-/<2</,
Hy — Acos[k°z(l—z)], E'z =— Acos[k° (I—z)] при /<z</,
(61.10)
335
получаем из формул (61.04) и (61.05) при х = 0 соотношения
7 7
J //,£•> = (! + /?) J E\H\dz,
-т
(61.11) I
I 1 I
J EtH\dz={\-R) J E\H\dz, I
— I •— I
откуда в силу граничного условия (61.09) будем иметь
7
J Y (z) E,Elxdz
. (61.12)
j EzHxy dz
Это соотношение является точным (Ег берется при х = 0).
Поскольку £'zf=«2£'‘ при R — 1, в правой части (61.12) можно
заменить Ег на Е1 и получить
^=-т(п5т+1Ъ1'-)- (6113>
где
7
2 А2 cos2 [kx (I — z)J dz _
g ==---I------------= еД2 ±=±; (61.14)
4 f dz
о
при вычислении интегралов мы пренебрегли членами порядка
—----- и —
k (/— I) Ы ер.
Правая часть (61.13) мала вследствие множителя поэтому
с той же точностью полагаем
к L1 г * 1 & е у ер.—-1
(61.15)
При 1=0 или е=оо мы возвращаемся к формуле (2.18), как это
и должно быть.
336
I
!
।
j
Собственное колебание резонатора, изображенного на
рис. 73, приближенно определяется выражениями
Hy = fx(kxx)fz(k^) при —-а<лг<а, —/<£</,
П — - (61.16)
Ну = fx (kxx) A cos [fc" (/ — z)] при — а <
Рассуждая, как в § 4, получим соотношение
/? = —(—l)me 2,**° (лг = 1, 2, ...),
откуда
g 1 Г <6117)
2Й[ +1+£ М *+gfale/^TJ
В силу формулы (61.07) уравнение (61.08) можно переписать
в виде
'f tgW-O-O. (61.18)
IZ \К г Е|Л1 Qm) * Г*
где величины
г _ & л k2x(i-i) r 1Q.
— 2kV^.' U —V5^ I (61.19)
выражаются через известную величину kx.
Уравнение (61.18) определяет собственные частоты резона-
тора. При его выводе мы считали зеркала идеально проводя-
щими; пренебрегая потерями в диэлектрике, т. е. считая е и ц
вещественными, получаем комплексные частоты вследствие
комплексности £т и t°m, т. е. вследствие излучения из зазоров
между диэлектриком и зеркалами. Уравнение (61.18) есть в сущ-
ности уравнение связанных колебаний двух резонаторов, одним
из которых является диэлектрический объем (точнее, в силу
симметрии, его половина 0<й</), а другим — зазор l<z<l
между диэлектриком и зеркалом; связь между резонаторами
осуществляется через грань диэлектрика z=l. При f2(Z) =cos/
это уравнение можно преобразовать к виду
sin (х - - ф = - R sin (хб + U - C°J, (61.20)
а при f2(/)=sinZ— к виду
cos (х - - С) = R cos (х0 + - ф, (61.21)
22—2547
337
где через R обозначен коэффициент отражения (60.27), который
не следует смешивать с коэффициентом R в формулах
(61.04) —(61.15), а
х = k (Т— 14-1 Иен) (61.22)
и ,
<6123)
l — I + I V «н
В двух предельных случаях, при R=0 и 7?=±1, уравнения
(61.20) и (61.21) допускают простые решения. При R=0 мы
имеем
+ (61.24)
где четные q соответствуют уравнению (61.20), а нечетные —
уравнению (61.21). При JA!] < 1 можно искать решение этих
уравнений в виде
х = ^4-ст4-г;0т4-дх; (61.25)
тогда для малой поправки Лх получаем выражение :
дх=/?51п[^±^+^(1+е)-^(1-б)], (61.26)
справедливое при любых q. Вследствие малости Ст и 5° можно на-
писать
х= f+я sin [ 1 + R (1 + в) cos 5!Ш!]+
-j-f [l — R(l— e;cos"’(12+ll>J. (61.27)
Мнимая часть х пропорциональна выражению
1Ц-Л?(6 — 0,)cosk<7(12+6). (61.28)
где
0, __УнМ7-*)-<.
У ер. (I — I) + I
Поэтому радиационное затухание оказывается зависящим от
продольного индекса q — оно как бы «промодулировано» по
индексу q.
338
Физический смысл этого результата становится ясным, если-
по формулам (61.12) и (61.15) вычислить величину
f z (& УА— t-m) (
cos [k(l — I) — ?°„]
(61.29)
определяющую отношение амплитуд поля в зазоре и в диэлек-
трике. При 7?=0 согласно формуле (61.24) получаем
(61.30)
а при малых /?, пренебрегая членами порядка /?Ст и R^m, мы по-
лучаем
А =± [1+2/? sin2 ==t [ 1 + 7? — R cos^±-9].
(61.31)
Таким образом, абсолютная величина А «промодулирована» по
индексу q примерно так же, как радиационное затухание.
Этот результат показывает, что модуляция радиационного
затухания по продольному индексу q обусловлена тем, что при
различных значениях q энергия колебания по-разному распре-
деляется между диэлектриком и зазором. Поскольку излучение
происходит только из зазора, появляется зависимость затухания
от q\ такая же зависимость будет и в том случае, когда потери
в зазоре будут обусловлены не излучением, а другими причина-
ми, например неполным отражением от зеркал.
Как видно из формул (61.28) и (61.31), глубина модуляции
радиационного затухания и отношения амплитуд по индексу q
тем больше, чем больше коэффициент отражения R от границы
диэлектрик—пустота. Этот коэффициент определяется форму-
лой (60.27), но при желании его можно изменять, нанося на
грани z—±l дополнительные слои — согласующие (для умень-
шения |/?|) или отражающие (для увеличения |/?|), и таким
образом изменять глубину модуляции. Формулы (61.27) и
(61.31) применимы только при малых R, поэтому ниже мы рас-
смотрим значения /?«П, а также (с качественной точки зрения)
промежуточные значения R и покажем, что модуляция радиа-
ционного затухания приводит к существенному разрежению
спектра собственных частот по продольному индексу q.
Прежде чем переходить к этому вопросу, рассмотрим колеба-
ния другой поляризации. Представляя Еу в виде
£i, = fx(kxx)fz(kzz) при — о<х<а, — /<£</,
Ey=fx (kxx) Bs'm [6° (/ — z)] при — a < x < a, I <z <7
339
22*
и пользуясь коэффициентом отражения (61.15), в котором е и р.
переставлены местами, получаем для kx выражение
kx ~ Г g РО+О. 1 1 * (61 ’33)
L 1+g М 1 + 8 карьер— 1.
Вместо уравнения (61.18) получаем
Г'« (61-34)
I z г '-ат)
которое при fz(/)=cos£ переходит в уравнение (61.21), а при
f2(f)=sin/— в уравнение (61.20), где положительная (при
е>|ц) величина определяется формулой (60.27). Таким обра-
зом, собственные частоты соответствующих колебаний находят-
ся из тех же уравнений, что и раньше; незначительное отличие
имеется лишь в величине <kx, а также в величинах t,m и £°т, вы-
числяемых по формуле (61.19). Все остальные соотношения и
сделанные из них выводы остаются без изменения.
При условии
Я = 1 (61.35)
решения уравнений (61.20) и (61.21) можно представить в виде
двух последовательностей
(б13б)
и
2^г+2^
1 + е
(61.37)
где <71 и q2—-целые числа. Первая последовательность опреде-
ляет собственные частоты диэлектрической призмы, поскольку
формулу (61.36) можно переписать в виде
(Я = О), (61.38)
а вторая — собственные частоты зазора между призмой и зеркалом
fc(/-/) = ^2 + C°
(g = oo).
(61.39)
Таким образом, при 7? = 1 мы имеем два изолированных резона-
тора, колебания в которых никак не связаны друг с другом.
Если положить
/? = 1 — ЛЯ, Д/?<1,
(61.40)
340
то между резонаторами возникнет слабая связь. Характеристи-
ческое уравнение (61.20) в этом случае можно переписать в виде-
2sin р(12—- — cos [ х(1~6) — = &R sin (хб + См — C°J,
(61.41)
а уравнение (61.21) — в виде
2sin р(12+ 6)—С] sitl[Х(12~6)~^]~Д^ cos(х6 + ~ О-
(61.42).
Корни этих уравнений будут близки к xi или хг, но требуется
особое рассмотрение в случае, когда какие-нибудь значения х>
и Х2 близки друг к другу. В последнем случае характеристиче-
ские уравнения (61.41) и (61.42) приводятся к квадратному
уравнению
(х-х1)(х-х2) = 1^. (61.43).
определяющему связанные колебания двух маятников или двух
контуров с близкими резонансными частотами. Решения этого
квадратного уравнения имеют вид
(6144)
причем при xi = X2 расщепление частот, вызванное связью меж-
ду колебаниями, определяется выражением
(61.45)
Формулами (61.43) и (61.44), учитывающими связь между
колебаниями xi и хг, нужно пользоваться при условии
|Xj — х2|<Дх, (61.46)
где Ах дается формулой (61.45). При противоположном условии
|Xj — х2| > Дх (61.47)
колебания можно считать независимыми и влияние слабой связи
между резонаторами учитывать, представляя решения уравне-
ний (61.41) и (61.42) в виде
х = х14“Д><1 (61.48)
или
х = х24-Ди2 (61.49)
344
и принимая во внимание малые поправочные члены Axi и Дхг
к значениям (61.36) и (61.37) только в тех функциях, которые
обращаются в нуль при Дх1 = 0 или Дх2=0. Таким образом
получаем
Ax.^^ctgZ,, (61.50)
где
7 х, (1 4-в) «0 / v \ 1 -Т б /С 1 К1 \
Z> -2------S-. —(jl ’•«JrTe —‘•m (61-51)
И
Дх2 = ]7Z~e tg Z2 ПРИ нечетных <у2;
+ (61-52)
Дх2 =—y-p-gdgZ2 при четных дг\
здесь
z2=^f^-cm=(^2 -c°j р=-| —(61.53)
Таким образом, Дх, и Дх2 в общем случае имеют порядок Д/?
или меньший. Исключение составляют случаи, когда Z,«^2 или
Z2 т. е. когда данный элемент х, или х2 последовательности
(61.36) или (61.37) близок к некоторому элементу другой после-
довательности; тогда эти колебания связаны и вместо фор-
мул (61.50) и (61.51) нужно пользоваться формулами (61.43)
и (61.44).
Рассмотрим теперь зависимость радиационного затухания
колебаний в диэлектрике от индекса q\. Поскольку в отсутствие
связи с зазором радиационное затухание колебаний в диэлек-
трике равно нулю, оно определяется формулой (61.50), причем
вследствие малости можно написать
?°
ctgZ, = ctg Z,-ф-(61.54)
sin2Z,
.где
(61-55)
"Таким образом, наименьшее затухание будет при
+ (61.56)
т. е. когда частота данного колебания в диэлектрике лежит при-
мерно посередине между собственными частотами зазора. Ясно.
.342
что тогда амплитуда колебаний в зазоре будет наименьшей и
излучение также будет минимально. При близости щ и хг мы.
полагаем
х2 = х'2— /х"2, х = х’~ in" (61.57У
и при условии
х"2<Дх (61.58>
приходим к выражению
х" = 441 ± -г, -|Х1~*21---------1, (61.59).
2 L *4x1 - х2)2 + (Ди)2 J
показывающему, что при будем иметь х"^.-^-. Величина,
х", вычисляемая по формулам (61.50) и (61.54), во много раз
меньше, а именно:
ff и '2 1 + ® Х,Г2 &R I ----- I ,
Таким образом, при /?«1 происходит существенное разреже-.
ние спектра по продольному индексу q. Это разрежение обу-
словлено тем, что колебания в диэлектрике, попадающие в резо-
нанс с колебаниями в зазоре, приобретают затухание того же-
порядка, что и колебания
в зазоре.
Рассмотрим теперь, как
меняются резонансные свой-
ства системы, если от пре-
дельного случая /?~0 пере-
ходить к другому предельно-
му случаяю R^\. Введем
переменные
? = x^ + U-4, (61.61)
tj^x-U-4,
связанные соотношением
g^+Ud+d)-:^]-^.
(61.62)
Кроме того, Е и т) связаны
уравнениями (61.20) и
(61.21), которые можно пе-
реписать в виде
(61.63)
cos tj — R cos Е.
РИС. 74. Кривые, определяемые уравне-
нием cos r)=/?cos £.
343
Второе уравнение дает семейство кривых, периодических по g.
Четыре такие кривые (две при J? = 0,2 и Хве при i/?=0,6) изобра-
жены на рис. 74, другие кривые получаются в результате сдвига
на 2пп (п='±1, ±2, ...) по оси тр Первое уравнение (61.63)
дает аналогичные кривые, но сдвинутые на ± — по осям коор-
динат. При IR —0 эти кривые вырождаются в семейство горизон-
тальных прямых т] = у , а при W=il они переходят в два семей-
ства взаимно ортогональных .прямых т1='±1£+л<7.
Собственные частоты связанных колебаний определяются
пересечением этих кривых с прямой (61.62),' образующей угол
<p=arctg0 с осью т|. Таким образом, рис. 74 дает качественное
представление об изменении резонансных частот системы при
изменении от нуля до единицы.
Результаты, полученные в этом параграфе, становятся не-
точными и даже неправильными, если зазор Г—I между диэлек-
триком и зеркалами слишком велик (т. е. Л4~1 или М << 1)
или слишком мал (т. е. I—ii~A.). Тем не менее эти результаты
охватывают большинство интересных случаев.
§ 62. Общие замечания о резонаторах
с диэлектрическими телами
Как видно из содержания предыдущих параграфов, теория
открытых резонаторов с диэлектрическими телами является бо-
лее сложной, поэтому здесь имеется сравнительно мало резуль-
татов. Многие трехмерные задачи, принадлежащие к числу
основных, не решены даже в приближении геометрической
оптики, например задача о собственных электромагнитных коле-
баниях прямоугольной призмы и кругового цилиндра в свобод-
ном пространстве (ср. задачу 6). Возникающие здесь математи-
ческие трудности обусловлены тем, что коэффициент отражения
полны от границы диэлектрик—пустота зависит от поляризации
волны, в то время как резонаторы с плоскими и изогнутыми
зеркалами практически не реагируют на поляризацию поля, и
поэтому все их свойства можно рассчитать, используя вместо
уравнений Максвелла скалярное волновое уравнение.
Если открытый резонатор образован зеркалами, между кото-
рыми помещено диэлектрическое тело, то теоретическое иссле-
дование колебаний в таком резонаторе оказывается довольно
трудным. Если эти трудности удается преодолеть, то обычно
получаются довольно громоздкие соотношения (ср. § 61). При-
чина этого заключается в сложности явлений, определяющих
свойства добротных колебаний в таких системах. Действительно,
наряду с отражением от границы диэлектрика здесь приходится
344
учитывать отражение от края зазора между диэлектриком и
зеркалом (§ '61) или отражение от краев плоских зеркал (см.
конец *§ 60), а если зеркала вогнутые, то и образование каустик.
Вследствие отражения от границы диэлектрика роль других
факторов может уменьшаться; так, допуски на параллельность
плоских зеркал, очень жесткие в оптическом диапазоне (см. §9),
при наличии диэлектрика должны смягчаться.
Очень часто, особенно в оптическом диапазоне, полное вну-
треннее отражение приводит к тому, что спектр собственных
частот открытого резонатора с диэлектриком оказывается — по
теоретическим оценкам — слишком густым, а фактическое раз-
режение достигается из-за шероховатости границы, резко увели-
чивающей потери на излучение для всех колебаний, за исклю-
чением тех, которые соответствуют скользящим лучам (ср. § 58).
Делая в системах, изображенных на рис. 72 и 73, боковые гра-
ни (х='±а) шероховатыми, можно достичь того, что высокую
добротность сохранят только колебания, удовлетворяющие
условиям (60.13); примерно к таким же результатам можно
прийти, окружая диэлектрическое тело оболочкой с близким
показателем преломления (ср. § 56).
В этой главе мы рассмотрели простейшие двухмерные зада-
чи, дающие представление об основных свойствах открытых
резонаторов с диэлектрическими телами. Из трехмерных задач
сравнительно просто решается задача о диэлектрическом ци-
линдре радиусом а, зажатом между двумя плоскими зеркалами
z='±t/; решение получится, если .взять уравнение (56.22) и
условие (60.33). Можно также учесть и отражение от краев
зеркал, если их радиус а>а (ср. замечания в конце § 60).
Задача, рассмотренная в § 61, также может быть решена в трех-
мерной формулировке — для диэлектрической призмы конечных
размеров или диэлектрического цилиндра, ось которого совпадает
с осью г, при условии, что колебания имеют вид лучевых пото-
ков, составляющих малые углы с осью г.
Основной вывод, вытекающий из теории открытых резонато-
ров с диэлектрическими телами, можно сформулировать следую-
щим образом: помещая диэлектрик между зеркалами, мы полу-
чаем, как правило, сложную резонансную систему, в которой
существуют связанные колебания. Решения частных задач здесь
ценны обычно лишь постольку, поскольку они позволяют разо-
браться во взаимодействии отдельных резонансных объемов,
образующих эту сложную систему, и в том, к какому спектру
собственных частот приводит это взаимодействие. Как видно из
§ 61, путем надлежащего варьирования параметров системы
можно изменить этот спектр и, в частности, добиться его допол-
нительного разрежения, как по продольному индексу а, так и по
поперечному индексу т, поскольку комплексные величины
определяемые формулой (61.19), пропорциональны и т2.
345
Нужно иметь в виду, что возможности сильного изменения
спектра открытого резонатора путем применения связанных ко-
лебаний рассматривались в литературе с довольно общих пози-
ций (см. {63]). Существенно, что резонаторы с диэлектрическими
телами дают самое естественное и простое конструктивное осу-
ществление связанных колебаний. Поэтому важно знать, что
можно получить в таких системах без их серьезного усложне-
ния: в этом заключается основная проблема, стоящая перед тео-
рией открытых резонаторов с диэлектрическими телами.
Задачи к гл. IX
1. Пользуясь результатами, полученными в задачах 3 и 6 к гл. V, вы-
В
вести уравнение (о8.10) и вычислить отношение д- для колебаний с большой
радиационной добротностью (58.15). Воспользоваться тем, что
w(t)=u(t) +iv(t), w'(t) =u'(t) +iv’(t),
причем при больших положительных t функции u(t) и o(Z) имеют асимптоти-
ческие выражения (см. [17], стр. 10 или [19], стр. 202):
_± -1,3/2 .1 -1,3/2
u(t) = t 4 е 3 , u\t) = t 4 е 3 ,
, _ L —1,3/2 _!_ __1,з/2
1 . 4 3 14 3
v (0= е , о'(0 = — У* е
Решение. Напишем, опираясь на результаты задач 3 и 6 к гл. V, для
функции Ханкеля формулу
/7<i’(x) = - I |/ 2Е* W (т),
2 о/п fTl
-у?/ thij), chij=—,
аналогичную формулам (25.18) и (25.19) для функций Бесселя. Для функции
. V - ( 1 \
„ и се производной будем иметь I полагая т = п + I
Лл’(х) = — /г^'(х) =, у/"ш-(т),
так как
dx___ sh ij
dx~~
В асимптотических выражениях для ш и w' мнимая часть экспоненциаль-
но мала по сравнению с вещественной (и даже по сравнению с поправочными
членами к вещественной части). Если мнимой частью пренебречь, то по фор-
муле (58.07) мы получим
В г---------. _Т
-д- = iey v sh ij o(t) е ,
346
е
— vshvj,
где t, v, Т и >] определяются формулами (58.09) и (58.11); таким образом, от-
В
ношение —д есть экспоненциально малая величина. Если такое же пренебре-
жение сделать в уравнении (58.06), то вместо уравнения (58.10) мы получим
уравнение
v'(t)
v(t)
определяющее вещественную частоту колебаний (радиационное затухание
в этом приближении равно нулю).
Множитель 1 —в формуле (58.10) получается при учете мнимых ча-
стей w(t) и ®'(т). Не следует рассматривать формулу (58.10) как нечто проти-
возаконное с математической точки зрения; хотя абсолютные погрешности ве-
щественной и мнимой частей функции, стоящей в этой формуле справа, совер-
шенно различны, их относительные погрешности примерно одинаковы, и по-
скольку они определяют различные физические величины — частоту колебания
и радиационное затухание — учет обоих слагаемых имеет смысл.
Правильность формулы (58.14), полученной таким образом, может быть
обоснована так: затухание должно быть пропорционально е~2Г, поскольку
амплитуда уходящей волны В пропорциональна е^г, и, следовательно, излу-
—2Т
чаемая мощность пропорциональна е .
2. Пользуясь асимптотическими формулами, использованными в предыду-
щей задаче, 'исследовать при условии (59.17) особый корень уравнения (59.14).
Вывести формулу (59.16) и определить мнимую часть То.
Решение. Из асимптотических формул для w' и w получаем
1+Те
Приравнивая это отношение согласно уравнению (59.14) положительной по-
стоянной g, получаем в первом приближении
Те = g2, T^/2= g\
Это приближение можно принять за основу, если g^> 1. Тогда во втором при-
ближении получаем
— g2(] + 2,е
мнимая часть То оказывается экспоненциально малой (оиа мала даже по срав-
нению с поправками к вещественной части, ср. задачу 1).
3. Пользуясь асимптотическими формулами задачи 1, вывести формулу
(59.20) для конечных положительных X.
Решение. Пренебрегая мнимой частью w и w', получаем
1
Л^'(х) п + Т
= — sh Tj, ch ij =-------
kci •
Из уравнения (59.13) мы легко получаем sh т]=А', ch г]=У1 + X2 и формулу
(59.20).
347
4. Показать, что, полагая в характеристическом уравнении (56.22)
kt = 0, kr = k°r Уцх,
получаем уравнения
= fт> pfm = Ет1 (fl)
определяющие комплексные собственные частоты со = ck® двухмерных колеба-
ний в диэлектрических цилиндрах. Показать, что при условиях
m^>l, ky^a^stn (fe=fe®)
первое из уравнений (а) принимает вид (58.10), если обозначить т= п -f-
Показать, что при условиях
т 1, ka =& т, Im k Уера = со
уравнения (а) принимают вид (59.14), причем
Z= или Z = у •
Показать, что для идеально проводящего цилиндра (е=<оо) собственные ча-
стоты внешних двухмерных колебаний определяются формулой
/ т \>/з / т \2/3
ka = m —1 -у I тп прим»! и |т„| (-у ) ,
где Тп (п=1, 2, ...) —корни уравнений (59.05) и (59.06).
5. Пользуясь результатами, полученными в задачах 7 и 8 к гл. VIII и
в предыдущей задаче, вычислить продольные волновые числа kz электрических
и магнитных волн, распространяющихся вдоль идеально проводящего цилиндра
(снаружи) и затухающих вследствие излучения. Ограничиться волнами, имею-
щими большой азимутальный индекс т и сравнительно небольшое затухание.
Решение. Мы имеем
причем для электрических волн под тп надо понимать 1° , для магнитных же
t'n (см. формулы (59.08) и (59.09)]. В первом случае мы имеем волны, кото-
рые МОЖНО Назвать ВОЛНаМН Етп, ВО ВТОРОМ — ВОЛЧЫ Нт„.
6. Показать, что если искать электромагнитные колебания в диэлектриче-
ской призме
—а<х<а, —b<y<b, —l<z<l
в виде:
Ех = Afx(kxx)f'y (kyy)f'z (kzz),
Еу = Bf’x (kxx) fv (kvy) f'z(kzz),
Ez = Cf'x (kxx) f'y (key) fz(kzZ),
Hx — Af x (kxx) fy (kyti) fz (kzz^f
Hy = Bfx(kxx) f'y (kvy) f, (kzz),
Hz = Cfx (kxX) fy (kytj) f’z (kzZ)
и ставить граничные условия так, как это сделано в § 60 (т. е. в приближе-
нии геометрической оптики), то мы придем к противоречию и не получим
интересующего нас приближенного решения. Считать kx, kv и kz отличными
от нуля.
348
Решение. Из волнового уравнения для электрического и магнитного
поля мы получаем соотношение
а из уравнения div Е = 0 — соотношение
kxA + kvB + kzC — 0.
Уравнение rot Е — ifep-H приводит к соотношениям
Л = ifepi kvC), В= (kxC kzA), С = ^2 (kvA kxB).
Поле в пустоте вблизи каждой грани мы представляем, пренебрегая диф-
фракцией, в виде уходящей плоской волны, (например, при х>а, —Ь<у<Ь,
—1<г<1 полагаем:
l/fl X
Ел == -До^ f у (feyl/) ffz
llfi X
Еу = Х fy(ky9) f'l
ik^ x
Ez= Coe x f'v (kyy)f'z(kzz)
81
1 ik° x
Hx = j^ (ktB0 —kvCt)e x fy(kvy) fz(kzz),
= ik°x С» — Л;Л) ekx Xfy(kvy) f^z),
1 л ik® x
Hz == (^у-До-)- x f
где постоянные Ло> Во, Со удовлетворяют соотношению
-До Ч~ kyB^-\-kzC= 0,
.а
х ’ угу е{1
Условие непрерывности составляющих Еу, Ег Ну, Нг дает четыре урав-
нения:
ife° а
Bfx(kxa)^B^ х ,
. ik° а
Cf'x(kxa) = CQe х ,
(kxC — kzA) fx (kxa) = p.(— ik°x Co — kz At) e x , (a)
(kvA — kxB) fx (kxa) = [x (kyAv 4-B0)e x .
349
которые вместе с предыдущими уравнениями образуют систему из шести Ч
уравнений для шести неизвестных А, В, С, До> В-э, Со. Комбинируя уравне- 1
ния (а), приходим к соотношению
A [kxfx (kxa) f’x(kxa)] = О,
которое при условиях
А #0, Д=0 (6) ’
приводит 'нас к характеристическому уравнению '
fx(kxa) . kx
f'x(kxa) —*kx‘
Условие Д=0 непосредственно следует из этого уравнения и формул (о), ко-
торые приводят к соотношению
ik® а 1
Afx(kxa)— цАе х ,
совместимому с дополнительным уравнением
ik® а
eAfx(kxa)=Ace х , j
вытекающим из предыдущих и выражающим непрерывность Dx=e,Ex на J
грани х=а, только при Д=йо-=0. При условиях 1
Л=0. А ./Д, (с>
лротивоположных условиям (Ь), мы приходим к характеристическому урав-
нению
f'x(kxa) . k°x
fx (kxa) le kx ’
Для kx получились характеристические уравнения, аналогичные уравне-
ниям (60.08) и (60.29), но при этом на постоянные коэффициенты приходится>
накладывать дополнительные условия (Ь) или (с). При выводе уравнений для»
ky и kz возникают другие дополнительные условия, которые приводят к тому»,
что все составляющие поля оказываются равными нулю. Таким образом, в дан-
ной форме получить решение поставленной задачи нельзя.
7. Рассмотреть, пользуясь граничными условиями вида (61.03), собствен- j
ные колебания в двухмерном открытом резонаторе, изображенном
рис. '15,6, три условии, что зеркало г=1 конечной ширины 2а имеет коэффи-
циент отражения
R = е~i2n₽ , р = р’ — ip''.
а зеркало z=0 — идеально проводящее. Показать, что получаемые результа-
ты эквивалентны тем, которые следуют из параболического уравнения (см.. '
задачи 3, 7 и 8 к гл. I).
Решение. Полагая внутри резонатора (при —а<х<а, 0<z</)
Ну = cos (kxx) cos (fe,z) или Hv = sin (kxx) cos (fe2z),
Ey = cos (kxx) sin (kzz) или Ev — sin (kxx) sin (kzz),
удовлетворяем граничным условиям при z=0. Учет неидеального отражения» !
от зеркала z=l приводит к соотношению (ср. § 4)
2kzl = r,q -J- 2яр,
откуда
350
где индексы q— четные для составляющей Ну и нечетные для составляю-
щей Ev. Граничные условия вида (61.03) приводят к характеристическим
уравнениям
ctelfea) — ka ₽<*+') ♦ /«, ч ь ₽(>+»), .. ]/2ка2
erg (пха) — пха——------tg(kxa) = — kxa----------’ М=у -j-r
имеющим при М ^>т приближенные решения
тп (
kxa — -g-l 1
тп
₽ м
м J
Частота колебаний определяется формулой
fe==fez + 2T’. 2W = ” (<7 + 2Р + 2/0-
где величина р дается формулой (4.11). Те же формулы для распределения
поля (т. е. для k2 и kx) и для частоты получаются из параболического урав-
нения, после введения соответствующих аппроксимаций (гл. I).
8. Обобщить результаты § 61 на случай, когда зеркала не являются иде-
ально проводящими (/?=!), а характеризуются коэффициентом отражения
R = e^l2np, р=р'— if".
Решение. При учете неидеального отражения формулы (61.16) и
<(61.32) принимают вид
Hv=Bfx (kx х) cos [k°(l — z) — пр].
Ev = Bfx (k°x x) sin ]fe° (Z — z) — пр].
Характеристические уравнения имеют тот же вид, но величина £°т теперь
р авна
0 (Ф2(/~0
&=----Г~
причем слагаемое пр учитывает потери на зеркалах.
9. Вывести характеристические уравнения для собственных частот двух-
мерного резонатора, изображенного на рис. 72,6, при условии, что зеркала
конечны и определяются соотношениями (60.34). Использовать «а краю зер-
кал граничные условия вида (61.03) или же выражение для коэффициента
отражения
R= — exp|i₽(l -Н)£°
/2Z1
k /’
использованное в гл. I. Сравнить полученные уразнения.
Решение. Используя коэффициент отражения, получаем характеристи-
ческое уравнение
0 2<Л° (о—-а)
Гх(^»а)_ 1 —Ее___х_____
fx(kxa) kx luPla-a)*
1 + Re x
351
обобщающее уравнение (60.08). Пользуясь приведенным выше выражением
для /?, мы можем переписать это уравнение в виде
f'x(kxa) __ kx t0
fx(kxa) kx g x
-«+₽(l+0)/ 2Г
Это —типичное уравнение связанных колебаний (ср. § 61): диэлектрический
объем и пространство между зеркалами, свободное от диэлектрика, являются
связанными резонаторами. Если пользоваться граничными условиями вида
(61.03), то получится уравнение (о), в котором
1-/₽(1 +i)k°x
R =—------------Х_
2k
< 1 два выражения для /? практически совпадают,
10. Вывести характеристическое уравнение для двухмерного открытого ре-
зонатора, изображенного на рис. '15,а, при условии, что на его стенке х=0
выполняется граничное условие импедансного типа [см. формулу (59.17)]
дФ <)Ф
^=-»Лгф или ^=-кХФ.
Решение. Поскольку граничные условия при z— ±1 остались прежними,
иной будет лишь функция }(£,), которая теперь при |=0 должна удовлетво-
рять граничному условию
df
~^ = -V2klX{.
Если искать функцию f(g) в виде
f(g)=sin(sog—а),
то для определения постоянных s0 и а мы получаем два уравнения
е ~ *<**<-*«) = — R, S(l ctg a =^2kiX.
Если, считая s0<Cl. для коэффициента отражения R от открытого конца взять
выражение (2.18), то мы получим для s0 выражение
пт 4- 2а
s° = Л4 + ₽(1 + i) = °’ 2’ 41 — >•’
Для параметра а получается уравнение
(пт + 2а) ctg a ^ViklX [М + ₽ (1 + «)].
При /п=0 оно имеет решение а~г'|а|, которое соответствует поверхностной
волне, запертой между двумя зеркалами z—±l, прилегающими к импедансной
плоскости х=0. Другие решения (т=2, 4, ...) соответствуют колебаниям,
отражающимся от края х=а и от импедансной плоскости х=0.
352
Глава X
Возбуждение открытых резонаторов
(общая теория)
§ 63. Затухающие свободные колебания
и собственные функции
непрерывного спектра
В предыдущих главах были исследованы свободные (соб-
ственные) колебания открытых резонаторов, причем в зависи-
мости от формы резонатора использовались те или иные аппро-
ксимации. Естественно возникает вопрос: как рассчитать вы-
нужденные колебания таких резонаторов? Ответ дает теория
возбуждения открытых резонаторов, которую в § 63—65 мы
излагаем для скалярного волнового уравнения, а в § 66—68 —
для уравнений Максвелла.
Теорию возбуждения открытых резонаторов можно строить
по-разному. Наиболее легкий путь — это расчет вынужденных
колебаний данного открытого резонатора в том же приближе-
нии, в каком найдены его свободные колебания (см. § 73 и 74
в следующей главе). Однако таким путем получаются резуль-
таты, имеющие весьма частный характер и не применимые
к резонаторам других типов. Поэтому наша цель будет заклю-
чаться в построении общей теории, которая позволит, не вводя
каких-либо специальных предположений и аппроксимаций, най-
ти резонансные свойства открытой системы в режиме вынуж-
денных колебаний, если известны ее свободные колебания, по
крайней мере те, которые обладают малым затуханием. Разу-
меется, при практическом применении теории возбуждения в ее
основные соотношения приходится подставлять поля свободных
колебаний, вычисленные в тех или иных предположениях, но
сами эти соотношения являются общими и точными. Такова же
ситуация в теории возбуждения объемных резонаторов (ср. [7],
гл. XVII или (64]).
23—2547
353
РИС. 75. Открытый резонатор и сфе-
рическая система координат.
Прежде чем излагать общую теорию возбуждения открытых
резонаторов, необходимо отметить, что эта теория, с одной сто- I
роны, в достаточной мере сложна и непривычна, а с другой сто- ’
роны, не обладает (по крайней мере в настоящий момент) до- J
статочной математической стро- •
гостью. По этим причинам з
чтение данной главы будет
трудным как для читателя i
с недостаточной математиче- '
ской подготовкой, так и для !
математика, не склонного удо-
влетворяться тем уровнем ма- j
тематической строгости, кото- J
рый обычен для физических 1
работ. Эти обстоятельства уве-
личивают значение частных ,
примеров, на которых прове- :
ряется и иллюстрируется об- ’
щая теория. Большое число
таких примеров приведено в
следующей главе, и читателю,
испытывающему указанные ;
выше затруднения, следует об- (
ратиться к гл. XI.
В гл. I—VII мы исследова- ;
ли свободные колебания в от- »
крытых резонаторах, решая j
скалярное волновое уравнение и лишь затем связывая
полученное решение с электромагнитным полем. В даль-
нейшем будем нумеровать свободные колебания с по- •
мощью индекса s (который в трехмерных задачах заменяет три
индекса mnq) и обозначать через <os частоту соответствующего
свободного колебания, через Ф6 — соответствующую собствен- !
ную функцию, которая удовлетворяет волновому уравнению ,
ДФв-|-^Ф8=0, (63.01)
граничному условию
Ф8 = 0 (63.02) \
на поверхности зеркал So и условию излучения
IkR,
Ф.=£.(», ?)-^- (63.03)
при 7? —оо. Здесь R, 8, <р— сферические координаты, начало ко-
торых расположено внутри резонатора (рис. 75), временная зависи-
—!«,* , о.
мость взята в виде е , ks= — есть волновое число собствен-
354
него колебания, с — скорость волн в свободном пространстве.
Формула (63.03) представляет сферическую волну, расходящую-
ся от резонатора при его свободном колебании; с этой волной
связаны потери на излучение, вследствие которых частоты <о8
будут комплексными:
сов = |<ов|е“'Тв, ke = \ke\e~‘'l‘, (63.04)
где
0<ys<n. (63.05)
Поэтому функции Фв экспоненциально возрастают при R —»оо
(ср. § 58).
Те же результаты получаются, если условие (63.02) заменить
условием
— = 0 (63.06)
на поверхности 50 или другими условиями, соответствующими
идеально отражающей или поглощающей поверхности зеркал;
для определенности мы будем ограничиваться условиями (63.02)
и (63.06).
Отметим, что наряду с собственной функцией Ф8 и частотой
<os всегда имеется комплексно-сопряженная функция Ф*в и часто-
та— w*s (ср. рис. 71 для идеально проводящего шара). Это свя-
зано с тем, что физический смысл имеет лишь вещественная
функция
Re (Ф6е~'“? )=4- (ф8е“гШ? + ф*«е ) = Re (Ф*8е'“%/). (63.07)
При рассмотрении вынужденных колебаний естественно восполь-
зоваться разложениями вида
Ф = £С8Ф*8, (63.08)
S
тем более что с помощью некоторых ухищрений [ср. ниже фор-
мулы (63.48) и (63.49), а также задачу 3] функции Фв можно
нормировать и доказать их ортогональность. Однако из самых
общих соображений следует, что поле в бесконечной области,
вообще говоря, нельзя разлагать в ряд по дискретной системе
собственных функций; формальное применение таких разложе-
ний приводит к неправильным результатам (см. задачи 4 и 5).
В теории объемных резонаторов, где поле занимает конечный
объем, а вне этого объема тождественно равно нулю, подобных
трудностей не возникает. Там функции Фк, удовлетворяющие
волновому уравнению (63.01) во всем объеме и граничным
условиям (63.02) или (63.06) на замкнутой поверхности, охва-
тывающей этот объем, образуют полную систему, и разложения
(63.08) позволяют без труда решить задачу о возбуждении.
23* 355
В теории открытых резонаторов функции Фв не могут образовы- '
вать полной системы (по этой причине их можно назвать «ква-
зисобственными») и вместо разложений вида (63.08) следует
применять разложения .по собственным функциям непрерывного '
спектра.
Собственные функции непрерывного спектра вводятся еле- :
дующим образом. Рассмотрим решения волнового уравнения i
ДФ+х2Ф=0 (63.09) j
при 0<и<оо, удовлетворяющие граничному условию
Ф = 0 или -^- = 0 (63.10)
на зеркалах и имеющие при —► оо следующий вид:
____________________________1Хр 1
Ф = х°(&1 (63.11) 1
Первое слагаемое в формуле (63.11) дает сходящуюся, вто-
рое— расходящуюся сферические волны. Расходящаяся волна
получается из сходящейся в результате рассеяния на зеркалах,
образующих открытый резонатор. Заданные на единичной сфере
функции %0 и х связаны соотношением
X=Sx°. (63.12)
где S—линейный интегральный оператор, который можно на-
звать оператором рассеяния. Воспользуемся теоремой Грина:
у(ф.дф(-ф,дф.)да= f (ф„^._ф(^)й, (63.13)
где Уд — объем, ограниченный сферой достаточно большого 1
радиуса R и поверхностью зеркал So, — производная по внеш-
ней нормали. Если функции Фа и Фр удовлетворяют соотношениям
(63.09)—(63.11) при одном и том же х, то интегралы по объему
Vp и поверхности будут равны нулю и для любой пары функ-
ций и /р получим соотношение
f Ха $xj dQ — J xJ,sx|^Q. (63.14)
в котором интегрирование производится по всей единичной сфере
(0<&<С~, 0 <2 <р 2-ге), a dQ — sin &dftd<f> есть элементарный те-
лесный угол. Применяя ту же теорему к функциям Фа и Ф*р
(Ф*р комплексно сопряжена с Фа), получим также
J SZ°aS*X°‘dQ= J Х°я xS’dQ. (63.15)
356
Комбинируя соотношения (63.14) и (63.15), получим
Jx°eSS*x;dQ=JZ0Bx^Q.
В силу произвольности ^функций /° и Хр произведение операторов
SS* должно быть единичным оператором.
Поэтому S-I=S*, где S-1—оператор, обратный 5, a S*—опе-
ратор, комплексно-сопряженный S:
Х°=5-'х, X*=S*X0*, (63.16)
т. е. S, равно как и «S-1, суть унитарные операторы. В дальней-
шем мы не будем пользоваться теорией унитарных операторов,
тем более что при наличии поглощения в зеркалах или в веще-
стве между зеркалами оператор S уже не будет унитарным.
Обозначим через gz=gz(^, ?) собственные функции, а через
Гт—собственные значения унитарного оператора S"1, тогда
= (63.17)
Индекс t в конкретных задачах заменяется двумя индексами тп
(ср. § 71). Полагая в соотношении (63.15)
Х° =5-^ = Г^, Sz° = Sz° (63.18)
будем иметь
)Г |г-= 1. (63.19)
Если форма, размеры ’и положение зеркал фиксированы, то
оператор S зависит только от х. Собственные значения и собст-
венные функции также будут зависеть от х, и мы будем их обо-
значать через ГДх) и £хх=£хх(&, <р). Соотношение (63.17) можно
переписать более подробно так:
5-’^.х=Г, (x)gT,x. (63.20)
Определим теперь собственные функции непрерывного Спектра
Ф1х как функции, удовлетворяющие уравнению (63.09) при 0<х<
<Z°°, граничному условию (63.10) и имеющие при —оо следую-
щий вид:
?) V’ (63-21>
где
<63-22>
357
Таким образом, при /? -> оо функции Фхх состоят из падающей
первое слагаемое в правой части (63.21)] и отраженной (второе
слагаемое) волн, причем величина Г”1 (х) есть в сущности коэффи-
циент отражения сферической волны от данной системы зеркал.
В силу того, что поглощение в зеркалах отсутствует, коэффици-
ент отражения согласно формуле (63.19) по абсолютной величине
равен единице, поэтому можно написать
Гт(х) = е2'^(х), (63.23)
где ах(и) есть вещественная величина.
С помощью разложения по этим функциям мы и будем ре-
шать задачу о возбуждении открытых резонаторов. Как видно
из предыдущего, функции Фх х вводятся чисто формально, т. е.
фактически их построить нельзя, если не считать нескольких
простейших систем (см. § 70 и 71); разложения по функциям
Фтх также имеют формальный характер, и лишь резонансные
члены, выделяемые из этих разложений, могут быть вычислены
в явном виде (см. § 64 и 65).
Легко, однако, понять, что именно такие функции необходи-
мо применить для того, чтобы получить общее решение постав-
ленной задачи. Действительно, окружим наши зеркала (рис. 75)
сферической оболочкой большого радиуса R, на которой ставит-
ся граничное условие Ф=0. Такая система уже будет закрытой,
и ее собственные частоты согласно формулам (63.21) — (63.23)
определятся соотношением
«6+-г)
х9=^---------(<7 = 0, 1, 2, ...), (63.24)
R — ах (хд)
а собственными функциями будут функции Ф, . При R -> оо ди-
*
скретный спектр (63.24) становится непрерывным (0< х<оо), и раз-
ложения надо вести не по дискретной системе функций Ф , а по
функциям непрерывного спектра Фх х. Здесь дело обстоит так же
как с рядами Фурье, которые при неограниченном увеличении размеров
области переходят в интегралы Фурье, являющиеся простейшими
примерами разложения по функциям непрерывного спектра.
Если на оболочке R — R выполняется граничное условие —
= 0, то мы получим формулу (63.24) в которой заменено
на q. При /? -> оо мы приходим к той же системе функций непре-
рывного спектра, которая, таким образом, не зависит от гранич-
ного условия, которое ставится на оболочке.
358
Базируясь на этих соображениях, можно ожидать, что система
собственных функций непрерывного спектра является полной, по-
скольку она возникает (в пределе 7?—*оо) из полной системы соб-
ственных функций, заданных в конечном объеме, окруженном обо-
лочкой R —R. Однако предельный переход R -> со нуждается
в строгом рассмотрении.
Из тех же соображений следует, что функции непрерывного
спектра образуют ортогональную систему. Ортогональность функ-
ций Фт х легко доказать непосредственно. Для этого применим
к двум функциям Фх х и Фх, х, теорему Грина (63.13) и восполь-
зуемся формулами (63.10), (63.21) и (63.22); тогда получим
( ф.. А у®=11 - г. W г,. Ml +
+sin(:t:?*11+г (х) г, (x')i+[rv (из - г (x)i+
+sln(;z-g*[r* +гх w} f *dQ- <63-25)
Полагая здесь х=х' и учитывая, что левая часть конечна при
конечных R, приходим к соотношению
[Г„ (х) - Г, (х)] J gx *gx, х dQ=0, (63.26)
которое следует также из формулы (63.14) и из которого выте-
кает условие ортогональности для собственных функций
при (63.27)
или
= (63.28)
где 8^,—символ Кронекера (8хх, — 0 при 8^=1), а
Gx(x) = J^xxdQ. (63.29)
Условие (63.27) следует из соотношения (63.26) лишь при
Г (х) #= Гт, (х), т. е. при отсутствии вырождения. При вырождении,
когда Гт(х) = Г1, (х) при 'условие (63.27) удовлетворяется
за счет надлежащего определения собственных функций g х. Дей-
ствительно, если данное собственное значение Гх(х) вырождено
и ему соответствует п различных собственных функций (п >2),
359
то, пользуясь произволом в их определении, всегда можно эти п-
функций дополнительно ортогонализировать так, чтобы условие
(63.27) выполнялось и для них.
Перейдем теперь в формуле (63.25) к пределу -оо. Мы
считаем
lim ty — х'), (63.30)
Д-»оо х *
где 6 есть дельта-функция Дирака, так как для любой достаточ-
но гладкой функции f(x), достаточно быстро убывающей при
к —— оо, сп р а ведливо тождество
lim [ f (к') sin(;3-;y dx' = «f (х). (63.31)
R-»oo J х х
0
Остальные тригонометрические функции при R—><x> мы заме-
няем нулями, так как
lim [ f (х') dx' = 0
R—»Оо J ’ * + *
о
и (63.32)
00
lim f f (x') cos (x ± x') dx' — 0.
R-»oo J
В результате получаем условие ортогональности для собст-
венных функций
i j Ф,. А,, =D, (х) 8„,8 (х - х'), (63.33)
где интеграл берется по объему Vа
D,(x) = lrjx)GJx). (63.34)
Отметим, что все условия ортогональности формулируются без
комплексного сопряжения: под интегралом стоит Ф, ХФТ, х,, а не
Ф, ХФ*,, Х,; поэтому функция О,(х), имеющая смысл нормы соб-
ственных функций непрерывного спектра, и другие нормы, вводи-
мые ниже, в общем случае комплексны. Так же обстоит дело
в теории возбуждения объемных резонаторов с потерями.
Заданную функцию р=р (х, у, г), убывающую при R —><х> до-
статочно быстро, теперь можно представить в виде
00
(б3-38)
х О
360
где суммирование производится по всем возможным значениям
т. Согласно условию (63.33) мы имеем
Интегралы вида
\ рФт xdV
£>х(х)
оо
О
(63.36)
(63.37)
возникающие при разложении по собственным функциям Фт х со-
гласно формулам (63.35) и (63.36), можно преобразовать, дефор-
мируя контур интегрирования в плоскости комплексного перемен-
ного х и при этом продолжая функции Фх х аналитически.
Определим сначала функции Фх х при —оо<х<0. Так как
при замене х на —х уравнение (63.09) не меняется и так как
функции Фх х определены условиями (63.21) и (63.22) с точностью
до постоянного множителя, то
<63-38)
где — постоянная, удовлетворяющая соотношению
€*=1, £т = +1. (63.39)
Отсюда
= (-х) = Г>)6» (63.40)
и
Dx(-k)=Dx(k), c,(-x) = gA(x), <63-41)
поэтому интеграл (63.37) можно переписать в виде
оо
Р, = J сх (х) Фх х dx. (63.42)
—00
Продолжая функции Фт х и сх(х) в нижнюю полуплоскость
1ш х < 0, придем к полюсам функции сх (и), которые соответствуют
корням уравнения
Г,(х)=0. (63.43)
Обозначим их через kw (индекс а есть номер корня), а соответ-
ствующие функции Ф, k — через Фто; последние при 7? -> оо
имеют вид
lknR
Ф« = ?) Чг~ - . k„ •
(63.44)
361
и, следовательно, они совпадут с „квазисобственными" функциями
Ф8, рассмотренными выше, а —с комплексными часто-
тами <os затухающих колебаний.
При вычислении вычетов в полюсах х = йто надо знать вели-
чину
I dD. I dr
N, (kJ (kJGx(k ), (63.45)
та ZTE ux V 4тг Ox 'та/ “S' -sa/’ X /
которая играет роль нормы функции Фта = Ф8. Действительно, по-
ложим в формуле (63.25) т = т' и х = х', тогда получим соотно-
шение
Vr
'e2ixR _ г2(х) е—2ixR
2/х
. (*)
1 dx
GJx), (63.46)
применимое и при комплексных х. В частности, при x=£w=£s
мы получаем
С SR Г
VR
гае gs — gw и NS — NXIJ. Таким образом.
(63.47)
(63.48)
РИС. 76. Путь интегрирования по Р в формуле (63.48).
где символ R -> оо еп означает, что после достижения больших
R, при которых выполняется асимптотическая формула (63.44),
дальнейшее изменение R производится в комплексной плоскости
(рис. 76) так, что
lira е * =0. (63.49)
R-»ooe‘H
Выражение (63.48) показывает, что величину NK, определен-
ную формулой (63.45), можно назвать нормой собственной функ-
ции Ф8. Вопрос о фактическом вычислении нормы будет рассмот-
рен в гл. XI.
362
§ 64. Вынужденные колебания
открытого резонатора
Рассмотрим колебания, которые возбуждаются источниками,
распределенными в пространстве с объемной плотностью р и ко-
леблющимися с вещественной частотой <i> = ck. Эта задача сво-
дится к определению функции Ф=Ф(х, у, z), удовлетворяющей
неоднородному волновому уравнению
AO-J-A2® = —4«р, (64.01)
граничному условию (63.10) на зеркалах и условию излучения;
последнее можно сформулировать, налагая на функцию Ф пре-
дельное условие
Нт/?Ф = 0 при 1т£>0 (64.02)
Р-»ос
и переходя к вещественному k лишь в окончательных формулах.
Условие (64.02) означает, что в свободном пространстве есть ма-
лое поглощение; при этом условии поставленная задача стано-
вится единственной (ср. (7], §10) и искомую функцию можно
представить в виде
Ф=£ J Сх(х)Фтх(Ьс.
т 0
(64.03)
Подставляя это разложение в уравнение (64.01) и учитывая
формулы (63.35) и (63.36), получаем
с (х) \ Р®х х &V
Ct (х) = — Л2_х2 = (Л«—x2)Dz(x)‘ (64.04)
Произведение с%(х)Фх х есть четная функция х, поэтому формулу
(64.03) можно переписать так:
(64Л5>
X — ОО
Определим теперь в комплексной плоскости х область Д не-
равенствами
kmin<Ren<kmax, — 6<Imx<0 (64.06)
и обозначим через Г контур, совпадающий при y.<kmin и х>
>kmax с вещественной осью и огибающий область Д снизу
(рис. 77). Формула (64.05) дает
Ф = У С8Ф6 + $,
д
(64.07)
363
где
C^-*dx,
К-----X
(64.08)
а сумма содержит все затухающие колебания, волновые числа
ks которых находятся в области Д. Коэффициенты Cs — ком-
плексные амплитуды этих колебаний — равны
\ ₽Фв dV
2k (k—ka)Nt
(64.09)
Они имеют резонансный характер, принимая большие значения
при k^ks. Резонансные знаменатели 2k(k—ks) отличаются от
знаменателей №—k2s, получающихся в теории возбуждения за-
крытых объемных резонаторов (см. [7] § 101 или (64]). При k~
^ks это отличие несущественно, однако из-за него колебания,
к min
-- ' О-—------о---------о
> — -о
кттп Г ^гпах "16
РИС. 77. Путь интегрирования Г и область Д.
у которых Re£s<0 (см. § 63), с большими амплитудами не воз-
буждаются.
Область Д не обязательно должна быть строго прямоуголь-
ной; kmin и kmax следует выбрать так, чтобы охватить интересую-
щий нас диапазон частот, а нижнюю границу области Д — так,
чтобы волновые числа ks для колебаний с перекрывающимися
резонансными кривыми оставались за пределами области Д.
Тогда сумма в правой части (64.07) дает резонансную часть по-
ля, а слагаемое Ф—нерезонансную часть, слабо зависящую от
частоты; это—фон, на котором проявляются резонансные свой-
ства открытого резонатора и который, в частности, обусловлен
волнами, непосредственно излучаемыми источником и не испы-
тывающими многократных отражений с суммированием
амплитуд.
Выделять резонансную часть поля не имеет смысла, если она
мала по сравнению с фоном и «забивается» им: так будет, если
в точке наблюдения или в области, занятой источниками, поле
затухающих колебаний является слабым. Если точка наблюде-
ния удаляется от резонатора, то при достаточно больших R со-
гласно формуле (63.03) вклад s-ro колебания в полное поле
определяется не резонансным знаменателем 2k (k—ks), а экспо-
ik„ R
нентой е , возрастающей приоо тем быстрее, чем боль-
ше затухание данного колебания. В этом случае поле также те-
364
ряет свой резонансный характер, и в выражении для Ф нецеле-
сообразно выделять резонансную часть — сумму вычетов.
Мы неявно предполагали, что подынтегральные функции (64.05)
в области Д никаких особенностей, кроме простых полюсов, не
имеют. В примерах, рассмотренных ниже в § 70 и 71, произведение
ст(х)Фт х является мероморфной функцией х, и это свойство, по-
видимому, сохраняется при весьма общих предположениях.
§ 65. Задача Коши
Задача Коши сводится к определению функции Ф=
= Ф(х, у, z, /), удовлетворяющей нестационарному волновому
уравнению
дф-^^> = °. (65.0!)
граничному условию (63.10) на зеркалах и начальным условиям
Ф = Ф°, ±^.=ф* при /=0, (65.02)
।
где Ф° и Ф1 — функции х, у, z, достаточно быстро убывающие
при R —>оо (ниже мы предположим, что они равны нулю при
R>Ro). Эти функции можно представить следующим образом:
где
Ф° = У J с* (х) Фх х dx,
t о
(65.03)
\ Ф°Ф, ,dV
С (х) = п ' ,
т ' ' (х)
•с 0
f [ф’Ф^У
С-№~ (х)
(65.04)
Будем искать функцию Ф в виде
Ф = у j" Сх (х, /) Фх х dx, (65.05)
1 6
тогда для функции Сх(х, t) в силу уравнения (65.01) мы получаем
уравнение ^+^,=0, (65.06)
откуда Сх (х, /)=С* (х) е-/хй + С; (х) е‘хс'. (65.07)
365
Функции С*(х) определяются из начальных условий (65.02)
сх++с; = < сх+-с;=±< (65.08)
следовательно,
сх+(х)=4[ ^(’<)+4-^(х)]=еа_ (-«к
, г f (65.09)
с; И=-2 [ с\ (х) — - с\ (z)j =Excz+ (— *)•
Используя также соотношения (63.38) и (63.39), мы получаем
для функции Ф выражения
со '
Ф = £ J С* (х) Фх Xe“lxrfdx (65.10) |
х —00
И 1
00 1
Ф = S j С- М ФЬ хе‘КС<ЙИ’ (65.1 1
Т -00
первое из которых позволяет выяснить поведение Ф при достаточно )
больших положительных t. Rm этого возьмем в качестве области
Д полосу
— oo<Rex<oo, —6<Чтх<0, (65.12)
тогда выражение (65.10) можно преобразовать к виду
ф=ЕсХе ‘**с/+ф+, д (65.13)
где Ф+ = £ 00 j6 С*(х) 1>х xe~'xrtdx (65.14)
и т —co—ib С* = (Y$° +-A Ф1^ dV. 3 8nWe И 1 k„ ) s (65.15)
Ряд вычетов в формуле (65.13) содержит свободные колеба-
ния с частотами ios=c£s, их комплексные амплитуды зависят от
начальных условий. В ряде вычетов Imfes>—6, а Ф+^е-м,
поэтому при достаточно больших положительных t функция Ф+
мала по сравнению с рядом вычетов.
Если функции Ф® и Ф1 отличны от нуля только в некоторой
конечной, области G (при R <С /?0), то в свободном пространстве
р" _
без зеркал Ф = 0 при t > — , где R есть наибольшее расстояние
366
точки наблюдения до точек области G. Многократные отражения
от зеркал приводят к тому, что Ф медленно убывает, осциллируя;
с этим связаны резонансы, рассмотренные в § 64. Физически ясно,
что возбуждение свободных колебаний в открытом резонаторе за-
канчивается при и поле этих колебаний доходит до точки
наблюдения, находящейся на большом расстоянии R от резонатора,
при —• Поэтому представлять функцию Ф в виде (65.13)
I D
целесообразно лишь при
Волновое уравнение (65.01) инвариантно относительно изме-
нения знака t, поэтому аналогичные отношения получаются при
/<0. Из выражения (65.11) следует, что
ф=^с;ф/'с'+.ф-,
д
где
оо—/Ь
С; (х)Фх яе,х^х
и
С~ =5-4" f (ф0 - Г- ф1^ ф« dV-
S 8nN, J k, J
(65.16)
(65.17)
(65.18)
Таким образом, при t—*—оо поле также убывает, осциллируя.
Выражения, аналогичные (65.13), выводятся в квантовоме-
ханической теории распада нестабильных состояний (ср. [65]
и [66]). Примененное выше разложение по собственным функ-
циям непрерывного спектра с последующей деформацией пути
интегрирования является естественным обобщением метода,
развитого в работе Крылова и Фока [65] (см. ниже § 71).
Обычно в открытых резонаторах радиационное затухание
колебаний тем меньше, чем выше их частота. С другой стороны,
комплексные амплитуды (65.15) должны, вообще говоря,
уменьшаться при переходе к все более высокочастотным коле-
баниям, поскольку они определяются интегралами от произве-
дений фиксированных функций ф° и Ф1 на функции Ф.«, все
более сильно осциллирующие в пространстве. Поэтому эволю-
ция волнового поля во времени происходит как бы по эстафете:
при увеличении t более низкочастотные колебания, возбужден-
ные с большими! амплитудами, постепенно выбывают из игры
вследствие их большего затухания и главную роль начинают
играть все более высокочастотные колебания, которые возбуж-
дены с малыми начальными амплитудами, но затухают слабее.
Для идеально отражающей сферы затухание колебаний тем
больше, чем выше их частота (см. § 59, рис. 71), хотя доброт-
367
ность этих колебаний, по формулам (59.04), (59.07) и (59.08)
равная
(65.19)
неограниченно растет с увеличением индекса п, т. е. частоты.
В этом случае поведение волнового поля при /—оо более просто,
а именно в нем главным будет член, соответствующий колеба-
нию с наименьшим затуханием (электрическому колебанию
с индексом п=1). Однако это простое поведение для открытых
резонаторов нетипично.
§ 66. Собственные функции
непрерывного спектра для
электромагнитного поля
Выше мы изложили теорию возбуждения открытых резона-
торов, исходя из скалярного волнового уравнения и простейших
граничных условий на зеркалах. Перейдем теперь к более обшей
постановке задачи, а именно рассмотрим электромагнитные
колебания в системе, заданной распределением в пространстве
комплексных проьицаемостей— диэлектрической и магнитной-
e = e(k) = e(k; X, у, г), ц = р. (&) = р. (fe; х, у, г), (66.01)
зависящих от волнового числа k—~ (или, что то же, от часто-
ты <и) и от координат х, у, г, причем мы будем считать, что
е = |л=1 при -\-уг-\-2г">R,
(66.02)
т. е. что за пределами сферы радиусом R — пустота, в которой
распространяются расходящиеся электромагнитные волны,
формирующиеся при электромагнитных колебаниях системы.
Комплексные проницаемости (66. 01) соответствуют поглощаю-
щим или непоглощающим веществам, шоэто-му
1m е 5» 0, 1тр>0.
(66.03)
Активных веществ (с отрицательными 'потерями) мы здесь не
рассматриваем.
Согласно этому определению открытым резонатором явля-
ется диэлектрический или металлический шар, равно как и
большинство других электродинамических систем, применяемых
на практике. Общая теория, изложенная ниже, охватывает
368
широкий классе систем, определяемых условиями (66.01) —
(66.03), однако она приводит к простым результатам, представ-
ляющим практический интерес, только в том случае, когда
данная система является резонансной, т. е. в ней возможны
собственные колебания с достаточно высокой добротностью.
Последнему требованию удовлетворяет диэлектрический шар
(см. § 58), в то время как металлический шар резонансных
свойств практически не имеет (см. § 59). Открытые резонаторы,
образованные зеркалами, расположенными в пустоте, очевидно,
охватываются приведенным выше определением: для них изла-
гаемая ниже теория является естественным развитием теории,
данной выше. Обычные объемные резонаторы превращаются
в открытые, если они связаны со свободным пространством.
Свободными (собственными) электромагнитными колеба-
ниями системы мы будем называть колебания, при которых
электромагнитное поле зависит от времени t по закону
_I <D t t
Е(0= Re{Ese s }, H(f)=Re{Hse * }, (66.04)
где
a>s=(o's—ivy"s (66.05)
есть комплексная частота собственного колебания с индексом s.
Векторные функции Es=Es(x, у, z) и H4=Hs(x, у, г) удовлет-
воряют однородным уравнениям Максвелла
rot Es = i£spHs, rotHg== — ikseEs = (66.06)
Проницаемости вир мы вводим в соответствии с формулами
(66.01) — (66.03), причем в дальнейшем будем брать k при
частоте возбуждения и только в конце § 68 нам понадобятся
векторы Es и Hs, удовлетворяющие уравнениям (66.06) с е=
= e(As) и р=р(&5), т. е. с проницаемостями на частоте самих
собственных колебаний.
Если е и р как функции х, у, г терпят скачки, то уравнения
(66.06) дополняются граничными условиями на поверхностях
раздела; как известно, эти граничные условия являются след-
ствиями уравнений поля, поэтому в общих рассуждениях мы
граничных условий вводить не будем, при необходимости рас-
сматривая вместо скачкообразного изменения 'е и р в простран-
стве непрерывное, но быстрое изменение. При /?—-со векторы
Es и Hs удовлетворяют условиям излучения, т. е. имеют вид
Es = gs (», ?) , Hs = [ngs (S, T)1 (66.07)
где R, &, <p — сферические координаты; n—единичный радиальный
вектор (nR = l, /?& = /z(jj=0); gs(&, ?)— векторная функция, одно-
24—2547
369
значная на единичной сфере и касательная к ‘ней, так что
ngs(&, «р) = 0.
Затухание собственного колебания во времени (его мерой
служит величина «",) определяется как излучением расходя-
щейся волны (66.07), так и потерями в самой системе (при ком-
плексности е или р.). Добротность колебания
= (66.08)
может быть весьма высокой (ср. § 58).
Следует также ввести собственные функции непрерывного
спектра. Для этого рассмотрим электромагнитные толя, удовлет-
воряющие (при 0<х<оо) однородным уравнениям Максвелла
rot Е = гхц Н,
rot Н = —txe Е
(66.09)
и имеющие при —оо следующий вид:
р—М
Е = Х°(&, <Р)-д-НХ(&. ЧО-д’
Н = —[пх°(&, ?)] +[пх (&, Т)]1^-’
(66.10)
где векторы х° и X однозначны на единичной сфере и касательны
к ней. Они связаны соотношением
Х = 5х°,
(66.11)
где оператор рассеяния S есть линейный интегральный оператор,
зависящий (при фиксированном распределении е и ц в пространстве)
от параметра х. Обозначим через gx х (&, <р) собственные векторные
функции обратного оператора S"1, а через 1\(х) — соответствую-
щие собственные значения. Мы имеем
5Х=ГЖх-
(66.12)
причем т есть дискретный индекс, нумерующий собственные
функции три фиксированном х.
Собственные векторные функции Ех х и Нх х непрерывного
спектра вводятся как решения уравнений (66.09), имеющие при
/?—«-оо следующий вид:
IxR ixR
Ех.х = бх,х(&Л)-д----|-gT,x(&, Т)^-’
(66.13)
о р—‘-'-R aixR '
Нх. х =- [ng,, х ?)] -R----F [ngz, х (&, ?)] - Д- ’
370
причем в силу соотношения (66.12)
£х(&. Ф)=Г»бх х(», ?)- (66.14)
Векторные функции Ет t и Н( к являются предельной формой
напряженностей электромагнитного поля собственных колеба-
ний в объемном резонаторе, который образуется, если поместить
нашу систему в идеально проводящую сферическую оболочку
большого радиуса /?. Так как при наличии поглощения (Im е>0
или Im ц>0 хотя бы в части 'пространства, занятого полем)
условие (63.19) уже не выполняется, то величина ах (х) в фор-
муле (63.23) будет комплексной. Поэтому собственные частоты,
по-прежнему определяемые формулой (63.24), будут комплекс-
ными, однако при /?—оо мы приходим к непрерывному спектру
0<х<оо.
Для функций Е, х и Н, х справедливо условие ортогональности
(66.15)
в котором интегрирование производится по всему бесконечному
пространству, а
DJx)=|r (x)G (х) (66.16)
и
(66.17)
причем последний интеграл берется по единичной сфере.
Соотношение (66.15) выводится из тождеств
div [Е Нт, x,J = ix'eEx xEv, ,, + гх„
(66.18)
div[E , х,Нх ] = <хеЕ XEV Х, + ^Н, хНх, х,
с помощью тех же рассуждений, что и в случае скалярного
волнового уравнения (см. § 63). Функция (66.16) играет роль
нормы собственных функций непрерывного спектра.
Векторные функции Ех х и Н, х можно продолжить аналитиче-
ски как на отрицательную часть вещественной оси, так и на всю
плоскость комплексного переменного х. При отрицательных х они
определяются формулами
Е,.-. = 6,Е,.,. = (66.19)
где
Ex==ti- (66.20)
24* 371
При комплексных х (а именно в нижней полуплоскости) функ-
ция ГДх) может обратиться в нуль. Каждый корень уравнения
Гх(х) = 0 совпадает с одним из значений ks, рассмотренных выше.
Кроме того, мы имеем
Exit=Es, Hxx = Hs при x=A*g. (66.21)
Действительно, в этом случае в соответствии с формулами
(66.13) и (66.14) имеет только расходящаяся сферическая
волна (66.07). Нормой затухающего собственного колебания
с индексом s является величина
i dDx : dl\
<66-22)
где
Gs = Gx (ks) == f g’ dCl. (66.23)
J
Величина Ns появляется при вычислении вычетов в точках х=
=ks (см. § 67 и 68). Можно доказать (ср. конец § 63), что
Ns= lim 1 [ rf?dV = - lim 1 [ ИН>, (66.24)
VR VR
где VR есть объем шара радиусом R, а угол у выбирается так,
чтобы интегралы сходились. При приближенном вычислении нор-
мы достаточно интегрировать по конечной области (см. гл. XI).
§ 67. Возбуждение открытых резонаторов
заданными токами
Пусть источниками поля являются сторонние электрические и
магнитные токи (с плотностями je и jm), колеблющиеся с часто-
той со = ck и находящиеся на конечных расстояниях. Возбуждае-
мое ими поле Е, Н должно удовлетворять уравнениям Мак-
свелла
rot E = i/epH — jm, rot H = — ifceE-f-y je (67.01)
и условиям в бесконечности
lim/?E = 0, lim /?Н = 0 при Imk> 0, (67.02)
R->co R-too
обеспечивающим единственность решения (см., например, [7],
§ 10) и позволяющим искать его (см. ниже) в виде интегралов.
(67.06) и (67.18) по вещественной оси; в окончательных форму-
лах (67.19) и (67.20) уже можно положить 1тй=0.
372
Так как векторы Ет х и Нх к удовлетворяют соотношениям
div(eE,>x) = O, div(nHxx)=O, (67.03)
вытекающим из уравнений (66.09), то искомые поля Е и Н сле-
дует представить в виде (ср. [7], § 101 или [64])
Е=Е'+Е», Н = Н' + Н\ (67.04)
где Е', Н' — поперечные (соленоидальные) поля, которые удов-
летворяют соотношениям
div(eE‘)=0, div(pH')=0 (67.05)
и могут быть представлены в виде
Е' = £ J Д (х) Ех /х, Н* = V J Вх (к) Нх /х, (67.06)
t 0 т 0
а Ег, Н‘ — продольные (потенциальные) поля, которые можно
записать так
Ег=—gradOe, Hz=—gradO”1. (67.07)
Здесь Ф' и Ф™— электрический и магнитный скалярные потен-
циалы, удовлетворяющие уравнениям
div (e grad Фв) =— 4яре, div (р grad Фт) = — 4ярго, (67.08)
где
ре =---r-divje, рт —------^-divi7" (67.09)
С/v v/v
— плотности сторонних зарядов.
Уравнения (67.08) решаются методами электро- и магнито-
статики (ср. § 71). Продольные поля не имеют резонансных
свойств. Так как все заряды находятся на конечных расстояниях,
то Фе и Фт при 7?—-со убывают, как или быстрее. Продоль-
ные поля ортогональны к векторным функциям непрерывного
спектра
J£Et xEzdV = O, JpH, xH'dV=0, (67.10)
поскольку, например,
J eEx>xEMV = —J еЕх xgrad®edV= —f div (еЕтхФ«)с/У +
Vr Vr Vr
+ 5 ®ediv(eEt x)dV= — фф'-пЕ, xdS, (67.11)
373
а интеграл no SR (сфере радиусом /?) при —оо исчезает, так
как Фе убывает, как -к- или быстрее, а радиальная составляющая
А
Ех.х~как
Подставляя разложения (67.06) в уравнения (67.01), получаем
соотношения
ie j* {kAx(х) — v.Bx(х)} Е, хdx = Je~ i^E1’,
t о
(67.12)
ip У {хД, (х) — kВх (х)} Н, х dx = — ~ jm+1 А>р.Н*,
т О
в которых справа стоят соленоидальные векторы; для них можно
написать разложения
7 je — ikeE‘ = Jах (х) Ех х dx,
’ ° „ (67-13)
—у F + «>Н-’ = 7 S J (х) Н, х dx,
х 0
причем коэффициенты at(x) и 6х(х)в силу формул (66.15) и (67.10)
имеют вид
M*)=7^peE,.:xdV, 6x(x) = ^-jrHx>xdV. (67.14)
Коэффициенты Дт(х) и Вх(к) должны удовлетворять уравне-
НИЯМ kAx (х) — иВх (х) = —у ах (х), 1 (67.15) хДх (х) — kBx (х) = — - Ьх (х),
откуда . , . i kaxM — ^xM АхМ= с ' (67.16) В (х) ~ — — ’!С’ — kt>x •
ГТользуясь соотношениями (66.19) и (66.20) и вводя коэффициенты
г , ч I М*)—М*)
(67.17)
374
мы можем заменить разложения (67.06) следующими:
E<=S J Н' = У J C»Ht xdx. (67.18)
х —эо г —оо
Сместим в этих интегралах путь интегрирования вниз и обо-
значим через Г новый путь, а через Д — область между старым
и новым путями (см. рис. 77 и § 64). Тогда получаем
E(=£csEs4-E, Н*=£с,Н,+Я, (67.19)
Д А
где суммирование распространено по всем затухающим собствен-
ным колебаниям, волновые числа ks которых лежат в области Д;
Ё и Н представляются интегралами (67.18), но не по веществен-
ной оси, а по пути Г. Коэффициенты Cs в силу формул (66.22)
и (66.23) получаются в виде
С8 = —(67.20)
где
(67.21)
При надлежащем выборе области А1 (см. § 64) суммы в фор-
мулах (67.19) определяют резонансную часть поля, а слагаемые
Е и Н вместе с продольными полями определяют нерезонансную
часть поля, на фоне которой проявляются резонансные свойства
данной системы. Может случиться, что данная система не имеет
резонансных свойств либо вообще, либо при определенном рас-
положении источников или точки наблюдения; тогда выделение
резонансной части не имеет смысла.
Формулы, выведенные выше, во многом аналогичны форму-
лам, которые получаются в теории возбуждения закрытых объ-
емных резонаторов.
§ 68. Задача Коши
для электромагнитного поля
Если (формально) причислить все токи проводимости к токам
смещения, то уравнения Максвелла для нестационарных полей
можно записать в виде
rot Е (/) = --го1Н(/)=---^Д. (68.01)
1 ’ с dt ’ ' ’ с dt ' '
Задача Коши сводится к интегрированию этих уравнений при
начальных условиях
D(0=D°, В(О = В° при t=0, (68.02)
37$
где D° и В0 — заданные векторные функции, достаточно быстро
убывающие при /?—оо.
Введем E(k)—векторную функцию координат х, у, z — по
формулам
E(k)=^eihctE(t)dt, e~ikctE(k)dk (68.03)
0 —ос
и аналогичным образом определим Н(&), D(k) и В(й). Из урав-
нений (68.01) получаем для этих векторов уравнения
rot Е(й) = г7гВ(й) + 1в°, rotH(&) = — ikD(k) — у D°. (68.04)
Если учесть соотношения
D(k)=E(k)E(k), E(k)=4x(Jz)H(k), (68.05)
в которых e(k) и ц(&) те же, что в формулах (66.01), то уравне-
ния (68.04) сводятся к уравнениям (67.01) со сторонними то-
ками
j₽ = -lD’, Г = -1В». (68.06)
Условия
divD° = 0, div В0=0 (68.07)
обеспечивают отсутствие продольных полей, поэтому полное по-
ле E(k), Н(&) получается в виде интегралов (67.06) и (67.18).
Однако для написания этих интегралов и для формулировки
условий (67.02), обеспечивающих единственность решения,
в формулах (68.03) надо считать 1т&>0 и интегрирование по k
производить несколько выше вещественной оси.
Выделяя в E(k) и Н(Ze) резонансную часть по формуле
(67.19) и выбирая область Д в виде полосы
—oo<iRex<oo, —6<Imx<0, (68.08)
переходим к Е(/) и Н(^) с помощью второй формулы (68.03).
Сдвигая путь интегрирования вниз, к прямой 1m х=—б, полу-
чаем выражения
E(0 = Scs(0Es + ..., H(/) = Scs(0Hs + -.., (68.09)
A А
в которых явно выписаны члены, убывающие при /—>оо по абсо-
v —let
лютнои величине медленнее, кчем е , причем
1 г 1 г (68.10)
D°E‘ f B»HS dV.
376
В формулах (68.09) и (68.10) фигурируют слабозатухающие
колебания с частотами cos=cks (Imfcs>—6), удовлетворяющие
уравнениям (66.06) при e=e(£s) и р,=р.(&6). Если вещества, за-
полняющие или образующие открытый резонатор, сами облада-
ют резонансными свойствами, вследствие чего появляется силь-
ная зависимость в и р, от k, то эти колебания могут существенно-
отличаться от колебаний, рассмотренных ранее. Даже число
этих колебаний может быть другим. Пусть, например, рабочая,
часть резонатора (скажем, пространство между зеркалами) за-
полнена однородным веществом, у которого
. »(*)=>. (68.11>
tv | «VQ
где во, Ао, ko и ро от частоты не зависят. Если ks~k0, то при за-
мене e(k) на s(ks) возможно расщепление частоты cks на две
частоты, соответствующие различным колебаниям.
Собственные значения ks распределены в плоскости комплекс,
кого переменного симметрично относительно мнимой оси, поэтому
частоте ш8 и векторам Е8, Hs всегда соответствует частота —<о*8
и векторы E*s, Н*8: это следует из выражений (66.04). В задаче
о возбуждении монохроматических полей (§ 67) значения ks, ле-
жащие вблизи отрицательной части вещественной оси, не пред-
ставляют интереса; в задаче Коши они обеспечивают веществен-
ность сумм (68.09).
Вывод формул (67.19) основан на допущении (ср. конец
§ 64), что подынтегральные функции (67.18) в области А, кроме
простых полюсов ks, никаких других особенностей не имеют.
В § 71 мы рассмотрим поведение этих функций в частном случае
однородного изотропного шара и убедимся, что это действитель-
но так. При выводе формул (68.09) и (68.10) сделано дальней-
шее предположение о том, что существенно особые точки функ-
ций z(k) и |т(&) лежат ниже прямой 1шх=—б, т. е. б достаточно-
мало. Полюсы функций e(k) и ц(&) могут лежать выше этой
прямой. Так, например, в случае применимости формул (68.11)
точки
k = ±yk[-p2Q-ip. (68.12)
могут лежать выше прямой 1птя=—б, т. е. может быть ро<б.
Таким образом, мы построили формальные решения задачи
о возбуждении открытой резонансной системы и задачи Коши
для нее путем разложения искомых полей по собственным функ-
циям непрерывного спектра. В этих решениях можно явно вы-
делить резонансную часть, обусловленную собственными колеба-
ниями с высокой добротностью. Простые выражения, получен-
ные для резонансной части, позволяют ее вычислить, если
377
известны соответствующие добротные колебания; эти выражения
дают возможность рассчитывать ряд свойств открытых резона-
торов примерно так же, как это делается для объемных резона-
торов.
Следует отметить, что теория свободных и вынужденных ко-
лебаний объемных резонаторов обычно основывается на пред-
ставлении о том, что резонатор есть «вещь в себе» — его поле
не проникает за пределы выделенного объема. Эта идеализация
не соответствует действительности. Если от нее освободиться, то
принципиальное различие между объемными и открытыми резо-
наторам1И исчезает, и колебания в объемных резонаторах сле-
дует рассматривать, учитывая связь резонаторов с линиями пе-
редачи; этот круг вопросов лежит за пределами данной книги
(см., впрочем, § 70).
§ 69. О возбуждении открытых волноводов
Задачу о возбуждении открытых волноводов (гл. VIII) мож-
но поставить следующим образом: при данной частоте возбужде-
ния (о=с& построить (формальное) решение уравнений Максвел-
ла (67.01), причем источники поля — сторонние токи je и jm —
заданы, а открытый волновод характеризуется комплексными
проницаемостями е и р, удовлетворяющими соотношениям
(52.03) и (52.04). Если источники поля je и jm находятся на ко-
нечном расстоянии от оси волновода (оси z), то искомые поля
должны удовлетворять условиям
lim^rE = 0, lim ]/rH — 0 при Im£>0, (69.01)
Г-+ОО r-»O0
аналогичным условиям (67.02); здесь
г = (69.02)
есть расстояние от оси системы.
Простейшим примером открытого волновода является волно-
вод, однородный по оси z, когда е и ц вообще не зависят от z
(в частности, диэлектрический волновод или обычный волновод
с бесконечной продольной щелью, ср. § 56 и 57). Однако в общей
теории возбуждения учет периодичности волновода по оси z не
должен приводить к серьезным осложнениям.
Мы не будем здесь рассматривать задачу о возбуждении
открытых волноводов во всех подробностях и лишь наметим
путь, позволяющий получить ее общее решение.
Прежде всего нужно иметь в виду, что по собственным вол-
нам в открытых волноводах, изученным в гл. VIII, нельзя разла-
гать поле, возбуждаемое в бесконечном пространстве, хотя бы
потому, что они образуют дискретную систему, которая в беско-
нечном пространстве всегда будет неполной.
378
г
Собственные волны, экспоненциально возрастающие при
г—»оо, часто называют «квазисобственными», в то время
как название «собственных» сохраняется только за поверхност-
ными волнами. Вследствие неполноты этих волн для решения за-
дачи о возбуждении необходимо ввести собственные волны не-
прерывного спектра. Всего проще это сделать, мысленно окру-
жив открытый волновод идеально проводящей цилиндрической
оболочкой большого радиуса г, вводя собственные волны в таком
«закрытом» волноводе и затем переходя к пределу г—оо
(ср. § 63 и 66). При этом наряду с волнами непрерывного спек-
тра надо отдельно учитывать поверхностные волны, которые обо-
лочкой г=г практически не возмущаются (ср. [7], стр. 453).
Поскольку теория возбуждения закрытых волноводов, одно-
родных по своей длине, развита в весьма общих предположениях
(см. [7], гл. XIV или [67]) и поскольку ее обобщение на случай
периодических структур не представляет труда (см. [68]), фор-
мальное построение решения возможно, после чего из этого ре-
шения выделяются слагаемые, соответствующие «квазисобствен-
ным» волнам, которые при определенных условиях дают глав-
ный вклад в волновое поле.
Способом, близким к указанному выше, Шевченко [69]
и Карбовяк (см. [70], стр. 857 и [71]) решили некоторые частные
задачи о возбуждении однородных открытых систем. Возмож-
ность более общей постановки задачи (в частности, для перио-
дических структур) представляется полезной, поскольку квази-
собственные волны в открытых структурах могут иметь разно-
образные физические и технические применения: они не только
передают электромагнитную энергию, но и могут формировать
излучение антенн, взаимодействовать с электронными пучками
и т. д. (ср. [70], стр. 837—856); оказывается также, что так на-
зываемые аномалии Вуда в диффракционных решетках связаны
с возбуждением квазисобственных волн (см. [70], стр. 887—890).
Задачи к гл. X
1. Пользуясь методом, примененным в § 68, свести задачу Коши для ска-
лярного волнового уравнения (65.01) к задаче о возбуждении, рассмотренной
в § 64. Сравнить получаемые таким путем результаты с результатами § 65.
Решение. Обозначим для краткости через Ф(/) решение уравнения
(65.01), стремящееся при t -»оо к нулю, и введем функцию
оо оо
Ф(/г) dt, Ф (0 = J е-{к^Ф (k)dk. (а)
I 0 — со
Умножая уравнение (65.01) на eiticidt, интегрируя по t от 0 до оо и пользуясь
начальными условиями (65.02) и тождеством
f д2Ф (0 дФ(Г) f ЭФ(П
1 eikc‘ at— — —— ick I егкс< -' dt — — сФ’ + /с/гФ0 — №Ф(1г),
1 (71 (/€ 1 t/t
О (=0 о
379
получаем уравнение
lk f i \
ДФ(£) + Л2Ф (k) = — Г Ф« + -у ФЧ,
эквивалентное уравнение (64.01). Если приравнять правые части этих уравне-
ний, то мы получим
Ст(Х) = Dt (х) ~ Т £ Ct(X) 4- 7Г ct(x) j »
где с°(х) и с*(х) определяются формулами (65.04). Согласно формулам (64.03),
(64.04) и (а) мы имеем
Ф(0 = 2^ J е-’*с<-----------------------Ф,.х dx,
—00 X 0
причем в соответствии с § 68 интегрирование по k производится немного вы-
ше вещественной оси. Изменяя в этой формуле порядок интегрирования и
учитывая тождества (при />0)
— f e-ihct -kdk-= — re— iM:t , eixrfj
2л J е k2— X2 2 -i-е Л
СО
2л J k2—х2 2х ' '
приходим к формуле (65.05).
2. Для скалярного волнового уравнения можно поставить задачу: решить
уравнение
1 й2Ф
ДФ— = — 4лр(х, у, z, t)
при «анальных условиях (65.02) и граничных условиях (63.10); функция р
задана при t 3* 0, причем при t -» оо она стремится к нулю. Показать, что эта
более общая задача 'сводится к задачам, решенным в § 64 и 65.
Решение. Вводя функцию Ф(£) согласно формулам (а) задачи I и
таким же образом вводя функцию р(А), придем к уравнению
ilk f i \
ДФ (k) + k2<S>(k) = — 4лр(£) + — ( фо + ф* k
которое решается так же, как в вадаче 1.
3. Показать, что собственные (квазисобственные) функции Ф», соответ-
ствующие затухающим свободным колебаниям и определенные в начале § 63,
удовлетворяют условию ортогональности
lim I Ф«Ф£,</1/ = 0 при s£s',
i?-»coe'T^
где смысл предела тот же, что в формулах (63.48) и (63.49).
Решение. Полагая в теореме Грина (63.13)
Фа=Ф. и Ф₽ = Ф4.,
380
н учитывая условие (63.02) или (63.06), получаем тождество
$ - %,) J ф.ф„ dV = i (ks,~k.) г(к-+ ks,)^8.gs,dQ.
VR
Если R -»oo e<7 так, что экспонента, стоящая справа, стремится к нулю, то мы
приходим к тождеству
(fe2-fe2)Hm. f Ф.Ф.,ЙК = О,
S s R-ооеП) s
VR
из которого при ks £ks, следует условие ортогональности (неравенства
ka£ — ks, особо оговаривать не надо, поскольку оба колебания должны быть
затухающими). Если же ks=ks,,m условие ортогональности может быть вы-
полнено благодаря надлежащему определению собственных функций, соответ-
ствующих данной вырожденной частоте.
4. Формально применяя разложение (63.08) и пользуясь условием ортого-
нальности, полученным в предыдущей задаче, найти коэффициенты Сг при
возбуждении монохроматическими источниками с плотностью р (§ 64). Срав-
нить получаемое выражение с формулой (64.09).
Решение. Представляя искомую функцию в виде ряда (63.08) и под-
ставляя этот ряд в уравнение (64.01), после формального дифференцирования
получаем
5’(/гг-^)С.Ф. = -4«р.
Умножая на какую-нибудь функцию Ф,, интегрируя по VR и полагая R-►сое'7
в силу формулы (63.48) и условия ортогональности находим коэффициенты С,
•в виде
JfrdV
(О)
Это выражение похоже на формулу (64.09) и отличается тем. что вместо
2k(k— ks) здесь стоит k2— k?. При k^k, (вблизи резонанса) выражения (а)
и (64.09) близки, но если рассматривать весь ряд (63.08) то при k^ks малый
резонансный знаменатель согласно формуле (а) имеет также член, соответ-
ствующий колебанию с комплексной частотой—ck*,, так как прн будем
>иметь k2 ^s(k*s)2.
Таким образом, формальное применение ряда (63.08) дает при резонансе
примерно вдвое большую амплитуду, чем в действительности (результаты
§ 64 подтверждаются решениями частных задач, рассмотренных в гл. XI).
Как мы увидим в следующей задаче, применительно к задаче Коши формаль-
ное обращение с рядом (63.08) приводит к явному абсурду.
5. Формально применяя разложение (63.08), найти коэффициенты С,=
=Cs(t) для задачи Коши, рассмотренной в § 65. Сравнить получаемое выра-
жение с формулами (65.15) и (65.18).
Решение. Уравнение (65.01) приводит к тому, что коэффициенты Ce(t)
должны удовлетворять дифференциальному уравнению
^ + ^2С = 0,
т. е. иметь вид
С8 (t) = С+е~'А«с + C~eik‘ct. (а)
381
Jiwwwwwbr! интегрирования С* я Cs должны определяться из начальных
условий (65.02), а именно
£(с++ С7)ф«= ф*.
£ke (С+-С7)Ф. = /Ф*.
Поступая так же, как в задаче 4,
приходим к выражениям
<7- ssrf ('- + <7 Ф')ф-Л'- С‘ - яУ С” - ф’) Ф-‘Я'-
Постоянные С* и С~ получились в соответствии с формулами (65.15) и (65.18).
Однако в выражении (а) фигурирует сумма затухающего колебания (первое
слагаемое, пропорциональное С*} и колебания, нарастающего во времени
(второе слагаемое). Таким образом, при t—> оо поле в резонаторе согласно
формуле (а) неограниченно возрастает. Этот результат физически абсурден,
он показывает недопустимость формального применения разложения (63.08).
Надо отметить, что формулы (а) задач 4 и 5 тесно связаны друг с дру-
гом: неправильный резонансный знаменатель приводит к появлению нарастаю-
щего колебания. Из § 66 видно, что вблизи начального момента времени t=Q
поле нельзя представлять (даже приближенно) рядом (63.08); в формулах
(65.13) и (65.16) ряды определяют главную часть поля только при достаточно-
/ R, + R \
больших |/| I а именно, при |/| >—-— 1.
6. Известно, что шарик, помещенный в однородное электростатическое по-
ле Е, приобретает в нем электрический дипольный момент
Шарик, помещенный в однородное магнитное поле Н, приобретает магнитный!
момент
Pm — X^iH,
___Р- 1 з
Xm — (х _|_ 2 Г0‘
В этих формулах гв — радиус шарика, е и ц — его диэлектрическая и магнит-
ная проницаемости. Эти формулы можно считать применимыми и в неодно-
родных переменных полях, если радиус г0 достаточно мал (по сравнению-
с длиной волны в окружающей среде и в шарике); при этом для идеально-
проводящего шарика следует считать е=оо и р=0.
Вычислить смещение собственной частоты открытого резонатора, вызывае-
мое таким шариком при внесении его в резонатор.
Решение. Считая шарик носителем сторонних токов, сосредоточенных
в малом объеме, мы должны положить
= — Zope, = — i<opm,
где интегрирование производится по объему шарика. Формулы (67.20) и (67.21)<
дают соотношение
k
С‘ = — 2(k — kt)N, <РеЕ' — ₽тН«)-
где Е, и Н, надо взять в точке, в которой расположен шарик. Полагая
Ре == XeC*eEs, Pm =; ХтС*аНа,
382
из этого соотношения находим частоту свободных колебаний системы, со-
стоящей из открытого резонатора и шарика. Искомое смещение частоты
Лю8=с(^—ks) определяется формулой
—=--------— (х Е2 —х Н2)
в, 2NB 1 m
(о)
Такая же формула 'получается и для закрытого объемного резонатора. Этот
эффект можно применить для измерения распределения полей в резонаторах.
7. Электрический диполь с моментом ре в свободном пространстве излу-
чает мощность
<04
Ре = Зс5 1Ре12’
а мощность излучения магнитного диполя равна
„ <04
Рт— зсз |Рт|2.
Считая, что пробный шарик в открытом резонаторе (см. задачу 6) на возбуж-
дение 'нерезонаноного фона тратит мощность Ре+Р,л, вычислить дополнитель-
ное затухание, вызванное излучением шарика. Сравнить между собой прира-
щение частоты (задача 6) и приращение радиационного затухания, вызванные
шариком.
Решение. Дополнительное затухание открытого резонатора с шариком
вычисляется по формуле
Ре+Р,п
2W,
Д<о"8
где Ws—энергия резонатора. Если в определении нормы [см. формулу (66.24)]
ограничить интегрирование объемом резонатора (ср. § 72) и считать норму
вещественной положительной величиной, то можно положить W, —-^Ns, и мы
получим
Д<о", k*
В том же приближении формулу (а) предыдущей задачи можно переписать
следующим образом:
Д<о'. 1
2Nb (xe|E,|2-|-Xm|H,|2).
Поэтому
Ьа>',
•X. (krty.
и так как шарик предполагается малым (kra<^. 1, см. задачу 6), то это отно-
шение мало. Тем не менее приращение радиационного затухания может быть
использовано для измерения распределения поля в открытом резонаторе.
Соотношения, выведенные в задачах 6 и 7, применимы лишь при условии,
что приращение частоты Дщ„ под действием пробного тела мало по сравнению
с разностью частот данного колебания и колебаний, близких ему по частоте.
В противном случае нужно учитывать взаимодействие колебаний (ср. § 76).
8. Пусть открытый .резонатор возбуждается электрическим диполем, по-
мещенным между его зеркалами. Сравнить мощность, затрачиваемую на воз-
буждение изолированного резонансного колебания при <d=w'„ и мощность,
383
идущую на возбуждение нерезонансного фона. Воспользоваться задачами 6 и 7.
Решение. Согласно задаче 6 диполь при k~Rek, возбуждает s-e коле-
бание с амплитудой
<д/в Qs
С« = — 2ю",ЛГ, РеЕе = — Л? РеЕ*’
где
Q* ~ 2ы”,
есть добротность колебания. Мощность, затрачиваемая иа возбуждение этого
колебания, равна
Р. = |С,|г2и".и7, = |C.|2<o".JV„
где норма N, положительна (см. задачу 7). Если векторы р, и Е, парал-
лельны, то
И Ы-.
Согласно -задаче 7 мощность, излучаемая диполем при отсутствии резонанса,
равна Ре — мощности излучения в свободном пространстве. Отношение мощ-
ностей Р, и Ре равно
Л_=_з_Л l£»l2 . Jk
Ре 2 kaN.~bn &V.'
где величину
можно назвать эффективным объемом s-го колебания. В миллиметровом Диа-
P. ,
пазоне отношение р— порядка единицы или больше.
Глава XI
Возбуждение открытых резонаторов
(частные задачи)
§ 70. Одномерная модель
открытого резонатора
В гл. X изложена теория возбуждения колебаний в открытых
резонаторах. В этой теории существенную роль играет разложе-
ние по собственным функциям непрерывного спектра. Продемон-
стрируем применение этого разложения на простейшем примере
открытого резонатора, а именно на системе, изображенной на
рис. 78. Эта система состоит из полубесконечной коаксиальной
линии /<z<oo и резонатора 0<х</, возникшего в результате
расширения коаксиальной линии. К ней применяется теория
длинных линий, основанная на телеграфных уравнениях, причем
для простоты потерн не учитываются и скорость волн в линии
принимается равной с. Мы получаем одномерную задачу, кото-
рая формулируется так. Напряжение Ф(а, t) в неоднородной ли-
нии, изображенной на рис. 78, удовлетворяет одномерному вол-
новому уравнению
при 0<2<оо (70.01)
и граничным условиям:
Ф(0, о = о,
Ф(/ —0, 0 = Ф(^ + 0, 0,
<(/-0,0=я>(/+0,0,
(70.02)
(70.03)
где g> 1 есть отношение волнового сопротивления коаксиальной
линии (резонатора) 0<2</ к волновому сопротивлению коакси-
альной линии /<2<ОО.
25—2547
385
Затухающие собственные колебания резонатора 0<z</,
связанного с полубесконечной линией /<z<oo, мы получим,
полагая
Ф = Re {Ф8 (z) е~ ik‘ct} (70.04)
и требуя, чтобы функция Ф4 удовлетворяла условию излучения
Ф8 = Де А“г при z>/, (70.05)
где В — постоянная. Собственные частоты определяются соот-
ношением
ksl = r.s — ib, (s = 0,=t 1,±2,...),
th 8=-у, (70.06)
а собственные функции равны
<Ds=sin&,z при 0<z</; (70.07)
при z>/ они определяются формулой (70.05), в которой
Д = . (70.08)
2t
Oj --------- -------
U-------I ---------
РИС. 78. Одномерная модель.
Те же собственные частоты и те же собственные функции
(70.07) имеет закрытый резонатор 0<г</, в котором граничные
условия (70.03) заменены импедансным граничным условием
-^(/-0,/)=—^-f-^-0,0. (70.09)
Для такого закрытого резонатора разложение по собственным
функциям (70.07) затруднено, так как условие ортогональности
имеет следующий вид:
J ф. (2)ф . (2) dz + Ф8 (/) Фв, (/) = -L V• (70. Ю)
386
Если же относить функции Ф6 к открытому резонатору
(рис. 78), то условие ортогональности можно записать так:
! ОоеЙ
dz + g j ФеФ^2=48^’ (70.11)
о I
причем угол у выбирается таким, чтобы интеграл сходился. Од-
нако формальное разложение заданной функции Ф°(г) в ряд
Ф°(2)^ £ с°Фе(2) (70.12)
s=—00
с коэффициентами
г=4[(ф.Ф,
о
(70.13)
не представляет, вообще говоря, этой функции. Например, если
фв<2) = 2ГпРи Z<zo —Л<2<2о + Д. (70 14)
Ф°(2) = 0 при других z,
то соответствующий ей ряд
с°Ф8=-^- е'*,(г°+г> (2>Z) (70.15)
S=—00 S=—00
определяет совершенно иную функцию.
Поэтому задача о возбуждении и задача Коши не могут быть
решены с помощью разложения по функциям Ф8 (и по любым
другим, образующим дискретную систему, ср. § 63). Для реше-
ния таких задач нужна другая система собственных функций,
а именно собственные функции непрерывного спектра.
Введем функции Фх (г) с помощью соотношений
Ф = sinx2 при 0<z<7.
(70.16)
Фх =— Л(—х)е ,хг-|-Д(х) е'хг при Z<z<Z°o,
где
А (и) = (sin xZ------cos xZ) e~ ы. (70.17)
Функция
Ф(г, Z) = Re {Фх(г)е'хс/) (70.18)
удовлетворяет уравнению (70.01) и граничным условиям (70.02)
и (70.03) при любом значении х. Если же х и х' — веществен-
25*
387
ные положительные числа, то функции Фх и Фх, удовлетворя-
ют условию ортогональности
I со
[ [фх Фх, dz +фх ®x,dz ]=D (х) 8 (х - х'), (70.19)
о I
где
D (х) =----А (х) А (— х) = i (cos2 х/ + g2 sin2 х/).
Функции Фх являются собственными функциями непрерывного
спектра*, D(x)— их норма. Появление непрерывного спектра ес-
тественно, поскольку мы рассматриваем поле в полубесконечном
интервале 0 < z < оо. По функциям Фх (z) можно разлагать лю-
бые функции z, достаточно гладкие и достаточно быстро убываю-
щие при z -► оо. Пусть, например, нам задана функция р (z); пред-
ставим ее в виде интеграла
оо
о
(70.20)
тогда из условия (70.19) получаем
i
с М = "0^0 [ (Рфхdz +£ |рФх dz
6 i
(70.21)
Интеграл (70.20) имеет тот же характер, что интеграл Фурье,
и переходит в него при g—1. Поэтому формулы (70.20) и
(70.21) позволяют разложить функции р (z) достаточно широ-
кого класса. Мы получим из функции Фх функцию Ф3, если
положим x=ifes, где ks определяется формулой (70.06).
С помощью собственных функций непрерывного спектра не-
трудно решить задачу о возбуждении рассматриваемой системы
* В силу одномерности задачи введенные функции Фх не зависят от
индекса т, вводимого в общей теории трехмерных открытых резонаторов
(§ 63). Падающая плоская волна отражается от резонатора согласно второй
' формуле (70.16) с коэффициентом отражения
с- Л(*>
----Л(-Х) ’
который в данном случае играет роль оператора рассеяния; мы имеем также
, А(— х)
Г (х) ----T7V
' ' А (х)
Собственные функции Фх можно построить, рассматривая собственные коле-
бания отрезка 0 < z
делу L -» со.
<2Ф \
0 или =0 при z = L 1 и переходя к пре-
388
заданными монохроматическими источниками. Эта задача сво-
дится к неоднородному уравнению
(70.22)
^ + ^2Ф = -4«Р,
в котором p = p(z) есть заданная функция, а <о — ck — заданная
частота колебаний. Функция Ф должна удовлетворять таким же
граничным условиям (70.02) и (70.03); если, кроме того, функция
p(z) достаточно быстро убывает при г —оо (в дальнейшем мы
будем для простоты считать, что p(z) = 0 при z>z0), то долж-
но также удовлетворяться условие
Ф —0 при z — оо и 1шА:>0. (70.23)
Как эту задачу, так и задачу Коши нетрудно решить элементар-
ными средствами вследствие простоты модели. Мы применим
аппарат собственных функций непрерывного спектра, чтобы про-
верить его действие на таком примере, где все принципиальные
вопросы легко выяснить до конца.
Если ’«[представить заданную функцию р в виде интеграла
(70.20), то искомую функцию Ф (z) можно найти при Im k > 0 в
виде
Ф=СС(и)ФхсЬс, (70.24)
о
где
= (70-25)
Пользуясь соотношениями
Ф_х=~ Фх, с (— х) = — с (и), (70.26)
можем переписать интеграл (70.24) в виде
Ф
1
2fe
С -^-Ф dx.
&- X X
(70.27)
Если все источники лежат в резонаторе (p-АО лишь при 0<
< z < Z) и если точка наблюдения также находится в резонаторе,
то интеграл (70.27) можно вычислить по вычетам в точках x=£s,
поскольку подынтегральная функция при Im и -* — оо убывает
быстрее, чем e-'*(Z-z). В результате мы получаем
Ф= V Cs$s,
S=—ОО
(70.28)
389
где
i
J рФ, dz
г-----------2______
s — 2k (k-k.)N,
и
кг i dD /1 \ *
Ns ~~ ~2Z ~d7 — 8S ’
(70.29) .!
(70.30) '
В соответствии с формулами (70.10) и (70.11) можно также на-
писать
(70.31)
о
и
I соей
^ф2</2_|_£ J tfdz], (70.32)
поэтому величину Ns можно назвать нормой затухающего собст-
венного колебания с индексом s.
Формулы (70.28) — (70.30) показывают, что данная система
при малых значениях б (т. е. при 1) имеет резко выражен-
ные резонансные пики, эквидистантно расположенные на оси
частот. Норма свободных колебаний, определяющих эти резо-
нансы, совпадает согласно формуле (70.30) с нормой колебаний
б закрытом резонаторе тех же размеров (т. е. при 6=0 и
g=oo); таким образом, волна (70.05), бегущая от резонатора,
не оказывает влияния на норму.
Формулы (70.28) — (70.32) отличаются от формул, опреде-
ляющих возбуждение обычных объемных резонаторов (ср. [7}
или [64]) тем, что в них вместо резонансного знаменателя k"2—k?
стоит 2k (k—ks). Нужно отметить, что импедансное условие
(70.09) означает наличие сосредоточенного «резервуара энергии»
при z=/, из-за которого в формулах (70.10) и (70.31) появляют-
ся слагаемые, пропорциональные g. В обычной же теории воз-
буждения объемных резонаторов предполагается, что все элек-
тромагнитное поле имеет конечный объем, т. е. оно заключено
внутри замкнутой поверхности So и не имеет таких резервуаров.
Отсюда и возникают различия в резонансных знаменателях,
в выражениях для нормы и т. д.
Применительно к закрытому резонатору с импедансным усло-
вием (70.09) все возможные случаи исчерпываются формулой
(70.28), которую трудно было бы получить непосредственно, опи-
раясь только на формулы (70.07) и (70.10). Возвращаясь к си-
стеме, изображенной на рис. 78, будем теперь считать, что источ-
390
ники расположены внутри резонатора (при 0<2<20</), а точка
наблюдения — вне резонатора; в этом случае переход от интегра-
ла (70.27) к ряду (70.28) возможен лишь при условии
/<г<2/—zo, (70.33)
причем формулы (70.29) — (70.32) также остаются в силе.
С другой стороны, при 2о<Л и z>/ из интеграла (70.27) мож-
но получить простое выражение
Ф = Се’*\ (70.34)
б котором постоянная С равна
С=-----kgA^-k)~ Jp(z)sinfe^ (70.35)
о
и резонансные свойства определяются функцией Л(—k).
Пусть теперь функция p(z) отлична от нуля только в интер-
вале
/<zi<z<z2 (70.36)
вне резонатора. Тогда при z>z2 мы будем иметь бегущую волну
вида (70.34), при /<z<2i — стоячую волну; обе волны не обла-
дают резонансными свойствами. При 0<z</ из интеграла
(70.27) получается выражение
Ф = Со sin kz, (70.37)
где
<70-38»
21
причем резонансы опять определяются функцией А (—k) в зна-
менателе. В случаях, когда применимы формулы (70.35) и
(70.38), можно в функции Ф выделить резонансную часть и не-
резонансный фон (см. § 64 и задачу 1).
'Перейдем теперь к решению нестационарного волнового урав-
нения (70.01) с начальными условиями
Ф = Ф°(г) и -1_-^-=Ф1(2) при t=0 (70.39)
и граничными условиями (70.02) и (70.03). Это — задача Коши,
в которой обычно интересуются функцией Ф(г, t) при t>0. Ре-
шение этой задачи дается формулой (ср. § 65)
Ф (г, /) = J С+ (х) Фх (2) е~,хс< dx, (70.40)
391
где;
с*<«^м^г|](‘1-+4ф';ф-й2 +
о '
оо
I
(70.41)
Пусть функции Ф° и Ф1 отличны от нуля только в интервале
0<z<z0, где z0^> I; тогда при 1шх->-—оо функция С+ (х) -~-
-V. е‘Х (го-2,) j и при условии
ct >• z0 -f- z — 21 (70.42)
интеграл (70.40) можно представить в виде ряда вычетов
Ф(М= £ Cs^se~ik,st,
S=—OO
(70.43)
где
(70.44)
Условие (70.42) справедливо как при z>l, так и при z</. При
z>l оно имеет следующий смысл: в линии z>/ возбуждаются
две волны: одна бежит направо, другая — налево. С течением
времени край волны, бегущей налево, дойдет от точки z0 до точ-
ки I, отразится от нее и пройдет мимо точки наблюдения z; толь-
ко после этого поле в точке наблюдения целиком определится
колебаниями, возбужденными этой волной в резонаторе. При
0<z</ условие (70.42) имеет другой смысл: колебания в резо-
наторе полностью сформируются только после того, как та же
волна дойдет до начала координат, отразится от него и затем от
точки I и, вторично отразившись от начала координат, пройдет
мимо точки наблюдения г.
Если функции Ф° и Ф1 отличны от нуля только внутри резо-
натора, то при 0<z</ разложение (70.43) применимо для лю-
бых положительных t, а при z>/ — для таких t, при которых
передний фронт волны успеет дойти до точки наблюдения.
Таким образом, ряд (70.43) пригоден при достаточно боль-
ших t, скажем, при Г>Т, где Т зависит как от положения точки
наблюдения, так и от начальных условий. В общей теории (см.
§ 65 и 68) представление поля в виде суперпозиции слабозату-
хаюших свободных колебаний имеет такой же характер.
Все полученные выше результаты легко проверить непосред-
ственно. В задаче Коши можно, например, взять в качестве
Ф°(г) функцию (70.14), вычислить в явном виде все интегралы
392
и проверить, что найденная таким образом функция Ф(г, t) дает
решение задачи. Полученные соотношения иллюстрируют мате-
матический аппарат, использованный в общей теории возбужде-
ния открытых резонаторов, и основные результаты этой теории.
Фактически все принципиальные вопросы были выяснены на
этой модели, и лишь после этого была построена общая теория,
изложенная в гл. X.
Эта простая модель показывает также, что реальные объем-
ные резонаторы, связанные с одним или несколькими волново-
дами, представляют собой системы с непрерывным спектром.
Это обстоятельство должно учитываться при построении общей
теории возбуждения таких систем.
§71. Возбуждение шара
радиальным диполем
Простейшей трехмерной системой, для которой можно по-
строить в явном виде собственные функции непрерывного спек-
тра, является однородный изотропный шар, свободные колебания
которого были исследованы в § 58 и 59.
Пусть однородный шар радиусом а с проницаемостями ей ц
возбуждается радиальным электрическим диполем, находящим-
ся в точке R—Ro, '©=0. Вне шара — пустота («=^.= 1 при R>a),
диполь может быть как вне шара, так и внутри него, р — мо-
мент диполя, (» = ck—частота. Возбуждаемое поле выражается
(ср. § 58) через скалярную функцию U=U (R, &):
• flssin» д» /’ » R дядй ’
Нужные нам собственные функции непрерывного спектра равны
и0п. х (R, 8) = [£<” (х) Л'1 ’ (х/?) - (х) Л'2) (х A?)] Pn (cos 8) при R > а,
UOn.t /?)Pn(cos&) при R<a, (71.02)
где функции jn, и hl„ определены так же, как в § 58, а
fiW(x)=^-у- ]'п (х j/eu. a) h^\%d) — jn (х a) h^' (на),
^2)(и)= v (х а) — jn (и /ер a) h^' (на).
(71.03)
393
Подставляя функции UOn * в формулы (71.01), где k заменено
на х, найдем векторные функции ЕОп х и НОп х. Функции Uтп х
зависящие от координаты <р, в нашей задаче не нужны.
Решение поставленной задачи имеет вид
[7 = 2 f7«P"(C0S&)’ (71.04)
л=0
где
Пп = (7'4-[7^ (71.05)
причем и*п соответствуют поперечному, a — продольному элек-
трическому полю. Величины Uln находим, решая электростатичес-
кую задачу. При R0^>a имеем:
2«+’ Я"+1
U” р (е + 1) «4-1 ^п+2 при/?<а,
T1i _„Fi । (Е—1)(«+ О f a \2n+,l Я"+1 r, n
P 1 + (fl J J Rn+2 ПрИ «<£</?„,
(71.06)
p i -f- (e + i)n+i «0 J J рп пРил;>/<0,
а при 7?0<a:
и1 — p Г1 j*-1)» / \2n+1] ^n+1 ппи p - p
Un e P (e + 1)«4- 1 ( a ) J Rn+2 ПРИ^^^о,
jP Г i (e — / R \2n + 11 n
U” el1 (e-|-l)n-|-l ( a J J ’ fl" nPH
(71.07)
[7* — П 2« + 1 Rn0~' D \ ZV
и — ^(е4-1)п+1 Rn
Величины и*п находим из общей теории (§ 67), заменяя диполь
сосредоточенным электрическим током и пользуясь выражениями
В(2)(х)
G..(x) = 4«(- 1)«'^±Ди-(В“’(х)1‘,
(71.08)
О„ (х)= - 2« « S»' (х) в;»(х).
394
В силу тождества Рп(1) = 1 результат можно записать так:
U4
п
kp
4я^о
(2«+1)
du.
(71.09)
Таким образом, полученное решение имеет вид интеграла по пе-
ременной и, имеющей смысл волнового числа. Правильность фор-
мулы (71.09) нетрудно проверить, дополняя ее слагаемым U1 и
пользуясь теоремой о вычетах; при R>a мы получаем явное
выражение
(71.10)
и формулы (71.01) и (71.04) дают нам решение в виде разложе-
ния по сферическим гармоникам, совпадающего с хорошо из-
вестными классическими рядами (ср. [17], § 1 или [19], стр. 192—
194).
Интеграл (71.09) можно преобразовать, деформируя путь ин-
тегрирования вниз. Подынтегральная функция в этом интеграле
мероморфна, что легко усмотреть из свойств функций (58.05),
причем в точке х=0 она регулярна. В нижней полуплоскости
Imx<0 ее полюсы совпадают с корнями уравнения Вл2) (х)=0,
т. е. с корнями уравнения (58.06). Возможность представления
интеграла (71.09) в виде суммы вычетов в точках knq — корнях
уравнения (58.06) — определяется только поведением подынте-
гральной функции при Imx—►—оо.
Ограничимся вещественными положительными значениями |/"ер..
При /?0 и R^>a подынтегральная функция в нижней полуплос-
кости возрастает как е‘х №+/?~2а>> поэтому интеграл по замыкаю-
щей полуокружности | х | = К при К со не исчезает и интеграл
(71.09) к одним вычетам свести нельзя. При Ro<a и R<a это
сведение всегда возможно. При Ro>a и R<a интеграл сводится
к вычетам при условии
Я0~л</^Г(л — R), (71.11)
аналогичном условию (70.33). Однако возможность сведения ин-
теграла (71.09) к сумме вычетов не связана непосредственно
с резонансными свойствами шара. Последние определяются су-
ществованием полюсов knq с достаточно малой мнимой частью,
а также существованием неперекрывающихся резонансных кри-
вых, т. е. расположением полюсов knq в области Д', примыкаю-
щей к вещественной оси (ср. § 64). В задаче Коши собственные
колебания проявляются более полно, в частности, даже для
395
идеально проводящего шара (§ 59) при достаточно больших
положительных t можно наблюдать любое колебание.
Для шара как функция Umn х, так и функция
ф = U™- * (71.12)
mnt х >
удовлетворяющая скалярному волновому уравнению (63.09),
являются целыми функциями х, а соответствующие им функции
I’mn(x), Gnin(x), Dmn(x)—мероморфные функции х. Эти свой-
ства сохраняются (см. [65] и [72]) в более общем случае, когда
уравнение (63.09) заменяется уравнением
ЛФ+[х2— У(7?)]Ф = 0, (71.13)
где функция V(R) удовлетворяет условию
У=0 при R>R. (71.14)
Заменяя V (/?) на V (х, у, г), мы приходим к квантовомехани-
ческим задачам, рассмотренным Титчмаршем [73] и другими авто-
рами. Если функция V (х, у, г) удовлетворяет условию (71.14), то
для построения решений можно применить собственные функции,
вводимые так же, как в § 63, однако исследование поведения
функций Фч х, Г (х), GT (х), DT (х) в плоскости комплексного пере-
менного х становится делом гораздо более трудным. К интере-
сующим нас задачам с зеркалами, на поверхности которых вы-
полняется граничное условие (63.02), можно перейти, полагая
У=оо в объеме зеркал и V=0 вне зеркал.
§ 72. Вычисление нормы Ns
В общей теории возбуждения открытых резонаторов фигури-
рует норма Ns, которая для скалярного волнового поля опреде-
ляется формулами (63.45) пли (63.48). Оба этих определения не
позволяют фактически вычислить норму Ns, поэтому вопрос о ее
вычислении следует рассмотреть особо. Поскольку Ns имеет
смысл энергии, запасенной в поле собственного колебания, мож-
но предположить [ср. замечание к формулам (70.30) — (70.32)],
что Ns фактически определяется не интегралом по бесконечному
пространству, а интегралом по рабочему объему резонатора,
т. е. по объему между зеркалами, а за пределами этого объема
поле сводится к слабым уходящим волнам, влиянием которых
на норму можно пренебречь. Результат, полученный ниже, под-
тверждает это предположение (см. также § 73).
Вычислим норму (63.45) для колебаний в резонаторах с плос-
кими зеркалами. Введем вспомогательную функцию Ф5 х, удовлет-
396
воряющую волновому уравнению (63.09), условию излучения
п₽и (72.01)
и переходящую в функцию Ф8 при х —* ks. Применяя к функциям
ФЛ. х и Фг формулу Грина (63.13) и пользуясь граничным услови-
ем (63.02), имеем
(х--^)Иш. (72.02)
R-»Ooe'T J "
VR So
где Ло — поверхность зеркал, а ----производная по нормали, на-
правленной внутрь зеркал. При х ks мы получаем выражение
1
8п£, Л ди
So
dS,
(72.03)
удобное для вычисления Ns.
Вычисляя норму в том же приближении, в каком рассчитаны
сами функции Ф,„ мы можем ограничиться интегрированием по
освещенной поверхности зеркал. Если они одинаковы, парал-
лельны и расположены друг против друга при z=±l, т. е. на
расстоянии 21, то справедлива приближенная формула
х I _ I дФ.
ди |x=*s ks дп
При 2 = ±/.
(72.04)
Она вытекает из того, что функцию Ф5 между зеркалами можно
представить в виде (см. гл. I)
фв = Ws (х, у, z) Р - (- 1)ч We (х, у, - z) , (72.05)
где функция зависит от координат х, у, z и волнового числа
ks гораздо слабее, чем множители е±,л,г ; поэтому функция Фа х
будет (при Kxks) приближенно определяться выражением (72.05),
в котором множители е±,А®г заменены множителями е* . При диф-
ференцировании этих множителей мы и приходим к формуле
(72.04)
Формулы (72.03) и (72.04) приводят к выражению
(72.06)
где интеграл берется по освещенной поверхности Si одного из
зеркал. Это выражение уже позволяет вычислить Ns> если функ-
ция Ф8 в объеме между зеркалами известна. При желании по-
верхностный интеграл (72.06) можно преобразовать в объемный.
397
Действительно, согласно результатам гл. I вместо формулы
(72.05) для функции <DS можно написать выражение
Ф6 — fs (х, у) cos —~ при нечетных <?,
(72.07)
<bs = fs(x, y)s\n~~ при четных q,
причем ks ~ -gp • Подставляя эти выражения в формулу (72.06),
получаем
He=^f2.(*,y)dS (72.08)
Si
или
(72.09)
Vo
где Vo — объем открытого резонатора, ограниченный зеркалами
z=±/ и образующими, параллельными оси г и проходящими
через края зеркал.
С помощью таких же рассуждений можно вывести формулу
(72.06) для колебаний в открытых резонаторах с цилиндриче-
скими и сферическими зеркалами, а также в цилиндрических и
бочкообразных резонаторах.
Пользоваться поверхностными интегралами (72.06) и (72.08)
для вычисления нормы удобнее, чем объемным интегралом
(72.09). В следующем параграфе мы покажем, что выражение
для нормы в виде поверхностного интеграла может быть выве-
дено непосредственно из интегрального уравнения, и вычислим
норму для колебаний в резонаторах с софокусными зеркалами
(гл. VII).
§ 73. Интегральное уравнение
и норма колебаний
между софокусными зеркалами
Рассмотрим возбуждение открытых резонаторов, пользуясь
интегральными уравнениями, выведенными в гл. I—V. Пусть
при каждом собственном колебании плотность тока f на отра-
жающих поверхностях, образующих открытый резонатор, удов-
летворяет уравнению
(73.01)
(73.02)
где
398
есть собственное значение этого уравнения, a G — линейный опе-
ратор, не зависящий от А и симметричный, т. е. удовлетворяю-
щий соотношению
<fe.Gf₽)=<f₽, Gfa)
(73.03)
для любой пары функций fa и fp; символ ( ) обозначает скаляр-
ное произведение функций.
Если и — собственные функции уравнения (73.01), и
— соответствующие им собственные значения, то из уравнения
(73.01) и соотношения (73.03) без труда выводится условие орто-
гональности
(73.04)
где 8^, есть символ Кронекера, а
(73.05)
— норма собственной функции Ц. Как всегда, условие ортогональ-
ности (73.04) выводится при а при Zx==Zv его выполне-
ние достигается путем надлежащего определения собственных
функций, соответствующих каждому вырожденному собственному
значению.
Теория свободных колебаний открытых резонаторов, образо-
ванных зеркалами, путем ряда аппроксимаций (параболическое
уравнение, параксиальность лучей и т. д.) приводит к уравне-
ниям вида (73.01). Например, для двухмерных колебаний откры-
того резонатора, образованного цилиндрическими зеркалами
шириной 2а (по оси х), выводится интегральное уравнение
(ср- § 14).
f (х) = е'х J G (х, х') f (х') dx', (73.06)
—a
являющееся частным случаем уравнения (73.01). Комплексная
частота ы — ck каждого колебания определяется формулой
2kl=nq+%,
(73.07)
где 2/ — максимальное расстояние между зеркалами, q— боль-
шое целое число. Комплексное ядро уравнения (73.06) является
симметричным
G(x, x') = G(x', х),
(73.08)
399
поэтому соотношение (73.03) удовлетворится, если скалярное
произведение определить формулами
7 (73.09)
(fa » Gf₽) = JJG Л') fa <*) f? (X'f dX dX'-
—a
Норма в этом случае равна
Nx = j fx(x)dx. (73.10)
В результате комплексности G собственные значения также в
общем случае комплексны. Ядро G зависит от волнового числа k,
, я<7
но в нем можно считать, что k = в теории возбуждения це-
лесообразно брать k соответствующим частоте возбуждения.
Аналогичные формулы можно написать для трехмерных ко-
лебаний, например для колебаний в открытых резонаторах со
сферическими зеркалами (ср. § 21). При этом функция f зависит
от двух переменных, так что уравнение (73.01) усложняется,
а индекс т есть краткая запись двух индексов (скажем, т
и п). Для резонаторов, обладающих симметрией вращения, усло-
вие ортогональности (73.04) выполняется, если зависимость от
<р взята в виде cos пир и sin т<р, а не в виде 屑""₽.
Во всех случаях норма Nx определяется интегралом по отра-
жающей поверхности.
Переходя от свободных колебаний к вынужденным, мы за-
меняем однородное уравнение (73.01) неоднородным уравнением
f=XG.f+/°, (73.11)
где заданная функция /° определяет локальную плотность тока,
создаваемую на отражающей поверхности источниками, воз-
буждающими поле (без учета взаимодействия токов на различ-
ных элементах поверхности). Параметр IX связан с вещественной
частотой возбуждения u>=ck формулами (73.02) и (73.07).
Известную функцию [° и искомую функцию f можно разло-
жить в ряды
Г = (73.12)
и
Г = (73.13)
400
Коэффициенты с° легко найти, если воспользоваться условием
(73.04); отсюда
Подставляя разложение (73.13) в уравнение (73.11), находим коэф-
фициенты <?х в виде
(73.15)
Полученные выше формулы по внешнему виду отличаются от
выражений, выведенных в гл. X, однако согласуются с ними прак-
тически. При этом следует учесть, что при резонансный
знаменатель 1 — в формуле (73.15) пропорционален резонанс-
ному знаменателю k — ks. Нормы Nx и Ne также пропорциональны,
как следует из результатов § 72. Выкладки, проведенные выше,
показывают, что выражение для нормы в виде интеграла по
освещенной поверхности зеркал (см. § 72) есть прямое следст-
вие интегрального уравнения, используемого для расчета диф-
фракционных явлений в открытых резонаторах. Таким образом
можно прийти к выводу, что во всех случаях, когда мы полу-
чаем интегральные уравнения данного типа (гл. I—V), норма
определяется формулой (72.06); этот вывод уже был сделан
в § 72.
В качестве примера вычислим нормы колебаний в резонато-
рах с софокусными зеркалами (гл. VII). Собственные функции
f(t), исследованные в гл. VII, удовлетворяют дифференциально-
му уравнению и определенным условиям при 1=0 и/=1. Пара-
метр © в дифференциальном уравнении подбирается так, чтобы
оба условия удовлетворялись одновременно. При произвольном
© мы вводим функцию F(t, ©), удовлетворяющую тому же диф-
ференциальному уравнению
^ + c27’(/,6)F = 0,
(73.16)
что и функция f(t), и одному из условий для последней, а именно:
(73.17)
26—2547
401
Для функции F можно написать асимптотические выражения
(49.07) и (49.08), но в силу произвольности © вместо выражения
(49.03) мы будем иметь
[/ j (jc) cos е-|-/z , (?c)sine],
m--2" т-~Г
где
П I (-«) = У -o-^raU)
(73.18)
(73.19)
есть второе решение уравнения (47.12), выражающееся через
функцию Неймана
При собственных значениях 0’мы имеем е = 0 и F = f. Комби-
нируя дифференциальные уравнения для функций f и F при разных
значениях 0 и затем неограниченно сближая эти значения,
ем тождество
1
t
dF dF
ре dt
р d'F
dQdt '
получа-
(73.20)
в правой части! которого после дифференцирований нужно взять
собственное значение © и е=0. Приближенно дифференцируя
функцию (73.18) и пользуясь тождеством
j' । (х)п I (х) — j J (Л-) п' ! (л-) = — 1, (73.21)
т_ __ — т- — т- —
получаем
1
с! р2 (0 dt = — Е'г . (73.22)
о
Величины В и определяются так. При ти> 1 и х^>т
формула (73.18) принимает вид
f=i7^s4ckr^‘®-+v]- <7323>
Отсюда (ср. § 49) мы получаем соотношения
С j/Жё) dt + £10 (у) - е = (2п + 1) ~ (л=0,1,2,...)
(73.24)
402
и
Г е2** I 1
В = i (-1)" 1/ е . (73.25)
Формула (73.22) принимает вид
(73.26)
о
где
H = + (73.27)
и
t,
J, __ 1 Г___________tdt____________
2 J W-ф (*?-<*)(<!-<*) ’
'° (73.28)
*2
J, ______1_ Г idt
— 2 J й*8 - Ф а1-Ф (*!-<’) ’
При т = мы имеем t0 = 0, и интегралы Г и J’ приводят-
ся к полным эллиптическим интегралам 1-го рода
(73.29)
с модулями k и k'. Формулы (73.28)
-i- и v <-----. В крайних точках
и (73.29) применимы при
они имеют вид
н= ' Г1п8с + 41п(1-4-)-О.(4-)1щ>н *=4-
4K'-T V (73.30)
Я— / 4^ + 4‘n(1 + 4)-O,(4)]n|«v=-4
Для колебаний переходного типа, при-< v < , можно
пользоваться приближенной формулой
/7 = 4-(ln8c-ni(v)l.
(73.31)
26*
403
согласующейся с формулами (73.30) с точностью до членов по-
рядка -i-. Функция Qj (v) в этих формулах определяется выраже-
ниями
Q, (v)_— In j/1 —4v2 =~^~ arcX(v)4-ln2v=
РИС. 79. Функция £2i(v).
-iv)+to2. (73.32)
Она изображена на рис. 79.
Функция Q] (v) является чет-
ной функцией своего аргу-
мента, причем
Q, (0) = — 1,2704,
, (73.33)
О,1750.
При больших положитель-
ных v мы имеем
(73.34)
и норма (73.26) экспоненци-
ально велика; это объясня-
ется тем, что функция f(t)
в середине зеркала прини-
мает значения, гораздо боль-
шие, чем у краев. При боль-
ших отрицательных v
<7335)
так что норма (73.26) мала.
Как показано в § 49, диффракционные потери при т—
= 0, 1,2,... можно в первом приближении рассчитывать по та-
ким же формулам, что и в случае т=±Ч2. В том же приближе-
нии величина Н определяется простыми выражениями (73.29) —
(73.35).
§ 74. Возбуждение открытого резонатора,
образованного параллельными дисками
Пусть открытый резонатор, рассмотренный в § 6, возбуждает-
ся сосредоточенным источником, помещенным в начало коорди-
нат, который в отсутствие зеркал (6.01) создавал бы сфериче-
скую волну
К Гг+г2 ’
(74.01)
404
а при наличии зеркал создает волновое поле, удовлетворяющее
волновому уравнению
ДФ +^2ф=—4лб (х)Ъ(у) б (г) (74.02)
и граничному условию Ф=0 на зеркалах, причем Ф есть четная
функция координаты г.
Поставленная задача в электродинамике соответствует [см.
формулы (3.55).— (3.57)] элементарному электрическому дипо-
лю, направленному по оси х или у и помещенному в точку х=
=y=z=0 между идеально проводящими дисками.
Если зеркала представляют собой бесконечные плоскости
z—±l, то искомую функцию из соображений симметрии можно
записать в виде ряда
Ф = ЪАЧ Н™ (krq г) cos (kzq z), (74.03)
в котором
kzq = ^-, krq = V~kr-k-zq , («7=1,3,...), (74.04)
а выбор функций Ханкеля диктуется условием излучения (рас-
ходящиеся волны при г-»оо). Постоянные Ад проще всего опре-
делить, применяя теорему Грина (63.13) к искомой функции Фик
функции
Jo(^?r)cos(^9z). (74.05)
Беря в качестве объема интегрирования цилиндр радиусом г
между плоскостями z—±l и учитывая, что функция Ф удовлет-
воряет неоднородному уравнению (74.02), а функция (74.05) —
такому же однородному уравнению, мы в силу тождества
J cos (kzq z) cos (kgq, z) dz = l\Q, (74.06)
—i
придем к соотношению
4л = 2rJAq krq r [H™ (krq r) J'„ (krq r) - Jo (krq r)H^’(krq r)]=
= — 4ilAq, (74.07)
откуда
Aq . (74.08)
Если зеркала конечны и представляют собой круглые диски
радиусом а, то в пространстве между дисками поле принимает
вид
Ф=Т У [^о1 г) + 2Г* 7о (krq r)l cos (kzq z). (74.09)
405
Постоянные Г, определяют амплитуды волн, возникших в ре-
зультате отражения первичных волн (74.03) от края г=а; вто-
ричное поле, обусловленное отражением от края, уже не может
иметь особенностей при г=0 и поэтому выражается через функ-
ции Бесселя Jo.
Вычислим постоянные Гч при условиях
(74.10)
когда согласно гл. I волна с индексом q должна испытывать
сильное отражение от края г—а. Формулу (6.16) для коэффи-
циента отражения этой волны можно переписать в виде
/?9>9 = _e'₽(1+'')s’, (74.11)
поскольку для симметричных волн допустимо положить
Q'o(von) = 1. Пользуясь другими аппроксимациями, использован-
ными в § 6, мы получим соотношение
(7412)
здесь согласно формулам (6.11) и (6.14) имеем
£}„ (х) = аге 77‘” (Л-) +-J-, (74.13)
(74.14)
где Von есть n-й нуль функции Jo(x).
Формулы (74.11) и (74.1,2) приводят к следующему выраже-
нию:
Г9 =-----, (74.15)
—' |2s0 (5- sq j + ₽(l + i)se j
® котором параметр M определяется формулой (6.08), причем вол-
новое число k соответствует частоте возбуждения. Пользуясь фор-
к» 2v
.мулой (6.15), при можно записать это выражение так:
Г<7 = ехр {«(М + ₽ + i₽)(sn, - s,)} - 1 ’ (74‘16)
.где комплексный параметр
О____
(74.17)
согласно формуле (6.09) соответствует собственной частоте ко-
лебаний, а вещественный параметр sq— частоте возбуждения.
406
Таким образом, коэффициент Г, имеет резонансный характер,,
и при sq~snq выражение (74.16) принимает вид
г =-------------------=
4 (Ж + Р + Ф><««—«•«>
I
(74.18)
Резонансное слагаемое в формуле (74.09) согласуется с об-
щей теорией возбуждения открытых резонаторов (§ 64); а имен-
но вычет функции (74.09) в полюсе k—ks равен (см. задачу 6)
вычету, вычисляемому по общим формулам (64.07) и (64.09).
Вместе с тем, формулы (74.15) — (74.18) позволяют найти форму
резонансной кривой, соответствующей взятому возбуждению.
Стандартная форма резонансной кривой определяется выраже-
нием
Г<7-ш --u'nq (74.19)
откуда
ip | г ___________________I I2_____
I (CO-+ (<->W
Выражение (74.19) получается, если полагать
^“^=£’1 (74.21У
w—co
1 nq
однако в некоторых случаях следует пользоваться более точны-
ми выражениями, например
Sq = 2 \/\k — kzq) I При k =b k2q.
(74.22>
Подобные вычисления представляют интерес потому, что при
экспериментальном исследовании открытых резонаторов с пло-
скими зеркалами часто получаются асимметричные резонансные
кривые (см., например, [74],стр. 411).
Задачи к гл. XI
1. Пользуясь тем, что при k^k, можно положить
А (—k) ~—А' (—k,) (k—k.), A (—k,) = 0
[функция А (х) определяется формулой (70.17)], показать, что вычеты функ-
ций (70.34) и (70.37) в полюсах k=k, равны вычетам функции (70.28) в тех
же полюсах. Вычет функции Ф(й) в простом полюсе k=ks определяется вы-
ражением
f, = lim (й —
k-*ks
Найти иерезонансный фон.
407
Решение. Согласно формулам (70.28)—(70.30)
I
4л f
re = lim(ft — £,)Ф = — I P®adz.
k~^k ® J
* о
(с)
В силу соотношений (70.06) мы имеем
А' (— ka) =
Ze8
2ch6*
откуда по формуле (70.34) получаем вычет
4 г°
г, = — Век“г Jp (z) sin ksz dz,
о
а по формуле (70.37) — вычет
za
4я Г , iksz .
r,=— £-j-sin&ezip(z)Be 8 dz,
Z,
где В определяется формулой (70.08). Оба выражения совпадают с формулой
(а). Разность
ф-£ А
&
определяет нерезонансный фон, который также можно представить в виде
интеграла, аналогичного (64.08).
2. Построить собственные функции непрерывного спектра для скалярного
волнового уравнения при отсутствии зеркал (т. е. в однородном свободном
пространстве). Вычислить величины , Г, и Gx для этих функций. Найти
оператор S.
Решение. Собственные функции непрерывного спектра зависят от ин-
дексов т, п и мепрерывного параметра %. С учетом формулы (58.05) их мож-
но записать в ваде
®ПИ. I— Рти (у, ’>) *
где Утп — сферические функции, которые можно определить так:-
Kmn = cosm^n (cos 6) (m = 0, 1.п).
Уmn= sin (— m<f) Р{п m)(cos6) (m=—1, —2,..., —n).
Таким образом, индекс т заменяется двумя индексами т к п. В силу асимп-
тотической формулы
/п (-*) = COS — (п + 1) J при X -► оо
мы имеем
rmn=(-l)n+>, Gmn = (- !)"+ e|m| (2п+ 1} [п + Ц,,
причем эти величины не зависят от х (ео=1, ei=e2= ... =2). Соотношение
in (—х) =(—!) n+ljn (х)
приводит к тому, что
£mn=(—1)"+*.
408
В свободном пространстве без зеркал оператор S превращает функцию
ф) в функцию %(©, ф)=—х°(л—О, л+ф); перемена знака обусловлена
(асимптотическим) скачком фазы в фокусе /?=0 (§ 22).
3. Построить собственные функции непрерывного спектра для скалярного
волнового уравнения при наличии шара, на поверхности R = а которого ста-
вится условие Ф = 0. Вычислить величины £х, 1\ и Gx.
Решение. Собственные функции непрерывного спектра определяются
формулой
Л _v ач ^\xa)h^(xR)-h^Xa)h^(xR)
Фтп, V) ---------------—--------------
где сферические функции Ymn те же, что ив предыдущей задаче. Величины £тп
те же, а
(хс)
Гтп (х) — (—1)" Л(2) ,
Gmn (х) - (—1)"+* (2n -J- 1) (п - |т!Я (х°Н2-
Функция Гтп (х) обращается в нуль при fi^(xa) = 0; корни этого уравнения
изображены на правой половине рис. 71.
4. Вывести выражение для нормы [аналогичное выражению (72.06)] при'
дФ. п
граничном условии = 0 на зеркалах.
Решение. В этом случае вместо соотношения (72.03) из формулы Гри-
на получается соотношение
•So
Заменяя в формуле (72.05) —(—1)’ на +(—1)«. получаем соотношение
<Э’Фвх I
дхдп |«=*. = ~ к‘1Ф° ПРИ 2 = ± 1'
аналогичное формуле (72.04). Отсюда имеем
N‘ = T^^dS-
Si
5. Установить связь между нормами (V, н Nx (§ 73) при условии, что функ-
ция fT(x, у) в формулах (73.05) и (73.10) и функция W,(x, у, z) в формуле-
(72.05) связаны соотношением
We(x, у, -l)=f^x.y).
Решение. Из формулы (72.05) при z = — / получаем
= 2iksW, (х, у, —I) e~‘k*1 = 2iktfz (х, у) е ‘k,t
поэтому по формуле (72.06)
N. = - J fl (х. у) dS = (- 1)«+* e~,ZTNx.
Si
409
Комплексная величина есть собственное значение интегрального уравнения
<73.01); она определяет комплексную частоту колебаний по формуле (73.07).
6. Показать, что вычет функции (74.09) в полюсе k—k, совпадает с вы-
четом, вычисленным по общим формулам (64.07) и (64.09). Воспользоваться
результатами задач 1 и 5.
Решение. Согласно формулам (64.07) и (64.09) мы имеем
г. = “ 2^» Фа f pa>sdV‘
В данном случае следует положить
(vOnr \ nqz
--------! 7~Г~ lcos “2Г ’
+₽~лг) /
поэтому по формуле (72.06)
тде мы применили приближенную формулу
-9. . . .9 , , 2 Von
/oW + 'i при х=--------j7p-===von;
’ + ₽~ЛГ
•следовательно,
В то же время из формул (74.17) и (74.18) вытекает, что при k -> k, можно
записать Г, в виде
.>2
______ISnq____________пд _____tVpn
« ~ 2von (sg — Snq) 2vOn/(/!— k*) 2kea2 (k—k„y
тогда согласно формуле (74.09) мы получаем ту же формулу для вычета г„
что и выше.
7. Обобщить формулы (74.03) и (74.08) на случай, когда источник рас-
положен в точке го на оси г.
Решение. В этом случае
^0 cos (^ze2o) cos (kIqz) +
9=1,3,...
9=2, 4, ...
sin (^igz0) sin (kzqz).
где klq и krq определяются формулами (74.04) при всех целых значениях <?.
8. Решить двухмерную задачу, аналогичную задаче, решенной в § 74;
а именно решить двухмерное волновое уравнение
(Рф ()2ф
д^+д^- + = - 4"8(x)3(z)
410
при граничном условии Ф=0 на зеркалах резонатора, рассмотренного в § 4
(рис. 6). Исследовать резонансы.
Решение. Мы ищем поле Ф между двумя бесконечными плоскостями.
z=±/ в виде
Ф = S>l9e1Ax«|JC'cos (&xgz),
где
^«9 = kxt — (<]— 1» 3, ...).
Применяя теорему Грина в прямоугольнике —х0<х <^х0. —/<z<^Z к функ-_
цин Ф н к функции
е tkx9x cos (kzqz),
получаем
2(эт
Л,== W'
Для зеркал конечной ширины 2а представим волновое поле в виде
Ф=ЕЛд [е£*х’М + 2гд cos (/гхдл)] cos (/г2дг).
При условии
мы получаем коэффициент Гд в виде
1
~ -<(M + ₽+<₽)sg *
е -f* I
Он имеет четко выраженный резонансный характер:
—1 „
Г’ ^(Al + p + ifXs,— smg) при s« =5=Sm’ = Л4+₽ + '₽ (m= *’ 3’ ")
9. Исследовать поведение волнового поля, полученного в предыдущей за-,
даче, при k-*kzq. Сравнить с поведением трехмерного волнового поля, най-
денного в § 74.
Решение. При k-*kzq, когда kxq -» 0, коэффициент Г, можно пред-
ставить в виде
1
Г« — 2
р + ikxqa + ₽ Л4
Коэффициент Aq стремится к бесконечности, однако q е слагаемое в выраже-
нии для Ф остается конечным, а именно:
2пГ Г 1 + i\ , 1
ф« I [а (j + ₽ М J ~
cos (kzqz) при kxq -»0.
(п).
В трехмерной задаче Aq и Гд конечны при k->kzq, поэтому первичное
поле, пропорциональное (krqr), при;/г-»^1д становится логарифмически
бесконечным. Этот результат неправилен, поскольку при г>0 полное поле
должно быть конечным; он показывает недостаточность примененных аппрок-
симаций при krq = 0 (правильное решение дано в задаче 11).
411.
10. Показать, что формулу (а) предыдущей задачи можно вывести еле- В
дующим образом: мы ищем поле Ф(х, г) в виде |
Ф = ^’₽,(х)СО8^(9=1,3,...) 1
9 Я
и получаем для функций V, обыкновенное дифференциальное уравнение ]
й’Ф, , 4л 1
-^- + ^ч=—Г8^- |
Решая это уравнение при kxq—G вместе с граничным условием 1
ЙФ, л/'~к 1—1
— прн^ = «. ]
аналогичным условию | (61.03), вывести формулу ,(а) задачи. 9. j
Решение. Умножая уравнение (а) задачи 8 на cos(kxqz), интегрируя I
по z от —I до I и пользуясь соотношением (74.06), получаем приведенное 1
выше уравнение для '1%. В силу соотношения '
jp |х| = 28 (х) *
.общее выражение для функции Ф5 (х) при kxq = 0 имеет вид <
2л ;
^^—(л-и). ;
-где А — неизвестная постоянная. Находя эту постоянную из граничного ус- .1
.ловия, которое можно переписать в виде у
₽(i + o 1
Фв=-------а-^ при х = а,
получаем <
f 1 + 1 \
Л-oHff м к
/•
11. Применяя метод, развитый в предыдущей задаче, исследовать q-e \
слагаемое в разложении (74.09) при krq—0. Сравнить значения этого слагае-
мого при krq=0 н прн резонансе, когда ?
/гГа = ~7 о . (n= 1, 2...(
Ч1+^) :
Решение. Представляя решение уравнения (74.02) в виде
Ф — ЕФ q (г) cos (klqz) (<7 = 1. 3, ...),
яолучаем для функции уравнение
-5^-+-^- + ^,=-—«(Х)8(Р).
412
Общее решение этого уравнения, зависящее только от г, имеет при krq“=O сле-
дующий вид:
2 г
= —Т1П-Л’
где А — неопределенная постоянная. Действительно, мы имеем тождество
дп ds~
4п
~г
для любого контура С, охватывающего начало координат г=0. Постоянная А
находится из граничного условия
*3 =
₽(1 + 0
— М а dr
при г = а
в виде
₽1±£
А = ае М = а
М
В резонансе функция ф9 по порядку величины в д— раз больше, чем при
'О 71
&rq — О-
12. Составить интегральное уравнение (73.11) для задачи, рассмотренной
в § 74. Показать, что решения согласно § 73 и 64 получаются эквивалентными
(т. е. что резонансные слагаемые практически равны). Воспользоваться резуль-
татом, полученным в задаче 5.
Решение. Обозначим полное поле через Ф+Ф°. -функцию Ф мы можем
представить в виде (ср. гл. I)
Ф = Г(г. z)e<*« + r (г,—z)e-<fts
а функцию Ф°, определяемую формулой (74.01), в соответствующем виде
Ставя граничное условие
ф фо == 0 при z= ±1, 0 < г < а,
приходам к соотношению
W(,r,—l) = — W (г. 1) es<hl — Ф° (г, 1)е‘*«.
которое приводит нас к интегральному уравнению
(Jt \ a Ik
)Г (krr’X
е (r’)r'dr' + fe(r)
о
для функции
f(r) = U7(r, -/).
причем
i*?
ег«м 21
f"(r) =— Ф° (г. /)е<Л,=— —— е
и
%=2feZ—nq
(q нечетное).
413
Полученное интегральное уравнение для функции f(r) можно записать,
в виде (73.11). Собственные функции соответствующего однородного уравне-
ния согласно § 6 приближенно равны
fn =
причем в силу условия М 1 можно положить
а . kr*
Г 1 2Г . . . , и .
I е f„ (г) rdr
о
это приближенное выражение получается, если проинтегрировать по частям и
учесть, что f«(r) меняется гораздо медленнее, чем экспонента. Таким образом,
исходя из § 73, мы можем написать
о 2я f л . , г . • 2яе2«*« . 2ле*х
С"~Л\г] fn(r)f^(r)rdr----------‘ ы/п -1 kNn'
О
Согласно задаче 5 при нечетных q
а
lV„ = 2n f f2n(r)rdr = -^-elnN.,
о
поэтому, образуя по формуле (73.15)
1 — е‘<х-х"’ ’
будем иметь
1
lim (А —Лв)с„ = —т-г7
й-»А, K»/v
или
lim (k k,) f (r)-------------. д, f„ (r).
(°)
В силу соотношений [ср. формулу (6.03)]
_ _ ,-х
Ф, = 2е 2 fn (г) cos , Ф = 2е 2 f (г) cos
для уравнения (74.02) имеем
fXn
p®.dV = 2e 2 ,
следовательно, соотношение (а) согласуется с формулами (64.07) и (64.09).
Таким образом, все три способа решения данной задачи, изложенные
в § 64, 73 и 74, приводят к эквивалентным результатам.
414
Глава XII
Открытые резонаторы
в физике и технике
§ 75. Применения открытых резонаторов
и открытых волноводов
Поскольку развитие теории открытых резонаторов и откры-
тых волноводов вызвано потребностями физики и техники, в кон-
це нашей книги мы кратко рассмотрим некоторые применения
открытых систем, не входя в экспериментальные детали и не
пытаясь исчерпать всех возможностей.
Как было отмечено в § 1, открытые резонаторы 'были впер-
вые предложены в качестве колебательных систем для оптиче-
ских квантовых генераторов. Это применение открытых резона-
торов не потеряло своей популярности до сих пор, поэтому в пер-
вую очередь мы рассмотрим применение открытых резонаторов
в электронике как квантовой, так и классической (§ 76). От-
крытые резонаторы широко применяются для различных изме-
рений, которым посвящен § 77.
Как неоднократно отмечалось ранее (§ 1, 7, 39 и т. д.), от-
крытые резонаторы имеют гораздо более редкий спектр собст-
венных частот, чем закрытые резонаторы тех же размеров.
Однако во многих применениях этот редкий спектр оказывается
слишком густым и возникает потребность в его дополнительном
разрежении. Открытые резонаторы с дополнительным разреже-
нием спектра рассмотрены в § 78.
Два следующих параграфа (§ 79 и 80) посвящены примене-
нию открытых резонаторов в качестве антенн, а § 81 содержит
решение задачи об оптимальной передаче энергии между двумя
апертурами; это решение тесно связано со свойствами открытых
резонаторов и открытых волноводов.
Открытые резонаторы определенной формы позволяют осу-
ществить фокусировку электромагнитных волн, благодаря чему
415
в небольшом объеме создается интенсивное высокочастотное по-
ле. В § 82 высказано предположение, что такая фокусировка
приводит к появлению шаровой молнии.
О применениях открытых волноводов мы в этой главе гово-
рить не будем и ограничимся сказанным в гл. VIII и § 69 (см.,
впрочем, конец § 76).
Отметим, что все полученные теоретические результаты без
всякого труда переносятся на звуковые волны, их можно рас-
пространить и на волны другой природы (в упругих телах, на
поверхности жидкости и т. д.). Что же касается практических
применений, то все они ограничиваются электромагнитными вол-
нами, а для звуковых, упругих и других волн почти ничего не
сделано: по-видимому, время для этого еще не пришло.
§ 76. Открытые резонаторы
в электронике
Рассмотрим применение открытых резонаторов в квантовой
электронике, ограничиваясь для определенности генераторами.
Самовозбуждение в таких системах можно трактовать как след-
ствие изменения комплексной диэлектрической или магнитной
проницаемости вещества, заполняющего открытый резонатор,
под влиянием накачки (при этом активное вещество, имеющее
отрицательные потери и способное поддерживать незатухающие
колебания, определяется условиями (76.12), см. ниже).
Пусть открытый резонатор, определяемый соотношениями
(66.01) — (66.03), имеет собственные колебания, электромагнит-
ное поле которых удовлетворяет уравнениям (66.06). Собствен-
ные колебания в возмущенной системе, проницаемости которой
®=е+бе и р.=ц+б|1 (76.01)
слегка отличаются от проницаемостей (66.01) исходной системы,
получаются из уравнений Максвелла
rot E = iA(p.-|-8|x) Н, rot Н = —zft(e-|-8e) Е, (76.02)
которые можно переписать в виде
rotE = f^H —у jm, rotH = — iteE + y je, (76.03)
где
Г = SsE. (76.04)
Таким образом, однородные уравнения в возмущенной системе
сводятся к неоднородным уравнениям в исходной невозмущен-
ной системе. Это обстоятельство позволяет, пренебрегая нерезо-
нансными членами, искать каждое собственное колебание в воз-
416
мущенной системе в виде линейной комбинации невозмущенных
собственных колебаний
Е —У С\Е(, Н~ (76.05)
5 S
Формулы (67.20) и (67.21) дают для коэффициентов Cs выражение
cs = - 8^ J (8sEEs - 8И HHS) dV, (76.06)
в правую часть которого надо подставить разложения (76. 05).
Тогда мы придем к системе однородных уравнений для коэффи-
циентов Cs:
(l-^G + J^C^O, (76.07)
sr
в которой величины
=ж j(Se EsEs’ -8[Х (76.08)
являются малыми в силу формулы (66.24) они имеют порядок
Й1Х
цли — , если изменение е или у. происходит во всем объеме, за-
Iх
нятом полемj.
Система (76.07) имеет нетривиальное решение, если волно-
вое число k, определяющее комплексную частоту колебания,
есть решение уравнения
Се,||(1-т) 8..-+'и.||=°- (76-09)
В формулах (76.05) — (76.09) должны учитываться все колеба-
ния, попадающие при данном k в резонанс. Уточнение этой
формулировки будет дано ниже, а сначала мы рассмотрим изо-
лированное собственное колебание, не взаимодействующее с дру-
гими при возмущении системы, вследствие чего в выражениях
(76.05) надо учитывать только один член, соответствующий это-
му колебанию с индексом $.
Уравнение (76.09) для изолированного колебания имеет корень
k= ks, где
(76.10)
Таким образом, под влиянием возмущения изменяется частота
каждого изолированного колебания. При вещественных значе-
27—2547 417
ниях де и dp величину £ss для добротного колебания в резонато-
ре с малыми потерями можно считать вещественной, так что по
формуле (76.10) мы .получаем в 'первом приближении смещение
частоты без изменения коэффициента затухания. При комплекс-
ных de и dp величина £ss также будет комплексной, и ее можно
записать в виде
?ss==,6ss-b^'nss- (76.11)
При отрицательных потерях, когда в активном веществе
Imde<0 или 1тбр<0, (76.12)
мы можем получить отрицательное значение t)ss, и при условии
1 Ь”
(76.13)
возмущенное колебание из затухающего становится нарастаю-
щим. 1 •
Для того чтобы выяснить, при каких условиях колебание
можно считать изолированным, учтем в формулах (76.05) 'два;
слагаемых, соответствующих колебаниям с волновыми числами
k\ и k2. Уравнение (76.09) тогда принимает вид
(1 - Т + “ Т )=U„. (76.14)
Вводя обозначения
С = 1/ ж KWT (76.15)
У (1 + «п)(1+ад * f
и
£ 0 + ^)0-У) ~ гДг ~ k° (S = 1 и 2), (76.16)
можно уравнение (76.14) переписать в виде
(а—а,)^—Аг)=еГ1Гг. (76.17)
Это — типичное уравнение связанных или взаимодействующих
колебаний (ср. § 61). Если положить
х = -^Ь-, A=^±^(l+{/), (76.18)
2 I k,kt
то решение квадратного уравнения (76.17) приводит к формуле
(76.19)
418
в которой, вообще говоря, все величины комплексны. Если вы-
полняется условие
<7б-2°)
то соответствующее колебание будет нарастать во времени.
Обозначим через kF> и А(2) корни уравнения (76.17), которые
определяются формулами (76.18) и (76.19). Нетрудно показать,
что при условии
И>П (76.21);
? 2
с относительной ошибкой порядка — можно полагать
k™ = ks, (76.22)
как если бы колебания были 'изолированными. Таким образом, при
условии
|fe1-\|>2/|C12C21feJ,| (76.23)
взаимодействием двух колебаний можно пренебречь и считать их
изолированными. Легко показать, что при k = k<l’> в этом случае
Cj>C2, а при k = k<-2’>, наоборот, С2 > Сг; здесь и в дальнейшем
при оценке различных коэффициентов Cs мы считаем, что все
рассматриваемые колебания нормированы одинаково (напри-
мер, все Ns=l или NS=V, где V — некоторый объем).
Это условие показывает, что даже очень слабое возмущение
приводит к взаимодействию колебаний, если спектр собственных
частот является достаточно густым. Под взаимодействием коле-
баний мы понимаем перестройку собственных функций под
влиянием возмущения, когда разложения (76.05) не могут быть
заменены одним членом, т. е. когда новые собственные функции
выражаются в виде линейной комбинации двух или большего
числа собственных функций исходной системы, причем коэффи-
циенты Cs в этой линейной комбинации имеют одинаковый по-
рядок. Взаимодействие колебаний, ведущее к перестройке си-
стемы собственных функций, происходит также вследствие не-
однородности зеркал (см. [94]).
Следует отметить, что в условие (76.23) входит разность
комплексных частот, а не просто разность частот. Поэтому ко-
лебания с существенно разными коэффициентами затухания не
взаимодействуют друг с другом, благодаря чему возможно раз-
режение спектра резонансных частот, о котором неоднократно
говорилось ранее (§ 1, 7 и т. д.).
Выше мы рассматривали самовозбуждение колебаний, ха-
рактеризуя активное состояние рабочего вещества величинами
бе и бц. В реальных системах малые возмущения бе и бц могут
27* 419
быть также вызваны неоднородностью среды, градиентами тем-
пературы и другими факторами, в результате которых собствен-
ные колебания отличны от колебаний идеальной системы. Соот-
ношения, полученные выше, позволяют ответить на вопрос: в ка-
ких случаях собственные функции мало изменяются под дей-
ствием малых возмущающих факторов, а в каких случаях изме-
нение собственных функций будет сильным. Этот ответ заклю-
чается в условии (76.23), примененном к любой паре колебаний
с близкими частотами; если условие (76.23) выполняется, то
собственные функции относятся к изолированным колебаниям
и изменяется незначительно, в противном случае возмущающие
факторы приведут к перестройке системы собственных функций,
т. е. к радикальному их изменению. Таким образом, резонаторы
со слишком густым спектром являются в каком-то смысле не-
определенными системами, поскольку их собственные колеба-
ния перестраиваются под влиянием ничтожно малых возмуще-
ний, эта перестройка не всегда сопровождается перекрытием
резонансных кривых (§ 7).
Выше были рассмотрены собственные колебания, зависимость
от времени предполагалась в виде e~z<0/ —e-iftci. В более слож-
ных случаях надо пользоваться выражениями для напряженностей
поля
Е (0 = Re { £ Cs (/) Ese-'“' }, Н (t) = Re {£ Cs (/) Н8е~'ш/}, (76.24)
s s
а не для их комплексных амплитуд, как ранее при написании
формул (76.05). В этих выражениях через со обозначена часто-
та, характеризующая данную совокупность колебаний (средняя
частота или какая-нибудь иная, в дальнейшем мы считаем
Imco = O), (причем коэффициенты Cs(t) — медленно меняющиеся
функции времени. Для функций Cs(t) можно написать систему
дифференциальных уравнений
+ -= (76-25)
S'
при постоянных Cs переходящую в систему (76.07). При обоб-
щении системы (76.07) на случай нестационарного (процесса
вместо (76.25) естественно написать более сложную систему
уравнений
".)С. +J C„.(<‘C,.+/^) = °, . (76.26)
S'
r dCs,
однако члены i,ss, являются произведениями двух малых вели-
чин и поэтому могут быть опущены. Правильность этих систем
всего проще проверить, полагая
Cs(0 = Cf(0)e-'w. (76.27)
420
Система уравнений (76.25), как мы видим, получается из
весьма общих .предположений, она применима как для открытых,
•так и для закрытых резонаторов. Эта система может быть при-
менена для построения нелинейной теории квантовых генерато-
ров, когда 'величины бе и др, а поэтому и коэффициенты Css,
являются медленно меняющимися функциями времени, причем
эту систему следует дополнить соотношениями, связывающими
де и др с электромагнитным полем и вытекающими из кванто-
вой теории излучения. Для оптических квантовых генераторов
в простейшем случае можно положить (ср. [75]):
де=—iKn, др=О, (76.28)
где п=«2—«1 (76.29)
есть так называемая плотность инверсной заселенности; п2 и
«1 — концентрация атомов, -находящихся на верхнем и нижнем
уровнях генерации, а коэффициент К определяется формулой
4^ (76.30)
в которой е и т — заряд и масса электрона, f— сила осцилля-
тора, у — ширина линии поглощения. Инверсная заселенность п,
входящая в первую формулу (76.28), удовлетворяет уравнению
где величина 1 характеризует интенсивность накачки, т — время
жизни возбужденного состояния, обусловленное спонтанным
излучением, а величина
“’=s|SC-WE*
S
(76.32)
есть плотность электромагнитной энергии, определяющей в фор-
муле (76.31) индуцированное излучение. А — квантовая постоян-
ная.
Взаимодействие колебаний в генераторе обусловлено тем,
что де зависит от координат и времени в соответствии с формула-
ми (76.28), (76.31) и (76.32). Поскольку при взаимодействии
колебаний система уравнений существенно усложняется, ее при-
ходится численно решать на электронных вычислительных ма-
шинах (лишь для двух колебаний 'некоторые результаты можно
получить аналитическим путем, см. {76]). Как показано в рабо-
тах {75] и [76], взаимодействие колебаний приводит к пульсациям
мощности генератора (в частности, к яичковому режиму). Та-
ким образом, работа генератора существенным образом зависит
от того, сколько добротных собственных колебаний имеется
в том диапазоне частот, где активное вещество способно поддер-
421
живать генерацию. Если таких колебаний много, то квантовый
генератор является сложной нелинейной колебательной систе-
мой со многими степенями свободы (каждому эффективно воз-»
буждаемому колебанию соответствует одна степень свободы).
Если же колебание только одно, то свойства генератора сущест-
венно упрощаются — его теория становится аналогичной теории
обычного триодного генератора с обратной связью, имеющего
одну степень свободы; ib частности, формулы (76.10) — (76.13)
позволяют рассчитать самовозбуждение такого квантового гене-
ратора.
Оптический квантовый генератор, работающий на одном ко-
лебании, по-видимому, будет обладать рядом преимуществ перед
генераторами со многими колебаниями. Осуществление такого
генератора требует создания открытого резонатора с достаточ-
но редким спектром (§ 78).
Характер спектра колебательной системы вблизи рабочей
частоты генератора имеет существенное значение и в вакуумной
электронике.
Так, в многорезонаторных магнетронах сантиметрового диа-
пазона обычно используется л-колебание, при котором поля
соседних резонаторов сдвинуты по фазе на л. Связь между
резонаторами приводит к появлению целого спектра собствен-
ных частот. Если не принимать особых мер, то вследствие того,
что связь между соседними резонаторами наиболее сильна,
спектр сгущается вблизи частоты л-колебания (см., например,
177]).
Разрежение спектра собственных частот в магнетронных ге-
нераторах приводит к более стабильной работе и к возможности
получать большие мощности. Обычно в магнетронах спектр
разрежается в результате применения связок, увеличивающих
связь между дальними резонаторами, или же в результате при-
менения колебательных систем, состоящих из разных резонато-
ров. В мощном магнетронном генераторе непрерывного дейст-
вия— ниготроне [78]—используется симметричное колебание
Н0{д в цилиндрическом резонаторе, первая пространственная
гармоника которого (возникающая вследствие того, что анод-
ный и катодный блоки имеют периодическую структуру) син-
хронна с электронным облаком, т. е. ее фазовая скорость близка
к скорости дрейфа электронов. В ниготронной колебательной
системе сгущения спектра вблизи частоты колебания HOiq нет,
так как другие колебания этой системы имеют иное распределе-
ние поля и зависят от других параметров. Колебание H0lq может
быть применено для стабилизации л-колебания в многорезона-
торных магнетронах [79], оно заменяет связки и увеличивает
добротность л-колебания (так называемый коаксиальный ма-
гнетрон) .
Из сказанного видно, что проблема разрежения спектра ко-
лебательных систем важна и в обычной вакуумной электронике
422
сверхвысоких частот. Возбуждение резонаторов электронными
потоками можно рассматривать как 'влияние сторонних токов
или же как .результат 'изменения проницаемости пространства
под действием электронов.
В вакуумных электронных приборах миллиметрового и суб-
миллиметрового (.диапазона весьма перспективно применение от-
крытых резонаторов. Если, открытый резонатор образован глад-
кими отражающими поверхностями, расположенными в вакууме
(ср. гл. I—VI), то надо учесть, что в таком резонаторе отсут-
ствуют медленные волны. Поэтому для синхронного взаимодей-
ствия полей и электронов целесообразно применять в соответ-
ствии с идеями Гапонова [80] криволинейные электронные пучки.
Так как .фазовая скорость поля вблизи каустики 'приблизительно
равна скорости света, то колебания с (каустиками могут быть
эффективно возбуждены релятивистскими электронными сгу-
стками, пролетающими вблизи каустики (ср. § 31).
Для синхронного взаимодействия с прямолинейными нереля-
тивистскими пучками электронов необходимо создать открытый
резонатор с медленной волпой, 'например, используя резонатор,
заполненный диэлектриком [81] или имеющий, как ниготронный
резонатор [78], медленные пространственные гармоники.
Поскольку до последнего времени экспериментальные работы
по применению открытых (резонаторов в вакуумной электронике
практически отсутствовали *, к высказанным выше общим сооб-
ражениям можно добавить только (следующее. Электронный при-
бор, использующий в (качестве колебательной системы открытый
резонатор, имеет целый ряд преимуществ по сравнению с обыч-
ными электронными приборами, которые используют объемные
резонаторы, связанные с (волноводами. Делю в том, что открытый
резонатор сам по себе может служить передающей или прием-
ной антенной; для этого .достаточно сделать одно из зеркал слег-
ка прозрачным (ср. § 79). Поле в открытом резонаторе легко
связать с направленной антенной, открытым волноводом или же
с измерительной системой (§ 77).
Говоря короче, практически все применения электромагнит-
ных волн миллиметрового и субмиллиметро1В01го диапазонов име-
ют квазиоптический характер, т. е. связаны с устройствами, раз-
меры которых гораздо больше длины волны. В этих диапазонах
волн электроника неизбежно должна основываться на квази-
оптических устройствах, т. е. открытых резонаторах и открытых
врлноводах.
Для полноты следует упомянуть об электромагнитных вол-
нах, излучаемых при прохождении прямолинейного электронного
пучка вблизи поверхности диэлектрика или вблизи периодиче-
ской структуры. Известно, что электроны, движущиеся равно-
мерно и прямолинейно в диэлектрике со сверхсветовой скоро^
* Лишь совсем недавно .появились статьи [99] и [102].
423
стью или вблизи диффракционной решетки, излучают (излуче-
ние Вавилова — Черенкова и излучение Смита — Парселла; по-
следнее используется в варотроне [84]). Поэтому электронный
пучок, предварительно промодулированный и пропущенный
вблизи диэлектрика или периодической структуры, создает элек-
тромагнитные волны. Если же электронный пучок 'первоначаль-
но однороден, то согласно теории Палоша и Олинера (см. [74],
стр. 217—233) излучение электромагнитной волны при неболь-
шой модуляции пучка сопровождается нарастанием модуляции
в самом пучке (нарастающая электронная волна), вследствие чего
рассматриваемая система подобна лампе с бегущей {или обрат-
ной) волной, т. е. .может быть превращена в усилитель или са-
мовозбуждающийся генератор (по крайней мере в принципе).
§ 77. Открытые резонаторы
в измерительной технике
Открытые резонаторы в последние годы используются (в мил-
лиметровом’и примыкающих к нему диапазонах) для измерения
частоты колебаний, диэлектрических и магнитных проницаемо-
стей различных веществ, а также для диагностики плазмы (см.,
например, [100]). Мы не будем приводить здесь ссылок на лите-
ратуру, поскольку публикации довольно многочисленны. Отме-
тим только, что все способы возбуждения колебаний в открытых
резонаторах можно разбить на две категории: распределенное
возбуждение и сосредоточенное возбуждение.
Распределенное возбуждение заключается, например, в том,
что слегка прозрачное зеркало открытого резонатора облучает-
ся волной, которая по своей структуре близка к плоской волне
и тем самым к волне, соответствующей собственному колебанию
в резонаторе; облучающая волна, как правило, формируется
с помощью рупора и линзы. Сосредоточенное возбуждение — это
возбуждение с помощью небольших антенн (диполей) или не-
посредственно открытым концом волновода (который целесооб-
разно диафрагмировать для уменьшения связи, ср. [82]).
Сравнивая распределенное возбуждение с сосредоточенным,
следует прежде всего сказать, что распределенное возбуждение
является для открытых резонаторов более естественным, при
нем потери на трансформацию малы, так как они обусловлены
главным образом той частью облучающей волны, которая про-
ходит мимо зеркала. При распределенном возбуждении резо-
нансные свойства системы проявляются даже в том случае,
когда она работает как интерферометр Фабри—-Перо, а не как
открытый резонатор (см. ниже). Сосредоточенное возбуждение
более естественно с точки зрения той аппаратуры миллиметро-
вого диапазона, которая применяется в настоящее время (гене-
раторы и усилители, связанные с волноводными трактами).
Однако при сосредоточенном возбуждении заметная часть мощ-
424
ности тратится на лрямое излучение (возбуждение нерезонанс-
ного фона). В миллиметровом диапазоне, при больших доброт-
ностях резонатора, мощность сосредоточенного возбуждения ре-
зонансного колебания по порядку величины равна мощности
нерезонансного излучения или превышает ее в несколько раз-
(ср. задачу 8 к гл. X). Резонансы при сосредоточенном возбуж-
дении наблюдаются только тогда, когда резонансные кривые
достаточно остры и четко отделены друг от друга.
Если в длинноволновой части миллиметрового диапазона из-
мерения можно производить в волноводах и объемных резона-
торах или сочетать измерения в открытых системах с волновод-
ными измерениями, то на более коротких волнах практически:
единственным волноводным элементом остается рупор, присоеди-
ненный к выходному волноводу генератора, а применение осталь-
ных волноводных узлов, широко используемых в сантиметро-
вом диапазоне, становится почти невозможным. Иначе говоря,,
все измерения приходится переносить в свободное .пространство,
применяя вместо волноводных элементов оптические (зеркала,
линзы, диффракционные решетки).
В последнее время для измерительных установок короткого
миллиметрового и субмиллиметрового диапазонов были предло-
жены и использованы (в работах Ирисовой и др. [83]) элементы,,
принципиально отличные от оптических, — решетки, образован-
ные тонкими параллельными металлическими проволочками и
имеющие период, значительно меньший длины волны; эти про-
волочки прикреплены к оправе—плоскому металлическому
кольцу, радиус которого гораздо больше длины волны (практи-
чески этот радиус а был равен 50 или '100 мм).
Такая решетка обладает анизотропной проводимостью: элек-
тромагнитная волна, поляризованная параллельно проволочкам,
почти полностью отражается от решетки, как от хорошо прово-
дящего зеркала, а электромагнитная -волна, поляризованная7
перпендикулярно проволочкам, проходит через решетку почти
без отражения. В диапазоне длин волн от 4 до 0,5 мм применя-
лись решетки с периодом от 150 до 40 мк и диаметром проволо-
чек от 15 до 8 мк. Коэффициент отражения по мощности от та-
ких решеток (при нормальном падении и параллельной поля-
ризации) был больше 0,998, причем коэффициент отражения
слабо зависел от длины волны.
Комбинируя такие решетки, можно осуществить поляризато-
ры, анализаторы, аттенюаторы и делители для волн, близких
к плоским. Две параллельные решетки, установленные на опти-
ческой скамье, образуют открытый резонатор с плоскими зер-
калами круговой формы или же интерферометр Фабри — Перо.
Вопрос о том, как называть систему из двух решеток при опре-
деленном расстоянии между ними — резонатором или интерфе-
рометром— легко решается при сосредоточенном возбуждении.
Если, например, при возбуждении диполем или малым отвер-
425
стием в центре одного из зеркал наблюдаются резонансы, то
систему следует считать резонатором, если же резонансы на-
блюдаются только при возбуждении плоской волной, причем ре-
зонансные кривые, соответствующие колебаниям с различными
радиальными индексами п, сливаются в одну кривую, то си-
стема работает как интерферометр. Конечно, граница между ре-
зонатором и интерферометром не является резкой, так как при
непрерывном изменении длины волны, или расстояния между
зеркалами, или других параметров свойства системы также из-
меняются 'непрерывно.
Поскольку система из двух параллельных решеток приме-
няется (см. [83]) и тогда, когда между решетками укладывается
сравнительно небольшое число .полуволн, теория, развитая в § 6
при ’условии
(77.01)
т. е. когда число полуволн q велико, нуждается в модификации.
Ниже мы рассмотрим собственные колебания между идеально
проводящими параллельными дисками радиусом а при произ-
вольных значениях q (q=\, 2, 3, ...), а затем оценим влияние
прозрачности и анизотропии решеток.
Как показано в гл. I, добротные собственные колебания
в открытых резонаторах с плоскими зеркалами круговой формы
определяются тем, что при условии
(77.02)
коэффициент отражения волноводной волны с радиальным волно-
вым числом kr от края г—а близок к единице. При условии <?>1
этот коэффициент отражения определяется формулой (2.18), кото-
рая при <7^1 уже неприменима.
Если к открытому концу плоского волновода, стенки которо-
го определяются соотношениями (3.01), подходит волна
(см. конец § 3), то согласно строгой теории диффракции на от-
крытом конце единственная составляющая Еу электрического
поля внутри волновода имеет вид
Ey = fE(x)cos -§- + • • • при q=l, 3, . . . ,
где
£» = M*)sin^4-. • - при 9 = 2,4, . . . ,
(77.03)
(77.04)
426
а коэффициент отражения /?£ равен
(77.05)
Многоточие в формуле (77.03) указывает на присутствие волн
других номеров (q±2, q±4, ...), амплитуды которых при усло-
вии s<^l малы; для распространяющихся волн это видно из за-
кона сохранения энергии. Все эти соотношения вместе с пара-
метрами и р"Е легко получаются из общих формул, приведен-
ных в книге [8]. В случае падения волны магнитное' поле
имеет единственную составляющую
Hv = fH(x)s[n^r + • • • ПРИ <7 = 1, 3, ... ,
Hy=fH(x)cos^-[-. . . при q = 2, 4, . . . , (77.06)
где
И
a z —Л ik
(77.07)
(77.08)
причем величины kx и s определяются теми же соотношениями,
что и выше. Параметры р', р"£, Р"я и р" —-----%--- зависят от
индекса q\ эта зависимость изображена на рис. 80, причем для
наглядности по оси ординат отложены разности р'—р и т. д.,
стремящиеся к нулю при q—-оо (р = 0,824).
Вместо того, чтобы пользоваться коэффициентами отражения
(77.05) и (77.08), можно подчинить функции fE и f н граничным
условиям
Z7 dfE
fE^'+irEWTk-rx
при х = + 0,
(77.09)
f / dfLj
427
аналогичным (4.23). Эти условия приводят к выражениям для коэф-
фициентов отражения, которые при s 1 практически совпадают
с формулами (77.05) и (77.08)*.
РИС. 80. Параметры, входящие в формулы (77.05) и (77.08), при различ-
ных q,
Переходя к собственным колебаниям между дисками, мы будем
выражать электромагнитные поля этих колебаний через составляю-
щие электрического и магнитного векторов Герца
Пе = — ГГ AJm № cos sin
* KK? Xt
при q= 1,3,...
II m= BJ„ (krr) sin (m<f> Д- <p0) cos
z UK?
(77.10)
* Отметим, что условия (77.09) справедливы и для поля, зависимость кото-
+ ik>J t. , L
рого от координаты у определяется множителем е v , cos kvy или sin kyy.
В этом случае составляющие Ev и Ну удовлетворяют в плоскости xz двухмер-
ному волновому уравнению с волновым числом j/”k2 — , поэтому, на-
пример, формула (71.08) остается справедливой (при s<^l). если считать
s = k
т.ц
k — 2/----2k~/ 1 ПрИ
Это обстоятельство позволяет исследовать собственные колебания в резо-
наторе, образованном дисками, при произвольном азимутальном -индексе т
(см. ниже).
428
или
п* = Д AJm (k,r) cos cos
при </ = 2,4, . . (77.11)
ПГ=WrBJm sin ^m<f + Vo) sin
fer
тогда окажется, что 'с относительной погрешностью порядка
зависимость составляющих Е и Нт от радиуса-вектора г опреде-
ляется функцией
f£(r) = CJm_I(^r)4-D/m+l(M,] I (77.12)
а зависимость Ег и Н,. — функцией
f н (г) = CJm _, (krr) — DJm+1 (k,.r), (77.13)
где
C = A-\-B, D = A — B; (77.14)
кроме того, имеются составляющие Ez и Л/2, которые пропорцио-
нальны ~А и ~В.
к к
Предполагая, что отражение цилиндрических волн от края г=а
происходит так же, как от открытого конца плоского волновода
(ср. § 6), мы подчиняем функции fE(r) и fH(r) граничным усло-
виям
при г=а, (77.15)
аналогичным (77.09). Эти условия приводят к характеристическому
уравнению
Лп-Лп+1 + (Лп-х + Лп+1)+ УБУН = °> (77.16)
в котором
<7717>
j ТП \Кги)
причем через М обозначен параметр (6.08), который мы считаем
большим. Величины
Уе + Ун________Р' + f'P"
2 2
429
в силу условия (77.02) малы; пренебрегая ими совсем, получаем
простое характеристическое уравнение
FTO-ifm+i=0, (77.19)
которое при /п=1, 2, ... имеет две серии корней
кго,—хт—\1П и kru='Vni+\,nt (7/.20)
где vmn есть n-й положительный корень уравнения /т(т)=0.
Пренебрегая квадратами малых величин (77.18) и записывая
решение характеристического уравнения так же, как в § 6, бу-
дем иметь две серии собственных колебаний, соответствующих
данному азимутальному индексу т=1, 2, ... Первая серия опре-
деляется соотношениями
=Й+У+Ф" • D=iC TST ~ ₽%)s < C- <77-21>
а вторая серия — соотношениями
s = TTJTTTF- • c= ® ТГ Ф "E - ?"„) s < C- <77.22)
В выражения для s входит P"— полусумма значений р"£ и $”н ;
для симметричных колебаний (т = 0) эти выражения неприменимы
и должны быть заменены другими, в которые входят параметры
р"£ и р"н, а не их полусумма (см. задачи 15 и 17 к гл. I).
Комплексные частоты собственных колебаний определяются
формулой
2kl = ^(q + 2р), /7=g, (77.23)
причем из выражений (77.21) и (77.23) для s видно, что часто-
ты, соответствующие корням V2n, тзп, ..., являются (в пределах
точности этих выражений) вырожденными, так как, например,
значению
_____2vzn
М + ₽'-Н₽"
(77.24)
соответствуют два колебания с различными азимутальными
индексами (/тг=3 и /72=1). Это вырождение отсутствует для та-
ких колебаний с индексом т=\, у которых
. _ 2v»n
М + ₽' + «₽"’
Для этих колебаний
ZB(r)«fH(r)^CJc(M.
(77.25)
(77.26)
430
поэтому при <р0 = 0 колебание поляризовано по оси х (Еу < Ех)
а при % —у — по оси У {Ех < Еу). Другие колебания имеют со-
ставляющие Ех и Еу одного порядка и сложное распределение
силовых линий.
Полученные результаты справедливы для бесконечно тонких
идеально проводящих зеркал, при переходе к зеркалам, толщи-
на которых сравнима с длиной волны, параметры р' и ip" могут
измениться; впрочем, поскольку р' и р" мало Отличаются от Р-
даже при q=I (см. рис. 80), это изменение должно быть незна-
чительным. Если зеркала не являются идеально проводящими,
а характеризуются комплексным коэффициентом отражения
^=е-'-2хР> р==р'_ (Р">0), (77.27>
то в формулах (77.10) и (77.11) зависимость от z надо брать
в виде cos(&2gz) и sm(kzqz), где
= + (77.28)
Формула (77.23) принимает в этом случае вид
2&/ = я(<7 + 2/?4-2р), (77.29>
где величина р учитывает диффракцию, а величина р — неидеальное
отражение от зеркал. Если же в качестве зеркал взяты прово-
лочные решетки, обладающие анизотропной проводимостью'
(см. выше), то из всех колебаний, рассмотренных выше, оста-
ются только колебания, определяемые формулами (77.25) и
(77.26) и поляризованные вдоль проволочек.
Таким образом, анизотропия решетки приводит к существен-
ному разрежению спектра собственных частот данной системы.
Впрочем, при возбуждении плоской волной, падающей нормаль-
но на одно из зеркал, все равно возбуждаются только колеба-
ния, определяемые формулами (77.25) и (77.26) и поляризован-
ные так же, как падающая волна. Если резонансные кривые,
соответствующие различными п, не перекрываются, то варьирова-
нием расстояния 2/ между зеркалами можно получить в откры-
том резонаторе распределение поля, соответствующее формуле
(77.26), причем
kr = —,----,-р„ , (77.30}
+ м )
Если же все резонансные кривые перекрываются, то при
возбуждается сразу несколько колебаний и распределение поля
в плоскости z=cons‘t близко к тому, которое имеет падающая
волна. В этом случае система из двух решеток работает как.
интерферометр.
431
§ 78. Открытые резонаторы
с дополнительным разрежением спектра
Как уже неоднократно отмечалось, открытые резонаторы по
сравнению с закрытыми резонаторами тех же размеров обла-
дают гораздо более редким спектром собственных частот.
Однако для некоторых целей спектр открытых резонаторов все
же является слишком густым, в связи с чем возникает пробле-
ма дополнительного разрежения спектра. Эта проблема особен-
но важна в оптических квантовых генераторах, где одновре-
менное возбуждение многих колебаний ухудшает когерентность
генерируемого излучения и его направленность; в частности,
диаграмма направленности при наложении многих колебаний
расширяется и становится изрезанной, поэтому теоретическая
направленность, определяемая отношением размеров аперту-
ры к длине волны, не реализуется. При использовании открыто-
го резонатора в качестве волномера паразитные резонансы не
позволяют однозначно измерять частоту.
В настоящее время имеется много работ, посвященных тео-
ретическому и экспериментальному исследованию конкретных
резонаторов с дополнительным разрежением спектра. Ниже мы
рассмотрим некоторые резонаторы такого типа, не стремясь
охватить всех имеющихся здесь возможностей, однако прежде
•всего скажем несколько слов о проблеме в целом.
Проблему разрежения спектра (или, как еще говорят, про-
блему увеличения селективности) можно формулировать по-
разному в зависимости от того, по каким параметрам произво-
дится сравнение различных колебаний и различных резонато-
ров. В дальнейшем мы будем сравнивать открытые резонаторы
одинаковых размеров, образованные двумя зеркалами, и ком-
плексные собственные частоты изображать точками на ком-
плексной плоскости (ср. рис. 14). Дополнительное разрежение
спектра заключается в том, что значительная часть точек отхо-
дит от вещественной оси, так как колебания приобретают боль-
шое радиационное затухание, а небольшая часть точек остается
вблизи вещественной оси, испытывая лишь сравнительно неболь-
шое смещение. Иначе говоря, дополнительное разрежение
спектра, которое достигается путем изменения конструкции от-
крытого резонатора, имеющего фиксированные размеры, мы
определяем так же, как разрежение спектра, реализуемое при
переходе от закрытого резонатора к открытому (§ 7).
Как правило, любое разрежение спектра, в том числе допол-
нительное разрежение, не дается даром, а достигается ценой
увеличения (или появления) радиационного затухания у наибо-
лее добротных колебаний, образующих разреженный спектр.
Увеличение радиационного затухания допустимо, если оно не
превышает затухания, вызванного другими причинами (непол-
ным отражением от зеркал, поглощением или рассеянием меж-
432
ду зеркалами и т. п.), и совершенно неощутимо, если оно гораз-
до меньше полного затухания. При конструировании открытых
резонаторов не следует добиваться чрезмерно малых диффрак-
ционных потерь; когда диффракционные потери станут малыми
по сравнению с другими видами потерь, частотный спектр будет
густым, так как обычно все виды потерь, кроме диффракцион-
ных, примерно одинаковы для самых различных колебаний.
Наоборот, умеренное увеличение диффракционных потерь
у наиболее добротных колебаний (приводящее, скажем, к сни-
жению их добротности на 10, 20 или 30%) приводит к более
редкому спектру, поскольку добротность других колебаний сни-
жается, как видно на примерах, гораздо сильнее.
Если отвлечься от простых (в теоретическом отношении) воз-
можностей разрежения спектра по поляризации (например,
с помощью пластинок, расположенных под углом Брюстера,
см. рис. 49) и по частоте (путем применения зеркал, коэффи-
циент отражения от которых сильно зависит от частоты), то
применительно к резонаторам, образованным двумя зеркалами,
проблема разрежения спектра состоит из двух частей: 1) раз-
режение по поперечным индексам т и п; 2) разрежение по про-
дольным (аксиальным) индексам q.
Из теории открытых резона.торов со сферическими зеркала-
ми (гл. IV, VI й VII) следует, что для достаточно коротких волн
и для зеркал, близких к софокусным (при с>1) существует
много колебаний, радиационное затухание которых экспонен-
циально мало, т. е. практически равно нулю. При уменьшении
кривизны зеркал радиационное затухание всех колебаний по-
степенно увеличивается, и для плоских зеркал мы получим кар-
тину, изображенную на рис. 14. При увеличении кривизны
зеркал радиационное затухание всех колебаний также увеличи-
вается, и для концентрических зеркал распределение комплекс-
ных частот будет отличаться от рис. 14 только тем, что прямые,
на которых расположены точки, будут составлять угол л+ф
с вещественной осью (а не угол — ф, как на рис. 14). Парал-
лельно с увеличением радиационного затухания усиливается его
зависимость от поперечных индексов т и п, в связи с чем про-
исходит разрежение спектра. Если разрежение спектра, реали-
зующееся в резонаторах с плоскими или концентрическими
зеркалами, недостаточно, то можно идти дальше и применять
слегка выпуклые или же короткофокусные зеркала (см. § II,
15 и 23).
В работе Микаэляна и др. [85] был осуществлен газовый
лазер, открытый резонатор которого состоял из плоского и сфе-
рического зеркал, причем радиус кривизны последнего был
близок к расстоянию между зеркалами. Экспериментально
показано, что в такой системе, не снижая существенно выходной
мощности, можно добиться генерации на колебаниях, отличаю-
щихся только продольными индексами q, и реализовать диа-
28—2547 433
грамму направленности, соответствующую теоретическому пре-
делу.
Спектр открытого резонатора с параллельными плоскими зерка-
лами можно сделать более редким, если уменьшить коэффициент
отражения волноводной волны от края резонатора. Если, как пока-
зано на рис. 81, плоские зеркала не обрываются на краях, а имеют
излом, то коэффициент отражения
от такого излома, как показано в
задаче 8, при q > 1 и — < 1 опре-
РИС. 81. Открытый резонатор
с плоскими зеркалами, имеющий
дополнительное разрежение
спектра.
деляется формулой
^ = -ехр^0(1 + Г/3)у},
(78.01)
где
з2/3г (4)
₽0 = —т^- = 1,37 (78.02)
г W
И (ср- § 9)
у = (4а)1/3, а —У2kl tg v
(78.03)
причем v есть малый угол излома (рис. 81).
Формула (78.01) применима при у < 1. Она показывает,
что i/?——1 при s —0. Все соотношения гл. I будут применимы
к данному резонатору, если в них произвести замену
(78.04)
В частности, для резонатора с квадратными или круглыми зер-
калами комплексные частоты будут лежать на прямых
(рис. 14), образующих угол —ф с вещественной осью, где
^=2arctg (78.05)
т ь Му + Ро тМу 7
Таким образом, малый угол ф можно изменять, варьируя угол
излома V.
Примерно такие же результаты можно получить и другими
способами *. Применяя в качестве зеркала призму, в которой
происходит полное внутреннее отражение вблизи критического
угла (для основного колебания с наименьшими поперечными
* Скажем, с помощью резонаторов, рассмотренных в задачах 6 и 7
к гл. III и IV, или резонаторов, изображенных на рис. 69 (ср. [97]).
434
РИС. 82. Открытый
резонатор, образован-
ный эшелеттом 'и пло-
ским зеркалом.
индексами тип), можно, как показано в работе [86], получить
существенное разрежение спектра, благодаря тому, что коэффи-
циент отражения вблизи критического угла .резко зависит от
угла падения. При этом диффракционные
потери основного колебания увеличиваются
неощутимо (их увеличение теоретически
оценить трудно, практически оно перекры-
вается поглощением в призме и другими
видами потерь).
Разрежение по продольным (аксиаль-
ным индексам q осуществляется Путем ис-
пользования колебаний в связанных резо-
наторах (см. § 61 и 62). В работе Косаре-
ва [87] показано, что спектр открытого ре-
зонатора, образованного эшелеттной диф-
фракционной решеткой и плоским зеркалом
(схематическое изображение этого резона-
тора дано на рис. 82), гораздо реже, чем
у обычного резонатора с плоскими зерка-
лами. Теоретически это можно понять так:
собственное колебание между параллель-
ными плоскими зеркалами имеет по оси z
характер стоячей волны (ср. рис. 9); если
эта волна поляризована по оси х, то замена нижнего зеркала
хорошо проводящей лестницей, высота ступенек которой равна
2/ 4/
Д2=7’7’- <78-06)
и одна из ступенек совпадает с зеркалом, не приведет к замет-
ному возмущению колебания с индексом q, так как горизон-
тальные поверхности ступенек совпадут с узлами электриче-
ского поля — плоскостями Еж=0, а вертикальные поверхности
ступенек будут перпендикулярны электрическому полю. Вместе
с тем, колебания с другими продольными индексами испытают
сильное возмущение и будут излучаться в стороны.
Резонатор с эшелеттом [87] был экспериментально исследо-
ван в диапазоне длин волн от 7,5 до 10,8 мм, где обнаружено
только одно основное колебание с добротностью Q=6 000 и два
колебания высших типов, отличающиеся распределением поля
в поперечном направлении (по оси х) и имеющие добротности
1 500 и 600.
Несомненно, что работа по созданию открытых резонаторов
со все более редким спектром будет продолжаться дальше
в соответствии с практическими потребностями в таких резона-
торах, причем каких-либо ограничений принципиального харак-
тера здесь пока не видно. Вопрос о практических ограничениях,
возникающих, например, при создании открытого резонатора
28* 435
с одним достаточно добротным колебанием в широком интерва-
ле частот, является более сложным, и на него в настоящее вре-
мя ответить нельзя.
§ 79. Открытые резонаторы
в антенной технике
Все резонансные системы, используемые в качестве передаю-
щих или приемных антенн, по существу являются открытыми
резонаторами. Так, например, антенный вибратор — тонкий
стержнеобразный проводник — имеет четко выраженные резо-
нансные свойства. При возбуждении вибратора монохромати-
ческой плоской волной или сосредоточенной э. д. с. в выраже-
ниях для тока и поля появляется резонансный знаменатель £>
(см., например, [8], § 62), принимающий вблизи собственных
частот • вибратора малые значения. Комплексные собственные
частоты вибратора определяются уравнением D=0, причем
чисто активное входное сопротивление вибратора реализуется
на частотах, равных вещественной части комплексных собствен-
ных частот.
Щелевые антенны также являются открытыми резонаторами
вне зависимости от того, прорезаны щели в стенке волновода
или же 'в оболочке объемного .резонатора, который, имея связь
со свободным пространством, становится открытым. В теории
щелевых антенн (88] учитываются резонансные свойства щелей.
Объемные резонаторы могут быть использованы не только для
возбуждения щелей, но и для создания определенного распреде-
ления электромагнитного поля на апертуре. Так, например,
в работе (89] использовался прямоугольный объемный резона-
тор с простейшим колебанием, одна из стенок резонатора была
слегка прозрачной и служила в качестве излучающей апертуры.
В такой системе фактическая характеристика излучения весьма
близка к теоретической, так как поле на апертуре известно
с большой точностью; в частности, фазовые ошибки, вызванные
непостоянством фазы на апертуре, практически отсутствуют.
Однако применение обычных объемных резонаторов не
позволяет осуществить антенны с большой направленностью,
поскольку для этого требуются апертуры, размеры которых
гораздо больше длины волны, т. е. резонаторы соответствующих
размеров. Поскольку объемные резонаторы больших размеров
обычно лишены резонансных свойств — в них нельзя возбудить
какое-то одно определенное колебание, то надо переходить к от-
крытым резонаторам, в которых удается создать одно колеба-
ние даже с помощью сосредоточенного возбуждения (см. нача-
ло § 77).
Как показано в гл. I—IV, в открытом резонаторе, образован-
ном двумя противостоящими зеркалами, собственные колебания
являются суперпозицией двух волн определенной конфигурации.
436
распространяющихся навстречу друг другу. Любой из таких
открытых резонаторов можно превратить в направленную
антенну, если одну из этих распространяющихся волн вывести
наружу, для чего достаточно, например, сделать одно из зеркал
слегка прозрачным. Таким образом, открытый резонатор пре-
образует электромагнитную энергию, подводимую к нему по
волноводу, в направленное излучение определенной конфигура-
ции. Чистота этого преобразования и его к. п. д. тем выше, чем
больше добротность колебания и чем реже спектр; преобразо-
вание происходит лишь на резонансных частотах, соответствую-
щих возбуждаемым колебаниям.
Рассмотрим излучение открытого резонатора более подроб-
но. Хорошо известно, что если в плоскости z=0 создать гауссо-
во распределение поля, пропорциональное
х'+у*
2г*.
е
то соответствующая ему характеристика излучения также будет
гауссовой, т. е. будет лишена боковых лепестков; таким обра-
зом, при условии
' kr^l (79.02)
мы будем иметь остронаправленное излучение, совершенно
лишенное побочных лепестков. Этот результат получается лишь
тогда, когда распреде-
ление (79.01) создано
на всей плоскости; ес-
ли же оно реализовано
лишь при г<г, а при
г>г поля на плоскости
равны нулю, то при
г > г* характеристика
излучения будет при-
ближенно гауссовой, но
появятся экспоненци-
ально малые боковые
лепестки.
Такая характери-
стика излучения в не-
которых случаях пред-
ставляет практический
интерес, поэтому сле-
дует указать на то, что
гауссово распределе-
ние поля на плоскости z=0 можно создать с помощью открыто-
го резонатора, изображенного на рис. 83,а. Этот резонатор об-
разован плоским зеркалом z=0, слегка прозрачным, и сфериче-
437
(79.01)
РИС. 83. Формирование характеристики излу-
чения с помощью сферических зеркал.
ским зеркалом круговой формы, находящимся на расстоянии I
от плоского и имеющим радиус кривизны г0. Согласно § 18 и 19
в таком резонаторе могут существовать колебания (с индекса-
ми т=п=0), при которых снизу вверх распространяется волна
— г (7 sh С-а)
Ф = Се 4 е .-.-у-----• (79.03)
аспц ' '
где С — постоянная; функция Ф согласно § 23 определяет век-
тор Герца и все составляющие электромагнитного поля этой
волны. Формула (79.03) на плоскости z=0 (£=0) принимает
вид
С ——
Ф=йе 2г*’, • (79.04)
где
г* —1^4’ d = r0sinacosa. — yi(r0 — l'). (79.05)
В волновой зоне формула (79.03) принимает вид
Ф=Се 2р* • (79.06)
где р есть угол, отсчитываемый от оси z, а параметр
р-==ё;=Й’ (7907)
определяет ширину главного лепестка. Уравнение
't = t0 = |Z2 (79.08)
есть уравнение каустической поверхности (§ 19), это — одно-
полостный гиперболоид вращения, пересекающий плоскость
z=0 по окружности г=г* и асимптотически приближающийся
к конусу, образующие которого составляют угол ру. с осью z.
Сравнивая формулы (79.01) и (79.04), мы видим, что в от-
крытом резонаторе может быть сформировано гауссово распре-
деление поля, приводящее к гауссовой характеристике излуче-
ния (79.06). Формула (79.03) позволяет проследить за развер-
тыванием (при £—•-оо, т. е. при R—-оо) гауссова распределения
на плоскости в гауссово распределение по направлениям. Гаус-
сову характеристику излучения можно получить и в резонаторе
с двумя сферическими зеркалами (рис. 83,6), если сделать одно
из зеркал слегка прозрачным. Возбуждая в открытых резо-
наторах колебания высших типов, можно получить характери-
стики излучения более сложной формы; так, например, несим-
438
метричные колебания с внутренней каустикой дают направлен-
ное излучение с провалом (до нуля) в центре.
Следует заметить, что соотношения (79.03)—'(79.07) спра-
ведливы лишь в той мере, в какой можно пренебречь диффр ак-
цией на краях зеркал, т. е. при условии, что экспоненциальные
функции (79.03) и (79.04) достаточно малы у краев. Если это
так, то отклонение фактического поля излучения от выражения
(79.06) будет экспоненциально малой величиной; в частнрсти,
побочные лепестки также будут экспоненциально малыми.
Выше мы рассматривали формирование полей излучения,
которые на языке геометрической оптики можно назвать луче-
выми потоками, ограниченными каустическими поверхностями;
такие поля легко выводятся из открытых резонаторов, в кото-
рых возбуждаются колебания с каустиками. В резонаторах
с плоскими (гл. I) или концентрическими (§ 15 и 22) зеркалами
добротные колебания существуют вследствие диффракции на
краях. Возникающее при таких колебаниях распределение полей
на зеркалах, несмотря на непостоянство фазы и небольшую
изрезанность, также может представлять интерес для антенной
техники; следует отметить, что для основного колебания с наи-
меньшими поперечными индексами тип изрезанность и фазо-
вые вариации невелики — порядка (гл. I).
Все антенны, использующие открытые резонаторы, являются
узкодиапазонными и работают фактически лишь на резонанс-
ных частотах соответствующих колебаний (эти частоты можно
плавно изменять, варьируя, например, расстояние между зерка-
лами). Поэтому для большинства применений эти антенны не
пригодны. Однако их следует рекомендовать для измерений
самого различного рода. Так как у антенн, изображенных на
рис. 83, поля в ближней и дальней зонах по существу не отли-
чаются и по своей структуре близки к полю бегущей плоской
волны, то с помощью этих антенн можно измерять такие вели-
чины, как коэффициент отражения плоской волны от плоской
пластинки (при нормальном падении), эффективную отражаю-
щую поверхность тел различной формы или эффективную по-
глощающую поверхность другой антенны (для падающей пло-
ской волны). Коэффициент отражения и отражающая поверх-
ность определяют волну, возвращающуюся назад в резонатор
и изменяющую комплексную частоту собственного колебания;
измеряемые величины можно выразить через соответствующее
смещение частоты (ср. задачи 6 и 7 к гл. X).
Открытый резонатор сочетает в себе приемную антенну и
волномер; его можно использовать для измерения частотного
спектра различных излучений.
В § 81 и соответствующих задачах будут рассмотрены неко-
торые диффракционные проблемы, связанные с построением
оптимальных антенн.
439
§ 80. Сверхнаправленная кольцевая антенна
как открытый резонатор
Исследуем иоле излучения тонкой кольцевой антенны. Элек-
тродинамические свойства кольцевого проводника мы рассмот-
рим ниже, сейчас же будем считать, что по бесконечно тонкому
кольцу — окружности, которая в цилиндрической системе коор-
динат г, ф, z определяется соотношениями
г —a, 2 = 0, (80.01)
течет азимутальный ток
(т=0, 1,2,.. .) (80.02)
(/— постоянная) и, следовательно, распределен заряд с линей-
ной плотностью
—J— — /е“
ср'' с₽
есть отношение фазовой скорости
(80.03)
(80.04)
(80.05)
с которой волна тока (80.02) бежит по окружности при частоте
возбуждения ы, к скорости света с.
Электромагнитное поле, создаваемое данной системой, все-
го проще вычислить, если сначала найти скалярный и вектор-
ный потенциалы, соответствующие заряду (80.03) и току
(80.02), а затем вычислить поле. Мы получим
ZK__™ _ 2л«/ Фтп.т- 1—’ Фтп,тп+1
— с₽ г — С 21
2ла/ ф , I ф (80.06)
Ар~ ~с 2 ’ —и’
где
2я
2п j е /?(ф) Щ — т,т 1, т-\-1), (80 07)
о
/? (Ф) — ]/~г2 — 2га cosO °2 + z2-
440
На весьма больших расстояниях от окружности, (80.01) можно
положить
/?(ф) = /?— a sin & cos ф, sin& = ^~, (80.08)
где
R = Vr2-\-z* (80.09)
есть расстояние точки наблюдения от начала координат — центра
окружности, и мы получаем
^fn = /-Vn(tesin&)-^- (80.101
Поле излучения в волновой зоне имеет составляющие
Ей = Н,. = i - ™+1 £ • ctg &Jm (ka sin &) — *
(80.11)
E^-Hb=-i-mk^J^(kasmb) -------------------
причем при условиях
р<1 и /п > 1 (m > h и m> 1) (80.12)
характеристика излучения является сверхнаправленной (см., напри-
мер, работы Кнудсена [90]): поле излучения прижато к плоскости
2 = 0 = тем сильнее, чем больше азимутальный индекс т.
Действительно, если кроме условий (80.12) наложить дополнитель-
ное условие
^у<ОТ-|-1, (80.13)
то функции Jm и J'm в формулах (80.11) можно заменить простыми
выражениями
7’”W==^f (т) ’ •/,™(-г) = 2(/и—l)i( у) * (80-14)
Поля излучения, пропорциональные sinm & и sinm-1&, быстро убы-
вают при удалении от плоскости & = Такой же результат,
(см. задачу 9) получается и без дополнительного условия (80.13).
Таким образом, при условиях (80.12) кольцевая антенна,
несущая ток (80.02), является сверхнаправленной; при ka=
= const ее направленность неограниченно растет с увеличением,
индекса т, т. е. с увеличением числа осцилляций тока на окруж-
ности. Вместе с тем, увеличение индекса т приводит к уменьше-
нию полной мощности излучения и даже к уменьшению поля
441
излучения в направлении '&= g* (ср. задачу 10). МоЖно также
показать (см. задачу 13), что с увеличением индекса т увели-
чиваются размеры ближней зоны, т. е. формулы (80.11) стано-
вятся применимыми на больших расстояниях R от антенны.
РИС. 84. Формирование сверхнаправ-
ленного излучения кольцевой
антенной.
Перечисленные свойства
характерны для всех сверхна-
правленных антенн (см. {91] и
[92]). Мы рассмотрели выше
сверхнаправленную кольцевую
антенну, поскольку на этом
примере яснее всего видно, что
сверхнаправленные антенны
представляют собой в сущно-
сти открытые резонаторы
с весьма большой радиацион-
ной добротностью.
Действительно, рассмотрим
собственное колебание тонкого
провода радиусом р, свернуто-
го в кольцо радиусом а, при
котором ток на проводе распределен согласно формуле (80.02).
Для того чтобы реализовать такое распределение, нужно замед-
лить волну тока, бегущую вдоль провода, так, чтобы ее фазовая
скорость (80.05) была значительно меньше скорости света в со-
ответствии с первым условием (80.12). Чтобы достичь такого
замедления в случае прямого провода, нужно, чтобы
индуктивный погонный импеданс Zo=—iX0, причем
§62)
он имел
(ср. [7],
= S (l-P)ln—-7 = 1,781.
СР Твр у 1 — р
Для изогнутого провода необходимый импеданс вычислить
труднее, однако нет сомнения, что для достаточно тонких про-
водов он мало отличается от (80.15).
Если необходимое замедление обеспечено, то по проводу бу-
дет циркулировать медленная волна тока, которая в окружаю-
щем пространстве создаст поле, экспоненциально уменьшаю-
щееся при удалении от провода (поверхностная волна). По-
скольку на расстоянии г от оси z фазовая скорость этого поля
в азимутальном направлении будет равна и г- (ср. конец § 58),
то на цилиндрической
поверхности
(80.15)
(80.16)
будет формироваться
больших расстояниях
442
₽ *
(рис. 84) поле излучения, которое на
описывается формулами (80.11). Из
рис. 84 ясно, что наибольшее излучение будет в плоскости "&=
и что его интенсивность будет быстро спадать при отклонении
от этой плоскости, поскольку излучение в направлении
формируется в результате просачивания поля до поверхности
(80.16) по кратчайшему пути.
Вычислим погонный импеданс кольцевой антенны
р
Z=R — iX^^
(80.17)
где Ео берется на поверхности провода. Для этого представим ин-
теграл (80.07) в виде
^.П=^П + ФВ).„. (80.18)
Первое слагаемое равно
= 1 Г -1пф М 1'Ы (-l)"^I/2(s)
где
2р р
(80.19)
(80.20)
р=^/(г — a)2-\-z2, p = j/(r-[-a)2-|-z2, (80.21)
причем р — минимальное, а р—максимальное расстояние точки на-
блюдения до окружности (80.01). В формуле (80.19) исполь-
зовано интегральное представление функций Лежандра (ср.
[41], раздел 37). Вблизи окружности, т. е. при условии
а -I
s ~ — > 1,
Р
(80.22)
формула (80.19) принимает вид
4’(Х>=ТГ!" (80-23)
Второе слагаемое в формуле (80.18) равно
о 0 0
(80.24)
443
при достаточно малых значениях р мы можем вычислить его непо-
средственно на окружности (80.01), полагая R (<р) = 2а sin у. В си-
лу соотношения (см. [93], стр. 341)
к 2л . [ ... Ф \
I С if-W+xsine) М 1 Г ‘ -«Ф+Х5ШГ
(*^) ^E2ri (-^) —Л е du — I е ' ' dty,
о о
(80.25)
где J2Jl— функция Бесселя, а Е2„— функция Вебера, мы можем
представить значение интеграла (80.24) на окружности г = а
в виде
^’n== £ f + iJ^ (2'^)1 dri- (80.26)
0
Составляющая вблизи окружности определяется выражением
-ik if ( ‘Г- “ ₽2 -ГО;ГО+1 +-Уго’т-1 ) • (80.27)
В силу тождеств
^2ТП-2 ^29П ~ 2J 2Гп _ 1? J2m ‘ZaW+ 2 '-’ 2J72^+11
^±2 + Л-2 =. J\m _ t - J'2m+, + J2m = 2J",ln + Jzm (80.28)
активная часть погонного импеданса (80.17) равна
R = - [ ₽’Лт (2/п₽) - т (1 - р) j‘ Jim (2тц) 1. (80.29)
о
Мы получим /?<0. Отрицательность R можно было предви-
деть заранее, поскольку поток энергии направлен из провода
наружу (кольцо излучает); для поддержания незатухающего
колебания с распределением тока (80.02) требуется непрерыв-
ный приток энергии. Величина —R есть в сущности погонное со-
противление излучения (поэтому в антенной технике обычно
определяют импеданс с обратным знаком), и полная мощность
излучения равна
Р=— ла/?|7|2. (80.30)
Эту мощность можно было бы вычислить путем интегрирования
потока энергии в волновой зоне, где поле определяется форму-
лами -(80.11), но в этом случае вывод формулы (80.29) был бы
много сложнее.
Если энергия не подводится (собственное колебание), то ко-
лебание будет затухать во времени, и волновое число
k=k'—ik‘
-(80.31)
444
будет комплексным. Вычислим добротность колебания
4 2k"
(80.32)
в том случае, когда она велика. Так как вычисление X по фор-
мулам (80.23) и (80.26) сопряжено с трудностями, заменим X на
Хо по формуле (80.15) и учтем, что при комплексных k в силу
соотношения
X (k) = X (k') — ik" (k') (80.33),
величина X влияет на значение ReZ. Условие
ReZ=0
(80.34)'
выражает отсутствие притока энергии и позволяет вычислить k"''
по формуле <80-35) . dk
откуда dx. „ k dk Q=~ur (80.36)
и при р< 1 Q = -^- (80.37)
Оценки показывают (см. задачу 12), что при выполнении
(80.12) радиационная добротность чрезвычайно велика, поэтому
сверхнаправленная кольцевая антенна представляет собой
открытый резонатор, почти не излучающий.
То обстоятельство, что сверхнаправленная кольцевая антен-
на является открытым резонатором, снимает только одну труд-
ность, возникающую при практическом осуществлении сверхна-
правленных антенн. Сложное распределение тока (80.02), даю-
щее сверхнаправленность, устанавливается в данной системе
само собой, если обеспечено надлежащее замедление р и если
возбуждение производится на частоте, близкой к резонансной
частоте системы *. Другие трудности — узкий диапазон и малый
к. п. д. — остаются. Действительно, в антенне неизбежны потери
* Наряду с резонансным полем, обладающим сверхнаправленностью,
возбуждается нерезонансный фон (гл. X). Для создания сверхнаправленного
излучения нужно, чтобы нерезоиансное излучение было пренебрежимо ма-
лым.
29—2547
445
других видов; если обозначить соответствующую им доброт-
ность через Q', то к. п. д. антенны
4=0^ (80.38)
при Q' < Q будет весьма низким. Если же удастся добиться того,
что Q' и Q будут одного порядка, то частотный диапазон, рав-
ный ширине резонансной кривой данного резонатора, будет
весьма узким. Кроме того, протяженность ближней зоны у дан-
ной антенны, как у всех открытых резонаторов, будет велика
(см. рис. 84 и задачу 13).
Направленность излучения растет гораздо медленнее, чем
радиационная добротность (см. задачи 9—11; впрочем, это
ясно уже из рис. 84). Поэтому большого практического значе-
ния данная система иметь не может, как, впрочем, и все сверх-
направленные антенны.
§ 81. Передача энергии
между двумя апертурами
Найдем распределение поля, реализующее оптимальную пе-
редачу энергии между двумя одинаковыми апертурами. Нач-
нем с двухмерной задачи, в которой апертуры определяются
соотношениями
—а<х<а, —oo<t/<oo, z=±l (81.01)
и будем искать такое распределение поля на первой апертуре
z=—I, при котором поток энергии через вторую апертуру z=l
был бы максимальным. Вводя безразмерные координаты
£ и функцию W по формуле (54.19), будем считать, что функ-
ция W(i, £) удовлетворяет параболическому уравнению, т. е.
что искомое поле имеет вид плоской волны с медленно меняю-
щейся амплитудой. Будем искать максимум мощности
М/2
р.= j |«?(«4)
—М/21
2
c/s,
(81.02)
проходящей через вторую апертуру, при заданной мощности
—М/2
(81.03)
проходящей через первую апертуру.
446
Поставленную вариационную задачу легко решить, если учесть,
что W (z, выражается через W (Е,— тЛ посредством формулы
к 2 J \ J
(54.23), и, следовательно,
Мс f 1 \
: I Г*(Е — V, 1)8Г*(Е',— yWE'. (81.04)
—М/2
8Г*
При варьировании выражения (81.02) мы пользуемся тем, что-
в выражениях вида
(81.05>
W и W* можно варьировать независимо (поскольку независи-
мо варьируются ReUZ и Iml^), и вводим в связи с условием:
(81.03) множитель Лагранжа
Т=Р£, (81.06),
имеющий смысл коэффициента передачи. Таким образом полу-
чается соотношение
М/2
[ [№(4)гг(*4)~ где (е,-4)8№* (у -4)]
—М/2
(81.07)
которое можно также получить как условие максимума коэф-
фициента передачи (81.06). В силу соотношения (81.04) мы
приходим к соотношению
М/2
TW(t,— -0= j Г*(Е —Е', 1)1Г^Е', у) dEz, (81.08)
—М/2
которое вместе с соотношением (54.23) приводит к интеграль-
ному уравнению
М/2
TWfi,-у) = j Я(Е, Е')Г(Е',—у) <#', (81.09)
—М/2
ядро которого в силу формулы (8.05) равно
М/2
Я(Е,Е') = f Г*(Е —Е", 1)Г(Е" —Е', 1)</Е"=
—М/2
= —е" 2
,. V-У sin
Е —Е'
(81.10)
29*
447
Если ввести обозначения
f(0=w(i,—0е'’. /=3,с=4'. (81.11)
то уравнение (81.09) примет вид
Tf «) = | j S-^7n f (П dt'. (81.12)
—i
Нетрудно показать, что это интегральное уравнение пред-
ставляет собой итерированное уравнение (41.06), определяющее
двухмерные собственные колебания в открытом резонаторе с со-
фокусными цилиндрическими зеркалами. Действительно, под-
ставляя вместо f(t') в уравнение (41.06) ее выражение в виде
интеграла и пользуясь соотношением
2 fz——/Л, Л =4772", (81.13)
справедливым для колебаний с индексом т (m = 0, 1, 2, ...), мы
придем к интегральному уравнению
(81.14)
—1
которое в силу соотношения
f(-'O = (-i)mf(O
(81.15)
эквивалентно уравнению (81.12), причем коэффициент передачи
определяется формулой
Т=е~*. (81.16)
Подведем итоги. Если мы выберем функцию /(/) такой же,
как при собственном колебании с индексом т=0 в открытом
резонаторе с софокусными зеркалами, то функция
/ \ -i —
2=f(f)e 2
(81.17)
будет реализовать нам оптимальную передачу энергии от одной
апертуры к другой с коэффициентом передачи (81.16), где Л
определяет диффракционные потери колебания с индексом т =
=0. Для колебаний с индексами т=1, 2, ... параметр Л больше
(ср. рис. 59 и 60), поэтому, хотя соответствующие функции
448
удовлетворяют уравнению (81.12), коэффициент передачи по
формуле (81.16) будет меньше.
Если мы знаем, что собственные функции софокусных зеркал
дают нам оптимум, то физический смысл формулы (81.16) стано-
вится совершенно прозрачным: поскольку энергия колебания изме-
—д —
няется по закону е т (см. § 41), то за время пробега от одной
апертуры к другой поток энергии умножится на е—Л, т. е. мощ-
ность Р,, вышедшая из первой апертуры, превратится в мощность
Р2=Р1е-л=Р1Т’, (81.18)
приходящую ко второй апертуре.
В гл. III мы показали, что резонатор с софокусными зерка-
лами имеет наименьшие диффракционные потери среди всех
резонаторов с цилиндрическими зеркалами, имеющих заданные
размеры 2а и 2/. Результаты, полученные выше, позволяют
утверждать, что софокусные цилиндрические зеркала являются
оптимальными по отношению к более широкому классу зеркал
(например, зеркал, имеющих изломы). Точно так же можно
утверждать, что открытый волновод, имеющий при заданных
размерах наименьшие потери, должен быть образован софокус-
ными линзами или софокусными зеркалами. Таким образом,
в периодических структурах, осуществляющих многократную
ретрансляцию полей, оптимум достигается при тех же условиях,
что и в системе однократной передачи энергии от одной апер-
туры к другой.
Выше мы ограничились двухмерной задачей. Все результаты
совершенно очевидным образом переносятся на трехмерные
задачи, причем для прямоугольных и круговых апертур могут
быть использованы результаты теоретического исследования
открытых резонаторов с софокусными сферическими зеркалами
прямоугольной и круговой формы (гл. VII). Нетрудно также
обобщить полученные выше соотношения на случай неодинако-
вых апертур (см. задачу 14).
Формирование полей, обеспечивающих оптимальную пе-
редачу, можно произвести с помощью линз и открытых резона-
торов (ср. § 79). Методом, развитым выше, можно найти опти-
мальные решения ряда других антенных задач (см. задачи 14—
18 к этой главе). Отметим, что исходное предположение о том,
что комплексная амплитуда W является медленно меняющейся
функцией, исключает из рассмотрения сверхнаправленные
антенны, у которых поле на апертуре есть быстро меняющаяся
функция. Такие системы обладают неограниченными теорети-
ческими возможностями, однако их практическая ценность весь-
ма ограничена (ср. § 80).
449
§ 82. Шаровая молния!
Этот параграф — последний в нашей книге — мы начнем
с того, что процитируем несколько фраз из статьи П. Л. Капицы
[95], посвященной природе шаровой молнии.
«Природа шаровой молнии пока остается неразгаданной.
Это надо объяснить тем, что шаровая молния — редкое явле-
ние, а поскольку до сих пор нет указаний на то, что явление
шаровой молнии удалось убедительно воспроизвести в лабора-
торных условиях, она не поддается систематическому изуче-
нию».
... «если в природе не существует источников энергии, еще
нам неизвестных, то на основании закона сохранения энергии
приходится принять, что во время свечения к шаровой молнии
непрерывно подводится энергия, и мы вынуждены искать этот
источник энергии вне объема шаровой молнии. Поскольку шаро-
вая молния обычно наблюдается «висящей» в воздухе, непосред-
ственно не соприкасаясь с проводником, то наиболее естествен-
ный и, по-видимому, единственный способ подвода энергии —
это поглощение ею приходящих извне интенсивных радиоволн».
«Местами, наиболее благоприятными для образования ша-
ровых молний, очевидно, будут области, где радиоволны дости-
гают наибольшей интенсивности. Такие места будут соответст-
вовать пучностям напряжения, которые получаются при разно-
образных возможных интерференционных явлениях».
В статье [95] показано, что гипотеза о происхождении ша-
ровой молнии за счет коротковолновых электромагнитных коле-
баний не только решает вопрос о подводе энергии к шаровой
молнии, но может объяснить ряд других явлений, связанных
с нею (фиксированные размеры, малоподвижное положение,
существование цепочек, взрывная волна при исчезновении, про-
никание в помещение). При этом, однако, возникают следующие
вопросы (см. [95]): 1. Почему во время грозы интенсивные элек-
тромагнитные колебания соответствующей длины волны, как
правило, не наблюдаются? 2. Если учесть, что шаровая молния
обычно возникает к концу грозы и после обычной молнии, то
каков механизм возбуждения этих колебаний?
Естественным дополнением к сформулированной выше ги-
потезе о происхождении шаровой молнии, позволяющим отве-
тить на первый вопрос, является следующее предположение: во
время грозы может образоваться открытый резонатор, одним из
зеркал которого является земля, а другим — туча, и в этом ре-
зонаторе возбуждаются электромагнитные колебания. При бла-
гоприятной конфигурации зеркал резонатор может обладать
большой добротностью. При определенных условиях в резона-
торе может достигаться сильная концентрация электромагнит-
ного поля; так, например, если резонатор образован плоским
участком земли и вогнутой поверхностью тучи, причем ее
450
радиус кривизны примерно равен ее высоте над землей, вблизи
земли образуется фокус (§ 22), где происходит высокочастот-
ный пробой и появляется шаровая молния.
Сделанное предположение объясняет как сравнительную
редкость явления шаровой молнии, так и локализацию электро-
магнитного поля в ограниченной области про-
странства, что, разумеется, затрудняет наблю-
дение поля.
Согласно этому предположению шаровая
молния возникает в результате фокусировки
электромагнитных волн. Это сближает шаро-
вую молнию со световой искрой (96], возникаю-
щей при фокусировке интенсивного светового
импульса от оптического квантового генерато-
ра. Аналогия между происхождением этих яв-
лений была бы более полной, если бы световая
искра образовывалась в том же открытом ре-
зонаторе с концентрическими зеркалами, ко-
торый является колебательной системой опти-
ческого генератора (рис. 85).
К сожалению, сейчас нельзя отметить на
второй вопрос — о механизме возбуждения
электромагнитных колебаний, создающих и
поддерживающих шаровую молнию, т. е. о
механизме превращения энергии обычной мол-
нии в энергию высокочастотных колебаний.
Этот неизвестный механизм в «эквивалентной схеме» на рис. 85
соответствует активному веществу А.
Так или иначе, но теория открытых резонаторов позволяет
с полной уверенностью утверждать, что с помощью открытых
резонаторов можно осуществить высокую плотность энергии вы-
сокочастотных электромагнитных полей. Будущее покажет, как
эта возможность может быть использована в физике и технике и
как она реализуется в природе.
РИС. 85. «Эквива-
лентная -схема»
образования ша-
ровой молнии.
Задачи к гл. XII
1. Исследовать влияние величин бе и бц (§ 76) на вынужденные коле-
бания открытого резонатора, для чего решить неоднородные уравнения Мак-
свелла
4л 4п.
rot Е = ik (р.-|-Зр.)Н— — jm, rot Н = — ik (е + Зе) Е + -у je
так же, как были решены однородные уравнения (76.02). Здесь je и jm—сто-
ронние токи заданной частоты <о = ck.
Рассмотреть случай изолированного колебания и двух взаимодействую-
щих колебаний.
Решение. Представляя 'искомое поле в виде (76.05) и вводя ве-
личины
с“ — i <S=W. J
451
аналогичные коэффициентам (67.20), получаем систему уравнений
определитель которой является левой частью уравнения (76.09).
Для изолированного колебания имеем
Й kg п
с» = (1 +U)—~с“,
k — ke
где к, определяется формулой (76.10). Таким образом, резонанс при k~
^k, заменяется 'резонансом при k~ks. В случае двух взаимодействующих
колебаний резонансный знаменатель имеет вид
(k — й(Ч) (й —й(2)),
где й(') и й(2)—корни уравнения (76.17). В зависимости от соотношений между
Re (fet1) — й(2)) и Im й(’), 1тй(2) резонансная кривая может быть либо двухгор-
бой (расщепление частот существенно больше затухания), либо одногорбой
(расщепление частот существенно меньше затухания).
2. Исходя из уравнений
d2P дР _ e2f „
dt2 dt +“ор —— т пЕ> (°)
дп
dt
1
— « +
2
Е,
(6)
= 7 —
использованных в работе {76], вывести соотношения (76.28)—(76.32) н
сформулировать условия их применимости. В этих уравнениях <Д) есть ча-
стота линии, Й 0)21—разность энергий верхнего и нижнего уровней, Р — по-
ляризация, обусловленная атомами рабочего вещества; остальные обозначе-
ния те же, что в § 76.
Решение. Если считать, что Р и Е пропорциональны e~lwi, то урав-
нение (а) приводит к соотношению
йе 4ne2fn
Р - -т- Е, Йе = —------------
4" со2-|-гу<о—<Од
Прн условии
|<о —ш0| << у
мы получаем первое соотношение (76.28); таким образом, оно применимо
при условии, что мгновенная частота поля отклоняется от о)п на величину,
значительно меньшую ширины линии.
В уравнении (6) при монохроматических колебаниях правая часть
содержит как постоянный член, так и слагаемое с частотой 2<о; пренебрегая
последним, мы можем написать это уравнение в виде
dn 1 1
. у
или, считая со st <o2i -g~ , в виде
i<oP-|--j- Р^Е*
дп 11/ йе \
— = —Re(t — |E|2J.
где Р и Е — комплексные амплитуды. Беря для йе выражение (76.28), прихо-
дим к формулам (76.31) и (76.32).
452
3. Вывести формулы (77.28) и (77.29); в случае затруднений использо-
вать решения задач 7 и 8 к гл. IX.
4. Вычислить поле, возбуждаемое в открытом резонаторе 'из слегка
прозрачных дисков (§ 77) плоской волной, падающей нормально на один
из дисков, который характеризуется комплексным коэффициентом прохож-
дения (прозрачности) Т. Возбуждением вследствие диффракции на дисках
пренебречь. Воспользоваться общей теорией возбуждения открытых резо-
наторов 1(гл. X), причем собственные функции брать в простейшем прибли-
жении (77.26), а собственные частоты—по формуле (77.29). Плоскую волну
Ех=—Ну=Еое~^
задать в виде плотности электрических и магнитных токов
Jx = —jp ПР" 2 = 1 + 0.
Решение. Будем искать резонансную часть поля при г<а и |г|</
в виде
- nqz . ^qz
n,q
. nqz nqz
ну = J] C„9Ja ^)[e' 21 + (- l)’e 21 ]
n, q
с неизвестными постоянными Cn9; составляющие £z и Hz не выписываем.
Поля, по которым производится разложение, при z=l+0 имеют состав-
ляющие
. 1^-
2,
их .норма без учета просачивания через зеркала и диффракции равна
АГП, = (- 1)’+*^8/? (von) (<7 = 1.2,.. .)•
поэтому
-4Ы+")
IP се'7
= — bnq = j jexEx, n9dS = — -^j-TEa Vcn/1(Vcn) ’
где использовано тождество
f/о C^}rdr^v-Ji (v^-
J \ и J
Мы получаем
1 е ' 7
С"« == Т TEa Von7i (Von) (й_Лпв)/-
5. Используя формулу (77.29) и результаты, полученные в предыду-
щей задаче, исследовать зависимость резонансных полей в дисковом резо-
наторе от индексов п тл q при условии, что радиальные резонансы .(по ин-
453
дексу п) не перекрываются. Рассмотреть два предельных случая: преобла-
дание диффракционных потерь и преобладание потерь на неполное отраже-
ние от дисков.
Решение. Если преобладают диффракционные потерн, то
и при k = Refe„, имеем
„5/2-3/2»
Если преобладают потери на отражение
р''» р".
то при £=Re£ng получаем
Cnv"y^’
причем зависимость от q отсутствует.
6. Исследовать поля, полученные в задаче 4, прн условии, что соб-
ственные значения knq не зависят от п (так будет при пренебрежении днф-
фракционными эффектами, ср. предыдущую задачу). Воспользоваться
тождеством
а
о
Дать физическую интерпретацию полученного результата н указать условия
его применимости.
Решение. Если knq=kq, то суммирование по индексу п приводит
к вычислению ряда
п=1
который сводится к постоянной величине. Действительно, считая S посто-
янной, получаем для нее разложение
следовательно, S = -ду- . Отсюда
__ ~уг+ М Г i i г'с,г 1
е(Д,)/ 1-е 21 -{“1),е 29(о>
—|(л/+-^-) р я?г ;ж9г1
,, - — TP V е "2Г , .
Hv~ 4 TEe2j (k — kq)l +(—1)«е ]•
я
При k^kq в этих выражениях становится большим q-е слагаемое, дающее
454
нам составляющие Ех и Ну, не зависящие от г. между зеркалами будет
стоячая плоская волна, возбуждаемая набегающей плоской волной. Такой
результат мы получим, решая задачу с самого начала как одномерную,
что при пренебрежении диффракцией допустимо.
Фактически ряд S сходится медленно, особенно плохой сходимостью он
обладает при r^-а, поскольку при г=а каждый член ряда стремится к нулю,
а сам ряд равен Вместе с тем, при больших п нельзя пренебречь диф-
фракцией, поскольку р-^-п2. Если при и=1, ..., п можно считать р<^р, а при
п>п уже нельзя, то первые п .радиальных колебаний будут иметь общую
резонансную кривую; соответствующее им поле при больших п будет от-
личаться от поля (а) главным образом вблизи края, при г~а.
Выше мы рассматривали систему нз двух зеркал при условиях, когда
она является интерферометром и диффракция возмущает поле в основном
лишь у края.
7. Показать, что если с помощью уравнения (55.09) решать задачу
о переходе плоского волновода в рупор, полагая
h (х) == 0 прн х > 0,
h (х) = х tg v при х < 0,
то при условиях (55.11) и при tgv< 1 уравнение (55.09) перейдет в урав-
нение (9.13), в котором надо считать /=0 и х<0.
Решение. Полагая
„а (*q VFi 2h(-*> 1 — ,2-vtgv\
I ] 21 ) + I )
tg2v
и пренебрегая величиной —g— по сравнению с единицей, получаем уравнение
Полагая далее
d2Q f r.q kx tg v \
+ 2Г—T-)(2 =
£ = — 2r.q =s§
и пользуясь формулой (9.03), мы легко преобразуем полученное уравнение
в уравнение (9.13) с индексом j=0.
8. Используя уравнение, полученное в предыдущей задаче, вывести
формулу (78.01) для коэффициента отражения волноводной волны от со-
членения волновода с рупором.
Решение. При g>0 для функции Q=Q(s) мы имеем уравнение
d2Q о
^2 + soQ — 0
с решением
Q = e-/s«* + Reis°\
где R— искомый коэффициент отражения. При 5<0 функция Q (?) удовлет-
воряет уравнению
d2Q
^g2 + ($Q 4а$) Q = 0,
455
выведенному в предыдущей задаче. Нужно взять решение этого уравнения,
соответствующее волне, бегущей в ща!правлении g —> — оо, поэтому согласно
§ 9 мы полагаем
Q=Tw(y(l—go)),
где
Неизвестные постоянные R и Т получаются из уравнений
Q(-0)=Q(+0), Q'(-0)=Q'(+0),
откуда
w (— ?£,,) я,
+ 1 w (— yEo) Y
__ . W (— YEo) Sq *
1 w' (— ySo) y
Аргумент функций Эйрн в последнем соотношении равен
е _ Ч
-- Y5o-----’
поэтому мы имеем (в соответствии с тем, что можно было ожидать из
физических соображений)
So
R-*—1 при —-*0 (т. е- ПР>1 so-*0).
R-*
n s°
О при —
оо (т. е. при v —»
0).
поскольку согласно формуле (9.26)
™ (— Yb) . Y
ш'(— yW^1 «о
«О v, ,
при ~ > 1.
Учитывая соотношение (см. [47], стр. 57 или [19], стр. 380)
З^Г (-тгЛ . п .к
w (0) _ \ 3 ) I—
w'(°) r(_L\ 6 -₽’е ’
Ч3 J
So
при условии — < 1 можно записать R в виде
(. \
1 T So I
2/рое -у-у,
что совпадает с формулой (78.01).
9. Исследовать поле излучения (80.11) при условиях (80.12) вблизи плос-
/ тс \
кости z=0 I ® —~2~)> не накладывая дополнительного условия (80.13). Вос-
пользоваться формулами (25.18) и (25.19) и асимптотическими формулами,
приведенными в задаче 1 к гл. IX.
456
Решение. При больших т функцию J„(ka sin ф) можно вычислять
по асимптотической формуле (25.18), в которой при функцию v(t)
можно заменить асимптотическим выражением, соответствующим большим
положительным t. Тогда зависимость Jm и J'm от О определится главным
образом экспоненциальным множителем
---к- m th Чо cos2 &
е—m (ij—th т]) __ е—т (7]0—th г0)е 2
где
т т 1
chl’ = ^IhTa* сЬЧ. = -^=-|-. cos’S «1.
Таким образом, поле убывает при удалении от плоскости 0 = п/2по закону
----~ mth ijocos5® _ JL m И—р»/&—у)
е---= е ' ',
т. е. тем быстрее, чем больше т.
10. Исследовать, как изменяется поле излучения (80.11) в направлении
П
0 = —g- при неограниченном возрастании индекса т, если произведение ka
или коэффициент замедления р остается постоянным.
л
Решение. При ka = const излучение в плоскости 8 = определяет-
ся функцией J'm(ka), которая согласно формуле (80.14) неограниченно убы-
вает при т -» оо. При p=const излучение определяется функцией
последняя, согласно результатам предыдущей задачи, пропорциональна
экспоненте
€—m (tjo—th ’Jo) _
geV1~Pa
1+/T=p
которая неограниченно убывает при т -» оо. Таким образом, чрезмерная
сверхнаправленность приводит к тому, что даже в направлении максималь-
ного излучения поле становится слабым.
11. Оценить радиационную добротность Q, определяемую формулой
(80.37), при условиях (80.12) и (80.13).
Решение. Применяя формулы (80.14) и (80.29), получаем
—/? =
2nkm(m— 1)
V (2m + 1)!
(mp)2m~*.
в то время как по формуле (80.15)
“ cP21п Yfep-
Отсюда
2Р
tkf (2m 4- 1)!
® 2п (тР)2"‘+'
Добротность Q
жения р2т+1 в
чаем, что
при больших т получается весьма большой из-за выра-
знаменателе. Действительно, из формулы Стирлинга полу-
(2m + 1)! „
—5, .i— =& 2е^ пт
Sm + l
при т^> 1,
457
поэтому (ср. задачу 10)
(2 Vm + l
W )
12. Показать, что при условии
kb -v ka 3> 1
интеграл (80.07) можно приближенно представить в виде
е< лф0)
Фт.„ = Л (kb) --------------------------,
где
b = -P-g— > Ro = R (Фо) = /рр,
. b‘ bR0 Ro
С05фо = — , Sin<J>0 = — , tg фо = -у' .
а р и р определяются формулами (80.21). Для этого исследовать, при каких
условиях в подынтегральной функции можно положить
R (Ф) — R0=kb sin (Ф — Фо)
(а)
1
и вынести при ф = ф0 за знак интеграла.
Решение. Введем обозначение
2 (Ф) = kR (ф) — пФ,
тогда
„ . kra
Q'^==R^)-n'
kra Г а
2"(ф> = w [Cos'1'-Wsina *]•
kra 2 га
°" (Ф) = -sin Ф — sin ф 2" (ф)
и, в частности,
2 (Фо) = kRo — «Фо, 2’ (Фо) — kb — п,
... 2kb*
2"(фо) = 0. 2"'(ф.) = -Ы>, й^(фо)==
1\о
Если в точной формуле
2 (Ф) = 2 (фо) + k [Я (ф) - Я»] - п (ф - ф„)
произвести замену (а),
члены
то это изменит лишь значение 21У(фо), т. е. изменит
1 kb*
12 Ro Фо?+...
(Ь)
в разложении Тейлора для функции (2(ф). Поскольку эффективный интер-
вал интегрирования по ф, определяемый предыдущим членом, равен
. ( 2 У/3
458
то членами (&) можно пренебречь при условии
ъ>
1У'3
kb )
(с)
Это условие может нарушаться только вблизи окружности, где оно принимает
вид
При том же условии (с) можно под знаком интеграла
и получить искомое выражение для функции п.
заменить
1
*(Ф)
на Ro
1-3. Показать, что выражение для ’Fm.n, полученное в предыдущей за-
даче, переходит в формулу (80.10), справедливую для волновой зоны;
исследовать условие, при котором происходит этот переход, и сравнить
с условием, вытекающим из рис. 84.
Решение. В волновой зоне можно положить
b = a sin 8, R0 = R, ф0 = -у
(а)
и прийти к формуле (80.10). Поскольку ф0 множится на большое число п,
напишем для ф0 более точное выражение, а именно положим:
я b a sin 0
$„ = -^--8, tg3^6 = -^ —£-
тогда условие mi < 1 при принимает вид
R^> та или R -у-.
(Ь)
По сравнению с обычным условием для дальней воны в условие (&)
входит малая величина Р, вследствие чего дальняя зона отодвигается.
С другой стороны, первое и второе соотношение (а) справедливы при
условиях
R > a, R > ka‘.
которые прн ka>l и ₽<1 являются более мягкими, чем условие (Ь).
Поскольку условие (й) выведено при ka^> 1 (см. задачу 12), можно
думать, что при ka<l оно заменится условием
а
вытекающим из рис. 84.
14. Обобщить результаты § 81 на случай двух апертур различной ши-
рины
—al<x<al, z=—l; —а2<х<а2, z=l.
Сравнить с соотношениями, полученными в задаче 8 к гл. VII.
Решение. Вводя параметры
459
заменяем формулы (81.02) и (81.03) выражениями
—MJ2 —MJ2
В соотношении (81.04) надо заменить М на Mi, а соотношение (81.07) пере-
писать в виде
М,/2 М,/2
J W(*’ 4“)ЙГ*0’ J r(£’-----------------------------------r)d5=0>
—Ma/2 -^Mt/2 .
откуда получаем уравнение >(81.08), в котором М—М2; в уравнении >(81.09)
’ надо положить М=МЬ а >в выражении (81.10)—опять Л1=Л12. Обозначая
i ?
( 1 \ 2
f(0 = U7^,-^Je
2$ МаМг
t = с = ~4~
приходим к тому же интегральному уравнению (81.12), со всеми вытекаю-
щими из него последствиями.
Таким образом, задача об оптимальной передаче энергии между двумя
апертурами различной ширины решается, в соответствии с задачей 8
к гл. VII, с помощью функции f(f), соответствующей собственному коле-
банию (т=0) в открытом резонаторе с софокусными зеркалами различной
ширины, у которого
С = , £1 = ga = 0.
Как распределение тока на зеркалах, так и радиационное затухание в таком
несимметричном резонаторе совпадают с соответствующими величинами для
симметричного резонатора (гл. VII).
15. Найти распределение поля на щели
—а<х<а, г=0,
при котором достигается (при постоянстве мощности, подаваемой к щели)
максимальная мощность излучения в интервале направлений
— ?0<?<?0 (?0<1),
где у— полярный угол, отсчитываемый в плоскости xz от оси г. Как изме-
няется относительная мощность, излучаемая в этот интервал, при у0 -* 0?
Считать ka 1.
Решение. Если на расстоянии г от щели поставить вторую щель
— а2<х<аа, z = r (г^>£а2),
причем положить
г=2(, О2=гфо, ai=a,
то задача сводится к предыдущей. Функция f (t), характеризующая распреде-
х
ление поля на излучающей щели в зависимости от /=—, совпадает с соб-
ственной функцией открытого резонатора с софокусными зеркалами, удов-
летворяющей интегральному уравнению (41.06) с параметром
kataa
с — —— или с = яа?о-
460
Коэффициент передачи Т по мощности от излучающей щели к приемной
в данной задаче есть относительная мощность, излучаемая в данной ин-
тервал направлений; Т по-прежнему определяется формулой (81.16). Если
у0 -* 0, то с уменьшается, Л (ср. гл. VII) увеличивается и, следовательно,
Т уменьшается.
16. Задача об оптимальной передаче энергии, решенная в § 81, привела
к формуле (81.17), т, е- к полю, имеющему сильное изменение фазы на
(. rf* \
фазовый множитель е J
Если искать такое (решение задачи об оптимальной передаче, которое
на излучающей апертуре имеет постоянную фазу, то естественно положить
м/2 м/2
р,= J р2= j 0’
—M/2 —M/2
I
и искать максимум отношения (81.06). Исходя из этих предположений, найти
оптимальное распределение W --.
Решение. Вместо соотношения (81.07) мы теперь получаем
М/2
j 6- 4’)8г(г> 4’)-"т'г(5’~4")8'г(5’-"т)]^=о’
—М/2
что приводит нас к интегральному уравнению (81.09) с ядром
М/2
К (5, Г) = J г (6 - Г. 1) г (Г - Г. 1) dl".
—М/2
Интегральное уравнение (4.19) для открытого резонатора с плоскими зерка-
лами можно переписать в виде (ср. § 8)
М/2
f($) = e,’2”T’ j Г (5-5', 1Щ?Х.
—М/2
Если его итерировать, то как раз получим уравнение (81.09) с выписанным
выше ядром KQ, £'). Таким образом, решение поставленной задачи имеет
вид
(1 \ лх л
И7 f ) = cos й1+'\ ’ Р = 4 (M+?-W ’
4 а(<1 + ₽_лг;
Т = еГ1^р, |7Ч = e~iKp" = е
Выражение, полученное для W ------2~у’ имеет небольшое изменение фазы
/ 1 X
I порядка -ду- ). Оптимальное чисто вещественное решение, очевидно, близ-
ко к полученному выше.
17. В результате решения задачи 15 мы получили синфазное поле f (<) на
излучающей щели. Исследовать функцию f (/) в предельных случаях 1 и
с 1, а также соответствующие характеристики излучения.
30—2547
461
Решение. Функция f (f) есть решение дифференциального уравнения
(41.07).-При t<^ 1 мы имеем (ср. конец § 47)
_ т2 _ <?/2
4* 2
f (/) = е == е (т -- 0),
причем при t ~ 1 и с>1 функция f (t) экспоненциально мала. Таким образом,
прн с^>1 оптимальное- распределение поля на щели близко к гауссовому
(ср. § 79). При с<1 уравнение (41.07) можно заменить уравнением
Kf = °, К = -ег0.
которое является дифференциальным уравнением Лежандра. Собственные
функции и собственные значения таковы:
К=— т(т+1) (т=0, 1, 2,...),
где Pm(t)—полином Лежандра, причем Ро(О='1. Таким образом, при
с«1 оптимальное решение есть константа (/(/)=='!). Этот результат мож-
но было предвидеть заранее, поскольку постоянное поле обеспечивает мак-
симальный 'коэффициент усиления антенны.
Гауссово поле на щели определяет гауссов}’ характеристику излучения
(§ 79), постоянное поле определяет поле излучения, пропорциональное
sin(^asinif) sin (ka<f)
ka sin <f kaip
18. Решить задачу об оптимальной передаче энергии между двумя ще-
лями (задача 14) со следующим изменением: мы требуем, чтобы излучение
из второй щели в направлении оси г было максимально, т. е. берем в ка-
честве Pi функционал
и ищем максимум Ра при Pj=const (Рх определяется так же, как в задаче 14).
Найти функцию W РеализУющУю этот максимум.
/ 1 \
Решение. Варьируя U7* ( £, i-g-l, получаем соотношение
Ма/2 М,/2
JJ 4*)^' —г ( w (*• ~
—Ms/2 —М,/2
которое дает явное выражение для искомой функции
M.J2
w(t,—-^=C J Г* (5l)rfg',
-Ма/2
где ма/2
1 <• / 1 \ f Рг \
С = у- I 1ГН, (7’ = рг)
-к/2
— постоянная. При ЛЬ -» оо мы получаем по второй формуле (8.06)
w(^ —г)=с’
как это и следовало ожидать (ср. задачу 17).
462
Заключение
Теория открытых резонаторов и открытых волноводов пред-
ставляет собой новую главу электродинамики и в более общем
смысле — новую главу теории волновых явлений. Здесь за ко-
роткое время (первые публикации математического характера
относятся к 1961 г.) получено много конкретных результатов,
развиты новые методы. Укажем прежде всего на то, что геомет-
рическая оптика применительно к резонаторным и волноводным
задачам радикально модифицируется, благодаря этой модифи-
кации ее можно применять для расчета собственных колебаний
и собственных волн (см. гл. VI и VIII).
Для теории открытых резонаторов и открытых волноводов
вообще характерно широкое сочетание лучевых и волновых
представлений. Такое сочетание возникает вследствие того, что
длина волны гораздо меньше всех существенных размеров рас-
сматриваемых систем, и дает основание для применения терми-
нов: квазиоптические устройства, квазиоптическая теория, ква-
зиоптика; терминология эта не очень удачна, и в нашей книге
мы ее старались избегать.
В открытых системах принципиальное значение имеют диф-
фракционные явления, исследование которых проведено мето-
дом параболического уравнения. Этот метод ведет к цели бы-
стрее, чем классические методы физической оптики (связанные
с именами Гюйгенса, Френеля и Кирхгофа), и является более
гибким и наглядным. Его можно рекомендовать для решения
многих диффракционных задач *, в частности для расчета
антенн (ср. § 81). В тех случаях, когда длина волны сравнима
с одним из размеров системы или больше его, уже нельзя
использовать приближенный (асимптотический) метод парабо-
лического уравнения, равно как и другие методы физической
оптики, и приходится прибегать к строгим методам (см., напри-
мер, § 56—59 и § 77).
Следует особо отметить математические и физические идеи,
связанные с теорией возбуждения открытых резонаторов и со
свойствами их собственных функций (гл. X и XI). Эти же идеи
могут быть использованы в теории объемных резонаторов, при-
соединенных к линиям передачи (§ 68 и 70), и в теории откры-
тых волноводов (§ 69). Существует тесная связь между задача-
ми, рассмотренными в этой книге, и задачами квантовой меха-
* Он применяется также в теории распространения радиоволн (ср. (8],
§ 58 и 59) и в нелинейной оптике [101].
30* *65
ники (ср. § 71); в частности, оператор рассеяния 5, введенный
в § 63 и 66, аналогичен квантовомеханической матрице рассея-
ния.
Читателя не должно смущать то обстоятельство, что методы,
применяемые в теории открытых систем, и получаемые с их
помощью результаты являются большей частью приближенны-
ми. Как всегда в теоретических исследованиях, корректное вве-
дение тех или иных аппроксимаций означает просто отделение
главных факторов от второстепенных — таких, которыми при
определенных условиях можно пренебречь. Теория открытых ре-
зонаторов и открытых волноводов приводит к надежным расчет-
ным соотношениям для ряда конкретных систем и вместе с тем
является основой для исследования других, более сложных
систем.
Несомненно, что открытые системы будут все шире приме-
няться как в экспериментальной физике, так и в технике, при-
чем эти применения могут скоро выйти за рамки, намеченные
в гл. XII. В теоретическом плане наибольший интерес сейчас
представляет исследование открытых резонаторов с диэлектри-
ческими телами (ср. гл. IX) и рассмотрение систем, обладаю-
щих дополнительным разрежением спектра (ср. § 78); здесь
следует ожидать новых результатов, имеющих как принципиаль-
ное, так и практическое значение.
Обзор литературы
В данном обзоре, ни в коей мере ще претендующем на полноту, мы пе-
речислим как работы, использованные при написании каждой главы, так и
работы, имеющие отношение к тематике каждой главы, но не упомянутые
в тексте.
Гл. I написана на основании работ автора (*> и ;2>, большинство задач
к ней возникло при более детальном рассмотрении вопросов, бегло затро-
нутых в этих работах. Задачи 7—9 к гл. II составлены на основании рабо-
ты (*>, в которой подробно исследованы свойства резонаторов, подобных изо-
браженным на рис. 20. Заметим, что применение интегральных уравнений
с бесконечными пределами в задачах 4—'6 эквивалентно использованию гео-
метрической оптики в параксиальном приближении (совместно с квантовыми
условиями, см. гл. VI); геометрическая оптика позволяет рассмотреть те
же вопросы более просто и наглядно (см. гл. VI). В частности, сведение
интегральных уравнений с ядрами Ki и К2 к уравнению с ядром Ко озна-
чает, что после двух отражений от разных зеркал система лучей становится
(в параксиальном приближении) такой же, как после двух отражений от
зеркал идентичных.
Гл. III представляет собой слегка переработанную статью автора (•*). За-
дача 5 к этой главе заимствована из работы (* 2 3 * 5), в которой рассмотрена более
общая задача о двух цилиндрических зеркалах, образующие которых состав-
/ it X
ляют произв ольный угол 1 0 < — ¥•<“2’)- Задачи 6 и 7 основаны на
статье Вахитова (6 *), в которой показано, что зеркала с переменным коэффи-
циентом отражения позволяют осуществить резонатор с сильным разрежением
спектра (по поперечным индексам).
Гл. IV написана на основании работы автора (7), а гл. V—на основании
его работ О) и <3>. Основные идеи и большая часть результатов гл. VI при-
надлежит В. П. Быкову; эта глава написана на основании работ (9), бо),
(Ц), (S) и (12). в частности, в .работе показано, что при условиях (36.13) и
(36.'14) лучевые потоки не могут быть ограничены каустиками.
Следует отметить, что в работе Келлера и Рубинов а оз) содержится ряд
результатов § 25, 28, 32, 33 н 34. В ней исследованы (с помощью лучевых
соображений) асимптотические свойства собственных функций в замкнутых
объемах и двухмерных областях, особенно детально рассмотрены двухмер-
ные задачи, в частности определена погрешность формул (24.27) и (24.28),
а также соотношений § 34. К сожалению, с этой работой автор познакомил,-
<> ЖЭТФ, 1963, т. 44, № 3, стр. 1050—1067.
(2) ЖТФ, 1964, т. 34, № 2, 193—204.
<3> А. Т. Ф в а л к о в с к и й, ЖТФ, 1966, т. 36, № 6, стр. 1100—1108.
<«> ЖТФ, 1964, т. 34, № 2, стр. 205—217.
(3) В. П. Быков. «Известия вузов», Радиофизика, 4966, т. 9, № 1,.
стр. 85—94.
<6> Н. Г. Вахитов. «Радиотехника и электроника», 1965, т. 10, № 9,
стр. 1676—1683.
,7> ЖЭТФ, 1963, т. 45, № 3(9), стр. 683—697.
<8 9> «Электроника больших мощностей», сб. 3. Изд-во «Наука», 1964.
стр. -176—215.
(9) В. П. Быков, Л. А. Вайнштейн. ЖЭТФ, 1964, т. 47, № 8,
стр. 508—517.
<10 * *> В. П. Быков «Электроника больших мощностей», сб. 4. Изд-во
«Наука», 1965, стр. 66—94.
<п> Л. А. В а й н ш т е й н. Ibid., стр. 95—105.
(12> В. П. Быков. «Радиотехника и электроника», 1966, т. 11, № 3,.
стр. 477—487.
<13> J. В. Keller, S. I. Rubinow. Ann. of Phys., 1960, v. 9, № 1,
p. 24—75.
46S
<я слишком поздно, когда основные результаты гл. III—VI были уже полу-
чены и приобрели законченную форму, поэтому работа’13 *) не была использо-
вана при написании книги.
Гл. VII 'базируется на двух статьях автора(,4), рис. 64 заимствован из
работы <15>. Следует отметить, что рассмотрение различных эквивалентных
систем (§ 40 и 51, а также задачи 8 и 9 к гл. VII) проведено Гордоном и
Котельником’16) и-с более общей точки зрения — Талановым’17 *), разработав-
шим операторный метод расчета лучевых потоков в открытых системах (см.
также(,8)). Свойства функций, удовлетворяющих дифференциальному урав-
нению (47.18) и интегральному уравнению (47.11), рассмотрены <в последней
•статье Слепяна ’19 *>, где также даны ссылки на предшествующую литературу.
Ряд новых численных результатов для сферических зеркал круговой формы
приведен в статье Лн(2°). При составлении гл. VI'II, наряду с работами, ука-
занными в тексте, была использована обзорная статья’21), а также работы <2)
Л ПЭ.
В гл. IX § 61 написан на основании работы Вахитова ’22>, которому при-
надлежат также некоторые результаты § 60 и обобщение результатов § 61
;на трехмерные задачи ((конечная призма или конечный цилиндр между
параллельными зеркалами). Следует отметить, что возможность разрежения
спектра собственных частот по продольному индексу с помощью связанных
колебаний рассматривалась рядом авторов <23 * 25> 124), однако только в рамках
одномерных задач. 'Некоторые- результаты для бесконечной призмы и ко-
нечного кругового цилиндра между бесконечными параллельными зеркалами,
прижатыми к граням призмы или торцам цилиндра, имеются в работе ’251;
статья <26 *>, посвященная собственным колебаниям конечной призмы в сво-
бодном '.пространстве, ошибочна. При написании § 58 и 59 использованы
некоторые результаты, полученные в работах (27> и (28>.
Гл. X и XI, посвященные теории возбуждения открытых резонаторов,
суммируют три работы автора’27) и <28>. Надо заметить, что данное в гл. X
определение собственных функций непрерывного оиектра не является един-
ственно возможным: можно, например, ввести эти функции так же, как
в квантовой механике, т. е. чтобы при Р~* оо они сводились к плоским
волнам. Однако данное определение является более естественным и удоб-
ным для задач, рассмотренных в этой книге. Задачи 6—8 к гл. X базиру-
(14> «Электроника больших мощностей», сб. 4. Изд-во «Наука», 1965,
•стр. 106—147.
<15> В. С. Авербах, С. Н. Власов, В. И. Таланов. «Радиотех-
ника и электроника», 1965, т. 10, № 6, стр. 1150—1153.
(,6) J. Р. Gordon, Н. Kogelnik. Bell Syst. Techn. Journ. ,1964,
v. 43, № 6, p. 2873—2886.
(17> В. И. Та лаков. «Известия 'вузов», Радиофизика, 1965, т. 8, № 2,
•стр. 260—271.
(,3) И. Kogelnik. Bell Syst. Techn. J., -1965, v. 44, № 3, p. 455—494
(1®> D. .SI epi an. Bell Syst. Techn. J., '1964, v. 43, № 6, p. 3009—3057.
(20> T. Li. Beil Syst. Techn. J., 1965, v. 44, № 5, p. 917—932.
(21) Б. 3. Каценеленбаум. УФН, 1964, т. 83, № 1, стр. 81—105.
(22) н р Вахитов. ЖТФ (в печати).
(23> D. A. Kleinman, Р. Р. К i s I i u k. Bell Syst. Techn. J., 1962, v, 411,
№ 2, p. 453—462.
(24> N. Kumagai, M. M a t s u h a r a, H. Mori. IEEE Journ. of Quan-
tum Electronics. '1965, v. QE-ll, № 2, p. 85—93.
(25) А. И. Ораевский, В. А. Щеглов. «Известия вузов», Радиофи-
зика, 1965, т. 8, № 1, стр. 81—90.
(2(i) А. Н. О р а е в с к и и, В. А. Щ е г л о в. «Радиотехника и электрони-
ка», 1965, т. 10, № 6, стр. 1140—1142.
<2т) ЖТФ, 1964, т. 34, № 9, стр. 1541—1555.
<23> «Электроника больших мощностей», сб. 4. Изд-во «Наука» 1965.
стр. 148—156; 157—172.
466
ются на работе <29>. В гл. XI особое внимание уделено возбуждению резо-
натора с плоскими зеркалами и, в частности, его свойствам вблизи крити-
ческой частоты (§ 74 и задачи 6—12), поскольку этот вопрос неоднократно
дискутировался.
В гл. XII теория собственных и вынужденных колебаний открытого ре-
зонатора, образованного круглыми параллельными дисками с произвольным
расстоянием между ними (§ 77 и задачи 3—6), изложена согласно работе
Фиалковюкого (30>; в этой работе использованы импедансные граничные усло-
вия (77.09), поскольку прямое использование коэффициентов отражения для
волн различной поляризации от края г—а (как в гл. I) становится практи-
чески невозможным. В связи с проблемой дополнительного разрежения
спектра, рассмотренной в § 78, следует также указать работу(й (см. выше)
и работу <3>, в которой показано, что в резонаторе, изображенном на рис. 20,
могут достигаться высокие радиационные добротности и, вместе с тем,
спектр собственных частот будет более разрежен, чем у резонатора с плос-
кими зеркалами тех же размеров. В работе <31’ исследованы связанные коле-
бания открытых резонаторов с диффракционной связью через общее плоское
зеркало; оказывается, что в такой системе также достигается дополнительное
разрежение спектра.
В § 78 отмечалось, что селективность системы можно определять по-
разному. В работе Власова и Таланова ,32> в качестве меры селективности
принята величина d=Ai—Ао, рассматриваемая как функция Ао; здесь
А/, характеризует затухание наиболее добротного колебания (энергия ^оле-
t
бання пропорциональна е , ср. начало § 41), a Ai— затухание колеба-
ния, следующего за ним по добротности, причем в принципе Ао и Ai дают
полное затухание, обусловленное всеми потерями. Величина d в какой-то-
мере характеризует .резонатор в оптическом квантовом генераторе при усло-
вии, что оба колебания одинаковым образом используют активное вещество.
Если учитывать только диффракционные потери, то оказывается, что наи-
большее значение d (при данном Ао) имеют софокусные зеркала, затем
идут .плоские зеркала, затем — зеркала с переменным коэффициентом от-
ражения, .рассмотренные в работе (6>. Между тем, согласно определению,
данному в § 78, софокусные зеркала имеют наиболее густой спектр, т. е.
наименьшую селективность, при переходе к плоским зеркалам селективность
(разрежение) увеличивается, а у таких систем, как система, изображенная
на рис. 81 или -рассмотренная в статье (6>, -разрежение спектра еще больше.
Противоречие .разрешается, если учесть, что, рассматривая d как функ-
цию Ао при учете одних диффракционных потерь, мы сравниваем между
собой резонаторы совершенно различных размеров. Вместе с тем, при доста-
точно малых диффракционных потерях они вообще ,-роли не играют, и ставить
их -на первый план нельзя. По этим причинам -нам представляется, что даже
для оптических квантовых генераторов данная в -§ 78 трактовка селективности
(разрежения спектра) в гораздо большей степени соответствует сути дела.
Рассмотрение сверхнаправленной кольцевой антенны в § 80 базируется
на статье автора (33>, посвященной излучению заряженной частицы при кру-
говом движении («светящийся электрон»). Изложение § 81 основано на ра-
ботах <21> и (34), откуда -взяты также задачи 14 и 15; в этих работах приве-
t29) Ю. М. Ц и п е н ю к. «Электроника больших мощностей», сб. 4. Изд-во
«Наука», 1965, стр. 173—175.
(зад д. Т. фиалковский. Докл. АН СССР, 1966, т. 168, № 6,
стр. 1300—1302.
<31> А. Т. Фиалковский. ЖТФ, 1966, т. 36, № 6, стр. 1109—1114.
(32> С. Н. В л а с о в, В. И. Т а л а н о в. «Радиотехника и электроника»,
1965, т. 10, № 3, стр. 552—554.
(Зз) «Радиотехника и электроника», 1963, т. 8, № 10, стр. 1698—4705.
<34> Н. Г. Бондаренко, В. И. Таланов. «Известия вузов», Радио-
физика, 1964, т. 7, № 2, стр. 313—327.
467
дены ссылки на предшествующую литературу, которые мы здесь опускаем.
Отметим лишь интересное обстоятельство, указанное Талановым'33': инте-
гральное уравнение (81.12) впервые было получено Л. И. Мандельштамом
в работе по теории оптического изображения (1912 г.), причем в этой же
работе был введен ряд понятий, играющих важную роль в ' современной
теории открытых резонаторов и открытых ^волноводов.
Задачи к каждой главе в большинстве своем содержат новые результа-
ты или позволяют по-новому подойти к вопросам, рассмотренным в основ-
ном тексте. В ряде случаев (особенно ,в 'последней главе) мы сознательно
вынесли часть выкладок в задачи, чтобы не загромождать основного текста. 3
(3S) в. И. Т а л а н о в. УФН, 1965, т. 87, № 1, стр. 23—28.
Цитированная литература
1, М. А. Ле он то вич. Статистическая физика. ОГИЗ, 1944 (§ 20).
2. Р. Курант, Д. Гильберт. Методы математической физики, т. 1.
Гостехиздат, 1933, гл. VI, § 4.
3. А. М. Прохоров. ЖЭТФ, 1958, т. 34, № 6, стр. 1658—1659.
4. A. L. Schawlow, С. Н. Townes. Phys. Rev., U9&8, v. 11*12, № 6,
p. 1940—1949.
5. А. И. Барчуков, A. M. Прохоров. «Радиотехника и электроника»,
1959, т. 4, № 12, стр. 2094—2095.
6. Н. Г. Басов, О. Н. Крохн н, Ю. М. Попов. УФН, 1960, т. 72, № 2,
стр. 161—209.
7. Л. А. Вайнштейн. Электромагнитные волны. Изд-во «Советское ра-
дио», 1957.
8. Л. А. Вайнштейн. Теория диффракции и метод факторизации. Изд-во
«Советское радио», 1966.
9. М. А. Леоитович. «Известия АН СССР», сер. физическая, 1944, т. 8,
№ 1, стр. 16—22.
10. М. А. Леонтович, В. А. Фок. ЖЭТФ, 1946, т. 16, № 7, стр. 557—
573. Сб. «Исследования по распространению .радиоволн», под
ред. Б. А. Введенского. Изд-во АН СССР, 1958, стр. 13—39.
11. Г. Д. Малюжинец. УФН, 1959, т. 69, № 2, стр. 321—334.
12. A. G. Fox, Т. Li. Bell Syst. Techn. J., 1961, т. 40, № 2, p. 453—488.
13. «Лазеры». Сборник переводов под ред. М. Е. Жаботинскопо. Изд-во
иностранной литературы, 1963.
14. В. П. Быков. «Электроника больших мощностей», сб. 3. Изд-во «Нау-
ка», 1964, стр. 148—153.
15. Г. Н. Ватсон. Теория бесселевых функций, ч. II. Изд-во иностранной
литературы, 1949.
16. М. Г. Белкина. Диффракция электромагнитных волн на диске. В сб.
«Диффракция электромагнитных волн на некоторых телах вращения».
Изд-во «Советское радио», 1957.
17. В. А. Фо к. Диффракция радиоволн вокруг земной поверхности. Изд-во
АН СССР 1946.
18. A. G. Fox, Т. Li. Proc. IEEE (IRE), 1963, v. 51, № 1, p. 80—88.
19. V. A. Foe k. Electromagnetic diffraction and propagation problems. Per-
gamon Press, 1965.
20. E. Янке и Ф. Эм де. Таблицы функций с формулами и кривыми
Физматгиз, 1959.
21. Д. Джексон. Ряды Фурье .и ортогональные полиномы. Изд-во ино-
странной литературы, 1948, гл. IX и X.
22. В. А. Фок. «Известия АН СССР», сер. физическая, 1950, т. 14, 1,
стр. 70—94 (§8).
23. Г. Д. Малюжинец, Л. А. В а й н ш т е й н. «Радиотехника и электро-
ника», 1961, т. 6, № 8, стр. 1247—1258.
24. Л. Д. Ландау, Е. М. Лифшиц. Теория поля. Физматгиз, 1960,
стр. 182.
25. Erdelyi, Magnus, Oberhettinger, Tricorn i. Higher Transcen-
dental Functions. Bateman Manuscript Project. Me. Graw-Hiil, 1953, v. 2.
26. W. Cuis haw. IRE Trans., 1962, v. MTT-'IO, № 5, p. 331—339.
27. А. Зоммер фельд. Оптика. Изд-во иностранной литературы, 1953.
28. А. Е. Siegman. Proc. IEEE (IRE), 1965, v. 53, № 3, p 277—286.
29. M. Born, E. W о 1 f. Principles of Optics. Pergamon Press, 1959, p. 436.
469
30. Дж. Сальмой. Конические сечения н новейшие алгебраические и гео-
метрические методы для исследования свойств кривых линий. 1860,
(§ 194 и 356).
-31. О. Staude. Die Focaleigenschaften der Flachen zweiter Ordnung. Leip-
zig, 1896.
32. Д ж. А. Стрэттон. Теория электромагнетизма. Гостехнздат, 1948,
стр. 61.
.33. Erdelyi, Magnus, Oberhettinger, Tricorni. Higher Transcen-
dental Functions. Bateman Manuscript Project. Me. Graw-Hill, 1955, v. 3,
p. 44.
34. G. D. Boyd, H. К о g e 1 n i k. Bell Syst. Techn. J., 11962, v. 41, № 4,
p. 1347—1369.
35. G. D. .Boyd, J. P. Gordon. Bell Syst. Techn. J., 196'1, v. 40, № 2,
p. 489—508.
36. К. Ф л а м м e p. Таблицы волновых сфероидальных функций. Вычисли-
тельный центр АН СССР, 1962.
37. Stratton, Morse, Chu, Little, Corbat6. Spheroidal wave func-
tions. Technology Press of M!IT, 'New York, 11956.
38. M. И. Петрашеиь. Ученые записки ЛГУ, сер. физическая, 1949,
вып. 7,1№ 120, стр. 59—78.
39. А. А. Д о р о д н и ц ы н. УМН, 1952, т. 7, № 6(52), стр. 3—96.
40. Ф. Т р и к о м и. Дифференциальные уравнения. Изд-во иностранной ли-
тературы, 1962, гл. IV.
41. Erdelyi, Magnus, Oberhettinger, Tricomi. Higher transcen-
dental functions. Bateman Manuscript Project. Me. Graw-Hill, 1953, v. 1.
Русский перевод: .Г. Бейтмен, А. Эрдейн. Высшие трансцендентные функ-
ции. Гипергеометрическая функция, функция Лежандра. Изд-во «Нау-
ка», 1965.
42. В. А. Фок. Теория диффракции от параболоида вращения. В сб. «Диф-
фракции электромагнитных волн «а .некоторых телах вращения». Изд-во
«Советское радио», 1957, стр. 5—56.
43. В. А. Фок, А. А. Федоров. ЖТФ, 1958, т. 28, № 11, стр. 2548—2566.
44. В. А. Фо к. «Радиотехника и электроника», 1956, т. 1, № 5, сгр. 560—
574.
45. Р. F. Byrd, М. D. F г i е d m a n. Handbook of elliptic integrals for
engineers and physicists. Springer Verlag, Berlin, 1954.
46. Л. H. Кармазина. Об асимптотике волновых сфероидальных функ-
ций. В сб. «Вычислительная математика». Изд-во АН СССР, 1959,
стр. 72—78.
47. Б. 3. К а ц е и е л е н б а у м. Теория нерегулярных волноводов с медленно
меняющимися параметрами. Изд-во АН СССР, 1961.
48. А. Д. Смирнов. Таблицы функций Эйри и специальных вырожденных
гипергеометрических функций для асимптотических решений дифферен-
циальных уравнений второго порядка. Изд-во АН СССР, 1955.
49. Ф. Клейн. Высшая геометрия. ГОНТИ, 1939.
50. G. Goubau, F. Schwering. IRE Trans., 1961, v. AP-9, Ns 3, p. 248—
256.
T. R. C h r i s t i a n, G. Goub a u. Ibid, p. 256—263.
51. Б. 3. К а ц e н e л e н б а у м. «Радиотехника и электроника», 1963, т. 8,
№ 9, стр. 1516—1522.
52. Н. Г. Бондаренко, В. И. Таланов. О лучевых волноводах зер-
кального типа. Доклад на II симпозиуме по диффракции волн. Горький,
июнь 1962.
.53. Н. Г. Бондаренко, В. И.. Таланов. «Известия вузов», Радиофи-
зика, 1964, т. 7, № 2, стр. 313—327.
54. Л. А. Вайнштейн. ЖТФ, 1957, т. 27, Ns 9, стр. 2109—2128.
55. М. Д. X а с к и н д, Л. А. Вайнштейн. «Радиотехника и электрони-
ка», 1964, т. 9, № 10, стр. 1800—‘1811.
56. А. Т. Фи ал ков с кий. «Радиотехника и электроника», 1966, т. 11,
Ns 2, стр. 178—186.
470
57. Г. ван де X ю л с т. Рассеяние света малыми частицами. Изд-во ино-
странной литературы, 1961, стр. 179—186.
58. С. G. В. Garret, W. Kaiser, W. L. Bond. Phys. Rev., П961, v. 124,
№ 6, p. 1807—1809.
59. P. Beckmann, A. S p i z z i c h i n o. The scattering of electromagnetic
waves from rough surfaces. Pergamon Press, Oxford, 1963, Chap. 2.
60. M. Г. Белкина, Л. А. Вайиште и н. В об. «Диффракции электромаг-
нитных волн на некоторых телах вращения». Изд-во «Советское радио»,
1957, стр. 88—91.
61. Р. Б. Ваганов, А. Б. Догадкин, Б. 3. К а ц ен е л ен б а у м. «Ра-
диотехника и электроника», 1965, т. 10, № 9, стр. 1672—1675.
62. Е. Snitzer. Journ. Optical Soc. Am., :J961, v. 51, № 5, p. 491—498;.
E. Snitzer, H. О s t e r b e r g. Ibid., p. 499—505.
63. J. R. Fontana. IEEE (IRE) Trans., 11964, v. MTT-12, № 4, p. 400—405.
64. Л. А. В а й н шт ейн. ЖТФ, 1953, т. 23, № 4, стр. 646—653.
65. Н. С. Крыло в, В. А. Ф о к. ЖЭТФ, 1947, т. 17, № 2, стр. 93.
66. Г. Ф. Д р у к а р е в. ЖЭТФ, 1951, т. 21, № 1, стр. 59.
67. Л. А. Вайнштейн. ЖТФ, 1953, т. 23, № 4, стр. 654—666.
68. Л. А. Вайнштейн. ЖТФ, 1957, т. 27, № 10, стр. 2340—2352.
"J В. В. Шевченко. «Акустический журнал», 1963, т. 9, № 2, стр. 215—
221.
7.'. Electromagnetic Theory and Antennas. Proceedings of a Symposium held
at Copenhagen, 1962. Pergamon Press, 1963.
71. A. E. Karbowiak. Proc. IEE (London), 1964, v. Ill, № 11, p. 1781—
1788.
72. R. G. Newton. Journ. of Mathemat. Phys., 1960, v. 1, № 4, p. 319.
73. Э. Ч. Титчмарш. Разложения по собственным функциям, связанные
с дифференциальными уравнениями второго порядка, т. I, 1960 и II,
1961. Изд-во иностранной литературы.
74. .Proceedings of the Symposium on Quasi-Optics, New York, June 1964.
Polytechnic Press, 1964.
75. А. Ф. Сучков. ЖЭТФ, 1965, т. 49, № 5(11), стр. 1495—1503.
76. Н. Г. Басов, В. Н. Морозов, А. Н. Ораевский. ЖЭТФ, 1965,.
т. 49, № 3(9), стр. 895—904.
77. «Электроника больших мощностей», сб. 2. Изд-во АН СССР, 1963,.
стр. 79—81.
78. П. Л. Ка п и ц а, С. И. Филимонов, С. П. Капица. «Электроника
больших мощностей», сб. 3. Изд-во «Наука», 1964, стр. 5—35.
79. Ф е й н ш т е й и и Колье. В сб. «Электронные сверхвысокочастотные
приборы со скрещенными полями». Пер. с англ., под ред. М. М. Федо-
рова, т. 2. Изд-во иностранной литературы, 1961, стр. 119—129.
80. А. В. Гапонов. «Известия вузов», Радиофизика, 1959, т. 2, № 3,
стр. 450—462; 1961, т. 4, № 3, стр. 547—559.
И. И. Анта ков, В. М. Боков, Р. П. Васильев, А. В. Гапонов.
«Известия вузов», Радиофизика, 1960, т. 3, № 6, стр. 1033—1044.
А. В. Гапонов, В. К. Ю лиатов. «Радиотехника и электроника»,
1962. т. 7, № 4, стр. 631—642.
81. Р. D. Coleman. IEEE (IRE) Trans., 1963, v. MTT-11, № 5, p. 271—
288.
82. Г. Д. Богомолов. «Электроника больших мощностей», сб. 3. Изд.-во
«Наука», 1964, стр. 154—175.
83. Н. А. Ирисова, Н. В. Карлов, А. М. Прохоров. Некоторые во-
просы квантовой электроники субмиллиметрового диапазона. Доклад на
Отделении обшей и прикладной физики АН СССР 14 апреля 1965 г.
Е. А. Виноградов, Е. М. Диалов, Н. А. И р н с о в а. Письма в ре-
дакцию ЖЭТФ, 1965, т. 2, № 7, стр. 323—326.
84. Electronics, 19/Х-1962, № 42, р. 74—76.
Electronic Design, 25/Х-1962, № 22, р. 16—17.
85. А. Л. Микаэлян, А. В. К о р о в и ц ы н, Л. В. Наумова. Письма
в редакцию ЖЭТФ, 1965, т. 2, № 1, стр. 37—41.
471
86. J. A. Giordmaine, W. Kaiser. Journ. Appl. Phys., 1964, v. 35, № 12,
p. 3446—3451.
87. E. Л. Косарев. Письма в ЖЭТФ, 1966, т. 3, № 7, стр. 295—298.
88. Я. Н. Фельд. Основы теории щелевых антенн. Изд-во «Советское ра-
дио», 1948.
Я. Н. Фельд, Л. С. Бенен с он. Антенно-фидерные устройства, ч. 2.
Изд. ВВИА им. Жуковского, 1959.
89. S. Jacobsen, Е. Andersen, М. G г о n 1 u n d. Proc. IEEE (IRE),
(1963, v. 51, Ks 1, p. 1431—1435.
90. H. L. Knudsen. IRE Trans., 11956, v. AP-4, Ks 3, p. 452—472.
H. L. Knudsen. Bidtrag til teorien for antennesystemer. Kobenhavn
1953, p. 145—159.
91. Я. H. Фельд, Л. Д. Бахрах. «Радиотехника и электроника», 1963,
т. 8, Ks 2, стр. 187—205.
92. С. Щелкунов, Г. Фрис. Антенны (теория и практика). Пер. с англ.,
под ред. Л. Д. Бахраха. Изд-во «Советское радио», 1955, (раздел 6.20).
93. Г. Н. В а т с о н. Теория бесселевых функций, ч. I. Изд-во иностранной
литературы, 1949, гл. XI.
94. R. J. Collins, J. A. Giordmaine. Quantum Electronics, Paris 1963
Conference, v. 2. Paris — New York, 1964, p. 1239—1246.
95. П. „Л. Капица. ДАН СССР, 1955, т. 401, № 2, стр. 245—248.
96. R. G. Meyerand, A. F. Haught. Phys. Rev. Letters, 1963, v. (Ill, Ks 9,
p. 401—403.
С. Л. Мандельштам, П. П. П a in и н и н, А. В. Прохиндеев,
А. М. Прохоров, Н. К. С уход рев. ЖЭТФ, 1964, т. 47, Ks 5(11),
стр. 2003—2005.
97. В. С. А в е р б а х , С. Н. Власов, В. И. Таланов, «Радиотехника
и электроника», 1966, т. 11, Ks 5, стр. 943—945.
98. S. Р. Morgan, Т. Li. Journ. Opt. Soc. Am., 1965, v. 55, Ks 9, p. 1128—
1132.
99. А. В. Гапонов, А. Л. Г о л ь д ен бер г, Д. П. Григорьев,
И. М. Орлова, Т. Б. Панкратова, М. И. Петелин. Письма
в редакцию ЖЭТФ, 1965, т. 2, Ks 9, стр. 430—435.
100. А. И. Анисимов, В. Н. Будников, Н. И. Виноградов,
В. Е. Гол ант. ЖТФ, 1965, т. 35, Ks II, стр. 2042—2051.
101. С. А. Ахманов, А. П. Сухоруков, Р. В. Хохлов. ЖЭТФ, 1966,
т. 50, № 2, стр. 474—486.
102. Ф. С. Русин, Г. Д. Богомолов. Письма в ЖЭТФ, 1966, т. 4, № 6,
стр. 236—239.
ОГЛАВЛЕНИЕ
Предисловие ...................................................... 3
Глава 1. Открытые резонаторы с параллельными плоскими зерка-
лами ........................................................ 5
§ 1. Основные свойства открытых резонаторов................. 5
§ 2. Диффракция на открытом конце волновода .... 9
§ 3. Параболическое уравнение и диффракция на открытом
конце волновода.............................................15
§ 4. Двухмерный резонатор, образованный плоскими зеркалами 27
§ 5. Открытый резонатор, образованный прямоугольными зерка-
лами ...................................................... 36
§ 6. Открытый резонатор, образованный круглыми зеркалами 38
§ 7. Спектр собственных частот..............................45
3 а д а ч и к г л. I....................................48
Глава II. Допуски для открытых резонаторов с плоскими зеркалами 63
§ 8. Интегральные уравнения для .произвольных зеркал . . 63
§ 9. Перекос зеркал.........................................65
§ 10. Параллельный сдвиг зеркал.............................75
§ 11. Прогиб зеркал.........................................77
Задачи к гл. II........................................79
Глава III. Открытые резонаторы с цилиндрическими зеркалами . 91
§ 12. Эллиптическая система координат и параболическое урав-
нение ......................................................91
§ 13. Каустики..........................................95
§ 14. Интегральное уравнение............................98
§ 15. Открытый резонатор с соосными зеркалами .... 102
§ 16. Цилиндрические зеркала конечной длины . ... 105
§ 17. Электромагнитные поля между цилиндрическими зерка-
лами ......................................................106
3 а д а ч и к г л. III................................109
Глава IV. Открытые резонаторы со сферическими зеркалами . . 115
§ 18. Сфероидальная система координат.......................115
§ 19. Сферические зеркала круговой формы...................118
§ 20. Сферические зеркала прямоугольной формы . 122
§ 21. Диффракционные явления............................. 124
§ 22. Концентрические сферические зеркала...................128
§ 23. Электромагнитные поля. Общие замечания . . . . 131
3 а д а ч и к гл. IV...................................134
Глава V. Цилиндрические и бочкообразные открытые резонаторы 139
§ 24. Цилиндрический резонатор..............................139
§ 25. Внутренняя каустика .................................144
§ 26. Бочкообразный резонатор в вытянутых сфероидальных
координатах................................................150
§ 27. Бочкообразный резонатор в сплюснутых сфероидальных
координатах................................................156
§ 28. Бочкообразный резонатор в сферических координатах . 159
473
§ 29. Интегральное уравнение для бочкообразных резонаторов 161
§ 30. Сектор бочкообразного резонатора . . .... 165
§ 31. Электромагнитные поля.................................168
Задачи к гл. V.........................................171
Глава VI. Геометрическая оптика открытых резонаторов ... 174
§ 32. Лучевые потоки в эллиптическом зеркале .... 174
§ 33. «Квантовые» условия...................................178
§ 34. Аналитический вывод квантовых условий . ... 181
§ 35. Зеркала и каустики....................................186
§ 36. Открытый резонатор, образованный зеркалами разной кри-
визны .....................................................189>
§ 37. Лучевые потоки в трехосном эллипсоиде . ... 193
§ 38. Асимптотические формулы для функций Ламе и кванто-
вые условия...............................................201
§ 39. Применение полученных результатов к открытым резона-
торам ......................................................205
§ 40. Возможности геометрической оптики.....................212
Задачикгл. VI.........................................217
Глава VII. Диффракция в открытых резонаторах с софокусными
зеркалами...................................................225
§ 41. Дифференциальное уравнение для софокусных цилиндри-
ческих зеркал...............................................225
§ 42. Метод эталонных уравнений. Исследование функции g(u, v) 229
§ 43. Колебания с каустикой..............................237
§ 44. Колебания переходного типа.........................240
§ 45. Колебания без каустики.............................242
§ 46. Численные результаты...............................244
§ 47. Дифференциальное уравнение для софокусных сфериче-
ских зеркал круговой формы..............................250
§ 48. Асимптотическое интегрирование уравнения (47.30) . . 254
§ 4<9 . Асимптотическое интегрирование уравнения (47.24) . . 258
§ 50. Диффракционные потери для софокусных зеркал круговой
формы......................................................262
§ 51. Диффракция .при произвольном отношении радиуса кри-
визны зеркал к расстоянию между ними .... 264
Задачи к гл. VII........................................269
Глава VIII. Открытые волноводы......................................275
§ 52. Основные свойства открытых волноводов .... 275
§ 53. Параксиальные лучевые потоки в открытых волноводах,
образованных линзами или зеркалами.........................282
§ 54. Диффракция в открытых волноводах........................289
§ 55. О диффракции на линзах в свободном пространстве. Ме-
тод приближенного разделения переменных . . . 296
§ 56. Диэлектрические волноводы...............................300
§ 57. Открытые волноводы других типов....................... 306’
Задачи к гл. VIII.......................................308
Глава IX. Открытые резонаторы с диэлектрическими телами . . 319
§ 58. Электромагнитные колебания диэлектрического шара . 319
§ 59. Внешние электромагнитные колебания идеально прово-
дящего и импедансного шара................................324
§ 60. Двухмерные электромагнитные колебания прямоугольной
призмы....................................................327
474
§ 61. Прямоугольная призма между плоскими зеркалами . 333
§ 62. Общие замечания о резонаторах с диэлектрическими те-
лами ....................................................344
Задачикгл. IX......................................346
Глава X. Возбуждение открытых резонаторов (общая теория) . 353
§ 63. Затухающие свободные колебания и собственные функции
непрерывного спектра.....................................353
§ 64. Вынужденные колебания открытого резонатора . . . 363
§ 65. Задача Коши...................................365
§ 66. Собственные функции непрерывного спектра для электро-
магнитного поля.....................................368
§ 67. Возбуждение открытых резонаторов заданными токами 372
§ 68. Задача Коши для электромагнитного поля .... 375
§ 69. О возбуждении открытых волноводов.............378
3 а д а ч и к г л. X...............................379
Глава XI. Возбуждение открытых резонаторов (частные задачи) . 385
§ 70. Одномерная модель открытого резонатора .... 385
§ 7'1 . Возбуждение шара радиальным диполем .... 393
§ 72. Вычисление нормы N,................................396
§ 73. Интегральное уравнение и норма колебаний между софо-
кусными зеркалами........................................398
§ 74. Возбуждение открытого резонатора, образованного парал-
лельными дисками........................................404
3 а д а ч и к г л. XI..............................407
Глава XII. Открытые резонаторы в физике и технике . . . . 415
§ 75. Применения открытых резонаторов и открытых волноводов 415
§ 76. Открытые резонаторы в электронике..................416
§ 77. Открытые резонаторы в измерительной технике . . . 424
§ 78. Открытые резонаторы с дополнительным разрежением
спектра..................................................432
§ 79. Открытые резонаторы в антенной технике .... 436
§ 80. Сверхнаправленная кольцевая антенна как открытый ре-
зонатор ................................................440
§ 81. Передача энергии между двумя апертурами . . . 446
§ 82. Шаровая молния?....................................450
3 а д а ч и к гл. XII..............................451
Заключение....................................................463
Обзорлитературы...............................................465
Цитированная литература.......................................469