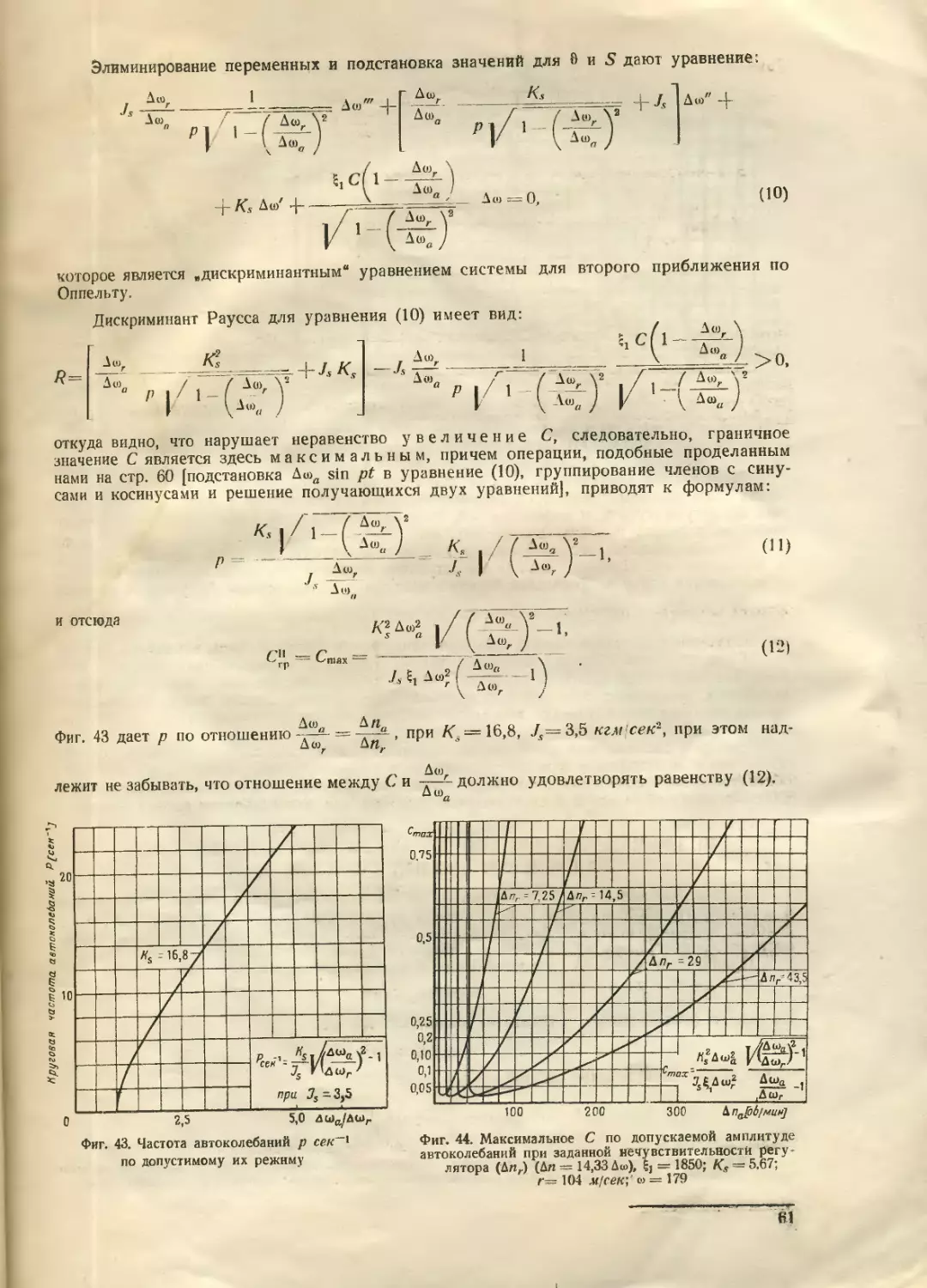
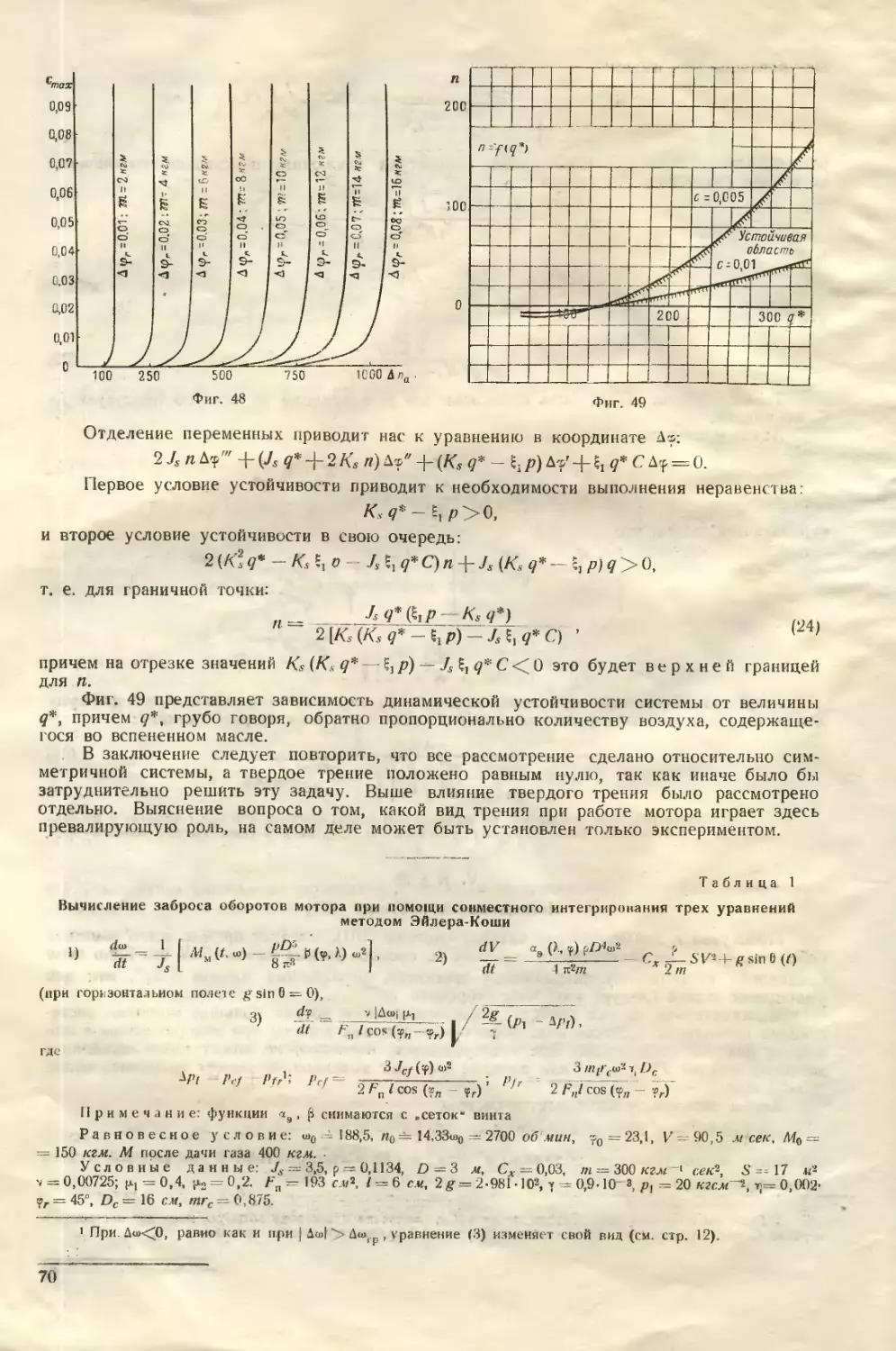
Text
МИНИСТЕРСТВО АВИАЦИОННОЙ ПРОМЫШЛЕННОСТИ СОЮЗА ССР
ЦЕНТРАЛЬНЫЙ АЭ°О-ГИДРОДИ Н AM ИЧ ЕСК И Й ИНСТИТУТ
им. проф. Н. Е. Жуковского
ТРУДЫ ЦАГИ
№ 602 *
ДИНАМИНА АВТОМАТИЧЕСКОГО
РЕГУЛИРОВАНИЯ СЁОРОТОВ АВИАМОТОРА
ПОСРЕДСТВОМ ВИНТА ИЗМЕНЯЕМОГО ШАГА
Е. Б. Левенталь
ИЗДАТЕЛЬСТВО БЮРО НОВОЙ ТЕХНИКИ
19 4 7
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
т — масса самолета.
Js — суммарный .осредненный* момент инер-
ций винта и кинематически связанных
с ним деталей, приведенный к оси вра-
щения винта.
сх — коэфициент лобового сопротивления
самолета.
S — несущая площадь самолета.
Р — плотность воздуха.
Ф — сила тяга винта.
ф — угол отклонения грузика центробеж-
ного регулятора.
Л1М , Маг — вращающий момент мотора.
Мв — тормозной момент винта.
Q — вес самолета.
6 — мгновенный угол траектории полета
к горизонту.
а — угол атаки самолета.
V — поступательная скорость самолета.
п - обороты мотора в минуту.
со — угловая скорость винта.
«у—показание центробежного регулятора.
<р — угол установки лопастей винта.
D — диаметр винта.
Dc — диаметр подшипников лопастн.
а9 — .коэфициент силы тяги* винта,
р — .коэфициент мощности* винта.
т, — коэфициент трения подшипников ло-
пастей.
гп{ — масса одной лопасти винта.
Гс — .-плечо* ц. т. лопасти.
— центробежный момент инерции лопасти.
f — площадь сечеиия поршня.
I — плечо кривошипа лопасти.
v — коэфициент сечения просвета золот-
ника.
|^оу| — действующее поперечное сечение зо-
лотника.
(J,1 — коэфициент расхода золотника при
.затяжелении* винта.
р.2 — коэфициент расхода золотника при
.облегчении* винта.
Р] — 1-й коэфициент упругости пружины
регулятора.
р2 — 2-й коэфициент упругости пружины
регулятора.
у — положение золотника регулятора.
<вд — угловая скорость вращения регулятора
/йг_ — масса грузика центробежного регуля-
тора.
т3 — масса золотника центробежного регу-
лятора.
/?0 — расстояние от оси вращения регулято-
ра до оси грузика.
/?1 — плечо ц. т. грузика регулятора отно-
сительно оси Ох л
/?2 — длина упорного дфючка.
— угол установки лопасти при централь-
ном положении поводка (развилки)
поршня.
пР2—показатель затухания колебаний р. п.
(регулируемого параметра).
nR—показатель затухания .изолированных*
колебаний индикатора регулятора.
уд-—собственная .изолированная* круговая
частота регулятора.
Ь — частота колебаний . затухающих* р. п.
Дю —малые отклонения р. п. от равновес-
ного положения.
Д<р — малые отклонения угла от равновес-
ного положения.
ДУ—малые отклонения скорости V от рав-
новесного положения.
Дпо — амплитуда автоколебаний р. п. в обо-
ротах.
Дпг — приведенная .зона нечуствительности*
регулятора.
Дшо — амплитуда автоколебаний, отнесенная
к угловой скорости винта.
Дшг — то же в отношении .зоны нечувстви-
тельности*.
ТРУДЫ ЦАГИ
№ 602
ДИНАМИКА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ОБОРОТОВ
АВИАМОТОРА ПОСРЕДСТВОМ ВИНТА ИЗМЕНЯЕМОГО ШАГА
Е. Б. ЛЕВЕНТАЛЬ
ПРЕДИСЛОВИЕ
Настоящая статья представляет собой несколько сжатое изложение основных резуль-
татов проделанного теоретического исследования динамики процесса автоматического ре-
гулирования ВИШ. Целью данной работы было создание сравнительно развернутой тео-
рии вопроса, но только в техническом аспекте, так как результаты предполагались быть
предоставленными для использования инженерам, работающим в авиапромышленности.
Сообразно со сказанным в работе применялись по возможности простые математи-
ческие средства, хорошо зарекомендовавшие себя в других областях, а иногда (например,
в вопросах автоколебаний) проводилось лишь приближенное исследование с целью избе-
жать привлечения громоздкого аппарата нелинейной механики.
Автор считает своим долгом принести глубокую благодарность проф. Д. Ю. Панову
за помощь и постоянную поддержку в проведении данной работы и проф. Г. М. Мусинянцу,
от4которого автор часто получал ценнейшие советы и указания.
‘Автор считает также необходимым выразить признательность В. Б. Коноваловой,
блестяще выполнившей всю вычислительную работу.
> I ч
S , ГЛАВА I
СО Ч/ КООРДИНАТЫ И УРАВНЕНИЯ ЗАДАЧИ
I
§ 1. Координаты системы
" I
Поскольку „снимаемая1* винтом мощность мотора (при заданном р) в любой момент
- А «И V \ I/
зависит только от X |Х — - — ^п\, ® и п, т. е. только от I/, <о, ф, постольку естест-
венно эти величины рассматривать как обобщенные координаты системы1, представляю-
щие собой независимые кинематические параметры, полностью характеризующие режим
работы винта.
Координата положения лопасти зависит от действия центробежного регулятора,
координатой же последнего мы будем считать Д_у = о>А. Последняя величина кинемати-
а— положение центробежного
регулятора я золотника при
постоянном (заданн ьм) числе
оборотов МО'; ора,
положение центробежного
регулятора и золо <ка при
повышении числа .оротов
мотора,
с -положение центробежного
регулятора мотора ' золотни-
ка при понижении исла обо-
ротов мотора
Фиг, 1
чески связана с углом отклонения ф центробежного грузика регулятора (фиг. 1). Всего,
следовательно, мы располагаем четырьмя независимыми координатами: V, ф/ и «р, что
- г Конечно, V и м представляют собой поступательную н угловую скорости. Для нас они, однако, играют
роль .обобщенных* координат.
позволяет нам установить, что рассматриваемая механическая система имеет четыре
степени свободы. Ввиду того, что в дальнейшем мы будем рассматривать процесс регу-
лирования при неизменном сх самолета, то четырех уравнений (см. ниже) в координатах
V, о>, <оу и ® соответственно будет достаточно для решения поставленной задачи
§ 2. Уравнение поступательного движения самолета
Мы привлекаем здесь общеизвестное уравнение поступательного движения самолета;
av о
т -фсх Л V2 = — Qsin 0(f) -(- а9 pCH/^cos а,
(1)
представляющее собой, по существу, очевидное условие равновесия между силой тяги
винта и всеми силами сопротивления движению, а также и реакцией инерции, каковое
условие по замене ns на «> записываем в форме:
т + Ся SV2 Q Sin 6 + Ю COS а’ а)'
где О рассматривается как заданная функция времени и при пикировании б<0.
Наличие зависимости силы тяги от переменной со (входящей и явно и неявно через
аэ) и переменной ф (входящей только неявно через а9) определяет связь уравнения (1а)!
с уравнениями в координатах со и
Для исследования процесса регулирования оборотов мотора достаточно рассматри-
вать лишь такие участки траектории полета, при прохождении которых можно считать
сх = const. В случае необходимости можно на каком-либо отрезке задать какой-либо
закон изменения сх. Как будет видно из дальнейшего изложения, практически в нашей
задаче в этом надобности не встречается.
§ 3. Уравнение вращения винтомоторной группы
Уравнение, о котором здесь идет речь, занимает, если так можно сказать, „цент-
ральное“ положение среди других, так как согласно самой постановке задачи и принятой
в теории регулирования терминологии оно является уравнением „регулируемого пара-
метра"1, поскольку регулируется именно угловая скорость вращения винта.
Подобно уравнению (1) оно также представляет собой условие равновесия, но в
данном случае между вращающим моментом мотора и тормозящим моментом винта*. Об-
щий вид этого уравнения таков:
УФ",2 ^ + ^№.?И==Ч,(<“.0.
(2)
или, заменяя ns угловой скоростью ш:
2Уп' ТГ+й₽ =м"' <“• 0.
и так как
то через „коэфициент мощности" 3 написанное уравнение связано
неявно с уравнениями в координатах V и <р.
Сумма S представляет сумму приведенных к оси винта моментов инерций всех
i
тел, кинематически связанных с винтом в его вращении при наличии передаточных чисел
П;. С достаточной для практики точностью можно для всех интересующих нас случаев
принять, что
_ /.«2 = const = Js,
1 Т. е. уравнением для w — resp для п об/мин.
3 Все угловые скорости и моменты сил мы рассматриваем приведенными к оси винта, таким образом,
.момент мотора (“.0 мы также рассматриваем в приведенной к оси винта форме
2
после чего уравнение регулируемого параметра принимает вид:
4^+^₽(М)«*=лМ“,о. <2а>
причем представляет собой некоторую, вообще говоря, табличную функцию <о, в
которой время t входит в виде параметра для общности, так как изменения Mdr по t
произвольно задаются.
При численных расчетах, проведенных ниже, мы пользовались так называемыми
„внешними -характеристиками" мотора, в которых представлена мощность мотора N в функ-
ции от <o = 2tws, и мгновенное значение функции МЛг(ш, t) вычислялись при заданной ш
и положении дросселя (положение дросселя являлось именно тем фактором, через кото-
75ДЛ
рый и вводился „параметр" f) как частные Mdr= ——Очевидно, что при этом опу-
скалась весьма „быстротечная" внутренняя (газовая) динамика мотора, учет которой чрез-
вычайно усложнил бы всю задачу и не был необходимым именно ввиду упомянутой
быстротечности газовых процессов в моторе сравнительно с процессами, подвергавшимися
изучению.
§ 4. Уравнение центробежного тахометра (индикатора) регулятора
Тахометры большинства регуляторов ВИШ по своему конструктивному оформлению
близки к типичной конструкции подобного прибора, изображенной на фиг. 2, где показан
центробежный тахометр регулятора Р-7.
Действие тахометра, управляющего перепуском масла на „затяжеление" и „облегчение"
винта, легко уяснить из фиг. 1, 2, З/и заключается оно в том, что для нормальной (задан-
ной регулятору) скорости вращения имеет место равновесие между моментом центробеж-
ных сил Мф вращающихся относительно оси Oz центро-
бежных грузиков, и упругим моментом реакции соответ-
ствующим образом установленной пружины.
При повышении скорости вращения выше заданной
увеличивающаяся центробежная сила, преодолевая пружину,
приводит грузики в положение, показанное на фиг. 1— Ь,
и наоборот, при понижении оборотов ниже норм—в поло-
жение, показанное на фиг. 1—с. В первом случае золотник (з)
центробежного тахометра открывает доступ масла во втулку
на „затяжеление" винта (угол <р возрастает), и винт вскоре
начинает снимать большую мощность, что и снижает обо-
роты, а во втором случае винт начинает „облегчаться", так
как угол <р уменьшается ввиду вытеснения масла из втулки
моментом центробежных сил лопастей винта, и винт начинает
снимать меньшую мощность, что и приводит к обратному
результату. Таким образом, этот процесс автоматически вы-
равнивает скорость вращения мотора и представляет собой
интересующее нас регулирование оборотов авиамотора по-
средством ВИШ.
Очевидно, что тахометр-индикатор, рассматриваемый
отдельно, представляет устройство с двумя степенями свобо-
ды, соответствующими вращению относительно осей Охи Oz.
Однако вращение относительно оси Oz не является незави-
симым, так как тахометр жестко связан шестеренной пере-
дачей с авиамотором. Поэтому нам остается написать урав-
нение-, для.координаты соответствующей положению
золотника и характеризующей „отклонение" индикатора
(тахометра).
Пользуясь системой осей, показанной на фиг. 3, и
крючка s, мы можем ввиду симметрии заметить, что оси Оу' и Oz', связанные с грузи-
ком, являются для последнего.главными осями инерции.
Мы напишем уравнение для тахометра, составив условие равновесия моментов на оси
вращения грузика Ох для <»/? = const. Эти моменты, как легко видеть, суть:
1) реактивный момент центробежной силы от переносного вращения центра тяжести
грузика:
Ml — Sin COS ф,
где/гаГр’-масса грузика;: ' -д— ‘ <•
/?0—расстояние оси грузика от оси вращения регулятора Oz, '
/?i—расстояние ц. т, грузика от оси Охр
3
2) момент центробежных сил грузика относительно оси, проходящей через центр
тяжести:
ЛГн = (/а— Л) cos ф sin ф,
где Ja и Jb —главные центральные моменты инерции относительно обеих центральных
осей Оу' Oz' соответственно.
В данном случае, так как этот момент вращает грузик в сторону увеличения
угла ф;
3) реактивный момент инерционных сил при ускоренном движении, включая эффект
от „выноса" центра тяжести грузика на плече Ru т. е.
Мп = -(ЛФ" + ^гР/?|ф"),
где Jc — главный центральный момент инерции грузика относительно оси Ох'-,
4) реактивный момент сил инерции ускоренного движения золотника:
Mv —-----tnJQ (cos2 фф" — sin ф cos ф ф'2),
где т3 — половина массы золотника и соединенных с ним деталей,
R— длина „крючка" г.
Это видно из того, что поскольку перемещение золотника Д_у = i»z и угол поворота (ф)
грузика связаны кинематически (см. фиг. 3 и 4) так:
Aj —/?281пф, (а)
рассматривая ф как функцию времени t и дифереицируя зависимость (а) по t последова
тельно, получим:
d*y
dP
dy
^г== R, cos фф ,
— /?2 (cos фф" — sin фф'2).
Отсюда следует., что реакция инерции золотника, выраженная в функции угла ф, будет:
Pt зол ~ -4- т3 Rz (cos фф" — sin фф'а).
/
.Усилие это на оси грузика порождает вращающий момент:
Mj — Pi 3ojiR2 cos ф — т. /^(С083фф"-~sin фcosфф'2);
5) момент упругих сил пружины регулятора:
Мпр^ЛпрСу)—/уПр(л4-^). причем sinф,
где /упр -вообще говоря, нелинейная функция прогиба.
4
В результате получаем:-
(4 4- wrp /?’-) ф" у m3R* 2(cos2 фф"—sin ф cos фф'9)—
=mtvRaR^Rcos ф + [(4 — Jb) -ф mгPZ?f] sin ф cos ф — /Иупр(у). (3)
Таково уравнение „собственных колебаний регулятора”, рассматриваемого изолиро-
ванно, для co/j. принятой за постоянную.
Предполагая в частном случае малых колебаний регулятора, что упругая реакция
пружины линейна относительно деформации (см. также дополнение), т. е. что функция
Pynp=jijj -ф- ц2у2 -ф р.8у8 -ф... может быть апроксимирована линейно в виде Pynp = р1у, п0'
лучаем, поскольку у=/?28шф, момент упругой реакции пружины, приведенный
к одному из двух грузиков, будет:
Мпр= у Н Sin Ф cos ф -фу- р ,У0А?2 cos Ф,
после подстановки выражения для которого в (3) мы можем написать уравнение1:
(У„-ф-wzrp/?i) ф"-ф -g-m3/?2(cos2 фф" — sin ф cos фф'2)-ф у V-tPisin Ф cos Ф —
((4"4) ~ф sin ф cos ф — mrpRoR^cos ф — P0R2 cos ф. (4)
Из этого уравнения находим условие статического равновесия, когда, следовательно,
Ф" = Ф' = О:
.у- sin Ф cos ф—и#[(Ja—4)-ф-лггр/?1] sin ф cos ф = mrp/?0₽i<»Rсоэф—Р0/?2 cos ф,
т. е.
-у H#oSin ф-т# ((4 — 4) -ф ОТгр/?1] sin ф=т,р R0Rxo>r — P0R.,,
Очевидно, что из этого равенства получается:
ц^гР R^Pi^'p РqR^
si» Ф == т—-----------------------•
4н;^-^[(4~4)+«гР/??|
Следовательно, равновесный угол:
ffirpRoRi^p РqR^
•Ь —arc sin у—------------------------------------------,
и в частности, если мы хотим привести это условие к отклонению золотника (Ду), так
как Ду — R2 sin ф, то
ffltpRoRi^P Р0^2 —
*У = j -------2-------------------• (5)
1(4-4) + "^^]
Фиг. 5 показывает для примера семейство полученных из равенства (5) так называе-
мых „равновесных" кривых регулятора при установке его на различные равновесные
обороты мотора. При этом величины постоянных были взяты следующие2:
тгр — 3-10 9 гсмл сек2; т3 = 1,05- 10~] гсм~х сек2; /?1 = 1,7 см; R2~\,7 см;
Rb — 2,5 см; ./с —3,28-10”3 гем. сек2; Уа = 3-10-9 гем сек2; Jb = 5,1 -10 3 г см секг;
u' = 8,12-103 гсм~х; <' = 8,77103 г см~г; «"'= 9,27-103 гсм~х (см. фиг. 5).
> Где Ро —сила натяжения начальной- (.установочной*) деформации, Рр= 'o' .RiJ’o-
2 Если учесть имеющую место нелинейность пружины, то .равновесные* кривые получаются более пря-
мыми (!) —регулятор Р-7 имеет на самом деле почти прямолинейные .равновесные* -кривые.
Различные значения у. взяты для частичного учета нелинейности пружины, показы
Фиг. 5. Кривая равновесных положений регулятора
Уравнение равновесия:
"ггрЯоЯ1(шя —“о)
2 ————
KS~^K4—4)+«rp*ll
Z г\2
— /(“/?)
Конструкция рассматриваемого регулятора такова, что в работе он отклоняется
мало — resp ф всегда остается малым углом. В связи с этим можно принять 81пф = ф,
совф = 1. Далее (cos2 фф" — sin ф cos фф'2) превращается сперва вф" —фф'2. Ввиду вы-
сокой частоты собственных колебаний данного регулятора и малости угла ф второе
слагаемое в последней скобке весьма мало по сравнению с ф" и может быть отброшено.
В отношении функции /И,1р принимаем, как уже было сказано (ввиду малости колеба-
ний), линейную форму:
^пр =, ~2~
Таким образом, окончательно уравнение малых колебаний тахометра регуля-
тора напишется в виде:
4+mrpR'i 4- '-у Rj) Ф"+ 1(4 - 4)4- ^гр/??]} ф - /Игр R0R^ - P()R2. (6)
Чтобы учесть влияние изменения w# на колебания регулятора, следует обратить
прежде всего внимание на то, что, представив <off в виде шп4-Дш, мы можем записать (6)
в форме:
Ф" + [°1 — °2 (ш0 + 2“од“ 4- Д Ф = «3 Н 4- 2о>0Д(0 + д 0?) — Я о-
В правой части вся постоянная часть первого слагаемого компенсируется начальной
установкой пружины, кроме того, квадратом малой величины Дю2 можно пренебречь.
В итоге получаем сперва (так как а3ш2— ^0 = 0):
ф" [«1 — (“о 4~ 2<%дД<о2)] ф = 2а3ш0Дш.
(6')
Но здесь следует принять во внимание, что, хотя правая часть уравнения меняется
пропорционально Ди, коэфициент при ф в левой части изменяется при малом изменении <о
очень мало, так, например, обычно величина порядка 200, следовательно, ч>2 порядка
40000, а Дю обычно не превышает 10, следовательно, Дю2 = 100, а обычно и того меньше.
Таким образом, величину
[а, — а2 (ю2 4- 2<ооД“ + д ш®)] ~ [«1 — а2 Н))
можно при малых колебаниях в скорости вращения («/?) практически считать постоянной.
в
Характеристика регулятора, снятая е натуры, либо вычисленная с учетом нелиней-
ности пружины, наоборот, еще ближе к прямолинейной (см. фиг. 7).
Таким образом, можно уравнение (6') написать так;
Ф"+/’«'к = 2ав%Дш. (6а)
и если учесть демпфирующее трение, взяв его в линейной форме, то
ф" 2rt₽ ф' ' р5?ф — 2п3ч)0Д<о. (6Ь)
Ввиду произвольности назначения „цены" отклонения регулятора, можно регулятору
придать такую „шкалу", что по его статическому отклонению непосредственно прочиты-
вать Д<о. Таким образом, введя координату <о/ = хф ’, напишем окончательно:
<о" -ф 2п/? 4~ P2R^f—PR& “• (6с)
При этом „частоту" регулятора (pR) вообще нет надобности вычислять и лучше, если
требуется, снять ее с натуры.
Вообще частота этого регулятора столь высока, что, как будет сказано ниже, она
не создает никакой практической угрозы для устойчивости процесса (см. § 24).
Что касается коэфициента то таковой подлежит определению опытным путем
и в настоящее время еще неизвестен. Учитывая,
однако, значительные усилия, уравновешивающиеся
в этом регуляторе при его работе, можно предпола-
гать, что силы трения, отраженные коэфициентом nR,
играют сравнительно небольшую роль и на собст-
венную его частоту влияют мало.
Дополнение к § 4
Эксперимент показал, что коническая пружина
регулятора Р-7 в действительности нелинейна
(см. фиг. 6)2. Эмпирическая формула, хорошо апро-
ксимирующая зависимость между упругой реакцией
и деформацией в форме Рупр = н у -4 h-2-V2> представ-
ляет собой в согласии с экспериментом:
Рупр ~ 5,67у 4” 2,5у2.
где у дано в см, Рупр — в кг.
При этом условие статического равновесия ре-
гулятора (когда ф" — ф' = 0) следует писать, учиты-
вая полную деформацию пружины и памятуя, что
полная деформация у представляет собой сумму
Фиг. 6. Характеристика пружины
регулятора Р-7
у=у04-Ду,
где у0— начальное поджатие пружины (для установки регулятора на заданное число
оборотов) и Ду = R2sinф — деформация, зависящая только от отклонения регу-
лятора.
Искомое условие равновесия представляет собой равенство моментов центробежной
силы (см. § 4) и момента от упругой деформации пружины, т. е.
{mtp Ro /?] 4- [(Jn — Jb) 4- отгр sin ф} cos ф = ~ РуПр /?, cos ф, (6d)
где Pynf — упругая реакция пружины [кг], так как
и Ду =sin ф,
то условие (6d) напишется так:
«л {'«гр Яо #1 +1(4 — 4) + «* 1>-р Я?] sln ф? cos ф = -L (р.| (у0 4- ду| 4- И2 (у0 ду)4 r„ cos ф ,
1 И, следовательно, «у —уф', ну—уф", где у" — коэфициен; мощности масштаба. Следовательно:
1 2
у — PR-
* Опытная кривая, изображенная на фиг. 6, любезно предоставлена профессором Г. М. Му синя ни.
7
сокращая которое на cos<]> и переходя в левой части от у к A> = /?2sin<p, получаем
равенство:
{Лип> Ro Ri 4- [(/„ — 4)+ffkp /?il ) 1н Су о 4- &у)+н Су о+д.у)2] >
разворачивая которое относительно Ду, приходим к квадратному уравнению:
Де._ ,^К4 ./,) i «^«tl I4,_
Z ( Z г\2 J
~т R R ы2 — И1 v У а
Выполнение условия, обращающего правую часть в нуль, тождественно, т. е. реше-
ние квадратного уравнения
^«1*2 , , ffsl»] r> г> 2
2 Уо 4~ 2 —/Пгр ’
и подстановка положительного его корня (соответственно необходимой начальной дефор-
мации пружины) в левую часть на место у0 обращает (7) в уравнение вида:
а Ду2-|-& Ду = 0, (7а)
для которого имеет место нулевой корень, соответствующий равновесной точке.
Полагая далее всегда, что у0 =/(«/?,о), мы равновесную кривую регулятора можем
построить по корням уравнения (7а), меняя в нем в качестве аргумента значение и
используя лишь корень созиачный с разностью «Ro> где wRo— заданная равновесная
угловая скорость, а «д; — переменная.
Построенные таким образом равновесные кривые регулятора представлены на
фиг. 7 и дают возможность видеть, что нелинейность пружины здесь действует в сторону
„спрямления" равновесных характеристик, вычисленных более приближенным методом.
Фиг. 7. Кривая равновесных положений регу-
лятора при учете нелинейности пружины
Уравнение равновесия:
R? 1^2 . ,
2 АУ1
+ К&гУо — ~ К4—4) -Ь mrD Ду 1
^2 )
-2- Уо + Яг Уо - «гр = О
§ 5. Уравнение сервосистемы регулятора
Масло, подающееся помпой под давлением 20 ат через регулятор во втулку винта,
приводит в движение поршень, соединенный со специальной развилкой („поводковой
муфтой"), передвигающей входящий в нее палец (фиг. 8) кривошипа комля лопасти.
Предположено (нормально это и имеет место), что масляная помпа во всех случаях
обеспечивает необходимый полезный расход масла, а наличие редукционного клапана
поддерживает давление на входе в регулятор, независимо от обстоятельств (за исклю-
чением „отрицательных перегрузок") на уровне 20 ат. Несложный расчет показывает,
что производительность помпы (15 л!мин) составляет примерно удвоенную величину
полезного расхода масла через золотник регулятора при полном его открытии, когда
лопасть меняет шаг со скоростью 6°—7° в секунду.
6
Фиг. 8 показывает, что имеется следующая кинематическая связь между углом
установки лопасти <р и положением поршня х:
х = I sin (<р —
(8)
где rfr — угол установки лопасти при центральном относительно оси комля положении
развилки поршня, обычно ср, = 45°.
Диференцируя последовательно уравнение кинематической связи (8) по времени t,
имея в виду, что получаем:
dx , , d<?
откуда
dy dx__________1 ч
dt dt /cos(«р — ср,) ’ '
I cos(<p - «,) — I sin (<p — cpr) () ,
•ткуда
dt'1 dt1 2 I cos (ср — ср,) ё ( dt
(8b)
Равенства (8), (8a) и (8b) выражают „кинематику" рассматриваемой передачи.
Составляя выражение элементарной работы М8<р = Р„ 8 х, где Рп — сила, приложенная к
поршню, и замечая (см. фиг. 8), что 8 x=l cos (ср — ср,) 3<р, находим:
М 8<р = Рп I cos (ср — ср,) 8<р, т. е. /И — Р.) / cos (ср — ср,).
(9)
Равенство (9) представляет собой „статику"
передачи от поршня на лопасть.
Переходя к составлению диференциального
уравнения движения сервосистемы регулятора,
примем, что:
1) потеря напора в маслопроводе может быть
апроксимирована квадратичным двучленом вида
Ра=^Ь1^ + Ь2^«,
где т;м — средняя объемная скорость масла в каком-
либо сечении маслопровода,
bt и Ь2 — коэфициенты, определяемые из экспери-
мента :
2) потеря напора „в очке"1 золотника — КВЗ- Фиг. 8. Кинематика передачи: поршень—лопасть
дратична относительно скорости масла в нем (по-
путно заметим, что сечение „очка" золотника весьма мало по сравнению с сечением
маслопровода), т. е.:
здесь р— коэфициент расхода,
vs—скорость масла в „очке" золотника, причем
/-----j
1 Т. е. в просвете.
2 KR и, следовательно, р легко определить из эксперимента, измерив рв при данном о4..
9
3) потеря напора в цилиндре от трения масла о стенки его пренебрежимо мала.
Противодавление Др, в цилиндре втулки винта равно алгебраической сумме давле-
ний, создаваемых:
а) моментами центробежных сил лопастей,
б) „ трения в подшипниках лопастей,
в) „ аэродинамических сил лопастей,
г) „ сил инерции при ускоренном проворачивании лопастей,
д) силами трения поршня о цилиндр,
е) радиальным градиентом давления масла во втулке из-за центробежной силы.
Из числа перечисленных факторов последние три (г, д и е), как было установлено,
относительно малы и могут быть в данном рассмотрении сразу опущены.
Таким образом, мы можем написать два нижеследующие равенства:
д „ = 37с/(<р)о>2 I 3/nfwa rc7jDc , 3Moer 9 .
Pl 2Fn I cos (<₽—<?,) 2Fn I cos (<f>—<f>) Fnl cos (<p — %) ’
= + + +
из которых последнее означает равновесие между располагаемым давлением и суммой
всех потерь при „затяжелении винта“.
Так как между скоростью масла v№ в каком-либо постоянном сечении /м маслопро-
вода и скоростью масла vs в переменном сечении „очка" золотника существует следую-
щая зависимость:
Vs.
Jw
Величину /м можно выбрать произвольно1, но коэфициенты сопротивления ЬА и Ь2
следует тогда „привести" к этому сечению. Причем /3ол = Чш/1> когда
и Дол = *| Д“гр |, когда о)у>Дшгр, и можно написать уравнение:
V2W2 \
bi -fT- т7- ~ ДА-
7м 7 7«
(9Ь)
Следовательно, скорость истечения vs через переменное сечение „очка“ золотника
отсюда определяется как положительный корень уравнения (9Ь):
V2 ш2.
Kr (А~дЛ)
(9с)
Равенство (9с) дает vs. Но так как общий расход масла Q=wyps по причине нераз-
рывности одинаков в любом сечении маслопровода и равен расходу в цилиндре, то ско-
рость поршня во втулке есть:
dx Q
Рп dt = F = ~~F ’
причем vs нам известно из (9с). Так как, с другой стороны, согласно (8а)
d<f dx ________1_______ dx
dt dt cos (<₽ — <fr) И dt ’
Таково уравнение сервосистемы при „затяжелении*. В дальнейшем мы упростим его,
приняв, что гидравлическое сопротивление маслопровода пренебрежимо мало по сравне-
1 В силу неразрывности.
10
Нию с сопротивлением золотника, в связи с чем следует положить ^ «== я= 0. Уравне-
ние (10а) тогда примет вид1:
./ 2^( Др) >0 (10b)
dt Fn / cos (ср — ср,) J у r ' 1
где попрежнему
д - । ЪМд„
Pl 2F„ I cos (ср -- <?,) 2Fn I cos (<? — ср,) “ Fn I cos (cp — cp,)
Для получения уравнения, соответствующего обратному процессу „облегчения*1
винта, когда доступ масла из помпы во втулку прекращен и происходит вытеснение
последнего под действием момента центробежных сил лопастей, в связи с чем активное
давление уже будет:
— 3 *^/(?)0)2 । зл/«ег 3/nfo3rfT)L>
2Fn I cos (ср — ср,) — Fn I cos (<р — ср,) 2Fn I cos (ср — ср,)
(полагаем U). Повторяя те же рассуждения, нетрудно видеть, что для облегчения
винта, имеющего место, когда Шу<0, при тех же допущениях имеем уравнение8:
= vro^ I / 2< О2
dt Fn / cos (ср — ср,) |/ y р ’
т. е.:
(Zcp _ VWy Р*2
dt Fa I cos (cp — <fr)
-3./(ср)со2 ! 3/ИП„ _ \
2Fn/ cos (cp — cp,) — Fn I cos (cp — cp,) 2Fn I cos (cp — <₽,)) ’
(Юс)
0,
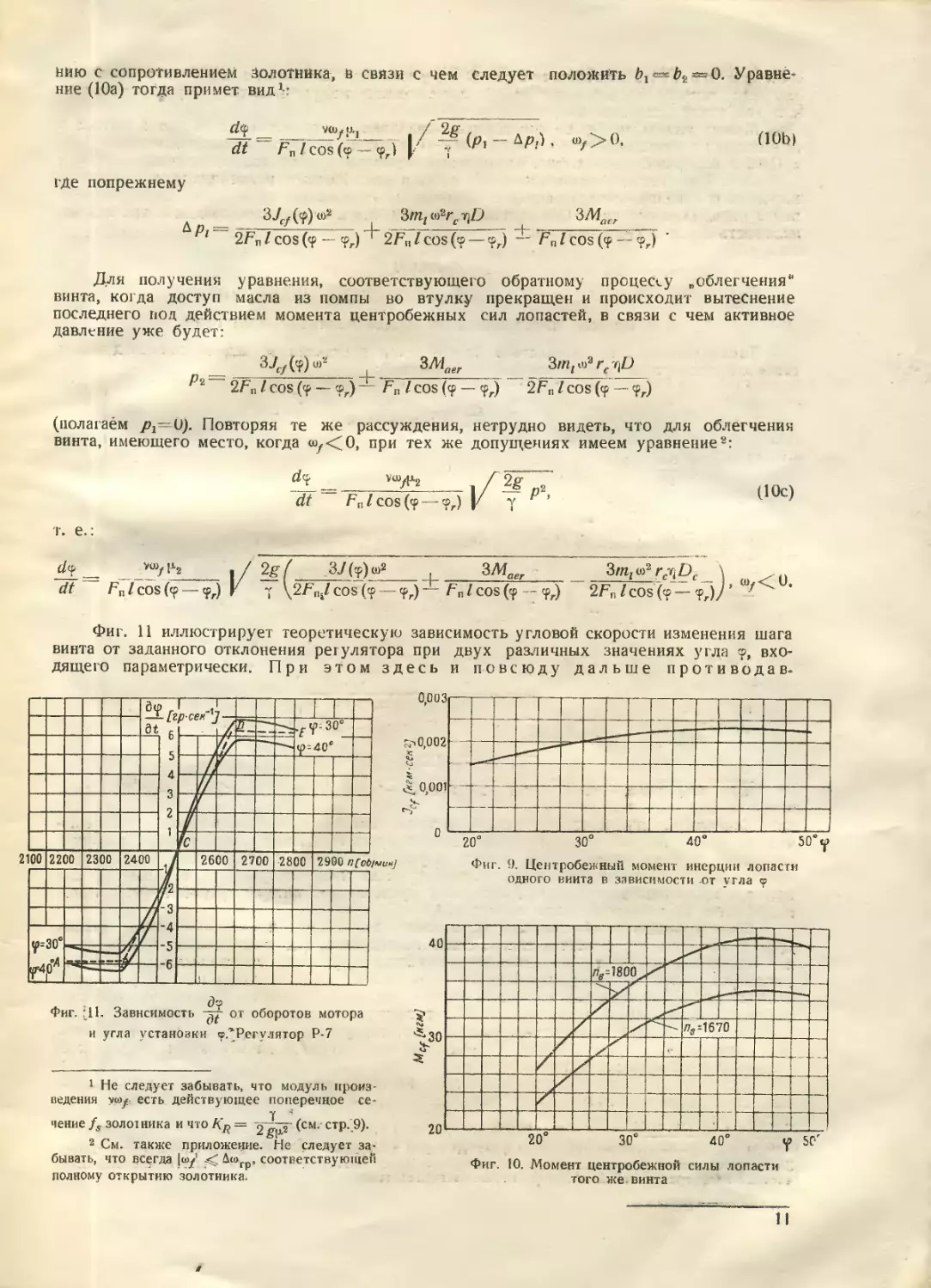
Фиг. 11 иллюстрирует теоретическую зависимость угловой скорости изменения шага
винта от заданного отклонения регулятора при двух различных значениях угла ®, вхо-
дящего параметрически. При этом здесь и повсюду дальше противодав-
1 Не следует забывать, что модуль произ-
ведения уи>, есть действующее поперечное се-
Т *
чение fs золотника и что Кр> = 2gpT (СМ/ СТР-^)-
2 См. также приложение. Не следует за-
бывать, что всегда [ay' ^ыгр> соответствующей
полному открытию золотника.
Фиг. 9. Центробежный момент инерции лопасти
одного виита в зависимости от угла е>
Фиг. 10. Момент центробежной силы лопасти
того же винта
II
ленмем от аэродинамического крутящего Момента пренебрегаете я,
так как таковой представляет собой сравнительно малую величину. Нужно помнить,
что при учете редукции получается п— 14,33 ю.
Можно видеть, что даже при довольно значительных отклонениях оборотов мотора п
от заданных и изменения угла в пределах + 5° функции, представленные равенствами (10b)
и (10с) и изображенные на фиг. 11, неплохо апроксимируются ломаной линией ABCD.
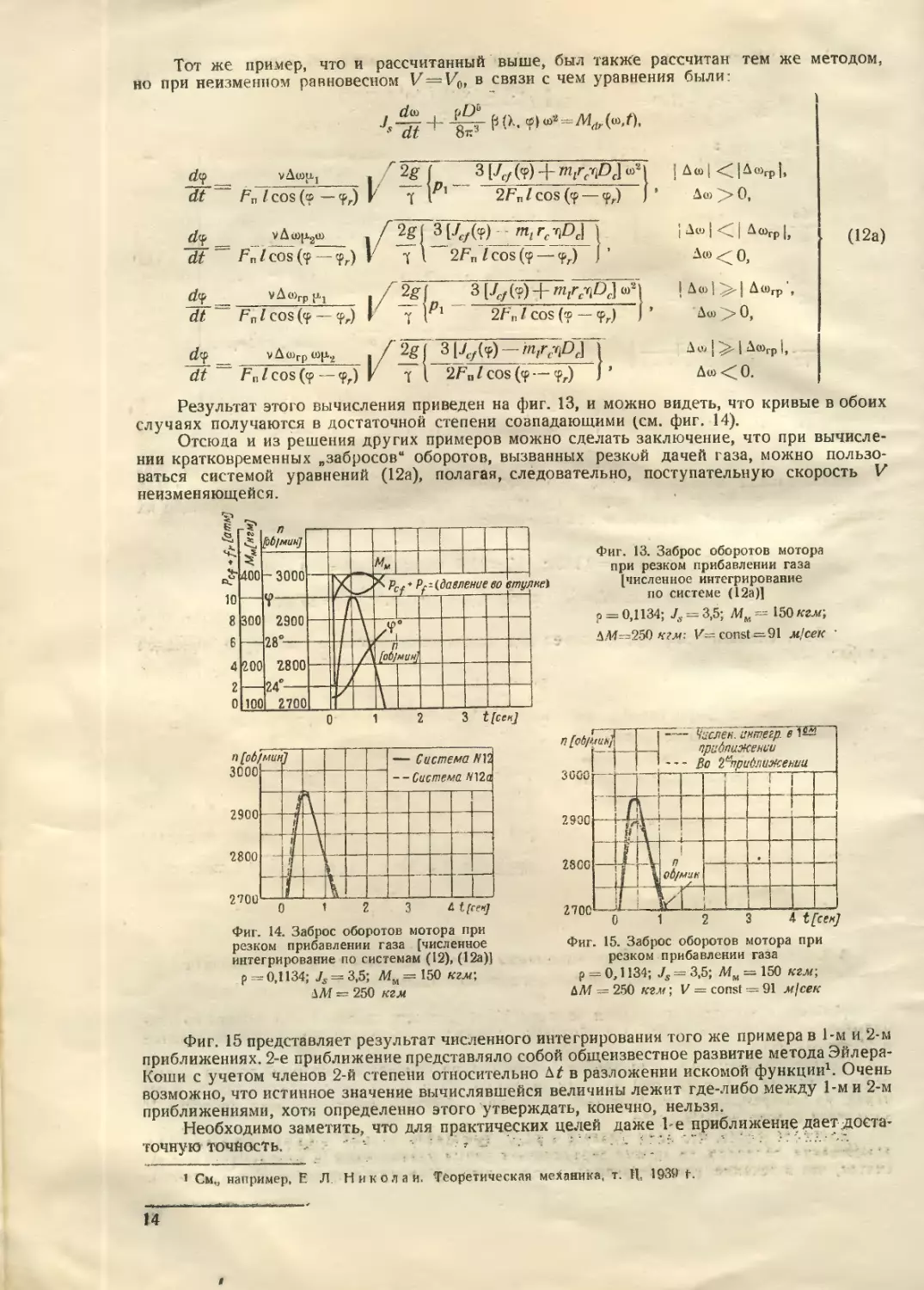
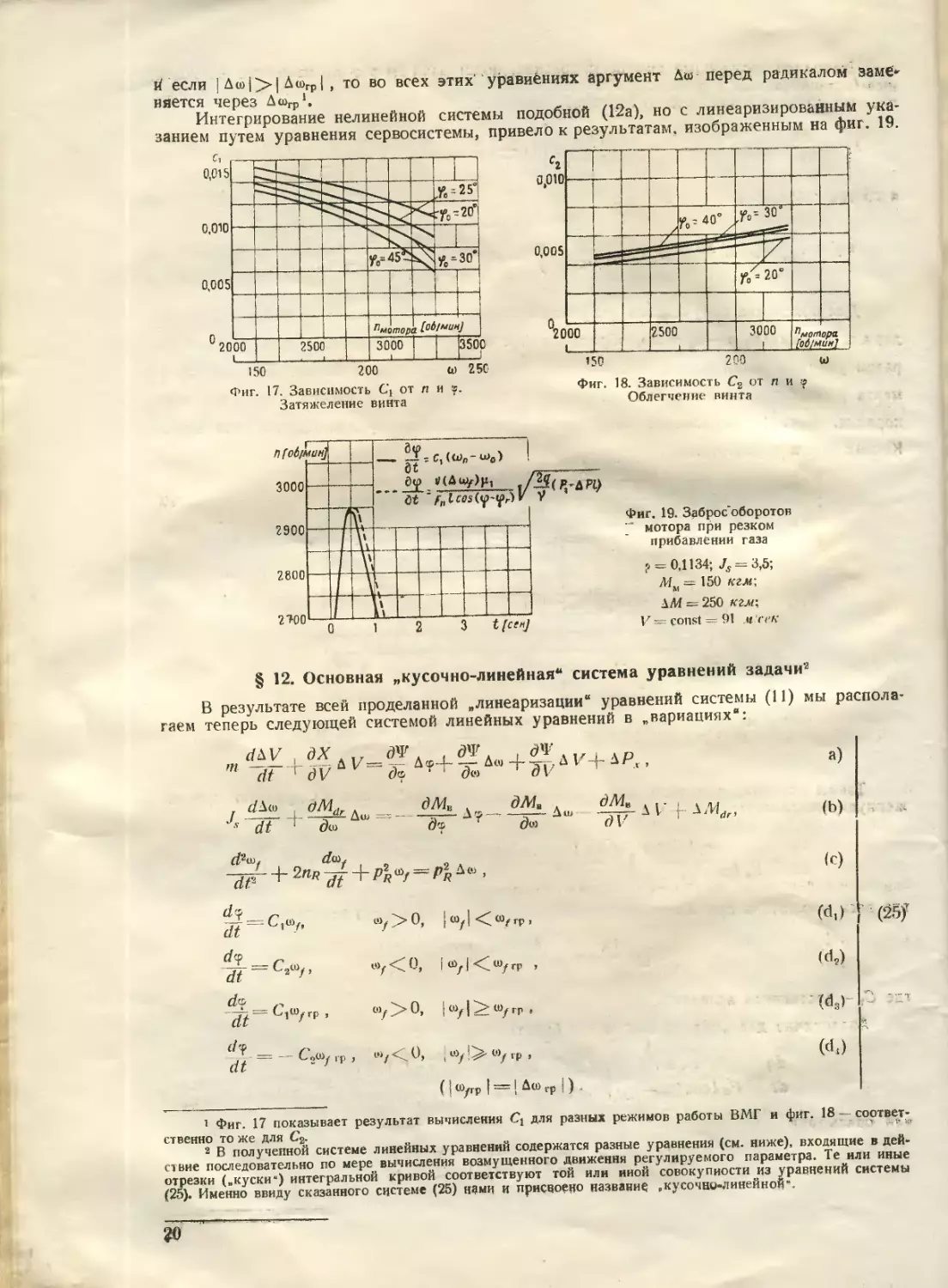
Фиг. 9 показывает зависимость Jcf от <р, и фиг. 10 дает возможность для двух пь
прочитывать величину вращающего момента центробежной силы для одной лопасти
винта определенного типа. Обе кривые являются, как известно, синусоидами, так как за-
висимость Jcf от ср синусоидальна.
ГЛАВА II
ОСНОВНАЯ НЕЛИНЕЙНАЯ СИСТЕМА УРАВНЕНИЙ
§ 6. Пример интегрирования общей нелинейной системы
Таким образом, мы располагаем для решения поставленной задачи нижеследующей
системой совокупных диференциальных уравнений:
dV „„ z-, . ч , аэ (>., <р) р£)4 о>2 , ,
т di f 1 * * р S 7 ~ sin 6 (ср) ~j----------------------------------- £----------- cos «, (а)
d2wf d&f
d± =______ W)/iX‘ i Z 2^ I __ 3[J</(<p)4-mfrc7iDc]«>a|
dt Fn/cos(cp —cpr) у 7 \f l 2Fn / cos (cp — cpr) j
rfcp i / 2g f 3 Г4/(ф) — j
dt F„ I cos (ср — cpr) I j 2Fn/cos(cp — cpr) j’
dep __ _ Wp H _ । / 2g f 3l4/(?) + ff¥77AJ 0)21
dt ~~ Fn l cos (cp — cpr) \ •( p 1 2Fn I cos (cp — cpr) i
d? = ш - / 2g I 3 [Jc/ (cp) — j
dt ~ F„ I cos (cp — cpr) | j 2Fn / cos (cp — cpr) j ’
(b)
(d>)
(d3)
(ds)
(d4)
(11)
Совершенно очевидно, что данная система, состоящая, за исключением (с), из нели-
нейных уравнений при наличии в них еще и функций, данных лишь в виде графиков
[например, аэ(Х,ср), £(Х,ср), /гу(ср)], может разрешаться лишь численно, что представляет
собой, ввиду сложности этой системы, работу очень кропотливую. Тем не менее мы для
примера проделаем этот процесс, поскольку представляло интерес сравнение результатов
применения различных методов вычисления.
Одно упрощение, совершенно безопасное, мы, однако, проведем с самое о начала.
Дело в том, что, как показали специальные исследования (см. ниже), ввиду весьма высо-
кой собственной частоты индикатора (тахометра) регулятора по сравнению с частотой
связанных колебаний регулируемой системы во всех случаях координата регулятора о>?
практически точно отражает вариацию Дю регулируемого параметра (ш), так как инертная
система регулируемого параметра (ВМГ) не дает себя заметно увлечь в весьма быстрое
колебание с высокой частотой Этот же большой разрыв между частотами обусловли-
вает также и то обстоятельство, что инерция индикатора в данной задаче не угрожает
условиям динамической устойчивости системы.
Эксперимент подтвердил теоретическое предположение, что данный центробежный
индикатор может рассматриваться как „быстродействующий", в связи с чем можно безо-
пасно принимать, что wf— Дю1.
1 Влияние запаздывания тахометра было изучено"и оказалось играющим малую роль в данной задаче.
Значительно важнее здесь запаздывание сервосистемы. Ввиду высокой .собственной" частоты тахометра даже
численная интеграция системы (11) практически затруднительна
12
В результате система нелинейных диференциальных уравнений будет:
dV , р . я, (к у) р£)*о>2
т dt +C^^SV QceMsin6 WH--------------------4^---------cosa’
d<f __ vAwp-j । f 2g I 3 [Jfy (y) -f- /nzrrv)jDJ w2|
dt ~ F„ Zcos (y — tfr) V ~ Г 1 2Fn I cos (y — yr) ) ’
d<i_____________vAo>p.2m । 2g | 3 [/fy (y) ]
dt~ F„l cos (y — yr) I 7 1 2F„ I cos (y — yr) J ’
d<P___ vAwrpH 2g( _____ 3 [/.у (у) 0)21
dt ~ Fn I cos (y — yr) I 7 Г1 2Fn / cos (y — yr) I
dy___ уДшгр wpE । / 2g J 3 [(y) — /rafrc7jOJ 1
dt F„l cos (у — y,) I 7 I 2F„ I cos (у — у,) J ’
j <J Al»rp I,
Au> 0,
Au> 0,
| Да>| >| ДшГр|,
Ды<0.
(12)
| Д« I < I A«rp I
Результат численной интеграции системы (12) для случая „внезапной" дачи газа
в горизонтальном полете методом Эйлера-Коши мы здесь приводим, причем, так как
функции аэ (к, у); В(к,у); Jt/(y) заданы графически, при вычислении соответствующие их
значения снимались с графиков в каждой точке.
Численные значения входящих в вычисление величин были следующие:
Js=3,5 кгм сек2; р=0,1134; Уо=9О,5 м1сек, AfM (0)=150 кгм,
ДЛ4м = 250 кгм, ZV0=377 л. с.-, /Vmax = 1050 л. с.; у0 = 23с,1.
Табл. 1 схематически представляет ход вычисления, результат которого приведен
на фиг. 12.
Фиг. 12. Заброс оборотов мо-
тора при резком прибавлении
газа [численное интегрирование
по системе (12)]: р = 0,1134;
— 3,5: Л1м = 150 кгм-,
ДАТ = 250 кгм
§ 7. Соображения о влиянии изменения поступательной скорости самолета
на величину возмущенных колебаний оборотов
Наблюдая за ходом изменения величин 17, ш, у, можно видеть, что в течение кратко-
временного процесса колебания в оборотах, вызванного внезапной дачей газа, изменение
в V весьма мало.
Только со временем, если прибавленный газ не убирается, скорость полета посте-
пенно приходит к новому равновесному значению. Если затем резко убрать газ, то в те-
чение кратковременного затухающего колебания оборотов поступательная скорость V
изменится сперва весьма слабо.
Возникла мысль, что если имеется в виду' вычислять только кратковременное,
возмущение оборотов, то можно ограничиться двумя уравнениями (в координатах <а и у),
считая, что в течение рассматриваемого короткого промежутка времени V — -Vfl — const.
Тот же пример, что и рассчитанный выше, был также рассчитан тем же методом,
но при неизменном равновесном V’=V'O, в связи с чем уравнения были:
dy vdwp.] । 2g Г 3 [/сД<р) Ц-wzzrfrj£)J w2i
dt F„ I cos (® — <pr) I 7 r 1 2F„ I cos (<? — <pr) J ’
d<f. vAw^w f 2g i 3 (Л/(®Г m;
dt ~ Ftil cos (cp — cpr) | 7 I 2Fn I cos (<p — <fr) ) ’
rfy _ vAwrp tx, . W 3[Jf/(®)4-mzrXjJ<72|
dt. F„lcos(cp — ®,) 1 7 p1 2FnZcos(® — J’
j Aw( <21A ojrp [,
Aw 0,
I Aw | < | A wrp I,
Aw < 0,
I A w i | A wrp',
Aw 0,
(12a)
dcp __ vAwrpw[x2
dt Fnl cos (cp — <pr)
V 7 I 2F„Zcos(cp —cpr) J’
Результат этого вычисления приведен на фиг. 13, и можно видеть, что кривые в обоих
случаях получаются в достаточной степени совпадающими (см. фиг. 14).
Отсюда и из решения других примеров можно сделать заключение, что при вычисле-
нии кратковременных „забросов” оборотов, вызванных резкий дачей газа, можно пользо-
ваться системой уравнений (12а), полагая, следовательно, поступательную скорость V
неизменяющейся.
Фиг. 13. Заброс оборотов мотора
при резком прибавлении газа
[численное интегрирование
по системе (12а)]
р = 0,1134; Js — 3,5; Мм = 150 кгле,
ДЛ4=250 кгм: V= const = 91 м/сек •
Фиг. 14. Заброс оборотов мотора при
резком прибавлении газа [численное
интегрирование по системам (12), (12а)]
р = 0,1134; Js = 3,5; Мм = 150 кгм-
\М — 250 кгм
Фиг. 15. Заброс оборотов мотора при
резком прибавлении газа
р = 0,1134; Js = 3,5; Мм = 150 кгм\
ЬМ — 250 кгм; V = const = 91 м/сек
Фиг. 15 представляет результат численного интегрирования того же примера в 1-м и 2-м
приближениях. 2-е приближение представляло собой общеизвестное развитие метода Эйлера-
Коши с учетом членов 2-й степени относительно AZ в разложении искомой функции1. Очень
возможно, что истинное значение вычислявшейся величины лежит где-либо между 1-ми 2-м
приближениями, хотя определенно этого утверждать, конечно, нельзя.
Необходимо заметить, что для практических целей даже 1-е приближение дает доста-
точную точность. ,* " •* ' ’ ' ' - " ' . .
> См„ например, Е Л Николаи. Теоретическая механика, т. Ц, 1939 г.
14
ГЛАВА Hi
УПРОЩЕНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
§ 8. Общие соображения о методике упрощения
В этой главе мы попытаемся настолько упростить нелинейную систему (12), чтобы
она стала разрешимой аналитически и чтобы можно было установить практически при-
годные формулы для предвычисления поведения регулируемого параметра (оборотов
нинта) в различных условиях полета.
Детальное изучение вопроса показало, что данная задача допускает применение
метода малых колебаний Лагранжа. В некоторых случаях приходится, правда, пользоваться
составным процессом вычисления (т. е. состоящим из нескольких этапов), тем не менее
основной процесс линеаризации дает здесь результаты, необходимые для всех случаев.
Так как мы проделали большое число примеров численного интегрирования неупрощен-
ных систем типа (12), некоторые из которых мы приводим здесь в виде графиков
(13, 14, 15), то станет ясным, что в нашем распоряжении все время имелся контрольный
материал для проверки практической применимости систем упрощенных диференциальных
уравнений, ибо целый ряд примеров расчислен разными методами для тех же самых
исходных данных.
Применение метода малых колебаний относительно „стационарного состояния" ока-
.алось здесь, пожалуй, столь же плодотворным, как и в теории динамической устойчи-
вости самолета. Именно благодаря этому удалось установить некоторые принципиальные
основы этой новой теории.
§ 9. Линеаризация уравнения поступательного движения самолета
Уравнение поступательного движения самолета (см. § 2)
,п s = cos а—Q sin 6 (0 (13)
представляет собой нелинейное уравнение. Для его линеаризации мы будем рассматривать
малые отклонения („вариации") величин V, uj и <р, представленные через Д V, Дад и Д^.
Таким образом, мы будем считать, что полёт происходит при установившихся „стацио-
нарных" условиях, когда V= Vo, w —1«0, <р = <р0, и изучать лишь упомянутые „малые
отклонения" от стационарных значений принятых координат.
Допуская, что полет происходит с неизменным углом атаки а и положив ввиду
малости угла а, чго соза—1 и представляя в (13) тягу винта в функции основных аргу-
ментов V, и и ф, получаем уравнение:
dV । Р ciz2 a, (V, a>,<p)pZ)4a>2 .
т ~gt + F* 2 5 1/2 = -Г^г-------------Q si« ° Ш
п . а, (I/, а>, <₽) р Z)4 а>2 _ „
Разложение функции —------------------- в ряд Тейлора по степеням вариации координат
(принимая во внимание промежуточные переменные) дает при следующем обозначении:
' 2 к2
/ d'F да3 дХ . dW\ , . dW da,
у da, dX dm г ди> у 01 да-я ду 1
d’F dX dX d4^ da, da,
причем производные 1 ~д\/ берутся аналитически, а производные ~gg~ > ~д^
вычисляются посредством графического диференципонанип, пользуясь „сетками" винта,
где представлена функция
; . /......... ? *•’ . - г. ' ~ У.....
a, (X, <р) — a, (V, а), <р), »
полученная опытным путем.
Ограничиваясь в разложении (14) лишь членами первой степени относительно вариа-
ции координат и проделав все показанные диференцирования, мы получаем нижеследую-
щее приближенное выражение для силы тяги винта:
. dW. d»F. . дФ...
'r='t«+ 7ьД?+*ГЛ" + <П741/'
в
(Иа)
что можно записать
виде:
(14b)
где коэфициенты
d'l’
^=d?
d4' дая pD* г да .
= ------5— = -тт“о-г 1кг1 -
da9 d<p 4?t2 dtp
„ -
Pt —
d*F da, dk d lK __ pD3 / .. дая . D аэ co0
d«> da9 d>- du> ' dw 2ft \ ° dk ‘ ~ ,
d’F d’F da9 d/. pD3 a>0 da9 r n
78 dV да, dk dV 2- dk 1 1
[кг сек]
(15)
„ dae das
Причем производные —и —получаются графическим диференцированием, так
как функция аэ (л, <р) графическая. Нужно всегда помнить, что эти производные берутся
при „стационарных" значениях всех аргументов.
Функция ctSV3, представляющая лобовое сопротивление, зависит только от V1.
Ее разложение пишется сразу:
сх | SV3 = сх ± S Vo + 2 сх £5У0 Д V+с, 5Д V*,
и поскольку мы везде отбрасываем члены степени выше первой относительно вариации
наших кинематических параметров, то полагаем, что для малых колебаний лобовое со-
противление будет:
РЛоб = ся S V$+ сх р 5У0 Д V.
Наконец, член Q sin 60 (<р), выражающий проекцию силы тяжести, обозначаем через
Рм и всякую вариацию этой величины, могущую происходить только из-за изменения
угла 6, через ДРЛ.. Таким образом, будет:
Теперь мы можем написать линеаризированное уравнение поступательного движения;
т.+ схSVl + схpSV^V^ Wo+Р1 Д? 4-р.г Дш4-р8 Д И+ Рх. + ДРХ.
Непосредственно в режиме невозмущенного стационарного движения, когда ДИ=
dV „
= Дш==Д(р —0, должно иметь место полное равновесие сил, ввиду чего —
Тогда остается:
cx-^SV^^PM, т. е. =
Таким образом, „стационарная" часть лобового сопротивления, равно как и постоян-
ная часть проекции силы тяжести на ось Ох, уравновешивает „стационарную" часть
силы тяги винта.
1 Так как допущено, что cr — const.
1ft
Для малых отклонений от. стационарного состояния остается, следовательно,
уравнение: • • . - «
я|/
+ ДА Д«) +ря Д V + ^Рх,
которое, можно записать еще в виде:
ДУЧ-р, Дш4-ДРГ1 (16)
где
причем все коэфициенты приведенных уравнений трактуются в дальнейшем как по-
стоянные.
§ 10. Упрощение уравнения винтомоторной группы
Уравнение винтомоторной группы, написанное для координаты со, имеет вид
(см. § 3):
р£)5
Член Л-т-PG-, <р) ш3 выражает тормозной момент винта, причем функция р(к, ср) называется
О
коэфициентом мощности и снимается с графика.
Таким образом, можно написать:
Мь = Л10+ДЛ4в=Л1в{Р[к(1<ш)?]} ,
где ДМ, — вариация момента Ма.
Разлагая функцию М в ряд Тейлора по степеням вариаций „координат" и принимая
внимание при этом промежуточные переменные Р и к, находим:
/И„ = М + Д М = Мв {рп [к0 (170, %) %] 03о} + Д т Д V+
во
Хззэ
дМв dp дк
др дк дсо
(17)
причем, как и в разложении (14), часть производных берется „на буквах", а производные
hr > вычисляются по „сетке" винта. Ограничиваясь в этом разложении членами пер-
ок (7ср
вой степени относительно вариаций координат и проделав все диференцирования, по-
лучаем:
л. Р&6 о X 2 . £>М др . . D4 со др
М -8яз Po(^o>?o)woH-p 8лз ^Дш-J-p 4л2 д)
а.+5ьи»+--.(!в)
” dk 1 it /
Что касается крутящего момента мотора Mdr, приведенного к оси винта, то таковой
на небольшом участке кривойрИ^Дш) по опытным данным зависит от со почти линейно1, и
поэтому из разложения:
1 :2 д®2 ^1-2-3 до3
достаточно взять только первые два члена, т. е. положить:
м^и^ж + ^До..
(19)
1 Рассматривая кривые .внешних характеристик* мотора, легко видеть, что на интересующих нас
участках аргумента ш = 2 ~ns таковые могут быть достаточно точно апроксимированы квадратичной функцией
вида N = а (6ш — /С, ш2). Тогда Mdr = 75 a (bt — К <») , и опять-таки = — аК„ Ьи>,;аКм = ~
м о) Дш
N
причем коэфициент а характеризует отношение _
/vtnax
3 БИБЛИОТЕК I?
I м I
I - *
„ о7Илг А
При »том, так как -^^--<0, т°, положив
дМ&
— | Kt |, получим:
Mdt(^ = M°dr - '/CJAw.
Вариацию моторного момента Mdr{t) мы будем считать заданной по времени
(вызванной, например, переводом сектора газа). Таким образом, окончательно будет:
Mdf (ш, Z) = ж -1 Кл | Дw + ДЖ(0. (2°)
где Кх —ftp, %) и зависит через ш0 и а от равновесной мощности.
Подставляя (18) и (201 в уравнение (2а), получаем сперва:
бА» / dMdr :
х dt Ц дш 1
Г ^4, дМв Х д =Л|« — м°-
d₽ Л дш dw J dr в
дМв d₽
dp drf
()Ma
dp
|*41л+лм„(Ч,
и так как стационарные моменты уравновешиваются по условию, то, применив для коа-
фициентов сокращенные обозначения, получим:
Л ~ А? + £3А V+ Д ЛЩ) ,
где
Ж=-- 1Ж И--^5- —. -
Причем, если проделать все показанные диференцирования:
t - = DB(Uq^
'3 d® dp d<p Р 8 л8 d® ’
s d7Wu d7W„ dp dk dAL pZ)4 / _ „ dp . Дрм0 \
dw dp dk do> 1 da> 4л2 0 d). ' л J ’
„ __ дМв dMB dp dk__ О*ы dp
4~'dV ““dp'dXdF*4^dT
(21)
(22)
§ 11. Упрощение уравнения сервосистемы регулятора
В § 5 мы установили следующие диференциальные уравнения движения сервоси-
стемы регулятора (т. е. механизма изменения шага винта):
и? ____ । з[7~(у)4-/у^]^2( w >0 (А)
dt Fn Z soc (<р — ®г) г у р 1 2F„ I cos (ф ?,) J '
d<? . / 2gj 3 И/(?) - т1ге‘Рг\ 0>aj (0 , 0, (В)
dt Fn Zcos (<р — %.) I 7 I 2Fn /cos (ф-- ?r) J
ГЛ Не-
очевидно, что в обоих случаях-г); зависит от трех переменных wf, <о, ф, т. е.
(рп
lit “
= 61,2 («>/, % <р). По ранее сообщенным соображениям мы примем Дш.
Имея намерение линеаризировать эти уравнения, вычислим вариацию этих функций
6i,2 (w, <р), применяя разложение по степеням вариации координат ш и ф. Таким образом,
получаем (шу = ш — а>о = Д<о):
Л , d6i,2 . , d6i 2 -л , 1 1 d26i,2 . „ , 2d26t 2 Дш Д<р . d26] 2 . , ,
Д® — ——Дш Я----— Дф-4- Дш------—Д-Д.—ид^ X (22э)
dw dep 2 1 do>2 d<o Д ® 1 дъг '
где 61,2 (ш, ?) представляет функции (А) и (В).
18
. . Выполняя показанные диференцирования, подставляя во все производные равновес-
ные („стационарные0) значения обобщённых координат и' ограничиваясь лишь членами
первого порядка относительно вариаций, находим:
Л (
дш = у Р-, Лео / 2g | 3[7f/cp0)4- nip^D1
Лп Z cos (cp0 — срг) |/ 7 И1 2FnZcos(cp0-cp„) J
и соответственно:
, C>62 , V|j.g Дш /~2g | 3[/fy (cp0) mzrciqZ)J(o2 |
? ~дш ^°’ ?0 ш ~ Fn Zcos (? — ?„) |/ 7 I 2ЛП I cos (cp0 — ?r) I ’
До> 4> 0,
Дш <4 0.
со-
об-
dtp
Для пояснения полученного результата заметим, что функция = 61>2 (ш, ср)
держит множитель <о —<о0 = Дш, обращающийся в равновесной точке в нуль и таким
разом уничтожающий вместе с собой производную в этой точке. Влияние аргу-
мента ср сказалось бы лишь при сохранении в разложении (22а) членов более высокого
tZcp
порядка. Фиг. 16 показывает зависимость от изменения ср для одного типа винта.
Кривая почти горизонтальна.
dv
Фиг. 16. Зависимость^^ от положения лопасти (угла ср)
=_____________ f . 1/2^1 3<°2 (Jcf (?) Ч 1)
dt Дп/со8(?-<рг)рДшН Г 2 \ /„/cos (? —<pr) ’
Таким образом, получаем для процесса „затяжеления" винта следующую прибли-
женную зависимость:
3И/Ы4-'«/гХ’М 1 Л zQo х
,т = ~ ---т----J/ — /’|--псд--------г' --ч—- / , Д<о>0, (23а)
dt F„ I cos (cp0 — cpr)у 7 I 2Fn Z cos (cp0 — cpr) J
где весь множитель при Дш — постоянный, благодаря чему можно писать:
~т — С, До>, Дш^>0,
fir *
где Cj — постоянная величина.
Аналогично для „облегчения" винта будет:
dep Дш______. /~2g f 3[Jf/(ср0) — Z)J <i>g
dZ ' FnZcos(cp0 —cp„) Г -pl 2Fn Z cos (cp0 — cpj
или опять-таки
~^С2Л(О, Дс£> <^0,
' Hr- ^.7
ri если | Дю|^>| Д(огр|, то во всех этих' уравнениях аргумент Дш перед радикалом заме*
няется через Дшгр‘.
Интегрирование нелинейной системы подобной (12а), но с линеаризированным ука-
занием путем уравнения сервосистемы, привело к результатам, изображенным на фиг. 19.
Фиг. 17. Зависимость С( от л и у. Фиг. 18. Зависимость С2 от л из
Затяжеление винта Облегчение винта
Фиг. 19. Заброс’оборотов
мотора при резком
прибавлении газа
? = 0,1134; /у = 3,5;
ЛГМ = 150 кгм;
\М = 250 к гм;
V = const ’= 91 .« сел’
§ 12. Основная „кусочно-линейная" система уравнений задачи2
В результате всей проделанной „линеаризации" уравнений системы (II) мы распола
гаем теперь следующей системой линейных уравнений в „вариациях”:
cMV'.dX... dW. .d’J'
W —j?—L- j Д V = Д Ф-*—Д°> ~}~ тгр Д I А ”
dt 1 dV do • 1 dw dV
. d±o> dMdr . дМв , дМв .
s dt do> do ’ dw
do>
a)
(b)
d2mf dwf
b ^nR~dt~^PZR^f~’
<s>j 0, j Wy ] <C ШГ гр >
, Wy <Z 0, | <£>y | <2 Wy rp ,
-^=C^u>yrp , ltoyl^S<o/rp •
= — Qwy ip , < o, , W/ !> W/ ,.p ,
( | Фугр | == I Aw rp I )
(c)
i Фиг. 17 показывает результат вычисления Cj для разных режимов работы ВМГ и фиг. 18- соответ-
ственно то же для С2.
2 В полученной системе линейных уравнений содержатся разные уравнения (см. ниже), входящие в дей-
ствие последовательно по мере вычисления возмущенного движения регулируемого параметра. Те или иные
отрезки („куски") интегральной кривой соответствуют той или иной совокупности из уравнений системы
(25). Именно ввиду сказанного системе (25) нами и присвоено название „кусочно-линейной"
д i - I д /и
Причем из уравнений (dv d2, dit dt) в каждый данный момент имеет место только
какое-либо одно из них.
Коэфициенты этих уравнений суть:
dxl' d’P daB pD* „ да ,
-5-—3-------Л"- = Р1 М ,
д<в до.3 дъ 4-2 0 д ф 1 1
d’F _ d4' da, d>. , dW pD3
dcu da, d). dco dcu 2т:
da, ZJas
0 ^dl ' -
I,=- [кг сек] ,
dT dU' да9 dl
dV ~ da, д). dV
pD^Wr. da, t ..
2_________—рЛкгсекм ’] ,
2я d).
дР лоб dV с,p5Ио = p< [кг сек м~х ], dPKOb dX dV dV
idV jdlZ dP i гт|=л1'£г сек м~11 s
dMB ~d^~ = dMB dp dp dcp p DW0 dp ‘8^dv — ?1 [кгм],
dMs dw dMB dp d>. , dp dX dcu dMB dco 4?r2 (- 1/^4- \ °d). '
дЛ1в dV — c)MB dp dk dp dk dV ~’p 4я2 Ф = d>. = ?s [кг сек] ,
£)р%
— $2 [кг м сек] ,
(26)
d/WM (co) 4 IZ r I
—d ’ — const =? л! [кг .и сек]
дМк , dMu r .
—s— - —\— = a . [кг м сек],
dcu dw
у Hi “>r [(4 Jb ) 4- mrp R]
Pr~ '
,2
2/ir определяется из эксперимента. Пока эга величина задается;
'Н
ды Fn I cos (<p — <pr) I
зИЛНадед I ~ . О1
Ру ~ —of -----i ci 1сек .
2rnZcos (ср — срл) ] 1 п
\dt) ^2c»‘J / 2g j 3 [Уг/(<р0)- тЛгД] i
do/ ~ Fn/cos(o-cpr) V 7 I 2Fn/cos(<p- cpr) j —Ч1^к|,
Как было уже сказано, функции ?/(<»), аэ(л, <р), ₽(>,?),
етвующих графиков, а производные
./с/(<р) снимаются с соответ-
dMdt __ d^ da, d^ dp
dw ’ ’ d>. ’ drf ’ d>. ’ d<p
VtX I
д
4+"4^+^
2J
‘также вычисляются графически1. При этом всегда надлежит помнить при численном вы-
числении всех этих коэфициентов, что их нужно брать для равновесных значений кине-
матических параметров нашей задачи, т. е. для/. = Х0, ₽==₽0 — resp, для Vo, woi ау = О.
Табл. 3 дает численные значения коэфициентов для некоторых случаев.
§ 13. Случай Уф const
Если, приняв во внимание весьма высокую собственную частоту- регулятора (рд),
пренебречь его изолированными колебаниями и полагать ш? = До>, то уравнение (25с) этим
будет по существу упразднено и система (25) примет вид:
d±V дЧ' л
дш
dV
дХ I
\dV i
—-С,дШгр,
Дсо^>0, I Дш I Дшгр ,
*Ш<0, Дш|<^Дшгр,
Дш >0, Дш I Дшгр ,
(27)
^?==------------------------------------ С2Дшгр, Дш<0, 'Дш!ф-Дшгр.
Ввиду особых свойств систем (25) и (27), в которых поочередно имеет место сово-
купность различных уравнений, процесс не является симметрическим, и пока у нас не
имеется методов для общей оценки сходимости колебаний (численный расчет показы-
вает, что таковые обычно имеют место) в обоих ветвях асимметрического колебатель-
ного процесса. Доказать сходимость этих колебаний нам удалось пока только для од-
ного частного случая. Тем не менее практически установить сходимость упомянутого
процесса можно всегда конкретно, проделав численную интеграцию2.
Необходимо указать, что накопленный вычислительный материал говорит о том, что
колебания рассматриваемой системы в условиях, хотя сколько-нибудь близких к нор-
мальным, всегда бывают сходящимися.
Таким образом, подтверждается при этом и чисто логическое предположение о том,
что если данная система является статически и динамически устойчивой в первой и
второй ветвях колебаний порознь, то она, по всей вероятности, устойчива и вообще.
Если колебания проходят в „зоне пропорциональности" регулирования, т. е. если
Дш| < | Дшгр |, то уравнения будут нижеследующими:
д Н4-ДРД0,
с7Д V 0W . , . ( дх
dt 1 дш у /Л
//Дш дМв дМ„ дМк дМв ...
' —п—=—д?-----------------т~ Д«^—i— Дш--------------Л1/- д1/-г ДЛ£.(/),
« dt дер т <9ш сДо dV i аг\ /•
d
dtp
dt
Дш = Cl,2 Дш
(рассмотрение будем вести сперва для симметрического случая, когда Ct — С2 = С).
1 Автором разработай метод „аналитической апроксимации" этих функций, пользуясь которым, вычи-
сление производных, например, • выполняется без труда на буквах, но здесь за отсутствием места про-
демонстрировать применение этого метода не представляется возможным.
2 Здесь само собой выдвинулась чисто математическая проблема, сводящаяся к нахождению критерия
устойчивости движения в случае кусочно-линейной системы, которая явилась бы естественным развитием
известных условий устойчивости для обыкновенных линейных систем по Routh’y-Hurwitz'y.
22
Отделение переменных (выкладки опускаются) приводит к независимым уравнениям,
левые части которых имеют вид:
дЧ>
dV
Д V" +
дМв \ . д/Ив
~д^~) W
дФ
дю
с)Мв
ДИ +
| дМв ( дХ дФ А дМв дФ
b [’ д? ^дИ ' дГ \) + dV д<р
Д V == правой части.
(29)
Если левые части уравнений в координатах ДК Дю, Дер обозначить через Р(У)^
F(w), F(cp) (левые части всех этих уравнений имеют одинаковый вид) и развить правые
части их, то будет:
,.... , . г, 1 д7Ив dAL„ , , r,i , дЛ-1,, ,, , дФ . , ,, дФ .
/?(К=4.држ+^+ |ДЛ- г -^-сдр. + ^дж+с-^ шаг1
F(w)=wa<+^£+|^ ^M'dr—
Р(ср) = СтД/И"4-С^ + |^ ДЛ^-С-^ДР,.
Здесь характерна неизбежность исчезновения правой части уравнения в коорди-
нате До) для случая Д/ИЛ. = const и ДРЛ = const.
Регулирование рассматриваемого типа в теории регулирования иногда называют
„скоростным", так как в зависимости от величины отклонения р. п. регулируется не
положение <р „регулирующего
д<₽
органа , а скорость изменения его положения.
В таких системах р. п. не дает постоянных отклонений при возмущениях, сохра-
няющих постоянную величину.
Возвращаясь к уравнениям (28) — (29) и положив
1 / дХ . I дФ । А Л dMdr
mJx ^dl/ 1 дк!Д)д^Г
, дМв \ , дМв (РГ , ,, д/Ив
+ дш J ' dV дю ' d'i
С дМв fdX. ,
а'л mJs д<₽ ^дР г
дФ А д/Ив дФ
dV ) ' dV д®
запишем уравнение для р. п. в виде:
Д<о"' -|-«i Ди>" 4- о2 Д+ а3 Д W = правой части.
Характеристическим для этого уравнения является алгебраическое уравнение:
г8 + аг г2 -|- а2 г ая = 0. (32)
На основании критериев Routh’a-Hurwitz’a мы можем установить, что в случае1 вы-
полнения следующих неравенств:
Я1>0; «2>0; а3>0; —а8>0, (33)
движение системы будет во всех трех координатах устойчивым, и если к тому же, со-
ставив количества:
di 2a3i а, аг ,
Pi — ? 27
i Только тогда, когда Q = С2 — С. В действительности может оказаться, что Cj ф Гогда практиче-
ски убедиться в устойчивости системы можно, только проделав вычисление для нескольких волн колебания
и наблюдая их затухание. Как уже было сказано, пока еще не доказано, что если система устойчива при
C«C'i и при С=С2, то она устойчива вообще. Опыт однако, го.ворит в пол.ьзу этого.
23
мцк обнаружим, что будет:
то движение будет носить колебательный, затухающий характер при наличии исчезаю-
щего с течением времени смещения. В случае же
будет иметь место апериодическое движение. Обычно наблюдается колебательное дви-
жение, в связи с чем общий интеграл движения в координате регулируемого параметра
имеет вид:
(^-«•'ф- е~п^ }С2cos bt-\-Cs sin bt }ф-/?(£), 1Д<ОК1 Д^гр), (34)
где частота b и „показатели затухания" Пу и /г2 находятся по корням характеристиче-
ского уравнения третьей степени (32), а функция R(t), представляющая собой ч а с т н ы й
интеграл, зависит в общем от приложенных через ДЛ1(/) и ДР(£) внешних возмущений.
Вычисление этой функции (если ДЛ1 и кР заданы) всегда может быть выполнено, хотя
бы методом „вариации постоянных" Лагранжа.
Для развития произвольных постоянных Су, С2, Cs напишем три уравнения [после-
довательно диференцируя интеграл движения (34)]:
Дю = Су е~п'* ф- е~п^ [ С2 cos bt-}- Cs sin bt} ф- R (t),
где R(t) уже полагается известным.
Дш' = — Су пх e~nt ф- [(C3ft — С2 п2) cos bt — (С8 п2 ф- С2 b) sin bt]4~ R’ (t),
W' = Су ri> e~nd ф- e j [C2 (и1 2 — b2) — 2C8 bn2] cos bt ф- [Cs (n2 - b2) ф-2C2 bn2] sin bt} ф- P'(t),
что для начального момента времени t — 0 даст три уравнения: •.а
^(0) = Cy + C2-}-R(0),
Дш' (0) = Су Пу 4- Cs b - С2 п2 ф- R' (0),
Дщ" (0) = С2 (и2 — ft2) — 2CS ftn2 ф- R" (0).
Теперь полезно сделать следующее указание: при таких вычислениях нужно
всегда сверять задаваемые начальные условия с исходной системой
у р а в н е н и й (29). Нужно помнить, что данная система допускает вве-
дение только трех произвольных кинематических параметров (или их производных),
все остальные1 будут от них зависеть. . „
Задав, например, начальные значения ДУ(0), Дю(0), Дер (0), мы для производных
До/(0), ДИ'(0), Д?'(0) уже не можем назначать произвольных значений, а получаем их
из основной системы (29). Если, например, вращающий момент Mdr изменяется скачком,
а наклон траектории полета к горизонту (т. е. угол В) не изменяется, то будем иметь:
7Wdr= const, Д/И;г= ДЛГ = 0, ДР—-ДР'= ДР" =0.
Уравнение в координате Д<о лишится тогда правой части (Р = 0), но исходная си-
стема для / —0 дает2:
Ды — 0, ДУ —0, Д<р==О,
rc\ 1 А ЛЯ
dt (°) ~ Js LMdr'
d2 Д<»
~dT{0)^ •
1 Параметры, либо их производные.
2 Влияние .скачка4 возмущающей функции сказывается подобно импульсу через начальные условия.
24
Таким образом, получаем для координаты р. й. следующие уравнения 'для вычисления
произвольных постоянных в этом случае:
О — С} ~|- С2,
^^~С.щ + С.Ь~С,п„ .
=С1^-ЬС,(/Н - Ь2)~2СяЬпп.
Zv
Еще в §§ 6- 7, вычисляя по точным нелинейным уравнениям, мы заметили, что в
отношении образования заброса оборотов явление развивается практически такг как
если бы поступательная скорость V не изменялась. - ди....г
v -у -Частота колебаний b и конфигурация возмущенного движения р. п. практически
сохраняются и при допущении, что V=const. Поэтому, поскольку нас интересуют именно
эти быстротечные явления, то основное применение системы (29) мы видим главным об--'
разом лишь в
а) проверке условий устойчивости системы, т. е. выполнения условий Hurwitz’a (33)7
б) выяснении типа корней характеристического уравнения, смотря по тому, какое’
из неравенств (33а) или (33b) имеет место.
Параметры же возмущенных колебаний могут расчисляться при допущении, что,
V—const, в связи с чем уравнение в координате V выпадает, но все же коэфициенты
уравнения в координате Дш попрежнему вычисляются для точек V = Уо, ш = ш0, <р = <р0.
с Подобное вычисление должно, однако, проводиться лишь для небольшого отрезка
времени (порядка 3—4 сек), пока скорость Vеще практически мало изменилась по сравнению
с Vj и чего обычно достаточно для вычисления возмущенных колебаний типа „заброса*.
Задача о поведении системы при пикировании самолета (когда нельзя уже пренебрегать
изменением V) будет рассмотрена ниже (см. § 21).
§ 14. „Техническая" система уравнения задачи
На основании сказанного в § 13 мы для вычисления быстротечных явлений „заброса*
оборотов мотора и близких по характеру иных динамических процессов рекомендуем при-
менять упрощенную „кусочно-линейную* систему диференциальных уравнений вида:
ш7 -(- Ks&ш = Д — $г Дср,
Дср7 = С1Дш, Дш^>0, |Дш|<^Дшгр,
Д<р7 = С2Д ш, Дш<^0, |Дш|<^Дшгр,
Д<р7 — Дюгр, |До>| Дшгр, Дш О,
Д<р7 =—•С3Д(огр, |Дш| Дшгр, Дш 0.
(36)
Как это выяснится ниже, система (36) и некоторые ее варианты пригодны для раз-
решения большинства практических задач динамики регулирования ВИШ. Следуя при-
меру проф. Б. И. Кудревича (в области теории гироскопических приборов), мы и в нашей
проблеме назовем систему (36) „технической системой* уравнений задачи.
Таким образом, техническая система в нашем случае есть простейший вариант общей
кусочно-линейной системы, причем техническая система может оказаться обыкновенной
линейной системой в случае С\ = С2 и лишь малых отклонений, т. е. выполнении условия
|Дш[<|Дшгр1. Вообще же при невыполнении какого-либо одного из этих условий техни-
ческая система также должна рассматриваться как вариант кусочно-линейной системы.
Ввиду важности для всего дальнейшего системы (36) развернем вычисление несколько
подробнее. Применим для отделения переменных операционный метод.
d d-
Введем оператор D — -^, следовательно, D2 — и т. д. и напишем символические
(Л/L (J t
определители для системы (36):
2.4. S ^0 , f^ + Ks -D ==_[J5D2 + ^,£) + S1C1.2]
0 — D | Дш | < Дшгр,
Дг = JP+k, д/и^О * -Л&Да.
0 . Л 1 U
из которых До называется „определителем системы*, а Д, и Д2 — „дополнительными
определителями*.
4
25
. Пользуясь теоремой Крамера,- пишем, символическое равенство в виде;'
^1(Ди>)=Д0Дш = Дп Л„(Д?) = Д0Д?= Д2,
и, наконец, подставляя До, Дг и Д2 и избавляясь от символа D, получаем два Независи-
мых уравнения в координатах Дм и Дер:
ЛДш" + ^Дм' 4- ^Дш = Д M'ar(t), (а) |
4Д?"+/W+^.-A? = c^Mdr{t). (b) j
Эти уравнения можно трактовать как приближенные, но практически вполне при-
годные для вычисления протекания кратковременных (длительностью до 5—6 сек) дина-
мических процессов. Если оставаться на уровне этого приближения, то для устойчивости
движения в случае С\ ф С2 (когда линейная система уже переходит в кусочно-линейную)
существует аналитический критерий сходимости колебаний (см. § 18).
Сначала рассмотрим простейший частный случай, когда Сг = С2 — С (симметриче-
ские колебания). Уравнения малых колебаний в этом случае представляют собой обыкно-
венные линейные уравнения второго порядка с постоянными коэфициентами. При выпол-
нении условия 4jJ;1C > (что в нашей задаче обычно имеет место) интегралы дви-
жения имеют вид;
Ды = е-п/{Лсок^-4-Ва1п bt}Fa[l^M'dr(t)\, | 8
т. Д<р = e~nt [Aj cos bt 4 sin bt] -J- Fb |C Д '
где
n==^7s И
В случае периодическое решение не имеет места и интеграл движения
имеет другой вид.
Отметим первую существенную особенность полученного решения. Частный инте-
грал, порождаемый вариацией вращающего момента мотора (хотя бы вследствие перевода
сектора газа) зависит в координате регулируемого параметра (До>) не от самой вариации
я dbMdr(t)
упомянутого момента, а только от ее производной по времени, т. е. от ------—- —
= Таким образом, если приращение вращающего момента мотора постоянно, т. е.
&Mdr — const, Д7И^г = 0, то равновесная угловая скорость (а, следовательно, и обо-
роты) остаются как бы без изменения (см. ниже § 15).
Частное решение в координате Д<р показывает тогда постоянное приращение угла <?,
так как новое положение равновесия, как легко видеть, будет (AAldr= const == ДЛ4*Г):
, ДЖ
% = Т<Н---₽— •
ГЛАВА IV
ПРОТЕКАНИЕ ДИНАМИЧЕСКИХ ПРОЦЕССОВ В РАЗЛИЧНЫХ ЧАСТНЫХ СЛУЧАЯХ
-§ 15. Скачкообразное увеличение вращающего момента
(резкое прибавление газа в полете)
Для этого случая F [ДMdr\ — 0 и на первый взгляд р. п. как бы не претерпевает
возмущения. Возмущение приходит, однако, через „начальные условия".
Исходная система (36) по подстановке начальных условий
4—0, Дш==0, Дт = 0, AMdr (0) — bMdr — const
дает;
/5Да>'=ДЛГ^,
откуда
“ - • АШ\О)=-Ц^—Дср'^О.
ati
Т^к как интегра*: движения эдест для ДЛ4—const имеет вид ,с т .
Д« = е‘ nt(A cos bt-\-B sinbt), (39)
TO; ' - '
Д ю' = e~nt [(Bfr -- An) cos bt — (Bn -f - Ab) sin bt\.
Подставляя в эти два равенства:
Л 714*
t = О, Дш (0) =-0, До/ (0) = t
•*s
находим:
Л М*.
Следовательно:
Теперь мы можем написать
начальными условиями):
г- = ВЬ.
D &JH3r
частный интеграл движения (в соответствии с принятыми
Л 714*
Дю = е-« — sin btt ... .О (40)
или в развернутой форме:
где
АЖ
Д о) = е 2 Js -------------------sin /._t
(40а)
dMdr дМв dMdr
до> ' дч> dw
. _ dMa____ D6wo dp
'* 8ks 1%
Для координаты Ду будет соответственно:
Д у — e~ni (Дг cos btBj sin bt) -f- ^^dr- ;
при тех же начальных условиях t=0, Дш(0)=0, До/(0)=
дает: Ду(О)=О, Ду'(О) = О, и мы получаем из (41) аналогичным образом (можно видеть,
что постоянные At и S зависят от А и Bi-
д*=—
где п и b имеют прежние значения.
Функция (40) изображает „заброс” оборотов под влиянием весьма быстрого прибав-
ления газа. Разыщем точку максимума этой Функции по времени. Диференцируем (40) И
получаем:
1 — e~nt(cos bt-\- ~ sin bt
(41)
система уравнений (36)
(41а)
« Д f __ „л
~e "~nt —j—-
В точке максимума должно быть Дшг = 0, Дш" <0. Следовательно, при максимуме
((^0) должно быть cos bt—sin bt — O. Таким образом, cos bt—-^- sinbt и время про-
хождения максимума найдется из равенства:
. 1 t с
о н :
и И . - L .
cos bt—— sin ^t
b
' 0 4лг
Следовательно^ самый мйксиму'М'найдем' посреди вбм подстановки (4?)в равёйСТво (40).
В результате получаем: <• . ... <
. / л . Ь\&Маг . ( . b\ ,.о,
Аа)шах = exp ( — у аге tg — \ f h sin (arc tg — L (42)
и в развитой форме:
wmax
К,
Л —---------.„arc tg-s-i----
К VIJ&C-K2
I
2ДЛС < Лат 1 47,6. С-
-7^-^=- sin-f ar&tg-’-'7-
zee-Л А-
К.
, J ZT- feS
(42а)
Течение „заброса", вычисленное по (40), в сравнении с тем же примером, расчислен-
ным по нелинейной системе, представлено на. фиг, 23. Видно, что для практических це-
лей формула (40а) достаточно хорошо иллюстрирует заброс.
г - § 16. Асимметрический процесс ч зоне пропорциональной 44
интенсивности регулирования ( —
*' /_,
’Ж-i Оставаясь пока в области таких колебаний, при которых |«у! < |Д<огр] и золотник ре-
гулятора полностью не перекрыт, т. е. когда (ввиду ранее принятого нашего допуще-
ния, что Дш = ау) ' 1 е а'
|Дш| < |Д<Огр|,
мы тем не менее сталкиваемся с возможным разрывом производной по «> от функциональной
зависимости ~Сг,2 Дш в точке Дш —0, так как при С, if- С8 уравнение ^ = С1Дш „скач-
dt г лг
ком" переходит в уравнение — С\Дш.
Фит. 20 доказывает соответствующие
кривые. Видны разрывы кривой ^^Идуглы"
у кривой = </ = о/(Дш) — СДш.
Вычисление поведения р. и. при пере-
ходе во вторую ветвь процесса (т. е. когда
имеет место „облегчение" винта) производим,
принимая во внимание, что:
, . в момент перехода во вторую ветвь (со-
ответствующей прекращению „затяжеления"
.Фиг.’ 20. Угловая скорость перекладки лопасти 4 и началу „облегчения" винта) коэфицйент Сх
’ " ' „скачком", превращается в С2, в связи с чем
’rfF — ч')п° кусочно-линейной системе система уравнений, описывающая новое дви-
- >цение, будет:
У, До/ 4- /<5Дш = ДМ* — 5, Дф,
Д^' = С., Дш,
I (43)
(ь) 1 * • ’
да'ющая общий(Интеграл.того же типа, что (39) и (41), т. е.
-: _• ..... " - - ’ \ -i ‘ *
Дш —g "• 4 [Д Pcos tn 4' fii2) Sin t2],
Д® = 4 [A(22) cos b2 4 4^ sin b2 4) 4- ,
« - ' : О- . , 4ЛТ ' :- R '
с тем, однако, отличием, что новое b2 у= b х, так как
1 ________________
ь, == 2J- f 4
(44)
1 Результат вычисления получается точнее, если вычислить для второй ветви новые значения и Л*#
ири не изменившемся V. Практически изменится (существенно) только Kg.
Что касается произвольных;достоянных^ то для шх/определения новыми начальными
условиями следует считать:
Л, = О,Д® —О, Дф=Д<р1,
причем Дер! есть то значение координаты Д<р, которое она имела при достижении коорди-
натой Де> значения До> = 0. 1 • "•
Укажем, как найти Дер,. Координата Дер в функции времени для первой ветви процес-
са дается равенством (41а). Спрашивается,' как найти соответствующий .момент времени?
Мы имели для координаты Лек
Д® = e~^nt - sin b} t\
Jx
положим Дш —0; находим, что, кроме корня t—О, следующее по порядку значение,
удовлетворяющее условию (Лад — 01, будет:
откуда интересующее нас значение Д<р1 найдем подстановкой в (40а) значения Л.г. Таким
образом,
Д Mdr I 1 I , — -г- /Д с»
Дер, — —-— 1Ч-е ь, . - (40).
Теперь развиваем новые произвольные постоянные Д|г) и В,2) при соответствующих
начальных условиях 4 = 0, Дю —0. Что касается До/, то оно теперь будет зависеть от
Д<Р1, т. е. уравнение (43 а) дает:
/>'фО=ЛЖ-Ч Д?| ,
следовательно:
Произвольные постоянные находятся из равенства:
уш(0) = 0= Л|2';
следовательно:
ЛР = 0, Л®' (0)^ --fr-J-1-
= В^Ь2 -А^п^В^Ь.,
и частный интеграл движения в координате Д® будет:
д со ~е~"^ sin b„ t
Jsb2
Для координаты Д? мы поступаем подобным же образом и получаем:
(46)
лдд«
?1----— ) COS t2
«•J Л
Д/Ил-
т р—
, (47)
Ь9
Это вычисление можно продолжать для любого числа
нашей задачи затухание колебаний обычно столь велико,
числять не приходится.
Характерными случаями таких колебаний являются
(см. фиг. 21 и 22). Пунктирная линия представляет для этого случая интегральную кри-
вую, вычисленную только что изложенным методом. Сравнение результатов численного
интегрирования нелинейных систем и применения линейных уравнений на фиг. 21, 22, 23
и 24 показывает не плохое совпадение результатов. Фиг. 25, 26 и 27 представляют очень
характерные примеры асимметрического движения, расчисленные для других числовых
данных.
Фиг. 28 представляет собой, результат применения формулы .(40а) для начальных ус-;
ловий, имевших место в действительности при опытах ЛИИ весной 1943 ,г. ' «?»':
колебаний, однако в условиях
что больше двух ветвей рас-
вычисленные нами примеры
испытаний характеризовался следующими данными: "•
1/0 = 326 км час, Js=3,5, ЛЛТ=211, W9 = 180 л. с., /Vmax = 7O0 л. с.,
b =» 2,49,_С= 0,013, = 23°,3.
Отсюда М0 — 77, и так как после дачи газа было Afmax = 288 мм (Nm№ — 7(X) л. с.),- те
граничные условия приближенно определялись.
У***' Таким образом, оказалось, что ^ = 1770, tg’=‘3,86, /^=4,38, и можно было приме-
нить формулу (40а).
Примечание » пичинм входившие в подсчет брали'п
при условии, ногдс v 123 *8 м
Фиг 21. Заброс оборотов мотора
' = ; ,5; 7 = 1000 ж; р = 0,121,
С = 0,0^6 У = 83,5; ДЛТ = 27-3 кгм
'Примечание'- 1 Численное интегрирование велось
с алронсимационной ф~ой для Я
2 Равновесное условие при Мо= 123 нг и
Фчг. 22. Заброс >боротов м< 'опа
7=3,5; /7= 1000 м; р = 0,121;
<? = <“,006, И=83,5; ЛЛГ = 273 л^и
при резком прибавлении газа
р = 0,1134; Js = 3,5; Мо = 150 кгм;
ДЛ4•= 250 кгм; V = 91 м/сек
Фиг. 24 Заброс оборотов мотора
* = 3,5; ’//=6000 м; р = 0,0636; С = 0,006;
V = 125 м/сек; ЬМ = 175 кгм
Фиг. 25.
Процесс асимметрического регулирования
без запаздывания
ЕДача -и уборка газа
при /5=7,5; ^ = 7,5; ^ = 2100; п = 0,5/
61 = 1,41; 6г = 0.94; Сг= 0,008; С2 = 0 004
___________________________t _______ * 28, который дает сравнение „теоретиче-
ского* недействительно имевшего в .этом случае место „заброса* оборотов мотора. Дру-
гой подобный пример представлен на фиг. 29 ’ -
яв
Фиг. 27, Возмущенны^ движения регудиру.е-, >.3
мой системы при манипуляциях сектором газа
(вычислено по кусочно-линейиой системе)
Уборка газа
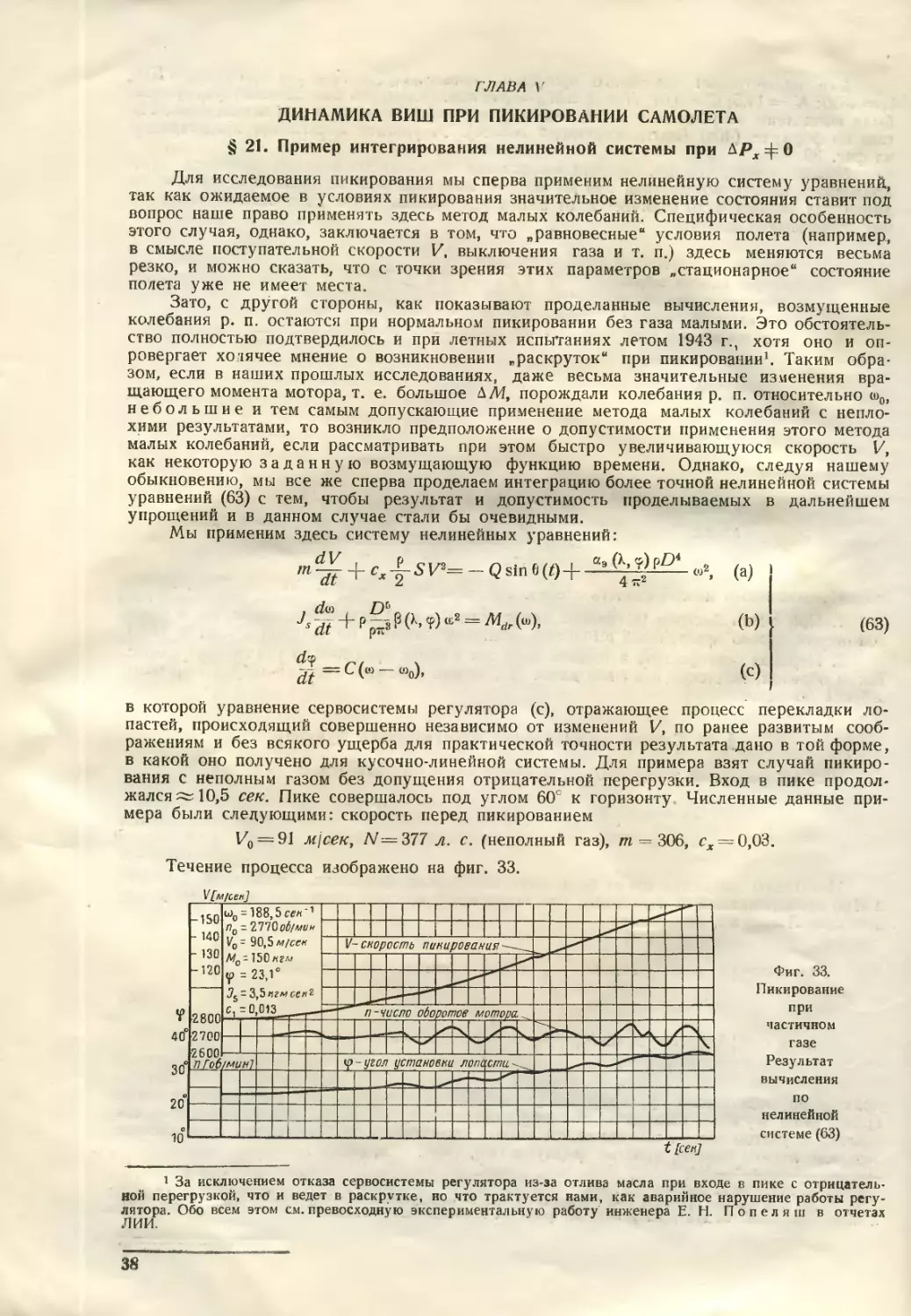
V = 136 м/сек-, if0 = 35°,3;
" п0 = 2700; Нм = 0; (7, = 0,01;
£, = 6250; " Ks = 17,4; С2 = 0,006
Фиг. 26. Возмущенные движения регулируе-
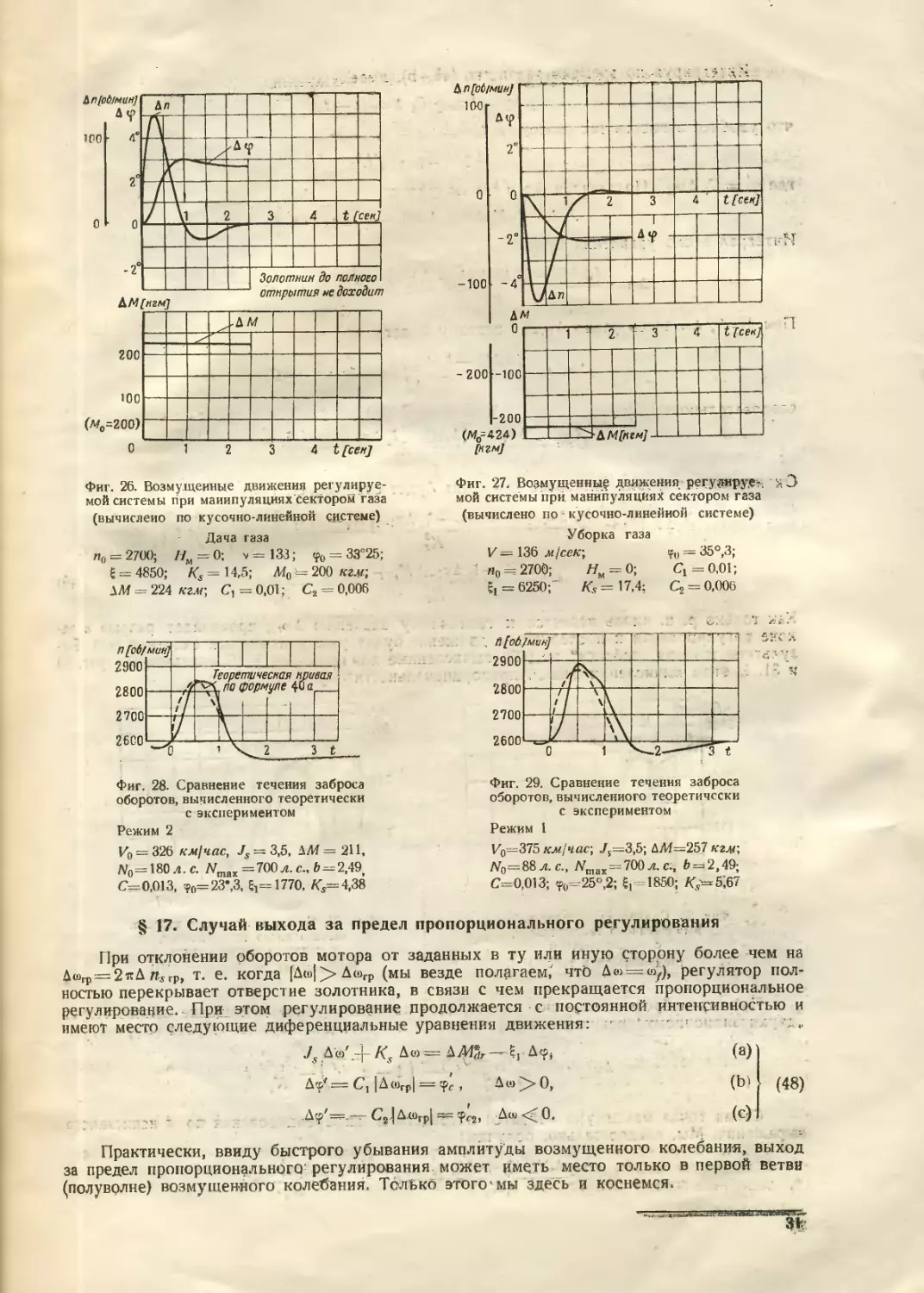
мой системы при маиипуляциях сектором 'газа
(вычислено по кусочно-линейной системе)
Дача газа
п„ = 2700; Нм =0; v = 133; <р0 = 33°25;
g = 4850; Ks = 14,5; Мо = 200 кгм\
SM = 224 кгм- С, = 0,01; С, = 0,006
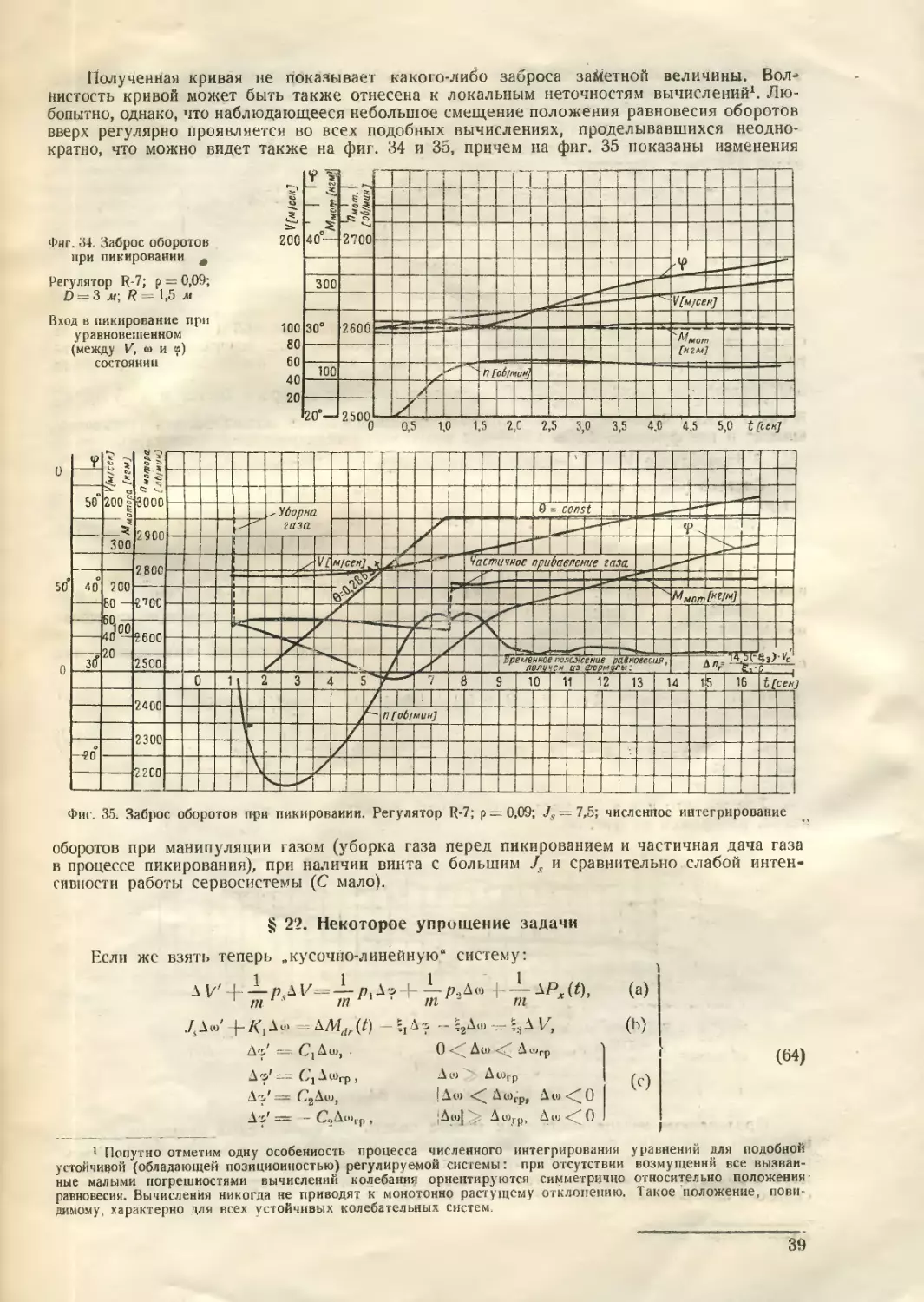
Фиг. 28. Сравнение течения заброса
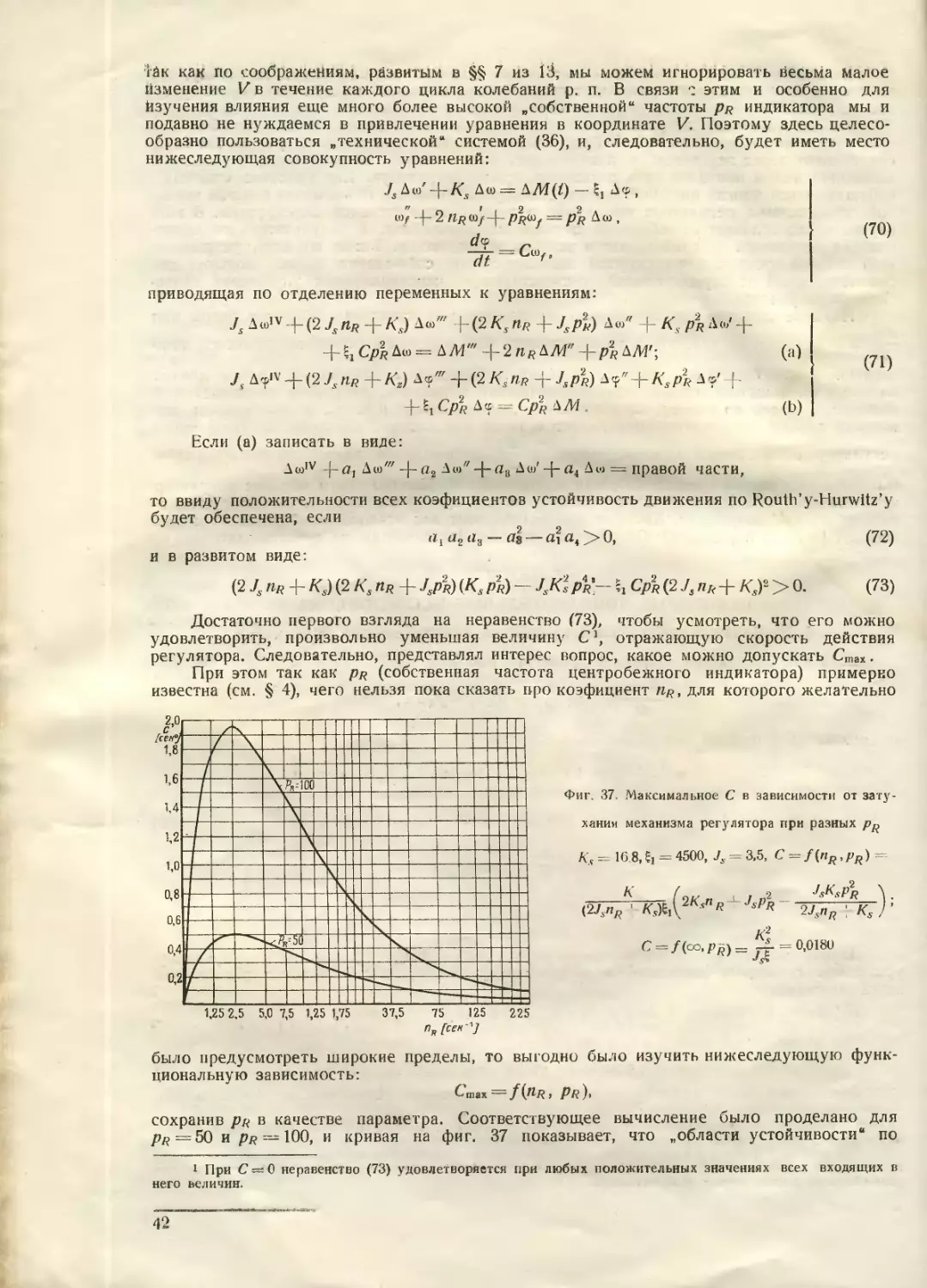
оборотов, вычисленного теоретически
с экспериментом
Режим 2
оборотов, вычисленного теоретически
с экспериментом
Режим 1
Vo — 326 км/час, Js = 3,5, ДЛ4 = 211,
Л?о=180л.с. Утах=700л. с., 6 = 2,49,
<7=0,013, ?й=23’,3, £,= 1770, К>=4,38
У0=375 км/час, Js=3,5; ДЛ4=257 кгм',
^=88 л. с., ^ах=700л.с;, 6 = 2,49;
<7=0,013; ?о=25°,2; £,=1850; Ks-=5,67
§ 17. Случай выхода за предел пропорционального регулирования
При отклонении оборотов мотора от заданных в ту или иную сторону более чем на
дШ1.р=:2лД njrp, т. е. когда [Дш| > Д<игр (мы везде полагаем,' чтй Ди = Шу), регулятор пол-
ностью перекрывает отверстие золотника, в связи с чем прекращается пропорциональное
регулирование. При этом регулирование продолжается с постоянной интенсивностью и
имеют место следующие диференциальные уравнения движения: • - - г • •
Js Дф'ф-А^ Дш = Д/И§Г-=Е, Д<р,
Дф' — С, | Д <urp | — сре, Д w о,
(а)
(ЬИ (48)
Д? =--= С2]Д<Огр| — '-рсг, Дв><4^0, (с)
Практически, ввиду быстрого убывания амплитуды возмущенного колебания, выход
за предел пропорционального регулирования может иметь место только в первой ветви
(полуволне) возмущенного колебания. Только этого'мы здесь и коснемся.
Интегрируя по времени равенство (48—Ь), имеем:
Д<р= Д?о 4~ С, Дигр (/ — /„),
что удобнее записать так (положив 1о — О):
д? = Д?о + ?^>
где <f'c~Cl Дшгр. Подставляя Д<р в (а), получаем:
Js До/ -j- Ks Ди — ДЖ - 4 (Д<р0 -j-<р't).
Интеграл этого уравнения будет:
д. = (д Л Е, i J, s. ъ t+&>-%.
Ks Ks
При £=0, Ди здесь равно Aw,-_t и поэтому будет:
Ди-
к1
следовательно:
С—k^Mdr — 4 Д?) Ka—J3 4
K2S '
Окончательная форма интеграла движения будет следующая:
Дш<-1 — k^Mftr 4 Д^г-i) Ks —- Js 4 <fc J * 11
— - —2--------------------exp । — -f- I/ Mf-
l\s *
। (ДЖ— 4 Д<р«-1) Kt 4~ Л4 & 4?c ( (49)
Ks Ks
Как только p. п. вновь вернется к граничному значению Дигр, произойдет разрыв в за-
коне регулирования и последующее движение будет уже описываться системой (43). Ре-
зультаты течения „заброса" по (49), вычисленные для примеров § 16, показаны на фиг. 30
и 31. В этом вычислении „зоной пропорциональности" пренебрегалось.
Фиг. 30. Сравнение течения заброса,
вычисленного теоретически,
с экспериментом
(подробности в тексте)
Фиг. 31. Сравнение течения заброса,
вычисленного теоретически,
с данными эксперимента
(вычисление по формуле (49)]
При пренебрежении „зоной пропорциональности" (такое допущение 'соответствует
„двухпозиционному" регулированию) Диг.„1 = 0 и будет для первого заброса (Д®0 —0): !
дж^+-/Л1 -£\ Ьъ,
к1 V / Ks
Самая точка максимума найдется посредством диференцирования по t написанного
выражения. Мы, следовательно, получим:
=0,
3?
отсюда:
t = _ A in________________ill'- 4----------
и, подставляя tm в равенство для Дшь находим:
ДЖ/С,4Ш , ^'cJsft
tOmax ‘ к* k2s vn дс^+^л?;
(49a)
Выбросы, вычисляемые по (49) и (49а), обычно получаются для регулятора Р-7 не-
сколько меньшими, чем истинные, и следует помнить, что настоящее свое применение эти
формулы должны найти для двухпозиционного регулирования.
§ 18. Соображения об устойчивости асимметричной системы
Как уже говорилось, пока мы не располагаем каким-либо общим критерием для
оценки устойчивости движения описываемого кусочно-линейной системой уравнений (27)
и (36). Практически выяснить такой вопрос мы можем, только проделав соответствующие
вычисления. Если в течение нескольких первых „полуколебаний" обнаружится резкое их
затухание, то обычно можно с практической точки зрения сделать заключен ае о сходи-
мости процесса, но этот „практический" критерий, ясное дело, не может претендовать на
замену ненайденного пока формального критерия.
К счастью, с инженерной точки зрения в этом пока нет большой необходимости,
тем более, что влияние тех или иных факторов, способных сделать систему „автоколеба-
тельной" или же и вовсе неустойчивой, можно изучить, соответствующим образом видо-
изменяя основные уравнения при пользовании предположением о симметричности процесса.
Таким образом, во всяком случае проявляется основная качественная (а во мно-
гих случаях и количественная) сторона явления.
В случае, если колебания происходят в зоне неполного открытия золотника (jwyl <4
<и/Гр) и если мы рассматоиваем регулятор, действующий без запаздывания, когда можно
считать, что иу=Ди и у'—Cj,2 Дю, т. е. когда дело сводится к асимметричной системе с
двумя степенями свободы, которой отвечают уравнения:
- -^1 Д '?» (*0
Да'—С} Дш, Дш^>0, (Ь)
Дс/=СгА.ш, д«<0, (с)
(50)
по которой в зависимости от знака Ди имеет место либо совокупность (а), (Ь), либо (а),
(с), то задача решается без затруднений. Так как системе (50) отвечают в координате Ди
два уравнения:
Js Д о>" 4 Ks Д и' 4 ct С] Д и = 0,
4 дш,;4 ks Ди 4 с2 ди=о,
(А)
(В)
(51)
которые каждое в отдельности представляют собой (так как /4>0; ^>0; ^Ci,2>0)
либо уравнение затухающих колебаний (когда 4 JsiA С1.2>/ф, либо апериодически зату-
хающего движения (когда 4 Js^ C\t2<ZK2), то нам следует выяснить, какими могут быть
последствия последовательного сопряжения интегралов движения по (А) и (В; с учетом,
однако, и того обстоятельства, что ввиду разных причин (см. ниже § 25) коэфициент Ks
может стать иногда малой, а иногда даже и отрицательной величиной.
Мы ограничимся здесь при этом рассматриванием пока только тех обычно встре-
чающихся на практике случаев, когда К2 <4 СЪ, т. е. когда для обеих ветвей асим-
метрического движения имеет место колебательное решение, и рассмотрим случай „дачи"
газа.
Так как при принятых предположениях колебания р. п. протекают так, что „разрыв"
в процессе регулиоования (соответствующий „скачкообразному" переходу от уравнения
ДУ=Сд Дсо к уравнению Д®'=С2Дш или обратно происходит точно в момент прохожде-
ния функции Д« через нуль1, то после полученного первого топчка р. п. будет изме-
няться в первой ветви по зависимости:
Д sin bxtx. (52)
где под tA понимается время, текущее от начала и до конца первой ветви процесса,
1 Мы будем говорить, что р. п. проходит в этой точке через .линию раздела*.
5
33:
Функция Aojj проходит максимум (см. § 15) в точке t= -J-arctg-^- и самое вира-
Р] /I,
жение для максимума имеет вид:
A°Jmax = f
— arctg — Дио . /
ъ' п> —— sin I arc tg
/7
n,
b
Очевидно, этот выброс пропорционален начальной скорости (Лсог) р. и. при прохож-
дении точки раздела.
Какова же будет начальная скорость к моменту первого переключения?
Так как согласно (52)
Ан,- = Ди;_ , f cos b, t, sin f ),
го к моменту окончания течения первой ветви, т. е. к моменту постижения равенства
b}t $= тг. окажется, что
Ди,- — е 1,1 Д«/(—1 0)— — е bi Ди,--I.
И если бы оказалось, что (но при выполнении прежнего условия <4/7,С), то
будет:
Т.П
Ди, е ь> Ди,--1, {bit — 7-
Во второй ветви при тех же предположениях о характере движения будет подоб-
ным же образом
Awy ~e ' nst sin (52a)
t/p
/ ЯИ14
и соответственный минимум так как здесь AwJ-i Ди, - Ди,-_1 е *, :
1Де>0
Д И/ min— т Sin
1?2
arc tg
n, bi
+ -£-arctg
€ в
V. 1Ц
bi
I Аир!
№
sin
r \ n. bj , Ц/7.
arc tg — '' e l,ja' s"» Л
n.J
(53)
Второй максимум будет [введя обозначение exp (...) = £(...)]:
, Ь-i \ f 1 Mj . Ь\ 1 “ ZZj , il /^2 1
2“s"’“ -+ -ГГ -Sln *8 ,,,)exp T,arc ,g 1' t7 “7'
Второй минимум в свою очередь:
A<y2min
Аир! I ь.
——L sin arc tg—'
\ n.
b., -кп
n9 — /7,
П.1 , -И
b2 “ ь}
Продолжая таким образом дальше, будем получать:
. ? A wo . 1 bx
Аи3,„ах= — Sin arc tg —
bi \ n}
• n, . b}
exp 7 7- arc tg , л
<71 ni
Hi
ь,
И,
т..
п9
К
Аи3
А ир| .
—,—- sin
Ь2
b
arc tg —
th
exp ^b-^arctg
p2
Ь..
п.,
, nx
- IT, - b~ ~~b.
П2
zh
bl
AP74max
Дир .
— sin
by
by
arc tg —
th i
«, , by
exp ±i6Jarclg-^
П., nx , И., , П; «2_
/7., ht — b2 — b{ “ b9
ni j «1
П
b
34
тричем закон образования этих выражений виден непосредственно. Так, например, при-
дав первому максимуму индекс г‘=1 и первому минимуму индекс /=1, будем иметь для
.всех остальных максимумов:
Awo . ( Ьг \
Аелшах = -т— SIH acr tg — J exp
t/j \ rl'i /
, «1 a. b\ 1
и для всех последующих минимумов:
, 1д<во! ( . &2\ , п2 * . / , Jni . (7~Un:
A®,- min = - -Ц- - sin arc tg -г- I exp + arc tg +«I + -v- ±------------------------------------т-----
и вспоминая, что при мгновенной даче газа Aw'
ДЖ
Л
то
, А/ИЗ, . ( L b, \ ( I «1 . bA . . I—1 . (г—1)п2
A^imaxS? -7-7—Sin afCtg-1 вХр{+ 7 ЭГС tg -А -f-7t + ~Т-”1 ± -1-
\ J | t/j c'l U2
. А/ИЗл . / i b2\ ( . П, bo , I . Jn. . (/—l)n,l) ,,,
^s’nv'c*g^ex₽l±'<'r g^+”l±V±_^—I)- (>
(54)
Если процесс в обеих ветвях затухающий, то все знаки плюс в фигурной скобке не
имеют места, в связи с чем при i^oo, Де>,гаах ->• 0 и процесс сходится быстро. В обратном
случае (когда система неустойчива в каждой ветви порознь) в фигурной скобке остаются
только положительные слагаемые, что, очевидно, указывает на расходимость процесса.
Оба эти обстоятельства могли бы считаться очевидными и без вышеизложенных рассуж-
дений. Интерес представляет тот случай (наблюдающийся иногда на практике), когда nt и
я2 имеют сами по себе разные знаки.
Рассматривая выражение (54), можно видеть, что в этом случае величина положи-
тельных выбросов (максимумов) будет при неограниченном возрастании указателя i убы-
вать в том, и только в том, случае, если при какой-либо комбинации знаков все же вы-
полняется нижеследующее неравенство:
±£-+-?-<0- (54а)
b-i
§ 19. Влияние плавности дачи газа на величину заброса оборотов
Для того, чтобы решить эту задачу, нужно апроксимировать какой-либо функцией
времени закон возрастания вращающего момента мотора при переводе сектора газа. В
конечном счете, поскольку это зависит от руки летчика, мы не можем дать уверенного
предпочтения той или иной функции.
Если ручку переводить равномерно, то вращающий момент мотора можно прибли-
женно апроксимировать на данном отрезке синусоидальной кривой, переходящей в точке
'^=~2 в прямую, параллельную абсциссе:
A/Mrfr(0=A Жет 17,
A Mdf (£) = А /ИЗ, = con s t,
(а)
(b)
(55)
Рассмотрим влияние на амплитуду заброса продолжительности процесса при подоб'
ной апроксимации в случае протекания колебаний в зоне пропорциональности.
Технические уравнения системы в этом случае будут иметь вид:
Js Aw' -|- Кв Аш= А/ИЗ, sin v t — ^Awj,
(36)
Aw'—CjAw, (|Дw| |Дсогр I), 1 q
Ao^CjAwrp , (| ^>| Aw|), J
35
Так как нас здесь интересует только сравнительное исследование, то ограничимся
малыми колебаниями, при которых второе неравенство 1Дю]У|Аю| не имеет места.
Интеграл движения в координате Аю при начальных условиях /=0, Аю=Дф=О тогда
будет иметь вид1:
( n cos г4-v sins
— --- ------------1 —COS г cos bt — --i---
V&c- j^+кр l b
A7W*cos(v£ — s)
и в координате Аэ соответственно:
. САЛ4*е ( ... rt Sin е - v COS г . 1 ,
Аэ = — J sin s cos bt 4-----------—-----sin bt
’ ) (EjC .b2)2 ' b J
CAM* sin(v£ — s)
|'&C- : АУ ’
при этом везде „сдвиг фазы"
__________________________________________
По достижении временем t значения ~ формулы (57) и (58) автоматически пре-
кращают свое действие, и вычисление продолжается по обычным общим формулам ку-
сочио-линейной системы, развитым для мгновенно приложенного и затем постоянного'
приращения вращающего момента, т. е. для АЛ4*г — const, которые для зоны пропорцио-
нальности регулирования суть:
j Аю/-1 cosft^y
A<4-AW/ 1(_/л /Q_?1A?i , 1.
-------------------------------- SIH bjt:
sin bjt
(a)
(59)
(b)
а за пределом „зоны пропорциональности":
Л^Дюп—1 (SMdr — i)As—Л^1?с j ns , I .
AW„=----------------——------------_---- exp (- f- t„ j
(д/и* } (60>
1 AJ - K,'1' (a)
a?„= Д?„-14-?Л- (b)
Причем „переходные" значения координат Дю;_1, A^_i, A<on_i и A<sn_i — суть те значения
искомых переменных, через которые они проходили в моменты наступления разрыва в
законе регулирования. В частности, например, Дюг_1 и Д®/-1 могут быть нулями. Сказан-
ное на стр. 34 о времени прохождения точек разрыва и о нахождении величины Аэ в мо-
мент разрыва остается в силе и здесь.
1 При выполнении условия 4 Js; С > , что обычно имеет место. Самый процесс интегрирования си-
стемы (56) опускаем, поскольку это является обычной задачей теории линейных чиференцнальных уравне-
ний с постоянными коэфициентами и с правой частью.
36
Для иллюстрации сказанного приведем пример. Пусть Уо — 133 м;сек\ п0 — 2700
—4850; ^=14,5; С = 0,01; Н = 0; ДЛ13^ = ЗОО кгм. Пользуясь выведенными формулами,
были вычислены забросы для v —3, v —0,76 и v = 0,3, а также и для мгновенной дачи
газа по формуле (40а) (соответствующей v = оо). Результаты вычисления представлены
на фиг. 32.
Можно видеть, что при быстром возрастании вращающего момента, например, если
продолжительность возрастания Д/И до полной величины Д/И* не превышает 0,5 сек, то
амплитуда заброса мало отличается от амплитуды такового при „мгновенном" возраста-
нии вращающего момента.
Фиг. 32. Сравнительный
график величин заброса
оборотов в зависимости
от плавности перевода
ручки сектора газа
V — 133 м/сек-,
ДЛ1 == 300 кгм-,
^=14,5;
5, = 4850;
/7=0;
С = 0,01;
А = 3,5;
b = 3,1;
п = 2,07
Из сказанного можно сделать следующий вывод.
1. При очень быстром (в течение менее, чем 0,5 сек) переводе сектора газа в новое
положение можно практически вычислять величину заброса по простой формуле (40а).
2. Перевод сектора газа в течение 3—4 сек и более практически уничтожает заброс
Таким образом, медленно и плавно давая газ, можно избежать сколько-нибудь заметного
заброса оборотов.
§ 20. Случай произвольной возмущающей функции
Для произвольной возмущающей функции мы имели равенства:
Aw = e~nt [ A cos bt-]- В sin bt} -ф I] (Д/И'Д/) ],
A'i = e~nt {Aj cos bt B} sin bt] -]-F2 [CAA4dr (/)].
Интегралы движения могут быть выписаны только формально, поскольку функция
ДЛ1(/) произвольна. Эти интегралы, при вычислении которых нами был применен метод
вариации Лагранжа, следующие1:
t
Дю = е~"*]А cosbt-\-B sin bt] -ф ~ e~nt f enf^M'{i) sin b (t — т) di,
t,
<
As = e~nt jAj cos bt-]-Bx sin bt] -ф-^~ e~nt J e~nt C±M(i) sin b(t— x) di,
t,
(62)
причем по подстановке функций ДТИ('х) и АЛТ (х) и разрешению определенных инте-
гралов (это нужно сделать сперва2) постоянные (А, В, A]( Bt) развиваются, как
обычно, с учетом общих замечаний, сделанных нами на стр. 24. Наибольшее практическое
значение имеют, однако, простые формулы (40), (40а), (52), (52а).
1 См. любой курс анализа.
- При подстановке пределов А и t получается вместо определенных интегральных какие-либо функции
t, после чего равенства диференцируются для развития произвольных постоянных.
37
ГЛАВА V
ДИНАМИКА ВИШ ПРИ ПИКИРОВАНИИ САМОЛЕТА
§ 21. Пример интегрирования нелинейной системы при АРд ф()
Для исследования пикирования мы сперва применим нелинейную систему уравнений,,
так как ожидаемое в условиях пикирования значительное изменение состояния ставит под
вопрос наше право применять здесь метод малых колебаний. Специфическая особенность
этого случая, однако, заключается в том, что „равновесные" условия полета (например,
в смысле поступательной скорости И, выключения газа и т. п.) здесь меняются весьма
резко, и можно сказать, что с точки зрения этих параметров „стационарное" состояние
полета уже не имеет места.
Зато, с другой стороны, как показывают проделанные вычисления, возмущенные
колебания р. п. остаются при нормальном пикировании без газа малыми. Это обстоятель-
ство полностью подтвердилось и при летных испытаниях летом 1943 г., хотя оно и оп-
ровергает ходячее мнение о возникновении „раскруток" при пикировании1. Таким обра-
зом, если в наших прошлых исследованиях, даже весьма значительные изменения вра-
щающего момента мотора, т. е. большое ДЛ4, порождали колебания р. п. относительно <о0,
небольшие и тем самым допускающие применение метода малых колебаний с непло-
хими результатами, то возникло предположение о допустимости применения этого метода
малых колебаний, если рассматривать при этом быстро увеличивающуюся скорость V,
как некоторую з а д а н н у ю возмущающую функцию времени. Однако, следуя нашему
обыкновению, мы все же сперва проделаем интеграцию более точной нелинейной системы
уравнений (63) с тем, чтобы результат и допустимость проделываемых в дальнейшем
упрощений и в данном случае, стали бы очевидными.
Мы применим здесь систему нелинейных уравнений:
л^+рй^(х,т)о;2=уи^(ш)’ (ь)
^?=С(е> — <о0), (с)
(63)
в которой уравнение сервосистемы регулятора (с), отражающее процесс перекладки ло-
пастей, происходящий совершенно независимо от изменений I/, по ранее развитым сооб-
ражениям и без всякого ущерба для практической точности результата дано в той форме,
в какой оно получено для кусочно-линейной системы. Для примера взят случай пикиро-
вания с неполным газом без допущения отрицательной перегрузки. Вход в пике продол-
жался^ 10,5 сек. Пике совершалось под углом 60е к горизонту Численные данные при-
мера были следующими: скорость перед пикированием
1/0 = 91 м[сек, N—377 л. с (неполный газ), т = 306, сх — 0,03.
Течение процесса изображено на фиг. 33.
[м/сек1
Фиг. 33.
Пикирование
при
частичном
газе
Результат
вычисления
по
нелинейной
системе (63)
1 За исключением отказа сервосистемы регулятора из-за отлива масла при входе в пике с отрицатель-
ной перегрузкой, что и ведет в раскрутке, но что трактуется нами, как аварийное нарушение работы регу-
лятора. Обо всем этом см. превосходную экспериментальную работу инженера Е. Н. Попеляш в отчетах
ЛИИ.
38
Полученная кривая не показывает какою-либо заброса заветной величины. Вол-*
Нис гость кривой может быть также отнесена к локальным неточностям вычислений1. Лю-
бопытно, однако, что наблюдающееся небольшое смещение положения равновесия оборотов
вверх регулярно проявляется во всех подобных вычислениях, проделывавшихся неодно-
кратно, что можно видет также на фиг. 34 и 35, причем на фиг. 35 показаны изменения
Фиг 34, Заброс оборотов
при пикировании л
Регулятор R-7; р = 0,09;
D = 3 л«; R =1,5 м
Вход в пикирование при
уравновешенном
(между И, ш и и)
состоянии
оборотов при манипуляции газом (уборка газа перед пикированием и частичная дача газа
в процессе пикирования), при наличии винта с большим Js и сравнительно слабой интен-
сивности работы сервосистемы (С мало).
§ 22. Некоторое упрощение задачи
Если же взять теперь „кусочно-линейную" систему:
А1/' + — pSV^ — р,А? + 1 т т Ап Д(о |-Ади т т (а)
4- Д’, = Шаг (t) - Д -д — :2Дш — % А (Ь)
А'х/ — Aw, . 0 До) Д о)„р
А (Sj А Юрр , Дш ' Дшгр (0
А'З* Дш <4 Аы1р, Ды< СО
Д'У = ~ CoAujpp , ;Дю| 4 Аи>|р, Дш< СО 1
1 Попутно отметим одну особенность процесса численного интегрирования уравнений для подобной
устойчивой (обладающей позиционностью) регулируемой системы: при отсутствии возмущений все вызван-
ные малыми погрешностями вычислений колебания ориентируются симметрично относительно полож-ния
равновесия. Вычисления никогда не приводят к монотонно растущему отклонению. Такое положение, неви-
димому, характерно для всех устойчивых колебательных систем.
(64)
39
и сделать предположение, что ДУ— заданная функция времени (ввиду превалирования
силы тяжести можно приближенно построить Д У(£), если сделать уравнение (а) незави-
симым от <о и ш и положив тягу винта постоянной на рассматриваемом участке, что для
винта фиксированного шага было бы недопустимым].
Тогда уравнение в координате ДУ не будет иметь места и останется система урав-
нений для двух координат:
J/<o' + К, д Ш = д Mdr (t) — ?! Д Т Д ы — Е3 Д У(£);
Дф'=С, Ды, Ды <Г Дыго 1
! > О,
До7 = CjДыгр , Ды Дыгр J
Дш'=С2Ды, Ды|<^|Аы1р;
Дф7= —С2Дыгр , (Ды I 1 Д ыгр |
(65)
Как видно по результатам численного интегрирования полной системы, вся первая
стадия пикирования (когда собственно только и предполагается возникновение опасности
раскрутки) в нашем численном примере протекает при мало изменяющемся ускорении
поступательного движения = V, численная величина которого близка к 6—8 м/сек2,
ll'l
В связи с этим будем исследовать отрезок, где пикирование можно считать „установив-
шимся,‘ и где функцию Д V— Д V70-|- Vct допустимо рассматривать как линейную.
В этом случае V— Vc = const (на малом отрезке). Положим С\ = С2 = С.
Система (65) по отделению переменных дает два уравнения:
.4Ды"4-л; ды'+^сды^ длг(о-£3а ।
^д/'-Ф^Дф'+^сдлр^сдм—а8ду(о. /
(66)
Когда Д7И= Д/ИЗл, то ДЛГ = 0. Если, кроме того, учесть сказанное о медленности
изменения Д V и положить, как имелось в виду, что на ограниченном участке Д V =
= const = Д то уравнения (66) покажут частные решения, определяющие смещения
положения равновесия колебаний.
Следовательно, для ограниченного участка кривой можно считать имеющими место
следующие интегралы движения:
Aoj == е п1 {A cos bt В sin bt} -у— У' ( Vc — const, ДМ — 0), |
А К i е I \ 1/' 1 f |
Лф = ent {Aj cos bt-]~Bt sin bt) + aJ2 c -j- Д Ус t.
?l ?1 с Ч
Тот же, что и в § 21, численный пример, вычисленный с помощью линейных урав-
нений, изображен на фиг. 36.
Фиг. 36. Пикирование при частичном газе
Результат вычисления по линейной системе (I/ — задано по таблице)
= 2715 кгм, Ks = 7,78 кгм сек, ₽3 = — 10.7 кг сек, С] = 0,013
§ 23. Выводы о роли пикирования
Проделанные исследования, как можно видеть по приведенным примерам, показы-
вают, что нормальный переход в пике не влечет за собой значительного „заброса*1 обо-
ротов мотора. Наблюдается лишь сравнительно небольшое повышение оборотов с тенден-
цией к сохранению такового в течение всего того промежутка времени, пока возрастает
скорость пикирования.
40
Физически и то и другое легко объяснимо. „Заброс" обычно мал здесь потому, что
переход в пике нормально происходит сравнительно медленно и регулятор вполне успе-
вает „сработать".
Заброс может все же развиваться сильнее, если при переходе в пике прибавить
газ (что обычно не делается). Заброс получается также, если резко убрать газ непо-
средственно перед переходом в пикирование. К подобному же результату приведет и
вызванное любой причиной запаздывание действия регулятора. Как выяснено опытами1,
наблюдавшаяся иногда при пикировании „раскрутка" оборотов объясняется отказом масля-
ной сервосистемы регулятора при входе в пике с отрицательной перегрузкой. В этом
случае масло отливает от заборного штуцера масляного бака, в результате чего серво-
система регулятора не срабатывает и винт не затяжеляется. Таким образом, устранение
этой главной причины для раскрутки зависит как от соблюдения правил эксплоатации
самолета, так и от осуществления соответствующих конструктивных улучшений серво-
системы регулятора.
Наличие стойкого (но неопасного ввиду малости) смещения оборотов вверх при
— /О объясняется тем, что в этом состоянии при малейшей остановке процесса затя-
CLL
желения винта, благодаря продолжающемуся возрастанию X, снимаемый винтом момент
начинает уменьшаться, отсюда обороты начинают возрастать, регулятор открывается и
пропускает масло во втулку, винт начинает, „затяжеляться" и т. п., и положением рав-
новесия образующихся колебаний является такое превышение оборотов, которое через
регулятор обеспечивает нужную скорость затяжеления винта, соответствующую
быстроте увеличения X — resp скорости возрастания Vz. Именно таким образом регулятор
автоматически „подстраивается" к условиям полета. При этом винт продолжает затяже-
ляться, пока V возрастает. Как уже говорилось, этот вид отклонения оборотов от нормы
невелик (обычно порядка 30- 60 об!мин) и опасности для мотора не представляет.
ГЛАВА VI
НЕКОТОРЫЕ ДОПОЛНИТЕЛЬНЫЕ ИССЛЕДОВАНИЯ
§ 24. Влияние собственных колебаний центробежного индикатора
Если для регулятора сохранить уравнение (см. § 4)
Ц- 2 nR Ц- pR = pR A «,
то система (27а) примет вид С2~Су.
т d^~ Р“ А V=Р1 А ? + Р2 А10 + ’
Js со == A Mdr А 0) — Ё3 А V,
СИ
d2Vif . dwf ,2 2 .
~dP + ^lRST^ pR»f=pR^,
(68)
d?
dt
Данная система при отсутствии возмущения (APx~bMdr~W) приводит к следующему
уравнению свободных движений в координате р. п. (процесс отделения переменных
здесь опускаем):
Acov4-(2/s /n/iR г Ksm |- pxJJ A<oiv -f-(2 KxmnR-}- Jsp2Rm~\ 2 Jsps tfR-] /<sps
+ A?3) (KspRm + ^KspjiR 7 JspRps-\-2nRpJQ + (.KxpRps-\- p'litn^C--^
PiPr 'я) A w -[• (ps pR C --|- /?j pR 5;t C) A co = 0. (69)
Однако нет необходимости изучать сложные условия устойчивости2 системы (68),
1 См., например, работу „Аппаратура и методика летных испытаний ВМГ на раскрутку и заброс"
инженера Г. И. Попеляш (Технический отчет филиала ЛИИ, 1943 г.).
г В известной части это проделано автором, для чего был использован критерий СгаштеРя для урав-
нения пятого порядка, полученный из общей теоремы Hurwitz’a. Сложность получившегося процесса не оп-
равдывается в данном случае необходимостью.
6
41
тйк как по соображениям, развитым в §§ 7 из 13, мы можем игнорировать весьма Малое
изменение И в течение каждого цикла колебаний р. п. В связи : этим и особенно для
изучения влияния еще много более высокой „собственной® частоты pR индикатора мы и
подавно не нуждаемся в привлечении уравнения в координате V. Поэтому здесь целесо-
образно пользоваться „технической" системой (36), и, следовательно, будет иметь место
нижеследующая совокупность уравнений:
Jj Aw — ДЛ4(() — Д<р ,
4- 2 nR w} 4 pR<uf = pR Д W ,
-di=c^’
приводящая по отделению переменных к уравнениям:
Js A<d,v4-(2 JstlR 4~ AiS) Aww/ 4~(2 KsnR 4“ JSP*R> 1 * Ksp2R^>'-\-
+ 11С^Дш=ДЖ"' 4-2пЛД7И"+р2/гД/И'; (a) (n)
A?«v-|. {2JsnR + Kz} Д®'" +(2KsnR 4- Jsp2R) M'+KsP2r Д?' +
4-Е1С^Д« -Cp^bM. (b) I
Если (а) записать в виде:
AwIV 4-«] Ды"'4~о2 Лш"4-а8 Дш'4“«4 Дщ = правой части,
то ввиду положительности всех коэфициентов устойчивость движения по Routh’y-Hurwitz’y
будет обеспечена, если
</j ti2 tzg — al — a2ai^> 0, (72)
и в развитом виде
(2 Js nR 4- Ks) (2 Ks nR 4- Jsp2R) (Ks p2r) - J,Ki PR-- 4 CpR (2 Л HR 4- Ksy > 0. (73)
Достаточно первого взгляда на неравенство (73), чтобы усмотреть, что его можно
удовлетворить, произвольно уменьшая величину С1, отражающую скорость действия
регулятора. Следовательно, представлял интерес вопрос, какое можно допускать Стах.
При этом так как pR (собственная частота центробежного индикатора) примерно
известна (см. § 4), чего нельзя пока сказать про коэфициент nR, для которого желательно
Фиг. 37. Максимальное С в зависимости от зату-
хания механизма регулятора при разных pR
Кх = 16 8, Ej = 4500, Js 3,5, С = f(nR ,pR) =
WsnR 1 itffaR JsPR ” 2JstlR ' Ks ) ’
C—f(ca,pR) — -± = 0,0180
было предусмотреть широкие пределы, то выгодно было изучить нижеследующую функ-
циональную зависимость:
Стах = f{nR> Pr\
сохранив pR в качестве параметра. Соответствующее вычисление было проделано для
p/j — 50 и pR 100, и кривая на фиг. 37 показывает, что „области устойчивости® по
1 При С’ = 0 неравенство (73) удовлетворяется при любых положительных значениях всех входящих в
него величин.
42
Routli’y здесь очень велики и, невидимому, с большим запасом перекрывают диапазон
МОКДУ flp niin И Л/? max» Даже для совершенно апериодического1 индикатора получающееся
при этом предельное значение С значительно больше применяемого на практике (обычно
С = 0,008-т-0,015).
Таким образом, видно, что в нашем случае можно игнорировать собственные коле-
бания индикатора и везде полагать
Ясно также, что запоздание самого индикатора также крайне мало и несущественно
(чего, однако, нельзя сказать про запоздание сервосистемы). Малость запаздывания инди-
катора определяется его высокой собственной частотой р^ и незначительным трением.
§ 25. Влияние запаздывания сервосистемы
По разным причинам регулирующее действие может запаздывать. В частности, заме-
чается накопление воздуха в виде пены в масле, благодаря чему масло становится сжи-
маемым и несколько „сдает", прежде чем преодолеется значительное сопротивление со
стороны поршня во время хода на затяжеление винта. При этом по опытным данным
наблюдается запаздывание „затяжеления" (при облегчении винта запаздывание сравни-
тельно мало), доходящее до 0,5—0,6 сек. Физически это можно понять, если заметить,
что после уравновешенного на малой мощности режима (resp на малом <ь) давление в
цилиндре сперва малое должно вслед за этим сильно увеличиться при открытии золотника
на затяжеление, что и приводит к сильному сжатию пузырьков воздуха.
При обратном ходе вытекание масла из цилиндра начинается сразу же после пере-
крытия золотника. При этом, так как режим после дачи газа остался усиленным (угол
теперь велик), происходящее в цилиндре с самого начала уменьшение давления из-за
вытекания масла через открывшийся золотник позволяет лопасти немедленно пойти на
облегчение (возможно лишь немного запоздав из-за влияния „сухою" трения).
Таким образом, запоздание здесь несимметрично и в основном имеет место в пер-
вой половине процесса при значительном прибавлении газа, когда режим противодавле-
ния в цилиндре необходимо должен возрасти на 1,5—2 ат.
Исследование влияния упругости вспененного масла требует введения дополнитель-
ной степени свободы, а, следовательно, и увеличения числа уравнений системы (25), (27)
или (36) на одно уравнение. Здесь мы проведем пока приближенный анализ влияния
вспененности масла посредством введения конечного запаздывания.
Привлекая для этой цели широко применяемый в теории регулирования метод „раз-
ложения по степеням малых запаздываний", сделаем предположение, что <?' остается
прежней функцией от отклонения р. п., но лишь в точке, сдвинутой по оси времени на
малый постоянный промежуток ДЛ Таким образом, скорость изменения шага винта
А?' = СТ(^-Д0,
трактуется как „запаздывающая" на интервал времени А/ по сравнению с той же ско-
ростью при отсутствии запаздывания. При этом:
»г(0 = д“; 'T'(0=Aw'; чг"(0= Дш" и т- д-
Введем вспомогательную, „запаздывающую" по отношению к Дю функцию Дюя и раз-
ложим ее в ряд Тейлора по степеням Д/. Мы получим:
Дю3 = Т (/ - ДО = 41‘ (0 - Ч" (0 д/ 4-^у- Т-" (0 д —-1^- (t) Д/« +... (74)
Замечая, что функции Ф (t), Ч'(0, Ч‘"(£) и т- Д- могут быть по условию заменены
через Дю, Дю', Дю" и т. д., соответственно пишем:
Дю3 = Дю — А о/ Д t “] :—5- Дю" Д /2-;—о q Д Ю " A Z8 . (75)
1*2 1*2*0
и, ограничиваясь членами второго порядка относительно А/, получим приближенное ра-
венство :
Дш3 — Дш — Дю' At —|“ Дю Д/’.
1 При чю на самом деле совершенно невозможно, так как трение в этом регуляторе по
сравнению с другими действующими силами крайне мало.
43
Таким образом, для запаздывающего действия сервосистемы будет иметь место уравнение:
Дф'=СДш3=='С | Дю- Лю' Д( -f-™ Дю" Д73
(76)
Подстановка Лу' в уравнение
/Л Л ю' 4- A’s. Л ю — А Л4 (t) — ?] Ду (76а)
дает независимое уравнение в координате Дю:
Л + 4£1СДН Дш" “ ’1СД0 д“'4ЛСДю= ДТИ'ДО, (77)
которое можно записать в виде:
w/jAo/' + uu<o’4-4iCAw-= лти;,до.
(78)
где величины U4 и W2 заменяют прежние коэфициенты: Js и Ks соответственно.
При запаздываниях
кроме того, так как
|^_^СД7|<|А4,
л+4$1Сл/г>л>
то условие, обеспечивающее колебательное движение, сохраняется и здесь, так что ин-
теграл движения здесь может иметь вид:
Дю — е 2vr, -zjyv- sin b3t,
Vy 1С?3
причем решение сохраняет свою форму и в случае W2<0, лишь бы сохранились усло-
вия, обеспечивающие колебательный тип решения, т. е.
>— -
’! 4W,
Формула максимума (42) теперь может быть записана так:
. I Ь3 \ /* п3 , Ь3 \ /'гол
Дютак==-—-—sin arctg—- exp I — K-arctg—-- , (79)
W j Рз \ П-3 J \ " 3 /
где я3 и b3 — новые значения прежних величин и соответственно суть
„3 = Л-, Ьз == 1 щ.
2(4 4~±?1сд^
Здесь необходимо заметить, что в случае симметричного запаздывания, одинакового
при затяжелении и облегчении и при Cj — C2 = C, может быть вычислено также и усло-
вие возникновения автоколебаний („раскачки")1.
Для чаще встречающегося случая полной асимметрии, когда не только самое запаз-
дывание Л( различно в обеих ветвях колебаний, но и С\ ф С2, вычисление поведения
системы может проводиться лишь методами численного интегрирования (более подробные
соображения по этому предмету см. приложение).
§ 26. Автоколебательные явления
Для случая Cj — С2 = С и симметричного запаздывания действия сервосистемы грубая
оценка параметров возможных иногда автоколебаний р. п. может быть сделана на основе
уравнения (77).
1 См. приложение.
44
Очевидно, что при запаздываниях At, достигающих такой величины, что
;1CAt>^s,
(80)
коэфициент при Дш' обращается либо в нуль, либо становиться отрицательным.
В первом случае мы имеем тогда условие для незатухающих колебаний, j т. е. урав-
Q \ ~ I
+ Аш"Ц-В1СДш== правой части j ,
что соответствует так называемой „критической" точке, а во втором же случае наступает
дивергенция колебаний.
Нужно указать, однако, на то обстоятельство, что происходящее при дивергенции
увеличение амплитуды колебаний обычно приводит к уменьшению запаздываний. Это
особенно относится к тому запаздыванию, которое имеет причиной какую-либо „мертвую
зону", образованную, например, твердым трением в системе поршень—лопасть.
Тогда в условиях уже начавшихся колебаний р. п. и вблизи критической точки мы
вправе сделать частное предположение о том, что имеет место равенство1:
Дю = Дшй sin pt.
С другой стороны, мы можем допустить, что для того, чтобы „стронуть с места" систему
поршень—лопасть и соответственно выбрать всю имеющуюся „слабину", необходимо для
преодоления трения Кулона пропустить какой-то определенный объем масла.
Пусть отклонение р. п. от заданного к этому моменту достигнет величины А %,
и отсюда начнем отсчет t, тогда будет к этому моменту времени
А юг = Дшв sin (р A t). (81)
Так как из этого следует, что
At= — arc sin - -, (82)
Р
то можно видеть, что при увеличении амплитуды автоколебаний (Аюа) продолжительность
запаздывания (At), происходящего по вине „твердого трения", будет уменьшаться. Это
легко понять и физически, так как очевидно, что при больших по амплитуде автоколе-
баниях р. п. и золотник регулятора совершает большие колебания (автоколебания обычно
не выходят за зону пропорционального регулирования) и, открываясь на большую вели-
чину, золотник каждый раз скорее пропускает необходимый для выборки „слабины"
объем масла.
В результате запаздывание (At) уменьшается и дивергенция колебаний прекращается.
С другой стороны, уменьшение амплитуды автоколебаний ввиду существования равенства
(82) приводит опять к росту запаздывания, а последнее обстоятельство вновь согласно (77)
раскачивает систему. Таким образом, может создаться режим довольно устойчивых авто-
колебаний и притом происходящих в точке, соответствующей равенству:
₽1CAt = ^s.
При этом вместо (77) остается уравнение:
с С
Дш" -j-----у-------Аш-правой части, (83)
4 + 4S1CA*2
где At уже можно приближенно рассматривать как величину „постоянную".
Аш"
Отсюда получаем вместо (83) при отсутствии правой части
’^2- Аш = 0,
‘ 2^ С
что определяет следующие параметры автоколебаний:
1) частота автоколебаний
(84)
Р<Г=
К]
2^С
1 Мы как бы предполагаем, что автоколебания «установились".
45
2) амплитуда автоколебаний
получено посредством подстановки р, в равенство Ди>„ —---------Ч-зЬ
" 1 “ sinptlbtj
Таким образом, можно видеть, что период автоколебаний Га = должен несколь-
ко превышать по величине период незатухающих колебаний р. п. Амплитуда устойчивых
автоколебаний обычно не на много превышает по величине „зону нечувствительности*.
Однако если по какой-либо причине достигло бы величины Д«гр, то запаздывание
при росте амплитуд колебаний р. п, более уже не могло бы уменьшиться ввиду невоз-
можности для золотника открываться еще больше. В этом случае создалась бы предпо-
сылка для возникновения полной дивергенции колебаний (прогрессивной „раскачки").
Формулы настоящего параграфа следует рассматривать только как „прикидочные". Под-
робнее об автоколебаниях см. приложение.
§ 27. О приближенной оценке эффективности работы регулятора Р-7
на основании тахограммы
Гак как (см. § 14) мы для |A«u|<Aiorp имели в первой ветви процесса:
и во второй ветви процесса:
Ь, = VVAOWmax) С8- [/C(Mmax)F >
1 ™ к 1 ’ 7Г 1 1
так как — 7] =7— и — 7 „=7—, и поскольку полупериоды -5-Л и — /., суть величины
O-t Z Ро Z Z
наблюденные, то
16kV* + [/<ЛЛ/(,)]3
4А’С|
*2
4/Л
Можно для различных условий начертить серии „тахограмм нормального заброса",
сравнивая с которыми наблюдаемые „забросы", нетрудно сделать заключение об эффектив-
ности работы испытываемого регулятора, так как не только полупериоды, но и ампли-
туды забросов непосредственно от этого зависят.
Помимо приближенных формул (87—а, Ь) можно построить для того же назначения
1 рафики посредством численного интегрирования основных нелинейных уравнений. Буду-
щее покажет, встретиться ли в этом надобность.
§ 28. О влиянии условий полета на динамическую возмущаемость системы
В этом вопросе пока проделана только небольшая часть необходимой работы. Ме-
тодика применялась следующая: использовалось выражение для максимума заброса:
K-s t 2^Mdr . f . V^W-^S\
^arctg ——- - —dr-— sin arc tg---------„-----), (42a)
Д1°тах — exp
46
которое при „физически" развитых коэфициентах имеет вид:
В этом выражении учтена вся динамика процесса и, рассматривая Аигтах как функ-
цию всех величин, породивших коэфициенты выражения (42а), можно было, варьируя
последние, изучать соответственные изменения АшП1ах.
При этом могло быть два пути:
1) варьирование каждого параметра правой части равенства (42а), входящего в коэ-
фициенты явно или неявно (например, р, V, о», N л. с. -о, Сит. д.), независимо от прочих
параметров (см. фиг. 38);
Равновесное условие: Л/=197; ДА/= 310 (р-?8”5';р-0,1134( 1000м) ы = 153,5; V= 86 м/сек
I1
ЕЧ
Фиг. 38. Величина максимального выброса оборотов (А“тах) по независимым
вариациям параметров V, ы, «, р
Js = 3,5; С = 0,012
, Выброс” вычислялся по формуле максимума:
^ытах
X ехр
г —____— sin arc tg k -------5
) 4^,6- К} \
I ,
Ks
— "7=^" ~arctg
К,
причем:
„ 2 д? . ?£Н
ч = % (И>- ®о); Л1=/(М)); с» - дг?
б?
(',z°’ “О’
IV 1
—— ' (Vo, о>0,
2) варьирование „равновесных условий" совместно, при котором, например, при
изменении угла наклона траектории (6) к горизонту, при постоянной мощности мотора
ч работающем регуляторе одновременно должны соответственно измениться и 1/0 и <р0.
Основное значение имеет, несомненно, второй путь, но вычислений было пока
проделано немного, а результат их поедставлен на фиг. 39 При этом варьирование
47
равновесных состояний производилось при фиксированной неполной мощности мотора
и величина заброса вычислялась как результат „мгновенного11 перехода мотора к полной
мощности. Имелось в виду установить влияние изменения режима полета в отношении
скорости V на динамическую восприимчивость системы к забросу. Так как стационарная
скорость самолета при постоянной мощности и ВИШ зависит от 0, то таковой и был
сделан аргументом варьирования.
Фиг. 39. Величина максимального выброса оборотов при варьировании
равновесных состояний по аргументу 0
Л 3,5; ДМ = 200 кгм-, С =0.012; р = 0,1134; N 300 л. с.
Оказалось возможным установить, что малая поступательная скорость (например,
при наборе высоты, когда 0>О) способствует большим забросам оборотов1.
Уменьшение р (повышение высоты полета) до тех пор, пока максимальная мощность
мотора еще близка к расчетной, также повышает величину Дюшах. Далее можно видеть,
что величина мало влияет на Дютах, но тем не менее штах [т е. (ю0-[~ Дштах)| будет иметь
место при наибольшем ш0. Варьирование равновесных условий должно быть в дальней-
шем распространено на все основные параметры, характеризующие состояние системы.
§ 29. О влиянии упругости рабочего тела регулятора
Как выяснилось при летных испытаниях в 1943 г., появление воздуха или картер-
ных газов в масляной системе регулятора Р-7 повторяется совершенно закономерно. До
этих испытаний мнения по этому вопросу расходились.
На сегодня, однако, остается невыясненным вопрос о физическом состоянии масла
непосредственно во время работы, в частности, содержится ли воздух в масле в виде
пены или сравнительно больших пузырей и каково процентное содержание воздуха
и других газов в масле во время полета.
Ввиду этого представлялось целесообразным подойти к исследованию влияния
указанных явлений на динамику процесса регулирования пока в свете некоторых, более
сильных упрощающих предположений.
Так, например, было сделано предположение, что упругая реакция сжатой масляной
пены линейна относительно величины ее деформации поршнем.
Второе предположение заключалось в том, что в течение всего интересующего
нас отрезка времени физические свойства этой „газовой эмульсии11 предполагались неиз-
менными.
Третье предположение, которое делалось, состояло в том, что для получения
необходимых результатов предполагалось К== const и рассматривался симметричный про-
цесс (С\ С8 = С), так как незначительная роль весьма малых изменений V при сравни-
тельно быстрых колебаниях р. п. очевидна, а симметрия процесса регулирования не
должна была затемнить специфики данного явления.
Приступая к установлению приближенных диференциальных уравнений задачи,
будем считать схематической моделью явления фиг. 40, на которой ха означает коор-
динату поршня при несжатом масле и х соответствует действительному положению
поршня. Таким образом, разность
л-а —(88)
можно рассматривать как „упругую деформацию11 вспененного-масла.
1 Как после оказалось, к этому же выводу приплел опытным путем и инженер Е. Н. П о п е л я ш,
проводивший ранее упоминавшиеся летные испытания в 1943 г.
48
При этом надлежит помнить, что координата ха подчиняется установленным ранее
законам для работы регулятора Р-7, в частности, например, допускаем, что
dxa
dt
Cjf ьЛЮ J
и так как
d<& 1 dx . ) C?n
---1»—= ------------1-----— ----- TQ Дф =—------------------------------
dt I cos (cp0 — tpr) dt ’ -a 1 cos (<p0 — %.)
следовательно,
/ COS (<p0 — <pr) ’
(88a)
(89)
где C„ — коэфициент „скорости регулирования", отнесенный к поршню.
Фиг. 40
Упругая реакция сжатой пены при сделанных
предположениях будет равна
Рупр = Qn ха = Яп (л'а (90)
и стремится оттолкнуть поршень и „затяжелить"
винт. При этом можно написать следующее равен-
ство сил:
д2х , dx , . _
/Пп — Г %пп — ?п (-^а — •*) — Рп , (91)
где qn — упругая постоянная вспененного масла,
зависящая вообще от многих факторов, но главным
образом.от относительного количества воздуха в
масле, тп—масса поршня и пп—коэфициент ли-
нейного трения поршня. Сила Рп есть приведен-
ная к поршню суммарная реакция лопасти винта.
Момент реакции одной лопасти (Мщ) при
затяжелении представляет собой
d‘l <? d ср Jcl (ср)
mi rc7j D' ^-
9 J . * Vlaer »
(92)
где Jz— момент инерции лопасти относительно продольной оси,
2п, — коэфициент „линейного трения",
Jcf — центробежный момент инерции лопасти.
При облегчении винта выражение для MRt изменяется только в том, что член
т, /' т D, w'2
-с % —— меняет знак. Роль твердого трения заключается в том, что оно здесь соз-
дает запаздывание сервосистемы, приближенно уже рассмотренное нами в § 1. Соответ-
ствующий член здесь опущен.
Вместо этого мы здесь коснемся запаздывания, вызванного большим „вязким" тре-
нием, отраженным коэфициентом nz.
Изменением аэродинамического момента также будем при малых колебаниях пре-
небрегать и полагать, что Maer — const.
Так как статика передачи поршень—лопасть (см. § 5) дает /И, — Рп I cos (<р — ®г), то
можно соединить равенства (91) и (92), так как должно быть:
MRl 4- Рп I cos (ср — <рг) = 0, MR1 = — М,\ (93)
На оси лопасти имеет место следующее равенство моментов:
J’ +2"' ~dt + — Maer +1COS (T “ + 2Ип 'S')
= Zcos (<p —- <pr) <7n (Xo-X),
(94)
1 Pn — суммарное давление, приходящееся на 1 лопасть.
7
49
и так как мы имели (см. § 5):
х — / sin (ср
d2x 1 i , d3® , . , / dcp>
Zcosfr ^~dp- /sinfr“^(
dt3
то уравнение для лопасти примет вид;
Л 4-2п( 4- 7ИГ/ Ч Malr +1 cos (ср - ф,) |
,d34>
да 'мп
4- 2nn I cos (cp — ©,) = Qn P cos (cp — ep,) [sin (cpa — cp,) — sin (® — cp,)].
Уравнение (95) весьма сложно и сохранение его в таком виде не оправдывается
необходимостью при исследовании малых колебаний. Целесообразно заранее упростить
входящие в (95) величины, пользуясь обычным методом. Так, с точностью до
первого порядка включительно имеем:
COS (ф — Ф,) = COS [(ср0 4- Дф) - ~ COS (<РО - Ф„) Sin (<р0 — срг) Дер;
sin (ср - ерф = Sin [(ср0 4- Дер) — cpj Sin (ср0- cpj-i- cos(®0 — срг) Дер,
(95)
величин
(96)
и далее:
/ИгДф,?) = М7„ ДЛ4Г/
2 । дМ tdJcf . дМ f
4“
V 1
т. e.
Mrf^ J-d^
-L ш2
2 0 <?ср
со() До) .
(97)
Подставляя эти величины последовательно в (94) и в (8), (8а) и (8Ь) и пренебрегая
всеми величинами высших порядков малости, мы и получим искомое уравнение в коор-
динате ср.
Ввиду того, однако, что численные данные, характеризующие основной коэфициент
qn , зависящий от количества воздуха в масле, могут быть известными лишь весьма
грубо, мы сперва еще более упростим задачу, имея пока в виду лишь область очень
малых колебаний.
Именно, мы позволим себе предположить, что „множитель передаточного отношения"
может быть апроксимиро-
допускаем существование
(8а), представляющий собой величину cos (ср— ср„), постоянен и
ван его средним значением cos(cp0 — ?г). Таким образом, мы
приближенного равенства:
Mt = Р„ I cos (срп - ср,).
Нужно заметить, что обычно cos(cpe —©,) есть величина
как второй член разложения sin (ср0 — ср,) при Дер, не превышающем 0,05, есть величина
примерно в 20 раз меньшая, чем cos (ф0-—©,).
Принимая для х, х' и х" и ха следующие приближенные
и (81))] значения:
порядка 0,80 — 0,95, тогда
[вытекающие из (8), (8а)
х I [sin (ф„ — ср,) 4- cos (% — ср,) Дср],
t' ~ I cos (фс ср,) Дф',
С"^/СО8(ср0-Ф,)Дср",
с I [sin (©£» — ©,) ф- cos (фСТ — ср,) Дф„ ]\
(98)
и подставляя их в (94), получаем следующее приближенное диференциальное уравнение
для движения в координате Д® в „вариациях":
[Л ф- тп I3 cos2 (®(| <рг)] Д<р" + 2 [п, ф- ип /2 cos2 (<?(| — ср,)] Лер' ф-
4 [4 “о fro) +l~ cos2 fro~
= qn Р cos (ф0 - ср,) cos (cpW — ®,) Дсро — Jcf (ф0) Ч?о Дю,
м
(99)
I Д<ро соответствует положению лопасти при несжатой пене.
50
в котором все „стационарные* величины уже исключены и которое можно при сокра-
щенных обозначениях записать в виде:
./; Д ср" 4- 2п* Д ср' 4- А ср = д™ Дсро - р* Д ш. (100)
Мы имели ранее (88а):
dXa Л
и если отнести это условие к координате (Д'-ра), то будет приближенно
. , Сп .
Дер <5; ------------ Ды
° I COS (ср0 — срг)
так как мы установили, что при очень малых колебаниях в этой задаче
cos (<р ?,)~cos(cp0 —cpj.
Таким образом, мы располагаем нижеследующей системой совокупных диферен-
цнальных уравнений для решения задачи о влиянии появления воздуха в маслосистеме
регулятора Р-7 на динамику процесса регулирования оборотов:
Дер" 4- 2п* Дер' 4- q*a Дер = q” Дерс - р* Дш,
У5Ас./4-^Д1й=Д2Ийг(0-^Д?,
Acs' — С Д<о,
где
Q__ бп_________
~ I cos (ер0 — срг) '
Исследование системы (101) будет дано в приложении.
(101)
§ 30. Некоторые выводы
I. В результате проделанной работы с несомненностью подтвердилось, что метод
малых колебаний Лагранжа к данной задаче вполне применим и при правильном его
использовании дает здесь во многих случаях не только качественные, но и количествен-
ные результаты с вполне достаточной для практики точностью. Это подтверждается, по-
мимо общих принципиальных соображений, основанных на изучении функций, с которы-
ми здесь приходится иметь дело, также и на многочисленных контрольных вычислениях,
проведенных по нелинейным системам уравнений, а также и при сравнениях с данными
летных испытаний. Некоторые из этих сравнений можно провести, рассматривая кривые,
представленные на фиг. 28 и 29.
Можно предположить, что очень хорошее совпадение теоретических и опытных кри-
вых на фиг. 28 и 29 при наличии в системе некоторого запаздывания из-за появления
воздуха в масле, не принимающегося во внимание, при построении теоретических кри-
вых, объясняется тем, что имеющаяся на самом деле нелинейность тормозного эффекта
винта относительно <« должна дать в действительности меньший заброс, чем полученный
при апроксимации явления линейными уравнениями. С другой стороны, имеющееся запаз-
дывание действует в сторону увеличения заброса, и в результате получается хорошее
совпадение с результатами вычислений по линейным уравнениям. Вычисление проводи-
лось здесь как раз по простейшим формулам (40а) и (49). Для вычисления последующих
ветвей колебаний подобный простой процесс, конечно, не пригоден. При вычислении
„заброса" формула (49) систематически дает результат несколько меньший, нежели экспе-
римент и формула (40а).
Нам представляется, что с точки зрения оценки эффективности действия регулято-
ров ВИШ в отношении предотвращения недопустимо больших забросов оборотов при
резких прибавлениях газа и т. п., невидимому, можно считать расчетный аппарат, выра-
жающийся в соответствующей методике и формулах уже достаточно определившимся.
Таким образом, при проектировании новых моделей регулятора ВИЩ, как мы на-
деемся, можно уже будет подойти к задаче с объективным расчетом.
II. С точки зрения устойчивости процесса регулирования задача пока строго решена
только при некоторых частных допущениях, например, при С1 = С2—С, или же в против-
ном случае при отсутствии запаздывания регулирования (однако большей частью вполне
51
позволительно использовать первое предположение, в связи с чем метод малых колеба-
ний и здесь дает достаточно убедительные результаты). Устойчивость процесса регули-
рования Р-7, как оказывается, имеет место с большим запасом по всем важнейшим па-
раметрам, так что нарушение устойчивости регулирования практически может иметь,
место только при возникновении каких-либо серьезных технических нарушений в работе-
системы регулятора, которые, к сожалению, часто все же имеют место. Это прежде
всего относится к подтвердившемуся по последнему испытанию факту — появлению зна-
чительного количества воздуха в маслосистеме регулятора, приводящего к повышению ве-
личин заброса и могущего породить раскачку, а также и случаев „масляного голодания"
при отрицательных перегрузках в полете, что является главной причиной так называемых
„раскруток" оборотов мотора. В случае полета в условиях большого холода возможное
загустевание масла во втулке может, вообще говоря, породить как большие забросы
оборотов, так даже (с теоретической точки зрения) и появления кратковременной раскачки.
III. Проведенное в работе приближенное исследование процесса регулирования при
запаздывании сервосистемы и возможных при этом состоянии „автоколебаний" дает кон-
структору возможность, хотя и грубо, но все же ориентироваться во взаимодействии
двух основных параметров, играющих здесь роль: скорости действия регулятора (пропор-
ционального коэфициенту С) и величины приведенной зоны нечувствительности регулятора
Дпг, из которых, например, увеличение С уменьшает забросы, но увеличивает при данной
Дп„ амплитуду возможных автоколебаний Дп„.
Как уже говорилось, в последнее время полагают, что в образовании Дпг основ-
ную роль играет появление воздуха в масле, что и приводит к запаздыванию серво-
системы.
ПРИМЕЧАНИЕ. Этот вопрос разработан подробнее в приложении, где также показано и приме-
нение метода Оппельта для исследования запаздывания регулирования.
IV. К числу достигнутых в работе результатов можно, невидимому, отнести обосно-
вание отказа от включения в общую систему уравнений задачи элементов, выражающих
инерцию чувствительного органа, т. е. центробежного тахометра, что значительно упро-
щает проблему и делает ее много „прозрачнее". Без всяких сомнений, можно здесь счи-
тать (см. § 4) центробежный индикатор в высшей степени „быстродействующим", что и
определяет указанное положение.
V. Можно еще указать на установление простых рабочих формул (87 а и Ь) для
анализа действия регулятора по наблюдающимся полупериодам колебаний р. п., если
иметь в своем распоряжении только тахограмму оборотов.
VI. В смысле оценки влияний условий полета на величину Аштах установлено, что
с теоретической точки зрения наибольшие забросы оборотов должны получаться при
полетах:
а) с наименьшей скоростью,
б) вблизи расчетной высоты мотора1.
При этом оказалось, что Дштах зависит от а>0 не очень сильно, в связи с чем наиболее
опасным в смысле появления чрезмерной скорости вращения мотора при забросе является
полет одновременно в условиях „а" и „б" и при наиболее высоких ш0.
Эти выводы совпадают с выводами инженера Е. Н. Попеляш в упомянутой его
работе.
СПИСОК НАИБОЛЕЕ ВАЖНЫХ УРАВНЕНИЙ И ФОРМУЛ
I. Основная система диференциальных уравнений задачи (нелинейная):
„,^+с45И-- Q
d'^> .99 2
4 ^nR~dt ~^PR PR (to~too) = /?«Ao>I
da ____ voypj_____/ 2g f 3 [Jef (<f>) rc у; ] <ug |
dt ~ FnZcos‘(<p—]/ у f 1 2Fn I cos (<p — <?r) j’ Дю>0.
1 Так как тогда ДЛ4тах велико, а р сравнительно мало (см. § 28).
52
dy
dt
VU)/ о.2 со
Fnl COS (ср—ср;
2р ( 3(ЛД?) —
7 j 2 Fn 7 cos (ср — cpr) j
°1< *"гр(,
А со < 0,
d'P ________vu)/ гр Hi_____। / [
dt A’n/cos(cf> — %.) | 7 |
Pi
3 [Л/ (?)+mi гс 5WZ
2 Tn I cos (ср — срг)
Асо'|> |Дсогр
Л Oj > 0,
(d8)
(Н)
db
dt ~ Falcos(ср—%)
rp
3(7/(?)—I
2 Fn I cos (ср — cpr) j ’
|Дсо! |Дсогр
(dj
II.
Общая кусочно-линейная система уравнений:
с7Д
т
d&w
dt
dt
- + ДК=-^- - dV d-ь (a)
^dr дЛ1в _ i d/WB J>~ ~dV Л S/^ar> (b)
to f)cp dco
1 o.. duif ! „2 2 c (c)
1 dt л
lt~c^f’ >0, 1w/l <C "/ rp > (d,)
«'cp <0, 1"/ < "/ rp , (d2)
r (ff C1 "rp, coz >0, |"rl^u)/rp, (ds)
d'p ,, ^-=- С2со/,.р, coy <0, 1"/ "/rp, (d4)
(си/1-р А со,.
1
I
(25)
111.
Техническая система уравнений задачи:
A/W)~Чд?<
А У = С, A co, A co >0. 1
As.' = C,Aco, A co < co, )
Дер' — C-i Acorp , |Aco| > Awrp ,
A ср' = — Cs Aco,.p , 1ЛЦ: >До)Гр ,
Дсо| </ Дсо1р ,
1
(36)
IV.
Система диференциальных уравнений с учетом
Дсо^>0,
Лео < 0.
колебаний регулятора:
Js До/ Ks До>= Д/И (t) — Дер,
coy 2 П% СО/ Рл? СО/ = рк Д ш,
d'b
м - с“> -
V. Технические уравнения с учетом запаздывания сервосистемы регулятора
вом приближении:
в
Л АЛ w /И (£) — Ej А ср,
Д<в' — С Aojs —С( Дю
(70)
пер-
(76а)
(76)
53
VL Диференциальные уравнения задачи при наличии воздуха в масляной
регулятора:
[./, 4- 7ПП /2 COS2 (<р0 — Ф,)] Д ср" 2 [и, - «п /2 COS2 (ср0 ср,)] Д ср' 4-
4-“S^fe)+
4-I2 cos2(cp0 — ср,) qn
Дер = ?n/2cos(cp0 — ср,)cos(cpsp* - ?,) А?„ — Jf/(cp0)co0 Aw,
системе.
1
(101)
./5Дсо' 4- Ks Дсо = Д Mdr(f) — ?! Дер, Acp)( —C^O>.
VII. Формула для вычисления течения заброса в зоне пропорционального регулиро-
вания:
к.. , ,
= е ----------sin I — I/ 4-/&С - К] t , (40а)
где К — К I E 1 dMB ~ dMdr kpZ)4/ < dp Dpw0\
Ж A j Нг di)i dw dot 1 4^2 \ ° 4^ 1 n )
дМв D" w2 dp
= -^F::=p_8^_d7-
VIII. Формула для непосредственного определения амплитуды заброса:
AcUmax == exp
ks
г-----—— arc tg------------,,------а
к2
2ШЛг ( I 47E]C-K2\
=- sin( arctg------ту--- ). (42a)
IX. Формула для вычисления течения „заброса“ при двухпозиционном регулировании:
^A^-(SMdr-^^)Ks-JsWc I Ks .\
--------------------------«’l-T'l"
(AMd,-51aT1,)K, + 7.c,T; t1?;,
№ Ks
X. Формула для вычисления амплитуды заброса при двухпозиционном регулиро-
вании:
, ^’CJS Л ’*?Ч
Ф K?s \ ажк5 + Ч<.
(49а)
XI. Общая формула для вычисления амплитуды t-го колебания при асимметрическом
процессе:
. АЖ
ZA C’J; -
J.b
.7 t ьл ।
sin t arc tg~ I exp +
«I * dj .
K“rclg4+’
. ДЛ45г . f , b?'^
А<оу ты =----------y-j— sin arc tg-A
«/ \ /C-4J J
t । «а
ехР ±тг
| ^2
b,.
пъ
ь.
(54)
i - 1 , i— 1
(/-- l)n2 1
b, I
ХП. Условие сходимости асимметрического процесса:
tr± 74<0-
Pi b2
(54а)
54
XIII. Общие формулы кусочно-линейной системы (мгновенное прибавление газа):
в зоне пропорциональности
cos Ь tj —
---------------jL-- — sin»/,,
CAu>rp —1~ tij
sin bjt
за пределами зоны пропорциональности
/<>гР (ДМ* - )KS- J^'t. | ns |
д“« = —-----_----—-------------------exp -j- tn i
(Дп* — ^Дсрп-i)
Ks К,
(60)
Д?» sg/г Дш.
XIV. Рабочие формулы для вычисления коэфициента скорости регулирования (Сп8)
но наблюдающимся полу периодам колебаний р. п.:
1 6^ + [< (м0)р 16^ ~+[Л7.ЛМ*
с’ = —ГТЛ’С(Я) : Сг = ШЖГахТ"
XV. Формула для теоретического вычисления:
3[/^0) + mtrcT)D>g | дш>о
’ ~ Fn/cos(<p()-?,.) | \р 2Fn / cos (ф0 — <р,) Г
2^2
FJ COS ('Ро - ?г)
/ 2gptjcX<Po) ~ Ш/Г^Ре Н
т I 2Fn I cos (<РО - ?,)
(23а*)
(24а*)
Д и> . о.
ПРИЛОЖЕНИЕ
I. АВТОКОЛЕБАНИЯ ИЗ-ЗА ТРЕНИЯ В СИСТЕМЕ. МЕТОД ОППЕЛЬТА
Сущность метода Оппельта заключается в следующем: считая экспериментально и
теоретически установленным, что колебания регулятора в случае наличия в нем „сухого
трения“ при синусоидальных (или близких к ним по форме) колебаниях регулируемого
параметра чаще всего имеют типичную „столообразную" форму (см. фиг. 41). Оппельт
апроксимирует эту функцию с помощью „ленты", заключенной между двумя синусоидами,
которые в нашем случае можно обозначить через Awj и Дш2, показанными пунктиром.
В этой „ленте" истинная кривая оказывается, по предположению, „погруженной" (пол-
ностью или почти полностью)
Следовательно, в основу метода положено предположение, что автоколебания регу-
лируемого параметра существуют, а также, что они имеют синусоидальную форму и ра-
зыскиваются условия их существования. Таким образом, этот метод, повидимому, не
пригоден для колебания типа релаксационных. В случае автоколебаний, происходящих
из-за трения в собственно регуляторе, а также в сервосистеме регулятора, обычно соз-
даются условия, подобные тем, которые имел в вид)' Оппельт при разработке своего ме-
тода, причем колебания регулируемого параметра в этих случаях чаще всего могут счи-
таться приближенно-синусоидальными. Хотя Оппельт не сделал попытки доказать это, и
поэтому описываемый метод не является математически строгим, нам все же представ-
ляется, что по „физическим соображениям" предположения Оппельта, повидимому, неда-
леки от истины. Дело в том, что мы рассматриваем колебания одной определенной ча-
стоты (так как в данном случае можно отрицать возможность суперпозиции колебаний
разных частот при сравнимой интенсивности).
Но при таких предположениях каждая полуволна кривой <oz не должна иметь каких-
либо заметных вогнутостей, если говорить о явлении, имеющем регулярный и периоди-
ческий характер.
В этом случае при сделанных предположениях (см. фиг. 41) очевидно, что площадь,
отсекаемая полуволной апроксимирующей синусоиды Д<о2, оказывается меньшей, чем
площадь полуволны «у, так как кривая Дю2 везде лежит внутри кривой «у. При этом
нужно помнить, что площадь полуволны этих кривых пропорциональна некоторой вели-
чине, которую можно назвать „импульсом", регулирующего действия за полцикла коле
бания. Что касается площади охватывающей кривой Дсвр то, принимая без оговорок упо-
мянутую „столообразную" кривую оу за истинную форму колебаний регулятора, все же
гораздо труднее утверждать, что площадь, отсекаемая полуволной Awj, должна быть
больше площади, отсекаемой соответствующим образом кривой Доу.
Естественно, что пригодность данного предположения зависит от параметров рас-
сматриваемой колебательной системы. Следовательно, и применимость метода Оппельта
должна поверяться экспериментальным наблюдением формы автоколебаний, либо в край-
нем случае численным интегрированием уравнений движения при наличии „сухого тре-
ния" на протяжении хотя бы полуцикла. Нам приходилось делать подобные вычисления
при предположении о существующих синусоидальных колебаниях р. п. Подобного рода
вычисления подтверждали предположения Оппельта о форме колебаний Доу,1, ввиду чего
мы в дальнейшем рассуждении встанем на его точку зрения и будем считать кривые,
представленные на фиг. 41, с достаточным приближением соответствующими действитель-
ности. В этом случае истинный регулирующий импульс за полпериода должен по вели-
чине лежать где-то между его апроксимирующими синусоидами Д«у и Д<»2, причем (что
весьма существенно) в расчет входит и вызываемое трением „запаздывание" регулирую-
щего действия.
Если До>г соответствует такому положению регулируемого параметра, при котором
регулятор „трогается", то будут иметь место соотношения (см. фиг. 41):
Доу—Aw„sin(pAZ) или
Да)а
sinpA£,
и, следовательно,
соз(рД0 —
М = — arc sin —-
р
1 На фиг. 42 показан результат такого вычисления (кривая II), а также при дополнительном учете
вязкого трения (кривая III) в сравнении с идеальной синусоидой (кривая I).
56
Первая апроксимирующая кривая представляется функцией:
Д<1А = ДоА sin (pt — p&t) — Д«А sin [ pt — arc sin
i Л Д«>о
Для второй апроксимирующей кривой делается предположение, что
д<оП = sin {pt — рД t) — 5До^ sin pt — arc sin . (a)
Дю*,1 = Дшй — Awr (здесь Aw1? — амплитуда); (b)
далее Оппельт вводит специальное промежуточное диференциальное уравнение’:
НДю^-(-До>у = 5Дю , (1)
в котором при первом приближении делается 5=1.
При предположении Дш = Д<оя sin pt частный интеграл (1) имеет вид;
— S Д<0 с.
Дщ = Sin {pt~ arc tg «»),
(la)
так как апроксимирующая синусоида должна по условию быть сдвинута по фазе на pkt,
то отсюда можно определить коэфициент так как
pkt = arc tg ftp.
Таким образом,
й==“ tg Pst>
Доз
и так как ранее было обусловлено, что p&t— arc sin - r , то
•A О),.
& = —- tg (arc sin
P V
Aw,
Д^
так как tg и = Л111^__= , то это равенство может быть написано так:
V 1 —sin2«
/ . Aw, \
sm ( arc sin ~-~-
&= —
P
(Д<о„
arc sin -т—-
Дшг
Д(ца______
/ А /л \ ®
(21
1
1 Причем описываемая этим уравнением функция Д«у может по желанию представлять либо Д»^ либо
Ди11-
8
67
Подставляя полученное значение И в амплитуду частного интеграла (1а), легко пока-
зать, что
/\ со
- — ° =Дшл cos pi^t.
/^р2 !
В самом деле, ранее было установлено, что
Дшг
'ДчГ/
а /
\ s
cos-рДЛ— cos ( arc sin
далее, так как
Дш2
Дш?'
Дш2
а
Дш2 \ ’
1
Д ш2
а
Дш2
а
то № р*=—-—¥
Дш2
1—Н-
Дш2
1Р
Р
и множитель при Дш„ в выражении для амплитуды частного интеграла (1а) представляет
собой:
Дш2
Дш?,
Другими словами:
Дш,
= А%
Дш^
--— Дша cos pAt,
Дшй
что и требовалось доказать.
Для второго приближения имеем, согласно (а) и (Ь) и фиг. 41:
Дш" = Дш"( - 1 = 5 Дш cos pkt — S Дш*
/о * \ 2 j
так как sin
= cos pkt ,
Д ш" — Д ш„ — Д ш ,
/о и
и отсюда
Дша— Дш,
5 = »---------*7
Дшй cos ръг
(3)
Но так как уже было
установлено, что cos рД^= |/
1 4“^
/ ^шг V
\'дшГ
AtU'- , го
Дш„
Дша — Дшг
। Л1_/Д“с.¥
I \ АМ
(За)
5 =
При этом для первого приближения легко доказать, что Дши— Дш
самом деле это расширенное неравенство означает, что
—- / Дш, \
Дш — Дш,.^= Дш, cos ars sin - ,
“ r ' " \ Дш, /
т. е.:
Дш Дш Дш
и Г Ct
или
Дш,
Дшг
А“«
Дш, ,
° хе-1
Дш,
В точках -т—-
Дш
А‘°«
Дш.
1 и -д —0 имеет место равенство, но эги случаи не представляют
интереса.
I
Если же -
видное неравенство:
есть положительная правильная дробь, то всегда имеет место оч-е-
Д<и,
1 д-1
-К
Д<»г \а
А <и
°
До
О,
и все эго означает,
второго приближения.
что амплитуда синусоиды первого
приближения больше амплитуды
Окончательно промежуточное уравнение Оппельта принимает вид:
(4)
Таким образом, построенное вспомогательное уравнение вводится как промежуточ-
ное в основную систему. Любопытным при этом является то, что получающиеся после
элиминирования переменных коэфициенты диференциальных уравнений становятся функ-
Д«Ц 1. П
циями отношения—и прочих основных физических параметров системы. При этом,
поскольку в самом начале было сделано основное предположение, что интегральная
кривая регулируемого параметра (необходима удовлетворяющая вообще основной системе
уравнений) представляет собой синусоиду (Дш), остается найти соотношения, допускающие
такое решение J. Это в частности может быть сделано посредством осцилляторной под-
становки.
Таким образом, можно выяснить условия для существования незатухающих авто-
колебаний, равно как и оценить их частоту и амплитуду.
Диференциальные уравнения, получаемые этим методом, мы будем называть „дискри-
минантными уравнениями" системы, все остальное выяснится на примере, излагаемом ниже.
ПРИМЕЧАНИЕ. Здесь следует иметь в виду, что легко показать, что
Ига Д’
Дю Д<о
г а
это означает, чю в случае большого (относительно) застоя, приближающегося к амплитуде До>а, регу-
лятор почти не сдвигается и коэфициент передачи S стремится к нулю, а это безусловно верно физи-
чески и составляет ценное место в концепции Оппельта, дозволяющее пользоваться ею для случаев, когда
Д<о
т— близко к единице.
В дальнейшем, когда Оппельт вводит уравнение (1), то произведение АДш фигурирует в его
правой части как амплитуда возмущающей функции, причем для первого приближения
S = 1 и искажения для амплитуды возмущающей функции не предусмотрено. Искажение амплитуды
uif из-за того, что & ф 0, связано только с тем, чтобы 8 обеспечивало нужный сдвиг фазы, при этом
оно одинаково для обоих приближений.
11. ПРИЛОЖЕНИЕ МЕТОДА ОППЕЛЬТА
а) Автоколебания как следствие трения в регуляторе ВИШ
Здесь мы принимаем, что координата р. и. есть Дш и координата регулятора Дш,.
Полагаем, что в регуляторе имеет место трение Кулона, благодаря которому он „запаз-
дывает". Задача рассматривается в свете концепций Оппельта, причем приведенная к
р. п. „зона нечувствительности" регулятора есть Д%., а амплитуда, автоколебаний р. п.
Аюс. Тогда получаем для первого приближения по Оппельту систему уравнений (для
Я = const):
,/$ Д Дш ^Д<р = О, OAwy'-j- Дш/~ Дш, Дф'= СД«у,
1 Если бы это оказалось невозможным, то это бы означало, что в рассматриваемых условиях предпо-
ложение о возможности автоколебаний не оправдывается.
59
причем
Ьшг_______L_
д<вй / /Док V
Р 1 / 1- ( -г-^-1
I \ Д°М
5
Элиминирование переменных и подстановка 6 дают уравнение:
}-?,CAiu = o,
(6)
которое мы условились называть „дискриминантным уравнением" системы для первого
приближения по Оппельту.
Если теперь ввести в уравнение (6) подстановку Доз—Дшд sin pt (соответствующую
нашему исходному предположению о существовании периодического решения), то в
результате группирования членов с синусами и косинусами и приравнивания их к нулю
получаем два уравнения:
J, 4?----“=к=Т5- +к.р=°- <»’
3 й / 1 ( ^шг V
I I J
(Ь)
которые должны быть удовлетворены.
Уравнение (а), кроме тривиального решения р — 0, обнаруживает корень:
Доз
а
представляющий частоту автоколебаний в том случае, если удовлетворено также и урав
нение (Ь), что может иметь только при определенном соотношении между р и С.
Исключая частоту р из (Ь) получаем (выкладку опускаем):
таким образом, граничное значение С оказывается квадратной функцией отношения
амплитуд автоколебаний и „застоя" регулятора, приведенного к координате р. п. Ниже
будет показано, что здесь Сгр — Стах.
Для второго приближения по Оппельту система уравнений будет следующая:
J, Доз' . Доз -|- 8, Д<5 = О,
<) Д ш'f Д — У Aoj,
А(в'=‘ С Аозг,
(У)
причем здесь 5 =
а й имеет прежнее значение.
60
Элиминирование переменных и подстановка значений для 8 и S дают уравнение:
которое является .дискриминантным" уравнением системы для второго приближения по
Оппельту.
Дискриминант Раусса для уравнения (10) имеет вид:
откуда видно, что нарушает неравенство увеличение С, следовательно, граничное
значение С является здесь максимальным, причем операции, подобные проделанным
нами на стр. 60 [подстановка sin pt в уравнение (10), группирование членов с сину-
сами и косинусами и решение получающихся двух уравнений], приводят к формулам:
и отсюда
(П)
(12)
Фиг 43 дает р по отношению = -т—— , при К — 16,8, Js—3,5 кгм сек~, при этом над-
r aw г апг
лежит не забывать, что отношение между С и должно удовлетворять равенству (12).
Фиг. 43. Частота автоколебаний р сек *
по допустимому их режиму
Фиг. 44. Максимальное С по допускаемой амплитуде
автоколебаний при заданной нечувствительности регу-
лятора (Дпг) (Дп = 14,33 До), uj — 1850; /<,=5.67;
г~ 104 м/сек', со =179
61
Фиг. 45. Максимальное С по зоне нечувствительности .. , Дя„
регулятора при постоянном Ьпа (Д/г = 14,ЗЗДш); 5, = 1850; Фиг. 10. Максимальное С по отношению
Ks = 5,67; V -= 104 .и/сек; о> = 179 /< == 5,67; = 1850; Js = 3,5
Зависимость допустимого C'max йо формуле второго приближения от различных ве-
личин „допускаемых" амплитуд автоколебаний оборотов мотора в виде семейства кри-
вых по аргументу Дпа и параметру Ага, (т. е. по приведенной к оборотам нечувствитель-
ности регулятора), представлена на фиг. 44.
Фиг. 45 представляет изображение той же зависимости, но только при аргументе \пг
и параметре Дпв. Наконец, фиг. 46 представляет результат развития концепции Оппельта
и вычисления сразу по формулам первого и второго приближений. Аргументом является
btl„ п
отношение . Причем, оставаясь на уровне развитых рассуждений, можно считать,
что неизвестная истинная кривая Стах проходит где-либо внутри заштрихованной области.
Следует в заключение заметить, что на практике автоколебания оборотов из-за
трения в регуляторе ВИШ, повидимому, имеют значительно меньшее значение, чем авто-
колебания, вызванные трением в исполнительном органе. Однако ввиду особенностей
данной системы возникновение этих автоколебаний возможно только в случае большей
или меньшей вспененности масла.
Отбором специальных проб масла, проведенным в 1944 г., было установлено, что
объем газов и пузырьков в масле регулятора в рабочем состоянии достигает 30%. Это
обстоятельство в сочетании с большими моментами трения, необходимыми для провора-
чивания лопастей, создает в свою очередь условия для возникновения автоколебаний.
III. ПРИМЕНЕНИЕ ДЛЯ ТОЙ ЖЕ ЗАДАЧИ МЕТОДА РАЗЛОЖЕНИЯ
ПО СТЕПЕНЯМ „МАЛЫХ ЗАПАЗДЫВАНИЙ-
Этот достаточно распространенный метод мы попытаемся для сравнения применить
и в только что рассмотренной задаче, однако видоизменив его так, чтобы выяснить па-
раметры автоколебаний, так как самое запаздывание, являясь в установившемся режиме
постоянной величиной, вообще говоря, является функцией упомянутых параметров1.
Принимая и здесь, что автоколебания р. п. синусоидальны, т. е. что
До == Дюа sin pt,
мы найдем (считая время текущим от нуля), что так как
Дшг = Д oje sin pit,
то величина „запаздывания" it найдется в виде:
1 .
at— — arc sin —- .
Р
1 Мы считаем, что если не учитывать этого, то ценность указанного метода невысока для практи-
ческих целей. Иное дело получается, если развить состав „запаздывания”, как и будет показано нитке.
Заметив себе сказанное, перепишем уравнения (36) так: !
4 Доэ' 4'Л.5Д<О—д<р, д</=сдоу,
причем в последнем уравнении введена „запаздывающая" координата До)у, исходя из сле-
дующих концепций: если Дю—/(/), то До>х —f(t—Ц), т. е. Дюу является той же функцией
времени, но запаздывающей на величину ор и, следовательно:
2-3
Но так как f(t) = Доз, то
д . До" Д<о"'
Д оэ^ -= ДО) — До) Ы --- ------
Л * О
Таким образом, имеем совокупность
До)' 4~ Ks До — —Дф,
Дер' — С До),(
До), = До) — Дш'^4- ---------- -р . . .
I о!
Ограничиваясь в разложении функции Дш^ членами второго порядка включительно \
отделяя переменные, получаем диференциальное уравнение:
До)
^ш2 Дш"4-IK, -Bj с эд д </ 4- е, с д w=о,
и так как
,, 1 • Д<Ог
о? ==— arc sm ,
Р &<»<,
то
| •/, 4~ — — f arc sin ~r-
I 2 Д<оо
Режим незатухающих автоколебаний возможен при удовлетворении условия:
К- L arc sin-г—г-~ О,
/' Д%
2
Дш"-4~/К, — £1 С — arc Sin -4^
\ Р
Дш'ф^СДо^О. (13)
или
С
До)
arc sin -г~- — р.
(а)
Потенцируя (а), имеем:
р^^-
7 K2S
С другой стороны, так как коэфициент при До/ равен нулю2, то остается уравнение:
2
Дог
arc sin -—-
Дшй
2
(Ь)
£s
2 "
До),
arc sin ——
Дш,
д«т
(с)
которое определяет частоту автоколебаний:
Р'
, I 1 - Z' 1 ( "
Js + Q- Ч С arc sin -г-?- з
2 р2\ Дшя /
а
(Ф
1 Величину U = — arc sin мы
Р Д<оя
будем считать величиной первого порядка малости. Нужно иметь
Дек,
в виду, что интересующая нас величина отношения (ввиду сравнительной малости Дюг) обычно здесь
не превосходит */г и соответствующая W обычно меньше >/4 сек> так как р Обычно больше 2.
2 На основании (а).
63
Подставляя в (d) (b), получим:
=------
2
£
2
______________
К2 f arc sin -т—
\ AoW
,2~я ( .
Ся arc sin -~-
\ д%
2
(И)
и, следовательно,
£,С
1
2
Далее мы должны подставить (е) в (Ь) и получить С в функции
(е)
Доз,
отношения -г—- или
Д<о„
наоборот.
Делая таким образом, последовательно находим:
С . Д<»г
1 Ks К. До>0
2 SjC
(L)
т. е.
С] С
С , До^
—------=— = arc sin -~-
1 К2 A(fl«
2
Следовательно, во-первых,
А“й = -----------------------------
sin,
Доз
Для нахождения Ста8 потенцируем (L):
Е, С £ С! / Дю
------Д---- —= 21_у i arc sin -7—
1 К2 X А®.
Л Г 2 Z •
АГ?
откуда и находим для граничного
tn ах
значения С—Сша8:
К*
JA, arc sin -г—-
\ &ша
Kl
2 '
(U)
2
Любопытно отметить, что если в (U) разложить arc sin - в степенной ряд и в по-
следующем выражении отбросить члены высших порядков, то получится:
г _ к2 д4
’ Js 5, Дш? ’
т. е. результат, тождественно совпадающий с первым приближением по Оппельту (см.
выше стр. 60). В самом деле, так как
Де>г __ Д<ог . 1 Дю)!
Дю*
то с точностью до членов четвертого порядка включительно
До) \2 Ди>? . 1 Ди>?
arc sin—г—М ==-—г + ’о'ТТ’
д<и«У Д«4 3 Д«4
64
подставляя, находим со сказанной точностью:
о/г2 __ r^f j J „2/9 _ Ао3'______L АшЛ
-АЛ \ 2 ‘ Ч Л 4 / .2 О * 4 )
z, \Дю« 6 л<«а / _ \ А “а 6 A°Ja /
Cmax ~ Z . 2 Г-1\ — / л 2 1 А 4 /
9/- I Ьыг . 1 Дю, \ , Ьшг , 1 X
z<?l ~Г~2 "Г -ц- ~Т Z1V1 . 2 г о . 4 ,
\ Дшд 9 Aujo \ А<оя •> Дшо !
Теперь, если ограничиться точностью до
„ . Д«
членов второй степени относительно и
До)2
принять, что----2 мало по сравнению с 2, то по-
Дюй
лучим, отбросив эти малые величины:
r _ 2/<s Ki Д<4
ад —: *1 д“'
Дадо
Таким образом, разложение по степеням
малых запаздываний дает результат тем более
„ Д°\
верный, чем меньше дробь , тогда как
Д<«„
а
использование обеих апроксимаций Оппельта
пригодно и для случая -» 1.
Фиг. 47
На фиг. 47 показан результат вычисления по формуле (U), который рекомендуется
сравнить с фиг. 46, отражающей результат применения метода Оппельта.
IV. АВТОКОЛЕБАНИЯ КАК СЛЕДСТВИЕ ТРЕНИЯ В ИСПОЛНИТЕЛЬНОМ ОРГАНЕ
СИСТЕМЫ ПРИ НАЛИЧИИ ВСПЕНЕННОСТИ МАСЛА
Для того, чтобы установить соотношения, характеризующие автоколебания, происхо-
дящие по причинам, указанным выше (в соответствии с данными последних эксперимен-
тов ЛИИ мы считаем эти обстоятельства основными для образования так называемой
„качки" оборотов1), перепишем уравнение (99) с добавлением в уравнение моментов
лопасти постоянного момента „сухого трения":
[Jt -j- ml'1 cos2 (<р0 — фг)] Дф" -ф 2 [п, пп cos2 (ф0 — фг)] А ф' 4~
I I 1 9
+ [ у “° (То) +12 cos2 (ф0 — ?,) ?п
= Z2 cos (ф0 — J cos («Я - ? г) А фя - Jcf (ф0) ю0 д <0 - Wfr sgtt A ©’,
Js A w' 4- Ks Аю = д A4dr(Z) — д ф, А ?я = С д 10,
или в сокращенной форме, отбрасывая \Mdr(t) и меняя порядок:
Л Aoj'4-/<t Дw = —— Дф,
Дф' = СДю,
1 а 1
Jt Дф" -|- 2 п* 4- q* Дф = q** Д—р* Дю 4- Wfrsgn Дф';
так как степень вспененности масла не является постоянной величиной, то коэфициенты
д№* и q* подвержены сильным изменениям. Следует отметить, что в связи с этим реше-
ние данной задачи должно рассматриваться как в значительной доле приближенное,
в силу чего не имеет смысла осложнять выкладки удержанием сравнительно малых
величин. Так, например, коэфициенты q** и q* — величины порядка 200 кгм]рад и члены
уравнений, их содержащие, при колебаниях с амплитудой 0,02 — 0,03 рад имеют порядок
1 Если не рассматривать устраненную теперь причину .качки* из-за гидравлической неуравновешенно-
сти золотника.
65
4 — 6 кгм, тогда как, например, член J* Д®" достигает всего лишь 0,0015^-0,0025 и, очевид-
но, может быть отброшен.
Коэфициент р* = Лг(?о)шо представляет величину порядка 0,002-200—0,4, и так как
Дю легко может достигать, например, 5 сек1, то член р* Доз имеет порядок 1 3 кгм гг
отброшен быть не может, что же касается коэфициента „вязкого" трения п*1, то, так как
к нему приведено трение обильно смазанной и двигающейся вообще со значительным
трением манжеты поршня во втулке винта, им вообще пренебрегать нежелательно, хотя:
установить порядок этой величины нам пока не удалось. Поэтому при установлении усло-
вий устойчивости системы (101) и при развитии критерия Раусса коэфициент п* нами
сделан аргументом, что дало нам возможность изменять его в широких пределах,
между которыми истинное его значение, по всей вероятности, должно лежать.
Для изучения же автоколебании, вызванных „сухим трением", мы рассматриваем
нижеследующую систему уравнений:
J Ли/ -ф Л s Дш = - - 5[ Д®,
А г - д?« Доз------------------sgn д</,
q q-r ь
Л® = const,
(а)
(Ь)
р* q* Дш Wfr > qi: ’ (с) 05*)
р* w*
<7* Дш (d)
где Wfr является приведенным к лопасти моментом „сухого трения", включающим как
собственно момент трения лопасти, так и приведенные к лопасти элементы трения, кине-
матически связанных с ней звеньев2. Функция Кронекера (sgri) указывает на знак этого
момента, зависящий от направления вращения лопасти.
Идея Оппельта прежде всего заключается в замене конечных уравнений:
А ® = A sin pt — sgii Л У,
Wfr
9*
Д® — const,
посредством специального промежуточного диференциального уравнения первого порядка
вида
«Да.'-4- Д® = Д®.
• 3 I • 3 1
Развивая в дальнейшем концепцию Оппельта, можно было бы попытаться вычислить
параметры автоколебаний в зависимости от физических постоянных системы. Такая попыт-
ка нами сделана, при этом оказалось, что неизвестные Сир входят в систему двух
нелинейных уравнений, что делает весьма затруднительным развитие для этих величин
каких-либо обозримых формул.
Ввиду сказанного нам пришлось прибегнуть к несколько видоизмененному методу
разложения искомой функции по степеням „малого запаздывания", учитывая, однако, что
самое запаздывание зависит от параметров, установившихся автоколебаний.
Принимая и здесь, что автоколебания синусоидальны (что для релаксационных коле-
баний не имеет места), т. е. что в интересующем нас режиме
Д?= A'fWSinp/1 и Дю = Aw„sin/K,
где t и т отличаются лишь на постоянное слагаемое, мы сперва апроксимируем функцию
Д® через функцию Д®з „запаздывающую", исходя из следующего допущения:
Д ®з = Д<р (t — ot).
3 Здесь q* положено равным q**, так как разность между ними мала
66
В этом случае б нашем распоряжении окажется следующая система уравнений1:
J s Дш' -j- /С, Ди) = ?!
Д®„ = СДш,
q* Д» — q* Д®п р* Д ш
(15а)
(так как q*^:q**),
к которым нужно присоединить разложение:
A?s Д? - д?'^4-А-Дср’о/4- Д?"'гИ:= + ...
2 2 ‘ о
Необходимо еще раз повторить, что здесь мы исследуем условия, допускающие
существование чисто периодического решения, т. е. установившихся автоколебаний, воз-
можность чего мы сперва принимаем как бы a priori.
В соответствии с этим здесь можно развить состав функции о/, так как согласно
допущению:
*? = ^„mpi^Pt, (а)
и, следовательно,
= ±'?ltmpi sin pit,
а отсю ia
gZ = — arc sin -----. it^>0.
P 'lampi
Теперь, рассуждая на основании принятого допущения о существовании периодиче-
ского решения, удовлетворяющего системе (15а), уравнение:
q* № = q* A<j/ р* Aw' (R)
ввиду того, что
Aw Awnsin(/>/ f- г),
а, следовательно, и
Aw' = Aw„p cos(pt -|-е\
и так как согласно уравнению (15* Ь)
Д's'z = С A w,
то после подстановки Aw (15* b) превратится в
Аз/— CAwnsin/K СЬшп sin (pt 4~ s)>
где e любой возможный сдвиг фазы координаты Aw по отношению к А? и, следова-
тельно, согласно уравнению (R):
А?' = CAw„ sin (pZ-f- г) Р-~£-а cos (pt { г).
ч
Отсюда мы находим приведенную амплитуду (после интегрирования):
Аз, — j J^P '" С" (16)
р J q*°- с '
Следовательно, основываясь на (а) и (16), мы можем считать, что при автоколеба-
ниях в координате Aw с амплитудой Дши координата А® подчинена зависимости:
\ л- л*®
Аз | Р2------t-Osin(^4e-|-o)-j-COnSt,
а, следовательно, разложение для производной от запаздывающей функции пред-
ставляющее собой
Аз' = Аз' \-fit ~^-^"'it2 (16а)
• з 1 1 2
1 Твердое трение здесь войдет уже через запаздыванье.
67
теперь по выполнении нижеследующих подстановок:
1 . А® 1 Аср.л
о г — — arc sin — -— = — arc sin-----------
P ^ampl P
A'%
p2 p*2
q*2
Дер' — Дер' — •—— До/ = СДю
До/'
Р* Л ,
— Aw,
q*
(17)
Е
q*
представит собой:
п*
д<р' == СДю-----х- Дю'
ТЗ д*
to'
' 1
— arc sin —------
P
A?rP
P2P*2
(18)
q*2 ' /
В этом нашем рассмотрении мы сохраним только два члена ряда (16а), в связи с
продиференцировав первое уравнение:
Js^"-YKS^' = А®',
и замещая Д^ полученным разложением, мы можем написать:
СДю — С Дю'- (СЬЛ — Aw
qv \ q
Л Дш"
—- arc sin-----
Р Л
До>«
Д(ЬР
чем,
Д <p" = С Д ю'
сд-"
q
।
что приводит к диференциальному уравнению автоколебаний, выписанному для коорди-
наты Дю и в развитом виде представляющему собой:
Л ( £1Р* • Д^гР
/ Л Н—arc sin----------
5 q*p
До/' 4-
q
p2 p*2
Bi с
—— arc sin --------
Р .
Дюа
*<?rP
ЧР*
м2 м*2
Р Р | Г*2
q*2 -’“С
Причем возможность существования автоколебаний
Дю' С Дю = 0. (19)
требует выполнения равенства:
&vrp
,r p2p*2
“ q*2
и в этом случае частота автоколебаний р найдется из трансцендентного уравнения, выте-
кающего из такого изменения (19) как следствие:
К,-----arc sin
5 Р
q*
(19a)
д‘°„],
q
_ ^P
„2 -----------------J——
f E л*
44--^-arc sin------
q p
Аю„
^гР
I q"-
Таким образом, для решения поставленной задачи мы располагаем системой из двух
трансцендентных уравнений:
p2=-
ДфгР
(20)
pq-
Д w„
a
р2 р*2
q*2
p* , c
-----arc sin------
q P .
Дюа
^trP
p2 p*2
— аг5 = о.
(21)
2
68
Из уравнения (20) имеем:
. ±ЪР (^С—Лр2)о*
. / „2П*г ЪР*Р
Л"'«| у, +С'
следовательно, arc sin (...) можно ввиду симметрии исключить, подставляя его значение
во второе уравнение. Мы находим:
Р*
q*
С_ (\C-Jsp^q^
Р
\Р*Р
— Ks-=d,
т. е.
4 MLC
7*
^Д-к^о,
или окончательно:
4Cfrj
/;? = ®(С) —___________________
р* ks+Js q*‘с,—р*2
вычислены все р, в функции от всех соответствующих
(22)
могут быть
Таким образом,
С,- по точкам.
Далее уравнение (19а) дает:
— arc sin
Pi
tyrPi
>2
Р*2Р
K-L ~
что означает также, что
sin
Р*
с, q*c;
Pi
...
Pi
т. е.
Д
1
I -^+й-
J q™ 1
Дч>о, получаем окончательно формулу
Ks Р*
Г
Разрешая полученное выражение относительно
для вычисления амплитуды автоколебаний в свете сделанных предположений1:
__________Д?,Р,-
/ Ks р*\р,
От О с
Л«>п= —
sin
Pi
*2
(23)
. — sin
Aw« Pi
ПРИМЕЧАНИЕ. При вычислении по формуле (23) нужно помнить, что подставляемые в нее зна-
чения для pj и С,- должны быть соответственными, т. е. должны удовлетворять равенству (22).
V. К § 29
Исследование системы (101)
Приступая к динамическому анализу системы (101), следует прежде всего заметить
себе, что ввиду незначительного влияния на процесс весьма малых (как это было нами
специально установлено) инерционных моментов, отраженных членом Л Дф", нам для
упрощения задачи следует этот член отбросить.
Действительно, на оси лопасти уравновешиваются весьма большие моменты, дости-
гающие нескольких десятков кгм, образуемых трением лопасти при поворачивании и мо-
ментом центробежной силы. При этих условиях, очевидно, не может иметь серьезного
значения момент У* Дф", так как порядок его, как выяснено, ие может превысить малой
доли 1 кгм.
Таким образом, у нас остается система:
2п* Дф'-\-q" Дф = q" Дфя — р* д“, Js Д«'-(- Ks Д® — — Дф. Дф„ — СДв>,
где ввиду малой разности положено q™ — q* и где в соответствии с постановкой задачи
мы возмущающую функцию положили равной нулю.
1 Здесь мы получаем зависимость Д<1>а = ф (С,), вычислив и построив которую, нетрудно построить и
обратно Cj — ф (Д«о), см. фиг. 48, где параметром семейства является момент трения.
99
Фиг. 48
Отделение переменных приводит нас к уравнению в координате Да;
2 Л п Д'/" 4- (Л Г + 2 Ks п) Да" 4- (Ks q* - L р) № -Hi С Д<р = 0.
Первое условие устойчивости приводит к необходимости выполнения неравенства:
К. q* -^/>>0,
и второе условие устойчивости в свою очередь:
2 (Ki q* - Ks о - Js С) я + Js (Ks q* - р) q > 0,
т. е. для граничной точки:
_____Л О* Р ~ Ks q*)
‘2[Ks(Ksq^-^p)-Js^q^C)
(24)
причем на отрезке значений Ks(Ksq* — ^р) — Js q* С< 0 это будет верхней границей
для п.
Фиг. 49 представляет зависимость динамической устойчивости системы от величины
q*, причем q*, грубо говоря, обратно пропорционально количеству воздуха, содержаще-
гося во вспененном масле.
В заключение следует повторить, что все рассмотрение сделано относительно сим-
метричной системы, а твердое трение положено равным нулю, так как иначе было бы
затруднительно решить эту задачу. Выше влияние твердого трения было рассмотрено
отдельно. Выяснение вопроса о том, какой вид трения при работе мотора играет здесь
превалирующую роль, на самом деле может быть установлен только экспериментом.
Таблица 1
Вычисление заброса оборотов мотора при помощи совместного интегрирования трех уравнений
методом Эйлера-Коши
1)
du> 1
rff Js
ад. «>)
dV а9(Х,
dt 1 n2m
r-~-SVM-g sin 6 (/)
2 in
(при горизонтальном полете g sin 6 = 0),
где
3) = 7 lAu>i H , / 1S_ (d,
dt Fn/cos (?„-?,) у
SPt Pef Pt J', Pcf — „7; ---------- Pfr
2 Fn I cos (?n ¥r)
- V/).
3 mfcoj- 1; Dr
2 Fnl cos (<p„ — -or)
О
Примечание: функции тэ , fs снимаются с .сеток" винта
Равновесное условие: «>0 = 188,5, пй = 14.33ш0 = 2700 об мин, ?0 - 23,1, V = 90,5 м сек, Мо —
= 150 кгм. М после дачи газа 400 кгм.
Условные данные: 4 = 3,5, р = 0,1134, D—3 м, Сх — 0,03, т = 300 кгм 1 сек2, S --- 17 м2
v = 0,00725; н = 0,4, На = F„ = 193 см2, I = 6 см, 2g= 2-981 • 10s, у = 0,9-10's Pl = 20 кгсм т;= 0,002-
= 45°, Dc — 16 см, тгс = 0,875.
1 При Ди><(0, равно как и при | A<of> Дш!р , уравнение (3) изменяет свой вид (см. стр. 12).
70
Вычисленные коноанты.
£^1 = 0,111, +£+= 0,000775, С. S = 0,0000964, 3 те rA D, 0,084
Я п-ч 4 т&т 2т
1 ll №№ и n | j 1 2 3 4 5 6 7 8 9 10 11 12 1 13 14 15
t- [сек] ю„ = 1433 Ю„ б!мин] V s 3 !l c <5 Л) зш Л1м 400+ +(9) [л-гл«у I дм dt (ei) + Um =-i‘H аэ
t ^Az' dt
1
С ' = i!
0 0 188,5 2700 90,5 1,003 23,1 0,038 0 0 150 0 0,1 0 188,5 0,029
1 0,1 188,5 2700 90,5 1,003 23,1 0,038 0 0 400 71,5 0,05 3,58 192,08 0,029
9 0,15 192,08 2755 90,5 0,987 23,1 0,041 3,58 9,3 391,7 6,4 0,05 3,9 195,3 0,031
3 — — — — — —T- — —• —. —
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
z~- ffl Cl ci"1 •I-
№ n/n дУ dt dt II + t^c ! см сек 1 s (20) 1 g s [кг c u~ К *£? + Pl — (24) (25) 7 V(26) (» (65) -4= l+ •
b.cH S- 8 s£ £ °e?4
0 0 0 90,5 0,167 21,9 0,9278 8,29 1,39 9,68 10,32 2,25-107 4750 0 i° 23,1
1 0 0 90,5 0,167 21,9 0,9278 8,29 1,39 9,68 10,32 2,25-107 4750 0 0 23,1
2 0,102 0,005 90,5 0,167 21,9 0,9278 8,6 1,45 10,05 9,95 2,17-107 4650 2,56 0,128 23,23
3 — — — — — — — — - — — —
— — — — — — —Mt
Таблица 2
4’=pD4a^ : р
£Га„ ш2
э
~~4^~
Основные функции
; ^=^^ = ^рш2; X = JL 2.;Рло6 = С^5И2;Лнот = «(днш~Л-й<и2).
дЧГ =
да
дЧ’ да дк
дЧ’___________
дш да дК
дю
Коэфициенты
дЧ" да ciDi ч да
-- --- = L--- ш,.
да да-4 л2 0
дЧ’ _ р О'л
дю 2л
- = Р1 = кг
дг
даэ 1)а9 ш„
° дХ л
== р., = кг сек,
дк р /Х3<1>(| дад
дУ 2 л дХ
дЧ __ дЧ' да9
дУ дад дХ
dV дУ
дМв_у
дм
р.А = кг сек .и'1, ’
ps = кг сек м
дР
лоб __ £;vp5v0 _ pt - кг ((>к м
дУ
с).
_
да . др d-f
8 л3
др
+7 = ^ = '"^
дМв др дк <ШВ р-О4
др дХ дю дю
4г2
др 7Хрш0
дХ 1
i2 = кг м рек.
ЭРМ = дЛД
дУ дУ
оЛ4в дЛ4в др
дУ др дХ
дХ ZM+ др „
— = q> _ — = t4•= кг сек,
дУ Т4лг дХ 3
4 т?
дМк (<>)
дю
д (
< dt,
дю
дМ
= const = Ку = кг м сек, -----я
дш
= Ks = кг м сек,
дю
V|lj
Fn I cos (<Fo - ог) I
Pt
3\Jcf (?о) + “>ol г гак°
-, -, — < 1_>1 — tntc .
2Fn Zcos fifn - ?г) -I
(it-; -______________-W4. . ... । ' 2g ( 31 fi'l |
дш - Fn I cos (?(, — cpn) 7 | 2 2Л"П Zcos (mn y2) J :
71
Таблица 3
Численные значения коэфициентов для рассмотренных примеров
№№ п/п । > М [кг л] сл- н р з V V [л/се«| || 11 31 3 $> о е <1) о ?0 Хе а0 Р\ [уаэ ио ?*J'd ||[лаэ ж гм] II 1 ! «3 [м сек] 1 1 1 Л й -’3 ах Примечание
1 150 73,2 0,027 6000 0,0636 1000 0,121 300 83,5 1 2200 153,5 26,16 1,135 0,05 0,033 2110 6,95 -10,3 1250 3,63 -4,92 0,8? —0,246
2 252 123 0,023 300 83,5 2200 153,5 25,75 1,135 0,044 0,028 39,40 12,8 —19,6 2360 6,7 —9,37 0,843 -0,246
3 350 171 0,021 6000,0,0636 450 125 2200 153,5 37,96 1.7 0,116 0,057 1510 9,14 -8,4 2150 7,44 -6,7 1,46 —0,32
4 710 346 0,041 60000,0636 450 125 2200 153,5 42,16 1.7 0,235 0,112 0,072 1800 9,3 —5,88 2590 9,38 -6 1,76 -0,3
5 820 400 0,026 1000,0,121 450 125 2200 153,5 38,96 1,7 0,143 4510 18.5 -15,95 3840 15,1 -12,2 1,37 -0,32
6 732,5 358 0,023 1000|0,121 450 125 2200 153,5 38,4 1.7 0,128 0,063 4720 17,8 -15,95 4000 14,6 -12,2 1,43 0,32
7 180 84,5 0,0377 6000,0,0636 300 83,5 2600 181,5 22,4 0,96 0,041 0,033 2750 7,3 -12,4 1410 3,24 -5 0,682 —0,212
8 810 334 0,0845 1000|0,121 1000,0,121 300 83,5 2600 181,5 26,06 0,96 0,086 0,074 4950 17,6 -23,6 3440 7,82 —9 0,88 -0,2
9 275 113,5 0,023 300 83,5 2600181,5 21.35 0,96 0,029 0,02 5410 13,8 —26 2640 5,4 -9 0,675 -0,2
10 710 293 0,043 6000,0,0636 450 125 2600 181,5 35,85 1,44 0,1425 0,084 2740 11,45 -10,76 2700 8,14 —7,1 1,31 —0,3
И 820 339 0,027 10000,121 150 125 2600,181,5 33,25 1,44 0,087 0,053 5080 20 - 22,1 4470 14,1 15 1,143 -0,344
12 710 293 0,023 10000,121 450 125 2600 181,5 32,72 1,44 0,075 0.045 5660 20,2 —23,6 4510 13,6 -15 1,155 —0,334
13 88 37 5168 0,0737 375 104 2570 179 25,15 1,2150,061 — — — — 1850 5,43 — 0,8 -0,32
14 700 294 5168 0,0737 375 104 2570,179 32,3 1,215 0,127 — — — — 2630 7,35 — 1.14 -0,259
15 180 79 » 5130 0,074 326 90,5 2600 181,5 23,3 1,04 0,033 — • - — — — 1770 3,86 —. 0,74 -0,217
16 700 290 51300,074 326 90,5 2600181,5 29,44 1 1 1,04 0,121 1 - 2220 6,32 0,93 —0,227
№№ п/п II W [Л. с.] L М [кг/м] С(. 7/ ₽ "3* 1Z [м/сек] п [об/жин] (О ?0 1 ! X» ао ! Р1 Р‘ р-л «1 1 ;3 ! 1 Oft до 1 ар ах Примечание
1 434 0,02 1 3000 0,09 580 161 2500 173 42,44 1,95 0,1645)0,072 4340 17,1 —13,4 5000 15,3 11 —
2 434 0,04 3000,0,09 460 127,5 2500 173 38 1,54 0.16450.09 3820 15,6 -13,4 3740 11,5 -8,8
3 434 0,06 3000 0,09 396 НО 2500 173'30,6 1,33 0,1645 0.Ю1 3310 15 -13,4 3260 105 -8,6
4 434 0,1 3000 0.09 330 92 2500 173:32,9 1,11 0,164510,115 2940 14,5 —13,4 2680 9,1 -7,65
5 1030 447 0,025 0 0,125 490 136 2500 173|37,6 1,65 0,1225 0,0642 5450 21,6 —20,2 5380 16,2 —14 1,47 —0,315
6 1050 424 0,025 0 0,125 490 136 2700 186 35,3 1,53 0,1 0,055 7250 20,65 -21 6250 14,6 - 13,65 1,47 -0,286
7 1050 424 0,04 0 0,125 420 117 2700 186'32 1,315 о,1 0,065 5420 22,5 25,9 4630 18,7 -22,4 1,09 -0,47
8 212 0,025 0 0,125 380 105,5 2700 186 27,12 1,19 0,05 0,033 5740 17,6 —25,4 3720 9,45 -12,6 0,875 -0,264
9 106 0,04 0 0,125 246 68,5 2700 18617,3 0,77 0.025 0,022 5640 10,6 —23.1 2340 4,45 9 0,55 -0,188
10 800 330 0,024 6000 0,0673 560 156 2600 181,540,5 1,8 0,152 .— 3940 11 1,81 —0,34
11 800 330 0.024 2000 0,122 450 125 2600 181,5 33,1 1,44 0,084 0,047 4500 14 1,145 -0,334
12 195 0,08 11000 0,1134 180 50 2600 181,5 17,17 0,575 0,053 0,0645 1780 3,7 0,485 -0,133 Кабрирование
13 — 195 0.024 1000 0,1134 528 147 2600 181,535,45 1,69 0,053 0,023 5450 14,15 1,48 -0,35 Пикирование
14 377 150 0,03 1000 0,1134 326 90,5 2700 188,5 23,1 1,003 0,038 0,029 —. — — 2715 6,78 — — —
15 100 41 0 0,125 0 0 2600 .181,5 1 ° 0,01 •— 2310 0,44 — 0,572 —• К экспер. ЛИИ от
1 ' 0 3/V 1943 г. Режим 1
16 815 337 0 0,125 0 0 2600 181,5 16.4 0,081 — — 2310 3,74 — 0,573 — К экспер. ЛИИ от
1 1 1 ! I 3/V 1943 г. Режим 2
ОПЕЧАТКИ
Стр. Строка Напечатано Должно быть По вине
4 7 15 17 17 23 23 24 24 34 36 15-я сверху 3-я снизу (сноска) 13 я сверху формула (18) 2-я снизу (сноска) формула (30) 1-я снизу 17-я 8-я . формула (57) R — длина .крючка' е у"—коэфициент мощности масштаба, систем типа (12) £>5u>n 75^75« CD F(V) = J^PX+ . . - Е(?) = СтЬМ" + - , dt jj км* (0) — Ч- • • • exp (...) = e ( . .) /?2 —длина „крючка* е у"— коэфициент масштаба. систем типа (12 а) 7ИВ = ..- +Р-Й-/ •• ОКЙ O'f СО F(V) = JsbP"x+ . . . Д(¥) = СиДЛ4^+ . . — ^^dr^s dt J2 &<!>' (0) = — CjZij ч~ • • - exp (...) = e~ ’ ’ ’ 1 автора коррек- тора
ДЛ4* cos (vi — e) /&С- J^y±f& J ДЛ1* cos (<7 — e)
37 53 62 63 70 71 71 72 формула (62) формула (25, Ь) 16-я сверху формула (13) 18-я сверху Табл. 1, графа 11 Табл. 1, графа 13 Табл. 3, 2-я сверху t 1 -nt f nt, . . . e 1 e ДЛ4 . . . b t дМв dMB •= д“+- • • объем газов и пузырьков л + 4-^с4(- •• )? • • А7 [ на самом деле может быть установ- лен только . . . 71,5 3,9 39,40 У^с-J^y+K2^ t . . ±е-"7гп/дм' .. b { cWR . . . — — "< Ди. — а Д«> г-. . . OS T o<o объем газовых пузырьков Л + ~2~ (••••) 2 • - • на самом деле может быть достиг- нуто только . . . 7,15 3,2 3940 автора я W коррек- тора автора м в
ОГЛАВЛЕНИЕ
Стр.
Предисловие ................................. 1
Глава I. Координаты и уравнения задачи . . . —
Глава II. Основная нелинейная система урав-
нений . . •.............................12
Глава III. Упрощение уравнений движения . . 15
Глава IV. Протекание динамических процессов
в различных частных случаях . • . . . • . 26
Глава V. Динамика ВИШ при пикировании са-
молета .................................... 38
Глава VI. Некоторые дополнительные исследо-
вания ......................................41
Приложение..................................56
Отв. редактор А. А. Горяйнов
Объем 9 печ. л., 42 880 зн в печ. л.
Г-81566 ~
Тип. изд-ва БНТ
Подписано к печати 24/1 1947 г.
Уче-но-ав’орских .листов 9,6
Зак. № 1?24