Author: Соболев О.С.
Tags: регулирование и управление машинами, процессами автоматика теория автоматического управления
Year: 1973
Similar
Text
БИБЛИОТЕКА ПО АВТОМАТИКЕ
Выпуск 483
О. С. СОБОЛЕВ
ОДНОТИПНЫЕ
СВЯЗАННЫЕ
СИСТЕМЫ
РЕГУЛИРОВАНИЯ
ш
«ЭНЕРГИЯ»
МОСКВА 1973
6П2.12
С 54
УДК 62-5$
РЕДАКЦИОННАЯ КОЛЛЕГИЯ:
И. В. Антик, Г. Т. Артамонов, А. И. Бертинов, А. А. Воронов,
В. С. Малов, Л. М. Закс, В. Э. Низе, Д. А. Поспелов,
О. В. Слежановский, Б. С. Сотсков, Ф. Е. Темников, М. Г. Чиликин,
А. С. Шаталов
Соболев О. С.
С 54 Однотипные связанные системы регулирования.
М., «Энергия», 1973.
136 с. с ил. (Б-ка по автоматике. Вып. 483).
Книга посвящена вопросам теории и методам инженерных иссле-
дований многосвязных систем автоматического регулирования, состоя-
щих из одинаковых сепаратных подсистем с перекрестными связями
через общие источники сырья или энергии или через общую нагрузку.
Рассматриваемые методы основаны на некоторых положениях линей-
ной алгебры и сводят расчет связанной системы регулирования к рас-
чету изолированных подсистем.
Книга рассчитана на инженеров и научных работников, занятых
исследованием, проектированием и расчетом сложных систем регули-
рования; может быть использована студентами вузов, специализирую-
щимися в области автоматического управления.
3313-072
6 051 (01)-73 29Ь72 6П2Л2
ОЛЕГ СЕРГЕЕВИЧ СОБОЛЕВ
Однотипные связанные системы регулирования
Редактор Л. Я. Серебрянский
Редактор издательства М. П. Соколова
Обложка художника Н. П. Стрельцова
Технический редактор Т. Я. Хромова
Корректор Л. К. Улегова
Сдано в набор 24/V 1972 г. Подписано к печати 3/1 1973 г. Т-00807
Формат 84Х1081/За Бумага типографская № 2 Усл. печ. л. 7,14
Уч.-изд. л. 8,86 Тираж 5 ООО экз. Зак. 1206 Цена 44 коп.
Издательство «Энергия». Москва, М-114, Шлюзовая наб., 10.
Московская типография № 10 «Союзполиграфпрома»
при Государственном Комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли.
Москва, М-114, Шлюзовая наб., 10.
ОБОЗНАЧЕНИЯ
Матрицы обозначены прописными буквами, их элементы — соот-
ветствующими строчными буквами с двойной индексацией, указы-
вающей номера строки и столбца элемента. Векторы обозначены
строчными буквами; их компоненты — теми же буквами с индексом,
указывающим номер компоненты. Символы матриц и векторов на-
печатаны полужирным шрифтом. Векторы исследуемой системы обо-
значены латинскими буквами; векторы эквивалентной системы — гре-
ческими.
Приведем основные обозначения, применяемые в тексте:
/ = у—1 — мнимая единица;
Е — единичная матрица типа пХп;
1 — вектор с единичными компонентами;
у, т| — вектор регулируемых величию;
и, | —вектор управлений;
f, ф — вектор возмущений;
х, х — вектор заданий;
А — матрица коэффициентов передачи перекрестных связей;
С — матрица канонического базиса;
Л— каноническая (Жорданова) форма матрицы А;
п — число регулируемых переменных;
р — оператор дифференцирования;
W0(p)—передаточная функция регулируемого канала объекта;
Wv(p)—передаточная функция сепаратного регулятора;
det — символ определителя;
со — угловая частота;
Xk — характеристическое число матрицы;
т — символ транспонирования (в индексе матрицы на-
верху) ;
* — символ сопряжения по Эрмиту (в индексе матрицы
наверху); между двумя функциями времени (скалярны-
ми или матричными) символ свертки.
ПРЕДИСЛОВИЕ
iB предлагаемой вниманию читателя книге рассматриваются ме-
тоды исследования многосвязных систем с идентичными сепаратными
каналами.
Такие системы широко распространены в различных областям
техники. |В промышленности, например*, типичной является схема
параллельной работы нескольких агрегатов, выполняющих одну и
ту же технологическую операцию. Установка нескольких агрегатов
(устройств) для параллельной работы может быть вызвана недо-
статочной мощностью отдельного агрегата (устройства); необходи-
мостью резервирования; одновременного выполнения одной и той
же операции в разных точках технологической схемы и т. д. Как
правило, параллельные агрегаты однотипны — одинаковы "по своим
конструктивным данным и, следовательно, характеризуются близкими
динамическими свойствами (в идеале — одинаковыми). Для примера
укажем, что на электрической станции средней мощности параллель-
но работают обычно однотипные котельные агрегаты, турбогенерато-
ры, питательные насосы, деаэраторы и т. д.; можно привести много-
численные примеры из областей химической, металлургической, пи-
щевой, бумажной и других отраслей «промышлености, где агрегаты
одинакового назначения, работающие параллельно, встречаются бук-
вально в каждом сколько-нибудь крупном цехе или отделении.
(Выполняя одну и ту же технологическую операцию, параллель-
ные агрегаты очень часто оказываются взаимосвязанными через
общую нагрузку или общие источники сырья или энергии.
Параллельные агрегаты или устройства вместе с индивидуаль-
ными регуляторами, одинаковыми в силу идентичности регулируе-
мых каналов, образуют многосвязную систему автоматического регу-
лирования. В этих многосвязных системах как отдельные регулируе-
мые каналы, так и их регуляторы одинаковы, т. е. одинаковы се-
паратные системы регулирования. Такие многосвязные
системы называют м н о г о с в я з н ы м и однотипными систе-
мами автоматического регулирования или, проще,
однотипными системами.
Идентичность связанных между собой систем регулирования
приводила исследователей к мысли о том, что допустимо ограни-
читься анализом отдельной сепаратной изолированной САР; при
этом авторы опирались на представления о синхронности действия
систем регулирования отдельных агрегатов |(так называемый «метод
эквивалентного генератора»). Дальнейшие исследования показали,
что такой подход не может быть обоснован и в ряде случаев при-
водит к тяжелым ошибкам. Однако, как оказалось, эту задачу мож-
но свести к задаче изучения некоторой достаточно простой экви-
валентной системы, которая состоит из нескольких изолиро-
ванных подсистем, каждая из которых аналогична сепаратной
САР, но может отличаться от нее коэффициентами передачи некото-
4
рых усилительных звеньев или наличием некоторых связей. Переход
к эквивалентной системе дает возможность провести исследование
с применением более простых методов и средств, чем это требуется
обычно для многосвязной системы, сделать его менее трудоемким.
Важными отличительными особенностями метода, основанного
на переходе к эквивалентной системе, являются: во-первых, сущест-
венное понижение 'порядка исследуемых дифференциальных уравне-
ний; -во-вторых, сохранение в эквивалентных уравнениях формальных
признаков уравнений изолированных сепаратных систем, что позволя-
ет интерпретировать их как уравнения простой эквивалентной си-
стемы регулирования.
Первые исследования однотипных связанных систем были вызва-
ны развитием энергосистем (Л. 1] и крупных электрических стан-
ций [Л. 3].
Теория однотипных связанных систем как раздел теории авто-
матического регулирования берет свое начало в работах А. А. Кра-
совского 1[Л. 2, 4], четко указавшего основные пути исследования
для важнейших видов систем с одинаковыми перекрестными связя-
ми между сепаратными системами (в настоящей книге они называ-
ются простыми симметричными) и двухканальных, с перекрестными
.связями, различающимися только знаками (двухканальных анти-
симметричных). В дальнейшем методы исследования простых сим-
метричных систем развивались в работах В. М. Матюхина [Л. 6],
Г. Ф. .Козловского и Г. В. Михневича [Л. 10, 13] и получили закон-
ченную форму в работах В. Т. Морозовского (Л. 7, 20]. Эта теория
успешно применялась для исследований энергетических систем в ра-
ботах В. Д. Миронова [Л. 3], В. М. Матюхина [Л. 6], 3. Я. Бейраха
и М. Д. Трахтенберга (Л. 5], ДА. Попова ![Л. 16], Г. Д. Меда [Л. 28],
В. Т. Морозовского {Л. 24] и др.
Теория двухканальных систем с антисимметричными перекрест-
ными связями разрабатывалась в трудах И. И. Ахметгалеева {Л. 8,
И, 12], С. Пашковского [Л. 9, 22], А. Н. Герасимова [Л. 26], а в по-
следние годы — А. А. 1Казамаровым, А. М. Палатником и Л. О. Род-
нянским [Л. 35], а также А. Г. Барским [Л. 32, 42], Г. А. Бенд*
риковым и В. И. Огородниковой [Л. 39, 40, 45], Г. В. Огородниковым
[Л. 44, 47].
Долгое время методы исследования двух видов систем основыва-
лись на индивидуальных рецептах и существовали независимо друг
от друга; отдельные работы, посвященные однотипным связанным
системам иных видов, касались только вопросов устойчивости
(А. Джеффри {Л. 18], Э. Бон [Л. 14, 23], Ту Сюй-янь [Л. 19],
О. €. Соболев [Л. 30], А. Г. Барский [Л. 38]).
Автору предлагаемой вниманию читателя книги удалось объеди-
нить отдельные методические ветви на основе теории линейных алге-
браических операторов. В книге делается попытка последовательно
изложить теорию линейных .многосвязных однотипных систем. В кни-
ге автор стремился показать, как основные задачи исследования
(анализа или синтеза) многосвязной однотипной системы могут быть
решены на значительно более простой эквивалентной модели; при
работе над книгой в центре внимания автора были скорее принципы
понижения размерности, чем конкретные вычислительные процедуры.
В то же время в книге достаточно внимания уделено применению
инженерных методов исследования, которые должны иллюстрировать
теоретические положения; изложение сопровождается примерами
конкретных расчетов.
5
Для исследования системы на эквивалентной модели необхо-
димо:
'1. Установить правила перехода от исследуемой системы к экви-
валентной.
2. Связать существенные для исследования свойства и характе-
ристики исследуемой системы со свойствами эквивалентной (т. е.
сформулировать методы исследования системы на эквивалентной
модели).
3. Оценить допустимость применения рекомендуемых методов
в условиях неизбежных индивидуальных различий сепаратных сис-
тем, в то время как теоретически сепаратные системы идентичны
(вопрос о грубости и чувствительности результатов анализа по отно-
шению к малым параметрам, вызывающим отличие системы от идеа-
лизированной модели).
Этим трем вопросам и посвящена книга. Содержание книги раз-
бито на пять глав.
В гл. 1 выясняются особенности уравнений многосвязных одно-
типных систем автоматического регулирования.
В гл. 2 приводятся необходимые вспомогательные сведения из
линейной алгебры и формулируются правила построения эквивалент-
ной модели.
Главы 3 и 4 посвящены методам решения задач исследования
многосвязных однотипных систем на эквивалентных моделях.
Глава 5 посвящена специальным вопросам теории однотипных
связанных систем: вопросам грубости систем и допустимости прове-
дения идеализации уравнений при исследовании; специальным мето-
дам исследования, позволяющим в некоторых случаях за счет за-
грубления решения обойти определенные вычислительные трудности.
iB этой же главе приводится обзор результатов в смежных раз-
делах теории автоматического управления; указываются некоторые
возможности для применения методов теории однотипных связанных
систем для исследования многосвязных GAP с -близкими по своим
динамическим свойствам сепаратными каналами.
В приложении приводятся результаты анализа матриц, необ-
ходимых при исследовании важнейших видов однотипных связанных
САР.
iB 'библиографии выделены разделы, относящиеся к теории мно-
госвязных однотипных систем регулирования и к смежным разделам
теории автоматического управления.
Чтение книги потребует от читателя знания основ линейной
алгебры и матричного исчисления (например, в объеме первого
раздела гл. 12 книги «Современная математика для инженеров» под
ред. Э. Ф. Беккенбаха, М., Изд-во иностр. лит., 1958; автор рекомен-
довал бы читателю также ознакомиться с соответствующими глава-
ми книги: К. Ланцош, «Прикладные методы практического анализа»,
М., Физматгиз, Г9&1). Имея в виду читателя, не знакомого с теорией
линейных операторов, автор счел своим долгом привести необходи-
мые сведения в тексте книги, стараясь при этом преподнести мате-
риал под углом зрения применения его в теории однотипных связан-
ных систем.
Автор признателен проф. В. Т. Морозовскому и канд. тенх. наук
А. Я. Серебрянскому за детальные обсуждения и полезные советы,
немало содействовавшие улучшению книги.
О. С. Соболев
ГЛАВА ПЕРВАЯ
ОДНОТИПНЫЕ СВЯЗАННЫЕ СИСТЕМЫ
АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
1. ОДНОТИПНЫЕ СВЯЗАННЫЕ СИСТЕМЫ В ТЕХНИКЕ
а) Вводные замечания
Многосвязная однотипная система автоматического регулиро-
вания состоит из нескольких одинаковых сепаратных систем с пере-
крестными связями между ними. Таким образом, основным призна-
ком, отличающим однотипные связанные системы от многосвязных
систем других типов, является то, что основные каналы передачи
воздействий в объекте одинаковы. Это обстоятельство имеет место
в одинаковых агрегатах, объединенных для совместной работы (и
в совокупности с объединяющими агрегаты технологическими ли-
ниями составляющих объект регулирования), либо в едином объек-
те симметричной конструкции при регулировании координат объекта
в симметричных относительно друг друга его частях и т. д. Иден-
тичность регулируемых каналов служит обоснованием, хотя и не-
строгим, для их оснащения одинаковыми регуляторами.
Перекрестные связи между сепаратными системами могут дейст-
вовать либо в объекте, либо в многосвязном регуляторе. 'В первом
случае они отражают существующее взаимодействие между сепарат-
ными системами регулирования через общие источники сырья, энер-
гии, через общую нагрузку и т. д. Во втором случае связи между
сепаратными системами накладываются для координации их дейст-
вий.
При исследовании однотипных связанных систем естественно
считать уравнения идентичных по конструкции элементов сепарат-
ных систем совпадающими, пренебрегая их неизбежными индиви-
дуальными отличиями. При этом особенности уравнений определя-
ются характером действующих между сепаратными системами пере-
крестных связей, их физической природой. Рассмотрим несколько
примеров, отличающихся характером перекрестных связей, получим
уравнения этих систем, что позволит в дальнейшем провести неко-
торые обобщения.
б) Регулирование параллельных агрегатов
Перекрестные связи между системами автоматического регули-
рования одинаковых параллельных агрегатов могут действовать че-
рез общие источники сырья или энергии или через общую нагрузку.
7
ч
От общего
источника
Пусть, например, включенные параллельно технологические агрегаты
объединены общим коллектором на стороне регулирующих орга-
нов {общий источник сырья или энергии (рис. il)]. (В каждом из
агрегатов регулируется од-
Л и\ на переменная технологиче-
к11 О IP/ 9j ского процесса, число агре-
7^Г~| гатов п.
(Перемещение любого из
регулирующих органов, на-
пример первого органа с ко-
ординатой «1, приводит к
изменению давления в кол-
лекторе -и как следствие
к .изменению расходов gi>
g2, ..., gn жидкого или га-
зообразного агента на все
агрегаты (а не только рас-
хода gi еа первый агрегат,
управляемый воздействием
ui). Таким образом, значе-
ние каждого из расходов
определяется положением
не только своего, но и со-
седних регулирующих орга-
нов. Поскольку процессы
з гидравлической «сети обыч-
но практически безынерци-
онны по сравнению с про-
цессами в агрегатах, то перераспределение расходов происходит
мгновенно вслед за изменением положения регулирующего органа;
в линейном приближении зависимость расходов от положений регу-
лирующих органов описывается алгебраическим уравнением
Рис, 1.
п
£и = Е амЩ> k==l> 2> •••» (1)
/=1
iB этом уравнении dkj — коэффициент передачи от /-го регули-
рующего органа к расходу через &-й агрегат. Коэффициенты переда-
чи прямых каналов ((/=.1, 2, ..., п) могут различаться из-за
индивидуальных особенностей характеристик регулирующих органов,
а перекрестных связей auj (кфу) — из-за особенностей характери-
стик гидравлической сети.
Изменение каждой из регулируемых переменных уи происходит
под действием изменения расхода на агрегат gh и может быть опи-
сано уравнением
yk=W„(p)gh + Wf(p)fk, £=1, 2, п. (2)
В уравнении i(2) fh — возмущение; Wd(p), Wfl(p) — передаточ-
ные функции агрегата по каналам управляющего расхода и возму-
щения; р — оператор дифференцирования (термин «передаточная
функция» применяется в книге в связи с тем, что .более уместный
термин «оператор» употреблен в ином значении). Исключив из урав-
8
нений (1) и (2) переменные gk, запишем уравнение объекта—сово-
купности агрегатов:
п
</* = 2 ahjW0 (р) щ + Wf (р) fh, к = 1. 2 п. (3)
/=1
Отметим, что вследствие безынерционности процессов перерас-
пределения расходов передаточные функции объекта по каналам от
каждого из регулирующих органов ко всем регулируемым перемен-
ным различаются только коэффициентами передачи ащ.
На каждом из агрегатов установлен регулятор с передаточной
функцией Wv(p) ^регуляторы считаем идентичными, одинаково на-
строенными), так что уравнение /-.го регулятора имеет вид:
Ui = Wp\(py(Xi-yi)t /=.1, 2, п, (4)
где Xi — задание.
В уравнениях (3), >(4) передаточные функции динамических
звеньев не отмечены индексами, поскольку динамические характери-
стики соответствующих звеньев сепаратных систем по крайней мере
в первом приближении могут считаться одинаковыми.
Идентичность сепаратных каналов передачи воздействий позво-
ляет в нашем случае вместо громоздкой полной структурной схемы
системы ограничиться изображением звеньев и связей, соответствую-
щих только одной сепаратной системе (рис. 2,а). Такое представле-
ние структурной схемы системы соответствует ее уравнениям (3),
9
(4), относящимся к одной сепаратной системе, при использовании
бегущего индекса для распространения уравненией на все п сепа-
ратные системы.
'Перейдем к более компактной матричной форме записи урав-
нений системы. Для этого введем векторы переменных:
У =
Ух
У2
Уп
х2
h
ft
(у — вектор регулируемых переменных, х — вектор заданий, и — век-
тор управлений, f — вектор возмущений) н передаточные матрицы:
■а^0(р) axiW0(p) . . .alnW0(p)
«1,^0(/>) anW0{p) . . .a2nW0(p)
LantW0(p) an2W0(p) . . .annW0(p)
a\\ a\2 • • • a\n
#21 #22 • • • a2n
= Wn(p)
W0 (p) A
(5)
— передаточная матрица объекта по основным каналам «передачи
воздействий;
-Wf(p) о ... о
О Wf (р) . . . о
о
= Wf(p)
О . . .Wf(p) J
"I о ... о
О 1 ... о
О 0 ... 1
(6)
— передаточная матрица объекта по каналам возмущении;
10
■Wt(p) о .
0 Wp(p).
о
■Щ(р)
о .
"1 о... о
О 1 ... о
О 0 ... 1
Щ (р) А
(7)
— передаточная матрица регулятора.
Одинаковые передаточные функции звеньев системы в переда-
точных матрицах вынесены в качестве скалярных сомножителей при
матрицах коэффициентов 'передачи: некоторой числовой А и единич-
ной Е; строение этих матриц показано в .(5)—*(7).
Каждая из передаточных матриц описывает всю совокупность
связей между переменными, входящими в состав соответствующей
пары векторов; передаточные функции каналов, связывающих между
собой компоненты векторов (отдельные переменные системы), игра-
ют роль элементов матриц и занимают в них вполне определенные
места.
Элементы матрицы в общем случае отмечаются двойным индек-
сом: первый из индексов соответствует номеру строки матрицы, или,
что то же самое, номеру вы-
ходной переменной; второй У1
индекс соответствует номе- * у ,р\ ф
ру столбца, т. е. номеру © I
входной переменной.
Теперь запишем уравне-
ния (3), (4) в -матричной
форме:
y=Wo'U>)Au+Wf(p)Et; (8)
И потребители^
У»
u=^p(/7)E(x-y). (9)
Матричным уравнениям
системы соответствует ма-
тричная структурная схема;
на ней векторные перемен-
ные в отличие от обычных
структурных «схем символи-
зируются двойными стрел-
ками (рис. 2,6).
Пусть теперь регули-
руемые агрегаты объеди-
нены коллектором на сто-
роне нагрузки (рис. 3). Перемещение любого из регулирующих
органов, например и\, во-первых, вызывает реакцию соответствующей
регулируемой переменной (например, у\) и, во-вторых, приводит
к изменению гидравлического режима коллектора. В рассматриваемом
случае соседние агрегаты воспринимают воздействие как пришедшее
Рис. 3.
11
со стороны нагрузки, так что формы процессов на возмущаемом и
любом из соседних агрегатов различны.
Предполагая по-прежнему, что процессы в коллекторе 'безынер-
ционны и, следовательно, передаточные функции перекрестных свя-
зей различаются только коэффициентами усиления, запишем для ре-
гулируемой переменной /-го агрегата
п, ]Ф1
yi = W0(p)ui + W1(p) S *tM + Wf(p)ft. *=1. 2,..., п.
/=1
Здесь W\(p) —передаточная функция перекрестного канала меж-
ду агрегатами; ац — значение коэффициента усиления перекрестного
канала от /-го управления к /-й регулируемой переменной.
Пусть уравнения одинаковых регуляторов имеют вид:
Ui = Wv(p) (Xi—yj),
тогда уравнения системы в матричной форме могут >быть записаны
следующим образом:
у = W0(p) Eu+ Wi (p)Au + WfEt; (10)
u=U7p(p)E(x-y). (14)
Как и в (б), (6), здесь передаточные функции динамических
звеньев идентичных сепаратных систем фигурируют в виде скаляр-
ных множителей «при числовых матрицах Е и А. Матричная струк-
турная схема системы показана на рис. 4.
в) Регулирование переменной, распределенной
по пространству
Регулирование распределенной переменной в идеале должно осу-
ществляться распределенным по пространству управлением при из-
мерении переменной во всех точках пространства. Практически же
переменная измеряется лишь в отдельных точках пространства и
управления также сосредоточены в отдельных точках. При этом
величина воздействия каждого из управлений на регулируемые зна-
чения параметра зависит от взаимного положения в пространстве
регулирующего органа и
датчика переменной (так
что динамические свойства
различных каналов «управ-
ление — переменная» при
одинаковом взаимном рас-
положении в пространстве
регулирующего органа и
датчика совпадают).
Примером может слу-
жить система автоматиче-
ского распределения дутья
по фурмам доменной печи,
задача которой—обеспечить
заданное распределение расхода горячего воздуха, вводимого в верх-
нюю часть горна Доменной печи через воздуховоды (фурмы), по ее
периметру [Л. 30, 36]. Взаимовлияние между регулируемыми кана-
лами определяется в этом случае общим регулируемым источником
Рис. 4.
12
воздуха (воздуходувкой) и распределенным по объему доменной
печи гидравлическим сопротивлением шихты и расплавов. iB (Л. 30,
36] математическое описание системы фурм уравнением вида (8)
основывается на экспериментальных данных. В простейшем варианте
системы при оснащении фурм индивидуальными сепаратными регу-
ляторами без дополнительных связей САР описывается уравнениями
(8), (9) и ее матричная структурная схема совпадает с изображен-
ной на рис. 2.
г) Регулирование координат симметричного
объекта
Примером объекта такого рода может служить однокамерная
двухпоточная трубчатая печь установки первичной переработки неф-
ти [Л. 125]. В печи подогревается нефть, прокачиваемая двумя пото-
ками через змеевики экранных поверхностей; температура каждого
из потоков на выходе из печи регулируется расходами топливного
газа на форсунки, расположенные в соответствующей части топочно-
го пространства. Каждый из змеевиков воспринимает тепло не
только «своего» факела, но и «чужого», т. е. между основными кана-
лами передачи воздействий в объекте имеются перекрестные связи.
Печь как объект регулирования описывается системой дифферен-
циальных уравнений:
yi = W0(p)ui + Wi (р) и2 +. Wt (р) и;
У 2 =Wi(p)Ui + W0 (р) и2 + Wf (р)
В этих уравнениях W0(p) —передаточная функция прямого ка-
нала передачи воздействий «расход газа — температура нефти на
выходе «своего» змеевика»; Wu(p) — передаточная функция по кана-
лу «расход газа — температура нефти на выходе «чужого» змее-
вика».
Совпадение динамики перекрестных связей в объекте является
следствием его симметрии.
Уравнения регуляторов следующие:
ui = Wp\(p){xi—yl)\
u2=Wv(р) (Х2—У2).
В матричной записи уравнения системы выглядят так:
у=[W0 (р) E+Wi (р) A]u+ Wf (р) Ef;
u=WpE(x-y).
Матричная структурная схема системы совпадает со схемой, по-
казанной на рис. 4.
В системах регулирования симметричных летательных аппаратов
между идентичными каналами регулирования углов тангажа и рыс-
канья действуют перекрестные связи, совпадающие по динамическим
характеристикам, но противоположные по знаку 1[Л. 65] (антисимме-
13
тричные перекрестные связи, [Л. 4]). Уравнения объекта регулирова-
ния в этом случае выглядят так:
yi = Wi(p) (ui+fi-W2(p)y2);
y2=Wii(p)iu2+f2+W2(p)yi)
или в матричной форме
y=UMp)E(u + f + HMp)Ay);
"О —1
А =
О
Ори использовании для регулирования переменных у\ и у2 оди-
наковых регуляторов с уравнениями (8) матричная структурная
схема системы имеет вид, показанный на рис. 5.
В приведенных примерах перекрестные связи действуют в объек-
те регулирования. iB некоторых случаях взаимодействие между се-
паратными системами осуще-
ствляется через связи в регуля-
торе, вводимые для координа-
ции их действий.
Рис. 5.
д) Регулирование общего
параметра
При необходимости стаби-
лизировать переменную, зави-
сящую от работы параллельно
действующих агрегатов, в си-
стеме регулирования применя-
ют общий регулятор, воздей-
ствующий на сепаратные САР. Таковы главный регулятор давления
пара в коллекторе котельной, воздействующий на системы регули-
рования параллельно работающих котельных агрегатов [Л. 3, 5];
корректоры частоты и напряжения на шинах параллельных электри-
ческих генераторов автономных систем электроснабжения [Л. 26];
регулятор давления газа в общем трубопроводе при параллельной
работе нагнетателей (Л. 28] и т. д.
Пусть передоточные функции по каналам от управлений отдель-
ных агрегатов к общей регулируемой переменной yn+i различаются
коэффициентами усиления bi, b2y ..bn ((зависящими, например, от
неравномерной загрузки агрегатов), так что
Уп+1=У(Р) И Ьм,
где V\(p) —общая передаточная функция (рис. 6).
Общий регулятор с передаточной функцией \R(p), описываемый
уравнением
ип+1=Щр) (Xn+i—yn+i),
воздействует в общем случае неравномерно на задания регуляторов
сепаратных систем, так что
Xq=X*g + gqUn + l.
14
Здесь x'q — составляющая задания сепаратного регулятора, вво-
димая вручную; gq — настраиваемый коэффициент усиления, опре-
деляющий интенсивность воздействия общего регулятора на задание
q-k сепаратной САР. В частном случае может быть gq=0 |(напри-
мер, при работе д-го котельного агрегата в базовом режиме).
Влияние со стороны у-й сепаратной системы на q-ю через общий
регулятор описывается передаточной функцией bjgqV(p)R(p) (см.
рис. 6), так что взаимосвязи в системе описываются передаточной
матрицей V(p)R(p)A, где
~ gA gA • • • gibn~
g2bx g2b2 . . . g2bn
A =
Lgtfii &A • • . grfin.
— GB.
(12)
Здесь gjbh = ajh\ G— матрица-столбец коэффициентов передачи
по каналам от управлений сепаратных систем к общему параметру;
В — матрица-строка коэффициентов передачи по каналам «выход
главного регулятора — задания сепаратных систем».
Полное уравнение связей через общий регулятор выглядит так:
при
x=x'+R(p)V(p)\u+Ii(p)r
r=Gxn+i.
Если сепаратные системы допустимо считать идентичными, то
передаточные матрицы звеньев системы, как и в предыдущих при-
мерах, представляются двумя
типами: скалярной и числовой,
с передаточными функциями
элементов системы в качестве
скалярных сомножителей.
Чи> (Р)\
г) Следящие системы
с перекрестными связями
между сигналами ошибок
В системах пространствен-
ного слежения отдельные коор-
динаты задания отрабатывают-
ся идентичными сепаратными
системами; иногда для согла-
сования их действий вводятся ЧИО, (р)\
жесткие перекрестные связи 1 1
между сигналами ошибок.
Примерами могут служить ра-
диолокационные системы про-
странственного сопровождения
[Л. 4]; следящие системы копи-
ровальных станков [Л. 43]; си
Рис. 6.
стемы автоматической синхронизации вращения двигателей {Л. 19];
следящие системы преобразователей координат [Л. 12] и т. д. Мно-
гомерный регулятор в рассматриваемом случае описывается урав-
15
[n, s^q
(х<1 — Уч)+ £ <*4а(Хш — Уз)
или в матричной записи
u=Wp(p)A(x-y). (13)
Рис. 7.
Матричная структурная схема для случая, когда регулируемые
каналы объекта независимы и описываются уравнением
y=W<,(p)Eu+Wt(p)t, (14)
показана на рис. 7.
2. ОСОБЕННОСТИ ОДНОТИПНЫХ СВЯЗАННЫХ СИСТЕМ
a)i Функциональные и структурные схемы однотипных
связанных систем
Материал предыдущего параграфа позволяет сделать определен-
ные выводы относительно особенностей функциональных и структур-
ных схем однотипных связанных GAP. Как обычно в задачах иссле-
дования многосвязных систем, здесь речь идет о многомерных
функциональных и матричных структурных схемах.
Многомерные блоки функциональных схем однотипных связан-
ных систем символически объединяют в себе идентичные по кон-
струкции элементы одинакового функционального назначения, рабо-
тающие в различных сепаратных системах. При этом структура свя-
зей между блоками определяется связями между элементами внутри
сепаратной системы и поэтому повторяет структуру обычной функ-
циональной схемы отдельной сепаратной системы. Используя иден-
тичность сепаратных каналов, вместо матричной для однотипной
связанной системы часто строят обычную функциональную схему
только для одной из сепаратных систем.
Пример il. Система автоматического распределения дутья по
фурмам доменной печи [Л. 29, 36].
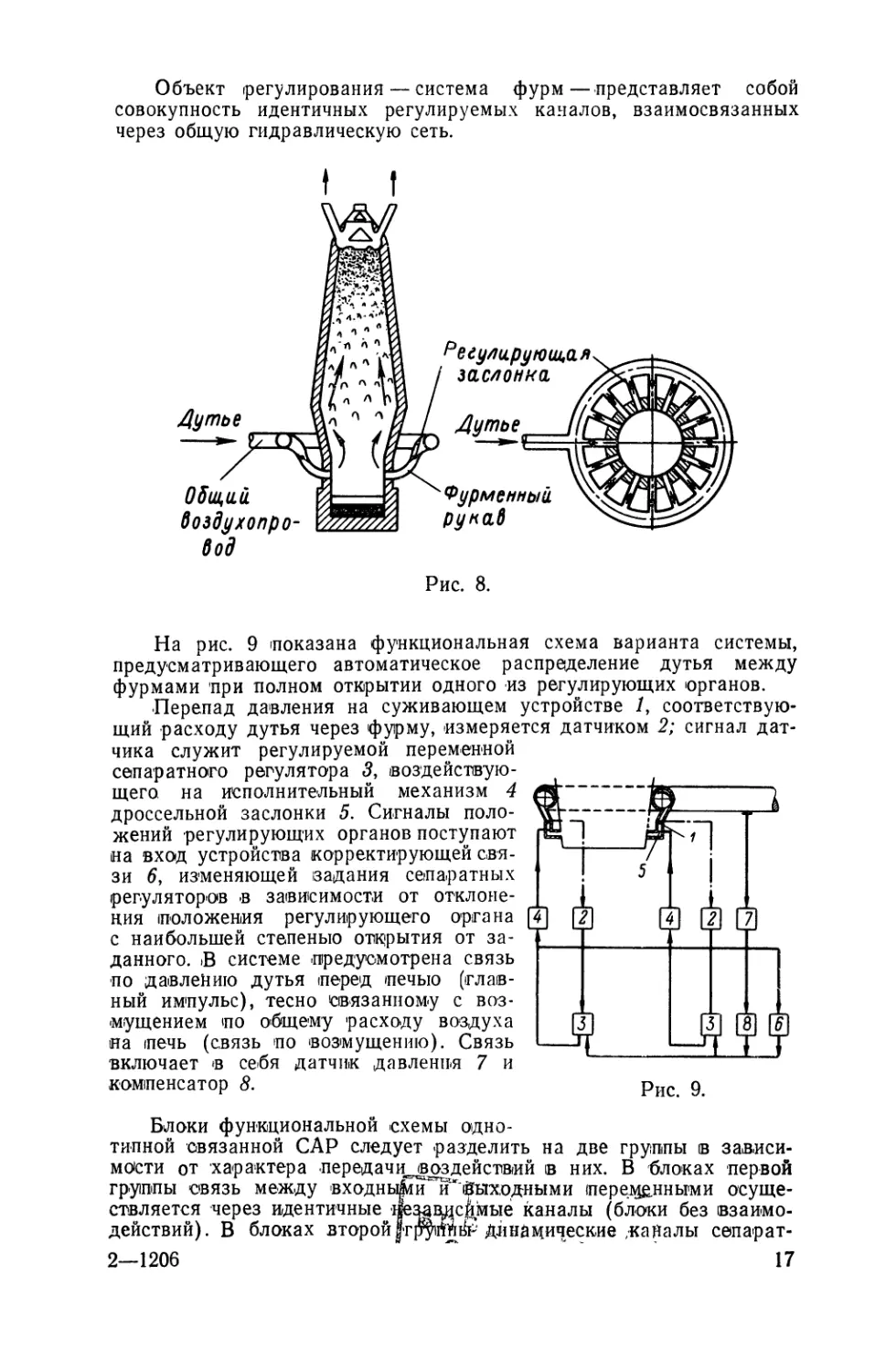
Воздух (дутье) подается в верх горна печи через ряд (обычно
14—(20) параллельных вводов — фурм )(рис. 8). По технологическим
причинам дутье распределяется между фурмами неравномерно, что
нарушает нормальный ход доменного процесса. Для управления рас-
пределением воздуха по^фурэдам применяются системы автоматиче-
ского распределения дутья, воздействующие на дроссельные-заслон-
ки в фурменных рукавах.
16
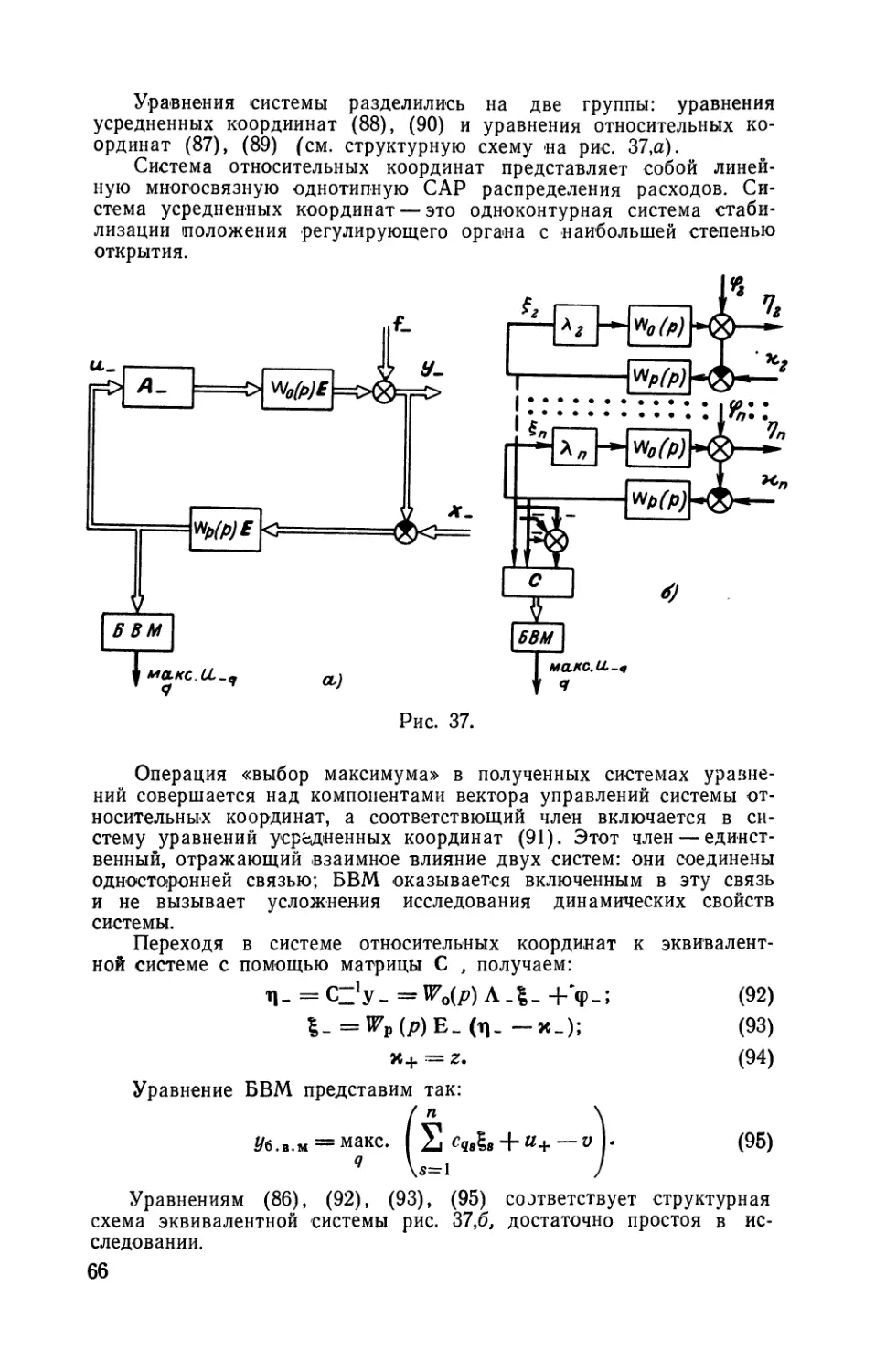
На рис. 9 показана функциональная схема варианта системы,
предусматривающего автоматическое распределение дутья между
фурмами при полном открытии одного из регулирующих органов.
Перепад давления на суживающем устройстве /, соответствую-
щий расходу дутья через фурму, измеряется датчиком 2; сигнал дат-
чика служит регулируемой переменной
сепаратного регулятора 5, воздействую-
щего на исполнительный механизм 4
дроссельной заслонки 5. Сигналы поло-
жений регулирующих органов поступают
на вход устройства корректирующей свя-
зи 5, изменяющей задания сепаратных
регуляторов в зависимости от отклоне-
ния положения регулирующего органа [4]
с наибольшей степенью открытия от за-
данного. В системе предусмотрена связь
по давлению дутья перед печыо (глав-
ный импульс), тесно связанному с воз-
мущением по О'бщему расходу воздуха
на печь (связь по возмущению). Связь
включает в себя датчик давления 7 и
компенсатор 8. рис g
Блоки функциональной схемы одно-
типной связанной САР следует разделить на две группы в зависи-
мости от характера передачи=гвоздействий в них. В блоках первой
группы связь между входными и*"выходными пере.м£нными осуще-
ствляется через идентичные фадвисймые каналы (блоки без взаимо-
действий). В блоках второй |труиШр динамические дсайалы сепарат-
2—1206 17
ных систем взаимосвязаны. Соответственно матричная структур-
ная схема однотипной связанной САР содержит матричные
звенья с передаточными матрицами двух типов. Передаточ-
ные матрицы (первого типа описывают динамические свойства
идентичных независимых каналов передачи воздействий в сепарат-
ных системах и представляют собой произведение скалярной пе-
редаточной функции отдельного канала на единичую матрицу Е
(скалярные передаточные матрицы). Передаточные матрицы второго
типа отражают взаимодействие между сепаратными системами и
представляют собой произведение общей скалярной передаточной
функции связей на матрицу их коэффициентов передачи А.
Здесь необходимо сделать следующее замечание.
'В 1большинстве приводившихся примеров элементы матрицы
представляют собой коэффициенты передачи перекрестных связей
между сепаратными системами и, как принято в теории многосвяз-
ных САР, имеют нулевые диагональные элементы. IB некоторых при-
мерах встречаем матрицу коэффициентов передачи А со знача-
щими диагональными элементами. Таковы матрицы в случаях
системы регулирования параллельно работающих агрегатов со свя-
зями между регулирующими органами; сепаратных систем регулиро-
вания, связанных через регулятор общей -регулируемой переменной.
Таким представлением матриц иногда пользуются в целях упро-
щения работы с уравнениями систем, объединяя в матричных
звеньях каналы передачи воздействий сепаратных систем с каналами
перекрестных связей, если передаточные функции прямых и перекре-
стных каналов совпадают хотя бы с точностью до коэффициентов
усиления. Для обозначения такой совокупности связей 'будем при-
менять термин «взаимосвязи». Математическая сторона методов, рас-
сматриваемых в настоящей книге, вовсе не требует равенства нулю
диагональных элементов матрицы А.
Матричные структурные схемы однотипных связанных систем
в основном повторяют скалярные структурные схемы сепаратных
систем, отличие появляется только в звене перекрестных связей. Это
позволяет рекомендовать следующую процедуру построения матрич-
ных структурных схем однотипных связанных систем. Сначала на
структурной схеме сепаратной системы скалярные связи между
звеньями заменяются векторными, а передаточные функции 'звеньев
сепаратных САР снабжаются матричным сомножителем Е. Затем на
структурную схему наносятся матричные звенья перекрестных свя-
зей; точки отбора и точки приложения векторных перекрестных свя-
зей на матричной структурной схеме определяются их положением
в структурных схемах сепаратных систем. Общая передаточная функ-
ция перекрестных связей служит сомножителем при матрице коэф-
фициентов передачи А.
Так как скалярная передаточная матрица перестановочна с лю-
бой квадратной, то при преобразовании матричных структурных схем
однотипных связанных систем можно менять местами последователь-
но соединенные матричные звенья — как звенья обычных структур-
ных схем линейных систем, если хотя бы одна из двух передаточ-
ных матриц звеньев скалярная. Напомним, что в общем случае такая
перестановка звеньев в матричной структурной схеме недопустима
из-за некоммутативности произведения матриц (Л. 48].
Пример 2. Рассмотрим пример трехканальной системы стабили-
зации, описанной в работе А. (Г. Барского 1[Л. 38]. Структурная
схема системы изображена на рис. 10,а.
18
Построим матричную структурную схему системы. На рис. 10,а
более толстыми линиями выделена структурная схема одной из
сепаратных систем. При переходе к матричной структурной схеме
системы (рис. 10,6) стрелки — символы обычных связей сепаратной
системы — заменены двойными стрелками, символами векторных свя-
зей; передаточные функции звеньев сепаратных систем получили
сомножитель Е. Векторные перекрестные связи на матричной струк-
турной схеме берут начало и приложены в точках единого вектор-
ного контура сепаратных систем, соответствующих точкам начал и
приложений перекрестных связей. Четыре матричных звена соответ-
ствуют четырем группам перекрестных связей между сепаратными
системами. Общая передаточная функция звеньев в каждой из групп
служит скалярным сомножителем в передаточной матрице соответ-
ствующего звена. Так как коэффициенты передачи звеньев перекрест-
ных связей каждой из групп на рис. 10,а одинаковы, то матрицы
коэффициентов передачи перекрестных связей содержат в качестве
значащих элементов только единицы; в обозначениях рис. 10,6
имеем:
бу Внешние воздействия в однотипных связанных системах
Анализ условий, в которых работают однотипные связанные
системы, позволяет сделать определенные выводы относительно ха-
рактеристик внешних воздействий в них.
'Внешнее воздействие может быть приложено либо к одной из
сепаратных систем, либо одновременно ко всем сепаратным систе-
мам.
Внешние воздействия, приложенные к сепаратной системе, опре-
деляются индивидуальными особенностями режима ее работы. 'Воз-
действия по заданию могут быть вызваны, например, необходимо-
стью изменения или коррекции режима работы сепаратной САР;
возмущения могут возникать в самом регулируемом агрегате. При-
чины появления воздействий в различных сепаратных системах тако-
вы, что их можно считать независимыми.
Если внешние воздействия на входах сепаратных систем пред-
ставляют собой независимые случайные процессы, то типичной можно
считать ситуацию, когда статистические характеристики процессов
совпадают (поскольку практически одинаковы условия работы от-
дельных сепаратных систем). При этом матрица корреляционных
функций стационарных входных воздействий i(t) [математическое
ожидание произведения f(/)fTi(rf+t)]
(15)
и
(16)
fyf.ro fyf2ro- • .fy,nW
L\f.ro vro. • .*,.,.(*) J
20
— является скалярной и представляет собой произведение общей кор-
реляционной функции внешних воздействий R (т) = ^ (х) = R^ ^ (т)=
= ...=/?,
f (т) на единичную матрицу Е:
'п ' п
R„(t)=iR(t)E.
(17)
Внешние воздействия, приложенные в целом ко всей системе,
вызываются причинами, общими для сепаратных САР. Они могут
поступать, например, со стороны линий, объединяющих агрегаты,
или вызываться общим для сепаратных систем изменением условий
работы. Такими возмущениями в примерах, рассмотренных в пер-
вой главе, являются: изменение аэродинамических условий — для
систем стабилизации курса летательного аппарата в вертикальной и
горизонтальной плоскостях; изменение калорийности топлива — для
двух систем регулирования температуры нефти в змеевиках труб-
чатой нагревательной печи; изменение потребления пара из котель-
ной — для систем регулирования котельных агрегатов и т. д.
В рассматриваемом случае возмущение является общим для
сепаратных систем, хотя может различаться в сепаратных системах
амплитудами воздействия (например, в системе с общим регулято-
ром, рис. 6, воздействие на задание общего регулятора распростра-
няется на сепаратные системы пропорционально коэффициентам пе-
редачи glf g2, ..gn). Поэтому внешнее воздействие может быть
представлено вектором вида
kx "
t(t)=f(t)
= /(0k.
(18)
где ku &2, ..kn — коэффициенты, с которыми общее воздействие
f(t) проявляется в сепаратных системах.
Если f\(t) — стационарная случайная функция времени, то ма-
трица корреляционых функций воздействий в САР имеет вид:
R//(t)=*//(t)kk*
(«19)
Здесь Rff(x)—автокорреляционная функция процесса l(t).
В частности, если воздействие распространяется на сепаратные си-
стемы в одинаковой мере, то /г1==^2= ... =kn = k:
R//(t)=*W//(t)I,
(•20)
где I — матрица пХп, каждый элемент которой — единица.
Таким образом, в характерных ситуациях векторные функции
внешних воздействий (или их матричные характеристики) могу г
быть представлены в виде произведения некоторой скалярной функ-
ции на вектор (или соответственно матрицу), состоящий (состоя-
щую) из постоянных элементов.
21
в) Однотипные связанные системы
\ЩР) *
Нам необходимо четко договориться о содержании понятия
«однотипные связанные системы», отличив предмет нашего исследо-
вания от многосвязной линейной системы любого другого класса по
структурным признакам.
Как уже подчеркивалось, основным признаком однотипных свя-
занных систем является идентичность звеньев сепаратных каналов
передачи воздействий. Однако это свойство систем само по себе
не создает предпосылок для применения специальных эффективных
методов исследования и тем самым не дает оснований для выде-
ления таких систем в отдельный класс. >В самом деле, перекрестные
связи между сепаратными
системами могут оказаться
настолько сложными по
своей структуре, что при
исследовании окажется не-
обходимым применять об-
щие методы теории много-
связных систем автоматиче-
ского регулирования.
В разобранных примерах
относительная «простота»
перекрестных связей отра-
жалась в различии переда-
точных функций связей
только коэффициентами пе-
редачи, так что перекрест-
ные связи описывались об-
щей передаточной функцией
и матрицей коэффициентов
передачи. Причины возникновения перекрестных связей разнообраз-
ны, так что во многих системах между сепаратными каналами
действует не одна, а несколько групп перекрестных связей, каждой
из которых соответствует звено на матричной структурной схеме.
Понятно, что появление на структурной схеме' САР нескольких
матричных звеньев перекрестных связей вместо одного (как в при-
мерах § 1) принципиально усложняет исследование. В этом случае
в качестве предпосылки для разработки специальных методов не-
обходимо наложить определенные условия на характеристики ма-
тричных звеньев; потребуем, чтобы передаточные матрицы различ-
ных звеньев (например, А и В) были перестановочными, т. е..в про-
изведении двух матриц их можно было менять местами: АВ — В А.
Благодаря этому условию оказывается возможным на струк-
турной схеме системы менять местами последовательно соединенные
фрагменты, содержащие различные матрицы коэффициентов пере-
дачи перекрестных связей 1(рис. 11,а и б). Таким образом, названное
условие усиливает аналогию правил преобразования структурных
схем однотипных связанных систем с несколькими звеньями пере-
крестных связей правилам преобразования структурных схем одно-
мерных систем. Отметим, однако, чго значение условия перестано-
вочности не ограничивается возможностью преобразования струк-
турных схем; по существу оно означает совпадение некоторой
внутренней структуры перекрестных связей и эффективно исполь-
зуется при исследовании. Свойство перестановочности обычно ока-
Рис. И.
22
Of, (р)£\
л.
II
wo IP)*
Рис. 12.
зывается проявлением органических свойств процессов в многомер-
ной системе и вовсе не является случайным.
Перейдем непосредственно к определению понятия «многосвяз-
ные однотипные системы автоматического регулирования».
К многосвязным однотипным 'будем относить системы автома-
тического регулирования, в которых
1) уравнения сепаратных САР совпадают;
2) передаточные функции перекрестных связей, берущих начало
и приложенных в идентичных точках сепаратных САР, совпадают
с точностью до коэффици- г-
ентов передачи; rfd
3) 'матрицы коэффици- L
ентов передачи различных
звеньев перекрестных свя-
зей системы перестано-
вочны.
Таким образом, к мно-
гоовязны'м однотипным отно-
сятся, например, системы,
в которых -между идентич-
ными САР действует одна
группа перекрестных связей !(возможно, различающихся коэффици-
ентами передачи), а также системы с несколькими группами пере-
крестных связей при условии, что их передаточные матрицы совпа-
дают с точностью до скалярных сомножителей и, следовательно,
перестановочны. Приводимые в § 1 матричные структурные схемы
(см. рис. 12, 4, 5, 7) соответствуют системам с одной группой пере-
крестных связей между идентичными сепаратными каналами и от-
вечают принятому определению однотипных связанных систем.
(В общем случае к однотипным не относятся многосвязные си-
стемы, матричные структурные схемы которых содержат несколько
звеньев с различными матрицами передаточных коэффициентов. Та-
ковы, например, САР параллельно работающих однотипных агрега-
тов, объединенных коллекторами одновременно на стороне регули-
рующих органов и на стороне нагрузки (рис. 12). К однотипным
рассматриваемая система относится только в том случае, если ма-
трицы Ai и А2 перестановочны.
Пример 3. Матричная структурная схема трехканальной системы
стабилизации из примера 2 |[Л. 38] содержит четыре матричных звена
перекрестных связей с попарно совпадающими передаточными ма-
трицами J и —JT; непосредственной проверкой устанавливаем, чтэ
матрицы J и —JT перестановочны:
J(_Jt) = (_Jt)J==_E
и поэтому система относится к однотипным связанным.
Подчеркнем, что в определении однотипных связанных САР не
накладывается ограничений на структуру сепаратной системы ре-
гулирования, которая может быть сложной, неодноконтурной, много-
связной.
Пример структурной схемы такой системы показан на рис. "13.
Объект представляет собой совокупность п агрегатов, в каждом из
которых регулируются две переменные у\ 'и воздействием на
управления Ui и Vi\ отдельный агрегат описывается передаточной
матрицей Wi(p) размером '2X2, сепаратный регулятор — матрицей
23
R(/7) размером 2x2. Управления и\ .различных агрегатов взаимо-
связаны между собой. Связи между агрегатами описываются матри-
цей коэффициентов передачи А.
и1
W,2
*U
—
1
/?,,
R21
о
1 Л |
1
H\2
P..
/
1
ы22
1 V,
On
"11
*22
R,2
R21
R22
2t
. 1*1
У»
Рис. 13.
г) О классификации однотипных связанных систем
Рассмотрим вопросы классификации однотипных связанных си-
стем по специфичному для них признаку — в зависимости от харак-
теристик взаимосвязей, точнее — от особенностей матрицы их ко-
эффициентов передачи, которые существенно отражаются на про-
цедуре исследования или расчета системы. При этом для обозначе-
ния различных видов систем будем пользоваться терминами, при-
меняемыми для соответствующих квадратных матриц.
Однотипная связанная система называется симметричной,
если матрица перекрестных связей симметрична:
ajk = ahj; k,j=\, 2, ..., п\
АТ = А.
Иными словами, однотипная связанная система является сим-
метричной, если взаимодействие между каждой парой сепаратных
систем |(/-й и k-n) в обоих направлениях (от /-й к k-n и от \k-u
к у-й) — одинаково.
Широко распространены симметричные многосвязные одно-
типные системы, в которых передаточные функции всех перекрест-
ных связей совпадают между собой (каждая сепаратная система
воздействует в равной мере на все остальные и реакции в каждой
из сепаратных систем на одинаковые возмущения в остальных оди-
наковы) :
aij = aqs; t, /, q, s = 1, 2, n,
1Ф\ q^s
24
Будем называть такие однотипные связанные системы просты-
ми симметричными.
Обозначив одинаковые коэффициенты передачи прямых каналов
а, а коэффициенты передачи перекрестных связей 6, запишем ма-
трицу коэффициентов передачи взаимосвязей простой симметричной
системы в виде
ь ь. . .ь
А =
а
Ь а Ь . . . Ъ
Ь Ъ а . . . b
Ъ Ъ Ь . . . а
(21)
Однотипные системы с антисимметричными матрицами переда-
чи перекрестных связей будем называть антисимметричными.
В антисимметричных системах взаимные воздействия между каждой
парой сепаратных систем одинаковы по форме, но противоположны
по знаку:
OLhs — —aSh\ k, 5=1, 2, ..., л.
Важнейший частный случай антисимметричных систем — систе-
мы с двумя регулируемыми переменными, называемые д в у х к а-
нальными антисимметричными (двухканальными систе-
мами с антисимметричными перекрестными связями, [Л. 4], {Л. 35]).
Матрица коэффициентов «передачи таких систем:
- О Г
~~ .-1 о.'
(22)
Следует выделить также циркулянтные однотипные свя-
занные САР с циркулянтными матрицами коэффициентов передачи
взаимосвязей:
А =
а т I
bam
с b а
с b
d с
. .d
(23)
т I
а т
b а
В циркулянтной матрице каждая последующая строка повторя-
ет предыдущую при сдвиге всех элементов (кроме /i-го) на одно
место вправо; п-й элемент предыдущей строки становится '1-м эле-
ментом следующей, т. е. элементы матрицы подчиняются условиям
ahj = ak+s, j+s; k, /=1, 2, ..., п\
ak\ = ak-\,n\ &=2, 3, п.
Циркулянтные матрицы (а вместе с ними и циркулянтные одно-
типные связанные системы) могут быть симметричными \(Ь = т, с—1
и т. д.) или антисимметричными (Ь = —т, с=—/ и т. д.).
К циркулянтным однотипным относится симметричная система
автоматического распределения дутья по фурмам доменной печи, ис-
25
следованная автором (Л. З'О] и В. Калиновски [Л. 36], и антисим-
метричная система автоматического регулирования- трехосной гиро-
скопической платформы, рассматривавшаяся в работах А. 'Г. Бар-
ского [Л. 38] и Г. А. Бендрикова и В. И. Огородниковой (Л. 45].
Среди прочих следует отметить системы с матрицей общей свя-
зи 1(12):
#А • • • gJn
g2bt g2b2 . . . g2bn , ^
gnbl gnb2
gnbn A
Особенностью матрицы является пропорциональность элементов
любой пары строк и любой пары столбцов, так как реакции общей
связи на одинаковые воздействия со стороны сепаратных систем
пропорциональны и воздействия общей связи на различные сепарат-
ные системы тоже пропорциональны. (К системам с рассматриваемой
матрицей взаимосвязей относятся системы, содержащие общую
связь.
ГЛАВА ВТОРАЯ
ЭКВИВАЛЕНТНАЯ СИСТЕМА
3. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ЗАМЕНЫ ПЕРЕМЕННЫХ
а) Примеры замен переменных
Особенности уравнений многосвязных однотипных систем по-
зволяют с успехом провести прием перехода к более простым экви-
валентным уравнениям с помощью специальных линейных замен
переменных. .
Общий метод исследования однотипных связанных систем со-
стоит в переходе к эквивалентным уравнениям, в проведении вы-
числений над эквивалентными уравнениями с последующим пересче-
том результатов для уравнений исследуемой системы. При этом
эквивалентные уравнения интерпретируются как уравнения некоторой
эквивалентной (в отличие от исследуемой, оригиналь-
ной в терминологии В. Т. Морозовского |[Л. 48]) системы ре-
гулирования, что определяет возможность применения для
исследования соответствующих приемов и методов теории автомати-
ческого регулирования. Эквивалентная система значительно проще
поддается исследованию и в то же время отражает все основные
свойства оригинальной системы.
Настоящая глава посвящена соответствию между оригиналь-
ной и эквивалентной системами регулирования. Сначала мы выяс-
ним общие правила перехода к эквивалентной системе и рассмот-
рим ее структурные особенности; затем обратимся к пересчету ре-
зультатов исследования эквивалентной системы для оригинальной;
в конце главы математические соотношения между свойствами ори-
гинальной и эквивалентной систем получат некоторую физическую
и структурную интерпретацию.
26
Рассмотрим на двух простых примерах, каким образом особен-
ности однотипных связанных систем могут быть использованы для
преобразования их уравнений к более простому виду.
Обратимся к системе автоматического регулирования п парал-
лельных агрегатов, взаимосвязанных через общую нагрузку (см.
рис. 4). Предположим, что сопротивление коллектора пренебрежимо
мало; тогда влияние любого из регулирующих органов на регули-
руемые переменные всех соседних агрегатов можно считать одина-
ковым, что выражается в равенстве между собой недиагональных
элементов матрицы А; в уравнении объекта (9) обозначим:
ahj = b; k, /=1, 2, п, кф\}.
Выпишем в развернутой форме уравнение объекта
у г = (р) "г + bwx (р) 2 щ + Щ (р) U;
/=2
п, \Ф2
y2 = W0(p)u2 + bW1(p) S u,+ Wf(p)fti
/-1
n—l
Уп = W0 (p) an + bW, (p) £ щ + Wf(p) fn.
/=i
Уравнения сепаратных регуляторов
u1 = Wp(p)(xl-y1);
u2--=Wv (p)(x2 — y2);
(25)
(26)
"n = Wv (p){xn — yn).
Проведем замену переменных, воспользовавшись методикой
[Л. 7]. Сначала введем так называемые усредненные коорди-
наты:
si
1
п
1
п
j_
п
п
п
k=l
п
n
S
(27)
27
Просуммировав почленно уравнения объекта (25), а затем —
регулятора (26) и выполнив простые преобразования, получим:
тц = [ИМ/*)+Мл—1) (р) ] Ei+wf (р) ф1;
Ei=^(P)(xi-t|i).
©ведем теперь относительные координаты:
y\q = yq
п
= хд -
/2=1
П
(28)
(29)
(30)
(Всего таких независимых переменных может быть я—1, так
что индекс q принимает значения q=2, 3, ..п.
Замену для относительных переменных легко выполнить, вычи-
тая почленно из уравнений для второй, третьей и т. д. переменных
объекта и регулятора соответствующие выражения для усредненных
координат (27). После выполнения над уравнениями 025), (26),
(28), i(29) указанных действий и подстановок получим:
% =- [Wo (Р)-Ь Vii(p) ] U + W, (р)<рв;
(31)
(32)
(Уравнения в новых переменых обладают двумя важными свой-
ствами. Во-первых, они сохраняют форму и коэффициенты урав-
нений сепаратных каналов объекта и регулятора и в совокупности
могут быть интерпретированы как уравнения некоторой оквивалент-
\
л)
Wp(p)
6)
Рис. 14.
ной системы регулирования. Во-вторых, уравнения эквивалентной
системы соответствуют сепаратным системам без взаимодействий,
поскольку в каждое из уравнений (28), 1(29), (31), (32) входят пере-
менные только с одним индексом; естественно, исследование эквива-
лентной системы уравнений оказывается существенно более про-
стым «по сравнению с исходной. Структурная схема эквивалентной
системы показана на рис. 14: а — система усредненных координат,
б — система относительных координат.
28
R качестве второго примера рассмотрим систему автоматиче-
ского регулирования курса летательного аппарата (см. § 1) с урав-
нениями
yl = W1(p)[ul + h-W2(p)y2]; \
У2 = Wi (Р) [«« + h + W2 (р) уг\; I (33)
u1=Wv(p)(x1-y1); |
u2 = Wj>(p)(x2 — y2). )
Следуя рекомендациям А. А. Красовского [Л. 4], введем новые
переменные
Ъ=У1 + 1У*> 5i = «1 + "v, ) (34)
*1 = *1 + 1*2', ?l=fl + if2 )
и
Ц2 = У\-^1У2\ g2==Wl—ш2 (35)
и т. д. (по единому образцу).
В соотношениях (34) и (35) / — мнимая единица; таким обра-
зом, новые переменные принимают комплексные значения <(в таких
случаях говорят, что rji(0, t]2i(0 и т. д. — комплекснозначные функ-
ции времени). После подстановок получим:
*|1=.ЯЧр) й1 + ф1 + ^2(р)г]1
(36)
(37)
Здесь выписано уравнение для первого сепаратного канала экви-
валентной системы; уравнение для второго канала отличается толь-
ко индексами переменных и знаком связи с комплексным коэффи-
циентом усиления. Как и ©пре-
дыдущем случае, в результате
замен переменных мы пришли
к уравнениям изолированных
сепаратных систем регулирова-
ния. Особенностями уравнений
(36), (37) является, во-пер-
вых, то, что переменные при-
нимают комплексные значе-
ния; во-вторых, передаточные
функции перекрестных связей
между сепаратными канала-
ми в эквивалентной системе
фигурируют с мнимой едини-
цей в качестве сомножителя. Можно ожидать, что эти осо-
бенности осложнят исследование или расчет; тем не менее до-
стижение — переход в результате замен к уравнениям независи-
мых сепаратных систем — несомненно. Структурная схема экви-
валентных сепаратных систем показана на рис. 15.
В обоих случаях линейные замены переменных формально при-
водили к уравнениям систем регулирования с одной регулируемой
величиной. Они иллюстрируют способы перехода к эквивалентным
системам уравнений, применявшиеся и ранее для исследования важ-
нейших из однотипных связанных систем — систем с простыми сим-
метричными и двухсвязных систем с антисимметричными -перекре-
Рис. 15.
29
стными связями. Замена переменных для систем каждого из этих
типов производится по специальному рецепту.
Что объединяет эти два различных способа замен переменных?
Почему в обоих случаях удается получить уравнения изолирован-
ных сепаратных систем? Как действовать в случае, если перекрест-
ные связи в однотипной многосвязной САР не относятся ни к одно-
му из двух .рассмотренных случаев?—Ответ на эти вопросы можно
получить с помощью теории линейных алгебраических операторов.
б) Замена переменных при исследовании линейных алгебраических
операторов
Действие связей в многосвязной однотипной системе характе-
ризуется матрицей коэффициентов передачи А, ставящей в соот-
ветствие каждому значению вектора на входе некоторого матрич-
ного звена определенное значение его выходного вектора. Например,
в случае однотипных агрегатов с коллектором на стороне регулирую-
щих органов ([см. рис. il, уравнения (1), (2)] каждому значению
вектора положений регулирующих органов и соответствует опреде-
ленное значение вектора расходов g.
(Рассмотрим матричное звено, преобразующее векторный сигнал
v в сигнал z (рис. 16):
z=Av. (38)
Принято /говорить, что вектор z является результатом действия
оператора Л на вектор v; матрица А описывает действие оператора
и называется матрицей опера-
тора Л.
Из линейной алгебры изве-
стно, что изучение линейного
оператора может быть суще-
ственно упрощено применени-
ем определенным образом по-
добранных линейных замен
входных и выходных перемен-
ных 'матричного звена (или,
- систем координат, в которых
V
Рис. 16.
как говорят, изменением базисов -
заданы векторы v и z).
При линейной замене векторной переменной z на новую g
компоненты вектора в старом и новом базисах связаны между со-
бой соотношениями
Zi = + A2S2 + ••• +"Pn£n>
Zl=/>2lSl + ... + Ръг&п*
(39)
*n = Pm ?! + РпЛ + . • • + Pnr£n f
или в матричной форме
z = Pg, (40)
где Р — матрица преобразования переменных. Имея в виду даль-
нейшее, будем допускать, что элементы матрицы Р — комплексные;
следовательно, новые переменные могут принимать комплексные зна-
чения. Для того чтобы набор компонент £1, £2, ..£п полностью
определял вектор z, т. е. соотношение между z и g было взаимно
30
однозначным, ни одно из п соотношений (39) не должно быть
следствием остальных. Это условие равносильно требованию невы-
рожденности матрицы Р; матрица Р невырождена, если ее опреде-
литель отличен от нуля:
detP^O.
При невырожденной Р значение £ выражается через z с по-
мощью соотношения
g = P-lz, (41)
где Р-1 — матрица, обратная матрице Р.
Соотношения между старыми и новыми переменными могут
быть записаны также в форме, представляющей разложение вектора
по векторам нового базиса:
z = £ipi + £2p2+ ... +£пр«. ('42)
Здесь векторы нового базиса pi, р2, ..., рп представляют собой
столбцы матрицы Р; компоненты £i, £2, ..£п являются проекция-
ми вектора z на соответствующие векторы нового базиса и опре-
деляются как скалярные произведения векторов
В этом соотношении p*jq — комплексное число, сопряженное
числу pjq. Если zq = (z, p<j) = 0, то говорят, что векторы Z И pq
взаимно ортогональны.
При замене базисов, в которых заданы векторы системы, изме-
няются выражения передаточных матриц звеньев системы. Так, на-
пример, уравнение (38) при замене
z = P£; (43)
v = Tv (44)
деформируется следующим образом:
g = p-iz = p-iATv = Bvf
где новая передаточная матрица перекрестных связей В выража-
ется через А так:
В = Р-4АТ.
При выборе замен переменных необходимо считаться с тем,
что в многосвязной однотипной системе существует обратная связь
через идентичные изолирован-
ные динамические цепочки.
Вычислив передаточную функ-
цию W(p) отдельной цепочки,
матричную структурную схему
многосвязной однотипной си-
стемы можно представить так,
как это показано на рис. 17. Рис. 17.
Заменив переменные с по-
мощью соотношений (43),
(44), придем к преобразованию скалярной передаточной матрицы
идентичных цепочек W(p)Ey так что ее новое значение F(p) выра-
зится:
Щр) =1-W(p) ЕР= W(p)T-*P.
31
Важно отметить, что только при использовании одинаковых
матриц преобразования для входного и выходного векторов звена
с передаточной матрицей А, т. е. при Р = Т, уравнения идентичных
.изолированных каналов не меняют своей простой формы:
Ft(p) = W(p)P-lP = W(p)E;
при этом передаточная матрица А умножается справа и слева на
взаимно обратные матрицы:
В = Р-4АР. (45)
Операция (45), осуществляемая невырожденной матрицей Р,
называется преобразованием подобия.
Таким образом, для всех векторов переменных систем следует
применять единообразную замену с одной и той же матрицей пре-
образования. Рациональный способ выбора нового базиса, а тем
/самым и преобразующей матрицы Р, указывает теория характери-
стических чисел и собственных векторов линейных алгебраических
операторов.
в) Характеристические числа и собственные векторы
Доказывается, что в пространстве векторов v, входных для
оператора А, существует такой вектор с4, что действие на него
оператора А равносильно умножению его на скаляр %i\
Aci=,XiCi, (46)
или е полной записи
«11^11 +«12^21+ ••• +alncnl = liCu; \
«21^11 + «22^21 ~4~ • • ' ~f" а2пСП\ — ^1с21» I
(47)
ап\С\\ ~1~ ап2С2\ + + апПСп2 ^1СП
Скаляр %i называется характеристическим числом
матрицы А; вектор Ci называется собственным вектором
матрицы, соответствующим характеристическому числу
Собственный вектор Ci матрицы А является решением одно-
родной системы линейных алгебраических уравнений, следующей
из (46):
(A-^iE)c1==0. (48)
Для того чтобы система (48) допускала решение, отличное от
тривиального (ci = 0), матрица А—Х\Е должна быть вырожденной,
т. е. характеристическое число является корнем так называемого
векового уравнения матрицы А:
deti(A—ЯЕ)=0,
или в полной записи
«и — X
«12
«13
• • «1П
«21
«22 ^
«23
. . а2п
«31
«32
«зз—^ •
«Зп
= 0.
(49)
«ш
«П2
«яз
• «пп — Ь
32
Вековое уравнение представляет собой алгебраическое уравне-
ние п-то порядка:
Xn + BiXn-4+ ... +ЯП=0,
где Ви Вг, ..., Вп — вещественные коэффициенты, алгебраические
функции элементов матрицы A. iB соответствии с основной теоремой
алгебры вековое уравнение матрицы имеет ровно п корней %и
А.2, ..., Яп ((среди которых могут быть кратные), вещественных или
комплексных, попарно сопряженных.
.Вырожденность матрицы ;(А—A,iE) приводит к тому, что собст-
венный вектор Ci определен системой уравнений (48) неоднознач-
но; в случае простого характеристического числа одно из уравнений
(47) является следствием остальных. Это значит, что вектор ci
определен своим направлением ^соотношениями между компонента-
ми), но не длиной, которая остается свободным параметром. Для
определения решения необходимо наложить одно дополнительное
условие ((например, задаться величиной какого-нибудь элемента).
Обычно собственные векторы нормируют по длине, наклады-
вая условие
|Ci| = УЫ2 + Ы2 + ... + Ы2 = 1.
т. е. полагая длину вектора |ci| равной единице.
Если все п характеристических чисел матрицы различны, то
каждому из них соответствует собственный вектор, так что имеется
п собственных векторов Ci, с2, с3, ..., сп. Доказывается, что все п
собственных векторов линейно независимы (ни один из собственных
векторов не может быть представлен линейной комбинацией осталь-
ных) и, следовательно, любой вектор на входе матричного звена
с оператором А может быть разложен по собственным векторам
его матрицы.
Линейной независимостью собственных векторов обеспечивается
отличие от нуля определителя (т. е. невырожденность) матрицы С,
составленной из векторов Ci, Сг, ..., сп:
С2\ С22 С23
«-1п
С2П
(50)
L. сш сп2 спг спп —!
Первый индекс д элемента матрицы cqs представляет собой
номер компоненты, второй s — номер собственного вектора cs.
г) Канонические формы и канонические базисы
квадратных матриц
При выборе в качестве нового базиса системы собственных
векторов матрицы А замена переменных определяется соотноше-
ниями
z = Cg, v = Cv,
а матрица А преобразуется в соответствии с выражением
С-*АС=Л. (51)
3—1206 33
Поскольку действие оператора на каждый из собственных век-
торов равносильно усилению с коэффициентом, равным собствен-
ному числу (ci усиливается в Xi раз, с2 — в Х2 раз и т. д.), то
матрица Л диагональна: на ее .главной диагонали стоят характе-
ристические числа матрицы А:
Г X, 0 0 ... О
Л
О х2 о
О О X,
ООО
Матрица преобразования С называется модальной мат-
рицей или матрицей канонического базиса опе-
ратора Л (матрицы А). Во многих практически важных
случаях векторы канонического базиса взаимно ортогональны, т. е.
при нормировании векторов по длине имеют место соотношения
(cj, cfe)=0, \фк\
(с,, Cj) = |cil2=l.
(52)
(53)
(54)
Канонический базис в этом случае называется ортогональным.
Обращение матрицы ортогонального базиса в соответствии с (52),
(53) сводится к замене ее строк столбцами при одновременном
переходе от комплексных величин элементов к комплексно-сопря-
женным; полученная таким образом матрица обозначается С* и
называется сопряженной по Эр ми ту по отношению
к матрице С:
С* = С-1; \
С*С=Е. /
Матрица С, обладающая свойством (54), называется уни-
тарной. При этом соотношение (51) может быть записано
в форме
С*АС = Л.
Если векторы нового базиса вещественны, то операция сопря-
жения заменяется транспонированием, т. е. заменой строк на
столбцы:
Ст = С"1; )
ОС=Е. } (55)
Важное свойство ортогонального преобразования состоит
в том, что оно сохраняет длины векторов в новом базисе:
М = 1Й.
т. е.
у г2 + 2|+... + 4= V\Ktf+ № + - +
Если Xq — комплексное характеристическое число, то компо-
ненты соответствующего собственного вектора ся — комплексные
34
числа. Для этого случая разделим комплексные сомножители
в (48) на вещественные и мнимые составляющие:
Имеем:
kq = (lq-\-i$q',
Cq = 'dq + lbq.
A(*q + ibq) = (Uq + ifiq) {SLq + tbq)
(56>
или, приравняв порознь вещественные и мнимые составляющие
(56), получим-
A2Lq = aqSLq—$qbq; (57)
Ab9 = p<7ag-f aqbq.
(58)
Соотношения (57), (58) характеризуют действие оператора Л
на вещественные векторы ая и Ъя. Нетрудно установить, что ком-
плексно-сопряженному собственному числу Xq+i = aq—L$q соответ-
ствует собственный вектор cg+i, комплексно-сопряженный по отно-
шению к cq: cg+i = a9—ibq\ анализ действия оператора Л на век-
тор Cq+i вновь приводит к соотношениям (57), (58).
Таким образом, если в матрице С заменить комплексно-сопря-
женные столбцы cq, Cq+i парой вещественных, представляющих
собой вещественную ад и мнимую части заменяемых, то с по-
мощью новой матрицы преобразования Т матрица А приводится
к виду, в котором клетка
OCq + /?q
о
о
** — ifo -
заменяется клеткой
Новую матрицу, подобную А, будем обозначать Q, так что
Q-T-iAT.
Матрица Q является вещественной канонической
формой матрицы А, матрица Т — ее вещественной модальной
матрицей; если все характеристические числа матрицы А вещест-
венны, то Q совпадает с Л, Т — с матрицей С.
Проводившиеся до сих пор рассуждения и выкладки верны
при условии, что среди характеристических чисел матрицы А нет
кратных. Если Кд — кратное характеристическое число, то усло-
вие (50) может не дать необходимого числа уравнений для опре-
деления собственных векторов матрицы А. Собственных векторов
оказывается меньше п, и базиса, составленного из них, не сущест-
вует (отметим, что хотя бы один собственный вектор, соответст-
вующий кратному характеристическому числу, существует).
В этом случае, однако, существует канонический базис, в ко-
тором матрица оператора А приобретает следующий вид: на глав-
ной диагонали расположены характеристические числа матрицы А;
кратному характеристическому числу Kq соответствуют в канони-
Z* 4 35
ческой форме Л так называемые клетки Жордана, субмат-
рицы вида
Xq 0 0 ... О
1 Xq 0 ... О
О 1 Xq . . . О
ООО
1 Xq J
Порядок клетки не превышает кратности характеристического
числа. Кратному характеристическому числу может соответство-
вать несколько клеток Жордана; сумма порядков клеток рацна
кратности характеристического числа (клетка 1-го порядка пред-
ставляет собой изолированный диагональный элемент). Описанная
каноническая форма матрицы называется Жордановой.
Двум кратным комплексно-сопряженным характеристическим
числам Xq и Xq+i=X*q соответствуют комплексно-сопряженные
клетки Жордана одинакового строения. Переход к вещественной
канонической форме принципиально осуществляется так же, как и
в случае некратных комплексных характеристических чисел; только
перенос на недиагональные места совершается уже над клетками,
а не над элементами матриц.
Например, блок клеток
заменяется блоком
+ ih о
1 0
0
1
ад + /рд
! о
0
Т
"о"
1 ад— /Рд
0
0
1 1
ад
~ aq 0
-h о -
1 ад
о _ря
•
ад " 0
- р h
1 ССд _
д) Некоторые свойства канонических форм и базисов
Как мы видели, задача нахождения характеристических чисел
матрицы, ее канонической формы и собственных векторов или век-
торов канонического базиса (полный анализ матрицы) связывается
с раскрытием определителя п-го порядка (49), решением алгебраи-
ческого уравнения я-й степени и решением системы я линейных
алгебраических уравнений. Эти вычисления для матриц невысокого
порядка (не выше четвертого) могут быть проделаны .вручную.
Методы решения полной проблемы характеристических чисел
изучаются в специальном разделе вычислительной математики
(см., например, [Л. 61, 63]).
При анализе матрицы А полезно иметь в виду некоторые важ-
ные соотношения между элементами матрицы, с одной стороны,
и ее канонической формой Л и модальной матрицей С — с другой.
36
1. Если вещественная матрица А перестановочна со своей
транспонированной Ат:
ААТ=АТА
(нормальная матрица), то она приводится к диагональной
форме преобразованием подобия унитарной матрицей С (т. е. ее
канонический базис ортогонален). К нормальным относятся сим-
метричные, кососимметричные и циркулянтные матрицы.
2. Характеристические числа симметричных матриц всегда ве-
щественны, кососимметричных — всегда мнимы.
3. Сумма характеристических чисел матрицы А равна сумме
ее диагональных элементов, называемой следом матрицы и обозна-
чаемой SpA:
п п
£ Ха = 2 ahh = Sp А.
4. Произведение характеристических чисел равно ее определи-
телю:
XiXdka... Яп == det А.
5. Среди характеристических чисел матрицы А имеются нуле-
вые в том и только в том случае, если матрица вырождена.
6. Если матрица А может быть представлена как полином от
некоторой матрицы В
A=^0B"+^1BW-1+ ... +gnE, (58а)
где go, gt, gn—скалярные коэффициенты, то характеристиче-
ские числа матрицы А являются значениями соответствующего ска-
лярного полинома, полученными в результате подстановки в (58а)
вместо В ее характеристических чисел (kj) в:
= (х*)2+я, (Wjr1+ ... + *».
Модальные матрицы для А и В совпадают:
С=СВ.
Здесь Св — модальная матрица для В.
При этом собственные векторы соответствующих друг другу
характеристических чисел %j и (Xj) в совпадают.
Полный анализ матриц для основных видов однотипных свя-
занных систем может быть выполнен на основе этих соотношений
без непосредственного проведения вычислений по формулам (48),
(49) (см. приложение).
Наконец, отметим, что относительно грубые оценки могут быть
весьма просто получены с помощью методов локализации харак-
теристических чисел матрицы в комплексной плоскости [Л. 62].
Применение некоторых оценок для исследования однотипных свя-
занных систем будет рассмотрено в § 11.
37
4. ЭКВИВАЛЕНТНАЯ СИСТЕМА АВТОМАТИЧЕСКОГО
РЕГУЛИРОВАНИЯ
а) Уравнения и структурные схемы эквивалентной системы
Проводя линейную замену переменных с помощью невырожден-
ных матриц преобразования, не зависящих от оператора дифферен-
цирования р, получаем систему дифференциальных уравнений,
эквивалентную исходной. Эквивалентность двух систем уравнений
означает, что между их решениями существует взаимно однознач-
ное соответствие, что и обусловливает возможность их взаимной
подмены при исследовании.
Замену переменных однотипной связанной САР будем рас-
сматривать на примере системы автоматического регулирования
параллельных агрегатов с коллектором на стороне нагрузки
(рис. 18) со следующими уравнениями.
Объект
у Н[Г0 (р) Е+ (р) A] u + Wf (р) Ef; (59)
регулятор
u = Wp(p)E(x-y). (60)
Выбор матрицы преобразования зависит от природы матри-
цы А, от постановки задачи исследования, от предполагаемого пу-
ти исследования. Как правило, замена переменных осуществляется
с помощью матрицы канонического базиса С, так что новое выра-
жение для вектора регулируемых переменных ц связано со ста-
рым у соотношением
У=Стг, (61)
для вектора управлений
и = С6; (62)
для вектора возмущений
f = Сф; (63)
для вектора заданий
х = Сх. (64)
В соотношениях (61) — (64) греческими буквами обозначены
значения векторов переменных системы в новых базисах.
Умножим слева обе части уравнений (59), (60) на мат-
рицу С-1 и введем формально перед векторными переменными
в правых частях сомножителем матричную единицу в форме Е =
= СС-1. Далее после несложных преобразований получим экви-
валентную систему уравнений:
H=W»{p)E+Wt{p)A]l+Wf{p)B^ (65)
— объект,
l = Wp(P)E(*-n) (66)
— регулятор.
Отметим, что полученная после перехода к новым переменным
эквивалентная система уравнений почти полностью совпадает
(с точностью до обозначений) с исходной, изменился лишь член
уравнений, содержащий матрицу А. Матричная структурная схема,
соответствующая эквивалентной системе уравнений, сохраняет
форму и передаточные функции структурной схемы исходной си-
38
#1
°fo(P)E\
У
Рис. 18.
стемы и отличается от нее лишь значением матрицы коэффициен-
тов передачи перекрестных связей (см. рис. 18). В эквивалентной
системе уравнения сепаратных каналов «объекта» и «регулятора»
сохранили свою форму и коэффициенты, т. е. эквивалентная си-
стема уравнений имеет очень удобную физическую интерпретацию:
система автоматического регулирования, аналогичная исследуемой,
но отличающаяся некоторыми характеристиками. Это дает основа-
ние сохранить за отдельными переменными и уравнениями экви-
валентной системы соответст-
вующую терминологию: регу-
лируемые величины, задания,
управления и т. д.; уравнения
объекта, регулятора, чувстви-
тельных элементов и т. д. Эту
систему регулирования будем
называть эквивалентной
в отличие от исследуемой,
оригинальной системы.
Сепаратная САР в
эквивалентной систе-
м е сохраняет в основных чер-
тах структуру сепаратной САР
оригинальной системы, что очень удобно при исследовании. В даль-
нейшем будем говорить о переменных, точках структурной схемы,
звеньях эквивалентной сепаратной системы, соответствующих анало-
гичным элементам структурной схемы сепаратной САР.
Сепаратные САР эквивалентной системы при выбранных нами
заменах переменных изолированы друг от друга (подобно тому,
как это было показано в примерах в начале главы) или связаны
между собой. Группу сепаратных САР эквивалентной системы, свя-
занных "между собой, будем называть подсистемой. Если се-
паратная САР в эквивалентной системе изолирована от других, то
она представляет собой подсистему.
Каждая из сепаратных САР эквивалентной системы соответст-
вует определенному характеристическому числу передаточной мат-
рицы взаимосвязей и его собственному вектору, играющим важную
роль в формировании свойств и характеристик эквивалентной се-
паратной системы. В дальнейшем канонический базис матрицы А
будем называть также каноническим базисом многосвязной одно-
типной системы.
Наличие связей между сепаратными системами эквивалентной
САР и их характер зависят от применяемого преобразования (С
или Т) и от формы канонической матрицы перекрестных связей.
Рассмотрим соответствующие случаи.
1. Если каноническая форма Л матрицы А диагональна:
*Х, 0 0 ... О
О Х2 О ... О
О О X, . . . О
__0 0 0 . . . Хп _
то уравнения эквивалентных объекта (65) и регулятора (66) диа-
гональны. Поэтому я-мерная оригинальная система эквивалентна
39
п изолированным сепаратным системам с одной регулируемой пе-
ременной в каждой. Уравнения эквивалентной сепаратной САР
получаются из (65), (66) заменой векторных обозначений на ска-
лярные и заменой матричных сомножителей Е и Л на скаляр-
ные 1 и Хд:
т|в=['^о(р)+Яд1Р|(р)Ед + ^/(р)фв, q=l 2, ...
h = Wp(p)(xq-«\q), Q=U 2, п.
(67)
(68)
Структурная схема эквивалентной сепаратной системы пока-
зана на рис. 19. Перекрестные связи оригинальной системы заме-
щаются в эквивалентной системе связями, замыкающимися внутри
сепаратных систем; характеристические числа Xi, Яг, ..., Хп мат-
рицы А играют роль коэффициентов усиления этих эквивалентных
связей.
2. Если каноническая форма Л матрицы А содержит клетку
Жордана с кратным характеристическим числом Xq:
Xg О О
1 Xg О
О 1 Xfl
О о
о о
о о
ООО
1 х0
то соответствующие эквивалентные сепаратные системы оказывают-
ся соединенными односторонними связями. В этом случае будем
говорить, что эквивалентная система кодиагональна.
Уравнения регулируемых каналов эквивалентного объекта
в этом случае имеют вид:
Ti^41^o(p)+Xgiri(/?)]gg+fe+^i(p)^+fe-i+^+^
Пример структурной схемы подсистемы, соответствующей клет-
ке Жордана второго порядка, показан на рис. 20.
Поскольку клетка Жорда-
на в канонической форме 'ма-
трицы — явление исключитель-
ное, то разобранный случай
имеет скорее теоретическое, чем
практическое значение.
Если среди характеристи-
ческих чисел матрицы А име-
ф« 1 ются пары комплексно-сопря-
женных, то при приведении
матрицы А к каноническому
виду мы приходим к систе-
ме уравнений с комплексными
коэффициентами. При этом для любых двух эквивалентных сепа-
ратных систем, соответствующих комплексно-сопряженным харак-
теристическим числам XQl Xq+u координаты и внешние воздействия
оказываются комплекснозначными, взаимно сопряженными. В этом
случае можно проводить исследование системы, применяя обычные
методы теории регулирования в их специальных модификациях
[Л. 4, 8, 35] к эквивалентным сепаратным САР с комплексными
40
Рис. 19.
Рис. 20.
*о(Р)
параметрами. Следует подчерк-
нуть, что в сепаратных систе-
мах с вещественными Xh функ-
ции внешних воздействий, а
следовательно, и функции вы-
ходных координат принимают
только вещественные значе-
ния.
Переход к уравнениям с
комплексными коэффициентами
оказывается выгодным именно
потому, что в этом случае эк-
вивалентная структурная схе-
ма принимает предельно про-
стой вид; переход к эквива-
лентным уравнениям * с веще-
ственными коэффициентами со-
провождается при этом возник-
новением дополнительных пе-
рекрестных связей между эк-
вивалентными сепаратными си-
стемами, а следовательно, к
значительному повышению
(удвоению) порядка исследуе-
мых уравнений.
Если по тем или иным при-
чинам переход к эквивалент-
ной системе с комплексными
параметрами оказывается не-
желательным или невозмож-
ным (например, при решении
задачи путем гмоделирования),
то, применяя замену перемен-
ных с помощью матрицы Т,
можно перейти к несколько
более сложной вещественной
эквивалентной САР. Таким об-
разом появляются еще два ва-
рианта подсистем эквивалент-
ной системы, дополняющие
рассмотренные выше.
3. В каждой из двух изо-
лированных сепаратных экви-
валентных систем, соответст-
вующих * комплексно-сопряжен-
ным характеристическим чи-
слам Xq=Mq+i$q\ Xq + i=aq—
—i$q (см. рис. 19), звенья
с коэффициентами усиления
Xq, Xq+i замещаются звеньями
с коэффициентами усиления ад,
охватываемыми прямыми антисимметричными перекрестными связя-
ми с коэффициентами усиления ±pq (рис. 21).
4. Паре клеток Жордана m-го порядка с комплексно-сопряжен-
ными характеристическими числами на главной диагонали Ял,л+1 =
%(Р)?к.
"p(PJ
Рис. 21.
41
='Ги±/0л соответствует эквивалентная подсистема, в которой две
группы по т сепаратных систем в каждой с односторонними еди-
ничными связями оказываются объединенными антисимметричными
перекрестными связями. Пример подсистемы эквивалентной САР
для т = 2 показан на рис. 22.
Первые два случая, как это следует из § 3, принципиально
исчерпывают все возможные варианты эквивалентной САР; они
являются основными и дальнейшее изложение будет опираться
главным образом на них.
Подытожим результаты.
42
Рис. 22.
Рис. 23.
Wp (р)
Переход от исходной системы уравнений в форме (59), (60)
к эквивалентной (65), (66) удобно производить, заменив матрицу
А подобной А или q и изменив обозначения переменных.
Структурную схему эк-
вивалентной системы легко
составить по матричной
структурной схеме исследуе-
мой системы, которая заме-
няется обычной по следую-
щему правилу; матричное
звено со скалярной переда-
точной матрицей заменяется
одномерным звеном с пере-
даточной функцией — сом-
ножителем Е; матричное
звено перекрестных связей
заменяется усилительным звеном с коэффициентом передачи Хд\
точки приложения внешних воздействий сохраняются; изменяются
обозначения переменных. Таким образом получаются структурные
схемы всех п сепаратные САР эквивалентной системы при q=
= 1, 2, п.
На рис. 23г—25 показаны
Wo(p) I-1 структурные схемы эквивалент-
ных сепаратных САР, соответ-
ствующие матричным струк-
турным схемам рис. 2, 4, 14.
В исключительном случае
наличия клетки Жордана вы-
сокого порядка эквивалентные
сепаратные системы соединя-
ются односторонней связью.
Антисимметричные связи меж-
ду сепаратными системами мо-
гут быть введены исследовате-
лем при желании избавиться от
необходимости работать с си-
стемами, описываемыми урав-
нениями с комплексными па-
раметрами; при этом комп-
лексный параметр Хя заменя-
ется его вещественной частью
ад, мнимая часть «д характе-
Ht ризует интенсивность действия
перекрестных связей. Восполь-
зовавшись прототипом такого
перехода между структурными
схемами рис. 17 и 19, читатель
Рис. 25. без труда воспроизведет струк-
турные схемы с антисиммет-
ричными связями для эквива-
лентных сепаратных систем рис. 23—25, соответствующих комплекс-
ным Яа.
Пример 4. Рассмотрим простейший вариант системы автомати-
ческого распределения дутья по фурмам доменной печи; описание
объекта приведено в примере 1.
*р (Р)
Рис. 24.
ft
\*11(P)*12(P)\
43
Дифференциальные уравнения объекта в операторной форме
y=№0(/?)Au+f, (69)
где у — вектор регулируемых величин (расходов); и — вектор
координат регулирующих органов; f — вектор нагрузок; А — квад-
ратная матрица коэффициентов передачи пХп не зависит от опе-
ратора дифференцирования р\ п — число фурм четное; W0(p) —
передаточная функция регулируемого канала, фурмы.
Основные особенности объекта, определяющие свойства мат-
рицы А, таковы.
Управления ии (& = 1, 2, п) влияют на распределение
дутья между фурмами (зависящее от соотношения сопротивлений
параллельных гидравлических каналов), но не влияют на общий
расход, поскольку сопротивление дроссельных заслонок мало по
сравнению с сопротивлением воздушно-га зов о го тракта доменной
печи, а общий расход дутья регулируется на воздуходувной ма-
шине. При этом синхронное движение регулирующих органов
в первом приближении не влияет на расходы на фурмах (не ме-
няются соотношения между сопротивлениями фурм и не меняется
общий расход). Следовательно, сумма элементов каждой строки
матрицы А равна нулю; введя вектор 1 с единичными компонен-
тами, запишем:
А-1 = 0-1, (70)
т. е. матрица А вырождена и ее нулевому , характеристическому
числу соответствует собственный вектор 1. Таким образом, объект
неуправляем по Р. Калману {Л. 66].
Регулируемые каналы идентичны, а интенсивность перекрест-
ных связей зависит только от взаимной удаленности фурм; по-
этому на каждой из кодиагоналей симметричной матрицы А рас-
положены равные друг другу элементы (фурмы пронумерованы
подряд по обходу печи), а циркулянтная матрица А симметрична:
- 1
ах
#2 • •
• Ял-1
ах
1
ах . .
. Дп-2
а2
а,
1 . .
• Яп-3
_ ап-\
Яп-2
. . 1
[коэффициенты передачи прямых каналов отнесены к передаточной
функции W0 (р), поэтому на главной диагонали стоят единицы].
При кольцеобразном строении объекта
ak = an-h.
Рассмотрим систему, содержащую идентичные несвязанные
регуляторы расходов воздуха через фурмы:
ti = Wp(p)E(y-x). (71)
Здесь Wv (/?) — скалярная передаточная функция регулятора.
Структурная схема системы показана на рис. 26.
Структурную схему эквивалентной сепаратной системы полу-
чаем из матричной структурной схемы рис. 26 'заменой матричных
44
звеньев с передаточными матрицами W0(p)k и Wv(p)E — одномер-
ными звеньями с передаточными функциями соответственно
XkWo(p), Wv(p)\ векторные связи между звеньями заменяются
одномерными, обозначения векторов у, х, f — обозначениями ска-
лярных переменных г\к, хл, ерь;
всего эквивалентных одномер-
ных систем п (&=1, 2,..п).
Эквивалентная сепаратная САР
отличается от сепаратной САР
расхода на фурме коэффициен-
том усиления в разомкнутом
состоянии, равным Хь, (рис.27).
Так как матрица А симме-
трична, то ее характеристиче-
ские числа Яг, ..., Яп веще-
ственны. Характеристические
числа циркуляптной матрицы А при известных ah могут быть под-
считаны по формуле
Рис. 26.
ah cos 2п
Ь(Я-1)
'л/2»
полученной из формулы (iTI-28) приложения при четном п. Из этой
формулы и из (70) непосредственно следует, что нулевое характе-
ристическое число A,i=0 единственное (только взятые с единичны-
ми весами коэффициенты к —
= 1, 2, п—1 в сумме дают—1).
Уже по результатам построе-
ния эквивалентной системы можно
сделать определенные выводы от-
носительно свойств системы.
При Xi=0 (т. е. из-за неуц-
равляемости объекта) соответст-
вующая эквивалентная сепарат-
ная система разомкнута вне зави-
симости от параметров W?(p) и
сепаратный регулятор не оказывает
управляющего воздействия на регулируемую координату r]i —сред-
нее значение расходов:
Рис. 27.
при этом координата регулирующего органа |i в сильной степени
зависит от усредненного расхода, а при применении астатических
регуляторов разомкнутая система нейтральна (не может быть сде-
лана асимптотически устойчивой). Эти обстоятельства приводят
к необходимости уточнить требования к системе (см. пример 7
в § 5).
б) Переменные эквивалентной системы
Рассмотрим соотношения, связывающие между собой функции
внешних сигналов и основные характеристики эквивалентной и ис-
следуемой систем. Эти соотношения в общем случае используются
45
при переходе к эквивалентной системе и при пересчете резулыатов
исследования эквивалентной системы для мпогосвязной однотип-
ной. Правда, во многих случаях, как это показано в последующих
главах, пересчетов на основе приводимых здесь соотношений уда-
ется избежать.
Соответствие между векторными функциями сигналов в каж-
дый момент времени / определяется соотношениями перехода
к новым координатам (61) — (64). Если, например, вектор возму-
щения f задан как детерминированная функция времени f(/)> то
в эквивалентной системе действует вектор возм\щения ср (t)i
ф(/) = с-'р(0-
Если задано начальное значение вектора регулируемых вели-
чин у(0), то соответствующее начальное значение вектора регули-
руемых величин в эквивалентной системе
i|(0) = C-'y(0)
и т. д.
Найдем соотношения между характеристиками стационарных
случайных процессов в исследуемой и эквивалентной системах.
Пусть, например, i(t) и у(0 — случайные стационарные фупк-
• ции времени; матрица корреляционных функций этой пары векто.-
ров R/y(t)—математическое ожидание произведения f(0yT(' + T)
(где индекс т наверху означает транспонирование, т — сдвиг во
времени) задана:
R,y W = A4{t(t)y*(t + z)} =
т
= lim If (О Ут + т) dt,
—Т
где М{-} — символ математического ожидания (равенство среднего
по ансамблю среднему по времени здесь является следствием ста-
ционарности процессов).
Матрица корреляционных функций соответствующих векторов
эквивалентной системы имеет вид:
*п М = Л{Ф(о л*+ =
т
= lim -туг- \ ф (0 if (t + dz.
—Г
Символ сопряжения по Эрмиту (звездочка наверху) векторов в
выражениях для матрицы корреляционных функций R (х) появляется
благодаря тому, что, возможно, переменные эквивалентной систе-
мы — комплекснозначные случайные функции времени; если экви-
валентная система вещественна, то звездочка заменяется символом
транспонирования. Заменяя переменные в выражении для (*)
в соответствии с (61), (63) и вынося постоянные множители за
46
символ математического ожидания (сохраняя при этом порядок
сомножителей!), получаем:
Яп <х) = м if (о ч* с + х)> = м <с! ^у1 с + с*> =
= С М {f (0 Г (f + х)} С* = CR,„ (х) С*,
т. е.
R„(t) = CRft,(x)C\ (72)
Обратный переход совершается по формулам вида
R,,(t)=C-«R„(t)(<>)-«.
Точно так же совершается переход для матриц корреляцион-
ных функций любой пары векторов, в том числе и для автокорре-
ляционной матрицы вектора, например, R//(t).
Перейдем к спектральным характеристикам сигналов. Матри-
ца .взаимных спектральных плотностей S/y(&g>) пары векторов f, у
определяется как преобразование Фурье соответствующей матрицы
корреляционных функций, так что
00
Sft (/«) = F {Riy (г)} = J e-*«Rft, W dx,
—00
здесь F{*} — символ преобразования Фурье, как обычно означает,
что преобразование Фурье совершается над каждым элементом
преобразуемой матрицы и полученные функции занимают соответ-
ствующие клетки матрицы-преобразования. Применяя преобразова-
ние Фурье к обеим частям (72), получаем:
F {R„ W> = F {CR,« (x) С*} = CF {Я,у (x)} С*
или
Sn (j») = CS/V (iw) С*
sft(to) = c-«sf4(ic.)(c')-».
Если канонический базис системы ортогонален, то соответст-
вующие друг другу матрицы корреляционных функций и функций
спектральной плотности исследуемой и эквивалентной систем свя-
заны друг с другом соотношением подобия
S„ (/<o) = CS^(/a>) С-*;
r^ W = cr/wwc-«.
Если компоненты вектора внешнего воздействия f (или х)
статистически независимы и характеризуются одинаковыми авто-
корреляционными функциями, то соответствующие матрицы функ-
ций статистических характеристик скалярны:
r//(t)=*(t)e;
S//(tco) =S(m)E,
где R(r), S (/о) — соответственно автокорреляционная функция и
функция спектральной плотности отдельного входного воздействия.
47
При переходе к эквивалентной системе с помощью ортогональ-
ного преобразования скалярные матрицы функций статистических
характеристик случайных процессов остаются неизменными:
8W (/») = Sf/(/©) = S(») Е;
В общем случае переход к эвивалентной системе проводится
в два этапа: 1) получение уравнений (или структурной схемы)
эквивалентной системы; 2) вычисление функций или характеристик
внешних воздействий.
Отметим, что если для построения структурной схемы экви-
валентной САР необходимо вычисление лишь канонической формы
матрицы Л (т. е. нужно знать характеристические числа матрицы
и знать порядки клеток Жордана, соответствующих кратным ха-
рактеристическим числам), то задача вычисления начальных зна-
чений, функций внешних воздействий и их характеристик связы-
вается с вычислением матрицы канонического базиса С, т. е. с пол-
ным анализом матрицы А.
в) Характеристики вход-выход
Характеристики вход-выход эквивалентной системы — времен-
ные, частотные характеристики или передаточные функции — удоб-
но получать непосредственно на математической модели эквива-
лентной системы. Для анализа однотипной связанной системы как
многомерной САР удобно иметь соотношения между характери-
стиками системы, записанные в матричной форме; к выводу этих
соотношений и переходим.
Пусть на входе системы, находящейся в покое, в момент вре-
мени /=0 возникает векторное возмущение f(/) [f(0=0 для
Тогда выходная векторная функция связана с входной интегралом
Дюамеля
00
у(/) = jB(M*('-'i)««i. (73)
О
где В(/)—матрица весовых (импульсных переходных) функций
системы. Как обычно, запись в правой части (73) означает, что
интеграл берется от каждого элемента вектора — произведения
В (/i)f —/i); результат интегрирования является соответствующим
элементом вектора у(/), так что
п 00
/=ioJ
Физический смысл элемента bi$(t) f-й строки и /-го столбца
матрицы В(0: импульсная переходная функция по каналу от /-го
входа системы к i-му выходу.
Применяя, как обычно, для интеграла свертки символ %, запи-
шем (73) в виде
У (О В (0* 1(0- (74)
48
После умножения слева на матрицу С и несложных преобразо-
ваний получим вместо (74) формулу, описывающую этот динами-
ческий процесс в эквивалентной системе:
с-у (Q - с - • [в (0 с * с- »| (0] = [с- >в (/) с] * [С- ■? (0]
или
i| (0 = г (0 *»(*)•
Здесь матрица весовых функций T(t) эквивалентной системы
связана с В(£) соотношением
сгсос-1 = в (0.
Итак, при переходе к эквивалентной системе матрица весовых
функций системы испытывает преобразование подобия, характери-
зуемое матрицей С.
Соответственно имеем:
с^в (ос = г(*).
Аналогичным образом связаны между собой матрицы переход-
ных функций (откликов на единичные ступенчатые возмущения)
оригинальной Bi (t) и эквивалентной Tt (t) систем:
СГ, (О С-1 = Bj (*); 1\ (0 = С- 1В1 (О С.
Запишем дифференциальные уравнения системы в виде
y«)-B(p)f(0; (75)
здесь В(р)—передаточная матрица системы. Элемент bqj(p) мат-
рицы представляет собой передаточную функцию по каналу от /-го
входа к <7-му выходу.
После умножения обеих частей (75) слева на С и преобразо-
ваний получим:
t|W = CBC-4(0 = r(p)q>(0,
гдеГ(/?)— передаточная матрица эквивалентной системы. Таким
образом,
СГ (/>)€-* = В (/>); Г(/>) = С-*В(/>)С.
т. е. передаточные матрицы эквивалентных систем связаны соотно-
шением подобия.
Если вход f(t) преобразуем по Фурье, то, совершив подста-
новку p—ixd, получим вместо (75):
у (/со) = В (/со) f (/со)
и
Tj(/co) = r(/co)<p(/co);
СГ (/со) С-1 = В (/со); Г (/со) = С- *В (/со) С.
Здесь у (/со), f(/co), т| (/со), ф (/со) — изображения по Фурьк
функций времени, В (/со), Г (/со)—матрицы частотных характеристи
Отметим, что если Л диагональна, то эквивалентные сепаратны©
системы изолированы, а Т (t), Г, (t), Г (р) и Г (/со) диагональны и
при этом связаны с матрицами В (t), Bt (t), В (р) и В (/со) соотноше-
нием подобия.
4—1206 49
Поэтому матрицы весовых функций, переходных функций, перс-
даточных функций и частотных характеристик эквивалентной си-
стемы, полученные преобразованием подобия соответствующих
матриц оригинальной системы, являются каноническими формами,
а их диагональные элементы — характеристическими числами этих
матриц при каждом значении своего аргумента; матрицей канони-
ческого базиса является одна и та же постоянная матрица С—мат-
рица канонического базиса системы.
Если матрица Л содержит клетки Жордана, то соответствующие
клетки матриц Г(/,) Г (р), Г (ю) треугольны, поскольку в пределах
подсистемы с односторонними связями воздействия распространя-
ются от каждой из сепаратных САР на все остальные с более
высоким номером. Диагональные элементы матриц по-прежнему
являются характеристическими числами соответствующих матриц
исследуемой системы при каждом значении их аргумента. Сказан-
ное выше о канонических формах и о канонических базисах мат-
риц для случая диагональной Л здесь уже недействительно, что
в ряде случаев затрудняет анализ системы при наличии клеток
Жордана.
г) Оригинальная и эквивалентная системы
Эквивалентная система представляет собой лишь некоторое
абстрактное построение, тем не менее ее «работу» можно обнару-
жить на самой многосвязной однотипной системе, например на
основе следующих рассуждений.
а) 6)
Рис. 28.
Выделим на структурной схеме системы звено с передаточной
матрицей А, охватываемое через систему векторной обратной
связью с передаточной матрицей W(p)E (рис. 28,а). Пусть на вхо-
де звена перекрестных связей действует векторный сигнал z(t);
разложим вектор z(t) по векторам канонического базиса матри-
цы А:
z(i)=Ci(0ci + E2(f)c2+ ... Hn(t)cn.
Каждый из членов разложения Zq(t)cq представляет состав-
ляющие в сигналах сепаратных систем, ординаты которых в каж-
дый момент времени относятся между собой как компоненты соб-
ственного вектора cq:
FZq (t) С1Ч
(t)Cq:
50
Kq (t) C2q
LZq(t)Cnq J
На каждую из переменных Z,q оператор Л действует как одно-
мерное усилительное звено с коэффициентом усиления, равным
соответствующему характеристическому числу:
или
vq(t)=KZq(t).
Каждая из составляющих £д(0< представленная в сепаратных
системах £g(Oci^ £д(0с2<?, tq(t)cnq (<7=1, 2 п), преоб-
разуется в сепаратной системе в соответствии с общей передаточ-
ной функцией идентичных динамических цепочек W(p) и прини-
мает вид:
L,q(t)cjq = W(p)vq(t)cjq^ /=1, 2, и; 17=1, 2, .... л.
В результате на входе звена с передаточной матрицей А
имеем составляющую ~'(t) векторного сигнала £>(t):
Z'(t)cq = W(p)v(t)cq.
Таким образом, результат действия вектора £q(t)cq на входе
звена с передаточной матрицей А после прохождения сигнала по
замкнутому контуру — векторная функция времени с тем же са-
мым соотношением между компонентами, что и у исходного век-
тора. Всего векторов £q(t)cq ровно /г, (<7=1, 2, п) они линейно
независимы; это означает, что любая входная векторная функция
времени может быть представлена как сумма составляющих, кол-
линеарных собственным векторам оператора (разложение по соб-
ственным векторам). В соответствии с принципом суперпозиции
результат действия каждой из составляющих может наблюдаться
независимо от действия остальных.
Физически это, означает следующее. Пусть в исследуемой си-
стеме измеряются все входные сигналы и выходные координаты.
Тогда могут быть замерены и их линейные комбинации, являющие-
ся входными сигналами и выходными координатами сепаратных
эквивалентных систем в соответствии с (61) — (64), т. е. например:
Л^=(С-1)мг/1+(С-1)й2«/2+ s.. +(C-*b»j/n. (76)
Здесь (C-1)feS — элемент матрицы С-1. В случае ортогонально-
сти канонического базиса системы коэффициенты соотношения (76)*
представляют собой элементы столбцов матрицы С.
Если среди характеристических чисел матрицы перекрестных
связей имеются пары комплексно-сопряженных, то элементы матриц
С, О1 — комплексные. При этом измерению подлежат отдельно Bej
щественные и мнимые составляющие переменных эквивалентной
системы:
Re тк = (Re c-*)k,0i + (Re C-*)hty% + ... + (Re C~*)hnyn;
Im ты = (Im С-')К1*л + (Im C-*)Myt + ... + (Im C-*)hnyn,
где Re — символ вещественной части; Im — символ мнимой части;
Полученные таким образом реализации не будут отличаться
от реализации в эквивалентной системе при действии на входах со-
ответствующих линейных комбинаций входных сигналов исследуе-
мой системы.
4*
51
Рис. 29.
Следовательно, дело обстоит так, как если бы в исследуемой
системе действовали п не зависящих друг от друга, эквивалентных
сепаратных САР. Это явление было отмечено впервые В. Т. Моро-
зовским для простых симметричных систем {Л. 7].
Аналогичным образом раскрывается смысл и перекрестных свя-
зей между сепаратными САР в эквивалентной системе для случаев
комплексных характеристических чисел матрицы А и наличия Жор-
дановых клеток в канонической форме Л.
Пример 5. Система со структурной схемой рис. 29,а описывает-
ся следующими уравнениями:
объект
1 _о,25 —0,1 0 т
А =
—0,25 1 -0,25 —0,1
—0,1 —0,25 1 —0,25
0 —0,1 —0,25 1
регуляторы
и= (о,384
Анализ матрицы А дает:
Г0,504 0
0,135
х).
0,93
0
0
0 0 '
о о
1,25 0
0 1,32
52
Структурная схема эквивалентной системы показана на рис.
29,6; переходные процессы в эквивалентных сепаратных системах
по выходным координатам *)k(t) и по управлениям £ь(0> вызван-
ные единичными ступенчатыми возмущениями фл(0» показаны на
рис. 30.
Рис. за
Следующий эксперимент демонстрирует связь динамики ориги-
нальной и эквивалентной систем. В модели САР наносились скач-
кообразные возмущения одновременно на идентичные входы сепа-
ратных систем; амплитуды возмущений относились между собой
как компоненты собственных векторов матрицы А. При этом в САР
возбуждались лишь движения, моделируемые соответствующей экви-
валентной сепаратной САР (рис. 31): переходные процессы по каж-
дой из регулируемых координат отличаются от переходного про-
цесса но регулируемой величине эквивалентной сепаратной САР
(рис. 31) только ординатами; при этом ординаты переходных про-
цессов в сепаратных системах относятся между собой как компо-
ненты соответствующего собственного вектора, т. е. как амплитуды
возмущений.
На рис. 32,-а—в показаны переходные процессы по регулируемым
величинам при поступлении на вход f (см. рис. 29) скачкообразного
возмущения, характеризуемого вектором
53
6)
Рис. 32.
54
На том же рисунке показаны результаты измерений на модели
САР регулируемых переменных эквивалентной системы в соответ-
ствии с (76):
т] 4 = 0,406 f/t+0,58 г/2+0,58 г/3+0,406 г/4;
Таким образом, наблюдаются переменные эквивалентной систе-
мы. В системе нанесено ступенчатое возмущение, характеризуемое
вектором «произвольного направления»; при этом возбуждены все
четыре эквивалентные сепаратные системы. Переходный процесс
в каждой из них четко прослеживается путем соответствующих из-
мерений.
Сопоставление осциллограмм соответствующих друг другу про-
цессов: в эквивалентной системе (см. рис. 30); в многосвязной си-
стеме при возбуждении переходных процессов, соответствующих
только одному из характеристических чисел (т. е. одной из эквива-
лентных сепаратных систем, см. рис. 31), а также составляющих,
соответствующих эквивалентным сепаратным САР при произвольном
векторе возмущения (см. рис. 32), дает представление о связи меж-
ду свойствами оригинальной и эквивалентной систем.
5. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ В ВАЖНЕЙШИХ СЛУЧАЯХ
Рассмотрим переход к эквивалентным системам для важней-
ших видов однотипных связанных систем, матрицы связей которых
относительно просто поддаются анализу; анализ матриц читатель
найдет в приложении.
Анализ матрицы простых симметричных систем
г]2=0,643 г/1 + 0,302 £/2—0,302 у г—0,643 #4;
т]3=0,58 f/i—0,406 г/2—0,406 г/з+0,58 г/4;
г)4 = 0,302 г/1—0,643 г/2 + 0,643 г/3—0,302 yit
а) Простые симметричные системы
А =
Га b Ь.
I b а Ь.
I b b а.
;!1
(77)
b b b
а
дает следующие результаты (см. приложение):
Л =
гл+(л- 1)6
а
0 0
— 6 0
0 л —6
0
о
о
a— b
55
с =
1 1
1
V~n Vn(n-
1 1
■1)
-1)(л
1
-2)
Уп Vn(n-
1 1
.1)
Vin
-\)(n-
1
-2)
Vn Vn(n —
1)
V(n
-l)(n-
-2)
n
0
1
1
о
(78)
0
Характеристические числа матрицы А принимают только два
значения:
^i=a+ (п— \)Ь\
Несмотря на высокую кратность характеристического числа
Яг— ... =Хп каноническая форма Л матрицы А диагональна
вследствие симметричности А. При этом, как отмечалось, собствен-
ные векторы, соответствующие кратному характеристическому чис-
лу, определены неоднозначно; следовательно, в выборе формы за-
мен переменных может быть допущен некоторый произвол. Экви-
валентная система представляется двумя структурными схемами.
Первая из них определяется характеристическим числом %i=a+
+ (n—l)b и соответствует системе усредненных координат [Л. 7];
вторая — кратным характеристическим числом ta=ta= ... =ЯП =
=а—Ь и соответствует системе относительных координат.
Следует уточнить, что число систем относительных координат
составляет п—1; структурные схемы их совпадают (что дает осно-
вание во многих случаях не различать их при исследовании), однако
характеристики функций внешних воздействий могут различаться.
Структурные схемы эквивалентных сепаратных САР для случая
простой симметричной системы со структурной схемой рис. 4 пока-
заны на рис. 14.
«Выделяют два важных частных случая матрицы взаимосвязей
простых симметричных систем [Л. 7]. При а—Ъ взаимосвязи назы-
ваются усредняющими. Непосредственно видно, что действие
усредняющих связей в системе относительных координат не отра-
жается (Я2=Яз= ... =Я»=0, коэффициент передачи замещающей
связи в каждой сепаратной системе относительных координат ра-
вен нулю) и структурная схема сепаратной эквивалентной системы
относительных координат совпадает со структурной схемой изолиро-
ванной сепаратной оригинальной системы. В системе усредненных
координат действие связи, замещающей перекрестную, оказывается
усиленным в п раз (Xi=nb).
Второй важный случай матрицы взаимосвязей имеет место при
а=—(п—\)Ь. Перекрестные связи в этом случае называются син-
хронизирующими. Действие синхронизирующих перекрестных
связей сказывается только на системе относительных координат
(А,2=Лз= ... =А,п=—я); структурная схема системы усредненных
56
координат совпадает со структурной схемой сепаратной системы
(Xi = 0).
Отметим, что способ определения относительных координат,
соответствующий матрице С (78), отличается от обычно применяе-
мого. Обычно относительные координаты вводятся с помощью про-
стейших соотношений, удовлетворяющих условию равенства нулю
суммы коэффициентов линейной формы в правой части формул
перехода [Л. 7] (пример рассматривался в § 3). В самом деле, для
координаты у формулы перехода определяются столбцами матрицы
С и имеют вид:
7)2 = Уп(/2—1) ^ + У2+ — + Уп'1 — 0*15
1
7,3 = |^(/г_ 1) (лг—2У [Ух + У* + + Уп~2 ~~ (/г"2) ^n"l];
■ toi—02).
(79)
Аналогичным образом должны выглядеть формулы перехода
для всех остальных координат системы. Указанное различие в спосо-
бах вычисления относительных координат определяется постановкой
задачи. Легко показать (и читатель может убедиться в этом
утверждении самостоятельно), что матрицы перехода, соответст-
вующие применявшимся в литературе правилам {Л. 7, 10] (см. так-
же § 3), не подчинены условию ортогональности. Условие ортого-
нальности в общем случае облегчает вычисление показателей каче-
ства регулирования исследуемой системы, поскольку при пересчетах
не возникает необходимости вычисления матрицы С-1 (напомним,
что С-!-Ст).
Во многих практически важных случаях вполне достаточно
ограничиться более простыми соотношениями (27), (30) между пе-
ременными исследуемой и эквивалентной систем (этого вопроса мы
еще коснемся в начале § 6).
б) Двухканальные системы с антисимметричными
перекрестными связями
Для матрицы перекрестных связей
*-[-?!]
о
1
имеем (см. приложение):
— 0 1
С =
V2
LW1
1
1
V2
57
Эквивалентные сепаратные системы наследуют от сепаратной
САР оригинальной системы уравнения и характеристики основных
каналов. Передаточные функции перекрестных связей в эквивалент-
ных сепаратных системах приобретают множители ±i (см. рис. 15).
Комплекснозначные координаты эквивалентной системы и функ-
ции внешних воздействий связаны с координатами системы соотно-
шениями, определяемыми матрицей С:
1
Y2
1
Ъ =-77т" (Ух—1У2)'>
' (fx + iftY.
VI
1
»eTT(fl~"/fe)
(80)
и т. д. Таким образом, как комплекснозначные функции внешних
воздействий, так и комплексные коэффициенты передаточных функ-
ций двух сепаратных систем взаимно сопряжены. Это приводит
к взаимной сопряженности комплекснозначных решений дифферен-
циальных уравнений, и при исследовании оказывается достаточным
рассмотреть одну из двух сепаратных систем.
Переход к уравнениям с комплексными коэффициентами сопро-
вождается потерей свойств симметрии нулей и полюсов передаточ-
ной функции относительно вещественной оси плоскости корней, сим-
метрии амплитудно-фазовых характеристик и годографа Михайлова
относительно вещественной оси и т. д.; поэтому приходится иссле-
довать расположение нулей и полюсов во всей плоскости, частот-
ные характеристики — во всем диапазоне частот (а не только по-
ложительных) и т. д. Объем исследования примерно удваивается
по сравнению с таковым для системы с вещественными парамет-
рами.
Следует обратить внимание на смысл вещественной и мнимой
составляющих комплексной координаты эквивалентной сепаратной
системы: это соответствующие координаты первого и второго кана-
лов оригинальной системы. Эта мнемоническая связь облегчает ин-
терпретацию результатов исследования или расчета. Аналогичным
образом мнимая единица служит «коэффициентом усиления» пере-
крестных каналов, параметры передаточных функций ^звеньев сепа-
ратных систем — вещественны. Поэтому если после преобразований
структурную схему двухканальной системы удалось представить
соединением звеньев с такими передаточными функциями, что мни-
мая единица фигурирует только в некоторых коэффициентах уси-
ления, то интерпретация результата для оригинальной системы
оказывается очень простой. Звенья с вещественными коэффициента-
ми усиления непосредственно переходят в прямые каналы; звенья
с мнимой единицей в качестве коэффициента усиления переходят
в перекрестные связи.
58
в) Системы с общей связью
Матрица общей связи
ё2*>1 g2b2 . . • g*bn
enbi gnb* • . . gnK
имеет только одно характеристическое число, отличное от нуля:
Х\ —Х2= ... —Хп—i = 0;
К = 2 ghbh
тор
Характеристическому .числу Хп соответствует собственный век-
~gi ~
g2
Lgn j
остальные собственные векторы ортогонапьны вектору
Ьг
т. е. удовлетворяют соотношению
Ь2
(Cq, Ь) = 2 Cjqbj = о, q = 1, 2,
/=1
.. ./1 — 1.
В эквивалентной системе общая связь представлена только в
одной п-й сепаратной САР; ее коэффициент передачи по сравнению
п
со связью в исследуемой системе увеличен в^] ghbh раз. Важно под-
бит 1
черкнуть, что было бы ошибочным переносить общую связь во все
остальные сепаратные системы с нулевым коэффициентом усиления
в соответствии с общим правилом перехода к эквивалентной САР.
Дело в том, что общая связь в исследуемой системе представляет
собой одну динамическую цепочку, а не п, как в других примерах.
Правило сохранения эквивалентной системой уравнений порядка
59
исходной приводит нас к выводу, что в эквивалентной САР такая
динамическая цепочка должна быть одна. Вырожденность переда-
точной матрицы взаимосвязей при ранге г = \ (только миноры пер-
вого порядка определителя матрицы отличны от нуля, любой минор
высшего порядка равен нулю) является органическим проявлением
этого обстоятельства: при вариациях параметров системы это свой-
ство матрицы сохраняется.
В то же время в общем случае вырожденность матрицы взаи-
мосвязей и наличие нулевых среди ее характеристических чисел
не означает, что в соответствующих эквивалентных сепаратных си-
стемах не представлены звенья перекрестных связей. При состав-
лении эквивалентной структурной схемы необходимо иметь в виду
правило сохранения порядка уравнений, и при наличии в системе п
динамических цепочек в каждой из эквивалентных сепаратных си-
стем должно быть представлено звено перекрестных связей хотя бы
с нулевыми коэффициентами передачи (связь разомкнута, см. при-
мер 3).
Примером общей связи могут служить корректоры частоты и
напряжения бортовых электроэнергетических систем, состоящих из
идентичных генераторов [Л. 7]. При условиях одинаковых взаимо-
действий со стороны каждого из генераторов на режим электро-
энергетической сети (bi — bz= ... =bn = l) и одинаковых воздейст-
вий корректоров на каждую из сепаратных систем (gi=g2=.. •
...=gn = l) имеем дело с простой симметричной системой, в которой
все взаимосвязи — одинаковы, aqj=l при всех q, /. В эквивалентной
системе звенья корректоров представлены только в сепаратной си-
стеме усредненных координат [Л. 7].
г) Переход к эквивалентной системе в общем случае
До сих пор предполагалось, что в структурной схеме исследуе-
мой системы имеется лишь одно звено перекрестных связей с пере-
даточной матрицей А, при этом остальная часть системы представ-
ляет собой изолированные идентичные динамические цепи. Может
ли прием линейных замен привести к построению простой, развя-
занной эквивалентной системы в более общем случае, когда струк-
турная схема с несколькими звеньями перекрестных связей не при-
водится к виду только с одним таким матричным звеном?
Очевидно, что если канонические базисы разных передаточных
матриц совпадают, то при соответствующих заменах переменных
матрицы одновременно приводятся к каноническим формам. Как и
ранее, многосвязная система оказывается эквивалентной простой си-
стеме с изолированными каналами.
Критерием возможности перехода к эквивалентной системе
в общем случае может служить перестановочность передаточных
матриц различных звеньев перекрестных связей. В соответствии
с теоремой линейной алгебры перестановочность матриц является
необходимым и достаточным условием для того, чтобы канонические
базисы матриц совпадали. Каждая из эквивалентных сепаратных
систем в таком случае отвечает конкретному вектору общего кано-
нического базиса; соответствующие собственные числа различных
матриц играют в ней роль коэффициентов передачи звеньев, заме-
щающих перекрестные связи.
Укажем некоторые практически важные случаи, когда оказы-
вается возможным применение сформулированных положений:
60
1. Передаточные матрицы перекрестных связей совпадают. С та-
ким случаем встречаемся при исследовании двухканальных систем
с антисимметричными перекрестными связями. Как показано
в (Л. -4, 12, 35], линейная замена переменных приводит к расчлене-
нию системы при произвольном расположении в системе любого
числа матричных звеньев антисимметричных перекрестных связей.
2. Матрицы коэффициентов передачи отличаются друг от друга
слагаемыми вида кЕ, где k — скалярный множитель. Канонические
базисы таких матриц, как известно, совпадают. Так обстоит дело
в случае однотипных систем с простыми симметричными перекрест-
ными связями, где матрицы могут входить в систему уравнений
с разными соотношениями между параметрами а и Ь матриц.
В обоих случаях переход к эквивалентной системе совершается
беспрепятственно в соответствии с рассматривавшимися правилами.
3. Если среди характеристических чисел матрицы А имеются
кратные, а ее каноническая форма — диагональна, то имеется не-
который произвол в выборе канонического базиса матрицы. Пусть,
например, найдены т собственных векторов, соответствующих крат-
ному характеристическому числу; тогда любой вектор, представляю-
щий их линейную комбинацию, может быть принят в качестве соб-
ственного, т. е. вектора канонического базиса [Л. 59]. Со случаем
кратных характеристических чисел матрицы сталкиваемся при изу-
чении однотипных систем с простыми симметричными взаимосвязями.
Если на структурной схеме системы кроме простой симметричной
матрицы вида (77) имеется матрица коэффициентов передачи Аг
иной структуры, то для успешного перехода к эквивалентной си-
стеме достаточно выполнить следующие условия: матрица Аг долж-
на обладать вещественным характеристическим числом с соответст-
вующим собственным вектором 1 (с единичными компонентами);
любой другой ее собственный вектор должен быть ортогонален век-
тору 1:
п
Ф=Е'.* = 0. (81)
Тогда, выбрав в качестве матрицы перехода к новым перемен-
ным матрицу канонического базиса оператора А2, приходим к экви-
валентной системе уравнений, в которой матрицы А и А2 заменены
их каноническими формами.
В некоторых случаях многосвязная однотипная САР может
представлять собой часть системы более крупных размеров. «Ос-
тальную» часть этой многосвязной системы условно назовем «внеш-
ней частью системы» и рассмотрим условия, при которых прием
перехода к эквивалентной системе может быть проведен беспрепят-
ственно. Итак, пусть между однотипными связанными системами и
«внешней частью системы» действует взаимная векторная связь
(рис. 33,а). Пусть воздействие со стороны системы на внешнюю ее
часть и обратное воздействие коллинеарны одному из собственных
векторов матрицы А (коэффициенты передачи по каждой из ком-
понент вектора воздействия пропорциональны компонентам собст-
венного вектора матрицы А). Тогда в эквивалентной системе взаи-
модействие существует лишь между одной из изолированных сепа-
ратных САР и «внешней частью системы» (рис. 33,6). Если указан-
ному условию подчиняется лишь один из двух векторов взаимодей-
ствий, то между внешней частью и другими сепаратными системами
61
возможны односторонние связи. Следует подчеркнуть, что указанное
свойство векторов очень часто вовсе не является случайным явлени-
ем, а определяется физикой процессов в элементах систем, объеди-
няющих сепаратные САР.
Внешняя часть
системы
Внешняя часть
системы
I
г-&>
Рис. 33.
Пример 6. Построим структурную схему эквивалентной систе-
мы для трехканальной САР из примера 2 [Л. 38]. Структурная схе-
ма и матричная структурная схема системы приведены на рис. 10,а
и б.
Характеристические числа матрицы J в соответствии с формулой
(П-24) приложения при я = 3:
\ч = е ' , q= 1, 2,3.
Для обратной ей (с точностью до знака) матрицы JT=—J"1
найдем характеристические числа
"* = — е 3 , </= 1,2,3.
№ = — К
Взаимно обратным характеристическим числам взаимно обрат-
ных матриц соответствуют одни и те же собственные векторы; сле-
довательно, jig и Хд должны фигурировать в структурной схеме
одной и той же "эквивалентной сепаратной схемы (рис.34).
Проведем теперь упрощение полученной структурной схемы, ис-
пользовав для этой цели прием перехода к эквивалентной системе.
Выделим в эквивалентной сепаратной системе ее двухканальную
Я* 1,2,3
62
Рис. 34.
часть (рис. 35,а); перекрестные связи между каналами характери-
зуются матрицей комплексных коэффициентов усиления
f при а = 2к ^ ) с характеристическими числами v, и v2:
Vi,2=±t.
Таким образом, эквивалентное звено двухканальной части
имеет вид рис. 35,6; вычисление передаточной функции всей цепочки
дает:
1 1
F (р) = (cos у + i sin ?) 1 _ ik
— [*2 + ikx]
при
1 +k:
0 = cp+arctg kv> &i = sin0, A!2 = cos0
(см. структурную схему на рис. 35,в). Очевидно, вещественная часть
F(p) представляет собой передаточные функции прямых каналов
двухканального звена, мнимая часть отражает действие перекрест-
ных связей; в передаточных функциях перекрестных связей мнимая
tisinp
—I |—-'"р
I 1
coscp
Н8>—н&н- /
б)
1
г)
Рис. 35.
часть F(p) должна стоять сомножителем при коэффициенте усиле-
ния ±_е±1Л (рис. 35,г) [но не в звеньях антисимметричных пере-
крестных связей (§ 5, п. «б»), поскольку переход к структурной схе-
ме на рис. 30,6 был совершен от системы с матрицей коэффициентов
передачи (81), но не от антисимметричной].
63
Теперь, имея в виду положение двухканальной части в струк-
турной схеме (рис. 34), легко вычислим передаточную функцию ра-
зомкнутой эквивалентной сепаратной системы:
2
^Раз (Р) = 2 Icos 9 + 1 sin а sin 0] W (Р)'
1 +
Пример 7. Неуправляемость объекта в системе автоматического
распределения дутья по фурмам доменной печи (см. пример 4) при-
водит к необходимости уточнить требования к системам и приме-
нить специальные меры для стабилизации эквивалентной сепарат-
ной системы усредненных координат. К системе предъявляются два
основных требования:
1. Система должна обеспечить заданное распределение дутья
по фурмам доменной печи, характеризуемое отклонениями расходов
от среднего значения у+:
0+ = ^-J]^; (82)
вектор распределения вводится с помощью соотношения
y_=y-i/+l. (83)
2. Гидравлическое сопротивление регулирующих органов долж-
но быть минимальным, т. е. по меньшей мере одна из заслонок
должна быть полностью открыта. Практически для регулирующего
органа с наибольшей степенью открытия заданным устанавливают
положение v, близкое к полному открытию:
макс. uh = v> к — 1, 2, ..., п.
k
Для выполнения второго требования в систему вводится нели-
нейная корректирующая связь (см. пример 1), получающая инфор-
мацию о положении регулирующего органа с наибольшей степенью
открытия с помощью блока выбора максимального сигнала (БВМ),
вычислительного устройства с п входами, состояние выходной ко-
ординаты которого зависит от входа, принявшего максимальное зна-
чение:
#б.в.м = ///макс. щ — vy (84)
В корректирующей связи применяется линейное корректирую-
щее устройство с передаточной функцией Wk(p):
z=Wk(p)y6.B.M. (85)
Корректирующая связь в равной степени воздействует на зада-
ния регуляторов расходов на фурмах
x=x_+zl. (86)
Здесь 1 — вектор с единичными компонентами; х_ — вектор
составляющих заданий регуляторов, соответствующих требуемому
неравномерному распределению дутья.
Теперь система распределения дутья описывается уравнениями
(69), (71), (84)—(86); структурная схема системы показана на
рис. 36.
64
Нелинейная корректирующая связь может рассматриваться как
«внешняя часть» системы, взаимодействующая с многоовязной одно-
типной САР расходов воздуха через фурмы.
\wo(p)yy
ОЪъект
6ВМ
-Л.
•Положение
регулируют, их\
органов
L__^Za
Корректируюсь*
св язь
ЦУ1
Рис. 36.
Рассмотрим разложение векторов системы на усредненные (кол-
линеарные вектору 1) и относительные (ортогональные вектору 1)
составляющие, определив их по аналогии с (82), (83).
Уравнение объекта (70) принимает вид:
y_ = №o(p)A_u +f-; (87)
У+-/+. (88)
Усредненные составляющие отмечаются индексом «+», относи-
тельные — индексом «—».
В уравнении (88) член, отражающий влияние регулирующих
органов, равен нулю из-за независимости среднего расхода дутья
от управлений (70). В уравнении (87) А_ — матрица, полученная
после разложения векторов на составляющие {(82), (83) и т. д.], она
описывает действие оператора А на относительные составляющие и
наследует его положительные характеристические числа и собст-
венные векторы.
Уравнения регуляторов
и_ = №р(р)Е_(у_-х_); (89)
u+ = Wv(p)(y+-x+). (90)
Уравнения БВМ представим в виде
Уб.1.* = ^«+ + макс. и.л— (91)
5-1206 65
Уравнения системы разделились на две группы: уравнения
усредненных коордиинат (88), (90) и уравнения относительных ко-
ординат (87), (89) (см. структурную схему на рис. 37,а).
Система относительных координат представляет собой линей-
ную многосвязную однотипную САР распределения расходов. Си-
стема усредненных координат — это одноконтурная система стаби-
лизации положения регулирующего органа с наибольшей степенью
открытия.
БВМ
*>
\Np(p).
1
MCLKC.LL-q
Рис. 37.
Операция «выбор максимума» в полученных системах уравне-
ний совершается над компонентами вектора управлений системы от-
носительных координат, а соответствющий член включается в си-
стему уравнений усредненных координат (91). Этот член — единст-
венный, отражающий взаимное влияние двух систем: они соединены
односторонней связью; БВМ оказывается включенным в эту связь
и не вызывает усложнения исследования динамических свойств
системы.
Переходя в системе относительных координат к эквивалент-
ной системе с помощью матрицы С , получаем:
Ч- -Cl'y- =WQ(p)\_\_ (92)
l-=Wv(p)b_(xi_ -х.); (93)
x+ = z. (94)
Уравнение БВМ представим так:
#б.„.м = макс. ц^8|8 + «+ — v - (95)
д ui J
Уравнениям (86), (92), (93), (95) соответствует структурная
схема эквивалентной системы рис. 37,6, достаточно простоя в ис-
следовании.
66
ГЛАВА ТРЕТЬЯ
АНАЛИЗ
6. УСТОЙЧИВОСТЬ
а) Анализ однотипных связанных САР и эквивалентная система
Эквивалентная система состоит из п изолированных (в исклю-
чительных случаях — односторонне связанных) САР. Поэтому она
оказывается значительно более простой для исследования, чем ори-
гинальная, многосвязная.
Однако переход к эквивалентной системе еще не решает задачи
анализа или синтеза САР; эквивалентная система — лишь средство
исследования, и вопрос о способах проведения исследования еще
подлежит обсуждению. Здесь нас прежде всего интересуют вопросы:
как связаны интересующие нас свойства оригинальной системы со
свойствами эквивалентной? Какие требования должны быть предъ-
явлены к эквивалентной САР, если известны требования к исследуе-
мой? Вообще, как следует проводить решение поставленной задачи,
используя прием перехода к эквивалентной системе?
Подчеркнем, что задача .исследования системы не сводится
к задаче исследования каждой из эквивалентных сепаратных систем.
Существенно, что только все п сепаратные САР эквивалентной си-
стемы в своей совокупности эквивалентны исследуемой системе; по-
этому при исследовании, вообще говоря, необходимо держать в поле
зрения все п эквивалентных сепаратных САР.
Настоящая глава посвящена вопросам исследования однотипных
связанных САР путем перехода к эквивалентной системе. Рассма-
триваются вопросы анализа устойчивости систем, качества регули-
рования.
б) Основной признак устойчивости многосвязных однотипных
систем
Можно сказать, что замена переменных системы, характеризуе-
мая невырожденной матрицей С, является по-существу изменением
точки зрения на динамические процессы в системе для целей ана-
лиза. При этом, естественно, «содержание» процессов, их основные
свойства сохраняются: как известно из теории обыкновенных ли-
нейных дифференциальных уравнений, характеристические уравнения
исследуемой и эквивалентной систем равносильны, т. е. их корни
тождественно совпадают.
Вопросы исследования устойчивости однотипных связанных си-
стем рассмотрим на примере системы регулирования параллельно
работающих агрегатов с коллектором на стороне регулирующих
органов (гл. 1, уравнение (5) (6), структурная схема рис. 2]. Урав-
нения объекта
у={W0 (р) E+Wi (р) A]u+ Wf (р) Ef;
регулятора
и=И7р(р)Е(х-у).
В эквивалентной системе уравнение объекта
5*
ц = [W0 (р) E + Wt (р) X]l + Wf (р) Еср;
67
уравнение регулятора
* = Тр<Р)Е(и-ч).
Запишем характеристические уравнения оригинальной системы
det {Е+ [W0 (р) E + Wt (р) A] Wv (р) Е} = 0;
эквивалентной системы
det {Е + [W0 (р) E + W, (р) Л] Гр (р) Е} = 0. (96)
Эти уравнения равносильны, поскольку в левых частях уравне-
ний стоят равные друг другу определители подобных матриц пере-
даточных функций:
С-« {Е + [W0 (р) E + Wt (р) A] Wv (р) Е} С =
= [Е + WQ (р) Е +W, (р) Л] Wv (р) Е.
Но эквивалентная система состоит из изолированных (или в ис-
ключительных случаях — односторонне связанных) сепаратных си-
стем регулирования; поэтому диагональный определитель в левой
части ее характеристического уравнения (96) представляет собой
произведение левых частей характеристических уравнений сепарат-
ных систем:
det {Е + [W0 (р) E + W, (р) A] Wv (р) Е} =
п
= П + 1Г° W + Х*Г1 гр </>»•
Таким образом, характеристическое уравнение оригинальной
системы равносильно п характеристическим уравнениям эквивалент-
ных сепаратных систем:
1+1^о(р)+^1Г1(р)]^р(р)=0, £=1, 2, п.
Отсюда следует основной признак устойчивости: для устойчи-
вости однотипной связанной системы необходимо и достаточно, что-
бы были устойчивыми все п эквивалентные сепаратные системы.
При исследовании проводится я-кратное применение какого-ни-
будь критерия устойчивости к эквивалентным системам. Порядок
исследуемых характеристических уравнений понижается примерно
в п раз, и исследование проводится относительно просто.
То обстоятельство, что эквивалентные сепаратные системы раз-
личаются лишь коэффициентами усиления отдельных звеньев, сле-
дует использовать при проведении аналитических или графо-анали-
тических исследований устойчивости: переход от характеристики
одной сепаратной системы к характеристике другой совершается
путем лишь деформации, вызываемой изменением соответствующего
коэффициента усиления.
Обсудим некоторые конкретные приемы исследования устойчи-
вости.
в) Применение критерия Найквиста
При исследовании устойчивости с помощью критерия Найквиста
структурную схему системы рационально привести к виду рис. 28,а,
где последовательно соединены матричные звенья с передаточными
матрицами А и W(p)E [W(p) — передаточная функция изолирован-
68
**
Рис. 38.
ной динамической цепочки звеньев], охватываемые единичной век-
торной обратной связью. Такое приведение осуществляется выде-
лением в матричной структурной схеме системы звена с передаточ-
ной матрицей А и вычислением передаточной функции W(p) одной
изолированной цепочки звеньев по каналу от выхода звена пере-
крестных связей до его входа. Структурная схема эквивалентной
сепаратной системы показа-
на на рис. 28,6. Эквивалент-
ные сепаратные системы от-
личаются лишь коэффициен-
тами усиления в разомкну-
том состоянии. При этом
оказывается удобным при-
менить критерий Найквиста
в формулировке, требую-
щей определенного поло-
жения амплитудно-фазовой
характеристики разомкнуто-
го контура относительно
точки (—>l/\k; /0), где к —
коэффициент усиления ра-
зомкнутого контура (Л. 68]. В нашем случае аналогичное требо-
вание относится к расположению годографа W(iod) относительно со-
вокупности точек —1Дь —. •—1ДП (при этом среди харак-
теристических чисел, следовательно, и их обратных величин могут
быть пары комплексно сопряженных [Л. 4]). Сформулируем теперь
результат.
Для устойчивости системы автоматического регулирования вида
рис. 28,а необходимо и достаточно, чтобы амплитудно-фазовая ха-
рактеристика W(m) охватывала каждую из п точек —
—1Д&, ..., —\/Хп в положительном направлении 1/2 раз, где I —
число полюсов W(p) в правой полуплоскости.
Если все Kk вещественны и положительны, а контур с переда-
точной функцией в разомкнутом состоянии W(p) теряет устойчи-
вость лишь при достижении коэффициентом усиления k некоторого
достаточно большого критического значения, то следует ограни-
читься исследованием расположения годографа W(m) относительно
точки —1Дмакс, где
Ямакс = макс, Хд, <7=1,2,
— максимальное из характеристических чисел. Таким образом, в рас-
смотренном частном случае о характеристических числах требуется
знать только то, что они вещественны и положительны, и распола-
гать численным значением наибольшего из них.
Для системы со структурной схемой рис. 4 (параллельные агре-
гаты, взаимосвязанные через нагрузку) исследование устойчивости
с применением полученного результата проводится в два приема.
Пусть число правых полюсов передаточных функций W0 (р), W\ (р),
wp(p) составляет соответственно mi, m2f m$. Сначала эквивалент-
ная сепаратная система размыкается по обратной связи .и по экви-
валенту перекрестной связи, т. е. в точках а и б (рис. 38). Затем
исследуется распределение корней сепаратной изолированной систе-
мы (без учета действия перекрестных связей) с характеристическим
уравнением
l + Wo(p)Wp(p)=0.
69
По обычному правилу подсчитывается число охватов tii ампли-
тудно-фазовой характеристикой W0(p)Wp(p) критической точки
(—1; ДО) с учетом их знаков. После этого система замыкается
в точке а и проводится окончательное исследование распределения
корней характеристического уравнения системы с учетом перекрест-
ных связей. Теперь распределение корней характеристического
уравнения системы, разомкнутой в точке б, известно (в правой
полуплоскости расположено т\ + т2Л-тг—щ полюсов) и непосредст-
венно может быть применен сформулированный признак устойчиво-
сти системы со структурной схемой рис. 28 при
Wip) УрСр)У.(р) .
Приходим к следующему правилу.
Для устойчивости системы со структурной схемой рис. 4 сумма
чисел положительных охватов п\ и п2 характеристикой
W0(i(x))Wp(m) критической точки (—1; ДО) и характеристикой
Wj> (/со) Wx (/со)
1 -|- и/р (до) (/(о) каждой из точек —1Дь должна быть равна
общему числу правых полюсов передаточных функций W0(p),
Wi(p) и W9(p).
г) Построение областей устойчивости
Так как сепаратные САР по предположению идентичны, то мо-
жет быть поставлен вопрос об определении области устойчивости
в плоскости какой-нибудь пары параметров сепаратной САР; при
этом предполагается, что при вариации соответствующие параметры
всех сепаратных САР изменяются одновременно (синхронно). Так
как все п эквивалентные сепаратные системы должны быть устой-
чивыми, то область устойчивости системы является пересечением
(общей частью) областей устойчивости, построенных для всех п
эквивалентных сепаратных систем.
Вообще при исследовании D-разбиения в плоскости какой-ни-
будь пары параметров сепаратный САР достаточно построить Л-раз-
биения для каждой из эквивалентных сепаратных систем и совме-
стить их. Тогда границы D-разбиения системы представляют собой
совокупность границ, построенных для эквивалентных сепарат-
ных систем; число корней характеристического уравнения в правой
полуплоскости, соответствующее конкретной паре исследуемых па-
раметров, равно сумме чисел правых корней для всех эквивалентных
сепаратных систем. Эти положения практически без изменения рас-
пространяются на случай /^-разбиения.
Сделаем несколько замечаний по поводу анализа областей
устойчивости для случая одноконтурных сепаратных систем вида
рис. 28. В эквивалентной системе одноконтурные сепаратные САР
отличаются друг от друга лишь коэффициентами усиления в разо-
мкнутом состоянии.
Если все характеристические числа матрицы А вещественны
(например, А — симметрична), то Л-разбиения удобно проводить
в плоскости параметров, пропорциональных коэффициенту усиления
передаточной функции W(p). Пусть, например, требуется построить
D-разбиение в плоскости параметров ku k2j причем W(p) =
= kiWi(p)+k2W2(p).
70
Характеристическое уравнение системы в форме
\+%кЩр)=0, 2, п
W{p)=-\IU\
приведем к виду
имеем уравнение границ D-разбиения:
1
(p) + k2W2(p)=-y-.
Решение этого уравнения при Xk — l дает границу D-разбиения
изолированной сепаратной системы:
&i = &i(o);
^2=^2(0)).
При этом для любого %дф® получим:
*.(•)•
Построение границы £>-разбиения сильно упрощается: граница
строится для одного из характеристических чисел Ки, для осталь-
ных — получается из построенной простым преобразованием подо-
бия с коэффициентом подобия Xkfkq, q=l, 2, ..., k—1, /г+1, ..., п.
Пример 8. Трехканальная система стабилизации (Л. 38] имеет
своей эквивалентной системой три однокон-
турные САР со структурной схемой вида
рис. 28 три
Aft = cos 0 + / sin 8 sin 2 ^
(см. пример 6). При конкретных характери-
стиках, принятых в статье А. Г. Барского:
£=20, 7=0,1 сек, а также при значениях
параметров (см. рис. 10,а): &р=1, ф=20°.
Амплитудно-фазовая характеристика
(рис. 39)
WW = m(iT*+l)
охватывает точку —1/Яг = —0,59—П,11, что свидетельствует о неус-
тойчивости системы (точка —1/А,3 =—0,59+П,11, не охватываемая
характеристикой, на чертеже не показана).
Пример 9. Устойчивость системы автоматического распределения
дутья по фурмам доменной печи |[Л. 30, 36]. Как показано в приме-
ре 7, структурная схема системы может быть представлена струк-
турными схемами двух взаимодействующих подсистем: распределе-
71
разомкнутой системы
ния расходов и управления положениями регулирующих органов.
Устойчивость подсистемы регулирования распределения расходов
анализируется методами теории однотипных связанных систем.
В результате экспериментального исследования объекта (Л. 36]
получено:
( 0,052\ п
aq = -( 0,037+ -^-). <7=1. 2,...,|-2--1;
ЛР)-
[0,5е~2>2Р
:[(2р+\Г
В качестве регуляторов расхода на фурмах применены ПИ-ре-
гуляторы с передаточной функцией
1
Щ(р)
где kv — коэффициент усиления регулятора; 7И — постоянная вре-
мени изодрома.
Расчет с помощью формулы (П-28) дает для п—1 характери-
стических чисел матрицы А
0,868<Яд< 1,164, ?=2, 3, п
(напомним, Х\—0).
Система с передаточной функцией XqW0(p)Wv(p) в разомкну-
том состоянии теряет устойчивость при достижении положительным
Xq некоторого достаточно большого значения. Поэтому устойчивость
системы следует проверять
0В_ кмакс по наибольшему из харак-
тер истичеоких чисел ХМакс =
=1,164. Таким образом:
1) устойчивость систе-
мы регулирования распре-
деления дутья достаточно
проверить по уравнениям
или характеристикам сепа-
ратной системы регулирова-
ния расхода на фурме с уве-
личенным на 16% по сравне-
нию с его действитель-
рис. 40. ным значением коэффициен-
том усиления разомкнутого
контура;
2) для устойчивости системы распределения дутья необходимо
и достаточно, чтобы АФХ разомкнутого контура W0 (/со) Wp (/со) не
охватывала точку (—1/1,16; Ю);
3) границы Л-разбиений удобно строить в плоскости параметров
регулятора kv, &Р/ГИ, пропорциональных коэффициенту усиления ра-
зомкнутого контура. На рис. 40 показан пример построения границы
устойчивости: сначала построена граница устойчивости для изоли-
рованной сепаратной системы регулирования расхода на фурме, за-
тем путем преобразования подобия с коэффициентом 1/1,16 найдена
Граница ДЛЯ |А = Амакс ; для любого другого Хн кривая D-разбиения
строится аналогично с коэффициентом подобия
72
7. КАЧЕСТВО РЕГУЛИРОВАНИЯ
а) Вводные замечания
Исследование качества регулирования в эквивалентных сепарат-
ных системах с вещественными параметрами может быть проведено
традиционными методами теории систем с одной регулируемой пе-
ременной. Эти же методы с некоторыми изменениями могут быть
применены для анализа качества в эквивалентных сепаратных си-
стемах с комплексными параметрами.
В* наиболее простых случаях исследование эквивалентной си-
стемы дает практически полный ответ на вопрос о качестве регу-
лирования в оригинальной системе.
Так обстоит дело, например, при анализе реакции простых сим-
метричных и двухканальных антисимметричных систем на ступен-
чатые входные воздействия.
Расчет переходного процесса в двухканальной системе на экви-
валентной модели с комплексными параметрами непосредственно да-
ет ординаты двух ее выходных переменных в виде вещественной
и мнимой составляющих комплекснозначной переходной функции
[Л. 4, 8, 35].
Анализ простых симметричных систем часто требует определе-
ния их реакции как на воздействия со стороны общих линий на все
сепаратные системы, так и на индивидуальные воздействия в от-
дельных сепаратных системах. В первом случае возбуждается толь-
ко эквивалентная сепаратная система усредненных координат; со-
ответствующая переходная функция характеризует одновременную
реакцию сепаратных систем, так что
M0=Yi(0. 2, л, <97)
где yt(t) —первый диагональный элемент переходной матрицы экви-
валентной системы Г(/), переходная функция первой эквивалентной
сепаратной САР, усредненное движение.
Во втором случае при возмущении одной из сепаратных си-
стем (для определенности — первой) ее реакция
Ух (0 = 4" Yi (0 + -^тг" ъ (0; (98)
реакции всех остальных сепаратных систем
M0=4"fti(0-Y2(0]. k=\,2 п. (99)
Здесь va(i) =7з(0 = ... =\n(t) — идентичные переходные функ-
ции эквивалентных сепаратных систем относительных координат. Со-
отношения (97) — (99) могут быть получены как при использовании
формул перехода к эквивалентной системе (28), (31), так и формул
(79); в обоих случаях следует вычислять амплитуды ступенчатых
воздействий на входах эквивалентных сепаратных систем и при об-
ратном пересчете учитывать ординаты их переходных функций с со-
ответствующими коэффициентами.
В общем же случае пересчеты характеристик внешних воздей-
ствий и отклонений на основе соотношений (61) — (64) могут ока-
73
заться затруднительными. Поэтому естественно поставить вопрос
о возможности оценки качества регулирования в системе непосред-
ственно по результатам анализа эквивалентной САР. Такая воз-
можность существует благодаря взаимно однозначному соответствию
между процессами в оригинальной и эквивалентной системах, вслед-
ствие которого большим отклонениям в эквивалентной системе
обычно соответствуют большие отклонения в исследуемой; исче-
зающе малые отклонения в обеих системах имеют место одно-
временно.
Рассмотрим применение показателей качества эквивалентных
сепаратных систем для оценки точности работы оригинальной си-
стемы.
б) Прямые оценки качества регулирования
Нам предстоит .выявить связь между показателями качества пе-
реходных процессов в многосвязной однотипной и эквивалентной
системах. Однако предварительно необходимо уточнить понятие
«единичного ступенчатого воздействия» в однотипных связанных
системах, вызывающего анализируемый переходный процесс. Дело
в том, что при анализе нет оснований ограничиваться рассмотре-
нием реакции на ступенчатое воздействие, нанесенное в какой-нибудь
сепаратной САР: как отмечалось в § 2, для однотипных систем ха-
рактерны ситуации, когда возмущение поступает одновременно на
идентичные входы нескольких (или всех) сепаратных систем.
Поэтому, рассматривая реакцию системы на самое тяжелое
единичное ступенчатое возмущение на конкретном векторном вхо-
де многосвязной системы, б>дем оговаривать только «модуль вектора
возмущения, не ограничивая соотношения между его компонен-
тами.
Будем говорить, что на векторном входе многосвязной однотип-
ной системы действует единичное скачкообразное возмущение, если
на идентичные входы сепаратных систем одновременно поступают
ступенчатые функции с амплитудами 1/1, fc,..., fn такими, что мо-
дуль вектора возмущения равен единице: у 2 Переход-
ам 1
ным процессом будем называть реакцию на единичное скачкообраз-
ное возмущение системы, находящейся до момента нанесения воз-
мущения в состоянии покоя.
Переходный процесс в системе описывается соотношением
у (0-в (Of, (loo)
где В (t) — матрица переходных функций системы; у (t) — вектор
отклонений регулируемых переменных от новых установившихся
значений.
При анализе будем предполагать, что, во-первых, сепаратные
системы изолированы (Л — диагональна) и, во-вторых, в новом ба-
зисе сохранены длины векторов (С — ортогональна). Эти два усло-
вия (при нормировании векторов нового базиса по длине) выпол-
няются по крайней мере в многосвязных однотипных системах
с симметричными, кососимметричными и циркулянтными передаточ-
ными матрицами перекрестных связей, т. е. практически во всех
известных по описаниям в литературе системах.
74
Таким образом, в эквивалентной системе действует единичное
ступенчатое возмущение ср:
|Ф| = Ш = 1;
П
И|т-*|2=1.
Символ модуля в этом соотношении необходим потому, что,
возможно, компоненты вектора <р — комплексные числа.
Переходный процесс в каждой из эквивалентных сепаратных
систем выражается так:
гДе Vqq (0 — переходная функция q-й сепаратной САР, диагональ-
ный элемент матрицы переходных функций Г(/) эквивалентной си-
стемы; фд представляет собой амплитуду ступенчатого воздействия
в q-и сепаратной системе:
4(0 = г (Оф.
Поскольку модули векторов при переходе к новому базису со-
храняются, то в каждый «момент времени t имеем:
п п п
E0?(o=Eh*(oi8 = E iY«wiai*«ie. (ion
/=.1 /=.1 q=\
Зафиксируем (момент времени t = t\ и будем варьировать по
направлению вектор воздействия f, т. е. ф, сохраняя его длину. Ана-
лиз соотношения (101) позволяет сделать следующий вывод. Макси-
мальное значение длины вектора выходных координат в момент вре-
мени ti, равное
п
макс. Е У2п Ci) = макс I Y« Ci) 12«
достигается при таком единичном воздействии, что вектор f совпа-
дает с собственным вектором Cj передаточной матрицы A; Cj соот-
ветствует эквивалентной сепаратной системе с максимальным зна-
чением регулируемой величины в данный момент времени, т. е.
|ф^| = 1. Таким образом, модуль вектора выходных координат си-
стемы в переходном процессе ограничен сверху наибольшим из мо-
дулей переходных функций эквивалентных сепаратных систем:
|у(0|<макс.|Тя(0|; \
1
/JL (102)
Е^(0<макс.|тгот(01-
/=1 q
Используя в качестве меры отклонений регулируемых перемен-
ных от устанавливающихся значений модуль вектора отклонений
выходных координат, определим основные показатели качества пе-
реходного процесса в системе следующим образом.
75
Перерегулирование умакс — это наибольшее из значений
модуля вектора выходных координат системы, наблюдаемых в пе-
реходном процессе:
Умакс = макс^ |у(0 [.
Время регулирования ТА — отрезок .времени с момен-
та нанесения единичного возмущения, достаточный для того, чтобы
модуль вектора выходных координат системы стал меньшим задан-
ного допуска Д:
макс. |у(01/=г = А;
|У(01/>г<А.
Из соотношения (102) следуют оценки для основных показате-
лей качества переходного процесса:
Умакс < Макс. | Yg(*)|. (ЮЗ)
q,t
г. е. перерегулирование в системе ограничено сверху наибольшим
из перерегулирований в эквивалентных сепаратных системах;
Гд<макс. Гд(7}8), (104)
S
т. е. время регулирования в системе ограничено сверху наибольшим
из значений времени регулирования в эквивалентных сепаратных
САР.
Эти оценки могут служить основанием для характеристики ка-
чества регулирования в -миогосвязных однотипных системах верх-
ними значениями указанных показателей качества в эквивалентных
сепаратных САР.
Таким образом, при анализе качества переходных процессов
в системе следует каким-нибудь способом получить п переходных
характеристик эквивалентных сепаратных систем и замерить наи-
большее из перерегулирований и наибольшее из значений времени
регулирования.
Подчеркнем, что в каждой из оценок (103), (104) знак равенства
достигается при определенном ступенчатом возмущении единичной
п
амплитуды 2 fq — 1, а именно при возмущении, вектор которого
9=1
совпадает с собственным вектором А, соответствующим эквивалент-
ной сепаратной САР с наихудшим значением этого показателя
(f=c„).
Так как модуль компоненты вектора не превышает его длины
i*«(oi<j/s*J(o.
5=1
то правые части оценок (103), (104) ограничивают сверху перере-
гулирование и время регулирования для любой выходной
76
величины системы. Эти оценки можно использовать при анализе
качества регулирования .в сепаратной САР при действии в этой САР
единичного ступенчатого возмущения.
Пример 10. В системе регулирования объект описывается урав-
нением
y=HMp)A(u+f),
регуляторы —уравнением
и = ИМр)Е(х-у)
прч
*о(р) =
А =
/ 0,135 \
*<Р>~(о.зв + —j;
" 1 —0,25 —0,1 0
— 0,25 1 —0,25 —0,1
— 0,1 —0,25 1 —0,25
0 —0,1 —0,25 1
Структурная схема эквивалентной системы и ее параметры при-
ведены в примере 5. Измерение наибольшего из перерегулирований
и наибольшего -из значений времени регулирования по допуску А=
=0,04 и эквивалентных сепа-
ратных
дает:
системах (рис. 41)
Умакс=0,72;
Гд = 26 сек.
26 сек
На рис. 42 показана реак-
ция системы на скачкообразное
возмущение f произвольного
направления:
0,93
f =
— 0,09
0,23
0
Рис. 41.
Результаты измерения па-
ра-метров качества регулирова-
ния наибольшего *из динамических отклонений, равного 0,63, и наи-
большего времени регулирования ^Р = 21 сек мажорируются соответ-
ствующими показателями качества регулирования в эквивалентной
системе.
в) Прямые оценки качества регулирования (продолжение)
Рассмотрим вопрос о качестве переходных процессов с более
общих позиций, применяя обобщенные характеристики длин векто-
ров — их нормы и нормы матриц — как характеристики усилитель-
ных свойств соответствующих операторов.
77
^1 21 сек
Рис. 42.
Норма вектора , z— это
мера его длины, неотрицатель-
ное число ||z||, удовлетворяю-
щее следующим требованиям:
1) норма вектора с нуле-
выми компонентами равна ну-
лю; если хотя бы одна компо-
нента вектора отлична от ну-
ля, то норма — число положи-
тельное
||z||>0 при z=^0 и ||0||=0;
2) умножение вектора на
скалярный множитель а при-
водит к умножению нормы век-
тора на модуль этого множи-
теля
l|az||=|a|||z||;
3) норма суммы двух векторов не превышает суммы норм этих
векторов (неравенство треугольника)
l|z+v||^||z|| + ||v||.
В качестве норм вектора применяются: его модуль (длина), ма-
ксимальный из модулей компонент, сумма модулей компонент и т. д.
Норма квадратной матрицы U — это неотрицательное число
IIUHi удовлетворяющее условиям:
1) норма матрицы положительна, если среди ее элементов име-
ются ненулевые; норма нулевой матрицы — нуль
||U||>0 при U#0, и ||0||=0;
2) при умножении матрицы на скаляр а норма матрицы умно-
жается на модуль этого скаляра |а|
||aU||=|a|||U||;
3) норма суммы двух матриц не превышает суммы норм этих
матриц
IIU + V|KI|U|| + ||V||;
4) норма произведения двух матриц не превышает произведения
их норм
IIUV||^||U||||V||.
При исследовании качества переходных процессов нормы векто-
ров характеризуют интенсивность внешних воздействий и амплитуды
реакций системы на эти воздействия; нормы матриц переходных про-
цессов определяют количественную связь между амплитудами внеш-
них воздействий и реакций выходных координат на эти воздействия.
Нормы векторов и матриц могут вводиться различными спосо-
бами. Говорят, что норма матриц согласована с нормой векторов, если
78
для любой матрицы U и любого вектора z выполняется неравенство
l|Uz||<||U||||z||. (105)
Если при каком-нибудь векторе z с нормой, равной единице,
в (105) имеет место равенство, то норма матриц называется под-
чиненной норме векторов.
Следует отметить, что нормы, удовлетворяя в соответствии
с определением требованиям весьма общего характера, представляют
собой некоторые оценки сверху усилительных свойств операторов и
длин векторов, иногда с большим запасом. Введение понятия подчи-
ненной нормы матриц имеет целью снизить запас в оценках.
Выражение для переходного процесса в системе (100) предста-
вим в виде
у(0 = СГ(0С-Ч, (106)
выразив переходную матрицу системы В (t) через переходную матрицу
эквивалентной системы Г (t).
При оценке реакций системы, определяемых соотношениями
(100), (106), будем пользоваться текущими значениями норм векто-
ров и матриц переходных характеристик, соответствующих фиксиро-
ванным моментам времени t\.
Пусть ||f||, Hy(^i)||—нормы векторов возмущений f и регулируе-
мых величин y(*i); ||B(ft)||, ||r(/i)||, ||С||, ||С-4|| — нормы соответст-
вующих матриц, согласованные с выбранной нормой векторов [нор-
мы у(/), В (4) и Г(t) зависят от t]. Имеем:
II у (МII < II в (<,) || н f || < || с || || Г (/,) || || с-> || || f ||.
При исследовании качества регулирования методом переходных
функций вектор f будем нормировать по длине так, что
1Ш1 = 1;
выбором длин векторов нового базиса может быть обеспечено:
ICI-1.
В этих условиях
II У II < || С-" || ||Г ||. (107)
Рассмотрим соотношение (107).
В правой части стоят два сомножителя: нормы матриц r(/i)
и С"1.
Норма диагональной матрицы переходных функций эквивалент-
ной системы T(^i)—это характеристика значений откликов эквива-
лентных сепаратных САР на единичные воздействия при конкретном
значении t—ti.
Норма матрицы С"1, обратной по отношению к матрице С, за-
висит от целого ряда свойств канонического базиса, из которых вы-
делим важнейшее — косоу гольность. В геометрической трак-
товке косоугольность базиса означает, что его векторы расположены
относительно друг друга под острыми или тупыми углами. Как след-
ствие, некоторые столбцы матрицы канонического базиса хотя и не
выражаются линейными комбинациями остальных (ведь матрица по
условию не вырождается), но довольно близки к ним и определитель
матрицы оказывается «довольно малым» по абсолютной величине.
79
При этом элементы матрицы С-1, обратно пропорциональные/бпреде-
лителю матрицы С, могут принимать большие значения, чтр'и приво-
дит к высоким оценкам нормы ||С_1||. /
В другой интерпретации: в косоугольной системе координат ма-
лые значения компонент вектора (ординат переходных функций
эквивалентной системы) не гарантируют малых значений модуля
вектора или значений компонент вектора в другой системе коорди-
нат (ординат переходных функций оригинальней системы).
Следовательно, оценка отклонений II у (О II /Определяется свойства-
ми эквивалентной системы ||Г(*)11 и степенью обусловленности матри-
цы С (||С_1||), т. е. косоугольностью канонического базиса матри-
цы А.
Перерегулирование при использовании аппарата теории норм
векторов и матриц определяется как максимум нормы ||у(0Н векто-
ра у(/) по t:
Умакс = макс. || у (О II-
Соответственно время регулирования ТА — как момент времени,
начиная с которого норма отклонения от установившегося значения
станет меньшей некоторого допуска А:
||У(ОН<>г<А. / (108)
В дальнейшем будем считать, что эквивалентные сепаратные си-
стемы изолированы и, следовательно, матрица переходных функций
эквивалентной системы Г (О диагональна.
Нормы матриц и векторов могут вводиться по-разному; каждый
способ определения норм приводит к своим оценкам показателей ка-
чества переходных процессов:
1. Если в качестве нормы векторов служит наибольший из моду-
лей компонент векторов (например, || У (^) IU = макс. | у9 (t) \ и т. д.),
я
то согласованная норма матриц —наибольшая из сумм модулей эле-
ментов строк: || В (t) ||j = макс. V | bq8 (t) | и т. д. Имеем:
Q
макс. |уд (01 < || С- « макс. | Y« (0 I- (109)
я я
2. Применив в качестве нормы векторов суммы модулей их компо-
п
нент (т. е. || у (0 ||2 = S I Уч. (0 I и т« Д-)> а в качестве согласован-
q=\
ной нормы матриц —наибольшую из сумм модулей элементов
их столбцов (|| В (0 ||2 = макс. V | bqs (t) | и т. д.), получим:
Я
п
£ I »я (0 КII С-1 Нв макс | Yn (0 I- О10)
3. Если в качестве нормы векторов выбраны их длины, то согла-
сованная норма для случая диагональной матрицы—наибольший из
модулем его элементов; полученные в п. «б» оценки можно рассма-
тривать как результат применения фтой нормы векторов и матриц.
Таким образом, при каждом t наибольший из модулей ординат
переходных функций макс. | Yqq (О I ограничивает сверху левые части
Я
неравенства с точностью до мнэжителя И С-1 II, не меньшего единицы.
Из (109), (110) следует, что при применении любой из рассмо-
тренных комбинаций норм векторов и матриц
Умакс<|| С-11| макс. |Yg<z(0 |. 1, 2, 0</<оо.
Оценим время регулирования в исследуемой системе. Пусть
||С-Ч|макс. |Уи(П1=А/||С-»||; \
II С~1 || макс. | YM (0 1/>г < А/ IJ С-«||. | (1И)
Я 1
Сравнивая (108) и (111), имея в виду (109), (НО), приходим
к выводу, что время регулирования в системе по допуску Д/||С1-||
не превышает времени регулирования в эквивалентной системе по
допуску А (время регулирования в эквивалентной системе для каж-
дой сепаратной САР измеряется отдельно).
Применение приведенных результатов затрудняется необходи-
мостью вычисления (или оценки) НС-1]!. Приводимые оценки могут
использоваться без вычисления ||С_1|| в качестве относительных ха-
характеристик отклонений в системе, известных с точностью до неиз-
вестного фиксированного параметра ||С_1||.
Перейдем к обсуждению методов исследования качества регули-
рования в однотипных связанных системах с помощью косвенных
критериев качества.
г) Косвенные критерии качества
Характеристики распределения корней. Как ука-
зывалось, корни характеристических уравнений оригинальной и экви-
валентной систем тождественно совпадают. Поэтому используемые
обычно при анализе показатели распределения корней характеристи-
ческих уравнений систем: степень устойчивости (Л. 67] и степень ко-
лебательности {Л. 69] тождественно совпадают.
Для того чтобы в исследуемой системе степень устойчивости и
степень колебательности имели значения не хуже заданных, необхо-
димо и достаточно, чтобы этот факт имел место для каждой из экви-
валентных сепаратных систем.
Как и обычно, при исследовании характеристик распределения
корней употребляются те же методы, что и при анализе устойчи-
вости.
Квадратичные критерии качества. Если качество
регулирования в системе оценивается интегральным квадратичным
критерием
п п 00 00
k-i k=\ о 6
6—1206 81
то для эквивалентной системы значение / выражается формулбй
00
Р=С*С
— положительно определенная Эрмитова матрица. Вообще говоря,
применение такой оценки весьма трудоемко. Однако если канони-
ческий базис ортогонален, то
С*С=Е
и выражение для квадратичного критерия / принимает предельно
простой вид:
оо п оо п
/ = jifETi^ = 2 ]>*ЪЛ = Е Ml). (ИЗ)
О k=\ 0 k=l
т. е. квадратичный критерий для системы (112) равен сумме крите-
риев, вычисленных для эквивалентных сепаратных систем. В частно-
сти, это имеет место для систем с симметричными и кососимметрич-
ными матрицами А в силу ортогональности их канонических базисов.
Эквивалентные сепаратные системы равноправны с точки зрения
квадратичной оценки для системы в целом: значения их интеграль-
ных квадратичных ошибок входят в сумму (ИЗ) с одинаковым
весом.
Интегральный квадратичный критерий / для переходного процес-
са в системе может быть выражен так:
л
' = 2 |¥*|ЯМТГ).
k=\
Здесь Jk (у) —квадратичный функционал качества на переходной
характеристике yh(t) k-й эквивалентной сепаратной системы.
Учитывая соотношение для амплитуд скачкообразных воздей-
ствий в эквивалентной системе (101), легко получить следующую
оценку:
мин, /д</<макс. /fc(Y)»
я ь
т. е. интегральный квадратичный критерий качества переходного про-
цесса заключен между наибольшим и наименьшим значениями квад-
ратичных критериев эквивалентных сепаратных САР. Знаки точного
равенства имеют место тогда, когда единичное ступенчатое воздей-
ствие характеризуется вектором канонического базиса системы, соот-
ветствующим эквивалентной сепаратной САР с наибольшим или наи-
меньшим значением критерия.
Для среднего квадрата ошибки в системе, находящейся под дей-
ствием стационарных случайных возмущений, имеем:
УЧ*Г= М {у- (0 у (/)} = М {V (О Р?) (0} (И4)
или при выполнении условия ортогональности канонического базиса
(например, в случае симметричной или кососимметричной А)
ГШ = м {т)* (о т) (/)} = hRF).
82
Как и в случае интегрального квадратичного критерия, вычисле-
ние среднего квадрата ошибки сводится к вычислению средних квад-
ратов ошибок для эквивалентных сепаратных систем.
Таким образом, наиболее употребительные параметры качества
регулирования для эквивалентных сепаратных систем, получаемые
сравнительно просто (путем расчета или моделирования), дают
исчерпывающие сведения о качестве регулирования в исследуемой
системе.
ГЛАВА ЧЕТВЕРТАЯ
СИНТЕЗ
В этой главе обсуждается применение метода эквивалентной
системы для синтеза однотипных связанных САР. Рассматриваются
общие вопросы перехода от задачи синтеза многосвязной однотипной
системы к задаче синтеза однотипных эквивалентных сепаратных си-
стем. Более детально рассмотрен расчет однотипных связанных си-
стем методом расширенных частотных характеристик, применяемым,
в частности, при проектировании и настройке САР объектов с за-
паздыванием.
8. ПРИМЕНЕНИЕ МЕТОДА ЭКВИВАЛЕНТНОЙ СИСТЕМЫ
ПРИ СИНТЕЗЕ
а) Общие положения
Исходными данными при решении задачи синтеза служат урав-
нения объекта, характеристики внешних воздействий; требований
к качеству регулирования; ограничения, накладываемые на структур-
ную схему системы регулирования из соображений простоты обслу-
живания, надежности и т. д.
Будем считать, что объект по формальным признакам может
быть отнесен к «однотипным связанным системам». В качестве при-
мера будем иметь в виду объект, описываемый уравнением
y=lWo(p)E+Wi(p)A]a+L
Структурная схема объекта изображена на рис. 43.
Входные воздействия представляют собой заданные детермини-
рованные функции времени или стационарные случайные сигналы
с известными характеристиками.
Требования к качеству регулирования могут формулироваться
как требования минимизации отклонений в той или иной метрике
(например, интегрального квадратичного критерия или средней квад-
ратичной ошибки) или как некоторые ограничения критериев каче-
ства (ограничения, накладываемые на распределение корней системы
или на показатели качества переходного процесса, и т. д.).
Рассмотрим три варианта ограничений, накладываемых на струк-
турную схему САР:
1. Из условий простоты обслуживания и надежности работы
САР требуется, чтобы каждый регулируемый канал был оборудован
6* 83
Рис. 43.
индивидуальной системой регулирования; перекрестные связи- между
сепаратными регуляторами не вводятся.
2. Допускается в целях улучшения качества регулирования вве-
дение простейших жестких перекрестных связей между идентичными
звеньями регуляторов сепаратных САР.
3. Ограничения на структурную схему регулирующей части си-
стемы не накладываются.
Ограничения структуры САР существенно влияют на процедуру
синтеза. Поэтому в дальнейшем будем говорить о трех постановках
задачи синтеза и соот-
Wf(p)f ветственно о трех проце-
дурах синтеза в зависи-
мости от характера огра-
ничений.
Как следует из пре-
дыдущей главы, задача
управления регулируемы-
ми переменными объекта
сводится к задаче управ-
ления регулируемыми пе-
ременными -эквивалентной системы: высокая точность синтезируемой
САР 'гарантируется высокой точностью эквивалентной САР.
Метод эквивалентной системы может быть применен для реше-
ния задачи синтеза при использовании следующей общей процедуры.
1. Поставленная задача синтеза формулируется применительно
к эквивалентной системе: вычисляются характеристики эквивалент-
ного объекта; формулируются требования к эквивалентной системе.
2. Проводится синтез эквивалентной системы.
3. Вычисляются характеристики регулятора оригинальной систе-
мы по полученным характеристикам эквивалентного регулятора.
Таким образом, приходим к задаче синтеза системы регулирова-
ния на несвязанных (если не принимать во внимание исключительные
случаи клеток Жордана в матрице Л) регулируемых каналах экви-
валентного объекта. Отсюда не следует, что в оптимальной системе
регулирования между регуляторами должны отсутствовать пере-
крестные связи: коррелированность внешних воздействий может
привести к тому, что такие связи окажутся полезными (Л. 67].
В целях упрощения задачи синтеза наложим дополнительные
ограничения на структурную схему САР: потребуем, чтобы эквива-
лентные сепаратные системы регулирования не были связаны между
собой (т. е. система уравнений эквивалентного многомерного регу-
лятора должна быть диагональной). Тем самым задача синтеза
многосвязной системы сводится к задаче синтеза диагональной экви-
валентной системы.
Обратимся сначала к общей характеристике решения задачи син-
теза на эквивалентной системе, а затем перейдем к особенностям
трех приведенных выше вариантов постановки задачи синтеза.
б) Решение задачи синтеза на эквивалентной системе
Как обычно, переход к эквивалентному объекту
ц = [W0 (р) Е + Wx (р) А] % + Wf (р) <р
осуществляется с помощью матрицы канонического базиса С: у = Сг\,
и = С|, f = Сф. Структурная схема эквивалентного объекта показана
на рис. 44.
84
Требования к качеству регулирования в эквивалентной системе
формулируются в соответствии с рекомендациями § 7. В общем слу-
чае формулировка требований к поведению ошибки регулирования
затрудняется необходимостью вычисления матрицы канонического
базиса. В практически же важных случаях, когда известно, что кано-
нический базис ортогонален , , ,
Wffp)pk
I—j*fW|-| у
Hg£-&
Рис. 44.
(напомним, что это условие
выполняется в симметрич-
ных, антисимметричных и
циркулянтных системах),
требования к качеству регу-
лирования практически непо-
средственно переносятся на
эквивалентную систему: ес-
ли требуется минимизиро-
вать квадратичный функционал (II2) или (114) в синтезируемой
системе, ю в эквивалентной системе следует минимизировать соот-
ветствующий квадратичный функционал; если заданы ограничения
на показатели качества переходного процесса (перерегулирование,
время регулирования) в синтезируемой системе, то они должны
быть выдержаны в каждой из эквивалентных сепаратных систем
в соответствии с (103), (104).
-На основе оценки сверху для интегрального квадратичного функ-
ционала качества на переходной характеристике наибольшим из
функционалов, вычисленных для эквивалентных сепаратных систем,
критерий
со п 00 п
' = J 2 У\ = | S hfc (О I2 dt -> мин.
О k=\
О k=\
может быть заменен более простым для вычислений критерием
макс
• JhgWI
2 dt мин.
При этом приходим к задаче с минимаксным критерием.
Ограничения на показатели распределения корней характеристи-
ческого уравнения системы вне зависимости от свойств каноническо-
го базиса должны выдерживаться в каждой из эквивалентных сепа-
ратных систем.
Формулировка структурных ограничений для диагональной экви-
валентной системы существенно зависит от характера ограничений
и будет рассмотрена ниже.
При синтезе эквивалентной системы определению подлежат
структурные схемы и параметры сепаратных регуляторов на изоли-
рованных сепаратных каналах эквивалентного объекта. Необходимо,
однако, подчеркнуть, что задача не сводится к обычному синтезу
изолированных систем вследствие двух обстоятельств. Во-первых,
как это следует из материала предыдущих глав, эквивалентные се-
паратные регуляторы должны содержать идентичные динамические
цепочки. Во-вторых, сепаратные системы взаимосвязаны между со-
бой через требования к качеству регулирования (необходимо удовле-
творить требования к заданным показателям одновременно во всех
эквивалентных сепаратных САР; минимизации подлежат не квадра-
85
тачные функционалы на реализациях переменных сепаратных систем,
а их суммы). Эти обстоятельства играют важную роль при синтезе
систем в первых двух вариантах задачи.
Будем иметь в виду задачу прикладного синтеза, заключающую-
ся в определении структуры и параметров простейшего (в некотором
конкретном смысле) регулятора, удовлетворяющего заданным требо-
ваниям к точности регулирования.
Для достижения заданных показателей качества регулирования
в эквивалентных сепаратных системах могут быть использованы
обычные приемы и средства теории автоматического регулирования
(введение интегралов и производных в закон регулирования, введе-
ние связей по возмущениям и т. д.).
Расчет параметров регуляторов в однотипных связанных систе-
мах, следующий за выбором схемы и законов регулирования, будет
рассмотрен в § 9.
После решения задачи синтеза эквивалентной системы вычисля-
ются передаточные функции оригинальной системы. Матрица пере-
даточных функций звеньев идентичного назначения (регуляторов,
связей по возмущениям и т. д.) О(р) определяется по полученным
из расчета элементам 6i(p), б2(/?), ..бп(р) диагональной матрицы
передаточных функций к(р) звеньев того же значения синтезирован-
ной эквивалентной САР с помощью соотношения подобия (гл. 1):
D(/?) = CA(/7)C-i. (115)
Матрица передаточных функций D(p) может быть реализована-
путем последовательного включения трех групп звеньев: усилитель-
ных с матрицей коэффициентов передачи С-1; звеньев с диагональ-
ной матрицей передаточных функций А(р); усилительных с матри-
цей коэффициентов передачи С. Такая реализация может оказаться
более простой, чем непосредственная реализация матрицы D(p).
Если А (р) — скалярная матрица (^ (р) — д2 (/?) = ...= 8П(/?)),
что встречается при решении' задачи синтеза в первой или во вто-
рой постановках, то
Ъ(р) = \(р). (116)
Таким образом, регуляторы эквивалентной системы непосредст-
венно переносятся в оригинальную систему, собственно «пересчет»
не требуется.
в) Задача синтеза изолированных сепаратных регуляторов
Если задано, что между сепаратными САР не вводятся пере-
крестные связи, то регулятооы эквивалентных сепаратных САР
должны быть идентичными. В самом деле, передаточные матрицы
регуляторов обеих эквивалентных систем должны быть диагональ-
ными; но это может быть тогда и только тогда, когда искомая матри-
ца передаточных функций регуляторов скалярная.
Для п сепаратных САР эквивалентной системы необходимо вы-
брать идентичные схемы регулирования с одинаковыми параметрами
(рис. 45,а, б).
Например, в случае связей в объекте между регулирующими
органами регулируемых каналов (см. рис. 2) нужно выбрать идеи
тичные регуляторы для одноконтурных САР, различающихся коэф-
фициентами усиления в разомкнутом состоянии.
86
При решении задачи выбираются одинаковые структуры и ве-
щественные параметры регуляторов для п изолированных регулируе-
мых каналов эквивалентного объекта, различающихся коэффициен-
тами усиления отдельных звеньев Xi, А,2 ..Хп. Число рассчитывае-
мых параметров многосвязной САР равно числу параметров настрой-
ки сепаратной САР:
/=г.
В соответствии с (116) структура выбранного регулятора экви-
валентной САР и его параметры непосредственно переносятся в про-
{ИЗ—&п I f>
ектируемую САР; необходимость вычислений по формуле (115) отпа-
дает. Поэтому знание матрицы С при расчетах не требуется, анализ
матрицы А достаточно ограничить вычислением характеристических
чисел.
г) Задача синтеза сепаратных* регуляторов
с оюесткими перекрестными связями
Если допускается введение простейших искусственных жестких
перекрестных связей между сепаратными САР, то для регулируемых
каналов эквивалентного объекта требуется выбрать идентичные схе-
мы регулирования, различающиеся коэффициентами усиления одина-
l |иШЬ-^7|—L=====(^<,=4J]^==s(^==
6)
а)
Рис. 46.
ково расположенных усилительных звеньев. Положения этих усили-
тельных звеньев в структурных схемах сепаратных САР эквивалент-
ной системы определяются местом введения жестких перекрестных
связей. Точки отбора жестких связей и точки их приложения в струк-
турных схемах сепаратных САР выбираются из соображений удоб-
ства реализации и эффективности действия связей на динамику
САР. На рис. 46,а, б показана структурная схема эквивалентной се-
87
паратиой САР при введении жестких перекрестных связей между
сигналами ошибок регуляторов; \xq, <7=1, 2, ..п — коэффициенты
усиления звеньев, замещающих жесткие перекрестные связи.
Параметры регуляторов сепаратных САР выбираются одинако-
выми, вещественными. Параметры усилительных звеньев эквивалент-
ной системы, замещающих жесткие перекрестные связи проектируе-
мой системы, выбираются для каждой из сепаратных САР индиви-
дуально, независимо от других; для регулируемых каналов с ком-
плексными параметрами передаточных функций — комплексными.
Число рассчитываемых параметров
l=r+nq,
где г — число параметров настройки сепаратной CAP; q — число
групп жестких перекрестных связей между сепаратными САР.
д) Задача синтеза при отсутствии
ограниченной структуры регулятора
Если на структуру САР в постановке задачи синтеза не накла-
дывается ограничений, то структура и параметры каждой из сепа-
ратных САР эквивалентной системы выбираются независимо от дру-
гих (рис. 47,а, б).
1 l*Mflh -&~:-4 4»frj |о=~=="==4><*==
а)
6)
Рис. 47.
Такой подход применялся В. Т. Морозовским при синтезе одно-
типных САР с простыми симметричными связями. В этом случае за-
дача сводилась к синтезу двух систем: относительных и усредненных
координат [Л. 48].
Структура и параметры каждой из сепаратных САР эквивалент-
ной системы выбираются независимо от других, что существенно
упрощает проведение соответствующих этапов синтеза. Число рас-
считываемых параметров
i=i г,.
(7=1
где Tq — число параметров настройки q-и сепаратной САР эквива-
лентной системы.
Три рассмотренные процедуры существенно различаются той сте-
пенью свободы, которой обладает инженер при проектировании си-
стемы; при прочих равных условиях различно и достижимое качество
88
регулирования. Естественно, удовлетворительный результат синтеза
при использовании первой или даже второй процедуры не всегда
достижим; в таких случаях необходимо идти на ослабление огра-
ничений, наложенных на структуру.
9. РАСЧЕТ ОДНОТИПНЫХ СВЯЗАННЫХ СИСТЕМ МЕТОДОМ
РАСШИРЕННЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
а) О методе расширенных частотных характеристик
Особенность расчета регуляторов сепаратных САР в каждом из
трех вариантов синтеза рассмотрим на примере применения процеду-
ры метода расширенных частотных характеристик, получившего рас-
пространение при проектировании промышленных систем регулирова-
ния 1[Л. 69, 70]. Будем рассматривать случай, когда каждый из п
регулируемых каналов содержит лишь одну регулируемую величину;
измеряются лишь регулируемые величины. Каждый из п регулируе-
мых каналов эквивалентного объекта представляет собой устойчивый
или нейтральный низкочастотный фильтр, не содержащий колеба-
тельных звеньев; с ростом частоты модули их амплитудно-фазовых
характеристик убывают, увеличивается отрицательный сдвиг по фа-
зе. В качестве регуляторов применяются стандартные с передаточной
функцией в виде одного из известных вариантов трехчленной фор-
мулы
1 w*(P) = -j- + sl + s1p.
где S0 — коэффициент при интегральной составляющей закона регу-
лирования; S{ — коэффициент при пропорциональной составляющей;
S2 — коэффициент при производной.
Методом расширенных частотных характеристик решается сле-
дующая задача: выбрать настройку регулятора заданной структуры,
минимизирующую некоторый критерий качества регулирования (инте-
гральный квадратичный критерий, абсолютную площадь регулирд-
вания или среднюю квадратичную ошибку) при заданных ограниче-
ниях на распределение корней характеристического уравнения САР
(обычно ограничиваются степени устойчивости и колебательности
[Л. 69]). В расчетной процедуре используется прием /^-разбиения.
Если разбиение производится в плоскости пары рядом стоящих
коэффициентов передаточной функции регулятора (Si—S0 или S2—
—Si), а по оси абсцисс откладывается коэффициент при старшем по
степени р члене, то для широкого класса возмущений оптимальная
настройка находится на границе области допустимых настроек (т. е.
на кривой равной колебательности), правее ее вершины*. Правилом
выбора параметров правее вершины путем визуальной оценки ха-
рактера кривой равной колебательности можно пользоваться, не
различая характера воздействий на изолированную САР. Это допу-
стимо в практических расчетах вследствие относительно низкой чув-
ствительности САР к вариации настройки в окрестности оптималь-
ной [Л. 70].
Если выбирается больше двух параметров настройки, то рассчи-
тываются- оптимальные значения какой-нибудь пары при ряде фикси-
* Если во входных колебаниях не преобладают высокочастотные состав-
ляющие [Л. 72]; это условие обычно выполняется на практике,
89
рованных значений остальных; путем сравнения качества регулиро-
вания при рассчитанных настройках определяется глобальный опти-
мум. Ограничимся случаем двух параметров настройки для каждого
из регуляторов.
Сделаем несколько замечаний относительно расчета методом
расширенных частотных характеристик сепаратной САР с комплекс-
ными параметрами. Граница -разбиения состоит из двух ветвей:
для положительных и отрица-
тельных частот (следствие не-
симметрии расширенных ча-
стотных характеристик регули-
руемого канала с комплексны-
ми параметрами, рис. 48). Гра-
ницы, построенные для двух
£ сепаратных САР с комилексно-
*_L- сопряженными передаточными
^ функциями, совпадают, но ча-
стотные отметки различаются
Рис. 48. знаками; поэтому каждая из
границ, как обычно, штрихует-
ся дважды. Построение гра-
ниц следует проводить либо для одной из двух систем с ком-
плексно-сопряженными характеристиками — для всего диапазона
частот, либо для обеих САР — только для положительных частот.
Будем применять второй из этих двух равносильных приемов.
Область допустимых параметров ограничивается одной из двух низ-
кочастотных ветвей границы -разбиения.
Если вещественная часть частотной характеристики эквивалент-
ного регулируемого канала объекта на нулевой частоте положитель-
на *, то САР с комплексно-сопряженными параметрами имеют во
втором и третьем квадрантах падающие амплитудно-частотные ха-
рактеристики; с ростом частоты отставание по фазе увеличивается.
При этом кривые равной колебательности имеют свой «обычный»
вид '[Л. 69, 70], оптимальная настройка, лежит правее вершины.
Отметим, что установка последовательно с регулируемым каналом
звена с комплексным коэффициентом усиления единичного модуля
jx = е1^ приводит к повороту частотной характеристики на угол
argp,=\|>. Если if>0, то при сделанных ранее оговорках на положи-
тельных частотах во втором и третьем квадрантах происходит умень-
шение модуля частотной (расширенной частотной) характеристики
и повышение частоты при фиксированных фазовых сдвигах; если г|э<0,
то наблюдаются обратные явления (рис. 49,а). Соответствующую
деформацию претерпевают кривые D—(\D^—) разбиения (рис. 49,6).
б) Расчет настройки идентичных изолированных регуляторов
Выбирается одна общая настройка для регуляторов эквивалент-
ных сепаратных САР. Вещественные части передаточных функций
регулируемых каналов при р=0 должны быть положительными во
избежание положительных связей в системе регулирования через ре-
гуляторы.
* Иначе через регуляторы в системе действуют положительные обратные
связи, и применение такой САР по меньшей мере нецелесообразно.
90
Область допустимых настроек в плоскости параметров системы
является пересечением (общей частью) выпуклых областей допусти-
мых параметров для п сепаратных САР, т. е. сама является выпук-
лой. Поэтому область допустимых настроек сохраняет в основном
свой обычный вид [Л. 69].
Рис. 49.
При выборе параметров настройки из допустимой области реко-
мендуется оптимизировать сепаратную САР эквивалентной системы,
имеющую наиболее близкие к мнимой оси корни (т. е. определяю-
щую общую границу -разбиения сепаратных САР). Основанием
для рекомендации служит то обстоятельство, что сепаратная система
с ближайшими к мнимой оси корням*, наиболее чувствительна к ва-
О а) 0 4>
Рис. 50.
риации настроек [Л. 72]; для сепаратных САР, близких по своим
характеристикам (с мало отличающимися от расчетного значения-
ми Я), приближенно будет осуществляться оптимум. Для остальных
эквивалентных сепаратных систем, обладающих удаленными от мни-
мой оси корнями, вариация настроек не приведет к существенному
изменению качества (см. примеры в |[Л. 70]). Выбор настройки про-
изводится на общей кривой равной колебательности, правее ее вер-
шины (рис. 50,а, точка /V).
Разберем частный случай, когда в объекте действуют перекрест-
ные связи между регулирующими органами (см. рис. 2), а характе-
ристические числа матрицы взаимосвязей А — вещественные, поло-
жительные (матрица А — симметричная, положительно определен-
ная). Расчет кривой равной колебательности производится лишь для
91
эквивалентной сепаратной системы, соответствующей наибольшему
характеристическому числу макс. Xq. Вместо численного значения
макс. kq в расчете может быть применена какая-нибудь его оценка
Я
сверху. Если кривая разгона отдельного регулируемого канала —
«типовая», то могут быть применены упрощенные методы расчета
настройки по кривой разгона (Л. 69, 70]; при этом расчет также
проводится по наибольшему из характеристических чисел (или по
его оценке сверху).
Пример 11. Для объекта с перекрестными связями между регу-
лирующими органами (рис. 51,а) требуется рассчитать систему регу-
лирования, состоящую из изолированных ПИ-регуляторов. Заданная
степень колебательности т=0,34.
f -0J5 -0,1 0
~0}5 f 0,25 -а/
'0,1-0,25 ' -QJ5
0 -0,1 -0,25 1
— ■ . . . .
'а, ли,г ttj а,
* I 1 А *1Г~Л 7
—1 °>93 гФ-Нст-—-
(EEL
а;
6)
Рис. 51.
Структурная схема эквивалентного объекта показана на рис. 51,6;
она состоит из четырех изолированных каналов регулирования, раз-
личающихся коэффициентами усиления в разомкнутом состоянии:
0,504-2
1,01
(Р+1)4
0,93-2
1,86
(/>+П4
1,25-2
2,50
(/>+1)4
(Z-+1)4
1,32-2
2,-64
(Р+1)4
Так как матрица А положительно определенная, то расчет на-
стройки проводится по характеристике эквивалентной сепаратной
САР, соответствующей наибольшему из характеристических чисел
А,4=1,32. Настройка выбирается на кривой равной колебательности
92
Qjl OA
Рис. 52.
(рис. 52), (правее ее вершины (точ-
ка N):
Si ==0,39;
S0=0,14.
Результаты моделирования систе-
мы приведены в 'примерах 5, 10.
Пример 12. Рассмотрим задачу
определения оптимальных параме-
тров настройки регуляторов системы
автоматического распределения дутья
по фурмам доменной печи. Как сле-
дует из результатов, полученных
в § 5, настройка регуляторов расхо-
дов на фурмах должна быть подчинена задаче стабилизации рас-
пределения расходов (в системе относительных движений). Заданы
конкретные параметры объекта [Л. 36]: л=20; коэффициенты ма-
трицы А:
/ 0,052\ п
Ян = —( 0,037 + —£—J, k= 1,2, ...,-2~— 1.
Расчет вещественных характеристических чисел матрицы А с по-
мощью формулы (П-28) дает:
0,868 < А* < 1,164, k=2, 3, я.
Динамические свойства сепаратного регулируемого канала —
фурмы — представлены ее экспериментальной переходной характери-
стикой, являющейся типовой S-образной кривой разгона [Л. 70]
(см. рис. 53). В системе применены ПИ-регуляторы:
Wv (р) = kv Y^-p '
В рассматриваемом случае может быть применен упрощенный
метод расчета оптимальной настройки регуляторов одноконтурных
систем по «спрямленным
кривой разгона k0, to и
Тя - беек
параметрам кривой разгона. Параметры
То определяются по отрезкам, отсекаемым
касательной и кривой в точке
перегиба от ее асимптот, как
показано на рис. 53. В [Л. 70]
приведены формулы для расче-
та настройки регуляторов, обе-
спечивающих минимум инте-
гральной квадратичной ошибки
при ограничении на колеба-
тельность замкнутой системы
(возмущение — скачкообразное
единичное, со стороны регули-
рующего органа).
В нашем случае колебатель-
ность системы относительных
движений определяется эквивалентной сепаратной САР, соответствую-
щей наибольшему из характеристических чисел Амакс = 1,164. Эта же
сепаратная система оказывается наиболее чувствительной (по инте-
гральной квадратичной ошибке) к изменениям параметров регулято-
0,5
У
г1 1
• 1 ^ 1
■Хд=3сек
\Л 6
в 10сек
Рис. 53.
93
pa. Поэтому расчет ведем по ее характеристикам. Параметры на-
стройки регуляторов
1
2,6 1-й—.»)
= 0,39;
Ги=0,8Го=4,8 сек.
С целью контроля качества регулирования в соответствии с ре-
комендациями § 8 проводим моделирование лишь двух систем с пре-
дельными характеристиками: ЯМакс = 1,164 и ЯМин=0,87. Результаты
моделирования показаны на
0,8
0,6
OA
0,2
0
'0,2
-OA
kk°f
\
>
макс
-0,6
V i
t
1
ту
'20 \
0^
50сек
рис. 54. Верхние значения по-
казателей качества переходных
процессов в двух системах (от-
носительное перерегулирование
#макс = 60%, время регулиро-
вания /Р=48 сек) являются
исчерпывающей характеристи-
кой точности работы многомер-
ной системы в переходном ре-
жиме.
Рис. 54.
Определить оптимальные
параметры ПИ-регуляторов на
объекте с типовой переходной
характеристикой, обладающем
комплексным коэффициентом передачи (случай комплексных харак-
теристических чисел матрицы взаимосвязей), можно по рис. 55*.
Графические рекомендации разработаны для колебательной фор-
мы переходного процесса (т=0,22); единичное скачкообразное воз-
мущение наносится по заданию.
На рис. 55,а показала зависимость оптимальных параметров на-
стройки ПИ-регулятора от параметров объекта: коэффициента уси-
ления &о. чистого запаздывания То, постоянной времени Го и фазы
комплексного коэффициента усиления г|х Критерий оптимальности —
интегральный квадратичный
00
dt.
На рис 55,6 представлены зависимости оптимальных значений
интегрального квадратичного критерия / от параметров объекта.
в) Расчет настройки регуляторов
при введении между ними жестких перекрестных связей
Ограничимся случаем, когда перекрестные связи вводятся после-
довательно с регуляторами (между сигналами ошибок, как на рис. 46,
или между выходными сигналами регуляторов). Необходимо вы-
* Расчет проведен в Вычислительном центре ЦНИИКА, вычислительные
программы разрабатывались инж. Н. Ростковской под руководством
инж. Е. Рабиновича.
94
брать п +1 параметров настройки САР< два общих параметра на-
стройки регуляторов и п—1 независимых* коэффициентов усиления
звеньев, замещающих систему жестких перекрестных связей.
В плоскости пары параметров настройки, пропорциональных ко-
эффициенту усиления регулятора (Si—S0 или S2—S4, рис. 50,6),
искомые параметры лежат на луче, исходящем из начала координат
и проходящем в первом квадранте (луч ON3 на рис. 50,6).
що
50,0
20,0
Ю,0
6,0
5,0
3,0
2,0
1,0
0,8
0,5
0,15
i—г-
ttod
0,52^
То
Рис. 55.
0,2 OJOfi 0,5 0,8 1
б)
Если параметры эквивалентного объекта вещественны, то при
расчете достаточно подобрать такой луч, чтобы он пересекал каждую
из кривых равной колебательности локальных САР правее вершины.
Точки пересечения * дают искомые параметры настройки (точки Nu
Ni, N3 на рис. 50,6). Вполне допустимо ограничиться довольно гру-
бым выполнением правила «правее вершины», если при выборе по-
ложения луча встречаются затруднения.
95
Пусть теперь среди характеристических чисел матрицы А имеют-
ся пары комплексно-сопряженных. В соответствующих эквивалентных
сепаратных системах следует выбрать комплексные коэффициенты
передачи усилительных звеньев. Число варьируемых параметров для
такой сепаратной САР увеличивается на единицу: комплексный ко-
эффициент усиления характеризуется двумя параметрами.
Рекомендуется для каждой пары комплексно-сопряженных САР
провести предварительный расчет с целью определить оптимальное
значение аргумента ф комплексного коэффициента усиления р.. При
расчете для ряда фиксированных значений ф выбирается настройка
на общей (для пары сепаратных САР с комплексно-сопряженнымч
параметрами) кривой равной колебательности, правее ее вершины;
затем перебором определяется «глобальный оптимум». Аргумент ко-
эффициента усиления той из двух САР с комплексно-сопряженными
параметрами, которая обусловливает общую кривую равной колеба-
тельности, выбирается положительным; это приводит к увеличению
допустимых коэффициентов усиления и повышению рабочих частот,
т. е. к улучшению качества регулирования [Л. 69, 70].
При увеличении ф кривые равной колебательности двух САР
с комплексно-сопряженными параметрами сближаются (обратно дви-
жению кривых равной колебательности, показанному на рис. 50,6);
наступает момент, когда они пересекаются и меняются местами —
внутренней становится та, которая прежде была внешней. Дальней-
шее увеличение ф приводит к снижению рабочих частот и уменьше-
нию допустимого коэффициента усиления, т. е. к ухудшению каче-
ства регулирования. Следовательно, ф следует выбирать таким, что-
бы обе кривые равной колебательности на участке правее вершины
внутренней из них располагались достаточно близко одна от другой.
В частном случае, когда звенья объекта и регулятора с комплексны-
ми коэффициентами усиления Хк и \Хк оказываются последовательно
включенными в цепь без разветвлений и точек суммирования, сле-
дует выбирать arg\ik=—argA,fc; две кривые равной колебательности
при этом совпадают.
После окончания предварительного расчета проводится выбор
настройки многосвязной САР как в случае вещественных характе-
ристических чисел матрицы А. Настройка для эквивалентных сепа-
ратных САР с комплексными параметрами по-прежнему выбирается
правее вершины кривой равной колебательности (в точке ее пересе-
чения с лучом).
Из полученной в результате расчета диагональной матрицы пе-
редаточных функций в качестве скалярного множителя выделяется
передаточная функция регуляторов (общая для всех сепаратных
САР); сомножитель — диагональная матрица с независящими от р
элементами представляет собой матрицу коэффициентов передачи
перекрестных связей в каноническом базисе. Она определена с точ-
ностью до скалярного множителя (до коэффициента усиления регу-
ляторов), который выбирается из тех или иных соображений (на-
пример, уменьшения влияния зоны нечувствительности регуляторов
и т. д.)
Если в объекте действуют перекрестные связи между регули-
рующими органами, то речь идет о расчете совокупности сепаратных
САР, в которых регулируемые каналы различаются коэффициентами
усиления. Пусть при этом эквивалентные сепаратные САР работают
в одинаковых условиях (например, на входе САР действует скачко-
образное возмущение lif|| = l) и существует единственный оптимум
96
для отдельно взятой сепаратной САР. Тогда оптимум в системе
реализуется путем оптимизации каждой из эквивалентных сепарат-
ных систем. Коэффициенты усиления рй обратно пропорциональны
характеристическим числам матрицы А. Матрица коэффициентов уси-
ления перекрестных связей в эквивалентной системе обратна матри-
це А (или отличается от А-1 скалярным множителем); оптимальной
является автономная система.
г) Расчет, при отсутствии ограничений
на структурную схему регулирующей части САР
При расчете не возникает осложнений, связанных с требования-
ми одинаковости параметров настройки различных сепаратных САР.
Для сепаратной САР с комплексными параметрами каждая на-
стройка регулятора должна полагаться, вообще говоря, комплексной.
При этом число выбираемых параметров удваивается; сложность
задачи расчета значительно возрастает. Задача может быть упроще-
на путем наложения ограничений на структуру рассчитываемой сепа-
ратной системы.
ГЛАВА ПЯТАЯ
СПЕЦИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ
ОДНОТИПНЫХ СВЯЗАННЫХ СИСТЕМ
10. ГРУБОСТЬ И ЧУВСТВИТЕЛЬНОСТЬ ОДНОТИПНЫХ
СВЯЗАННЫХ СИСТЕМ
а) Постановка вопроса.
Грубость однотипных связанных систем
В этой главе рассматриваются вопросы влияния отличий системы
от идеализированной модели на свойства системы и способы учета
этих отличий при расчете (§ 10), а также вопросы приближенного
исследования однотипных связанных систем с применением методов
локализации характеристических чисел передаточной матрицы взаи-
мосвязей (§ 11). В заключение коснемся вопроса о месте метода
эквивалентной системы в общей теории автоматического управления
(§ 12). .
Метод эквивалентной системы предполагает идентичность сепа-
ратных систем регулирования и совпадение передаточных функций
перекрестных связей с точностью до коэффициентов усиления.
Естественно возникает вопрос: насколько правомерна такая
идеализация уравнений многосвязных однотипных систем, если ре-
альные сепаратные системы неизбежно отличаются индивидуальными
особенностями, а их характеристики медленно меняются во времени
(старение), оставаясь при этом «близкими» между собой? Этот во-
прос является частью более общей проблемы грубости и чувствитель-
ности однотипных связанных систем по отношению к «неидеально-
стям» — малым параметрам двух групп: малым изменениям коэффи-
циентов уравнений системы и малым паразитным постоянным вре-
7—1206
97
мени в элементах системы. Принципиальное различие этих двух
групп малых параметров в том, что появление первых приводит лишь
к малым изменениям коэффициентов уравнений системы, появление
вторых вызывает повышение порядка уравнений. При этом возни-
кают два принципиальных вопроса [Л. 73, 74]:
1. Не может ли появление малых параметров привести к суще-
ственному изменению свойств системы, т. е. груба ли система по
А. А. Андронову?
2. В каких случаях и как следует учитывать влияние малых па-
раметров при расчете?
От того, груба ли система, принципиально зависит допустимость
применения идеализации при исследовании, т. е. методов расчета
однотипных связанных систем, рассматривавшихся выше в гл. 2—4.
Решение второго вопроса должно очертить границы области приме-
нения рассматриваемых методов исследования в координатах параме-
тров, определяющих различия передаточных функций сепаратных си-
стем и перекрестных связей.
. Пусть малые параметры таковы, что сепаратные системы оста-
ются идентичными, а перекрестные связи по-прежнему различаются
лишь коэффициентами усиления. Например, в каждой из сепаратных
систем могут иметь место неучитываемые при анализе малые по-
стоянные времени одинаковых инерционных звеньев; коэффициенты
передачи перекрестных связей могут отличаться от их расчетных
значений по тем или иным причинам и т. п. Как легко видеть, в этом
случае вопросы грубости и чувствительности относительно просто
решаются на эквивалентной сепаратной системе. В самом деле, появ-
ление малых параметров не препятствует переходу к эквивалентной
системе регулирования с независимыми сепаратными каналами пере-
дачи воздействий.
Эквивалентная система отличается ит исследовавшейся нали-
чием малых параметров, характер которых, положение в структур-
ных схемах сепаратных САР и численные значения определяются
обычным образом с помощью правил из гл. 2.
Если в идентичных элементах системы имеются различные по
величине паразитные постоянные времени, то грубость системы сле-
дует из ее грубости по отношению к одинаковым паразитным по-
стоянным времени. В самом деле, важно установить сам факт грубо-
сти, что можно выполнить, предположив, что малые параметры
в идентичных цепочках одинаковы. К системе с реальными соотно-
шениями между паразитными постоянными (в том числе с малыми
параметрами разных порядков) можно затем перейти за счет малых
деформаций коэффициентов системы, грубость которой уже установ-
лена.
Таким образом, приходим к следующему простому правилу
проверки системы на грубость.
Грубость однотипных связанных систем по отношению к малому
параметру следует из грубости эквивалентных сепаратных САР по
отношению к малому параметру.
Пусть, например, в канале объекта /-й сепаратной САР системы
со структурной схемой рис. 2 имеется не учитываемое при анализе
звено с передаточной функцией W(p, где \i — малый параметр,
соответствующий малой постоянной времени, см. рис. 56,а. Тогда
анализ грубости системы по отношению к малому параметру можно
проводить на эквивалентной системе со структурной схемой рис. 56,6.
Встречающиеся в инженерной практике однотипные связанные
98
системы являются грубыми, и, следовательно, применение рассматри-
ваемых методов их исследования и соответствующая идеализация
их уравнений принципиально допустимы.
б) Вариации параметров и дополнительные движения
Рассмотрим подробнее вопрос о влиянии малых параметров на
динамику системы. Предположим сначала, что динамические свой-
ства звеньев сепаратных систем, предполагавшиеся при анализе
идентичными, отличаются друг от друга. Диагональная передаточная
матрица звеньев W*(p) теперь отличается от принимавшейся при
анализе скалярной передаточной матрицы W(p)E:
W.(p) = ^(p)E+AW(p). (117)
Здесь W (р) — передаточная функция, описывающая идеализиро-
ванную модель звена сепаратной системы; AW (р) — {AW# (р)У{ —
/Г q-a системе
От к-и
састелш\
wp(p)\
4А
Wf(p)f>,
6)
Рис. 56.
диагональная передаточная матрица, отражающая индивидуальные
отличия каналов, — вариация передаточной матрицы W(p) Е.
Таким образом, имеем дело с варьированной системой; поведе-
ние этой системы отличается от поведения идеализированной моде-
ли, так что, например, реализации yv(t), yi{t) и т. д. (варьиро-
ванное движение) отличаются от соответствующих результа-
там нашего анализа t/i(t), y2(t) ... (основное движение) на
так называемое дополнительное движение:
л</1 (0 = fi (0-01 (0;
At/a (0 = Гг (t) — y2 (t);
(здесь применена терминология теории чувствительности {Л. 74]).
7* 99
Вариациям в исследуемой системе соответствуют вариации в эк-
вивалентной системе и, естественно, варьированное и дополнитель-
ное движение.
Новая передаточная матрица звена в эквивалентной системе
имеет вид:
C_1W* (р) С =W (р) Е+С-* Д Wi(p) С.
(Первое слагаемое в этом соотношении соответствует эквивалент-
ной системе для идеализированной модели, второе (представляет со-
бой вариацию передаточной матрицы соответствующего звена экви-
валентной системы; она далее обозначается AW3i(p):
Ат(р)=С-*АЩр)С.
Так как на главной диагонали AW(p) стоят не равные друг
другу элементы, то AWa,(p)—недиагональная матрица; для ее эле-
ментов имеем:
п п
А*/* (Р) = £ {С"1}*.*.* (Р) = £ (Р). (118)
где
4? =• (С"(Н9)
Диагональные элементы матрицы AW3(p) представляют собой
вариации передаточных функций соответствующих звеньев эквива-
лентных сепаратных систем; недиагональные элементы матрицы
отражают действие перекрестных связей между сепаратными систе-
мами и представляют собой вариации нулевых передаточных функ-
ций перекрестных связей. На основе выражения (lil9) можно вы-
писать матрицу коэффициентов передачи Kj, с которым вариация
AWii'(p) входит в соответствующие звенья эквивалентной системы:
Каждая строка матрицы, как и каждый столбец, составлена из
элементов у-й строки матрицы С с сомножителем, представляющим
собой определенный элемент из этой же строки; на диагонали ма-
трицы стоят квадраты модулей элементов строки.
На рис. 57 показана структурная схема, отражающая форми-
рование дополнительных движений в эквивалентных сепаратных си-
стемах при малых вариациях идентичных звеньев системы с урав-
нениями
*i=(W(P)v*, / = 2, п.
100
Вариация звена в /-й сепаратной САР (рис. 57,а) приводит
к появлению связей в эквивалентной системе |(рис. 57,6);, структур-
ная схема рис. б7,в соответствует обозначениям ('М8).
В случае двусвязной антисимметричной системы вариация од-
ного из двух прямых каналов (первого, например) в эквивалентной
системе имеет матрицу коэффициентов передачи:
Таким образом, в эквивалентной системе рассматриваемая вари-
ация -представлена с одинаковым коэффициентом передачи 7г в се-
паратных каналах и в «слабых» симметричных перекрестных связях
между каналами.
Для простой симметричной системы в случае вариации в у-м
канале AWjj(/>) ее матрица коэффициентов передачи, соответствую-
щая матрице С 1(78), имеет вид:
1 1 1
/-я
строка
1
п Уп-
1
nVn— 1
1
п(п—1)
Vn(n—\)(n—2)
1
(n—l) Vn(n—2)
Vn(n-l)(n-2) (n—\) Vn (n—2) J"-*) 2)
V
n—j + \
n(n—\)(n—j—2)
В эквивалентной системе оказываются варьированными п—/+2
сепаратных САР. (Каждая из вариаций входит в эквивалентную си-
стему усредненных координат с коэффициентом передачи \/п; ко-
эффициенты передачи в других эквивалентных. сепаратных САР
зависят от способа перехода к эквивалентной системе ((напомним,
что в простой симметричной системе замена переменных может
быть осуществлена различными способами). Действие каждой из
вариаций «распределено» в эквивалентной системе «неравномерно»,
так что одна из сепаратных систем получает наиболее весомую долю
вариации; соответствующие коэффициенты принимают значения меж-
ду */г и (я—-1)/л.
Рассмотрев вариации сепаратных каналов исследуемой системы,
перейдем к случаю, когда элементы уточненной матрицы коэффици-
ентов передачи перекрестных связей А(р) являются передаточными
функциями устойчивых звеньев с малыми постоянными времени, так
что
А(/?)=А(0)+АА(р). .(120)
Здесь А соответствует идеализированной модели; модули ЛА(р)
В диапазонах существенных для системы частот достаточно малы.
101
После перехода к новому базису имеем:
С-1 А\(р) С=Л+ С-1.АА (р) С.
•Как и в предыдущем случае, C-^AAfpJC— недиагональная пе-
редаточная матрица.
Вариации АА,ц, ая22, ..., А^пп коэффициентов передачи %и
Яг, ..., Хп в эквивалентных сепаратных системах выражаются фор-
мулой
п
&Kl = (С"'ЛАС}*, = 2 {С-^дАЛда*?,,, Л./= 1,2. .... я. (121)
Таким образом, появление малых параметров в системе приво-
дит: 1) к вариации передаточных функций соответствующих звень-
ев сепаратных САР эквивалентной системы и 2) к появлению ела-
v1
*1
К j-й системе
Wfp)
w(p)
б)
Рис. 57?
102
бых перекрестных связей между изолированными при отсутствии
малых параметров сепаратными системами.
Соответственно в дополнительном движении Ar\k(t) каждой из
п эквивалентных сепаратных систем следует различать составляю-
щую, вызванную вариацией звеньев этой системы Аг]//1(/), и со-
ставляющую, -определяемую слабыми перекрестными связями
Поскольку форма перехода к эквивалентной системе (т. е. ма-
трица С) для варьированной^ CAjP сохранилась прежней, то дейст-
вительны все соотношения между характеристиками двух систем,
рассматривавшиеся в предшествующих главах; при определении по-
казателей качества в исследуемой системе с помощью соотноше-
ний (103), ('104), ((1'13) и т. д. за основу необходимо принимать ха-
рактеристики варьированного движения эквивалентной системы.
в) К оценке дополнительных движений ,
Непосредственное исследование вариаций и дополнительного
движения в эквивалентной системе затрудняется необходимостью
вычисления матриц С и С-1 и громоздкостью выражений (117) —
(121).
Если канонический базис системы ортогонален, то для вариаций
операторов эквивалентной системы легко вывести относительно же-
сткие оценки. Так, вариации звеньев исследуемой системы AWa(p)
входят в вариацию k-и эквивалентной сепаратной системы AW9kk(p)
с неотрицательными весами, дающими в сумме единицу {см. (118)]:
и
Весовой коэффициент auj представляет собой квадрат модуля
/-й компоненты вектора с&.
Таким образом, вариации передаточных функций в эквивалент-
ных сепаратных системах претерпевают некоторое осреднение; для
точек из правой полуплоскости и мнимой оси имеем по крайней
мере оценку
|ДП^ (/,)!< макс. \№„(р)\. (122)
/
Обычно для идеализации уравнений сепаратных систем их ха-
рактеристики усредняют в том или ином отношении, так что в диа-
пазонах рабочих частот вариации AWjj(p) в сумме погашают друг
друга:
п
Е №ц(р)
и макс. \AWit(p)\
103
При атом и модули АЩк(р) взвешенной суммы (118) в диапазо-
нах существенных для системы частот оказываются довольно малы-
ми, так что оценка (Ш2) определенно имеет некоторый запас.
Для коэффициентов передачи перекрестных связей имеем:
ags = {c-1}g^s = c*jqcjs;
каждый из коэффициентов ограничен
I «#} К (I си |} V\-\cul* < 4" '
Радикал V \ — | Cjs |2 представляет собой оценку сверху для моду-
ля компоненты Cjs вектора единичной длины; оценка 1/2 легко полу-
чается путем анализа функции | Cjs | V\ — | Cjs |2 на интервале 0 ^
<|сЛ|<1:
Для модулей коэффициентов в выражениях для недиагональ-
ных элементов матрицы вариаций (.1(18) имеем оценку вследствие
известного неравенства (Коши — Буняковского:
Si«j2>i<i.
5=1
Дашее можно вывести определенные суждения относительно роли
каждой из вариаций AWjj(p) в вариациях звеньев эквивалентной
системы на основе анализа матрицы ее коэффициентов передачи
Kj. Имея в виду свойства ортогональных нормированных базисов,
легко получить следующие выводы:
1. -Вариация звена у-й сепаратной системы AWjj(p) входит
в вариации эквивалентных сепаратных систем AW*s(p) с неотрица-
тельными весами, в сумме дающими единицу:
п
S 1'л1я = 1-
k=\
2. Сумма квадратов модулей коэффициентов передачи при ва-
риации AWjj(p) в связях, берущих начало или приложенных в k-й
эквивалентной сепаратной системе, равна квадрату модуля /-го эле-
мента вектора Си:
п
£ |^к|2 = 1^12.
5=1
3. Сумма квадратов модулей коэффициентов передачи при ва-
риации AWjj(p) в связях эквивалентной системы равна единице:
Эти соотношения во многих случаях дают возможность доста-
точно просто оценить сверху характеристики дополнительного дви-
жения системы из-за неидентичности сепаратных систем.
Аналогичным образом могут быть получены оценки для вариа-
ций в эквивалентной системе в случае, если претерпевает изменения
104
матрица А (121). Не останавливаясь на этом вопросе подробно,
подчеркнем только, что обычно вариации различных элементов ма-
трицы являются зависящими друг от друга и это существенно для
анализа.
г)' Оценка смещения корней характеристического уравнения
Рассмотрим вопрос о смещении основных корней характеристи-
ческого уравнения системы, определяющих ее динамику, под влия-
нием малых параметров. Путь к получению оценки смещения корня
состоит в следующем: составляется характеристическое уравнение
системы с учетом малого параметра ц |(т. е. полное характеристи-
ческое уравнение)
D(p, [г) =0, (123)
где D(py ц)—левая часть характеристического уравнения системы,
зависящая от \i. (При |х=0 имеем вырожденное характеристическое
уравнение идеализированной модели системы:
D(pt 0)=0.
Характеристическое уравнение в форме ((123) можно рассматри-
вать как неявную зависимость его корней от малого параметра ц.
Рассмотрим вопрос об оценке 'смещения г-го корня характеристиче-
ского уравнения q-й эквивалентной сепаратной системы рдг, пред-
полагая, что в точке pgr нет корней других эквивалентных сепарат-
ных систем. Искомая оценка при конкретном значении малого пара-
метра ijx получается путем разложения неявной зависимости (ЮЗ)
в ряд Тейлора [Я. 11, 27]:
(124)
Здесь частные производные (dD/dV]o, [dD/dp]Q определяются при
д=0в точке pqr'i Я — остаточный член:
R=-T^bW№' 0<8<1-
Обычно имеется возможность не учитывать остаточный член за
малостью.
Различая в системе по методическим соображениям многомер-
ные звенья со скалярной и числовой передаточными матрицами, бу-
дем считать, что структурная схема системы приведена к виду
рис. 28. На этой структурной схеме последовательно соединенные
звенья с передаточными матрицами числовой А и скалярной W(p)E
охвачены единичной обратной связью.
При исследовании чувствительности систем ограничимся случаем,
когда характеристические числа матрицы А различны (следователь-
но, Л — диагональна).
Пусть передаточные функции идентичных изолированных цепо-
чек отличаются от принятых при исследовании (117). IB линейном
приближении рассматриваемые вариации передаточных функций лро-
8—1206 105
порциональны малому параметру |i. Характеристическое уравнение
эквивалентной системы представим в форме
det [E+W(p)A + [xAW9 (р) А] = 0.
IB нашем случае D(p, ц) представляет собой полином по ц.
При вычислении производной [dD/d)\i] достаточно знать коэффициент
полинома при члене в первой степени |i, поскольку производные
старших членов в точке р,=0 обращаются в нуль. Но члены первой
степени имеют своими коэффициентами только (Произведения диа-
гональных элементов матрицы вариаций AW3(p) на элементы диа-
гональной характеристической матрицы эквивалентной системы Е-Ь
+ W[(p)A, так что
D(p, ^) = det][E + W(p)A] +
п п%\Фк
+ к- S (р) п t1 + ^w </oi + - <125>
k=l /=1
Имеем:
dD
фГ= J] (р) П 11 + Х^ (Л1 + -
k=zl /=1
В исследуемой точке p=pqr имеет место корень характеристиче-
ского уравнения (7-й эквивалентной сепаратной системы, так что
l+KqW{pqr)=0. ('126)
Окончательно имеем искомое значение производной:
«. Маг
[ЗГ ] = AW*lfo) П t1 + х^ '
/=1
При вычислении производной |^—^ J воспользуемся раз-
ложением (125) и учтем условие (126); получим:
«»М<?
] (Лг) П П+МПЛг)]. (127)
Окончательно получаем при ц.= 1 (т. е. при заданных вариациях
передаточных функций):
Aftr =5s Х#"(/>вг) ' (128)
Обратим внимание на то обстоятельство, что линейная часть
смещения r-го нуля характеристического уравнения q-й эквивалент-
ной сепаратной GAP определяется вариацией ее передаточной функ-
106
ции и не зависит от вариаций передаточных функций других сепа-
ратных систем и от передаточных функций возникающих «слабых»
перекрестных связей.
Аналогичным образом рассмотрим случай, когда элементы ма-
трицы А являются передаточными функциями с малыми постоян-
ными времени (120). Характеристическое уравнение системы
det {Е + ГС»[Л + цДЛ (р)]}^-0.
В рассматриваемом случае
D(p, (x) = det [E + W(p)\] +
п п,\Фк
k=\ /=1
Отсюда при условиях, что Л диагональна и что в исследуемой
точке только одна эквивалентная сепаратная САР имеет некратный
корень, следует:
п п,\Фк
П п+мп/>)] + ...
i=i
Учитывая условие (126), получаем:
Имея в виду выражение для [dD/dp\0 (127), получаем после
подстановки в (124) при р.=Л:
AAgg (Рйг)
bpqr^-XqWf (pqry (129)
Как и в предыдущем случае, смещение корня характеристиче-
ского уравнения эквивалентной сепаратной системы определяется
только вариацией звеньев этой системы и не зависит от других ва-
риаций.
С помощью соотношений (128), (129) можно оценить изменение
степеней устойчивости и колебательности системы под влиянием
малого параметра.
Смещения расчетных нулей характеристического уравнения си-
стемы тем больше, чем больше модули дополнительных членов
в расчетных нулях и чем меньше абсолютные значения производ-
ной передаточной функции W(p).
8* 107
Использование оценок (128), (129) затрудняется необходимостью
вычисления матриц С и С-1.
Если канонический базис системы ортогонален, то, используя
оценку для вариации передаточных функций эквивалентных сепарат-
ных САР (122), приходим к оценке сверху для модулей линейной
части смещения корня:
Оценки смещения корней характеристического уравнения отно-
сительно их расчетных значений могут быть использованы для кон-
троля допустимости идеализации уравений системы. В частности,
контролю могут быть подвергнуты допущения о возможности счи-
тать идентичными близкие но своим динамическим характеристикам
элементы одинакового назначения сепаратных GAP.
Контроль выполняется после проведения исследования я заклю-
чается в оценке смещения нулей характеристического уравнения.
При анализе САР оценки смещений дают уточненное распределение
корней характеристического уравнения; при синтезе смещение корня
должно сравниваться с допустимым, задаваемым из тех или иных
соображений. Если смещение не укладывается в допуск, то возмож-
ны следующие решения:
1) вводится такая поправка в найденные параметры системы,
что основные корни характеристического уравнения, определяющие
динамические характеристики САР, возвращаются в расчетные
точки;1
2} проводится повторный расчет для уточненной модели систе-
мы; способ уточнения зависит от характера неблагоприятного сме-
щения нулей.
Пример 113. Рассмотрим систему уравнений
Передаточные функции W0(p)t Wv(p) и матрица А те же, что а
в примере 5; WH(p) —диагональная передаточная матрица инер-
ционных звеньев с малыми постоянными времени, не учитывавшихся
ранее при анализе:
макс. | /Wu(pri)\
y=№0(p)WHi(p) [Att+f];
u-lMp)E'(x-y).
1
О
О
О
0,02/?+ 1
1
о
о
0,1/7+1
о
w.(/>)
о
о
0,2/7+ 1
о
1
о
о
о
0,02/?+ 1
108
Вычислим вариацию AW(p) передаточной матрицы W>(p) иден-
тичных изолированных цепочек сепаратных систем:
AW (р) = W0ip) Wv (р) (W. (р) -Е].
В соответствии с (128)
л
Щ (Л) (A) S (С-1)* [»м (А) - Ч 'л
. <?-1
h Wo (Ро) Wp(Po) + W'v (Ро) W0 (p.)}
S (C-^g Kqg(/?)o — 1] Cqs
^o(A) ^ ^p(A) J
025
0,580
\-0A06
0,580
0,25
30 с etc
025V
Рис. 58.
109
«Расчетный корень характеристического уравнения системы ро
в примере И определяется 4-й эквивалентной сепаратной САР; ро=
= (—0,34+/)0,6. Имеем:
°'302 0,02/70+1+0'6432 0Ла+ 1+
Д/?о^ — -
/ 4 0,39/^—0,14/70 \
1,25\a+i o,i4 ;
Г0,2/7о 0,02 /70
+ °'6432 Ж2^ТГ + °>3022 0,02/>0 + 1
-> = 0,015-/0,017.
Уточненное положение расчетного корня
Ро+Аро=1(—0,34+00,6+0,015^Ю,017=.(—0,33+/)0,58.
Появление неучитываемых в расчете инерционных звеньев при-
водит к снижению рабочей частоты до 0,58 рад/сек (по сравнению
с расчетным значением 0,6 рад/сек) -и к уменьшению степени коле-
бательности до 0,33 (по сравнению с 0,34), что вполне допустимо.
На рис. 68 показаны процессы в модели САР при скачкообраз-
ных возмущениях, характеризуемых различными собственными век-
торами матрицы А. Их сравнение с переходными процессами в си-
стеме без дополнительных инерционных звеньев (см. рис. 31) пока-
зывает, что система сохранила свои свойства; по-прежнему резуль-
таты исследования эквивалентной системы (см. рис. 41) вполне ха-
рактеризуют динамику САР.
11. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ
а) О применении методов локализации
Приближенные методы исследования основаны на локализации
характеристических чисел матрицы коэффициентов передачи взаимо-
связей. Они применяются в тех случаях, когда проведение трудоем-
t кого анализа матрицы при переходе к эк-
вивалентной системе не оправдывает
себя из-за низкой точности задания
исходных данных для расчета и '(или)
невысокой чувствительности системы
jRe X к вариации элементов матрицы Д в не-
которых — достаточно широких — пре-
делах.
Применение методов локализации
дает возможность путем несложных вы-
числительных операций определить
в комплексной плоскости область G распределения корней векового
уравнения матрицы, а не точные их значения. При этом задача
исследования формулируется для эквивалентной системы регулиро-
вания (например, со структурной схемой рис. 19), о коэффициентах
усиления отдельных связей в которых Ai, Яг, ..., Хп известно толь-
ко, что они принимают значения из некоторой области G.
Рис. 59.
ПО
Рассмотрим применение наиболее простой оценки области рас-
пределения характеристических чисел — оценки С. А. (Гершгорина.
Для простоты будем считать, что диагональные элементы А равны
между собой: аль=<а, &=1, 2, ..., п. В этом случае все характери-
стические числа матрицы А расположены в круге радиуса Я с цен-
тром в точке а ((круге |Гер,шгорина, рис. 59).
\a—\\<^\R.
Радиус R — это меньшая из двух величин, ^? = мин.'(Р, Q), одна
из которых представляет собой наибольшую из сумм модулей не-
диагональных элементов строк:
Р = макс. Р8;
s
л= Е к
й=1
(130)
вторая — наибольшую из сумм недиагональных элементов столбцов
матрицы А:
Q = макс. Qs;
n,k=s
I "hs |.
(131)
Если А симметрична, то ее характеристические числа веществен-
ны и область G представляет собой
отрезок вещественной оси
Im Я=0.
Опособ применения оценок обла-
сти распределения корней характери-
стического уравнения зависит от осо-
бенностей конкретной задачи.
б) Анализ устойчивости
Здесь ограничимся анализом
устойчивости систем со структурной
схемой рис. 28. Критерий устойчи-
вости Найквиста в приводимой выше Рис. 60.
формулировке (§ 6) должен выпол-
няться при всех возможных коэффи-
циентах усиления разомкнутых эквивалентных сепаратных систем
А.1, Яг, ..Яп.
Значения—\/Xh в силу признака Гершгорина в случае а>#
могут располагаться на комплексной плоскости в круге с центром
a R ~
ач #2. и с радиусом, равным ~TZT^T* Этот КРУГ
представляет собой образ Gi круга Гершгорина G (рис. 60), полу-
в точке —
Ш
ченный отображением инверсии z——1Д. В случае симметричной А
имеем дело с отрезком вещественной оси:
1 1 1
о, — R <-lГ<"■5T^, ImX==0e
При a = R образом круга Гершгорина является полуплоскость
1 1
Re -у ^ -г^. При я < /? значения 1Д в соответствии с признаком
С. А. Гершгорина могут располагаться вне круга с центром в точке
a R ^
R2_a2 и с радиусом ^2__Д2 • Среди характеристических чисел
матрицы могут быть и нулевые ^(область Gt сдержит бесконечно уда-
ленную точку).
Перейдем к формулировке условия устойчивости.
Система регулирования исследуемого типа устойчива, если
амплитудно-фазовая характеристика W(m) охватывает каждую точ-
ку G\ т. е. область G' в положительном направлении т/2 раз, где
т —число полюсов передаточной функции W(p) в правой полупло-
скости (рис. 60).
Этот критерий является достаточным (но не необходимым), по-
тому что область распределения характеристических чисел матрицы
А указывается «с избытком». Невыполнение критерия для части
области не означает еще потери устойчивости системой, поскольку
в этой части число точек—\ЦКк может оказаться равным нулю.
Если значения диагональных элементов матрицы А не равны
друг другу (ац=ац), то область G распределения характеристиче-
ских чисел матрицы А по С. А. Гершгорину представляет собой
пересечение областей D' и D", первая из которых D' представляет
собой объединение кругов
\ац-Ц<Ри
а вторая D" — объединение кругов
где величины Pi и Q* определены ранее i(il30), (il&l). В этом случае
область G и соответственно область >(?i могут представлять собой
несколько изолированных «островков», т. е. быть несвязными.
Формулировка достаточных условий устойчивости системы при этом
не меняется; выполнение критерия требуется для каждой из связных
частей
Вернемся к случаю an = ajj=a>0. Из непрерывности годографа
W(m) следует, что для устойчивости системы достаточно, чтобы
выполнялся критерий Найквиста для системы с передаточной функ-
цией aW\(p) в разомкнутом состоянии и, кроме того, не было
общих точек у АФХ W(m) и у образа круга Гершгорина <?'. Гра-
ничным i(c точки зрения достаточных условий устойчивости) следует
считать случай, когда годограф АФХ касается окружности, ограни-
чивающей iG'. Определив параметры передаточной функции W(p),
при которых имеет место касание, получим точку границы обла-
сти гарантированной устойчивости. Здесь в случае
a>R нетрудно видеть формальную аналогию с методом расчета
112
систем автоматического регулирования из условия заданного пока-
зателя колебательности М — максимума модуля частотной характе-
ристики замкнутой системы по каналу управляющего воздействия.
Метод основан на выявлении условий касания годографом разо-
мкнутой системы некоторой окружности, расположенной в левой
полуплоскости; в нашем случае применимы соответствующие расчет-
ные приемы (Л. 7)1]. Расчет проводится так, как если бы система
с передаточной функцией aW(p) =aW0(p)Wv\(p) в разомкнутом
состоянии рассчитывалась на показатель колебательности M=,a[\R.
Действительно, как следует из предыдущего, система устойчива,
если выполняются условия числа обходов годографом W(i(d) обла-
сти Gi и, кроме того, на всех частотах выполняется неравенство
W (/со) -
a2 — R*
^ a2 — R2
(условие отсутствия общих точек у годографа W^m) и' области Gi).
Положив в этом выражении W/,(p)=aWi(p) и a/R=M, после
несложных преобразований получим:
Неравенство (132) означает, что точки годографа W'(m) долж-
ны лежать вне окружности радиуса М[(м2—1) с центром в точ-
ке М2/(М2—,1), что совпадает с условием расчета при ограничении
допустимого значения максимума модуля.
Если а^1/?, то устойчивость системы при использовании оценок
Гершгорина может быть гарантирована только в тех случаях, когда
разомкнутая система устойчива (полюсы передаточной функции
Wi(p) расположены в открытой левой полуплоскости]; в частности,
не может быть гарантирована устойчивость систем вида рис. 28,а
с астатическим объектом или с астатическим регулятором. Этот вы-
вод станет очевидным, если заметить, что метод Гершгорина в этом
случае допускает наличие нулевых '(при a=R) .или отрицательных
(a<R) характеристических чисел матрицы А, т. е. наличие эквива-
лентных сепаратных систем (рис. 28,6) с незамкнутой обратной свя-
зью (а=</?, Xfc=0) или вообще с положительной обратной связью.
Если диагональные элементы матрицы А не равны между собой,
то область гарантированной устойчивости определяется как пере-
сечение областей, полученных для п кругов Гершгорина (соответст-
вующих разным диагональным элементам матрицы). Примеры при-
менения оценок /Гершгорина для анализа устойчивости оистем можно
найти в (Л. 14, 23, 49]; в [Л. 43] затронуты вопросы использования
других оценок характеристических чисел для той же цели.
в) Оценка качества регулирования
Так как известна лишь область распределения характеристиче-
ских чисел матрицы А, то приходится ограничиться оценками каче-
ства регулирования (предполагается, что достаточные условия устой-
113
чивости выполняются). При этом оказывается важным знание ха-
рактера зависимостей интересующих нас показателей качества ре-
гулирования в сепаратной системе от переменного коэффициента
усиления X. В большом числе практически важных случаев (напри-
мер, в «типовых» одноконтурных системах) указанные зависимости
имеют либо монотонный (динамическое отклонение, колебательность,
статизм), либо выпуклый (интегральный критерий) характер (см.
примеры в (Л. 70]). iB этих случаях достаточно провести контроль
показателей качества для граничных значений X, расположенных на
окружности Гершгорина.
В практических расчетах достаточно исследовать качество для
максимального вещественного Xi = a+\R (точка рис. 59), мини-
мального вещественного А,2=я—R (точка М) и для Х3 с наименьшим
запасом устойчивости — в смысле наименьшего расстояния между
АФХ разомкнутой системы и образом окружности С. А. Гершгорина,
полученным отображением инверсии (значение 1Д3 характеризуется
точкой Q, рис. 60). Если значение Хз близко значению Яг, то при
контроле качества вместо Я3 можно взять точку окружности с ма-
ксимальной мнимой частью Xi=a+iR (точка L, рис. 59). Если ма-
трица А симметрична, то контроль для Я4 не проводится, поскольку
все Xq вещественны.
Исследование качества производится в соответствии с рекомен-
дациями § 7.
Использование методов локализации при синтезе приводит к не-
обходимости проектировать систему с таким расчетом, чтобы задан-
ные требования к системе выполнялись при всех значениях коэффи-
циентов усиления X из области G.
Пример 14. В примере 11 система
y = №0(p)[Au + Ef];
u = Wp(p) (х-у)
при
<гттг*
«Мр) = -(*, +у)
рассчитана методом расширенных частотных характеристик.
Проведем теперь расчет с помощью оценки Гершгорина области
распределения характеристических чисел матрицы А. Составим сум-
мы модулей недиагональных элементов строк матрицы А:
р1==0,35, Р2 = 0,6, Р3 = 0,6, Р4 = 0,35, Р = макс. |/>в| = 0,6.
В силу симметрии матрицы А получение соответствующих ха-
рактеристик для столбцов матрицы не дает новой информации о рас-
пределении характеристических чисел X. Так как А симметрична,
то ее характеристические числа вещественны и заключены в замкну-
том интервале [0,4; 1,6]:
0,4<^Ag<l,6, q=\t 2, 3, 4.
А =
1 —0,25 —0,1 0
— 0,25 1 —0,25 —0,1
— 0,1 —0,25 1 —0,25
0 _0,1 —0,25 1
114
Теперь об эвивалентном объекте известно только, что он состоит
из четырех изолированных каналов регулирования с передаточными
функциями вида 2 V(P+ 04, где значения X заключены в указанном
выше интервале.
Расчет проводится по верхней оценке характеристических чисел
макс. Ль «^1,6. „Оптимальную" настройку находим, вводя в найден-
k
ные ранее параметры для Л=1,32 поправочный множитель 1,32/1,6:
Sj=0,31; vS0=0,ll.
Рис. 61.
Моделирование эквивалентной системы (рис. 61) показывает, что
качество регулирования незначительно уступает качеству в САР, на-
строенной в соответствии с точным расчетом (увеличение динамиче-
ской ошибки до 0,74 по сравнению с 0,63 и времени регулирования
до 35 сек по сравнению с 21 сек).
12. ЗАКЛЮЧЕНИЕ
а) Метод эквивалентной системы
в теории автоматического управления
Итак, в книге рассмотрены методы исследования однотипных
связанных систем регулирования, состоящих из идентичных сепарат-
ных ^систем. Методы основаны на трансформации поставленной зада-
чи исследования для эквивалентной системы, состоящей из изолиро-
ванных сепаратных систем. Между уравнениями, структурными схе-
мами исследуемой и эквивалентной систем существует прозрачная
мнемоническая связь, что удобно при исследовании, расчете. Как
показано в книге, основные задачи линейной теории регулирования,
сформулированные для однотипной связанной системы, могут быть
решены на эквивалентной системе; при этом достигается существен-
ное упрощение исследования.
115
В заключение остановимся на некоторых вопросах, выходящих
за рамки теории однотипных связанных систем, однако имеющих
к ней непосредственное отношение.
Сначала в обзорном порядке коротко коснемся состояния смеж-
ных проблем в теории автоматического управления однотипными
связанными объектами. Затем попытаемся провести параллель меж-
ду рассматривавшимися методами и некоторыми методами, позво-
ляющими понизить размерность дифференциальных уравнений систе-
мы автоматического управления путем их преобразований и «рас-
щепления». И, наконец, коротко рассмотрим возможность исследова-
ния некоторых многосвязных систем путем аппроксимации их урав-
нений уравнениями однотипных связанных систем.
Следует подчеркнуть, что метод эквивалентной системы предна-
значен для исследования линейных однотипных связанных систем
регулирования, поскольку он опирается на принцип суперпозиции, на
возможность независимого исследования составляющах реакций на
каждую из составляющих воздействий. Поэтому в задачах исследо-
вания систем с существенными нелинейностями рассматривавшийся
прием может применяться только при линеаризации нелинейной
зависимости в той или иной форме. Однако уже применение метода
гармонического баланса в общем случае многосвязной однотипной
системы встречает определенные затруднения, поскольку обычно за-
ранее нет оснований предполагать единственность гармонического
режима в многосвязной системе. Метод гармонического баланса
использовался для анализа периодических движений в простых сим-
метричных системах В. Т. Морозовским (Л. 24]; в целом ряде работ
исследовались периодические режимы в двухканальных антисимме-
тричных системах с реле в общем тракте переменного тока |Л. 15,
32, 35]; автоколебаниям в двухканальных антисимметричных систе-
мах посвящены работы И. И. Ахметгалеева {Л. 12], Г. В. Огородни-
ков а [Л. 44].
В нескольких работах рассматривается вопрос об абсолютной
устойчивости однотипных связанных систем. А. Линдгрен и Р. Пин-
кос {Л. 33] исследовали вопрос об абсолютной устойчивости простой
симметричной нелинейной системы с двумя регулируемыми перемен-
ными методом В. М. Попова. Абсолютной устойчивости двухканаль-
ных антисимметричных нелинейных систем посвящены работы
И. И. Ахметгалеева [Л. 34, 46], применившего методы А. М. Ля-
пунова и В. М. Попова. Можно сказать, что исследование абсолют-
ной устойчивости однотипных связанных систем с нелинейностями,
заключенными в секторах, облегчается при ортогональном преобра-
зовании уравнений, поскольку в эквивалентной системе при этом
имеются нелинейные звенья с перекрестными связями между ними,
причем нелинейности заключены в соответствующих секторах.
В ряде работ разрабатываются вопросы оптимального^ перевода
однотипных связанных объектов из одного состояния в другое (за-
дача оптимального управления). В исследованиях О. И. Ларичева
эффективно использован прием синтеза оптимальных управлений на
эквивалентном объекте (Л. 51]; О. И. Ларичеву принадлежит термин
«метод эквивалентной системы» [Я. 55]. Р. Т. Янушевским развиты
процедуры синтеза оптимального управления для простых симме-
тричных объектов при эффективном использовании расщепления
квадратичного функционала качества; им же рассмотрены вопросы
аналитического синтеза регуляторов для простых симметричных си-
стем (Л. 53]. Вопросы синтеза оптимальных управлений для двухка-
116
нальных антисимметричных объектов (в том числе нестационарных)
подробно исследованы Ю. В. Александровым, разработавшим проце-
дуры решения вариационных задач для нестационарного эквивалент-
ного объекта с комплексными переменными [Л. 52, 56].
В последние годы в связи с постановкой задач управления объ-
ектами высокой размерности интенсивно разрабатываются методы,
основанные на заменах переменных, приводящих к независимым
эквивалентным подсистемам уравнений; при этом есть основания
говорить об «эквивалентной системе управления». Эта система, одна-
ко, уже в значительной мере утрачивает сходство с исследуемой;
становится более опосредствованной связь между свойствами двух
систем.
Методы декомпозиции многосвязных систем развиваются для
целей исследования систем с большим числом переменных. Деком-
позиция состоит в разбиении многосвязной системы на подсистемы;
взаимодействие каждой из подсистем с остальными через разрывае-
мые перекрестные связи учитывается введением дополнительных чле-
нов в уравнения подсистем. Поскольку дополнительные члены долж-
ны определяться решениями и заранее неизвестны, то оказывается
необходимым применение итерационной процедуры, в ходе которой
устраняются невязки между дополнительными членами и решения-
ми уравнений. Можно сказать, что переход к эквивалентной систе-
ме в нашем случае представляет собой декомпозицию многосвязной
однотипной системы, осуществляемую единым вычислительным прие-
мом благодаря особенностям уравнений и структурной схемы си-
стемы.
А. И. Кухтенко указывает на возможности применения алге-
браической теории групп для выявления возможности одновремен-
ного приведения матриц различных частей многосвязной системы
к квазидиагональному или квазитреугольному виду [Л. 57]. Посколь-
ку при этом переменные отдельных матричных звеньев системы не
исключаются, то соответствующие звенья оказываются представлен-
ными и в эквивалентной системе, что позволяет сохранить сходство
в > структуре уравнений и в структурных схемах эквивалентной и
исследуемой систем.
Р. А. Нелепин разработал метод «сечений фазового простран-
ства» для исследования1 систем со многими нелинейностями [Л. 58].
Сечения пространства означают по существу анализ уравнений в но-
вых переменных (на координатные оси которых и «натянуты» сече-
ния). Сечения выбираются так, чтобы каждый раз в уравнениях бы-
ла представлена только одна нелинейность. Можно сказать, что
каждому сечению соответствует своя эквивалентная сепаратная си-
стема; исследование каждой из них достаточно просто, и по сово-
купности результатов можно составить отчетливое представление
о свойствах системы (хотя и неполное, поскольку свойства фазовых
траекторий системы вне сечений остаются неизвестными).
б) Приближенные методы исследования многосвязных систем
Рассмотрим некоторые возможности применения метода экви-
валентной системы для расчета многосвязных систем, состоящих из
близких по своим динамическим свойствам сепаратных САР. По
своему содержанию это расширение области применения метода вы-
ходит за рамки теории однотипных связанных систем, хотя непос-
редственно на нее опирается.
117
Подчеркнем, что проблема расчета многосвязной системы воз
никает прежде всего в случае близости собственных частот (или
частот среза) сепаратных систем, объединенных перекрестными свя-
зями через объект. При исследовании взаимосвязанных систем
с различным быстродействием во многих случаях допустимо: 1) для
малоинерционной сепаратной системы пренебрегать связью с инер-
ционными контурами и 2) для инерционной системы пренебрегать
инерцией взаимодействующих с ней малоинерционных систем. Кри-
терием допустимости такого развязывания может служить значи-
тельное различие собственных частот (или частот среза) взаимо-
действующих сепаратных систем; прием может успешно проводить-
ся уже при трех—пятикратном различии их собственных частот.
Здесь рассмотрим случай близких резонансных частот взаимосвя-
занных систем (отличающихся не более чем в 1,5—2 раза).
Предполагается, что амплитудно-частотные характеристики
разомкнутых сепаратных систем и перекрестных связей представ-
ляют собой монотонно падающие функции частоты; частотные ха-
рактеристики разомкнутых сепаратных систем (регулируемых кана-
лов в задаче синтеза) не слишком сильно отличаются вблизи их
частот среза.
При этом, как хорошо известно, важнейшие параметры и ха-
рактеристики замкнутых сепаратных систем (показатели качества
переходного процесса при возмущении по заданию, положения до-
минирующих полюсов, координаты экстремумов амплитудно-частот-
ных характеристик по каналам заданий и т. д.) оказываются близ-
кими, что создает условия для их аппроксимации одинаковыми урав-
нениями.
Приближенное решение задачи исследования проводится в три
этапа:
1) идеализация условий задачи с целью приведения исходных
данных к условиям систем с идентичными характеристиками в се-
паратных контурах;
2) решение задачи на идеализированной модели;
3) перенесение результатов на исследуемую систему.
Идеализация состоит в приближенной замене действительных
уравнений и характеристик одинаковыми для основных каналов
передачи воздействий и совпадающими с точностью до коэффици-
ентов передачи для перекрестных связей. Средствами идеализации
являются: 1) выбор из совокупности нивелируемых характеристик
каналов наихудшей, т. е. в наибольшей степени ограничивающей
качество регулирования; 2) пренебрежение слабыми перекрестными
связями; 3) в задаче синтеза — изменение масштабов регулируемых
переменных с целью нивелирования требований к отклонениям от-
дельных регулируемых координат; изменение масштабов координат
регулирующих органов с целью выравнивания усилительных свойств
регулируемых каналов в существенных диапазонах частот.
Решение задачи анализа проводится на идеализированной таким
образом модели с применением методов теории однотипных свя-
занных систем.
Обсудим несколько подробнее вопросы решения задачи синтеза,
ограничившись важнейшим для приложений случаем изолированных
сепаратных регуляторов. Здесь затруднения может вызвать необ-
ходимость определения индивидуальных операторов каждого из
этих регуляторов. Для этого случая рекомендуется следующий при-
ем. Определяется эквивалентная сепаратная система идеализиро-
118
ванной модели с наиболее неблагоприятными характеристиками;
в ней звено сепаратного канала идеализированной модели пооче-
редно заменяется звеньями соответствующих каналов объекта и
проводится я-кратный синтез сепаратных регуляторов. Требования
к качеству должны выполняться в каждой из синтезированных та-
ким образом систем.
Каждый из синтезированных сепаратных регуляторов применяет-
ся для регулирования на том из каналов объекта, на котором про-
водился синтез. После синтеза следует проверить предположение
—г*
c*z>4^ { 7i 1
г 1 ^на-Ч17>ЧШ-А
Уг иг
6)
г)
Рис. 62.
о близости динамических параметров сепаратных систем, которое
должно выполняться вследствие близости характеристик сепаратных
каналов и требований к качеству регулирования. Если условие
близости не выполняется (например, собственные частоты систем
различаются более чем в 1,5—2 раза), то возможны два решения:
1) коррекция характеристик синтезированных регуляторов с целью
выравнивания собственных частот; 2) применение общей методики
синтеза многосвязной системы. Во многих практических случаях
достаточно ограничиться первым решением.
Обратимся к вопросу расчета систем регулирования с двумя
регулируемыми переменными, в которых безынерционные перекрест-
ные связи действуют между регулирующими органами, а для регу-
лирования применены независимые сепаратные регуляторы. Струк-
турная схема системы показана на рис. 62,а. После несложных пре-
образований она может быть приведена к структурной схеме
рис. 62,6. Будем предполагать, что «оптимально» настроенные без
учета перекрестных связей сепаратные системы характеризуются
близкими частотами и близкими характеристиками затухания пере-
ходных процессов. Это условие означает, что амплитудно-фазовые
характеристики разомкнутых сепаратных систем &nWi ('<*>) #i (ОД и
ЛггИМОД^МОД могут быть аппроксимированы одной характери-
стикой W(m). Полученная расчетная модель соответствует некото-
рой однотипной связанной системе со структурной схемой рис. 62,в.
На рис. 62,г показана структурная схема эквивалентной системы.
119
Коэффициентами передачи в ней %i и Х2 служат характеристические
числа матрицы
kii
иычисляемые по формуле
1
&21
k22
1
Хь2 =
Под радикалом здесь стоит так называемая «передаточная функ-
ция связи» Wcb(p) —важная характеристика объекта с двумя регу-
лируемыми переменными.
Wn (Р) V* (р) '
Xl1W1
В нашем случае Wcв(р) = Ксъ -— вещественное число. Если пе-
рекрестные связи одного знака, то /Ссв>0, и оба коэффициента пе-
редачи в эквивалентной системе вещественны; если знаки перекрест-
ных связей противоположны, то параметры эквивалентной системы
оказываются комплексными.
После обратной замены W(p)—+kjjW}(P)Rj(P)> /=1> % пере-
ходим к расчетной схеме, соответствующей изолированным одно-
контурным системам (рис. 63).
Расчет каждого из двух регулято-
ров проводится для одного из двух
л,,-, лимитирующего в данном кон-
туре достижимые показатели за-
паса устойчивости или качества ре-
гулирования в соответствии с ре-
комендациями § 7.
Естественно, расчет, выпол-
ненный по предлагаемой .методике,
носит приближенный характер
вследствие допущений, принятых
при ее разработке и действующих
обычно в «запас прочности» ((на-
пример, различие собственных ча-
стот систем—ослабление «резонан-
гса»—содействует увеличению запа-
са устойчивости системы). Однако
расчет может дать удовлетворительные результаты во многих практи-
ческих задачах. В задачах, требующих более точного решения, опи-
санный метод расчета может быть применен для определения на-
чального приближения перед применением итерационной вычисли-
тельной процедуры.
Отметим, наконец, что прием аппроксимации сепаратных кон-
туров многосвязной системы однотипными может служить эффек-
тивным средством качественного анализа динамики системы. Напри-
мер, эмпирическое исследование влияния знаков перекрестных свя-
зей на динамику системы с двумя переменными, проведенное Мит-
челлом и Уэббом [Л. 75], могло быть весьма просто выполнено на
эквивалентной модели.
Рис. 63.
120
Пример 15. В качестве примера рассмотрим расчет системы ре-
гулирования одного из участков температурного профиля ректифи-
кационной колонны с боковыми отборами. Объект по результатам
экспериментальных исследований описывается уравнениями
["'1=
L у 2 J
(4,4/7+1)2
0,Бе~3р
(7,35/>+1)2
1.2*-2'
(3,7/7+1)2 (3,7/7+1)2
«Близость» динамических характеристик отдельных каналов
передачи воздействий в объекте определяется тем обстоятельством,
что речь идет 6 регулировании температур паров и жидкости в об-
щем объеме.
Выбор прямых каналов осуществлен путем анализа передаточ-
ной функции связи №св(р), которая при распределении каналов объ-
екта в соответствии с приведенным уравнением имеет модуль ча-
стотной характеристики, .всюду меньший единицы, и монотонно па-
дающие по частоте амплитудную и фазовую характеристики:
(4,4/7+1)2
. «2 J
/с*(Р)-{)>'06 (7,35р+ l)2 е
ония перемет
Для регулирования переменных ух и у2 применены ПИ-регуляторы
(рис. 64, а):
1 #2 — У2 J
Рассмотрим расчет системы на эквивалентной модели; приме-
няется метод расчета на заданный показатель колебательности М=
= 1,62 [Л. 71].
Предварительно проводится расчет независимых сепаратных си-
стем; результаты расчета:
&i = l,96; £2=0,96;
7i=5 мин; Г2=5 мин;
Юр 1=0,3 рад/мин; сор2=0,25 рад/мин.
Здесь copj — резонансная частота /-го контура, абсцисса макси-
мума амплитудно-частотной характеристики системы по каналу за-
дания. Несмотря на существенное различие в параметрах изолиро-
ванных сепаратных систем, их частотные свойства при «оптималь-
ной» настройке близки (резонансные частоты относятся между собой
o)pi: с0р2=0,3 : 0,25 = 1,2). Расчет сепаратных систем может быть вы-
полнен на эквивалентной модели (рис. 64,6).
9—1206 121
В качестве эквивалента перекрестной связи в сепаратных конту-
рах представлено звено с передаточной функцией V W0B (р), что
является естественным обобщением (и уточнением) основного мате-
риала параграфа, в котором применялось звено с коэффициентом пере-
дачи У/Сев* В расчетной модели знак связи с передаточной функцией
У^еш(р) »+" соответствует увеличению модуля и увеличению отри-
а) б)
Рис. 64.
дательного сдвига по фазе частотных характеристик эквивалентного
объекта, т. е. в расчет приняты эквивалентные сепаратные системы,
ограничивающие запас устойчивости.
Расчет параметров регуляторов проводится по стандартной ме-
тодике, разработанной для одноконтурных систем |[Л. 71] На рис.65
показано определение допустимого по условию М^1,62 коэффициен-
та усиления регулятора ki при разных значениях времени изодрома
Рис. 65.
122
регулятора 7\ путем построения окружности, касающейся АФХ ра-
зомкнутой системы и луча, исходящего из начала координат под ут-
лом 0=38° к отрицательной вещественной полуоси; оптимальная на-
стройка выбирается на границе области
допустимого запаса устойчивости в пло 0»*П,
скости параметров k\, kifTi в точке е?
вершины (рис. 66, точка N). Результаты
расчета:
^=1,7; £2=0,7;
7\=10 мин; Г2 = 6 мин.
0,1
Действие перекрестных связей при-
водит в данном случае к необходимости
снижения коэффициентов усиления и
увеличению времени изодрома в сел арат- I , кр х
ных «регуляторах. Л 1 2
На рис. 67 показаны переходные
процессы в системе ио регулируемой ко- рис gg
ор(динате первого канала при единичном
ступенчатом воздействии но заданию
первого регулятора (кривая /) и второго регулятора (кривая 2, рас-
считано -методом трапеций). По своим качественным характеристи-
кам процессы могут быть признаны вполне удовлетворительными;
некоторая затянутость и наличие отрицательного перерегулирования
процесса по прямому каналу
могут быть объяснены влияни-
ем близких к началу координат
нулей характеристического
уравнения, соответствующих
эквивалентной сепаратной си-
стеме со знаком «—» в перед а -
точной функции У Wcbi(p); на-
стройка может быть легко
скорректирована.
При оценке результатов
р п. расчета следует иметь в виду,
что он основан на минимакс-
ном критерии «.минимум боль-
шего из линейных интегральных функционалов качества двух экви-
валентных сепаратных систем» при общем ограничении на общий по-
казатель колебательности М, как это следует из рекомендаций [Л. 71]
и из содержания § 7. Реакция системы на конкретные воздействия
при таком расчете может быть «неоптимальной».
ПРИЛОЖЕНИЕ
АНАЛИЗ МАТРИЦ КОЭФФИЦИЕНТОВ ПЕРЕДАЧИ
1. Матрица простых симметричных однотипных связанных си-
10
го
30 м и *ч
стем
А =
abb
b a b
b b а
(П-1)
123
ЪЬЬ
Характеристическое уравнение
[а — X Ь Ь
Ь а — Х Ь
Ь Ь а — Х
а — Х
= 0.
(П-2)
Определитель в левой части уравнения легко раскрывается
путем эквивалентных преобразований. Вычтем последний столбец
определителя из каждого предыдущего, получим:
•Ь]—Х о о
0 а—Ъ — Х 0
0 0 a—b—Х.
-а + Х Ь — а + Х Ь — а + Х . . . Ъ — а + Х а — \
= 0.
Воспользуемся тем, что элементы последней строки определите-
ля повторяют диагональные элементы с противоположным знаком;
прибавляя каждую из строк к последней строке, получаем:
а—Ь—Х 0 0
0 a—b—Х 0
0 0 ^а — Ь—Х,
О
О
О
О
О
О
О а+(п— \)Ь—Х
= 0.
Полученный треугольный определитель равен произведению его
диагональных элементов:
(a—b—Х) п~\а+ (п—\)Ь—Х]=0.
Таким образом, характеристические числа матрицы (П-1)
Xi=a+(n— \)Ь; (П-3)
Х2=Х3= ... =Хп=а—Ь) (П-4)
а ее каноническая форма диагональна (поскольку А симметрична)*
(П-5)
~ а + (п —
\)Ь 0
0 . .
. о -
0
а — Ь
0 .
. 0
А =
0
0
а — Ь .
. 0
0
0
0 .
. а — Ь_
Собственный вектор с, соответствующий характеристическому
числу Xi, должен удовлетворять системе линейных алгебраических
уравнений
(А—XiE)ci=0. (П-6)
124
После подстановки в это уравнение Я* и сокращения на b си-
стема может быть записана в развернутой форме
— (л — 1) с1Х + с21 + с31 + ... + сп1 = 0;
Си (л 1) £2i + с31 + ... + сп1 = 0;
Си + c8i + Съ\ + .- — (« — О *п1=0.
Легко видеть, что система уравнений имеет решение сц =
= c2i=...=Cni (предположив, что ски cqi не равны друг другу,
приходим к противоречию, сопоставив к—е и q—е уравнения). Нор-
мируя вектор Ci по длине, т. е. накладывая условие
V с21 + с|1 + ... + Л = СпУп= 1,
получаем:
Vn
Для остальных сь. имеем:
(А—ЯлЕ)сА=0. fc = 2, 3,..
(П-7)
или после подстановок и сокращений
п
2 cih = 0. 6 = 2, 3 л. (П-8)
i=i
Условие (П-7) дает для компонент каждого из п—1 собствен-
ных векторов п одинаковых уравнений вида (П-8), т. е. лишь одно*
уравнение (которое, кстати, означает только, что необходимо брать
векторы, ортогональные к Ci). Вектор с2 определим, положив
С12 = С22=Сз2= *.. =£71-1,2;
тогда из условия (П-8)
Сп2 = — (Л— 1)С12,
а из условия нормирования по длине
V с\2 +42+... + с\п = с12 Vn{n- 1) = 1
1
fn\n-\)
(/2-1)
125
Для вычисления с3 наложим условие ортогональности векторов
с3 и с2:
(С3, C2)=Ci2Ci3 + c22c23+ ... +Сп2СпЗ=0. (П-9)
или
Cl3 + C23+ . . . Cn-i,s— (п— 1)сп3 = 0. (П-10)
Уравнения (П-9) и (П-10) не определяют с3; наложим допол-
нительные условия, облегчающие вычисления:
Ci3 = C23 = C33= ... =сп-2,3;
сп3=0.
Сп-1,з=—(л—2)ci3.
После нормирования с3
Тогда из (П-8)
У 4 + 4+- + с«-1,з = ^зК(п-1)(Аг-2) =1;
следовательно,
с3 =
V (л — 2)
-(/1-2)
О
Продолжая этот процесс (при вычислении компонентов каждого
вектора накладываются условия ортогональности к уже полученным;
полагаются равными нулю последние k—2 компоненты, где k — но-
мер вектора), приходим к результату:
С =
- 1
1
1
1
K2"
Vn
Vn(n— 1)
1/ (n
-1)("-
2)
1
1
1
1
Vn
Vn(n— 1)
V (n
-l)(/z-
2)
V2
1
1
л — 2
... 0
Vn
Vn (AZ — 1)
V (n
-l)(/2-
2)
1
n — 1
0
... 0
Vn
V n(n— 1)
Очевидно, матрица С определена не единственным образом;
в качестве С может быть принята любая матрица, в которой первый
столбец составлен из одинаковых элементов, остальные п—1 ортого-
нальны ему. При решении многих задач бывает важно наложить
также требование взаимной ортогональности п—1 векторов, соответ-
ствующих кратному характеристическому числу %2, и нормировать
векторы по длине.
126
2. Матрица двухканальных систем с антисимметричными пере-
крестными связями:
г п 1 i
(П-И)
_ - 0 — 1
" L 1 о /
Характеристическое уравнение
— X
1 —X
характеристические числа
„ 1 —A J
= Х2+ 1 =0;
(П-12)
Xif2 = ±L (П-13)
Компоненты собственного вектора, соответствующего характери-
стическому числу Xi = i, должны удовлетворять уравнению
—icn—Ci2=0.
Таким образом, в качестве компонент первого вектора могут
быть взяты любых два комплексных числа, удовлетворяющих един-
ственному условию:
,**/2
■ = е
(равные модули и относительный фазовый сдвиг величиной jt/2).
Принимая первую компоненту вещественной и проведя опера-
цию нормирования вектора по длине, получаем:
Ci=Vf[\\
Аналогичные выкладки приводят к
и, следовательно,
-Г1 1 1
3. Матрица общей связи
gibi gib2 gib3 . .
g2bl #2^2 g2b3 • •
gibl g*b2 . .
A =
gibn
g2bn
gbK
(П-14)
(П-15)
. gffil gj>2 gnb3 • • • gnbn J
Строки матрицы, как и столбцы, пропорциональны друг другу;
поэтому матрица А вырождена, и ее ранг равен единице. Следова-
тельно, имеется единственное ненулевое характеристическое число,
так что
А.1 = Х2 — ... = An_! = 0;
п
Xn = SpA ==Ц gqbq.
(П-16)
(П-17)
127
Для вычисления сп в уравнении
(А-ЛпЕ)с„=0 (П-18)
выразим А и Хп следующим образом:
A=gb*;
X«=gTb
и перепишем уравнение в виде
gbTcn=(gTb)cn.
Воспользовавшись законом ассоциативности в произведении мат-
риц, запишем:
g(bTc«) = (gTb)cn,
откуда при (Ътсп)фО, (gTb)^=0 с точностью до скалярного сомно-
жителя следует:
cn=g. (П-19)
Для вычисления остальных п—\ векторов матрицы имеем .един-
ственное уравнение
Ас* = 0; / = 1,2 п—\\
abTc* = 0;
Ьтс* = 0;
(П-20)
т. е. любой вектор, ортогональный вектору Ь, является собственным
вектором матрицы A=gbT, соответствующим нулевому характери-
стическому числу.
4. Циркулянтная матрица
А =
а\\ &2 аг • • • ап
ап-2
(П-21)
Матрица характеризуется двумя особенностями: 1) на каждой
из диагоналей матрицы стоят одинаковые элементы; 2) диагонали,
отстоящие на одинаковом расстоянии от левого нижнего угла и от
главной диагонали, состоят из одинаковых элементов. Простейшая
из циркулянтных матриц
0 1 0 ... 0 0
0 0 1 ... 0 0
J==| 0 0 0 ... 0 0
1 0 0
0 0
(П-22)
128
Вековое уравнение матрицы J
— X 1 О
О —X 1
О 0 —X
1
О
О
О
= 0
(П-23)
или [например, после разложения определителя в левой части
(П-23) по элементам первого столбца]
Я"—1=0,
откуда для п характеристических чисел матрицы J имеем:
f2»(fe-l)
ХА = * п , £=1,2,п. (П-24)
Собственный вектор cq матрицы J удовлетворяет соотношению
0 10 0
0 0 10
0 0 0 1
0 0 0 0
. о -
. О
. О
. О
1 0 0 0 ... О
ciq
C2q
v4q
i
= e
2*07-1)
ciq
C2q
Czq
<43
(П-25)
Выполнив действия в левой и правой частях уравнений (П-25),
получим:
12к
<7~1
c6q = e п c8-.uq; s = 2, 3, п\
ciq = e п cnq.
Последнее соотношение является очевидным следствием пре-
дыдущих п—1; как обычно, оказывается необходимым доопределить
векторы канонического базиса каким-нибудь условием. Приняв пер-
вые компоненты векторов вещественными положительными, после
нормирования векторов по длине получим:
г 1
1
1
1
, 2*
I —
Л П
1
1
1Аъ
п—\
п—\
(П-26)
/2—1
П—\
12%
129
Вычислим степени матрицы J:
- 0
0
1
0
0 .
. . о -
- 0
0
0
1
0
. . . о-
0
0
0
1
0 .
. . 0
0
0
0
0
1
. . . 0
0
0
0
0
1 .
. . 0
; J3 =
0
0
0
0
0
... 0
1
0
0
0
0 .
. . 0
0
1
0
0
0
... 0
_ 0
1
0
0
0 .
. • 0 -
_ 0
0
1
0
0
. . . 0_
и т. д.
Таким образом, при повышении степени матрицы J обе знача-
щие ее диагонали передвигаются на один ряд вправо. Это позволяет
представить циркулянтную матрицу А как полином от матрицы J:
А=а1Е+а2Л + а3^+ ... +anJn-*. (П-27)
Характеристическими числами полинома от матрицы являются
все значения этого полинома от характеристических чисел матрицы;
в соответствии с этой теоремой для матрицы А имеем:
* а« <?-'>(«-'>
Ая = а, + 2|Яа* п , q = l,2, ...,п. (П-28)
Что касается канонического базиса, то он наследуется от мат-
рицы J, т. е.
С=С7.
ЛИТЕРАТУРА
Теория и применение однотипных связанных систем
1. Лебедев С. А. Объединение станций при расчетах статической
устойчивости.— «Электричество», 1939, № ,12.
2. Красовский А. А. О процессах автоматического регулирова-
ния в однотипных связанных линейных системах. Труды ВВИА им.
Н. Е. Жуковского, вып. 576, 1955.
3. Миронов В. Д. О свойствах барабанных котлов по давлениям
и расходам пара.— «Теплоэнергетика», 1955, № 12.
4. Красовский А. А. О двухканальных системах автоматического
регулирования с антисимметричными связями.— «Автоматика и теле-
механика», 1957, № 2.
5. Бейрах 3. Я., Трахтенберг М. Д. К вопросу об автоматическом
регулировании параллельно работающих котлов.— «Энергомашино-
строение», 1957, № 4.
6. Матюхин В. М. О статической устойчивости электропередачи
в связи с наличием нескольких генераторов на передающей стан-
ции.—«Известие АН СССР. ОТН», 1957, № 10.
7. Морозовский В. Т. Избирательная инвариантность в однотип-
ных связанных системах.— В кн.: «Теория инвариантности и ее при-
менение в автоматических устройствах». М., Изд-во АН СССР, 1959.
8. Ахметгалеев И. И. О переходных процессах в двухканальных
системах автоматического регулирования. Труды Казанского авиа-
ционного института, вып. 45, 1959.
9. Paszkowski S. Stabilnosc wielowymiarowych ukladow ze spze-
zeniami skrosnymi miedzu kanalami.— «Archiwum automatyky i tele-
mechanikb, 1959, т. 4, № 3, 4 1см. «Механика». Периодический сбор-
ник переводов, № 1, 1962 (71)].
10. Козловский Г. Фм Михневич Г. В. О пределе статической
устойчивости многоагрегатной станции при интенсивном регулирова-
нии возбуждения.— В кн.: «Проблемы энергетики», М., Изд-во АН
СССР, 1959.
11. Ахметгалеев И. И. Об оценке малой неидентичности в ли-
нейных двухканальных системах с антисимметричными перекрест-
ными связями. Труды Казанского авиационного института, вып. 58,
1960.
12. Ахметгалеев И. И. К теории двухканальных систем автома-
тического регулирования с антисимметричными перекрестными свя-
вями. Канд. диссертация, Казань, 1960.
13. Михневич Г. В., Козловский Г. Ф. Устойчивость и качество
переходных процессов регулирования возбуждения многоагрегатной
электростанции. М., Изд-во АН СССР, 1960.
14. Bohn Е. V. Stabilization of linear multivariable feedback cont-
rol systems — «IRE Trans, on Aut. Contr.», 1960, v. AC-5, № 4.
131
15. Красовский А. А. К теории двухканальных следящих систем
с релейным элементом в цепи переменного тока. — «Автоматика и
телемеханика», 1960, № 9.
16. Попов Д. А. Исследование устойчивости параллельной рабо-
ты однотипных генераторов постоянного тока. — «Известия АН
СССР. Энергетика и автоматика», 1960, № 5.
17. Гунь Бинь-цынь. Исследование вопросов автоматического ре-
гулирования промышленных объектов с двумя взаимосвязанными
регулируемыми величинами. Канд. диссертация. М., 1960.
18. Джеффри А. Устойчивость взаимосвязанных систем регулиро-
вания. Труды первого Международного конгресса ИФАК. М., Изд-во
АН СССР, т. 1, 1961.
19. Ту Сюй-янь. Теория гармонически действующей системы уп-
равления со многими регулируемыми переменными. Труды первого
Международного конгресса ИФАК. М., Изд-во АН СССР, 1961.
20. Морозовский В. Т. К теории однотипных связанных систем
автоматического регулирования с симметричными связями. — «Авто-
матика и телемеханика», 1961, № 3.
21. Красовский А. А. Двухканальные следящие системы с анти-
симметричными связями при наличии случайных возмущающих воз-
действий.— «Автоматика и телемеханика», 1961, № 2.
22. Пашковский С. Выступление по докладу А. Джеффри на пер-
вом Международном конгрессе ИФАК. Труды первого Международ-
ного конгресса ИФАК. М., Изд-во АН СССР, т. 1, 1961.
23. Bohn Е. V. Design and synthesis methods for a class of пнй-
tivariable feedback control systems.— «Appl. and Ind.», 1962, № 6i.
24. Морозовский В. Т. Динамика параллельной работы генера-
торов постоянного' тока. Труды ВВИА им. Н. Е. Жуковского,
вып. 938, 1962.
25. Абилов А. Г. Автоматизация однокамерной двухпоточной
трубчатой печи атмосферной трубчатой установки, работающей на
газообразном топливе. Канд. диссертация, Баку, 1962.
26. Герасимов А. Н. О выборе параметров двухканальных сле-
дящих систем с антисимметричными связями. — «Известия АН СССР.
Энергетика и автоматика», 1962, № 1.
27. Морозовский В. Т. Анализ и синтез корректирующих пере-
крестных связей многомерных автоматизированных систем. Тру-
ды ВВИА им. Н. Е. Жуковского, вып. 1000, 1963.
28. Мед Г. Д. Регулирование давления параллельно работающих
нагнетателей на общий газопровод.— «Энергомашиностроение», 1963,
№ 10.
29. Морозовский В. Т. К вопросу об эквивалентировании генера-
торов автономных электрических систем при расчетах статической
устойчивости.— «Известия АН СССР. Энергетика и транспорт»,
1964, № 2.
30. Соболев О. С. Анализ структуры многомерной автоматичес-
кой системы с нелинейной связью.— «Автоматика и телемеханика»,
1964, No 3.
31. Соблев О. С. Эквивалентирование систем автоматического
регулирования параллельно работающих идентичных агрегатов.—
«Известия АН СССР. Энергетика и транспорт», 1965, № 2.
32. Барский А. Г. Периодические режимы в двухканальных ав-
томатических системах с нелинейным элементом в одноканальной
части контура.— «Автоматика и телемеханика», 1966, № 9.
132
33. Lindgren A. G., Pinkos R. F. Stability of symmetric nonlinear
multivariable systems.— «Journ. of Franklin Inst.», 282, 1966, № 2.
34. Ахметгалеев И. И. Абсолютная устойчивость равновесия си-
стем с антисимметричными связями.— В кн.: «Применение второго
метода Ляпунова в энергетике», Новосибирск, «Наука», 1966.
35. Казамаров А. А., Палатник А. М., Роднянский Л. О. Динами-
ка двумерных систем автоматического регулирования. М., «Наука»,
1967.
36. Kalinowski W. Systeme der automatischen Regelung der Wind-
verteilung an Hochofen.— «Messen — Steuern — Regeln», 10, 1967,
№ 10.
37. Соболев О. С. Вопросы синтеза однотипных взаимосвязанных
систем автоматического регулирования.— В кн.: «Приборостроение,
средства автоматизации и системы управления». М., «Наука», 1967.
38. Барский А. Г. Устойчивость трехканальных систем автомати-
ческого регулирования с антисимметричными связями.— «Автомати-
ка и телемеханика», 1967, № 1.
39. Бендриков Г. А., Огородникова В. И. Траектории корней
двухканальных систем с антисимметричными перекрестными связя-
ми.— «Автоматика и телемеханика», 1967, № 4.
40. Бендриков Г. А., Огородникова В. И. О выборе параметров
симметричных перекрестных связей двухканальных систем.— «Вест-
ник Московского университета», серия П, № 6, 1967.
41. Sobolev О. S. Applied methods of multivariable control system
study.— «1FAC Symposium uber Mehrgrossen — Regelsysteme. Verab-
druck der Beitrage. Band I», Dusseldorf, 1968.
42. Барский А. Г. Устойчивость двухканальных систем автома-
тического регулирования при неограниченном коэффициенте усиления
антисимметричной связи — «Автоматика и телемеханика», 1968, № 1.
43. Баранчук Е. И. Взаимосвязанные и многоконтурные регули-
руемые системы. Л., «Энергия», 1968.
44. Огородников Г. В. О вынужденных периодических режимах
нелинейных двумерных систем. «Известия вузов. Приборостроение»,
1968, № 3.
45. Бендриков Г. А., Огородникова В. И. Исследование трехка-
нальной системы автоматического управления с антисимметричными
перекрестными связями методом траектории корней.— «Автоматика
и телемеханика», 1968, № 9.
46. Ахметгалеев И. И. Абсолютная устойчивость двухканальных
систем с антисимметричными перекрестными связями при неидентич-
ных нелинейностях. Труды Казанского авиационного института,
вып. 99, 1969.
47. Огородников Г. В. Об исследовании периодических режимов
нелинейных двухканальных систем с антисимметричными перекрест-
ными связями. Труды Казанского авиационного института, вып. 99,
1969.
48. Морозовский В. Т. Многосвязные системы автоматического
регулирования. М., «Энергия», 1970.
49. Лихтциндер Б. Я., Широков С. М. Об устойчивости автома-
тического уравновешивания многомерных мостовых цепей.—«Авто-
матика и телемеханика», 1971, № 5.
50. Соболев О. С, Фундатор Ю. В. Исследование динамики па-
раллельной работы редукторов.— В кн.: «Пневмоавтоматика». М.,
«Наука», 1972.
133
Оптимальное управление однотипными связанными объектами
51. Ларичев О. И. Оптимальное управление одним классом мно-
госвязных систем. Канд. диссертация. Институт автоматики и теле-
механики АН СССР, 1965.
52. Александров Ю. В. Аналитическое конструирование регуля-
торов для двухканальных систем с антисимметричными перекрест-
ными связями. Труды Казанского авиационного института, вып. 87,
1965.
53. Янушевский Р. Т. Оптимизация многосвязных систем управ-
ления. Канд. диссертация. Институт автоматики и телемеханики. М.,
1967.
54. Александров Ю. В. О формировании оптимальных управлений
в линейных двухканальных взаимосвязанных системах — «Известия
вузов. Авиационная техника», 1967, № 3.
55. Ларичев О. И. Метод эквивалентной системы. Труды III Все-
союзного совещания по автоматическому управлению (технической
кибернетике). М., «Наука», 1968.
56. Александров К). В. Оптимальные процессы в двухканальных
системах при ограничении на вектор управляющих воздействий.
Труды Казанского авиационного института, вып. 99, 1969.
Смежные вопросы теории автоматического управления
57. Кухтенко А. И. Основные задачи теории управления слож-
ными системами.— В кн.: «Сложные системы управления», Киев,
вып. 1, 1968.
58. Нелепин Р. А. Точные аналитические методы в теории нели-
нейных автоматических систем. Л., «Судостроение», 1967.
Литература по линейной алгебре и теории матриц
59. Гантмахер Ф. Р. Теория матриц. М., «Наука», 1966.
60. Современная математика для инженеров. Под ред. Ф. Бе-
кенбаха. М., Изд-во иностр. лит., 1958.
61. Ланцош К. Прикладные методы практического анализа. М.,
Физматгиз, 1961.
62. Пароди М. Локализация характеристических чисел матриц
и ее применения. М., Изд-во иностр. лит., 1960.
63. Фаддеев Д. К., Фаддеева В. Н. Вычислительные методы ли-
нейной алгебры. М., Физматгиз, 1960.
Общие вопросы
64. Мееров М. В. Системы многосвязного регулирования. М.,
«Наука», 1965.
65. Боднер В. А. Теория управления полетом. М., «Наука», 1964.
66. Воронов А. А. Основы теории автоматического управления,
ч. 1—3, Л., «Энергия», 1965—1970.
67. Катковник В. Я., Полуэктов Р. А. О задаче синтеза опти-
мальных многомерных систем автоматического управления.— «Авто-
матика и телемеханика», 1965, № 1.
68. Основы автоматического регулирования. Теория. Под ред.
В. В. Солодовникова. М., Машгиз, 1954.
134
69. Дудников Е. Г. Основы автоматического регулирования теп-
ловых процессов. М., Госэнергоиздат, 1956.
70. Стефани Е П. Основы расчета настройки регуляторов теп-
лоэнергетических процессов. М., Госэнергоиздат, 1960.
71. Ротач В. Я. Расчет настройки промышленных систем регули-
рования. М., Госэнергоиздат, 1961.
72. Цирлин А. М. Настройка регуляторов в промышленных систе-
мах автоматического регулирования с учетом характера возмуще-
ний.— В кн.: «Комплексная автоматизация химических производств»,
М., Машгиз, 1963.
73. Мееров М. В. Синтез структур систем автоматического регу-
лирования высокой точности. М., Физматгиз, 1959.
74. Митчелл Д. С, Уэбб К. Р. Исследование взаимодействия
многоконтурных систем регулирования. Труды первого Международ-
ного конгресса ИФАК, т. I, М., Изд-во АН СССР, 1961.
ОГЛАВЛЕНИЕ
Обозначения 3
Предисловие 4
Глава первая. Однотипные связанные системы автома-
тического регулирования 7
1. Однотипные связанные системы в технике .... 7
2. Особенности однотипных связанных систем ... 16
Глава вторая. Эквивалентная система 26
3. Математические основы замены переменных ... 26
4. Эквивалентная система автоматического регулирования 38^
5. Эквивалентные системы в важнейших случаях ... 55
Глава третья. Анализ 67
6. Устойчивость 67
7. Качество регулирования 73
Глава четвертая. Синтез 83
8. Применение метода эквивалентной системы при син-
тезе 83
9. Расчет однотипных связанных систем методом расши-
ренных частотных характеристик 89
Глава пятая. Специальные вопросы теории однотипных
связанных систем 97
10. Грубость и чувствительность однотипных связанных
систем 97
11. Приближенные методы исследования НО
12. Заключение 115
Приложение 123
Литература 131