Теория упругости - Демидов С.П.

Author: Демидов С.П.
Tags: механика деформируемых тел упругость деформация физика теория упругости
Year: 1979
Similar
ANSYS в руках инженера
Неравенства в механике и их приложения. Выпуклые и невыпуклые функции энергии
Пространственные деревянные конструкции
Радиационная газовая динамика спускаемых космических аппаратов. Многотемпературные модели
Text
                    С. П. ДЕМИДОВ
ТЕОРИЯ
УПРУГОСТИ
Допущено
Министерством высшего и среднего
спецнального образования СССР
в качестве учебнике для студентов вузов,
обучающихся по специальности
«Динамика и прочность машин»
МОСКВА «ВЫСШАЯ ШКОЛА» 1979

ББК 22.37
ДЗО
УДК 539.3@75.8)
Рецензенты:
кафедра сопротивления материалов Леиииградского
кораблестроительного института (зав. кафедрой — проф. В. С. Калинин)}
Н. Д. Тарабасов — докт. техи. наук, проф.
(Московский станкоинструментальный институт]
НЕ БОЛЕЕ »И КНИГИ В
ОДНИ РУКИ И 2ХВДВЕ
КОЛОХ2А
ОСКОРЩк
Демидов С. П.
ДЗО Теория упругости: Учебник для вузов. — М.: Высш. школа,
1979. —432 с, ил.
В пер.: 1 р. 20 к.
В книге иа современном научном уровне изложены основы теории упругости,
а также основные задачи и методы их решения, общие теоремы и вариационные
принципы; подробно рассмотрены: теория кручения и нзгяба прямого бруса, илоская
и контактная задачи теории упругости, задача определенна напряжений в кривых
круговых брусьях при произвольной нагрузке иа нх торцах; многочисленные задачи
с анализом решения; прилагается программа для ЭВМ иа языке FORTRAN решения
задачи кручения прямого бруса; широко использован тензорный анализ, небходнмые
элементы которого даиы в приложении.
20304—125
Д 84—79 1734000000 531
001@1)—79 ББК 22.37
© Издательство «Высшая школа», 1979

Посвящается 150-летию
Московского высшего технического
училища имени Н. Э. Баумана
' A830—1980)
ПРЕДИСЛОВИЕ
Одной из основных задач в области машиностроения, по-
поставленной XXV съездом КПСС, является повышение надеж-
надежности машин и снижение их материалоемкости и стоимости
на единицу мощности.
Для решения.этой проблемы требуется расширение теоре-
теоретических и экспериментальных исследований по вопросам
прочности и соответствующая подготовка инженеров. В учеб-
учебные планы втузов по некоторым специальностям машино-
машиностроения включены курсы «Теория упругости», «Теория пла-
пластичности» и другие дисциплины по механике деформируемых
твердых тел. В ряде втузов за последние годы введена новая
специальность «Динамика и прочность машин».
За основу учебника взяты лекции, читаемые студентам
специальности «Динамика и прочность машин» в МВТУ
им. Н. Э. Баумана, а также лекции по этому курсу — на фа-
факультете повышения квалификации для преподавателей ка-
кафедр «Сопротивление материалов».
Изложение материала ведется на уровне втузовского кур-
курса математики; в отдельных случаях приводятся крат-
краткие напоминания некоторых вопросов математики или дела-
делаются ссылки на соответствующую литературу. В частности,
в книге используется тензорное исчисление, элементы которо-
которого даны в приложении I. В основном тексте делаются ссылки
на формулы, приведенные в двух пунктах этого приложения
A°и2°).
Автор считает своим долгом выразить глубокую призна-
признательность профессору С. Д. Пономареву за полезные сйветы
по содержанию книги, а также профессорам | Л. И. Балабуху j
и Н. Н.Малинину за ценные замечания по рукописи. Искрен>
нюю благодарность за внимательный и большой труд автор
приносит рецензентам: профессору Н. Д. Тарабасову и кол-
коллективу кафедры сопротивления материалов Ленинградского
кораблестроительного института, возглавляемой профессором
В. С. Калининым.
Автор

ВВЕДЕНИЕ
Задачей теории упругости, как одного из разделов механики сплош-
сплошной среды, является определение деформаций и напряжений в твердом
упругом теле, которое подвергается силовому или тепловому воз-
воздействию.
Эта же задача среди других рассматривается и в курсе «Сопротив-
«Сопротивление материалов». Однако методы решения этой общей задачи в том
и другом курсах существенно отличаются друг от друга. Сопротивле-
Сопротивление материалов решает ее главным образом для бруса, базируясь на ря-
ряде гипотез геометрического или физического характера. Такой метод
позволяет получить хотя и не во всех случаях вполне точные, но до-
достаточно простые формулы для вычисления напряжений.
Теория упругости ограничивается только задачей определения
напряженно-деформированного состояния тела и, не используя недо-
недоказанных предпосылок, позволяет получить возможно более точное
ее решение для тел, вообще говоря, любой формы.
Результаты решений задач методами теории упругости позволяют,
в частности, оценить применяемые в сопротивлении материалов гипо-
гипотезы и установить границы их правомерности. Наиболее же сущест-
существенным является то, что методами теории упругости можно решить
ряд задач, имеющих важное практическое значение, что недоступно
для элементарных приемов сопротивления материалов. Это, например,
задачи о концентрации напряжений, задачи кручения брусьев некруг-
некруглого или переменного ноперечных сечений, задачи определения напря-
напряжений в кривых брусьях при произвольном их нагружении, контакт-
контактные задачи, имеющие исключительную важность в машиностроении.
Не принимая каких-либо вспомогательных гипотез, теория упру-
упругости не может все же обойтись без абстрагирования изучаемого объек-
объекта. Реальные твердые тела рассматриваются в виде модели, наделяемой
лишь их основными и общими свойствами, характерными при опре-
определенных условиях. В зависимости от особенностей принимаемой мо-
модели твердых тел теория упругости подразделяется на классическую,
линейную и нелинейную.
Предметом классической теории упругости является напря-
напряженно-деформированное состояние твердых тел, модель которых имеет
следующие свойства: 1) сплошность, 2) идеальную упругость, 3) ли-
линейность зависимости между напряжениями и деформациями, 4) дос-
достаточную жесткость.(малость перемещений), 5) однородность, 6) изо-
изотропность.
Классическая теория упругости представляет собой простейщий
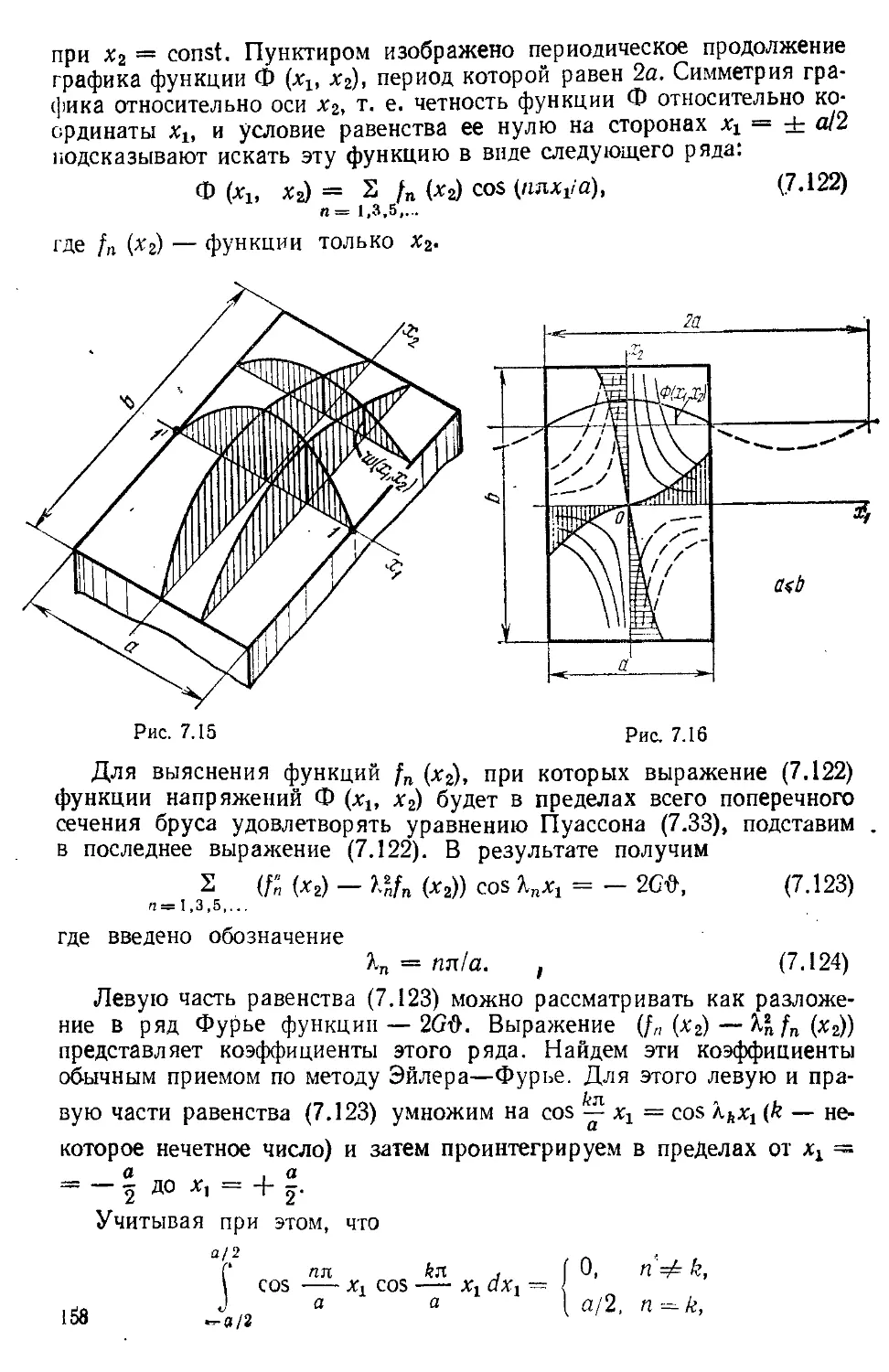
вариадт линейной теории упругости, рассматривающей более широкий
круг задач. Линейная теория упругости изучает напряженно-
деформированное состояние твердых тел, которые могут быть неодно-

родными и анизотропными, т. е. неотъемлемыми свойствами их модели
будут только первые четыре из шести перечисленных.
Развитие техники за последние десятилетия связано с применением
новых материалов и широким использованием в конструкциях различ-
различного рода гибких элементов и вызвало необходимость решения задач,
которые являются предметом нелинейной теории упругости.
Эти задачи могут быть либо геометрически нелинейными (когда тела
не обладают достаточной жесткостью, например гибкие стержни), либо
физически нелинейными (когда тела не подчиняются закону Гука), а
также геометрически и физически нелинейными (когда детали изготов-
изготовлены из резины или некоторых пластмасс). Во. всех этих задачах не-
непременными свойствами модели являются сплошность и идеальная
упругость, а возможность других свойств, конкретизирующих ее,
определяется особенностями абстрагируемого твердого тела. Нелиней-
Нелинейная теория упругости, таким образом, имеет еще более общий характер
и решает весьма широкий круг задач, постоянно и неизбежно выдвигае-
выдвигаемых современной техникой. Это не принижает фундаментального зна-
значения линейной теории упругости и не обязывает получать зависимос-
зависимости последней как частный случай значительно более сложных соотноше-
соотношений нелинейной теории упругости. Напротив, познания теории упру-
упругости должны начинаться с изучения исторически первой и наиболее
разработанной линейной теории упругости, которая в этом отношении
должна носить как бы пропедевтический характер.
Основы теории упругости были разработаны почти одновременно
Навье A821), Коши A822), Пуассоном A829). Независимо друг от дру-
друга они получили по существу все основные уравнения этой теории.
Особо выделялись работы Коши. В отличие от Навье и Пуассона, при-
привлекавших гипотезу молекулярных сил, Коши, опираясь на метод, в
котором используется статика твердого тела, ввел понятия деформации
и напряжения, установил дифференциальные уравнения равновесия,
граничные условия, зависимости между деформациями и перемеще-
перемещениями, а также соотношения между напряжениями и деформациями
для изотропного тела, первоначально содержавшие две упругие пос-
постоянные. В эти же годы появились исследования М. В. Остроградско-
Остроградского о распространении волн в упругом теле при возмущении в его ма-
малой области. На эти исследования ссылается в своих работах Пу-
Пуассон, впервые A830) доказавший существование в однородной изот-
изотропной среде двух типов волн (волны расширения и искажения).
Дальнейший весьма существенный вклад в теорию упругости внес-
внесли Ламе и Клапейрон. Наряду с разработкой основ теории упругости,
а также постановкой и решением ряда проблем практического значе-
значения Ламе написал первую книгу по теории упругости — «Лекции по
математической терии упругости твердых тел» A852).
Весьма большое значение имела работа Грина A829), посвященная
выводу соотношений между напряжениями и деформациями, которая
базировалась на принципе сохранения энергии без введения какой бы
то ни было гипотезы о поведении упругих тел. Эта работа позволила
разрешить дискуссионный в то время вопрос о числе упругих постоян-
постоянных.

Даже такое поверхностное перечисление всех важнейших работ по
теории упругости.потребовало бы многих страниц. Отсылая читателя,
желающего ознакомиться с историей развития теории упругости, к ув-
увлекательной книге [55], здесь назовем еще лишь некоторых зарубеж-
зарубежных и отечественных выдающихся ученых, труды которых имели опре-
определяющее значение в становлении теории упругости. Это прежде всего
Сен-Венан, Кирхгоф, Ляв, Фойгт, Герц, Мичелл, G. П. Тимошенко,
И. Г. Бубнов, Б. Г. Галеркин, П. Ф. Папкович, Г. В. Колосов,
Н. И. Мусхелишвили. Так, Г. В. Колосов и Н. И. Мусхелишвили раз-
разработали эффективный метод решения задач теории упругости с по-
помощью аналитических функций комплексного переменного.
В ходе развития теории упругости, определяемого обычно прак-
практическими потребностями, некоторые ее проблемы впоследствии яви-
явились предметами специальных дисциплин механики деформируемого
тела: «Теория оболочек и пластин», «Устойчивость деформируемых си-
систем», «Колебания упругих систем», «Экспериментальные методы ис-
исследования напряжений», «Термоупругость» и др.
Бурное развитие современной техники неизбежно выдвигает перед
механикой деформируемого тела новые, все более сложные задачи.
Традиционные материалы ставятся в чрезвычайно сложные условия
высоких температур и давлений, внедряются новые материалы — раз-
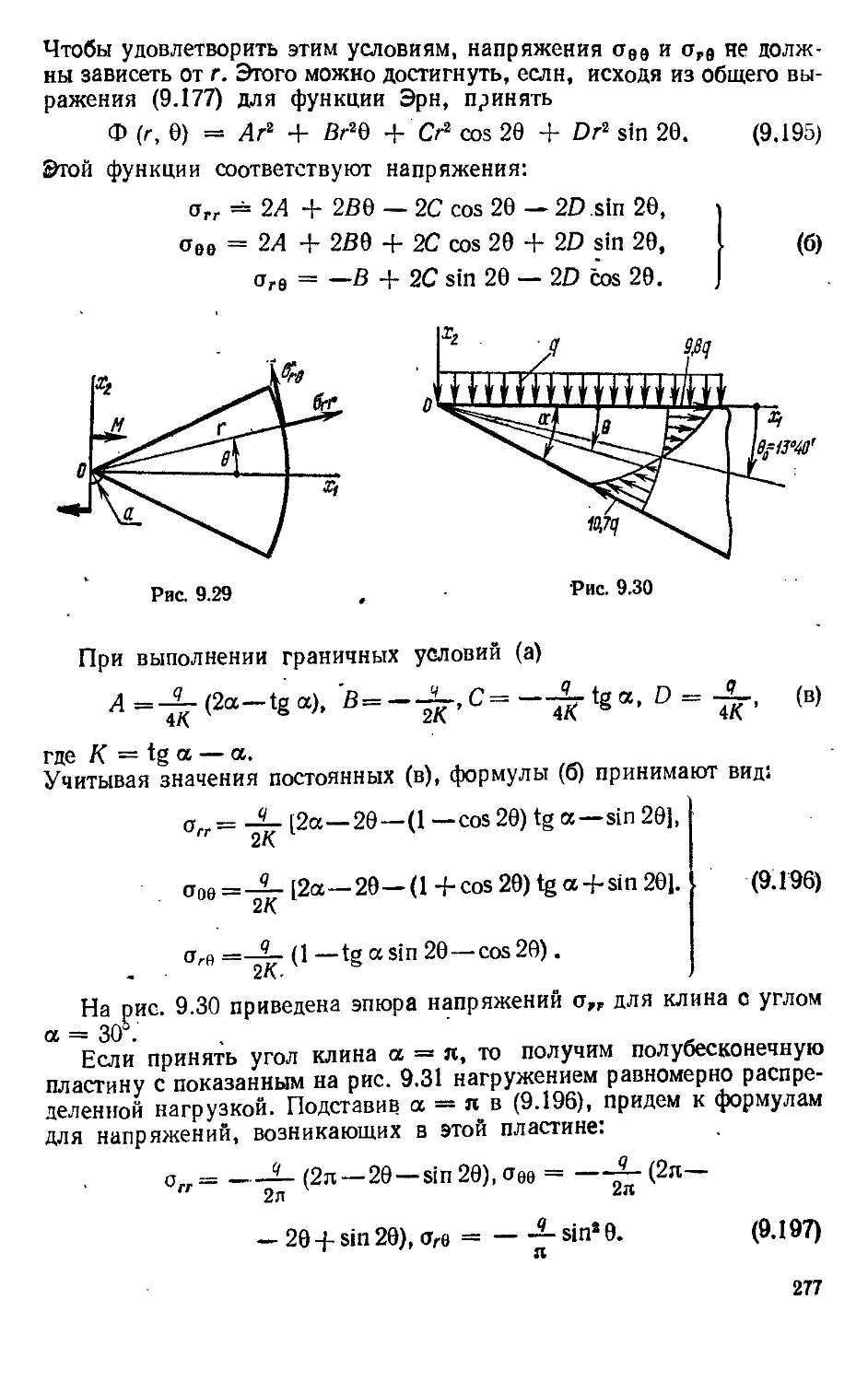
различные высокожаропрочные сплавы, композиционные материалы, вы-
высокопрочные и высокомодульные волокна. Это привело к необходимос-
необходимости, наряду с моделью упругого тела, рассматривать другие модели де-
деформируемого тела, широко применять в инженерных расчетах уже дав-
давно сложившиеся методы теории пластичности, ползучести, вязкоупру-
гости, статистические и вероятностные методы при переменных напря-
напряжениях и т. д. За последнее время определилось новое направление ме-
механики твердых тел, которое получило название механики разруше-
разрушения. Развитие этого направления будет опираться на перечисленные
теории деформируемого тела, причем они приобретают новое, более
широкое значение. Это относится и к теории упругости. В этой связи
академик Ю. Н. Работнов в одной из своих статей заметил: «Теория
упругости нашла в наши дни новую область приложения: в физике
кристаллов, в теории разрушения; теория упругости в известном
смысле переживает второе рождение и истинная ценность ее только
теперь раскрылась в полной мере».
По-прежнему теория упругости сохраняет свое неоценимое значе-
значение при исследовании напряженно-деформированного состояния эле-
элементов обычных инженерных конструкций, в частности машинострои-
машиностроительных, детали которых, как правило, описываются моделью линей-
линейно-упругого тела.

Глава I
ТЕОРИЯ ДЕФОРМАЦИИ
§ 1. ВЕКТОР ПЕРЕМЕЩЕНИЯ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ
Под действием внешних сил или в результате изменения теплового
состояния тело меняет евои размеры и форму, т. е. деформируется.
Пусть тело, как сплошная среда, в начальном состоянии (до внеш-
внешнего воздействия) занимает в трехмерном евклидовом пространстве
область У(рис. 1.1). Положение произвольной точки М тела, которую
в отличие от точки пространства будем называть материальной точкой,
определяется радиус-вектором х в компонентами xt (i— I, 2, 3) в де-
декартовой системе осей Ох^хгхъ.
Допустим, что в результате какого-либо внешнего воздействия на
тело произошло смещение его точек и тело заняло новую область V.
При этом некоторая материальная точка М (xt) ? V (напомним, что
знак ? означает «принадлежность», т. е. в данном случае точка М, при-
принадлежащая области V) сместится в положение точки М' (x't) ? V.
Вектор а = ММ', соединяющий начальное и конечное положения
материальной точки М {xt), называется ее вектором перемещения.
Каждая материальная точка М (х() ? V переместится в некоторую
точку М' (x't) ? V, за исключением, быть может, отдельных точек,
например закрепленных, которые будут общими для областей V и V".
При этом тело, занявшее новую область V, по предположению, оста-
остается сплошной средой. Поэтому координаты x'i точек области V долж-
должны быть непрерывными и однозначными функциями координат xlt х2,
ха материальных точек в начальном состоянии V:
Xi = Xt (Xlt X%i Х8). A.1)
Будем предполагать, что функции A.1) имеют непрерывные про-
производные по всем координатам х*. (k = 1, 2, 3) и якобиан\дх\ /dxh\ Ф
Ф 0, т. е. уравнения A.1) можно разрешить относительно xt:
xt = xt (x'u x'i, х'я). A.2)
Компоненты иг вектора перемещения и на основании A.1) и A.2)
могут быть выражены либо как функции хи хг, х3:
щ = x't — Xt - x't (*„ х2, х3) — Xi = ut (xh), A.3)
либо как функции x'v х'„, х'3\ ¦ *
Щ = Xt —Xi= X't — Xt(x',, Х'г, X'3) = Uj (Xk) A.4)
Способ описания перемещений функциями A.3), когда за независимые
переменные принимаются координаты Xk материальной точки М (хь)
в начальном состоянии V, называется лагранжевым. Другой способ
описания движения сплошной среды с помощью функций A.4), в ко»

торых независимыми переменными являются координаты х* точек
W (х'ь) € У. называется способом Эйлера. За основной параметр дви-
движения сплошной среды в способе Эйлера принимается скорость v (**, t)
материальных точек, проходящих в каждый момент времени t через
рассматриваемую точку пространства. Способ Эйлера имеет преиму-
преимущество в тех случаях, когда важно знать все данные о движении мате-
материальных точек (частиц) сплошной среды, которые с течением времени
йрйходят в рассматриваемое пространство. Независимые переменные
Эйлера: координаты х'ь точек про-
пространства и время t использу-
используются, например, в гидромеханике.
В теории упругости обычно при-
применяется способ Лагранжа, по-
позволяющий определить перемеще-
перемещение фиксированной материальной
точки М (xh), которое она полу-
получает из начального состояния в
_?> результате внешнего воздействия
на тело.
Переход тела из начального со-
состояния У в новое состояние V
возможен вследствие перемещения
Рис. 1.1. тела, как абсолютно твердого, т. е.
без изменения расстояния между
любыми двумя его точками. Такое перемещение тела называется же-
жестким смещением.
Если переход тела из начального состояния V в новое V происходит
вследствие изменения расстояний между его точками, то новое со-
состояние V' называется деформированным щтоянием тела.
Очевидно, что деформированное состояние тела вполне определяет-
определяется, если известны функции щ — и\ (xh)-
Деформированное состояние, определяемое линейными функциями .
щ = щ (Xh), называется однородным. Так как в этом случае функции
x't = хг + щ будут также линейными, то любая прямая или плоскость,
которые можно вообразить в состоянии V тела, переходят в прямую
или плоскость тела в состоянии V1.
§ 2. ТЕНЗОР ДЕФОРМАЦИИ
При неоднородном произвольном деформировании тела функции
иг — щ (Xh) будут нелинейными. Однако и в этом случае в весьма малой
окрестности любой точки тела деформированное состояние может рас-
рассматриваться как однородное, т. е. прямолинейные материальные
элементы в окрестности некоторой точки М ? -V преобразуются в
прямолинейные элементы деформированного состояния окрестности
точки М' € V.
Пусть при общем случае деформирования тела его две бесконечно
близкие точки М (хг) и N (xt + dxt), расстояние между которыми
ds=\dx\ в начальном состоянии V (рис. 1.2), перемещаются в положе-

ния М' (x't) и N' (х} + dx'i) состояния V. В результате линейный эле-
элемент ds = | dx], ограниченный точками М uN, преобразуется в линей-
линейный элемент ds' = \dx'\, ограниченный точками М' и N'.
Проекции на координатные оси элемента ds равны компонентам dxt
вектора dx, а элемента ds1 — компонентам dxt = dxt + dut вектора
dx'. Тогда в рассматриваемых координатах
ds* = dx\ + dx\ + dx\ ** dxtdXi
и, аналогично,
ds'2
xj
x (dxt + dut),
A.6)
или
ds" = ds2 + 2dxr,d«j + dutd
Компоненты d«r вектора du, пред-
представляющего собой вектор перемеще-
перемещения точки Af относительно точки М,
определяются
din - (dtiiidx^Xi. + (дщ/дхъ)йхг +
+ (du,/dxa)dx8 — utjdxj. A.7)
Учитывая формулу A.7) и прини-
принимая во внимание, что
dHjdH* => d«ftd«h = uhJdxtuhJdxj,
равенству A.6) можно придать вид
ds'2—ds* = Buu + uk,tukj)dxtdX}
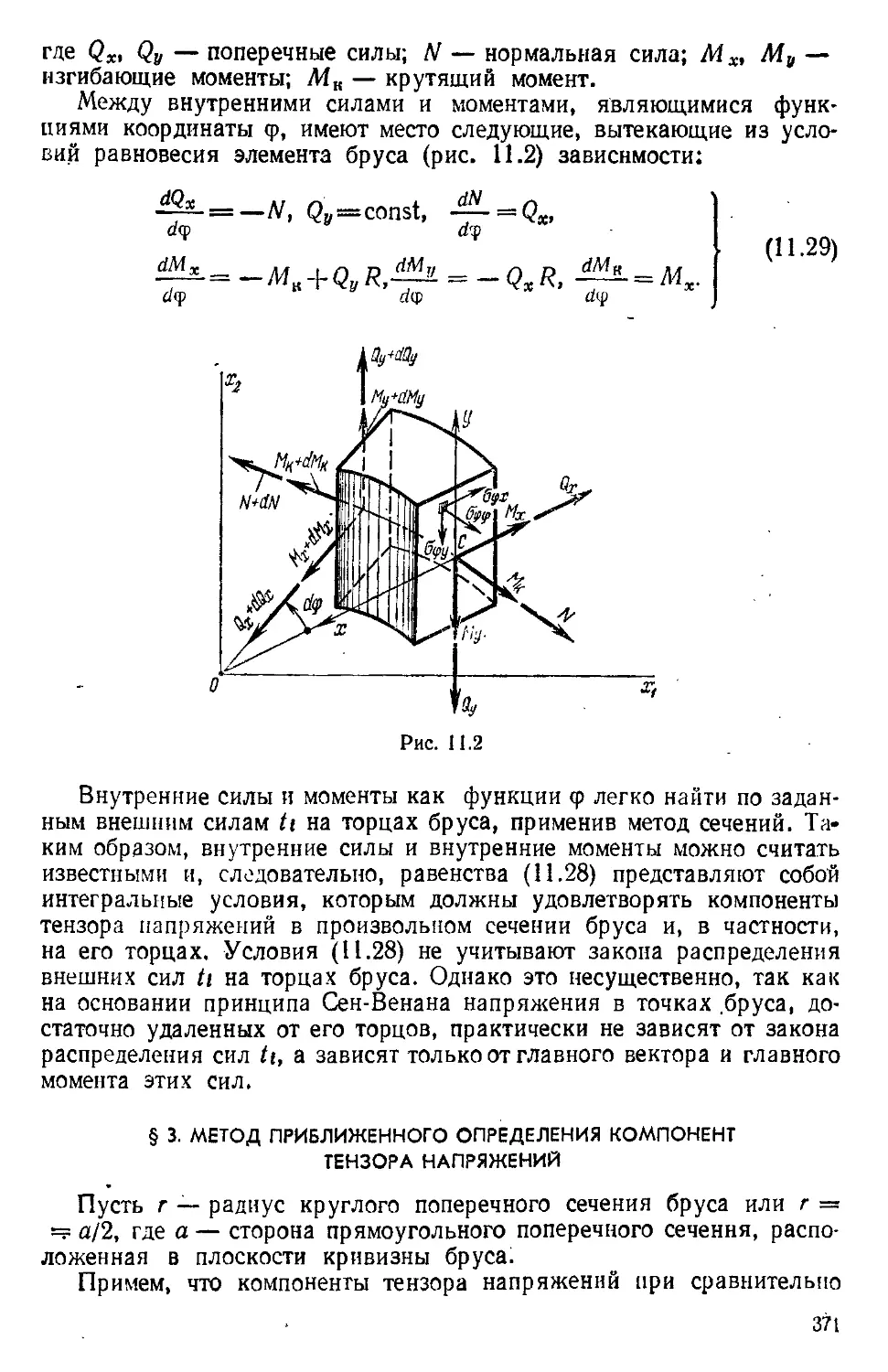
Рис
A,8)
Левая часть равенства A.8) представляет собой скаляр (инвариант).
Поэтому на основании A°.36) выражение в скобках при dx^Xj в пра-
правой части равенства A.8) является тензором второго ранга. При этом
(«и)—несимметричный тензор, так как щ,)Фщ,ь а (ым"ы) —
симметричный тензор, поскольку UkjUhj — uhjuhti. Несимметрич-
Несимметричный тензор (uij), через компоненты которого по формуле A.7) оп-
определяются компоненты вектора относительного перемещения, назы-
называется тензором относительного перемещения; его можно разложить
на симметричную и кососимметричную составляющие A°.33):
«и " "(и) + "['.я - ("и + uj.iV2 + ("м — ииI2> О «Я)
На основании A°.34) имеет место равенство
= (ии + Uj.iyiXidxj/2, A.10)
учитывая которое, формулу A.8) можно записать в следующем виде:
ds'1 — ds* = 2(etJ)dxtdx}, " A.11)
где (вц) — симметричный тензор второго ранга а компонентами
( + uJ.i + "ft.*

которые нелинейно зависят от производных компонент вектора пец?-
мещения и, вполне определяющего деформированное состояние тела.
Поэтому тензор (ei}) называется нелинейным тензором деформации.
На основании формулы A.12) шесть независимых компонент сим-
симметричного тензора (etj) определяются равенствами:
[dxJ
дХз
12 ~
дих
ij dui диг a«s , ди3 ди3 \ ,
_ j—_ ___ -j—__ —— 11
\ aXi oXl ojcs oxi oXj I
' 1 / a«g . da3 . dul da1 . a«a аиа ¦ ди9 ди3 \.
2 ^ а^3 5jcs 5xs ax3 a*s a^3 axj а^8 /
i \ С*! GJt3 Cjtg Cjt1 OJtj 0Xi 0X3 CIX{ ]
Компоненты тензора {etj) образуют симметричную матрицу
23
81
A.13)
L/si e32 e38j
A.14)
Выясним геометрический смысл компонент тензора 1ец).
Относительное удлинение линейного элемента da обозначим через
es% тогда
г*в = (ds'— ds)/ds A.15)
или
Отсюда имеем
+ej)ds. '
BеГ
Сопоставляя равенства A.11) и A.17), находим
A.16)
A.17)
A.18)
где а,- = dXf/ds, a} = d^/ds — направляющие косинусы элемента ds.
Пусть линейный элемент^ по деформации направлен параллельно коор"
динатной оси xt. Тогда at = 1, а} = 0 при / Ф i, ej = e? и по форму-
формуле A.18) получим
2е; +ef =2еп, A.19)
где ец — диагональная компонента тензора (et])t т. е. е^ — одна из
компонент еи, егг, е88 тензора (е,у) в отличие от е„ = еи + е82 + е88-
Решая квадратное уравнение A.19), найдем относительное удлине*
ние элемента, параллельного в недеформированном состоянии оси xt:
е^УТ+Щ-К A.20)
ю

Теперь рассмотрим два линейных элемента d% и ds2, выходящих из
данной точки М тела и образующих до деформации угол 0. Направ-
Направления этих элементов определяются направляющими косинусами:
аи = dxt/dSi и а2/ = dxt/ds2.
Угол между элементами ds\ и dsz после деформации обозначим через
0', а их направляющие косинусы — через
а'ц = dxl/ds'i и <хы = dxitds%.
Поскольку
djc/ = dxt + du( = dxt + utJ dx},
то, принимая во внимание соотношение A.16), получим
a'u = (dxt/dst + ult)dx1ldsx)dsllds[ =»
= («u + uu 04^/A + el).
Аналогично,
Тогда
Изменяя обозначения немых индексов, имеем:
— ui,t аиаг]\
— Uk,i Uh,i a
Учитывая последние соотношения и равенство au<xi} = cos 9, а
также формулу A.12), получим
cos У-
Если линейные элементы dst и ds2 до деформации направить парал-
параллельно координатным оеям xt и Х), то cos9 =0, е\ == е/, е5 = е/,
Оц = afl = 1, a^ = a^ = 1 и на основании формулы A.21) имеем
cose'-cos f-i- y//W ^ , A.22)
\2 х") (l+8j)(l+ej) v ;
где уц — угол сдвига, представляющий вобой уменьшение первона-
первоначально прямого угла между элементами dst и dsh выходящими из точки
М тела параллельно осям xt и х}.
Из формул A.20) и A.22) следует, что диагональные компоненты
41 (еш e22*i взз) тензора деформации характеризуют относительные
удлинения, а компоненты elt (i Ф1) — углы сдвига; е-ц — линейные
компоненты тензора деформации, или линейные деформации, etj
И

?*f) — угловые компоненты тензора деформации, или угловые деформа-
деформации. На основании A.22) и A.20) угол едвига определяется формулой
v,, = a rosin '• A.23)
V(«+*7H'+*7)
Компонента тензора (ef,), как тензора второго ранга, при повороте
координатных овей преобразуются по закону A°.16):
е'г. чш arta4leth A.24!
где аГ| — коеинув угля между новой овью *.' я «тарой %\, а,? — коти
нув угла между ооями х, и xt.
Поскольку координатные ови можно повернуть как угодно, то
формула A.24) позволяет определить el и в' для "любых взаимно
перпендикулярных направлений, выходящих из данной точки тела!
,a¦+
A.26)
Зная t~ и е„, на основании A.20) и A.23) найдем отноаительное
удлинение е; в произвольном направлении г, а также угол едвига у^
отновительио взаимно перпендикулярных произвольных направлений
t a si
A.28)
A.27)
Таким образом, тензор деформации аолноатью определяет дефор-
деформированное «овтоянне окревтновти точки тела.
§ 3. ПРЕДСТАВЛЕНИЕ НЕЛИНЕЙНОГО ТЕНЗОРА ДЕФОРМАЦИИ ЧЕРВЭ
ЛИНЕЙНЫЙ ТЕНЗОР ДЕФОРАААЦИИ И ТЕНЗОР МАЛОГО ПОВОРОТА
На основании равенства A.9) выполняется разложение тензора
относительного перемещения (ul%f) на «имметричный тенвор в ком-
аонентвми
и кососнмметричный тенвор, компоненты которого определяютвя фор-
формулой
Л/--?-(«и ;—««!)• A29)
Используя обозначения A.28) я A.29), равенвтву A,9) придадим
вид
12

Тогда компоненты нелинейного тензора деформации, которые опре-
определяются по формуле A.12), можно представить в следующем виде:
cow)/2, A.31)
где величины вц (так же как eftJ и ею), определяемые формулой A.28),
представляют собой компоненты линейного тензора деформации.
На основании разложения A.30) вектор относительного перемеще-
перемещения da = Uijdxfti точки /V относительно точки М тела (рис. 1.2) пред-
представим суммой двух векторов:
йп =» etjdx}9t + (ot)dX)9t *= us.+ a»,
вдесь dXj — координаты точки /V в локальной системе координат с на-
началом в точке М. Введем обозначение lj = dxit тогда
и8 - егД,э,; а® = ©,Др,. A.32)
Для фиксированной точки М тела компоненты etj и «oj; вуть неко-
некоторые конвтанты. На основании формулы A.28) найдем компоненты
тензора деформации, воответвтвующие векторам а8 и emi
ди? dt
Отсюда вледует, что вектор аа предвтавляет вобой перемещение
точки Л^ относительно точки М не в результате деформации окрестнос-
окрестности точки М, а вследствие ее малого поворота, как абсолютно твердого
тела. Поэтому тензор (со^), компоненты которого определяютвя форму-
формулой A.29), называетвя тензором малою поворота.
Косооимметричный тензор (со(>) можно представить вектором <о,
компоненты которых ввязаны соотношениями (ем. l°.31)i
A.33)
где et)h — тензор Леви-Чивита.
Вектор со называется вектором поворота; его компоненты юь —
углы поворота вокруг овей координат х%.
На основании A.33) и A.29) получим!
(О, = —©а8 = С08а = (Ы3,8 — «а.8У2'. '
йJ = -ш81 = «i, = (и1Л — и8Д)/2; A.35)
(Oj-ss —со12 = сои = (Иад — ulit)/2.
Из равенств A.35) вытекает, что вектор поворота ю равен половине
ротора вектора перемещения а точки М тела, т. е.
о = (l/2)rottt. . A.36)
Таким образом, еогласно равенству A.31) можно представить не-
нелинейный тензор деформации (etj) через линейный тензор деформация
(ец) и тензор малого поворота (иц).
13

§ 4. ТЕНЗОР МАЛОЙ ДЕФОРМАЦИИ
Большинство материалов (исключение составляют резина и некото-
некоторые пластмассы), используемых в технике, остаются полностью упру-
упругими лишь при весьма малых относительных удлинениях и сдвигах,
т. е. при малых деформациях. Следовательно, этот чаще встречающий-
встречающийся случай деформирования тела представляет наибольший практичес-
практический интерес.
Деформации называются малыми, если относительные удлинения
е* и углы сдвига у<; являются малыми порядка г\ <^ 1, т. е. когда для
произвольной точки М (Xh) тела абсолютные значения е<* и уц при
любых i u j удовлетворяют условиям
I е? | < г) и | у?/1 < г],
а величина х\* пренебрежимо мала сравнительно с х\.
В случае малых деформаций тензор (etj) называется тензором ма-
малых деформаций. Компоненты его eti определяются формулой A.31), из
которой следует, что при малых е1} должны быть малыми компоненты
линейного тензора деформации (ги) и компоненты тензора малого по-
поворота (<йи).
При некоторых условиях нагружения тел, у которых один размер
существенно отличается от двух других измерений (тонкий длинный
стержень, тонкая оболочка), могут возникать большие перемещения
и при малых деформациях. В этих случаях компоненты ек} имеют бо-
более высокий порядок малости, чем юй;, и в формуле A.31) необходимо
сохранить квадратичные слагаемые относительно <ahf, т. е. компоненты
тензора малой деформации будут определяться формулой
ец — Ц) + (oh,wk1/2, A.37)
На основании формулы A.37) и соотношений A.34) шесть незави-
независимых компонент тензора малой деформации в этих овобых влучаях
определяются следующими равенствами:
e»t ~ егг + (щз + ffliV2; еЯ8 = eg8 — юа<»8/2; I A.38)
е88 = 88з + (К + «гУ2; е81 == 881 — ©„(дуг. j
При незначительном деформировании тел, размеры которых сущест-
существенно не отличаются друг от друга, малые компоненты ъц и а>и яв-
являются величинами малости одного порядка, т. е. их абсолютные зна-
значения удовлетворяют увловиям
»1. П« 1. * A.39)
В этом наиболее часто встречающемся случае компоненты тензора
малой деформации (еи), как это следует из формулы A.31) и условий
A.39), совпадают g компонентами линейного тензора деформации:
е,у = (и,,, + uiit)/2. A.40)
14

Условия A.39) эквивалентны условию малости перемещений
для произвольной точки М (xk) тела при всех значениях I и /
|И|,,|<а при б < 1. A.41)
Условие A.41) допускает пренебрежение квадратами и произве-
произведениями компонент тензора (utJ) по сравнению с их первыми степеня-
степенями. При таком допущении формула A.12) приводится к формуле A.40).
Таким образом, в случае малых перемещений деформации будут так-
также малыми, при этом тензор малой деформации еовпадает с линейным
тензором деформации, который в дальнейшем называется тензором
деформации. В последующем рассматриваются случаи малых переме-
перемещений, а следовательно, и малых деформаций.
Поскольку при малых деформациях s? « 1 и е/2 <^ е? на основа-
основании формул A.19) и A.22), в которых теперь et) заменено обозначением
&1}, выясняется простой геометрический смысл компонент тензора де-
деформации (8j>). Из формулы A.19) имеем
8й=е?, A.42)
а из формулы A.22) находим
cos (у—v*/) = sin у*„ = т/, = 2е„ или в,,«-у ?*/. A,43)
Следовательно, линейные компоненты тензора деформации (ли-
(линейные деформации) суть относительные удлинения линейных элемен-
элементов окрестности точки М. тела, выходящих в направлении координат-
координатных осей, а угловые компоненты etJ(i Ф /) равны половине угла сдвига
между линейными элементами в направлении координатных осей Х\
И X].
Величина у1} = 2г1} (i Ф /) называется угловой деформацией, ко-
которая равна углу вдвига.
Шесть независимых компонент тензора деформации на основании
формулы A.40) определяются равенствами
A.44)
Дифференциальные зависимости A.44) между малыми деформация-
деформациями и малыми перемещениями были непосредственно получены впер-
впервые О. Коши A789—1857). Поэтому обычно равенства A.44) называют-
называются дифференциальными зависимостями Коши.
§ 5. ПРЕОБРАЗОВАНИЕ КОМПОНЕНТ ТЕНЗОРА ДЕФОРМАЦИИ
ПРИ ПОВОРОТЕ КООРДИНАТНЫХ ОСЕЙ
При повороте координатных осей компоненты тензора деформации
(8|>), так же, как и нелинейного тензора деформации (ef/) (тоже второго
ранга), преобразуются по закону A°.16):
tit ~ aria,fit]. A.45)
15
+ dusf,dxif уя1 = 2гй1 = дия(дхх

Таблица J.I
к
/,
'8
*,
/П,
^8
я*
П8
Для направляющих коеинусов art и a,> повернутых осей введем
иные, часто используемые обозначения, которые приведены в табл. 1.1.
Тогда компоненты тензора деформации (ги) отноеительно поверну-
повернутых осей на основании A.46) и A.43) определяются формулами:
-f
1 f
2гЯ9п1пг +
«i«i + ВД) + Тя («i'i +
+ 2е,%гт%ть + 2essn2ns +
Vts
Tii =
Y81
Формулы A.46) позволяют вычислить линейную деформацию 8Г- и
угловую деформацию y^'s относительно произвольных перпендикуляр-
перпендикулярных направлений г и s, выходящих из данной точки тела.
§ 6. ОДНОРОДНАЯ ДЕФОРМАЦИЯ. ПОТЕНЦИАЛ ПЕРЕМЕЩЕНИЯ
При однородной деформации компоненты щ вектора перемещения tt
произвольной точки являются линейными функциями ее координат:
щ = иЧ +в„Х], A.47)
где и/ и си — постоянные.
При однородной деформации компоненты тензора деформации .A.40)
и компоненты тензора-малого поворота A.29) будут постоянными ве-
величинами:
вИ)/2;
A.48)
т: е. все частицы тела деформируются одинаково.

До деформаций тела рассмотрим его точки в плоскости, которая оп-
определяется уравнением
+ bi =0. A.50)
При однородной деформации рассматриваемые точки тела опреде-
определяются координатами
. х', = х, + Ut^Xi-h вих, + uf, A.51)
или относительно х%
xt =xi +d,)X'i + ui, ' A.52)
где dtj к ei — постоянные.
Подстановка х{ согласно выражению A.52) в уравнение A.50) пре-
преобразует его в уравнение, линейное относительно «J, т. е. в уравне-
уравнение плоско*ти
a'txl + Ы = 0. A.53)
Следовательно, точки пловкооти, которую можно вообразить в теле
до его деформирования, при однородной деформации переходят в точ-
точки плоскости тела в деформированном состоянии.
Таким же путем можно показать, что при однородной деформации
прямые линии остаются прямыми после деформации, параллельные
плоскости и параллельные прямые преобразуются в параллельные
плоскости и параллельные прямые поеле деформации, а сфера пре-
преобразуется в эллипсоид.
Рассмотрим линейные завизимовти A.47) при увловии, что все ком-
компоненты тензора деформации г1} равны нулю, т. е. когда тело не дефор-
деформируется. В этом случае, сославшись на формулу A.48), получим cty=»
« —йц% вд = 0, а по формуле A.49) находим щ} = Сц = —о# и тог-
тогда зависимости A.47) принимают вид
И/ = ы" + щ,Х{. A.54)
Приняв во внимание A.34), последнее равенство запишем так:
и/ = и? —ei)k(Akxh A.55)
или
«I =» Ul + «>2*8— 6>»*2, |
| 0-56)
un3-\r щхг —
Равенства A.56), в которых и\, и°г, и"„ — компоненты поступатель-
нбго перемещения, а сох, <ог, со,— углы поворота окрестности точки
вокруг осей координат, определяют «жесткое смещение тела»..
¦ Теперь рассмотрим такую деформацию, когда все компоненты тен-
тензора поворота cot; равны нулю, т. е. когда
= Щ: ,;, . ... . ...... . . A.-57)
17

Из равенства A.57) вытекает, что выражение tiidxi является полным
дифференциалом некоторой скалярной функции ? (xi), т. е.
m^dW/dxi A.58)
или
0 = ai&Vldxt = grad ?. A.59)
Таким образом, в рассматриваемом случае поле перемещений —
градиент скалярного поля ? {xi), т. е. будет потенциальным полем,
а функция ? — потенциал (точнее, скалярный потенциал) перемеще-
перемещения. Деформация, являющаяся результатом таких перемещений, назы-
называется чистой деформацией.
§ 7. ГЛАВНЫЕ ДЕФОРМАЦИИ И ИНВАРИАНТЫ ТЕНЗОРА ДЕФОРМАЦИИ
Главные значения тензора деформации (е^), как симметричного
тензора второго ранга, равны корням кубического уравнения
(см. (l°.50)J:
8« - /х (8„)8? + /2 (8»,)8 - /3 (8,;)= 0. A.60)
Здесь It (stj), /2 (stj), /8 (8|>) — соответственно первый, второй
и третий инварианты тензора деформации, которые определяются ра-
равенствами 1см. A°.57Ij
— (ess)8]/3 + {гцгИ — et)et,)(eas)!2. ,
A.61)
Главные значения тензора деформации, которые называются также
главными деформациями, обозначим через ej.
Компоненты единичного вектора п в направлении главных осей тен-
тензора деформации или, что то же самое, направляющие косинусы век-
вектора п, которые обозначим через nJt определяются из уравнений
[см. A9.48)]
0 A.62)
и соотношения
= 1. A.63)
Подставив в уравнения A.62) вместо 8 главное значение тензора
j), например 8!, и решив их совместно с A.63), найдем направляющие
косинусы пи для первой главной оси. Аналогично определяются на-
направляющие косинусы второй и третьей главных осей тензора (е^).
Если координатные оси направить по главным осям тензора (е^), то
его диагональные компоненты, т. е. линейные деформации ед, будут
совпадать с главными значениями тензора е1э е2, е8 [см. A°.3), с. 4001.
а угловые деформации v*/ = 2е{/ будут равны нулю.
Наряду с инвариантами, которые определяются равенствами A.61),
имеет место другая тройка инвариантов тензора (ei;) — линейный, квад-
18

ратичный и кубичный [см. A°.58)]:
A.64)
Между инвариантами A.61) и другой тройкой инвариантов A.64)
имеют место зависимости A°.б9):
2/, (eo)t . A.65)
Л (eii) - I\ (е„) - 3/, (e,,)/, <е„) + 3/, (e,,). )
При направлении координатных осей по главным осям тензора (е,7)
его компоненты будут определяться равенствами
ап = в|, vu = 2гц = 0, A.66)
а формулы A.61) и A.64) для инвариантов примут такой вид:
h (ety) — ех -f ег + е8, |
h (ejy) = е^г + еге8 + 8,8!, I A.67)
(8ij )= ex -f- е2 + е ^
(ei,) - ej + ej +в», I A.68)
)
Первый (или линейный) инвариант тензора малой деформации имеет
простой геометрический смысл, а именно представляет собой объемную
деформацию окрестности точки тела. Действительно, вообразим в ок-
окрестности точки М (xt) 6 V элементарный параллелепипед со сторона-
сторонами dxu dxt, dxa, направленными по главным осям тензора (ej;). Объем
этого элемента dV = dxxdx^tx^. После деформации элемент также будет
прямоугольным параллелепипедом, объем которого
dV1 = dx[dx'2dx: = A + 8^A + ег)A + Bjdx^dx,.
Поскольку 8ц 82, е, являются малыми величинами, то с точностью
до малых первого порядка имеем
Относительное объемное расширение элемента, называемое также объ-
объемной деформацией окрестности данной точки тела,
0 = (dV1 — dV)IdVt
ИЛИ
0 ^ ^(егу) = J, (8,;) = 8м, A.69)
что и определяет геометрический смысл линейного (или первого) инва-
инварианта тензора (е^).
19

Приняв во внимание дифференциальные зависимости Коши A.44).
получим
I =7i(e(j) = в = ei««= dujdxt+dut/dx^ + dujdxs = div a. A.70)
. § 8. ПОВЕРХНОСТЬ ДЕФОРМАЦИИ
Тензрру деформации (е<>) в точке М тела, как симметричному тен-
тензору второго ранга, соответствует характеристическая поверхность о
центром в точке М [см. A°.62)]:
Я.Ф-в|,&|&,=»:ЬЛ 0-71)
где it — компоненты радиус-вектора г относительно локальной си-
системы координат с началом в точке М.
Учитывая значения направляющих косинусов г
«„ - Si/1гI, а,) = У\г |,
уравнение центральной поверхности второго порядка A.71) приведем
к виду
[rret/xr,ccr, = ±е2-. A.72)
На основании A.45) имеем
е~, A.73)
где е,~ — относительное удлинение в направлении г.
Принимая во внимание A.73) и уравнение A.72), получаем
A.74)
Отсюда следует, что модуль радиус-вектора г, определяющего ха-
характеристическую поверхность тензора деформации, обратно пропор-
пропорционален корню квадратному нэ абсолютного значения относительного
удлинения в точке М тела по направлению п
М-*/]/Ш- 0-75)
Характеристическая поверхность тензора деформации A.71) назы-
называется поверхностью деформации Коши.
Главные оси характеристической поверхности тензора (et/) совпа-
совпадают с его главными осями, в которых уравнение A.71) принимает ка-
канонический вид A°.63)
8,1? = ±Ф. A.76)
Если в точке М тела главные деформации е< все одного знака и раз-
различны по величине, то поверхность деформации A.76) представляет
собой эллипсоид (рио. 1.3)!
»!« +e,!t+е ,&«+*». A.77)
Если же главные деформации ei имеют различные знаки, то поверх-
поверхность деформации представляет совокупность однополостного и дву-
двуполостного гиперболоидов с разделяющим их асимптотическим кону-
конусом. ¦"•*.¦¦
2Q ¦

\gradf
Рис. 1.3
Дифференцируя (l.Ti) no it,
получим
df/dlt - etil, и
grad f — в|у!,»|. A.78)
Рассмотрим в окрестности
точки М тела иа направлении
вектора г бесконечно близкую
точку N о координатами г,.
Пусть gj = аг,, где а — постоян-
постоянная. Тогда равенство A.78) при-
принимает вид
grad f =¦ a&tfra, A.79)
или, ссылаясь на A.32),
grad f-ott». (t.80)
Равенство A.80) означает, что вектор относительного перемещения
W точки N относительно точки М в результате чистой деформации
параллелен нормали (вектору grad/) к поверхности деформации в точ-
точке К, определяемой радиус-вектором г (рие. 1.3).
в 9. ШАРОВОЙ ТЕНЗОР И ДЕВИАТОР ДЕФОРМАЦИЙ
Иногда выгодно тензоо деформации (ац) раяложить на шаровой
тензор и девиатор [ом. (l*.S)]i
ei» - вов*| + ёц, A-81)
где ejOjj — компоненты шарового тензора деформации; ?tf—компо-
?tf—компоненты цевиатора деформации; в0 — среднее относительное удлинение,
равное
_ 1 I I /„ » /1 0О\
Bj""-*- в||^"Т" *1\™Ш« V**0'*'
Первый, второй и третий инварианты шарового тензора деформации
ооределяютоя равенствами A*.68)|
Зе,-
A.83)
A84)
равны
21
Главные значения девиатора деформации равны
*t — главные деформации.
Первый, второй и третий инварианты девиз юра
\т. (l\76)ii

h Ы = '.(M-.-f
П Ы-
A.85)
Вторая тройка инвариантов девиатора деформации — линейный,
квадратичный и кубичный — определяется равенствамиA°.77):
= 3/а
= 3/, (е„) -
-Н. /»(в„).
A.86)
§ 10. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПО КОМПОНЕНТАМ ТЕНЗОРА
ДЕФОРМАЦИИ. УСЛОВИЯ СОВМЕСТНОСТИ ДЕФОРМАЦИЙ
Компоненты вектора перемещения ш (перемещения) и компоненты
тензора деформации &t} связаны между собой дифференциальными зави-
зависимостями Коши A.44) или, что то же самое, формулой A.40). Эти зави-
зависимости позволяют вычислить компоненты тензора деформации Zij
непосредственным дифференцированием перемещений ui, которые в
соответствии с предположением о сплошности тела являются непре-
непрерывными и однозначными функциями координат xh произвольной точки
тела A.3). Естественно, что компоненты тензора деформации должны
быть также однозначными функциями xk и иметь непрерывные произ-
производные.
Для решения обратной задачи, т. е. задачи определения трех функ-
функций щ по компонентам тензора деформации eij, имеем шесть уравнений
A.44). Очевидно, что эта задача не может иметь решения, если компо-
компоненты тензора деформации е^ не подчиняются некоторым дополнитель-
дополнительным зависимостям. Эти необходимые зависимости обнаружатся при рас-
рассмотрении решения поставленной задачи.
Пусть в занятой телом области V, которую пока полагаем односвяз-
ной, заданы функции et} и требуется определить функции щ.
Все частные производные искомых функций ui на основании ра-
равенства A.30) определяются в зависимости от известных компонент тен-
тензора деформации е,^ и компонент тензора малого поворота со^. По-
Последние, как легко показать, связаны с компонентами тензора дефор-
деформации дифференциальными зависимостями
(Oijh — Zlhi] — Bih,l' A.87)
Действительно, дифференцируя по xh равенство A.29), получим
(Ojj h = (ut jh — u}th)/2 — (uth) — Uj ,й|)/2 -f (uh tj — uhij)l2 =s
22

Интегрируя уравнение A.30) по любой кривой М0М, не выходящей
из области V, получим
м м
и, = и? + (! ги dx) + J &u dx]K A.88)
где н* — перемещения точки Мо (xf), совпадающей с началом кривой
интегрирования; х1 — координаты текущей точки М* (*/) кривой
M. Полагая
dx' = — d (X) — х*,),
где Xj — координаты фиксированной точки М (xj), последний инте-
интеграл в равенстве A.88) вычислим по частям и учтем равенство A.87):
мм и
. f (ou dxj = — f ©у d {х,—к)) = — <в„ {xj—х))
Mo Uc
M M
Me
A.89)
Подставив в равенство A.88) значение интеграла A.89), получим
формулу Чезаро
м
щ = и1+<о!,{х,-х1)+[ l*th+(xj-xt)(eihJ-ejhii)dxl A.90)
Мо
которая позволяет определить перемещения любой точки M(xj)f тела
по известным функциям е^.
Шесть постоянных и? и со?/, входящих в формулу Чезаро, опре-
определяют произвольное бесконечно малое жесткое смещение тела как
целого.
Действительно, если во всех точках М (х}) ? V имеем e^j = 0, то
на основании A.90), совмещая ради простоты точку Мо (*/) с началом
координат, получим выражение
ui = н? + <at,x, - и? — eiik(uokx}, A.91)
определяющее жесткое смещение.
Таким образом, при заданных компонентах тензора деформации
Btj перемещения т определяются а точностью до произвольного беско-
бесконечно малого «жесткого смещения».
Постоянные н?, со/} находятся из условий, вытекающих из способа
закрепления тела. В случае незакрепленного тела перемещения опреде-
определятся единственным образом, если потребовать, чтобы в некоторой
точке, например, совпадающей с началом координат, перемещения ы?
и углы поворота <в|! ее окрестности были равны нулю.
Перемещения произвольной точки М (х/) тела должны быть функ-
функциями ее координат и не должны зависеть от пути интегрирования
MQM. Поэтому подынтегральное выражение в формуле Чезаро должно
23

быть полным дифференциалом, т. е. во всех точках М* (xj) области
V необходимо и достаточно соблюдение условий
'. >i* + (*j — x'№ihj—»л.|I.|-[вц+ (Х)—х))(г1и—гПл)\,к. A.92)
Выполняя дифференцирование левой части равенства A.92) по '*/
и правой части по х\, получим
ejft,/ — (ejft.i — 6гм) + (xi — x*i)(elhi)l — eihtl) =
'.'[. — «п.* — (8n.ft — 8ftu) + (xj — Xi)(eili<№ — eJuh),
откуда вытекает
е«лл + Bn,ik — eu.jh — eJk,n = °« П -93)
Равенство A.93) определяет те дополнительные зависимости между
компонентами тензора деформации, необходимость которых отмеча-
отмечалась выше. Эти дифференциальные зависимости, как это следует из
способа их получения, представляют собой необходимые и достаточные
условия интегрируемости уравнений A.30).
Легко обнаруживается, что выражение левой части A.93) меняет
знак, во-первых, при перестановке индексов I и /, а во-вторых, при
перестановке индексов k и /. Поэтому оно тождественно обращается
в нуль при i = / и при k = /. Кроме того, это выражение остается без
изменения при одновременной перестановке индексов: 1) I и k, j и 7,
2) i я /, / и А, 3) /и /, k и /.
Тогда среди соотношений A.93), не повторяющихся и не обращаю-
обращающихся тождественно в нуль, будет только шесть при следующих значе-
значениях индексов ЩЩ\ A212), B323), C131), A213), B321), C132). Эти
шесть соотношений образуют две группы дифференциальных зависи-
зависимостей между компонентами тензора деформации.
Одну из зависимостей первой группы получим, положив I — k = 1,
/ = I = 2:
д2ги/дхга + dhiS/dxl — 2&в1,/(дх1дхй = 0- A-94)
Две другие зависимости этой группы получаются путем круговой
перестановки индексов.
Принимая ( = k = I, ] = 2, I — 3, получим одну из зависимостей
второй группы:
¦ &гХ11(дхгдх8) + д (d&^s/dxj, — деа1/дхг — дг^дх^дху. = 0. ' A.95)
Выполняя круговую перестановку индексов, получим еще две зави-
зависимости второй группы.
Необходимые и достаточные условия интегрирования уравнений
A.30), выраженные дифференциальными зависимостями A.93), полу-
получены исходя из предположения о непрерывности функций щ. Поэтому
зависимости A.93) являются также условиями сплошности тела.
,Необходимость существования зависимостей между компонентами
тензора деформации можно обосновать также геометрически. Предпо-
Предположим, что в начальном состоянии тела оно мысленно разделено на
элементарные параллелепипеды (исключая элементы у поверхности
24

тела). Если, эти параллелепипеды подвергнуть деформации при незави-
независимых между собой компонентах г%}, то из деформированных таким про-
произвольным образом элементов не удается, естественно, сложить сплош-
сплошного тела, каким оно должно быть в действительности. Между некото-
некоторыми элементами образуются зазоры, а для других из них не окажется
достаточного места. Это и показывает, что компоненты тензора деформа-
деформации не могут быть произвольными, а должны подчиняться установ-
установленным аналитическим путем зависимостям A.93).
Шесть соотношений, вытекающих из зависимостей A.93): три типа
A.94) и три типа A.95), — называются условиями неразрывности или
совместности деформаций. Впервые A864) они .были получены Сен-
Венаном A797—1886) и часто называются
дифференциальными зависимостями Сен-
Венаиа.
Если тело ограничено односвязной обла-
областью V, то условия A.93) не только необхо-
необходимы, но и достаточны, чтобы определяемые
функции щ были однозначными, так как в
этом случае при выполнении условий A.93)
интеграл в формуле A.90) не зависит от вы-
выбора пути интегрирования. Рис. 1.4 :
В случае же многосвязного тела диффе-
дифференциальные зависимости Сен-Венана A.93) являются необходимы-
необходимыми и достаточными условиями интегрируемости уравнений A.30) и
лишь необходимыми, но недостаточными условиями однозначности
перемещений ии
Рассмотрим простейшее многосвязное тело, например двусвязный
цилиндр, поперечное сечение которого показано на рис. 1.4.
Любое многосвязное тело можно превратить в. односвязное, мыс-
мысленно производя необходимое число разрезов: для m-связного тела тре-
требуется (т — 1) разрезов.
Рассматриваемое двусвязное тело превращается в односвязное путем
одного продольного разреза ab, два берега которого условно обозначим
знаками (—) и (+). Для полученной таким образом односвязной об-
области при выполнении зависимостей A.93) определяемые перемещения
«г будут однозначными функциями координат точки М (xh), если путь
интегрирования MqM (точка Мо начала пути на рис. 1.4 не показана)
не пересекает разреза, т. е. не выходит из полученной односвязной
области. Однако если точку М приближать к какой-либо точке М±
разреза, то перемещения будут принимать, вообще говоря, различные
значения в зависимости от какого берега приближается точка М к точ-
точке Ali.
Пусть ui+) — перемещения точки Л^ при приближении к ней точки
М (хк) с берега (+), a «J"' — при приближении с берега (—). Тогда
для получения однозначных перемещений в случае многосвязного тела
наряду с зависимостями A.93) необходимо вдоль всех разрезов выпол-
выполнение дополнительных условий
и\+) - и\-\ A.96)
25

Если при определении перемещений в мйогосвязном теле условия
A.96) не будут соблюдены, то перемещения и при выполнении условий
A.93) окажутся многозначными функциями xh.
Рассмотренный путь определения перемещений не является един-
единственным. Следующий параграф посвящен другому, более удобному,
способу определения перемещений.
§ 11. ОПРЕДЕЛеНИЕ ПЕРЕМЕЩЕНИЙ ЧЕРЕЗ КОМПОНЕНТЫ
ТЕНЗОРА ОТНОСИТЕЛЬНОГО ПЕРЕМЕЩЕНИЯ
Формула Чезаро ввиду громоздкости подынтегральных функций
обычно не используется для определения перемещений. Значительно
проще перемещения можно определить через компоненты тензора от-
относительного перемещения (u(j;) по заданным компонентам тензора
деформации (ег-;). Из дифференциальных зависимостей Коши A.44) не-
непосредственно находятся три компоненты тензора (ut ,-):
«1. 1 = 8И, иг 2 = 822, «з. 3 = 833. A-97)
а остальные компоненты uitj (i ф j) определяются дак функции по
их полным дифференциалам в зависимости от заданных компонент eij.
Дифференцируя по xh равенство A.30) и учитывая зависимость
A.87) , получим формулу
Щ. ih = е*л ft + 8»ft,) — &jh. h A-98)
определяющую все производные компонент тензора относительного
перемещения через производные заданных компонент -Тензора дефор-
деформации, удовлетворяющих условиям совместности 1.93).
Тогда
м
Щ, 1 = "?,/ + j (ew,й + Bikii — e/ft, г) dxh. A.99)
При соблюдении дифференциальных зависимостей Сен-Венана кри-
криволинейный интеграл A.99) не зависит от пути интегрирования MJA.
Как известно, наиболее удобно интегрировать по не выходящей из
области V ломаной, звенья которой параллельны осям координат. Сов-
Совмещая начало Мо пути интегрирования М0М с началом координат,
имеем
Ui.J="?.i+ \ (ви.1 + 8|1,, — 8/x.i
J
0 • 0
dx2+ f (8,AB + 8,Bf,—eja,t)dxs. A.100)
2
x, = 0
Вычислив компоненты utj (i Ф f) по формуле A.100) и учитывая
компоненты A.97), перемещения ш произвольной точки М тела можно
определить как функции по их полным диффенциалам;
26

j
о о ' о
Если окрестность точки Мо тела не может иметь жесткого смещения,
то постоянные Ui,j и ifi, входящие в формулы A.100) и A.101), равны
нулю.
В дальнейшем перемещения будут определяться преимущественно
этим способом. Поэтому рассмотрим его применение на следующем при-
примере.
Пример. В произвольной точке М (#/) призматического бруса компоненты
тензора деформации
v 1
вц=>8М="— *5! s33=—— x3i ei2 = 8!3«=«e31 = 01
где гир — постоянные.
Требуется найти перемещения точки М (xj), считая, что окрестность точки
Мо (*у). совпадающей g началом координат, не имеет жесткого смещения.
Решение. Данные компоненты еу, как легко видеть, удовлетворяют диф-
дифференциальным зависимостям Сен-Венана A.93). На основании A.97)
«1.1=—--*»» «2.&=— — *»» "з,8-— Ч-
Учитывая производные заданных компонент ец, по формуле A.100) вы-
вычисляем остальные компоненты uj, j (I ф j)\
«i,»-«i,»— ~хй «i,8 = ui,s»
"
v
—
3,2
1
+—-«8.
По формуле A.101) находим перемещения!
*S—
Поскольку, по условию, окрестность точки Мв, совпадающей с началом ко»
ординат, лишена жесткого смещения, вое пойтоянные а^и ш^ равны нулю. Тот»
¦а окончательно
v 1 1
«1-— *!*!,¦ «2-— — [Х%— V (ДС|— Х%)]> U3~. — X2X3.
9 2р Р

Глава II
ТЕОРИЯ НАПРЯЖЕНИЙ
§ 1. ВНЕШНИЕ СИЛЫ
Внешние силы, действующие на тело, бывают двух видов: массо-
массовые и поверхностные.
Массовыми называются силы, действующие на частицы объема те-
тела, например сила тяжести, силы инерции. Пусть / (да) — массовая
сила, отнесенная к единице массы в окрестности точки М (да) тела, т =
= pdV— масса частицы тела, объемом dV, p — массовая плотность,
тогда mf (да) — сила, действующая на массу в элементарном объеме
dV, а величина р/(да) =/о(#0 представляет силу, отнесенную к еди-
единице объема, которая называется объемной силой.
В линейной теории упругости при рассмотрении равновесия де-
деформированного тела (или его части) принимают, что размеры и форма
его такие же, как и в начальном состоянии, т. е. полагают V( = V и
& = 5.
Следовательно, главный вектор массовых сил, действующих иа те-
тело, занимающее область V, равен1
B.1)
а главный момент относительно начала координат определяется ин-
интегралом:
B.2)
Поверхностные силы — силы, распределенные по поверхности 5,
ограничивающей область V, занятую телом. Поверхностные силы яв-
являются результатом действия на рассматриваемое тело других тел,
с ним соприкасающихся.
Вектор внешней поверхностной силы, приходящейся на единицу
площади поверхности 5 тела, обозначим через t. Тогда поверхностная
сила, действующая на элемент поверхности площадью dS, будет tdS.
Главный вектор Rt и главный момент Mt поверхностных сил опреде-
определяются интегралами по поверхности S:
' B.3)
B.4)
1 Область, занимаемая телом, и объем тела обозначаются одной буквой V,
так же, как поверхность тела и ее площадь обозначаются буквой S.

§ 2. ВЕКТОР НАПРЯЖЕНИЯ И НАПРЯЖЕННОЕ СОСТОЯНИЕ
Расположение частиц в недеформированном теле соответствует со-
состоянию его теплового равновесия. При этом каждая мысленно выде-
выделенная часть тела находится и в состоянии механического равновесия,
т. е. главный вектор и главный момент всех сил, действующих на эту
часть со стороны смежных частей, равны нулю.
Под действием внешних сил Тело деформируется, т. е. происходит
изменение относительного расположения его частиц. В результате меж-
между частицами тела возникают дополнительные силы взаимодействия,
стремящиеся вернуть тело в на-
начальное состояние. Эти внутрен-
внутренние силы выявляются методом
сечений.
Мысленно рассечем тело
(рис. 2.1) гладкой поверхностью
S', проходящей через его неко-
некоторую точку М (xt), на две ча-
части: /и //. Силы взаимодейст-
взаимодействия между расположенными по
обе стороны поверхности S' со-
соседними частицами тела до его Рис: 2.1 • :
рассечения представляли собой
внутренние силы. Эти, силы после рассечения тела необходимо прило-
приложить к его частям /и // на поверхностях сечения,чтобы эти части, ка*
и до рассечения, находились в равновесии (рис. 2.2). Тем самым эти
силы мысленно переводятся в категорию внешних поверхностных сил,
распределенных на поверхностях сечения S'' обеих частей тела. Они
представляют собой действие одной части тела на другую его часть.
Например, на часть / тела объемом Vx, ограниченную поверхностями
Si и S', действуют приложенные к ней заданные массовые и пове'рх-
нбстные силы на поверхности Si (на рис. 2.1 и 2.2 они не показаны), а
также поверхностные силы на S' как результат действия части // те-
тела, на часть /. Под действием всех этих сил часть / тела находится в
равновесии. >
Рассмотрим" на поверхности S' части / элементарную площадку пло-
площадью AS, содержащую точку M{xi) ? S1. Обозначим главный, век^-
тор и главный момент поверхностных сил на этой площадке соответст-
соответственно через АР и AM, а единичный вектор по внешней нормали к по-
поверхности S'- в точке М (xi) — через п. •
! Классическая теория упругости базируется на модели сплошной
среды, между частицами которой по разделяющей их площадке^ осу-
осуществляется лишь центральное силовое взаимодействие, т. е. когда при
.стягивании элементарной площадки в точку М (xt) имеем
Игл (АР/AS) = dP/dS =pn, lim (AM/AS) = 0. B.5)
AS-*0 . > . AS-s-0
Заметим, что в 1887 г. Фойгт A850—1919) при исследовании напря-
напряжений в кристаллах ввел другую модель сплошной среды, между час-
частицами'ко'гбрЪй пЬмимр' центрального имеет место еще и вращательное

взаимодействие, т. е. в этом случае lim AM/AS = dMIdS — m ф 0.
AS-s-O
Теория упругости, построенная на модели среды Фойгта и называемая
моменгной или несимметричной, разработала в 1910 г. братьями Кос-
сера [43, 40]. Ограничившись этим замечанием, будем рассматривать
только модель сплошной среды классической теории упругости.
Вектор рп, определяемый первым равенством B.5), называется век-
вектором напряжения в точке М (xt) на площадке с нормалью п.
На основании принципа равенства действия и противодействия часть
/ действует на часть //по площадке dS, содержащей точку М (xt)t си-
силой р-п dS, равной по величине силе pndS, но противоположно на-
- правленной (рис. 2.2), т. е. p-ndS = —pndS, откуда
Р-п = — Рп-
B.6)
5"
Рис. 2.2
Вектор напряжения/^ не зависит от вида секущей поверхности, т.е.
если рассечь тело другой поверхностью S", отличной от S', но проходя-
проходящей через ту же точку М (xt) тела и имеющей общую касательную пло-
плоскость Sk в этой точке, то вектор напряжения не изменится.
Очевидно, что в некоторой точке тела на различных площадках,
проходящих через нее, будут иметь место различные векторы напряже-
напряжения/7,! — рп (xi, n). Множество векторов напряжения на всевозможных
площадках, проходящих через рассматриваемую точку тела, опреде-
определяет напряженное состояние в этой точке. Напряженным состоянием
тела называется совокупность напряженных состояний во всех точках
тела. Если вектор напряжения зависит только от вектора и, а от коор-
координат xt точки тела не зависит, то напряженное состояние тела назы-
называется однородным.
§ 3. ТЕНЗОР НАПРЯЖЕНИЙ
Рассмотрим некоторую точку М (xt) деформированного тела и про-
произвольно проходящую через нее площадку, положение которой опре-
определяется вектором,». Покажем, что в данной точке вектор напряжения
рп на рассматриваемой произвольной площадке полностью определяет-
определяется, если известны в данной точке векторы напряжения/»» на трех коор-
координатных площадках.
30

Начало координатных осей совместим с точкой М и за положитель-
положительные направления внешних нормалей к координатным площадкам при-
примем положительные направления координатных осей.
В окрестности точки М мысленно выделим элементарный тетраэдр
(рис. 2.3), три грани которого проходят через точку М и перпендику-
перпендикулярны координатным осям, а четвертая грань перпендикулярна век-
вектору л. Площади dSi координатных площадок элемента равны
dSi = (XnidS — mdS, B.7)
где ni — компоненты единичного век-
вектора, которые равны его направляю-
направляющим косинусам ani; dS — площадь
перпендикулярной вектору п грани
элемента.
Помимо поверхностных сил, дей-
действующих на грани элемента со
стороны тела, на элемент, вообще
говоря,' действует также массовая
сила fpdV. Поскольку элемент, вос-
воспринимающий все эти силы, нахо-
находится в равновесии, их главный век-
вектор должен быть равен нулю:
pndS
P.zuSz
B.8)
Рис. 2.3
B.9)
где объем элемента
dV = hdS/3.
Здесь h — длина перпендикуляра, опущенного из точки М на пер-
перпендикулярную вектору п грань ABC.
Учитывая равенства B.7) и B.9) и принимая во внимание, что /?_* —
= —pi, находим
Рп = Pint + fph/З. B.Щ
Для отыскания вектора напряжения рп в точке М на площадке, оп-
определяемой вектором л, грань ABC тетраэдра будем перемещать к точ-
точке М так, чтобы она оставалась перпендикулярной вектору л. При этом
А, а следовательно, и последнее слагаемое в равенстве B.10)устремляют-
ея к нулю. В результате получим
B.11)
Таким образом, вектор напряжения рп на произвольной площадке,
перпендикулярной вектору л и проходящей через точку М тела, пол-
полностью определяется тремя векторами напряжения pi на координат-
координатных площадках, проходящих также через точку М. Вектор рп и три
вектора р% разложим по векторам базиса Э{.
Рп =¦ РщЭ?, B.12)
Pi = оцэи B.13)

где pnj — три компоненты вектора напряжения рп на произвольной
площадке; oi} — девять компонент трех векторов напряжения pi на
координатных площадках.
Учитывая разложения B.12) и B.13), формула B.11) принимает вид
Pnfii = Oijnt3j. B.14)
Отсюда имеем
Рп) = °tjtii, B.15)
где «,• = ani — компоненты определяющего положение произволь-
произвольной площадки единичного вектора л.
На основании обратного тензорного признака A°.37) из равенства
B.15) следует, что девять компонента^ трех векторов/?* являются ком-
компонентами тензора второго ранга, который называется тензором на-
напряжений.
Первый индекс у компонент а%] тензора напряжений, как это выте-
вытекает из равенства B.13), соответствует индексу координатной оси хи
перпендикулярной площадке, на которой имеет место вектор напряже-
напряжения pi, второй индекс указывает направление компоненты at] по коор-
координатной оси Xj. Следовательно, компоненты а^ при / = i, т. е. а? t,
являются нормальными напряжениями, а компоненты otj при I Ф / —-
касательными напряжениями на координатных площадках.
Таким образом, компоненты тензора напряжений предетавляют
собой нормальные и касательные напряжения в данной точке тела на
площадках, параллельных координатным плоскостям. Из равенства
B.15) следует, что тензор напряжений полностью определяет напря-
напряженное состояние в данной точке, т.е., зная тензор (oi}), можно оп-
определить проекции вектора напряжения рп на любой площадке, про-
проходящей через рассматриваемую точку тела:
B.16)
Pm — °iini ~г CT2in2 ~г ^ai^s'i
Pni = 0"l2^1 T" O2^2 I" O'es'^e!
Pn 3 == "l S^l T" ^28^2 T" ^SS^S"
Компоненты тензора напряжений образуют матрицу]
B.17)
где диагональные элементы аи, агг, qS3 — нормальные напряжения на
координатных площадках, которые называют нормальными компонен-
компонентами тензора {ог]), а остальные элементы матрицы — касательные на-
напряжения на координатных площадках или касательные компоненты
тензора напряжений.
32

§ 4. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ
И СИММЕТРИЯ ТЕНЗОРА НАПРЯЖЕНИИ
Пусть на деформируемое тело объемом V, ограниченное поверх-
поверхностью S, действуют массовые и поверхностные силы, которые вызы-
вызывают малые перемещения его точек, а следовательно, и малые дефор-
деформации.
Рис. 2.4
Деформируемое тело, как целое, будет находиться в равновесии,
еели главный вектор /? и главный момент М массовых и поверхност-
поверхностных сил будут равны нулю:
= 0, B.18)
B.19)
где г — радиус-вектор произвольной точки тела.
При равновесии тела любая его мысленно выделенная часть должна
находиться в равновесии под действием сил, к ней приложенных. В слу-
случае деформируемого тела на поверхности его выделенной части необхо-
необходимо приложить силы/?пй5 как результат воздействия на нее осталь-
остальной части тела. Вектор напряжения рп -в некоторой точке М (хг) тела
на площадке с нормалью п, как уже известно, вполне определяется
тензором напряжений (ptj) в данной точке тела.
Естественно, что компоненты тензора (сгг>) являются функциями
координат точки М (xt) тела. Будем считать эти функции непрерыв-
непрерывными и имеющими непрерывные частные производные во всей области
V, занятой телом.
Из находящегося в равновесии тела, занимающего область V, кото-
которая ограничена поверхностью S, мысленно выделим произвольную об-
область V*, ограниченную поверхностью S*, не имеющей общих точек
в поверхностью S тела (рис. 2.4).
2 Зак. &14
НЕ БОЛЕЕ 1Й КНИГИ В
ОДНИ РУКИ И 2Х В ДВЕ '
33

На поверхности S* выделенной части тела распределены силы pndS,
которые являются внутренними для данного тела, т. е. для области V,
и внешними силами для выделенной области V*. Под действием по-
поверхностных сил pndS, а также массовых сил fpdV выделенная про-
произвольная часть объемом V* находится в равновесии. Поэтому глав-
главный вектор и главный момент этих сил относительно, например, нача-
начала координат О должны быть равны нулю:
B.20)
O, B.21)
где г = Xi9t — радиус-вектор произвольной точки замкнутой области
V*, т. е. включая точки поверхности S*.
На основании формулы Остроградского A°. 106), а также приняв
во внимание равенство B.11), имеем
Тогда согласно равенству B.20) получим
ДО
Поскольку область V* произвольная, то последнее равенство воз-
возможно лишь тогда, когда подынтегральная функция во всех точках об-
области V равна нулю.
Таким образом, для каждой точки тела имеем
dpt/dxt + р/ = 0. B.22)
Учитывая разложение B.13) векторов р% и разложение f =*/>Э^ по-
получим
doij/dxt + pfj =• 0,
или
°ил + P/i = 0- B.23)
Равенство B.23) представляет собой три дифференциальных урав-
уравнения равновесия деформированного тела.
Теперь по формуле Остроградского преобразуем поверхноетный
интеграл в равенстве B.21):
34

Внося это значение поверхностного интеграла в равенство B.21)
и учитывая B,22), получим
Из произвольности области V* следует
dr/dXiXpt — 0.
Так как drldxt = э* то, принимая во внимание B.ГЗ), получим
это равенство можно записать и такз
(э,хэ})аи + {aiX9j)atj =? 0.
Если во втором выражении последнего равенства заменить немой
индекс f на / и / на i, то получим
(ЭгХЭ})ои+ CjX3i)an = 0
или, учитывая, что (а,хэг) = —(ЭгХэ,), будем иметь
(eixa,)(ow —о„) =0.
Поскольку при i Ф jэгX 9j<ф 0, то из последнего равенства сле-
следует, что
его - а„, B.24)
т. е. тензор напряжений является симметричным тензором.
Равенство B.24) выражает также известное из курса сопротивле-
сопротивления материалов свойство парновти (взаимноети) касательных напряже-
напряжений Oij (i Ф /): касательные напряжения на двух взаимно перпенди-
перпендикулярных площадках, перпендикулярные линии пересечения этих
площадок, численно равны между еобой. Свойство парности касатель-
касательных напряжений представляет частный случай общей теоремы. Пусть
через некоторую точку тела проходят две произвольные площадки,
нормали к которым обозначим через п' vtn", а векторы напряжения на
них — соответственно через рп- и ра«. Тогда теорема утверждает;
проекция вектора напряжения рп- на нормальй? равна проекции век-
вектора напряжения ра» на нормаль п'.
Для доказательства теоремы обратимся к формуле B.15), опреде-
определяющей компоненты вектора напряжения на произвольной площадке,
проходящей через некоторую точку, в зависимости от компонент тен-
вора напряжений в данной точке. Эту формулу, учитывая симметрию
тензора напряжений, можно записать также в следующем виде:
Pni = ОцП}. B.25)
Вспоминая, что проекция вектора на некоторое направление равна
сумме проекций его компонент на то же направление, на основании
B.15) и B.25) получим:
Щп»Рп' = Рп' i п'1 = аи га/ я?,
пр„< р„г = pa"i nl = atj n'i ni.
2« 35

Последние равенства доказывают утверждение теоремы:
прП"Рп- — прпРп'-
В силу симметрии тензора напряжений дифференциальные урав-
уравнения равновесия B.23) можно записать так:
°пл + Ph = °-
Заменив в последнем равенстве свободный индеко / иа I, a
немой индекс i на /, получим уравнения равновесия в следующем виде:
°uj + ?h=0 B.26)
пли
дап!дхг + до12/дхг + daiS/dxB + pft = 0; '
дап1дх1 + дог2/дх2 + до2Ь/дха + р/2 = 0; B.27)
дат/дхх + даа2/дх2 + <9as3/dx3 + р/3 = 0. ,
Шесть независимых компонент ои симметричного тензора
напряжений, как уже отмечалось, предполагаются непрерывными
функциями координат произвольной точки тела, включая и точки его
поверхности. Следовательно, функции ai;, которые удовлетворяют
уравнениям равновесия B.26), должны также удовлетворять усло-
условиям равновесия элемента, выделенного в окрестности любой точки
поверхности тела.
Мысленно выделим элементарный тетраэдр в окрестности некото-
некоторой точки поверхности S тела так, чтобы его три ортогональные
грани были параллельны координатным плоскостям, а четвертая грань
совпадала бы с поверхностью S в данной ее точке. Единичный вектор,
направленный по внешней нормали к этой грани, обозначим через п.
Внешняя поверхностная сила на этой грани, совпадающей g поверх-
поверхностью тела, равна tdS.
Условия равновесия элементарного тетраэдра выражены равенет-
вом B.15) или B.25). Если в равенстве B.25) заменить pni на tu то по-
получим условия равновесия элементарного тетраэдра в окрестности точ-
точки поверхности тела:
оф, = h B.28)
или
a21rt, + a22n2 + aisn3 = t2; 1 B.29)
°31«1 + O32«2 + Os3tls = t3, ]
где щ — компоненты единичного вектора п, которые равны его на-
направляющим косинусам ani — tit.
. Равенства B.29) устанавливают связь искомых функций ои с при-
приложенными к телу внешними поверхностными силами. Эти равенства,
так же как и формула B.28), их определяющая, называются краевы-
краевыми или граничными условиями.
Заметим, что в некоторых случаях граничные условия определяют-
определяются заданными перемещениями точек поверхности тела (см. гл. IV, § 1).
36

Дифференциальные уравнения равновесия B.26) и граничные усло-
условия B.28) являются необходимыми условиями рав-
равновесия деформируемого тела. Если во всей области V, занятой
телом, будут удовлетворены уравнения B.26), а на поверхности 5 тела
выполняться условия B.28), то тогда будут удовлетворены и уравне-
уравнения равновесия деформируемого тела B.18) и B.19). Действительно,
подставив в B.18) и B.19) вытекающее из B.26) значение р/ = р/гэ4- =
= — oUj3i, получим:
Применяя формулу Остроградского, приходим к следующим вы-
выражениям главного вектора и главного момента, которые обращаются
в нуль в силу условий B.28):
R = jT tt эь dS - ff аи п} 9, dS = 0;
М= ff (rx9,)ttdS— f [(rXdJouiijdS = 0.
V "У
В случае движения деформируемого тела в уравнения B.26) надо
по началу Даламбера включить силы инерции (массовые силы) и тогда
получим уравнения движения деформируемого тела
o«., + p-(fi-ui) = 0, B.30)
^ — проекция на координатную ось xt ускорения частицы тела, ко-
которая в момент времени t находится в точке М (*&).
Если тело движется так, что перемещения иг всех его чаетиц ос-
остаются малыми, то flj = д2щ/дР и уравнения малого движения имеют
вид
°tu + Pft = рРщ/di3. B.31)
§ 5, СТАТИЧЕСКАЯ НЕОПРЕДЕЛИМОСТЬ ЗАДАЧИ ОПРЕДЕЛЕНИЯ
ТЕНЗОРА НАПРЯЖЕНИЙ
При равновесии деформируемого тела в каждой его точке шесть
независимых компонент симметричного тензора напряжений а1} долж-
должны удовлетворять трем дифференциальным уравнениям в частных про-
производных B.27), а на поверхности тела — граничным условиям, на-
например B.29).
Очевидно, что система трех уравнений B.27), содержащая шесть не-
неизвестных, имеет неоднозначное решение.
Действительно, можно подобрать множество разнообразных решо
ний этих уравнений, в которые войдет необходимое число произвола
ных постоянных, удовлетворяющих граничным условиям B.29). Каж-

дое решение из этого множества представляет собой статически воъ
ножное напряженное состояние.
Таким образом, условий статики недостаточно для нахождения теь
зора напряжений, определяющего действительное напряженное состоя
ние тела, соответствующее заданной совокупности внешних сил, т. t
данная задана является статически неопределимой. Это обстоятель
ство вполне очевидно. В самом деле, тело под действием приложенные
к нему внешних сил деформируется и, как уже известно, возникающие
деформации должны подчиняться условиям совместности A.93). По-
Поэтому действительное напряженное состояние, будучи статически воз-
возможным, должно также находиться в соответствии с условиями сое
местности. Выполнение условий совместности и учет физических свойств
рассматриваемой модели сплошной среды позволит, очевидно, получит*
необходимые дополнительные уравнения для раскрытия статической
неопределимости задачи определения тензора напряжений {оц
(см. гл. III и IV).
§ 6. ПРЕОБРАЗОВАНИЕ КОМПОНЕНТ ТЕНЗОРА НАПРЯЖЕНИЙ
ПРИ ПОВОРОТЕ КООРДИНАТНЫХ ОСЕЙ
Компоненты тензора напряжений (ai}), как тензора второго рангг.
при повороте координатных осей преобразуются по закону (см. 1°. 16>
а« = ariasjai}. B.32
Принимая для направляющих косинусов ari и aSj обозначения
приведенные в табл. 1.1, на основании закона B.32) получим следую-
следующие формулы для1 компонент тензора напряжений относительно повеь-
нутых осей:
2;
а
12
аз (тгп2 + /я2п,) + о
31
B.33)
assn2ns + oI2 (l2m3 + lsm2) +
.+ огз {т2п3 + msn2) + a31 (n2/3 + n3/2);
a3i — auUh + оггт3тх + a^n^ + 0i2 (ls/щ + 1хт3) +
+ Огз И3«1 + mxtis) + a31 (n3/, + njg).
Координатные оси могут быть повернуты как угодно, поэтому фор-
формулы B.33) позволяют вычислить нормальное напряжение ал и каса-
касательные напряжения atJ (i Ф /) на любой площадке, проходящей через
рассматриваемую точку тела.
38

§ 7. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ИНВАРИАНТЫ ТЕНЗОРА НАПРЯЖЕНИЙ
Как и в случае любого симметричного тензора второго ранга, глав-
главные значения тензора напряжений (аи) равны корням кубического
уравнения [см. A°.50I:
os - h (^/)oa + h (<fu)<f - h Ш = 0, B.34)
где /, (oij), /2 (ои), /а (ст;/) — первый, второй и третий инварианты
тензора напряжений.
Эта тройка инвариантов определяется равенствами 1см. A°.57)]:
Л(аи) = ан>
) (o ° а)
h(°V>—~
B.35)
Корни уравнения B.34), т. е. главные значения тензора (ai;) обо-
обозначим через аг. Обычно принимается нумерация главных напряжений
в порядке их убывания в алгебраическом смысле (о учетом знака): ах>
> ста> ая.
Компоненты nf единичного вектора п в направлении какой-либо
главной оси тензора (а^), которые равны направляющим косинусам
вектора п, определяются из уравнений [см. A°.48I
(аи - оЬи)п, = О B.36)
и равенства
П/П, = 1. B.37)
Подставив в B.36) вместо о поочередно главные значения alt a2, а3
тензора (ai}) и решив каждую из трех полученных групп уравнений
совместно g равенством B.37), найдем три группы направляющих ко-
косинусов п1}, п2), пя}, определяющих направления трех главных осей
тензора напряжений.
При совмещении координатных осей с главными осями тензора
(с^) его касательные компоненты Оц (i Ф /) будут равны нулю, а диа-
диагональные компоненты, т. е. нормальные напряжения ад, будут сов-
совпадать с главными значениями аг тензора напряжений [см. (Iе.3), с.400],
которые называются главными напряжениями. Следовательно, пло-
площадки, проходящие через данную точку тела и перпендикулярные глав-
главным осям тензора (ai;-), свободны от касательных напряжений, а нор-
нормальные напряжения на них есть главные значения тензора напряже-
напряжений или главные напряжения. Эти площадки называются главными
площадками.
Помимо инвариантов тензора (otj), определяемых равенствами
B.35), можно рассматривать другую тройку инвариантов тензора на-
напряжений, которые называются линейным, квадратичным, кубичным
инвариантами и определяются следующими равенствами [см, A°.58I.
39

J.2 (au) = auau\
B.33)
Линейный, квадратичный и кубичный инварианты связаны в пер-
первым, вторым и третьим инвариантами тензора (atj) завиеимостями [ем.
19]
Л (Оо) *= h (°иУ,
B.39)
3/
•^з (°и) = /f (°u) — ЗА (оиIг
Если координатные оси направить по главным осям тензора (огД то
его нормальные компоненты будут главными напряжениями аи а2, ав,
а касательные компоненты atj (i Ф- j) равны нулю, т. е. матрица B.17)
компонент тензора напряжений будет диагональной;
О 0\
о, 0 ). B.40)
0 aj
При таком направлении координатных осей формулы B.35) и B.38),
определяющие две тройки инвариантов тензора (atj), примут вид:
А (аи) -
h (О и) =
/q (Ои) — О,ОяОя',
*Л (оц) = ог + о2 + а3;
•^2 (ст*у) = of + а! + а§;
•^з (о</) = of + оЕ + о^.
B.41)
B.42)
§ В. ПОВЕРХНОСТЬ НАПРЯЖЕНИЙ
Тензору напряжений (аи) в некоторой точке М тела соответствует
характеристическая поверхность с центром в точке М [ем. A°.62)], ко- :
торая определяется уравнением
2/ (Ik) = оиЫ} = ±с4 B.43)
и называется поверхностью напряжений Коши.
Здесь lt — компоненты радиус-вектора г относительно локальной ,|
системы координат с началом в точке М. |
Направляющие косинусы г равны t
Уравнение B.43) можно, следовательно, записать так!
B.44)
40

или, ссылаясь на B.32),
|г|аа~ = ±с2, B.45)
где агу — нормальное напряжение в точке М тела на площадке, пер-
перпендикулярной г.
Из уравнения B.45) следует, что модуль радиус-вектора г, конец ко-
которого расположен на поверхности напряжений, обратно пропорцио-
пропорционален корню квадратному из абсолютной величины нормального на-
напряжения в точке М на площадке, перпендикулярной г:
kH ° • B.46)
' I гг |
Главные оси поверхности напряжений Коши совпадают с главными
осями тензора (oif). Относительно этих осей уравнение B.43) имеет
канонический вид [см. A°.63)|:
Oil! = ±с2. B.47)
Для точки тела, в которой главные напряжения стг различны по ве-
величине, но одного знака, поверхность напряжений B.47) представ-
представляет собой эллипсоид:
(Tig? + о2Ц + а ,11 = +fla. B.48)
Если в точке тела главные напряжения имеют различные знаки, на-
например at> 0, стг> 0, а3< 0, то поверхность напряжений опреде-
определяется уравнениями:
аЛ\ +о2Ц-\ов\Ц -+?*, B.49)
a,g? +aa6J-|a8|g; =-с2, B.50)
т. е. поверхность напряжений представляет совокупность однополост-
ного гиперболоида B.49) и двуполостного гиперболоида B.50), кото-
которые разделены асимптотическим конусом:
oJJ + o.gJ-IOaie-O. B.51)
Располагая поверхностью напряжений для некоторой точки тела,
можно найти нормальное и полное напряжения, а следовательно и,
касательное напряжение на площадках, проходящих через данную точ-
точку тела.
Если конец радиус-вектора г = МС (рис. 2.5), направление кото-
которого перпендикулярно рассматриваемой площадке, располагается на
поверхности однополостного гиперболоида B.49), то в силу формулы
B.45) нормальное напряжение на данной площадке равно
оРг=<*1\г\\ B.52)
и будет напряжением растяжения.
В том случае, когда конец радиус-вектора г = МК располагается
на поверхности двуполостного гиперболоида B,50) на соответствующей
41

площадке, проходящей через
точку М тела, имеет место на-
напряжение сжатия
\\ B.53)
На площадках, нормаль к
которым совпадает с образую-
образующей асимптотического конуса
(г = оо и о- = 0), действует
только касательное напряже-
напряжение.
Теперь, дифференцируя
B.43) по ij, имеем
df/dl, = Oijlj и grad/ =
Так как
arj \r\, то
B.54)
Рис. 2,5
На основании B.13)
=Р;, а в силу B.11) p,-arj = рт
и тогда равенство B.54) прини-
принимает вид
-—grad / =рг, B.55)
т. е. вектор напряжения рт на площадке, перпендикулярной радиув-
вектору г, параллелен нормали (т. е. вектору grad /) к поверхности
напряжений в точке, соответствующей концу г (рис. 2.5).
Зная нормальное напряжение сг~ и направление векторарп, можно
определить величину \рг\ напряжения на рассматриваемой площадке,
а также и проекцию на эту площадку вектора рт, т. е. касательное на-
напряжение аге.
§ 9. ЭЛЛИПСОИД НАПРЯЖЕНИЙ
Наряду с поверхностью Коши можно дать другое геометрическое
представление о напряженном состоянии в точке тела, которое предло-
предложено Ламе A795—1870).
Координатные оси совместим с главными осями тензора (агу) для
некоторой точки М тела. При таком направлении координатных осей
касательные компоненты atj (i ф ]) тензора напряжений будут равны
нулю, а нормальные компоненты будут главными напряжениями
Рассмотрим проходящую через данную точку тела произвольную
площадку, положение которой определяется направляющими косину-
косинусами anj — я,- единичного вектора п, нормального к данной площадке
(п, — компоненты вектора п).
42

Проекции на координатные оси вектора напряжения рп на этой
Площадке есть координаты х, точки, совпадающей с концом вектора/>п.
На основании B.16) они-равны:
Л1 Нп1. и1> Л2 ' ИП2 — и2''2> -*а —• Рпа ~~ Cjiij, ^s.OOJ
Подставив значения Я/ из последних равенств в зависимость между
направляющими косинусами
п\ + nl + nl = 1, B.57)
получим уравнение эллипсоида а полуосями, равными главным на-
напряжениям а1( а2, аа:
х?/о1 + 4/о| + 4/о§ = 1. B.58)
Этот эллипсоид называется
эллипсоидом напряжений или
эллипсоидом Ламе.
Поверхность эллипсоида на-
напряжений представляет, как
это следует из предыдущего,
геометрическое место концов
векторов напряжений рп на
всем множестве площадок, про-
проходящих через данную точку М
тела.
Эллипсоид Ламе (рис. 2.6)
позволяет сделать еледующие рис 2 б
выводы о напряженном состоя-
состоянии в точке тела.
Наибольшее напряжение в рассматриваемой точке тела равно наи-
наибольшему их трех главных напряжений в этой точке. Это следует из
того, что полуосями эллипсоида Ламе являются главные напряжения,
а у эллипсоида одна из полуосей представляет наибольшее расстояние
от его центра до поверхности.
Если ни одно из трех главных напряжений не равно нулю, то векто-
векторы полных напряжений на всем множестве площадок, проходящих через
данную точку тела, располагаются в объеме эллипсоида Ламе. Такое
напряженное состояние в точке тела называется объемным или трех-
трехосным. В зависимости от знаков главных напряжений это еоть растяже-
растяжение или сжатие в направлениях трех главных осей тензора (ац).
Когда одно из главных напряжений равно нулю, то поверхность
эллипсоида Ламе обращается в геометрическое место точек плоской
замкнутой области, ограниченной эллипсом с полуосями, равными
отличным от нуля главным напряжениям в рассматриваемой точке те-
тела. В этом случае векторы напряжений на всех площадках, проходящих
через точку тела, располагаются в одной плоскости и напряженное
состояние называется плоским или двухосным. Тензор (ai}) плоского
напряженного состояния характеризуется, как это вытекает из B.34),
равенством нулю третьего инварианта /3 (о^) = | а^|, что имеет место,
когда соответствующие элементы двух столбцов или двух строк опре-
определителя из компонент тензора (оц) пропорциональны.
43

Если два главных напряжения равны нулю, то эллипсоид напряже-
напряжений превращается в отрезок прямой линии, расположенной на одной
из главных осей тензора напряжений. Напряженное состояние в этом
случае называется одноосным. Необходимым условием существования
одноосного напряженного состояния в некоторой точке тела является
одновременное равенство нулю второго и третьего инвариантов тен-
тензора (аи).
§ 10. КРУГОВАЯ ДИАГРАММА
Поверхность напряжений Коши дает полное геометрическое пред-
представление тензора напряжений. Другой геометрический образ напря-
напряженного состояния — эллипсоид Ламе—представление о векторах
напряжений на всем множестве площадок, проходящих через рассмат-
рассматриваемую точку тела.
Существуют и другие геометрические представления напряженного
состояния в точке тела. Среди них заслуживает внимания круговая
диаграмма напряженного состояния, предложенная О. Мором A835 —
1918), которая, являясь условным геометрическим образом, так как
любое напряженное состояние изображается диаграммой на плоскос-
плоскости, позволяет сделать ряд полезных выводов.
Координатные оси совместим с главными осями тензора (ai}) в не-
некоторой точке тела. Тогда проекции на координатные оси вектора на-
напряжения рп в данной точке на произвольной площадке о нормалью
п будут определяться равенствами B.56).
Спроектироваврп на направление нормали л к площадке, получим
нормальное напряжение ап на этой площадке, а проекция вектора рп
па плоскость площадки есть касательное напряжение, которое обозна-
обозначим хп.
Ставится задача определения положения площадки, на которой
имеют место некоторые заданные наперед значения ст„ и хп.
Исходя из B.56), находим
ап = сх,л? + cx2rti + cx3/i§. - B.59)
Ссылаясь на те же равенства B.56), очевидное соотношение
\рп I2 = ап + Vi = рп\ + Рп2 + Pn'i
приведем к виду
el + т* = а\п\ + o-i/21 + а\п\. B.60)
Таким образом, поставленная задача сводится к определению п? из
линейных уравнений B.59), B.60) и уравнения
1 = п\ + п| + п\. B.61)
Умножив уравнения B.59), B.60), B.61) соответственно на
произвольные постоянные а, Ь, с и сложив результаты, получим
Ьо% + ааа + с + Ьх\ = (Ьо\ + аа, + с)п\ +
+ (Ьа\ + ааг +_ с)щ + фа\ + ао, + с)п\. B.62)
44

В полученном уравнении B.62) коэффициенты при nf, как и первые
три слагаемых в его левой части, представлены многочленом второй
степени с одинаковыми коэффициентами:
F (г) = Ьг3 + аг + о. B.63)
Будем считать вначале, что в рассматриваемой точке тела главные
напряжения ah различны и а±> а%> ст8.
Для определения п\ достаточно принять многочлен B.63) в следую-
следующем виде:
F (г) = (г — аг)(г — а3) = гг—(o2+as)z + о2о8,
т. е. а = —(аа + ва), b = 1, о = стгст8.
Аналогично, для определения п| и п\ вледует соответетвенно принять
a = — (os + ог), Ь = 1, в — Oscv,
a = —(Oj + Оа), Ь = 1, в = а^а.
Тогда из B.62) находим:
П\ =•
— О2)(О„— 03)
О,)(О,—08)
п—oa)t°n—Qi
3 — Ol)(Og— O2)
Легко убедиться, что
B.64)
B.65)
Учитывая еоотношение B.65) и принимая в нем значения svir для пер-
первой формулы B.64) s = 2, г = 3, для второй — s = 3, г = 1, для
¦ третьей — s = 1, г = 2, найдем из них
B.66)
рде
^ J
— o3)n\,
Rl =
B.67)
45

Равенства B.66) представляют собой уравнения трех семейств кон-
концентрических окружностей в осях ап, -сп с центрами в точках
С, I——^—1-. Ог. С
Уравнения окружностей содержат т*п, и поэтому напряжение тп
определяется с точностью до знака. Следовательно, можно ограничить-
ограничиться рассмотрением полуокружностей в полуплоскости т„ ^ 0.
Радиусы Ri этих полуокружностей зависят от главных напряжений
Oh и соответствующего направляющего косинуса nt.
ж
Рис. 2.7
Поскольку квадраты направляющих косинусов и? ^ 0 и аг >
о.г > о8, то на основании B.67) должны выполняться неравенства:
о,
— °з
2
—о.ч
2
-0-2
^зо-
B.68)
где через /?10, i?20, /^ обозначены радиусы полуокружностей /, //, ///
для частных случаев, когда соответственно пг = 0, пг = 0, п8 = 0.
Отсюда следует, что область осуществимых значений ап и тп пред-
представляет собой замкнутую область, ограниченную полуокружностями
/, // и /// (рис. 2.7). Эта область (на рисунке она заштрихована)'на-
заштрихована)'называется круговой диаграммой напряженного состояния или кругами
Мора. Координаты точек круговой диаграммы определяют-в масштабе
диаграммы нормальное (ап) и касательное (т„) напряжения на всем мно-
множестве площадок, проходящих через рассматриваемую точку тела.
Главные оси тензора (а,-Д по направлениям которых действуют глав-
главные напряжения аи сг2, оя, будем называть соответственно первой,
второй и третьей главными осями. Тогда множество площадок, про-
проходящих через первую главную ось, т. е. площадок, для которых пх — 0,
назовем площадками первой серии. Площадкам первой серии соответ-
соответствуют трчки полуокружности / круговой диаграммы.
46

Таблица 2.i
±41/2
±1/У2
0
±1/У2"
±1/У2
0
Аналогично площадки, проходящие через вторую главную ось
(п2 = 0), образуют площадки второй серии. Им соответствуют точки
полуокружности //. Площадкам третьей серии, т. е. проходящим через
третью главную ось (п3 = 0), соответствуют точки полуокружности ///.
Абсциссы точек пересечения полуокружностей с осью ап равны зна-
значениям главных напряжений oh.
Нормальное и касательное напряжения на «несерийных» площадках,
пересекающих все три главные оси тензора (аг Д т. е. когда nt Ф 0, п#Ф
ф 0, п3 Ф 0, определяются координатами внутренних точек области,
ограниченной полуокружностями /, //, ///. Для нахождения точки
N диаграммы (рис. 2.7), определяющей напряжения на площадке о
нормалью п, следует по формулам B.67) вычислить радиусы i?a, R2, /?з
соответствующих окружностей, пересечение которых и определяет ис-
искомую точку N. Возможно и чисто графическое отыскание точки N',
этот прием подробно изложен в работе [44].
Анализируя круговую диаграмму, можно сделать ряд выводов о
свойствах напряженного состояния в точке тела.
Отметим два наиболее важных вывода.
1. Алгебраически наибольшее главное напряжение ох больше всех
остальных нормальных напряжений, существующих в расематривае-
мой точке тела, а наименьшее главное напряжение а3 меньше всех ос-
остальных нормальных напряжений в'данной точке тела; это следует из
того, что наибольшая абсцисса диаграммы равна аи а наименьшая
2. Для площадок первой, второй и третьей серий касательные на-
напряжения имеют экстремальные значения:
Tl = (а2 — а3)/2, тг = (ах — о8)/2, т3 = (ох — аг)/2, B.69)
которые иногда называют главными касательными напряжениями.
Главные касательные напряжения действуют на площадках, кото-
которым соответствуют точки А, В и С круговой диаграммы. На этих пло-
площадках имеют место также нормальные напряжения!
о' = (а2 + а8)/2, о* = (о, + о8)/2, &" = (а, + ог)/2. B.70)
Подставив в формулы B.64) вместо о„ и тп соответствующие значе-
значения нормального и касательного напряжений на площадках, которым
отвечают точки А, В и С круговой диаграммы, найдем направляющие
косинусы нормалей к этим площадкам, приведенные в табл. 2.1.
47

Таким образом, площадки, на которых действуют главные касатель-
касательные напряжения, проходят через одну из главных осей и биссектрису
угла между двумя другими главными осями.
Из круговой диаграммы (рис. 2.7) и формул B.69) следует, что наи-
наибольшее касательное напряжение в данной точке тела
тшах = Х2 = (Ci — О3)/2. B.71)
Взаимно перпендикулярные площадки, на которых возникают
tmax. проходят через вторую главную ось и биссектрисы углов между
первой и третьей главными осями тензора (а^).
§ 11. ШАРОВОЙ ТЕНЗОР И ДЕВИАТОР НАПРЯЖЕНИЙ
Тензор напряжений (ai}), как симметричный тензор второго ранга
[ем. A°.5I, можно разложить на шаровой тензор и девиатор напряже-
напряжений:
оц = ао8и + а„, B.72)
где o08ij — компоненты шарового тензора напряжений; а*/ — компо-
компоненты девиатора напряжений; о„ — среднее нормальное напряжение,
равное
а0 = а88/3 = /j (a,^)/3. B.73)
Первый, второй н третий инварианты шарового тензора напряжений на
основании A°.68) определяются равенствами:
h (о<А;) = Зо0.= h {Оц)\
h (оо^и) = За3 = I\ (at,)/3; B.74)
fa (°оЬц) = ог: '- Л (аи)/27.
Главные значения девиатора напряжений на основании A°.73) оп-
определяются формулой
а, =ог —/1(а,/)/3, B.75)
где ot —главные напряжения, т. е. главные значения тензора (otj).
Первый, второй и третий инварианты девиагора (о4>) равны
(см. 10.76):
-Л (о„) /2(о„)/3 + B/27) /f (a,,).
B.76)
Три других инварианта девиатора напряжений — линейный, квад-
квадратичный и кубичный — связаны с предыдущей тройкой инвариантов
девиатора напряжений и могут быть выражены через инварианты тен-
тензора (аи) следующими формулами [см. A°.77I:
2/.2(о?/)=B/3)/? (о„)—
(a4J) -f- B/9)/»
B.77)

Глава III
СООТНОШЕНИЯ МЕЖДУ КОМПОНЕНТАМИ
ТЕНЗОРА ДЕФОРМАЦИИ
И КОМПОНЕНТАМИ ТЕНЗОРА НАПРЯЖЕНИИ
Геометрическая теория деформации (Гл. I) и статическая теория
напряжений (Гл. II) рассмотрены при предположении о деформируе-
деформируемом теле лишь как о сплошной среде. Поэтому эти теории и полученные
зависимости справедливы для любой сплошной среды, которая может
быть и газообразной, и жидкой, и упругим или упругопластическим
твердым телом.
Из соображений физического характера ясно, что деформированное
состояние тела (сплошной среды) и era напряженное состояние, вы-
вызванные внешними силами или тепловым воздействием, взаимно обу-
обусловлены, т. е. должны иметь место некоторые соотношения между ком-
компонентами ои тензора напряжений и компонентами еи тензора дефор-
деформации.
Эти соотношения необходимы и с математической точки зрения. Дей-
Действительно, деформированное состояние тела описывается тремя не-
непрерывными функциями ut (Хь), через которые на основании зависимос-
зависимостей Коши A.40) определяются компоненты тензора деформации, а на-
напряженное состояние тела определяется шестью независимыми компо-
компонентами а;; тензора напряжений. Однако для определения этих девяти
функций (щ (Хъ) и ои (xh)) в зависимости от внешнего воздействия на
тело пока что имеем лишь систему трех дифференциальных уравнений
равновесия B.26), решение которых должно удовлетворять граничным
условиям, например B.28). Такая система уравнений называется не-
незамкнутой, так как не позволяет найти функции и-г (хн) и atj (*&), ка-
каковы бы ни были для них граничные условия. Это вполне понятно, по-
поскольку не учтены физические свойства рассматриваемой сплошной
среды.
Таким образом, для математической формулировки задачи описа-
описания напряженно-деформированного состояния тела необходимо иметь
по крайней мере еще шесть зависимостей между перечисленными де-
девятью функциями. Очевидно, что недостающие зависимости между функ-
функциями должны отражать физическую сторону данной задачи для кон-
конкретной модели сплошной среды, наделенной определенными свойст-
свойствами ее механического поведения. Эти зависимости называются зако-
законом поведения или законом состояния рассматриваемой сплошной
среды.Установление закона состояния приводит к замкнутой системе
уравнений, которая позволяет определить реализуемое в теле поле
напряжений и поле перемещений при заданном внешнем воздействии
на тело.
43

§ 1, ТЕРМОДИНАМИКА УПРУГОГО ДЕФОРМИРОВАНИЯ
Твердые тела под действием приложенных к ним сил изменяют свою
форму и размеры, т. е. деформируются. Если деформация тела срав-
сравнительно мала, то при снятии вызвавших деформацию внешних сил
тело возвращается в начальное недеформированное состояние. Способ-
Способность тел восстанавливать свою начальную форму и размеры при устра-
устранений внешнего воздействия называется упругостью, а снимаемые при
этом деформации называются упругими.
При больших деформациях после снятия'их вызвавших внешних
сил тело в большинстве случаев (исключение представляют тела типа
резины) не возвращается в свое начальное состояние, т. е. этот про-
процесс деформирования является необратимым. Полученные в этом слу-
случае деформации при разгрузке тела частично сохраняются, и эти ос-
оставшиеся деформации называются остаточными иди пластическими
деформациями.
В дальнейшем будут рассматриваться малые упругие деформации
твердого тела, т. е. обратимый процесс его деформирования.
Для полного определения состояния тела необходимо знать не толь-
только его деформированное состояние (конфигурацию), но также и тем-
температуру в каждой его точке. Деформирование тела может происходить
при изменении и без изменения температуры в его точках. При этом
изменение температуры тела может быть не только вследствие притока
тепла от внешнего источника, но, вообще говоря, и в результате самого
процесса деформирования.
1 Если тело деформируется сравнительно медленно путем постепен-
постепенного увеличения нагрузки (статическое нагружение), то при сохранении
равновесия температур в теле и окружающей среде изменение его со-
состояния, т. е. процесс деформирования, является изотермическим.
Если деформирование тела происходит без поглощения или потери
тепла элементами тела, как это имеет место при малых быстрых коле-
колебаниях тела, то процесс деформирования является адиабатическим.
Деформирование тела, строго говоря, является термодинамичес-
термодинамическим процессом. Поэтому даже в случае малых упругих деформаций при
изучении деформированно-напряженного состояния тела предпочти-
предпочтителен термодинамический подход, который впервые применил Томсон
A824—1907).
Если под действием приложенных внешних сил тело находится в
состоянии движения, то оно обладает кинетической энергией К, кото-
которая зависит от скоростей и масс элементарных частичек тела. Кроме
кинетической энергии тело обладает еще внутренней энергией U, зави-
зависящей от его деформированно-температурного состояния. Полная
энергия тела определяется суммой кинетической и внутренней
энергий.
В случае равновесия тела его полная энергия будет равна внутрен-
внутренней энергии.
Пусть тело, находящееся под действием массовых сил ft и поверх-
поверхностных сил t(," обладает кинетической энергией К и внутренней ^ер-
гией U. При переходе тела в другое состояние за элемент времени &t
50

полная энергия тела получит изменение 8К + Ы/, а внешние силы
(массовые и поверхностные) совершат при этом работу 6Л.
Согласно первому закону термодинамики, изменение полной энер-,
. гии тела равно сумме работы внешних сил ЬА при данном элементарном
процессе и сообщенному телу количеству теплоты 8Q, измеряемому
эквивалентной ему работой, т. е.
б/С + б[/= 6Л + 6Q. C.1)
Найдем изменение кинетической энергии ЬК тела при его элемен-
элементарном переходе в новое состояние. До этого перехода тела проекции
скорости его элемента объемом dV на координатные оси xt в случае
малых перемещений равны дщ/дГ^ щ. Тогда кинетическая энергия те-
тела до'перехода его в новое состояние определяется равенвтвом
C.2)
v
где интеграл берется по объему V тела в недеформированном состоя-
состоянии.
Изменение кинетической энергии за элемент времени 61
д/с=(д/с/ао»=ПТй,И|<
Учитывая, что изменение перемещений щ за то же время Ы Ьщ =
= (дщ1д1) Ы = щЫ, на основании предыдущего равенства получим
C.3)
Теперь вычислим работу, еовершаемую внешними вилами за тот
же элемент времени Ы, т. е. на перемещениях Ьщ рассматриваемого
элементарного процесса. Очевидно, имеем ¦
ЬА = JSJf, би, pdV + iyt бй, dS. C.4)
v s
Заметим, что это выражение для работы не связано в предположе-
предположением об упругом или неупругом состоянии тела.'
Интеграл по поверхности S тела в последнем равенстве преобразу-
преобразуем по формуле Остроградского в интеграл по объему V тела. Прини-
Принимая во внимание равенство B.28), имеем
J\tt 8щ dS =Ц оа 8Ui n, dS = Ц$ {аи Su^jdV.
S S V
Тогда
Ш JJJw6w,.,dV. C.5)
Исходя из равенства C.3) и C.5), находим приращение затрачивае-
затрачиваемой на деформацию тела при рассматриваемом элементарном процессе
Ы

деформирования работы внешних сил:
6Л—в/С = JJJ (о|Л^ + р/,—рм,) ««
V V
Принимая во внимание B.31) и равенство A.30), имеем
6Л-6К = JJ j о„ 6 (е„ + со„) dV.
v
Поскольку (Oij) — симметричный тензор, a (<d^) — кососиммет-
ричный тензор, оида>и — 0 [см. A°.32)] н, следовательно,
6Л-6К= JJJo06efjdV. C.6)
v
Интеграл в равенстве C.6) представляет собой приращение работы,
затраченной на деформацию или, что то же, приращение работы дефор-
деформации.
Если под действием внешних сил тело находится в равновесии,
то 8К == 0 и в этом случае приращение работы внешних сил равно прн-
ращению работы деформации:
6А = J J J аи 5eudV = J J J бх WdV. C.7)
v v
Очевидно, что
б, IF = аибви C.8)
есть приращение удельной работы деформации, т. е. приращение ра-
работы деформации, отнесенной к единице объема тела в окреетноети
его произвольной точки.
Подставив значение ЬА—6Я по формуле C.6) в равенство C.1),
получим
u8eudV + 8Q, C.9)
v
т. е. приращение внутренней энергии тела равно сумме приращения
работы деформации и тепловой энергии, сообщаемой телу.
Для единицы объема тела в окрестности его произвольной точки
равенство C.9) примет вид
dU - a,M} + 6iQ» C.10)
где dU — приращение удельной внутренней энергии; о/;бегу — при-
приращение удельной работы деформации; 6XQ — приращение тепловой
энергии, отнесенной к единице первоначального объема тела.
Заметим, что dU представляет собой полный дифференциал, так как
внутренняя энергия U определяется начальным и конечным состоя-
состоянием идеально упругого тела и не зависит от конкретного процеееа
перехода из одного состояния в другое. Напротив, количество теплоты
и, вообще говоря, работа деформации не определяются однозначно
начальным и конечным состоянием тела, а зависят также от пути пе-
перехода из начального состояния в конечное.
52

Известно, что не все процессы, удовлетворяющие требованиям пер-
первого закона термодинамики (выполнимость закона сохранения энер-
энергии), действительно могут быть реализованы. Поэтому необходимо
обратиться ко второму закону термодинамики, согласно которому,
в частности, в случае обратимых процессов отношение SiQ/T, где Т —
абсолютная температура, является полным дифференциалом функции
состояния системы, которая называется энтропией s:
ds = 81Q/T. C.11)
Учитывая] соотношение C.11) и равенство C.10), получим
dU = atf8etj + Ids. " C.12)
Равенство C.12) является основным термодинамическцм еоотноше-
нием для деформируемых тел.
Внутренняя энергия U является функцией компонент 8^ тензора
деформации и энтропии s (etf и s являются параметрами состояния) и,
следовательно,
C.13)
Сопоставление выражений C.12) и C.13) дает
аи = (ди/дга)„ C.14)
Т = (dU/ds),. C.15)
Вместо функции U (ei}, s) введем другую функцию состояния тела
(системы), которая называется свободной энергией Гельмгольца и
определяется равенством
F = U — sT. C.1G)
Свободная энергия F есть функция параметров состояния е^ и Т.
Поскольку
dF = dU — sriT — Ids,
соотношение C.12) принимает вид
dF = otjdRtj — sdT. C.17)
Так же как и внутренняя энергия U (в1}, s), свободная энергия
F (еи, -Т) является термодинамическим потенциалом.
Тогда из C.17) имеем
аи = (dF/d&uh, C.18)
s « —(dFldl)s. C.19)
Таким образом, компоненты оц тензора напряжений в зависимости
от компонент еи тензора деформации можно получить по формуле
C.14), дифференцируя внутреннюю энергию U (etj, s) по компонентам
тензора деформации при постоянной энтропии s, или по формуле C.18)
дифференцируя свободную энергию F (ег,-, Т) при постоянной темпера-
температуре Т. Свободная энергия F и внутренняя энергия U являются, сле-
следовательно, потенциалами для тензора напряжений (аи).
53

§ 2. УПРУГИЙ ПОТЕНЦИАЛ И ДОПОЛНИТЕЛЬНАЯ РАБОТА
Твердое тело называется идеально упругим, если напряженное сос-
состояние в любой его точке в произвольный момент деформирования ва-
висит только от деформаций в этой точке.
В случае адиабатического деформирования идеально упругого
тела 6Q = Tds = О, т. е. когда s = const, потенциалом тензора напря-
напряжений является внутренняя энергия U:
а„ = (dU/deu)s. C.20)
При этом равенство C.12) принимает вид
dU = ацйеи, C.21)
т. е. в этом елучае приращение удельной работы деформации C.8)
будет полным дифференциалом
dW = a(jdeu. C.22)
Отсюда вытекает, что
аи = дИР/дец. C.23)
Функция W (8j,-) называется упругим потенциалом и представляет
собой удельную работу деформации или удельную потенциальную
энергию деформации.
Равенство C.23) называется формулой Грина. Оно од-
однозначно определяет шесть независимых компонент atj тензора нап-
напряжений через компоненты &и тензора деформации и представляет
собой общее выражение закона упругости.
Если деформирование совершается изотермически, т. е. в процессе
деформирования температура Т остается постоянной, равной темпера-
температуре То тела в его естественном состоянии, то в этом случае потенциалом
тензора напряжений является свободная энергия F:
C.24)
Равенство C.17) при Т = То принимает вид
dF = Oijdetj, C.25)
т. е. при изотермическом процессе деформирования (поскольку dF —
полный дифференциал) приращение удельной работы деформации
будет также полным дифференциалом и, следовательно, имеет место
формула Грина C.23).
Однако при изотермическом деформировании упругий потенциал
W (еи) определяется свободной энергией F = U — TqS, а при адиаба-
адиабатическом деформировании упругий потенциал определяется внутрен-
внутренней энергией 0. Поэтому соотношения между ац и ei;-, определяемые
формулой Грина, при изотермическом и адиабатическом процессах
деформирования не будут тождественными, т. е. упругие постоянные
для данного материала тела, которые содержатся в этих соотношениях,
будут различными. Но это различие несущественно, поскольку в елу-
чае твердых тел (в отличие от газообразных тел) величина TjS зна-
значительно меньше величины U.
54

Шесть соотношений C.23) между пи и ци вместе с тремя дифферен-
дифференциальными уравнениями равновесия B.26) и шестью дифференциаль-
дифференциальными зависимостями Коши A.40) составляют замкнутую систему
уравнений теории упругости, ч'исло которых равно числу неизвестных
функций: utt Rtj, au.
Очевидно, что соотношения C.23) могут быть разрешены относи-
относительно компонент Rtj тензора деформации. Наиболее просто это дости-
достигается путем введения функции
Л = atfitJ - W, . C.26)
которая называется удельной до-
дополнительной работой.
Название этой функции опре-
определяется следующими соображе-
соображениями. Пусть для некоторого не-
нелинейно упругого тела при испы-
испытании образца на растяжение
экспериментально уетановлена за-
висимовть между напряжением ст
и соответствующей упругой де-
деформацией е, которая характери-
вуется кривой О А (рие. 3.1). Оче-
Очевидно, что площадь О A3 этой диа-
диаграммы еоответствует удельной по-
потенциальной энергии деформации
W
«§•
Рис. 3.1
Площадь О АС будет равна
j ads.
=аи80—W
(ОС)
и в масштабе диаграммы представляет работу, которая является
дополнением до удельной работы, равной аоео, вычисленной в пред-
предположении, что в процессе деформирования напряжение а0 сохраняет
постоянное вначение.
Очевидно, что для упругих тел выражение
dA = BtJdou C.27)
является полным дифференциалом, так же как и dW — o-i7dei7-.
В самом деле, имеем
dW + dA = audeu + ei}dau — d @цВц) — dA*,
где А* = otfiij — удельная работа, вычисленная в предположении,
что на протяжении всего процесса деформирования компоненты а^
сохраняют постоянные значения, равные их окончательным значе-
значениям в положении,рассматриваемого равновесия.
Тогда на основании C.27) имеет место равенство
еи = дА/дац. C.28)
96

, Действительно, дифференцируя равенство C.26) по ohl как слож-
сложную функцию Л (oi}), получим
да hi Sahi дгц дам
Последние два слагаемых в полученном равенстве на оснований
формулы Грина взаимно уничтожаются, и, следовательно, подтверж-
подтверждается равенство C.28), т. е. дополнительная работа Л (ои) является
потенциалом для тензора деформации (е,-;).
Заметим, что к этому выводу можно было бы прийти путем введения
термодинамического потенциала Г и б б с а
G = F — atflU = U — Ts — otfiU. C.29)
§ 3. ОБОБЩЕННЫЙ ЗАКОН ГУКА
Соотношения между компонентами aiS тензора напряжений и компо-
компонентами Btj тензора деформации для определенной модели упругой
сплошной Среды могут быть получены на основании формулы Грина
*.!.23), если для данной сплошной Среды известен упругий потенциал
If (ev) как функция компонент тензора деформации.
Естественно, что эта функция зависит от свойств упругой сплошной
,среды и, следовательно, она может быть выявлена на основании дан-
данных соответствующих экспериментов.
В случае твердых тел имеют место очевидные затруднения в экспе-
экспериментальном определении интересующих величин. Действительно,
совершенно невозможно непосредственное измерение не только нап-
напряжений, но и деформаций во внутренних точках твердого тела.
Сравнительно просто с помощью различных тензометров эксперимен-
экспериментально можно определить только средние значения относительных
удлинений линейных элементов на поверхности образцов, испытываю-
испытывающих определенного вида нагрузку, которую, лишь как равнодейст-
гующую, можно замерить с достаточной точностью.
Как известно, наиболее легко осуществимыми экспериментами яв-
являются испытания образцов при одноосном растяжении и одноосном
сжатии, а также испытание трубчатых образцов на кручение. При
этих простейших нагружениях образцов их основная («рабочая») чавть
находится в условиях однородных простейших напряженных еов-
тояний (одноосного и чистого сдвига).
Результаты этих экспериментов показывают, что в определенных
пределах нагружения для большинства твердых тел деформации про-
пропорциональны нагрузкам, т. е. при увеличении нагрузки измеряемая
деформация увеличивается в том же отношении. Эта закономерность
известна как закон Гука A635—1703).
Обобщая результаты этих и некоторых других экспериментов, т. е.
гридерживаясь индуктивного метода, приходим к обобщенно-
обобщенному закону Гука, согласно которому компоненты ои тензора
напряжений в каждой точке тела являются однородными линейными
функциями компонент eif тензора деформации в той же точке рассмат-
рассматриваемого состояния равновесия тела.
56

Однако следует иметь в виду, что опыты, которые приводят к закону
Гука, не дают исчерпывающего доказательства этого закона. Напро-
Напротив, для некоторых материалов он носит приближенный характер.
Вместе с тем выводы, которые можно получить на базе закона Гука,
как правило, имеют достаточно хорошее экспериментальное подт-
подтверждение.
Итак, компоненты 9ц тензора напряжений согласно закону Гука есть
линейные функции компонент г{} тензора деформации и вмевте g тем
в соответствии g формулой Грина являются частными производными
первого порядка упругого потенциала W (etj) по соответствующим
компонентам тензора деформации. Отсюда становится очевидным, что
упругий потенцил W (ец) представляет собой функцию второго поряд-
порядка компонент тензора деформации. Общее выражение этой функции
можно представить в следующем виде:
W (е»>) = Ъы + Cl)hfilfihln. C.30)
Здееь на основании обратного тензорного признака Сц— тензор
второго ранга, Сим — тензор четвертого ранга.
При ограничениях линейной теории упругости тензор деформации
(etj) является симметричным. Поэтому при перестановке индексов
I и /, k и / величины е,ц и е^е^ не должны меняться.- Следовательно,
тензоры Си и Cfjki также должны удовлетворять условиям симметрии:
C.31)
Подставив выражение C.30) для упругого потенциала W (eti)
в формулу Грина C.23), найдем
аи = Си + СшРн- C-32)
В начальном состоянии тела гц = 0, atj = 0 при всех f и / (внеш-
(внешние силы отсутствуют). Поэтому W @) = 0 и Сц — 0. Тогда выраже-
выражение C.30) для упругого потенциала принимает вид
№(е„) = (ЩС1}к1еиеы, C.33)
а соотношения C.32) между компонентами а^ тензора напряжений и
компонентами е^ тензора деформации будут определяться равенством
C.34)
Выражение C.33) для упругого потенциала W (вц) и равенство
C.34) являются общими для анизотропного линейно-упругого тела.
Тензор (Cijki) называется тензором упругих постоянных (в случае
однородного тела компоненты этого тензора не зависят от координат
точек тела) и как тензор четвертого ранга имеет, вообще говоря,
З4 = 81 компоненту. Однако, учитывая условия C.31) симметрии тен-
тензора (Ci}ki), число независимых компонент (упругих постоянных)
будет 36. Кроме того, из условия
57

вытекает еще 15 соотношений:
Chuj.
C.35)
Таким образом, тензор упругих постоянных (С,-ум) В самом общем
случае анизотропии линейно-упругого тела имеет 21 независимую
компоненту (упругую постоянную), которые можно представить
в виде следующей симметричной матрицы:
1122
С
183
'2283
¦П123
J2323
2281
^
2881
'2212
'3312
'2812
W212
C.36)
В общем случае анизотропии тела упругие постоянные Сцы зависят
от ориентации координатных осей.
Структура анизотропного тела может обладать некоторой упругой
симметрией, в каждой точке тела обнаруживаются симметричные в от-
отношении упругих свойств направления. В этих случаях оказывается
возможным выбрать такую ориентацию осей координат, при которой
некоторые упругие постоянные оказываются равными нулю или ли-
линейно зависящими от других упругих постоянных.
Пусть тело обладает плоскостью упругой симметрии, с которой сов-
совместим координатную плоскость xtx2. Это означает, что если направле-
направление оси х3 изменить на противоположное, т. е. сделать замену коорди-
координат: х[ = Xi, х'2 = х2, х'а = —xs, то упругий потенциал W (е,-;-)
не изменится. Поскольку при данной замене координат компоненты
% и ы2 вектора перемещения не меняются, а компонента и8 изменяет
знак, т. е. и[ = иъ и'г = иг, u't = —u3, то в этом случае у компонент
&U тензора деформации, для которых индекс «3» фигурирует один раз,
изменится знак, а остальные компоненты тензора деформации оста-
останутся неизменными:
628 "~"8
2 3>
счт с
31»
8II — 811> 822 — 822>
Очевидно, что произведение 8^eft! будет менять знак, если среди
индексов ijkl индекс «3» содержится нечетное число раз. Следова-
Следовательно, при этом же условии меняют знак члены в выражении C.33)
упругого потенциала W (ги). Поэтому упругий потенциал не изме-
изменится, если компоненты Cuki тензора упругих постоянных, среди ин-
индексов которых индекс «3» входит либо один раз, либо три раза, будут
равны нулю.
Таким образом, для тела с одной плоскостью упругой симметрии
при указанной ориентации осей координат матрица упругих постоян-
постоянных имеет вид

'1122
'2222
С
1133
'2233
'3838
0
0
0
!828
С
с
0
0
0
2881
О1 Oi
Clll2
^•2212
с
312
0
0
C.37)
Следовательно, у тел, имеющих одну плоекость упругой симмет-
симметрии, g которой совмещается одна из координатных плоскостей, число
упругих постоянных сокращается до 13.
Если тело имеет две взаимно перпендикулярные плоскости упру-
упругой симметрии, то в этом случае при совмещении g ними координат-
координатных плоскостей, например XiX2 и XiX8, очевидно, обращаются в нуль те
упругие постоянные Сим, у которых индекс «3» или индекс «2» со-
содержится нечетное число раз. Матрица упругих постоянных в этом
случае
^1122
'2222
2233
3333
0
0
0
0
0
0
0
^3131
0
0
0
0
0
121 li
C.38)
Следовательно, в данном случае число упругих поетоянных будет
равно 9. Из рассмотрения матрицы C.38) легко заметить, что при на-
наличии у тела двух взаимно перпендикулярных плоскостей упругой
симметрии (л^и #i#8) обращаются в нуль также упругие постоянные
СцъЬ среди индексов которых встречается один или три раза индекв «1».
Отсюда следует, что если в теле имеют место две ортогональные плоско-
плоскости упругой симметрии, то и ортогональная к ним третья плоскость
также будет плоскостью упругой симметрии.
Тело, обладающее тремя ортогональными плоскостями упругой
симметрии, называется ортотропным.
Следует иметь в виду, что при наличии у тела плоскостей упругой
симметрии число упругих постоянных сокращается только при сов-
совмещении координатных плоскостей в плоскостями упругой симметрии.
Если координатные плоскости не совпадают, например, g ортогональ-
ортогональными плоскостями упругой симметрии ортотропного тела, то число
упругих постоянных будет равно 21, т. е. как и в общем влучае ани-
анизотропного тела.
Существуют и другие виды упругой симметрии; необходимые све-
сведения по этому вопросу приводятся в книгах [36, 37].
59

§ 4. ОБОБЩЕННЫЙ ЗАКОН ГУКА ДЛЯ ОДНОРОДНОГО ИЗОТРОПНОГО ТЕЛА
Тело' называется однородным в отношении упругих свойств, если
эти свойства одинаковы во всех точках тела, т. е. если упругие постоян-
постоянные lie зависят от координат точек тела.
Однородное тело может быть анизотропным и изотропным.
Тело называется изотропным, если упругие свойства его, которые
характеризуются упругими постоянными, одинаковы для всех направ-
направлений, выходящих из произвольной точки тела.
Следовательно, для однородного изотропного тела компоненты
тензора упругих постоянных (Сцьд не должны зависеть от направления
координатных осей.
Тензор, компоненты которого не изменяются при повороте коор-
координатных осей, называется изотропным тензором.
Поскольку упругий потенциал W (ео) является инвариантом и для
линейно-упругого тела представляет собой функцию второго порядка
компонент тензора деформации, то в случае однородного изотропного
тела эту функцию можно образовать из линейного и квадратичного
инвариантов тензора деформации:
И7 - -j [1Д (ем) + 2yiJt (в„I. C.39)
где к и (j — постоянные; J1 (eu) и У2 (е^) — линейный и квадратичный
инварианты тензора деформации, которые определяются равенства-
равенствами A.64):
"б" б- е е = — (б б +б б I C>40)
Учитывая, что
•^i (в//) = bifibfiifihi, C.41)
а также последнее равенство C.40), выражению C.39) для упругого
потенциала можно придать вид
W = -1 [Щ, Ьм + |х (бй Ь}1 + btt 6jh)} eu ekl. C.42)
Сопоставляя выражение C.42) упругого потенциала для однород-
однородного изотропного тела с выражением C.33) для упругого потенциа-
потенциала-в общем случае, находим, что тензор упругих постоянных в случае
однородного изотропного тела определяется равенством
С mi = М, fihl + |i Fih6n + 6tfiJh). C.43)
Это есть изотропный симметричный тензор четвертого ранга [см.
A*.42I, компоненты которого определяются через две упругие посто-
постоянные 7i и ц, называемые постоянными Ламе. Симметричная матрица
компонент тензора (Cuhi) в этом случае имеет вид

A,
к
-2*
0
0
i 0
ц.
0
0
0
0
0
0
0
0
0
и-
C.44)
• Подставив выражение C.42) для упругого потенциала W в форму-
формулу Грина C.23), получим
оц = lM(?ki + Ц Ф1к6„ + 6tfitk)\ ehl. C.45)
Учитывая, что 6ft геьг — efefe = в — объемная деформация, а
Sih&jfiki — Ц} и ^ifijh^ki — ел = ъц> равенство C.45), представляю-
представляющее собой соотношения между компонентами тензора напряжений и
компонентами тензора деформации, принимает вид
аи = Ши + 2цеи. C.46)
Формула C.46) выражает обобщенный закон Гука для однородного
изотропного тела и определяет шесть алгебраических уравнений
этого закона:
а22 = Я0
ст88 = Я0
а12
crai =
C.47)
'33 — «¦" "Г <Ч*О88> и31
Очевидно, что эти уравнения справедливы и для неоднородного
изотропного тела. В этом случае упругие постоянные Ламе Яиц будут
функциями координат Xi рассматриваемой точки тела (К и \\ — «пос-
«постоянные» в том смысле, что они характеризуют упругие свойства
материала тела, которые в случае неоднородного тела в каждой его
точке могут быть различными).
Если координатные оси совместить в главными осями тензора де-
деформации, то при этом у12 = V28 — Yei — 0- Тогда на основании
уравнений C.47) ст12 = сг28 = ст81 = 0, а это означает, что площадки,
проходящие через рассматриваемую точку тела и перпендикулярные
принятым координатным осям, являются главными площадками, т. е.
координатные оси оказались совмещенными и G главными осями тен-
тензора напряжений. Отсюда следует, что в каждой точке изотропного
тела главные оси тензора деформации совпадают g главными осями
тензора напряжений.
§ 5. УПРУГИЕ ПОСТОЯННЫЕ И ДРУГИЕ ФОРМУЛЫ ЗАКОНА ГУКА
ДЛЯ ОДНОРОДНОГО ИЗОТРОПНОГО ТЕЛА
При изотермическом деформировании тела упругий потенциал
ТУ определяется свободной энергией F = U — Tos, которая в состоянии
термодинамического равновесия, как известно, минимальна. Если
к телу не приложены внешние силы, то свободная энергия F, как функ-

ция компонент тензора деформации, должна иметь минимум при 8tj = О,
т. е. в естественном состоянии тела. Отсюда следует, что упругий по-
потенциал, как квадратичная форма компонент тензора деформации
C.89), должен быть существенно положительным, т. е.
• W (е„) > 0. C.48)
К этому же выводу можно прийти и в случае адиабатического де-
деформирования, когда упругий потенциал W определяется внутренней
энергией U.
Этот вывод следует также из следующего соображения. Упругий
потенциал W, как уже отмечалось, представляет собой удельную по-
потенциальную энергию деформации, за счет которой единичный объем
тела возвращается в недеформированное (естественное) состояние
как только силы, вызвавшие деформацию, снимаются. Это и подтвер-
подтверждает соотношение C.48), в котором знак равенства соответствует не-
деформированному состоянию.
Из равенства C.39) и соотношения C.48) вытекает, что
1>0иA>0, C.49)
Действительно, если деформированное состояние определяется
тензором (eti) таким, что У( (ei7) — 0, то в выражении C.39) остается
только второе слагаемое. Тогда, поскольку У2 (еи) > 0, неравенство
C.48) будет иметь место, если ц> 0. Так как J\ (eu) > 0 при любом
упругом деформировании, то из выражения C.39) находим, что и дру-
другая постоянная Ламе Я,> 0.
Теперь произведем операцию свертывания в равенстве C.46) по
индексам I и /:
а и = ЗШ + 2цв|,-.
Используя в дальнейшем для линейного инварианта тензора нап-
напряжений Jj (otj) обозначение 2, а для линейного инварианта тензора
деформации-. 1Х (е^) обозначение G [см. A.70)], т. е.
он = Ji (ou) - 2, C.50)
е» = Щ.1 = Л Ы =» ©, . C.51)
из предыдущего равенства находим
в - 2/(ЗЛ + 2\х) = 2/(ЗЛ) = ao!k, C.52)
где о0 = Y°it ~ "з"^ — среднее нормальное напряжение, а величина
?=а+-1и>0 C.53)
О
— модуль объемного сжатия.
Из соотношения C.52) следует, что объемная деформация G при
любом упругом деформировании изотропного тела зависит исключи-
исключительно от линейного инварианта 2 тензора напряжений, причем эта
зависимость определяется только модулем объемного сжатия k> 0.
Рассмотрим тензор напряжений чистого сдвига, например, в пло-
62

скости хух.2. В этом случае ьсе компоненты аи равны нулю, за исклю-1
чением о12 = ап. Следовательно, 2 =0 и на основании C.52) в == 0.
Тогда, по закону Гука C.46), все компоненты etJ равны нулю, исклю-
исключая в12 = в21, а это дает единственное соотношение
о12 = 2це12 = [-I7i г»
Где 7i2 — 2е12 — угол сдвига между направлениями осей Oxt и Ох2.
Упругую постоянную Ламе \i называют модулем упругости при сдви-
сдвиге и обозначают G, т. е.
И =• G. C.54)
Рассмотрим другой частный случай тензора напряжений при рав-
равномерном одноосном растяжении призматического тела (бруса). Если
ось Ох8 совместить с осью бруса, то только crs8> 0, а остальные ком-
компоненты oi} равны нулю. Тогда по формуле C.52) найдем
0 = 1 о
3X+2G
На основании закона Гука C.47) можно записать:
а,.,, C.55)
3
8 = kt9.— о C.56)
88 О (ЗЯ + 20) 33> '
812 = Е2 3 — 8 81 = 0. C.57)
Заметим, что при одноосном тензоре напряжений тензор деформа-
деформации не являеся одноосным.
Введем обозначения:
v= . C.59)
2(^+0)
Поскольку, как было показано, 1>0 и ц = G>0, из равенств
C.58) и C.59) вытекает, что
Е > 0 и v > 0. C.60)
Величина Е называется модулем продольной упругости или моду-
модулем Юнга A773—1829), a v — коэффициентом поперечной деформации
или коэффициентом Пуассона A781—1840).
Используя обозначения C.58) и C.59), формулы C.56) и C.55)
приводят к простому виду, известному из курса сопротивления мате-
материалов:
е83 = ст83/Е,_ C.61)
8и = 822 = —vo83/E = —ve33. C.62)
Среди введенных пяти упругих постоянных А,, ц = G, k, E, v для
изотропного тела только две из них являются независимыми.
63

Если принять за основные независимые упругие постоянные Е
и v, которые наиболее просто определяются экспериментально, то
упругие постоянные X и \х = G найдем из формул C.58) и C.59):
С= , C.63)
2(l+v) . '
vS . C.64)
)(l2v) '
l~2v
Подставим эти значения G и X в равенство C.53):
к-щ=»>- <3-65>
Поскольку X> 0 и Е> 0, из равенства C.64) следует, что
!+v>0h 1 — 2v > 0.
Отсюда определяются пределы значений v:
—1 < v < 0,5.
Однако вследствие неравенства C.60) для всех изотропных мате-
материалов коэффициент Пуассона v имеет значения в пределах
0 < v < 0,5, C.66)
что подтверждается экспериментально.
Строго говоря, при изотермическом (W = F = U — Tos) и адиа-
адиабатическом (W — U) процессах деформирования одного и того же
изотропного тела его упругие постоянные несколько отличаются по
величине. Например, для различных металлов при температуре 20° С
в случае адиабатического и изотермического процессов деформирова-
деформирования соотношение между модулями объемного сжатия &ад и k сле-
следующее:
km = A,004 -f- 1,038) k.
Такие же небольшие различия имеют место между адиабатическим
?ад и изотермическим Е модулями Юнга, а также между адиабатиче-
адиабатическим vaa и изотермическим v коэффициентами Пуассона. И только
модуль сдвига имеет одинаковое значение при адиабатическом и изо-
изотермическом процессах деформирования: бад = G.
Экспериментальное определение упругих постоянных при изо-
изотермическом деформировании и при адиабатическом деформировании
дзет, действительно, несколько различные результаты, но это разли-
различие незначительное. С допустимой при практических расчетах точ-
точностью можно не делать различия между изотермическими и адиаба-
адиабатическими упругими постоянными. Более подробно по этому вопросу
см. [3, 4, 341.
При решении некоторых задач необходимо иметь формулу, поз-
позволяющую непосредственно определить компоненты тензора дефор-
деформации по известным компонентам тензора напряжений. Решая линей-
61

ное уравнение C.46) относительно г() и учитывая равенства C.52) и
C.54), найдем
1 к
ъи ~— °ц ; B) btj\. C.67)
20 ЗА. -f* 2G
Подставив в формулу C.67) значения G и X, из C.63) и C.64), получим
формулу закона Гука
8у= 4-К1 +v)aM — vB)ew],' C.68)
позволяющую найти компоненты е^ по известным компонентам ои:
—[au — v (а2г + a88K, Vi,= 2elt = 2Ag+v) al2,
e83 -4"fCT» —v(ffu + ff«i)l. Ysi = 2e3l =
с
C.69)
В некоторых случаях удобно иметь соотношения между компонен-
компонентами тензора напряжений и компонентами вектора перемещения. Ис-
Используя дифференциальные зависимости Коши A.40) и произведя
подстановку C.54), формула закона Гука C.46) приводится к виду
ot) = \®&tl+G(uu+ult), C.70)
где в = иа, „.
Отметим еще характерную зависимость для линейно-упругого
изотропного тела. ¦
Оказывается, что между компонентами ati девиатора напряжений
и компонентами ги девиатора деформации имеет место простое соот-
соотношение
аи=2вв,/. C.71)
В самом деле, если в уравнение C.46) закона Гука подставить сог-
согласно формулам A.81) и B.72)
°и + -ao fi«
то получим ¦
° и + °о &и = ^efii> + 2Овг> + 2Ge0 Ьи
Учитывая, что е0 = -yess = -3* ®. будем иметь
-|- G) ввм.
Вторые слагаемые в левой и правой частях последнего равенства
на основании C.52) взаимно уничтожаются, следовательно, прихо-
приходим к соотношению C.71).
3 Зак. 514 65

§ 6. ФОРМУЛА КЛАПЕЙРОНА И ФОРМУЛА КАСТИЛЬЯНО
Поскольку упругий потенциал W (е^) для линейно-упругого тела
является однородной функцией второго порядка относительно^ ком-
компонент е,-; тензора деформации, то на основании теоремы Эйлера
об однородных функциях имеем
dW
Или с учетом формулы Грина C.23) получим равенство
2W = ацгц, C.72)
которое называется формулой Клапейрона A799—1864).
Тогда для линейно-упругого тела на основании C.26) и формулы
Клапейрона получим
Л (ац) = Oijeij — W = W,
т. е. в случае линейно-упругого тела дополнительная работа Л (oij)
равна по величине упругому потенциалу:
А= W. C.73)
Следовательно, упругий потенциал для линейно-упругого тела
можно представить как функцию второго порядка компонент aij
тензора напряжений.
• Поэтому на основании равенств C.28) и C.73) имеем так называе-
называемую формулу Кастильяно A847—1884)
ei} = dW/datj. C.74)
Подчеркнем, что если формула Грина C.23) и формула C.28)
применимы для любого упругого тела, то формула Кастильяно спра-
справедлива лишь для упругого тела, следующего обобщенному закону
Гука.
§ 7. ФОРМУЛА БЕТТИ
Рассмотрим два различных напряженно-деформированных состоя-
состояния одного и того же линейно-упругого тела. Пусть одно состояние
определяется тензорами (aij) и (е/у), а другое — тензорами (ah)
и &,)¦
Оба состояния должны удовлетворять обобщенному закону Гука
C.34), т. е.
°'ц = СикМи ¦* C.75)
°Ь = Сиые'н. C.76)
Здесь тензор упругих постоянных (djhi) один и тот же, так как оба
состояния рассматриваются для одного и того же тела.
Умножим равенство C.75) на ъ"ч, а равенство C.76) — на е'ц:
o'ii е'и, =
вв1

Отсюда, приняв во внимание C.35), получаем формулу Бет-
Бетти .
а//е// = а?,е//, C.77)
т. е. для двух различных напряженно-деформированных состояний,
которые могут возникнуть в некоторой точке тела, следующего обоб-
обобщенному закону Гука, суммы произведений компонент тензора напря-
напряжений одного состояния на соответствующие компоненты тензора де-
деформации другого состояния взаимно равны.
§ 8. УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
И УДЕЛЬНАЯ ДОПОЛНИТЕЛЬНАЯ РАБОТА ЛИНЕЙНО-УПРУГОГО ТЕЛА
В случае линейно-упругого тела удельная потенциальная энергия
деформации W (etj) и удельная дополнительная работа Л (ац) равны
между собой C.73). Однако и в^том случае все же полезно различать
эти функции.
На основании C.72)
W = (l/2)aijeij. • C.78)
Заменив в последнем равенстве компоненты aij по формуле C.46),
получим удельную потенциальную энергию деформации как функцию
компонент тензора деформации е;;-:
W (е„) = A/2) (кв* + 21*8,/»!,). C.79)
Если в равенство C.78) подставить значения компонент е,^ по
формуле C.68), то получим удельную дополнительную работу как
функцию компонент тензора напряжений Oij, равную в случае линейно-
упругого тела удельной потенциальной энергии деформации:
Л (аи) = A/2?) [A + v) atjotj — v BJ]. C.80)
§ 9. СООТНОШЕНИЯ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ
ИЗОТРОПНОГО ТЕЛА ПРИ ИЗМЕНЕНИИ ЕГО ТЕМПЕРАТУРЫ
Рассмотрим деформирование однородного изотропного тела, соп-
сопровождающееся изменением его температуры.
Предположим, что в естественном состоянии (е^ = 0, aij = 0)
тело имеет некоторую постоянную температуру То.
Представим себе в окрестности произвольной точки М (Х{) тела его
единичный элемент, который можно считать нагретым равномерно.
Пусть ¦& = Т — То есть изменение температуры в этой точке тела, за-
зависящее от координат xt. Тепловая деформация элемента встречает
упругое сопротивление тела, поэтому дополнительно возникают
Упругие деформации. В результате деформированное состояние ок-
окрестности точки М (xi) будет определяться тензором деформации, ком-
компоненты которого Btj представляют сумму тепловой деформации
г/j и «силовой» упругой деформации е//:
e/j = efi + e/J. C.81)
я* ¦ 67

Будем рассматривать малые изменения температуры ¦& = Т — То
в точках тела, при которых тепловая деформация имеет величину од-
одного порядка малости по сравнению с ег7-, а упругие постоянные мате-
материала и коэффициент линейного расширения а остаются при этом
такими же, как и при То.
Термодинамическими параметрами, описывающими состояние уп-
упругого тела, будут компоненты г-1} тензора деформации и температу-
температура Т - То + 0.
Свободная энергия F {tij, T) является инвариантом, а тело рассмат-
рассматривается изотропным. Поэтому F (&ij, T) может зависеть только от ин-
инвариантов тензора деформации /х (е,^) = 0, J2 (ztj) = ег^ и от тем-
температуры. Поскольку при изменении температуры элемент будет де-
деформироваться даже при отсутствии воздействия на него окружаю-
окружающей среды, то выражение для F (&tj, T) должно содержать слагаемое
линейное относительно Jt (e-,j) '— в с коэффициентом, пропорцио-
пропорциональным $ = Т — То, так как это слагаемое должно обращаться
в нуль при ¦& = 0. Тогда выражение для свободной энергии можно
принять в следующем виде:
F(bu, Г) =-?¦ [Xe»-J-2|i8w еи-Щв]. C.82)
Свободная энергия является потенциалом для тензора напряже-
напряжений. Поэтому имеем
а„ = -^ = *еб„ + 2цв рвб C.83)
Выполняя свертывание левой и правой частей равенства, получим
оц = 3A.0 + 2це« — 3$Ъ
или
2 = 3 (/г в — Щ, C.84)
Q
где k — X + ^fi — изотермический модуль объемного сжатия.
Из равенства C.84) имеем
e=-f- + -f», ¦ C.85)
где второе слагаемое в правой части равенства представляет объемное
тепловое расширение и, следовательно,
Р.'* = За. C.86)
Тогда, учитывая обозначения C.54) и C.86), равенство C.83) при-
приведем к виду
аи = Явбу + 2Gei} — 3kaUtj. C.87)
Решая это линейное уравнение относительно etj и принимая во вни-
внимание C.85) и C.86), получим
Ч = ~ [ои ~ -~ B) «„] + ~~ 3«0б,,, C.88)
68 •

Учитывая вытекающие из C.53), C.63), C.64) и C.65) следующие
соотношения между упругими постоянными:
к v ±z±L
20 ? ' 2G-3k Б' 2G "* 3 '
равенству C.88) можно придать вид
ец = (НЕ) [A + v) ац — v (S) 81}) + аМп. C.90)
Первое выражение в правой части последнего равенства представ-
представляет собой «силовую» упругую деформацию в}), а второе—тепловую
деформацию е'ц.
Соотношения, определяемые формулами C.87) и C.90), впервые
A838) были получены Дюамелем A797—1872) и несколько позднее
Ф. Нейманом A798—1895). Поэтому эти формулы называют законом
Дюамеля—Неймана.

Глава IV
к ОСНОВНЫЕ УРАВНЕНИЯ И ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
§ 1. ОСНОВНЫЕ УРАВНЕНИЯ
В предыдущих трех главах уже получены основные уравнения
теории упругости, представляющие замкнутую систему уравнений
которая позволяет выяснить напряженно-деформированное состоя-
состояние тела как результат внешнего воздействия на него.
Вначале дадим общую сводку основных уравнений для задач рав-
равновесия упругого тела, которые составляют содержание раздела тео-
теории упругости, называемого обычно статикой упругого
тела.
Деформированное состояние тела вполне определяется тензором
поля деформации г{} — eij (xh) или полем перемещений щ = щ (jtft).
Компоненты тензора деформации Бг^ связаны с перемещениями щ
дифференциальными зависимостями Коши A.40):
*tj=-y(ui,j + uj.t)' DЛ)
Компоненты1 тензора деформации должны удовлетворять дифферен-
дифференциальным зависимостям Сен-Венана A.93):
е*л.я + ejMh — ?ii,jh — ejftiij = 0, D.2)
которые являются необходимыми и достаточными условиями интег-
интегрируемости уравнений D.1).
Напряженное состояние тела определяется тензором поля напря-
напряжений oij — Oij (xh). Шесть независимых компонент симметричного
тензора (aij) должны удовлетворять трем дифференциальным уравне-
уравнениям равновесия B.26):
он,} + p/i = 0. D.3)
Компоненты тензора напряжений at) и перемещения т связаны
шестью уравнениями закона Гука C.70):
оц = Шц + G (щ,} + uj,,), D.4)
где
® = Л (eij) = ess — uss = div и.
В некоторых случаях уравнения закона Гука приходится исполь-
использовать в виде формулы C.68)
гц = 1A + v) ots — v B) ЬцУЕ, D.5)
где
'2 = Л (oij) — ass.
Уравнения D.1)—D.5) являются основными уравнениями стати-
статических задач теории упругости. Иногда уравнения D.1) и D.2) на-
70

зывают геометрическими уравнениями, уравнения D.3) статиче-
статическими уравнениями, а уравнения D.4) или D.5) — физическими урав-
уравнениями.
К основным уравнениям, определяющим состояние линейно-упруго-
линейно-упругого тела в его внутренних точках объема V, необходимо присоединить
условия на его поверхности S. Эти условия называются граничными
условиями. Они определяются либо заданными внешними поверхност-
поверхностными силами tt, либо заданными перемещениями u\s) точек поверх-
поверхности тела. В первом случае граничные условия выражаются равен-
равенством B.28):
tit D.6)
где tt (xa) — компоненты вектора t поверхностной силы, п} — компо-
компоненты единичного вектора п, направленного по внешней нормали
к поверхности S в рассматриваемой ее точке.
Во втором случае граничные условия выражаются равенством
Щ = и}°, D.7)
где и\$) = ы'5) (*„) — заданные на поверхности функции.
Граничные условия могут также иметь смешанный характер, когда
на одной части St поверхности тела заданы внешние поверхностные си-
силы tt (xs), а на другой части Su поверхности тела заданы перемещения
Возможны и иного рода граничные условия. Например, на некото-
некотором участке поверхности тела заданы только некоторые компоненты
Ш вектора перемещения и, кроме того, также не все компоненты U
вектора поверхностной силы.
§ 2. ОСНОВНЫЕ ЗАДАЧИ СТАТИКИ УПРУГОГО ТЕЛА
В зависимости от вида граничных условий различают три типа ос-
основных статических задач теории упругости.
Основная задача первого типа состоит в опре-
определении компонент тензора поля напряжений atj (xh) внутри области
V, занятой, телом, и кэмпонент щ (xk) вектора перемещения точек
внутри области V и точек поверхности S тела по заданным массовым
силам ft и поверхностным силам tt.
Искомые девять функций должны удовлетворять основным уравне-
уравнениям D.3) и D.4), а также граничным условиям D.6).
Основная задача второго типа состоит в опреде-
определении перемещений «г (хк) точек внутри области V и компонент тензо-
тензора поля напряжений atj (xk) по заданным массовым силам /г и по за-
заданным перемещениям u\s) (ха) на поверхности тела. '
Искомые функции щ (хк) и atj (xk) должны удовлетворять основным
уравнениям D.3) и D.4) и граничным условиям D.7). .
71

Заметим, что граничные условия D.7) отражают требование о непре-
непрерывности определяемых функций т (хь) на границе S тела, т. е. когда
внутренняя точка М (xk) стремится к некоторой точке поверхности
S, функция ui (xh) должна стремиться к заданному значению u\s) (xs)
в данной точке йоверхности.
Основная задача третьего типа или смешан-
смешанная задача состоит в том, что по заданным поверхностным си-
силам tt (xs) на одной части поверхности тела St и по заданным переме-
перемещениям h{s) (xs) на другой части поверхности тела Su, а также, вообще
говоря, по заданным массовым силам fi требуется определить компо-
компоненты тензора напряжений atj (xh) и перемещения tit (xh), удовлетво-
удовлетворяющие основным уравнениям D.3) и D.4) при выполнении смешан-
смешанных граничных условий D.8).
Получив решение данной задачи, можно определить, в частности,
усилия связей на Su, которые должны быть приложены в точках по-
поверхности Su, чтобы реализовать заданные перемещения u\s) (xs)
на этой поверхности, а также можно вычислить перемещения щ то-
точек поверхности St.
§ 3. ПРЯМАЯ И ОБРАТНАЯ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Различают две постановки задач теории упругости: прямую и
обратную.
Прямая задача состоит в решении одной из основных задач
указанных трех типов (см. § 2), т. е. в определении девяти функций
Qi} (xh) и щ (xk), определяющих напряженно-деформированное сос-
состояние тела в зависимости от внешнего воздействия иа него.
Решение прямой задачи часто сопряжено с большими математи-
математическими трудностями.
Обратная задача состоит в том, что, задавшись либо пе-
перемещениями ut как непрерывными функциями ut = и-, (xh), либо
компонентами тензора напряжений, т. е. шестью функциями а,-; =
— Oi} (xk), определяют из основных уравнений D.1)—D.4) и соответ-
соответствующих граничных условий все остальные функции, а также внешние
силы, осуществляющие заданные перемещения «* или заданные функ-
функции Oi].
Решение обратной задачи значительно проще, чем решение прямой
задачи. Особенно просто решается обратная задача, если задаться
перемещениями «г. При заданных непрерывных функциях. щ —
= «г (хи) дифференциальные зависимости Сен—Венана тождественно
удовлетворяются и, следовательно, в этом случае они не используют-
используются. Решение этой обратной задачи выполняется в следующем порядке:
на основании формулы закона Гука D.4) определяются компоненты тен-
тензора напряжений aij (xh), соответствующие принятым функциям
и, (xk), а из уравнений равновесия D.3) и граничных условий D.6)
определяются внешние силы, при которых осуществляются заданные
перемещения.
72

Если задаваться компонентами тензора напряжений аи (xk), то
решение обратной задачи будет несколько сложнее. В этом случае
перемещения т (xk) находятся интегрированием уравнений D.1),
что возможно, если компоненты тензора деформации е^ (xk), которые
определяются формулой D.5) закона Гука по принятым функциям
oi) (Xh), будут удовлетворять дифференциальным зависимостям Сен-
Венана D.2). Следовательно, компонентами тензора напряжений
oi] (xk) надо задаваться так, чтобы выполнялись условия совместности
D.2). Это обстоятельство и осложняет решение данной обратной
задачи. Но решение и этой обратной задачи для односвязной области
проще, чем решение прямой задачи.
Представим, что для определенной простой формы упругого тела
при некоторых ограничениях его нагружения, задаваясь различными
вариантами, например, функций а} {xk), определили реализующие
их внешние силы. Располагая набором таких решений обратной задачи,
путем их комбинирования можно подобрать функции at) (xh), кото-
которые будут соответствовать заданным конкретным нагрузкам, прило-
приложенным к рассматриваемому телу. Таким приемом можно решить,
например, некоторые задачи для прямоугольных полос, различно на-
нагруженных по контуру (см. гл. IX, § 9). Однако в более общем случае
упругого тела приходится решать прямую задачу теории упругости.
Прямую задачу удобно решать, если за основные неизвестные
функции, определяемые в первую очередь, принимаются либо переме-
перемещения ut (xk), либо напряжения аи (xk). Эти два пути решения прямой
задачи называют соответственно решением в перемещениях и решением
е напряжениях.
§ 4. УРАВНЕНИЯ УПРУГОГО РАВНОВЕСИЯ В ПЕРЕМЕЩЕНИЯХ
Некоторые прямые задачи, в частности задачи второго типа, удоб-
удобно решать в перемещениях. При этом основные уравнения следует
выразить через перемещения.
Уравнения упругого равновесия в перемещениях получим путем
исключения компонент тензора напряжений aij (хь) из уравнений рав-
равновесия D.3), используя формулу закона Гука D.4).
Продифференцируем равенство D.4) по координате ху.
ai/,} = a Q,fiij + G (Ui,}} + Uj,ij). D.9)
Учитывая, что в^б^ = 0,,-; uittj = Ujjt и
ии} = dujdxi + Ьи^дхг + ди3/дх3 = div и = 0, D.10)
а также используя дифференциальный оператор Лапласа
щ,„ =¦ д*щ/дх\ + д2щ/дх1 -f д1щ1дх\ = Vzuu
равенство D.9) приводится к виду
ai],j = GV'ut + (K + G) 0,,.
73

На основайии соотношения C.64) X + G = . 'G и тогда
Используя равенство D.11), дифференциальные уравнения равно-
равновесия D.3) приводятся к виду
^+TZi70-<=-i'<- DЛ2)
Равенство D.12) определяет три дифференциальных уравнения:
= ?-/3,
D.13)
которые представляют собой уравнения упругого рав-
равновесия в перемещениях, т. е. они выражают условия
равновесия каждого элемента тела в зависимости от функций ut (хь)
и в (хк), характеризующих деформированное состояние тела, и при
этом учитывают соотношения между atj и zi} для однородного изотроп-
изотропного тела. Можно сказать, что эти уравнения отражают геометриче-
геометрическую, статическую и физическую стороны задачи теории упругости.
Уравнения D.13), или равенство D.12), определяющее их, назы-
называются уравнениями Ламе. Они могут быть записаны в виде
.одного векторного уравнения.
Умножая равенство D.12) на орт Эг и учитывая, что
Q,iBi - grad в, D.14)
а также используя равенство D.10), получим
graddiv«= —9-f. D.15)
graddiv«
Если принять во внимание тождество A°.1ОЗ), то уравнение D.15)
можно записать в другой, иногда более удобной, форме:
^^ivtt- rot rot и = —?-/. D.16)
Во многих задачах массовые силы можно считать равными нулю
и тогда уравнения Ламе D.12) принимают вид
Продифференцировав равенство D.17) по координате xt, получим
+ e 0
74

Отсюда, поскольку щ^ = в и в,ti = V29, вытекает, что
V2e-0, D.i8)"
т. е. объемная деформация 9 (при отсутствии массовых сил или когда
они постоянны) удовлетворяет уравнению Лапласа и, следователь-
следовательно, в является гармонической функцией.
Применяя к равенству D.17) дифференциальный оператор Лап-
Лапласа и учитывая свойство D.18), получим
V?V2«i = 0, D.19)
т. е. компоненты щ вектора перемещения являются бигармоническими
функциями. Это заключение справедливо и при постоянных массовых
силах, так как в этом случае при выполнении операций дифферен-
дифференцирования правая часть равенства D.12) исчезает.
Заметим,, что уравнения D.19) не означают, конечно, что перемеще-
перемещения ui (при отсутствии массовых сил) являются произвольными би-
бигармоническими функциями; эти функции должны удовлетворять так-
также и дифференциальным уравнениям более низкого порядка — урав-
уравнениям Ламе D.12).
При решении в перемещениях основной задачи первого типа для
искомых функций щ (xh) необходимо иметь условия на границе тела
в зависимости от приложенных поверхностных сил.
На основании формулы D.4) закона Гука имеем
at}n3= Wnfitj + G (ut,}nj + u
или, если учесть, что п,-6?7- = гц, а
+ (dui/dx2) n2 + (дщ/дх3) п3 = dui/dn
представляет собой производную функции щ (xh) по нормали к по-
поверхности тела, то
G (дщ/дп + Uj,itij). D.20)
Тогда граничные условия D.6) принимают вид
Шщ + G (dutldn + щ,щ}) = и. D.21)
Уравнения Ламе D.12) вместе с граничными условиями D.21),
т. е. в случае основной задачи первого типа, или вместе с граничными
условиями D.7) основной задачи второго типа вполне определяют
все три компоненты т вектора перемещения. Далее, по формуле D.1)
вычисляются компоненты е^ тензора деформации, а по формуле D.4)
находятся компоненты otj тензора напряжений. *
Совершенно ясно, что решение в перемещениях основной задачи
первого типа, т. е. при граничных условиях D.21), более затрудни-
затруднительно, чем решение основной задачи второго типа при значительно
более простых граничных условиях D.7). Поэтому для задач первого
типа обычно предпочтительнее решение в напряжениях,
75

Очевидно, что уравнения движения при малых перемещениях
B.31) могут быть записаны в перемещениях в любом из трех видов:
D.23)
2A~v) grad div a - rot rot и = - JL f/ ^-). D.24)
1—2v О \ от2 /
В приведенных уравнениях движения перемещения и* являются,
естественно, функциями координат xh точек тела и времени t: ui =
Решение уравнений движения D.22) должно удовлетворять началь-
начальным условиям — условиям в начале движения, т. е. при t = 0 пере-
перемещения Ui и их производные по времени / (скорости «О должны иметь
заданные значения щ0 и Ui0'-
Ш (xh, 0) = т0,
т {xh, 0) = ui0.
§ 5. ОБЩЕЕ РЕШЕНИЕ УРАВНЕНИЙ В ПЕРЕМЕЩЕНИЯХ
D.25)
Общее решение уравнений Ламе было получено П. Ф. Папковичем
A887—1946) в 1932 г., а позднее A934) другим путем получил Нейбер.
При равновесии однородного изотропного тела в случае отсутст-
отсутствия массовых сил уравнения Ламе определяются равенством D.17).
Решение этих уравнений будем искать в следующем виде:
Щ = ф< + i|>,f, D.26)
где фг (/ = 1, 2, 3) — гармонические функции, т. е. V\i = 0; ф —
некоторая скалярная функция, подлежащая определению.
В соответствии с D.26) объемная деформация
в = Uj,j = <pj,} + i|>,w = фЫ + VY D.27)
Подставляя в уравнения Ламе D.17) выражения для «г и в по фор-
формулам D.26) и D.27) и учитывая, что У2ф< = 0, найдем
или
Легко видеть, что последнее равенство будет удовлетворяться, ес-
если функцию г|з подчинить уравнению
v**==~Tubr(p'-i< D>29)
76

Так как V"q>i = 0 и V2 (Фы) = (У2Ф,),, =0, то из уравнения D.29)
следует, что функция г|) должна быть бигармонической, т. е. должна
удовлетворять уравнению V? (V2ty) = V4ty = 0.
Любая гармоническая функция <pi является также и бигармонн-
ч€ской функцией:
У4Ф| = V» (Vty) = 0. D.30)
Можно показать, что если q>i — гармонические функции, то функ-
функции
D.31)
будут бигармоническими.
Действительно, рассмотрим, например, первую функцию D.31).
Поскольку
то, учитывая, что У2фх = фШ1 + ф1J2 + ф1)88 = 0, получим
Щ\ = V? (^Фх) = (х1ф1),11 + (^ф,),» + (*1ф1),88 = 2Ф1>1 D.32)
и, следовательно,
V^i = V^ (V2%) = V? BФь1) = 2 (VVi),i = 0. D.33)
Из равенства D.33) следует, в частности, что производная гармо-
гармонической функции есть также гармоническая функция.
' На основании D.31) частное решение уравнения D.29) примем
в следующем виде:
Ф = Cxkyh, D.34)
где С — постоянная.
Последовательно дифференцируя равенство D.34), найдем
\p,i = С (xhyk),t = С (ф? + xhyh,i), ty,u = С (xhq>h),u =
= С (ф|,^ + ф^| + xk(fhi}). D.35)
Свертывая последнее равенство по индексам i и /' и учитывая, что
Фй.и = ^2фй = 0, получим
у*ф = CV2- (xk<ph) = 2СФ(,(. D.36)
Из сопоставления равенств D.29) и D.36) находим
С = — . D.37)
4A—v) K '
Общее решение уравнения D.29) должно представляться суммой его
частного решения D.34) и произвольной гармонической функции фО|
т. е.
* = —ГаЬт{Xh ф"+Фо)> D<38)
Топа общее решение уравнений Ламе D.17) на основании D.26)
и D.36) будет выражено через четыре произвольные, независимые
77

друг от друга гармонические функции <р0, Фл (к — li 2, 3):
«f Фг4A—v) (*"Ф
Однако это равенство правильнее называть не общим решением
уравнений Ламе, а функциональным представлением в форме Папко-
вича—Нейбера вектора перемещения и в упругом изотропном одно-
однородном теле.
В представлении Папковича—Нейбера D.39), не нарушая его общ-
общности, как было показано в работах М. Г. Слободянского A954),
Р. Юбенкса и Е. Стернберга A956), можно сохранить только три гар-
гармонические функции, т. е. принять его в таком виде:
«! = Фг—4A*_v) (*>Ф&),<- D.40)
Но в случае конечной односвязной области последнее представление
допустимо при условии, что v Ф 0,25.
В некоторых случаях сохранение функции ф0 в D.39)*оказывается
полезным, поскольку за счет произвольного ее выбора можно до-
достигнуть упрощения выкладок при решении конкретной задачи.
Исходя из D.26) и учитывая D.35), D.37), получим формулу для
компонент тензора относительного перемещения:
t№ + V+xVk.ti)- D.41)
Свертывая последнее равенство по индексам i и / и вспоминая, что
Ч>*.<* = V2q>ft = 0, найдем
"'¦' = в"^Г4''-" D-42)
Подставив теперь равенства D.41) и D.42) в формулу закона Гука
D.4), получим представление компонент тензора напряжений через
гармонические функции ф&:
[2уфб + A2уНФ + )-*йФь.Ы- D-43)
§ 6. ОСНОВНЫЕ УРАВНЕНИЯ В НАПРЯЖЕНИЯХ
При решении задачи первого типа обычно выгодно за основные не-
неизвестные принять компоненты тензора напряжений, т. е. решать
задачу в напряжениях. При этом для упрощения решения задачи ос-
основные уравнения следует представить только через искомые функ-
функции Oij.
Система трех дифференциальных уравнений равновесия D.3),
содержащая шесть искомых функций aij (xh), имеет неоднозначное
решение. Функции oij (xh), определяющие действительное напряжен-
напряженное состояние тела, будучи статически возможными и связанные за-
законом Гука D.5) с функциями etj (xh), должны подчиняться, как и
функции Btj (Xft)i уравнениям, выражающим условия совмест-
78

н о с т и. Очевидно, что эти уравнения можно получить из диффе-
дифференциальных зависимостей Сен-Венана D.2) путем исключения функ-
функций ец с помощью формулы D.5) закона Гука. Однако эти необходимые
уравнения более просто находятся из уравнений Ламе D.12).
Продифференцировав равенство D.12) по координате'*у, получим
Выполняя в равенстве D.44) операцию свертывания по Индексам
i И /', приходим к равенству
которое, учитывая, что
Ut,i = в,
принимает вид
2A—-
1 i\
е,н
= v2e,
D.45)
Используя вытекающее из C.52) и C.65) соотношение
e-i=2L2, D.46)
а также зависимость C.63), из равенства D.45) получим
V22 = -i±lp/s>s. D.47)
В формуле D.12), определяющей три дифференциальных уравне-
ния Ламе D.13), свободный индекс i можно заменить любой другой
буквой, например /, т. е.
Дифференцируя последнее равенство по кординате Х(, найдем
vf«« + T=57e-""—o/w- Dl48)
Сложив равенства D.44) и D.48), получим
V2 (и,., + ",.,) +~^ в.м = —р- (fu + fu). D.49)
На основании D.1) и D.5) имеем
ulti + ujtt = 2г1} = 2 [A + v) оц - v B) 8i}]/E. D.50)
Учитывая равенства D.50), D.46) и C.63), уравнение D.49) приведем
к виду
A + v) V2aij - v6iyV22 + S,(i = -A + v) p (ftti + f)tt).
79

Используя равенство D.47), окончательно получим
Это равенство определяет шесть соотношений, которые образуют
две группы дифференциальных зависимостей между компонентами
тензора напряжений at) (xh). Одна из зависимостей первой группы
имеет вид
"".' i+v дх\ 1+v
а первая зависимость второй группы представляется уравнением
¦= —Р ТГ + 1Г- • <4'53)
Остальные зависимости получаются путем круговой перестановки ин-
индексов в уравнениях D.52) и D.53).
В наиболее часто встречающихся задачах, когда массовые силы
fi постоянны или, в частности, равны нулю, равенство D.51) упроща-
упрощается;
„2ст . 1 ¦
и определяет установленные в 1892
дифференциальных уравнений:
/=0 D.54)
Бельтрами следующие шесть
V2a.
1 + v дх\
1 а2 2
= 0.
= 0,
dxz dxt
= 0.
D.55)
Три уравнения типа D.52) и три уравнения типа D.53) были полу-
получены Дж. Мичеллом в 1900 г. Поэтому уравнения, определяемые
равенством D.51), называют уравнениями Бельтрами—
М и ч е л л а. Они представляют собой условия совместности!- вы-
выраженные через компоненты тензора напряжений at}.
Таким образом, при решении прямой задачи в напряжениях
первоначально находятся шесть функций ots (xk), которые должны
удовлетворять дифференциальным уравнениям равновесия D.3),
уравнениям Бельтрами—Мичелла D.51) или D.54) и граничным усло-
80

виям D.6). Далее по полученным функциям at) (xh) находятся функ-
функции e(j (xh) из алгебраических уравнений D.5) закона Гука. Так как
при нахождении функций oi} (xk) удовлетворялись условия совмест-
совместности Бельтрами—Мичелла, то функции е*у (xh) будут удовлетворять
дифференциальным зависимостям Сен-Венана, т. е. необходимым и
достаточным условиям интегрируемости уравнений D.1). Тогда путем
интегрирования уравнений D.1) определяются перемещения т (xk).
Выполняя операцию свертывания по индексам i и /в равенстве
D.54) и учитывая, что
аи = 2 и 2,и = V22,
найдем
V2 2=0, D.56)
т. е. первый, или линейный, инвариант тензора напряжений 2 = аи
представляет собой (при отсутствии массовых сил или когда они по-
постоянны) гармоническую функцию.
Применяя к равенству D.54) оператор Лапласа и учитывая, что ли-
линейный инвариант тензора напряжений — гармоническая функция,
получим
ФФои=*0, D.57)
т, е. компоненты тензора напряжений at] являются бигармоническими
функциями, когда массовые силы постоянны или, в частности, равны
нулю.
§ 7. ПОЛУОБРАТНЫЙ МЕТОД СЕН-ВЕНАНА
Решение прямой задачи как в перемещениях, так и в напряжениях
требует интегрирования довольно сложной системы дифференциаль-
дифференциальных уравнений в частных производных и, как правило, сопряжено
со значительными математическими трудностями. Поэтому при реше-
решении прямой задачи часто используют приближенные методы.например
метод сеток, прямые методы вариационных задач (методы Ритца, Буб-
Бубнова—Галеркина, Канторовича и др.), а также получивший за пос-
последнее время широкое применение метод конечных элементов. В неко-
некоторых же случаях решение можно эффективно получить с помощью
так называемого полуобратного метода Сен-Венана.
Сущность полуобратного метода Сен-Венана состоит в том, что при
решении конкретной задачи, например, в напряжениях задаются
из соображений физического характера задачи некоторыми компонен-
компонентами тензора напряжений и затем определяют остальные компоненты
otj (xh) из уравнений равновесия D.3) при выполнении условий сов-
совместности Бельтрами—Мичелла D.51) или D.54) и граничных условий
D.6).
Может случиться, что сделанные предположения о значениях не-
некоторых компонент тензора напряжений будут противоречить или
уравнениям равновесия, или граничным условиям, или условиям
совместности Бельтрами—Мичелла. В этих случаях следует сделать
81

иные предположения о значениях части компонент oij (xh), исходя,
например, из известных решений аналогичных задач. В этом смысле
полуобратный метод Сен-Венана не является совершенным. Однако ког-
когда сделанные предположения о значениях некоторых компонент тен-
тензора напряжений или для некоторых компонент вектора перемещения,
если задача решается в перемещениях, не противоречат всем основным
уравнениям граничной задачи, то полученное решение полуобратным
методом является точным и на основании теоремы о единственности
(см. гл. V) однозначным.
Сен-Венан применил A855) полуобратный метод при решении за-
задачи об упругом равновесии призматического бруса произвольного по-
поперечного сечения, находящегося под действием поверхностной наг-
нагрузки на его торцах. Эта задача, представляющая большой прак-
практический интерес (кручение и изгиб призматического бруса), назы-
называется задачей Се н-В е н а н а (см. гл. VII и VIII).
§ 8. ПРИНЦИП СЕН-ВЕНАНА
Существенные математические осложнения при решении прямой
задачи возникают вследствие необходимости удовлетворения конк-
конкретным ее граничным условиям. Вместе с тем из соображений физи-
физического характера ясно, что точное осуществление распределения
поверхностных сил на некоторых участках поверхности S( тела,
на которых это распределение предпо-
предполагается заданным, как определенные
граничные условия, практически вряд
ли осуществимо. Во многих задачах по-
поверхностные силы, приложенные к не-
некоторым участкам поверхности тела,
известны только суммарно, т. е. как
их главный вектор и главный мо-
момент, а закон распределения поверх-
поверхностных сил известен лишь примерно
или вообще неизвестен. Таким образом,
наряду с математическими трудностями,
с которыми приходится встречаться при
решении граничных задач теории упру-
упругости, имеют место затруднения и в точной формулировке граничных
условий. Эти трудности значительно уменьшаются благодаря так на-
называемому принципу Сен-Венана, который опубликован в известном
мемуаре Сен-Венана «О кручении призм» A855).
Принцип Сен-Венана утверждает, что если к небольшому
участку поверхности тела приложена система сил, главный вектор и
главный момент которой равны нулю, то эта система сил вызывает ло-
локальное напряженно-деформированное состояние, быстро убывающее
по мере удаления от участка приложения сил.
В порядке подтверждения этого принципа Сен-Венан ссылается
на свои опыты с каучуковыми стержнями. На рис. 4.1 приведен один
из примеров, когда две равные и противоположно направленные
82

силы, действуя на каучуковый стержень, вызывают tto существу
лишь его местную деформацию, а на основной своей длине стержень
практически не деформируется.
Принцип Сен-Венана можно сформулировать также следующим об-
образом: если некоторую совокупность поверхностных сил на сравнитель-
сравнительно малой части поверхности тела заменить статически эквивалент-
эквивалентной системой сил, действующих на той же части поверхности, то та-
такая замена- сил практически не изменит напряжений и перемещений
в точках, удаленных, от площадки приложения сил на расстояния, не
меньшие наибольшего линейного размера этой площадки.
Принцип Сен-Венана позволяет удовлетворять граничные условия
интегрально, т. е. удовлетворять на конкретному закону распреде-
распределения поверхностных сил, а их главному вектору и главному моменту.
Принцип Сен-Венана достаточно хорошо подтверждается экспе-
экспериментально, хотя еще и сейчас не имеет законченного теоретического
обоснования. Обзор работ, посвященных исследованию и математиче-
математическому обоснованию принципа Сен-Венана, можно найти в статье [231.
§ 9. ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Задачи, в которых компоненты тензора напряжений aij (xh), a
следовательно на основании D.5) и компоненты тензора деформации
eij (Xk)< определяющие напряженно-деформированное состояние упру-
упругого тела, являются линейными функциями координат xh его точек
или постоянными величинами, называются простейшими задачами тео-
теории упругости.
В тех случаях, когда массовые силы ft можно считать равными
нулю, условия совместности Бельтрами—Мичелла D.54) при линейных
функциях otj (xh) удовлеторяются тождественно. Следовательно, если
эти функции не будут противоречить уравнениям равновесия D.3),
то они представляют точное решение рассматриваемой задачи при вы-
выполнении ее граничных условий D.6). При этом в силу теоремы о един-
единственности .(см. гл. V) это решение будет однозначным.
Простейшие задачи теории упругости решаются или полуобратным
методом Сен-Венана, или как обратные задачи в тех случаях, когда ре-
решение фактически сводится к проверке решений задач, известных
из сопротивления материалов.
Растяжение призматического бруса. Рассмотрим призматический
брус (рис. 4.2), длина / которого значительно больше наибольшего ли-
линейного размера поперечного сечения произвольной формы. Начало
координат О совместим с центром тяжести левого торца бруса, напра-
направив ось х3 по оси бруса. Боковая поверхность бруса свободна от по-
поверхностных сил, а к торцам приложены распределенные равномерно
поверхностные силы ts = a [tx = /2 = 0), которые растягивают брус
равнодействующими Р = aF, где F — площадь поперечного сечения.
Полагаем, что массовые силы /(- равны нулю.
Решая задачу полуобратиым методом, примем, что в произвольной
точке М (xk) бруса
Оц = СТ22 — Оц = (J23 = <*31 = 0| а83 = Я + Ьхз, (а)
• - 83

где а и Ь — постоянные, которые подлежат определению.
Принятые компоненты at} тождественно удовлетворяют уравне-
уравнениям совместности Бельтрами D.54) и первым двум уравнениям рав-
равновесия D.3). Третье уравнение равновесия удовлетворяется при
условии
да33/дх3 =-6 = 0, т. е. а33 = «• (б)
Обратимся к граничным условиям D.6). Для любой точки боковой
поверхности бруса ns = 0 и, следовательно, на этой поверхности
граничные условия выполняются при любом
значении а. Для точек левого и правого
торцов щ = пг = 0, п3 = =F1, поэтому на
торцах первые два граничных условия удов-
удовлетворяются тождественно, а из третьего
находим
а38 = а = о = PIF. (в)
По формуле D.5) закона Гука находим
еа — е22 = —(v/E)a, е33 = A/Е) а,
«12 = е23 = е31 = 0- (Г)
e
tan
a
. 7
Рис. 4.2
Рис. 4.3
Будем считать, что окрестность точки тела, совпадающей с нача-
началом координат О, не имеет жесткого смещения, т. е. при ху = х2 =
= х3 = 0 uf = 0 и и?,/ = 0. Тогда по формулам A.97), A.100) полу-
получим:
«1д — «2,2 — —(v/?) а, и3,з = A/?) а,
«1,2 = «1,3 ^ «2,1 — М2,3 — «3,1 — «3,2 = 0.
Теперь по формуле A.101) найдем перемещения точки М (xh):
их = —(v/?) ахи иг — —(\1Е) ах2, и3 = A/Е) ох3. (д)
Из последней формулы (д) следует, что поперечные сечения бруса-
остаются плоскими. Этот вывод подтверждает предположение, которое
является исходным (гипотеза плоских сечений) при рассмотрении дан-
данной задачи в курсе сопротивления материалов. По этой же формуле
находим удлинение бруса:
д/ = „j (/) =» аи в = Pll(EF). (е)
84

Таким образом, полученные из основных уравнений теории упру-
упругости результаты, являясь точным решением рассматриваемой задачи,
совпадают с решением, известным из курса сопротивления материалов.
Однако это решение будет точным при условии, что силы, растя-
растягивающие брус, распределены по его торцам равномерно. Но согласно
принципу Сен-Венана это решение можно считать точным и при ином
способе приложения растягивающих сил Р.
Допустим, что один из торцов рассматриваемого бруса заделан, а
к другому приложена растягивающая сила. В этом случае все точки
заделанного, например левого, торца не должны иметь перемеще-
перемещений и, следовательно, формулы (д) не соответствуют этому случаю,
так как определяемые по ним перемещения Wj и «2 не равны нулю при
х3 = 0, т. е., строго говоря, полученное решение не будет точным для
этого случая. Если же при записи граничных условий в перемеще-
перемещениях D.7) учитывать также некоторую гибкость, которая на основа-
основании принципа Сен-Венана допустима относительно граничных условий
D.6), то в данном случае вместо требования равенства нулю перемеще-
перемещений во всех точках левого торца можно ограничиться использован-
использованными условиями отсутствия жесткого смещения окрестности одной
точки О этого торца. Это не отразится на деформированном.состоянии
бруса в целом и скажется только на его левой концевой части длиной
порядка наибольшего размера поперечного сечения.
Растяжение призматического бруса под действием собственного
веса Вертикально расположенный призматический брус (рис. 4.3)
длиной / закреплен по верхнему торцу и находится под действием
собственного веса. Начало координат О совместим с центром тяжести
нижнего торца недеформированного бруса,- направив ось х3 вверх
по оси бруса.
Итак, на брус действуют только массовые силы
h = h = O, f, = -g (a)
и реактивные поверхностные силы на верхнем закрепленном торце,
суммарно равные весу бруса pglF, где F — площадь поперечного се-
сечения бруса.
Очевидно, что дифференциальные уравнения равновесия D.3) и
условия совместности Бельтрами—Мичелла D.51) будут удовлетво-
удовлетворены, если в произвольной точке М {хк) бруса принять
Оц = 022 = 012 = О23 = 031 = 0. 033 = Р?*3- (б)
Легко убедиться, что граничные условия D.6) на боковой поверх-
поверхности бруса и на его нижнем торце {ха = 0, п8 = —1), свободных от
внешних поверхностных сил, выполняются. На верхнем торце (xs = I,
п8 = +1) граничное условие a33ns — h принимает вид
pgl = *,, (в)
т. е. решение (б) будет точным для данной задачи, если уравновешиваю-
уравновешивающие вес бруса поверхностные силы на закрепленном верхнем торце
распределены равномерно. Согласно принципу Сен-Венана, это ре-
решение будет хорошим приближением и при ином способе распреде-
85

лени я реактивных поверхностных сил с равнодействующей pglF,
направленной по оси х3.
По формуле D.5) получим:
4l = е22 = F Р№> «33 = -Г PgX3> е12 = е23 = е31 = 0- (Г)
С С
Примем закрепление верхнего торца такое, при котором окрест-
окрестность точки Ж0@,0,/), совпадающей с центром тяжести торца, не имеет
перемещения и поворота, т. е.
При *! = Л;2 = О, Х3= I
т = 0 и utj = 6. (д)
По формулам A.97) и A.100), совмещая начало пути интегрирования
с точкой Мо @, 0, /), найдем:
«i,i = «2,2 = —(v/?) pgxs, «з,з = (pglE) xz, «li2 = 0, |
«1,з = —(v/?) pgxu «ад = 0, «2,3 = —{уIE) pgx2, 1 (e)
«3,1 = (V/^) PgXlt «3,2 = (V/^) PgX2. )
Тогда, выполняя интегрирование от точки Мо @, 0, 7), по форму^
ле A.101) получим перемещения точки М (xh):
«1 = —(vpg/E)x1x3, «2 = —(vpg/E) x2x3, )
«з - (pgJ2E) Ixl + v (x\ + xl) - /2J. j (Ж)
Из формул (ж) вытекает, что точки оси х3 имеют только вертикаль-
вертикальные перемещения
«3 = -(pg/2E) (I* - х\).
Произвольная точка М (xh) перемещается в радиальном направле-
направлении к оси бруса на величину, пропорциональную ее расстоянию
г от оси х3, а в окружном направлении / не перемещается (рис. 4.3);
и, = «xcos a + «2sina = —(vpg/E) rx3, щ — h2cos a — «jSin a = 0.
Отсюда следует, что «волокно» (геометрическое место точек), парал-
параллельное до деформации оси х3, после деформации наклоняется к этой '
оси пропорционально расстоянию г.
Поперечные сечения после деформации искривляются и принима-
принимают поверхность параболоида вращения. Например, точки сечения
х3 = с после деформации будут иметь координаты точек параболоида
*; = с + «з = с + (pgl2E) [v (x\ + х\) - (Р - <?)].
Эта поверхность будет перпендикулярна всем продольным «во-
«волокнам» бруса, которые после деформации наклоняются к оси х3,
что соответствует отсутствию угловых деформаций у12 = 2ei2, yi3 =
= 2е13 и у2з = 2е2з.
Отмеченные выводы схематически отражены на рис. 4.4, где
пунктиром показана форма бруса после деформации.
Чистый изгиб прямого бруса постоянного сечения. Ось х3 направим
по оси бруса из центра тяжести О левого торца, а осилс! и х2 совместим
с главными осями поперечного сечения (рис. 4.4). К. торцам бруса
приложены поверхностные силы, которые приводятся к равным по ве-
86

личине и противоположно направленным моментам М, действующим
в плоскости хг0х3. у ш. «•
Такое нагружение бруса, как известно из курса сопротивления
материалов, называется чистым изгибом, а компоненты аи тензора нап-
напряжений в произвольной точке К (xh) равны:
0ц = 022 = 012 = 02з = 031 — 0. 0зз — Ехг/р, (а)
где р — радиус кривизны изогнутой оси бруса.
Выясним, удовлетворяет ли это решение (а) основным уравнениям
теории упругости, т. е. является ли оно точным. Очевидно, что урав-
уравнения Бельтрами—Мичелла D.51) и дифференциальные уравнения рав-'
новесия D.3) выполняются при отсутствии массовых сил. Граничные
условия D.6) при данном решении (а) принимают вид
h = 0, tz — 0, t3 — а39п8. (б)
н
0
х2
^\ р'
J
1
-
поперечное
сечение
Рис 4.4
Так как для любой точки боковой поверхности бруса пя — 0, то
граничные условия (б) удовлетворяются, если боковая поверхность
свободна от внешних сил, что соответствует условию задачи.
Для левого и правого торцов бруса п3 ~ ±1 и, следовательно,
U — ±0зз = ±ЕхУр, (в)
т. е.. на торцах поверхностные силы, приводящиеся к моментам М,
должны распределяться так же, как напряжение 038 на поперечном
сечении.
Только при этих условиях, строго говоря, решение (а) является
точным. Но из принципа Сен-Венана следует, что решение (а) будет
справедливо для точек основной части бруса, достаточно удаленных
от его торцов, и в том случае, когда поверхностные силы на торцах,
приводящиеся к моментам М, имеют любой другой закон распреде-
распределения.
Изгибающий момент в поперечном сечении бруса
ххйхг = — {[xldXldx.2 =^Ь-,
Р JJ р
где Jr,— момент инерции поперечного сечения относительно главной
оси xv .
,=М=\\ а
\\
83
87

Отсюда кривизна изогнутой оси бруса
1/р = М/?Уч. (г)
На основании формулы D.5) при данном решеипи (а) имеем
= v_ a = \_x c =zJ_a =J_X
22 ? 33 ^ 2' 33 ? J3 p
(д)
Тогда при условии, что окрестность точки О @, 0, 0) не имеет
жесткого смещения, перемещения произвольной точки К. (xh) будут
определяться равенствами (см. с. 27):
U] = х,х2, и, = [х'з — v (xi—х2)], и3 = — х2х8. (е)
р 2р р
Для точек оси бруса (*] =• А'2 = 0) получаем
И| = «, = 0, Н.,= — = —; ¦•
Последнее равенство представляет собой уравнение изогнутой оси
(упругой линии) бруса. . t
Рассмотрим некоторое поперечное сечение бруса х3 = с. После де-
деформации точки этого сечения будут находиться в плоскости
Л'з = С + U3 '— С + СХ2/р,
т. е. при чистом «изгибе поперечное сечение остается плоским, а тан-
тангенс угла его наклона к оси х3 равен
tgO = dxt/dxi = р/с = EJX]/(Mc).
Угловой коэффициент упругой линии при х3 — с равен
tg а = (du2/dx3) хз „е = —Mc/(EJX{y
Следовательно, tgd tg a = —1,
т. е. при чистом изгибе поперечные сечения переходят в плоские сече-
сечения, перпендикулярные упругой линии.
Представим, что до изгиба бруса в его поперечном сечении х3 — в
выделен прямоугольник со сторонами b и h, параллельными осям
л', и х% (рис. 4.4, б). Тогда после изгиба стороны этого прямоуголь-
прямоугольника #] = ± Ь/2, оставаясь прямыми:
а-;= ±6/2 +«!=±(б/2)A —Hi
V р
повернутся, как показано на рис. 4.4, б пунктиром.
Две другие стороны прямоугольника jc2 — ±ft/2 обратятся в дуги
параболы:
*?= ± h/2 + u, =± ft/2 — (l/2p)[c2 — v(*f — й*/4)].
Всестороннее равномерное сжатие тела. Пусть к поверхности про-
произвольной формы тела, не имеющего внутренних полостей, приложено
равномерное давление р, а массовые силы отсутствуют.
S.8

Естественно предположить, что все точки тела будут испытывать
одинаковое напряженное состояние, определяемое шаровым тензором
o pS т. е.
Оц = 022 = О3з — Р» 012 — 023 — <?31 = 0- (в)
Действительно, уравнения совместности Бельтрамн D.54) и диффе-
дифференциальные уравнения D.3) будут удовлетворяться, а граничные
условия принимают вид:
t2
что соответствует условию задачи.
Значит при данном нагружении тела решение (а) является точным.
На основании D.5) компоненты тензора деформации равны:
6ц = е22 = ess = —[A — 2v)/E] р, е12 = е23 = е31 = 0. (в)
Пусть окрестность некоторой точки тела, о которой совместим на-
начало координат, закреплена и не может иметь жесткого смещения:
при хх «= х2 = х3 = 0 uf = 0 и uait j := 0.
Тогда по формулам A.97) и A.100) имеем:
«1,1 = «2,2 = «з,8 = — Ц1 — 2v)/?] p,
«1,2 = «1,3 — «2,1 = «2,3 = «3,1 = «3,8 = 0»
По формуле A.101) находим перемещения произвольной точки:
ui = —[A — 2v)/?] рд:г. (г)
Таким образом, перемещение любой точки происходит по направ-
направлению радиус-вектора г = xi3i данной точки, т. е.
и = —[A — 2v)/?] pr.
§ 10. МЕТОД СУПЕРПОЗИЦИИ
Для линейно-упругого тела при однозначных малых перемещениях
щ, удовлетворяющих условию A.41), справедлив метод суперпозиции.
Предположим, что линейно-упругое тело при выполнении A.41)
находится в двух состояниях нагружения. В первом случае испытывает
действие массовых сил // при граничных условиях а'цП) = t[ на St
и и! = «{s)/ на Su, а во втором случае находится под действием массо-
массовых сил f'l при граничных условиях ацп.) = ti на St и и'! == u\s) на Su.
Тогда на основании суперпозиции функции т = и[ + и'!, aij =
= ofi + oi'j определяют решение для данного тела под действием
массовых сил ft = // + f'i при граничных условиях oijtij — tl + t]
на St и Ui = u\sY + u\s)" на. Su.
Например, для призматического бруса, растягиваемого собственным
весом и силой, равномерно распределенной на его торце, решение бу-
будет определяться суммой соответствующих решений, которые при-
приводятся в § 9 гл. IV.
69

Главе V
ОБЩИЕ ТЕОРЕМЫ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ
§ 1. ТЕОРЕМА КЛАПЕЙРОНА
Пусть упругое тело, которое ограничено поверхностью S и имеет
объем V, находится в равновесии под действием массовых сил ft и по-
поверхностных сил tt. Работа этих сил на произведенных ими переме-
перемещениях будет равна
И1 1]ЧМ5* E.1)
Последний интеграл, учитывая D.6), преобразуем по формуле
Остроградского:
U|*S = JJ *„«,«,<« =JfJ(aw«,)./^. E-2)
Преобразуем интеграл в правой части последнего равенства:
j ff (otu
Ш a".t u
t uidv+j|j
Щ E.3)
где учтено, что oijcaij = 0, так как (aij) — симметричный тензор, а
' и) — кососимметричный тензор.
Теперь равенство E.1) приведем к виду
V. E.4)
Приняв во внимание дифференциальные уравнения равновесия
D.3) и формулу Грина C.23), получим
А =
Равенство E.5) представляет собой теорему Клапейрона
для любого упругого тела. Здесь W — упругий потенциал, который
при изотермическом деформировании определяется свободной энерги-
энергией F — U — TqS и представляет собой удельную работу деформации.
Если упругое тело подчиняется закону Гука, то упругий потенци-
потенциал является квадратичной функцией гц C.39). В этом случае, учитывая
90

уравнения равновесия D.3) и формулу Клапейрона C.72), равенство
E.4) приведем к виду
Следовательно, согласно теореме Клапейрона для линейно-упруго-
линейно-упругого тела, работа деформации равна половине работы внешних сил
на произведенных ими перемещениях.
§ 2. ТЕОРЕМА О ЕДИНСТВЕННОСТИ РЕШЕНИЯ
Как уже известно, при решении конкретной задачи полуобратным
методом Сен-Венана задаются, например, некоторыми компонентами
оц тензора напряжений из каких-либо интуитивных соображений,
а затем из основных уравнений определяют остальные компоненты
oij. При этом может возникать естественный вопрос об однознач-
однозначности полученного решения. Этот вопрос, возникающий также при ре-
решении обратной задачи, снимается теоремой Кирхгофа
о единственности решения основных задач
статики упругого тела.
Теорема Кирхгофа A824—1887), как и равенство E.6) теоремы
Клапейрона, базируется на предположениях, что упругое тело под-
подчиняется закону Гука, а перемещения являются однозначными и
малыми A.41).
Доказательство теоремы о единственности решения проведем от
противного, ссылаясь при этом на равенство E.6) теоремы Клапейрона,
которое, учитывая E.1), представим в следующем виде:
E.7)
Предположим, что одна из трех сформулированных основных задач
статики упругого тела (см. гл. IV, § 2) имеет два различных реше-
решения:
1) ulMi.ofo 2) и], г?,, о», E-8)
которые удовлетворяют основным уравнениям при одинаковых гранич-
граничных условиях и массовых силах. В частности, должны подчиняться
уравнениям равновесия функции а// и а//, т. е.
и должны выполняться граничные условия;
а) в случае задачи первого типа
• o'it n}\s = tt и а"ц nj \s = (t; E.1
б) в случае задачи второго типа
.иЛв = и$*> и «;|s = «<sM EЛ
91

в) в случае задачи третьего типа
oilп} \st = /„ ui \su = и}»> и el,n, \st=tt, u' \su = u<>$). F.13)
Рассмотрим разности допускаемых двух решений E.8):
ut = и! — u'is eij = г'ц — г"ц, at/ = ex// — at). F.14)
Очевидно, что функции atj должны, как это следует из E.9), E.10)
и E.14), удовлетворять уравнениям равновесия при ft — О
аг^ = 0. E.15)
Следовательно, для функций E.14) равенство E.7) получает упро-
упрощение:
JJJJJ«"'& (М6)
Граничные условия для функций E.14) в случае основных задач
первого, второго и третьего типов соответственно принимают вид
а) а„я,|5 = 0; б) и,|в = 0; в) aunf\st^0, u^s^O. E.17)
Тогда интеграл в правой части E.16)
во всех трех случаях E.17) обращается в нуль, так как либо ti = О
на S или на St, либо Ui = 0 на S или на Su, т. е. для функций E.14)
будем иметь
~~*WdV=*0. E.18)
Но упругий потенциал И^ представляет собой положительно опре-
определенную квадратичную функцию компонент eif (см. с. 62). Поэтому
равенство E.18) возможно только в случае, если во всех точках облас-
области V, занятой телом, W = 0. Это означает, что во всех точках тела
eij — 0, а на основании закона Гуна и aij = 0, т. е. во всех точках тела
г'ц = е"/ и at) — a"/.
При ги = 0 в случае задачи первого типа перемещения щ могут
быть отличными от нуля и представлять собой «жесткое смещение»
упругого тела A.56). Если по условию задачи исключается «жесткое
смещение», то и щ = 0, т. е. и/ = и'.
Таким образом, предположение, что поставленная задача может
иметь различные решения, опровергается, и следовательно, теорема
о единственности решения основных задач трех типов доказана. Одна-
Однако эта теорема утверждает единственность решения, если оно сущест-
существует.
Доказательство теоремы существования решения задач теории
упругости представляет значительные математические трудности.
Первоначальные сведения о доказательствах теоремы существо-
существования решения, которые даны Корном A907) и Лихтенштейном
A924), можно получить в работах [5, 3].
92

§ 3. ТЕОРЕМА БЕТТИ
Рассмотрим линейно-упругое тело в двух состояниях.
Пусть в первом состоянии тело находится под действием массовых
сил // и поверхностных сил //, которые вызывают напряженно-де-
напряженно-деформированное состояние тела, характеризуемое функциями и*',
е//, at,-.
Во втором состоянии тело подвергается действию массовых сил
ft и поверхностных сил //, а напряженно-деформированное состояние
тела определяется функциями u"i, г,), а°/.
Теорема Бетти утверждает: работа сил первого состояния
на перемещениях второго состояния равна работе сил второго совтоя-
ния на перемещениях первого состояния.
Работа А1г сил первого состояния ft, t[ на перемещениях второго
состояния и, равна
Шр f:  dV+Я''"; dS-
Учитывая, что t't •= ацп}; и'[ — г'ц + со//; а\\<ац = О, и выпол-
выполняя преобразования интеграла по поверхности S аналогично преобра-
преобразованиям E.2) и E.3), а затем ссылаясь на D.3), получим
Щ. F-20)
Точно так же можно убедиться, что работа А21 сил второго состоя--
ния //, t'i на перемещениях первого состояния и[ будет равна
«-WpnuSdV
j J t! и! dS - J j J a/- e/, dV. E.21)
Принимая во внимание формулу Бетти C.77), из сопоставления по-
последних равенств E.20) и E.21) приходим к' заключению
Ап=Аг1. E.22)
С помощью теоремы Бетти весьма просто можно решить некоторое
задачи об упругом теле, находящемся в равновесии под действием мас-
массовых сил // и поверхностных /(. В качестве первого состояния рас-
рассматриваемого тела примем некоторое простейшее его напряженно--
деформированное состояние, а за второе — состояние под действием
заданных сил fi и it.
Приведем примеры использования формулы E.22), которую полез-
полезно записать в следующем виде: левую часть формулы E.22) заменим
выражением E.20), а правую—выражением E.21). Опуская при
этом двойные штрихи для величин второго состояния, получим
l, ги dV= j j J pf, ul dV + ^j /, щ dS. F.23)
1 Требуется найти изменение объема V тела произвольной формы
под действием массовых сил ft и поверхностных сил ti,
93

В качестве простейшего первого состояния тела примем однородное
напряженное состояние, определяемое шаровым тензором a'ij =
= —pbtj, т. е. при котором тело находится в условиях всестороннего
равномерного сжатия (см. с. 89), а значит, и остается геометрически
себе подобньцц»
В этом случае перемещения
u'i = — [A — 2v)/?] pxi
и тогда приращение объема тела согласно формуле E.23)
-2v ГССГ - „, . ГГ. .„1 E 241
где G = zifotj = ?ti — относительное изменение объема,
X,
Рис. 5.2
В частности, при сжатии тела произвольной формы двумя силами
Р, расстояние между элементарными площадками приложения которых
равно h (рис. 5.1), объем V тела при отсутствии массовых сил на осно-
основании формулы E.24) уменьшится на величину
Д1/ = —1A — 2v)/?] Ph,
так как интеграл по объему в правой части равенства E.24) равен
нулю, а интеграл по поверхности Ph [58].
2. Для призматического бруса с произвольным контуром попе-
поперечного сечения площадью F необходимо найти изменение его длины /
под действием приложенных к нему сил /, и ti.
За первое простейшее состояние бруса примем равномерное растя-
растяжение вдоль его оси х3, которое характеризуется напряжениями;
°11 = °2S — »"l2 = °!
o'3l = 0, а'аз » а = PIF
и перемещениями:
«1 = — (v/?) axlt и', = — (vlE) oxz, ul3 = (l/E) oxa.
В этом случае интеграл в левой части равенства E,23) примет вид
o $fj$ e83 dV = a (es3)cp V,
и
94

где (е33)ср — среднее относительное удлинение вдоль оси бруса.
Тогда, подставив значения и/ в правую часть равенства E.23),
получим формулу для изменения длины бруса
А' = (езз)ор / = ~г (f f f P f/з х3 — v (f, xx +
9—\{$xxl-\-ttx^\dS\. E.25)
Найдем, например, изменение длины / и объема V призматиче-
призматического бруса произвольного поперечного сечения площадью F под
действием его собственного веса Q = Flpg, когда брус поставлен своим
основанием на горизонтальную плоскость и когда тот же брус положен
на горизонтальную плоскость своей боковой поверхностью (рис. 5.2)
В первом случае при принятом направлении координатных осей
имеем /i = /г = 0. /з — —§¦ Интегралы по поверхности в формулах
E.24) и E.25) равны нулю, так как на боковой поверхности бруса и
на его верхнем торце ty = t2 = t3 = 0, а на нижнем торце ix = /2 =
= 0, t3 = —Q/F, но х3 = 0. Интегралы по объему в этих формулах
равны
i
* QI
Тогда
М = —QI/2EF, AV - —[A — 2v)/2?] Ql.
Во втором случае, направив ось х3 по образующей бруса, совпадаю-
совпадающей с горизонтальной плоскостью, а ось хх вверх, имеем fl = —g,
f2 = fa = 0, поверхностные силы на всей поверхности tx = /2 = t9 =
= 0, исключая силы tu распределенные по образующей хг = 0. Поэто-
Поэтому интегралы по поверхности S в E.24) и E.25) равны нулю, а интегра-
интегралы по объему V — соответственно
Р ( — ё) *i dxi йхг dx3 = — р
= — pglFc= —Qc,
.где с — расстояние центра тяжести поперечного сечения от оси
= vQc.
Следовательно, по формулам E.25) и E.24) имеем:
Теорема Бетти имеет весьма общий характер. Она позволяет пост-
построить методы интегрирования уравнений теории упругости, основан-
основанные на использовании функций Грина [4].
05

§ 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ
Как известно, многие законы механики, и частности механики,
сплошной среды, наряду с описанием их дифференциальными уравне-
уравнениями сводятся к утверждению, что некоторый функционал в рассмат-
ртдемом процессе должен достигать экстремума. В такой формули-
формулировке эти законы называются вариационными прин-
принципами механики. Задачи, в которых требуется исследовать функ-
функционал на экстремум, называются вариационными зада-
задачами.
Напомним, что функционалом называется переменная величина, за-
зависящая от функции, принадлежащей определенному классу (мно-
(множеству) функций. Обычно функционал представляет собой некоторый
определенный интеграл. Например, простейший функционал, зави-
зависящий от функции одной переменной, имеет вид
J= \f(x,u(x),u1 (х)) dx, E.26)
•Со
где F — непрерывная и дифференцируемая функция.
Необходимым условием экстремума функционала является равен-
равенство нулю его первой вариации б/, т. е. главной части приращения
функционала, которая линейна по отношению к вариации функции 8«.
В вариационном исчислении доказывается 149], что функция
и (х), реализующая экстремум функционала, должна удовлетворять
определенному дифференциальному уравнению. Например, для функ-
функционала E.26) условие экстремума 8J = 0 будет выполнено, если функ-
функция и (х) удовлетворяет дифференциальному уравнению
Fu - dFu.ldx = О; E.27)
где Fu =* dF/du, /v = dFldu'.
Дифференциальное уравнение второго порядка E.27) называется
уравнением Эйлера. Две постоянные общего интеграла этого уравне-
уравнения определяются из граничных условий и (*0) = и0, и (xt) = uv
Для функционала, зависящего от функции трех независимых пе-
переменных и (хи х2, х3),
* *а. *s. «. "*,> «*,> uXt)dV E.28)
дифференциальное уравнение, которому должна удовлетворять функ-
функция и (Xi), реализующая экстремум функционала, имеет вид
Fu-Wuxjd*- дРиХг/дх,- dFUxjdxa = 0, E.29)
где Fu = dF/ди, dFUxjdxt = д (dFldu,t)/dxlt
uXl
Дифференциальное уравнение второго порядка в частных произ-
производных E.29) называется уравнением Эйлера—Остроградского. По-
Постоянные, которые войдут в общее решение этого уравнения, опреде-
96

льются из граничных условий на поверхности S, ограничивающей
область V.
Например, для функционала
J = ,f.[J [(ди/dxj* + (du/dx2f + (du/dxsn dV E.30)
уравнение Эйлера—Остроградского имеет вид
дги!дх\ + д*и/дх* + дги/дх23 = V2« = 0, E.31)
т. е. является уравнением Лапласа, причем надо найти непрерывное
в области V решение и (xt) этого уравнения, обычно принимающее
заданные значения на границе этой области. Это одна из основных
граничных задач математической физики, называемая задачей
Дирихле.
Краткие сведения некоторых основных понятий вариационного
исчисления приведены с целью напомнить, что решение вариационной
задачи эквивалентно решению граничной задачи для дифференциаль-
дифференциального уравнения, которое является уравнением Эйлера или урав-
уравнением Эйлера—Остроградского для данного функционала.
Обычно дифференциальные уравнения вариационных задач интег-
интегрируются в конечном виде лишь в исключительных случаях. Поэтому
возникает необходимость решения вариационных задач непосредст-
непосредственными или прямыми методами, т. е. без решения соответствующих
дифференциальных уравнений.
Основная идея прямых методов состоит в том, что вариационную
задачу можно рассматривать как предельную для некоторой задачи
на экстремум функции конечного числа параметров.
Допустим, что искомая функция u(xi), от которой зависит функцио-
функционал, может быть представлена в виде функции
ип = ип (аи аг, ...,ап, хх, х%> xs), E.32).
зависящей от п параметров а,, ..., ап так, что при любых значениях
этих параметров функция ип удовлетворяет граничным условиям и
обычно требованию непрерывности. При таком представлении искомой
функции функционал окажется функцией конечного числа парамет-
параметров и вариационная задача сведется к задаче на экстремум функции
конечного числа параметров, которая решается обычными методами.
Затем, совершая предельный переход при л —> оо, получим (в случае
существования предела) функцию, являющуюся тэчным решением
рассматриваемой вариационной задачи. Полученное решение будет
также, ввиду отмеченной эквивалентности, точным решением граничной
вадачи для дифференциальных уравнений, которые являются уравне-
уравнениями Эйлера или Эйлера—Остроградского для данного функционала.
Если не представляется возможным совершить предельный переход
и приходится ограничиться функцией ип, то получим приближенное
решение вариационной задачи.
Среди прямых методов решения вариационных задач наиболее
широкое применение получили метод Ритиа, метод Канторовича и
метод Бубнова—Галеркина — метод приближенного решения диффе-
Зак. 514

ренциальных уравнений, не связанных, вообще говоря, с вариационны-
вариационными принципами.
В теории упругости рассматриваются преимущественно два вариа-
вариационных принципа — принцип минимума потенциальной энергии
и принцип минимума дополнительной работы (принцип Кастильяно).
§ 5. ПРИНЦИП МИНИМУМА ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
Пусть под действием массовых сил ft и поверхностных сил 1г тело
объемом V, ограниченное поверхностью S, находится в равновесии,
а его деформированное состояние определяется перемещениями щ.
Согласно принципу возможных перемещений для сплошных сред,
работа Вч'ех внешних и внутренних сил на малых возможных пере-
перемещениях точек тела из состояния его равновесия равна нулю. Эта
формулировка принципа возможных перемещений для сплошных сред
эквивалентна следующему утверждению.
Рчбота всех внешних сил на малых возможных переметениях рав-
равна изменению потенциальной энергии деформации тела, т. е.
' /, 6н4 dS, E.33)
где W — удельная потенциальная энергия деформации тела, которая
равна свободной энергии при изотермическом процессе деформи-
деформирования и внутренней энергии при адиабатическом деформировании.
Возможными перемещениями Ьщ в случае сплошного тела явля-
являются любые малые перемещения, которые удовлетворяют условиям
непрерывности тела и условиям перемещений на поверхности тела,
т. е. бн; непрерывны вместе со своими производными первого порядка и
должны обращаться в нуль на части Su поверхности тела, где заданы
перемещения «|s).
Поэтому
[ /, 6щ dS = JJ /, быг dS + W t, бы. dS = j J /, бы, dS. E34)
si $u S<
При сообщении точкам тела малых возможных перемещений 8ut ea-
данные силы /; и tu при которых тело находится в равновесии, рас-
рассматриваются постоянными. Поэтому в области V, занятой телом,
б (pfi) = 0, а на части St поверхности тела 6 {tt) = 0. Следовательно,
имеем
pfibui = б (p/jUj), tfiui — б (/,-«/). E.35)
Тогда знак вариации б в равенствах E.33) и E.34), поскольку
V и St фиксированы, можно вынести за знак интегралов и равенство
E.33), учитывая также E.34) и E.35), можно привести к виду
б / f f j WdV - j f j p/, щ dV-jj tt ut dS\ = 0. E.36)
98

Уравнение E.36) называется вариационным уравне-
уравнением Лагранжа.
Предыдущие рассуждения и уравнение E.36) справедливы для лю-
любого упругого тела.
Вариационное уравнение Лагранжа E.36) в влучае консерватив-
консервативных внешних сил можно записать в еледующем виде:
S/7 = 0, E.37)
где величина
П = J f J WdV - J f J 9h «i dV - J J tt ut dS, E.38)
равная разности потенциальной энергии деформации тела и работы
приложенных к нему внешних еил на втатически соответствующих
им перемещениях, называется потенциальной энергией системы.
Как уже известно, удельная потенциальная энергия деформации
W (гц) представляет собой в случае линейно-упругого тела положи-
положительно-определенную квадратичную функцию C.33) компонент тен-
тензора деформации ztj> которые ввязаны о перемещениями дифферен-
дифференциальными зависимостями D.1).
Потенциальная энергия системы /7 представляет собой функцио-
функционал, зависящий от функций щ и их производных.
Из равенства E.37) следует, что из всех вочможных перемещений
действительными, соответствующими равновесию гела при заданных
внешних силах, будут те перемещения, при которых функционал /7
принимает стационарное значение.
Покажем, что в случае линейно-упругого тела условие E.37)
превращается в условие минимума потенциальной энергии. Для этого
доетаточно убедиться, что при сообщении вариаций Ьщ действительным
перемещениям щ приращение функционала П будет положительным,
%. е.
ДЯ = JJj SW (ги) dV-Щ Д (р/, щ) dV-
(<,«,)d5>0, E.39)
Jj
st
Поскольку внешние вилы ft и tt постоянны, то при сообщении ва-
вариаций but имеем:
A (Phut) - S (pftut), Л (ttut) = б (/<И<). E.40)
Для определения приращения удельной потенциальной энергии
деформации функцию W (еи +[6&ц), где бег/= A/2) (быг,/+быу,;)—
вариации компонент тензора деформации, соответствующие вариаци-
вариациям 8uit разложим в ряд Тейлора:
W (ги + Ьги) - W (в|/) + ^^М. Ьги + A /2) ?*&*- 6вм бвА, E.41)
Cejj 08lj Рид;
i. 99

Здесь в правой части равенства второе слагаемое представляет со-
собой первую вариацию удельной потенциальной энергии деформации,
которая с учетом C.23) равна
бй7(е1у) = -^М-б8,у=а,^Р,/; • E.42)
д
третье слагаемое есть вторая вариация W (8i7), которая g ссылкой на
ту же формулу и C.34), C.33) равна
б2 И7 (e») = ~S- 371П) бе^ ^и, = 4 C,ift!6Bj/ 6eft, = W Fв„). E.43)
Следовательно,
&W(bu) = IF (8,, + 6eiy) - W(e,tj) = Ш (efy) + W Fе„), E.44)
где U7 (бегу) — удельная потенциальная энергия деформации, которая
имела бы место, если бы тело подверглось только перемещениям биг;
как положительно-определенная квадратичная форма бегу, W (бе;у) >
>0. ¦
Учитывая .E.40) и E.44), приращение функционала П будет
- J J *f Uf dSJ + f Д V/ Fetf) dV. E.45)
Принимая во внимание E.36) и то, что № Feti-) > ),
А/7-
что и требовалось показать.
Отсюда следует, что из всех возможных перемещений, т. е. удов-
удовлетворяющих условию сплошности тела и принимающих заданные
значения на Su, действительными будут те, при которых функционал
П имеет минимум. В этом и состоит принцип минимума
потенциальной энергии.
Таким образом, задача определения функций щ, соответствующих
равновесию линейно-упругого тела при заданных внешних силах ft
и tt, сведена к вариационной задаче.
Теперь покажем, что уравнениями Эйлера—Остроградикого и ес-
естественными граничными условиями для функций ut, реализующих
минимум функционала П, являются уравнения равновесия D.12) и
граничные условия D.21).
В самом деле, используя E.42), имеем
JJJ Г (е„) dV = Ш
JJJ 6W Ы dV = j| J си Ыи dV.
100

Поскольку 6e;-; = S«jf}—Ьш1} и ои8соц — 0, то
SJJJ W(Bti)dV=tyouuuudV = ty(oti6ut.,-.ty oiU6ut dV.
По формуле Остроградского,
(atJbut)tldV =
Jfj
и, следовательно,
7 (в„) dl/ = Ij a,, л, Ьщ dS -Mj oiU
Учитывая D.20) и D.11), получим
6 ^ W (8„) dl/ = JJ [А,0Я| + G ^ + uu
Подставив последнее выражение в уравнение E.36), найдем
uidS==0. E.46)
Так как в объеме V и на части S( поверхности тела вариации би{
произвольны, то последнее равенство, т. е. условие стационарности
функционала П, будет выполняться, если подынтегральные функции
в равенстве E.46) равны нулю.
Отсюда получаем уравнения упругого равновесия ъ перемещениях
v2"i + 7Zi70^-T'* E'47)
и граничные условия на поверхности St
KQn. + GB!h.+un nt) = /„ E.48)
\ an I
которым должны удовлетворять функции щ, чтобы функционал П
имел минимум.
§ 6. ПРИНЦИП МИНИМУМА ДОПОЛНИТЕЛЬНОЙ РАБОТЫ
Тело объемом V и ограниченное поверхностью S, находится в равно-
равновесии под действием приложенных к нему массовых еил ft и поверх-
поверхностных сил tt на части St. Пусть деформированное состояние тела
определяется перемещениями ut, а его напряженное еовтояние — ком-
101

понентами ст,-у тензора напряжений, которые в объеме V должны удов-
удовлетворять уравнениям равновесия
°и,, + 9fi = 0 E.49)
и граничным условиям
oun,\st = tt. E.50)
Подвергнем компоненты а^ действительного тензора напряжении
произвольной вариации, но такой, чтобы смежное наряженное
состояние, характеризуемое'компонентами а1} + ба^, было статически
возможным при тех же заданных внешних силах, т. е. должны удовлет-
удовлетворяться уравнения равновесия и граничные условия:
iPu + 6а„),, + р/, = 0, E.51)
frt, + 6oa)n,\st-ti.' E-52)
Из сопоставления равенств E.49) и E.51), а также E.50) и E.52)
следует, что вариации 6а it в объеме V должны удовлетворять однород-
однородным уравнениям равновееия
boihi = 0 E.53)
и граничным условиям
6atin,\s. =0. E.54)
На остальной части Su поверхности тела, на которой заданы не по-
поверхностные силы, а перемещения, вариации Ьаа могут быть произ-
произвольными:
8a»n>|su-8<,. E-65)
При переходе к смежному напряженному состоянию изменение
дополнительной работы деформации тела будет
б J f J Л (аи) dV = J Г J Л (<jw + ва„) dV - J J J Л (а,,) dV. E.56)
Разложим выражение удельной дополнительной работы для изменен-
измененного напряженного состояния в ряд Тейлора:
i i fAf) 6aiy6aft,.E.57)
Последнее слагаемое равенства E.57) является второй вариацией
удельной дополнительной работы, в учетом формулы C.80) и прини-
принимая во внимание, что оиаи = б1к8наиак1, BJ = (<*ji)a=s6f A,
его можно записать так:
— v6iy 6fti] бо„ 5айг e-i- [(l + V) §o.; 6af/-v (баг,)г] = Л (баи). E.58)
Следовательно, вторая вариация 62Л (otj) — Л (bati) — сущест-
существенно положительная величина второго порядка малости по сравне-
сравнению с 8аи,
102

Принимая во внимание формулы C.73) и C.74), дифференциальные
зависимости Коши D.1), а также учитывая, что вариации даи ~
~ 8оц должны удовлетворять уравнениям E.53), второе слагаемое
в правой части равенства E.57), представляющее собой первую ва-
вариацию 6Л (<т,-у), приведем к виду
6Л (аа) = dAJ?ll) 8аи = eti 8ati = ~ (И|>, + ии)
j—u, 8aifJ = {и, 8au)j. E.59)
Опуская последнее слагаемое в равенстве E.57) и используя E.59),
упростим равенство E.56):
8 Г Г Г Л (ot]) dV = Г Г Г (и, 8аи)„ dV. E.60)
Щм.,^-фо.
Интеграл в правой части последнего равенства преобразуем по
формуле Остроградского и учтем условия E.54) и E.55):
J[j (и, bou)jdV = jj и, 6atin,dS =
= \[ut8at,n]dS=\fut6ttdS. E.61)
s" s
Поскольку на поверхности Sa заданы перемещения uj5), то 6«,- = 0
и знак вариации можно вынести за знак последнего интеграла.
Тогда равенство E.60) можно представить в виде
0 E.62)
или
8W = 0, E.63)
где величина
m^u?)dS E.64)
называется дополнительной работой.
Так как 62Л (alV) == Л (бст^) > 0, приходим к следующему вы-
выводу, называемому принципом минимума дополни-
дополнительной работы или вариационным принципом
К а о т и л ь я н о: из всех статически возможных напряженных сос-
состояний тела при заданных внешних силах в действительности реали-
реализуется то напряженное состояние, для которого функционал Ч*1 над
тензором напряжений (atj), называемый дополнительной работой,
имеет минимум.
Можно показать, что условие E.63) влечет за собой выполнение
уравнений Бельтрами—Мичелла, представляющих уравнения Эйяе-
ра—Оароградского для функционала W, а также выполнение геомет-

рических (кинематических) граничных условий на части Su поверхно-
поверхности тела, как естественных граничных условий вариационной задачи.
Вариации бсг^ должны подчиняться условиям E.53) и E.54), т. е.
их нельзя рассматривать независимыми. Эти условия являются, таким
образбы, уравнениями связей и, следовательно, имеем связанную
задачу вариационного исчисления.
Следуя методу неопределенных множителей Лангранжа и учитывая
/5.Г4), представим условие стационарности E.63) в следующем виде»
S = 0, E.65)
su
где ht — неопределенные множители, представляющие собой компо-
компоненты некоторого вектора % в произвольной области V, занятой телом.
Ссылаясь на C.80), имеем
ЗА (оу)/д<т„ = (УЕ) 1A + v) а„ - vohft8,yl. E.6(э)
Применяя формулу бстроградсхого, преобразуем объемный интег-
интеграл:
E.67)
ff lidoiitijdS — ^Hku6audV,
где (ki,j) — несимметричный тензор второго ранга, который можно
разложить на симметричную и кососимметричную части:
1 1
Учитывая равенства E.66), E.67), E.68), E.54) и принимая во вни-
внимание, что (бст,^) — симметр-ичный тензор, условие стационарности
E.65) приведем к виду
audV +
E.69)
Шесть вариаций 8ot], связанных тремя уравнениями E.53), при
соответствующем выборе трех компонент К{ лагранжева вектора X
Можно считать произвольными. Приравнивая нулю множители в по-
подынтегральных выражениях перед вариациями б"ст(;- в условии стацио-
стационарности E.69), получим соотношения
(УЕ) [A + v) а„ - vokh6u]=(№) (h,, + *„,); h \su = u(,s). E.70)
Правая часть первого соотношения представляет собой симметрич-
симметричный тензор, определяемый вектором "к; второе соотношение E.70)
показывает, что вектор К должен быть равен вектору перемещения
104

tt, заданному на поверхности Su тела. Очевидно, что вектор h можно
отождествить с вектором перемещения и в области V, т. е. считать, что
тензор, определяемый правой частью первого равенства E.70), 'есть
тензор деформации (ег/) и, следовательно, компоненты его должны
подчиняться зависимостям Сен-Венана D.2). Подставив в эти зависимо-
зависимости значения компонент е.1}, выраженные левой частью первого соот-
соотношения E.70), придем к уравнениям Бельтрами, как уравнениям
Эйлера—Остроградского для функционала W, второе соотношение
E.70) — естественные граничные условия вариационной задачи.
§ 7. ВАРИАЦИОННЫЙ ПРИНЦИП РЕЙССНЕРА
В принципе минимума потенциальной энергии рассматривается
функционал, зависящий от функций ии непрерывных и принимающих
заданные значения u\s) на части 5„ поверхности тела.
В принципе минимума дополнительной работы рассматривается
функционал, зависящий от компонент а/у тензора напряжений, которые
должны быть статически возможными, т. е. должны удовлетворять
дифференциальным уравнениям равновесия в объеме V и граничным
условиям на части St поверхности тела а заданными поверхностными
силами.
В вариационном принципе Рейввнера предполагается,
что заранее выполняетея равенство
ги = ИЛ (ati)/datf, E.71)
устанавливающее однозначную зависимость между компонентами
otf тензора напряжений и величинами sti, природа которых не уточня-
уточняется, т. е. не вводится предположение, что они определяются полем
перемещений щ.
В этом принципе рассматривается функционал, зависящий от пе-
перемещений щ и от компонент atf тензора напряжений, причем фу«к-
ции щ и aij предполагаются независимыми:
J~ Щ
^-iti^dS. E.72)
Вычислим вариацию функционала J-,
j bou-pnSu^dV-
s
t
IS. E.73)
105

Применяя формулу Остроградского, преобразуем объемный интег-
интеграл:
jjj A/2) ои{Ьии + Ьии) dV = J ГJ otJbuudV = JJ J
= fJa1/«j6M,dS4-JJa,,rt,6M,dS —JJJa,M6ii,dV\ E.74)
Тогда условие стационарности функционала принимает вид
6/= Г Г Г {[A/2) (щ *+и, Л—дА/даи\ ба^—(oi}j + pfi) bu^dV -\-
и
Поскольку Ьоц и б«( произвольны, то
дА/даи = еи = A/2) (ии + им), E.76)
otjj +- p/i = 0, E.77)
a,yn7|S/ = /,, E.78)
и, |.sB = «}">. E.79)
Таким образом, для вариационного уравнения б/ = 0 уравнения-
уравнениями Эйлера—Остроградского являются дифференциальные зависимо-
зависимости Коши E.76) и дифференциальные уравнения равновесия E.77), а
естественными граничными условиями — условия E.78) и E.79).
§ 8. ПОЛНЫЙ ФУНКЦИОНАЛ СТАТИКИ ЛИНЕЙНО-УПРУГОГО ТЕЛА
Покажем, что основные уравнения статики линейно-упругого
тела:
дифференциальные зависимости Коши
в/у = ("ь/ + ии)/2, E.80)
дифференциальные уравнения равновесия
Oim + Ph = 0, E.81)
соотношения между напряжениями и деформациями
аи = dW/дгц E.82)
и граничные условия ¦
°и п> Is, = U, E.83)
«4|5и = и}»>, E.84)
являются уравнениями Эйлера—Остроградского и естественными гра-
граничными условиями некоторой вариационной задачи,
106

Построим функционал Э = Э (щ, ef/, atJ) от функций и,, eih ou,
которые рассматриваются независимыми:
i
— Jj/,u,dS —fJo^nHH, —w}4))iS. E.85)
st su
Приравняем нулю вариацию этого функционала:
- JJ /, 8u, dS — JJ 6оап,(щ — u]s)) dS—JJ a,, n, 6wf dS = 0. E.86)
Так как вариации batj и бе^ независимые и произвольные, то вы-
выражения при ба,-у и при 6е^ под знаком объемного интеграла равны
нулю. Отсюда получим соотношения E.80) и E.82).
Эти соотношения, учитывая преобразование объемного интеграла
E.74), дают возможность условие стационарности функционала E.86)
записать в следующем виде:
(oUJ+ p/,)fiuf dV + JJ (аип,-и) бы, dS-
s
Отсюда ввиду независимости и произвольности вариаций б«г и
batj получим дифференциальные уравнения равновесия E.81) и гра-
граничные условия E.83) и E.84).
Таким образом, вариационное уравнение 65 = 0 содержит все
основные уравнения статики линейно-упругого тела E.80)—E.82)
и граничные условия E.83) и E.84).
Если некоторые условия стационарности полного функционала Э
считать выполняющимися заранее, то получим частные вариационные
принципы теории упругости. Так, 'принимая, что заранее выполняют-
выполняются соотношения между ai; и 8^ и учитывая соотношение C.26).
Oifiu — W (ef/) = Л (a,,),
на основании равенства E.85) получим функционал Рейсснера E.72).
Если предположить, что заранее выполнены зависимости E.80)
и граничные условия E.84), то полный функционал Э превращается
в функционал /7 принципа минимума потенциальной энергии.
Наконец, пвлагая, что заранее выполнены соотношения E.82),
дифференциальные уравнения равновесия E.81) и граничные условия
E.83), полный функционал Э превращается в функционал Кастилья-
но V.
107

§ 9. МЕТОД РИТЦА
Одним из прямых методов решения вариационных задач
метод Ритца. Рассмотрим метод Ритца применительно к нахождению
минимума функционала П E.38):
77=Ш г {8;/) dV ~ Шp/i щ dV~llh Ui dS> {5-87)
гдо W (eu) — квадратичная функция C.79) компонент тензора де-
деформации вц = A/2) {Ui,j+ uhi), т. е. квадратичная функция произ-
производных функций ut.
Допустимыми функциями щ будут такие, которые вместе со своими
производными непрерывны в замкнутой области V + S и удовлетво-
удовлетворяют заданным геометрическим граничным условиям
Заметим, что удовлетворять заранее статическим граничным уело-
виям, вообще говоря, нет надобности, так как функции uh реализую-
реализующие минимум функционала П, будут удовлетворять, как уже извест-
известно, уравнениям равновесия Ламе E.47) и статическим граничным
условиям E.48), т. е. будут решением граничной задачи, эквивалент-
эквивалентной принципу минимума потенциальной энергии.
Идея метода Ритца состоит в том, что значения функциона-
функционала рассматриваются не н2Г произвольных допустимых функциях, а
лишь на семействе функций, линейно зависящих от нескольких пара-
параметров:
"ы = ut + J] ak (u,)k (k = 1,2,.... n), E.89)
где ah — произвольные параметры, подлежащие в дальнейшем опреде-
определению; и?—функции, удовлетворяющие^граннчным условиям E.88);
(д — функции, удовлетворяющие однородным граничным условиям
k = 0. - E.90)
Очевидно, что при таком выборе класса допустимых функций
они будут удовлетворять граничным условиям E.88) при любых пара-
параметрах ah: Среди этих функций uin надо найти ту, которая сообщает
функционалу E.87) наименьшее значение. Если подставить в функ-
функционал вместо ui выражение E.89) и выполнить интегрирование, то
функционал превратится в квадратичную функцию и параметров ah:
П* = /7* К, а,, .... ак ап). E.91)
Чтобы эта функция достигала минимума, параметры ah должны
удовлетворять системе уравнений
дП*/дак = 0 (k = 1, 2, ..., я). E.92)
Система E.92) является линейной относительно искомых парамет-
параметров ah, причем число уравнений равно числу неизвестных. Решив
систему E.92), получим определенные значения параметров а\, при
108

которых функция E.91) будет иметь минимум. Тогда приближенное
решение вариационной задачи, а следовательно, и приближенное
решение ей эквивалентной граничной задачи E.47), E^48) будут оп-
оеделяться сЬсгомулой
г
ределяться формулой
Методом Ритца можно получить ряд последовательно все более
точных приближений. Вопрос о сходимости эти-х приближений к ис-
искомому решению вариационной задачи, а также об оценке погрешности
этого метода представляет собой относительно трудную задачу 128, 41].
Обычно для оценки точности приближенного решения, полученного
методом Ритца или другими прямыми методами, пользуются следующим
теоретически, конечно, несовершенным, но практически достаточно
надежным приемом: вычислив utn и «Kn+i)> сравнивают их между собой
в нескольких точках рассматриваемой области. Если в пределах
требуемой точности их значения совпадают, то считают, что с тре-
требуемой точностью решением вариационной задачи будет uin. Если же
значения uin и Mj(n+1) в пределах заданной точности не совпадают, то
вычисляют ыг(п+2) и сравнивают с ««(„+!>•
Точность приближенного решения методом Ритца в большой сте-
степени зависит от удачного выбора координатных функций и, вообще
говоря, возрастает с увеличением их числа. Если удачно задаться
координатными функциями E.89), то хорошую точность для переме-
перемещений щ можно получить даже при п =1. Однако производные функ-
функций щ, найденных методом Ритца, а следовательно, и напряжения
at] D.4) имеют меньшую точность.
Заметим, что приближенное значение функционала П* E.91),
получаемое методом Ритца, всегда не меньше действительного функ-
функционала П E.87). В самом деле, значение минимума функционала
находится с избытком, так как минимум функционала на любых допус-
допустимых функциях не больше, чем минимум того же функционала на
части этого класса допустимых функций E.89).
Далее будут приведены решения конкретных задач методом Ритца,
а также другими приближенными методами.
§ 10. МЕТОД ЁУБНОВА—ГАЛЕРКИНА
И. Г- Бубнов A872—1919) впервые в 1913 г. изложил новый приб-
приближенный метод интегрирования дифференциальных уравнений тео-
теории упругости, который широко применялся затем Б. Г. Галеркиным
A871—19.45) для решения ряда задач теории упругости. Метод Буб-
Бубнова—Галеркина, как общий приближенный метод интегрирования
дифференциальных уравнений, не связан, вообще говоря, с каким-
"либо вариационным принципом.
Общий прием этого метода рассмотрим применительно к обык-
обыкновенному линейному уравнению второго порядка
/ + Р (*) У' + Ч W У = / (*) E-94)
109

с граничными условиями
У(х0) - Уо< УМ = У\- <5-95)
Уравнение E.94) кратко запишем так:
L(y) = f {х), E.96)
где L ¦— дифференциальный оператор.
Приближенное решение уравнения E.96) будем искать в виде
0, = Фо(*) + |;а*Ф*(*). E-97)
где ф0 (х).— функция, удовлетворяющая граничным условиям E.95);
Фа (х) — удовлетворяющие однородным граничным условиям первые
п функций пооледовательности координатных функций ф1 (х), фг (х),
.... ф„ (х), ..., обладающей полнотой на отрезке [х0, л;,]; ah — коэффи-
коэффициенты, подлежащие определению.
Подставим в уравнение E.96) вместо у приближенное решение
уп с неопределенными коэффициентами ah. Очевидно, что при этом
уравнение не будет тождественно удовлетворяться и получим функцию
F (х, ah) = L (ф0) + ZakL (фй) — / (х) Ф 0, E.98)
* к = I
которую можно назвать невязкой.
Если случайно уп окажется точным решением, то F (x, ak) = 0 и
невязка будет ортогональна ко всем координатным функциям, т. е.
будем иметь
2 \F(x,ah)<pk(x)dx = 0. E.99)
k=\ К,
Для получения приближенного решения, близкого к точному ре-
решению, согласно методу Бубнова—Галеркина требуем, чтобы функция
F (x, aft) была ортогональна ко всем п функциям фь (х). Таким образом,
получим систему п уравнений
F(x, ah)(fh(x)dx = 0 (k=l,2,...,n) E.100)
к— \ х0
ИЛИ
2 ak J Фй (x)
L (Фь) dx = | Фь (x) [f (x) - L (щ)] dx. E.101)
Определив из системы п уравнений коэффициенты ak, получим
приближенное решение:
&, = Фо (*) + S а* Ф* (*)• (
Уравнения E.100) или E.101) называются условиями Буб-
Бубнов а—Г алеркина. Аналогичные условия используются при
решении дифференциальных уравнений в частных производных или
110

системы этих у^ав ;ений. При решении задач теории упругости методом
Бубнова—Галеркина необходимо функции приближенного решения
выбирать так, чтобы заранее были удовлетворены все граничные ус-
условия (статические и геометрические).
§ 11. МЕТОД КАНТОРОВИЧА
Прямой метод решения вариационных задач, предложенный
Л. В. Канторовичем A933) и названный методом приведения к обык-
обыкновенным дифференциальным уравнениям, представляет собой разви-
развитие метода Ритца, когда функционал зависит от функций несколь-
нескольких переменных.
Сущность метода состоит в том, что при координатных функциях
принимаемого приближенного решения берутся не постоянные пара-
параметры, а неопределенные функции одной из независимых переменных,
например хх. Тогда функционал J [и (хи х2, х3)] на классе функций
п
«п = «о (*i, х2, х3) + 2wft (хх) uh (xv x2, xa), E.103)
где м0 (*;) — функция, удовлетворяющая граничным условиям за-
задачи; Mft {Xt) — функции, удовлетворяющие однородным граничным
условиям; wh (Xj) — неизвестные функции одной переменной, прев-
превращается в функционал J \wh (*,))> зависящий от п функций wh (xj
одной независимой переменной.
Функции wh {Xi) находятся из условия стационарности функционала
J [wk (x,)], уравнениями Эйлера при этом будет система обыкновен-
обыкновенных дифференциальных уравнений относительно этих неизвестных
функций. Решая эти уравнения точно или численно, что вполне дос-
доступно современным вычислительным средствам, получим приближен-
приближенное решение рассматриваемой вариационной задачи.
С помощью метода Канторовича удается получить приближенное
решение значительно более точное, чем по методу Ритца с теми же
координатными функциями и с тем же числом членов ряда. E.,103).
Это достигается благодаря тому, что класс функций E.103) значи-
значительно шире класса функций E.89) с постоянными коэффициентами
йь и, следовательно, среди функций E.103) можно подобрать функ-
функции, лучше аппроксимирующие решение вариационной задачи, чем
среди функций E.89).
§ 12. МЕТОД ТРЕФФЦА
В тех случаях, когда уравнение Эйлера—Остроградского является
сравнительно простым, а контур рассматривааемой области имеет до-
достаточно сложное очертание, оказывается целесообразным приме-
применение прямого метода Треффца. Сущность метода состоит в том, что
за координатные функции приближенного решения принимаются ре-
решения уравнения Эйлера—Остроградского, а коэффициенты ah в их
линейной комбинации определяются из соображений возможно наибо-
наиболее полного удовлетворения граничных условий. Рассмотрим метод
1П

Треффца на примере задачи о стационарном значении функционала
E.30), зависящего от функции" и (xt), для которого уравнением Эйле-
ра---Остроградского является уравнение Лапласа E.31), а функция
и (xt) должна удовлетворять заданному граничному условию
«|s = «(s>. E.104)
Приближенное решение будем искать в виде
иг= 2 akUh, E.105)
где uh — гармонические функции, представляющие частные решения
уравнения E.31).
Коэффициенты ah ряда E.105), при которых функция иг будет
наиболее полно удовлетворять граничному условию E.104), будем
находить из требования минимума следующего интеграла:
/ =- JJJ" l(ttr.f — ult) (нгЛ — иш1)\ dV, E.106)
т. е. из условий
д11дат = 0 (т = 1, 2, ..., г) E.107)
Заметим, что в равенстве E.106) индекс i — немой.
С учетом E.106) и E.105) условия'E.107) принимают вид
2 ak4,t — «,f J
т. е.
или
2
J jJ "ft. t «„,, dV = J f J uj wm,, <
2 аь [ \ [ иъ , ит , dV = [ IT и , и„., dV
fr=i
ak Г Г Г gradHfe-gradumdK = ГГГ gradH.gradum dV.
На основании формулы Грина A°. 113), учитывая, что функции
uh и ит гармонические, последнее равенство можно привести к сле-
следующей системе уравнений, из которых определяются коэффициенты
ah приближенного решения и/.
или
= 0 (m=l,2, .... r). E.108)
112

Как уже отмечалось, получаемое методом Ритца приближенное
значение функционала всегда не меньше действительного. Напротив,
приближенное значение функционала, -получаемое методом Треффца]
никогда не превосходит действительного. Докажем эти особенности
методов Ритца и Треффца.
Пусть в плоской области F, ограниченной контуром L, требуется
найти функцию Ф (д-j, лг2), удовлетворяющую уравнению Пуассона
V2O> = С E.109)
и граничному условию
Ф \l = Фг.. E.110)
С помощью подстановки
Ф (дг„ хг) = Фо (хъ хг) + х (v,. *2), E.111)
где Фо (хи х2)— любое частное решение уравнения E.109), ах(*ъ хг)—
неизвестная функция, удовлетворяющая уравнению Лапласа
V^x-O, E.112)
поставленная задача сводится к задаче о нахождении гармонической
функции х. которая в соответствии с граничным условием E.110)
должна на контуре удовлетворять условию
X U = (Ф —Фо) к = Фг.. E.ПЗ)
Приближенное решение %п по методу Ритца в виде
%п = Хо (*i. xt) + ^ahtk (xv хг),. ( 5.114)
Где Хо (*i> ' ^г) — функция, удовлетворяющая условию E.113);
5U (xi> *г) — функции, удовлетворяющие на контуре L условию
XftU = 0, E.115)
при соответствующей совокупности коэффициентов ah должно мини-
минимизировать функционал
n/dxtf + (dxJdx2f\ йх.йхг, E.116)
для которого, ссылаясь на E.30) и E.31), уравнение E.112) является
уравнением Эйлера—Остроградского.
Функционал E.116) можно записать в следующем виде:
Dn = J|(grad lnf dXldxz. E.117)
» Обозначим через а> (Xi, x2) невязку приближенного решения Хп:
w = x — Х«. E.118)
где х — действительное решение уравнения E.112) при выполнении
условия E.ПЗ).
из

Подставив %п из E.118) в E.117), найдем
dXl dXt>= 1J [grad (X—
= И
j J (grad xJ dxx dx2 + J J (grad wJ d^ dx2 —
x2. E.119)
На основании-формулы Грина A°.ПЗ) для области F, ограниченной
контуром L, имеем
Я grad со • grad %dxt dx2 — ф со —— dL — A a)Va idxt dx2. E.120)
J dn JJ
F L F
По определению, функция со на ,контуре L равна нулю, поэтому
первый интеграл в правой части равенства E.120) обращается в нуль;
последний интеграл этого равенства, принимая во внимание уравнение
E.112), также равен нулю. Тогда равенство E.119) получает вид
Dn = J J (grad %nJ dxj, dx2 = j J (grad %f dx1dxt + ^ (grad соJ dxv dx2,
F F F
E.121)
откуда следует, что значение функционала Dn E.117) при любом %n,
полученном методом Ритца, не может быть меньше функционала при
действительном значении %.
Следуя методу Треффца, решение уравнения E.112) при граничном
условии E.113) находим в виде ряда
г
У == ^ ^ь Уь (x-t X ) * ('
где %h (хихг) — гармонические функции, т. е. удовлетворяющие
уравнению E.112), а коэффициенты ah в соответствии с E.108) опреде-
определяются из системы уравнений
^-dL = 0 (m = l, 2,..., г). E.123)
Принимаем, что приближенно удовлетворяющее граничному усло-
условию E.113) решение у_г по методу Треффца имеет невязку и, опреде-
определяемую равенством E.118). Тогда имеем следующее выражение для
истинного значения функционала:
D = JJ(grad х)" dXldx2 = JJlgrad (Хг + а>)]2 dXldx, =
= JT(grad %rJ dxjdxz + Jj"(grad <oJ dxxdxz + 2jJ grad %r ¦ grad (adx^dxz.
E.124)
114

На основании A°. 113) имеем
grad Xr-gradайхг dx2 = фи ^- dL—NaV*%r dxx dx2. E.125)
F L F
Последний интеграл в равенстве E.125) равен нулю, поскольку
по определению V2xr = 0, а интеграл
обращается в нуль на основании уравнений E.123), из которых опре-
определяются коэффициенты aft.
В результате получаем соотношение
D = JJ(grad X)- <W*i = I/ (grad ъ?- йх^хг + jj (grad ш)« d^dx*
E.126)
из которого следует, что значение функционала при приближенном
решении %г по методу Треффца никогда не может быть больше, чем
значение функционала при действительной функции х«

Глава VI
УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
При решении задач теории упругости существенно необходимо удов-
удовлетворять граничным условиям. Например; при решении основной
задачи первого типа граничные условия налагают определенные ог-
ограничения на напряжения в точках поверхности тела. Если поверх-
поверхность тела имеет криволинейное очертание, то удовлетворение гранич-
граничных условий при использовании декартовых координат обычно вы-
вызывает затруднения. Часто в этих случаях выгодно использовать со-
соответствующую систему криволинейных координат, при которой кри-
криволинейная поверхность тела совпадала бы с координатной поверх-
поверхностью.
§ 1. ОСНОВНЫЕ УРАВНЕНИЯ И СООТНОШЕНИЯ
В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
Если входящие в основные уравнения в декартовых координатах
обычные частные производные заменить ковариантными производ-
производными, то получим уравнения в криволинейных координатах.
Дифференциальные зависимости Кош и в криволинейных коорди-
координатах. Заменим в равенстве D.1) обычные частные производные кова-
ковариантными:
^ ,). F.1)
где VtUj — ковариантная производная B°.65 или 2°.6О):
Viu, = diuj — Г?/***. F.2)
Здесь dtUj — обычная частная производная по криволинейной
1 d d/d'
j
координате х1, т. е. j j
Тогда дифференциальные зависимости Коши в криволинейных ко-
координатах F.1) примут вид
et]. - A/2) (dtui + д,т) — Г?,ык. F.3)
Объемная деформация в криволинейных координатах. В декарто-
декартовых координатах объемная деформация 0 определяется равенством
A.70):
в = div й = т и F.4)
В криволинейных координатах дивергенция вектора определяется
ковариантной производной контравариантного вектора B°.88):
0 = div й = ViW = dtw + r'iku* F.5)
116

или, согласно B°.90),
=
F.6)
где g'k — контравариантные компоненты метрического тензора; g =
— \gik I — определитель из компонент метрического тензора.
В случае ортогональных криволинейных координат, ссылаясь на
B°.91), имеем
где ЫD) — физические компоненты вектора а.
Выполняя суммирование по немому индексу I в формуле F.7),
получим
F.8)
Компоненты тензора малого поворота и вектора поворота. Заменяя
в формуле A.29) обычные частные производные ковариантными, по-
получим формулу для компонент тензора малого поворота в криволи-
криволинейных координатах:
F.9)
В трехмерном евклидовом пространстве тензору (со*/) соответствует
вектор поворота с контравариантными компонентами:
«хEы5ы) uii{du^Ы)
F.10)
В случае ортогональных криволинейных координат имеем:
2 V822S33
{Vila "(з)) —^з {Vgtt "B)) J.
со(8) =
F.11)
Уравнения совместности деформаций. После замены в уравнениях
D.2) обычных частных производных ковариантными получим урав-
уравнения совместности деформаций в криволинейных координатах:
Vifcey< — VMet, —
0.
F.12)
117

Выполнив ковариантное дифференцирование по формуле B".65),
получим
дп eift + dik ея — d}h еп—ди ем — 2еаР {Г?к Г% — Г,™
+ 2ГЛе,*« + 2Г?*8/,в-2Г7*8„а-2Гйе/*в = 0, F.13)
где
е«а = A/2) (dh?ia + дыа — daeih). F.14)
Еще раз подчеркнем, что дкг1а = dsia/dxkt т. е. дифференцирова-
дифференцирование в формулах F.13) и F.14) производится по криволинейным коор-
координатам jc*. Например,
Уравнения равновесия. Дифференциальные уравнения равновесия
D.3) в декартовых координатах преобразуем в уравнения равновесия
в криволинейных координатах путем замены обычных частных произ-
производных ковариантными производными. Кроме того, эти уравнения
запишем через контравариантные компоненты тензора напряжений
и контравариантные компоненты вектора массовой силы:
V,o" + pf = 0, F.15)
где VjO11 — ковариантная производная контравариантного тензора
напряжений, которая в силу B°.98) равна
V, a'i = д, а'/ + Г{« а"» + Г',в о/«. F.16)
Тогда уравнения равновесия в криволинейных координатах мож-
можно записать так:
«3; оЛ + Г/, о/а + Г/в о/в + {>Г = 0. F.17)
Используя B°.99), уравнениям равновесия придадим более удоб-
удобный вид:
^а^^ ; 0. F.18)
Соотношения между напряжениями и деформациями. В прямоли-
прямолинейной прямоугольной системе координат соотношения между напря-
напряжениями и деформациями были записаны в форме C.45) и C.46),
В произвольной системе криволинейных координат соотношения между
напряжениями и деформациями имеют вид
о" = XQg'i + |i (gkgU + giigi*) Ekl. F.19)
В случае ортогональных криволинейных координат формула F.19)
принимает вид
a" = Wg4 + 2\igllgHetj. F.20)
Переходя к физическим компонентам тензора напряжений
и тензора деформации б(г)(Л по формуле B°.84), получим
нЛ. F.21)
П8

Таким образом, закон Гука в оргогональных криволинейных коор-
координатах представляется такой же формулой, как и в декартовых
координатах. По аналогии с C.68), следовательно, имеем
е(|)(/> = (НЕ) [A + v) ог{|)(Л - v B) б|Д F.22)
где Е — первый инвариант тензора напряжений.
Уравнения упругого равновесия в перемещениях. Учитывая вы-
выражение лапласиана вектора перемещения я в криволинейных коор-
координатах по формуле B°. 100) и выражение компонент градиента скаля-
скаляра div а = в по формуле B°.87), получим векторное уравнение Ламе
D.15) в криволинейных координатах:
_га д"а г* dUk га а"а
дх1 дуР ' дх'
F.23)
Уравнения Бельтрами. Полученные в декартовых координатах шесть
скалярных уравнений Бельтрами D.55), определяемых формулой D.54)
можно записать одним тензорным уравнением,
Умножим равенство D.54) на орт э}. Учитывая B.13) и соотношение
получим три векторных уравнения:
уг^+ТТ^(у2)(=0' F'24)
Используя представление тензора второго ранга (о,,) в виде суммы
трех диад (otj) = Эфх и соотношение V (VE) = э% (V2)л, векторные
уравнения F.24) можно заменить одним тензорным уравнением
V(v2) 0> F'25)
которое является инвариантным (бескоординатным) представлением
уравнений Бельтрами.
С помощью тензорного уравнения F.25) можно записать шесть
скалярных уравнений Бельтрами в любой системе координат.
§ 2, КОМПОНЕНТЫ МЕТРИЧЕСКОГО ТЕНЗОРА И СИМВОЛЫ КРИСТОФФЕЛЯ
ДЛЯ НЕКОТОРЫХ ОРТОГОНАЛЬНЫХ КРИВОЛИНЕЙНЫХ КООРДИНАТ
Различные системы ортогональных криволинейных координат на
плоскости можно построить, воспользовавшись аналитическими функ-
функциями комплексного переменного ?-^ + ix2:
113

действительные и мнимые части которых, как известно, подчиняются
условиям Коши—Римана
Ф,« = Ч>.2 и Ф.2 = — Ул- F-27)
Рассмотрим в плоскости хххг семейства кривых
ср (х1гх2) = а и г|з (xltx2) = р, _ F.28)
представляющие линии уровней действительной и мнимой частей
функции / (?). С помощью F.27) легко показать, что во всех точках
рассматриваемой области плоскости XjX? имеем
grad ф-grad 1|з = ц>лЦл + <Р.*Чл = — Ф^Ф.а + Ф.гФд = °- F-29)
Рис. 6.2
Рис. 6.1
Так как градиент ортогонален линии уровня, то отсюда следует,
что семейства кривых F.28) взаимно ортогональны.
Рассмотрим например, аналитическую функцию
= 1/5 =
Xlt(x\ + x\) - i
F.30)
В этом случае получим следующие семейства окружностей!
x,/tf + xl) = а и хг1(х\ + х\) = р F.31)
соответственно с радиусами 1/Bа) и 1/Bр). Окружности первого
семейства касательны к оси х2 в начале координат, а окружности вто-
второго семейства — к оси хг также в начале координат (рис. 6.1).
Зависимость между декартовыми координатами (л^ и х$ на пло-
, скости и ортогональными криволинейными координатами (а, Р или
к1, х2) удобно представить в следующем виде:
хг + /*г = F (х1 + ix2). F.32)
Например, в рассмотренном случае зависимость F.32) принимает,
как это следует из F.30), следующий конкретный вид?
*i + iXi = \l(xl — ix2). F.33)
120

Точка К, определяемая декартовыми координатами хи х2, х3, мо-
может быть определена также некоторыми ортогональными криволиней-
криволинейными координатами х1, хг в плоскости Оххх2 и координатой х9.
Такую систему координат называют цилиндрическими ортогональ-
ортогональными криволинейными координатами х1, хг, х3 — х3. В зависимости от
системы криволинейных координат на плоскости Ох&г цилиндрическим
координатам приписывается соответствующее название. Например,
полярные цилиндрические координаты (рис. 6.2), эллиптические ци-
цилиндрические координаты (рис. 6.3) и т. д.
Рис. 6.3
Рис. 6.4
Положение точки К можно также определить некоторыми орто-
ортогональными криволинейными координатами в плоскости, проходя-
проходящей через точку К и ось Oxz. Положение этой плоскости определяется
углом 8, который отсчитывается в плоскости Ох^ от оси хг к оси хг.
Такую систему координат 'называют осесимметричными ортогональ-
ортогональными криволинейными координатами, примером которых являются
сферические координаты (рис. 6.4).
Для некоторых ортогональных криволинейных координат найдем
компоненты метрического тензора и символы Кристоффеля.
Полярные цилиндрические координаты
(рис. 6.2).
Формула F.32), устанавливающая связь между декартовыми ко-
координатами Xi, Кг и криволинейными координатами х1 = г, х%- — 0 в
плоскости 0x^2, в этом случае имеет вид
txs = re'° = r (cos 6 + i sin 6). • F.34)
Xl
Таким образом, имеем:
хг = г cos 0, хг = г sin 0, хй = х3 — г.
Координатными линиями являются окружности
х\ + xl — Н
F.35)
121

и прямые
х2 = х, tg 9.
Исходя из B°.78), имеем формулу
A. A tг* о f*\
?Ti~~Ii —t' (о.оЬ)
определяющую ковариантные компоненты метрического тензора, по
которой находим:
?п = 1. g22 = Л g33 = 1; g = gug2zgas = r%- ¦ (б-37)
Символы Кристоффеля второго рода (отличные от нуля) на осно-
основании B° .82)
2-2 '» ' 12 1 21 • V"'W/
Частный случай полярных цилиндрических координат, когда
х1 = г, х2 = 0, х3 = г = 0, представляет собой полярные координаты.
Они используются при плоской задаче или когда изучаемые величины
не зависят от координаты х3 = z.
Эллиптические цилиндрические координаты
Зависимость между декартовыми координатами хи и эллиптическими коор-
координатами х1 устанавливается формулой
хх + »х2 = a ch (х1- + ix2) = а (ch x1 cos х2 + i sh x1 sin x2). E.39)
Отсюда
*1 = а ch х1 cos х", х2 = a sh x1 sin *2, х:! = *з = г, F.40)
Координатными линиями (рис. 6.3) являются эллипсы
и гиперболы
a2 cos2 х2 a2 sin2
По формуле F.36) находим:
gu =g22 = a2 (sh2 x1 cos2 x2 + ch2 xl sin2 x2) = (a2/2) (ch 2a:'—cos 2a:2) . \
fe = '; g = glt?2!!g33 = (^/4)(ch2xi-cos2x2J. |
На основании формул B°.82) находим символы Кристоффеля второго родш
F'42)
Биполярные цилиндр, ическис координаты
Связь между декартовыми {xlt jt2) и биполярными {Xх, х2) координатами в пло-
плоскости Oxjjt,; устанавливается формулой
x1-\-ix2 sh x'-(-: sin а:2
122

т. е. имеем:
к, — а
sin
F.44)
chx'4-cosx2' ~* Chxi + cosxa> 3 "
Координатные линии х1 = b = const представляют собой эксцентричные
окружности (рис. 6.5), центры которых находятся на оси Ох^,
{xt — a cth bf + к\ = a2/sh2 b.
Координатные линии х2 = с = const суть дуги окружностей с центрами на
оси 0*2 и проходящие через две точки ^ = ± а, которые называются полюсами;
sm'o
alshb
Рис. 6.5
B°.82)
Ковариантные компоненты метрического тензора находим по формуле F.36)
Su = Sn = «2/(ch xl + gos *2J, ft,, = Г,
в = Biting** = fl4 /(ch я1 + co's x2L. F.45)
Отличные от нуля символы Кристоффеля второго рода в соответствии с
Ghx>+cos*2
F.46)
ty, x3 =
F.47)
r cos ф. F.48)
Сферические координаты (рис. 6.4).
Связь между декартовыми (xt, х2, *3) и сферическим {хх = г, зР
== 6) координатами определяется формулами!
xs + Ф = г (cos ij) + i sin »f) = г/*;
Xi = p cos 0 = /• sin гр cos 8, x2 = p sin 0 = r sin ф sin 8, jc8
Ковариантные компоненты метрического тензора
Stt = I. ^2 = г2. §зз =» Iя sin 2ф; g = Щуе„&п = И sin2 г|>. F.49)
Символы Кристоффеля второго рода (отличные от нуля) по формулам
B^.82) имеют значения:
ri = rsin2\|> ri-.-iin^cos^ |
123

Тороидальные координаты (рис. 6.6)
Соотношения между декартовыми (xt, хг, лг3) и тороидальными (х1 = а.
р", х? — 0) координатами:
= да cth
а-Ир" sinP-f-'. sh a.
—-— а —
2
x = t> cos 0 =
sh a cos 8
ch a—cosp1
—;
en а—cos A
sh а sin 0
sin p
ch a—cos fS
ch а—c
F.51)
F.52)
Рис. 6.6
Ковариантиые компоненты метрического тензора!
al1 5Z2 (cha-
Символы Кристоффеля второго рода!
ёзз"
аг sh2 a
(ch a—cos|iJ
sh n
П, = 1
2 ch a—cos $
•i -p'-- sini'
12 п cha—cosf)
sh a A —ch a cos P)
1
ch a—cos В
-ch a cos p1
sh a(cha— i
sh2 a sin P
ch a—cosli
cha—cosP
F.53)
Среди различных систем криволинейных координат наиболее широко ио«
пользуются полярные цилиндрические и сферические координаты.
124

§ 3. УРАВНЕНИЯ В ПОЛЯРНЫХ ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
1. Соотношения" между ковариантными щ и физическими и^ ком-
компонентами вектора перемещения и определяются по формулам B°.83):
«1 = «A) = "г, «2 = ГиB) = Шв, «з = "(8) = «г- F.54)
2. Соотношения между ковариантными ?,\j и физическими е(!)(Л
компонентами тензора деформации устанавливаются на основании
B°.84):
eIl = fe'(l) (l) = err> e22==f2e<2) B) = ''2еС0, е33.== ЕC) C) = ?
ei2 = '"ed) B) — гггв, е23 = геB, C) = ле/)г, е31 = еC) {1) = е2Г
3. Дифференциальные завиашости Коши определяются формулой
F.3). Найдем, например, зависимости для компонент евв и ег6- На
основании F.3), принимая во внимание F.38) и F.54), находим:
.„ „ч
e12 = A/2)(ди1/дх2 + диг/дх1) — Г«2 иа = A /2) (dur/dQ + rduti/dr -f «e) —
— «я r = A /2) (диг/дв -\- гдиа/дг — нн).
Учитывая соотношения F.55), получим:
Аналогично определяются зависимости для остальных компонент
тензора деформации. В результате имеем следующие дифференциаль-
дифференциальные зависимости Коши в цилиндрических координатах:
ет = "IT"' еое = due/rdQ + «/•/r> szz = dujdz,
or
вл = A/2) (диг/гдв + диц/дг- ив/г), ет =
+ dujrdd),
6.5б)
4. Объемная деформация вычисляется на основании формулы F.8).
Учитывая равенства F.37), находим
диг , 1 а";1 . диг аг
— ~Т~ г — -Г--Г —Г~-Г—'
F.57)
5. Компоненты тензора малого поворота и вектора поворота опре-
определяются формулами F.11). Учитывая F.37), получим:
г дв дг
даг диг '
~дТ дг
д"а 1 d»r
125
F.58)

6. Уравнения совместности деформаций определяются формулами
F.13) и F.14). Принимая i = k = 1, / = I = 2, найдем
в„« +2Г« в2г«-2Г«. е12а-2Г
Учитывая соотношения F.55) и выполняя в последнем равенстве
суммирование по немым индексам а и р\ приняв во внимание значения
символов Кристоффеля второго рода F.37), получим
—2-
г)еш
е122 =
Выполняя дифференцирование и учитывая, что по формуле F.14)
найдем одно из шести уравнений совместности деформаций:
д^ ёаа I Л2 а 9 (^ 8 i>
U U r A W bff с, /-у
J_B^i—
/- \ дг
дг
Остальные уравнения можно получить, принимая последователь-
последовательно значения индексов: i = k = 2, / == I = 3; i = k = 3, / = / = 1;
(: = fe = l, / = 2, Z = 3; / - k = 2, / = 3, / = 1; / = k = 3, / = 1,
/ = 2, т. е. имеем следующие шесть уравнений совместности деформа-
деформаций в цилиндрических координатах:
2 З2 ег0
дг*
1 »еа
г2 ао2
вео , 1 5е
, _1_/2^!ее____5еП1 2 aer9 \ ^ Q
Д дг дг г -дО /
дг2
52егг
дг2
+
дг~
о д2вг,
дгдг
= о,
1
г 06 дг
Ь6г
ьг0
дга
1 д-ег,
дгдг г дгдд г
dgfl
дгдг
1 д2 вл9 1 да в9г 1
с ооог с огоо /¦
ьое
дг
1 №9г ОвГГ i __п
г д9 дг '
1 д2в7
г д9дг
F.59)
126

7. Уравнения равновесия определяются по формуле F.18).
Предварительно пользуясь формулами B°.83) и B°.84), найдем
соотношения между контравариантными и физическими компонентами
вектора массовой силы, а также тензора напряжений;
/1=/„ P=~h, /3=/г; F.60)
F.61)
При I — 1, учитывая F*37), имеем
L * № дг
Приняв во внимание соотношения F.60), F.61) и F.38), получим
дг г dQ дг '
Выполняя аналогичные действия при i — 2 и / = 3, получим еще
два уравнения равновесия, т. е. в результате будем иметь;
дг
дг
да..
90
дг
I --tin , ~2Н
г ае а?
a©
F.62)
8. Уравнения равновесия в перемещениях;
По формуле B°.25), ссылаясь также на F.37), имеем;
g« = lf g« e I/,-*, g33 = !t gfl = о (/ ф д# F.б3)
Учитывая F.63), F.38) и то, что х1 — г, хг- — 0, г' = г, на осно-
основании F.23) получим
oi
at . 1 а2 их , а2 щ , 1_ дах 2^ да$ а^ ,
2 . г2 аег а?2 г дг г» ае г2
1 —2v
, 2
ав
ае +i—2v
— """ 4- *
г дг rl-2v
F.64)
Используя лапласиан скаляра в цилиндрических полярных коор-
координатах, который согласно B°.93) имеет вид
дг*
дг*
F.65)
ДО

2
и принимая во внимание соотношения F.54), на основании вектор-
векторного уравнения F.64) получим три скалярных уравнения Ламе:
див Uf i бе , р - *
ае 7г" 1—2v дг g
2 диг ив 1 дв j
1 ае р
1 —2v дг
¦+i'.-°-
F.66)
Заметим, что на основании D.15) и F.66) компоненты вектора V2tt
в цилиндрических полярных координатах определяются формулами:
F.67)
_L.?E-, (V9J = —. F.68)
а компоненты вектора grad 9 = V9 равны:
д€>
дг '
9. Уравнения Бельтрами получим на основании тензорного урав-
уравнения F.25).
Векторные компоненты в цилиндрических полярных координатах
тензоров V2 (oij) и V (V2), входящих .в уравнение F.25), соответст-
соответственно равны V2pr, V2pe, V2/>z и -^r (V2), -A- -^ (V2), -^ (V2). Эти
определения аналогичны определениям V2a как вектора с компонен-
компонентами (V2a)r, (V2a)e., (V2aJ и градиента скаляра 2 как вектора, имею-
имеющего компоненты д-2,—:-5тг2, -3—2. На основании этих аналогий
Of T Oxj OZ
векторные компоненты тензоров V2 (oij) и V (V2) найдем, восполь-
воспользовавшись формулами F.67) и F.68). В формулах F.67) вектор и нуж-
нужно заменить тензором (atj), компоненты иг, ив, uz — векторными ком-
компонентами рг, рв, рг тензора (btj). Векторные компоненты тензора
V (V2) определятся формулами F.68), если в них вместо в подста-
подставить V2. При этом производные в формулах F.67) и F.68) необходимо
заменить ковариантными производными ковариантных векторов по
формуле B°.60). В результате тензорное уравнение F.25) можно за-
заменить тремя векторными уравнениями:
V2pr-^I2V2 ощ +рГ) + -4- Vx 2,=.0,
F.69/5
каждое из которых можно заменить тремя скалярными уравнениями.
128

Спроектируем векторы первого уравнения F.69) на координатную
ось г. На основании первого равенства^F.67) имеем
<*,,,,_*.„_-1(8-?-+„„),
а по формуле B°.60) при / = 1, учитывая F.38) и F.54), получим:
V2CTe/ = —— Г^а о02= —— aee, Vj 2, 7 =—i = ——,
В результате будем иметь . -
Если спроектировать первое уравнение F.69), например, на ось г,
то аналогично получим скалярное уравнение, которое будет совпадать
с уравнением, полученным в результате проектирования третьего
уравнения F.69) на ось г. Непосредственно можно убедиться, что сре-
среди девяти скалярных уравнений, эквивалентных системе F.69), толь-
только шесть будет различных — это следующие уравнения Бельтрами:
«"
-О,
1 м as 1 * s\
i+v \ r ¦ ar r* aes /
0,
52 2
1+V
= 0,
дг (г а&
i+v. r аеаг
д 2 е, - агг 1 »И
"" г' ае га i+v агаг
= 0.
F.70)
ком-
ком§ 4. УРАВНЕНИЯ В СФЕРИЧЕСКИХ КООРДИНАТАХ
1. Соотношения между ковариантными щ и физическими
понентами вектора перемещения и по B°.83):
их = иг, иг = гпц, и$= г sini|)ue. F-71)
2. По формулам B°.84) находятся соотношения между ковариант-
ковариантными &ij и физическими e(i)(^ компонентами тензора деформации:
И гг< 14 Wi 33 98» Л E.72)
е12 = r&rq, e2s = г sin i|)e^e. e8l = r sin i|389r. J
3. Дифференциальные зависимости Коши устанавливаются по
5 Зек. 514 129

формуле F.3). Например, найдем зависимости для е^ и ег6 по формуле
F.3), принимая во внимание равенства F.50) и F.71):
1 / . , , . , Ьи« . дит\
^тг&т^+Г51П^-дУ+~жГ
1
— «osin\|) = — г sin 1J3
дг
Ссылаясь на соотношения F.72), найдем:
1 ди$ ит 1 "
г difc г ' °' ~ 2
—+"
1 дцг
дг
г sin if дВ
Аналогично находятся зависимости для других компонент тензо-
тензора деформации от компонент вектора перемещения. В результате по-
получим следующие дифференциальные зависимости Коши в сфериче-
сферических координатах:
1 д"в . «г , "ч
гтг —
диг
д
Л);
еее —
г sin
69
rtg\|3
8rifc =-
\ (ди* , \ диг Ц\ 1/1 С«е
ди,,
"е
2 V дг
4-
диг
г sin tf
F.73)
4. Объемная деформация определяется формулой F.8).
Приняв во внимание равенства F.49), по формуле F.8) найдем
di|; r sin \)з dQ r
и»
F.74)
5. Компоненты тензора малого поворота и вектора поворота опре-
определяются по формулам F.11):
F.75)
6. Уравнения совместности деформаций устанавливаются форму-
формулами F.13) и F.14). Они имеют громоздкий вид.
7. Уравнения равновесия получим по формуле F.18), определив
соотношения между контравариантными и физическими компонентами
вектора массовой силы и для тензора напряжений 1B°.83) и B°.84I:
130

fi = / n= — f P— l
F.76)
F.77)
' r2sm\f * г si n ij-
Используя F.18) при i = 1 и учитывая равенства F.49), получим
.
г2 sin ф L дг * ду дВ J +
+ Г\а о'« + Па о2» + П. а3а + р/Г = 0.
Учитывая соотношения F.76), F.77), а также значения символов
Кристоффеля второго рода F.50), последнее равенство приводим к виду:
Проделав аналогичные операции при i — 2 и 1 = 3, найдем еще
два уравнения равновесия и получим систему трех дифференциальных
уравнений равновесия:
30 r v rr
CVi|>Ctg\|>)-t-p/r=0,
F.78)
Зг г дф г sin if a9 r
8. Уравнения равновесия в перемещениях.
На основании B°.25) и F.49) конгравариантные компоненты метри-
метрического тензора:
g" = 1, g™ = 1/га, g83 = l/H sin2\|). F.79)
Учитывая последние равенства, значения символов Кристоффеля
второго рода F.50) и принимая во внимание, что в сферических ко-
координатах дифференциальный оператор Лапласа имеет вид [B°.93I
w дг* ^ г* ,3ф2 ^ (г sin ф)а дв*
+ i!iliU.\ F.80)
' Зф .'
уравнения равновесия в перемещениях можно получить по F.23).
6* 131

Главе VII
КРУЧЕНИЕ ПРЯМЫХ БРУСЬЕВ
§ 1. ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ УРАВНЕНИЯ
Выяснение напряженно-деформированного состояния призматиче-
призматического бруса, находящегося под действием поверхностных сил, прило-
приложенных только к его торцам, называется задачей Сен-Венана.
Частными случаями ее являются задачи растяжения, кручения и из-
изгиба призматического бруса силами, приложенными к его торцам.
Решения задачи растяжения и задачи чистого изгиба призматиче-
призматического бруса уже рассмотрены в гл. IV, § 8. Задача изгиба призмати-
призматического бруса будет рассмотрена в следующей главе, а в этой главе
рассмотрим кручение прямых брусьев.
Пусть имеем брус постоянного поперечного сечения с произволь-
произвольным контуром L (рис. 7.1). Предполагается, что массовые силы от-
отсутствуют (ft = 0), боковая поверхность бруса свободна от внешних
сил, а к его торцам приложены поверхностные силы, которые приво-
приводятся к противоположно направленным моментам М вокруг оси бру-
бруса.
Начало координат О совместим, например, с центром тяжести од-
одного из торцов, направив ось хь по оси бруса, а плоскость Охххг прой-
пройдет по плоскости торца х3 = 0.
Чтобы исключить поворот и поступательное перемещение бруса,
как' твердого тела, будем считать, что при xt = хг = х3 = 0 выпол-
выполняются равенства
и\ = п\ = п% = 0, G.1)
со? = а>2 = о>э = 0. G.2)
Ставится задача: найти для данного бруса компоненты тензора
напряжений и компоненты вектора перемещения произвольной его
точки К (xt), т. е. выяснить напряженно-деформированное состояние
бруса при заданных условиях.
Поставленную задачу будем решать в напряжениях полуобратным
методом Сен-Венана. По аналогии с известной из сопротивления мате-
материалов задачи кручения бруса круглого поперечного сечения допу-
допустим, что
Оц = °22 = О83'= О12 = 0. G.3)
Остальные компоненты тензора напряжений о28 = о82 и о31 == о13
будем находить так, чтобы при выполнении условий совместности
Бельтрами D.55) и граничных условий D.6) удовлетворялись урав-
уравнения равновесия D.3).
132

Так как. по условию ft = 0, то при принятых значениях для части
компонент тензора напряжений G.3) первые два (i =^ 1 и i = 2) урав-
уравнения равновесия D.3) принимают вид
о188 = 0, с28 8 = 0, G.4)
а третье (i = 3) —
О31.1 + О82,2 = 0- G.5)
Из уравнений G.4) вытекает, что искомые компоненты тензора
напряжений о31 и оз2 не зависят от координаты л:3 и являются функция-
функциями только хг и хг.
Рис. 7.2
Рис. 7.1
Функции о31 = osl (xlt xz) и о82 = о82 (xlt #г) должны удовлет-
удовлетворять условиям совместности Бельтрами D.55). При принятых зна-
значениях напряжений G.3) 2 = oss = 0 и, следовательно, первые четы-
четыре уравнения Бельтрами удовлетворяются тождественно, а два по-
последних принимают вид
V2o31 = 0, ^о„ = 0. G.6)
Здесь и в дальнейшем в этой главе
V2 ( ) = д* (Iдх* + д2 ( )/dxl — оператор Лапласа.
Таким образом, искомые функции о81 (xlt хг) и о2з (*i> -*г2) долж-
должны удовлетворять дифференциальным уравнениям G.5) и G.6). Легко
убедиться, что уравнение G.5) будет удовлетворено, если ввести та-
такую функцию Ф = Ф (xt, х2), что
о31 = дФ/дх^ = Ф-2; о2з = — дФ/dxt = — Фл. G.7)
Функция Ф, с помощью которой определяются компоненты тензо-
тензора напряжений a3i и о2з, называется функцией напряже-
напряжений.
Принимая равенства G.7), уравнения G.6), изменяя порядок диф-
дифференциальных операций, приведем, к виду
(У2Ф).2 = О, (У2Ф)Л =» 0.
{НЕ БОЛЕЕ 1И КНИГИ В I
t ОДНИ РУКИ И 2ХВДВЕ \
133

Из последних равенств следует, что функция напряжений должна
удовлетворять уравнению Пуассона
V*<b = с, G.8)
где с — постоянная, значение которой будет выяснено в следующем
параграфе.
Обратимся теперь к граничным условиям D.6):
oijti, = U. G.9)
Вначале рассмотрим условия на боковой поверхности бруса, ко-
которая по условию задачи свободна от внешних сил (tt = 0).
Рис. 7.3
Рис. 7 4
В любой точке боковой поверхности внешняя нормаль я к ней
перпендикулярна образующей, т. е. л3 = 0. Поэтому первые два усло-
условия G.-9) (при i = 1 и i = 2) удовлетворяются тождественно, а третье
принимает вид (рис. 7.2)
^31^1 ~Ь ^з2^2 = 0, G.10)
где
пх = cos a = dxJdL = dxxldn\ n2 = sin а = — dx-JdL = dxjdn, G.11)
Равенство G.10) означает, что полное касательное напряжение
в контурной точке направлено по касательной к контуру сечения. Дей-
Действительно, левая часть равенства G.10) представляет собой скалярное
произведение вектора касательного напряжения в контурной точке
х = o8i эг + о3г э2 и единичного вектора по внешней нормали к
контуру п = nidi + пгэ^. Так как т • п = 0, то вектор т перпен-
перпендикулярен вектору я.
Принимая во внимание равенства G.11) и G.7), условие G.10)
представим в следующем виде:
дФ dx2 , до dxx _ с/Ф „п у 12j
dL
U. Л j t( Vf /л
d/.
dL
Последнее равенство показывает, что на контуре L поперечного се-
сечения функция напряжений Ф должна иметь постоянное значение.
Если поперечное сечение бруса представляет собой односвязную
область, т. е. сплошное сечение, то величина «той постоянной может
134

быть принята произвольно, поскольку значения напряжений о31 и о82,
как это следует из равенств G.7), при добавлении к функции напряже:
ний Ф (*,, х2) любой постоянной не изменяются. Поэтому в случае
сплошных поперечных сечений бруса постоянное значение функции
напряжений на контуре принимают обычно равным нулю, т. е.
Ф (*i, x2) \L = 0. G.13)
Если поперечное сечение бруса представляет собой многосвязную
область, т. е. брус имеет продольные цилиндрические полости и,
следовательно, граница поперечного сечения будет состоять из не-
нескольких замкнутых контуров Lv L2, L3, ..., /,„,- охваченных внеш-
внешним контуром Lo (рис. 7.3), то в этом случае функция напряжений
Ф (х1у х2) на контурах Lh (k = 0, 1, 2, ..., п) принимает постоянные,
но на каждом контуре, вообще говоря, различные значения Фк (k =
= 0, 1, 2, ..., п). При этом постоянные Фй на контурах Lk не могут
быть выбраны произвольно. Можно произвольно выбрать лишь одну
постоянную, например, принять постоянную Фо на внешнем контуре
Lo равной нулю, а остальные постоянные ФЛ (k = 1, 2, ..., п) на вну-
внутренних контурах получат конкретные значения, которые определяют-
определяются на основании теоремы Бредта о циркуляции касательного напряже-
напряжения, изложенной ниже в § 2 этой главы.
Граничные условия для функции напряжений в случае многосвяз-
многосвязного поперечного сечения имеют вид
Ф'(*i. хг) к„ = Q. ф(*1>*2)кй = фь (&=1,2 п). G.13')
Рассмотрим теперь граничные условия на торцах бруса.. Внешние
нормали к торцам параллельны оси х3. Поэтому щ = щ = 0, п3 ==
= ± 1 и граничные условия G.9) на торцах бруса принимают вид
± о si = к, ± оа2 = tz, ts = 0, G.14)
где знак плюс принимается для торца, внешняя нормаль к которому
совпадает с положительным направлением оси х3.
Из равенств G.14) следует, что искомые напряжения оп и о3г
распределяются по поперечным сечениям таким же образом, как и по-
поверхностные силы к и t2 на торцах бруса. Следовательно, внутренние
силы на поперечных сечениях бруса, как и поверхностные силы на его
торцах, должны приводиться только к моменту относительно оси бру-
бруса, т. е. к крутящему моменту М.
Покажем, что проекции на оси хг и хг внутренних сил в любом по-
поперечном сечении действительно равны нулю.
Пусть имеем некоторое многосвязное поперечное сечение бруса
(рис. 7.3), причем на наружном контуре Lo функция напряжений
Ф (хъх2) имеет постоянное значение Фо, а на внутренних контурах —
постоянные значения Ф,, Ф2, ..., Фп- Проекция на ось хг внутренних
сил в произвольном поперечном сечении, т. е. поперечная сила QXi,
будет равна
— dxxdxv G.15)
135

Воспользуемся формулой Грина
— ) dx1 dx2 == ф Pdxx + Qdxif G.16)
где Р и Q — функции, непрерывные вместе со своими частными про-
производными первого порядка в замкнутой области F, и преобразуем
интеграл в правой части равенства G.15) в интеграл по контуру L
области F.
В нашем случае Р (хъ х2) = — Ф {xlt хг), Q (хи х2) = 0. Тогда
' GЛ7)
где интеграл по контуру L в случае многосвязной области F представ-
представляется, как известно, суммой интегралов по внешнему контуру Lo
и всем внутренним контурам Lh области F; причем каждый контур
обходится в положительном направлении, т. е. так, чтобы область F
все время оставалась по левую сторону линии обхода. Это достигается,
если внешний контур обходить против часовой стрелки, а внутрен-
внутренние — по часовой стрелке (рис. 7.3).
Учитывая, что функция напряжений Ф (xlt #2) и на внешнем конту-
контуре и на внутренних контурах принимает постоянные значения Фк
k = 0, 1, 2, ..., п), равенство G.17) можно привести к виду
dXl = 0. G.18)
На основании G.15) и G.18) Q*, = 0. Аналогично можно показать,
что QX2 также равна нулю.
Найдем момент внутренних сил в произвольном поперечном сече-
сечении относительно оси xs, т. е. крутящий момент М:
м = SS
F
SS аз1 *i) dJh. dxt. G.19)
F
Используя равенства G.7), получим
М = -JJ (Xl Фд + х2 Ф,2) dXl. dx2 = - JS [fa Ф),! -f
F
F F
+ fa Ф),J dXi dx2 + 2 Ц (bdxi dx» G.20)
Первый интеграл в правой части последнего равенства преобра-
преобразуем по формуле Грина G.16) в интеграл по контуру, .ограничивающий
многосвязное сечение. В данном случае Р = — х2Ф, Q = хгФ и, учи-
136

тывая сделанное выше напоминание об интегрировании по многосвяз-
многосвязному контуру, получим
).i-<-*.<I>),J dXl dx^
— 2 фк & (—4 dxx + xx dxj. . G.21)
Криволинейные интегралы
(— xjdx, + лг^г) (* - 0, 1, 2, ..., я)
преобразуем по формуле Грина G.16).
В этом случае Р — — х%, Q = xt и, следовательно,
fj A + 1) ^ldX2 e 2^ft> G.22)
где Fft — площадь, ограниченная контуром Lk,
Тогда равенство G.21) примет вид
O)it\dx1dx2 = 2O0F0—2 S Фй^ G.23)
и формула G.20) для крутящего момента приводится к виду
М => 2 JJ Odx, d«, - 2Ф0 f 0 + 2 2 Фй f*. G.24)
Положим Фо = 0, что, как отмечалось, допустимо. Тогда формула
G.24), устанавливающая связь между крутящим моментом и функцией
напряжений в случае многосвязного поперечного сечения бруса, при-
примет вид
G.25)
<!=]
Этой формуле можно дать простое геометрическое истолкование.
Пусть имеем, например,-двусвязное поперечное сечение бруса (рис.7.4),
для которого известна функция напряжений Ф (хи х2). Если из каж-
каждой точки поперечного сечения в направлении оси х3 отложить в не-
некотором масштабе соответствующие значения функции напряжений
Ф (*i, Хг)> то получим некоторую фигуру, ограниченную поперечным
сечением с контурами Lo и Llt поверхностью, изображающей функцию
137

Ф (xi> xz) и цилиндрической поверхностью с контуром основания L^.
Очевидно, что интеграл \j(bdx1dx2 определяет объем этой фигуры; про-
F
ижедение Ф^ равно объему цилиндра, основание которого очерчено
контуром Lu а его высота соответствует значению функции напряже-
напряжений Ф\ на контуре ?*.
Следовательно, крутящий момент М будет равен (в принятом мас-
масштабе) удвоенному объему фигуры («холма»), ограниченной поверх-
поверхностью, изображающей функцию напряжений, и плоскостями
ф = ф0 = о и Ф = Фх.
В случае бруса с односвязным поперечным сечением (сплошным),
т. е. без внутренних полостей, формула G.25) принимает вид
М = 2$fodxldx2. G.26)
§ 2. ПЕРЕМЕЩЕНИЯ ПРИ КРУЧЕНИИ ПРИЗМАТИЧЕСКИХ БРУСЬЕВ
И ТЕОРЕМА О ЦИРКУЛЯЦИИ КАСАТЕЛЬНОГО НАПРЯЖЕНИЯ
При значениях компонент тензора напряжений, определяемых
равенствами G.3), имеем 2 = ass = 0. Объемная деформация в на
основании формулы D.46) будет равна нулю:
в = 1-2v 2 = 0. G.27)
Тогда уравнения закона Гука D.4) примут вид
oij = G (uij + Ujt). G.28)
Отсюда, учитывая равенства G.3) и G.7), находим:
"l.i = ,2 = «з.з = 0, и1Л + .1 = 0; G.29)
,3 + «3,2 = О23/С = — Фд/G,
«зд + «1,з = опЮ = Ф.в/С G.30)
Искомые функции uL и и2 будут удовлетворять уравнениям G.29)
и условиям закрепления G.1), если их принять в следующем виде:
«! = — §X2XS, U2 = §Х!Ха, G.31)
где ¦& — постоянная.
Функции Их и и2 характеризуют перемещения точек поперечного
сечения в его плоскости. Найдем радиальное иг и окружное и, переме-
перемещения произвольной точки поперечного сечения (рис. 7.5). Спроекти-
Спроектировав на радиальное направление г перемещения их и и2 точки К, по-
получим
иг --= «! cos a + u2 sin a — — дхгх^/г + ¦дх1х3х2/г =*0,
т. е. произвольная точка поперечного сечения не перемещается в ра-
радиальном направлении.
138

Проектируя их и иг на направление t, перпендикулярное радиаль-
радиальному направлению, найдем окружное перемещение:
«t = «2 cos a — «! sin a =
Отсюда следует, что при фиксированном значении х3, т. е. в не-
некотором поперечном сечении, перемещение ut прямо пропорционально
расстоянию г точки К от оси бруса. Это означает, что при кручении
бруса произвольного поперечного сечения радиальные лучи остаются
прямыми и поворачиваются на угол ftx3, который называется углом
закручивания на длине х3; $ — относительный угол закручивания,
т. е. угол закручивания на единицу длины бруса.
х2\
Рис. 7.5
Рис. 7.6
Обратимся к уравнениям G.30). Продифференцируем первое из
них по *i, а второе — по хг, вычтем результаты и получим
— «1,32—
G.32)
С учетом равенств G.31) последнее уравнение принимает вид
VM) = — 2GO. . G.33)
Сопоставляя уравнения G.33) и G.8), находим, что постоянная в
уравнении G.8) с = — 2Gb.
Из G.29) следует, что функция и3 не зависит от координаты х9,
а ее частные производные по Xi и х2 согласно G.30) равны:
«3,1 = ФУС — "l.s'i «3,2 = — Фд/С— И2,3 ' G-34)
или, принимая во внимание G.31),
и3,1 = Ф.,/6 + ®х2; ' G.35)
«3.2 = - (O.i/Q + tt.*i).
Таким образом, при кручении прямого бруса произвольного по-
постоянного сечения можно определить и перемещения, и напряжения
о31 и 0з2, если известна функция напряжений Ф (хи х2), удовлетворяю-
удовлетворяющая уравнению Пуассона G.33) и граничному условию G.13).
Поскольку уравнение Пуассона получено исходя из уравнений
совместности Бельтрами, то уравнения G.35) всегда интегрируются
и в результате находится функция и3 (хи х2), определяющая искрив-
4 139

ление (депланацию) поперечного сечения бруса при его кручении.
Если поперечное сечение сплошное (односвязная область), то урав-
уравнения Бельтрами или соответствующие им дифференциальные зависи-
зависимости Сен-Венана D.2) являются не только необходимыми и достаточ-
достаточными условиями интегрируемости уравнений G.35), но также необ-
необходимыми и достаточными условиями, чтобы определяемая функция
us была однозначной. В случае многосвязного поперечного сечения
уравнения Бельтрами являются необходимыми, но недостаточными
условиями однозначности функции и3 (х1у х2). Необходимым и. доста-
достаточным условием однозначности функции и3 в этом случае является
равенство нулю следующего интеграла по любому замкнутому конту-
контуру L', не пересекающему контуров сечения (рис. 7.6):
2 = 0. G.36)
Учитывая выражения G.35) и G.7), имеем
.2dxi—xldx2)^0. G.37)
L'
Второй интеграл в последнем равенстве преобразуем по формуле
Грина:
,-xxdx.) = \\( °l~*'' ^¦)dxldxi=-2Ft
J ^ \ дх, дх, )
где F' — площадь, ограниченная контуром V'.
Тогда условие однозначности перемещения G.37) принимает вид
o32dXi - 2G$F*. G.38)
Поскольку — dxi = dL' sin a, dxz = dL' cos a, подынтегральное
выражение в равенстве G.38) приводится к виду
оsi^i + as2dxz = (— a31 sin a + a32 cos a) dL1.
Выражение в скобках последнего равенства представляет собой
проекцию полного касательного напряжения т в рассматриваемой
точке на направление касательной ( к контуру L' в этой точке, т. е.
напряжение т( (рис. 7.6). В результате условие однозначности переме-
перемещения «з G.38) принимает вид
§TtdL' = 2G$F'-. G.39)
Интеграл в левой части равенства G.39) называется циркуляцией
касательного напряжения при кручении. Равенство G.39) выражает
содержание теоремы Р. Бредта, которую можно сформули-
сформулировать так: для всякого замкнутого контура, расположенного в преде-
пределах поперечного сечения бруса и не пересекающего его границ, циркуля-
циркуляция касательного напряжения при кручении равна площади, ограничен-
ограниченной этим контуром, умноженной на 2GO.
Теорема Бредта выражает необходимые и достаточные условия
однозначности определяемых с помощью функций "напряжений
140

Ф (хъ хг) осевых перемещений и9 при кручении бруса. Циркуляцию
касательного напряжения можно выразить непосредственно через
функцию напряжений Ф. Действительно, имеем
/ дФ , дФ \
—a31sma= — —— cosa-f —_Sina),
\ дх! дх2 /'
т.е.
т, = —-
дФ
дп
G.40)
Формула G.39) принимает вид
—
дп
G.41)
Совмещая замкнутый контур 1} с каж-
каждым внутренним контуром многосвязного
поперечного сечения, получаем -п уравнений,
позволяющих определить п постоянных зна-
значений функции напряжений на п внутрен-
внутренних контурах поперечного сечения:
— dL= -2G&Fk.
дп
Рис. 7.7
G.42)
Здесь Fh (k = l, 2, ..., n) — площади, ограниченные внутренними
контурами Lfe.
Отметим, что при постановке рассматриваемой задачи начало коор-
координат О было совмещено с центром тяжести одного из торцов бруса.
Однако начало координат можно совместить с любой точкой торца
бруса. Рассмотрим новую систему координатных осей О*х[х'лх'а, па-
параллельных системе ОхххгХй, с началом О' {аъ а%), где аг,а2 — коор-
координаты относительно старых осей (рис.7.7). Тогда перемещения и{
и «2 будут определяться равенствами
u'i ~ — #*2*я = — * (*2 — аг) х3 = «! + $а2Ха, )
1 ( _ * * _ а / _ а | G.43)
а для определения перемещения и'3 имеем уравнения
и'3 , =
— а,),
Напряжения определятся по формулам
о;2= -аФ'/а^; = с (и,., + «;.,) = с («;it +
Отсюда
7а (л;а'J =
- G.44)
G.45)
G.46)
141

Граничное условие G.10) принимает вид
оз1 П1 + Оз?«?=-—- т—2- -f-—-—-*_ = —_ =0. G.47)
сЫ d/. d* 4/ -7/
Из последних равенств вытекает, что функция напряжений Ф' сов-
совпадает с Ф и, следовательно, изменение начала координат не отражает-
отражается на напряжениях.
Поскольку Ф'' = Ф, то уравнения G.44) запишутся так:
Интегрируя первое из этих уравнений, получим
и3 = на - &a2Xl + f (хг). G.49)
Продифференцировав это равенство по Хг и сопоставив полученный
результат со вторым уравнением G.48), найдем
df (хг)/дх2 — $av,
интегрируя которое, получим
/ (#г) = ^«1-^2 + const.
Тогда
и, = и3 — Ъа.гХ\ + ^atxz + const. G.50)
Из равенств G.43) и G.50) следует, что перемещения и[, и'г, и'3
отличаются от перемещений ии и2, и3 на величину жесткого смещения.
§ з. функция кручения
Задача кручения призматического бруса произвольного попереч-
поперечного сечения может быть решена полуобратным методом в перемеще-
перемещениях. Именно такой путь был принят Сен-Венаном, когда в 1847 году
он впервые решил эту задачу.
Задавшись перемещениями
иг = flx,A-3, G.51)
из уравнений Ламе D.13) и граничных условий-D.21) будем определять
перемещение н3 в следующем виде:
и3 = #Ф (*i. х2). . G.52)
Из G.51) и G.52) вытекает, что
в = uij = 0. G.53)
Тогда первые два уравнения Ламе удовлетворяются тождественно,
а третье принимает вид
V2qp = 0, G.54)
т . е. функция ф (*!, хг), при помощи которой находится перемещение
«з (*ъ хг), должна быть гармонической функцией, определенной в об-
области поперечного сечения бруса.

На боковой поверхности, свободной от внешних сил, первые два
граничных условия D.21) удовлетворяются тождественно, а третье
(t = 3) приводится к равенству
дфп | L = *2«i — xxn2. G.55)
Таким образом, задача кручения призматического бруса сводится
к определению гармонической функции ф (хи х2), определенной вну-
внутри ограниченной области, производная которой по нормали к грани-
границе этой области должна подчиняться условию G.55), т. е. к решению
внутренней задачи Неймана.
Применив формулу Грина A°. 113) к частному случаю \|з = 1> по-
получим, что если ф — гармоническая функция, то
[
^-dL = 0. G.56)
an
Следовательно, задача Неймана имеет решение, когда соблюдается
условие G.56).
В нашем случае, учитывая G.55) и используя соотношения G.11),
убеждаемся, что условие существования решения задачи Неймана со-
соблюдается, а именно:
U
г
l
Предположим, что получили два различных решения данной зада-
задачи ф<х> и фB>. Разность этих решений обозначим через ф = ф<х> —
— Ф<2>. Очевидно, что У2ф = 0 и df/дл | ?. = 0. Тогда, применяя
формулу Грина A°. 113) для случая ф = ф иг|> = ф, найдем
^grad ф-grad фс^ йхг — 0. G.57)
Данное равенство может иметь место только тогда, когда ф — по-
постоянная. Этим показано известное положение, что внутренняя зада-
задача Неймана имеет сколько угодно решений, причем разность любых
двух из них равна постоянной.
Таким образом, функция кручения ф (xlt xz) определяется с точ-
точностью до постоянного слагаемого. Однако эта постоянная не отра-
отразится на напряжениях, возникающих при кручении бруса, так как
на основании формулы G.28) закона Гука находим, что отличные от
нуля компоненты тензора напряжений зависят от производных функ-
функции ф (*,, х2):
а„ = G® (ф 1 — х2), ом = G® (ф,2 + хх). G.58)
Очевидно, как это вытекает из формулы G.52), замена ф на ф + const
приведет лишь к жесткому поступательному перемещению бруса
вдоль оси х3.
143

Гармоническая функция ер (хи х2) называется функцией кручения.
Она характеризует депланацию поперечных сечений бруса и поэтому
ее называют также функцией депланации. Известно, что гармониче-
гармоническая функция достигает своего максимального значения на границе
области ее определения (теорема, называемая «принципом максималь-
максимального значения» [49]). Это означает, что депланация поперечного сече-
сечения бруса при его кручении достигает наибольшего значения на кон-
контуре сечения.
Принимая во внимание G.58), формула G.19) для крутящего мо-
момента принимает вид
М = Gii |J (к2, + х\ + л^ф 2 — х2ф j) dx^dx% G.59)
F
или
М = Ср, G.60)
т. е. крутящий момент пропорционален относительному углу закручи-
закручивания Ь.
Коэффициент пропорциональности С называется жесткостью при
кручении. Жесткость при кручении равна произведению модуля сдви-
сдвига G на величину Ук, зависящую только от геометрии поперечного се-
сечения бруса:
C = GJK, . G.61)
где величина JK, называемая геометрической характеристикой жест-
жесткости при кручении, определяется формулой
•'к = Я (А + xl + х&л — хвфд) dx^xi = Jp—D. G.62)
F
Здесь Jp = JJ (x\ + x\) dxrdx2 = Л, + Л, — полярный момент
инерции поперечного сечения бруса относительно начала координат
(центра тяжести поперечного сечения), а величина D определяется
формулой
D = Я [(дс«Ф)д - (*1<р)?,1 dxtdxt. G.63)
F
Применяя формулу Грина G.16), получим
D = j Ф (х^ + xidxt) = A/2) | ydr\ G.64)
где г2 = х\ + х\.
Можно показать, что для всех форм поперечных сечений
Ja < JP. G.65)
Действительно, согласно теореме Клапейрона E.6), работа дефор-
деформации U равна половине работы внешних сил на произведенных ими
перемещениях:
1ЯТл' GМ)
144

Внешними силами в рассматриваемой задаче являются только по-
поверхностные силы на торцах бруса, приводящие к моментам М. По-
екольку взаимный угол поворота торцов бруса длиной / {рис. 7.1)
равен bl, то
А = МЫ G.67)
или, учитывая G.60),
А = Ст. G.68)
Тогда
U = СЬЧ12. G.69)
Поскольку при деформированном состоянии U > 0, то из равен-
равенства G.69) вытекает, что жесткость при кручении положительна:
C = GJS=G (Jp - D) > 0. " G.70)
Покажем, что величина D, зависящая от депланации поперечного
сечения, не может быть отрицательной. В самом деле, в силу G.64)
и соотношений G.11) имеем
D = j ф (*,d*, + x2dx2) = j ф (— ххпг + лг2«х) dL. G.71)
Учитывая равенство G.55), находим
Теперь на основании формулы Грина A°.ПЗ), в которой в данном
случае надо принять q> = <р, ф = ф и учесть уравнение G.54), получим
dL
= JJ [(Ф,1)г + (ч- J2i dxx dx2 ^ 0. G.73)
Из неравенств G.70) и G.73) вытекает соотношение G.65), в котором
знак равенства имеет место только для поперечных сечений в форме
круга и кругового кольца, для которых депланация и3 = Фф = 0,
а в силу G.64) и D = 0.
Введем теперь гармоническую функцию г|; (хи х2), сопряженную
с функцией кручения ф (хи х.г), т. е. удовлетворяющую условиям Ко-
ши—Рпмана:
Ф.1 =<Ф.г; Ф.г = —Ул, G-74)
Подставив в формулы G.58) вместо производных функции ф (xlt x2)
производные функции г)з (xlt х2) в соответствии с условиями Коши—Ри-
мана G.74), получим следующие формулы для напряжений:
о31 = G& ДО,, — xt), о32 - — СдA|гд — хх). G.75)
Выясним граничное условие для гармонической функции г}э (хь х
которая называется сопряженной функцией кручения.
145

По определению, имеем
Ji.=_^n] + i5.n2. G.76)
on дх\ дх2
Исходя из условий G.74) и ссылаясь на G.11), получаем
д(р dty с1хг . д\\> dx, _ с/гр ,т jj.
дп дх2 dL dxt dL dL
Тогда на основании G.55), учитывая G.77), находим
dL L » dL dL
или после интегрирования
$\l = (x}+ xl)/2 + Co. G.78)
Таким образом, если для нахождения гармонической функции кру-
кручения ф (хи х2) необходимо решать задачу Неймана, то нахождение,
сопряженной функции кручения \|; (*,, х2) сводится к задаче Дирихле,
которая, как известно, при весьма общих условиях имеет решение,
и притом единственное.
Из того, что сопряженная функция кручения яр (xlt x2) является
гармонической, т. е. V2\|5 = 0, а также исходя из равенств G.33),
G.13) и G.78) непосредственно устанавливается следующее соотноше-
соотношение между функцией напряжений Ф (хи х2) и сопряженной функцией
кручения:
ф = СО ly — (jcf + х\I2\. G.79)
В случае многосвязного поперечного сечения граничное условие
для функции \р (хх, х2)
Ф U = (х\ + х\I2 + Chr G.80)
где Сь — постоянные, вообще говоря, различные на каждом из всех
контуров Lh, ограничивающих поперечное сечение бруса.
Одна из этих постоянных, например Со, на внешнем контуре может
быть выбрана произвольно, а остальные должны определяться из усло-
условий G.42), которые, учитывая соотношение G.79), приводятся к виду
Ссылаясь на G.11) и G.22), получаем
G.81)
Решение задачи кручения бруса сводится, следовательно, к опре-
определению в области его поперечного сечения одной из функций: Ф, ф
или \|). В дальнейшем будем пользоваться функцией напряжений Ф.
146

§ 4. ТЕОРЕМА О МАКСИМУМЕ КАСАТЕЛЬНОГО НАПРЯЖЕНИЯ
При практических расчетах екрученного брува важно найти мак-
еимальное касательное напряжение, а также знать точку поперечного
сечения, в которой оно возникает.
Докажем теорему: касательное на-
напряжение на поперечном сечении бру-
бруса при его кручении всегда достигает
максимального значения в точке кон-
контура поперечного сечения.
Одно из доказательств этой теоре-
теоремы состоит в следующем. Пусть в про-
произвольной внутренней точке М попереч-
поперечного сечения касательное напряжение
равно т,м. Направим ось хх параллель-
параллельно тм (рис. 7.8). Тогда хм = (as,),w =
= (дФ/дх2)м' Поскольку функция на-
напряжений Ф (#!, х2) удовлетворяет
уравнению Пуассона G.33), то
Рис. 7.8
дх9
. (V2 Ф) = 0 или V2
дф
= V2 (а„) = О,
G.82)
т. е. а3) = Ф2 — гармоническая функция.
В теории гармонических функций доказывается теорема (мы на
нее уже ссылались, см. о. 144), согласно которой гармоническая функ-
функция не может принимать экстремальное значение во внутренней точке
области ее определения. Поэтому в окрестности произвольно выбран-
выбранной точки М всегда найдется такая точка N, для которой будем иметь
Так как
(СГ31)м.
(а,х)дг
G.83)
G.84)
G.85)
то на основании соотношений G.83), G.84) и G.85) заключаем, что
т„ > хм. G-86)
Поскольку точка М является внутренней произвольной точкой
поперечного сечения, то неравенство G.86) означает, что касательное
напряжение при кручении бруса не может достигать максимума во
внутренней точке его поперечного сечения и, следовательно, макси-
максимальное касательное напряжение имеет место в какой-либо точке
контура сечения.
На основании равенства G.10) было отмечено, что полное каса-
касательное напряжение на поперечном сечении в его контурной точке
всегда направлено по касательной к контуру сечения. Отсюда, в ча-
частности, следует, что в точке Л (рис. 7.8), которая является вершиной
выступающего угла, касательное напряжение на поперечном сечении
равно нулю. Действительно, если предположить обратное и разложить
147

вектор касательного напряжения т в точке на составляющие х'п и т?
по нормалям к пересекающимся в точке А кривым контура, то обе
составляющие, будучи нормальными к контуру, должны быть равны
нулю. Следовательно, и т = 0.
Отметим еще одну особенность распределения касательных напря-
напряжений на поперечном сечении. Через произвольную точку М в сече-
сечении проведем кривую Ф (хг, х2) — const. Очевидно, что вдоль этой
кривой должно быть
дФ дФ dxx , дФ dx2 ~
' dL dx, dL дх% dL
Принимая во внимание равенства G.7) и G.11), получим
т. е. касательное напряжение в произвольной точке поперечного се-
сечения бруса направлено по касательной к кривой Ф (хи х2) — const,
проходящей через эту точку. Эти кривые называются траекториями
касательного напряжения. Очевидно, что контур поперечного сечения
является траекторией касательного напряжения.
§ 5. МЕМБРАННАЯ АНАЛОГИЯ
Оказывается, что задача определения функции напряжений Ф (xlt
х2) при кручении бруса и задача нахождения прогибов однородной
идеально гибкой мембраны, равномерно натянутой на жесткий кон-
контур и нагруженной равномерным давлением, являются одной и той
же математической задачей, если контур, на который натянута мем-
мембрана, совпадает с контуром поперечного сечения бруса.
Рассмотрим упомянутую мембрану, равномерно натянутую на
плоский жесткий контур L, совпадающий с контуром односвязного
поперечного сечения скручиваемого бруса и с координатной плоско-
плоскостью Охгх2 (рис. 7.9). Пусть q— растягивающее усилие, приходящее-
приходящееся в каждом сечении мембраны на единицу его длины, р — давление
на единицу площади мембраны, w (хъ х2) — перемещение точки средин-
срединной поверхности мембраны в направлении оси х3, перпендикулярной
плоскости контура. Предполагается, что начальное натяжение мембра-
мембраны равномерным усилием q настолько велико, что при деформировании
мембраны под действием давления р это усилие q практически нигде
не изменится.
Выделим элемент abed мембраны, стороны которого параллельны
осям координат, и рассмотрим условия его равновесия в деформиро-
деформированном состоянии, соответствующем давлению р. Элемент находится
в равновесии под действием приложенных к его граням сил натяжения
и силы давления. Спроектируем эти силы на ось х3. На грань элемента
¦ ab действует сила натяжения qdx2, направленная к оси хх под углом а,
который ввиду малости перемещений w (xlt x2) можно считать равным
а — dw/dxu а усилие qdx2 на противоположной грани cd направлено
под углом а + gj dxr — g^- + ^р dx^ Силы на гранях ab и cd дают
148

не ось х3 проекцию
Аналогично, силы на гранях ad и bo даюг на ось ла проекцию
~dXl
Уравнение равновесия элемента принимает вил
Отсюда находим
___ dXi dx% + q —^- dxi dxz + pdxx dx\ — 0.
OX% OX
p
дхг, дх%. q
или
У2ш = — plq. G.87)
Перемещения (прогибы) w (xlt хг) мембраны на жестком контуре L
равны нулю. Поэтому граничное условие будет
w (xu x2) U - 0. G.88)
Таким образом, граничное условие G.88) для перемещений мем-
мембраны тождественно с граничным условием G.13) для функции напря-
напряжений, а дифференциальные уравнения G.87) и G.33) становятся так-
также тождественными, если принять
Ф (х„ х2) = хы> (хи хг), G.89)
где коэффициент пропорциональности
х =? 2G$q/p. G.90ч
i
Итак, значения функции напряжений Ф (хи х2) при кручении
бруса сплошного сечения пропорциональны прогибам мембраны, рав-
равномерно натянутой на жесткий контур, повторяющий контур попереч-
поперечного сечения скручиваемого бруса, и находящейся под действием
одностороннего равномерного давления. В этом и заключается мемб-
мембранная аналогия, установленная в 190S году ПрандтлемA875—1953).
Мембранную аналогию можно использовать и при кручении бру-
бруса с многосвязным поперечным сечением. На каждом внутреннем кон-
контуре Lk функция напряжений Ф (хи хг), как уже известно, должна
иметь постоянные значения Ф,{, определяемые из уравнений G.42).
Поэтому и прогибы w (дг,, хг) мембраны в точках, соответствующих
точкам контура Lh поперечного сечения бруса, должны быть одинако-
одинаковыми и в силу соотношения G.89) равными
wk = Фь/х. G.91)
Этого можно достигнуть, если мембрана будет натянута на непод-
неподвижный жесткий внешний контур и на жесткие невесомые диски,
контуры которых соответствуют внутренним контурам поперечного
149

сечения бруса, причем эти диски должны иметь возможность переме-
перемещаться только поступательно в направлении, перпендикулярном к пло-
плоскости внешнего контура (рис. 7.10).
Если теперь вместо функции напряжений Ф (хи х2) подставить ее
значение согласно равенствам G.89) и G.90) в G.42), то получим
—q&j-dL = pFh. G.92)
Здесь pFk — сила давления р, воспринимаемая диском, соответст-
соответствующим внутреннему контуру Lft; Fk — площадь, .ограниченная кон-
контуром Lk. Левая часть равенства G.92) представляет собой сумму
Рис. 7.10
проекций на ось х3 сил натяжения мембраны, действующих на конту-
контуре Lh.
Мембранная аналогия позволяет наглядно представить характер
функции напряжений, а также сделать заключения о распределении
напряжений на поперечном сечении скрученного бруса. Действитель-
Действительно, в ряде случаев весьма легко представить форму выпученной мем-
мембраны, а следовательно на основании G.89) и характер функции на-
напряжений.
Если рассечь поверхность выпученной мембраны плоскостями
w (хи дг2) = const, то получим на ней горизонтали, которые будут со-
соответствовать линиям Ф fa, x2) = const, т. е. траекториям касатель-
касательного напряжения на поперечном сечении скручиваемого бруса. Полное
касательное напряжение в некоторой точке поперечного сечения на-
направлено, как это уже отмечалось, по касательной к кривой Ф (хих2) —
= const, проходящей через данную точку, и на основании G.40)
и G.89) равно
^^ G.93)
дп
дп
Таким образом, величина касательного напряжения xt в некоторой
точке определяется уклоном мембраны dw/dn по нормали к горизонта-
150

ли w (х1} х2) = const. Отсюда становится очевидным, что касательное
напряжение достигает максимума в тех точках, где горизонтали наи-
наиболее сгущаются.
Из выражения G.26) с учетом соотношения G.89) ясно, что крутя-
крутящий момент пропорционален объему V, ограниченному изогнутой по-
поверхностью мембраны и плоскостью ее контура:
М =
= 2kV.
G.94)
Мембранная аналогия позволяет экспериментально определять рас-
распределение касательных напряжений на поперечном сечении любого
очертания путем измерения прогибов мембраны. Ряд исследователей
х,
Рис. 7.11
Рис. 7.12
в качестве мембраны использовали мыльную пленку, в которой вели-
величина постоянного натяжения q определяется силами ее поверхностно-
поверхностного натяжения. Другие исследователи использовали резиновые мем-
мембраны. В лаборатории испытания материалов МВТУ им. Баумана
имеется прибор с резиновой мембраной конструкции С. В. Брярши-
нова. Описание этого прибора и порядок определения ттах с его по-
помощью приводятся в книге [45].
Помимо мембранной аналогии Прандтля имеют место гидродинами-
гидродинамические аналогии с ламинарным течением вязкой жидкости (аналогия
Буссинеска), с потенциальным течением идеальной несжимаемой жид-
жидкости (аналогия Томсона и Тета) и аналогия Гринхилла с вихревым
течением идеальной несжимаемой жидкости.
Аналогия Гринхилла основана на том, что функция напряжений при
кручении бруса математически тождественна с функцией тока при
движении идеальной несжимаемой жидкости в трубе того же сечения, ¦
чго и поперечное сечение скручиваемого бруса. Это означает, что рас-
распределение скоростей гидродинамической задачи математически тож-
тождественно с распределением касательных напряжений при кручении.
Гидродинамические аналогии позволяют сделать некоторые каче-
качественные выводы о распределении касательных напряжений при кру-
ченйи призматического бруса. Если, например, в поперечном сечении
скручиваемого бруса имеется отверстие — след круглой цилиндриче-
цилиндрической полости (рис. 7.11), диаметр которого значительно меньше харак-
151

терного линейного размера поперечного вечения, то при обтекании
такой полости скорости в точках а и b будут равны нулю, а в точках
cud — значительно больше скорости натекающего потока. Отсюда
заключаем, что в окрестности точек с и d будут возникать касательные
напряжения, значительно большие (удваиваются) тех, которые были
бы в точках в и d при отсутствии полости. Рассматривая циркуляцион-
циркуляционное течение идеальной несжимаемой жидкости в трубе g поперечным
сечением в виде прямоугольника (рис. 7.12), легко убедиться, что
скорости жидкости в угловых точках а, Ь, о и d равны нулю, а вблизи
середин длинных, сторон (точки тип) скорости будут наибольшими.
Следовательно, при кручении бруса прямоугольного сечения макси-
максимальные касательные напряжения будут возникать в точках тип.
Подробное описание гидродинамических аналогий и электродина-
электродинамических аналогий приводится, например, в книге ПО].
§ 6. БРУС ЭЛЛИПТИЧЕСКОГО СЕЧЕНИЯ
Контур поперечного сечения (риа. 7.13) определяется уравнением
х\1аг + хЦЬ' = 1. G.95)
Очевидно, что граничное условие G.13) функции напряжений
Ф (хъ х2) будет удовлетворяться, если ее взять в аледующем виде:
Ф (хх, xj = А (х\/аг + х\№ - 1), G.96)
где А — постоянная.
Подставив принятое выражение G.96) для функции напряжений
в уравнение Пуассона G.33), найдем
А = — GMW/ta9 + W). G.97)
Тогда функция напряжений, удовлетворяющая граничному усло-
условию и основному уравнению G.33), имеет вид
L) G.98)
Теперь выражения G.98) для функции Ф (хъ х2) подвтавим в фор-
формулу G.26):
Так как первый интеграл в правой части последнего равенства есть
площадь поперечного сечения
F = l\dxxdxz = nab, G.99)
а два другие интеграла — осевые моменты инерции сечения:
Л, = ft" x\ dxy dx2 = nab"/4,
JXt = f f x\ dxx dxi=na* t/4, G.100)
152

то получим
М = G$na*b8/(a* + Ьг) = СФ.
G.101)
Здесь С —жесткость при кручении, которая вавивит от модуля
сдвига материала бруеа и от геометрии его поперечного «ечения:
С = GncPbPKa* + Ьа) = GJM
G.102)
гдеУк = aVV6a — геометрическая характеристика жесткости при кру-
кручении.
Учитывая G.101), выражение G.98) для функции Ф (хи яа) мож-
можно привести к следующему виду:
*| дс|_\
а2 Ьг )'
G.103)
Рис. 7.13
По формулам G.7) находим напряжения!
nabs
G.104)
Легко подметить, что отношение компонент напряжения onlaSi
пропорционально х^х1. Отсюда следует, что отношение osl/oSi оста-
остается постоянным по длине любого радиуса, например ОК (рив. 7.13).
Это означает, что во всех точках некоторого радиуса ОК полные ка-
касательные напряжения имеют одинаковые направления, очевидно,
параллельные касательной к контуру сечения в точке К. На рис. 7.13
показаны также эпюры напряжений по большой и малой полуосям
сечения. Можно доказать, что максимальное касательное напряжение
хтях возникает в точках, которые совпадают о концами малой ови эл-
эллипса @, ± b). Величина этого напряжения равна
Ттах = I О311 тм = 2М/паЬ* = M/WK, G.105)
где №„ = паЬ2/2 — момент еопротивления кручению.
Для рассматриваемого бруеа эллиптического сечения жестковть
при кручении С, определяемая формулой G.102), может быть пред-
представлена в таком виде:
r n (nab)*
153

т. е,
C = GF*l(\n4p), G.106)
где F — площадь поперечного сечения, Jp — Jxi + /*2 — полярный
момент инерции.
Сен-Венан отметил, что по формуле G.106) можно вычислять жест-
жесткость не только в случае эллипса, но с достаточно хорошей точностью
и для многих других односвязных сечений. Поэтому иногда формулу
G.106) используют для приближенного вычисления жесткости для
любого односвязного сечения.
Перемещения ых и цг определяются равенствами G.31):
«1 = — $х2х3, иг = Флг^з,
где в данном случае на основании G.101) относительный угол закру-
закручивания
О = М (а2 4- b2)/Gna3b3 = М/С. G.107)
Теперь найдем перемещение и3. По формулам G.35), принимая во
внимание G.98), находим:
Тогда, совмещая начало координат с центром тяжести одного из
торцов и считая окрестность этой точки закрепленной так, что выпол-
выполняются условия G.1) и G.2), по формуле A.101) найдем
J^ZfgLxlxv "G.108)
т. е. поперечные сечения искривляются и обращаются в поверхности,
горизонталями которых (линии равной депланации и3 = const) яв-
являются равнобокие гиперболы, которые показаны на рис. 7.13. Асим-
Асимптотами этих гипербол являются оси xL и х2, точки которых остаются
а плоскости поперечного сечения.
Формулы G.105) и G.107) для ттах и $ при а — b ~ r (брус круг-
круглого поперечного сечения) дают:
ттах = 2М/(яг>) = M/Wp, О - 2MliGntA) = M/(GJP), G.109)
а из равенства G.108) следует, что us = 0, т. е. в случае круглого
бруса его поперечные сечения не искривляются.
§ 7. КРУЧЕНИЕ БРУСА, ПОПЕРЕЧНОЕ СЕЧЕНИЕ КОТОРОГО
ПРЕДСТАВЛЯЕТ СОБОЙ РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК
Совместим начало координат с вершиной угла А поперечного се-
сечения, направив ось хи как показано на рис. 7.14. Тогда стороны АВ
и АС сечения определяются уравнением х2 = ± ~?Л хъ а сторона
О'
164

ВС — уравнением xx = L^.a, где а — размер стороны треуголь-
треугольного сечения.
В случае бруса эллиптического сечения функцию напряжений
Ф (х,,х2) весьма просто выбрали так, что она сразу удовлетворяла
граничному условию.
В данном случае функцию Ф (хъ х2) можно в помощью G.79)
выбрать так, что сразу будет выполняться уравнение Пуассона G.33).
• В формуле G.79) функция i|> (xu хг) — гармоническая. Известно,
что действительная" и мнимая части любой аналитической функции
Рис. 7.14
/ (г) комплексной переменной г = хх -\- ix2 являются гармоническими
функциями. Рассмотрим, например, функцию
/ (г) = г" = (*!
при некоторых частных значениях п:
1) п = 1, } (z) = г = Xi + ix2,
т. е. х1 и х2 — гармонические функции;
2) п = 2, / (г) = г2 = (дт, + гдт2J = х\ — х\ + i2x,x2,
т. е. (дг| — xl) и 2x^2 — гармонические функции;
3) п = 3, / (г) = г3 = (хг + j^ = х\ — 3Xlxl + i CxU, — х\\
т. е. (дт? — Ъххх\) и C*!хг — xl) — гармонические функции;
4) п = — 1, / (г) = Г1 = (х, + /дгг) = хх/(х\ + х\) — 1х.гЦх\ + х\),
т. е. Xi/(x\ + xl) и х2/(дт^ + х\) — гармонические функции.
155

Любая линейная комбинация гармонических функций является
функцией гармонической. Подбирая различные линейные комбинации
гармонических функций, можно решить многие практически важные
задачи.
Для рассматриваемой задачи, исходя из G.79), функцию напряже-
напряжений Ф (хъ хг) примем в следующем виде:
Ф = G$ [/Cj (jet — х\) + Кг (Jcf — Зххх%) — (jcf + xi)/2], G.110)
где Ki к Кг — постоянные.
Это выражение функции Ф (хи х2) удовлетворяет уравнению Пуас-
Пуассона G.33), так как при постоянных К\ и Кг имеем гармонические
функции, а дифференциальный оператор Лапласа от последнего сла-
слагаемого в квадратных скобках этого выражения равен — 2.
Постоянные Ку и Кг найдем так, чтобы выражение G.110) для
функции Ф (jfj, хг) удовлетворяло условию на контуре G.13).
На сторонах АВ и АС сечения, т. е. при хг = ± (У~3/3) хъ имеем
/Ct B/3) xf — B/3) jcf = -0.
Отсюда К\ — 1 и выражение G.110)' принимает вид
Ф = Gtf [A/2) (х\ — Зх22) + КгХ\ (А — Зх|I- G.'111)
На стороне ВС контура сечения, т. е. при хг = (уз/2) а, функция
Ф (*i, х2) также должна быть равна нулю. Выражение G.111) для функ-
функции Ф (хи хг) будет рано нулю при хх = (КЗ/2) а, если коэффициенты
при (х\ — 3x1) будут численно равны и противоположны по знаку.
Из этого условия 1/2 = — Кг A^3/2) а получим Кг = — Кз/Cа).
Тогда выражение для функции Ф (хъ х2), удовлетворяющее урав-
уравнению Пуассона и условию на контуре, примет вид
Ф = (GO/2) U? - ЗА - BXl/V3a) (x\ - 3x1)]. G.112)
Подставив это выражение в формулу G.26), найдем
*, = (У'З/80) G&a*^ G$JK, G.113)
где JK — геометрическая характеристика жесткости, равная
JK = (/3/80) а\ G.114)
В выражение G.112) подставим значение д из формулы G.113).
В результате получим
Тогда на основании G.7) для произвольной точки поперечного се-
сечения найдем следующие формулы для компонент напряжения:
^[^ G.116)
156-

Для точек высоты AD сечения, т. е. при #2 = 0, имеем
o»i ¦- 0. ои = {MUJ Q/Txjd — l)xt. G.17)
На рис. 7.14 приведена эпюра напряжения по высоте AD попереч-
поперечного сечения бруса. Наибольшее напряжение ттах возникает в точках,
являющихся серединами сторон сечения (например, точка D), причем
согласно G.117) при % = УЗа/2
ттах = 20М/О8 = M/WH, G.118)
где момент сопротивления кручению WK = a?f20.
В точках стороны ВС сечения, т. е. при хг — У~За/2, на основании
G.116) аи = О, а приведенный на рис. 7.14 график изменения а,2
¦ определяется уравнением
<js2= B0M/as) (I — Axlld1). * G.119)
Перемещения иг и м2 определяются по общим формулам G.31),
в которых надо принять значение ¦& из формулы G.113).
Теперь по формулам G.35), используя G.112), находим:
W -x\) -2Xl\.
Накладывая условия G.1) и G.2) на окрестность точки, с которой
совмещено начало координат, по формуле A.101) получим
«з = о [ ~-
На рис. 7.14 изображен характер линий уровня («8 = const) де-
планированного поперечного сечения, которые представляют собой
кривые третьего порядка.
§ 8. КРУЧЕНИЕ БРУСА ПРЯМОУГОЛЬНОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
При решении данной задачи удобно обратиться к мембранной ана-
аналогии Прандтля, которая позволяет наглядно представить характер
функции напряжений.
Поверхность мембраны, равномерно натянутой на жесткий прямо-
прямоугольный контур и находящейся под действием некоторого постоян-
постоянного давления, очевидно, будет иметь вид, показанный на рис. 7.15,
на котором заштрихованные области изображают эпюры прогибов
w {хъ *2) мембраны при Xi = const, а также и при хг = const. Из рас-
рассмотрения поверхности мембраны легко заключить, что наибольший
угол наклона мембраны — в контурных точках / и /', которые яв-
являются средними точками длинных сторон прямоугольника."
Следовательно, при кручении бруса прямоугольного поперечного
сечения наибольшее касательное напряжение будет возникать также
в средних точках длинных сторон сечения.
В соответствии с характером упругой поверхности мембраны и со-
соотношением G.89) на рис. 7.16 показан график функции Ф (хъ х2)
157

при х2 = const. Пунктиром изображено периодическое продолжение
графика функции Ф (хг, х2), период которой равен 2а. Симметрия гра-
графика относительно оси х2, т. е. четность функции Ф относительно ко-
координаты хи и условие равенства ее нулю на сторонах хг = ± а/2
подсказывают искать эту функцию в виде следующего ряда:
Ф (хъ х2) = 2 L (x2) cos (tmxiia), (.7.122)
n= 1,3,5,...
где /„ (хг) — функции только х2.
Рис- 7Л5 Рис. 7.16
Для выяснения функций fn (хг), при которых выражение G.122)
функции напряжений Ф (хи х2) будет в пределах всего поперечного
сечения бруса удовлетворять уравнению Пуассона G.33), подставим
в последнее выражение G.122). В результате получим
Д (fn (хг) — Щп (х2)) cos Кх! = - 2Gb, G.123)
где введено обозначение
К = «л/а. , G.124)
Левую часть равенства G.123) можно рассматривать как разложе-
разложение в ряд Фурье функции — 2G&. Выражение (/„ (х2) — %гп fn (x2))
представляет коэффициенты этого ряда. Найдем эти коэффициенты
обычным приемом по методу Эйлера—Фурье. Для этого левую и пра-
правую части равенства G.123) умножим на cos ^ Xl = cos khXl (k — не-
некоторое нечетное число) и затем проинтегрируем в пределах от хх =
= -| до х, = + |.
Учитывая при этом, что
а/ 2
f COS^
158 Ja/2 а
cos — лгх
а
О, пФ к,

а также, что
0/2
cosJJLjc ^«
a
ч
0/2
Г
kn 2 \h
-an
придем к следующему уравнению для определения fk (x2)'*
, П(* — 1)/2
/* (*,) - Л-1 /* (*,) = - 8G0 i^il . G.125)
Aft a
Общий интеграл этого дифференциального уравнения с правой
частью имеет вид
/* (*«) = Ah ch Xh х2 + Bh sh lh x% + 8Gd J—bL , G.126)
4°
График функции Ф (xt = const, хг), как это следует из мембранной
аналогии (см. рис. 7.15), симметричен относительно оси хъ т. е. эта
функция является четной относительно координаты хг. Поэтому функ-
функция fk (Хг) должна быть четной относительно хг и, следовательно, сла-
слагаемые в равенстве G.126), содержащие sh ~к^х^ должны отсутство-
отсутствовать, т. е. необходимо Bk = 0. Постоянные Ak найдем из условия, что
функция напряжений, а поэтому и функция /ft (лг2) должны обращать-
обращаться в нуль при Хг = ± Ь/2. Из этого условия на основании G.126) по-
получим
G.127)
1а
Тогда
ch/eh
и выражение G.122) для функции напряжений принимает вид
G.128)
•а
G.129)
Это выражение для функции Ф (хи х2), удовлетворяющее урав-
уравнению Пуассона G.33) и граничному условию G.13), подставим в фор-
формулу G.26):
я3 ^7б «
»/2
ял a
пл
-0/2 -ft/2
159

Учитывая, что
получим
М = 32GO•
n= 1^375,...
2
ra= t ,3.5,...
2a
(
n4 \ 96 nb
la
ft, G.130)
где p — безразмерный коэффициент, зависящий от отношения сторон
прямоугольного поперечного сечения;
= _L/i __L?i_-2_ У _!
.4 тт5 h _¦«_ п5
G.131)
Значения коэффициента р для некоторых отношений Ыа
приведены в табл. 7.1.
Таблица 7.1
Ь/а
1
1.5
1,75
2
2,5
3
а
0.208
0.231
0,239
0,246
0,258
0,267
0,1406
0,196
0,214
-0,229
0,249
0,263
6
1,000
0,859
0,820
0,795
0,766
0,753
Ь/а
4
6
8
10
IX)
а
0,282
0,299
0,307
0,313
0,333
&
0,281
0,299
0,307
0,313
0,333
¦'-
0,745
0,743
0,742
0,742
0,742
Исключив с помощью равенства G.130) величину Gd из выражения
G.129), получим
1-D/2
X 1— ch-
2а
G.132)
Тогда компоненты напряжения в произвольной точке поперечного
сечения определяются по формулам
м
а2 Ь п2
(-1)
(п —1)/2
sh
1,3,5,...
nub
2а
¦COS
G.133)
1С0

JL 2 .(-
G.134)
Уже отмечалось, что наибольшее касательное напряжение тгаах
на поперечном сечении возникает в средних точках длинных сторон
прямоугольника. Так, при Ъ > а ттах возникает в точках 1 (а/2, 0)
и 1- (— а/2, 0). Подставив в G.133) и G.134) *, = а/2, *г = 0, получим
— О - Л} 8
"81 — u> Tmai — 0.4-1 т~Г. —"
или, поскольку
2 1 _ Я2
а= Е , G.136)
Обозначив
п=1,3.6,... / \ 2а
формулу G.135) можно записать так:
ттах = M/WB, G.137)
где WK — момент сопротивления кручению, который равен
WK = aazb (а<Ь). G.138)
Значения безразмерного коэффициента а, определяемые по фор-
формуле G.136) в зависимости от отношения Ыа, приведены в табл.7.1.
Напряжение в средней точке короткой стороны сечения получим,
подставив в G.133) и G.134) *, = 0, хг = 6/2:
7. —г ш , 0.0 = 0.
Приняв во внимание равенство G.136), приходим к формуле
** = —СТтах, G-139)
где ^ — безразмерный коэффициент, значения которого определяют-
определяются формулой
(I)/2 nnb
!1 G.140)
О п=1,3.6,...
в Зак. 514

и некоторые из них приведены в табл. 7.1.
Перемещения щ и ы2 определяются формулами G.31), в которые
надо подставить значение ¦& из равенства G.130).
Для определения перемещения и3, характеризующего депланацию
поперечного сечения, по формулам G.35) находим:
и. 1==Ф 2/G + bx2 = — На— х
л4
,и^?г.
X ^ V - COS -
п' ¦ nnb
сп
2а
х
я" в-lX».... П
Выполняя интегрирование, найдем
«,=»
V
ch
2a
На рис. 7.16 приведены горизонтали («3 = const) депланирован-
ного поперечного сечения. Точки осей сечения Охх и Ох2 остаются в
его плоскости.
§ 9. КРУЧЕНИЕ БРУСА КРУГЛОГО СЕЧЕНИЯ С ПРОДОЛЬНОЙ
ПОЛУКРУГЛОЙ КАНАВКОЙ
Решение данной задачи раовмотрим в полярных координатах х1 = г, х* = 6
(рис. 7.17), которые связаны g декартовыми координатами равенствами F.35):
Xf = г cos 8, х2 = г sin G. G.141)
Компоненты напряжения в полярных координатах ои, ог9 и в декартовых
координатах о31, о82 связаны равенствами!
alT = a3l cos 6+ a32 sin G, 1
ozB = o32cosO— a3lsin6. j
Принимая во внимание равенства G.141) и G.7), запишем!
дФ J_ дх2 , дФ _1_ dxt _ J_ дФ
°zr= дх, ~7 60 дх{ г ~дп 'г W '
дФ dxj дФ дх2 _ дФ
Z(J dxt dp дхг дг дг
162

Итак, имеем следующие соотношения между компонентами напряжения в
полирных координатах и функцией напряжений:
1 дФ дФ
<V = 7~^-. °*в--—• G.143)
Функция напряжений Ф должна удовлетворять граничному условию
Ф|г. = 0 G.144)
и уравнению Пуассона, которое в полярных координатах записывается [см
F.65)] так:
д^ Ф 1 д* Ф 1 дФ
УаФ = 1 1 =i— 2Gft. G.145)
дг2 га д№ г дг
Контур поперечного сечения рассматриваемое бруса очерчен двумя ок-
окружностями — малой окружностью радиуса а с центром О на большой окруж-
окружности радиуса Ь (рис. 7.17). Уравнения этих окружностей в полярных коорди-
координатах g началом в точке О
г — 2Ъ cos 0 = 0, G 146^
г — г. — Э. G.147)
Функцию напряжений примем в следующем пндес
Ф = (Kir) (г2 - а2) (г — 2b cos й). G 148)
Выражение G.148) обращается в нуль во всех точках контура сечения при
любой постоянной К.
Подставив это выражение для функции иапряжений Ф в уравнение Пуассо-
Пуассона G.145) найдем значение постоянной К,, при которой последнее будет удовлет-
удовлетворяться:
К «= - Gd/2. G.149)
Тогда функция напряжений, удовлетвориющая уравнению G.145) и гра-
граничному условию G,144), будет иметь вид
G& I аг Ь . \ ,„ . .„,
Ф = — [ г2—a2— 26rcos9 + 2 cos 9 . G.150)
2 \ ' I
По формулам G.143) находим компоненты напряжения в пронзвольной точ-
точке поперечного сечения:
а0 ^^ . <7Л51)
G.152)
в дг
Анализ формул G.151) и G.152) позволяет установить, что наибольшее на-
напряжение будет при 9 = 0, г — а, т. е. в точке Р (рис. 7.17):
тшах=»(ого)р= — G96 B—а/Ь). G.153*
Если а < Ь, то
G.154)
а жесткость бруса о небольшой канавкой можно считать такой же, как у бруса
круглого поперечного сечения без канавки, т. е. равной GJp Тогда относитель-
относительный угол закручивания бруса равен
d= Ml (GJP), G-155)
а наибольшее касательное напряжение ттах, возникающее а гочке Р, на основа-
основании G.154) в G.155)
6* 163

где Wp = Jp/b — ntPi2 — момент сопротивления кручению, Jp = пЬ*/2 — по-
полярный момент инерции круглого сечения -
На рнс. 7.17 приведена эпюра касательных напряжений. В окрестности
точки Р (у дна канавки) имеет место концентрация напряжений. Отношение наи-
наибольшего напряжения (тшах = IMIWp) к номинальному (тном = AVWp), как
известно, называется теоретическим коэффициентом концентрации ?т. В данном
случае имеем
fe 2. G.157)
Отметим, что рассмотренная задача впервые A921) была решена Вебером.
§ 10. КРУЧЕНИЕ БРУСА С ПОПЕРЕЧНЫМ СЕЧЕНИЕМ В ВИДЕ
СЕКТОРА КРУГА (РИС. 7.18)
Эта задача была решена Сен-Венаном A878) и А. Гринхиллом A879).
В 1912 р. А. Н. Диниик решил эту задачу при помощи функций Беоселя. В даль-
дальнейшем она была изучена иными методами рядом других авторов Рассмотрим
решение Сен-Венана.
Ссылаясь на G.79), функцию напряжений возьмем в следующем виде!
ф = Gfl. до _ (Х\ + х*I2\ = Gtf№ — rV2), G.158)
Рис. 7.17
Рис. 7.18
где г)> — сопряженная функция кручения, которая должна удовлетворять урвв*
нению Лапласа.
Функцию i|> можно принить в виде следующего ряда!
ЧтГ
япб
а,
П—1.3,6,...
и тогда функция напряжений будет иметь.вид
cos 26
cos»
= 1,3,5,...
/ г \™>a nnQ ) cos 26 \
„ — eos 1*[\ . G.
V о. I a \ cos a / I v
159)
Выражение G.159) для функции напряжений обращается в нуль па ради>
альных сторонах контура сечения, т. в, при 9 = ± а/2 Чтобы функция напря-
напряжений обращалась в нуль и на круговой части контура (г = а), необходимо при-
принять
V , плЬ ссь2й
п-&....Ал"*~-1-~- (?Л60)
164
eos a

Левую часть равенства G.160) можно рассматривать как разложение в ряд
Фурье функции, стоящей в правой части этого равенства. Определим обычным
приемом коэффициенты Фурье этой функции:
а/2 (
2 Г I cos 26 \ ллб , 2 2а пп
Л„ = — I 1— cos а0 = —{ sin
a J \ • cosa / а а «л 2
—а/2 I
-а/2
а/2
1
2 cos a
1 Г 1 I . пп пп \ . 1
sin ——• cos a—gos —r- sin a I -f
L IT"
eosa _^L_2 V 2 / J^.jl.2
La a
U . пп пл . \ I /4 2 2 N
sin—— coscc + ces—— sin a I =( —— 1
\ 2 ^2 jl) \nn nn—2a. nn + 2a}
X
n—i
2
sin —— ^з 16 • 5 '-
2 я» л (n—2а/л) (л + 2а/я) *
Теперь функция напряжений будет иметь вид
«("-2а/я)(п+2а/я)
а / а \ юза /|
Для выяонения жесткости бруеа GJK подотавим функцию напряжений
G.161) в формулу для крутящего момента!
= G./R», - G.162)
ff(
где JK = ka* — геометрическая характеристика жесткости; k — безразмерный
коэффициент, величина которого зависит от урла а; для некоторых значений a
величина k приведена в табл. 7.2.
Компоненты напряжения найдем по формулам G.143);
1 дФ
Г_!_
ллв г sin
Ksin
a - a eosa
дг
G.163)
[ 2
(т
165

ппб . г / cos 26 \\
Xcos 1 A — .
a a \ cos a J\
G.164)
Наибольшие касательные напряжения на круговой и радиальных частях
контура сечения определяются соответственно формулами
G.165)
где k-i и k2 — безразмерные коэффициенты, величины которых для некоторых
значений а приведены в табл. 7.2.
a
П/4
я/3
л/ 2
2 п/3
0
0
0
0
,0181
,0349
,0825
,148
0,490
0,652
0,
0,
А*
452
622
3
5
a
п
л/2
л/2
2 л
0
0
0
0
к
,298
,572
,672
,878
Та бли
ft.
0,849
—
па
0
7.2
,728
—
—
—
§ 11. КОМПЛЕКСНАЯ ФУНКЦИЯ КРУЧЕНИЯ
При решении задачи кручения часто выгодно использовать функ-
функцию комплексного переменного г = хЛ + ix2, определяемую следую-
следующим образом:
/(г)-ф(*1, **) + «¦(*!. х2), G.166)
где ф (хъ х2) — функция кручения, а \|э (хг, *2) — сопряженная функ-
функция кручения.
Функция / (г) называется комплексной функцией кручения.
Поскольку функции ф (хг, х2) и ур (*!, х2) удовлетворяют условиям
Коши—Римана G.74), функция / (z) будет аналитической в области
поперечного сечения.
Граничное условие для комплексной функции кручения / (г), ссы-
ссылаясь на G.78), можно записать так:
lm / (г) = —- гг + const.
G.167)
Исходя из формул G.58) и учитывая условия Коши—Римана G.74)
находим
или
— ix2)\
°3i — 'O32 = G# if B) — iz\.
Если уравнение
Ira / B) = -ф (Xl, x2) = (x\ + 4)/2 + const
G.168)
G.169)
G.170)
будет представлять собой уравнение некоторого контура поперечно-
поперечного сечения скрученного бруса, то тогда
B) == Ф (xL, Хг)
G.171)
166

будет, очевидно, соответствующей функцией кручения для данного
поперечного сечения и задача решена.
Конечно, можно поступить и наоборот, т. е. принять;
Re / (г) =: — -ф (xlf х2),
lm / (г) ~ q> (xlf хг),
так как и в этом случае выполняются условия G.74).
Рассмотрим, например, аналитическую функцию
f (Z) = /(г2 = К (XI - ж§) + ЙД7^», G.173)
где К — действительная постоянная.
Тогда, принимая в соответствии g G.172)
Re f(z) = K {xl — x\) = — ф («lt д^г) G.174)
и
Im f (г) = 1Кх&г = Ф (xb хг), G.175)
получим, что уравнение
±С G.176)
К(х\х\)
представляет собой уравнение эллипса с полуосями
G-177)
Из соотношений G.177) находим
1^!^ G.178)
Тогда функпия кручения ф (xlt x2) для бруса эллиптического се-
сечения имеет вид
*=iwXiX* GЛ79)
Перемещение «3. определяющее депланацию поперечного сечения,
находится по формуле G.52):
и $J^Z±XxXv G.180)
3 a2 + 62 l 2
Геометрическая характеристика жесткости /к определяется по
формуле G.62):
' F'
2Ь*
-JJ xf^d^-j- -j-.j-jj^l^^.^^^. G.181)
167

Напряжения находим по формуле G.168):
a3l=-G#-^-, ая = GO J?*-. G.182)
Естественно, что результаты данного решения совпадают с резуль-
результатами решения, приведенного в § 6 данной главы.
Если принять комплексную функцию кручения в виде
/ B) = /Сг3,
то можно аналогично решить задачу кручения бруса, поперечное
сечение, которого — равносторонний треугольник. Несколько иное
решение этой задачи было рассмотрено в § 7.
Сен-Венан решил этим приемом целый ряд задач. Принимая, на-
например, комплексную функцию кручения в виде полинома четвертой
степени, Сен-Венан получил решение для бруса с поперечным сечени-
сечением, имеющим форму различных криволинейных четырехугольни-
четырехугольников [8].
Решение задачи кручения для многих сложных профилей попереч-
поперечных сечений значительно проще можно получить методом конформного
отображения.
§ 12. МЕТОД КОНФОРМНОГО ОТОБРАЖЕНИЯ
Допустим, что имеем однозначную аналитическую функцию ком-
комплексного переменного ? = ? + щ = ре10
г = <о (С), G.183)
которая отображает область s плоскости ? на область S плоскости
г = хг + iXi. Будем считать, что функция G.183) однолистная, т. е.
такая что каждой точке ? области s соответствует одна и только одна
точка г области S, и, обратно, каждой точке г области S соответствует
только одна точка ? области s. В этом случае говорят, что функция
G.183) определяет взаимно-однозначное (однолистное) конформное
отображение области s в область S, и обратно.
Как известно, конформное отображение характеризуется следую-
следующим свойством аналитической функции G.183): если в области s рас-
рассмотреть два линейных элемента (прообразы), выходящие из точки ?
под некоторым углом а друг к другу, то соответствующие им элементы
(образы) в точке г области S будут составлять между собой такой же
угол а, причем направление отсчета углов сохраняется. Напомним
также, что угол поворота каждого элемента (образа) в точке z по от-
отношению к соответствующему элементу (прообразу) в точке ? будет
равен аргументу производной arg со' (?), а отношение длин соответст-
соответствующих элементов будет равно модулю производной | а1 (?) |.
Из теоремы Римана (основная теорема конформного ото-
отображения) следует, что если конечная односвязная область S ограни-
ограничена простым замкнутым контуром, то всегда можно найти аналитиче-
аналитическую функцию G.183) в круге |?| < 1, отображающую однолистно
168

круг | ? К 1 на область S. Эта функция будет определена единствен-
единственным образом, если
со (?0) = z0, arg ш' (Q = а0,
где ?0 ? s, г0 ? S и а0 — заданное действительное число. Геометри-
Геометрически это означает, что единственность отображения будет обеспечена,
если для некоторой точки ?0 области s будет указан ее образ z0 и задан
угол, на который при этом отображении поворачивается бесконечно
малая окрестность точки ?0.
Заметим, что при взаимно-однозначном отображении производная
го' (?) не может обращаться в нуль в области s. Кроме того, поскольку
отображение непрерывно вплоть до контуров, функция со (?) непрерыв-
непрерывно продолжима на границу области s.
В дальнейшем обычно область s будем рассматривать в виде кру-
круга с радиусом р = 1. Окружность этого круга обозначим через Y>
а ее точки — через % = е'е. Тогда граничное значение функции со (?)
будем обозначать Через © (%).
Пусть функция G.183), конформно отображающая круг ,|?|< 1
на область S плоскости г, известна и при этом точка 5 = 0 переходит
в точку г — 0. Пучок радиусов (9 = const), ортогональных семейству
окружностей (р = const) единичного круга плоскости ? = ре'9
(рис. 7.19), преобразуется на плоскость г в кривые (9 = const), вы-
выходящие из точки г = 0 и доходящие до контура L, который соответст-
соответствует окружности V- Остальные же окружности (р = const) преобразую-
ся на плоскость г также в замкнутые линии, окружающие точку г.
Эти два семейства кривых на плоскости г, получаемые в результате
конформного отображения, будут взаимно ортогональны и их можно
рассматривать как координатные линии ортогональных криволиней-
криволинейных координат р и 9 точек г. Обозначим касательную к кривой 6 =
= const, проведенную в сторону возрастания р через (р), а касатель-
касательную к кривой р = const в сторону возрастания 9 через (9). При кон-
конформном отображении направление отсчета углов не изменяется, по-
зтому ориентация осей (р) и (8) должна быть такой же, как и осей
Охх и Охг соответственно. Угол, образованный положительными на-
направлениями осей (р) и Охг, обозначим через а.
Рассмотрим некоторый вектор а с началом в точке г = а (ре16)
^рис. 7.20), проекции которого на оси Охг и Ох2 обозначим через
аХх и flX2, а на оси (р) и (9) — через ар и ав. Пусть р1—угол между на-
направлением вектора а и осью (р). Тогда ср = | а \ cos (}, се = J a | sin 0,
и, следовательно,
Отсюда
= (oo-Mae)e'e ' G-184)
или
x.) e~ia. G.185)
163

Если точке z придать смещение dz в направлении (р), то соответст-
соответствующая точка ? получит смещение dt, в радиальном направлении, т. е.
при 0 = const. Поэтому будем иметь
dS = |dS|e*e, dz = \dz\e«*
и, следовательно,
la»'
Тогда
_• плоскость z
\ «' (U
плоскость ? хг
= -L, ®>(S) , G.185')
Р la'QI
' @ |
Рис. 7.19
Рис. 7.20
и формулы G.184), G.185) примут вид
aXt+iax,= Sw,(?) (a
р I (о) (D i
I ш
G.186)
G.187)
Отметим, как это следует из теоремы Римана, что конформное ото-
отображение многосвязной области на односвязную невозможно, а допу-
допустимо отображение друг на друга только областей одинаковой связ-
связности. Например, область S, ограниченную двумя замкнутыми глад-
гладкими контурами, можно всегда однолистно отобразить на круговое
кольцо, отношение радиусов граничных окружностей которого долж-
должно быть определенной величины, зависящей от вида области S.
Пусть функция G.183) конформно отображает область F попереч-
поперечного сечения скрученного бруса на единичный круг |?|< 1 плоско-
плоскости ?. Выражая комплексную функцию кручения G.166) через С ="
= рет, получим функцию /0 (?):
/ (z) = ф + tip = / [со @1 = f0 (Q,
G.188)
которая будет аналитической внутри окружности у единичного круга.
170

Из соотношения G.188) имеем
-L д, (?) = гр—(ф, G.189)
Используя принятое обозначение % = е'е для точек окружности
у, граничное условие для действительной части я|) функции /0 (?)/i,
ссылаясь на G.78) и принимая во внимание G.183), можно привести
к виду (без произвольной постоянной)
*Hv = -l-zi=-i-co(x)Hxb <7Л9°)
Таким образом, задача кручения свелась к определению аналитиче-
аналитической функции f0 (t)/i внутри окружности у с радиусом р = 1 при гра-
граничном значении G.190) ее действительной части.
Очевидно, можно принять, что определенное граничное значение
на у, т. е. при ? = х» будет иметь также функция ф, а следовательно,
и функция /0 (?)/*. Граничное условиеG.190) в этом случае можно за-
записать так:
h Ш + /о (Х)А' = со (X)«(X). G.191)
Умножая равенство G.191) на ж-т *~7 й интегрируя по у, по-
получим
х—? 2л/ J X—?
V V V
G.192)
Первый интеграл в левой части равенства на основании интеграль-
интегральной формулы Коши равен -rf0 (?). Второй же интеграл равен постоян-
постоянной на основании следующей теоремы теории аналитических функций:
для того чтобы непрерывная на окружности у функция f (%) была гра-
граничным значением аналитической функции внутри окружности ?»
необходимо и достаточно, чтобы
1
1 С l(l)d
2т J х-?
где С — постоянная, которая равна значению аналитической функции
в точке I = 0 (см. гл. IX, § 23).
Тогда из равенства G.192) получим
const. G.193)
171

Подынтегральная функция интеграла в формуле G.193) представ-
представляет собой функцию Q (у) и интеграл легко можно вычислить по теоре-
теореме о вычетах:
Г р(х)та d% = f Q(x)dxe2ra. у Res(Q(x); ak\, G.194)
где аь — изолированные особые точки функции Q (х).
Основная формула G.193) для функции /0 (?), определяющей реше-
решение задачи кручения, принимает вид
М0=' i Res[Q(x);aftJ. G.195)
Если функция Q (x) инеет конечное число простых полюсов ah
и ее можно представить в виде
р (Y) = °i(x)
то вычеты относительно простых полюсов удобно определять по фор-
формуле
Res [Q(x); «»] = -??*{•. G.196)
Выразим геометрическую характеристику жесткости JR через
и со (х). Согласно равенствам G.62) и G.64), имеем
JK=JP—D=§(x\+xl)dx1dxt—A/2M
GЛ97)
Преобразуем первый интеграл в последнем равенстве с помощью
формулы Грина G.16):
JP =
W (*i + 4) ^, ^2 = J j" [-^-
Y (Y JY «
L *^2 V 1 1
Учитывая, что
*! = (г +г)/2, дса- = (г -г)/B/),
получим
•¦=—±-&{z*dz-<
+ гг zdz — ? dz) .
По теореме Коши имеем:
172

Далее, интегрируя по частям, находим
где учтено, что функция (гг?/2)? является однозначной.
Тогда формула для полярного момента инерции принимает вид
, -1. ф г« ate = JL ф и. (х) со Ос) dco (х). G.198)
Поскольку на контуре г? = гг = со (х) со (х) и ф = -у [f0 (x) +
+ /о (x)Ji формула для величины D, зависящей от депланации попе-
поперечного сечения бруса, запишется так:
GЛ99)
Учитывая выражения G.197), G.198) и G.199), для геометрической
характеристики жесткости получаем-- формулу
G.200)
Обозначим вектор касательного напряжения в произвольной точ-
точке поперечного сечения бруса через t, а его проекции на оси (р) и
@) — через тр и т9, проекции же на оси Охх и Ох&, как обычно, — через
Ом и сг22. Тогда, переходя к сопряженным значениям, на основании
G.187) имеем
или, ссылаясь на формулу G.169) и учитывая, что в соответствии о
G.188)
рф-г- df(z) - dfui® l G.201)
получаем
тр-he = u | ^Q | [> (О -МО сог (S)J. G.202)
Можно также находить а81 иаз2по формуле G.169), которую, при-
принимая во внимание G.201), можно привести к виду
G.203)
Рассмотрим пример решения задачи кручения методом конформного ото-
отображения,
173

С помощью функции
(а>0,
G.204)
имеем отображение на круг | L | < 1 области, ог-
ограниченной так называемой лемнискатой Бута.
При Ь, мало отличающемся от единицы, эта об-
¦ ласть мало отличается от двух кругов, касаю-
- щихся друг друга. Рассмотрим поперечное сече-
' ние скрученного бруса, когда Ь= 3 (рис. 7.21).
Решение задачи сводится к определению по
формуле G.193) функции/0 (?).
Так как для точек С, = х = е'в единичного
круга
~
Ч
то формула G.193) пригишаст вид
G.205)
Подынтегральная функция Q (у) имеет вне у Два простых полюса:
yb и х-, = —i~\/b. Вычеты
муле G.196) В данном случае
^i-(x) =а2 X2. 9i (X) = 2х A + bf) (х-
и вычеты равны:
Подынтегральная функция Q (у) имеет вне у Два простых полюса: xi =
= ( yb и х-, = —i~\/b. Вычеты относительно этих полюсов определяем по фор-
форG.196) В
21A—ь*)иуь —I
Res[Q(x);xtJ = -"
2((i-*2) 0 /<» + E)
Так как простые полюса вне у, то по формуле G.195) находим
г
По формуле G.203), используя G.204) и G.206), найдем
G.206)
<7.207)
Учитывая, что ? = рг1д, и отделяя действительную и мнимую части в ра-
равенстве G.207), получаем!
o3l
о32 = Сда
Р4 — 2*р cos20
_2Ь Ь—р!
* — 26р cos2Q
cos2q
; sin0,
cos 9.
G.208)
174

Координаты xt и х2 поперечного сечения в плоскости г, соответствующие
координатам р и 6 единичного круга | ? | < 1 плоскости ?, определяются исходя
113^G.204) по формуле
, , а (И-1) cos 0 , а F—1) sin 6
г = х,-\-<хч = — ;—1-/ ; ' -. G.209)
В точках 1 и V (р = 1, 8 = 0 и 6 = л) возникает наибольшее касательное
напряжение!
В тЬчках 2 и 21 (р=1, 8=л/2 и -9=3 я/2) касательное напряже-
напряжение составит
Геометрическую характеристику жесткости находим по формуле G.200):
, m^ + O ,72Ш
J"Z 2(Ь>-\у • G'212)
Для оечепия, изображенного на рио. 7.21, Ь = 3. В этом случае
JB- 0,0315а4, ттах= 19,9/И/а3. (оа}8. 8, =» Т 9,95Л}/а3. G.213)
На рис. 7.21 приведены эпюры напряжений в точках малой и большой по-
полуосей сечения.
Отметим, что рассмотренная задача решена Н. И. Мусхелишвили A929)
и другим путем, более сложным, решена Т. Хиггинсом A942) [18].
§ 13. НАПРЯЖЕНИЯ В ВЕРШИНАХ ВЫСТУПАЮЩИХ И ВХОДЯЩИХ
УГЛОВ КОНТУРА ПОПЕРЕЧНОГО СЕЧЕНИЯ
Пусть скручиваемый брус имеет поперечное сечение (рис. 7.22),
у которого в точке О контура касательные к контуру образуют угол а.
Если а < я, то угол называют выступающим, а при а > я — входя-
входящим.
Вместо действительного очертания контура сечения в окрестно-
окрестности точки О рассмотрим контур этой окрестности, образованный ка-
касательными (рис. 7.23). Очевидно, что на характер особенности в рас-
рассматриваемой точке О эта замена не скажется.
Принимая, что распределение напряжений в окрестности точки О
определяется комплексной функцией кручения вида
^ie"'ael2"+lCl" G'214)
мы удовлетворим граничному условию G.167):
Im /о = zz/2 + ch = r?/2+ ск. . G.215)
Действительно, легко убедиться, что для функции G.214)
^_ cos^~a) +ch G.216)
и, следовательно, при 9 = 0 и 9 = о условие G.215) выполняется.
175

Очевидно, что к решению G.214) можно прибавить произвольную
функцию /, (г), если Im ft (z) обращается в нуль на сторонах Оа и Ob
угла о. Эту функцию можно принять в виде ряда
= 2
G.217)
Поскольку при В = 0 и б = а должны иметь Im /t = 0, то при
вещественных коэффициентах ah необходимо, чтобы sin к/to = 0 и,
следовательно, и = л/а.
Рис. 7.22
Рис. 7.23
Тогда общий вид комплексной функции кручения будет
2 cos i
а
G.218)
Поскольку, исходя из G.142), имеем
ая1 — Огт cos 0 — агв sin 0, азг = ozr sin 0 -f- огв cos 9, G.219)
формула G.169) приводится к виду
azr — шгй = GO [f (г) — /zl е<\ G.220)
Тогда, учитывая, что г — г&ь, а производная в полярных коорди-
координатах вычисляется по формуле
найдем
176

, или
-fa^gO (Гг sin(a~26) + У ak^r*«>«-> cos-^il
IL cosa «?i a « J
+ ,Г cos(a
co
L
-2Q) j.
cosa *ы a
Отсюда
cos -^-1, G.222)
a
[ V cosa / ^-J a a j
G.223)
Если теперь a < л, т. е. угол контура сечения — выступающий,
то lim azr = 0 и lim aiB = 0. Этот результат уже был элементарно до-
'-¦0 г->-0
казан в § 4 этой главы.
При a = п в окрестности точки О контур поперечного сечения
будет гладким и в этом случае lim azr = Gdai cos 8, lim ozq =
r-t-O . - r-*0
¦= —Gfta! sin 8; касательное напряжение в точке О будет равно т =
= Gftflj (at — некоторая постоянная) и направлено по касательной
к контуру.
В случае входящего угла, т. е. когда a > я, имеем lim огг = оо,
г-*0
lim | оге | = о». Следовательно, в точке вершины входящего угла на-
пряжения оказываются бесконечно велики. Этот результат нельзя
воспринимать буквально. Он получен в предположении, что материал
бруса идеально упруг и следует закону Гука. Реальные же материалы,
как известно, при некоторых конечных напряжениях уже не следуют
закону Гука и в случае пластичных материалов при достижении пре-
предела текучести испытывают заметные пластические деформации. По-
Поэтому действительные повышенные местные напряжения в таких осо-
особых точках, как вершины входящих углов, не могут быть определены
только методами- теории упругости.
§ 14. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ ВАРИАЦИОННОЙ ЗАДАЧИ КРУЧЕНИЯ
Один из способов вариационной постановки задачи кручения осно-
основан на применении принципа минимума дополнительной работы
(см. гл. V, §6).
- Поскольку в задаче кручения все компоненты тензора напряжений,
за исключением a3i = Ф, а и а3г = — Ф. i, равны нулю, то в соот-
177

ветствии с C.80) удельная дополнительная работа определяется фор-
формулой
Исходя из решения задачи кручения бруса полуобратным методом
Сен-Венана в перемещениях, следует считать известными перемещения
«1 и н2 на торцах х3 = 0 и ха = / (рис. 7.1). На основании G.51)
при х3 = 0 н<5> = h<2s) = 0;
при х3 = / «(/> = — #/д:2, н<*> = #/хх. G.225)
Тогда второй интеграл в выражении E.64) функционала сводится
к интегралу на торце х3 = / (nt = п2 = 0, п3 = +1) по площади F
поперечного сечения бруса. Учитывая G.14), имеем
JJ tmpdXidxt = — Ы Д (^Ф,, + х2Ф, z) cbddxt, G.226)
" Интеграл в правой части последнего равенства представляет собой
выражение крутящего момента через функцию напряжений Ф (хи х%),
которая, если ограничиться рассмотрением односвязных поперечных
сечений, должна удовлетворять граничному условию G.13). Поэтому
на основании G.20) и G.26) имеем
г + х2Ф а) dxxdxi = 2 f Г ®dXldx2. G.227)
f f
Ссылаясь на формулу E.64), получаем следующее выражение для
функционала:
Согласно принципу минимума дополнительной работы, напряжен-
напряженное состояние, реализуемое в упругом теле, отличается от всех стати-
статически возможных напряженных состояний тем, что оно сообщает мини-
минимум функционалу W. Поэтому функция напряжений Ф (хъ хг), опре-
определяющая действительное напряженное состояние скрученного бруса,
должна удовлетворять вариационному уравнению E.63), т. е.
6 ГИ—[(ФAJ+(Ф1гJ] — 2Gd0ldx1dA;2 = O. G.229)
Как уже было показано (см. гл, V, § 6), вариационное уравнение
E.63) влечет за собой выполнение условий совместности Бельтрами,
которые в случае задачи кручения выражены уравнением G.33).
Легко установить, что уравнение Пуассона G.33) является следствием
вариационного уравнения G.229), т. е. представляет собой уравнение
Эйлера—Остроградского для функционала G.228). Действительно,
исходя из уравнения G.229), имеем
178
Я [Фд FФ) ,i + Ф.| FФ)., — 2G<^j йхгйхг =5 0.

Интегрируя по частям и принимая во внимание, что на контуре
сечения 6Ф | L = 0, получаем
дУ = JJ (У2Ф + 2GU) ЬФйх^х^ = 0, G.230)
откуда ввиду произвольности вариации 6Ф в области F вытекает урав-
уравнение G.33).
Таким образом, вместо решения уравнения Пуассона G.33) при
граничном условии G.13) функция напряжений Ф, минимизирующая
функционал Ч;, может быть приближенно определена одним из прямых
методов вариационной задачи кручения при выполнении граничного
условия G.13).
Другая вариационная постановка задачи кручения бруса бази-
базируется на принципе минимума потенциальной энергии системы
(см. гл. V, § 5). В этом случае приходим к функционалу П, уравнением
Эйлера—Остроградского которого является уравнение Лапласа G.54)
для функции кручения ср (оно получено из уравнений равновесия Ламе),
естественными граничными условиями — граничные условия G.55)
для функции ф. Читателю, желающему ознакомиться с такой поста-
постановкой вариационной задачи кручения, можно рекомендовать кни-
книгу [35].
Рассмотрим примеры решения вариационной задачи кручения пря-
прямыми методами.
Брус прямоугольного поперечного сечения (рис. 7.16).
1. Решение методом Ритца.
Значение функционала V будем рассматривать на семейотве функций
Ф (*j, д?2), линейно зависящих от параметров а^ и удовлетворяющих грайичному
условию Ф \L = 0. Руководствуясь мембранной аналогией т. е. учитывая сим-
симметрию функции Ф (хь хг) = ух: (*,, х.2'< относительно осей Ох^, Од-2 ее, оче-
очевидно, мож1!о принять в следующем виде:
, х\ +а2 х\ +а, х\ x'i + ...) G.231)
В первом приближении ограничимся одним параметром, т. е. примем
Ф-ао(л:?— аг/4)(*1— 6г/4). G.232)
Подставив принятое выражение G.232) для Ф в формулу G.228) и выпол-
выполняя интегрирование, получим
а/2 Ь/2
81 С Г
[а2 х\ (х\— &2/4J+ajf x\ (*2 —с
G
о
—Gftao («f —а2/4) (х% — Ь2/4)],
Si а3 Ь3
= 0 144
Из условия минимума функционала V
dV/da0 = (а„/5) (а1 + б2) — Gd = О
находим
а0 = 5Gd/(aa + й2),
179

т. е. в первом приближении функция напряжений получает вид
Тогда
а/2 6/2
М = 2 Г Г «Dd*! dx2 = -^~Г \ f (xi-аЩ) (х% -62/4) dxt dx
Например, в случае квадратного сечения (Ь = а) геометрическая характе-
характеристика жесткости будет JH = E/36) a* = 0,1388a4, а максимальное касатель-
касательное напряжение, возникащее в точке ! (а/2, 0), равно ттах = (a32)maxc=9iM/2a3.
Сравнивая полученные результаты % а] точным, решением (gm. § 8 дайной
главы), убеждаемся, что ошибка в величине /к составляет около 1,2%, а в на-
напряжении ттах — порядка 6,2%
Желая получить лучшее приближение, возьмем первые три вдена ряда
G.231). Ограничиваясь рассмотрением квадратного сечения и при этом учиты-
вая условия симметрии, принимаем
(**+*2))- G-233)
Подставив выражение G.233) в G.228) и выполнив интегрирование, из усло-
условий минимизации V получим систему двух линейных уравнений относительно
аа и щ., откуда найдем:
_ 1295 GO* 527 Gft
а°- 554 ~'а1=1т7 а' '
В результате получим JK = 0,1404a*, ттах = 5,0Ш/а3, ошибки составляют
соответственно'0,2% и 4,3%, т. е., как и следовало ожидать, с возрастанием чио-
ла параметров а^ ряда G.231) точность решения повышается.
Большая погрешность в напряжении, чем в Реомэтрической характеристике
жесткости, вполне объяснима. Геометрическая характеристика жесткости пред-
представляет собой интегральную характеристику и оценивается объемом «холма»
функции напряжений Ф (дгъ х2), напряжение же определяется точечными значе-
значениями производных функции Ф (*i, Vj), т. е. зависит от рельефа «холма», что
трудно учесть и не учитывается при выборе функции Ф (*j, aj2).
2. Решение методом Канторовича.
Выражение вариации минимизируеморо функционала ? определяется ра-
равенством G.230). Следуя методу Канторовича, будем искать первое приближение
функции Ф (хь х2) в виде
Ф (jflf *а) = (я=/4 - х\) ! (х,), G.234*)
где / (х2) — неопределенная функция только д:2, которая должна удовлетво-
удовлетворять граничному условию
/ (*2) = 0 при х2 = ± ЫЧ. G.235)
При таком выборе функции Ф (дг1> дг2) ее граничное условие Ф и = 0 удов-
удовлетворяется.
Подставив
180

в выражение G.230) и проинтегрировав по *а, получим
6/2 а/2
№ = 4 j 6f{xa)dXi j
6/2
J
6/2
о
fiQJ б/ (*2)
— / (*s) + "^- fiQJ б/ (*2) а*, - 0,-
Так как вариация б/ (дг2) произвольная, Jto приходим к уравнению с по-
постоянными коэффициентами
f («а) — A0/а2) / (*a) = — A0/а2) GO. . G.236)
Частное решение этого неоднородного уравнения Очевидно; /0 (д:2) = Gft.
Тогда общее решение "уравнения G.236) имеет вид
/га /га
dch jc + CSh—
. . .
Из граничного уоловия G.235) находим:
C^-GO/chJ&JL,
и, еледовательно,
Ф (*i, *»)= G*f-7" -*!) ( l-ch-^ *2/ch 1/ -2- 4- |. G.237)
Тогда по формуле G.26) получим
0/2 6/2
М=8
f.e.
Напряжение
о^-Ф,.—G*(-f >,.) J^sh^-^ch yqjlA. G.239,
Например, в случае квадратного поперечного сечения бруаа (Ъ = а) полу-
получаем /к = 0,140а4, а наибольшее касательное напряжение, воаникающее в точ-
точке @, а/2), ттах = — 0,723G$a = — Ь,\ЬМ1Ф; ошибки составляют соответст-
соответственно около 0,7 и 6%, т, е. решение методом Канторовича уже в первом прибли-
приближении дает почти такую же точность, как второе приближение при решении ме-
методом Ритца. Это вполне закономерно, так как решение по методу Канторовича
разыскивается а более широком классе функций [функция / (хг) ие назначалась
наперед] и, следовательно, среди этого класса функций можио подобрать функ-
функцию Ф (х%, хг), лучше аппроксимирующую решение вариационной задачи.
3. Решение методом Треффца,
181

За частное решение Фо (*х> xa) уравнения Пуассона G.33) можно взять
Фо = - A/2)G» (х\ + х
В соответствии с равенствами E.111) и E.122) и ограничиваясь первым при-
приближением, для функции ii принимаем выражение
которое удовлетворяет уравнению V2Xf — 0.
Функция напряжений представится в следующем виде:
Ф [* (xl+xD+a, (**+**-6*?
2a2
Здесь коэффициент од находится на основании E.123) из уравнения
Г , . йу,
Ф lfli Xi—ЭС1 -**- dL*=Q,
i дп
которое, учитывая E.113) и G.13), принимает вид
д
Г
Выполнив интегрирование в последнем уравнении, найдем aj = 7/9,
Подставив выражение функции напряжений Ф в G.26), получим
М — GW, 1533а4, т. е. /к = 0,1533а4'
вместо точного значения JK= 0,1406а4.
Наибольшее касательное напряжение оказывается меньше действительногв
и равно
«max = 4,45M/fir*.
Поперечное сечение бруса — равносторонний треугольник (ом. рно. 7.14),
ограниченный прямыми' х2 •=» ± (|^3/3) х^ и хх = A^3/2) о, рде а — сторона
треугольника.
Решая задачу методом Канторовича, будем искать функцию напряжений
Ф (хь хг) в виде
[(^J] G-240)
где неопределенная функция f (xj) должна удовлетворять условию
/ {хх) = 0 при х, = (У3/2)а. G.241)
При таком выборе функции Ф (д^, х2) она удовлетворяет граничному уоло-
вию Ф \L = 0.
Подставив
в выражение G.228) функционала Y и выполнив интегрирование по ^2, найдем
._ (УЪ/2)а
8 Л/3 I С
? = ~405~"g J l*il''L5^1l'TlMiJ4l5GW)<(«i. G.242)
о
182

Уравнение Эйлера f> — ^ Ff = 0 1см. E.27)] для функционала V при-
приводится к уравнению
х\Г + 5V' - 5/ = A5/2) G*. G.243)
одно частное решение которого очевидно: /0 = — C/2) GO. Решение соответст-
соответствующего однородного уравнения ищем в виде /= х[" итогда общимрешением
уравнения G.243) будет
- / = ClXl + Са*г5 - C/2) .GO.
Рис. 7.24
Рис. 7.25
Поскольку в окрестности точки х? = О функция f должиа быть ограничен-
ограниченной, то необходимо принять С8 = 0, а из условия G.241) находим Ct = ]/GO/a.
Тогда
Ф(*,,
Это выражение для функции напряжений
Ф (х\, хг) совпадает с выражением G,112),
полученным точным решением.
Брус круглого поперечного сечения со
срезанным сегментом (рис. ? 24).
При решении задачи методом Ритца
функцию напряжений следует искать в сле-
следующем виде:
Ф (*1. Ч) = /
аъх\
G.244)
2а
,n=4
*n=2
G.245) ,
Рис. 7.26
где / (jffj, *2) = 0 — уравнение контура поперечного сечения бруса.
Для рассматриваемого поперечного оеченни уравнение линии АВ: xi + Ь —
= 0, а уравнение линии АСВ х\ + xl — га = 0. Так как функция напряжений
Ф (J6i, «2) в данном случав должна быть, как это подсказывается мембранной ана-
аналогией, симметричной относительно оси л^, то ряд в выражении G.245) hi
должен содержать членов с х2 в нечетной степени.
Тогда функцию Ф (х± хг), удовлетворяющую граничному условию Ф |L =
^ 0, можно принять в следующем виде:
Ф (xi, Ч) = (xi + Ь) (х\ + к\ - г*! (аа + atxt + а»х\ + а3х\ + ...). .
Дальнейшее решение аналогично решению задачи методом Ритца для бруса
прямоугольного поперечного сечения (см, о. 179).
Брус круглого поперечного сечения со шпоночной канаикин (рис. 7.25).
Заметим, что уравнение

при и = 1 — уравнение эллипса, а при п = 4 — уравнение прямоугольника
со скругленными углами (рис. 7.26).
Тогда уравнение контура шпоночной канавки (рис. 7.25) можно принять
в виде
*i/aS+xg/&8 —1=0,
а уравнение линии ABC (окружности) контура поперечного сечения — в виде
*i + (*2 — г? — г2 = 0.
Учитывая, что функция напряжений должна быть симметричной относи-
относительно оси jt2, ее следует принять в следующем виде:
Ф(х1г *,) = [*? + (*a-rJ-^](x?/a8+*?8/68- Otan.+Qt «s + Os^H-«в*? +•••)•
Постоянные параметры а^ определяются согласно методу Ритца нз условия
минимума функционала G.228).
§ 15. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ (МЕТОД СЕТОК)
Решение задачи кручения сводится к определению функции напряжений
Ф (хь хг), которая должна удовлетворять уравнению Пуассона G.33) н гранич-
граничному условию G.13).
Аналитические методы, а также классические приближенные методы (Рит-
(Ритца, Канторовича, Бубнова—Галеркнна и т. д.) позволяют найти функцию
Ф (*!, *2) лишь для сравнительно простых поперечных сечений бруса.
Существенно более универсальным, более гибким, в частности в отношении
геометрии поперечного сечения (области F), является метод конечных разностей.
Однако этот метод требует выполнения большого числа однотипных арифмети-
арифметических операций. Возникающие при этом трудности преодолеваются с помощью
ЭВМ и совершенствованием вычислительных алгоритмов.
Прн решении задачи методом конечных разностей искомая функция Ф оп-
определяется на некотором достаточно большом конечном множестве точек области
Г, которые называются расчетными точками и являются узлами сетки (обычно
прямоугольной нлн квадратной), покрывающей область F.
Для иллюстрации рассмотрим, например, двусвязную область F, ограничен-
ограниченную наружным контуром Lo и внутренним контуром Ц, покрытую прямоугольной
сеткой с шагом ft, по направлению оси ^ не шагом h2 по направлению оси х2
(рис. 7.27).
Узлы сетки, наиболее близкие к контуру L (Lo + LY), называются гранич-
граничными (на рис. 7.27 они обозначены знаком «X»), Все остальные узлы, попавшие
внутрь области F, называются внутренними (на рис. 7.27 они обозначены точ-
точками). Каждый внутренний узел имеет четыре соседних, среди которых могут
быть граничные. Множество граничных (соответственно внутренних) узлов
обозначим через L^ (соответственно Г^), подчеркнув зависимость от шагов сет-
сетки Максимальное число расчетных точек вдоль оси хх обозначим через КТ,
а вдоль оси х, — через МТ. Отметим, что Л; = AilNi, где А( —размер области
F r направлении xt (i = 1, 2), Wj = КТ — 1, N.2 = МТ — 1.
Расчетная точка xk.m, находящаяся на пересечении 6-го {k = 1 КТ)
столбца и m-ой (/л=1, ..., МТ) строки, имеет координаты х;^ и х2т. Значение
фукции Ф в точке xk т будем обозначать Ф^;т, т е. Фк.т = Ф (xlh, xim).
После выбора сетки дифференциальное уравнение G.33) и граничное условие
G.13) тем или иным способом приближают алгебраическими соотношениими
в расчетных точках. При этом, естественно, можно получить только приближен-
приближенные значения Ф^.т, которые будем обозначать Ф?.т. Функцию, определенную
в узлах сетки и принимающую значения $>%.т в точке xkm, называют сеточной
функцией; обозначим ее Ф*.
Приближение дифференциального уравиеннн алгебраическим осущест-
осуществляется путем замены производных коиечно-разностными соотношениями,
184

Рис. 7.27
Учитывая что Фй±1, т — Ф(дс^;г ± ftj, xim), по формуле Тейлора имеем
31
Ль.
41
дх\
рде 0 < 6 < 1,
" Отсюда
~и т __
Щ
где через О (hi) обозначена величина, удовлетворяющая условию | О (h\) \
< const • h\.
Аналогично,
4-0 (А*). G.247)
186

Введем следующий простейший разностный оператор Лапласа:
Ч+U тЧ; т Ч-.и т , Ф1: т+ !
h\ Г
V*im h\ Г А|
G.248)
Заметим, что точные решения дифференциального уравнения
у=Ф + / = 0 * G.249)
удовлетворяют условию
где fkm = / (х1к, xim) (в нашем случае / = \k.m = 2G&).
Соотношение G.250) не является алгебраическим, гак как о правой части
его известно лишь то. что она близка к нулю; точнее \О (hi 4- ft?) I < corrt X
X (h\ + h\) -+ 0 при ftlt ft2 -» 0.
Поэтому говорят, что разностная система линейных алгебраических урчв-
нений
аппроксимирует с точностью до /*2 дифференциальное уравнение G.249).
Граничное условие для функции Ф например, в случае дьусвязной области
F имеет вид
где Ф{ — некоторая постоянная. •
Это граничное условие можно непосредственно перенести на множество L^,
». е. положить
ф*|, =0, Ф*1, =©!. G.253)
Если нг все точки Lh лежат на L, то при таком представлении граничных
условий возникает ошибка порядка h = (h\ + hs)/2. Можно улучшить аппрок-
самацию граничных условий до порядка к2 с помощью линейной интерполяции
(см. [141, с. 443).
Таким образом, приходим к разностной задачг G.251), G.253). аппроксими-
аппроксимирующей дифференциальную G.33), G.13)
Отметим, что постоянная Ф, может быть определена при непосредственном
счете на ЭВМ как решениь уравнения G ¦'<'>).
Порядок системы линейных алгебраических уравнений G.251), G.253),
которую надо решить, сравним с ЛГ, где Л' ~ 1/Л Для юстнжения хорошей точ-
точности решения нужно брать h достаточно малым. Если h ~ 1M00, то порядок
системы ~104. При решения системы столь высокого порядка общими методами,
например методом исключения Гаусса, нужно выполнить около Л/^6 =¦ (>V2)B ариф-
арифметических операций. На машине, делающей ~103 onepaiuift в секунду для этого
вгтребуетск несколько месяцев машинного времени. Это время можно сократить
до 20—30 мин, если воспользоваться методом матричной прогонки (см. [241,
с. 100—102), учитывающим специфику матрицы разностной задачи (ее тридн-
агональность); этот метод требует ~ ЛГ: операции
Чтобы еще более существенно сократить машинное время, нужно использо-
использовать не только специфику матрицы системы но и отказаться от нахождения ее
точного решения. На самом деле точное решение разностной задачи не столь уж
U4HHO, поскольку оно само лишь приближается к решению исходной дифферен-
дифференциальной задачи с точностью ~ Л2. Поэтому имеет смысл искать решение раз-
разностной задачи тоже приближенно с точностью е ~ ilN1.
В такой постановке задачу можно решать итерационными методами, проде-
проделав порядка N* In N операций.

Общая схема итерационных методов выглядит так Задается некоторое на-
начальное приближение Ф*9 сеточной функции Ф*, а затем производят последова-
последовательный пересчет:
1,2,3,...).
G.254)
так, чтобы Ф*; •* Ф* при / -» ос •
Конкретный вид формулы G 254) определяет гот или иной итерационный
метод. Достаточно подробный обзор современных итерационных методов решения
разностных эллиптических уравнений содержится в статье [57].
Для задания в памяти вычислительной машины множества внутренних
расчетных точек области Fh можно поступить, например, так. Для каждой строки
с номером т = 2, .,., N2 (на первой и последней строке находятся только гра-
граничные точки) указывается числе интервалов INT (m) на этой строке, попавших
Рис. 7.28
в область Затем нужно указать начальное и конечное значения k для внутренивх
точек, находящихся на к ждом из этих интервалов, т. е. нужно задать массивы
чисел KSTART (/, т) н KFIN1S (/, т), где / — номер интервала в /n-и строке.
Йапример, на рис. 7.27 для т = 4 имеем /Л?Г D) =2 прячем Для /= 1
KSTART A, 4) = 2, KFINIS A, 4) =5; для / = 2 KSTART '2 4) = 8,
KFINIS B, 4) =11.
В приложении II приводится программа решения задачи кручения брусьев
о поперечными, сечениями, показанными на рис. 7.28, а, б. Решение уравнения
G 33) проводилось по модифицированному методу Ричардсона [57J Программа
составлена на языке FORTRAN. Счет выполнялся на машине БЭСМ-b. Время
счета (при N1 = N2 = 15) составило ~ 3 о. Численные результаты решения
приведены в приложении II и в виде эпюр касательных напряжений i = k Mia*—
на рис. 7.28, где приведены значения коэффициента * .
Отметим, что для повышения точности результатов можно проводить эвс-
траполяцию по h результатов счета, полученных, например, при h ~ Ш5,
Ь ~ 1/30 и h ~ 1/60. Кроме того, можно применять разностные схемы более вы-
высокого порядка.
§ 16. КРУЧЕНИЕ БРУСЬЕВ МНОГОСВЯЗНОГО ЗАМКНУТОГО
ТОНКОСТЕННОГО ПРОФИЛЯ
Решение задачи кручения брусьев, у которых поперечное сечение
представляет собой многосвязный замкнутый тонкостенный профиль,
наиболее просто достигается, исходя из мембранной аналогии.
187

Вначале рассмотрим простейший случай — кручение тонкостен-
тонкостенной трубы, т. е. когда поперечное сечение — тонкостенный двусвязный
профиль, изображенный на рис. 7.29. Толщина стенки б может быть
переменной вдоль средней линии L профиля, т. е. б = б (L).
При малой толщине б стенки трубы по сравнению с остальными раз-
размерами ее поперечного сечения поверхность мембраны, натянутой на
жесткий неподвижный контур, совпадающий с наружным контуром
Lo сечения, и на диск, соответствующий внутреннему контуру L3
сечения, можно считать конической поверхностью, соединяющей оба
контура: Lo и Lx. Это допущение, обусловливающее приближенность
решения, равносильно предположению, что касательные напряжения
постоянны по толщине стенки и во всех точках направлены параллель-
параллельно касательной t к средней линии профиля.
Рис. 7.29
Тогда в точках сечения на нормали п к средней линии L касатель-
касательное напряжение т будет определяться уклоном мембраны в данном ме-
месте. Поскольку на наружном контуре Lo функция напряжений Фо =
. = хшо = 0, имеем
т = xwJ8 = Оуб, G.255)
где Фг = v.wl — постоянное значение функции напряжений на вну-
внутреннем контуре Lx профиля.
Согласно мембранной аналогии, крутящий момент М пропорцио-
пропорционален объему, ограниченному поверхностью мембраны. Поэтому, учи-
учитывая G.255), получим -
М =
или
т = М/BРЪ),
G.256)
где F — площадь, ограниченная средней линией L профиля..
На основании теоремы о циркуляции касательного напряжения
G.39) имеем
G.257)
183

Из последнего равенства, сделав подстановку G.256), получим
М
L
Отсюда геометрическая характеристика жесткости
G-259)
В случае трубы с постоянной толщиной стенки б получим
fl = ML/DGF26) = xUBGF). ¦ G.260)
Если поперечное сечение трубы имеет входящие углы (рис. 7.30, а),
то в этих углах имеет место концентрация напряжений.
Для определения наибольшего местного напряжения в точках А,
следуя С. П. Тимошенко A878—1972), используем мембранную ана-
аналогию. На рис. 7.30, б заштрихованные области представляют эпюры
прогибов w мембраны. Поверхность мембраны по биссектрисе OOt
выкружки приближенно можно считать поверхностью вращения с осью,
перпендикулярной плоскости поперечного сечения и проходящей че-
через точку О. Тогда уравнение G.87) поверхности мембраны в зоне вы-
выкружки в полярных координатах имеет вид
с/2 w , I dw в
л—
фг , р ф
Так как
dw cP w I dx р ,
ар dp'1 ¦ x dp
получим
eh . 1
G.261)
Рассматривая трубу с постоянной толщиной б стенок и обозначая
через т0 напряжение в контурных точках, значительно удаленных от
угла профиля сечения, получаем из равенства G.260)
2GxJ = x0UF.
Последнее равенство дает возможность преобразовать уравнение
G.261);
^1 + JLT.J^.. G.262)
dp p F
Частное решение этого уравнения, очевидно, %0Lp/BF) и, следова-
следовательно, общее его решение будет
х = С/р + r0Lp/BF). G.263)
Постоянную интегрирования С можно найти из следующих сообра-
соображений. Очевидно, если предположить, что выступающие углы попе-
189

речного сечения имеют закругления радиуса (г + б), то это существен-
существенно не отразится на распределении напряжений в окрестности точ-
точки А. Тогда на основании гидродинамической аналогии имеем ра-
равенство
= то6, . G.264)
означающее, что количество идеальной жидкости, протекающей через
каждое сечение профиля, должно быть постоянным. Подставив выраже-
выражение G.263) для т в равенство G.264), после интегрирования найдем
In-
G.265)
и тогда напряжение в точке А (р = г) будет равно
хА = kx0, G.266)
где k — коэффициент концентрации напряжений, определяемый фор-
формулой
2F
G.267)
Например, для сечения (рис. 7.30) с размерами а = b = 10 см,
б = 1 см, г = 0,5 см, имеем F = 80,2 см2, Ь = 34,2 см и коэффи-
коэффициент концентрации напряжений k = 1,54.
Рассмотрим теперь поперечное сечение, представляющее собой трех-
связный тонкостенный профиль (рис. 7.31), у которог^в пределах каж-
каждого участка толщина стенки постоянна. Обозначим на участке ABC
толщину стенки б1? напряжение xit длину средней линии Llt на уча-
участке ADC — б г, т2, L2, а на участке АС — б3, т3, L3.
В соответствии с мембранной аналогией (рис. 7.31) имеем:
^бь т2 = К1Юч1Ьъ G.268)
190

т3 = х (Wi — и»2)/в8 = (тД — т2б2)/б3. G.269)
Применяя формулу G.39) теоремы о циркуляции касательного на-
напряжения к контурам АСВА и ADCA и учитывая при этом, что
| x3dL = — f radL, найдем:
СА АС
| 3 f
СА АС
J
т3 dL -f- J xt dL — т3 L3 + тх Lx —'.
ЛСС С7 \ G.270)
J x2dL+ )x3dL =
\DC CA
J 3 , 2—x8 L3 =
HOC СЛ
где FjH^ — площади, ограниченные средними линиями замкнутых
контуров.
Крутящий момент пропорционален объему, ограниченному мем-
мембранной, а принимая во внимание выражения G.268), получим
М = 2х (/>! + FwJ = 2 (fAfi + Fzbzc2). G.271)
Решая совместно уравнения G.269), G.270) и G.271), найдем:
G.272)
x8 = (M/Q) (
О = (M/G2Q) («iLjL, + бг^3^ + Sj^L»), G.273>
где
Q = 2 [e^jLjFf + 62831/1 + 6162^3 (Fi + ^гJ1. G.274)
§ 17. КРУЧЕНИЕ КРУГЛЫХ БРУСЬЕВ ПЕРЕМЕННОГО ДИАМЕТРА
В машиностроении широко применяются круглые валы перемен-
переменного диаметра. При этом диаметр может иметь резкие изменения, на-
например, в случае ступенчатого вала с галтелью (рис. 7.32), вала с раз-
различными кольцевыми выточками (рис. 7.33).
Круглый брус переменного диаметра — тело вращения, форма ко-
которого может быть представлена как результат вращения плоской кри-
кривой ABC вокруг оси Oz, расположенной в плоскости этой кривой
(рис. 7.34). При решении задачи кручения такого бруса, очевидно,
удобно воспользоваться цилиндрическими координатами г, 0, z, сов-
совмещая ось Ог с осью бруса.
Рассмотрим кручение бруса силами, приложенными на его торцах
и приводящимися к противоположно направленным моментам М вокруг
оси бруса.
Эха задача была впервые A900) решена Дж. Мичеллом полуобраг-
ным методом Сен-Венана. Предполагается, что, как и при кручении
круглого бруса постоянного диаметра, перемещения произвольной точ-
точки К бруса в радиальном направлении ит и в осевом направлении иг
равны нулю. Перемещение же по касательной к окружности радиуса
г в плоскости поперечного сечения есть некоторая искомая функция
191

«e *= "в (''. z), которая в силу осевой симметрии задачи не должна за-
зависеть от координаты в. Итак, предполагается, что
иг = иг = 0, щ = ив (г, г). G.275)
Используя F.57), убеждаемся, что объемная деформация
диг + J_ дщ _j_ _да1
г dQ
Q:
= 0.
G.276)
дг г dQ дг г
Тогда, считая, что массовые силы равны нулю, из трех уравнений
равновесия в перемещениях F.66) останется одно:
у2ы„ — ui/i* = 0, G.277)
которому должна удовлетворять искомая функция н9.
J
ta
1
I
Рис. 7.32
Рис 7.33
Решение задачи упрощается путем введения функции
W (г, г) - ив/г, G.278)
которая называется функцией перемещений и представляет собой угол
поворота вокруг оси скрученного бруса всех элементов его попереч-
поперечного сечения, расположенных на окружности радиуса т.
Компоненты тензора деформации в зависимости от функции пере-
перемещений ? на основании F.56)
г с
егг = еее = е„ = еа.~0, в,-о— -^
дг
дг
G.279)
и, следовательно, по формуле F.21) закона Гука найдем:
= GrdW/dz. G.280)
Подставив из G.278) ив = г? в уравнение G.277) и принимая во
внимание F.65), получим
д"* W" 3 дЧ? a2 W
. dr2 r
—4—
G.281)
ложить
G.282)
¦' Очевидно, что это уравнение будет удовлетворено, если положить
64 I дф дЧ 1 дФ
дг Grs дг ' дг Gr% дг '
где функция Ф (г, г) называется функцией напряжений.
192

Из G.280) и G.282) имеем:
i дФ
Orb =
1 дФ
= -T ^Г - G-283)
Функция Ф (г, г), разумеется, не может быть произвольной. Диф-
Дифференцируя первое уравнение G.282) по г, а второе — по г и прирав-
приравняв смешанные производные, получим следующее уравнение, которому
должна удовлетворять функция напряжений:
з *ф +_*ф 0.. G>284)
дг*
дг
Рис. 7.34
Выясним теперь граничное условие для функции Ф, к определеу
иию которой свелось решение рассматриваемой задачи. Посколько
боковая поверхность бруса свободна от внешних сил, очевидно, чта
полное касательное напряжение т9 в произвольной точке В контур-
меридионального сечения бруса (рис. 7.34) должно быть направлено
по касательной t к контуру. Поэтому проекция оге и o&z на нормаль я
к контуру должна равняться нулю, т. е.
йг dr п
ds ds
G.285)
где ds — элемент дуги контура меридионального сечения бруса.
Подставив в G.285) значения агв и о9г из G.283), получим
дФ йг , дФ dr л dФ
= 0 или
дг ds ds
дг
"f +
ds
= 0,
G.286)
т. е. функция напряжений Ф (г, г) должна быть постоянной на контуре
меридионального сечения бруса:
Ф (R, г) = С, = const, G.287)
где R — наружный радиус поперечного сечения бруса.
Далее, так как при кручении бруса сплошного поперечного сече-
сечения напряжения ozo и агв в точках оси бруса равны нулю, то из
формул G.283) следует, что при г — 0 производные дФ/дг, дФ/дг
7 Зак. 514
193

должны равняться нулю. Это означает, что функцию Ф (г, г) необхо-
необходимо подчинить еще условию
Ф @, г) = Со - const. G.288)
Таким образом, функция напряжений Ф (гг г) должна удовлетво-
удовлетворять уравнению G.284) и условиям G.287) и G.288).
¦ Крутящий момент М, т. е. момент, который дают напряжения az9
в поперечном сечении, связан о функцией напряжений следующим со-
соотношением:
я у
= 2n f-^-dr = 2л [Ф(/?, г)—
-Ф(О,г)]. G.289)
Отметим, что перемещение ив, как это легко видеть из уравнения
G.278), нелинейно зависит от г. Поэтому радиусы поперечного сече-
сечения бруса переменного диаметра при его кручении искривляются, что
составляет отличие от кручения цилиндрического бруса. Об искривле-
искривлении радиусов поперечного сечения свидетельствует также наличие
напряжений ог9, т. е. различных по интенсивности вдоль радиуса сдви-
сдвигов в плоскости поперечного сечения.
Рассматриваемую задачу можно решить также путем непосредствен-
непосредственного определения функции перемещений ?, удовлетворяющей урав-
уравнению G.281) и граничному условию
дШп - 0, G.290)
вытекающему из равенства нулю проекции на нормаль п к контуру
меридионального сечения бруса напряжений овг и o9z, значения кото-
которых определяются равенствами G.280). Однако этот путь решения вви-
ввиду более сложного граничного условия G.290) менее рационален.
Функция перемещений ? (г, г), представляя собой угол поворота
элементарного кольца радиуса г поперечного сечения, легко находится
из уравнений G.282) после определения функции напряжений Ф (г, г).
Очевидно, что, положив
? = const, G.291)
получим поверхность, у которой элементарные кольца радиуса г
при кручении бруса будут иметь один и тот же угол поворота. Лз ус-
условий симметрии следует, что поверхности, определяемые уравнением
G.291), являются поверхностями вращения. Эти поверхности ортого-
ортогональны поверхностям Ф = const, поскольку, как легко убедиться,
функции ? и Ф удовлетворяют условию
^ J5L + J31 J* 0. G.292)
дг дг дг дг
В частности, на основании G.287) линия пересечения поверхности,
? = const с плоскостью меридионального сечения бруса, представ-
представляя собой меридиан ВВ' (рис. 7.34) этой поверхности вращения, долж-
должна быть ортогональна к контуру этого сечения.
194

Покажем, что в произ-
произвольной точке Ki (рис. 7.34)
меридионального сечения бру-
бруса полное касательное на-
напряжение т9, как и в кон-
контурной точке В этого сече-
сечения, направлено по норма-
нормали к меридиану ВВ1, прохо-
проходящему через точку К и Дей-
Действительно, рассмотрим про-
произвольное направление s,
проходящее через точку Кх
и образующее угол р* с на- Рис lib
правлением те. Тогда имеем
Tg cos p = <jfj2dz/ds + oerdr/ds.
Учитывая G.280), последнее равенство принимает вид
% cos $ =
ds
откуда следует, что если направление «будет совпадать с меридианом
ВВ , то dWIds — 0, следовательно, cos ft = 0, т. е. напряжение т9
в точке /Ci меридиана ВВ1 направлено по нормали v к последнему и,
очевидно, равно
т9 = GrdY/dv. G.293)
Таким образом, в любой точке меридиана ВВ'- имеет место чистый
сдвиг в плоскости, перпендикулярной меридиану.
Если для некоторой точки меридионального сечения бруса окажет-
окажется возможным найти значение производной dW/dv, то напряжение тв
в этой точке легко получить по формуле G.293)
В качестве примера рассмотрим кручение бруса, имеющего форму
кругового усеченного конуса (рис. 7.35)
Очевидно, что величина
на контуре меридионального сечения конического бруса будет по-
постоянной, равной cos а. Тогда любая функция от этой величины будет
удовлетворять условию на контуре G.287) для функции Ф (г, г).
Непосредственной проверкой можно убедиться, что функция
где д _ постоянная, удовлетворяет основному уравнению G.284)
и, следовательно, является функцией напряжений рассматриваемой
задачи. *
Величина постоянной А должна быть такой, чтобы выполнялось со-
7. 195

отношение G.289). Подстановка функции G.294) в равенство G.289)
дает
А** ^ . G.295)
2.".B —3cosa+cos3«)
Теперь определим напряжения огв и ar9 по формулам G.283):
о* = ^ =-. G.296)
¦2п B—3 coi a+coss a) У(г*+г«M *
ЗМг3
,_
°М1 ~" 2я B — 3 cos a + coss a)
Вычислим по этим формулам напряжения, например, в точке К
При Г ва 2/?i И 2 = 8Ri.
агв - 0,235М/(л/??), ае, = 0,059M/(n#;)-
По формуле для цилиндрического бруса касательное напряжение
на поперечном сечении в той же точке К
_16УИ_==О25_М_ 7298
2 лDЯ)з п^? ' v '
т. е. абсолютная погрешность формулы G.298) в данном случав
составляет 6,3%.
При указанных размерах бруса угол при вершине конуса 2а == 28е.
Вычисления показывают, что при 2а = 20° абсолютная погрешность
при определении напряжений по формуле G.298) будет около 2%.
Угол закручивания характеризуется функцией перемещений
? (г, г), которую находим из уравнений G.282):
г^А G.299)
Следовательно, поверхности равного угла закручивания представ-
представляют собой сферы, центр которых совпадает с вершиной конуса (с на-
началом координат О).
Аналогично можно получить решение задачи кручения бруса, имею-
имеющего форму эллипсоида вращения, а также гиперболоида и параболои-
параболоида вращения. Эти задачи решены в 1920 г. Е. Меланом [46].
Встречающиеся в практике машиностроения многие задачи круче-
кручения валов переменного диаметра, например, с концентраторами напря-
напряжений в виде галтелей или коль-
кольцевых выточек различной формы
(см. рис. 7.32 и 7.33) оказывают-
оказываются значительно более трудными.
Поэтому эти практически важные
задачи решались приближенными
методами или экспериментально
многими исследователями. Доста-
Достаточно полный список работ по это-
этому вопросу и их обзор можно най-
Рис 7.36 ти в книге [50].
196
SL В
с 1 X
г*
К
2

Современная вычислительная техника позволяет успешно решать
эти задачи численным методом сеток. Весьма полезные результаты
и выводы о концентрации напряжений при кручении можно получить
на основе предложенной в 1925 р. Л.. С. Якобсеном электрической ана-
аналогии.
Пусть имеем тонкую однородную пластинку переменной толщины
t (рис. 7.36), контур которой совпадает с контуром половины меридио-
меридионального сечения вала переменного диаметра. Соединяя стороны пла-
V-
гз
2,0
1,6
1
11
\\
\
2,00
ч*
^^
¦
¦нтвим
0,04 Ц08 VI OJS
Рис. 7.37
стинки 2 = 0иг = /с источником электрического тока и поддерживая
определенной величины разность потенциалов Vo — Vi на этих сто-
сторонах, в пластинке получим стационарное электрическое поле, по-
потенциал V которого должен удовлетворять уравнению
dv\. а.л sv\ :0 G300)
Если при этом толщина / пластинки будет пропорциональна кубу
расстояния г от ее кромки, совпадающей о осью г (о осью вала): * = осЛ
то уравнение G.300) приводится к виду
i!L + -LiL + i!L = 0, G.301)
т. е. в этом случае оно совпадает с уравнением G.281) для функции пе-
перемещений ? задачи кручения круглого бруса переменного диаметра.
Условия на контуре для линий равного потенциала '/ = const
также совпадают с условиями на контуре линий равного угла закру-
закручивания ? = const. Действительно, при постоянной разности потен-
потенциалов на сторонах ОА и СК пластинки линии тока электрического
197

поля будут совпадать с ее контурами АС и ОК, а изопотенциальные ли-
линии, нормальные к линиям тока, будут перпендикулярны к контурам
АС и ОК, т. е. как и линии W = const в меридиональном сечении бру-
бруса. Таким образом, изопотенциальные линии тождественны линиям рав-
равного угла закручивания. Это позволяет представить картину распре-
распределения напряжений в скручиваемом брусе путем исследования рас-
распределения потенциала по соответствующей пластинке. В частности,
на основании электрической аналогии из формулы G.293) следует, что
касательное напряжение в точках
контура ABC вала пропорцио-
пропорционально относительному падению
потенциала dVldv вдоль кромки
ABC пластинки. Замеры с помо-
помощью чувствительного гальваномет-
гальванометра падения потенциала по контуру
rA'№M/nd3 галтели (выкружки) позволяют об-
обнаружить место наибольшего па-
Рис. 7.38 дения потенциала и определить
его величину. Тогда отношение
этого наибольшего падения потенциала к падению потенциала в доста-
достаточно удаленной от галтели точке Л будет определять величину коэф-
коэффициента концентрации напряжений в галтели:
k = ттах/тд. G.302)
где хА = 16М/{п(Р) — напряжение в точке А.
Коэффициент концентрации напряжений k, зависящий от отноше-
отношений laid и Did, можно определить по кривым рис. 7.37, построенным
по результатам экспериментов на основе аналогии Якобсеиа. На
рис. 7.38 приведен график, отражающий характер изменения каса-
касательных напряжений в меридиональном сечении бруса в точках кон-
контура галтели при laid = 0,15, Did — 1,5.
§ 18. КРУЧЕНИЕ АНИЗОТРОПНЫХ БРУСЬЕВ
Рассмотрим кручение призматического бруса сплошного попереч-
поперечного сечения моментами М, к которым приводятся приложенные толь-
только к торцам бруса поверхностные силы tt. Считаем, что массовые силы
ft = 0.
Как и в случае изотропного бруса, направим ось Ох3 по оси бруса,
начало координат О совместим с центром тяжести одного из его тор-
торцов.
Для исключения перемещений бруса как абсолютно твердого тела
будем считать
и\ = и\ = и\ = 0, со;1 = со» = cog = 0 при #! =
= 0.
G.303)
Предполагается, что компоненты тензора упругих постоянных
Cijki, называемые модулями упругости, являются непрерывными
функциями лишь координат хъ Хгпв каждой точке имеет место пло-
198

скость упругой симметрии, совпадающая е плоскостью попереч-
поперечного сечения бруса. При выполнении последнего ограничения в равен-
равенстве
G.304)
выражающем закон Гука, модули упругости Cim представляются ма-
матрицей C.37).
Решая уравнения G.304) относительно компонент тензора деформа-
деформации, получаем
- G.305)
где упругие постоянные Akiij образуют матрицу податливости.
При принятой упругой симметрии элементы матрицы податливости
Akitj, среди индексов которых встречается один или три раза индекс
«3», равны нулю.
Так же как и при кручении изотропного однородного бруса, зада-
задачу будем решать полуобратным методом Сен-Венана в напряжениях,
предполагая, что
On = 022 = Озз = о12 = 0. G.306)
Остальные две компоненты тензора напряжений а23 — о32 и
сг31 — ffi3 должны удовлетворять уравнениям равновесия B.27), гра-
граничным условиям B.29) и, имея в виду G.305), условиям совместности
Сен-Венана A.93)
С учетом условий G.306) уравнения равновесия B.27) принимают
вид:
Oi3,3 = 0, а2з.з = 0, G.307)
аил + °з2.г = 0. G.308)
Из равенств G.307) следует, что
о si = o3l (*i, хг), а32 = сгз2 (*,, хг). G.309)
Принимая во внимание предположения G.306) и сказанной относи-
относительно коэффициентов податливости A kit}, на основании формулы
G.305) определим компоненты тензора деформации:
ЁЦ = «1,1 = °. 822 — «2,2 = °i еЗЗ = «3,3 = 0. Yl2 = 2б12 =
= «Li + «2.ь
Уг3 = 2б23 = иг з + «3,2 = ^2323023
Y31 = 2е31 = Ы3,1 + «1,8 = ^2331028 + ^O
По условию Ahiu = Ahlij (хъ х2), следовательно,
е31 = e3i (^1. хг), ез2 = ез2 (xlt x?. G.312)
Тогда условия совместности Сен-Венана A.93) принимают вид
а^ а' а2 а2ег8 G 313)
дд'
дх\
199

Подставив в них значения е31 и ез2по формулам G.311) и выполнив
затем интегрирование, найдем
Т~ (Л2823 °23 + Л23а1 °8l) ~ Т~ И2331 °23 + Л3131 °3l) = COI1St- G.31 4)
Уравнение равновесия G.308), очевидно, будет удовлетворено,
если положить
о31 = дФ1дхъ оз2 = — дФ/дхи G.315)
где Ф = Ф (х1У х2) — функция напряжений.
Подставив значения о31 и оз2 по формулам G.315) в уравнение
G.314), найдем, что условия совместности будут выполнены, если
функция Ф (хг, х2) удовлетворяет уравнению
д I . дФ . дФ\ . д f . дФ . . дФ\ .
¦j- Лгзаз A.i33l —- + —- — Азш —* -f Лз181 —- = const.
д*, \ dxt dxt I ox2 \ dxi дхг J
G.316)
По условию, боковая поверхность бруса свободна от поверхност-
поверхностных сил, а поверхностные силы на его торцах приводятся к моментам
М, скручивающим брус. Поэтому, исходя из граничных условий
B.29), найдем, что функция напряжений Ф (хг, х2), как и при круче-
кручении изотропного однородного бруса, должна удовлетворять гранично-
граничному условию
O|l = 0 ' G.317)
и быть связанной с моментом М равенством
xt. G.318)
F
Уравнения G.310) и условия закрепления G.303) будут удовлет-
удовлетворяться, если принять
«1 = — #*2*3> «2 = ft*l*3> G.319)
где ¦& — относительный угол закручивания.
Если первое уравнение G.311) продифференцировать по хи а
второе — по х2 и результаты вычесть, то, приняв во внимание равен-
равенства G.315) и G.319), получим дифференциальное уравнение, которо-
которому должна подчиняться функция напряжений Ф:
д (л дф A -^W д ( А дф л А дф
G.320)
Уравнение G.320) отличается от уравнения G.316), выражающего
условие совместности, конкретностью постоянной в правой части.
Из равенств G.311), учитывая G.31,5) и G.319), находим частные
производные функции и3 (хх, х^):
u д "^
a' яз dxi ' Л1<" дхг
А О
иа,г— Л2згз "Г т^гзз! ^
200

Тогда функция иа (xlt x?, характеризующая депланацию попереч-
поперечного сечения бруса, находится по формуле
и» = "з + | («»д)*1-odXi +J («а.2) ^8. G.322)
о о
Основное уравнение задачи G.320), разумеется, упрощается для
ортотропного бруса. В этом случае в формуле закона Гуна G.304)
модули упругости представляются матрицей C.38) с числом независи-
независимых упругих постоянных, равным девяти. Упругие постоянные Cijm
и Аьц] (в случае ортотропного тела), у которых среди индексов встре-
встречаются один или три раза индекс «1», «2» или «3», равны нулю. Поэтому
при кручении ортотропного бруса коэффициент податливости А гза1 = 0
и равенства G.311) упрощаются:
Угз¦= Агз2яо2я, уя = Лата81, G.323)
а уравнение G.320) принимает вид
?)--»• <М24>
Если брус изотропный, но неоднородный, то]
А гага = Л п»1 = А (*„ х? — UG (xv x?,
где G (xlt х2) — модуль сдвига.
Для такого бруса функция напряжений Ф должна удовлетворять
уравнению
J_/± 1*) + J_f_L^)= _2O. G.325)
дх, \G dxj dxAG dxj v '
В случае изотропного однородного бруса модуль сдвига G не зави-
зависит от координат хъ хг и тогда функция Ф подчиняется уравнению
Пуассона G.33).
Рассмотрим простейший пример — кручение анизотропного одно-
однородного бруса с одной плоскостью упругой симметрии, совпадающей
с плоскостью его эллиптического поперечного сечения с полуосями
а и Ь (см. рис. 7.13).
Для однородного бруса коэффициенты податливости Акц) не за-
зависят от координат и уравнение G.320) при рассматриваемой упругой
симметрии имеет вид
Чтобы удовлетворить граничному условию G.317), функцию напря-
напряжений примем (см. § 6 данной главы)
Ф = А (х\1аг + xl/b* — 1), G.327)
где постоянная А находится из условия подчинения функции урав-
уравнению G.326):
А =- Ъа*ЬЧ{А Л31аг + АШзЬ2). G.328)
201

Следовательно, функция Ф, определяющая решение рассматривае-
рассматриваемой задачи, имеет вид
Ф = _ $а*Ь* A _ х\1аг — хЦЬ2)/(А пшФ 4- Агъгф% G.329)
Подставив это выражение для Ф в G.318), найдем относительный
угол закручивания:
О = -~ (ЛШ1 в1 + А,323), G.330)
где с = alb.
Ссылаясь на G.315), находим:
2Л1 2М .
/7OQM
G'33l)
Перемещения иг и иг определяются равенствами G.319), а переме-
перемещение «з. считая, что для окрестности точки, совпадающей с началом
координат, выполняются условия ее закрепления G.303), находим
по формуле G.322):
4 alo*)Xl xj. G.332)
Полученные результаты показывают, что напряжения не зависят
от упругих постоянных материала бруса и определяются по таким же
формулам, как и в случае однородного изотропного бруса (см. § 6
данной главы). От упругих постоянных зависят жесткость бруса и,
следовательно, перемещения. ¦ • • '
Достаточно много примеров решения задачи кручения анизотроп-
анизотропных брусьев можно найти в книге 137].

Глава Vlll
ИЗГИБ ПРЯМЫХ БРУСЬЕВ
§ 1. ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ УРАВНЕНИЯ
Имеем брус постоянного поперечного сечения, ограниченного про-
произвольным контуром L (рис. 8.1). Начало координат совместим с цент-
центром тяжести закрепленного левого торца бруса, направив по его оси
координатную ось х3, а оси х± и хг — по главным осям поперечного се-
чения так, чтобы система осей Оххх2ха была правая. Длину бруса обоз-
обозначим через /.
Рассмотрим изгиб бруса силой Р, направленной параллельно оси
х2, к которой приводятся поверхностные силы U на незакрепленном
правом торце (ха — /)• Предполагается, что массовые силы /; = О,
а боковая поверхность бруса свободна от сил tt.
Задачу будем решать в напряжениях полуобратным методом Сен-
Венана, т. е. сделав определенные предположения относительно значе-
значений некоторых компонент тензора напряжений. Допустим, что
<7ц = <3гг = <7i2 = 0. ass = — P (I — xs) X2/J, (8.1)
где J — момент инерции поперечного сечения относительно оси х,.
Остальные две искомые компоненты тензора напряжений а2з и оп
должны удовлетворять уравнениям равновесия D.3), условиям сов-
совместности Бельтрами D.55) и граничным условиям D.6).
Уравнения равновесия D.3) с учетом предположений (8.1) примут
вид:
ai3,3 = 0, а2з,3 = 0; (8.2)
Из уравнений (8.2) вытекает, что компоненты а31 и а3г не зависят
от координаты х3 и, следовательно, во всех поперечных сечениях каж-
каждая из них является одной и той же функцией только хх и хг. Эти функ-
функции а31 (*i, *г) и а3г (*i> хг) должны удовлетворять уравнению равно-
равновесия (8.3) и условиям совместности Бельтрами, При принятых зна-
значениях (8.1) для других компонент тензора напряжений первые четыре
уравнения D.55) удовлетворяются тождественно, а остальные два при-
приводятся к виду
Обратимся теперь к граничным условиям D.6). Для боковой поверх-
поверхности бруса, свободной от внешних сил ti, первые два условия удовлет-
удовлетворяются тождественно, поскольку ns — 0, а третье принимает вид
= 0. (8-5)
203

Так как (рис. 8.1)
пх = cos (я, хх) = dxz/dL, tit = cos (я, *2) = — dx-Jdt,
то условие (8.5) на контуре L сечения приводится к следующему:
aadxJdL — osZdxxldL = 0. (8.6)
Итак, решение поставленной задачи сводится к нахождению функ-
функций о9Х (хх, х2), оз2 (•*!, х2), подчиняющихся уравнению равновесия
(8.3), условиям совместности (8.4) и условию (8.6) на контуре L по-
поперечного сечения.
Для всех точек торцов бруса (ха = 0, xs = /) пх = пг = 0, па — =F 1,
поэтому граничные условия D.6) на торцах запишем так:
= 4-
h =
= + °зз
(8.7)
поперечное сечение
Рис. 8.1
т. е. напряжения о31 и og2 на поперечных сечениях бруса должны рас-
распределяться так же, как и соответствующие поверхностные силы tx
и t2 на его торцах.
Легко обнаружить, что уравнение равновесия (8.3) удовлетворяет-
удовлетворяется при условиях
= _зф_ р_. г г/х)| о =_j?!5. /g g)
где Ф (Хц х2) —. функция напряжений; / fo) — введенная С. П. Ти-
Тимошенко произвольная функция только координаты хх.
Подставив выражения (8.8) для о81 и оз2 в граничное условие
(8.6), получим
дФ dx3 дФ dxx _ P ,v2_fiYx,jbh_
т. е. граничное условие для функции Ф
dl 2J *
dL
(8.9)
204

Принимая выражения (8.8), условия совместности (8.4) приводим
к следующим уравнениям:
= 0. (8.10)
Согласно второму уравнению (8.10), У*Ф не зависит от дс2. Поэтому
интегрирование первого уравнения (8.10) по хг дает
¦*--?•(¦&¦«-?)+<;• (8Л1)
гае С — постоянная интегрирования.
Покажем, что постоянная С имеет простой механический смысл.
Производная по х3 угла поворота со3 произвольной элементарной пло-
площадки в плоскости поперечного сечения вокруг оси х8 на основании
A.35) и A.87) равна
Заменяя в последнем равенстве егз и е18 их значениями по форму-
формулам закона Гука C.69) и учитывая равенства (8.8), получаем
. 2G(o3i3 = V2 Ф + — —. (8.12)
Подстановка значения У2Ф из уравнения (8.12) в (8.11) приводит
к равенству
0)о «= 1 . (О. lO)
3 s E J 2G К '
Из этого равенства следует, что угол поворота на единицу длины
бруса со33 состоит из двух относительных углов поворота элементар-
элементарной площадки. Один из них линейно зависит от координаты хг элемен-
элементарной площадки и является результатом искажения поперечного се-
сечения в его плоскости при изгибе бруса (см. рис.4.4, б); другой — по-
постоянный, на который поворачиваются все элементарные площадки
поперечного сечения, т. е. так же, как и при кручении бруса. Напри-
Например, для элементарных площадок поперечного сечения в окрестностях
точек оси Хг (хх = 0) на основании равенства (8.13) имеем
С <= 2Gcos 3 = 2GO, (8.14)
т. е. указанные элементарные площадки, как и поперечное сечение
в целом, получают относительный угол поворота ft, с которым по-
постоянная С связана равенством (8.14).
Подставим полученное выражение для С в уравнение (8.11):
2/ \ 1 +v dxx j
Таким образом, поперечный изгиб бруса силой Р, приложенной
в направлении главной центральной оси его поперечного сечения, мо-
может сопровождаться кручением бруса. Однако путем параллельного
переноса линии действия силы Р кручение бруса можно устранить.
205

Тогда постоянная С = 2СФ будет равна нулю и основное уравнение
(8.11) примет вид
?•© = -?-/_?_*,-. *L\ (8.16)
2/ V l+v dxi I
Уравнение (8.16) и граничное условие (8.9) определяют функцию
напряжений Ф, когда указанным приемом кручение бруса устранено.
Произвольную функцию / (*i) можно выбрать таким образом, что-
чтобы правая часть уравнения (8.9) обращалась в нуль. При этом функция
Ф на контуре L поперечного сечения будет постоянной величиной, ко-
которую можно принять равной нулю. В этом случае задача изгиба бруса
будет аналогична задаче определения прогиба равномерно натянутой
мембраны на жесткий контур, совпадающий с контуром поперечного
сечения бруса, и испытывающей непрерывною нагрузку, определяв-'
мую правой частью уравнения (8.16).
§ 2. ЦЕНТР ИЗГИБА
Как уже было отмечено, поперечный изгиб бруса может сопровож-
сопровождаться кручением. Это происходит, как правило, твгда, когда главная
центральная ось поперечного сечения, с которой совпадает линия дей-
действия изгибающей силы Р, не является осью симметрии сечения. Воз-
Возникающее в этом случае кручение мож-
можно устранить путем приложения изгиба-
изгибающей силы Р по линии, параллельной
главной центральной оси и проходящей
через определенную точку в плоскости
поперечного сечения, называемую цент-
центром изгиба.
Центром изгиба называется точка,
относительно которой сумма моментов
всех касательных сил о^кх^Хг, a^dxidx^,
возникающих при поперечном изгибе,
равна нулю. Очевидно, что для опре-
определения положения центра изгиба не-
решить задачу изгиба, т. е. определить
Рис. 8.2
обходимо предварительно
функции о31 (*!, хг) и аз2 (хи х2).
Обозначим координаты центра изгиба Си через х\, х2 (рис. 8.2).
Тогда, по определению, имеем
Я Ь.ц (х2 — xi) — a9Z (X! — х\)} dxxdx2 = О
(8.17)
или
Здесь М — момент сил
координат О:
-*2<2,,=0, C.18)
и a3ifixidx2 относительно начала
ijiozxH-
(8.19)

и Q», — поперечные силы в направлениях осей л^ и х2!
Q*. =gaMd*id*8, (8.20)
3*dxidx2' ' (8-21)
Если брус изгибается только силой Р, параллельной главной цен-
центральной оси х2, то Q*, = 0, Qx7 = Р и равенство (8.18) принимает вид
М + х\Р = 0. (8.22)
Учитывая выражения (8.8) для о31 и оз2, формуле (8.19) можно при-
придать вид
М:
= -JJ(*iФд +х, Ф,2)dxx dxt +—- f J
Первый интеграл в последнем равенстве преобразуем таким же
образом, как и интеграл в формуле G.20). Тогда в случае односвязного
(сплошного) поперечного сечения имеем
М = 2 fjW*! dx2 + -^-N \x\ -/ (Xl)] xi dXl dx2. (8.23)
Формулы (8.22) и (8.23) позволяют определить координату х\ цент-
центра изгиба, когда брус изгибается силой Р, линия действия которой
параллельна главной плоскости хгх3.
Центр изгиба всегда расположен на оси симметрии сечения. Если
сечение имеет две оси симметрии, то центр изгиба совпадает с точкой
их пересечения, т. е. с центром тяжести сечения.
§ 3. ИЗГИБ БРУСА ЭЛЛИПТИЧЕСКОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Рассмотрим поперечный изгиб консольного бруса силами, распре-
распределенными на его торце и приводящимися к силе Р, направленной по
оси Хг (рис. 8.3).
Контур эллиптического поперечного сечения определяется урав-
уравнением
xVa2 + х\№ = 1. (8.24)
На основании (8.9) функция напряжений Ф на контуре сечения
обращается в нуль:
Ф|1. = 0, (8.25)
если произвольная функция
/ {Xj) = A - xlla1) b\ (8.26)

Уравнение (8.16) с учетом выражения (8.26) для функции f (xt)
принимает вид
Граничное условие (8.25) выполняется, если функция напряжений
Ф, которая должна также удовлетворять уравнению (8.27), имеет вид
и (8.28)
Рис. 8.3
Подставив выражение (8.28) в уравнение (8.27), найдем, что по-
последнее удовлетворяется при следующем значении постоянной А:
(8.29)
Итак, функция напряжений Ф, определяющая решение рассматри-
рассматриваемой задачи, представляется в виде
ф = _^
По формулам (8.8) находим:
оз1 = --
362) ,/
_ L
6я—xl —
A—
х\
a2+2(l+v)
Для точек оси лгх (х2 = 0) поперечного сечения получаем
(8.31)
(8.32)
т. е. имеем неравномерное, зависящее от коэффициента Пуассона, рас-
распределение напряжений по горизонтальному диаметру.
Касательное напряжение в центре сечения {хг = 0) равно
_ 2Р 1-й
~ F
+ 2 —
(8.33)
203

где F = nab — площадь поперечного сечения.
В точках / и /' (дг, = ± а) имеем
Так как v ^ 0,5, то 2v /A + v) ^ 1/A + v). Из сопоставления фор-
формул (8.33) и (8.34) вытекает, что наибольшее касательное напряжение
будет в центре сечения: ттах = тЛ
Если а существенно больше Ь, то имеем
1^-v F 1+v F V
Распределение напряжений по оси Xj в этом случае оказывается
заметно отличным от равномерного, предположительно . принимае-
принимаемого в сопротивлении материалов. Например, при v = 0,3 получим
х' = т,„а1 = 1.54P/F, т" = 0.92P/F.
Максимальное напряжение примерно на 14% превосходит напря-
напряжение, определяемое по формуле сопротивления материалов: ттах =
А
— РI /**
з '
При а ^> Ъ максимальное значение напряжения <х31 может оказать-
оказаться больше (а3а)тах. Наибольшей величины напряжение asl достигает
в точках, для которых выражение
хххг = XxbVl — х\1а2
1/2 Т/2
имеет максимум, т. е. при хх = ± -у- а, хг = ± '-тр Ь. Эти точки яв-
являются точками пересечения контура эллиптического сечения с диа-
диагоналями описывающего его прямоугольника, т. е. точки Кг, Кг, К3,
/С4 (рис. 8.3). В этих точках имеем
vaa4-(l+v)b2 Pab___ 2P a v/( I + v) + (b/af
^a3^max~ (I+v) (a"+ 3b») г! — F b
(8.36)
На рис. 8.3 приведены эпюры напряжений а3г вдоль оси хг и на-
напряжений <т31 по линиям КхКъ и КsKi при v = 0,3 и Ыа = 1/3,
Отметим, что касательные напряжения значительно меньше мак-
максимального нормального напряжения a3S в сечении ха = 0, равного
на основании (8.1)
(a33W=~-=4-i--?-. (8.37)
С уменьшением отношения alb уменьшается неравномерность рас-
распределения оз2 вдоль оси хх. Например, для круглого поперечного се-
сечения (Ь — а) при v = 0,3 по формулам (8.33) и (8.34) имеем
т« = TmnT = 1.38P/F, Xя- = 1.23P/F.
209

В этом случае абсолютная погрешность элементарной теории из-
изгиба в величине наибольшего «асательного напряжения составляет
около 4%.
В произвольной точке круглого поперечного сечения ф = а) на
основании формул (8.31) имеем:
l+2v P
31 4(J + v) •/ *'»
3+2v Я
¦7("-*|-Т^4 <а38)
Найдем перемещения tit произвольной точки круглого бруса при
его поперечном изгибе.
По формулам закона Гуна C.69), учитывая формулы (8.1) и (8.38),
получаем:
_ _?_,._ _ _Р_ _' Р_
11 EJ 3 г' м EJ . з г» зз gj
г, 3+2v P. I .. 2 1—2v
» ?V \ 3+2v
-—-^-^^
(8.39)
На основании A.97) и A.100) найдем:
«1,1 =т (/~*з) *., "... - V -?- (/ -
«1,2 «1,2+ V ?^ ( А;8)^1. «1,8
р
' ' EJ 2'
+ —— [v(x\— x'i) + 2lx3 — x
«з,1 ~ и%. 1 —ТрТ Xl x*'
«8,2 = «1,2 — "^-(y X' + Y ;
Теперь по формуле A.101) получим;
(8.40)
21Q

-j-w+***«)]•
(8.41)
Заметим, что если линия действия силы Р проходит через центр
изгиба, то выражения (8.41) для перемещений их и м% справедливы и
при любой другой форме поперечного сечения (см. §6 данной главы).
Если окрестность точки, совпадающей с началом координат, за-
закреплена так, что при хх = хг — хг = 0 и, = иг-— us = О и <»!=
= ©2 = ©8 == 0, то все постоянные интегрирования и] и ui,)t входя-
входящие в равенства (8.41), равны нулю.
§ 4. ИЗГИБ БРУСА ПРЯМОУГОЛЬНОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Длины сторон прямоугольного поперечного сечения бруса обозна-
обозначим 2я и 1Ъ, как показано на рис. 8.4.
На вертикальных сторонах хх = ± а, параллельных изгибающей
силе Р, производная dxJdL = О, поэтому если положить
f (Xi) - b\ (8.42)
то правая часть равенства (8.9) обращается в нуль на всем контуре L
поперечного сечения и постоянное значение функции напряжений
Ф (*х, хг) на контуре L можно принять равным нулю:
Ф | L = 0. (8.43)
Подставляя принятое выражение (8.42)
для функции / (х,) в уравнение (8.16), по-
последнее получает вид
(8.44)
1 + v .! L
Функция напряжений Ф (хх, дг2), как от-
отмечалось в § 1 данной главы, подобна функ-
функции прогибов w (xi, *2) мембраны, равномер-
равномерно натянутой на жесткий, в данном случае
прямоугольный, контур и находящейся вод
действием нагрузки, пропорциональной пра-
правой части уравнения Пуассона (8.44). На
рис. 8.4 показаны эпюра этой нагрузки и
кривая s, представляющая пересечение мемб-
мембраны с плоскостью ххх3. Из такой аналогии
« 2а ¦-
с
хг
Рис. 8.4
211

легко заключить, что функция Ф (хх, х? должна быть нечетной от-
относительно хг и четной относительно х2. Тогда решение уравнения
(8.44) можно~ искать в виде следующего ряда, удовлетворяющего ус-
условию (8.43) на сторонах хг = ± а:
^ . V чп у # \ • ППХХ -о .ел
п= 1
Если потребовать, чтобы функции Yn (xz), входящие в последний
ряд, удовлетворяли условию
Yn (± Ь) = 0, (8.46)
то принятое выражение (8.45) для функции Ф (xit xz) будет подчинять-
подчиняться условию (8.43) также и на сторонах хг — ± Ь.
Подстановка выражения (8.45) для функции Ф в основное урав-
уравнение (8.44) приводит к уравнению
| [? ] f (8.47)
правую часть которого разложим в ряд Фурье:
' (8-48>
п= 1
где коэффициенты Ап определяются, как обычно, методом Эйлера —"
Фурье:
Ап = — f XxSin^fLrf*!--^. (-!)»+«. (8.49)
a J a nn
—о
Учитывая значения коэффициентов Ап и. равенство (8.48), на ос-
основании (8.47) получим линейное дифференциальное уравнение
Y"«(*>--^Г- уп Ы = у ^ (-О"+1. (8.50)
общее решение которого следующее:
Так как функция У„ (х2) должна быть четной, то коэффициенты
Dn — 0, а коэффициенты С„ на основании (8.46) равны
Тогда выражение (8.45) для функции напряжений Ф, удовлетво-
удовлетворяющее уравнению (8.44) и граничному условию (8.43), принимает
вид
1+v. У я? n^J n? ^ ch (ллб/а) / а
212

Учитывая равенство
(-1)"
2а»
плх.
(8.54)
(в справедливости которого легко убедиться, разложив его правую
часть в ряд Фурье по sin -1), выражение (8.53) приводим к виду
(-1)"
ch
плх3
л8 плЬ
¦ ch
(8.55)
Ссылаясь на (8.8) и учитывая, что J — Ух, =-§ ab* =-^Fb2, имеем:
р ( а V v
. _ 6 р ( а V
* n2 F \ b j
I+v
a -
°8%~
L
п2
2 F
( — 1)" sh (nnxt/a)
81П
n2 ch (плЬ/а) ¦ a
14-v \~b
•COS
n=\
n2 ch (плЬ/а) а
(8.56)
В центре сечения С @, 0) и в точках / и V' (-± а, 0) (середины вер-
вертикальных сторон сечения), в которых угол подъема мембраны наи-
наибольший, напряжения на основании (8.56) равны:
а) в точке С
, 4 ?, (-!)»>
 1 
Ch
(8.57)
б) в точках / и /'-
——
(у) [т-
(8.58)
213

Ыа
2
1
1/2
0,983
0,940
0,856
0,805
<
0,981
0,944
0,856
0,805
Та
ft,
1,033
1,126
1,396
1,988
блица 8.1
*,'
1,041
1,144
1,435
2,065
3 Р
Первые слагаемые в формулах (8.57) и (8.58), равные -jj> совпада-
совпадают с величинами касательных напряжений, которые даются элемен-
элементарным решением сопротивления материалов, исходящим из предпо-
предположения равномерного распределения напряжений по ширине сече-
иия. Вторые слагаемые в этих формулах, уточняющие элементарное
решение, пропорциональны квадрату отношения сторон прямоуголь-
прямоугольного сечения (albf. Очевидно, если высота 2Ъ прямоугольного сечения
заметно превосходит другую его сторону 2а (ширину), то вторые слагае-
слагаемые в формулах (8.57) и (8.58) будут малы и в этом случае элементар-
элементарное решение достаточно хорошо согласуется с точным решением. На-
Напротив, если ширина сечения велика по сравнению с его высотой, то
величины поправочных слагаемых точного решения могут оказаться
весьма существенными.
Формулы (8.57) и (8.58), определяющие касательные напряжения
в точках С и У, можно записать в следующем виде:
_L JL
2 F
_3__Р_
2 F '
(8.59)
где kt и kx — безразмерные коэффициенты, величины которых для
некоторых отношений сторон прямоугольного сечения при v = 0,25
приведены в табл. 8.1. В этой же таблице приведены значения коэффи-
коэффициентов k'c и k{ формул (8.96) и (8.97) приближенного решения данной
задачи.
Из табл. 8.1 видно, что при Ыа ^ 2 элементарное решение дает
достаточно точные величины касательных напряжений. Однако уже
для квадратного сечения погрешность элементарного решения в наи-
наибольшем напряжении составляет около 12%, а для случаев, когда ши-
ширина прямоугольного сечения превосходит его высоту, элементарное
решение оказывается неудовлетворительным.
Следует отметить, что при изгибе бруса сравнительно большой дли-
длины наибольшее нормальное напряжение о38 значительно превосходит
наибольшее касательное напряжение. Поэтому погрешность при опре-
определении касательных напряжений по элементарной теории изгиба не
отражается (или почти не отражается) при решении задачи о прочности
бруса. Однако выяснение действительной картины распределения каса-
касательных напряжений имеет существенное значение при определении
центра изгиба.
214

§ 5. ЦЕНТР ИЗГИБА ДЛЯ БРУСА С ПОЛУКРУГЛЫМ
ПОПЕРЕЧНЫМ СЕЧЕНИЕМ
Предполагается, что изгибающая сила Р приложена в центре ич-
гиба Са (рис. 8.5) в направлении, перпендикулярном к оси симметрии
Xi сечения, и, следовательно, брус не скручивается.
Чтобы иметь наиболее простую запись уравнения контура сеченин,
начало координат О совместим не с центром тяжести сечения, как ра-
ранее, а с центром полуокружности АВК контура. Тогда уравнение (8.16)
запишется так:
где х] = 4#/(Зя) — координата центра тяжести С поперечного се-
сечения.
Примем
f (xj *-#* — х|, (8.6И
тогда граничное условие (8.9) для функции напряжений Ф на пол>-
окружности АВК контура сечения приводится к виду
йФ/dL = 0. (8.62)
Постоянное значение функции Ф (хи х? на полуокружности
АВК можно принять равным нулю:
ф|,=/? = 0. (8.63)
На прямолинейном участке А К контура сечения хх — 0, поэтому
согласно граничному условию (8.9) функция Ф на участке АК должна
удовлетворять также и условию (8.62), а с учетом непрерывности
функции Ф принимаем
Фи, =о = О. ^ .(8.64)
Подставим выражение (8.61) для функции / (х^) в уравнение ($.60):
8Ш= Xi + A, . (О.DO)
1 4-V «/
где
v PvQ ттДО
гг v ' ¦*! / 4ЬЛ- /О сс\
Д = , J = . ^о. 00)
1-f v J «
На основании мембранной аналогии правая часть уравнения (8.65)
пропорциональна нагрузке на мембрану, равномерно натянутую на
жесткий полукруглый контур. Это обстоятельство позволяет заклю-
заключить, что функция напряжений Ф должна быть четной относительно
координаты х2, поэтому будем искать ее в следующем виде:
!(l+cos20)+ 2 anr"cos/i9 . (8.67)
Ссылаясь на F.65), убеждаемся, что
V"< (СУ* cos 29) = 0, V2 (С, S anr" cos «0) = Ои V2 (Сх/?2хх) = 0,
215

поэтому подстановка выражения (8.67) для функции Ф в уравнение
(8.65) дает
8С, *,
-5-*, +/С.
Отсюда находим, что при постоянных
,, _l+2v Р г _± к___
,- 4 А- _
Рх\
1+v SJ
(8.68)
1+v 4/
выражение (8.67) для функ-
функции Ф удовлетворяет урав-
уравнению (8.65).
Обратимся к граничным
условиям для функции Ф.
Очевидно, что на прямо-
прямолинейном участке А К кон-
контура {хг = 0, 0 = ± я/2)
условие (8.64) выполняется
только при нечетных значе-
значениях п = 1, 3, 5, ...
Следовательно, выраже-
выражение (8.67) на полуокружно-
полуокружности АВК контура (г = R,
—я/2 ^ 0 <; я/2) принимает
вид
Рис. 8.5
(I)L=/?==C2[^a(l4-cos26)+ ^
/i-l, 3, 5...
а чтобы удовлетворялось условие (8.63), необходимо
R2 A + cos 26) + 2 а«Я" cos «е = 0.
(8.69)
Для определения коэффициентов ап ряда равенства (8.69) умножим
последнее на cos kQ dQ (k = 1, 3, 5, ...) и проинтегрируем в пределах
от — я/2 до 4- л/2.
Учитывая, что
ъ
A4-cos26)cosfterf0 = —sin-j- —
k(k*—4)
2—4)
_ (л/2 при
0 при
.находим
(8.70)
216

Тогда выражение (8.67) для функции напряжений Ф принимает
вид
+ _Ш у (-!)<-¦>/. „ cosne1
" -м..... «(««-4)/?»- J
Определим координату х\ центра изгиба Си. Для этого предвари-
предварительно вычислим момент М по формуле (8.23), которая с учетом выра-
выражения (8.71) приводится к виду
z
Поскольку dxxdxt = dF = rdBdr, то
Г Г (г«—/?2) Xi dxx rfx2= Г Г (г»—R2) г2 dr cos
15
0 ~}i
Nr*(l+cm26)dxldxM=( Г ,
Р 0 —я/2
Я/2 Ц
rn cos яб^*! rfx2 = I I;
н —я/ 2 О
«(л + 2)
Тогда '
м^ Г'8 3+4v I 4v A I 128
(8.72)
и на основании равенства (8.22) находим координату х\\
гм _ ад
Р
. (8.73)
217

Ряд в последнем равенстве сходится весьма быстро. Ограничиваясь
первыми четырьмя членами ряда, находим
При v = 0,25 получим к\ = 0,511/? и расстояние между центром
изгиба Си и центром тяжести поперечного сечения С будет х{ — к\ =»
= 0,087/?.
' § 6. ВАРИАЦИОННАЯ ПОСТАНОВКА ЗАДАЧИ ИЗГИБА
Рассмотрим вариационную постановку задачи изгиба бруса, ос-
основанную на применении принципа минимума дополнительной работы
(см. гл. V, § 6), допускающего сравнение статически возможных напря-
напряженных состояний.
Как известно, из всех статически возможных напряженных состоя-
состояний в действительности реализуется то, для которого вариация функ-
функционала W E.64), называемого дополнительной работой, равна нулю;
6? = б {Ш Л (°и) dV - JJ tt «</> dS\ = 0. (8.75)
В рассматриваемой задаче удельная дополнительная работа А(ац),
определяемая формулой C.80), с учетом выражений (8.1) и (8.8), равна
(8.76)
При вычислении вариации первого интеграла в равенстве (8.75)
в выражении (8.76) варьируются только слагаемые, зависящие от
функции напряжений Ф, т. е. получаем
- ~ (*2-/ (*i)) Ф. i] dxt dx2. (8.77)<
На контуре L поперечного сечения функция Ф должна подчиняться
граничному условию (8.9), поэтому в рассмотрение следует вводить
только функции, удовлетворяющие этому условию. Это означает, что
на контуре L ^32;1^ = ^;бФ|1 = О, откуда можно принять, что
на контуре L поперечного сечения выполняется условие
6ФЦ = 6Ф^ = 0. (8.78)
По условию задачи на боковой поверхности бруса U = 0 и, сле-
следовательно, остается найти работу вариаций поверхностных, сил ^
218

и /2. определяемых равенствами (8.7) и (8.8), на торцах бруса (t3 —
— ± «за не варьируется, поскольку напряжение о88 задано).
Перемещения их и иг произвольной точки бруса и, в частности, пе-
перемещения u[s) и u\s) точек его торцов оказываются независимыми
от функции напряжений Ф и могут быть получены в общем виде. По
формулам закона Гука C.69), принимая во внимание (8.1) и (8.8), по-
получаем
8ц — 8г2 —
Хя) Х%
(/ Х3)
— О,
(8.79)
На основании A.97) и (8.79) имеем
а по формуле A.100), учитывая (8.79), находим:
«2., =-«;,,+ ^ D-
(8.80)
i / ?_ 1 у
Используя A.101), получаем:
(8.81)
Заметим, что перемещение иа также определяется в общем виде,
но через функцию напряжений Ф или через так называемую-гармониче-
скую функцию изгиба Сен-Венана % (хх, хг) 12].
Перемещения щ и м2 не зависят от функции Ф, поэтому Ьиг = 0
и б«2 = 0. Тогда работа вариаций поверхностных сил tr и U на торцах
(ха = 0, х3 = /) определяется вариацией интеграла:
б JJ Uu\s)dS = б {JJ [tlU['> @) +
JJ
@)] dXldx2 +
ia (u[s) (I) -
- «1*J @)) + a23 («<s» @ - «<s> @))]
(8.82)
где «(,s) @), u[s) @) и u[s) @, «^s) @ — перемещения точек торцов
бруса соответственно при ха = 0 и хь — I.
219

По формулам (8.81) находим:
vPl
«kSl (О-«Г (O)-ttJ.,/- -^-
Учитывая последние равенства и соотношения (8.8) и опуская при
этом в выражении для о2з члены, не зависящие от функции Ф, так
как их вариации равны нулю, приведем равенство (8.82) к виду
1:)Ф11-и13Фл)йх1йх,. (8.83)
Последние два интеграла в равенстве (8.83) преобразуются по фор-
формуле Грина G.16).в контурные интегралы, обращающиеся в нуль вслед-
вследствие условия (8.78). Тогда в силу этого обстоятельства, а. также на
основании (8.75), (8.77) и (8.83) получи^ для функционала У следую-
следующее выражение:
((ф)а+(ф>2J ~т [x*~f {ХгI
х1 dx2. (8.84)
Таким образом, вариационная постановка задачи изгиба, базирую-
базирующаяся на принципе минимума дополнительной работы, сводится к опре-
определению подчиненной граничному условию (8.9) функции напряжений
Ф (хи х2), минимизирующей' функционал (8.84).
Найдем вариацию функционала W. Варьируя и интегрируя по ча-
частям члены выражения (8.84)при условии (8.78), найдем:
- Г Г 6Ф ~- dXl dx2 = - Г Г 6Ф V2 Фйхх dx2,
220

j
F F
Последние равенства и условие E.63) позволяют записать:
-l-L.Xl + -L.p{Xl)J8Odx1dx2. (8.85)
F
Поскольку вариация 6Ф произвольна в области F, а иа контуре t
этой области удовлетворяет условию (8.78), из равенства (8.85) вы-
вытекает уравнение Пуассона (8.16),полученное из условий совместности
Бельтрами.
Функцию напряжений Ф (хи хг), минимизирующую функционал Y,
можно приближенно найти одним из прямых методов вариационной
задачи изгиба при выполнении граничного условия (8.9).
Рассмотрим простейший пример — изгиб консольного бру-
бруса прямоугольного поперечного сечения (рис. 8.4)
силой Р, приложенной в направлении оси дг2 на торце х$ = /,
Правая часть уравнения (8.9) будет равна нулю, если
/ (*i) - Ь\ (8.86}
и, следовательно, можнв принять
<t>|L = 0. (8.87)
Следуя методу Канторовича, решение вариап^оннпго уравнения (8.85)
будем искать в виде
Ф (% Ч) = (&2 - *5) Q (*i> <8-88>
Условие (8.87) выполнится, если функцию Q (xi), подлежащую определению
подчинить требованию
Q (± а) = 0. (8.89)
Подставив (8.86) и (8.88) в уравнение (8.85), получим
[
-j Xxj (&»-*?) 6Q (Xl) dxt dxt =
Г Г 16 vP\4
~ \ 6Qw[l6~&SQS(Xl) -BQ^+T+VTJCljT&8
Ввиду произвольности вариации 6Q (x{) приходим к дифференциальному
уравнению
(8.90)
821

общий интеграл которого имеет вид
м (xj-Ach Т/571 ^-+в sh V572 у —р+7 7 *• (8<91)
Так как функция Q (ц) — нечетная (см. §4 данной главы.}, то принимаем
А = 0.
Из условия (8,89) находим
В У—-^- rL=— (8.92)
1+v У shV5/2a/6
в выражение (8.88) для функции напряжений Ф принимает вид
} (8-93)
По формулам (8.7) находим:
31 1+v 1 %shV572a/b " '
!+v 2У b 2l\f shi/5/2a/& v a /
Напряжения а точках С @, 0) и 1 (a, 0) определяются следующимя форму-
формулами:
а) в точке Ш
в точке
;
Здесь it н ij — безразмерные коэффициенты, зависящие от отношения
Ыа в коэффицвеята Пуассона v. Для некоторых отношений Ыа при v = 0,25
значения kc и k[ приведены в табл. 8.1, из которой видно, что формулы (8.96) и
(8.97) приближенного решения удовлетворительны по своей точности.
§ 7. НЕКОТОРЫЕ ЗАМЕЧАНИЯ
В этой главе рассмотрены решения задачи изгиба консольного бру-
бруса, один конец которого закреплен.а другой на торце нагружен рас-
распределенными силами tt, которые приводятся к силе Р, проходящей
через центр изгиба параллельно главной центральной оси х2 сечения.
Полученные решения являются точными лишь при выполнении ус-
условий (8.7). Если эти условия не будут выполнены, т. е. приводящие-
приводящиеся к той же силеР поверхностные силы tt будут распределены на тор-
торце иным образом, то в концевых поперечных сечениях бруса распре-
распределение напряжений <jn и a82 отличается от полученных решений.
В этом случае напряжения a3i и а3г оказываются зависящими также
и от координаты х8. Однако эта зависимость будет существенной только
на небольшой длине бруса от места приложения к нему нагрузки.
Полученные решения для о31 и а3г в поперечных сечениях на рас-
расстояниях от нагруженного торца, превышающих наибольший его ха-
222

рактерный размер, на основании принципа Сен-Вена*на можно рассма-
рассматривать точными при любом распределении на торце поверхностных
сил U , которые приводятся к указанной силе Р.
Если силы tt на торце бруса приводятся к изгибающей силе, линия
действия которой наклонена к главным осям поперечного сечения,
то ее можно разложить на составляющие в направлениях главных осей
и рассмотреть изгиб отдельно в каждой из двух главных плоскостей.
Результирующие напряжения и перемещения получатся путем нало-
наложения этих двух решений на основании принципа сложения действия
сил.
Пользуясь принципом Сен-Венана, полученные решения для
консольного бруса можно распространить и на случаи иного закрепле-
закрепления бруса, например для бруса на двух опорах с нагрузкой в каком-
либо сечении между опорами. В этих случаях можно допускать с до-
достаточной степенью точности,что напряжения на поперечных сечениях
бруса, значительно удаленных от месга приложения сил, зависят от
поперечной силы и изгибающего момента, как и в случае консольного
бруса.
Вблизи приложения внешних сил распределение напряжений в
поперечных сечениях заметно отличается от распределения в осталь-
остальных сечениях. Однако это отличие носит локальный характер, что
будет показано на'примере изгиба бруса узкого прямоугольного*поие-
речного сечения (см. гл. IX, §9).
Задача изгиба бруса нагрузкой, распределенной по его длине, в ча-
частности под действием собственного веса, впервые A901) рассмотрена
Мичеллом [3, 4]. Было показано, что в этом случае кривизна оси бруса
вообще не пропорциональна изгибающему моменту, а длина оси бру-
бруса несколько изменяется. Эта последняя характерная особенность будет
показана на примере изгиба равномерно распределенной нагрузкой
бруса узкого прямоугольного поперечного сечения (см. гл. IX, §9

Главе IX
ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
В машиностроении приходится встречаться с довольно обширным,
практически очень важным классом задач, в которых на форму тела
и на приложенные к нему внешние силы можно наложить определен-
определенные ограничения, приводящие к так называемой плоской задаче тео-
теории упругости.
Плоская задача теории упругости включает в себя задачи плоской
деформации, плоского напряженного и обобщенного плоского напря-
напряженного состояния. Эти задачи, отличающиеся по своей сущности,
объединяются идентичной математической формулировкой, что поз-
позволяет решать их одинаковыми методами.
§ 1. ПЛОСКАЯ ДЕФОРМАЦИЯ
Рассмотрим значительной длины цилиндрическое или призматиче-
призматическое тело (рис. 9.1) с основаниями (торцами), нормальными к его оси
х8 и закрепленными так, что их точки могут свободно (без трения) пере-
перемещаться в своей плоскости и не могут перемещаться в направлении оси
х3. Начало координат совместим с центром тяжести поперечного сече-
сечения, равноудаленного от торцов тела, направив оси хх и хг по главным
осям сечения. Внешние силы, приложенные нормально к боковой
поверхности тела, равномерно распределены по его длине, т. е.
ix =*= tx (xu Xz),tz = t2 (xi, x2), t8 = 0. Эти поверхностные силы вместе
е массовыми силами ft = fx {хъ хг), fz = fz (*ъ хг), f3 = 0 (если при-
приходится с ними считаться) должны быть статически эквивалентны
нулю.
При этих ограничениях в отношении формы тела и нагрузки, дей-
действующей на него, все сечения, перпендикулярные оси х3 (поперечные
сечения), оставаясь плоскими, находятся в одинаковых условиях
плоского деформированного соспюяния, которое характеризуется переме-
перемещениями:
 — Щ \Х\, Х%), «2 —  V*li Ху, «з — УЗ- Хр-1)
Это позволяет вместо рассмотрения всей области, занятой телом,
ограничиться рассмотрением его элемента, выделенного двумя попереч-
поперечными сечениями /—/ и //—// (рис. 9.1), расстояние между которыми
равно единице. Главный вектор и главный момент относительно оси х8
внешних сил, приложенных к этому элементу, по условию должны
обращаться в нуль:
= 1,2),
г (9.2)
I (*л — хгк) dL + Яр to/» -A'*/i)dF=г
I F -
224

где F — площадь поперечного сечения (тела), ограниченного конту-
контуром L.
Исходя из равенств (9.1) и уравнений закона Гука D.4)
где
-f
©1 = ««,! = «1,1 + «2,2,
(9.3)
получим следующие выражения для компонент тензора .напряжений:
аи = X6X + 2Gutl, a22 = Wt + 2Gu2ii, o12 = G (u12 + игл), (9.4)
а33 == Х9и а28 = о31 = 0.
(9.5)
Отсюда следует, что компо-
компоненты тензора напряжений,
как и перемещения, не зави-
зависят от координаты хь.
Из первых двух уравне-
уравнений (9.4), принимая во вни- Ь
мание C.64), имеем
=2 (к + фОц = Ш,Л\ (9.6)
Учитывая последнее ра-
равенство, получим
о88 = 1
Рис. 9.1
, = v (а„ + а2г).
(9.7)
Дифференциальные уравнения равновесия D.3) в случае плоской
деформации принимают вид
= 0, <т21Д + а222 + р/г = 0.
(9.8)
Граничные условия D.6) на боковой поверхности рассматривае-
рассматриваемого тела сводятся к условиям на контуре L его поперечного сечения:
"Г"
(9.9)
Граничные условия на торцах тела определяются их закреплени-
закреплением, которое приводит к возникновению на торцах тела и в его попереч-
поперечных сечениях напряжений а83 = а3з (хи х2), определяемых равен-
втвом (9.7). Наличие этих напряжений обусловливает плоское деформи-
деформированное состояние (плоскую деформацию) тела.
Усилия на торцах приводятся в общем случае к продольной силе
N =
= Я
«22)
8 Зам. SI4

и к моментам относительно главных центральных осей хх и хг:
мх, = Я x2o33dF = v |J (оц + о22) хфсхйхг,
' (9.11)
= v jj (ou + аг2) x,dj;A2.
Часто приходится иметь дело с призматическими телами, торцы
которых не закреплены и, следовательно, свободны от усилий. В этом
случае при условии, что длина тела велика по сравнению с его по-
поперечными размерами, решение можно получить путем наложения на
решение задачи о плоской деформации решений задач растяжения
и изгиба данного тела (при tx = t2 = A = /2 = 0) силой — N и момен-
моментами — MXi и —МХг, абсолютные значения которых определяются
равенствами (9.10) и (9.11). Последние задачи являются простейшими;
решение их было рассмотрено в гл. IV, § 8. В результате получим ре-
решение для данного тела при заданных нагрузках it = tx (xx, x?),
t2 = t2 (xi, x2) на его боковой поверхности и, вообще говоря, при не-
некоторой нагрузке на его торцах, главный вектор и главный момент ко-
которой равны нулю. Согласно принципу Сен-Венана, полученное реше-
решение для точек, удаленных от торцов, будет совпадать с решением для
данного тела, торцы которого полностью свободны от усилий. Дефор-
Деформация в этом случае уже не будет плоской; иногда ее называют обоб-
обобщенной плоской деформацией.
§ 2. ФУНКЦИЯ НАПРЯЖЕНИЙ
• Решение задачи о плоской деформации в напряжениях сводится
к определению функций ап = Оц (х1у х2), а2г = а2г (xlt x2), а12 =
= Оц fa, хг), которые должны удовлетворять уравнениям равновесия,
граничным условиям и условиям совместности.
Будем исходить нз однородных уравнений равновесия
Оц,1 + О12.8 = 0, O2i,i + О22.2 = °. (9-12
т. е. полагать, что fi~fz = 0.
Если массовые силы соизмеримы с поверхностными силами и их.Ц
необходимо учитывать, то эту, более общую, задачу можно свести так- i"
же к однородным уравнениям равновесия (9.12). Пусть afj{i = 1, 2; Щ
/ = 1,2) — какое-нибудь частное решение неоднородных уравнений Щ
равновесия (9.8), тогда общее решение уравнений (9.8) можно пред- - ';
ставить в виде
o°f = 0?, + оц d = 1, 2; / = 1, 2), (9.13)
где oij — функции, удовлетворяющие однородным уравнениям (9.12).
Частное решение of/ при обычно встречающихся на практике мае
совых силах (собственный вес тела, силы инерции) находится весьма
просто. Если, например, необходимо учитывать собственный вес при-
призматического тела (рис. 9.1), то уравнения равновесия (9.8) прини-
принимают вид
«ид + о12л = pgXl, о21д + аг2л = pg*a, (9.14) ,,
226

где gXi, gXa — компоненты ускорения силы тяжести соответственно
по осям xt и х2.
Очевидно, что уравнения (9.14) будут удовлетворяться, если при-
принять, например,
о?1 = oh = 0, ah = pgx,x2 + pgx,xi. (9.15)
При рассматриваемых массовых силах это частное решение удов"
летворяет уравнениям Бельтрами—Мичелла D.51) и, следовательно,
реализуемо в линейно-упругом теле. Остается найти функции oit,
удовлетворяющие однородным уравнениям равновесия (9.12).
Непосредственной подстановкой легко убедиться, что уравнения
(9.12) удовлетворяются, если принять
оп = Ф 22; СХ22 = ФД1;о12 = — Ф,12. (9.16)
Введенная здесь функция Ф = Ф (хъ Хг) называется функцией
напряжений или функцией Эри A801—1892).
Три соотношения (9.16) можно записать одним равенством
°и = ЩкПл®. ki, (9-17)
где illft — кососимметричный тензор второго ранга (t]l1 == т]22 = 0,
Tli2= + 1, Ла = — !)•
Чтобы функции aij были не только статически возможными, но и
реализуемыми в линейно-упругом теле, они помимо уравнений равно-
равновесия должны еще удовлетворять однородным уравнениям Бельтрами
D.55).
Принимая соотношения (9.16) и ссылаясь на (9.7), имеем:
(9:18)
рде Vs ( )=»—г 1—: .
ах\ ox*
Учитывая равенства (9.18), уравнения Бельтрами приводим к виду
(последние три уравнения D.55) удовлетворяются тождественно):
vV2Va<D = 0 )
Из (9.19) вытекает следующее уравнение для функции напряжений:
JliL д'Ф =0, (9-20)
у^Ф= + 2 +
дх\ ^ дх\дх\ ^ дх\
которое называется бигармоническим уравнением, а удовлетворяющая
ему функция Ф (*!, х2) — бигармонической функцией.
Подставив соотношения (9.16) в (9.9) и учитывая, что пг = dx2/dL,
п2 = — dxi/dL, получим граничные условия для функции напряжений
Ф на контуре L:
dx, даФ rtx{ _ d I дФ_\(
d a dL dL\dXbJ
дх\ dL dxt ax9 dL
д*Ф йхх d ( дФ
(9.21)
dxLdxt 4L дх\ dL a
В» 227

Таким образом, решение задачи о плоской деформации свелось
к определению бигармонической функции Эри, которая должна
удовлетворять условиям (9.21) на контуре L.
§ 3. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Пусть призматическое тело (рис. 9.1) с незакрепленными торцами
находится под действием уравновешенных поверхностных сил, прило-
приложенных нормально к его боковой поверхности (t3 = 0). Массовые силы
из рассмотрения исключаются, так как частное решение, соответствую-
соответствующее их действию, можно считать известным.
По определению, тело будет находиться в плоском напряженном ео-
стоянии, если во всех его. поперечных сечениях
оаз = оя = ои = 0. (9.22)
Отличные от нуля компоненты тензора напряжений ot} (I = 1, 2;
/ = 1, 2) должны подчиняться однородным уравнениям равновесия
(9.12). Последние будут удовлетворяться, если функцию напряжений
Ф° ввести следующим образом:
ои = Фи», а2г = Ф?ц, а12 - -Ф?12- (9.23)
В данном случае в отличие от плоской деформации перемещения
«1. «2» «8> а следовательно,- at) (i = 1, 2; / = 1, 2) и Ф° зависят от ко-
координаты хъ, т. е. задача о плоском напряженном состоянии является
трехмерной.
Можно показать (см. [3, 4J), что при симметричном нагружении
тела относительно его среднего поперечного сечения, с центром тя-
тяжести которого совмещено начало координат, бигармоническая функ-
функция напряжений Ф° представляется в следующем виде:
Ф° (xt, xt, xH) = Ф (*ь х2) -^—. х\ V8 Ф (хг, х.г), (9.24)
где Ф {хъ х2) — бигармоническая функция, не зависящая от х3.
Следовательно, напряжения, определяемые равенствами (9.23),
будут также квадратично зависящими от хь. Отсюда вытекает, что пло-
плоское напряженное состояние осуществляется при внешних силах/х и t^
на боковой поверхности рассматриваемого тела, распределенных по
такому же закону симметрично относительно среднего поперечного
сечения.
Уравнения закона Гука D.4) при плоском напряженном состоянии
принимают вид:
оп = № + 2GuMl-a2i = *е + 2G«a,a, о33 = № + 2Gu8i, = 0; (9.25)
о12 = G (ииг + «2Д), сг2з = G («2 й + ы3,а) — °>
о31 = G (и31 + uli8) = 0, (9.26)
где
© = «ia + «2.2 + «3.3- (9.27)
228

Поскольку 6 = 0! + иьь, где 9 х •= «1Д + игг, из третьего
выражения (9.25) находим
«8)8 = - Лв^Л, + 20), (9.28)
Тогда
9 = 2GQJQ. + 2G) (9.29)
и соотношения закона Гука приводятся к виду
on^%*@1 + 2Gulu a22 = 'K*el+2QuZt2, al2 = 0 («1>2-f «2Д), (9.30)
где
2° '2v v? ' (9.31)
—v)
Соотношения (9.30) по форме совпадают G соответствующими урав-
уравнениями (9.4) задачи о плоской деформации; если в (9.4) заменить ко-
коэффициент Ламе I другой постоянной X*, определяемой равенствами
(9.31), то получим соотношения (9.30). Вместе с тем в отличие от задачи
о плоской деформации задача о плоском напряженном состоянии явля-
является, как уже отмечалось, трехмерной, поскольку напряжения и пере-
перемещения в этом случае зависят и от координаты хь. Однако при очень
малом расстоянии между торцами тела по сравнению с его поперечными
размерами, т. е. когда тело представляет собой пластину (рис. 9.2),
зависимость напряжений от ха (в этом случае ха весьма мало), как это
усматривается из соотношения (9.24), будет несущественной.
Это позволяет, как показал Файлон, сделать важное обобщение
задачи о плоском напряженном состоянии, приводящее в случае тон-
тонкой пластины к двумерной задаче. Основная идея Файлона состоит
в том, что знание средних значений компонент тензора напряжений
и вектора перемещения по малой толщине пластины равноценно зна-
знанию их действительных значений в каждой точке.
§ 4. ОБОБЩЕННОЕ ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Рассмотрим тонкую пластину толщиной 2h (рис. 9.2), нагружен-
нагруженную только по ее контуру поверхностными силами tx и ^2, симметрич-
симметричными относительно срединной плоскости пластины, с которой совме-
совмещена координатная плоскость Ох^Хг. При таком нагружении пластины
в ее внутренних точках все компоненты тензора напряжений,
вообще говоря, будут отличны от нуля и должны удовлетворять трем
однородным]уравнениям'равновесия (принимается, что массовые силы
к = h = U = о):
ffll.l + СТ12.2 + а13,3 = 0» а21,1 + CT-22,8 + ff28,8 = 01 (9.32)
<*31.1 + ff32,2 + СТ33.3 — 0- I (9.33)
Однако по условию нагружения на торцовых плоскостях пласти-
пластины, т. е. во всех точках (xt, x2, ± h), должно быть
Отсюда, в частности, следует, что во всех точках (xi, x» ± ft)
o8i I l±ft = о82,а |±*> - °. (9-35>
229

поэтому из уравнения равновесия (9.33) для этих течей *юлучим
о3з,з1±й=0. (9.36)
По формуле Тейлора разложим функцию а33 (хи #2, *а) в РЯД по
х3 при фиксированных значениях хх и х%:
\( h) + a\(x
hf + ...
Учитывая (9.34)
(9.36),
имеем
Рис. 9.2
= у%,33М^-/1)г + ... (9.37)
Следовательно, для тонкой пла-
пластины компонента а99 весьма ма-
мала и с достаточным приближе-
приближением можно считать оаа = 0 во
всех точках пластины.
Остальные^ компоненты тензо-
тензора напряжений aij представим
их средними значениями с^ п0
формуле
=^г 1 °udx»
(9.38)
По условию, пластина нагружена симметрично относительно ее
срединной плоскости, поэтому компоненты ош а2г, сцг — четные функ-
функции относительно xs, компоненты аа1 и в3г — нечетные. Отсюда выте-
вытекает, что средние значения компонент osi и о3г равны нулю:
аоз1==(г32=0. (9.39)
Таким образом, при замене компонент тензора напряжений оц их
средними значениями а), отличными от нуля и независимыми от ха
будут только три компоненты о% (i — 1, 2; / = 1, 2), т. е. при осред-
осреднении компонент тензора напряжений рассматриваемая пластина при"
ближенно будет находиться в плоском напряженном состоянии, кото-
которое принято называть обобщенным плоским напряженным состоянием-
Поскольку а83 = о?1 =• о^г = 0» уравнения равновесия при ис-
использовании средних значений асц принимают вид
(9.40)
!,2 '
а соотношения закона Гуна будут следующими:
(9.41)
230

где л. — постоянная, определяемая равенствами (9.31);
Щ = «i.i + uln (9.42)
«Так как средние значения компонент тензора напряжений oft
не зависят от х3, то уравнения равновесия (9.40) можно удовлетворить
введением функции Эри Ф (хъ xz):
on = Ф.22, а°22 = Ф.п, а\2 = -Ф>12. (9.44)
Функции afj должны подчиняться условиям совместности Бель-
трами, а функция Эри, следовательно, должна быть бигармонической,
т. е. удовлетворять уравнению (9.20).
Граничные условия для функции Ф (лсь Хг) на контуре L пластины
выражаются равенствами
(9.45)
где
h
ft=— {t.dxo ft = 12). (9.46)
i 2h J t з /
Если на контуре L заданы не внешние силы, а перемещения, т. е.
граничные условия
«•|L-«}'> 0=1,2), (9.47)
то в этом случае задачу удобнее решать в перемещениях, используя
уравнения равновесия Ламе, которые для задачи о плоской деформа-
деформации имеют вид
уам,ч !—в, ,= 0 (/==1,2), ' (9.48)
I I « л lit \ ' / 9 \ г
а для задачи о плоском напряженном состоянии
V*««+-r-L-re°, = 0 (/ = 1,2), (9.49)
где постоянная v* на основании соотношений (9.31)
v* = v/(l + v). . (9.50)
Из сопоставления основных уравнений задачи о плоской деформа-
деформации о соответствующими уравнениями задачи об обобщенном плоском
напряженном состоянии видно, что они математически идентичны.
Заменив в уравнениях первой задачи комионенты щ и atj(i —1,2;
} — I, 2) их средними значениями по формуле типа (9.38), а коэффицн-
231

ент Ламе к — постоянной к*, определяемой равенствами (9.31), по-
получим уравнения второй задачи. Эти две различные по содержанию за-
задач» сводятся к одной и той же бигармонической краевой задаче, ко-
которая называется плоской задачей теории упругости.
Приведем еще формулы закона Гука, определяющие деформации
по компонентам тензора напряжений.
В случае плоского напряженного состояния имеем
2 = Оц + О22
и на основании D.5) получим
en =— (°u— vo22), е22 =— (о23 —von), ек = —il a12. (9.51)
С 12 С
В случае плоской деформации согласно (9.18)
2 = Оц + 022 + О33 = A + V) (Оц + О22),
а по формуле D.5) найдем:
ец=-?7-(°и—v'o22), еа2=—(о2г—v*au), е1г = —^- о12, (9.52)
где
~ 1—v2 ' V ~" 1 —V ~ 1 — 2v* ' <
Формулы закона Гука для плоского напряженного состояния (9.51)
и для плоской деформации (9.52) можно привести соответственно к сле-
следующим видам:
1 1
еи =-5—1A —v*) Оц—v*aa2L 8512 *= К*—v*) °аа—v*°nli
ela = -i-a12; (9.54)
=-—- [A — v) au — vo22], e22 =-^- [A — v)
(9.66)
В дальнейшем рассматривается, как правило, задача о плоской де-
деформации, при этом не имеющий значения размер тела вдоль оси хь
принимается равным единице длины. Имея решение задачи о плоской
деформации, путем указанной замены получим решение соответствую-
соответствующей задачи об обобщенном плоском напряженном состоянии при тех
же граничных условиях.
§ 5. ПЕРЕМЕЩЕНИЯ В ПЛОСКОЙ ЗАДАЧЕ
Если определена бигармоническая функция Эри, удовлетворяю-
удовлетворяющая граничным условиям (9.21), то соответствующие напряжения на-
находятся по формулам (9.16), а перемещения их и иг определяются инте-
интегрированием системы трех уравнений (9.4). Эти три уравнения, со-
232

держащие две определяемые функции их и и2, интегрируемы, так как
бигармоническое уравнение (9.20), которому должна удовлетворять
функция Эри, получено из условий совместности Бельтрами.
Равенство (9.3) позволяет записать уравнения (9.4) в следующем
виде:
оц = (I + 2G) вк — 2Gm2i2, саг = (Я + 2G) Qx — 2Gu1>lt
orit-G^M + o,,,). (9.56)
Из первых двух уравнений (9.56) с учетом равенств (9.16) и (9.3)
имеем
<тц + о22 = У2Ф = 2 (X + G) вг = Р, (9.57)
где введенная функция Р (хи х?) — У*Ф является гармонической,
поскольку Ч2- (ЧЩ = V2 Р = 0.
Учитывая соотношения (9.16) и значение вх из формулы (9.57),
уравнения (9.56) представляем в следующем виде:
—Ф,22, G(m1>2 + h21) = —Ф.12. (9.58)
Если обозначим через Q гармоническую функцию, сопряженную
с Р, то функция
f(z)=*P + iQ (9.59)
будет аналитической и интеграл этой функции по г будет аналити-
аналитической функцией. Тогда функция
ф(г)= p-\-iq=—\f(z)dzf (9.60)
также будет аналитической и, следовательно, функции р и q будут
подчиняться условиям Коши—Римана. Отсюда, учитывая (9.59),
имеем
дхг длг, дх2 дх.г 4 4
т. е.
Р = 4ра = 4<7,2, Q = 4<7д = - 4р,2. (9.61)
Используя соотношения (9.61), первые два уравнения (9.58) пре-
преобразуются так:
ZOH1A = ! — р х — Ф,ц» 2ОН2B = 9i2 — ^i22" ("•*3^)
Выполняя интегрирование уравнений (9.62), получим:
(9.63)
где /х (xz) и /2 (хх) — некоторые функции.
233

Подставляя выражения (9.63) в третье уравнение (9.58) и учиты-
учитывая, что р_4 = — <7д> получаем
. П {хг) + ft (*0 = 0.
Так как ft (х2) — функция только х2, а /2 (х{) — функция только
хъ то
/i (X2) = A,f2 (Xl) = - А, (9.64)
где А — постоянная.
Интегрируя уравнения (9.64), найдем:
h (хг) = Ахг + В, /2 (х,) = — Ах, + С
где В и С — постоянные.
Таким образом, функции /х (х2) и /2 {х{) в выражениях (9.63) со-
соответствуют жесткому смещению тела. Полагая, что на тело наложе-
наложены связи, запрещающие его жесткое смещение, эти функции следует
положить равными нулю. В этом случае выражения (9.63), учитывая
соотношение C.64), принимают вид
^ ^(D,2|. (9.65)
В случае задачи о плоском напряженном состоянии в равенствах
(9.65) надо заменить v на v* по формуле (9.50). Если еще учесть соот-
соотношение C.63), то для плоского напряженного состояния получим:
«i = -^[4p—(l+v)O,Il. «8 = 1[4?-A+у)ФД (9.66)
с Ь
Исходя из того, что р и q — гармонические сопряженные функции,
непосредственно находим:
V2 (Xlp) = 2рд = Р/2, V2 (*, q) = 29>8 = Р/2, (9.67)
где, как уже отмечалось, Р'= У2Ф — гармоническая функция.j
Тогда
V2 (Ф - ххр - x2q) - 0,
т. е. Ф — Хцр — хгц = pi — некоторая гармоническая функция.
Отсюда следует, что любая бкгармоннческая функция и, в част-
частности, функция Эри, через производные которой определяются на-
напряжения и перемещения в плоской задаче, может быть представлена
в общем виде через три гармонические функции, две из которых
(р и q) сопряженные:
Ф = хф + Xiq + px. (9.68)
§ 6. МЕХАНИЧЕСКИЙ СМЫСЛ ФУНКЦИИ ЭРИ
И ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ НЕЕ
Из пластины толщиной 2h = 1 мысленно выделим ее часть, огра-
ограниченную произвольной гладкой кривой s (рис. 9.3). Выделенная
часть будет находиться в равновесии под действием напряжений со
стороны остальной (внешней) части пластины. Составляющие рпг
234

и рпг вектора напряжений рп в произвольной точке контура s на осно-
основании B.15) и (9.16) равны:
dxt дхг ds дх\ ds
ИЛИ
РП2 ds
Проинтегрируем равенства (9.69) по некоторой дуге s в положитель-
положительном направлении, при котором выделенная часть остается слева, т. е.
от некоторой начальной точки А до произвольной точки В (рис. 9.3).
В результате получим значения производных функции Эри в про-
произвольной точке В:
-* +
(9.70)
где К = (Ф ib, Л^ = (Ф 2)л — постоянные, равные значениям про-
в
изводных функции Эри в начальной точке А дуги s; Pi = J Pni^s.
в
Рг = J pn2ds—компоненты главного вектора поверхностных сил,
А
приложенных на дуге АВ.
Знание производных Ф i и Ф 2 в произвольной точке контура s
позволяет найти производные функции Эри по касательной и по нор-
нормали к контуру выделенной части:
dO) __ дФ dx1 ¦' дФ йхг АФ дФ dxx дФ dx2 /о 71)
ds dxt ds дхъ ds ' dn ддс, dn дх^ dn
Интегрируя первое равенство (9.71) по дуге А В, получаем
J \ х1 ds дх2 ds
А
где М = (Ф)л — постоянная, равная значению функции Эри в на-
начальной точке А дуги s.
Вычисляя интеграл в последнем равенстве по частям и принимая
во внимание (9.69) и (9.70), находим
$
-xfN+\(xlPlia-xtpnl)ds. (9.72)
л
235

Последний интеграл в равенстве (9.72) представляет собой глав-
главный момент М° поверхностных сил на дуге АВ относительно начала
координат О:
в
М° = J (хг pni — xzpni) ds. (9.73)
Равенство (9.72) можно записать так:
Ф = М + (х? — xf) К + (*? - xf) N — х*Рг + xf Px +M °, (9.74)
Рис. 9.3
Рис. 9.4
или в другом виде
Ф = М + (х,в — х?) К + (xf — xf) N + Мв, (9.75)
где
А
f) рпг~\хг -
xf)
рпЛ] ds
(9.76)
есть главный момент поверхностных сил, приложенных на дуге АВ,
относительно точки В.
Таким образом, значение функции Эри в произвольной точке В
дуги АВ с точностью до несущественной для напряжений линейной
функции равно взятому относительно точки В главному моменту Мв
внутренних сил на дуге А В, а производные функции Эри определяют-
определяются по формулам (9.70) проекциями на оси хг и хг главного вектора
этих сил.
Приведенные рассуждения, естественно, применимы и к наружно-
наружному контуру L пластины. В частности, значение функции Эри в произ-
произвольной точке Ь контура L пластины (рис. 9.3) с ссылкой на формулы
(9.75) и (9,76) определяется равенством
Ф = М
\ — х\) К
N
- (хг - х<>) tx\ dL,
(9.77)
236

r.ie M = (Ф)а, К — (Ф,1)а, N = (Ф2)а — значения функции Эри
л ее производных в произвольной начальной точке а контура L.
Второе равенство (9.71) на контуре L принимает вид
Л)-5-- <9'78)
а равенства (9.70) запишутся так:
Фд = ~ J /2dL + /С, Ф,а = \ hdL + N, (9.79)
о . о
где Ф 1 и Ф 2 — производные функции Эри в произвольной точке
контура, значения которых в фиксированной- точке контура, от ко-
которой отсчитывается дуга контура L, обозначены
/С = (Фд)о, # = (Ф,а)о
Итак, решение плоской задачи может быть сведено к определению
бигармонической функции Ф (хъ х2) по значениям этой функции на
контуре L и ее производной по нормали к контуру L, определяемым
формулами (9.77) и (9.78) в зависимости от заданных поверхностных
сил ti и tz.
Если контур L ограничивает односвязную область, то входящие
в формулы (9.77) и (9.78) постоянные /С, N, М можно принять равны- ¦
ми нулю. В случае же многосвязной области (рис. 9.4) эти постоянные
можно считать равными нулю только на одном, например наружном
контуре Lo, а на внутренних контурах их следует находить из условия
однозначности перемещений их и иг, определяемых равенствами (9.65).
Это означает, что при положительном обходе (в указанном на рис. 9.4
направлении) каждого контура Lh приращения функций Hi и и2
должны быть равны нулю, т. е.
На основании (9.70) производные — Фл и Фа при обходе конту-
контура Lfc получают приращения, равные соответственно Рг и Р1г пред-
представляющие собой суммы проекций на оси х2 и хх внешних сил, при-
приложенных к контуру. Поэтому функции
4 A — v) р = A — v) j \Pdxi — Qdx2) и 4 A — v) q = A —
— v) J (Qdxx + Pdx2)
при обходе контура Lk должны получить приращения соответствен-
соответственно — Р2 и Pi. Следовательно, необходимо выполнение условий
A - v) I (Pdxl — Qdx2) = - Р2, A — v) J (Qdxt + Pdx2) = Pl (9.80)
Еще одно условие для определения трех постоянных на каждом
контуре Lft, входящих в граничные условия (9.77) и (9.78) для Ф
237

и дФ/дп, получим, исходя из легко устанавливаемого кинематиче-
кинематического смысла гармонической функции Q. В самом деле, угол малого
поворота относительно оси х$ элемента пластины, как целого, на ос-
основании A.35) и (9.65) равен
® ("«) ^pfo PJ = f ®
Отсюда следует, что функция Q пропорциональна углу малого по-
поворота ©з элемента.
Приращение функции Q при обходе по дуге АВ определяется, оче-
очевидно, формулой
А
Поэтому при однозначных перемещениях на контурах L& должны
соблюдаться равенства
Ld ^L^UC^^O. (9.81)
dx дп
Таким образом, в случае многосвязной области равенства (9.80)
и (9.81) позволяют определить постоянные, входящие в граничные
условия для Ф и дФ/дп.
Заметим, что в случае односвязной области функция Эри является
однозначной функцией. Действительно, из (9.2) (массовые силы ft
принимаются равными нулю) и из (9.21) вытекает, что производ-
производные Ф,1 и Фл при обходе контура L, ограничивающего односвязную
область, не получают приращений. А на основании (9.77) и последнего
равенства (9.2) следует, что при обходе контура L не получит при-
приращения и функция Эри. В случае же многосвязной области функ-
функция Эри и ее производные будут однозначными лишь при условии,
что на каждом контуре внешние силы статически эквивалентны нулю;
если на каждом контуре Lk только главный вектор внешних сил
равен нулю, то производные Фд и Ф 2 будут однозначными функ-
функциями, а сама функция Ф будет," вообще говоря, неоднозначной.
§ 7. ТЕОРЕМА ЛЕВИ—МИЧЕЛЛА
Напряжения в плоской задаче, когда на контуре L заданы внешние
силы, определяются формулами (9.16) в зависимости от функции Эри,
которая должна удовлетворять бигармоническому уравнению (9.20)
и граничным условиям (9.77) и (9.78). Во все эти уравнения не входят
упругие постоянные материала. Это обстоятельство позволяло Мори-
Морису Леви A838—1910) сформулировать следующую теорему: распре-
распределение напряжений в плоской задаче при данном погружении на кон»
туре является одинаковым для всех изотропных материалов.
Эта теорема, как показал Дж. Мичелл, справедлива для односвяз-
ных областей, а в случае многосвязных областей она имеет место лишь
238

тогда, когда главные векторы внешних сил, приложенных к каждому
отдельному контуру, равны нулю.
Теорема Леви—Мичелла является основой оптического метода
исследования напряжений, так как согласно этой теореме вместо изу-
изучения напряжений в изотропных металлических телах можно изучать
напряжения в прозрачных изотропных телах, оптически чувствитель-
чувствительных к возникающим в них напряжениям.
§ 8, ПРЕДО*АВЛЕНИЕ БИГАРМОНИЧЕСКОЙ ФУНКЦИИ
В §5 гл. IVбыло отмечено, что любая гармоническая функция / и ее
производные /./ представляют собой бигармонические функции. Там
же было показано, что если ft, — гармонические функции, то функции
ф, = xifu Ф2 = x2f2 (9.82)
являются бигармоническими.
Покажем теперь, что если / (хх, х2) — гармоническая функция, то
функция
Ф = г2/, (9.83)
где г2 = х* + х% = xtxt, является бигармонической.
Действительно, имеем:
г2/,,; (/¦»/).о = 2&tjf + 2xi/j + 2x,f,, +
Свертывая последнее равенство по индексам I и / и учитывая, что
6*/= 6Ц + б22 = 2, fJt = V2/ = 0, получим
. уг (г2/) = 4/ + ixtfj = 4 (/ + хх/д + xjj. (9.84)
Поскольку /, а следовательно, и ftt — гармонические функции,
то на основании D.32) имеем:
V2 (jc/д) = 2/,и, V3 (x2ft2) = 2/,e.
Сложив последние равенства, получим
V2 to/., + АГг/>2) = 2V2/ = О,
откуда следует, что правая часть равенства (9.84) есть гармоническая
функция, поэтому функция Ф = г2/ — бигармоническая, т. е.
V2V2(r2/)=0.
Очевидно, что сумма бигармонических функций также удовлетво-
удовлетворяет бигармоническому уравнению. Следовательно, функции
Ф = *i/i + /4, Ф = Ыг -И», Ф = г2/3 + /6) (9.85)
при условии V2/j = 0(/ = 1, 2, ..., 6) — бигармонические функции.
Любая бигармоническая функция может быть представлена через
две независимые гармонические функции в одном из трех видов (9.85).
Например, бнгармоиическую функцию
ф = xj-x -f x2F2, (9.86^
23!)

где F-l (Хи хг), Fz (л'ь x2) — произвольные гармонические функции,
представим в следующих видах:
Ф - х^ + x2F2 ¦= xl (F, + Ft) + (x2Fz — xxF3), (9.87)
Ф = х^г + x2F2 = х2 (Ft + Ft) + {xtFt - x^Fd (9-88)
Принимая введенные в равенствах (9.87) и (9.88) функции F3 (хх, х2)
и Ft (*ь Xz) гармоническими, сопряженными соответственно с функ-
функциями Fz (х\, Хг) и Fi (хи х2), т. е. удовлетворяющими условиям Коши—
Римана;
dF<Jdxx = dFz/дхг и д/удх2 = дрх1дхъ
функции /4 = XzFz — xxF8 и /5 = ^i ~ х^\ будут гармонически-
гармоническими и выражения (9.87) и (9.88) для бигармонической функции (9.86),
используя обозначения гармонических функций /х = Fx + F9 и /г —
= ^г + ^4. приводятся к первым двум видам (9.85).
Общее представление (9.68) бигармонической функции также при-
приводится к этим двум видам:
Ф = 2Xlp + (x2q — ххр + р^ =» 2хц + (Хф — хгц + pt), (9.89)
где выражения в скобках — гармонические функции, так как р и q —
сопряженные гармонические функции.
При решении многих плоских задач удобно принимать гармониче-
гармонические функции fi (xu хг) в выражениях (9.85) в форме однородных гар-
гармонических полиномов, определяемых вещественной Re и мнимой Im
частями функции ю = гп комплексного переменного г = xt + ix2.
В этом случае представления (9.85) бигармонической функции Ф при-
принимают вид:
Ф = Сххх Re гп + С2 Rez"+', Ф = С3хг Im г" + С4 Im z"+! \
Ф = С5 (х\ + xl) Re г«-! + С6 Re г"+!. ) (9.90)
Очевидно, что полином ниже четвертой степени удовлетворяет би-
гарионическому уравнению при любых постоянных коэффициентах.
Суммируя равенства (9.90) и выражая в них z через модуль и аргу-
аргумент: г — г (cos 6 + l sin 6), придем к представлению бигармонич-
ской функции, которое используется при решении некоторых плоских
задач в полярных координатах:
Ф (г, 9) = (dr* + С2г"+2 + С3г-" + С4г-«+2) cos «9 +
+ (ZV" + ZV+2 + D3r-» + D4r-"+2) sin «9, (n > 2) ( '
§ 9. ПЛОСКАЯ ЗАДАЧА В ДЕКАРТОВЫХ КООРДИНАТАХ
При решении "плоской задачи для прямоугольных пластин и длин-
длинных прямоугольных полос естественно использовать прямоугольные
координатные оси, направленные параллельно сторонам пластины
(рис. 9.5). В этом случае граничные условия (9.9) на прямоугольном
контуре существенно упрощаются. Действительно, на вертикальных
240

сторонах пластины, т. е. при Xl = 0, хх = /, имеем Я1 = + 1, п2 = 0 и,
следовательно, на этих сторонах условия (9.9) принимают вид:
к = Т аи = =f Ф 22, *2 = q= а21 - ± Ф 12. (9.92)
На продольных кромках пластины (хг = ± й/2) ftj = 0, о2 = ± 1
и условия (9.9) сводятся к равенствам:
к ~ ± а12 = ± Ф 12, ^ = ± а22 == ± Ф,ц. (9.93)
Однако отыскание бигармо-
нической функции Эри, удов-
удовлетворяющей даже простым
граничным условиям (9.92) и
(9.93), при заданных tx и t2
обычно вызывает затруднения.
Поэтому иногда обращаются к
решениям обратной задачи. За-
Задаваясь различными бигармони»
ческими функциями, опреде-
определяют, какому виду нагружения
они соответствуют. Имея набор Рис. 9.5
таких решений, путем их линей-
линейного комбинирования можно установить вид функции Эри, соответ-
соответствующей данному конкретному нагружению пластины.
Решение с помощью полиномов. Менаже в 1901 г. предложил за-
задаваться функцией Эри в виде полиномов различных степеней. Это
позволило получить решения для некоторых практически важных
задач.
Примем функцию Эри в виде полинома второй степени
Ф = агх\ + bzxix2 + в2х1, (9.94)
(
который удовлетворяет уравнению (9.20) при любых значениях его
коэффициентов. По формулам (9.16) находим:
°а = ф,»2 = 2с2, а22 -Ф„ = 2а2) а12 = — Ф,18 = — Ьг, (9.95)
т. е. функция (9.94) соответствует постоянным значениям компоиент
тензора напряжении во всех точках пластины, на сторонах которой
приложены постоянные силы к и tz, показанные на рис. 9.6, а, б.
Примем теперь функцию Эри в виде полинома третьей степени
Ф = а^с\ + 6 з*?*2 + CgXj*! + djxs, (9.96)
который также удовлетворяет уравнению (9.20) при любых коэффи-
коэффициентах.
В этом случае по формулам (9.16) находим:
<*и = ^gXj 4- 6d3X2, a22 — 6а3*1 + 26з*2, ffi2 = — 2^3^ — 2с8х2.
(9.97)
Рассмотрим полином (9.96) при некоторых частных значениях его
коэффициентов. Принимая, например, все коэффициенты, за исклю-
исключением d3, равными нулю, имеем оп = 6d3x2, о22 = о12 = 0, т. е.
241

, J, I
ST
-С:
i i p |
it
X,
xi
t,--bt.
I'
Рис.
функция Ф = d3x2 соответствует чистому изгибу пластины (рис. 9.7).
На рис. 9.8 показано нагружение пластины, соответствующее функ-
функции Ф = бз*?-*^; в этом случае имеем:
а22 = 2bsxit а12 = — 26^, ап = 0. (9.98>
Возьмем функцию Эри в виде полинома четвертой степени:
ф=а^\ +btx \хг + Ci х\ х% + di хг х\ + е4 х\. (9.99)
г х\
Подставив это выражение для функции Ф в уравнение (9.20)
убедимся, что оно удовлетворяется лишь при условии
Ч =¦ — («4 + Ф),
т. е. в выражении (9.99) произвольно можно принимать только четыре
коэффициента: ait bit c4 и d,. Придавая им различные значения, по-
получим условия нагружения на сторонах прямоугольной пластины. На-
Например, принимая с4 = 64 = с4 = 0, d4 ?=0, т. е. Ф = d&xl, по
формулам (9.16) получим!
ац = б^^хп ае2 = 0, aJ2 = — 3d**», (9.100)
г
Рис. 9.7
242
Рис. 9.8

В соответствии с граничными условиями (9.92) и (9.93) напряже-
напряжения (9.100) в пластине осуществляются при следующем ее нагружении
(рис. 9.9). На продольных сторонах х2 =* ± ft/2 действуют равномер-
равномерно распределенные касательные усилия ^ = =F т dji*; на сторонах
Xi = 0 и хх — I распределены по параболическому закону касатель-
касательные усилия t% =¦ ± М^1 и, кроме того, на стороне хх = I действуют
меняющиеся по линейному закону усилия tx = =F Bdjx-i.
2 %-Щ<к
/
Рис. 9.9
Рассмотрим функцию Эри в виде полинома пятой степени
Ф = аьх\ + Ьъх\х2 + о^хЬ + d5^f^32 + е^х\ + Ы> (9.101)
который будет удовлетворять бигармоническому уравнению (9.20)
при следующих соотношениях между коэффициентами:
еъ => - Eа5 + с&), /5 » - (&,
ш*
4ш
шгжнжж
ЖЖТТЖН
—- — ^/_
\ x,
Рис. 9.10
Здесь также только четыре коэффициента: а5, Ъъ, св и йъ — можно
принимать произвольно. Пусть аъ == Ьь = св — 0, dj ^= 0, т. е.
Ф «s d5 (xf ^l — х\1Ъ) и, следовательно, имеем
а15 = - Ф,ц =- - 6йлх|. (9.102)
&ги напряжения реализуются при нагружении пластины (рис. 9.10, а,
б), постоянными нормальными усилиями ti = dbfi3l4 и линейно
243

изменяющимися касательными усилиями tv = =F MJi*xJ2 на ее про-,
дольных сторонах хг = ± Л/2, нормальными усилиями tx = Мьх% на
стороне хг = 0, касательными t2 = — Ыь1х\ и нормальными усилия-
усилиями tx = d, FZ2*a — 4*1) на стороне *i = I.
При другом выборе значений независимых коэффициентов рассмо-
рассмотренных полиномов придем к иным условиям нагружения прямоуголь-
прямоугольной пластины. Линейно комбинируя эти элементарные решения, по-
получим новые решения, имеющие практическое значение.
. Рассмотрим некоторые примеры применения этого метода наложе-
наложения.
1. Изгиб консоли силой приложенной на конце.
Рис: 9.11
Имеем консоль длиной I с прямоугольным поперечным сечением
шириной, равной единице, и высотой h (рис. 9.11). Правый конец кон-
консоли закреплен, а на её левом торце (х± = 0) распределены поверхност-
поверхностные силы t2, главный вектор которых равен Р.
Распределению сил t% = —ап на торце хг = 0 отвечает функция
Эри Фа = b2x1xt (см. рис. 9.6, б). Однако этой функции соответствуют
постоянные касательные силы tt и на продольных сторонах консоли,
которые в рассматриваемой задаче должны быть свободны от поверх-
поверхностных сил. Для устранения сил /х на сторонах х2 = ±Л/2 добавим
функцию Ф4 = d&ixl (см. рис. 9.9), которой на этих сторонах соот-
соответствуют также постоянные силы tv Путем надлежащего выбора ко-
коэффициентов Ъг и d4 можно достигнуть освобождения сторон хг =*
= ± Л/2 от поверхностных сил и удовлетворить условиям нагруже-
нагружения консоли. Поэтому функцию Эри примем в следующем виде:
(а)
Ф = Ь2Х!Ха +
По формулам (9.16) найдем
ап =
= 0, а12 = — (b2 + 3d4x%).
(б)
Ha основании равенств (9.93) на продольных кромках консоли
(х2 = ± Л/2) по условию должны иметь
= =Ь
= =F (ft, + 3dji4i) ~
= ± ои = 0;
244

отсюда
b2 = — C/4) dth\ ¦ (в)
На левом торце (xY = 0) по условию нагружения, ссылаясь на
(9.92), имеем
ft/2 ft/2 h/2
Г Г j
/
= Г
ft/
j
—'[/2 —ft/2 -ft/2
Из последнего равенства, приняв во внимание выражение (в), на-
находим
d4 = 2Plh\ Ъг =— 3P/{2h),
и формулы (б) принимают вид
аи=Рлг! х^У, ам = 0, а12 = ~- (Л8/4—4), (г)
где J — 1 • /г3/12 — осевой момент инерции поперечного сечения кон-
еоли. Полученное решение (г) совпадает в решением, известным из
курса «Сопротивление материалов». Это решение является точным
только в том случае, когда повер'хностные силы t2 на торцах консоли
распределены по тому же закону, что и касательные напряжения а1е,
а поверхностные силы tv на закрепленном торце (хх = Z) пропорцио-
пропорциональны х2. Однако на основании принципа Сен-Венана решение (г)
можно считать точным для точек консоли, удаленных от ее торцов на
расстояниях больших к, и при ином статически эквивалентном рас-
распределении поверхностных сил на торцах хх = 0 и xt = I.
Найдем перемещения, соответствующие решению (г).
Из уравнений D.5) закона Гука
тогда
eu Р х,х г v P х,
E.I ' 2> 22 ?У
По формулам A.97)' имеем;
Р
«Li- ?/ *i*t,
а по A.100) получим:
2Р./ '
«a,i .1 2?у х\
¦°г
/1 1 ,Л ^ /^
Р
-v~e7 lXi>
р р )
х\.
(a)
(е)
(ж)
245

Используя теперь формулу A.101), найдем:
(з)
Производные и\,ч и и\,\ в точке О @, 0) консоли, входящие
в уравнения (з), на основании последнего равенства (д) связаны соот-
соотношением
2е?2 = v?2 = u?,2 + «8.1 = Ph4(8GJ). (и)
Следовательно, независимых постоянных интегрирования, содер-
содержащихся в уравнениях (з), будет три, которые можно определить из
трех уравнений связей, необходимых для исключения жесткого сме-
смещения консоли.
Три связи на закрепленном сечении консоли, устраняющие ее жест-
жесткое смещение, можно осуществить различными способами. Рассмотрим
несколько вариантов:
1) две связи запрещают перемещения их и и2 точки К (К 0), тре-
третья — поворот вертикальной? линейного элемента (uli2) окрестно-
окрестности точки К\
2) две связи запрещают перемещения их и щ точки К (I, 0), третья —
поворот горизонтального линейного элемента (и2Л) окрестности точ-
точки К, т. е. элемента оси консоли;
3) одна связь запрещает перемещение и2 точки К (I, 0), две дру-
другие — перемещения иг точек A (I, hl2) rt В (I, — ft/2).
Рассмотрим первый из этих способов закрепления, при котором
уравнения связей принимают вид
«1U = "I =0, «j \к = и% + ut, /--?- - 0,
bEJ
Из этих уравнен ш и соотношения (и) находим:
0 РР о РР , Ph? 0 PI3 Plh*
и равенства (з) преобразуются, а именно:
" х+А х
PI3 Plh* , РР Рп-
+Х+
—V —— Х1Х2.
6?7 2EJ
246

Изогнутая ось консоли определяется уравнением
/.. ч . _ PI* Plh* , PI2 ,. , Ph2 ..
&GJ
2EJ
8GJ
6EJ
Х\,
а прогиб нагруженного торца консоли равен
,„ v Pi3 Pih*
тГ
(м)
(н)
Первое слагаемое в правой части равенст-
равенства (н) совпадает с величиной прогиба, полу-
получаемой методами сопротивления материалов,
а второе слагаемое выражает влияние на
прогиб поперечной силы, которое обычно не
учитывается в сопротивлении материалов.
При изгибе консоли ее поперечные се-
сечения искривляются (мх зависит от xl). Ге-
Геометрия искривления закрепленного (рас-
(рассматриваемым способом) торца (рис. 9.12)
характеризуется выражениями:
р
eGJ
р
9.FJ
Jfl + v
Р з
бя/ Хг'
Р Ya
2ОУ ' 2"
Рис.
9.12
(о)
В действительности при защемлении торца по всей его высоте h он
не будет искривляться и распределение напряжений на нем отлично
от того, что дают формулы (г). Однако для сравнительно длинных кон-
консолей решение (г), для сечений, значительно удаленных от защемлен-
защемленного торца, на основании принципа Сен-Венана можно считать точ-
точным.
2. Изгиб двухопорной балки узкого прямоугольного сечения рав-
равномерно распределенной нагрузкой.
Балка с показанным на рис. 9.13 прямоугольным сечением свобод-
свободно опирается по концам и изгибается равномерно распределенной по
всей ее длине 21 нагрузкой интенсивности q. Начало координат совме-
совместим с центром тяжести среднего сечения балки, направив оси коорди-
координат, как показано на рис. 9.13, а.
Опорные реакции, равныеmql, представим как распределенные по
торцам силы ti. Граничные условия на верхней и нижней кромках
балки имеют следующий вид:
*i = ± Oi21*,= ± л/2 = 0. к — + °22 к= + ч/г = —q,
*г=— а2гк=-л/2 = 0, (а)
а на левом и правом торцах (д^ = — / и х1 = + t) необходимо иметь:
ft/2 -1/2 /i/2
-А/2 _ft/e -ft/2 -ft/2
247

ft/2
ft/2
= 0. (б)
—fill ' —hi г
Функция Эри, удовлетворяющая условиям (а) и (б), может быть
установлена, как и в предыдущей задаче, комбинированием слагае-
слагаемых рассмотренных полиномов:
Ф = <цх\ + Ь&ХХг 4- d^i\ + db (x\x\ — A/5) х%). (в)
Тогда на основании (9.16) компоненты тензора напряжений опре-
определяются формулами:
an = GdgXz + dfl (&х\хг — 4*2), )
ап = 2аг + 2ЬзХ„ -f 2dbx%, 1 (г)
о12 == — "'
Рис. 9.13
Условия (а) выполняются, если коэффициенты в формулах (г)
подчиняются равенствам:
Ь, + C/4) db№ = 0, 2а, + bsh + A/4) d-h? = — q, 2ай — bah —
— A/4) d,hs - 0,
откуда
Подставив полученные значения коэффициентов в формулы (г)
и учитывая, что 1'/гУ12 = J —осевой момент инерции сечения, по-
получим:
,_±_'( 2 2_ Л
•§У \ 3 /
022 = 17 v"l i ПГ/'
(д)
Выражения (д) для компонент тензора напряжений удовлетворяют,
как легко проверить, первому и второму условиям (б) при любом зна-

чении d3, а третье условие (б) удовлетворяется при ds, определяемом
из равенства
Л/2
1
x2 d3h + (l
! ! 2 ' т У ( 12 120
т.е. при ds= q—(p-—\
V 3 12/ \ 10 7
Формула (д) для ап принимает вид
Здесь первое слагаемое представляет собой напряжение, получае-
получаемое на основании элементарной теории изгиба в курсе сопротивления
материалов, а второе слагаемое следует рассматривать как поправку
к этой теории. Величина поправки не зависит от координаты xt и при
21 ^ h она пренебрежимо мала по сравнению g величиной первого сла-
слагаемого формулы (е). Например, при hl2l = 0,1 поправка для наиболь-
наибольшего напряжения ои в среднем сечении составляет всего 0,3% от на-
напряжения, определяемого элементарной теорией, а при Л/2/ = 0,25—
На рис. 9.13, б приведены эпюра напряжений ап в среднем сече-,
нии балки и эпюра поверхностных сил t2 — =F ol2 на ее торцах (хг =
Полученное решение является точным, строго говоря', лишь при
наличии на торцах (xi = =F /) поверхностных сил /2 == =F oVi, рав-
равнодействующие которых равны ql, а также поверхностных сил
представляющих собой системы взаимно уравновешивающихся сил
на каждом торце. Поэтому согласно принципу Сен-Венана влиянием
поверхностных сил tt на напряжения в сечениях, удаленных от тор-
торцов на расстояниях больших, чем высота Л, можно пренебречь и, сле-
следовательно, для этих сечений полученное решение является достаточно
точным, когда на торцах сил tx нет.
Элементарная теория изгиба базируется на предположении, что на-
напряжения о22 отсутствуют, в действительности они имеют место. Эпю-
Эпюра этих напряжений, не зависящих от координаты хъ приведена на
рис. 9.13, в.
На основании уравнений закона Гука D.5) и формул (д) и (е)
имеем:
249

ла лз yi
"Т*—li")]
? *,--?.+ v (/•*,-*!*,+
(ж)
Пользуясь формулой A.100), получаем:
«1,,
~ X, ~'X, + 2A-, X\ -
C)
Учитывая последние равенства и принимая во внимание, что
И1д — ен и "ад Xst еаа> по формуле A.101) найдем:
% = «?+ иТ.2 жв—
3 10
2BJ [2 1 12
Так как начало координат совмещено с центром тяжести средне-
среднего сечения (с плоскостью симметрии балки), то постоянные и\, и? 2
и и\ л, входящие в выражения (и), равны нулю.
Для точек оси балки (хг — 0)
(к)
250

Вследствие сжимающего напряжения ог2 | ,1==0 = — q/2 ось рас-
рассматриваемой балки получает удлинение, которое на основании пер-
первого равенства (к) равно ~.
Второе равенство (к) представляет собой уравнение изогнутой оси
балки. Постоянную и°, входящую в это уравнение, найдем из условия,
что прогибы осевой линии при хх = =F / равны нулю:
24
Здесь выражение перед квадратными скобками равно прогибу, ко-
который находится по элементарной теории тгиба, базирующейся на
гипотезе плоских сечений, а второе слагаемое в этих скобках определя-
определяет влияние на прогиб поперечной силы.
мм mmti<
I
Рис. 9.14
Кривизна изогнутой оси (упругой линии)
,о EJ [ 2 { б Т 8
т. е. кривизна не вполне пропорциональна изгибающему моменту
(M)
Второе слагаемое в скобках равенства (м) выражает влияние ва
кривизну поперечной силы и сжимающих напряжений о2а, которые по
высоте балки распределены неравномерно (рис. 9.13, s). Удлинения
в направлении оси хъ возникающие в результате этих напряжений,
уменьшаются от верхней кромки балки к нижней, и это обусловливает
обратную кривизну с выпуклостью вверх.
3. Изгиб консоли равномерно распределенной нагрузкой.
Для консольной балки, показанной на рио. 9.14, граничные ус-
условия на верхней и нижней кромках
=±л/2 = 0, tt = 4- а22 |хг
— =fc°i
2 k
а на левом торце (xt — 0)
ft/2 »i/2
§ ol2dxa = 0, \
Л/2 -Л/2
(a)
Л/2
-Л/2
251

Принимая функцию Эри в таком же виде, как в предыдущей ана-
аналогичной задаче, и удовлетворяя граничным условиям (а), получим для
напряжений, как и в случае двухопорной балки, формулы (д). Постоян-
Постоянная ds, входящая в выражение для схи, определяется из третьего усло-
условия (б) (первые два условия (б) удовлетворяются'при любом значении
d,):
d - qhi
3
d
3 120/
и формулы для рассматриваемой балки примут вид:
ст =л_х%х !_VJLr-> 'L.
11 11 % 2J { 3 10
22 ~ 2./ ( 3 ^ - 4 ^2 12
(в)
Первое слагаемое в формуле для ои совпадает с величиной напря-
напряжения, даваемой элементарной теорией изгиба, а второе слагаемое
является поправкой к этой теории.
Согласно полученному решению напряжения оц на свободном тор-
торце балки {хх = 0) отсутствуют, а напряжения ап имеют место и пред-
представляют собой взаимно уравновешенные силы
при наличии которых решение (в) является точным.
При отсутствии этих сил решение (в) уже не является точным для
конца консоли, но на основании принципа Сен-Венана его можно счи-
считать точным для остальных ее поперечных сечений.
Решение Рибьера и Файлона. Рассмотренное решение Менаже пло-
плоской задачи для прямоугольной полосы при помощи функции Эри в вида
алгебраических полиномов имеет ограниченные возможности. Оно при-
применимо для случаев непрерывной нагрузки на кромках (х2 = ± Л/2)
полосы и практически при сравнительно простом законе ее изменения.
Произвольное распределение поверхностных сил на кромках по-
полосы можно представить разложением в тригонометрический ряд.,
Тогда, очевидно, и функцию Эри следует разыскивать в виде тригоно-
тригонометрических рядов.
Рибьер предложил A898) находить функцию Эри в виде ряда
(9.103)
п~ I
где % = «л//: п —• любое целое число, /„Щ —функция только ко*
ординаты ла.
252

Подставив выражение (9.103) и (9.20), получим следующее урав-
уравнение для определения функции /„ (хг):
^^n = 0. (9.104)
Общее решение этого дифференциального уравнения известно и
смеет следующий вид:
/» (х2) = Сы ch Хх2 + С2п sh Kxt + Сапх2 ch Хх.2 + Cinx2sh kx2,
(9.105!
где Cin (i — 1, 2, 3, 4; п — 1, 2, ..., оо) — постоянные.
Напряжения, соответствующие функции (9.103), на основании
(9.16)
2 f« (**)cos ^Xi
n=l
2 Wn (.4) cos
(9.106)
CTi2= 2 Vb (*j) sin Я,*!,
n= 1
где fn (x2) определяется равенством (9.105).
Постоянные Cin, которые будут содержаться в выражениях (9.106),
определяются из граничных условий.
Из граничных условий (9.92) и выражений (9.106) вытекает, что
на торцах полосы, т. е. при ^ = 0 и *! = /, поверхностные силы долж-
должны подчиняться условиям
d#0,<,-0. (9.107)
Если в выражениях (9.103) и (9.106) заменить cos Xxt на sin Kxt,
а в выражении для о12 изменить знак и заменить sin Кхг на cos hclt то
получил! другое решение, предложенное A903) Файлоном.
В решении Файлона в отличие от решения Рибьера на торцах
полосы {Xi = 0, Xi = I) для поверхностных сил имеем условия
/1=»0, ЬФО. (9.108)
Более общее выражение для функции Эри получим суммированием
решений Рибьера и Файлона:
ф = S fn («i) cos Ь, + 5 /; (х2) sin Xxlt (9.109)
1 1
4 = 1 . П=1
где fn{x2) — функция, определяемая выражением (9.105), в котором
постоянные Cin необходимо заменить на C*tn.
Очевидно, что к выражению (9.109) при необходимости (й'ожно до-
добавить бигармонический полином.
Решение Рибьера и Файлона более подробно обсуждаются, напри-
например, в книге [7]. Здесь ограничимся рассмотрением характерного при-
примера, поясняющего применение этих решений.
2S3

Пусть полоса длиной 21 нагружена на верхней и нижней кромках,
как показано на рис. 9.15, т. е. в пределах от — /до — а и от + а
до -f / на верхней и нижней кромках t2 = 0, в пределах от — о до
+ а на верхней кромке t% — — q, а на нижней t2 = q-
Эти нагрузки, симметричные относительно плоскости среднего
сечения полосы, представим разложениями в ряды Фурье: на верхней
кромке
к = — («о + 2 ап cos
1
на нижней кромке
= К
&n cos
(9.140)
(9.111)
jgfe.
й
Рис. 9,15
где
(9.112)
—; —а
/ . а
о„ == Ьп =я — Г t% (x±) cos ^^ dx1= — \ cos Я^! d
= -g-sinba, (9.113)
* = -y-. (9.114)
Слагаемые а0 и b0, равные qall, представляют собой равномерную
сжимающую нагрузку, вызывающую напряжения оЦг = — qall.
Напряжения, возникающие под действием симметричной нагрузки,
определяемой тригонометрическими рядами (9.110) и (9.111), найдем,
принимая функцию Эри в виде решения Рибьера (9.103) и, следова-
следовательно, используя формулы (9.106) и (9.105):
X ch Кхг)
sh
B ch \xt +
sh
-*Л B sh
cos Xxu .
X
254

2 № iCln ch Xx2 + 6'27! sh to2 + C
X хй sh Хл:2] cos Xxlt
= 2 ^ ГСщЯ, sh Xx2 -f C27!X eh \x2
sh Я x2) + C4n (sh Л.л:2 + \хг ch
x, ch Xx2
4n
(9.115}
(ch X*2
sin Ххг.
Постоянные Ctn необходимо определить из граничных условий на
продольных кромках {хг = ± е) полосы:
± сЧа к=±* = О»
п=1
п=>1
COS
(9.116)
(9.117)
Из условий (9.116) имеем:
ClnX shXc + C9ni ch Xo + C3n (ch Xe -f Xe sh M -f C4n fsh
+ Xc ch Xo) =0,
— Cln?L sh Xe + С27Д ch Jle + C87! (ch Xe + Xe sh Лс) —
— C4n (sh Лс + Xc ch Xc) = 0,
откуда
Xch
¦Чп
(9.118)
' sh U 4- U ch
Используя условия (9.117), получим
К* (Cln ch Хв + С%п sh Xe + Сзп в eh Хв + Cinc sh Ы = ап,
Хг- (Cln ch Xe — C2n sh Xo — С3„ в ch Xe + Cin« sh Хв) = й„,
или
2X* (Cln ch Хя + О4П о sh Xo) = an + bn,
2X? (C2n sh Ь + C.lne ch Xe) — an — fen.
Из последних равенств, принимая во внимание соотношения (9.118)
и (9.113), найдем:
г
. «
sh
Gan = 0, C8n=0,
- -^j sin Xa
sh 2U
(9.119)
255

Формулы для напряжений, учитывая, что аа2 = о§2 + агг. при-,
мут вид: -
00
оа = 4<7 — Y An fte ch Xc ch Я.лг2 — sh Яс (ch Ъс2 +
-f ^2 sh ^2)]cos ^1»
{- »
1+4 ^ A,,ftechtechLe2 —
(9.120)
— sh ?lc (кхг sh Ъг2—ch %х%)] cos
cr12 = 4^ — V ftn (Яс ch Xc sh Яд:2—sh
n = l
ch
sin
где
*»¦
sin "ka
Xa (sh
1U) '
(9.121)
Представляет интерес распределение напряжений аа2 в средней
плоскости (х% — 0) полосы:
(oa)r,-o = — 9 ~ И + 4 2 К (te ch Xc + sh Яс) cos Ux .
(9.122)
Для бесконечно длинной полосы при очень малом размере а, т. е.
когда полоса нагружена .сосредоточенными силами Р = 2qa, это рас-
распределение характеризуется кривой (рис. 9.16). Легко видеть, что
напряжение (а22)*2=о очень быстро уменьшается с удалением от
сечения, в котором приложены силы Р. Это подтверждает заключение,
обычно принимаемое на основании принципа Сен-Венана.
Рассмотрим противоположный случай, когда высота h = 2в пла-
пластины, нагруженной сосредоточенными силами Р = 2qa (размер а
очень мал), значительно больше длины 2/ (рис. 9.17). В этом случае чис-
число %с = ппс/1 большое и им можно пренебречь по сравнению g величи*
ной sh Kc. Также с достаточно большой точностью можно принять
sh Ic — ch
A/2) е
К
(9.123)
Полагая, что sin Ka — Ка, выражение (9.121) для коэффициента
&я примет вид
К = 2/е2Ч (9.124)
Для сечений х2 — const на значительном расстоянии от средней пло-
плоскости (х2 = 0) можно принять
sh hc2 = ch
(9.125)
256

Тогда для напряжений waa в этих сечениях на основании формул
(9.120), а также учитывая (9.123)—(9.125), получим
*= —ТГУ
cos
(9.126)
При величинах (о — х^ > 112 ряд в формуле (9.126) сходится до-
достаточно быстро. Приведенные на рис. 9.18 эпюры напряжений ог2
на еечениях хг — о — 1/2, хг яа д — / и хг — о — 2/ наглядно убеж-
р
0
1.0
ол
р
i
1
г
f
х
\
¦
*
BP/i
X,
хс
ус
р
L
0
Р
L
j
X,
Рис. 9.16
Рис. 9.17
дают, что при удалении от места приложения силы распределение на-
напряжений о22 быстро приближается к равномерному. На расстоянии
(о — х^ — 21, равном ширине пластины, распределение напряжений
практически равномерное, что находится в соответствии с утверждением
принципа Сен-Венана.
Решение (9.109) Рибьера и Файлона для конечной полосы можно
обобщить и получить решение для бесконечной полосы. Если пара-
параметр % = nnll, который в решении (9.109) принимает дискретные зна-
значения, рассматривать непрерывным в пределах от — со до + со, то
функцию Эри для бесконечной полосы можно представить в следую-
следующем виде [7J:
(9.127)
(9.128)
257
Зак.
(Ал.) =
(кхг) =
514
Ф
= (
С
-Tf кх
—аз
^l(k) Ch кХъ~
Г (к) ch кхг +
+ с
cos AjfjdA, -f J. F
f C2 (A;) sh А.д:2 +
2 Ы
C3(k)
+ Сд (к) kx% sh Ax,.
CJMshUs + Cs
4 (X) Xx2 Sh kx2.
(к) кхг
sin
kx
ch
kx^dk,
г ch А.д;2 -j-'
kx2 +

2,575^
ув-
увив?
1
1
х.=с-1
X2<-2L
¦Zw. vffi
Рис. 9.19
Рис. 9.18
Коэффициенты Ct (l) и С/ (X) функций /^ (hc2) и F2 (Лдг2) опреде-
определяются из граничных условий (9.93) на кромках хг = ± о полосы,
законы изменения поверхностных сил tx (#i) и 4 (jf2) на которых пред-
представляются с помощью интеграла Фурье D9);
fa) = — Г dX Г ф (a) cos Я (а—
—се —со
+с« +ео
= ' I cos fax dk [ ф (a)
—ос
—со
+00
¦f — Г sin Ялг, dX Г ф(а)$1пАайа.
(9.129)
258

Например, одно из двух условий на верхней кромке (хг — + с)
получит вид
1 С С
(xi) — \ cos ^xi dk \ t2 (a) cos kada -f-
—<z> . —ел
Г sin kxt dk Г t2 (a) sin kada = -j- Ф_ n =
—СЛ —^Э
+c« +oe
= — \ гх (лс) л2 cos кхг dk— \ F„(kc) к2 sin kxxdk,
J J
(9.130)
откуда находим:
1 f
{kc) = — \ t2 (a) cos Xa da,
+=*
t.2 (a) sin
(9.131)
Из остальных трех граничных условий (9.93) аналогично получим еще
шесть уравнений для определения С, (к) и С/ (к).
Ограничиваясь сделанными замечаниями (подробное изложение
см. [7]), отметим что этот метод решения для бесконечной- полосы был
использован рядом авторов (Ламб, Карман, Зеевальд и др.) для неко-
некоторых практически интересных задач.
Рис. 9.21
259

Зеевальд A927), применив его к случаю балки, нагруженной сосре-
сосредоточенной силой Р (рис. 9.19), показал, что
где ос, р, у — безразмерные коэффициенты, зависящие от координат
хх и х2. Некоторые значения этих коэффициентов представлены кри-
кривыми на рис. 9.20 и 9.21, которые показывают, что местные напряже-
напряжения очень быстро убывают с удалением от среднего сечения балки, к ко-
которому приложена сила Р, и на расстоянии хх — ± 2с ими можно пре-
пренебречь.
Распределение напряжений в окрестности точки приложения силы
-рассмотрено на с. 278.
§ 10. ПЛОСКАЯ ЗАДАЧА В ПОЛЯРНЫХ КООРДИНАТАХ
При решении плоской задачи для тел, имеющих круговое очерта-
очертание (круговые кольца и кривые брусья узкого прямоугольного сече-
ння, круглые диски и т. п.), выгодно использовать полярные коорди-
координаты х* = г, х2 = Q (см. гл. VI, § 2), связанные с декартовыми коорди-
координатами хъ х% равенствами F.35):
хх — г cos 6, х2 = г sin 8. (9.132)
Основные уравнения плоской задачи в полярных координатах
Зависимости между компонентами тензора напряжений в поляр-
полярных координатах (огг, Оее. Ore) и в декартовых координатах (ош ow,
о12) на основании B.32) определяются равенствами
Огг — ^ri^rjO,), oee = ^вг^в)Оц, огв — апав]ои (i =* 1, 2;
/ - 1. 2),
где ап -— cos 0, ага = sin 8, ав1 = — sin 8, ав2 = cos 6, или
ori. = o11cosa8-fo22Sinll0-f.alisin 20
one — 0tl sin2 6+ 022cosiS A—a12sin 20'
ore =o18 cos 28— au~°22 sin 20.
Si
(9433)
Аналогично на основании B.32) получим обратные зависимости:
схх~оп cos2 0 + aeo sin2 0—агв sin 20,
a22 = а„ sin2 8 + aee cos2 0 + a,e sin 20,
а12=а>е cos 20-f
sin 20.
(9.134)
Принимая массовые силы равными нулю и исходя из уравнений
F.62), в которых положим о« = авг — azr = 0, получим дифферен-
дифференциальные уравнения равновесия в полярных координатах:
(9.135)
260
dOrr
dr
dr
¦ +
1
r
1
r
оагв
dQ
¦ +
2-
~aeo
r
r" _ r\
- — U.
r
o,

Ссылаясь на F.56), получаем зависимости между компонентами
тензора деформации и компонентами вектора перемещения в полярных
координатах:
диг I Ч , кг 1/1 диг ,
дг г дЬ t 2[f й Т
дий tip, \
+ -~ . (9.136)
дг г ]
Уравнения закона Гука в ортогональных криволинейных коорди-
координатах имеют такой же вид, как и в декартовых координатах. Поэтому
в случае плоского напряженного состояния в соответствии с (9.51)
имеем:
е,г= — (агг —vaee), еее = — (аее — VO. ere = „ огв, (9.137)
а в случае плоской деформации по аналогии о (9.52)
еГг= -^7 Кг—V аов), еее = ~-{овв —V агт), ег9 = ' 1"/ аг8, (9.138)
СП С
где
Е' = ?/A — v2), v« = v/(l — v). (9.139)
Если в равенствах (9.133) напряжения ап, аа2, аХ2 заменить их пред-
представлениями (9.16) через функцию Эри, а затем в полученных выраже-
выражениях производные функции Ф по х2 и хг заменить производными слож-
сложной функции Ф (г, Э) по г и 6, то получим
1 дФ . 1 а2 Ф а2 Ф
*0
д ( 1 дФ \ /о
^ Г"( ^ГЬ (9-
а/- \. г ао /
где Ф (г, 8)—функция Эри в полярных координатах.
Непосредственной подстановкой можно убедиться, что выражения
(9.140) удовлетворяют уравнениям равновесия (9.135).
Чтобы функции аг„ оее, огв, определяемые выражениями (9.140),
удовлетворяли бы и условиям совместности Бельтрами F.70), в кото-
которых надо принять аг2 = абг — о1Т — 0, функция Эри Ф (г, 8) долж-
должна подчиняться бигармоническому уравнению 1см. (9.20)]:
У2У2Ф (г, 6) = 0, (9.141)
Оператор Лапласа \РФ в полярных координатах на основании
F.65) имеет вид
Vb-++, (9.142)
поэтому бигармоническое уравнение (9.141) можно записать так:
/_ + -L-?.+_LJLU.™+J-?2. + J_-^ Wo. (9.143)

Задачи, в которых напряжения зависят только от г
Для некоторых задач является вполне очевидной независимость
напряжений от полярного угла 6, и в этом случае функцию Эри сле-
следует принять в виде
Ф(г, 0) = Л0 + ф(г), (9.144)
где А — произвольная постоянная; ф (г) — функция только г.
Подставив выражение (9.144) для функции Ф в уравнение (9.143),
последнее примет вид
JL+JL±)(*2. + ±«L.)-O. (9,145)
dr* r dr j\ dr* r dr j v '
Введем обозначение
^+т2--»"> <9:'46>
и уравнение (9.145) упростим:
dr [ dr.
интеграл которого
ф (г) = С, In r + С%. (9.147)
Тогда уравнение (9.146) приводится к виду
(r) C1Hnr+C2r. (9.148)
dr \ dr I
Интегрируя последнее уравнение и принимая С,/4 = Ао, (Сг —
— Са)/4 = Во, получим
<F (г) « Лог2 In г + Вог2 + С„ In г + Do. (9.149)
Постоянную Do в равенстве (9.149) можно отбросить, так как на-
напряжения определяются производными функции Ф. Тогда для рас-
рассматриваемых задач функция Эри получит вид
Ф = -40 + АогЧп г + В/? + Сп In r. (9.150)
Компоненты тензора напряжений, соответствующие функции Эри
(9.150), на основании формул (9.140) равны:
on AQ(l + 2\nr) + 2B0 + C0/r\]
аее = /40C + 2 In г) + 2В0 - CJr\ (9.151)
ore = Air. j
Компоненты тензора деформации (9.136) в случае плоского напря-
напряженного состояния, ссылаясь на (9.137) и (9.151), будут определяться
выражениями:
262

E
2 U ae ^ dr r ) e
Интегрируя первое уравнение (9.152), найдем
(9.152)
(9.153)
Из второго уравнения (9.152), используя равенство (9.153), найдем
див/дв = ге9в — иг = 4Л//? — a (Э)
и, следовательно,
и9 = 4Л/е/? — fa F) 60 + р (г), (9.154)
где Р (г) — функция только г.
Подставив выражения (9.153) и (9.154) в третье уравнение (9.152),
получим
откуда
или
= о и 4r~r~
Решая последние уравнения, найдем!
. (9.155)
и равенства (9.153) и (9.154) принимают вид
ив =
(9.156)
! cos 8— C2sinG-{-C3r— -^ —, (9.157)
где постоянные С,, Са, С3 определяются из уравнений связей.
2R3

Первое слагаемое в выражении (9.157) для перемещения ие при
обходе по замкнутому контуру, т. е. при изменении В от 0 до 2л, по-
получит приращение — '2л. Следовательно, в случае неодносвязной
области (замкнутое кольцо) перемещение не будет однозначным толь-
только при Ао = 0, поэтому в выражении (9.150) для функции Ф и в форму-
формулах (9.151) для напряжений в случае^ замкнутого кольца необходимо
принять Ай = 0.
Рассмотрим решения некоторых типовых задач.
1. Полый цилиндр под действием равномерного внутреннего
и внешнего давления (задача Ламе)-
Рис 9.22
Рис. 9.23
Пусть гх и г2—внутренний и наружный радиусы цилиндра со
свободными торцами (рис. 9.22), рх и pt — равномерные внутреннее
и внешнее давления.
Напряжения в точках окружности радиуса г рассматриваемой дву-
связной области получим, положив в формулах (9.151) Ао = 0:
а„ = 250 + Со/Л аее = 250 — Сй1г*, о>6 = Alt*. (9.158)
Это решение должно подчиняться граничным условиям
arr\r==r, — —pi, <xrr|r=r, = —р2> O
которые позволяют определить значения постоянных, А, Во, Со из
равенств
2Я0
CJr\ = - pi, 2B0 + CJrl = - рг, Alr\ .=- A/rl = 0.
Учитывая значения постоянных А, Во, Со, формулы (9.158) при-
принимают такой вид:
_.
r\-r\
¦+
(Pt—Pt)rir'i
(r\-r\)r* '
(9.159)
264

Равенство нулю касательных напряжений аг9 можно было заранее
предвидеть из условия осевой симметрии задачи.
Поскольку перемещения не должны зависеть от 6 по формулам
(9.156) и (9.157), получим
i^s]l*=lC-r- (9Л60)
Перемещение ив представляет собой поворот цилиндра вокруг его
оси, как абсолютно твердого тела.
2. Равновесие кольцевой плйстины под действием касательных
усилий на внутреннем и внешнем контурах.
Равномерно распределенные касательные усилия ql на внутреннем
контуре радиуса гх и усилия q^ на внешнем контуре радиуса г2 пласти-
пластины (рис. 9.23) приводятся к противоположно направленным моментам
М = 2nrf<7i = 2nr\q%.
Напряжения в точках окружности произвольного радиуса г дву-
связной области определяются формулами (9.158), которые в данном
случае должны удовлетворять следующим граничным условиям:
приводящим к равенствам
250 + CJr\ = 0, 250 + С0/г1 =- 0, Alr\ =qlt Alr\ - q2,
откуда
Вп = Cft = 0, А = <ы\ = q%r\ = М/Bя),
и формулы (9.158) принимают такой вид:
Огг = 0. а9в - 0, <хге = М/Bпг% .(9.161)
Перемещения на основании равенств (9.156) и (9.157)
«r = 0, Ue = C,r—i±2-^. (9.162)
где постоянная С3 определяется из условия закрепления пластины.
3. Чистый изгиб кривого бруса узкого прямоугольного сечения
(задача X. С. Головина).
Кривой брус (рис. 9.24) с круговой осью радиуса р = (гг + гг)/2,
где гх и гг — внутренний и наружный радиусы, изгибается в плоско-
плоскости своей кривизны моментами М, приложенными к его концам.
Напряжения в рассматриваемой задаче, как и в предыдущих за-
задачах, не зависят от 8, поэтому для функции Эри принимаем выраже-
выражение (9.150), которому соответствуют напряжения, определяемые фор-
формулами (9.151).
Постоянные, входящие в формулы (9.151), найдем из граничных
условий на криволинейных контурах бруса:
orr\r==ri = arr\r==,t = 0, Огв\г=г, = огв\г=г, = 0 (а)
265

и на его торцах:
Г2 '!
Г аоо dr=0, \ am rdr = М.
(б)
Принимая во внимание формулы (9.151), условия (а) приводим
к уравнениям
Ло A + 2 In г,) + 250 + CJr\ = О, Ло A + 2 In rj + 250 +
+ Co/rl = 0, . (в)
А1г\ = /1/г| = 0, т. е. А - 0. (г)
Рис 9.24
Из первого условия (б) находим
'2
- [Ао A + 2 In r,) + 250 + C0/r2] n = О,
что удовлетворяется тождественно вследствие равенств (в).
* Из второго условия (б) приходим к равенству
(Д)
р а2 ф , во
\ rdr — —
J дгг дг
— Ф
которое, учитывая выражения (9.150), (г), (д), приводим к уравнению
n^^-M. (e)
г
Определив из уравнений (в) и (е) постоянные Ао, Во, Со, по форму-
формулам (9.151) найдем напряжения в точке N (л, 0):
arr =-=-(/¦» in — + r» In —+ -V" ln —).
(9.163)
266

где
Таблица 9.1
'а/г»
1,3
2
3
Приближенное реше-
решение
+72,98
-61,27
+7,725
—4,863
+2,285
— 1,095
Точное решение
+73,05
—61 ,-35
+7,755
-4,917
+2,292
-1,130
Перемещения иг и ие произвольной точки N (г, 8) определяем по
формулам (9.156) и (9.157), в которых постоянные Си С2, С3 находим
из условий закрепления бруса, а постоянная /4=0.
Чтобы исключить жесткое смещение бруса потребуем, например,
для точки No (р, 0) выполнения условий иг — не = див/дг = 0, из
которых найдем:
Формулц для перемещений примут такой вид:
A + v) ^1 + С2 cos 6,
= ^»ге —C2sin
(9.164)
Из второй формулы (9.164) вытекает, что при чистом изгибе рассма-
рассматриваемого бруса его поперечные сечения остаются плоскими, т. е.
одно из предположений элементарной теории изгиба кривого бруса
подтверждается, а другое предположение (отсутствие напряжений
агг), на котором базируется элементарная теория, ие соответствует
действительности. Последним обстоятельством объясняется некоторое
расхождение между напряжениями аОе элементарного и точного реше-
решений. В табл. 9.1 приведены значения коэффициента k, с помощью кото-
которого определяются наибольшее и наименьшее значения напряжения
а9е элементарного и точного решений по формуле
овв=кМ/г]. (9.165)
267

Эта задача решена в 1880 г. X. С. Головиным A844—1904).
Задачи, в которых напряжения зависят от г и в
Среди этих задач имеют место задачи для кругового кольца или его
части, в которых напряжения пропорциональны sin 0 или cos 0, т. е.
являются функциями вида /х (г) sin Э или f2 (г) cos 8. Такому распре-
распределению напряжений соответствует функция Эри
ф (,-, 6) = (#х cos Q + Br 6 sin 6) + (#а sin 9 + B'rQ cos 6). (9.166)
где J)] и J?, — функции только г; В и В' — постоянные.
Непосредственно легко убедиться, что функции r0 cos 8 и лб sin 0
являются бигармоническими, т. е. удовлетворяют уравнениям
V* (r8 cos 9) = 0, V4 (r9 sin 8) = 0.
Тогда подставив выражение (9.166) в уравнение (9.141) и ограни-
ограничившись частным случаем, когда /?2 (г) — 0, В' = 0, получим
) +
r dr г* J\ dr* r dr r*
Следовательно, функция Rt (r) должна удовлетворять уравнению
/_?,_!__! 1 \(diRl . 1 dR, L
\ dr* r dr ti}\ dr* ~1~ r dr г*
ИЛИ
±\±JH±\L±]\]0. (9.167)
dr [r dr \ dr
Общее решение уравнения (9.167)
Rl(r)->Alr* + B1r\nr + O1-l-+Dlr. . (9.168)
По формулам (9.140), принимая функцию Эри в следующем виде:
Ф (г, 0) = (a^ + Bs In r + Ct -J-f-JVJcos 0 + BrO sin 0, (9.169)
получим:
= BAl r + B, — — 2CX —) cos 8 + 2B — cos 0,
V • т гз I t
2d—\sin9.
r & I
(9.170)
В формулы (9.170) для напряжений не входит постоянная Dlt что
вполне понятно, так как слагаемое DYr cos 8 в выражении (9.169)
функции Эри представляет собой линейную функцию хг.
Компоненты тензора деформации (9.136) в случае плоского напря-
напряженного состояния на основании формул (9.137) определяются равенст-
равенствами
268

/¦3
—]cos8,
/• J
+ 2A + v)C, JL + 2vB -i-1 cos6, -
(9.171)
(9.172)
Интегрируя уравнения (9.171), найдемг
Иг = -— 1A — 3v) Аг г3 cos 6 -f Вх [A — v) In r cos i
+ 2F sin6 —cos 6)J +A +v)C!~ cosl
+ A— v) (9 sine-cose)]},
+ 2У cos UJ + A -f- v) Cx -i sin в—В [2 In r sin в + 2v sin 0—
— A —v)ecos6]}.
Из выражений (9.172) следует, что перемещения иг и «в в случае
замкнутого кругового кольца будут однозначными при условии
2ВХ + A — v) В = 0, (9.173)
в этом случае первая формула (9.170) принимает вид
1—V
i- 2С,—
(9.174)
т. е. напряжение атт оказывается зависимым от упругой постоянной v.
Мичелл показал, что распределение напряжений будет независимым от
упругих постоянных, если равнодействующая усилий, приложенных
к каждому контуру замкнутого кольца, равна нулю (см. § 7 данной
главы).
Если рассмотреть другой частный случай функции Эри (9.166), ког-
когда R, (г) = 0, В — 0, то получим зависимости, аналогичные (9.167)—
(9.174).
269

Объединив эти два частных случая, функцию Эри (9.166) предста-
представим в следующем виде:
(9.175)
где в случае замкнутого кольца постоянные Бх и В подчиняются за-
зависимости (9.173), а постоянные В[ и В' также связаны равенством
25i + A — v) В' = 0. (9.176)
I
1 -М sin 9+ В'гв cos 9,
Рис. 9.25
Суммируя выражения (9.150), (9.175), (9.91) и присоединяя еще
бпгармоническую функцию D/29, получим удовлетворяющее бигар-
ионическому уравнению (9.141) общее выражение функции Эри в по-
полярных координатах, которое было дано в 1899 г. Мичеллом:
Ф {г, 6) = AQ + Ао г* In г + Во г2 + Со In г + Do г2 6 +
г-1) cos9+ fir9 sin 0+ (Л
гп+г + С3п г"» + Cin
+ Din r"+
*) cos пв + 2 (Dln
D3n r-» + Dtn r-«+2) sin лв.
Слагаемому Dor2Q, как легко установить, соответствуют напряже-
напряжения стг^ = 2DO9, ст99 = 2Do9, ore = — Do, т. е. в случае замкнутого
кольца напряжения сггг и сг9в окажутся многозначными и поэтому для
этого случая следует принять Do = 0. Кроме того, для замкнутого
270

кольца необходимо, как уже отмечалось, положить Ло = 0, а постоян-
постоянные fli, В и В[, В' подчинить равенствам (9.173) и (9.176).
Определив напряжения агг, о9в. «re. a затем и перемещения иг,
«е, соответствующие представленным рядами в выражении (9.177)
бигармоническим функциям, можно убедиться, что последние удовлет-
удовлетворяют условиям однозначности перемещений.
Постоянные, входящие в выражение (9.177) функции Эри, опреде-
определяют из условий на контурах, учитывая сказанное относительно по-
постоянных Ло, Do, В,, В, В\, В'.
Подбирая соответствующим образом члены выражения (9.177), мож-
можно получить решения многих практически важных задач.
1. Изгиб кривого бруса узкого прямоугольного сечения силой, при-
приложенной к незакрепленному концу (задача X. С. Головина). Пусть
кривой брус (рис. 9.25, а) с круговой осью радиуса р = (rY + г2)/2,
торец mm которого закреплен, изгибается силой Р, приложенной к не:
закрепленному торцу пп в его плоскости. При данном нагружении бру-
бруса изгибающий момент в его произвольном сечении, определяемом уг-
углом 9, пропорционален sin 0. Естественно предположить, что в этом
случае напряжение 0вв = д*Ф/дг2, а следовательно, и функция
Ф (г, 0) будут также пропорциональны sin 0.
Принимая функцию Эри в виде
ф(Л) 0) = (Л,73 + B\r\nr + CJr-1) sin 9, (9.178)
по формулам (9.140) получим:
orr=r2Alr + Bl -l-2C;-
_!_ + 2С;— Ysin9,
Т 1*3 J
(9.179)
Постоянные А\, В{, С[ найдем из граничных условий
Учитывая (9.179), условия (а) принимают вид:
f f2 fS
откуда
Л1 = P/BK0), Bi = — (Р/АГо) (г? + rj), C[ = — (Р/2К0) г\г\, (в)
где
/Со = А — Л Л- (''f + rl) 'п ('гАг)« (Г)
271

Подставив значения (в) постоянных А[, В\, С{ в равенства (9.179),
получим следующие формулы для напряжений:
(9.180)
—iM^
гч П
)
На рис. 9.25, б приведены графики (эпюры) напряжений о9в и а„
в сечении II для случая г.г = Zrx, где в скобках даны значения напря-
напряжения о8е в крайних точках
сечения, подсчитанные по
элементарной теории изгиба
данного бруса, базирующей-
базирующейся на гипотезе плоских се-
сечений и допущении, что на-
напр яженяя агг отсутствуют.
Можно считать, что элемен-
элементарная теория дает вполне
удовлетворительные резуль-
результаты. Отметим, что распре-
распределение касательных напря-
Рис. 9.26 жений стг8 в сечении 0 = л
характеризуется такой же
кривой, как для напряжений агг в сечении //.
Рассмотрим теперь нагружение бруса силой Р, направленной пер-
перпендикулярно свободному торцу (рис. 9.26). В этом случае в произ-
произвольном сечении изгибающий момент пропорционален eos 6.
Принимая
Ф'(г, в) = (А^ + Byr In г + Q r-1) cos в,
по формулам (9.140) имеем;
(V » BV + Bjr — 2C!/r3) cos 9,
ст0в = FV + Brfr + 2d/f*) cos в,
ore = BAxr + Bjr — 2Cjrs) sin 6.
Из граничных условий
найдем постоянные:
272
(9.181)
— Р
(9.182)
(д)
= (Р/Ка) {г\ + r|), d = (Р/2/Со) Лг\ (е)

и формулы (9.182) примут вид:
(9.183)
где К9 определяется по формуле (г).
Из (9.183) следует, что при принятой функции Эри (9.181) в сече-
сечении 9 = л/2 имеют место только касательные напряжения огв, кото-
которые приводятся к поперечной силе | <тге | е = л/2 dr = Р, а на сво-
сво't
бодном торце распределенные силы оЯ9 (е=о приводятся к силе Р, при-
приложенной к центру тяжести сечения и еще к моменту М = Рр (рис.
9.26, а, б). Прикладывая момент М = Рр = Р (гг + гг)/2 в обратном
направлении, т. е. учитывая (9.163), получим решение рассматривае-
рассматриваемой задачи:
а
r\+r\ In— + Л Ini-—13- ln-^-V
P / r? 4- r\ r\r\ N. о
в^-тг- ^ 2 ^ —^ sin 9.
Ко \ Г f8 У
(9.184)
Имея решения (9.180) и (9.184), на основании принципа сложения
можно получить решение задачи изгиба рассматриваемого кривого
бруса силой, произвольно направленной в его плоскости.
Решение задачи изгиба, а также кручения кривого бруса о прямо-
прямоугольным поперечным сечением, стороны которого соизмеримы, при-
приведено в гл. XI, §5.
2. Сжатие симметричного клина силой, приложенной к его вер-
вершине (задача Мичелла). К вершине клина (рис. 9.27), толщина кото-
которого равна единице, приложена сжимающая сила Р по оси симметрии
Охх. Вследствие симметрии задачи функцию Эри примем четной отно-
относительно отсчитываемого от оси 0^ полярного угла 9 в следующем
виде:
Ф (г, 9) = Вгд sin 9. (9.185)
273

По формулам (9.140) получим:
а„ = BB/r) cos 9, (Гее = 0, <тг9 = 0. (9.186)
Граничные условия на кромках клина сгее | е= ± а — 0, Стгв г е = ± а = 0
выполняются, так как всюду <т8е — агв — 0.
Постоянная В определяется из условия равновесия части клина,
отсеченной цилиндрической поверхностью радиуса г (рис. 9.27 а, б)\
а
Р= — Г а„ acos(M0= — 2В (а + — sin 2аV
щ
Рис. 9.27
откуда
В = —PI Ba + sin 2а).
Решение (9.186) принимает вид
2Pcos6 _'
"" г Bcc-|-sin2a) ' °Й ~"
(9.! 87)
Это решение будет точным, если сила Р представляет собой равно-
равнодействующую распределенных по закону (9.187) сил на цилиндричес-
цилиндрической поверхности малого радиуса а у вершины клина.
Компоненты тензора напряжений в декартовых координатах, ис-
используя формулы (9.134) и (9.132) и введя обозначение k0 =
= Ba + sin 2a)/2, определяются выражениями
\1 (№), ог2 = -РхххЦ (к„г*), о1а =• -Px\x%l(k^), (9.188)
где г* = [х\ + х\)\
Для клина при a = 15° на рис. 9.27, б приведены эпюры напря-
напряжений сггг на цилиндрическом сечении радиуса г и напряжений оа и
а1г на поперечном сечении л;г = с, из которых видно, что нормальное
напряжение ои на поперечном сечении распределяется неравномерно.
Наибольшее напряжение crn возникает в центре сечения и превышает
274

вреднее напряжение (ou) op = PIF при а = 15° на 4,3%. С увеличе-
увеличением а это отклонение увеличивается.
3. Изгиб клина силой, приложенной к его вершине. Сила Р, изги-
изгибающая клин (рис. 9.28), представляет собой кососимметричную на-
нагрузку относительно оси симметрии клина Охх. Поэтому функцию Эри
примем нечетной относительно 9 в следующем виде:
Ф (г, 9) = ?79 cos 9. (9.189)
Этой функции соответствуют напряжения
агг = —BB'/r) sin 9, стеб = агв = О,
* S)
Рис. 9.28
при которых граничные условия на кромках клина выполняются.
Постоянная В' определяется из условия равновесия отсеченной
части клина (рис. 9.28, б):
откуда
и, следовательно,
Р+
В' = PI Bа — sin 2а)
агг —
2Р sin 6
г Bа—sin 2а)
-, стее = Ого = 0.
(9.190)
Для компонент тензора напряжений в декартовых координатах,
приняв обозначение k = Bа — sin 2а)/2, получим:
<*„ = PAxJ (/гг4), а„ = Р*%1 (Ьг4), а1г - Рххх\! {kr*), (9.191)
где г4 = (х\ + х%)\
На рис. 9.28, а, в представлены эпюры напряжений агг на сечении
радиуса г и напряжений оа и о12 на поперечном сечении xv = с при
а = 15°. Отметим, что наибольшее касательное напряжение а1г возни-
возникает в крайних точках сечения, причем оно почти в два раза превыша-
превышает то, которое дает элементарная теория в центре тяжести прямоуголь-
275

ного сечения балки. Напротив, по элементарной теории изгиба наи-
наибольшее нормальное напряжение аи получается несколько больше,
чем по первой формуле (9.191).
Решение данной задачи получено в 1902 г. Мичеллом. Оно являет-
является точным при условии, что на закрепленном конце клин испытыва-
испытывает усилия,.распределенные по закону (9.190). При невыполнении это-
этого условия решение будет точным только для точек, отстоящих на до-
достаточном расстоянии от закрепленного конца.
Имея решения (9.187) и (9.190), можно получить решение при лю-
любом направлении силы Р, приложенной в плоскости клина к сто вер-
вершине.
4. Изгиб клина моментом, приложенным к его вершине (задача
Инглиса). Принимая, исходя из (9.177), функцию.Эри нечетной отно-
относительно 6 в виде
ф (Г, 6) = Л6 + Di2 sin 26, (9.192)
по формулам (9.140) найдем:
°гг=— -—-sin26,oee=0,or0=-^-+~2-cos29. (9.193)
Из граничного условия сгг81 е = ± а = 0 получим Di2 = —А/ B cos 2a).
Постоянная А, учитывая последнее равенство, находится из условия
равновесия отсеченной части клина (рис. 9.29)
а а
{rorerdd^A 1A ——)dd=M,
J J \ cos 2a /
—об —a
откуда
M
А = — —:— и Di
2а — tg 2а м 2 Bа—tg 2а) cos 2а '
Формулы (9.193) принимают вид:
2Msin20
raBa—tg 2а) cos 2а '
Онп = 0,
Это решение Инглиса будет точным, если к закрепленному концу кли-
клина и к цилиндрической поверхности малого радиуса а при его вершине
приложены распределенные по закону (9.194) силы, приводящиеся к
противоположно направленным моментам М.
5. Изгиб клина равномерно распределенной нагрузкой (задача
М. Леви). При указанном нагружении клина (рис. 9.30), толщина ко-
которого равна единице, граничные условия имеют вид:
oeete=a--=0, aoe|e=o— — q, о,е|е=и = Огб|а=а = 0. (а)
276

Чтобы удовлетворить этим условиям, напряжения ав9 и сгг9 не долж-
должны зависеть от г. Этого можно достигнуть, если, исходя из общего вы-
выражения (9.177) для функции Эрн, принять
Ф (г, 6) = Агг + Вг2в + Сг2 cos 29 + Dr* sin 26. (9.195)
Этой функции соответствуют напряжения:
атг = 2Л + 2В6 — 2С cos 26 — 2D sin 26,
(Tee = 2Л + 2В9 + 2С cos 29 + ID sin 29, [ (б)
агв = —В + 2С sin 26 — 2D ?os 29.
Г
,,, / Г.
Рис. 9.29 , Рис. 9.30
При выполнении граничных условий (а)
, D =
(в)
где /С = tg а — а.
Учитывая значения постоянных (в), формулы (б) принимают вид:
Оп= JL. [2а—26—A -cos 29) tg а—sin 291,
аое=_?_ [2а-29-A +cos29)tg
2К
агв =-?- A —tg а sin 26—cos 26).
(9.196)
Ha рис. 9.30 приведена эпюра напряжений а„ для клина с углом
а = 30 .
Если принять угол клина а = л, то получим полубесконечную
пластину с показанным на рис. 9.31 нагружением равномерно распре-
распределенной нагрузкой. Подставив а = яв (9.196), придем к формулам
для напряжений, возникающих в этой пластине:
о„= q-Bn — 29 — sin 29), A99= —^
- 29 + sin 29), orr9 = — -J- sin* 9.
(9.197)
277

6. Действия некоторых нагрузок на прямолинейную кромку по-
полубесконечной пластины. Первоначально рассмотрим действие силы
Р, приложенной в плоскости полубесконечной пластины перпендику-
перпендикулярно ее прямолинейной кромке (рис. 9.32, а). Решение этой задачи
Фламана A892) получим, рассматривая ее как частный случай задачи
Мичелла (см. с. 273), в которой надо принять а = л/2. В этом случае,
исходя из (9.187), получим:
агг = —2Р cos 0/ (пг), авв = агв = 0.
(9.198)
Для произвольной точки Л/ окружности диаметра d, касающейся
прямолинейной кромки пластины в точке О, имеет место соотношение
г = d cos 8, поэтому согласно
(9.198) в любой точке данной
окружности, за исключением
точки О, напряжение а„ оди-
одинаково, а именно:
V" о„ = — 2Р/ (jid).
В окрестности точки О пред-
предполагается цилиндрический вы-
вырез малого радиуса а, по по-
поверхности которого распреде-
Рис. 9.31 лены по закону (9.198) силы
tr, приводящиеся к действую-
действующей силе Р (рис. 9.32, б).
Компоненты тензора напряжений в декартовых координатах, ссы-
ссылаясь на (9.188). и учитывая, что в данном случае k0 = я/2, определя-
определяются равенствами
п , 0РгН1пгл\ п 9Рг г?/1тхг4\ п ¦ 9Pr?v /(тгг*\ <Q IQ№
Если вместо силы Р приложить единичную силу,к кромке пласти-
пластины в точке О, то напряжения будут равны: а'ц = ап/Р, а'^ = агг1Р,
Oi2 = <W- На рис. 9.33 приведены графики (эпюры) а'ц, о[2 на
сечении mm пластины, взятом на расстоянии Ь от ее кромки, а также
график изменения а22 на сечении, параллельном линии действия силы
Р и проходящем на расстоянии с от этой линии. Следовательно, в не-
некоторой точке К\ сечения mm напряжение ап от действия силы Р бу-
будет равно Phi, где hx — ордината эпюры Стп в точке Kv
Приведенные графики ad, a22, <j[2 позволяют определить напря-
напряжения, возникающие под действием нескольких сил Р, Рх, Р2, ..., при-
приложенных ,к кромке пластины (рис. 9.33), путем суммирования напря-
напряжений от каждой из них. Например, график а'ц от единичной силы,
приложенной в направлении Plt представлен пунктирной кривой.
Тогда напряжение au, взываемое силой Рх, в точке К равно Pxhu а при
совместном действии сил Р, Pt(i — 1, 2, ..., п) напряжение ап в точ-
точке К определяется суммой:
on = Ph + V pthf. (9.200)
278

Располагая эпюрами а[{, о^, можно найти напряжения аи и сти
в точке К и от распределенной нагрузки, приложенной к кромке плас-
пластины. Например, от равномерно распределенной нагрузки интенсив-
интенсивности q на участке пп (рис. 9.33) напряжение ап в точке К равно про-
произведению интенсивности q на площадь заштрихованной части эпюры
aii на участке п^пг.
Имея решение (9.198), можно найти перемещения ит, м9, вызыва-
вызываемые действием силы Р. В случае плоского напряженного состояния
на основании (9Л36) и (9.137) получим:
Рис. 9.32
я Ег
2 \ г
30
пЕе
Интегрируя первое уравнение (9.201), находим
иг=—-~ lnrcose + ф, (9).
л с
(9.201)
Подставив последнее выражение во второе уравнение (9.201) и затем
проинтегрировав его, получим
U8= J^-sin9 +—
пЕ пЕ
InrsinS— Г Ф1 (9) afe + ф4 (г).
Подстановка выражений для ит и «е в третье уравнение (9.201)
приводит к заключению, что
ф|
Э si n 0, ф, (г) = Сг.
1, следовательно,
Ф, @) = Л sinO + B cos9 —¦
па

Для перемещений получим выражения:
«г=— — lnrcosG—
я.Е
пЕ
пЕ
(9.202)
пЕ
_(i-v)P
пБ
где постоянные А, В, С определяются из уравнений связей. Пусть свя-
связи, наложенные на пластину, исключают перемещения ив точек на ли-
линии действия силы Р и, кроме того, запрещают перемещение и, одной
Рис. 9.33
из этих точек, находящейся на расстоянии d от кромки пластины. При
этих условиях из второго выражения (9.202) вытекает, что А = 0,
С = 0, а из первого выражения (9.202) находим
IP
~~Е
и, следовательно, для перемещений получим формулы:
иг = — [2 In — cos6— <1—v) sine],
nEl ¦ г J
„fi = JL [21n— sine — A— v)9cos6 + (l— v)sin el.
яЕ[ d J
Точки прямолинейной кромки (в = ±я/2) получают перемещения:
(9.203)
2?
, (9.204,
т. е. все точки кромки смещаются в ее плоскости к точке приложения
силы Р на одинаковую величину A — v)P/ BE) и, кроме того, на раз-
различную величину в вертикальном направлении. Наличие малого ци-
цилиндрического выреза в окрестности начала координат О, о котором
упоминалось выше, исключает бесконечные значения перемещения
ие | е = ± я/2-
280.

Рассмотрим теперь действие на полубесконечную пластину силы
Р, приложенной вдоль ее прямолинейной кромки (рис. 9.34). Эта за-
задача представляет собой частный случай задачи изгиба клина силой
(см. с. 275), и ее решение будет определяться формулами (9.190) и
(9.191), в которые надо подставить а = я/2 и k = я/2:
Рис. 9.34
а„ — 2Р sin 6/ (яг), (Tee = огв = 0; (9.205)
аи = 2Рх\хУ (пг*), а2г = 2РхЦ (пг4), а1г = 2РхххУ (пг4). (9.206)
Имея решения (9.198) и (9.205), легко получить формулы для напря-
напряжений при действии на кромку пластины в ее плоскости произвольно
направленной силы Р (рис.
9.35). р
В случае действия в пло- 0>
скости пластины момента М,
приложенного к ее кромке
(рис. 9.36), решение получим,
подставив в формулы (9.194)
а = я/2:
¦н
а„ = — 2М sin 26/ (яг2), о99 = 0, ргв = М A + cos 26)/ (яг2). (9.207)
7. Сжатие круглой пластины. Круглая пластина, толщина кото-
которой равна единице, сжимается двумя силами Р, направленными по ее
диаметру ОХО^ (рис. 9.37). Предположим, что каждая из этих сил вы-
вызывает радиальное распределение напряжений, определяемое решени-
решением (9.198), и выясним, какие силы необходимо приложить на контуре
281

пластины для осуществления в ней такого распределения напряжений.
Согласно (9.198), в произвольной точке К контура пластины во взаим-
взаимно перпендикулярных направлениях гаг' имеют место напряжения
сжатия: а„ = — 2Р eos Ql{nrh) и o>'r = — 2Р cos Q'/(nr'k). Посколь-
Поскольку диаметр пластины d = rj cos 6 = nl cos 6', упомянутые главные
напряжения в точке К оказываются одинаковыми и равными
—2PI (nd). Это означает, что
на любой площадке, прохо-
проходящей через произвольную
точку К контура пластины
перпендикулярно ее плоско-
плоскости, действуют такой же вели-
величины напряжения сжатия.
Следовательно, предполагае-
предполагаемые два радиальных рас-
распределения напряжений в
пластине будут реализованы,
если к ее контуру прило-
приложить радиальные сжимаю-
сжимающие силы постоянной интен-
интенсивности 2P/nd. Распределе-
Распределение напряжений в рассмат-
рассматриваемой пластине, контур
которой свободен от внеш-
наложения радиальных распределе-
пластины усилиями
Рис. 9.38
них сил, получим путем
ний напряжений на однородное растяжение
2P/nd. В результате напряжения в произвольной точке М, коорди
й О
ру р
наты которой относительно системы
тельно системы 02*i *2 равны х[, x'i
ются формулами
^хг равны *,, —хг, а относи-
относина основании (9.199) определя-
определя0"»=
2Р
л V /¦?
op / r2 r r'2 r \
(9.208)
или
2Р /cos» б, , cos» 6г 1 \
1 I ~ It
я \ rx rt d j
2Р /
f
я \
2Р /sin2 6, cos
f ¦
sin2 04 cos I
IP /sfn Gi cos' 6t
—
sin H, cos» е
)¦
(9.209)
282

На рис. 9.38 приведена эпюра напряжений ои на горизонтальном
диаметральном сечении АВ пластины, а также график изменения а,,
в точках линии действия сил Р. Если радиус а цилиндрических выре-
вырезов в окрестностях точек Оу и Ог принять равным d/50, то ап наиб5«
« —100Р/ (nd). Приведенные числовые значения на рис. 9.38 пред-
представляют собой коэффициенты при —Р/ (nd); эпюра на горизонталь-
горизонтальном диаметре изображена в увеличенном масштабе.
8. Температурные напряжения в длинном круговом цилиндре. Рас-
Рассмотрим стационарное тепловое состояние цилиндра g осесимметрич-
ным распределением температуры Т, не зависящим от координаты
Xs = г; воспользуемся полярными цилиндрическими координатами
г, 0,г, совмещая ось г с осью цилиндра. Предположим вначале,
что торцы цилиндрической трубы с внутренним радиусом гх и наруж-
наружным радиусом гг закреплены таким образом, что е„ = 0, т. е. рас-
рассматриваем задачу плоской деформации. В этом случае отличными
от нуля будут три компоненты тензора напряжений: атт, о8в и агг,
зависящие только от координаты г.
При стационарном режиме и при отсутствии внутренних источни-
источников теплоты уравнение теплопроводности в полярных координатах
имеет вид
V2 7=—+ — -4Г = 0. (9.210)
Используя обозначение Ф = Г — То, где То — начальная тем-
температура, уравнение (9.210) приводим к виду
dr \ [dr ,
интегралом которого является выражение
ft = С, In r -f Ca.
Определяя постоянные С, и С2 из условий
ft |,=r, = ftx И ft|r«*/-s = ft2
найдем, что
*
где слагаемое Ф2, соответствующее равномерному нагреву, не вызы-
вызывающему напряжений, можно отбросить и принять
(M^-dJ-lH-f^L (9.211)
i (V)
Считая, что при рассматриваемом изменении температуры ft, характе-
характеристики материала остаются постоянными, на основании C.87) и C.89)
имеем:
• 283

2Gerr—
aH0 = Я.6 4- 2Geefl —
l-2v!
1—2v
(9.212)
где
в = 8rr + 8е9. (9.213)
Из уравнений (9.212) находим
azz — v (arr + aee) — aEft. (9.214)
Уравнения равновесия (9.135) в рассматриваемом случае приводят-
приводятся к одному уравнению
darr/dr + (arr—авв)/г — 0, (9.215)
а зависимости (9.136) принимают вид:
8rr = dujdr, 8ее = иг/г. (9.216)
Подставляя в (9.215) значения агг и ae9 по формулам (9.212) и учи-
учитывая равенства (9.213) и (9.216), получаем уравнение
ит . 1_ d«r___ffr_ 1 + v di}
r* r ~dr ~~r*~a 1 v dT'
dr* r dr r*a 1— v
которое можно также представить в виде
f f-LlM]-al±l^. .(9.217)
dr I r dr J .1—v dr
Интегрирование уравнения (9.217) дает выражение
подставляя в которое значение в по формуле (9.211), получим
Первые два уравнения (9.212), используя (9.213) и (9.216), можно
переписать в следующем виде:
Огг = (*. + 2G)durldr + %ur/r — a?W A — 2v),
a99 == (X + 2G)«r/r + Ыыг/с!г — аЕЫ A — 2v).
Подставляя в последние уравнения значение и, по формуле (9.218),
найдем:
n + 4
U-2v г г»
284

rn4ln+
—2v г г* rt 2r2
agft E ( Dt РЛ
,l-2v ~I~ 1 + v U-2v "*" rV'
где
A 2(l-.v)!n(^x)- (9'220)
Постоянные Dt и D2 определяютоя из уоловий
огг|/.=ьЛ, = 0 и o^Ur.-O,
которые дают воотношения1
откуда вледует
d+v)(i-2v) Vi-^? a 2 r
Учитывая последние равенства, формулы (9.219) примут вид:
Принимая во внимание равенства (9.222) и (9.211), по формуле
(9.214) получим
(HdV (9.223)
Чтобы выполнялось условие плоской деформации (г1г « 0), к торцам
цилиндрической трубы нужно приложить нормальные усилия, распре-
распределенные по закону (9.223).
Если торцы трубы свободны, то на распределение усилий по фор-
формуле (9.223) можно наложить- такие постоянные усилия а'гг, при ко-
которых равнодействующая сил на каждом торце цилиндра будет равна
нулю. Величина о1г, следовательно, должна удовлетворять условию
г.
[К (v-2 In-2—v—^i— in-^+o;,bnrdr=»0,
. J \ ' r\-r\ rx )
285

откуда
Тогда при свободных торцах трубы на основании (9.223) и (9.224)
получим.
W?LM (9.225)
Остающиеся при этом самоуравновешенные усилия на торцах
трубы, согласно принципу Сен-Венана, будут вызывать вблизи их
только местные особенности.
Напряжения агг, Оев в этом случае определяются по формулам
(9.222), а е правой части формулы (9.218) для перемещения иг добав-
добавляется слагаемое—v~-r, соответствующее равномерному распреде-
распределению напряжений о'2г.
§ 11. КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ ФУНКЦИИ НАПРЯЖЕНИЙ
Многие плоские задачи теории упругости предпочтительно решать
используя функции комплексного переменного.
Вместо декартовых координат xlt x2 за независимые переменные
принимаются комплексные переменные:
г = *j + ix2, z = хх — ix2. . (9.226)
Тогда функцию напряжений Ф можно рассматривать как елож-
ную функцию от независимых переменных хи хг. По правилам диффе-
дифференцирования сложных функций имеем:
dxL дг дху дг дхх \ дг дг j
~дГ дг
и, наоборот,
X (9.228)
дг 2 { дх, дхг ) дг 2
Производные второго порядка определяются равенствами
дгдг
*¦-—
дг2
286

Отсюда имеем
Ф1и+Ф.и = *«Ф-4-^,*Ф-И-^.. (9.230)
Следовательно, бигармоничесжое уравнение (9.20) представляем
следующим образом:
w -а <9231>
Общий интеграл уравнения (9.231) можно найти путем последователь-
последовательного интегрирования по аргументам гиг. Однако тот же результат
получим, используя представление функции напряжений через три
гармонические функции (9.68):
Ф = хф + хд + ръ (9.232)
где, как уже известно, р и</ — гармонические еопряженные функции
и согласно (9.60)
р + iq = Ф (г), (9.233)
а Рх — некоторая гармоническая функция, которую теперь будем рас-
рассматривать действительной частью аналитичевкой функции комплекс-
комплексного переменного г;
X (г) = р, + Ь/,. (9.234)
Легко установить, что действительная qaGTb (Re) функции
(*! — lx2) (р 4- t?) 4- /?х 4- u?j
совпадает в правой частью равенства (9.232).
Тогда, осыпаясь на равенства (9.233) и (9.234), функцию напряже-
напряжений можно представить в виде
Ф (г, г) - Re li <р(г) + х (*I. (9.235)
Напомним, что некоторой аналитической функции со (г) соответ-
соответствует ей еопряженная функция со (г), которая получается из.функции
со (г) в результате вамены г на г, а также замены ввех поатоянных ко-
коэффициентов вопряженными им величинами; другими вловами, со (г)
получается из со (г), если всюду i заменить на —it. Используются еще
и такие обозначения; со (г) и со (г), имеющие следующий смысл; функ-
функция со (г) получается из со (г) заменой только коэффициентов на сопря-
сопряженные, а функция со(г) — путем замены только г на г. Например,
если to (г) — полином
со (г) = а0 + atz -f a^ -f ...,
то
ci (г) = а0 4- ^г + а^ + ...,
со (г) = <2р +'<V + а2?г + •¦•.
со (г) = <з0 + ахг 4- <згга + ....
.287

По определению, имеем
со (г) = со (г) и со (г) = со (г).
Очевидно, что
со (г) + йГ(г) = 2Reco (г). (9.236)
Для функции [гср (г) + х (г) 1 ей сопряженная функция, будет
lap (г) + х (г) 1 и, следовательно, на овновании (9.236) равенвтво
(9.235) запишем так:
2Ф (г, г) = г Ф(г) + гф (г) + х (*) + ~% (г). (9.237)
Равенство (9.237), которое называется формулой Руре а, яв-
являясь общим интегралом уравнения (9.231), выражает собой пред-
представление функции напряжений через две аналитические функции
комплексного переменного ф (г) и х (*)•
§ 12. КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ КОМПОНЕНТ ТЕНЗОРА
НАПРЯЖЕНИЙ И ПЕРЕМЕЩЕНИЙ
Согласно (9.57), оп + о22 = УгФ и, следовательно, приняв во вни-
ыание (9.230) и (9.237), имеем
аи + а22 = 4 -Ц- = 2 [<р< (г) + ф' E) ] = 4 Re Ф< (г). (9.238)
Комбинируя выражения (9.229) для производных второго поряд-
порядка и учитывая (9.237), найдем
Ф.ц-Ф.м-2М>.« = 4 -^|- = 2 [гФ" (г) + Х" (г)].
Тогда, ссылаясь на соотношения (9.16), получим
<*22 — On + 2ia12 = 2 [iip* (г) + х" (г) 1. (9.239)
Отделив действительную и мнимую части в последнем равенстве,
можно получить выражения для (о2г — оп) и 2о1г, которые вмевте в
равенством (9.238) позволяют определить компоненты тензора напря-
напряжений.
Обращаясь к представлению перемещений, воспользуемея равен-
равенствами (9.65) и образуем комплексную комбинацию:
2G («! + шг) = [4A— v) (р + iq) — (Фд + *Ф 2I. (9.240)
Дифференцируя (9.237) в соответствии в (9.227), находим
Ф,1+Ю\. = 2-|р8ВВФB)+гф' (i)+j?(z). (9.241)
Учитывая, последнее соотношение, а также (9.233), преобразуем
равенство (9.240), которое и приводит к представлению перемещений
через те же две аналитические функции ф (г) и х B):
2G (иу + iu,) = хф (г) - г? E) - х' (г), (9.242)
288

где
и = 3 — 4v. (9.243)
Если в формуле (9.242) отделить действительную и мнимую части,
то можно получить выражения для компонент щ и иг вектора переме-
перемещения я.
Формулы (9.238), (9.239) и (9.242) получены Г. В. Колосовым 1311.
В случае плоского напряженного состояния в формуле (9.242) вмес-
вместо к согласно равенству (9.50) надо принять
и* - 3 — 4v* = C — v)l (I + v). (9.244)
Поскольку в формулы Колосова входят только первая и вторая
производные функции % (г), удобно ввести обозначение
X' (г) = dyjdz = ф (г) (9.245)
и записать эти формулы в вледующем виде!
оп + о22 = 2 [<р~- (г) + ф« E)] = 4Re <р? (г),1 {
°и-°ц + 2iau = 2 [г Ф" (г) + ф« (г)] ; |
2G (И1 + ш2) = иф (г) — гф' (г) — f (г). (9.247)
Аналитические комплексные функции ф (г) и ф (г), через которые
представляются напряжения и перемещения, называют функциями
Колосова—Муохелишвили.
Уатановим комплексные предвтавления главного вектора и глав-
главного момента сил, приложенных к дуге АВ (см. риа. 9.3).
Компоненты главного вектора вил, приложенных к дуге А В, еог-
лавно (9.70) равны:
Здесь квадратные вкобки 11д означают приращение заключенной в
них функции при перемещении по дуге АВ от А к В.
Образуем комплексную комбинацию:
Рх + 1РШ = |Ф2 - 1Фл\а =-« [Ф.1 + №.,Й,
которую, ввылаявь на равенетва (9.241) и (9.245), вапишем так?
рг + fpg = —i |ф B) + гф' (г) + ф (г)!3. (9.248)
Главный момент М° аил на дуге А В относительно начала координат
О определяется формулой (9.73), которая, евли учесть равенвтва (9.69),
принимает вид
Л!0 = - f [Xyd (ФЛ) + хф (Ф.,)].
Вычисляя пооледний интеграл по частям, получим
10 8ав. 5U 289 __]__

Так как
и учитывая (9.235), получим комплексное представление главного
момента сил на дуге А В относительно начала координат О в следую-
следующем виде:
Ма = Re fx (г) — гф (г) — ггф' (z))%. (9.249)
§ 13. СТЕПЕНЬ ОПРЕДЕЛЕННОСТИ ФУНКЦИЙ <р(г) И ф(г)
По первой формуле (9.246) сумма напряжений ап -Ь а22 опреде-
определяется только действительной частью производной ф' (г), поэтому к ее
мнимой части без изменения напряжений можно добавить постоянную
С. Отсюда следует, что при заданных напряжениях производная
ф' (г) определяется с точностью до слагаемого iC, а функция ф (г), сле-
следовательно, — с точностью до iCz + а + ф.
Тогда из второй формулы (9.246) вытекает, что при заданном тен-
тензоре напряжений производная ф' (г) определяется единственным об-
образом, а функция ф (г) — с точностью до слагаемого а' + t{J',
Таким образом, при замене
Ф (г) на ф (г) + iCz + (а + if,),
Ф (г) на ф (г) + (а' + ф')
напряжения не изменятся, а комплексная комбинация перемещений
(9.247) получит следующее приращение:
20 (А«х + iAu2) = i A + х)Сг + х (а + ф) — (а' — #'). (9.251)
Отделяя действительную и мнимую части в равенстве (9.251), найдем
что перемещения ut и ы2 определяются с точностью до слагаемых
Аи^~[-(\ +х)С
(9.252)
выражающих собой, как и следовало ожидать, жесткое вмещение те-
тела.
Из (9.251) вытекает, что при заданных перемещениях постоянные
С, (а + Ф) и (а' — ф') должны подчиняться условиям
С = 0, х (а + ф) - (а' - ф') = 0. (9.253)
Соответствующим выбором постоянных а, р, а', Р' функции ф (г) и
ф (г) можно подчинить условиям
Ф @) = 0 или ф @) = 0, (9.254)
каждое из которых исключает произвол в выборе функций ф (г) и ф (г)
при заданных перемещениях.
290

При заданных напряжениях можно распорядиться всеми пятью
постоянными С, а, р1, а', р" и их можно подобрать так, что получим
условия
Imcp' @) = 0, ф @) = 0, г|> @) = 0, (9.255)
которые фиксируют обе функции: <р (г) и ф (г).
Если область S, представляющая сечение тела плоскостью х3 = 0,
односвязна, то функции ф(г) иг|)(г) в ней однозначны."В случае много-
многосвязной области S функции ф (г), гр (г) могуть оказаться многознач-
многозначными.
Предположим, что имеем конечную многосвязную область S с на-
наружным контуром Lo и внутренними контурами Lh (см. рис. 9.4).
Пусть на одном из внутренних контуров L& компоненты Plh и P2ft
главного вектора внешних сил имеют определенные значения. Тогда
функции ф (г) и ty (г) должны обладать такими особенностями, чтобы
при обходе контура Lk комплексная комбинация компонент главного
вектора внутренних сил была равна — (Рх^ + iP^k)- Далее, из того,
что компоненты тензора напряжений и перемещения должны быть од-
однозначными, вытекает необходимость однозначности выражений в
правых частях формул Колосова (9.246) и (9.247). Эти условия будут
удовлетворены, если принять
Ф (г) = A k In (z-2k) + Ф1 (г), Ц) (г) = Bk In (z~zk) + % B), (9.256)
где Ah = ah + ip\, Bh = al, + i% — постоянные; zh — произволь-
произвольная точка внутри контура Lk; Фх и % — голоморфные, т. е. однознач-
однозначные аналитические функции.
Очевидно, что производные функций ф (г) и т]) (г), определяемых
выражениями( 9.256), однозначны, а сами функции при обходе конту-
контура Lk получат приращения:
[Ah In (г - zh)]Lk =• 2niAk, [Bh In B - zk)]Lk = 2niBh. (9.257)
Тогда используя формулу (9.248) для главного вектора внутренних
сил на контуре Lf, и учитывая сказанное выше, получим
Plk + iP,k = -2л (Ak - Bk), (9.258)
где Bk = a'k — tfH.
Из условия однозначности перемещений на основании (9.247) по-
получим еще уравнение для определения постоянных Ah и Bh:
xAh + B~h = 0, (9.259)
откуда
А _Ьл±Ет g =ilLh±l?*.t (9.260)
2A+) 2лA+х)
Учитывая значения постоянных, формулы (9.256) примут вид
^ (г) = x P?~*? In {z-zh) +b (z). (9.261)
10* 291

Если к другим внутренним контурам приложены также неуравнове-
неуравновешенные силы, то соответствующие логарифмические члены суммиру-
суммируются.
Обратимся теперь к многосвязной бесконечной области S, которую
можно рассматривать как предельный случай конечной многосвязной
области, наружный контур Lo которой целиком уходит в бесконечность.
Формулы, полученные для конечной многосвязной области, будут
справедливы для любой конечной части рассматриваемой области и
необходимо только выяснить поведение функций ф (г) и ф (г) в окрест-
окрестности бесконечно удаленной точки.
Для любой точки вне окружности L, охватывающей все внутрен-
внутренние контуры Lft, имеем |г| > \гк\, поэтому
In (г — 2ft) = In г + In A — zkz~\
где In A —zhz~l) — голоморфная функция вне L.
Тогда формулы (9.261) в случае бесконечной многосвязной облавти
примут вид
(9.262)
1пг+*'<*>•
где ф* (z) иг)э* (г) — функции, голоморфные вне L, т. е. в круговом
кольце L •< г ¦< Lo (Lo — бесконечно большая окружность).
Следовательно, функции <р* и \|з* можно представить в кольце L <
<г< Lo сходящимися рядами Лорана:
Ф* (г) = ^ ап г". Г(г)=%Ьпг\ (9.263)
— с^ — ел
Потребуем, чтобы компоненты тензора напряжений на бесконеч-
бесконечности были ограниченными, и выясним, каковы должны быть функции
ц> (г) и г|з (г) при выполнении этого требования.
Подставив в первую формулу (9.246) выражение (9.262) для функ-
функции ф (г) и заменив ф* (г) рядом (9.263), получим
откуда легко ваключить, что сумма ап + аг2 будет ограниченной, ев-
ли ап = ап = 0 при п > 2.
При выполнении этого условия таким же образом можно устано-
установить, что комбинация о22 — ou + 2ta12 будет ограниченной, еели Ъп =¦
= 0 при п > 2.
Итак, имеем
Ф* (г) - п1г + Фо (г), ф* (г) = btz + ф0 (г),, (9.264)
292

где at = а + t{$, bt = ах + t'Pi — постоянные, a функции
Фо (z) = 2 а" г""' ^о (г) = 2 6п г~" (9-265)
являются голоморфными вне L, включая бесконечную точку.
Не изменяя тензора напряжений, можно принять р = 0.
Теперь по формулам (9.246) при \z\ -> u~> находим:
Оп + 0'й = 4Re ф^ (г) = 4а; а=» — а~ + 2/а~ = 2bL = 2at + 2фь (9.266)
откуда
of, = 2a — a1( of, = 2a + at, ofs = fc, (9.267)
т. е. в бесконечно удаленных частях области имеем равномерное рас-
распределение напряжений.
На основании (9.247) можно установить, что перемещения при
|г| -*- оо будут равны нулю при выполнении равенств
р1 + iPt = 0, a = 0, ctj + t"P, = 0, (9.268)
т. е. при условиях, что главный вектор сил, приложенных к контурам
области, равен нулю и напряжения на бесконечности a'fj = af3 =
= of, = 0.
§ 14. ГРАНИЧНЫЕ УСЛОВИЯ, КОТОРЫМ ДОЛЖНЫ УДОВЛЕТВОРЯТЬ
ФУНКЦИИ КОЛОСОВА—МУСХЕЛИШВИЛИ
Из формул Колосова (9.246) и (9.247) следует, что решение плоской
задачи сводится к отысканию аналитических функций ф (г) и г|> (г) в
рассматриваемой области. Очев'идно, что эти функции должны удов-
удовлетворять определенным условиям на контуре L рассматриваемой об-
области.
Будем считать, что функции at) и щ непрерывны вплоть до грани-
границы L области.
1. Конечная односвязная область, ограниченная простым замкну-
замкнутым контуром L.
В случае основной задачи первого типа, т. е. когда на контуре тела
заданы поверхностные силы tx и t2, граничные условия можно выра-
выразить следующим образом.
Исходя из равенств (9.79), образуем комплексную комбинацию:
Ф х + г"Ф , = i | ft + U2)dL + Co, (9.269)
' о
где L — дуга контура, соответствующая его произвольной точке, от-
отсчитываемая в положительном направлении (область остается слева)
от некоторой начальной точки контура; Со = К + iN — постоянная.
Комплексная комбинация в левой части равенства (9.269) опреде-
определяется выражением (9.241) и, следовательно, учитывая (9.245), име-
имеем
Ф (г) + гфг (г) + "ф (г) 11 - L + if г + С* (9.270)
293

h + If2 - t Hh + «г)^ « * (Pi + H»g). (9.271)
где
Было показано, что в случае односвязной области замена (9.250)
не меняет тензора напряжений. При этой замене выражение в левой
части равенства (9.270) заменяется на
Ф (г) + гф1 G) + ф E) + (а + /р) + (а' - Ф')-
Следовательно, при подходящем выборе постоянных а + /р и
а*—гр', можно придать любое значение постоянной Со. Напротив, если
определенным образом зафиксировать постоянную Со, то произвольно
можно принять одну из двух постоянных а + /р, а1 — ip', т. е. мож-
можно считать
Ф @) = 0 или ф @) = 0, 1тф8 @) = 0. (9.272)
В случае основной задачи второго типа, т. е. когда на контуре за-
заданы перемещения иУ\ граничное условие для функций Колосова—
Мусхелишвили, согласно (9.247), принимает вид
хФ (г) — ajJ* (г) — у (z) | L = 2G («<»> + 1иф).^ (9.273)
2. Бесконечная область, ограниченная простым замкнутым кон-
контуром L (бесконечная плоскость с отверстием).
Задачи в рассматриваемой области на основании выражений (9.262)
и (9.264) можно привести к определению в ней голоморфных функций
Фо B) и 1|?0 {г).
В случае первой основной задачи граничное условие (9.270) для
функций фо (z), фо (г) принимает вид
Фо (z) + гф,; (S) + фо (г) | L = /J + i/J U + Со, (9.274)
где
/? + ifl = f 1 + f/« + 9Pl + ',P\ A n z-x In i) -f-
й ^ ~(ai +Б1) 2-^- (9l275)
г
Легко установить, что выражение в правой части (9.275) является
однозначной функцией на контуре L. Действительно, при обходе кон-
контура L в положительном направлении функция /г + t'/г на основании
равенства (9.271) получит приращение i (P1 + iP2), а приращение
функции In г1— к In г будет — 2ш — х2ш = —A + хJш.
Отметим, что при заранее принятом значении Со необходимо счи-
считать, что
ф0 (оо) = 0 или -фо (оо) = 0, Ima'i = 0. (9.276)
В случае второй основной задачи граничное условие (9.273) при-
принимает вид
хФо (z) — гф,' (г) -фо (г)k = 2G (и, + ш2)ft., (9.277)
294

где
20 W+'•"•>=20 <«!"+'<•>+Й^'"(^^& t
(9.278)
Непосредственно можно убедиться, что правая часть (9.278) пред-
представляет собой на контуре L однозначную функцию.
§ 15. формулы колосова в ортогокальных
'криволинейных координатах
При решении многих задач выгодно пользоваться криволинейны-
криволинейными координатами \, г\, которые связаны о декартовыми координатами
хъ хг соотношениями F.32):
2 = Xl + iX2 = F (С) = F (I + щ). (9.279)
Угол между осью Xi и осью (|) обозначим через а (рис. 9.39). Тогда
компоненты тензора напряжений ац, ат, а^ в системе осей (Е), (г\)
на основании B.32) связаны с ап, Ом, а12 следующими соотношениями:
<J|g == Оц cos^ а + а22 sin* а + ац sin 2а,
Ощ = сгц sin? а + огг cos2 а — ai2 sin 2a,
(9.280)
а12 cos 2а „- (ап — а22) sin 2a.
Отсюда получим:
= (а22 - а„ + 2^а)е'^ J l ' ;
Пусть точка г (точка М) получает в направлении (Е) смещение &| =
= F1 (S)d|. Если представить производную Fc (?,) в точке М как ком-
комплексную величину в показательной форме /7'(?)=&е'а, то поскольку
F1' (?) = fee-'a, получим _ _
g/2a = р'- fa,pl (^ (9.282)
Тогда формулы Колосова (9.246) в ортогональных криволинейных
координатах, учитывая (9.282), запишутся так:
(9.283)
Компоненты «|, ил вектора перемещения и точки М (рис. 9.39) на ос-
основании G.185) связаны с компонентами этого вектора ult uz в декар-
декартовых координатах соотношением
щ + 1щ = («1 + Ш2)е~1а. (9.284)
Учитывая, что _
e-'a = Fl Qlk = Fl (S)/1 fг (?) [, (9.285)
295

на основании равенств (9.284) и (9.247) получим
В случае полярных координат \ = г, г\ = б формулы (9.283) и
(9.286) получают вид:
о„ + аей = 2 [Фе (г) + ф* (г)] = 4Re?'(z),
а09 - агг + 2iare = 2е'2е [яр« (г) + ф«B)];
(9.287)
2G (иг + ш6) =
[хф (г) — гф* (г) — г|> (г) ]. '(9.288)
Если контур L тела является
окружностью и начало полярных
координат совмещено с ее цент-
центром, то компоненты единичного
вектора п по внешней нормали к
контуру равны пг = \, п$ = 0. В
этом случае на основании
= ti(l = г, 0; j = г, 0)
имеем:
Рис. 9.39
(9-289)
формулы
Вычитание второй
(9.287) из первой дает
оГт — ^ее = ф' (г) + ф~' (г) — [гф? (г) + ? (z) \em. (9.290)
Подстановка согласно равенствам (9.289) дает граничное условие
для функций Колосова—Мусхелишвили в полярных координатах:
Ф< (г) + ? (z) — [гф" (г) + ф{ (г) У2в | L = t, — ite. (9.291)
§ 16. ОБЩЕЕ РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ПЕРВОГО ТИПА
ДЛЯ БЕСКОНЕЧНОЙ ПЛОСКОСТИ С КРУГОВЫМ ОТВЕРСТИЕМ
В этом случае удобно воспользоваться полярными координатами
с началом в центре отверстия радиуса а.
Для рассматриваемой бесконечной многосвязной области функции
Ф (г)и 1|) (г) определяются выражениями (9.262).
Обратимся к граничному условию (9.291), которому должны под-
подчиняться эти функции.
С учетом равенств (9.264) и разложений (9.265), которые имеют
место во всей области вне контура Lx отверстия, находим
= к
- 2"»--
Сг+1)
(9.292)
296

Для коэффициентов в последних выражениях введем следующие
обозначения:
^^ (9.293)
(9.294)
. Bh=*-nba
и примем z~<n+l) = z~k.
Тогда выражения (9.292) запишутся так;
Ф!й=|4 г"*, ^s' (z) =|fift г"»
(9.295)
ф"(г)=_ v
(9.296)
Для точек контура отверстия г — ое'8 и, следовательно, по фор-
формулам (9.295) и (9.296) получим:
Ф'(г)
(9.297)
—zem ф
ое
'(г)
д
D
—
ее
= 2 ^ka'
«=.0
i
ся
Sft+2
Считая 1Т и /в на контуре Li отверстия заданными, разложим функцию
(^, — Uq) в комплексный ряд Фурье 149]:
+ СЯ
/,-tfe= 2 Cheik\ (9.298)
*=—со
где
2л
Ch = -~( (tF— it») e-m d0.
о
Подставив (9.297) и (9.298) в (9.291), получим
"ci О+k) Ак c^tk0 , -у ^ft_e««e 'V
(9.299)
^1
(9.300)
297

Сравнивая коэффициенты при е"*д в обеих частях равенства (9.300)
при k = 0, 1, 2, найдем:
А о + Л о — Вг/а2 = Со, ЛУа — BJa = d, AJ& — Во = Cz
(9.301)
а при fe > 3
Лк/а* = Cft. (9.302)
Сравнение коэффициентов при erm (k > 1) приводит к соотношению
A + k)Ah/a« - Bk+i/ak+* = C.ft. (9.303)
Напомним, что тензор напряжений не изменится, если принять
Im Ло = Р = 0 (см. с. 293). Следовательно, Ло— действительное чис-
число, причем Ло + Ло = 2Ло = 2а.
Коэффициенты Ло = ее, fl0 = «i + 'Pi, определяющие по форму-
формулам (9.267) напряжения на бесконечности, будем считать известными.
Чтобы обеспечить однозначность перемещений, необходимо удов-
удовлетворить условию (9.259), которое при единственном внутреннем кон-
контуре L\ рассматриваемой области принимает вид
кЛ, + В, = 0. (9.304)
Из этого условия и второго равенства (9.301) находим:
Ai = Cia/ (I + к), By = —Kda/ A + к;. (9.305)
Из первого и третьего равенств (9.301) получим
Л2 = (So + CV)^, fl8 = BЛ0 — С0)аа, (9.306)
а из равенства (9.302) следует
Л ft = Cfta" (& > 3). (9.307)
Наконец, уравнение (9.303) дает
Вк = (* - 1) ааЛй_, - а"С_й+г (* > 3). (9.308)
Таким образом, все коэффициенты рядов (9.295) определены и при
• заданном нагруженни (tr — itg) на контуре 1г отверстия задача пол-
полностью решена.
Заметим, что в случае плоского напряженного состояния , т. е. ког»
да рассматривается бесконечная пластина с отверстием, необходимо
всюду к заменить на х* по формуле (9.244).
§ 17. ПЛОСКОСТЬ С КРУГОВЫМ ОТВЕРСТИЕМ, К КОНТУРУ
которого приложено равномерное давление
К контуру расположенного в центральной части плоскости мало-
малого отверстия радиуса а приложено постоянное давление р (рис. 9.40),
т, е. имеем tr = —р, t(, = 0. На бесконечности напряжения принима-
принимаем равными нулю и, следовательно,'по формулам (9.267) получим а =я
— «1 — Pi — 0, т. е.
Л„-=Яо = О. (9.309)
298

Так как tT = —г79 — Р, то из (9.298) следует
Со = — р, Ck = 0 при k ф О.
Теперь по формулам (9.305)—(9.308) находим:
Ах = Й! = Аг = 0, fi2 = /ш2, Ак = Bk = 0 при & > 3 (9.310)
и разложения (9.295), учитывая (9.309) и (9.310), принимают вид
Ф* (z) = 0, ф» (z) = раУг\ (9.311)
По формулам (9.287), принимая г — ге'°, получим
а„ == —раг/Н, авв = ра'2//-?, аг9 = 0, (9.312)
Рис. 9.40
а по формуле (9.288), опуская несущественную постоянную, найдем:
"'вм 1 "в = 0-
На рио. 9.40 приведены эпюры напряжений а„ и
§ 18. ДЕЙСТВИЕ НА ПЛОСКОСТЬ СОСРЕДОТОЧЕННОГО МОМЕНТА
Пусть к контуру отверстия радиуса а приложены только постоян-
постоянные силы te = в, а на бесконечности о^ = afa — <rfa =s 0.
Следовательно,
Ао = fl0 = 0. (9.314)
Очевидно, что компоненты Ри Р2 главного вектора приложенных
еил равны нулю, а главный момент
2я
(9.315)
Поскольку (if, — ite) = —fe, из формулы (9.298) вытекает, что отлич-
отличным от нуля будет только один коэффициент при А == 0
Со = —io.
299

По формулам (9.305)—(9.308) находим
а все остальные коэффициенты Аи, Bk равны нулю.
Таким образом, принимая во внимание равенство (9.315), имеем!
q/(z) = O, ^(zH-i-Jjip (9.316)
и по формулам (9.287) находим:
о>, = аее =-0, аг9 « — М/ Bпл2). (9.317)
Представим, что радиус а отверстия беспредельно уменьшается,
а силы /в увеличиваются так, что момент М остается постоянным. При
таком предельном переходе формулы (9.317) будут соответствовать дей-
действию сосредоточенного момента М, приложенного в начале коорди-
координат.
§ 19. ДЕЙСТВИЕ НА ПЛОСКОСТЬ СОСРЕДОТОЧЕННОЙ СИЛЫ
На бесконечности плоскости, имеющей отверстие, напряжения рав-
равны нулю, т. е.
Л 0 = Во = 0, (9.318)
а к контуру отверстия радиуса а приложены распределенные постоян-
постоянные силы tt — clt ti = Ъъ (рис. 9.41).
Главный момент этих сил, очевидно, равен нулю, а компоненты
Pi, P2 их главного вектора равны:
Pi = 2пасъ Р2 = 2пась (9.319)
т. е. приложенные силы приводятся к силе|Р| = 2лаУе? + el, на-
направленной под углом р = arctg (г,г!с\)к оси хл.
Нормальная tT к контуру и касательная (э составляющие сил tx ==
= Ci, tz = Сг равны
/, =— (t'i cos 0 + е2 sin 6), te = Ci sin 6 — c2 cos 9,
откуда
. tr — ite = — (Cl — /c2)e«>.
На основании (9.298) устанавливаем, что отличным от нуля будет
только один коэффициент
Ci = — (ci — ic2) = — A/2по) (Pj — (Р2). (9.320)
Приняв во внимание равенства (9.318) и (9.320), по формулам (9.305)—
(9.308) находим отличные от нуля коэффициенты разложений (9.295I
2яA+х)
Тогда интересующие нас функции принимают вид:
-1_ ,.,'(;)- >'-(Р.-/Р3) 1 P.+ iP, а*
(9.321)
ф(г) (;)
2яA + х) г 2иA+н) г я
(9.3 22)
300

Если теперь радиус а беспредельно уменьшать, &tx—cx и t% = с2
увеличивать так, чтобы компоненты Рь Р2 главного вектора "остались
неизменными, то придем к случаю действия сосредоточенной силы,
приложенной в начале координат. В этом случае функции (9.322) при-
ыут вид:
2лA
Рис. 9,41
Подставляя выражения ф{ (г) и г|>* (г) в формулы (9.287) и учиты-
учитывая, что г = relti, получаем:
(9.324)
(9.325)
Вспоминая, что в случае плоского напряженного состояния необхо-
необходимо заменить к на и* = C — v)/ (I + v), и отделяя действительнш
и мнимые части в равенстве (9.325), находим:
(9.326)
301

§ 20. ОДНОСТОРОННЕЕ РАСТЯЖЕНИЕ ПЛАСТИНЫ С МАЛЫМ '
КРУГОВЫМ ОТВЕРСТИЕМ (ЗАДАЧА КИРША)
Пластина значительной ширины с малым отверстием радиуса а в
ее центральной части подвергается равномерному растяжению напря-
напряжениями о в направлении оси х3 (рис. 9.42), следовательно,
0=1 = 0, af2=of2=0.
Рис. 9.42
Из формул (9.267) находим:
А о = a = о/4, Во = a, + $i = —а/2. (9.327)
Поскольку на контуре отверстия отсутствуют внешние силы, т. е.
tr = /9 = 0, все коэффициенты Фурье Ch (9.299) оказываются равны-
равными нулю. Тогда из формул (9.305)—(9.308), учитывая (9.327), нахо-
находим, что
At = Bt = О, А 2 = — в/2а\ Вг = о/2а\ A h = 0 при k > 3,
В8 = 0, В, = —C/2)aa4, Bh = 0 при k > 5.
Следовательно, функции (9.295) принимают вид:
ф' (Z) = (о/4) A — 2а2/22), ф* B) = -(а/2) A — аг/га + З^/г*). (9.328)
Теперь по формулам (9.287), принимая г = ге'е, получаем:
о
+ a09 = a (l — 2 -^i cos 29] ,
|— 3^-jsin 29,
302

откуда
(9.329)
В точках контура отверстия (г == а) имеем
агг = аге = 0, а9е = а A — 2 cos 29).
Рис. 9.43
Ha рис. 9.42, б приведена эпюра напряжений аее в точках конту-
контура отверстия, откуда видно, что в точках B) имеют место напряжения
растяжения (<Tee)max = За, a в
точках (/) — напряжения сжатия
соо = —о. На рис. 9.42, а приве-
приведены также эпюры напряжений-
агг и аее в точках осей хх и х2.
Любопытно, что в точке К оси
Xi на расстоянии г = У 6/Ъа имеет
место сжимающее напряжение
агг — ап = —а/24. В этой же
точке напряжение а8в — Огг так-
также сжимающее, т. е. эта точка
вблизи отверстия (она не единственная) находится в условиях двух-
двухосного сжатия.
Эпюры напряжений наглядно показывают, что влияние малого от-
отверстия на распределение напряжений носит локальный характер. С
удалением от отверстия в точках оси х2 напряжения а99 = ап быстро
приближаются к а.
Задача Кирша A898) является характерным примером того, что
наличие резких изменений формы тела (различного рода надрезов: ма-
малые отверстия, выточки,.канавки и др.) приводит к значительным мест-
местным напряжениям, быстро затухающим по мере удаления от этих гео-
геометрических концентраторов напряжений. Обычно местные напряже-
напряжения характеризуют коэффициентом концентрации
напряжений к, представляющим собой отношение наибольшего
местного напряжения к номинальному напряжению, т. е. к напряже-
напряжению, вычисленному в предположении отсутствия концентратора. В
рассматриваемом случае k = (aee)max/c = 3.
Наличие концентраторов напряжений не только ведет к повыше-
повышению напряжений вблизи них, но и изменяет характер напряженного
состояния.
Для определения перемещений найдем функции ср (г) и гр (z) по их
производным (9.328). Отбрасывая несущественные постоянные, по-
получаем:
Ф (г) = (а/4) (г + 2а2Iz), $ (г) = -(а/2) (г + аЧг — aVz3).
309

Теперь по формуле (9.288), заменив и величиной и* = C — \I A + v)
(рассматривается плоское напряженное состояние), найдем
откуда, выделив действительные и мнимые части, имеем:
м, = ¦
4G |_ 1+v $ \ 1+v
= __?_ B -1=1 "*. +г _ *-) Sin 29.
(9.330)
Поскольку с удалением от отверстия напряжения быстро прибли-
приближаются к о, приведенное решение применимо к пластине конечной ши- ¦
рины b > 10а. *
Если диаметр отверстия оказывается соизмеримым с шириной
пластины, то распределение напряжений отличается от того, что дают
формулы (9.329). Решение последней задачи, выполненное Р. Хаулен-
дом A930), дает при а = 0,25Ь распределение напряжений,о9е = Си
на сечении, совпадающем с осью Хг, представленное эпюрой на рис.
9.43.
§ 21. ПЛАСТИНА С МАЛЫМ КРУГОВЫМ ОТВЕРСТИЕМ
ПРИ НАГРУЖЕНИИ В ДВУХ НАПРАВЛЕНИЯХ
Решение этой задачи можно получить методом суперпозиции (см.
гл. IV, § 9), используя решение задачи Кирша.
Растяжение пластины в направлениях осей хг и хг с одинаковым
напряжением а (рис. 9.44). Суммировав напряжения, определяемые
по формулам (9.329) в произвольной точке К (г, 0) пластины при ее
растяжении вдоль оси хл с соответствующими напряжениями при рас-
растяжении в направлении оси Xz, которые можно вычислить по тем же
формулам (9.329), подставив в них вместо угла 9 угол (я/2 + 6), по-
получим
( ) ( ) (9-331)
На рис. 9.44 приведены эпюры напряжений огг и о9е в точках се-
сечения хл = 0.
Аналогично, исходя из (9.330), при рассматриваемом нагружении
пластины найдем:
М^) "9=0- (9-332)
Растяжение пластины напряжением а в направлении оси хг и
ее сжатие напряжением — о в направлении оси х2 (рис. 9.45). При-
Применяя метод суперпозиции и используя формулы (9.329) для рассмат-
304

Рис. 9.44
1
h
11AШ"Н1
ttfftttiff
|f|j. ¦
Рис. 9.45
805

риваемого нагружения пластины, находим:
а„ = о A — 4а2//-8 + За4//-4) cos 20, J
о99 = _оA + За4//-4) cos 2©, (9.333)
аг0 = __0 A + 2а2//-2 — За4//-4) sin 26. J
Характер изменения напряжений агг и а9е в точках сечений хх —
= о и х2 = 0 отражается эпюрами, приведенными на рис. 9.45. Точ-
Точка (/) находится в условиях одноосного сжатия при напряжении а99 —
= О22 = —4а, а точка B) — в условиях одноосного растяжения при
напряжении а8е = °и = 4а. В этих точках наибольшее касательное
напряжение на основании B.71) тшах = 2а.
Рис. 9.46
Перемещения определяются по формулам
г 20 \ 1 +v >- гз j
(9.334)
Результаты решения этой задачи можно применить и к случаю кру-
кручения тонкостенной цилиндрической трубы, имеющий малое радиаль-
радиальное отверстие (рис. 9.46, а). Выделенный из трубы элемент abb1 а'' на-
находится в таких же условиях (рис. 9.46, б), как и рассмотренная плас-
пластина (рис. 9.45). В точках (/) и B) наибольшее касательное напряже-
напряжение ттах = М I (jtD2S), где D — средний диаметр трубы, S < D —
толщина ее стенки.
§ 22. КОНФОРМНОЕ ОТОБРАЖЕНИЕ
Пусть функция
z - © (С)
(9.335)
определяет однолистное конформное отображение области s плоскости
? на область S плоскости z (см. гл. VII, § 12).
306

Ограничимся рассмотрением области S двух видов:
1) односвязная конечная область S ограничена простым замкну-
замкнутым контуром L;
2) бесконечная область S ограничена простым замкнутым внутрен-
внутренним контуром L.
Область S первого вида будем отображать на круг |?] <Г 1, а об-
область второго вида — на область | ?| > 1, т. е. на бесконечную плос-
плоскость с круговым отверстием радиуса р = 1.
Окружность круга | ? | < 1, как и в гл. VII, § 12, будем обозначать
через у, а ее произвольную точку — через
% = е'е. ' (9.336)
Отметим, что область второго вида можно также отображать на круг
1С|<1.
При решении плоской задачи методом конформного отображения
функции ф B) и i|) B) необходимо выразить через новую переменную
t, вводимую соотношением (9.335), а также необходимо преобразо-
преобразовать основные формулы плоской задачи.
Функции Колосова—Мусхелишвили примут вид:
Ф B) = Ф [<о (С) 1 = Ф1 @. Ч> («> = 1» I© @1 = *i @. (9-337)
Ясно, что функция ф! отлична от функции ф, а также % отлична
от tp. Однако ради простоты обозначений для функций cpi (?) и ifo (?)
условно сохраним обозначения соответственно ф (^) и г]з (?). Принимая
это соглашение, имеем
(9.338)
dl dz ш' (О .» @
= ^ = J~.
Аналогично, имеем
2)= ФШ, Рде ф- ®=±\SLM\ = ю> И Ф' (О ~Ф' @ »' @, (9.339)
W dz dl dz ш' (О .»' @
где» учтено, что &Ц&г = ^ = J~.
Учитывая равенства (9.337) и (9.338), формула (9.247) принимает вид
2G (И1 + /Ul) = жр (С)- 4== ФЧО-те- (9-340)
Относительно ортогональных криволинейных координат р, 9 на плос-
екости 2, получаемых при конформном отображении, на основании
G.187) имеем
20 (ыр + /ив) - j- -^Щ- Г1СФ @ - Щ VW-Ш ]. (9-341)
В формулах (9.281), связывающих компоненты тензора напряже-
напряжений в криволинейных координатах и в декартовых координатах, в дан-
данном случае необходимо заменить | на р, а г\ на 9. Тогда на основании
307

выражений (9.246), (9.337), (9.338) и формулы G.185'), согласно кото-
которой
Р2 1<й'(Ша Р2 со' (?) ш' (У "р*" <^Ш'
получим:
ф' С)
= ^ ——— + . ¦_¦ —
(9.342)
)-Срр+ 2/аро = ¦
Из формул (9.342) следует
appfapA 4S+=J=rR!b-(?) +^@]
«> (О со' (О р2 «о (О
Теперь преобразуем граничные условия.
Для основной задачи первого типа в случае конечной односвязной
области 5, ограниченной простым контуром L, ссылаясь на (9.270) и
учитывая, что на окружности у согласно равенству (9.336) С = %, по-
получаем - ~~
<Р (X) + -^т 7Ъ) + Ш = h + ift + со на v, (9.344)
с,' (у.)
где выражение /\ + ifz следует рассматривать, как заданную функцию
точки х — б'й окружности y-
Граничное условие основной задачи второго типа для конечной од-
односвязной области S на основании (9.340) получит вид
— Ш) = 2G (Ц« + toi5>) на V. (9-345)
где m(js> -f ш</> — заданная функция точки % = е'0 окружности у.
Условия (9.344) и (9.345) удобно записать одной формулой -
(,) (у)
*Ф (X) + =- Ф' (X) + Ф (X) = ^ (X). (9.346)
«' (у.)
где в случае первой основной задачи
k = 1, К (X) = h + ih + Co, (9.347)
а в случае второй основной задачи
k = -и, /С (х) = —2С («\s> + /м«*)). (9.348)
§ 23. ИНТЕГРАЛЫ КОШИ. ГРАНИЧНЫЕ ЗНАЧЕНИЯ ГОЛОМОРФНЫХ ФУНКЦИЙ
Напомним некоторые свойства интегралов Коши [33, 49].
Пусть гладкий замкнутый контур L, точки которого обозначим че«
рез /, делит плоскость г на внутреннюю конечную область S+, остаю*
308

щуюся слева при обходе L против часовой стрелки, и на внешнюю бес-
бесконечную область 5".
Если в области S+ задана голоморфная функция /(г), которая
непрерывна в 5+ + L, то, кдк известно, имеет место формула Коши
(9.349)
2л/J t-г { 0, г ?5-.
Если функция / (г) голоморфна в S~ (включая бесконечную точку)
и непрерывна в 5" + L, то формула Коши имеет вид
J_ Г *Ш?. = I f (°°)' г 6 s+> (9.350)
2ni{Lt-z l-/(z)+ /(«), г 6 S-.
Если в подынтегральном выражении формул Коши- (9.349) и (9.350)
функция f (/) представляет собой значение /(г) на Ь, то интегралы в
этих формулах называются интегралами Коши.
Если функция" f (t) непрерывна на L, но не является контурным
значением f (г), то интегралы называются интегралами типа
Коши.
Имеют место следующие теоремы.
1. Чтобы непрерывная на L функция f (t) была граничным значени-
значением некоторой функции, голоморфной в S+, необходимо и достаточно
условие
fmt = 0, г е S~. (9.351).
I — г
2. Чтобы непрерывная на L функция f (t) была граничным значени-
значением некоторой функции, голоморфной в S~ (включая бесконечную точку),
необходимо и достаточно условие
1 С / (/) dt . _ ^ OJ- (9.352)
9.Ы I
2niJl t—г
где а — постоянная, равная f (сю).
Необходимость условий (9.351) и (9.352) непосредственно следует
из формул (9.349) и (9.350), а их достаточность доказывается, исходя
из формул Сохоцкого—Племея [49, 33],
Обозначим область круга | ? | < 1 плоскости ? через Х+, а область
вне окружности у этого круга — через X". Пусть F (?) — голоморф-
голоморфная функция в Х+, представленная рядом
F (?) = во + сг? + 02?? + ... (9.353)
Рассмотрим функцию .Fa (?) в X", определенную следующим образом:
Foil) =F(l/?) или, что то же самое, Fo (?) = F A/?). (9.354)
Последнее равенство показывает,' что Fo (?) принимает значения,
сопряженные е F (?) в точках 1/?, являющихся отраженными в окруж-
окружности у (рис. 9.47).
309

Принимая выражение (9.353), функцию Fo (?) представим рядом
^о (O=co + Ci 7"+ c2-rj + ...» (9.355)
абсолютно сходящимся в X".
Очевидно, что если F (?) в Х+ имеет граничное значение F+ (%)
на у, то на основании (9.354) функция Fo (?) в Х~ имеет граничное
значение F^t (x)» причем
(9.356)
где учтено, что % = \1%.
Тогда из условий (9.351) и (9.352) выте-
вытекает следующие теоремы:
1. а. Необходимое и достаточное условие
для того, чтобы непрерывная на у функция
f(%) была граничным значением некоторой
функции, голоморфной вне у, имеет вид
1 С77Й7^=О) S€X_# (9<357)
f (X)
Рис. 9.47
2. а. Для того чтобы непрерывная на
окружности у функция f (у) была граничным
значением некоторой функции, голоморфной внутри у, необходимо
и достаточно, чтобы
— \ IM^L = С, С 6
х-Е
(9.358)
где С — постоянная, равная значению голоморфной функции в точ-
точке С = 0.
Пусть теперь функция / [г) в точке г = а имеет полюс порядка пи
Тогда разложение этой функции в ряд Лорана в окрестности z = а,
как известно, имеет вид
(9.359)
т. е. главная часть ряда Лорана представляет конечную сумму.
Разложение (9.359) можно записать в следующем виде!
/ (г) = /о (г) + G (г), (9.360)
где /о (г) = Со + Ci (г + а) + ... — функция, голоморфная в S+j
G (г) — главная часть ряда Лорана, которая представляет собой функ-
функцию, голоморфную в S" и исчезающую на бесконечности.
Применяя формулу Коши (9.349) к функции /0 (г), получаем
2т
CGJjydt
А t—г
(9.361)
310

где последнее слагаемое на основании (9.350) равно нулю. Тогда из
равенств (9.361) и (9.360) получим
Ш={Цг)-0(г), г 6 5+ (9 362)
Аналогично можно показать, что если f (z) голоморфна в S~ и не-
непрерывна в 5~ + L, за исключением точки z = а (включая бесконеч-
бесконечную точку) этой области, где она имеет полюс с главной частью G (г),
то
\_ С fj?dt_ t-f(g) + G (z), z6 S- (9>363)
2m { (~* { G(z), г ?S+.
Пусть, например, ф (?) = c0 -f- Ci? + c2?? + ... — срункция, голо-
голоморфная внутри у и непрерывная вплоть до у. Тогда имеем
I— ¦ и ¦¦ i
ы J Л =с°? + ci +'" (9'364)
Действительно, %тФ (%) — граничное значение функции С^Р (D =
= ?тф f-r-) = coSm + c1?m't+ ..., голоморфной вне у и имеющей в
точке г = оо полюс порядка т. Следовательно, формула (9.364) не-
непосредственно вытекает из (9.363).
§ 24. ОБЩЕЕ РЕШЕНИЕ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ
ОДНИМ ЗАМКНУТЫМ КОНТУРОМ
Конечная область. Рассматривается конечная область S на пло-
плоскости г, ограниченная одним простым замкнутым контуром L, имею-
имеющим непрерывно изменяющуюся кривизну. Отобразим область S на
круг | ? | < 1 плоскости ? с помощью голоморфной функции
г = со (?). (9.365)
Будем считать, что точке г = 0 соответствует точка ? = 0, т. е.
со @) = 0. (9.366)
Граничные условия основных задач первого и второго типов запи-
записываются формулой (9.346):
где для первой
а для второй
k
*Ф(Х) + -
основной
fe = l,
= —X, Л
ш'(х)
задачи
*(Х) =
:(х)="
(х) + Ч«Сх) /С(х).
= fi + //2 + Со,
—2G («<s) + f«Bs)).
(9.367)
(9.368)
(9.369)
311

Переходя к сопряженным значениям, условие (9.367) запишется
так:
*Ф (X) + ^ Ф' (X) + $ (X) = К (X).
Умножим уравнения (9.367) и (9.370) на-s^r-^r, где S ?
и проинтегрируем их по окружности у единичного круга
В результате получим
Г ¦+ (х) rfy. + _L Г м (х) ф' (х) d , _L Г f (x) rfx = л (t), (9.371)
-(i)dx_ =B(q (9372)
v
где обозначено
Л(Г)=-1 Г-1ША, 5=_Lf JLfiJ^L. (9.373)
Ы J x—ё 2я( J x—С
v v
Считая, что голоморфные функции <р E) и ip (С) непрерывны в кру*
ге 111 < 1 вплоть до его окружности у, и учитывая, что граничными
значениями функций <р (?) и ip @ являются ф (х) и iM (x), на основании
формулы Коши (9.349) имеем
^ 1), (9-374)
а на основании (9.358)
2Я1 J х—? 2л.»
V
ГЖх. = р-Ие(,П<1). (9.375)
.» J х—С
Принимая постоянную Со в равенстве (9.368) равной нулю, на ос-
основании (9.272) можно считать ij) @) = ¦ф~@) = 0 и, кроме того, для
первой основной задачи Im ц>'(г) |г==0 = 0, т. е. 1тф{ @)/сог @) = 0.
Тогда с учетом (9.374) и (9.375) уравнения (9.371) и (9.372) принимают
вид:
/ (X) (Х-С)
(9.376)
*(С) + "Г" f Vfu{Jl d* + kW) = B &. (9.377)
2m J ш'(х)(х— t)
v
Заметим, что уравнение (9.376) можно привести к интегральному урав-
уравнению Фредгольма второго рода из которого и определяется функция
<р (?), а затем из уравнения (9.377) находится функция яр (?). Однако
312

в простейших случаях, функцию ф (?) можно определить непосредст-
непосредственно из функционального уравнения (9.376).
Бесконечная область с отверстием. Рассматривается бесконечная
область на плоскости г, ограниченная одним внутренним замкнутым
контуром L, имеющим непрерывно изменяющуюся кривизну. Отобра-
Отобразим эту область 5 на область |?| > 1, т. е. на бесконечную область g
круговым отверстием радиуса р = 1, с помощью функции
г = о> @ = R\ + фо (О, (9.378)
где R — постоянная; соо @ — функция, голоморфная в бесконечной
области.
При этом отображении бесконечно удаленные точки плоскостей
г и ? соответствуют друг другу.
Считая, что на бесконечности напряжения остаются ограниченны-
ограниченными, голоморфные в S функции ер (г) и ij) (г) на основании (9.262) и
(9.264) имеют вид
о*)- j (9.379)
Принимая функцию (9.378), формулы (9.379) приводятся к виду
где ф0 (S) и <|>0 (?) голоморфны при | ? | > 1, причем на основании (9.276)
•можно считать ф0 (оо) = 0; кроме того, при решении первой основной
задачи можно принять 1т аг = р «=» 0, что, как отмечалось в § 13 дан-
данной главы, не изменяет тензора напряжений.
Ограничимся рассмотрением первой основной задачи (k = I,
К (%) = (/i + t/2) = / (х))- Подставив функции (9.380) в граничное
условие (9.367) н учитывая, что х = 1/х» получим
(9.381)
(9.382)
Если теперь написать условие (9.381) через сопряженные значения
и затем выполнить преобразования, аналогичные сделанным с уравне-
уравнениями (9.367) и (9.370), и учесть, что на основании (9.350)
3K

а на основании (9.357)
1 С 4'о (Х) d% n I С Фо(х)^Х _п
¦у V
то получим
===: , ^ "X—ло и)» (У.Joci)
)-50(С), (9.384)
. у
где
JL Г .Ш<Ь., до@в^_ГЛ1ЙД. (9.385)
v v
Определив из (9.383) и (9.384) ф0 (О и i|}0 (Q. искомые функции
Ч? (D и iM (?) найдем из соотношений (9.380).
§ 25. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ПЕРВОГО ТИПА ДЛЯ КРУГА
Обозначим радиус круга S через R, а его контур — через L. При-
Примем
г = ш (S) = /?Е, (9.386)
тогда м(х^ = х и уравнение (9.376) при * == 1, /С (х) = / (х) ДЛЯ пеР*
и*(х)
вой основной задачи приводится к виду
Ф @ + -f f *?Ш- dX- ^- f ^f . (9.387)
v v
Голоморфная внутри у функция ф (?) может быть представлена
рядом
Ф (Q = сх1 + с2? + .... (9.388)
откуда
Ф' (D = с, + 2б2!; + ... (9.389)
Тогда на основании (9.364) получим
V
а равенство (9.387) примет вид
314
—-L Г -^-f-. (9.390)
2л( J х—&

Для определения постоянных Су и Сг правую часть последнего уравне-
ния представим следующим разложением:
I ^ х X' 7 X
j_cf{t)dx=j_c fii)dt =_±_
2я« J х-? 2и/ J хA—С/Х) 2я/
_ 1 С fd% ¦ S С fd% . ?* Г fd% .
2я( J x 2я« J хг 2л< J x3
Y Y 7
Подставим последнее разложение и разложение .(9.388) в уравнение
(9.390) и сравним коэффициенты при ? и С2:
f, С2. (9.39i)
v v
Левая часть первого равенства (9.391) равна 2Reci. На изменяя тен-
тензора напряжений, как было показано в § 13 данной главы, можно при-
принять Imci = 0, тогда
Cl = ; > ГА-, ' (9.392)
4го J х2
Y
где правая часть должна быть также действительной. Можно показать,
что это возможно при равенстве нулю главного момента внешних сил,
приложенных к контуру L круга.
Поскольку постоянные слагаемые в выражениях для <р (?), г|з (?)
не влияют на напряжения, величину Сг можно отбросить в равенстве
(9.390) и последнее примет вид
Функцию iJj (?) определим из уравнения (9.377). Используя (9.362),
находим
v v
и тогда, принимая во внимание, что
X
Y
получаем
4,@ = J- Г JfiL_J!LfflL+5.. (9.394)
2зи J X—t -
7
Выражения (9.393) и (9.394) для функций ip (Q и i|) (?) определяют
решение рассматриваемой задачи.
315

§ 26. КРУГЛАЯ ПЛАСТИНА, ЗАГРУЖЕННАЯ ПО КОНТУРУ
НЕКОТОРОЙ СОВОКУПНОСТЬЮ СОСРЕДОТОЧЕННЫХ СИЛ
Пусть в точках zt = Re1'®*, z2 — Re1*', ,.., гп = Re'an @ ^
<Xx < a2 <. ... < an < 2я). контура L круглой пластины радиу-
радиуса R приложены в ее плоскости сосредоточенные силы соответственно
РОК Р(а\ ..., Р™ (рис. 9.48), проекции которых на оси xt и х2 равны
и P\,k) (k = 1, 2, ..., /г). Главный вектор этих сил и главный мо-
момент равны нулю.
Точкам 2^ = Relah соответствуют точки %h = е'°й окружности
V на плоскости ?•
Для определения функций ф (?) и д|) (?) необходимо вычислить ин-
интегралы, входящие в формулы (9.393) н (9.394), и определить постоян-
постоянную cv
При обходе-окружности у выражение f = Д + if г в её точках %h
изменяется скачком, равным на основании (9.271) величине i (P\k* +
+ iP[k)). Примем, что на дуге x«Xi /(л) ^ 0« Тогда при обходе ок-
окружности у на ее Дуге Х1Х2 получим р) = i (P[l) + iPin), на дуге
з Р = i (Pi1' + M>il)) + i (^i2) + iP?}) и т. д.
Следовательно,
1
2л ¦
-S 2л/
\ Г+1 г + "-+ \ ;
] у I 1 v —' ] V — L
+ J х-;
Последний интеграл в этом равенстве равен нулю, так как /М^
Выполняя интегрирование, получаем
_\_
V
jPi-2-i) In I
iPW) In (х»—01
A = 1
Аналогично,
-?)J = ^" 2'<pi*J~
ln (^ft~
(9.396)

Приняв во внимание (9.395), продифференцируем (9.393):
ф< (?) = _1_ у (Р(*> + ipw\ —[ c (9.397)
2я <«¦ " v>,—С
Поскольку Ci = ci и согласно (9.389) ct == ф'(°)> из уравнения
(9.397) находим
>—. (9.398)
=-2- у (pi*)+i
4я /*J
4=1
Постоянную Ci можно было определить и по формуле (9.392).
рШ
Рис. U48
Рис. 9.49
Учитывая равенства (9.395)—(9.398), выражения (9.393) и (9.394)
приведем к такому виду:
Ф (г\ — .,, ' 'V (Pi*) ^-ip(bn jn (у g\___±_ у (P(*)_i_ /Pi,*)) —-
(9.399)
(t)-_iLy/P(*)_,
- i!r 2(P"
ln (Xft ~?) ~
(9.400)
Рассмотрим частный случай, когда пластина сжимается парал-
параллельными оси Oxi силами Р, приложенными в точках гг — Reia a
гг = /?е<(я-<х) (рИс. 9.49). В этом случае Р,A) = — Р, Р{1} = 0, Р[г) =
= Я, ЯB2) =0и формулы (9.399), (9.400) при переходе к переменной
г = R? примут вид:
<p(^)='?'[lnBi~2)~ln(?2~2)+i(i:~"i')]> (9-40I)
. (9.402)
817

Подставляя выражения (9.401), (9.402) в формулы (9.246) и учиты-
учитывая, что
г2—z=—
(9.403)
находим:
2P t cos 9t , cos8j cos a \
G22 — au + 2/olg =-?•
. / sin 6,
(
j .
cos 02 + cos 30g
)]•
Отделив действительную и мнимую части в последнем равенстве
н выполнив элементарные преобразования, получим:
2Р I cos» 0t . cos302 ces a
022 = —
IP I sin2 0i cos 0i . sin2 % cos 02 cosa
sin 9a cos2 0S
_ 2P ( sin 6t cos2
(9.404)
Подставив функции ф (г) и ф (г) в формулу (9.247), получим
zu^м1-t-ш2^ = xin^—- + in 4?—rr+41—=—
2п [ г! —г zi—г гх— г
cos a
•г.
Теперь, заменив в последнем равенстве инах*=C — v)/(l +.v) и при-
приняв во внимание равенства (9.403), после отделения действительной
и мнимой частей найдем:
Hi= — Г—^— 1п-^- + — (соз 26! — cos262) —
1—v cosa
1+v 2R
-T(sin 261+sin 26^~
1 — v cos a
1 + v 2Я
(9.405)
Если в формулах (9.404) и (9.405) примем a = 0, то получим реше-
решение для случая сжатия пластины силами Р по ее диаметру OiO2 (см.
рис. 9.37). Легко видеть, что в этом случае формулы (9.404) совпадают
318

с формулами (9.209), полученными другим способом решения этой
частной задачи.
Используя формулы (9.399) и (9.400), аналогично можно получить
решение для многих других случаев загружения круглой пластины
самоуравновешенной системой сосредоточенных сил, приложенных
к ее контуру. Впервые эти и подобные задачи были решены другими
способами Герцем A883) и Мичеллом A901).
§ 27. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ПЕРВОГО ТИПА ДЛЯ БЕСКОНЕЧНОЙ*
ПЛОСКОСТИ С ЭЛЛИПТИЧЕСКИМ ОТВЕРСТИЕМ
Бесконечная плоскость с эллиптическим отверстием отражается
на бесконечную плоскость с круговым отверстием радиуса р = 1 с по-
помощью функции
г = со @ - R (? + mil), (9.406)
где /?>0, 0<т< 1.
Выбирая различные значения Rum, получаем различные эллипсы
с центром в начале координат и полуосями
а = R A + т), b - R A — т). (9.407)
В частности, при т = 0 — плоскость с круговым отверстием ра-
радиуса R, а при т = I — плоскость с прямолинейной щелью длиной
4/?.
Вначале рассмотрим случай, когда главный вектор внешних сил,
приложенных к контуру L эллиптического отверстия, равен нулю.
Кроме того, на бесконечности плоскости напряжения считаем также
равными нулю; последнее означает, что аг = Ьх = 0.
В этом случае функции ф (С), ф (?), определяемые выражениями
(9.380), будут совпадать с голоморфными вне y (Y — окружность кру-
круга |?| < 1) функциями ф0 (С). Фо it), которые задаются выражениями
(9.383) и (9.384), причем можно считать ср (оо) = 0.
При отмеченных условиях на основании равенства (9.382) /0 = f
и, следовательно,
V
Исходя из функции (9.406), имеем:
(9.409)
ш'(Х) х A—/пх3) ' со'(х) f-m ' ' %
и тогда уравнения (9.383) и (9.384) принимают вид:
319

Первый интеграл в равенстве (9.410) на основании формулы Коши
(9.349) равен нулю. Действительно, выражение
Ф (X)
% 0 —
представляет собой граничное значение функции
которая голоморфна внутри у и обращается в нуль при ? = 0. В са-
самом деле, поскольку функция ф (?) голоморфна вне у и ф (с/э) =я 0, ее
можно представить рядом
Ф (?) - Сх/5 + оЛ2 + .... С € (|С|>1).
Тогда
Фс (С) = -сЛ*- - 2сЛ3 - .... ? 6 (I ? I > О (9-412)
и
Фг (-1) = -^?2 - 2с2?? - ..„ ? 6 (IS К 1).
Таким образом, уравнение (9.410) принимает вид
Ф@=_^_Г-^-. (9.413)
v
Далее, выражение
представляет собой граничное значение функции
которая, ссылаясь на (9.412), голоморфна вне у и исчезает на беско-
бесконечности.
Следовательно, на основании формулы Коши (9.357) имеем
и уравнение (9.411), отбрасывая не влияющую на тензор напряжении
постоянную ф (оо), принимает вид
.(О. » fJfiL. (9.414)
2л1 J х—С
Y
В общем случае, когда на бесконечности плоскости напряжения
остаются ограниченными, функции ф (?) и vp (?) определяются выра-
выражениями (9.380), в которых ф0 (?) и г]50 (С) на основании уравнений
(9.413) и (9.414) находятся по следующим формулам:
• (М15>
320

где о учетом (9.382) и (9.409)
Напомним, что при решении основной задачи первого типа, не из-
изменяя тензора напряжений, можно считать аг = Reo^ = а.
§ 28. ОДНООСНОЕ РАСТЯЖЕНИЕ ПЛАСТИНЫ С ЭЛЛИПТИЧЕСКИМ ОТВЕРСТИЕМ
Рассмотрим пластину с эллиптическим отверстием, растягиваемую
на бесконечности равномерными усилиями интенсивности а в направ-
направлении, составляющим угол р с осью 0х\. Контур L эллиптического от-
отверстия свободен от внешних сил, т. е. Pi = Р2 = 0.
Формулы (9.281), если принять ортогональные направления (?) и
Щ соответственно за первую и вторую главные оси тензора напряже-
напряжений, т. е. положить сгц = оь ат == сг2» <*&ti — 0, можно привесш
к такому виду:
ои + ои-ог + о,.- J
сгц — вгг + 2юц = (а2 — ~.v<r-/2B i v '
где р — угол между осью Охх и направлением (|), совпадающим с пер-
первой главной осбю тензора напряжений.
Сопоставляя формулы (9.418) с формулами (9.266), определяющими
напряжения на бесконечности, и учитывая условия нагружения плас-
пластины (of = a, of = 0), получаем:
а = Rea, = A/4) (of + of) = a/4, |
й, = A/2) (of — of )er-w = —(a/2)e-'2P / ( '
Поскольку / = /i + t/i = it (Pt + iPz) ~ 0, по формуле (9.417)
имеем
(9.420)
и, вспоминая, что х — 1'х» находим
Выражение rn—myi)" представляет собой граничное значение
функции •g(i_<aM)'t которая голоморфна внутри у, за исключением
И Зек. 814 321

точки t, — О, являющейся для нее полюсом с главной частью rn.lt,. По-
Поэтому на основании (9.362) имеем
1 Г *2+т dt — — '942П
2я, J хA-«Ха) (х-0 t * '
Функция ? - Jl?^ голоморфна вне v» за исключением точки ? =я
= «>, где она стремится к т?, поэтому на основании (9.363) получим
. (9.422)
с,"—т
Наконец, по формулам Коши (9.349) и (9.350) имеем:
Теперь, используя равенства (9.420)—(9.423), по формулам (9.415)
и- (9.416) находим:
^- '**»?-'* . . (9.424)
J'jL-J'L J!±2U1. (9.425)
По формулам (9.380), учитывая равенства (9.407), (9.424) и (9.425)
и выполняя элементарные преобразования, получим:
(9.426)
(9-427)
Компоненты тензора напряжений определяются формулами (9.342),
а перемещения—формулой (9.341).
Найдем, например, сумму двух компонент тензора напряжений:
В наиюм случае юе (?) = — ^ ' И> учитывая, что I = ре'",
находим
_
82?

Отделив действительную часть числителя последней дроби (знамена-
(знаменатель — действительная величина), получим
1 "op-
ГТ
»'(D
На контуре отверстия р == 1 и ав
р4—2mp2cos26 + *
рр = 0, поэтому в точках контура эл-
эллиптического отверстия пластины имеем
1— m2 + 2mcos2fl— 2 cos 2 (9— ft)
(9.428)
При растяжении пласти-
пластины в направлении оси Ох?,
(Р = :fc п/2) получаем
1—m2—2m-f-2cos 29
1 4- т2—2т cos 29 '
(9.429)
Для этого случая на рис.
9.50 приведена эпюра напря-
напряжений dee в точках контура
эллиптического отверстия
при т = 1/2 (alb — 3). Наибольшее напряжение (а9в)max, возника-
возникающее в точках Л, равно
Рис. 9.50
(оее)тах= -Н—
1 —т ¦
(9.430)
т. е. коэффициент концентрации напряжений k в этом случае (т =«
-1/2) равен fe - @ее^т" = 7.
Если т = 0, то эллиптическое отверстие, как отмечалось, обра-
обращается в круговое радиуса /?. Принимая для этого частного случая
Р = 0 (растяжение в направлении оси O*i), формула (9.428) дает вы-
выражение
ав0 = а A — 2 cos 29),
совпадающее со второй формулой (9.329), в которой надо принять г =«
= а (задача Кирша).
§ 29. ВСЕСТОРОННЕЕ РАСТЯЖЕНИЕ ПЛАСТИНЫ
С ЭЛЛИПТИЧЕСКИМ ОТВЕРСТИЕМ
В случае всестороннего растяжения пластины усилиями а решение
можно получить методом суперпозиции, используя предыдущее реше-
решение при р = 0 и р = п/2.
В результате получим
и*
823

Отсюда по формулам (9.342) можно найти напряжения. Например,
в точках контура эллиптического отверстия
ow = a—-—:— ^Ti (9.432)
а для точек оси Охг получим:
о ,.,,а -М*?-"')
U (x2
-, (9.433)
где а и Ъ — полуоси эллипса.
Рис. 9.51
На рис. 9.51 изображены эпюры напряжений Оц, о%г в точках оси
Охх и напряжений а99 на контуре отверстия для случая alb = 3 (т «а
= 1/2). Наибольшее напряжение (ст9е)таХ возникает в точках А,
совпадающих с концами большой оси эллипса, и равно
__9_L+?L
\—т
= 6(Т,
(9.434)
т. е. коэффициент концентрации напряжений k = 6.
При m = 0 имеет место случай всестороннего растяжения пласти-
пластины с круговым отверстием; по формуле (9.434) получим величину
(оее)тах = 2о, совпадающую с результатом формулы (9.331) при г »
= а.
Отметим, что решения задач о концентрации напряжений в окрест-
окрестности различных отверстий пластины можно найти в книге Г. Н. Са-
Савина 147J.
§ 30. О КОНЦЕНТРАЦИИ НАПРЯЖЕНИИ НА КОНЦАХ ПРЯМОЛИНЕЙНОЙ ЩЕЛИ
Предположим, что в рассмотренных задачах о растяжении плас-
пластины с эллиптическим отверстием интенсивность усилий а фиксирова-
фиксирована,,а параметр эллиптического отверстия т ->- 1, т. е. отверстие вырож-
вырождается в прямолинейную щель длиной 4?? по оси Охх (см. § 27 данной
главы). В этом случае напряжение оее на концах щелн (в точках А,
см. рис. 9.51) согласно формулам (9.430) и (9.434) неограничено воз-
возрастает при любом конечном значении о как при одноосном, так и при
всестороннем растяжении пластины.
В местах очень высокой концентрации напряжений возникают плас-
пластические деформации и, следовательно, линейная теория упругости
324

для этих зон неприменима. Для описания действительного механи-
механического поведения материала в зонах большой концентрации напря-
напряжений, на которое оказывают влияние не только сами деформации,
но и их градиенты, необходимо использовать нелинейную теорию уп-
упругости, а также теорию пластичности и ползучести материала.
Вместе с тем теоретические .и экспериментальные исследования по-
показывают, что размер зоны очень большой концентрации напряжений
весьма мал и уже в достаточной близости от концов щели линейная тео-
теория упругости и полученные выше решения правильно описывают рас-
распределение напряжений. Например, Г. Нейбер"[42] отмечает, что у
острых надрезов стальных образцов характерный размер зоны, в ко-
которой действительные характеристики состояния материала сущест-
существенно отличаются от полученных результатов по линейной теории уп-
упругости, имеет порядок 0,5 мм.
§ 31. ВАРИАЦИОННАЯ ПОСТАНОВКА ПЛОСКОЙ ЗАДАЧИ
Вариационную постановку плоской задачи при заданных на кон»
туре L поверхностных силах tlt t2 рассмотрим, исходя из принципа ми-
минимума дополнительной работы (см. гл. V, § 6).
В этом случае силы tt и t2 не подвергаются вариации и вариаци-
вариационное уравнение E.62) принимает вид
6? = 6 Я Л (ai^dXidxz = 0, (9.435)
где Л (atj) — удельная дополнительная работа, которая определяет-
определяется формулой C.80).
В случае плоского напряженного состояния по формуле C.80) по-
получим
Л (а„) = JLfal 1 + а\2 + 2 A + v) <rf, -2wu а„\. (9.436)
Если в равенстве (9.436) заменить Е на Е1 и v на v* по формулам
(9.139), то получим следующее выражение для удельной дополнитель-
дополнительной работы в случае плоской деформации:
Л(о|У) [(lv)(a
(9.437)
При исследовании односвязной области, ограниченной контуром
L, согласно теореме Леви—Мичелла распределение напряжений яв-
является одинаковым для всех изотропных материалов и, следователь-
следовательно, в этом случае коэффициент Пуассона v в равенствах (9.436) и
(9.437) можно принять равным нулю. Учитывая это обстоятельство и
представляя компоненты тензора напряжений через функцию напря-
напряжений Ф (xi, Хг);
„ (9.438)
325

для функционала ? получаем следующее .выражение:
w=~h JJ [(ф-п)а+(ф-мI+2 (фда)г'dXx d
JJ [
(9-439)
Таким образом, вариационная постановка плоской задачи сво-
сводится к определению подчиненной граничным условиям (9.21) функции
напряжений Ф (хъ х2), минимизирующей функционал (9.439).
Решение этой вариационной задачи можно найти, например, ме-
методом Ритца.
В качестве примера приведем решение методом Ритца. следующей
задачи С. П. Тимошенко [81.
Для прямоугольной пластины (рис. 9.52), ограниченной кромка-
кромками Xi = ±а, Хг = ±Ъ, требуется найти компоненты тензора напря-
напряжений при нагружении пластины на кромках Xi = ±я силами
/,=.етA-^/&2). (а)
В этом случае граничные условия (9.21) для функции Эри прини-
принимают вид:
на кромках хг = ±а
дх\
А
на кромках х^ =
дхх
(б)
Искомую функцию Ф представим в виде ряда
(в)
где Фо — функция, удовлетворяющая граничным условиям (б), име-
имеет, как легко установить, следующий вид:
0 2 л\ W)
Фк — базисные функции, которые должны удовлетворять однород-
однородным граничным условиям:
д* Фь дг Oft n
¦ ^= ————— =^ \) ПОИ Х\ *==* ^j^Q.
(Д)
^' = '^"=0 при ^=±&;
а» — произвольные лараметры, которые подлежат определению из
условий
¦Й- = 0- (е)
326

При рассматриваемом нагружении пластины распределение нап-
напряжений должно быть симметрично относительно осей *, и хг, Поэтому
функции Фь, подчиненные условиям (д), должны содержать только
четные степени Xi и хг. Принимая это во внимание и учитывая выра-
выражение (г), представление (в) для функции Ф можно взять в виде
Ф
- -gfa) + (х\-а2J (**-
+ агх\ +
(ж)
•о
f 0
а
*
а т
^*
Рис. 9.52
Рис. 9.53
Если ограничиться одним членом аг в последних скобках, то из ус-
условия
= 0
найдем
Для квадратной пластины (а = Ь) получим ах = 0,04253^0* и ком-
компоненты тензора напряжений определятся формулами
(з)
0,1703аA —
=-Ф,1а=-0,6805а
центральной точки пластины (xt =* х2 — 0) получим:
ац = 0,8298а, а22 = —0,1702а, 6п — 0.
На рис. 9.53 кривая / соответствует закону изменения tt на кромке
Xi = а, а кривая // характеризует распределение напряжений аи на
сечении xi = 0.
827

Если взять три члена в последней скобке равенства (ж), то для квад-
квадратной пластины уравнения (е) дают:
at = 0,04040а/а«, аг = а8 = 0,01174а/а8.
При этом приближении распределение напряжений ап на сечении
хг = 0 характеризуется кривой /// на рис. 9.53 (в центре пластины
ои = 0,8619а).
Вариационная постановка плоской задачи, основанная на прин*
ципе минимума потенциальной энергии, обстоятельно рассмотрена в
книге [35]. Отметим, что при определении температурных напряже-
напряжений во многих случаях также эффективно применение вариационных
методов [11, 30].
Наряду с классическими вариационными методами решения задач
плоской теории упругости широко используют численный метод ко-
конечных разностей и метод конечных элементов, реализуемые с по-
помощью ЭВМ.
§ 32. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ Ч
Если метод конечных разностей (см. гл. VII, § 15) представляет со-
собой приближенный метод, который аппроксимирует дифференциаль-
дифференциальные уравнения рассматриваемой задачи разностными уравнениями,
то метод конечных элементов связан с приближенной минимизацией
функционала той же задачи в вариационной постановке.
Отметим, что в случае плоской задачи бигармоническое уравнение
(9.20) аппроксимируется разностной системой алгебраических урав-
уравнений, которую можно получить на основании формулы G.248). По-
Повторив операцию разностного оператора Лапласа для квадратной сет-
сетки, получим следующую систему алгебраических уравнений: ¦
Ряд примеров решения плоской задачи методом конечных разно-
разностей с использованием ЭВМ можно найти в книге [56]. Ограничившись
сделанными замечаниями о методе конечных разностей применитель-
применительно к плоской задаче, кратко остановимся на другом численном мето-
методе — методе конечных элементов (МКЭ).
МКЭ в общих чертах состоит в следующем:
1. Область,- занимаемая рассматриваемым телом, мысленно раз-
разделяется на ряд конечных подобластей, которые называют конечными
элементами. В случае плоской задачи за конечные элементы (КЭ) ча-
чаще всего принимают треугольники, а в случае пространственной зада-
задачи — тетраэдры.
2. Предполагается, что КЭ взаимодействуют между собой лишь
в узлах, т. е. в вершинах треугольников или тетраэдров. К узлам
КЭ прикладываются силы, уравновешивающие напряжения на грани-
границе элемента.
328

3. Так же как в методе перемеще-
перемещений строительной механики, за основ-
основные неизвестные принимаются переме-
перемещения узлов, которые определенным
образом должны быть связаны с узло-
узловыми силами.
4. Выбирается система функций,
однозначно определяющая перемеще-
перемещения в пределах рассматриваемого КЭ в
зависимости от перемещений его узлов.
5. Зная перемещения любой точки
внутри КЭ, на основании дифферен-
дифференциальных зависимостей Коши и зако-
закона Гука можно получить выражения
/
/
У\
А
/
7
л
/
V
Рис. 9.54
для компонент тензора деформации и тензора напряжении.
Основные зависимости МКЭ рассмотрим на примере плоской
Пусть тонкая пластина находится в условиях обобщенного
го напряженного состояния (рис. 9.54). Мысленно разобьем ее
угольные конечные элементы и рассмотрим один из них с
/, т, п (на рис. 9.54 этот элемент выделен точками). Перемещен
дого узла, например /, имеют две компоненты:
-и:;!-
задачи.
плоско*
на тре-
узламй
и я каж-
(9.440)
а шесть компонент узловых перемещений элемента образуют шести-
шестимерный вектор-столбец:
{«} =
/ = 1,2).
(9.441)
Пусть перемещения ш произвольной точки внутри элемента в зави-
зависимости от узловых перемещений {и} одноэначно определяются век-
вектор-столбцом
, (9-442)
где элементы прямоугольной матрицы [А] размером 2x6 являются
функциями координат х, рассматриваемой точки. ;Эти функции долж-
должны быть выбраны так, чтобы при подстановке в (9.442) координат уз-
узлов элемента получались соответствующие узловые перемещения, сото-
сотого можно достигнуть, в частности, если принять их линейными отно-
относительно X).
Для рассматриваемой плоской задачи примем
ш = at
(9.443)
где коэффициенты at и рг/ сохраняют постоянные значения в пределах
каждого конечного элемента, а индекс / — немой.
329

Выбранные таким образом- функции перемещений обеспечивают
непрерывность перемещений на границах смежных элементов, так как
вдоль любой стороны треугольника они изменяются линейно и, еле*
довательно, из равенства перемещений в узлах следует их равенств»
по всей границе. Заметим также, что принятому распределению пере-
перемещений соответствует однородная деформация элемента.
Подставив в (9.443) вместо х} координаты х[, xf, xf узлов элемен-
элемента, получим две системы уравнений:
= at
u? = at + Pnxf + Pi*?, (I = 1.2).
a? = at + pV? +
(9.444)
Решая систему уравнений (9.444) относительно постоянных коэф-
коэффициентов по правилу Крамера, найдем:
а,=
«{ А х\
itfl vftl vftt
1
1
1
«I1
A2
1 xf и?
1 x\w\
2A
2Д
2Д
где Д — площадь треугольника:
Д =
1
1
1
х\
xf
xf
xf
X"
(9.445)
(9.446)
Подставив значения коэффициентов ai, $ilt Pj2 из равенств (9.445)
в выражение (9.443), получим формулу для компонент перемещения
произвольной точки конечного элемента:
"/ = T7-I
bl
с'
и{
и?
где
а' = xf х"—х\ xf, bl = xf—х\, с' = xi—xft
(9.447)
(9.448)
а остальные коэффициенты находим в результате круговой переста-
перестановки индексов 1,т,п.
Равенство (9.447) можно записать в матричной форме}
uf
(9.449)

где
at+Ыxy+et я,
2A
>4m и Л" определяются аналогично.
Зная перемещения во всех точках конечного элемента, определя-
определяем компоненты деформации о помощью соотношения, которое в мат-
матричной форме можно записать так:
{е} - [5] {и}, (9.451)
где {в} — вектор-столбец компонент деформации, которые определя-
определяются через перемещения tit дифференциальными зависимостями Ко-
ШИ2
(9.452)
Исходя из равенств (9.449) и (9.452), получаем
(е}=
(9.453)
Из сопоставления равенств (9.451) и (9.453) следует, что в правой
части последнего из них матрица размером 3x6, умноженная на 1/2Д,
есть матрица '1В], которую можно записать в следующем виде:
[В] т W1, Я«, В"}, (9.454)
где, например,
[S'] =
(9.455)
Как и следовало ожидать, при принятых выражениях (9.443) для
функций И| матрица [В], определенная явным образом в равенстве
(9.453), не зависит от координат точек внутри конечного элемента, т. е.
деформации в его точках постоянны.
Для определения компонент напряжения используем закон Тука
в матричной форме
{а} = [С] {е}, <9.456)
SS1

где [с] — матрица упругих постоянных материала, которая для плос-
плоской задачи в случае однородного изотропного тела на основании C.36)
и C.44) имеет следующий вид:
Г% + 2G ' X 0 '
[С]= К X+2G 0 . (9-457)
[О О G
Подставив зиачения упругих постоянных G и X по формулам C.63)
и C.64), получим матрицу упругих постоянных для задачи плоской
деформации:
, -JL-' О
1—V
[С]=-
(l-v)fi
A + v) A - 2v)
1-v
1
1
О
О
1 — 2v
2A—v) J
(9.458)
В случае обобщенного плоского напряженного состояния в матри-
матрицу (9.457) надо вместо X подставить значение X* по формуле (9.31). В
результате получим
1 v О
Е v 1 0 (9.459)
О О (I —v)/2
1—л
Исключая из равенства (9.456) вектор-столбец {е} с помощью со-
соотношения (9.451), найдем
{а} =. [D] {«}, (9.460)
где [D] = [С] [В] — матрица, которую иногда называют матрицей
напряжений.
Для однородного изотропного тела в случае обобщенного плоского
напряженного состояния матрица [D] имеет вид
\D\=
vc'
1—V
2
с'
1—V
2
Ы
ст
1
vcm
с
— V
2
¦1
ft"
— V
2
С"
с"
1—V
2
(9.461)
Таким образом, перемещения ui, компоненты деформации и компо-
компоненты напряжения определяются равенствами (9.449), (9.451) и (9.460)
в зависимости от перемещений узлов конечного элемента.
Напряженно-деформированное состояние элемента, описываемое
зависимостями (9.451) и (9.460), можно рассматривать как результат
действия узловых сил, которые должны быть статически эквивалентны
напряжениям на границе элемента.
332

Узловые, силы, компоненты которых совпадают по направлению о
компонентами узловых перемещений {и}, представим вектор-столб-
ком
Rf
1*7
(9.462)
Естественно, что между узловыми силами и узловыми перемещени-
перемещениями существует определенная зависимость. Для" установления этой
зависимости воспользуемся принципом возможных перемещений. При-
Придадим узлам конечного элемента некоторые кинематически возмож-
возможные перемещения {бн}, которым будут соответствовать вариации ком-
компонент деформации {бе}. Тогда работа внешних сил {R}, равная сум-
сумме произведений компонент узловых сил на соответствующие компо-
компоненты узловых перемещений, в матричной форме запишется в виде
а работа внутренних сил в единице объема с учетом (9.451) будет
{бе}7" {о} = ([В] {8и})т {о} = {8и}т [В]т {о}. (9.463)
Приравнивая работу внешних сил работе внутренних сил по все-
всему объему конечного элемента, имеем
{бн}7" {R} = {8и}т fff IB]7 {a}dV = {6м}7" jT WV {o}hdx1dx2, (9.464)
где h — толщина конечного элемента.
После подстановки значения {а} согласно равенству (9.456) с уче-
учетом (9.451) получим
{6«}г {R} = {бн}г JJ IBF [С] 1В] {и} Ыхг dx2. (9.465)
Поскольку уравнение (9.465) справедливо для любых кинемати-
кинематически возможных перемещений {бн}, выражения при них в левой и пра-
правой частях должны быть равны. Учитывая при этом, что матрицы в
подынтегральном выражении не зависят от xt и х2, найдем
{R} = WV [С] [В] {u}hA,
или
{R} = Ik] {«}. (9.466)
Здесь матрица
[Щ = [В]7" [С] [В]ЛА,
где Д — площадь треугольного элемента, называется матрицей
жесткости конечного элемента
Матрицу жесткости элемента можно представить в следующем ви-
виде:
•nl j^inm k"
m forim form
(9.467)

где подматрицы, имеющие размериостть 2x2, образуются следующим
образом:
[к'т] = [В']т [С) [В«]АД. (9.468)
Такая форма записи удобна для вычислений на ЭВМ.
Зависимость (9.466) между узловыми силами и узловыми переме-
перемещениями представляет собой систему канонических уравнений в мат*
ричной форме известного в строительной механике метода переме-
щений, а элементы матрицы жесткости суть коэффициенты этих урав-
неиий.
Рассмотрим теперь дискретную модель пластины, представляю-
представляющую собой систему конечных элементов,-соединенных между собой шар-
шарнирами в узлах.
Если к пластине приложены внешние сосредоточенные силы, то
разделение пластины на элементы надо произвести так, чтобы эти си-
силы оказались приложенными к узлам сетки конечных элементов. Рас-
Распределенную внешнюю нагрузку на границе пластины следует заме-
заменить статически эквивалентными сосредоточенными силами, прило-
приложенными к граничным узлам.
Через {Р} обозначим вектор-столбец приложенных к узлам внеш-
внешних сил (включая силы, заменяющие распределенные нагрузки)
{/>} = {Р№ ... Р\}, , (9.469)
а через
{«о} = {и]и} ... и\) (9.470)
— вектор-столбец узловых перемещений всех узлов I.
Применяя принцип возможных перемещений к дискретной модели
пластины, имеем
1|{б8}г {о)Ыххйхг - {б«0} т {Р} = 0. (9.471)
Здесь
{бе} = Ш {8и0}, (9.472)
где [Во] — матрица, элементы которой В{ = В1, если узел принадле-
принадлежит рассматриваемому элементу, и В'о = 0, если узел / не принадле-
принадлежит элементу.
С учетом (9.456) и (9.472) равенство (9.471) можно привести к виду
{б«0} т {Р} = {6ио}г jj Шо) т [С\ [fi0] {«о} hdXidxt, (9.473)
где интеграл берется по всей плоскости пластины.
Из равенства (9.473) получаем основное соотношение
{Р} = (/С! Ы, (9.474)
где (/С) — общая матрица жесткости.
Произвольный элемент матрицы [/С! определяется равенством
{Krs\ = 2 tfe"J, " (9.475)
где суммирование выполняется по всем элементам, примыкающим к
узлам г и s, а матрица [krs] определяется соотношением (9.468).
134

Заметим, что в уравнении (9.471) первое слагаемое представляет
собой вариацию потенциальной энергии деформаций, а второе — ва-
вариацию работы внешних сил при варьировании узловых перемещений.
Поскольку при этом внешние силы и напряжения не варьируются,
уравнение (9.471) можно записать так:
6Л = 0, (9.476)
где величина П, равная разности потенциальной энергии деформации
и работы внешних сил, называется потенциальной" энергией системы
(см. гл. V, § 5).
Равенство (9.476) означает, что для обеспечения равновесия систе-
системы ее потенциальная энергия должна принимать стационарное зна-
значение. В случае линейно-упругого тела условие стацибнарноети
(9.476) превращается, как было показано в гл. V, § 5, в условие мини-
минимума потенциальной энергии системы.
Следовательно, метод конечных элементов представляет собой оп-
определение минимума потенциальной энергии системы среди возмож-
возможных перемещений заданной формы внутри конечных элементов. Сис-
Система уравнений метода конечных элементов (9.474), отражающая, по
существу, тот факт, что варьирование перемещений осуществляется
по конечному числу параметров {и0}, может быть записана в виде
дП
дП
duj
дП
duf
(9.477)
Таким образом, метод конечных элементов в такой постановке име-
имеет сходство с методом Ритца (см. гл. V, § 9). Разница состоит в способе
выбора координатных функций. В методе Ритца они задаются опреде-
определенными во всей области тела через некоторые параметры, а в МКЭ —
в пределах элемента через узловые перемещения. Если в методе Рит-
Ритца изменение любой из координатных функций вызывает изменение
перемещений по всей области тела, то в МКЭ изменение любого из уз-
узловых перемещений сказывается на перемещениях лишь внутри ко-
конечных элементов, сходящихся в этом узле. В частности, поэтому при-
применение метода Ритца ограничивается относительно простыми форма-
формами тела, а в МКЭ простую геометрию должны иметь лишь конечные
элементы.
Естественно, что решение задач МКЭ может быть реализовано о
помощью ЭВМ. Для программирования решения задач МКЭ широко
используется алгоритмический язык FORTRAN. Типичная програм-
программа, реализующая МКЭ, состоит из нескольких общих блоков. Такими
блоками являются, например, ввод исходных данных, вычисление
жесткости элементов, решение уравнений, вычисление напряжений.
Эти специальные вопросы программирования достаточно подробно об-
обсуждаются в книгах [26, 44].
335

В качестве примера использования МКЭ приведем результаты ре-
решения задачи о концентрации напряжений, взятые из книги [441. Пря-
Прямоугольная пластина конечной шириной В, длиной L имеет квадрат-
квадратный вырез bxb со скруглениями радиуса г и растягивается равно-
равномерно распределенными поверхностными силами интенсивности tt =s
= 20 кгс/см2, как показано на рис. 9.55, а. Пластина разбивалась на
треугольные элементы, причем вокруг выреза размеры элементов приш
z
—5?
, Г"
Л
J
• ГЛ.
>
21
-21
Рис. 9.55
нимались достаточно малыми, чтобы обеспечить возможно большую
точность определения напряжений в зоне их концентрации. С удале-
удалением от'выреза размеры конечных элементов увеличивались (рис.
9.55, б). Заметим здесь, что число элементов и их размеры зависят от
желаемой точности результатов, от характера изменения напряжений,
от вида нагрузки и от ограничений, связанных с объемом памяти ЭВМ.
На рис. 9.55, в изображена эпюра напряжений в точках контура вы-
выреза для пластины с ЫВ = 0,25, rib = 0,125 и L = В по результатам
числового расчета, запрограммированного на ЭВМ «Минск-22» [44].

Глава X
КОНТАКТНЫЕ ЗАДАЧИ
Контактные задачи являются практически важнвши примерами
пространственных задач теории упругости.
Рассмотрим решение этих задач использвуя функциональное пред-
представление Папковича—Нейбера D.40).
Задаваясь различными гармоническими функциями q>ft, входящи-
входящими в представление D.40), можно получать различные частные реше-
рия граничных задач. Имея частные решения, с помощью суперпо-
суперпозиции получаем новые решения.
Два частных решения, для которых вблизи особых точек перемеще-
перемещения неограниченно возрастают, Буссинеск A842—1929) назвал эле-
ментарными решениями первого и второго типов.
§ 1. ЭЛЕМЕНТАРНОЕ РЕШЕНИЕ ПЕРВОГО ТИПА
Входящие в представление Папковича—Нейбера D.40) гармони-
гармонические функции cpft примем следующими:
<Pi = Фа = 0, ф3 = 4 A — v)A/r, A0.1)
где А — постоянная, г =}^хкхк — расстояние произвольной точки
К (Хь) от начала координат.
Функция 1/г, как известно, является гармонической. Действитель-
Действительно,
A/г)(| = -xt/r3, A/г8), , = -Зх}-/г*, A/г), и = -б^/г3 + ZxiX/t* A0.2)
и, свертывая последнее равенство A0.2), имеем
A/г) и = v»(i/r) = _з/г> + Зх^/г5 = 0. A0.3)
Подставив принятые значения (ЮЛ) для функций q>ft в D.40) и при-
приняв во внимание равенства A0.2), получим
A0.4)
По формулам D.43) найдем компоненты тензора напряжений, соответ-
соответствующие функциям A0.1):
JI-Bv-l-3fy olt=-BAG
A0.5)
ззт

Перемещения щ и компоненты тензора напряжений atj, как сле-
следует из A0.4) и A0.5), неограниченно возрастают при г ->0, т. е. на-
начало координат представляет собой особую точку. Следовательно, рас-
рассматриваемое решение имеет смысл для всех точек бесконечного тела
кроме начала координат. Исключим эту особую точку, положив на-
начало координат центром сферической полости малою радиуса г0. На
поверхности S этой полости должны иметь место силы
U = оипи A0.6)
где п} = —х/г„.
Учитывая выражения A0.5), по формуле A0.6) находим
, t2 6AG^, t36AG-^ + 2(l — 2v)-^- .
ra ro ro ro
A0.7)
Компоненты главного вектора этих сил
A0.8)
Поскольку в четырех из восьми квадрантов сферической поверх-
поверхности *з*1 > 0 и *аЛ;3 > 0, а в остальных четырех квадрантах лс3дс1<0
и дсадс3 < 0, то \\ x&x&S — 0 и jT ^a^3dS == 0.-
Далее, ввиду центральной симметрии поверхности сферы имеем
ff*fdS=JJxidS=Jj4dS, A0.9)
откуда
N
-L jjгг0 dS = -^L rj. A0.10)
Тогда
Pj = pa = 0, P3 = P - 16яЛС A - v), A0.11)
т. е. соответствующие рассматриваемому решению силы tt на поверх-
поверхности малой сферической полости с центром в начале координат ста-
статически эквивалетны направленной по оси х3 силе Р.
Подставив значение постоянной А из A0.11) в выражения A0.5),
получим
338

СТц=-
—v)f«
8яA—\
8яA—v)r3
ЗР
8л A- v)
8яA—>
Л
(Ю.Г2)
Эта решение для бесконечного тела, находящегоея пэд действием со-
сосредоточенной силы Р, приложенной в начале координат н направ-
направленной по оси Оха, Буссинеск назвал элементарным решением первого
типа. Отметим, что на координатной плоскости ха = 0, согласно фор-
формулам A.0.5), нормальные напряжения отсутствуют, а касательные на-
напряжения на этой плоскости
f»
-^. A0.13)
§ 2. ЦЕНТР РАСТЯЖЕНИЯ (СЖАТИЯ) В БЕСКОНЕЧНОМ ТЕЛЕ
Гармонические функции ср& в представлении Папковича—Нейбера
D.40) примем в следующем виде:
A0.14)
где В' — постоянная.
Этим функциям соответствуют перемещения в произвольной точ-
точке бесконечного тела
щ = -?^- —(—) =-^-, (ЮЛ5)
* е» 4 A -v) V i )л г» к ¦ '
где
Свертывая выражение производной
найдем
0.
339

Следовательно, согласно D.42) объемная деформация 0 » 0. Тог-
Тогда по формуле D.4), учитывая равенство A0.15), получим следующие
ВБ1ражения для компонент тензора напряжений:
«у 3-^L) A0.17)
Г8 Г& J
или
\
rl
¦ О—— I , O; ; — — DZXJ ¦
A0,18)
Ц R
Из полученных выражений A0.15)
и A0.17) следует, что при г -»-0 пе-
перемещения и напряжения неограни-
неограниченно возрастают, т. е. начало коор-
координат является особой точкой. Иск-
Исключим эту особую точку путем об-
образования сферической полости ма-
малого радиуса г0 с центром в начала
координат, на поверхности которой
имеют место силы
tt = aun, (п} = —х//г0), A0.19)
или с учетом формулы A0.17)
Рис- 10Л tt = 4BGxt/r±. A0.20)
' Из выражений A0.20) следует, что равнодействующая сил tt в про-
произвольной точке поверхности сферической полости направлена по
нормали к ней, т. е. в радиальном направлении, и равна
tT = Unt = ABGxtriilrb = — IBGxtxJrl - — ABG/rl A0.21)
Аналогично, в произвольной точке тела получим
а- = —ABGl/r3 = С/г5, A0.22)
где С = —ABG — постоянная.
Рассмотренное решение Буссинеск назвал центром растяжения
или центром сжатия. Если постоянная В < 0, то tT > 0 и в этом слу-
случае имеем центр растяжения; при В > 0 tT < 0 — центр сжатия.
Этим решением можно воспользоваться для определения напряже-
напряжений в толстостенной сферической оболочке, нагруженной равномер-
равномерными внутренним и наружным давлениями. Пусть г± и г2—внутренний
и наружный радиусы сферической оболочки, а ру и ра—внутреннее
и наружное равномерные давления (рис. 10.1).
Накладывая на решение A0.22) равномерное сжатие или растяже-
растяжение во всех направлениях, получим общее выражение для радиаль-
радиального нормального напряжения:
а„ = Clr* + D,
A0.23)
340

где С и D — постоянные, величины которых определяются из условий
на внутренней и внешней поверхностях оболочки:
Glr\ + D = —ри Ctrl + D = —р2.
Из последних равенств находим:
С=—(Pi-p2)rfrl/(rl-rf), D==(Plrf-p2ri)/(rl-rf) A0.24)
и, следовательно,
В рассматриваемой задаче, симметричной относительно начала ко-
координат, помимо агг в сферических координатах будут отличными от
нуля еще две компоненты тензора напряжений, равные между собой
а99 = ощ. Тогда из первого уравнения равновесия F.78), учитывая
равенство A0.23), находим
— _ г dorr . С_ , п
2 йг гг 2/*
Подставив значения постоянных С и D, получим
A0.26)
Формулы A0.25) и A0.26) впервые другим путем получены Ламе.
§ 3. ЭЛЕМЕНТАРНОЕ РЕШЕНИЕ ВТОРОГО ТИПА
В предыдущем параграфе было рассмотрено решение.с особенно-
особенностью, называемой центром растяжения (сжатия). Перемещения и нап-
напряжения оказались пропорциональными постоянной В, которую мож-
можно назвать мощностью центра растяже-
растяжения (сжатия).
Найдем теперь перемещения и напря-
напряжения в произвольной точке бесконечно-
бесконечного тела, возникающие под действием
центров растяжения (сжатия), равномер-
равномерно распределенных вдоль отрицательной
полуоси х3 (рис. 10.2).
Интенсивность мощности распреде-
распределенных центров растяжения обозначим
через Ь. Тогда перемещения точки К, воз-
возникающие под действием центров растяже-
растяжения на элементарном отрезке 'dt,, будут
равны:
duy = (bdt,)xM, du2 = (bdt,)x2frl
dua - (bdj) (x3 + l)lr\, A0.27)
где rx =Vx\ + x\ + {xs + 0a-
Проинтегрировав выражения A0.27) по ?, получим перемещения
точки К под действием центров растяжения, распределенных вдоль
отрицательной полуоси х3:
341
Рис. 10.2

щ = vxx
'<•¦ оо
Вычислим интегралы, входящие в равенства A0.28I
</> С/5
A0.28)
где
'*
S~ *1+** и
ds
и, следовательно,
(*з + Оа (*з + 03
о
2 (*!+«!)
I
Теперь
Г fa + 0 rfg _ l Г rfM+
Таким образом, перемещения определяются выражениями
«!= ^ , и% = ~^—, щ=>-у, A0.29)
или
uj = Ьф,„ A0.30)
где ф = In (г + х8) — гармоническая функция.
Поскольку объемная деформация
в = и i j = Ьф, u = М72ф = 0, A0.31)
компоненты тензора напряжений на основании D.4) определяются
формулой
°и — О (щ j + иу t) =» 2^Оф( jj, A0.32)
которая дает:
р _
A0.33)
342

Выражения A0.30) или A0.29), как легко убедиться, представля-
представляют собой решение уравнений D.17) во всех точках бесконечного тела,
ва исключением начала координат и отрицательной полуоси *,. Это
решение Бусеянеск назвал элементарным решением второго типа.
По формуле A0.19) найдем силы tt на поверхности сферы малого
радиуса г0 о центром в начале координат:
^ Ъ. , u = 2bG~ . (Ю.34)
§ 4. ДЕЙСТВИЕ СОСРЕДОТОЧЕННОЙ СИЛЫ НА ПЛОСКУЮ ГРАНИЦУ
ПОЛУБЕСКОНЕЧНОГО ТЕЛА (ЗАДАЧА БУССИНЕСКА)
Пусть к упругому изотропному телу, ограниченному плоскостью
х3 — 0, приложена в начале координат сила Р, направленная вдоль
оси х9 (рис. 10.3). Поскольку местное влияние силы Р слишком вели-
велико, удалим объем части тела, заключенной в полусфере малого радиу-
радиуса /"о о центром в начале координат.
Если все линейные размеры тела велики по сравнению а размера-
размерами той площадки плоскости х3 = 0, на которой приложена сила Р,
то можно считать, что тело ограничено бесконечной плоскостью и по-
поверхностью малой полусферы.
В соответствии с элементарным решением первого типа в рассмат-
рассматриваемом теле будем иметь распределение напряжений по формулам
A0.5) и перемещения, определяемые формулами A0.4), если на полу-
полусфере действуют силы, которые задаются формулами A0.7):
, t'3 - MG**/rJ + 2 A —
t3
A0.35)
а на плоскости х3 = 0 приложены касательные усилия, представля-
представляемые формулами A0.13):
а'31 = — 2AG A — 2v)xx/r3, a'3i - — 2AG A — 2v)xi/r*. A0.36)
В нашем случае плоскость х3 = 0 свободна от усилий, поэтому,
чтобы снять усилия A0.36), иа элементарное решение первого типа
наложим элементарное решение второго типа, согласно которому на
плоскости xs = 0 имеют место усилия, представляемые формулами
A0.33):
а1 - -26GV3, *3\ - -2W/xa/r», A0.37)
а на поверхности полусферы—силы, определяемые формулами A0.34):
*' ¦ ti = 2bG * . «-26G ' (Ю.38)
Составив суммы соответствующих усилий: <j'31 + о'п и а'яг 4- о"9г,
легко заключить, что плоскость х8 = 0 будет свободна от усилий, ес-
если произвольные постоянные А и Ь подчинить соотношению
Ь = -А A - 2v). A0.39)
343

Постоянную Л найдем из условия, что распределенные по полусфери-
полусферической поверхностисилы A0.35) и A0.38) статически эквивалентны при-
лпженной вдоль оси ха силе Р.
Очевидно, что силы t[ и Г„ как и силы ([ и Гг% етатичееки эквива-
лентны нулю, а силы Г, и С3 должны приводиться к силе Ft
P = po = ff(/; + QdS, A0.40)
5/2
s/
0'
IP""""
.
1
Рис. 10.3
где символ S/2 означает, что интегрирование производится по поверх-
ности полусферы (S - площадь поверхности сферы радиуса г0)
Учитывая соотношение A0.39), на основании равенств A0.35) н
A0.38) имеем
m A0.41)
и, используя A0.10), получаем
Из последнего равенства и соотношения A0.39) находим!
4лО
A0.42)
A0.43)
Учитывая эти значения постоянных Л, Ь и суммируя решения A0.4)
и A0.29), найдем перемещения произвольной точки рассматриваемого
тела:
344

" —A —2v) ^ 1,
_p
4jiG | f3
P
A0.44)
Аналогично, на" основании A0.5), A0.33) и A0.43) получим:
•»-
?
?§_
]}¦
°зз= —
2я
ЗР
2я
зр
A0.45)
В произвольной точке К на горизонтальной площадке возникают
напряжения (рис. 10.3):
Полное касательное напряжение т8 в точке К направлено по ра-
радиусу г* = Ух\ + х\ и равно
^y^T^^^L, A0.47)
а вектор напряжения рг направлен по линии ОК и модуль его равен
\ря j = Уа2яя + xf = — -й- = ~- cos2 0. A0.48)
Представим себе сферическую поверхность диаметра d, проходя-
проходящую через произвольную точку К и касающуюся плоскости хг — 0
в начале координат 0. Для любой точки этой поверхности имеем г —
= d cos 9 и. следовательно, в каждой из них модуль вектора напря-
напряжения на горизонтальной площадке будет один и тот же, равный ве-
величине
\р9\ =
A0.49)
345

Перемещения произвольной точки Ко граничной плоскости х8 = О
определяются выражениями
«9 =
Р 1—v
2я Ос
Р I—2v ху
1 4зх G <¦« ' 2
A0.50)
Из первых двух равенств A0.50) следует, что точка Ко смещается
в плоскости х3 = 0 к началу координат О по линии КоО на величину
l_2v Я A -4-у) A — 2v) Р
иг=-
A0.51)
G 4nr Е
а последнее равенство A0.50) определяет ее вертикальное смещение
piQ и3 = — ~v'. A0.52)
Из формулы A0.52), называе-
называемой формулой Буссинеска, выте-
вытекает, что для всех точек плоскости
х3 = 0 имеем uj — const, т. е.
радиусы О/С0, проведенные в этой
плоскости из начала координат,
после деформации становятся ги-
гиперболами в плоскости К00ха. От-
Отметим, что решение этой задачи
Буссинеска является трехмерным
аналогом решения задачи Фламана для полу бесконечной пластины
(см. с. 278).
Располагая решением при действии сосредоточенной силы на плоо-
кую границу полубесконечного тела, с помощью суперпозиции можно
найти перемещения и напряжения, вызванные распределенной нагруз-
нагрузкой, действующей на некоторой части Q плоской границы полубеско-
полубесконечного тела (рис. 10.4).
Пусть в произвольной точке Ki (i. л) площади Q интенсивность
распределенной нагрузки равна р (|, ц). Тогда от действия элементар-
элементарной силы dP = p (|, r\)d%dr) = pdQ перемещения произвольной точки
К (*„) определяются формулами A0.44), а от действия всей распреде-
распределенной нагрузки — выражениями
Рис. 10.4
1
_1_
—
4яО
—A— 2v)
F
pdQ,
A0.53)
где г
расстояние между точками

Перемещения произвольной точки Ко (Xi, хг, 0) граничной плоскос-
плоскости определяются равенствами
(ю.55)
где г = ^/ (*i — IJ + (-«г — ЛJ — расстояние между точками Kt и
Ко,
р = A _ v)/ BjiG) - A — v2)/ (п?).
Интеграл в формуле A0.55) называется потенциалом простого слоя
плотностью р, нанесенного на поверхность Q [49].
Используя формулы A0.45), можно получить выражения для ком-
компонент тензора напряжений при действии распределенной нагрузки
интенсивности р (?, г\).
§ 5. ДАВЛЕНИЕ МЕЖДУ ДВУМЯ СОПРИКАСАЮЩИМИСЯ ТЕЛАМИ
(ЗАДАЧА ГЕРЦА)
Два однородных изотопных тела / и // с различными упругими по-
постоянными соприкасаются в точке О, расположенной на гладких участ-
участках их поверхностей (рис. 10.5). В точке касания О, не являющейся
особой точкой поверхностей тел, имеет место общая касательная плос-
плоскость.
Обозначим координатные оси с началом в точке касания О для тела
/ через хи г/,, гх, а для тела // — через ха, уг, г2. Положительные на-
направления осей гх и гг совместим с внутренними нормалями тел / и //,
а осн~х,, г/, и х2, у% направим по линиям пересечения общей касатель-
касательной плоскости с главными нормальными сечениями поверхностей тел.
Пусть тела сдавливаются по нормали к общей касательной плос-
плоскости так, что результирующая сил между ними равна Р. Части обоих
тел вблизи точки касания О будут деформироваться, а тела касаться
уже не в одной точке, а по некоторым малым, но конечным участкам
их поверхностей. Участок поверхности касания называется площад-
площадкой контакта, а ограничивающая ее кривая — контуром площадки
контакта. Чтобы выяснить контур площадки контакта и установить
распределение давления по ней, необходимо располагать некоторыми
геометрическими соотношениями поверхностей тел вблизи их точки
касания.
Уравнение криволинейной поверхности, например, тела / вблизи
точки касания можно записать в виде г, = /-(jclt г/0-
Функцию г, = / (хи у^ разложим в ряд Маклорена:
/(•*!, Vl)
о
о
о 2 dxl
2 ду\
<la66)

где индекс «О» означает значение функции f и ее производных в нача-
начале координат. -
Так как поверхность проходит через начало координат и плоскость
касательна к поверхности в начале координат, то f/0 = 0 и
lo = df/dy^o = 0, а при выбранном направлении осей xlt ytvi
l^ilo= 0- Далее, поскольку рассматривается небольшая часть
поверхности тела вблизи точки касания О, то члены ряда A0.56), со-
содержащие малые величины хи ух третьей и высших степеней, можно
отбросить. Учитывая эти замечания, равенство A0.56) принимает вид
2Х = A/2) (Knxi+K12yl), (Ю.57)
и К
1г
где Кп = /? |0 1г
— d2f/dyl\0— кривизны главных
нормальных сечений поверхно-
поверхности тела /.
Рис. 10.5
Рис. 10.6
Аналогично можно получить для тела /7
гг = A/2) (/^ + Kity\), A0.58)
где Кп и /С22 — кривизны главных нормальных сечений поверхности
тела //.
Преобразуем теперь уравнения A0.57) и A0.58), отнеся их к неко-
некоторой общей системе координат х, у в плоскости касания (рис. 10.6).
Обозначим угол между осями xt и х% через ф, угол между осью х и осью
ху — через iplt а угол между осями х и х2 — через -фа. причем i|) =
= Th — я|>2. Тогда по известным формулам преобразования координат
при повороте координатных осей
ух = х sin г|>х + у cos г^
*! = х cos % — у sin i^
х2 = х cos -§2 — у sin г|зг, у2 — х sin ^2 + у cos
уравнения A0.57) и A0.58) приводятся к такому виду:
l
sin2
К» cos8 ф^-
A0.60)
х2 (Кп cos2 ф! + Kl2 sin2 ^
— «У (/Си — К12) sin apj,
г,'= A/2) U2 (/Cn cos2 ярг + К22 sin2 ф2) + у* (Ки sin2 tj>a +
+ Кгг cos2 г|J) — Ху [Кп — /C22) sin 2iJJ!. A0.61)
Рассмотрим точку Мх поверхности тела / и точку Мг поверхности
тела //, расположенные на одной прямой, перпендикулярной общей
343

плоскости касания и отстоящей на малом расстоянии от точки касания
О (рис. 10.5). Расстояние между точками Мх и Л4г до сдавливания
тел равно zt + z2, т. е. сумме правых частей равенств A0.60) и A0.61),
зависящей от геометрии поверхностей тел вблизи точки касания и от
углов 1|5Х и ijv
Направление общих осей х, у, определяемое углами г]^ и i]52 =
«<pj—ty можно выбрать произвольно; направим эти оси так, что-
чтобы в сумме правых.частей равенств A0.60) и A0.61) коэффициент при
ху.был равен нулю:
(Кгг — /Cia) sin Щ + (Кп ~ ^ 22) sin 2фг = 0. A0.62)
При таком направлении осей х, у, если дополнительно ввести обозна-
обозначения
А = (Ки cos2 Ч»х + Яи sin2 % + Кп cos2 фг + /Сга sin2 ф2)/2, A0.63)
В = (Кп sin2 i]v+ /С12 cos2 ih + /Си sin2 ф, + /Сга cos2 ^2)/2, A0.64)
расстояние между точками Мх и Мг будет определяться равенством
гх + гг = Л*2 + Бг/2. A0.65)
Складывая и вычитая почленно равенства A0.63) и A0.64), получим:
А + В = (Кп + /С1г + /Си + К,«)/2, A0.66)
б — Л = t (/Cia — /Си) cos 2ih + (/С22 — Кп) cos 2ф,]/2.
A0.67)
Если квадрат равенства. A0.67) сложить с 1/4 квадрата равенства
A0.62) и учесть, что ф = tpx —\|зг, то для разности В — Л получим
выражение, не зависящее от произвольных углов ^ и ijv
В - А = A/2) [ (/Си - /С12J + (/С„ - /СИ)г + 2 (/Си -
- Kia) (/Си - *См) cos W8. A0.68)
Введем величину 0, определяемую формулой
(Ю.70)
Из последних равенств и равенства A0.66) получим:
А = A/2) (/Си + К1Ш + Ки + K,l sin2 @/2), A0.71)
В = A/2) (/Си + /С„ + Кп + /См) cos2 @/2). A0.72)
Поскольку сумма гх + г2, как расстояние между двумя точками,
существенно положительна, а величина Л и В, как следует из равенств
A0.71) и A0.72), одного знака, то на основании A0.65) Л и В должны
быть положительными. Это позволяет сделать заключение, что проек-
проекции на общую касательную плоскость точек поверхностей соприкаса-
349

нхцихся тел с одним и тем же расстоянием гх + г2 = С лежат на эл-
эллипсе
Ах2 + By* = С. A0.73)
При сдавливании соприкасающихся тел контур площадки кон-
контакта, очевидно, также эллипс.
Перемещения точек Л^ и Ма в направлениях осей гх и z8, происхо-
происходящие вследствие деформации частей тел вблизи точки касания О,
обозначим через wt и w2, а перемещения точек в начале координат —
через w\ и w\. Очевидно, что величина а = w\ + w\ представляет со-
собой сближение соприкасающихся тел в результате их сдавливания,
при котором расстояние между точками Мх и Мг уменьшится на вели-
величину а — (оу, + w2).
Таким образом, для точек площадки контакта имеем равенство
2l + гг = а — К + ш2), , A0.74)
которое, учитывая A0.65), принимает вид
Wi + щ = а — Ах* — By*. A0.75)
Для точек вне площадки контакта имеем неравенство
гх + zt>a — (wl +ы>г). A0.76)
Поскольку размеры площадки контакта весьма малы по сравнению
с.общими размерами соприкасающихся тел, последние можно пред-
представить упругими полупространствами, нагруженными давлением
Р (?» Л), распределенным по площадке контакта Q.
Пренебрегая силами трения по площадке контакта и обозначая
для Тела / упругие постоянные через Еи vlf а для тела // — через
Е2, va, перемещения wx и w2 находим по формуле A0.55) и равенство
A0.75) приводим к виду
(Рх + Pa)"o = а-Ах1-By*, A0.77)
где
, Ра = A - v=)/(.n?2), A0.78)
а функция и0, определяемая формулой
iLju*. A0.79)
Q
представляет собой потенциал простого слоя, нанесенного на площад-
площадку контакта Q с плотностью р (I, г\).
Таким образом, решение контактной задачи Герца A857—1894)
приводится к нахождению потенциала простого слоя и„.
Один из приемов решения подобных задач состоит в том, что потен-
потенциал простого слоя рассматривается как предельный случай потенци-
потенциала непрерывного распределения массы в некотором объеме.
Согласно интегральному уравнению A0.77), потенциал и„ в точках
площадки контакта представляет квадратичную функцию координат.

Вместе о этим потенциал для внутренних точек однородного эллип-
эллипсоида
xVa2 + у*1Ьг + zW = 1 A0.80)
о плотностью р = const является, как известно, также квадратичной
функцией координат и определяется выражением
-.паЬсрЬ\- * у2 г* V ^
A0.81)
Поэтому за потенциал и0 можно принять потенциал однородного эл-
эллипсоида, размер с которого в направлении оси г стремится к нудю,
а плотность р неограничено возрастает, так что величина ср остается
постоянной. В пределе получим простой слой, распределенный по по-
поверхности эллипса с полуосями а и Ь, т. е. по площадке контакта Q.
Плотность этого слоя р (|, г)) будет равна той части массы эллипсоида,
которая заключена в призме с едииичиым основанием и высотой 2г =
-!--?, т.е.
ylL? A0.82)
Очевидно, что сила Р, которой сдавливаются тела, будет равна мас-
массе эллипсоида, т. е.
Р = D/3)лаЬ (ср). A0.83)
Исключая из A0.82) и A0.83) величину (ср), остающуюся постоянной
при указанном предельном переходе, найдем
Подставив в равенство A0.77) вместо потенциала простояго слоя и0
потенциал эллипсоида A0.81) при переходе к пределу, когда с-*-0
3 Р
B = 0) и учитывая, что (ср) = х~3б = cons^> получим
(ft 46 )± Ъ
о
= а—Лж»-вг/2. A0.86)
Последнее уравнение должно выполняться тождественно при всех зна-
значениях х, у внутри площадки контакта, поэтому должны иметь место
такие равенства:
со
а = — Р (В. 4- р.) Г ^ , A0.86)
О
В51

со
f — -——======- . A0.88)
4
о
Уравнения A0.87) и A0.88) позволяют определить полуоси а и Ь
эллиптической площадки контакта по заданной силе Р в зависимости
от Л и в, определяемых геометрией поверхностей соприкасающихся
тел. Зная а и Ь, из уравнения A0.86) определяется величина сближения
тел а при заданной силе Р.
Преобразуем интегралы, входящие в равенства A0.86) и A0.87),
введя новую переменную ср с помощью соотношения % = Ьг tg2 ф
и используя эксцентриситет контура эллиптической площадки кон-
контакта:
k = У\ —k*, где k0 = Ыа < 1. A0.89)
Интеграл равенства A0.86) преобразуется следующим образом!
ел я/2
Г Ар
/
С dk _2_ Г
J Ук{а2 + к){Ьг + \) ~ a J
) J V(q + 0 sin2
л,»
—^- ^., —g-/r(ife)t (Ю.90)
q J У1 — б2 sina ф а
где
я/2
Г
/
J
есть полный эллиптический интеграл первого рода.
Интеграл равенства A0.87) приводится к виду
сп л/2
Г Л __^_ Г COS2 ф^ф
J (аЧЧ1/Ц<1ЧЧ(*Ч^ а3 J V(cos^4-fe2 sin4)8 ' ^
Исходя из равенства A0.90), производная F (k) no k0 равна
Я/2
Я/2
<#¦(*) _ Г *osin2
sin2 ш)з
Умножая последнее равенство на k0, преобразуем входящий в него ин-
интеграл:
я/2
dF(k) __ _ Г1 (cos2 ф-ffeg sin2ф—cos2 ф) tftp _
/
, dF(k) __ _ С
4ko J
352

я/г я/г
Г dq> , Л cosa фЛр
J I/(cos2 ф + &() sin3 ф) J l/(coss ф-J-ft? sin* шK
0 T)
откуда, приняв во внимание A0.90), находим
Л/2
С cos3 yd<p , dF(k) , -,,.
\ , ~ К ., + F (k). (i o.93)
J у (cosa ф4"^о s'na ф)8 °
0
Используя доказываемую в теории эллиптических интегралов форму-'
лу
где E(k)
E(k)= Г VI— k*sin*<pdy A0.94)
о
есть полный эллиптический интеграл второго рода, равенство A0.93)
приводим к виду
Я/2
С «вафЛр F{k) — E(k)
j CQsa fel sin2 3 = tf * <10-95)
о
Введя новую переменную соотношением \ = a* tga ф, интеграл в ра-
равенстве A0.88) аналогично преобразуем к виду
J
cosa
о
в _2_ ЫБ {k) — k\ F {к)\ 1096
Учитывая равенства A0.90), A0.92), A0.95), A0.96) и вводя обозна-
обозначение i
I 2
формулы A0.86)—A0.88) приводим к виду
L
S = -L g ? feo(g(fe)-fe§f(fe)] A0.98)
йз посгтедних двух равенств, принимая во внимание A0.89), находим;
<10.99)
Зак. 514 353

откуда
!И^]$1- A0100)
Из первого равенства A0.99), учитывая, что
6» -= о1 A — Л"), A0.101)
получаем формулу для наибольшей полуоси контура эллиптической
площадки контакта
а = т\/ — -&-
у 2 v.
A0.102)
где п^у-ИЖ., A0.103)
и - 2М + В) = Ки + К1г + Кк + Кп. (Ю.104)
Опираясь на равенства A0.101), A0.102) и введя обозначение
- k\ A0.105)
получаем формулу для малой полуоси контура площади контакта
Ь = п\/ — А Р . A0.106)
Г 2 и
При подстановке значения а из равенства A0.102) в первую форму-
формулу A0.98) формула для величины сближения тел принимает вид
a = -?i*L|/±pgxp2. A0.107)
urn у -4
Закон распределения давления р (|, tj) по площадке контакта опре-
определяется формулой A0.84), из которой следует, что наибольшее дав-
давление имеет место в центре площадки контакта при | = х\ = 0 и равно
Рт** = Ро = (Ш)Р/паЬ. A0.108)
Давление в произвольной точке площадки контакта можно предста-
представить в следующем' виде:
Р = РоУо, A0.109)
где
Цс = у\ — 1Ча2 - V/b2. A0.110)
Подставив в A0.108) вместо а и Ъ их значения по формулам A0.102)
и A0.106), получим
\/ I Y . A0.111)
птп у 2 U /
Из формул A0.102), A0.106), A0.107) и A0.111) следует, что полу-
полуоси а и Ь контурного эллипса, величина сближения тел а и давление
р0 нелинейно зависят от силы сдавливания Р (а, Ь и р0 пропорцио-
пропорциональны Я1/3, а величина а пропорциональна Р2/3).
354

Таблица 10.1
0, град
18
20
25
30
35
40
45
50
jn
4,15(э
3,850
3,152
2,731
2,397
2,136
1,926
1,754
n
0,394
0,410
0,456
0.493
0,530
0,567
0,604
0,641
в. урад
55
60
65
70
75
80
85
90
от
,611
1,486
,378
,284
1,202
1,128
,061
1,000
п
0,678
0,717
0,759
0,802
0,846
0,893
0,044
1,000
Итак, зная кривизны поверхностей соприкасающихся тел и угол
tjj между их главными нормальными сечениями, по формуле A0.69).
можно вычислить cos 9. Тогда, пользуясь таблицами полных эллип-
эллиптических интегралов, из уравнения A0.100) можно определить k. Зная
k, по формулам A0.103) и A0.105) найти коэффициенты т и п, затем
по формулам A0.102) и A0.106) получить полуоси а и Ь контурного
эллипса, а по формулам A0.107) и A0.111) —величины а и р0.
Для облегчения перечисленных вычислений Г. Виттемор и С. Пет-
Петренко составили A921) таблицу (табл. 10.1), позволяющую сразу опре-
определить коэффициенты т и п в зависимости от 0.
Рассмотрим некоторые характерные поверхности соприкасающих-
соприкасающихся тел.
Пусть тела / и // имеют сферические поверхности о радиусами Rx
и /?г. В этом случае
Ки = К„ = ±l//?i, К„ = K2i = 1/Я„ A0.112)
где знак минус берется при сферической выемке радиуса Rt (рис. 10.7).
Подставим эти значения в формулу A0.104):
к = 2(±l/tfx + VR2) = 2(/?! ± #2)/ (#!#*), A0.113)
а по формуле A0.69)-найдем, что cos 9 = 0, т. е. 0 = 90°, и по табл.
10.1 имеем т = п = 1.
Тогда формулы A0.102) и (ГО.106) дают
а = Ъ = 0,9086
R,±Rt
[10.114)
т. е. контур площадки контакта, как и следовало ожидать, оказыва-
оказывается окружностью радиуса а и поэтому k = 0.
По таблицам эллиптических интегралов при k — 0 находим F @) =
= Е @) = л/2, а по формулам A0.107), A0.111) получаем:
a = 0,8255]/ (p0 Pf
, = 0,57841/ ^
12»
A0.115)
A0.116)
355

В частном случае, когда материала сферических тел одинаковы:
Ел = ?2 = Е, vt = v2 = v и коэффициент Пуассона v ¦= 0,3,
р 0 = 2 A -va)/? = 1,82/Е
н формулы A0.114)—A0.116) принимают вид:
3 / р р D 3 A PL' P. 4- Р.
A0.117)
Рис. 10.7
Рис 10.8
Если тело / — полупространство, а тело // — шар радиуса R% = R,
то
/<и = ки = о, /<:21 = Ki2 = 1//?; к = 2/R
и формулы A0.114) —A0.116) принимают вид:
а = 0,9086 V$oPR, а =0,8255]/Ф„/У/Л , /?0 = 0,6784
0,3 на ют:
ро = 0,388
A0.118)
которые при
а== 1,109 v
A0.119)
Контур площадки контакта будет также окружностью при сдавли-
сдавливании двух круговых цилиндров с перпендикулярными осями и рав-
равными радиусами Ri = Лг = R (рис. 10.8). В этом случае Кп = 0,
'Кп = 1/Л, Къ. = 0, /Саг = 1/Л; « = 21R; ф = л/2 и cos 6 = 0, т. е.
6 = 90° н, следовательно, т = « = 1. В результате имеем:
а = 0,9086 у^рТЖ, ро = 0,5784/Р/(Р0^, а = 0,8255 К(Ро/>)'/*,
A0.120)
а при Ег = Е2 = Е и Vi = v2 = 0,3 получаем:
1,109
= 0,388
. A0.121)
356

Отметим, что при Rx ф /?2 площадка контакта будет эллиптической
Другой предельный случай эллиптической площадки контакта,
когда а/Ь-*- оо и &-»¦ 1, соответствует контакту двух тел с круговыми
цилиндрическими поверхностями, соприкасающимися по образующим.
Эллиптическая площадка контакта в этом случае превращается в узкую
полосу шириной 2Ь, Давление по ширине 2Ь полосы контакта будет
распределяться по закону полуэллипса с полуосями Ь и о:
Р — РоУо, где ?/а = Vl — nW-.~
Обозначим через q нагрузку на единицу длины полосы контакта:
— b — b
откуда наибольшее давление в средней линии полосы
я о
Сила Р, сжимающая цилиндры, на основании A0.108) и A0.122) выра-
выразится через q следующим образом:
P^ — nabpn = — щ. A0.123)
3 3
Подставляя выражение A0.123) в формулы A0.102) и A0.106) и.
учитывая при этом равенства A0.103) и A0.105), а также что Ыа =
= 1 — k2, находим:
К пA —fe2)x
(lo.i24)
При fe = 1 имеем ? (^) = 1, и из первой формулы A0.124) следует, что
выражение для большой полуоси а контурного эллипса действитель-
действительно обращается в бесконечность, а выражение для малой полуоси Ь, т. е.
для полуширины полосы контакта, принимает вид
± А. ,= 1,128 -i/J^lM^., (Ю.125)
п х V R±R
где знак минус берется при соприкасании цилиндра радиуса /?2 с ци-
цилиндрической выемкой радиуса Ri.
Заменив в равенстве A0.122) величину b по формуле A0.125), по-
получим
(Ш26)
Для случая, когда Еу = ?2 = Е и vt = v2 = 0,3, формулы A0.125)
и A0.126) дают:
357

При контакте цилиндра радиуса R2 = R с плоскостью (Ri = оо),
когда Ei =» Ей = ? и vx = v2 = 0,3, имеем;
1,522 l/-f-!, Д, = 0.418 l/^f.
Зная размеры площадки контакта Q и распределение на ней давле-
давления р A, г)), можно определить перемещения ш и компоненты тен-
тензора напряжений atj.
Соприкасающиеся тела, как уже отмечалось, можно представить
полупространствами, загруженными распределенной нагрузкой
р (I, г|) по малой площадке Q. Тогда перемещения будут определяться
формулами A0.54) и A0.55).
Используя же формулы Буссинеска A0.45), подставляя в них вмес-
вместо Р элементарную силу dP = pdQ и выполняя интегрирование по
площадке Q, можно определить компоненты тензора напряжений. Это
интегрирование и исследования напряженного состояния соприкаса-
соприкасающихся тел в случае круговой площадки контакта выполнены
А. Н. Динником A876—1950), а при эллиптической площадке контак-
контакта — Н. М. Беляевым A890—1944).
Приведем некоторые результаты этих исследований. С точки зре-
зрения оценки прочности контактирующей детали наибольший интерес
представляют напряженные состояния в точках центральной оси г (ли-
(линии действия силы Р) и в точках контура контактной площадки.
В случае круговой площадки контакта в точках оси г компоненты
тензора напряжений определяются равенствами
v) (l — ^-arctg-g-)—
из которых следует, что компоненты o~t являются главными напряже-
напряжениями, причем, как легко убедиться, во всех точках осей гх и гг
ох = а2 == а,, = а22 < 0, а3 = а33 < 0,
т. е. эти точки находятся в условиях трехосного сжатия. Заметим,
что здесь индекс «1» соответствует х, «2» — у и «3» — г, например
ап — охх- Максимальное касательное напряжение в точках @,0, z)
определяется равенством
A0.130)
Формулы A0.129), A0.130) можно представить в следующем виде:
О,г = Ог2 = —ktfo, О33 = —k2p0> Tmax = ?3Ро, A0.131)
где ku k2, k3 — безразмерные коэффициенты, зависящие от отношения
г/а.
Для некоторых отношений г/а при v = 0,3 значения коэффициен-
коэффициентов ?ь k2> k3 приведены в табл. 10.2, а на рис. 10.9 изображены эпюры
358

г/а
0
0,1
0,2
0,3
0,4
0,5
0
0
0
0
0
0
ft,
,800
.614
,462
,342
,250
,180
1
0
0
0
0
0
k.
,000
,990
,962
,917
,862
,800
ft,
0,109
0,188
0,250
0,288
0,306
0,310
г/а
0,6
0,7
0,8
0,9
1,0
*,
0,129
0,091
0,063
0,043
0,029
l a
0,
0,
0,
0,
0,
ОЛИ
ft.
735
671
610
552
500
ц a i и. с
*,
0,304
0,290
0,273
0,255
0,236
напряжений ап — агг, a3S и ттах в точках оси г. Наибольшее макси-
максимальное касательное напряжение, равное тшах = 0,310/?0, -возникает
в точке г = 0,48а.
В точках кругового контура площадки контакта имеет место чистый
сдвиг, причем главное напряжение ог является радиальным напряже-
напряжением, а ст8 — окружным:
<Ti = -^-po.<*a = °r=0. СТа= -"±TL/J°- A°Л32)
При v = 0,3 в этих точках имеем:
а,'= 0,133р„, сгг - 0, ст8 = — 0,133/Эо.
= 0,133ро- A0.133)
В случае эллиптической площадки контакта в точках оси г компо-
компоненты тензора напряжений определяются формулами
2v
-\kl
k\
-2Sf(l-v) F (k, ф) -(l--?
E (k,
"F x
(Ю.134)
X
-v)F(k, ^)-
0 0,1 OX 0J 0,4 gf 03 0,7 03 0,5 Щ
2a
3a
/
/
/
/
1—
——
,
Рис. 10.9
359

l — k%, 6 = z/a,
a8i = °»
=» arctg 6,
У(\+&)(Ц+№)
Все точки осей гг и z2 находятся в условиях трехосного сжатия.
Зависимости напряжений оп, агг, оаа и т^ах — A/2) (сг22—о88) от
отношения z/а наглядно характеризуются эпюрами, приведенными на
рис. 10.10 для случая, когда k0 = bla = 0,5 и v = 0,3.
L
0,1
•V
«7j
w\
1
/
1
7
/
1
0,2
J
/
/
о
f
I
/
/1
/
/
/
f
o,
/
/
6
/
f
0,8
%
/
/
/
zja
Рис. 10.10
Кривые на рис. 10.11 - показывают, что отношение k0 = Ь1а несу-
несущественно влияет на величину ттах и заметно сказывается на поло-
положении точки оси г, в которой возникает ттах. Наибольшее значение
Ттах, равное примерно 0,325р0. имеет место при fe0 = Ыа =¦ 0,5 и г/а =*
= 0,31.
Компоненты тензора напряжений в точках эллиптической площад-
площадки контакта определяются следующими выражениями (ось х направ-
направлена по наибольшей полуоси эллипса а):
=—а22 = —A—2v)
_ilL arctg-
kb &
ky
kob
¦)¦
Л _
X
"Та
arcth
aM == - A -2v) -2a*!L ^L pL arcth -^- -
la ' № ab \ka a
kb
A0.135)
360

Все точки контура площадки контакта находятся в условиях чистого
сдвига.
Наибольшее касательное напряжение в точках площадки контак-
контакта значительно меньше наибольшего касательного напряжения.в точ-
точках оси z и не превышает величины 0,2р0-
В случае, когда площадка контакта — полоса шириной 2Ь, т. е.
при сдавливании соприкасающихся по образующим цилиндров, в
точках плоскости, проходящей через среднюю линию площадки кон-
контакта перпендикулярно последней, компоненты тензора напряжений
определяются формулами
Рис. 10.11
Рис. 10.12
/ 1+2(г/йJ п ,,\
о22 = —р0 , v ' — — 2z/b },
стзз = — Ро
-, я12 = o23 = ст81 = 0.
A0.136)
На рис. 10.12 приведены графики функций aij и тгаах при v = 0,3
для точек указанной плоскости.
Наибольшее максимальное касательное напряжение ттах возни-
возникает в точке на глубине г = 0,786, и его величина равна 0,304р0.
Формулы A0.136) получены для цилиндров неограниченной дли-
длины при предположении, что сжимающая нагрузка равномерно распре-
распределена по длине образующей цилиндра. Однако эти формулы можно,
использовать и при конечной длине соприкасающихся цилиндров.
Рассмотрим некоторые примеры контактных задач.
Пример 1. Найти радиус а площадки контакта, наибольшее давление рл
и наибольшее максимальное касательное напряжение т,^ах при сжатии силой
Р = 1 кгс стальных цилиндрических роликов (R = 10 мм), оси которых взаим-
взаимно перпендикулярны (см. рис. 10.8).
361

В этом случае площадка контакта будет круговой, ее радиус найдем по нер-
нерпой формуле A0.121):
з
. 1,109
2.10»
= 0,008 см.
Наибольшее давление в центре площадки контакта можн? вычислить по
формуле A0.108):
3 Р
Ро= — — = 6170 крс/см3 .
При круговой площадке контакта наибольшее максимальное касательное
напряжение возникает в точке на линии действия силы Р на расстоянии г =
-- 0,48а — 0,004224 см от центра площадки контакта и равно тшах = 0,310^>0 я*
= 1910 кгс/см2.
! I ; Рис Ю.13
Пример 2. Найти наибольшее давление р0, наибольшее максимальное
касательное напряжение ттах и сближение а между двумя" стальными (Е = 2 - 10е
кгс/см2, v = 0,3) цилиндрическими роликами одинакового диаметра d = 20 мм,
оси которых образуют угол \f = 30° (рис. 10.13), если ролики сжимаются силой
Р = 2 кгс, направленной по нормали к плоскости касания и проходящей через
точку начального касания 0.
Вначале необходимо определить полуоси а и Ь эллиптической площадки кон-
контакта. Кривизны поверхностей роликов: Ku = Q, К\г = 2/d, Кц = 0, fB2 = lid.
По формуле A0.69) получим cos 9 = У~3/2, т. е. 6 = 30°. Тогда из табл. 10.1
найдем т = 2,731, п — 0,493 и по формулам A0.102), A0.106) и A0.108), учиты-
учитывая, что Ро = 2(-1 — v2)/? = 0,91. Ю-6 и к = 4/d = 2, получим:
а = 0,0302 см, b — 0,00546 см, Ро = 5780 кгс/см2.
По кривым рис. 10.11 при Ыа = 0,181 найдем, чтоттах ж 0,32ро= 1850кгс/см2
и это напряжение имеет место на глубине г « 0,14а = 0,423-10~2 см. При k =
= У 1 — (ЫаJ = 0,985 по таблицам полных эллиптических интегралов найдем
Г (k) = 3,1534 и тогда по формуле A0.107) получим а. = 0,905-Ю-4 см.
Пример 3. Определить ширину 1Ь площадки контакта, наибольшее давле-
давление рц и наибольшее максимальное касательное напряжение ттах при сжатии
¦ силой Р= 125 кгс соприкасающихся по образующим стальных (Е = 2-10° кгс/см2,
v = 0,3) цилиндров длиной / = 125 мм, если их диаметры одинаковы d, = d2 =
-- d = 20 мм.
На основании формул A0.127), учитывая, что q = Pll = 10 кгс/см и Rx =
= R2 = R = 1 см, получаем
Ъ =
= 0,241-Ю-2 см, р0 = 0,59/q?/i? = 2640 кгс/смг.
Наибольшее максимальное касательное напряжение ттах = 0,304р0 = 800 кгс/см2
имеет место на глубине г — 0,786 = 0,188-10—? см.

Пример 4. Найти размеры площадки контакта и наибольшее давление меж
ду рельсом, имеющим цилиндрическую головку радиуса /?j = 300 мм, и колесом
с цилиндрическим ободом радиуса R2 = 450 мм, если колесо передает на рельс
силу Р «= 6000 кго (рис. 10.14).
Главные кривизны головки рельса равны: Кц = l//?t = 1/30 см-1, Ки в °-
а у обода колеса Кц = 1//?2 = 1/45 см-1, /B2 = 0. Плоскости главных кривизн
взаимно перпендикулярны, т. е. ф = я/2. Тогда по формуле A0.69) получим
cos б = ¦
- = 0,2, tr.e. 6 = 78° 35'
По габл. 10.1 путем интерполяции находим! т = 1,149, п = 0,Е
Рис. 10.14
Рис. 10.15
Упругие постоянные материала рельса и колеса примем одинаковыми'
Е = 2-10 крс/сма, v =» 0,3, гогда Ро = 2 A — v?-)/E = 0.91-10-«.
Подставляя значения. Р, т, п, р„ и и = 1/30+ 1/45= 148 в формулы.
A0.102)- и A0.106), получим полуоси эллиптической площадки контакта!
а = 0,606 см, Ъ — 0,464 см,
а по формуле A0.108) найдем наибольшее давление!
3 6000
Рй ' 2 пО.606-0,464
= 10. 200KPG/CM».
Пример 5. Определить размеры площадки контакта и наибольшее давление
между наиболее нагруженным шариком и дорожкями качения наружного и вну-
внутреннего колец радиального одиоридного шарикоподшипника (рис 10.15), вос-
воспринимающего статическую нагруяку Q= 3400 кго [45!.
Усилив, воспринимаемое наиболее нагруженным шариком, определяется по
формуле
Р = 5Q/1 =. 1700 кго,
рде i = 10 — число шариков подшипника.
Главные кривизны шарика диаметром d0 = 19,84 мм равны! Кц = Кь ~
» 2/d,, = 1,008 см-'; главные кривизны дорожки качении!
aj ааружного кольцт К„, = — \i'R = — "
- L/
— 0,9775
363

в) внутреннего кольца: К$ = Ь #„ = 0,2048 см~М
KS2 = — \h = — 0.9775 ом-1.
Тогда при соприкасании шарика с дорожкой наружного кольца к =» Кц +
+ /Ciz + К21 ¦+¦ Ла2 = 0,8929 и по формуле A0.69) получим cos В = 0,9317,
т. е. 6 = 2г42 Интерполируя по табл ЮЛ, найдем! т= 3,616, п= 0,4257.
Упругие постоянные материала (хромистая сталь) шариков и колещ Е =
= 2,12.10е кгс/см2, v= 0,3 и, следовательно
2A—Vй)
Ро= „ ^0.858-10-«.
Теперь по формулам A0 102), A0.106) и A0.108) найдем!
0 = 3,616 у — ¦ °'85яооп ' '700 = 3,616-0,1348 = 0.485 см>
6 = 0,4257.0,1348 = 0.0574 см,
3 1700
Аналогично, при соприкасании шарика а дорожкой внутреннего кольца по-
вледовательно найдем*.
к = 1,2433, cos В = 0,951, В = 18Q, m = 4,156,
п = 0,394; а = 0,502 см, b = 0.0476 ем,
р0 = 34000 кгс/см2.
' Следовательно, внутреннее кольцо испытывает несколько большее давление,
чем наружное.
Отметим, что наибольшие допускаемые контактные напряжения для под-
подшипниковых сталей при начальном касании а точке принимают порядка
50 000 кгс/сма.

Главе XI
КРИВЫЕ КРУГОВЫЕ БРУСЬЯ
Некоторые детали машин (различного рода кольца или их части)
представляют собой плоские кривые брусья большой кривизны с кру-
круговой осью с поперечными сечениями в форме круга или прямоуголь-
прямоугольника. Условия нагружения этих деталей могут быть самыми различ-
различными. Ниже рассматриваются решения задачи определения тензора
напряжений для кривых круговых брусьев (круглого и прямоуголь-
прямоугольного поперечных сечений) при произвольной нагрузке на их торцах.
При таком нагружении бруса внутренние силы в его поперечных се-
сечениях приводятся, вообще говоря, к изгибающим моментам как в плос-
плоскости кривизны бруса, так и в перпендикулярной ей плоскости, к
крутящему моменту, а также к поперечным силам и. к нормальной си-
силе.
§ 1. КОЛЬЦЕВЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
При определении тензора напряжений в кривых брусьях (кольцах)
удобно воспользоваться специальной осесимметричной системой орто-
ортогональных криволинейных координат х' (назовем ее кольцевой):
xi = к, хг = у, Xs = ф. A1.1)
Координата г* = <р (полярный угол) определяет положение попе-
поперечного сечения бруса, а координаты х1 = х, х? = у с началом в цент-
центре тяжести С поперечного сечения определяют положение произволь-
ной точки К в этом сечении (рис. 11.1).
Между этими криволинейными координатами г и декартовыми
координатами х& с началом О в центре кривизны бруса имеют место
очевидные соотношения (направление осей tf и *& показано на рис.
И-1):
Xi = (/? — х) cos «р. Хг = у, х3 = —(R — х) sin ф, A1.2)
где R — радиус кривизны оси бруса.
Ковариантные компоненты метрического тензора для рассматри-
рассматриваемой системы криволинейных координат х' на основании B°.76) и
B°.7-7) равны:
gu = 1, ёгг = 1, ?зз = (R — xf n g = gugzzgss = (# — *J.
A1.3)
а отличными от нуля символы Кристоффеля второго рода в соответст-
соответствии с B° .82) будут
Пэ = {R - X), Hi = Пэ = -1/ (R - X). A1.4)
365

Найдем в криволинейной системе координат A1.1) формулы для
дифференциальных операторов: градиента, дивергенции и лапласиана.
На основании B°.87), учитывая A1.3), получим:
(grad( ))jt =
, (grad(
ду
(grad( ))9 = .
)
A1.5)
R—x д<р
п, следовательно, для градиента скаляра имеем следующую формулу:
grad( ) = V( ) =
Рис. 11.1
Используя физические компоненты а<5) (ах, ау, av) вектора а и при-
принимая во внимание A1.3), по формуле B°.91) находим
diva =
дх
ду
R—x
A1.7)
V
Формула оператора Лапласа для скаляра в ортогональных криво-
криволинейных координатах A1.1) на основании B°.93) принимает вид
~ дх2 ду> {R—x) дх (R—x)* о
¦•A1.8)
Лапласиан вектора а в криволинейных координатах определяется
формулой B°. 100). Входящие в нее контравариантные компоненты мет-
метрического тензора g'l на основании B°.25) и A1.3) равны:
(П.9)
Принимая во внимание равенства A1.1), A1.4), A1.9) и учитывая
суммирующее действие немых индексов i'= j, k, a и E, по формуле
B°. 109) получаем
366

ai I ^ai ¦„. ' dai ¦
a a/2 (/?) a* ^
!— J
(#-xJ \|
+ —!— 2 i* !— J+e
(#)J аФ (#J \|
o2
a* a2 a» a2
a2 a a2
2 ay2 ~~
**.+. »
(tf-x) Эх (Я—*)г Зф2
(/г-хг * at/a («_x)s аф3
!«a !2a] - A1.Ю)
R — x nx (R-xI
Согласно B°.83), ковариантные компоненты а, вектора а, содержа-
содержащиеся 8 последнем равенстве, связаны g его физическими компонен-
компонентами a!s) (ax, aff, Оф) равенствами
at = ax, a3 = a»i «s — (# — *)<*p« A1.11)
Векторное уравнение A1.10), учитывая равенсггво A1.11) и форму-
формулу A1.8), можно заменить следующими тремя скалярными равенст-
равенствами;
A1.12)
S 2. ОСНОВНЫЕ УРАВНЕНИЯ
Установим дифференциальные зависимости Коши, дифференциаль-
дифференциальные уравнения равновесия и уравнения совместности деформаций
в рассматриваемой системе криволинейных координат.
Соотношения между ковариантными компонентами «« и физичес-
физическими компонентами Щп (их, ии, мф), вектора перемещения а на основа-
основании A1.11) будут следующими»
иъ = ях, иг = «у, «8 =з (R — х)нф. A1.13)
Соотношения между ковариантными компонентами ei) и физичес-
физическими компонентами еии„ (гхх, виу, гт, гхи, еуф, 8ФХ) тензора дефор-
деформации (ejy) определяюгся формулой B°,84), которая о учетом A1.3)
дает!
81 f == 8 хх* ® 22 == ®иУ» ^38 ^= ' ^ """" ^ °фф*
р — о р. — / D _^ v^j/ о — f /? _^ у\р и
Дифференциальные зависимости Коши в криволинейных коорди-
координатах определяются формулой F.3), на основании которой, прини-
принимая во внимание A1.1) и A1.4), получаем!
36?

ди,
дх
(
2 V а<р
ду
dv j R-* 8*
A1.15)
Учитывая соотношения A1.13) и A1.14), зависимости Коши A1.15)
примут следующий вид:
ди -,
dUy 1 / dU<f \
axW
_ I / 1
¦ dun
A1.16)
Соотношения между контравариантными компонентами а11 тен-
тензора напряжений (atj) и его физическими компонентами Ощи) (ахх,
ОуУ, афф, ажг/, арф, афж) устанавливаются формулой B°.84), по которой,
учитывая A1.3), находим:
a11 = oxx, o2? = ov
T12 _ „28 _
O88^
'-*),
«W (Л — *).
A1.1
Пренебрегая массовыми силами, дифференциальные уравнения
равновесия в криволинейных координатах на основании F.18) запи-
запишем
A1.18)
Учитывая равенства A1.3), A1.4), соотношения A1.17) и суммирую-
суммирующее действие немых индексов / и а, по формуле A1.18) получим диф-
дифференциальные уравнения равновесия:
дх
даху
ду
дх д,
do~r da,,
R(l—x/R)
R{l-x/R)
1
дх
(Н.19)
368

Уравнения совместности Бельтрами получим на основании тензорно-
тензорного уравнения F.25M
V*(o,,) + -J—V(V2)e0. A1.20)
Векторные компоненты тензора V2 (otj) найдем по формулам A1.12),
в которых вектор а нужно заменить тензором (а^), а компоненты ах,
йу> °ф — векторными компонентами рх, ру, />ф тензора (ai}). Вектор-
Векторные компоненты тензора V (VS) определятся формулами A1.5), если
положить, что не записанная в них функция равна VS. При этом про-
производные в формулах A1.12) и A1.5) следует заменить ковариантными
производными ковариантных векторов на основании B°.60):
дР<?
15Г
A1.21)
В результате тензорное уравнение A1.20) можно заменить тремя век-
векторными уравнениями. Для дальнейшего достаточно иметь только два
из них:
^) + VS0 (ll22)
каждое из которых можно с помощью тех же формул A1.12) и A1.5)
заменить тремя скалярными уравнениями, т. е. вместо двух уравне-
уравнений A1.22) получить шесть скалярных уравнений. Непосредственно
легко убедиться, что из этих шести уравнений только пять будут раз-
различными. Следовательно, не хватает еще одного уравнения совмест-
совместности. Недостающее уравнение можно получить, если учесть, что при
отсутствии массовых сил функция 2 = ахх -\- аУу + ow должна удов-
удовлетворять уравнению Лапласа
V22 = 0,
откуда на основании A1.8) имеем
где
VI 2= ! -2 L_?l, (Ц.23)
Заменяя уравнения A1.22) скалярными уравнениями и учитывая
A1.21), A1.23), A1.24) и A1.8), получаем уравнения Бельтрами:
369

дох
I
дх*
Я<1—*/Я) дх Я2 (I —л
¦X
n
иУУ
1
l+v
R(l—x/R) дх R4i—x/R)*
дЪ I #S
дхду R(\—xlR) dx R> A—
^ оф,
R(\-xlR){ дх
X
R'(\-x,l<y
дх
A1.25)
Компоненты тензора напряжений otj должны удовлетворять гра-
граничным условиям D.6I
ацп} - U. A1-26)
При рассматриваемом нагружении бруса его боковая поверхность
свободна от внешних сил ti и для любой точки пв =« пф = 0, поэтому
на боковой поверхности бруса граничные условия A1.26) принимают
вид
аип, = 0 {i => х, у, ф; / = х, у). A1.27)
Рассмотрим теперь граничные условия на торцах бруса, к которым
приложены поверхностные силы tt (i *» х, у, ц>).
В соответствии с определением внутренних сил Qx, Qy% N и внут-
внутренних моментов Мх, Ми, Мк, положительные направления которых
показаны на рис. 11.2, имеемз
офф ydx dy =s Mx, j J am xdxdy
J J (°ч>у x — а^»у) axdy == Mut
= — AfB
A1.28)
370

где Qx, Qy — поперечные силы; N — нормальная сила; Мх, Ми —
изгибающие моменты; Мк — крутящий момент.
Между внутренними силами и моментами, являющимися функ-
функциями координаты ф, имеют место следующие, вытекающие из усло-
условий равновесия элемента бруса (рис. 11.2) зависимости:
^*- = -N, Qff=const, ^ = QX,
cftp dy
dM
= M,
A1.29)
Внутренние силы и моменты как функции <р легко найти по задан-
заданным внешним силам ti на торцах бруса, применив метод сечений. Та-
Таким образом, внутренние силы и внутренние моменты можно считать
известными и, следовательно, равенства A1.28) представляют собой
интегральные условия, которым должны удовлетворять компоненты
тензора напряжений в произвольном сечении бруса и, в частности,
на его торцах. Условия A1.28) не учитывают закона распределения
внешних сил ti на торцах бруса. Однако это несущественно, так как
на основании принципа Сен-Венана напряжения в точках .бруса, до-
достаточно удаленных от его торцов, практически не зависят от закона
распределения сил tt, а зависят только от главного вектора и главного
момента этих сил.
§ 3. МЕТОД ПРИБЛИЖЕННОГО ОПРЕДЕЛЕНИЯ КОМПОНЕНТ
ТЕНЗОРА НАПРЯЖЕНИЙ
Пусть г — радиус круглого поперечного сечения бруса или г =
=?= а/2, где а — сторона прямоугольного поперечного сечення, распо-
расположенная в плоскости кривизны бруса.
Примем, что компоненты тензора напряжений при сравнительно
371

малом отношении rlR < 1 можно разложить в ряд по возрастающим
степеням параметра MR:
' ' ^ою+...+ ±-оиш + .... A1.30)
где oi)a — функции координат х, у, ф, не зависящие от параметра /?;
i = х, у, ф; j=x, у, ф; s = О, 1, 2, ..-.
Преобразуем основные уравнения A1.19), A1.25), A1.27), A1.28),
подставив в них выражения A1.30) для компонент тензора напряжении.
Рассмотрим, например, первое уравнение A1.19). Подставив в него
выражения A1.30) и разложив функцию 1_x/d в бесконечный ряд
l—x/R = ' + я ~*~ яг ""*" ••• + 7р + ••"
что допустимо, поскольку \x/R\ ^ r/R < 1, получим
7хх4 i д°хуо ¦ ' /*""асж1 . ^".rai \ i 1 f дах
Параметр \/R — независимая величина, поэтому выражения при оди-
одинаковых степенях 1/R в левой и в правой частях последнего равенства
должны быть равны между собой. Следовательно, имеем равенства:
до*
дх
дах
Подобным же образом преобразуются второе и третье уравнения рав-
равновесия A1.19). В результате вместо уравнений A1.19) получим неог-
неограниченное множество групп уравнений:
= 0,
дх
A1.31)
372

A1.32)
A1.33)
Е<зли подставить выражения A1.30) для компонент тензора напря-
напряжений в уравнения Бельтрами A1.25), а функции A — xlR)~l,
A — xlR)"* заменить их разложениями в ряды:
A-
и затем приравнять выражения при одинаковых степеня?; параметра
1/R, как это было сделано при преобразовании уравнений A1.19), то
вмевто уравнений A1.25) получим неограниченное число групп урав-
уравнений следующего вида!
оххо
-о,
1 + v дхг
1-J- v дхду .
;+
=о,
A1.34)
373

ь.
1
V?
1+ v дхду д)
да 1 ра
дх "~1+ V
1+ v
A1.35)
. "°уу 1 1ш_ ™ Оууо
дх дф» '
дх ' йл
дх ' &с
— 2-
A1.36)
V? а„ф2 *= л -
дх
1 + v дг/ <?ф
v ф йф
1 а» 2Х
+ v дф дх
й* 1 + v
I dZ0 с
1 + v ^ф
.
Здесь и в дальнейшем приняты обозначения:
2« ^ 0**« + Ода» + оФф4 E = О, 1, 2,
374
A1.37)

Граничные условия A1.27) на боковой поверхности бруса после
подстановки в них выражений A1.30) и последующего разделения
уравнений примут вид
ailsn, =- 0, A1.38)
где t = х, у, ф; / = х, у; s — 0, 1, 2, ...
Остается рассмотреть условия A1.28), которым должны удовлет-
удовлетворять компоненты афф, афзс, аФУ в произвольном поперечном сечении
бруса и, в частности, на его торцах.
Выражения A1.30) для компонент афф, оФзс, ато будут удовлетво-
удовлетворять условиям A1.28), если потребовать, чтобы внутренние силы, оп-
определяемые слагаемыми omjRs, афзи!//?\ OvyJR* этих компонент,
были бы статически эквивалентны: 1) при s=0 — изгибающим мо-
моментам Мх, Му и крутящему моменту Ма; 2) при s = 1 — попереч-
поперечным силам Qx, Qy и нормальной силе N; 3) при s = 2, 3, ... — нулю,
т. е. при s = 2, 3, ... создавали бы статически уравновешенную систе-
систему внутренних сил. При выполнении указанных требований, вместо
равенств A1.28) получим следующие условия:
1) ДЛЯ фуНКЦИЙ ОффО, ОфН),
A1.39)
aw0 dxdy=0, f f афф0dxdy = 0,
= 0, jjawO<&d(/=O, JJ
f f °фф о ydx dy = Mx, Г f аффо xdxdy =
f f (Oi-yo x—Стф,-о у) dxdy =AfK;
2) для функций оффЬ афл,
Г Г
F
t—Oyxi У) dxdy=0;
t* с ее jj re
\ Ошш1 ydxdy = 0, ii афф! xdxdy = 0, II
V F P
A1.40)
3) для функций афф5, оф^, ата (s — 2, 3, ...)
f f oVKSdxdy = 0, f Г aws dArdy = 0, f f афф5 dxdy = 0,
A1.41)
Таким образом, основные уравнения A1.19), A1.25) и условия
A1.27), A1.28) с помощью разложений A1.30) разделяются на отдель-
отдельные группы уравнений. Функции oi]s, входящие в эти группы уравне-
уравнений, зависят лишь от координат х, у, ф и не зависят от кривизны
375

l/R бруса. Полученные группы уравнений связаны между собой. Эта
связь состоит в том, что например, в (k + 1)-ю группу уравнений
помимо функций оци входят также функции aijs (s =0, 1, 2, ..., k — 1)
всех предыдущих групп. Поэтому для нахождения функций огд,
соответствующих (k -f 1)-му приближению, необходимо последова-
последовательно, начиная с первой, решить все предыдущие группы уравнений.
В этом последовательном решении полученных групп уравнений и со-
состоит метод последовательных приближений, или, иначе, метод раз-
разложения искомых функций в ряды по параметру. Такой метод решения
уравнений A1.19) и A1.25) позволяет определить компоненты тензора
напряжений с достаточной степенью приближения.
§ 4. БРУС КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Задача определения компонент тензора напряжений atj при про-
произвольном нагружении на торцах кривого бруса круглого поперечно-
поперечного сечения является частным случаем решенной Н. А. Чернышевым
A906—1963) общей задачи о напряженном состоянии и деформации
цилиндрических пружин, свитых из круглого прутка [60].
Определение функций aij0. Функции аио должны удовлетворять
уравнениям A1.31), A1.34), граничным условиям A1.38) при s = 0 на
боковой поверхности бруса и условиям A1.39), которые должны быть
выполнены в произвольном поперечном сечении бруса.
Непосредственной проверкой можно убедиться, что выражения
о =о' =о =0 о = — -tb±
Jp \ (П.42)
Мкх 1 ... ., , ' '
- э = — (Мху—Мух),
Jp w J
где J — ^-, Jp = 1J — ^g осевой и полярный моменты инерции
круглого поперечного сечения бруса радиуса г, удовлетворяют всем
уравнениям A1.31), A1.34) и условиям A1.38) и A1.39).
Определение функций агд. В правые части уравнений A1.32) и
A1.35), которым должны удовлетворять функции а,д, подставим зна-
значения функций atjo из формул A1.42) и учтем зависимости A1.29). В
результате получим уравнения, которые удобно разделить на две сле-
следующие системы:
A1.43)
376

dx
dx
i
dy
=0.
1+V
fl = O,
A1.44)
Функции owi должны подчиняться также граничным условиям
A1.38) при s = 1 и условиям A1.40), которые разделим на две группы:
у \l. = 0,
dxdy = RQX,
dxdy = RQy,
x—o9xi g) dxdg = 0;
ny \l = 0, оУх1 пх
dxdy =
avvl nv \L = О,
= 0,
= о,
A1.45)
A1.46)
где пх = dyldL и «у = —dxIdL (рис. 11.3); L—контур кругового
поперечного сечения.
Таким образом, определение функций atil сводится к решению двух
граничных задач. Первая задача состоит в определении функций
°ф*1 и ouvi, которые должны подчиняться уравнениям A1.43) и усло-
условиям A1.45), а вторая — в нахождении функций axxU am\, a^i,
аку1, которые должны удовлетворять уравнениям A1.44) и условиям
A1.46).-
Первую граничную задачу решим путем введения функции напря-
напряжений Фь принимая
— ~ (x +y —
A1.47)
Выражения A1.47), удовлетворяющие первому уравнению A1.43),
подставим во второе и третье уравнения A1.43)s
откуда, опуская постоянную интегрирования, найдем
. A1.48)
377

Граничное условие для
функции Фх получим, под-
подставив выражения A1.47) в
первое уравнение A1.45).
. Поскольку на контуре попе-
поперечного сечения бруса хг +
-f- у2 — г2 — О, получим
d&xIdL — 0. Согласно выра-
выражениям A1.47), функции
офх1 и ат\ зависят от произ-
производных функции, поэтому
можно принять
Рис. 11.3
= 0.
A1.49)
Уравнение A1.48) и контурное условие A1.49) для функции Ф! тож-
тождественны с уравнениями поверхности идеально гибкой мембраны на-
натянутой на жесткий круговой контур радиуса г и подверженной дав-
давлению, меняющемуся по закону, выраженному правой частью равен-
равенства A1.48). Легко найти, что функция Ф, имеет вид
-">- 0..50,
Тогда выражения A1.47) преобразуются:
l+2v M
—— ху
4(l+v) * J
+ 2v
8A+v) ч
М« 3 + v
X
xy,
xy
_ RQy_ [• 3 + 2v
l + v)
8(l+v)
A1.51)
Из вывода формул A1.51) следует, что они удовлетворяют всем урав-
уравнениям A1.43) и первому условию A1.45). Подстановкой выражений
/11.51) в остальные условия A1.45) можно убедиться, что они также
удовлетворяются.
Вторую граничную задачу решим также с помощью функции нап-
напряжений Ч*!, вводимую равенствами
°xxl =
Мх
A1.52)
которые удовлетворяют первым двум уравнениям A1.44).
378

Исключив из остальных уравнений A1.44) ^-~ и з~г, получаем
Из последнего равенства и первых двух формул A1.52) вытекает
l±^ik A1.53)
1+v J
Подставляя выражения A1.52) в первые два условия A1.46), получаем:
dL \ дх j ' dL \ ду
Можно принять, что dx?Jdx и dWJdy на контуре L поперечного се-
сечения бруса равны нулю. Тогда производные функции Ч^ по нормали
к контуру и по дуге контура будут:
^ ^^^?^21^ = 0 ^i _dyi dx ¦ ЗУ, rfy __0
' dL д dL д dL
0
0л йд; dn ду dn ' dL дх dL ду dL
Отсюда следует, что на контуре L функция 1\ сохраняет постоянное
значение, например равное нулю. Итак, на контуре L функция % и ее
производная дЧУд/z равны нулю. Эти контурные условия вместе с урав-
уравнением A1.53) для функции ?, тождественны с уравнениями упругой
поверхности равномерно нагруженной круговой пластины, защем-
защемленной по контуру. Уравнение упругой поверхности такой пластины
известно и дает следующее выражение функции %:
у * L±^L_ ik (x* + у«- г*)*, .A1.54)
1 64(l+v) ^ V
учитывая которое, на основании равенств A1.52) получаем:
Л
J'
L±2v_
)
A1.55)
xyL iJ N J ' ' J 81
Чтобы определить функцию аффь найдем из третьего, четвертого
и шестого уравнений A1.44) ее производные ¦ ^ , д®® , ——
Вспоминая, что 2, = аЛх1 + ауг/4 + афф1, и принимая во внима-
внимание формулы A1.55), получаем:
My
2(l+v) J ' дуг 2 A+v) J
= A + v)-^-. A1.56)
379

Проинтегрировав уравнения A1.56) и подобрав постоянные ин-
интегрирования так, чтобы удовлетворялись последние три условия
A1.46), найдем
24-v
41+v)
41+V)
, RN
A1.57)
где F = яг? — площадь поперечного сечения бруса.
Компоненты тензора напряжений. Если в правые части уравнений
A1.33) и A1.36) подставить функции ат по формулам A1.42) и функ-
ir ' ции аг;1 по формулам A1.51),
A1.55) и A1.57), то, принимая
во внимание зависимости A1.29),
получаем систему уравнений,
которую можно разделить на
две группы уравнений. Эти
две группы уравнений вместе с
условиями A1.38) и A1.41) при
s = 2 позволят аналогичным об-
образом, как и при определении
функций oiix, найти функции
Oijz. He останавливаясь кон-
конкретно на вопросе определения
функций aU2, но учитывая их
значения и ограничиваясь вы-
вычислением трех первых сла-
слагаемых соответствующего ряда A1.30), можно с достаточной для
технических расчетов точностью получить формулы для компонент тен-
тензора напряжений atj (см. [60] ). Анализ этих формул показывает, что
опасной точкой оказывается точка К (рис. 11.3), в которой отличные
от нуля компоненты тензора напряжений при v = 0,3 определяются
следующими выражениями:
о„- - -~ [0,154 Mv S- + @,246 Му — 0.0705RN) (J-)*].
w I R ^ . \ R J 1
1Г" ¦'««"¦' ««-«.» Z_ _|_@,642Ми —
н + @,635/И„ + 0,615RQU) -^ + @,345Мк -{
+ 0,527RQy)
R
A1.58)
где W = пг'/А и Wp = nr*/2 — осевой и полярный моменты сопротив-
сопротивления поперечного сечения бруса, а внутренние моменты Ми, Мк и
380

Таблица 11.1
R/-
2
3
4
5
6
ft
1,844
1,514
1.367
1,285
1,233
R/r
8
10
15
20
OS
k
1,170
1,134
1,087
1.065
1,000
внутренние силы Qv> N зависят от полярного угла <р, определяющего
положение рассматриваемого поперечного сечения. В частности, при
нагружении бруса, показанном на рис. 11.4, а, во всех его поперечных
сечениях внутренние силы приводятся к крутящему моменту Мк =»
= PR и к поперечной силе Qy = Р. При таком нагружении, харак-
характерной для витков цилиндрических пружин растяжения (с малым уг-
углом подъема витков), в опасной точке К имеет место чистый сдвиг (рис.
11.4, б), причем
Оф„ = kPRIW9, A1.59)
где ft — безразмерный коэффициент, зависящий от отношения Rlr.
Для некоторых отношений Rlr, называемых индексом пружины,
значения коэффициента k приведены в табл. 11.1.
§ 5. БРУС ПРЯМОУГОЛЬНОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ [20]
Определение функций atJ0. Уравнения A1.31) и A1.34), которым
должны удовлетворять функции otjo, распадаются на две независимые
группы:
до
A1.60)
A1.61)
В первую группу уравнений A1.60) входят только функции аф*о и
>> которые должны подчиняться условиям на боковых поверхно-
поверхностях бруса
0,
A1.62)
381

условиям в произвольном поперечном сечении бруса и, в частности, на
его торцах:
If a^adxdy = О, ff amodxdy = 0, Jf (alfyox—a4,xoy)dxdy = Мк A1.63)
Функции охх0, оиу0, аЧф0, охуо, входящие во вторую группу урав-
уравнений A1.61), должны удовлетворять соответственно условиям:
+ Охч0П„ = 0, Oxmtl
ljawudxdy = О,
+ О„пПи = 0, A1.64)
, jj awQxdxdy = — М». A1.65)
Таким образом, задача определения функций atjo сводится к двум
независимым граничным задачам. Первая из них, т. е. уравнения
A1.60) вместе с условиями A1.62) и A1.63), представляет собой зада-
задачу кручения прямого бруса прямоугольного поперечного сечения (см.
гл. VII, §8). Эта задача, как уже известно, решается путем введения
функции напряжений, которая определяется формулой
rfi
1—ch
пли
——
, плЬ \ ппх
ch cos —,
2a j a
A1.66)
где а — длина стороны поперечного сечения бруса в плоскости его кри-
кривизны; Ь — длина другой стороны сечения, перпендикулярной плос-
плоскости кривизны; Р — безразмерный коэффициент, определяемый фор-
формулой G.131).
Функции афжо и о9уо определяются формулами:
ду
dfl>o
<Vo= — - —
дх
_8_
я*
(-1)
(п-П/2
X
п=!7з,5...
2a
X
A1.67)
Непосредственной подстановкой легко убедиться, что выражения
^¦vrn7== Q'/yo == ^эс^О == ^> ^ффО == —— ~~ , A1.68)
11'
Jxx0~
аЬ9
г аЬ9 ФЬ
где J х = -J2" и Jy = ^— осевые моменты инерции поперечного се-
сечения, удовлетворяют всем уравнениям A1.61) и условиям A1.64) и
A1.65) второй граничной задачи.
Следовательно, функции otH представляют собой решение задачи
кручения и чистого изгиба прямого бруса прямоугольного сечения.
332

Определение функции atjl. В правые части уравнений A1.32) и
A1.36), которым должны подчиняться функции aiji, подставим зна-
значения функций at)o по формулам A1.67) и A1.68) и примем во внима-
внимание зависимости A1.29). В результате получим систему уравнений,
которые разделим на две следующие группы:
= 2
f (MK-RQV)-^- RQX
A1.69)
A1.70)
Входящие в первую группу уравнений A1.69) функции афЛ] и
должны удовлетворять условиям на контуре Ь поперечного се-
сечения
о<$х\Пх + o<pyiny = 0, A1.71)
условиям в произвольном поперечном сечении бруса и на его торцах:
= RQX, Jj avyidxdy = ЯQj,, П (оф!/1л; — афЛц/) dxdy = 0.
A1.72)
Функции второй группы уравнений A1.70) ахзЛ, oyyl, awi, a^i долж-
должны удовлетворять соответственно следующим условиям*
х1Пх + 0^1% = 0, О„х\Пх + Oyyltlg = 0, A1.73)
JJ omXydxdy = 0, jf ow\xdxdy - 0. A1.74)
Таким образом, определение функций о/д сводится также к двум
независимым граничным задачам. Первая из них состоит в определе-
определении функций ОфЛ, cr<pj,i из уравнений A1.69) и условий {П-71) и
A1.72), а вторая — в определении из уравнений A1.70) функций ахх1,
°уп> awi> °xw удовлетворяющих условиям A1.73) и A1.74).
Первую задачу удобно решить путем введения функции напряже-
напряжений Фх (х, у) следующими равенствами:
2J»
883

которые тождественно удовлетворяют первому уравнению A1.69).
Если подставить выражения A1.75) во второе и третье уравнения
A1.69) и учесть G.33) и G.130), то получим следующие зависимости:
Jy
v MK — RQV . Мк
—- _ 4 —
где JB = fia3b — геометрическая характеристика, жесткости при кру-
кручении прямого бруса прямоугольного сечения.
Интегрируя последние равенства соответственно по у и лох, полу-
получаем выражения
из сравнения которых находим, что
Следовательно, функция напряжений Фх (л:, у) должна удовлетво-
удовлетворять уравнению
+v У„
A1.76)
Подставляя выражения A1.75) в условия A1.71) и учитывая, что при
х = +а/2 ия = ±1, иу = 0, а при у = ±&/2 пх = 0, иу = ±1,
приходим к заключению о граничном условии для функции d>i
OiL^O. A1.77)
Искомую функцию Ф1 удобно представить в виде "трех слагаемых!
'ф! = Ф1а + Ф1Й + Ф1о, A1.78)
удовлетворяющих уравнениям:
^-/?Qy4^N > )
(П.80)
384

Здесь, как и прежде, под символом Vf( ) понимается дифференци-
дифференциальный оператор
Учитывая далее, что
уравнение A1.81) можно привести к следующему виду:
угфЪ^Лкх, - (П.82)
где
Ф\с = Фи — *Фо/2. A1.83)
Итак, искомая функция Фь согласно равенствам A1.78) и A1.83)*
представится следующей суммой:
где функция Фо определяется равенством A1.66), а функции Ф1я,
Ф\ь и Ф°с подчиняются уравнениям A1.79), A1.80) и A1.82).
Так как функция Фх должна удовлетворять условию A1.77), то
можно потребовать, чтобы функции Ф1а, Ф1Ь и Ф\с на контуре L по-
поперечного сечения бруса также были равны нулю. Тогда уравнения
A1.79), A1.80) и A1.82) вместе с контурными условиями для функций
Ф1а, Ф1Ь и Ф\о тождественны с уравнениями поверхности идеально
гибкой мембраны, натянутой на жесткий прямоугольный контур, сов-
совпадающий с контуром поперечного сечения бруса, и подверженной
давлению, изменяющемуся по законам, выраженным правыми частя-
частями уравнений A1.79), A1.80) и A1.82).
Определив, -используя аналогию с мембраной, функции Ф1а, Ф(г>,
Ф^ и внеся их выражения, а также выражение A1.66) для функции
Фо в равенство A1.84), получим
v MK-RQy .3 МИ аз ^ (-1)" „
4-v 4JX 4 J
_ch *™L I ch -^) sin i^H. + ^L_ 3R*. x
I a ) a 1+v My
у ich /ch
яз ^ газ V a / 2a
n= 1, 3» 5,.••
A1.85)
Располагая выражением- функции Фх (л:, у), легко найти на осно-
основании равенств A1.75) формулы для функций (Уф*1 и ат\, которые, как
это следует из их вывода, удовлетворяют всем уравнениям A1.69) и
18 Зак. 614 385

условию A1.71). Подстановкой формул для функций a^xi и awi в уг
ловия A1.72) можно показать, что они также удовлетворяются.
Решение второй группы уравнений A1.70), из которых вместе с у
ловиями A1.73) и A1.74) определяются функции охх1, оууи офф,
охУ1, разделим fta две задачи. Каждую из искомых функций предсть
вим в виде суммы двух функций:
Oxxi
= O'xxl + Oxxl» Oyyl — o'yyl -f- aUit\>
A1.86
Потребуем, чтобы функции а'хх\, оУУи
уравнениям
$'ху\ удовлетворял!.
да
xxl
дх
ду
V! O'xxl +
1
Мух
дх
д*2'.
ду
1+v дх*
= 0,
1+v ay2
дхду
A1.87)
где
Тогда функции ахх\, a'vv\, am\, оху\, как это вытекает из ра-
равенств A1.70), A1.86) и A1.87), должны удовлетворять уравнениям
дх
|
ду
дсрду
1 +v а^
да'ху\
дх
до1'
= 0, (П.{
1
I + v дхду
= 0,
где
Потребуем также, чтобы функции oi*i,
A1.73), удовлетворяли условиям
о'*х\ nx
а функции a"xxi, oyo\, o"xyi — условиям
«+0^1 nu=0,
'yi/i пу—0,
, исходя из
A1.89)
у=»0. .A1.90)
Аналогично, исходя из равенств A1.74), можно положить, что
функция офф1 в произвольном поперечном сечении бруса, а также на
386

его торцах удовлетворяет условиям
J J o9Vi dx dy = RN, jj ovl>i ydx dy=0, J J or^, xdxdy = 0,
A1.91)
а функция о^ф| — условиям
j J афф i dx dy =s 0, J J o"mi ydxdy = 0, J J o^i jcdxdy = 0.
A1.92)
Первая задача, заключающаяся в определении функций о'хх\, ...,
о'хщ, удовлетворяющих уравнениям A1.87) и условиям A1.89) и
A1.91), представляет собой задачу растяжения и чистого изгиба кри-
кривого бруса в плоскости его кривизны. Эта задача решена в работе [211
путем введения соответствующей функции напряжений, с помощью
которой она приводится к уравнению.и граничным условиям, экви-
эквивалентным задаче определения изогнутой поверхности защемленной
по контуру прямоугольной пластины, находящейся под действием
равномерно распределенной нагрузки.
Вторая задача, состоящая в определении из уравнений A1.88) и ус-
условий A1.90), A1.92) функций о"хх\, .... о"ку\, представляет собой за-
задачу изгиба кривого бруса в плоскости, перпендикулярной плоскости
его кривизны. Эта задача путем введения функции напряжений, как
и первая, также сводится к бигармоническому уравнению, но при иных
граничных условиях [22].
Окончательные формулы для функций о'хх\, ..., о[у\ и а'т, ....
o'tyi, довольно сложные, здесь не приводятся.
Компоненты тензора напряжений atJ при решении задачи были
разложены в'бесконечные ряды A1.30). С достаточной для инженерных
расчетов точностью можно, как показывают вычисления, ограничить-
ограничиться первыми двумя слагаемыми этих рядов, т. е. можно принять
ои = ош + ~-аи1 (f = x,0,<p; l=x, #,ф). (Н.93)
к
Анализ напряженного состояния позволяет заключить, что при
различных случаях нагружения на торцах рассматриваемого бруса
напряжения оуу и оху не оказывают существенного влияния на проч-
прочность, а остальные напряжения представляют интерес лишь для трех
точек поперечного сечения: Ki (а/2, 0), Кг (а/2, Ы2), К.ь @. Ы2) (см.
рис. 11.1).
В точке Ki существенное значение имеют напряжения ат и аФУ,
которые можно определить по формулам:
^ 0*S*+*^' {1L94)
где Wy — (Pb/Ъ — момент сопротивления изгибу; WK = аа?Ь — мо-
момент сопротивления кручению; F = ab — площадь поперечного се-
сечения; kx и k% — безразмерные коэффициенты, некоторые значения
13* • 387

R/a
2
2,5
3
3,5
1/6
—1
—1
— 1
—1
,171
,135,
,112
,096
•
-1
—1
— 1
-1
/3
,172
,136
,113
,097
1/21
—1
-1
—1
—1
,175
,138
,114
,100
0,
—1,
-1,
—1,
-1.
8
177
143
119
102
1.0
-1,183
—1,147
—1,122
—1,105
1,25
—1,192
—1,154
—1.129
—1.111
Таблица
;¦ i
—i
—i
—i
-i
,8
,201
.163
,13b
,115
11
—1
—1
—1
—1
.2
2
,223
,180
,1Ы)
,130
2
2,5
3
3,5
1
1
1
1
1/6^
,326
,261
,217
,186
1
1
1
1
1/3
,275
,220
,183
,157
1
1
1
1
1/2
.232
,186
,155
.133
b/a
0,8
1.162
1,129
1.108
1,093
1
1
1
1
1,0
,135
.109
,090
,077
1
1
1
1
1
1,25
,114
.091
.076
,065
T аблица
1
1
1
1
1
1,5
,098
,079
,066
,056
11.3
2
1,079
1,063
1,053
1.045
b/a
1/6
1/3
1/2
0.8
0,
0,
0.
0.
о
067
107
1Ь5
193
k
4.
4,
2,
1,
82'
67
19
83
1
1
1
1
ft.
,347
,322
,258
.092
1
1
1
1
ft.
,51
,53
,56
.64
1
1
1
2
b/a
,25
,5
0.
0-,
0.
0,
a
208
221
231
246
1
1
1
1
,72
,65
.61
,56
Таблиц.
ft.
1,000
0.916
0,859
0.795
3 11
k
1,
1,
1.
2,
.4
I
72
83
95
19
R/a
2
2,
3
3,
5
5
b/a
' —
1
1
1
1
1/6
,210
,168
,140
.120
1
1
1
1
i/3
,214
,171
,143
,122
1
1
1
1
1/2
.223
,178
,149
,128
1
1
1
1
0,8
,280
,224
,187
,160
1
1
1
1
1
.340
,272
,227
,194
T а б;л и ц а
1,25
1,395
1,316
1,264
1,226
1
1
1
1
1,5
,425
,340
,283
.243
11
1.
1,
1,
1,
.5
2
454
367
306
262
2
2
3
3
5
5
—1
—1
1
1/6
,167
,133
,111
,095
—1
1
—1
—1
1/3
.164
.131
,109
,094
—1
—1
—1
-1
1/2
,160
.128
.107
,092
...1
-1
-1
0,8
,151
,121
,100
,086
b/a
—1
—1
-1
1
,142
,113
,094
,081
l.
—1
—1
-1
—1
25
,128
,102
,085
,073
Таб
1
1
—1,
1
-1,
ЛИ 1
,5
110
088
074
063
*а 11.6
—1
-1
|
2
,067
,053
,045
,038
388

R/a
2 "
2,5
3
3,5
0
0
0
0
1/6
,088
,070
,058
,050
0
0
0
0
1/3
,091
,073
,060
,052
0
0
0
0
1/2
,094
,073
,030
,054
0
0
0
0
b/a
0,8
,100
,080
,067
,057
0,
0,
0,
0,
i
105
084
070
060
0
0
0
0
1,25
,112
,090
,075
,064
1'a
0
0
0
0
блица
1.6
,123
,098
,082
,070
0
0
0
0
11.7
2
,155
,124
,103
,089
К/а
2
2
3
3
5
5
1/6
-0
—0
-0
—0
127
101
085
073
1
—0
Q
—0
~о
р
,128
,102
,086
,074
1
-0
—0
-0
о
/2
132
105
087
075
0
—0,
—0,
—0,
—0,
b/a
,8
135
108
090
077
—0
—0
—0
—0
1
,137
,109
,091
,078
1
-0
-0
-0
—0
,25
,138
,110
,092
,079
Г а б лица 11.8
1
-0,
о
-0,
-0,
.5
139
111
093
080
-0
—0
—0
—0
2
,140
,112
,094
,081
которых в зависимости от отношений RIa и Ыа приведены в табл. 11.2
и 11.3; значения безразмерных коэффициентов k3 и а, зависящих толь-
только от отношения Ыа, приведены в табл. 11.4.
При произвольном нагружении бруса в точке Кг возникает только
напряжение афф, определяемое формулой
аФФ = ?4-^ +k6-J- + —, .A1.95)
где k4 и кь — безразмерные коэффициенты, зависящие от отношений
RIa и Ыа (табл. 11.5 и 11.6).
В точке /С3 возникают напряжения офф, афХ и акх, которые можно
вычислить по формулам:
афф = MJWX + KMyIWy, аф, = k7MKIWK + ksQx/F,
oxx = KMuiWy, .; A1.96)
где безразмерные коэффициенты fee и fe8 в зависимости от отношений
R/a и Ыа определяются по табл. 11.7 и 11.8, а коэффициенты k7 и ks,
зависящие только от отношения Ыа, даны в табл. 11.4.
Приведенные здесь результаты могут быть использованы при рас-
расчете цилиндрических винтовых пружин с витками прямоугольного
сечения, угол подъема которых не превышает 10°. Однако при Ыа > 2
пружину следует рассматривать как цилиндрическую оболочку. Та-
Такой подход к расчету пружин с витками прямоугольного сечения рас-
рассмотрен в работах [15, 16].
Отметим также, что расчет ортотропного кривого бруса прямо-
прямоугольного сечения дан в работе [17].

ПРИЛОЖЕНИЕ I. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
Физические и геометрические величины, характеризующие состоя-
состояние сплошной среды, не зависят от выбора системы координат, т. е.
представляют собой инвариантные объекты. Однако эти величины
удобно изучать-в некоторой системе координат. При этом инвариант-
инвариантный объект определяется совокупностью величин, называемых его
компонентами, которые зависят от системы координат. Например,
из курса сопротивления материалов известно, что напряженное сос-
состояние в точке тела определяется девятью компонентами — напряже-
напряжениями на трех координатных площадках. Такие многокомпонентные
инвариантные объекты и называют тензорами, определения которых
даны ниже.
1°. ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ В ПРЯМОУГОЛЬНЫХ ДЕКАРТОВЫХ
КООРДИНАТАХ
§ 1. ОПРЕДЕЛЕНИЕ ТЕНЗОРА
Систему ортогональных декартовых осей в трехмерном евклидо-
евклидовом пространстве будем обозначать Охххгхъ, а их ортонормированный
базис— через 9t (i = 1, 2, 3). По определению,
где 8и — символ Кронекера.
Произвольный вектор а в данном базисе представляется разложе-
разложением
з
а - а^ + агэг + а3э3 = "Е A°2)
где величины at (i = 1, 2, 3) — компоненты вектора.
В целях удобства правую часть равенства A°.2), как и в других
подобных случаях, записывают без знака суммы, т. е.
" а = а^и A°.3)
где дважды повторяющийся индекс i, по которому производится сум-
суммирование, называется немым и в случае трехмерного пространства
принимает все три значения: 1, 2, 3.
Немой индекс можно обозначить любой буквой, т. е.
а = ai9i = ajBj = ahah = ... = а,э, + агэг
Рассмотрим систему декартовых осей Oxix^x' с ортонормирован-
ным базисом э/, повернутых относительно исходных (старых) осей во-
вокруг начала координат О.
390

Косинус угла между новой осью Ох] и старой Oxjt равный скаляр-
скалярному произведению ортов э\ и Э], обозначим через atj:
э! -Э] = аи. A°.5)
Так как косинус atj равен проекции единичного вектора э\ на на-
направление единичного вектора э} и, с другой стороны, alt = at} ра-
равен проекции вектора Bj на направление вектора э[, то разложение
орта э1 по старому базису Э] имеет вид
а/ = alldi °6
а разложение орта Э; по новому базису э\ будет
Э) = апэ{ 4-
Дважды повторяющийся индекс / в правой части равенства A°.6) яв-
является немым, а неповторяющийся индекс i называется свободным.
Свободный индекс принимает поочередно одно из трех значений 1, %
3 и в обеих частях равенства обозначается какой-либо одной буквой,
отличной от буквы, принятой для немого индекса. В равенстве A°.7)
индекс / — свободный, а индекс i — немой.
Коэффициенты а^ в формуле A°.6) образуют матрицу перехода от
одного ортонормированного базиса к другому, которая является ор-
ортогональной, т. е. обратная ей матрица равна транспонированной:
Элементы ортогональной- матрицы удовлетворяют условиям
<*th<*>jh = &ij и akiak} = 8и, A°.8)
а определитель ортогональной матрицы
|a«l-±l, • A°-9)
где знак плюс принимается, когда базисы д] и Э] имеют одинаковую
ориентацию, и минус, если один базис правый,- а другой левый.
Приведем теперь формулы преобразования компонент вектора а.
Разложения вектора в каждом из рассматриваемых базисов имеют
вид
а = ajBj = aia't A°.Ю)
Подставляя в равенство A°. 10) значение Э} по формуле A°.7), полу-
получим закон преобразования компонент вектора при переходе 'От ста-
старых к новым осям:
A°.П)
Подстановка значения э/ по формуле A°.6) в равенство A°. 10) дает
закон преобразования компонент вектора при переходе от новых осей
к старым:
Исходя из закона преобразования компонент вектора как объекта,
не зависящего От поворота координатных осей, вытекает его опреде-
определение.
¦391

Инвариантный объект, который в системе декам-.-ооых oce^ харак-
характеризуется тройкой чисел ait преобразующихся при повороте осей по
закону A°.11), называется вектором или тензором первого ранга, а эти
три числа — его компонентами.
Тензор первого ранга имеет истолкование не только как вектор.
Рассмотрим, например, инвариантную линейную форму
ajxj = m'x( = 1, AМЗ)
представляющую собой уравнение фиксированной плоскости, не про-
проходящей через начало координат.
Здесь Xj, xl — компоненты радиус-вектора произвольной точки
плоскости относительно старых и новых осей; а/, а! — коэффициенты
линейной формы в старых и новых осях.
Внося в A°. 13) вместо Xj выражение согласно закону A°. 12), полу-
получим
откуда ввиду произвольности х'ц вытекает закон преобразования ко-
коэффициентов инвариантной линейной формы:
а/
который совпадает с законом A°Л1) преобразования компонент тен-
тензора первого ранга. Следовательно, коээффициенты инвариантной ли-
линейной формы образуют тензор первого ранга.
Найдем закон преобразования коэффициентов инвариантной би-
билинейной формы:
О0-15)
где ац, a'kt — коэффициенты билинейной формы, Хи У} и х\, yl — ком-
компоненты векторов х и у в старом и новом базисах.
Подставив в равенство A °. 15) значения компонент х% и yj по форму-
формуле A °. 12), получим закон преобразования коэффициентов инвариант-
инвариантной билинейной формы
a'kl =
который аналогичен закону A °. 14) преобразования коэффициентов
инвариантной линейной формы.
Подстановка в A°.15) значений компонент xk и у[ согласно A°. 11)
приводит к закону обратного преобразования коэффициентов инва-
инвариантной билинейной формы
аи = oi,klauaki. A°Л7)
По аналогии с определением тензора первого ранга определяется
тензор второго ранга.
Инвариантный объект, который в системе декартовых осей трех-
трехмерного пространства характеризуется девятью числами ац, преоб-
преобразующимися при повороте осей по закону A°.16), называется тензО'
ром второго ранга, а эти девять чисел с двумя в определенном порядке
индексами называются его компонентами.
392

Если рассматривать полилинейную форму, то аналогично придем
к понятию тензора любого ранга.
f Тензором ранга р называется инвариантный объект, который в сис-
системе декартовых осей трехмерного пространства характеризуется 3''
j числами atu it... ip, занумерованными в определенном порядке р ин-
| дексами, причем при повороте осей эти числа, называемые компонента-
| ми тензора, преобразуются по закону
По аналогии с A°Л7) обратное преобразование определяется фор-
формулой
аН h--tp = а/> '•а/.'. • • • % ip a'h /.-/Р. О0-19)
Тензор, например, второго ранга с компонентами ац символически
обозначают соответствующей заглавной жирной буквой А или а, а
также путем записи его компонент в круглых скобках, т. е. (ац). Та-
Таким образом, можно встретить следующие обозначения тензора вто-
второго ранга:
А = а -
Иногда для тензора используется обозначение его компонент, на-
например Ьць — тензор третьего ранга (ранг тензора совпадает с числом
свободных индексов при его компонентах).
§ 2. ТЕНЗОРНАЯ АЛГЕБРА
Над тензорами можно производить некоторые инвариантные опе-
операции, т. е. такие, результаты которых не зависят от системы коорди-
координат, в которой они .выполняются.
Сложение и вычитание тензоров. Эти операции применимы лишь
к тензорам одинакового ранга.
Суммой (разностью) двух тензоров одинакового ранга называется
тензор того же ранга, компоненты которого равны суммам (разностям)
соответствующих компонент рассматриваемых тензоров. Например,
сумма двух тензоров второго ранга (а,-у) и (btJ) есть тензор также вто-
второго ранга (с1}), компоненты которого определяются равенством
сц = ац + Ь„. A°.21)
Умножение тензоров. Эта операция применима к любым двум или
нескольким тензорам, заданным в определенном порядке.
Тензорным (внешним) произведением тензора (cul...ip) ранга р т
тензор (bti... /ч) ранга q называется тензор (с<х... tpil... iq) ранга (р + q),
компоненты которого образуются путем умножения каждой компо-
компоненты первого тензора на каждую компоненту^ второго тензора, т. е.
393

Компоненты тензора-произведения (мультипликативного тензора),
как это следует из равенства A°.22), снабжаются индексами, снятыми
поочередно с компонент тензоров-сомножителей в заданном порядке.
Например, в результате тензорного (внешнего) умножения двух
тензоров первого ранга (at) и (Ь}), т. е. векторов, получим тензор вто-
второго ранга (сц), который называется диадой. Компоненты диады
образуют матрицу
Си
С13
^23
а2 Ьг аг Ьг аг Ь3
а3 bi а3 Ьг а3 Ь3
Умножение тензора ранга р на скаляр Я, приводит к тензору ранга
р, все компоненты которого умножены на к.
Свертывание тензоров. Операция свертывания состоит в отождест-
отождествлении (приравнивании) двух индексов у компонент данного тензора.
Отождествленный индекс оказывается немым и, следовательно, по
нему производится суммирование. В результате получается тензор,
ранг которого меньше на две единицы ранга исходного тензора. Так,
свертывая тензор четвертого ранга (аг;ьг)> например по первому и вто-
второму индексам (/ = i), получаем тензор второго ранга с компонента-
компонентами bxi = аИк1.
Заметим, что свертывание тензора (a^fti) по индексам / и / равно-
равносильно умножению компонент данного тензора на символ Кронекера
6
= bhl. (P.24)
Свертывание тензора (ailti... ^ _li2P) четного ранга 2/> по р па-
парам индексов приводит к тензору нулевого ранга, т. е. к инварианту
(скаляру). Следовательно, операция свертывания является одним из
способов получения инвариантов тензора четного ранга.
Например, свертывая тензор второго ранга (ai}), получим инва-
инвариант аи = ап + а22 + я33 — $Р (^o')> который называется следом
тензора (а^).
Производится также свертывание тензора с тензором. Эта опера-
операция, называемая внутренним .произведением тензоров, состоит в пред-
предварительном тензорном (внешнем) умножении тензоров, а затем полу-
полученный мультипликативный тензор свертывается по индексам, при-
принадлежащим тензорам-сомножителям. Например, перемножая тен-
зорно два вектора (а,) и (bj), а затем свертывая полученную диаду
(с;;) = (at) (bj), приходим к инварианту
Сц = atbi = аД + агЬг + аф3 = (a,)- (bj), (P.25)
т. е. к скалярному произведению векторов.
Аналогично определяется скалярное произведение тензоров, во-
вообще говоря, любых рангов. Так, скалярное произведение тензоров
394

(аи) и (bki) в заданном порядке, например, по индексам i и ft приво-
приводит к тензору (ел) второго ранга:
(аи)' (bki) = 8ikCiijbki — афп = сп. A°.26)
Скалярное умножение тензоров (ai}) и (bki) по двум парам индек-
индексов j и k, / и /, называемое бискалярным произведением тензоров, при-
приводит к скаляру d:
(ац)--(Ьк1) = Ь1к8}1аиЬы = аиЬи = d. A».27)
Перестановка (транспозиция) индексов. Эта операция состоит в
том, что из тензора, например, (aiik) образуется того же ранга другой
тензор (bijk) путем перестановки индексов у компонент тензора {aijk).
Пусть переставляются, например, 1-й и 3-й индексы, т. е. i и ft. В ре-
результате получим тензор (btjk) с компонентами Ь^к '= ahii. Поскольку
у тензора строго определенный порядок индексов при его компонен-
компонентах, то операция перестановки индексов приводит, вообще говоря,
к тензору, отличному от исходного, т. е. (Ьць) = (akji) Ф (aiJh). Од-
Однако некоторые тензоры не изменяются при перестановке индексов
у компонент или изменяют лишь свой знак.
Тензор, который не меняется при перестановке любой пары индек-
индексов, называется симметричным.
Тензор (atj) второго ранга называется симметричным, если его ком-
лоненты удовлетворяют условию
а„ = а„. A°.28)
Очевидно, что из девяти компонент симметричного тензора второ-
второго ранга только шесть являются независимыми.
Тензор второго ранга (Ь^) является 'кососимметричным, если его
компоненты подчиняются условию
Ьи = -b,t. A°.29)
На основании A°.29) при / = с имеем Ь^ — —Ь^1, т. е. % = 0.
Таким образом, кососимметричный тензор второго ранга имеет лишь
три независимые компоненты и, следовательно, его можно рассматри-
рассматривать как вектор с компонентами
Ьх == —&2з = ^зг. Ьг = —bsl = bl3, bb = —612 = Ьи. A°.ЗО)
или
bh = -(\ЩетЬц, A°.31)
где ецк — компоненты тензора Леви-Чивита A873—1942): вць. =
=• +1 (—1), если индексы Ijk. образуют четную (нечетную) переста-
перестановку чисел 1,2, 3, и et}h = 0, если среди индексов ijk по крайней ме-
мере два повторяются, т. е.
а остальные компоненты равны нулю.
1 Для дважды повторяющегося индекса, по которому суммирование ие про-
производится, принято обозначение 11. Например, а~ — одна из диагональных ком
понент тензора [аф aiv an, a,3, a ahk = «и + ags + а,з.
ч 395

Отметим, что если тензор (аи) симметричный, а тензор фц) косо-
симметричный, то
atfit, = 0. . A°.32)
Действительно, выражение а^Ь^ не изменится, если немой индеко
i заменить на./, а немой индекс / — на i, следовательно, ацЪц = аф^\
и в силу условий а.ц = а.ц и Ьц = —Ьц а^Ьц = —афц или 2aubi} «а
= 0, что и подтверждает равенство A°.32).
Любой тензор второго ранга а1} может быть разложен, и притом
единственным образом, на симметричную составляющую Щф и косо-
симметричную составляющую щц\ : at] = Щт 4- Д[//], где
(а + а) a = (a
Покажем, что квадратичная форма а,^г*/не изменится, если тен-
зор (ац) заменить его симметричной составляющей сШ). В самом де-
деле, имеем
о»»xiХ1 = -j (°ij+ ан)*t Х/=— (ciijXix}+ анх,х}).
Поскольку в последнем выражении индексы i и / немые, то пере-
переменные хх и X] можно записать в обратном порядке и затем, заменяя
немой индекс / на i, at — на /, получим
ан) xi x>=-j (аи xt xi + ап X3xi) =¦ -у (auxt х> +
Сложение (вычитание), умножение, свертывание тензоров и лю-
любая комбинация этих операций приводит, вообще говоря, также к тен-
тензорам. Следовательно, тензорный характер какого-либо объекта мож-
можно распознать, подметив, что он определяется совокупностью чисел,
которая образуется в результате операций над известными тензорами.
В работах по тензорному исчислению [29] доказывается следующая
теорема, которая именуется обратным тензорным признаком.
Теорема. Если в каждом ортонормированием- базисе имеем сово-
совокупность Зр+<? чиселCix fg... fp /, /8... / такую, что в результате сверты-
свертывания ее с произвольным тензором (в^ ^... / ) ранга р получается тен-
тензор {bjx /s... j ) рангаq, то эта совокупность чисел образует тензор ран-
ранга р + q:
в
частности,
если
•¦• 'р /. 1*
имеем
atjbi
... iq о/, /,... /
равенство
, = QijXiXj
p = °liU
== с,
••/в.
A°.3б)
A°.36)
в котором (bij) = (xt) (xj) — диада (тензор второго ранга), ас — ска-
скаляр (инвариант), то совокупность девяти чисел ai} образует тензор
второго ранга.
396"

Аналогично, если для произвольного вектора (xj) и вектора (yt) вы-
выполняется равенство
У1 = aljXj, A°.37)
то числа ai} являются компонентами тензора второго ранга.
Например, символ Кронекера 6tJ определяет компоненты единич-
единичного тензора второго ранга. Действительно, очевидное тождество
доказывает, что (8t}) — тензор второго ранга, причем тензор (8i}) яв-
является симметричным, так Как 8ц = 8jt. Относительно новых (по-
(повернутых) осей */ компоненты 8'ц тензора (8feJ) определяются по фор-
формуле A°. 16). Учитывая при этом равенства A°.8), имеем
в</ = atkVifiki == ccikajk = 8tJ, A°.39)
т. е. компоненты тензора (8^), а следовательно, и тензора (Лбг;), где
Я, — скаляр, не меняются при переходе от одной системы координат
к другой. Тензоры, обладающие этим свойством, называют изотроп-
изотропными. Изотропным тензором третьего ранга является тензор Леви-
Чивита (e(jk), а также тенвор (hetjk).
Компоненты изотропного тензора четвертого ранга определяются
формулой, содержащей три скалярных множителя Я,, у, v:
- 8tl8jk). (l°.4O)
В случае симметрии тензора
Оцы = Опы = otm = e]m A°.41)
имеем F/ft6yt — Sn6yft) = 0, т. е. изотропный симметричный тензор
четвертого ранга содержит два скалярных множителя:
ет1 - MtJ8kl + у (бгйбя + 6tl8]k). A°.42)
§ 3. ГЛАВНЫЕ НАПРАВЛЕНИЯ И ГЛАВНЫЕ ЗНАЧЕНИЯ ТЕНЗОРА
ВТОРОГО РАНГА. ИНВАРИАНТЫ ТЕНЗОРА
На основании соотношения A°.37) тензор второго ранга {ац) мож-
можно определить как линейный оператор А, посредством которого про-
произвольному вектору х ставится в соответствие некоторый вектор у:
у = Ах, A°.43)
где А, как линейный оператор, обладает свойствами:
А (х + х0) = А (х) + А (х0), V
А (Кх) = Ы (х). | ( '
Здесь х и х0 — произвольные векторы; А. — скаляр.
Особую роль играет частный случай линейного оператора:
3» - Ах =* 1х, A°.45)
397

т. е. когда направления векторов у и х совпадают, а модуль вектора
у в X раз отличается от модуля вектора х.
В координатной форме равенство A °.45) запишется так:
Из сопоставления равенств A°.46) и A°.37) имеем
ацх, = Xxt. A°.47)
Если вектор л: при преобразовании посредством'тензора (atj), как
линейного оператора, изменяет только свою величину в X раз, а на-
направление его не меняется, то это направление называется главным
направлением тензора (аи), а величина X называется главным значени-
значением тензора.
Главные направления и главные значения тензора находятся ре-
решением системы уравнений A°.47), которую, поскольку xt = 6tiXj,
можно представить так:
(а„ - М,,)х, - 0. A«.48)
-Вектор х, указывающий главное направление тензора, не может
быть нулевым, т. е. xlt x2, xa не могут одновременно обращаться в нуль.
Следовательно, система однородных линейных уравнений A°.48) не
должна иметь нулевого решения. Поэтому определитель из коэффи-
коэффициентов этой системы должен быть равен нулю, т. е.
В развернутом виде уравнение A°.49), которое называется харак-
характеристическим уравнением тензора (at}), запишется так!
(an~X)
«31
«31-
«12 «13
(«22 "~ ^) «23
«
32
(«33—*)
= 0.
(Г°.49г)
Раскрыв определитель, получим кубическое уравнение относитель-
относительно X:
Хд- — /, (aw)A,* + h (at])X — /8 (atj) = 0, (l°.5O)
где
h (аи) =
«и
«21
«12
«22
+
«*
«3
«22 +
2 «23
2 «33
«33.
+
«чч
«13
«31
«и
а
11
«
14
а
13
«Л «42 «4S
йЛ «34 а88
Уравнение (Iе.50), как уравнение нечетной степени с действитель-
действительными коэффициентами, имеет по крайней мере один вещественный ко-
корень. Покажем, что в случае симметричного тензора (ац) все три корня
398

уравнения A°.5О) являются вещественными. Допустим противополож-
противоположное, т. е. два корня уравнения A°.5О) являются комплексными. Пусть
X* — один из них. Тогда, подставив Я* в систему A°.48) вместо X, най-
найдем комплексные значения х\, х\, xl, удовлетворяющие также равен-
равенству A°.47):
ai}x) = X*xh
Умножив обе части последнего равенства на х), комплексно-сопря-
комплексно-сопряженное с */, получим _
= Х*хп*1. A°.52)
Произведения комплексно-сопряженных чисел х\х\, как известно,
вещественные и положительные. Поэтому и те члены суммы в левой
части равенства A°.52); для которых / = г, будут вещественными. Ос-
Остальные члены, для которых / Ф i, рассмотрим попарно, объединяя,
например, члены с/ = 1,/ = 2ис/ = 2, /== 1. Учитывая симметрию
тензора (аЬ]), получим
= ^12 (xiX\ 4- x\xl). A°.53)
Выражение в скобках равенства A°.53) есть сумма двух комплекс-
комплексно-сопряженных чисел, и поэтому это выражение вещественное. Сле-
Следовательно, левая часть равенства A°.53) вещественная, как и выраже-
выражение при X* в правой части равенства A°.52). Поэтому и X* должно быть
вещественным, т. е. предположение, о существовании комплексных кор-
корней уравнений A°.5О) не подтверждается.
Таким образом, все три корня Х\, Хг, Х3 уравнения A°.5О) действи-
действительные и являются главными значениями тензора {аи).
Подставив в систему A°.48) вместо X главное значение Xh тензора
(atJ), найдем компоненты xf1 вектора xlk), определяющего соответст-
соответствующее главное направление тензора. Три главных направления тен-
тензора (главные оси тензора) являются ортогональными [29].
Как известно, корни Х^, Х2, Х3 кубического уравнения связаны'с
коэффициентами 1и 1г, 1д уравнения соотношениями
Ч, A°-54)
0
0
Х2
К
0
h
0
х.
=
0
0
^•з
0
0
х%
0
0
^¦1
0
0
Jig
Определитель из компонент тензора второго ранга .является инва-
инвариантом преобразования координатных осей. Действительно, имеем
\ац\ = |а^аг^,| - \ahi\ \au\ Hi\ = |а«|. 0°-55)
так как на основании A°.9) \aht\ = 1 и |аг;| = 1. Тогда
Iаи - X6tl | = Xs - 11 (аи)Х* + 1г (аи)Х - /8 (д„) Aв.5б)
есть инвариант, поскольку (аи — Я,б^) — тензор второго ранга.
399

Отсюда можно заключить, что коэффициенты Ilt /4, h уравнения
A°.50) и его корни %i, Хъ, А,,, т. е. главные значения тензора (аи), яв-
являются инвариантами относительно поворота координатных ¦ осей.
Тогда из сопоставления соотношений A°.51) и A°.54) следует, что
если координатные оси направить по главным осям тензора (atj), то
его диагональные компоненты au, a2a. я88 будут совпадать с главными
значениями тензора Xlt kif к3, остальные компоненты тензора будут
равны нулю, т. е. аи = 0 при i Ф /.
Равенства A°.51), определяющие инварианты Л, 1%, /з> которые
называются соответственно первым, вторым и третьим инвариантами
тензора, можно записать в следующем виде:
h (аи) = аи,
h (аи) = -у (ан ан—а„ аи),
U (au) = I fly | = — [% aih aJh — (aj3] +
Инварианты тензора четного ранга, как уже отмечалось, можно
также получить путем операции свертывания. Так, свертывая тензор
(аи), получим линейный инвариант «/х (ati) = аи, совпадающий с пер-
первым инвариантом /х {al}) = ait.
Образовав тензор-произведение (ati) {ahl) и свернув его по двум
парам индексов i и k, / и /, получим квадратичный инвариант Jt (ац) =>
= пцпц. Если образовать тензор-произведение (a;;) (amh) (а„я) и свер-
свернуть его по трем парам индексов i и т, /и п, k и s, to получим кубич-
кубичный инвариант Js{atj) = atjathalh.
Число независимых инвариантов тензора ограничено. Для тензо-
тензора второго ранга в трехмерном пространстве независимых инвариан-
инвариантов только три. Поэтому между линейным, квадратичным и кубичным
инвариантами тензора (аи)
Л (аи) = аш |
У4 (at,) = cttflts, A°.58)
и другой тройкой инвариантов, которые определяются равенствами
A°.57), имеют место зависимости
Jt (аи) - I\ (at}) — 2/8 (ati),
Jз (atj) — /f (atj) — 3/х (flj/)/4 (а^/) + 3/s
Если координатные оси направить по главным осям тензора (atj)t
то его компоненты а1} при i Ф j будут равны нулю, а диагональные ком-
400

ионенты apt будут главными значениями тензора К1г А.а, ка и в этом слу-
случае равенства A°.57) и A°.58) примут вид:
/i (ац) = К + К + К }
h (аи) = КК + К^ь + ^вК, [ A°.6О)
ls (аа) ¦¦=• ^ЛА»-
Л Ш = К + К + К )
А (а») - М + М + М, (l°.6l)
= X, + Ц + Ц. j
§ 4. ХАРАКТЕРИСТИЧЕСКАЯ ПОВЕРХНОСТЬ СИММЕТРИЧНОГО
ТЕНЗОРА ВТОРОГО РАНГА
Симметричному тензору второго ранга (а1}) соответствует централь-
центральная поверхность второго порядка, которая называется характеристи-
характеристической поверхностью тензора:
2/(У = а„^=±са, (Р. 62)
где atJ — компоненты тензора; |, и Ъ} — координаты произвольной
точки поверхности относительно декартовых осей с началом в центре
поверхности; в — постоянная.
Как известно из теории поверхностей, координатные оси всегда
можно направить так, что в уравнении A°.62) коэффициенты ai} при
/ Ф i относительно таких осей, называемых главными, обращаются
в нуль и уравнение центральной поверхности второго порядка приво-
приводится к каноническому виду
где at =з а^ — коэффициенты at] при / = L
Очевидно, что главные оси характеристической поверхности тензо-
тензора (fljj) совпадают в главными направлениями тензора, а коэффици-
коэффициенты at — g его главными значениями, т. е. at «== Kt.
При положительных и различных главных значениях тензора
(^ > "къ > ^з > 0) ег° характеристическая поверхность представ-
представляет собой эллипсоид
Если все три главные значения тензора одинаковы, например в
случае тензора (abtj), где а — действительное положительное число,
то характеристической поверхностью является сфера, а тензор назы-
называется шаровым. У шарового тензора все направления главные и, сле-
следовательно, его компоненты не меняются при повороте координатных
осей, т. е. шаровой тензор является изотропным.
Когда главные значения тензора имеют различные знаки напри-
например %i > ^г > 0, ^8 < 0, уравнение A°.63) необходимо записать в
двух видах:
К1\ + КЫ - |х„| U
14 Зак. 614 401

т. е. в этом случае характеристическая поверхность тензора представ-
представляется поверхностью однополостного гиперболоида A°.65) и поверх*
ностью двуполостного гиперболоида A°.66).
§ 5. РАЗЛОЖЕНИЕ СИММЕТРИЧНОГО ТЕНЗОРА ВТОРОГО РАНГА
НА ШАРОВОЙ ТЕНЗОР И ДЕВИАТОР
Симметричный тензор второго ранга (а^) можно разложить на два
симметричных тензора:
(аи) = (а&и) + (dit), A°.67)
где а — действительное число и, следовательно, (a8tj) — шаровой
тензор, главные значения которого ах = аг = а3 = а.
Если принять а — A/3)/,. (аи), то на основании A°.6О) первый,
второй и третий инварианты шарового тензора (абц) определяются
равенствами
1г (а&и) = За = Л (аи), - |
1, (а&1}) = За2 = A/3O! (а„), A«.68)
/, (а8и) = а3 = A/27O? (а„) )
Главные значения тензора {dij) с компонентами
dt, = ati - а8и A°.69)
определяются как корни характеристического уравнения
\dif - v6o| - О, A°.7О)
которое, учитывая A°.69), принимает вид
\аи — (v + аMи\ = 0. A°.71)
Из сопоставления характеристического уравнения A°.71) для тен-
тензора (dij) с характеристическим уравнением тензора
следует, что главные значения тензора (dtj) определяются формулой
Компоненты вектора л:, определяющего главное направление тен-
тензора (di}), т. е. величины^, находятся на основании A°.48) из системы
уравнений
(da - v&u)xj = fail—(v + а)8и]Х} = 0. A°.74)
Подставив в уравнения A°.74) вместо v главное значение v^ тензо-
тензора (dij) по формуле A°.73), получим систему
(аи - Ми)*/Л> = 0,A«.75)
из которой-следует, что главные направления тензора (dtj) совпадают
с главными направлениями тензора (atj).
402

Исходя из формул A°.6О) и учитывая A°.73), первый, второй и тре-
третий инварианты тензора (di}) определяются равенствами
Л (du) ="Vi + v2 + vs = О,
h (di}) = v4v2 + v2v3 + v8Vl = /2 (atJ) - A/3)/?
h (du) = V!V2vs = /s (als)—A/3)/, (at]) I2(au) + B/27)/? (a,,).
Тензоры, первый инвариант которых равен нулю, называются де-
виаторами. Таким образом, тензор (dt]) является девиатором тензора
(аи), т. е. (du) = Dev alt.
Линейный, квадратичный и кубичный инварианты девиатора
Dev au = (di}) на основании A°.59) и A°.76) равны:
Jx (Dev аи) = /х (Dev ati) = О,
J2 (Dev at]) = —2/2 (Dev ai7) = B/3)/? (au) — 2/2 (atl),
Ja (Dev flW) = 3/3 (Dev at]) = 3/8 (a,,) — A (a»)/, (aw) +
+ B/9)/'Паи).
§ 6. ТЕНЗОРНЫЕ. ПОЛЯ
Если в каждой точке М (хе) ? V (т. е. в точке М, принадлежащей
области V) задан тензор одного и того же ранга р как функция ее коор-
координат jcs, то область V называется тензорным полем ранга р, а тензор
называется тензором поля.
Примеры простейших тензорных полей.
1. Тензорное поле нулевого ранга (скалярное поле) задается од-
одной функцией трех переменных
а = a (xs), A°.78)
определяющей значение скаляра а в каждой точке М (ха) ? V.
2. Тензорное поле первого ранга (векторное поле) задается тремя
функциями трех переменных
at = at (xs), A«.79)
которые определяют компоненты вектора a = at9i (тензора первого
ранга) в каждой точке М (xs) ? V.
¦ 3. Тензорное поле второго ранга задается девятью функциями трех
переменных
в« = flu (*.), ' 0°.80)
которые представляют собой компоненты тензора поля второго ранга.
Примерами тензорных полей второго ранга являются поле нап-
напряжений и поле деформаций твердого тела.
Рассмотренные алгебраические операции над тензорами примени-
применимы и к тензорным полям, т. е. к тензорам поля в произвольной его точ-
точке.
Помимо алгебраических действий над тензорами поля производят-
производятся еще операции тензорного анализа — дифференцирование и интег-
интегрирование.
14* . 403

Пусть задано тензорное поле, например, третьего ранга
ат =• atjk (xt).
При переходе из точки М (xs) в произвольную бесконечно близ-
близкую точку М' (x$+dxs) компоненты тензора поля получат приращения,
главные линейные части которых равны
dauh = (datjh/dxi)dxi + (dat]h/dxz)dx2 + (dai]h/dx3)dx3 =
= (datik/dxt)dxa.
Величины йпць являются компонентами тензора третьего р'анга.
Действительно, при переходе к новому базису э\ — ait3t компоненты
тензора поля преобразуются по закону
а'1тп = auamJanhaUh, A°83)
где ан, ат}, anh — косинусы углов между ортами старого и нового
базисов, а значит, и не зависящие от координат xs.
Тогда, дифференцируя равенство A°.83), получим
т. е. при переходе к новому базису величины dai]k преобразуются по
закону A°.83) для тензора третьего ранга.
Тензор {йа.цк) называется абсолютным дифференциалом тензора
поля (aijh).
В левой части равенства A°.82) — компоненты тензора третьего
ранга, а в правой части компоненты dxs произвольного вектора dx =
>¦
= ММ' свертываются с величинами да^к/дх6. Тогда на основании
обратного тензорного признака величины daijh/dxa являются компонен-
компонентами тензора четвертого- ранга, который называется абсолютной про-
производной тензора поля.
Для компонент абсолютной производной используется обозначение
даак/дх, =
где после запятой ставится индекс той координаты точки М (xs), по
которой производится дифференцирование.
Для тензора поля аналогично можно получить абсолютный диф-
дифференциал и абсолютную производную второго и высших порядков.
Так, для тензора поля {aijk) вторые частные производные его компо-
компонент по координатам xs и хг, aijhsr образуют тензор поля пятого ран-
ранга, который называется абсолютной производной второго порядка.
В результате свертывания тензора (aljk eT) с dxe и dxr получается
тензор третьего ранга, который называется абсолютным -дифферен-
-дифференциалом второго порядка тензора поля (а^к):
сРа11Ч = aijhtST dxsdxT. ' A°.86)
Таким образом, независимо от порядка абсолютный дифференциал
является тензором того же ранга, что и исходный тензор поля, а аб-
абсолютная производная представляет собой тензор, ранг которого боль-
больше ранга исходного тензора на порядок производной.
404

§ 7. ФОРМУЛЫ ВЕКТОРНОГО И ТЕНЗОРНОГО АНАЛИЗА
Как известно, со скалярным полем ф (ха) связывается векторное
поле, определяемое вектором
grad ф = 9id<p/dxt = фл &и A°.87>
который называется градиентом скалярного поля ф (xs).
С векторным полем a (xs) связываются скалярное поле, определяемое
дивергенцией векторного поля
div a = dajdxi = alit,
и векторное поле, определяемое ротором вектора-
rot а = (а3,г — йг,зM1 "+" (а1,з — аздM2 + («гд ~~ ai,z)?
или
rot а = ei}hah<j9i,
где ет — компоненты тензора Леви — Чивита.
Операции вычисления градиента, дивергенции и ротора можно
записать g помощью символического вектора V — оператора Гамиль-
Гамильтона
A°.88)
A°.90>
следующим образом:
grad ф = Уф = фл-э,-,
div a = V-a = at t,
д
дх,
ai
д
дх,
о*
д
дх3
«я
rot a =
Напомним, что при действиях с оператором V надо пользоваться
правилами векторной алгебры и правилами дифференцирования. На-
Например,
. у (фг|)) = фУф + ф\7ф = ф grad i|) + t|? grad ф, V A°.95)
V x (a + b) = V x a + V X b = rot a + rot b. A°.96)
Приведем основные тождества, которые используются в книге:
div (фа) = V-(q>a) = ф\7-а + а-Уф = ф div а + а • grad ф, (Iе.97)
rot (фа) = V х (фа) = фУ X а + Уф X а = ф rot a +grad ф х а. A°.98)
div (о х ft) = S7-(axb) = b'V х а — а-У xb = &• rot а — а -rot b,
div (rot а) = У- (V X а) = О,
rot ( grad ф) = У X (Уф) = 0, ,
div ( grad q>) = У- (Уф) = У2ф = ф,„,
A°.1ОО)
A°.101)
A°.1О2)
405

rot (rot a) = V x (V x a) = V (V • a) — V2a = grad (div a) — V4a,
r V r?i
Лапласа (лапласиан); V2cp == ф_ц — скаляр; V2a — вектор с ком-
компонентами п) Ц.
Дифференциальные операции в векторном поле обобщаются на
тензорные поля любого ранга.
Например, для тензора третьего ранга (aiJh) градиентом, обозна-
обозначаемым V (Qjjfc) или grad (aijh), является тензор четвертого ранга g
компонентами ацк t.
Дивергенция тензорного поля представляет собой тензор, получае-
получаемый свертыванием двух последних индексов у компонент градиента
тензора поля. Так, для тензора второго ранга (at]) его дивергенция
V- (а„) = div (аи) = (atJJ) A
есть тензор первого ранга, т. е. вектор с компонентами аи].
Если тензор поля ранга п, то его дивергенция будет тензор ранга
(п - 1).
Из векторного анализа известна формула Остроградского
A801—1861)
\ §l § A405)
v» v s
или в прямоугольных декартовых координатах
)))ai^dV = ))ainidS> . (l°-106)
где V — односвязная область, ограниченная замкнутой гладкой или
кусочно-гладкой поверхностью 5; компоненты вектора (тензора пер-
первого ранга) at — непрерывные функции в замкнутой области (V + 5);
производные at t непрерывны в каждой точке области V; п — единич-
единичный вектор внешней нормали к поверхности S, компоненты кото-
которого «г = cos (я, xt).
Формула Остроградского применима к тензорам любого ранга.
Например, для тензора второго ранга (а(;)
¦(аи) dV = §n-(au) dS A°.1О7)
v
и соответственно
utijdS. A °.1О8)
В частности, для шарового тензора
406

и, так как (y&v)j = ф,|, б^ ns — nt, получим
S, AМ09)
или в векторной форме
yjgradcpfi[V= Jjcp/icfS. . A °.l 10)
Формула A°.1О8) для тензора второго ранга с компонентами emah
(«о* a*)j dV Г 1Д *<л flft.> dl/ = 1J еи* 'a^,dS, A». 111)
учитывая A°.90> и то, что eiihaknj = п X а, принимает вид
rot a fifK=
a) dV*= ff(»xa)dS. A°.I12)
Пусть функции ф (jcs) и v|) (л;8) имеют непрерывные производные вто-
второго порядка в (V +,S). Тогда, вычисляя поток векторного поля
t grad ф через S, но формуле Остроградского A°. 106) получим
Ф.» п, dS = j| j Инр.,)., dV =
Поскольку (pttnt — dq> Idn— производная по направлению п, по-
последнее равенство можно записать в следующем виде:
== f f f §rad^-grad<PdV + Crr
Равенство A°.113) называется первой формулой Грина. Переста-
Перестановка местами функций ф и v|) в равенстве A.113) и составление раз-
разности приводят ко второй формуле Грина:
2°. ТЕНЗОРЫ В КОСОУГОЛЬНОМ БАЗИСЕ
§ 1. КОНТРАВАРИАНТНЫЕ И КОВАРИАНТНЫЕ КОМПОНЕНТЫ ВЕКТОРА
Систему координат зададим с помощью некомпланарных векторов
et, модули которых, вообще говоря, различны. Эти векторы, направлен-
направленные по касательным к координатам линиям, образуют основной базис.
Взаимный базис определяется векторами
е' * е} х eh , B».1)
407

где V = <v(e2 X ?з) — объем параллелепипеда, построенного на
векторах еь основном базиса; i, /, k — составляют циклическую пере-
перестановку чисел 1, 2, 3.
Из этого определения вытекают соотношения
*' l==kt B°.2)
Любой вектор а можно представить его разложениями в основном
и во взаимном базисах:
а = a'ei = с,-е', B°.3)
где а' — контравариантные, «^ — ковариантные компоненты век-
вектора а.
Здесь и в дальнейшем дважды повторяющийся индекс (наверху и
внизу) является немым индексом, т. е. индексом суммирования.
Из-равенств B°.3) и B°.2) вытекает:
ак = а-ек, B°.4)
а* = а-е*. B°.5)
Установим зависимость между компонентами вектора в двух коор-
координатных системах, связанных формулами взаимно-однозначного пря-
прямого и обратного преобразования координатных векторов:
е* =» «*е, B°.6)
где eh 6i — векторы базиса старой системы координат; e'k, e} — векто-
векторы базиса новой системы координат; al и pi — коэффициенты соответ-
соответственно прямого и обратного преобразования.
Исключая из равенства B°.6) векторы е* на основании B°.7), а из
равенства B°.7) — векторы е/ на основании B°.6), получим:
h et =
Ввиду линейной независимости векторов e'k, как и векторов et, име-
имеем:
а1ф{ = fijL а/Р! == б(, B° .8)
где б* и б' — символы Кронекера, т. е.
B0.9)
Рассмотрим преобразование контравариантных компонент вектора
а, который в старой и новой системах координат представляется раз-
разложениями
а = а'е, = а'*е*. B°. 10)
С учетом формулы B°.7)
'i = a'ke'k.
408

Так как векторы ек линейно независимы, то
Используя формулу B°.6), из равенства B°. 10) аналогично полу-
получим
а1 = alka'k. B°. 12)
Таким образом, прямое преобразование B°. 11) контравариантных
компонент вектора а выполняется через коэффициенты обратного пре-
преобразования координатных векторов еи а обратное преобразование
B°. 12) — через коэффициенты прямого преобразования. Этим и объ-
объясняется название «контравариантные компоненты»."
Формулы преобразования ковариантных компонент вектора а по-
получим на основании равенств B.°4) и B°.7)
или, поскольку а-е\ = а/,
Исходя из B°.13), B°.8) и B°.9), находим
т. е.
alk = a'ka,. B°. 14)
Отсюда следует, что прямое преобразование B°. 14) ковариантных
компонент выполняется через коэффициенты прямого преобразования,
а обратное преобразование B°. 13) — через коэффициенты обратного
преобразования. Этим и объясняется название «ковариантные компо-
компоненты».
§ 2. МЕТРИЧЕСКИЙ ТЕНЗОР
Скалярное произведение векторов а и ft в косоугольной системе ко-
координат можно представить в бедующих формах:
Введем обозначения для скалярных произведений векторов ос-
основного и взаимного базисов:
gu = еге}, ёы = е*-е<, g\ = еге', & = е*.^. B°.16)
Очевидно, что
8ч = 8th ё" = в*, gl = 8t - «i- B°-17)
Равенства B°.15) принимают вид
аь — gua'bi == gklahbi = g^a'ft, = 6{a'bj = а1Ъ%. B°.i8)
'Косинус угла между векторами а и b
409

Квадрат модуля вектора а
| а |2 = о-о = gtjcta! = g4a,a, = ? а' а, = dat. B°.2O)
Квадрат расстояния между двумя точками евклидова пространства
М (х\ х2, х3) и iV (х1 + Ах\ х2 + Ах\ х* +
| MN |2 = As2 = gl}Ax{Ax< > 0. B°.21)
Положительно определенная квадратичная форма B°.21), харак-
характеризующая расстояние между двумя точками пространства, называ-
называется фундаментальной квадратичной формой. Коэффициенты gtj фун-
фундаментальной квадратичной формы полностью определяют метрику
пространства, т. е., зная эти коэффициенты, можно определить рас-
расстояние между двумя точками пространства (модуль вектора), а также
угол между двумя произвольными направлениями.
Величины gn представляют собой компоненты ковариантного тен-
тензора второго ранга, который называется метрическим тензором. Ана-
Аналогично, (g11) — контравариантный метрический тензор, (g'.j) — кон-
траковариантный метрический тензор и (gj!) — коконтравариантный
метрический тензор.
На основании B°. 17) метрический тензор является симметричным.
С помощью метрического тензора можно установить соотношения
между контравариантными и ковариантными компонентами вектора
а. Исходя из B°.4) и B°.3) имеем
а{ = a-et = e^eja1,
или
я, = gifif. B°.22)
Используя B°.5) и B°.3), найдем
а* = eka = ek-e!at,
или
а* = g*'a,. B°.23)
Равенство B°.22) можно рассматривать как систему линейных ал-
алгебраических уравнений относительно контравариантных компонент
а> вектора о. Решая эту систему, получим
ai = afi'l/g, B°.24)
где g — определитель матрицы метрического тензора, С— алгебраи-
алгебраическое дополнение элемента gtj определителя g.
Сопоставляя равенства B°.23) и B°.24), получим
gti = G"/g = (l/g) (dg/dgt,). B°.25)
§ 3. ТЕНЗОРНАЯ АЛГЕБРА В КОСОУГОЛЬНОМ БАЗИСЕ
По аналогии с представлением вектора (тензора первого ранга),
контравариантные и ковариантные компоненты которого при повороте
координатных осей преобразуются по формулам B°. 11) и B°. 14), можно
дать следующее определение тензора любого ранга и любого строение
(контравариантный, ковариантный).
410

Некоторый инвариантный объект называется т. раз контравариант-
ный и п раз ковариантный тензор ранга т + п, если в любой системе
координат трехмерного пространства он определяется совокупностью
Зт+" чисел Л/';"'".'. /™, которые называются компонентами тензора и
при повороте координатных осей преобразуются по закону
Обычно принимается общая нумерация мест индексов верхних и
нижних, так что каждому номеру отвечает лишь один индекс верхний
или нижний. Если, например, 1-й, 3-й и 4-й индексы расположены
наверху, то внизу под ними остаются «пустые» места, что отмечается
точками, и наоборот, т. е. используется обозначение Л'/.*1..
Отметим некоторые особенности алгебраических операций над тен-
тензорами в косоугольном базисе.
Сложение -тензоров. Складывать можно только тензоры
одинакового ранга и одинакового строения, т. е. с одинаковым чис-
числом верхних индексов и с одинаковым числом нижних индексов. На-
Например, при сложении тензоров (Л'/.'*}) и (B'J.'k'i) получим тензор
также четвертого ранга и того же строения с компонентами.
С1й= А'&+*& . Bо.27)
Умножение тензоров. Перемножать можно любые тен-
тензоры (любого ранга и любого строения) в заданном порядке. Ранг тен-
тензора-произведения равен сумме рангов тензоров-сомножителей. На-
Например, в результате тензорного умножения тензора второго ранга
(Л'/) на тензор третьего ранга В.['т получим тензор пятого ранга, ком-
компоненты которого определяются равенством
С??т=А[,В^т B°.28)
Свертывание тензора возможно только по индексам,
один из которых верхний (контравариантный), а другой нижний (ко-
(ковариантный). Свертывание по паре индексов приводит к снижению
ранга тензора на две единицы.
Свертывание тензора с тензором состоит в предварительном тен-
тензорном умножении их, а затем свертывании по соответствующим ин-
индексам тензоров-сомножителей.
Путем свертывания данного тензора с метрическим тензором вы-
выполняется операция «опускания» или «поднятия» индексов у данного
тензора. Эту операцию для вектора (тензора первого ранга) иллюстри-
иллюстрируют равенства B°.22) и B°.23). Пусть, например, два раза контрава-
контравариантный тензор a'i дважды свертывается с ковариантным метричес-
метрическим тензором. В результате получим два раза ковариантный тензор
(t'gmgji = ai'gn = «he B°-29)
Отметим, что операция перестановки индексов
'возможна только ковариантных индексов между собой либо контра-
вариантных индексов между собой.
411

§ 4 ТЕНЗОРНЫЙ АНАЛИЗ в КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
Пусть точки трехмерного пространства определяются тремя пара*
метрами х (i — 1,2,3), называемыми криволинейными координатами.
Кривые, вдоль которых изменяется лишь одна из трех координат, на-
называются координатными линиями.
Радиус-вектор г произвольной точки будет функцией криволиней*
ных координат
г "
Через каждую точку пространства проходят три координатные ли-
линии g касательными векторами
et - дг/дх' = dtr, . B°.31)
Векторы е,, являютвя функциями координат »' и имеют, вообще
говоря, различные модули, отличающиеся от единшда. Эти векторы
образуют локальный координатный базис.
Установим формулы преобразования векторов ви полагая, что ои*-
темя координат подвергается взаимно-однозначному точечному пре-
преобразованию,
х = х' (х'\ х' - x'J (х% B°.32)
И меем!
е, - дг/дхJ = (drldv) (дхЧдх'') -. et (дх1дх\ B°.33)
et = riridx' =. (дг/дх f) (дх Jldx<) = е) (dx'tdx'). B°.34)
Коэффициенты прямого преобразования B°.33) и обратного пре-
преобразования B°.34) являются функциями координат **,
Обозначим их соответственно!
а} - дхЧдх'' - а$ (**), B°.35)
pi « dx'Udx1 « 0i (х*). B°.3б)
Очевидно, что-.
ajpi - fi* и а?Э' = б|. Bе.37)
Рассмотренная тензорная алгебра в косоугольном базисе полностью
применима в случае криволинейных координат к тензорам в одной в
той же точке пространства с локальным базиеом et =* dtr.
В частности, метрический тензор gi} а случае криволинейных ко-
координат определяет метрику окрестности рассматриваемой точки и
является функцией- координат»
gu - ere, - (it, (x*). Bй.38)
Для двух бесконечно близких точек М (Xе) я N {$' + dxe) согласно
B».ЗО) и B°.31) имеем
dr - (drldx')dx' «- etdx*. B°.39)
Квадрат расстояния между этими точками
ds* « dr*dr ** eidx'-ejdxi « gtJdx'dxh Bu.4O)
412

Рассмотрим векторное поле, которое определяется вектором
а = а (г) =» а (*'), B°.41)
заданным его контравариантными компонентами
а = ехаК B°.42)
Найдем дифференциал вектора а, учитывая при этом , что его ком-
компоненты of зависят от базиса, векторы которого et — функции коор-
координат хН
da — eidaf + aldet. - B°.43)
Контравариантные компоненты дифференциала da обозначим че-
через Dai. По определению,
Da = ei*da, B°,44)
тогда
Da = ei-eida* + e^deia'. B°.45)
Учитывая, что
еье, = б'/ и ЬШ = da', B°.46)
а также
det = (detldxk)dxk, B°.47)
равенство B°.4б) принимает вид
Dd> - dd + ё!*(де№хк)а4х\ B°.48)
Введем обозначение!
eUdetldxk = е'*&гШдхк = T]k. B°.49)
Величины Г|а = rL называются вимволами Кристоффеля вто-
второго рода, учитывая которые, равенство B°.48) запишем
Da = М + Г|* a'dxK B°.5O)
Если векторное поле определяется ковариантным вектором
а = е%, B°.51)
то
da = e'dat + arfe1. B°.52)
Ковариаитные компоненты векхора da равны
D ddid + e,-de'at = da} + aiejt(de4dxk)dxk. B°.53)
Так как е^е1 = б) — тензор с постоянными компрнентами, то
или
егдеУдх" = -e''de,ldxk = —Г}». B°.В4)
Учитывая B°.54), равенству B°.53) придадим вид
Da, = daj- Т\к aidxk. B°.55)

Формулы B°.50) и B°.55) определяют контравариантные и кова-
риантные компоненты вектора da— абсолютного дифференциала век-
вектора а.
Поскольку дифференциалы компонент вектора а определяются ра-'
венствами
da' = (da<ldxk)dxk = dkaJdxk и
' da} - (da,/dxk)dxk - dhajdx", B°.56)
то формулы B°.5О) и B°.55) можно записать в следующих видах!
Dal = (дьа< + Т{к oQd**, B°.б7)
Da, = (dha, — T'lk at)dxk. B°.58)
На основании обратного тензорного признака выражения в скоб-
скобках равенств B°.57) и B°.58) представляют собой компоненты тензо-
тензоров второго ранга, которые называются ковариантными (абсолютны-
(абсолютными) производными вектора а. Для них принимают следующие обозна-
обозначения.
Ковариантная производная контравариантного вектора
Vhai •= dha' + Г{* а'. B°.59)
Ковариантная производная ковариантного вектора
Vka} = dha, — Тк of. Bе.60)
Теперь рассмотрим тензор поля воторого ранга (S1.)) (один раз кон-
травариантный и один раз ковариантный) и' произвольные векторы
(ai) и (Ь>). Образуем скаляр
Ф = S'.jatbl B°.61)
и найдем его дифференциал!
dq> = aibldS1.) + SV, tfdai + S1.) atdbl B°.62)
Подставим в B°.62) значения dai и db> из B°.5О) и B°.55)i
^ф ^ atbidS'.) + S'.j Ы (Dai + Г?3 Oadx») 4- S\)ai (Dbl — ltP badx^).
Производя в последнем равенстве переобозначение немых индексов
в членах о символами Кристоффеля, получим
dtp = S':,bi Dai + S'.jatDV + atV (dS'.j + S?/ Г^р dx* — S'.« Г^Р).
Левая часть полученного равенства и первые два члена в его пра-
правой части — скаляры. Следовательно, и последний член в правой чао-
ти — скаляр. Тогда на основании обратного тензорного признака вы-
выражение в скобках определяет компоненты некоторого смешанного
тензора второго ранга. Этот тензор называется абсолютным дифферен-
дифференциалом тензора (S'i'.):
ds'.) = ds1:, + rip sa;dx* — r%s':adxt. B°.63)
Легко подметить, что в формуле абсолютного дифференциала DS1.)
контравариантному индексу i соответствует со знаком плюс член с сим-
414

волом Кристоффеля второго рода, а ковариантному индексу / — со зна-
знаком минус. Тогда аналогично можно написать общую формулу для
абсолютного дифференциала тензора любого ранга и любого строения:
- т% Cg? dx* -... B4)
Ковариантная производная тензора ранга г является тензором ран-
ранга (г + 1) и на основании B°.64) определяется формулой
+Та?,Сц... + ГарC,/#* -f...
/3^a/.- — l0/C/a... —... B°.65)
Помимо символов Кристоффеля второго рода используются также
символы Кристоффеля первого рода:
= е, -(^r/ {dxidxk)=.et >(dek/dxt) = r,ih;, B°.66)
которые связаны с символами Кристоффеля второго рода.
Действительно, учитывая, что
el=g"et, . B°.67)
на основании B°.49), B°.67) и B°.66) получим •
Имеет место и обратная зависимость
Г,.,* = gurjk. B°.69)
Символы Кристоффеля можно выразить через компоненты метри-
метрического тензора. Исходя из B°.66)
Г|<й = A/2) ififdejldx" + ecdejdxi) = A/2) [д {ei-e})ldxk +
+ д (et-eh)/dxi — e}'detldxk — eh'det/dxU = A/2) (dgti/dxk +
+ dgtk/dxt — e,<deh/dx' — eh'de}ldxl) = A/2) (dgtj/dx" + dgtk/dxi —
- dgSkldx% B«.70)
Тогда
r'« (dgai/dxk + дёаЛШ - dgihldx«). B».71)
- При ковариантном дифференцировании используется теорема Рич-
чи A853—1925): ковариантная производная метрического тензора рав-
равна нулю.
Докажем это для ковариантного метрического тензора. На основа-
основании B°.65), B°.69) и B°.7О)
ta=-^~r/,,p-r<</B^0. B«.72)
Отсюда, в частности, вытекает
ГиР + Г,,,р. B°.73)

B°J4)
Можно также получить равенства V^g1' — 0, Vpg; == 0, т. е. при
ковариантном дифференцировании метрические тензоры ведут себя
как постоянные величины.
При ковариантном дифференцировании справедливы следующие
правила:
D (а-д) = a-Db + b'Da,
D (A + В) =DA + DB,
D (AB) « ADB + BDA,
D (aA) = ADa + aDA,
где a, b — векторы; А, В — произвольные тензоры; a — скаляр, при-
причем Da = da, т. е. абсолютный дифференциал скаляра совпадает a
обыкновенным дифференциалом.
§ 5. НЕКОТОРЫЕ ДИФФЕРЕ .ЦИАЛЬНЫЕ ОПЕРАЦИИ
В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
Ковариантное дифференцирование пригодно для любой системы
координат и имеет тензорный характер. Поэтому, выражая какую-ли-
какую-либо векторную операцию через ковариантные производные, получим вы-
выражение, справедливое в любой системе координат.
- В трехмерном евклидовом пространстве от общих криволинейных
координат, в которых квадрат расстояния между двумя бесконечно
близкими точками определяется формулой B°.40), всегда можно пе-
перейти к прямолинейной прямоугольной системе координат Хь =
= Хь (х'), в которой
ds2 = dxh dxb=—*- dx> ^% dxl. B°.75)
дх' дх'
Из сопоставления B°.40) и B°.75) имеем
gti = (dxh/dx') (dxjdxi). ¦ B°.76)
В случае ортогональных криволинейных координат компоненты
метрического тензора удовлетворяют соотношениям
где Hi — коэффициенты Ламе;
Ht = Vg^ = V(dxh/dxl)/(dxh/dx<) = | et [. B°.78)
Элемент объема в ортогональных криволинейных координатах
dV = e^'iezdx2- x e^dx3) = HxH^H^ih x i3)dxldx4x3- =
= H1H2H3dxldxidx'i = ygdxldx*dx\ B°.79)
где l$ = eJHs = ejVgTs — единичные векторы, направленные по ка-
касательным к координатным линиям в данной точке;
НгНгНъ - Vgng22g33 = >% B°.80)
413

В ортогональных криволинейных координатах символы Кристоф-
феля с тремя различными индексами на основании соотношений B°.70),
B°.71) и B°.77) равны нулю, а остальные определяются формулами
в которых не следует суммировать по одинаковым.индексам.
Если обозначить ортогональные проекции вектора а на направ-
направления единичных векторов ts локального базиса через ща), называемые
физическими компонентами а, то между ними, контравариантными и
ковариантными компонентами вектора имеют место соотношения
± ± B°.83)
У e?s
?s
Аналогичные формулы можно получить для тензоров второго и
более высокого рангов. Так, для тензора второго ранга имеем
«К,, (r)
Теперь перейдем к рассмотрению дифференциальных операций.
Градиент скаляра. На основании B°,65) ковариантная производ-
производная тензора нулевого ранга (скаляра) совпадает с частной производ-
производной
Угф = а«ф. B°.85)
Частные производные dty представляют собой ковариантные ком-
компоненты вектора, который называется градиентом скалярной функции:
(grad ф)| = дщ> = дфхК B°.86)
В случае криволинейных ортогональных координат, переходя от
ковариантных компонент к физическим по формулам B°.83), получим
^^. . B0.87)
Дивергенция вектора. Ковариантная производная контравариант-
ного вектора представляет собой смешанный тензор второго ранга.
Свернув этот тензор, получим скаляр, называемый дивергенцией век-
вектора
div a = Vta' = did + Y\kak. _ B°.88)
На основании B°.71) имеем
Г« = №ё1а [dgijdx\ + dgajjdx' - dgihldx%
где слагаемые
bdt -gladgth/dx«
417

уничтожаются; тогда,р ссылаясь на B°.25), получим
Г' =±
2 дхк 2g dgia dxk 2g dxk
dxk у^ dx»
Подставляя B°.89) в B°.88) и изменяя немые индексы 6 на i, полу-
получим
= V, а' = ^L- д, {а> Vg) = y^ dt {g« ak V^). B«.9О)
В ортогональных криволинейных координатах, пользуясь физи-
физическими компонентами, в силу B°.83) имеем
^Y B0.91)
Лапласиан скаляра. Подставив в формулы B°.9О) и B°.91) вектор
(grad ф), т. е. принимая в них а* = (grad ф)й == dhq> и а({) =
= (grad ф)({) = : dtcp, получим оператор Лапласа в произволь-
У8П
ных криволинейных координатах:
\72Ф == div grad Ф = -L dt (\/gglk dhq>) B°.92)
Vb
и в ортогональных криволинейных координатах:
B°'93)
Ротор вектора. В декартовых координатах компоненты rot а оп-
определяются выражениями вида
( rot a)t = да3/дхг — даг/дхй. B°.94)
Заменяя в случае криволинейных координат обыкновенные про-
производные ковариантными, получим компоненты ковариантного косо-
симметричного тензора второго ранга:
ath = V(ah — Vfta* = dtah — Гааа — dhat + T%Oa. = dtak — dhai.
B9.95)
Следовательно, компоненты rot а не зависят от метрики простран-
пространства. В трехмерном евклидовом пространстве тензору (coth) эквивален-
эквивалентен вектор с контравариантными компонентами:
w1=-Jy (д2 а3—д9 аг), со2 =—U (д3 а1—dt a3),
@3 = -pj(^a2—dtcQ. B0.96)
418

В случае ортогональных криволинейных координат в силу формул
B°.83) и B° .96) ^
=(rota\t)^ -^====-[д,{У^ка{к))—дк{У^aU))}, B°.97)
где ct(j) — физические компоненты вектора а, а индексы /, /, k прини-
принимают последовательно значения 1, 2, 3; 2, 3,1; 3, 1, 2.
Дивергенция тензора второго ранга. В декартовых координатах
дивергенция тензора (at]) определена [см. A°.1О4) ] как вектор с ком-
компонентами atjj. Следовательно, в криволинейных координатах дивер-
дивергенцию тензора получим, заменив обыкновенную производную кова-
рнантной, т. е. будем иметь вектор с компонентами
+ Т'а/а*' + Г/в о"*. B°,98)
Сделав подстановку согласно B°.89), получим
Yg дх*
или окончательно
V, oil = -L- BiVffn + Ki a«\ B0.99)
/ OX'
Выражения дифференциальных операций второго порядка над век-
векторами и тензорами весьма громоздки. Например, лапласиан вектора
определяется следующей формулой:
B°.1ОО)

ПРИЛОЖЕНИЕ II. ПРОГРАММА ДЛЯ ЭВМ НА ЯЗЫКЕ FORTRAN
РЕШЕНИЯ ЗАДАЧИ КРУЧЕНИЯ
1°. ПЕРЕХОД К БЕЗРАЗМЕРНЫМ ВЕЛИЧИНАМ
Функция Ф [кгс/см], удовлетворяющая G.33), G.13), G.26), зави-
зависит от следующих размерных величин: Ху [см], х% [см], Ау [см], Л г [см],
2Gb = К [кгс/см3], М [кгссм|, где Ау и Л2 — размеры области F в
направлениях соответственно Ху и хг,
В случае областей, показанных на рис 7.28 а, б, Аг = Аг = а [см]
и, кроме того, первая из них характеризуется еще размером Ъ [см], т. е.
Ф = Ф (xlt хг, а, Ь, К, М). A)
Осуществим переход к безразмерным величинам ( [48], т. 1, с. 393—
403).
За основные величины с независимыми размерностями примем
а [см] и К [кгс/см8]. Изменим их единицьГизмерения соответственно в
аа и <хк раз. Численные значения величин в новой системе единиц из-
измерения будут равны:
х\ = аахи Х2 = аахг, с? = ааа, Ь1 = aabt
К1 = аКК, М1 = а&кМ, Ф' = а1акФ.
Соотношение A) примет вид
Фг- = а|акФ = ф (х[, х'ч, а', Ь'\ К1, М'% B)
так как оно не зависит от выбора системы единиц измерения.
Положим, что аа = \1а, ак = \1К. При таком выборе масштабов
аа и ак значения а' и К1 будут равны 1, поэтому
Ф' = Ф/а2К =• ф (ху/а, хг/ау 1, Ыа, 1, М/а*К). C)
Для безразмерных величин введем обозначения;
U = Ф/а2К, Ху = Xyla, Ха =¦- хг!а, р = Ыа, у, — M/tfK. D)
Заметим, что
KU) ,, д* U Э2 Ф ,, d8 U
E)
дх]
Следовательно,
имеем
д(а
U+ 1
¦А дх> и
= 0, U\L
dxl
= 0.
Условие G.26) примет вид
М = а4Л> = Щ#Ки<1
Для жесткости С и напряжения а91 получим
М = а4Л> = Щ#Ки<1 (aXjd (аХг), т. е. ц =» 2^UdX1dX2. F)
Таким образом, задача сводится к нахождению у, — коэффициента
1 dt'
жесткости и - ^ параметра «сигма».
420

JO, ПРОГРАММА ДЛЯ ЭВМ (Б9СМ6) НА ЯЗЫК! PORTRAN
PROGRAM SIGMA
6OMM0N/B/ U (91. Щ. Y (91), Z (9Ц INT (90), KSTART B, 90), KFTNFS
(*. 90),
• JAU От, ТЛ A28). Ai, А2. N1, N3, В, ЦТ, МГ, HI, Ш. HHl, HH2, iV,
Sw, NT, RQ, T
• /Bl/ KVR
Аи s
— 1. | •) Задание манеимальных размеров облаоти F по Xj и Xs.
1
Nl-15
N2-15
Задание чиола интервалов оетка ао Xj в Хв (ем примеча-
примечание 4 а подпрерраммв NTAU).
Е = 0.00011 Задана* течнвотн решения равиэотнвй задачи.
ТО
т
71
DG 66 KVR - 1,2
РО 2 М «- 2. N2
INT 4Mi - !
KSTART (I, M)
RFINIS(l.M) -N12
IP(KVR=»JO0.70, 71
N23 — (N2/3)* 2
N123 - 1 + N23
DO 7 М- 123. N2
KPINIS A. M)»N23
KT =¦ N1+ !
MT - N2 + i
Задание облаоти F, т. e.I =¦ INT (m), KSTART
(I m), KPINIS (I, m) (ом о. 256). В данной
программе уаасматриаают две области Pi при
KVR=-1—рно.7.28,а, при KVR =2—рио. 7.28,-6
Примечание 1. Валн облаоть миоросвязная и через
Was обозначить максимальное значение INT (/л)
?я т "= 2, .... N2(cm. с 256), то а операторах
IMMON должны быть маовнвы KSTART Aшах,
„,), KPINIS (fraM. ...).
DO 1 К = 1, KT
D© 1 M => 1. MT
U (К, M) = 0.
GALL LAPLASr
Задание
начального
Примечание 2. В алучае многосвязной
области пользователь должен задавать
иа границах Ья (к > 1) постоянные Ф№
каюры» можно найи: ятерацнонно, ио>
приближения хчия иа формулы G,42).
DO 5 М = 1, МТ
IN - INT (M)
D0 4 К - I. KT
Z (К) - U (К, М)
Y (М) => 0.
DO 3 1 - 1, IN
KS1 = KSTART (I, M) - 1
KF1 = KPINIS (I, M) + I
Y ^M) = Y (M) + S(KS1. KP1, HI, Z)
SMOMEN=SA, MT, H2, Y) * 2.
Подсчет u =- SMOM E N
XX
((при этом попользуется подпро-
подпрограмма — функция S (Lj, ьР,
н. хи.
Задается польаова1елем.
421

80
31
32
41
81
33
40
66
DO 8 К = 1, 14
Y (К) = HI * К
PRINT 6, SMOMEN, (Y (К), К = 1, 14)
FORMAT (/, ' коэффициент жесткости = ',
El.2,11,' значения параметра «сигма» на границе
сечения F при указанных значениях Хг Y X, '
X, '! 14F 8.3)
РН2 = 0.5 /(Н2 * SMOMEN)
IF (KVR - 1) 80, 80, 81
DO 31 К = 2, N 23
Y (K)= PH2 * D.* U (К, N2)—3.* U (К, МТ) —
—U (К, N2—1))
20
21
22
2, N 23)
3.*U(K, N123)—
PRINT 40,- 1., (Y (К), К
DO 32 К = N123, N1
Y(K) = PH2* D.* U (К, N23)
—U(K, N23 — 1))
Ха = N 23* Н2
.PRINT 41, 42, (Y, (К), К = N123, N1)
FORMAT (F 5.3, F 83.2, 4F8.2)
DO 33 К = 2, N1
Y (К) = РН2 * D. * U (К, 2) — 3. * U (К, 1) —
-U (К, 3))
PRINT 40, 0., (Y, (К.;, К= 2, N1)
FORMAT (F 5. 3, '¦', 14F8!2, /////////)
Печать ц.= SMOMEN,
подсчет и печать гра-
граничных значений
dU
а также
абсцисс вычисляемых
производных.
CONTINUE
RETURN
END
SUBROUTINE LAPLAS
COMMON/В/ U (91,91), Y (91), Z (91), INT (90), K.START B. 901,
KFIN1SB, 90),
TAU B56), TJ A28), Al, A2, N1, N2, E, KT, MT, HI, H2, HHI, HH2, SV,
SW, NT, RC, T-
/Bl/ KVR
HI = A17N1)
H2 = A2 /NT2
Вычисление шагов сетки по Xj и Х2<
HHI = 1 . /(HI * HI)
НН2 = 1 . /(Н2 * Н2)
IF (KVR — 1) 20, 20, 21
SV = 24 . 6/ (Al * A2)
GO TO 22
SV = 20. /(Al * A2)
SW = 4 * (HHI + HH2)
Задание нижней границы спектра разност-
разностной задачи (см. 157]); при KVR = 1 —
рис. 7.28, a, npnKVR = 2 — рис. 7.29, 6.
Вычисление верхней границы спектра —
см [57].
NU = 0
DO I L = 1,3
CALL NTAU
DO 2 JNU = 1, NT
T = TAU (JLU)
CALL ITERA
NU = NU + NT
CALL RCR
IF (RC — E) 6, 6, 1
CONTINUE
Решение разностной задачи модифицированным
итерациониым методом Ричардсона [57].
Примечание 3. За счет цикла DO I L = 1, 3
итоговое число итераций имеет вид NU = 2NS'-^
+ 2 г + 2NS', где NS; считается в подпрограм-
подпрограмме NTAU. Благодаря этому итоговое NU (при
Nx, N2 ~ 100) можно сделать не слишком боль-
большим, например 216 + 64 4- 16 = 296 вместо
21" = 512.
422

6
8
PRINT 8, Л1. N2, RG, NU
FORMAT (' число интервалов по X2 Y X2 i N1=', 13, ', N
итоговая невязка в метрике * G *| RG = ', E7, 2. * : общее
раций: N NU = ' 13)
RETURN
END
N2 = ', 13, ';
число и'те-
SUBROUTINE NTAU
COMMON /B/ U (91, 91),
KFIN1S B, 90),
• TAU B56), TU A28), Al, A2, N1,
SV, SW, NT, RO, T
CALL" RCR
NS = 1 . 5* @ . 5*
+1)) - 0.5 IF (NS - 1)
1 NS= 2
GO TO 3
2 IF (NS - 8) 3, 3,
4 NS = 8
3 NT = 2**NS
TAU A) = 1.
TAU B) = 2.
NSi = NS— 1
TJU = 1.
DO 5 N = 1, NSI
TJN = TJN + TJN
JNT = TJN
DO 9 К = 1, JNT
9 TJ(K) = TAU(K)
DO 5 К = 1, JNT
K2 <= К + К
TAU (K2 — 1) = TJ (K)
5 TAU (K2) = TJN +TJN+1. — TJ (K)
TN = 1./NT
DO 6 I = 1; NT
6 TAU (I) = 2./((SW + SV) + (SW — SV)*
(I) -1 )) * TN))
RETURN
END
Y (91), Z (91). INT (90), KSTART B, 90).
N2, E, KT, MT, HI. H2, HH1, HH2.
ALOG (SW/SV) + ALOG (ALOG (RC/E + J.) -f
I, 1, I
В подпрограмме NTAU вычисляются; г
а) параметр NT, при этом 4 < NT < 256;
б) итерационные параметры щ (j — 1, ,.,, NT).
Примечание 4. Первая строчка оператора COMMON
резервирует в памяти машины массивы: U, Y, Z,
INT, KSTART и KFINIS в предположении, что
Nf и Na < 90. Если Ы1 и Na желательно взять боль-
большими, то нужно резервировать большую память.
COS (A,5708* (TAU (I) + TAU
SUBROUTINE ITERA
COMMON/B/U (91, 91), Y(91), Z (91), INT (SO), KSTART B, 90),
KFINIS B, 90),
TAU B56), TJ A28), Al, A2, N1, N2, E, KT, MT, HI, H2, HH1, HH2,
SV, SW, NT, RG. T
DO 1 К = 1, KT
г (к) = о.
DO 2 M = 2, N2
К = I, KT Подпрограмма ITERA осуществляет итерацию
Z (К) матрицы U с текущим итерационным параметром
Т = %j (см. [57]).
М)
DO
Y(K)
Z (К) = U (К,
IN = INT (M)
DO 2 I = 1, IN
KS = KSTART (I, M)
KF= KFINIS (I, M)
DO 2 К = KS, KF
Z2 = Z (K) + Z (K)
I/ (K, M) = Z (K) + T* ((Z (K-l)-Z2 + Z (K + 1)) * HHI
— Z2 + U (К, М + 1)) * HH2 + 1.)
(Y (K) -
42.3

3°. РЕЗУЛЬТАТЫ СЧЕТА ДЛЯ СЕЧЕНИЯ,
Число интервалов no XtnX2i N1=l5, Л/2=15; итоговая иевязка в метрике
Матрица U:
0.00+00 0.00+00 0.00+00 0.00+00 0.00+00 0.00+00 0.00+00 0.00+OQ
0.00+00'
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00 0.00+00 0.00+00 0.00+00 0.00+00 0.00+00 0.00+00 0.00+00
6.33—03
1.05—02
1.34—02
1.54—02
1.68—02
1.78—02
1.84—02
1.85—02
1.82—02
1.74—02
1.60—02
1.39—02
1.09—02
6.57—03
1.04—02
1.78—02
2.31-02
2.70—02
2.97—02
3.16-02
3.27—02
3.30—02
3.24—02
3.09-02
2.83—02
2.44—02
1.88—02
1.09—02
1.30—02
2.27—02
2.98—02
3.52—02
3.91—02
4.18—02
4.33—02
4.38—02
4.31—02
4.11—02
3.74—02
3.20—02
2.44—02
1.39-02
1.46—02
2.56-02
3.40—02
4.04—02
4.51—02
4.86—02
5.07—02
5.14—02
5.07—02
4.83—02
4.40—02
3.74—02
2.83—02
1.60—02
1.51-02
2.68—02
3.58—02
4.27—02
4.81—02
5.22—02
5.49—02
5.61—02
5.56—02
5.31—02
4.83—02
4.11—02
3.09—02
1.74—02
1.48—02
2.62—02
3.51—02
4.22—02
4.80—02
5.28—02
5.63—02
5.81—02
5.79—02
5.56-02
5.07-02
4.31—02
3.24—02
1.82—02
1.34-02
2.36—02
3.17—02
3.84—02
4.45-02
5.03—02
5.48—02
5.76—02
5.81—02
5.61—02
5.14—02
4.38—02
3.30—02
1.85—02
Матрица невязок, т. е. матрица A + лапласиан (U) в области ГО);
7.2—08
4.3—09
7.5—08
2.2—07
2.6—07
2.9—07
2.2—07
7.7—08
1.8-07
1.6—07
1.4—08
4.0-08
1.6—07
1.0—07
5.6-08
6.4—08
•1.7—07
4.1-07
5.2-07
5.7—07
3.9—07
2.0-07
3.5-07
3.1—07
1.0—07
1.2-07
3.2-07
1.6—07
1.4—07
2.6-07
3.8—07
6.4—07
8.0—07
8.0—07
4.4—07
1.7—07
3.6—07
3.3-07
2.3—08
6.3-08
1.2—07
4.0—08
2.8—07
4.4—07
5.4—07
8.0—07
1.0—06
9.8—07
5.2—07
2.3—07
5.0—07
5.2—07
2.0—07
2.3—08
1.0—07
1.4—08
2.5—07
4.2—07
4.9—07
7.1—07
9.6—07
9.3-07
5.2—07
2.7-07
5.5—07
6.9-07
5.2-07
3.3-07
3.1—07
1.6—07
7.9-08
2.9—07
3.4—07
5.2—07
7.9—07
7.1—07
3.4—07
1.5—07
4.0—07
5.5-07
5.0—07
3.6—07
3.5-0?
1.8—07
—1.2—07
4.8—08
6.2—08
1.5—07
3.8—07
3.6—07
9.7—08
—7.6—09
1.5—07
2.7—07
2.3—07
1.7—07
2.0—07
7.7—08
Коэффициент жесткости = 4.88—02
Значения параметра «сигма» на границе сечения FO при указанных значениях
x*\x,
0.000
.667
!ooo
0Л67
2.28
2.36
0
3
3
,133
.65
.83
0.
4.
4.
200
51
82
0
5.
5
.267
01
49
0.333
5.19
5.93
0.400
5.07
6.19
0.467
4.62
6.29
424

ПОКАЗАННОГО НА РИС. 7-28, а
«С»: RC=1, 02— Об,; общее число итераций: NU
0.00+00 0.00+00 0.00+00
1.08—02 6.61—03
1.88—02 1.J2—02
2.52—02 1.48—02
3.09-02 1.85-02
3.70—02
4.44—02
5.07—02
5.48—02
5.63—02
5.49—02
5.07—02
4.33—02
3.27—02
1.84—02
2.38—02
3.52—02
4.44—02
5.03—02
5.28-02
5.22—02
4.86—02
4.18—02
3.16—02
1.78—02
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00 0.00+00 0.00+00 0.00+00 0.00+00
-о.оо+оо
0.00+00
0.00+00
0.00+00
0.00+00
'0.00+00
0.00+00
0.00+00
о.оо+оо
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
0.00+00
о.оо+оо
0.00+00
0.00+00 0.00+00 0.00+00 0.00+00
0.00+00
о.оо+оо
0.00+00
0.00+00
0.00+00
о.оо+оо
о.оо+ео
о.оо+оо
0.00+00
0.00+00
0.00+00 0.00+00 0.00+00 0.00+00 0.00+00 0.00+00 0.00+00 0.00+00
2.38—02
3.70—02
4.45—02
4.80—02
4.81—02
4.51—02
3.91—02
2.97—02
1.68—02
1.85-02
3.09—02
3.84—02
4.22—02
4.27-02
4.04—02
3.52—02
2.70—02
1.54-02
1.48—02
2.52—02
3.17—02
3.51-02
3.58—02
3.40—02
2.98—02
2.31—02
1.34—02
1 .12—02
1 .«8—02
2.36—02
2.62—02
2.68-02
2.56—02
2.27—02
1.78—02
1.05-02
6.61-03
1.08—02
1.34—02
1.48—02
1.51—02
1.46—02
1.30—02
1.04—02
6.33-03
—1.7—07
—3.7—08
—6.7—08
—8.8—08
7.3-08
8.7—08
—1.3—08
9.7-08
3.4—07
5.2—07
5.2—07
4.4—07
5.9—07
2.0—07
-7.9—08
1.7—08
3.6—08
2.2-09
5.5—08
3.4—08
8.7—08
3.6—07
7.1—07
9.3—07
9.8—07
8.0—07
5.7—07
2.9-07
5.5—08
7.3—08
3.8—07
7.9—Q7
9.6—07
1.0—06
8.0—07
5.2-07
2.6—07
2.2—09
—8.8—08
1.5-07
5.2—07
7.1^-07
8.0—07
6.4—07
4.1—07
2.2—07
3.6-08
—6.7—08
6.2—07
3.4—07
4.9—07
5.4—07
3.8—07
1.7—07
7.5-08
1.7—08
—3.7—08
4.8—08
2.9—07
4.2—07
4.4—07
2.6-07
6.4—08
4.3—09
—7.9—08
—1.7—07
—1.2—07
7.9—08
2.5—07
2.8—07
1.4—07
5.6—08
7.2—08
X!
0
3
6
и Ха:
.533
.76
.26
0
2
6
.600
.35
.09
0
8
5
.667
:эз
.79
Р.
6
5
733
.61
.32
О
5
4
.800
.24
.66
0.867
3.97
3.71
О
2
2
.933
.40
.29
425

RETURN
END
SUBROUTINE RCR
COMMON /В/ О (91, 91), Y (91), Z (91), INT (90), KSTART B, 90),
KF-IN1S B, 90),
* TAU B56), TJ A28), Al, A2, N1, N2, E, KT, MT, HI, H2, HH1, HH2,
SV, SW, NT, RC, T
RC= 0.
DO 1M = 2, N2 Подпрограмма RCR считает невязку RO
IN = INT (M)
DO1I = 1, IN в метрике С, т. е. RC = max| VJ)/n U|F+ 1|.
k; m I I I
KS = KSTART (I, M)
RF= K.FINIS (I, M)
DO 1 К = KS, KF
U2 = U (К, М) + U (К, М)
А = (U (К — 1, М) - U2 + U (К + 1. М))* НН1 + (U (К, М — 1) —
— U2 + U (К, М + 1)) * НН2 + 1.
. R = ABS (А)
IF(RC- RK,.l, I
3 RC = R
I CONTINUE
END
FUNCTION S (LS, LF, H, X)
DIMENSION X (91)
L = LF — LS
M = L/2 Подпрограмма — функция S (LS, LF. H, X)
M2 = M + M
S = 0. считает одномерный интеграл с использо
S2 = 0.
S4 = 0. ванием формулы Симеона.
IF (L — М2) 2, 2, 1
1 S= 1.5 *(X(LF— 1)+(X (LF))
2 LF2 = LF - 2
DO 3 1 = LS, LF2, 2
S2 = S2 + X (I)
3 S4 = S4 + X A + I)
4 . S = S + (S2 + S2) + 4. * S4 + X (LS -f M2) - X (LS)
S = H* S/3.
RETURN
END

ЛИТЕРАТУРА
Основная
1. Амензаде Ю. А. Теория упругости. М., 1976.
2. Лейбенэон Л. С. Курс теории упругости. М., 1947.
3. Лурье А. И. Теория упругости. М., 1970.
4. Ляв А. Математическая теория упругости. М., 1935..
5. Мусхелишвили Н. И. Некоторые основные задачи математической теории
упругости. М., 1966.
6. Новожилов В. В. Теория упругости. Л., 1958.
7. Папкович П. Ф. Теория упругости. Л., 1939.
8. Тимошенко С. П., Гудьер Дж. Теория упругости. М., J975,
9. Филоненко-Бородин М. М. Теория упругости. М., 1959.
Дополнительная
10. Арутюнян Н. X., Абрамян Б. Л. Кручение упругих тел. М.> 1963.
11. Балабух Л И., Шаповалова Л. А. О вариационных уравнениях термоуп-
термоупругости. — ПММ, 1960, № 24.
./ 12. Безухое Н И. Примеры и задачи по теории упругости, пластичности
и ползучести. М., 1965.
13. Безухое Н. И., Лужин О. В. Применение методов теории упругости и
пластичности к решению инженерных задач. М., 1974.
14. Березин Н С, Жидков Н П. Методы вычислений. М., 1962, т. 2.
15. Бидерман В. Л. Винтовая пружина прямоугольного оечения, как ци-
цилиндрическая оболочка. — Изв. АН СССР. Механика и машиностроение, 1963,
№4.
16. Бидерман В. Л., Шитиков В. Н. Растяжение и кручение ленточных
цилиндрических пружин при больших перемещениях. — Изв. АН СССР. Меха-
Механика твердого тела, 1970, № 1.
17. Бидерман В. Л., Князева В. А. Антиплоская деформация ортотропиого
кривого бруса прямоугольного сечения. — Изв. вузов. Машиностроение, 1972,
№6.
18. Ван Цзи-де. Прикладная теория упругости. М., 1959.
19. Галин Л. А. Контактные задачи теории упругости. М., 1953.
20. Демидов б. П. Исследование напряжений плоского кривого бруса лря-
моугольиого сечения. — В кн.: Расчеты на прочность в машиностроении. М.,
1953.
21. Демидов С. П. Чистый изгиб кривого бруса прямоугольного сечения. —
Науч. тр./МВТУ, 1953, кн. 26.
22. Демидов С. П. Расчет на прочность кривого бруса прямоугольного се-
сечения. — Науч. тр./МВТУ, 1955, кн. 31.
23. Джанелидзе Г, Ю. Принцип Сен-Веиаиа. — Науч. тр./ЛПИ им. Кали-
Калинина, 1958, № 192.
24. Дьяченко В, Ф« Оеновиые понятия вычислительной математики. М.,
1972.
,25. Жермен П. Механика сплошных сред. М., 1965.
26. Зенкевич О. Метод конечных элементов в технике. М., 1975.
27. Ильюшин А. А. Механика сплошной среды. М., 1971.
28. Канторович Л. В., Крылов В. И Приближенные методы высшего ана-
анализа. М., 1962.
29. Кильчевский Н. А. Элементы тензорного анализа и его приложение к
механике. М., 1954.
30. Коваленко А. Д. Основы термоупругости. Киев, 1970,
427

31. Колосов,Г. В. Применение комплексной переменной к теории упругости.
М., 1935.
32. Купрадзе В. Д. Методы потенциала в теории упругости. М., 1*964.
33. Лаврентьев М. А.,Шабат Б. В Методы теории функций комплексного
переменного. М., 1964.
34. Ландау Л. Д., Лифшиц Е. М. Теория упругости. М., 1965.
35. Лейбензон Л. С. Вариационные методы решения задач теории упруро-
сти. М., 1943.
36. Лехницкий С. Г. Теория упругости анизотропного тела. М., 1950.
37. Лехницкий С. Г, Кручение анизотропных и неоднородных стержней.
М., 1971.
38. Лурье А. И. Пространственные задачи теории упругости. М., 1955.
39. Me из Дж. Теория и задачи механики сплошных сред. М., 1974.-
40. Миндлин Р Д Влияние моментных напряжений на концентрацию на-
напряжений. — Механика, 1964, Л"» 4.
41. Михлин С. Г. Вариационные методы в математической физике. М., 1957.
42. Нейбер Г. Концентрация напряжений. М., 1947.
43. Цовацкий В. Теория упругости. М., 1975.
44. Постное В. А., Хархурим И. Я Метод конечных элементов в расчетах
судовых конструкций. Л., 1974.
45. Расчеты на прочность в машиностроении/ Пономарев С. Д., Бидер-
ман В. Л., Лихарев К- К. и др. М., 1956—1959, т. I—III.
/ 46, Рекач В. Г. Руководство к решению задач по теории упругости. М., 1966.
47. Савин Г. Н. Распределение надряжений около отверстий, Киев., 1968.
48. Седов Л. И Механика сплошной среды. М., 1970, т. 1. 2.
49. Смирнов В. И. Курс высшей математики. М., 1954—1957, т. I—IV.
50. Соляник-Красса К В. Кручение валов переменного сечения. М., 1973.
61. Справочник по теории упругости/ Под ред. Варвака П. М., Рябо-
Рябова А. Ф Киев, 1971
52. Справочник. Прочность, устойчивость, колебания/ Под ред. Бирге-
ра И. А., Пановко Я. Г. М., 1968, т. I.
53. Тарабасов Н. Д. Расчеты напряженных посадок в машиностроении. М.,
1961.
54. Тарабасов Н. Д. Новый прием решения задач прессовых сондинений. —
В кн.: Расчеты на прочность. М., 1969, вып. 14.
55.-Тимошенко С. П. История науки о сопротивлении материалов. М.,
1957.
56. Угодников А. Г., Длугач М. И., Степанов А- Е. Решение краевых задач
плоской теории упругости на цифровых и аналоговых машинах. М., 1970.
57. Федоренко Р. П Итерационные методы решения разностных эллиптиче-
эллиптических уравнений. — В кн.г Успехи мат. наук, 1973, т. 28, вып. 2.
58. Феодосьев В. И. Избранные задачи и вопросы по сопротивлению ма-
материалов. М., 1953.
59. Филин А. П. Прикладная механика твердого деформируемого тела. М.,
1975, т. I.
60. Чернышев Н, А. Напряженное состояние и деформации пружин, свиты;
из круглого прутка. — В кн.: Динамика и прочность пружин. М., 1950.

ОГЛАВЛЕНИЕ
Предисловие 3
Введение , 4
Глава I. Теория деформации 7
§ 1. Вектор перемещения и деформированное состояние 7
§ 2. Тензор деформации - 8"*
§ 3. Представление нелинейного тензора деформации через
линейный тензор деформации и тензор малого поворота 12
§ 4. Тензор малой деформации 14
§ 5. Преобразование компонент тензора деформации при
повороте координатных осей 15
§ 6. Однородная деформация. Потенциал перемещении ... 16
§ 7. Главные деформации и инварианты тензора деформации 18
§ 8. Поверхность деформации 20
§ 9. Шаровой тензор и девиатор деформации ....... 21
§ 10. Определение перемещений по компонентам тензора де-
деформации. Условии совместности деформаций ... 22
§ 11. Определение перемещений через компоненты тензора
относительно перемещении 26
Глава 11. Теория напряжений 28
§ 1. Внешние силы .... 28
§ 2 Вектор напряжения и напряженное состоиние .... 29
§ 3. Тензор наприжений 30
§ 4. Дифференциальные уравнения равновесия и симметрия
тензора наприжений 33
§ 5. Статическаи неопределимость задачи определения тен-
тензора иаприжений 37
§ 6. Преобразование компонент тензора напряжений при
повороте координатных осей 38
§ 7. Главные напряжения и инварианты тензора наприжений 39
§ 8. Поверхность наприжений 40
§ 9. Эллипсоид ¦ напряжений 42
§ 10 Круговая диаграмма 44
§ 11. Шаровой тензор и девиатор напряжений . 48
Глаза 111. Соотношения между компонентами тензора деформации и
компонентами тензора напряжений 49
§ 1. Термодинамика упругого деформирования 50
§ 2. Упругий потенциал и дополнительнаи работа ..... 54
§ 3. Обобщенный закон Гука 56
§ 4. Обобщенный закон Гука для однородного изотропного
тела 60
§ 5. Упругие постоянные и другие формулы заиона Гука для
однородного изотропного тела 61
§ 6. Формула Клапейрона и формула Кастильяно .... 66
¦ § 7. Формула Бетти 66
§ 8 Удельная потенциальная энергия деформации и удель-
наи дополнительнаи работа линейно-упругого тела ... 67
§ 9. Соотношении между напряжениими и деформациями изо-
изотропного тела при изменении его температуры 67
429

Глава IV. Основные уравнения и задачи теории упругости ...... 70
§ 1. Основные уравнения 70
§ 2. Основные задачи статики упругого тела ....... 71
§ 3. Прямая и обратная Задачи теории упругости 72
§ 4. Уравнения упругого равновесия в перемещениях . . 73 ¦
§ 5. Общее решение уравнений в перемещениях ..... 76
§ 6. Основные уравнения в напряжениях 78
§ 7. Полуобратный метод Сен-Венапа 81
§ 8. Принцип Сен-Веиана 82
§ 9. Простейшие задачи теории упругости . 83
§ 10. Метод суперпозиции 89
Глава V. Общие теоремы и вариационные принципы 90
§ 1. Теорема Клапейрона 90
§ 2. Теорема о единственности решения 91
§ 3. Теорема Бетти 93
§ 4. Вариационные принципы 96
§ 5. Принцип минимума потенциальной энергии 98
§ 6. Принцип минимума дополнительной работы 101
§ 7. Вариационный принцип Рейсснера 105
§ 8. Полный функционал статики линейно-упругого тела 106
§ 9. Метод Ритца 108
§ 10. Метод Бубнова—Галеркнна 109
§ 11. Метод Канторовича 111
§ 12. Метод Треффца 111
Глава VI. Уравнения теории упругости в криволинейных координатах 116
§ 1. Основные уравнения и соотношения в криволинейных
координатах 116
§ 2. Компоненты метрического тензора и символы Кристоффе-
ля для некоторых ортогональных криволинейных
координат . 119
§ 3. Уравнения в полярных цилиндрических координатах 125
§ 4. Уравнения в сферических координатах 129
Глава VII. Кручение прямых брусьев 132
§ 1. Постановка задачи и основные уравнения 132
§ 2. Перемещения при кручении призматических брусьев
и теорема о циркуляции касательного напряжения ... 138
§ 3. Функция кручения _ 142
§ 4- Теорема о максимуме касательного напряжения ... 147
§ 5. Мембранная аналогия '. 148
§ 6. Брус эллиптического сечеиия . 152
§ 7. Кручение бруса, поперечное сечение которого пред-
представляет собой равносторонний треугольник 154
§ 8. Кручение бруса прямоугольного поперечного сечения 157
§ 9. Кручение бруса круглого сечения с продольной полу-
полукруглой канавкой 162
§ 10. Кручение бруса с поперечным сечение^ в виде сек-
сектора круга (рис. 7.18) . 164
§ 11. Комплексная функция кручения J66
§ 12. Метод конформного отображения 168
§ 13. Напряжения в вершинах выступающих и входящих
углов контура поперечного сечения 175
§ 14. Прямые методы решения вариационной задачи кручения 177
§ 15. Метод конечных разностей (метод сеток) ¦ . . 184
§ 16 Кручение брусьев многосвязиого замкнутого тбнко»
стенного профиля 187
§ 17. Кручение круглых брусьев переменного диаметра ... 194
§ 18. Кручение анизотропных брусьев .198
430

Рмыа VIII. Изгиб прямых брусьев 203
§ 1. Постановка задачи и основные уравнения 203
§ 2. Центр изгиба , 206
§ 3. Изгиб бруса эллиптического поперечного сечения . . . 20?
§ 4. Изгиб бруса прямоугольного поперечного сечения ... 211
§ 5. Центр изгиба для бруса о полукруглым поперечным ее-
чением 215 ,
§ 6. Вариационная постановка задачи изгиба 218
§ 7. Некоторые замечания 222
Глава IX. Плоская задача теории упругости 224
§ I. Плоская деформация 224
§ 2. Функция напряжений .- 226
§ 3. Плоское напряженное состояние 228
§ 4. Обобщенное плоское напряженное состояние 2$
§ 5. Перемещения в плоской задаче ............ 232
§ 6. Механический смысл функции Эри и граничные условия -
для нее 234
§ 7. Теорема Леви—Мичелла ".'.... 238
§ 8. Представление бигарм^нической функции 239
§ 9. Плоская задача в декартовых координатах 240
§ 10. Плоская задача в полярных координатах 260
§ 11. Комплексное представление функции напряжений . . 286
§ 12. Комплексное представление компонент тензора напря-
напряжений и перемещений 28&
§ 13. Степень определенности функций ф (z) и if (г) .... 290
§ 14. Граничные условия, которым должны удовлетворять
функции Колосова—Мусхелишвили 293
§ 15. Формулы Колосова в ортогональных криволинейных
координатах 295
§ 16. Общее решение основной задачи первого типа для бес-
бесконечной плоскости с круговым отверстием 296
§ 17. Плоскость с круговым отверстием, к контуру которого
приложено равномерное давление . . . . 298
§ 18. Действие на плоскость сосредоточенного момента . . . 293
§ 19. Действие на плоскость сосредоточенной силы .... 300
§ 20. Одностороннее растяжение пластины с малым круговым
отверстием (задача Кирша) 302
§ 21. Пластина с малый круговым отверстием при нагруже-
нии в двух направлениях 304
§ 22. Конформное отображение 306
§ 23. Интегралы Коши. Граничные значения голоморфных
функций 308
§ 24. Общее решение для областей, ограниченных одним
замкнутым контуром 311
§ 25. Решение основной задачи первого типа для круга . . 314
§ 26. Круговая пластина, загруженная по контуру некоторой
совокупностью сосредоточенных сил 316
§ 27. Решение основной задачи первого типа для бесконечной
плоскости с эллиптическим отверстием 319
§ 28. Одноосное растяжение пластины с эллиптическим от-
отверстием ... 321
§ 29. Всестороннее растяжение пластины в эллиптическим
отверстием -. 323
§ 30. О концентрации напряжений на концах прямолинейной
щели 324
§ 31. Вариационная постановка плоской задачи 325
§ 32. Метод конечных элементов 328
Глава X. Контактные задачи 337
431

пая просьба
|ъ и рассматриваю
л ф«лграф|иит д.
. ра^краши-
§ 1. Элементарное решение первого типе 337 '
§ 2. Центр растяжения (сжатия) в бесконечном теле ". ,¦ . 339
§ 3. Элементарное решение второго типа 341
§ 4. Действие сосредоточенной силы на плоскую границу
полубесконечного тела (задача Буссинеска) 343
§ 5. Давление между двумя соприкасающимися телами (за-
(задача Герца) 347
Глава XI. Кривые круговые брусья 365
§ 1. Кольцевые криволинейные координаты "... 365
§ 2. Основные уравнения 367
§ 3. Метод приближенного определении компонент тензора
напряжений . -, 371
§ 4. Брус круглого поперечного сечения . 376
§ 5. Бруо прямоугольного поперечного сечения [20] .... 381
Приложение I. Элементы тензорного исчисления
1°. Тензорное исчисление в прямоугольных декартовых коорди-
координатах 390
§ 1. Определение тензора 390
§ 2. Тензорная алгебра 393
§ 3 Главные направления и главные значения тензора вто-
второго ранга. Инварианты тензора 397
§ 4. Характеристическая поверхность симметричного тензора
второго ранга 401
§ 5. Разложение симметричного тензора второго ранга на
шаровой тензор и девиатор . . . .» 402
§ 6. Тензорные поля 403
§ 7. Формулы векторного и тензорного анализа ..... 405
2°. Тензоры в косоугольном базисе 407
§ 1. Контравариантные и ковариантные компоненты вектора 407
§ 2. Метрический тензор 409
§ 3. Тензорная алгебра в косоугольном базисе 410
§ 4. Тензорный анализ в криволинейных координатах . . . 412
§ 5. Некоторые дифференциальные операции в криволиней-
криволинейных координатах 416
Приложение И. Программа для ЭВМ на языке FORTRAN решения
задачи кручения . 420
1°. Переход к безразмерным величинам 420
2°. Программа для ЭВМ (БЭСМ—6) на языке FORTRAN .... 421
3°. Результаты счета для сечения, показанного на рис. 7.28, а . 424
Литература 427
Сергей Петрович. Демидов
ТЕОРИЯ УПРУГОСТИ
Редактор Г. Н. Самошкина
Художник В. 3. Казакевич
Художественный редактор И. К. Гуторов
Технический редактор Э.' М. Чижевский
Корректор Г. И. Кострикова
ИБ № 1624
Изд. № ОТ-266. Сдано в набор 18.D7.78. Подп. в печать 26.12.78.
Формат 60x90'/i6. Бум. тип. № 2. Гарнитура литературная. Печать высокая.
Объем 27 усл. печ. л. Уч.-изд. л. 23.11. Тираж 20 000 экз. Зак. № 514. Цена 1 р. 20 к.
Издательство «Высшая школа». Москва, K-5I, Неглинная ул., д 29/14
Московская типография № 4 Союзиолигрэфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли
г. Москва, 1290-11, Б. Переяславская ул., д. 46-