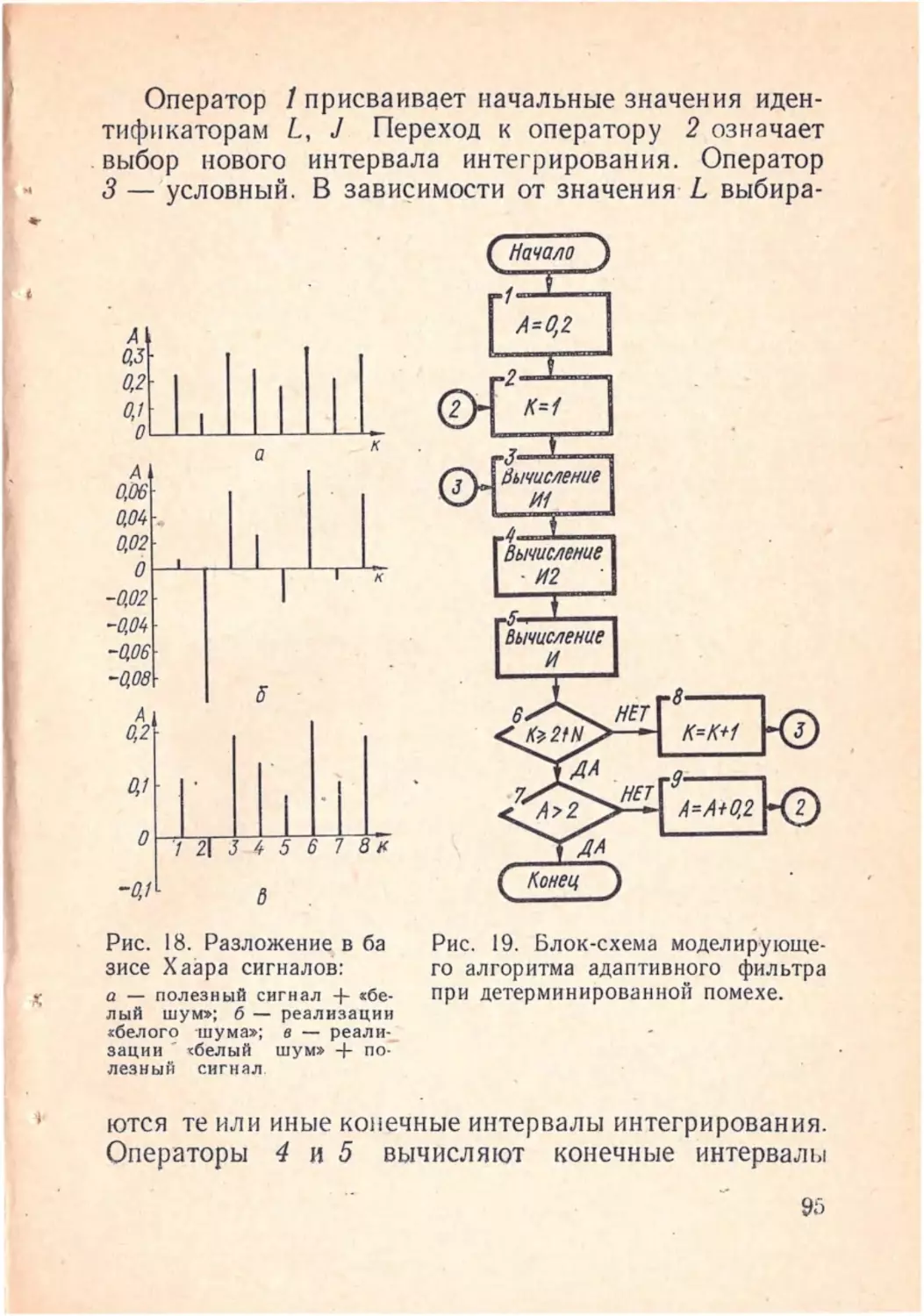
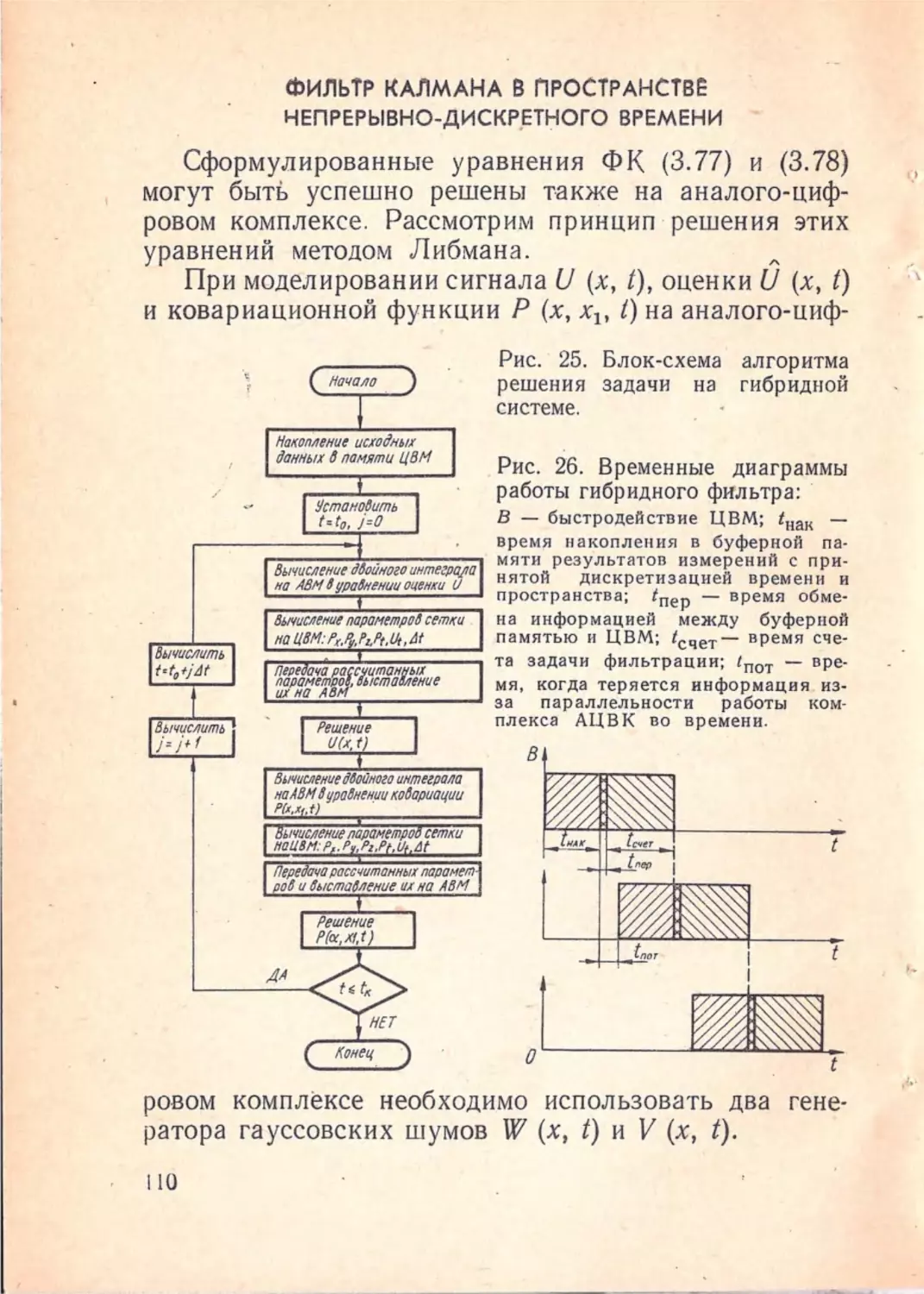
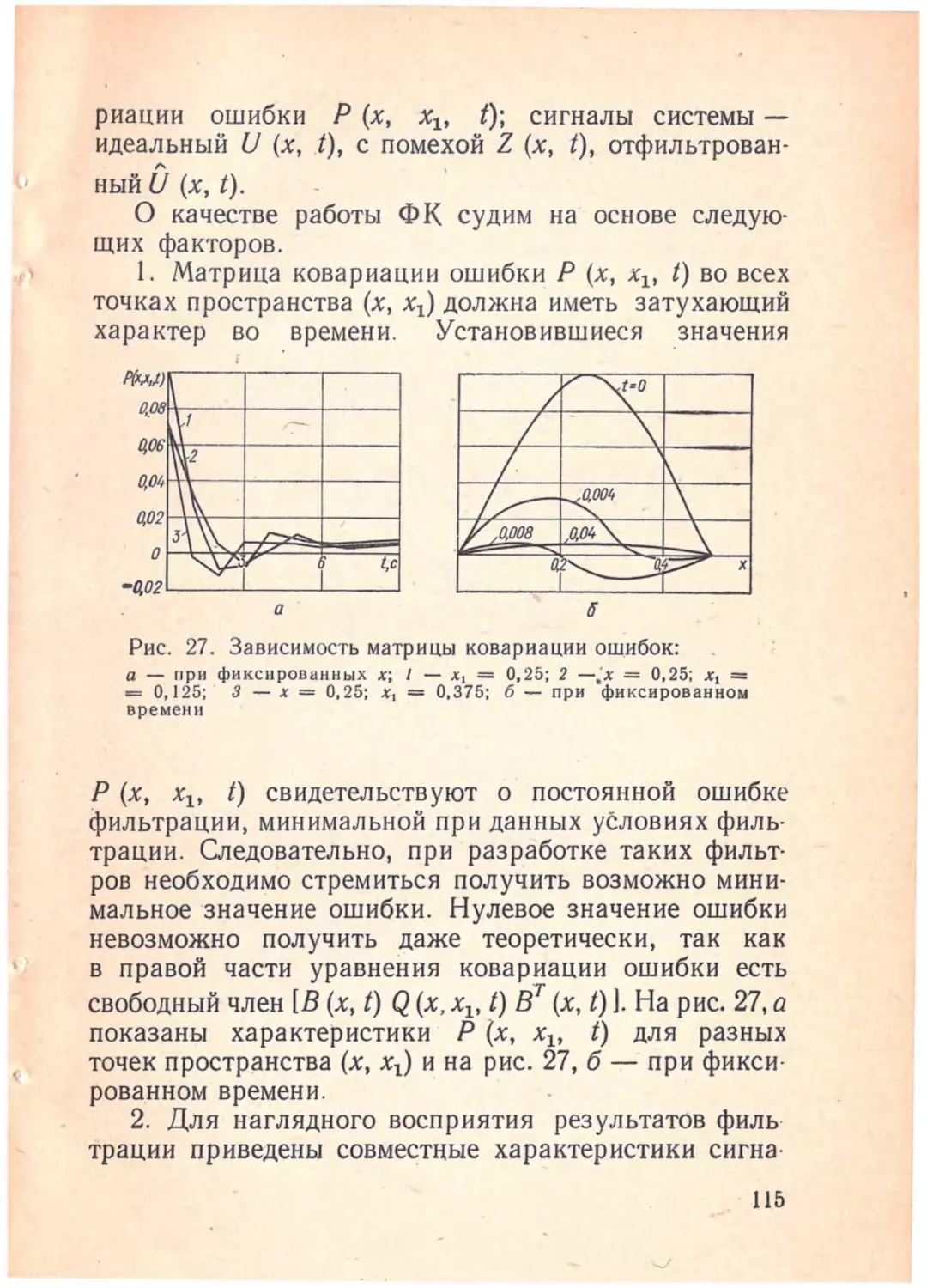
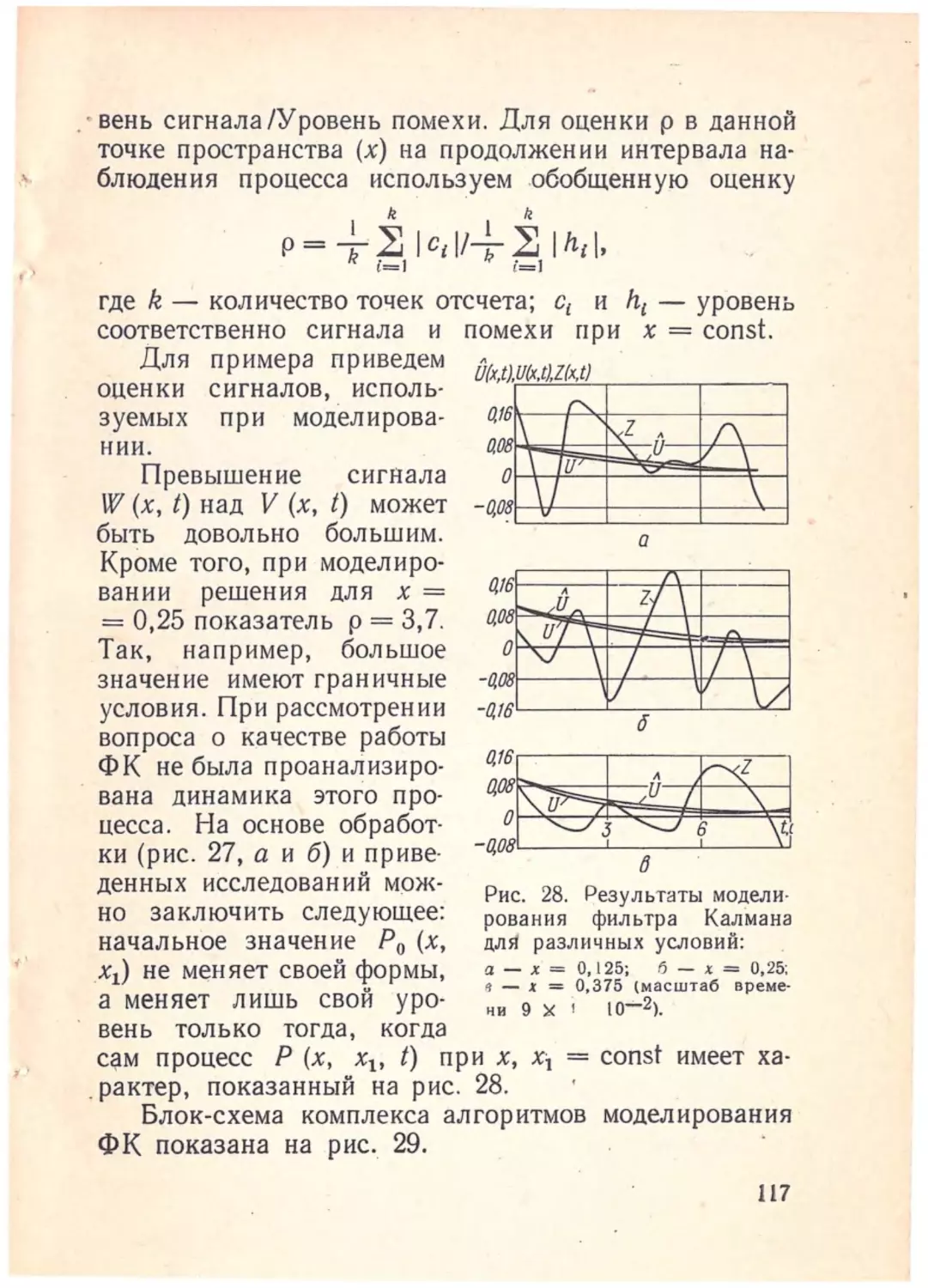
Author: Полонников Р.И. Костюк В.И. Краскевич В.Е.
Tags: электротехника электроника обработка сигналов кибернетика теория автоматического управления
Year: 1977
Text
\)
j
·~
/',
ПS 8~37 .
.
1
1
1(
Р . И. ПОЛОННИКОВ,
в. и: костюк,
В. Е. КРАСКЕВИЧ
МАТРИЧНЫЕ
МЕТОДЫ
ОБРАБОТКИ
СИГНАЛОВ
О SH-43 7
-
1
6ФО.1
П52
УДК
•
621 .391
Матричные методы обработки сигналоn. П о л о н •
н и к о в Р . И., К. о с т ю к
В. И . , К р а с к е.
в и ч )3 . Е. Киев, !<Технiка», 1977. 136 с .
Изложены новые матричные методы обработки сиг
налов и показано их применение при комплексной
микроминиатюризации
_радиоэлектронной
аппара
туры . В основу этих ме:годов положен обобщенный
спектральный ан<\ЛИЗ, предоставляющий исследова
телям широкий
класс систем ортонормированных
базисных функций для получения спектров сигнала .
Показано, что наиболее удобными в практической
реализации при построении радиоэлектронной ап
паратуры
на
интегральных микросхемах
являются
функции Уолша и Хаара. Рассмотр е ны устройства
цифровых фильтров и обуча е мых распознающих
устройств для систем с сосредоточенными и распре
деленными
параметрами.
Рассчитана на инженеров, работающих в области
технической кибернетики, радиоэлектроники и си
стем автоматического управления , и может быть
полезна
студентам
. соответствующих
специальнос
тей .
Табл.
7.
Ил.
32.
Список лиt.:
31
назв.
Рецензент д-р техн . наук Р. М . Юсупов
Редакция
литературы
по энергетике, электронике,
кибернетике и связи
_.
Зав. редакцией З. В. Божко
30401 -105
П М202 (04)-77
46"77
@издательство «ТеJ1нiка», 1977
:-
ПРЕДИСЛОВИЕ
Основным направлением развития радиоаппар.ато
строения
ция,
является
комплексная ,
предполагающая
широкое,
микроминиатюриза
комплексное
ние методов и средств микроэлектроники,
ральной электроники,
в
Jо\ли
внедре
интег
развитие технической базы
радио- и электронного приборостроения' в схемос
и системотехнику. С внедрением этих методов и средств
открываются новые, чрезвычайно широкие возможнос
ти
по «крупноблочному строительству» аппаратуры
самого разнообразного назначения и, что само'е су
щественное, увеличивающейся функциональной слож
ности.
С появлением микроэлектроники стало возмож
ным реализовать практически большое разнообразие
схем с переменными параметрами, что в значительной
мере способствовало повышению интереса
к другим
системам полных и ортогональных базисных функций.
Наибольшее
полным
предпочтение,
прямоугольным,
однако,
отдается · сейчас
ортонормированным
систе~
мам базисных функций и в' первую очередь функциям
Уолша и
Н<!
<.'
основе
Хаара. Обобщенный спектральный анализ
использования
этих
и
некоторьтх
других
функций является в настоящее время математиче
ским аппаратом на-иболее адекватным как современной
элементной базе микроэлектроники, так и основным
тенденциям ее развития. Использование в качестве
3
базисной системы функщ1й Уолша, принимающих на
+
всем интервале только два значения
1 и -1,
избавляет от необходимости реализации операций
умножения функций и позволяет синтези·ровать циф
ровые фильтры, всевозможные спектральные анализа
торы и другие устройства обработки сигналов без при
менения индуктивностей, тем самым исключая один
из наиболее сложных в микроэлектронике элементов.
Весьма интересные перспективы, связанные также с
применением функций Уолша, открываются и при по
строении фазированных антенных решеток (ФАР),
при синтезе оптимальных сигналов, при разработке
обучаемых распознающих систем, при решении цеJю
. го
ряда
9адач
оптимизации
и
численного
анализа.
Данная книга является попыткой систематизиро
ванного,
хотя
и
краткого,
изложения
последних
до
стижений в области обобщенного спектрального ана
лиза
и
матричных
методов
применительно
к
решению
задач обработки сигналов. При ее написании прихо
ди'Jюсь учитывать то обстоятельство, что методы обоб
щенного спектрального анализа, применение функций
Уолша и быстрого преобразования Адамара еще ма
ло зю:1комы широким кругам инженеров-разработчи
ков и поэтому нуждаются в подробном раз~;,яснении
и популяризации.
Глава 1 написана совместно Р . И . Полонниковым,
В . И . Костюком, В. Е. Краскевичем; глава 2 Р. И. Полонниковым; глава 3 - совместно В. И. Кос
тюком, В. Е. Краскевичем и Р. И. Полонниковым;
глава 4 - Р. И. Полонниковым.
·
Замечания и отзывы просьба направлять по адресу:
252 601,
во
Киев,
«Технiка».
1,
ГСП, Пушкинская,
28,
издательст
_
·
Гла в а
1
ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
В ПРЯМО УГОЛЬНЫХ
ОРТОГОН~ЛЬНЫХ БАЗИСАХ
t.
ДИСКРЕ Т НЫЕ ФУНКЦИИ УОЛШД
И ПРЕОБРА З ОВАНИЕ
АДАМАРА
Появление
новых
экономичных
методов
спек
тральн. ого анализа позволило ускорить процесс полу
чения спектра в сотни и даже тысячи раз
без увели
чения
роль здесь
быстродействия
ЭВМ .
Решающая
принадлежит методам быстрого преобразования Фурье ,
Адамара и Хаара.
·
Представление сигнала в виде суммы синусоидаль
ных
и
косинусоидальных
единственно
составляющих
возможным. _В
наиболее
не
является
общем
виде,
оставаясь в рамках· линейных представ.Пений, любой
сигнал
можно
рассматривать
как
совокупность
эле
ментарных функций (сигналов), взятых с некоторыми
весами . Совокупность элементарных функций обычно
называют системой базисных функций, а - представле
ние сигнала в
виде суммы
-
разложением сигнала
по
системе базисных функций . Набор весовых коэффи
циентов называют спектром сигнала . Используя эти
представления, удобно рассматривать сигнал как век
тор в многомерном пространстве.
Тогда
система
базисных функций образует в этом пространстве сис
тему координат (координатных функuий), а спектр
являетс;я
проекцией вектора-сигнала на соответст
вующие оси координат .
Рассмотрим преобразование Адамара и представ
ление
сигнала
с
использованием
базисных функций
Уолша.
5
Дискретные, функции Уолша (ДФУ) образуются
равномерной выборкб'Й непрерывных функций Yoл-
ша. Пронумеруем моменты выборки i
общем
N=I
= ~
·
ik2k при
k=O
количестве _ моментов выборки и
дИскретных
. функций Уолша N = 2п. Обозна,Чим ДФУ:
wi (i, N), wal (i, N);
J
са!
~j,
i,
N),
sal
(j,
i,
N);
1
h; (t, N).
r;
Для. описания свойств дискретной функции Уол
ша примем следующую форму записи:
(i, N) =
W;
W; (т:/Т0) б (t- iт:) .
.
К основным свойствам ДФУ относятся:
ортогональность
N-1
~ W; (i, N) Wk (i,
N) =
2nбik,
j=O
где б1k
..,..... символ
Кронекера;
полнота
N-1
~ W; (i, N) W; (k, N) = 2nбlk;
i=O
симметрия
W; (i, N)
= wi (j, N);
мультипликативность
W;
(i, N) wk (i, N) = W;fIЭk (i, N).
Прямое и обратное преобразования Адамара оп
ределяются
соотвЕ:!тственно
f* (j)
N-1
= ~
f (t) = 2-п
6
i=O
N-1
следующим
-
w, (i, N) f (i);
~ W; (i,
i=O
N) f* (j).
обрс;~зом:
Пара преобразований обозначается
f* (j) +- ~ f (i).
(1 .1)
Преобразования Адамара можно записать
в
мат-
ричной форме:
f* == HNf; f = (IJN) HNf*,
f* = [f* (О), f* (1), ... , f* (N - l)]r
f (1), .••. , f (N - 1)] - векторьнтолбцы;
где
т
('•
ца
Адамара
порядка
и
.f = [f (О),
N- матри-
Н
определяемая из
N,
условия
нNн~ =NI.
Строки матрицы Н соответствуют дискретным функциям· Уолша и принимают значения ± 1. В соответствии с различными формами записи функций Уолша
строки матрицы Н размера N х N могут быть упорядочены согласно с номерами функций :
wi (i,
N); HN - hi (i, N) - собственно
Nwal - wal (j, i, N).
Для N = 8 (п = 3)
1
~
нw
=
1
1
1
1
1 -1 -1
1
~1
Адамара;
1
1
1
-1 -1 ...:._ 1
1
1
1 -1 -1
1 -1 - J -1 -1
1
1
1
1 -1
1 -1
1 -1
.1 -1
1 -1 -1
1
1 -1
1 -1
1 -1 -1
1
1 -1 -1
1
1 ...:._ 1 -1
1 -1
1
1 -1
1
1
1
1 -1
1
1 -1
HN= 11 -11 -11
1 -1
1
1 -1
1
1 -1 - 1
1
'-.-(
1
1
Hw -
матрица
1
-1
-1
1
1
1
1
1 -1
1 -1
1 -1 -1
1
1
1 -1 -1
1
1 -1
-1 -1
. :. .__ 1 -1
-1
1 -1
1
-1
-1
1 -1
- 1
1
1
1
1 -1
7
1
1
1
1
1
1
1
11
1
1
1 -1 -1 -1 -1
1
1 -1 -1 -1 -1
1
1
1
1 -'- i -1
1
1 -1 -1
1 -1 -1
1
1 -1 ...:._ 1
1
1 -1 -1
1 -1
1
1 -1
1' - 1
1 -1
1 -1 -1
1
1 -1
1 -1
1 -1
1 -1
Hwal =
Перечисленные ниже основные свойства преобра
зования Адамара справедливы независимо от способа
упорядqчения матрицы Н.
f
1. Преобразование Адамара
(i) отличается от
функции
(i EFJ k) только множителем, равным зна
чению ДФУ wi (k, N) (теорема сдвига):
f
N-1
~ wi (i, N)
Dk {f (i)}
= wi (k, N)
f* (j),
1=0
.
Dk {f (i)} = f (i EFJ k) - двоичный оператор сдвига.
2. Преобразование Адамара от диодной (логической) свертки двух дискретных функци~ f (i) и g (i):
где
N-1
N-1
~ wi (i, N) .~
преобразование
g* (j),
Адамара · от двоичной
двух функций равно произведению
преобразований (теорема свертки).
3. Если
функции
.
(j)
k=O
i=O
т. е.
f (i ЕJЭ· k) g (k) = f*
f (i)
и
g (i) -
их
произвольные дискретные
и
f (i) +- -+f* (k); g (i) +--+ g* (k), .
N-1
то
~
1=1
8
f (i) g (i)
свертки
дискретных
N-1
= 2-п ~
k=\
f* (k) g* (k)
1
'
"
или
в
матричном
виде
( g = 2 -п(Т g*
(теорема Парсеваля).
4. Сложение вектора с постоянной:
·>
(/) + Nаб (l).
составляющая вектора f*
f (i)
5.
Нулевая
+а+--+ f*
с точностью
до множителя 2-п есть среднее составляющих вектора f:
f* (О)
N-1
= ~
f (i).
i=O
Среднее суммы составляющих вектора
нулевую составляющую вектора f:
f (О) =
6.
N-1
2-п ~
i=O
f*
f*
(j) .
Свойство симметрии. Если f +--+ f*, то ~
2.
дает
+--+ f.
ФАНТОРИЗАЦИЯ МАТРИЦ дДАМдРд
Быстрое преобразование Адамара (БПА) можно по
лучить разложением матрицы НN
f
>
ние
матриц
Гуда
G, [28]
отличных от нуля членов
числение
спектра
f*
с
(N -
2п) в произведе-
небольшим
п-1
HN .
п
количеством
.
G,. Поэтому вы-
r=О
можно
представить
следующим
образом:
9
ИJIИ в виде · последовательности преобразований
',
!1 = Gof;
!2=G1f1;
1·
f* = f ~ = Gn-lfn-1·
Матрица. G,, представленная
нальной матрицы
-
А (r)
1
1
2n-r-t
l)_.
виде
блочно-диаго
1 ]
1А(r)1
G=
r
содержит
2, . ", п -
в
(1.2)
1
11
А (r)
-
отличных от нуля блоков (r
Подматрицы А
(r)
= 1,
находятся кais Кро
некерово произведение ]\1атриц:·
А
(r) = Н2 @/2 •
(1.3)
Для п = 3 и N = 8 на основании выражений (1.2)
и
(1.3) .
А(О) =Н2 ;
A(l)
=Н2 @/2 ; _ А(2) =Н2 @/4;
Н2
. Go (8)
Н_2
1
----:-'
1
2
Н
= i-;----1 --;--1
1
10
1
/
1
1
где Н2_ = [ 11
1].
-1
Граф БПА, соответствующий этому разложению,
пою1зан на рис. 1. Ввиду симметриЧности матриц
Адамара
Рис.
1. Граф бь1ётроrо преобразования Адамара .
Из выражения
(1.4),
представляющего собой одlс\У из
возможных мqдификаций матриri Адамара, следует,
что
БПА
f!Меет
два
- алгоритма;
-с;оотgетствующих
прямой и обратной последовательности сомножителей
в произведении матриU: G,. Друrой подход к синтезу
БПА состоит в. разбиении HN на б.т~оки с последующей
11
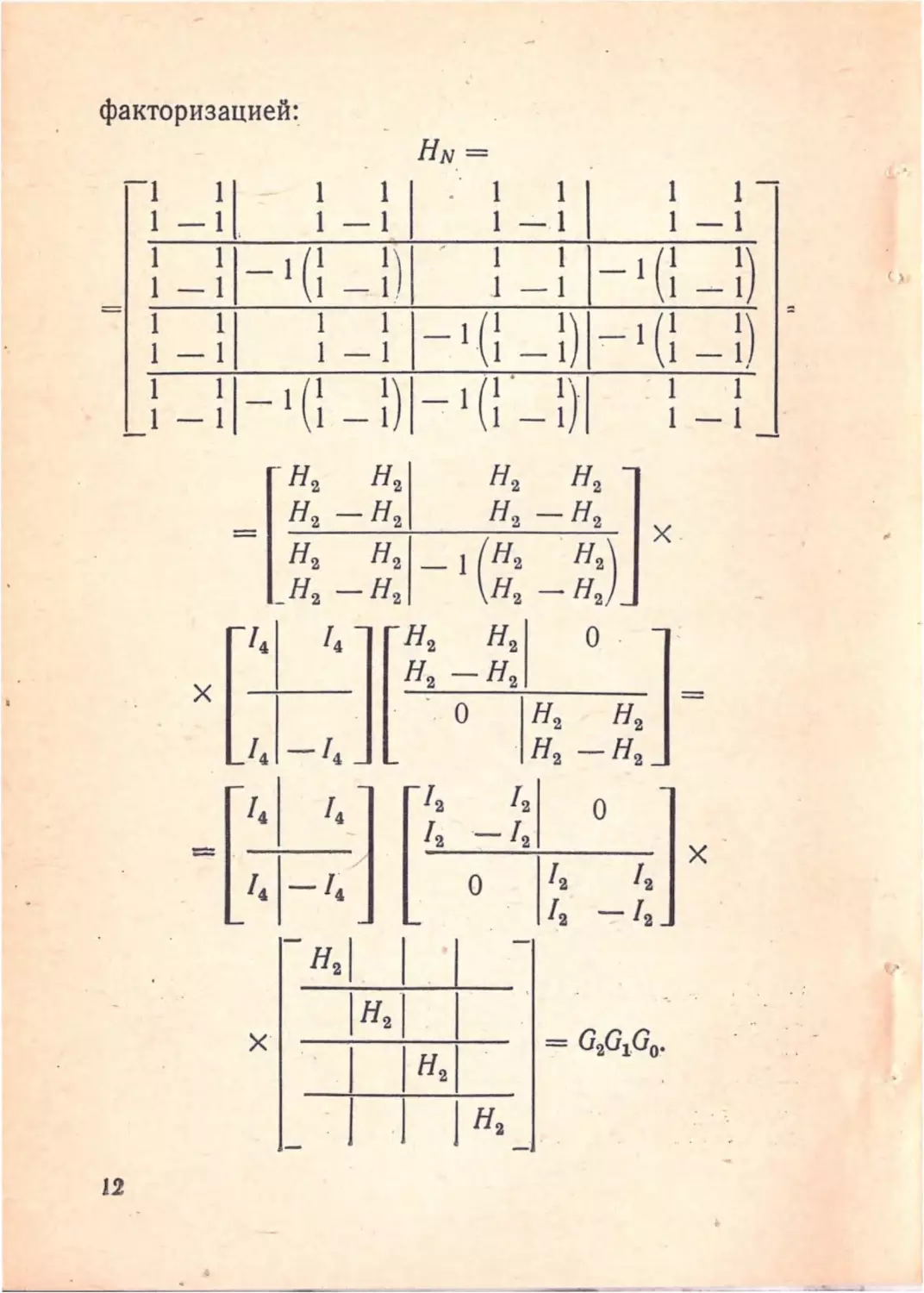
факторизацией :
HN=
-1
11 1-1 ,
1
1
1-1
1
1
11 1( 1
1\ 1
1 - 1 - 1-1 !
1
11
1- 1
.
,
1
1
1-1
1
1
1 1 1 (1
1)
1-1 1~1
1
1 1-1(1
l)l-1(1
1)
1- 1
.1- 1
1 - 1,
l')·i
1
11-1(1
l)J-1(1 ·
_1 - 1
1- 1
1- 1
12
1
11-1
(>
=
: 1
1
1 - 1_ -
поэтому Нн =
оп.
Каждая строка матрицы Гуда содержит два от
личных от нуля элемента, равных
1 или -1 . По
этому умножение на одну матрицу Гуда размером
+
2п х 2п требует всего
2п арифметических операций
(сложение и "вычитание), а из матрицы
(1.5)
следует,
что общее число операций при нахождении спектра
равно nN. Непосредственное же вычисление пре
образования Адамара потребовало бы
метических операций. Аналогичные
· соответствующие
N (N -1) ариф
разложения
и
им быстрые алгоритмы можно полу
чить и для других д1;1скретных линейных преобразо
ваний, таких как Фурье,_ Хаара , причем наименьшее
число операций , равное
2 (N - 1),
нео_бходимо при
использовании преобразования Хаара.
Рассмотрим
еще
одну · модификацию БПА.
Если
1)
. 13
'·.;
12
-12
о
о
12
12
о
Матрицу
(1.6)
· Нв
=
о
(1.6)
MOЖifO записать в виде
= (Н2 014) (/2 0 Н2 012) (/4 0 Н2) =
(Н4 012 012) (/2 0 Н2 012)
U2 012 0 Н2)
или в общем :виде
Н 2п = (Н3 Q9
/ 2 0 · · · ® 12) (!20
Н2 012
· · · ®/2) · ·· (/20120 ·· · 0Н 2 ),
®
(1.7)
где чис,110 член.ов (скобок) в правой части выражения
(1. 7) равно п.
·
Введем оператор «идеальной перетасовки»
l1:_,J ~ ::::::
X
р -
·-
lj
-хо
XN/2
. _XN-1
!·!
.
тогда
Н2п = (СР)п,
/:
(1.8)
·где С =Н2 @!2 @ · ·· @! 2.
Для п =
1
3
и
N ----' 8
(
1
Gв=
1
1 -1
о
о
о
о
о
о
о
о
1
о
о
о
о
о
о
Пользуясь
т
о
о
о
о
1 - 1
о
о
о
о
1
1 -
1
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1 о
1
выражениями
преобразования
fi
1
1 -1
о
о
о
о
о
о
о
о
(1 .8)
и
.
о
(1.9)
(1. 9)
находим
Адамара:
=[ifo+f4),
(fo-f4), (f1+fs), U1-fs),
U2+fв), (f2-fв), (fз+f1), '(fз-f1)]т;
f2 + fв + f1 + fs + f з + f1h+~+~+~-h-~-~-~
f1 + f4 - f2 -fв + f1 + f5 - fз - f1
h+~-~~~-h-~+~+~
f1 - f4 + f2 - fв + f1 - fs + fз - f7
f1 - f4 + f2 - fв - f1 + fs -fз + f7
f 1- f4 - f2 + fв + f1 --fs - fз +f.i
_f1 -f4 - f2 fв -/1 fь f з - f7
Известна также модификация БПА [14, 151,
-f1 + f4 +
.
r=
+
водящая к спектру,
1 •
+ +
при-
инвариантному относительно цик
лических сдвигов вектора, зеркальных отражений, .из
менений масштаба и смещений. Здесь вместо операций
сложения и
вычитания
проводятся
чисто
ЛОГ?Ч~ские
15
.
операции, что более удобно при технической реа
лизации. Так, вместо сложения . используется опера-
ция И--'-НЕ:
а
<-
1+ 1 =
О;
О
--()+о=
1;
1 +о= 1,
вычитания
вместо
+ 1=
1;
операции НЕРАВНОЗНАЧ
НОСТЬ:
-
х,
х,
1- 1 =О;
1-0 = 1;
0-0 =0;
0-1=1 . .
Рис.
2.
Поэтому .данное пре
образование назвали
логическим БПА (ЛБ
ПА). Устройство, осу
ществляющее ЛБПА,
Фувкциональная схема эле
ментов,
выполняющих
операции
И-НЕ и НЕРАВНОЗНАЧНОСТЬ.
просто
реализуется
на
интегральных
микросхемах-
И обладает большой однородностью структуры. Функ
циональная
схема элементов,
выполняющих операции
И-НЕ и НЕРАВНОЗНАЧНОСТЬ, показана на рис.
.
2.
Структурная схема всего устройства показана на
рис. 3. Число разнообразных выходных кодов . после
ЛБПА может быть . найдено по формуле
Nвых =
где
N -
(N-3) log2 N + (N2/4)-(5N/2) +}О,
размерность
преобразуемого входного век
тора.
Свойство инвариантности
ся
возмущениям
ЛБПА к упоминавшим
типа сдвига,
переносов,
изменения
масштаба и толщины линий изображения можно проде
монстрировать с помощью рис.
16
4, 5, 6.
f
1
2
2
3
4
J
4
5
6
5
6
,J
;)
7
7
8
--<>8
g
9
10
!О
11
12
13
14
15
18
Рис. 3. Структурная схема
автоустройства,
реализующего
логическое быстрое преобразование Адамара:
ЯI - ЯЗ2 ~ячейки .
""
3. ЛОГИЧЕСКАЯ КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
И КОРРЕЛЯЦИОННЫЙ АНАЛИЗ В БАЗИСЕ УОЛШд
Пусть имеются выборочные функции х (j} и у (j)
(j = О, 1, ... , N - 1) некоторых дискретных случай
ных процессов Х (j) и У (j). Логическая корреляцион
ная функция этих двух выборочных последователь
ностей
I N-1 .
L (k) = N ~ х (j
(f) k) у (j),
(1.10)
f=O
где
k = 0,1, .. . , (N - 1) и N = 2п; j и k - целые
- 1.
положительные числа, меньшие, чем 2п
Рассмотрим ряд таких чисел:
{О, 1, 2, ••. , (2п...,. nJ = z_~:
(1.11)
":- !(:,._
п~ в }•) '4 .
· 1~J -
'1 tJ
.1 ;;
.
__ " "
~·
~.
Q
~ • • . • ,.. ~ •
;:_:"~"
, . '{J i ' :!
~
ct
:-1···
• ...
.•.:;.17
i
о
о
о
о
о
о
о
о
о
о
о
о
о
(}
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
р
о
о
о
о
о
о
о
о
о
о
о
о
о . о
о
о
о
О.
о
о
о
1
1
о
о
о
о
о
о
1
-о . о
о
о
о
о
о
о
о
1
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о ·
о
о · о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о ·
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
.. о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
.
О · О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
· о·, о
о
о
о
о
о
о
о
о
о
о
.О
о
о
о
25 13 13 13 15 13
13 1 1 1 3 .1
11 .
1 1 1 1,
11
1 1 1 1
13 3 3 3 3 3
9 . 1 r 1
1
1
11 1 1 1
11 1 1 1 1 1
15 3 3 .. 3 5 3
1 1
11 1 1
3
13 ..1 1
13 ' 1 1
3
15 3 3 . 3 5 3
. 1i ·. 1 1 1 1
13 1 1 t 3
3
13 1 1
13
1
1
1
3
1
1
1
3
1
1
1
3
а
"
13 15 13' 13
1 3 1 1
1 1 1 1
1 1 1 1
3 3 3 3
1 1 1
1 1 1
1 1 1 1
3 5 3 3
1
1
1.
3
3·
1
3 5 3 3
1 1 1 1
1 3
1 3
13
1
1
1
3
1
1
1·
3
1
1
1
3
15 13 13 13
·з
1 1 1
1 1 1 1
1 1 1 1
3 3 3 3
1 1 1 1
1 1
1· 1
1
5 3 3 3
1 1 1 1.
3 1 1 1
3 1 1
5 3 3 3
1
1 i
1
3 1
!
3 1
б
18 •
•)
о
о
о
о
о
о
о
о
о
о
о
о
·о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
·о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
()
о
о
·о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о·
о
о
о
о
о
о
о
о
о
о··
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
01
1
1
о
о
о
о
·о
о
о
о
· о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
О . о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
. О
о
о
о
о
')
'1
1/
о
о
о
о
о
о
о
о
о
о
о ' о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
13
1
1
1
3
1
1
1
3
'!
·1
1
3
'I
13
;
'}
о
о
25 13 13
13 1 1
11 1 1
11 1 1
13 3 3
9 ' 1 1
11 1 1
11 1 1
15 3 3
11 1 1
13 ' 1 1
i3 1 1
15 3 "3
1.
н
iз
13
13
13 13 13 15
1
1 3
1 1
1
1
1 1 1 1
3
3 3 3 3
1·
1
1
1 1
1
1
1 1 1
3 3 3 5 .3
1
1 1 1' 1
1, 3
1
1 J
1 1 г -з ' 1
з- - 5 - з
3 3 5 "'З-"
1 1 1 1 1 ' 1
1 3 1 1 1 3
3 1 1 1 3
13 15
3
1 1
1 1
3 3
l
1
1 1'
3 5
1 1
1 3
1 3
lq
1
1
1·
3
1
1
3
1
1
1
3
13 15 13
3 1
1 1
1
1
3 3 3
1
1 1
1 1
3 5 .,3
l 1 ,1
1 3 1
1 3 )
3 5 3
1 1 ~1
'1 3 1
1 3 ,1
1
1
3
1
'!
1
3
1
i '
!
3
I
J }
\ .;.
1 ~
\'
19.~
о
о
о
о
о
о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1
о
о
о
1
о
о
о
1
1
1.
о
о
о
l
· о
о
о
о
о
о
о
о
1
о
.О
о
о
о
1
о
о
о
о
о
1
о
о
о
о
о
l
l
l
l
1
l
11
1
1
1
1
1
1
1
о
о
.1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1
1
о
о
о
о
о
о
о
о
о
l
о
о
о
о
о
о
1
l
l
l
l
1
о
о
о
о
о
о
о
1
о
1
1
1
1
1
о
о
о
о
о
о
о
о
о
о
о
,Q
о
о
о
о
о
о
о
1
1
о
о
о
о
о
1
.
v
о
1
о
о
-'J
в
Рис.
4.
о
о
Код фигуры в виде креста на входной матрице (16Х 16)
rический адамаров спектр (в},до
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
О.
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
О·
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
·о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о ·о
о
о
о
о
о
l
1
о
о
о
о
о
о
о -
· о
о
о
о
о.
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
О 'О
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
-l
·j
l
о
о
о
а
20
·-
·
-~
г)
о
о
о
о
о
о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1
1
l
l
1
l
1
1
1
1
о
о
о
1.
1
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
()
о
о
о
о
о
о
о
1
1
о
о
о
о
о
о
l
1
.
1
1
1
1
1
1
1
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
l
1
о
о
о
о
о
о
о
l
о
о
о
о
о
1
1
1
1
l
о
о
о
о
1
1
о
о
о
о
о
о
о
о
о
о
о
о
1
о
о
о
о
о
1
1
о
о
о
о
о
о
о
о
1
1
о
о
о
о
о
о
1
о
о
1
1
1
элементов (а), адамаров спектр
и uосле смещения изображения .
этого
изображения
(6),
ло-
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
9
о
о
о
о
о
о
о
о
1-11
о
о
о
о
о
о
о
о
о
о
о
о
1о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
. <.;,)
1
о
о
о
- ,-
о
о
о
11
1_
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
_о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
()"
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
-о
о·
о
о
о
о
о
о
о
о
О.
о
о
о
О -О
о
о
о
о
о
о
о
о
о
о
о ·
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
6
о
о
о.-· о
о
о
о
о
о
21
13
5
5
5
7
1
1
1
7
7
7
7
1
1
1
13
5
5
5
7
7
7
7
7
1
1
7
7
1
r
.,
7
1
1
1
7
7
1
7
1
1
1
1
1
1
1
- 1
1
1
7
5 1
5 •1
·5 1
7
1
7
7
13
7
1
1
1
7
1
1
7
7
7
7
7
1
1
1
1
13
,7
5
5
5
7 7
1 1
1
1
7
1
1
1
7
7
1
7
,,
,,
7
7
7
1
1.
7
1,
7
7
1
1
1
1
7
7
1
1.
1
-1
7
7
1
б
о
о
о
о
о
1
о
о
о
о
о
о
1
о
о
1
1
о
о
о
о
о
о
о
о
1
о
о
о
о
о
1
1
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
· О
1
1
о
d
1
1
1
1
1
!'
о
о
о
о
о
о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о . о
о
о
о
о
о
о
о
о
о .О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1
о
о
1
о
о
о
1
1
1
1
.О
о
о
о
1
о
о
о
t
о
о
.О
о
о
о
1
.
11
1.
1"
1
- 1-
_о
о
о
о
.о
о
о
о
О о
о
о
о
1
1
1
1
1
1
1
о
о
о
о
о
о
1
1
1
о .- 1
о
.1
()
о
1
1
1
1
1
1
1·
1
1
о
о
о
о
1
о
о
1
о
о
1. о
1- 1
в
Рис. 5.
2~
Код фигуры' в виде креста на свходнсiй матрИце (16Х'
адамаров спектр этих изображений (б), логиче-
·•
-,•t
3
3
1
1
1
1
3
1
1
1
1
5
1
3
3
3
1
1
1
3
1
1
1
3
5
3
1
3
1
3
1
3
3
1
1
1
1
1
1
5 ' 3
1 1
3 1
3 1
3
1
1
3
1
1
1
1
1
1
1
1
1
3
1
1
1
3
1
1
1
5
1
3
3
3- 3
1 1
1 1
1 1
3 _5_ 3
1
1 1
-1
3 т
1
3 1
5
1
3
3
3 3
1/ 1
1
1
1 1
5
1
3
3
3 •3
-1 1
1 1
1
1
3
1
1
1
5.
1 '
3
3
5
1
3
3
3
1
1
1
--
3
1
1
1
3
3
1
1
1
1
1
1
1
1
3
1
1
1
1
1
3
1
1
1
5 3
1 1
3 ' 1
3 1
3
1
1
1
3
1
1
1
5 3
1 1
3 1
3 •\
3
1
1
3
1
1
о
о
1
1
1
о
о
1
1
о
о
1
1
о
1
о
о
1
о - 1
о
о
о
1
о
о .
о
о-
о
о
1
1'
о
о
о
о
о
1
о
о
о
о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1
о
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
элементов
до и после
1
5
1
3
3
1; о
1 о
1 о
1 о
1 о
16)
-1
3
о
1
1
3
1
о
о
3
3
1
1
1
о
о
i
1
О ·
1
3
1-
1
о
· о
3
1
1
1
·3
1
О -
1
5
1
1
1
3
1
3
о
1
1
1
3
1
1
1
1
о·
о
о
о
3
1
1
3
1
-
о
1 1
5
1
3
. 3
3
1
3
1
1
1
о
1
)
5 3
1' 1
3 1
3 1
5
1
3
3
-1
1
1
1
•1
1
смещения
о
о
о
о
о
о
о
о
о
1
о
о
о
1
1
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1
о
1
1
1
1
о
1
1
1
о
о
О ,
о
о
о
о
о
1
1
о
о
о
о
о
о - о
о
о
1
О.
1
1
1
1
1
и изменения
1
1
1
1
1
1
1
о
о
о
о
о
о
о
о
о
о
1
1
1
о
1 ' 1
1
масштаба (а) ,
ск.ий адамаров спектр тех же изображений (в) .
23
--
-· .
-
~----~--
о
о
о
о
о
о
о
·О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о .
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
9
о
о
/ 1
10
о
о
о
о
о
о
о
о
о
о
о
О . о
о
о
о
,О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
')
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
-О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
..
' -' 1
,_,
о
а
13
7
5
5
5
7
7
7
7
13
5
5
5
7·
7
7
7
7
1
1
1
7
1
1
1
-1
7
1
1
1
7
7
1
1
1
7
1
1
1
1
1
7
7
1
1
7
1
1
' 1-
7
1
1
1
1
1
1
7
1
1
1
1
1
1.
1 1
1. 1
'1
1
1
1
1
1
1
1
1
1
1
1
7
1
1
1
1
1
13
7
1
13
5
5
5
7
7
7
7
5
5
5
7
7
·7
7
7
1
1
1
1
1
7
7
1
7
1
1
1
7
. 1
7
1
1 1
1 .1
1
-1
7
7
1
1
. 1
7
7 7
1 1
1
1
1 1
1 1
1 . 1
1 1.
7
1
1
7
1
1
7
1
;}
1 1
1.
1 1-
"1
1
1
б
24
!)
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1:
1,
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
'о
о
о
о
о
о
о
о
о
о
:
. 1
-1
.
(
о
о
о
о
о
о
о
-о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
(j
: 1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
52
о
28
о
28
о
28
о
28
о
28
о
28
о
28
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
20 .
о
4
о
4
о
4
о
4
о
4
о
4
о
4
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
20
о
4
о
4
о
4
о
4
о
4
о·
4
о
4
о
о
о
о
о
о
о
о
о
о
о
о
-о
о
о
о
о
20
о
4
о
4
о
4-
о
4
о
4
о
4
о
4
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
28
о
4
о
4
о
4
о
4
о
4
о
4
о
.4
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
28
о
о
4
о
4
о
4
о
4
о
4
о
о
4
с о
о · о
28
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
4
о
4
о
4
о
4
о
4
о
4
о
4
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
28
о
4
о
4
о
4
о
4
о
4
о
4
о
4
о
о
о
о
о
о
о
(L
о
о
о
о
о
о
о
о
о
25
О
о
1
О
о
о
1
·'1
1
О
о
о
О
о
о
.О
о
о
1
1
.1
0010001
0010001
.о
о
1 о о о
1
1010001
0010001
lJIOOOl
0010001
1 о
1' '0
о
о
1
о
о
1 о о о
1
0010001
0010001
1010001
о
о
1 о
о
о
1
о
о
о
о
1
1
1
1
о
1
1
о
о
о
J
1
1
I
1
1
1
1
1
1
о
о
о
о
о
о
о
о
о
о
о
о
1
' о
1
1
о
о
о
О
о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
о
.О
о
о
о
о
о
о
1
1
1
1
1
1
.1
1
1
1
1
1
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о .
о
о
о
о
о
о
.о
о
о
о
о
о
о
1
о
о
о
о
о
о
о
1
о
о
о
1
в
Рис.
6.
К:од фигуры в виде креста на входной матрице (16Х 16)
ны линий (а), адамаров спектр этих изображений (б),
КаЖдь{й элемент ряда ( 1.11) можно представить в дво'~
ичной системе . В ·табл .
1 приведена матриuа IJОразряд
2 (j Ef) k) длЯ ряда Z4 =
ного сложения по модулю
= {O;l, ... , 15}.
Если . для
какого-то определенного
п матрица делится на четыре матриuы 2п 12 х 2п 12 ,
to
каждая из них является симметричной относитель
но обеих диагоналей . Это позволяет расширять таб
лицу для п
4. Если в выражении (1"1О) у (j) = x(j),
>
to L<m> (k) ' - логическая функuия
. для j-й выборки длины
N,
автокорреляции
которую можно определить
как математическое ожидание по ансамблю локальных
автокор·реляционных функuий :
• L (k) = М {L<m> (k)},
В частноспl, для
k =О, 1, ... , (N .:.;___ 1)."
N = 4 логическая .автокорреляцион
ная функuия в матричной форме имеет вид
·rL (О)]
LN __:._
·.
~ (1)..
L (2)
L (3)
26
.
= м _1
· . 4
rx (О)
х (1)
х (2)
х
(3)
х (1) х (2)
x(3)l
х (О)
~ (3)
х (3)
х (О)
х
х
х
х (О)
(2)
( 1)
х (2)
(1)
'•
х
о
о
о
1
о
о
о
о
о
1.
1
1
1
1
о
т
о
]
-о
1
1
О.
о
о
о
о
о
о
1
о
о
о·
.
о
1
о
о
о
о
о
о
о
о
·_О
1
1
1.
1
о
f.
_ о
1
1
1
о
о
о
о
о
о
о
о
··- . о -···-
о
·о
о
-о
··о · -- -
-о
о
о
о
о
о
о
о
о
о
()
о
о
о
элементов до и , после
,Q
1
1
о
а
о
о
о
о
о
1
1
о
о
о
о
о
о
о
о
о
о
о
о~
о
о
о
о
1
i
о
о
о
1
1
1
1
1
_)
1
1
1
1
1
1
1
1
1
1
1
1
1
.!
1
1
о
о
о
о
о
_)
1
1
--
о
о
о
о
о :
о
о
о
1
1
о
о
1
о
о
-т
1
-- 1
1
о
о
о
о
- О
о
о
о
l
1
о
о
о
О-
О
О-
о
О'
о
о
о
J·-
1
.
о
о
о
о
о
l
х
~
о
о
о : о
о
о
--о
- l
Q
11
!
! '
1
о
о
о
о
о
1
о
1
о
о - ь -- о
d
смещения, изменения масштаба
x (0)
х (1)
1
J
о
о
о
- -о
1 ··- о
о- -
о
о
о
о
о
логический адамаров спектр тех же изображений (в).
х
1
-~~г · т
о
о
о
о
о -
о
о
о
о
о
о:- - о
1 -. о
1 _о
1.
1
1
о
о
и
толщи
•
(1 . 12)
(2) "
х (3)
::Значения аргумента у элементов 'квадратной матриuы
в правой части определены с ПОМОЩЬЮ таб.ri.
1
rзо
].'
~читывая ~ыраж~ние (1.12) и табл.}, rюлучаем лог.и:
ческую ковариационную матрицу, которая для N =
= 4 имеет. вид- -
- ll
CL .=
:
(J2
.
(О)
l (1)
l (2)
l
l ( 1-)
l (2)
(3}~
l (3)
l (О)
l (1)
ЦО) - l (3) - l (2)_-_-
'
__1(3) L(2) . l(l) _l(O) - где
l (k) = L (k)/a 2 ;
-
l (0) _:-1;
L (0) = 0-2 •
Если Имеется матричное уравнение У- = ТХ, .пред
rтавляюшее линейное ортонормированное преобраз_о
вание .входного
случайного
-век1·ора_
Х в
выходной
27
)
Таблица
k
1
о l 1 I з 1 41 I ·б-1
1
2
s
71
в1
9
1
l l 1з l 14 l
l ·10 11
12 ,
1s
oj ol 1l 2l зl 4l -5l 6l 1\ вl 9l1ol11!12l1зl14l15
11 1I о 1 з 1 2I 51 41- 1 I 61 9j в l 11 l 10 l 1з I·12 j 15 l 14
2 I 2I з 1 о 1 1I 61 1 I •41 5110 l 11 I в 1 9l 14 j 15 l 12 l 1з
з 1 з\ 2111 ol 11 61 51 4111l101 91 в\ 15l 14l 1зl 12
41. 41 51 61 1 \ о 1 11 2I з 1·12 l 1з l 14 l 1s I в 1 9l 10 l 11
51 51 41 11 6/ 1j oj зl 2j 1зl 1~l 15l 14 l .9I вl 11_110
.61 61 1 I 41 51 2I з j о 1 1l 14 l 15 / 12 l 1з l 10 l 11 1 в 1 9
71 1 I 61 51 41 з 1 2I 11 о l15 l 14 l 1з l 12 l 11 j 101 91 в
в 1 в 1 9110 l 11 l 12 l 1з l 14 l 15 j о 1 1I 2I з 1 41 51 61 7
9 / 91 в\ 11 l 10 jiз Ir2 l 15 l 14 I 11 о 1 з 1 2I 51 41 1 / .6
10 / 10 l 11 I в j 9l 141 'i~ l 12 l 1з I 2/ з 1 о 1 1/ 6_1 71 41 5
l1 /11l1ol 9l вl15l14l1зl12l зl 2l 1I o/ 1j 6 514
12 / 12 l1з 114 / 15 I в 1 9i10 l11 / 41 51 61 71
1з l 1зl 1_2\ 15l 14l
9l
28
1 2i з
вl 11\101514171611 / о/ .з\
J14[15/12/1зi1ol11/ sl 9\
15115 \ 14 / 1з \ 12l11\101 91 в/
14
о/
6/ 7141512\
1/
з/ о\
~ 1 s / 41 з / 2 \
2
1
1/ о
вектор 'У, то ковариационная матрица выходного век
тора У
Су= ТСхТ*,
где Сх - коварщщионная матриuа Х. а и.ндекс · «*»
означает сопряженное транспонирование. Если Т -
=
=
матриuа Адамара, .а Сх
CL, то матрица Су
HCLH*
является диагональной. Для N = 4 ее элементы
Л00 = Na 2 { 1
9'.11
=№ 2
=
Л33 ·=
Л 22
+ l (1) + l (2) + l (3)};
{1
+l(H-1(2)-1(3)};
l (1) -1 (2) + l (3)};
Na 2 {1 -1 (1) + l (2) - l (3)}.
№2 { 1 -
Таким образом, в рассмотренном случае преобр 0 -
зование Адамара эквивалентно преобразованию Корунена - Лоэва.
.
Спектр плотности мощности в базисе Уолша есть
преобразование Адамара для логической автокорре
ляционной функuии [13]
L~ = Рн +- -+LN
или
L~ (j) =
N-1
1} LN (i) W; (i,
N).
i=O
Дискретные спектры плотности в обычном базисе
тригонометрических функций (sin, cos) и в базисе
Уолша для речевого сигнала исследовали·сь в работе
[30 ].
Из непрерывной речи. (текст из пяти предложений
читали мужчина и женщина) в течение 30 с были сде
ланы выборки на частоте 8 кГц при N = 16 и найдены
арифметическая и логическая автокорреляционные
функuии, а также собственные величины ковариацион
ной
матрицы.
релляционных
Затем значения
функций
выборочных автоко
взвешивались
с
помощью
29
ядер Парзена р (/г) =
=
1 - 6 (k/(N - 1))+61k!(N-1)1 3
2- (1-1 k/(N - 1) /3 ) при (N Опри/k\>N--:--1
·
·
i
при
lk/
< (N-'----
1)/2;
1)/2</k 1<N ~1;
.
.
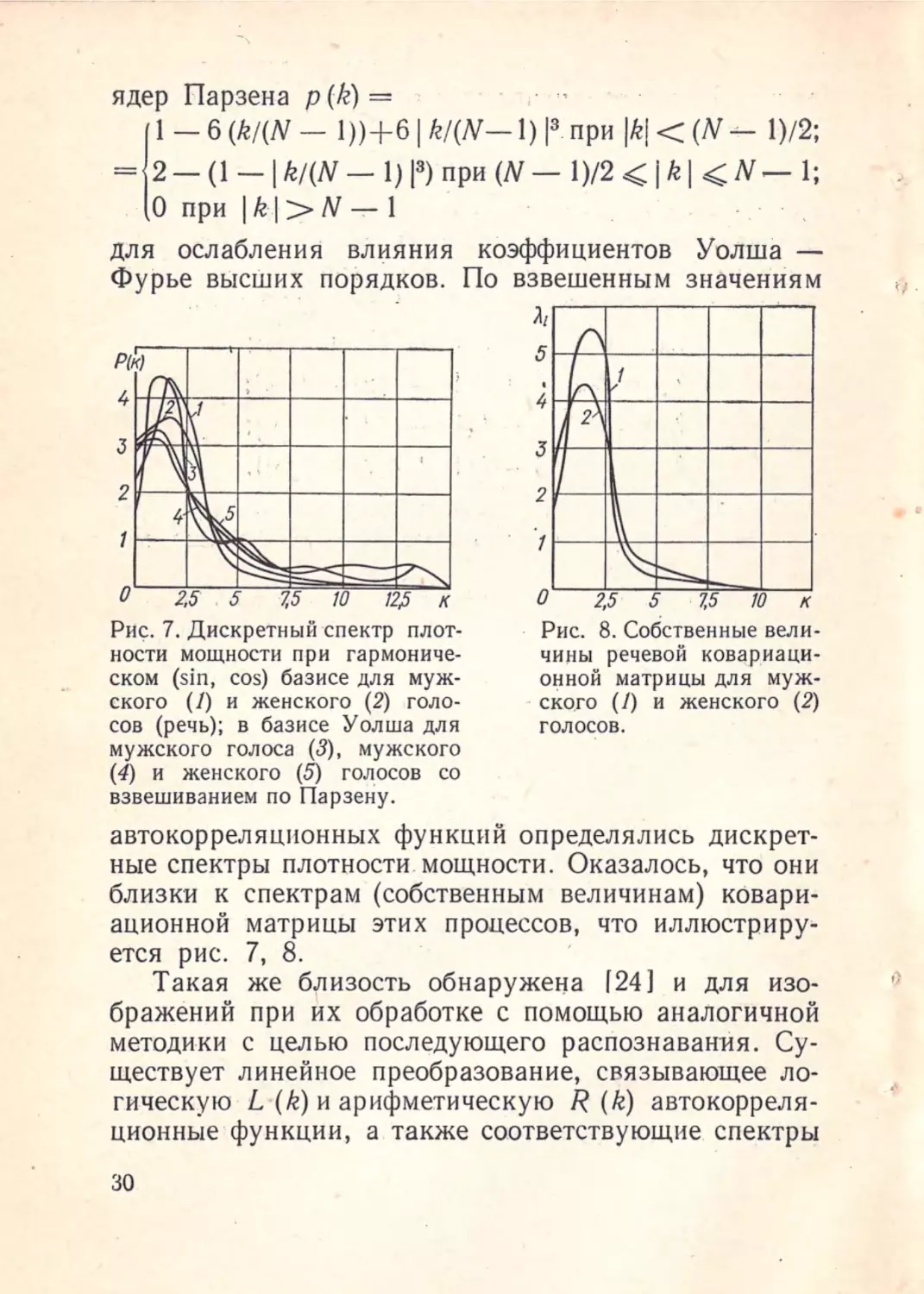
для ослабления влияния коэффициентов Yo.tiшa Фурье высших пьрядков . По взвешенным значениям
л,
5
'
4
'1 ·
r
1
IA /
2'
3
2
~
~~
о
Рис .
7.
ности
Дискретный спектр плот
мощности
при
гармониче
ском (sin, cos) базисе для муж
екого (1) и женского (2) голо
сов (речь); в базисе Уолша для
мужского голоса (3), мужского
(4) и женского (5) гол. асов со
взвешиванием по Парзену.
2,5
5
' 7,5
10
к
Рис. 8. Собственные вели
чины речевой
ковар,иаци
онной матрицы для муж
ско.го (1) и женского (2)
голосов .
автокорреляционных функций определялись дискрет
ные спектры плотности . мощности. Оказалось, что они
близки к спектрам (собственным величинам) ковари
ационной матрицы этих процессов, что иллюстрируется рис.
7, 8.
·
Такая же б{!изость обнаруже!jа [24] и для изображений при их обработке с помощью аналогичной
методики с целью последующего распознавания. Су
ществует линейное преобразование, связывающее ло
гическую L -(k) и арифметическую R (k) автокорреля
ционные функции, а также соответствующие спектры
30
•}
плотности мощности. Это преобразование можно з·а
писать в матричной форме в виде матрицы .
(1.13)
где индекс «ал» означает переход от арифметической
;!
к логарифмической форме; DN - диагональная матрица
размерностью N х N и элементами d (j, j). = т- 1 , j =
-- О , 1, 2, , .. , (N - 1),. mi -- 2v.-1+6u.o).
1
,
vi - число
единиц в двоичном представлении j; б (j, О) - символ
Кронекера.
В табл . 2 [30] приведены элементы mi и vi для об- ·
ратной матрицы DN-J при N = 16 и п = 4. Матрицу
Т N . ( 1.13) можно сформировать рекуррентно с помощью
матрицы SN(2 , у которо_й все элементы - нули , не
Таблица
Значения
десятичные
о
1
2
3
4
5
6
7
8
,,.
·g
10
11
12
13
14
15
~\
2
;
vl
т;
о
1
1
1
1
1
2
2
1
2
1
2
2
2
3
1
4
1
2
2
2
2
двоичные
о
о
о
о
о
о
о
о
о о о
о о 1
о 1 о
о 1 1
1 о о
1о 1
1 1о
1 1 1
·1 (') о о
1о о 1
1о 1о
1о 1 1
1 1о о
1 1о 1
1 1 1о
1 1 1 '1
3
4
2
2
3
3
4
4
4
8
~1
считая единиц, размещенных впр аво
от элемента нег лавной диагонали :
rro
o0 0о 0о
о]
о
о
r
5 =
о
4
О)(П \1 элемент
о
1
1.
1 о
о
Рекуррентность матрицы начинается с Т1 =
Т~ =
. Обратный
[
1
0 ]
TN12
TN12SN12
TN/2 •
переход от логической формы к арифме
тической производитсЯ с помощью матрицы
(1.14)
Для
N = 16
1о о о
о 1 о о
о о 1 о
о 1 о 1
о
о
О
о
о
о
о о о
о о 1
О 1 О
1о 1
о о о
о о о
о
о
о
о
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
О
о
о
о
о
о
о
О
о
о 1
О. О 1
о 1 о 1
о о о о 1
о о о 1 о
о
о
о
о
о
о
О
о
о
1
о
о
о
о
о
о
О.
о
о
о
о
о
о
о
о
о
О
о
о
о
о
о
о
о
о
о
О
о
о
о
.о
о
о
о
о
о
О
о
о
о
о
о
о
о
о
о
О
о
о
о
о
о
о
о
о
о
О
о
о
о
0000001000100000
о· о о о о 1 о 1 о 1 о 1 о о о о
о о о о 1 о о о о о о о 1 о о о
о о о 1 о 1 о о о о о 1 о 1 о о
о о 1 о о о 1 о о о 1 о о о 1 о
О 1 О 1 О 1 О 1 О 1 0_1 О 1 О 1
1
Т N-I = .10о
32
о
о
о
о
1
о
1 О -0
о
О
о
о
О
о
о
О
о
00
00
00
о
О
о
о
О
о
.
00
о о
00
0001 ·
о о о
о о о
00 о о 00 о о о
00 о о 00 о о о
1 0-1 о 1
00 о о 00 о о о
о о о
0-1 о о о 1 00 о о 00
0-1 о о 0-1 о 1 о о о 00 о о о
о
о
00
о о о
о
о
о
о
о
о 1
о
о
1 о о о 1 0-1 о 1 о 00 о о о
о
о
о о о
о
1 о о 0-1 00 о 1 00
0-1 о 1 0-1 о 00-1 о 1 о
о о о
0-1 о о 00 о · О о 1 о о о
о
о
о
1о о
о
1 0-1 о о о 00 1 0-1 о
о
0-1 о о о о 00 0-1 00 о 1 о
0-1. о о о о о 00-1 о - 00 -1 о 1
0-1
о
о
о
т
N-1
о
о
о
1
о
о
1
Арифметическую
о
о
о
о
о
функцию _ RN
Пусть имеем т-ю вы.
корреляционную
находим следующим образом.
бор ку временной функции x<rn> (i), i = О, 1, ... , N - 1 и N = 2п, для -которой спектр Адамара
N-1
х
J - 1}
*(rn) (") -
х
t wi ("t, N) .
(rn) (")
i=O
Спектр плотности мощности в базисе Уолш1:1 опреде
ляется как среднее из локальных энергетических спек-
··
тров Адамара:
-
-
1
Рн (j) =~
s.
[Х
1}
*(
m)
(j)] 2 •
0 rn=l
Обрап~ое преобразование Адамара, аналогичное пря:
MJMY от вектора Рн
= {Рн (О), Рн (1), ... , Рн (N - l))т, дает вектор (логическую автокорреляцион-
"
ную функцию)
LN =
2 7-
14 03
~
L (О)
~ (1)
,
L (N -
l
:___
НРн.
-
1)
- 33
Используя
R (1),
матрицу
l)j
.. . , R (N -
находим_
'(1.14),
т
-
)
RN = ( R (0),
.
арифметическую
1
корреля-
ционную функцию:
RN = TN-1DN- 1LN.
Применение БПА
позволяет здесь сократ!!ть число
операций сложения и вычитани·я.
ОРТОГОНАЛЬНОЕ
РАЗЛОЖЕНИЕ СИГНАЛОВ
В БАЗИСЕ ХААРА ·
4.
Система функций Хаара является полной орто
нормированной системой функций, определенных . на
промежутке
[0,1 ].
Непрерывные функuии Хаара упо: ·
рядочиваются по двум индексам
дующим
1:! определяются сле
образом:
х~ (t) =
V 2п
1V
= . -
О
Индекс
периода
хождение
[0,1 ].
при
2)/2п+\
(2k- 1)/2п+l];
1);2п+ 1 ,
2k;2п+ 1 1; ~
при остальных
п- указывает
функции
амплитуды,
ле
t Е [(2~ -
2п пр11 t Е [(2k на
Хаара;
равной
данного
V 2n,
t,
на отрезке
длительность
[0, l].
ненулевого
равного
индекс
ненулевого
- 1/2п, и ее
k ~на местона
периода
на
интерва-
·
Для определения : дискретных функций Хаа·ра необходимо выбрать значения непрерывных - функций
Хаара в равноотстоящих точках - в точках перехода
через нуль функций Хаара первого (по п) отбрасыва
емого порядка . Полученные таким образом дискретные . функции также являются _ полной ортогональной
системой функций, определенной на выбранной ре-
34
•'
шетке. МножитеJtъ
1/V2п+ 1 (где 211+1
количество
-
точек в рещетке) делает систему ортонормированной .
На рис. 9 показаны графики первых непрерывных
и дискретных функций Хаара. Здесь ~Х~) - функции
первого
отбрасываемого
порядка,
нули
которых
определяют рещеrку дискретных функций Хаара, ха·
(;
рактеризующиеся
щими
следую-
осоfiенностями:
они
кусочно-постоянны, на зна
чительной
ла
части
определения
лю,
-·
равны ну
значение функции по-
V 2n
рядка п ращю
+
всех
особенности
Эти
k.
дают
при
возможность сущест
венно
сократить
с
помощью
V2[n
V21x
о
перемно
жения вектора .на матрицу.
Такая
.
ОГШ ·
число
арифметических операций
до 2 (!'{ - 1) при нахож
дении коэффициентов раз
ложения функции в ряд Ха
ара
1. t
интерва
экономия опера
ций достигается с помощью
t
ГП х:
liJt
:rtl_=tlJ
t
t
быстрого
преобразования
Рис. 9. Графики первых не
Хаара (БПХ) в связи с тем,
прерывных
и
дискретных
что большинство членов ма
функций Хаара.
трицы преобразования рав
ны нулю. В результате уменьщаются затраты ма
шищюго времени, например, по сравнению" с преоб
разованием
Фурье,
жение на 2м 12 -
так
как
при
четных
п
-
умно
является просто сдвигом двоичного
члена на п/2 разрядов влево. ··
Любую ' непрерывную функцию S (t), удовлетворя·
ющую условиям Дирихле, МОЖНО ра:}ЛОЖИТЬ в рав-
2*
35
номерно сходящийся ряд Фурье в базисе Хаара. Так .
как эта система я·вляется ортонормированной, то коэф. -
фициенты этого ряда при любой функции
k
Хаара 'Хп·
(t)
можно найти по формуле
1
. а~
= ~ s (t) х~ (t) dt,
(1.15)
·
о
а функция
S (t)
=
1J ап'Хп (t).
k k
(l .J 6)
п.k
При каждом фиксированном
'v'tE[O, 1]
-
3k:X~(t 0)::p0.
t
Другими словами, в окрестности точки
0 функция
интегрирует!:я п раз.
Чтобы . умен_ьшить количество операций интегри
рования при вычислении коэффициентов ряда (1.15)
S (t)
в
п
раз
(1.16)
При
огранич~нии
количества
членов
ряда
функциями порядка п и ниже, рассмотрим мат
рицу, строками которой являются ненормированные
дискретные функции Хаара соответствующего поряд
ка . Обозначим эту матрицу Arc. Построим вектор
1;2п+1
7
S
= (
(Т
-
JS
знак
l+i S
2;2n+l
(t) dt,
112
1
(t) dt, ... ,
l-l~n-l S (t) dt
)
транспонирования).
-
•
-
k
Вектор Sx. = ArcS состоит из коэффициентов ап разложения функции s' (t) в ряд Фурье - Хаара . При
этом функuия (при нахождении вектора S) интегри
руется однократно на интервале
36
[0,1 ].
Матрицей дискретного преобразования Фурье будет
матрица А:п. умноженная на
l!V 2п+ 1
(для нормирова-
'
·1 системы
ортогональных векторов, составляющих матрицу). Обозначим Ал!V 2п+~ через А~. С по:
ния к
мощью дискретного
преобразования
Хаара
сишал
(определим его как вектор, элементами которого будут
Р
значения функции S {t) в 2n+t равноотстоящих точках
интервала [О, 1]) можно представ1пь
дискретных функций Хаара:
-o
S _
-
"1
kxk(D)
~ап п
в
виде
суммы
( 1.17)
•
п.k
Так как строки матриuы А~ - ортонормированная
система векторов, являющихся дискретными функ
циями Хаара, коэффиuиенты суммы (1.17) будут ска-
ляр,ные произведения вектора
-v
S на строки матрицы
- А~- Обозначив вектор коэффициентов суммы (1.17)
-о
-v
D D
через Sx, получим S х = АлS .
Точность приближени~ непрерывными функuиями
Хаара равна Mh, где М - максимум первой произ
водной приближаемой функции (для гармоники М
равно круговой частоте сигнала cos
sin wt); h =
wt,
= 1/2п+~
- величина шага ступенчатой функЦии, ко
образует частичная сумма ряда Фурье - Ха
торую
ара для приближаемой функции .
В случае дискретного приближения, если количест
во членов ряда Фурье - Хаара взято равным коли
честву отсчето:/3 приближаемого сигнала, представ
ление является точным, без погрешности (так как это
просто разложение вектора из Евклидова пространства
Еп по п линейно независимым векторам).
-
Период
аппроксимируемого
ся по формуле Та
=
2-п
сигнала
определяет
l с, где 2~" - длите.т~ьноСТ!>
37
\
соответствующей функuии Хаара; l - число функuий
Хаара (п = const), укладывающихся в периоде ап
проксищ1руемого сигнала.
Абсолютная
погрешность в определении · периода
определяется по формул~ ЛТ = Т. - 2-nl
Т
период аппроксимируемой ·,функции.
-
Относительная погрешность
откуда 2п ~ 1/(уТ), а
п
Формула
между
·
l/(2пТ),
:;;;;.-- - (ln '\' - ln T)/ln 2.
(l.18)
(l . 18) устанавливает аналитическую связь
периодом
но~тью
< ЛТ/Т <
'\'
2п, где
<:
базиса
представления
анализируемого
Хаара
и
периода
сигнала,
допустимой
размер- ·
погрешностью
анализируемого
сигнала.
Реализуемость. методов анализа сигнала в базисе
Хаара определяется возможностью - вычислительных .
маiпин . .Рассмотрим аналитическую связь·
входящих в формулу
(1 . 18),
период~в,
с быстродействием ЦВМ.
Если задана частота сигнала и относительная погреш~
ность разложения у, то по. формуле
(l .18)
можно опре
делить необходимую · размерность базиса Хаара.
Для · выбора вычислительной · машины необходимо
знать быстродействие ЦВМ при выполнении элемен
тарных операций :
рости
Б(+)• Б{l), Б<2»
Б<х» Б<уп>
выполнения операuии соответственно
ско
-
сложения,
сдвига на один разряд, сдвига на два разряда, умноже
ния,
условного
перехода.
Время, затрачивае!\юе вычи г лительной машиной
на ра з ложение сигнала, _определяется формулой
.
Тцвм
/
1 -+-d-+~)n+
(-d-+Б<+~
2Б(l)
'LБ(
Б(упJ
21
+ __!____
+-.-2-.
2 п,
6(уп 1
Б (х1
1:де п
38
-
количество дискретизаций интервала
[Q, l l.
·
,..
Если вре мя Т превышает допустимое время обра
ботки 'сигнала Т 0 , то данная ЦВМ не удовлетворяет
поставленным требованиям. Если Т
Т 0 , то быстро
действия ЦВМ достаточI:Iо, чтобы с заданной точностью
-<
разложить сигнал в базисе
Глава
Хаар11 .
·
1
ОБРАБОТКА СИГНАЛОВ
С ИСПОЛЬЗОВАНИЕМ ФУ~КЦИЯ
УОЛША
1. РЕШЕНИЕ ДИФ.ФЕРЕНЦИАЛЬНЫХ
И ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
С ПРИМЕНЕНИЕМ ФУНКЦИЙ УОЛША
Имеется дифференциальное уравнение п-го порядка
d(n)x
. dti1 + а1 (t)
d(n-l)x
dfl-1
+ .. . + ап (t) х =
f (t)
с начальными условиями, определенными для ·
х (to) =Хо,
х' Uo)
= х~ •
•• . ' х<п:...1) (to)
t
= t0 ,
= хьn-1>.
Положим, что
d(n)
_х_= И(t)
dfl
где И
t,
.
(2.1)
'
(t) - известная функция.
.
Проинтегрировав обе части выражения
(2.1),
най-
дем
t
x<n-I! =
.
Ин1егрир у я
I И(~) d~ + x<n-I) (t
t
о
0).
(2.2)
.
аналогичцо выражение
(2.2), пол у чаем
39
Х(п~2) = ·
i t
.
.
ssИ (;) d~2 + х(~-1) (to) . t
1 to
+ х(11-2) (to):
fo fo
;·
т-й интеграл от
(2: 1)
r . . . sи ш dsm + x<n-1) (to)
1
x(n-m) =
1
J
(t -
to)m-1
(tn- 1) 1
10
fo
+ x<n-2) (t )
о
т-2
(t - to) .
(m-2)1
+
+ ... + x<n-m) (to)
или в более компактной форме
Искомая функция х
при
т
=
х (t) =
находится и~ выражения
(t)
(2.3)
(2.3)
п
t
s
to
(2.4)
Если в исходное · уравнение (2.1) подставить значения
функции х (t) и производных, определенных выраже
ниtм (2.3), то получим
1
И (t)
'
t
1
+ а1 (t) SU(s) d; + а2 (t) SSИ Ю ds +
2
·'
lo f o
fo
t
1
10
10
+ . . . + S . . . SИ (s) dsn + а1 (t) x<11-I> Uo) +
.+ а2 (t) x(n-I> {t0)
*о
1
1
10
+ а2 (t) хт- 21 (t + · · · +
0)
п
k
·+вп Щ ~ .x<n-) (t-o)
(t -
(п -
to)n-1'
k) 1
= f (t).
(2.5)
· k=I
Все ·слагаемые, не содержащие интегралов в выраже
нии (2.5), запишем в виде суммы :
а кратные интегралы сведем к простым по формуле
(' . r
J ... J и (Ю d6
t
t
fo
т
t
=
fo
('
J
(1 -
~)т-1
<т _ l) 1 _ и (6) d6.
(2.6)
fo
С учетом формулы
( t)
содержащие И
(2.6) слагаемые в. выражении (2.5),
под знаком интеграла,
следующим образом:
п
t
(t-~)т-1
(m -1) 1
('
~ ат (t) J
т=I
запишутся
и (6) d6.
10
Положив
g (t)
п
.
получим
•,
+~
·
т-1
x<n-k) Uo)
ат (t)
(t _
fo)т-k
(m _ k) J
k= I
следующее
п
И (t)
т
= f (t)-..:. ~ ~
выражение:
t
.
(;~t~) 1 ~ (t -6)т-l И (6) d~ = g (t),
m.=1
,
(2.7)
t0
которое является уравflением Вольтерра второго рода.
Решение это~о уравнения с использованием функций
· Уолша [27) требует представления в виде рЯда Фурье
по
функциям
Уолша
множителя,
с:гоящего
под
41
Б
3
1
о
1
00
1
• 01 .
о
2
10
о
3
ll
о
4
100
о
5
101
о
6
110
о
1
.1
1
2
1
7
-15
31
-192
31
-256
15
-128
691
-6144
1
3
16·
32
27 •
256
512
127
-2048
63
-1024
ll 971
- 196 608
..
1
-в- --в
о
1
~
1
-16 -15
о
о
1
3
64
111
2048
1
3·
128
123
4096
64
100~ о /- ;2 j- 3~
42
3
3f:
-
1
-
1
6
-32
1
-4 -4
1
1
5
4
3
1
-
3
256
55
255 1
8192
-
235
4096
'
1-+вl
511
1
16 384 -
-
295.
8192
-
535
16384
195 331
6291456
(,•
Таблица
8
б
1
-7-
1
1
9
8
9
-54
-
3
-
2l9
2048
1
127
1024
85
-768
13 231
131 012
-
9325
93 304
.
429
4096
-
3939
65 536
7659
131 072
18 565
196 608
819
8192
-
993 007
!6 777 216
15 309
262 144
-
731 725
12 582 912
1 454 125
25 165 824
'
-
10 749
262 144
-
1-
23 499
524 288
. 645
16 384
. 46 179
1 048 576
64 899
66 198 511
2 147483 648
-:- 2 "097 152
.·
2 390 725
60 331 648
37 065
786432 ..
1.
49324 845
1610612 736
43
знаком суммы во втором слагаемом
1
•
(2. 7),
.:,:, •.
·-· -
.
-
.
(т ~ 1) 1 s(t - s)m-I и ш ds =~с, (т, п) w, (t),
t
r=O
о
•
(2.8)
.
что в свою. очередь требует представления в виде ря
да Фурье по функциям Уолша функции tm (О
и
интегрирования
Запишем ряд для
tm =
функций
('
Уолша .
<;: t
<
Покажем
1)
это.
в виде
~ Dn (т) w~ (t),
О<;:
t< I.
n= O
Коэффициенты ряда
Dn
(т) определяются из уравне
ния
1
Dn (т)
= Stmwn (t) dt.
(2.9)
о
=
Можно показать, что, например, для п
2 (или в
двоичной форме записи двойки - «10») интегрирова
ние по частям уравнения (2.9) и выполнение простей
ших преобразований с использованием свойств функ
ций Уолша дает
t т
.
Jr t W10· (t). dt =
Х [ 1-2m+I + 3m+l
Dio (т) =
.
о
+1
4т
-+
2
+ 1)
(т
х
4m+I].
В табi 3 [10] приведены значения Dп (т)' дл:Я целых п ил~ в. пределах от О до
8.. .
Для интегрирования функций Уолша
t
=
t, о < t < I;
Swa1 (s) ds = t, о < t <
о
... ... ·-· . .
t
Sw00 (!;) ds =
+; S
'
о
t .
.
-
wo1 (s)-ds =
о
/·
=
1 - t, 2
т
=
1
1
<t<
'
1
используем
табл.
3,
откуда при
находим
t
1
1
l
-
2 w00 (t)- 4 w01 (t)-тw10 (t) -
=
1
(2.10)
- 16 W100 (t)- ''' '
Учитывая выражение (2.10) и правило умножения ·
функций Уолша, получаем
Jw
1
t
(S) d~ = 4W00 (t)- 8
01
1
1
W 11
1
-16 W101 (f) - 32 W1001 (t) -
(t)... ,
или в общем виде
t
00
~ w~ (~) d~ = ~ dn (т) wm (t).
,
о
m=O
Коэффициенты разЛо:Жения dn (т) сведены в табл. 4
Разложим интеграл
[27].
вида
(2.8),
где
И,(~)
=
· = Wo1 Ш ·; в ряд Фурье по функциям Уолша:
t
~1 ~ (t -
G)m Wo1
(~) d~ =
1
о
-
_1_.
ml.
r· (t -
s)m+l
m+ l -
f"+l -
'
2 (t (т+
]t =
f"+l
(т+
_l_)т+!
!)!
2
'
1)1
1
'
2<t<1.
Используя функции Уолша, получаем (для интервi].ла
45r,
'
$;
.·
. '>\ о
1
,
,
l
1
1
~
1
3
1
4
.
1 '5
.
1
1
6
7
1
~
1
9
1
10
1
11
1
1~- 1 ·
Таблица
13
1
14
' 1.
4
15
оо 1+1- +1~ +1 1- ~ 1 о 1 ° 1 О; 1- Тz 1 °· 1 'о 1 ° 1 ° 1 ° 1 о 1 °
1-+1 о l 1° 1- +1 о 1- ~ 1 () 1 о 1 о 1~i1 о 1 о 1 о 1 о 1 о 1 о
1 ~ 1 ° 1 ° · 1 ° 1 ° 1 ° , 1- ~ 1 . о 1 °\ 1
1-·i 1 ° 1 ° 1 ° 1 ° 1 ~
1 о 1- ~1 . (' 1 о 1 о 1 о 1 о
~ 1 о 1: о 1 1- ~ 1 о 1 о 1 о 1 о
1~ 1 1 о
о о: 1 о 1 а 1 1 о 1 · о 1 о 1- ~ 1 о 1 о 1 о ,
1 о 1 ~ 1 о 1 о 1 о 1 о 1 о 1 о 1 о 1: о 1 о 1 о 1 о 1- i 1 о 1 о
'
•
n ,
-.
OI
10
.
!
11
0
,\-
loo
n
\
\
1)
n
\·u
'
.101
11О 1 о 1 ~ 1 ~ 1 о
1
1 u 1
- 1
1
1
·1
.,.
1
1
_.;
1
о
1
1 u 1 u 1 u 1 "' 1
1
1
1 .
1
1
1
о
1
1
о
1-
i1о
1
1
.
_
~1~
о
'
о
о
о
1-- ----.--.--- --.-.-.-.- - - - - - --- ---.-. - ---. --..
о
о
о
о
о
о
о
о
о
о
о
о
с
о
- О
о
о
о
о
о
о
о
о
о
о
о
о
о
с
о
о
о
о
'о
о
о
•
,
с
о
_
о
о
о
о
с
о
-1~
о
о
о
о
о
о
-1~
-1~
о
-1~
о
о
с
о
о
о
о
о
о
о
о
о
~
о
о
о
о
--
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
---- ---·-- ---- ---- ---- --- --- ----1~
о
§
47
'Таблица
о
01
10
100
11
. 101
110
5
l ll
· - - -·
о
01
10
11
100
101
110
1
1
-т
6
1
-8-
1
1
1
1
1
о
о
1
128 .
1
-128
'
1
о
о
о
-43
о
1
-128
о
о
1
-128
о
1
-192
о
о
о
о
о
1
-128
О ·
1
-192
о
о
о
о
о
о
о
192
о
о
о
о
о
1
128
-54
о
о
1
1
1
о
32 -54
64
1
--.ш
о
32
1
-32 64 128
1
о
1
1
о
1
зг
-12 -32
16 32
ш
1
-16
1
128
1
о
1
-192
(0, 1 ])
1
t
.
тг S(t - s)
т
wo1 (s)
ds =
f"+' .
<т + l) 1 wo (t) -
о
(t-+(+1
-
(т
+ !) 1
... fwo (t) -Wo1 (t)].
Раскладывая каждую степень t и t - 1/2 с использованием табл. 3, перемножая функции Уолша и группируя члены, можно получить коэффициенты разложения
Gr (т, 1). Значения этих коэффИциентов для т = 1
и т = 2 приведены соответственно в табл . 5 и 6 [27].
х (1)
48
Пример 1. Решим дифференциальное уравнение х
= 1.
- ·х =
О;
"
-.,;.
Таблица б
о
1
()
24
7
<О
10
11
100
101
110
111
.
7
-""192
1
01
192
-"'"32
10
31 1536
-64:
11
64
17
- . 1536
100
127
12 288
-128
101
1
~
-
110
1
~
-512
ш
1
5Т2
о
1
~
01
1
-
1
127
12 288
64
-
1
17
1536
-128
1
1
~
-54
-128
1
1
128
256
-
1
-
1
256
1
512 .
65
12 288
1
'5Т2
1
5i2
17
' 12 288
о
о
1
1
-512.
о
о
.-
1
256
о
-
1
256
1
512
-
1
512
1
1024
о
-
1
1024
о
о
1
2048
-
1
2048
о
о
о
1
2048
о
о
1
65
12288
31
1536
1
-512
1
-
17
12288
о
о
-
17 .
12288
о
/
-
17
12 288
о
2048 '
Пусть И
х, тогда соответствующее интегральное -урав
(t) =
нение
t
\ -}
и и1-= 1+ ~ и <s> ds.
о
Возьмем первое приближение в виде
мощью таб~ . 6
U0. (t) = ;v0 (t),
тогда с по
t
Ui (t) =
r
Wo (t) + J.Wo {S) ds =
3
2
1
Wo (/) -т Woi (/) .
о
J?торое
·
· приближение
И2UJ =
t
woU)
+Л ·~
wo<SJ-+woi
(s)] ds =
о
27
=
-
.
3
l6 Wo (t) - 8
..
~oi (t)
3
1
. .
-16 Wio (t) + 32 Wii (/) -
•••
Этот процесс можно продолжать до получения требуемой точности.
!{ля определения х (t) необходимо полученное для . И (t) выра·
жение проинтегрировать с помощью табл. 4. Это дает ступенча·
тую · функцию. Для
восьмичленного
приближения результат
приведен в табл. 7. Здесь же для сравнения приводятся значения,
соответствующие точному решению в точках,
лежащих
на
сере·
дине двоичных отрезков.
Таблица
Двоичные отрезки
0-1/8
1/8-2/8
2/8-3/8
3/8-4/8
4/8-5/8
5/8-6/8
6/8_:_7/8
.Z/8-1 ~
50
х
(/}
(восьмнчленное
7
приближение)
el (точное решение;
J,065 19
1,207 01
1,367 73
1,549 83
1,756 21'
1,990.03
2,254 99
2,555 25
1,064 49
1,206 23
1,366 84
1,548 83
1,755 05
-1,988 74
2,253 53
2,553 59
Таким образом, с помощью предварительно рас"
считанных таблиц (вида табл. 3_..:...5) можно достаточно
просто
находить
решения дифференциальных _ и инуразнений . При этом в каждом малом ин
. тегральных
тервале
приближенное · решение
среднему
значению
истинного
будет стремиться
решения
для
_i:9r.o
к
же
интервала. Способы построения эле1пронных С!'ем
для реализации табличных функций подрОбно изложены в
[23].
2.
· ·
,,.
НСПОЛЬЗОВАННЕ
ПРЕОБРАЗОВАНИЙ АДАМАРА
ПРН РЕШЕНИИ СИСТЕМ
АЛГЕБРАИЧЕСКИХ YPABHEH11Jit
Если имеются результаты замеров полезного полиномиального сигнала S ( t) в аддитивной смеси с помехой ~ (t):
·
х
(t) = s (t)
где
s (t) =
+ h (t),
(2.11)
,..
п
~ k/, оценки К. 1 коэффициентов k1, полуi=О
ченные с помощью обработки замеров
в дискретные моменты времени
. tm
(2. l .I ),-
(т =т
взятых
по ме
1, N)
тоду наименьших квадратов (МНК), есть. результат
решения системы нормальных уравнений
(2.12)
ЗдесQ
А=[:. :: -~ _:)];
.·
1 tн
ti ... _t'N
'· : ·
;,
5t
.
"Т
К
"
,..
= [k 0 , k1 ,
"
•• • ,
kп];
Х
Т
,
= [х (t1), Х (t2),
• •• ,
Х (tн)J .
При этом корреляционная матрица оценок
D (k) = cr2 (Ат АГ 1 "
где
cr 2
-
дисперсия помехи .~ (t) .
Хорошо известны трудности,
~.
возникающие при
практическом решении системы (2.12) и .связанные
с плохой обусловленностью матр цы А [25] при боль
ших
N
и чувствительностью
решения
к
вариациям
значений элементов матрицы и правь1х частей исход
ной системы, вызванных помехами и вычислиrельны
ми погрешностями .
Наиболее эффективные методы преодоления у казан"
ных трудностей (метод ортогонализации и метод ре
гуляризации А. Н . Тихонова) не просты в технической
реализации. Поэтому здесь будет рассмотрен, хотя и
менее эффективный, но бoJ,Iee просто реал изуемый на
практике метод решения в частотной области. Пусть
имеется система у равнений
АК=Х.
(2. 13)
Преобразуем ее По Адамару, для чего умножим слева
обе части равенства
(2. 1.3)
на матрицу Н размерности
N х N (N =-= 2k):
(2.14}
Ада!'4аров
спектр· вектора замеров
обозначим
через
Х* = НХ, а матрицу НА через А*, тогда равенство
(2. 14)
запишем в виде
·
A*k= Х*.
Образуя из выражения
52
(2.15)
(2.15)
систему нормальцых
уравнений и решая ее, найдем
f<: = [(А*) 7 А*Г 1 (А*)т Х*.
·1
Корреляционная матрица оценок в этом случае остается той же. Действительно,
·
D (К)= [(А*) А*Г 1 _(а*) 2
=
=
l(HA/ НАГ 1 Na2
=
[А 7 ННАГ 1 Na 2 =[А' А] Na 2/N = а 2 [Ат А].
Однако переход к новой матрице системы А* приво
дит к новому спектру матрицы. Обусловленность
системы
улучшается,
так
как
происходит
проектиро
вание векторов-строк матрицы А.
Пример
2. Пусть дана плохо обусловленная система
[ 10.04 19,98]
19,98 40,01
Собственные значения матрицы
'J..2
-
[к]
к:
. [10050] .
системы
50,05Л
(2.16)
=
находим из . уравнения
+ 2,5 =О, '
от~уда Лi = 50, Л 2 = 0,05 и число обусловленности Z0 = 50/0,05=
= 1000, что говорит о высокой чувствительности решения к ва
риациям числовых значений правых частей системы (2.16). Гео
метрически это означает, что система (2.16) описывает две прямые,
пересекающиеся
под очень
прямые). Преобразуем
малым
систему
углом
(2.16)
(почти параллельные
по Адамар. у
J [11 · -
·[ 1
1] [ 10,04 19 ,98}-l f(0
1 - 1 19,98 40 ,01 J кi =
1] [ 50]
1 100 ·
В результате получаем
[ 30,02
- 9,94
59,99][g~]=[
- 20,03
Ki
Собственные значения м.атрицы системы
150]·
- 50
(2.17)
(2.17)
находятся из урав-
нения
'J..2
-9,991..-5 =О,
53
·
10,46 и Л2. = - 0,48, откуда чис
10,46 1 i\ 0,48 / ~ 22. Выигрыш, ко
торый при этом получается, составляет Z0 /Z0 н = 1000/22 = 45 раэ.
решая которое, найдем Лi
ло обусловленности Z0 н =
=
1
Обратим внимание еще на одну особенность пре
образованной системы. Fассмотрим для этого случай,
когда влиянием помех в выражении (2.11) можно пре
небречь. · Пусть
s (t)
=
k 0 +~k 1 t
Представлены в виде вектора
S
т
=
+kt
2 2
и
замеры
[s (t1 ), s_(t2 ), s,(t 3), s (/4)].
(2.18)
· Если использовать только первые три уравнения систе
м.ы (2.18), что вцолне достатрчно (система становИтся.
опр.~деленной), то приходим к системе с треугольной
матрицей. Решение такой систеМЬI не tГредставляет
за.труд!itЩИД и .fte требует обращения матрицьl.
54 ,•.
~
...
Гnава
3
СИНТЕЗ СТРУКТУРЫ ФИЛЬТРОВ
1.
·
ЦИФРОВАЯ ФИЛЬТРАЦИЯ СИГНАЛОВ
Цифровые фильтры (ЦФ) по сравнению с аналого
выми
1.
имеют ряд преимуществ.
ЦФ не имеет реактивных элементов,
поэтому
при его разработке исключаются все проблемы, свя
занные с точностью изготовленИя
и стабйльностыq
этих элементов.
2. ЦФ мо:щно выполнять на интегральных схемах
или в виде нескольких (или даже одной) интегральных
субсистем. Такие фильтры экономичны, имеют неболь
шие размеры.
3.
ЦФ могут быть запрограммированы в тех слу
чаях, когда для обработки сигналов применяется ЦВМ,
работающая в реальном масштабе времени. Такая ре
ализация ЦФ особен1ю удобна, коrда ЦВМ исполь
зуется для моделирования динамических систем.
4. Характеристики ЦФ прогнозируются и вьцюл
няются' с высокой точностью.
5.
Характеристические
частоты
ЦФ
зависят
от
внешней тактовой характеристики (частоты). Изме
няя эту частоту, можно легко перестраивать фильтр.
Можно также легко изменять и другие параметры
фильтра (ширину полосы пропускания), что дает воз
можность использовать их в
системах
6.
мую
адаптивных и следящих
. .
ЦФ имеют высокую ,стабильность,
стабильностью
генератора
определяе
тактовой
частоты,
Это позволяет реализовать фильтры с очень высокой
добротностью ил w чрезвычайно больши11:1и постоянны
ми времени .
·
7.
ЦФ можно выполнять
характеристиками,
с линейными фазовыми
что важно в тех
случаях
синтеза
55
систем, когда необходимо иметь постоянную задерж
ку на всех частотах ил.и хорошую импульсную харак
теристику.
При разработке ЦФ не возникает проблем с фи
зической реализацией отрицательных индуктивностей,
поэтому можно увеличить разнообразие структур
фильтров..
.
.
8.
9.
При разработке ЦФ не возникает
задача
со
гласования нагрузок.
10.
Преимущества ЦФ особенно видны на сверх
низких частотах, где габаритные размеры аналоговых
фильтров недоступно велики .
11. ЦФ не имеет дрейфа, присущего активн.1:>1м
фильтрам.
.
12. В случае реализации фильтровых гребенок
OJI.HO управляющее устройство и один арифметический
· блок могут обслуживать много ЦФ, что дает существен
ную экономию оборудования:
В то же время следует иметь в виду, что в отличие
от аналоговых фильтров работа ЦФ сопровождается об
разованием специфического шума за счет недостаточ
но
четкого ограничения
логового
сигнала,
дискретизации
и
полосы частот
неточного
применения
входного
определения
квантования,
ана
частоты
а
также
· за счет неизбежного округления чисел при проведении
вычислений. Обла~ти применения ЦФ и вообще циф·
ровых методов обработки сигналов в значительной
степени определяются возможным быстродействием
используемых вычислительных средств.
Математические схемы цифровых фильтров опи
сываются с пом9щью разностных схем подобно тому,
как схемы аналоговой фильтрации описываются с по
мощью дифференциальных уравнений. Для решения
разностных уравнений и синтеза ЦФ удобно исполь
зовать математический аппарат z-преобразований, вы
полняющий в дискретном .анализе ту же роль, что и
_56.
·)
(
преобразование Лапласа в непрерывном анализе.
Некоторые типы ЦФ можно рассматривать. как аппро
ксимацию J!Звестных аналоговых фильтров . В общем
же случае ЦФ составляют широкий класс устройств,
которые можно 1 1 роектиров~пь непосредственно , не .опи
раясь на
-)
Цф,
аналоговые прототипы,
не имеющие себе
т. е.
подобных
можно создать
среди
аналоговых
фильтров.
В ЦФ
входной и
выходной сигналы квантуются
по времени и по уровню и системная функция реали
зуется
в числовом виде
так же,
как
и в вычислитель
ных машинах . Цифровой фильтр по существу реали
зует
решение разностных уравнений, с
помощью
которых связывается требуемый вы}.{ одной сигнал и
текущие
значения
входного,
а
также
предыдущие
значения входного и выходного сигналов . Его основны
ми элементами являются
линии задержки, умножители
на константу и сумматоры . ~' равнение, описывающее
ЦФ, можно записать в виде
00
у
[NJ =
00
~ akx [п ·
~=0
k]
+ ~у [п -
k] bk.
(3. 1)
n=I
Из этого уравнения следует, что
текущее
значение
выходн·ого сигнала у 1п1 находится взвешиванием и
последующим суммированием текущего значения вход
ного сигнала х [п] и предыдущих значений х [п и выходного сигнала у [п - k].
k]
Фильтр, выходной сигнал которого является функ
ц-ие.й только зна-qений входного сигнал а и не зависит
от предыдущих значений · выходного ( bk = О), назы
вается поперечны~ или нерекурсивным. Однако, ес
ли выходной сигнал ЦФ з ависит хотя бы от одного
предыдущего значения
называется
выходного сигнала, то фильтр
рекурсивным.
Рекурсивные UФ в основном· бывают прямой или
канонической формы (рис. 10, а, 6). Обычно отдается
57
предпочтение фильтру канонической формы, поскольку
он
имеет
вдвое
меньше
задержек
и,
следовательно,
меньший уровень собственных шумов, хотя
оба вида
--[В-
Вход
Gт
а
а,
Структур
ная
схем11
прям : й
(а) и канонической
(6) форм цифрово
го фильтра ..
б
Рис. 11. Об.общенная структура цифрqвоrо фильтра ЦФ.
фильтров описываются
одним и тем же . разностным
уравнением. Фильтры высших порядков любой фор
мы · чувствительнее к неточности · ве.1ичин коэффици
ентов, вызванной ограниченной длиной слова.
Рассмотрим., принцип действия цифровых
58
фильт-
ров-;' выполняющих одни и те же операции . Фильтр
ЦФ, схема которого показана на рис.
трех частей:
преобразователя аналог
цифрового счетного устройства
теля цифра - аналог ЦАП.
11,
состоит из
-
цифра АЦП;
ЦСУ;
преобразова
Входным и выходным сигналами ЦФ являются
узкие модулированные по амплитуде
одному за период стробирования Т 5
менты времени
счеты
t
= nT5
непрерывного
мгновенно
входного
импульсы
= 2n/ffi5 ).
(по
В мо
производятся от
сигнала
и
на
входе
ЦФ появляется импульс х (пТ 5 ). В преобразователе
АЦП амплитуда импульса переводится в кодовое
слово, являющееся кодированной последовательностью
бинарных единиц (бит), которые представляют ам
плитуду х (nT5 ). Точность ее представления опреде
ляется длиной слова, т . е. количеством содержащихся
в нем бит . Все работы производятся ' над· этими слова
ми, а выход вычислительного
устройства
-подключа
ется к преобразователю ЦАП - для того, чтобы полу
чить выходной импульс фильтра у [nT 5 ]. Вслед за
ЦФ размещена схема затягивания ЗЦ, превращаю~
щая
· пос.Ледовательность
импульсов в непрерывный
выходной сигнал. Ступеньки, получающиеся при та
кой аппроксимации, могут бьiть устранены последу
ющей аналоговой фильтрацией.
Для того чтобы ЦФ работал
в аналоговых схемах
в реальном масштабе времени, требуются промежуточ
ные цепи. Типичные входн1>rе и выходные цепи вмес
те с ЦФ показаны на рис 12.а. Спектры сигналов в
отмеченных буквами точках .qтой схемы изображены
на рис.
но
12,
б. Входной спектр А показывает, что мож
ожидать
присутствия
сигнала
любой
частоты.
Поскольку стробирование по сути является моду:П яци
онным
процессом, частспа его должна выбираться
вдвое выше верхней частоты входного сигнала, иначе
произойдет· перекрытие спектров. 'Эта минимальная
59
частота стробирования является частотой Н аiiквиста.
Поэтому, чтобы подготовить аналоговый сигнал к про-
ФНЧ
в
ЦФ
п
цессу
:~11111111111111111111111111
'
'
:
.
_
с~
g)
о~
~~
.
i
~~·
•
:~г----,'Ь---;--.,, .к--
FI
ограни
следует
тром низких частот ФНЧ.
В зависимости от задан
ной фазовой характерис
тики может потребовать
ся фазовый корректор
ФК (фильтр, пропускаю
щий все частоты) для
компенсации
фазовых
искажений,
вносимых
.Фильтром низких
час
тот .
/
!
о.~
вначале
сигнал
чить по полосе частот
путем фильтрации филь
а
:•
последовательной
дискретизации,
· Для
иллюстрации •
, предположим, что циф
ровой фильтр имеет ха
рактеристику
f
го
полосового
ОТ
(!)
Рис. 12. Структурная схема ци·
фрового фильтра (а), работаюLце·
го· в аналоговых схемах,
и
спек
тры сигналов в Х'арактерных точ·
ках этой схемы
тотах,
(6).
,
фильтра
ДО (!)
Выходной спектр
=
=W 5 /5.
идеально
(!) 5 /
=
1О
напоминает
входной
спектр тем ; что и его по
лоса
пропускания
как
+бь1 модул-ируется на час-
кратных частоте стробирования.
-
Обычно используемые затягивающие цепи ЗЦ
-
это цепи нулевого порядка . Такая цепь задерживает
величину
последнего
импульса
до
появления
следую
щего. Передаточная функция затягивающегося устрой
ства
нулевого
Н0 (w)
60
порядка_ имеет
вид
= sin (wT/2)/(WT /2) <
5
-(wT 5 /2) ,
Абсолютная величина А ЧХ этой функuии показана
(
на рис. 12, 6, где хорошо заметна фильтрация высщих
гармоник. В зависимости от применения может быть
желательной
последующая
фильтраuия
обычным
фильтром низких частот (срезаются ступеньки функ
ции) .
Полный фазовый сдвиг равен сумме фазовых сдви
гов, вносимых в ЦФ затягивающей uепью, обычными
аналоговыми фильтрами и задержкой в uепи сигна
ла . Фазовый угол, обусловленный временной задерж
кой fg, возрастает линейно с ростом частоты и имеет
величину -(J)fg рад. Временные задержки возника!ОТ
в АЦП и в счетном устройстве. Время счета уменьша
ется с ростом стоимости и
сложности и увеличивается ·
с ростом требований к точности. Поскольку счет дол
жен быть· закончен за период стробирования, время
счета накладывает ограничения на верхнюю частоту
стробирования .
Для анализа ЦФ используется
которое записываем
в
следующем
z-преобразование,
виде:
00
х (z)
=
~ х (nT 5 ) z-п.
n=O
С учетом этого выражения перепишем уравнение
в
(3.1)
виде
у (z)
=
х (z)
±
akz-k
k=O
+у (z)
i; bkz-k.
(3.2)
k=O
Уравнения (3.1) и (3:2) идентичны и одно из них мож·
но . легко получить из другого. Для этого нужно пре·
-k , где k дыдущие значения сигнала умножить на z
1
количество
периодов
':!астоты
стробиров;шия,
которое следует сдвинуть импульсы или слово .
на
Из
61
уравнения
(3.2) можно
функuию сисrемы
о"пределить
n~редаточную
Н (z) =у (z)/x (z) = ~ aliz-kt(1 ::- ~о bkz-k).
.
(3.3)
·'
С полюсами и нулями этой функции в z-плоскости
можно оперировать так же, как с полюсами и нулями
передаточной. функuии.
1.
МЕТОДЫ УПРОЩЕl;IИЯ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
ЦИФРОВЫХ ФИЛЬТРОВ
Передаточная функuия uифровых фильтров может
оказаться сложной - иметь высокий порядок, обла
дать f!еминимально фазовыми свойствами.
Для упрощения структуры
математических мо
делей синтезируемых uифровых фильтров применя
ются методы теории rомоморфизмов.
Рас.смотрим некоторые методы синтеза структуры
гомоморфных фильтров, полученных эквивалентным
упрощением исходных моделей.
МЕТОД ЦЕПНЫХ ДРОБЕЙ
Пусть имеется исходная структура фильтра с ха
рактеристикой Kv. Известно, что час:тотные характерис
тики устойчивой системы,
ной
функuии
при
Времени К (z) ПрИ
р
== jw
полученные из передаточ
(в
Z = ejruT),
случае
дискретного
ОJi.НОЗНаЧНО ОПредеЛЯЮТ
ее динамические свойства. Поэтому iз качестве крите
рия
для
понижения
дифференuиального
порядка
передаточной функuии
(разностного)
ура1:1нения
мо.щет
быть принято усJювие, состоящее в том, что мало от-
62
·
•/
личающимся
ствуют
частотным
мало
характеристикам
отличающиеся
переходные
соответ
проuессы .
Рассмотрим устойчивую линейную с истему, . вы
ходная величина которой в форме z-преобразования
имеет
вид
х
·1
где х
У
(z),
ходыой
(z) -
.
.-
z-изображения
величины
У (kЛt); Лt
(z)' = К (z) У (z),
х (kЛt)
период
-
-
К (z) =
b1nZm
·п
апz
и
(3.4)
соот ветственно
внешнего
дискретизации,
вы
воздействия
а
+ bm-1~-I+ + b1Z +Ьо
+. an-I ~-I + ··· + aJz + 1
(3.5)
передаточная функция.
Задача заключается в том , чтобы достаточно точно
описать переходные процессы в этой системе переда
точной функции пониженного порядка
К1
d5-I
(z) =
,
q,z
+ d 1zs-I + ··· + d z + do
,_
,
+ c,_1Z 1 + ' .. + C1Z + 1
5_
1
(s
< r<
п) ,
(3.6)
которая
с
достат_очной
точностью
аппроксимируе1
исходную.
Из теории
дробно " рациональных
приближений
функций в комплексной области и з вестно, что наилуч
шее приближение, не требующее сложных выкладок,
получается при помощи цепнь1х дробей
Передаточным функциям
(3.4)
и
(3 .5)
[7] .
соответству.ют
АЧХ
К (eiWT)
Ьт (e j wT)m
ап (eiwT)n
=
+ ьт-1 (ejwT)m-1 + ... + bi (ejwT) + hl)
+ an-I (e.jrиT)n-1 +
К1 (eiwT ) =
63
где Ь 0 и d0 - коэффиu.иенты усиления, определяющие
статические свойства системы, поэтому d0 = Ь 0 при
условии тождественности статических свойств.
Для
С2 ,
•• "
определения
с" d 1 , d2 ,
.. ,
остальных
.
ds А Ч Х К (e 1
с1 ,
коэффиu.иентов
т
(J)
)
выражение
(3. 7)
пр~образуем в соответствующую цепную дробь
К (eiUJT)
=
а
_:_!_
1 .о
+
а · (e;ffiт)
2,0
а1.о
+
а
2п.о
+
а
(eiUJT)
з,о
· а2.о
+ ...
(eiUJT)
(Э. 8 )
а,2п-1.О
при условии ak,o =#=О;
a1.k = bii (k = О, 1, 2, ... , т);
ao.k = ak (k = !, 2, ... , п). Если ak.o =О, то u.епная
дробь имеет вид
Коэффиu.иенты
ловии а 00
a.k.o
в выражениях (3.8)" и (3.9) при ус:
= 1 определяем
по формуле
ak,i = ak-1.oak-2.i+1-:- ak-2.oak-l.i+I·
-"
Если вместо каждой пепной дроби (3.8) и (3.9) взять
необходимую дробь,
и
имеющую тот же
(3. 7}, то получим
К 1 (eiUJT) =
64
порядок,
что
".
pk
(е;шт)/[Q (eiUJT)J,
где
порядо1< подходящей дроби, которую . нахо
k -
дим по формуле
· т
Pk (e 1w ) _
р
jwT)
ak-1 ,0 k-1 (е
Qk (efwT) -
а
Q
k-1 ,0 k- 1
+ ak.O (е jwT) рk-'f (е iwT)
(efwT) +аk,0 (efwT) Qk-2 (efwT) •
>-
спра ведливой при всех k
2. При этом Р0 (efwT)/[Q 0 х
Х (efwT)J = 0/1; P1(eiwT)/ [Q1(efwT)] = а10/аоо·
Величину погрешности,
В()ЗНикающую при пони
можно оце
жении порядка передаточной функции,
нить
при
помощи
1
К (efwT) -
неравенства
К1 ( efwT)I <; 1f[VSQ% ( efwT)J .
По данному методу можно , найти выражения для
коэффициентов упрощенной модели передаточной функ
ции
через коэффициенты передаточной функции
в общем виде при любых з начениях т, п, s,,.,r,
т. е ." можно последовательно понижать порядок пере
даточной функции(3.5) на единицу.
Рассмотрим цифровой фильтр. для системы иденти
(3.6)
(3.5)
фикаuии,
рабочий
сигнал
последовательностью
которой
представляется
радиоимпульсов
длитель
>
ностью fи, следующих с периодом повторения Т 11
fи.
Радиоимпульс на интервале t = t11 достаточно точно
описывает(: я аналитиЧеским выражением
S 11 (t) =
Ат COS Ш
cos rot.
Работа цифрового фильтра описывается линейным
разностным уравнением
т
у [nT]
='
п
~ А 1 Х [пТ- iT]
~1
Нерекурсивный фильтр,
+
~ Biy [nT- iTJ . (3. 10)
81
~1
=
.
О в уравнении
(3. 10),
не может быт1;> использован для фильтрации разрыв
но й последо·вательности импульсов с периодом повто
рения Т 11
з
7-1403
))
111
вследствие очистк и р егистров хранен и я
65
предыдущих
значений
значениями,
~.:оответствующими
tи . входного сигнала .
входного . сигнала
При
нулевыми
интервалу
времени
использовании рекурсив-
, наго
фильтра (даже при полной очистке регистра хра
предыдущих значений входного сигнала) на
выход фильтра будут поступать значения выходного
нения
сигнала,
.
полученные
сложением·
предыдущих
зна
чений выходного сигнала, умноженных на коэффиuи
шт, соответс·~вующий элементу" задержки
Таким образом, для фильтрации заданной после
довательносп~
разрывных
импульсов
необход11мо
использовать рекурсивный ЦФ, структура которого
учитывает запаздывание импульсов : Проектируемый
.
цифровой фильтр должен
характеристику,
лей . и
иметь линейную фазову10
что соответствует расположению ну
полюсов . передаточной функции
на · единичной
окружности (расположение полюсов на границе-устой
чивости является признаком резонанса в системе) .
Описанные в литературе методы синтеза рекур
сивных фильтров . во временной области · позволяют
синтезировать фильтры с хорошими
рактеристиками
и
менее
временными ха
качественными
характеристиками . Фильтры,
частотными
синтезированные в час
тотной области,
обладают
хорошими
частотными
и худшими временнь1ми характеристиками. Кроме
того, большинство из разработанных методов сйнте
за в ча·стотной области основано на дискретизации
предварительно рассчитанных аналоговых фиJ1ьтров,
в
результате
чего
часто
возникают отклонения
ченных характеристик от проектируемых.
Выполнение
всех
требований,
проектируемому фильтру,
полу
·
предъявляемых
к
возможно при нспоJ1ьзова
нии классического метода синтеза передаточной функ
ции, определяемой как отношение изображения вы
ходного сиги.ала 1< изображению входного:
W(z) = Y(z)/X(z).
06
,._
(3.11)
'· '
Для определени51 z-преобразованиs:~ вхощюtо сиг
нала необ ходимо определить изображение одного ра
диоимрул?са, а затем изображение периодической по
следоватеJ1ыюсти
пользоваться
Лапласа
Если
импульсов,
методикой
непериодических
z-преобразование
тельности
для
чего
определения
радиоимпульсов
можно
вос
изображения
разрывных функций . .
непрерывной последова
определяется
выр-ажением
z (Ат"' cos Qt cos wt) =
2
гДе ai, bi - постоящше 1юэффициенты, представля
ющие собой периодические функции периода к'ванто
ван~1я Т, а .изображение смещенной на длительность
импульса fи = kT, где k - количество целых . перио
дов,
непрерывной
последовательности
имеет
вид
.
Zсм ( А m 8 x COS 2 Qf COS wt)
А
= ·-
твх
4-
.
-ks
(z),
. Z
то изображение одного радиоимпульса
Z1 ( Атвх
cos 2 Qt cos wt}
.
z (Атвх COS2 Qt cos wt} - ·
.
А
-
Zсм (Атнх
cos Qt cos wtf
2
=-
твх
4-
.
( 1-
На основании теоремы запазды~ания
z-преобразование
входного сигнала,
k
Z- )
S (z).
оригиналов
представляюще
го собой периодическую последовательность импуль
сов ,
принимает
вид
Zвх_ ( Атвх COS 2 Qt
cos wt j = .
67
ZM
zM-k
;;
7
S(z)
1
-
=
а изображение выходного сигнала,
гармониче кое колебание,
(3.12)
Х (z).
представляющего
. собой
.
Zвых {Атвых SIП
z sin (j)T
Аm8ЫХ z2 - 2z cos (j)T
ron =
+
1=
у (z).
(3.13)
Таким образом, передаточная функция цифрового
фильтра на
основании выражений (3.11) - (3.13)
определ.яется следующим
W (z)
=
выражением:
k(
Х
+
с омножитель.(z
A6 z0 -
8 7z7 -B"z6
~~k ) Х
MZM
l
-z
+
+
+
л-1
)
· - 1 /(z
М
+
во
входном
( 3 l-4)
'
'
M-k)
- z
передаточной функции определяет
пульсов
+
A5 z" A4 z' - A3 z"
A2 z2 - A1 z Ао
Br,z 5 - B4z4
B~z 3 - B2z2 8 1 z1 - 8 0
в выражении для
запаздывание им
сигнале.
Цифровой фильтр с передаточной функцией (3. 14)
физически нереализуем, так ка1< оператор z-преобра
зованиЯ в положительной степени указывает на зави
симость выходного сигнала фильтра от последующих
значений входного и · выход~:юго сигналов . Разде
лив выражение (3.14) на z в максимальной степени,
получим физически реаJJизуеМ,ую передаточную фун
кцию
W(z)=
68
где М
-
количество
у кладывающи хся
на
uе.лых
периодов
период
< +
квантования,
повторени я
в ходного
сигнала Т -<: МЛt
Т
1; k - количество uелых
периодов непрерывной последовательности tn = kT.
Используя
учи.тывая,
Рис.
для .
13.
опредtление передаточной функuии
что z-преобразование
· вло1< -схема алгоритма вычисл ений, необходимых
определения зна ~ ения ВЫ)\Одноrо сигна л а .
задержанной на
u
исходнои
i
выбо_рок,
равно z-преобразованию
.
последовательности,
записываем
боту
и
последовательности,
u
умноженнои
разностное . уравнение,
на
' -i
z ,
описывающее
ра
проектируемого фильтра:
. у [nT] = L 6 x [пТ-Т]
+ · · · + L 0 x [nT- 7Т] +
+
+ " . +L~x[nT
+ .L~x[nT-(M
l)T]
-(M + 7)Т] + k0 y[nT-T] +
· · · + li y[nT-7TJ+
+ k;y [пт_-:- kT] + " : + k'y [пТ -(k + 7) Т] . (3. Jб)
0
Алгоритм определения каждого значения выходного
сигнала,
соотв етствующий
разностному
уравнению
и передаточной фун кuии (3.15) и составленный
по способу - прямого программирования . показан на
(3.1r.)
рис. 13. Блок- схема алгоритма моделирования дан
ного фильтра показана на рис. 14.
69
Начал(!
X[7]=0,0, .. .0,"A[7}.A!CZ
Y[7NJO, ... Д8Щ8f[7}
T=(l- f)xTк4
,,
"
Y4 =Z (Y[l(Jx82[Lf-K+!J)
l(:ЦcNf
Цикл
l(= [· ·f
Шае=-f
Рис.
14.
фильтра.
Блок-схема
Y[к+fl=V[кl
х[к1ti= пк1
алгоритма
моделирования
,..
Если принять, что М и
()
- ·z-м ;
и
( 1 - z-k)
.k
uелые числа, то можно
разложить :
-z-1) (} +z-1 + z-2 +
1-z-'' =(1-Г 1 )(1 +z-' +z- 2 +
1 -z-М
=
(. }
в результате чего получим
+ z=- 1 + ·· + z-M+I) (А 0 Г 1 - Аьz-2 +
• • -4 + А - 5
А -6 + А -7)
А 4Z- 3 -:tt,,z
+
W(z-J)=k
· "22
iZ
oz
, (! + z-1 + .. +гk+i) (В1 - в6г~ + в,г2 +.
+ В4Г 3 + Взz- 4 - B2z-5 + B1z-5 +.вог- 7 )
(1
Если
выполним умножение полиномов и сделаем
переход от W (z- 1) к W (z), то получим
А'
zk+б +А'
zk+s +А',М+4 zk+4 +
М+б
М+5
W (z)
... + A:W_izk-i + .. + A;i-M+I + Aiik-M
, k+?
,
k+o .
,
k-i
Bk+7z
+ Bk+бz
+ ... + Bk-iz
+ ...
... + в;z+в~·
=k
Коэффиuиенты со штрихами вычисляем по форму·
лам:
1)
для
k
=
м
k-1
k-l
B~+rk-1)-i
A~+1k-11-• = ~ Aб(i-z);
1=0
где
i~
+ (k -
О,
= ~ - B1~u-I),
1=0
+
+
1, 2, ... , (7
(k-'-- 1)J; j = О, 1, 2, .. , [6
1)]. Если (i - l) <О и 7 - (i -!) <О, то
Аб-u-1 1 = B1-(i-t1 = О;
2) для k =/= М и k
>
.
М Aб<k-1)-i·
. ·
Имея выражение для коэффициентов передаточной
функuи~ как некоторых периодических функций Q~
рJюда квантования, можно, варьируя частотой кван·
тования,
корректировать
частотные
характеристики
фильтра. В данном сJ1учае условие резонанса в системе
71
Начало
ffET
>----i
Вычислитk,
.
As+rк-tJ"i~tA!,- fi-1! ,
Bi+rк- tJ-i = ,fo 81-ri-1)
Вычи~лить
сiок=А;; Cio= f; cir,к= .8t;
f = 7 +(l-f); ol.к,i=«к-r,otXк-1JfГ
- Оlк-2,0 tXк- tiff
i.
Вычислить
1
B1 =. r.
vo
f
- Q( 2
1
2m-1 Z
НЕТ
!(онец
,_
Вычислить
k= k-f
M=M-f
Рис.
путем
15.
Алгоритм
понижения
ее
упрощения
порядка.
передаточной функции
определяется самим подходом к синтезу передатоЧной
функuии. Кроме того, условию резонанса соответству·
ет распоJюжение полюсов
на единичной окружности,
что является условием линейности фазовой характе·
ристики фильтра .
Представленный пример требует большого числа
вычислительных операuий и поэтому задачи такого
рода удобнее решать на ЦВМ. Общий алгоритм ре·
шения порядка К (z) показан на рис. 15. По этому
алгоритму может быть успешно решена задача со·
кращения W
(z)
при фиксированных
k
и М.
МАТРИЧНЫЙ МЕТОД
Представим модель дискретного во времени ста·
ционарного фильтра
x(j+
l)=Фх(j)+ЛИ(j)
(3.17)
в виде разбиения
(j +
[ х1
X2U+
l)J- [Ф1
1) = Фз
Здесь Ф и Л
Ф2] [х1 (j)J
Ф4 X2(j)
+
[Л1]
Л2 U(j). ( 3.lB)
п х •п и п Х т постоянные матрицы;
-
И - т-мерный вход системы; х - п-мерный вектор,
состоящий из /-мерного вектора х 1 и (п - /)-мерного
вектора
х2 •
•
Необходимо построить упрощенную модель
X1(j
-
~
+ 1) = ФRХ1 (j) =
заданного порядка
l,
ЛRИ
(j)
(3.19)
в которой подлежат определению
матрицы соответствующих порядков Фk и Лk.
_
Известно,
что существует п Х п
ТОР.аЯ ПОЗВОЛЯеТ
преобразовать
матрица М, ко
уравнение
(1 .14) 1<
жордановой канонической форме [31 ). Запишем это
преобразо~ание в виде х (j) = Mz (j) и в блочной
73
форме
(3.20)
где
21
Z - канонический вектор состояния, а векторы
и Z2 имеют размерность l и п - l соответственно.
Столбцы матрицы М будем считать упорядочен
ными слева направо в порядке убывающей значимости
соответствующих
собственных
значений
переходной
матрицы Ф. Это всегда можно сделать подходящей
перестановкой столбцов. Так как система (3.17) пред
полагается устойчивой, го все собственные значения
Ф лежат в единичном круге. Следовательно, столбцам,
расположенным
слева,. соо:гветствуют
собственные
значения Ф, лежащие ближе к единице (по абсолют-
,
· ной величине), а расположенным
справа
-
лежащие
ближе к нулю. Если Ф имеет п различных собствен
ных значений, то
столбцами
М
являются
собствен
ные векторы Ф, а М называется модельной матри
цей. Подставив выражение (3.20) в уравнение (3.18),
получим . систему в жо.рдановой канонической форме
J (j)J [б2t\J U(j);
О l. Z2(j)
Z1
а2
а=
где а -
[ а1
О
О
а2
J = М _1ФМ
.
и б
(3:21)
·
= [б~]
= V Л, (3.22)
62
блочно-диагональная матрица; б
-
матрица;
(3.23)
- блочное представление обратной
матрицы М..,.. 1 •
Вследствие предполагаемого упорядочения столб-цов преобразования М жордановая каноническая . мат
рица а имеет . следующую структуру:
74
в ее левом верх-
'·
нем блоке
0:1
размера l х l сосредоточен·ы собственные
значения Ф, расположенные ближе к единице, а в
(п - l) х · (п - l) блоке сх 2 сосредоточены собствен
ные значения, расположенные ближе к нулю. Из ска
занного и" уравнения
(3.21)
з.аключаем, что каноничес
кие координаты Z1 характеризуют медленное движе
ние систем, а Z2 - быстрое, т. е. после приложения
входного возмущения координаты Z2 стремятся к сво
им установившимся значениям быстрее, чем коорди- .
наты Z1 . Из уравнения (3 .2 1) видно, что движения,
характеризуемые координатами
Z1 , и Z2 , не связаны.
Для систем с линейно независимыми собственными
векторами а является ди а гонально~ матрицей и по
этому Z1 и Z2 всегда будут несвязанными. Если же- чис
ло линейно независимых собственных векторов меньше
п, то представление исходной системы в матричной
форме в виде пыражения (3.18) следует произво
дить так, чтобы не расщеплял ·ись жордановые блоки
а; тогда Z1 и Z2 остаются независимыми.
Для решения поставленной задачи сокращения раз
мерности дискретной модели воспользуемся подхо
дом Маршалла
131 ], который применяется дл.Я р~шения
аналогичной задачи в пространстве непрерывного вре
мени.
Идея
метода состоит в пренебрежении
движения в исходной модели
высокого порядка . Для координаты х 1 из уравнения
(3.18) имеем
динамикой
.
Х1 (j
этого
быстрого
+ 1) =
Выражение для х 2
уравнения
(3.19)
и
Ф1Х1 (j)
(j)
+ Ф2Х2 (j) + Л1И (j).
можно
получить,
(3.24)
комбинируя
(3.23):
х20)= v:;- 1 !Z2U)-V3x1 (i)J.
Реакция координаты 2 2 на · входное возмущение
оказывается более быстрой, чем реакция координаты
Z1 ,
так как собственные значения блока сх 2 расположе-
75
ны ближе к нулю, чем собственные зн.ачения блока
а 1 . В качестве приближения предположим, что 2 2 (j)
немедленно достигает
яния,
т . е.
нового
обладает
установившегося
мгновенной
реакuией .
состо
Тогда
из уравнения (3.24) получаем
· Z2(j
+ 1) = Z2(j) = ( 1 -
а2 Г 1 б 2 И (j).
(3.25)
Объединяя теперь уравнения (3.24) и (3.25), находим
модель
системы
пониженного
ФR = фl
ЛF = Л 1
+
-
порядка,
где
Ф2V4 1 V3;
а2
ФУ:t 1 (/ -
(3.26)
)- 1
б2 •
(3.27)
При постоянных входах координаты х 1 исходной
и упрощенной системы достигают одного и того же
'установившегося з начения .
Другой метод анализа непрерывных систем, пред
ложенный Дэвисоном
[31 ],
основан
на
предположе
нии, что вклад несущественных собственных значе
ний исходной системы в ее реакuию незначителен
и им можно пренебречь . Решение записывается в сле
дующем виде:
x(j
+ 1) ·=
i-1
Фiх(О)
+ k=O
~ фkЛU(k),
где х (О) ~· начальное состояние системы .
Следуя Дэвисону , рассмотрим случай, когда х (О)
=О. Тогда
=
j- 1
x(j
Используя
можно
преобразование
переписать
x(j
76
+ 1) .= .~
ФkЛU(k).
k=O
в
(3.28)
(3.22), выражение (3.28)
следующем
виде :
+ 1) = м (~: аkм- 1 ли (k)).
После
разбиения
это
уравнение
l
x1 (j
X2(j
+
+
принимает 'форму
1)) =
J)
=[:: ::JI%{(~ :~)(~: - ~:)~иk}).(3.29)
Предположим, что собственные значения а 2 ' не ока·
зывают существенного
влияния
на
реакцию системы,
а потому ими можно пренебречь (т. е. а 2 =О) . Уравнение
в результате упрощается:
·
(3.29)
[ xl(j
. (.
Х2 J
!)] =' [мlл;-I
+ !)
+
М
k
'
]
~ (а1 (V 1 V2) ли (k)} . (3.30)
2
k=~
/=1
Определим l х 1 вектор
s .~
k=O
подставив его в уравнение
{(a~)(V 1 V 2 ) ли (k)) и,
(3.30),
·
получим
[~: ~~: ~~J = [::J sПосле преобразований из последнего уравнения полу·
чаем
s= м;-lxl (j + !);
.
Х2 (j
+ 1) =
M 8Ml 1Х1 (j
+ 1).
Для вычисления Фk подставим
выражение
невозмущенное уравнение
т. е.
и
(j)
=О:
(3.24),
(3.31)
(3.31) в
примем в нем
·. (3.32)
rогда Фя
= Ф1 + Ф 2 М 3М! 1 •
Для вычисления
Лk
ср·авним решения
•
исходной
. # . упрощенной . М.QД~.JJe.iit дри х (О) =о~ E~JJ.И дрен~·
17
бречь а. 2 , то решением исходной модели fiудет
X1U
+ 1) = М1 1 ~~ {а.~'(V1Л1 + V2Л2)И(k)))'
а решением уnрощенной
(3.33)
i= l
Х1(j+1) = ~ {Ф~ЛRИ (k) }.
k=O
=1 Ма V и VМ· == f, можно
= M 1a 1MI , в результате чего реше-
Используя соотношения Ф
•
(Iоказать., что ФR
ние упрощенной модели принимает вид
х1 (j- + 1) = М 1 (~'
{a.~M! 1 ЛRV (k)J \/ .
11=0
Сравнивая уравнения
•
ЛR =
(3 .33)
М 1 (V 1 Л 1
При разбиении на блоки
и
(3.34),
+ V2 Л 2 ) =
(3.34)
получаем
М/) 1 •
выра':жения
(3.35)
VМ = / пере
ходная матрица из уравнения (3.32) Эквивалентна пе
реходной матрице (3.26), полученной методом Мар
шалла.
Рассмотрим
модели
кого
задачу
преобразования
высокого ·порядка
порядка .
Пусть
непрерывной
в дискретную модель низ
модель
физической
системь~
представлена · в виде системы - линейных дифференци
альных уравнений
х =АХ +ви.
(3.36)
Для решения поставJ1енной задачи можно предло
жить два подхода. Согласно первому непрерывная
модель высокого порядка (3 .36) преобразуется в не
прерывную модель более низкого, а ун<е от нее произ
води.тся переход к дискретной модели низкого поряд
ка вида (3.19). В соответстsии же со вторым подходом
поступают
наоборот - аппроксимируют
непрерыв-
78
ную модель (3.36) дискретной моделью высокого по
рядка (3 . 17), а за тем, используя изложенный выше
метод, переходят к дис1<ретной модели низrюго порядка
(3.19). Для полноты изложения приведем методы Мар
шалла и Дэвисона
систем,
'"
которые
понижения порядка непрерывных
используются
в
первом
Известно, что существует матрица
образующая
уравнение
1{
подходе.
М [31 ],
пре
жордановой канонической
форме:
x=MZ;
\
где J
.
(J1
Z = JZ+ РИ = , О
= м- 1 АМ; Р = м- 1 8 = VB.
Как и в случае дискретного времени для получ·е
ния упрощенной модели, уравнение (3.36) следует
представить в блочном виде типа уравнения (3.18)
Далее необходимо упорядочить столбцы матрицы м .
Теперь столбцы слева должны соответствовать собст·
венным значениям матрицы А с действительными час
тями, расположенными ближе к нулю, а столбцы спра
ва - собств нным значениям · А, действительная часть
которых ближе к
прерывная
=
ARX1
-
модель
+ ВRИ,
оо. В результате получаете~ не
пониженной
размерности
х1 =
где по методу Маршалла
AR = M1J1Ml 1;
(3.37)
BR = 81 - A2V4 1J2 1P2,
(3.38)
а по методу Дэви·сона
.(
AR = А 1
+ А 2 М 3 М\ 1 ;
В~= М 1 Р1 .
(3.39) (3.40)
Рассмотренные подходы различаются между собой
порядком щагов сокращения размерности и дискрети
зации.
Так
как
шаги
содержат
только
линейны<-
7':J
операции, то
можно
ожидать, что указанные подходы
приводят 1< эквивалентным · результатам . Эту эквива
лентность можно показать аналитически, если
испоJ}ь· ·
зовать соотношения
т
Ф= ехр(АТ);
Л = ~ ехр(А(Т-т))Вdт (3.41)
о
и выразить Фя и Ля через Ая и
BR
по формулам
т
Фя = ехр (ART);
Ля = ~ ехр (AR (Т - т)) BRdт.
о
Для сравнения . результатов дискретного и непре
рывного подходов к упрощенИю модели высокой раз
мерности
можно
выражений
Ф
=
воспользоваться
Ма V
и
М V·=
/
представлением
и
показать,
что
дискретная переходная· матрица ~ выражении !.3.26)
эквивалентна
Фя = Ф 1
-
Ф2V4 1 V 3 = М 1 а1 М! 1 •
(3.42)
Учитывая это И сравнивая уравнения (3.42) и (3.37),
и (3.27), (3.32) и (3 .39), (3 .35) и (3.40), замечаем,
(3.38)
что имеется прямое почленное соответствие между
ре
зультатами
по
нижения
'
Пример
дискретного
размерности
3.
и
непрерывного
методов
модели.
Дана непрерывная система второго порядка
х = (х1 ) = (
Х2
0 -51)'х + (0)1 И,
(3.43)
-4
которую желательно аппроксимироваать
одномерной системой
относительно х 1 . Собственными значениями матрицы системы
(3.43) являются -1 и -4, так что
J=r-~ -~J;м=[~:~: -:~:1; V=[~
:J.
Модель эквивалентности дискретной системы с периодом Т имеет
80
ВИД
x(i+O=
1
=
3
·l
4 е,хр (-Т) -4 ехр (-Т,\
Х х (j)
ехр (-4Т),
ехр (-Т) - ехр (-4Т)
J
+ 4 ехр (-4Т) , --ехр (-Т) + 4 ехр (-4Т) Х
+-1_ [з/ 4
ехр (- Т) + i; 4 ехр (- 4Т)] Х ·и (j); (З.4 41
3 l
ехр (- Т) - ехр (- 4Т)
-
Уравнение
ехр (-4Т).
имеет
(3.44)
с9бственные
значения
ехр
(-Т)
и
Вначале для
аппроксимации непрерывной дву
мерной системы (3.43) Дискретной одномерной моделью
восполь з уемся первым Подходом и методом Маршалла.
Используя уравнения
(3.37)
и
(3.38),
получаем
AR ~ M1J1Ml 1 = - 1; BR = 81 -- A2V4 1J2 1P2 =
1 /4 •
Таким образом, непрерывная м·одель имеет вид
Х1 = -Х1
+ И/4,
а соответств у ющзя ей дискретная ,модель
х 1 (j
+ 1) = е хр (- Т) х 1 (j) + [1 -
txp (Т)]
И
(j)/4.
(3.45)
Если же воспользоваться вторым подходом сокраще
ния размерности, то из уравнений (3.26), (3.27) и (3.44)
найдем
ФR = Ф 1 -Ф 2 V4 1 V 3 = ехр(-Т);
ЛR = Л 1 + Ф 2 V4i (/ - сt2 Г 1 <\ = [1 - ехр (- Т)]/4.
В этом случае дискретная модель имеет вид
х 1 (j
+ 1) =
~хр (- Т) х1 (j)
т. е. она идентична модели
мощью первого
+ [1 .:.___ ехр ·(T)J И (j)/4,
(3.45),
полученной с по
метода.
Решим эту задачу с помощью метода Дэвисона
81
При . первом подходе из уравнений (3.39) и (3.40)
имеем
AR = А1
+AM
2
3
Ml 1 =
-
BR = М 1 Р 1 =
1;
1/ 3 .
j·
В этом случае непрерывная модель первого порядка
получается
=· -
Х1
+
Х1
· J'
И /3,
а соо!ветствующая ей дискретная модель
х1
+ !) =
(j
При
(3.35)
ехр(-Т) х 1
(j)
втором подходе с
и (3.44) находим
+ [! -
помощью
ехр(- Т)] И
(j)/3.
уравнений
(3.32),
+ Ф 2 М 3Мl 1 = ехр(-Т);
М1 (V 1 Л 1 + V2Л2) = [1 - ехр (- T)J/3,
ФR = Ф 1
ЛR
чему
х (j
=
соответствует
одномерная
+ 1) =
Т) х 1
ехр
(-
совпадающая с моделью
(j)
дискретная
+ [1 -
ехр (Т)] И
модеJiь
(j)/3_,
(3.45).
ЦИФРОВЫЕ ФИЛЬJРЫ В БАЗИСЕ УОЛША
3.
Кроме рассмотренного дискретного преобразования
Фурье, большое значение для цифровой обработки
сигналов представляет дискретное
преобразование
Уолша (ДПУ), которое может быть определено сле
дующим образом
.,
[6].
Рассмотрим конечную аппроксимацию случайного
процесса х ( t)
N-1
XN
(t)
=;=
~
XzCfJt
(t),
(3.46)
1=0
где ср 1
(t) -
набор ортогональных функций; х 1 ....,. со-
,
"
ответствующий коэффиuиент Фурье для данного про
цесса.
Если рассмотреть процесс (3.46) в дискретные мо
менты времени в точках t =О, T/N, ... , (N - 1/N) Т,
Т - интервал набщодения, то получим набор дискрет-
(i ~ ). которь1й
ных значен~~й случайного процесса . х
обозначим f (j), и днскретных функций ср 1 (j), j =
=О, 1, - 2, "" N -1 , удовлетворяющих условию
N-1
•
,,..,
(')
(')r=o
ЧJ1 1 CfJk 1 •
( N
при l = k;
l О · при L=F k, cpk (j)
{
=
(347)
ер; (k).
·
Исходя из рассмотренных вводных определений,
сформулируем прямое и обратное дискретные пре
образования соответственно:
+
N-1
F (k)
=
~о f (j) cpk (j);
(3.48)
N-l
~ F (k) ЧJ; (k),
f (j) =
j
=О,
1, 2, ... , · N -
1. .
• k=O
(3.49)
Среди набора дис1<ретных ортогональных функ
ций очень удобным является набор дискретных функ
ций Уолша,
которые определяются следующим обра-
.
зом:
wal
(О,
j) = 1
. 1
wal (1, j) =
1
-1
где N = 2р, р
-
для
j
=О,
1, ' 2, ... , N -
1;
для j = О, 1, ... , ~ - 1;
для
j
=
~
,
~
.+ 1,
натуральное число.
... , N -
1,
·
83
,
/
ПоследуЮщие функции набора
получаем по ре
куррентной формуJ1е вида
.
wal tk, J)
=
{ wal (2 [k/2], i) = cal (k, j);
wal (k - 2 [k/2], j) = sal (k, j),
где
[ ] - функция entier.
Если для функции Уолша выполняются соотноше
ния (3.47) - (3.49), то прямое дискретное преобра
зование Уолша прИ:нимает вид
N-1
=
F (k)
-fr ~ f (j) wal (k, j),
i=O
а обратное
N -1
f (j) =
N-1
~ F (k) wal (k, j) =
~ F (k) wal (j, k),
k=O
k=O
N-1
где f(O) = ~ f(k), а f(O) =
11=0
-F
N-1
~ f (j).
i=O
ИспОJiьзуя определение так назьiваемой логиче- ской свертки, можно определить следующую величину:
·
Lн (j) = f (j) * f (j) =
N-1
-Jv ~- f (j ЕВ т) f (т),
m= O
*-
где Lн - логическая свертка;
сИмвол свертки;
Ef) - сумма по модулю двух _соответствующих битов
двоичного разложения чисел
После преобразований
j
и т.
получаем соотношение
N- l
Lн (j) :__ ~ (f (k)) 2 wal (k,j),
- (3.50)
k=O
аналогичное результатам, полученным в теории Ви
нера - Хинчина, где Lн (j) является аналогом функ
ции автокорреляции, а (F ( k)) 2 - аналогом фун1щ1щ
мощносп1 сле1пральной плотности.
84 -
Если обозначить
=
(F (k)) 2
Р
(k),
то обратное
npe·
образование
N-1
P(k)=
При
-k-· ,~ Lн(i)wal(ll,
k=O, 1, 2, .. "
N-1
j).
и
P(k)>O
Lн(О)=
N-1
=
~ Р (k), где Lн (О) представляет полную мощность
k=O
•
последовательности
fm·
Рассмотрим простейшую задачу фильтрации по
лезного сигнала на фон~ помехи типа «белый шум» -
~
<: 1.
где О<: t
Предположим, что полезный сигнал неизвестной
формы можно приближенно Представить отрезком
(t),
Фурье по функциям Уолша
N-1
~ ckwk (t),
S (t) ,
k=O
(3.51)
·
где ck - случайные величины с началы1Ь1ми момента·
ми второго порядка ·Rkt·
Переходя к дискретному времени t, - r = 1, 2, .", N,
имеем вектор замера процесса Хт = [x(t 1 ), x(t 2 ),
••. , х(tн)], где x(t, ) = s(t,)
~(t,).
,
+
Преобразуем вектор-столбец х по Адамару: х*
•• •
=
= НХ, где Н - матрица Адамара размером N х N~
а N = 2п, приЧем п = 1, 2, .:.
.
Необходимо с помощью диагоналыюй матрИцы
'
Q ;__
= diag !q,z) так трансформировать спектр Х*, чтобы
при обратном преобразовании вектора QX* иметь оценку вектора
кую
(в
"
,. .
S = [s (t 1 }, s(/2 ) •.• .
т
л
среднеквадратическом
13еюору sт = ts(t1), s (t 2),
••• ,
"
, s(tн )], наиболее близ-
смысле)
к
тр~буемому
s(tN)J. В.ыражение . для
&)
вектора ошибки фильтрации
(3.52)
e =S-HQX*/N
преобразуем к виду
е = [НС- HQH (S + Z)]/N =
= [HC-HQC-HQHZJ/N= f(H-HQ)C-HQHZJ/N
при условии, что С = [с 0 , с 1 , с 2 , ••• , cN-1] - неизвестный с пектр сигнала (3.51); zт =~ [~(t 1 ) ; ~(t 2 ), ".
т
~(tн)] - вектор шума .
Найдем выражение для ковариационной матрицы
". ,
ошибок оценок М {еет), где М - оператор математи
ческого ожидания (осреднения по реализации). Опре
делим сначала матрицу для
еет
=
[(Н
одной реализации
- HQ) С - HQHZ]
[(Н
- HQ)
С
-
-HQHZ]т/№=[(H-HQ)C-HQHZ] [Ст(Н-НQ) ,-
- zт (НQН)т]!№. = [(Н -HQ) ССт (Н - НQ)т - (Н - HQ) czT (HQH{- HQHZCT (Н - HQ{
+ HQHZZт (НQН)т j /№.
--
+
(3.53)
Полагая, что сЛучайные величины С; и ~ (t1) некор
релированы, найдем
М {еет) = М {(Н ~ HQ) ССт (Н -НQ)т)/№
+ М {HQHZZ 7 (HQH{)/№.
+
(3.f>4)
Если считать, что известн~1 коррещщионные матрицы
в
виде
R, =
~
Rg0Rg1 . . . R'O(N-I )
RfoR.f 1 ••• Rf(N-1)
R(N-1)0 ••• R(N-l)(N-1)
86
]
=
-1
l
СсСоС1
-;1--2
_
/
"
С1СоС1
=
.
--
R~oR~1
J
. .
"
•
'
RZ1N-11
R~N~:)D
1
(3.55)
-2
CN-1
C1 N-1JCo .. .
[
R, =
СоС " C1C N-I
]
~~~~1)(N~I;
0
=
rr·~ ~~1)_1 2 • ~:(t~)~ U2} ·.. : ~ U1~ ~и.N )] '
~(t1)~{t2)
то в выражении
(3.54)
Q,
элементы матрицы
(3.56)
... fЦtN)] 2
определению подлежат ·только
которые находятся
путем ми
нимизации величин ковариационной матрицы ошибок
М \еет}.
В матрицах (3.55) и (3.56) черта сверху означает
операцию усреднения по т реали з ациям Дифферен-
цируя элементы матрицы М \ее
.,...... g,,
и приравнивая
т
}
по элементам
результат нулю,
Q-
получаем систе·
му . № уравнений Для определения
д [М \еет) j/дgп =О,
- Пример
r =О, N ~ 1.
4 . .Пусть N = 2 и
-[Rб1
Rcо-
Пользуясь выражениями
О
Rf1
о
] ., Rz .= a2
О а2
r
1
•
(3.53) и (3.54), находим
М {ее т} =
87
1 [2 (q5o + qf1J а2 2С45о -
+т
2
. 2 (qoo
-
~
2
2
q!!) а~
2 (qoo
qf1) а2 ].
2
+ qн)
а2
·
•
д l~q~:eт)] = - 2(1- qoo) /i6 + 4q00<Т 2 = OJ
д [М {еет)]
д
q11
(3.57)
= -
2 (1 -
-2
q11) с1
+ 4q11a
2
=О
Система уравнений (3.57) получена в результате
цирования толъко одного элемента матрицы М {еет} -
диффер е н
элемента,
стоящего на пересечени и первой строки и первого столбца.
уравнения (3.57), найдем
qii =
ёi;сёf + 2а2) =
Rf1!(Rf1 + 2а2) .
Таким образом, если известны
матрицы
Решая
(3.58)
Rc
и
Rz•
то фильтр имеет достаточно простую структуру и рас
чет его не представля.ет затруднений. Однако такой
случай на практике не встречается. Рассмотрим ре
альный случай, когда матрицы R, и R2 неизвестны.
Здесь для синтеза фильтра потребуется использовать
свойство адаптации . Адаптивный блок фильтра дол
жен обладать памятью: необходимо вначале запомнить
т реализаций вектора х* (р) (р
=
1,
т) . Далее в бло
ке следует определить и запомнить выборочные сред
ние значения из компонент вектора .х*
т
xi =
-1
m
~ х7 (р),
i=O, 1, . .. , N-I, (3.59)
P=I
а затем найти приближенную к
(ха)2
Rx-
=
- xix~
Rc
.
ХоХ2
матрицу
-• --•
XoXN-1
-
хiхм- 1
(xi)2
;
- _ XN-IXo
88
• •
XoXJ
- •-
(x!v-1> 2_
..,,
ПрибЛижением к
R,
будет матриr.iа
R,..,
z
торой
"'
где ~<PJ (t;) ~
J
N
,.. •
hi~(P>;
h1 -
элементы ко-
вектор~ строка, компоненты
которого равны :~лементам i-й строки матрицы Адамара,
а вектор-столбеu
;. -
\,(р)-
[
J
ха - хо (р)
x*-xi(p)
х~-1
(3.60)
•
- хЛц (р)
Таким образом, совершив обратное преобразование
Адамара над вектором (3.60), необходимо для получе
ния R,.. найти корреляuию между полученными ком-
z
понентами.
Чтобы
облегчить
расчеты
элементов
~ii• можно с некоторого номера j считать · их ну~евыми.
Для проверки справедливости такой гипотезы следует
воспол&зоваться аппроксимацией
. .
с.
торая для дисперсии ~i:
D(~ii/~ii) =
Если в выражение
,..
'
\
,..
D
(с.
~i~
Бартлетта
)
(3.61)
ко-
дает
*[+ ~1 ~7vl~7t].
1
[3 ],
2
вместо ~iv и ~it
(3.61)
подставить
<
~iv и ~ii и задаться q
j, то квадратный корень из
полученного числа даст стандартную ошибку, которая
не должна превосходить ~ir /~ii, где r
>
q.
Итак ; адаптивный цифровой фильтр с памятью вы
дает первый результат (отфильтрованный неизвест
ный полезный сигнал), спустя (тТ
iсч) с, и далее
+
89
+ tc"
будет его возобновлять через каждые Т
Т - время, приходящееся на ннтерва.п
по функuиям
Уолша
(на
интервал
0-, !);
с. Здесь .
разложения
т - число
реализаuий, т. е. число повторений интервала (пред
полагается, что пелезный сигнал повторяется на каж
аом интервале Т);
t,.4 -
время счета, необходимое для
практической реализаuии описанных вычислений, на
правленных
на
получение значений
превосходит Т, то фильтр
штабе времени.
4.
qг,.
Если
lсч
не
работает в реальном мас
АДАПТИВНАЯ ЦИФРОВАЯ ФИЛЬТРАЦИЯ
В БАЗИСЕ .ХААРА
По анало'гии с фильтрами Уолша можно строить
цифровые
фильтры
Хаара
Коэффициентам
фильтров присваиваются
значения
матр' иuы
Хаара.
преобразования
Уолша, отношение
величиной 1/Т
Us -
таких
элементов строки
Как
и
в фильтрах
f0 /j_,_ приближенно
частота
определяется
квантования сигнала,
Т - период, на котором функции Хаара не равны
нулю), поэтому для практиqеского си·нтеза этих фильт
ров необходимо за ранее снимать их А Ч Х и заносить
в таблиuу · Пользуясь этими !аблиuами, можно под
бирать фильтр с необходимой центральной частотой
пропускания,
а
также
количество
последовательных
однотипных фильтров, необходимое для
заданного качества фильтраuии.
достижения
Адаптивную фильтраuию в базисе Хаара
·
можно
Проводить по алгоритму, иллюстрируемому структур
ной схемой (рис. 16, а).
На вход блока А подается смесь полезного сигна
ла и помехи. В блоке
А поступивший сиrнал разла
rает~я в . ряд Хаара, а коэ:рфиuиенты этого ряда вычис
ляются -~етодом, описанным ранее.
Блок весовых
90
,,
коэффициентов БВК, исходя из имеющихся в памяти
ЦВМ коэффициентов ра з л ожения в ряд Хаара полез
ного сигнала, умнож а ет коэффициенты Хаара посту
пившего сигнала таким образом,
Рис.
чтобы на ·выходе
16.
Адаптив н ый фильтр:
а структурная схема в бази
се
Хаара;
А спектр-анали
затор Хаара ;. БВК . - блок ве
совых коэффициентов , С -- син
тезатор;
БП · _ блок подстрой
ки весовых коэффициентов; 6 устройство.
·
а
1
1
1
1
1
1
1
1
1
1
1
1
L. - - - - - -- - - -_J
r5
блока были коэффициенты ряда Хаара полезного сигнала
вида
_а~ = Х~ (~)/[~ (s + N)J;
где а~ енты
весовые коэффициенты; х~ (s) -
разложения
в
ряд
Хаара
коэффици
полезного сигнала,
хран:Ящиеся в памяти ЦВМ; х~ (s
+ N) -
циенты Хаара фильтруемого сигнала.
коэффи
·
Блок синтеза С умножает функции Хаара на по
ступившие из БЕК коэффициенты, в результате чего
~J
может быть получен .отфильтрованный сигнал. В . за·
висимости от требуемого качества фильтрации, блок
подстройки БП изменяет весовые 1<0эффициенты.
Рассмотрим пример синтеза устройства фильтра·
ции смеси радиосигнала и помехи в виде «белого шума»
и гармонического сигнала.
Структурная схема устройства адаптивной фильт
рации в базисе Хаара
представлена на рис.
16, 6 .
. Сигналы
и помеха, постуuающие на вход адаптивного
фильтра,
обрабатываются
в
отсчетном устройстве
ОУ, предназначенном для пqлучения отсчетов огиба
ющей, и преобразуются к форме, удобной для дальней
шей обработки и анализа сигн.алов.
Для обнаружения радиосигнала на фоне
помех по-
следний раскладывается по базисным функциям Хаара
(схема
разложения
•
СР),
где
коэффициенты
опреде-
1
. ляются по формул,е а. = ~ f (t) xk (t) dt.
n
дЛ>я реализации указанной зависимости служат:
блок ключей БК, блок интеграторов БН, генератор
длИтельностей функuий Хаара ГФХ. Количество ко
эффициентов разложения выбирается в зависимости
от точности представления сигнала в пространстве ба
зисны х функний Хаара. Генератор длительностей
функuий Хаара управляет временем интегрирования
блока интеграторов , на выходе которого получаются
значения коэффициентов разложения принятого сиг
нала, т. е. получаем некоторый вектор
ния сигнала в пространстве
ара.
f}°
представле
базисных функций
Ха
·
· Синхронизация
временной диаграммы принимае
мых сигналов с временной диаграмl\;ой адаптивного
фильтра осуществляется следующим обрцзом.
92
Устройство опенки у() анализирует полученные
ранее компоненты вектора j3, в результате чего прини
мается
решение
в данном
если
о
наличии
отрезке
сигнал
н~
обнаружен,
УО вьiдает команду
ния,
ра
1i
в
противном
или
временного
отсутствии
интервала .
то
сигнала
При этом
устройство
оценки
на сдвиг интервала интегрирова
случае
значение
компоненты
поступает на вход следующего
векто-
устройства. На
этом процесс обнаружения заканчивается.
Устройство точной фильтрации сигнала УТФ со
стоит из функциональных блоков (рис .
Значения элементов вектора
устройства
БВКС,
j3
16, 6).
поступают на вход
представляющего
собой
некоторых матриц А, элементы которых весовых
набор
значения
коэффициентов суммирования .
В устройстве БВКС происходит поиск и выделение
не искаженных помехой составляющих вектора j3,
т . е. при умножении ~ на матрицу А получаем но·
вый вектор а, содержащий только не искаженные по
мехой компоненты вектоr_а
только одна из матриц А
13.
При этом выбирается
указанного
выше набора.
Набор матриц (блок БМ) позволяет восстановить ис
каженные компоненты вектора отфильтрованного сиг
нала в пространстве базисных функций Хаара.
Устройство сравн.ения УС позволяет получить
оценку
тора
рассогJ1асован11я
1i · С
полученных
компонент
КОМПОНеНТаМИ вектqра , ВЫХОДНОГО
век
СИГНаЛа
модели (устройство МС). Величина получаемой в ус
."
тройстве сравнения ошибки оценивается
устройством
управления УУ, которое выбирает матрицы А и
В
таким образом, чтобы сигнал ошибки был минималь
ным. Модель сигнала МС запускается при обнаруже
нии сигнала , т.
е. в
момент
совriадения фазы прини
маемого сигнала и начала отсчета функций Хаара [10) :
93
Рис. 17. Блок-схема
делирующего
мо.
алгоритма
адаптивного
фильтра при
помехе типа «белый шум»:
J -
счетчик
ний
к массиву · · Р;
-4----.
8ыч11сл11ть
tO,
tM
числа
обраще
L - если
то значение
функ
· ции Хаара равно
Х, если
L = 2, то значение функ
ции Ха ара равно - Х; N N -
L =
1,
число
+
участ1<ов
участков
б
N
разбиения
интегрирования;
-оставшееся число
ков
tM -
участок
интегри
К номер функ
ции Хаара;
мя;
ла;
участ
интегрирования;
конечный
рования;
И И!
-
t-
грирования
лолуnолны
И2 -
текущее вре
значение интегра
результат
интеположительной
функции
результат
Хаара;
интеrрирова ·
нил отрицательной
по11 увол
ны функции Хаара; А ко
фун1щии
Хаара
эффициент
2
С целью проверки
работоспособности из
ложенного
rоритма
дено
выше
было
tro
ал- ·
про_ве
частичное
моделирование .
Моделировались
конеч
следующие
режимы
работы: обнаружение
сигнала на фоне «бе
лого шума» и на фо ·
не детерминированной помехи. В качестве генератора
«белого шума» была использована программа выделе~
ния
п_севдослучайных
чисел
с
математическим
ожи
данием, равным О, 11, дисперсией - 1, 13, показателе1У1
асимметрии _,_ 0,22. В · качестве полезного сигнала
была выбрана . синусоида с частотой колебаний 8 Гц.
На рис . 17 показана схема моделирующего алго
ритма при помехе_ тип~ «белый шум».
94
Оператор 1 присваивает начальные значения иден
тификаторам L, J Переход к оператору 2 означает
. выбор нового интервала интегрирования. Оператор
3 - · условный. В завщ:имости от значения· L выбира-
л\ci~'---'---'---'-\.__.____.___\1 I
1
1 .__.____.__
·
к
А
О.06
0.04 .
0,02
о._.--.~~~~~~к
- 0.02
-0,04
-0,06
-0,08
о.11
0,1
о
1 2
-0.1
Рис.
!(онец
д
18.
Разложение в ба
зисе х аара сигналов:
+
- полез ный сигнал
<бе
ш ум» ; б реализ а ции
~: белого -ш ума»;
в реали·
а
лый
эации • <белый
лезный
ются
шум»
сигнал
+
Рис. 19. Блок-схема моделирующе
го алгоритма адаптивного фильтра
при детерминированной помехе.
по:
те или иные конечные интервалы интегрирования.
Операторы
4
и
5
вычисляют
конечные
интерваJJы
95
интегрирования, т . е .
вания
функции
определяют интервал существо
Хаара
Оператор
б
производит
' М
интегрирование И =
f f (М) Х (t) dt,
t.
В программе значение t0 сразу же присваивается
значению текущего времени t. Оператор 7 - услов
ный
переход.
поЛуволна
Если
функции
интегрирования
интегрировалась
Хаара
(L = 1),
запоминается
положительная
то
(оператор
результат
_8)
и затем
интегрируется отрицательная полуволна.
Если
интегрировалась отрицательная полуволна
то результат также запоминается (оrтератор 9)
и затем вычисляется коэффициент функции Хаара
(оператор 10). Оператор 11 - условный пер~од.
Если К максимально, то решение прекращаете~, если
нет - К увеличивается· на единицу (оператор 12) и уп
равление передается оператору 2. Резу .Льтаты разло
жения по функциям Хаара изображены на рис . 18.
Таким образом, синтезированное устройство, поз
воляет фильтровать сигнал. При нал ичии сигнала
коэффициенты функций Хаара приблизительно на по
рядок больше тех же функций без сигн ала .
Моделирование работы устройства обнаруженttя
(L
=
2),
сигнала при воздействии детерминированной помехи
проводилось . по алгоритму, показанному на рис. 19.
Программы моделирования показаны на рис . 20.
Полезный сигнал представлен син усоидой с часто
той 8 Гц, а аддитивная помеха - оин усоидой с частотой 1 гц;
··
,
Оператор 1 (рис . 19) присваивает идентификатору
амплитуды помехи значение, равное 0,2. Оператор
, 2 выбирает
на отрезке [О,
1 1 первую из восьми функций
Хаара. Операторы 3 и 4 производят интегрирование
в соответствии со з н а I<ом функции ,.., Х а ар а. Оператор
5 вычисляет зна чение коэфф1щиента функ ции Х аара.
96
"РАЗ"б. "ДЛЯ"М=1"Ш"1"ДО"16"ВЫП"" ДЛН"J =1 "Ш" ! "ДО"2t (М-1)"ВЫП"
(K=2t(M-1)+J;C[K]=(1/'1.W)x\(I=(J-1)/2t(M-1)x111-3,(J-1/2)/2t
(M-,:.)x1ю-3,20,2t((M-1)/2)xS(I))+(1/'1.W)x\(I=(J-1/2)/2t(М-1) .
i'
•1
х!~-:З,J/2t(М-1)х1ю-3 ,20,-(2+( (М-1)/2) )xS(I)); ".ВЩ!'"'ЗНА"К,"
ПРОБ"!,С[К],"ПРОБ"З)"ГдЕ"А=1;МЮ=2;ТМЮ=80ю-б;омс=2х7[х1 11 5;ТО
=1ю-З;S(Т)="Е"Т<i60ю-6"ТО"(Ах(Т/ТМЮ)tМЮхЕХР(МЮ-МЮх(Т/ТМЮ))
xCOS(OMCxT))"ИH"(O);C[1035]"ROH"
. .
--
а
"РАЗ"5 .L=i ;K=i; М2 ~N="EC":Т(6(NN)/2)=0"TO"(!i(NN) )"ИН" (!i(NN)+i
);"EC"L=1"TO"(T=(K-1)/2tNX;'lМ=(2xK-1)/(2tNX+i);L-2)"ИН"(T=(
2xK-1)/2tNX +1); Thl=K/2tNX; L=i); H=('IМ-T)/N; N=N-1; И=F(T)+P[I];
I=I+-i;M.T=T+H;И=И+4x(F(T)+P[I]);I=I+1;T=T+H;"EC"N=,1"TO"(И=(
И+(F(T)+P[I]) )хН/З; I=I +1; "НА "Мi)"ИН"(И=И+2х(F(Т)+Р[I]); I=I+J
);N=N-2;"НА"М;М1."ЕС"L=2"ТО"СИ1=И;"НА"М2)"ИН"(И2=И);А=(И1~И
2)хV(2tNХ);"ВЫВ"К,"ПРОБ"2,А,"СТРОК";"ЕС"К=2tNХ"ТО"("СТОП")"
ИН"(K=K+1;"НA"M2)"ГдE"F(J)=SIN(2x1lx8xJ);NN=10;NX=З;P[200]"K
ОН"
"РАЗ"5.К=1;Х=V(2tН); "длн"D=18"Ш"~8"ДО~2"БЫП"("ВЫБ'"'СТРО"4,D
;"длН"F=О"Ш"1"ДО"ЗО"БЫП"("ЕС"F=8"ТО"(F=:9);"БЫВ""СТРО"З,F;"д
ЛЯ"А=.2"Ш".2"ДО"2".БЫП"("ВЬIБ""СТРО"2,А;"длн"К=1"Ш~f"ДО"2tН"В .
ЫП"(И!=\ (T=(IH)/2tH, (2><K-l)/2t(H+1) ,D,S);И2=\ (Т=(2хК•1)/2t
(H+i) ,K/2tH ,D,S);И=(И1-И2)хх; ".БDJB"K, "ПРОБ"Э,И, "стРоj;)))),;Гд
E"H=З;S=SIN(2x7[x8xT);Л=SIN(2x7[xFxT)"KOH"
в
Рис.
20.
Программы
моделирования
адаптивного
фильтра:
а вычисления коэффициентов Фурье Хаара функции S (Т);· б прн помехе типа 'белый шум»; в
при детерминированной помехе:
Х абсолютное значе~ие функции
Хаара; KN иидексы функции
Каара; D дискретность
численного интегрирования; F ~ частота
помехи; А амплитуда помехи; И значение коэффициента фун1<
-
ции
Хаара;
S -
сигнал + _ помеха.
97
Операторы 6,
7, 8
и 9 образуют циклы для изменения
амплитуды помехи и для выбора следующей функции
К:аара .
Результаты проведенного моделирования показаны
на рис. 21.
Таким образом, при действии помехи коэффициенты
функций - Хаара сохраняют свои положительные зна
4~t
1
1
111
чения, которые приобрели
колебательный характер с
частотой,
равной частоте
помехи, но сдвинутой на
.
atWШl_LL
,о
1 2 J
4
б
s
7
вк
четверть периода. Амплиту
да Помехи ослаблена в 10
раз. Учитывая, что коэффи
Рис. 21. Результаты , моде.пи·
рования фl!льтра по блок·
схеме рис. 19 (А
1,6).
=
циенть~ сохраняют положи
тельные значения при дей
сrвии _ детерминированной помехи, можно сделать вы
вод о наличии
полезного сигнала.
Следовательно,
для
ортогонального
разложения
сигналов в задачах цифровой фильтрации целесообраз
но применять базисные функции Хаара, позволяющие
уменьшать время обработки сигна.тiа и являющиеся
наиболее удобнь1ми дл:Я обработки на ЦВМ.
5.
АНАЛИЗ НЕЛИНЕЙНЫХ СИСТЕМ
В БАЗИСЕ УОЛША
В винеровской теориИ анализа нелинейных систем
выход нейзвестной системы представляется в виде
суммы полной системы ортогональных функционалов
Gn
!Кт х (t)
1,
где
характеризующих
{Кп) - последовательность ядер,
нелинейную систему; х
(t) -
вход
системы .
Функционалы G,., являются ортогональными в том
смысле, что если на вход системы поступает «белый
98
,
шум » ,
то
8 (Gп[Кп, x(t)JGmfKm, x(t)J) =О,
n=f=m,
где символ 8 обозначает усреднение по совокупности
Последовательность ядер Кп можно определить
путем конструирования параллельных фильтров с им·
пульсными характеристиками, образующими полную
систему ортогональных функций
{Fn (t)}.
На входы
анализ.ируемой системы и фильтра поступает. «белый
шум» х (t). Выход системы умножается на выходы па·
раллельных филиров и результирующий сигнал по·
ступает в блок, интегрирующий по t (усреднение).
Пусть п - число параллельных фильтров, тогда ре·
зультат
усреднения
ложения
ядра
п- го
есть
коэффициент
порядка
произведений функций
Fi
-
(Х1
.02=Q
п-кратных
•• • '
Ип) =
00
~ ~ .•. ~ Ср,р" ..рпFР, (U 1)
/J1=0
Ср,р, ... Рп раз·
виде суммы
(И):
Кп (И1, И2,
'?О
в
Рп=О
•••
.
Предлагаемый метод
FP (Ип)· .
п
[26), основанный на · исполь·
зевании свойства функции Yoлilla, представляется на·
ибQлее эффективным с точки зрения
практических
применений винеровской теории нелинейных систем .
Для практических целей удобно использовать вы·
ражение функций ·Уолша через функции Paдel\Jaxepa.
Известно, что функции Уолша wn (t) обладают следующими свойствами:
.. ,.
а) W2kп(f) = Wп(2k,
f);
б) Wn, (t) Wn, (t) = W~,nffi, (t);
-
в) Wn (t~) Wn U2) = Wn U1 ЕВ f2);
~/
r)
о
~ Wn(t)wт(t)dt =
{ 1
О
при т =О;
при т
=f: О;
99
д) w(2n, t)= w(n, 2t-1)
·}
1
w1 (2п+ 1, t)= -w(n, 2t-i) при 2
<t< ~;
1
е) SWп (t) Wm (t1 Ef>
апw.п,
f 2 ) dt1 =
о
где ап - коэффициенты Уолша - Фурье функции wn .
. Знаком ЕJЭ обозначено поразрядное сложение по
mod 2 величин, которые представлены в двойн·ой си
\о
стеме счисления и определяются так:
d ЕЕ> е =
P=I
~ (d1 Ef> е 1 ) 2i,
i=O
P=l
где d
=
P=I
~ d121;
·
i=O
о ЕЕ>
е = ~ е 121 •
Например, О ЕJЭ О= О:
i=O
1 = 1 ЕJЭ
о =
ЕJЭ ( -
е)
1; 1 ЕЕ> 1 = о.
dие
Для отрицательных чисел
( - d)
= d ЕJЭ е; . ( - d)
ЕJЭ е
= d
ЕJЭ ( -
е)
=
= -(d ЕJЭ е). ·
. Из свойств функций Уолша, указанных в пп. б),
в) и е), следует:
..
1
о
sWп U1) w U1 Е1Э f2) dt1 = s
Е1Э t2) w (t1) dt1,
является
интеграла свертки
wn (t1
о
1
что
аналогом
свойств
00
00
5 w U1) w (t2-
t1) dt1 =
5 w (t2 -
t1) w U1) dt1.
-оо
Эта аналогия, как и соответствующая аналогия с тео-
ремой Хинчина
-
Винера, является основой предла
гаемого подхода к а~ализу нелинейны х систем ,
100
~
В винеровской теории параллельными фильтрами
· являются фильтры Уолша, осуществляющие преоqра·
зование входа
(t)· в ' выходную функцию .
f
.
y(t) =
1
~ Wп(u)w(t ЕВ u)du,
п
или в другой фазе записи
у (t)
= anwn (t).
(3.62)
В случае, когда на входе фильтра
Уол ша
-
«бе
лый шум» с нулевым средним и дисперсией А, коэф·
фициенты ап выхода фильтра имеют гауссовские рас
пределения с параметрами, определяемыми формулами
8 (ап} · О;
8 {апат)
=
Абпт,
(3.63)
где . бпт - символ Кронекера.
Так как 8 {x(t1 )x(t 2 ) ." х(tп)) =О при нечетных п
и 8{x(t1 )x(t2 )
."
х(tп )} =~ПS{x(t;)x(ti))бц при
i
четных п,
где- суммирование
i
осуществляется
по
всем
произведениям двух сомножителей, из этого следует,
что
8
{ар,ар, ". аР;,} =О, если п -
нечетное, и
(3.64)
если
п-четное.
Пусть сигнал на выходе нелинейной системы свя
зан с входным сигналом х (t) уравнением
00
(3.65)
где {Gп) -: система ортогональных функционалов с
соответствующей заменой интегралов свертки опе
ратором ЕВ.
lOJ
=
При п
.
О,
1, 2, 3, ...
имеют место следующие со-
отношения:
1
G0 [H 0 x(t)] =Н 0 ;
G1 [H 1 , x(t)]
S Н 1 (и);
=
.
о
G2 [Н 2 , x(t)] =
1 1
=
.
SSН 2 (и, v)x(tEEJu)x(tEf)v)dudv-AS H 2 (u,u)du;
о
.
о
о
G3
1 1 1
=
1
SSSH
o
о
3
о
[Н8 , Х (t)]
=
(u,v,w)x(t ® u)x(t ® v)x(t Ef) w)dudvdwl 1
- ЗА S S Н3 (и, v, w) х (t ® и) dudv.
о
(3.66)
о
Ядра {Нп} определя19тся путем разложения в ряд
Уолша - Фурье следующим образом:
00
Н1 (и)
=
00
.
~ ckwk (и);
(3.67)
k=O
00
(3.68)
При подаче на вход системы «белого шума» х
(t)
=
00
= ~ akwk (t) выходной сигнал ~ожет быть выражен
k=O
[с учетом подстановки · уравнений
(3.68), (3.65)) в следующей форме:
(3.66), (3.67)
и
00
y(t) = Н 0
00
+~
00
00
~ aiaidi;Wi (t) W; (t) - А~ di ,
i=O i=O
102
+ k=O
~ akckwk(t) +
·
i=O
+
(3.69)
Используя основное мультипликативное свойство
функции Уолша, указанное в . п . б, выходной сигнал
неизвестной системы можно представить в виде
(3.70)
Коэффициенты
bk
вычисляются путем сравнения ко·
эффициентов при ffik
и
(t), k =!= О, в формулах (3.69)
(3.70)
(3.71)
где
ЕВ
i
*j
=
двойная сумма по тем индексам, для которых
k.
z(t)
а
f{t]z(l)dt
а,а.Ь,,.,. ::::(а,а.ь,,,,,.} 2A'd,,,,:AZ(4J4..
о
Рис. 22. Алгоритмы оценки
(б) порядков.
ядра первого (а) и второго
Поскольку по предположению k =!= О, из свойств
оператора· следует, что i =!= j. При k = О
Ь0 = Н0
00
00
i=O
i=O
+ а0с0 + ~ afd1;-A ~ d1; + ··· (3.72)
Из последней формулы следует, что 8(Ь0 }
t·
•
=
Н0 , так
как второй член в правой части выражения (3. 72)
равен нулю (в соответствии с формулой (3.63) 8{а0 } =
103
= О и В (а7) = А; остальные члены по той же при
чине также равны нулю).
Как видно из рис . 22, а, коэффициенты Уолша
Фурье для Н 1 (и) определяются из уравнения
-
Сп= В (апЬп)/А
Для
доказательства
этого
рассмотрим
ф ильтра Уолша. rt:з формулы
anw,1 (t), и, следовательно ,
.=
1 .
S У (t) Z {t) dt = ~
О
Поскольку
bkan
z (t)
z (t) =
SWk (t) Wn (t) dt .
О
ортогональная система функций
1
в интервале [О, 1 ], то Sу
лы (3.71) при
что
1
k=O
( wn (t)} -
выход
(3.62) следует ,
-
(t)z (t) dt =
апЬп. Из форму-
О с;едует
k' =
1
В {апЬп) =В {апап) с 11 +~~ · В {а 1 а;ап) di; + · · ·,
,:
;
откуда, с уЧетом формулы (3.64), вытекает, что .
В{апЬп) = А сп, что и требовалось доказать .
Рис. 22, б иллюстрирует методику определения
ядра второго порядка Н 2 (и, v) . Коэффициенты разложения Н2 (и, v) находятся по формуле
·
r
1
!i! {апатЬпвэт) . _
d11т -_ _
д2
2
8
{Ь 0 } б
А
пт
]
•
(3. 73)
Доказательство этого результата основывается на
использовании свойства мультипликативности и ор
тогональности функции Уолша.
Пример 5. Рассмотрим систему второго порядка общего вида,
изображенного на рис. 23,
где крайние блоки соответствуют
фильтрам Уолша.
104
/
Выход системы может быть представлен
ч (tJ =
)'
1 '
Jj° J
w (t 2 ) w (t 2
о
п
в следующей форме:
Е1Э и J w (1 2 Е1Э ~) х u, Е1Э ~) х
п
Х х (1 1· Е1Э v) dt 2 dиdv
(3. 74)
Из этоii формулы можно выделить ядро второго порядка,
поло·
ЖИ 13
1
Н 2 (и,
Jw
v) =
(1 2 ) w (t 2
Е1Э и) w (t2 Е1Э
v) dt 2 .
u
x(I)
.---.z(tj.----. y(t}
w2
g(t}
Рис.
ма
23.
рога
П ос кольку Н 0
=
8 {Ь 0 )
и 8 { Ь0 )
=
Структурная схе·
анализа
вто·
8 {у (t)), можно записать
1
выражение для ядра нулевого порядка Н0 = А
Следовательно, у
системы
порядка.
JН2 (и, и)
du.
о
представляется в виде суммы ортогональ:
(t)
ных функцион а л о в :
1 1
у (t)
= f-10
+ JJН 2 (и,
о
х (ti Е1Э и) х (ti Е1Э
v)
v) dudv
~
.
о
1
-
А
JН
2
(и, и)
du.
п
Представляют
интерес
два следующих · случая:
1) w (t1 ) =
= б (t) и 2) w (t2) = б (/), для которьiх проведены расчеты ядра
·
второго порядка.
·~
В первом случа е н д ро имеет вид н; (и, v) =
где б (и - v) - дельта -функция Дирака .
w
(и) б (ц
-
Таким обр аз ом, ядро равно нулю всюду вне прямqй и
на которой оно совпадает с ' функцией w (и).
5 7- 1403
v),
= v,
ФИЛЬТР КАЛМАНА В СИСТЕМАХ
С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
6.
ФИЛЬТР КАЛМАНА
В ПРОСТРАНСТВЕ НЕПРЕРЫВНОГО ВРЕМЕНИ
Пусть задано некоторое л.инейное
стохастическое
дифференциальное уравнение
дU (х,
дх
1)
LP (х,
=
t)
+ В(х, t) W (х, t),
~р (х, t) = _ О,
Zx
(х, t)
=
xED;
хЕ
М (х, t) И (х,
t)
+ V (Х,
t),
(3.75)
nD;
xED,
>-
определенное при t
t 0 в п--=-мерной области D с по
верхностью nD. В этом уравнении ~ (х, t) - некото
рая неизвестная матрица входных сигналов; Zx ( ·)
и ~х ( • ) - заданные линейные операторы в D и nD.
Эти операторы могут быть дифференциальными, ин
тегральными и интегро-дифференциальными; М (х, t) известный оператор наблюдений, воздействующий на
пространственные переменные; W (х, t), V (х, t) -
-
регулярные гауссовские случайные процессы, распре
деленные
в
пространстве
и
удовлетворяющие
следу
ющей системе равенств:
Е= [V(x, t)]
E[W(x, t)] =0;
= -0;
.
)
Е [W (х, t) wт (х1 • .-)1 = Q (х, Х1, t) б и- •);r1
т
E[V(x,t)VT(X1,•)]=R(x,x1,t)б(t--•);
1
Е
'
[V (х, t) W
при всех
t, •
~
(х 1 ,
t0
l)I
=О
(3.76) '
-
-
и x:r> х1 Е D. Здесь Е [ . ] обознача
Q (х, х 1 , t) - симметриче
ет операцию усреднения;
ская
положительно
R (х,
х1 ,
ленная
!Об
t) -
по.iтуопрелеленная.
матрица,
а
симметрическая положительно . опреде
матрица.
Для систем
(3. 75)
и
задача
(3. 76)
оnтимальной
фильтраuии формулируется следующим образом [31 ]:
- при заданных уравнениях и наблюдаемости системы,
имеющейся реализации Z (х, t) (при х Е D) наблюде
~ий в интервале t 0
т
t найти оптимальную оuенку
< <
И (х,
"
t .>-
х Е D для И (х, t) и при
t);
Уравнения
фильтра
Калмана,
t0 .
-. которые
так сф~ормулированную
задачу,. имею;г'
вид
.
\
.
дU (~t t;tj
решаю1
+ Sf Р (х, х1 , t/t) М 7 (х, t) х
= LP (xt/t)
DD
(3. 77)
дР(х,d; 1 • l/t) =
LxP(x,
+ В (х, t) В 7 (х, t) -
х1 ,
tit)
+ Р(х, Х1 , t/t)L[, +
f f Р (х, х;, t/t) М 7 (х', t) х
D D
Х Q7 (x',x",t)M(x",t)P(x",x1 , t/t)dD'dD"; (3.78)
~)J (х, t/t)
z (х, t/t)
=
О; х Е nD; И (х, i0 /t 0 ) = Е [V 0 (х)],
= z (х,
t) -
М (х, t) О (х, t/t);
=
где
t /t -
момента
мент t;.
означает,
/t
Р (х, х 1 , t/t) =
Р 0 (х, х 1 ),
что
на
основе
наблюдений
до
принимаем . решение о значениях х в мо-
Уравнения
'J
х Е D;
·
(3. 77)
и
(3. 78),
описывающие Ф К, яв-
ляются дифференциальными уравнениями в ·частных
производных. Их решение на универсальной аналого
вой технике требует применения ряда специальных
приемов. Если же решать эту задачу на специальн_р1х
типа сеточных АВМ, то приходится разрабатывать со
вершенно новые подходы к ее решению .
Кроме того,
107
при решении этой задачи. нужно выполнять большой
объем трудоемких вычислений. Весь этот комплекс
трудностей и послужил толчком для рассмотрения
других способов решения поставленной Калманом за
дачи фильтрации. Пqэтому рассматривается дискрет
ный вариант Калмащ1, описываемый системой разност
ных
уравнений,
которые
легко
представить
в
виде
алгоритма для решения на ЦВМ . Учитывая недостатки
,,
аналогового и цифрового моделирования. фи:льтров
Калмана, ниже предложен алгоритм решения уравне
ний фильтра на гибридньтх вычислительных системах
и, в
частности, на аналого-цифровых вычислительных
комплексах .
ФИЛЬТР КАЛМАНА
В ПРОСТРАНСТВЕ ДИСКРЕТНОГО ВРЕМЕНИ
Рассмотрим случай, когда измерения производят·
ся в дискретные моменты времени, т. е. t = Лtk и в
дискретных точках пространства, т. е. х = lЛх; l =
= 1, 2, .. . , L; k = 1, 2, . . , К Для этого случая урав
нения (3. 75), (3 . 77) и (3. 78) принимают вид
И
[l, k
+ !] =
~р
Z[L., k]
где
[ 1
=
L,U [l, k] +В [l, .kJ w [L, k];
IL, k]
М
[L, k]
= / + ЛtL 1 ;
P[l, п, k +
\] =
=О;
И
l = l, L;
[L, kl
В [l, kJ
-
Lp[l, п, k]
+ В [L, kJ Q [L, п, k]
L
N
(3.79)
=
+ V fL,
ЛtВ [L, k];
+ P[l,
В7
k],
-7
п, k]Lп
' (3.80)
+
\п, k] -
1-
,
-~ ~ Pfl, r, klM 7 [r, k]Qlr, т, kJM/m, k] х
'=lm;=I
х Р
l08
[m,
п,
kj,
(3,81)
'·
Рис.
тра
Общая структур11ая схема филь·
24.
в
пространстве днскрепюrе>
времени:
РО процедура rенср~цни псевдослучайных
rауссовс1шх
проц~ссов
\f; (х, t) н V (х, /);
Р1 про11едура рсш~. ния урапнения (3. 79);
Р2 процедура решения коuар!iации ошиб·
"" (3.81 ); Р.1 - ГJроцсдура решения уравне·
lfava110
8808: IJ, и (.r, t)
PO(l,;(f); UOM
orx. xt, о: щr,ru;
(3.80)
ния
где
Q 1 1=Q 1 1/Лt;
п = l, 2, ... , N;
Р
1 1=
Р
[
]/Лt;
B1 U JL, kJ =О;
РО
UJl, l]=E(U 0 fl]);
l = 1, 2, ... , L; z Jm, k] = z fm
l= l, L;
kl·- м 1т, kl
Р
п,
JL,
1] =
ЫVllC/11Jmь:
D1т. kJ;
Р0
Z[L,kl=M[L,k]X
U[L,k]• V[L,k]
[l, nJ.
Задачу фильтрации в такой поста·
новке
ЦВМ.
Выч11с1111ть Р2
целесообразно решать на
Общий алгоритм решения
задачи показан на рис. 24.
такой
Фильтр Калмана, синтезирован
ный
для
по
предложенному алгоритму
систем
с
распределенными
раметрами, може т найти
па·
свое п ри-
менение в тех областях, где инфор·
маuия
о
протекающем
время
является
u.rJ,z,P, V
процессе
распределена в пространстве (ме·.
теорология, ·радиоастрономия),
а
"
печать масс11808:
непрерывным
или
конец
дискретным.
При последовательном решении уравнений ФК (чисто цифровая реализация)
ограничено
количество
возможных узлов . пространственной сетки (конечная
память ЦВМ) и необходимо длительное время решения.
109
ФИЛЬТР КАЛМАНА В ПРОСТРАНСТВ!:
1-!ЕПРЕРЫВНО-ДИСКР.ЕТНОГО ВРЕМЕНИ
Сформулированные уравнения Ф К
(3. 77)
и
(3. 78)
могут быть успешно решены также на аналого-циф
ровом комплексе. Рассмотрим принцип решения этих
уравнений методом Либмана.
л
При моделировании сигнала И (х, t), оценки И (х, t)
и ковариационной функции Р (х, х 1 , t) на аналого-uифРис.
25.
решения
fi(JЧQЛO
Блок-схема
алгоритма
задачи
гибридной
на
системе.
НакопЛеtfие ucxotlнмr
dа1111ш В памяти ЦВМ
. Рис. 26.
Временные диаграммы
работы гибридного фИ'льтра:
!lcmattoOumь
В -
f=lo, }=0
быстродействие ЦВМ;
врем11
Вычисление ddodнoгo uнmeгдlljla
на А8!16 ураdнежщ оценки
U
8ыl./11сле1ше лоранетроd сетки
8и11ислvть
.
11aЦBl1:1',,li.ЛP1.lft,Jt
в
с
па
при
на информацией
между
буферной
памятью и ЦВМ; lсчет- время сче
задачи
фильтрации;
lпот
-
вре
мя, когда теряется информация из
эа
параллельности
работы
ком
плекса АЦВК во времени.
Вычислить
j=j+I
в
ДА
0
1.._____,~~
- ~.
t
ровом комплексе необходимо использовать два
ратора rауссовских шумов
110
lнак
буферной
измерений
нятой
дискретизацией времени и
пространства;
lпер время обме
та
l•t,+jJt
накопления
мяти результатов
W
(х,
t)
и
V
(х,
t).
гене
,"
'\
Двойные интегралы в правых - частях уравнений
ФК (3 .77) , (3.78) предполагается вычислять на АВМ.
Выражения Р (х, х', t!t), Р (х", х, t/t) и Z (х, t/t) не
делают данные уравнения нелинейными, так как пр·и
методе Либмана время является дискретным, а,
ме того, на данном этапе
все вычисления
кро
ведутся
при
=
Лt = const. Исходными данными при вычисле
нии интегралов являются начальные значения функ-
j
цийР (х, х 1 ,
t0 /t 0 )
"
и И (х,
.t"0 /t 0 ).
Для решения задачи фильтрации на гибридной си
стеме предполаr-ается следующая блок-схема алгорит
ма решения, показанная на рис. 25.
Временные диаграммы работы такого гибридного
фильтра Калмана можно представить в . виде диаграм
мы (рис. 26).
Определяющим фактором практической пригод
ности фильтра при его работе в реальном масштабе
времени является . время
потери lпот· ДQпустимая
. величина lпот, а тем самым величина погрешности
фильтра, является разной при решении определенных
задач.
МОДЕЛИРОВАНИЕ ФИЛЬТРА КАЛМАНА
В
качестве примера
проведенным
моделирования
алгоритмам
рассмотрим
филь'"!'ра
по
решение задачи
фильтрации распределенных помех [10] .
Процесс описывается стохастическим дифференци
альным
1,
1.)
уравнением в частных
аи (х, t) = 1 5 дИ 2 (х, t)
дt
,
дхz
производных
+ w (х, t)·'
для
которого граничные
условия И (О, t)
И (R, 1) = О, а начальные И (х, О) = O,J sin
Наблюдаемый
процесс
аддитивно связан с
=
О;
(:rtx).
помехой
111
V
(х,
t):
Z (Х; t)
=И (х, t)
+ V (х,
t).
Дополнительно заданы
характеристики случайных распределенных процессов W (х, t) и . V (х, t)
в
виде
ковариационных
матрин
Q(x, х1 , t) =О, 5ехр1 - (х- Х 1 ) 2 ]; Q(x, х 1 , t) = б(х, х 1 );
R (х,
х 1 t)
=
б (х
д'
. l,S дх2
В этом примере Lx
.'
;
·-'
х 1 ).
-
В (х, t)
= 1;
М (х, t)
= 1.
Уравнения ФК принимают вид
дИ ~;·
t)
= д2 Uд~,
+ ~ Р (х, х 1 , L/t) i (х1 , t/t)-dD;
t)
D
дР (х,
xi, t/t)
=
д2 Р
дt
(х, х 1 , l/t)
·
+
д 2 Р (х, х 1 , t/t)
дх 2
+
дхf
+ Q(x, х1 , t)- j ~ Р(х, х 1 , t/t) Q(x', х", t) Х
D D
х Р(х", х 1 , t/t) dD'~D".
При моделировании ФК приняты
D(О
'
и
'
t) = О·
'
начальные
·
граничные
условия
л
U(k,z) = O;
Р(х, О,
P(O,V 1 ,t)=0;
t) :==О
условия
л
U(x,O)
= 0,1
sin(лx), Р(х, х 1 , О)=
0,1 sin(лx 1 )s i n (лх).
1•
Отметим ряд особенностей моделирования этой задачи .
1.
Моделирование
процессов
случайных
распределенных
W (х, J) и V (х, t).
Так как такие процессы в каждой точке пространст
ва и во времени (х, t) характеризуются своей плот-
112
."
ностью
распределения,
то
в
данном
случае
сделано
упрощение, заключающееся в следующем. Принято,
что плотность распределения в каждой точке (х, t)
является постоянной . Такое упрощение делает моде·
лирующий алгоритм более быстродействующим. Для ·
обоих процессов W (х, t) и V (х, t) принят нормаль
ный закон распределения с нулевым математическим
ожиданием
и
различными
дисперсиями.
Присутствие в задаче трехмерных массивов .
Эта задача решена методом, близким к методу Либ
2.
мана,
который применяется
при
решении дифферен
циальных уравнений в частных производных на гиб
ридных
комплексах
заключается
(АЦВМ).
в фиксировании
Содержание
времени
t=
метода
tФ и
хождении значения Р (х, х 1 , tФ), т. е: массива Р
на
[l, k].
Выводом из памяти ЦВМ tФ и соответствующего мас
сива Р делается следующий шаг во времени и находит·
ся соответствующий массив Р.
3. Д.hя решения уравнений в частных производ·
ных применен метод прогонки, обладающий преиму·
ществами
по
сравнению
с другими
численными
мета·
дами решения таких уравнений.
4.
При любом численном методе решения диффе
ренциальных
уравнений
в
час~;ных
производных
необходимо рассмотреть два
вопроса: пригодность
разностных схем и условия устойчивости.
Если дифференциальное уравнение аппроксими·
руется
двумя
различными
то даже при одном
и
том
разностными уравнениями,
же шаге сетки можно
полу
чить значительное расхождение . . Кроме того, не всег·
да
возможно
улучшить
аппроксимацию
путем . умень·
шения Шага сетки, даже если разностное уравнение
допускает точное решение. Пригодны только такие
'·'
схемы ; в . которых при уменьшении шага сетки решение
разностного уравнения
сходится
к решению рассмат
риваемого дифференциального уравнения.
Для пара-
113
болических и гиперболических
производных такая
тогда,
когда
шаги
удовлетворяют
уравнений в частных
сходимость
сетки
имеет
по
некоторому
место
обеим
только
координатам
условию
.J
устоичивости.
Так, решение разностного уравнения
И (х
+ Лх,
+ И (х -
2И (х, t)
t) -
Лх, t)
-;..
Лх 2
=
сходится
к
И (х,
1
t. -
Лt)
-
решению
уравнения
д2U (х, t)
t)
те п лопроводности
дИ (х, t)
=
дх 2
а2
при Лt-+ О, Лх-+ О, если Лх
•
ностного
И (х,
Лt
(j2
дt
' 1
< -2
Лх 2 • Решение раз-
+И (х
-
а
уравнения
И (х
+ Лх,
2И (х,
t) -
t)
Лх,
t)
Лх 2
=
И (х,
t-
лt)
С2
-
2И (х, t) И (х,
t-
лt)
Лf2
сходится к решению волнового уравнения
д 2 U (х,
дх2
· 1
= С2
при Лt-+ О, Лх-+ О,
если Лt
'
t)
д 2 U (х,
t)
дt2
< -1
с
Лх.
Такие условия устойчивости обеспечивают также
лучшую
аппроксимацию
при
конечном
В данном случае при О< х
л.t =
1
2а2
1
Лх 2 = 2-Т,5О,125 2
шаге
и Лх
< 0,5
сетки.
= 0,125
'
= 0,0052.
r·.
гiри моделировании ФК было принято Лt = 0,004 с,
в
результате чего получены следующие данные:
114
кщза-
риации ошибки
идеа~ьный И (х,
Р (х, х1 ,
t); сигналы системы с помехой Z (х, t), отфильтрован-
t),
ный И (х, t).
О качестве работы ФК судим на основе следую·
щих факторов.
,'
1. Матрица ковариации ошибки. Р (х, х1 , t) во всех
точках пространства (х, х 1 ) должна иметь затухающий
характер
во
времени.
Установившиеся
значения
P(x,x"t)
О,_08
406
2
0,04
о
t,c
6
х
-402
о
а
Рис.
Зависимость матрицы ковариации ощибок:
а при фиксированных х; 1 х1 =
0,25; 2 -:х = 0,25; х 1 =
= 0,125; · 3 - х
0,25; х,
0,375; б - при фиксированном
27.
=
=
времени
Р (х, х 1 , t) свидетельствуют о постоянной ошибке
фильтрации, минимальной при данных условиях филь
трации. Следовательно, при разработке таких фильт·
ров необходимо стремиться получить возможно мини
мальное ·значение ошибки. Нулевое значение ошибки
невозможно
•'
получить
в правой части
даже
уравнения
теоретически,
так
как
ковариации ошибки есть
т
свободный член [В (х, t) Q (х, х 1 , t) В (х, t) ]. На рис. 27, а
показаны характеристики · Р ~х, х 1 , t) для разных
точек пространства (х, х1 ) и на рис. 27, б - при фикси
рованном времени.
2.
Для наглядного восприятия
трации
приведены
совместн:ые
результатов филь
характеристики
сигна-
. 115
лов И (х, t),
U(х,
t) и Z (х, t) при фиксированной точ
ке пространства (рис. 28).
На основе пол у ченных результатов можно сделать
следующие
1)
U (х,
2)
выводы:
фильтр
не
дает
искажения
формы
сигнала
t);
достигнута высокая с практической точки зр~
ния степень близости сигнала И (х,
t) 1< V
(х,
t). Эту
близость в установившемся режиме оцениваем на ос
нове значения Р (х, х 1 ,
ставить
t) .
Меру близости можно пред
как
л
0 = 1_
1 И (х,
t) И (х .
И (х, t) 1
t)
В точках х = 0,375 наблюдается самое большое рас
хождение в момент t = 0,008 с. Для этого момента
о=
Для
оценки
1-
0,038489 - 0,0354464
качества
о
О,О.'-154464
= •9
фильтрации
на
23
.
всем
отрезке
рассматриваемого времени при фиксированной точ
ке пространства можно применять обобщенную меру
близости в виде
о= 1
-+ [~1 D(Х;,
i = 1, 2, ". , k;
= 0,375
где
Для х
W
W
Лt
t;)-
=
Лti;
~1 и (Х/;) ]/~!и (Х;, t;),
j = 1, 2, ". , L;
0,982 .
х
=
Лх;.
получено о ~·
Рассмотрим оценку превышения уровня сигнала
(х , t) над уровнем помехи V (х , t). Так как сигналы
(х, t) и V (х, t) являются случайными процессами,
то в
каждой
точке
(х) соотношение
уровня
сигнала
и помехи во времени будет различное. Для его оценки
в данный момент времени (t) и в данной точке про
странства (х) можно определить показатель р = Ур оц.ш
. • вень
сигнала /Уровень помехи. Для оценки р в данной
точке пространства (х) на продолжении интервала на·
блюдения процесса используем .обобщенную оценку
+~
k
Р=
•'
i=J
k
j Ct IJ+ ~ 1ht \,
i=J
где k - количество точек отсчета; с1 и
соответственно сигнала и помехи при
Для примера приведем
оценки
сигналов,
зуемых
при
h1
уровень
-
х
= const.
исполь
моделирова
нии.
Превышение
сигf!ала
над V (х, t) может
быть довольно большим.
Кроме того, при моделиро·
W (х, t)
вании
решения
для
х
а
=
= 0,25
Так,
показатель р = 3, 7.
например,
большое
значение
имеют граничные
условия. При рассмотрении
вопроса о качестве работы
Ф К не была проанализиро·
вана
динамика
этого
про·
цесса. На основе обработ
ки {рис. 27, а и 6) и приве·
денных исследований мож
но
заключить
следующее:
начальное значение
<'
Р 0 (х,
х1 ) не меняет своей формы,
а меняет лишь свой уровень
только
с;;~м процесс
-рактер,
тогда,
Р (х,
/}
Рис.
28.
рования
Результаты модели
фильтра
Калмана
длЯ различных условий:
О, 125;
б х = 0,25;
0,375 tмасштаб време
"и 9 }( i
10~2).
а • -
х·
х
=
=
когда
х1 ,
t) при х, х1
показанный на рис.
Блок-схема
_}ьj,6fsJ
= const
имеет ха
28.
комплекса алгоритмов моделирования
ФК показана на рис.
29.
117
<'
!·
- Рис.
29.
Блок-схема. алгоритмов моделирования фильтра Калмаиа.
Глава
4
РАСПОЗНАВАНИЕ - СИГНАЛОВ
НА ОСНОВЕ ПРЕОБРАЗОВАНИЙ
АДАМАРА
1.
ОПТИМАЛЬНЫЕ РАВНОУДАЛЕННЫЕ
СИГНАЛЫ
В
теории
идеального
приема
доказывается,
что
в условиях действия гауссовской помехи условная ве
роятность регистрации сообщения j вместо i опреде
ляется расстоянием между сигналами этих сообщений
Это соответствует метрическим соотношениям для
пространства Гильберта. Если s; (t) = О, то
,
Р10 =
-. f
V
+
1.+т
.
~ sf (t) dt = V Е i/T,
(4.1)
1,
где PiO - длина вектора или расстояние между точкой
пространства, представляющей функцию s; (t), и нача
лом координат; Е; - энергия i-го сигнала.
Если s; (t) и s1 (t) ортогональны, то
р;; =
v
2
р;о
+ Р10.
2
Так как вероятность трансформации
(4.2).
i -+ j
опреде-
119
ляется значением
достоверности
то при требовании одинаковой
т сообщений uелесо.образно по
Pi;,
всех
строить такую систему сигналов, для которой выпал·
няется
условие
Pi 1 = р
т. е.
расстояние
Такие
= const,
между
сигналы
всеми
называются
ij
= 1,
т,
сигналами
(4.3)
одинаково.
равноудаленными,
или
эквидистантными .
Если энергия всех ортогональных сигналов оди
накова, т . е . Е 1 = Е 2 = . .. = Ет = Е, то из формул
и (4.3) имеем р; 1 = V2E /Т. ·
В. А. Котельников впервые сформулировал и ре
шил важную для теории связи задачу [9]:
(4.1), (4.2)
найти систему равноудаленных сигналов, обладаю
щих одинаковоj:\ энергией и обеспечивающих мини
мальную
или
вероятность
заданную
неправильного
вероятность
опознания
неправильного
их
опознания
при минимальной энергии.
Такая с·истема сигналов называется оптимальной.
Доказано, что скалярное произведение оптимальных
равноудаленных
сигналов
+I
' ,+т
V;;
=
si (t) s; (t) dt = .
1.
{
=
где Еопт
-
Еопт/Т
-Еопт/ [Т(т-1)1
при
i = j;
при
i =F j,
энергия оптимальных равно удаленны х сиг
налов .
Таким образом,
жет
120
служить
проверкой на оптимальность мо
величина
отношения
\•
Симплексный
сигналов.
код
Для
(т -
=-
vii/v,
является
них
строго
1г1 •
(4.4)
системой
оптимальных
выполняется
отношение
(4.4).
.
•
Двоичные сигналы, равноудаленные по Хеммингу,
являются также равноудаленными по Котельникову.
При проверке на оптимальность по формул е (4.4)
следует
пользоваться
двоичных чисел : О
·
О
правилом
= ·1 • 1 =
= -1.
умножения
+ 1; О
разрядов
· 1= 1•
О
=
Таким образом, идеальными условия м и работы
классификатора в распознающем автомате будут та·
кие, при которых каждому классу объектов соответ
ствует сигнал с выхода блока сложных (или простых)
признаков,
записаннь1й
симплексного кода.
будут
поступать
в
соответствующей
строке
В этом случае на классификатор
всегда
сигналы,
системе оптимальных сигналов,
соответствующие
а это гарантирует ми ·
н и мальное число ошибок при их распознавании. Впер·
вые было предложено использовать симпл ексные ко·
ды в качестве универсальной системы эталонов при
распознавании сигналов в работа х
(17, 18, 19].
Симплексный код (Нэ) просто может быть полу·
чен и.з нормализованной матрицы Адамара путем вы·
черкивания первого столбца, состоящеrо из .
+1. _,
Flpuмep
6.
Пусть имеем
н,{
'
1 -1
-1
'J .
1 -1
-1
1
1 -1
-1
'
121
·
тогда
Нэ=
l
I
-1
-1
-1
-1
= 4, vii = - 1/3, V;; =
v;/vu = -1 /3 = -1/4-1.
Здесь т
(4.4)
дает
2.
_:1
1
•
1,
-1
и проверка по формуле
1!·
АЛГОРИТМ РАСПОЗНАВАНИЯ СИГНАЛОВ
Рассмотрим схему распоз_нающего автомата (РА),
изображенную на рис . 30, Пусть имеется т сигналов,
подлежащих классификации
Выше было показано,
Матрица
.
рецептороО
!(ласси!рЦ!(Оmор
R
И11tl11кация решенця
матрица памят11 (G1)
_
'-----1
Omtfop цнrрорматцд
ных кooptl1111am
Рис.
122
30.
Структурная схема распознающего автомата.
.
(
1
1
что
идеальными
условиями
работы
классификатора
в РА будут такие, при которых каждому классу объек-
,;,
тов
соответствует
сигнал с выхода
блока
сложных
(или простых) пrизнаков, записанный в соответствую
щей
строке матрицы
Н3 матрицы
универсаль
ных эталонов. Покажем, как, пользуясь Н 3 , строить
процесс
минимизации
описания
или
отбора
при
знаков.
Результат
мых
накопления
сигналах
можно
информации
представить с
о распознавае
помощью
матрицы
j = П (L - размерность сиг
нального вектора XL), где g;; = (2пt - s)/1;; - 1
g;i
1, пt - число
1 образовавшихся на j-м
GL
=
<
(g;iJ, i
1, т;
=
<
+
<
выходе блока · формирщ10-ния признаков при предъявле
нии в процессе обучения 1; объектов i-го класса.
Образуем матрицу отбора информативных координат
Ф
==
»
H~GL (n х L~ L
п);
sup 1 cp;i /; j = 1, L.
Ф ={ер;;).
Критерий для
отбора
i
i
Отметим в матрице Ф соответствующие элементы
знаков
():
1
2
1
2
L
k
3
1
1
1
1 ()
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1 () 1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Ф=з
.
п
Расположим отобранные .элементы в порядке воз
растания индекса строки:
C(J1k, C(J2i,
С(Jзр,
.•• ,
C!Jnt·
.123
Пользуясь указанием вторых индексов, образуем
матрицу
весов
G=
.g,k
f g2k
g11
g,p ••• g11
g21 g2p ••• g21
. . .
. .
gml gmp
gmt
gmk
Вторые индексы
k, l,
р, ... ,
t
J
1,
указывают на номера
информативных разрядов вектора
Х L (номера столб-
цов G:z).
,
Действительно, например, k-я координата вектора
XL при предъявлении объектов .1 класса чаще будет
выдавать символ,
лении объектов
2
совпадающий с h 1k , при предъяв
класса - символ, совпадающий
х 1 , Хр, : . "
= (xk,
с h2k, и т. д" а весь вектор Х
х1 }
при предъявлении объектов 1 класса будет больше по
хож на вектор, записанный в первой строке Н 3 , при
предъявлении объектов
2
класса
-
похожий на век
тор, записанный во второй строке, и т. д. Решаю
щая процедура здесь получается очень
простой .
Отыскав
вектор
"" Rm1 7 , где G0
R
•1
= . GX 7 -
2 G0
=
[R1 , R2,
столбец, образованный из . диаго
нальных эЛементов матрицы G* = GG 7 , по sup R1
-
i
определяют класс i.
Надежность распознавания по каждому из т классов Pi (i = 1, . т) также можно приближенно оценить
по сравнительно простой формуле
i;
pt,....,
1
п
v=O
где Р; = 2п ~ (gi;hi ,
явления
1=1
.
~ c~-vp7-v ( 1 ~ pJv,
+ 1)- средняя
необходимого
кодового
при предъявлении объектов
124
вероятность по-
слова
.
(вектора Х)
'! ""= I(d -
n-ro класса;
( ~
-
1)/2) -
число
допустимых
хэммингово расстояние;
•
1~
[ ·] -
ошибок
в
коде;
d-
наибольшее целое.
В ряде случаев оказывается удобней работать с
отображением r. игнала (или его преобразования ли·
нейного или нелиней ·
4
наго) на фазовой пл ос·
кости · (s~
si.
Для по·
иска подходящих пре·
образований сигнала
и отображения,
из·
бавляющих от вл111я·
ния
ных,
неинформатив ·
мешающих
па·
раметров,
требуется
индивидуальный под·
у .
,Z
Рис. 31 . Схема 11реобразований сиг
нала s (1) для формирования фазово
го изображения.
х.од [12 ]. Ранее fiыла
показана полезность преобразования Адамара и его ло·
гической модификации для получения инвариантностн
к возмущениям типа сдвига, изменения масштаба и др
Рассмотрим еще одну возможность. Пусть имеется
сигнал (рис. 31), аналитическая запись которого
s (t) =И 1 а (t) cos (w 0t + ср 1 ) +
+ U2a(t - т) cos Jw0 (t - т) + ср 2 ],
. где a(t)
ср 2 -
= t 2e- 21
случаиные
мерения,
модулирующая функция; И 1 , И 2 , ср 1 ,
-
величины,
время
из·
но медленно меняющиеся от измерения к
постоянные
во
из·
мерению. Требуется оценить i;. Постараемся исклю·
чить влияние мешающих параметров U 1, cpi (i = 1, 2).
Запишем, используя преобразование Гильберта, выра·
жение для квадрата огибающей сигнала
д2(t)
=
Ufa2 (t)
+ Иа2 (t -
т)
+ 2U U2а (t) а (t ~ т) cos ( w0т + ср1
1
+
-
ср 2 ).
125
Мгновенное значение фмы
s (t)
~(t)
_
t
- arc g
откуда
И 1а
=
+ ср 1 ) + И 2 а(t)(t -
(t) sin (w 0t
т)
sin [w0 (t.
5
мгнов е нное
w
0 A2
зн а чение
(t)
т)
+ (p2 j ,
частоты
+ И 1 И 2 siп (w 1 + ср 1
0
ср 2 ) Х
-
.i, (t) _: __
х_[а_
· (_t)_a_(t__ •)_'_ a_(t_)_а~(1_-_т_)J_
'У
A2t
Из последнего выраЖения пол 'учим
c0 (aa,-atl,,), где
x(t)=A 2 (t)[.\p(t)-w 0 ]
с0 =
Up 2 sin(w 0.- + ср1 -
<р 2 );
а =
a(t);
а, =
a(t-•).
Все мешающие параметры являются составляющи
ми случайной а мплитуды с0 сигнала х ( t) . Чтобы до
биться инвариантности к изменени ~м мешающих па
рам~тров, достаточно в качестве фазовых координат
выбрать отношение двух линейных преобразований
процесса х
(t).
Выбираем такие преобраз ования в виде
у= 4 + ~
z= 4 + ~
Так как х (t) =
чательно
[ln x(t)] ..
(ln
_
x-i: 4х
;
[Ух (t)]) = х' +: 8х + 16
.
х+ 4х
ct (t--: •) е- 41 ;
с=
-
2с 0 .-е 2 ',
то окон
получи~
у=
(2t- 't)/[t(t - •)];
Следовательно,
значения
Z зависят только от
t
z = 2/(2t- •).
фазовых
координат
!26
У,
и · • и фазовое изображение ин
вариантно к неизвестным параметрам Л'lj.J и у =
Уравнение фазового отображения
У=
~)
8Z/( 4 - • 2Z 2 );
У = О;
О
<:. Z <:. 2/т:.
U2 /U 1 •
"
Натр11ца
рецепторов
."
блок11 rрормцроВа·
HllЯ СЛОЖНЫХ
лрцзнакоО
х,
х"
Грулпо otl l(ЛОС
сшрцкатор #а
Zt
,J
Инilикшщя
решен11я
Рис.
32.
Блок-схема
распознающего автомата при груп
повом методе обучения.
Схема преобразований еигнала s (t) показана на
рис. 32. Хараюерной особенностью рассмотренного ал
горитма
распознавания
является
использование
од
нотипных операций (умножение на матрицу Н или Н 3
и G) на всех этапах решения задачи. Действительно,
на этапе формирования сложных признаков, инвари
антных
к определенным
возмущениям
входа,
исполь
зуется преобразование Адамара или его логическая мо
дификация, на этапе отбора информативных призна
ков - умножение на матрицу Н 3 , полученную из
матрицы Адамара, и на этапе принятия решения -
на матрицу весов G. Однотипность операций обуслов
ливает однородность структуры РА, что очень ценно,
так как f!аиболее полно удовлетворяет требованиям
интегральной технологии, считающейся сейчас
наи
более прогрессивной при производстве радиоэлектрон
ной аппаратуры (РЭА) на интегральных и больших
интегральных микросхемах. Вопросы аппаратурной
реализации подобньiх РА с использованием новей
ших достижений
ботах
микроэлектроники освещены
в
ра
[2, 16, 21 ].
3. Г 0РУППОВОй МЕТОД ОБУЧЕНИЯ
ПРИ РАСПОЗНАВАНИИ
Структура Н э такова, что каждый столбец содер
жит одинаковое число элементов со значением
1
и -1. Это является основанием для разработки груп
+
пового метода обучения
[20 ].
Идея его. состоит в том,
что информация об объектах (сигналах) записывается
в п матриц Gт.а (а =
размерность 2 х L
gii
128
=
I:n), ){аждая из которых имеет
и образуется
(2пt -- 0,5m6)/0,5m6,
i
элементами
= 1, 2;
j
=
1, L.
+1,
Здесь пtj _:_ число
образовавшихся на j-м
выходе блок# формирования признаков при предъяв·
лении в процессе обучения распознающему устройст
ву
0,5
ms
объектов
i-й
группы;
объектов в каждом классе; т
Объединение
объектов
в
--,
s-
полное число
число классов.
группы
при
обучении
производится в соответствии со структурой Н 9 • На·
пример, для Н 9 вида 8 Х 7
1
-l
1
l
1
-1
-1
-1
-1
и r:x
= l
рице
1
l
-1
1. - l
-1 -1
-1
-1
-1
-1
-1
-1 -1
-1
1
l-1
-1
l
-1
( 4.5)
-1
(т. е. рассматривается первый стоЛбец) в мат·
(4.5)
в первую группу войдут объекты
1,3, 5, 7,
а во вторую - , 2, 4, 6, 8 классов . Соответственно
для этого же случая, но длЯ rx = 7 (предпоследний
столбец), в первую группу войдут объекты l, 4, 6, 7,
во вторую - 2, 3, 5, 8 классов. .
·
Матрица отбора при групповом обучении строит·
ся с использованием простейшей матрицы
. .= [_ 1]l .
Нэ(2Хl)
Процесс отбора должен быть повторен .для каждой
из матриа G'l:.a
Фа= H~2x1iG'f.a·
Критерий для отбора тот же: sup/cp~\,
i
i= 1; j = l, L.
12~
Отбор можно повторять, считая каждый раз исклю- .
ченными
элементами
отмеченные
как
наибольшие
iз
предыдущем шаге. При этом для останова можно ру-
ководствоваться соотношением 8
= 2-
1
(fJ~
1
<;: бmах,
где 8 - допустимое отклонение от идеального сходства
столбцов Gr.a со столбцом Н э(2 Х I» а бmах - заданное
максимальное допустимое отклонение . Отмеченные
элементы расположим в порядке их убывания (по ве-
.
)а
а
а
(fJJq,
ср 1
,,
а
З
(fJ ic, ..• , rp1 s·
начения
индексов
q, r, с, ... , s указывают на нам-ера информативных раз
рядов L-мерного вектора признаков и из них формиру
личине
ется матр.ица весов
Ga = [glq
g11q
g1,
gr,
.. · gis ]
g11r
gri c • • •
grrs ·
Решение за номером а об отнесении предъявленного
объекта к первой или ко второй группе формируется
подачей на групповой классификатор сигнала (ин
формативн~1х разрядов):
( 4.6)
или
Ra =
+G~
Ga.X~ -
=
1;; ] ,
где G~ матр Ица - столбец, образованная из диапщаль
ных элементов матрицы G~ = GaG~.
Выход детектора ,наибольшего напряжения груп
пового классификатора
Za={+l,
·
>
Rf <
ес4и R~
- - 1,- если
R~.
R~.
Этот выход можно рассматривать как сложный п'ри
знак. Сово1<упность сложных признаков образует
вектор Z
130
= (za.) (а =-Г:-п), информация о котором
''
1"
может быть записана в виде матриuы
?z =
,
2
(gia)
{
+1,
п~ - число
ра
= 2п/t~- ~ },
наибольшего
i
= -1,
т,
-
а:= 1,
n,
образовавшихся на выходе детекто
напряжения
группового
классифи
катора под номером а: при предъявлении автомату
s
объектов i-го класса. Окончательное решение об от
несении объекта к классу _ принимается в · соответствии
с расположением элемента с наибольшим значением
у
вектора
Блок-схема структуры РА для этог_о варианта по
казана на рис. 32. Хотя в этом варианте процесс обу
чения РА значительно больше по времени, тем не ме
нее такое построение РА имеет преимущества, главны
ми
из
которых
являются
следующие:
значительная экономия
элементов памяти, так как
матрица памяти РА должна здесь иметь размерность
2 Х L, а не т Х L;
задача
нилась
на
на
п
распознавание т
параллельно
классов
решаемых
здесь
расчле
альтернативных
задач, для решения которых разработаны весьма эф
фективные методы классификации.
Поясним последнее с помощью частного примера .
Вектор Ха можно преобразова'ть в линейную дискри· .
минантную функцию. Для этого необходимо провести
многомерный
дисперсионньтй
анализ
над
выборкой,
относящейся к первой Х~ и ко второй Х~ группам.
Схема анализа такова. Определяются функции
0,5т_;
Wu =
~
j=I
(х);) 2
+
IJ.5m'
~ (x)f) 2 i=I
' 131
-
-
[с~~ х!; у с~· x)l) о ,5ms), .
2
}(
i = .q, r, с, .. . ,
Wik
+
i=I
i=I
;;
~
x)ix)k-
i=I
+ ·~ х)/ о.~; x~k)!(0,5ms~l •
x)k
i=I
i =f=. k;
(4.6)];
0,5m ':
= ~ X~1X:k
-[( 0 '~' х!. · i~
[см.
1>
. · ,5т ~
'=·1
i=I
r,
i, k = q,
с,
.• • , s.
Затем определяются расстояния
d1 =
( 0 '~' х}1 - ') ,~' x~i)/(0,5m"S),
i=1
где
'
а
1, 2 Далее
i=1
t =
q, r.
, i>.
с,
по-п.режнему, номера групп
решается система уравнений
объектов.
относительно
неиЗвестных весов Л 1 . В матричном виде эта система
записывается следующим образом:
WЛ
где
W = {W;;\ ;
л~ r ~.
=
D, ·
Лql
( 4. 7)
. rdq]
о~
,
:.
Линейная дискрйминантная решающая функuия стро
ится на основе данных рещен ия
(4; 7)
рого поро~:а для Уа: Ra = Ха.А
и выбора некото
Уа. 1 то
Если Ra
объект относят к первой группе, если
>
Ra <
У-:х
-
то
ко второй . Решающим устройством здесь может быть
обычный пороговый элемент. Его вы х од следует рас
сматривать
132
как некоторый
информативный
признак .
f.\
СП"IСОК ЛИТЕРАТУРЫ
1. Адаптивные системы идентификации. Под ред. В. И. Кос
тюка. Киев, «Технiка», 1975. 284 с.
2. Александров В. В., Полонников Р. И., Трофимов Е. И.
Оптоэлектронное устройство распознавания образов.- В кн.:
Оптическая и электрооптическая обработка информации. М.,
«Наука», 1971, с. 66-71.
3. Брюс Р. Цифровая обработка сигналов.- «Зарубежная
радиоэлектроника», 1971, № 12, с . 18- 31.
4. Голд Б., Рейдер Ч. Цифровая обработка сигналов. М.,
«Сов. радио», 1973. 367 с.
5. Гольденберг Л. М., Левчук Ю. П., Поляк М. Н. Цифро
вые фильтры. М., «Связь», 1974 160 с.
6. Гусев В. Д. Процедуры быстрого преобразования Фурье
и Уолша.- В кн.: Вычислительные системы. Под ред. Н. Г . За
горуйко. Выл. 45. Новосибирск, «Наука», 1971, с. 107- 116.
7. Зеленский К. Х. Упрощение моделей, идентифицирующих
объекты с распределенными параметрами .- «Вести. КПИ. Сер.
Автоматика и электролриборостроение».
Киев, Изд-во КГУ,
1974, No 11, с. 18-21.
8. Клейбанов С. Б Стабилизация коэффиЦиентов в дискрет
ном фильтре Калмана.- «Автоматика и телемеханика», 1974,
No 3, с. 76-82.
9. Котельников В. А. Теория потенциальной помехоустой
чивости. М., Госэнергоиздат, 1956.
(1
10. Краскевич В. Е., Корбич Ю. С. Дискретный фильтр
Калмана для систем с распределенными параметрами.- «Вести.
КПИ. Сер. Автоматика и электроприборостроение». Киев, Изд
во КГУ, 1975, No 12, с. 79-81.
11. Крутько П . Д. Оптимальная фильтрация в дискретных
автоматических
системах.- «Автоматика
и
вычислительная
техника», 1970, No 4, с. - 39~41.
12. Основы разделений и измерения сигналов по структур·
ным свойствам. Под ред. А. М . Заездного. М.
Изд-во М-ва свя
зи СССР, 1971. 123 с.
133
13. Пирл Г. Обработка случайны х сигналов
Уолша.- «Зарубежная радиоэл ектроника», 1972, No
функциями
8, с. 42-50.
14. Полонников Р . .И. Адаптивные однородные структуры
для распознавания сliгналов:- В кн.:
Ада.птивные системьr
автоматического управления. Вып. 1. Киев,
«Технiка», 1973,
с. 23-31 .
.
r'I
15. · Полонников Р. И . Быстродействующий распознающий
автомат.- В кн . : Автоматическое управление и регулирование
в различных отраслях народного хозяйства .
изд . МВ и ССО РСФСР, 1971 , с. З9-47 .
'
16.
nолонников
рецепторного
поля,
Р.
И.
Вып.
1.
'
1
Куйбышев,
Логическое преобразование сигнал а
инвариантное
к
некоторым
ям . - «Вопросы
радиоэлектроники.
вып. 5, с . 84-95.
Сер.
его
возмущени
общетехн.»,
1973,
17. nо.Лонников Р. И . , Александров В. В. Некоторые методы
выделения информативных параметров и их применение в адап
тивных системах.- В кн . : Теория
систем. Алма-Ата, Изд-во Каз. ПИ,
и
применение
адаптивных
1971.
18. nолонников Р. И . , Александров В . В . Об одном спосо
бе решения задач опознания объе ктов . - «Из вестия АН СССР.
Сер. Техническая кибернетика», 1967, No 1, · с . 92-102.
19. nолонников Р. И., Александров В. В. Обучаемые клас
сификаторы и устройства опознавания, использующИе симплекс
ные коды. - «Вопросы радиоэлектроники. Сер . общетехн.», 1971,
вып . 19, с. 56-66.
.
20. nолонников Р. И . , Александров В. В. Обучаемый распоз
нающий автомат на основе адаптивных матричных структур.
В кн . : Технические средства для адаптивной переработки инфор
мации и аналоговые запомин а ющие устройства .
Труды ин-та
электронных управляющих машин . М" «Наука», 1969, с . 35,
21. nолонников Р. И" Трофимов Е. И. Применение методов
rеории чувствитель~ости при разработке устройств классифика
ции, выполненных на основе бескорпусных
оптоэлектронных
элементов . - В · кн .:
Чувствительность
систем
управления.
Труды Всесоюзной школы-семинара по · теории чувствительности
систем управления и ее применению. Т. 2. Владивосток , ДВНЦ
АН СССР, 1975, с. 204-209.
22. Романов В. А., Селяран В. А. Идентификация динами
ческих характеристик многомерЯы х объектов с помощью орто
гональных разложений · Уолша.- «Автоматик а и телемеханика»,
1974, No 11 , с . 173-178.
23. Смолов В. Б., Фомичев В. С. Аналогс 'цифровые и цифроаналоговые
нелинейные
вычислительные устройства.
Л.,
«Энергия», 1974. 264 с.
134
·
1•
2~ . Уинтц П. А . Коднр о омше
111ю 1 Jр 11 :юна 11ий. - В кн . : Об р а ботка
1lBM. М . , « Мир» , 1973, с. 98- 110.
25.
~()()
"
Хсммнн r
Р.
2П . Л11drewJ Н.
изображений посредством
изобр ажений при помощи
ЧнсJ1 ш1ые методы. М ., «Наука», 1972,
С ., Caspari К. Z. А Geпeralized techпique
В.
[01 Sp •·t1·<1 J Aпalysis. !Е ЕЕ !1·а пs. Comput., vol. С-19, N 1, 1970,
р . /() 25.
27. Corri11gton М. s·. So llltioп of Differeпtioпal апd Iпtegral
Е ч1111li о п. \Vith Walsh Fuпc tioпs. IEEE Iraпs оп circuit theory,
vol. 1. 20, N 5, 1973, р. 470- 476.
2Н. Good J, Т. The iпt rac tioп algorithm апd practical Fourl ' Г Лш1l ys is. Т . Roy Statigtica l Sos (Lопdоп) vol. В 20, 1959,
р . ЗG I .
29. Kalman R. New Methods апd Results in Li neare Precll 11 011 а пd Fie lteriп g Tl1eory . . Res. Tпst. Advaпce d Studieпs.
f3 11lll111orc. Md. Tech. R р., 1961, р. 1-61.
30. Roblпsoп G. S. Logical Coпvolutioп а пd discrete Walsh
п п сl 1: urier power Spectra. !ЕЕЕ Tra пs. Оп Audio апd Electroa 11sli s, vol. AU-20 , N 4, 1972, Р - 271 - 280.
3 1. Tzafestas S. G. Оп Optimum distribllted Parameter Fillcri 111( а пd Fixed - lпl e r va l Smootl1ig for covered Noise. IEEE
T 1·11 11s оп Automatic Со пtго l , vol. АС-17, 1972, N 4, р. 448-558.
~
Содержанне
'·
",,
:'i
Стр.
Предисловие
Глава
1.
Представление сигналов в
тогональных
1.
2.
3.
4.
Глава
Глава
2.
3.
•
•
прямоугольных ор-
5
базисах
Дискретные функции Уолша и преобразование Адамара
Факторизация матриц Адамара
Логическая корреляционная функция и кар·
реляционный анализ в базисе Уолша
Ортогональное разложение сигналов в базисе Хаара
Обработка сигналов
кций Уолша
с
использованием
Решение дифференциальных и интегральных
уравнений с применением функuий Уолша
2.
Использование преобразований Адамара при
решении сисi-ем алгебраических уравнений
Синтез структуры фильтров
1.
2.
Цифровая фильтрация сигналов
Методы упрощения математических моделей
3.
4.
Цифровые фильтры в базисе Уолша
Адаптивная цифровая фильтрация в базисе
Хаара
...
Анализ нелинейных систем в базисе Уолша
цнфровых фильтров
Распознавание сигналов на основ~
1.
2.
3.
34
39
51
55
55
62
82
90
98
106
преобразо- .
ваний Адамара
119
Оптимальные равноудаленные сигналы
Алгоритм распознавания сигналов
Группщюй метод обучения при распознава
119
нии -
Список
17
39
1.
ными .параметрами
4.
5
9
фун·
5.
6. Фильтр Калмана в системах с распределенГлава
литературы
~ч
3
122
128
133
/
1
Реаольд Иванович Полонников, канд. техн. наук
Dсеоолод Иванович Костюк, д-р техн . наук
Валерий Евгеньевич Краскеви•1, канд. техн . наук
1
Матричные методы обработки сигвалоn
Редактор издательства Л. О. Полянская
Оформление художников В. А. Потиевского,
А. А . Шурховецкого
Художественные редакторы Е. А . Ильницкий,
В. С. Шапошников
Технический редактор Л. И. Л евочкин.а
Корректор Г. Г. Бондарчук
ИБ №
441
Сдано в набор 22. 11. 1976 г. Подписано в печать 25. 03.
1977 г. Формат 70Х100 1/". Бумага тнпогр. No 3. Усл. печ.
л . 5,48. Уч.·изд. л. 5,22. Тираж 4500 экз. БФ 02918. Зак.
№
7-1403.
Цена
32
коп.
Издательство «Техника•,
ская,
252601,
!(иев,
1,
ГСП, Пушкин
28.
тп с•1nта 110 с матриц головного предприятия республи1Са 11с коrо производственного объединения сПолиrрафкви·
rn• Госкомиздата УССР, г. !(пев, ул. Довженко, 3 на
1(11 ооскоn фабрике печатной рекламы, Киев, Выборг
С !СОЯ,
84. ·