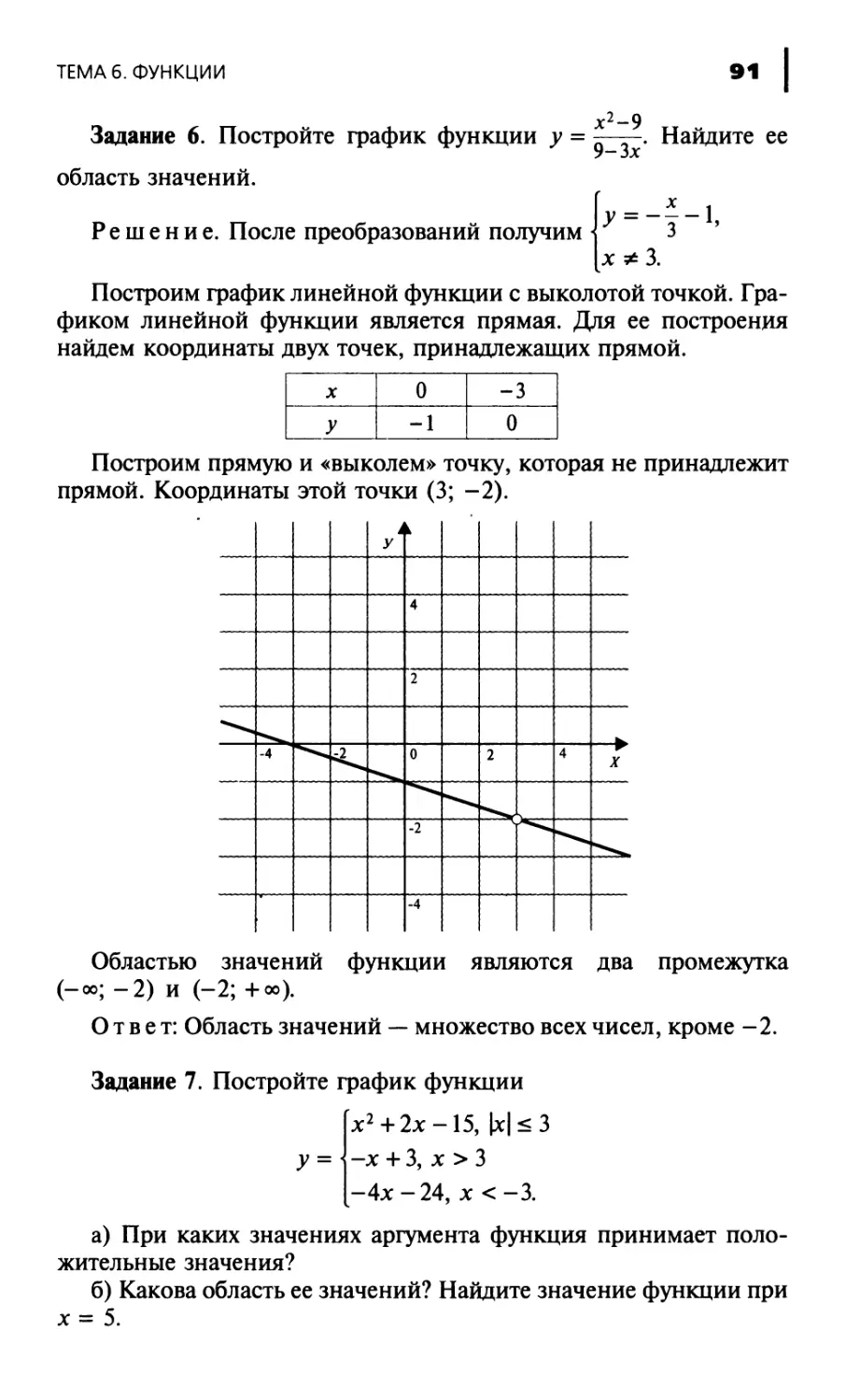
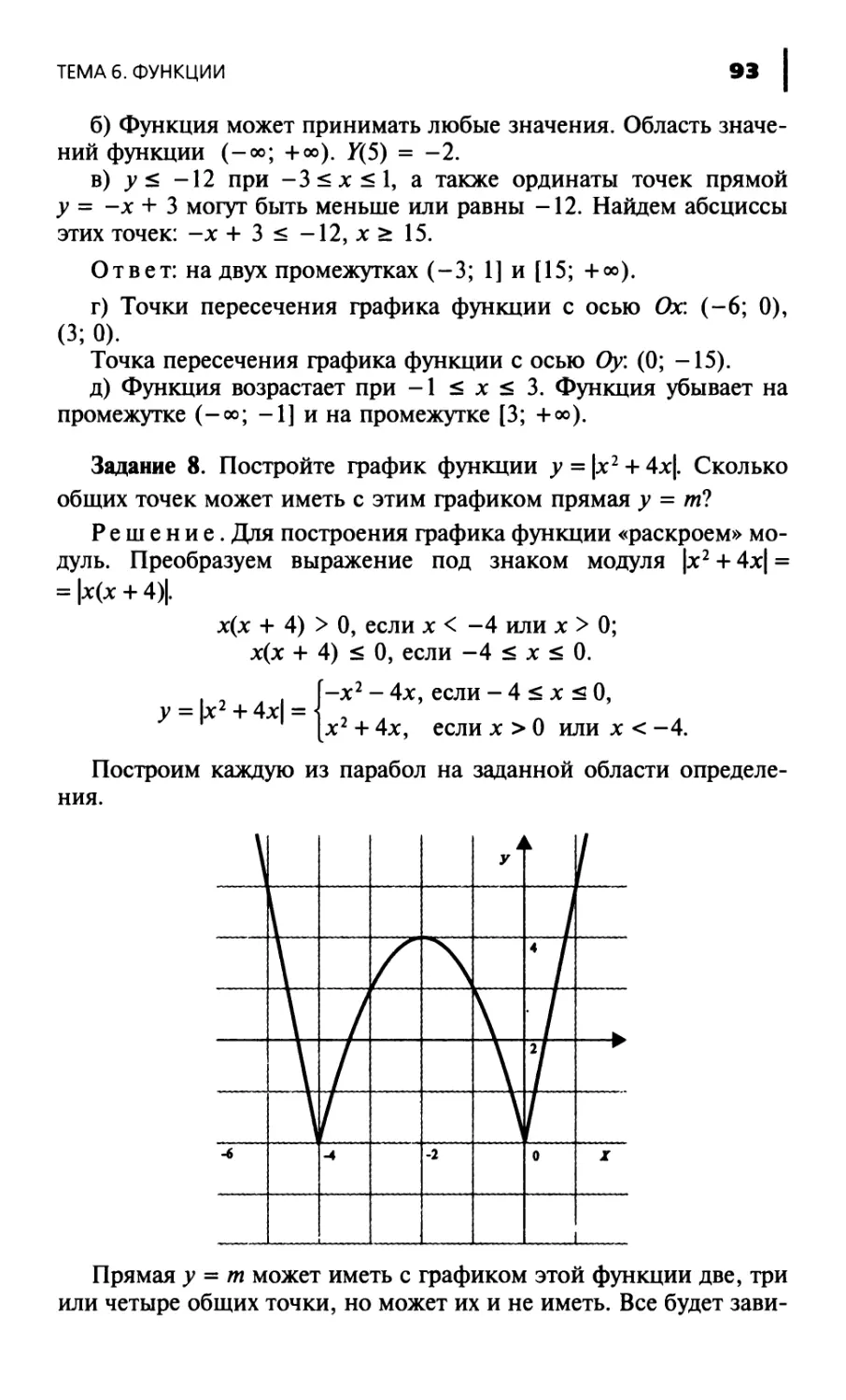
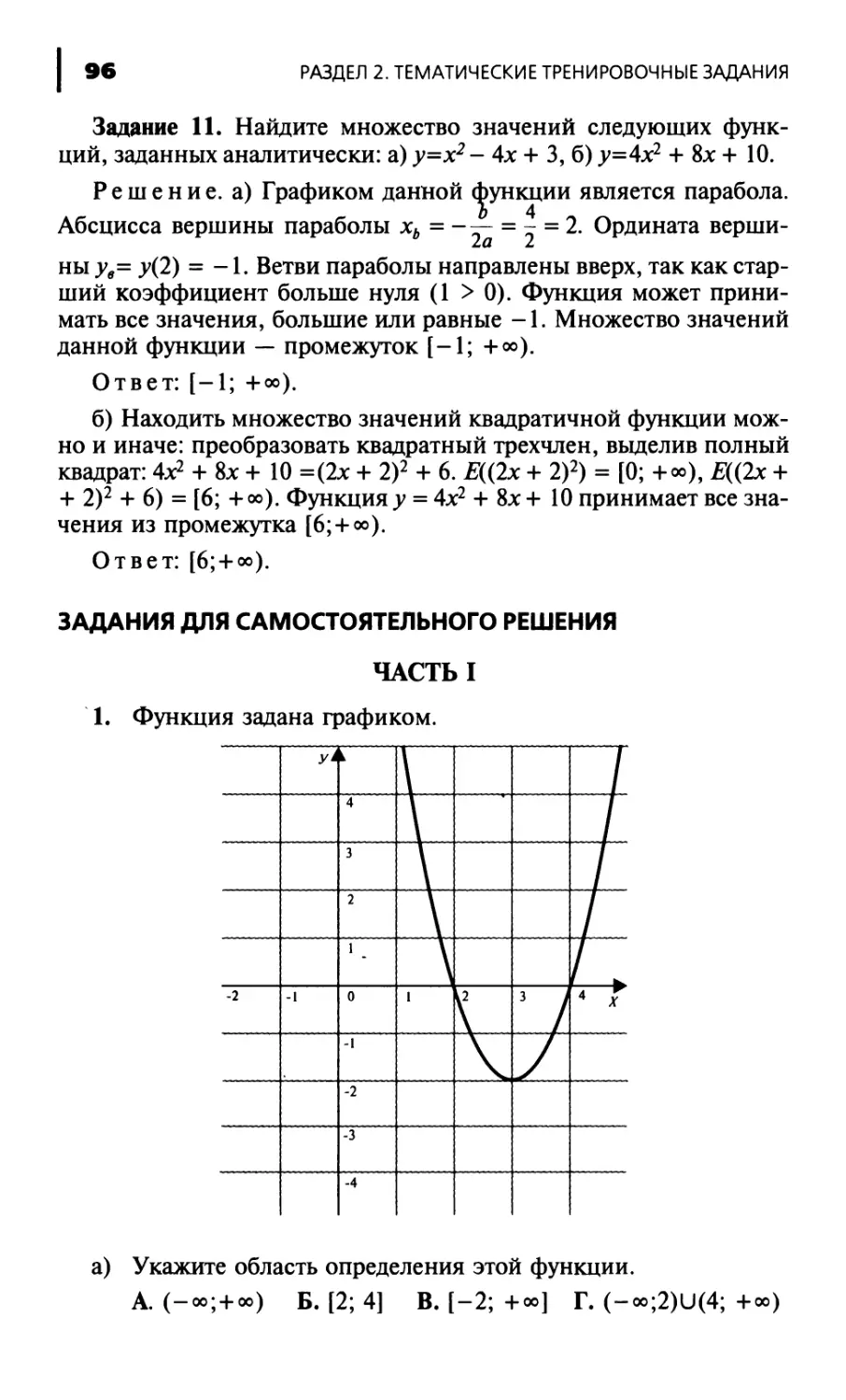
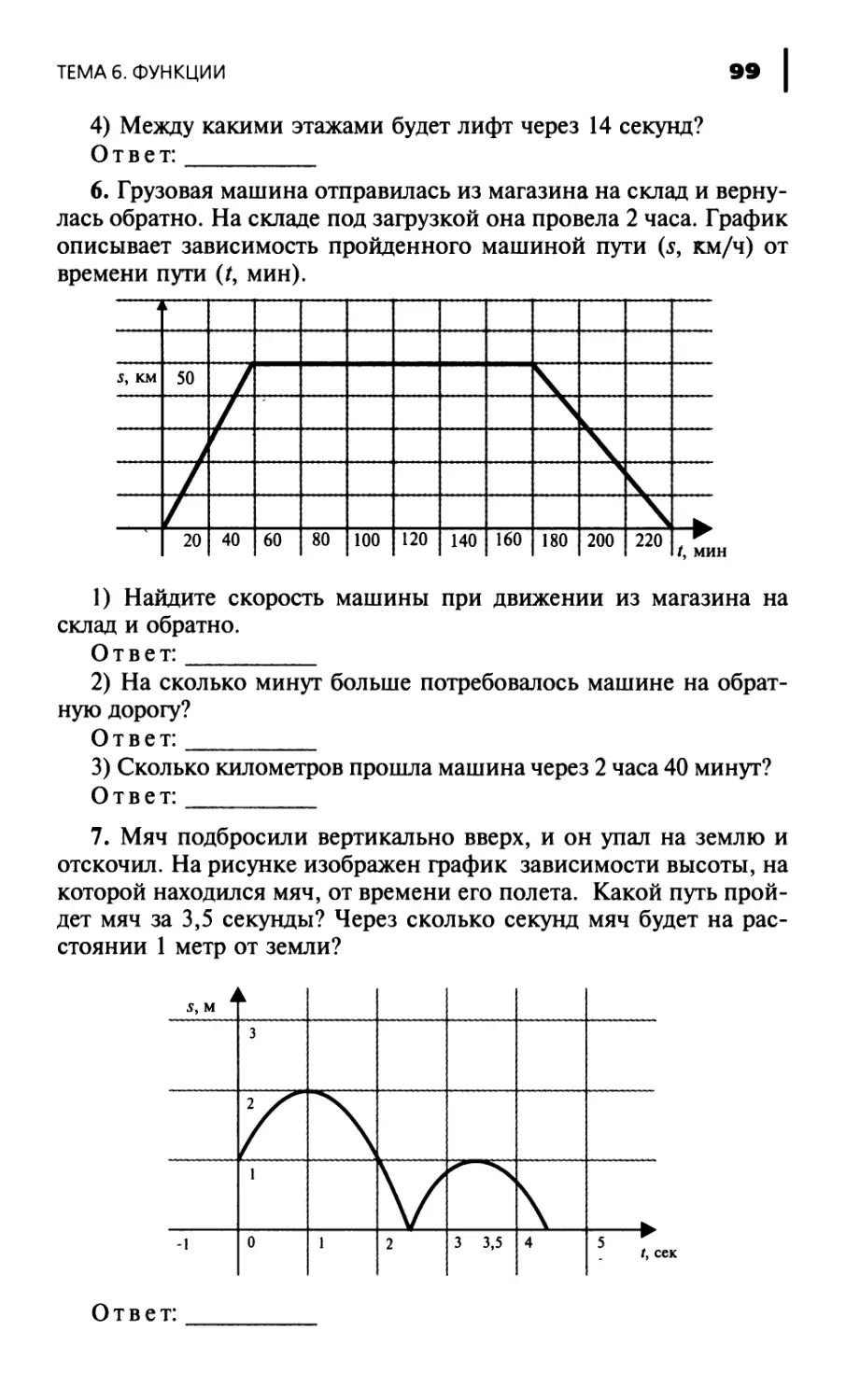
Author: Кочагина М.Н. Корчагин В.В.
Tags: общее школьное образование общеобразовательная школа математика учебные пособия и учебники по математике подготовка к экзаменам пособие для учителей
ISBN: 978-5-699-37597-4
Year: 2009
Text
УЧИТЕЛЯ
М. Н. Кочагина
В. В. Кочагин
гид
ПО МАТЕМАТИКЕ
Подготовка учащихся
к государственной
итоговой аттестации
9 класс
класс ДЛЯ УЧИТЕЛЯ
М. Н. Кочагина
В. В. Кочагин
гид
ПО МАТЕМАТИКЕ
9 класс
Подготовка учащихся
к государственной
итоговой аттестации
эксмо
МОСКВА
2009
УДК 373.167.1:51*09
ББК 22.1я721
К 55
Кочагина М. Н.
К 55 ГИА по математике : 9 класс : Подготовка учащихся к итоговой
аттестации / М. Н. Кочагина, В. В. Кочагин. — М. : Эксмо,
2009. — 192 с. — (Мастер-класс для учителя).
ISBN 978-5-699-37597-4
Пособие адресовано учителям математики — для подготовки выпускников 9-го
класса к государственной итоговой аттестации.
В книге подробно рассказано об особенностях структуры и содержания этого
нового вида итоговой аттестации выпускников основной школы.
В пособии представлены все учебные темы, которые входят в экзамен. По каждой
теме даются:
♦ основной теоретический материал;
♦ задания для активного обучения (с комментариями, решениями, ответами);
♦ задания для самостоятельного решения;
♦ указания и ответы ко всем заданиям.
Задания для самостоятельного решения полностью соответствуют ГИА по
математике.
УДК 373.167.1:51*09
ББК22.1я721
© Кочагина М.Н., Кочагин В.В., 2009
ISBN 978-^5-699-37597-4 © ООО «Издательство «Эксмо», 2009
СОДЕРЖАНИЕ
Введение 5
РАЗДЕЛ 1. «МАЛОЕ ЕГЭ» ПО МАТЕМАТИКЕ
ДЛЯ УЧАЩИХСЯ 9-х КЛАССОВ: ОСОБЕННОСТИ
СТРУКТУРЫ И СОДЕРЖАНИЯ 6
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Тема 1. Числа и выражения. Преобразование выражений 10
Теоретические сведения 10
Задания для активного обучения
(с комментариями, решениями, ответами) 12
Задания для самостоятельного решения 21
Тема 2. Уравнения 27
Теоретические сведения 27
Задания для активного обучения
(с комментариями, решениями, ответами) 29
Задания для самостоятельного решения 38
Тема 3. Системы уравнений 41
Теоретические сведения 42
Задания для активного обучения
(с комментариями, решениями, ответами) 42
Задания для самостоятельного решения 48
Тема 4. Неравенства 55
Теоретические сведения 55
Задания для активного обучения
(с комментариями, решениями, ответами) 55
Задания для самостоятельного решения 63
Тема 5. Координаты и графики 67
Теоретические сведения 67
Задания для активного обучения
(с комментариями, решениями, ответами) 70
Задания для самостоятельного решения 75
4
СОДЕРЖАНИЕ
Тема 6. Функции 82
Теоретические сведения 83
Задания для активного обучения
(с комментариями, решениями, ответами) 85
Задания для самостоятельного решения 96
Тема 7. Арифметическая и геометрическая прогрессии 102
Теоретические сведения 103
Задания для активного обучения
(с комментариями, решениями, ответами) 103
Задания для самостоятельной работы ПО
Тема 8. Текстовые задачи 113
Задания для активного обучения
(с комментариями, решениями, ответами) 114
Задания для самостоятельного решения 123
Тема 9. Уравнения и неравенства с модулем 130
Теоретические сведения 130
Задания для активного обучения
(с комментариями, решениями, ответами) 131
Задания для самостоятельного решения 141
Тема 10. Уравнения и неравенства с параметром 144
Теоретические сведения 144
Задания для активного обучения
(с комментариями, решениями, ответами) 144
Задания для самостоятельного решения 154
РАЗДЕЛ 3. УКАЗАНИЯ 158
РАЗДЕЛ 4. ОТВЕТЫ 182
ВВЕДЕНИЕ
Итоговый письменный экзамен по математике сдают все
учащиеся 9-х классов. В последнее время в России появилась новая
форма организации и проведения итоговой аттестации за курс
основной школы: малое ЕГЭ.
Особенности такого экзамена:
♦ состоит из двух частей;
♦ на выполнение каждой части дается ограниченное
количество времени;
♦ первая часть экзаменационной работы содержит задания в
тестовой форме;
♦ вторая часть - в традиционной форме;
♦ оценивание работы осуществляется отметкой и рейтингом.
Структура экзаменационной работы и организация
проведения экзамена отличаются от традиционной системы аттестации,
поэтому и подготовка к экзамену должна быть другой.
Эта книга адресована учителям математики, с ее помощью вы
сможете подготовить учащихся 9-х классов к успешной сдаче
этого экзамена.
В данном пособии представлены все темы, которые входят в
экзамен. По каждой теме даются:
♦ основной теоретический материал;
♦ задания для активного обучения (с комментариями,
решениями, ответами);
♦ задания для самостоятельного решения;
♦ указания и ответы ко всем заданиям.
Задания для самостоятельного решения в данном пособии
полностью соответствуют уровню заданий обоих частей «малого
ЕГЭ».
Надеемся, что данное пособие поможет девятиклассникам
систематизировать свои знания по математике, узнать
особенности заданий, предлагающихся на экзамене по математике, и
научиться их выполнять.
Авторы выражают благодарность учащимся гимназии № 1534
г. Москвы и студентам математического факультета Московского
городского педагогического университета за неоценимую помощь
при подготовке данного пособия.
РАЗДЕЛ 1
НОВАЯ ФОРМА ИТОГОВОЙ АТТЕСТАЦИИ
ПО МАТЕМАТИКЕ ДЛЯ УЧАЩИХСЯ 9-х КЛАССОВ:
ОСОБЕННОСТИ СТРУКТУРЫ И СОДЕРЖАНИЯ
С 2005 года письменный экзамен по алгебре в 9-м классе в ряде
регионов России, участвующих в эксперименте Министерства
образования и науки РФ, проходит в новой форме. Все изменения в
содержании и формах проведения экзамена связаны с
необходимостью предъявления общих требований к уровню подготовки
учащихся по математике и независимой процедуры оценки
учебных достижений учащихся. Кроме того, в связи с введением
профильного обучения в 10-11-х классах отбор учащихся в
профильные классы может осуществляться по результатам экзамена без
дополнительных испытаний.
Рассмотрим основные изменения в структуре
экзаменационной работы по математике, организации ее проведения, ее
оценивании и в методике подготовки к этому экзамену.
Структура работы. Текст экзаменационной работы печатается
на индивидуальном бланке для каждого ученика. Предусмотрено
4 варианта работы для класса. Экзаменационная работа состоит
из двух частей.
Первая часть содержит 16 заданий в тестовой форме. Учащиеся
должны фиксировать ответы, полученные при решении заданий,
в бланке с текстов работы. В этой части работы предлагаются
задания трех типов:
— задания, в которых требуется выбрать из четырех
предложенных ответов один верный;
— задания с кратким ответом, в которых требуется записать
только ответ;
— задания на сопоставление, в которых требуется соединить
пары объектов некоторыми линиями.
Приведем примеры заданий каждого типа.
1. Запишите 0,00019 в стандартном виде.
А. 0,019 • 10"2 Б. 0,19 • 10"3 В. 1,9 • 10"4 Г. 19 • 10"5
РАЗДЕЛ 1
2. Найдите значение выражения ^— при т = -л/7.
Ответ:
3. Соотнесите дроби, которые выражают доли некоторой
величины, и соответствующие им проценты.
1. 4% 2. 50% 3. 20% 4. 25%
Вторая часть содержит 5 более сложных заданий, требующих
записи хода решения. Уровень сложности заданий определяется
баллом, который можно получить при правильном решении
задания, — 2, 4 или 6 баллов. Этот балл проставляется рядом с
формулировкой самого задания. При выполнении заданий второй части
нужно применять нестандартные приемы, уметь грамотно запи^
сывать решение, обосновывать свои рассуждения. Оформлять
решения заданий второй части нужно на отдельных листах.
Время на выполнение работы. На выполнение всей работы
отводится 4 часа, но выполнять разные части работы предлагается в
разное время. Тексты первой и второй частей работы выдаются в
начале экзамена. Время на выполнение первой части работы
ограничено и составляет 1 час. После этого первая часть работы
сдается для проверки. Оставшееся время отведено для выполнения
второй части работы (к выполнению второй части работы можно
приступить раньше, если ученик быстрее справился с заданиями
первой части).
Содержание, проверяемое экзаменационными заданиями.
Экзаменационные задания проверяют основные блоки содержания:
числа, буквенные выражения, преобразования выражений,
уравнения и текстовые задачи, неравенства, последовательности и
прогрессии, графики и функции.
Система оценивания заданий. По результатам выполнения
работы выставляются две оценки: отметка «2», «3», «4» или «5» и
рейтинг — сумма баллов за верно выполненные задания первой и
второй частей.
Оценка «2» выставляется, если учащийся дал менее восьми
верных ответов.
За каждое правильно решенное задание первой части
начисляется 0,5 балла. За каждое правильно решенное задание второй
части начисляется то количество баллов, которое указано
непосредственно рядом с заданием. Для подсчета рейтинга учащегося
нужно сложить количество баллов за первую и вторую части
работы. Например, ученик правильно решил 9 заданий первой части,
8 РАЗДЕЛ 1
поэтому за эту часть он получил 9 х 0,5 = 4,5 балла. Из второй
части этот же ученик решил задание на 2 балла и на 4 балла,
поэтому за вторую часть он получил 2 + 4 = 6 баллов. Рейтинг этого
ученика 4,5 + 6 = 10,5 баллов. Округляем с избытком, получаем,
что рейтинг ученика — 11 баллов. Как узнать, какую оценку
получил ученик на экзамене? Для этого посмотрим на таблицу
перевода рейтинга в оценку по пятибалльной шкале.
Количество набранных баллов
4-7
8-15
16-30
Оценка
«3»
«4»
«5»
Рейтингу в 11 баллов соответствует оценка «4».
Рекомендации по подготовке к экзамену с помощью пособия.
Наиболее эффективно работу по подготовке к сдаче экзамена по
математике можно построить по следующему плану:
1) Ознакомиться с разделом пособия «О новой форме экзамена
по алгебре для учащихся IX класса» с целью выяснения структуры
экзаменационной работы.
2) Изучив (или повторив) теоретический материал первой
темы основных вопросов содержания «Числа и выражения.
Выражения и их преобразования», разобрать комментарии по решению
типовых заданий этой темы и решить последовательно все
предложенные задания.
3) Сравнить полученные ответы с ответами, приведенными в
конце пособия. Обязательно разобраться с причинами появления
ошибок (если такие будут), при необходимости повторив
теоретический материал или воспользовавшись указаниями к решению
задач, которые предложены в разделе «Указания».
4) Работая так и дальше, последовательно переходить от одной
темы к другой, от одного раздела к другому. Стараться запоминать
основные приемы решения заданий.
5) Решать подготовительные варианты к экзамену или
варианты экзамена по математике прошлых лет, которые можно найти в
литературе, например: Кузнецова Л.В., Суворова СБ., Бунимо-
вич Е.А. и др. Алгебра: Сборник заданий для подготовки к
итоговой аттестации в 9-м классе. — М.: Просвещение, 2006.
В случае ошибок в ответах или незнании способа выполнения
какого-то задания повторить соответствующий теоретический
вопрос по данному пособию и вернуться к решаемому варианту.
РАЗДЕЛ 1 9
Рекомендации по поведению на экзамене. Во время проведения
экзамена старайтесь не волноваться. Чем быстрее у вас получится
сосредоточиться на решении заданий, тем скорее вы вспомните
необходимые математические факты и приемы решения типовых
заданий, а также поймете, что подготовка к экзамену на уроках в
школе и с помощью данного пособия не прошла даром и вы
можете многое решить. Однако все же не стоит забывать о
самопроверке.
И еще, внимательно читайте условие и требование
выполняемого задания. В заданиях первой части работы оценивается
только ответ на поставленный вопрос\
Перед тем как приступить к выполнению заданий,
просмотрите всю первую часть предложенной вам работы. Далее, не теряя
времени, начинайте выполнять одно за другим задания первой
части. Если какое-то задание вызвало затруднения, оставьте его и
переходите к решению следующего. К пропущенным заданиям
можно будет вернуться позже. Рекомендуем проверять себя после
выполнения каждого задания, а также после выполнения заданий
каждой части. Перед тем как сдать первую часть работы, еще раз
проверьте правильность заполнения бланка ответов: не осталось
ли нерешенным какое-то задание. Теперь первую часть работы
можно сдать и переходить к выполнению второй части работы.
Рекомендации по выполнению этой части работы такие же, как и
для первой части, однако здесь еще следует следить за
правильностью оформления решенных заданий. Очевидно, что надо
стараться решить большее количество заданий, причем правильно.
Желаем успешной сдачи экзамена!
РАЗДЕЛ 2
ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Тема 1. Числа и выражения.
Преобразование выражений
При выполнении заданий по преобразованию выражений
используются различные свойства степени и арифметического
квадратного корня. Вычисления и преобразования требуют
повышенной концентрации внимания.
В первой части экзаменационной работы обычно требуется
выполнить одно или два действия для получения результата по
преобразованию целых и дробных выражений. Во второй части —
преобразования многошаговые, причем часто приходится
применять различные методы разложения выражений на множители.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определение. Степенью числа а с натуральным показателем п
называется число, записываемое как а" и определяемое по правилу:
а- а...а, если п > 2;
(f = ' л раз
а, если п = 1.
Определение. Степенью числа а (а * 0) с целым показателем т
называется число, записываемое как сГ и определяемое по правилу:
а а-...-а,если т —натуральное число, т > 2;
v '
т раз
а, если л = 1;
оГ = \
1, если а * 0 и т = 0;
— ,если т = -п,(-п) — целое отрицательное число.
сГ
Выражения 0° и нуль в отрицательной степени не определены.
Определение. Арифметическим квадратным корнем из
неотрицательного числа а называют неотрицательное число 4а, квадрат
которого равен а, т.е. (4а)1 = а, а>0
ТЕМА 1. ЧИСЛА И ВЫРАЖЕНИЯ. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ 11
Свойства арифметического корня квадратного {4а > 0)
(D
(2)
(3)
Для любого действительного числа х\4х* = |х| (4)
Свойства степени с целым показателем
(/и, п — целые числа, я * 0)
оГ • (f = п™*" (5)
оГ'.сГ = оГ~п (6)
(7)
) (8)
(9)
Формулы сокращенного умножения
(12)
(13)
(14)
(15)
(16)
Формула разложения квадратного трехчлена на множители
ах2 + Ьх + с = а{х - хх)(х - х2), (17)
где хх и х2 — корни трехчлена ах2 + Ьх + с.
Некоторые степени чисел 2, 3, 4, 5
2°= 1
3°= 1
4°= 1
5°= 1
2' = 2
З' = 3
41 = 4
51 =5
22 =
З2 =
42 =
52 =
4
9
16
25
23 = 8
З3 = 27
43 = 64
53 = 125
24= 16
34 = 81
44 = 256
54 = 625
25 =
35 =
32
243
2б
З6
= 64
= 729
12 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
ЗАДАНИЯ ДЛЯ АКТИВНОГО ОБУЧЕНИЯ
(С КОММЕНТАРИЯМИ, РЕШЕНИЯМИ, ОТВЕТАМИ)
Стандартный вид числа
Если положительное число а представлено в виде д, • 10я, где
1 < ах < 10, п — целое число, то говорят, что число а записано в
стандартном виде.
Задание 1. Запишите 0,0032 в стандартном виде.
Решение.
Чтобы представить число 0,0032 в стандартном виде (см.
определение стандартного вида числа), нужно перенести запятую в
числе 0,0032 на три знака вправо. Получим число от 1 до 10. Итак:
0,0032 = 3,2 • Ю-3.
Ответ: 3,2-10"3.
Перевод единиц измерения
Задание 2. Перевести 155,4 м; а) в километры; б) в сантиметры;
в) в миллиметры.
Решение.
A) Так как 1 км = 1000 м, то надо решить пропорцию:
1 км = 1000м v _ М55,4 _
у X — inr\t\ — U,l JJ4.
jckm = 155,4 м 100°
Ответ: 0,1554 км или 1,554-10"' км.
Б) Так как 1 м= 100 см, то 155,4 м= 155,4 • 100 см =15540 см.
Ответ: 15540 см или 1,554-104 см.
B) Зная, что в 1 метре 1000 миллиметров, найдем, что в
155,4 метрах 155400 миллиметров.
Ответ: 155400 мм или 1,554-105 мм.
Нахождение значений выражений
■Ч
5~
Задание 3. Найдите значение выражения — - при х = -V5.
Решение.
Подставим значение х в выражение.
/f *3V5 (-V5)3V5
При х = -V5 значение выражения —— равно —— .
(_У5)3У5 - (V5)4 V5^ V625 25
5 5 "5 5 5
Ответ: -5.
ТЕМА 1. ЧИСЛА И ВЫРАЖЕНИЯ ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ 13 I
Задание 4. Найдите значение выражения у!а2 - Ь2 при а = 8;
Ь = -6.
Решение.
Подставим значения аи b в выражение.
При a = S,b = -6
(-б)2 = №^& = V(8-6)(8 + 6) =
Ответ: 2V7.
Выражение переменной из формулы
Задание 5. Выразите из формулы скорости равноускоренного
движения v = v0 + at время t.
Решение.
Выполним два шага: 1) сначала выразим at; 2) затем время /.
\)at = v-vQ;
Ответ: / = ^A
Задания на соотнесения
Задание 6. Каждое из чисел VT5, VT7, V38 соотнесите с
соответствующей ему точкой на координатной прямой.
А В CD
Решение.
Определим, между какими двумя соседними целыми числами
находится каждое из чисел VT5, -ЛУ, V38.
3 < Vl5 < 4, значит, числу VT5 соответствует точка А.
4 < л/ТУ < 5, поэтому числу >/Г7соответствует точка В.
6 < V38 < 7, следовательно, числу V38 соответствует точка D.
Ответ: Vl5 -» A,Jl7 -» 5,V38 -> Z).
Непосредственное применение свойств арифметического
квадратного корня и степени с натуральными
целым показателями
Задание 7. Вычислите: 1-1 - 4"3:4"5 + 2007°.
Решение.
Преобразуем каждое слагаемое.
14 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
(iY2
В выражении - перейдем к степени с натуральным показате-
гг4
В выражении 4~3: 4~5применим свойство (6):
Л-Ъ . Дг-5— Л-Ъ-i-S) — Л2
По определению степени с целым показателем 2007° = 1.
Окончательно имеем: | -1 - 4~3: 4~5 + 2007° = 42 - 42 +1 = 1.
Ответ: 1.
Задание 8. Вычислите: ^81-0,0001.
Решение.
1-й способ
Подкоренное выражение равно 0,0081. Так как 0,092 == 0,0081,
то по определению арифметического квадратного корня д/0,0081 =
= 0,09.
2-й способ
По свойству (1) получим V81-0,0001 = V8T • ДООШ = 9 • 0,01 =
= 0,09.
Ответ: 0,09.
Задание 9. Вычислите: (-3V2)4.
Решение.
По свойству (8) имеем: (-3V2)4 = (-3)4(Л)4 = 81 • 4 = 324.
Ответ: 324.
Задание 10. Вычислите:
Решение.
Чтобы вычислить арифметический корень из смешанного
числа, переведем смешанное число в неправильную дробь и
применим свойство (2).
/Т2Г_ /4-25+21 _ Ш _ VT2T _ 11 -1 _0
V4 25 " V"1T" ~^~Ж~75- l'L
Ответ: 2,1
Если сразу не удается вычислить арифметический квадратный
корень, то часто помогает разложение подкоренного выражения на
множители.
ТЕМА1 ЧИСЛА И ВЫРАЖЕНИЯ ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ 15
Задание 11. Найдите значение выражения л/12-15-20.
Решение.
1-й способ (непосредственно)
Vl2-15-20=V3600 = 60.
2-й способ (с помощью разложения на множители)
V12 -15 • 20 = V2 • 2 • 3 • 3 • 5 • 2 • 10 = V4 • 9 • 100 = 2 • 3 -10 = 60.
Ответ: 60.
Задание 12. Упростите выражение yj(\0x -1)2 - д/(Юх +1)2 и
найдите его значение при:
а) х < -2008; б) -0,007 < х < 0,007; в) х > 2008.
Решение.
Преобразуем исходное выражение.
-1)2 - V(10x +1)2 = |10х -1| - |10х +1|;
а) при х < -2008 \\0х -1| - |10х +1| = -(10х -1) + 10х +1 = 2;
б) при -0,007 < -х < 0,007 |10х -1| - |10х +1| = -(10х -1) -
(
в) при х > 2008 |10х -1| - |10х +1| = 10* -1 - (10* +1) = -2.
Ответ:|10*-1|-|10* + 1|;а)2;б) -20*; в) -2.
Приемы разложения на множители
При преобразовании степенных выражений часто приходится
применять различные приемы разложения на множители. Напомним
основные из них: 1) вынесение общего множителя; 2) группировка;
3) формулы сокращенного умножения; 4) формула разложения
квадратного трехчлена на множители.
Вынесение общего множителя
Задание 13. Упростите выражение * а , если ^ = 7 — иа>0,
у/ао-Зо о о1
Ь>0.
Решение.
Разложим на множители и числитель и знаменатель дроби, а
затем сократим на общий множитель.
а-Ъ4аЬ ()
причем Vfl * Ъ4Ь, а * 9Ь, - * 9.
о
16 РАЗДЕЛ 2 ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
~ а -58 а п a-?>4ab
Таккак - = 7- и - *9, то ^_
Переведем смешанное число в неправильную дробь и
применим свойство (2).
25
9
Ответ: ^, а*9Ь,27-.
Группировка
Задание 14. Упростите выражение ———--— и найдите его
значение при х = у = 2007.
Решение.
В числителе четыре слагаемых. Очень часто при разложении на
множители выражения, содержащего четыре слагаемых,
используют группировку.
ху-х-у + Х = х(у-\)-у + \ = х(у-\)-(у-\) = (у-\)(х-\) =
JC-1 JC-1 JC-1 JC-1 У '
Так как х = 2007 * 1, то при у = 2007 имеем: у -1 = 2006.
Ответ: у-\, х * 1; 2006.
Формулы сокращенного умножения
Для упрощения выражений с помощью формул сокращенного
умножения используют формулы (10) - (16). Чтобы выбрать
соответствующую формулу, следует обратить внимание на показатели
степени одночленов, входящих в выражение.
Задание 15. Упростите выражение -£ -:^—- и найдите его
значение при х = 101.
Решение.
К выражению (х2 - 4) применим формулу разности квадратов,
а к выражению (х3 - 1) — разности кубов.
При х = 101 имеем: (х - 2)(х -1) = 99 • 100 = 9900.
Ответ: (х-2)(х-1), х * 1; 9900.
ТЕМА 1. ЧИСЛА И ВЫРАЖЕНИЯ ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ 17
— 3 1 и—3
Задание 16. Упростите выражение —j—ггт-Ой)"1 и найдите
а 1+Ь '
его значение при а = V20, b = V5.
Решение.
Сначала заменим степени с отрицательными целыми
показателями на.степени с натуральными показателями, т.е.
Теперь избавимся от «двухэтажности» в числителе и в знаменателе
первой дроби, т.е.
1 1
^У 1 (ЬЧа*)аЬ 1
=
I+I ab a?bl(b+a) ab'
а Ь
Обратим внимание на показатели степеней. Применим в
числителе первой дроби формулу суммы кубов и сократим и
числитель и знаменатель на общий множитель: ab(a + Ь\ Тогда
выражение будет иметь вид
(b3+a3)ab j__ a2-ab+b2 _ J_
ab~~~^b2 Vtf ° *
Приведем дроби к общему знаменателю:
a2-2ab+b2 = (a-b)2
a2b2 " аЧ1 '
Итак, при а = V20, b = V5 значение исходного выражения равно
(V20-V5)2 (2V5-V5)2
(V20)W
Ответ: a2l2 , a * -b\ 0,05.
= 0,05.
При преобразовании дробных выражений полезно разложить на
множители числитель и знаменатель каждой дроби, затем сократить
дробь. И далее приводить к общему знаменателю.
г* +т лт Q~~\6b G\a — \J-ris\ и
Задание 17. Упростите выражение -=—-= ^— и
найдите его значение при а = 4 и b = 0,04.
18 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Решение.
„ - a-\6b {Ja-A4b){Ja+A4b) г л Гп л П
Первая дробь: -= j= = -= = = ыа + 4v0, а * 4vо,
JaЩЬ JaЩЬ
Вторая дробь:
д_16, = у
а * 16*.
Тогда исходное выражение имеет вид:
a-\6b ayfa-64lhfb г- . пг a+4y[ab+\6b
Т^ЧЛ a-\6b "Vfl
При а = 4 и b = 0,04 имеем
_ 4-ДТб _ 1,6 _ 4
" 2+4^2 " 2,8 " 7"
. 4
; г
Разложение квадратного трехчлена на множители
Задание 18. Какое выражение надо подставить вместо
многоточия, чтобы было верным равенство Зх2 -2х -1 = 3(х -1)(...)?
Решение.
Чтобы разложить на множители квадратный трехчлен
Зх2 - 2х -1, решим уравнение Зх2 - 2х -1 = 0 (см. формулу
разложения квадратного трехчлена на множители (17).
Уравнение имеет корни 1 и - -, поэтому
Ответ: х + -.
При преобразовании-иррациональных выражений иногда удобно
воспользоваться заменой Vx =а. Это позволяет свести
преобразование выражений к действиям с многочленами.
Задание 19. Упростите выражение —1=—— и найдите его зна-
Vjci
чение при х = (l2^ +1 ^-0,8-зМ-12.
Решение.
Пусть Vx = а, тогда исходное выражение будет иметь вид:
2 тт _
. Чтобы разложить на множители числитель, решим урав-
ТЕМА 1. ЧИСЛА И ВЫРАЖЕНИЯ. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ 19
нение а2 - 1а + 6 = 0 и применим формулу разложения квадратного
трехчлена на множители (17).
а2-7а+6 (а-\)(а-в) ,
—- = - '\—- = а-6, а*\.
а-\ а-\
Вернемся к переменной х.
Осталось найти значение выражения 4х - 6.
Найдем значение х из выражения 112 —hi — — 0,8 — 3 — 1-12.
Обратите внимание, что можно рационально вычислить значение чи-
4
елового выражения в скобке, если заметить, что 12- = 12,8.
0,3)12 fl2,80,8f3l
12 3) { V 12 п
Итак, при х = 121 4х -6 = 5.
Ответ: 4х -6, х * 1; 5.
Покажем применение всех основных приемов разложения на
множители при решении следующего задания.
Задание 20. Упростите выражение
25jc3-10x2+jc
5х2-16х+3 *х3-Зх2-9х+27
и найдите значение выражения при х = 3,1.
Решение.
25х3 — 10х2+х
Рассмотрим первую дробь 2 ——.
В числителе все три слагаемых имеют общий множитель (х).
После вынесение общего множителя получим выражение
25х2 - 10х +1, которое представляет собой квадрат разности, т.е.
2
В знаменателе используем формулу разложения на множители
квадратного трехчлена, т.е. 5х2 - 16х + 3 = 5(х - х])(х - х2), где хх и
х2 — корни уравнения 5х2 - \6х + 3 = 0.
Окончательно имеем:
25jc3-10jc2+jc jc(5jc-1)2
5jc2-16jc+3 5(jc-3)(jc-0,2)'
Рассмотрим выражения (5х -1) и (х - 0,2). Если первое
выражение продолжим раскладывать на множители, то получим
• 20 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
5х -1 = = 5(х - 0,2). Учитывая это, преобразуем знаменатель:
5(х -3)(х -0,2) = (х -3)(5х -1). Итак, после сокращения на
общий множитель, дробь будет иметь вид:
yiSy — 1i y^Sy—1^
5(x-3)(x-0,2) = x-3 ' X * U'
Рассмотрим вторую дробь
x3-3x2-9jc+27*
В числителе вынесем общий множитель (х).
В знаменателе обратим внимание на число слагаемых: их
четыре. Используем группировку, т.е.
= (х2-9)(х-3).
В первом множителе применим формулу разности квадратов:
(х2 - 9)(х - 3) = (х - 3)(х + 3)(х - 3) = (* - 3)2(х + 3).
После сокращения на общий множитель вторая дробь будет иметь
вид:
jc3+3x2-9x+27 (х-3)2'
Вернемся к исходному выражению:
25jc3-10x2+jc jc2+3x
5x2-16jc+3 'jc3+3x2-9jc+27 jc-3 (x-3)2 V
x ^±3, x *0,2.
При x = 3,1 значение исходного выражения равно
(5-3,1-1)(3,1-3) = 1,45.
Ответ: (5х - 1)(х -3), х * ±3, х * 0,2; 1,45.
Нетрадиционные задания
Для вычисления значения выражения вида V^ + Vb ±V<3-Vb,
a > 0, b > 0 рассматривают квадрат этого выражения.
Задание 21. Выражение V7-V24 - V7 + V24 является целым
числом. Найдите его.
Решение.
Пусть А = V7-V24 - V7 + V24. Найдем А2.
= 14-2^/(7 + 724X7-л/24) =14-2725 = 4.
ТЕМА 1. ЧИСЛА И ВЫРАЖЕНИЯ. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ
Итак, А2 = 4.
Так как А < 0 (почему?), то А = -V4 = -2.
Ответ: -2.
21
При преобразовании дробных выражений, содержащих
арифметические квадратные корни, иногда умножение на выражение,
сопряженное знаменателю, позволяет упростить вид всего выражения.
Задание 22. Вычислите , - + V35.
V6+V35
Решен
V6+V55
Ответ:
ие.
6.
V6+V35-
л/б-л/35 /r^ _ 6-V35
л/б-л/35 1
При преобразовании выражений, содержащих корни, можно ис-
| пользовать введение новой переменной. Это позволяет сделать
выражение компактным.
Задание 23. Найдите значение выражения
л/х - 4Vx - 4 - V* + 4Vx - 4 при х =; 2008.
Решение.
Пусть л = л/Т- 4, тогда х = л2 + 4. Исходное выражение имеет
вид
Применим свойство (4)
При х = 2008 имеем |V2008-4 - 2| - |V2008 - 4 + 2| = -4.
Ответ: -4.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЧАСТЫ
1. Запишите 0,00019 в стандартном виде.
А. 0,019 • Ю-2 Б. 0,19 • Ю-3 В. 1,9 • 10"4 Г. 19 • 10"5
2. Расстояние от Земли до Солнца равно 1,5 -1011 метров.
Выразите это расстояние в километрах.
А.1,5-1010 Б. 1,5-109 В. 1,5 108 Г. 1,5-107
22 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
3. Расстояние от Земли до Солнца равно 1,5-10" метров.
Выразите это расстояние в миллиметрах.
А. 1,5-1015; Б. 1,5 1014; В. 1,5-1013; Г. 1,5-1012.
4. Найдите значение выражения ^—— при т = -V7.
Ответ:
5. Найдите значение выражения л/д2 - 4Ь2 при а = 10; Ъ = -4.
Ответ:
fflV2
6. Из формулы кинетической энергии Ек = -у- выразите
скорость.
A. v = ^ Б. v = #*- В. v = ,Щ Г. v =
2 V
2/и
7. Из формулы мощности автомобиля Р = —А где Р —
16
мощность в лошадиных силах, D — диаметр цилиндра, п — число
цилиндров, выразите п.
А. л = -^ E.n = l6PD2 В.п = -Г 1.я
8. Одна из точек, отмеченных на координатной прямой,
соответствует числу V34 . Какая это точка?
А В С D
1 •+■*—•+• ►
А. А Б. В В. С Г. D
9. Соотнесите дроби, которые выражают доли некоторой
величины, и соответствующие им проценты.
А 1 Б 1 В 1 Г *
А' 5 Б' 4 В' 2 Г' 25
1. 4% 2. 50% 3. 20% 4. 25%
10. Найдите разность выражений т—тт ~;—л-
(д-2) (2-д)
А. — Б. — В. -^- Г.
2-е а-2 (а-2)2 а+2
11. Выполните умножение -щ^ъ~г ' ~^Г2~-
А
Б ___ в г ___
2Ь-2с # ЗЬ+Зс2 ' 2Ьс-2с2 ' ~2Ьс-6с2
12. Найдите значение выражения — ^— - —- -щ.
А' ~5~ Б' ТО В- " 16 Г' °
ТЕМА 1. ЧИСЛА И ВЫРАЖЕНИЯ. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ 23
сгх+Ь-х
13. Упростите выражение
а+Ь
А. -2 Б. аЬ В.а + b Г. -L
ab
14. Вычислите: V54 • V6.
Ответ:
15. Вычислите: (-3J-) .
Ответ:
16. Вычислите: —=-.
V2
Ответ:
17. Сократите дробь —.
А. а2 - ЪаЬ + 9Ь2 В. а2 - ЪаЬ + Ь2
Б. я2 + Зяй + W Г. я2 + dab + й2
18. Сократите дробь
s/fl-9VZ>
X2X5
19. Представьте в виде степени с целым показателем ^.
А. х2 Б. X"2 В. х1 Г. х
20. Упростите выражение * у и найдите его значение при
х = 100 и у = 299.
Ответ:
21. Вычислите: ^) +5"3:5-4 - 2005.
Ответ:
(2-3)4
22. Вычислите: ' .
Ответ:
2-2-54-10-5
23. Вычислите: 2.3.5з.10-4-
Ответ:
24. Вычислите: VV730 -1 • VV730 +1.
Ответ:
24 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
25. Упростите выражение \[12а + V48fl - >/147д.
Ответ:
26. Представьте в виде степени с целым показателем х2: х~3.
Ответ:
27. Представьте в виде степени с целым показателем (/и3)4.
Ответ:
ЧАСТЬ II
Задания на 2 балла
28. Вычислите: (2Л)4+ (-2V5)2.
29. Вычислите: V742 - 702 +(Vl5 - 5)(5 + Vl5).
30. Вычислите: V529 -2 • 23• 14 +196 + VU2 -1,22.
31. Расположите в порядке возрастания 5л/5; Зл/7; 3-ЛТ; -4V5;
-Зл/Ш.
32. Вычислите: ^(5-л/ГТ)
33. Сократите дробь
2 +
,,. л/ jc2+10jc+25 jc2-25
34. Упростите выражение —^—:
з
,,- л, jc3+2jc2-jc-2 jc+3
35. Упростите выражение ^——-.
VJC2 V
36. Упростите выражение -—-у - ;—^т и наВДите его
значение при х = 11, у = 0,1.
37. Упростите выражение -—-т + ^ и найдите его значе-
(/и-1) (1-/и)
ние при т = 0,75.
38. Упростите выражение - + 2007 + 3".
39. Докажите, что значение выражения не зависит от допусти-
„ х2—36 jc-6 o -
мых значении переменной -^——-: -т—- - 8х - х2.
v jc2-2jc+4 jc3+8
40. Упростите выражение —^=+3 (9-6Vx +x) и найдите его
\3-Vjc Г
значение при х = 169.
ТЕМА 1. ЧИСЛА И ВЫРАЖЕНИЯ. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ 25
Задания на 4 балла
41. Значением выражения —j= 1= + V3 + VH) является целое
3vlO—10V3
число. Найдите его.
/о //'о
42. Значением выражения , + V63 + 2007 является целое
V8+V63
число. Найдите его.
43. Выражение v6 + 2V5 - V5 является целым числом. Найдите
его.
44. Упростите до целого числа выражение V3 - V4 + 2V5.
45. Выражение V3 - V8 - V2 является целым числом. Найдите
его.
46. Упростите до целого числа выражение 4 - 3V2 + V34 - 24V2.
ап х/ /V-27 9jc \(л 6 \
47. Упростите выражение 2 : 11 I.
Ао л, 5 / jc-4 16 \
48. Упростите выражение — -— -у-—— ——^ .
к 1+4JC1 \jc2+4jc 16—л:2 /
49. Упростите выражение т= + -j=— • ^ ^ - ТУ и
найдите его значение при у = 6,25.
50. Найдите значение выражения
V2
- 4(Vx + 2) + 4)2при х = 2007.
51. Докажите, что значение выражения
х2-2(т+а)х+4та х2-4Ь2 (х+2а)2
x2+2(a+b)x+4ab ' х2-4а2 ' х-2т
не зависит от значений переменной а.
52. Докажите, что значение выражения
х2-3(т+п)х+9тп х2-9Ь2 (х + Зп)2
x2 + 3(n + b)x+9nb x2-9n2 х-Зт
не зависит от значений переменной п.
53. Найдите значение выражения д/(Зх-12)2 ~v(3x + 12)2 при
х < -2007.
54. Значение выражения 5о(У* -6Vx -9 -у/х + 6Vx -9) при
х = 9,0169 является целым числом. Найдите его.
26
55.
56.
57.
58.
59.
Вычислите:
Вычислите:
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Задания на 6 баллов
17б+175+174+173+172+17+1
17М '
135+134+133+132+13+1
136-1
Упростите выражение
Упростите выражение
п5-\ пъ+\ '
т4-т3+т2-т+\ т2+т+\
Найдите значение дроби
f =0,25.
т3-1 •
хъ-Ах2у+5ху1-уг
если
60.
61.
Упростите до целого числа выражение
V4 + 2V3-V4-2V3.
Упростите до целого числа выражение
(2V6-5) -10V49-20V6.
62. Найдите значение выражения л/19-д + л/10-д, если
63. Найдите значение выражения л/74-д4 -VlO-л4, если
-fl4 =16.
64. Найдите значение выражения л/60-д4 + 4д2, если
/6 +л2 + Vio-л2 = 6.
65. Упростите до целого числа
если 0 < л < 0,2008.
66. Сравните V2005 + V2008 и V2007 + V2006.
л4+4
67. Сократите дробь
а2-2а+2'
68. Найдите значение выражения
а4+ 4
, если известно, что
69. Вычислите:
\_
6
х(732
7Ю24 _ (7512 + 1)(7256 + 1)(7128 + Щ-JM + Ц х
+ 1)(78 + 1)(74 + 1)(72 + 1)(7 + 1).
ТЕМА 2. УРАВНЕНИЯ 27
70. Вычислите:
1 . 6Ю24 _ (6512 + 1)(6256 + 1)(6128
Х(632 + 1)(616 + 1)(68 + 1)(64 + 1)(62 + 1)(6 + 1).
71. Упростите выражение
(jc+10)(jc+20)(jc+30)(jc+40)-10000
2 _
X
jc2+50jc+500
72. Сократите дробь
(jc2 - х + 1)(jc4 - х2 + 1)(х* - jc4 + 1)(jc16 - x8 + 1)(jc32 - jc16 + 1)(jc2 + x +1)
JCM+JC32+1
73. Сократите дробь
Тема 2. Уравнения
Все уравнения школьного курса, изучаемые в курсе алгебры
7-9-х классов, можно разбить на несколько больших групп: 1)
линейные; 2) квадратные и сводимые к ним; 3)
дробно-рациональные; 4) уравнения высших степеней. В первой части
экзаменационной работы требуется решить уравнения без дополнительных
условий. При решении уравнений из второй части работы часто
требуется выполнить алгебраические преобразования выражений,
упрощающие решение уравнения, или решать уравнения с
дополнительными условиями, или использовать специальные приемы
решения уравнений, такие как разложение на множители или
введение новой переменной.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определение. Корнем уравнения с одним неизвестным называют
значение неизвестного, при котором уравнение обращается в
верное равенство.
Определение. Решить уравнение с одним неизвестным — значит
найти все его корни или доказать, что корней нет.
Определение. Линейным уравнением с одним неизвестным х
называют уравнения вида ах = Ь, где х — неизвестное, аи b —
некоторые числа; а называют коэффициентом при переменной, Ь —
свободным членом.
Определение. Квадратным уравнением с одним неизвестным х
называют уравнения вида ах2 + Ьх + с = 0, где х — неизвестное, а, Ъ
и с — некоторые числа (коэффициенты уравнения), причем а * 0.
а называют первым (старшим) коэффициентом, Ъ — вторым
коэффициентом, с — свободным членом.
28 РАЗДЕЛ 2 ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Если в квадратном уравнении хотя бы один из коэффициентов
равен 0 (кроме, конечно, коэффициента при х2), то уравнение
называют неполным квадратным уравнением.
Выражение
D = b2-4ac (1)
называют дискриминантом квадратного уравнения ах2 + Ьх + с = 0.
По дискриминанту квадратного уравнения определяют, сколько
оно имеет корней:
если D > 0, то уравнение имеет два корня;
если D = 0, то уравнение имеет один корень (или два
совпавших корня);
если D < 0, то уравнение не имеет корней.
Формулы корней квадратного уравнения
Корни уравнения ах2 + Ьх + с = 0 находят по формуле
-b±4D
х = -^-. (2)
Корни квадратного уравнения, в котором второй
коэффициент — четное число, можно вычислять по формуле
D
Теорема Виета
Если приведенное квадратное уравнение х2 + рх + q = 0 имеет
корни, то сумма корней этого уравнения равна второму
коэффициенту, взятому с противоположным знаком, а произведение
корней равно свободному члену, т.е. если х, и х2 — корни уравнения
х2 + рх + q = 0, то
к+*> = -/>;
Обратная теорема Виета
Если сумма двух чисел равна второму коэффициенту
приведенного квадратного уравнения, взятому с противоположным
знаком, а их произведение равно свободному члену, то эти числа
являются корнями приведенного квадратного уравнения, т.е., если
выполняются условия
Где, + х2 = -р\
\хх -x2=q,
то *! и х2 — корни уравнения х2 + рх + q = 0.
ТЕМА 2. УРАВНЕНИЯ 29
ЗАДАНИЯ ДЛЯ АКТИВНОГО ОБУЧЕНИЯ
(С КОММЕНТАРИЯМИ, РЕШЕНИЯМИ, ОТВЕТАМИ)
Линейные уравнения
I При решении линейных уравнений слагаемые с неизвестным обыч-
| но переносят в левую часть уравнения, а остальные слагаемые - в
I правую часть. При этом переносе надо изменить знак всех слагаемых
на противоположный.
Задание 1. Решите уравнение 2 - 3(х + 2) = 5 - 2 х.
Решение.
Сначала раскроем скобки.
2-3jc-6 = 5-2x
-х = 9.
Уравнение еще не решено (почему?). Надо найти значение
переменной х, а не (-х).
х = -9.
Ответ: -9.
Задание 2. Найдите корни уравнения ^ + ~ = 3,75.
Решение.
В левой части уравнения — дроби с разными знаменателями.
Приведем их к общему знаменателю.
- + S.3,75
£ = 3,75
Остается разделить и левую и правую часть уравнения на
коэффициент при неизвестном, т.е. на —.
* =3,75: 1
О-7С 12
т = 3,75 • —
При умножении можно либо число 3,75 перевести в
обыкновенную дробь (полезно знать, что 0,75 = - ), либо **исло — пере-
4 5
вести в десятичную (разделив 12 на 5).
15 12
W=ST'T
т =9.
Ответ: 9.
30 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Квадратные уравнения
При решении неполных квадратных уравнений важно понимать, что
уравнение можно решить, и не применяя основную формулу (2)
корней квадратного уравнения.
Задание 3. Каждое уравнение соотнесите с множеством его
корней.
1) 0,5х2 - 2х = 0 2) 0,5х2 -2 = 0 3) 0,5х2 = О
а) 0 б)-2 и 2 в)0и4
Решение.
Решим сначала первое уравнение. Вынесем за скобки общий
множитель.
х(0,5х - 2) = О
х = 0 или 0,5х -2 = 0
х = 0 или х = 2 : 0,5
х = 0 или х = 4
Итак, корнями первого уравнения являются числа 0 и 4.
Решим второе уравнение. Выразим х2, т.е.
х2 = 2 : 0,5
х2 = 4.
Корнями второго уравнения являются числа 2 и -2.
Осталось решить третье уравнение. При решении его тоже
выразим х2.
х2 = 0.
Только число 0 является его корнем.
Остается записать ответ.
Ответ: 1) - в, 2) - б, 3) -а.
Замечание: соотнести данные уравнения с множеством их
корней можно и проще, с помощью следующих рассуждений: первое
уравнение имеет два различных корня — нуль и другое число,
корнями второго уравнение являются два противоположных числа,
корнем третьего уравнения является только число нуль.
Рассмотрим решение квадратных уравнений, в которых ни
один из коэффициентов не равен 0.
Задание 4. Решите уравнение Зх2 - 2х -1 = 0.
Решение.
По основной формуле корней квадратного уравнения (2)
х = —=—. В данном уравнении д = 3, Ъ = -2, с = -1, поэтому
ТЕМА 2. УРАВНЕНИЯ
Имеем:
Ответ: 1;
1
~3*
X
-(-2)±VI6
2-3
_ 2±4
31
Замечание: подсчитаем сумму коэффициентов этого уравнения
3+(-2)+(-1) = 0. И число 1 является корнем этого уравнения.
Это верно и в общем случае, т.е. если мы решаем квадратное
уравнение ах2 + Ьх + с -0и сумма его коэффициентов равна нулю
а + b + с = 0, то один из корней уравнения равен 1.
Задание 5. Решите уравнение -х2 + 0,1 = 0,9х. В ответе укажите
произведение его корней.
Решение.
Перенесем слагаемые в левую часть уравнения.
-х2+0,1-0,9х = 0
х2 + 0,9х-0,1 = 0
Чтобы избавиться от десятичных дробей, умножим обе части
уравнения на 10.
10х2+9х-1=0
/> = 92 - 4 • 10 (-1) = 121
_-9±Vl2l
Х~ 20
х = -1 или х =0,1
Не забудем, что в задании есть дополнительный вопрос.
Произведение корней уравнения равно -0,1.
Ответ: -0,1.
Замечание: на дополнительный вопрос в задании можно было
ответить, даже не находя корней уравнения. Вспомните
формулировку теоремы Виета (3).
После того, как вы убедились в существовании корней (D > 0),
можно просто найти их произведение. Из двух уравнений
х2 + 0,9х - 0,1 =* 0 и Юх2 + 9х -1 = 0 только первое является
приведенным, поэтому теорему Виета применяем к первому уравнению:
32 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Задание 6. Не решая уравнения 2х2 + 2х - 3 = 0, найдите:
а) х, + х2; б) х, • х2; в) — + —; г) х\ + х\\ д) х,2х2 + х,х22;
е) х| + Xj3; ж) х£ + xf, где Xj и Х2 — корни уравнения.
Решение.
Известно, что Xj и х2 — корни квадратного уравнения.
Применим теорему Виета.
а), б) сначала необходимо сделать исходное уравнение
приведенным, т.е. разделить на первый (старший) коэффициент 2.
Имеем: х2 + х-1,5 = 0.
По теореме Виета:
Гх, +х2 = -1,
|х,-х2 = -1,5.
поэтому в пункте а) х, + х2 = -1; а в пункте б) х, • х2 = -1,5.
Чтобы вычислить значения выражений в пунктах в)—ж),
выразим слагаемые в них через х, + х2 и х, • х2.
1 f 1 =ъ+х2= -1 =2
jcj x2 jcj -jc2 -1,5 3'
г) х22 + х,2 = (х, + х2)2 - 2х, • х2 = 1 + 2 • 1,5 = 4.
д) х,2х2 + х,х22 = XjX^x, + х2) = 1,5.
е) х23 + х,3 = (х, + х2)(х2 - х,х2 + х22) = -1 • (4 +1,5) = -5,5.
ж) х24 + х,4 = (х2 + х2)2 - 2(х, • х2)2 = 16 - 2 • 2,25 = 11,5.
Ответ: а) -1; б) -1,5; в) |; г) 4; д) 1,5; е) -5,5; ж) 11,5.
Если в квадратном уравнении коэффициент при х — четный,
можно использовать формулу (4) для нахождения корней
квадратного уравнения с четным вторым коэффициентом.
Задание 7. Решите уравнение х2-32х + 31=0.
Решение.
В уравнении а = 1, Ъ - -32, с - 31.
1-й способ.
Применим формулу для уравнений с четным вторым
коэффициентом (3).
^ = (-16)2 -1-31 = 256-31 = 225
16±V225
■у- —
х = 31 или х = 1
ТЕМА 2. УРАВНЕНИЯ 33 |
2-й способ.
Применим основную формулу (2)
D = (-32)2 - 4 • 31 = 1024 -124 = 900
32±V900
Х = -2Л-
х = 31 или х = 1.
Ответ: 1, 31.
Замечание: В уравнении х2 - 32х + 31=0 сумма коэффициентов
1 + (-32) + 31=0, поэтому 1 является корнем уравнения. А второй
корень можно найти по теореме Виета, так как х, • х2 = 1 • х2 = 31,
тох2 = 31.
Задание 8. Решите уравнение (Зх - 2)(4х - 3) = 0. В ответе
укажите больший корень.
Решение.
В левой части уравнения записано произведение, причем
произведение равно 0.
(Зх-2)(4х-3) = 0
Зх - 2 = 0 или 4х - 3 = 0
2 3
х = - или х = -
3 4
Чтобы выбрать больший корень, можно либо привести дроби к
, uf2 8 3 9 \
одному знаменателю и сравнить числители дробей - = —;- = — ,
\3 12 4 12/
либо перевести обе дроби в десятичные дроби - = 0,666... = 0,(6),
Ответ: 0,75.
В курсе алгебры рассматривают также различные уравнения,
сводимые к решению квадратных уравнений.
Дробно-рациональные уравнения
Решениедробно-рациональных уравнений основано на следующем
утверждении: дробь -равна нулю тогда и только тогда, когда ее
числитель равен нулю, а знаменатель не равен нулю.
34 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Задание 9. Решите уравнение ——^— = 0.
А. -1 Б. 2,5 В. -1; 2,5 Г. -1; 2,5
Решение.
Дробь равна нулю, значит, числитель равен 0, а знаменатель не
равен 0, т.е. 2х2 - Зх - 5 = 0 и х +1 * 0. Или
|2х2-Зх-5 = 0,
[х + 1 * 0.
Решим квадратное уравнение и произведем отбор его корней.
х = 2,5 или х = -1.
Но х * -1, число (-1) является посторонним корнем.
Итак, уравнение имеет единственное решение х = 2,5. И в
ответе пишем букву «Б».
Ответ: Б.
Задание 10. Найдите корни уравнения
1 х -5х+2
+
~х~+2 + х2-2х+4 "
Решение.
Перенесем все слагаемые в левую часть, а затем приведем к
общему знаменателю. При этом желательно разложить знаменатели
дробных выражений на множители. Один из знаменателей равен
х3 + 8. Переменная возводится в третью степень, поэтому
целесообразно к выражению х3 + 8 применить формулу суммы кубов
х3 + 8 = х3 + 23 = (х + 2)(х2 - 2х + 4).
Имеем
х+2 jc2-2jc+4 jc3+8
jc2-2x+4 , jc-(jc+2) , 5jc-2
(jc+2)(jc2-2jc+4) (x+2)(jc2-2jc+4) (jc+2)(jc2-2jc+4)
2x2+5jc+2
Уравнение имеет единственный корень (-0,5).
Ответ: -0,5.
ТЕМА 2. УРАВНЕНИЯ 35
Уравнения высших степеней
Уравнения, степень которых выше второй, обычно решаются двумя
основными методами: введением новой переменной и
разложением на множители.
Метод введения новой переменной
Задание 11. Найдите корни уравнения х4 -11х2 -12 = 0.
Замечание: уравнения вида ахл + Ьх2 + с = 0, где а * 0,
являющиеся квадратными относительно х2, называют биквадратными
уравнениями.
Решение.
Это уравнение можно свести к квадратному с помощью замены
а = х2.
х4-11х2-12 = 0
а = х2
а2-Па-12 = 0
а = -1 или а = 12
Вернемся к переменной х.
х2 = -1 или х2 = 12.
Первое уравнение решений не имеет (почему?), а второе
уравнение имеет два корня VU = 2V3 и -VU = -2V3.
Ответ: ±2<Л.
Замечание: уравнение x-llVx-12 = 0 тоже можно свести к
квадратному а2 -1 \а -12 = 0 заменой а = Jx. Правда, тогда, после
решения уравнения с переменной а, придется решать простейшие
иррациональные уравнения: Vx = -l,Vx = 12. И корнем
исходного уравнения будет только 122 = 144.
Не всегда замена переменной так очевидна, как при решении
биквадратных уравнений.
Задание 12. Найдите наименьший корень уравнения
Решение.
Рассмотрим первое слагаемое (х + 3)4. Вспомним, что(х + 3)2 =
Сгруппируем второе и третье слагаемые Зх2 + 18х. Если вынести
общий множитель 3 за скобки, тогда имеем 3(х2 +6х).
36 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Введем новую переменную а = (х + З)2, а > О, тогда
Исходное уравнение будет иметь вид а2 + За - 27 -1 = 0.
Получили квадратное уравнение относительно переменной а. Решим
его.
а = -1 или а = 4
а - -1 — посторонний корень (почему?).
Вернемся к переменной х.
(х + 3)2 = 4.
Как проще решить это уравнение?
1-й способ. Раскрыть квадрат суммы и применить основную
формулу корней квадратного уравнения.
2-й способ. Перенести 4 в левую часть и применить формулу
разности квадратов.
3-й способ. Извлечь квадратный корень из обеих частей
уравнения.
х + 3 = 2 или х + 3 = -2.
х = -1или х = -5
Прежде чем записать ответ, вспомните, на какой вопрос
требуется ответить в задании.
Ответ: -5.
Метод разложения на множители
Прежде чем приступать к решению уравнений с помощью данного
метода, советуем повторить тему «Числа и выражения.
Преобразование выражений».
Задание 13. Сколько корней имеет уравнение
х3-Зх2-32х + 96 = 0?
А. 0 Б. 1 В. 2 Г. 3
Решение.
В левой части уравнения четыре слагаемых, поэтому
применяем метод группировки.
(*3-Зх2)-(32х-96)=0
х2(х-3)-32(х-3) = 0
(х-3)(х2-32) = 0
ТЕМА 2. УРАВНЕНИЯ
37
Произведение равно 0, значит, х - 3 = 0 или х2 - 32 = 0.
Уравнение имеет три корня: 3; ± 4>/2.
Ответ: Г.
Задания второй части экзаменационной работы на 4 и 6 баллов по
теме «Уравнения» часто содержат уравнения с параметром.
Рассмотрим примеры решения двух таких заданий.
Уравнения с параметром
Задание 14. При каких значениях параметра а уравнение
х2 + 2х + а = 0 имеет: 1) два различных корня; 2) имеет корень,
равный 2?
Решение.
1) Так как уравнение х2 + 2х + а = 0 имеет два различных корня,
то D > 0.
D = 4-4a>0, a<\
Ответ: при а < 1 уравнение имеет два различных корня.
2) Так как 2 является корнем уравнения х2 + 2х + а = 0, то
22 + 2-2 + я = 0,я = -8.
Ответ: при а = -8 уравнение имеет корень, равный 2.
Задание 15. При каких значениях параметра т оба корня
уравнения х2 - тх + 2 = 0 лежат в промежутке (0; 3) ?
Решение.
Рассмотрим функцию f(x) = х2 - тх + 2. Графиком данной
функции является парабола. Изобразим параболу с указанными
свойствами.
Запишем условия, соответствующие этому расположению
параболы.
Г/(0)>0,
^ ^ -^вершины
D>0.
38 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Решим отдельно каждое из этих неравенств.
/(0) = 2 > 0, значит, первое условие выполняется
автоматически.
= 9-3/и+2>0, -3/и>-11, m<j.
0<<3°<<6
и
^вершины =~2а= Т
Z) = /w2-8>0, wg(-oo;-2V2]u[2V2;+oo).
Решением системы неравенств будет промежуток 2>/2; 3- .
Ответ: при т G 2V2; 3 - оба корня уравнения лежат в
промежутке (0; 3).
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЧАСТЫ
1. Решите уравнение х - 5(х - 4) = 6х + 5.
Ответ:
2. Найдите корень уравнения 4 - - = 3.
Ответ:
3. Какое из уравнений имеет бесконечное число корней?
1)0-х=0 2)0-х = 1 3)0 + х=0 4)0-х=0
4. Решите уравнение — — = -1.
Ответ:
5. Найдите корни уравнения 1-х + 3 (0,2х -1) = 0.
Ответ:
6. Решите уравнение An -10,5 = 5п- 3(2п -1,5).
Ответ:
7. Корнем квадратного уравнения -5х2 = -25 является число
А.-5 Б.1 B.--L Г. -VI
8. Найдите корни уравнения -2к2 + 32 = 0.
Ответ:
9. Найдите корни уравнения -2к2 + 32к = 0.
Ответ:
ТЕМА 2. УРАВНЕНИЯ 39
10. Решите уравнение -9х2 + — х = 0. В ответе укажите
наименьший из его корней.
A. -f Б. 0 В.-1 Г.1
11. Укажите верную формулу корней квадратного уравнения
кх2 + тх + п = 0.
А -т±л1т2-4кп _
А. х = Б. х =
Тх=
"•*=2*Тх= 2k
12. Решите уравнение х2 - 6х + 7 = 0.
A. 3-V2; 3 + V2 В. 6-2V2; 6 + 2V2
Б. 3-V3; З + л/3 Г. -3-V2; -3 + V2
13. Каждое уравнение соотнесите с множеством его корней.
1.)0,2х2-5х=0; 2)0,2х2-5 = 0; 3)0,2х2 = 0.
а) 0; б) -5 и 5; в) 0 и 25.
14. Найдите положительный корень уравнения 2с2 - Зх - 5 = 0.
А. 2 Б. 5 В. 1 Г. 2,5
15. Укажите наименьший корень уравнения х2 + 2х = 24.
Ответ:
у+7
16. Решите уравнение 7—!Чт \ = 0.
Ответ:
У_7
17. Решите уравнение 7—ч-, ^ = 0.
(у-7)(у+9)
Ответ:
(у_7)(у+9)
18. Решите уравнение -^—- = 0.
Ответ:
19. Решите уравнение v^ '^ = °-
Ответ:
20. Решите уравнение —- = —-.
Ответ:
21. Решите уравнение — = 0.
Ответ:
4О РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
/»/» г» 2jc2-5x-7 л
22. Решите уравнение — = 0.
Ответ:
jc2 —8 2х
23. Укажите количество корней уравнения —— = -—.
Ответ:
24. Найдите сумму корней уравнения х2 - 28х + 27 = 0.
Ответ:
ЧАСТЬ II
Задания на 2 балла
25. Укажите общий корень уравнений
-1=0 и х2 - 5х - 24 = 0.
26. Решите уравнение -х3 + 5х2 + Юх - 50 = 0.
27. Решите уравнение х3+ 2х2 - 18х - 36 = 0.
28. Решите уравнение (х2 + 2)(х2 - 8) = 11.
29. Решите уравнение (х2 - 4)(х2 + 3) = 18.
30. Решите уравнение —- —=—- = 3.
J* jc+3 jc2-9
31. Решите уравнение —- —j-— + 2 = 0.
jc+2 jc2—4
Задания на 4 балла
„„ г» 1 jc 5х+2
32. Решите уравнение —- + -y-z—- = -т—^-
JK jc-2 jc2+2jc+4 jc3-8
33. Решите уравнение (х - 2)4 - 4х2 + 16х - 61 = 0.
34. При каком значении а уравнение х2 - 4х + а = 0 имеет один
корень?
35. Один из корней уравнения х2 + рх -15 = 0 равен 5.
Найдите сумму корней этого уравнения .
36. Произведение корней уравнения (х2 + Зх)2 - х2 - Зх = 12
равно...
37. Решите уравнение х - 17>/х -18 = 0.
38. Не решая уравнения Зх2 + Зх - 1=0 , найдите Х!2х2 + х22хь
где Xj и х2 — корни уравнения.
39. Не решая уравнения Зх2 + Зх - 1=0, найдите х,2 + х22, где х,
и х2 — корни уравнения.
42. При каких значениях параметра Ъ уравнение — = О
ТЕМА 3. СИСТЕМЫ УРАВНЕНИЙ 41 I
40. При каких значениях а уравнение х2 - Зх + а = 0 имеет
корень, равный 3?
х2-Ь
41. При каких значениях параметра Ь уравнение —^ = 0 име-
х—о
ет единственное решение?
42. При каких значен
имеет единственное решение?
л** гт l x2-bx+4 л
43. При каких значениях параметра о уравнение — = 0
х—6
имеет единственное решение?
Задания на 6 баллов
44. Укажите наибольшее целое значение д, при котором
уравнение х2 - 2ах + 2а + 24 = 0 имеет различные отрицательные корни.
45. Укажите наибольшее значение а, при котором уравнение
х2 - (а+7)\х\ + а2 - 5а = 0 имеет три решения.
46. Числа 13 и -24 являются корнями уравнения
х4 -745х2 +97344 = 0. Укажите наибольший корень уравнения.
47. Укажите все значения а, при которых уравнение
х3 - 2ах2 - (2а - 3)х = 0 имеет три различных корня.
ло п jc2+5jc+2 jc2+5jc+3 ,
48. Решите уравнение -~—-—- + —~—i—- = 1.
JV jc2+5jc+4 jc2+5jc+9
49. Решите уравнение - + —- + —- + —- = 0.
х jc+2 jc+3 jc+5
3jc-6 x—2x2
50. Решите уравнение 2_ = -^- 2.
51. Докажите, что уравнение (х2 - 2x + 7)(x2 + 6x +11) = 11
не имеет корней.
52. При каких значениях b оба корня уравнения х2 - Ъх + 2 = 0
лежат в промежутке (l; 3)?
Тема 3. Системы уравнений
Системы уравнений можно решить различными методами.
В первой части экзаменационной работы требуется решить
системы уравнений либо методом подстановки, либо методом
сложения, либо графическим методом.
При решении систем уравнений из второй части
экзаменационной работы приходится применять специальные приемы
решения систем уравнений, в частности, метод введения новых
неизвестных, а также решать системы уравнений с параметром.
42 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определение. Решением системы уравнений с двумя
неизвестными называется пара значений неизвестных, обращающая каждое
уравнение системы в верное равенство.
ЗАДАНИЯ ДЛЯ АКТИВНОГО ОБУЧЕНИЯ
(С КОММЕНТАРИЯМИ, РЕШЕНИЯМИ, ОТВЕТАМИ)
Метод подстановки
Задание 1. Решите систему уравнений
\х-2у = 1.
Решение.
Рассмотрим второе уравнение системы. Выразим неизвестное х
через у и подставим в первое уравнение.
Решим первое уравнение системы.
Z) = 1 -4-2 (-10) = 81
_ -1±9
у = 2 или у = -2,5
Соответствующие значения х можно найти, подставив
найденные значения у в одно из уравнений исходной системы, например,
во второе уравнение.
= -2,5,
= 2-(-2,5) + 1; [х = -4.
Ответ можно записать в виде пар: (5; 2), (-4;-2,5) — или так:
х, = 5, у{ = 2;х2 = -4, у2 = -2,5.
Ответ: (5;2), (-4;-2,5).
Метод сложения
Задание 2. Найдите решения системы уравнений
торое уравнение.
\у = 29 h = 2, h = -2,5 Г
[х = 2-2 + 1; [х = 5. ИЛИ |х = 2-(-2,5) + 1; [
Зх-5>> = -7.
ТЕМА 3. СИСТЕМЫ УРАВНЕНИЙ 43
Решение.
1-й способ. Метод сложения
Сложим оба уравнения исходной системы
Найдем соответствующее значение у, подставив найденное
значение х в любое из уравнений системы, например, в первое.
J3.1 + 5>> = 13, (у = 2,
[х = 1; [х = 1.
2-й способ. Метод подстановки
Выразим х]
рое уравнение:
Выразим х из первого уравнения х = —т-^- и подставим во вто-
Решим второе уравнение системы.
13 -5у -5у = -7
-\0у = -20
у = 2
Найдем соответствующее значение х из первого уравнения
_ 13-5-2
х - 3 , х - 1.
Ответ: (1; 2).
Задание 3. Вычислите координаты точки пересечения прямых
Решение.
Точка пересечения прямых принадлежат как первой прямой,
так и второй прямой, поэтому чтобы найти ее координаты, надо
решить систему уравнений:
Метод подстановки в данном случае не удобен, так как надо
выражать переменные и при этом придется делить либо на 6, либо
на 5, либо на 7, либо на 3.
I 44 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Попробуем применить метод сложения. Как получить
слагаемые, отличающиеся только знаком?
Умножим первое уравнение на (-7), а второе на 6.
\бх + 5у = -1, | х (-7) J-42JC- 35^ = 7,
l42x-18j> = -60.
Почленно сложим уравнения.
-42х - 35у + 42х -18^ = 7 + (-60)
-53у = -53
у = \
Подставим найденное значение у в любое из уравнений
исходной системы, например во второе.
[7х - 3 • 1 = -1
Ответ: (-1; l).
Метод введения новых неизвестных
Задание 4. Найдите решения системы уравнений
10 2 =-
= -1.
х-у х+у
4 15
х+у х-у
А. (-3,5; -1,5) Б. (3,5; 1,5) В. (3,5; -1,5) Г. (-3,5; 1,5)
Решение.
Введение новых неизвестных позволяет упростить вид
выражений, входящих в систему уравнений. В данном случае можно ввести
1 , 1
следующие неизвестные а = , о = , тогда получим систему
[4я-15й = -1. ^
Далее применяем уже известные методы: метод подстановки
или метод сложения. Учитывая коэффициенты при неизвестных,
выберем для решения метод сложения.
Чтобы получить слагаемые, отличающиеся только знаком,
умножим первое уравнение на 2.
4a-\5b = -L
(20b-4a = 2,
[4a-l5b = -L
ТЕМА 3. СИСТЕМЫ УРАВНЕНИЙ 45
Сложим уравнения. Получим 5b = l,b = 0,2. Найдем
соответствующее значение переменной д, подставив в любое из уравнений
системы значение Ь. (*).
Вернемся к переменным х и у.
05
— = 0,2.
х-у
Далее систему уравнений можно решить либо методом
сложения, либо методом подстановки. Окончательно получаем:
х = 3,5,
У = -15.
В ответе укажем букву «В».
Ответ: В.
Замечание: получить правильный ответ в задании 4 можно и
иначе, например, поочередно подставив возможные решения под
буквами А, Б, В, Г в систему и проверяя, не получили ли мы
верное равенство. Здесь главное не ошибиться в вычислениях.
Задание 5. Сколько решений имеет система уравнений?
f + 4-^ = 5
у х
Решение.
Рассмотрим второе уравнение системы. Если обозначим - = а,
у 1 4
то - = -. Имеем уравнение а + - = 5. Это дробно-рациональное
х а а
уравнение (см. решение таких уравнений в теме «Уравнения»).
Решим его.
д2-5д+4
— U.
а
Его корни 1 и 4.
Вернемся к неизвестным хи у. Исходная система распадается
на две системы:
46
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
( I ) или
х + у = 8,
(I ) или
(Н)
(И)
[х = Ay.
Решением системы ( I) является пара чисел (4; 4). Решением
системы ( II ) является пара чисел (6,4; 1,6). Исходная система
имеет два решения.
Ответ: два решения.
Графический метод
Задание 6. На рисунке изображены парабола и три прямые.
Укажите систему уравнений, которая имеет 2 решения.
[у =
В.
Б
х + 10. [х-6 = 0.
Г. Все три указанные системы.
Решение.
Каждая система содержит уравнение параболы у = х2 + 7 и
уравнение прямой. Если система имеет два решения, то парабола и
прямая должны иметь две общие точки. Проанализируем рисунок.
Прямая у = х + 10 и парабола не пересекаются. Система под
буквой А решений не имеет.
Прямая х - 6 = 0 и парабола пересекаются в одной точке (это
можно заметить, если мысленно продлить параболу и прямую).
Система под буквой Б имеет одно решение.
Прямая у - 8 = 0 и парабола пересекаются в двух точках (это
можно заметить, если мысленно продлить параболу и прямую).
Значит, ответ на вопрос задачи — система под буквой В.
Ответ: В.
ТЕМА 3. СИСТЕМЫ УРАВНЕНИЙ
47
Задание 7. На
у = х2 + 4х + 3 и у =
уравнений
(у = х2 + 4х + 3,
рисунке изображены графики функций
х + 3. Используя графики, решите систему
(у =
\
\
\
-5
/
\
\
/
\
/
-2 >
ут7
у
/
/
-1
2
1
0
-1
-2
-3
-4
Z
1
—
2
3
4 £
Решение.
Координаты каждой из
точек пересечения
параболы у = х2 + 4х + 3 и
прямой у = х + 3
удовлетворяют как первому уравнению
системы, так и второму,
т. е. являются решением
исходной системы.
Остается найти координаты этих
точек.
Ответ: (-3; 0), (0; 3).
Системы уравнений с параметром
Задание 8. При каких значениях т имеет решение система
уравнений
Зх - у = О,
- 4х + 5у = 19,
5-т=х?
Решение.
Все три уравнения системы — это уравнения прямых. Чтобы
система имела решение, нужно, чтобы все три прямые
пересекались в одной точке. Сначала найдем координаты точки
пересечения первых двух прямых, т.е. решим систему
Зх-у = 0,
4х + 5у = 19.
Эту систему можно решить методом подстановки. Ее решение
(1; 3). Подставим х = 1 в третье уравнение исходной системы и
найдем значение т.
Получим 5 - т = 1, следовательно, т = 4.
Ответ: при т = 4.
48
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Задание 9. При каких значениях т система
у2 =
[х = т - 4.
имеет два решения?
Решение.
Первое уравнение системы задает окружность с центром в
точке (0; 0) и радиусом 2. Второе уравнение задает множество прямых,
перпендикулярных оси абсцисс. Эти прямые должны пересекать
окружность в двух точках. Обратимся к рисунку.
Итак, переменная х должна принимать значения от -2 до 2,
исключая -2 и 2, так как при таких значениях х система будет иметь
единственное решение.
-2</и-4<2
-2 + 4</и<2 + 4.
2 <т <6
Ответ: при т е(2; 6).
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЧАСТЫ
\х-2у = -7,
1. Решите систему уравнений <„
[3x + 4j' = 19.
Ответ:
Г
2. Решите систему уравнений \
ху = -6,
[
Ответ:
3. Вычислите координаты точки пересечения прямых
2х-Зу = -8, 4
Ответ:
ТЕМА 3. СИСТЕМЫ УРАВНЕНИЙ 49
4. Решите систему уравнений
Ответ:
5. Решите систему уравнений
Ответ:
6. На рисунке изображены парабола и три прямые. Укажите
систему уравнений, которая имеет 2 решения.
.у + 4 = О
{
[у = -х +10.
Б.
в
Г. Все три указанные системы.
7. На рисунке изображены парабола и три прямые. Укажите
систему уравнений, которая не имеет решения.
у + 4 = 0
50
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
А.
Б.
8. На рисунке изображены парабола и три прямые. Укажите
систему уравнений, которая имеет одно решение.
>> = -х + 10. ' [у+ 4 = 0.
' Г. Все три указанные системы.
=-х + 10
А.
Б.
R
у + 4 = 0.
Г. Все три указанные системы.
= х2-2,
_
9. Из данных уравнений подберите второе уравнение системы
4
так чтобы система имела 2 решения (используйте графические
представления).
А. у = -х Б. у = х В. -у = х2 Г. у = х2
10. Из данных уравнений подберите второе уравнение системы
_ 4
х '
так чтобы система не имела решения (используйте графические
представления).
А. у = -х Б. у = х В. -у = х2 Г. у = х2
ТЕМА 3. СИСТЕМЫ УРАВНЕНИЙ
51
11. Укажите рисунок, на котором приведена графическая
иллюстрация решения системы уравнений
А.
В.
ч-2
ч-2
Б.
г.
-2,
= х-2,
= -х-2.
12. Укажите рисунок, на котором приведена графическая
иллюстрация решения системы уравнений
А.
В.
v-2
-2
Б.
1\
t У
-2.
52
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
13. На рисунке изображены графики функций у = х2 - Ах + 3 и
у = х -1. Используя графики, решите систему уравнений
(у = х2 - 4х + 3,
(у = х2 -
Ответ:
ЧАСТЫ1
Задания на 2 балла
14. Решите систему уравнений
4 +6 А
- у - -2 5
4~ '
15. Решите систему уравнений
16. Решите систему уравнений
\х + У = 6,
|х2 + у7 = 16 + 2лу.
17. Сколько решений имеет система уравнений
+ у2 = 29,
ТЕМА 3. СИСТЕМЫ УРАВНЕНИЙ
18. Решите систему уравнений
53
-^2 = -11.
19. Решите систему уравнений и укажите наименьшую сумму
ук, где (л^; ук) — решение системы
[2х2-у2 = 46.
20. Решите систему уравнений и укажите наибольшую сумму
+ ук, где (хк; >>к) — решение системы
Задания на 4 балла
21. Решите систему уравнений
[х-у = 12,
[у х
22. Решите систему уравнений
9 4
х-у х+у
х-у х+у
23. Решите систему уравнений
= 1,
\х2-2ху = 5.
24. Сколько решений имеет система уравнений
25. Решите систему уравнений
2х -4y = S,
- %у2 = -4.
54 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
26. При каких значениях а система уравнений
х + у-а = 5
имеет решение.
Задания на 6 баллов
27. Решите систему уравнений
\х2у + ху2 = -2.
28. Сколько различных решений имеет уравнение
(х2 + 2ху + у1)2 + (х2 - 5у- I)2 = О?
29. Сколько решений имеет уравнение
-37 =0?
30. Решите систему
31. Решите систему
32. Решите систему
х + у = 3,
+ х = 4.
J
[x2-2xy = S.
33. При каких значениях b система
не имеет решения?
34. При каких значениях Ъ система
х + у = 6
имеет одно решение?
ТЕМА 4. НЕРАВЕНСТВА 55
Тема 4. Неравенства
Решение большинства неравенств сводится к решению
соответствующих уравнений. Рассмотрим решение линейных и
квадратных неравенств, а также специальный метод решения
неравенств — метод интервалов.
В первой части экзаменационной работы обычно требуется
решить неравенства без дополнительных условий. Во второй части
часто приходится совершать алгебраические преобразования,
выбирать решения, удовлетворяющие дополнительным условиям, а
также решать неравенства и системы неравенств с параметром.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определение. Всякое значение неизвестного, при котором
данное неравенство с неизвестным обращается в верное числовое
неравенство, называется решением неравенства. Решить неравенство —
значит найти все его решения или доказать, что их нет.
Определение. Неравенства вида ах + Ъ > О (< 0, > О, < 0), где
х — неизвестное, аи b — некоторые действительные числа (а * 0),
называются неравенствами первой степени или линейными
неравенствами.
Определение. Неравенства вида ах2 + Ъх + о 0 (< 0, > 0, < 0),
где а ^ 0, называют неравенствами второй степени с одним
неизвестным или квадратными неравенствами.
Свойства числовых неравенств
(а,Ь,с — действительные числа)
Если а > b и Ъ > с, то а > с. (1)
Если а> Ь,то а + с> Ь + с. (2)
Если а > b и с — положительное число (с > 0), то ас > be. (3)
Если а > b и с — отрицательное число (с < 0), то ас < be. (4)
ЗАДАНИЯ ДЛЯ АКТИВНОГО ОБУЧЕНИЯ
(С КОММЕНТАРИЯМИ, РЕШЕНИЯМИ, ОТВЕТАМИ)
Использование свойств числовых неравенств
Задание 1. Если а < Ь, то верно неравенство:
А. -2Ь > -2а Ъ.а-2<Ь-2 В. 5 - а < 5 - Ь Г. | > |
Решение.
Попытаемся получить из неравенства а < b каждое из
неравенств под буквами А, Б, В, Г.
56 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Так как -2 < 0, то из неравенства а < Ъ следует -2а > -2Ь
(свойство (4). И неравенство под буквой А неверно.
Так как а < Ь, то по свойству (2) верно а-2< b -2. И
неравенство под буквой Б верно.
Так как а < Ь , то -а + 5 > -Ь + 5 (свойства (4) и (2). И
неравенство под буквой В неверно.
Так как - > 0, то из неравенства а < b следует неравенство | < -.
И неравенство под буквой Г неверно.
Ответ: Б.
Линейные неравенства
Задание 2. Укажите наименьшее целое решение неравенства
-х + 0,5(х + 4) < 4.
Решение.
Сначала раскроем скобки.
-х + 0,5х + 2 < 4.
При решении линейных неравенств обычно переносят
неизвестные слагаемые в левую часть неравенства, а известные — в
правую часть и приводят подобные слагаемые.
-0,5х < 2.
Чтобы выразить х, надо разделить обе части неравенства на
(-0,5). Знак неравенства меняется на противоположный.
-0,5х < 2
х > -4.
Отметим решение неравенства на координатной прямой.
-4
Наименьшим целым решением является число (-3), а не (-4).
(Почему?)
Ответ: -3.
Задание 3. Найдите число целых решений неравенства
-3<4-1<1-
4
А. 14 Б. 15 В. 16 Г. 17'
Решение.
Исходное неравенство называется двойным неравенством. Его
можно решать разными способами.
ТЕМА 4. НЕРАВЕНСТВА 57
1-й способ (непосредственно).
-3<^-1<1
4
4
-8<х<8
2-й способ (с помощью системы).
Исходное неравенство равносильно системе неравенств
--1>-3
;-!<!.
Решим первое неравенство.
±г-3 + 1
Решим второе неравенство.
!<■♦■
х<8
Отметим решения и первого и второго неравенства на
координатной прямой.
-8
Решением системы неравенств будет промежуток [-8; 8).
Количество целых чисел, входящих в промежуток, равно 16.
Ответ: В.
Квадратные неравенства
гных неравенств ах2 + Ьх Л
1. Вводим соответствующую функцию у = ах2 + Ьх + с.
Решение квадратных неравенств ах2 + Ьх + о 0 (< 0, > 0, < 0)
состоит из 5 этапов:
58 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
2. Определяем направление ветвей параболы у = ах2 + Ьх + с
(при а > 0 ветви параболы направлены вверх; при а < О ветви
параболы направлены вниз).
3. Находим нули функции, т.е. решаем уравнение
ax2 + bx + c = 0.
4. Если уравнение имеет корни, то отмечаем корни на
координатной прямой и схематически рисуем параболу в соответствии с
направлением ветвей. Если уравнение не имеет корней, то
схематически рисуем параболу в соответствии с направлением ветвей.
5. Находим решение неравенства с учетом смысла знака
неравенства.
Решение квадратных неравенств, в зависимости от дискриминанта
соответствующего квадратного уравнения, разбивается на 3 случая:
1)D>0; 2)D=0;3)D<0.
Рассмотрим первый случай: D> 0.
Задание 4. Решите неравенство -х2 - 2х + 3 > 0.
Решение.
1. Пусть у = -х2 - 2х + 3.
2. Так как а = -1, то ветви параболы направлены вниз.
3. Решим уравнение -х2 - 2х + 3 = 0.
Его корни: х = 1 и х = -3.
4. Отметим числа 1 и (-3) на координатной прямой и построим
эскиз графика функции
5. Так как знак неравенства (>), то решением его будет отрезок
-3; 1].
1 Г
Ответ: [-3; 1].
Рассмотрим случай, когда D = 0.
Задание 5. Решите неравенство: 4х2 + 4х +1 > 0.
Решение.
В соответствии со схемой решения квадратного неравенства
получаем:
1. Пусть f(x) = 4х2 + 4х +1.
2. а = 4 > 0, значит, ветви параболы f(x) = 4х2 + 4х +1
направлены вверх.
ТЕМА 4. НЕРАВЕНСТВА 59 I
3. Уравнение 4х2 + 4х +1 = 0 имеет совпавшие корни
х^ = х2 = -0,5. Парабола касается оси абсцисс.
4.
-0,5
5. Так как знак неравенства (>), то решением его являются все
числа, кроме х = -0,5.
О т в е т: (- оо; - 0,5) U(-0,5; + оо).
Замечание: Решением неравенства 4х2 + 4х +1 > 0 является
промежуток (-оо; + оо). Решением неравенства 4х2 + 4х +1 < 0
является только число (-0,5). Неравенство 4х2 + 4х +1 < 0 решений
не имеет.
Рассмотрим случай, когда D< 0.
Задание 6. Решите неравенство -х2 - 6х -10 < 0.
Решение.
Имеем:
1)/(х) = -х2-6х-10;
2) ветви параболы направлены вниз (почему?);
3) уравнение -х2 - 6х -10 = 0 решений не имеет. Парабола не
пересекает ось абсцисс.
4) ►
Г\
Так как знак неравенства (<), то решением его являются все
числа.
Ответ: (-оо; +<»).
Замечание: неравенство -х2 - 6х -10 > 0 решений не имеет.
Область определения выражения
Значения переменной, при которых выражение имеет смысл,
называют допустимыми значениями переменной. Множество всех
допустимых значений переменной называют областью определения
выражения.
Задание 7. При каких значениях х имеет смысл выражение:
1) tFx + 6; 2)
60 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Решение.
1) Так как выражение 4а имеет смысл при а > 0
(арифметический квадратный корень определен только для неотрицательных
чисел), то решим неравенство -х + 6 >0. Областью определения
исходного выражения будет промежуток (-оо;б].
2) Так как выражение - имеет смысл при д*0,то-х + 6*0и
а
х * 6. Областью определения исходного выражения будет
объединение промежутков (-<»; б) и (б; + оо).
3) Решим систему
-х + 6 > 0, \х < 6,
Г—jc + 6 > 0, Г
[х -1 * о, \
Отметим решения системы на координатной прямой.
1
// //? // Д *
Областью определения исходного выражения будет
объединение промежутков (-<»; l) и (l; б].
Ответ: 1) (-«>; б]; 2) (-«>; б) и (б; + «>); 3) (-«; l) и (l; б].
Метод интервалов
При решении более сложных неравенств используют метод
интервалов. Поясним его на примерах.
-4
Задание 8. Решите неравенство 7 -^г—~>—т\ > 0.
(-х+5)(*2-4)
Решение.
Так как числитель дробного выражения отрицателен, то
решение исходного неравенства сводится к решению неравенства
(-х + 5)(х2 - 4) < 0. Решим неравенство методом интервалов.
Рассмотрим функцию/(х) = (-х + 5)(х2 - 4). Найдем нули
функции, т.е. решим уравнение (-х + 5)(х2 - 4) = 0. Числа 5; -2; 2
являются нулями функции.
Отметим нули функции на координатной прямой.
-2 2 5
В каждом из промежутков, на которые область определения
функции разбивается нулями функции, знак функции
сохраняется, а при переходе через нуль функции, т.е. через точки -2, 2, 5, ее
знак меняется.
ТЕМА 4. НЕРАВЕНСТВА
61
Определим знак функции в каком-нибудь из четырех
промежутков. Например, рассмотрим ДО) = (-0 + 5)(02 - 4) = 5 • (-4) =
= -20 < 0, значит, в промежутке (-2; 2; значения функции
отрицательны.
-2 2 5
Далее происходит чередование знаков.
Итак, мы решаем методом интервалов неравенство
(-х + 5)(х2 - 4) < 0. Решением неравенства будет объединение
промежутков (-2; 2) и (5; +оо).
Ответ: (-2; 2) и (5;+оо).
Задание 9. Решите неравенство х4 - 9х2 £ 0.
Решение.
Рассмотрим функцию f(x) = хА -9х2. Ее нули 0; -3; 3.
Отметим эти числа на координатной прямой и определим знак
функции, например, на промежутке (0; 3).
Найдем значение функции в точке I, I e (0;3).
-3 О 3
Так как
/(*) = х2(х2 - 9) = х • х - (х - 3)(х + 3) = (х - 0) • (х - 0) • (х - 3)(х + 3),
то число 0 является, говорят, нулем двойной кратности. При
переходе через него знак функции не меняется.
-3 0 3
У исходной функции только 0 является нулем двойной
кратности, поэтому и при переходе через точку 3 и при переходе через
точку (-3) знак функции меняется.
-3 0 3
Решением исходного неравенства является не только
объединение промежутков (- оо; - з] U [3; + оо), но и точка 0.
Ответ: (-оо; -3]и{0}и[3; +«).
62 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Замечание: решением неравенства х4 - 9х2 > О является
объединение промежутков (- оо; - з) U (3; + оо).
Решением неравенства х4 -9х2 < О является объединение
промежутков (-3; 0) U (0; 3).
Решением неравенства х4 -9х2 < 0 является отрезок [-3; 3].
Неравенства с параметром
Задание 10. При каких значениях а система неравенств
Г-5х < 10,
[х + а > 2х
1) не имеет решений; 2) имеет ровно два целых решения?
Решение.
Решим первое неравенство и приведем подобные слагаемые во
втором неравенстве.
Г*>-2,
[х <а.
Сравним взаимное расположение точек (-2) и а на
координатной прямой и рассмотрим три случая: а = -2; а > -2; а < -2.
1) При а--2 имеем
s s / а
'"f//// >
-2
При а = -2 система решений не имеет.
2) При а > -2 имеем
При а > -2 решением системы является промежуток (-2; а].
3) При а < -2 имеем
/ / / /
-2
При а <—2 система решений не имеет.
Получаем, что при а<-2 система решений не имеет.
2. Система может иметь решения только при а > -2. Чтобы
система имела ровно два целых решения, необходимо, чтобы в
промежутке (-2; а] (см. рисунок ко второму случаю) лежало только
два целых числа: -1 и 0. Это выполняется, если 0 < а < 1.
Ответ: 1) при а < -2; 2) при 0 < а < 1.
ТЕМА 4. НЕРАВЕНСТВА 63
Задание 11. При каких значениях а неравенство ах2 + х -1 > О
выполняется при всех значениях х?
Решение.
Данное неравенство не при любых значениях параметра а будет
квадратным.
При а = 0 имеем: 0 • х2 + х -1 > 0. Получаем линейное
неравенство х -1 > 0, которое выполняется не при всех значениях х
(например, при х = -2: -2 - 1 < 0).
При а * 0 исходное неравенство будем квадратным. Графиком
функции f(x) = ах2 + х — 1 является парабола. Для того чтобы
неравенство выполнялось при всех значениях х, нужно, чтобы
парабола была расположена выше оси абсцисс.
Запишем условия, соответствующие данному положению
параболы:
\а>0,
[D<0.
Z) = I2 + 4 • я.
Решением неравенства/) < 0является промежуток (-оо; -0,25).
[а>0,
[а < -0,25.
Система решений не имеет.
Ответ: таких значений а не существует.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЧАСТЫ
1. Сколько целых чисел входит в промежуток (-1; 5]?
А. 6 Б. 7 В. 5 Г. 4
2. Число 5 является решением неравенства
A. (2х -10)2 < х2 - 26 Б. (2х -10)2 < х2 + 25
B. х2<2х-10 Г. х2-50>(х-5)2
3. Решите неравенство 1х + 5 < 4х -7.
Ответ:
64 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
4. Решите неравенство ^ - ^-— < 1.
2 4
Ответ:
5. Для любых значений х верно неравенство:
А. (х-2)2<0 В.х2<2
Б.(х + 3)2>0 Г. х2-10х + 25>0
6. При каких значениях переменной х имеет смысл выражение
А. х > О В. х > О
Б. х < О Г. х — любое действительное число
7. При каких значениях переменной х имеет смысл выра-
2V^O
жение —-?
А. х > О В. х * О
Б. х < О Г. х — любое действительное число
8. На рисунке изображен промежуток
-5 3
А. [-5; 3] Б. (-5; 3] В. (-5;3) Г. [-5; 3)
9. Если а < Ь, то для любых аи b верно неравенство:
А. -5Ь > -5а; В. 2 - а < 2 - Ъ\
Б.а2<Ь2; Г. а + 4 < Ъ + 4.
10. Если д > /и, то для любых аи т верно неравенство:
А. -Зя>-3/и В. Ъ-а<Ъ-т\
Б.->1; Г. а-Ъ<т-Ъ.
т
11. Если 2 < х < 5, 4,5 < у < 6, то значение выражения х + >>
принадлежит промежутку:
А. (7; 10,5) Б. (6,5; 11) В. (9; 30) Г. [7; 10,5]
12. Решите двойное неравенство -30<3-11>><-8.
Ответ:
13. Решите систему неравенств
|5х-2>-12,
|0,5х < 4.
Ответ:
ТЕМА 4. НЕРАВЕНСТВА 65 |
14. Решите систему неравенств
1^ + 2 > О,
[х -1 > 2х.
Ответ:
15. Решите неравенство (х+5)2 < 25 - х2.
Ответ:
16. Решите неравенство 8х - Зх2 + 3 > 0.
Ответ:
17. Решите неравенство х2 - 10х + 25 > 0.
Ответ:
18. Решите неравенство х2 - 10х + 25 < 0.
Ответ:
19. Решите неравенство х2 - 10х + 26 < 0.
Ответ:
ЧАСТЬ II
Задания на 2 балла
20. Найдите наибольшее целое значение п, при котором
разность (3 - 2л) - (8 - 1,5л) положительна.
21. При каких значениях t выражение 3 - 2t принимает
положительные значения, меньшие 2.
22. Укажите наименьшее целое решение системы неравенств
23. Укажите наибольшее целое решение системы неравенств
Г5х-4(2х-1)>3(х + 2),
[9-х2 >0.
24. Найдите корень уравнения х2 + 4х + 3 = 0,
удовлетворяющий неравенству - (х-1) < -(5х+3).
25. Решите неравенство: (т -1)2 + (т +1)2 > 2(т - \){т +1).
26. Найдите область определения выражения Vl-x2.
27. Найдите область определения выражения
jc + 5
66 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
jc2-3jc+2
28. Найдите корень уравнения —2 = 0, удовлетворяющий
неравенству - (5 - 2х) > -(6,5 - Зх).
29. При каком значении а решением неравенства ах < 5
является Промежуток (-оо; + оо)?
30. Укажите число целых решений неравенства
(2х-1)2-3(2х-1)<0.
Задания на 4 балла
31. Решите неравенство ( * -2 (6х +12) > 0.
32. Найдите целые решения системы неравенств
|6-V3x<0,
[l6-V8x>0.
33. Решите неравенство т-^)—Y < 0.
34. Решите неравенство (Vx - 4) < 7.
х
2'
35. Решите неравенство (Vx + 4) < -.
-, тт и _ V-jc2+36
36. Найдите область определения выражения —2 .
37. Сколько целых чисел входит в область определения
выражения V9 -х2 + у/х + 1?
Задания на 6 баллов
38. Решите неравенство х4 - 10х2 + 9 > 0.
39. Решите неравенство х4 - 10х2 > 0.
40. Решите неравенство х3 - 6х2 + 9х < 0.
41. Найдите наибольшее натуральное решение неравенства
)
42. Решите неравенство х - 5Vx + 4 > 0.
43. При каких значениях а система неравенств
|4х-12<0,
|-х + а < 0
имеет решения.
ТЕМА 5. КООРДИНАТЫ И ГРАФИКИ
67
44. При каких значениях а < О система неравенств
Г4х-12 <0,
\-х + а < О
имеет ровно пять целых решений?
45. Укажите наименьшее целое значение а, при котором
неравенство -х2 - 4х+ 3 - д < 0 выполняется при любых значениях х.
Тема 5. Координаты и графики
В первой части работы чаще всего представлены задания,
требующие установить соответствие между графиком функции и ее
аналитическим заданием, т.е. формулой, задающей функцию.
Среди графиков функций встречаются прямые, параболы и гиперболы.
Для выполнения заданий по этой теме из любой части работы
полезно:
— знать уравнения прямых, парабол и гипербол;
— знать геометрический смысл коэффициентов к и Ъ для
уравнения прямой у = кх+b и коэффициентов аи с уравнения
параболы у = ах2 + Ьх + с;
— уметь находить координаты вершины параболы, точки
пересечения прямых или прямой и параболы, точки пересечения
параболы с осями;
— уметь проверять принадлежность некоторой точки прямой
или параболе.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Графиком линейной функции является прямая. Уравнение
у = кх + b является уравнением прямой, пересекающей ось Оу в
точке, ордината которой равна Ь. Коэффициент к называется
угловым коэффициентом прямой.
у=х+ 1
к=\>0
= -х+ 1,
Две прямыеу1 = kjX + b1 иу2 = к2х + Ь2 являются
параллельными, если их угловые коэффициенты к} и к2 равны и Ъх * Ь2.
Например, прямые у = 5х — Зи>>=5х — 4 параллельны.
Две прямые ух = кх х + Ъ\ и у2 = к^ х + Ь2 являются
пересекающимися, если кх * к2. Например, прямые у = 4х~Зиу=5х — 4 пере-
68
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
секаются. Две пересекающиеся прямые имеют одну общую точку,
координаты которой удовлетворяют каждому из уравнений прямых.
Точка лежит на прямой, если ее координаты удовлетворяют
уравнению этой прямой. Например, точка М (2; 7) лежит на
прямой у = 5х - 3, так как координаты точки удовлетворяют
уравнению прямой: 7 = 5-2-3.
Если точка лежит на оси абсцисс (Ох), то ее ордината равна
нулю (у = 0).
Если точка лежит на оси ординат (Оу), то ее абсцисса равна
нулю (х = 0).
Для построения прямой достаточно знать координаты двух
точек.
График квадратичной функции называется параболой.
Уравнение у = ах2 + Ьх + с, где а, Ь, с — действительные числа и д * 0,
является уравнением параболы, пересекающей ось Оу в точке,
ордината которой равна с. Коэффициент а называется старшим
коэффициентом. Если а > 0, то ветви параболы направлены вверх, если
а < 0, то ветви параболы направлены вниз.
у — ддг+ bx + с
а >0
7
у = ах*+ Ьх + с
а <0
\
Координаты вершины параболы (хв; ув) находят с помощью
формул:
Хь=~~2а' Уь=ахь+Ьхь+С
Координаты точек пересечения параболы с осями находят с
помощью следующих рассуждений.
Абсцисса точки пересечения параболы с осью Оу равна нулю, а
ордината точки пересечения равна с (т.к. у = а • О2 + b • 0 + с, у = с).
Ордината точки пересечения параболы с осью Ох равна нулю, а
абсциссу точки пересечения можно найти, решив уравнение
0 = ах2 + Ьх + с.
На рисунке парабола пересекает ось OYb точке С(0; - 1), а ось
ОХ в точках А(-\; 0) и В(3; 0).
ТЕМА 5. КООРДИНАТЫ И ГРАФИКИ
69
Парабола может иметь одну точку пересечения с осью Ох,
может иметь две точки, а может не иметь таких точек. Определить
количество точек пересечения параболы у = ахг + Ьх + с с осью Ох
можно с помощью исследования дискриминанта квадратного
уравнения ах2 + Ьх + с = 0:
если дискриминант D = Ь1 - 4ас равен нулю, то точка
пересечения одна;
если дискриминант D = Ь2 - 4ас больше нуля, то точек
пересечения две;
если дискриминант D = Ь2 - 4ас меньше нуля, то точек
пересечения нет.
У*
\
\
i
D=0
а>0/
/
/
►
X
У*
\
/)>0
а>0 J
\ ^
1 V.
х
1
У а>0
X
Для нахождения координат точек пересечения (или касания)
прямой и параболы нужно решить в системе уравнения прямой и
параболы (см., например, решение задания № 10).
к
График обратной пропорциональности у = - называется
гиперболой. Число к — коэффициент, к * 0. В зависимости от знака
коэффициента к гипербола будет располагаться либо в I и III
квадранте, либо во II и IV квадранте.
70
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
ЗАДАНИЯ ДЛЯ АКТИВНОГО ОБУЧЕНИЯ
(С КОММЕНТАРИЯМИ, РЕШЕНИЯМИ, ОТВЕТАМИ)
Задание 1. На рисунке изображен график функции у =
= 4х2 - 19х +12. УкалогГе координату точки М.
A. (0,75; 0)
Б. (4; 0)
B. (0; 4)
Г. (0; 0,75)
Решение. Точка Л/, координаты которой нужно найти,
является точкой пересечения параболы с осью абсцисс. Ордината
точки М равна 0, так как точка лежит на оси абсцисс. Абсциссу точки
Мможно найти из уравнения: 4х2 - 19х +12 = 0, х = 0,75 или х = 4.
Так как точка Af расположена на оси Ох левее другой точки
пересечения параболы с осью, то абсцисса точки М меньше
абсциссы другой точки пересечения: х = 0,75. Точка Мимеет координаты
(0,75; 0).
О т в е т: А.
Задание 2. График какой функции изображен на рисунке?
A. у = -х - 2
Ъ.у = 2-х
B. у = х-2
Г. у = х + 2.
—
—
—
—
-4
-2
—
У
—
—
4
0
У"
—
—
—
—
—
—
X
4 *
_—
Решение. 1-й способ. Прямая, являющаяся графиком
функции, проходит через точки с координатами (2; 0) и (0; 2).
Подставим эти координаты в общее уравнение прямой у = кх + Ъ\
[b = 2.
Получим уравнение прямой у = -х + 2.
ТЕМА 5. КООРДИНАТЫ И ГРАФИКИ 71 |
2-й способ. Точки лежат на прямой, значит их координаты (2; 0)
и (0; 2) удовлетворяют уравнению этой прямой. Можно проверить
принадлежность этих точек каждой из четырех прямых.
3-й способ. Прямая, изображенная на графике, получена
сдвигом прямой у = -х на две единицы вверх. Поэтому на графике —
прямая у = -х + 2.
Ответ: Б.
Задание 3. Прямая у = кх + Ъ пересекает ось Ох в точке (3; 0), а
ось Оу в точке (0; 9). Запишите уравнение этой прямой. Проходит
ли эта прямая через точку (-1; П)?
Решение. Если задана точка, лежащая на оси Оу, то
коэффициент Ь известен и равен ординате точки, т.е. Ъ = 9. Для того чтобы
найти коэффициент к, нужно подставить координаты точки (3; 0)
в уравнение у = кх + 9, к = -3.
Уравнение прямой можно найти и другим способом. Прямая
проходит через две точки, поэтому их координаты (3; 0) и (0; 9)
удовлетворяют уравнению прямой:
9 = A; [b = 9.
Уравнение прямой у = -Зх + 9.
Прямая >> = -Зх + 9 не проходит через точку (-1; 11), так как ее
координаты не удовлетворяют уравнению прямой. Действительно,
И * -3(-1)+9.
Ответ: у = -Зх + 9. Прямая не проходит через точку (-1; 11).
Задание 4. Парабола с вершиной в точке (-1; 2) проходит через
точку с координатами (1; 8). В каких точках парабола пересекает
ось абсцисс?
Решение.
Уравнению параболы удовлетворяют координаты двух
заданных в условии точек:
■с, \2 = a-b + c, \2 = a-b + c, J7> = 3,
= 2b;
Точка (-1; 2) является вершиной параболы, значит по формуле
координат вершины параболы хп = - —, -1 = - —, b = 2а. Полу-
2а 2а
чили, что b = 2а = 3, значит а = 1,5.
Имеем b = 3, а = 1,5, коэффициент с найдем из второго уравнения
системы с = 3,5. Уравнение параболы имеет вид у = 1,5л2 + Зх + 3,5.
72
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Для того чтобы определить, в каких точках парабола пересекает
ось абсцисс, нужно решить уравнение 1,5^ + Зх + 3,5 = 0.
Дискриминант этого уравнения меньше нуля, поэтому уравнение
корней не имеет, следовательно, парабола не пересекает ось абсцисс.
Ответ: у = 1,5л2 + Зх + 3,5; пересечений с осью Ох нет.
Задание 5. При каком значении параметра к парабола
у = Ах2 + 12х + к касается оси абсцисс?
Решение. 1-й способ. Найдем абсциссу точки касания. Так
как касание возможно только в вершине, то найдем абсциссу вер-
b 12 3
шины:*в=-- = -у = --.
Вершина параболы лежит на оси абсцисс, поэтому ордината
вершины равна нулю: 0 = 4- (—у) +1 ^ * (- ~) + £• ОТСК)Да найдем к.
к = 9.
2-й способ. По условию парабола с осью абсцисс имеет только
одну общую точку. Это возможно только в том случае, если
дискриминант квадратного уравнения 4х2 + 12х + к = 0 равен нулю.
Так как D = 144 - \6к = 0, то к = 9.
Ответ: 9.
Задание 6. На рисунке изображен график функции
>> = х3 + х2-5х-5. Найдите координаты точек А, В, и С.
Решение. Точки А и В являются точками пересечения
графика функции с осью Ох. Для того чтобы найти их координаты,
решим уравнение:
х3 + х2 - 5х - 5 = 0, х2(х +1) - 5(х +1) = 0, (х2 - 5)(х +1) = 0.
ТЕМА 5. КООРДИНАТЫ И ГРАФИКИ
73
Решениями уравнения являются числа -V5, V5 и -1. Все эти числа
являются абсциссами точек пересечения графика функции с осью
Ох. Так как -V5 < -1, то точка В имеет координаты (-V5; 0),
точка А имеет координаты (-1; 0).
Координаты точки С найти проще: абсцисса равна нулю, а
ордината равна у(0) = -5.
Ответ: А (-1; 0), B(S; 0), С(0; -5).
Задание 7. Изобразите на координатной плоскости множество
точек, координаты которых удовлетворяют уравнению
Решение. Решением уравнения (\х\ + у)(ху-2) = 0 является
решение уравнения у = -\х\ или уравнения у = -. Точки,
координаты которых удовлетворяют уравнению (|х| + у)(ху - 2) = 0, лежат
на гиперболе у = -, на луче у = х, х Е[-оо; 0] и на луче у = -х,
хе[0; оо].
Ответ: Графиком является объединение гиперболы у = - и
графика функции у = -\х[
Задание 8. Графиком квадратичной функции у = ах2 + Ьх + с
является парабола с вершиной в точке А (-5; 9). Определите
знаки коэффициентов а, Ь, с, если а + Ь +с >0.
Решение. Запишем все условия. Так как вершина параболы
имеет координаты (-5; 9), то верно, что -5 = - —, Юа = Ь, т.е.
коэффициенты аи b имеют один и тот же знак. Имеем следующие
условия:
1) а и Ъ одного знака, т.е. возможны только два случая о>0и
Ъ > 0 или а < 0 и Ъ < 0;
2) а + Ъ + с > 0.
Изобразим схематически графики.
74
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
-5.
У
1) Для первого случая у > 9, значит с > 9, значит коэффициент
с> 0.
2) Во втором случае, так как .у < 9, значит и с < 9, значит
коэффициент с может быть или отрицательным, или положительным.
Если с < 0, то неравенство а + b + с>0 неверное, значит с > 0.
Получаем, что л < 0, Ь < 0, с > 0.
Ответ: Возможны два случая: д >0, й >0, с >0 или а < 0, 6 < 0,
с> 0.
Замечание. Если заметить, что для любых чисел а, 6, с,
являющихся коэффициентами квадратичной функции f(x) = ах2 + bx+c,
а + Ь + с =/(1), то задание № 8 можно решить проще. Так как по
условию а + Ь + с > 0, тоД1) > 0. Это означает, что точка графика
с координатами (1;/(1)) лежит в первой четверти, поэтому с > 0.
Задание 9. Прямая х = 2 — ось симметрии параболы у = ах2 +
+ (а2 + 4)х - 4, ветви которой направлены вниз. Найдите
координаты вершины параболы.
Решение. Так как, по условию, ветви параболы направлены
вниз, то старший коэффициент а < 0. Так как прямая х = 2 — ось
симметрии параболы, то абсцисса вершины равна 2. Найдем
ординату вершины, для этого подставим в уравнение параболы х = 2.
Получим у = 4а +(а2 + 4)2 - 4, у = 2а2 + 4а + 4.
Ордината выражена через параметр а. Найдем его. Известна
формула, связывающая абсциссу вершины параболы и
коэффициенты квадратного трехчлена:
хь = - ^, 2 = - ^, 4а = -а2 - 4, а2 + 4а + 4 = 0, а = - 2.
Подставим найденное значение параметра в выражение для
ординаты вершины, получим >>=8-8 + 4, у = 4.
Получаем, что вершина параболы имеет координаты (2; 4).
Ответ: (2; 4).
ТЕМА 5 КООРДИНАТЫ И ГРАФИКИ 75
Задание 10. Прямая, параллельная прямой у = -4х, касается
параболы у = х2 - 2. Вычислите координаты точки касания.
Р е ш е н ие. С помощью условия параллельности прямой у = -4х
и касательной к параболе получим, что уравнение касательной
имеет вид у = -4х + Ъ.
Касательная к параболе и парабола имеют одну общую точку,
следовательно, система уравнений должна иметь единственное
решение:
[у = -4х + Ь, (у = -4х + Ь, \у = -4х + Ь,
[у = х2 - 2; [х2 - 2 = -4х + /
Второе уравнение системы имеет единственное решение, когда
его дискриминант равен нулю 24 + 4Ъ = 0, Ъ = -6.
Уравнение касательной к параболе имеет вид у = -4х - 6.
Найдем координаты точки касания:
• = -4х - 6, [у = -4х - 6, \у = -4х - 6, \х = -2,
'I 'I ' L-'
Ответ: (-2; 2).
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЧАСТЫ
1. Установите соответствие между функциями и их
графиками. Функции заданы формулами:
—4
а) у = —; б) у = -4х2 - х; в) у = -4х - 1.
1) парабола; 2) гипербола; 3) прямая.
2. Графику функции у = — принадлежит точка
А. (0; 1) Б. (10; -2) В. (-10; 0,2) Г. (25; -\)
3. Графику функции у = - принадлежит точка
А. (0; 3) Б. (-10; 0,3) В. (-10; -0,3) Г. (18; 1-)
4. Графику функции у = - - принадлежит точка
А. (0; -7) Б. (49; \) В. (-10; 0,7) Г. (14; 2)
5. В каких координатных четвертях расположен график
к
функции у = -, если ему принадлежит точка (-2; -5)?
А. III Б. I и III В. 1и1Г Г. III и IV
76
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
6. В каких координатных четвертях расположен график
к
функции у = -, если ему принадлежит точка (-5; 2)?
А. III Б. II и III В. II и IV Г. I и IV
7. В каких координатных четвертях расположен график
функции у = -, если ему принадлежит точка (2; -5)?
АЛ Б. I и IV В. II и IV
Г. III и IV
8. По графику квадратичной функции у = ах2 + Ьх + с
определите знаки коэффициентов аи с.
А. д < 0 и с < О
Б. о < 0 и с > О
В.о>0ис<0
Г.о>0ис>0
\
9. По графику квадратичной функции у = ах2 + Ьх + с
определите знаки коэффициентов а и с.
А. а < 0 и с < О
Б. о < 0 и с > О
В.о>0ис<0
Г.а>0ис>0
У
\
i
)
/ *
10. На каком из рисунков изображен график квадратичной
функции у = ах2 + Ьх + с, если известно, что а < 0 и квадратный
трехчлен имеет корни разных знаков?
\
L
Б.
у'
Г
I
\
\
X
в.
У'
1 \\
г.
I \
ТЕМА 5. КООРДИНАТЫ И ГРАФИКИ
77
11. На рисунке изображена парабола. Графиком какой из
функций она является?
А. у = (х + 2)2
Б.у = х2-2
Ъ.у = (х-2)2
Г. у = (х + 2)2 + 2
-2
12. Установите соответствие между функциями и их графиками.
\)у = -; 2)у = 2х2; 3)у = х-2; 4)у = 2х.
А. Б.
-4
\
\
\
-2
ч
4 1 Т
2 /
/
0
-2
-4
2
4
В.
-4
/
-2
/
/
4
2
0
-2
-4
/
/
2
/
/
4*
-2
\
\
\
\
2
0
-2
-4
2
4
Г.
-4
А
-2
у
/
1
1
4
у
/
0
-2
-4
/
/
/
2
4 '
Ответ:
78
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
13. По графику линейной функции у = кх + Ъ определите
знаки коэффициентов к и Ь.
A. к < О и Ь< О
Б. к<0и Ь>0
B. к>0иЬ<0
Г. к>0иЬ>0
14. По графику линейной функции у = кх + Ъ определите
знаки коэффициентов к и Ь.
A. А;<0ий<0
Б. А;<0и6>0
B. к>0иЬ<0
Г. к> Ои Ь> О
15. При каком значении параметра а прямая у = а-А-(а
проходит через начало координат?
А. -2 Б. 4 В. -6 Г. О
16. При каком значении параметра а прямая у = а + 6-(а + \)х
проходит через начало координат?
А. -1 Б. -5 В. -6 Г. О
17. Графики функций у = 5х -7 и у = 2х-1 пересекаются в
точке
А. (2; 3) Б. (-2; 3) В. (3; -2) Г. (-3; -2)
18. Графики функций у = 12х -5 и у = 3х + 4 пересекаются
в точке
А. (-7;1) Б. (7; -1) В. (1; 7) Г. (7; 1)
19. На рисунке изображен график функции у = х2-Зх-4.
Укажите координату точки М.
A. (0;-1)
Б. (0; 1)
B. (1;6)
ТЕМА 5. КООРДИНАТЫ И ГРАФИКИ
79
ЧАСТЬ II
Задания на 2 балла
20. Прямая у = кх + Ъ пересекает ось Ох в точке (-2; 0), а ось
Оу в точке (0; 6). Запишите уравнение этой прямой. Проходит ли
эта прямая через точку (1; 9)?
21. Прямая у = кх + b пересекает ось Ох в точке (4; 0), а ось Оу
в точке с ординатой -1. Запишите уравнение этой прямой. В
какой координатной четверти нет точек этой прямой?
22. По графику квадратичной функции у = ах2 + bx+с
определите знаки коэффициентов af b, с.
23. По графику квадратичной функции у = ах2 + Ьх + с
определите знаки коэффициентов а, Ь, с.
х J
24. При каком* значении к парабола у = 2х2 + 3х л-к касается
оси абсцисс?
25. При каком значении т парабола у = 2х2 - 4х + т касается
оси абсцисс?
26. При каком значении к парабола у = -5х2 + 4х + к касается
оси абсцисс? Найдите точку касания.
27. При каком значении к парабола у = 4х2 +кх + 9 касается
оси абсцисс?
28. Проходят ли через одну точку прямые у = 8-2х, у = 2х,
у = Зх-2.
Задания на 4 балла
29. Найдите уравнение прямой, параллельной прямой у = Зх и
проходящей через точку А (2; -2).
80
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
30. Найдите уравнение прямой, параллельной прямой у = 2х и
проходящей через точку А (-2; 5).
31. Прямая у = кх + Ь проходит через точки (-3; -2) и (1; 2).
Запишите уравнение этой прямой. В каких точках прямая
пересекает оси координат?
32. Парабола с вершиной в точке (1; 2) проходит через точку с
координатами (-2; -1). В каких точках парабола пересекает ось
абсцисс?
33. Парабола с вершиной в точке (3; 2) проходит через точку с
координатами (6; -1). В каких точках парабола пересекает ось
абсцисс?
34. На рисунке изображен график функции у = хъ + х2 — х — 1.
Найдите координаты точек А, В, и С.
35. На рисунке изображен график функции у = х3 + х2 - Зх - 3.
Найдите координаты точек А, В, Си D.
ТЕМА 5. КООРДИНАТЫ И ГРАФИКИ 81
36. Используя графики, определите число решений системы
[х2 + у2 = 8.
37. Используя графики, определите число решений системы
[х2 + у2 = 4.
38. Используя графики, определите число решений системы
[х2 + у* = 49.
39. Используя графики, определите число решений системы
ix = y2-2y,
40. Используя графики, определите число решений системы
\х = у2-12у+ 36,
[х2 + у2 = 4.
41. Используя графики, определите число решений системы
\х = 4у2-16,
\х2 + у2 = 100.
Задания на 6 баллов
42. Графиком квадратичной функции у = ах2 + Ьх + с является
парабола с вершиной в точке А (3; -7). Определите знаки
коэффициентов а, Ь, с, если у(0) > 0.
43. Графиком квадратичной функции у = ах2 + Ьх + с является
парабола с вершиной в точке А (2; 8). Определите знаки
коэффициентов а, Ь, с, если а - Ъ + с > 0.
44. Прямая, параллельная прямой у = 4х, касается параболы
у = х2 +3. Вычислите координаты точки касания.
45. Прямая, параллельная прямой у = -6х, касается параболы
у = -х2 + 2. Вычислите координаты точки касания.
46. Прямая х = 1 — ось симметрии параболы
у = ах2 + (л2 - 8 )х + 2,
ветви которой направлены вверх. Найдите координаты вершины
параболы.
I 82 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
47. Прямая х = 2 — ось симметрии параболы
у = ах2 + (а2+4)х + 2,
ветви которой направлены вниз. Найдите координаты вершины
параболы.
48. Прямая х = -1 — ось симметрии параболы
у = ах2 + (а2 - 8)х + 2,
ветви которой направлены вниз. Найдите координаты вершины
параболы.
49. Изобразите на координатной плоскости множество точек,
координаты которых удовлетворяют уравнению
(2х + у)(ху-2) = 0.
50. Изобразите на координатной плоскости множество точек,
координаты которых удовлетворяют уравнению
51. Изобразите на координатной плоскости множество точек,
координаты которых удовлетворяют уравнению
4х2 + 4ху + у2-1 =0.
52. Изобразите на координатной плоскости множество точек,
координаты которых удовлетворяют уравнению (х2 + у2 - б)2 = 4.
Тема 6. Функции
В первой части экзаменационной работы чаще всего
представлены задания, проверяющие:
а) умение «считывать» свойства функции по ее графику;
б) умение анализировать графики, которые описывают
зависимость между величинами, например, между расстоянием и
временем, между объемом выполненной работы и временем и т.д.,
умение установить соответствие между графиком функции и ее
аналитическим заданием.
Во второй части работы практически во всех заданиях по этой
теме требуется сначала построить график функции, а затем его
исследовать и ответить на дополнительные вопросы.
Чаще всего в заданиях встречаются квадратичные, линейные
или кусочно-заданные функции.
ТЕМА 6. ФУНКЦИИ 83 I
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
D{y)—область определения функции у — множество, на
котором задается функция. При графическом способе задания
функции ее область определения может считываться по графику. Если
функция задана аналитически (формулой) и ее область
определения не указана, то это означает, что функция задается на
естественной области определения.
Е(у) — множество значений (область значений) функции у,
которые она принимает при всех значениях аргумента из ее области
определения. Проще всего находить множество значений
функции, если задан ее график. В этом случае надо спроектировать все
точки графика функции на ось Оу. Получившееся множество
точек будет множеством значений функции. Это множество может
задаваться конечным числом точек, состоять из одного или
нескольких промежутков.
Нули функции. Для функции f[x), заданной графически,— это
абсциссы точек, в которых график функции пересекает ось
абсцисс или касается ее. Чтобы найти нули функции, заданной
аналитически, надо решить уравнение Дх) = 0.
Функция Дх) возрастает на множестве X, если для любых х7 и х2
из множества X, таких что х7 < х2, выполняется неравенство
Axi) <ЛХ2)- Иными словами, функция называется возрастающей на
множестве X, если для любых двух значений аргумента из этого
множества большему значению аргумента соответствует большее
значение функции.
Функция fix) убывает на множестве X, если для любых х1 и х2 из
множества X, таких что х, < х2, выполняется неравенство Дх,) > fx2).
Иными словами, функция называется убывающей на множестве X,
если для любых двух значений аргумента из этого множества
большему значению аргумента соответствует меньшее значение функции.
Функция у = f{x) называется четной, если для любого х из
области определения функции выполняется равенство/-х) = f[x).
Свойство графика четной функции — симметричность
относительно оси ординат.
Функция у = fx) называется нечетной, если для любого х из
области определения функции выполняется равенство Л-х) = -Дх).
Свойство графика нечетной функции — симметричность
относительно начала координат.
Свойства линейной функции y = kx + b,kER,beR
1) Область определения: /)(у)=(-<»; +оо).
2) Область значений: Е(у) = (-оо ; + <»), если к * 0.
Е(у) = {Ь}, если к = 0.
84
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
3) Монотонность:
если к > О, то функция у возрастает на всей области
определения;
если к < О, то функция у убывает на всей области
определения.
ч
\ О
kx+b,
k<0
\ JQ
Свойства обратной пропорциональности у = -,Л * О
1) Область определения: Z) (у) = (-<»; 0)U(0; +<»).
2) Область значений: £(у)=(-оо; 0)U(0; +oo).
3) Монотонность:
если к > 0, то функция у убывает на промежутке (0; +<») и на
промежутке (-»; 0);
если Л < 0, то функция >> возрастает на промежутке (0; +<») и
на промежутке (-<»; 0).
4) Функция является нечетной.
щ
*—t
та
' I ■ >
Свойства дробно-рациональной функции у = j~,
Q\x)
где Р(х) и Q(x) — многочлены от х
1) Область определения D(y) — любые действительные х, не
обращающие знаменатель Q(x) в нуль.
2) Множество значений Е(у) зависит от конкретной функции.
ТЕМА 6. ФУНКЦИИ
85
Свойства квадратичной функции у = ах2 + Ъх + с
а Е R, Ь Е R, с Е R — коэффициенты, а * О
1) Область определения D(y)= (-<»; +<»).
2) График квадратного трехчлена — парабола с вершиной в
точке с абсциссой хь = -
2а9
направленная ветвями вверх, если а > 0;
направленная ветвями вниз, если а < 0.
3) Множество значений: Е{у)=\ув\ +<»), если а > 0;
Е(у)=(~°°', Ув\> если л ^ 0> Л ~ ордината вершины параболы.
у г Qx2+bx+$, a<0
Свойства функции у = л[х
1) Область определения D(y)=[Q; +oo).
2) Множество значений Е(у)=[0; +оо).
3) Монотонность: функция у возрастает на всей области
определения.
ЗАДАНИЯ ДЛЯ АКТИВНОГО ОБУЧЕНИЯ
(С КОММЕНТАРИЯМИ, РЕШЕНИЯМИ, ОТВЕТАМИ)
Задание 1. График описывает движение парусной яхты, которая
первую часть пути прошла под парусом. Спустив парус, она
продолжила движение.
1) Найдите скорость яхты «под парусом» и «без паруса»
(выразив ее в км/ч).
2) На каком расстоянии от начала движения находилась яхта
через 50 минут, через 2 часа?
3) Сколько эремени потребуется яхте на обратный путь, если
она будет двигаться с той же скоростью, что и на первом участке
«под парусом»?
86
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
А
-10
S, KM
50
40
30
20
10
0
/
10
у
20
/
30
/
40
/
50
60
——
70
.-—
80
90
100
no
/, мин
120*
Решение. 1) Под парусом яхта прошла 30 км за 60 минут, т.е.
за 1 час, значит ее скорость была v = - = 30 км/ч. Без паруса яхта
прошла 5 км за 60 минут, значит ее скорость была 5 км/ч.
Ответ: скорость яхты «под парусом» 30 км/ч, скорость яхты
«без паруса» 5 км/ч.
2) На графике найдем точку с абсциссой, равной 50. Найдем
ординату этой точки. Она равна 25. Получили, что за 50 минут
яхта пройдет 25 км. Аналогично, за 120 минут — 35 км.
О т в е т: за 50 минут яхта пройдет 25 км, за 120 минут — 35 км.
3) Обратный путь составляет 35 км. Скорость яхты 30 км/ч.
Найдем время обратного пути: / = - = — = - ч, что составляет
v 30 6
1 час 10 минут.
Ответ: 1 час 10 минут.
Задание 2. Функция задана графиком.
—i
f
Г
У/
4
0
jO..
s
4
/
/
X
ТЕМА 6. ФУНКЦИИ
87
Укажите: а) область определения функции;
б) область значений функции;
в) промежутки, на которых функция
принимает только положительные значения;
г) нули функции;
д) промежутки возрастания функции.
Решение, a) D(y)=(-4; 7). Для того чтобы найти область
определения функции, заданной графически, надо спроектировать
все точки графика на ось Ох. Полученный промежуток и будет
областью определения функции.
б) Ду)=(-2; 4). Для того чтобы найти множество значений
функции, заданной графически, надо спроектировать все точки
графика на ось Оу. Полученный промежуток и будет множеством
значений функции.
в) Надо найти те промежутки оси Ох, на которых график
функции расположен выше оси Ох. Положительные значения функция
принимает на промежутке (-3; 5) и на промежутке (5; 7). В точке
х = 5 функция обращается в нуль.
г) Надо найти те точки, в которых график функции пересекает
ось Ох или касается ее. Нулями функции будут 5 и -3.
д) Для определения промежутков возрастания функции можно
воспользоваться определением, но для того, чтобы прочитать
график, достаточно знать графическую интерпретацию возрастания
функции на промежутке: график функции «поднимается вверх».
Получаем, что функция возрастает на промежутке (-4;1] и на
промежутке [5; 7).
Задание 3. Используя график функции у = f(x), определите,
какое утверждение верно.
j А. Нулями функции
являются числа -7; -2; 4.
""Ц. Функция убывает на про-
I межутке [-2; +<»).
< 0 при -7 < х < 0.
88
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Решение. Нулями функции являются числа -7 и 4.
Л-2) = 6 * О, поэтому х = -2 не является нулем функции.
Л0)=5.
Функция принимает положительные значения(Дх) > 0), т.е.
график функции расположен выше оси абсцисс, при -7 < х < 4.
Функция возрастает на промежутке (-»; -2]. Функция убывает
на промежутке [-2; + оо).
Ответ: Б.
Задание 4. Постройте график функции у = -х + 2.
а) При каких значениях аргумента функция принимает
положительные значения?
б) Какова область ее значений?
в) Какие значения принимает функция, если -3 < х < 1,5?
г) Найдите координаты точки пересечения графика с осями.
Решение. Построим график функции и с помощью его
ответим на вопросы. Графиком линейной функции является прямая.
Для построения прямой достаточно знать координаты любых двух
точек, принадлежащих этой прямой. Найдем их.
X
У
-3
0
3
4
-2
у '
У
4
2
0
-2
-4
2
Ответим на вопросы:
а) Функция принимает положительные значения (у > 0).
Графически это можно определить следующим образом:
— выше оси абсцисс находится та часть прямой, ординаты
точек которой больше нуля;
— найдем абсциссы этих точек: (-3; +оо).
Ответ: (-3; +оо).
ТЕМА 6. ФУНКЦИИ
89
б) Функция может принимать любые значения, поэтому
область значений (-»; +оо).
Ответ: (-<»; +<»).
в) у(-3) = О, >>(1,5) = 3. Если -3 < х < 1,5, то 0 < у < 3.
Ответ: [0; 3].
г) Точка пересечения с осью абсцисс уже найдена: (-3; 0).
Точку пересечения с осью ординат найдем по графику: (0; 2).
Ответ: (-3; 0) — точка пересечения с осью абсцисс и (0; 2) —
точка пересечения с осью ординат.
Задание 5. Постройте график функции у = х2 - 6х + 5.
а) При каких значениях аргумента функция принимает
положительные значения?
б) Укажите наименьшее значение функции.
в) Какова область ее значений?
г) Найдите координаты точек пересечения графика с осью Ох.
д) Укажите промежутки возрастания и убывания функции.
е) Какие значения принимает функция, если 0 < х < 4?
Решение. Построим график функции у = х2 - 6х + 5.
Графиком квадратичной функции является парабола. Для ее построения
найдем координаты вершины параболы и точки пересечения с
осями координат.
хв = -— = 3, уъ = >>(3)= -4. Ветви параболы направлены вверх,
координаты вершины (3;-4).
Найдем точки пересечения с осями координат:
X
У
0
5
1
0
5
0
90
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
а) выше оси абсцисс (у > 0) находятся точки графика с
абсциссами больше 5 или меньше 1.
Ответ: (-«>; 1) и (5; +<»);
б) наименьшее значение функции у = -4 функция принимает
в своей вершине.
Ответ: -4 — наименьшее значение функции;
в) функция может принимать все значения, большие, чем
значение в своей вершине.
Ответ: [-4; +оо).
г) Точек пересечения с осью Ох две. Их координаты (1; 0) и
(5; 0).
Ответ: (1; 0) и (5; 0).
д) Правее абсциссы вершины функция возрастает, а левее —
убывает.
Ответ: промежуток возрастания функции [3; + оо),
промежуток убывания функции (-<»; 3].
е) Изобразим график функции у = х2 - 6х + 5, если 0 < х < 4.
-4
-2
У Т
\
\
2 1
0
-2
■А
\
\
2
\
/
4
X
Для того чтобы найти значения функции, можно найти
ординаты всех точек получившегося графика. Спроектируем точки
графика на ось ординат, получим отрезок [-4; 5].
Ответ: [-4; 5].
Замечание. Обратите внимание на то, что для нахождения
области значений недостаточно было найти значения функции на
концах промежутка [0; 4]: >>(0) = 5, у(4) = -3. Функция убывает на
промежутке [0; 3] и возрастает на промежутке [3; 4], поэтому на
промежутке [2; 4] принимает значения, меньшие -3.
ТЕМА 6. ФУНКЦИИ
91
jc2-9
Задание 6. Постройте график функции у = jr^-- Найдите ее
область значений.
Решение. После преобразований получим
Построим график линейной функции с выколотой точкой.
Графиком линейной функции является прямая. Для ее построения
найдем координаты двух точек, принадлежащих прямой.
X
У
0
-1
-3
0
Построим прямую и «выколем» точку, которая не принадлежит
прямой. Координаты этой точки (3; -2).
Областью значений функции являются два промежутка
(-оо;-2) и (-2;+оо).
Ответ: Область значений — множество всех чисел, кроме -2.
Задание 7. Постройте график функции
х2 + 2х-15, М<3
у = - -х + 3, х > 3
-Ах -24, х < -3.
а) При каких значениях аргумента функция принимает
положительные значения?
б) Какова область ее значений? Найдите значение функции при
х= 5.
92
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
в) При каких значениях х выполняется неравенство у < -12?
г) Найдите координаты точек пересечения графика с осью Ох и
осью Оу.
д) Укажите промежутки возрастания и убывания функции.
Решение. Построим график кусочно заданной функции.
Для этого на каждом из трех заданных интервалов построим
заданную на нем функцию.
1) На интервале -3<х<3 построим график функции
у = х2 + 2х -15. Графиком этой функции является парабола.
Найдем ее вершину. хв = -19ув= -16. Одна точка пересечения
графика с осью Ох (3; 0) принадлежит интервалу, другая — (-5; 0)
не принадлежит ему.
2) На интервале х > 3 построим график функции у = -х + 3.
Для построения прямой, являющейся графиком этой функции,
достаточно знать координаты двух точек.
X
У
4
-1
-2
3) На интервале х < -3 построим график функции у = - 4х - 24.
Для построения прямой, являющейся графиком этой функции,
достаточно знать координаты двух точек.
X
У
-4
-8
-6
\
|\
\
\
\
-4
\
\
\
\
\\
у
у
\
\
-2
/
i
0
-2
-4
-6
-8
2 14
/
/
/
/
/
/
-10 /
/
\
М I
16
4
S
ч
6
ч
8
ч
X
\
По графику ответим на дополнительные вопросы.
а) Функция принимает положительные значения при х < -6.
ТЕМА 6. ФУНКЦИИ
93
б) Функция может принимать любые значения. Область
значений функции (-<»; +оо). Y(5) = -2.
в) у< -12 при -3<х<1, а также ординаты точек прямой
у = -х + 3 могут быть меньше или равны -12. Найдем абсциссы
этих точек: -х + 3 < -12, х > 15.
Ответ: на двух промежутках (-3; 1] и [15; +<»).
г) Точки пересечения графика функции с осью Ох: (-6; 0),
(3; 0).
Точка пересечения графика функции с осью Оу: (0; -15).
д) Функция возрастает при -1 < х < 3. Функция убывает на
промежутке (-»; -1] и на промежутке [3; +оо).
Задание 8. Постройте график функции >> = |х2 + 4х|. Сколько
общих точек может иметь с этим графиком прямая у = ml
Решение. Для построения графика функции «раскроем»
модуль. Преобразуем выражение под знаком модуля \х2 + 4х\ =
х(х + 4) > 0, если х < -4 или х > 0;
х(х + 4) < 0, если -4 < х < 0.
-х2 - 4х, если - 4 < х < 0,
если х > 0 или х < -4.
у = х2 + 4х
) ,
1-х2 - 4х,
[х2 + 4х,
Построим каждую из парабол на заданной области
определения.
-6
\
\
\
\
/
/
V
-4
-2
i
У
\
\
к
/[
4 I 1
2/
0
I
Прямая у = т может иметь с графиком этой функции две, три
или четыре общих точки, но может их и не иметь. Все будет зави-
94
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
сеть от расположения прямой. Для того чтобы определить
значения параметра т в каждом случае, надо «перемещать» прямую
у = т вдоль оси Оу и замечать количество пересечений графика
функции и прямой.
\|
\
1
-6
\
\
/
/
V
-4
-2
yi
\
4 I
/
/
21
V
0
(
У =
^ =
= m
= т
■• т
: т
Ответ: при т = 0 и т > 4 прямая у = т может иметь с
графиком функции две общие точки. При т = 4 < 4 прямая >> = /и может
иметь с графиком функции три общие точки. При 0 < т <4 прямая
у = т может иметь с графиком функции четыре общие точки. При
т < 0 прямая у = т не имеет с графиком функции общих точек.
Задание 9. Задайте аналитически функцию, график которой
изображен на рисунке.
\
-4
\
\
\
\
\
i
4
2
0
-2
-4
2
6
8
X
ТЕМА 6. ФУНКЦИИ 9Б
Решение. График заданной кусочной функции состоит из
трех прямых, заданных на своих интервалах. Зададим
аналитически каждую из прямых.
1) На интервале -4 < х < О прямая проходит через точки с
координатами (-4; 4) и (-2; 0). Уравнение прямой у = кх + Ь. Найдем
коэффициенты к и Ь, решив систему уравнений
(к = -2,
\
Уравнение прямой на этом интервале имеет вид у - -2х - 4.
2) На интервале 0 < х < 8 прямая проходит через точки с
координатами (0; -4) и (4; -1). Аналогично первому интервалу,
получим у = 0,75х - 4.
3) На интервале х > 8 прямая проходит через точки с
координатами (8; 2) и (9; 2). Уравнение прямой имеет вид у = 2.
Зададим функцию, изображенную на рисунке:
У =
-2х-4, -4<х<0,
0,75х - 4, 0 < х < 8,
2,х>8.
Замечание. Если задана кусочная функция, то концы областей
определения включаются только в один из. интервалов, причем не
имеет значения в какой.
Задание 10. Найдите область определения следующих
функций, заданных аналитически:
a)^ = V6x-x2-8; б) у = ^.
Решение, а) Областью определения функции у = 4х является
промежуток [0; +оо), поэтому область определения функции
у = \1бх-х2 -8 можно найти из неравенства 6х - х1 - 8 > 0,
л^-бх + в^О, 2<х<4.
Ответ-: [2; 4].
б) Областью определения дробно-рациональной функции
у = -^ являются любые действительные х, не обращающие зна-
менатель Q(x) в нуль. Поэтому областью определения функции
у = -у—- являются все действительные числа, кроме корней
уравнения х2 - 9 = 0: х = 3 или х = -3.
Обратите внимание на то, что сокращение дроби на общий
множитель привело бы к неверному ответу.
Ответ: (-»; -3)U(-3; 3)U(3; +«>).
96
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Задание 11. Найдите множество значений следующих
функций, заданных аналитически: а) у=х2- 4х + 3, б) у=4х2 + 8х + 10.
Решение, а) Графиком данной функции является парабола.
Абсцисса вершины параболы хл =-— = - = 2. Ордината
вершины ув= у(2) = -1. Ветви параболы направлены вверх, так как
старший коэффициент больше нуля (1 > 0). Функция может
принимать все значения, большие или равные -1. Множество значений
данной функции — промежуток [-1; +оо).
Ответ: [-1; +оо).
б) Находить множество значений квадратичной функции
можно и иначе: преобразовать квадратный трехчлен, выделив полный
квадрат: 4х2 + 8х + 10 =(2х + 2)2 + 6. Е((2х + 2)2) = [0; +оо), Е((2х +
+ 2)2 + 6) = [6; +оо). функция >> = 4х2 + 8х+ 10 принимает все
значения из промежутка [6; + оо).
Ответ: [6; + оо).
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЧАСТЫ
1. Функция задана графиком.
а) Укажите область определения этой функции.
А. (-оо;+оо) Б. [2; 4] В. [-2; +оо] Г. (-oo;2)U(4; +»)
ТЕМА 6. ФУНКЦИИ
97
б) Укажите область значений этой функции.
А. (-оо; +оо) Б. [2; 4] В. [-2; + оо] Г. (-оо; 2)U(4; + oo)
2. Функция задана графиком.
а) Укажите область определения этой функции.
А. [-2; 5] Б. (3; 1) В. (-1; 8) Г. [0; 8)
б) Укажите область значений этой функции.
А. [-2; 5] Б. (3; 1) В. (-1; 8) Г. [0; 8)
3. Используя график функции у = f(x), определите, какое
утверждение верно.
-4
-2
/
/
/
/
У*
/
/
4
2
0
-2
-4
\
\
2 \
\
\
\
\
= 0.
Б. Функция убывает на промежутке (0; +<»).
В. Наибольшее значение функция принимает при х = 3.
4. На рисунке изображен график функции у=А*)- Из
приведенных утверждений выберите верное.
98
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
\
\
\
\
—
\
-2
-/.
У*
1
/
4
2
0
-2
-4
^^
2
4 J
А. Наименьшее значение функции y=f(x) равно -2.
Б. Функция возрастает на промежутке [-2; +»).
В.Д-1)>Л-4).
Г./х) < 0 при х< 0.
5. Лифт поднимался со второго этажа и останавливался на
требуемых этажах.
1) На высоте какого этажа окажется лифт через 12 секунд от
начала движения?
Ответ:
этаж
у
-1
12
II
10
9
8
У
6
5
4
3
2
0
^^
2
3
*^
4
^^
5
6
7
8
9
10
11
12
13
*^-
14
15
-^
16
17
се
18
19 W
2) На сколько этажей поднялся лифт за все время движения?
Ответ:
3) Какова скорость дифта, если высота этажа 3 метра?
Ответ:
ТЕМА 6. ФУНКЦИИ 99
4) Между какими этажами будет лифт через 14 секунд?
Ответ:
6. Грузовая машина отправилась из магазина на склад и
вернулась обратно. На складе под загрузкой она провела 2 часа. График
описывает зависимость пройденного машиной пути (s, км/ч) от
времени пути (t, мин).
S, КМ
50
J
/
/
20
/
/
Г
40
60
80
100
120
140
160
ч
N
180
\
200
\
220
W
/, мин
1) Найдите скорость машины при движении из магазина на
склад и обратно.
Ответ:
2) На сколько минут больше потребовалось машине на
обратную дорогу?
Ответ:
3) Сколько километров прошла машина через 2 часа 40 минут?
Ответ:
7. Мяч подбросили вертикально вверх, и он упал на землю и
отскочил. На рисунке изображен график зависимости высоты, на
которой находился мяч, от времени его полета. Какой путь
пройдет мяч за 3,5 секунды? Через сколько секунд мяч будет на
расстоянии 1 метр от земли?
V
3 3,5
t, сек
Ответ:
1ОО РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
ЧАСТЬ II
Задания на 2 балла
8. Постройте график функции у = - - + 4. Какие значения она
принимает при 0 < х < 6 ?
9. Постройте график функции у = -0,2х -1. Какие значения
она принимает при 2 < х < 5 ?
10. Постройте график функции у = 2х + 5. Какие значения она
принимает при -2 < х < 1 ?
11. Постройте график функции у = —^. Какие значения она
принимает при -1 < х < 4?
12. Постройте график функции у = (х - З)2 - 2. Укажите ее
область значений.
JC2+JC
13. Постройте график функции у = . Укажите ее область
значений.
14. Постройте график функции у = Ъх2 - х + 5. Какие значения
принимает функция, если 1 < х < 2 ?
15. Постройте график функции >> = -Ах1 + 5х - 8. Какие
значения принимает функция, если 2 < х < 3 ?
16. Постройте график функции >> = -х2 + 6х - 1. Какие
значения принимает функция, если 0 < х < 4 ?
Задания на 4 балла
17. Постройте график функции f(x) = (х + 1)2 + (х -З)2.
Укажите ее область значений.
jc4-4
18. Постройте график функции у = -j^w- При каких значениях
аргумента функция принимает положительные значения?
19. Построит*
чений функции.
х2-9
20. Постройте график функции у = -—. При каких значениях
аргумента выполняется неравенство у > 3 ?
2jc2+jc-10
21. Постройте график функции у = —-у—j--. Найдите ее
область значений.
jc4-4
19. Постройте график функции у = —-у. Найдите область зна-
ТЕМА 6. ФУНКЦИИ 1О1
22. Постройте график функции f(x) = \
При каких значениях х значения функции у = /(х)
неотрицательны?
{2-х2, |х|< I
2\х\- I, рс| > I.
Укажите промежутки возрастания функции у =f(x).
24. Постройте график функции f(x) =х + 7,х<-2
х - 5, х > 2.
Укажите промежуток, на котором функция у =f(x) убывает.
3,х>2
25. Постройте график функции f(x) =
Найдите значение функции у = f{x) при х = 10.
Задания на 6 баллов
26. Постройте график функции
[х2 +1, если х > 0
[-Х2 - 2х +1, если х < 0
При каких значениях х выполняется неравенство ^ > 1?
27. Задайте аналитически функцию, график которой
изображен на рисунке.
-8
•
/
/
/
/
-4
\
\
-2
У i
\
i
б
4
2
0
-2
/
/
2
1O2
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
28. Задайте аналитически функцию, график которой
изображен на рисунке.
\
\
\
-4
\
\
-2
\
\
У*
I
/
/
i
4
7
У
1
-2
-4
/
/
2
« х
29. Постройте график функции у = \х2 - 4х|. При каких
значениях т прямая у = т имеет с графиком этой функции четыре
общие точки?
30. Постройте график функции у = х2 - 8|х|. Сколько общих
точек с графиком функции может иметь прямая у - пР.
Тема 7. Арифметическая
и геометрическая прогрессии
В школьном курсе алгебры изучается арифметическая и
геометрическая прогрессии. В первой части экзаменационной
работы обычно представлены задачи, решаемые либо с помощью
формулы л-ого члена прогрессии, либо с помощью формулы
суммы «-первых членов прогрессии. Эти формулы надо знать
наизусть.
Во второй части экзаменационной работы предлагаются
задания, требующие применения рекуррентных формул,
характеристического свойства прогрессий, а также задания, решение
которых сводится к решению уравнений и их систем, неравенств и их
систем.
ТЕМА 7. АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
ЮЗ
Определение
Рекуррентная формула
Формула
л-ого члена
Характеристическое
свойство
Сумма
л-первых
членов
Арифметическая
прогрессия
Арифметической
прогрессией (ап) называется
последовательность, каждый член
которой, начиная со
второго, равен предыдущему
члену, сложенному с одним и
тем же числом d (d —
разность прогрессии) .
Для любого
натурального п
<>n+i=an+d (1)
ап = ах + d(n - 1)
(2)
а„-ап-1 + а"+\п> 1 (3)
Эп-а>\пп-п (4)
Sn = 2a^(n-l).n (5)
Геометрическая
прогрессия
Геометрической
прогрессией (Ьп) называется
последовательность
отличных от нуля чисел,
каждый член которой,
начиная со второго, равен
предыдущему члену,
умноженному на одно и то
же число q (q
—знаменатель прогрессии).
Для любого
натурального п
bn+l = bn-q,bn*O (6)
(7)
bl = K_x • *я+1, п > 1 (8)
^ = ^fA,,*l (9)
Зп-Ь?—j,q*\ (10)
q-\
ЗАДАНИЯ ДЛЯ АКТИВНОГО ОБУЧЕНИЯ
(С КОММЕНТАРИЯМИ, РЕШЕНИЯМИ, ОТВЕТАМИ)
Формула л-ого члена
Арифметическая прогрессия
Задание 1. В арифметической прогрессии (ап) ах = -5, ^ = -7.
Найдите двадцать первый член этой прогрессии.
Решение.
По формуле я-ого члена (2) д^ = о, + d(2l -1) = ц + 20d. Так как
по условию пу =-5, то а2х =-5 + 2(W. Осталось найти разность
прогрессии:
d^c^-a^ т.е. d = -7 - (-5) = -2.
а2] =-5+ 20-(-2) = -45.
Ответ: а21 = -45.
104 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Задание 2. Какое число не является членом арифметической
прогрессии 4; 7; 10; ...?
А. 28 Б. 64 В. 95 Г. 127
Решение.
Запишем формулу я-ого члена: ап = я, + d(n -1). В исходной
прогрессии я, = 4, d = 7 - 4 = 3, поэтому я„ = 4 + 3(л -1) = Ъп +1.
Проверим: является ли число 28 членом исходной прогрессии.
Для этого решим уравнение 28 = Ъп +1. Получаем, что п = 9, т.е.
28 — девятый член прогрессии (сц = 28).
Проверим: является ли число 64 членом исходной прогрессии.
Для этого решим уравнение 64 = Ъп +1. Получаем, что п = 21, т.е.
64 — двадцать первый член прогрессии (^ = 64).
Проверим: является ли число 95 членом исходной прогрессии.
94 1
Для этого решим уравнение 95 = Ъп +1. Получаем, что п = — = 31 -,
т.е. п — не натуральное число и число 95 не является членом
прогрессии.
Проверим: является ли число 127 членом исходной прогрессии.
Для этого решим уравнение 127 = Ъп +1. Получаем, что п = 42, т.е.
127 — сорок второй член прогрессии (я42 = 127).
Итак, только число 95 не является членом исходной
прогрессии. Правильный ответ под буквой «В». Эту букву и запишем в
ответ.
Ответ: В.
Задание 3. Бригада в январе изготовила 8 деталей, а в каждый
следующий месяц изготавливала на 7 деталей больше, чем в
предыдущий. Сколько деталей бригада изготовит через п месяцев?
Решение.
Так / как бригада каждый следующий месяц изготавливала на 7
деталей больше, чем в предыдущий, то мы имеем арифметическую
прогрессию с разностью 7. Первый член прогрессии равен 8.
Формула я-ого члена для данной прогрессии будет иметь вид
ап = 8 + 1(п -1), т.е. ап=7п +1.
Ответ: 7л+ 1.
Задание 4. Сколько отрицательных членов содержит
арифметическая прогрессия (ап): -18; -17,3; ...?
Решение.
Что требуется найти? Сколько членов прогрессии
отрицательны, т.е. требуется найти п.
Запишем формулу я-ого члена для данной прогрессии
ап = -18 + d(n -1). Как найти разность прогрессии?
d = a2-a] =-17,3-(-18) = 0,7.
ТЕМА 7. АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ 1O5
Подставим значение d в формулу л-ого члена:
ап = -18 + 0,7(я -1). При каких п члены прогрессии отрицательны?
Решим неравенство ап < 0.
-18 + 0,7(л-1)<0
-18,7 + 0,7л<0
In < 187
ж 26*
Значит, двадцать шестой член прогрессии — последний
отрицательный член прогрессии, а двадцать седьмой — первый
положительный член прогрессии.
В этом можно убедиться, используя формулу я-ого члена.
я26 =-18+ 0,7(26-1) = -18 + 0,7-25 = -18+ 17,5 = -0,5
О27 =-18 + 0,7(27-1) = -18+ 0,7-26 = -18+ 18,2 = 0,2
Ответ: 26.
Задание 5. Известно, что в арифметической прогрессии (яп)
а^+сц =-4, 02*д6 =-16. Найдите разность и первый член
прогрессии.
Решение. По условию известно, что
Га,+<%=-4,
[02-о6 =-16.
Чтобы решить систему уравнений, выразим каждый из членов
прогрессии через ах и d. Используем формулу я-ого члена для
«2» Д>> ав-
02 = Я, + d
сц = я, + 4df
а6 = я, + 5d
Подставим в систему:
{я, +я, +4rf = -4,
(a]+d)-(al+5d) = -\6.
Решим систему методом подстановки, для этого выразим из
первого уравнения я, и подставим во второе уравнение:
U=-2-2d,
{(-2 - Id + d){-2 -2d + 5d) = -16.
Решим второе уравнение системы — квадратное уравнение
относительно переменной d.
106 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
(-2-d)(-2 + ld) = -l6
4 + 2d-6d-3d2 = -l6
-3d2-4d + 20 = 0
4d-20 = 0
Его корни: 2 и -3-.
Система имеет два решения:
, или
ах = -6
Ответ
: ах = -6, d = 2; q = 4^, rf = -3^.
Геометрическая прогрессия
Задание 6. Найдите шестой член геометрической прогрессии
-2; 6;...
А. 243 Б. 336 В. 486 Г. 546
Решение.
1-й способ (с помощью формулы я-ого члена)
По формуле я-ого члена геометрической прогрессии (7)
Так как Ьх = -2, а? = ^ = -^ = -3, то Z>6 = -2-(-3)5 = 2-243 =
= 486. В ответе пишем букву «В».
2-й способ (с помощью рекуррентной формулы) ,
Так как знаменатель прогрессии равен -3, то
*3 = 6(-3) = -18
Z>4=-18-(-3) = 54
Ь5 = 54(-3) = -162
Ь6 =-162(-3) = 486
Ответ: В.
Задание 7. Между числами 2 и 32 вставьте такие три числа,
которые вместе с данными числами образуют геометрическую
прогрессию.
Решение.
Из условия задания имеем Ьх =2,Ь5 = 32. Следует найти b2, b3, bA.
ТЕМА 7. АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ 1O7
По формуле я-ого члена Ь5 = 6, • #4, т.е. 32 = 2 • <?4 и q* = 16. Для
знаменателя прогрессии две возможности: 1) # = 2; 2) # = -2.
В первом случае имеем геометрическую прогрессию 2; 4; 8;
16; 32.
Во втором: 2; -4; 8; -16; 32.
Ответ: 2; 4; 8; 16; 32 или 2; -4; 8; -16; 32.
Рекуррентная формула
Задание 8. Геометрическая прогрессия (Ьп) задана условиями:
Ьх = 4,Ьп+] = Ъп • 3. Найдите пятый член прогрессии.
Решение.
1-й способ (с помощью рекуррентной формулы)
По рекуррентной формуле имеем:
^ = Ар3 = 4-3 = 12
Z>3 = V 3 = 12-3 = 36
bA =63.3 = 36-3 = 108
65 =64-3 = 108-3 = 324
2-й способ (с помощью формулы п-ого члена)
Необходимо найти Ь5. Так как в геометрической прогрессии
q = -уЦ то # = 3. Формула л-ого члена имеет вид Ъп = 4 • З""1 и
65 =4-35"1 =4-81 = 324.
Ответ: 324.
Характеристическое свойство
Характеристическое свойство устанавливает связь между каждым
членом прогрессии, кроме первого, с предыдущим и последующим
членами (см. формулы (3) и (8).
Задание 9. В арифметической прогрессии (дп) а7\=3%,
я73=-128. Найдите семьдесят второй член этой прогрессии.
Решение.
Для арифметической прогрессии характеристическое свойство
имеет вид а,, = п~х я+1, п > 1, поэтому aj2 = 71 73. Подставим
известные данные.
38+(-128)
а = = —45
Ответ: -45.
Задание 10. В геометрической прогрессии (Ьп) Ь9=4п, 6П=413.
Найдите знаменатель и первый член этой прогрессии.
I 108 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Решение.
Так как заданы девятый и одиннадцатый члены прогрессии, то
можно найти десятый член прогрессии. Воспользуемся
характеристическим свойством: bl = bn_x • bn+].
Н0 |0
Тогда знаменатель прогрессии равен
Запишем формулу л-ого члена для десятого члена прогрессии
610 = Ьх • q\ т.е.
1) 412 = Ьх • 49 и Ьх = 412:49 = 412"9 = 43 = 64.
2) -412 = Ьх • (-4)9 и 6, = -412:(-4)9 = 412"9 = 43 =^ 64.
Ответ: знаменатель прогрессии равен 4 или (- 4); первый
член прогрессии равен 64.
Сумма л-первых членов
Задание 11. В арифметической прогрессии (ап) ап=Ъп- 4.
Найдите сумму шестнадцати первых членов.
Решение. Для нахождения суммы «-первых членов арифме-
а, + а
тической прогрессии используют две формулы Sn = п • п и
о 2аг+(1(п-\) „ -.
Sn - —-— п. Какую из них в данном случае удобнее
применять?
По условию известна формула л-ого члена исходной
прогрессии: ап = Ъп - 4. Можно найти сразу и о,, и а]6 без нахождения d.
Поэтому воспользуемся первой формулой.
где ах = 3 • 1 - 4 = -1, а о,6 = 3 • 16 - 4 = 44.
— 14-44
516 =—;р-16 = 43-8 = 344.
Ответ: 344.
Задание 12. Найдите сумму всех натуральных чисел, кратных 4
и не превосходящих 170.
Решение. Число а называют кратным числу />, если число а
делится на число Ъ.
ТЕМА 7. АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ 1O9
Первое число, кратное 4, — это само число 4. Найдем число,
кратное 4 и не превосходящее 170. Это число 168.
Итак, мы име£м арифметическую прогрессию (дп), в которой
а, = 4, ап = 168 и d = 4. Чтобы найти сумму всех натуральных
чисел, кратных 4 и не превосходящих 170, найдем значение п.
По формуле л-ого члена q, = а, + d(n -1) = 4 + Цп -1). С другой
стороны, ап = 168.
Решим уравнение
Ап = 168,
л = 42.
Значит, в искомой прогрессии сорок два члена.
4^42 = 172-21 = 3612.
Ответ: 3612.
Комбинированные задачи
Задание 13. Четыре числа образуют геометрическую
прогрессию. Если из этих чисел вычесть соответственно 1,2, 11, 44, то
получим четыре числа, образующих арифметическую прогрессию.
Найдите числа, образующие арифметическую прогрессию.
Решение.
Подобные задания являются одними из самых сложных
заданий на прогрессии, так как приходится применять формулы и
арифметической и геометрической прогрессий.
Пусть члены геометрической прогрессии имеют вид 6,, bxq, bxq2,
bxql. По условию задания числа Ъх - 1, bxq - 2, bxq2 -11, bxql - 44
являются последовательными членами арифметической прогрессии.
Применим характеристическое свойство арифметической
прогрессии, связывающее каждый член прогрессии (кроме первого) с
двумя «соседними» членами.
г
Упростим первое выражение (1).
(1) и ^2-п= ■* 2ЭД— (2)
=8
Упростим второе выражение (2).
11О РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
+ b]q = 24
2q + l) = 24 (2')
Из (Г) и (2') имеем: q = 3.
Тогда, например, из (Г), 6,(3-1)2 = 8, Ьх = 2.
Четыре числа, образующих геометрическую прогрессию: 2; 6;
18; 54.
Четыре числа, образующих арифметическую прогрессию: 1; 4;
7; 10.
Ответ: 1; 4; 7; 10.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
ЧАСТЫ
1. Найдите девятый член арифметической прогрессии 3; 7; ...
А. 33 Б. 34 В. 35 Г. 36
2. Найдите восьмой член арифметической прогрессии
ап=5-0,5п.
Ответ:
3. В арифметической прогрессии (ап) я, = -1, д2 = -3. Найдите
двенадцатый член этой прогрессии.
Ответ:
4. Какое число не является членом арифметической
прогрессии: 5; 8; 11;...?
А. 53 Б. 62 В. 82 Г. 95
5. Найдите шестой член геометрической прогрессии 128; 64;...
А. 2 Б. 4 В. 6 Г. 8
6. Найдите пятый член геометрической прогрессии Ъп =
= 2-3"-1.
Ответ:
7. Какое число не является членом геометрической
прогрессии: -; -; ...?
А. 8 Б. 12 В. 16 Г. 32
8. Найдите сумму девяти первых членов арифметической
прогрессии 4; 11; ...
А. 286 Б. 288 В. 290 Г. 292
9. Найдите сумму семи первых членов геометрической
прогрессии 4; 8; ...
Ответ:
ТЕМА 7. АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ 111
10. Ракета за первую секунду пролетела 300 метров. За
каждую следующую секунду ракета пролетала на 200 метров больше,
чем за предыдущую. Какое расстояние (в километрах) пролетела
ракета за шестую секунду?
Ответ:
11. Ракета за первую секунду пролетела 300 метров. За
каждую следующую секунду ракета пролетала на 200 метров больше,
чем за предыдущую. Какое расстояние (в метрах) пролетела ракета
за шесть секунд?
Ответ:
12. Поезд за первую минуту прошел 200 м. За каждую
следующую минуту поезд проходил на 100 метров больше, чем за
предыдущую. Какое расстояние (в метрах) прошел поезд за п минут?
А. 100л +200; Б. 100л +100; В. 200л +100; Г. 200л +200.
13. Найти шестой член последовательности, заданной
рекуррентным способом й, = 1, Ь2=\, bn+l=bn_x + Ъп (п > 2).
А. 5; Б. 6; В. 7; Г. 8.
14. Последовательность ап задана формулой ап=п2 - 2п -1.
Найдите номер члена последовательности, равного 7.
Ответ:
ЧАСТЬ II
Задания на 2 балла
15. Длины сторон треугольника ABC образуют
арифметическую прогрессию (ЛВ < АС < ВС). Периметр треугольника ABC
равен 36 см. Найдите длину стороны АС
16. В арифметической прогрессии (ап) известно, что а3=3,
а5 = 4. Найдите сумму семи первых членов прогрессии.
17. В геометрической прогрессии (Ьп) Ьх = 8, Ьъ = 24.
Найдите Ь5.
18. В арифметической прогрессии (ап) известно, что ап = 4,
д,4 = 16. Найдите тринадцатый член прогрессии.
19. Сколько отрицательных членов содержит арифметическая
прогрессия (ап): -16; -15,6...?
20. Дана арифметическая прогрессия: 3,3; 2,9... Сколько
положительных членов она содержит?
21. Найти шестой член арифметической прогрессии: ах\ а2\ 9,4;
я4; 11,6...
22. Между числами 3 и 48 вставьте такие три числа, которые
вместе с данными числами образуют арифметическую
прогрессию. В ответе запишите найденные три числа.
112 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
23. В геометрической прогрессии (Ьп) Ь7=5и, Ь$=5п. Найдите
первый член этой прогрессии.
Задания на 4 балла
24. Между числами 3 и 48 вставьте такие три числа, которые
вместе с данными числами образуют геометрическую прогрессию
25. Сумма второго, восьмого и одиннадцатого члена
арифметической прогрессии равна 69. Найдите седьмой член этой
прогрессии.
26. Дана арифметическая прогрессия: -2,8; -2,5 ... Укажите
наименьший по абсолютной величине член арифметической
прогрессии.
27. Дана арифметическая прогрессия: -2,8; -2,5 ... Укажите
наименьший положительный член арифметической прогрессии.
28. В геометрической прогрессии (Ьп ) известно, что 56 = 85,
q = -0,5. Найдите bj.
29. Известно, что в арифметической прогрессии (ап)
а\ + аъ = ~4, а4 • сц = 8. Найдите первый член прогрессии.
30. Найдите сумму отрицательных членов арифметической
прогрессии: -10; -9,8 ...?
31. На одной стороне угла от вершины отложены шесть равных
отрезков и через их концы (кроме вершины угла) проведены
параллельные прямые, пересекающие вторую сторону угла. Найдите
сумму длин всех параллельных отрезков, заключенных между
сторонами угла, если длина наименьшего из них равна 10 см.
32. Первый член геометрической прогрессии равен 4. Разность
между третьим и вторым ее членами равна 8. Найдите знаменатель
этой прогрессии, если известно, что прогрессия не содержит
равных членов.
33. Найдите сумму первых пяти членов геометрической
прогрессии, третий член которой равен 3, а пятый равен 27.
34. В геометрической прогрессии (Ьп) известно, что Ъп = 4,
6U = 16. Найдите шестнадцатый член прогрессии.
35. В арифметической прогрессии (ап) а34 = 54, а36 = 80.
Найдите разность прогрессии.
36. В возрастающей геометрической прогрессии (Ьп) известно,
что Ьх + ЬА = 27, Ь2- Ь3 = 72. Найдите четвертый член прогрессии.
37. Найдите сумму всех натуральных чисел, кратных 3 и не
превосходящих ПО.
38. Найдите сумму членов арифметической прогрессии с
двадцатого по двадцать восьмой включительно, если ап = 4п + 3.
ТЕМА 8. ТЕКСТОВЫЕ ЗАДАЧИ 113
39. Какое наибольшее число последовательных четных чисел,
начиная с 2, можно сложить, чтобы получившаяся сумма осталась
меньше ПО?
Задания на 6 баллов
40. Представьте в виде степени с натуральным показателем
41. Вычислите:
1+3+ЗЧ...+313
1+3+32+...+36*
42. Четыре числа образуют геометрическую прогрессию. Если
к ним прибавить соответственно 2, 5, 7 и 7, то получим четыре
числа, образующих арифметическую прогрессию. Найдите числа,
образующие геометрическую прогрессию.
43. Сумма утроенного второго и четвертого членов
арифметической прогрессии равна 12. При каком значении разности
прогрессии произведение третьего и пятого членов прогрессии будет
наименьшим?
44. Вычислите сумму 432 - 422 + 412 - 402 + ... + 22 -12.
45. Найдите сумму первых десяти совпадающих членов
арифметических прогрессий 3; 5; 7 ... и 8; 15; 22...
46. Сколько существует натуральных двузначных чисел,
которые делятся только на одно из чисел 3 или 4?
47. Найдите сумму всех четных двузначных чисел, кратных 3,
но не кратных 7.
48.Найдите сумму всех натуральных чисел, не превосходящих
150, которые при делении на 4 дают остаток 1.
49. Произведение пяти последовательных членов
геометрической прогрессии равно 243. Найдите третий член этой прогрессии.
Тема 8. Текстовые задачи
Среди задач, предлагаемых в первой части работы, могут быть
задачи на движение, на работу, на проценты, на части, задачи
геометрического содержания. В этих задачах может требоваться
решить задачу или выбрать среди предложенных уравнений (или
выражений) то, которое является математической моделью задачи. Те
задачи, которые требуется решить, могут решаться с помощью
составления уравнения (системы уравнений) или арифметически.
Во второй части работы предложены более сложные задачи,
например, задачи на движение по окружности, на концентрацию
и т.д.
114 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
ЗАДАНИЯ ДЛЯ АКТИВНОГО ОБУЧЕНИЯ
(С КОММЕНТАРИЯМИ, РЕШЕНИЯМИ, ОТВЕТАМИ)
Задачи на проценты
Процентом числа называется его сотая часть, например,
1% — это одна сотая числа, 1% от числа 500 — это число 5,
3% — это три сотых числа, 3% от числа 500 — это число 15.
Отсюда легко получаются соотношения, которые полезно
помнить:
50% числа х — это его половина (0,5 х);
числа х — это его четверть (0,25 х или -х);
числа х — это его пятая часть (0,2 х или -х);
75% числа х — это его три четверти (0,75 х или .х);
числа х — это все число (х).
Решение любых задач на проценты сводится к основным трем
действиям с процентами:
— нахождение процентов от числа
Пример. Найти 15% от числа 60.
0,15 -60 = 9.
Ответ: 9.
— нахождение числа по его процентам
Пример. Найти число, 12% которого равны 30.
12% искомого числа нам известны — это 30. Какое же это
число? Это число (х) принимаем за 100% и находим его из пропорции:
Ответ:
250.
12
Fob "
30
12% -
100%
х =
- 30
— х
30-100 _
~ п~ "
— нахождение процентного отношения чисел
Пример. Сколько процентов составляет 120 от 600?
120
600 100% = 20%.
Ответ:
Среди задач на проценты, предлагающихся на экзамене, можно
выделить несколько типов.
ТЕМА 8. ТЕКСТОВЫЕ ЗАДАЧИ 115
Задание 1. Спрос на товар увеличился в 5 раз. На сколько
процентов увеличился спрос?
А. 500% Б. 100% В. 200% Г. 400%
Решение. Первоначальный спрос на товар (а) составлял
100%. Спрос увеличился и стал 5а. Произошло увеличение на 4а.
Увеличение составило 400%.
Ответ: Г.
Задание 2. Объем товаров увеличился на 200%. Во сколько раз
произошло увеличение?
А. В 2 раза Б. В три раза В. В четыре раза Г. Вполовину
Решение. Первоначальный объем товаров (а) составлял
100%. Он увеличился и стал а + 2а = За. Произошло увеличение в
три раза, по сравнению с первоначальным объемом.
Ответ: Б.
Задание 3. Квартплата составляла 2000 рублей. Какой стала
квартплата после ее увеличения на 120%?
Решение. 2000 рублей составляют 100%,
х рублей составляет 120%.
Найдем из пропорции, какой стала квартплата после
увеличения: х = (2000 • 120) : 100 = 2400.
Ответ: 2400 рублей.
Задание 4. Магазин в первый день продал 40% имеющихся
овощей. За второй день он продал 80% овощей, проданных в первый
день. В третий день — оставшиеся 28 кг. Сколько килограммов
овощей было в магазине первоначально?
Р е ш е н ие. Обозначим за х (кг) — вес имевшихся в магазине
овощей. Тогда в первый день магазин продал 0,4л: (кг), а за второй
день — 0,8(0,4х) кг. Зная, что в третий день было продано 28 кг
овощей, составляем уравнение:
0,4-х + 0,8-(0,4-х) + 28 = х,
0,28 х = .28,
х= 100.
Ответ: 100 килограмм.
Задание 5. Цена изделия составляла 1000 рублей и была
снижена сначала на 10%, а затем еще на 20%. Какова окончательная
цена товара?
Решение. Подобные задачи, на наш взгляд, удобно решать с
помощью такой схемы рассуждений:
116
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
-10% -20%
1000 р.
-180 рч
1000 р.
1000-100=
I - 900 р.
900-180 =
- 720 р.
Первое снижение цены товара было на 0,1 1000 = 100 руб.
После первого снижения цена товара составила 1000 - 100 = 900 руб.
Второе снижение цены товара было на 0,2 • 900 =180 руб. После
второго снижения цена товара составила 900 - 180 = 720 руб.
Ответ: 720 рублей.
Задание 6. Цену товара повысили на 25%, затем новую цену
повысили еще на 10% и, наконец, после перерасчета произвели
повышение цены еще на 12%. На сколько процентов повысили
первоначальную цену товара?
Р е ш е н ие. Обозначим первоначальную цену товара за х (руб),
тогда после первого повышения цена товара стала — 1,25х. Второе
повышение цены было на 0,1 • 1,25х. После него цена товара
стала — 1,25* + 0,1 • 1,25* = 1,375*. Третье повышение цены на 12%
производилось от цены, полученной после второго повышения, и
составило 0,12 • 1,375х = 0,165х. После последнего повышения
цена товара составила 1,375х + 0,165 х = 1,54х
Схема рассуждений была следующей:
+25% +10% +12%
*+0,25* =
1,25*+
+0,125* =
= 1,375*
1,375*+
+0,165* =
= 1,54*
Осталось выяснить процент повышения первоначальной цены.
Цена была повышена на 1,54х - х = 0,54х рублей, что составляет
54% от первоначальной цены.
Ответ: 54%.
Задание 7. Сберегательный банк в конце года начисляет 3% к
сумме, находившейся на счету. На сколько рублей увеличится
первоначальный вклад в 1000 рублей через 2 года?
Решение. Эта задача на так называемые «сложные
проценты». Так говорят, когда в задаче идет речь о поэтапном изменении
некоторой величины. В данном случае рассмотрим два этапа — на
ТЕМА 8. ТЕКСТОВЫЕ ЗАДАЧИ 117 |
первом начисляется процент на сумму, находившуюся на счету
первый год, а на втором этапе производится начисление
процентов на сумму, получившуюся после первого этапа, т.е. на сумму с
уже начисленными процентами после первого года.
1000 рублей — первоначальная сумма вклада. Начисленные
проценты после первого года составят 0,03 • 1000. По окончании
первого года на счету окажется 1000 + 0,03 • 1000 = 1030. По
окончании второго года проценты составят 0,03 • 1030 = 30,9. Таким
образом, после двух лет сумма вклада составит ЮЗО+30,9 = 1060,9.
Первоначальный вклад был увеличен на 60,9 рублей.
Ответ: 60,9 рублей.
Задание 8. После истечения двух лет сумма банковского
вклада, положенного под 3% годовых, выросла на 304,5 рубля.
Найдите первоначальную сумму вклада.
Р е ш е н ие. Пусть А рублей — первоначальная сумма вклада.
Тогда через год сумма вклада составила А + 0,03 А = А(\ + 0,03) =
= 1,03-Л руб. За второй год проценты составили 0,03(1,03 А). Через
два года сумма вклада станет равной 1,03 Л + 0,03(1,03А) =
= 1,03-1,03-А Получаем уравнение:
1,03-1,03-Л=Л + 304,5,
0,0609vl = 304,5,
А = 5000.
Ответ: 5000 рублей.
Задачи на «концентрацию», на «смеси и сплавы»
В таких задачах часто встречаются понятия процентного
содержания или концентрации. Например, если в задаче идет речь о
девятипроцентном растворе уксуса, то можно понять, что в этом
растворе 9% чистого уксуса, а остальные 91% приходится на воду, с
которой смешивался чистый уксус. Также можно сказать, что 0,09
части составляет в этом растворе чистый уксус, а 0,91 части
приходится на воду. Понятно, что объем всего раствора принимается за
100% (или за 1).
В задачах этого типа обычно присутствуют три величины,
соотношение между которыми позволяет составлять уравнение:
— концентрация (доля чистого вещества в смеси);
— количество чистого вещества в смеси (или сплаве);
— масса смеси (сплава).
Соотношение между этими величинами следующее:
Масса смеси х концентрация = количество чистого вещества
I 118 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Задание 9. Сколько литров воды надо добавить к 20 литрам
пятипроцентного раствора соли, чтобы получить
четырехпроцентный раствор?
Решение. Соль содержится в каждом из растворов. В 20
литрах пятипроцентного раствора соли содержится 20 х 0,05 = I (ед)
соли. Ее количество не меняется. Доливается только вода.
Узнаем, каково ее количество.
Обозначим х (л) — количество добавленной воды. Из.условия
задачи получаем, что 4-процентную концентрацию раствора
характеризует уравнение —— = 0,04. Решением уравнения является
х = 5.
Ответ: 5 литров.
Задание 10. Имеются два куска сплава меди и цинка с
процентным содержанием меди 42% и 65% соответственно. В каком
отношении нужно взять эти сплавы, чтобы, переплавив, получить
сплав, содержащий 50% меди?
Решение. Изобразим схематически условие задачи:
концентрация 0,42
масса сплава х
количество меди
0,42л:
концентрация 0,65
масса сплава у
количество меди
0,65>>
концентрация 0,5
масса сплава х+у
количество меди
Количество меди в каждом сплаве найдено с помощью
соотношения (1). Можем составить уравнение: 0,42 х + 0,65 у = 0,5(х+у).
В этом уравнении две неизвестных, а в задаче требуется найти
их отношение -. Решая уравнение, получим 42 х + 65 у = 50(х+у),
\5у = 8х, х: у= 15:6.
Ответ: Нужно взять первый и второй сплавы в отношении
15 к 6.
Задачи на «движение»
Действие движения характеризуется тремя компонентами:
пройденный путь, скорость и время. Известно соотношение между
ними:
Путь = скорость х время
Задание И. Скорость велосипедиста от поселка до станции
была на 1 км/ч больше, чем на обратном пути. На обратный путь он
затратил на 2 минуты больше. Расстояние между пунктами 7 км.
Найдите первоначальную скорость велосипедиста.
ТЕМА 8. ТЕКСТОВЫЕ ЗАДАЧИ 119
Пусть х км/ч — скорость велосипедиста. Какое из уравнений
соответствует условию задачи?
А 7 -7- Х В 7 +7-2
jc+I jc 30 jc-I х
Б L_Z-1 г -1 7-i
i-l х~30 1 х
*~зо
Р е ш е н ие. Если х км/ч — скорость велосипедиста от поселка
до станции, то (х — 1) км/ч — скорость велосипедиста на обратном
пути. Время велосипедиста от поселка до станции -, а время
обратного движения ——. Так как время обратного движения на 2 мину-
/ 1 v * 7 7 1
ты (т.е. на — ч) больше, составим уравнение: —- — = —.
Ответ: Б.
Задание 12. Катер прошел 20 км по течению реки и такой же
путь обратно, затратив на весь путь 1 ч 45 мин. Скорость течения
реки равна 2 км/ч. Найдите время катера в пути.
Пусть х (км/ч) — собственная скорость катера. Какое из
уравнений соответствует условию задачи?
.20 1у|. п 20 20 7
А. —- = 1,45 В. —- + —- = -
х+2 х-2 х+2 4
Б^-^°_ = 145 Г -*-+ -*- = !
'х-2 х+2 ' '2-х 2+х 4
Решение. Скорость катера по течению (х+2) км/ч, а
против течения (х - 2) км/ч. Время движения катера по течению —-,
20 „ 20 20
а против течения —-. На весь путь катер потратил —- + —- или
1 ч 45 мин. Переведем 1 ч 45 мин в часы: 1 ч 45 мин = 1 + - = - (ч).
Уравнение под буквой В соответствует условию задачи.
Ответ: В.
Задание 13. Два тела, движущиеся в разные стороны по
окружности длиной 500 м с постоянными скоростями, встречаются
каждые 125 секунд. При движении в одну сторону первое догоняет
второе каждые 12,5 секунд. Найдите скорости каждого тела.
Р е ш е н ие. При движении в одном направлении время, через
которое одно тело догонит второе, можно найти по формуле:
. Пусть скорости тел равны х и у (м/с)> тогда получим первое
v2-v,
уравнение: = 125.
у-х
12O РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
При движении навстречу друг другу время, через которое тела
встретятся, можно найти по формуле: . Получим второе урав-
500 ,-_
нение: = 12,5.
у+х
Решением системы
*» = 125,
у-х
-^ = 12,5
у+х
является пара х = 18 (м/с) и
у = 22 (м/с).
Ответ: Скорость первого тела — 18 м/с, скорость второго —
22 м/с.
Задачи «на работу»
Работу характеризуют три компонента действия:
— время работы,
— объем работы,
— производительность (количество произведенной работы в
единицу времени).
Существует следующее соотношение между этими
компонентами:
Объем работы = время работы х производительность
Задание 14. Две копировальные машины печатают рукопись.
Если всю рукопись будет печатать первая машина, то работа будет
выполнена на 4 минуты позже, чем две машины, работая вместе.
Если печатать всю рукопись будет вторая машина, то она
напечатает на 25 минут позже, чем обе машины, работая вместе. За
сколько минут может напечатать эту рукопись вторая машина?
Решение. 1-й способ. Примем за единицу работу по печати
всей рукописи. Пусть время печати всей рукописи первой
машиной — х (мин.), а второй — у (мин.). Тогда производительность
первой машины -, производительность второй машины -, общая
х у
их производительность I - + -1. Получаем время их общей работы:
V УI
-<—J-. Можем составить два уравнения относительно времени работы:
у
х-4 =
у-25 =
' У
1
тгт
х у
у = 15 или у = 35,
у + 25 = ^-~'; 1х = -6илих = 14.
ТЕМА 8. ТЕКСТОВЫЕ ЗАДАЧИ
121
В соответствии с условиями задачи решение (-6; 15) является
посторонним. Вторая машина может напечатать рукопись за
35 минут.
2-й способ. Пусть время печати всей рукописи первой
машиной — х (мин.), а второй — у (мин.). Тогда время общей работы
двух машин можно найти двумя способами: х - 4 и у - 25.
Поэтому получим первое уравнение: х - 4 = у - 25.
Примем за единицу работу по печати всей рукописи.
Производительность первой машины — --, производительность второй
машины , общая их производительность
, Зная их общее
, -(и)
время работы (х - 4), можно составить второе уравнение
I —I— I • (х — 4) = 1. Решая систему
\х УI
У
получим, что вторая машина может напечатать рукопись за 35
минут.
Ответ: вторая машина может напечатать рукопись за 35
минут.
Задачи геометрического содержания
Задание 15. Балкон имеет форму прямоугольника. С двух
меньших сторон он утеплен одним слоем утеплителя, а с третьей
стороны — двумя слоями. Площадь всего балкона 8 м2. После утепления
балкон имеет размеры 3,6 м х 1,8 м. Какую толщину имеет слой
утеплителя? Выберите уравнение, соответствующее условию задачи.
A. 8 = (2х+ 3,6)(1,8 + х)
Б. 8 = (х + 3,6)(х + 1,8)
B. 8 = 3,6* + 1,8 х
Г. 8 = (2х+ 3,6)(2х+ 1,8)
и
3,6
1,8
Решение. Для нахождения площади прямоугольника
нужно найти произведение его длины и ширины. Если х (м) толщи-
122 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
на утеплителя, то длина прямоугольника 2х+3,6, а его ширина
2х + + 1,8. Можно составить уравнение: 8 = (2х+3,6)(2х+1,8).
Ответ: Г.
Другие задачи
(на составление уравнения, системы, отношения)
Задание 16. Из 42 поездов, приходящих на станцию, отношение
пассажирских к скорым поездам составляет 4:3. Сколько скорых
поездов приходит на станцию?
А. 7 поездов Б. 14 поездов В. 24 поезда Г. 18 поездов
Решение. Из всех поездов 4 части составляют пассажирские
поезда, а 3 части — скорые. Получаем, что из 7 частей
складывается число поездов, приходящих на станцию. На одну часть
приходится 42 : 7 = 6 поездов. Так как скорых — 3 части, то их 3 х 6 = 18
поездов.
0 т в е т: Г.
Задание 17. Два карандаша и три ластика были куплены за 45
рублей, а три карандаша и четыре ластика — за 65 рублей.
Сколько стоит один карандаш и один ластик?
Р е ш е н ие. 1-й способ — арифметический. 2 карандаша и 3
ластика стоят 45 руб., поэтому 6 карандашей и 9 ластиков стоят в три
раза дороже: 45 х 3 = 135 руб.
Так как 3 карандаша и 4 ластика стоят 65 руб., то 6 карандашей
и 8 ластиков стоят 65 х 2 = 130 руб.
6 карандашей и 9 ластиков стоят 135 рублей.
6 карандашей и 8 ластиков стоят 130 рублей.
1 ластик стоит 5 рублей.
„ 45-15 1С -
Получаем, что карандаш стоит —-— = 15 руб, а вместе они
стоят 20 рублей.
2-й способ — алгебраический. Пусть один карандаш стоит х
рублей, а один ластик у рублей, тогда составим систему уравнений по
условию задачи:
\2х + 3^ = 45, Г6х + 9>> = 135, (у = 5,
Один карандаш и один ластик стоят х+у= 15+5=20 (руб.)
Ответ: 20 рублей.
ТЕМА 8. ТЕКСТОВЫЕ ЗАДАЧИ 123 |
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЧАСТЫ
1. Цену товара повысили на 100%, а затем снизили на 50%.
Как изменится цена товара?
А. Не изменится В. Возрастет в половину
Б. Возрастет в 2 раза Г. Снизится на 25%
2. Цену товара повысили на 50%, а затем снизили на 50%.
Как изменится цена товара?
А. Не изменится В. Возрастет на треть
Б. Снизится на четверть Г. Снизится на треть
3. Некоторое число уменьшили на 20%. На сколько
процентов надо увеличить результат, чтобы получить первоначальное
число?
А. На 20% Б. На 25% В. На 50% Г. На 120%
4. Вкладчик положил в Сбербанк 10 000 рублей из расчета
1 % годойых. Каким будет его вклад через один год?
А. 10 001 Б. 10 010 В. 10 100 Г. 11 000
5. Сбербанк в конце года начисляет 4% годовых к сумме,
находящейся на счету в начале года. Каким станет первоначальный
вклад в 2500 рублей через один год?
А. 2504 Б. 2550 В. 2580 Г. 2600
6. На три полки поставили 278 книг. На первую из них
поставили на 14 книг больше, чем на вторую! На третью полку —
в 2 раза больше, чем на вторую. Сколько книг поставили на
первую полку?
А. 68 Б. 80 В. 132 Г. 70
7. На склад привезли 126 тонн яблок, груш и слив. Яблок
оказалось в 4 раза больше, чем груш. Слив на 18 тонн меньше, чем
груш. Сколько тонн яблок привезли на склад?
А. 6 Б. 24 В. 82 Г. 96
8. Скорость пешехода от поселка до станции, расстояние
между которыми 4 км, была на 1 км/ч больше, чем на обратном пути.
Время его обратного пути на 12 минут больше. Чему равны
скорости пешеходов?
Пусть х км/ч — скорость пешехода от поселка до станции.
Какое из уравнений соответствует условию задачи?
А.
Б.
4
jc+1
4
jc-1
4
X
4
1 X
_ 1
~ 5
_ 1
5
В.
Г.
X
4
jc-1
jc-1
4 _
JC
12
12
124 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
9. Скорость машины от поселка до Станции была на 20 км/ч
меньше, чем на обратном пути. Расстояние между пунктами
40 км, а время ее обратного пути на 10 минут меньше.
Пусть х км/ч — скорость машины от поселка до станции. Какое
из уравнений соответствует условию задачи?
4^ В.
х х+20 6 х
J10 40 _1 JfL-40-
+20~ х 6 ' х+20 х
10. Моторная лодка прошла по течению реки 15 км и вернулась
обратно, затратив на обратный путь на 40 минут больше. Скорость
течения реки 3 км/ч.
Пусть х км/ч — собственная скорость лодки. Какое из
уравнений соответствует условию задачи?
А _15 ^ = 2 BJ5 Я_ = 2
" х-Ъ х+3 ~~ 3 ' х+3 х-3 ~ 3
11. Катер прошел 3 км по течению реки на 30 минут быстрее,
чем 8 км против течения реки. Собственная скорость катера
15 км/ч.
Пусть х км/ч — скорость течения реки. Какое из уравнений
соответствует условию задачи?
12. Найдите периметр прямоугольного участка площадью
192 м2, одна из сторон которого больше другой на 4 м.
Ответ:
13. Найдите периметр прямоугольного участка площадью
91 м2, одна из сторон которого больше другой на 6 м.
Ответ:
14. Найдите периметр прямоугольного участка площадью
252 м2, одна из сторон которого больше другой на 4 м.
Ответ: ^
15. На одном и том же расстоянии от стен комнаты
прямоугольной формы площадью 24 м2, находится ковер размерами
3 м х 2 м. Каково расстояние от ковра до стен комнаты? Выберите
уравнение, соответствующее условию задачи
ТЕМА 8. ТЕКСТОВЫЕ ЗАДАЧИ
125
A. (2х + 2)(2х + 3) = 24
Б. (х+2)(х+3) = 24
B. 3(2х+2) = 24
Г. 2(х+3)(х+2) = 24
3
2
X
16. Численности рабочих, работающих в двух цехах завода,
относятся как 3 : 4. Сколько человек работает в меньшем цехе, если
всего на заводе работает 4900 рабочих?
Ответ:
17. Один за другим с интервалом в 20 минут из города выехали
в одном направлении два велосипедиста и встретились на
расстоянии 15 км от города. Скорость движения второго,
велосипедиста была на 1 км/ч больше скорости первого.
Пусть х км/ч — скорость движения первого велосипедиста.
Какое из уравнений соответствует условию задачи?
Б
х х+1 3
г 15 _ 15 = 1
# х+Т х 3
18. Две байдарки начали свое движение по озеру из одного
пункта с интервалом в 10 минут и встретились через 2 км.
Скорость движения первой байдарки была на 4 км/ч больше, чем
скорость второй. Найдите скорости байдарок.
Пусть х км/ч — скорость движения первой байдарки. Какое из
уравнений соответствует условию задачи?
.221 „ 2 2 ,Л
В.
X
2
х-
х-
4
4
2
X
6
1
6
Б-
х х-4
19. Две машины, работая одновременно, могут выполнить
некоторую работу за 5 дней. Первая машина может справиться с
этой работой на 24 дня быстрее второй. Какой объем работы
выполнит первая машина?
Пусть х дней — время работы первой машины. Какое из
уравнений соответствует условию задачи?
I R 1 1 1
5
х х+24
R 1
х х+24
х х-24 5
х-24 5
126 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
20. Две машины, работай одновременно, могут выполнить
некоторую работу за 8 минут. Вторая машина может справиться с
этой работой на 30 минут быстрее первой. Найдите время работы
второй машины.
Пусть х минут — время работы второй машины. Какое из
уравнений соответствует условию задачи?
А I + _L_ = l в Il l
' 30 8
+ в =
х х-30 8 х х+30 8
Б 1 + _^ = 1 г I !_ = 1
х х+30 8 х х-30 8
21. Две машинистки, работая одновременно, могут выполнить
некоторую работу за 6 часов. Вторая машинистка может
справиться с этой работой на 16 часов быстрее первой. Найдите время
работы первой машинистки
Пусть х часов — зремя работы первой машинистки. Какое из
уравнений соответствует условию задачи?
Ai, i J в i_ 1 _'
X JC + 16 6 X JC + 16 6
Б ' + 1 -1 Г '- ' -1
JC JC-16 6 X JC-16 6
22. Сберегательный банк в конце года начисляет 2% к сумме,
находившейся на счету. На сколько рублей увеличится
первоначальный вклад в 5000 рублей через 3 года?
Ответ:
23. Сберегательный банк в конце года начисляет 5% к сумме,
находившейся на счету. На сколько процентов увеличится
первоначальный вклад в 2000 рублей через 2 года?
Ответ:
ЧАСТЬ II
Задания на 2 балла
24. Изделие, цена которого 500 рублей, сначала подорожало на
10%, а затем еще на 20%. Какова окончательная цена изделия?
25. Цену на некоторый товар сначала снизили на 30%, а затем
повысили на 20%. На сколько процентов изменилась
первоначальная цена товара?
26. Цену некоторого товара снизили на 15%, а потом еще на
20%. Найдите общий процент снижения цены.
27. Найдите первоначальную сумму вклада (в рублях), если
после истечения трех лет она выросла на 765,1 рубля при 2% годовых.
28. За январь выпуск продукции обувной фабрики составил 30%
квартального плана. За февраль — 120% продукции, выпущенной в
ТЕМА 8. ТЕКСТОВЫЕ ЗАДАЧИ 127 I
январе. Чтобы выполнить квартальный план, в марте фабрика
изготовила 680 пар обуви. Каков квартальный план фабрики?
29. За апрель выпуск продукции завода составил 40% плана за
II квартал, за май — 130% продукции, выпущенной в апреле.
Чтобы выполнить план за II квартал, завод в июне изготовил 240
машин. Каков квартальный план завода?
30. В первый день со склада было отпущено 20% имевшихся
яблок. Во второй день — 180% от того количества яблок, которое
было отпущено в первый день. В третий день — оставшиеся 88 кг
яблок. Сколько килограммов яблок было на складе первоначально?
31. Моторная лодка прошла 10 км по озеру и 4 км против
течения реки, затратив на весь путь 1 ч. Найдите собственную
скорость лодки, если скорость течения реки равна 3 км/ч.
32. Катер прошел 15 км по течению реки и 4 км по озеру,
затратив на весь путь 1 ч. Найдите собственную скорость катера, если
скорость течения реки равна 4 км/ч.
33. Два пешехода отправляются навстречу друг другу
одновременно из двух пунктов, расстояние между которыми равно 50 км,
и встречаются через 5 ч. Определите скорость каждого пешехода,
если скорость у одного из них на 2 км/ч больше, чем у другого.
34. Два мотоциклиста отправляются навстречу друг другу
одновременно из двух пунктов, расстояние между которыми равно
200 км, и встречаются через 4 часа. Определите скорость каждого
мотоциклиста, если скорость одного из них была на 10 км/ч
больше, чем у другого.
35. Два туриста отправляются навстречу друг другу
одновременно из двух пунктов, расстояние между которыми равно 44 км,
и встречаются через 4 часа. Определите скорость каждого туриста,
если скорость одного из них на 1 км/ч больше, чем у другого.
36. Расстояние между морскими пристанями 300 км. Два
катера начали свое движение с одной и той же пристани с интервалом
в 5 часов, а в конечный пункт прибыли одновременно.
Определите время движения каждого катера, если скорость движения
одного из них на 10 км/ч больше скорости другого.
37. Расстояние между двумя городами 90 км. Два
велосипедиста одновременно выезжают из одного города и направляются
в другой. Найдите скорости велосипедистов, если первый делает в
час на 1 км больше другого и прибывает в конечный пункт на
1 час раньше.
38. Два велосипедиста отправляются навстречу друг другу
одновременно из двух пунктов, расстояние между которыми равно
54 км, и встречаются через 2 ч. Определите скорость каждого
велосипедиста, если скорость у одного из них на 3 км/ч больше,
чем у другого.
128 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Задания на 4 балла
39. Для распечатки 302 страниц были использованы две
копировальные машины. Первая машина работала 8 мин, вторая —
10 минут. Сколько страниц в минуту печатает первая машина,
если первая печатает в минуту на 4 страницы больше, чем вторая?
40. Двое рабочих изготавливают по одинаковому количеству
деталей. Первый выполнил эту работу за 6 ч, второй за 4 ч, так как
изготовлял в час на 14 деталей больше первого. Сколько деталей
изготовил второй рабочий?
41. На строительстве стены первый каменщик работал 5 дней
один. Затем к нему присоединился второй, и они вместе
закончили работу через 4 дня. Известно, что первому каменщику
потребовалось бы на выполнение этой работы на 5 дней больше, чем
второму. За сколько дней может построить эту стену первый
каменщик, работая один?
42. За определенное время на заводе собирают 90 автомобилей.
Первые три часа на заводе выполняли установленную норму, а
затем стали собирать на один автомобиль в час больше. Поэтому за
час до срока уже было собрано 95 автомобилей. Сколько
автомобилей в час должны были собирать на заводе?
43. На швейной фабрике израсходовали 204 м ткани на 24
пальто и 45 костюмов. На 24 пальто и 30 костюмов израсходовали
162 м. Сколько ткани расходуется на пошив одного пальто?
44. Две бригады, работая одновременно, могут выполнить
некоторую работу за 6 дней. За какое время каждая машина может
выполнить эту работу, если известно, что вторая может
справиться с этой работой на 9 дней быстрее первой?
45. Два тела, двигаясь по окружности в одном направлении,
встречаются через каждые 112 минут, а двигаясь в
противоположных направлениях — через каждые 16 минут. Во втором случае
расстояние между ними уменьшилось с 40 м до 26 м за 12 секунд.
Сколько метров в минуту приходит каждое тело?
46. К 40%-ному раствору соляной кислоты добавили 50 г
чистой кислоты, после чего концентрация раствора стала равной
60%. Найдите первоначальный вес раствора.
47. Какое количество воды нужно добавить в 1 литр 9%-ного
раствора уксуса, чтобы получить 3%-ный раствор?
48. Сплавили два слитка, содержание цинка в которых было
64% и 84% соответственно. Получился сплав, содержащий 76%
цинка. Его вес 50 г. Сколько весил каждый из сплавленных
слитков?
ТЕМА 8. ТЕКСТОВЫЕ ЗАДАЧИ 129
49. Имеются два куска сплава меди и цинка с процентным
содержанием меди 30 и 55% соответственно. В каком отношении
нужно взять эти сплавы, чтобы, переплавив, получить сплав,
содержащий 40% меди?
50. Какое количество воды надо добавить к 2 литрам 18%-ного
раствора соли, чтобы получить 16%-ный раствор?
51. При повышении цены билета на 25% число зрителей в
кинотеатре уменьшилось на 22%. На сколько процентов изменилась
выручка театра?
52. Цена первого товара повысилась на 30%, а потом еще на
5%. Цена второго товара повысилась на 25%. После повышения
цены товаров сравнялись. Найдите, на сколько процентов
первоначальная цена одного товара больше первоначальной цены
другого товара.
53. Зарплата была повышена два раза за один год на один и тот
же процент. При таком повышении вместо 100 руб. за один день
рабочий стал получать 125,44 руб. Определите, на сколько
процентов повысилась зарплата.
Задания на 6 баллов
54. Швея Ольга может сшить за 3 часа 15 фартуков, швея Нина
за 2 часа — 12 фартуков, а швея Тамара за 30 минут — 4 фартука.
Как должны распределить швеи между собой работу, чтобы
закончить ее одновременно, если им осталось сшить 59 фартуков?
55. На фабрике в коробки упаковывают елочные игрушки.
Первый упаковщик может упаковать 15 коробок за 0,5 часа,
второй упаковщик — 40 коробок за час, третий — 20 коробок за
40 минут. Осталось упаковать 88 коробок. Как упаковщики
должны распределить между собой оставшуюся работу, чтобы
закончить ее одновременно?
56. Две бригады выполняют некоторую работу. Если всю
работу будет делать первая бригада, то она затратит на 9 дней больше,
чем две бригады вместе. Если эту работу будет делать вторая
бригада, то она затратит на 4 дня больше, чем обе бригады вместе. За
сколько дней выполнит эту работу первая бригада?
57. Мастер и его ученик выполняют некоторую работу. Если
всю работу будет делать мастер, то он затратит на 9 часов больше,
чем мастер и ученик вместе. Если эту работу будет делать ученик,
то он затратит на 25 часов больше, чем мастер и ученик вместе. За
сколько часов выполнит эту работу ученик?
58. Два крана разгружают баржу. Если всю работу будет
выполнять первый кран, то работа будет выполнена на 16 часов позже,
13O РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
чем два крана, работая вместе. Если разгружать баржу будет
второй кран, то работа будет выполнена на 9 часов позже, чем оба
крана, работая вместе. За сколько часов может разгрузить эту
баржу первый кран?
59. Один сплав содержит два металла в отношении 2:3, другой
сплав содержит те же металлы в отношении 3 : 4. Сколько частей
каждого сплава надо взять, чтобы получить третий сплав,
содержащий эти металлы в отношении 15 : 22?
Тема 9. Уравнения и неравенства
с модулем
Уравнения и неравенства с модулем встречаются во второй
части экзаменационной работы. При решении большинства
уравнений и неравенств с модулем приходится использовать определение
модуля, реже — свойства модуля и его геометрический смысл.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определение. Модулем числа а называется само это число я,
если а > 0, и противоположное число (-а), если а < 0. Модуль
числа а обозначается \а[
к если я>0, (1)
\-а, если а < 0.
Геометрически модуль числа а означает расстояние на
координатной прямой от точки с координатой а до начала координат.
0
Запись \х-а\ можно понимать как расстояние от точки с
координатой х до точки с координатой а на координатной прямой.
Свойства модуля
Для любого действительного числа а
W^O (2)
W = M (3)
W2 = а2 (4)
ТЕМА 9. УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ 131
ЗАДАНИЯ ДЛЯ АКТИВНОГО ОБУЧЕНИЯ
(С КОММЕНТАРИЯМИ, РЕШЕНИЯМИ, ОТВЕТАМИ)
БЛОК1. Уравнения и неравенства с модулем вида |f(x)|=b, Их)|<Ь,
\f(x)\> Ь, где f(x) - некоторая функция, а Ь - положительное
число (Ь>0).
Задание 1. Решите уравнение \х - 7| = 2.
Решение.
1-й способ
Исходя из геометрического смысла модуля, следует найти на
координатной прямой точки, расстояние от которых до точки с
координатой 7 равно 2.
Получим х = 5 или х = 9.
2-й способ
По определению модуля х - 7= -2 или х - 7 = 2.
Получим х = 5 или х = 9.
Ответ: 5; 9.
Задание 2. Решите неравенство \х - 7| < 2.
Решение. 7-w способ.
Исходя из геометрического смысла модуля, следует найти
точки на координатной прямой, расположенные на расстоянии,
меньшем 2 от точки с координатой 7.
Получим промежуток (5; 9).
2-й способ.
Найдем нули выражения, стоящего под знаком модуля
х -1 - 0, х = 7. Отметим число 7 на координатной прямой.
Число 7 разбивает координатную прямую на два промежутка.
Рассмотрим отдельно два случая и объединим результаты.
132 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
1) Если х < 7, то выражение под знаком модуля принимает
отрицательные значения, и по определению модуля имеем систему
\х < 7, \х< 7, \х < 7,
Н*-7)<2; l-*<-5; \x > 5.
Решение системы — промежуток (5; 7).
2) Если х > 7, то выражение под знаком модуля принимает
неотрицательные значения, и по определению модуля имеем систему
[х > 7, Гх > 7,
[U-7)<2; [х<9.
Решение системы — промежуток [7; 9).
Объединим решения в пунктах I) и 2). Получим промежуток
(5; 9).
3-й способ.
Неравенства вида \f(x)\ < b, где fix) — некоторая функция, а
число Ъ > 0, можно решить с помощью равносильных
преобразований. Неравенство |/(х)| < Ь равносильно системе
\Дх) > -Ь.
Неравенство \х - 7| < 2 равносильно системе
Гх-7<2,
[х-7>-2.
Ее решением является промежуток (5; 9).
Ответ: (5; 9).
Задание 3. Решите неравенство \х + 7| > 3.
Решение.
1-й способ.
Исходя из геометрического смысла модуля, требуется найти
числа, находящиеся на расстоянии, большем или равном (не
меньшим) 3, от точки с координатой (-7).
-10 -7 -4
Получаем два промежутка (-<»;-10] и [-4; + «>).
2-й способ.
Найдем нули выражения, стоящего под знаком модуля:
7 = 0, х = -7.
ТЕМА 9. УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ ЛЪЪ
Число (-7) разбивает координатную прямую на два
промежутка. Решим исходное неравенство на каждом из промежутков.
1) Если х < - 7, то выражение под знаком модуля принимает
отрицательные значения, и по определению модуля имеем систему
х<-т7, Гх<-7, Гх<-7,
-(х + 7)>3; [-X > 10; [х<-10.
Решением ее будет промежуток (-оо;- ю].
2) Если х > -7, то выражение под знаком модуля принимает
неотрицательные значения, и по определению модуля имеем
систему
{х>-7, [х>-7,
(х + 7)>3; [х>-4.
Решение системы — промежуток [-4; + оо).
Объединяем решения в пунктах 1) и 2). Получаем объединение
промежутков (- оо; - ш] U [-4; + оо).
3-й способ.
Неравенства вида |/(х)|>£, где/(х) — некоторая функция, а
число Ъ > О, можно решить с помощью равносильных
преобразований. Неравенство |/(х)| > Ъ равносильно совокупности неравенств:
f(x)>b или /(х) < -Ь.
Неравенство |х + 7| > 3 равносильно совокупности неравенств:
х + 7 > 3 или х + 7 < -3. Решением является объединение
промежутков (- оо; - ю] U [-4; + оо).
Ответ: (-оо;-Ю]и[-4;-
БЛОК 2. Уравнения и неравенства с модулем вида \f(x)\=g(x),
\f(x)\<g(x), \f(x)\>g(x), где f(x) и д(х) - некоторые функции.
Задание 4. Решите уравнение |х - 4| = 4х + 1.
Решение. 1-й способ.
Найдем нули выражения, стоящего под знаком модуля:
х - 4 = 0, х = 4.
Число 4 разбивает координатную прямую на два промежутка.
134
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Решим исходное неравенство на каждом из промежутков.
I) Если х < 4, то то выражение под знаком модуля принимает
отрицательные значения, и по определению модуля имеем систему
[х < 4, ix < 4, \х < 4,
\-{х - 4) = 4х +1; {-5х = -3; [х = 0,6.
Решением системы будет число 0,6, так как 0,6 Е(-оо; 4).
0,6 4
2) Если х > 4, то выражение под знаком модуля принимает
неотрицательные значения, и по определению модуля имеем систему
Iх ~ 4'
x > 4,
> 4,
Система не имеет решений, так как -- £ [4; +«>).
2-й способ
Уравнение вида |/(х)| = g(x) равносильно системе
0.
Уравнение \х - 4| = 4х +1 равносильно системе
- 4 = -4х -1,
4х +1 > 0,
решением которой является число 0,6.
Ответ: 0,6.
Задание 5. Решите неравенство \1х + 4| + х < 2. В ответе укажите
сумму всех его целых решений.
Решение. 1-й способ.
Найдем нули выражения, стоящего под знаком модуля:
2х + 4 = 0, х = -2.
ТЕМА 9. УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ 135
Число -2 разбивает координатную прямую на два промежутка.
Решим исходное неравенство на каждом из промежутков.
1) Если х < - 2, то имеем систему
{г < —9 \х < —2 (х < —2
-(2х + 4) + х < 2; \-х < 6; |х > -6.
Решением системы неравенств является промежуток (-6; -2).
2) Если х > -2, то имеем систему
|**-2, Г**-2, j^"2'
[2х + 4 + х<2; [Зх<-2; U<-|.
Г 2
Решением системы неравенств является промежуток -2; - -
Объединяем промежутки, являющиеся решением каждой
системы в пунктах I) и 2), получим промежуток -6; - - .
Целые решения, входящие в этот промежуток: -5; -4; -3; -2;
-I. Их сумма равна -15.
2-й способ.
Неравенство вида |/(х)| < g(x) равносильно системе неравенств
[/(*) < «(*),
[/(*) > -g(x).
Неравенство \2х + 4| < 2 - х равносильно системе неравенств
I? д _ 1 Решением которой является промежуток -6;
Осталось выбрать целые числа, входящие в этот промежуток, и
найти их сумму.
Ответ: -15.
Задание 6. Решите неравенство \х2 - 4| > Зх.
Решение.
Найдем нули выражения, стоящего под знаком модуля:
х2 - 4 = 0, х = ±2. Числа —2 и 2 разбивают координатную прямую
на три промежутка.
-2
136 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
I) Если х < -2, то имеем систему
\х ^ -2,
[х2 - 4 > Зх.
Решим второе неравенство системы х2 - Зх - 4 > 0.
Решением неравенства является объединение промежутков
oo;-l]u[4; + oo).
Решением системы неравенств является промежуток (- оо; - 2].
2) Если -2 < х < 2, то имеем систему
Г-2 < х < 2, Г-2 < х < 2,
[4 - х2 > Зх; {-х2 - Зх + 4 > 0.
Решим второе неравенство системы -х2 - Зх + 4 > 0.
Решением неравенства является отрезок [-4; l].
Решением системы неравенств является промежуток (-2;1].
3) Если х > 2, то имеем систему
Jx>2,
[х2 - 4 > Зх.
Решением второго неравенства является объединение
промежутков (-оо; - l] U [4; + ооj.
Решением системы неравенств является промежуток [4;+ оо).
Решением исходного неравенства является объединение
решений в пунктах 1), 2) , 3): (-оо; l] и [4; +оо).
Ответ: (-оо; l]u[4; +»).
Замечание: неравенство вида |/(х)| > g(x) равносильно
совокупности неравенств /(х) > g(x) или /(х) < -g(x). В задании 6
неравенство |х2 - 4| > Зх равносильно совокупности неравенств
х2 - 4 > Зх или х2 - 4 < -Зх.
БЛОКЗ. Уравнения и неравенства с модулем вида |f(x)|=|g(x)|,
\f(x)\<\g(x)\.
Задание 7. Решите уравнение |2х + 5| = |х - \[
Решение.
Два числа, модули которых равны, либо равны между собой,
либо отличаются только знаком, т.е. если \а\ = \Ь[ то либо а = Ь, ли-
ТЕМА 9. УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ 137
бо а = -Ь. Применим это свойство модулей к решению исходного
уравнения.
2х + 5 = х -1 или 2х + 5 = I - х
х = -6 или х = --
4
Ответ: -6; - -.
Замечание. Уравнение вида |/(х)| = \g(x)\ можно решать с
помощью равносильных преобразований. Так как обе части
уравнения неотрицательны, то уравнение равносильно уравнению
/2(х) = g\x), тогда (/(х) - g(x))(f(x) + g(x)) = 0.
Например, в задании 7 уравнение \2х + 5| = \х -1| равносильно
уравнению (2х + 5)2 = (х -I)2. Далее применяем формулу разности
квадратов и условие равенства нулю произведения:
(2х + 5 - (х -1)) х х (2х + 5 + х -1) = 0.
Задание 8. Решите неравенство \х2 -2х| < \х + 4[ В ответе
укажите число целых решений неравенства.
Решение.
Так как обе части неравенства неотрицательны, то возведем обе
части неравенства в квадрат. Имеем:
Перенесем слагаемые в левую часть неравенства и применим
формулу разности квадратов.
(х2 - 2х - х - 4)(х2 - 2х + х + 4) < 0
Данное неравенство не является ни линейным, ни квадратным.
Решим его методом интервалов.
Рассмотрим функцию fix) = (х2 -Зх -4)(х2 -х + 4). Найдем
нули функции, для этого решим уравнение
(х2-Зх-4)(х2-х + 4) = 0.
Числа -1,4 являются нулями функции.
Отметим нули функции на координатной прямой. Они
разбивают координатную прямую на три промежутка.
В каждом из промежутков знак функции сохраняется, а при
переходе через нуль функции (т.е. через точки -1,4) ее знак меняется.
Определим знак функции в каком-нибудь из трех промежутков.
Например, рассмотрим /(0) = (0 - 4)(0 + 4) = -16 < 0, значит, в
промежутке (-1; 4) значения функции отрицательны. Далее
происходит чередование знаков.
138
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Решением исходного неравенства является промежуток (-1; 4).
В этот промежуток входит четыре целых числа: 0; 1; 2; 3.
Ответ: 4.
БЛОК 4. Уравнения, содержащие несколько модулей.
Задание 9. Решите уравнение \х - 7| +19 + х\ = 18.
Решение.
Найдем нули каждого из выражений, стоящих под знаком
модуля: х - 7 = 0, х = 7 и 9 + х = 0,х = -9. Числа -9 и 7 разбивают
координатную прямую на три промежутка.
-9
Определим знаки каждого из выражений, стоящих под знаком
модуля в каждом из промежутков.
Составим таблицу знаков.
х- 7
jc + 9
х< - 9
-
-
-9<х<7
-
+
х> 7
+
+
1) Если х < -9, то имеем систему
\х ^ -9, Гх < -9,
[-(х - 7) - (х + 9) = 18; [-2* = 20.
Решением системы является число -10; -10 Е (-«>; -9].
2) Если -9 < х < 7, то выражение х - 7 принимает
отрицательные значения, а выражение х + 9 принимает положительные
значения, т.е. имеем систему
(-9
]-(* - 7) + (х + 9) = 18; [16 = 18 (неверно).
Система не имеет решений.
3) Если х > 7, то имеем систему
\х > 7, (х > 7,
Юс-7) +(х+ 9) = 18; {2* = 16.
<х<7, Г-9 < х < 7,
* - 7) + (х + 9) = 18; [16 = 18 (нев!
ТЕМА 9. УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ 139
Решением системы является число 8 Е [7; +оо).
Итак, исходное уравнение имеет два решения: -10 и 8.
Ответ: -10; 8.
БЛОК 5. Сложный модуль (к этому блоку отнесем такие уравнения и
неравенства, в которых под знаком модуля находится выражение,
в записи которого содержится один или несколько модулей).
Задание 10. Решите уравнение \\х -1| - 2| = 3.
Решение.
Решение можно начать с раскрытия «внутреннего» модуля.
1) Если х - 1 > 0, то \х -1| = х -1. И имеем следующее
уравнение \х -1 - 2| = 3, \х - 3| = 3, решением которого являются числа 0
и 6.
Так как х > 1, то число 0 является посторонним корнем
уравнения. Значит, при х - 1 > 0, получаем только один корень 6.
2) Если х - 1 < 0, то \х - 1| = -(х -1). И имеем следующее
уравнение \-(х -1) - 2| = 3, \-х - 1| = 3, решением которого являются
числа 2 и (-4). Так как х < 1, то число 2 является посторонним
корнем уравнения, т.е. при х - 1 < 0 получаем только один корень
(-4).
Итак, исходное уравнение имеет два корня (-4) и 6.
Ответ: -4; 6.
БЛОК 6. Системы уравнений с модулем.
Задание 11. Решите систему уравнений
[2х + у = 7,
\\х-у\ = 5.
Решение.
Рассмотрим второе уравнение системы. Так как |л: - ^| = 5, то
х-.у = 5 или х- у = -5
Г2х + у 7,
В первом случае имеем систему j которую можно
решить методом сложения или методом подстановки. Решением
системы является пара чисел (4; -1).
14O РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
[2х + у 7,
Во втором случае имеем систему j _ которую тоже
[х — у — — j,
можно решить методом сложения или методом подстановки. Ре-
(2 2)
шением системы является пара чисел | -; 5 -1
Ответ: (4; —I), Г|; 5^
БЛОК 7. Использование свойств модуля при решении иррациональных
уравнений.
Задание 12. Решите уравнение х2 + V*2" -12 = 0.
Решение.
Так как yfb2 = |й|, то исходное уравнение равносильно
уравнению х2 + |х|-12 = 0.
Решим его двумя способами.
1-й способ.
Решим уравнение на каждом из двух промежутков X > 0 и х < 0.
1) При х >0 получим уравнение х2 + х-12 = 0. Его корни:
-4 и 3. С учетом условия х > 0, имеем только один корень 3.
2) При х < 0 получим уравнение х2 - х -12 = 0. Его корни: 4 и
(-3). С учетом условия х < 0, имеем только один корень (-3).
Исходное уравнение имеет два корня: 3 и (-3).
2-й способ. Введем новую переменную. Пусть |х| = а. Так как
х2 = |х|2, то имеем квадратное уравнение относительно а.
я2+я-12 = 0.
а = -4 или а = 3.
|х| = -4 или |х| = 3.
Первое уравнение корней не имеет (почему?). Второе
уравнение имеет два корня ±3.
Ответ: ±3.
Замечание: уравнение х2 + (Vx) -12 = 0 внешне практически
не отличается от уравнения х2 + ^/х2 -12 = 0. Тем не менее при
решении его используется другое свойство арифметического
квадратного корня. А именно: (Vft) = b,b > 0.
ТЕМА 9. УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ 141
И его решение будет следующим:
Корни квадратного уравнения: 3 и (-4). Но х > 0, поэтому
решением уравнения х2 + (Vx) -12 = 0 будет только число 3.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЧАСТЫ
1. Модуль числа (-12) равен...
Ответ:
2. Модуль числа V3 - 2 равен...
Ответ:
3. Упростите выражение \х -6|-7 при х > 14.
Ответ:
4. Упростите выражение \х - 6| - 7 при х < 2.
Ответ:
5. Упростите выражение \х - 6| + \х\ при 0 < х < 4.
Ответ:
6. Упростите выражение \х - 6| + |х| при х < -4.
Ответ:
7. Упростите выражение |х - 6| + [х| при х > 15.
Ответ:
8. Решите уравнение |х| = 5.
Ответ:
9. Решите уравнение \х\ = -5.
Ответ:
ЧАСТЬ II
Задания на 2 балла
10. Решите уравнение |3х - 2| = 4.
11. Решите уравнение |3х - 2| = 4 - VT7.
12. Решите неравенство \х - 3| < 4.
13. Решите неравенство \х +1| > 2.
14. Укажите число целых решений неравенства \х +1| < 7.
I 142 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
15. Укажите наименьшее натуральное решение неравенства
|х-2|>1.
16. Решите неравенство |3х - 2| < 4.
17. Решите неравенство |3х - 2| > 4.
18. Решите уравнение \х - 3| = Ъх + 2.
19. Решите уравнение \х - 5| = 2х + 3.
20. Решите уравнение \1х - 3| = х.
21. Решите неравенство \х - 5| < 0.
22. Решите неравенство \х - 5| > 0.
23. Решите неравенство \х - 5| > 0.
24. Решите уравнение |х2 -6| = 15.
25. Решите уравнение \х2 -9| = 8х.
26. Решите уравнение |х2 - 9| = -8х. В ответе укажите сумму его
корней.
4 балла
27. Решите систему неравенств
fix +1| < б,
28. Решите систему неравенств
fix -1| < 5,
В ответе укажите число целых решений системы.
29. Решите неравенство \х2 + 2jc| < |х + 6[ В ответе укажите
длину промежутка, являющегося решением неравенства.
30. Решите неравенство \х2 - х\ > |2х +10|.
31. Решите уравнение \х2 -9| = |8х|.
32. Решите уравнение \х + 2007| = 2007 + х.
33. Решите неравенство \х + 2007| > 2007 + х.
34. Решите неравенство |х + 2007| < 2007 + х.
35. Решите неравенство \х + 2007| < 2007 + х.
36. Укажите середину промежутка, являющегося множеством
решений неравенства |х +1| < 0,5х + 2.
37. Решите неравенство \х - 5|(х - 3) > 0.
38. Решите неравенство \х + 5|(х - 3) > 0.
ТЕМА 9. УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ 143
Задания на 6 баллов
39. Решите уравнение ||х| +1| = 4.
40. Решите уравнение ||х| + 2| = 6.
41. Решите уравнение |х-8| + |7 + х| = 16.
42. Решите уравнение \х - 5| +16 + х\ = 13.
43. Решите уравнение \х - 5| +16 + х\ = 11.
44. Решите уравнение х2 + ЪлГх2 -10 = 0.
45. Решите уравнение х2 + 3(Vx) -10 = 0.
46. Решите уравнение х2 + 6^/х2 -7 = 0.
47. Решите неравенство х2 + 6|х|- 7 > 0.
48. Решите уравнение х2 + 6\^) -7 = 0.
49. При каких натуральных значениях т верна система
неравенств
{(т -1)2 + (т +1)2 > 2(/и - \)(т +1),
[[4-2/и|<3.
50. Найдите наибольшие и наименьшие целые числа,
принадлежащие промежутку, который является множеством решений
системы неравенств
7 3(jc-1) jc-2 13
51. Решите уравнение |7-21х| + |9 + 21х| = 16.
52. Решите уравнение |15х - 3| + |14х - 9| = 6 + х.
53. Решите неравенство \х + 1| + \х + 2\ + \х -1| + \х - 2| < 5х -15.
54. Решите неравенство \х + 3| + \х + 2| + |х - 2| + |х - 3| < 6х -18.
55. Решите уравнение (х2 -9х + 8)2 + 5|х -1| = 0.
56. Решите уравнение \х2 - 4| + \х - 2| = 0.
57. Решите систему уравнений
58. Решите систему уравнений
+ у = 25,
144 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Тема 10. Уравнения и неравенства
с параметром
Уравнения и неравенства с параметром встречаются только в
четырех или шести балльных заданиях второй части
экзаменационной работы.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Решить уравнение (неравенство) с параметром — это значит
установить соответствие, позволяющее для любого значения
параметра найти соответствующее множество решений уравнения
(неравенства).
ЗАДАНИЯ ДЛЯ АКТИВНОГО ОБУЧЕНИЯ
(С КОММЕНТАРИЯМИ, РЕШЕНИЯМИ, ОТВЕТАМИ)
Линейные уравнения и неравенства
Задание 1. Решите при всех значениях параметра а уравнение
ах = 2х + 5.
Решение.
Необходимо решить линейное уравнение с параметром.
Сначала перенесем все неизвестные слагаемые в левую часть уравнения
и приведем подобные слагаемые. Получим (а - 2)х = 5.
Чтобы найти значение х, в данном случае надо разделить
уравнение на (а - 2). При всех ли значениях параметра а мы можем
уравнение разделить на (а - 2)?
Нет. При а = 2 выражение а - 2 обращается в нуль, поэтому
значение параметра а = 2 является «особым» — контрольным
значением параметра. Рассмотрим это значение отдельно.
При а = 2. (2 - 2)х =5; Ох = 5 — уравнение решений не имеет.
Теперь а ** 2, и, чтобы выразить х, делим обе части уравнения
на (а - 2).
При а ** 2 получим х = —-.
а—2
Ответ: при а - 2 решений нет; при а ** 2 х = —-.
а—2
Задание 2. Решите при всех значениях параметра а
неравенство ах < 2х + 5.
Решение.
Необходимо решить линейное неравенство с параметром.
Перенесем все неизвестные слагаемые в левую часть неравенства и
приведем подобные слагаемые. Получим (а - 2)х < 5.
ТЕМА 10 УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРОМ 145
Чтобы найти значения х, надо разделить обе части неравенства
на (а - 2). При всех ли значениях параметра а мы можем
неравенство разделить на (а - 2)?
При а = 2 выражение а—2 обращается в нуль.
Рассмотрим это значение отдельно.
При а = 2 (2 - 2)х < 5; Ох < 5. Это неравенство верно при
любых значениях х, поэтому решением исходного неравенства при
а = 2 является промежуток (-«>; +«>).
Теперь а * 2. Для того чтобы выразить х, надо разделить
неравенство на (а - 2). Существенным отличием решения линейного
неравенства с параметром от решения линейного уравнения с
параметром является то, что знак неравенства при делении обеих
частей неравенства на выражение с неизвестным может
измениться на противоположный или не изменится. Поэтому при делении
неравенства на выражение с параметром надо учитывать знак
этого выражения.
Если а - 2 < О, то знак неравенства придется изменить; если
а - 2 > О, то знак неравенства не меняется.
При а <2 х > —- (знак неравенства изменился).
а—2
При а>2 х < —- (знак неравенства не изменился).
а—2
Ответ: при а = 2 х Е (- оо; + оо); при а <2 х > —-; при
а > 2х < -Л-.
а-2
Квадратные уравнения и неравенства
Число корней квадратного уравнения определяют по знаку
дискриминанта:
если D > 0, то уравнение имеет два различных корня;
если D = 0, то уравнение имеет один корень (или два совпавших);
если D < 0, то уравнение не имеет корней.
Задание 3. При каких значениях параметра а уравнение
4х2 - 4ах + 1 = 0: 1) имеет два различных корня; 2) имеет два
корня; 3) не имеет корней?
Решение.
Найдем дискриминант исходного уравнения.
1) Так как уравнение имеет два различных корня, то
D = 16а2 — 16 > 0, о2 > 1 (см. решение квадратных неравенств в
теме «Неравенства»). Получим а Е (-<»;-1) U (l; + °°).
146 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
2) Так как уравнение имеет два корня, не обязательно
различных, то/) = 16я2-16>0, я2>1 и яе(-оо; — l]u[l; +оо).
3) Так как уравнение не имеет корней, то D = 16я2 -16 < О,
а2<\ и яе(-1; l).
Ответ: при а е(-оо; -l)u(l; + оо) уравнение имеет два
различных корня; при a G (- оо; -1] и [l; + «>) уравнение имеет два
корня; при a G (-1; l) уравнение не имеет корней.
Задание 4. При каких значениях параметра уравнение
(Ь - l)x2 + (b + 4)х + 6 + 7 = 0 имеет только один корень?
Решение.
При всех ли значениях параметра данное уравнение будет
квадратным?
Нет, при Ъ = 1 уравнение становится линейным (6 = 1 —
контрольное значение параметра). Подставим значение Ь = 1 в
исходное уравнение.
(1-1)х2 + (1 + 4)х + 1 + 7 = 0,5*+ 8 = 0. Это уравнение имеет
один корень -16.
При Ъ * 1 имеем квадратное уравнение. Так как квадратное
уравнение имеет один корень, то D = 0.
Находим дискриминант и приравниваем его к нулю.
= -3b2-\6b
Уравнение имеет корни 2 и -
Ответ: при b = 1; b = 2; b = -— уравнение имеет только один
корень.
Задание 5. При каких значениях параметра неравенство
ах2 + 4ах + 5 < 0.
не имеет решений?
Решение.
Данное неравенство не при любых значениях параметра а будет
квадратным. Какое значение параметра является в данном случае
контрольным?
(I) Пусть а = 0. Имеем: 0х2+0х + 5<0. Получаем 5 < 0. Это
не верно. Значит, при а = 0 исходное неравенство решений не
имеет.
(II) При а * 0 исходное неравенство будем квадратным и
графиком функции f{x) = ах2 + 4ах + 5 является парабола. Чтобы нера-
ТЕМА 10. УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРОМ 147
венство ох2 + 4ах + 5 < 0 не имело решений, надо, чтобы парабола
была расположена выше оси абсцисс.
Запишем условия, соответствующие данному положению
параболы.
J
[D<Q.
Решением неравенства D < 0 является промежуток (0; 1,25).
\а>0,
[0<а< 1,25.
Решением системы является промежуток (0; 1,25).
Объединяем полученные решения и получаем ответ.
Ответ: при а е[0; 1,25) неравенство не имеет решений.
Применение теоремы Виета
Если приведенное квадратное уравнение х2 + рх + q = 0 имеет корни,
то сумма корней этого уравнения равна второму коэффициенту,
взятому с противоположным знаком, а произведение корней равно
свободному члену, т.е. если х-,\лх2- корни уравнения х2 + рх + q = 0, то
\х} + х2 = -р;
\ _ (теорема Виета).
1*1 ' Х2 ~ Я-
Задание 6. Найдите все значения параметра Ь, при которых
уравнение
х2 - 2&с + Ъ + 6 = 0
имеет положительные корни.
Решение. 1-й способ.
Чтобы квадратное уравнение имело корни, необходимо, чтобы
дискриминант его был неотрицателен (D > 0).
В каком случае оба корня положительны. Например, если и
сумма корней положительна (х1 + х2 > 0) и произведение корней
положительно (xj • х2 > 0).
Пусть хх и х2 корни уравнения, тогда, по теореме Виета:
х, + х2 = 2Ъ и х, • х2 = Ь + 6. И имеем систему неравенств:
148
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
jc, + x2 = 2b > 0,
x, • x2 = b + 6 > 0,
4b2-4(b-
Решим квадратное неравенство
4b2-4b-24>0
Ь2-Ь-6>0
////\ Л
-2
Решением системы неравенств будет промежуток [3; + «>).
2-й способ.
Рассмотрим функцию/(*)= х2 - 2Ьх + Ъ + 6. Ее графиком
является парабола. Изобразим параболу, удовлетворяющую
условиям задачи.
Запишем условия, соответствующие этому расположению
параболы.
Д0)>0,
х > О
вершины v*
Решим каждое из этих неравенств.
ДО) = 6 + 6 > О, Z>>-6.
/) = 4Z>2-4(Z> + 6)>0, Z>e(-oo;-2]u[3;
*вершины
-2Ь
2
Отметим решения каждого неравенства на координатной
прямой и найдем пересечение решений.
I ,.
—►
—►
-6 -2
ТЕМА 10. УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРОМ
149
Решением системы неравенств будет промежуток [3; + оо).
Ответ: при b Е [3; + оо) уравнение имеет положительные корни.
Задание 7. Найдите все значения параметра/7, при которых
разность корней уравнения х2 + рх +12 = 0 равна 1.
Решение.
Пусть х{ и х2 корни уравнения, тогда, по теореме Виета, имеем
систему:
х, -х2 = 12,
Выразим корни уравнения из первого и третьего уравнений
через параметр р и подставим во второе уравнение.
х -
2 '
с, -х2 = 12,
с2 = =у^;
1 ~
2 '
1-/1,-1-/1
2 2
-\-р
= 12,
Решим квадратное уравнение относительно параметра /?.
1 -/?2 = -48
Уравнение имеет два корня 7 и (-7).
Ответ: при р = ±7 разность корней уравнения равна 1.
Расположение корней квадратного уравнения
относительно заданных точек
Задание 8. При каких значениях параметра а оба корня
уравнения х2 - ах + 7 = 0 меньше 7.
Решение.
Рассмотрим функцию /(х) = х2 - ах + 7. Графиком данной
функции является парабола. Изобразим параболу с указанными
свойствами.
15O
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
./<*)
Запишем условия, соответствующие этому расположению
параболы.
/)>0,
х < 7
■^вершины *
Решим каждое из этих неравенств.
/(7) = 49-7о + 7 > 0, ж 8.
D = а2 -28 > 0, а2 > 28, а Е (-«>;-
_ b _ -а _ а а _ ..
•^■вершины "" ~2д ~ 2~ ~ 2^' 2^ и < 1Ч-.
Отметим решения каждого неравенства на координатной
прямой и найдем пересечение решений.
-2V?
2л/7 8 14
Решением системы неравенств будет объединение промежутков
(-oo;-2V7]u[2V7;8).
Ответ: при а е(-оо; -2>/7]U[2>/7; 8) оба корня уравнения
меньше 7.
Задание 9. При каких значениях параметра а число 7
находится между корнями уравнения х2 - ах + 7 = 0.
Решение.
Рассмотрим функцию Дх)= х2 - ах + 7.
Изобразим параболу, удовлетворяющую
условиям задачи, и опишем
соответствующие условия.
Чтобы число 7 разделяло корни
уравнения, достаточно, чтобы /(7) < 0.
Решим неравенство /(7) = 49 - 1а + 7 < 0, я > 8.
Ответ: при а > 8 число 7 находится между корнями уравнения
х2 - ах + 7 = 0.
,/М
ТЕМА 10. УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРОМ 151
Системы линейных уравнений
Задание 10. При каких значениях параметра а система уравнений
1) не имеет решений; 2) имеет бесконечно много решений.
Решение.
Графиком каждого из уравнений системы является прямая. Две
прямые на плоскости могут быть: 1) параллельными (система не
имеет решения); 2) могут пересекаться (система имеет одно
решение); 3) совпадать (система имеет бесконечно много решений).
Прямые у = куХ+Ьу \лу=к2х+к)2 1) параллельны, если ^ = к2 и Ь^ * Ь2;
2) пересекаются, если /с, ** к2\ 3) совпадают, если к, = к2 и Ь, = Ь2.
Выразим в каждом уравнении системы переменную у.
= 0,5я2х - я,
Сравним коэффициенты при х. При равенстве коэффициентов
при х (угловых коэффициентов) прямые могут либо совпадать,
либо быть параллельными.
0,5я2 = 2, я2 = 4, а = ±2.
При а = 2 имеем систему
= 2х-2,
и прямые параллельны (система не имеет решений).
При а = -2 имеем систему
и прямые совпадают (система имеет бесконечно много решений).
Ответ: при а = 2 система не имеет решений; при а = -2
система имеет бесконечно много решений.
Уравнения с модулем
Уравнения и неравенства с модулем можно решать графически. Для
этого выражения, содержащие параметр, переносят в одну часть
уравнения (неравенства) и строят графики функций левой и правой
частей уравнения (неравенства).
152
РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
Задание 11. Решите уравнение |х + 3| - а\х - 1| = 4 при а > 0.
Решение.
|х + 3| - а\х - 1| = 4
|х + 3| - 4 = а\х - 1|.
Будем строить в одной системе координат графики функций
у = |х + 3| - 4 и у = а\х - 1|.
Рассмотрим четыре случая: 1) а > 1; 2) а = 1; 3) 0 < а < 1; 4) а = 0.
1) При я > 1 графики выглядят следующим образом.
у = а\х - l|, a > 1
)>=|jc+3|-4
Графики пересекаются в одной точке: (1; 0), т.е. при а > 1 х = 1.
2) При л = 1 графики выглядят следующим образом.
у = \х + 3| - 4
При х > 1 графики совпадают, т.е. система имеет бесконечно
много решений.
При а = 1 решением уравнения будет промежуток [l; + «>).
3) При 0 < а < 1 графики выглядят следующим образом.
ТЕМА 10. УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРОМ
153
У
Графики пересекаются в двух точках. Одна точка имеет
координаты (I; 0).
Чтобы найти координаты второй точки, надо решить систему
Так как х < -3, то модули выражений раскрываются
следующим образом: |х + 3| = -(х + 3) = -х - 3; |х - \\ = -(х -1) = -х +1.
Осталось решить уравнение:
ах-х = д + 7
Так как 0 < а < 1 (поэтому а * 1), то х = —-.
Итак, при 0<д<1х= 1их = —-.
а— 1
4) При а = 0 график у — а\х - 1| совпадает с осью абсцисс и
уравнение имеет два решения. Решения можно найти из
уравнения |х + 3| - 4 = 0.
|х + 3| = 4
х + 3 = 4 или х + 3 = -4
х = 1 или х = -7
При а = 0 уравнение имеет два корня: 1 и -7.
Ответ: при а > 1 х = 1; при а = 1 х > 1; при 0 < а< 1 х = 1 и
х = ^—г; при л = 0 х= 1 и х = -7.
154 РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЧАСТЫ
1. При каком значении параметра а корнем уравнения х - а = О
является число 4?
Ответ:
2. При каком значении параметра а корнем уравнения
5х - а = 0 является число 4?
Ответ:
3. При каком значении параметра а корнем уравнения
х2 - 2х - а = О является число 4?
Ответ:
4. При каких значениях параметра а уравнение х2 = а не имеет
решений?
Ответ:
5. При каком значении параметра а уравнение Ох = а имеет
бесконечно много решений?
Ответ:
6. При каком значении параметра а уравнение Ох = а не имеет
решений?
Ответ:
х-2
7. При каком значении параметра а сократима дробь ?
Ответ:
ЧАСТЬ II
Задания на 2 балла
8. При каком значении параметра а уравнение ах = 3 не имеет
решений?
9. При каком значении параметра а уравнение ах = 1 - х не
имеет решений?
10. При каком значении параметра а уравнение ах2 = 0 имеет
бесконечно много решений?
11. При каком значении параметра а уравнение = 0 не
имеет решений?
12. При каких значениях параметра а неравенство ах > 8 имеет
бесконечно много решений?
13. При каком значении параметра а неравенство ах > 8 не
имеет решений?
ТЕМА 10. УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРОМ 155
Х2 _25
14. При каких значениях параметра а сократима дробь ?
х2-а
15. При каких значениях параметра а сократима дробь —- ?
х2 —х—2
16. При каких значениях параметра а сократима дробь — ?
17. При каких значениях параметра а уравнение х2 - ах +16 = 0
имеет два различных корня ?
18. При каких значениях параметра а уравнение х2 - ах +16 = 0
имеет два корня?
19. При каких значениях параметра а уравнение х2-ах + 16 = 0
не имеет корней?
Задания на 4 балла
20. При каком значении параметра а уравнение (а2 - 4)х =
= а2 + а - 6 имеет бесконечно много решений?
21. При каком значении параметра а уравнение (а2 - 4)х =
= а2 + а - 6 не имеет решений ?
22. При каком значении параметра а неравенство 2ах < 1 - х
выполняется для любых значений xl
23. При каком значении параметра а неравенство х • а2 < а + х
не имеет решений?
24. При каком значении параметра а неравенство х • а2 < а + х
выполняется для любых значений х?
25. При каком значении параметра а уравнение 2а(а - 2)х =
= а-2 имеет бесконечно много решений?
26. При каком значении параметра а уравнение 2а(а - 2)х =
= а - 2 не имеет решений?
27. При каких значениях параметра а неравенство 2а(а - 2)х <
< а - 2 не имеет решений?
28. При каких значениях параметра а неравенство
2а(а-2)х >а-2 имеет бесконечно много решений ?
29. При каких значениях параметра а неравенство
2а(а-2)х >а-2 выполняется для любых значений х?
30. При каких значениях параметра Ъ уравнение
(26 - 5)х2 - 2{Ь - \)х + 3 = 0 имеет единственное решение ?
31. При каких значениях параметра Ъ уравнение
(2Ь - 5)х2 - 2(Ь - \)х + 3 = 0 имеет два различных корня ?
156- РАЗДЕЛ 2. ТЕМАТИЧЕСКИЕ ТРЕНИРОВОЧНЫЕ ЗАДАНИЯ
32. При каких значениях параметра а неравенство
х2 + 2ах +1 < 0 не имеет решений?
33. При каких значениях параметра а множеством решений
неравенства х2 + 2ах +1 < О является отрезок?
34. При каких значениях параметра а множество решений
неравенства х2 + 2ах +1 < О состоит из одной точки?
35. При каких значениях параметра а неравенство
х2 - (а + 2)х + $а +1 > 0 выполняется при всех значениях xl
36. При каких значениях параметра а неравенство
х2 - (а + 2)х + 8д +1 > 0 не имеет решений?
37. Найдите все значения параметра Ъ , при которых уравнение
х2 - 2Ъх +6 + 6 = 0 имеет отрицательные корни.
38. Найдите все значения параметра Ъ , при которых уравнение
х2 - 2Ъх +6 + 6 = 0 имеет корни разных знаков.
39. Найдите все значения параметра р, при которых разность
корней уравнения 2хг - рх +1 = 0 равна 1.
40. Найдите все значения параметра /?, при которых отношение
корней уравнения х2 + рх + 2 = 0 равно 2.
41. Найдите все значения параметра а, при которых оба корня
уравнения х2 - ах + 4 = 0 лежат в промежутке (1; 4).
42. Найдите все значения параметра а, при которых 4 разделяет
корни уравнения х2 - ах + 4 = 0.
43. Найдите все значения параметра а, при которых оба корня
уравнения х2 - ах + 4 = 0 больше 4.
44. Найдите все значения параметра а, при которых оба корня
уравнения х2 - ах + 4 = 0 отрицательны.
45. Найдите все значения параметра а, при которых разность
корней уравнения х2 - ах + 4 = 0 равна 4.
46. Найдите все значения параметра а, при которых отношение
корней уравнения х2 - ах + 4 = 0 равно 4.
47. При каких значениях параметра а система уравнений
Гя + у - 0,5а2х = 0,
[8х - .у + 4 = 0
имеет бесконечно много решений?
48. При каких значениях параметра а система уравнений
\а + у - 0,5я2х = 0,
[8х - у + 4 = 0
не имеет решений?
ТЕМА 10. УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРОМ 157
49. При каких значениях параметра а система уравнений
[а + у - 0,5я2х = 0,
\%х - у + 4 = О
имеет единственное решение?
Задания на 6 баллов
50. При каких значениях параметра а неравенство
ах2 - 4ах - 3 £ 0 выполняется при всех значениях х?
51. При каком значении параметра а неравенство
ах2 + (2а + 3)х + а -1 > 0 не имеет решений?
52. Найдите все значения параметра а, при которых 2 разделяет
корни уравнения ах2 + х + 1 = 0.
53. При каких значениях параметра а уравнение
[х-1| + |х-3| = д имеет бесконечно много решений?
54. При каких значениях параметра а уравнение
\х -1| + \х - 3| = а не имеет решений?
55. При каких значениях параметра а уравнение
|х-1| + [х-3| = д имеет ровно два .решения?
56. Укажите число решений уравнения а\х + 3| - 2\х - 1| = 2 в
зависимости от а при а > 0.
РАЗДЕЛ 3
УКАЗАНИЯ
Тема 1. Числа и выражения.
Преобразование выражений
28. См. решение типового задания № 9.
29. В первом слагаемом примените формулу разности
квадратов. Во втором слагаемом сначала поменяйте местами слагаемые,
чтобы в дальнейшем не ошибиться в применении формулы
разности квадратов.
30. В первом слагаемом подкоренное слагаемое представляет
собой квадрат разности. Во втором слагаемом примените формулу
разности квадратов.
31. Сначала в каждом выражении внесите множители под знак
корня. Далее сравните подкоренные выражения.
32. В каждом слагаемом примените формулу (4). Не забудьте,
что |3 - VlT| = VlT - 3.
33. В числителе примените формулу разности кубов. В
знаменателе — квадрата суммы.
34. Сначала разложите на множители числитель и знаменатель
каждой дроби. В числителе первой дроби примените формулу
квадрата суммы. В числителе второй дроби — разности квадратов.
35. Сначала разложите на множители числитель и знаменатель
каждой дроби. В числителе первой дроби обратите внимание на
число слагаемых. Это подскажет вам прием разложения на
множители. В знаменателе второй дроби примените формулу
разложения квадратного трехчлена на множители. В случае
затруднения смотрите решение типового задания № 20.
36. Приведите дроби к общему знаменателю, учтите, что
(1-х)2 = 0с-1)2.
37. Приведите дроби к общему знаменателю, учтите, что
(/n-l)3 = -(l-m)\
38. Разложите на множители числитель дроби, применив
формулу разности кубов.
39. См. решение типового задания № 15.
ТЕМА1. ЧИСЛА И ВЫРАЖЕНИЯ. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ 159 I
40. В первой скобке приведите к общему знаменателю. Полу-
9
чите -—г=. Во второй скобке примените формулу квадрата
разности.
41. В знаменателе дроби вынесите множитель V30 и сократите
дробь на V30. Далее избавьтесь от иррациональности в
знаменателе, умножив и числитель и знаменатель на V3 + Vlo.
42. См. решение типового задания № 22.
43. Представьте подкоренное выражение 6 + 2V5 в виде
квадрата суммы, т.е. 6 + 2V5 = (l + V5) , и примените формулу (4).
44. Представьте подкоренное выражение 4 + 2^1Ъ в виде
квадрата суммы, т.е. 4 + 2V5 = (l + л/з) , и примените формулу (4).
45. Представьте подкоренное выражение 3 - 2V2 в виде
квадрата разности, т.е. 3 - 2V2 = (l - V2) , и примените формулу (4).
46. Представьте подкоренное выражение 34 - 24V2 в виде
квадрата разности. Для этого возведите выражение 4 - 3>/2 в квадрат.
47. Выполняйте действия последовательно и аккуратно. В
первой скобке сначала разложите на множители и числитель, и
знаменатель первой дроби, а затем приведите дроби к общему
знаменателю х + 3.
48. Сначала преобразуйте множитель -.-^--т» заменив
отрицательный показатель степени на положительный показатель. Далее
избавьтесь от «двухэтажное™» в знаменателе. В случае
затруднений смотрите решение типового задания № 16. В скобке, прежде
чем приводить дроби к общему знаменателю, разложите на
множители знаменатели каждой дроби.
49. В первой скобке разложите на множители знаменатели
каждой дроби, для этого вынесите множитель Jy. В выражении
49-\4у+у2
—-дг- выделите в числителе квадрат разности.
50. Не торопитесь с решением. Внимательно посмотрите на
выражение в скобках и сравните его с выражением а2 - 4а + 4,
которое представляет собой квадрат разности.
51. В первой дроби и в числителе, и в знаменателе раскройте
скобки и примените группировку. Во второй дроби примените
формулу разности квадратов.
52. В первой дроби и в числителе, и в знаменателе раскройте
скобки и примените группировку. Во второй дроби примените
формулу разности квадратов.
53. Смотрите решение типового задания № 12.
160 РАЗДЕЛ 3 УКАЗАНИЯ
54. Смотрите решение типового задания № 23.
55. Примените в знаменателе следующую формулу для
любых значений а и Ь и произвольного натурального числа п:
а" -Ъп =(а- b)(a"-] + сС~2Ь +... + аЬп~2 %
56. Примените в знаменателе следующую формулу для
любых значений а и Ъ и произвольного натурального числа я:
сС - Ъп = (а- b)(cf-] + cf-2b+...+abn-2 + bn~x)
57. Примените в знаменателе первой дроби формулу
cf-bn =(a-b)(a"~l +cf~2b+... + abn~2 + bn~l), а в знаменателе
второй дроби примените формулу суммы кубов.
58. Примените в знаменателе первой дроби формулу для
любых а и b и произвольного нечетного натурального числа п:
a"+bn =(a + b)(a"-]-an-2b+...-ab"-2+bn-]\ где a = m,b = l а в
знаменателе второй дроби примените формулу разности кубов.
59. Сначала выразите х через у из соотношения --- = 0,25,
\3х+у )
т.е. у = 0,25 <=> у = - и х = у. Подставьте х = у в вы-
\3х+у) \2x-y) 4
х3-4х2у+5ху2-у3
ражение т—тЛ— •
ЛГ-6.Г
60. Представьте каждое подкоренное выражение виде квадрата
и не ошибайтесь в применении свойства (4).
61. Возведите 2>/б - 5 в квадрат и обратите внимание на
подкоренное выражение. Представьте подкоренное выражение в виде
квадрата разности и, не забывая свойства (4), закончите решение.
62. Рассмотрите произведение
и примените формулу разности квадратов.
63. Рассмотрите произведение
(л/74 - а* - л/Ю-я4) • (л/74 - а* + VlO-04).
64. Рассмотрите квадрат выражения л/б
65. Попробуйте представить каждое подкоренное выражение в
виде квадрата, для этого введите новую переменную b = 4а. В
случае затруднений смотрите решение типового задания № 23.
66. Пусть А = V2005 + V2008 и В = V2007 + V2006. Возведите А
и В в квадрат и сравните V2005 • 2008 и V2006-2007. Обозначьте
а = 2005, выразите через а 2006, 2007, 2008.
ТЕМА 2. УРАВНЕНИЯ 161
67. Разложите на множители числитель дроби, дополнив его до
квадрата суммы. Далее примените в числителе формулу разности
квадратов.
68. Преобразуйте выражение - + °-^-. Получите, что - + ~ = 3.
а 2 а 2
Далее рассмотрите - + - .
\а 2}
69. Умножьте выражение (7512 +1)(7256 +1)(7128 + 1)(764 +1) х
х(732 +1)(716 +1)(78 +1)(74 +1)(72 +1)(7 +1) на (7 - 1) и примените
формулу разности квадратов.
70. Умножьте выражение
(б512 +1)(6256 +1)(6128 + 1Х664 +1) х
х(632 +1)(616 +1)(68 +1)(64 +1)(62 +1)(6 +1)
на (6 - 1) и примените формулу разности квадратов.
71. Разложите на множители числитель дроби. Для этого
преобразуйте выражение (х + 10)(х + 20)(х + 30)(х + 40) следующим
образом:
(х + 10)(х + 20)(х + 30)(х + 40) = (х + 10)(х + 40)(х + 20)(х + 30) =
= (х2 + 50* + 400)(х2 + 50* + 600).
И введите новую переменную / = х2 + 50х + 500.
72. Преобразуйте числитель дроби, сгруппировав первое и
последнее слагаемые и применив формулу разности квадратов.
Далее получите
Теперь уже сгруппируйте первые два слагаемых и т.д.
73. Примените формулу х]2 -1 = (х -1)(хп +х10 +... + * + l).
Эта формула непосредственно следует из формулы d1 -Ъп =
Тема 2. Уравнения
25. 1-й способ. Решите каждое уравнение в отдельности.
Корнями первого уравнения будут числа - и 8. Второго — 8 и 2. 2-й способ.
Решите сначала одно уравнение, а затем его корни подставьте в
другое уравнение.
26. См. решение типового задания № 13.
27. См. решение типового задания № 13.
28. См. решение типового задания № 11.
162 РАЗДЕЛ 3. УКАЗАНИЯ
29. См. решение типового задания № П.
30. Приведите дробные выражения к общему знаменателю и
перенесите число 3 в левую часть.
31. См. решение типового задания № 10.
32. См. решение типового задания № 10.
33. См. решение типового задания №12.
34. Уравнение имеет один корень, если D = 0.
35. Примените теорему Виета и найдите другой корень
уравнения. Он равен (-3).
36. Введите новую переменную а = х2 + Зх и решите уравнение
й2 - а -12 = 0. Корни исходного уравнения 1; - 4; —^—.
37. См. замечание к решению типового задания № 11.
38. Выражение х,2х2 + x22*i разложите на множители и
примените теорему Виета. Не забудьте, что теорема Виета применяется
для приведенного квадратного уравнения.
39. В выражении хх2 + х22 выделите полный квадрат, т.е.
х\2 + Х22 = (*i + xi) ~ 2х,х2 и примените теорему Виета. См.
решение типового задания № 6.
40. См. решение типового задания № 14.
41. Уравнение х2 -Ъ = 0 имеет единственное решение х = 0
при 6 = 0. Уравнение ^—р = 0 имеет единственное решение еще в
X — О
одном случае: корень знаменателя является корнем числителя,
т.е. при Ъ = 36.
42. Уравнение х2 - 36 = 0 имеет два корня 6 и (-6), поэтому
исходное уравнение имеет единственное решение только в одном
случае: корни числителя является корнями знаменателя.
43. Уравнение х2 - Ъх + 4 = 0 имеет единственное решение при
D = 0. Уравнение — = 0 имеет единственное решение еще в
х—6
одном случае: корень знаменателя является корнем числителя.
44. Уравнение имеет различные корни, если D > 0. Уравнение
[х, + х2 = 2а < 0,
имеет отрицательные корни, если \ ^
1*1*2 = 2л + 24 > 0.
Окончательно имеем промежуток (-12; -4).
45. Функция Дх)= х2 - (а + 7) |х| + а2 - 5а является четной,
поэтому, чтобы уравнение имело нечетное число корней (в
данном случае — три), необходимо, чтобы один из корней был равен
0. Получаем, что а = 0 или а = 5. Проверкой убеждаемся, что оба
эти значения а подходят.
ТЕМАЗ. СИСТЕМЫ УРАВНЕНИЙ 163
46. Функция J{x) = х4 -745х2 +97344 = 0 является четной,
поэтому уравнение имеет корни ±13; ±24.
47. Вынесите общий множитель. Уравнение х2 - 2ах - (2а - 3) = О
имеет два различных корня при а Е (-«>; -3)и(1; +«>). Чтобы
исходное уравнение имело три различных корня, надо, чтобы
нуль не был корнем уравнения х2 - 2ах - (2а - 3) = 0, т.е.
02-2я0-(2я-3)*0.
48. Введите новую переменную а = х2 + 5х.
49. Сгруппируйте первое и четвертое, второе и третье
слагаемые. Приведите их к общему знаменателю и получите один из
корней — (-2,5).
х—2
50. Введите новую переменную т = —^—.
51. Рассмотрите первый множитель х2 -2х + 7. Докажите, что
он принимает значения большие или равные 6. Рассмотрите
второй множитель х2 + 6х +11. Докажите, что он принимает значения
большие или равные 2. Из этого следует, что левая часть
уравнения больше или равна 12.
52. См. решение типового задания № 15.
Тема 3. Системы уравнений
14. Умножьте и первое и второе уравнение на 12 и приведите
подобные слагаемые.
15. 1-й способ. Метод подстановки. Выразите из первого
уравнения х или у и подставьте во втрое уравнение. 2-й способ.
Рассмотрите второе уравнение и попробуйте «увидеть» формулу
квадрата суммы. Только не забудьте, что уравнение а2 = 25 имеет два
решения.
16. Преобразуйте второе уравнение системы. Перенесите все
слагаемые в левую часть и примените формулу квадрата разности.
17. Удобнее решать систему методом сложения. Получаем, что
х2 = 25, у2 = 4 и исходная система распадается на четыре системы.
18. При сложении уравнений получите, что х2 = 25. Далее
исходная система распадается на четыре системы.
19. Сложите уравнения и получите, что.х2 = 25. Система имеет
четыре решения.
20. Решите систему методом сложения, при этом получите
квадратное уравнение х2 + х - 6 = 0.
21. См. решение типового задания № 5.
22. См. решение типовбго задания № 4.
23. Рассмотрите первое уравнение системы. Получите возмож-
164 РАЗДЕЛ 3. УКАЗАНИЯ
ное решение системы (5; -2). Проверьте, удовлетворяет ли эта
пара чисел второму уравнению системы.
24. Во втором уравнении примените формулу разности
квадратов и замените выражение х1 + уг числом 13.
25. См. решение типового задания № 8.
26. См. решение типового задания № 8.
27. Умножьте второе уравнение на 3 и сложите с первым
уравнением. Далее примените формулу куба суммы. Получите, что
х + у = 1.
28. Сумма квадратов двух выражений равна нулю тогда и
только тогда, когда каждое из выражений равно нулю. Учитывая это
утверждение, получите систему уравнений
x + J> = l,
ху(х + у) = -2.
29. 4а + 4Ь = О тогда и только тогда, когда \, '
[о = U.
30. Сложите все три уравнения системы и получите
х + у + z = 6. Теперь из этого уравнения последовательно
вычитайте каждое уравнение исходной системы.
31. Перемножьте все три уравнения системы и получите
(xyzf = 36.
32. Рассмотрите первое уравнение системы. Попробуйте
«увидеть» сумму квадратов двух выражений.
33. См. решение типового задания № 9.
34. Сложите уравнения системы. Получите уравнение
х2+х-Ь-1 = 0. Квадратное уравнение имеет единственное
решение, если его дискриминант равен нулю.
Тема 4. Неравенства
20. Раскройте скобки и получите неравенство -0,5я > 5.
21. Решите двойное неравенство 0 < 3 - 2/ < 2.
22. Из первого неравенства системы получите х > -1,4. Из
второго неравенства: х > 1.
23. Решением первого неравенства является промежуток f - оо; - -1.
Решением второго неравенства — отрезок [-3; 3].
24. Корни уравнения — (-1) и (-3). Решение неравенства —
промежуток (-оо; -1). Произведите отбор корней, принадлежащих
этому промежутку.
ТЕМА 4. НЕРАВЕНСТВА 165 I
25. Раскройте скобки и приведите подобные слагаемые.
Получите 2 > -2.
26. См. решение типового задания № 7.
27. См. решение типового задания № 7.
28. Уравнение имеет корни I и 2. Решением неравенства
является промежуток (-оо; 1,5).
29. Решением линейного неравенства при а ** О является луч.
А если а = О?
30. Вынесите общий множитель. Исходное неравенство
равносильно Неравенству (2х - 1)(2х - 4) < 0, которое можно решить
методом интервалов. См. решение типового задания № 8.
31. Рассмотрите первый множитель. Приведите слагаемые к
^ V5+V5-4 _
общему знаменателю. Определите знак множителя . Для
этого сравните числа V5 + V5 и 4. Или (V5 + V5) и 42.
32. Решение первого неравенства (2V3; + оо). Решение второго —
(-ос; 4V2].
33. См. решение типового задания № 8.
34. Так как (Vtf ) = а при а > 0, то исходное неравенство рав-
\х - 4 > 0,
носильно системе {
[х - 4 < 7.
35. Так как (Vtf ) = а при а > 0, то исходное неравенство равно-
х + 4 > 0,
сильно системе
36. См. решение типового задания № 7.
[9-х2 >0;
37. Область определения можно найти из системы \
[х +1 > 0.
38. Решите неравенство методом интервалов. Для этого решите
уравнение х4 - 10х2 +9 = 0. Отметьте корни на координатной
прямой и используйте правило чередования знаков.
39. См. решение типового задания № 9.
40. Решите неравенство методом интервалов. Для этого решите
уравнение х3-6х2 + 9х = 0. Отметьте корни на координатной
прямой, один из них будет корнем двойной кратности. См.
решение типового задания № 9.
41. Разделите на коэффициент при х и освободитесь от
иррациональности в знаменателе. Получите: х < 3 + 2V2.
42. Введите новую переменную а = V*. Решите квадратное не-
166 РАЗДЕЛ 3. УКАЗАНИЯ
равенство а2 - 5а + 4 > 0. Вернитесь к переменной х. Осталось
решить неравенства Vx < l,Vx > 4.
43. См. решение типового задания № 10.
44. См. решение типового задания № 10.
45. См. решение типового задания № 11.
Тема 5. Координаты и графики
20. Смотрите решение типового задания № 3.
21. Смотрите решение типового задания № 3.
22. Ветви параболы направлены вниз (а < 0), ордината точки
пересечения с Оу отрицательна (с < 0). Абсцисса вершины
отрицательна, значит - - - < 0. Определите знак коэффициента Ь.
2а
23. Смотрите решение задачи № 22.
24. Смотрите решение типового задания № 5.
25. Смотрите решение типового задания № 5.
26. Смотрите решение типового задания № 5.
27. Смотрите решение типового задания № 5.
28. Запишите уравнение прямой, проходящей через две точки.
Проверьте, принадлежит ли третья точка этой прямой.
29. Уравнение прямой имеет вид у = Ъх + Ъ. Найдите Ъ.
30. Уравнение прямой имеет вид у = 2х + Ь. Найдите Ь.
31. Найдите коэффициенты к и Ь. Для этого подставьте
координаты каждой точки в общее уравнение.
32. Смотрите решение типового задания № 4.
33. Смотрите решение типового задания № 4.
34. Смотрите решение типового задания № 6.
35. Смотрите решение типового задания № 6.
36. График первого из уравнений постройте в каждой из
четырех координатных четвертей — это квадрат с диагональю, равной
4V2. График второго уравнения — окружность с центром в начале
координат и радиусом, равным 2V2.
37. График первого из уравнений постройте в каждой из
четырех координатных четвертей — это квадрат с диагональю, равной
4V2. График второго уравнения — окружность с центром в начале
координат и радиусом, равным 2.
38. График первого из уравнений постройте в каждой из
четырех ^координатных четвертей — это квадрат с диагональю,
равной 16. График второго уравнения — окружность с центром в
начале координат и радиусом, равным 7.
ТЕМА 6. ФУНКЦИИ 167
39. Графиками уравнений являются парабола с вершиной в
точке (-1; I), пересекающая ось Оу в двух точках, и окружность с
центром в начале координат и радиусом, равным 3.
40. Графиками уравнений являются парабола с вершиной в
точке (0; 6), ветви которой направлены вправо, и окружность с
центром в начале координат и радиусом, равным 2.
41. Графиками уравнений являются парабола с вершиной в
точке (-16; 0), пересекающая ось Оу в точках (0; 2) и (0; -2), и
окружность с центром в начале координат и радиусом, равным 10.
42. Смотрите решение типового задания № 8. Заметим, что
коэффициент с задан, в условии, и коэффициент а должен быть
положительным.
43. Смотрите решение типового задания № 8. Выражение
а - Ъ + с > 0 можно прочитать как у(-1) > 0. Во всяком случае
коэффициент с > 0.
44. Смотрите решение типового задания № 10.
45. Смотрите решение типового задания № 9.
46. Смотрите решение типового задания № 9.
47. Смотрите решение типового задания № 9.
48. Смотрите решение типового задания № 9. Ветви параболы
направлены вниз, значит а < 0.
49. Смотрите типовое задание № 7.
50. Смотрите типовое задание № 7. Обратите внимание на
область определения уравнения.
51. Смотрите типовое задание № 7. Разложите на множители
левую часть уравнения, применив формулы сокращенного умножения.
52. Смотрите типовое задание № 7. Замените уравнение двумя
следующими уравнениями: х2 + у2 -6 = 2и х2 + у2 -6 = -2.
Тема б. Функции
8. Смотрите решение типового задания № 4.
9. Смотрите решение типового задания № 4.
10. Смотрите решение типового задания № 4.
11. Смотрите решение типового задания № 4.
12. Смотрите решение типового задания № 5.
13. После преобразования выражения у = —— получим
у =х+ 1, х* 0.
14. Смотрите решение типового задания № 5.
15. Смотрите решение типового задания № 5.
168
РАЗДЕЛ 3. УКАЗАНИЯ
16. Смотрите решение типового задания № 5.
17. Преобразуйте выражение к виду квадратного трехчлена.
18. Смотрите решение типового задания № 6.
19. Смотрите решение типового задания № 6.
20. Функцию можно задать формулой у = х + 3, где х ** 3.
Графиком функции является прямая у = х + 3 без точки с абсциссой,
равной 3.
21. Функцию можно задать формулой у = х - 2, где х ** -2,5.
Графиком функции является прямая у = х - 2 без точки с
абсциссой, равной -2,5.
22. Смотрите решение типового задания № 7.
-2
6\
\
4 \
2
0
\
\
ч
\
\
6
X
23. Смотрите решение типового задания № 7.
\
\
-4
\
\
V
\
-2
6
4
N
0
/
/
/
/
2
/
/
/
ТЕМА 6. ФУНКЦИИ
24. Смотрите решение типового задания № 7.
169
У
/
/
-6
/
-4
л
\
|\
\
\
-2
У *
[
\
8
6
4
2
0
-2
-4
у
2
/
/
X
25. Смотрите решение типового задания № 7.
—
/
■4
)
/
/
1
-2
yi
2
0
-2
■4
2
\
\
\
26. Смотрите решение типового задания № 7.
—
-6
-4
/
/
/
/
/
1
-2
4
J
2 У
0
-2
-4
/
/
2
4
X
17O
РАЗДЕЛ 3. УКАЗАНИЯ
27. Смотрите решение типового задания № 9.
28. Смотрите решение типового задания № 9. Графику
функции принадлежат, например, точки (I; 2), (0; -I), (-3; 0), (-2; -2)
и т. д.
29. Смотрите решение типового задания № 8. При т > 4 и
т = 0 — две общих точки, при т - 4 — три общих точки, при
т < 0 — нет общих точек.
-6
-4
\
\
\
i
У
1
-2
\
\
\
\
8
6
4
/
У
I
0
-2
2
\
\
/
/
/
/
/
/
/
4
X
30. Смотрите решение типового задания № 8.
ТЕМА 7. АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ 171
Тема 7. Арифметическая
и геометрическая прогрессии
15. Пусть АВ = аи тогда АС = ax+d и ВС = ax+2d. Периметр
треугольника ABC равен АВ + АС + ВС = 3a{+3d или 36, поэтому
ax + d= 12.
16. Используя характеристическое свойство арифметической
прогрессии, найдите а4, а затем по формуле л-ого члена и я,, и df.
17. Z>3 = bxq2, значит, q2 = 3. Выразите b5 через b3.
18. Используйте характеристическое свойство арифметической
прогрессии или см. решение типового задания № 9.
19. См. решение типового задания № 4.
20. Запишите формулу я-ого члена. Получите неравенство
ап <0, п <41.
21. Найдите я4» используя характеристическое свойство
арифметической прогрессии. Далее найдите разность прогрессии.
22. Имеем: ах = 3 и а5 = 48. Используйте формулу л-ого члена.
23. См. решение типового задания № 10.
24. См. решение типового задания № 7.
25. Запишите формулу л-ого члена для а2, я8, аи. Получите:
ах + 6d = 23.
26. Используйте формулу л-ого члена. Найдите член
прогрессии, наиболее близкий к нулю. Для этого определите
последний отрицательный и первый положительный член прогрессии.
См. также решение типового задания № 4.
27. См. решение типового задания № 4.
28. Используйте формулу суммы л-первых членов геометриче-
()
ской прогрессии. Получите: 6, ^—'-— = 85.
-г1
29. Получите систему уравнений: {(^)(^+4</) = 8.
Систему можно решить методом подстановки. См. также
решение типового задания № 5.
30. Найдите последний отрицательный член прогрессии, для
этого решите неравенство ап < 0. Получите, что п < 51.
31. Используйте свойство средней линии треугольника и
средней линии трапеции. Получите арифметическую прогрессию: 10;
20; ... 60.
32. Используйте формулу л-ого члена для Ьъ и для Ь2. Получите
уравнение на q : q2 - q - 2 = 0. Почему один из корней уравнения
является посторонним?
172 РАЗДЕЛ 3. УКАЗАНИЯ
33. Используя характеристическое свойство геометрической
прогрессии, найдите ЬА. Получите два значения 64» и »
соответственно, два значения d. Задача имеет два решения.
34. Выразите 614через Ьп. Далее выразите bl6 через Ьн.
35. Используйте характеристическое свойство арифметической
прогрессии для нахождения а35. Затем найдите разность
прогрессии.
. _4 = 27,
36. Решите систему уравнений ' '
•Й3=72.
Преобразуйте второе уравнение и получите, что Ьх • Ь4 = 72.
Система имеет два решения, но одно из них является посторонним.
37. См. решение типового задания № 12.
38. 1-й способ. Найдите 528 и 519. Искомая сумма равна 528 - 519.
2-й способ. Найдите а^ и а^. Получите конечную
арифметическую прогрессию: 83; ...; 115 и найдите сумму ее членов.
39. Рассмотрите арифметическую прогрессию (ап): 2; 4; 6 ...
Запишите формулу л-го члена и решите неравенство ап< ПО.
40. Представьте и числитель, и знаменатель в виде степени с
натуральным показателем. В числителе — х1+2+ +17. В знаменателе
— х1+3+ +17. Найдите сумму членов конечных арифметических
прогрессий: 1; 2; ...; 17 и 1; 3; ...; 17. Далее разделите степень на
степень.
41. В числителе и в знаменателе представлены суммы
конечных геометрических прогрессий со знаменателем 3. Найдите их.
314-1
Получите: vrrp
42. Пусть члены геометрической прогрессии имеют вид
6,, bxq, bxq2, bxql. Используйте характеристической свойство
арифметической прогрессии и получите систему уравнений
Раскройте скобки, приведите подобные слагаемые и сгруппируйте
слагаемые, содержащие Ьх. См. также решение типового задания
№ 13.
43. Из первого условия получите: ах = 3 - l,5d. Исследуйте
квадратичную функцию f(d) = (3 + 0,5df)(3 + 2,5d) на наименьшее
значение. Для этого найдите координаты вершины параболы.
44. Примените формулу разности квадратов. Получите сумму
конечной арифметической прогрессии 85 + 81 +... + 3.
45. Формула л-ого члена для первой прогрессии имеет вид:
ап = 2п +1; для второй — ат = 1т +1. Члены прогрессий
совпадают, если ап = ат, 2п = 1т. Так как тип— натуральные числа, то
по свойствам делимости т делится на 2, а л делится на 7. Итак, т
ТЕМА 8. ТЕКСТОВЫЕ ЗАДАЧИ 173
может быть равно 2; 4; ... 10. Получаем арифметическую
прогрессию с первым членом 15 и разностью 14.
46. Двузначные натуральные числа, которые делятся на 3,
таковы: 12; 15;... 99. Их 30. Двузначные натуральные числа, которые
делятся на 4 таковы: 12; 16; ..>; 96. Их 22. Двузначные натуральные
числа, которые делятся и на 3 и на 4, таковы: 12; 24; ...; 96. Их 8.
Имеем: 30 + 22 - 8 = 44.
47. Все четные числа, кратные 3, имеют вид 6 я, где п —
натуральное число. Сумма двузначных чисел такого вида равна 810.
Четных двузначных чисел, кратных 3 и кратных 7, всего два: 42 и
84. Имеем: 810 - 42 - 84 = 684.
48i Любое натуральное число, которое дает при делении на 4
остаток 1, можно записать в виде 4л + 1, где п — натуральное
число. Сколько таких натуральных чисел не превосходят 150? Решите
неравенство 4л+ 1 < 150. Их 37. Остается найти сумму тридцати
семи членов арифметической прогрессии ап = 4л +1.
49. Запишите формулу я-ого члена для каждого, кроме
первого, члена геометрической прогрессии. Получите Ь5Х • д]0 = 243,
значит, bx-q2 = 3.
Тема 8. Текстовые задачи
24. См. решение типового задания № 5.
25. См. решение типового задания № 6.
26. См. решение типового задания № 5.
27. См. решение типового задания № 8.
28. См. решение типового задания № 4. Пусть х — объем
продукции, выпущенной в январе.
29. См. решение типового задания № 4.
30. См. решение типового задания № 4.
31. Если собственная скорость лодки — х км/ч, то выразить
время движения по озеру и по реке, а затем составить уравнение.
32. См. решение задачи № 31.
33. Если скорость первого пешехода — х км/ч, то скорость
второго пешехода (х + 2) км/ч. Движение навстречу друг другу харак-
S
теризуется соотношением —— — = /, где / — время до их встречи,
a S — путь сближения.
34. См. решение задачи № 33.
35. Кроме способа, описанного в указании к задаче № 33,
задачу можно решить и другим способом. Пусть х км — путь,
пройденный до встречи первым туристом, тогда (44 - х) — путь второго
w 44- х х i
до их встречи. Можно составить уравнение ——- = - +1.
174 РАЗДЕЛ 3. УКАЗАНИЯ
36. Если х ч — время движения первого катера, то (х - 5) —
„ 300 300
время второго. Скорость первого —, скорость второго ——.
37. См. решение задачи № 36.
38. См. решение задачи № 36.
39. Если х — производительность первой машины, тогда (х - 4) —
производительность второй. Найдем объем работы, выполненный
первой машиной, объем работы, выполненный второй машиной,
и их сумму.
40. Пусть А — объем работы, тогда производительность работы
первого —, производительность работы второго —. Известна их
разность.
41. Если х — время работы первого, тогда (х - 5) — время
работы второго. Производительность первого -, производительность
второго —-. Если учесть, что первый работал 9 дней, а второй 4,
можно составить уравнение.
42. Пусть х автомобилей — норма выпуска в час, a t ч — время
для производства всех автомобилей по плану. Получим первое
уравнение, х • t = 90. Завод перевыполнял план: за 3 часа
произвел Зх автомобилей, а за оставшиеся (/ - 4) часов — (/ + \)(х + 1)
автомобилей. Так как в действительности завод выпустил 95
автомобилей, составим второе уравнение. Решим систему из двух
уравнений.
43. См. решение типового задания № 17.
44. Если х — время работы первой бригады, тогда (х - 9) —
время работы второй. Производительность первой бригады -,
производительность второй ——. Найдем двумя способами их
общую производительность: - и - + —-. Составим уравнение.
45. См. решение типового задания № 13.
46. См. решение типового задания № 9.
47. См. решение типового задания № 9.
48. См. решение типового задания № 10.
49. См. решение типового задания № 10.
50. См. решение типового задания № 9.
51. Выручка театра получается умножением числа зрителей на
цену билета. Ее нужно считать дважды — до и после повышения
цены билета.
52. Уравняйте цены товаров после повышения цены.
ТЕМА 9. УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ 175
53. Пусть р — процент повышения зарплаты, тогда после
первого повышения зарплата стала (р + 100), а после второго ■ .
1UU
54. Найдем производительность каждой швеи и их общую
производительность. Зная общий объем работы (59 фартуков), можно
найти время совместной работы, а затем, в соответствии с
производительностью каждой швеи, найдем вклад каждой в общий
объем работы.
55. См. решение задачи № 54.
56. См. решение типового задания № 14.
57. См. решение типового задания № 14. 2-й способ. Пусть
время совместной работы мастера и его ученика х ч, тогда мастер
работал (х + 9) ч, а ученик (х + 25) ч. Можно составить уравнение
относительно их производительности:
58. См. решение типового задания № 14. 2-й способ. Пусть
время совместной работы кранов х ч, тогда первый кран работал
(х + 16) ч, а второй — (х + 9) ч. Можно составить уравнение
относительно их производительности: —— + —- = -.
х+16 х+9 х
59. Используйте при решении типовые задания № 10 и 16.
Обозначьте массу первого сплава — jc кг, а массу второго — у кг.
Найдите количество двух видов чистого металла в первом и
втором сплавах. Запишите общие количества первого и второго
металлов и найдите их отношение. Отношение — показывает, что в
полученном сплаве 15 частей первого металла и 22 части второго.
Тема 9. Уравнения и неравенства
с модулем
10. См. решение типового задания № 1.
11. Сравните число 4 - VT7 с нулем.
12. См. решение типового задания № 2.
13. См. решение типового задания № 3.
14. Решите неравенство. См. решение типового задания № 2.
Решение неравенства — промежуток (-8;б).Сколько целых чисел
входит в этот промежуток?
15. Решением неравенства является объединение промежутков
(-оо;1)и(3;+оо).
16. См. решение типового задания № 2.
17. См. решение типового задания № 3.
176 РАЗДЕЛ 3. УКАЗАНИЯ
18. См. решение типового задания № 4.
19. См. решение типового задания № 4.
20. См. решение типового задания № 4.
21. Примените следующее свойство модуля: для любого
действительного числа а \а\ > 0.
22. Используйте следующее свойство модуля: для любого
действительного числа а \а\ > 0.
23. Примените следующее свойство модуля: для любого
действительного числа а \а\ > 0, причем \а\ = 0 тогда и только тогда,
когда а = 0.
24. См. решение типового задания № 1.
25. См. решение типового задания № 4.
26. См. решение типового задания № 4. Корни уравнения: (-1)
и (-9).
27. Решите отдельно каждое неравенство системы.
Решение первого неравенства — (-7; 5); второго неравенства —
( 1][3)
28. Решите отдельно каждое неравенство системы.
Решение первого неравенства — (-4; 6); второго неравенства —
(][)
29. См. решение типового задания № 8. Решением неравенства
является отрезок [-3; 2].
30. См. решение типового задания № 8.
31. См. решение типового задания № 7.
32. См. решение типового задания № 4.
33. См. решение типового задания № 5.
34. См. решение типового задания № 5.
35. См. решение типового задания № 5.
36. См. решение типового задания № 5. Решение неравенства —
отрезок [-2; 2].
37. 1) Если х > 5, то получите неравенство (х - 5)(х - 3) > 0,
которое можно решить методом интервалов (смотрите тему
«Неравенства»). Решением в случае 1) является промежуток [5; + оо).
2) Если х < 5, то получите неравенство (-х + 5)(х - 3) > 0.
Решением в случае 2) является промежуток [3; 5).
38. 1) Если х > -5, то получите неравенство (х + 5)(х - 3) > 0,
которое можно решить методом интервалов (смотрите решение
неравенств методом интервалов в теме «Неравенства»). Решение в
случае 1) {-5}и[3; +«>). 2) Если х < - 5, то получите неравенство
(-х - 5)(х - 3) > 0. Решений в случае 2) нет.
39. См. решение типового задания № 10.
40. См. решение типового задания № 10.
41. См. решение типового задания № 9.
42. См. решение типового задания № 9.
ТЕМА 9. УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ 177
43. См. решение типового задания № 9.
44. См. решение типового задания № 12.
45. См. замечание к решению типового задания № 12.
46. См. решение типового задания № 12.
47. Введите новую переменную а = |х|. Решите
квадратное неравенство д2+6д-7>0 (смотрите решение
квадратных неравенств в теме «Неравенства»). Получите, что
яе(-оо; -7Ju[l; +oo). Учтите, что а >0. Вернитесь к
переменной х и решите неравенство \х\ > 1.
48. См. замечание к решению типового задания № 12.
49. Решите отдельно каждое неравенство системы. Решением
первого неравенства являются все действительные числа.
Решением второго — промежуток (0,5; 3,5), значит, решением системы
является промежуток (0,5; 3,5).
50. Решите отдельно каждое неравенство системы. Решением
первого неравенства является промежуток (-«>; 5,25]. Решением
второго — промежуток (-4; б), значит, решением системы
является промежуток (-4; 5,25].
51. Используйте следующее свойство модулей: |д| + |й| = \а + Ь\
тогда и только тогда, когда или а и Ъ одного знака, или одно из
них равно нулю, или каждое из них равно нулю, т.е. аЪ > 0.
Получите систему неравенств
Г7-21х>0,
[9 + 21* >0.
Или решите уравнение методом, рассмотренным в решении
задания № 9.
52. Используйте следующее свойство модулей: |а| + |й| = \а + Ь\
тогда и только тогда, когда аЪ > 0. Или решите уравнение
методом, рассмотренным в решении задания № 9.
53. Так как 5х -15 > 0,х > 3, то все выражения, стоящие под
знаком модуля, неотрицательны. Решение исходного неравенства
сводится к решению системы неравенств
54. Так как 6х - 18 > 0, х > 3, то все выражения, стоящие под
знаком модуля, неотрицательны. Решение исходного неравенства
сводится к решению системы неравенств
J
|4х<6х-18.
55. Так как при любых значениях х (х2-9х + 8) >0 и
5|х-1|>0, то уравнение имеет решение, если слагаемые
178 РАЗДЕЛ 3. УКАЗАНИЯ
(х2 - 9х + 8) и 5\х - \\ обращаются в нуль одновременно. То есть
исходное уравнение равносильно системе уравнений:
|(х2-9х+8)2 = 0;
[5|х-Ц = 0.
56. Учтите, что при любых значениях х \х2 - 4| > 0 и \х - 2| > 0.
57. См. решение типового задания № П.
58. См. решение типового задания № 11.
Тема 10. Уравнения и неравенства
с параметром
8. См. решение типового задания № 1.
9. См. замечание к решению типового задания № 1.
10. Контрольное значение параметра а = 0. При а * 0
уравнение имеет единственное решение.
11. Контрольное значение параметра а = 0. При а ** 0
уравнение имеет единственное решение.
12. См. решение типового задания № 2.
13. См. решение типового задания № 2.
14. Дробь сократима, если х = а — корень числителя.
15. Дробь сократима, если х = 5 — корень числителя.
16. Дробь сократима, если х = а —. корень числителя.
17. См. решение типового задания № 3.
18. См. решение типового задания № 3.
19. См. решение типового задания № 3.
20. Коэффициент при х равен (д-2)(д + 2). Имеем два
контрольных значения параметра: а = 2иа = -2. Подставьте их в
исходное уравнение.
21. Коэффициент при х равен (д-2)(я + 2). Имеем два
контрольных значения параметра: а = 2и а = -2. Подставьте их в
исходное уравнение.
22. См. решение типового задания № 1 и замечание к нему.
Контрольное значение параметра: а = -0,5.
23. См. решение типового задания № 1 и замечание к нему.
Контрольные значения параметра: а = 1иа= -1.
24. См. решение типового задания № 1 и замечание к нему.
Контрольные значения параметра: а = 1 и а = -1.
25. Коэффициент при х равен 2а(а - 2), поэтому контрольные
значения параметра а = 0 и а = 2. Подставьте их в исходное
уравнение.
ТЕМА 10. УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРОМ 179 I
26. Коэффициент при х равен 2а(а -2), поэтому контрольные
значения параметра а = 0 и а = 2. Подставьте их в исходное
уравнение.
27. Коэффициент при х равен 2а(а-2), поэтому контрольные
значения параметра а = 0 и а = 2. Подставьте их в исходное
неравенство.
28. Коэффициент при х равен 2а(а - 2), поэтому контрольные
значения параметра а = 0 и а = 2. Подставьте их в исходное
неравенство.
29. Коэффициент при х равен 2а(а - 2), поэтому контрольные
значения параметра а — 0 и а = 2. Подставьте их в исходное
неравенство.
30. Дискриминант исходного уравнения равен (26 - 4)2 при
Ъ * 2,5. См. решение типового задания № 4.
31. Дискриминант исходной) уравнения равен (2Ь-4)2 при
Ъ * 2,5. См. решение типового задания № 4.
32. См. решение типового задания № 5. D < 0.
33. См. решение типового задания № 5. D > 0.
34. См. решение типового задания № 5. D = 0.
35. См. решение типового задания № 5. D < 0.
36. Решением исходного неравенства может быть либо вся
координатная прямая (D < 0), либо одна точка (D = 0), либо отрезок
(/)>0).
37. См. решение типового задания № 6.
38. См. решение типового задания № 6.
39. Теорема Виета применяется для приведенного квадратного
уравнения. Получите систему уравнений:
х, -х2 = 1,
х, + х2 = 0,5/7,
х, • х2 = 0,5.
См. решение типового задания № 7.
40. Получите систему уравнений:
х] • х2 = 2,
х] + х2 = -р.
Из первого и второго уравнений найдите корни уравнения.
41. Рассмотрите функцию f(x) = х2 - ах + 4. Графиком данной
функции является парабола. Изобразите параболу с указанными
свойствами.
18O
РАЗДЕЛ 3. УКАЗАНИЯ
О
Запишите условия, соответствующие этому расположению
параболы.
(1)
(2)
ы < 4> (3)
(4)
1 < х
Решите каждое из этих неравенств.
42. См. решение типового задания № 9.
43. См. решение типового задания № 8.
Получите систему неравенств
/<4)>0,
^вершины "•
44. См. решение типового задания № 6.
45. См. решение типового задания № 7.
46. Получите систему уравнений
х, + х-у = а.
Из первого и второго уравнений найдите корни уравнения.
47. См. решение типового задания № 10.
48. См. решение типового задания № 10.
49. См. решение типового задания № 10.
50. Получите систему неравенств:
J
[D<0.
См. решение типового задания № 5.
ТЕМА 10. УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРОМ
181
51. Получите систему неравенств:
[ж 0,
[D<0.
См. решение типового задания № 5.
52. Рассмотрите два случая: 1) а > 0; 2) а < 0. Изобразите
параболу, соответствующую условию задания в каждом из случаев.
См. также решение типового задания № 9.
53. Изобразите график функции f(x) = \х -1| + \х - 3|.
1
При а = 2 решением уравнения будет отрезок [l; 3].
54. См. указание к решению № 53. При а < 2 прямая у = а не
пересекает график функции f(x) = \х -1| + \х - 3|.
55. См. указание к решению № 53. При а > 2 прямая у = а
пересекает график функции f(x) = \х -1| + \х - 3[ ровно в двух точках.
56. См. решение типового задания № 11. Постройте в одной
системе координат графики функций у = 2\х- 1| + 2 и у = а\х + 3|.
Рассмотрите четыре случая: 1) а > 2; 2) а = 2; 3) 0,5 < а < 2;
4) 0 < а < 0,5.
Например, в первом случае графики выглядят следующим
образом.
у = а \х + 3f, a > 2
\
2--
2|х-1|+2
При а > 2 графики пересекаются в двух точках.
РАЗДЕЛ 4
ОТВЕТЫ
Тема 1. Числа и выражения.
Преобразование выражений
1
в
8
15
3
22
в
29
14
36
Xjc+1).
х-Л ' '
1
50
2007
57
Ja
64
10
71
500
2
В
9
А-З.Б-4,
В-2,Г-1
16
8
23
1
30
9,5
37
44 1
-1
51
58
2
65
6
72
1
3
Б
10
Б
17
А
24
27
31
-3VI6;
-4V5;
Зл/7;3-ЛТ;
5V5
38
2009
45
-1
52
х-ЗЬ
59
37
49
66
первое
меньше
73
X2 + X = 1
4
-7
11
Г
18
25
32
2
39
12
46
0 ,
53
| к
60
2
67
а2+2а + 2
5
6
12
6
В
13
л г
19
г
26
X5
33
4х-3
40
9(3-^)-90
47
[ "3
ы
-3
61
68
1
32
20
0,01
27
тп
34
х2
х-5
41
0
48
55
1
16
62
9
69
1
6
7 I
А
14
»
- ■ ■ ■
21
-1975
28
76
35
JC-1
42
2015
49
^•28
у;2,8
56
1
12
63
4
70
1
5
ОТВЕТЫ
Тема 2. Уравнения
183
1
| 1.5
«
15
"6
22
-3,5
1 29
±л/б
36
12
I 43
50
±1
2
2
9
0; 16
16
-7
23
1
30
37
324
44
-5
51
корней
нет
3
1
10
Б
17
Решений
нет
24
28
31
38
|
45
5
52
(2л/2;3)
4
-30
И
г
18
25
■
32
0,5
39
5
3
46
24
-6; 5
12
А
19
-9
26
5;±Vl6
33
-1;5
40
0
47
(-5-3)
(1; 15)
(1,5; +со)
6
3
13
1-в,
2-6,
3-а
20
-32
27
-2; ±Зл/2
34
4
41
0;6
7
Г
14
Г
21
3, |
28
±3
35
2 !
42
±6.
48 49
-2;-3
-5±л/29
2
-2,5;
-5±-ЛЗ
2
184
РАЗДЕЛ 4
Тема 3. Системы уравнений
1
(i;4)
5
(i; -3)
Б
13
(1; 0), (4; 3)-
17
4
21
(24; 12), (16; 4)
" 25
(2;-i)
4
| 33
(-оо; -7) U(-l; +оо)
2
(-3; 2), (4;-1,5)
6
А
10
А
14
(1; 12)
18
(5; 6), (5; -6),
(-5; 6), (-5; -6)
22
(2,5; -0,5)
26
-10
30
(1; 2; 3)
34
-1,25
3
(-i;2)
7
В
И
А
15
19
"7
23
(5; 2,5), (0; -2),
(-4; -2)
27
(2;-1), (-1;2)
31
(1; 2; 3),
(-1; -2; -3)
4
(2, -3)
8
Б
12
Г
16
(1; 5), (5; 1)
20
4
24
4
» J
2
(2; -1)
ОТВЕТЫ
185
Тема 4. Неравенства
186
РАЗДЕЛ 4
Тема 5. Координаты и графики
г .
а-2, 6-1, в-3
6
В
11
А
16
В
21
у = 0,25х- 1,
II четв
26
-0,8; (0,4; 0)
31
У = х + 1,
(0; 1), (-1; 0)
36
4
41
4
2
Г
7
В
12
1-Б, 2-А,
3-В, 4-Г
17
А
22 U
я < 0, Ь < 0,
с<0
27
±12
32
,->■-
-2*-5)
0
42
л > 0, А < 0,
с>0
3
в
8
А
13
Б
18
В
гг
я > 0, £ < 0,
с>0
28
да;
(2; 4)
33
>> = --*2 +
+2jc-1
8
4
В
9
В
14
В
19
Г
24
■S
29
>> = Зх - 8
34
Ж-!;0),
Я(0;'-1),
С(1;0)
39
2
43 44
а > 0, b < 0,
с > 0 или д < 0,
b > 0, с > 0
(2; 7)
5
Б
10
Б
15
Б
20
у = Ъх + 6, да
25
2
30
у = 2х + 9
35
Л(-л/3;0;
Ж-кО)
С(л/3; 0)
ДО; -3)
40
0
45_ J
(3; -7)
46. а = 2; (1; 0).
47. я = -2; (2; 10).
48. При а = -2 у = -2х2 - 4х + 2, (-1; 4) — координаты
вершины параболы.
2
49. Объединение гиперболы у = - и прямой у = -2дс.
50. Гипербола у = - без двух точек (1; 1) и (-1; -1),
принадлежащих двум параллельным прямым дс=1идс=-1.
51. Две параллельные прямые у = 1 - 2х и у = -1 - 2х.
52. Две концентрические окружности с центром в начале
координат и радиусами 2 и 2л/2.
ОТВЕТЫ
Тема 6.
1. а) А
2. а) В
Функции
; б) в.
; б) а.
3.
4.
А.
Б.
5. 1) на вйсоте пятого этажа; 2) на пять этажей; 3) - этажа в
секунду или 1 м/с; 4) между пятым и шестым.
6. 1) 75 км/ч и 50 км/ч; 2) на 20 минут; 3) 50 км.
7. 4 м; на расстоянии 1 м от земли мяч будет в начальный
момент, через 2 секунды и через 3,5 секунды.
8. Если 0 < х < 6, то 2 < у < 4.
9. Если 2 < х < 5, то -2 < у < -1,4.
10. Если -2 < х < 1, то 1 < у < 7.
11. Если -1 < х < 4, то 0,5 < у < 3.
12. Область значений — промежуток [-2; +«>).
13. Область значений — множество всех чисел, кроме 1.
14. Если 1 < х < 2, то 7 < у < 15.
15. Если 2 < х < 3, то -24 < .у < -14.
16. Если 0 < х < 4, то -1 < у < 8.
17. Область значений — промежуток [8; +«>).
18. у > 0, если х — любое число, кроме х = V2 и х = -V2.
19.[2;4)и(4;+оо).
20. ^ > 3, если х > 0, кроме х = 3.
21. Область значений — множество всех чисел, кроме -4,5.
22. у > 0, если х < 2 и х = 4.
23. Функция возрастает на промежутке [-1; 0] и на
промежутке [1; + оо).
24. Функция убывает на промежутке [-2; 1].
25. Я Ю) = -17.
26. у > 1 при х > -2.
3, х>3
х+ 6,х < -3
Зх -1, х > -1
27.^ =
28. у = л .
' |-2х-6,
29. Прямая имеет с графиком функции четыре общие точки
при 0 < т < 4.
30. При т > Опт =-16— две общих точки, при -16 < т < 0 —
четыре общих точки, при т = 0 — три общих точки, при т < -16 —
нет общих точек.
188
РАЗДЕЛ 4
Тема 7. Арифметическая и геометрическая
прогрессии
1
в
6
162
11
4800
1 »
24,5
1 « '
12,7
-0,1
31
. 210
36
24
41
2188
44
2
1
7
Б
12
Б
17
72
22
14,25; 25,5;
36,75
27
-0,2
32
2
37
1998
42
1; 2; 4; 8
47
684
з
-23
8
Б
13
Г
18
10
23
55
28
128
33
40 i или
20 з
38
891
43
-3,6
48
2849
4
В
9
508
14
4
19
40
24
3; 6; 12; 24; 48
и 3; -6; 12;
-24; 48
29
-н
34
64
39
9
44
1012
49
3
5
Б
10
1,3
15
12
20
9
25
23
30
-255
35
13
40
45
780
ОТВЕТЫ
189
Тема 8. Текстовые задачи
*
А
6
Б
11
Б
16
2100 человек
21
Б
26
32%
31
15 км/ч
36
15 ч,
10 ч
41
15 дней
46
100 г
уменьшилась
на 2,5%
56
15 дней
2
Б
7
Г
12
56 м
17
В
22
306,04 р
27
12 500 р
32
16 км/ч
37
9 ч,
10 ч '
42
6
автомобилей
47
2л
52
на 9,2%
57
40 ч
3
Б
8
Б
13
40 м
Г' ш
в
23
10,25%
28
2000 пар
33
4 км/ч,
6 км/ч
38
12 км/ч,
15 км/ч
43
3,25 м
48
20 г,
30 г
53
12%
58
28 ч
4
В
9
А
14
64 м
19
А
24
660 р
29
3000 машин
34
20 км/ч,
30 км/ч
39 j
19 страниц
в минуту
44
9дн,
18 дн
49
3:2
54
24, 20, 15
5
Г
10
А
15
А
20
Б
25
16%
30
200 кг
35
5 км/ч,
6 км/ч
40
1
168 деталей
45
40 м/мин
30 м/мин
50
0,25 л
55
32, 24, 32
59
30 частей первого и
7 частей второго
РАЗДЕЛ 4
Тема 9. Уравнения и неравенства с модулем
1
12
-2х+6
Решений
нет
16
(-N
21
5
26
-10
31
±1; ±9
36
0
41
-7,5; 8,5
46
±1
51
№
56
2
г .
2-Л
7.
2х- 6
12
(-1;7)
17
H-f]u
и[2; + оо)
22
(_оо;+оо)
- v—;■
(-7;-1]и[3;5)
32
[-2007; + »)
37
[3; + со)
42
7; 6
47 -
(-оо;-1]и
и[1; + »)
52
57
(2; 1),
(0,5; -3,5)
3
х- 13
8
±5
13
(-005-3] и
&; + ») •
18
0,25
23
(-оо;5)и(5;+оо)
28
8
33
(-OOJ + с»)
38
{-5}и[3; + »)
43
[-6; 5]
48
1
53
(15; + »)
58
4
-х- 1
9
Решений нет
14
13
19
2
3
24
±л/2Т-
29
5
34
[-20U7; + оо)
39
±3
44
±2
49
1; 2; 3
54
•fo+oo)
5
у'
10
15
4
20
1;3
25
1;9
30
(-оо;-2]и[5; + «>)
35
Решений нет
40
±4
45
2
50
-Зи5
55
1
ОТВЕТЫ
Тема 10. Уравнения и неравенства с параметром
4
6
0
16
-1;2
21
-2
26
0
31
Ь *2,5; 4
36
Не
существует
41
[4; 5)
46
±5
51
1 9\
V Ш
2
20
7
2
12
а*0
17
(-со;-8) и(8;+оо)
22
-0,5
27
0;2
32
И;1]
37
3
8
8
0
13
0
18
(-оо;-8]и[8;+оо)
23
-1
28
0;2
33
(-oo;-l) u(l;+oo)
38
И;-2] (-~;-б)
42
(5;+ос)
47
-4
52
(-0,75; 0)
43
Не существует
48
4
53
2 •
4
а<0
д
-1
14
±5
19
(-8; 8)
24
1
29
0;2
а = 0
10
0
15
25
20
2
25
2
30
2,5; 4
34 35
±1 (0; 28)
39
±2>/3
40
±3
44 45
(-оо;-4] ±4л/2
49 50
а* ±4
JJ—,
54
а<2
[-0,75; 0]
55
а>2
56
При д > 2 и 0,5 < д < 2 два решения;
при а = 0,5; 2 одно решение;
при 0 < а < 0,5 решений нет.
Учебное издание
Мастер-класс для учителя
Кочагина Марина Николаевна
Кочагин Вадим Витальевич
ГИА ПО МАТЕМАТИКЕ
9 класс
ПОДГОТОВКА УЧАЩИХСЯ К ИТОГОВОЙ АТТЕСТАЦИИ
Зав. редакцией И. Федосова
Ответственный редактор А. Жилинская
Художественный редактор Г. Федотов
Технический редактор Н. Тростянская
Компьютерная верстка Г. Ражикова
ООО «Издательство «Эксмо»
127299, Москва, ул. Клары Цеткин, д. 18/5. Тел. 411-68-86, 956-39-21.
Home page: www.eksmo.ru E-mail: info@eksmo.ru
Оптовая торговля книгами «Эксмо»:
ООО «ТД «Эксмо». 142702, Московская обл., Ленинский р-н, г. Видное,
Белокаменное ш., д. 1, многоканальный тел. 411-50-74.
E-mail: receptionOeksmo-8ale.ru
По вопросам приобретения книг «Эксмо» зарубежными оптовыми
покупателями обращаться в отдел зарубежных продаж ТД «Эксмо»
E-mail: Internatlonal9eksmo-8ale.ru
International Sales: International wholesale customers should contact
Foreign Sales Department ofTrading House «fiksmo» fortheir orders.
intemational9eksmo-sale.ru
По вопросам заказа книг корпоративным клиентам, в том числе в специальном
оформлении, обращаться по тел. 411 -68-59 доб. 2115,2117,2118.
E-mail: vlpzakaz9eksmo.ru
Оптовая торговля бумажно-беловыми и канцелярскими товарами для школы
и офиса «Канц-Эксмо»: Компания «Канц-Эксмо»: 142700, Московская обл.,
Ленинский р-н, г. Видное-2, Белокаменное ш., д. 1, а/я 5. Тел./факс +7 (495) 745-28-87
(многоканальный), e-mail: kanc9eksmo-sale.ru, сайт: www.kanc-eksmo.ru
Полный ассортимент книг издательства «Эксмо» для оптовых покупателей:
В Санкт-Петербурге: 000 СЗКО, пр-т Обуховской Обороны, д. 84Е.
Тел. (812) 365-46-03/04. В Нижнем Новгороде: 000 ТД «Эксмо НН», ул. Маршала
Воронова, д. 3. Тел. (8312) 72-36-70. В Казани: Филиал 000 «РДЦ-Самара»,
ул. Фрезерная, д. 5. Тел. (843) 570-40-45/46. В Самаре: 000 «РДЦ-Самара»,
пр-т Кирова, д. 75/1, литера «Е». Тел. (846) 269-66-70.
В Ростове-нэ-Дону: 000 «РДЦ-Ростов», пр. Стачки, 243А. Тел. (863) 220-19-34.
В Екатеринбурге: 000 «РДЦ-Екатеринбург», ул. Прибалтийская, д. 24а.
Тел. (343) 378-49-45. В Киеве: 000 «РДЦЭксмо-Украина», Московский пр-т, д. 9.
Тел./факс (044) 495-79-80/81. Во Львове: ТП 000 «Эксмо-Запад», ул. Бузкова, д. 2.
Тел./факс: (032) 245-00-19. В Симферополе: 000 «Эксмо-Крым», ул. Киевская,
д. 153. Тел./факс (0652) 22-90-03, 54-32-99. В Казахстане: ТОО «РДII-Ал маты»,
ул. Домбровского, д. За. Тел./факс (727) 251 -59-90/91. rdc-almaty@mail.ru
Подписано в печать 15.07.2009
Формат 60x901/i6. Гарнитура «Тайме». Печать офсетная.
Бумага тип. Усл. печ. л. 12,0.
Тираж 5000 экз. Заказ № 530.
Отпечатано в ГП ПО «Псковская областная типография».
180004, г. Псков, ул. Ротная, 34.
ГИА
ПО МАТЕМАТИКЕ
Подготовка учащихся
к государственной
итоговой аттестации
Тестовые задания полностью соответствуют ГИА по математике.
В пособии представлены все темы, которые входят в экзамен.
По каждой теме даются:
• основной теоретический материал
• задания для активного обучения (с комментариями,
решениями, ответами)
• задания для самостоятельного решения
• указания и ответы ко всем заданиям