Author: Аршинов М.Н. Садовский Л.Е.
Tags: исследование операций математика рассказы кодирование криптография библиотечка квант москва наука
Year: 1983
Text
@
БИБЛИОТЕЧКА .КВАНТ.
ВЫПУСК ЗА
М. Н. АРШИНОВ
л. Е. САДОВСКИЙ
КОДЫ
И МАТЕМАТИКА
рАсскАзы
О КОДИРОВАНИИ
МОСКВА «НАУКА»
r ЛАВНАЯ РЕДАКUИЯ
ФИЗИКО.МА ТЕМА ТИЧЕСКОfl ЛИТЕР А ТУРЫ
1 9 в э
22.18
А 89
УДК 519.8
РЕДАКЦИОННАЯ КОЛЛЕrия;
Академик и. К. КИКОИН (председатель), академик А. Н. Колмо-
ropo8 (заместитель председателя), доктор физ.-мат. наук Л. r. Аела-
мазов (ученый секретарь), член-корреспондент АН СССР А. А. Абри-
I\OCOB, академик Б. К. Вайнш тейн, заслужен ный учитель РСФСР
Б. В. ВОЗДВИll{енс ий, академик I B. 1\1. rлушков f, академик П. Л. Ка-
пица, профессор С. п. Капица, академик с. п. Новиков, академик
'10. А. Оеипьян, акадеМИI{ АПН РСФСР В. r. Разумовский, академик
Р. 3. Саrдеев, Кандидат ХИМ. наук М. Л. Смолянский, профессор
Я; А. Смородинекий, академик С. Л. Соболев, член-корреспондент
АН СССР Д. К. Фадеев, член-корреспондент АН СССР И. С. ШКЛО8СI(ИЙ.
М.. Н. Аршинов, л. Е. Садовский
А89 Коды и математика (рассказы о кодировании). . М. I
Наука, r лавиан редакция физико-математической
литературы, 1983. 144 с. (Библиотечка «Квант».
Вып. 30). 25 . коп.
Б популярноЙ форме книrа знакомит читателя с основными понятиямв
И идеями теории эффективноrо и помехоустой.чивоrо l{одирования важ.
поrо направления математики,
Имея своими первоисточниками криптоrрафию (искусство засеI<речи..
вания истинноrо содержания сообщения), но rлавным образом решая
различные проблемы, возникающие при передаче информации по линиям
связи, теория н:одирования в настоящее время выросла в обширную и
разветвленную область знания со своим KpyroM объектов и задач.
Не ставя перед собой цели систематичеСI{оrо изложения теории, авторы
стремятся отразить rлавные ее черты.
Л 1702070000 075 186.82
053 (02)-83
ББК 22.18
6ФО.1
А 1 702070000 075 186-82
053 (02).8.3 J
<g Издательство «Наука,.
fлавиая редакция
Фиэико-математическоВ
литературы, 1983
ПРЕДИСЛОВИЕ
Право же, не будет ошибкой предположить,
TO у большинства читателей слова «КОД», «кодирование»
вызывают примерно одинаковые представления. Ведь все
хорошо знают, что коды или шифры используются для
передачи секретной информации. Менее известно, однако,
что в наше время коды приобре и и иное значение, быть
может, более обыденное, но зато куда более важное и ши
рокое. В этой их новой роли '{оды И кодирование пре}кде
Bcero средство для экономной, удобной и практически
безошибочной передачи сообщений. Новые прим:енения
кодов сложились в результате бурноrо развития различных
средств связи, неизмеримо возросшеrо объема передаваемой
информации.
Решать возникшие в связи с этим задачи было бы невоз-
можно без привлечения самых разнообразных математиче
ских методов. Неслучайно поэтому теория кодирования
считается сейчас одним из наиболее важных разделов
прикладной математики. Желание познакомить широкий
Kpyr читателей с задачами и методами этой теории и являеТ
ся основной нашей целью. Все же HeMHoro места уделили
мы также кодам в их Изначальном смысле как средству
обеспечения секретности.
Первая часть книrи (ЭЭ l lO) написаиа вполне элемен-
т.арно, и для ее понимания читателю достаточно озиако
миться с приложеиием 1, содержащим простейшие CBeдe
ния о сравнеииях.
В дальнейшем изложении, одиако, существенно исполь-
зуются основные факты линейной алrебры, а также факты,
связанные с поня-тиями поля и rруппы. Все иеобходимые
определения и теоремы содержатся в приложениях 2 5.
1*
3
Не освоившись с материалом этих приложений, читатель
не crvIor бы свободно ориентироваться во второй части книrи..
В заключение отметим, что в конце большинства пара..
rра-фов меется раздел «Задачи И дополнения», rде рассмат-
риваются некоторые более специальные и, как правило,
более трудные вопросы, а также приводятся задачи для
самостоятельноrо решения. Читателю, желающему основа-
тельно разобраться в содержании книrи, мы рекомендуем
не пренебреrать этими аадачами.
М. Н. Аршинов> Л. Е. Садовский
1. КОДИРОВАНИЕ ИСТОРИЯ
И ПЕРВЫЕ ШАrи
I{оды появились в rлубокой древности в виде
криптоrрамм (по-rречески тайнописи), коrда ими поль..
зовались для засекречивания важноrо сообщения от тех,
кому оно не было предназначено. Уже знаменитый rрече
скип историк rеродот (V век до н. э.) приводил примеры
писем, понятных лишь для одноrо адресата. Спартанцы име..
ли специальный механический прибор, при помощи KOToporo
важные сообщения можно было писать особым спосоБОl\1,
обеспечивающим сохранение тайны. Собственная секретная
азбука была у Юлия Цезаря. В средние века и эпоху Воз
рождения над изобретением тайных шифров трудились
мноrие выдающиеся люди, в их числе философ Фрэнсис
Бэкон, крупные математики Франсуа Виет, Джероламо
Кардано, Джон Валлис.
С течением времени начали появляться по"настоящему
сложные шифры. Один из них, употребляемый и поныIе,'
связан с именем ученоrо аббата из Вюрцбурrа Тритемиуса,
KOToporo к занятиям криптоrрафией побуждало, быть
10жет, не только монастырское уединение, но и потреб..
ность сохранять от оrласки некоторые духовные тайны.
Различные хитроумные приемы кодирования применяли
шифровальщики при папском дворе и дворах европейских
королей. Вместе с искусством шифрования развивалось
и искусство дешифровки, или, как rоворят, криптоанализа.
Секретные шифры являются неотъемлемой принадлеж..
ностью мноrих детективных романов, в которых деЙСТВУIОТ
изощренные в хитрости шпионы. Писатель"романтик Эдrар
По, KOToporo иноrда причисляют к создателям детективноrо
жанра, в своем рассказе «Золотой жук» В художественной
форме изложил простейшие приемы шифрования и расшиф..
рОБКИ сообщений. Эдrар По относился к проблеме расшпф..
ровки оптимистически, вложив в уста cBoero rероя следую-
щую фразу: «.. .едва ли разуму человека дано заrадать та..,
кую заrадку, которую разум друrоrо ero собрата, направ-
ленный должным образом, не cMor бы раскрыть. Прямо
скажу, если текст зашифрован без rрубых ОШlJбок и доку-
:мент в приличной сохранности, я болЬше ни в чем не нуж-
даюсь; последующие трудности для меня просто не сущест-
вуют». Столетие спустя это высказывание было опроверrну-
то ученым, заложившим ОСН,овы теории информации, Кло-
дом Шенноном. Шеннон показал, как можно построить
криптоrрамму, которая не поддается никакой расшифровке,
если, конечно, не известен способ ее составления.
О некоторых приемах криптоrрафии и криптоанализа
мы расскаж'ем в следующем параrрафе, в остальных частях
книrи речь будет идти в основном об ином направлении
в кодировании, которое возникло уже в близкую нам эпоху.
Связано оно с проблемой передачи сообщений по линиям
связи, без которых (т. е. без телеrрафа, телефона, радио,
телевидения и т. д.) немыслимо наше нынешнее существо-
вание. В задачу TaKoro кодирования, как уже rОВОРИJ!ОСЬ,
входит отнюдь не засекречивание сообщениЙ, а иная цель:
сделать передачу сообщений быстрой, удобной и надежной.
Предназначенное для этой цели кодирующее устройство со-
поставляет кюкдому символу передаваемоrо текста, а иноr
да и целым словам или фразам (сообщениям) определеНI1ую
комбинацию сиrналов (приемлемую для передачи п дан-
ному каналу связи), называемую кодом или КОДОБЬПv1 сло-
вом. При этом операцию перевода сообщений в определен-
ные последовательности сиrналов называют кодированием,
а обратную операцию, восстанавливающую по принятым
сиrналам (кодовым словам) передаваемые сообщения,
декодированием.
· Заметим сразу же, что различные символы или сообще-
ния должны кодироваться различными кодовыми словами,
в противном случае по кодовым словам нельзя было бы вос-
становить передаваемые сообщения.
Исторически первый код, предназначенный для переда..
чи сообщений, связан с именем изобретателя телеrрафноrо
аппарата Сэмюэля Морзе и известен всем как азбука Морзе.
В этом коде каждой букве или цифре сопоставляется своя
последовательность из кратковременных (называемых точ-
ками) и длительных (тире) импульсов тока, разделяеМЬJХ
паузами. Друrой код, столь же широко распространенный
в телеrрафии (код Бодо), использует для кодирования два
элементарных сиrнала импульс и паузу, при этом со-
6
поставляемые -буквам кодовые слова состоят из пяти таких
сиrналов.
КОДЫ, использующие два различных элементарных сиr-
нала, наз'ываются двоичными. Удобно бывает, отвлекаясь
от их физической природы, обозначать эти два сиrнала сим-
волами О и 1. Тоrда кодовые слова можно представлять как
последовательности из нулей и единиц.
Двоичное кодирование тесно связано с принципом дихо-
томии (деления пополам). Поясним этот \ принцип на при..
мере.
Некто задумал число, заключенное между О и 7. Уrады..
вающему разрешено задавать вопросы, ответы на которые
даются лишь в форме «да» или «нет». I{аким образом следует
задавать вопросы, чтобы возможно быстрее узнать задуман..
ное число?
Саlv1ЫЙ бесхитростный путь перебирать числа в любом
порядке, надеясь на удачу. В этом случае при везении МО"
жет хватить и одноrо вопроса, но если не повезет, то может
понадобиться и целых семь. Поэтому не будем рассчитывать
на везение и постараемся построить такую систему вопро-
сов, чтобы любой из ответов «Д(l)} или «нет» давал нам
одинаковую (пусть сначала и неполную) информацию о за..
думанном числе. Например, первый вопрос Mo eT быть та..
!{им: «3а,ключено ли задуманное число в пределах от О до
3?» Оба ответа и «да» И «нет» одинаково приближаю"r
нас 1{ цели: в любом случае рстаются четыре возможности
для неизвестноrо числа (а первоначально их было восемь).
Если на первый вопрос получен утвердительный ответ,
то во второй раз можно спрос.ить: «Не является ли заду..
!\iaHHOe число нулем или единицей?»; еСли же ответ был от..
рицательным, спросим: «Не является ли задуманное число
четвер'кой или пятеркой»? В Лlобом случае после ответа на
второй вопрос останется выбор из двух возможностей. Для
Toro чтобы ero осуществить, достаточно одноrо вопроса.
Итак, для уrадывания зздуманноrо ЧИСJIа, кац:им бы оно
1 ни было, достаточно трех вопросов (каждый из них выяс..
, вяет, содержится ли задуманное число в «нижней» половине
, заключающеrЬ ero ПрОI\1ежутка). Можио показать, что мень-
ll1ero числа вопросов недостаточно.
Если возмо}кные ответы «да» или «нет» обозначить ус-
ловно символами О и 1, то ответы запишутся в виде после..
довательности, состоящей из нулей и единиц. Так, напри..
мер, если задуманное число было нулем, то на каждый из
Трех вопросов ответом будет «да». Трем «да» соответствует
последовательность 000.
7
Если было задумано число 3, то ответами будут «да»,
«нет», «нет», Т. е. числу 3 соответствует последоватеJ1Ь-
ность 011. По результатам ответов можно составить слеп,уЮ-
щую таблицу:
Таблица 1
I
Задуманное число О 1 2 3 4 5 6 7
,
t I
I
Отв еты 000 001 010 011 100 101 11 О I 111
I
!
Читатель, знакомый с двоичной системоЙ счисления t
узнает в нижней строке двоичную запись соответствующих
u
чисел верхнеи строки.
Заметим, что вместо множества чисел от 0- до 7 можно
рассматривать любое множество из во ьми сообщений,
и каждое из них мы можем закодировать последовательно..
стями из нулей и едиииц длины 3. Если ИСПОt!Iьзовать более
ДЛИННI:>Iе двоичные последовательности, то ими в принципе
можио закодировать любое конечное мно)кество сообщений.
Действительно, число двоичных последовательностей
длины 3 равио 23==8 (все они приведены в таблице 1), двоич-
ных последовательиостей длины 4 вдвое больше число
их. равно 24== 16. Вообще, число двоичных последователь-
ностей длииы п равио 2 n . Поэтому, если требуется закоди-
ровать нулями и едииицами, к примеру, 125 сообщениЙ,
то дЛЯ этоrо с избытком хватит двеичных последователь-
ностей длины 7 (их в нашем распоряжении имеется 27 ==
:=:::: 128). Из этоrо примера становится ясно, что М сообще-
ний можно закодировать двоичными последовательностями
длииы п тоrда и Т9ЛЬКО тоrда, коrда выполняется условие
2n M, т. е. коrда n>log2M.
Первый, кто понял, что для кодироваиия достаточно
двух символов, был Фрэисис Бэкон. Двоичный код, I{OTO-
рый он использовал в криптоrрафических целях, содержал
лятиразрядиые (как и в коде Бодо) .слова, составлеиflые из
символов О, L. '
Сказанное здесь это лишь первые подступы к пробле-
ме кодирования, которой посвящеиа эта КИиrа. Пока же
отметим только, что наряду с двоичными кодами примен ю'r
коды, и пользующие не два, а большее число элементарных
сиrиалов, или, как их еще называют, кодовых символов. Их
число d называют основанием кода, а множество кодовых
8
СИlVIВОЛОВ КОДОВЫМ алфавитом. При этом общее число п.
буквенных слов, использующих d символов, вычисляется
пн алоrично прежнему и равно d n .
Задачи и дополнения
1. Часто по разным соображениям для кодирования
сообщений испол зуют не все последовательности в данном алфавите, а
только некоторые из них, удовлеТВОРЯJ:Qщие тем или иным оrраничени
ям. Будем рассматривать, например, n буквенные двоичные слова с
фиксированным числом t единиц (или, как rоворят, слова постоянноrо
E€ca i). Сколько Bcero тzких слов нетрудно подсчитать. Ка,кдос из
них получится, если мы выберем некоторым образом t позиций из n, и
запишем в них единицы, а в остальных п t позициях нули. Значит,
число всех слов постоянноrо веса совпадает с числом сочетаний из n
эле ментов по t, т. е. равно
t n!
Cn..== t!(n t)! '
2. С 7Jожнее наЙти число всех двоичных слов длины n, не содержа"'--
щих несколько нулей подряд. Обозначим это число через 8n. Очевидно,
S1 == 2, а слова длины 2, удовлетворяющие нашему оrраничению, таковы:
1 О, 01, 11, т. е. 82==3' Пусть а1а2 . . . an 1aп такое слово из п сим
волов. Если символ а п == 1, то а1 а 2 . . . aп ! может быть произвольным
(п l)-буквенным словом, не содер)кащим нескольких нулей подряд.
Значит, число слов длины n...c единицей на конце равно 8п 1.
Если же символ ап==О, то обязательно а n "':1== 1, а первые п 2 сим-
вола а1а2 . . . an 2 MorYT быть произвольными С учетом рассматривае
Moro оrраничения. Следовательно, имеется 8n 2 слов длины n с нулем
на конце. Таким образом, общее число интересующих нас, слоз равно
8n== 8n f +8п 2'
Из полученноrо соотношения (подобные соотношения называют
рекуррентными) леrко можно найти числа 8 п для любоrо n. ПОСКОЛЬКУ
51 И 82 известны, то 8з== 81+ S 2== 5; 84==82+sз==8, 8б==8 з +8 4 == 13 И т. д.
Полученная последовательность чисел
2, 3" 5, 8, 13, 21, 34, . . . ,
Б которой каждый пос едующий член р'!вен сумме двух преДЫДУIЦИХ,
это хорошо известный в математике ряд Фибоначчи. О мноrих интерес-
ных свойствах чисел Фибоначчи и их разнообразных приложениях мож
но прочесть в популярной брошюре [21], а также в недавно изданной
книrе [6]. В частности, можно убедиться (см. [21]), что п-ый член ряда
Фибоначчи вычисляется по формуле:
(( 1+ У-б ) n+2 ( 1 У-б ) n+2 ) ( l 6 ) п+2
Bп. У5 2 2 У5 ' z .
3. Соединим оба предыдущих оrраничения и найдем число двоичных
слов постоянноrо веса t, не содержащих нескольких нулей подряд.
Рассуждать можно так. Пусть q . n t ---- число нулей в рассматри
Баемых словах. В любом слове имеется q l промежутков между бли
tJ
жаишими нулями) в каждом из которых находится одна или несколько
9
единиц (см. рис. 1). Предлолаrается, KOHetIHO, что q...s;;п/'2. Б ПрGrн нvМ
случае (при q>n/2) нет ни одноrо слова без рядом стоящих нулей.
Если из кзждоrо промежутка удалить ровно по одной едини;,:,с,
ТО получим слово длины n q+ 1, содержащее q нулей. Леrко ВИДСТЬ,
О что любое такое слов о может быть
О О О. .. получено указанным образом из не-
KOToporo (и притом только одноrо)
п-буквенноrо слова, содержащеrо
q нулеЙ, никакие два из которых
не стоят рядом. Значит, искомое
число совпадает с числом в сех слов
длины n q+ 1, содержащих ровно
q нулей, т. е. равно (см. допол.
нение 1)
C Q С п t
п Q+l == t+l.
4. И пользуя результаты дополнений 2, 3, убедиться в справед-
ливости тождества:
[п/2] q 1 (( 1+У 5 ) n+2 ( 1 Y5 ) n+2 )
L Cn q+1 y 2 2
0 5.
q=
(символ [п/2] означает наибольшее целое число, не превосходящее п/2).
5. При каком q число двоичных слов из дополнения 3 максимально?
6. Показать, что число всех п-буквенных d ичных слов, В которых
один из символов встречается фиксированное ЧИС.по t раз, равно
ch (d 1)n t (ер. дополнение 1).
7. Обобщить результаты дополнений 2 и 3 применительно к d-ично"
му алфавиту,
2. ШИФРbI, ШИФРbI, ШИФРbI...
Приемов тайнописи великое множество, И,
скорее Bcero, это та область, rде уже нет нужды придумы-
вать что-нибудь существенно новое. Наиболее простой тип
криптоrрамм это так называемые подстановочные крип-
TorpaMMbI. Составляя их, каждой букве алфавита сопостав-
ляют определенный символ (иноrда тоже букву) и при ко-
дировании всякую букву ,текста заменяют на соответствую-
щий ей символ. В рассказе «Золотой жук» Эдrара По при-
водится как раз пример подстановочноrо шифра.
Автор рассказа наrлядно демонстрирует, что расшиф-
ровка подобных криптоrрамм не составляет большой про-
блемы. Все основывается на том (за подробностями отсы-
лаем читателя к ориrиналу), что различные буквы естест-
BeHHoro языка анrлийскоrо, PycCKoro или какоrо-либо
друrоrо встречаются в осмысленных текстах неодинако-
во часто. Следовательно, то же Cal\10e верно для соответст-
вующих им знаков. В еще большей мере это относится к
буквосочетаниям из двух или нескольких букв: лишь
некоторые из них часты, мноrие же вообще не употребля-
ются.
/ТfJОl1еЖ!lтffll
с еОllllllцаl1l1
Рис. 1.
10
Анализируя частоту появления тех или иных знаков
я их сочетаний (именно так поступает rерой Эдrара По),
можно с большой уверенностью восстановить буквы зашиф..
pOBaHHoro текста. Даже если в каких-то частях текста воз..
никает неоднозначность, она леrко устраняется по смыслу.
Этот метод (он именуется частотным анализом) основывает-
ся, таким образом, на заранее известных частотах зашифро..
ванных знаков. В следующей таблице указаны относитель-
ные частоты букв pyccKoro языка.
Буквы «е» и «ё», а также «ь», «ъ» кодируются обычно
одинаково, поэтому в таблице они не различаются. Как
явствует из таблицы, наиболее частая буква pyccKoro язы..
ка .......... «о». Ее относительная частота, равная 0,090, означа..
ет, что на 1000 букв pyccKoro текста приходится в среднем
90 букв «о». В таком же смысле понимаются относительные
Таблица 2
М!! Букв а Относит. М!! Буква Относит. М!! Буква Относит"
частота частота частота
О а 0,062 10 к 0,028 20 Ф 0,002
1 б 0,014 11 .л 0,035 21 х 0,009
2 в 0,038 12 м 0,026 22 ц 0,004
3 r 0,013 13 н 0,053 23 ч 0,012
4 Д 0,025 14 о 0,090 24 ш 0,006
5 е, ё 0,072 15 п 0,023 25 щ 0,003
6 ж 0,007 16 Р 0,040 26 ы 0,016
7 3 0,016 17 с 0,045 27 ь, ъ 0,014
8 и 0,062 18 т 0,053 28 э 0,003
9 й 0,010 19 У 0,021 29 ю 0,006
30 я 0,018
частоты и остальных букв. В таблице 2 не указан еще один
«символ» .......... промежуток между словами. Ero относитель-
ная частота наибольшая и равна 0,175.
С помощью таблицы 2 читатель сумеет, по-видимому,
расшифровать такую крицтоrрамму (расшифровку и пояс-
нения см. в дополнении 1 на стр. 15):
Цярснсмщи ямякзж онкдждм мд снкыйн rкю онrр ямнб-
нцмщФ ЙПЗ0СНВПЯЛЛ мн б rптвзф рктцяюф нм ркнемдд.
Ненадежность подстановочных криптоrрамм (сравни-
тельная леrкость их расшифровки) была замечена уже ,цав-
11
НО, И потому в разное время предлаrались различные дру...
rие методы шифрования. Среди них важное место заНИl\1ают
перестановочные криптоrраммы. При их составлении весь
текст разбивается на rруппы, состоящие из одинаковоrо
числа букв, и внутри каждой rруппы БУI{ВЫ HeKOTOpbIl\I
образом переставляются. Если rруппа достаточио длинная
(иноrда это весь текст целиком), то число возможных пере-
становок очень велико, отсюда большое мноrообразие пере-
становочных криптоrрамм. Мы рассмотрим один тип пере-
становочной криптоrраммы, которая составляется при
помощи так называемоrо ключевоrо слова. Буквы текста, ко-
торый должен быть передан в зашифрованном виде, перво-
начально записываются в клетки прямоуrольной таблицы,
по ее строчкам. Буквы ключевоrо слова пишутся над столб-
цами и указывают порядок (нумерацию) этих столбцов спо-
собом, объясняемым ниже. Чтобы получ'ить закодированный
текст, надо выписывать буквы по столбцам с учетом их ну..
мерации. Пусть текст таков: «В связи С создавшимся ПОJfО.
жением отодвиrаем сроки возвращеиия домой. Рамзай».
Используем для записи текста, в котором 65 букв, прямо..
уrольную таблицу 11 х 6, в качестве ключевоrо возьмем
слово из 6 букв «запись», столбцы занумеруем в соответст"
вии с положением букв ключевоrо слова в алфавите. В Jpe..
зультате получится следующая кодовая таблица:
Таблица 3
3 а п и с ь
2 1 4 3 5 6
в с в я 3 И
С с о 3 Д а
в ш и м с я
п о л о ж е
н и е м о т
о Д в и r а
е м с р о к
и в о э D Р
а щ е н и я
Д о м о й р
а м з а й
Выписывая буквы из столбцов таблицы 3 (сначала из
nepBoro, затем из BToporo и т. д.), получаем такую шиф
ровку:
Ссшо идмвщ о l'vl В свп Н оеи ад ая з 1\10 l'vlИ Р з Н оаВ9 ил ев соемззд с-
}коrовийииаяетакряр
Кл!Очевое слово известно, конечно, и адресату, который
поэто лу без труда расшифрует это сообщеиие. Но для тех,
кто этим ключом не владеет, восстановление исходноrо
TeKcri a весьма проблематично (хотя в принципе и возмо)кно). ,
LlастотныЙ анализ здесь по вполне понятным причинам не
решает задачи. В лучшем случае, поскольку частоты букв
примерно такие, как в таблице 2, он позволяет предполо
)I(ить, что было применено перестановочное кодирование.
Использование ключевоrо слова, конечио, не обязатель
но, можно было указать нумерацию столбцов цифровым
ключом, в данном случае числом 214356. Слово удобнее,
если' ключ надо хранить в памяти (что немаловажно для
конспирации) .
Имеется ряд шифров, в которых совмещеиы приемы под
становочноrо и перестановочноrо кодирования. Шифр можно
еще более усложиить, если дополнительно к этому каждую
букву заменять ие одним, а двумя или несколькими симво
лами (БУI{вами или числами). Вот пример. Расположим бук '
вы pyccKoro алфавита в квадратной таблице 6 х 6 произ
вольным образом, например так, как в слецующей таблице.
Таблица 4
о 1 2 3 4 5
О з и ы р с
1 а т у й ь э
2 б в Ф к л
3 м ю я r х Ц
4 ч н о Д е
5 ж ш Щ п
Каждую букву шифруем парой цифр: первая цифра ЭТО
номер строки, в которой стоит данная буква, вторая..........
номер столбца. Например, букве «б» соответствует обозиа-
чение 21, а слову «шифр» обозиачение 51022304.
Еще большие трудиости для криптоанализа представ-
lIяет шифр, связываемый с именем Тритемиуса. Этот шифр
13
является раЗВf!тием рассмаrриваемоrо в дополнении 2 кода
Цезаря и состоит в следующем. Буквы алфавита нумеруют-
ся по порядку числами 0,1,...,30 (см. табл. 2). При шиф..
ровании ключевое слово (или номера ero букв) подписы-
вается под сообщением с повторениями, как показано ниже:
всвязиссоздавшимсяположениеIvIотодвиrаемср окивозв р а
записьзаписьзаписьзаписьзаписьзаписьзаписьзаписьэ
щениядомойрамзай
аписьзаписьзапис
Каждая буква сообщения «сдвиrается» вдоль алфавита
по следующему правилу: буква с номером т, под которой
стоит буква ключевоrо слова с номером k, заменяется на
букву с номером l==т+k (если т+k<31) или букву с но-
мером l==т+k 31 (если т+k>31). Например, первая
буква «в» сдвиrается на 7 букв и заменяется буквой «й»,
слеДУlощая буква «с» остается без изменения и т. д. т аким
образом, номер 1 кодирующей буквы вычисляется по фор-
муле:
l==т+k (mod 31).
(1)
в цифровых обозначениях исходное сообщение и повт<?..
ряемое ключевое слово запишутся в следующем виде:
Таблица 5
Сообщение I 2 ]7 2 30 7 8 17 17 14 7 4 О 2
Кл 10 Ч I 7 О 15 8 17 27 7 О 15 8 17 27 7
Сообщение I 24 8 12 17 30 15 14 1 1 14 6 5 13 8
Ключ I о 15 8 17 27 7 О 15 8 17 27 7 О
Сообщение I 5 12 14 18 14 4 2 8 3 О 5 12 17
КЛIОЧ I 15 8 17 27 7 О 15 8 17 27 7 О 15
Сообщение I 16 14 10 8 2 14 7 2 16 О 25 5 13
КЛIОЧ I 8 17 27 7 О 15 8 17 27 7 О 15 8
Сообщение I 8 30 4 14 1'2 14 9 16 О 12 7 О 9
КЛIОЧ I 17 27 7 О 15 8 17 27 7 О 15 8 17
Ilосле суммирования верхней и нижней строки по
модулю 31 получаем последовательность чисел:
14
9. 17. 17 . 7.24.4.24. 17.29.15.21.27.9.24.23.20.3.26.22. 14.26.
22.23. 1.20.8.20.20.0.14.21.4.17.16.20.27.12.12.1.24. 0.6.
15.2.29.15.19.12.7.25.20.21.25.26.11.14.27.22. 26.12. 7.
12.22.8.26.
Наконец, заменяя числа на буквы, приходим к закодиро
ванному тексту:
йссзшдшсюпхьйшчфrыцоыцчбфиффаохдсрфьммбшажпвю
пумзщфхщылоьцымзмциы
Если ключевое слово известно, то дешифровка произво
дится безо всякоrо труда на основе равенства:
т===l k (mod 31).
Чрезвычайно трудно расшифровать подобный текст, если
ключ неизвестен, хотя в истории криптоrрафии были
случаи, коrда такие тексты разrадывались. Дело в том, что
повторяемость ключевоrо слова накладывает некоторый OT
печаток на криптоrрамму, а это может быть обнаружено
статистическими методами, которые позволяют судить о
длине ключевоrо слова, после чеrо расшифровка значи
тельно упрощается.
Мы рассмотрели лишь некоторые способы составления
криптоrрамм. Заметим, что комбинируя их, можно полу
чать шифры, еще более труднодоступные для расшифровки.
Однако вместе с этим возрастают трудности пользования
шифром для отправителя ceKpeTHoro сообщения и адресата,
поскольку сильно усложняется техника шифровки и дe
шифровки даже при наличии ключа.
Задачи и дополнения
1. Для расшифровки криптоrраммы на стр. 11 под
считаем, сколько раз встречается в ней каждая буква. Результаты поц
счета приведены в следующеЙ таблице:
Таблица 6
Буква н м я к Д с р r о п з Ф ц б в Л{ Й Л Т Щ 10 е и ы
Число ПО яв- 11 9 6 6 5 5 4 3 3 3 3 3 3 2 2 2 2 2 2 2 2 1 1 1
лений в тек-
сте
Наиболее часто встречаюIЦИЙСЯ символ «н» скорее rcero означает
букву «о». Сделав такое предположение, рассмотрим сле,vJЮIЦИЙ по ча-
стоте символ «м». В криптоrрамме имеется двубукв I:tное сочетание
«мн», и так как «н» это «о», то символ «м» соответству,\ r соrласной.
Среди соrласных в PYCCI\O:Vl языке выделяются по частоте буквы ({Т»
И «н» (см. табл. 2), и потому «м» скорее Bcero означает одну из этих сукв.
Разберем случай, коrда «м» означает «н», предоставляя читателю само-
стоятельно убедитьс5L, что друrа,Я возможность не приводит к осыыслен-
ной расшифровке криптоrраммы.
Если «М» зто «н», TC B сочетании «мд», встречающемся в крип-
TorpaMMe, «д» означает скорее cero rласную, Из наиболее вероятных
для «д» вариантов «а», «е», «и» выбираем «е», потому ч3'О лишь В этом слу-
чае имеющееся в криптоrрамме слово «ркнемдд» допускает осмысленную
расшифровку. Итак три знака разrаданы: «н» это «о», «м» «н»,
«д» «е». Обращаемся к сочетанию «ямякз)к». В нем «я» может означать
лишр rлаСНУIО «а» или «и». Любые друrие вОЗможности заседомо не
допускают разумноrо прочтения слова «ямякзж». Испытаем БУКЕУ «а».
Подставляя вместо «я» букву «а», вместо (1М» «н», вместо друrих зна-
ков . точки, получим недописанное слово «ана. . .». В словаре имеется
Bcero .т:lИШЬ несколько слов из 6 букв с таким началом: «анализ», «ана-
Лоr», «ананас», «анатом». Из них rодится лишь первое (почему?). Если
вместо «я» подставить букву «И», то получится шестибуквенное сочетание
с началом «ини», но В словаре нет ни одноrо TaKoro слова. Расшифрова-
H )I СJде четыре буквы: «Я», «к», «з», <ОК» означают соответственно «а»,
«л», «и», «з».
В слове «онкждм» известны все символы, кроме nepBoro. Заменяя
их буквами, получаем: «.олезен», Ясно, что неизвестная 'буква это «п».
Значит, «с» расшифровывается как «п».
Не разrаданы еще ДВ'а сравнительно часто встречающиеся знака
<\0» и «р». Рассмотрим сочетание «ркнемдд», означающее «.ЛО.нее».
Имеется HeMHoro вариантов ero прочтения, один из них «сложнее», и
следовательно, скорее Bcero «р» это «с», «е» ЭТО «ж».
Из нерасшифро!3анных еще знаков чаще Bcero встречается «с».
В соответствии с таблицей 2 среди оставшихся соrласных наибольшую
частоту имеет «т»,. Естественно поэтому предположить, что «с» означа-
ет «т».
f}опытаемся восстановить зашифрованный текст, подставляя вместо
разrаданных знаи:ов соответствующие .им буквы:
.зстотн..анаЛИЗ полезен H ТОЛ..О .л. ПО.стано.О.Н.. ..ИПТО..а..
110 . ....и. сл..а.. он сложнее
Ясны (по контексту), по крайней мере, три слова: «.астотн..» озна-
чает «частотный», «тол..О» «только», «.л.» «для». С учетом новой
информации текст примет следующую форму:
Частотный анализ полезен не только для подстано.ОЧНЫ. К.ИПТо..а..
но . Д...и. СЛ.чая. он сложнее
Окончательная расшифровка не представляет труда. Текст таков:
Частотный анализ полезен не только для подстановочных крипто-
r рамм, но в друrих случаях он сложнее
2. Шифр, пр.имененный в предыдущем примере, это так назы-
ваемый шифр Цезаря. Он состоит в том, что весь алфавит сдвиrается
на определенное число букв вправо или влево. В данном случае был
применен сдвиr влево на одну букву, т. е. каждая буква заменялась
предшествующей буквой алфавита (при этом для буквы «а» предшеству-
ющей считалась буква «я»). Для шифра Цезаря имеется более простоЙ
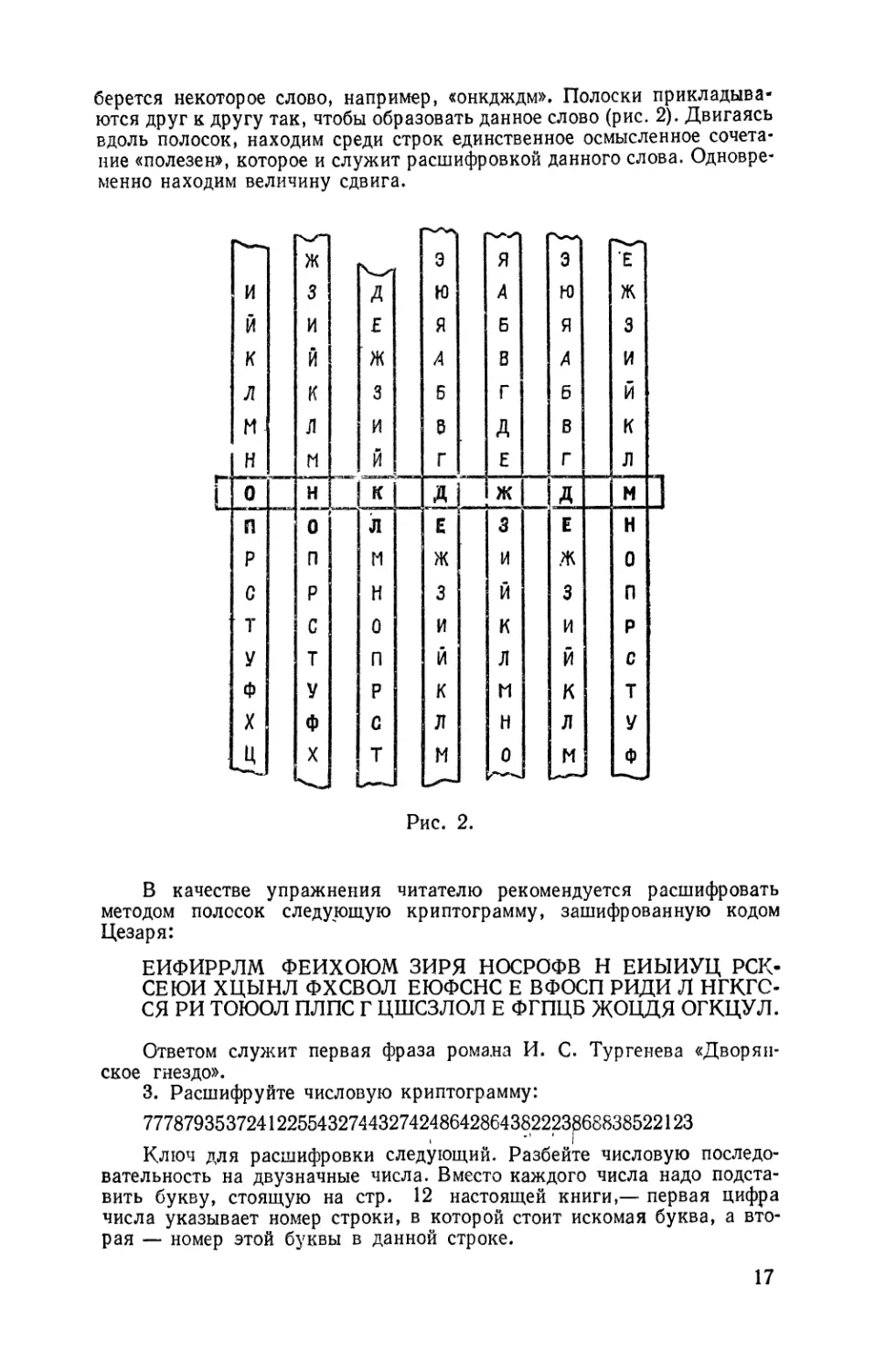
способ расшифровки так называемый метод полосок. На ка*дую
полоску наносятся по порядку все буквы алфавита. В кр"иптоrрамме
16
берется некоторое слово, например, «онкдждм». Полоски прикладыва"
ются друr к друrу так, чтобы образовать данное слово (рис. 2). Двиrаясь
вдоль полосок, находим среди строк единственное осмысленное сочета-
ние «полезен», которое и служит расшифровкой данноrо слова. Одновре"
менно находим величину сдвиrа.
f'./'"" """"""'"
.............
ж '\......". Э я э 'Е
И 3 Д to А н) Ж
Й и Е Я Б Я 3
к Й I ж А В А И
Л К 3 Б r б й
Н л и 6 Д в к
н N Й r Е r л
i !д
о н к Д ж м I
.
n о п Е а Е н
Р n м ж и .IК О
G Р Н 3 Й 3 n
т с о и к и р
у т n й л й с
Ф у р к м к т
Х Ф с л н л у
-i х т м о м ф
............. l.,.;--- ,.,.,.. ..........
Ри с. 2.
в качестве упражнения читателю рекомендуется расшифровать
методом полосок следу'..ЮЩУЮ криптоrрамму, зашифрованную кодом
Цезаря:
ЕИФИРРЛМ ФЕИХОЮМ ЗИРЯ НОСРОФВ Н ЕИЫИУЦ РСК.
СЕЮИ ХЦЫНЛ ФХСВОЛ ЕЮФСНС Е ВФОСП РИДИ Л HrKrC-
СЯ РИ ТОЮОЛ ПЛПС r ЦlliСЗЛQЛ Е ФrПЦБ ЖОЦДЯ оrкцУЛ.
Ответом слу)кит первая фраза рома.на и. С. Турrеиева «Дворян-
ское rнездо».
3. Расшифруйте числовую криптоrрамму:
7778793537241225543274432742 86428643 22f3 68838522123
Ключ для расшифровки следующий. Разбейте числовую последо-
вательность на двузначные числа. Вместо каждоrо числа надо подста-
БИТЬ букву, стоящую на стр. 12 настоящей книrи, первая цифра
числа указывает номер строки, в которой стоит искомая буква, авто"
рая номер этой буквы в данной строке.
17
Это пример криптоrраммы, для составления и расшифровки котор ой
используется некоторый заранее условленный текст, известный и от-
пр авителю, и адресату.
4. Друrим примером шифра, использующеrо заранее условленный
текст, является так называемый шифр «беrущеrо ключа». При шифрова-
нии по этому методу УСЛQ енный текст накладывается на передавае-
мый так же, как в шифре Тритемиуса.
3. КОД ФАНО ЭКОНОМНЫЙ КОД
Алфавита из двух (а подавно из большеrо
числа) символов, как мы убедились в Э 1, достаточно для
кодирования любоrо множества сообщений. Устанавливая
этот факт, I\lbI кодировали все сообщения словами одинако-
вой длины, что, однако, далеко не всеrда бывает выrодно.
Представим себе, что одни сообщения приходится пере
давать довольно часто, друrие редко, третьи совсем
в исключительных случаях. Понятно, что первые лучше за-
кодировать тоrда короткими словами, оставив более длин-
ныIe слова для кодирования сообщений, появляющихся ре-
,ке. В результате кодовый текст станет в среднем короче,
и на ero передачу потребуется меньше времени.
Впервые эта простая идея была реализована упоминав-
шимся нами американским инженером Морзе в предложен-
ном им коде. Рассказывают, что создавая свой код, Морзе
отправился в ближайшую типоrрафию и подсчитал число
литер в наборных кассах. Буквам и знакам, для которых
литер в этих кассах было припасено больше, он сопоставил
более короткие кодовые обозначения (ведь эти буквы BCTpe
чаются чаще). Так, например, в русском варианте азбуки
Морзе буква «е» передается одной точкой, а редко встречаю
щаяся буква «ц» набором из четырех символов.
В математике мерой частоты появления Toro или иноrо
события является ero вероятность. Вероятность события А
обозначают обычно символом Р (А) или просто буквой Р.
Не останавливаясь на определении вероятности, заметим
только, что вероятность HeKoToporo события (сообщения)
можно предст-авлять себе как долю тех случаев, в которых
оно появляется, от общеrо числа появившихся событиЙ
(сообщеНИI) .
Так, если заданы четыре сообщения А 1 , А2' Аз, А4
С вероятностями Р (А 1 )== 1/2, Р (А 2)== 1/4, Р (Аз)==Р (А 4 )==
== 1/8, то это означает, что среди, например, 1 000 передан
ных сообщений около 500 раз появляется сообщение Аl'
около 250 сообщение А 2 и примерно по 125 раз каж..
дое из сообщениЙ Аз и А4.
18
Эти сообщения нетрудно закодировать ДВОИЧНЫМИ сло-
вами длины 2, например так, как показано в следующей
таблице:
Таблица 7
I А 1 А 2 Аз А4
I 00 01 10 11
Однако при таком кодировании вероятность появления сооб-
щений никак не учитывается. Поступим теперь иначе. Разо-
бьем сообщения на две равновероятные rруппы: в первую
попадает сообщение A f , во вторую сообщения А 9, Аз, А4'
Сопоставим первой rруппе символ О, второй символ 1 (см.
таблицу 8; во второй rрафе таблицы указаны вероятности
сообщений) .
Таблица 8
Aj ")./2 О
А 2 1/4
Аз 1/8 1
А4 ")./8
о 1
о
1
1
Это вполне в духе принципа, применявшеrося в задаче с
уrадыванием. Действительно, символ О соответствует отве-
ту «да» на вопроо «принадлежит ли сообщение "'первой
rруппе?», а 1 ответу «нет». Разница лишь в том, что рань-
ше все множество разбивалось на две rруппы с одинаковым
числом элементов, теперь же в первой rруппе один, а во
ВТОрОЙ три элемента. Но, как и раньше, разбиение это
таково, что оба ответа «да» И «нет» равновозможны. Продол-
жая в том же духе, разобьем множество сообщений А 2, А 3,
А4 снова на две равновероятные rруппы. Первой, состоя..'
щей из одноrо сообщения А 2, сопоставим сим ол О, а второй,
в которую входят сообщения А; и A4' символ 1. Наконец
оставшуюся rруппу из двух сообщений разобьем на две
rруппы, содержащие соответственно сообщения Аз и А4'
19
СОПОС'"i'НВИВ перDОЙ из них о, а второй символ 1. Сообще-
ние А 1 образовало «самостоятельную» rруппу на первом
шаrе, ему БыIл со оставлен символ о, слово О и будем счи-
тать кодом этоrо сообщения. СообщеНlJе А 2 обраЗCJвало са-
мостоятельную rруппу за два шаrа, на первом шаrе el'vlY со-
поставлялся СИl\ ВОЛ 1, на BTOp01\tI о; поэтому буде .л коди-
ровать сообщение А 2 словоrvI 10. Аналоrично, для Аз и А4
выбираем соответственно коды 110 и 111. В итоrе получа::т-
ся СJ1ЕДУlощая КJдовая таслица:
Таблица 9
А 1 А 2 Аз А4
I
О 10 110 111
Указанный здесь способ кодирования был предложен
американским математиком Ф но. Оценим тот выиrрыш,
который дает в нашем случае код Фано по сравнению с рав-
номерным кодом, коrда все сообщения кодируются словами
длины 2. Представим себе, что нужно передать в общей слож-
ности 1000 сообщений. При использовании paBHoMepHoro
кода на их передачу потребуется 2000 двоичных символов.
Пусть теперь используется код Фано. ВСПОl\1НИМ, что из
1000 сообщений примерно 500 раз появляется сообщение А 1 ,
которое кодируется Bcero одним символом (на это уйдет 500
символов), 250 раз сообщение А 2, кодируемое двумя
символами (еще 500 символов), примерно по 125 раз
сообщения Аз и А4 С кодам:и длины 3 (еще 3 х 125+3 х 125==
:=:750 символов). Bcero придется передать примерно 1750
символов. В итоrе мы экономим восьмую часть Toro време-
ни, которое требуется для передачи сообщений равномер-
ным кодом. В друrих случаях экономия от применения кода
Фано 'dожет оказаться еще значительнее.
Уже этот пример показывает, что показателем эконом-
ности или эффективност HepaBHoMepHoro кода являютс
не длины отдельных кодовых слов, а «средняя» ИХ длина т;
определяемая равенством:
N
7 == li P (A i ),
i= 1
rде li длина кодовоrо обозначения для сообщения А"
р (A i ) вероятность сообщения A i1 N оБLЦее число CO
общений.
20
Наиболее экономным оказывается КОД с наимень-
шей средней длиноЙ Т. в примере для кода Фано
1=== 1 х 0,5+2 х 0,25+3 х 2 х 0,125== 1,75,
в то время как для paBHoMepHoro кода средняя длина [===2
(она совпадает с общей длиной кодовых слов).
Нетрудно описать общую схему метода Фано. Распола-
raeM N сообщений в порядке убывания их вероятностей:
р (Al) P (A2) ' . . P (A N ). Далее разбиваем множество
сообщении на две rруппы так, чтобы суммарные вероятно..
сти сообщений каждой из rрупп были как можно более
БЛИЗI(И друr к ,друrу. Сообщения:м из одной rруппы в каче.
стве первоrо символа кодовоrо слова приписывается сим-
ВОЛ О) сообщени ям из друrой символ 1. По тому же прин-
ципу ка}l{дая из полученных rpynn снова разбивается на две
части, и это разбиение определяет значение BToporo символа
кодовоrо слова. Процедура продолжается до тех пор, пока
все множество не будет разбито на отдельные сообщения.
В результате каждому из сообщений будет сопоставлено
кодовое слово из нулей и единиц.
Понятно, что чем более вероятно сообщение, тем быстрее
QHO образует «самостоятельную» rруппу и teM более КОРОТ-
ким словом оно будет закодировано. Это обстоятельство
и обеспечивает высокую экономность кода Фано.
Описанный метод кодирования можно применять и в
случае произвольноrо алфавита И3 d символов с той лишь
разницей что на ка}l{ДОМ шаrе следует производить разбие-
ние на d равновероятных rрупп.
" А{lfОрИТМ кодирования Фано имеет очень простую rpa.
фическую иллюстраЦИfО в виде множества точек (вершин)
на плоскости" соединенных
отрезками (ребрами) по опре-
деленному правилу (такие фи
rypbI в математике называют
срафамu). rраф для кода Фа..
но строится слеДУIОЩИ1\1 оора..
30М (см. рис. 3). Из нижней
(корневой) вершины rрафа ис-
ходят два ребра, одно из кото-
рых ПОlVlечено символом О, дру-
roe символо!-.1 1. Эти два реб-
ра / соответствуют разбиеНИIО
множества сообщений на две равновероятныеr руппы, ОДНОЙ
из которых сопоставляется символ О, а друrой ....... символ 1.
Ребра, Исходящие йз вершин следующеrо «этажа», соответ-
ие
"7
Рис. 3.
21
ствуют разбиению получившихся rрупп снова на равнове-
роятные подrруппы и т. д. Построение rрафа заканчивается,
коrда множество сообщений будет разбито на одноэлемент-
ные подмножества. Каждая конце-
вая вершина rрафа, т. е. верши-
на, из которой уже не исходят
ребра, соответствует некоторо-
му кодовому слову. Чтобы ука-
зать это слово, надо пройти путь
от корневой вершины до соответст- .
вующей концевой, выписывая в по-
рядке следования по этому пути
символы проходимых ребер. На-
пример, вершине аз на рис. 3 ,со-
ответствует слово 100, а вершине а 6 слово ] 110 (вер-
шины, соответствующие кодовым словам, помечены на
рисунке кружками).
[раф для pacCMoTpeHHoro выше примера представлен
на рис. 4.
Получающиеся для кодов Фано rрафы всеrда обладают
тем свойством, что они не содержат замкнутых контуров.
Такие rрафы называют деревьями (мы будем называть их,
учитывая происхождение, кодовыми деревьями). Кодовые
деревья можно строить не только для кодов Фано, но и для
друrих кодов. Независимо от алrоритма кодирования каж-
дому дереву соответствует определенное множество кодовых
слов. Например, для кодовоrо дерева, изображенноrо на
рис. 3, имеем:
ai==OO, а2==01, аз== 100, а 4 == 101, а 5 == 110,
а в == 111 О, а7 == 1111.
Кодовое дерево может быть построено для кода с произ-
вольным основанием d. Каждое ero ребро помечается тоrда
одним из d символов алфавита
и из каR<ДОЙ вершины "TaKoro
дерева исходит самое большее
d различных ребер. Напри-
мер, на рис. 5 представлено
кодовое дерево для ТР9ичноrо
кода со следующим множест-
вом кодовых слов: О, 1 О, 11,
120, 121, 20, 21, 220, 221, 222.
Кодовые деревья дают удобное rеометрическое представ-
ление для мноrих ажных понятий и облеrчают, как мы уви",
дим, решение различных задач, возникающих при построе-
нии экономных кодов.
Рис. 4.
Рис. 5.
22
Задачи и дополнений
1. Закодировать двоичным кодом Фано следующие мно-
жества сообщений:
а) семь сообщений с вероятностями
Рl==Р2== 1/4; РЗ==Р4==Р&== 1/8; Рв==Р7== 1/16;
б) десять сообщений с вероятностями
Pi== Р2== 0,22; Рз== Р 4== РБ== Рв== 0,1; Pi== Рв== Р9== РI0== 0,04.
Найти среднюю длину каждоrо из полученных кодов.
Выяснить, каков выиrрыш по сравнению с равномерным кодирова-
нием.
2. Приведем пример троичноrо кодирования методом Фано для
множества из 8 сообщений с вероятностями
Рl==0,3; Р2==РЗ==Р4==0,15; Р5==Рв==Р7==0,О7; рв==0,О4 А
Таблиuа 10
Со об -
щения:
Веро-
ятно-
СТИ
А 1 0,3
А 2 0,15
Аз 0,15
А4 0,15
АБ 0,07
Ав 0,07
А7 0,07
Аа 0,04
................
о
о
1
1
О
О
1
2 1
О
2
1
Кодо -
вые
слова
о
10
11
20
210
211
220
221
3. Закодировать троичным кодом Фано следующие множества сооб.
щений:
а) 9 сообщений с вероятностями
1/3; 1/9; 1/9; 1/9; 1/9; 1/9; 1/27; 1/27; 1/27;\
б) 1 О сообщений с вероятностями
0,2; О, 15; О, 1 5; О, 1; О, 1; О, 1; 0,05; 0,05; 0,05; 0,05.
2а
4. CBofH:l'BO ПРЕФИКСА,
или КУДА ИДТИ РОБОТУ
При использовании неравномерных кодов
приходится сталкиваться с одной проблемой) которую мы
поясним на примере кодовой таuлицы 9 предыдущеrо пара..
rрафа. На первый взrляд разумно было бы укоротить второе
и третье кодовые слова, отбросив в них последний СИ 1ВОЛ,
так как при этом основное наше требование сохраняется:
по-прежнему различные сообщения кодируются разными
словами, как это видно из получившейся новой кодовой
таблицы.
Таблица 11
А 1 А 2 Аз А4
О 1 r 11 111
Но пусть, к примеру, данные сообщения это команды)
выдаваемые электронному роботу: А 1 идти прямо, А 2
повернуть назад, Аз свернуть влево, А4 свернуть
вправо. Предположим, что проrрамма поведения робота
задается следующей последовательностью:
Al Аз Al А4 Al А 2 Аз ... (1)
в результате кодирования эта последовательность пре-
образуется в такой двоичный техст:
01101110111 ... .
Леrко вообразить себе, в какое недоумение привели ББJ
мы робота, снабдив ero подобноЙ инструкцией. Куда же
ему идти? Ясно, что сначал а надо идти прямо. А дальше
свернуть влево или повернуть назад, потом еще раз назад?
Впереди же еще большая путаница...
Естественно возразить, что следовало бы отделить одно
кодовое слово от друrоrо. Разумеется, это можно сделать,
по лишь используя либо паузу между словами, либо спе-
циальный разделительный знак, для KOToporo необходимо
особое кодовое обозначение. И тот и друrой путь приведет
к значительному удлинению KoJtoBoro текста, сводя на НеТ
наше предыдущее «усовершенствование».
24
Друrое дело, если мы будем пользоваться прежними
кодовыми обозначениями для сообщений А i. Тоrда пОСJlе:-:
доваrельность (1) будет закодирована так:
О 11 00 111 О 1 О 11 00 ... .
Здесь уже не может быть разночтений. Первое слово О .......
идти прямо, второе слово 110 свернуть влево, так как Б
списке кодовых слов не значатся слова 1 и 11. В этом сплош-
ном тексте одно за друrим однозначно выделяются кодовые
слова, и нет сомнений, что робот найдет правильную до-
pory.
Итак, суть проблемы в том, что нужно Y 1eTb в ЛI{)БО!\I
кодовом TeK Te выделять отдельные кодовые слова без
использования специальных разделительных знаков. Иначе
rоворя, мы хотим, чтобы код удовлетворял следующему
требованию: всякая последовательность кодовых символов
может быть единственным образом разбита на кодовые сло-
ва. Коды, для которых последнее требование выполнено,
называются однозначно декодируемыми (иноrда, их назыа..
ют ,кодами без запятой).
Наиболее простыми и употребимыми кодами без запятой
являются так называеМl?Iе префиксные коды, обладающие тем
ствойством, что никакое кодовое слово не является началом
(префиксом) друrоrо кодовоrо слова. Если код префиксный,
то, читая кодовую запись подряд от начала, мы всеrда смо-
жем разобраться, rде кончается одно кодовое слово и начи-
нается следующее. Если, например, в кодовой записи встре-
тилось кодовое обозна1!fение 11 О, то раз-
ночтений быть не может, так как в силу
префиксности наш код не содержит кодо-
вых обозначений 1, 11 или, скажем, 1101.
Иl\1енно так обстояло дело для рассмотрен-
u
Horo выше кода, которыи очевидно явля-
ется префиксным. Рис. 6.
Нетрудно понять, как отражается свой-
ство префиксности или ero отсутствие на кодовом дереве.
На рис. 6 представлено дерево для кода из таблицы 11 (круж.
ками, как и раньше, помечены те вершины, которые соот.
ветствуют кодовым словам). Таким образом, если свойство
префикса не выполняется, то некоторые промежут6чные вер-
шины дерева MorYT соответствовать кодовым словам. Для
кода Фано это невозможно, так как по самомх алrоритму
кодирования построение кодовоrо слова заканчивается од-
новременно с достижением концевой вершины. Следова.
тельно, КОД Фано является префиксным кодом.
25
Задачи и дополнения
1. Префиксный код называют полН,ым, если добавление
к нему любоrо HOBoro кодовоrо слова (в данном алфавите) нарушает
свойство префиксности. Убедиться, что двоичные коды, деревья кото"
рых изображены на рис. 3, 4, являются полными.
На рис. 7 представлено кодовое дерево префиксноrо, но неПОЛНОI'О
двоичноrо кода. Действительно, добавив к кодовым словам О, 10, 111
слово 11 О, получим снова префиксный код.
2. Доказать, что двоичный код Фано является полным кодом.
Верно ли аналоrичное утверждение для кода Фано с произвольным ос..
нованием?
3. Проанализировав задачи I и 2, сформулировать необходимое
и достаточное условие, которому должно удовлетворять кодовое дерево
полноrо префиксноrо кода, и доказать ero необходимость и достаточ-
ность.
4. Используя кодовое дерево, доказать, что всякий префиксный
код может быть расширен до полноrо oдa добавлением к нему некото"
poro множества кодовых слов.
5. Пусть k максимальное значение длин кодовых слов префик-
cHoro кода. Показать, что число кодовых слов не превосходит величины
2k'B случае двоичноrо кода и величины d k в случае кода с произвольным
основанием d. При каких условиях достиrается равенство?
6. Код, представленный на рис. 7, можно сделать более экономным,
отбрасывая в слове 111 последний символ. При этом свойство префикс-
ности не нарушится. Подобная операция, СОСТОЯlцая в том, что каждое
q)
OJ
Рис. 711
Рис. 8.
слово префиксноrо кода заменяется наименьшим ero началом, не явл}!-
ющимся началрм друrих кодовых слов, называется усечением. Очевидно,
что в результате усечения получается префиксный код и при этом более
экономный, чем исходный. Возникают такие два вопроса:
1. Возможно ли усечение полноrо кода?
2. Можно ли утверждать, что 8' результате усечения получается
полный код?
7. На рис. 8,а представлено кодовое дерево префиксноrо I{ода, для
KOToporo усечение невозможно. В то же время мы получим более эк о..
номный префиксный код (рис. 8, б), если в словах 110 и 111 вычеркнем
второй символ 1.
Справедливо следующее утверждение: префиксный код является
полным тоrда и только тоrда, коrда ero невозможно сократить (т. е.
вычеркнуть хотя бы один знак в любом из кодовых слов), не нарушив
СВойства префикса.
8. Любопытно рассмотреть примеры однозначно декодируемых
кодов, не обладающих свойством префикса. Пожалуй, простеЙII.tИМ при
мерам TaKoro рода является двоичный код {l, 10}. Ясно, что в любой
кодовой последовательности, составленной из этих слов, всякое появле"
26
ние символа 1 ознсн!ает начало HOBoro кодовоrо СЛова. lIоследнее ос.1'а"
ется справедливым для кода, каждое СЛОБО KOToporo есть единица с по.
следующими нулями. Разумеется, подобные коды далеко не самые эко-
номные.
Приведем M Hee тривиальный пример однозначно декодируемоrо
кода: {01, 1 О, 011}. Рекомендуем читателю указать алrоритм одноз-
начноrо выделенJi кодовых слов из кодовой последовательности для
9Toro кода.
9. Как узнать, является ли произвольный код однозначно декоди-
руемым? Для этоrо можно предложить следующий способ. Возьмем
всевозможные пары кодовых слов, в которых одно слово является
префиксом друrоrо. Для каждой такой пары найдем «повисший» суффикс,
который остается после удаления префиксноrо слова из начальной части
бо.пее ДЛинноrо слова. Например, повисший суффикс для пары 10 и
, 10010 есть 010. Выпишем все повисшие суффиксы. Далее проделаем то
же самое для каждой пары слов, состоящей из повисшеrо суффикса и
кодовоrо слова, в которой одно слово является префиксом друrоrо. Выпи-
шем все новые повисшие суффиксы, которые при этом получатся. Будем
продолжать этот процесс До тех пор, пока будут появляться новые
суффиксы. Код является однозначно декодируемым тоrда и только
тоrда, коrда никакой суффикс не совпадет ни с одним кодовым словом.
10. Выяснить, обладают ли свойством однозначной декодируемости
следующие коды:
{ 11 О, 11, 1 00, 00, 1 О} ;
{ 1 00, 00 1, 1 01, 11 01, 11 011 }.
11. Префиксные коды иноrда называют меновенными (или MrHoBeH-
но декодируемыми), поскольку конец кодовоrо слова опознается сразу,
как только мы достиrаем конечноrо символа слова при чтении кодовой
последовательности. В этом состоит преимущество префиксных кодов
перед друrими однозначно декодируемыми кодами, для которых конец
ка:>кдоrо кодовоrо слова, как мы видели, MOJKeT быть найден лишь после
анализа одноrо или нескольких последующих символов, а иноrда и всей
кодовой последовательности. Таким образом, в отличие от префиксноrо
кода декодирование здесь осуществляется с запаздыванием по отноше-
НИIО к передаче сообщения.
5. ЕЩЕ О СВОЙСТВЕ ПРЕФИКСА
И ОДНОЗНАЧНОЙ ДЕКОДИРУЕМОСТИ
Возникает вопрос: каковы возможные ДЛИНЫ
кодовых слов однозначно декодируемоrо, в частности, пре-
фиксноrо кода? Понятно, например, что не существует дво-
ичноrо префиксноrо кода с длинами кодовых слов 1, 1, 2.
Несколько труднее ответить на такой вопрос: существует
ли префиксный двоичный код, содержащий 100 слов с дли-
нами от 1 до 100? Оказывается, существует. Кодовое дерево
для требуемоrо кода, содержащее 100 «этажей», изображено
на рис. 9 (пунктиром отмечены пропущенные этажи).
Вопросы TaKoro рода можно было бы продолжить, отве-
I
чая на них в каждом конкретном случае. Но на самом деле
можно установить общие условия (необходимые и достаточ-
27
пые) для существования префиксноrо и вообще ПРОИ3ВОЛЬ"
Horo однозначно декодируемоrо кода.
Пусть V=={al' а2, ..., аN} префиксный двоичный
код, дерево которото схеl\1атически изображено на рис. 10.
100
t1N 1 ан
98 VV 1
\ I
а 4
If
;; 3
2 2
, 1
О
Рис. 9. Рис. 10.
Пусть nп число кодовых слов длины k (nп совпадает с
числом концевых вершин k..ro этажа). Конечно, справедливо
неравенство
пk 2k, (1)
так как 2 k максимально возможное число вершин на
k-M этаже двоичноrо дерева. Однако в случае префиксноrо
кода для nп можно получить rораздо более точную оценку,
чем (1). В самом деле, если ni, n2, .., , nп....l число конце-
вых вершин 1; 2; ... ; k 1 этажей дерева, то число всех
вершин k-ro этажа кодовоrо дерева равно
2k 2k lпl 2k '2п2 ' . . 2пk i,
и потому
N 2 k 2 R 1 2 k 2 2
k пl п2 "' пk jJ
(2)
или иначе
2 k 1 +2 k 2 t + " + 2 /
п 1 п2 -... ,-пk l пk ·
Деля обе части последнеrо HepaВ€HCTBa на 2 k , получаем:
k
пi2"i l (3)
i=l
28
НеравеНСТБQ (3) верно для любоrо k, L (L макси.
ма.п:ьная длина КОДОВЫХ слов), в частности
L
пi2 i 1. (4)
i = 1
'Если 11, 12' ... , lN длины кодовых слов аl, а2, о.. ; aN,
то нераве'НСТВО (4) запишется в таком виде:
2 11+2 l2., ...+2 lN 1. (5)
Это и есть то условие, которому обязаны удовлетворять
ДЛИНЫ КОДОВЫХ с.пов ДВОИ1. ноrо префиксноrо кода.
Оказывается, что неравенство (5), называеIVlое в теории
кодирования неравенством Крафта, является также доста-
точным условием Toro, чтобы существовал префиксный код
длинами кодовых слов 11, 12' ... ,7 N .
Рассуждаем так. Если среди чисел 1j, 12' ... , lN имеется
ровно пi чисел, равиых i, то неравенство (5) можно перепи-
С:1ТЬ в виде (4), rде L максимальное из данных чисел. Из
, ' ., '4t , tt, , , ,.. , , , l
I \ J \ , I , I \ l' , 1
Х ' / \ J \ J , I " , у у \ \ , \ , "
, 1t l' У 1 \
I \ I \ I \ I
4
5'
Рис. 11.
справедливости (4) подавно следует, что верны неравенства
(3) для всех L, а, следовательио, и неравеиство (2).
Обратимся к рис. 11, на котором изображено дерево «вы-
соты» L, имеющее иаибольшее число вершин и ветвей (ре-
бер). Все концевые вершины (их 2L) TaKoro дерева находят-
ся на последием L-OM этаже, а' из каждой вершины промежу-
, точноrо этажа исходят ровно две в, тви.
Для построения иужноrо префИRсноrо кода мы должны
подходящим образом выбрать пi слов длины 1, n2 слов дли-
'вы 2, вообще nk слов длины k (1 <,k L) или, иными слова-
МИ, n1. концевых вершин на первом, n2........ на втором, ... t
nk на k-OM этаже.
29
Из неравенства (2) при k== 1 получаем пl<2, т. е. требуе-
мое число не превосходит общеrо числа вершин первоrо
этажа. Значит, на этом этаже MO}I{HO выIратьь какие-т<? п!
вершин в качестве концевых (п 1 рапно О, 1 или 2). Если
это сделано, то из общеrо числа вершин BToporo этажа
(их 2 ==4) для построения кода можно использовать лишь
4 2пl (почему?). Однако нам хватит и этоrо числа вер-
I
шин, так как из нерааенства (2) при k==2 вытекает
п2<4 2пi.
Аналоrично, при k==3 имеем неравенствот
пз<23 4пl 2п2.
Правая часть ero вновь совпадает с допустимым для по-
строения префиксноrо кода числом вершин TpeTbero этажа,
если на первых двух этажах уже выбраиы пl и п 2 концевых
вершин. Значит, снова можно выбрать пз концевых вершин
на .третьем этаже. Продолжая этот процесс вплоть до k==L,
мы и получим требуемый код.
Если кодовый алфавит содержит d символов, то подоб-
ным же образом доказывается, что необходимым и достаточ-
ным условием для существования префиксноrо кода с дли-
нами слов 1i, 12' ... , 1 N является выполнение неравенства
d...11+d 12+...+d lN 1. . (6)
Оказывается, неравеиству (6) обязаны удовлетворять и
длины кодовых слов произвольноrо однозначно декодируе-
Moro кода. Поэтому, если существует однозначно декоди-
руемый код с длинами C OB 1 t , 12' ... , 1 N , то существует и
префиксный код с теми же длинами слов. Префиксными же
кодами пользоваться удобнее по причине, указанной в до-
полнении 11 к 4.
Задачи и дополнения
1. Каково минимальное число слов полноrо двоичноrо
префиксноrо кода с максимальной длиной L? Какими будут длины Ко-
довых слов TaKoro минимальноrо кода? (Ответы на эти вопросы подска..
зывает рис. 9.)
Решить те же вопросы в случае d ичноrо кода..
2. Доказать, что префиксный !{од является полным тоrда и только
тоrда, коrда в неравенстве Крафта достиrается равенство:
d ll+d li+... +d lNc:: 1.
у к а З а н' и е. То, что из предыдущеrо равенства вытекает по..Ч"
нота, очевидно. Для доказательства обратноrо утверждения следует
предположить, что неравенство (6) cTporoe! Тоrда из иеrо выводится'
ЭQ
CTporoe }Ке неравенство
nL < d L dL lnl dL 2n2 dnL 'f.,
которое показывает (почему?), что можно добавить по крайней мере
еще ОДНО слово, не нарушая префиксности.
3. Утверждение предыдущей задачи допускает следующую забав-
ную интерпретацию, являющуюся одновременно./ и ero доказательством
(она заимствована из книrи [6]).
Рассмотрим дерево, соответствующее полному префиксному коду.
Представим себе, что на это дерево взбирается обезьяна. Начав с корня,
она науrад выбирает любую из d исходящих из Hero ветвей; вероятность
raKoro выбора равна l/d. Добравшись до очередной развилки, обезьяна
снова науrад выбирает некоторую ветвь с вероятностью l/d (напомним,
что из каждой промежуточной вершины дерева полноrо кода исходит
ровно d ветвей). Тоrда вероятность Toro, что обезьяна достиrнет какой-
то определенной концевой вершины, находящейся на высоте k, равна
(l/d)k. Если таких вершин ntt, то с вероятностью nkd k обезьяна оста-
новится на высоте k. На какой-то высоте от 1 до L обезьяне придется
L
остановиться (вероятность этоrо равна 1). Поэтому nkd k === 1.
k=l
(8 приведенном рассуждении мы использовали правила сложения и
умножения вероятностей.)
4. Префиксный код с данными длинами кодовых слов может быть
построен далеко не единственным способом. Пусть d ичный префиксный
код (не обязательно полный) имеет nk слов длины k (1 <k<L). Доказать,
что число различных таких кодов с фиксированными L и nk равно про
изведению
( ) х (d2 2dnf)
( d 3 d2nl dп2 )
Х Х...
па
Х ( dL dL J.nf '" dnL i ) _
t . . ,
пL
rде (;) ==с! число сочетаний из i элементов по j.
Например, число двоичных префиксных кодов с L===4, ni==O, n2== 1,
nз==2, n 4 ==4 равно
cgclc:c: == 4200.
5. Выше было доказано, что если для чисел lf, 12' . . .., l N выполня-
ется неравенство Крафта, ТО' существует префИI{СНЫЙ код с длинами
11, 12, . · ., 1 N. Найти этот код можно, строя этаж за этажом ero кодо.
Бое дерево. Друrой более удобный метод решения этой задачи был при"
думан UUeHHoHoM, и (применительно к двоичным кодам) он состоит в
следующем.
Пусть числа 11, 12' I . ., IN удовлетворяют неравенству
N
2 li 1.
i= 1
.можно, считать, что li</ 2 <. . . <1 N' Рассмотрим последовательность
чисел
j--l N--l
1 l. l.
q О . q 2 1.- · q 2 l q 2 l
1 , 2...... ,..t, j=::З ".., N=:::' .
i= 1 i= 1
(7)
81
Заметим, что все эти числа заключены в прсделах O q i < 1, поэтому
каждое из них может сыть представлено двоичной дробыо вида
п
(X,k2 k, rде каждое (х, k есть О или 1. Пр и этом из (7) МО}К но заклю-
k= 1
ЧИТЬ, что все эти дроби конечны, и двоичная запись для q j имеет не бо-
лее lj значащих цифр.. Такиf\. образом, любое число qj однозначно
представимо в виде:
l}
q ........ С ., . 2 1
J....... l J '
i = 1
rде всякое Cij есть О или 1. Следовательно, каждому q J однозначно от-
вечае'l слово Vi CljC2j . . . C l .; длины [j. Рассмотрим код v {t'l, Т)2', ".
... , и N}' Покажем, 9ТО он обл дает свойством префикса. Пусть V j и Vk два
l.
слова (k>j). Тоrда, соrласно (7), qk qJ 2 J, а это означает, что .1j-Й
символ слова v j не совпадает с 1 j-M символом слова Vk. Следовательно,
V j не является началом Vk, откуда и вытекает префиксность кода У.
Разъясним сказанное на примере. Построим преф",ксный код с ДЛИ r
нами слов 11== 1, [2 lз==3, 14==4. В этом случае
1 5
ql == О , ' q q
2 2; З 8;
3
q4 == 4.
Двоичная запись этих чисел с нужным числом lj знаков следующая:
I О О 1 О 1
q1 == О, Q2::::'T+"22+ 23 ; qз:=: 2+22'+2"3 :
. 1 1 О О
Q4==2+W+F+2i'
в результате ны получим искомый код:
01==0; v 2 ==lOO; vз==lОl; v4==1100.
6. Используя метод Ше. .fOHa, найти префиксные KOДЬ с указанными
ниже длинами слов:
а) 11==12==2; 1 З ==[4==3; 15==l6==[7==4
б) /1 ---;- 1; 12== 2; 1 з == 14,== 15 == [6== 4.
Построить кодовые деревья для полученных кодов. Определить, какой
из этих кодов является полным.
6. ОПТИМАЛЬНЫЙ КОД
Как уже rоворилось, общее правило при по-
строении экономноrо кода следующее: чаще встречающиеся
сообщения нужно кодировать более короткими кодовыми /
словами, а более длинные слова использовать для кодиро-
вания редких сообщениЙ. Это правило и было реализовано
в paccIvIoTpeHHoM выше методе кодирования Фано. Но всеrда
ли метод Фана приводит к наиболее экономному коду? Ока-
82
ЭБlвается, нет. Способ построения оптимальноrо кода, кото-
рый мы здесь изложим, потребует от нас более тонких
рассуждений,
Пусть сообщения Af, Ai, ... ., AN имеют вероятности Рl,
P2j ... , PN (Pi;;:::P2 ... PN) И кодируются двоичными сло
вами йl, й2, ... , aN, имеющими длины 11, [2, ... , lN. Поста
раемся выяснить, какими свойствами должен обладать
двоичный код, если он оптимален.
1. В опти:мальном коде менее вероятное сообщение не
может кодироваться более коротким ,словом, т. е. если Pi<
<Pj, то li?3 1 j.
Действительно, в противном случае поменяем ролями
кодовые обозначения для A i и AJ. При этом средняя длина
кодовых слов изменится на величину
Pili + Р jl j Pil j p jli == (Pi P j)(li l j»O,
т. е. уменьшится, что противоречит определению оптималь-
Horo кода.
2. Если КОД оптимален, то всеrда можно так перенуме-
ровать сообщения и соответствующие им кодовые слова, что
pf. p ?;;;''' PN и при этом
ll<J2 ...<JN' (1)
В самом деле, если Pi>Pi+l' то из свойства 1 следует, что
..
li<:li+l' Если же Pi==Pi+l, НО li>li+i, то переставим сооб
щения А ; и Ai+l И соответствующие им кодовые слова. По-
вторяя эту процедуру нужное число раз, мы и получим
требуемую нумерацию.
Из неравенств (1) следует, что сообщение AN кодируется
словом aN наибольшей длины lN'
3. В оптимальном двоичном коде всеrда найдется, по
краЙней мере, два слова наибольшей длины, равной lN,
и таких, что ОНЦ отличаются друr от друrа лишь в послед-
нем символе.
Действительно, если бы это было не так, то можно было
бы просто откинуть последний символ кодовоrо слова aN,
не нарушая свойства префиксности кода. При этом мы, оче-
видно, уменьшили бы среднюю длину кодовоrо слова.
Пусть слово at имеет ту же длину, что и aN и отличает-
ся от Hero ЛИШЬ в последнем знаке. Соrласно свойствам 1
и 2 можно считать, что lt===lt+l=='" ==lN' Если t=l=N-----l,
то можно поменять ролями кодовые обозначения 'at и aN...l,
не нарушая при этом неравенств (1).
Итак, всеrда существует такой оптимальный КОД, в !<о-
тором кодовые обозначения двух (наименее вероятных)
2 м. Н. Аr1 ИПОВ Л. Е. Садовсний 33
сообщенwа AN l и AN отличаются лишь в последнем сим.
воле.
Отмеченное обстоятельство позволяет для решения за-
дачи рассматривать только такие двоичные коды, у кото-
рых кодовые обозначения aN..f и aN для двух наименее ве-
роятных сообщений AN--i и AN имеют наибольшую длину,
отличаясь лишь в последнем символе. Это
значит, что KOHцeB e вершины aN__l и aN кодо-
Boro дерева искомоrо кода должны быть соеди-
нены с одной и той же вершиной а предыдущеrо
«этажа» (см. рис. 12).
Рассмотрим новое множество сообщений
Рис. 12. A<J,)== {Ai, А 2 , ... , AN--i, А} с вероятностями
Р1' Р"2, ... , PN...i, P==PN...l+PN' Оно получается
из множества {A i , А 2, ... , A N __"2, A N __ 1 , A N } объедине-
нием двух наименее вероятных сообщений A N __ i , AN в од-
но сообщение А. Будем rоворить, что АЦ) получается сжа-
тием из {А 1, А"2, ... , А N ... 2., А N __ i, А N }.
Пусть для А (1) построена некоторая систем'а кодовых
обозначений К(l)== {ai, а2, ... , aN..."2, а}, иными словами,
указано некоторое кодовое дерево с концевыми вершинами
аl, а"2, .. . , aN... 2, а. Этой системе можно сопоставить код
K=={ai, ai, .., aN....i,aN...i, аN}ДЛЯ исходноrо множества со-
общений, в KOTO pOM слова aN__i и aN получаются из слова
, а добавлением соответственно О и 1. Процедуру
ан t ( Oн перехода от K(l) К К назовем расщеплением.
\! Справедливо следующее утвержден е, откры-
вающее путь для построения оптимальноrо
J а кода:
J Е сли код K(l) для множества сообщений А ( 1 )
Рис. 13. является оптимальным, то оптимален также
u код К для исходНО20 множества сообщений.
Для доказательства установим связь между средними
длинами Т и l' слов кодов К и КО). Она, очевидно, такова:
1 == l' + р. (2)
Предположим, что код К не является оптимальным, т. е.
сущестаует код К1 со средней длиной ll<1. Как отмечалось.
.... ...
можно считать, что концевые вершины aN--i и aN ero кодо-
Boro дерева (см. рис. 13) соответствуют кодовым обозначе-
ниям для наименее вероятных сообщений AN...i и AN' Тоrда
эти обозначения отличаются лишь' в последнем символе.
Рассмотрим код K 1)== {ai, ... , aN...i, а}, в котором слово а
получается из aN...l и _ aN отбрасыванием последнеrо СИМ-
иN l ан
V
I
I
34
вола. Средние ДЛИНЫ l; и l связаны соотношением, анало-
rичным (2):
11 == l + р.
Из неравенства li<l следует l;<I' j что противоречит оп-
тимальности кода K("J). Утверждение доказано.
Теперь ясно, что для построения оптимальноrо кода
можио использовать последовательные сжатия исходноrо
множества сообщений.
Проиллюстрируем процесс последовательных сжатий и
расщеплений на примере множества из пяти сообщений с
вероятностями pi==O,4; Р2==РЗ==Р4==рs==О,15. Процесс этот
отражен в .следующей таблице:
Таблица 12
Вероятности и кодовые обозначения
Сооб- Сжатые множества
ЩЩIИЯ Исходное множество
А(1) А(а) А(8)
А 1 0,4 1 0,4 1 0,4 1 -+0,6 О
А 2 0,15 010 -+0,3 ( 00 О , 3 00 0,4 1
Аз 0,15 011 О, 151 010'........ -+0 , 3J-----or
А4 о · 151 000 011
О , 15
А5 О, 15 001
Каждое из множеств А (1), А ( ), А (3) получается сжатием
предыдущеrо множества. Множество А (8) состоит из двух
сообщений, поэтому оптимальный код К(З) содержит два
кодовых обозначения О и 1. Последовательное расщепле-
ние К(З) дает оптимальный КОД для ИСХQДНОЙ системы сооб-
щений. I
Средияя длина 1 кодовых слов, равиая 0,4+4 х 3 х О, 15==
:=:2,2, является, как это следует из предыдущеrо, мииималь-
но возможной для данноrо множества сообщений.
Описанный метод кодирования был предложен в 1952 r.
американским математиком Д. А. Хаффменом.и называется
ero именем. Сравним теперь оптимальный код из таблицы 12
с кодqм Фано для Toro же множества сообщениЙ, который
строится ниже.
2.
85
Т а б л и ц а 13
Сообщения В е ро ятности К9довые
слова
А 1 0,4 О O
о
А 2 0,15 1 01
J .....
Аз 0,15 О 10
А4 0,15 1 О 110
А5 0,15 1 1 111
Подсчитаем среднюю длину lF КОДОВЫХ СЛОВ В этом слу-
чае:
lF ==2 х 0,4+2 х2 хО,15+2 х 3 хо, 15==2,3.
Следовательно, метод кодирования Фано не всеrда ПрИВОДИТ
к оптимальному коду.
Как и метод Фано, метод кодирования Хаффмена может
быть распространен на случай KoAoBoro алфавит , состоя-
щеrо из произвольноrо числа символов. Этот вопрос рас-
смотрен в книrе [2].
Задачи и дополнения
1. Доказать, что всякий оптимальный КОД является
полным.
2. Закодировать двоичным кодом Х ффмена множество сообщений,
имеющих вероятности:
Pi==O,25; Р2==0,2; РЗ==Р4==рь==О,15; P6==O,J.
Построить соответствующее кодовое дерево.
3. Основываясь на алrоритме Хаффмена, найти способ непосред.
CTBeHHoro построения кодовоrо дерева оптимальноrо кода.
у к а з а н и е. Построение дерева надо начинать не с корня, а
с концевых вершин.
4. В некоторых случаях результаты двоичноrо кодирования ПО
методу Фано те же, что и по методу Хаффмена, в том смысле, что длины
соответствующих кодовых слов для обоих методов совпадают. Так,
например, обстоит дело для множества сообщений с вероятностями:
Pi== 1/4; Р2==РЗ==Р4==РЬ== 1!а; Р6==Р1==Рэ==Рg== 1/16.
На самом деле справедливо следующее утверждение: если Pi==2 171
(Т. е. .если вероятности являются степенями двойки), ТО длины соот"
ветствующих кодовых слов в кодах Фана и Хаффмена одинаКОВЪJ и
равны 1Ц.
5. Не всеrда по..'!ныА код является оптимальным для данноrо MHO
тества сообщеf[ИЙ. Можно J.\оказаТЬ J однако; ЧТО I3СЯКИЙ полный КОД
36
является оптимальным для HeKoToporo множества сообщений с подхо-
дящим образом подобранными вероятностями. Так, если кодовые слова
полноrо кода с основанием d имеют длины n'i., n2' . . ., nN, то он оптима-
лен для множества сообщений с верояrностями d пl, d nl; t . ., d п N.
7. ОБ ИЗБЫТОЧНОСТИ, ШУМАХ
И кРиптоrРАММЕ, КОТОРУЮ НЕЛЬЗЯ
РАСШИФРОВАТЬ
Напомним читателю, что при кодировании
сообщений нужно заботиться о том, чтобы их передача была
достаточно быстрой, удобной и надежной. До сих пор мы
интересоваЛИСh лишь требованием быстроты. В этой связи .
были рассмотрены различные эффективные методы коди
рования: коды Фано, Шеннона, Хаффмена. Последний, как
было выяснено, является даже оптимальным при заданном
множестве сообщений с заданными вероятностями. Указан-
ные методы можно рассматривать как cBoero рода искусст
венные языки, предназначенные для экономной передачи
информации. Оказывается, что привычные нам естественные
языки (русский, анrлийский и т. д.) являются В этом
\
плане слишком расточительными и не выдерживают конку-
ренции с искусственными языками. Подтвердим это следую-
щим мысленным экспериментом. Произвольный русский
текст разобьем на куски одинаковой длины n (промежуток
между словами можно по желанию либо иrнорировать,
либо считать отдельным символом). Получающиеся при этом
различные буквосочетания из n букв будут встречаться,
как это отмечалось прежде, не одинаково часто. Представим
себе, ЧТО, мы располаrаем таблицей, в которой указаны
всевозможные n-буквенные сочетания и их вероятности в \
русском тексте. Применяя метод Фано, закодируем их ко-
довыми словами, также использующими русский алфавит.
Возвращаясь к исходному тексту, заl'4..еним каждый ero ку-
сок длины n соответствующим ему кодовым словом. Расчеты
показывают, что действуя таким образом, мы смоrли бы
при достаточно большом n сократить исходный текст более,
чем наполовину, сохранив при этом всю содержащуюся в
нем информацию.
Было бы однако неОСТОРОЖНЬПvl на основе СК3З8нноrо об..
,, .
винить русскии язык или друrие естественные языки в не..
совершенстве. В теории информации имеется понятие, име..
нуемое избыточностью языка или текста. Избыточность"
"
точноrо определения которои мы не приводим, можно
представлять себе как долю тех символов текста, которые
37
MorYT быть искажены или стерты без ущерба для ero пони..
мания, или иначе, как степень возможноrо «сжатия» текста
в случае применения к нему методов оптимальноrо коди-
рования. Мы вправе сказат поэтому, что естественные язы-
ки обладают высокой избыточностью (более 50%). Напро-
тив, оптимально закодированные тексты имеют избыточ-
ность, близкую к нулю. Но именно высокая избыточность
естественных языков позволяет с леrкостью пользоваться
ими в письменной и устной речи, например, свободно вни-
кать в смысл написанноrо, несмотря на содержащиеся в тек-
сте сокращения или опечатки, без особоrо труда понимать
человека, rоворящеrо с акцентом или на каком-нибудь диа-
лекте и т. д. [ерои известноrо романа Жюля Верна «Дети
капитана rpaHTa» счастливой развязкой своих приключе-
ний также во MHoroM обязаны избыточности языка.
Одним словом, избыточность позволяет языку противо-
стоять влиянию всякоrо рода мешающих воздействий, в то
время как оптимально закодированные тексты, оказывает-
ся,. перед ними совершенно беззащитны. Подтвердим это
приведенным в таблице 13 примером текста, закодирован-
Horo двоичным кодом Фано.
Возьмем последовательность сообщений А iА з А 5 Аr;А 1 А 4
и отвечающий ей кодовый текст 011011111100110. Пусть
, произошло искажение одноrо только первоrо СИМВQла.
Получившаяся тоrда кодовая последовательность
111011111100110 после расшифровки будет воспринята как
последовательность сообщений А5А2А5А4А2Аз.
Произошла непоправимая путаница, и ее виновником
был Bcero лишь один неверно принятый кодовый символ.
Аналоrично обстоит дело с любым оптимальным кодовым
TeKCTOM ошибки (одна или несколько) переводят ero в дру-
rой также вполне осмысленный кодовый текст, НО смысл
получившеrося текста может быть совершенно отличен от
первоначальноrо. Такова расплата за оптимальность кода.
В то же время в реальных каналах связи, по которым
происходит передача информации, ошибки неизбежны. Они
являются следствием помех или, как иначе rоворят, шумов,
которые MorYT иметь самую различную физичеСКУIq при-
роду. Действие этих шумов на передаваемый текст можно
ослабить, но устранить ero полностью нельзя. ОТСI-Dда вы-
вод: оптимальные коды в чистом виде неприrодны для
передачи сообщений по каналам связи с шумами, так как
передача в этом случае становится ненадежной. С друrой
стороны, ясНО; что надежность можно обеспечить только
за счеrr неКQrорой избыточности кодовото текста. В Д Jrf
Э8
u u
неишем речь поидет как раз о таких системах кодирования,
которые предусматривают введение избыточности для борь- \
бы с теми или иными видами ошибок. При построении по-
добных кодов всеrда приходится идти на компромисс: с од-
ной стороны, избыточность (т. е. количество дополнитель..
ных, «лишних», символов) не должна быть слишком велика,
чтобы не растяrивать время передачи; с друrой стороны,
помехоустойчивость (т. е. способность кода корректировать
ошибки) должна быть достаточной, чтобы обеспечить надеж-
ность передачи.
[Iрежде чем переходить к рассмотрению помехоустойчи-
вых кодов, ПQЗВОЛИМ себе еще одно небольшое отступление
в криптоrрафию. К этому нас ПQбуждает понятие избыточ",
ности, которое, оказывается, имеет прямое отношение к
степени секретности криптоrраммы. Подстановочные крип"
TorpaMMbI, например, потому-то и столь леrки в расшифров-
ке, что они, по существу, сохраняют избыточность перво..
начальноrо текста.
Друrие методы шифрования уменьшают эту избыточ-
ность, ыо все же не полностью ее устраняют, к тому же появ..
ляется избыточность, связанная со специфическими особен..
настями применяемоrо ключа. Совершенно секретная, Т. е.
недоступная для расшифровки, криптоrрамма должна быть
освобождена как от избыточности исходноrо текста, так и ОТ
избыточности ключа. Способ составления такой КрИПТО
rраммы был предложен, как об этом уже упоминалось,
К. Шенноном, и состоит он в следующем. Сначала устра-
няем избыточность текста, применяя к нему какой"нибудь
из методов эффективн r'd кодирования. Вслед за этим к по-
Jlучившемуся безызбыточному тексту применяем шифр со
случайным ключом. Он похож на шифр Тритемиуса, для
KOToporo (применительно к русскому алфавиту)
li=:;;тi+k, (mod 31).
В этом равенстве т" и l, по-прежнему являются номе..
рами i-ой буквы шифруемоrо текста и криптоrраммы соот-
ветственно, а каждое k, выбирается случайным образом сре..
ди чисел О, 1, 2, ... , 30 так что выбор любоrо из этих чи-
сел в качестве k i одинаково возможен.
Недостатком такой совершенно секретной системы ЯВ-
ляется то, что вместе с шифрованным сообщением требуется
посылать такое же по объему сообщение, содержащее ин-
формацию о случайном ключе, поскольку он заранее
неизвестен адресату. Поэтому практически эта спстема ма-
, ло риеМJIема.
39
Существуют, однако, системы шифрования, не И ПОЛЬ..
ЗУlощие случайноrо ключа, и в то же время близкие к со-
вершенно секретным. Необходимая система, например.
может быть получена усовершенствованием шифра беrу-
щеrо ключа (CM дополнение 4 к 9 2). Она состоит в том, что
u u
на предварительно сжатыи передаваемыи текст наклады-
вается друrой текст, также предварительно сжатый.
Наконец, и от хлопотливой процедуры предварительноrо
сжатия также можно отказаться, если в качестве ключа для
шифровки испо.пьзовать не один, а несколько (три или боль-
ше) условленных заранее текстов, прибавляя все их к пере-
даваемому сообщению_
8. КОДЫ...... АНТИПОДЫ
Мы выяснили, что при построении помехо-
устойчивых кодов не обойтись без дополнительных симво-
лов, которые должны быть присоединены к кодовым словам
безызбыточноrо кода. Эти СИI\lВОЛЫ уж е не несут информа-
ции о передаваеI\1ЫХ сообщениях, но MorYT дать информа-
цию о происшедших при передаче ошибках. ИНЫ1\1И словами,
их назначение контролировать правильность передачи
кодовоrо слова. Вводимые дополнительные символы так и
называют контРОЛЬНblми (или провеРОЧНblми).
Самый незатейливый способ, позволяющий исправлять
ошибки, состоит в том, что каждый информационный сим-
вол повторяется несколько раз, скажем, символ О заl\1.еняет-
си блоком из п нулей, а символ 1 ........ блоком из n' единиц.
При декодировании п-буквенноrо блока, содержащеrо,
быть может, ошибочные СИМВОЛ I, решение принимается
«большинством rолосов». Если в принятом блоке нулей боль-
ше, чем единиц, то он декодируется как 00...0 (т. е. счи-
тается, что был послан нулевой символ), в противном слу-
чае........ как 11.. .1. Такое правило декодирования позволяет
верно восстановить посланные символы, если помехи в ка-
нале искажают менее половины символов в ка)l{ДОМ пере-
дав&емом блоке. Если длину блока п вьюрать достаточно
большой, то мы практически обезопасим себя от возможиых
ошибок, однако передача сообщений будет идти черепашь-
ими темпами. По этой причине указанныlй код (ero называют
кодом с повторением) не имеет большоrо практическоrо
значения, однако правило ero декодирования (<<rолосова-
иие») содержит в себе BeCb1\1a полезную идею, которая с ус-
пехом прим няется в друrИХ t практически более интересных
поl\tlехоустойчиJ3ЫХ кодах. Об этом речь пойдет Д8J1ьше (см.
40
17, 18), а сейчас постараемся выяснить, на что мы можем
рассчитывать при минимальной избыточности, коrда к каж
дому кодовому слову добавляется Bcero лишь один прове
рочный символ. Пусть аlа2' . .а n двоичное кодовое сло
БО. Выберем проверочный символ а n +l с таким расчетом,
чтобы на ero значение одинаково влиял каждый из символов
данноrо слова. Это естественное требование будет выпол-
нено, если, например, положить a n +l==a 1 +a2+. . .+а п
(mod 2). Тоrда проверочный символ an+i будет равен нулю,
если в кодовом слове ala2. . .а п содержится четное число
единиц, и единице в противном случае.' Например,
присоеДИЕЯЯ таким образом проверочный символ к слову
1010, получаем слово 10100, а из слова 1110 получим слово
11101.
Нетрудно видеть, что все удлиненные кодовые слова
(XIC't2" . .anC'tn+l содержат четное число единиц, т. е.
сх 1 +а 2 +... +а п +а п + 1 ==0 (mod2). (1)
LLопустим, что в процессе передачи в удлиненное кодовое
слово аlа2.. .а п а п +l вкралась одна ошибка (или даже
любое нечетное число ошибок). Тоrда в искаженном слове
a a;. . .a a +l число единиц станет нечетным:. Это и служит
указанием на искажение в передаче слова. В конечном
итоrе все сводится к проверке соотношения (1) для символов
принятоrо слова, что леrко сделает простейшее вычисли-
тельное устройство сумматор по h10ДУЛЮ 2. Итак, прави-
ло приема следующее: еСJIИ равенство (1) выполняется, счи-
таем, что сообщение передано правильно, в противном слу-
чае отмечаем, что ПрОИЗОШilа ошибка и, к<;>rда это возможно,
требуем повторить передачу кодовоrо слова. Понятно, что
иначе ошибки не' исправить. Haf!plJMep, если принято «He
правильное слово» 11100, то одинаково возмо)кно, что было
послано любое из кодовых слов:
01100, 10100, 110001 11110, 11101.
Каждый из перечисленных случаев соответствует одной
ошибке, а ведь ошибки моrли произойти даже в трех, а то
и в пяти символах.
Еще большая неприятность подстереrает нас в случае
двойной ошибки или вообще четноrо числа ошибок. Ведь
тоrд соотношение (1) не нарушится, и мы восприме!d иска-
женное олово как верное.
ОписанныЙ код, который называют кодом с общей про-
веркой на чеТНОСТЬ J ПОЗВОJIяет, следовательно, обнаружить
, 1
- любое нечетное число ошибок, но «пропускает» искажения,
если число ошибок четно.
Код с повторением и код с общей проверкой на чет-
ность до некоторой степени антиподы. Возможности
первоrо исправлять ошибки теоретически безrраничны, но
он крайне «медлителен». Второй очень быстр (Bcero один
дополнительный символ), но зачастую «леrкомыслен». В ре-
альных каналах связи, как правило, приходится считаться
с возможностью ошибок более чем в одном символе, поэтому
в чистом виде код с общей проверкой на четность приме-
няется крайне редко. rораздо чаще применяют коды с не-
сколькими проверочными символами (и, соответственно,
с несколькими проверками на четность). Они позволяют не
только обнаруживать, но и исправлять ошибки, и не только
одиночные, но и кратные, и притом делать это rораздо
эффективнее, чем упоминавшийся нами код с повторением.
Эrо можно проиллюстрировать на одном красноречивом
и в то же время простом примере. ,
Рассмотрим множество всех двоичных слов длины 9 (с ИХ
помощью можно закодировать 29==512 сообщений). Распо-
ложим символы каждоrо слова alai. . .а в в квадратной
таблице следуюIЦИМ образом:
т а б л и ц а 14
at а! аз
а. а5 аа
I as I
(1,
к каждой строке и к каждому столбцу этой таблицы до-
бавим еще по одному (проверочному) символу с таким рас-
четом, чтобы в строках и столбцах получившейся таблицы
(таблица 15) было четное число единиЦ.
При этом, например; для первой строки и первоrо столб-
ца будут выполняться проверочные/ соотношения:
i==аi+а,2+аз (mod 2),
P4==af+a,+a? (mod 2)
и аналоrично для остальных строк и столбцов. Заметим, что
Pi+Pi+P8== +P5+ 8 (mod 2).
Обе эти суммы равны О, если в слове aicti. . .ct 9 четное число
единиц) в QРОТИDПОМ СJIуча-е обе они равны 1. Это дает воз..
42
Т а б л и ц а 15
аl I азl pj
.
а4 а5 аа Р2
а.; ав а9 Ра
Р4 Р5 Ре Р7
можность поместить в таблице 15 еще один проверочный
символ р" равный
Р,==Рi+Р2+ З==Р4+Р5+Ре (mod 2).
Например, слову 0110 lOOOl отвечает следующая таблица:
Таблица 16
о 1 1 О
О 1 О 1
О О 1 ]
I I
О О О О
I
Эти «маленькие хитрости» позволяют, оказывается, испра-
вить любую одиночную ошибку, возникшую в процессе
передачи, а сверх Toro и обнаружить любую двойную
ошибку. В самом деле, если произошла одна ошибка, то на-
рушаются проверочные соотношения ровно для одной стро-
ки и ровно для одноrо столбца, как раз Той строки и Toro
столбца, на пересечении которых стоит ошибочный символ.
Если же произошла двойная ошибка, то это приводит К на-
руш нию проверок на четность либо в двух строках, либо
в двух столбцах, либо сразу в двух строках и двух столб-
цах. По этим признакам мы и обнаруживаем двойную
ошибку. (Однако исправить ее мы не можем почему?)
Добавим к сказанному, что данный код позволяет обна..
руживать мНоrие, хотя и не все, ошибки более высокой
43
кратиости (в трех, четырех и т. д. символах). Например,
обиаруживаются тройные ошибки в символах (Xi, (Xi, аз
или в символах (Xi, (Х2, (Х6' А вот тройная ошибка в символах
(%:i, (Х2, (Хб не мо}кет быть обнаружена, она будет воспринята
как одиночиая.
Продемонстрированиое в этом примере сочетание про-
верок иа четиость, по строкам и столбцам допу кает широ-
кие обобщения. О простейшем из иих rоворится в дополие.
нии 3t
Задачи и дополнения
1. Для разобранноrо в данном параrрафе примера най-
ти число необнаруживаемых тройных ошибок. Какую часть они состав-
ляют от общеrо числа тройных ошибок?
2. Кодовые слова в примере на стр. 42 содержат 9 информацион-
ных символов /и 7 проверочных, так что общая длина кодовоrо слова
равна 16. TaKoro числа символов достаточно, чтобы исправлять любые
одиночные и обнаруживать любые двойные ошибки. Чтобы достичь
Toro же эффекта для кода с повторением, нужно каждый информацион-
ный символ повторить 4 раза, так что общая длина кодовоrо слова будет
равна 36. Сравнение явно не в пользу кода с повторением. Справедли-
вости ради надо все же отметить, что код с повторением обладает по
сравнению с использованным в примере кодом некоторыми преимущест-
вами в смысле обнаружения ошибок более высокой кратности. Предла-
raeM читателю найти, например, долю необнаруживаемых тройных оши-
бок для указанноrо кода с повторением и сравнить ответ с результатом
задачи t. Интересно найти также долю исправимых (1) тройных ошибок
для этоrо кода.
3. Пример из данноrо параrрафа обобщается следующим образом
(смотри также дополнение 12 к 11). Пусть каждое сообщение кодиру-
ется двоичным словом длины тn. Расположим все символы в прямоуrоль-
ную таблицу (матрицу) с т строками и 'n столбцами:
Таблица 17
аl1 (1,1 2 (1,in (l,f, п+1
а 2 , СХ 2 2 СХ 2п СХ 2 , п+1
а т l СХ т2 а тп а т , n+l
"'m+l, 1 I а. т +l, 2 I I а. й +1, 11 ;
т + 1, n+1 I
I i
&4
Как Jf прежде, добавим к каждой строке и К Кё'л{дому столбцу ПО QДНОМУ
прорерочному символу, так чтобы во всех строках и столбцах олучи"
JIИСЬ четные CYMМbI. Аналоrично прежнему выбираем СИМВQЛ а,n+l' n+l-
Полученное множество слов образует код, исправ"тrяющий Лlо5ые оДИ.
ночные и обнаруживающий Лlобые двойные ошибки.
9. КОД ХЕмминrл
Пусть количество сообщений, которые тре..
буется передавать абоненту, равно 16. Для их безызбыточ-
Horo кодирования можно использовать двоичные слова дли-
ны 4, но тоrда код не будет корректировать ошибки. При
использовани,И слов длины 5, как мы уже знаем, мо)кно об-
наружить, но не исправить любую одиночную ошибку.
Впрочем, из дополнения 3 предыдущеrо параrрафа вытекает,
TO если добавить 5 проверочных символов, то код Сl\ложет
не только исправлять одиночныI,, но и обнаруживать
двойные ошибки. Возникает вопрос: нельзя лl'! для этой цели
обойтись меньшим количеством проверочных символов?
Вычислим сначала, каково минимальное число прове-
рочных символов, необходимое для исправления любых,
одиночных ошибок. Нетрудно убедиться, что двух добавоч-
ных символов для этоrо недостаточно (пре,цлаrаем читате.
лю проверить это самостоятельно).
Попробуем обойтись тремя проверочными символами,
Т. е. будем использовать для кодирования сообщений двоич.
ные слова аlаiаsа4аБCtва7 длины 7. Наша задача опреде.
лить, произошла ли ОШИ,бка, и если произошла, то в каком
месте. Но это то же самое, что указать одно из восьми
чисел от О до 7 (О соответствует отсутствию ошибки).
Пусть требуется передать сообщение, кодируемое словом
(Хlсх'2аза4. Добавим к этому слову три символа а5, а в , (Х 7 ,
определяемые равенствами (здесь и до конца параrрафа все
равенства берутся по модул.О 2):
Ctб==а2+Cts+а4,
ав==а1+Ctз+а4, (1)
а 7 == а l +а2+ а 4.
Если теперь нужно выяснить, допущена ли при передаче
слова CtlCt2CtвCt4CtБCtвCt7 одиночная ошибка в одном ИЗ СИМВО,.
лов а4, СХБ, а в , (Х 7 , то для этоrо достаточно вычислить сумму:
Sl==Ct4+аб+Ctв+а7' (2)
Ее значение, равное 1, соответствует ответу «да», значение
О ........ ответу «нет» (почему?).
,4,
В случае «да» проверим, нет ли ошибки в символах (%8.
й 7 , В случае «нет» ....... не содержится ли ошибка в символах
а2, аз. В каждом И3 этих случаев ответ дает значение
суммы:
S2==СХi+СХз+СХо +СХ 7 8 (3)
Если, например, значения обеих сумм (2) и (3) равны 1, то
ошибка содержится либо в СХ 6 , либо в СХ 7 8 Bcero имеется
четыре комбинации значений сумм 8f, 82; они приведены в
следующей таблице:
т а б л и ц а 18
8. 8! Место ошибки
1 1 ао или а7
1 О а4 или а5
О 1 а 2 ИЛИ аз
О О нет ошибки или at I
Наконец в каждом из четырех случаев нужно выбрать одну
из двух возможностей. Это позволит сделать значение суммы
SЗ===СХi+аЗ+СХ5+а7' (4)
Итак, мы имеем три проверочных соотношения:
Sl==CX'+ CX 5+ a O+ a ,==O,
8j==СХi+аЗ+СХ8+а7==Оt (5)
8з ==аl +а.з+а.5 +СХ 7 ==0,
которые позволяют' либо установить, что ошибки нет, либо
однозначно УI{аэзть ее место.
Отметим особо, что если произошла одиночная ошибка,
то ее положение укаэывается числом с двоичной записью
SlS2SЗ. Пусть, например, 81 == 1, 8а==0, Sa== 1. Соrласно табли-
це 18 ошибка допущена в четвертом или пятом разрядах
поскольку 5з== 1, она......... в пятом разряде, но 81828з== 101
как раз и есть двоичная запись числа 5.
Изученный здесь кОД......... это код Хемминrа длины 7 с
четырьмя информационными символами.
В общем случае кодовые слова двоичноrо кода Хеммин..
ra, позволяющеrо исправить одиночную ошибку, имеют
длину 2т......} (т...... натуральное). Для определения поло.
жения ОШ lбки TorAa ун(е нущцо т прове ОКj Т, е. т ПРОБе.
f(i
рочных символов. Оставшиеся 2m 1 m символов явля
ются информационными. Проверки строятся по аналоrии
с рассмотренным случаем. Значения т проверок, как Тl BЫ
ше, образуют номер положения ошибки.
Вернемся, однако, к вопросу, поставленному в Н3 1 }але
этоrо параrрафа. Добавим к кодовым словам кода ХеМl\/.tИJI
ra длины 7 еще один проверочный символ ао, а к провероч
ным соотношениям (5) еще одно (общую проверку на чет..
ность):
80==ао+аl+а2+аз+а4+аБ+ав+а7==О, (6)
Новый код по-прежнему будет содержать 16 кодовых слов,
потому что, как и раньше, символы ai, а 2 , аз, а 4 MorYT быть
взяты какими уrодно; по ним из соотношений (1) опреде..
ляются символы аБ, а в , а" а из равенства (6) и символ а о .
В случае одиночной ошибки добавленное соотношение (6)
нарушается, а значения 8i, 82, 8з образуют номер положения
ошибки. Если же произошла двойная ошибка, то соотно"
шение (6) будет выполнено, а хотя бы одно из равенств (5)
нарушится (почему?). Это и позволяет обнаружить любую
двойную ошибку. Итак, для исправления одиночных и об
наружения двойных ошибок к четырем информационньпv1
символам достаточно добавить четыре проверочных симво..
ла. Можно показать, что обойтись меньшим числом прове..
рочных символов невозможно.
Построенное множество кодовых слов аоаlа2('Хза4аБа6(Х7'
удовлетворяющих соотношениям (5) и (6), пример рас-
ширенноrо кода Хемминrа (длины 8 с четырьмя информаци
онными символами).
Задачи и дополнения
1. Определить положение одиночной ошибки виска.
)кенном слове 1100011 кода Хемминrа длины 7.
2. Пусть 110.10011 и 11001111 искаженные слова расширенноrо
кода Хемминrа длины 8. Какое из этих слов содержит одиночную, а
l{aKOe двойную ошибку? В случае одиночной ошибки определить ее
положение.
3. К проверкам кода Хемминrа длины 7 добавим (не меняя длины
кода) общую проверку на четность: '
CG:i+CG2+CGЗ+СХ4+СХБ+CGв+СХ,== О. (7)
Сколько слов удовлетворяет соотношениям (5) и (7)?
4. Доказать, что код из задачи 3 исправляет одиночные и обна-
руживает двоЙные ошибки.
5. Построить систему проверок для кода Хемминrа длия:ы 15.
Сколько кодовых слов содержит этот код? Сколько информационных
и сколько проверочных символов имеется в кодовом слове?
6. Если задан код Хемминrа длины п==2т 1, то существуют два
простЫХ способа получить из Hero коды с исправлением одиночных и
обнаружением двойных ошибок.
Первы-й из них (он аналоrичен способу, разобранному в конце этоrо
параrрафа) таков: к кодовым словам добавляем проверочный символ
ао, а к проверочным соотношениям кода Хемминrа общую проверку
n
на четность: ai == О.
i= О
Во втором способе (см. задачу 3) длина кодовых слов не меняеТСЯi
n
но добавляется общая проверка на четность: ai == о.
i= 1
Сколько информаЦИОНl!ЫХ и проверочных символов содержится
в каждом из описанных здесь кодов?
10. НЕОБЫЧНОЕ ОБЫЧНОЕ РАССТОЯНИЕ
Известно, что расстояние между точками в
1lространстве определяется как длина отрезка прямой,
соединяющей эти точки. Оно служит мерой близости то-
чек чем меньше расстояние, тем ближе друr к друrу рас-
положены точки. Если обозначать расстояние между точ-
ками а и Ь через р (а, Ь), то для любых точек а, Ь и с имеем:
1) р (a,b) O;
2) р (а,Ь)==О 0знач ет, что а==Ь;
3) р (а,Ь) ==р (Ь, аl
4) р (а,Ь)+р (b,c) p (а,с).
(Последнее условие, называемое неравенством 'треуrоль..
ника, означает, что длина любой стороны треуrольника не
превос:&одит CyrvlMbI длин двух друrих сторон.)
Иноrда удобно бывает определить меру близости или
расстояние для элементов Toro или иноrо множества, даже
если эти элементы и не являются точками в обычном смысле.
При этом считается, что расстояние между элементами
множества определено, если любым двум элементам а и Ь
сопоставлено действительное число р (а, Ь) и для любых
элементов а, Ь и с данноrо множества выполняются усло-
вия 1) 4).
Вернемся теперь к нашей основной TeM . Мы уже знаем,
что код тем лучше приспособлен к исправлению ошибок,
чем больше отличаются друr от друrа кодовые слова. Эту
мысль можно будет выразить точно, если ввести расстояние
на множестве п-буквенных слов.
Расстоянием р (х, у) между двумя словами х и у назовем
число несовпадающих позиций этих слов. Например, рас..
стояние ежду словами x;;Ol101 и y:;;OOl11 равно 2"
48
Определенное так расстояние называют расстоянием
Хемминса. He составляет большоrо труда проверить, что
все своЙства 1) 4) расстояния в данном случае выпол-
нены. Вопрос лишь в том, в какой мере это понятие помо-
жет оценить способности кода исправлять и обнаруживать
ошибки. Чтобы ответить на этот вопрос, введем для произ-
вольноrо кода понятие кодовосо расстояния.
Кодовое расстояние d (V) определим как минимальное
расстояние между различными кодовыми словами из V:
d (V) == min р (х, у).
x=I=y
Введенная только что величина является основным по-
" u
казателем корректирующих возможностеи кода, посколь-
ку верно следующее утверждение:
Код способен исправлять любые комбинации из t (и .мень-
шеео числа) ошибок тОсда и только тОсда, КОсда е20 кодовое
расстояние больше 2t.
В самом деле, если d (V»2t, то для любых кодовых слов
Х, у имеем р (х, y) 2t+ 1. Пусть при передаче HeKoToporo
слова х произошло r<.t ошибок, и в результате было приня-
ТО слово z. Тоrда р (х, z)==r<t, и в то же время расстояние
р (z, у) до любоrо друrоrо кодовоrо слова у больше t. Послед-
нее вытекает из неравенства треуrольника:
р (х, z)+p (z, y) p (х, y) 2t+ 1.
Значит, для восстановления посланноrо слова (декодиро-
вания) необходимо найти кодовое слово х, «ближайшее»
к ПРИ!:IЯТОМУ слову z в смысле расстояния Хемм:инrа. Под-
черкнем, что это правило декодирования приводит к пра-
вильному результату, если число ошибок в передаваемом
слове действительно не превосходило, t.
Если же условие d (V»2t нарушается, то найдутся та-
кие кодовые слова х и у, расстояние между которыми
р (х, y)<2t. Тоrда может найтись такая комбинация И3 t
ошибок в одном из слов Х, что принятое слово z будет на-
ходиться от ДРуrоrо слова у не дальше, чем от х. Поэтому
нельзя будет ОПI;>еделить, какое из слов х или у было
на самом деле передано
Задачи и дополнения
1. Имеется 8 ДВОИЧНЫХ слов ДЛИНЫ 3. ИХ можно изоб..
{)азить в пространственной системе координат как вершины куба со
стороной 1. Каков в этом случае «rеометрический смысл» расстояния
Хемминrа между л ами?
2. Доказать, что для обнаружения s (или меньшеrо числа) ошибок
необходимо и достаточно, ЧТобы кодовое расстояние удовлетворяло не-
равенству d (V»s+ 1.
3. Доказать, что для исправления t (и меньшеrо числа) ошибок и
вместе с этим обнаружения s (и меньшеrо числа) ошибок (s t) необ- r
ходимо И достаточно, чтобы кодовое расстояние удовлетворяло нера-
венству d (V»t+s+ 1.
4. Показать, что кодовое расстояние для кода с общей проверкой
на четность равно двум, а для кода Хемминrа трем. Чему оно равно
для кода с повторением, чему для расширенноrо кода Хемминrа?
11. ЛИНЕЙНЫЕ ИЛИ rРУППОВЫЕ КОДЫ
Большинство рассмотренных выше кодов об-
ладало следующим свойством: сумма (и разность) двух ко-
довых слов также являлась кодовым словом. Для кода с
повторением это свойство очевидно. Ясно оно и для кода
с общей проверкой на ч тность, потому что сумма двух слов
с четным числом единиц есть также слово с четным числоМ
единиц.
В 9 был рассмотрен код Хемминrа с системой прове-
рочных соотношений (5). Обобщим теперь этот пример, вы-
брав в"качестве кодовоrо алфавита некоторое конечное по-
ле Р. Каждое слово Х1Х 2. . .Х п этоrо алфаL4I{1та будем отож-
дecTBляTь с вектором (Х 1 , Х2, ... , Х п ) n-мерноrо пространства
L n (в котором координаты векторов являются элемент ми
Р). Вектор, соответствующий кодовому слову, будем назы-
вать кодовым. Систему проверочных соотношений запишем
в виде системы уравнений:
b 1 i X 1+ b 12 X 2+. . .+Ь 1п х п ===О,
Ь21Х1+Ь22Х2+. . .+Ь 2п х n ==О,
(1)
.................
Ьт1Х1+Ьт2Х2+. . .+Ьтпхп==О
с коэффициентами b ij из Р. Код, состоящий из всех слов
Х1Х2. . .Х п , для которых справедливы соотношения (1),
называют кодом с nроверками на четность.
Для TaKoro кода выполняется следующее свойство: если
векторы (а1' а2, ... , аn) и (Ь 1 , Ь.;" ... , Ь п ) Я:QЛЯЮТСЯ кодо-
выми, а значит, решениями системы (1), то и их сумма (а1+
+Ь 1 , а2+Ь2, . . . , ап+Ь п ) также является решением этой
системы и потому кодовым вектором. Справедливо и друrое
свойство решений системы (1): если а элемент поля F
и (ai, а2, ... ,а п ) решение системы (1), то и вектор (аа1'
аа21 ... , аа n ) также является решением системы (1).
50
Оба отмеченных свойства проверяются непосредственноА,
подстановкой в систему (1) векторов
(а 1 + Ь:1, а 2 + Ь 2, . . . , а n + Ь n ) и ( (Ха1, (Ха 2, . . . , (Ха n ) .
Вместе эти свойства означают, что ,код с проверками на чет-
ность образует линейное подпростраиство в пространстве
Ln всех n-буквенных слов. По этой причине коды с провер..
ками на четность называют линейными кодами (двоичные
линейные коды называют также срупповыми). Если кодовое
подпространство в пространстве Ln имеет размерность k,
то употребляют для большей определенности термин ли-
иейный (п, k) код.
Имеется очень MHoro причии, по которым лииейные коды
являются важнейшими в теории кодироваиия. Одна из них
связана с удобствами в обнаружеиии и исправлении оши
бок, как это видно из примера, рассмотреииоrо в 9. Друrая
причииа это возможность компактиоrо задания кода.
Действительно, в случае линейноrо кода нет иеобходимо-
сти указывать полный список кодовых слов, ведь код впол..
не определен системой лииейных уравнений (1) или матри-
l ей этой системы (проверочной матрицей):
( bif.
Н == b 2 i
. !
bmf.
bi.s
Ь 22
. . . Ь 1п )
. . . Ь 2 п.
.
! ! ! . .
. . . Ь тп
! . !
Ь т2
в дальиейшем мы будем предполаrать, что строки этой
матрицы линейно незввисимы.
К числу друrих достоинств линейных кодов, которые
связаны с предыдущими, относятся простые алrоритмы КО-
дироваиия и декодирования, леrко реализуемые электрон-
ными переключательиыми схемами. Вообще, можно ска-
зать, что буриое развитие теории кодирования, которое
происходило ВI последние десятилетия, объясияется rлав-
ным образом тем, что к линейным кодам приложим XOpOIIIO
развитый аппарат линейной алrебры и теории конечных
полей.
Возвращаясь к рассмотреиным ранее кодам, леrко най-
дем их проверочные матрицы. Так, для кода с общей про-
в ркой на четность имеем одно проверочное С00тношеи е
xl+xs+. . .+хп==О; соответственно этому проверочная Marr"
рица состоит из одной строки и имеет вид
H==(111.. .1).
51
Из проверочных сuqтношений для кода с повторевием;
Xl X2==O,
Хl ХЗС:О'
. . . . . . , ,
Xl Xn==O
получаем следующую проверочную маТРИЦУJ
(1 1 О . . , . )
Н== 1 О .......1 .
. t .
. ! ! . ! , t I I
1 О О . . . 1
Наконец, проверочная матрица двоичноrо кода Хем-
минrа длины 7, как это следует из соотношений (5) 9, вы-.
r лядит aK:
( О О О 1 1 1 1 )
Н== о 1 1 О О 1 1 .
1 О 1 О 1 О 1
(2)
Имеется и друrой способ матричноrо задания линейноrо
кода. Он основан на том, что во всяком лодпространстве ли-
нейноrо пространства можно выбрать базис, т. е. такую ли-
и u
неино незави имую систему векторов, через которые линен-
но выражаются все вообще векторы подпространства. Пусть
а 1 ==(аll' а12, . . . , аln)'
а2==:;(а21, а22, . . . J а2n)' (3)
..............
а h =;= (ah,l, ah 2, · · · , ahn)
базисные векторы линейноrо 1{ода. Тоrда всевозможные
кодовые векторы исчерпываются линейными комбинациями
аlаl+а2а2+' . .+rthah, (4)
rде коэффициенты rti любые элементы исходноrо поля.
Таким образом, сиетема базис ых векторов (3) пол:'
ностью определяет линейный (п, k)-код. Матрица О, состав-
ленная из них,
I ali а12 . . . а 1п )
G == ( а 21 а22 · · · а 2п
.......!. ,
akl ak2 .., akn
(5)
называется порождающей. Atamptll{ea кода.
52
Заметим, что базис можно выбрать не единственным об..
разом, поэтому порождающая матрица G определена неод-
нозначно. Последнее, впрочем, верно и в ОТНОIIIении про-
верочной матрицы Н.
Леrко указать порождающую матрицу кода с повторе-
jiием; она имеет вид:
O==(l 1 1. . .1).
в качестве базисных векторов двоичноrо кода с общей
проверкой на четность MorYT быть взяты, например, сле-
дующие п l векторов:
а 1 == (1 1 О О ... О),
аз == (1 О 1 О ... О),
аз == (1 О О 1 ... О),
.......... .
aп 1 == (1 О О О ... 1).
Поэтому матрица
1 1 О О '.' О
1 О 1 О ,.. О
й== 1 О О 1 ,.. О
." '!'
1 000 .... 1
. u u
является порождающеи матрицеи этоrо кода.
При использовании линейноrо кода для передачи сооб-
щений полезно знать и пор ождающую , и проверочную мат-
рицу. С помощью порождающей матрицы удобно кодиро-
вать сообщения. Поскольку линейный (п, k)-код с порож-
дающей матрицей (5) имеет qk кодовых слов (любой из k
коэффициентов в (4) можно выбрать q способами), он позво-
ляет закодировать все сообщения длины k в алфавите из q
символов. Если А == СХ 1 (Х 2. . .а1l .......... такое сообщение (а;
информационные символы), то самое удобное сопоста-
u u u
вить ему кодовыи вектор а, совпадающии с линеинои ком-
бинацией (4) строк порождающей матрицы. Вектор а не-
трудно записать в матричном виде, используя правило УМ-
ножения матриц:
( ::: : : : : ) (6)
а==А ' й== ( а 1 (Х2 t . . as.) \ .
,. 11ft!'
aki akl akn
53
При м е р. Пусть дана порождающая матрица двоич-
u
Horo линеиноrо кода:
( 1 1 1 О О О О )
1001100
а== О 1 О 1 О 1 О ·
1101001
Этот код содержит 24== 16 К9ДОВЫХ слов, которыми можно
вакодировать все двоичные сообщения длины 4. Если, на-
пример, А==(0101), то для соответствующеrо кодовоrо век-
тора имеем:
( 1 1 1 О О О О )
1001100
а == (О 1 О 1) о 1 О 1 О 1 О == (О 1 О О 1 О 1).
1101001
о роли проверочной матрицы мы скажем в дальнейшем .......
она используется в основном при декодировании получен-
ных сообщений и для исправления ошибок.
Выясним, как связаны порождающая и проверочная
матр,IЦЫ, и как по одной из них найти друrую. Обратимся
к соотношениям (1). Всякая строка порождающей матрицы,
являясь кодовым вектором, удовлетворяет каждому из
соотношений (1), т. е. для любых i и i
bi1aji+bi i a j2+. . . +binajn ==0.
Друrими словами, любая строка порождающей и
строка проверочной матриц ортоrональны друr
Матричная запись равенств (7) выrлядит так:
ОНТ==О
(7)
любая
друrу.
(О озиачает здесь нулевую матрицу).
Заметим также, что из соотношений (1) вытекает равен-
ство
'VHT ==0,
справедливое для каждоrо кодовоrо вектора fJ.
Для отыскания порождающей матрицы нужно факти-
чески найти k==n т линейно независимых решений сис-
темы (1). Эти решения как раз и будут строками порождаIО-
щей матрицы.
При м е р. Найдем порождающую матрицу кода Хем-
минrа длины 7 с проверочной матрицей (2). В данном случае
требуется найти 4 независимых решения следующей
64
Gистемы:
Х 4 +Х 5 +Х в +Х 7 ==0,
х 2 +х з + Х 6 +Х 7 ==0,
Х 1 + Ха + Х 5 + Х 7 == о.
Разрешаем систему относительно неизвестных Xt, Xi, X4
Хl==ХЗ+ Х 5+ Х 7f
Х2==ХЗ+Х6+Х7t (8)
Х4==Х5+ Х 6+ Х 7 8
Неизвестным Хз, Х5, Х в , Х 7 можно придавать любые значения;
тоrда из равенств (8) MorYT быть определены оставшиеся
неизвестные Xi, Х2, Х 4 . Придавая поочередно одному из неиз..
вестных Хз, Х5, Х в , Х 7 значение 1, а остальным....... О, получим
4 решения:
а 1 == (1110000) , а 2 == (1001100) f а 3 == (О 1 О 1 О 1 О) t
а 4 == (1101001),
которые, как читатель может убедиться, линейно независи-
мы. Составленная из этих решений матрица
1110000
1001100
О 1 О 1 О 1 О
110 1 О О 1
й==
и и и
И является искомои порождающеи матрицеи.
По поводу СК8занноr<? в этом параrрафе возникает мно.
жество вопросов. Например, как, зная порождающую и
проверочную матрицы, выяснить корректирующие способ-
ности данноrо кода; как реализовать эти способности (т. е.
каким должен быть 8лrоритм декодирования, исправляю..
щий или обнаруживающий ошибки); как, наконец, после
исправления ошибок выделить информационные символы?
Остановимся вначале на последнем вопросе. Пусть,
исправив ошибки, мы получили некоторый кодовый вектор
a==(ai, ai, . . . , а п ). Тоrда соответствующие ему информа..
ционные символы (ti, а2' . . . , (tk определяются из равен..
ства (6). Иными словами, вектор (af. а2, . . . , rtk) есть ре..
шение (как можно показать, единственное) системы ли..
и и
неиных уравнении:
ail(Z1+ a 21(ti+. . .+akl rt k==ai,
а12аl+ а 22(Х2+' . .+аkЗС%k==аi,
.................
aln a l+ a in a i+. · .+aAn A==an.
бl
, Хотя задача отыскания этоrо решения и не содержи.
. принципиальных трудностей, она может потребовать rpo..
моздких вычислений. Однако выделение информационных
символо предельно упрощается, если использовать для
кодиров ния так называемые систематические линейные
коды. \
Линейный (п, k)-код называется сuстеlrtатuчески.м, если
ero порождающая матрица имеет вид
1 . . . о . . . о Plf · .. Рlт
G == О... 1 · '. О Р21 · .. РВт
. . .
.
. . . .
(9)
о о ... 1 Pki ... Pkm
или вид
( Plf . . . Рlт 1 О 11" 0\
G P:f .. : · / т. ? :.: ? ) ,
Pkl ... ТJkm О О ... 1
т. е. если она получается приписыванием к единичной мат-
. рице порядка k некоторой матрицы из k строк и т==n k
столбцов (иначе rоворя,' матрицы порядка kxm).
В случае (9) равенство (6) принимает вид:
( 1 О '" О Рll '" Рl т )
( ) о 1 ... О Р21 .. . Р2т
а == а 1 а 2 ... tX k ==
.. ........
O -о ... 1 Pkl... Pkm '
== (а 1 а!. · · fXkak+ f' · · а n ).
Та им: образом, первые.k символов любоrо кодовоrо
слова как раз и оказываются информационными, а осталь-
ные (они являются проверочными) связаны с информаци-
онными символами соотношениями:
ak+l==Pl1 fX l+P21 EX i+" .+Pkl(Xk,
аk+З==Р12 tX l+Р2Z(Х2+. · .+Pk2 tX k,
(9') )
(10)
............,......
а n ==Рlт(Хl+Р2т а 2+. · .+PkтCXk'
Равенства (10), очевидно, образуют систему проверочных
соотношений систематическоrо линейноrо кода. Очень важ-
но, что всякий линейный код в некотором смысле эквива-
лентен системаrическому (Clvl. дополнение 9).
Дальнейшее прольет свет и на друrие вопросы, постав-
ленные ВЬ1ше.
56
Задачи и дополнения
1. Весо,М вектора и (обозначается w (и» называют
число ero не нулевых .координат. Понятно, что расстояние Хемминrа
, между двумя векторами "1 и "2 равно весу их разности w (иl и2)' Это
позволяет упростить отыскание кодовоrо раССТ0ЯНИЯ пинейноrо кода.
Именно, справедливо следующее утверждение:
Кодовое расстоянuе линейноео кода равно .минимально,Му весу еео
Н,енулевых кодовых слов.'
d (У) == min w (f1).
'VEV
v=#=o
Предоставляем читателю доказать это утверждение.
2. Пусть двоичный линейный код V содержит хотя бы одно слово
нечетноrо веса. Доказать, что число всех таких слов составляет TorAa
ровно половину от общеrо числа кодовых слов.
У к а з а н и е. Убедиться, что множество всех кодовых слов чет-
Horo веса есть подпространство и найти смежные классы кода V по
этому подпространству.
3. Рассмотрим матрицу порядка qkX n, в качестве строк которой
взяты все кодовые векторы q-ичноrо линейноrо (n, k)-кода. Будем пред-
полаrать, что ни один столбец этой матрицы не является нулевым (ина-
че, вычеркнув нулевой столбец, мы получили бы код с тем же кодовым
расстоянием, но меньшей длины).) Показать, что в каждом столбце
этой матрицы каждый из q;элементов поля встречается ровно qk J раз.
Пользуясь этим, убедиться, что суммарный вес всех кодовых слов ра-
вен n (q l)qk J.
у к а з а н и е. Проверить, что множество всех кодовых слов,
содержащих О в некоторой фиксир ованной позиции, есть подпростран-
СТБО, и найти разложение кода в смежные классы по этому подпростран-
ству.
4. Предположим, что кодовый вектор со== (Xi, Х2' . . ., Х п ) имеет
вес, равный w, и Xk1' Xki' . . ., Xk ero ненулевые координаты. Из
W f
проверочных соотношений (1) получаем тоrда:
_ , b 1 k1 X k 1 + b 1 k2 X k2 + · · · + blkwXkw == о,
4>'
, . . .. . . . . . . . . . . . . . . .
" ь тk 1 Xk l + b т k2 X k; · · · + bтkwxkw ==0...
'Это означает, что столбцы проверочной матрицы с номерами k 1 , k 2 , . . .
. . ., kw линейно зависимы. Следовательно, каждому кодовому Беl{ТОРУ
веса w соответствует w линейно зависимых столбцов проверочной мат-
рицы. Верно и 'обратное утверждение.
Отсюда вытекает, что кодовое расстояние линейноrо кода равно d
тоrда и только тоrда, коrда в проверочной матр ице найдется d линейно
зависимых столбцов, а всякая система из меньшеrо числа столбцов
линейно независима.
5. Доказать, что двоичный линейный код исправляет Лlобые оди-
ночные ошибки тоrда и только тоrда, коrда все столбцы ero провероч-
ной матрицы не нулевые и различные. Верно ли это для ЛIобоrо линей-
Horo кода?
6. Как изменится кодовое расстояние двоичноrо линейноrо кода
при добавлении ко всем ero словам одноrо лроверочноrо символа, зада-
ющеrо общую проеерку на четность?
м
7. Двоичный (8,4) KOД задан порождающей матрицей
( 1 1 1 О 1 О О О )
01011100
a О О 1 1 О 1 О 1 ·
1 О О 1 1 О 1 О
(11)
Найти ero проверочную матрицу и кодовое расстояние.
То же задание для троичноrо (6,3) Koдa с порождающей матрицей
( О О 1 1 2 2 )
а:== 1 1 1 2 О О .
1 2 1 1 О 1
8. Два кода V f и V 2 называются эквивалентными, если KOДOBЫ
слова одноrо кода' получаются из кодовых сл 08 друrоrо некоторой
переС1'ановкой символов (одной н той )I{e для всех кодовых слов). По-
скольку при этом веса кодовых слов остаются без изменений, то кодо-
JЗые расстояния двух эквивалентных кодов совпадают, поэтому одина-
ковы также их возможности исправлять или обнаруживать ошибки.
Ясно, что если порождающие матрицы кодов получаются одна из дру-
rой путем перестановки столбцов, то коды эквивалентны.
Эквивалентными являются, например, коды Vi и V 2 со следующими
порождающими матр ИI',ами:
( 1 О 1 1 О О ) ( 1 О О 1 1 О )
О! == О О 1 О 1 1 и а 2 == О 1 О 1 О 1 .
О 1 1 1 1 О О О 1 111
Однако связь между матрицами эквивалентных кодов может быть
и более сложной. Причина заклЮчается в том, что порож.цающая мат-
р ица данноrо кода определена неоднозначно.
9. В предыдущем пр и мере код Vr эквивалентен систематическому
коду V 2. Это не исключение, а прарило, поскольку справедливо след}t..'О..
щее утверждение: '
Всякий линейный код эквивалентен систематическому коду.
Доказательство, которое рекомендуется продумать читателю, ос-
новывается, в сущности, на известном современному школьнику методе
raycca исключения неизвестных.
Последовательность действий, приводящих произвольный код к
систематическому, продемонстрируем на при мере матрицы (11) (задача 7).
Вычитая из четвертой строки матрицы (11) первую, получим:
( 1 1 1 О 1 О О О )
О 1 О 1 1 1 О О
00110101 ;
,О 1 1 1 О О 1 О
далее, вычитая из первой строки вторую, приходим К матриц
/1 О 1 1 О О О О )
\ 0 1 О 1 1 1 О О
00110101 ·
01110010
riолучающиеся при этих преобразованиях матрицы также лорождают
Qa
исходный код. Осуществим теперь перестановку столбцов, чтобы слева
получить единичную матрицу пятый столбец поставим на место ВТО-
poro, восьмой на место TpeTbero, седьмой на место четвертоrо столб-
ца. В итоrе получим порождающую матрицу систематическоrо кода
( 1 О О О О 1 1 О )
О 1 О О 1 011
О О 1 О О 1 11.
О О О 1 1 1 1 О
10. Показать, используя соотношения (7), что для систематическоrо
кода с порождающей матрицей (9) в качестве пр о вер очной можно взять
следующую матрицу:
( Pif P2f . .. Р kf 1 О . t 1) О )
Н == Pi2 Р22 ... Pk2 О 1 .. t О
:... i ''':' P'2 '.:. ..:... k: · о' <> · .:: i ·
11. Пусть V произвольный линейный (n, k) код. Рассмотрим
множество V всех векторов пространства Ln, ортоrональных каждому
из кодовых векторов t1 Е У. Нетрудно проверить, что У1. является под-
пр ост ранс тв о м в Ln И, следовательно, может рассматриваться как ли-
нейный код. Код y называется дуаЛЬНblм' к исходному коду V.
Убедиться, ЧТQ если G и Н порождающая и проверочная матрицы
кода V, то они служат соответственно проверочной и порождающей
матрицей дуальноrо кода V".
Простейший пример кодов, дуальных друr к друrу, это код с
повторением и код с общей проверкой на чеТН9СТЬ.
12. Одним из способов получения кодов, обладающих большим ко-
довым расе. тоя ни ем, а значит, и высокой корректирующей способно.
стью; является комбинирование двух или нескольких кодов. Примером
TaKoro комбинирования является рассматриваемая, здесь конструкция.
Она дает код, который является обобщением матричноrо кода из Э 8
с пр о верками на четность по строкам и столбцам.
Пусть дано слово, содержащее k==k 1 k 2 информационных символов.
Разобье множество этих символов на k 2 блоков по ki. символов в ка){{дом
и запишем результат в виде квадратной матрицы порядка k 2 Xk 1 :
( : : : ::: : :: ) . (12)
a.:k2 (1"k 2 2 '. .'. ! d k2 'kl
В первой строке этой матрицы выписаны по порядку символы nepBoro
блока, во второй символы BToporo и т. д.
Рассмотрим теперь произвольный систематический линейный код
V f длины n! с ki информационными символаМfi и с тем же самым кодо..
вым алфавитом. Строки матрицы (12) закодируем указанным КОДом
ДЛЯ этоrо к ка)кдой строке припишем ni ki проверочных символов та-
ким образом, чтобы выполнялись проверочные соотношения кода Vi.
Далее каждый столбец получившейся матрицы порядка k 2 X пl.
((1,,11 (1,,12 IXlа1 . . . CXinl
! СХ 2 1 а 2 2 . . . IX 2 k 1 ' . . (1..2 nl
\ . . . . . ! . . . I . . . . . . )
\ (1" k '1.1 ak29 , " , Ct..k 2 k 1 ! , . а k 2 n1 /
,59
закодируем точно таким же способом с помощью линейноrо (n2' k 2 )..
кода У 2 .
В результате получим матрицу порядка n2Х nl:
( CXli CXi2 · .. . (Xlkt · .. CXlпt )
СХ2! СХ 22 CX 2 k 1 " .... СХ2п.
. . . . .. . .. . . . .. . .
CXk21 CXk22 С. k2kl CXk2пt .
. . . . . .
. . . . . . . . . . . . . . . .
t СХ nЗ l а n22 .. · · a n2 kt · · · а n2п.
Выписывая элементы этой матр ицы «по строкам», мы и составим кодовое
CJIOBO, отвечающее исходному слову. Оно, очевидно, однозначно опре-
ДeJIяется матрицей (12).
Построенный код называется произведением кодов V 1 и V'A И обоз-
начается V 1 Q9 V 2.
Пусть теперь k, ki, k 2 ....... числа информационных символов кодов
VtQ9V 2 , Vi и У 2 а n, ni, n2 длины этих КОДОВ. Из построения кода
V 1 QS)V 2 сразу же вытекает, что
k==k t k 2 и n==ntn2'
Менее очевидно аналоrичное соотношение между кодовыми рас-
стояниями d, di, d 2 тех же кодов: d==di .d'A' Доказательство этоrо факта
предоставляем читателю.
Предлаrаем читателю также выяснить, какова связь между количе
ством ошибок, исправляемых кодами Vi, У 2 и V 1 Q9V 2 .
ПРОИЛЛlострируем сказанное примером. Пусть k==8, k 1 ==4, ka==2.
В качестве кода Vi возьмем (7,4)-код Хемминrа, записав предварительно
ero порождающую матрицу в систематической форме:
а == ( ! g i ! ) , I
,О О О 1 1 1 1
в качестве V 2 (З,2)-код С общей проверкой на четность. Составим ко..
довое слово кода V t QS)V 2 , соответствующее исходному слову 00101110
с восемью информационными символами. Запишем ero в виде матрицы
порядка 2Х4:
( О О 1 О,
11 1 О).
В результате код рования строк (7,4)-кодом Хемминrа (см. праВИJIО
{6» получим матрицу порядка 2х 7:
( О О 1 О О 1 1 )
1110000 ·
Кодирование столбцов этой матрицы сводится к добавлению в каждом
столбце символа общей проверки на четность. Получившейся в ИТОI'е
матрице порядка зх 7
( О О 1 О О 1 1 )
1110000
1100011
соответствует следующее кодовое слово кода V 1 Q9V 2 :
001001111100001100011.
6(1
12. ДЕКОДИРОВАНИЕ ПО СИНДРОМУ
И ЕЩЕ РАЗ О КОЛЕ ХЕмминrл
Слово «синдром» означает обычно совокуп-
ность признаков, характерных для Toro или иноrо явлеция.
Такой же примерно смысл имеет понятие «синдром» и В тео-
рии кодирования. Синдром вектора, содержащеrо, быть мо-
жет, ошибки, дает возможность распознать наиболее веро-
ятный характер этих ошибок. Правда, определение, кото-
рое мы приводим ниже, не сразу позволяет это увидеть.
Синдромом вектора" называется вектор s(и), опреде-
ляемый равенством:
s (и) == "НТ.
Из правила перемножения матриц следует, что синдром есть
вектор длины т, rде т число строк проверочной матри-
цы. В силу определения синдрома вектор и тоrда и только
тоrда является кодовым (и Е У), коrда ero си НДрОfvl равен
нулевому вектору. В самом деле, равенство
иНТ == О
равносильно тому, что координаты Хl, Х2, . . . , Х п вектора '
удовлетворяют проверочным соотношениям (1) из 11.
Пусть теперь вектор " не является кодовым, тоrда этот
вектор обязательно содержит ошибочные символы. Вектор
tt можно представить тоrда в виде суммы посланноrо кодо..
Boro вектора (1 (которь.й пока не известен) и вектора ошиб.
ки е:
u==v+e.
(1)
ЯСНО, что вектор е==(Е 1 , 82, ... , Е п ) содержит ненулевые СИМ-
волы в тех позициях, в I{OTOPbIX вектор U содержит иска.
женные символы.
Важным обстоятельством является то, что синдромы
принятоrо вектора и и вектора ошибки совпадают. Дейст-
вительно,
s (и) == ('l1 + е) НТ === fJHT + еНТ === еНТ == s (е). (2)
Рассмотрим теперь MHOJi<ecTBO U всех векторов и', имею..
щих тот же синдром, что и вектор и. Пусть а==и' и. Тоrда
s (а) == (и' ....... и) НТ == и' НТ иНТ == s (и') s (Е:) == О.
Так как s (а)==О, то а ....... кодовый вектор. Обратно, если
и' и кодовый вектор, то s(и )==s(u). ТаКИ l образом,
для интересующеrо нас множества и имеем: .
U=={u+aiaEV}.
61
На языке теории rрупп это означает, что и есть смеЖНJj»IЙ
класс по подrруппе V (пространство Ln и ero кодовое под-
простраиство V можно рассматривать соответственно как
rруппу и ее подrруппу относительно операции сложения
векторов) .
Сказаииое позволяет сделать слеДУЮIЦие выводы:
1. Два вектора имеют одинаковый синдром тоrда и толь-
ко тоrда, коrда они принадлежат одному смежному классу
по кодовому подпространству. Таким образом, синдром век-
тора одиозначно определяет тот смежный класс, которому
этот вектор принадлежит.
2. Вектор ошибки е для вектора u иужио искать в силу
равенства (2) в том же смежном классе, которому принадле-
жит и сам вектор а.
Разумеется, указание смежноrо класса, которому при-
надлежит вектор е, еще не определяет caMoro этоrо вектора.
Естественио выбрать в качестве е тот вектор смежноrо клас-
са, для KOToporo вероятиость совпадения с е наибольшая.
Такой вектор называют лидером смежиоrо класса. Если
предположить, что большее число ошибок совершается с
меньшей вероятностью, то в качестве лидера следует взять
вектор наименьшеrо веса даиноrо класса и в дальнейшем
лидер б fдет пониматься именно в этом смысле.
При реализации алrоритма декодирования по синдрому
составляют таблицу, в которой указываются синдромы 5i
И лидеры ei соответствующих им смежных классов. Алrо-
ритм декодирования заключается тоrда в следующем:
1. Вычисляем синдром 5 (и) принятоrо вектора ".
2. По сиидрому s(a)==81 определяем из таблицы лидер
е, соответствующеrо смежноrо класса.
3. Определяем посланный кодовый вектор fJ как разиостъ
'lJ == " el'
Может случиться, что в некоторых смежных классах
окажется более одноrо лидера. Если искаженный вектор и
попал в один из таких смежиых классов, то разумнее от-
казаться от исправления ошибки, оrраничившись ее обиа-
ружением.
При всей своей простоте и прозрачносТИ алrоритм сии-
дромноrо декодирования обладает серьезным недостатком. .
Заключается он в том, что устройство, реализующее этот
способ декодирования, должно хранить информацию о ли-
дерах и синдромах. Объем же этой информации может ока-
в аться очень большим даже при умереиных длинах кодо-
вых CJIOB (порядка нескольких десятков). В этом нетрудио
(j
убедиться ........ ведь число лидеров и синдромов совпадает
с числом смежных классов, которое по теореме Лаrранжа
равно qn: qk==qn k. Так что, например, для двоичноrо
(50, 40)-кода получится 1024 лидеров и столько же синдро"
мов, а для (50,30)-кода число их превзойдет миллион.
Таким образом, мы либо придем к чрезмерному усложне-
нию аппаратуры для синдромноrо декодирования, либо
практически вообще не сможем ее построить. К счастью,
имеются коды, декодирование которых не требует обраще-
ния к таблице лидеров и синдромов. Простейшие из них
ЭТО код Хемминrа и ero расширенный вариант, рассмотрен-
ные в Э 9.
Как мы уже знаем, двоичный код Хемминrа является
линейным, в общем случае имеет длину n== 2т 1, исправ-
ляет одиночные ошибки и обходится минимально возмож"
ным для этой цели числом проверок (это число равно т).
Таким образом, проверочная матрица кода Хемминrа имеет
порядок mx(2т 1). При этом все столбцы этой матрицы
должны быть ненулевыми и различными (см. Э 11, задача 5).
Кажд й столбец есть двоичный вектор длины т; Bcero име-
ется 2т таких векторов, поэтому для построения провероч-
ной матрицы кода Хемминrа длины 2т 1 нужно выписать
(в качестве столбцов этой матрицы) все ненулевые двоичные
векторы длины m. Порядок столбцов безразличен, но чаще
Bcero их упорядочивают так, чтобы содержимое каждоrо
столбца являлось двоичной записью ero номера (сравни с
матрицей (2) из Э 11). Вот как выrлядит проверочная мат-
рица кода Хемминrа длины 15 (т==4):
( О О О О О О О 1 1 1 1 1 1 1 1 )
О О О 1 1 1 1 О О О О 1 111
011001100110011 ·
1 О 1 О 1 О 1 О 1 О 1 О 1 О 1
Алrоритм исправления одиночных ошибок в этом случае
удивительно прост. Если вектор "' содержит ошибочный
символ в i-й позиции, то синдром s(u) этоrо вектора совпа-
дает с i-M столбцом проверочной матрицы. Таким обраЗОl\f,
этот синдром, читаемый как двоичное число, и есть номер
ошибочноrо символа,
Код Хемминrа и в общем случае допускает усовершенст-
вование Toro же рода, что и (7,4)-код из Э 9. Добавление
проверочноrо символа (хо, осуществляющеrо общую провер-
ку на четность, приводит, как и там, к расширенному коду
Хемминrа с дополнительной способностью обнаруживать
двойныI'' ошибки. Ero проверочная Ь1атриqа леrко может
'рЗ
быть получеиа из матрицы кода ХеМl\1инrа: к каждой строке
последней следует впереди приписать нулевой символ, а
к получившимся строкам строку из единиц, соответст-
вующую общей проверке на четность:
а о +а 1 +а 2 +. · .+ап===О.
Например, из приведенной выше проверочной матрицы
для (15,11 )-кода Хемминrа получается следующая про-
верочная матрица для расширенноrо (16,11 )-кода:
1 1 111 1 111 1 1 111 1 1
О О О О О О О О 1 111 1 1 1 1
О О О О 1 1 1 1 О О О О 1 1 1 1
О О 1 1 О О 1 1 О О 1 1 О О 1 1
О 1 О 1 О 1 О 1 О 1 О О t О 1
При вычислении синдрома искажеиноrо вектора возмож..
ны две основные ситуации: либо синдром совпадает с одним
ИЗ столбцов проверочной матрицы, либо это не так. Чита-
тель леrко проверит, что первая ситуация соответствует
нечеrНО IУ числу ошибок в слове, а вторая четному.
В первом случае считаем, что ПРОИ30luла одиночная
ошибка, и ее положение определяется номером столбца, с
которым совпадает синдром.
Во втором случае считаем, что допущены две или любое
большее четное число ошибок, если s (и) =1= О. Если же
8 (и)==о, то, как обычно, полаrаем, что ошибок при
передаче не было.
Задачи и дополнения
J. Построить таблицу индромов и соответствующих
пидеров дпя (7,3)-кода с порождающей матрицей
( О О 1 1 о 1 1 )
й== О 1 О О 1 1 1 .
1 О О 1 1 О 1
2. Доказать, что алrоритм синдромноrо декодирования позволяет
[ d....... 1 J
исправить любое количество ошибок, не превосходящее ,rде
d .....кодовое расстояние.
[ d 1 ]
Ъ( к а з а н и е. Достаточно проверить, что все векторы веса
и меньше попадают в различные смежные классы и, следовательно, явля-
ются лидерами в своих смежных классах,
64
3. Код с проверочнон матрицей
1 О 1 О О О О
1 l О 1 О О О
Н== О 1 О О 1 О О
О О О О О 1 О
0000001
используется для исправления всех одиночных ошибок. Определить,
какие еще ошибки MorYT быть в данном случае исправлены или об на..
ружены при декодировании по синдрому.
4. Проверить, что для обычноrо (нерасширенноrо) кода Хемминrа
лидеры не нулевых смежных классов исчерпываются всеми векторами
веса 1. Верно ли это для расширенноrо кода Хемминrа? \
IS. О КОДАХ, ИСflРАВЛЯЮЩИХ
НЕСИММЕТРИЧНЫЕ ОШИБКИ
На практике нередко встречаются каиалы,
отличающиеся асимметричным характером ошибок, скажем,
такие, в которых преобладают замещения вида О --+ 1 (Т. е.
вместо нуля при ии мается единица), а зам еще и и я 1 О
u
краине редки.
Конечно, и в этом случае можно использовать коды, пред-
назначенные для исправлеиия замещений обоих видов, в
частности, рассмотренный нами код Хемминrа. Но это было
бы слишком расточительно, так как корректирующая спо-
собность кода наполовину расходовалась бы тоrда вхоло-
стую.. Придуманы поэтому коды, приспособленные специ-
ально к испр авлеиию несимметричных ошибок.
Исходное соображение здесь очень простое: если в ка-
нале невозможны ошибки вида 1 О, то в принятом двоич-
ном слове нет нужды проверять позиции с нулевыми сим-
волами они наверняка переданы без искажений. Будем
поэтому производить проверку таким образом, чтобы ее
u
результат зависел только от позиции с единичнЫМИ симво-
лами, точнее, от номеров этих позиций. С этой целью для
произвольноrо двоичноrо слова U==XIXi...Xn составим сумму
n
S (и) == xii.
l = I
(1)
в сумме (1) ненулевые слаrаемые соответствуют только еди-
ничным символам и каждое из них совпадает с номером
этоrо символа, т. е. число S (и) равно сумме иомеров еди-
u
ничных позиции слова и.
Как обычно, постараемся найти простое условие, выде-
ляющее кодовые слова среди прочих. Будем искать это ус.
э М. Н. Аршинов. Л. Е. СаДОВСRИЙ
65
JIовие в виде сравнения по некоторому модулю l. Предста-
вим себе] что число 1 уже выбрано, и рассмотрим КОД,
u
состоящии из всех таких слов V===Xl Х! ... Х n , для которых
S (V) == O (mod 1),
(2)
т. е. из слов, для которых сумма номеров единичных пози-
ций делится на 1 без остатка. Обозначим указанный код че-
рез V n, l' Так, при n==4, 1==5 получим следующее множе-
ство кодовых слов:
V 4 ,5== {ОООО, ]001, 0110, 1111}.
Нетрудно убедиться, хотя бы перебором всех возможных
случаев, что данный код исправляет лю(5 Iе одиночцые
Оlпибки вида О --+ 1. Например, ошибка в третьем символе
слова 1001 переводит ero в слово 1011. -При этом никакое
друrое кодовое слово не моrло преобразоваться в резуль.
тате одиночной ошибки в слово 1 О 11. Поэтому получатель
декодирует слово 1011 однозначно, считая, что было по-
слано слово 1001. Аналоrично обстоит дело с друrими
двоичными наборами, содержащими одиночные замещения
нуля на единицу. Отметим, что в некоторых случаях (но
не всеrда!) возможно исправление также и двойных заме-
щений нуля на единицу. Один из таких случаев ошибка
в двух первых символах слова 0000. Получающееся при этом
слово 1100 не является кодовым и не моrло получиться ни
из KaKoro кодовоrо слова в результате одиночной ошибки.
К тому же имеется единственный вариант двойноrо заме.
щения, переводящеrо кодовое слово в слово 1100, именно
тот, который был указан выше.
Подобные свойства сохраняются и для произвольноrо
кода Vn,l' если l n+l. В частности, такой код исправляет
любые одиночные ошибки вида О 1; при этом алrоритм их
исправления чрезвычайно прост. Действительно, пусть в
кодовом слове V==Xi Xi. . .Х n произошло не более одной
ошибки и получилось слово а. Если ошибка произошла в
j-M символе, то понятно, что S (U)==S (V)+j. Поскольку
S (V) =.: O (mod l), то вычет числа S (и) по модулю 1 равен j,
т. е. номеру позиции, в которой произошла ошибка. Если
же ошибки не произошло, то вычет S (и) по модулю 1 равен
нулю.
Проиллюстрируем исправление одиночной ошибки на
l1римере paCCMoTpeHHoro выше кода V 4 ,5. Пусть принято
слово u===0111. Тоrда S (u)==2+3+4==9 4 (mod 5). Сле-
довательно, ошибка произошла в четвертой позиции, т. е.
передавалось кодовое слово 0110.
66
Наиболее употребимы коды V n.' при минпмально В03-
fОЖНОМ 1 : l==n+ 1. Именно они впервые были предложены
советскими специалистами по кодированию Р. Р. Варша-
мовым и r. м. Тененrольцем.
Коды Vn,z обладают способностью исправлять еще
один тип искажений кодовых слов, характериый для не-
симметричных каиалов. Это так называемые выпадения
и вставки символов.
Предположим, что в некотором слове V==X1X2'. 'Х п
произошло выпадеиие одноrо символа, в результате чеrо
получилось слово U==Y1Y2. . .Уп--! длины n 1. Пусть ni
число единиц, а по ............ число нулей, расположенных правее
выпавшеrо символа. Оказывается, числа nl и по MorYT быть
определены с помощью суммы
n l
S (и) == iYi.
i= 1
в самом деле, если выпал символ О, то S (V) S (u)==ni,
а если выпал символ 1, то S (v).........S (и)==n no. Если w (и)
вес слова и, то, очевидио,
nl<w(u)<n no n. (3)
Так как S (v) == O (mod 1), то вычет числа S (и) по
модулю 1 равен либо nl (в случае выпадеиия иуля), либо
n............nо (в случае выпадения единицы). Неравенства (3) пока-
зывают, что если этот вычет ие превосходит w (и), то выпал
символ О, если же это не так, то символ 1. В первом случае
выпавший символ О иадо вставить в слово u так, чтобы пра-
вее иеrо было число едиииц, равное вычету числа S (и)
по модулю 1. Если же этот вычет больше, чем w (и), то встав..
ляем в слово u ед ииицу так, чтобы правее нее было число
нулей, равиое раз иости n и вычета числа............ S (и). Если,
например, при использовании кода V 4 ,s принято слово u==
== 101, то S (и)==4, а w (u)==2, вычет числа............ S (и) по моду..
JIЮ 5 равен 1, и, следовательио, выпал символ о. Вставить
ero надо так, чтобы правее Hero была одиа единица. Полу-
чается кодовое слово 1001.
Аиалоrичио исследуется случай одиночной вставки сим..
вола. Читателю предлаrается обосиовать следующий алrо
ритм восстаиовления кодовоrо слова, отвечающий этому
случаю.
Пусть прииято СЛОВОU===УIУ2. . .Уn+! длины n+ 1 и k
вычет числа S (и) по модулю 1. Тоrда
1) если k==O, то отбрасывается последний символ сло..
ва и;
З*
67
2) если O<k<w(u), то отбрасывается любой нулевой
символ, правее KOToporo в слове и ровно k единиц;
..3) если k == w (и), отбрасывается первый символ слова и;
4) если k > w (и), отбрасывается любой единичный сим-
вол, правее KOToporo имеется n+l k нулей.
Задачи и дополнения
1. Сравнить коды V 56 И V 5 10' а также коды V 6 ?,
V V б '. u ,
6 8' . .., 6 12 по их спосо ности испраВЛЯТh двоиные замещения Еида
О"";" 1 _ t
2. Для кода V n, "+ i сформулировать признак исправимости заме-
щения двух или большеrо числа символов. Каким будет этот признак
для кода V n 2n?
3. Найти алrоритм исправления (исправимоrо) двойчоrо замеще-
ния для кодов V n, "+ 1 и V п, 2n'
4. I(оды V n k можно использовать для исправления одиночных
замещений вида'l О. Каково в этом случае правило декодирования?
5. Построив код V 7 8, убедиться, что на местах с номерами 3, 5,
6, 7 встречаются всевозможные наборы из нулей и единиц и, значит
символы с этими номерами иrрают роль информационных.
6. Утверждение задачи 5 можно обобщить на случай любоrо кода
V n n+l' для KOToporo n==2m 1.
, Рассмотрим т позиций с номерами 1, 2, . ..., 2т --;1.. Выберем про-
извольную комбинацию из нулей и единиц в оставшихся n т позициях.
Тоrда существует единственное заполнение позиций 1, 2, . . ., 2т, для
KOToporo получившееся слово удовлетворяет условию (2), Т. е. является
кодовым_ Отсюда вытекает, что чисЛО слов кода V n, "+l равно 2 п -- т ,
Т. е. совпадает с числом слов в коде Хемминrа длины n==2т 1.
7. Пусть k n+ 1 есть простое число. Через V n, k обозначим код,
состоящий из всех слов V==Xi Х2 .. . Х N ' дЛЯ которых вы,полняются
два соотношения:
n
iXi == О (mod k),
i= 1
п
i2Xi == О (mod k).
i= 1
Построить КОД V 6 1- Убедиться, что он исправляет любые одиночные
и двойные замещения вида O l.
8. Показать, что всякий код V n k (СМ. задачу 7) исправляет лю-
бые одиночные и двойные замещения вида 0....1. Сохранится ли ЭТО
свойство для COCTaBHoro k?
14. ЦИКЛИЧЕСКИЕ КОДЫ
Среди линейных кодов особо важную роль
иrрают так называемые циклические коды. По ряду причин
они являются наиболее ценным достоянием теории КОДИ..
рования. Во-первых они допускают еще более компактное
описание, чем произвольные линейные коды. BO-ВТОРbIХ f
имеющиеся для линейных кодов алrори мы кодирования и
декодирования MorYT быть в применении к циклическим
68
кодам ЗНi чите.JIЬНО упрощены; более Toro, для циклически'!
кодов существуют свои особые методы декодирования, не..
приложимые к друrим линейным кодам. Наконец, по своей
структуре эти коды идеально приспособлены к реализации
u
в современных технических устроиствах.
Простые в реализации, они, однако, не столь просты в
теории. Для полноrо разъяснения большинства вопросов,
связанных с построением и методами декодирования цик-
лических кодов, требуется довольно сложный алrебраиче-
ский аппарат. Поэтому наше предстоящее знакомство с цик-
лическими кодами будет далеко не полным. .
Начнем с понятия циклическоrо сдвиrа вектора. Пусть
задан произвольный:n-мерный вектор а==(ао, аl, а2, . . ., an f)
с координатами из любоrо поля F (нумерацию коорди-
нат в случае циклических кодов удобно начинать с нуля).
Циклическим сдвиеом этоrо вектора назовем вектор а':::::8
==(an__f, ао, аl, а2, ... , an 2). Например, для вектора
(01101) последовательными циклическими сдвиrами являют-
ся такие вектора:
(10110), (01011), (10101), (11010).
Циклическим кодом называется линейный код, который
вместе с любым своим вектором содержит также Ц ero цик-
лический сдвиr. Иными словами, циклический код обладает
следующим свойством: циклический сдвиr любоrо кодовоrо
вектора снова является кодовым вектором.
Циклическим является, например, код с порождающей
u
матрицеи
( 1 О 1 О )
а== о 1 О I ·
Менее тривиальным примером циклическоrо кода (проверка
предоставляется читателю) является код, эквивалентный
(7,4)-коду Хемминrа, с проверочной матрицей
( 1 1 1 О 1 О О )
Н== о 111 О 1 О .
0011101
(1)
При рассмотрении циклических кодов кроме обычных
действий над векторами мы имеем дело фактически еще с од-
ной операцией, сопоставляющей каждому вектору ero цик-
лический сдвиr. Удобным алrебраическим средством для
, ее описания являются мноrочлены. t каждым вектором а==:с
,r:=(ao, af, . . . ; an 1) свяжем мноrочлен а (х):::зао+аlХ+. . ."+
аn..lХп--lj коэффициенты KOTop ro совпадают о соответ..
,
69
ствующими координатами вектора. В дальнейшем будем
отождествлять вектьр а с соответствующим ему мноrочле-
ном а(х), свободно переходя от векторной записи к записи
в виде мноrочлена. Циклическому сдвиrу а' ==(an--i, ао, аl,
. . . , а п __ 2) вектора а соответствует тоrда мноrочлен а' (х)==
==an__i+aOx+alx2+. . .+a n __ 2 x п -- 1 . Сравним мноrочлены а(х)
и а' (х). Если сумму первых n 1 слаrаемых а (х) умножить
на х, мы получим сумму последних n l слаrаемых MHoro-
члена а' (х). Вообще, нетрудно заметить, что
а'(х) ==х a(x) an 1 (xп 1). (2)
Будем теперь считать, что х......... образующий элемент
циклической rруппы порядка n. Тоrда n-я степень х равна
единице:
х n == 1,
(3)
а все меиьшие степени, 1, Х, х 2 , ... , xп l, являются различ-
ными элементами. При этом правило умножения степеней х
следующее:
XkXm == x r ,
(4)
тде r == k+т (mod п) и O r<n.
С учетом (3) равеиство (2) дает:
а' (х) == ха (х),
т. е. циклический сдвиr любоrо вектора получается умно-
жением этоrо вектора на х.
Из равенсти (3) и (4) BbITeKaeT следующее правило умно-
жения любых двух мноrочленов от х степени п ......... 1. Если
а (х) == а о +а 1 х + . . . + а n __ 1 х n -- !
и
ь (х) == Ь о + Ь 1 х + . . . + Ь n __ 1 х п ....ж
....... два таких мноrочлена, то чтобы найти их произведение,
сначала обычным образом раскрыраем скобки, умножая
степени Xk и Х т по правилу (4), а коэффициенты ak и Ь т
по правилу умножения в поле Р, после чеrо приводим по-
добные члены.
При м е р 1. Пусть n==5 и a(x)==I+x+x +x4 и
Ь (х)== 1 + х з + х 4 ........ двоичные мноrочлены. Тоrда
а (х)Ь (x)==(l +x+x +x4)(1 +х В +х4)==
;:;; 1 + х+ x + х 4 + х В + xx + x x + х 4 х В + х 4 + хх 4 + х 2 х 4 + х 4 х' ===
=:;: 1 +x+x + x4+x +x4+ 1 +х!+х 4 + 1 +х+х з == 1 +х 4 .
70
При м е р 2. Пусть п==4, a(x)==1+2x+x и b(x)
==2+x+x мноrочлены над полем Z8. Имеемt
а (х)Ь (х) == (1 +2х+ х 2 )(2+ х+ хз) ==
==2+2 .2x+2x +x+2x +x3+x +2xx3+x2x3==
==2+х+2х +х+2х +2хЗ+2+х== 1 +x +2x3.
1-1так, для мноrочленов кроме операции сложения опре-
делена также и операция умножения (напомним, что сло-
жение мноrочленов не нуждалось в специальном определе-
нии, поскольку мноrочлены понимаются нами как векторы).
При этом, очевидно, операция умножения мноrочленов ком-
мутативна, ассоциативна и дистрибутивна относительно
операции сложения. Поэтому множество Р п всех мноrочле-
нов степени n образует относительно указанных операций
кольцо. Но тоrда циклический код может быть описан в
чисто алrебраических терминах следующим образом:
Линейный код V является циклическим тоrда и только
тоrда, коrда V является идеалом в кольце F n'
В самом деле, если V ....... идеал, то для всякоrо кодовоrо
вектора (мноrочлен ) а(х) Е V имеем ха(х) Е V, Т.е. цикличес-
кий сдвиr снова является кодовым вектором.
Обратно, если V циклический код, то для всякоrо кодо-
Boro вектора а(х) ero последовательные циклические сдви-
rи ха(х) , х 2 а(х) , .. ., xn--1a(x) также являются кодовыми век-
торами.
Остается показать, что для всякоrо мноrочлена
Ь (х) == Ь о + Ь 1 х + Ь 2 х 2 + . . . + bп__ixп--
произведение Ь(х)а(х) является кодовым вектором. Мы
имеем:
Ь (х) а (х) ==
== Ьоа (х) + Ь 1 ха (х) + Ь 2 х 2 а (х) + . . . + bп...lxп lа (х). (5)
Соrласио сказанному выше, каждое слаrаемое в (5) прииад-
лежит кодовому пространству, но Tor да и вся сумма обла-
дает этим свойством. Итак, V........ идеал.
Не вполне ясно пока, какова польза получеииоrо нами
описаиия циклическоrо кода. Следующее утверждение про-
JIивает свет на этот вопрос.
Во всяком идеале V кольца F п существует фиксирован-
ный мноzочлен, g(x), которому кратен всякий мноеочлен идеа-
ла V.
Иными словами, любоЙ мноrочлен а(х) Е V можио пред-
ставить в виде произведения фиксированноrо мноrочлеиа
71
g(x) Е V и HeKOToporo подходящеrо мноrочлена s(x) Е F п:
а(х)== g(x)s(x). (6)
Для доказательства рассмотрим ненулевой мноrочлен
g(x) наименьшей степени, принадлежащий идеалу. Если
а(х) произвольный мноrочлен из V, то разделим ero на
g(x) с остатком:
а(х) == g(x)s(x)+ (х).
(7)
Это можно сделать по обычным правилам деления MHoro-
члена на мноrочлен; степень остатка (х) будет меньше сте.
пени делителя g(x). Первое слаrаемое в правой части (7)
принадлежит V (в СИ-lIУ определения идеала). Поскольку и
мноrочлен а(х) принадлежит. V, то остаток ((х), равный раз-
ности
а(х)...... g(x)s(x)
двух элементов из V, также должен принадлежать идеалу.
Если предположить, что ,(х) ненулевой мноrочлен, то
приходим к противоречию: мноrочлен ,(х), принадлежа-
щий идеалу, имеет степень, меньшую степени g(x). Следо-
вательно, ,(х)==О и выполняется равенство (6).
Мноrочлен g(x) на ывается nорождающuм' .м.Н,О20членом
идеала V (или соответствующеrо циклическоrо кода).
Таким образом, если известен порождающий MHoro-
член кода, то тем самым известны и все кодовые мноrочле-
ны ........... их список исчерпывается всевозможными произведе-
ниями g(x)s(x) , rде s(x) ...... произвольный мноrочлен степе-
ни, меньшей n.
Вспомним, что для задания произвольноrо кода нужно
u u
указать полныи список кодовых слов, а для задания линен-
Horo кода...... список базисных кодовых векторов. Для цик-
лическоrо же кода, как мы выяснили, достаточно указать
Bcero лишь один кодовый мноrочлен, а именно ........ порож-
дающий мноrочлен g(x).
По порождающему мноrочлену леrко найти порождаю-
щую матрицу циклическоrо кода. Пусть
g(x)==go+glX+." +gт xт
........ мноrочлен степени т и k==n........т. Рассмотрим следующие
мноrочлены:
g (х), xg (х), x 2 g (х), ..., x k -- 1 g (х). (8)
Все они являются кодовыми, степень их очевидно не пре-
восходит п........l. Нетрудно убедиться, что рассматриваемые
72
как векторы, они образуют линейно независимую систеМУt
и всякий КОДОВЫЙ вектор является их линейной комбина-
цией. Следовательно, матрица а, составленная из векторов
(8), является порождающей матрицей циклическоrо кода.
Порядок ее равен k Х п и она имеет следующий вид:
( go gi , · . gm О . . . о ) ( g (Х» )
0== о, ,e ,еl, :.: , , , .e . :': , . == .. e,(X .(9)
о ... о go gl ... gm xk lg(x)
В качестве примера рассмотрим двоичный циклический
код длины 7 с порождающим мноrочленом g(x) == 1 + X + х 8 ::::;
== (1011000). Так как
хg(х)==х+х З +х 4 ==(01ОllОО),
x2g(x)==x2+x4+x ==(OOl0110),
хЗg(х)==хЗ+х +х8==(ООО1011 ),
то порождающей будет следующая матрица:
( 1 О 1 1 О О О )
О 1 О 1 1 О О
G == \ о о 1 О 1 1 О ·
\0 о о 1 О 1 1
Нетрудно убедиться, что данный циклический код эквива..
лентен коду Хемминrа с проверочной матрицей
( О О О 1 1 1 1 )
0110011.
1 О 1 О 1 О 1
Вообще, можно показать, что для всякоrо кода Хемминrа
u u
имеется эквивалентныи ему циклическии код.
Очень важно, что среди циклических кодов имеются
такие, которые исправляют любое заданное количество
ошибок. Именно, справедлива следующая теорема:
( 2т 1 )
Для любых значений т и t t < 2 существует дво-
ичный циклический код длины 2 m .......l, исправляющий все КОМ-
бинации из t или меньше20 числа ошибок и содержащий не
более, чем mt проверочных символов.
Доказательство этой теоремы мы здесь не приводим.
Скажем лишь, что построение указанных кодов основано
на использовании упоминаемых в приложении полей ra-
пуа OF(q) (см. также дополнение 8 к этому параrрафу).
78
Задачи и дополнения
1. В теории циклических кодов мноrочпеllы удобно
трактовать не только как элементы кольца F п' но tf как элементы кольца
мноrочленов F [Х] с обычной операцией умножения мноrочленов. Ус.
ловимся в последнем случае вместо обозначения а (х) пользоваться обо-
значением а (Х). Необходимость различать ии обозначения видна хотя
бы из TaKoro примера: если в кольце F п имеет место xп l==O, то в коль-
це F[X] мноrочлен xп l, разумеется, не является нулевым элементом.
Для циклических кодов существенно следующее свойство порожда-
ющеrо мноrочлена g (х):
Если в качестве g (х) выбран м,ноеочлен наименьшей степени, при-
надлежащий идеалу V, то м,ноеочлен, g(X) Е F[X] является делителем
1I1н,оеочлена xп 1.
Для доказательства разделим xп 1 на g (Х) с остатком. Получаем:
Хп.....l == h (Х) g (Х) + r (Х), (10)
rде степень, (Х) меньше степени g (Х). в кольце F n равенство (1 О) при.
обретает вид:
h (x)g(x)+r(x)==O,
откуда заключаем, что r (х) должен принадлежать идеалу V, в то время
как ero степень меньше, чем степень g (х). Следовательно, , (х)==О, но
тоrда и , (х)==о, т. е.
Xп 1 ==h (Х) g (Х). (11)
Мноrочлен h (Х), удовлетворяющий равенству (11), называется
nроверочным, м,ноеочленом.
2. Воспользуемся определением проверочноrо мноrочлена для по..
строения проверочной матрицы циклическоrо кода.
k
Пусть h (х) == h JX! .....проверочный мноrочлен кода. Из (11) еле..
j=O
дуеТ t что если т ..... степень мноrочлена g (х), то h (х) имеет степень п т,
т. е. k==п m. В силу (11) имеем также, что в кольце F n проверочный и
порождающий мноrочлены связаны равенством
h(x)g(x)==O. (12)
Рассмотрим матрицу
( О ,.,
В == О . .. 11
. .
h k
н порядка тХ n, имеющую следующий вид:
О h k . . . ht h O )
,О, k. . . :': . h . h .0.. (13)
. . . h! ho о... о о
Первая строка этой матрицы составлена из коэффициентов мноrочлена
h (х), записанных в обратном порядке (т. е. в порядке убывания степе"
ней). Последующие строки составлены аналоrичным образом из коэф-
фициентов мноrочленов xh (х), . . ., xт--Jh (х).
Докажем, что матрица Н является проверочной.
п..l
Действительно, пусть а (х) == aixl...... произвольный кодовый
i=O
мноrочлен. Рассмотри tvI идеаn У"== (h (х», порожденный проверочным
74
п '
мноrочленом h (х) и ьозьмем ПрОИЗВОЛЬНЫЙ мноrочлен: Ь (х) == ь Jx'
j=O
из этоrо идеала. Тоrда а (x)==s (x)g(x) , Ь (x)==q (x)h (х) и соrласно (12)
а (х)Ь (x)==s (x)q (x)g (x)h (х)==О.
С друrой стороны, умножая мноrочлены а (х) и Ь (х) по правилам умно-
жения в F n (см. равенства (4», получаем:
а (х) Ь (х) == (ао+аlХ+... + а п .:. 1 x п -- 1 ) (Ь О + Ь 1 х+. " + bп__i xп -- J ) ==
== (llob o +a 1 b n -- 1 +... +а n --1 ы 1) + (lloЬ 1 +a1b o +... +a п -- 1 b 2 )x+...
... + (a O b n -- 1 +a 1 b n -- 2 +.... +an--1b o ) x n -- 1 .
Так как мноrочлен а (х)Ь (х) нулевой, то и все ero коэффициенты равны
нулю, в частности
llobn--1 +a 1 b п -- 2 +.,. +an--iЬО ==0.
Эrо равенство означает, что всякий кодовый вектор ортоrонален вектору
(b n -- 1 , Ь n -- 2 , · · ., Ь о ), который получается из произвольноrо мноrочлена
Ь (х) Е V , если ero коэффициенты записать в обратном порядке. Таким
образом, в силу построения матрицы (13), каждая ее строка opToro-
нальна любому кодовому вектору и, стало быть, эта матрица является
проверочной.
3. Вернемся снова к примеру циклическоrо (7,4)-кода с порождаю-
щим мноrочленом g (х)== 1 + х 2 + х8. Как было доказано, мноrочлен
g(X)== I+Х 2 +Х З является делителем мноrочлена X'1 I. Леrко прове-
рить, что
X'1 I==(X I) (ХЗ+Х+l) (ХЗ+Х 2 +1).
Следовательно, для проверочноrо мноrочлена h (х) имеем:
h (х)== (x l) (х3+х+ 1)== l+x +x8+x4== (1011100).
I Поэтому проверочной будет следующая матрица:
( О О 1 1 1 О 1 )
Н== О 1 1 1 О 1 О .
1 1 1 О 1 О О
4. Исходя из равенств
(X9 1) == (X I) (Х2+Х+l) (Х6+ХЗ+l),
(Xl I)==(X l) (X +X+l) (Х 4 +ХЗ+Х 2 +Х+l) (Х4+Х+l)Х
х(Х4+Х З +l),.
найти порождающие и проверочные матрицы всех двоичных циклически"
кодов длины 9 и длины 15.
5. Пусть f (X)==fo+fi Х +. .. .+ fkXk произвольный мноrочлен
степени k. Мноrочлен t'" (Х) == Xkt ( l ) называют двойствеНЯЫItI
к f (Х).
Покаэать, что проверочная матрица циклическоrо кода может быть
записана в виде:
( h* (х» )
Н== xh*(x) t
х'т l .h; (;)
75
rде h* (х) ...... мноrочпен, двойственный к проверочному мноrочлену
Il (х).
6. Убедиться, что код, дуальный к циклическому (см. 11, допол..
нение 11), также является циклическим. Как связаны между собой
порождающие и проверочные мноrочлены двух дуальных кодов?
7. Пусть е* (х) ...... мноrочлен, двойственный к мноrочлену g (х).
Показать, что
а) коды, порожденные мноrочленами g (х) и g* (х), эквивалентны;
б) если для кода с порождающим мноrочленом g (х) выполняется
условие g (х)==е* (х), то кодовое подпространство TaKoro кода вместе
с каждым вектором "== (ао, af, . " ., aп l) содержит также и вектор
"*==(an 1' aп 2' · "ао).
8, Среди циклических кодов особую практическую важность имеет
один специальный класс кодов, предложенных американскими матема-
тиками Боузом, Чоудхури и Хоквинrемом. Эти коды так и называЮТСЯ
кодами БЧХ ...... по начальным буквам фамилий этих математиков. Тео-
рия кодов БЧХ выходит за рамки настоящей книrи, и мы только объяс..
ним в нескольких словах, каким образом они определяются. Для этоrо
нам потребуются некоторые дополнительные сведения из теории полей.
Будем rоворить, что подмножество F является nодnодем поля J'i;
если F есть поле относительно операпий на Р. Справедлива такая тео.
рема:
Для любою конеЧНО20 поля F .мОЖНО указать конечное поле Р , удов.
леmворяющее следующим УСЛ08Ия.м,:
1) F ecrпb подполе поля Р;
2) F содержиrп n корней уравнения Xn......l==O;
3) не сущесrпвуеm п оля , обладающе20 свойсrпва.ми 1 и 2 и и.меющеzо
меньше эле.менrп08, чем Р.
Пусть теперь для поля F указано поле F со свойствами 1)..... 3).
Пусть (х. ...... примитивный элемент поля F i а числа s и 1 таковы, что ЭЛе-
мент (Х.$ имеет порядок n и 5+I<q, rде q...... число элементов поля Р.
Циклический код называется кодом БЧХ (с параметрами n, 5, 1), если
он состоит из всех мноrочленов CTeneH!1 <.n......l с коэффициентами из F t
среди кор ней которых содержатся все элементы
па nS+;I. ",8+2 n 8 +1
vw,vw ,vw ,'..,VII .
l\t\ожно доказать, что кодовое расстояние TaKoro кода не меньше
1+2. Следовательно, варьируя параметры n, 5, 1, мы имеем возможность
получать коды БЧХ с любым расстоянием, а значит, исправляющие лю-
бое заданное число ошибок. Это обстоятельство счастливо дополняется
тем, что для указанных кодов разработаны удобные алrоритмь(декодиро"
вания, основанные на вычислениях в конечных полях:и леrко реализуе.
мые автоматическими электронными устройствами.
9. До сих пор мы rоворили о кодовом расстоянии кода и макси-
мальном числе t исправляемых ошибок как об основных показатeJIя"
корректирующей способности кода. Однако ясно. что более весомым
показателем является величина t/n, показывающаЯj какова доля числа
ошибочных символов от общеrо числа символов принятоrо слова, при
которой возможно еще правильное декодирование (исправление оши-
бок). С друrой стороны; отношение k/n (k...... число информационных
спмволов) характеризует избыtо'Чность кода: чем меньше это отношение,
тем; очевидно, больше избыточность,
76
li .от здесь коды БЧХ обнаруживают некоторыА изъян. Оказ*
вается, при заданной корректирующей способности, т. е. заданной
величине t/n, коды БЧХ большой длины имеют слишltом высокую из-
быточность. Более Toro: если отношение t/ n фиксировано, а n---+ со, то
k/n O.
Стремление исправить этот недостаток привело к появлению таких
кодовых конструкций, как коды-произведения (СМ. дополнение 12 к
11) и их обобщение каскадные коды. Строящиеся, как правило,
на базе кодов Б Ч Х, они в значительной степени сохраняют их досто-
инства, но одновременно избавлены от упомянутоrо выше дефекта.
15. О rРАНИЦАХ возможноrо
в КОДИРОВАНИИ И СОВЕРШЕННЫХ КОДАХ
Одна из основных проблем теории кодирова-
ния (и, пожалуй, самая интриrУЮЩ8Я) формулируется сле-
дующим образом:
Каково максимальное число кодовых слов в двоичном
коде длины п, если наименьшее расстояние между кодовы-
ми словами равно d? (Для укаЗ8нноrо числа, завися-
щеrо от значений п и d, будем применять обозначение
М(п, d).)
Ответ на поставленный вопрос позволил бы во всех слу-
чаях выяснить, какой наименьшей длины должен быть код,
чтобы можно было, во-первых, передать нужное число сооб-
щений, и во-вторых, rарантировать исправление (или обна-
ружение) данноrо числа ошибок.
Однако здесь мы сталкиваемся с явлением весьма рас-
пространенным в математике, коrда простая по формули-
ровке задача оказывается далеко не столь простой для ре-
шения. И, хотя указанной проблеме было посвящено немало
интересных и rлубоких исследований, хотя для ее решения
были испытаны самые разнообразные математические мето-
ды (вплоть до весьма COBpeM HHЫX .......... таких, как линейное
проrраммирование), исчерпывающеrо решения пока не П9-
лучено. Более Toro, сейчас, по-видимому, уже ясно, что
едва ли удастся найти сколько-нибудь обозримую формулу
для числа М (п, d). Более реальный, хотя тоще нелеrкий
путь, по которому и идут исследования, заключается в том,
чтобы достаточно точно оценить это число.
Мы расскажем здесь о самых простых oцeHK X для ЧИС-':l,а
М(п, d), которые MorYT быть получены из itеOJtожной ком-
бинаторики.
Будем называть шаром радиуса r с центром в слове х
множество всех лов у, YA8 PHQJX: ,2?:.?С рассtояние, lJe
большее " т. е. таких, ЧТО р(х, у)<:,' (анаЛО Яfl а обычным
Шаром) .
77
Во всяком шаре радиуса r содержится одно и то же I{O"
личество ДВОИЧНЫХ слов, зависящее только от " посколь-
ку t как нетрудно проверить, оно совпадает с количеством
слов шара Toro же радиуса с центром в нулевом слове. По-
следний же шар содержит все те двоичные слова, у которых
число единиц не превышает '. Число различных п-буквен-
. U
ных слов С t единицами равно числу сочетании из п эле-
ментов по l (СА). Поэтому, обозначив число всех слов в ша-
ре радиуса r через V rt получим:
r
V ,. == 1 + C + C + . . . + с:; == c .
i= О
Рассмотрим теперь код длины п с кодовым расстоянием
d===2t+ 1, содержащий максимальное число М (п, d) ==
== м (п, 2t+ 1) кодовых слов. Иными словами, это наиболь-
ший по объему код, исправляющий любые t (и меньшее
число) ошибок.
«Окружим» каждое кодовое слово шаром радиуса t.
Очевидно, что эти шары попарно не пересекаются, и, следо-
вательно, общее число слов во всех шарах равно V t .М(п, d).
Разумеется, оно не может превосходить числа всех n-
буквенных двоичных слов, т. е. V t .М(п, d) 2n, откуда мы
и получаем верхнюю оценку для максимальноrо числа ко-
довых слов:
2 п
1\1 (п, 2t + 1) .
V t
(1)
Эта rраница, предложенная Хемминrом, называется ero
имеием. Друrое ее название ераница сферической упаков-
ки связано с тем, что равенство в (1) достиrается в ТОМ
случае, коrда непересекающиеся шары (или сферы) радиу.
са t с центром в КОДQВЫХ словах целиком заполняют все
множество n-буквенных слов. Коды, облад ющие таким
свойством, называют совершеНн'ыми или плотно упакован-
ными, и к ним мы еще вернемся чуть позже.
Чтобы получить оценку снизу, рассмотрим для каждоrо
кодовоrо слова шар радиуса 2t с центром в этом слове. Из
максимальности кода следует, чтр любое n-буквенное сло-
во принадлежит хотя бы одному такому шару. Будь иначе,
мы смоrJIИ бы добавить к нашему коду еще по крайней мере
одно слово, не уменьшая кодовоrо расстояния. Итак, объ-
единение всех рассматриваемых шаров совпадает с множе-
ством всех n..буквенных слов.
Произведение V 2tM(n, d) есть число слов, содержащихся
ВО всех зтих шарах. Но при этом мноrие слова MorYT при-
7&
надлежать не одному, а нескольким шарам, и значит, в
произведении учитываются несколько раз. Поэтому спра..
в дливо неравенство
V 2t M(п, d) 2 n ,
которое дает теперь уже нижнюю оценку для максималь-
Horo числа кодовых слов:
2 n
М (п, 2t + 1) Y . (2)
2t
Оценки, аналоrичные (1) и (2), справедливы и для не-
двоичных кодов. В случае произвольноrо. основания q они
имеют вид:
qп qn
........... у М (n, 2t + 1) Y ;
21 t
при этом число слов в шаре радиуса, вычисляется по фор-
му ле:
V r == 1 + C (q 1) + C (q 1)2 + . I . + C (q 1)'.
На примерах можно убедиться, что указанные rраницы да-
,леко отстоят одна от друrой, т. е. являются весьма rрубы-
ми. Имеется MHoro их уточнений, а также оценок друrоrо
рода, но это вопросы более специальные.
Скажем теперь несколько слов о совершенных кодах,
с которыми связана целая эпоха в теории кодирования. Мы
отмечали уже, что число кодовых слов М совершенноrо
кода, исправляющеrо t ошибок, достиrает наибольшей воз-
можной величины (верхней rраницы Хемминrа). В случае
двоичноrQ кода имеем, следовательно,
t
М == 2 n / C . (3)
l=O
Тривиальным примером совершенноrо кода является код
с повторением нечетной длины n==2t+ 1. В этом случае
верхняя rраница (1) равна
t
2 2t + 1 / C t+l == 22t+l/22t == 2,
i=O
что совпадает с числом кодовых слов кода с повторением.
Более интересный класс совершенных кодов являют со..
бой хорошо известные нам коды Хемминrа длины 2т 1 с
исправлением одиночных ошибок. rраница сферической
упаковки для этих параметров (n==2т 1, tz::l) равна
2 n /(l + п) == 2 n /2 т ;=; 2 n -- т .
79
Столько же КОДОВЫХ СЛОВ имеет двоичный ({од Xervf
минrа.
Из равенства (3) вытекает, что совершенные двоичные
коды MorYT существовать лишь для таких параметров п »
t
t, для которых C является степенью
ё= о
u
двоики
(так
именно и было в рассмотренных выше примерах).
Понятие плотно упакованноrо кода появилось уже в пер-
вых работах по теории кодироваиия, тоrда же возникла про-
блема описания всех совершеиных кодов. Поиск плотно
u u
упакованных кодов казался весьма замаичивои задачеи, но
лишь однажды ои увенчался успехом. Новый совершениый
двоичный код был открыт в 1949 f. американским учеиым
rолеем. Этим кодом (ero так и называют......... код rолея)
оказался (23, 12) KOД, исправляющий три ошибки. Как впо-
следствии выяснилось, этот код является циклическим с по..
рождающим мноrочленом g(X)==X 11 +X 9 +X 1 +X!+X + 1
(мы уже знаем, что этот миоrочлен служит делителем MHoro-
члена X 3........1).
Дальнейшие поиски совершеиных кодов к удаче не при-
вели. Это не зиачит, однако, что ие появлялось интересных
работ о совершеины-х кодах. Самой значительной и rлубо-
кой из них была опубликоваиная в 1957 r. статья Ллой-
Да, в которой иа изучение проблемы были брошены мощиые
средства теории функций комплексноrо перемеиноrо и диф-
ференциальиых уравиений. В результате вопрос существо.
ваиия совершенноrо кода с теми или ииыми параметрами
был сведеи к чисто алrебраической задаче, связаиной со
свойствами корней HeKoToporo мноrочлеиа.
Под влиянием этой и ряда друrих работ стало склады.
u
ваться впечатление, что иных двоичных линеиных совер-
шенных кодов, кроме перечисленных, и не существует. Это
предположение оказалось справедливым, но ДОК8заио оно
было лишь в начале семидесятых rодов финскими учеными
А. Тиетявяйненом и А. Перко и независимо от них совет..
скими учеными В. А. Зииовьевым и В. К. Леонтьевым. Ре-
шению проблемы предшествовала мноrотрудная подrотовка,
в которую внесли вклад мноrие специалисты, инемалую
u
роль здесь сыrрали результаты и методы упомииавшеися
выше работы Ллойда.
Что касается кода rолея, то он является во мноrих от..
ношениях важным и замечательным кодом и остается ис-
u u
ТОЧНИКОМ мноrих идеи и исследовании в теории КОДИDования
(см. [12]) . .
80
3адачи и дополнения
1. Убедиться, что не существует кода длины 20, содер-
жащеrо 1000 кодовых слов и исправляющеrо любые комбинации из
трех и менее ошибок.
2. Использовать верхнюю оценку Хемминrа для доказательства
следующеrо утверждения:
Для вСЯКО20 q-UЧНО20 линеЙНО20 (n, k)-Koдa с кодовым расстоянием
d == 2t+ 1 величuна logq V t служит нижней ераницей для числа т прове-
рочных символов "
т logq Vt.
3. Для оценки «качества» линейноrо кода можно пользоваться так
называемой rраницей Варшамова rильберта. Применительно к дво-
ичным кодам указанная оценка основывается на следующем утвержде-
нии:
Е ели выполняется неравенсmво
l+C l+C l+"'+C = < 2т,
(4)
то существует линейный (n, k)-Koд с кодовым расстояние.М" не меньшим
d, имеющий не более т проверочных символов.
Для доказательства достаточно построить матр ицу Н пор ядка
тХ n, в которой любые d 1 столбцов линейно независимы; она и будет
служить проверочной матрицей искомоrо кода (см. 11, дополнение 4).
В качестве первоrо столбца Н можно взять любой ненулевой вектор ДЛf{-
ны т. Пусть уже выбрано i<n столбцов, любые d 1 из которых линей-
но независимы. Всевозможных линейных комбинаций этих i столбцов,
содержащих ровно j слаrаемых, имеется не более С{, и, следовательно,
число всех линейных комбинаций, содержащих d 2 или меньше столб.
цов, не превосходит числа
С 1 С 2 C d 2
#Е + i + · .. + i ·
Но в силу (4) это чисJ.JО меньше величины 2т 1, т. е. общеrо количества
ненулевых столбцов. Поэтому мы можем добавить по крайней мере еще
один столбец, не равный ни одной из указанных линейных комбинаций.
В получившейся при этом системе из i+ 1 векторов любые d 1 векторов
по-прежнему будут линейно независимы. Продолжая эту процедуру при-
соединения столбцов, мы и построим искомую матрицу Н.
4. Утверждение, доказанное в дополнении 3, обобщается на слу-
чай линейноrо кода над произвольным полем из q элементов; неравен-
ство (4) заменяется при этом на следующее неравенство:
d 2 '
C l (q l)i < qт.
i= О
5. Можно указать Еще одну простую оценку для }{одовоrо расстоя-
ния. Поскольку суммарный вес ненулевых кодовых слов q-ичноrо ли"
нейноrо (n, k)-кода есть nqk...;1(q l) (см. 11, дополнение 3), то средний
вес ненулевых кодовых слов равен nqk l(q I)/(qk I). Ясно, что он не
может быть меньше минимальноrо веса, совпадающеrо с кодовым рас-
стоянием d. Таким образом,
d nqfl l (q 1) . (5)
qk 1
Мы получили rраницу t называемую вер хней rраницей Плоткина.
81
Оценка (5) обобщается на случай произвольноrо q- ичноrо кода
ДЛИНЫ n, содержащеrо М КОДОВЫХ слов. В этом случае
d (q l) пМ (6)
q (M I) ·
6. Из оценки Хемминrа (1) также можно получить rраницу для
кодовоrо расстояния. Пусть код ДЛИНЫ n, исправляющий t и меньшее
число ошибок, содержит М кодовых слов. В силу определения
М (п, 2t+ 1) и оценки (1) М -<:М (п, 2t+ l)-<:qn/V t. Отсюда получаем:
1 t qп
l+Cп+,.,+Cп м . (7)
Неравенство (7) дает верхнюю rраницу для " а значит, и для кодовоrо
расстояния d== 2t+ 1.
fраница Хемминrа точнее rраницы Плоткина для кодов, избыточ-
ность которых не слишком велика (отношение числа проверочных сим-
волов к общему числу символов не превосходит 0,6). В остальных слу-
чаях точнее rраница Плоткина.
Например, для двоичноrо (16,5) Koдa оценка (5) дает d<.8, а из
оценки (7) получается t-<:4, т. е. d-<:9. .
7. Имеются и нелинейные совершенные коды, но их также HeMHoro.
Во всяком случае известно, что любой нетривиальный совершенный код
над любым полем должен иметь те же самые параметры (длину, KOДO
вое расстояние и число кодовых слов), что и один из кодов Хемминrа
или fолея. Все же полное описание нелинейных совершенных кодов,
исправляющих одиночные ошибки, пока не получено (см. по этому по
воду [12], задача 6.6).
16. КОДИРУЕТ И ДЕКОДИРУЕТ ЭВМ
3аrоловок этоrо параrрафа не следует понимать
буквально. Вряд ли было бы целесообразно привлекать
универсальные ЭВ дЛЯ кодирования и декодирования с
помощью линейных и циклических кодов. Однако устрой-
ства или схемы, предназначенные для этих
целей, состоят из тех же элементов, что и
любая ЭВ , так что такие схемы, если уrод-
но, можно рассматривать как специализи-
рованные мини-ЭВ . В случае двоичных
кодов применяются элементы двух основ-
ных типов:
Ячейка памяти (или три22ер), которая
может находиться в двух состояниях: одно
из них соответствует символу О, друrое символу 1.
Я чейка памяти имеет один вход и один выход.
Двоичный сумматор, осуществляющий сложение по мо-
дулю 2. Сумматор имеет два входа и один выход.
Устройства, составленные И3 этих элементов, позволя-
ют леrко перемножать и делить двоичные мноrочлены, а
это как раз те операции, которые приходится выполнять
при использовании циклических кодов.
82
в качестве nepBoro примера рассмотрим схему, осущест-
вляющую умножение произвольноrо двоичноrо мноrочлена
f(X) на мноrочлен 1 + X + Ха. Эта схема представлена на
рис. 14 и состоит Bcero из трех ячеек памяти и двух сумма-
торов. Поясним принцип ее работы.
f'(:c}
Рис. 14.
Первоначально все ячейки памяти содержат нули, а на
вход поступают коэффициенты мноrочлена '(Х)==апх п +
+а п __ 1 х п -- 1 +. . . +а о , начиная с коэффициентов при старших
Оп
а)
Oh"Z
6)
о)
(/п..,+а п
о)
a.'1 t
в)
е)
ж)
Рис. 15.
степенях. Коэффициент а п без изменений передается на вы-
ХОД и запоминается в первой ячейке памяти (рис. 15, а)
В следующем такте работы (рис. 15, б) в первую ячейку
памяти попадет коэффици нт а п --l, а коэффициент а n
83
сдвиrается в следующую ячейку памяти. При этом на
входах первоrо сумматора окажутся значения а п и а п -- 1 ,
а на выходе их сумма по модулю 2.
В третьем Ч'акте (рис. 15, в) произойдет даJ!ьнейший
сдвиr коэффициентов в ячейках памяти, а на выходе пер-
Boro сумматора и всей схемы появится сумма aп 2+an--l"
На рис. 15, z показано состояние схемы на i- л такте,
коrда на вход подан коэффициент aп ; (i<n).
Последние три такта отражены на рис. 15, д ж.
Итак, на выходе схемы ПОЯВИТGЯ следующая последова-
тельность из n+3 коэффициентов: ,
а п ; aп i + а п ; an 2 + an 1; а n -- з + an 2 + a ; "..; а п -- i +
+ an 1+1 + аn--i+з; ...; а о +а 1 + аз; а о +а 2 ; a 1 ; а о .
Эта последовательность соответствует мноrочлену
апХn+З + (а п -- 1 + а n ) Хn+2 +(an 2 + a n -- 1 ) Х п + 1 +
+(ап з+аn 2+аn)хп+... +(an--i+an--i+i+
+аn i+з)Хn--l.+З+... +(а о +а 1 +а з )Х 3 +
+ (а о + а,) Х 2 .+ а 1 Х +а о .
Непосредственно проверяется, что этот мноrочлен как
раз и есть НУ1Кное нам произведение
(апХn + an__iXn--1 + . .. +а 2 Х 3 +a1X +а о ) (ха + Х2 + 1).
Аналоrично устроена схема умножения на произволь-
ный мноrочлен
.
g (Х) == gm Xm + gт__l Хт -- 1 + . . · +gl X + go
над любым полем (рис. 16). В этой схеме ячейки памяти хра-
нят элементы поля Р, так что число различных состояний
ячеек должно совпадать с числом элементов в Р. Ячейки
памяти, как это видно из предыдущеrо описания, не только
вхоа
. . .
, . .
Рис. 16.
«запоминают», НО И «сдвиrают» поступающие в HJJX коэct>Фи-
циенты (иrрают роль сдвuzающеzо рееuстра). CYMMaToppl.
осуществляют сложение по правилам СJ10жения в поле Р.
84
кроме Toro, в схе лу введены добавочные устройства, произ-
водящие умножение на элемент gl Е F (на рис. 16 эти уст-
u
роиства, ПОК8заны кружками, помеченными соответствую-
щими множителями). В двоичном случае особых устройств
для этоrо не требуется: если gi== 1, то в соответствующеl\1I
u
месте схемы имеется «вертикальное» соединение и двоичныи
сумматор, в противном случае они отсутствуют.
Столь же просты схемы деления мноrочлена на MHoro-
член с остатком. Вот, например, как устроена схема деле..
ния на мноrочлен l+Х +ХЗ (рис. 17).
На вход поступают коэффициенты делимоrо, начиная со
u
старших степенен, на выходе последовательно появляются
Вхоо.
/{e,tllltfO / ;+;
BbI,fO!/
.'
"астноl.l
Рис. 17.
коэффициенты частноrо. После окончания деления в ячей-
ках памяти слева направо оказываются записанными коэф-
фициенты остатка, начиная с младших степеней. Просле-
дим последовательность работы схемы при делении на х з +
+ X +l мноrочлена Х +Х4+ХЗ+Х+l. Деление уrлом
дает:
X +X4+X3+0.X2+X + 1 'Х З +Х 2 +ОХ + 1
Х 5 +Х 4 +О.Х 3 + Х 2 Х 2 +О.Х + 1
ОХ 4 +Х 3 +Х II j +X+l
ОХ 4 +ОХ 3 +ОХ 2 +ОХ
Х 3 +Х 2 +Х + 1
Х 3 +Х 2 +ОХ + 1
I ОХ2+Х +0
(рамочками выделены последовательные частичные остат-
ки).
В первые три такта работы схемы старшие коэффициен-
ты делимоrо сдвиrаются по ячейкам памяти. При этом
старший коэффициент (при Х 5 ) окажется в крайней пра-
вой ячейке (рис. 18, а). Все это время на «нижних» входах
85
сумматоров сохраняются нулевые элементы, не ВЛИЯЮЩlfе
на работу схемы. В следующем такте (рис. 18, б) старший
коэффициент сдвиrаеrся на выход схемы, одновременно по-
падая на нижние входы сумматоров. На вход схемы посту..
пает нулевой коэффициент при X . в первую ячейку запи-
сывается выход nepBoro сумматора, равный 1 +0== 1, во
.!
tJ) 6)
i
Рис. 18.
вторую.......... содержимое первой ячейки в предыдущем такте
(т. е. 1), а в третью выход BToporo сумматора, равный
1 + 1 ==0. В итоrе в ячейках памяти сдвиrающеrо реrистра
оказываются записанными коэффициенты nepBoro И3 обве-
денных рамочкой остатков.
На рис. 18, в показано состояние схемы после еще
одноrо такта ее работы. Теперь уже содержимое ячеек
коэффициенты BToporo из заключенных в рамочку ос-
татков.
Еще один такт работы схемы переводит ее в конечное
состояние (рис. 18, е). В ячейках памяти получены коэффи-
циентыI остатка, а последовательность символов 1, О, 1 на
выходе.......... это коэффициенты частноrо.
Приведем без комментариев схему, осуществляющую де-
ление- с остатком на произвольный мноrочлен g(X) (рис.
19), предоставляя читателю самому разобраться в принци-
пе ее действия.
Схемы умножения и деления мноrочленов, рассмотрен-
ные нами, это, по существу, уже rOToBbIe кодирующие
устройства (или, как их называют, кодеры) для цикличес-
ких кодов. В самом деле, вспомним правило кодирования
линейцым (п, k)-кодом. Если А ==схо. . .ak"'l произвольное
сообщение длины k, то ему сопоставляется кодовый вектор
a==(cxO...cxk__i)G, (1)
rде а......... порождающая матрица линейноrо кода.
86
Разумеется, правило остается в силе и для любоrо ЦИК-
лическоrо кода, но на языке мноrочленов ему можно при-
да.ть теперь ииую, rораздо более удобиую форму.
Если а(х) миоrочлен, соответствующий вектору а, и
А (х) == (ХО + a,iX + . . . + a,k__lX "'l
мноrочлен, соответствующий сообщению А, то равенство
(1) перейдет в равенство миоrочлеиов
a(x)==A(x)g(x), (2)
rде g(x) порождающий миоrочлен циклическоrо кода.
.еКОО +
1t7/J -
. . .
BhlXOi
l/qcт""
Рис. 19.
Для Toro чтобы убедиться в этом, достаточно подставить
в (1) матрицу G из формулы (9) 11 и проверить, что коор-
дииаты получающеrося вектора служат коэффициентами
миоrочлеиа А (x)g(x).
Итак, операция кодирования сводится к умножению мно-
rочленов. При этом можно считать, что речь идет об обыч-
ном умн ожении миоrочленов, поскольку степеиь g(x) равиа
т, а степень А(х) меньше n т, так что сумма степеней
этих миоrочленов меньше n. Но схемы, которые мы здесь
рассмотрели (рис. 14 и 16), как раз и вычисляют обычиое
произведение миоrочленов. Первая из иих может служить
кодером для циклическоrо (7,4)-кода с порождающим мно-
rочлеиом x3+x + 1, а вторая для произвольиоrо цикли...
ческоrо кода с порождающим мноrочлеиом g(x). Если на
вход последией поступают информационные символы (хо,
CXi,. . ., сх'п--l (коэффициеиты миоrочлеиа А(х», то на выходе
соrласио (2) будем иметь коэффициенты кодовоrо миоrо-
члена а(х).
На осиове схем деления чрезвычайно удобио строить ко-
деры для систематических циклических кодов, в которых
ииформационные символы отделены от проверочиых (см.
дополиеиие 4 к этому параrрафу).
Даже наше беrлое зиакомство с устройствами кодирова...
НИЯ показываеТ J что все ОНИ имеют унифицированную СТРУК-
87
туру. Как видно из РИСо 16, путем определенных видоизме-
нений схемы, предназначенной для одноrо кода, можно по..
лучить схему кодирования для друrоrо кода. Поэтому в ря-
де случаев целесообразно использовать не конкретные схе..
мы для каждоrо кода, а достаточно разветвленное устрой-
ство с большим набором стандартных элементов, работу
KOToporo можно было бы перестраивать, вводя в Hero ту
или иную nporpaMMY. Такое устройство, в сущности; и есть
специализированная мини-ЭВМ с проrраммным управле-
н и ем. '
в задачу декодирования входит исправление и обнару-
жение ошибок, и эта процедура MHoro более сложная, чем
кодирование. Но устройства, подобные рассмотренным: «ми-
ни-ЭВМ», позволяют решить и эту задачу. В отличие от
кодеров, которые выrлядят более или менее стандартно
для всех циклических кодов, декодирующие устройства
(или декодеры) отличаются большим разнообразием, и то
как они устроены, зависит и от типа кода, и в особенно-
сти, от способа декодирования.
Кроме синдромноrо декодирования, о котором мы рас-
сказывали в 12, существуют еще ряд друrих методов, так
или иначе связанных с вычислением синдрома. Для любо..
ro из них принципиальная схема декодера выrлядит так,
как показано на рис. 20.
Наиболее сложной частью TaKoro декодера является
комбинационная лоrическая схема, которая по вычислен.
ному синдрому находит положение ошибочных символов I
Устроост60
илн ВЬ/ЧUС.llенI./Я
ClIHOpOHfl
ffOIfOllHQl(1I0HHllR
/!OBUlIec/(oR
c,tel1o
DОЛ/Jllенное
c//IJdo
J'опОIfUНQlQщее !/l"тfJoиcтdo
НО li сunВолоВ
Hcn,oqd/lellNiJe
:+: C/lO O
Рис. 20.
Устройство этой лоrической схемы целиком определяетсй
алrоритмом декодирования, а мноrообразием лоrических
схем в свою очередь определяется большое разнообразие
декодеров. Сложность практической реализации декодера
всецело зависит от характера лоrической схемы. Комбина-
ционная схема исключительно проста, как мы увидим, в
случае декодеров, только обнаруживающих ошибки или ис-
правляющих лишь одиночные ошибки, но существенно
88
сложнее для декодеров, исправляющих кратные ошибки.
В следующих двух параrрафах мы познакомимся с метода..
ми так иазываемоrо мажоритарноrо декодирования, кото-
рые позволяют значительно упростить комбинационную ло.
rическую схему,
Что же касается устройств для вычисления синдрома,
то здесь особой проблемы нет: они реализуются по тому же
принципу, что И кодеры циклических кодов. Для этой цели,
оказывается, MorYT быть использованы схемы деления мно-
rочленов.
Чтобы убедиться в этом, рассмотрим матрицу В, по
столбцам которой стоят коэффициенты остатков (;(Х) от де-
ления мноrочленов х; (i ==0, 1, . . ., п 1) на порождающий
мноrочлен g(x). Запишем ее условно в виде:
Н == (, о (х), f i (х), '2 (х), ..., 'n...f (х».
Можно показать, что матрица Н является проверочной для
рассматриваемоrо кода (см. дополнение 2 к этому пара-
rрафу).
Если и== (и о , Ui, . . ., и п -- 1 ) принятый вектор, то ero
синдром иВТ будет равен
И о ' о (х) + и 1 , 1 (х) + · · · + и п -- 1 , n-- i (х). (3)
Выражение (3) совпадает с остатком от деления MHoro.
члена
u (х) == и о + и 1 х + . . . + и n ... iXn--!
на порождающий мноrочлен g(x). Таким образом, Лlобая
схема деления, вычисляющая OCTaTOK, например, схема,
представленная на рис. 19, может быть использована как
составная часть декодера для получения синдрома.
JаЛОI1ЦН(JlOщее !/строастОи
На п СЦ/1ВО//ОО
>1
...
, . .
Рис! 21,
На рис. 21 приведена схема декодера, преднаэначенноrо
только для обнаружения ошибок.
Полученное слово одновременно вводится в запоминаю-
щее устройство и в схему деления. К моменту заполнения
89
запоминающеrо устройства в ячейках сл мы деления будет
получен остаток от деления на g(x), который равен синдро-
му. Если синдром равен нулю, то слово передается адреса-
ту, в противном случае прием прекращается и передающей
стороне посылается запрос на повторную передачу.
Не памноrо сложнее схема декодера для кодов Хеммин-
ra, исправляющих одиночные ошибки. В качестве примера
рассмотрим декодер для (7,4) Koдa с порождающим MHoro-
членом 1 +х 2 +х З . Ero схема представлена на рис. 22. Она
I!слро8'//f?ющuti
С!/I1патор
+ I1слра6ленное
сдо60
l/o.I/9'I/BH/l1l8
С.IIоОи
J't1ЛОI1UН(1/{)щее #строистВо
но 7 cl/t1Do/lCJd
Рис. 22,
включает в себя наряду со схемой деления и запоминающим
устройством также и лоrическую схему. Последняя устрое-
на так, что на ее выходе появляется 1, только если на вход
из ячеек памяти подается комбинация 011, равная послед..
нему столбцу проверочной матрицы
( 1001110 )
Н=== 0100111
0011101
(которая построена указанным выше способом из остатков
. u
от деления мноrочленов x t на порождающии мноrочлен
1 +x +x3). I
Предположим теперь для примера, что ошибка в слове
ио Иi И2 ИЗ и 4 и б Ив произошла в символе ИЗ четвертом по
порядку. Как мы знаем, синдром в этом случае будет сов..
падать с четвертым столбцом матрицы Н, Т. е. будет равен
вектору (1 О 1). Следовательно, после семи тактов работы в
u
запоминающем устроистве окажется слово и о Иl И2 Uз и 4 И 5 Ив,
u
а в трех последовательных ячеиках схемы деле..
ния комбинация 1 О 1. На восьмом такте из запоминаю..
щеrо устройства на исправляющий сумматор поступит сим.. I
вол и в, на вход лоrической схемы сдвинется комбинация I
90
1 О 1, на ее выходе окажется О, и символ Ив без изменений
поступит на выход всей схемы. При этом, как нетрудно про..
верить, в ячейках схемы деления окажется комбина ция 1 1 1
(на вход всей схемы, начиная с BocbMoro- такта поступают
нули). В следующих трех тактах из запоминающеrо устрой-
ства будут последовательно поступать символы U б , И 4 ' из,
на вход лоrической схемы комбинации 111, 110, 011,
а на ее выходе получатся поочередно О, О и 1. Поэтому сим-
волы И 5 И И 4 поступят на выход неисправленными, а оши..
бочный' символ из исправится. Проследив дальнейшие три
такта, можно убедиться, что символы И2, иf И ио исправ-
ляться не будут. В результате на выходе схемы окажется
слово, в котором будет исправлен только ошибочный сим...
вол из.
Совершенно аналоrично происходит исправление ошиб-
ки в любой друrой позиции.
Задачи и дополнения
1. Построить кодеры для двоичных циклических кодов
длины 15 с порождающими мноrочленами
а) Х 4 +Х+l; б) Х 8 +Х 7 +Х 6 +Х 4 +1.
2. Всякий циклический (n, k) код с порождающим мноrочленом
g (х) можно представить в систематической форме следующим образом.
ПУСТЬ'j (х) остаток от деления xi на порождающий мноrочлен g (х), Т.е
х' ==.. qi (х) g (х) +, i (х).
Рассмотрим мноrочлены
xi 'i (х) ==qi (х) g (х)
при i==т, т+ 1, . . 'f n l, rде т==n k степень порождающеrо мно"
rочлена g (х). Все эти мноrочлены кодовые, так как они кратны g (х).
Кодовый вектор, соответствующий мноrочлену xi 'i (х), имеет вид:
( 'iO' 'i1, ..., 'iJт l, О, ...,1, 'f', О),
rде 'io, 'н., 'i. m 17'"" коэффициенты остатка 'i(X), а символ 1 стоит в
позиции с номером l.
Мы получили n т==k векторов, которые, как нетрудно видеть,
линейно независимы. Если составить матрицу а, строками которой
являются указанные векторы, то она и будет порождающей (ее строки
образуют базис кодовоrо подпространства). Если через R обозначить
матрицу, строками которой являются коэффициенты мноrочленов '; (х),
то матрица G получается приписыванием к матрице R справа единич"
ной матрицы Е k порядка k и ее можно условно записать в виде:
G== R!Ek. (4)
Отсюда леrко следует (ср. 9 11, задача 10), что в качестве провероч-
нои можно взять матрицу
Н == Е IЛ i R,T .
91
По столбцам М8ТР ИЦЫ 11 стоят КОЭффti иенты остатков от делен ия МНО"
rочленов х О , х 1 , . . " х n 1 на g (х).
8. Чтобы проиллюстрировать метод, изложенный в дополнении 2,
рассМОТрИМ снова (7,4)-код с порождающим мноrочленом 1+х 2 +х 3 .
Имеем:
х з === (х З +х 2 + 1)+х2+ 1,
х 4 == (r+x2+ 1) (х+ 1)+х2+х+ I j
х 6 == (r+x2+ 1) (х2+х+ 1)+х+ 1,
х 6 === (х3+х2+ 1) (r+x2+x)+x2+x.
Строками порождающей матрицы являются, следовательно, }{оэффици"
енты мноrочленов:
Таким образом,
( 1 1 1 О 1 О О ) ( 1 О О 1 1 1 О )
G :Z :: : : : и н == о 1 О О 1 1 1 .
0110001 0011101
4. Метод, рассмотренный в дополнении 2, MO HO использовать для
построения кодера систематическоrо циклическоrо кода.
При кодировании с помощью матрицы (4) кодовое слово получается
умножением информационноrо слова на эту матрицу (см. (6), Э 11). В
этом случае последние k символов а т , а m +l' . . ., aп l кодовоrо слова
совпадают с информационными символами, а все кодовое слово явля-
ется линейной комбинацией строк порождающей матрицы (4) с коэффи-
циентами а т , а т +l, . . ., aп l' Учитывая, что по строкам матрицы R
1 + +х 2 +х З ,
1 +х+х2+ +х 4 ,
1 +х+ +х 5 ,
x+x2 ,. + х 6 ,
А
rg
КоооВое
В С.I!оОо
t1зtЧ,Оsdв А
RНtpОрIlОЦIlОJ/Нh/е
Сlll1Dолы В
Рис. 23.
стоят коэффициенты остатков от деления мноrочленов х; на порождаю-
щий мноrочлен g (х), мы убеждаемся, что величины llo, af, · . ., а т 1
являются коэффициентами остатка от деления мноrочлена
....... (атх т + а т +l Хtn + 1 + , .. + aп lXn l)
на мноrочлен g (х) (в случае двоичных мноrочленов знак минус перед
скобкой можно опустить).
Следовательно, схемы деления MorYT БЬ1ТЬ использованы для на-
хождения проверочных символов кодовых слов ЦИКJ1ическоrо кода в сис-
теМатической форме и, в конечном итоrе, для построения ero кодера.
На рис. 23 приведена схема кодера двоичноrо (7, 4) Koдa с порождаю..
щим мноrочленом l+x +x3, основанная на указанном принципе, .
92
Проследим вкратце работу этой схемы в течение семи тактов. Пер-
вые четыре такта переключатели схемы находятся в положении А,
следующие три в положении В. В первые четыре такта информацион
ные символы поступают (без изменений) на выход всей схемы и на ,выход
схемы деления. В течение этих четырех тактов в последовательных ячей-
ках схемы де.1!ения получаются коэффициенты остатка ао, ai, а2 от деле.
ния мноrочлена авх6+аьх5+а4х4+азх3 на порождающий мноrочлен
1 + х 2 + х З , т. е. проверочные символы (в схеме на рис. 18 на это ушло
бы семь тактов, НО в данной схеме три такта «экономятся», так как по-
следовательность коэффициентов а6, аь, а 4 , аз подается не на вход, а
сразу на выход схемы деления). В последующие три такта проверочные
сиыволы снаЧала а2, затем аl, затем ao поступают из схемы деления
на выход всей схемы. Таким образом, по истечении семи тактов на вы-
ходе всей схемы получаем целиком кодовое слово.
Рекомендуем читателю проследить по тактам работу рассматривае-
мой схемы для случая аз== О, а 4 == а 5 == а в == 1.
17. rОЛОСОВАНИЕ
Хотя в процедуреl1РИНЯТИЯ решения большин-
СТВОМ rолосов нет для нас ничеrо необычноrо, может все же
показаться неожиданным, что метод rолосования исполь-
зуется при декодировании помехоустойчивых кодов. Отча-
сти мы уже коснулись этоrо вопроса в 8, коrда рассказы-
вали о коде с повторением, решение о посланном симво-
ле принималось там как раз большинством rолосов. Теперь
же мы покажем, как применяется rолосование в случае
u
произвольноrо линеиноrо кода.
Обратимся сначала к примеру. Здесь нам поможет не-
однократно упоминавшийся ранее (7,З)-код, получающий..
ся из (7,4)"кода Хемминrа добавлением общей проверки на
четность. Ero проверочная матрица имеет вид:
Н == ( 1111 : : ) .
1 О 1 О 1 О 1
Удобнее, однако, рассмотреть эквивалентиый цикличеСI\ИЙ
код с порождающим мноrочленом g(x)==(x+l) (х З +х+l)
и с проверочной матрицей
Н 1 == ( 1 11 ) t
О О О 1 1 О 1
Эта матрица получеиа способом, указанным в дополнеЦJIИ
9 к 11. В том, что коды с проверочными матрицами Н И
Н} действительно эквивалентны, читатель может убедить-
ся самостоятельно.
93
Пусть принято некоторое слово схо аl (Ха аз СХ 4 (Х5 СХ 6 , со..
держащее, быть может, ошибочные символы. Для каЖД04
ro символа CXi будем в отдельности решать, верен он и.НИ
нет, используя те соотношения, которыми этот символ свя-
зан с остальными. Начнем с символа СХ О и выпишем некото-
рые содержащие ero проверки. Первой строке матрицы Н!
отвечает проверочное соотношение СХ О +СХl +c'tз==О, сумме
первой, второй и третьей строк соотношение СХо+СХ 4 +
+СХ 5 ==0, а сумме первой, второй и четвертой строк........ соот-
ношение СХО+СХ2+СХ6==0. Итак, имеем:
C't о ==СХ 1 +СХ з ,
сх о ==сх 4 +сх 5 , (1)
СХ О ==сх 2 +сх 6 .
Если ошибки при передаче отсутствовали, то в приня-
том слове будет выполняться каждое из соотношений (1)
а правые их части дадут верное значение для СХо. Соотноше.
ния (1) для символа сх о выбраны с таким расчетом, что вся-
кий друrой символ входит в правую часть ровно одной про-
верки. Поэтому если лишь один из них ошибочен, то толь-
ко J3 одном из соотношений (1) будет нарушено равенство.
Учитывая это, можно предложить следующее правило для
определения BeplIoro значения символа схо: если среди зна-
чений СХl+СХЗ, сх 4 +сх 5 , СХ2+СХ6' ао большинство составляют
нули, то полаrаем, что нуль и есть верное значение для
<%0, если же большинство из них....... единицы, то верным
значением для схо считаем единицу. Такое rолосование ra 4
рантирует верное решение, если принятое слово содержит
не более одной ошибки. Возможно и равенство rолосов (на-
пример, в случае двойной ошибки), и в этом случае прихо-
дится довольствоваться ее обнаружением.
Аналоrичные проверки MorYT быть составлены и для
друrих символов. Например, дЛЯ CX:i имеем соотношения:
СХ 1 ==сх 2 +сх 4 ,
СХ 1 == СХ 5 + сх 6 ,
СХ 1 == СХ О +c't з ,
также обладающие тем свойством, что каждый символ вхо-
ДИТ в правую часть не более одноrо раза. Эти проверки по-
лучаются из системы (1) циклическим сдвиrом на одну по-
зицию. Последующие циклические сдвиrи дают системы
подобных проверок для остальных символов.
Анализируя указанным способом каждый символ при-
нятоrо слова, мы правильно восстановим посланное кодо-
вое слово, если произошло не более одной ошибки, и обна-
94
ружим люБУIО двойную ошибку. Тем самым полно-
стью используются корректирующие способности дан-
Horo кода ведь ero кодовое расстояние равно 4.
Разобранный нами метод исправления и обнаружения
ошибок называют мажоритарным декодированием (т. е.
де.кодированием по принципу большинства). Применим он
тоrда, Коrда........ как в нашем примере ......... для каждоrо сим-
вола а} существует система проверок
rl j == alkrtk'
k
а } == a 2 k rt k' (2)
k
. . . . . .
rt j == askrtk'
k
обладающая тем свойством, что в правую часть каждой
U U
проверки входят символы, отличные от a j , и всяким такои
символ входит не более чем в одну проверку. Такая систе-
ма проверок называется ортО20нальноu (или разделенной).
Если число проверок, входящих в каждую ортоrональную
систему, не меньше s, то путем rолосования MorYT быть ис-
правлены любые t ошибок, rде t«s+ 1 )/2. В самом деле,
ошибка в одном символе влияет в силу ортоrональности не
более чем на одну проверку, следовательно, среди значе-
ний символа a j , которые даются всеми СООТ}iошениями (2),
неправильными MorYT оказаться не более t, т. е. не более
половины значений. Тоrда, сравнивая значения правых
частей проверок, а также значение caMoro символа a j ,
мы по большинству rолосов определяем верное значение
этоrо символа. Если же (при нечетном s) t== (s+ 1 )/2, то
имеет место равенство rолосов, ошибка при этом хотя и об-
наруживается, но не исправляется.
Случай, коrда число s проверок в каждой ортоrональной
системе на единицу меньше кодовоrо расстояния d, т. е.
коrда s==d-----l, является в известном смысле идеальным. В
этом случае rолосование позволяет, как и в рассмотренном
u
примере, полностью реализовать корректирующие своист-
ва кода. КОД, дЛЯ каждоrо символа KOToporo существует
система из (d l) ортоrональных проверок, называется пол-
ностью ортО20налuзуеМblМ.
Чем хорош метод rолосования? Прежде Bcero тем, что
ero техническая реализация предельно проста (особенно в
случае двоичных циклических кодов). Наряду с обычными
сумматорами и ячейками паl\1ЯТИ схема декодирования дол-
95
жиа со ржать мажоритарный элемент (лоrическую схему,
осуществляющую выбор значения а! по большинству ro-
посов).
Вот как устроена принципиальная схема мажоритарно-
ro декодирования для (7,З)-кода, упомянутоrо выше (рис.
24, а).
В этой схеме М мажоритарный элемент, осуществ-
ляющий rолосование, К переключатель, находящийся в
" 10%00
81(
О
BhI.fot7
+
+
о)
ВЫХОIl
tt.'
"()
+
0)+
Рис. 24.
положении О во время приема сообщения и в положении 1
при ero декодировании. Рис. 24, а соответствует моменту,
коrда сообщение полностью поступило в запоминающий ре-
rистр и ключ К переводится в положение 1. Начинается де-
кодирование. На первом ero шаrе (первый такт) на вход
маЖоритарноrо элемента подаются значения схо, СХ 1 +СХ Зt СХ 2 +
+ а 6 , (Х4+а5' На выходе ero появляется символ CX , являю-
щийся итоrом rолосования. В следующем такте происходит
сдвиr сообщения в реrистре, а символ a поступает в по-
следнюю ячейку памяти. Этому моменту соответствует рис.
24, б.
96
Теперь уже rолосование осуществляется по значениям
(Хl, (Xz+a 4 , аз+а , а5+а6, и в результате получается зна-
чение CX следующеrо символа сообщения. Дальнейшие так-
ты работы схемы совершенно аналоrичны. Если произошло
не более одной ошибки, то последовательность (a , a ,. . .
. . ., сх;) и есть верное кодовое слово.
Как мы видим, в схеме используется только информа-
ция о принятом слове; никакой дополнительной информации
не требуется. А это очень важно, потому что именно необ-
ходимость хранения большоrо объема данных служит ос-
новным препятствием для применения некоторых методов
декодирования (например, синдромноrо декодирования).
Еще одно немаловажное достоинство rолосования по
сравнению с друrими методами декодирования заключается
в том, ЧТО этот метод зачастую позволяет исправлять или
обнаруживать мноrие ошибки, кратность которых превы
шает (d 1)/2.
Задачи и дополнения
1. Доказать, что код из примера 9 8 с проверками на
четность по строкам и по столбцам является полностью ортоrонализуе"
мым, составив для каждоrо из символов систему из трех ортоrональных
проверок (например, проверки
а1==а 2 +аэ+Рt,
a1==a4+CX1+ 4'
Q:1 == сх 5 +а в +сх в +а о + 3+ 5+ 6+P7
образуют требуемую систему для символа СХl).
2. Проверить, что (7,4)-код Хемминrа не является полностью ор-
тоrонализуемым, показав, что для символа а1 не существует пары орто-
rональных проверок. '
Будет ли полностью ортоrонализуемым расширенный {8J4) KOA
Хемминrа?
3. Решить те же вопросы, что и в задаче 2, для произвольноrо ДBO
ичноrо кода Хемминrа и ero расширенноrо варианта.
4. Построить систему ортоrональных проверок и мажоритарный
декодР.р для троичноrо циклическоrо (l3,6)-кода с порождающим мно-
rочленом
е(х)==(х+2) (х3+2х2+2х+2) (x3+x +2).
18. мноrОСТУПЕНЧАТОЕ rОЛОСОВАНИЕ
и КОДЫ РИДА.... МАЛЛЕРА
Мы расскажем здесь о кодах, для которых най-
ден замечательный алrоритм исправления ошибок, cblrpaB-
ший важнейшую роль в развитии методов мажоритарноrо
декодирования.
4 и. Н. Аршинов, л. Е. СаДОВСRИЙ
97
Проще Bcero начать с расширенноrо (8,4) Koдa Хеммин-
ra. Нетрудно убедиться, что этот код дуален самому себе,
Т. е. что ero проверочная матрица служит для Hero и по-
рождающей:
( 1 1 I I ] I 1 1 ) ( gO )
G о о о о 1 1 1 I == g1
О О 1 1 О О 1 1 g2'
О 1 О 1 О 1 О I з
Этот код не является полностью ортоrонализуемым (см.
17, задача 2). Значит ли это, что rолосование для этоrо
кода невозможно? Оказывается, нет.
Идея, которую l\1bI проиллюстрируем на данном при-
мере, состоит в следующем. Если нельзя составить нужной
системы ортоrональных проверок для каждоrо символа в
отдельности, то, может быть, это удастся сделать для опре-
деленных линейных комбинаций этих символов.
Пусть 11== (СХ о , СХ1, а 2 , аз, (Х4' СХ 5 , (Х.6' СХ 7 ) произвольное
кодовое слово. Оно, как обычно, может быть записано в
виде:
t1== a o g O +a 1 g 1 + Q2g2+азgз.
(1)
Выясниrvl, как связаны координаты СХ; вектора 11 с коэф-
фициентами равенства (1). Заметим, что сумма первых
двух координат каждоrо из векторов go, g1 И g2 равна О,
тоrда как для вектора gз она равна 1 i Поэтому cYlVIMa соот-
ветствующих координат вектора 11 равна аз, Т. е.
. аз==Ctо+а 1 .
(2)
(:овершенно T8I{ же убеждаемся, что верны равенства:
й з ==а 2 +а з ,
а з ==(1,4+ а IН
а з ==а 6 +(1,7.
(3)
Нетрудно понять, что соотношения (2) и (3) представляют
систему ортоrональных проверок для коэффициента аз. Для
коэффициентов а2 и а1 дело обстоит аналоrично и opToro-
нальные проверки для них таковы:
а 2 ==сх о +сх 2 ,
а 2 ==(1,1+ а з,
а 2 ==(1,4+ а в,
а 2 ==а 5 +(1,7'
аl ==а о +(1,4'
а 1 ==а 1 +(1,5'
a t ==Cl 2 +(1,6'
а 1 ==а З +СХ 7 8
(4)
98
Применяя к полученным проверкам принцип большин-
ства, мы найдем верные 8начения коэффициентов аl, ai,
аз, если произошло не более одиой ошибки. В случае двой-
ной ошибки при определеиии хотя бы одиоrо из коэффици-
еитов rолоса распределятся поровну и ошибка будет толь-
ко обиаружена.
Предположим, что верные значеиия коэффициеитов ai,
а2, аз найдеиы. Тоrда еще одии этап rолосоваиия позволяет
определить также и верное зиачеиие коэффициента ао. Сде..
пaTЬ это совсем иесложио. В самом деле, рассl'ЛОТРИМ раз..
ность
'V 1 =='О аlg1 а2g2 азgз.
В случае безошибочной передачи, в силу равеиства (1),
l[Jl==a o g o , т. е. все коордииаты вектора '01 равиы ао.
3иачит, либо все они равиы нулю, либо все равиы единице.
Поэтому в качестве вериоrо зиачеиия а о выбираем то, ко..
торое преобладает среди коордииат вектора iJ 1 .
Определив зиачеиия коэффициентов ао, ai, а2, аз, м:ы
без труда восстанавливаем кодовое слово соrласио равеи-
ству (1).
При м е р. Пусть прииято слово 01110110, содержа..
щее одиночиую ошибку. Для декодирования обращаемся
к равеиствам (2), (3) и (4), которые в данном случае дают
следующие результаты: I
а 1 == О, а 2 == 1 , аз == 1 ,
а 1 ==0, а 2 ==0, аз ==0,
а 1 == О, а 2 == 1, аз == 1,
а 1 == 1 , а 2 == 1 , аз == 1 .
По большинству зиачений находим: аl==О; а2==аз==l. Тоrда
"'1 ==(01110 11 o) (oo 11 00 11 ) (o 1 О 1 0101) == (00010000),
откуда ао==О. Следовательио,
'lJ==g2+gз==(0110ОllО).
Этот изящиый метод декодироваиия ..10жет быть приме
неи к так называемым кодам Рида Маллера (сокращен
но РМ-коды), которые мы и хотим сейчас рассмотреть.
РМ-код первоrо порядка определяется как код, дуаль
ный к расширеииому коду Хеммииrа, т. е. как код, порож
дающая матрица KOToporo совпадает с проверочной матри
цей расширеииоrо кода Хеммииrа. Таким образом, расши-
рениому (п, k)-коду Хемминrа (п==2 т , k==2т т l) отвечает
(n, n k)-код Рида Маллера, При т 3 оба кода сов..
4'
99
падают: расширенный (8,4)-код Хемминrа дуален самому
себе. При т==4 получаем (16,5)-код Рида Маллера пер-
Boro порядка с порождающей матрицей
111 I 1 1 1 11] ) J 1 ] I
000000001) 11111
о== О о о о 1 ] 1 1 О О О О 1 1 1
001100110011001
О I О 1 О 1 О ] О 1 О ] О 1 О
i )
1 I
go
gl
g2
gз
g4
Алrоритм декодирования для этоrо кода практически
не отличается от paccMoTpeHHoro выше алrоритма для (8,4)-
кода. ДеЙствительно, если
v == aog 0+ a 1 g 1 + a 2 g 2 + Qзgз + a 4 g 4 ,
то, например,
а4 == Ctt.t+ a . == a 2 +a S ==CX 4 +СХ 5 == а 6 +а? == (ХЭ+СХ 9 ==сх ц )+а 11 ==
==CG12+СХlз==а14 +а 10 .
т аким образом, для коэффициента а 4 имеем 80ртоrональных
проверочных соотношений. Такое же число ортоrональных
проверок о.пучается и для каждоrо из коэффициентов аl,
а2, аз-
Следовательно, если произошло не более трех ошибок;
то в первом «туре» rолосования удается восстановить вер-
ные значения коэффициентов аl, а2, аз, а 4 . Во втором «туре»,
действуя совершенно так же, как и в случае (8,4)-кода, по..
лучаем верное значение для а о . После этоrо по найденным
значениям коэффициентов целиком восстанавливаем кодо-
вое слово. Итак, (l6,5)-код Рида Л\аллера исправляет
любые ошибки, если они имеются не более чем в трех сим-
волах, и обнаруживает ошибки в четырех символах. Мо?Кно
убедиться,' что двух этапов rолосования достаточно для
любоrо РМ-кода первоrо порядка.
При построении кодов Рида Маллера более высоких
порядков используется покомпонентное ,умножение векто-
ров, определяемое следующим образом: если 'V==(al' (Х2, ...
· .. .., а п) , и == ( :i , 2,. . ., п) , то
cv о и== (CX1 1' a2 2" . . , aп n)'
Покажем теперь, как по произвольному РМ-коду пер-
Boro порядка строятся PM KOДЫ ,-ro порядка (r>l). Пусть
строками порождающей матрицы РМ-кода первоrо порядка
являются векторы go, gj,. . .,gm' Составим из этих векторов
всевозможные произведеиия, содержащие не более r со-
множителей. Добавим эти произведения в качестве допол-
100
нительных строк к строкам go, gi, . . .,gт- Полученную в
результате матрицу и будем считать порождающей матри-
цей PM Koдa r ro порядка. Например, для РМ-кода BToporo
порядка, соответствующеrо (l6,5)-коду Рида........ Маллера
nepBoro порядка, эта матрица имеет вид
1111111111111111)
О О О О О О О О 1 1 1 111 1 1
О О О О 1 1 1 I Q о о о 1 1 1 1
0011001100110011
1 О 1 О 1 О 1 О 1 О 1 О 1 О 1
a 0000000000001111
О О О О О О О О О О 1 1 О О 1 1
О О О О О О О О О 1 О 1 О 1 О 1
О О О О О О 1 1 О О О О О О 1 1
О О О О О I О 1 О О О О О 1 О 1
\0 О О 1 О О О 1 О О О 1 OU О 1 J
Ко
gl
Kg
1'8
К4,
gl о g2
111 о Ка
1/1 о 8".
1/2 0 К8
Kg о К,
\ К8 о 1/4
)
.
Этот код исправляет любые одиночные и обнаруживает
двойные ошибки, а мажоритарное декодирование дЛЯ Н8'0
может быть осуществлено в три этапа. Если 'lJ кодовое елО-
во, то
fJ==aogO+a1g 1 +. · .+a4g4+a12gtog2+
+аlзgl0gз+. · .+a s4 g s og l . . (5)
На первом этапе определяем верные значения козффици-
tHTOB aij, для каждоrс из которых имеем четыре opTor9-
нальных проверочных соотношения. Например, дЛЯ КО9ф-
фициента а З4 они таковы:
а З4 ==CXO+CX 1 +ct 2 +сх з ,
а З4 ==СХ 4 +СХ Б +СХ в +СХ 7 ,
а З4 ==ав+сх о +СХ 1о +СХ 11 ,
а З4 ==СХ12+СХlЗ+СХi4 + CX f5"
После определения коэффициентов aij составляем разность
fJl==fJ a12g10g2 - . . аЗ4gзоg4==(СХ ' cx ,. · .,a 6).
'.....
Поскольку при безошибочной передаче
fJ 1 == aog o + a 1 g 1 + a 2 g 2 + азg:) + a 4 g 4 ,
то проверочные соотношения для определения ai., а2, q,t,
а 4 (это второй этап rолосования) таковы Же, как дЛЯ РМ..
кода первоrо порядка. К примеру,
а, ;;::: CX + a == а; + a == a + a == a + а; == a + a =s
== a o + a l == a 2 + a =: CXf4 + af".
101
Наконец, на третьем этапе составляем разность
( "'1 " )
V 1 alg1 a2g2 азgз a4g4 === а о , СХ 1 , ..., СХ 15
И ПО большинству значений координат а,'; определяем зна-
чение а о . После завершения TpeTbero этапа кодовое слово
восстанавливается по формуле (5).
Подобная процедура декодирования распространяется
на РМ-коды произвольных порядков; при этом для кода
,-ro порядка число этапов rолосования равно '+ 1 и ДЛЯ
кода длины 2т число ортоrональных проверок на пеРВО:\1
этапе равно 2 т -- , (на каждом последующем этапе число
проверок удваивается). Таким образом, может быть исправ.
лено 2m r 1 1 ошибок, а 2m r 1 ошибок всеrда обнаружи-
вается.
В настоящее время открыто достаточно MHoro кодов,
для которых применимы подобные алrоритмы декодирова-
НИЯ. ИХ описание и способы построения ортоrональных
проверок базируются на различных комбинаторных и reo
метрических конструкциях.
Задачи и дополнения
t. Для (8,4)-кода Рида Маллера первоrо порядка
ИСПР811ИТЬ или обнаружить ошибки в следующих словах:
11 О 1 О 11 О, 111 0000 1 .
2. Анализируя соотношения (2), (3), (4), найти число обнаруживае-
мых и число необнаруживаемых тройных ошибок в (8,4)-коде Рида
Маллера. Имеются ли исправимые тройные ошибки? Решить те же во-
просы для ошибок в четырех символах.
3. Для (16,5)-кода Рида Маллера первоrо порядка исправить
или обнаружить ошибки в следующих словах:
1110010100100111, 1010010110101010, 1001001001001001.
4. Считая, что используется РМ-код BToporo порядка длины 16,
исправить или обнаружить ошибки в тех же словах, что и в задаче 3.
Чем объясняются расхождения с результатами задачи 3?
5. Доказать, что код Рида Маллера '-ro порядка длины n== 2т
имеет 1 +cln+. . .+C информационных символов, 1 +с:п+. . .+C r l
проверочных символов, а ero кодовое расстояние равно 2т r.
19. ЛАТИНСКИЕ КВАДРАТЫ И КОДЫ
Латинские квадраты долrое время были изве-
стны лишь математикам и любителям rоловоломок и, в ос-
новном, блаrодаря одной знаменитой задаче Л. Эйлера *).
В 1782 r. Эйле р предложил следующую проблему.
*) Леона рд Эйлер (1707 1783) один из великих математиков
XVIII века, создавших основы математическоrо анализа, IIJвейцарец
102
Среди 36 офицеров находится по шесть офицеров шести
различных званий из шести полков. Можно ли построить
этих офицеров в каре так, чтобы в каждой колонне и каж-
дой шеренrе встречались офицеры всех званий и всех пол-
ков?
Лишь в 1901 r. удалось доказать, что это невозмож-
но. Однако связанные с задачей Эйлера латииские квадраты
не потеряли интереса, так как вскоре обнаружилось, что
они имеют миоrообразные практические применения. А сов-
сем недавно (конец шестидесятых rодов) они были примене-
ны и в теории кодирования. Получающиеся иа их основе
коды, хотя и далеки по своим параметрам от оптимальных,
но зато допускают простые алrоритиы декодирования (ro-
лосование в один шаr).
Будем рассматривать квадратные матрицы порядка n,
элементы которых числа 1, 2, . . ., n. Такую матрицу Ha
зывают латинским KBaapafпOM, если всякий элемент входит
ровно один раз в каждую строку и в каждый столбец.
Следующие матрицы являются примерами латинских
квадратов (соответственно порядка 2, 3 и 4):
(; ) ,
( 1 2 3\
2 3 1 ),
3 1 2)
( 1 2 3 4 )
3 4 1 2
. 2 3 4 1 I
\4 1 2 3
Существениым при построеиии кодов является свойство
ортоrональности матриц, которое определяется следующим
образом.
Две матрицы порядка n называются ортО20наЛЬНblМU (не
путать с ортоrональностью векторов!), если при наложении
любой из них иа друrую мы получим множество всех упо..
рядочеиных пар (i, j), l<i n, I J<n.
Вот пример ортоrоиальных латинских квадратов по-
рядка 3:
( 1 2 3 )
2 3 1 ,
3 I 2
( 1 2 3 )
3 1 2 ,
231
по происхождению, он жил и- работал преимущественно в России.
Эйлер, выделявшИЙСЯ своей исключительной интуицией и разносто..
ронностью интересов, оставил rлубокий след практически во всех об.
ластях современной ему математики. Большое количество ero замеча-
тельных результатов явилось ОСНОВОЙ АЛЯ дальнейшеrо развития МНО-
rих разделов математики!
103
OpтorOHaпbHbI также и следующие две матрицы:
( 1 I 1... 1\ ( 123 ... п
222 ,.. 2 ) I 2 3 ... п
А=== 333...3, [З==\ 123...n
\n' n'n' . . . \, l' 2' 3' ....
(1)
Леrко видеть, что матрица порядка n является латинским
квадратом тоrда и только тоrда, коrда она ортоrональна
обеим матрицам А и В.
При построении кодов используются матрицы (1) и им
ортоrональные. Способ построения обеспечивает нужное
для декодирования число ортоrональных проверок; состоит
этот способ в СJ1едующе l.
Для матрицы С указанноrо типа и для любоrо ее эле..
мента k определим двоичную матрицу С k' которая получа..
ется из С заменой всех элементов, равных k, единицами,
а' всех остальных элементов нулями. Таким образом,
по матрице С порядка n строятся матрицы С 1 , С 2 , ..., Сп.
КаждоЙ из этих матриц C k сопоставим вектор 'V k , первые п ко-
ординат I{OTOpOro ЯВЛЯIОТСЯ последовательными "элементами
первой строки матрицы C k , следующие п координат эле
ментами второй строки и т. д. Иными словами, п 2 коорди
нат вектора fJk это все элементы матрицы С k' «вытяну..:
той» В одну общую строку. Образуем, наконец, матрицу С
порядка n Х п 2 , строками которой являются векторы fJ k :
( f/ 1 '\
ё == ? J .
\.f1 n
Например, для матрицы
С === ( ; )
3 I 2
имеем:
Cl== ( ) ' C2== ( ) ' сз== ( ) ,
010 001 100
v 1 === (100001 О 1 О), v 2 ==(0 101 00001), vз ==(00 1 О 1 О 100)
( 1 О О О О 1 О 1 О )
ё== о 1 О 1 О О О О l .
О О 1 О 1 О 1 О О
104
Пусть теперь А и В матрицы (1), а D 1 , D 2 ,. . .,D, ..
попарно ортоrональные латинские квадраты. Образуем из
них указанным выше способом матрицы 11, В, ы1' Ь 2 , . . .
. . . , D"'" а затем построим матрицу Н, которую можно ус.
ловно представить в виде:
( -- . \
,А
В
Ь1 . Вт
Ь 2 .
Н==
. I
I
....Ь, I
. )
(матрицы 11, B,D i ,D 2 ,.. .,D,подписываютсяоднаподдру-
rой и к получившейся матрице приписывается справа еди-
ничная матрица Е т соответствующеrо порядка т).
Матрицу Н будем считать проверочной матрицей кода,
построенноrо с помощью латинских квадратов. Число строк
этой матрицы, как вытекает из построения, равно (r+2)n,
а число столбцов составляет n 2 +(r+2)п. Кодовое расстояние
полученноrо кода, как мы увидим, будет не меиьше
,+3.
В качестве примера рассмотрим код, построенный с по..
мощью двух ортоrональиых латинских квадратов поряд-
ка 3: ·
( 1 2 3 )
D 1 == 2 3 1 .t
3 I 2
в этом случае
( 1 I 1 )
А=== 222,
333
I I 1 1 О О О О 6 О )
А==(ООО 111000,
\0 о о о о о I I I
( 1 О О О О 1 О 1 0\
D 1 :::::: \ 0 I О 1 О О О О 1 ) '
О О 1 О I О 1 О О
( I 2 3 )
D 2 == 3 1 2 .
231
( I 2 3 )
В== 123.
\1 2 3
( 1 О О 1 О О I О О )
В== 010010010 t
О О 1 О О 1 О О I
( 1 О О О 1 О О О 1 )
Ь 2 == О 1 О О О 1 1 О О .
О О 1 1 О О О 1 О
105
l aKOHeц) проверочная 1атрица искомоrо кода такова:
{111000000
О О О 1 ] 1 О О О
О О О О О О 1 1 I ()
1 О О 1 О О 1 О О
О 1 О О 1 О О 1 О
О О 1 О О 1 О О 1
Н=== 100001010
О 1 О 1 О О О О 1 I
О О 1 О 1 О 1 О О 1
1 О О О 1 О О О I 1
010001100 1
,,001100010 IJ
Леrко видеть, что для каждоrо из 9 информационны
симв€>лов может быть составлено четыре ортоrональных про-
верки. Например, перва.я, четвертая, седьмая и десятая 1
1
1
1
1
.:!
()
а,
«2
(/,0
aJ
а8
«12
«о
«5
"7
{f,
а4
«8
ал
ао
Рис. 25.
строки матрицы Н дают слеJ.ующие проверки для пер-
Boro символа ао:
сх. о ==а 1 +а 2 +а о ,
ао==аз+а6+а12'
а о ==а 5 +а 7 +а 15 ,
а о ==а 4 +а э +а 1э .
Ортоrональность этих соотношений, как можно убедиться,
как раз и объясняется свойством ортоrональности исход-
ных матриц. При этом число таких соотношений для
каждоrо символа всеrда равно числу матриц, использу- I
емых для построения, т. е. ,+2. А значит, кодовое рас- I
стояние не может быть меньше, чем '+3; в нашем примере
оно не меньше пяти.
106
На рис. 25 мы ПРИВОДИМ часть декодирующей схемы,
предназначенную для декодирования символа ао (буквой
М, как и раньше, обозначен мажоритарный элемент).
20. МАТРИЦЫ АДАМАРД И КОДИРОВАНИЕ
Важную роль в алrебре и комбинаторике
иrрают матрицы Адамара, которые впервые были введены
в латематический обиход в конце прошлоrо века *). Срав-
нительно недавно (в 1960 r.) было замечено, что эти
матрицы MorYT быть "использованы для построения кодов
с большим кодовым расстоянием (d;;::: [ ] ) ·
Квадратная матрица Н порядка п с элементами + 1 на-
зывается .fJ,tаmрuцей Адамара, если выполняется условие
ННТ==nЕn.
Вот несколько примеров матриц Адамара:
(1 )t
с ) "
п= 1 п= 2
{ 1 1 I I 1 I I I '\
I 1 1 I 1 l 1 1
(! ) I 1) I I I 1 I 1 l 1
l 1 1 I l l 1 1 I l 1
1 l I , 1 1 I I l 1 1 I .
l 1 1 1 l 1 1 l 1 l 1
п=4 1 1 l 1 l l 1 1
" 1 1 I 1 I 1 I l
п=8
Рассмотрим произвольную матрицу Адамара
(h 11 h 12 h 1n '\
Н == h 21 h 22 ' · · h 2n
. . . .
! . . .
h..==+l.
lJ
\ h п1 h n2 · · · h nn J
Из определения следует, что для любой пары СТрок с но..
мерами 1 и J (i=l=j) верно равенство:
h i1 h j1 + h i2 h j2 + · · · + hinh jn == о. (1)
*) ЖаI{ Адамар (1865 1963) один из крупнейших француэ
ских математиков конца XIX и первой половины ХХ века, аВТОр ря..
Аа основополаrающих работ в области теории чисел, алrебры и матема..
rическоrо анализа.
107
Таким образом, различные строки матрицы Адамара по..
парно ортоrоиальны. Далее, число слаrаемых В (1), рав-
иых + 1, должно совпадать с числом слаrаемых, равных
1. Следовательио, n четно и любые две строки совпадают
РОВИО в n/2 позициях и различаются в остальных.
Пусть теперь А двоичиая матрица, получающаяся из
матрицы Н замеиой элемеита + 1 иа О 1 на 1. .Ll\1иожество
векторов-строк матрицы А образует тоrда код с расстоя-
нием Хеммииrа между любыми кодовыми словами, paBHЫ 1
п/2. Так, из матрицы Адамара порядка 8 получаем мат-
рицу А, задающую код длииы 8 с кодовым расстоянием 4:
о О О О О О О О)
О 1 О 101 О 1
00110011
01100110
А == О О О О 1 1 1 1 · (2)
01011010
00110011
01101001
Не меияя кодовоrо расстояиия, можио УlVlеиьшить длииу
кода, если отбросить п рвый (нулевой) символ каждоrо
слова.
Указаниым образом из всякой матрицы Адамара поряд-
ка n можно получить двоичиый код Адамара, типа (n l, n,
п/2) (n l длииа кодовоrо -слова, n число слов кода,
п/2 кодовое расстояиие). Это, как правило, код, ие яв-
ляющийся лииейным.
С .матрицей А связаиы еще два кода, которые тоже на-
зывают кодами Адамара.
Первый из них получается так. Перейдем от матрицы
А к матрице А , заменив все элеl\1еиты матрицы А их допол-
нениями (т. е. замеиив единицы иулями, а иули едини-
цами). Тоrда строки l\1атриц А и А в совокупиости образуют
код типа (n, 2n, n/2), что леrко проверяется с помощью ра-
веиства (1).
Друrой код Адамара получается из предыдущеrо от-
брасываиием первоrо символа в каждом кодовом слове.
Это будет код типа (п l, 2п, 1) .
Например, из матрицы (2) можио получить таким спо-
собом коды Адамара типов (8,16, 4) и (7, 16,3).
Коды Адамара, как видио из их определеиия, обладают
иитересной особеииостью: расстояиие между любыми двумя
кодовыми словами одииаково и совпадает поэтому с кодо-
108
БЫМ расстоянием. Подобные коды называют эквuдuсmаnmны-
МИ, и в некоторых случаях их использование дает особые
преимущества.
Коды Адамара, обладая большим кодовым расстоянием,
позволяют соответственно исправить и большое количество
ошибок (первые два из них исправляют ошибки примерно
в четверти позиций кодовоrо слова). Достиrается это, ко-
нечно, ценой высокой избыточности.
Для построения и реализации кода Адамара той или
иной длины необходимо построить сначала матрицу Ада-
мара соответствующеrо порядка. Надо сказать, что такое
построение является совсем нелеrким делом, и этому воп-
росу посвящен внушительный раздел современной комби-
наторики. Некоторые методы построения будут рассмотре-
ны ниже в разделе «Задачи И дополнения» (см. также [4]).
С матрицами Адамара связан ряд нерешенных проблем,
одна из которых состоит в следующем. Мы уже видели, что
порядок n матрицы Адамара при n 3 может) быть лишь
четным. Более Toro, нетрудно доказать, что при n 4 по-
рядок обязаи делиться на 4 (см. дополнение 3). До настоя-
щеrо времени остается открытым вопрос: для любоrо ли
n, KpaTHoro 4, существует матрица Адамара порядка п?
Неизвестно, в частности, существует ли матрица Адамара
порядка 268 (это наименьший порядок, кратный 4, для ко..
Toporo матрица Адамара еще не построена).
Задачи и дополнения
1. У кажем наиболее простой способ построения матриц
Адамара сколь уrодно больших порядков. Пусть Н n матрица Ада-
мара порядка п и H п матрица с противоположными элементами.
Составим из них матрицу порядка 2п следующим образом:
Н ( Н п Нп )
2п== Н п Hп ·
Именно таким образом nолучались одна из друrой матрицы порядков
1,' 2, 4, 8, приведенные в начале этоrо параrрафа.
Доказать, что матрица Н 2n является матрицей Адамара.
2. Следующие две операции преобразуют матрицу Адамара снова
в матрицу Адамара:
1) перестановка строк (или столбцов);
2) 'умножение строки (или столбца) на 1.
С помощью этих операций любую матрицу Адамара можно преоб-
разовать в так называемую нормализованную матрицу Адамара, у
которой первая строка и первый столбец состоят из одних единиц.
3. Докажем, что если Н матрица Адамара порядка n>2, то n
кратно 4.
109
Действительно, можно считать матрицу Н нормализованной мат..
рицей Адамара. Переставляя ее столбцы, всеrда можно добиться"
чтобы первые три строки матрицы имели вид:
11 ."l 1 1
11.,.1 1 1
1 1 , , . 1 1 1
" , .
111
1 l l
l 1 1
, . .
. . .
. . .
111
l 1 1
1 l l
. , .
. . .
1
l
l
. , ,
. . .
Получается четыре типа столбцов. Пусть i, j, k, 1 означают соответст-
венно число столбцов nepBoro, BToporo, TpeTbero и четвертоrо типов.
Свойство ортоrональности строк влечет тоrда также равенства:
i+j k l==O,
i J+k l==O,
l j k+l==O,
Кроме Toro,
I+J+k+l==n.
И .. k 1 n
3 этих равенств получаем t == 1 == == == 4' откуда и следует наше
утверждение.
4. Изложим еще один метод построения матрицы Адам ар а метод
Пэли. Рассмотрим поле 7l р вычетов по модулю р, rде р простое
ЧИCJIо. Всякий элемент 7l Р' являющийся квадратом какоrо-либо эле..
Мента Toro же поля, называется квадратичны'м' вычетом, всякий дру"
rQii квадратичным невычетам. Определим на Zp следующую функцию
X (l ) , Н8зываеМУlО символом Лежандра *):
f О, если Т ==0;
Х (i) == 1, если i квадратичный вычет;
t 1, еrли i квадратиqный невычет.
Исходя из этоrо определения, можно доказать, что для всякоrо c O
выполняется равенство
% ( 1) Х (i + с) + х ( 2) Х (2 + с) + · · . + х (р 1) Х ( р 1 + с) == 1. (3)
Рассмотрим теперь квадратную матрицу Q порядка р, элементы
которой qij (i, j== 1, 2, . . ., р) определяются следующим образом:
Qij==X (j i) .
Пусть Е единичная матрица порядка р, а J квадратная матрица
Tor9 же порядка, все элементы которой равны 1. Тоrда, пользуясь (3),
.,. , .
можно доказать равенства
QQT==pE J, QJ==JQ==O. (4)
*) Адриен Мари Лежандр (I752 1833) французский матема-
тик, плодотворно работавший в теории чисел и в ряде разделов мате-
матичес){оrо анализа и механики!
110
Пусть теперь p==4k l. В этом случае матрица
tl 1 1 ...1)
1 ..........
.
H 1
. Q E.
.
\ I
..........
r
является матрицей Адамара порядка Р+ 1. Действительно, вычисляя
произведение Н Нт, получаем:
р+l
О
о ,.. о
ННТ==
j8,.............i'...
.
.
. .. '!I
.J+(Q E) (QT E).
.
о
................'.i..
Далее, как нетрудно проверить, матрица Q порядка p==4k 1 совпадает
с матрицей QT. Отсюда с учетом (4) имеем:
J +(Q E) (QT E) J + QQT Q QT +Е==
==J +pE J Q+Q+E==(p+ 1) Е.
Таким образом, Н НТ == (р+ l)Е.
5. В качестве примера построим матрицу Адамара порядка 8.
При этом р==7. Функция X(i) задается следующей таблицей:
70123456
Х (i) О 1 1 1 1 l l
Матрицы Q и н имеют тоrда вид:
о 1 1 1 1 l 1
1 О 1 1 1 1 1
I I О 1 1 1 1
Q== 1 l I О 1 1 l
1 1 l l О 1 1
1 l 1 1 1 О 1
1 1 l 1 l 1 О
[l 1 1 1 1 1 1 1)
1 ........1 1 1 ........1 1 ......1 1
1 l l 1 1 l 1 1
Н== 1 l 1 l 1 1 .......1 1
1 1 1 l 1 1 1 ......} .
1 1 1 1 1 ........1 1 1
1 1 ......1 1 1 1 l 1
1 1 1 1 1 l ......1 ....l}
6. Построить методом Пэли матрицу Адамара порядка 12 и найти
соответствующие коды Адамара. ' .
111
21. ЗАДАЧА ОБ ОЖЕРЕЛЬЯХ,
функция М.ЕБИУСА
И СИНХРОНИЗИРУЕМЫЕ КОДЫ
Некоторые вопросы теории кодирования
связаны с известной комбинаторной задачей, называемой
«задачей об ожерельях». Эту задачу можно сформулиро
вать следующим образом.
Пусть ожерелье состоит из бусинок нескольких цветов.
Спрашивается, сколько существует различных ожерелий,
если задано число бусинок ка)кдоrо цвета.
Располо}ким n бусинок по окружности, указав для
каждой бусинки' Hor..1ep ее цвета. Если обойти эту
окружность в определенном направлении, начав с не-
которой бусинки, то ожерелью
из n бусинок будет сопостав-
лено слово (аl а2.. .а n ), rде ai
есть номер цвета i-й бусинки. Но
обход можно начать с любой бу-
синки, поэтому любому ожерелью
соответствует n слов, получаемых
одно из друrоrо циклическими
сдвиrами. tIапример, для оже-
релья, представленноrо на рисун-
ке, получаем следующие слова:
12213, 31221, 13122,
21312, 22131 .
Вообще rоворя, среди n слов, сопоставленных ожерелью,
MorYT быть и одинаковые. Нас, однако, будут интересовать
не все ожерелья, а только такие, которые нельзя составить
из двух ил!l более одинаковых «кусков». Таким ожерельям
отвечают слова, которые нельзя составить из нескольких
одинаковых слов меньшей длины. Будем называть подоб-
ные слова основными. Например. слова 11, 100100100 не
являются основными, а слово 1011 основное. Ясно, что
каждому «несоставному» ожерелью отвечает n различных
основных слов.
Чтобы указать удобную формулу для числа основных
слов, нам потребуется так называемая функция Мёбиуса *),
*) ABrYCT Фердинанд Мёбиус (1790 1868) немецкий матема-
тик и астроном, известный, rлавным образом, своими работами по "роек..
тивноА rеометрии. Им были впервые систематически изучены свойст.
ва функции lA{n).
112
определяемая следующим образом:
J 1, если n == 1;
( l)k, если n произведение
ft(n) 1 простых чисел;
\. о в остальных случаях.
Обозначим через Р п(т) общее число осиовиых слов дли
ны п алфавита из т символов. Тоrда, как можно доказать,
Р n (т) == f.t (d 1 ) m п / d1 +!! (d 2 ) m п / d ! + . . . + (d k ) m п / dk , (1)
k различных
rде d 1 , d 2 ,. . ., dk все различиые делители числа п.
Формула (1) позволяет найти число интересующих нас
о}керелий, которое, очевидио, равно Р п(т)/п.
Выясним теперь, какое отношение имеет задача об оже
рельях к проблемам кодирования. Дело в том, что при пере
даче закодированных сообщений должна соблюдаться опре
деленная синхронность работы на передающей и приемной
сторонах канала связи, которая обеспечивается дополни
тепьными устройствами тактовыми rенераторами. Пря
сбоях этих reHepaTopoB происходит нарушение синхрони
зации, и в качестве начальноrо символа кодовоrо слова BOC
прииимается символ, который начальным не является. ОТ-
сюда актуальность задачи построения кодов, способных BOC
станавливать синхронизацию. Один из возможных путей
ее решения (если отвлечься от исправления ошибок в сим
волах) состоит в следующем. Будем рассматривать множе
ство п буквенных кодовых слов, удовлетворяющее такому
оrраничению: если (аl а2. . .а n ) и (Ь 1 Ь 2 . . .Ь п ) кодовыIe
слова (не обязательно различные), то никакое из «переи:ры..
тий» между ними
. (а 2 а з ...а n Ь 1 ), (а з ...а n Ь 1 Ь 2 ), ..., (aпbl...bп l)
не является кодовым словом. Коды с этим свойством назы
вают синхронизируеl\1ЫМИ, и они, как леrко понять, отве-
чают поставленной цели.
Как и обычно, платой за усовершенствование кода яв-
ляется уменьшение числа кодовых слов и, как обычио, воз..
никает вопрос, насколько велика эта плата. Для ответа иа
этот вопрос как раз и можно использовать решение задачи
об ожерельях. В самом деле, если а==(аl а2 аз. . .а n ) ко-
довое слово синхронизируемоrо кода, то кодовым словом не
может быть никакой ero циклический сдвиr, так как он яв.-
ляется перекрытием для пары (а, а). Кроме Toro, по той
же причине всякое кодовое слово должно быть основным.
t м.. Il. АрmИfIОВ. Л. Е. Садовсний
113
Поэтому маКСИlVlальное число п-буквенных слов синхрони-
зируемоrо кода, использующеrо алфавит из т символов,
не превосходит числа несоставных ожерелий с n бусинка-
ми т различных цветов. Обозначив это число через Wп(m),
имеем, следовательно,
1
W п. (т) n Р n (т).
rаким образом, пользуясь (1), получаем такую верхнюю
rраницу для числа п буквенных кодовых слов синхронизи-
pyeMoro кода:
W n (т) (I! (d 1 ) m n / d , + . . . + I! (d k ) mn/dk); (2)
(здесь di,. . .,d k по прежнему все различные делители п).
Можно доказать (но это достаточно сложно), что при не-
четных п rраница (2) действительно достиrается, и что это,
вообще rоворя, не так, если n четно. Относительно простые
выкладки показывают, что при больших п СУl\лма в скобках
близка к т Тl , т. е. к общему числу слов длины n в т-буквен-
ном алфавите, так что число допустимых слов синхронизи-
pyeMoro кода ПрИl'l1ерно в п раз меньше общеrо числа слов
длины n.
Задачи и дополнения
1. Доказать следующее свойство функции Мёбиуса:
Jl (пm)== fl (n)fl (т) для любых взаимно простых n и т.
2. Функция f называется СУ'м'маторной функцией для g, если
t (n) === }J g (d)
dtn
(запись dln означает, что суммирование распространяется на все раз-
личные делители числа п).
Показать, что сумматорная функция для функции Мёбиуса равна
нулю при n>1 и единице при n===1.
3. Пусть f....... сумматорная функция для g (см. задачу 2). Верна
следующая замечательная формула обращения Мёбиуса, лежащая в
основе всех приложений функции Jl(n):
g ===}J f .
dtn
Действительно,
}J J.t (njd) f (d) ==}J f.t (n/d) g (k) ==}J }J J.t (n/d) g (k). (4)
dln dln ktd dln kld
В получившейся двойной сумме изменим порядок суммирования. За-
метим для этоrо, что aprYMeHT k функции g (k) при двойном суммирова..
114
нии пробеrает всевозможные делители числа n, и если k фиксировано,
то d пробеrает все делители n, которые в свою очередь делятся на k.
Поэтому двойную сумму (4) можно переписать в виде:
g (k) f1 (njd) == g (k) 1-" (njd), (5)
kln kldln kln kld\п
при этом запись kfdln обозначает, что d пробеrает все делители n, деля.
щиеся на k. Введем обозначения m==n/d и t==n/k, тоrда т пробеrает все.
возмо)кные Делители t и в силу утверждения задачи 2
f1 (n /d) == f1 (т) == { 1, если t == 1 ,
kldln mlt О, если t > 1.
Следовательно,
f1 (njd) == { 1, если k == n, (k делитель n).
kldln О, если k < n
Обращаясь теперь к выражению (5), мы видн;ч, ЧТО в сумме по k
имеется лишь одно ненулевое слаrаемое, отвечающее значению k===n,
и потому
g (k) р, (njd) == g (n),
kln k'd"1
что равносильно (3).
4. Назовем число d периодом (Д ;)a и, если а получается сочленением
одинаковых слов длины d и не является сочленением одинаковых слов
меньшей длины. Пусть Р d (т) означает общее число слов длины n в
алфавите из т символов, имеющих период d.
Убедиться, что
,:. Pd(m)==mn,
dln
и, пользуясь формулой обращения (3), получить оценку (2).
S.
ЗАКЛЮЧЕНИЕ
Наши рассказы о кодировании подошли
к концу. Мы познакомились, конечно, далеко не со всеми
задачами этой теории, но в той или иной мере затронули
три ее основных направления.......... кодирование с целью
засекречивания сообщений, кодирование с целью сжатия
информации, наконец, кодирование с целью исправления
и обнаружения ошибок. Нам хотелось дать представление
читателю, сколь широки. и мноrообразны связи этой тео-
рии с разными разделами математики, и как порой самые
абстрактные математические теории MorYT с успехом при-
меняться для решения практических задач.
Дальнейшее проникновение в проблем:атику теории ко-
дироваиия (подробное изучение циклических кодов и их
обобщениЙ, знакомство с кодаl\tlИ, исправляющими пакеты
ошибок, и специфическими алrоритмами их декодирования
и т. д..) требует уже значительно более серьезной математи-
ческой подrотовки. Впрочем, интересующийся читатель мо-
жет при желаиии обратиться к литературе, список которой
приводится В конце книrи.
ПРИЛОЖЕНИЕ
в ШКО..тIЬНОЙ математике рассматриваются раЗЛИЧНt) е
операции над числами. Простейшие из них сложение и обраТIIа к
нему операция вычитания, и умножение, для KOToporo обратной опера-
цией является деление. Подобные действия приходится производить
не только над числами, но и над друrими, более СJIО)КНЫМИ объектами.
Это можно обнаружить уже и в школьном курсе: на уроках rеометрии
и физики учат складывать и вычитать векторы, а на уроках алrебры
рассматривают операции сложения и умножения мноrочленов. Однако
список таких объектов rораздо обширнее. Мы познакомимся с неко.
ТОрЫ IИ из НИХ, наисолее важными для наших целей.
1. Сравнения и классы вычетов
Исходным материалом для нас остаl<Л ся пока все }ке
числа. Два целых числа а и Ь называют срдвниМ,ыМ,и по м'одулю n (n
натуральное), ес..тIИ их разность а b делится на n без остаТ1<:а *}.
Это выражают следующей записыо:
а == ь (mod n).
(1)
Число n называют МОДУЛЕМ сравнения (1). Например, 35 == 2 (mod 11),
так как разность 35 2== 33 делится на 11; аналоrично, 25 == 1 1 (mod 9).
так как 25 ( II)== 36 делится на 9.
Запись а == О (mod n) означает тоrда, что само число а делится на n,
1. е. a==k.n.
Если зафиксировать некоторый модуль сравнения n, то всякое
натуральное число с можно единственным образом представить в виде
c==kn+r, (2)
rAe k частное от деления на n, а r octaToK, совпадающий с одним
*) Понятие сравнимости впервые было введено великим немец..
ким математиком Карлом Фридрихом rayccoM (1777 1855) в ero трак..
тате «Арифметические исследования» и является ОДНИМ из основных
понятий теорИИ чисел.
117
из чисел
О, 1, 2, . i ., n 1.
(3)
Остаток, называют также вычетом числа с по модулю n. Заметим,
ч '1 о запись вида (2), rде OEQ" n.......l j допускают не только натуральные,
н о и любые целые числа. Очевидно, из равенства (2) следует, Что с==
=== ,(mod n), т. е. всякое число сравнимо со своим остатком (вычетом) по
модулю n. Пусть теперь а и Ь ....... два произвольных числа, 8аписанные
в виде (2):
а== ktn+'i, b==k 2 n+'2'
Ка)кдый из остатков '1 и '2 это ОДНО из чисел (3), поэтому И
разность может делиться на n лишь в одном случае, коrда '1=='2' Но
тоrда и разность а Ь== (k1 k2)n+'i '2 может делиться Н1 n тоrда
и только тоrда, коrда '1=='28 Отсюда следует, что а == Ь (mod n) '}'оrда
и 'Iолько тоrда, коrда числа а и Ь имеют одинаковые остатки при делении
l1а n.
В теории чисел (см., например, [5]) доказывается ряд свойств
сравнений, во MHoroM аналоrичных свойствам обычных равенств. По-
добно тому, как мы это делаем с равенствами, сравнения по одинако-
вому модулю можно складывать; перемножать и т. д. (так, перемножив
сравнения 17 == 5 (mod 4) и 7==3 (mod 4), получим, как нетрудно убедить-
ся, верное сравнение 119 == 15 (mod 4). Вообще, если а1 == Ь 1 , а2 :::=' Ь 2 , то
а1+ а 2 -:= Ь 1 +Ь 2 ' а1 а 2 ==' Ь 1 Ь 2 .
Значение этих свойств заключается в '10М, ЧТО при рассмотре ии
ЕОПРОСОВ делимости чисел и различных числовых арифметических
выра,кений мы можем входящие в эти выражения числа заменять на
друrие, сравнимые с ними по данному модулю n; в частности, каждое
число может Бы1ь заменено своим вычетом. Проиллюстрируем сказан-
ное следующей задачей.
Доказать, Ч10 число (1981)k+ (1982)k при любом нечетном нату"
ральном k делится на 3.
Замечаем, что 1981 ==. 1 (mod 3), 1982==2 (mod 3). Заменяя в исход-
ном выражении числа 19В1, 19В2 их вычетами по модулю 3, по.пучаем
(19В l)k + (1982)1l == 1 + 2 k (mod 3).
Следовательно, левая часть сравнения делится на 3 тоrда и только
тоrда, коrда на 3 делится сумма 1+2k. Для степеней двойки имеем:
22 ==. ], 23 ==2 , 24==1, 20 == 2 и т. д. Вообще, применяя индукцию по k,
беждаемся, что 2 k =:1 при k четном и 2 Я ::= 2 при k нечетном. Таким
образом, при нечетном k
1+21ls=1+2e=O (mod3).
'1'. е. eC H k нечеТНО J ТО исходное выражение делится на 3,
118
В разобранной задаче числа 1981 и 1982 моrли быть заменены
JIюбыми числами а и Ь, дающими пр и делении на 3 остатки COOTBeTCT
Бенно 1 и 2. Ни утверждение задачи, ни способ ero доказательства от
этоrо не изменились бы. Таким образом, в некоторых вопросах все
числа, имеющие один и тот же вычет, по модулю п, и, следовательно,
сравнимые между собой по этому модулю, оказываются взаимозаме-
няемыыи. Объединим все их в один класс, обозначаемый ,:
r {с I с ==. , (mod n)}.
(4)
Иными словами, класс r состоит из всех тех целых чисел, которые
записываются в Биде (2). Класс, определяемый равенством (4), назы
I Бают классом вычетов. Каждому вычету О, 1, 2, . . ., n 1 отвечает свой
класс вычетов, так что имеется ровно n различных классов
О,
1 , 2,
. . . ,
n l.
(G)
Ясно, ЧТО эти классы попарно не пересекаIОТСЯ и каждое це IJО ЧИС<IIО
попадает ровно в один класс.
Мы обнаруживаем, далее, что используя операции сложения и
( множения чисел, можно производить аналоrичные операции и над
классами вычетов.
В самом деле, пусть '! и два класса вычетов. Выберем любые
два числа из этих классов: а1 Е '1 , а2 Е'2' Пусть оказалось, что сумма
: аl+а2 имеет вычет " а произведение аlа2 вычет s:
аl + а2 Е , ,
а1 а 2 Е S:-
Тоrда будем считать, что «сумма» классов 'i. и '2 равна" а их «произ-
\ ведение» равно s:
\
'1+'2=="
'1"2==S.
Законность этоrо определения обосновывается тем, что класс, KoropoMY
принадлежит сумма а1 +а2 (соответственно произведение аlа2) не за.
висит от выбора элементов аl и а2 в .классах '1 и '2 .
Поясним данное определение на примере, взяв за модуль срав-
нения число n== 2. В этом случае имеем два класса вычетов О и
а операции над ними выrлядят так:
0+ 0== 0;
о · 0== 0;
0+1 == l-1 O 1 ; т + т == 0 ;
о !! Т == Т · 0 == о; 1. Т == 1:
Часто, коrда 9ТО не вызывает путаницы, в обозначениях классоPi
вычетов опускают черту, записывая их как обычные натуральные
числа. В основном тексте книrи это делается без специальных oroBopoK. ,
Выпншем, например, таблицw сложения и умножения классов по
119
+ о 1 2 1 з
I I
О О 1 2 3
1 1 2 3 О
2 I 2 3 I о 1
I
3 3 О 1 2
. о 1 2 3
О О О О О
1 О 1 2 3
2 О 2 О 2
3 О I з 2 1
Эти таблицы можно пони мать и буквально, считая, что они опре..
дел нют две опер ации Н.1 множестве {О, 1, 2) 3} ....... СЛО}l{ение и умножение
110 модулю 4,
2. rруппы
Прежде чем дать определение rруппы, рассмотрим один
важныи пример.
Будем исходить из понятия взаU.МJ10 однознаЧНО20 оmображеиuя
множества на себя. В случае конечноrо множества такое отображение
называют обычно пoдCтaH06КfJй. Пусть множество М состоит из чисел
1, 2, 3: М== {t, 2, 3}, Чтобы задать какую-либо подстановку множе-
ства М, достаточно указать для каждоrо из чисел 1, 2, 3 то число, в
которое оНо 010бражается этой подстановкой. Удобнее Bcero сделать
это, использовав таблицу из двух CTpOK, В первой CTpOI{e выписы.
ваются (в любом порядке) числа 1, 2, 3, а во второй под каждым из них
ПИIllется соответствующее ему при данной подстановке число. Скажем,
обе табл ИЦЫ
( 1 2 3 )
2 3] ·
( 2 3 1 )
312
задают одну и ту же подстановку: число 1 переходит в число 2, 2
в 3, 3 в 1. Нетрудно указать все различные подстановки множества
А1. их будет шесть:
( 1 2 3 )
01 == 1 2 3 J
( 1 2 3 )
о, == 2 З) ,
( 1 2 3 )
О, == 1 3 2 '
( 1 2 З )
06 == 3 1 2 I
( 1 2 З )
аз == 2 1 3 '
( 1 2 3 )
06 == 3 2 1 !
120
операцию умножения (или ко.мпозuцuю) подстановок. Именно, произ-
ведением подстановок аЁ и а j будем называть подстановку (Jk, получаю-
щуюся в результате последовате.пьноrо выполнения сначала подста-
новки 0i) а затем а j (записывается: (Ji(J j== (Jk). Например,
( 12 3 ) (12 3 ) == ( 12 3 )
3 1 2 \1 3 2 2 1 3
(первая подстановка переводит число I в число 3, после чеrо вторая
подстановка переводит число 2 в число 3, так что в результате после-
довательноrо выполнения подстаНОБОК число 1 перейдет в число 2
11 Т, д.). Читатель может проверить, что
( 1 2 3 ) ( 1 2 3 ) ( 1 2 3 )
132 312 == 321'
и тем самым убедиться, что произведение двух подстановок зависит,
вообще rоворя, от порядка сомножителей.
Множество S с определенной выше операцией умножения называlОТ
еру ппой подстаново1\, множества М.
Операция умножения на S обладает следующими свойствами.
В о-первых, эта операция ассоциативна: для любых (Ji, Oj! (Jk
(о ,а j) (J k == (J i (о j(J k).
BO-Вl0РЫХ, тождественная подстановка
( 1 2 3 )
а1 == 1 2 3 '
лереводящая каждый элемент в себя, иrрает роль единицы в обычном
умножении, а именно, для люсой подстановки а;
а 1 О i == о , а 1 == (J i .
Наконец, BM€CTe с каждой подстановкой О; множество S содержит
обратн)'ю ей подсrановку (Jj' которая переводит число а в число Ь тоrда
и только тоrда, коrда а; переводит число Ь в число а. При этом, понятно,
каждое из произведений aiOj и О}О; будет тождественной подстановкой:
о i a j == а jO i == а 1.
Эти три свойства сохранятся, если распространить определение
множения подстановок множества {l, 2, 3} на случай подстанов(н{
Jlюбоrо конечноrо множества.
Более Toro, выяснилось, что имеются самые разнообразные си-
стемы объеl<:ТОВ с операцией, обладающей указанными свойствами.
121
Это привело к следующему (общему) определению rруппы *}.
Множество а, на котором определено умножение элементов, назы-
вается ёруnnОЙ, если выполняются три аксиомы:
1. Умножение ассоциативно: для любых элементов а, Ь, с из а
а (Ьс)== (аЬ)с.
2. В множестве G существует такой едuничный элемент е, что
еа== ае== а.
3. Для каждоrо элемента а !\!ножества G существует в а такой
обрапl1iЫЙ элемент а 1, что
aa l ==a a==e.
Ос ращаем внимание читателя на то, что в приведенном опреде-
лении rоворится об умножении элементов и используется связанная
с обычным умножением терминолоrия и символика. Этой «мультипли-
катив ной» терминолоrии мы и будем в дальнейшем придерживаться.
Однако термин «умножение» нельзя понимать буквально; речь идет
о любой операции, удовлетворяющей данным аксиомам. В частности,
в ряде случаев естественнее называть операцию сложением и соот-
ветственно переформулировать аксиомы rруппы, пользуясь термино-
лоrией, связанной со сложением (<<аддитивной» терминолоrией):
1. Сложение ассоциативно: для любых ЭЛементов а, Ь, с из G
(а+Ь)+с==а+ (Ь+с).
2. Существует такой нулевой элемент О, что для любоrо элемента а
из G
а+О==О+а== а.
3. Дл я каждоrо элемента а существует такой противоположныЙ
элемент ( a), что
а+ ( a)== ( a)+a==O.
rруппа подстановок, определенная выше, является, как мы видим,
одним из примеров rруппы. Вообще взаимно однозначные преобразо..
nания ЛIобоrо множества образуют rруппу относительно операции
умножения преобразований (эти rруппы сыrрали основную роль в
формировании общеrо понятия rруппы).
Читатель обнаружит далее, что мноrие примеры rрупп ему уже
известны. Перечислим некоторые из них:
*) В виде, близком к современному, определение rруппы было
впервые сформулировано а r!II:Ii1 J\ИМ математиком А. КЭJlИ в 1854
rоду.
122
1. Множество всех не нулевых действительных чисел относительно
операции умножения «мультипликативная rруппа действительных
чисел» IR * .
2. Множество всех целых чисел относительно операции сложе-
ния «аддитивная rруппа целых) чисел» Z.
3. Множество всех векторов в пространстве относительно опера-
ции сложения векторов.
4. Множество всех мноrочленов с действительными коэффициен-
тами относительно операции сложения мноrОЧЛенов.
rруппы в примерах 1 4 имеют бесконечно MHoro элементов, а
rруппа S конечная (6 элементов). Число элементов конечной rруппы
называется ее порядком.
Из аксиом rруппы можно вывести, что в rруппе существует только
один единиЧный элемент. Можно доказать таюке и единственность
обратноrо элемента для всякоrо элемента rруппы.
Пример rруппы подстановок показывает, что умножение в rруппе
может быть некоммутативным. Те rруппы, для которых опера-
ция коммутативна, так и называются коммутативными (примеры
1 4) .
Если некоторое подмножество Н rруппы G само образует rруппу
относительно операции, определенной в а, то подмножество Н назы-
BalOT nодеруnnой rруппы а.
Например, подмножества Н 1 == {O'i, 0'2} и Н 2 == {O'i, 0'4' а 5 } rруппы S
ЯВЛЯ..JТСЯ подrруппами этой rруппы. Подмножество четных целых
чисел есть подrруппа аддитивной rруппы Z всех целых чисел, а под-
множество нечетных чисел не будет подrруппой этой rруппы (сложение
на Z не задает операцию на этом подмножестве, так как сумма двух
,печетных чисел есть число четное).
Имеет место следующая теорема.
Длл ,поео чтобы подмножество Н являлось nодеруппой еруппы а,
необходuмо и достаточно, чтобы выnолнялuсь два условия:
1) nроuзведенuе любых элемеНlnов hi, h 2 из nOaMHOJfCeClпBa Н также
является эле/11.ентом из Н (h 1 h 2 Е Н);
2) если hEH, то u обратный 1(, нему элемент прuнаiJАежuт
/1 (11, lEH).
Наиболее просты так называемые циклические nодеруппы, кото-
рыми обладает любая rруппа а. Со всяким элементом g Е G можно свуо-
зать ( порожденную» им циклическую подrруппу, которая, по существу,
представляет собой наименьшую из подrрупп, содержащую данный
элемент. Чтобы определить ее, введем понятие степени элемента g,
полаrая gO== е и для любоrо натуральноrо k
gk == gg. . . g, g.... k == (gk) -- J!.
k сомножителей
Пр 11 таком определении степени выполняются орошо знакомые
)23
нам правила действий со степенями: для любых целых чисел т и п
gmgn==gm+n, (gm)n==gmn.
ЯСНО, что всякая подrруппа, содержащая элемент g, должна со..
держать любые ero степени. С друrой стороны, у?Ке само множество
степеней образует, как нетрудно уб.едиться, rруппу.
Указанную rруппу называют циклической подrруппой, порож..
денной элементом g; ее обозначают символом (g), а сам элемент g назы-
вается образующим элементом этой rруппы.
Может случиться, что для HeKoToporo элемента g циклическая
подrруппа (g) совпадает со всей rруппой О, и тоrда rруппа G также
называется циклической. Например, аддитивная rруппа целых чисел
есть циклическая rрупла с образующим элементом 1 (или ......1)' а ее
лодrруппа четных чисел..... циклическая с образующим элементом 2.
Являясь наиболее простыми, циклические rруппы служат важным
инструментом для изучения rрупп, имеющих более сложное строение.
Между rруппой и любой ее подrруппой существует определенная
связь, которую можно охарактеризовать с помощью понятия с меж"
Horo класса по подrруппе.
Пусть Н...... подrруппа rруппы G и gEG ..... произвольный элемент
rруппы G (мы не требуем, чтобы он обязательно принадлежал ПОД"
rруппе). 1\1ножество всевозможных произведений gllj rде h ЛIобой
элемент подrруппы Н, называется смежным клаССОJt (точнее, левым
смеЖНЫАt классом) по подrруппе Н, а элемент g ero nредспzавителем.
Обозначая левый смежный класс через gH, имеем, следовательно,
gH=={gh I hEH}.
Аналоrично определяются правые смежные классы l/g. Если rруппа
G коммутативная, то Hg==gH.
Для смежных классов, безразлично, левых или правых, справед"
ливы два основных факта.
1. В случае конечной подrруппы /1 число элементов в любом смеж-
ном классе одно и то же и совпадает с порядком подrруппы.
2. Любые два смежных класса glH и g2H либо совпадают, ли(jо
вовсе не имеют общих элементов.
Для иллюстрации понятия смежноrо класса рассмотрим следующий
пример.. ПУС1Ь z..... аддитивная rруппа целых чисел, а Н..... ее под-
rруппа, состоящая из чисел, кратных пяти. Тоrда можно «BbInI C'aTb»
следующие смежные классы:
Н+О=={..., .......10' ----5' О, 5,10, ...},
Н + 1 == { . . ., ---- 9, .......4, 1, 6, 11, ...},
н + 2 == { . . ., ...... 8, .......3' 2, 7, 12, .. 11 },
Н+3=={...,..... 7, .......2' 3,8,13, ...},
Н+4=={\!"....... 6, lJ 4,3,14, ...}.
124
Читатель сразу )ке заыетит, что это классы вычетов О, 1 J 2t З, 4 по мо-
дулю 5. Леrко видеть, что всякий смежный класс Н+п совпадает с
одним ИЗ этих пяти) и что классы эти не Пересекаюtся! Непосредственно
видно также, что
Z==(H+O) U (H+l) U (Н+2) U (Н+8) U (Н+4).
Оказывается, то же самое верно для любой rpYnnbI: если Hgf,
Hg 2 , · · ., Hg r ...... все различные (правые) смежные классы rруппы G по \
подrруппе Н, ТО
a Hel U Hg 2 Utt U Hg,.
в случае, коrда G и Н конечные труппы порядков т и 11" из
fl0.следнеrо равенства вытекает, что т==п 'f. }.\ы пришли к слеДУlощей
теореме Лаrранжа *):
П орядок; любой подёруnпы конечной еруппы является де лuтелем.
порядка еруппы.
Мы привели здесь простейшие определения и факты теории rрупп.
За дальнейшими сведениями читатель может обратиться, например, к
квиrам [8J, [9J.
3. Кольца и поля
Часто приходится рассматривать множества, на кото-
рых определены две операции, например, различные числовые множе-
ства, множества мноrочленов, множества классов вычетов с опреде-
ленными на них операциями сложения и умножения. Выделяя ое-
которые свойства этих операций, общие для всех указанных множеств,
мы приходим К еще одному важному алrебраич€скому поняТию..... по..
нятию кольца.
Кольцом. называется (не пустое) множество К, на КОТОрОМ опре..
делены две операции (СЛОjJ{ение и умножение), обладающие следующими
свойствами:
1) множество К относительно сложения образует коммутативную
rруппу;
2) умножение ассоциативно: для любых й, Ь, с Е к
(аЬ)с==а(Ьс);
*) Лаrранж (l736 1813) великий французский математик;
ero труды по математическому анализу, механике и теории чисел име-
ют важнейшее значение для развития этих дисциплин. лаrранж.......
один из создателей дифференциальноrо исчисления, КJ1ассичес ой
1еории дифференциальных уравнений и вариационноrо ИСЧИСJ1ёния.
12
3) сложение и умножение подчиняются дистрибутивному закону:
(а+ Ь) с== ас+ Ьс, с (а+ Ь) ca+ сЬ
для любых а, Ь, сЕК.
При этом множество К, рассматриваемое лишь относительно опе"
рации сложения, называется аддитивной еруnnой кольца,
Приведем некоторые примеры колец.
1. Множество целых чисел с операциями сложения и умножения
кольцо целых чисел Z.
2. Множество мноrочленов от oAHoro неизвестноrо с действитель-
ными коэффициентами с операциями сложения и умножения MHoro.
членов кольцо мноrочленов IR[X].
3. Множество классов вычетов по модулю n с операциями сложе-
ния и умножения классов кольцо классов вычетов Zn'
Читаlелю предлаfается проверить выполнимость аксиом кольца
в каждом из примеров. Остановимся подробнее на примере 3.
Поскольку операции над классами вычетов сводятся к операциям
над числами из этих классов, то свойства ассоциативности и комму-
тативности ЭТИХ операций вытекают из аналоrичных свойств числовоrо
сложения и множения. То же замечание относится к свойству Дистри.
бутивности. Роль нулевоrо элеменrа при сложении иrрает класс о.
Проти воположным элементом для класса вычетов r=i= O является класс
n (. Из определения сложения классов следует, что
r+(n r )== O .
в общем определении кольца не содержится требование комму.
тативности умножения. В том случае, если умножение обладает этим
дополнительным свойством, кольцо называется коммутативным. В при-
мерах 1......3 мы имеем как раз коммутативные кольца, а позднее (в при..
ложении 5) познакомимся с важным примером некоммутативноrо
кольца.
УМНО.iкение в кольце, как и в rруппе, является асеоциативноЙ
операцией, но друrие свойства rрупповоrо умножения в кольце MorYT
не БЫПОЛВя.ться. Правда, большинство важных колец содержат еди-
ничный элемент относительно умножения (скажем, кольца из примеров
1 3), но и такие кольца заведомо содержат элементы, для которых
не существует обратноrо (необратимые элементы). В любом кольце
необратим элемент О....... нулевой элемент относительно сложения, так
как доказывается, Что он отличен от единичноrо и ЧТО дЛЯ Лlобоrо а Е к
имеет место:
о ,а==а .0==0.
Как показываЮi примеры 1 и 2а необратимыми MorY1 быть и ненулеВЫ6
12а
елементы. Так, в кольце целых чисел обратимы лишь 1 и 1) всякое
друrое n:tf:O в кольце Z не имеет обратноrо, так как l/n Z.
Рассмотрим таблицы wмножения ненулевых sлементов в КО.пьцах
вычетов Z 4 и Z 5'
Таблица 19
. I 1 2 3
1 1 2 3
2 2 О 2
3 3 2 I
т а б л и ц а 20
. 1 2 З 4
1 1 2 З 4
2 2 4 1 3
3 3 1 4 2
4 4 3 2 f
Таблица 19 показывает, что в кольце MorYT существовать ненуле-
вые элементы, произведение которых равно нулю: в Z4 2-2==0. Из
8ТОЙ же таблицы видно, что класс 2 необратим. Вообще, можно дока-
зать, что ненулевые элементы, произведение которых равно нулю (на-
8ываемые делителями нуля), всеrда необратимы. С друrой стороны,
таблица 20 показывает, что в кольце Z5 всякий не нулевой элемент
обратим. Кольца с этим СВОЙСТItОМ имеют особое аначение. Примем
такое определение.
Коммутативное кольцо с единицей, в котором всякий ненулевой
элемент обратим, называется полем.
Множество ненулевых элементов поля относительно умножения
образует в силу определения поля коммутативную rруппу, которая
называется мультunлuкатuвной еруnпой поля.
Простейшими примерами числовых полей являются поле рацио..
нальных чисел Q и поле действительных чисел /R (разумеется, отно"
сительно операций сложения и умножения чисел). Полем, как ясно из
предыдущеrо, является и кольцо Z5' Вообще, можно доказать, что при
любом простом р (и 10ЛЬКО В этом случае) кольцо вычетов Z р является
полем. Оно называется полем вы.четов по .модулю р. В таблице 21 указаны
элементы, обратные к ненулевым элементам поля вычетов Z 7.
21
Поля вычетов Zp являются простейшими примерами конечных
полей. В алrебре .р.оказывается, что в произвольном конечном поле
число элементов q всеrда есть степень простоrо числа: q== рn. Справед-
ливо и обратное утверждение: для любоrо q, являющеrося степенью
npOCToro числа, существует поле с q элементами.
т а б л и Ц а 21
k 1 2 3 4 5 6
k ). 1 4 5 2 3 6
Конечные поля часто называют полями rалуа (их обозначают
ОР (q)); важное их свойство, используемое, в частности, и в теории
кодирования, состоит в следующем:
Мульmиnликаlпивная еруппа поля Талуа являеmся циклической
ерупnой порядка q 1.
ОбраЗУIОЩИЙ элемент МУЛЫИП.i'1икативной rруппы поля fалуа
наэываIОТ примитивным элементом. Так, в поле Z'1 примитивным
ЭЛемеН10М является класс вычетов 3. ДеЙствительно, ero степени
3, 32 == 2, 33 == 6, 34 == 4, 35 == 5, 36 == 1
исчерпывают все ненулевые элементы поля.
Заметим, что класс :2 не является пр имитивным элеМентом в Z 7'
так как среди ero степеней нет, например, класса 3. в то же время
имеется очень MHoro простых чисел р, для которых элемент 2 прими..
'Сивев в Zp' Так обстоит дело в полях Zз, Z5' Zii И т. д. В теории
чисел известна следующая до сих пор не решенная задача:
Бесконечно ли множество тех простых чисел р, для которых 2
является примитивным элементом в Z р?
Интересно, что с ответом на этот вопрос свяаано решение неко-
'сорых проблем теории кодирования.
В заключение определим еще одно важное понятие, связанное с
кольцом, понятие идеала,
fl0дмножество J КОJlьца К наэывае1'СЯ ero (двусторонним) идеалом,
если оно само является кольцом относительно операпий на К и если
для любых элементов а Е /( и Ь Е I оба произведения аЬ и Ьа принад-
лежат J.
Так, МНО)l{ество четных чисеJf есть идеал кольца Z. Читатель
JIerRU провеРИТ I что и вообще ВСЯКое, множество qИС Jl: KparHbIX ка-
кому-нибу ДЬ числу k, является идеалом кольц' Ж.
Рекомендуем читателю иаiIтn идеалы, КQлед вые1'QI; Z . Zat Zs
tJ КОЛЬ1\8 мноrочленоа R(X),
128
4.. Арифметическое п-M pnoe
векторное пространство
Всякая точка на плоскости при выбранной системе
координат задается парой (а, ) своих координат; числа а и можно
пони мать также как координаты радиуса вектора с концом в этой точке.
Аналоrично, в пространстве тройка (а, , ,\,) определяет точку или
вектор с координатами а, , 1'. Именно на этом основывается хорошо
известная читателю rеометрическая интерпретация систем линейных
уравнений с двумя или тремя неизвестными. Так, в случае системы
двух линейных уравнений с двумя неизвестными
аl Х + Ь 1 У == Сl'
а2 Х + Ь 2 У == С2
каждое из уравнений истолковывается как прямая на плоскости (см.
рис! 26), а решение (а, ) как точка пересечения этих прямых И.,1И
:с
Рис. 26.
как вектор с координатами а и (рисунок соответствует случаю, коrда
система имеет единственное решение).
Аналоrично можно поступить с системой линейных уравнений с
тремя неизвестными, интерпретируя каждое уравнение как уравнение
плоскости в пространстве.
В математике и различных ее приложениях (в частности, в теории
кодирования) приходится иметь дело с системами линейных уравнений,
содержащих более трех неизвестных. Системой линейных уравнений с n
неизвестными Xf, Х2' · · ., Х N называется совокупность уравнений вида
аl1 Х l + а12 Х З + !I' t +аlnХn
а21 Х l --t а22 Х З + ' ! , + а2n Х п
== b 1 .
== Ь з .
(1)
,.! !t.".. ".!I
а т l Х l + а т 2 Х 2 + ! t t + а;'nхn == Ь т t
129
rде aij и bi произвольные действительные числа. Число уравнений
в системе может быть любым и никак не связано с числом неизвестных.
Коэффициенты при неизвестных аи имеют двойную нумерацию: первый
индекс i указывает номер уравнения, второй индекс j номер неиз-
BeCTHoro, при котором стоит данный коэффициент. Всякое решение
системы понимается как набор (действительных) значений неизвестных
«(;(i, (;(2, · · ., (;(n)' обращающих каждое уравнение в верное равенство.
Хотя непосредственное rеоме1рическое истолкование системы (1)
при n >3 уже невозможно, однако вполне возможно и во мноrих от-
ношениях удобно распространить на случай произвольноrо n reoMeT-
рический язык пространства двух или трех измерений. Этой цели
и служат дальнейшие определения.
Всякий упорядоченный набор из n действительных чисел (CXil СХ2, . . .
.. . ., СХ n ) называется n-мерным арифметическим вектором, а сами числа
(;(1, 0:2, . . ., СХ п координатами 9Toro вектора.
Для обозначения векторов используется, как правило, жирный
шрифт и для вектора а с координатами СХl' а 2 , . . ., СХ п сохраняется
обычная форма записи:
а == ( СХ l, СХ2, ... СХ n )'
По ана.п:оrии с обычной плоскостью множество всех п-мерных век..
торов, удовлетворяющих линейному уравнению с n неизвестными,
называют еиnерnлоскостью в n-мерном пространстве. При таком оп-
ределении множество всех решений системы (1) есть не что иное, как
пересечение нескольких rиперплоскостей.
Сложепие и умножение n-мерных векторов определяются по тем
же правилам, что и для обычных векторов. А именно, если
а == (аl, СХ2, '.', (;(n)' Ь == ( 1' 2' "', n)
(2)
два n-мерных вектора, то их суммой называется вектор
а+Ь== ( СХ l + 1' (;(2+ 2' ..., сх n + n)'
(3)
Произведением вектора а на число л называе1СЯ вектор
ла==( ла l' Л(;(2, .", лап)'
(4)
Множество всех n-мерных арифметических векторов с операциями
сложения векторов и умножения вектора на число называется apи
метическим n-мерным векторным nространством L n'
Используя введенные операции, можно рассматривать произволь-
ные линейные комбинации нескольких векторов, т, е. выражения вида
lal + Л2 а 2 + '.. + Лkаk,
rде лi действительные числа. Например, rлинейнЗ'я комбинаций
векторов (2) с коэффициентами л и f..t это вектор
ла + !1Ь == ( ла l + fl l' ЛCt2 + fl 2' !,. J лап + !1 п)'
130
В трехмерном пространстве векторов особую роль иrрает тройка
векторов i, jj k (координатные орты), по которым разлаrается любой
вектор а:
a==xi+y}+zk,
rде х, у, z действительные числа (координаты вектора а).
В n.MeprioM случае такую же роль иrрает следующая система век-
торов:
еl==(1, О, О,
e ==(O, 1, О,
ез==(О, О, 1,
. . .
, О),
, О).
, О).
(5)
. . .
. . .
. . . .
еп==(О, О, О, . . . , 1).
Всякий вектор а есть, очевидно, линейная комбинации векторов ei,
е2, !!., е п :
а ==аlеl +а2е2+... +а п е 1l ,
(6)
причем коэффициенты ai, а 2 , . . ., а п совпадают с координатами век-
тора а.
Обозначая через О вектор, все координаты KOToporo равны НУЛIО
(кратко, нулевой вектор), Rведем следующее важное определение:
Система векторов ai, а2, . . ., ak называется линейно зависимой,
если существует равная нулевому вектору линейная комбинация
Лl а l +Л2 а 2+'.. +Лkаk==О,
в которой хотя бы один из коэффициентов Лf) ""2, . . ., Лk отличен от
нуля. В противном случае система называется линейно llезависимоu.
Так, векторы
.al==(I, 0,1,1), a2==(I, 2,1,1), аз==(2, 2,2,2>
линейно зависимы, посколы{у
аl+а2 аз==О.
Линейная зависимость, как видно из определения, равносильна
(при k 2) тому, что хотя бы один из векторов системы является ли-
нейной комбинацией остальных. '
Если система состоит из двух векторов af, а2' то линейная зави-
симость системы означает, что один из векторов пропорционален дру-
rOMY, скажем, аl==ла2; в трехмерном случае это равносильно коллине-
арности векторов а1. и а2. Точно так же линейная зависимость системы
из трех векторов в обычном пространстве означает компланаРН(lсть
этих векторов. Понятие линейной зависимости является, таким обра-
зом. естественным обобщением понятий коллинеаРllОСТИ и компланар"
ности.
131
Нетрудно убедиться, что векторы ei, е2, i 1'; Сп из системы (5)
линейно независимы. Следовательно, в n-мерном пространстве сущеет.. I
BYIOT системы из n линейно неззвисимых векторов. Можно показать,
что всякая система из большеrо числа векторов линейно зависима.
Всякая система ai, а2, . . ., а n из n линейно независимых векторов
ll-мерНОrо пространства Ln называется ero базисом.
Любой вектор а пространства L n раскладывается, и притом един-
ственным образом, по векторам произвольноrо базиса af, а2, j . ., а п %
а == ЛI Q l + Л2 Q 2 +.,! +лnа n .
Этот факт леrко устанавливается на основании определения базиса,.
Продолжая аналоrию с трехмерным пространством, можно и в
п-мерном случае определить скалярное произведение а.Ь векторов,
полаrая
а.Ь ==al l +a2 2 + ,. t +an n.
При таком определении сохраняются все основные свойства скаляр-
Horo произведения трехмерных векторов. Векторы Q и Ь называются
ортоzонаЛЬНblМИ, если их скалярное произведение равно нулю:
al i+a2 2+' · .+an n==O.
в теории линейных кодов используется еще одно важное понятие .......
понятие подпространства. Подмножество V пространства L п называ-
ется подпространством 910ro пространства, если
1) для любых векторов а, Ь, принадлежащих V, их сумма а+Ь
также принадлежит V;
2) для любоrо вектора а, принадлежащеrо V, и для любоrо дей-
ствительноrо числа 'А вектор ла также принадлежит V.
Например, множество всех линейных комбинаций векторов ei, ез
из системы (5) будет подпространством пространства Ln.
В линейной алrебре доказывается, что во всяком подпространстве V
существует такая линейно независимая система векторов а1.' а2, . . .
. . ., Qk, что всякий вектор а подпространства является линейной ком-
бинацией этих векторов:
а == Лl ах + Л2 а 2 + · · · + Лk а k'
Указанная система векторов называется базисом подпространства У.
Из определения пространства и подпространства непосредственно
следует, что пространство L п есть коммутативная rруппа относительно
операции сложения векторов, а любое ero подпространство V яв.пяется
подrруппой этоЙ rруппы. В этом смысле можно, например, рассмат-
ривать смежные классы пространства Ln по подпространству У.
В заключение подчеркнем, Ч10 если....в теории n-мерноrо арифме.
тическоrо пространства вместо действительных чисе,lI (Т. е. элементов
132
поля действите..ТIЬНЫХ чисел) рассматривать элементы произвольноrо
поля Р, то все определения и факты, приведенные выше, сохранили
бы силу.
В теории кодирования важную роль иrрает с.пучай, коrда поле F
есть поле вычетов Z р' которое, как мы знаем, конечно. В этом случае
соответствующее n-мерное пространство также конечно и содержит,
как нетрудно ВИдеТЬ, рп элементов.
Понятие пространства, как и понятия rpYnnbJ и кольца, допускаст
также и аксиоматическое определение. За подробностями мы отсылаем
читателя к любому курсу линейной алrебры.
5. Алrебра матриц
Большую роль в линейной алrебре и мноrих друrих
осластях математики иrрают так называемые матрицы.
Под матрицей понимают прямоуrольную таблицу вида
( аl1 а12 · '! а1n )
й21 а22 · .. а2п , (1)
. . .. . .
й т l ат2 · · .а тп
rде буквы Qij обозначают некоторые элементы. Эти обозначения содер-
жат два индекса, первый из КОТОРЫХ указывает номер строки, а вто-
рой номер столбца, на пересечении которых находится соответст"
вующий элемент. Про матрицу, у которой т строк и n столбцов, ro..
БОрЯТ, что она имеет порядок тХ n. В случае, коrда число строк и
столбцов одинаково (т== n), матрица называется квадратной порядка n.
Если т== 1, то матрицу можно понимать как вектор, координаты
KOToporo записаны1 в строку; ее тоrда так и называют вектор-строка.
Точно так же в случае одностолбцовой матрицы пользуются термином
вектор-столбец. Иноrда матрицу обозначают одной буквой (А, В и
Т. д.), а вместо (1) часто используется сокращенное обозначение (a;j)'
Если в ЕСХОДНОЙ матрице А строки и столбцы поменять ролями,
то получим матрицу, называемую транспонированной к А (обознача-
ется А т). Матрица, транспонированная к матрице (1), имеет вид:
( аl1 й21' · · Q'!'l )
а12 й22' · .а т 2
.
. ! . ! ! . .
аln а2п" .а тп
Для матриц с действительными элементами определяются опе-
рации С 'Iоя(ения матриц и умножения матрицы на число, аналоrичные
операциям над векторами, а именно, для Лlобых двух матриц порядка
тХn
( йl1 ... й 1 n ) ( ы11 ... ы1) . ...... ( йl1 + Ь 1 1 ... аlп + b i n )
"!" + '!!.' !e'!ttttt.i
а m 1 ... а тn Ь т 1 " t Ь m n а т 1 + ь т i ... а тп + ь n.
133
, и для любой матр l'ЦЫ и любоrо числа CG
1> ( а1! ... а 1 n ) ( (Ха1! ... a,ain ' )
а, ...... \ . . . . . . . .
ат! ... а тn JY..ami ... аа тn /
Определение этих операций выrлядит вполне естественно. Иначе
обстоит дело с довольно своеобразной операцией умножения матриц.
Рассмотрим сначала умножени квадратных матриц одноrо порядка n.
Если
A==(aij) и B==(bij)
...... две таких матрицы, то их произведением
С == А.В == (Cij)
называется квадратная матрица порядка n, произвольный элемент
которой вычисляется по правилу:
Cij == ai1 b 1j + ai2 b 2j + · · · + ainbnj. (2)
Иначе rоворя, чтобы получить элемент i-й строки и j-ro СТОol'Iбца MaT
рицы С==А ,В, нужно взять сумму произведений элементов i-й строки
матрицы А на соответствующие элементы j ro столбца матрицы В.
Например,
(ь ) ( )==( ).
Умножение матриц некоммуrативно, т. е., вообще rоворя, А . В =1= В .А.
Так, перемножив две предыдущие матрицы в обратном порядке, полу-
чим иную матрицу:
( ). (ь п==( ).
Вместе с тем, нетрудно доказать, что умножение матриu ассоциативно:
(А. В). С===А. (В. С).
Особую роль (п одобную числовой единице) иrрает так называемая
единичная маmрu ца
1 О О
О l' ""
Е==
.
.
.
о о 1
Действительно, из формулы (2) следует, Ч10
ЕА==АЕ==А
для любой квадратной матрицы А!
134
Можно убедиться, что множество всех квадратных матриц задан-
Horo порядка образует относительно введенных операций сложения и
умножения (некоммутативное) кольцо.
Правило умножения матриц можно распространить и на прямо-
I уrольные матрицы, не являющиеся квадратными. Формула (2) по-
зволяет это сделать, если число столбцов первой матрицы А совпадает
с числом строк матрицы В. Например,
( 1 2 ) , 2 О ) ( О 2 )
3 1 ,( 1 1 == 5 1.
О l 1 1
При этом получаюи аяся матрица имеет столько же строк, сколько
первый сомножитель, и столько же столбцов, сколько второй. Поль..
еуясь операциями над матрицами, мы получаем возможность записы-
вать произвольные системы уравнений в краlКОЙ матричной форме.
Действительно, пусть матрица
( аll а12 ... ain )
А == а21 а22 ... а2n
...!....
атl а т 2 ... а тп
сост влена из коэффициентов при неизвестных системы (1) приложения 4
(в этом случае она называется матрицеЙ системы). Рассмотрим векторы-
столбцы неизвестных и свободных членов, обозначая их соответственно
через х и Ь:
Ь!
Х2 Ь 2
х== Ь== t
..
Х п Ь т
Тоrда произведение Ах есть матрица с т строками и одним столбцом;
т. е. вектор столбец, элементы KOToporo вычисляются соrласно фор-
муле (2). Таким образом,
( аllХl + а12 Х 2 + ' · · + а 1nх п )
Ах == 21 1 , a:2 2 : : ' ', 2:X: .
а т l Х i + а т 2 Х 2 + · · · + а т пХп
Каждое из уравнений системы (1) означает равенство соответствующих
координат вектора Ах и вектора Ь, и вся система в целом означает тоrда
равенство
Ах==Ь.
JЗ5
Полученная краткая запись и есть матричная форма системы линей.
ных уравнений. Подобная матричная запись встречается во множестве
друrих ситуаций, и она широко используется в математической, физи-
ческоЙ и технической литераl уре.
Все сказанное о матрицах с действительными элементами в равной
мере относится к матрицам с элементами из произвольноrо поля Р.
Так, в теории кодирования приходится рассматривать матрицы, со-
ставленные из элементов конечноrо ПО.,1Я. Естественно, что при опери-
ровании с такими матрицами их элементы складываются и умножаются
в соответствии с «арифметикой» поля Р. ВОТ, к примеру) как перемно"
жаются две матр ицы с Э..'Iементами из Z2:
I 1 О О 1 ( 1 0\ о 1
( О 1 1 О ) . ь: 1== ( 1 О ) .
\1 1 1 О 1./ о О
6. Задачи и дополнения
1. Покажите, что преобразование, обратное па аллель.
ному перенесу в направлении вектора а, есть параллельный перенос
е противоположном направлении (на вектор а).
2. Пусть f симметрия плоскости относительно оси Ох, g пово.
рот плоскости на nj2 против часовой стрелки. Проверьте, что преоб-
разование fg есть симметрия относительно биссектрисы I-ro и 3-ro
координатных yr Лов. Найдите также п реобразование gf и убедитесь,
что t g :j::. gl.
3. Операция произведения преобразований обладает свойством
ассоциативности, это значит, что для любой тройки преобразова-
ний 11' t 2' 1з выполняется paBeHCfBo
(/1/2) t 3 == f 1 (f 21 3) ·
Справедливость соотношения вытекает из Toro, что обе ero части
есть результат последовательноrо выполнения трех преобразований
сначала 11' затем '2, затем 1з.
4. Какие из следующих множеств образуют rpynny преобразова-
ний плоскости:
а) множество всех параллельных переносов;
б) множество всех вращений относите,,'!ЫIО фиксированноrо центра;
в) множество всех вращений п.аоскости;
r) множество всевозможных осевых симметрий.
5. Напсмним, что совокупность всех подстановок n-элементноrо
множества сбразует rруппу. Она называется симме rрической rруппоЙ
степени n и обозначается S n. Найдите все подстановки из 5з, не
меняющие значения функций
а) ерl == Х1 Х 2 + Х2 Х З + Х1 Х З;
б) <Ра == (Хl Х2){Хl ХЗ){Х2 Ха).
136
Лроверьте прямым вычислением, что найденные в ка)l ДОМ из случаев
подстановки образуют rруппы.
6. т ранспозuцuей называется подстановка, переставляющая ка-
кие-либо два символа, а все прочие оставляющая на месте. Например,
из двух подстановок
с
2 3 4 )
3 2 4 '
( 1 2 3 4 )
234 1
первая является транспозицией, вторая нет, но она может быть пред"
ставлена в виде пропзведения транспозиций следующим образом:
( 1 2 3 4 ) ( 1 2 3 4 ) ( 1 2 3 4 ) ( 1 2 3 4 )
2 3 4 1 == 2 1 3 4 3 2 1 4 4 2 3 1 ·
(1)
Справедлив общий факт: всякая подстановка разлаrается в произведение
транспозиций.
Это разложенне неоднозначно, например, вместо (1) мы моrли бы
написать
(; ; )==(:
2 3 4 ) ( 1
3 2 4 1
2 3 4 ) ( 1 2 3 4 )
432 2134.
Однако можно доказать, что при всех представлениях подстановки
в виде произведения транспозиций число сомножителей имеет одина..
ковую четность.
Подстановка называется четной, если число транспозиций и
в разложении четно, в противном случае подстановка называется
нечетной.
7. Покажите, что lY.HO)l{CCTBO всех четных подстановок образует
rруппу, она сбозначается Аn и называется знакопеременной ёруппой.
8. Убедитесь, что множество подстановок из задачи 5 (6) совпа-
дает со знакопеременной rруппой Аз-
Восбlце рассмотрим ФУНКЦИIО
F (Хl, Х2' · ", Х n )== П (Xi Xj),
i < I
" j, == ), 2, ..., п.
(2)
Тоrда множество всех под стано во к переменных, не меняющих зна.
чения этой. функции, совпадает со знакопеременной rруппой Аn. Это
вытекает из Toro, что при любой транспозиции значение функции (2)
меняется на противоположное, например,
F (Х2, Хl,"', Х n ) == p (Хl, Х2, ..., хn)'
Сказанное объясняет и происхождение термина «знакопеременная
rруппа».
lЗi
9. Для числовых rрупп типичной является такая ситуация, KOrn1!
все степени одноrо элемента g =1= 1 различны *). Если же обратиться
к rруппам преобразований, то в них зачастую бывает так, что две
различные степени одноrо элемента (пр образования) совпадают.
В качестве примера таких элементов рассмотрите преобразования:
а) симметрию относительно оси; б) поворот плоскости на уrол n/3
(вообще на уrол 2лjk).
Что касается конечных rрупп, то здесь для JIюбоrо элемента g
существуют такие натуральные k и т (k i= т), что
gk==gm. (3)
Если бы это было не так, то rруппа содержала оы бесконечно
MHoro элементов.
Пусть в равенстве (3) k > т. Умножим Gбе ero части на элемент
g т, это даст слеДУЮШ,ее равенство gk m==e, или gn==e, rде
n==k m > о.
в описанной ситуации обязательно найдется наименьшее нату-
ральное n со свойством gn==e, которое называется порядком элемен-
та g.
Если же все степени элемента g
gO == е, g, g2, ..., gk
различны, то g называется элементом бесконечноrо порядка.
10. Найдите порядки следующих подстановок:
( 1 2 3 4 5 )
2 3 4 5 I ,
( 1 2 3 4 5 )
\2 3 1 5 4 ,
с
2 3 4 5 )
4 5 2 3 .
11. Пусть G == (g) ...... конечная циклическая rруппа, и ее образую-
щий g имеет порядок n. Рассмотрим произвольную степень gm.
Если показатель кратен n (т == sn), то gт == gnS == (gn)S == e S == е.
Если }I(e показатель т произволен, то ero всеrда можно записать
в виде: m==sn r, O r n 1, rде r ccTaToK от деления 'n на n.
Но тоrда gт == gSn + r == gSn. gr == е. gr == gr. Это значит, что все элемен-
ты rруппы G == (g) исчерпываются следующими n элементами:
е, g, g2, ..., gn 1.
Мы доказали, что порядок конечной циклической rруппы совпадает
с порядком ее образующеrо. Как, использу я сказанное, вывести из
теоремы Лаrранжа следующие утверждения:
а) порядок любоrо элемента конечной rруппы является делителем
порядка этой rруппы;
б) всякая rруппа простоrо порядка является циклической?
*) в случае, если rрупповая операция сложениеl приходится ro-
воrить не о степеНЯХ l а о кратных элемента.
13&
12. Найдите возможные порядки элементов в rруппах 8з, 85' цик-
лической rруппе liорядка 12.
13. Проверьте, что всякая подrруппа Н циклической rруппы
G == (g) сама является циклической.
у к а з а н и е: рассмотрите наименьшую положительную степень
gk Е Н, покажите, что Н == (gk).
14. Покажем, пользуясь законом дистрибутивности, что нулевой
элемент аддитивной rруппы кольца иrрает роль нуля и при умноже-
нии.
Рассмотрим произведение любых двух элементов а и Ь и преоб-
разуем ero следующим образом:
аЬ == (а+О) Ь === аЬ+ОЬ.
Второе слаrаемое, как видно из равенства, иrрает роль нейтраль-
Horo элемента при сложении. В силу ero единственности ОЬ === О для
всякоrо Ь Е К.
15. Какие из следующих числовых множеств являются кольцами
относительно обычных операций сложения и умножения:
а) множество четных чисел;
б) множество чисел, кратных данному п;
в) множество мноrочленов степени n с действительными коэф-
фициентами;
r) множество всех мноrочленов с целыми коэффициентами;
д) множеС1ВО неотрицательных действительных чисел;
е) множество всех чисел вида а+Ь У2,rдеаиЬ рациональные.
в каких случаях мы имеем дело с кольцом с единицей, в ка-
ких с полем?
16. Покажем, (что делитель нуля (левый или правый) не может
быть обратим. В самом деле, пусть ха== 1 и аЬ == о. Тоrда
хаЬ == { (ха) - Ь == 1 · Ь == Ь J
Х (ab)==x-О===О.
Следовательно, Ь == О и а не является делителем нуля_
Из сказанноrо непосредственно вытекает, что никакое поле не
содержит делителей нуля.
17. Показать, что если n==пl.п2 ЧИСЛО составное, то Zn не
является полем.
18. Показать, что ненулевой элемент kE Zn обратим тоrда и толь-
ко тоrда, коrда числа k и n взаимно прссты, и что В противном случае k
является делителем нуля.
19. Пользуясь предыдущим утверждением, найдите обратимые
элементы и делители нуля в кольцах вычетов Z 6, Z 8, Z 11, Z 12.
Для обратимых элементов найдите обратные. Д.ля элемеJJТОВ k 1 ЯБЛЯ..
139
ющихся делителями ну ля, найдите т :/= О такой, что k · iii == о. Явля-
ется ли такой класс т единственным?
20. Уже самые простые сведения о кольцах и rруппах MorYT быть
применены в различных математических вопросах. Прекрасной иллю-
страцией этоrо является теория чисел. Рассмотрим, например, хорошо
извеСl ную теорему (малую теорему Ферма):
Если р простое, то для Лlобоrо натуральноrо а число aP a
делится на р.
Рассуя<даем так:
аР a==a (aP l 1).
Если а делится на р, то утверждение очевидно.
Пусть а не деJIИТСЯ на р и а ==mp 'rr (О < , p 1). Тоrда
n поле вычетов р аЕ' и r ;.. О. J1елимость числа ap l l на р рав-
носильна тому, что в p справедливо равенство ,p 1 1 ==0 или
равнссильное ему
,Р 1 r::: 1.
(4)
Так как порядок мультипликативной rруппы поля 2 р равен
p 1 t то из теоремы Лаrранжа вытекает справеДЛIlВОСТЬ равенства
(4), и это доказывает малую теорему Ферма.
21. Подумайте (это не простая задача), как с помощью указан-
ных методов можно доказать утверждение: если р простое, то
(p 1) ! + 1 делится на р. Это теорема Вильсона, одна из наиболее
изящных теорем элементарной теории чисел.
22. Функция Эйлера ер (п) определяется в теории чисел как ко.
личество натуральных чисел, меньших n и взаимно простых с ним.
Например, ер (4) == 2, q> (8) == 4 и Т. Д. ДЛЯ всякоrо простоrо р очеви-
дно <р (р) == р 1. Обобщением малой теоремы Фер а является теоре-
ма Эйлера, которая формулируется так:
Дли любоrо натуральноrо а, взаимно прсстоrо с п, а Ф (п) 1 де-
лится на n. Например, при п==8, а==5 имеем 54 1==624==8X78.
Можно предложить следующий план доказательства теоремы Эйлера
(детали на усмотрение читателя):
а) ноказать, что множество обратимых элементов любоrо кольца
образует rруппу относительно умножения;
б) рассмотреть кольцо вычетов Z n И убедиться, что rруппа ero
обратимых элементов имеет порядок <р (п) (ВСПОМНИТе утверждение
пункта 18);
в) дальнейшие р2.ссуждения таковы же, как и при доказатель-
стве малой теоремы Ферма.
23. Найти все решения системы линейных уравнений
к + 2 z == 1, у + 2z == 2, 2х + z =: 1
в поле ВЬ1чеrов: а) по модулю 3; б) по модулю 5.
149
24. Мноrочлев р (Х) Е F [Х] называется неприводимым, если
не существует разложения р (Х) == t (Х) g (Х), в котором t (Х), g (Х) Е
ЕР [Х] и степени СОМНО)i{ителей меньше, чем степень мноrочлена
р (Х).
Выяснить, являются ли следующие мноrочлены:
Х 3 +Х2+ 1) Х4+Х 2 + 1, X2 2
неприводимыми над полем: а) Z2; б) ZЗ; в) а; r) IR.
25. Разложить на неприводимые множители мноrочлен
X4+X 3 +X+l
над полем: а) Z 2; б) Z 3; в) Q.
26. Найти наибольший общий делитель мноrочленов
f (Х) ==X +X2+2X +2; g (Х) ==Х 2 +Х + 11
J1ад полем: а) Z 3; б) а.
27. Доказать что в конечном кольце с единицей любой ненуле-
вой элемент либо обратим, либо является делителем нуля. Верно ли
это утверждение без предположения конечности (вспомните кольцо Z)?
28. Используя предыдущее утверждение, докажите, что конечнсе
коммутативное кольцо без делителей нуля, содержащее более одно-
ro элемента, является полем.
29. В вопросах, связанных с решением систем линейных урав-
нений, особую роль иrрает понятие определителя квадратной матрицы.
Введем здесь это понятие применительно . к матрице 2-ro порядка
( )
(5)
с элемента и из произвольноrо поля Р. Ее опрсделителем называ-
ется величина
д ==аб у.
(6)
Доказать, что в кольце всех матриц 2-ro порядка матрица (5) обра-
тима TorAa и только TOr[I.a, коrда ее определитель отличен от нуля
(указать способ отыскания обратной матрицы). В противном случае
матрица (5) являеrcя делителем нуля.
30. Какие из перечисленных ниже матриц обратимы или явля-
ются деЛИ1елями нуля
( ;)
( ):
(; ;)
H Д полем: а) Z 3; б) Q?
В случае, если матрица обра1има, найти обратную.
ЛИТЕРАТУРА
.,....
1. ШеflflОfl К. Работы по теории информации и кибернеТике......
М.: ИЛ, 1963.
2. Я2ЛОIIl А. М., Яелом и. М. Вероятность и информация. М.:
Наука, 1973.
3. БрИЛЛЮЭfL л. Наука и теория информации. М.: Физматrиз, 1959.
4. Холл М. Комбинаторика. М.: Мир, 1970.
5. Оре о. Приrлашение в теорию чисел. М.: Наука, 1980.
6. РеflЬИ А. Трилоrия о математике. М.: Мир, 1980.
7. Кострикин, А. И. Введение в алrебру. М.: Наука, 1977.
8. КаЛУЖflИн, л. А. Введение в общую алrебру. М.: Наука, 1973.
9,. Фано Р. Передача информации. Статистическая теория связи.........
М.: Мир, 1965.
10. rаллаеер Р. Теория информации и надежная связь. М.: Совет..
ское радио, 1974.
11. Питерсон, У., Уэлдон, Э. КОДЫ, исправляющие ошибки. М.:
Мир, 1976.
12. Мак Вилья.мс Ф., Слоэн, Н. Дж. Теория кодов, исправляющиХ!
ошибки, М.: Связь, 1979.
13. Каса,М,u Т., Токура Н., Ивадарu Е., Инаеакu Я. Теория кодиро"
вания....... М.: Мир, 1978.
14, Берлекэ.мn э. Алrебраическая теория кодирования. М.: Мир,
1971 .
15. Колесник В. Д., МИРОНЧИКО8 Е. Т. Декодирование циклических
KOДOB. М.: Связь, 1968.
16. Стиффлер Дж. Теория синхронной связи......... М. : Связь, 1975.
11, ЯБЛОflСlаиl С. В. Введение в дискретную математику. М.: Н ау..
Ка, 1979.
18" Блох Э. Л., Зяблов В. В. Обобщенные K CKaДHыe коды......... М.:
Связь, 1976.
19" МаР1(,()8 А. А. Введение в теорию кодирования. М.: Наука,
1982.
20, Нови/( д. А. Эффективное кодирование......... М. Л.: Энерrия, 1965.
21. Воробьев Н! Н. Числа фибоНаччи,.... М.: Наука, 1972,
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ 3
1. КОДИРОВАНИЕ ИСТОРИЯ И ПЕРВЫЕ ШАrи 5
2. ШИФРЫ, ШИФРЫ, ШИФРЫ I 10
3. КОД ФАНО ЭКОНОМНЫй КОД 18
4. СВОйСТВО ПРЕФИКСА, ИЛИ КУДА ИДТИ РОБОТУ 24
5. ЕЩЕ О СВойСТВЕ ПРЕФИКСА И ОДНОЗНАЧНОй ДЕ КОДИ..
РУЕМОСТИ 21
6. ОПТИМАЛЬНЫй КОД 32
7. ОБ ИЗБЫТОЧНОСТИ, ШУМАХ И кРиптоrРАММЕ. КОТОРУЮ
НЕЛЬЗЯ РАСЩИФРОВАТЬ 37
8. КОДЫ АНТИПОДЫ 4 О
9. КОД ХЕмминrА 45
10. НЕОБЫЧНОЕ ОБЫЧНОЕ РАССТОЯНИЕ 48
11. ЛИНЕйНЫЕ или..--.rРУППОВЫЕ КОДЫ 50
lf. ДЕКОДИРОВАНИЕ ПО СИ'ИДРОМУ И ЕЩЕ РАз 6 КОДЕ ХЕМ-
\ минrА 61
13. О КОДАХ, ИСПРАВЛЯЮЩИХ НЕСИММЕТРИЧНЫЕ ОШИБКИ 65
14. ЦИКЛИЧЕСКИЕ КОДЫ 68
15. О tРАНИЦАХ возможноrо В КОДИРОВАНИИ И СОВЕРШЕН-
HI:\тX КОДАХ 77
16. КОДИРУЕТ И ДЕКОДИРУЕТ ЭВМ 82
17. rОЛОСОВАНИЕ 93
18. мноrОСТУПЕНЧАТОЕ rОЛОСОВАНИЕ И КОДЫ РИДА.......
МАЛЛЕРА 97
19. ЛАТИНСКИЕ КВАДРАТЫ И КОДЫ 102
20. МАТРИЦЫ АДАМАРА И КОДИРОВАНИЕ 107
21. ЗАДАЧА ОБ ОЖЕРЕЛЬЯХ, ФУНКЦИЯ мЕБИУСА И СИНХРО
НИ3ИРУЕМЫЕ КОДЫ 112
ЗАКЛЮЧЕНИЕ а 16
ПРИЛОЖЕНИЕ ] 17
1. СРАВНЕНИЯ И КЛАССЫ ВЫЧЕТОВ 117
2. rруппы 120
3. КОЛЬЦА И ПОЛЯ 125
4. АРИФМЕТИЧЕСКОЕ n MEPHOE ВЕКТОРНОЕ ПРОСТ..
РАНСТВО 129
5. АлrЕБРА МАТРИЦ 132
6. ЗАДАЧИ И ДОПОЛНЕНИЯ 136
ЛИТЕРАТУРА 142
м uхаuл Н ау.м.О8UЧ Аршuнов
Леонuд ЕфUАtовuч Садовскuй
КОДЫ И МАТЕМАТИКА
(рассказы о кодировании)
(Серия: Библиотечка «Квант»)
Редактор Ф. Л. ВарпаХО8СКUЙ
Технический редактор Е. В. МОРОЭО8й
Корректор В. В. Сидоркина
ИВ Ng 12096
Сдано в набор 13. 12. 82. Подписано к печати 04. 04. 83. Т-О8318. BYMara
84Х 1081/32' Бумаrа тип. Н2 3. Лите r атурная I'арнитура. Высокая печать.
Условн. печ. JI. 7,56. Уч.-изд. n. 8,2 . Тираж 150 000 экз. Заказ NII 1067.
иена 25 коп.
И дательство «Наука:.
rлавная редакция физико-математической литературы
t 17071. Москва, В-71. Ленинский проспект, 15
Ордена Октябрьской Революции и ордена Трудовоrо KpacHoro Знамени Первая
Образцовая типоrрафия имени А. А. Жданова СОЮЗПОJlиrрафпрома при rocy"
дарственном комитете СССР по делам издательств, полиrрафии. и книжной тор-
rовЛи. Москва, М-54, Валовая, 28 .
Отпечатано в rипоrрафии NII 2 иэд-ва «Наука., Москва, Wубинский пер., 1 С. 2688