А. И. КИТАЙГОРОДСКИЙ
РЕНТГЕНОСТРУКТУРНЫЙ
АНАЛИЗ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 195 0 ЛЕНИНГРАД

АННОТАЦИЯ
Ё книге излагаются основные проблемы
современного рентгеноетруктурного анализа: кристаллографические
основы структурного анализа, получение рентгеновских
лучей н взаимодействие их с веществом.
Книга рассчитана на научных работников, инженеров,
аспирантов и студентов-физиков и химиков старших курсов.
Редакторы А. А. Семёнов в Е. Е. Кузнецова. Техн. редактор Я. Я. Мурашова.
Подписало х печати 26/1V 1950 г. 40,75 пет. л. 20,375 бух. л. 46,86 уч.-нзд. л.
46 984 тип. зи. в печ. листе. Т-00269. Тираж 4000 экз. Цена книги 16 р. 40 к. Переплёт 2 р.
Заказ № 1143.
*"* типография и*. Евг. Соколовой Главполиграфвздата при Совете Министров СССР.
Ленинград. Измайловский пр., 29

ОГЛАВЛЕНИЯ
Предисловие 9
Глава I. Кристаллографические основы структурного анализа . . 13
А. Элементы, теории пространственной решётки 13
§ 1. Описание пространственной решётки 13
а) Понятие пространственной решётки 13
б) Узловая прямая 14
в) Узловая плоскость. Индексы семейства узловых плоскостей 15
г) Обратные векторы If»
д) Некоторые формулы структурной кристаллографии 19
е) Различные способы выбора основных векторов или осей
координат решётки 22
§ 2. Липейное преобразование пространства . 28
а) Параллельный перенос или трансляция 29
б) Поворот вокруг оси . . . '• 29
в) Инверсия 31
г) Отражение в плоскости 32
д) Общий случай линейного преобразования 33
3 3. Симметрические преобразования 37
а) Закрытые симметрические преобразования, возможные у
решётки 37
б) Поворотные и инверсионные оси 38
§ 4. Точечные группы или острова 42
а) Возможные углы между одноимёнными осями симметрии . . 43
б) 11 точечных групп с поворотными осями 46
в) 32 точечные группы 48
г) Описание точечных групп • • • 49
ji 5. Кристаллические системы 62
§ 6. Трансляционные группы 67
а) Введение 67
б) Обзор трансляционных групп 68
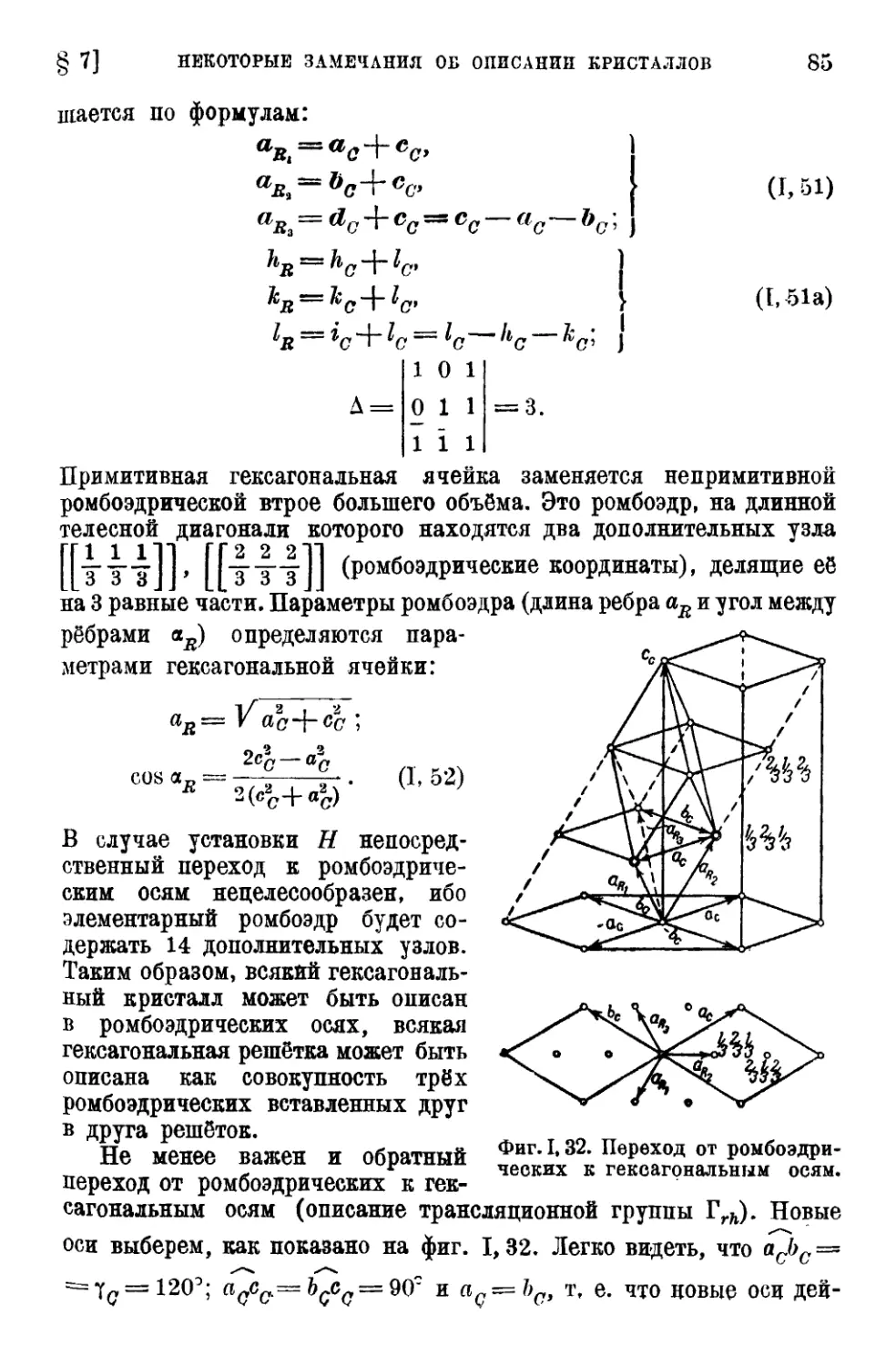
§ 7. Некоторые замечания об описании кристаллов гексагональной
и ромбоэдрической систем . . . 80
а) Четвёртый индекс 80
б) Два способа выбора гексагональных осей, С- и Я-установки 82
в) Связь ромбоэдрической и гексагональной систем координат 84
§ 8. Открытые симметрические операции 87
а) Винтовые оси и плоскости скольжения 87
б) Общие соображения о взаимном расположении элементов
симметрии в решётке. Класс симметрии 91
в) Трансляция и другие элементы симметрии 92
§ "9. Преобразования, производимые элементами симметрии решётки 94
а) Преобразования координат точки 94

4 ОГЛАВЛВНИЕ
б) Генерирование новых элементов симметрии
в) Расположение элементов симметрии и трансляционная группа
§ 10. Пространственные группы ....'.
а) Перечень пространственных групп класса Cgft
б) Номенклатура пространственных групп
в) Положения точек
г) Симметрия и число возможных островов
д) Подгруппы ...... (
Б. Элементы геометрической кристаллографии
§ 1. Опытные законы кристаллографии
а) Закон плоскогранности и пряморёберности кристаллов . . .
б) Закон постоянства yi лов кристаллов
в) Закон рациональности отношений осевых отрезков
г) Закон зон
д) Закон развития форм
е) Закон симметрии
ж) Закон однородности и анизотропности кристаллов
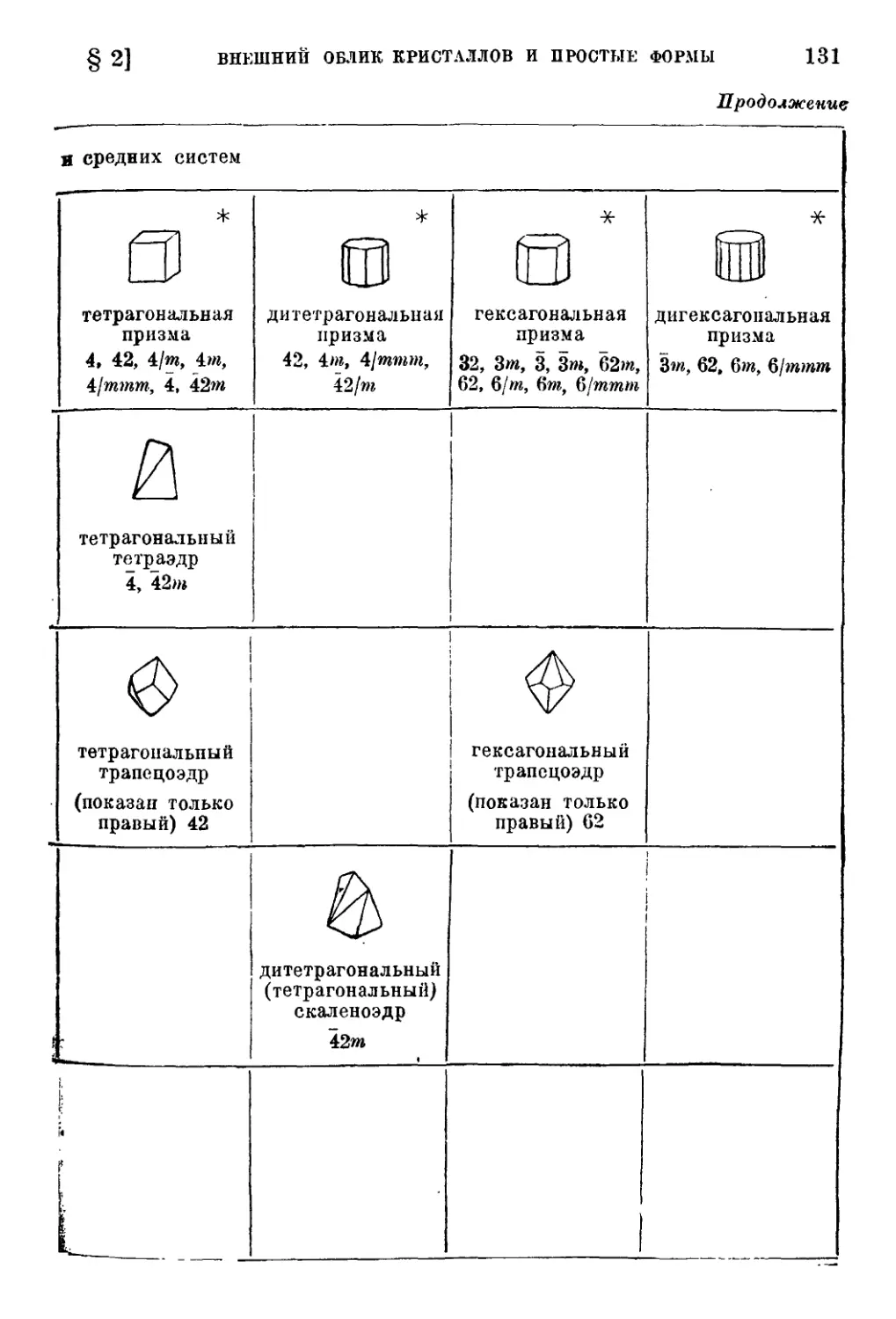
§ 2. Внешний облик кристаллов и простые формы
§ И. Кристаллографические проекции
а) Линейная проекция
б) Гномоническая проекция
в) Стереографическая проекция
г) Гномостереографическая проекция
§ 4. Сетка Вульфа
§ 5. Гониометрическое изучение кристаллов
§ 6. Обработка результатов гониометрических измерений
а) Вычисление кристаллов
б) Черчение кристаллов .•
§ 7. Работы Фёдорова. Кристаллохимический анализ
а) Теория параллелоэдров • . .
б) Закон кристаллографических пределов Фёдорова
в) Кристаллохимический анализ •
Глава II. Получение рентгеновских лучей и их взаимодействие
с веществом
§ 1. Рентгеновская трубка . . . . •
§ 2. Спектр рентгеновских лучей
а) Общие замечания. Разложение в спектр. Измерение длины-
волны
б) Непрерывный спектр рентгеновских лучей
в) Характеристический спектр .
^ 3. Общая картина взаимодействия рентгеновских лучей и вещества
& 4. Коэффициент ослабления (поглощения)
а) Вычисление коэффициентов ослабления
б) Измерение коэффициента ослабления
в) Зависимость поглощения от длины волны и менделеевского
числа • ...»
г) Фильтры
§ 5. Фотографическое действие рентгеновских лучей и измерение
интенсивности по почернению плёнки
а) Фотографическое действие рентгеновских лучей
б) Визуальная оценка интенсивностей
в) Фотометрирование рентгенограмм
г) Светящиеся и усиливающие экраны
§ 6. Ионизирующее действие рентгеновских лучей и ионизационный
метод измерения интенсивностей

ОГЛАВЛЕНИЯ 5
Глава III. Диффракцня рентгеновских лучей в кристалле .... 203
§ 1. Направление рентгеновских лучей, диффрагированных кристаллом 203
§ 2 Рассеяние рентгеновских лучей электроном . 209
§ 3. Атомный фактор • 214
а) Атомный фактор и распределение электронов 214
б) Расчёт атомного фактора для свободных атомов 219
в) Температурная поправка 222
§ 4. Структурный фактор 223
а) Основные формулы 223
б) Частные случаи формул структурного фактора 228
§ 5. Рассеяние рентгеновских лучей малым кристаллом (абсорбция
и экстинкция отсутствуют) 231
а) Условие возникновения и величина максимума
интенсивности «#, 231
б) Ширина максимума интенсивности • . • 236
в) Перечень упрощений, сделанных при расчёте (абсорбция,
экстинкция) 237
г) Некоторые представления в обратной решётке 238
§ 6. Рабочие формулы интенсивностей 240
а) Метод Лауэ • • • 241
б) Метод вращения кристалла 244
в) Метод «порошка» • 248
§ 7. Учёт поглощения 252
а) Сечение луча меньше сечения кристалла 252
б) Сечение луча больше сечения кристалла '. . . 255
§ 8. Учёт экстинкции (вторичной) 262
§ 9. Идеальный кристалл. Первичная экстинкция 266
а) Интегральное отражение идеального кристалла 266
б) Учёт первичной экстинкции. Условия идеальной мозаичной
структуры 269
§ 10. Влияние тепловых колебаний 269
§ П. Температурный фактор 274
§ J 2. Тепловые диффузные максимумы 278
а) Основные факты 2*8
б) Тепловые волны 280
в) Геометрические условия диффракции на тепловых волнах • 284
г) Связь между картиной диффузных максимумов и
структурой 291
Глава IV. Методы получения и расчёта рентгенограммы
монокристалла 294
§ 1. Введение 294
§ 2. Метод Лауэ 295
а) Идея метода i 295
б) Геометрия интерференционной картины. Зональные кривые.
Гиомоническая проекция лауэграммы 298
в) Индицирование лауэграмм 303
г) Нахождение и уточнение ориентировки кристалла 307
д) Некоторые замечания о симметрии рентгенограмм 312
е) Симметрия лауэграммы 314
») Астеризм 318
з) Исследование формы узлов обратной решётки 322
§ 3. Методы вращения и качания кристалла 323
а) Идея метода. Слоевые линии. Измерение периода вдоль оси
вращшия 323
б) Интерференционные кривые 330

6 ОГЛАВЛЕНИЙ
в) Индицирование рентгенограммы качания 336
§ 4. Практические замечания 345
а) Камеры 345
б) Выбор спектра и образца 350
§ 5. Методы уточнённого определения Периодов идентичности по
рентгенограммам качания и вращения 352
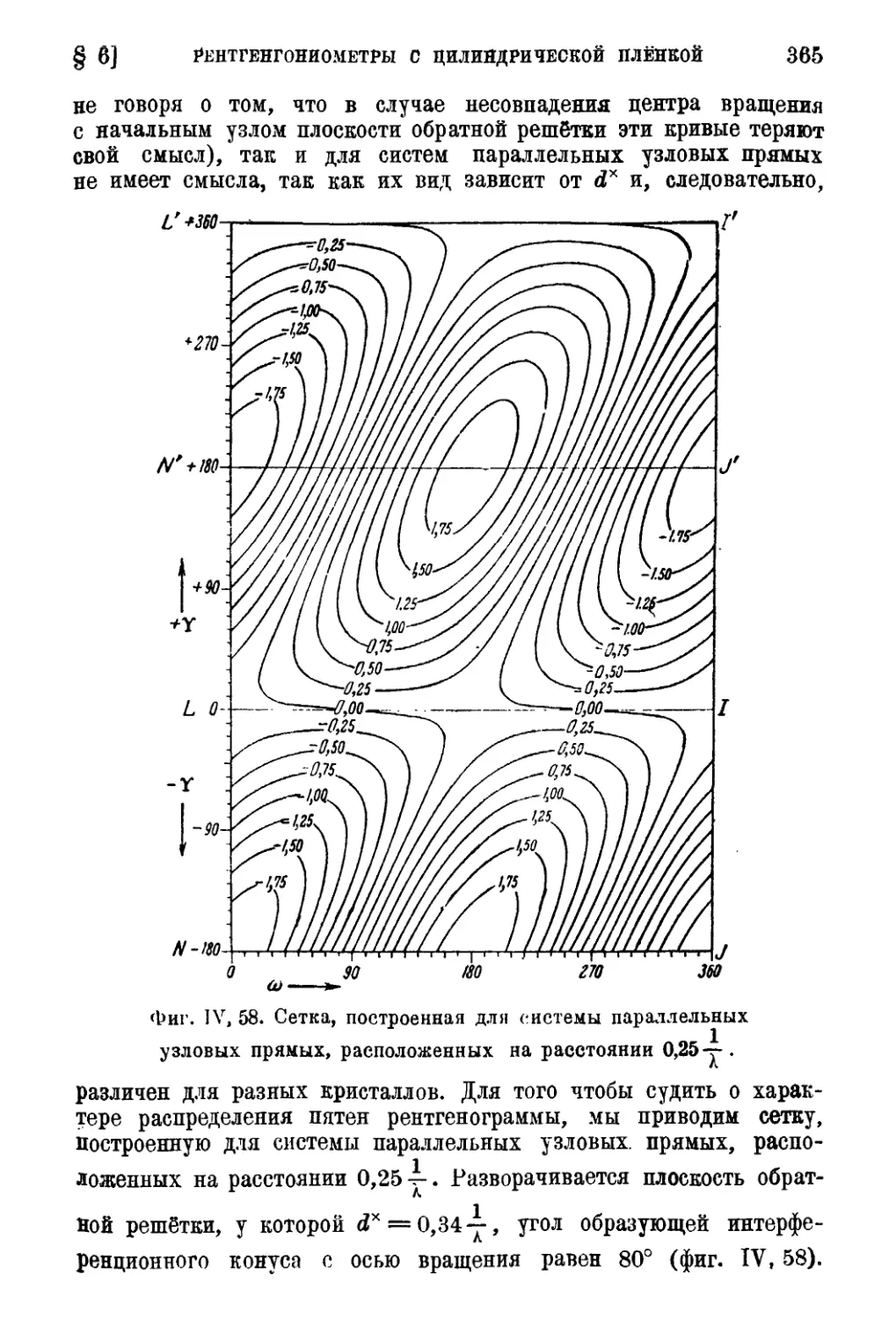
§ 6. Рентгенгониометры с цилиндрической плёнкой 355
а) Общие замечания. Классификация • 355
б) Цилиндрический гониометр (прямая съёмка) 356
в) Получение рентгенограмм по эквинаклонному методу и их
расшифровка 366
§ 7. Рентгенгониометры с плоской плёнкой 371
а) Метод фотографирования обратной решётки 371
б) Круговой гониометр 380
§ 8. i ентгенспектрограф 383
Глава V. Структурный анализ без оценки интенсивностей . . . 389
Л. Теория плотной упаковки 389
§ 1. Введение 389
§ 2. Топологическая характеристика кристаллов 390
а) Классификация 390
б) Атомные и межмолекулярные радиусы 392
в) Координационное число 394
§ 3. Теория плотнейшей шаровой упаковки 405
а) Симметрия упаковки 405
б) Пустоты в шаровых упаковках 409
в) Правила строения ионных кристаллом 412
г) Область применения 413
§ 4. Теория плотной упаковки молекул 414
В. Определение размера и симметрии ячейки кристалла и заключения,
которые могут быть сделаны из этих данных. 420
§ 1. Определение размеров элементарной ячейки кристалла и
трансляционной группы 420
§ 2. Размеры ячейки и заключения о структуре кристалла 429
а) Вычисление коэффициента упаковки 429
б) Тождественные и подобные ячейки 435
в) Определение молекулярного веса и плотности 437
§ 3. Определение пространственной группы 438
§ 4. Пространственная группа, симметрия расположения атомов и
молекул в ячейке и химическая формула 457
В. Геометрический анализ 460
§ 1. Учёт конечного размера атомов при размещении их в ячейке . 460
§ 2. Геометрический анализ ионных кристаллов на основе теории
плотной упаковки ♦ 462
§ 3. Геометрический анализ молекулярных кристаллов 463
» •
Глава VI. Структурный анализ с оценкой интенсивностей . . . 468
§ 1. Сравнение с опытом возможных моделей структуры 468
а) Измерение интегрального отражения и вычисление Ъ'изм . . 468
б) «Испытание» модели. Метод проб • • • . * г . . 470

ОГЛАВЛЕНИЕ 7
§ 2. Метод рядов электронной плотности 474
а) Формула ряда для общего случая. Область применения
метода 474
б) Трёхмерные ряды и их сечения 477
в) Проекции ряда электронной плотности 481
§ 3. Техника подсчёта двумерных рядов Фурье 484
§ 4. Симметрия двумерного ряда электронной плотности 493
а) Центросимметричные плоские группы 493
б) Симметрия ряда 510
§ 5. Точность F-рядов и возможности их применения ....... 512
а) Заключения о строении молекулы • • 512
б) /-кривая и атомная функция. Влияние обрыва ряда на вид
атомной функции • .... 515
§ 6. Ошибка ряда электронной плотности 523
а) Значения электронной плотности 523
б) Значения координат максимумов 525
в) Разрешающая способность ряда электронной плотности ■• • 530
§ 7. Ряды межатомных векторов — ,Р2-ряды 533
а) Основная формула 533
б) Частные случаи ^2-рядов 535
§ 8. Анализ проекций ^-рядов 538
§ 9. Методы уточнения структуры, основывающиеся на идее
максимального сближения Fna6„ и FBil4 547
§ 10. Определение знаков Fj&i по данным об их величине 549
§ 11. Автоматизация расчётов в структурном анализе 556
Глава VII. Исследование поликристаллических веществ 561
§ 1. Сущность и цели исследования 501
§ 2. Обычный метод исследования поликристаллических веществ . . 563
а) Вид рентгенограммы 563
б) Индицирование 565
в) Точность определения межплоскостных расстояний и меры
к её увеличению 567
§ 3. Фазовый анализ 572
а) Общие замечания 572
б) Химический анализ по рентгенограммам 574
§ 4. Съёмка в фокусирующих камерах 577
а) Принципы фокусировки и схемы камер 577
б) Определение диаграмм состояния 580
в) Контроль термической обработки стали 582
§ 5. Исследование текстуры 583
а) Сущность метода исследования 583
б) Построение полюсных фигур по рентгенограммам . . . • . 584
в) Плоская и аксиальная камеры 585
г) Текстуркамера 586
I 6. Определение размера частиц по рентгенограммам 588
8 7. Измерение напряжений 596
§ 8. Определение радиального распределения плотности вещества
в кристалле 600
§ 9. Структурный анализ газов, жидкостей и аморфных тел .... 602
а) Введение 602
б) Структурный анализ газообразного вещества 603
в) Структурный анализ одноатомной жидкости 605
§ Ю. Исследования строения решёток с элементами беспорядка и,
сверхструктурой 608
§ И. Исследование строения волокнистых веществ 611

8 ОГЛАВЛЕНИЕ
Глава VIIL Примеры рентгеноструктуриого анализа кристаллов 614
§ I. Исследование структуры по рентгенограмме порошка.
Кубический кристалл Zn(CN)a 615
§ 2. Определение структуры метил- и этилхлоридов ртути CH3HgCl и
C2H6HgCl 617
§ 3. Исследование структуры карбида кремния на основе теории
плотной упаковки 622
§ 4. Исследование структуры карбида бора 625
§ 5. Структурный анализ органического соединения, проведённый
количественно геометрическим методом (2,6-дифенилнафталин) . 631
§ 6. Исследование структуры CgH^HgClBr методом ^-рядов .... 634
§ 7. Кристаллическая структура «глобулярных» протеинов 6S7
Алфавитный указатель ... • . • • 646

ПРЕДИСЛОВИЕ
За сравнительно небольшой промежуток времени применение
рентгевоструктурного анализа в физике, химии, биологии, технике
стало таким же обычным, как использование микроскопа. Без
данных, полученных на основании наблюдения диффракционных
картин, создаваемых рентгеновскими лучами, не существовало бы
стройного здания учения о строении кристаллов из молекул,
молекул из атомов, поликристаллических тел из кристаллитов,
полимеров из молекул.
В течение первых 20—25 лет существования рентгеноструктур-
ного анализа применение его ограничивалось относительно простыми
случаями. За последние 10 лет были развёрнуты мощные методы
исследования, позволившие включить в качестве объектов молекулы,
содержащие многие десятки атомов; удалось приступить к изучению
строения белковой молекулы; усовершенствовались методы
исследования поликристаллических веществ.
Определение взаимного расположения атомов удаётся в
некоторых случаях проводить у аморфных и поликристаллических тел.
Однако основными объектами, на которых изучаются закономерности
атомной структуры молекулы и кристалла, являются монокристаллы.
Поликристаллическое вещество даёт значительно менее богатый
экспериментальный материал, обработка которого исключительно
проста в принципе и в то же время в редких случаях
практически выполнима.
Поэтому вполне понятно, что центром тяжести учения о рент-
геноструктуряом анализе является рентгеновское исследование
монокристалла.
В подавляющем большинстве случаев рентгеновский анализ
поликристаллов и не используется для определения атомной структуры.
Обычно его применяют тогда, когда хотят провести фазовый
анализ вещества, исследовать текстуру образца, уточнить параметры
сплава.
Цель предлагаемой книги дать описание хода рентгеноструктур-
ного анализа во всех его стадиях для всевозможных объектов.
Естественно, что большее внимание уделено изучению монокристалла.
Рентгеноструктурный анализ основывается на трёх больших
главах физики: кристаллографии, физике рентгеновских лучей и

10
ПРЕДИСЛОВИЕ
учении о диффракции волн. Эти три вспомогательных вопроса
изложены в нашей книге. При этом мы ставили перед собой задачу
изложить лишь тот минимум знаний, который необходим для
практической деятельности работников в области рентгеноструктурного
анализа. В совершенно конспективном виде изложена глава,
посвященная физике рентгеновских лучей; по нашей мысли она должна
носить скорее справочный характер. Кристаллография не является,
конечно, частью курса рентгеноструктурного анализа. Мы изложили
подробно лишь вопросы теории симметрии пространственной
решётки, мало или совсем не освещенные в существующих курсах
кристаллографии. Остальные кристаллографические вопросы
изложены лишь в том объёме, который потребуется при изучении
рентгеноструктурного анализа. Мы тем более могли не излагать чисто
кристаллографических и кристаллофизических вопросов, имея в виду
наличие на книжном рынке превосходного курса трёх авторов*).
О такой же точки зрения мы подходим и к главе о теории
диффракции рентгеновских лучей. Например, мы не излагали
математических основ динамической теории интерференции
рентгеновских лучей.
В то же время мы старались не вводить в книгу без достаточно
строгого обоснования «такие положения или формулы, которые
практически важны и находят своё применение в дальнейших частях
курса.
Основное содержание книги — описание хода
рентгеноструктурного анализа — это остальные пять глав. При изложении этого
материала автору не пришлось придерживаться каких-либо
образцов. Со времени появления на пашем книжном рынке аналогичной
книги**) прошло уже 10 лет, а предмет изложения претерпел за
это время коренные изменения; за границей также не издано
какой-либо книги, достойной быть рекомендованной советскому
читателю. Следует отметить, что пути, по которым развивается рентгено-
структурный анализ в Советском Союзе и за границей, довольно
резко расходятся. Развитие плодотворных идей плотной упаковки
частиц в кристаллах советскими учёными наложило отпечаток на
рентгеноструктурные исследования, проводимые в СССР. Именно
поэтому за последний год было три случая опровержения нашими
работниками структур, найденных, казалось, крупными западными
специалистами.
Книга не претендует на охват всей области рентгеновского
структурного анализа со всеми его приложениями и результатами
его применения. Здесь изложена лишь теория метода. В
дальнейшем предполагается выпуск в свет ещё двух книг. Одна из них
*) Шубников А. В., Флинт Е. Е. и Б о к и й Г. Б., Основы
кристаллографии, 1940.
**) Г. С. Жданов, Основы рентгеноструктурного анализа, 1940.

ПРЕДИСЛОВИЕ
11
должна быть посвящена технике эксперимента и конструкции
приборов, а другая должна содержать развёрнутое обсуждение
результатов применения рентгеновского структурного анализа в ряде
областей. В неё должны войтн:
1) Рентгенография неорганических веществ,
2) Рентгенография органических веществ,
3) Рентгенография металлов,
4) Рентгенография полимеров.
Советская школа рентгенографов имеет почётное право считать
себя наследницей трудов А. В. Гадолина и в особенности Е. С.
Федорова— основателей кристаллографии, а также Ю. В. Вульфа —
основоположника рентгеновского исследования кристаллов.
Преемственность — одна из важнейших причин, благодаря которой в
молодой области рентгеновского структурного анализа мы идём
собственными путями, и притом более глубокими и совершенными, чем те,
которые развиты на Западе.
Автор надеется, что это своеобразие нашло отражение в его
курсе, являющемся плодом не только его собственного опыта, но
и опыта всего дружного коллектива советских рентгенографов.
Эта книга предназначается для студентов старших курсов
физических и химических факультетов университетов, аспирантов и
начинающих научных работников. Книга написана как учебник,
и автор предполагает лишь общую физическую и математическую
грамотность читателя. В книгу введён целый ряд таблиц и
справочных данных, это позволяет нам надеяться, что книга сможет
служить и рабочим пособием.
В составлении этой книги мне оказал большую помощь Ю. Т.
Стручков. Им написан ряд параграфов гл. I и И, в частности весь
второй раздел гл. I. Им также выполнена большая работа по подбору
и составлению большинства рисунков. В технической работе над
рукописью мне помогали члены коллектива моей лаборатории
Б. В. Ненарт и Т. Л. Хоцянова. Ряд ценных советов в отношении
гл. VII я получил от проф. В. И. Ивероновой. Всем этим лицам—
моя искренняя благодарность.

ГЛАВА I
КРИСТАЛЛОГРАФИЧЕСКИЕ ОСНОВЫ СТРУКТУРНОГО
АНАЛИЗА
А. ЭЛЕМЕНТЫ ТЕОРИИ ПРОСТРАНСТВЕННОЙ РЕШЕТКИ
§ 1. Описание пространственной решётки
а) Понятие пространственной решётки. В основу
исследований кристалла кладётся следующее фундаментальное утверждение:
распределение вещества в
кристалле может быть
представлено трёхмерной
периодической функцией.
На фиг. I, 1 изображён
рисунок обоев. Имеется
некоторый элемент этого рисунка,
повторяющийся в двух
направлениях. Выберем любую
точку рисунка А, назовём её
узлом. Мы можем провести на
рисунке систему линий,
проходящих через выбранные узлы.
Элемент, повторением
которого строится весь рисунок,
заключается в ячейке
возникшей сетки. Очевидно, что, зная
ячейку, можно построить весь
рисунок при помощи
параллельных переносов на
величину векторов ячейки а и Ь.
Кристалл представляет
собой пространственную
решётку. Неповторимым
элементом—«атомом кристалла»
является параллелепипед,
построенный на трёх векторах
переноса или трансляции а, Ь, с,
воторые, вообще говоря, могут быть выбраны бесчисленным
количеством способов. Этот параллелепипед мы будем называть элемен-
Фиг. 1,1. Обои, как пример двумерной
решётки.

l4 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [гл. t
тарной ячейкой, векторы а, Ь, с — основными векторами или
основными трансляциями, а их длины а,Ь, с—основными периодами
повторяемости или идентичности решётки. Решбтка описывается
в системе координат, за оси которой приняты направления основных
векторов. Различные способы выбора основных векторов, т. е.
элементарной ячейки, иллюстрируются для двумерного случая фиг. I, 2.
Элементарная ячейка в общем случае представляет собой косоугольный
параллелепипед с рёбрами а, Ъ, с и углами а = 6, с; {3 = с, а; -у = а, Ъ.
Шесть величин а, Ь, с, а, {3, f, однозначно характеризующие
элементарную ячейку, называются её параметрами. Поскольку задание
элементарной ячейки определяет всю решётку, эти величины иногда
называют параметрами
решётки.
Если один из узлов выбран
за начало отсчёта, то радиус-
вектор любого другого узла
может быть представлен
формулой
Bmnp = ma-\'4ibb-\-рс, (Т, 1)
где т, п, р— целые числа,
нумерующие узлы и
называемые индексами узлов.
Совокупность трёх индексов,
характеризующих узел,
называется символом узла и
записывается в виде [[m»jp]].
Принцип пространственной решётки утверждает, что распределение
вещества в решётке, скажем электронная плотность, определяется
формулой
РИ =Р (*• + «)> (1.2)
где г — радиус-вектор любой точки решётки. Следовательно,
электронная плотность есть трёхмерная периодическая функция с
периодами а, Ъ, с.
б) Узловая прямая. Существует бесчисленное количество
узловых плоскостей и узловых прямых. Прежде всего несомненно, что
как узловые прямые, так и узловые плоскости представлены
в решётке бесконечными параллельными семействами. Переход от
одной прямой к другой прямой того же семейства, или от одной
плоскости к другой происходит параллельным переносом
(трансляцией) вдоль любого вектора, соединяющего два узла этих прямых
или плоскостей.
Каждое семейство узловых прямых характеризуется периодом
идентичности вдоль узловой прямой и направлением, т. е. накло
Фиг. I, 2. Различные способы выбора
элементарной ячейки (двумерный
случай).

§1]
ОПИСАНИЙ ПРОСТРАНСТВЕННОЙ РЕШЁТКИ
15
жш к выбранным осям координат. Для описания семейства
выбираем прямую, проходящую через начало координат. Узловая
прямая однозначно характеризуется индексами т, п, р первого узла,
лежащего на этой прямой. Индексы этого узла называют индексами
прямой. Период повторяемости или идентичности вдоль прямой
равен R и определяется формулой
jfmnp = w2aa -{- n2b2 -{- р2с2 -\- 2 mnab cos i -f-
-j- 2 npbc cos a -\~2pmea cos p. (I, 3)
Принято символ узловой прямой заключать в квадратные скобки
[тпр].
в) Узловая плоскость. Индексы семейства узловых
плоскостей. Пространственная решётка может быть построена следующим
образом. Двумя трансляциями строится бесконечная сетка —
узловая плоскость, третьей трансляцией, не лежащей в этой плоскости,
строится решётка. Пространственная решётка кристалла может быть
представлена семействамиу зловых плоскостей бесчисленным
количеством способов. Всякое семейство узловых плоскостей состоит из
параллельных плоскостей, расположенных на одинаковом
расстоянии друг от друга.
Для данной решётки исчерпывающей характеристикой семейства
узловых плоскостей будет указание ориентации одной из этих
плоскостей относительно выбранных осей координат и
межплоскостного расстояния. Достаточно также задать ориентацию по
отношению к выбранным осям плоскости, наиболее близкой к началу
координат. Расстояние этой плоскости от начала координат будет
равно межплоскостному расстоянию рассматриваемого семейства.
Пусть эта ближайшая к началу плоскость отсекает на осях
решётки доли основных периодов идентичности -~-, -г- и -т-.
Числа /*, к, l, характеризующие ориентацию плоскости, назовём
индексами плоскости. Нетрудно видеть, что h, к, I — целые числа.
Это следует хотя бы из такого рассуждения. Рассмотрим плоскость
семейства АВ, проходящую через начальный узел, и другую CD,
сдвинутую на вектор а. Это показано па фиг. I, 3. Между этими
узловыми плоскостями будзт проходить и другие, но они должны
быть расположены на равных расстояниях друг от друга.
Следовательно, период идентичности будет делиться узловыми плоскостями
на целое число h частей. Такое же рассуждение справедливо и для
других периодов идентичности.
Ближайшая к началу координат плоскость, отсекающая целые
значения шх, %х, р* периодов идентичности по осям координат,
найдётся, очевидно, по уравнению

1С КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. t
причём тх, тех, р* будут целыми числами, лишёнными общего
для всех трёх чисел множителя.
Например плоскость (236) отсекает по осям отрезки -£-, -х- и
-g-. К этому семейству принадлежит любая плоскость, которая
отсекает по* осям отрезки, в целое число раз большие приведённых.
Так в нашем случае следующие
с а плоскости будут отсекать такие
отрезки по осям:
«'¥ Ь«Т
3 7 С
2а, -^ Ь, -j с;
— а, -5-6, -—с; За, 26, с
2 о о
и т. д. Здесь mx = 3, wx = 2
и р* = 1. Это иллюстрируется
фиг. I, 3 для двумерного случая.
Если плоскость отсекает по
осям отрицательные отрезки, то
это отмечается знаком минус над
соответствующим индексом.
Совокупность трёх индексов
плоскости называется её символом.
Условимся также заключать
символ плоскости в круглые скобки,
а именно так: (Ш).
Очевидно, что плоскости (КкТ)
n(hkl) принадлежат к одному
и тому же семейству. Поэтому
можно у индексов плоскости
менять все знаки на обратные.
Если плоскость параллельна
оси координат, то
соответствующий индекс равен 0. Таким
образом (101) есть плоскость, параллельная оси Ь, (100) есть
плоскость Ъс решётки и т. д.
г) Обратные векторы. Для описания семейства узловых
плоскостей, в особенности в косоугольных системах координат (а основные
векторы решётки зачастую образуют такую систему),
исключительно целесообразно ввести в рассмотрение так называемые
обратные векторы, определяющиеся следующими уравнениями.
Если а,Ъ, с — основные векторы решётки, а а*, 6х, сх —векторы,
в в
Фиг. I, 3. Семейство узловых
плоскостей (230). Плоскость ЛВ
проходит через начало координат,
плоскость CD выводится из неё
трансляцией а.

S 1] описмшк ui'OuiivvHCTBEtmoii решетки
им обратные, то *)
17
(1,4)
(abx) = (ас*) = (6ах)= (&сх) = (ca*) = (с&х) = 0. {*, -5>
Из этого определение следует, что вектор а* перпендикулярен
плоскости Ьс, вектор Ьх—плоскости еа и вектор сх— плоскости aft,
(фиг. I, 4). В случае прямоугольной
системы координат «прямой», вектор а и
обратный ему вектор а* антипараллельны.
Векторы ах, Ьх, сх называются
основными обратными векторами, ибо они об-
ратны основным векторам решётки а, Ь, е.
Написанные условия определяют также
длину основных обратных векторов
а =
1 = ИМ = |[М
a cos act* (a [be]) Г
(U)
Фиг. I, 4. Прямые и обратные
где I —объём элементарной ячейки. векторы.
Так как направление ах совпадает
с направлением \Ъс], то можно заипсатт, и в векторной форме
4 v
и аналогично
&х =
i^J, С*=ВД. (1,7)
Фиг. I, 5. Нахождение
направления нормали к
любой плоскости (ЬЫ).
tt
Зная основные обратные векторы,
можно найти направление в пространстве
нормали к любой плоскости (Ш).
Действительно, из фиг. 1,5 следует, что
вектор нормали ДГ(аи) должен быть
с и
перпендикулярен векторам — г- п
Ь а _,
у —д . Следовательно, направление
mi) должно совпадать с направлением векторного произведения
17JL __ Bl W (SL _ Ml _ I*HJ j_ (£^3 _l Иц1
|Д k h )A \ l k )\~ Id "i ih i hlc '
*) Круглые скобки означают скалярное, квадратные—векторное
проведение векторов.

18 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА |>Л. I
Помножал на у, мы получим некоторый вектор
%>hn = Uf+.kV + lc\ (1,8)
параллельный нормали к плоскости (hkl). Этот вектор назовём
обратным вектором плоскости (hid). Вектор 4рш позволяет, таким
образом, находить ориентировку в пространстве семейетва узловых
плоскостей.
Однако, более того, при сделанной нами нормировке этот
вектор получил длину, равную обратной величине межплоскостного
расстояния
♦«-ssr- (1>9)
Для доказательства этой весьма важной формулы поступим
следующим образом.
Вне зависимости от характера системы координат уравнение
плоскости (hhl), проходящей через начало координат, запишется
так:
Ятпр ё~) — О, (1,10)
$hkl /
где ttmnp*=ma-\-nb-{-pc есть радиус-вектор узла, лежащего
в этой плоскости (hkl), a Фш/Фш— единичный вектор нормали
к этой плоскости. Подставляя $ш = ha* -f- кЪ* ~\- 1с? и учитывая
условия, определяющие обратные векторы, получим:
Лт+ *»+*? = <). (1,11)
Как известно, первая плоскость может быть получена из
нулевой трансляцией на у, или у , или -~. Сдвинем начало
координат на вектор —т-. Нумерацию узлов оставим прежней. Тогда
радиус-вектор узла [[т»р]] будет равен
Уравнение первой от начала координат плоскости имеет вид
*-.f£f)-rf»* (U2)
где dhkl— расстояние ее* от начала координат, т. е. меишлоскостное
расстояние. Подставляя значение *£>ш, получим:
(hm ^-кп-\-1р~\-1)'^-г= dm
или, принимая во внимание равенство нулю hm-\-kn-\-lp для
плоскости, проходящей через начало, имеем: d1M = -— .
Vhkl

8 И
ОПИСАНИЕ ПРОСТРАНСТВЕННОЙ РЕШЁТКИ
10
Итак, доказано, что обратный вектор плоскости (ЬЫ),
определяемый уравнением (1,8), направлен по нормали к ней и численно
равен межплоскостному расстоянию семейства (Ш).
д) Некоторые формулы структурной кристаллографии.
1. Объём элементарной ячейки. Как известно из
аналитической геометрии, объём косоугольного параллелепипеда
выражается формулой V=(a[bc]). По формулам векторного исчисления
квадрат смешанного произведения равен
Fa=(afo)2 — а2 (6с)'
т. е.
62 (га)2 — с2 (aft)2 -f- 2 (ab) (6с) (со),
V = abc \fl —cos2 а — cos2J3— cos2 *f -j- 2 cos a cos [3 cos 7. (1,13)
2. Связь между параметрами обратной и прямой
ячеек. Параметры ах, Ьх, с* и ах, {Зхдх параллелепипеда,
построенного на основных обратных векторах, связаны с параметрами
соответствующей элементарной ячейки, построенной на основных
прямых векторах а, Ь, с, ос, (3, *f следующим образом.
Непосредственно из (1,7) имеем:
ах = -у be sin а,
/>х — -трг ас sin (3, ,
х 1 1. •
с =-тг absmf. }
Для косинуса одного из углов, например чх, имеем:
РЛ-.,.х_ (*»»*) _QMM)
Пользуясь формулой векторного исчисления
([6с] [са]) == (be) (еа) — фа) с2,
(Г\14)
получим:
cos ^ = -
аналогично получаем
Ъс~а • cos а • cos ft — be^a cos y cos a cos 5 —cos 4
Ъс1 a sin a sin ft
sin о sin ft
COS а
x cos ft cos у — cos a ]
sin ft sin у '
ox COS a COSY—COS ft }
COS 8 = -: -. , '
r em a sm y
cosy
cos a cos ft — cos y
sin a sin ft
(1Д5)

20 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [о. Т
3. Длина обратного вектора и межплоскостное
расстояние. Длину обратного вектора семейства плоскостей
(Ш) вычисляют по формуле:
$!« = /t2 а*2 + № &*2 + Р сХ2 + 2 Ш*Ь* cos ?* +
+ 2Mb* с* cos асх-Ь2^сх ах cos?*. (1,16)
Эта же формула служит для определения межплоскостного
расстояния, так как &м = jj— • Однако, если надо определить dhPl,
то целесообразно заменить параметры обратной решётки
параметрами прямой. Проделывая эти преобразования при помощи только
что выведенных формул, получим:
-L = -£, [ЪЧЧ* sin2 a + с%2*2 sin2 (3 + а2/>2/2 sin27 -\-
-4- 2а6с2 (cos а cos (3 — cos 7) hk ~\- 2cPbc (cos 8 cos 7 — cos a) M J-
-{-2а62с (cos f cos а — cos(J)JA]. (1,17)
4. Закон зон (условие параллельности узловой прямой п
плоскости). В предыдущем разделе было показано, что уравнение
плоскости (hkl), проходящей через начало координат, имеет вид
Нт-\-кп-{-1р = 0. (Г, 11)
Это уравнение может быть также трактовано следующим
образом: это есть условие того, что узловая прямая [тпр] лежит
в плоскости (hkl). Можно сказать н иначе: это есть условие для
индексов плоскостей, пересекающихся по прямой [тпр]. В последней
форме это условие называется законом зон. Серия плоскостей (hkl),
пересекающихся вдоль одной узловой прямой, называется зоной,
и прямая [тпр] называется осью зоны.
Условие зональности позволяет определить неизвестный символ
[тпр] оси зоны, если известны символы двух её плоскостей (hjc^)
и (hqk2l2). Действительно, написав уравнение 1.11 для обеих
плоскостей :
hym -\- кхп -\- 1гр = О и Ji2m -\- k2n -[-l^p — О,
находим из них три неизвестные ?n, n и р с точностью до
постоянного множителя:
т = кг12 — 1хка, п = 1^о — /i^2> j0-=='*i&2 — ^i^2- (I» И а)
Эти решения суть миноры матрицы \\ l 1 г
ibq, Л/о la
получаемые при
отбрасывании соответственно первого, второго или третьего столбца
(второй минор берётся с обратным знаком).

§ 1] ОПИСАНИЕ ПРОСТРАНСТВЕННОЙ РЕШЁТКИ 21
Совершенно аналогично решается и обратная .задача об
определении неизвестного символа плоскости (hkl), в которой лежат
две (непараллельные) прямые с известными символами [^п,/»,]
й [щп&ъ]-
5. Условие перпендикулярности узловой прямой
и плоскости. Очевидно, такое условие может быть записано
в форме
№тпр &hkl)
R>mnp Qhkl
Это означает, что радиус-вектор точки
[тпрЦ
Bmnp = ma-\~nb^rpc
совпадает с обратным вектором &ш = ha*-\-hb*-^-1ех плоскости (Ш).
Перемножая, получим:
hm + kn-\-lp . /Т10\
~7? сч ==1* U-18)
■Ятпр 'УНЫ
В общем случае это уравнение не имеет решения. Только для
простейших случаев нормалью к узловой плоскости будет узловая
прямая.
Особенно простым будет случай, когда решётку можно
описывать в кубических осях, т. е. если а = Ь = е и а = |3 = у — 90°.
В этом случае
Условие перпендикулярности имеет вид
hm -f kn + lp = 0Ara2 + w2+j92) (/Д2+"^+72).
Это равенство превращается в тождество при m — h, п — к, р = 1.
Таким образом, в кубической решётке узловая прямая [тпр]
перпендикулярна узловой плоскости (тпр).
6. Вычисление углов между узловыми прямыми
ж плоскостями. Угол между двумя узловыми прямыми JB и JB'
ищем по формуле
™Ч=(-ТПЪГ- (1'19)
Длины векторов В и R' находятся по формуле (1,3), а
скалярное произведение раскрывается так:
(.В • R') = (ma -\- nb -j- рс, т'а-\- п'Ъ -\-р'с) =
— mm'a?-\-mri(db)-\- •• •
Для вычисления угла нужно знать параметры решётки и сим-
ы [тпр] и [т'п'р'] прямых, образующих искомый угол.

22 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
Совершенно аналогично определяется угол между плоскостями
(Ш) и (h'k'V) по формуле
c„s? = «-^f> (1,20)
и угол между прямой и плоскостью — по формуле
«*?-■*££*• (1,21)
е) Различные способы выбора основных векторов или осей
координат решётки. Для описания решётки могут быть приняты
различные тройки векторов а, бис. Если внутри элементарной
ячейки нет узла, то такая ячейка называется примитивной.
Различные способы выбора примитивной элементарной ячейки
показаны на фиг. I, 6. На каждый узел решётки приходится
одинаковый объём. Это объясняется периодичностью пространственной
Фиг. I, 6. Различные способы выбора примитивной
элементарной ячейки.
решётки. Объём, приходящийся на один узел, равен объёму
примитивной элементарной ячейки независимо от способа выбора её.
Действительно, каждый из восьми узлов, находящихся в вершинах
такой ячейки, «поделён» между восемью ячейками, т. е.
принадлежит каждой из них на 1/8. Таким образом, на каждую ячейку
приходится 8--£-=1 узел. В ряде случаев целесообразен выбор
алементарной ячейки большего объёма, чем примитивная, т. е.
содержащей дополнительные узлы, помимо узлов в вершинах.
Сложную, т. е. непримитивную, элементарную ячейку,
характеризуют координатами узлов. Совокупность координат узлов,
входящих в элементарную ячейку, называют базисом ячейки.
По причинам, которые станут ясными из дальнейшего, весьма
часто целесообразно вместо примитивной элементарной ячейки
выбрать элементарную ячейку, у которой дополнительные узлы
находятся в центрах граней или в центре «бъёма *). Три случая
являются распространёнными.
*) Понятие центрированной ячейки иногда употребляют в более
широком смысле, понимая под «центрированной» всякую непримитивную
элементарную ячейку, дополнительные узлы которой необязательно, нахо»
дятся 8 центре объёма, центрах граней или рёбер.

1]
ОПИСАНИЯ ПРОСТРАНСТВЕННОЙ РЕШЁТКИ
23
1. Объемноцентрированная ячейка. Дополнительный
узел находится в точке пересечения телесных диагоналей ячейки.
На каждую ячейку приходится два узла: Г [000] J и hir"|"¥j Г
Координаты узлов указываются в долях периода. Если основные
векторы примитивной ячейки суть а, Ъ
и с, то ту же ячейку можно
представить в виде объёмноцентрированной
с основными векторами а', Ъ', с'.
Соотношение между векторами очевидно из
фиг. 1,7:
а ~а,
Ь' = Ь,
с' = 2с
а
а
Ь
а,
Ъ',
и' f Ъ' + С
(1,22)
(1,22а)
_*
Фиг. I, 7. Объёмноцентри-
рованная ячейка.
На объемноцентрнрованную ячейку приходятся 2 узла. Один
узел (в центре) целиком принадлежит ячейке; 8 узлов — вершин
парраллелепипеда — принадлежат каждый 8 ячейкам (т. е. данной
ячейке каждый из таких узлов принадлежит на 1/8).
2. Гране центрированная ячейка. Дополнительные
узлы находятся в центре одной пз пар граней, например, аЬ. На
[[OOOjl и |[|-70]|* Связь
каждую ячейку приходятся два узла:
между основными векторами а, Ь, с примитивной и а', Ъ', с
гранецентрированной ячеек даётся
формулами (см.
фиг. 1,8):
а'=а,
Ъ'^2Ъ —
а,
Фиг. J, 8. Гранецентриро-
ванная ячейка.
*=4(«ч-»'),
е = с'.
На эту
два узла,
ячейку
так как
также
узлы
(1,23)
(1,23а)
приходятся
в центрах
противоположных граней принадлежат каждой ячейке
наполовину.
3. Всестороннецентрированная ячейка.
Дополнительные узлы находятся в центрах всех граней, Как показывает

24 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
фиг. ■ 1,9, связь между основными векторами примитивной и все-
етороннецентрированной ячеек даётся формулами:
а' = —а ~\- Ъ -\- с,
_^.—""^
с
ь\
З-"""^
i ^ ^^^^~
од /
"~c"~*V
b'
Ь'— ст— Ь-\-с,
с' = а-±~Ь — с;
Ъ'-\-с'
ст =
с —
(Г,24)
(1,24а)
Фиг. I, 9. Вееетороннецентри-
рованная ячейка.
2 '
2
Каждой ячейке принадлежат 4 узла:
[ооо]], [[Но]], [[|о!]] и
При написании полного символа пространственной группы (об
этом ниже) мы будем пользоваться следующими обозначениями:
Р— примитивная ячейка; А, В, С—ячейки, центрированные
в гранях be, ас и аЪ; F—всестороннецентрированные ячейки и
J—объёмноцентрированные. Эти наиболее распространённые случаи
центрировки сведены в таблицу I.I.
Т а блиц a I, I
Символ
р
А
В
С
J
F
Базис
| [000]]
[[000]] ,
[1000]],
[[000]],
[[000]] ,
Ш\
ХЫ]]
вн
\j 2" 2" J J
[Ю(ю1],[[оЛ1]]
[[Щ[Ш
Число узлов
на ячейку
1
2
2
2
2
4
Объём ячейки
Ур
VA=2Vp
VB = 2VP
Vc = 2Vp
Vj~2Vp
T>=4FP

§1]
ОПИСАНИЕ ПРОСТРАНСТВЕННОЙ РЕШЁТКИ
25
4. Общий случай. В произвольном случае, переходя от
описания решётки в осях а, Ь, с к описанию в осях »', Ь' с', мы
производим преобразование по формулам:
а' = °11« + а126 + °13С»
Ь' =a21<j-j-a22&-J-°23c> \ (1,25)
^ = 031«+а326 + °33^ •
Решая эти уравнения относительно а, Ъ и с, находим формулы
перехода от новых осей к старым:
6 = T2i^'+'"22&'+ "2з'Л (1,25а)
0 = T3lrc'-f-T3a&'-f<:3sc'.
Величины оЛ. и т<ь называются коэффициентами преобразования.
Первый индекс указывает номер строки, второй — номер столбца.
Это скаляры, могущие нриниматг, целые и дробные, положительные
и отрицательные значения. Формулы преобразования не содержат
свободных членов. Следовательно, начало координат при
преобразовании не меняется.
Таблицы, характеризующие преобразование старых осей в новые
и обратно, записываются в виде ,
ТП Т12 Т13
Х21 Т2о Т^
~31 "32 "38
Определители утих таблиц AJ и Ат называются определителями
преобразования. Зная коэффициенты о1Ъ находят коэффициенты -iK
по формуле
°11
°21
°31
°12
°22
°32
°13
°23
°33
И
Чк Т7~ ' \ 1) >
(1,26)
где &L — минор определителя Аа, получаемый из него
вычеркиванием &-й строки и г-го столбца. Справедлива и обратная формула
'ы
Чк
(-1)
i + k
(1,26а)
Кроме того, между коэффициентами преобразования существует
ещё следующая зависимость;
V ( 0 при ъфк, v ( ° ПРИ ьфк, /то«^ч
ZiQuxu = \ * • , и 1°^ = L • , 0.266)
1«! I 1 при г = & ^ (1 при ;, = 7с.
Формулы (1,25) и (1,25а) являются векторными равенствами и
Потому не могут служить для определения абсолютных величин

26 кристаллограф, основы структурного анализа [гл. i
осей а, а' и т. д. Коэффициенты преобразования сит даже
в случае прямоугольной системы координат не являются
направляющими косинусами. Для нахождения абсолютных величин осей
следует пользоваться формулами скалярного произвецения
(а' • а') = а'~ = з'па~ -\- а{ф~ -\- о^с2 -j- 2ot ^12 ab cos ab -j-
4" 2o12o18/>c cos he -f- 2o13onca cos ca. (1,27)
Определитель преобразования Дт (ташке Ат) имеет наглядный гео-
v
метрический смысл, а именно А7 = -—■——, т. е. определител!.
аЪс
преобразования а -> а', Ъ-+Ъ', с ->• с' равен отношению объёма
элементарной ячейки, построенной на векторах а', Ъ\ с', к объёму
элементарной ячейки, построенной на векторах а, Ь, с. Дадим
простое доказательство:
Va'b'c = (a' [6V]) =
= (а11« + а12& "Г а13^) [о2,« -t" °22fo + °23<% °31« + 3326 4~ аЗЗС1 =
= (аТ1^ 4" ~126 + а13С) (°21312 [«&] "Г °21°83 iaC] -Г а22331 [&«] 4*
+ °22а33 [&С] 4- °23°31 [€а) 4" 323С32 [<*] ) =
-=(1 [ЬС] [6j ,(033033— Зо;^32)+а12(°23^31 — б21в8з)+а1»(0Й13За—°2233l)] —
= а [Ьс] • Дт = УаьЛ*
А*. (.[,28)
Д\ (Т,28а)
Легко проверить, что если системы осей a, ft, л и а\ Ь', <•'
одноимённы (правая и правая, левая и левая), то определители
положительны; если же они разноимбнны, то определители
отрицательны.
Если примитивная ячейка преобразуется в примитивную же
(f/=F'), то определитель преобразования равен единице. Если же
она переходит в сложную ячейку, содержащую и узлов, то
определитель равен п (целое число). -)то и понятно, ибо на каждый
узел в решётке приходится одинаковый объём- Дробные значения
определителя преобразования получаются при переходе от сложных
ячеек к примитивным, или к сложным же ячейкам меньшего объёма.
Эти правила легко проверить на данных преобразованиях
примитивных ячеек в ячейки Л (В, С), J и F. Формулы
преобразования основных векторов иди осей координат решётки определяют
v
ubc
Совершенно аналогично:
v
abc
1 а'Ъ'е'

ft l] ОПИСАНИЕ ПРОСТРАНСТВЕННОЙ РВШЁТКИ 27
формулы преобразования: 1) обратных векторов, 2) символов
узловых плоскостей, 3) символов узловых прямых.
Для нахождения формул преобразования обратных векторов
воспользуемся формулами (1,4):
(аа*) + (ЬЬХ) + {ссх) = 3 - (а'а'х) -f (&'&'*)-f {c'cfX). (1,29)
Подставляя значения а', Ъ' и с' из (1,25), получим:
(<шх) + (&&х) + (ссх) = а'х (oua -f а]2& 4- °1вс) 4-
+ &'Х (a2i«4- °22& + °аз<-*) -f С* (а31я + о326 4" ^33^) =
4-е(ах/о13 + &х/"м + ех,°м).
Приравнивая коэффициенты при a, ft и с в левой я правой частях
уравнения, получим:
a* = sn,/*'4-^x/4-°3iCx', )
ftx = a12ax/4-^26x4-c32^x/, (1,30а)
с* = о1Ъах' + o^bx' A-o^c*', )
Это и есть формулы преобразования новых обратных векторов
в старые.
Воспользовавшись для подстановки значений а, Ь п с в
формулу (1,29) формулой (I, 25а), найдём аналогичные формулы
преобразования старых обратных векторов в новые:
а*' = хиах 4- %&х 4- Vх*
ft*' = ^12«х -И22&х 4-%>сх,
cx'==T13ax4-x23&x+Vx- J
(1,30)
Сравнивая формулы (I, 25) с формулами (I, 30а) и формулы (Г, 25а)
с формулами (1,30), легко видеть следующее: новые обратные
векторы получаются из старых с помощью тех же коэффициентов
преобразования, что и старые прямые векторы из новых, но только
коэффициенты преобразования записываются не по строкам, а по
столбцам; аналогично, старые обратные векторы получаются из
новых с помощью тех лее коэффициентов преобразования, что и
новые прямые векторы из старых, но записанных не по строкам,
а по столб цам.
Чтобы найти формулы преобразования индексов узловой прямой
или узла, воспользуемся инвариантностью вектора, проведённого
ЙДОль прямой или соединяющего узел с началом координат:
R — та 4- пЬ +ре = т'а' -\- u'V ~\-p'v't (1, 31)
[т'п'р'] —- новый символ прямой или узла.

28 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
Как и при выводе формул преобразования для обратных
векторов, подставим в эту формулу значения а\ Ъ', с' из (1,25);
приравнивая коэффициенты при а, Ь, с в левой и правой частях,
найдём формулы преобразования новых индексов в старые. Если же
в формулу (1,31) подставить значения а, Ь, с из (1,25а) и
приравнять коэффициенты при а'', Ь'', с', то получим*формулы
преобразования старых индексов в новые:
т = опт' + 02У-Г3зУ> J
п = опт' -\- Оооп' -\- o32i>', V (1,32а)
w, = x11m + T21w-{-T3j^, j
л' = т12и»-|- Тда»-J-1^, > (1,32)
/ = T18j»4-x28« + T8a^. )
Таким образом, формулы преобразования индексов узла или
прямой совершенно аналогичны формулам преобразования
обратных векторов.
Остаётся вывести формулы преобразования индексов узловых
плоскостей. Для этой цели воспользуемся инвариантностью вектора
обратной решётки:
ф = ha* + 1сЪх + 1сх = к'а*' + КЪ*' + 1с*'. (I, 33)
Совершенно аналогичным приёмом (подставляя значения ах, Ъх, с*
или а*', &х/, сх' и приравнивая коэффициенты при а*', ft*', сх/
или при стх, 6х, сх) получим формулы:
/*' =
7с'=
/' =
Ь =
fc =
г =
:On/t-f <
621fc-i-c
V*+e
xnfc' +
xeifc' -f
^Л' +
»i2fc + o13i,
!22& + °2B^
J32"' ~T~ °33^'
x12fc -f~x13i ,
X22* "T^S^ »
T32^ H~'C33^-
Следовательно, формулы преобразования индексов узловых
плоскостей совершенно аналогичны формулам преобразования осей:
применяются не только те же самые коэффициенты преобразования,
но и не происходит замены строк столбцами.
§ 2. Линейное преобразование пространства
В этом параграфе мы для простоты повсюду будем применять
прямоугольную систему координат. Это, однако, не уменьшает
общности выводов, ибо свойства того или иного преобразования

ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЙ ПРОСТРАНСТВА
20
8*1
пространства, конечно, не зависят от того, в какой системе
координат описывается это пространство и его преобразования.
а) Параллельный перенос
или трансляция. Это
преобразование пространства
заключается в движении всех его
точек по параллельным
прямым в одну и ту же сторону
и на одну и ту же величину.
Любая точка М{х, у, г)
переходит при этом в точку
М'(х', у', г') по формулам:
.'/'—?/о + ?/»
(I, 35)
I, 10. Параллельный перенос или
трансляция.
Формулы эти справедливы и Фиг.
для косоугольной системы
координат.
Вектор t0 с компонентами г0, у0, г0 (фиг. 1,10) называется
вектором переноса или трансляции. Очевидно, что перенос точек
пространства на t0 при неподвижной
системе координат
эквивалентен параллельному переносу
системы координат на —tQ при
неподвижном пространстве,
т. е. изменению начала
координат при сохранении
направления осей.
б) Поворот вокруг оси.
Вращение пространства вокруг
оси координат (например, Оу)
описывается следующим
образом. Все точки пространства
не изменяют своих
координат по оси вращения
(фиг. I, И). Проекция М (хОз)
любой точки пространства
7"(жг/г) повернётся на некоторый угол <? (положительным считается
Вращение против часовой стрелки) и перейдёт в М' (х'Ог'). Проведём
РИомогательную прямую О А, образующую с осью Оз угол <р. Со-
ю построению OS = OS' и SM = S'M'. Из прямоугольных
^угольников NS'M/ и OPS' находим NS' — S'M' sin © = х sin ®
OP = arcose=,grcos?. Но s' = OP — NSft У = NAT-^ PS'.
Фиг. 1, 11. Поворот вокруг осн.

Я(>
КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА
|1'Л. 1
Следовательно, формулы преобразования координат при повороте
вокруг оси Оу на угол » таковы:
х' = х cos » -j- з sin »,
</' = ?/, | (1,36a)
#' — — х sin » -f- £ cos ».
Аналогичные формулы получаются и для поворотов вокруг осей ог
(на <*>) и о.г (на Ф):
.г' = .?; cos а) — ?/ sin ш, I
//ssa'SUUe + il/COSa», } (1,366)
(Г, Звв)
?/ =?/ cos Ф — £ sin Ф,
^' = г/ sin Ф -}~ ^ cos Ф-
Таблица коэффициентов преобразования для первого случая имеет
вид:
cos» О sin»
О 1 О
— sin » О cos»
Определитель преобразования А = cos3 » -j- sin2 » = 1. Это
справедливо и для поворотов вокруг осей Ох и Or.
Легко видеть, что поворот пространства вокруг оси координат
(скажем, Оу) на некоторый угол » при неподвижной системе
координат эквивалентен повороту системы координат вокруг той же оси
на угол — ». Если на фиг. Т, 11 принять О А за новую ось 0~',
а перпендикуляр к ней за новую ось Ох', то координаты точки М
в новой системе координат будут (замена » на —»):
хх = — z sin » -\~ х cos »,'
?/х«У, (1,37)
£х = г cos » -f- x sin ».
Поворот пространства вокруг произвольной осп (не оси
координат) на любой угол может быть описан как результат трёх
последовательно .произведённых поворотов: вокруг оси Ох на Ф, вокруг
оси Оу на » и вокруг оси Oz на <о. Применяя формулы (Т,36в),
(1,36а) и (1,366), имеем:
х!" = х cos со cos » — у sin to cos <o-\-z sin «; I
у'" = .-r (sin со cos Ф 4~ cos (о sin » sin Ф) -j- I
-f- ?/ (cos <o cos «1» -j- sin <o sin » sin 0) — r cos » sin Ф;
£w = # (sin со sin Ф — cos a) sin » cos Ф) -|-
-f- ?/ (cos <o sin Ф -j- sin a) sin » cos Ф) ~\- ~ cos » cos Ф. J
(I, 38)

2]
ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА
31
А^=
Определитель преобразования
oos u> cos о — sin u> с »s 4» sin (p
sia u> oos ф +ons u> sin <p sin ф cos u) cos >1>—sin u> sin о sin ф —cos <p sin ф
sin u> sin ф— cos u> sin c? cos ф cos u> sin ф -]- sin u> sin о cos ф cos cp cos ф
=i. (I, 38a)
Подробное проведение выкладок предоставляем читателю.
Итак, при любом повороте пространства определитель
преобразования равен единице. Справедливо и обратное положение:
преобразование первой степени относительно всех переменных, не
содержащее свободных
членов, определитель
которого Д = -1-1, есть
поворот (или
совокупность поворотов).
в) Инн ej) сия. Под
инверсией понимается
своеобразное
«отражение в точке», которая
называется центром
инверсии (фиг. I, 12).
Если центр инверсии
принять за начало
координат, то
преобразование инверсии
заключается в том,
тао любая точка
М С'", У> -) переходит
в точку М' (г',!/',~')-
инверсия меняет
направления векторов,
соединяющих точки,
за. обратные, не
изменяя их величины.
Формулы преобразования
имеют вид:
У = —?/, (
(Г,:*0
Фиг. I, 12. Инверсия.
&ни справедливы и для косоугольной системы координат.
Определитель преобразования
-1 О О
А =
О —1
О О
о
— 1

32
КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА
[ГЛ. I
Очевидно, что инверсия пространства при неподвижной системе
координат эквивалентна перемене направлений всех трёх осей
координат на обратные при неподвижном, неизменном пространстве.
Можно произвести сложное преобразование пространства,
состоящее из поворота и инверсии. Последовательность проведения
поворота и инверсии безразлична. Комбинируя (I, 38) и (I, 39), имеем:
х'" = — х cos (о cos « -\- у sin со cos ^ — з sin <p:
у"' = — х (sin <o cos ф -\- cos <о sin 9 sin ty) —
— у (cos (о cos ф — sin <« sin cp sin ty) -j- s cos ® sin J>;
#'" = — x (sin со sin ф — cos со sin 9 cos <b) —
— ?/ (cos со sin <1> -j- sin (o sin 9 cos <!>) -4- 5? cos 9 cos ty.
Определитель этого преобразования равен — 1.
Справедливо и обратное положение: преобразование первой
степени относительно Rcex переменных, пе содержащее свободных
членов, определитель
которого Д = — 1, есть
инверсия с поворотом
(или чистая инверсия).
г) Отражение в
плоскости. Это
преобразование заключается в том,
что любая точка
пространства Ъ\{х, у у з)
переходит в точку
ЗГ (х', у\ z'\, лежащую
на перпендикуляре,
опущенном из точки Ж на
отражающую плоскость,
на том же расстоянии от
неб, что и исходная точка М, но по другую сторону её.
Следовательно, если за отражающую плоскость принять координатную
плоскость, например хОз, то преобразование отражения не изменяет
координаты по осям, лежащим в плоскости отражения, а координата
по оси, перпендикулярной этой плоскости, изменяет знак на
обратный. Это иллюстрируется фиг. I, 13. Формулы преобразования
имеют вид:
х' = х, | х' = — х,
, I (отражение f
У ——?/> | R плоскости У —,'/,
3=3 ) " .?==*•
Фиг. I, 13. Отражение в плоскости.
(отражение
в плоскости
Oyz);
У' = ?/,
(отражение
в плоскости
а-уО).
(I, 40)

§2]
линейное преобразование пространства
33
Определитель преобразования равен
А =
1
О
О
О
— 1
О
О
О
1
Очевидно, что отражение пространства в плоскости при
неизменной системе координат эквивалентно изменению направления одной
из осей на обратное при неподвижном, неизменном пространстве.
Можно доказать следующие теоремы:
1. а) Отражение в плоскости эквивалентно повороту вокруг оси,
перпендикулярной этой плоскости, на 180° с последующей инверсией
(центр инверсии — точка пересечения оси и плоскости). Это видно
уже из фиг. I, 13 и из того, что комбинация (I, 36) (при ?= 180°)
и (I, 39) приводит к (I, 40).
б) Инверсия эквивалентна отражению в плоскости с
последующим поворотом на 180° вокруг оси, перпендикулярной этой
плоскости (фиг. I, 13).
2. Поворот вокруг оси на 180° эквивалентен отражению в
плоскости, перпендикулярной атой оси, с последующей инверсией
(фиг. 1,13).
3. Инверсия эквивалентна отражению « трёх взаимно
перпендикулярных плоскостях.
Итак, за основные исходные преобразования можно принять:
повороты и инверсию (тогда отражения в плоскостях оказываются
производными) или отражения в плоскостях (повороты и
инверсия— производные). Мы примем за исходные преобразования
повороты и инверсию.
д) Общий случай линейного преобразования. Под
преобразованием пространства следует понимать всякое изменение его,
например поворот, перенос, деформацию и т. д.
Преобразуем пространство по формулам:
Х* = Х0 + аПЖ + «12?/ + а13^ = Х0 И" Х'>
У* =Уо~Ь <*21Х + а22*/ + V = У0 + У'>
*х = *о + а31ж + *тУ + атг = *o + s'-
(Ui)
Поскольку преобразуется пространство, не только одна точка
M(xyz) переходит в точку М* (жх, у*, z*) по формулам (1,41),
но и любая другая точка N{XYZ) переходите точку Nx (X*rxZ*)
по тем же самым формулам:
Хх=я0+а11Х+а12Г4-«1з^
Y* = У0 + «21X -Н а22 Y + а23&
Z* =5'o + a3lXH-a32*r-ba33^
(1,414)

31
КРИСТАЛЛОГРАФ. ОСНОТШ СТРУКТУРНОГО ЛНАЛНИЛ
[гл. г
NWfZ*)
M'(x'y*z'>
Преобразование (1,41) будем называть линейным, если оно
не «деформирует» пространства (не растягивает, не сжимает, не
скручивает). Иными словами,
преобразование пространства (1,41)
называется линейным, если оно ^не
изменяет расстояний между точками.
Расстояние между двумя любыми
точками М и Лг до преобразования
равно расстоянию между
полученными и я них после преобразования
точками Мх и /Vх: ^я = ^ж*лт><
(фиг. 1,14).
Выясним, каковы должны быть
свободные члены х0, у0 и ~0 и
коэффициенты <хи., чтобы
преобразование (1,41) было линейным. Для этого
подставим в выражение d2 значения гх, у*, гх, Xх, Ух, Z* и:ч
(Т,41) и (1,41а):
М(хуг>
Фиг. Т, 14. Общий случай
лилейного преобразования.
^=(Х—г)«+(У—?/)а+(^—rr)e =
= X2-}-y2-f &-[-x*-\- //а-|-г2 — 2(X.f-r- Yy-\-Zs), (Г,42)
d^* = {X*-х*)* + (Y* - у*)*+(Z*-**)* =
= X2 («и + «и + «зО + Г2 (я?-.- Н- <4 -|- =4) -h ^ («is + «аз -г а»з) ~Ь
Н- х" («и + a"i + «зг) -г /Г № + °& + °&) -Ь ~" (а?з -Ь «23 + *'зз) +
-f- 2Х Г (аиа12 -f- а21а22 Jr %i732) + 2 УЯ («i2«ia f я22а28 + а32азз) "Г
+ 2ZX (a13an-f-a23a2r!-a33a3i) ~г 2ж.'/ (au2i2-f «21*22 "f а31азз) +
4-2?/-(ot12alS + a22<z23-ba3^33) + 2лг (a18au-f «o^-fa^i)'!-
— 2Хж(а21+*л+ a'si) — 2Ху/ (anai2 + a2ia22 + asia32) —
— 2К~ («na]3 -j- a21a23 -j- а81а83) — 2 >^(а12ац-Ь'а22а2г1-а32^:я) —
— 2 >г//(а?2+424-азз)—2 Уг (*,2ai3+ а22а23 4" а32*зз) —
— 2Zc (a18au + а28аЭ1 + а83а81) — 2/у (а18а]2 -\- а<2Ъ*<,2 •{• ЧъЪч) ~
— 2У,г (а?3 + «гз Ч" «зз). (1,42а)
Мы требуем, чтобы a- т=иесР^хлх» и поэтому должны приравнять
коэффициенты при соответствующих членах в уравнениях (1,42) и
(1,42а). Это даёт следующие соотношения между коэффициентами

§2]
линейное преобразование пространства
Щ
преобразования:
ац -J- a»i + «3i = 1 ] 3 3
ai24-«"2 + 4s=l } SaHa/<= Saff=l (* = 1» 2, 3); (I,43a)
ais T" a23 ~т~ азз = 1 J
alla12 + a21<*22 + a3la32 = 0
aJ2a13 + а22Я23 + a32a33 = °
а11 + a23a2l + a33a3l = °
lB^ll
2 a7<a7* = 0;
z=i
i^fc
г=1, 2,3
fc = l, 2, 3
(1,436)
^Г*" io
Итого G уравнений, выражающих условие того, что
преобразование (1,41) является линейным. Легко показать, что все эти
уравнения независимы друг от друга и что кроме них нет других
независимых от них уравнений между aik. Все шесть уравнении
могут быть записаны одной формулой
„p,i_i /*-1,2,.8\
при 1фк \к = 1, 2, 3/.
В случае прямоугольной системы координат коэффициенты
преобразования агк являются направляющими косинусами; в случае
косоугольной системы они зависят ещё и от углов между
координатными осями.
Что касается свободных членов ^0, у0, *0, то линейность
преобразования не накладывает на них никаких условий: они могут быть
взяты, любыми (при подстановке (1,41) и (1,41а) в (1,42) они
уничтожаются). Это показывает, что линейное преобразование в
общем случае включает в себя перенос. Действительно, сам вид
формул (1,41) показывает, что линейное преобразование может быть
разложено на 2 стадии: 1) линейное преобразование без
переноса (х-» х'; у -> у'; 8-+s')\ 2) перенос (х' ->• жх; у' ~* ух; в' ->г*).
Докажем следующую важную теорему: определитель,
составленный, из коэффициентов линейного преобразования без перс-
носа at7f, может принимать только два значения: ztl.
То-есть требуется доказать:
А =
41 ^12 "13
'21 a22 a23
а.
= =£1.
(1,44)
131 "32 и33
Если провести преобразование (1,41) в «обратном направлении»
(т. е. считать точки Л/Х(жх, ?/*, sx) и iVx(Xx, Гх, Z*) за
исходные, а точки М{хуз) и N(XYZ) за получающиеся в результате

m
КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА
|ГЛ. I
преобразования), то требование линейности преобразования даст
следующие соотношения между <*«:
s^*=i;:::,^.,. u=1~,'iJ).
/=i
1 при i = k fi = l, 2, 3N
О при id-h
(1,45)
Уравнения (1,45), согласно сказанному выше, являются следствиями
уравнений (1,43). Определитель этого «обратного» преобразования
Д' =
И "21 "31
:12 «22 а32
а.
а,
13 "23 "33
а*
= Д.
Этот определитель равен определятелю преобразования (1,41), ибо
отличается от него только заменой строк столбцами и наоборот.
Вычислим квадрат определителя линейного преобразования
112 "13
А2 -= Д . Д = А • А' = | ссц1 «оц а2з
а
31 а32 а33
'll а21 а31 I
42 "*22
43 «23 "33
Л.,.,
а..
Применяя правило умножения определителей (производя
умножение построчно) и принимая во внимание уравнения (Г,45), имеем:
I "?1 + «;2 +«?3' а11а21+а12а22+а13в23' а11а31 + а12п32+я13азЗ
Д' = а21аИ + в22в12+а9Вв18' atl+als +<4 » a2ia31+a22a32+V3S
а31а11 + а82а12+а33а13. а31а21+«32а22+а33в23 , 4l+a32 +<4
1 О О
0 10 =1.
О 0 1
Следовательно, Д= У^2 = — 1> что и требовалось доказать.
Справедлива и обратная теорема: если определитель преобразование
Д = :±:1, то это преобразование является линейным.
Все рассмотренные выше преобразования (перенос, поворот,
инверсия, поворот с инверсией, отражение) являются линейными,
ибо определители их равны -[■ 1 или — 1 • В формулы переноса
входят свободные члены, но, как показано выше, требование
линейности преобразования не накладывает на них никаких ограничений-:
Линейность этих преобразований видна и из того, что их можно
рассматривать как преобразование системы координат при
неподвижном неизменном пространстве. Если же пространство остаётся
неизменным, то расстояния между точками, безусловно, не меняются.

§3]
СИММЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
37
Если соответствующее преобразование переводит «левый» объект
в «правый» (меняет левую систему на правую и наоборот, если
его рассматривать как преобразование координат, а не пространства),
хо его определитель равен —1. Если же «левое» переходит в
«левое», а «правое» в «правое», то определитель
преобразования равен -}-1. Действительно, перенос и поворот не меняют
«знака» системы, а инверсия, инверсия с поворотом и отражение
меняют его.
Покажем, что всякое линейное преобразование без переноса
состоит из поворотов вокруг осей и инверсии*).
Действительно, определитель линейного преобразования без
переноса (л*о — г/0 —- *о — 0) может принимать лишь 2 значения: Д = zt i.
Но всякое преобразование первой степени без свободных членов
с А = -j-1 есть поворот (или совокупность поворотов), а всякое
преобразование первой степени без свободных членов с А=-1 есть
инверсия с поворотом (или чистая инверсия). Следовательно,
линейное преобразование без переноса есть в общем случае лишь
поворот и инверсия.
Преобразование идентичности является тривиальным линейным
преобразованием без переноса: х' = х; у' = у; s' = z. Для целей
систематизации оно может рассматриваться как повброт на 360°
вокруг произвольно выбранной оси.
Содержание данного параграфа можно суммировать в виде
следующей теоремы.
В общем случае преобразования пространства, при которых
остаются неизменными расстояния между точками (линейные
преобразования), могут быть проведены переносами, поворотами и
инверсией.
§ 3. Симметрические преобразовании
а) Закрытые симметрические преобразовании, возможные
У решётки. Рассмотрим произвольную пространственную решётку
и линейно преобразуем это пространство. Если при этом
преобразовании каждая точка М (х, у, з} ячейки перейдёт в точку М' (.г', у\ г'),
обладающую той яге плотностью электронов, то мы назовём такое
преобразование симметрическим. Обычно под координатами хуз
понимаются координаты, выраженные в долях периодов вдоль
основных осей (относительные координаты).
Иными словами, симметрическим преобразованием называется
такое линейное преобразование кристаллического вещества, которое
совмещает его с самим собой, ибо если все его точки переходят
в точки с той же плотностью электронов, то мы не можем
различить кристаллическое вещество до такого преобразования и после
) В другой формулировке — из отражений в плоскостях.

38 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
,'„./„/
него. Естественно, что если симметрическое преобразование
переводит одну узловую прямую в другую, то периоды идентичности
вдоль них должны быть одинаковы. Простейшим и тривиальным
симметрическим преобразованием является преобразование
идентичности (поворотная ось симметрии первого порядка), которое
попросту оставляет точки в покое. Точки, переходящие друг в друга
при симметрическом преобразовании, называются эквивалентными
или гомологическими.
Совокупность всех симметрических преобразований,
свойственных данной пространственной» решётке, называется её
пространственной или фёдоровской группой. Основное свойство
пространственной решётки— её периодичность — ограничивает число и характер
симметрических преобразований.
Для того чтобы вывести все возможные пространственные группы
(а их 230), нужно рассмотреть все допустимые симметрические
преобразования и выяснить правила возможного их сочетания.
Если повторение симметрического преобразования хуг ->• х'у'
-+%"\fz" и т. д. через конечное число операций приводит все
точки решётки к совмещению с ними самими, то такое
преобразование называется закрытым*). Остальные симметрические
преобразования мы будем называть открытыми.
Простейшим открытым симметрическим преобразованием является
трансляция решётки вдоль оси на величину периода. Однако это
преобразование является тривиальным, так как этот результат
очевиден из самого устройства решётки и свойственен каждой
решётке.
Очевидно, что трансляция не участвует в закрытом
симметрическом преобразовании. Таким образом все подлежащие здесь
рассмотрению симметрические преобразования сводятся к поворотам
около осей и инверсии. Геометрический образ симметрической
операции называется элементом симметрии.
б) Поворотные и инверсионные оси. Построение
пространственной решётки накладывает ограничение как на направление оси
поворота, так и на угол симметрического поворота.
Прежде всего очевидно, что ост, симметрического поворота
(поворотная ось симметрии, короче — поворотная ось) должна совпадать
с узловой прямой решётки и одновременно являться нормалью
к узловой плоскости решётки.
Для того чтобы показать, что поворотная ось должна совпадать
с узловой прямой, достаточно доказать, что па ней должны
лежать два узла. Для того чтобы показать, что поворотная ось
) Поскольку симметрия внешней формы идеальных монокристаллов
(идеальных форм роста) описывается закрытыми симметрическими пре-
??!!^?инями' они м°гут быть названы макроскопическими
симметрическими операциями.

§3]
СИММЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
?9
Фиг. I, 15. Поворотная ось
симметрии всегда
перпендикулярна узловой плоскости.
перпендикулярна узловой плоскости, достаточно показать, что
в какой-либо плоскости, перпендикулярной поворотной оси, лежат
три узла.
Для доказательства достаточно вспомнить, что любые линии,
в том числе и поворотные оси, образуют в пространственной решётке
семейство эквивалентных параллельных
прямых.
Рассмотрим две такие поворотные оси
(фиг. 1,15). Поворачивая решётку около
одной оси, мы переведём узел 1 в узел 2,
поворачивая узел 2 около второй оси,
мы переведём его в узел 3. Узлы 1 я 2
лежат на линии, перпендикулярной
первой оси, узлы 2 и 3— на линии,
перпендикулярной второй оси. Так как
поворотные оси симметрии параллельны, то
все три узла лежат в плоскости,
перпендикулярной поворотной оси.
Отложим доказательство того
обстоятельства, что поворотные оси должны
совпадать с узловыми прямыми решётки,
и перейдём к рассмотрению ограничений, налагаемых на углы
симметрического поворота принципом пространственной решётки.
Рассмотрим поворот одной
плоскости решётки. Повороты,
невозможные для плоскости, будут тем более
невозможными для всей решётки.
Мы будем называть поворотной
осью симметрии %-го порядка ось сим-
360°
метр ми с углом поворота а = .
Пусть ось п-то порядка проходит через
узел решётки В и ближайшая к ней
идентичная—через узел решётки Л
(фиг. 1,16). Поворот около оси В
переводит узел А.в узел А', поворот около А переводит В в В'. Согласно
построению В'А' = АВ (1 -f- 2 cos а). Однако расстояние между
узлами А'В' должно быть кратно периоду идентичности АВ, ибо
АВ параллельно АгВ'. Следовательно, 2 cos а должно равняться
целому числу. Из этого условия следуют для cos а только лишь
следующие возможные значения 0, _1г—и±1, т. е. углы ново-
fcJ
рота 60°, 90°, 120V 180° и 360°. Как и следует из определения
закрытой симметрической операции, все углы поворота равны
частному от деления 360° на целое число. Таким образом в кристалле
возможны поворотные оси симметрии 6-го, 4-го, 3-го, 2-го и 1-го
Фиг. 1,16. Возможные порядки
поворотных осей симметрии.

4U КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
порядков, или, по общепринятой номенклатуре, оси 6, 4,' 3, 2 и 1.
Ось 1-го порядка упоминается в целях систематизации.
Теперь мы можем без труда доказать, что поворотная ось
является узловой прямой решётки. Действительно, пусть
поворотная ось проходит через узел О; узел А (фиг. 1,17) не лежит
на поворотной оси. Производя поворот на 180° (такой поворот
возможен для осей 2, 4 и 6),
получим точку Аг. Таким образом
о' через О А А' проходит узловая
плоскость с ячейкой, строящейся
на векторах О А и О А''. Так как
эти векторы равны и наклонены
под одним углом к оси, то
узел 0[ попадает на
поворотную ось. В случае оси 3 около
неб возникают три узла,
образующие равносторонний
треугольник (фиг. 1,17а). Эти три узла
вместе с начальным определяют
три вектора элементарного
параллелепипеда, телесной диагональю
которого явится поворотная ось.
Следовательно, во всех
случаях поворотная ось симметрии
совпадает с узловой прямой
решётки.
До сих пор мы рассматривали
чистые повороты решётки, т. е.
такие, для которых детерминант преобразования равнялся -f-l.
Наряду* с возможными поворотными осями симметрии 1, 2, 3, 4, 6
будут существовать инверсионные оси симметрии 1, 2, 3, 4, О,
которым соответствуют преобразования кристаллического
пространства с детерминантом — 1.
Инверсия всегда совместима с принципом построения решетки.
Поэтому вполне очевидна возможность осуществления разрешённых
поворотов с последующей инверсией*). _
Инверсионная ось первого порядка 1 иначе
называется центром симметрии или центром инверсии. Элементом
симметрии является не линия, а точка. Если эта точка принята за
Фиг. 1,17.
Поворотная ось
симметрии всегда
совпадает с
узловой прямой.
Фиг. 1,17а.
Поворотная ось
симметрии как
узловая прямая
(случай оси 3).
*) Иногда вместо инверсионных осей употребляют в качестве основных
элементов симметрии так называемые зеркально-поворотные оси. Операция
зеркально-поворотной оси есть один из разрешённых симметрических
поворотов с последующим отражением в плоскости, перпендикулярной оси
поворота.

/
/
/о
<,л
**,«■:
Фиг. I, 18. Симметрические преобразования:
а — ось 1^ б — ось 1, в — ось 2, г — ось 2, д — ось 3, е — ось 3, ж — ось 4,
з — ось 4, и — ось 6, к — ось 6. М, М± — точки, связанные элементом
симметрии. М', М\ — те же точки в стереографических проекциях.

42 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
начало координат, то операция инверсии переводит точку хуг
в точку хуг («отражение в точке»).
При этом симметрическом преобразовании лишь одна точка — сам
центр симметрии (000) переходит сама в себя (фиг. J, 12).
Инверсионная ось второго порядка 2=т иначе
называется плоскостью симметрии. Точки, связанные операцией 2,
находятся во взаимном положении предмета и отражения его в
зеркальной плоскости. Эта зеркальная плоскость перпендикулярна оси
поворота. Точки, лежащие на плоскости, переходят при этой
операции сами в себя. Поэтому операция 2 задаётся для решетки но
осью, а плоскостью (фиг. 1,13). Если ось ()>) есть ось симметрии,
а центр симметрии есть начало координат, то точка хцз
переходит в хуг.
Инверсионная ось 3-го порядка 3 может быть задана
поворотной тройной осью и центром симметрии ца нен. Инверсионную
ось третьего порядка молгно рассматривать поэтому как совокупность
двух операций З-j-l. Лишь одна точка (выбранный центр
симметрии) переходит в этом преобразовании сама в себя.
Инверсионная ось 1-го порядка 1 задаётся
расположением оси н расположением на ней «центра», не являющегося
центром симметрии. Этот «центр» есть единственная точка,
переходящая при этом преобразовании сама в себя.
Инверсионная о с ь . (> - г о порядка (> може/i' быть задана
расположением простой тронной оси и плоскости, перпендикулярной
этой тройной оси. Ось 0 можно рассматривать поэтому как
совокупность двух операций: оси третьего порядка и зеркального
отражения: 6 —З+w. При совокупности этих операции переходит
сам в себя опять-таки один «центр» — точка пересечения оси
о плоскостью.
Итак, мы ириходим к следующим независимым закрытым не
тривиальным симметрическим преобразованиям, возможным для
пространственной решётки: 2, 3, J, о, 1, 2 и 4.
Элементы симметрии, совершающие эти закрытые
симметрические преобразования, их графические обозначения и
соответствующие стереографические проекции показаны на фиг. 1,18. Форт
мулы всех симметрических преобразований, совершаемых этими
осями, сведены в таблицу 1,VII.
§ 4. Точечные группы или острова
Выведенные нами возможные в решётке элементы
симметрии—простые и инверсионные осп — могут пересекаться и не
пересекаться в решетке. Элементы симметрии, пересекающиеся в одной
точке решётки, образуют так называемую точечную группу, а эта

§4]
ТОЧЕЧНЫЕ ГРУППЫ ИЛИ ОСТРОВА
43
точка называется центром или особой точкой точечной группы.
Это число должно быть конечным. Исходя из любой заданной
точки, можно симметрическими операциями притти к любой из
эквивалентных ей точек. Эта исходная точка должна
находиться в общем положении, т. е. не лежать ни на одном из
элементов симметрии. В противном случае кратность группы окажется
заниженной. Это видно, например, из того, что ось (плоскость,
центр) «не действует» на лежащие на ней точки. Совокупность
эквивалентных точек, возникающих применением к одной точке
всех элементов симметрии группы, называется островом, а число
этих точек—кратностью острова или точечной группы.
Итак, точечная группа — это совокупность закрытых
симметрических преобразований. Она называется точечной, ибо по крайней
мере одна точка пространства (центр группы или особая точка)
преобразуется точечной группой сама в себя (т. е. попросту не
меняет своего положения). В некоторых точечных группах таких
точек имеется бесконечное число. Это имеет место в тех точечных
группах, где элементы симметрии пересекаются по прямой (особые
точки заполняют всю прямую), или если точечная группа состоит
из одного элемента симметрии (ось, плоскость). В этом случае все
точки, лежащие на элементе симметрии, оказываются особыми.
Элементы симметрии точечной группы переводят друг в друга
системы эквивалентных узловых прямых и плоскостей.
Следовательно, точечная группа кристалла предопределяет взаимное
расположение узловых прямых и плоскостей (§ 5).
Для того чтобы вывести все возможные для решётки точечные
группы, необходимо проанализировать возможности сочетания
закрытых элементов симметрии. Уже сразу очевидно, что число таких
возможностей ограничено; ясно, например, что ось 3 не может
лежать в плоскости симметрии (т. е. пересекаться под углом 90°
с инверсионной осью 2).
а) Возможные углы между одноимёнными осями симметрии.
Пусть в узле О пространственной решётки пересекаются оси п-то
порядка. Эти оси могут быть или поворотными, или
инверсионными, или часть из них может быть поворотными, а другая
инверсионными. Выводы, которые мы получим ниже, справедливы для
всех этих случаев, ибо инверсия не изменяет ориентации прямой
в пространстве, а лишь меняет положительное направление на
отрицательное и наоборот.
Если число осей, проходящих через узел, более одной,, то оно
ь общем случае уже и больше двух, так как две оси обязательно
вызовут существование третьей. В общем случае добавление
второй оси должно приводить к созданию точечной группы, состоящей
из некоторого ограниченного числа осей. Это число может быть
ограниченным только в том случае, если в конце концов новые
оси, выводимые применением операции первой оси ко второй,

U КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [гл. I
второй к третьей, вновь полученной третьей ко второй и т. д.,
будут становиться на место ранее полученных. Одноименные оси
могут быть равнозначными и неравнозначными. Если две (или
более) оси п-то порядка переводятся друг в друга каким-либо
третьим элементом симметрии, то, следовательно, они совпадают
с узловыми прямыми, периоды идентичности вдоль которых равны.
Такие оси симметрии называются равнозначными. Если же
одноименные оси не переводятся друг в друга третьим элементом
симметрии*) (узловые прямые с разными периодами), то они
называются неравнозначными.
Рассмотрим две равнозначные оси н-го порядка, пересекающиеся
иод наименьшим возможным углом чп в узле О решетки. Пусть О А
Фиг. 1,19а. Получение осей ОС и 01) Фиг. 1,196. Сферический тре-
поворотом вокруг равнозначных осей О А угольник,
и ОВ.
и ОВ будут равные периоды идентичности вдоль этих осей.
Поворачивая около оси О А ось О В, получим ось ОС; поворачивая около
оси ОВ ось О А, получим ось OD (фиг. I, 19а); О, А, В, С и
В — узлы решётки.
Из сферического треугольника, построенного на тех же
отрезках (фиг. I, 196), находим, что угол между осями определяется по
формуле (удобно применить формулу Деламбра)
s
oos J£_ = i .
sin -g-
*) Перевод одной оси в другую каким-либо элементом симметрии не
следует путать с генерированием осей в результате комбинирования
одной из осей с этим элементом симметрии. О генерировании элементов
симметрии смотри ниже.

•о
ТОЧЕЧНЫЕ ГРУППЫ ИЛИ ОСТРОВА
45
Из фиг. 1Д9а видим, что на вспомогательный угол е принцип
решётки накладывает ограничения, а именно: так как CD = а • АВ,
где N—целое число, а из чертежа очевидно, что CD — AB{\-\-
2cose), то
cos s
1.
Угол е может принимать
значения 0°, 60°, 90°, 120° и
180°, и, следовательно, sin-77 мо-
1 \г2
жет иметь значения 0, -=-, -~,
2
Решения уравнения для y»
сведены в таблицу I, II, откуда
видно весьма ограниченное число
возможностей взаимного расположения одноимённых равнозначных
осей симметрии.
Таблиц а I, И
Возможные углы у,» между одноимёнными равнозначными осями
(дополнительные до 180° углы fn должны считаться за один).
Фиг. I, 20. Нахождение угла Ъп.
^\"w
0°
60^
90°
120°
180э
180°
-> 180э
120° *-
90°
60° *-
-* о>
120°
-> 180°
J 09° 28' *-,
70° 32' -<-'
-> оэ
■—
90°
-> 180°
901
-> О1
—
—
60°
.-> 180э
Ц 0°
—
—
—
Рассмотрим теперь возможные углы Ьп между одноимёнными
осями О А и ОВ, не делая никаких предположений о том, что они
равнозначны. Ось О В переводит ось О А в равнозначную ей ось О А!',
ось О А переводит ось 08 в равнозначную ей ось ОВ''. Из
сферических треугольников ABB' и АА'В имеем (фиг. I, 20):
1) /.АА' = чА = ^ВВ' = чв, t- е- возможные углы -\п будут
одинаковы для обоих семейств равнозначных осей А и В; 2) cos f» =
= cos28n + sin2Sncosan, где
а„ =
или
cos^o
п
COS Yn—COS ап
1 — COS ап

46 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗ \ flVI. T
Решения этого уравнения сведены л таблицу 1,111. Поскольку
мы рассмотрели общий случай, углы оп суп, углы между
неравнозначными одноименными осями. Таблица 1Д11 показывает, что
они совпадают с углами fw между равнозначными осями и только
для неравнозначных осей 2 возможны ещё два угла 30° и 45°.
Таблица I, III
Возможные углы оп между неравнозначными одноимёнными осями
90° | Г>()э
оэ
60°
70° 32'
90>
109° 28'
120^
180°
0°
30'
—
45'
—
60°
90°
Следует различать полярные и неполярные оси симметрии.
Полярной называют ось, на которой можно различить
положительное и отрицательное направления, т. е. концы которой не
переводятся друг в друга никакими симметрическими преобразованиями
(ось является вектором). В противном случае ось называют нено-
лярной. Все инверсионные оси являются неполярными, ибо инверсии
обращает направление вектора. Поворотная ось является неполяр-
нои, если помимо неб имеется инверсионная ось 1 или 3 любого
направления, или параллельная ей инверсионная ось 2 или 6, или
перпендикулярная ей поворотная ост, чётного порядка (2, 4, 6),
или инверсионная ось 4.'
б) 11 точечных групп с поворотными осями. На основании
полученных только что таблиц 1,ТТ и 1ДТГ нетрудно будет
рассмотреть все возможные сочетания поворотных осей разных иорядког..
Это рассмотрение сильно облегчается тем обстоятельством, что
из всех возможных комбинаций осей 3, 4 и 6 могут существовать
только комбинации осей 4 и 3. Действительно, комбинации с осью
6 невозможны, так как 6 равнозначных осей 3 или 4 не могуч1
образовать между собой углы, разрешённые таблицей I, II*).
) Напомним, что в общем случае ось n-го порядка выводит из любой
другой оси » равнозначных ей осей. Максимальные углы между шестью
направлениями, связанными осью 6 (60°), меньше минимальных углов
между равнозначными осями 3 или 4.
'In
180'
120'
0е
-> 109° 28'
> 70° 32'
ж-
-> 180°

$ 4|
ТОЧЕЧНЫЕ ГРУППЫ ИЛИ ОСТРОВА
47
Таким образом возможны следующие комбинации:
а) ось 6 и оси 2,
б) ось 4 и оси 2,
в) ось 3 и оси 2,
г) оси 2,
д) оси 4, оси 3 и оси 2.
Простейшими из них будут комбинации tocefi 6, 4, 3 или 2
с перпендикулярной к ним осью 2. Возникают четыре точечных
группы 622, 422, 322 и
222, обозначаемые так-
же 2>в, i>4f А» и D2 (V).
В случае DQ вновь
возникшие оси 2 образуют
между собой углы 00°,
1$ случае Dn —120° в
случае />4 — -i5" и н случае
7i2 — 90°, т. е.
разрешённые таблицами.
Никаких других групп,
содержащих только ось
(> и оси другого
наименования, кроме группы
i)6, а также групп,
содержащих только оси 2,
кроме группы D.2, быть
не может.
К оси 4 двойная ось
может быть добавлена
иод углом 45° (этим она , тп, ,, ,
„;■„,„ ,.ч Фиг. 1,21. К объяснению
отличается от оси 0). возможных сочетаний
Тогда углы между ося- поворотных осей, а —
ми 2 будут равны 60° определение угла между
(см. фиг. 1, 21, а; сфери- осями - ^-возникно-
<» - вение осей четвертого
ческии прямоугольный ]10рядка; е_Сщё одна
треугольник даёт: cos f— ось второго порядка;
^ 0 1 г — ось третьего поряд-
COS45 , COS 45 ~~т>> т« в. ка образует одинаковые
fi.o\ " углы со всеми двойными
т? и четверными осями:
Вполне очевидно, ЧТО д — сферический тре-
в этом случае возни- угольник,
кают ещё новые оси
четвёртого порядка, которые образуют между собой углы в 90э
(фиг. I, 21, tf). Однако и на этом вывод новых осей не кончаете»,
так как вновь полученные оси симметрии 4 создадут новые
оси 2 (фиг. I, 21, в). Вглядываясь в фиг. I, 21, в, видим, что
группа обладает также осью третьего порядка, образующей

48 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
одинаковые углы со всеми двойными и со всеми четверными осями
(фиг. 1,21, г).
Решая сферический треугольник, показанный на фиг. 1,21, <?,
... 360°
находим из уравнения cos 90 = cos if cos «у -j- sin 7 sin y cos —g- , что
tgY = V2~/, т. е. угол между осями четвертого и третьего порядка
равен 54°44'8". Угол между осями 3, связанными симметрической
операцией 4, будет, следовательно, равен так называемому тетраэд-
рическому углу 109°28'16". Угол между осями 3, связанными
симметрической операцией 2, равен 2 (90°—54° 44' 8"), т. е. 70° 31'44"
также в соответствии с выведенным ранее значением.
Рассмотренная точечная группа называется группой октаэдра
и обозначается либо 0, либо 43.
Итак, комбинация осей 4 и 2 под углом в 45° привела к
комбинации осей 4, 3 и 2. Другой такой комбинации (содержащей
только оси этих порядков) не существует.
Остаётся рассмотреть комбинацию осей 3 и 2 (без 4) иную,
чем в /)3. Если в группу D2 ввести тройную ось тем же способом,
как мы это только что сделали, т. е. так, чтобы оси 3
образовывали одинаковые углы с тремя взаимно перпендикулярными осями 2
(во всех квадрантах), то новые осп не возникнут, а углы между
осями 3 будут тетраэдрическими, т. е. разрешёнными таблицей 1, II.
Эта точечная группа называется группой тетраэдра и обозначается
Т или 23 (в отличие от 32 = D3).
Этим исчерпаны все возможные комбинации поворотных осей
друг с другом.' Приб.авляя сюда ещё простейшие группы,
состоящие из одной только поворотной оси (циклические группы),
получим всего 11 точечных групп, содержащих одни лишь поворотные
оси симметрии: С1(1), С2(2), С3(3), С4(4), С6(6) (содержат ось
лишь одного наименования), />2, D3, Dit D6, T (содержат оси двух
наименований) и О (содержит оси трёх наименований).
Выведенные точечные группы сведены в таблицу I, IV.
в) 32 точечные группы. Добавкой центра инверсии или заменой
тех или иных поворотных осей на инверсионные в выведенных
11 группах мы придём к полному перечню возможных в решётке
островов, т. е. выведем все возможные точечные группы.
Добавляя центр симметрии к группе Си лишённой симметрии,
получим группу С<=1. В группе С'2 = 2 можно либо заменить
ось 2 на ось 2 — возникает группа Са=т=2, либо добавить центр
симметрии — это значит наложить ось 2 на ось 2. Возникшая
группа обозначается C2ft = —.
В группе D2= 7=222 две оси 2 можно заменить на оси 2.
Эта группа с двумя взаимно перпендикулярными плоскостями сим-

§ 4] точечные группы или острова 49
метрии, проходящими через ось 2, обозначается Ca„ = 2mm =
= 2т = тт.
К этой же группе Z)2 можно добавить 1. Этот центр
симметрии создаёт три взаимно перпендикулярные плоскости симметрии.
Группа обозначается D2h, У и пли ттт. Эта же группа
получается добавлением 1 к C2v или заменой в группе В2 одной оси
2 на ось 2.
Добавляя к группе (73 центр инверсии, получим группу (7Sf.
Из группы Db получим две группы: одну С®, = Зт, заменив оси
2 на 2, и другую D3d = 3m добавлением центра инверсии (замена
оси 3 на 3 эквивалента добавлению центра инверсии).
— А.
Группа (74 приводит к группам 54 = 4иС41( = -; в первой
из них произведена замена 4 на 4, в последней добавление центра
инверсии привело к образованию плоскости симметрии,
перпендикулярной оси 4.
Из группы D4 = 422 получим группу Civ = 4тт— заменой
оси 2 на 2, далее группу Т)ы = Vd = 4 2m заменой оси 4 на 4 и,
наконец, Д^ —^^; добавлением центра инверсии.
Из группы CQ получим (7374 = 6 заменой оси 6 на 6 и(?№=-
добавлением центра инверсии. Как и в остальных подобных
случаях (оси чётного порядка), генерируется перпендикулярная оси
плоскость симметрии.
Группа De —622 аналогично группе D4 даёт три группы:
C6v = 6mm, Da,, = 62m и DRh = .
В группе тетраэдра лишь замена оси 3 на 3 приводит к новой
группе Th = m3.
В группе октаэдра новые группы получаются двумя способами:
одновременной заменой на инверсионные оси осей 4 и 2—это
будет группа Тй=\ Вт и заменой оси 3 на 3 (или на 6)— это
будет группа Oh = mSm. Итак, всего имеется 32 различных
острова или точечные группы. Все точечные группы собраны
в таблицу I, IV.
г) Описание точечных групп. Точечная группа задаётся своим
символом. В структурном анализе употребляют два типа символов.
В более старой номенклатуре буквой С с цифровым индексом
обозначаются точечные группы с одной осью (циклические), буквой Dn—
группы с осью п, перпендикулярно к которой добавлена ось 2.
Буквы v и h в индексе означают добавленные к осям вертикальные
и горизонтальные плоскости симметрии.

Q
С:
» я
3 I
tc
J3
° £
а £
— »тз
w-
со
■а
н*
2=1
о я S
hxs а
ш о »
р о a
-з
TJ -5
S3 О
Я -С
1 Я
р
© О


народный
о
к я
2.*
5* СО
38
Я О
я а
Е ®
о о
о я
со W
3 к
ф
со
е S
•fe о
о н
Элементы
симметрии
точечной
группы
Их число
Кратность
точечной группы
о
о
о
с\
р
м
о
я
р
прое
я
ция
в
ере
огра
>е<
я
CD
А
Я
О
»
я
S
I *iu]
vcHirvHV ол.онльшылхо иаоноо 'фудлоьтухэшя
09

Продолжение

Кристаллическая
система
ная
Символ
точечной группы
по Шен-
флису
Со
с,
Cwi


народный
2
т
2/эд
Название
соответствующего

кристаллического класса
но Болдыреву
Диэдрический
осевой
Днэдрический
безосный

Призматический
Элементы
симметрии
точечной
группы
2
2 = т
2 = т
2
1
Их число
1
1
1
1
,1
Кратность
точечной группы
2
2
4
Особая точка
оси
Любая точка
плоскости
Центр
инверсии

Стереографическая проекция
ГЛ
vJ
л
(
VJ
г\
и
(7^
? V
Ч
Т
J
Изображение
точечной группы
л _,, й
л
_
V
-р-р
V

Продолжение

Кристаллическая
система
Символ
точечное группы
по Шен-
флису
2 Я Я
Название
соответствующего

кристаллического класса
но Болдыреву
S
» Й В
О Ф й
3 я £
S § *
Ь Он
Особая точка

Стереографическая проекция
Изображение
точечной группы

Ромбическая
С?г
D«=V
я2л=т
ч>
222
Ромбопирами-
дальный
Ромботетра-
эдрический
Ромбодипира-
мидальньтй
_ 2
2 = т
_2
2 = m
Любая точка
оси

Точкапересечения осей
Центр
инверсии
-Г
^-ч

Продолжение

Кристаллическая
система
Символ
точечной группы
по Шен-
флису
*а*
Ф ев 3
Название
соответствующего

кристаллического класса
по Болдыреву
а н
ф © «
39 Я дэ
2 Я t£
Ч я О
:.«
о Я
с
Е* ft
Si
а"
Особая точка

Стереографическая проекция
Изображение
точечно! группы

Тетрагональная
Jih
4tjm
Тетрагональ-
нотетраэдри
ческий
Тетрагонально

пирамидальный
Тетрагонально-
дипирами-
дальный
Особая точка

инверсионной оси
Любая точка
оси
Центр
инверсии
□
Mr

-*^
i-1 H
43 43
Я P
►с я
С» Ф
о е
Й О
я '
Яс
н
о
я
Р
н)
С*
я
о
s я s
Сг« О
Е я
9 о
«1
а я
~ ф
°^
о ф
в»?
о 5
О OV
Я Р
Й
Я Н
Р Я>
U -Э
Я Р
S3 П
И О
^J
43
я
л
со
п>
я
я
о
у?
р
«
ф
я
о
'
4-ч
п
о
я
р
t=i
сг
Я= Я
Ю1
[I со *.'
я
о
я=
я
я
СО
ф
О 43
о
я
п
я
о
я
о
о
Г,\
Р
й
н
о
кС
р
я
>е< о
я Е
о
а>


народный
1=)
а
о
О
Я Я
» ю
ч §
43 Я
=<! Н
Я О
о ° я
° К 43
о 2 °
V О Н
Е М д
43 Р Я
Ф О jj
а о а
<< р •
А Р
Н W
О Ю
Н р
ю я
<< я
8 ф
£ о
Ф О
■л о
о н
Элементы
симметрии
точечной
группы
Их число
Кратность то
чечнойгруппы
О
о
о
о О
и ^
о
-1
43
Р
>е<
я
х
й
н
о
л
Си
х
я
о
»
41
43
Я
Я
Е
ф
К
о
о\
43
Р
Й
CD
Я
я
О)
I *1TJ] VSHLTHT ОЛОМЛХЯЛЛХО ИЯ0Н00 •фУЛХОТПГУХОШЯ f%

Продолжение
ооо

Кристаллическая
система
Символ
точечной группы
по Шен-
флису
Kg
й ft*
<в ее Я
яка
Название соот
ветствующего

кристаллического класса
по Болдыреву

Тетрагональная

Ромбоэдрическая или
тригональ-
ная
подсистема
Д
ih
С,„
4:Jmmm
Дитетраго-
нальнодипи
рамидальный
Тригонально-
пирамидаль-
ный

Ромбоэдрический
Я 2 ®
2 s v
Л о н
' Я
°и
^ и
л >»
Н ft
о и
go
* 3
Особая точка

Стереографическая проекция
Изображение
точечной группы
4
2
2 = т
1
3 = 3 + 1
16
6'
Центр
инверсии
Любая точка
оси
Центр
инверсии

Гекса
налън
£?
Р
Oil
3=1
to н
р уз*&
Ь| Я Я
гональ
пирам
ьный
Я И
1 о
Сб"
II
+
СО'
н*
OS
О
и sg
2 й о>
» Ю р
о« w
о о ч
к я о
о >в
и и
< р
^*'*в"^
/>
( А
\
V А
V ^
4—У
ь
ее
а.
021
5
3=1
Аоч
^ я я
S в 1
►a 5 о
CD Я) Я
одр
Я ' U*
» 3
о
со.
ь»1 II
j| to со
3 +
1—1
W ЮН
ь-
со
j=5
1 ч
—
^
i ЛчА
lf^f^
Ji—->IRs^
г V ^/Tvs^
V/l\ ;
пЧ
W~\xA « ^Г"*' Л
\Р
4^1
ь
со
со
со
-3
Я) 43 Д
2 £ о
я я =;
£ 2 «S
to 5
я
coco

Свеса
^
Я ^
М я
°£
° ©
»о
*я>
^Г"~" >
\/\7
м V
It я.—
/ \ /\
/ \ / \
V/ \
V >
\|
k 4 J
J Л >^
i
^
\
\
а н ,д >т)
р 43 CD гГ
3 Э 2 £ о4
*S 2 * »
*£>£яЙ
■Si
О
to
СО
$
3=t
s
to н
Р я ^3
й s s
5 » 2
и1
я
о
COI
II со
3
СО •—
OS
^
о 8
о о\
Я Р
о
л
я
р
\ А/Л
\f jy,—)
г \ А /
/ \ / \ /
У \ / \ У
У х/ \/
г ^<^ _^^
ч£Эг
ч и
/ л*
1 Г
'
о Й я
" о 2
z Я р
- S •?
а


народный
О
я а
© к
^§
►с»
я 2
я л
Е 2
■
я о и » И
W2 5 о ю
О 2 ° Н 8»
S ° н ю а
Е Ь g g в
в о j o> о
» 2 » ч °
=<! Р i о Н
Элементы
симметрии
точечной
группы
Их число
Кратность
точечной группы
о
о
р
So
О
А
Я
Р
о О
я н
Р CD
"* CD
я 2
CD P
Я ^
с я
S ?
о
►Д js)
CD ф
►4 о
а о
О ^
Я= р
t-^ Я
ь>-3 CD
^ 5
Я К
а •
С
I TJ]
V8HL'VHV ОЛОНсТАХЯЛсТЮ ИЯОНОО -ФУЛЛОГГУХОИсТЛ
9С

Продолжение
coo

Кристаллическая
система
Символ
точечной группы
по Шен-
флису
(В и Я
Название
соответствующего

кристаллического класса
по Болдыреву
в
и^§ д
(1) <V
FE
Я й л) И
ё 2 ? >»
Ч Я о р,
о
Ч
чис
И
К
Л Я
о Я
в
Л >>
6- р,
о сГ
атно
ной
Особая точка

Стереографическая проекция
Изображение
точечной группы

Гексагональная
"6h
п
'8Й
6'w
6 2/»
Гексагонально

пирамидальный
Гексагонально-
дипирами-
дальный
Дитригонально
дипирами-
дальный
6
6
2 = т
1
6 = 8 + »»
2
2 = т
1
1
1
1
1
8
3
6
12
12
Любая точка
оси
Центр
инверсии
Особая точка

инверсионной оси

Продолжение

Кристаллическая
система
Символ
точечной группы
по Шен-
флису
*5
03 5в Я
й ю к
Название
соответствующего

кристаллического класса
по Болдыреву
к
н о*
К ь м
<15 (В Ц
я я S
2 * р
ГО о н
О
чис
и
S
►А >»
ё&
атно
ной
»ч
к £
Особая точка

Стереографическая проекция
Изображение
точечной группы

Гексагональная
-6и
6»ш
lh
I)
6Л
621
б/
jtnnim
Днгексаго-
нальнопира-
м и дальний
Гексагонально

трапецоэдр и чес кий
Дигексаго-
нальнодилн-
рамидальны*
6
2 = т
6
2
2 = »»
1
12
12
24
Любая точка
оси
Точка
пересечения осей
Центр
инверсии

"Продолжение,

Кристаллическая
система
Символ
точечной группы
по Шен-
флису
ео ев 3
Я Я Я
Название
соответствующего

кристаллического класса
по Болдыреву
я
Я я.*
2 но
И Н м
© <в р
33 33 ф
-5 я °
С5 о ь
' Я
S н
н С
л >>
О U
я*
* Й
Стаз
J5 pi
Особая точка

Стереографическая проекция
Изображение
точечной группы
Кубическая
Та
23
ыЪ
4 3?»
Пентагонтри-
тетраэдри-
ческии
Дидодекаэдри-
ческий
Гексатетра-
эдрпческий
3*)
2
2 = w
1
4
3
12
24
24
Точкапересе-
чения осей
Центр
инверсии
Точка
пересечения осей
*) Здесь ось 3 есть вместе с тем ось 6.
ел
«о

Продолжение

Кристаллическая
система
Символ
точечной группы
по Шеи-
флису


народный
Название
соответствующего

кристаллического класса
по Болдыреву
Я Я в
Е4 Р< л
я Р2 я
2 2 F н
Ш 2 « в
£75 о tr и
1 Я
ь К
Е* Л
s«
5 <=>
Особая точка
Кубическая
43
п&т
Пентагонтри-
октаэдриче-
ский
Гексаоктаэдри-
ческий
8*)
4
2
2 = т
I
24
48
Точка
пересечения осей
Центр
инверсии

Стереографическая проекция
Изображение
точечной группы
*) Здесь ось 3 есть вместе с тем ось 6.

§4]
ТОЧЕЧНЫЕ ГРУППЫ 1ТЛИ ОПТРОЙА
61
При наличии единственной оси она считается вертикальной,
при наличии нескольких осей вертикальной считается ось высшего
наименования. Следовательно, индекс v обозначает параллельность,
а индекс h — перпендикулярность оси к плоскости.
Другие так называемые международные символы более ясны.
Чтобы ими сознательно пользоваться, нужно помнить лишь
следующее. Символы, написанные рядом, указывают на симметрию трёх
пространственных направлении, принимаемых за основные. Этим
одновременно указываются и оси, в которых целесообразно
описывать точечную группу. Плоскость симметрии т,
перпендикулярная оси, отделяется дробной чертой. Таким образом, символ группы
т> 6 2 2 „
De7,= означает, что в ней имеется ось шестого порядка и
wt то m m ' г-*-*—
перпендикулярная к ней плоскость, а также оси 2-го порядка,
к которым также перпендикулярны плоскости. Если плоскость
параллельна оси или другой плоскости, их символы пишутся рядом
без отделения дробной чертой.
Например, символ группы 4mm означает следующее: вдоль
одного направления идёт ось 4, вдоль двух других — инверсионная
ось 2 (иначе говоря, перпендикулярно двум другим имеются
плоскости симметрии, параллельные оси 4).
Выбрав определённым образом оси координат, мы можем
охарактеризовать точечную группу координатами точек образуемого
ею острова. Начало координат всегда выбирается в центре (особой
точке) точечной группы. Центром точечной группы считается
точка пересечения составляющих её элементов симметрии (точка
пересечения осей, оси и плоскости, центр инверсии, особая точка
инверсионной оси). В случае пересечения не в точке, а по прямой
или наличии только одной оси (циклические группы) — любая точка
линии пересечения или оси, в случае группы Cs = m—любая
точка плоскости симметрии, в случае группы d = 1— любая точка
пространства могут служить началом координат.
Если, например, рассматривается группа С2Л = 2/т, то элементы
симметрии совершат следующие преобразования над точкой xyz
(т совпадает с плоскостью xOz, 2 с осью у).
Двойная ось 2: (1) xyz —► (2) xyz
I плоскость т I плоскость т
4_ _4__ (фиг. 1,22)
(3) осу2 (4) xyz
Нетрудно видеть, что точки (1) и (4) оказались связанными
центром симметрии. Два элемента симметрии породили третий. Этот
факт является частным случаем общего правила. Взаимодействие
двух элементов симметрии порождает (генерирует) по крайней мере
один новый элемент симметрии. Вполне понятно, что мы получили

С>2 КРЙОТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
ХШ
ту же точечную группу, если бы исходили из центра инверсии и
оси 2 или центра инверсии и плоскости т.
Пусть точка хуз не лежит ни на одном из элементов
симметрии точечной группы. Такую точку принято называть находящейся
в общем положении.
Если из этой точки xyz применением всех элементов симметрии
точечной группы возникло ещё п — 1 точек, то число п есть
кратность общего положения данной
точечной группы, иначе кратность точечной
&9М. группы или острова.
_^ По крайней мере одна точка острова
-4*7 переходит сама в себя. В случае групп
с одними поворотными осями такими
точками будут все, лежащие на оси;
ири наличии только плоскости т — все
точки, лежащие на ней.
Если точка лежит на элементе
симметрии, т. е. подвергается преобразованию
только другими элементами симметрии
группы, то такое положение называется
частным. Разумеется, кратность частного
положения будет в целое число раз меньше кратности общего
положения.
Такое частное положение имеет, например, место в группе
2/т—С2л, если точка лежит на оси или на плоскости симметрии.
В первом случае преобразование имеет вид:
в;.
(X.Q.Z)
fc!AV
Фиг. I, 22. Преобразование
элементов симметрии груп-
пы Cih = — .
во втором
(1)0?/0 -> (2) ()//(),
В обоих случаях кратность частного положения равна 2.
В группах с одной особой точкой имеется одно особое частное
положение— особая точка, не подвергающаяся преобразованию ни одним
элементом симметрии. Кратность особого частного положения,
очевидно, равна 1.
Максимальная кратность общего положения равна 48, она имеется
у высоко симметричной группы Oh.
§ 5. Кристаллические системы
Если в пространственной решётке существуют определённые
острова, то этим накладываются некоторые условия на векторы
решётки. Действительно, мы доказали, например, в § 3, что ось
симметрии совпадает с узловой прямой и перпендикулярна узловой

§5]
КРИСТАЛЛИЧЕСКИЕ СИСТЕМЫ
6 3
плоскости. Это значит, что при наличии оси симметрии всегда
имеется возможность выбрать ячейку так, чтобы один из векторов
был перпендикулярен двум другим.
Вполне очевидно, что при отсутствии в решётке каких-либо
элементов симметрии или при наличии только центра инверсии
на векторы а, Ь, с не накладывается никаких условий.
Элементарная ячейка образует в общем случае косоугольный
параллелепипед. Кристаллы этого типа принадлежат к триклиннои
системе.
При наличии в решётке островов 2, т плп 2/т имеется
возможность выбора оси Ь перпендикулярно осям а л е. Ось Ь идёт вдоль
оси 2 или 2 (т. е. перпендикулярно т). Кристаллы этого тина
относятся к моноклинной системе.
Возможность выбора ячейки в виде прямоугольного
параллелепипеда появляется при наличии в решётках островов 222, mm и
ттт. Эта система называется ромбической.
Рассмотрим теперь решётки, содержащие острова с осью 4-го
порядка. Вектор с решётки направим вдоль оси 4 и проведём
вектор а в узел, лежащий в плоскости, перпендикулярной оси 4 на
соседней оси симметрии 4. Симметрическое преобразование этого
узла приведёт его в другую точку, которую можно принять за
конец вектора Ь. Очевидно в кристаллах этого типа имеется
возможность выбора ячейки в виде параллелепипеда с квадратным
основанием. Такие кристаллы принадлежат к тетрагональном
системе.
Наше рассуждение относится и к решёткам с островами,
содержащими ось 4. Чтобы ото было очевидным, надо выбрать начало
координат в особой точке оси 4.
В случае классов с осями 3, 3, С и 6 выбираем за начало
координат особую точку инверсионной оси или любую точку простой оси.
Вдоль указанных осей направляем ось с. Ось а, идущая в
плоскости, перпендикулярной оси с, поворачивается при симметрической
операции на 120° или 60°. Таким образом, в этих случаях имеется
возможность выбора осей а и Ь, равных но величине и
расположенных под углом 120° друг к другу. Кристаллы этой системы
Рйзываются гексагональными.
Следует отметить, что принято выделять решётки с тройными
Осями в подсистему, называемую ромбоэдрической. Для этой системы,
*роме указанного выше, употребляется ещё и другой выбор ячейки,
% именно вектор а выбирают под некоторым углом к тройной оси,
симметрический поворот около которой создает оси Ь и с, идущие
■од тем же углом к оси симметрии. Элементарная ячейка предста-
Гяет собой косоугольный параллелепипед с тремя равными углами
тремя равными рёбрами (ромбоэдр).

Таблица I,V
Кристаллические системы
Система
Входящие
в неё точечные
группы
Три-
клинная
С
Моно- [ С\ = 2
клиннал С8 = т
G*h = 2/»г
Правила выбора
осей
За а, Ь, с,
принимают три
некомпланарных наименьших
вектора решётки
Параметры
ячейки
Объём
ячейки
Обратные векторы
и углы между
ними
Межплоскостные
расстояния
За Ь принимают
направление 2 или
перпендикуляра к
т, за а и
с—наименьшие векторы
решётки,
перпендикулярные к Ь
а, Ь, с a, S, -f

произвольны
а, Ь, с и р

произвольны
а = f = 90е
Общие формулы, данные в § I, 1
V=abc sin Э
«sin [
J_
= Ь '
1
csm p
ах = у* = 90°
&* = 18(Р — р
с sin
2 ?Л cos
ca sin!

Ромбическая
J)2 = F = 222
^2,t-Fh =
= mmm
3a a, 6, с
принимают направления 2
или направления
перпендикуляров к т
а, Ъ, с

произвольны
а=р=т=90'
V ~ a be
a ' о
^х= —
• — с '
а* = рх =7Х=9Ь°
1)а+

Продолжение <**
ел
Система

Тетрагональная


эдрическая или
триго-
нальная

подсистема
Входящие
в неё точечные
группы
С4 = 4,
Сы = 4/m;
D4 = 422
Giv = 4mm,
Did = 42m
7)4/j = Цттт
C3 = 3
C3< = 3
D3 = 322
Ozv = 3»»
DBa = 3w
Правила выбора
осей
За ось с
принимают направление
4 или 4, за а и &
наименьшие векто-
рырешётки.перпен-
дикулярные с и
связанные операцией
4 или 4
Гексагональная
установка: за ось
с принимают
направление 3 или
3, за а и Ъ —
наименьшие векторы
решётки,
перпендикулярные с и
связанные операцией
3 или 3
Параметры
ячейки
с
произвольно;
а=р=т=90°
с
произвольно;
а = Ь
Т = 120°
а = В = 90°
Объём
ячейки
V = а2г
Обратные векторы
и углы между
ними
х hx ^ •
~ а
X _ 1
с '
а* = рх=7ч==90°
Межплоскостные
расстояния
d*~ а2 ^ 1 с)
'■
Смотри гексагональную систему
■
<

Продолжение
Система


эдрическая или
триго-
нальная

подсистема
Входящие
в неё точечные
группы

Гексагональная
CV
('вк
А»
Jhh
С;
6;
• 6/ш;
:622;
6mm;
■ Qm2;
Qlnwnn
Правила выбора
осей
Параметры
ячейки
Объём
ячейки
Ромбоэдрическая
установка: за оси а,
Оно принимают
три некомпланарные
наименьшие
векторы решётки,
связанные операцией 3
или 3. а, Ь и с не
перпенди кулярн ы
а не параллельны
3 или 3
а = ft
V = а*Х
X(l — cosa)X
XV"l+2cosa
Обратные векторы
и углы между
ними
Межплоекостньн
расстояния
.IS = С =
— COS2 7Г
а 2
Id2"
С08^
За
■( ф 90:
cos a =
COS a
1 -f" COS a
За ось с
принимают направление 6
или 6, за а и Ь
наименьшие векторы
решётки, перпенди-
I кулярные с и
связанные операцией
6 или 6

Кубическая
Т
Th
О
Та-
23
= m3
;43
43>«
mSm
с
произвольно;
а =■ Ь;
7 = 120°
a = В = 90°
V =
Уз
= ь =
с
'б0°
Y's
90е
За оси а, Ь и с
принимают
направления трёх
эквивалентных, ортого-
нальных_ осей 2
(Т Гл).4 (Т„) или
4 (О, 0А)
a = ft =s <•;
о = jii = ^
F =
= ft = с
= _1
:90С
о . « . За
й- sin — sin -^~
X
=[«
—(l—tg^(^+
+ гл + м-)1
ie^*« + *'-r
+ **) +
1 Л2 _|_ fcS _|_ J2

§6)
ТРАНСЛЯЦИОННЫЕ ГРУППЫ
67
Точечные группы наиболее высокой симметрии позволяют выбрать
кубическую ячейку. К кубической системе относятся решётки с
островами тЗ, 43, 43m, mSm и 23.
Правила выбора осей и распределение точечных групп по
системам иллюстрируется вышеприведенной таблицей I,V.
В этой же таблице приведены специализированные формулы
векторов обратной решётки, межплоскостного расстояния и объёма
элементарной ячейки для всех систем.
Выбор осей определяет правила выбора элементарной ячейки,
которые могут быть сформулированы следующим образом: 1)
симметрия элементарной ячейки должна совпадать с симметрией
наиболее высокосимметричной (голоэдрической) точечной группы той
системы, к которой относится кристалл; 2) при соблюдении первого
условия число прямых углов между осями ячейки должно быть
максимальным; 3) при соблюдении первых двух условий объём
элементарной ячейки должен быть минимальным.
§ 6. Трансляционные группы
а) Введение. Трансляционной группой называется
совокупность операций параллельного переноса (трансляций) элементарной
ячейки кристаллической решётки. Иначе, это подгруппа
параллельных переносов данной пространственной группы. Такое абстрактное
определение имеет весьма простой смысл: говоря о трансляционной
группе, мы говорим по существу о центрировке элементарной ячейки.
Действительно, если среди операций переноса данной решётки нет
других переносов, кроме оставляющих узел в пределах ячейки а,
бис (оси выбранной ячейки), то выбранная ячейка является
примитивной. Если, помимо этих переносов, имеется перенос
(трансляция) —у—, то выбранная ячейка оказывается центрированной
в грани аЪ и т. д. Число возможных способов центрировки очень
невелико, как мы увидим ниже, и определяется кристаллической
системой. Может показаться, что трансляционная группа зависит
от выбора ячейки, но на деле это не так. Определённая
трансляционная группа свойственна данной решётке; конечно, мы всегда
можем выбрать примитивную ячейку, но это не значит, что
исчезнут переносы, переводившие начальный узел, скажем, в центр
грани аЪ или в центры всех граней ячеек, которые прежде были
выбраны за элементарные. Переносы эти остались, но часть их
теперь совпадает с осями ячейки, а другая часть выносит начальный
узел за пределы выбранной ячейки, оставляя её примитивной.
Отметим ещё следующее. «Непримитивная» (т. е. с
непримитивной элементарной ячейкой) решётка может рассматриваться как
совокупность нескольких примитивных решёток, параллельно встав-

Г)8 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [гл. t
ленных друг в друга. («Непримитивная» решётка расщепляется па
несколько «примитивных».) Число этих примитивных решёток равно
числу узлов, приходящихся на ячейку непримитивной решётки, а их
начальные узлы лежат в узлах ячейки непримитивной решётки. Так
«всесторонне центрированная решётка» (решётка с ячейкой F) есть
<i А
т '
. -А
"ь
Ншштшттф.,
О 0 0
1 ° Т ° Т
Т 1
b'\W a
,, __, i * 1
0 0 0 О 0 0
,__ , А J
b
0 0 0 it ° °
, А (ф&——*f—
A i
0 0 О
А ■ ■<
о 0 0
Фиг. I, 23а.
Дополнительный узел 1
находится в центре грани.
Вектор d является
вектором переноса; он
переносит узел 1 в один
из основных узлов
решётки.
Фиг. 1,236. Если дополнительный узел 1 не
находится в центре грани, то вектор d.
являющийся вектором переноса, создаёт новые
дополнительные узлы в новых точках решётки, что
приводит к уменьшению размера ячейки.
Новая уменьшенная ячейка оказывается
примитивной. На фигуре узел 1 имеет координаты 1/4,
1/3 (в долях периодов). Новая ячейка а'Ь'
получается по условию
4
*' = т-
совокупность четырёх параллельных примитивных решёток с теми
же периодами вдоль основных осей и с начальными узлами в (000),
(■й<0.(*От) ■(•**)•
6) Обзор трансляционных групп. В предыдущем параграфе был
указан возможный выбор симметричных ячеек при описании
решёток, построенных из тех или иных островов. Однако ничего ещё
не было сказано о том, являются ли эти ячейки примитивными. Не
приходится, за очевидностью, доказывать, что эти ячейки могут
быть примитивными. Напротив, следует рассмотреть вопрос о том,
могут ли выбранные указанным способом элементарные ячейки
быть непримитивными и, если да, то какими.
Для ясности рассмотрим все кристаллические системы по
отдельности.
Триклинная система. Так как на углы и длины периодов
элементарной ячейки не наложено каких-либо ограничений, то
очевидно, что элементарная ячейка должна быть примитивной.
Действительно, если узел решётки попал внутрь ячейки, то выбор основных
трансляций можно переменить, сделав этот узел вершиной ячейки.

§6]
ТРАНСЛЯЦИОННЫЕ ГРУППЫ
СО
Моноклинная система. В плоскости, перпендикулярной
оси 2 или 2, лежат основные векторы решётки а и с, выбор
которых не диктуется симметрией. Поэтому сторона ячейки,
построенная на векторах а и с, всегда может быть сделана примитивной.
Рассмотрим теперь прямоугольное сечение ячейки, построенное на
векторах атЪ или с и Ъ. Вдоль оси Ь идёт ось симметрии. Нетрудно
видеть, что прямоугольная плоская ячейка этого сечения решётки
может быть непримитивной, но только
единственным способом — она может
быть центрирована. Наличие
дополнительного узла в центре грани ячейки
не противоречит принципу решётки,
так как симметрические операции
решётки переводят один такой узел
в аналогичные (фиг. 1,23а). Напротив,
дополнительный узел, расположенный
в другом месте сечения (грани ячейки),
симметрическими операциями
переводится в другие ячейки в новые
положения, что невозможно, так как ячейки
должны остаться элементарными (фиг.
1,236).
Таким образом, кроме примитивной
моноклинной ячейки существует одно-
стороннецентрированная (иногда
говорят: базоцентрированная) в паре
граней аЪ или Ъс. Вполне очевидно, что, выбрав оси а и с по-
иному (например так, как показано на фиг. 1,23в), мы можем
получить объёмноцентрированную ячейку. Итак, между ячейками Л,
С и J в случае этой системы нет принципиальной разницы: иным
выбором осей они могут быть переведены друг в друга. Все
эти ячейки составляют, как мы говорим, одну трансляционную
группу.
В моноклинной системе существуют, следовательно, две
трансляционные группы: примитивная Гт и центрированная Гта.
Ромбическая система. Все три оси ячейки выбраны
в соответствии с требованиями симметрии. Поэтому любая из
плоскостей ячейки может содержать дополнительный узел. Этот узел
опять-таки может быть только в центре грани, так как в противном
случае применённые к нему симметрические операции перенесут
его в другие ячейки в иные положения. Таким образом, все
основания ромбической ячейки могут быть центрированы.
Имеется, однако, ещё одна возможность введения
дополнительного узла в ячейку. Ячейка может быть центрирована по объёму.
9то возможно потому, что любые симметрические операции, свой-
/\/к
1
X
i
\А/~
Фиг. I, 23в. Гране- и объёмно-
центрированная ячейки
моноклинной системы выводятся
друг из друга простой
переменой осей а и с. Они
равноценны, ибо обладают
одинаковой симметрией и объёмом.

70 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
ственные решётке, перенесут один такой узел в аналогичные места
соседних ячеек.
Итак, кроме примитивной ромбической решётки Г0 существует
центрированная по одной паре граней Го, центрированная по всем
граням Г0 и центрированная по объёму Г0". Ромбическая ячейка,
центрированная по двум парам граней, невозможна. Чтобы убедиться
в этом, достаточно посмотреть на фиг. 1,24, из которой очевидно,
Г
л
а+с\
2 \
/а
■*;
н-
/
]h
/
с
'4
ь
/
0.1
гл< */
4o.t
# i>
1~'п
' /
Ь/ &/
f /'
UK- У' 1,
0.1
'гГ 2
01
У-^Ф
А /
/ /
/
/4
l/f4 /л, Щ
/ /
/ /
4 t
4
ty
Фиг. I, 24. Цифры указывают координату вдоль оси г,
(период с принят за 1). Плоские чертежи это — проекции
на плоскость Ъа ячейки.
что принцип построения решётки требует наличия узла в центре
основания решётки. То же самое получается, если мы вспомним,
что сумма векторов решётки есть вектор решётки.
Складывая
видим, что конец диагоиали параллелограма, построенного на
векторах ОА\ н Oio, лежит в центре основания (узел А%).
Следовательно, мы приходим к ячейке Го.
Тетрагональная система. Очевидно, что в этом случае
возможно в принципе существование ячеек, центрированных в гранях
и центрированных по объёму. Все эти ячейки сводятся к двум
трансляционным группам — примитивной 1\ и объёмноцентрированной Г*.
Действительно, на векторы а и Ъ накладываются лишь
следующие условия. Вектор а есть кратчайший вектор в плоскости,
перпендикулярной оси четвёртого порядка. Вектор Ь есть вектор,
возникший совершением над а операции четверной оси. Если поэтому
у тетрагональной решётки центрировано основание аЪ, то переменой

6]
ТРАНСЛЯЦИОННЫЕ ГРУППЫ
71
осей она сводится к примитивной (при этом именно последняя
установка является общепринятой), что видно жз фиг. 1,25,а. По этой
же причине всестороннецентрированная ячейка сводится к
центрированной по объёму (фиг. 1,25,(5). Ячейки, центрированной по одной
паре граней ас (или Ьс),
не может быть: ось
четвёртого порядка
центрирует тогда и грань Ьс
(или ас). Но такая ячейка
невозможна по тем же
причинам, что и
соответствующая ромбическая.
Гексагона л ьная
и ромбоэдрическая
системы. Решётки
обеих систем могут быть
представлены
гексагональными ячейками.
Центрировка
основания ab таких ячеек
приводит к ячейке
вчетверо меньшего размера #/ос
(фиг. 1,26). Центрировка
граней, параллельных
шестерной оси, также не
даёт ничего нового.
Доказательство
примерно такое же, что и для
тетрагональной системы.
Чтобы из поля
зрения не выпала какая-
либо иная возможность,
решим в этом случае задачу более 'строго (подобный метод можно
было бы применить и к ячейкам других систем. Ввиду простоты
этих случаев мы опустили подобные доказательства).
Найдём условия, накладываемые принципом решётки на
координаты ху узла внутри ячейки. Пусть координаты этого узла
(гексагональные) *) равны и'нип. Уравнения преобразования этого узла
осью 6 будут (фиг. I, 27)
Фиг. I, 25. а) Сведение базоцентрированной
решётки к примитивной; б)
всестороннецентрированная ячейка сводится к центрированной
по объёму.
хн = Ую
>/h = Vi
(1,46)
'н- J
) О гексагональных координатах смотри в § 7.

72
КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА
[ГЛ. I
Эти формулы мы получим из (1,366), давая а> значение 60° и
перейдя от прямоугольной системы координат к гексагональной по
формулам:
_ , 1 \
хн~х~Т!>Ун>
Уи-yfV-
(1,46а)
Фиг. I, 26. Центрировка основания
гексагональной ячейки. Вектор t, соединяющий
дополнительный узел х с основным
узлом о, есть вектор решётки. Поэтому
возникают новые дополнительные узлы о
в срединах рёбер (при наличии оси 6 они
выводятся ею). Новая уменьшенная
вчетверо ячейка заштрихована.
Диагональ парадлелогра-
ма, построенного на
векторах с компонентами х'ну'н
и %ную должна попасть
в узел основной решётки,
ибо сумма векторов
решётки также есть вектор
решётки, т. е.
х'н + хн = т'
У'н + Ун = п*)>
где т и п — целые
числа. Отсюда имеем:
т-\-п 2п — т
Ун^-11-^-, хн = ~~. (1,466)
Давая различные значения парам целых чисел m и м, получим
следующие возможные значения
1_ .
3 '
координат:
з
возможные
±
хн— з '
А •
3 '
Ун =
Ун =
Хн—Т
я
= а» !/н = Т'Систе-
Ун =
ма вновь образовавшихся узлов
показана на фиг. 1,27а. Так как
речь идёт о простой поворотной
оси, то, следовательно, все новые
узлы лежат в одной плоскости,
перпендикулярной оси, что приводит
к новой простой гексагональной
ячейке втрое меньшего объёма.
Для других осей, *
существующих в этих системах (6, 3 и 3),
если и возможны узлы внутри ячейки, то только с уже найденными
для оси 6 координатами х и у.
Фиг. I, 27. Преобразовании
осью 6.
*) Напомним, что здесь х, у, ■>н, ун— относительные координаты.

§0]
ТРАНСЛЯЦИОННЫЕ ГРУППЫ
73
Вели ячейка центрирована, то только таким образом, чтобы
12 2 1
координаты этих узлов были -о"?^i и "я"Т^2« Из фигуры 1,27а
очевидно, что наличие внутри ячейки одного из этих узлов вызывает
с необходимостью существование второго и, более того, так как
Фиг. I, 27а. Наличие узла
*/з 2/з требует наличия узла
2/з 1/3. В случае оси 6 это
понятно из того, что угол
симметрического поворота
равен 60°. В случае оси 3, 3
и 6 это происходит
потому, что т есть вектор
решётки.
Фиг. I, 276. Цифры
указывают координаты по
вертикали в долях периода.
Указанное расположение узлов
не противоречит оси 3, или
оси 3, проходящей в точке
О, ибо узлы, лежащие на
одной высоте, выводятся
друг из друга поворотом
на 120°.
Фиг. I, 27в.
Указанное
расположение узлов
(примитивная ячейка) не
противоречит
наличию в точке О
оси 3 или 3,
нормальной к
плоскости чертежа. Узлы
О связаны осью 3.
Узлы х выводятся
из них вектором
решётки т
перпендикулярным оси 3.
В свою очередь
узлы х связаны
между собой
осью 3.
узлы эти могут лежать только на пространственной диагонали (если
они лежат на плоскостной, то это будет уже разобранный случай
1 2
оси 6), то зи z0 равны соответственно ■=- и -^. Вполне очевидно
(см. фиг. 1,276), что такое расположение не противоречит оси 3
и 3. Не следует делать обратного вывода. Из наличия оси 3 или
3 вовсе не следует существования центрированной ячейки. Это
иллюстрируется совершенно отчётливо фиг. I, 27в.
Рассмотрим теперь возможность центрировки в случае 6. Кроме
12 12 12
точек v 7 -.» и т п- 7 должны возникнуть точки, связанные с ними
1 ° 7 2 12
плоскостью симметрии, т. е. -^ 1Г "з" и я" ¥ ¥'
Как видно из фиг. I, 27г, мы пришли к уменьшенной простой
гексагональной ячейке.

74
КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА
[ГЛ. I
Итак, доказано, что для кристаллов гексагональной системы
(содержащих, по определению, точечные группы 6 и 6) возможна
лишь одна трансляционная группа Гл, характеризующаяся
примитивной гексагональной ячейкой. Решёткам же ромбоэдрической
системы (содержащим, по определению, 3 или 3) отвечают две
трансляционные группы: Гй, характеризуемая примитивной гексагональ-
Фиг. 1, 27г. Случаи оси С.
узлы с координатой 1
» » » i/g
'/в
/з [ вдоль оси G.
Расположение узлов О и + друг над другом получается потому, что
в решётке координата — ]/з эквивалентна +2/з и */з эквивалентна — 2/:s»
ибо — 1/з+1 = + 7з и i/з
•3/з- При таком расположении узлов
имеется вектор решётки т. Следовательно (см. правый чертёж), в
показанные точки проектируются узлы с координатами 0, */3 и h> T- е. период
с уменьшается в 3 раза; приходим к уменьшенной простой
гексагональной ячейке (заштрихована), объём которой в 9 раз меньше объёма
первоначальной ячейки.
ной ячейкой и ГгЛ (читать ромбоэдрическая), характеризуемая цен-
трированной гексагональной ^чейкой с базисом (000, -д- •— -^ , -^ о"*т]-
Обе трансляционные группы могут быть, разумеется, описаны
в ромбоэдрических осях. Как показано в § 7, примитивная
гексагональная ячейка Vh преобразуется в три раза большую по
/ XXX 2^2\
объёму ромбоэдрическую с базисом (000, — -» у, т^у , а цен-
/ Х2Х 2 1 2 \
трированная гексагональная ячейка с базисом (000, -«--«--»■ > Т "о"?)
может быть преобразована в три раза меньшую по объёму
примитивную ромбоэдрическую ячейку (отсюда и название трансляционной
группы). Такая ячейка обозначается символом 7?.
Отметим здесь, что из ромбоэдрических кристаллов
группу Th имеют те, решётки • которых содержат только поворотные

Таблица I, VI
Трансляционные группы
CD
Кристаллическая
система
Триклпннан
Моноклинная
Символ
трансляционной группы
Г или Г7Г
Базис элементарной
ячейки
(000)
(000)
ооо,||о
Симметрия
элементарной ячейки точечной
решётки
Ci = l
1h
^/, = fr
Изображение

трансляционной группы
U
В 90'
Ш
м
ш

Продолжение
Кристаллическая
система
Ромбическая
Символ
трансляционной группы
1\
Базис элементарной
ячейки
(000)
(000;Н°)
Симметрия
элементарной ячейки точечной
решётки
JL1.
2 2
ooa-s-fojfo^of,
LI
2< 2
I)i}l = w»mw
I)y( = №IN№
7)2/l = mmw
Изображение

трансляционной группы
*fcp'
5*
гГ

Продолжение
GO©
С5
Кристаллическая
система
Символ
трансляционной группы
Ромбическая
Тетрагональная
Г'о'
Базис элементарной
ячейки
«*kkk
(000)
ЫН)
Симметрия
элементарной ячейки точечной
решётки
D«h = mmm
*hh =
J>*h =
mmm
Изображение

трансляционной группы
Я
а
+-—*
*
Щ
f

Продолжение
Кристаллическая
система
Ромбоэдрическая или
тригональная
подсистема
Гексагональная
Символ
трансляционной группы
Frk
Г/,
1\
Базис элементарной
ячейки
(000) в ромбоэдрических осях;
/12 1 2 1 2\
1°°0,з з з ' з з з)
в гексагональных осях
(000) в гексагональных осях;
в ромбоэдрических осях
Vю ' з з з'з з з)
в ромбоэдрических осях; (000)
в гексагональных осях
Симметрия
элементарной ячейки точечной
решётки
1)ы = з«*
утроенная ячейка
J)bli = Qjmmm
утроенная ячейка
Изображение

трансляционной группы
rrf>
•
с
Щ*р<

ирооолжение
Кристаллическая
сиотема
Кубическая
Символ
трансляционной группы
Базис элементарной
ячейки
Симметрия
элементарной ячейки точечной
решётки
000
000'Y!04°i;0iir)
Oh = /«3»*
v°°°;T-fl)
0/t = ч-дш
Oh = тЗш
Изображение

трансляционной группы
с
ш
Ш2:

80 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
с;=а
Cf'fiJ
Фиг. I, 28. Если решётка имеет поворотные
и винтовые оси, она может быть
охарактеризована простым ромбоэдром.
(или инверсионные или те и другие) оси или только винтовые оси
третьего порядка. При наличии же в решётке и поворотных
(инверсионных) и винтовых осей
она имеет
трансляционную группу ГГ7„ т. е.
может быть
охарактеризована простым ромбоэдром.
Это иллюстрируется фиг.
1,28. Определение
винтовой оси будет дано
ниже (§ 8).
Кубическая
система. Центрировка
пары граней кубической
решётки приведёт
благодаря симметрии к всесторонней центрировке. Поэтому здесь
возможны следующие трансляционные группы: примитивная Г0, все-
стороннецентрированная Гс и объёмноцентрированная Гс.
Всего трансляционных групп всех кристаллических систем
оказалось 14. Они иллюстрированы чертежами и охарактеризованы
значением базиса в таблице Т, VI.
(Об обозначениях для
гексагональной сингонии см. в следующем
параграфе.)
§ 7. Некоторые замечания об
описании кристаллов гексагональной
и роибоэдрической систем
а) Четвёртый индекс.
Кристаллическая решётка является
трёхмерным образованием.
Поэтому для описания её обычно
применяются системы координат с
тремя осями. В самом деле, для
определения положения точки в
трёхмерном пространстве,
необходимо и достаточно знать три её
координаты. Только в случае
кристаллических решёток, относящихся к гексагональной системе,
мы применяем для описания реального трёхмерного объекта
координатную систему с четырьмя осями. Целесообразность этого
приёма иллюстрируется фиг. 1,29, изображающей узловую
плоскость, перпендикулярную оси 6. Направления ох, оу и ои
совершенно равноценны, а периоды повторяемости a b, d по этим
направлениям равны. Поэтому, приняв за одну ось координат (с)
Фиг. I, 29. Узловая плоскость
перпендикулярна оси 6.

§ 7] НЕКОТОРЫЕ ЗАМЕЧАНИЯ ОБ ОПИСАНИИ КРИСТАЛЛОВ 81
направление оси 6, мы за две другие оси с равным правом могли
бы взять пары направлений Ох и Оу, или Ох и Ои, или Оу и Ои.
В силу этого мы пользуемся не тремя, а четырьмя осями
координат: а (Ох), Ь(Оу), d(Ou) с одинаковыми периодами а, и с(Оз)
с периодом с. При этом узлы, узловые прямые и плоскости
характеризуются не тремя, а четырьмя индексами. Естественно, что
четвёртый индекс не является независимым. Для доказательства
этого рассмотрим фиг. 1,29. Узловая плоскость пересекает оси а,
Ь и d в точках А, В ж D' соответственно (она может пересекать
или не пересекать ось с). Проведя прямую DD', параллельную ОВ,
получим равносторонний треугольник ODD' (OD'= OD). Из
подобия треугольников ADD' и ЛОВ имеем:
ов ~ о а или от>'~ ол-ов '
По определению, индексы равны:
. d a j a j Ъ 7J-7 ^ ^" ^
г~ ~~Ъ~В'~-~ ОП''> к~ОА; "~~OB 11^'С — а1)А^ОВ'
Следовательно,
h + k=—i или h -f- h -j- г = 0. (1,47)
Аналогичное соотношение можно доказать для индексов [тпгклр]
узловой прямой:
m Л~п Н~ ш == о*
Равнозначные кристаллографические направления разбивают
узловые плоскости, перпендикулярные осям 6, на шесть
равноценных полей. Четвёртый индекс
выразительно подчёркивает
этот особый характер
гексагональных сеток, что
иллюстрируется следующим
примером (фиг. 1,29а). Узловая
плоскость параллельна осям с
и 6 и пересекает ось а. Если
не интересоваться
расстоянием этой плоскости от
начала координат, то символ
её можно написать как (100).
Ось 6 создаёт из этой
плоскости ещё пять плоскостей
,- - /\А *иг* *■ 2^а* Пример выражения харак-
(100), (010), (ПО). Охватить твра гексагональных сеток четвёртым
эти шесть плоскостей, связан- индексом,
ных осью 6, общим символом
не удаётся. Введение четвёртого индекса позволяет записать
символы этих 6 плоскостей как (1010), (0110), (1100), (1010), (0П0),

82 кристаллограф, основы структурпого анализа [гл. i
(1100) и охватить их общим символом {1010}. Меняя местами
первые три индекса, получим символы всех плоскостей. Поскольку
число перестановок из трёх равно 6, ясно видно, что число
связанных плоскостей равно 6.
Подчеркнём ещё раз, что для описания кристаллов достаточно
трёх координат и трёх индексов. Четвёртый индекс вводится для
большего удобства и наглядности описания. Иногда предпочитают
обходиться без него.
6) Два способа выбора гексагональных осей. С- и
Ж-установки. Гексагональные оси могут быть выбраны двумя способами,
ибо в случае гексагональной сетки имеются 2 возможности выбора
Фиг. I, 30. С-установка и -//-установка.
тройки направлений (узловых прямых), образующих углы по 120°
(60°). В первом случае (установка С) за оси выбирают узловые прямые
с минимальным (в гексагональной узловой плоскости) периодом ас,
во втором случае (установка К) за оси выбирают узловые прямые
с периодом aH—aoyY. Переход от установки С к.установке If
и наоборот совершается путём поворота осей на 30 или 90°.
Сказанное иллюстрируется фиг. 1,30. Причиной введения 2-х
установок является то обстоятельство, что по направлениям аа и ап
могут проходить разные элементы симметрии (классы Ся„, I)3, 1)м,
У)зл) и монокристалл может быть огранён или по направлениям ас,

§7]
НИКОТОРЫЕ ЗАМЕЧАНИЯ ОБ ОПИСАНИИ КРИСТАЛЛОВ
83
или по направлениям ан, так что заранее неизвестно, выбор какой
из двух троек направлений явится более удобным.
Переход от установки С к установке Н совершается по
формулам:
ан=ас—dc = 2ас -\- Ъс,
bH = bc — ao='2bcJrdc'
а
н
ь0—ас
2Ьс~\-а
с
Формулы преобразования индексов таковы:
(1,48)
к
н
*с К
"н ~~ пс
»Я = '(Г
Детерминант преобразования
Д =
2kc-\-ic,
гс == ^ Н~ ^с»
(1,48а)
2
1
0
1
1
0
0
0
1
= 3.
В* случае установки Н примитивная гексагональная ячейка
заменяется непримитивной гексагональной же ячейкой втрое большего
объёма. В основаниях этой ячейки находится по 2 дополнитель-
12 2 1,
ных узла: •^■-т 0 и -тО (сравните с возможностью центрировки
о о о о
гексагональной ячейки).
Как в случае установки С, так и в случае установки Я мы
можем перейти к прямоугольной системе координат, называемой
ортогексагональной. Ортогексагональных ячеек одинакового
размера существует две, оси которых повёрнуты на 60° друг к другу.
Разумеется, в случае оси 6-го порядка эти ячейки будут
эквивалентны. Принято связывать одну из них с установкой И, а
другую с установкой С. Способ перехода показан на фигуре I, 30.
В случае установки С формулы перехода т:шовы:
а„
— dc = aG-{-bc,
Ъо = -ас-^ьо = 2Ьс + (1
с>
^о~ сс5
с
(1,49)
(I, 49a)

64
КРИСТАЛЛОГРАФ. ОбНОВЫ СТРУКТУРНОГО АНАЛИЗА
[гл. 1
Детерминант преобразования равен:
1 1 О
Д= 110
О 0 1
В случае установки Н формулы перехода таковы:
ан~ьп 2ан + ан
а0— 3 3
*i = —<*я = ая + *я'
_ hH — kn 2hH + iH
л0 — з — ■ з"
^ = —«я = /<я4-/гя,
Детерминант преобразования
(1,50)
(I, 50а)
Д =
1
3
1
0
V
3
1
0
0
0
1
Фиг. I, 31. Описание
гексагональных кристаллов в
ромбоэдрических осях.
Ортогексагональной системе
координат отвечает базоцентрированная
(С) прямоугольная (ромбическая)
ячейка с осями
ая/3
b0 = aaYJ =^ан.
в) Связь ромбоэдрической и гексагональной систем
координат. Весьма важным является описание гексагональных
кристаллов в ромбоэдрических осях. Выберем новые оси aR, aR и
«Да, как показано на фиг. I, 31. Относительно них можно сказать,
что
и что
Следовательно, это — ромбоэдрические оси. Преобразование совер-

§7]
НЕКОТОРЫЕ ЗАМЕЧАНИЯ ОБ ОПИСАНИИ КРИСТАЛЛОВ
85
шается по формулам:
ав1 = «(? + ссг>
lR==iC + lC =
1 О 1
д =
'с j
lc—]lc
"С
(1,51)
(1,51а)
= 3.
О 1 1
111
Примитивная гексагональная ячейка заменяется непримитивной
ромбоэдрической втрое большего объёма. Это ромбоэдр, на длинной
телесной диагонали которого находятся два дополнительных узла
ГГ-g--з""^! 1» ItTtII (ромбоэдрические координаты), делящие её
на 3 равные части. Параметры ромбоэдра (длина ребра ав и угол между
рёбрами aR) определяются
параметрами гексагональной ячейки:
aR= Va2c-\-cc ;
2с% — а%
cos a,
Ч4+4)
а. 52)
В случае установки Н
непосредственный переход к
ромбоэдрическим осям нецелесообразен, ибо
элементарный ромбоэдр будет
содержать 14 дополнительных узлов.
Таким образом, всякий
гексагональный кристалл может быть описан
в ромбоэдрических осях, всякая
гексагональная решётка может быть
описана как совокупность трёх
ромбоэдрических вставленных друг
в друга решёток.
Не менее важен и обратный
переход от ромбоэдрических к
гексагональным осям (описание трансляционной группы Trh). Новые
оси выберем, как показано на фиг. 1,32. Легко видеть, что асЬс —
= 7(7 = 120°; a(fic.= bQcQ = W и ас=Ьа, т, е. что новые оси дей-
Фиг. 1,32. Переход от
ромбоэдрических к гексагональным осям.

8C
КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА
[ГЛ. 1
ствительно являются гексагональными. Преобразование совершается
по формулам:
ас=ап:
lR.;>
)
bC = aR—aRS
4 + ^,+ ^'
h,C~^lR *Я»
)
In
(1,58)
(I 5,4a)
1
О
1
]
1
1
О
1
1
д =
Примитивный ромбоэдр В заменяется на ненримитивную
гексагональную ячейку утроенного объёма. Дополнительные узлы,
находящиеся на длинной телесной диагонали и делящие ее на три
1 2 1
2 1
3 3 3 И 3 3 3
равные части, имеют координаты (гексагональные):
Параметры гексагональной ячейки определяются параметрами
ромбоэдра:
ас=ал/2(1 — сова-);
сс = aR у 3 (1 + 2 cos aR). (I, 51)
От ромбоэдрических осей можно
перейти и к ортогональным по
формулам
ао aR1 aRt
aRl-3T2aRi — aR/ f (1,56)
k0 = hR
U
— hR~\-'2kR lR,
1 n ~ ^
\ (I, ooa)
I
Фиг. I, 33. Ортогексагональный
элементарный параллелепипед.
Д =
I
1
1
0
2
1
1
1
1
= 0.
Ортогексагональный элементарный параллелепипед содержит 5 до-
полнительных узлов: I±0; i{|, \ ||-, О I-J , of |. Это
изображено на фиг. ], 33.

§ 8] ОТКРЫТЫЕ СИММЕТРИЧЕСКИ!) ОПЕРАЦИИ 87
Следовательно, всякий ромбоэдрический кристалл можно описать
в гексагональных осях, всякую ромбоэдрическую решётку можно
представить как совокупность 3 гексагональных, вдвинутых друг
в Друга.
Указанные переходы от ромбоэдрических осей к
гексагональным и наоборот часто применяются в практике рентгеноструктур-
ного анализа и кристаллографии. Так, например, ромбоэдрическим
(тригональным) кристаллам часто придают не только
ромбоэдрическую, но и гексагональную установку. Объясняется это тем, что
ось 3 является частным случаем оси 6.
Разумеется, новый выбор осей приводит только к иному
способу описания, рассмотрения кристалла, но отнюдь не изменяет
ни его точечной, ни его трансляционной, ни его пространственной
группы. Это утверждение справедливо и во всех других случаях
перемены осей.
§ 8. Открытые симметрические операции
а) Винтовые оси и плоскости скольжения. В § 2 было
показано, что в общем случае симметрическое
преобразование состоит из вращения, инверсии и
трансляции. Симметрические преобразования, в кото- ^^[—«^ //
рых перенос решётки отсутствовал, были названы
закрытыми. Здесь мы хотим рассмотреть
симметрические операции, в которых принимает
участие трансляция.
Подобные открытые симметрические операции
могут заключаться в общем случае в
повороте + трансляция. Простейшей и тривиальной
операцией этого типа является чистая трансля- J- [ t
ция на величину периода.
Открытая операция будет совершаться в два
360°
приема: поворот точки около оси п на угол и
/ "
Л
последующее смещение точки вдоль оси на
величину tn. n поворотов, сопровождающихся
смещениями, должны быть эквивалентны трансляции
вдоль оси. Иные возможности несовместимы
с принципом решётки.
Действительно, после п поворотов точка 1
поворачивается на 360° и смещается в
направлении оси на величину ntn, переходя в
точку N. Точки N и 1 трансляционно-идентичны; следовательно,
расстояние между ними равно трансляции t вдоль оси. Таким
Образом, tn = -t- (фиг. I, 34).
^Я^"
Фиг. I, 34.
Винтовая ось.

88 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
Комбинации поворота-с трансляцией вдоль оси создают подобие
винтового движения и называются винтовыми осями. Винтовые
оси могут быть правыми и левыми.
Итак, винтовой осью п-то порядка мы называем элемент сим-
360°
метрии, совершающий следующее преобразование: поворот на —-
и перенос параллельно оси на — , где t — период в направлении
оси. При этом должно быть указано направление вращения.
Если, смотря вдоль винтовой оси навстречу смещению, мы
видим, что поворот совершается против часовой стрелки, то эта
ось считается правой.
Левая и правая винтовые оси второго порядка совпадают.
Поэтому винтовые оси сводятся к следующим (о номенклатуре осей
смотри несколько ниже): 21г 32 и 32, ^ и 4S, 62 и 6Б. Большими
индексами обозначены правые оси.
Очевидно, что некоторые поворотные оси могут быть совмещены
с винтовыми так, чтобы это пе противоречило принципу решётки.
Возможны следующие совмещения: 1) ось 2Х и ось 2, что даёт
ось 2 и уменьшение периода вдвое; 2) ось 2 и ось 4j или 4S, что
даёт ось 42; 3) ось 3 и ось 6а или 65, что даёт ось 63; 4) ось 2
и ось 6j, что даёт ось 62; 5) ось 2 и ось 65> что даёт ось 64-
Согласно общепринятой номенклатуре винтовая ось
обозначается символом па, где п указывает порядок оси: м = 1, 2, 3,
4, 6, a s = 0, 1, 2, 3, 4, 5, 6s^w. Отношение s/n равно
смещению, выраженному в долях периода вдоль оси, которое
сопровождает каждый поворот. При 5 = 0 или s — п имеем поворотную ось
порядка п, которая может рассматриваться как винтовая ось со
смещением, равным 0.
Две винтовые оси порядка п, для которых sv -\- s2 = п,
отличаются лишь направлением вращения. Левой считается ось с
меньшим значением s. Только оси с s=l считаются независимыми.
Это левые оси. Оси с s = n—1 представляют собой
соответствующие им правые оси. Остальные винтовые оси с яфп—1, szjtzl
являются комбинациями осей поворотных и винтовых. Ось %
является комбинацией винтовой оси п1 с поворотной осью
порядка s. Если s>-g-, то это комбинация соответствующей правой
оси с поворотной осью порядка п — s. Комбинация поворотной оси
с винтовой приводит к уменьшению периода вдоль оси в s раз.
Все возможные элементы «винтовой» симметрии показаны на
фиг. I, 35, а совершаемые ими преобразования координат даны
в таблице I, УП (см. ниже).
Из других независимых симметрических операций может
сочетаться с переносом лишь плоскость симметрии.
Соответствующие открытые симметрические операции носят название

8]
ОТКРЫТЫЕ СИММЕТРИЧЕСКИЕ ОПЕРАЦИИ
89
отражения в плоскостях со скольжением (иначе операций
плоскостей скользящего отражения).
IX i
г х i
ffu^.y iL-^Ло <,.~.:«;:у jr^-fry
3 J
3 J
4
д 6
б,
#
Обозмбчрнаевинтовых осей.
параллельных плоскости
чертежа
JHHh
Пример обозначения
поворотных осей, параллель
ных плоскости чертежа
h
4J
Фиг. I, 35. Винтовые оси. Вверху показаны винтовые оси; внизу даны
проекции расположения точек на плоскость, перпендикулярную оси. Цифры
указывают координаты точек вдоль оси в долях периода. Ещё ниже даны
графические символы винтовых осей. Для осей 62, 63, 64 и 6Б даны только
проекции и символы.
Плоскость скольжения показана на фиг. I, 36. Вдоль плоскости
должна быть указана линия переноса, называемая линией скольжения.
Величина трансляции равна */з периода вдоль линии трансляции.

90 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
Выбор системы координат при описании решёток всегда таков,
что мы будем встречаться с плоскостями скольжения, со
скольжением (переносом) либо вдоль основного ребра ячейки (оси), либо
вдоль плоскостной диагонали. Во втором случае мы можем
встретиться с двумя возможностя-
3(x*t z) ми: скольжение вдоль центри-
• роваыной или нецентрирован-
t ——-_) н0^ Гра1Ш- Период диагонали
центрированной грани равен
половине длины диагонали.
Таким образом, скольжение
в этом случае будет
происходить на х/\ длины
диагонали. Плоскости диагонального
скольжения обозначаются
буквами d (скольжение на ili
длины диагонали) и п (на половину длины диагонали). Плоскости
скольжением вдоль осей а, Ь, с обозначаются а, Ь и с.
Фиг. 1, 36. Плоскость скольжения.
I
XT*
р-2
Ш«i
а\
а(ОШ)
*x,yj
<W*
a i n (010)
*x,y,z+j
1
i
и/
j y*+Uz+]i
d(010)
Фиг. I, 36a. Изображение плоскостей скольжения. Плоскости
скольжения, перпендикулярные плоскости проекции,
изображаются штриховыми (компонента скольжения лежит в плоскости
чертежа), пунктирными (компонента скольжения
перпендикулярна плоскости чертежа) и тптрихпунктирными (компонента
скольжения наклонена к плоскости чертежа) линиями.
В ромбических и более симметричных ячейках, где выбор oceii
определяется симметрией, существует объективное различие между

§ 8] ОТКРЫТЫЕ СИММЕТРИЧЕСКИЕ ОПЕРАЦИИ 91
плоскостями с диагональным и осевым скольжениями. Напротив,
в моноклинных ячейках, меняя выбор осей а ж с, всегда можно
диагональную плоскость превратить в осевую и обратно.
Итак, мы описали все комбинации закрытых симметрических
операций с переносом, т. е. открытые симметрические операции.
6) Общие соображения о взаимной расположении элементов
симметрии в решётке. Класс симметрии. В кристаллической
решётке бесконечными параллельными группами расположены
различные элементы симметрии. В одной элементарной ячейке может
быть расположено несколько островов, принадлежащих к разным
точечным группам симметрии; между этими островами могут
проходить, кроме того, различные открытые элементы симметрии
(винтовые оси и плоскости скольжения).
Пусть размеры периодов кристалла стремятся к нулю. Тогда
все параллельные оси симметрии сольются в одну ось, а плоскости
симметрии в одну плоскость.
Если параллельные оси симметрии пространственной группы
были двух тип (или более) порядков, то возникающая ось
будет иметь высший из имевшихся порядков. Так, например, в ряде
пространственных групп тетрагональной системы имеются
параллельные оси порядков 4 и 2. Макросимметрия кристалла
характеризуется наличием (в данном направлении) оси 4. Винтовые оси
превратятся в простые и плоскости скольжения в плоскости
зеркальной симметрии, ибо величины трансляций обратятся в 0.
Возникает точечная группа, характеризующая макроскопическую
симметрию кристалла, как целого. Эту точечную группу мы будем
называть классом симметрии кристалла. Номенклатура классов
симметрии, разумеется, совпадает с таковой для точечных групп
(или островов).
Отсюда следует, что все точечные группы, существующие в
данной решётке, суть подгруппы класса симметрии и, далее, что
винтовые оси порядка п возможны в кристалле данного класса
симметрии лишь в том случае, если класс симметрии содержит
параллельную поворотную ось того же порядка. Аналогично, в
решётке могут проходить плоскости скольжения лишь в том случае,
если класс симметрии кристалла содержит параллельную плоскость
зеркальной симметрии.
Это обстоятельство практически важно, так как класс симметрии
определяет внешнюю симметрию свободно растущего
кристаллического образца (это так называемая симметрия идеальной формы
роста или макросимметрия кристалла) и зачастую определяется
^независимо от исследования структуры.
Приведём примеры соотношения пространственной группы и
класса симметрии.
Кристалл йодоформа СШ3 принадлежит к пространственной
группе Св = И. В элементарной ячейке проходят параллельные

92 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
оси 63, 2t и 3. В соответствии со сказанным выше, кристалл
относится к классу симметрии Св = 6. Другой кристалл диметилового
эфира гидрохинона СН30—^Г \— 00Н3 относится к
пространственной группе Vln = РЬса. В элементарной ячейке проходят три
взаимно перпендикулярные семейства плоскостей скольжения a, b
и с и три взаимно перпендикулярных семейства винтовых осей 2t;
кроме того имеются центры инверсии. Кристаллический класс этого
кристалла Vh, т. е. (ттт).
Из сказанного делаются также понятными пути вывода всех
возможных пространственных групп данного кристаллического
класса. Для этого, очевидно, следует рассмотреть все возможные
х/Г
(а) (6)
Фиг. I, 37. Возникновение в ячейке новых центров инверсии
(см. текст к фиг. I, 38).
случаи «расщепления» макроскопических элементов класса
симметрии па параллельно расположенные соответствующие
«микроскопические» элементы симметрии. Например,класс Cih= 4/mможет
дать пространственные группы, содержащие оси 4, 4lJP 42, 43,
параллельные тетрагональной оси идеальной формы роста и зеркальные
плоскости симметрии и плоскости скольжения, перпендикулярные
этой оси. Для вывода всех пространственных групп класса надо
перебрать все возможные способы взаимного сочетания и
взаимного размещения этих элементов.
в) Трансляция и другие элементы симметрии. Все элементы
симметрии выступают в решётке в виде бесконечного семейства
параллельных линий или параллельных плоскостей или решётки
(в случае центра инверсии).
Таким образом, помещая вершину ячейки в центре симметрии,
беря ребро ячейки вдоль оси симметрии, а грань её вдоль
плоскости симметрии, мы автоматически получаем те же элементы
симметрии в других вершинах, рёбрах и гранях ячейки; это —
тривиальный факт, следующий из принципа построения решётки.
Однако на самом деле элементы симметрии в решётке
расположены более часто. Применение симметрической операции переноса

§ 8] ОТКРЫТЫЕ СИММЕТРИЧЕСКИЕ ОПЕРАЦИИ 93
к элементам симметрии порождает новые элементы симметрии,
точнее — аналогичные элементы симметрии, расположенные внутри
элементарной ячейки.
Рассмотрим возникновение в ячейке новых центров инверсии.
Если в ячейке имеется центр симметрии с координатами (а, Ъ, с),
то координаты точек, связанных центром инверсии, подчиняются
условию х-\-х1 = 2а, у-\-у1 = 2Ъ и z-\-zt — 2c (см. фиг. 1,37).
Предположим, что начало ячейки есть центр симметрии. Это
значит, что любая точка (xys) переходит в точку {руг).
Транслируем вторую точку вдоль пространственной диагонали; получаем
точку с координатами 1 — ху 1—у, 1— z. Нетрудно видеть, что
первая точка хуг связана с третьей центром инверсии в точке
¥"2 ¥* Транслируем вторую точку вдоль плоскостной диагонали ху;
она получит координаты 1 — х, 1 — у, з. Эта точка связана с пер-
1 1
вой центром инверсии в точке у у О. Аналогичным образом
показываем, что если в начале ячейки имеется центр инверсии, то
центры инверсии имеются в серединах рёбер, граней и объёма
ячейки. Таким образом, на каждую ячейку приходится 8 центров
инверсии. Эти центры инверсии при отсутствии иных элементов
симметрии независимы между собой или, иначе говоря,
симметрически не связаны. Это значит, что в реальной кристаллической
решётке все 8 семейств центров инверсии могут быть заполнены
или окружены разными атомами. Точно так же посередине между
2 соседними особыми точками инверсионной оси (расстояние
между ними равно периоду вдоль оси) возникает новая особая точка.
Аналогичным способом можно доказать, что при наличии в
кристалле только двойных осей и плоскостей симметрии (моноклинная
и ромбическая системы) имеет место следующее: если ось второго
порядка (поворотная или винтовая) проходит через ребро ячейки,
то возникает ещё 3 независимых семейства таких же осей; выходы
этих осей на перпендикулярную плоскость будут в центре грани
ячейки и в серединах рёбер (см. фиг. 1,38). Если через грань ячейки
проходит плоскость симметрии (простая или скольжения), то
возникнет независимое семейство таких же плоскостей, проходящих
через середину ребра, перпендикулярного этим плоскостям (см.
фиг. 1,39).
В случае других кристаллических систем дело обстоит несколько
сложнее. Как бы то ни было, и там внутри ячейки генирируются
новые элементы симметрии.
Во всех этих случаях термин «независимые» аналогичен термину
«не связанные симметрической операцией». Две бесконечные
последовательности взаимно перпендикулярных осей 2, связанных
осью 4, представляют собой одно семейство.

<ц
КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА
[гл. т
Следует различать тождественные и нетождественные семейства
элементов симметрии. Мы будем называть тождественными такие
Ш •&
(а)
SK
Ш .&
ш
(б)
Фиг. 1,38. а) Ось/, проходящая вдоль ребра ft ячейки (оси 11,
III, ZT трансляционно идентичны оси/), выводит из
произвольной точки 1 точку 1'. Кроме этих точек, разумеется,
имеются трансляционно идентичные 2, ,?, 4 и 2', 3', 4'.
Легко видеть, что точки 1 и 2', а также /' и 2 связаны осью,
проходящей через середину ребра с и параллельно Ъ.
Аналогично точки 2 и 3' (2' и 3) связаны осью, проходящей
в середине ребра а, точки 4 в. 2' (4\ 2; 1Г, 3; 1, 3') связаны
осью, проходящей через центр грани ас; б) здесь показаны
дополнительные оси V, VI, VII, VIII и /X.
/ •
Фиг. I, 39. Возникновение в ячейке новых плоскостей
симметрии. Точки 1 и 2', а также V и 2 связаны новой
плоскостью III, проходящей через середину ячейки.
семейства, которые переводятся друг в друга параллельным сдвигом
решётки.
Примеры нетождественных семейств центров инверсии будут
приведены ниже при рассмотрений пространственной группы С\ь.
• /
/
2''
Ш
§ 9. Преобразования, производимые элементами
симметрии решётки
а) Преобразования координат точки. Каждая пространственная
группа характеризуется взаимным расположением элементов
симметрии в элементарной ячейке.
При различном выборе начала координат элементы симметрии
могут, вообще говоря, находиться в произвольных точках ячейки
и отсекать произвольные отрезки на осях координат.
Однако при описании пространственной группы всегда
целесообразно выбрать начало координат ячейки либо в центре инверсии,
либо в точке пересечения каких-либо элементов симметрии (пред-

§ч
ПРЕОБРАЗОВАНИЯ, ПРОИЗВОДИМЫЕ ЭЛЕМЕНТАМИ
95
почтительно закрытых). Если же имеются только семейства
параллельных осей или плоскостей симметрии, то начало координат
выбирается в любой точке оси или плоскости. Естественно, что
при наличии параллельных поворотных и винтовых осей начало
выбирается на поворотной оси.
Точно так же при наличии зеркальной плоскости симметрии и
плоскости скольжения начало выбирается на первой из них. При
этом координаты других элементов симметрии будут выражаться
простыми дробями. Так мы будем встречаться с центрами симметрии,
расположенными в центрах граней, в серединах рёбер, в точках,
находящихся на одной четверти диагонали ячейки, и т. д.
В таблице 1, VII приводятся наиболее часто встречающиеся
расположения элементов симметрии в решётке. В таблице
указывается, какие координаты получит точка xyz при совершении
симметрической операции данным элементом симметрии,
расположенным в данном месте ячейки.
Таблица I, VII
Преобразования, совершаемые элементами симметрии *)
А. Оси симметрии
а) Оси симметрии, проходящие через начало координат вдоль оси z
2 хуг -?-*■ хуг;
2i хуг—+хуг + - ;
3 xyz —»- у, х — у, г —*■ у — х, х, г;
32 xyz —+ у, х — у, — + * —-* У — х, х, — -{- .?;
3i хуз —» у — х, х, —■ + г —* у, х — у, — -\г ,?;
4 xyz —*■ ух г —*■ хуг —*-ухг;
к *У* —+У,*, j + * —+ я, У, * + — —*■ V, х, J + г;
4t xyz —► у, х, — + г —*■ х, у, —• + г —► J'. я*. J + ~5
42 ги/^—*■ ?/> ,т. -К" + г—*-хуг—>-?/, .т, -— -j- ,г;
4 ж?/»—»• у,аггг —*-#2/,? •■—*-ухг;
6 a?j/£ —»■ а; — j/, а-, .г, —>- у, х — у, z —► хуг —*■ у — х, х, z —*■ yf у — ее, z;
*) В книге принята правая система координат. Выражение для
преобразования осью Si в левой системе координат будет совпадать с
формулой преобразования Зг в правой системе. В интернациональных таблицах
•меньшими индексами обозначены первые оси.

96 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [гЛ. I
Продолжение
6Ь xyz-^x — y, х, — -|-*—* у/, а-— у, -g-+ *-^ а'> У» ^ + z ~"
- 2 . 5 .
—" ?/ — а*, ж, - -{- с —► ;</, 1/ — х, j + г;
1 , - 1
6t аму.г —* У, у — *> -Q + * —- 1/ — а>, а-, — -f s —*
1 , - 2 , 5 .
—* я» У» у + г ~~"?/' а? ~ у' "з" + * "~* Ж~~ У' *' "б" "*" ''
1 - 9
64 vyZ—+X — y, X, -£-\rS—+y, X — y, j--\--Z—+xy.r—>
—► ?/ - ?", а?, - -j- г —+ у, у — х, — + z;
1 , ~ 2 .
б2 ауз —* у, у — х, ~ + г —> ?/ — а?, х, - -|-.: —* а-у~ —+
- г , 2 ,
—+у, х — у, -д+^—*-а! —у, ж, д--Ь?;
1 . - --1
а;у~—>х — у, х, — -\-г—» у, х — у, г—+ху-?-
1 ,
—► У — х, *, г-—*у, у — ж, -J + 2-;
i-yг —> у — х, х, г —»■ у,'я- — у, z —»■ xyz —>• у -
!-.:—>
-X, X, Z
у, х— у, z.
б) Некоторые оси симметрии, не проходящие через начало координат
или не параллельные осям координат.
Оси 2, параллельные оси г, проходящие через точки:
аЬ xyz—*2а— х, 26 — у, г\
п 1 ~ 1
О, ~ xyz —+х, — — у, с;
11 1 1
а проходящие через точки: 0 — и — -^- то же, что и для осей, проходя-
щих через начало координат.
в) Оси 2, проходящие через начало координат вдоль плоскостной
диагонали
[110] xyz —*- yxz;
[101] xyz—*■ zyx.
г) Оси 2 в гексагональной системе, идущие в плоскости г = О вдоль
следов координатных плоскостей, и оси 2\ в гексагональной системе,
идущие в плоскости .г = 0 между следами координатных плоскостей:
110 xyz —»• yxz;
120 xyz —► у — х, у, z
210 xyz —► х, х —у, z
010 xyz—*-х, у — х, z
110 . xyz —у yxz.

§ 9] ПРЕОБРАЗОВАНИЯ, ПРОИЗВОДИМЫЕ ЭЛЕМЕНТАМИ 97
Продолжение
1 2
д) Оси 3 и оси 6, параллельные оси .г, проходящие через точки -п--^- и
о о
—• •--, совершают те же преобразования, что и оси, проходящие через
начало координат.
е) Оси 3, проходящие вдоль диагонали [111] (в кубической системе)
хуг —► гху —► угх.
ж) Оси 4, параллельпые оси г, проходящие через точку — —
1 11 1
-П1г -^>--к — У,х,г, —ь — — х, — — у, г —► ?/, у — хг.
Б. Плоскости симметрии
а) Являющиеся координатными плоскостями хг:
т хуг —у хуг;
. 1 -
a хуг —* .т -f — . у. г;
- , 1
c «yz—ух, у, г + -2- ;
, 1 - , 1
н хуг —> я- -]- — , у, г -\- -- •
X — , X 1 .1 . 3 - , 3
(I ауг—t-x-{---, у, sJr~^—*х ~\~ "2» V- » 'Т~^ —» 'г "Г f. ?/. ~+ ~^ ;
^ 1
о) отсекающие отрезок - - по оси у:
1
ж ж г/^ —>- х, — —у, .г;
а хуг —•• ж + "2 J ~ У' z>
с xyz—*x, ~ — у, y + S;
.11 1 ...
п хуг —у х ^- - , — — у, — + ~,
в) параллельны плоскости (НО) и проходят через начало координат
(в тетрагональной системе)
т хуг —► ухг;
; l 1 _1_ 1 -
а, Ь я-?/г —*-?/ + -^ , a? + -J » *:
, 1
,1 , 1 . , 1
п хуг —► ?/-{- — , •'£ + — » -+«■;

08 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [гл. I
Продолжение
а а а Ь
и проходят через точки -^- О и 0 —
1 ! 1 .
т хуг —*■ — -f у, — -f- ar,
а, Ь xyz —> у, х, г;
с хуг—+у-\- — , .г + —
, 1 .
п xys —*■ у, х, * + -г- ,
г\
•>+ь
г) в гексагональной системе.
Плоскости ш, проходящие через начало и параллельные плоскостям
(110) xyz —+ ухг\
(120) xyz —*■ у — х, у. :;
I (210) xys—>х, х — у, -;
(010) xyz —*• х, у — х, .:;
(ПО) xyz—+ yxz.
Плоскости с, проходящие через пачало и параллельные плоскостям
(ПО) хуг—yx,z-\--\
(120) xyz—>?/ — х, у, ~+—;
II (210) :гуг—+х, х — у, ~ + \;
(010) хуг —> х, у — х, - + у ;
(110) хуг—^ ух, г-\- --.
Плоскости Ь, проходящие посредине между координатными плоскостями,
совершают те же преобразования, что и (I); плоскости п, проходящие
посредине между координатными плоскостями, совершают то ;ке
преобразования, что и (II).
В. Центр симметрии
В точке 000, — - - — и т. д.
ш di &
В точке —
xyz -> xyz.
4 4 4
1 1 I
•'?/'"* 2 *. j — У> у-

К 91 ПРЕОБРАЗОВАНИЯ, ПРОИЗВОДИМЫЕ ЭЛЕМЕНТАМИ <)У
б) Генерирование новых элементов симметрии. При помощи
таблицы, обсуждённой в предыдущем разделе, нетрудно научиться
находить аналитическим способом элементы симметрии, возникающие
как следствие некоторых исходных элементов, условно принимаемых
за основные.
Покажем это па примере.
Пространственная группа C?v = Рпа
(фиг. I, 40) (об обозначениях ниже)
задаётся следующим образом: плоскости
скольжения и отсекают отрезки \\ и 3,4
(в долях периода) по оси а п
перпендикулярны ей, а плоскости
скольжения « отсекают отрезки 1 \ и 3;4 по
оси Ь и перпендикулярны ей. Так как
каждый из этих элементов симметрии
удваивает число точек, то в
рассматриваемой группе из одной точки
возникнут 4, а именно, отражением в v
дш получим точку
(1).^/:-(2)т-Л ?/+Y'~+T'
а отражением в а обеих точек
получим точки
(3) у-Ь'', | — г/, .г, (4) .г, уу .r-f 1.
Рассматривая внимательно
совокупность этих точек, мы замечаем, что
точка (1) переходит в точку (4), а
точка (2) в точку (3) при помощи
двойной винтовой оси, параллельной
оси с и проходящей через начало
координат. В соответствии со сказанным
в разделе в) § 8, эта ось вызовет существование ещё 3-х семейств
осей 2и проходящих через середины рёбер и центр грани аЪ.
Само собой разумеется, что можно было бы принять в качестве
исходных элементов симметрии ось 21% и п, или 2t и а. Третий
элемент симметрии появится как следствие наличия двух первых.
в) Расположение элементов сим-метрии и трансляционная
группа. Предположим, что в решётке имеются параллельно
расположенные оси 2 и 2j. Пусть ось 2 проходит через ось координат
ячейки, а ось 2Х имеет координаты тип (оси параллельны оси с).
Тогда точка .njz подвергается следующим преобразованиям:
2 - - 2Y 1
(1) .г у г —* x\js —> Ъп -4- •*, 2» + у, г-\- — .
Фиг. Т. 40. Ромбическая
пространственная группа Ctv —
— Рпа (проекция на
плоскость аЪ). Имеются: 1)
винтовые оси 2i, параллельные
оси с и проходящие в начале
координат, серединах рёбер
а и Л и в центре грани ab. Это
оси 2i [001] , iii
СО; — 0; 0 — ; -- —
„ли 00,, 1.0.-. 0i,„||,:
2) плоскости скольжения а,
перпендикулярные оси и
отсекающие отрезки 1ji и 3/4 по оси
Ь. Это плоскости а (010)у ,,4
или х г/4 г и х 3/4 г. 3)диагональ-
ные плоскости скольягения н,
перпендикулярные оси а и
отсекающие • отрезки ]Д л 3/4
по оси а. Это плоскости п (100)
i/4; з/4 или 1/* У* и 3/4 у*.

100 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [о. I
При т = —, п = -^ точка хуг переходит в точку х-\- — , i/ -f- т»
я + Т ; ПРИ m = 0, w = — она переходит в х, у-\--^, ^ +у,
наконец при т = — и » = о имеем дг-f- —, #, я-Ну. Но это
означает, что указанная комбинация элементов симметрии приводит
к центрировке .объёма или грани ячейки.
Положим теперь, что в ячейке имеются две параллельные
плоскости: т, совпадающая с плоскостью ху, и а, проходящая от неё
на расстоянии 1/4 по г. Тогда точка хуг может быть подвергнута
следующему преобразованию:
т —а 1 1
хуг —> хуг —*• ж+у, у, -%-\-г.
В этом случае два указанных элемента симметрии приводят к
центрировке грани. Если бы вместо плоскости скольжения а мы взяли
плоскость скольжения п, то пришли бы к центрировке объбма.
Аналогичным способом можно показать следующее: если в решётке
имеется два параллельных семейства плоскостей или осей симметрии
таких, что эти плоскости или оси принадлежат одному и тому же
классу (т. е. их различие исчезает при стремлении периода решётки
к нулю), то ячейка такой решётки будет центрирована по объёму
или по грани.
Наличие той или иной трансляционной группы есть, таким
образом, также следствие из характера взаимного расположения
элементов симметрии решётки.
§ 10. Пространственные группы
а) Перечень пространственных групп класса С27, (фиг. 1,41).
Как было указано в конце § 8, для вывода всех пространственных
групп данного класса симметрии следует перебрать все способы
взаимного расположения элементов симметрии, получающихся
«расщеплением» макроскопических элементов симметрии класса. Класс
С & характеризуется наличием оси 2 и перпендикулярной ей
плоскости симметрии т (в точке их пересечения лежит центр
инверсий 1). Следовательно, в пространственных группах класса (72й мы
можем встретиться со следующими элементами симметрии: 1, 2, 2t,'
т и плоскостями скольжения. Поэтому мыслимы следующие
пространственные группы: 1) группа, содержащая оси 2 и плоскости т;
2) группа, содержащая оси 2Х и плоскости т; 3) группа,
содержащая оси 2 и 2„ а также плоскости т; 4) группа, содержащая оси 2
и плоскости скольжения; 5) группа, содержащая оси 2Х и
плоскости скольжения; 6) группа, содержащая оси 2, оси 2, и плоскости
скольлсения. Во всех случаях оси, естественно, перпендикулярны
плоскостям.

i О 1
0 fl 1
a\ Cjh=P2/m
a\ &-Р2,А
a\ C*,-C2/m
c£-"&
4 =P2,/c
1
l—~i
, /
&
, /
й ' *
/
*
/
4
1
b
/
4
f
4
M i * i
6 ! r-o ! о
■ с г/с
Фиг. I, 41. Пространственные группы класса C2h- (Проекции на ллоскосгь аЪ.) Кружочком обозначен центр
инверсии. Цифры 1/4 указывают координаты осей вдоль с. Двумя параллельными линиями обозначены
зеркальные плоскости, перпендикулярные плоскости чертежа.

102 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [lM. I
Кроме того, мы можем добавить к первым трём группам
плоскость скольжения, а к последним трём плоскость т. Однако все
возможности исчерпываются приведенными шестью группами.
Прибавление плоскости зеркальной симметрии к группам, уже
содержащим плоскости скольжения, приводит во всех случаях к третьей
группе. У класса С2Л существует только 6 пространственных групп.
С1ь = Р2;'т. Эта пространственная группа возникает простой
трансляцией точечной группы C2h=2!m. В решётке имеется 8 семейств
центров инверсии, 4 семейства осей 2 и два семейства плоскостей т.
Сгл = Р21 im. Решётка строится трансляцией плоскости
симметрии т вдоль оси Ъ. Оси 2Х идут вдоль оси Ь ячейки. Между
плоскостями симметрии на осях 2t возникает новый элемент
симметрии— центр инверсии.
Центры инверсии попарно связаны плоскостями симметрии, таким
образом в решётке имеется 4 семейства пар центров- инверсии.
Плоскости симметрии также связаны между собой (операцией 2г). Оси 2,
симметрически не связаны. Аналогично предыдущей группе имеется
1 семейства осей 2t.
C2h = C2;m. В этой группе мы должны разместить оси 2 и 2,,
а также плоскости т. Последние расположатся перпендикулярно
оси Ь, на расстоянии Ь 2. Оси 2 и 2г параллельны оси Ь. Если одну
из осей 2 выбрать за ребро ячейки, то другие оси 2 будут иметь
выходы в середине рёбер с и а и в середине грани ас так же, как
и в группе Со/». Оси 2Х можно разместить только посредине между
осями 2'"").
Из фиг. I, 42 видно, что расположения осей 2! вдоль диагонали ас,
п вдоль оси (а или с) ячейки приводятся друг к другу переходом
к иной системе координат и, следовательно, представляют одну и
ту же пространственную группу. Размещение oceii 2X вдоль двух
осей ячейки приведёт к генерированию новых oceii 2 и,
следовательно, к уменьшению ячейки. Уменьшенная ячейка даст опять то
же самре распределение элементов симметрии. Таким образом
в рассматриваемой группе из трех направлений двух — осей и
диагонали— только одпо состоит из чередующихся осей 2 и 21.
В ячейке возникает плоскость скольжения, проходящая между
плоскостями т. Это очевидно из следующего преобразования
координат произвольной точки хцг. Точка пересечения 2 и т есть
центр инверсии. Эта точка выбрана за начало координат. Инверсия
*) Это легко доказать от противного. Если бы оси -\ не располагались
строго посредине между осями 2, то оси 2 не переводили бы оси 2i друг
в друга, а создавали бы новые оси 2\. Эти новые оси 2] создавали бы.
в свою очередь, новые ойи 2, те, в свою очередь, новые оси 2i и так далее
до бесконечности. В результате мы пришли бы к бесконечно малым
периодам в плоскостях, перпендикулярных осям 2 и 2*. что. конечно,
бессмысленно.

§10]
ПРОСТРАНСТВЕННЫЕ ГРУППЫ
103
в ней даёт: ./•//■? -* щг. Ось 2,, которой придадим координаты
-г У 0 *) (удобство этого выбора станет ясным ниже), даёт
1 . 1
т. е. действительно имеется плоскость скольжения а, имеющая
координаты х -г z **).
Из раздела в) предыдущего параграфа ясно, что решётка
принадлежит к трансляционной группе Г' . Это значит, что в зависи-
Фиг. I, 42. Возможные случаи взаимного расположения параллельных
семейств осей 2 и 2\. а) оси 21 располагаются посредине между осями 2
вдоль одного из рёбер ячейки (например а). Размер ячейки не
уменьшается; б) оси 2i располагаются посредине между осями 2 вдоль одного
из рйбер (а) и вдоль диагонали. Возникновение новых осей приводит
к уменьшению периода вдоль с вдвое. Новая ячейка, заштрихованная на
чертеже, отвечает случаю а); в) оси 2] располагаются посредине между
осями 2 вдоль обоих ребер (а и с). Происходит уменьшение ячейки;
заштрихованная новая ячейка отвечает случаю а), если направить ось с вдоль
диагонали исходной ячейки.
мости от выбора осей ячейка центрирована по грани, проходящей
через ось Ь или по объёму. Мы выбрали координаты так, что
центрированной является грань аЬ.
*) Точки, лежащие на прямой, параллельной оси у и пересекающей
1 1
О, имеют координаты —- у 0. Поэтому
плоскость xOz в точке х =
4 '
об оси 2i мы говорим, что она имеет координаты —г- у 0. Аналогично ось
4
«11
с координатами -г-г з параллельна оси 2 и пересекает плоскость ху()
в точках х = — -, I/ = — .
4 ' 4
**) Точки, лежащие на плоскости, параллельной плоскоетм хО: и
пересекающей ось ;/ и ючко у—-- , имеют координаты х - .?, поэтому об
4 4
Этой плоскости молено указачь, что oii координаты суть х —- .?.
4

104 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
В ячейке группы С^й возникает 16 центров инверсии, но они
не образуют 16 семейств. В ячейке имеются центры симметрии
двух сортов. Это, во-первых, центры симметрии, возникающие
в точках пересечения оси 2 и зеркальной плоскости. Один из этих
центров попадает в начало координат (в этом причина указанного
выше выбора координат оси 2j). Центры симметрии этого типа
существуют в ячейке парами. Действительно, как ось 2{, так и
плоскость а переносят точку 000 только в точку у у 0. Таких
пар центров симметрии имеется ещё три. Точка 0 -0- 0 имеет лишь
1 пп п„ 1 111 /ч 1 1 1 Л
одну эквивалентную -^-00; 00 -^ w - - ти0- -у к- 0-тг •
<U U Lk Li Li Li Li Li Li
«Другие» центры симметрии находятся в точке пересечения
осей 2j и плоскости а. Подчеркнём, что эти центры симметрии
генерируются другими элементами симметрии, так что центр
симметрии может и не появиться в месте такого пересечения (в
противоположность пересечению 2 и т). Каждый из таких центров имеет
еще 3 эквивалентных центра. Тот, который находится в -г -т- О,
1 3
преобразуется плоскостью симметрии в -г - - 0. Эти два центра пере-
3 1 3 3
водятся осью 2 в точки — -■ 0 и — -г 0.
4 4 4 4
Итак, в группе Cj|h имеется 4 тождественных семейства пар
центров инверсии и 2 тождественных семейства квартетов центров
/ 1 1 1 1 '3 1
инверсии (второе семейство имеет координаты — v у ; ТТ~2 '
А -1 jL • JL A _L
4 4t 2 ' 4 4 2
C*ft —P2/c. Семейство простых двойных осей пересекается
семейством плоскостей скольжения. Возникают, как это объяснялось
выше, вставленные посредипе оси и плоскости.
Плоскости скольжения симметрически не связаны. Таким
образом существуют два семейства плоскостей с. Оси 2 оказываются
связанными попарно плоскостями скольжения. Имеем 2 семейства
пар осей второго порядка. Появление восьми центров инверсии
вызывается основными элементами симметрии. Центры инверсии
расположены на плоскостях скольжения между двойными осями.
Поэтому эти 8 точек разбиваются на 4 пары.
C\h — P2jc. При пересечении системы осей 2, плоскостями
скольжения с возникают вставные плоскости и оси. Как оси, так
и плоскости попарно связаны. Имеем поэтому одно семейство
плоскостей скольжения и два семейства осей. Если оси имеют коорди-
13 1 1 1 1
наты 0 у -£- и 0 у -4- — первая пара и у у -т- и - -у — вторая

§ 10] пространственные группы 105
пара, то один из центров симметрии попадёт в начало координат. Всего
центров симметрии 8 и они опять разбиваются на 4 семейства.
Каждая пара центров симметрии связана осью 21 или плоскостью
скольжения (обе операции совпадают). Центры инверсии находятся
посредине между осями 2Х и между плоскостями скольжения.
С®й = С2/с. Систему чередующихся осей 2 и 2, мы пересекаем
плоскостью скольжения. В отношении расположения осей уже всё
сказано при рассмотрении группы C\h. В группе C%h пересечение
двойных осей плоскостью симметрии вызвало появление плоскости
скольжения. Если мы пересечем систему осей такой плоскостью,
линия скольжения которой будет параллельна тому направлению,
в котором чередуются оси 2 и 2Х, то мы придём, разумеется,
опять к группе C%h. Здесь же мы сделаем другой выбор, а
именно примем, что линия скольжения направлена вдоль линии
одноимённых осей.
Если выбрать координаты одной из осей 2 в 0 у -т- и одной из
11
осей 2Х в - - у --, то это значит, что оси надо пересечь
плоскостью скольжения с. Пусть ее координаты будут x()z. И в этом
случае, как и в группе C|ft, между двумя плоскостями возникает новая
плоскость (с координатой — но оси у), но это уже будет не
плоскость т, а плоскость скольжения п. Что это действительно так,
видно из следующих преобразований точки xQz:
двойная ось (1) xOz _> (2) ж, у -^ z;
ось 2t (2)xy, i— z —►(3)«-f--j.y+Y'3'
плоскость с (3) .г -f- у, у + у, г -- (4) х -\- —, у — уг z -f —.
Действительно, первая и последняя (1 и 4) точки связаны плоскостью
скольжения п.
Ячейка центрирована по плоскости аЬ, что видно из того же
преобразования (первая и третья точки).
Центров инверсии в ячейке 16, так же как и в группе CJft .
Распределение их на семейства иное, а именно, имеются 4 семейства
Квартетов центров инверсии. Любой из центров инверсии
применением к нему элементов симметрии даёт ещё 3 центра. Например,
Центр инверсии, попадающий в начало координат (как видим, и здесь
выбор координат осей диктуется тем же желанием иметь в начале
координат центр инверсии), переносится элементами симметрии
в точки 00 ^ , i- 2- о и 4 » 4-- .

106 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [г.1. I
Указанные -А семейства тождественны попарно. Одна пара
квартетов переводится друг в друга сдвигом на — но оси Ь. Другая пара
переводится сдвигом на ~ по оси с. Не существует параллельного
сдвига, переводящего одно из семейств первой пары в семейство
второй.
Подобным же образом, т. е. путём всех возможных комбинаций
существующих элементов симметрии выводятся все
пространственные группы.
Как видно, пространственная группа характеризуется
совокупностью элементов симметрии, взаимное расположение которых
указано. Всевозможные характеристики кристалла (класс,
система, трансляционная труп на) определяются пространственной
группой.
Число пространственных групп равно 230. Первый вывод всех
пространственных групп был осуществлён великим русским
кристаллографом Е. С. Федоровым. В, связи с этим пространственные
группы называются также фёдоровскими группами.
Ввиду существования как правых, так и левых винтовых осей
существуют энантиоморфные пространственные группы, т. е. группы,
отличающиеся только направлением поворота вокруг винтовых осей.
Энантиоморфных групп 22 (11 «правых» и 11 «левых»).
6) Номенклатура пространственных групп. Существуют
старая и международная номенклатуры. По старой
номенклатуре символ пространственной группы иолучается путём
добавления индекса к символу соответствующего кристаллического класса.
Так, например, С°>п есть символ одной из пространственных
групп класса С2Л. Старая номенклатура не является рациональной,
ибо индекс указывает лить порядковый номер пространственной
группы данного кристаллического класса при одном из весьма
многочисленных способов вывода их. Напротив, международная
номенклатура является рациональной. Международный символ состоит
из большой латинской буквы, указывающей трансляционную группу
данной пространственной группы (Р, А, В, С, J, F) и одного,
двух или трёх числовых и буквенных символов, указывающих
симметрию главных направлений данной пространственной группы
(о символах элементов симметрии говорилось выше). Такими
направлениями являются: 1) для моноклинной системы—ось Ь; 2) для
ромбической — направление трёх взаимно перпендикуляр пых осей;
3) для тетрагональной — «главная» (тетрагональная) ось, две
другие оси, перпендикулярные к ней и друг к другу, и диагонали
между этими последними осями; 4) для гексагональной и тригональ-
ной системы — главная ось (шестого или третьего порядка) и три
другие, иорцецдикулнрныс к ней и образующие углы друг с другом
в 60'; 5) для кубической — направления [001J, [M1J н '[По). Дли

•10]
ПРОСТРАНСТВЕННЫЕ ГРУППЫ
107
хриклинной сингонии достаточно указать наличие или отсутствие
центра инверсии.
Символы, указывающие симметрию главных направлений,
пишутся рядом и не отделяются друг от друга дробной чертой, даже
если соответствующие направления взаимно перпендикулярны.
Первым пишется индекс, указывающий симметрию вдоль оси а,,
вторым — вдоль оси Ь, третьим — вдоль оси с (если все три оси являются
главными направлениями. Если главное направление одно, то пишется,
естественно, один индекс). Конечно, можно изменить наименование
осей, а следовательно, и порядок символов. Однако этого не
принято делать, когда одно ив главных направлений является особым,
т. е. единственным в своём роде (например, оси с в классе C.2v и во
всех классах тетрагональной, гексагональной иромбоэдрической син-
гопии). Если симметрия главного направления может быть
охарактеризована одним элементом симметрии, то символ, указывающий
симметрию этого направления, состоит из одной буквы или
цифры. Если же для характеристики одного элемента симметрии
недостаточно, то символ состоит из двух знаков: обычно цифра и
буква, указывающие ось и перпендикулярную ей плоскость
(например, 4:jlb).
Международный символ сразу позволяет сказать, к какому
кристаллическому классу принадлежит данная пространственная
группа. По существу символы, характеризующие симметрию главных
направлений, являются «расширенными» символами
соответствующих кристаллических классов. Международный символ однозначно
(если не говорить о различных способах наименования осей)
характеризует пространственную группу. При вдумчивом рассмотрении
символа всегда можно указать расположение элементов симметрии
в элементарной ячейке данной пространственной группы. Символы
(старые и международные) 230 пространственных групп приведены
в таблице I.VIII. Международную номенклатуру полезно пояснить
примерами.
1) Cm (Cj). Указание симметрии только одного главного
направления и определение этой симметрии только плоскостью
зеркального отражения т говорит о принадлежности пространственной
группы к классу т моноклинной системы. Ячейка центрирована
в грани С, что говорит о наличии помимо плоскости ж (010)
плоскости скользящего отражения (легко показать, что это плоскость
а (010),,). Других элементов симметрии нет.
2) lJ2Jm(C-ih)- Указание симметрии только одного главного
направления и определение её осью второго порядка говорит о
принадлежности к моноклинной системе. Указание, кроме того,
перпендикулярной плоскости говорит о принадлежности к классу 2\т.
Примитивность ячейки говорит о наличии осей второго порядка
только одного типа (только 2^) и плоскостей только одного тина (т).

108 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
Таблица I, УШ
Фёдоровские группы
Кристаллическая
система
Триклинная
Моноклинная
Ромбическая
Старый символ
с;
с\
С*
Cj
61
с\
ск
<&
ск
°к
о',
Г3
°2и
Со
Г*
Международный символ
полный
Р1
Pi
Pm
Pc
Cm
Cc
P2
P2X
C2
P2
ш
p-h
m
ol
m
с
. P2i
с
cA
с
сокращённый
PI
pi
Pm
Pc
Cm
Cc
P2
P2t
G'2
P 21 ni
P2llm
С2-т
P2/c
G2\c
Pmin
Pmc
Per,
Рта
Pea
Pnc
Pmn

§ 10] ПРОСТРАНСТВЕННЫЕ ГРУППЫ 100
Продолжение
Кристаллическая
система
Ромбическая
.
■—■—
Старый символ
3,
ol
/-.10
fill
b2v
^13
°2«
f,U
1 2v
4u
/lis
°2«
<#,
e£
/V21
eg
Dj-F1
D* = F3
D* = F3
Di-V*
Щ = F5
2>5=Гв
7); = F7
7)* = F8
d;-f9
П1 — F1
D2 — V'1
l)ih ■- > 7»
»2*=t1
Международный символ
полный
РЬа2
Pna 2t
Pnn2
Cmm2
Cmc21
Ccc2
Amm2
AbtnH
Ama2
Ahn2
Fmm2
Fdd2
Jmm2
Jbn2
J>ua2
P222
P222t
P2L2X2
P212l2l
C222t
сокращённый
РЪа
Pna
Pnn
Cmm
Cm с
См
Л mm
A hut
A ma
Aba
Fnim
mi
J mm
Jba
Jma
P222
P222x
P2A2
• P2i2t2i
C222t
C222 C222
7^222
/222
/212x2!
pill
m m m
2 2 2
n n n
2 2 2
p "
rem
J7222
J222
.71212121
Pmmm
Pnnn
Perm
...

110 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА flVI. 1
Tlpodruj/reniir
Кристаллическая
система
Ромбическая
Старый символ
/&-1
^ь»1
//■', —. I
":>.h
/>~, -■
' ih
>Ъ -
"Ь-i
<-
К =
«а =-i
"й=
»и=
*>а-
"й-
BS=
7)19 __
yy2A —
D21 -
17 2A ~
-4
h
и
it-
-i'.
/i
/7
^ A
h
A
•10
A
' A
A
1 A
'a
r15
1 A
1 A
r17
y h
A
r19
1 A
r'_>0
A
r-21
A
Мел;дународный символ
полный
|
0 0 О I
p-f--
/> a n
| )/ П fJ
! pL2.li
! /// » n
i f с а
I 2< 2i 2
h a in
! pzlrl r.
j с о к
! 2 2i 2,
It С III
1 ]> fi -t ~.
I n w ?//
■ ш in п
1 p 2i _2_ 2t
1 hen
■ 2i 2i 2i
b с а
■ Ph*ih
и hi, a
ш с ш
! m с а
.' О 9 '>
i с - - --
III 111 III
1
О о О
! с с /у/
j w, /// a
1
сокращенный
J'ban
Vmma
Pima
Рит а
Peru
pli/i/ii,
Vccv
PllClH
PVIIII)
PllUI/ll
Phcn
Phca
Tnma
С me hi
С и/г а
Смит),
С с, с m
Спина

§1<>1
IIPOCTPAHCTHF.TTHME ГРУПП Г,Г
111
Продолжение
Кристаллическая
система
Ромбическая
Старый
лй«
"£ =
»х~
л£=
"й-=
л& =
символ
If
•t
If
'■»'
'f
•т
•■г
Международный символ
полный
О 9 9
С- — -
с с а
/;- 2 2 2
Ш Ш W
9 9 9
f/ д Л
9 9 9
.7 ~ — ~
9 9 9
b a m
b с а
j Ъ h h
m ш а
сокращённый
Coca
l-'onnm
Fddd
Jmm in.
Jbmii.
Jhca
.J чипа
Тетрагональная
Л'!
C\
G\
C\
c]
p.\
C\n
a;
U i.
c':,
Г4
./4
74
14±
?h
.71
pi
pi
p
J±
a
14
.74
P4
*4i
P4o
Р4:.
/4
J4t
I»4/m
P42;w*
7М/Д-
I>4..;»i
.74/ m
.74,/"

112 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
Продолжение
Кристаллическая
система
Тетрагональная
Старый символ
Dld=yd
Ad-Vd
Г)3 _ тгЗ
uld — y d
7)* _ XT*
■'-'ad— Kd
7)5 _ T/r>
4d=K
Dld=n
7)8 _ T-R
u2d — ' d
1 jf — г0
l,'ld ~ ' d
TvlO I/10
D2d = Vd
I 7)11 _ T-ll
^2 «J — ' d
1 "2d — ' d
i ,,1
! °4г>
1 Civ
| °4t>
°4v
| C4v
U4t;
С4и
Ъ
/ч10
°4t;
Г11
Dl
Hi
л}
D\
Международный символ
полный
1Ч2т
Р~42с
P42im
P42ic
C42m
(742c
C42&
C42«
F42w
F42c
^42»i
J42fZ
P4mm
Pibm
Р4ъап
P4<>nm
P4ec
P4nc
P4*me
P42bc
JAmm
J4cm
J4tfnd
J4xcd
P422
P42t2
P4t22
P4t2i2
сокращённый
P42w
P42c
P~42\m
P42xc
C42m
C42c
G42b
C42n
F42m.
F42c
J~42m
J42d
P4mm
P4bm
P4cm
P4nm
P4cc
P4nc
P42w»c
P42bc
J4mm
J4cm
J4\md
J4cd
P42
P42i
P4t2
PWi

10]
ПРОСТРАНСТВЕННЫЕ ГРУППЫ
113
Продолжение
Кристаллическая
система
Старый символ
Тетрагональная
л;
D\n
D
В
Г/
nih
[>Ш
D't
ih
I)
4h
D
lh
ЫО
Международный символ
полный
P4222
P4322
P432!2
У422
/4222
m m tn
4 2 2
pZ_
m <■' с
± о »>
P±y-~
и о т
„ 4 2 2
Р-71--
т о т
i. 2i 1
ш п с
Л г.1 1
Р
Р
пес
4>> 2 ->
р 1* — л
42_2 _2
п b с
П 11 Ш
422t_2
т. Ь с
сокращённый
P4V2
Р422х
Р432
Р432!
.742
Ji{2
Р4, пинт
Pi-тсс
P±}ibm
Pi'tmc
Pi'mbm
Pij тис
P\\nmm
Piincc
Pijmi/w
P4 in cm
Pi/nbc
Pi/nnui,
Pijmbc
Pljhwut

114 КРИСТАЛЛОГРАФ. ОСНОВЫ СГРУКТУРНОГО АНАЛИЗА [гл. I
lip одолжение
Кристаллическая
система
1
Тетрагональная
Гексагональная
Старый символ
1Jih
К
Dg
Л18
JJ4h
Я19
JJih
<>{
<-l
cl
ci
°f
CS(
4
(•6v
Gtv
Ctv
G-AV
4
p,
*,
4
D\
«5
Dl
Международный символ
полный
p hh -.
n m с
■n с т
m m m
сокращённый
P4/W«e
P4 не»*
.74 mmm
4 2 2 i
J '. ,74-1 mem
m с j»
4, *> '> '
/ — — -^ J4iamd
о »>, d
J *1 - --
а с d
C3
C*
JAijacd
сг
C6X
C-h \ C32
tftf j 7?3
C3
R'S
C'iml
mmi
6'3cl
Л3с1
/?3w
H3c
Я321
03
№
C3m
mm
СЪс
IfSr
R3rn
№c
//32
C321 j C32
mgi
C3i21
#3221
C3?21
Я32
//3i2
C3i2
Я322
C322
i?32

§10]
ПРОСТРАНСТВЕННЫЕ ГРУППЫ
115
Продолжение
Кристаллическая
система
Гексагональная
'
Старый символ
Я«
Dla
Via
»м
i)6
1JAd
ol»
cl
ol
o\
ci
ci
Of:
CGh
D\n
»ln
J,3h
u'Ah
Glv
C2
C»
»l
*
Международный символ
полный
#3 — 1
m
ЛЗ-1
с
C-6- I
■m
C-A -=-1
ДЗ-
- 2
ЯЗ —
с
(.6
C6
C6t
сокращённы
iyaiwi //3w*
язс1 тс
G'A:n\ СЗ/w.
C3fl C3c
/Юм*
#3e
c»;
C6
Он
C65 С65
C62 ! C«2
C64 , <?64
C6.$ • r»«3
m
1'6*«2
C6/m
C(>; JM
C6///2
C6c2 '. Cb>2
7/6w2 №*2
//f;«2 /Л^З
СЬшм Cfimm
Свес ' C'6<v
1
1
C6timc С time
i C622
1 C6,23
C62
a\{2

116 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [гл. I
Продолжение
Кристаллическая
система
Гексагональная
Кубическая
Старый символ
»t
D\
Dl
Dl,h
D\h
Dtn
23
7,2
n
n
n
Международный символ
полный
C6522
C6222
C6422
C6a22
m tn m
C~- -
m с с
m с in
G^ 1 i
m m с
P23
F23
J23
P2,3
J2t3
pi»
F-3
m
FP
m
2i
P^3
a
PA'Am
сокращённый
C652
C622
C642
C632
CQImmm
C6jmcc
C&lmcm
CQimmc
P23
F23
J23
P2t3
• J2i3
P«3
Pn3
Fm3
Fd3
Jm&
PaS
Ja'i
PiSm

§10] ПРОСТРАНСТВЕННЫЕ ГРУППЫ 117
Продолжение
Кристаллическая
система
Кубическая
Старый символ
ш2
d
rpb i
d !
7'-* !
1d i
mb \
/ji6
d !
О1 1
О2 j
03
1
0. ;
О'
1
О6 j
07
08
oi :
1
°i i
OS
o4
* !
1 ol \
\ \
■
■
ol
°l i
i
<* !
ol°
1
Международный символ
полный
FiSm
J43m
PiZn
FiSc
Ji3d
P432
Р4г32
F432
F4i32
/432
сокращённый
F43wi
J43w
P48w
F43c
J43d
P43
P423
F43
FitS
J43
P4332 1 Р4зЗ
Р4х32 | P4,3
74i32 Mx3
P -3— P»»3»t
m m
P—3 — : РпЗи
n n
4<>-2
P-^3 —
m n
n m
те »»
»i С
a m
РжЗп
РпЗм
Fm3m
FmZc
FdBm
F^d- W3c
a c '
m m
JmZni
Дз1 | JaU
a a \

118 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА ]ГЛ. I
3) P222t{V2). Указание симметрии трёх главных направлений
и притом симметрии осей второго порядка говорит о
принадлежности пространственной группы к классу 222 ромбической син-
гонии. Примитивность ячейки говорит о наличии в каждом из
трёх главных направлений только одного типа осей второго
порядка: вдоль осей а и b идут только оси 2, вдоль оси с—
только оси 2V
4) Jmm2 (С^). Указание симметрии трех главных
направлений и среди них двух плоскостей и оси второго порядка говорит
о принадлежности к классу 2тт ромбической системы.
Перпендикулярно осям а и Ь идут плоскости т, вдоль оси с — ось 2.
Центрировка в объеме говорит о наличии по крайней мере ещё одного
семейства плоскостей (осей) симметрии. Легко видеть, что это
семейство w(100)i_, или /г (010)i, или 2j(001) ц. В действитель-
4 Т IT
ности все три семейства элементов связаны указанными в
символе элементами т, т и 2 и потому обязательно существуют
вместе.
Для вывода всех существующих в этой пространственной группе
элементов симметрии достаточно записать её символ в виде Jmm.
Это так называемый сокращённый символ. Эти символы, наряду
с полными, приведены в таблице I, VIII.
4 - 2
5) F — 3 — (0J). Ячейка всесторонне центрирована. Вдоль
направления [100] идёт ось 4, а перпендикулярно ему зеркалвная
плоскость. Вдоль направления [111] идёт ось 3, вдоль
направления [ПО].—ось 2, а перпендикулярно ему плоскость
скольжения с. Центрировка ячейки указывает на наличие и других
элементов симметрии, не упомянутых в символе.
Рассмотрим ещё, как преобразуется символ пространственной
группы при изменении наименования осей. Возьмём
пространственную группу РЬса. Произведём круговую перестановку: х' — у;
y' = z; z' =<я. Символы плоскостей преобразуются следующим
образом: Ь (100)-+ а' (001); с (010)-»?/ (100); а (001)~>с' (010).
Символ примет вид РЬса. Итак, при круговой перестановке символ
не изменился. Взаимно переменим теперь наименования осей х и
z\ ж' —г; z' = x; у' = у. Символы плоскостей преобразуются
следующим образом:
&(100)-> &'(001); с (010) ->а' (010); а (001)-► с' (100).
Символ примет вид Pcab. Рассмотрим, что произойдёт с символом
пространственной группы с непримитивной трансляционной
группой (центрировка в паре или во всех гранях) при круговой
перестановке осей. Возьмём группу Ссса. Изменим названия осей
x'z=y; y' = z; z' = x; с (100) -+ Ь' (001); с (010) -+ Ь' (100);

§10]
ПРОСТРАНСТВЕННЫЕ ГРУППЫ
119
-а(001)->с' (010). Грань ab имеет теперь символ са, т. е.
центрировка С в новых осях является центрировкой В. Итак, новый
«имвол таков: Bbcb. Эти примеры показывают, в чём заключается
единственный недостаток международного символа: при изменении
наименования осей в общем случае изменяется вид символа
пространственной группы.
в) Положения точек. Про точку ячейки, не лежащую на каком-
либо закрытом элементе симметрии, говорят, что она находится в
общем положении. Все элементы симметрии решётки деятельны по
отношению к такой точке, т. е. образуют из неё эквивалентные точки
и не переводят её самоё в себя. Понятно, что такая точка, вообще
говоря, может лежать на винтовой оси или на плоскости
скольжения, так как эти элементы симметрии производят преобразование
и в этом случае (в данном случае преобразование сводится,
очевидно, к трансляции на долю периода вдоль оси).
Если применением всех элементов симметрии пространственной
группы из одпой точки, находящейся в общем положении,
возникает ещё п — 1 точка, то п называется кратностью общего
положения. Минимальная кратность общего положения равна 1 в группе
без элементов симметрии; максимальная равна 192 в некоторых
группах кубической системы.
Если точка лежит на каком-либо элементе симметрии, то такое
положение называется частным. Кратность частного положения,
разумеется, в целое число раз меньше кратности общего положения.
Например, в только что рассмотренной группе dh имеется
восьмикратное общее положение и 4 четырёхкратных частных положения.
В группе Gift имеется четырёхкратное общее положение и
4 двукратных частных положения. Частное положение кроме
-своей кратности должно быть охарактеризовано элементом
симметрии, на котором находится точка. Так, в группе Cf*
все частные положения одного типа — точка занимает центр
инверсии. В группе C\h имеются 4 частных положения, в которых точка
занимает центр симметрии и одно частное положение, в котором
точка лежит на оси 2.
В связи с этим мы .можем различать частные положения с двумя,
с одной и без степеней свободы. Точка, лежащая на плоскости
зеркальной симметрии, обладает двумя степенями свободы, так как
это частное положение осуществляется, вообще говоря, в любом
месте плоскости. Точка, лежащая на поворотной оси, обладает
одной степенью свободы и, наконец, точка, лежащая в центре
инверсии, в месте пересечения осей, оси и плоскости или в особой
точке инверсионной оси, не обладает степенями свободы. Выбор
частного положения в последнем случае полностью определяет
координаты точки, в случае оси остаётся неопределённой одна, а
£ случае плоскости —две координаты (параметра).

120 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. 1
Следует подчеркнуть во избежание недоразумении, что группа
обладает конечным числом частных положений без степеней
свободы. Что же касается частных положений с одним или двумя
параметрами, то их в решётке имеется, строго говоря,
бесчисленное множество, так как параметру могут быть приданы любые
значения.
Мы всё же будем говорить (это общепринято), что в решётке
имеется одно или несколько частных положений со- степенями
свободы, если речь идёт об одном или нескольких семействах
элементов симметрии.
Частные положения симметрически не связаны между собой*
Поэтому, если речь идёт о заполнении решётки атомами, то
частные положения одинаковой симметрии и кратности могут быть,
вообще говоря, заселены разными частицами, а часть из них может
остаться незаполненной.
г) Симметрия и число возможных островов. Рассматривая
симметрическую структуру пространственной группы, мы без труда
определяем число, симметрию и расположение островов,
существование которых будет возможно в данной пространственной группе.
В обсуждавшейся выше пространственной группе С|й из
макроскопических элементов симметрии имеется только центр инверсии.
Следовательно, в решётке с этой пространственной группой могут
быть расположены острова 1 (без симметрии) и 1. Центр острова 1
попадает в положение центра инверсии. В группе С1н, кроме
центров инверсии, в ячейке имеются оси второго порядка. Острова
1,1 и 2 могут быть размещены в решётке с этой пространственной
группой.
Про точку, в которую может быть помещён центр острова (или
плоскость, или ось острова) говорят, что она обладает симметрией
острова. Таким образом про. точку 000 в группе Cth можно
сказать, что она обладает симметрией Г; про точку 000 в группе
Сал можно сказать, что она обладает симметрией 2,'т. Про все
точки, лежащие на двойной оси, мы говорим в этом смысле, что-
они обладают симметрией 2.
Точки любого частного положения обладают симметрией выше
тривиальной (1). Кратность положения, обладающего той или иной
симметрией, показывает, сколько островов того или иного типа может
разместиться в решётке. Как мы уже говорили, в группе С\ь
имеются 4 частных положения, в которых точка занимает центр
инверсии, и 1 частное положение для точек, лежащих на оси 2.
Соответственно с этим, в ячейке группы С\н могут быть размещены 16-
островов симметрии Г. Кратность 4 положений с центром
симметрии разрешает группировать эти острова по четыре. Таким
образом острова с центром симметрии могут быть четырёх сортов.

§ 1] ОПЫТНЫЕ ЗАКОНЫ КРИСТАЛЛОГРАФИИ 121
При заполнении решётки веществом совершенно не обязательно-
занимать все четырёхкратные частные положения. Поэтому в
решётке могут существовать 4 симметрически связанных острова
1 (три положения не заняты), 4 острова сорта а и 4 острова,
сорта б (два положения не заняты) и т. д.
Независимо от наличия островов 1 в этой решётке могут
существовать острова типа 2 (также по 4 эквивалентных) и
несимметричные острова (по 8 эквивалентных).
Таким образом в ячейке решётки группы С\ь можно в
принципе разместить любое число по 8 одинаковых островов 1, любое
число по 4 одинаковых острова 2 и 4 группы по 4 одинаковых
острова 1. Возможна, разумеется, любая комбинация, являющаяся
частным случаем данной. Например, 4 острова 1 и 8 островов 1
или 4 острова 2, 4 острова 1 и 16 островов 1 и т. д.
Этих замечаний должно быть достаточно для составления списка
возможных островов для любой пространственной группы.
Т) Подгруппы. Если у пространственной группы вычесть какой-
либо элемент симметрии, притом так, чтобы он не генерировался
вновь оставшимися, то полученная группа будет называться
подгруппой данной группы.
Так, например, подгруппами C\h являются группы: С|!=С2
(отняты плоскости симметрии), (*-=Сс (отняты оси симметрии),.
Ct = Pl (оставлен один лишь центр инверсии). Тривиальной
подгруппой является СХ = Р\, т. е. группа без элементов симметрии.
Б. ЭЛЕМЕНТЫ ГЕОМЕТРИЧЕСКОЙ КРИСТАЛЛОГРАФИИ
§ 1. Опытные законы кристаллографии
В результате многолетнего изучения внешних форм кристаллов удалось
установить ряд опытных законов, которые, однако, оставались чисто
феноменологическими до появления теории пространственной решётки. После
Появления этой теории и подтверждения её рентгеновскими
исследованиями опытные законы геометрической кристаллографии получили вполне
естественное объяснение.
Прежде чем перейти к этим законам и их теоретическому обоснова-
"нию, необходимо остановиться на различии между идеальными и
реальными кристаллами. Идеальные кристаллы представляют собой твёрдые
Тела, построенные из материальных частиц (атомов, молекул, ионов) с
абсолютной правильностью согласно теории пространственной решётки^
Реальные кристаллы, встречающиеся в природе или получаемые
искусственно, отличны от кристаллов, построенных по законам идеальной
пространственной решётки. Неизбежные в реальных условиях малые
деформации приводят к искажению внешней формы и внутренней структуры
реального кристалла; к аналогичным последствиям приводят
неправильности роста. В подавляющем большинстве случаев кристалл обладает
Мозаичной структурой, т. е. состоит из субмикроскопических блоков».

122 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
построенных весьма совершенно («осколков» идеального кристалла), но
несколько дезориентированных друг относительно друга (см. стр. 262).
Законы геометрической кристаллографии, установленные опытным
путём на основании изучения реальных кристаллов, являются известной
идеализацией опытных фактов и вполне строго выполнялись бы только
в случае идеальных кристаллов. Реальные кристаллы несколько
уклоняются от этих законов, причём это уклонение является мерой
несовершенства данного реального кристалла.
а) Закон плоскогранности и пряморёберности кристаллов. Грани
нормально образованных кристаллов суть плоскости, а рёбра —прямые-
линии. Этот закон является очевидным следствием того факта, что
кристалл можно рассматривать как правильное расположение строящих его
материальных частиц по узловым плоскостям и;А прямым, образующим
параллельные семейства. Грань кристалла является граничной узловой
плоскостью, ребро — граничной узловой прямой. Встречаются отступления
от этого закона — кристаллы с искривлёнными гранями и рёбрами —
вызванные деформациями, несовершенством кристаллообразования.
б) Закон постоянства углов кристаллов. У различных кристаллов
одного и того же вещества величина и форма граней, их взаимное расето-
Фиг. I, 43. Кристаллы кварца; несмотря на большое разнообразие внешних
форм кристаллов, углы между соответственными гранями постоянны.
Например, углы между гранями призмы равны 120:'.
яние и даже их число могут изменяться, но углы между
соответственными гранями и рёбрами остаются при этом постоянными.
Прекрасной иллюстрацией этого закона являются, например, кристаллы
кварца (фиг. I, 43). Кристалл, вообще говоря, может ограняться узловыми
плоскостями различных семейств. Поэтому число граней может быть
различным. Расстояние между гранями, их величина и форма определяются
в значительной степени ростом кристалла (размер кристалла, скорости
роста разных граней и т. п.). Постоянными характеристиками кристаллов
данного вещества (вернее его определённой модификации, существующей
при данных термодинамических условиях) являются углы между
соответственными гранями и рёбрами. С точки зрения теории решётки, это углы
между соответствующими узловыми плоскостями и прямыми. Так как
опытом установлено, что кристаллам каждого вещества отвечает своя
решётка, то эти углы должны быть постоянными у всех кристаллов
данного вещества.
В силу анизотропии теплового расширения кристаллов этот закон,
строго говоря, выполняется для разных кристаллических индивидов лишь
при одинаковой температуре.
Незначительные отступления (порядка нескольких минут) от этого
-закона также объясняются несовершенством реальных кристаллов.

§1]
ОПЫТНЫЕ -ЧАКОНЫ КРИСТАЛЛОГРАФИИ
123
в) Закон рациональности отношений осевых отрезков. Выберем три
ребра кристалла О А, ОБ и ОС за координатные оси (фиг. I, 44). Одну из
граней abc, пересекающую все три оси, назовём единичной, а отсекаемые
ею по осям отрезки Оя, ОЬ, Ос назовём осевыми единицами и примем
за единицы измерении длин но соответствующим осям. Существенной
характеристикой кристалла является отношение осевых единиц. Оно,
очевидно, равно обратному отношению косинусов углов, образуемых нормально
111
к единичной грани с кооординатными осями а:Ь:с== : -: •
^ ^ cos a cos р cos у
Величину b обычно принимают равной единице. Возьмём любую другую грань
а'Ь'с', отсекающую осевые отрезки
Оа', ОЬ' и Ог'. Закон рациональности
отношений осевых отрезков
утверждает, что осевые отрезки любой грани,
измеренные в соответствующих осевых
единицах, являются рациональными
числами, и, следовательно, их
отношение можно представить как отношение
целых чисел
Оа/ . ОЬ'_ щ Ос^_
~0~а '• ОЬ '' Ъ»
■ p:q:r,
(1,56)
где /j, q, r—целые числа. Величины
р, q. r иногда называют параметрами
грани. Кристаллографическими
индексами грани называют величины ft, fc, I,
обратные параметрам р, q, r:
h : к
1 = 1:
Р
_ Оа_
~ Оа'
2L-9L
ОЬ''' Ос'
ЯК/'-пГ/- (1.57)
Фиг. ]
ности
44. К закону рациональ-
отношений осевых
отрезков.
Отношение h:k:l есть также
отношение трёх целых чисел. Совокупность
трёх индексов грани называют её
символом. Поэтому этот закон называют
также'законом рациональности символов. Символ грани обычно записывают
в круглых скобках: (Ш). Поскольку Оа = Ar/cos а, Оа' = iV'/cos а', можно
написать
со? <*' cos {3' . cos y'
h:k:l^
cos а ' cos p" ' cos y
(1,58)
где N и Nr — величины нормалей к единичной и любой другой грани, а а
р\ y и а.', $', Y — углы, образуемые ими с осями координат. Символ
единичной грани, очевидно, всегда будет (111). Грань, параллельная одной из
осей (например, а), имеет символ ((Ш); грань, параллельная двум осям
(а и Ъ), имеет символ (00Z). Выбор единичной грани определяется
условиями, различными для разных кристаллических систем:
триклинная — единичная грань отсекает произвольные отрезки по всем
трём осям;
моноклинная — единичная грань отсекает произвольные отрезки по всем
трём осям;
ромбическая — единичная грань отсекает произвольные отрезки по всем
трём осям;

124 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
тетрагональная — единичная грань отсекает равные отрезки по осям а и Ь
и произвольный по оси с;
гексагональная — единичная грань отсекает равные отрезки по осям а и &
и произвольный по оси с (гексагональная установка),-
кубическая — единичная грань отсекает равные отрезки по всем трём
осям.
В ряде случаев изучаемый кристалл не имеет грани, пересекающей
все три оси (или если она и есть, то эта грань не удовлетворяет
вышеизложенным правилам). В таком случае достаточно взять пару граней,
пересекающих все три оси попарно. Например, грань 1 пересекает оси
а и Ъ, грань 2 — оси Ъ н с. Этим граням приписываются символы (110)
и (011). Всякая другая грань получит два неполных символа (hkl) и
(?fc7); положив к — к', найдём и в этом случае полный символ (hk'l).
Отношение осевых отрезков можно найти и в этом случае: сперва находим
по (110) «:1, затем по (ОН) 1:с и, следовательно, «:1:с. Если имеется
лишь одна зона граней (другие плохо выражены), параллельная
координатной оси, достаточно одной «единичной» грани типа (110).
Выбор единичной грани по указанным правилам является
однозначным только в случае кристаллов кубической системы. Критерием
правильности выбора единичной грани (при соблюдении указанных правил)
будет простота получаемых символов (индексы не превосходят 6 — 8).
Если получаемые символы сложны, следует выбрать, соблюдая правила,
другую единичную грань.
Теория пространственной решётки даёт простое объяснение этого
закона. Рассмотрим для простоты двумерную решётку (плоскую сетку).
Пусть единичная грань совпадает
»i по направлению с узловой прямой,
J проходящей через второй узел по
0 «в о о оси а и первый по оси Ь (фиг. I, 45).
Определим отношения параметров
0 0 0 о 0 Двух других граней 1 и 2:
2 2
2) Р : q = -g
= 3:4,
Единичная грань
Фиг. I, 45. Двумерная решётка.
а их символы (21) и (43).
Легко видеть, что так как
грани кристалла параллельны узловым
плоскостям, то параметры и индексы
должны быть рациональными
числами. Действительно, отрезок,
отсекаемый узловой плоскостью по
данной оси, есть целое кратное параметра решётки по этой оси, являющегося
специфичной для данного кристалла единицей длины.
В § 1 (стр, 15) индексы узловой плоскости были определены как числа,
обратные долям периодов, отсекаемым по выбранным осям первой от начала
координат плоскостью семейства. Таким образом определение индексов
узловой плоскости аналогично определению индексов грани. Отличие
состоит в том, что в первом случае за единицу длины берётся период по
соответствующей оси, а во втором — отрезок, отсекаемый гранью,
выбранной за единичную. Если бы за единичную грань всегда можно было
выбрать грань, параллельную узловой плоскости (111), то символы граней
и параллельных им узловых плоскостей совпадали бы. Однако в
действительности это бывает не всегда (за исключением кристаллов кубической

§1]
ОПЫТНЫЕ ЗАКОНЫ КРИСТАЛЛОГРАФИИ
125
системы). Всё сказанное о рациональности отношений осевых отрезков
граней относится и к рёбрам кристалла. В этом случае под осевыми
отрезками понимают отрезки, отсекаемые на осях перпендикулярами,
спущенными из любой точки ребра.
г) Закон зон. Всякая плоскость, параллельная каким-либо двум
возможным или действительным рёбрам. кристалла, есть возможная грань
кристалла. Всякая прямая, параллельная линии пересечения двух воз-
ложных или действительных граней* кристалла, есть возможное его ребро.
Возможными гранью или ребром кристалла называют такие грань или
ребро, которые не присутствуют на данном кристалле, но могут
встретиться на других кристаллах данного вещества. Объяснение этого закона
таково. Линия пересечения двух граней есть узловая прямая, т. е.
потенциальное ребро; плоскость, проходящая через два ребра, есть узловая
плоскость, т. е. потенциальная грань. Поскольку плоскость симметрии
•совпадает по направлению с узловой плоскостью или перпендикулярна
к узловой прямой, а новоротная ось симметрии (кроме 1) совпадает с
узловой прямой и нормалью к узловой плоскости, всякая плоскость симметрии
лараллельна возможной грани, а всякая ось симметрии параллельна
возможному ребру кристалла.
Ценность закона состоит в том, что он позволяет, зная четыре грани
или четыре ребра кристалла (из которых никакие три не пересекаются
в параллельных рёбрах, соответственно гранях) вывести все возможные
грани или рёбра кристалла. Для этого применяют правило зональности
и стереографическую проекцию. Подробнее об этом будет сказано при
описании обработки гониометрических измерений.
д) Закон развития форм. Закон развития форм утверждает, что обычно
на кристаллах развиваются грани с простыми символами (индексы редко
превышают 6 и никогда 10). Этот закон позволяет если не предсказать,
какие грани будут встречаться у данного кристалла, то по крайней мере
почти наверняка сказать, какие грани встречаться не будут.
Закон развития форм легко понять на основании теории решётки и
простых энергетических соображений. Чем плотнее данная узловая
плоскость, т. е. чем гуще она усажена частицами, строящими крцсталл, тем
больше её стабильность и, следовательно, вероятность появления.
Наоборот, чем плотнее узловые плоскости данного семейства, тем больше
расстояние между ними *), т. е. тем слабее силы притяжения между
частицами, находящимися в отдельных узловых плоскостях данного семейства.
Естественно, что в процессе роста стремление к минимуму
поверхностной энергии требует, чтобы кристалл огранялся наиболее
стабильными, т. е. наиболее плотными сетками. Наоборот, при механическом
воздействии кристалл будет колоться параллельно сеткам, которые-слабее
других связаны друг с другом, т. е. расстояния между которыми
наиболее велики.
Из формул межплоскостных расстояний (формула I, 17 и таблица I, V)
•следует, что чем проще символ узловой плоскости грани, тем больше
межплоскостное расстояние и тем плотнее сетка. Следовательно, как при
росте, так и при разломе кристаллов преимущественно должны возникать
грани с простыми символами, соответствующие плотным сеткам.
е) Закон симметрии. Фактически этот закон является простым
перечислением тех элементов симметрии, которые могут встречаться у
кристаллов. Для кристаллов возможны лишь одинарные, двойные, тройные,
*) Действительно, объём элементарной ячейки V = S^i - йш, где S^j—
площадь элементарной ячейки узловой плоскости, а <2Л^ —
межплоскостное расстояние данного семейства (hkJ).
„ a const.
Поэтому 8Ш = -j— .

126 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
четверные и шестерные поворотные и инверсионные оси симметрии. Как
уже говорилось, принцип пространственной решётки запрещает другие
элементы симметрии (см. стр. 42).
ж) Закон однородности и анизотропности кристаллов. Все кристаллы
являются однородными телами, что является результатом правильного
периодического строения их. Кристаллы анизотропны, т. е. векторные
свойства их (теплопроводность, коэффициент теплового расширения,
коэффициент преломления и т. и.) зависят от направления. Исключением в
отношении некоторых векторных свойств являются только кубические
кристаллы.
§ 2. Внешний облик кристаллов и простые формы
Внешний облик кристалла определяется двум^я обстоятельствами:
внутренним строением данного кристаллического вещества и внешними
условиями, в которых протекал рост данного кристалла. Первое
определяет возможные и наиболее вероятные грани кристалла и углы между
ними. Второе— определяет образование вполне конкретных граней из
числа возможных, их размеры и форму, так
же как и размеры и форму всего кристалла
в целом *).
Весьма большое значение имеет скорость
роста граней, определяемая как структурой
самого кристалла (внутренний фактор), так и
растворителем, температурой, концентрацией
(внешние факторы). Пусть грани Л, В и С
возможны с точки зрения закона развития форм,
но имеют разные екорости роста. Рост кристалла
можно представлять как наслоение узловых
плоскостей: каждая грань растёт параллельно
себе самой. Тогда из построения фиг. 1,46
очевидно, что наиболее развчтыми окажутся
наименее быстро растущие грани. Быстро
растущие грани могут быть даже совсем «поглощены»»
если кристалл растёт достаточно долго.
Условия роста кристаллов могут привести к
неодинаковому развитию соответственных граней
разных кристаллов одного и того же вещества,
к отсутствию некоторых граней на одном и присутствию их на другом
кристалле. Тем самым реальная форма кристалла не всегда додает
очевидной его симметрию. Строго говоря, внешняя симметрия кристаллов
проявляется лишь в угловых величинах. Именно поэтому геометрическая
кристаллография характеризует кристаллы угловыми константами. Для
выявления симметрии кристаллов данного вещества необходимо построить
их идеальную форму роста. Идеальной формой роста называют ту форму,
которую кристалл получил бы при равномерном развитии всех его граней.
Идеальную форму находят с помощью сферической проекции, которая
строится на основании гониометрических измерений. Для этого проводят
плоскости, касательные к шару проекции во всех точках — полюсах
граней (о сферической проекции сказано ниже). Полученный
многогранник и представляет собой идеальную форму роста. Конечно, уже сами
гониометрические измерения позволяют сделать вывод о симметрии идеаль-
Фиг. I, 46. Изменение
внешнего облика
кристалла в процессе роста;
Va* vb и ^ —
скорости роста граней
Л, В, С.
*) Здесь же следует отметить, что форма кристалла отчасти
определяется и его внутренним строением. Кристалл обычно имеет
наибольшие линейные размеры в направлении наиболее частого повторения слоев
частиц, в большинстве случаев совпадающем с минимальной трансляцией.

§ 2] ВНЕШНИЙ ОБЛИК КРИСТАЛЛОВ И ПРОСТЫЕ ФОРМЫ 121'
ной формы роста кристалла. Поэтому фактически её построение обычно
не производится. Идеальная форма соответствует одной из реально
возможных форм.
Однако идеальная форма роста не всегда правильно характеризует
симметрию кристалла. Например, кристаллу, имеющему форму
прямоугольного параллелепипеда, соответствует в качестве идеальной формы
куб. Однако этот кристалл может относиться не к кубической, а к
тетрагональной и даже к ромбической сингонии. В таких случаях на помощь
приходит рентгеновское исследование. Весьма часто результаты
гониометрических измерений завышают симметрию кристалла на центр
симметрии. Это имеет место по той причине, что появление граней (fikl)
и (hkl) равновероятно с точки зрения закона развития форм, так как они
параллельны узловым плоскостям одного и того же семейства. Поэтому
появление таких «пинакоидальных» нар граней происходит довольно часто,
даже если кристалл и не обладает центром симметрии.
Идеальные формы роста кристаллов относятся по своей симметрии
к одной из 32-х точечных групп симметрии, ибо внешняя форма кристалла
может обладать лишь закрытыми элементами симметрии и притом только
теми, которые разрешены принципом решётки (так как внешняя форма
есть лишь «оболочка» решётки). Поэтому эти точечные группы симметрии
называют иногда группами симметрии идеальны? форм роста, а
кристаллы по их внешней симметрии относят к одному из 32
кристаллических классов.
Простые формы и их комбинации. Простой формой
называют многогранник, вес грани которого выводятся из одной данной
комбинации элементов симметрии этого многогранника. Если, например,
кристалл обладает осью симметрии 4, то он будет иметь по четыре
соответственных грани, выводимых друг из друга этой осью и образующих
в совокупности простую форму.
Если исходная грань взята в общем положении, то выводимая из неё
простая форма называется общей. Если же она взята в частном положении
(параллельно или перпендикулярно элементу симметрии или сечёт
симметрично связанные элементы симметрии под равными углами), то
выводимая простая форма называется частной. Одна и та лее простая форма
может быть общей для одного класса симметрии и частной для другого
более богатого элементами симметрии.
Если простая форма образует замкнутый многогранник, она
называется закрытой; простая форма, не замыкающая пространства,
называется открытой.
Энантиоморфные простые формы выводятся друг из друга отражением
(например, левый и правый нентагонтритетраэдры). Поэтому они могут
встречаться лишь в тех классах симметрии, которые не содержат
элементов симметрии с отражением (т. е. центра и плоскости симметрии и
инверсионных осей). Из самого определения простой формы следует, что
все её грани кристаллографически и физически равны друг другу (равная
скорость роста в равных условиях, одинаковый наклон относительно
осей и т. и.). Однако в силу неравноморностей условий роста они могут
различаться геометрически, т. е. ч размером и формой. Кристалл редко-
бывает ограничен одной простой формой; чаще встречаются сочетания
нескольких простых форм или, как говорят, комбинации. Открытые
простые формы, очевидно, могут встречаться только в комбинациях. Простых
форм существует 47 (из них 15 принадлежат только кристаллам
кубической системы), комбинаций простых форм огромное число. На фиг. I, 47
<стр. 134) приведены некоторые комбинации простых форм.
В таблице 1, IX указаны названия всех простых форм, даны их
•изображения и перечислены кристаллические классы, в которых каждая.
из них может встречаться.

КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
Т абл и ца
Простые
Простые формы низших
•
Вид сечения
Пирамиды
Дипирамиды
1
моноэдр
1, 2, т, 2т, 4, 4»<,
3, Зт, 6т
•4>
ромб
ромбическая
пирамида
2»»
ромбическая
дипирамида
ттт
тригон
(правильный
треугольник)
*
А
тригональная
пирамида
3, Зш
0
тригональная
дипирамида
32, 6, 62 т
1
диэдр
2, т, 2т
\
дитригон
ж
дитригональная
пирамида
дитригональная
дипирамида
Зт, 62»»

8 2]
ВНЕШНИЙ ОБЛИК КРИСТАЛЛОВ И ПРОСТЫЕ ФОРМЫ
129
I, IX
формы
и средних спетом
1
■й-
1
тетрагон
(квадрат)
тетрагональиия
j пирамида
4, 4»»
- тетрагональная
дипирамида
42, 4!т, ijmmnt,
42»»
*
С-,'
CZJ
инпакоид
1, 2, т, 2\т, 22, 2т,
ттт, 42, 4/wt,
А,ттт, 4, 42м, 32,
3, Зм», 6, 62м», G2,
6/;», Gjmmm
-ф-
i
дитетрагон
*
А
д тетрагональная
пирамида
4м»
i
1 днтетрагональная
1 дипирамида
4! ттт
1
1
i
1
■# !
гексагон
(правильный
шестиугольник) !
-V-
гексагональная
пирамида
3»*, 6»г
1
гексагональная
дипирамида
3'», 62т, 62. 6/ю,
Gfmmm
дигексагон
•*
дигексагональная
пирамида
дигексагональная
дипирамида
(з!ттт

130 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. 1
Призмы
Тетраэдры
Трапецоэдры
грани, трапеци,
т. е.
произвольные
четырёхугольники
Л
Скаленоэдры
грани, скалены,
т. е. произвольные
треугольники
Д
*
(Г
ромбическая
призма
2jm, 22, 1т, тшт
^и>
^7 «)
ромбические
тетраэдры:
а) правый
б) левый 22
Простые формы низших
*
0
тригональная
призма
3, 32, Згс, 6, 62ш
1
i
1
i
1
1
j
j
/\ триго-
(V--1 нальние
\/ i\ трапецо-
^ а) эдры:
/ v\ а) правый
уу/ б) левый
\1/ б) 32
ромбоэдр
(грани, ромбы)
32, 3, Зш
*
0
Ш
дитригональная
призма
32, Sm, 62w
I
1
i
А
Фп
V
дитригональнын
(гексагональный)
скаленоэдр
Зт

§ 2] ВНКШНИЙ ОБЛИК КРИСТАЛЛОВ И ПРОСТЫЕ ФОРМЫ 131
Продолжение
я средних систем
*
-
)
тетрагональная
призма
4, 42, 4/ад, 4т,
4\ттт, 4, 42т
£1
тетрагональный
тетраэдр
4, 42т
тетрагональный
трапецоэдр
(показан только
правый) 42
1:
[:
Р
*
(f=Pf|
ш
дитетрагональная
призма
42, 4м, 4jmmm,
42/m
дитетрагональныи
(тетрагональный)
скаленоэдр
42т
-Х-
fn4
l_U
гексагональная
призма
32, Зт, 3, 3»*, 62w,
62, 6/m, 6m, 6/mmm
гексагональный
трапецоэдр
(показан только
правый) 62
*
fffrffi
ши
дигексагональная
призма
Зм, 62, 6>и, 6/www

132 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
Простые формы
Основные формы
тетраэдр 23
43 т
куб (гексаэдр)
жЗ, 23, 43w, 43,m3w
Форма грани
гексатетраэдр
43w»
тетрагексаэдр
43w, 43, тЗт
тригон
тригонтритетраэдр
23, 43w
тетрагон
тетрагонтритеграэдр
23, 43w
Пентагон
а) б)
пентагонтритетраэдр:
а) левый, б) правый
23

2] ВНЕШНИЙ ОБЛИК КРИСТАЛЛОВ И ПРОСТЫЕ ФОРМЫ 133
Продолжение
кубической системы
октаэдр
>»3, 43, шЗт
ромбододекаэдр
(двенадцатигранник
с ромбическими
гранями)
23, шЗ, 43т, 43, тЗт
пентагондо декаэдр
(двенадцатигранник
с пятиугольными
гранями)
23, тЗ
гекеаоктаэдр
шЗт
дидодекаэдр
»»3
тригонтриоктаэдр
тЗ, 43, тЗт
тетрагонтриоктаэдр
тВ, 43, тЪт
а) б)
Пентагонтриоктаэдр:
*) левый, б) правый
43

134 КРИСТАЛЛОГРАФ. ОСН01Ш СТГУКТУРНОГО АНАЛИЗА [lVf. I
Примечания к таблице I, IX. Таблица содержит изображения
простых форм, их названия и перечень кристаллических классов, в
которых встречается каждая из них. Открытые формы отмечены звёздочкой.
I. Простые формы низших и средних систем. Все простые формы (за
исключением трёх: моноэдра, диэдра и пинаконда) располагаются в
вертикальных столбцах. Все простые формы одного столбца имеют
одинаковое сечение горизонтальной плоскостью. В одну горизонтальную строку
входят простые формы, относящиеся или к одному типу многогранников
(пирамиды, призмы), или имеющие грани сходной формы (трапеца, скалена).
Фиг. I, 47. а) Образование комбинации тетрагональной призмы
и тетрагональной бипирамнды; б) образование комбинации
куба и ромбического додекаэдра; в) кубический кристалл грос-
суляра (силикат), представляющий комбинацию
ромбододекаэдра и тетрагонтриоктаэдра; ») кристаллы правой (7) и левой (II)
винных кислот. Комбинация четырёх пинакоидов а, с, г, р и
трёх диэдров т, [a, q; д) кубооктаэдр или комбинация куба и
октаэдра.
Название каждой простой формы (кроме указанных трёх и ромбоэдра)
представляют собой сочетание названия её сечения и типа многогранника
(или формы грани). Например, дитригональная дипирамида,
гексагональный трапецоэдр.
II. Простые формы кубической системы. В первой строке находятся
основные простые формы. Во второй строке находятся простые формы
с двойным названием. Приставка указывает, во сколько раз число граней
данной простой формы больше числа граней соответствующей основной
(стоит в начале столбца). В трёх остальных строках расположены тритет-
раэдры и триоктаэдры, различающиеся по форме граней. Формы грани
(помещены в первом столбце) входят в названия этих простых форм.
Таким образом название основной простой формы входит в названия всех
остальных, находящихся в том же столбце.

§3]
КРИСТАЛЛОГРАФИЧЕСКИЕ ПРОЕКЦИИ
135
Поскольку все/ грани простой формы выводятся из одной, они должны
иметь сходные символы: инцексы символа могут менять знаки и меняться
местами, но их числовые значения должны быть одинаковыми для всех
граней одной простой формы. Так, например, символы граней октаэдра
таковы: (111), (Ш), (ill), (111), (111), (111), (111}» (Ill)- Если желают
отметить, что символ относится не к одной грани, а ко всей простой форме
в целом, его заключают в фигурные скобки {111}.
§ 3. Кристаллографические проекции
Для графического изображения кристаллов и кристаллической решётки
широко пользуются проекциями. Проекции применяются и для решения
ряда задач кристаллографии и рентгеноструктурного анализа: графические
расчёты, индицирование лауэграмм и т. д. Проекции изображают не сам
Фиг. I, 48. а—кристаллическая решётка; б1—комплекс решётки;
в—полярный (обратный) комплекс решётки.
кристалл или кристаллическую решётку, а их комплекс. В целом ряде
случаев вполне достаточно знать лишь взаимную ориентацию граней и рёбер
кристалла или узловых
плоскостей и узловых прямых решётки,
а не расстояния между ними.
Поэтому все параллельные
плоскости можно заменить одной
плоскостью, все параллельные
прямые — одной прямой. Так,
путём параллельных переносов
заменяют кристалл или решётку
совокупностью плоскостей и
прямых, проходящих черев одну
точку; эта совокупность
называется комплексом, а точка —
центром комплекса. Фиг. I, 49. Линейная и гномоническая
Если в комплексе заменить проекции,
плоскости их нормалями, а
прямые перпендикулярными к ним плоскостями, то получим так называемый
полярный (обратный) комплекс. Полярный комплекс тесно связан с
обратной решёткой, широко применяемой в рентгеноструктурном анализе.
Переход от кристалла или решётки к комплексу и к полярному
комплексу иллюстрируется фиг. I, 48.
Для изображения кристаллов и решётки применяются следующие виды
проекций: линейная, гномоническая, стереографическая, гномостереогра-
фическая.
а) Линейная проекция. Плоскость проекции Р находится на
некотором расстоянии d = 00' от центра комплекса О (фиг. I, 49). Точки пере-

136 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
Фиг. 1,50. Линейная проекция зоны
плоскостей.
сечения М и N прямых комплекса ОМ и ON с плоскостью проекции
считаются проекциями этих прямых, линия пересечения Q'Q" плоскости
комплекса Q с плоскостью проекции — проекцией этой плоскости. Итак,
плоскости проектируются прямыми,
прямые — точками. Зона плоскостей
Q, R, Т проектируется как пучок
прямых Q'Q?', R'R", ТТ",
веерообразно расходящихся из одной
точки А' — проекции оси зоны О А'
(фиг. I, 50). Неудобство этой
проекции состоит в том, что для
изображения всех плоскостей и
прямых (с любыми углами наклона
к плоскости проекции а)
необходим не ограниченный участок
плоскости, а бесконечно большая
плоскость. Эта проекция применяется
редко.
б) Гномоническая проекция. Эта
проекция весьма тесно связана с
линейной проекцией. Отличие состоит
в том, что комплекс решётки
заменяется полярным комплексом. Следовательно, плоскость Q проектируется
точкой N(ON—нормаль к плоскости Q), а прямая ON—прямой же Q'Q"
(фиг. I, 49). Зона плоскостей проектируется как серия точек,
расположенных на прямой, являющейся проекцией оси зоны. Неудобство этой проекции
то же, что и родственной ей линейной проекции. Гномоническая проекция
широко применяется в рентгеноструктурном анализе для расшифровки лауэ-
грамм (см. главу IV). Следует
отметить, что гномоническая проекция
может рассматриваться как особая
проекция обратной решетки
кристалла.
в) Стереографическая проекция.
Принцип проектирования состоит в
следующем (фиг. I, 51). Центр
комплекса совмещается с центром шара
проекции О. Плоскость проекции Р
также проходит через центр шара
проекции, т. е. сечёт его по экватору.
Это сечение называется основным
кругом проекции. Точки пересечения
диаметра шара, перпендикулярного
плоскости проекции, с поверхностью
шара, называются полюсами
проекции; северный полюс N лежит над
плоскостью проекции, южный полюс
S — под ней. Через любую точку М,
которую нужно спроектировать,
проводят радиус ОММ'. Точка пересечения М' этого радиуса с поверхностью
шара (сферическая проекция точки М) соединяется прямой с полюсом
проекции. Если Ж (и М') лежит над плоскостью проекции, то прямую проводят
через полюс 8, если под ней, то через полюс N. Точка пересечения М\
этой прямой с плоскостью проекции называется стереографической
проекцией точки М. Для различения точек, лежащих над плоскостью
проекции и под ней, проекции первых из них обозначаются точками,
вторых—крестиками. Легко видеть* что проекции всех точек, находящихся
Фиг. I, 51. Стереографическая
проекция.

§3]
КРИСТАЛЛОГРАФИЧЕСКИЕ ПРОЕКЦИИ
137
внутри шара проекции (и даже вне его), находятся в пределах
основного круга проекции. В этом состоит одно из достоинств
стереографической проекции: стереографическая проекция любого объекта имеет
конечные размеры, определяемые радиусом взятого шара проекции. Зная
принцип проектирования точки, легко показать, что стереографическая
проекция M'Q' прямой MQ, проходящей через центр шара проекции, есть также
прямая (фиг. 1,51а), а стереографическая проекция MQ'RT плоскости MQBT
есть дуга большого круга (фиг. I, 516), кривизна которой тем больше,.
Фиг. I, 51а. Стереографи- Фиг. I, 516.
Стереографическая проекция прямой. ческая проекция плоскости.
чем меньше угол проектируемой плоскости с плоскостью проекции. Дугой
большого круга называют дугу окружности, пересекающую окружность
основного круга проекции в диаметрально противоположных точках. Те
части прямой, или плоскости, которые находятся ниже плоскости проекции,
изображаются на стереографической проекции штриховыми линиями.
Плоскость, перпендикулярная плоскости проекции, проектируется как диаметр
основного круга проекции, совпадающая с ней, — как окружность
основного круга проекции. Прямая, перпендикулярная плоскости проекции,
проектируется как центр основного круга проекции, лежащая в ней—как
диаметр его. Зона плоскостей проектируется как серия дуг больших круговг
пересекающихся в двух диаметрально противоположных точках; ось зоны—

138 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
как прямая, соединяющая эти точки. Стереографическая проекция обладает
рядом важных свойств; например, 1) окружности на шаре изображаются в
стереографической проекции окружностями же; 2) углы между линиями на
шаре равны. углам между стереографическими проекциями этих линий.
Стереографической проекцией часто пользуются при описании
симметрических преобразований и точечных групп. Для этой цели она
применяется и в данной книге.
г) Гномостереографическая проекция. Эта проекция строится так же,
как и стереографическая, только вместо комплекса берётся полярный
-(обратный) комплекс. Следовательно, соотношение этих проекций такое
же, как гномонической и линейной проекций. Прямые проектируются
дугами больших кругов, плоскости — точками, называемыми полюсами
плоскостей, зона плоскостей — серией точек, расположенных по дуге большого
круга — проекции оси зоны. Гномостереографическая проекция обладает
тем же достоинством, что и стереографическая, а именно конечными
размерами. Гномостереографические проекции, называемые иначе полюсными
фигурами, применяются в рентгеноструктурном анализе для определения
ориентации монокристаллов и расшифровки текстур (см. гл. IV и VII).
Интересно отметить, что в случае кристаллов кубической^системы
гномостереографическая проекция совпадает со стереографической, а гно-
моническая—с линейной. Это происходит потому, что в этом случае индексы
плоскостей совпадают с индексами нормалей к ним и наоборот.
Описание практических применений (например, определение углов
между кристаллографическими направлениями и вычерчивание
кристаллов) с помощью гномостереографической проекции (сетки Вульфа)
читатель найдёт несколько ниже.
Следует отметить, что ввиду сходства принципа стереографической
и гномостереографической проекции чёткоеразличие между ними проводится
не всегда. Часто терминохМ «стереографическая» обозначают обе эти
проекции.
§ 4. Сетка Вульфа
Для практического применения гномостереографической и
стереографической проекции необходимо располагать проекцией семейств
координатных линий. Как известно, такими координатными линиями на шаре
являются параллели и меридианы. Если спроектировать систему параллелей
и меридианов на плоскость, проходящую через полюсы шара, поместив полюс
проекции иа экваторе (на нормали к этой плоскости), то получим сетку,
изображённую на фиг. I, 52. Эта сетка была предложена Юрием Викторовичем
Вульфом и носит его имя. Прямая АН называется горизонтальным
диаметром или экватором сетки, прямая CD — вертикальным диаметром.
Окружность ACBD носит название основного круга, точки С и D — верхнего и
нижнего полюсов, точка О — центра сетки. Дуги сетки, проходящие через её
полюсы, называются меридианами, дуги типа MN— параллелями.
Сетка Вульфа позволяет решать на плоскости задачи, относящиеся
к шару.
Сетка печатается на плотной бумаге; дуги (являющиеся дугами
окружностей) наносятся через интервалы в 2°, чем и определяется точность
построений. Все построения производятся на кальке, накладываемой на
сетку, на кальке отмечается центр сетки и конец одного из диаметров, что
позволяет всегда привести её в первоначальное положение.
Изложим некоторые основные задачи, решаемые с помощью сетки
Вульфа. Укажем, что все перемещения, связанные с построениями,
производятся путём концентрического вращения кальки.
1. Построить стереографическую проекцию точки, заданной
сферическими координатами р и <?• Отсчёт р ведётся от центра сетки (р = 0°)
по одному из её диаметров к основному кругу (р = 90°) и далее по

ЮРИЙ ВИКТОРОВИЧ В У Л Ь Ф
(1863-1925 гг.).
Автор многочисленных работ по геометрической
кристаллографии. Предложенный им графический метод вычисления
кристаллов (сетка Вульфа) является общепринятым. Пионер
рентгенографии кристаллов в России. Вывел основную формулу
реитгеноструктурного анализа 2dsinO = nA. (1913 г.).

140 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
тому же диаметру к центру сетки (р = 180°). Изменение р от 90 до 180°
надо предбтавлять происходящим под плоскостью чертежа. Отсчёт <р
ведётся по основному кругу от правого конца горизонтального диаметра
(ср = о°) по часовой стрелке (фиг. I. 52).
Для построения точки р, у откладываем по основному кругу угол <р.
Концентрическим поворотом кальки приводим полученную точку на конец
Р'90* с ?'270°
О'90° D
Фиг. I, 52. Сетка Вульфа.
одного из диаметров и, отсчитав по нему угол р, находим искомую
точку р, у.
Если р>90°, продолжаем отсчёт за основной круг. В этом случае
точка находится под плоскостью чертежа; такие точки, в отличие от
точек, находящихся над плоскостью чертежа и отмечаемых кружками,
отмечаем крестиками,
2. Измерить угловое расстояние о между двумя заданными точками.
Поворачивая кальку (не смещая её центра с центра сетки), приводим обе
точки на один (если они лежат в одном полушарии, например верхнем
или нижнем) или на симметричные (если они находятся по разные
стороны от плоскости чертежа) меридианы. Отсчёт угла производим по этому
меридиану, или но одному меридиану до полюса, а от полюса по другому.
Сказанное поясняется фиг. I, 53.
Две точки являются гномостереографическими проекциями двух
граней. Таким образом мы измерили угол между гранями (рёбрами).

§41
СЕТКА ВУЛЬФА
141
3. Через две заданные точки провести дугу большого круга. Обе
точки приводим на один или симметричные меридианы, согласно
сказанному в задаче 2. Этот меридиан (или совокупность двух симметричных
меридианов) и есть искомая дуга большого круга. Очевидно, данная задача
служит для отыскания оси зоны (грани, проходящей через пару рёбер).
Часть дуги большого круга, проходящая по нижнему полушарию,
прочерчивается пунктиром.
Фиг. I, 53. Определение углового расстояния а между
двумя точками. Точки А и В л^ежат в одном полушарии
(верхнем). Точки Е и D лежат в разных полушариях,
в этом случае о = а± -f- а2.
4. Построить точку, диаметрально противоположную данной.
Точка приводится на один из меридианов и по нему отечнтываетея от неё
угол 180°.
5. Найти полюс дуги большого круга (переход от гномостереографи-
ческой проекции к стереографической и обратно). Полюсом дуги большого
круга называют точку, отстоящую от всех точек дуги на 90°.
Дуга совмещается с одним из меридианов, от точки пересечения дуги
с экватором отсчитывают угол 90° в сторону центра сетки. Найденная
точка и есть полюс.
6. Измерить угол между двумя дугами больших кругов. Угол между
дугами равен углу между, их полюсами. Поэтому поступаем согласно
указаниям задач 5) и 2). Применение этой задачи то же, что и у задачи 2).
7. Совместить путём поворота две заданные точки.
Концентрическим поворотом приводим точки на одну параллель; ось поворота есть

142 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
вертикальный диаметр; угол, поворота равен углу между точками,
измеренному по параллели.
8. Совместить данную точку с центром сетки путём поворота.
Приводим точку на экватор. Ось поворота — вертикальный диаметр; угол
поворота р — координата дайной точки.
9. Совместить поворотом две дуги большого круга. Дуги совместятся,
если совместятся их полюсы. Поэтому поступаем согласно 5) и 7).
Фиг. I, 54. Построение малого круга; а и
Г—действительные центр и радиус малого круга; R и /"—сферические
радиусы и центр его; NP' = NrPr — В, NP^fiN'P.
10. Заменить плоскость проекции новой плоскостью, полюс которой
есть заданная точка. Ута задача есть вариант предыдущей. Приводим
заданную точку на экватор. Переносим стереографические проекции всех
точек по соответствующим параллелям на величину р полюса новой
плоскости проекции в том направлении, в котором он совмещается с центром
сетки (точки нижнего полушария движутся в противоположном
направлении). Задача применяется при черчении кристаллов и формулируется
так: 1) поворот на угол р* вокруг горизонтальной оси (вертикального
диаметра) точками верхнего полушария влево и 2) поворот плоскости
проекции на угол а вокруг вертикальной оси (центра сетки) по часовой
стрелке. В данном случае полюс новой плоскости проекции имеет
координаты <р = — а, р == р.
11. Совместить заданную дугу большого круга с основным кругом
сетки. Вариант задачи 8. Строим полюс дуги и поступаем, как указано
выше.

4]
СЕТКА ВУЛЬФЛ
14а
12. Построить стереографическую проекцию дуги малого круга с
радиусом а и с полюсом в заданной точке. Дугой малого круга называется
окружность, проведённая на шаре, но не проходящая (в
противоположность дуге большого круга) через его диаметрально противоположные
точки.
Приводим заданный полюс Р на любой из диаметров сетки.
По этому диаметру по обе стороны от полюса откладываем по углу а
(фиг. Т, 54). Полученный отрезок есть диаметр искомого малого круга*
Фиг- 1,55. Дуга малого круга пересекает основной круг;
ABCD — дуга малого круга; Р— её полюс;
ZPB = zPMD = a.
Окружность на шаре в стереографической проекции изображается
окружностью же. Поэтому, разделив найденный отрезок Ж^Г'понолам, строим на,
нём, как на диаметре, с помощью циркуля окружность — искомый малый
»руг. Чертёж показывает, что действительные центр (заданный полюс) и
радиус (а) малого круга не совпадают со сферическими (т. е. фактически
^принятыми при построении) полюсом Р' и радиусом В.
Если угол а достаточно велик, так что дуга пересекает основной
круг, то построение приводят несколько иначе. Этот более общий способ
•вполне применим и в первом случае. Поворачивая кальку, приводят заданный
оолюс последовательно на разные меридианы и каждый раз откладывают
"От него углы а в обе стороны. Таким образом получают достаточное
число точек, через которые и проводят дугу (фиг. I, 55).

144 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
Если полюс дуги малого круга совпадает с центром сетки,
сферический и действительный центры и радиусы совпадают.
Отложив
Р = «,
проводят из центра сетки окружность этим радиусом (фиг. 1,56).
Фиг. 1,56. Полюс дуги малого круга совпадает
с центром сетки.
Если полюс лежит на основном круге сетки, его совмещают с одним
из полюсов её и, отложив о по вертикальному диаметру, проводят
соответствующую параллель, которая и является искомой дугой малого круга
.{фиг. 1,57).
13. Найти полюс дуги малого круга. Находим сферический центр дуги
простым геометрическим построением (отыскание центра окружности).
Совмещаем его с одним из диаметров сетки.
Измерив диаметр 2а дуги малого круга и отложив а по диаметру
•от любой нз точек пересечения круга с диаметром внутрь его, находим
полюс.
14. Измерить длину дуги малого круга f. Согласно 13) измеряем
радиус а малого круга. Через концы Л я В дуги малого круга проводим
дугу большого круга (задача 3) и измеряем согласно 2 её угловую
величину р.

4]
CKTIiA ЛУЛТ.ФЛ
M5
Угол y находим по формуле
■ Р
sin-^
S1I1 "-г = — .
2 sin о
Читатель без труда выведет её, воспользовавшись фиг. 1,58а и 1,586 и
припомнив, что радиус шара и круга проекций равен единице.
15. Определить, не связаны ли данные п точек осью симметрии п-го
порядка. Если данные п точек действительно связаны осью симметрии,
Фиг. I, 57. Полюс лежит на основном круге сетки.
то они должпы лежать на одной дуге большого или малого круга и
делить её на п равных частей.
Поэтому в соответствии (^предыдущими задачами прежде всего пытаются
провести через все п точек дугу большого или малого круга. Если это
удалось, измеряют отрезки этой дуги между точками и при равенстве их
Друг другу заключают о наличии оси или псевдооси симметрии. Выход оси
симметрии находится как полюс соответствующей дуги; при желании его
можно совместить с центром сетки.
16. Найти плоскость или псевдоплоскость симметрии (фиг. 1,59). Для
этого необходимо наличие по меньшей мере четырёх точек Р, Р', Q и Q'
(полюсов граней). Приводим точки Q и Q' на одну параллель. Если при
этом точки РиР' также легли на одну параллель, то, возможно, имеется

146 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. t
М
Фиг. I, 58a. ABCD — малый круг радиуса а, Р — его полюс, 'Р — его
сферический полюс, О — центр сетки. Через концы дуги ЛЕВ малого
круга, угловую величину ? которой хотят определить, проводят дугу
большого круга MABN и измеряют угловую величину (3 еб участка А В.
Фиг. 1,586. Малый круг сечёт шар проекции по дуге AEBCD; Р — полюс
дуги малого круга; О — центр сферы; О' — центр сечения. 0'КА.АВ; т
&ООгА: ЛО'=8ш а; из CSAO'K: AK=AOf sin 1= sin4" sin а; из &ОАК:
4JT=sin|-.

$ 5 J ГОНИОМЕТРИЧЕСКОЕ ИЗУЧЕНИЕ КРИСТАЛЛОВ 147
плоскость симметрии — дуга большого круга, — проходящая через верхний
и нижний полюсы. Она действительно имеется, если, проведя дугу СЕВ
так, чтобы о = а', найдём одновременно, что и 6 = В'. Если этого нет, то
Фиг. I, 59. Отыскание плоскостей симметрии.
и плоскости симметрии между точками Р и Р\ Q и Q' не существует.
Тогда её следует искать аналогичным образом между точками Риф,
Р' и Q'.
§ 5. Гониометрическое изучение кристаллов
Гониометрическое изучение кристалла состоит в измерении углов
между всеми его гранями или в измерении сферических координат р и <р
всех граней.
Для этой цели применяются приборы, называемые отражательными
гониометрами. Схема отражательного гониометра изображена на фиг. 1,60.
Кристалл Е укрепляется в центре вращающегося лимба Л. Коллиматор
посылает на кристалл параллельный пучок света. Наблюдатель, смотрящий
в трубу, увидит зайчик, (сигнал), отражённый от грани » кристалла, если
'её нормаль совместится с биссектрисой угла, образованного осями трубы
а коллиматора. Если кристалл прикреплён так, что ось зоны граней^, i^...
совпадает с осью вращения, а оси трубы и коллиматора перпендикулярны
ей и пересекаются в ней, то при полном повороте лимба Ж можно
измерить углы между нормалями ко всем граням этой зоны, а следовательно,
и дополнительные им углы между соответствующими гранями. Такой,

148 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [гл. 1
Фиг. I, 60. Принцип устройства
отражательного гониометра.
гониометр называется однокружным: измерение сопровождается только
одним вращением (кристалла вокруг одной оси). Без переклейки кристалла
можно измерить углы между гранями
лишь одной зоны.
Большее распространение получили
двукружные отражательные
гониометры Фёдорова и' Чапского. В этих
гониометрах измерение сопровождается
двумя вращениями: 1) кристалла
вокруг одной из осей, 2) кристалла же
вокруг другой оси, перпендикулярной
первой (гониометр Фёдорова) или трубы
с коллиматором вокруг оси,
перпендикулярной оси вращения кривталла
(гониометр Чапского). Располагая таким
образом двумя степенями свободы,
можно замерить сферические
координаты р и ср всех граней без переклейки
кристалла. В этом состоит основное
преимущество двукружных
гониометров, обусловливающее их широкое
применение.
Гониометр Чапского изображён на фигуре 1,61 и 1,61а. На массивной
подставке укреплены горизонтальный и вертикальный лимбы Л^ и Л?. Оси
вращения лимбов JIi и Л% взаимно
перпендикулярны и
пересекаются в точке О, называемой
оптическим центром
гониометра. Отсчёт углов производится
по нониусам Нг и Д"2. На оси
лимба Jfi укрепляется
гониометрическая головка Г с
кристаллом К. Коллиматор и
труба Т жёстко связаны друг
с другом и прикреплены к
лимбу Жч. Их оптические оси
образуют между собой некоторый
угол; они перпендикулярны
оси лимба Л2 и пересекаются
в оптическом центре О *).
Коллиматор и труба
поворачиваются вместе с лимбом Л*.
В трубе коллиматора (фиг. 1,62)
помещаются осветительная
лампочка, экран с
крестообразной щелью и линза, дающая
параллельный пучок света
(щель обусловливает
крестообразное сечение его).
Зрительная труба (фиг. 1,62) со-
Фиг. I, 61. Гониометр Чапского: /—ось лим- стоит из окуляра, двух
ба Л±, 2 — ось лимба Л2, 3—4 — оптическая взаимноперпендикулярных ни-
ось коллиматора, 5—6—7 — оптическая ось тей Н, пересекающихся на
трубы; остальные обозначения в тексте. оптической оси трубы, объек-
t) Ради удобства конструкции зрительная труба направлена парял-
лельно оси лимба Л"а; однако призма или зеркало направляют лучи,
идущие по оси трубы, в оптический центр гониометра (фиг. 1,62).

5]
ГОНИОМЕТРИЧЕСКОЕ ИЗУЧЕНИЕ КРИСТАЛЛОВ
149
тива и откидной линзы О. Ж. При введённой линзе О. Л. фокусное
расстояние трубы уменьшается, и в неё виден кристалл, находящийся
в оптическом центре О. Для
лучшего наведения на
фокус окуляр можно
перемещать вдоль оси трубы. При
выведении линзы О. Ж.
фокусное расстояние сильно
увеличивается («установка
на бесконечность») и при
соответствующем
положении кристалла (нормаль к
грани — биссектриса угла
оптических осей
коллиматора и трубы) наблюдатель
видит сигнал, т. е.
изображение источника света,
отражённое от грани кристалла.
Сигнал представляет собой
более или менее яркий и
чёткий светлый крест на
тёмном фоне. Для
небольших и точных поворотов
лимбов Ж\ и Ж2 служат
микрометрические винты Вх
и Б2; ими можно иользо- ^ „ . ., .
ваться, закрепив стопорные ф11Г- ].Ь1а. 1 ониометр Мапского (другой вид),
винты Bs и В4.
Гониометрическая головка (фиг. [, 63а) представлязт собой механизм,
позволяющий перемещать кристалл в двух взаимно перпендикулярных
направлениях, перпендикулярных оси головки (центрировка), и наклонять
его в двух взаимно перпендикулярных плоскостях, проходящих через ось
головки (юстировка). Головка
Колмттор
Линза
Ламла\
навинчивается на ось лимба
Ж1 и может быть несколько
приподнята или опущена на
этой оси. Головка
оканчивается выступом В, на котором
с помощью кусочка воска
укрепляется кристалл К.
Центрировочный механизм
гониометрической головки
состоит из двух линейных
салазок, перемещаемых виптамп
В\ и .В2. Котировочный
механизм состоит из двух
цилиндрических салазок,
перемещаемых винтами 7?з и Б4.
Головки других конструкций
(фиг. I, 63 и I, 636) построены
но аналогичному принципу.
Для измерения выбирают
небольшой (0,5—2 дел), по
возможности хорошо
образованный кристалик. С помощью кусочка воска его укрепляют на выступе
головки; воск должен закрывать как можно меньшую часть поверхности
кристалла. Кристалл укрепляют так, чтобы какое-либо важное кристал'
Призма
Объектив
fJOA
Фиг. 1,62. Схема устройства коллиматора
и зрительной трубы гониометра.

150 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [гл. I
.юграфическое направление (видимая ось симметрии, ось богатой гранями
зоны, иногда нормаль к наиболее развитой грани) было примерно
параллельно оси головки 00'. Толовку с кристаллом навинчивают на ось
лимба Л\. Наблюдая кристалл
через трубу Т с введённой
линзой О.Л., поднимают или
опускают головку так, чтобы
кристалл пересекался
горизонтальной нитью Н. Затем
приступают к центрировке.
Поворотом лимба Л\ ставят винт
В\ примерно перпендикулярно
плоскости осей трубы Т и
коллиматора; поворачивая винт,
приводят кристалл на верти-
Фиг. 1, 63. Гониометрическая головка. Si52£HH!HПоставив в ана-
' у логичное положение винт В2,
поступают аналогичным
образом. После этих операций кристалл оказывается в оптическом центре О
и будет оставаться в нём при любых поворотах лимбов JTj и Л%.
Затем приступают к юстировке, состоящей в точной установке
выбранного направления кристалла по оси головки, а значит, и лимба Л^ Если
выбранное направление является осью зоны, то, повернув лимб Л% так, чтобы
биссектриса осей трубы Г и
коллиматора была
горизонтальна *)
(перпендикулярна оси лимба Л{),
добиваются, чтобы сигналы от
всех граней зоны прохо-
Фиг. I, 63а. Гониометрическая головка Фиг. I, 636. Гонио-
другой конструкции (обе применяются метрическая головка
при рентгеносъёмке,). (третья конструкция).
дили через крест нитей Л. Для этого, повернув лимб Ж^ так, чтобы
один из юстировочных винтов Въ или J?4 смотрел примерно вдоль плоскости
осей трубы Т и коллиматора, поворачивают его, приводя ближайший сигнал
на крест нитей. Аналогично поступают с другим котировочным винтом.
р) Это положение является константой прибора.

5] ГОНИОМЕТРИЧЕСКОЕ ИЗУЧЕНИЕ КРИСТАЛЛОВ 151
После этого небольшими поворотами 2>3 и J>'4 производят точную установку.
Если кристалл имеет ряд граней равнонаклонённых к выбранному
направлению, устанавливают (поворотом лимба Л%) биссектрису угла осей трубы
Т я коллиматора примерно по нормали к поверхности конуса, описываемого
этими гранями при вращении лимба Лг. Далее поступают аналогично
предыдущему случаю за тем исключением, что приходится слегка
поворачивать и лимб Л%. Если имеется грань, нормальная к оси головки, то юстировка
очень проста. Ставят (поворотом лимба Ж<^ биссектрису угла осей трубы Г
и коллиматора вертикально (на 90° от положения, отвечающего первому
Фиг. 1,64. Двукружный^гониометр конструкции К. С. Фёдорова.
случаю). Вращая лимб Л\ и котировочные винты, добиваются, чтобы
единственный сигнал всё время оставался в пересечении нитей при полном
повороте кристалла.
После того как кристалл сцентрирован и"съюстирован, приступают
к измерениям. Для этого, поворачивая кристалл (лимб Л±) и трубу с
коллиматором (лимб Jr2), приводят сигналы от всех граней на крест нитей и
отмечают соответствующие сферические координаты грани: <? по Л\ (начало
отсчёта безразлично) и р по J5 (0° при вертикальной биссектрисе угла
осей трубы Т и коллиматора и 90° при горизонтальной). Конструкция
гониометра такова, что можно измерять углы у в пределах от 0 до 360° и р
в пределах от 0 до (примерно) 130—140°. «Мёртвый» интервал р (140—180°)
соответствует, однако, граням, заклеенным воском. Поэтому, вообще
говоря, и двукружный гониометр требует двух приклеек кристалла.
Практически измерение производят следующим образом (аналогично
Действуют и при отыскании сигналов при юстировке). Сначала отыскивают
(вращая лимбы Л± и Л"2) сигнал или, вернее, ярко блестящую грань
с введённой откидной линзой. Затем уточняют координаты сигнала,
выведя линзу и действуя микрометрическими винтами. Полный обзор
кристалла производят с выведенной откидной линзой. При данном
положении лимба Лг медленно поворачивают кристалл на 360°. При обнаружении
сигналов несколько поворачивают лимб Лг и уточняют их координаты.

152 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
Повернув затем лимб Жг на угол а (угол поля зрения трубы, обычно
равный 2,5°), повторяют полный поворот кристалла. Снова поворачивают лимб JT2
на угол а и т. д. Таким образом проходят весь интервал р при всех
значениях <р, не пропустив ни одного сигнала.
Следует отметить, что центрировка и юстировка кристалла должны
выполняться весьма тщательно, ибо этим в значительной степени
определяется точность измерения кристалла на гониометре и качество
рентгенограмм.
В результате измерения кристалла на гониометре получают таблицу
сферических координат риф для всех его граней, в которой также
зарисовывают грани, отмечают яркость и чёткость сигнала.
Гониометр Фёдорова (фиг. 1,64) отличается тем, что труба Т и
коллиматор неподвижны, а кристалл может вращаться вокруг двух взаимно
перпендикулярных осей.
Оптические оси зрительной трубы и коллиматора горизонтальны,
образуют друг q другом тупой угол и пересекаются в оптическом центре О
прибора. Они перпендикулярны оси основного лимба Л^
(отсчёт р). Вокруг оси этого лимба может вращаться
массивная шина Ш, на которой укреплена стойка С.
Стойка С служит опорой для оси другого лимба Л2
(отсчёт ф), на которой укрепляется гониометрическая
головка Г с кристаллом Е. По принципу ориентировки
и измерения кристалла гониометр Фёдорова не отличается
от гониометра Чапского: вращению коллиматора и трубы
соответствует в данном случае вращение шины Ш,
а вместе с ней и кристалла вокруг оси лимба Лг;
гониометр Фёдорова применяется исключительно для
измерения кристаллов, так как гониометрическая головка
неотделима от оси лимба Л%.
Фиг. I,G5a.
Кристалл каламина
Zn2H2SiOa (класс
2т).
Комбинация моноэдра с,
двухпинакоидов
а и Ь,
ромбической призмы т,
четырёх диэдров
-s, r, t, l и
ромбической
пирамиды q.
§ 6. Обработка результатов гониометрических
измерений
Обработка результатов гониометрических измерении
оказывается наиболее простой в том случае, если
измерению подвергался целесообразно ориентированный
кристалл. Как уже указывалось, кристалл следует
ориентировать так, чтобы с осью головки совпадало какое-либо
ярко выраженное кристаллографическое направление:
обычно видимая (и могущая оказаться действительной)
ось симметрии, ось богатой гранями зоны, иногда
нормаль к хорошо развитой грани.
Результаты гониометрического измерения
кристаллов позволяют: 1) вычислить кристалл, т.е. найти
отношение осевых единиц, угловые константы, символы всех граней,
отклонения от закона рациональных отношений; 2) построить гномостереогра-
фнческую (или стереографическую) проекцию, идеальную форму роста и
вычертить кристалл.
На основании этого определяется симметрия идеальной формы роста,
т. е. принадлежность к одному из 32 классов симметрии.
Построение гномостереографической проекции кристалла производится
с помощью сетки Вульфа и состоит в простом нанесении на сетку полюсов
всех граней по их сферическим координатам р и ср. Гномостереографическая
проекция правильно ориентированного кристалла позволяет сразу же
сделать вывод о его симметрии (по крайней мере о принадлежности к той или
иной кристаллической системе). Если кристалл ориентирован
произвольно, то, пользуясь приведенными выше задачами на применение сетки

§ 6] ОБРАБОТКА РЕЗУЛЬТАТОВ ГОНИОМЕТРИЧЕСКИХ ИЗМЕРЕНИЙ 153
Вульфа, можно выяснить, не являются ли данные направления или
плоскости осями или плоскостями симметрии. Если это окажется так, то
можно (как указано там же) произвести требуемый поворот плоскости
проекции (а значит, и самого кристалла), приводящий его к правильной
ориентации. Стереографическая проекция позволяет измерить углы между
осями кристалла и между его гранями и рёбрами (см. раздел: Сетка Вульфа),
а также найти символы всех его граней и вычертить кристалл (об этом
несколько ниже). Для примера приводим стереографическую проекцию
кристалла каламина (фиг. I, 65а и б).
Фиг. I, боб. Стереографическая проекция (схема).
а) вычисление кристаллов. Чтобы можно было сделать определённые
выводы из гониометрических измерений, необходимо произвести установку
кристалла, т. е. согласно определённым правилам выбрать координатные
оси и единичную грань.
Из закона рациональности 'отношений осевых отрезков следует:
для того, чтобы символы всех граней и рёбер были рациональными,
необходимо за координатные оси и плоскости выбирать три возможные или
действительные рёбра и грани кристалла.
Правила выбора осей кристалла по существу совпадают с правилами
выбора осей решётки (таблица I, V); достаточно лишь слова «вектор» или
«наименьший вектор» заменить словом «ребро». Единичная грань
выбирается, как указывалось на стр. 123,124. Этот выбор прост, но неоднозначен.
Так, например, выбор единичной грани для кристаллов всех систем, кроме
кубической, остаётся в значительной степени произвольным. Действительно,

154 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
например, любая грань ромбического кристалла, пересекающая все три оси,
может быть принята за единичную. Единственным (и опять-таки
неоднозначным) критерием правильности выбора единичной грани является
простота получаемых символов. Если символы сложны, их можно
упростить, выбрав другую единичную грань. Однозначной является установка,
предложенная Е. С. Фёдоровым. Однако она мало распространена ввиду
её сложности.
После того как установка кристалла произведена, приступают к его
вычислению. Существуют два способа вычисления кристаллов:
аналитический, основанный на применении сферической тригонометрии, и
графический с применением сетки Вульфа.
1) Аналитический способ. Угол между двумя направлениями
в пространстве &13, задаваемыми их сферическими координатами р^ q> и
(>2, ?& определяется по формуле
cos Ь12 = cos px cos pa + sin p j sin p2 cos (^ — f2). (1,5У)
С помощью этой фо'рмулы определяются углы а, р, f между выбранными
осями, а также углы а^ fo f0 и а.', р', у', образуемые с этими осями
единичной н любой другой гранью. Здесь р и <р представляют попросту
отсчёты по двум лимбам гониометра. Зная а0, р0, ^о> находят отношение
осевых единиц (см. стр. 123). Зная, кроме того, а', р', ff для всех
граней, находят их символы по уравнению (1,58). Таким образом
аналитическое вычисление кристалла является весьма простой, хотя иногда и
длительной работой.
2) Графический способ. С помощью стереографической
проекции находят углы между выбранными осями и между ними и единичной
гранью. На основании последних, находят отношение осевых единиц.
Определение символов производится путём так называемого развития
поясов. Для проведения его необходимо выбрать три координатных
грани (или ребра) и единичную грань. Далее, проводя через проекции
пары граней (например, (100) и (111)) дугу большого круга, находим
возможное или действительное ребро (в данном случае [011]). Четыре
исходные грани дают 6 рёбер'. Точки их пересечения есть проекции
действительных или возможных граней (110), (011) и (101). Привлекая эти грани,
получаем новые действительные или возможные грани и рёбра,
группирующиеся по поясам. Символы их определяем, пользуясь правилом
зональности (стр. 20). Его удобно применять следующим образом. Друг под
другом пишут символы двух граней (рёбер), повторяя в конце первые два
индекса и отбрасывая первый индекс в начале:
XXX
^2 *2 'h '••'г
Производя перекрёстное умножение и беря первое произведение с плюсом,
второе с минусом, получим символ ребра (грани):
(ОД— ?ifc2): {hlh — hh): CM» — Ms) = »»!И 'Р>
Например, найдём символ грани, проходящей через рёбра (211) и (302).
1121 , ч ,
(1 • 2 — 1 • 0) г (1 • 3 — 2 • 2): (2 • 0 — 1 • 3) = 2 :1:3 или [21 3].
0230
Решение, естественно, неоднозначно, ибо, поменяв местами верхний и
нижний символы, получим символ центросимметричной грани или ребра. Цен-

§ 6] ОБРАБОТКА РЕЗУЛЬТАТОВ ГОНИОМЕТРИЧЕСКИХ ИЗМЕРЕНИЙ 155
тросимметричное ребро является попросту продолжением того же ребра,
напротив, центросимметричная грань присутствует Гне всегда. Правильное
решение выбирается с помощью проекции. Таким образом мы получим
проекции всех возможных граней кристалла. Совпадение ряда из них
с проекциями реально промеренных граней определяет символы последних.
Последовательное развитие поясов иллюстрируется фиг. 1,66.
Для кристаллов кубической системы можно заранее изготовить
стереографическую проекцию с обозначениями символов всех граней и
применять ее для определения символов граней любого кубического кристалла.
Фиг. I, 66. Развитие поясов (зон). Квадрант /: выбраны исходные
грани (100), (010), (001) и (111). Квадрант II: проведены все
возможные рёбра и определены их символы. Квадрант ///: определены
символы граней, найденных как точки пересечения этих рёбер.
Квадрант IV: проведена ещё серия рёбер, для чего привлечены
найденные грани (110), (011) и (101). Возникают ещё новые точки
пересечения, соответствующие граням (211), (112) и (121). Операции
затем продолжают в таком же порядке.
Это возможно потому, что в данном случае положение единичной грани
фиксировано. Для кристаллов гексагональной н тетрагональной систем
ножно дать лишь примерные проекции с символами, так как в этом случае
единичная грань имеет одну степень свободы. Проекция с развитием
поясов для кубических кристаллов представлена на фиг. I, 67.

156 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [ГЛ. I
6) Черчение кристаллов. Под черчением кристаллов понимают их
изображение в ортогональной проекции. Такое изображение обычно даёт
отчётливое впечатление о внешнем виде кристалла, нередко заменяя модель.
Наиболее отчётливо кристалл представляется в том случае, если,
исходя из наиболее простого его вида (главное направление вертикально,
нормаль к одной из характерных главных граней или другое важное на-
Фиг. I, 67. Развитие поясов для кубических кристаллов.
правление смотрят прямо на наблюдателя), повернуть его вокруг
горизонтальной оси на 10э (так чтобы верхняя часть кристалла наклонилась
вперёд) и вокруг вертикальной оси на 20э (по часовой стрелке). Сказанное
иллюстрируется фигурой I, 68.
Соответствующий поворот плоскости стереографической проекции
разъяснялся в одной из задач на сетку Вульфа.
Как известно, при ортогональном проектировании полюс проекции
находится в бесконечности, так что все точки изображаемого объекта
(кристалла) проектируются на плоскость чертежа параллельными лучами.
Параллельные друг другу рёбра кристалла изобразятся при этом
параллельными же отрезками. Равенство углов и отрезков в проекции в общем
не будет соблюдено; только равные углы с параллельными сторонами и
равные параллельные отрезки останутся равными и на проекции.

в]
ОБРАБОТКА РЕЗУЛЬТАТОВ ГОНИОМЕТРИЧЕСКИХ ИЗМЕРЕНИЙ
157
\В fa)
Для получения ортогональной проекции кристалла необходимо
располагать эскизом кристалла или самим кристаллом и его гномоствреографн-
ческой проекцией.
Соотношение между ортогональной и
стереографической проекцией очевидно из фигуры ], 69,
где О А — изображаемое ребро, 8— полюс
стереографической проекции; А' — стереографическая
проекция ребра О А; О А" — его ортогональная
проекция (в этом случае полюс проекции
находится в бесконечности). Так как луч SA лежит
в одной плоскости с
лучами, ортогонально проек- ур?0
тирующими отрезок О А, то
очевидно, при совпадении
плоскостей ортогональной
и стереографической
проекций ортогональная
проекция ребра есть прямая,
проходящая через его
стереографическую проекцию и
центр сетки.
Изложим теперь
практические правила черчения
кристаллов. Во-первых,
производим изменение
плоскости проекции путём
поворота вокруг
вертикального диаметра сетки влево
на 80° и затем вокруг центра
сетки на 110° по часовой
стрелке (это отвечает по-
о°
Фиг. 1,68. Наиболее
простой вид
кристалла,
являющегося комбинацией
тетрагональной
призмы и бипирамиды.
Фиг. I, 69. Связь
ортогональной и
стереографической проекций:
о — вид «сбоку»;
б—вид «сверху».
воротам вокруг горизонтальной оси на 80° и вокруг вертикальной на 110";
читатель сообразит, что от наиболее простого вида кристалл повернётся
соответственно на 10 и 20°).
После этого концентрическим
вращением кальки приводим
преобразованные проекции каждой пары
граней а' и V на один меридиан
или на симметричные меридианы
(см. стр. 141). Тогда гномостерео-
графическая проекция ребра их
пересечения а' — Ь' есть этот
меридиап; стереографическая
проекция его есть точка экватора
К, отстоящая от этого меридиана
на 90°, а ортогональная проекция
направлена по экватору сетки КО
(фиг. 1,70). Прочерчивая отрезки,
соответствующие по направлению
ортогональным проекциям рёбер вне
сетки {К'СУ) и находя с помощью
эскиза их относительную
величину и взаимное расположение,
получаем ортогональную проекцию
кристалла.
В ряде случаев очень полезно
построить сперва ортогональную
Фиг. 1,70. Черчение кристаллов.
Преобразовав стереографическую
проекцию (изменив плоскость проекции),
приводим последовательно полюса
всех граней (a'V) попарно на один
меридиан. Проводя линии вдоль
экватора ОК, находим ортогональную
проекцию ребра, по которому
пересекается данная пара граней а'Ь'.

158 КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА [гл. 1
проекцию кристалла на первоначальную (до поворотов) плоскость
проекции. Это—так называемый вид сверху. Эта проекция сразу же
определит взаимное расположение ортогональных проекций
вертикальных рёбер кристалла после поворота; а именно, они будут исходить из
соответствующих точек этого «вида сверху»,
§ 7. Работы Фёдорова. Кристаллохимнческий анализ
а) Теория параллелоэдров. Теория параллелоэдров была создана
в конце XIX века. Параллелоэдрами Фёдоров называл одинаковые
выпуклые многогранники, целиком выполняющие пространство в
параллельном положении. Параллелоэдры центросимметричны и имеют четырёх-
или шестиугольные грани. По числу пар граней различают три-, тетра-,
гекса- и гептапараллелоэдры. Наиболее симметричными параллелоэдрами
этих типов являются куб, гексагональная призма, ромбический додекаэдр
и кубооктаэдр. Все другие получаются из этих основных путём
деформации, растяжения и сдвига.
С современной точки зрения параллелоэдр может рассматриваться как
область, приходящаяся на каждый узел решётки. Совершенно очевидно также,
что современное представление о так
называемых координационных полиэдрах (см. главу V)
является, по существу, развитием теории
параллелоэдров Фёдорова. На фиг. 1,71
представлена объёмноцентрированная кубическая решётка
и трактовка её как
выполнение пространства кубо-
октаэдрами.
Решёткам кубической и
гексагональной систем
соответствует выполнение
пространства параллелоэдрами
четырёх наиболее
симметричных типов. Решёткам
тетрагональной и низших
систем соответствует
выполнение пространства
менее симметричными
параллелоэдрами. Эти
параллелоэдры могут рассматриваться как результат деформации четырёх основных.
Растягивая куб вдоль оси 4, придём к тетрагональной призме, сжимая её
перпендикулярно оси 4, придём к прямоугольному параллелепипеду,
производя сдвиг вдоль одного из его рёбер, получим «моноклинный»
параллелепипед; производя затем сдвиг вдоль другого ребра, получим триклинный
параллелепипед. Все эти многогранники могут выполнять пространство без
промежутков, т. -е. являются параллелоэдрами, отвечающими
соответствующим решёткам тетрагональной, ромбической, моноклинной и триклинной.
Таким образом все кристаллы тетрагональной и низших систем по
Фёдорову рассматриваются как деформированные кристаллы кубической и
гексагональной систем. Все кристаллы делятся на два больших типа:
кубический и гексагональный.
На основании теории параллелоэдров Фёдоров дал подробную
классификацию решёток, рассматривая каждую из них как деформированную
решётку кубической или гексагональной системы. Данная решётка
считается производной той из основных, из которой она выводится путём
минимальной деформации.
> \—у
^
Фиг. I, 71. Объёмноцентрированная
кубическая решётка и её трактовка.

ЕВГРЛФ СТЕПАНОВИЧ ФЁДОРОВ
(1853-1919 гг.).
Великий русский кристаллограф. Творец теории
пространственных групп — основы современного исследования строенин
кристаллов (первый вывод 230 пространственных групп
содержится в работе «Симметрия правильных систем фигур», 1890 г.).
Им изобретён двукружный гониометр и предложен
универсальный оптический метод исследования кристаллов. Кри-
сталлохимический анализ Фёдорова был первым методом,
позволившим судить о строении кристаллов.

Ш) КРИСТАЛЛОГРАФ. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА (гл. I
б) Закон кристаллографических пределов Фёдорова. Этот закон,
установленный Фёдоровым на основании изучения богатого опытного
материала и являющийся, таким образом, одним из опытных законов
кристаллографии, является дополнением и подтверждением теории парал-
лелоэдров.
Кристаллы тетрагональной, гексагональной и тригональной систем
Фёдоров называет идеальными. Кубические кристаллы также идеальны и
могут быть отнесены с равным правом к одному из первых двух типов.
Неидеальные кристаллы (ромбические, моноклинные, триклинные)
приближаются к идеальным. В этом и состоит закон кристаллографических
пределов. Действительно, углы между гранями главной зоны этих
кристаллов обычно близки к 120, 90 или 60 . Половина угла отклонения от
120 нли 90° и полный угол отклонения от GO0 называется ромбической
анортогональноетью. Триклинная и моноклинная анортогональности равны
отклонениям координатных углов от 90°. Опыт показывает, что все
кристаллы идеальны или близки к ним, так как величины анортогональностей
обычно не превосходят 0—6°.
в) Кристаллохимический анализ. Кристаллохимический анализ
Фёдорова есть способ определения вещества по геометрии внешней формы его
кристаллов. Разработка его относится к началу XX века.
Кристаллохимический анализ базируется на трёх других открытиях Фёдорова: теории
параллелоэдров, законе кристаллографических пределов и «правильной»
(выражение самого Фёдорова) установке.
Фёдоровская установка, т. е. выбор осей и единичной грани, является
однозначной. В этом состоит её большое преимущество, однако она мало
распространена ввиду большой сложности. Для пользования кристалло-
химическим определителем Фёдорова необходимо, однако, пользоваться
именно этой установкой, что сильно затрудняло применение этого
определителя в его первоначальном виде. Для определения вещества по
таблицам Фёдорова нужно провести гониометрическое измерение его кристаллов,
построить стереографическую проекцию, отнести кристалл к кубическому
или гексагональному типу, придать ему правильную установку и
определить символы всех граней, определить по найденным символам структуру
в фёдоровском смысле, определить величины анортогональностей.
Таблицы Фёдорова содержат данные о громадном числе кристаллов
(5000 не считая кубических) и относятся главным образом к минералам.
Советские учёные школы Фёдорова упростили его метод кристалло-
химического анализа, устранив в частности необходимость применения
сложной однозначной установки. «Определитель кристаллов» Горного
института в Ленинграде содержит все угловые величины, замеренные
иа кристаллах громадного количества веществ, стереографические
проекции, чертежи наиболее распространённых комбинаций простых форм и
оптические константы.

ГЛАВА И
ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ
И ИХ ВЗАИМОДЕЙСТВИЕ С ВЕЩЕСТВОМ
§ 1. Рентгеновская трубка
Для производства рентгеноструктурного анализа необходимо
располагать рентгеновским аппаратом, рентгеновской трубкой и
рентгеновской камерой.
На фиг. II, 1 а, б, в изображены трубки для
рентгеноструктурного анализа. Стеклянная трубка откачана до высокого вакуума,
т. е. до давления ниже 10-6.*M*Hg. В трубку вделаны два электрода:
массивный анод в виде медного стержня и катод в виде
накаливаемой током вольфрамовой нити, окруженной фокусирующим
цилиндром или чашечкой. В трубке сделаны четыре окошка из
специального стекла, мало поглощающего рентгеновские лучи. На
анодный конец трубки навинчивается стальной цилиндр с четырьмя
отверстиями, устанавливающимися против окошек трубки. Через
эти отверстия рентгеновские лучи выходят из трубки. Анод—полый
внутри—охлаждается проточной водой. Анодный конец трубки
имеет один электрический вывод, катодный — два.
Принцип работы рентгеновской трубки заключается в
следующем: нить катода накаливается током и выделяет электроны.
Накладывая высокое напряжение на катод и присоединяя к земле анод,
мы создаём внутри трубки сильное электрическое поле, ускоряющее
электроны в сторону анода. Попадая в зеркало анода — пластинку,
напаянную на конец анодного стержня, электроны создают
рентгеновские лучи, исходящие от анода и распространяющиеся, вообще
говоря, во все стороны. Окошки трубки расположены с таким
расчётом, чтобы пропустить наиболее интенсивную часть пучка лучей.
Выделяется часть пучка, идущая примерно под углом 11 градусов
к горизонтальному направлению (фиг. II, 2). Зеркало анода
изготовляется из самых различных металлов; наиболее употребительны
Фрубки с медным и молибденовым анодами, а также трубки с
железным и хромовым анодами.
Свойства лучей, испускаемых данной трубкой, зависят от
наложенного на трубку напряжения, силы тока в трубке (анодный ток)
и материала анода. В свою очередь, анодный ток определяется

* \
шк-
Фиг. И, la. Рентгеновская
трубка типа БСВ с защитным
цилиндром и трубками
охлаждения.
Фиг. II, 16. Рентгеновская
трубка типа БСВ без
защитного цилиндра. Видны окна
из специального стекла.
Защитный }
потух I
> Заземлены
s&HOd~ I
"Ъеталгшч \ Стеклянный баллон
! трубка J
водяное
охлаждение
Патрон
Выход пучеи
через графитовые окна
Опошко из специального стекло
Фиг. II, 1в. Разрез рентгеновской трубки типа БСВ.

1]
РЕНТГЕНОВСКАЯ ТРУБКА
163
Фиг. II, 2. Э — электронный луч; Р —
выпускаемый из трубки пучок рентгеновских
лучей; В—стеклянный баллон; О —
окошки из специального стекла; Т —
металлическая трубка; Г — графитовые окошки;
А — анод; Я — нить накала; Ф —
фокусирующий стакан.
током накала нити (фиг. И, 3). Сила тока накала заводских трубок
указывается в их паспорте; обычно изменения тока накала от 3,7
до 3,9 ампер покрывает
весь допустимый диапазон
в силе анодного тока.
Максимальный анодный ток
в описываемых трубках
при вапряжении 30
киловольт—15—25 миллиампер.
Переход за эту границу
влечёт за собой быстрое
прогорание зеркала анода—
охлаждающая вода не
успевает отводить тепло,
выделяемое при бомбардировке
анода электронами. Забыть
включить проточную воду,
охлаждающую анод,—это
значит испортить трубку.
Достаточно указать, что
при напряжении в 50 кв температура анода в этом случае под*
нималась бы с большой скоростью. Четверть часа достаточно, чтобы
нагреть анод до белого каления и этим
погубить трубку. Следует всегда помнить,
что лишь ничтожная доля энергии пучка
электронов переходит в энергию
рентгеновских лучей (менее 1%); практически вся
энергия, поступающая в рентгеновский
аппарат, идёт на выделение тепла.
Напряжения, накладываемые на трубку
при структурном анализе, невелики. На
железных трубках удобнее всего работать
при 25—30 кв, на медных при 30—35 кв
и молибденовых при 45—50 кв. Цифра 60 кв,
даваемая как максимум для заводских
трубок, вполне удовлетворительна.
При наличии сильного насоса,
обеспечивающего вакуум 10"6 мм ртутного
столба, исследователь может приняться за
изготовление металлической разборной
рентгеновской трубки. Было предложено очень
большое число подобных конструкций.
Разборные трубки, если они хорошо
сделаны, обладают некоторыми преимуществами
перед запаянными трубками: несколько бблыпая интенсивность
излучения, возможность иметь трубку с переменными анодами,
»
Трансформопср
напала
I
• ■ivy il
/иодпь/й топ
Топ попало
Фиг. II, 3. Схема
направления токов накала и
анодного в
рентгеновской установке.

164 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [ГЛ. II
возможность сильно перегружать катодную нить и анод, имея
в виду относительную лёгкость замены, и пр. Однако все эти
достоинства будут действительно таковыми лишь при наличии
высококвалифицированного экспериментатора, непрерывно ухаживающего
за трубкой. Работа же запаянных трубок требует не большего
присмотра, чем работа электрической лампочки.
Рентгеновский аппарат может быть собран без труда в любой
лаборатории. Для этого необходимо располагать высоковольтным
трансформатором, позволяющим при заземлении одного полюса
получить напряжение до 55 кв, понижающим трансформатором для накала,
Нити рентгеновской трубки, дающим на выходе около 6 в. Мощность
повышающего трансформатора может не превышать 2 киловатт
(что соответствует анодному току 40 миллиампер), мощность
понижающего трансформатора должна быть порядка 30 ватт. Кроме
этих трансформаторов необходимо располагать измерительными
приборами и приборами, позволяющими менять напряжение на
выходе обоих трансформаторов. Для этой цели -применяются для
высокого напряжения автотрансформатор и для низкого — реостат.
Описанная схема изображена на фиг. II, 4а. Анод рентгеновской
трубки, охлаждающийся проточной водой из водопроводного крана,
приходится заземлять; поэтому заземлен и один из полюсов
высоковольтного трансформатора. Регулировка качества рентгеновских
лучей осуществляется двумя рукоятками — одна из них позволяет
менять напряжение на трубке (на старых моделях рентгеновских
аппаратов ступенчато, на новых непрерывно), другая меняет ток
накала и этим силу анодного тока. Изменение напряжения на трубке
позволяет изменить соотношение интенсивностей
характеристического и белого излучения, а также кортоковолновую границу
излучения. Изменение тока накала позволяет изменять суммарную
интенсивность излучения.
Рентгеновская трубка в описанной схеме работает лишь на
одной полуволне переменного тока — электрический ток через трубку
идёт только в те моменты времени, когда на анод падает плюс,
а на катод минус. Только в этот полупериод электроны,
освобождающиеся катодом, движутся по направлению к аноду. Вторая
половина периода будет нерабочей, так как анод не выделяет
электронов.
Довольно часто последовательно с рентгеновской трубкой в цепь
включается выпрямительная лампа —кенотрон (фиг. II, 46). В этом
случае трубка находится в менее жестких условиях во время работы,
и срок ее" жизни удлиняется. Предложено большое число схем,
позволяющих использовать рентгеновскую трубку во время обоих
полупериодов переменного тока. Эти способы позволяют увеличить
в 1,5—2 раза интенсивность рентгеновского излучения.
Борьба за увеличение интенсивности рентгеновских лучей за
счёт изготовления специальных рентгеновских трубок и усложнён-

1] РЕНТГЕНОВСКАЯ ТРУБКА
Фиг. 11,4а. Схема рентгеновской установки без
кенотрона: Р — главный рубильник; Am —
автотрансформатор; 11— регулятор напряжения на трубке;
V—вольтметр (напряжение на первичной обмотке Тр);Тр—
высоковольтный трансформатор; Тп — трансформатор
накала трубки; R — реостат — регулятор тока накала;
А — амперметр (ток накала трубки); тА—
миллиамперметр (анодный ток); Т — трубка.
Фиг. И, 46. Схема рентгеновской установки
« кенотроном: Р — главный рубильник; Am —
автотрансформатор; П — регулятор напряжения на
трубке; Tpi — высоковольтный трансформатор;
Tpi — трансформатор накала трубки;
Тр$—трансформатор накала кенотрона; Я\ — реостат —
регулятор тока накала трубки; _ft2 — реостат —
регулятор тока накала кенотрона; Vi — вольтметр
напряжения на первичной обмотке Тр^\ У2 —
вольтметр напряжения накала кенотрона;
Л—амперметр тока накала трубки;
тА—миллиамперметр анодного тока; Т—трубка; К — кенотрон.

166 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [ГЛ. II
ных схем рентгеновских аппаратов имеет значение лишь для
некоторых специальных проблем в рентгеноетруктурном анализе. Для
решения большинства проблем обычная трубка и простейший
аппарат являются вполне удовлетворительными. Дело в том, что обычно
расчёт рентгенограмм и обработка полученных результатов
занимают много больше времени, чем съёмка рентгенограмм. Поэтому
сокращение времени
экспозиции, скажем, с двух часов до
о'дного часа (усиление
интенсивности лучей вдвое), вообще
говоря, не имеет
принципиального значения. Это
положение совершенно бесспорно для
исследования монокристаллов;
при работе методом порошка
интенсивность лучей играет
бблыпую, а иногда и
решающую, роль (см. стр. 578).,
Щ Возвращаясь к рентгенов-
щ ским аппаратам, следует от-
ж метить, что для структурного
ж) анализа желательно пользо-
^ ваться готовыми
промышленными рентгеновскими
аппаратами. Эти аппараты бывают
настольными или имеют вид
небольшого (70 см)
квадратного стола. Такие аппараты
« совершенно безопасны как в
отношении рентгеновского
излучения, так и в отношении
высокого напряжения — все
подводки сделаны внутри
аппарата. Аппараты включаются
. тт е Т1 л ,. непосредственно в сеть, и
Фиг. II, 5. Настольный рентгеновский „„„„,«£,-„„„ „л „<пп „„,,.
аппарат. У трубки установлены каме- инструкция по ооращению
ры для съёмки рентгенограмм порошка. С ними может быть усвоена
весьма быстро. На фотографии
(фиг. II, 5) изображён настольный аппарат производства
рентгеновского завода.
Несколько замечаний относительно фокуса рентгеновской
трубки.
Под фокусом рентгеновской трубки понимается та часть анода,
из которой исходит излучение. Для получения хороших диффрак-
ционных рентгенограмм, существенно лишь, чтобы рабочая площадь
фокуса излучала равномерно. С другой стороны, для получения малых:

§2]
СПЕКТР РЕНТГЕНОВСКИХ ЛУЧЕЙ
167
экспозиций существенна острота фокуса, определяющая плотность
излучения. В этом отношении хороший результат даёт «штрих-
фокус», при скошенном аноде прямоугольный фокус проецируется
в квадрат (фиг. П, 6). Употребляется также крестообразный фокус,
возникающий при катоде, состоящем из двух перекрещённых
спиралей. В случае кругового фокуса, проецирующегося в виде эллипса,
выгодно устанавливать прямоугольную диафрагму с отношением
Фиг. II, 6. При скошенном аноде
прямоугольный фокус проецируется
в квадрат.
сторон 6:1—таково будет примерно отношение осей эллипса.
Распределение интенсивности в фокусе и, следовательно, форму
фокального пятна определяют събмкой по методу камеры-обскуры.
§ 2. Спектр рентгеновских лучей
а) Общие замечания. Разложение в спектр. Измерение длины
волны. Как показывает опыт, рентгеновское излучение
представляет собой электромагнитные волны. Малость длины волны делает
весьма яркими их квантовые свойства. Поэтому законны два
описания рентгеновского излучения. Во-первых, рентгеновские лучи
могут быть разложены в волновой спектр, характеризующийся
функцией 1{к), т. е. интенсивностью в функции длины волны. С
другой стороны, рентгеновские лучи представляют собой поток
фотонов энергии fo>, где частота v = -r- (с — скорость распространения
излучения 3 • 10ю см/сек). Величина Дту — число фотонов частоты
у — соответствует I (X) в волновом описании. Полная интенсивность
рентгеновского излучения равна
Jl(X) dl или |A"vfcvdv.
Таким образом,, охарактеризовать данное рентгеновское
излучение, — это значит сказать, из каких длин волн оно еостоит (или

168 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [ГЛ. 1*
из каких фотонов) и указать интенсивность каждой из длин волн
(количество фотонов каждого сорта).
Как мы увидим ниже, приходится сталкиваться как со сплошным,
так и с прерывным спектрами рентгеновских лучей. Сплошной (или
непрерывный, или «белый») спектр описывается видом кривой I (X).
Прерывный (или характеристический) спектр характеризуется
совокупностью спектральных линий, имеющих определённые длины волн
и определённые интенсивности.
Фиг. II, 7. Диффракция рентгеновских лучей на
отражательной решётке; UW — первичный луч; R,B\,
Вп, Вш—лучи диффрагированные в нулевом,
первом, втором и третьем положительных порядках;
Р — диффракционная решётка.
Измерение длин волн рентгеновских лучей может быть
выполнено так же, как и для световых лучей, с помощью диффракциопной
решётки.
Коэффициент преломления рентгеновских лучей меньше 1 на
величину порядка 10~6. Было показано, что при падении на стекло
под углами скольжения 6' 10" рентгеновские лучи претерпевают
полное внутреннее отражение.
Если под углами меньше указанного заставить падать
рентгеновские лучи на диффракционную отражательную решётку (200
линий на 1 мм), то, несмотря на малость длины волны, удастся
добиться прекрасного разрешения и измерить длины волн
рентгеновских лучей с достаточной точностью. Схема опыта показана на
фиг. II, 7. Если угол отражения равен а0, то кроме луча,
отражённого под этим же углом а0, возникнут диффрагированные лучи
под углами a0z+zou а0±«2 и т. д. Следует отметить, что
отрицательные порядки обладают слитком малой интенсивностью, и
измерение проводится по положительным порядкам.
Разность хода между лучом отражённым и лучом диффрагирован-
пым в положительном %-ом порядке равна: acosa0 — acos(a0-|-<pn),
где a — постоянная решётки. Деля эту величину на п, найдём
длину волны спектральной линии.

§2]
СПЕКТР РЕНТГЕНОВСКИХ ЛУЧЕЙ
169
Измерения при помощи диффракционной решётки, как метод
исследования спектра, имеют смысл лишь для очень длинных волн
(более 20 ангстрем). В остальных случаях эти измерения имеют
лишь метрологический смысл, позволяя установить
непосредственным измерением длины волн спектральных линий в долях
сантиметра (ангстремах). Само же'исследование спектра проводится,
как правило, отражением рентгеновских лучей от грани кристалла.
Взаимодействие рентгеновского луча и кристалла изучается
весьма детально в дальнейших главах. Здесь нам будет достаточно
провести элементарное
рассуждение, которое сделает
понятным сущность метода
измерения длины волны.
Грань кристалла
параллельна узловым плоскостям
решётки. Рассеяние
рентгеновских лучей кристаллом
можно рассматривать как
создание каждым узлом
решётки элементарной сфери- ^иг. 11,8. Отражение плоской волны,
ческой волны.
Если бы существовала одна узловая плоскость, на которую под
углом скольжения 0 падает плоская волна, то благодаря
интерференции элементарных волн возникала бы волна, «отражённая» иод
тем лее углом Ь (фиг. 11,8). Но рентгеновские лучи проникают
в глубь кристалла. Ноэтому «отражение» происходит от серии
параллельно расположенных узловых плоскостей.
Интерференция этих отражённых волн приводит к тому, что
отражение становится возможным лишь при некоторых строго
определённых углах скольжения &. Действительно, как видно из
фиг. IT, 9, разность хода между лучами, отражёнными от первой
и второй, второй и третьей и т. д. плоскостей равна 2d sin 0, где
d — межплоскостное расстояние. В отражении участвует
практически бесконечное число узловых плоскостей. Поэтому лишь при
строгом соблюдении условия — разность хода равна целому числу
длин волн — будет возпикать вторичный луч. Уравнение Вульфа-
Брэгга
2dsinft = wX (11,1)
является основной формулой рентгеноструктурпого и рентгеноспек-
трального анализов.
Очевидно, что при данном 9- кристалл отразит какую-то
определённую волну спектра. Исследование всего спектра может
производиться вращением кристалла под падающим рентгеновским
лучом: Каждому зпачению угла будет соответствовать некоторая
Длина волны X. Спектр может фотографироваться, а может также
лучяоааащии
S/уч ffmpaMsuitofLL

170 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [ГЛ. II
измеряться при помощи ионизационной камеры (ионизационный
рентгеноспектрограф).
Зная точное значение длины волны из измерений при помощи
диффракционной решётки, можно из измерений углов скольжения
вычислить d для грани употребляемого стандартного кристалла.
На практике пользуются в" качестве стандартных веществ каменной
солью (d — 2,8143 А), кальцитом (d = 3,03 А), сахаром {d = 10,57 А),
слюдой (d = 9,93A).
Исторически дело развивалось не совсем так. Рентгеновские
спектры были уже тщательно изучены, прежде чем были
проведены хорошие измере-
Луч падающий ^ Луч отраженный ния на
дифракционных решётках. Каким
же образом были
оценены в абсолютных
единицах длины волн?
Это было сделано
примерным вычислением
межплоскостного
расстояния граней таких
кристаллов как
кальцит и каменная соль.
Для кристалла
хлористого натрия это
вычисление является
весьма простым;
однако, несмотря на свою
нростоту, идея этого
вычисления является
весьма замечательной,
если учесть, что в то
время строение
кристаллов было
совершенно неизвестно. Хлористый натрий является ионным
соединением, следовательно, его кристаллы построены из ионов Na+ и С1~.
Было сделано предположение (которое является наиболее
естественным и вероятным), что в решётке кубического кристалла
хлористого натрия катионы и анионы чередуются, т. е. что
ближайшими непосредственными соседями катиона являются
анионы, и наоборот. Если поместить в узлы примитивной
кубической ячейки ионы Na+, разделив их ионами С1~ (которые
будут находиться в серединах рёбер куба), то, чтобы разделить
ионы С1~, придётся поместить ионы Na+ ещё и в центры всех
граней. Чтобы разделить эти ионы Na+, придется поместить ион С1
ещё и в центр ячейки. После этого между каждыми двумя ионами
Фиг. II, 9. К выводу уравнения Вульфа-Брэгга
АО = ОВ = -А-й ; АС = 2AD cos Ь = 2d *^-2 .
sin & sin о
Разность хода лучей, отражённых от
соседних плоскостей параллельного семейства,
равна Д = {АО + OB) — AC = 2d sin &. Разность
хода лучей, отражённых от несоседних
плоскостей, кратна Д.

§2]
СПЕКТР РЕНТГЕНОВСКИХ ЛУЧЕЙ
171
Na+ оказывается ион С1", и наоборот, и сделанное предположение
оказывается выполненным. Последовательные стадии этого
заполнения ячейки ионами и окончательный результат изображены на
фиг. II, 10. Межплоскостное расстояние d100 равно расстоянию
между центрами соседних ионов Na+ и С1~, расположенных ни
ребре куба. Оно вдвое меньше периода повторяемости в этом
направлении. dm является ребром куба, в вершинах которого
находятся 4 иона Na+ и 4 иона С1~. Следовательно, на него приходится
половина «молекулы» (ибо частица, находящаяся в вершине куба,
принадлежит ему лишь на 1/8). Этот куб в восемь раз меньше
элементарного куба.
Фиг. II, 10. Последовательные стадии «заполнения ячейки»
NaCl ионами.
Теперь dm легко вычисляется из уравнения
. М-1,65- К)"24
о = з ,
2- dl00
где М — молекулярный вес; 1,65 • 10-24 г — масса атома водорода,
а 2 — плотность.
Аналогичным образом было вычислено межплоскостное
расстояние для кристалла кальцита: 3,029 • 10~8 см = 3,029 А.
Мы видим, что эти вычисления требуют знания массы атома
водорода и величины плотности. Измерение последней особо трудно,
так как по идее нам требуется знать истинную плотность кристалла,
не содержащего трещин и включений.
Сознавая невозможность точного абсолютного измерения,
исследователи ввели особую единицу длины для длин волн рентгеновских
лучей и межплоскостных расстояний кристаллов. Эта новая
единица, длины, называемая килоиксом (кХ), определяется следующим
Образом: межплоскостное расстояние d100 кальцита равно 3,029 кХ.
Таким образом, приближенное вычисленное значение межплоскост-
о
ного расстояния кальцита, выраженное в А, считается вполне
точным при выражении его в килоиксах. Кальцит был
выбран в качестве стандарта в виду того, что его кристаллы
являются обычно весьма совершенными, вследствие чего ошибка
в определении плотности мала. Кроме того, и применение

172
ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ
[ГЛ. II
кристаллов кальцита представляет ряд практических преимуществ
(лёгкая доступность и др.).
Последующими измерениями длин волн рентгеновских лучей
непосредственно в абсолютных единицах (диффракционные решётки)
было показано, что кХ—единица, близкая к величине 1А = 10~нем,
поэтому в очень многих случаях не делают различия между кило-
иксом и ангстремом. Это явилось прекрасным подтверждением
правильности идеи, положенной в основу примерного вычисления
межплоскостных расстояний в абсолютных единицах. Последние
опыты с диффракцией рентгеновских лучей от решётки показали,
что 1кХ отличается от 1А на 0,2%- Следует иметь в виду, что
в книгах и статьях, вышедших до 1947 г., говорили об ангстремах,
хотя имелись в виду килоиксы. Все таблицы длин волн, вышедшие
до этого времени, составлены в килоиксах (хотя авторы таблиц
пользуются словом «ангстремы»). Начиная с 1947 г. между двумя
названиями начинает проводиться различие. Соотношение между
килоиксом и ангстремом таково:
1 кХ = 1,00202 А.
Точность самого фактора перехода порядка 0,003%. Так как
длины волн в килоиксах были измерены с точностью до 0,001%,
то, вычисляя длины волн в ангстремах, мы можем давать цифры
с точностью до 0,004%.
Для примера приведём значения длин волн К« — дублета меди:
в ангстремах Kt —1,54050, К^ —1,54434, в килоиксах Kt—
1,53743, Аа,—1,54122.
Можно предложить ряд способов измерения интенсивности
различных участков сплошного спектра, а также спектральных линий.
Совершенно безупречным способом явилось бы измерение
количества тепла, выделяющегося в теле, полностью поглощающем
рентгеновский луч. Для этой цели можно воспользоваться болометром,
термостолбиком, радиометром. Практическое осуществление
подобных измерений весьма сложно. Поэтому на практике пользуются
либо оценкой почернения на фотоплёнке, либо измерением
ионизационного тока в камере, куда падает рентгеновский луч.
Зависимость этих величин от интенсивности рентгеповских лучей
различных длин волн исследовалась достаточно тщательно, и указанные
измерения с успехом служат для сравнения интенсивностей, а при
тарировке могут быть использованы и для измерения
интенсивности в эрг/см*. Об измерениях интенсивности мы будем говорить
подробней на стр. 192.
6) Непрерывный спектр рентгеновских лучей. Типичный
спектр рентгеновской трубки показан на фиг. II, 12 (средняя
кривая). При рассмотрении этой картины создается впечатление, что
на плавную, сплошную кривую накладываются несколько острых
пиков (спектральных линий). Сравнение спектров, создаваемых

§2]
СПЕКТР РЕНТГЕНОВСКИХ ЛУЧЕЙ
173
анодами из разных элементов, показывает, что сплошной спектр
присутствует всегда, а спектральные линии, накладывающиеся на
него, характерны для данного элемента. Таким образом опыт
приводит к следующему суждению: рентгеновский спектр, возникающий
от вещества, можно рассматривать как сумму непрерывного спектра
и характеристических для данного вещества спектральных линий.
Опыт показывает далее, что характеристический спектр возникает
лишь, начиная с некоторого критического напряжения. Для
некоторых металлов оно может быть очень высоким (например, для
вольфрама это 70 кв).
Рентгеновские лучи распространяются от места возникновения
(места, куда попадают электроны, бомбардирующие анод) во все
стороны. Интенсивность лучей зависит от угла а, образуемого
рентгеновским лучом с электронным лучом. Интенсивность лучей
зависит от менделеевского числа материала анода Z, от
приложенного к трубке напряжения V, от силы анодного тока и от X. Таким
образом интенсивность луча
1=1 (X, V,Z,a,iA).
Рассмотрим по отдельности характер зависимости интенсивности
сплошного спектра от этих факторов.
Зависимость от длины волны показана на фиг. II, П. Кривая
имеет резкую коротковолновую границу, возрастает до максимума
при средних длинах волн и затем плавно спадает в сторону
длинных волн.
Возникновение сплошного спектра обязано своим
происхождением торможению электронов в материале анода. Электроны,
обладающие энергией Е1г полученной за счёт ускорения в электрическом
поле, теряют свою энергию, благодаря торможению, до величины Е2-
Разность энергий выделяется в виде излучения
El— #2 = Ь.
Величина Е% может принимать любые значения от Ех до 0. Таким
образом частоты возникающих лучей лежат в границах от
%ах = Г ДО vmin = 0-
Очевидно, что не перешедшая в излучение энергия электронов Е.2
Ьереходит в тепло. Эта последняя часть энергии много больше
части, превратившейся в излучение. Коэффициент полезного
действия рентгеновской трубки — мы ещё будем говорить о нем
ниже—ничтожно мал.
Теоретические расчёты, указывающие на вероятность перехода
Данной части энергии в энергию излучения, а также на вероятность
того или иного направления рентгеновского кванта, наталкиваются

174
ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ
[ГЛ, II
на большие трудности и проведены лишь для упрощённых условий,
сильно отличающихся от действительных.
Значение максимальной частоты или, что то же,
коротковолновой границы спектра есть функция напряжения, приложенного
к трубке. Действительно,
(11,2)
, ch
Amin jjj^ у
где с— скорость распространения излучения (3 • 1010 см/сек), а Ех
есть кинетическая энергия электрона
которая возникает за
вольфрам
0,2 03 ОА O.S 0.6 0,1 ОД Q9
Фиг. II, 11. Распределение
интенсивности белого спектра в
зависимости от напряжения на трубке.
Анод — вольфрам.
счбт работы eV электрического
ch
поля. Таким образом ^miD = -rp.
Подставляя известные значения
констант, получим формулу
К-^Ц?-, (п,з)
где XraiD выражено в ангстремах,
а V в киловольтах. Таким
образом при напряжении 30—40
киловольт, наиболее часто
употребляющемся в рентгеноструктур-
ном анализе, спектр начинается
о
примерно с 0,3 А.
Зависимость кривой
сплошного спектра от напряжения на
трубке иллюстрируется фиг. II, 11.
Кроме сдвига границы спектра
в коротковолновую часть, о чём
мы только что говорили, при
увеличении напряжения происходит
сдвиг максимума к коротким
волнам и возрастают все ординаты кривой. На этом рисунке показаны
кривые, имеющие место при постоянном напряжении. Если
напряжение пульсирующее, что имеет место во всех обычных
установках, работающих от трансформатора; то спектр представляет собой
наложение непрерывного ряда спектров. Коротковолновая граница
определяется, разумеется, максимальным значением напряжения.
Форма кривой искажается таким образом, что увеличивается
удельный вес длинных волн.
Мы не можем привести каких-либо удобных формул,
позволяющих определить, во сколько раз увеличивается интенсивность той
или иной длины волны при увеличении напряжения.
Сравнение спектральных кривых различных анодов,
проиллюстрированное на фиг. II, 12, позволяет утверждать, что ординаты

§2]
СПЕКТР РЕНТГЕНОВСКИХ ЛУЧЕЙ
175
кривой /(X) для данного напряжения примерно пропорциональны
первой степени менделеевского числа Z.
Зависимость интенсивности от направления луча изображена
на фиг. II, 13. Излучение рентгеновских лучей происходит с
максимальной интенсивностью под углом порядка 60° к пучку
электронов. Это обстоятельство используется при изготовлении трубок
со скошенным анодом. Такие трубки имеют лишь одно окошко
для выпуска лучей. В трубках с
четырьмя окошками
используются лучи, идущие под углом 100°
к пучку электронов. Как видно
из приведённого рисунка, в этих
трубках интенсивность белого
излучения будет в 2—3 раза
меньше при прочих равных
условиях.
Мы не будем вдаваться в
детальное рассмотрение вопроса.
Укажем только, что нами
приведено лишь типичное
распределение интенсивности по углам.
Исследования показывают, что
характер этого распределения
зависит от длипы волны,
напряжения па трубке и менделеевского
числа.
Весьма полезной
характеристикой сплошного спектра
является значение интегральной
интенсивности, т. е. полной
энергии, выделяемой анодом в виде
рентгеновского излучения, кото-
рая равна Г / (X) dK С достаточной точностью выполняется формула
со
полная энергия Е% = аг ZV2, (II, 4)
где г — сила тока в трубке, Z—менделеевское число,
V—напряжение, а — постоянная.
Так как энергия, доставляемая аноду электронами, равна iV,
то коэффициент полезного действия рентгеновской трубки равен
Y) = aZr, (П,5)
где a — постоянная, определяемая на опыте. Рядом измерений для
Фиг. II, 12. Зависимость
интенсивности белого спектра от материала
анода. Показаны две
характеристические линии Мо-излучения.

176
ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ
[ГЛ. II
/"ГУ* 9°° *Л°
Направление злгнтрохноео луча
Фиг. П, 13. Азимутальное распределение интенсивности для
различных X при постоянном (31 кв) напряжении на трубке
1 : X = 0,43 А, 2 : X = 0,53 А, 3 : X = 0,73 А.
;оо° У м»
Фиг.
Направление электронного луча
II, 13а
интенсивности X . при
mm c
Азимутальное распределение
различных
напряжениях на трубке:
I 37,8 кв (X . = 0,326 А),
II 31,0 кв (а = 0.398 А),
III 24,0 кв (Х"1!^ 0,514 А),
Х ПИП о'
IV 16,4 кв (к . = 0,753 А).

§2]
СПЕКТР РЕНТГЕНОВСКИХ ЛУЧЕЙ
177
этой величины было установлено значение
a=:(10d=3) • Ю-10.
Для вольфрамового анода и напряжения 100 кв к. п. д. равен 7°/00!
Практически вся энергия тратится на нагревание анода.
в) Характеристический спектр. Рентгеновский
характеристический, спектр послужил одним из основных орудий в изучении
строения атома. Полное обсуждение его особенностей связано поэтому
с вопросами строения атома. В этом курсе мы не имеем возможности
вдаваться в
подробности и изложим поэтому
лишь те данные,
знание которых
необходимо для лиц,
работающих в области
рентгеновского
структурного анализа.
Под ударами
электронов катодного
пучка атомы анода
могут притти в
возбуждённое состояние.
Возвращаясь в исходное
невозбуждённое
состояние, атом отдаёт
энергию в виде
излучения. Так как
энергия атома может
принимать только
дискретные значения, то
излучение будет
состоять из отдельных
спектральных линий—
возникает характеристический спектр. Картина энергетических
уровней атома и схема возникающих переходов показаны на фиг. 11,14.
Энергетические уровни собраны в слои. Наиболее низким является
/Г-слой, имеющий 1 уровень, далее Х-слой — 3 уровня, Ж-слой—
б уровней и т. д. Возбуждение заключается в удалении электрона
с данного уровня и переходе его на более высокий уровень или
удалении за пределы атома. Излучение состоит в переходе другого
электрона с одного из более высоких уровней на освободившийся
более низкий уровень.
Предположим, что скорость электронов, бомбардирующих анод,
постепенно возрастает (растёт напряжение на трубке). Как только
энергия летящего электрона достигнет величины, позволяющей
удалить один из атомных электронов за пределы атома, сразу же
Nw
Ы¥1
Nv
NIV
N„ —i
A/,
4;
W<-
!V"fc
n I
4 3 Ц *?Ъ
4 3 $/ 2Fto
4 2 & Ч3/г
4 / 3/г Р3Я
4 1 1/2 22P'/2
■4 0 1/2 S't
My —
MIV —
м„ —
M, -
.3 2
3 г
■ з i
■ 3 i
■з о
5/2
p
3/2
1/2
\dS/2
43/2
iP*2
2 Si/2
2 J
2 f
-2 0
3/2
V2
1/2
\P3/2
2 PI/2
St/2
К
1 О
s%
Фиг. 11,14. Схема энергетических уровней, элек»
тронных переходов и излучаемых при этом
спектральных линий.

178 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [гл. II
возникнет серия спектральных линий, соответствующая переходам
электронов с более высоких уровней на освободившийся. Таким
образом для каждого из уровней можно указать напряжение
возбуждения. Очевидно, что в спектре будет содержаться одна jff-серия
линий, три Х-серии, пять Ж-серий и т. д. К-серия будет возникать
последней по мере возрастания напряжения.
Интенсивности линий определяются так называемыми
вероятностями перехода электрона с одного из уровней на другой, которые
могут быть теоретически вычислены.
Число сильных линий в каждой серии не велико (это главные
линии серии); имеются линии особо выделяющиеся по
интенсивности. Линии ЙГ-серии много сильнее линий Х-серии, в свою очередь,
линии Х-серии интенсивнее линий М-серии.
Линии if-серии имеют наиболее короткие длины волн.
Самой сильной линией К- сери и любого элемента является
а- дублет. Это две очень близкие (в большинстве опытов сливающиеся
в одну) спектральные линии, возникающие благодаря переходам
с уровней Хш и Хц на уровень К. Разность К, — К, не
превышает 0,005 А. Если дублет расщепить, то окажется, что aj-линия
примерно в два раза сильнее а2-линии. Второй по силе линией
является более коротковолновый р-дублет А'-серии, к которому
примыкает ещё одна (3-линия. Из трбх р-линий наиболее сильной
является линия р, (в структурном анализе именно о ней идёт речь,
когда говорят о бета-линии), возникающая в результате перехода
Mm —► К. р-линия слабее аглинии примерно в б раз. Остальные
линии ещё в несколько раз слабее и не имеют значения в
структурном анализе.
В таблице II, I приведены длины волн /С-серии (в,, а9 и р) для
употребляющихся на практике анодов. Из этой таблицы видно, что
весь характеристический спектр закономерно сдвигается в сторону
коротких волн с возрастанием менделеевского числа.
Длины волн Х-серии тяжёлого элемента могут оказаться короче
длин волн .ЙТ-серии лёгкого. Например, Х-серия вольфрама начи-
о
нается с длины волны 1,03 А, в то время как, скажем, ЯГ-серия меди
с
начинается с 1,4 А.
Напряжение возбуждения серий также закономерно возрастает
с увеличением порядкового номера. Так, напряжения возбуждения
для ЯГ-серии: Ti (Z = 22) — 4,9 кв, Cr(Z=24) — 6,0 кв, Fe(Z=
= 26) — 7,1 «в, Си (Я =29)—8,9 кв, Mo(Z=42) — 20*в, W(£=
=з 74) —69,3 кв.
• Мы. говорили об относительных значениях интенсивности линий*
характеристического спектра. Что же касается абсолютной
интенсивности характеристического спектра, то она возрастает с
увеличением напряжения пропорционально (V—F0)«, где
V0—напряжение возбуждения, a w лежит в пределах 1,5 — 2. Для практической

Таблица II, I
Некоторые данные о /С-излучанви для различных анодов, находящих
применение в рентгеноструктурном анализе
ту.»
ГО
Элемент
Мен-
де-
леев-
ское
число
24
25
26
27
28
29
3)
42
45
46
47

Символ
Сг
Ми
Fe
Со
Ni
Си
Zn
Mo
Rh
Pd
Ag
^
Длина волны
вА
2.28962
2,10174
1,93597
1,78891
1,65783
1,54050
1,43510
0.70926
0.61326
0,58545
0,5o941
в kX
2,2850
2,0975
1,9321
1,7853
1,6545
1,5374
1,4322
0.7078
0,61202
0,58427,
0.56267
Линия
/r3
Длина
волны
в А
2,29352
2,10570
1,93991
1,79279
1,66168
" 1.54434
1.43894
0,71354
0,6Ш
0,5843
0,5583

Относительная
интенсивность *)
51
55
49
53
48
46
49
51
51
52
52
а;.2)|
Длина Длина
волны волны
в А в А
2,2909
2.1031
1,9173
1,7902
1,6591
1,5418
1,4364
0,7107
0,6147
0,5869
0.Е609
2,08479
1,91016
1,75654
1,62073
1,50008
1,39217
1,29520
0,63225
0,54559
0,52052
0,49701
**

Относительная
интенсивность г)
21
22
18
19
17
16
18,5
23
25
25
24
Граница К-
полосы
поглощения
в А
2,0701
1,8954
1,7429
1,6072
1,4869
1,3802
1,2831
0,6197
0,5341
0,5090
0,4855
•

Напряжение
возбуждения К-
серии в
киловольтах
6,0
6,5
7,1
7,7
8,3
8,9
9,6
20,0
23.2
24,4
25,5

Оптимальное
напряжение на
трубке
тах 3)
20—25
25
25—30
35—45
50
I
о
со
а
я
к
X
Ьа
«<
л
•ЕВ
ВС
Примечания: 1) Интенсивность Ка -линий принята за 100. 2) Ввиду незначительной разности длин волн
линий Ка и Кл пятна, отвечающие этим линиям излучения, часто не разрешаются на рентгенограммах. Поэтому
вводят некоторую условную длину водны ХЙГв, лежащую примерно посредине между XJfai и ХК"ад. Этой средней
длиной волны Xjfife пользуются при расчётах. 3) Оптимальное в смысле соотношения интенсивностей линий /f-серии .*-.
и остального спектра. .«с

180 получение Рентгеновских лучей [гл. it
работы* существенно найти такой режим трубки, при котором
характеристический спектр наиболее резко выделялся бы на фоне
сплошного; Эти условия ищут опытным путём для каждого
материала анода. Они и приводят к наиболее часто употребляемому
напряжению 30—40 киловольт для железного и медного анодов.
§ 3. Общая картина взаимодействия рентгеновских
лучей и вещества
При встрече рентгеновского луча с веществом происходят весьма
разнообразные и сложные процессы. В общем случае часть энергии
падающего рентгеновского луча, потерянная при прохождении луча
через вещество, может .пойти на создание вторичных, третичных
и т. д. рентгеновских-лучей (рассеянные лучи), на вырывание из
атомов веществ электронов и на выделение тепла. Для излагаемого
здесь предмета главнейшей и изучаемой потерей энергии
падающего луча является рассеяние рентгеновских лучей электронами
без изменения длины волны (так называемое классическое
рассеяние). Проходя через вещество, рентгеновская волна приводит
в состояние колебания электроны атомов этого вещества.
Колеблющиеся электроны становятся источниками элементарных сферических
волн, распространяющихся во все стороны.
Наряду с этим возникают вторичные рентгеновские лучи иного
происхождения. Как под действием бомбардирующих электронов,
так и под действием падающих рентгеновских квантов может
возникнуть характеристический рентгеновский спектр. Для
его возникновения необходимо лишь выполнение условия
&Уц»дающ. > Характер. Например, квант К, излучения меди (X = 1,54 А),
попадая в железо, возбудит атомы железа и, таким образом,
попадание такого кванта в атом железа явится причиной возникновения
характеристического спектра. Более мягкие кванты могу! возбуждать
лишь Х-серию или Л/-серию вещества.
Наконец, кроме этих двух типов вторичного излучения имеется
и ещё один: это излучение со слегка увеличенной длиной волны.
При попадании кванта Ь» . в электрон может произойти упругое
соударение фотона с электроном, при этом фотон может потерять
часть своей энергии. Если энергия фотона после столкновения
равна Av'<fev, то это и означает возникновение рассеянного
излучения, у которого частота стала меньше и, следовательно, длина
волны больше. Появление вторичного излучения этого вида (с
уменьшенной частотой) называют квантовым рассеянием. Итак,
интенсивность вторичного излучения /вторщн. слагается из следующих частей:
^ вторит. == -/клаоскч. ~\~^характер* ~у"-*Евангов.
Естественно, что вторичные лучи могут вызвать появление
третичных и т. д. Скажем, вторичное характеристическое излучение,

.3] ОБЩАЯ КАРТИНА ВЗАИМОДЕЙСТВИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ 181
созданное в атомах вещества, будет рассеиваться в других атомах
опять-таки всеми тремя механизмами. В некоторых случаях*(но не
в структурном анализе) роль таких третичных лучей может быть
немаловажной.
При взаимодействии первичных рентгеновских фотонов с атомами
часть энергии может быть передана электронам. Во-первых, это
имеет место при квантовом эффекте. Электроны, принимавшие в нем
участие, называются электронами отдачи. Во-вторых, энергия
фотонов переходит к электронам, выбитым из атома. Как и в оптике,
выбитые из атома электроны называются фотоэлектронами.
Отношение числа электронов отдачи к числу фотоэлектронов
исключительно резко зависит от длины волны. Для мягких лучей,
употребляющихся в структурном анализе, число электронов отдачи
практически равно нулю; при длине волны 1МоКа это отношение
о
равно ОД, при Х = о,4 оно уже равно 1, а при Х = 0,13А число
фотоэлектронов в 72 раза меньше числа электронов отдачи.
Если электронам, получившим дополнительную энергию, не
удалось выбраться из вещества, то эта добавочная энергия пойдёт на
увеличение скорости электронов и атомов вещества, т. е. перейдёт
в форме тепла во внутреннюю энергию вещества. Кроме того, эти
электроны с повышенной энергией будут переходить на более низкие
уровни, которые освободились вследствие выбивания с них
электронов рентгеновскими квантами. При этом, естественно, разность
энергий электрона будет выделяться в виде кванта
характеристического излучения. Таким образом появление характеристического
излучения непосредственно связано с появлением в веществе
фотоэлектронов.
Итак, все «события», происходящие в веществе при попадании
в него рентгеновского луча, могут быть представлены следующей
схемой:
Падающий луч
Клисси-
ческое
р ассея-
ние
1
Зторичные лу
1
1


ристические
лучи
чи
1

Квантовое

рассеяние
Прошел
1
Электроны
1
1
Тепло
ший луч
Электроны,
вышедшие нз вещества
1
I I
Электроны Фотоэлек
отдачи троны
Рассеяние с изменённой длиной волны является помехой для
рентгеноструктурного анализа и иногда существенной. Поэтому сле~
дует отметить некоторые детали квантового эффекта,

182 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [ГЛ.- II
Кристалл Ионизационная
номера
Схвма установки, позволяющей изучать рассеяние
рентгеновских лучей веществом, показана на фиг. II, 15. На образец R
падают лучи из трубки Т. Диафрагмы выделяют лучи, рассеянные
под интересующим нас
углом, скажем, 90°. Эти лучи
падают на кристалл,
поворачивая который, мы
можем выяснить
спектральный состав рассеянного
излучения.
Опытами этого рода,
а также квантово-механи-
ческими расчётами
(которые в этом случае удаётся
довести до конца)
установлен ряд интересных
фактов. При данном угле
рассеяния . изменение длины
волны одинаково для всех
веществ. При угле
рассеяния 90° оно равно 0,0242 А.
Соотношение величин квантового и классического рассеяния
невыгодно у лёгких элементов. Интенсивность квантового
рассеяния в данном направлении у органических веществ в 5 — 6 раз
больше интенсивности
классического рассеяния,
а, например, у меди
в пять раз меньше. На §
фиг. II, 16 приводится §
Фиг. II, 15. Схема излучения рассеяния
рентгеновских лучей.
К„ с
измененной А
Фиг. 11,16. Спектральный состав
квантового рассеяния графитом излучения МоЛГ.
Угол рассеяния 90°.
типичная кривая, полу- «
ченная при помощи уста- $
новки, схема которой бы- <5
ла изображена на пре- ^
дыдущем чертеже, для
рассеяния от графита
под углом 90°.
Разумеется, что для
наблюдения должно быть
выбрано такое направление, которое не удовлетворяет условию
диффракции (уравнение II, 1).
Квантовое рассеянное излучение некогерентно; таким образом
порядок в расположении атомов, вообще говоря, не влияет на
характер квантового рассеяния. Этот сорт рассеянных рентгеновских
лучей участвует в создании общего фона на рентгенограмме.
Зависимость интенсивности этого фона от угла рассеяния молсет
быть теоретически вычислена. Эти формулы не имеют, однако,

§4]
КОЭФФИЦИЕНТ ОСЛАБЛЕНИЯ
183
практического применения в рентгеноструктурном анализе, так как
причин возникновения фона несколько, и общее его значение не
поддаётся лёгкому расчёту.
Если делить энергию падающего луча на поглощённую,
прошедшую и рассеянную, то обычно под последней понимают энергию,
уносимую электронами отдачи, классическим и квантовым
рассеянием. Энергию -фотоэлектронов и характеристических лучей относят
к поглощению. Разумеется, деление носит условный характер,
и наиболее важным для практики является суждение об ослаблении
рентгеновского луча.
§ 4. Коэффициент ослабления (поглощения)
а) Вычисление коэффициентов ослабления. Вследствие всех
процессов, рассмотренных в предыдущем параграфе, рентгеновский
луч интенсивности J, пройдя в веществе путь dx, ослабеет по
интенсивности на величину, пропорциональную толщине dx и
интенсивности I. Таким образом
—dl—pldx,
где коэффициент пропорциональности р называется коэффициентом
ослабления. Интегрируя это уравнение, мы сможем вычислить
ослабление, которое испытывает луч, проходя слой вещества конечной
толщины х. Получим:
' 7=j0e-^, (11,6)
где 1о — интенсивность падающего, а / — прошедшего через слой
х луча.
Коэффициент jx принято разбивать на две части и полагать
H = *-f-o, (И,7)
где т— коэффициент поглощения, учитывающий потери энергии
за счёт возникновения характеристических лучей и фотоэлектронов,
а а—коэффициент рассеяния, учитывающий потери энергии за счёт
классического и квантового рассеяния, а также электронов отдачи.
Коэффициенты {*, г и о измеряются в обратных сантиметрах.
Весьма часто вместо коэффициентов ц, т и о используют так
называемые массовые коэффициенты
7' 7' 7'
где р — плотность вещества. Дело в том, что взаимодействие
рентгеновского луча с веществом определяется числом молекул,
приходящихся на единицу объёма, и составом этих молекул. Таким
образом взаимодействие рентгеновского луча с веществом и в
частности его ослабление зависит от плотности вещества. Однако плот-

l.S'i ПОЛ У ЧИНШ'! L'EHrrLMOirOBCK.llX ЛУЧЕЙ |ГЛ. II
ность, т. е. число молекул в единице объёма мозкет быть более
или менее случайной. Так-, например, плотность зависит от
температуры и агрегатного состояния, следовательно, пришлось бы давать
зависимость \i, -сиз от температуры. Чтобы избавиться от этих
неудобств, вводят массовые коэффициенты, которые характсризую'1'
ослабление, вызываемое определённым числом атомов. Поэтому
массовые коэффициенты не зависят от температуры и
агрегатного состояния, а зависят лишь от типа атомов, т. е. от
менделеевского числа.
При желании мозкпо закон ослабления применять в форме
п.
Г=Го'~^'т, (И,8)
где ш(=.гр) есть количество вещества в граммах, приходящееся
на площадку в 1 см2 слоя, пронизываемого лучами.
Наряду с массовыми коэффициентами в существующих таблицах
приводятся также атомные (молекулярные), равные произведению
V1* = 7 " М ' шн> (11,9)
где Ъ1 — атомный (молекулярный) вес и та—вес атома водорода.
Так как Мтп есть вес атома (молекулы) в граммах, то у^—
есть число атомов (молекул), находящееся в 1 см2 слоя вещества,
пронизываемого лучами. Подставляя значение (ха в закон
ослабления, имеем:
/= /0 oxpf — \ia -j^-\ , (11,10)
Mm
*t
hi.
где --гг-— есть число атомов (молекул), приходящееся на 1 см2
площади слоя, пронизываемого лучами. Разумеется, коэффициенты \ia>
•za и ап также не зависят от агрегатного состояния, плотности и
температуры вещества, как и массовые коэффициенты.
Коэффициенты |xw, xa, za имеют размерность площади.
Так как процессы рассеяния и поглощения определяются
свойствами атомов и не зависят от способа соединения атомов в
веществе, то коэффициенты а, ц« и — аддитивны (т. е. зависят лишь
от состава, а не от строения вещества), во всяком случае с
точностью до 10—20%- Такие отклонения от аддитивности наблюдаются
во многих случаях. Поэтому приводимыми ниже формулами
следует пользоваться лишь тогда, когда требования к точности
цифр не превосходят указанных выше. В противном случае следует
прибегнуть к непосредственным измерениям.
Коли даны атомарные коэффициенты ]а(Д $ и т. д., то ра —
молекулярный коэффициент поглощения вещества, состоящего из

§ и
КОЖЧГЦНИНТ 00ЛЛПЛ И1П1.Н
185
молекул, содержащих Si атомов первого сорта, Е2 атомов второго
сорта и т. д., равен
Если плотность вещества р, то коэффициент поглощения
химического соединения вычисляется по формуле
Mm-,
^1^Ч-^2|Л3)+...
(11,12)
При известной элементарной ячейке лучше пользоваться
рентгенографической плотностью. В этом случае формулу молено
преобразовать к такому виду:
1А
U)
V
К;%
>Ы''(<? -
(ПДЗ)
где V — объём элементарной ячейки, а пл и %> — количества атомов
данного сорта в ячейке.
Наконец, если определяется коэффициент поглощения смеси,
состоящей из ду весовых частей вещества с плотностью р{, д2 частей
вещества с плотностью р2 и т. д., то
Р _ "'I n _U1J'2// 4-
(И, 14)
D
"
J P
1К
г—J
.......
ш
1
*
i
б) Измерение коэффициента ослабления. Как мы увидим
ниже, коэффициент ослабления очень резко зависит от длины
волны излучения. Поэтому
измерения <х имеют смысл лишь
в том случае, если падающий
луч монохроматизирован
предварительным отражением от
кристалла. Пучок таких лучей
заставляют проходить через
объект, имеющий форму
пластинки с толщиной х,
нормально к ней. Лучи, прошедшие
через объект, попадают в
ионизационную камеру. Следует
обращать внимание на то,
чтобы в щель камеры не
попадало излучение, рассеянное образцом. Это достигается тем, что
щель ионизационной камеры располагается в некотором отдалении
от исследуемой пластинки (фиг. II, 17). Нет нужды в абсолютных
измерениях. Достаточно измерить величину ионизационного тока
при прохождении луча через пластинку и его величину при убран-
Фиг. II, 17. Принцип измерения
коэффициента поглощения. D— диафрагма,
11— пластинка, V— рассеянные лучи,
11. К. — ионизационная камера.

186 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [ГЛ. II
ной пластинке. Величины этих ионизационных токов
пропорциональны интенсивностяы I и 70. Отношение сил ионизационных
токов равно отношению интенсивностей. Поэтому, зная толщину
образца, найдём коэффициент ослабления по формуле
1 In Г»
.(ИД5)
в) Зависимость поглощения от длины волны и
менделеевского числа. Ниже будет показано, что из теории классического
рассеяния следует постоянство массового коэффициента рассеяния.
Более того, из теории следует числовое значение —, а именно 0,2
(см. стр. 214).
Для лёгких элементов квантовое рассеяние увеличивает эту
величину в 5—6 раз. В то же время поглощение веществ, состоящих
из легких элементов,
меньше. Таким образом,
чем больше
менделеевское число вещества, тем
меньше различие между
коэффициентами
поглощения и ослабления.
Однако даже для
органических соединений
массовый коэффициент
поглощения много
больше 0,2. Например, дли
углерода коэффициент
поглощения К- излучения
меди равен 5,5. Считая,
что коэффициент
рассеяния может стать равным (из-за квантового эффекта) даже 1,
мы веб же и здесь имеем право с точностью до 15—20%
приравнять друг другу коэффициенты ослабления и поглощения. Что же
касается элементов с менделеевским числом более 10, то там это
равенство будет уже выполняться с точностью опыта. При Z > 20
равенство ^ = х можно считать вполне точным.
Таким образом в последующем, говоря о закономерностях,
строго справедливых для поглощения, мы получаем право применять
их и для ослабления рентгеновских лучей.
Изменение р с длиной волны определяется характером процесса
вырывания фотоэлектронов из атомов вещества.
На общую тенденцию увеличения проницающей способности
кванта по мере возрастания его энергии (т. е. уменьшения
коэффициента поглощения с уменьшением длины волны) накладываются
так называемые скачки поглощения, возникающие в том случае,
О 0/ 0JQ3MQ5Q6Q7QSQ9WV U13 И ISA
Фиг. II, 18. Поглощение рентгеновских лучей
в платине. Зависимость коэффициента
поглощения от длины волны.

4]
КОЭФФИЦИЕНТ ОСЛАБЛЕНИЯ
187
если величина падающего кванта становится равной энергии,
необходимой для удаления электрона из атома.
Число скачков поглощения должно равняться числу уровней.
Так должен существовать один скачок поглощения К (удаление
электрона с /i-уровня), три скачка L, пять скачков М и т. д.
Типичная кривая показана на фиг. 11,18. При уменьшении длины волны
от 1,6 А до 1,1 А проницаемость кванта возрастает, но при Х= 1,1 А
энергия кванта становится равной той энергии, которая необходима
для удаления электрона с уровня Ъщ. Поглощение возрастает
скачком и опять начинает уменьшаться до следующего скачка.
Скачки поглощения называют также краями полос поглощения.
Если разложить в спектр пучок белых рентгеновских лучей, то
после прохождения лучей через вещество на фотопластинке образуется
система абсорбционных полос с резкими краями, соответствующими
скачкам в значении ц.
Ход коэффициента поглощения с длиной волны между двумя
скачками поглощения ближе всего передаётся кубической параболой,
т. е. уравнением ак*-\-Ъ. Например, поглощение А1 в
интервале от 0,1 до 0,4 А хорошо передаётся формулой: 14,45 A.3 -j- 0,15;
поглощение никеля в том же интервале — формулой 145 Xs-\- 0,20
(это значения массового коэффициента поглощения). Впрочем, на
практике пользуются не формулами, а таблицами. Приводим выборку
из такой таблицы; для примера даны коэффициенты поглощения V,
Mn, Ni, Zr, Pd для Ка-линий разных анодов (таблица 11,11).
Табл ица II, II
Массовые коэффициенты поглощения — (—j ванадия, марганца,
никеля, циркония и палладия для Ка излучения наиболее
распространённых анодов
Элемент
23 V
25 Мп
28 Ni
40 Zr
46 Pd
Излучение
•<
S
Ю
О
II
13.3
17,4
25,0
01,1
13.8
СО
о
II
17,7
22,6
32,3
80,9
17,6
г—
о
?
о
II
26Д"
33,5
47,4
17,2
26,7
ее
^+<
ю
Г-Г
II
227
284
49,2
143
207
OS
r-i
II
2Й"
275
348
61,0
173
254
•<
со
t-
СО
OS
II
422
63,0
93,1
260
376
8
о»
II
77,3
99,4
145
391
545

188 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [ГЛ. II
Зависимость поглощения от менделеевского числа носит
примерно такой же характер, что и зависимость от длины волны.
Общая тенденция заключается, очевидно, в увеличении поглощения
по мере возрастания менделеевского числа: чем больше число
электронов атома, тем он менее проницаем для данного кванта. Скачки
поглощения делают кривую \i = \l(Z) очень похожей на кривую ft =■ ji (a).
На фиг. II, 19 показан ход поглощения в зависимости от Z для
X = 1 А- Кривая для другой длины волны была бы вполне подобна
этой, но только границы
поглощения были бы сдвинуты. Скачки
поглощения смещаются к
коротким волнам по мере возрастания Z.
И здесь в промежутке между
скачками поглощения кривая идёт
примерно по кубической
параболе.
г) Фильтры. Механизм
явления поглощения делает понятным
следующий очень важный для
практики факт: длина волны
скачка поглощения очень близка (и
немного меньше) к длине волны
самой коротковолновой линии
соответствующей серии.
Действительно, скачок поглощения
соответствует энергии, которую нужно
затратить на удаление электрона, скажем, с 7£-уровн# за пределы атома,
самая же короткая линия JBT-серии соответствует переходу на К -уровень
С наиболее далёкого уровня атома. Разумеется, последняя энергия
должна быть немного меньше первой и, следовательно, длина волны
наиболее коротковолновой линии Х-серии должна быть немного
больше длины волны скачка JT-поглощения. В таблице длин волн,
которую мы приводили выше (таблица 11,1), даны также значения
границ полос поглощения. Как мы видим, длина волны jK^-линии
больше длины волны, соответствующей границе /i-полосы поглоще-
о
ния всего лишь на 0,01 — 0,02 А.
Такое соотношение в расположении /{"-линии и границы if-полосы
поглощения приводит к заключению, что наиболее выгодным
условием рентгеносъёмки будет исследование медного образца при
помощи излучения Ка меди, железного образца при помощи
излучения Ка железа и т. д. В этих случаях поглощение будет
минимальным.
Границы .йГ-полос поглощения приводят к возможности
применения специальных фильтров, ослабляющих |3-линию. Действительно,
например, Кг-линия меди имеет длину волны 1,54 А, кулиния 1,39 А
Ю 20 30 40 60 60 70 80 90
Фиг. 11,19. Зависимость атомного
коэффициента поглощения ра от
менделеевского числа Z поглощающего
вещества для X = 1 А.

§4]
КОЭФФИЦИЕНТ ОСЛАБЛЕНИЯ
189
Если только найти элемент, у которого скачок поглощения лежит
между этими длинами волн и использовать его в качестве фильтра,
более короткая Щ-линия будет ослабляться много более, чем 7Г„-линия.
Таким фильтром всегда может служить элемент, порядковый номер
которого на единицу меньше. Так, для медного излучения
фильтром является Ni (границя Ji-полосы поглощения 1,48 А).
Употребляющиеся для этой цели фильтры сведены в следующей
таблице И, III.
Таблица II, III
Фильтры для выделения Д^-линий
Материал анода и его
менделеевское число
, Вещество фильтра
и его менделеевское
число
Толщина
фильтра
в мм
Количество
вещества в t на
1 см2
Хром (Сг)—24
Железо (Fe) — 26
Медь (Си) — 29
Молибден (Мо) — 42
Серебро (Ag) — 47
Ванадий (V) — 23
Марганец (Мп) — 25
Никель (Ni) — 28
Цирконий (Zr) — 40
Палладий (Pd) — 46
0,005
0,007
0,03
0,03
0,004
0,0067
0,020
0,036
Если вещество фильтра не может быть получено в чистом виде,
то применяют любые химические соединения его. Фильтр
употребляется в виде фольги или
изготовляется нанесением
тонкого слоя вещества на какую-либо
прозрачную для лучей
подкладку.
Изменение белого спектра,
происходящее из-за поглощения,
выражается в том, что мягкая
часть излучения не проходит:
лучи становятся жестче. Для
примера на фиг. II, 20 приводится
непрерывный спектр
рентгеновских лучей, пропущенных через
1,5 и 10 мм алюминия.
Нетрудно рассчитать толщины
тех или иных материалов,
поглощающих лучи практически целиком. Пусть, например, требуется
определить толщину свинца, поглощающего практически нацело лучи,
исходящие из трубки, работающей при напряжении 40 кв. Самые
жёсткие лучи имеют при таком напряжении длину волны 0,3 А.
J0
Д?
ООк
V
ч
щ
——■
0.2
\6Л
0.6
0.8
Фиг. II, 20. Изменение интенсивности
белого спектра при фильтровании
через пластинки алюминия
различной толщины.

190 полу чади к рентгеновских лучей [гл. it
о
Коэффициент поглощения свинца для X = 0,3 А примерно
равен 100 ем-1. Будем считать практически полным поглощение,
при котором пройдет лишь 1/10 000 доля интенсивности падающего
луча. Тогда е_1СОж —Щоо или 1()0-г1£е = 1& 10 000 = 4. Отсюда
§ 5. Фотографическое действие рентгеновских лучей
и измерение интенсивности по почернению плёнки
а) Фотографическое действие рентгеновских лучей. Как
известно, результатом фотохимического процесса, происходящего
в фотоплёнке или фотопластинке под действием видимых и
рентгеновских лучей, является разложение бромистого серебра, причём
металлическое серебро выделяется в виде мельчайших частичек.
Однако для получения заметного почернения плёнки требуется
исключительно сильное и длительное освещение. При практически
же осуществляемых экспозициях никаких следов почернения плёнки
заметить нельзя. Первичное фотохимическое действие лучей лишь
подготовляет те места плёнки, на которые падали лучи, к более
или менее интенсивному выделению металлического серебра
(образование «скрытого» изображения). Действуя далее на пластинку
соответствующими реактивами, можно вызвать восстановление
металлического серебра в тем большей степени, чем сильнее было
освещено соответствующее место плёнки. В этом и заключается
процесс проявления. После проявления остаток неразложепного
бромистого серебра (из неосвещавшихся участков плёнки) удаляют
обработкой раствором гипосульфита и тем самым предохраняют
фотоплёнку от дальнейших изменений на свету (фиксирование).
Рентгеновские лучи вызывают в общем то же фотохимическое
действие, что и видимые лучи, ибо не существует плёнок,
чувствительных к рентгеновским и нечувствительных к видимым
лучам и обратно. Однако необходимо указать и существенные отличия
фотографического действия рентгеновских и видимых лучей.
Микроскопическое изучение поперечных разрезов фотоплёнок показывает,
что рентгеновские лучи вызывают появление зёрен металлического
серебра равномерно по всей толщине эмульсии; видимый же свет
вызывает появление зёрен лишь на освещенной поверхности
эмульсии. Это объясняется непрозрачностью светочувствительной
эмульсии для видимых лучей и прозрачностью её для рентгеновских.
Поэтому чувствительность плёнки к рентгеновским лучам возрастает
с увеличением толщины эмульсии. Специальная рентгеновская
плёнка вследствие этого изготовляется с более толстым
светочувствительным слоем, чем обычная, и кроме того обычно является
двухсторонней, т. е. покрывается эмульсией с обеих сторон. "Другое
отличие состоит в том, что плёнки с мелким зерном, мало чув-

§ 5] ФОТОГРАФИЧЕСКОЕ ДЕЙСТВИЕ РЕНТГЕНОВСКИХ ЛУЧИЙ 191
ствительные к видимым лучам, очень чувствительны к
рентгеновским. С увеличением зерна растбт чувствительность плёнки к
видимым и падает чувствительность к рентгеновским лучам.
Для количественного определения интенсивностей диффрагирован-
ных рентгеновских лучей необходимо знать зависимость почернения
плёнки S от интенсивности падающего излучения /. Почернение
определяют следующим образом:
S = lg%, (11,16)
где «о есть интенсивность пучка света, падающего на проэкспони-
рованную и проявленную плёнку, а г—интенсивность пучка света,
прошедшего через плёнку. Для данной фотоплёнки при данном
способе проявления и при данной длине волны почернение является
функцией экспозиции, т. е. произведения интенсивности падающих
на плёнку лучей на продолжительность их действия t:
S=S(E) = S(H). (11,17)
Поэтому кривые S = S(I) и S=S(t) имеют идентичный вид.
Формула II, 17 выполняется только в области нормальных почернений,
т. е. при #<2. Более широкая область почернений охватывается
формулой S=S(Itp), где р— постоянная. В области нормальных
почернений для рентгеновских лучей р = 0,99 =t 0,02. Зависимость
S=aS (E) не может быть выражена аналитически; существует, однако,
несколько приближённых формул. Характерная кривая S^=S(E)
изображена на фиг. II, 21. Кривая не проходит через нуль, ибо
проявление вызывает незначительное почернение даже совершенно
неэкспонировавшейся плёнки. Это — вуаль, обусловленная самим
проявлением. Типично отсутствие зависимости почернения от
экспозиции для очень малых экспозиций. Ото так называемая область
инерции. По достижении некоторой экспозиции почернение
начинает возрастать. Это—порог почернения. Начиная с некоторого
момента, почернение становится пропорциональным экспозиции,
а при больших экспозициях—пропорциональным логарифму
экспозиции. Зависимость S=kE выполняется обычно в интервале
0,2 <&<0,7; зависимость S=k'\gE—в интервале 0,7 < #< 1,8.
Величины этих интервалов зависят от ряда факторов (спектральный
состав излучения, сорт плёнки). При дальнейшем увеличении
экспозиции кривая проходит через максимум, так что почернение
начинает уменьшаться. Это явление называется соляризацией. Оно
наблюдается обычно в месте попадания на плёнку первичного пучка
(почернение в .этом месте слабее, чем диффракционные пятна).
Рабочим интервалом является приблизительно прямолинейный
участок кривой от S — 0,4 до S = 2,0. Интервал экспозиций,
отвечающий прямолинейному участку, называется широтой эмульсии
и является характерным для данного сорта плёнки. Другой важной

192 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [ГЛ. II
характеристикой данной плёнки является её* контрастность, т. е.
наклон прямолинейного участка кривой 4f = tga. Чем больше
широта эмульсии, тем меньше контрастность, и наоборот. Сильно
контрастную плёнку легко переэкспонировать, мало контрастная
h
Максимальный интервал
допустимых экспозиций
Логарифм экспозиции
Фиг. 11,21. Типичная кривая почернения S = S(K).
требует большой экспозиции. Обычная широта эмульсии
допускает правильное воспроизведение внтенсивностеи в интервале
—^я^ЮО—120. Если желают охватить более широкий интервал,
необходимо делать несколько снимков с разными экспозициями.
Почернение резко зависит от длины волны применяемого
излучения. Чувствительность плёнки тем больше, чем сильнее
поглощаются ею падающие лучи,.поэтому чувствительность меняется
с длиной волны примерно так, как и коэффициент поглощения
бромистого серебра. Чувствительность претерпевает резкие скачки
у краёв полос поглощения брома (0,918 А) и серебра (0,485 А)
(фиг. II, 22).
Если рентгенограмма фотометрируется, то необходимо построить
кривую почернения данной плёнки. Для этого пускают на плёнку
лучок лучей, имеющий форму вытянутого прямоугольника (необ-

§'г>]
ФОТОГРАФИЧЕСКОЕ ДЕЙСТВИЙ РЕНТГЕНОВСКИХ ЛУЧЕЙ
198
ходимо, чтобы интенсивность была постоянной по всему сечению
пучка). Между пленкой и диафрагмой, вырезающей пучок,
вращается секторная заслонка (фиг. II, 23), благодаря чему
продолжительность экспозиции оказывается различной для разных участков
пленки. В зависимости от
формы заслонки можно
варьировать экспозицию в
любых пределах.
/4
10
в
*?.
л
„/
X
j
/
А
0,5 0.9 1,3 П
Фиг. II, 22. Зависимость почернении
от длины волны.
Фиг. 11,23. Секторная
заслонка.
б) Визуальная оценка интенсивностей. Как правило, при
измерениях интенсивности пятен на рентгенограммах вращения
рли рентгеногониометра пользуются одним из двух
полуколичественных методов. Самый простой, но менее совершенный, это метод
3-пятеп. Отношепие между интенсивностями а- и ^-пятен, возникших
ври отражении от одной и той же плоскости, есть величина
постоянная (она равна, например, 5,7 для медного излучения). Выберем на
илёнке самое интенсивное а-пятно и присвоим ему номер 10, его
р-пятну присвоим помер 7. Найдём а-пятно той же интенсивности,
что и пятпо номера 7, его {3-пятно имеет интенсивность,
обозначаемую номером 4. [3-пятно, которое соответствует а-пятпу с
интенсивностью номер 4, будет самым слабым пятном на
рентгенограмме и получит номер 1. На-глаз выбирают пятна с
промежуточными интенсивностями, присваивая им помера 8, 9 (6, б и 3, 2). Мы
присвоим пятну номер 5 в том случае, если его интенсивность лежит
между номером 4 и номером 7, но ближе к номеру 4. Отношение
интенсивпостей пятен номер К), 7, 4 и 1 должно быть примерно
100 : 18 : 3,5 :0,5. Опыт показывает, какие цифры надо приписать
промежуточным номерам. В результате возникает следующая оценка
интенсивностей:
Номера . . . .
Интенсивности
1
0,5
3
1,8
4 5
3,5 Г,
G
10
7
18
33
9
55.
10
1С О

194 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ flMt. It
Разумеется, этот метод не может претендовать на точность,
большую 50%.
Метод шкал со стандартными почернениями*) требует
специального эксперимента, но несравненно точнее. На исследуемую плёнку
(после того, как съёмка рентгенограммы окончена) заставляют
падать рентгеновский луч и на свободном месте плёнки создают
ряд пятен, снятых при разных экспозициях. Лучше всего выбрать
экспозиции пятен так, чтобы они удовлетворяли закону
геометрической прогрессии со знаменателем \г2. Вполне достаточна шкала
из 17 пятен — она позволяет сравнивать интенсивности,
различающиеся более чём в 200 раз. Оценка интенсивности
интерференционных пятен заключается в сравнении их почернений с
почернениями пятен шкалы.
Возможная ошибка при работе с подобной шкалой не может
превышать разницы между двумя соседними пятнами шкалы,
т. е. ~40%-
Такая точность вполне достаточна для обычных проблем
структурного анализа.
в) Фотометрирование рентгенограмм. Фотометрирование
рентгенограмм редко применяется при структурном анализе
монокристалла. Это объясняется тем, что необходимо определять
интегральное почернение отдельных интерференционных пятен. Для этого
необходимо промерить почернения в разных частях пятна, а затем
просуммировать результаты этих измерений. С практической точки
зрения эта задача является весьма трудной. Значительно проще
фотометрирование рентгенограмм порошка, ибо здесь достаточно
промерить почернение вдоль экваториальной линии рентгенограммы.
Принцип фотометрирования заключается в том, что узкий
параллельный пучок света постоянной интенсивности ?0
направляют на плёнку. Тем или иным способом (фотоэлемент, болометр,
радиометр) измеряют интенсивность прошедшего через плёнку
пучка г. В таком случае S = lg — есть почернение в данном месте
плёнки. Почернение можно характеризовать двояким способом.
Если i0 есть интенсивность падающего пучка света, то S есть
суммарное почернение (фон или вуаль -f- почернение пятна). Если же
i0 есть интенсивность пучка, прошедшего через соседний с пятном
участок плёнки, то S есть почернение собственно пятна. Для целей
структурного анализа интересно знать интенсивность только диф-
фракционного пятна, а не фона. Поэтому почернение определяется
по второму способу.
Наиболее удобен фотоэлектрический фотометр, принципиальная
схема которого показана на фиг. П, 24. Система диафрагм и линз
*) Г. С. Жданов и В. П. Котов, Журнал Физ. Химии 15, 918, 1941.

§5]
ФОТОГРАФИЧЕСКОЕ ДЕЙСТВИЙ РЕНТГЕНОВСКИХ ЛУЧЕЙ
195
^ллллллл-
п
rlilililililililili-
«шин-)
выделяет узкий параллельный пучок света, даваемого лампочкой,
накал которой поддерживается постоянным. Этот пучок проходит
через рентгенограмму порошка, двигающуюся с постоянной
скоростью в направлении
экваториальной
линии. Прошедший
пучок света попадает в
фотоэлемент.
Возникающий ток
усиливается обычной трбхэлек-
тродной лампой и
подаётся на
саморегистрирующий
гальванометр. Иногда
применяют зеркальный
гальванометр; пучок
света, отражённый от
зеркальца, попадает
на движущуюся с
постоянной скоростью
фотоплёнку.
Типичная кривая,
полученная при фото-
метрировании
рентгенограммы
поликристалла, представлена
ад
4rTtZ- I
Фиг. II, 24. Фотоэлектрический фотометр: О —
осветитель; Р — рентгенограмма; М—моторчик;
Ф — фотоэлемент; Л—усилительная лампа;/7 —
зеркальный гальванометр; Л" — фотоплёнка.
на фиг. 11,25. Каждому интерференционному кольцу отвечает острый
пик, фон монотонно убывает с углом 0. Для определения величины
Фиг. II, 25- Кривая фотометрирования рентгенограммы порошка. Величина
максимума 1 определяется площадью между кривой фотометрирования и
касательной.
Данного максимума проводят касательную, как это показано на
фигуре, и определяют площадь между ней и кривой. Если работают

196 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [гл. It
в прямолинейной области кривой почернения, то интегральная
интенсивность данного кольца пропорциональна логарифму
площади максимума фотометрической кривой.
г) Светящиеся усиливающие экраны. Рентгеновские лучи
вызывают фосфоресценцию ряда веществ. Свет фосфоресценции
характеризуется большей длиной волны, чем возбудившие его
рентгеновские лучи, так что часть его спектра зачастую лежит
в видимой области. Это явление используется для изготовления
экранов, позволяющих обнаруживать
невидимые глазом рентгеновские лучи.
Для получения экрана
фосфоресцирующее вещество наносится тонким слоем
на картон. Наиболее часто
применяются платиноцианид бария (зеленое
свечение) и вольфрамат кальция
(фиолетовое свечение). Светящиеся экраны
могут применяться для усиления
фотографического действия
рентгеновских лучей, что позволяет уменьшить
экспозицию в 4—10 раз.
Для этого светящийся экран
помещают за плёнкой, вплотную к ней,
так что фотографическое действие
оказывают не только рентгеновские
лучи, но и свет фосфоресценции.
Отрицательная сторона применения
экранов заключается в том, что при
недостаточно тесном контакте экрана и
плёнки (чего нельзя избежать при двусторонней плёнке) пятна
становятся размытыми. Экран даёт тем меньшее размытие, чем
мельче зёрна флюоресцирующего вещества, однако при этом его
усиливающее действие уменьшается. Результаты применения
флюоресцирующего экрана иллюстрируются фиг. 11,26.
Z8
Z*
§ го
116
1»
Q8
ом
0
4
J
/
г
\
1
I
1
Г
/
/
/
У
'
<
/
/
1
J
7
/
/
t
}
О 0,3 0,6 Q9 1.2 1.S 18 2.1 Zk
Логарифм интенсивности пучна
Фиг. 11,26. Действие
усиливающего экрана, кривая А
характеризует зависимость
почернения от интенсивности
пучка при применении
экрана, кривая В—без него.
§ 6. Ионизирующее действие рентгеновских лучей
и ионизационный метод измерения ннтенсивностей
Проходя через газ, рентгеновские лучи ионизируют его.
Рентгеновские фотоны, сталкиваясь с молекулами или атомами газа,
выбивают из них фотоэлектроны. Кинетическая энергия этих
фотоэлектронов обычно настолько велика, что при столкновении с
другими молекулами или атомами газа они также вышибают из них
электроны. Таким образом, рентгеновские фотоны, проходя через
газ, вызывают появление определённого числа электронов и поло-

6] ИОНИЗИРУЮЩЕЕ ДЕЙСТВИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ 197
жительных ионов. Наряду с ионизацией, как и воегда при
прохождении рентгеновских лучей через вещество, имеют место
квантовый эффект и появление характеристического и рассеянного
излучения.
Ионизация газа под действием рентгеновских лучей может быть
использована для весьма точного измерения их интенсивности.
k и насосу
Фиг. И, 27. Схематический разрез ионизационной камеры:
К—металлический кожух; Э — эбонитовые пробки; б—стеклянный баллон; ц — ла.уи-
ный цилиндр (катод); О — слюдяные окошечки; II— стальная проволока
(анод).
Для этой цели применяется ионизационная камера, состоящая
из двух электродов, помещённых в запаянный стеклянный сосуд.
Конструкция камеры схематически изображена на фиг. 11,27.
Внутри запаянного стеклянного цилиндра находится латунный
цилиндр, являющийся отрицательным электродом. По оси цилиндра
натянута стальная тонкая проволока, являющаяся положительным
электродом. Проволока тщательно изолирована от металлического
цилиндра эбонитовыми пробками. На конце камеры имеется окошко
для впуска рентгеновских лучей, изготовленное из малопоглощаю-
щего вещества (целофан, слюда, алюминиевая фольга, специальное
стекло). Камера помещается в защитный металлический цилиндр,
обычно заземляемый, и снабжается выводом с хорошим краном для
наполнения требуемым газом и частичной эвакуации. На камеру
накладывается постоянное напряжение, варьируемое в зависимости
от требуемого режима работы. При попадании в камеру рентге.

198 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [ГЛ. II
новских квантов (или других ионизирующих частиц) происходит
ионизация газа в камере, и через неб начинает течь ток. Измеряя
этот ток, определяют интенсивность рентгеновских лучей. Обычные
размеры цилиндрической ионизационной камеры таковы: длина 16 см,
диаметр 5 см. Размеры камеры должны быть достаточны для
практически полного поглощения газом попадающего в неб пучка
рентгеновских лучей. Рентгеновские кванты не должны
бомбардировать электродов камеры, ибо это приводит к вырыванию из
них фотоэлектронов и другим процессам, нарушающим
правильную работу камеры. Размеры камеры, кроме того, должны
быть сравнимы (но не меньше) с длиной свободного пробега
электронов (около 10 см) для того, чтобы фотоэлектроны могли
проявить своё" ионизирующее действие, прежде чем они будут
поглощены анодом.
При любом режиме работы камеры необходимым условием
пропорциональности ионизационного тока интенсивности
рентгеновского пучка является полное поглощение всех рентгеновских
квантов газом. Поэтому в случае применения жёсткого излучения
(например, Шо) камеру необходимо наполнить каким-либо тяжёлым
газом, обладающим значительным коэффициентом поглощения. В
качестве такого газа особенно удобно применять ксенон из-за его
химической инертности или смесь его с воздухом. В случае
медного излучения достаточно наполнять камеру аргоном; в случае
железного излучения камера может быть наполнена воздухом. Число
положительных ионов и электронов, порождаемых одним
рентгеновским квантом, вообще говоря, тем больше, чем меньше энергия
ионизации молекулы газа. Энергия ионизации, характеризуемая
потенциалом ионизации, в общем падает с ростом молекулярпого
веса, т. е. изменяется симбатно с коэффициентом поглощения. Чем
тяжелее газ, тем больше ионизационный ток при той же
интенсивности рентгеновского пучка. К сожалению, применение таких
газов, как Br2, CH3J, CC14, имеет ряд неудобств (они легко
разлагаются и разъедают стенки камеры). Поэтому, в качестве тяжёлых
газов применяют инертные криптон и ксенон. Ионизационный ток
при полном поглощении лучей мало зависит от их частоты. Это
иллюстрируется таблицей II, IV. Если рентгеновские лучи полностью
поглощаются газом, то его давление не играет роли. Увеличивая
давление газа в камере, мы повышаем его плотность, а
следовательно, и поглощающую способность, и уменьшаем длину свободного
пробега электронов. Благодаря этому можно уменьшить размеры
камеры. Однако в некоторых случаях выгодно работать при несколько
пониженном давлении газа в камере, ибо при этом работа камеры
становится более стабильной.
Режим работы камеры определяется прежде всего приложенным
напряжением. Как известно, зависимость силы тока, протекающего
через ионизированный газ, от разности потенциалов изображается

§ 6] ИОНИЗИРУЮЩЕЕ ДЕЙСТВИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ 199
кривой, показанной на фиг. II, 28.Горизонтальный участок кривой
отвечает току насыщения; на этом участке ток не зависит от
разности потенциалов, ибо все
ионы и электроны достигают
электродов и участвуют в
создании ионизационного
тока. Для этого падение
напряжения на камере
должно быть достаточно велико,
но не должно превышать
некоторого предельного зна-
V
чения Е= —р, где Ги0„ —
потенциал ионизации газа,
наполняющего камеру, I —
длина свободного пробега
электронов. Если падение
напряжения превышает эту
величину, то вторичные
электроны разгоняются в
поле настолько, что могут вызвать ударную ионизацию новых
молекул газа. Наступает так называемая ударная ионизация, и кривая
Таблица И, IV
Ионизация газов рентгеновскими лучами
Фиг. И, 28. Зависимость силытока от
разности потенциалов в ионизированном
газе.
Газ или нар
н2
со2
CgH6Cl
Ar
ССЦ
Ni(CO)4
C2H5Br
CH3J
HgfCH3)2
Плотность по
отношению к
плотности воздуха
0,07
1,53
2,24
2.78
5,35
5,9 J
' 3,78
1 4,96
7,93
Ионизация по отношению к
ионизации воздуха
мягкие лучи
0,01
1,57
18,00
21,80
67
89
72
145
425
жёсткие лучи
0,18
1,49
17,3
—
71
97
118
125^
* (Е) идёт резко вверх. Напряжения, отвечающие режиму
насыщения, зависят от ряда факторов (ионизационный потенциал газа,

200 ПОЛУЧЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [ГЛ. II
заполняющего камеру, его давление, форма и размеры
ионизационной камеры и т. д.). При наполнении камеры воздухом или
аргоном при давлении, близком к атмосферному, эти напряжения
лежат обычно в интервале 200—400 вольт.
Ионизационная камера, работающая в режиме насыщения,
называется собственно ионизационной камерой. Многочисленные
эксперименты показывают, что в этом случае величина ионизационного
тока строго пропорциональна интенсивности ионизирующего
рентгеновского пучка. Поэтому ионизационная камера может с успехом
применяться для точного измерения интенсивностей. Рентгеновские
лучи обычной в структурном анализе интенсивности создают в
ионизационной камере токи Ю-11 — 10"иа. Между тем обычные
зеркальные гальванометры измеряют токи не ниже Ю-9— 10~8а.
Необходимо поэтому усиливать ионизационный ток в 10~3—К)-6 раз.
Этого можно избежать, заряжая ионизационным током некоторую
ёмкость в течение более или менее длительного времени. В
качестве такой емкости можно пользоваться обычным электроскопом
или квадрантным электрометром, делая отсчёты через равные
интервалы времени. Чувствительным электрометром можно
непосредственно измерять ток, измеряя падение потенциала на большом
сопротивлении, один конец которого заземлён. Обычно, однако,
прибегают к ламповому усилителю с электрометрическими лампами.
Усиленный ток регистрируют обычным зеркальным гальванометром,
зайчик которого может служить .самописцем (медленно двигающаяся
фотоплёнка).
Если повысить напряжение на камере, то можно перейти
в область ударной ионизации, где ток резко изменяется с
напряжением. Ионизационная камера, работающая в этом режиме,
называется пропорциональным усилителем*). Оказывается, что и при
работе в этой области ионизационный ток пропорционален
интенсивности рентгеновского пучка. Однако в этом случае первичный
ионизационный ток значительно усиливается за счёт ионизации
г
ударом. Это газовое усиление характеризуется отношением к = -Д-,
*нас
где гус—усиленный в камере ток, w — ток насыщения.
Коэффициент к может достигать нескольких тысяч. Таким образом,
пропорциональный усилитель даёт токи Ю-11—10~8а. В этой
повышенной чувствительности состоит его преимущество перед
ионизационной камерой. Ионизационный ток усиливается ламповым
усилителем и регистрируется зеркальным гальванометром.
Принципиальная конструкция пропорционального усилителя ничем не
отличается от конструкции ионизационной камеры, описанной выше.
Камера обычно (при работе на медном пзлучении) заполняется
*) Боке л о j) В. И. и И с а с и Б. М., ДАН, стр. 369, 193^.

§ 6] ИОНИЗИРУЮЩЕЕ ДЕЙСТВИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ 201
Юом
6« Zr~2000V
аргоном под давлением 760—200 мм Hg. Усиление при
достаточных размерах камеры в общем несколько увеличивается с
уменьшением давления; при этом также значительно возрастает
стабильность работы. Схема лампового усиления, применяемая при работе
с пропорциональным усилителем, показана на фиг. II, 29. Эта схема
успешно применяется и при работе в режиме тока насыщения.
Усиление достигает 10б раз.
В качестве усилительных ламп применяются четырёхэлектрод-
ные лампы специального типа, так называемые электрометрические
лампы с малой величиной сеточной утечки и другими
особенностями. Схема построена
по мостиковому принципу. JT
Зеркальный гальванометр "Mv^^
включается в аподные цепи
обеих ламп. При равных
потенциалах на
управляющих сетках обеих ламп
гальванометр, естественно,
будет стоять на нуле, ибо
при одинаковых условиях
питания анодные токи
обеих ламп одинаковы.
Управляющая сетка одной из ламп
(левой на схеме) соединена с
отрицательным электродом
(проволокой) камеры. В
качестве источника
напряжения на камере применяются
сухие батареи. Напряжение
можно изменить, выключая
часть батарей. В отсутствии
ионизации ток в камере
равен нулю, и потенциал на
управляющей сетке левой
лампы остаётся постоянным
и равным потенциалу на
сетке первой лампы;
гальванометр стоит на нуле.
Ионизация газа в камере
рентгеновскими л учами
приводит к появлению ионизационного тока в камере. Положительные
ионы, выделяясь на отрицательном электроде, понижают его
потенциал, а значит, и отрицательный потенциал управляющей
сетки. Анодный ток в левой лампе увеличивается, и
гальванометр регистрирует разность анодных токов правой и левой ламп.
Эта разность пропорциональна разности сеточных потенциалов,
bn~300v
£
^HimifciiKJ
1—^Щ|1ь4_
Фиг. 11,29. Лринципнальная схема
лампового усилителя к пропорциональному
усилителю: Л\ и Л...--электрометрические
лампы; Г—гальванометр,
чувствительностью Ю-7— Ю-10 а/дел.;
тЛ—миллиамперметры тока накала ламп;
V—вольтметр сеточного смещения; Ь'к— батарея,
дающая высокое напряясение на камеру;
/>А, />q , 7>и — анодная, сеточная, накаль-
ная батарея питания ламп.

202 ПОЛУЧВНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ [ГЛ. II
т. е. ионизационному току и в конечном счёте интенсивности
рентгеновского пучка. Другие детали схемы служат для питания
ламп, создания правильного режима их работы и измерения
сеточных напряжений и токов накала. Для питания ламп применяются
аккумуляторы. Для измерения интенсивности рентгеновских лучей
применяются также счётчики, регистрирующие отдельные
рентгеновские кванты. Неудобство применения их заключается в том,
что для измерения слабых интенсивностей требуется весьма
продолжительное время.
Точность ионизационного измерения интенсивностей по любому
из трёх методов (камера, пропорциональный усилитель, счётчики),
вообще говоря, является очень высокой и может быть доведена
до 2—5%.

ГЛАВА III
ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ
§ 1. Направление рентгеновских лучей, диффрагированных
кристаллом
Электромагнитная волна, падающая на кристалл, приведёт
к возникновению элементарных шаровых волн, рассеиваемых
каждым элементом объёма вещества. Периодическое распределение
вещества в пространстве приведёт к возникновению резких фазовых
соотношений между этими волнами. Только в некоторых определённых
направлениях волны, рассеянные всеми частицами кристалла, будут
действовать в одной фазе. Поэтому возникнет лишь ограниченное
число диффракционных лучей. Направление их в пространстве
будет определяться периодами решётки, её ориентацией
относительно падающего луча и спектральным составом излучения.
В этом параграфе мы хотим остановиться только на
геометрической стороне явления. Вопрос об интенсивности того или иного
диффракционного луча мы оставляем открытым. В таком случае мы
можем рассмотреть рассеяние точечной пространственной решёткой,
полагая всё «содержимое» элементарной ячейки сосредоточенным
в узле. Действительно, опуская это предположение (как мы и сделаем
в следующих параграфах), мы не получим при прочих равных
условиях новых (в смысле направления) диффракционных лучей, а,
напротив, лишь можем свести к нулевой интенсивности некоторые из
них, возможные для точечной решётки.
В § 4 этой главы это положение будет доказано строго.
Пространственную решётку можно представить в виде различных
бесконечных семейств прямых, например в виде семейств,
параллельных основным векторам а, Ь и с решётки.
Рассмотрим, например, узловую прямую с периодом а. Пусть на
эту прямую в направлении t0 падает плоская волна. Рассмотрим
фронт волн, рассеянных всеми узлами прямой в направлении t.
Если элементарные волны, идущие от узлов, действуют в одной
фазе, то t будет направлением сильного луча. В противном случае
в направлении t вторичный луч распространяться не будет. у.
Для того чтобы все волны действовали в фазе, необходимо,
чтобы разность хода между волнами, рассеянными от двух сосед-

204
ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
них узлов, равнялась целому числу длин волн. Как видно из фиг. III, 1,
разность хода равна
acosa — acosa0 или a(t— *0).
Условием сильного луча будет a (t — t0) = ИХ, где Н—целое число.
Подобное рассуждение можно провести для любой узловой
прямой.
Для определения направления t (при
достаточно иметь три уравнения, которые, разумеется, проще всего
записать для семейств
основным векторам.
Итак, направление
определяется уравнениями:
a{t — t0)=m,
b{t — t0) = K\,
с (t—t0)=*L\
где Ну К, L — целые числа, называемые
индексами диффракции (или интерференции). Каждое
направление диффракции характеризуется таким
образом тремя целыми числами.
Вместо векторов t и t0 введём, как это при-
волновые векторы к = -г- t и
заданных а, Ъ, с и t0)
всего
прямых, параллельных
диффракционного луча
(III, 1)
Фиг. III, 1. Диф-
фракция на
узловой прямой.
Разность хода равна
AC—BD =
=о cos а — a cos a0.
нято в оптике,
^° == Т 'о* ^ти вект0Ры удобны тем, что они
одновременно характеризуют как направление, так и
длину волн. С их помощью (III, 1) запишется
в виде
Ь (к—к0) = 2кК, (III, 1а)
с (к—к0) = 2t:L.
Искомое направление t можно определить и одним уравнением.
Это уравнение имеет следующий вид:
* _ t0 = X (На* -4- КЪ* + £сх).
Нетрудно видеть, что это векторное уравнение эквивалентно написан*
ным выше трём скалярным. Действительно, помножая поочерёдно
это уравнение скалярно на а, 6 и с, получим, используя
соотношения (1,8), тройку уравнений (III, 1).
Вспомним, что обратным вектором системы узловых плоскостей
(Ш) мы назвали вектор ha* ~\- kb* -}- 1сх = фш, где индексы
hM — целые числа, лишённые общего множителя.
Индексы интерференции Н, К, L могут содержать общий
множитель.

§ lj НАПРАВЛЕНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ 205
Очевидно, H = nh, К=пк и L = nl, где п — целое число.
Поэтому условие интерференции в векторном виде может быть
записано так:
< —*0 = A«$ftW, (III, 2)
где &ш — обратный вектор плоскости (Ш). Итак, единичный
вектор t, характеризующий направление диффрагированной волны,
может быть получен как сумма двух векторов
Зная взаимное расположение решётки и падающего луча, зная
основные векторы решётки и вместе с этим направление и величину
обратных векторов, можно определить направления возникающих
диффракционных лучей.
Вектор t — единичный вектор, а не вектор произвольной длины,
поэтому, очевидно, условие (III, 2) может, вообще говоря, и не
выполняться ни для одного из векторов &ш, а в общем случае
будет выполняться лишь для некоторых из векторов &Ш.
Для того чтобы сделать условия диффракции наглядными,
поступим следующим образом.
Представим себе решётку, к основным граням ячейки которой
построены нормали. Нанесём точки на этих линиях через
расстояния, равные длинам обратных векторов. Считая эти точки за узлы,
мы можем построить на них пространственную решётку, каждый
узел которой будет определяться уравнением
(J9T—радиус-вектор узла обратной решётки). Каждое направление И
этой решётки есть узловая прямая с периодом повторяемости — ф.
Вектор, соединяющий узел HKL такой решётки с началом
координат, будет равен n$frhM. Назовём эту решётку обратной решёткой
кристалла, а вектор п&ш = Д—вектором обратной решётки
(в отличие от в целое число раз меньшего обратного вектора *рш)«
Итак, каждому семейству узловых плоскостей прямой решётки
отвечает узловая прямая обратной решётки. Справедливо и
обратное: каждой узловой прямой решётки отвечает серия узловых
плоскостей обратной решётки. Обратная решётка, в отличие от
прямой, не имеет реального физического смысла, а является
математическим образом, весьма удобным для истолкования явлений
диффракции рентгеновских лучей в кристаллах.
Условие диффракции
*-(* — t0)=H[ или t = t0-{-kH

2()6 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ (гл. Ill
или также
к — к0=2т:Н и fc = *0 + 2irJT*) (III, 16)
имеет следующий геометрический смысл: это есть условие образо-
вания треугольника тремя векторами у , у и Я.
Проведём в начало координат обратной решётки вектор —-'
(направление падающего луча по отношению к векторам обратной
решбтки однозначно связано с направлением *0 по отношению
к кристаллу). Из начала координат мы должны для выполнения
условия диффракпии провести тот из бесчисленного количества
векторов .ВТ, который заканчивается в точке (узле обратной решётки),
отстоящей от начала вектора ~ на расстоянии — . Проще всего
это построение можно проделать, проводя из начала вектора -°
(конец его находится в начале координат) сферу радиусом .
(сфера отражения). Если на эту сферу попадёт узел обратной
решётки, то соответствующий вектор Ш будет удовлетворять диф-
фракционному условию. Вектор t, т. е. направление диффракцион-
ного луча мы найдём, соединяя начало вектора -Д- с концом
вектора Ш.
Если на сферу радиуса у не попадёт ни один узел обратной
решётки, то, следовательно, при данном взаимном расположении
падающего луча с длиной волны X и решётки диффракционные
лучи не возникают. Напротив, если сфера проходит через несколько
узлов решётки, то это значит, что в рассматриваемом случае
возникает одновременно несколько диффракционных лучей. Радиус
сферы, соединяющий центр сферы с узлом на сфере, указывает
направление диффракционного луча; индексы узла представляют
собой индексы интерференции.
Описание диффракции построением сферы отражения в
пространстве обратной решбтки является основным методом
расшифровки рентгенограмм.
На фиг. III, 2 изображена обратная решётка кристалла й
показано направление прямых и обратных основных векторов. Пусть
падающий луч длины волны а падает на кристалл перпендикулярно
к оси Ь (идущей перпендикулярно к плоскости чертежа) и образует
углы е2 и е2 с осями а и с кристалла. Эти условия однозначно
определяют расположение и радиус сферы отражения. Сфера всегда
(по определению) проходит через центр комплекса, т. е. через
*) Разность векторов k — kQ будет нам весьма часто встречаться
в дальнейшем. Вводя обозначение s — ft — ft0, можем записать условие
диффракции ещё короче: s=Hr.ff.

l| Направление рентгеновских лучей £ol?
начало координат обратной решётки. На фиг. III, 2 изображены
направления возникающих в этом случае диффракционных лучей.
Совершенно очевидно, что характер диффракции резко меняется
при изменении угла, под которым луч падает на кристалл — это
соответствует повороту обратной
решётки по отношению к сфере
(или повороту в обратном
направлении сферы по отношению
к решётке), а также при
изменении длины волны рентгеновского
луча это соответствует изменению
диаметра сферы. Чем больше
длина волны, тем меньше размер
сферы. Если длина волны станет
2 -
такой, что диаметр — будет
меньше самого малого периода
обратной решётки (внутри сферы узлов
нет), то диффракция становится не-
о
возможной. Например, при X = 2 А
диффракция невозможна для
решёток, у которых обратные векторы
о _
больше 1А и, следовательно,
межплоскостные расстояния в кристалле
о
меньше 1 А.
Другой предел наблюдаемости
диффракции будет соответствовать
случаю, когда сфера отражения
содержит очень много узлов, т. е.
2
Y много больше величины обратных векторов. При
относительном увеличении диаметра сферы отражения наступит
предел, когда практически нри любом положении сферы она будет
равномерно усеяна узлами*). Это значит, что рассеяние будет
происходить при любом падении луча равномерно во все стороны.
Этот предел наступит нри падении на кристалл весьма жёсткого
излучения. Для точности следует отметить, что равномерного
распределения интенсивности рассеянного излучения при этом не
наступит; во всяком случае справедливо, что диффракция
практически исчезнет.
То обстоятельство, что каждое диффракционное направление
определяется индексами H = nh, К — пк и Ь = п1,ще
(Ш)—символ семейства плоскостей кристалла, показывает, что каждое диф-
*) Как мы увидим ниже, узлу обратной решётки следует приписать
конечные размеры.
Фиг. III, 2. Кристалл К, его оси а
и с. Обратная решётка с осями
ах и с*. Узлы 001,300,201
находятся в отражающем положении.
таком

208 ДЦФФРАКЩШ РЕНТГЕК0ВС1ШХ ЛУЧЕЙ В КРИСТАЛЛЕ [гл. III
фракционное направление связано каким-то способом с
расположением в кристалле той или иной системы плоскостей. Нетрудно
видеть, что это за связь.
Проведем через вершину равнобедренного треугольника,
построенного на векторах у, -,- и FT, плоскость, перпендикулярную к Н
(фиг. III, я). Эта плоскость,
очевидно, параллельна семейству
плоскостей (hkl). Из построения
очевидно, что лучи t0 и t образуют
один и тот же угол & с
плоскостью (hkl). Отсюда следует, что
диффракционный луч с индексами
интерференции HKL можно
рассматривать, как луч «отражённый»
от системы плоскостей кристалла
(hkl). Углы «скольжения» «>
(дополнительные углам падения и
отражения) связаны с
межплоскостным расстоянием (1Ш и длиной
волны. Действительно, из
равнобедренного треугольника находим
2 sin О
Фиг. 111, 3. Истолкование
уравнения Вульфа с помощью обратной
решётки. t0, t — первичный и
диффрагированный лучи; А А' —
плоскость (hkl); Hhlii — её
обратный вектор; О — начальный узел
обратной решётки, Р — узел в
отражающем положении.
= ТТШ (III,:*)
или
2dftWsin !> = пХ,
(III, Па)
где п — целое число — множитель,
связывающий индексы плоскости
h, к, I с индексами интерференции Н, К, L, называемый порядком
«отражения» *).
Итак, условие возникновения диффракционного луча может быть
сформулировано следующим образом: такой луч возникает только
в том случае, если одно из семейств плоскостей (hkl) наклонено
к лучу под углом 0, удовлетворяющим уравнению (III, 3), которое
называется уравнением Вульфа-Брэгга.
Каждое семейство плоскостей кристалла дает несколько
отражений под углами 0,, 02, 03, ..., определяемыми условиями:
sin r>,
2d
■ш
sin»2 = 2 • -к-,-
sin »» = :-j-
ы
ш
*) В дальнейшем мы будем пользоваться обозначением hkl как для
индексов плоскостей, так и для индексов интерференции. К путанице это
привести не может.

§ 2] РАССЕЯНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ ЭЛЕКТРОНОМ 209
Очевидно, что наиболее высокий порядок отражения определяется
условием nk^.2d. Каждой системе плоскостей (Ш) свойствен
свой набор возможных углов скольжения ft.
Это селективное отражение можно наглядно объяснить фиг. 1П, 4.
Полагая, что диффракционный луч получается как сумма лучей,
отражённых (уже без кавычек) всеми плоскостями семейства, мы
получим уравнение Вульфа-Брэгга,
если учтём, что сильный луч
возникнет лишь в том случае, если
разность хода лучей,
отражённых от двух соседних
плоскостей, равна целому числу длин
волн. Как видно из фиг. III, 4,
2d sin 0 и есть эта разность хода.
Таким образом, селективное
отражение, скажем 3-го порядка, есть
такое отражение, при котором
разность хода лучей, отражённых Фиг. III, 4. Разность хода
от двух соседних плоскостей, рав- ь — Ав + ВС — Ы sin Ь.
на ЗХ.
Предыдущие рассуждения молено рассматривать как
доказательство правомочности представления явлений диффракции,
как явлений отражения от узловых плоскостей решётки. Такой
метод рассмотрения обладает большими удобствами и
наглядностью и будет многократно применяться в дальнейшем.
Рассматривая богатую диффракционными лучами картину, мы
всегда имеем возможность указать, от какой системы плоскостей
(Ш) отразился луч и в каком порядке произошло это отражение.
Поворачивая кристалл, мы изменяем картину диффракции потому,
что подставляем в отражающее положение то одни, то другие
семейства плоскостей. Изменяя длину волны, мы гасим одни отражения
и даём. возникнуть другим, для которых данная волна является
подходящей в смысле уравнения (Ш, 3).
§ 2: Рассеяние рентгеновских лучей электроном
Здесь и в последующем мы пользуемся классической
электродинамикой, которая даёт превосходные результаты не только для
качественного понимания, но и для количественной оценки
явлений взаимодействия рентгеновского луча с кристаллом.
Квантовые эффекты создают лишь некогерентное рассеяние и
участвуют лишь в создании фона рентгенограммы. Заметим,
впрочем, что частично фон объясняется и классическими
представлениями. Во всяком случае интересующая нас задача —
сопоставление интенсивности диффрагированного рентгеновского луча со
структурой кристалла решается классической теорией
электромагнетизма.

210 диффракция рентгеновских лучей в кристалле [гл. ill
В этом параграфе мы рассмотрим рассеяние рентгеновского
луча электроном. Электрическое поле падающей волны приводит
электрон в колебание с частотой самой волны. Колеблющийся электрон
представляет собой диполь с переменным электрическим моментом и
создаёт, в свою очередь, переменное электромагнитное поле.
Интенсивность этого поля и есть интенсивность излучения, рассеянного
электроном.
Как известно из электродинамики*), средняя интенсивность
•излучения / (энергия, проходящая через площадку в 1 см2 в
единицу времени) в данной точке пространства связана с
напряжённостью электрического поля Е в этой же точке соотношепием
Г = — F2
где с—скорость распространения электромагнитных волн (3-ю10 си/сек).
Вычисление интенсивности сводится к вычислению электрического
поля, создаваемого колеблющимся электроном.
Пусть на электрон заряда е и массы т падает плоская
поляризованная волна
Е=^Е0 cos Ы.
Условимся здесь и в дальнейшем пользоваться комплексным
представлением волны
Е = Е0еш,
имея в виду, что длина вектора Е даётся действительной частью
этого выражения (напомним, что е*'а = cos а -|— i sin а).
Обратим внимание на то, что если Е^ окажется комплексной
величиной, то мнимая её часть получит отчётливый физический смысл.
Действительно, если Е0 = ае*<р, то Е=а&№+9). А так как смысл имеет
действительная часть этого выражения, то Е ~ a cos (u>t -|- cp). Таким образом две
волны, обладающие комплексными амплитудами Е0, с отличными друг от
друга мнимыми частями, отличаются друг от друга по фазе. Основной
вид расчётов, которые приходится производить в теории диффракции,—это
вычисление интенсивности излучения в точке наблюдения, причём
излучения, созданного взаимодействием большого числа когерентных волн.
Интенсивность определяется нахождением суммы типа
2 = ai cos (&t -f ?!) + а2 cos (<ot -f s2) -f a3 cos (<*>t + '•?3) + • • •,
возведением этой суммы в квадрат и нахождением среднего по времени
значения, так как именно это среднее значение служит объектом
эксперимента.
Бели записать выражения волн в комплексной форме, то все операции
значительно упростятся; действительно,
*) См. Тамм И. Е., Основы теории электричества, стр. 496,М. — Л.,
1946.

$ 2] РАССЕЯНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ ЭЛЕКТРОНОМ 2ll
где Л — комплексное число, которое запишем в форме А^ -\- гА'тК Тогда
результат суммирования примет вид cos a>t — А^т* sin &t. Возведём
в квадрат и возьмём среднее за период (2') от этого выражения:
Т т т
— AW cos2Wdt-f-i-A{mf I sin2^^ — 1-AWaW sin 2<»t dt;
о о о
T
последний интеграл равен нулю, а первые два —. Таким образом
интенсивность равна -0- (А(и)' -f- Л(т* )• Коэффициент -— может быть введён в
величину А.
Однако и этого вычисления можно не производить, если обратить
внимание на то, что то же выражение мы получим, умножив At на
комплексно-сопряженную величину А*с~гш*,
(А® -,- iAbn) (А{0)) — iA{m)) • eiint е~^ = А(дГ + А^\
Следовательно для подсчёта интенсивности суммарной волны
справедливо правило: представим все волны в форме комплексных чисел adf,
где о — амплитуда, а <р — фаза волны, сложим их значения и помножим
сумму на комплексно-сопряжённое число.
Примем, что сила, связывающая электрон с атомом, мала по
сравнению с внешней силой еЕ, действующей со стороны
рентгеновской волны. Пренебрегая также торможением электрона,
составим уравнение его движения
d-x
m j-^ = eE = eE0 cos Ы.
Величина х есть смещение электрона, происходящее вдоль вектора Е
волны. Решение этого уравнения даёт
е_ jp
Дипольный момент электрона ре = — еэс0, где х0—максимальное
смещение электрона
е -,-,
Хп — ^ Л/о.
Как доказывается в электродинамике, максимальное значение
электрического поля диполя Ее на расстоянии 7? от его центра и
под углом о к оси диполя (т. е. к направлению колебания
электрона) равно:
Поле представляет собой элементарную шаровую волну длины
волны X той же, что и у падающей волны. Направление электри-

212
ДИФФРЛ.КЦИЯ рентгеновских лучей в кристалле [гл. ш
ческого вектора рассеянной волны перпендикулярно радиусутвек-
тору и вектору Е (которому параллелен вектор ре).
Вычисляя квадрат Ее, получим:
Таким образом интенсивность волны, созданной электроном
под действием линейно-поляризованной волны Е, равна
I_*[**bA%_Il*_*!1V (Ш4)
где 10 — интенсивность падающей волны.
Волна, падающая на электрон, не является, однако,
поляризованной. Следовательно, все значения sin2© будут встречаться
одинаково часто. Это не значит, что интенсивность рассеяния не будет
зависеть от угла рассеяния. Действительно, электрический вектор Ее,
как мы указывали только что, во всяком случае перпендикулярен М.
Поэтому в случае, если JB перпендикулярен плоскости колебания
вектора Е для неполяризованной волны, то угол ? может иметь
значение лишь 90°. В этом случае sin2<p=i, и рассеянная
интенсивность равна
т =i(-*A2 ._L
Если JB лежит в плоскости колебания вектора Е, то угол
принимает любые значения, sin2cp меняется от нуля до 1 и sin8 с? =— .
Каково же будет значение sin2 <р для произвольного направления JB?
Очевидно, это значение будет
определяться углом между JB и плоскостью
колебания вектора Е, или иначе — углом
рассеяния, т. е. углом между
рассеянным лучом (направление JB) и
лучом падающим. Обозначим этот
угол через 20. Между углом ft и
углом со имеется следующая связь
(фиг. III, 5):
cos2«p==sin22&cos2^,
k где ^ есть пере'менный угол,
указывающий мгновенное расположение
вектора Е неполяризованной волны
по отношению к плоскости,
проходящей через падающий н рассеянный лучи. Этот угол <|> при
любых утлах рассеяния меняется от 0" до 360° и, следовательно,
волна
Фиг. 111,5. Рассеяние
троном.
элек-

2J
РАССЕЯНИИ) РЕНТГЕНОВСКИХ ЛУЧЕЙ ЭЛЕКТРОНОМ
213
cos84* == -J- Таким образом cos2c?=» -g sina2*> и sina©= 1—-5-sina2&==
= у+ \ cos2 20.
Итак, мы доказали, что интенсивность рентгеновского луча,
рассеиваемого электроном под углом 2Ъ к падающему лучу, равна
1 + cos2 2ft mT M
-о (П1, 5)
в точке, находящейся на расстоянии В от электрона (фиг. Ш, 6).
В сделанном выводе не учитывалась возможность близости
между частотой падающей волны и собственными частотами
связанного электрона. Если частота падающей волны ш близка к
собственной частоте электрона а>0,
то наступает явление
резонанса. Включая в уравнение
движения электрона члены,
содержащие упругую силу — <а0х
и силу «трения» — к -j-,
мы получим для дипольного
момента иное решение, а
именно:
Рв =
2?о
Фиг. Ill, 6. Рассеяние электроном. Ог —
падающий луч; О А — рассеянный луч;
2& — угол рассеяния; f — угол между
осью диполя и рассеянным лучом.
Кривая I. Падающая волна линейно
поляризована вдоль Ox. I*v^»v sin 29
Картина обладает симметрией тела
вращения (ось вращения Ох). В
направлении оси диполя рассеянная
волна не распространяется.
Кривая II. Падающая волна неполяри-
яована. Электрон колеблется в плоско-
л Т l-f-cos22& 7[& = 0]
стяхОу.1 g ;/[&==450] = 2.
Картина имеет симметрию тела
вращения (ось вращения Оз).
Выражение интенсивности
рассеянного излучения будет
теперь зависеть от констант
данного атомного электрона
к и %.
В структурном анализе,
как правило, не учитывается
влияние связанности
электронов на картину рассеяния.
Подробнее об этом будет
сказано па стр. 315.
Здесь уместно будет
рассмотреть вопрос о суммарном
рассеянии электрона. Интегрируя (III, 5) по всем углам 0, можно
найти отношение энергии, рассеянной электроном, к падающей, т. е.
определить коэффициент рассеяния <? (см. стр. 186),
Интегрирование по сфере приводит к формуле
■1о6ц
8?
$ п№ '
(Ш,<'>)

214 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
Предположим теперь, что па пути рентгеновских лучей
ставится пластинка толщины d, содержащая п электронов в 1 см*.
Если полагать рассеяние некогерентным, то оно равно
лплаот ~—' ДОЛIобщ*
На 1 см2 пластинки в одну секунду падает энергия /0, из
которой рассеивается /пласт- Это значит, что коэффициент рассеяния
Массовый коэффициент рассеяния
|«0,2. (Ш, 7а)
6,02 -102{ ,
Действительно, в 1 грамме находится .— атомов веса .1:
6 02 • 1023
в единице объёма их будет -^—-? р. Число до электронов в
единице объёма равно произведению числа атомов на число
электронов в атоме Z, т. е. до — -^—^— pZ. Полагая Zzz -~ ,
получим (III, 7а).
§ 3. Атомный фактор
а) Атомный фактор и распределение электронов. Фактором
атомного рассеяния или, короче, атомным фактором f называется
отношение амплитуды волны, рассеянной атомом, к амплитуде
волны, рассеянной электроном при тех же условиях, т. е. под тем
же углом и для той же длины волны. Если бы все электроны
рассеивали в одной фазе, то атомный фактор равнялся бы
менделеевскому числу Z.
Если атом содержит Z электронов, мгновенное расположение
которых в пространстве описывается векторами rit то мгновенное
значение амплитуды, рассеянной атомом, будет
.КИ = ^2^Ю. (Ш, 8)
» = 1
Величина s?\ учитывает разность фаз, возникающую между
волнами, рассеянными электроном г и электроном, находящимся
в начале координат. Действительно, рассмотрим электрон,
находящийся на расстоянии ri (ОМ) от начала координат. Пусть на этот
электрон падает плоская волна, характеризующаяся волновым
вектором /<?р и рассеиваемая в направлении к. Напомним, что эти
векторы указывают направление волн, а их длина обратно
пропорциональна длине водны,

§3]
АТОМНЫЙ ФАКТОР
215
Из фиг. 111,7 очевидно, что волна к0 в ходе к электрону
в точке М пробегает путь, больший на ВМ, чем к электрону
в пачале координат. Также ясно, что рассеянная волна к от
электрона М делает путь, меньший
на АО, чем от электрона в
начале координат.
Таким образом разность хода
равна О А — ВМ, а разность фаз
1сг{ — 7с0г4. Введём обозначение
8=(7с~ Я?0). (Ш,9)
Абсолютное значение вектора 8
можно выразить через угол рас-
сеяния, Так как 7с = 1с0 = ^ , то
ко
ho
В
У
^^ъ-
N /
^М
* = 4~
sin Ь
(Ш, 10)
Фиг. III, 7. К выводу атомного
фактора.
Итак, разность фаз между волнами, рассеянными электронами
в точке J/ив начале коордияат, равна srt, чем и доказана
формула (III, 8).
Подчеркнём, что в этом рассуждении, так же, как и далее, мы
пользуемся представлением об интерферирующих плоских волнах,
что справедливо при малости рассеивающего объекта по сравнению
с расстоянием от него до точки наблюдения. Размеры длины волны
рентгеновских лучей сравнимы с расстоянием между электронами.
Поэтому величинами «1% пренебречь нельзя и Eat<,ZEe- .
На опыте измеряются, разумеется, не мгновенные значения
интенсивности рассеяния, а усреднённые.
Каждый из электронов характеризуется своей «функцией
распределения» Pi{xyz), указывающей плотность того «электронного
облака», которое возникает при наложении друг на друга
бесконечного числа его траекторий "(мысленных мгновенных фотографий
этого атомного электрона). Общая плотность электронов в атоме
(в числах электронов на единицу объёма) равна
z
о(*г/.?) = 2р*(^).
Величина pdi', где dv— элемент объёма, есть количество
электронов, приходящихся в среднем на объём dv.
Рассеяние элементом объёма dv выразится, очевидно,
следующим образом: pdi?e'<*r>, где г — радиус-вектор, соединяющий начало
координат с элементом dr. В соответствии с определением фактора
атомного рассеяния, пмоем:
('(*) = f ре* M<ivi (Ш,П)

216 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ Л У ЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
Знание функции р (#*/£) определяет атомный фактор. В общем
случае атомный фактор есть функция вектора s; это значит, что
атомное рассеяние зависит от аргумента —^- (см. (III, 10), а
также от ориентировки атома в положении рассеяния.
Мы ниже вернёмся ещё к этому общему случаю. А сейчас
введём основное упрощение, вводимое всегда при подсчёте
атомного рассеяния-, предположение о сферической симметрии
электронного распределения. Вполне очевидно, что в этом случае
значение / не зависит от ориентировки атома, и рассеяние становится
функцией скалярного аргумента
Подобное допущение, очевидно, вполне хорошо передаёт
особенности электронного распределения свободного атома.
При наличии сферической симметрии выражение (III, 11)
атомного фактора удобно преобразовать, вводя в рассмотрение функцию
£/(»•) = 4™-2р (г). (Ш, 12)
Начало координат берётся в центре атома.
Очевидно, U(r)dr есть число электронов, заключённых между
сферами радиусов г и r-\-dr. Функция U(r) называется
радиальным распределением и очень паглядно, как мы увидим далее,
характеризует атом.
Как известно, элемент объёма в сферических координатах
(фиг. Ш, 8)
dv — г2 sin я da dr dy.
Выбирая направление s за радиус сферы, от которого
происходит отсчёт а, получим: ^«^= а. Подставляя значение р из (III, 12)
и пользуясь написанным выражением для dv, получим:
f(s) = -L Г ( f [J(r)efbroosar2sinadrdaab.
о о о
Производя интегрирование но углам, получим без труда
оо
f(s) = jU(r)™^dr.p (111,13)
о
Итак, атомный фактор есть функция ^^ ; вид этой функции
определяется радиальным распределением электронов в сферически
симметричном атоме,

§3]
атомный фактор
217
Если распределение рассеяния атома по углам известно для той
или иной длины волны, то U (г) может быть найдено на опыте.
На основании известной теоремы обратимости интеграла Фурье
имеем:
оо
U(r)=* Г st(s)aiu(sr)ds.
(Ш,Н)
Для многих целей структурного анализа полезно вычисление
проекции электронной плотности атома на плоскость.
,
/dr
1 г
^
---*\\^\
х>?<Д \
df~~3c^K.
Vy
// d<p^y^
г / \ s
/ / \s
/ / \ N
ч/\/аг \ \
Фиг. 111,8. Элемент объёма имеет рёбра dr,
rda, rsinadip. Считая его прямоугольным
параллелепипедом, имеем dv = г2 sin о dr darff.
Проекция плотности вдоль направления, проходящего на
расстоянии а от центра атома, равна:
оо оо
о(а) = 2 [ о (V^ + tf) dx = 2 J Z_ P (r) dr. (Ill, 15)
О а
На практике приходится прибегать к интегрированию в конечных
разностях. Кривая о (а) имеет большое значение в рентгеновском
структурном анализе, так как соответствует очень распространённой
картине атома в проекциях электронной плотности на грань
элементарной ячейки.

218
ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
Кривая о (а) может быть вычислена из, опытной или
теоретической f -кривой. Форма кривой а (а), в особенности при больших а,
чувствительно зависит от /-кривой.
На фиг. III, 9 првводятся две кривые о (а) для атома углерода.
Они подсчитаны из f-кривой для атома углерода с температурной
,мМ7
О 0.2 О.и 06 0$ Ю U 14 1.6
Фиг. 111,9. Кривые а (а) для атома углерода.
поправкой е v х ' при Ь' = 4А~2; первая кривая о (а) построена по
/"-кривой, оборванной прв —^- =0,5, а вторая по /'-кривой,
сведенной к нулю при ~- = 0,7. Общий характер кривых а (а)
разумеется тот же, по средние различия в а достигают 0,2 эл/Ар.
Кривые сходят к нулю лишь на расстоянии 1,7 А от атома.
Для ряда расчётов бывает удобно выразить кривую о (а)
приближённой формулой. Для этой цели подходят уравнения типа
о(а) = Ле-кг"; о(а) =
sur г
а(а) =
(аН-г«)2'
где г — расстояние от центра атома, А и а — параметры-
Дтом углерода, например, хорошо аппроксимируется рлсдующим

§3]
атомный фактор
219
выражением:
о (а) = 77 ,
V ' (0,12 + e*)*-
здесь а — в ангстремах (подробнее см. стр. 522).
б) Расчёт атомного фактора для свободных атомов.
Распределение электронов около свободного атома можно рассчитать.
Действительно, квантово-механический смысл p(xyz) это $2(хуг), где
ty(xyz)— волновая функция, удовлетворяющая уравнению Шредин-
гера. Как известно, строгое решение может быть дано только для
атома водорода. Были предложены приближённые методы расчёта
и по ним были' вычислены атомные факторы для всех свободных
атомов.
Первый заключается в рассмотрении всех Z электронов атома
как газа, энергия которого складывается из притяжения электронов
и ядра, отталкивания электронов друг от друга и кинетической
энергии электронов. Плотность этого газа исключительно высока и
нулевая энергия электронов настолько велика, что тепловой
энергией можно пренебречь. Таким образом при обычных температурах
газ рассматривается, как находящийся в состоянии полного
вырождения: кипетическая энергия электронов полагается равной нулевой
энергии и вместо статистики Больцмана к газу применяется
статистика Ферми.
Расчёт, проведенный в этих предположениях, приводит к
следующему результату:
Здесь а = Z 3 [&>£*) о—2=== °»47 Z 3 к называется
характеристическим радиусом атома, х—расстояние от центра атома в единицах а.
Функцля J-L-~ измеряет электрический потенциал системы; её
значения были вычислены для всех х = г\а.
Переходя от функции р(г) к значению атомного фактора,
приходим с помощью (111,13) к следующему результату.
Атомный фактор атома с менделеевским числом Z равен
/ = £Ф,
4* sin Ь
где Ф есть универсальная функция аргумента sa = —г-—а, где
а — характеристический радиус атома.
Значения Ф приведены в таблице III, I, в функции sa. Вычисляя
1
— о" °
л =*= 0,47 Z 8А, мы можем построить при помощи этой таблицы
кривую /(-Т-) для любого атома.

220
ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ
И В КРИСТАЛЛЕ [ГЛ. Ш
Примером такой кривой является кривая, изображенная на
фигуре III, 13 (стр. 222).
Таблиц a III, I
Универсальная функция атомного фактора Ф = Ф (sa)
sa
0,00
0,16
0,31
0,47
0,62
0,78
0,93
•
-i
1.000
0,922
0,796
0,684
0,589
0,522
0,469
sa
1,09
1,24
1.40
1,55
1,71
1,86
2,02
-4
0,422
0,378
0,342
0,309
0,284
0,264
0,240
sa
2,17
2,33
2,48
2,64
2,80
2,95
3,11
-i
0,224
0.205
0,189
0,175
0,167
0,156
0,147
Итак, рассеяние атома максимально (все электроны рассеивают
в фазе) в направлении падающего луча (при ft = 0; f = Z). С
возрастанием 0 рассеяние
падает и притом тем
быстрее, чем короче длина
волны.
Вполне очевидно, что
рассмотрение
электронного распределения по
этому методу довольно
грубо уже хотя бы
потому, что оно не
учитывает наличия К, L и
т. д. уровней.
Этого недостатка
лишён метод Фока-Хартри.
Этот способ вычисления
позволяет найти кривую
распределения
электронной плотности для
каждого электрона в
отдельности.
На фиг. III, Ю
изображено радиальное
распределение электронов
U (г) для различных электронов иона К+. На фиг. 111,11
изображены доли участия разных электронов в атомном факторе.
Мы видим, что доля .ЙТ-электрона остаётся существенной и при
больших —. Напротив, рыхлая 3/-оболочка даёт заметное рассеяние
г.(Д)
Фиг. 111,10. Радиальное распределение U(r)
различных электронов в ионе К+.

§ 31
АТОМНЫЙ ФАКТОР
221
лишь при малых углах. Это обстоятельство оправдывает
аппроксимацию атомов сферически симметричным распределением даже и
в случае наличия химиче-
Ю
ской связи. Действительно,
в связи участвуют внешние
электроны, а рассеяние в
основном определяется
внутренними электронами.
Такая аппроксимация,
вероятно, менее справедлива для
химически связанных
лёгких атомов, у которых, как,
например, у углерода, из 6
электронов лишь 2 не
участвуют в химической связи.
Вычисления по методу
Фока-Хартри весьма
громоздки. Оказывается, что
для атомов с Z > 20
можно пользоваться с успехом
упрощённым вышеописан-
г
0,5-
W
Зр\\3$
7Г
\\z
is\
h
/Y +
s&
5m ■$
- , A
0,5 10
Фиг. 111,11. Доля участия различных
электронов иона 7С+ в атомном факторо.
ным методом. В этих случаях индивидуальные особенности
электронного распределения атома хорошо усредняются универсальной
функцией.
60 г-U **/ам
— Фок-Хартри
Первый метод
0J
U 0.6 0.8
г в единицах с=0,53А
W 10 ХО \0
Фиг. 111,12. Радиальное распределение U(r) в атоме Rb,
рассчитанное по двум методам.
На фигуре III, 12 показано радиальное распределение для
рубидия, вычисленное обоими методами. Усреднённый характер упро-

222 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. lit
щбняой кривой совершенно очевиден. Фигура III, 13 показывает,
что значения /"-фактора, рассчитанные по обоим U (г)-кривым,
практически совпадают.
Следует подчеркнуть, что при необходимости рассчитать атомный
фактор для иона, а не для нейтрального атома, приходится
пользоваться исключительно методом Фока-Хартри.
в) Температурная поправка. Электроны атома находятся в
тепловом движении вместе с атомом или молекулой. Картина среднего
во времени
электронного распределения, которую
даёт опыт, включает в себя
и эти движения электрона,
так же, как и движения
электрона по отношению
к ядр^ атома.
Следовательно, определяемый на опыте
атомный фактор / есть
характеристика рассеяния
атомом, колеблющимся в
решётке.
§!п* Формулы раздела а)
I , , * справедливы и для атома,
О #5 Ю находящегося в тепловом ко-
Фиг. 111,13. Кривые атомного фактора, лебании. Электронное рас-
рассчитанные по двум U(r) кривым. нределение и (г) или р (г)
будет характеризовать
среднее во времени распределение электронов, созданное движениями
всех типов. Если колебания атома изотропны, то атомный
фактор будет функцией абсолютного значения вектора \s\ и
формулы (III, 12), (III, 13) и (III, 14) сохранят свою силу.
В случае анизотропии тепловых колебаний атомный
фактор будет зависеть от вектора s и определяется формулой
(III, 8) и (III, 11).
Таким образом анизотропия тепловых колебаний и отклонение
электронного облака от сферической симметрии благодаря
химической связи могут привести к одинаковым изменениям. Лишь
исследование при разных температурах может установить различие между
этими искажениями.
Что же касается расчётов, о которых мы говорили в разделе б),
то они сделаны для покоящегося атома. Естественно, что теория и
опыт будут значительно расходиться.
На фиг. Ш, 14 показаны /"-кривые для углерода: (а)—
рассчитанная для покоящегося атома и (<5) — опытная.
Не представляет труда ввести поправку на изотропные коле-
бания. Как будет показано ниже, она имеет форму с ^ *• ' .
Г
30-
Фон-Хартри
Перми метод
20-
10

4] бтруктурный Фактор 223
Показанная на рисунке /"-кривая переходит в опытную при
умножении на указанную поправку (ii = 4A~a).
Эта поправка позволяет пользоваться табличными /"-кривыми для
реальных случаев. Коэффициент В определяют на опыте, т. е.
подбирают его таким, чтобы совпадение теории с опытом было наилуч-
Теоретичесная кривая для покоящегося
атома (а)
Зксперименталыюя кривая (б)
Фиг. III, 14. Атомный фактор для углерода; теоретическая
кривая для покоящегося атома (а); экспериментальная кривая (б).
шим. Такая процедура вполне законна, так как исследуется
интенсивность очень большого числа отражений.
Коэффициент В обратно пропорционален температуре. Чем выше
температура, тем быстрее спадает рассеяние с увеличением угла Ь.
Если желают учесть анизотропию тепловых колебаний, то нельзя
пользоваться универсальной константой В. Как будет видно из
дальнейшего (стр. 277), в этом случае каждой из плоскостей (Ш)
надо будет приписать своё значение В.
§ 4. Структурный фактор
а) Основные формулы. Рассеяние элементарной ячейки,
выраженное в электронных единицах, т. е. отнесенное к рассеянию
электрона в тех же условиях (те же & и Я), называется структурной
амплитудой FhM. Если мы говорим, что рассеяние элементарной
ячейки в направлении, определяющемся индексами
интерференции Ш, равно, скажем, 32, то это значит, что такой же
величины рассеяние дали бы под углом рассеяния 2& 32 электрона,
действующих в фазе. Таким образом амплитуда волны, рассеянной
одной элементарной ячейкой кристалла, равна Ь\ыЕе. Каждому

224 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
отражению hkl будет соответствовать своя структурная амплитуда.
Квадрат структурной амплитуды Fm принято называть структурным
фактором. Впрочем, иногда это название применяется и к FbU.
Очевидно величина Fbn должна быть связана с характером
распределения электронов в элементарной ячейке.
Действительно, повторяя рассуждения, приведшие нас к формуле
атомного фактора (III, 11), мы можем предположить, что каждый
элемент объёма dv элементарной ячейки даёт волну с амплитудой,
пропорциональной числу электронов p(xys)dv и фазой, равной sr.
Следовательно, в соответствии с опрецелением
F = j j j p (хуг) е* <")<*« (III, 17)
t?
г — попрежяему расстояние элемента объёма dv до начала
координат, которое берётся, как правило, в узле [000] ячейки.
Мы рассматриваем рассеяние кристаллом («отражение» от
кристалла). В этом случае вектор s—к — к0 равен 2пНькь где
Нш—вектор обратной решётки узла Ш, попавшего на сферу отражения.
Таким образом, действительно, для каждой интерференции (т. е. для
каждого узла обратной решётки) имеется своя структурная
амплитуда
Fm = j j j P (хуг) е**К <ншг> dv. (Ill, 18)
V
Электронную плотность элементарной ячейки можно представить
как сумму атомных функций, т. е. электронных плотностей
отдельных атомов, входящих в ячейку.
Пусть центр атома номера к находится в точке гк ячейки,
тогда его атомную функцию удобно записать в виде рк(г— гк)
(г — гк — аргумент функции р). Электронная плотность в ячейке
N
р {xyz) = 2 н (г — гк). (III, 19)
Лт—число атомов в ячейке. Подставляя (111,19) в (111,18), получим:
11 »и = S / / / р*{г ~ **> e<i* {Нш'Г) dv' №20)
Учитывая, что атомный фактор Jc-ro атома может быть представлеп
в виде
h = / f / р» О— П) е* С '- **> dv, (III, 21)

j? 4J структурный фактор 225
получим:
I-m==kf/2r-(n'^]- (Ш,22)
A = l
Раскрывая скалярное произведение, можем записать эту очень
важную формулу в виде
*ш = 2 fLetir-{hXk 'г*у* :'"*) > ("Т. 23)
где хк1 ук и zk— относительные, т. е. измеренные в долях
периодов, координаты центра атома в элементарной ячейке.
Если ячейка обладает центром симметрии, выбранным за
начало отсчёта, то каждому атому хк ук гк соответствует атом хк ук зк.
Поэтому
Рыл = 22 //, cos 2- (lixk -j- kyk + tek). (Ш, 24)
Как мы говорили в предыдущем разделе, атомный фактор бывает
известен исследователю лишь приблизительпо. Поэтому для многик
целей вполне допустимо ввести следующее предположение: значения
атомных факторов разных атомов для всех отражений относятся,
как соответствующие менделеевские числа
Это значит, что /'-кривые всех атомов, входящих в кристалл,
предполагаются «параллельными». Введём в рассмотрение
единичный атомный фактор /'. Тогда fr — fZr, fk = fZk (TIT, 25) и т.д.
для любого атома. Выражение структурной амплитуды приобретёт
вид
N
Разделим обе части равенства на 7А\ где Z= 2 %* есть полной
*•—1
число электронов в ячейке. Величину
Рш = ^ = V ЩС^ ^Щ + Ч (1П> 2у)
назовём единичной структурной амплитудой. Отношение пк = -~
можно назвать «весом» данного атома. Очевидно, что максимальное
значение Fhkl (все атомы рассеивают в одной фазе) равно I. Если
кристалл состоит из атомов одного сорта, то пк одинаково для
•всех атомов и равно обратной величине числа атомов в ячейке.

226 ДИФФРЛКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [гл. Ill
Для того, чтобы ещё более отчётливо представлять себе смысл
выведенных формул структурной амплитуды, проведём следующее
рассмотрение. На фиг. III, 15 показана плоскость семейства (Ш),
отражение от которого мы рассматриваем. Допустим, что в
элементарной ячейке находятся два одинаковых атома, один из которых
находится в начале координат.
А (hkl)
Фиг. III, 15. Атом А находится в
плоскости (hkl), атом В сдвинут на А по
нормали к ней. Разность хода о = ЛС-\-
+ ЛП = Д2 sin » = ЫНШ = 1гкНш.
о а
Разность фаз = ~ = 2ъгъНш-
Помещая второй атом в разные точки ячейки, мы будем
создавать, вообще говоря, различные разности фаз 2ъЦшгк между
волнами, рассеиваемыми этими двумя атомами. Для разных
расположений Fhici будет принимать значения, колеблющиеся в пределах
от 0 до -f- 2/. Легко видеть, что влияние второго атома на
величину структурного фактора можно охарактеризовать одной
координатой Ь — Ншгк, отсчитываемой в направлении нормали к
отражающей плоскости. Иначе говоря, сдвиг атома вдоль отражающей
плоскости не меняет значения структурного фактора. Очевидно
также, что при сдвиге вдоль Нш А будет обращаться в 1, как
только мы попадём на одну из плоскостей семейства (hkl).
Пересечём элементарную ячейку несколькими плоскостями
семейства (hkl), проходящими через неё (фиг. III, 16), и рассмотрим
некоторое расположение центров атомов. Имеется возможность
быстро и наглядно оценить, какие из этих^ отражений должны быть
сильными, какие нет. Действительно, чем ближе атомы к плоскостям,
тем ближе значения А к 1, значение фазы к нулю и
значение единичной амплитуды к 1. Чем ближе атомы к
середине между плоскостями, тем ближе значение Д к „-, значение
^азы — к 180° и значение амплитуды к — 1. Следует запомнить
Фиг. III, 16. Сечение
элементарной ячейки
несколькими
плоскостями семейства hkl.

4}
СТРУКТУРНЫЙ ФАКТОР
227
фигуру III, 16; она очень помогает в практической работе, по
расшифровке структур. Если А и Е—две ближайшие плоскости
семейства (Ш), то атомы, лежащие на плоскостях В и D, ничего
не добавят к этому отражению, атомы в Л к Е будут
«поддерживать» друг друга, а в Л и С «погашать» друг друга.
Фиг. III, 17. Положения атомов углерода в проекции на грань
ас находятся как точки пересечения плоскостей, дающих
отражения, выделяющиеся по силе.
На фиг. III, 17 изображен скелет структуры одного
органического соединения. Все атомы его попали на плоскости (Ш):
(16.00), (16.01), (14.08), (10.03), (602), (405"), (207). Отражения
от этих плоскостей были самыми сильными.
Разумеется, отражение будет одинаковой силы в том случае,
если все атомы лежат на плоскостях или все атомы лежат
посередине между плоскостями. В одном случае амплитуда будет-}-1,
а в другом — 1. На интенсивности это различие сказаться не может.
Впрочем, это очевидно и из того соображения, что выбор начала
координат произволен, а от этого выбора значения структурных
амплитуд измениться не могут.
Исследование отражений более высоких, чем первого порядка,
удобно производить, рассматривая их как отражения от вставных

228
ДИФФРЛКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕН В КРИСТАЛЛЕ [гл. III
плоскостей. Если плоскость (234) ближайшая к началу координат
отсекает по осям отрезки -_•, — и --, то «плоскость (468)» от-
и, таким образом, поделит все истинные
сечёт отрезки
1
"в и
атомы нахо-
на рас
межплоскостные расстояния пополам. Если поэтому
дятся, например,
1 2
стояниях -=-,-=- и т. д. от
о о
плоскостей ilikl), то можно
утверждать, что отражение
5-го порядка от этой
системы будет сильным. В
указанном смысле мы и далее
будем говорить о
«плоскостях» (Ш) в случае, когда
индексы h, к и / содержат
общий множитель.
При рассмотрении
проекций на грань ячейки
изучаются, как мы узнаем
позже, структурные
факторы тех плоскостей (Ш),
которые перпендикулярны
плоскости проекции. Тогда
можно представить себе
характер изменения
структурной амплитуды вдоль точек проекции в виде «плоской»
косинусоиды (см. фиг. ITI, 18), период которой равен с(ш для отражения
первого порядка .и — для отражения и-го порядка.
б) Частные случаи формул структурного фактора. Так как
в кристалле центры атомов связаны симметрическими операциями,
то всегда возможно разбить атомы на две или несколько групп
с одинаковыми аналитическими выражениями для структурных
амплитуд.
Для каждого положения определённой кратности любой,
пространственной группы имеет смысл записать специализированное
выражение структурного фактора. Для вывода этого выражения
надо знать координаты точек, занимающих в ячейке то или иное
положение.
Выведем выражение структурной амплитуды для общего
положения в группе C\h = Р2, с. Координаты точек общего положения стгь
Фиг. Ш, 18. Наглядное представление
структурных амплитуд в виде плоских
косинусоид.

§ 4] структурный фактор 229
По определению
// = f (ei2r'{hxJr *У-''1е) 4- e~iir-(Ьж+kil+ls) -i_
e
'2tz (—hx-rky — lz-\—-—) —Uk ( — hx^-hy—lz-j —— )
Пользуясь формулой еы -\-в *а = 2 cos а, а также приводя сумму
косинусов к виду, удобному для логарифмирования, получим:
Fm = tfcos 2« (te + ^ -f ^) cos 2- (fy — *±i).
Ксли в рассматриваемой ячейке содержится — iV таких групп
атомов, то структурная амплитуда ячейки равна
4
Fhkl = 4 J /г COS 2it (/ia?r -j- for -f ^J COS 2- (&yr — Цр).
Ксли в этой же пространственной группе другими атомами
занять двукратное положение, скажем 1 [000] и Г?? » т0
к написанному выражению надо добавить структурную амплитуду
для этого частного положения, которая будет равна
Эта часть структурного фактора может принимать всего лишь два
значения — нуль при к-]-1 нечётном и 2f при к-\-1 четном.
В том случае, если в ячейке нет центра симметрии,
структурная амплитуда остаётся комплексной (сравни (III, 23) и (Ш, 24)).
В этом случае удобно представить Fhkl в виде Л -4- Въ. Вычислим,
например, структурную амплитуду для общего положения группы
Cl = C2. Координаты точек таковы:
— 1 , 1 , , 1 1 , -
■W, ->W, уЬ''» у+•'/, ~; у — Л у "Г?/, *•
Единичная структурная амплитуда имеет вид:
Fm = cos 2~ (hx -j- Jcy -{- 1г) -f- cos 2n (— hx -f- Jet/ — h) -f-
-f cos 2~ (lrx+hj -; lz |-^y^)-| cos 2* (-Нх+ку-1г-\- ^) -|-
-j- i sin 2tz (hx -j- hj -j- Iz) -[- sin 2тс (— hx -{- fo/ — /^) -|-
-Lsin 2т: (Aa.-pt//-Lfe-i-*±*)-Lsin 27Г (-hx~'rhj—fc+^JU
= 4 cos2 2- (~У - ) COS 2ic (Aa? 4~ ^) cos 2т: % -4-
■i-i[4cos8 2s(A+i.)cos2«(*ar + fo)sin2ictyJs=J[fcW+»i/fcM.

230 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЧИ В КРИСТАЛЛЕ [ГЛ. III
Если в ячейке находится несколько групп атомов, то (сравни (III, 27))
*"ш = 2*г(4г+ВД, (Ш, 28)
г
ИЛИ
/<ш = 2 fr (A + /^f). (Ш, 28а)
При отсутствии центра симметрии структурная амплитуда может
быть также представлена в действительной форме
к
*ш = EfrC03 2ic(fojr+ tyr + kr + аш), (Ш, 29)
ГД6 аш—Фаза данного отраженшг. Связь с комплексным
представлением даётся в виде:
2/г*Й7
tff2ita/lW =
r=i
У
(ИГ, 29а)
2 ^Й*
Структурный фактор Fm равен произведению Гш на комплексно
сопряжённую величину F*hki (см. на стр. 211)
F'm = FfcW • *ш = (2 /*^г)2 + (2 fr Br? (III, 30)
или для единичного структурного фактора /<ш =
А'2
(Zff
Ъ\ы = №* = (2 nrArY + (2 »г Яг)2- (Ш, 30а)
г г
При записи структурной амплитуды в виде (III, 29) надо
обращать внимание на связь между фазами отражений Ш. Эту связь
находят по уравнению (III, 29а). Например, для группы С»— /'2,
к = 2п
А = 2 cos 2* (кг |- U) cos 2ф/ «ш = — <хйы- = — айй,
\В = 2 cos 2« (Ля? -f te) sin 2**// а-ш = о^т :£ яЛЙ,
/;=2W fl'
^ = — 2 sin 2тг (йж + fe) sin 2'ky am = — аш = т: — aft,7,,
/>' = 2 sin 2- (fee -h te) cos 2irfci/ Чы = т: -f- аЛж7 ^ аш.

« 5]
РАССЕЯНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ
231
0г~,
*
7\~
9
-40
Ьм2пх,Ш2пхь
-100
-99
■80
■70
^kr-60
-50
-Щ-40
\\35
Ш-30
■25
-20
20
2}
22
-- 13
-- 7
'-'- в
--5
-- 4
§ 5. Рассеяние рентгеновских
лучей «малым» кристаллом
(абсорбция и экстинкция
отсутствуют)
23
Д4
Уже сейчас мы обратим внимание на то, что ряд отражений га«-
сится интерференцией волн, исходящих от симметрически связанных
атомов. Например, в формуле F
для группы С\ отражения hkl при
h-\-h нечётном будут
отсутствовать. Очевидно наличие связи
между пространственной группой и
формой структурного фактора. Как
будет показано ниже, именно это
•обстоятельство даёт возможность
опытным путём определить
пространственную группу.
Подсчёт структурных факторов
и амплитуд приходится весьма
часто производить в практике
структурного анализа. Так как
структурную амплитуду можно
представить в виде произведения
трёх косинусов или синусов (с
аргументами ЧтЛьх, 2ъку, 2к1г) между
собой, то для проведения такого
подсчёта рекомендуется
номограмма Белова, показанная на
фиг. III, 19. Слева и справа
отложены аргументы косинусов в
сотых долях длины окружности,
в середине величина произведения.
Произведение любого синуса на
косинус также найдётся без труда, если
.вспомнить, что sin a = cos (90° — а).
4-
6
id»
ям
п
12
О
/4
-15
9
29
21
22
23
*2&
Фиг. 111,19. Номограмма Белова
для расчёта структурных
амплитуд.
а) Условие возникновения и
величина максимума
интенсивности. Рассмотрим теперь рассеяние маленького кристалла. Примем
следующее предположение: падающая электромагнитная волна
действует одинаково на все атомы кристалла. Полагая, кроме того,
кристалл малым по сравнению с расстоянием В до точки
наблюдения ■■), мы можем подсчитать суммарное поле, рассеянное всеми
*) В этом случае лучи, идущие от всех точек кристалла, могут считаться
параллельными.

232 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ |l\r. Ш
-ячейками, путём сложения амплитуд рассеянных волн, созданных
всеми N ячейками кристалла.
Амплитуды волн, рассеянные каждой ячейкой решётки, равны Fhkl;
фазы их будут разными для разных ячеек. Разность фаз вычисляется
по отношению к началу координат (узел ООО) тем же способом,
которым мы действовали выше, и равна sRvlnp, где, как и ранее,
в = & — Ал0, а М.тпр = та -f- nb-\~pc есть радиус-вектор А:-й ячейки.
Итак, амплитуда волны, рассеянной всем кристаллом, равна;
EKp = EcFm S e'(eJW, (Ш, 81)
так как EeFhkl равна абсолютной величине амплитуды волны,
рассеянной одной ячейкой.
Суммирование происходит по всем N элементарным ячейкам.
Чтобы произвести суммирование, допустим, что кристалл имеет
форму параллелепипеда со сторонами A", a, N2b и У$с;
произведение NtN2Ns равно числу ячеек А7. Тогда последнее выражение
можно переписать следующим образом, подставив значение ЛтПр-
Екр = Е^м%\<™яУ%\шь*Л±\»". (LIT, 32)
т—о »=о р—о
Каждая сумма представляет собой геометрическую прогрессию,
суммирование которой легко проводится, и мы получаем следующее
выражение:
Екр = EeFm ei8a__x ->«ь_1 ei*c_1 ' (m> :33)
Мы ищем значение интенсивностей рассеянной волны в точке
наблюдения. Как известно, интенсивность равна произведению Е
на комплексно сопряжённую величину Е* (см. стр. 211)
I £''-7'2 2 — 2 cos Nxsa 2 — 2 cos N^sb 2 — 2 cos У-двс mr .. \
Ы — J^hil ' 2 —2cos*a " 2 —2cos*fc 2 —2cos*« ' <Ш> Mf
или
sin2 — X^sa sin2 — X„sb sin2 — X-^sn
/Kp = E'iF'm ^ ^ L . (in, 34a)
sin2 — sa sin2 — sb sin2 — sc
£i J, 2i
Функция типа ът« а изображена на фиг. Til, 20 для N = Ь.
sin в А
Уже при N более 100 вся интенсивность практически
сосредоточивается в главных максимумах. При увеличении Л' высота
максимума возрастает пропорционально АГ2, площадь — пропорционально А"
и ширина убывает обратно пропорционально N.

§5]
РАССЕЯНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ
233
Эти положения доказываются без труда. Значение функции
в максимуме находим, применяя правило Лопиталя:
-т-(Sin2 .ЛГа)
L do
•Sin-a
= Л'
r sin 2Va cos JVa
Sin а cos а '
Л'
sin 2Xa
-,— sin 2а
= I l\2 CQS 2Л'«
L cos 2а
= X*.
(Ш, 35)
Главные максимумы значения N2 имеют место тогда, когда и
числитель и знаменатель обращаются в нуль, т. е. при условии
а = *к(л = 0, з:1, ±:2...).
Sin'* 'TV3
rir «л т sin-iVa •
Фиг. Ш, 20. Функция ——— при .V=5.
sm- а 1
Высоты побочных максимумов анализировать не будем. Вполне
очевидно, что они уменьшаются при увеличении N. То, что вся
энергия при большом Лг будет сосредоточена в главных макоюгумах,
следует из такого вычисления.
sin2 Na
Проинтегрируем функцию
Sin-a
в пределах от 0 до т.. Это
значит, что мы суммируем энергию, приходящуюся на один

234 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. Ш
главный максимум и на все побочные, лежащие между двумя
главными.
sin2 Na
Для вычисления этого интеграла вспомним, что ——— равно
Л*, —1
Е0Е0, где Е0 = 2 еЫа (слг< СТР- 232). Величину, пропорциональ-
т = о
ную E0Eq, можем получить и иначе, а именно, перемножив
выражения Е0 и Ео, не производя суммирования. Имеем
IV,— 1 Ns — 1 Ni — I N,— 1
£'o#u'::'= 2 eima 2 e-<'w= 2 2 e<(»»-»>«. (Ill, 36)
,r „ „ _ sin2iVa
Переходим к действительной части и приравниваем —г-,—
значению, равному Е0Е0:
"в^'г ^S 2cos (w~~w) а- (1Т1,37)
Теперь мы можем вычислить интересующий нас интеграл
J lln"8rda==S 2] J cos(ro —n)ada,
W—0 n = 0 0
Г cos (m — n) a da. = 0 при тфп.
\ (TIT, 38)
При т = п этот интеграл равен ти. В двойной сумме случай т = п
повторится 2Х раз. Следовательно,
о
Теперь подсчитаем энергию, сосредоточенную в главном
максимуме. Ближайшие к этому максимуму нулевые значения функции
.лежат при a = zt — > (все нулевые значения лежат, естественно,
жри siniVa=0). Следовательно, надо подсчитать интеграл
da.
' Л*
J-
г.
sin2 iVa
sin2 a
2г
s) Таким образом ширина главного максимума равна -=

5] РАССЕЯНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ 235
• "к
cos (т — n)ada. (111,40)
п
IV
Вычислим последний интеграл
sin (ад — п) о"]
Л*
Если X очень велико, то синус можно заменить аргументом и
интеграл становится равным -тт. Это значение получится как при
т = п, так и при тфп. Всего двойная сумма имеет N2 членов.
Следовательно, вычисляемый интеграл приближённо равен 2лЛт.
На опыте это приближённое равенство выполняется весьма точно,
так как даже у небольшого кристаллика числа N имеют порядок
величины 100 000. Поэтому практически вся интенсивность
оказывается сосредоточенной в главных максимумах.
Иначе говоря, интенсивность излучения, рассеянного
кристаллом, отлична от нуля только в строго определённых направлениях.
Эти направления определяются превращением в нуль знаменателей
формулы (III, 34а). Условия, определяющие направления
рассеянных кристаллом лучей, имеют вид
sa = 2rJi, )
s1> = 2t:1;, \ (Ш, 41)
8С = 2гЛ, )
но ведь это условия диффракции, рассмотренные нами в § 1
(формула Ш, 1а), эквивалентные условию в = 2-.ЕГш. Итак, мы еще
раз доказали, что рассеяние рентгеновских лучей кристаллом (во
всяком случае его часть, существенная для структурного анализа)
сводится к «отражению» от семейств узловых плоскостей решётки.
Интенсивность каждого такого отражения будет равна
hn = EilAuX\ (Ш, 42)
т. е. определяется соответствующим структурным фактором.
Величина N2 попадает в эту форму по той причине, что значение
sin2 - JS\sa
в максимуме равно N'-v Подставляя значение E\—IeJ
sin2 — sa
2
Пользуясь (III, 38), имеем:
.1 sin2 a AJ jLJ
2 sin -^- {m — n)
(HI, 40a)

236 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. Ill
получим:
т -п.-2 л?2 е* 14-cos22ft mT ,.л
Если нас интересует распределение интенсивности излучения
около максимума, т. е. для векторов s = 2*JET-|-A8, то
формулу (111,43) удобно преобразовать. Вектор Дз раскладывается по
осям обратной решётки и представляется в виде
As =Pla* +рф* +1V>X. (ITT, 4 i)
Тогда характер распределения интенсивности вблизи максимума
будет задан выражением
sin2 — Nxpi sin2 — ХгРъ sin2 j N3p3
/Kp = IeFiki ^ fj 1 . (Ш, 44a>
sin2 -у/>1 sin2 — ^2 »'»' у />l5
6) Ширина максимума интенсивности. Хотя условия диффрак-
ции соблюдаются очень строго, но все же отражение рентгеновских
лучей происходит не при каком-то единственном значении * или ft,
а в небольшом угловом интервале около значения 0В,
удовлетворяющего уравнению Вульфа-Брэгга (III, 3). Диффракционный максимум
обладает некоторой шириной, которую можно подсчитать.
Рассмотрим для простоты отражение (100), происходящее в
ромбическом кристалле под углом *>в- Интенсивность излучения,
«отражённого» от этой плоскости под углом От? ~\- Д$, будет равна
sin8-7r JV"jf«A*
sin2— a^s
где
4л COS&g Aft
\ *
За полуширину этого интерференционного максимума примем
полуширину максимума функции
где L — размер кристалла в направлении оси a (L = Хга) и X — Х2Х,3.
Основанием для этого является то обстоятельство, что площади и
величины максимумов функций 1К9 и Г одицаковы. Подставляя
вместо &# его значение, получим условие, определяющее полу-
вирину Д#1
cos* Ь
€ > >

3 5]
РАССЕЯНИЕ РЕНТГЕНОВСКИХ ДУЧЕИ
237
откуда
Д{> t = Х1^!' • (ш> 45)
Эта приближённая формула показывает, что идеальные крж7
сталлы размером всего лишь в Од мм при углах &, близких к 90°
(cos 0 «0,1), дают полуширину порядка 10" — 10~б радиана, т. е.
порядка нескольких секунд дуги. Повторим ещё раз, что
выполнение диффракционных условий очень строго; размытие отражений
начинается лишь у кристаллов коллоидальных размеров.
в) Перечень упрощений, сделанных при расчёте (абсорбция,
экстинкция). Как указывалось в начале параграфа, основное
предположение, использованное при расчёте, заключалось в допущении
одинакового действия электромагнитной волны на все узлы
кристаллической решётки (на все атомы кристалла).
Это, конечно, неверно потому, что луч, попадающий в кристалл,
Судет взаимодействовать с атомами вещества и интенсивность
излучения, подходящего к атомам, лежащим на поверхности и в
глубине кристалла, может коренным образом различаться.
Ослабление рентгеновских лучей в кристалле происходит
по-разному, в зависимости от того, находится ли кристалл в
отражающем положении или нет. Если кристалл не находится в
отражающем положении (ни один узел обратной решётки не попадает на
<зферу отражения), то проникающий в кристалл луч ослабляется,
благодаря рассмотренным в предыдущем разделе явлениям (энергия
идёт на выбивание фотоэлектронов, электронов отдачи,
характеристическое излучение и квантовый эффект). Ослабление луча
характеризуется коэффициентом р. Если кристалл находится в
отражающем положении, то кроме того становится весьма заметной доля
энергии, идущая на вторичное когерентное рассеяние (см. ниже).
Это добавочное поглощение, происходящее только в том случае,
когда кристалл находится в отражающем положении, называется
экстинкцией. Чем сильнее отражает кристалл, тем больше
экстинкция; вполне ясно, что экстинкция будет иметь разное значение
для разных отражающих положений кристалла.
Таким образом ослабление луча в кристалле описывается
коэффициентом t* + s> коэффициент поглощения «х одинаков для любого
положения кристалла по отношению к лучу, коэффициент экстинк-
ции е равен нулю в неотражающем положении кристалла и имеет
разные значения в различных отражающих положениях.
Пренебречь поглощением и экстинкциен можно в том случае,
если f* L <С 1 и zL <С 1. Как будет показано ниже, экстинкциен
можно пренебречь в том случае, когда размер кристалла меньше
10"4 см. Право на пренебрежение истинным поглощением всегда
легко оценить, зная ja и L. Например, для органических объектов
коэффициенты поглощения для медного излучения примерно равжы

238 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. Ш
6 см~1. Таким образом кристаллы органических соединений
размером до 0,1—0,2 мм являются «малыми» в отношении поглощения;
они обычно не являются малыми в отношении экстинкции.
г) Некоторые представления в обратной решётке. 1.
Интерференционная функция в пространстве обратной
решётки. Как мы только что видели (IIT, 34а), интенсивность
рассеянных кристаллом рентгеновских лучей можно представить
в виде произведения структурного фактора на функцию
sin2 -jr- Nxsa sin2 -JV^ sin2— JV^sc
L (*) = i \ \ . (Ill, Щ
sin2 — sa sin2 — sb sin2 — sr,
*J Ci dt
Если кристалл велик, то возникают острые диффракционные
максимумы; в противном случае начинает играть роль вид L{s)
в окрестностях максимума, а при совсем малом числе частиц и
побочные максимумы L («).
Возникающие при этом эффекты удобно рассматривать тем же
методом обратной решётки (стр. 205). Вектор разности волнового
вектора падающей и волнового вектора рассеянной волны s = (к — fe0)
имеет размерность, обратную длине, и может быть представлен
в пространстве обратной решётки:
e=(tex-H&x + Ccx)2ic,
где £, тг), С — текущие координаты в пространстве обратной решётки.
При обращении этих чисел в целые числа h, к, I конец вектора 8
попадает в узел обратной решётки (s обращается в 2ъЖт).
Функция L (s) может быть теперь также представлена в пространстве
обратной решётки
L (Вд - sin2^f • si"'<ff • *™'<р™ . (Ill, 46a)
v ' ' SID2 (тг;) sin2 (гст;) sin2 (<) v ' '
Если число частиц в кристалле не очень велико, то £($*}С)
имеет максимум конечной ширины. Размытию интерференционного
максимума соответствует расширение соответствующего «узла»
обратной решётки.
Рассмотрим небольшой кристалл в форме параллелепипеда со
сторонами Nlt N2 и N3 частиц. Было доказано выше, что
полуширина максимума равна -^-; следовательно, более или менее
значительная интенсивность будет рассеиваться и в том случае, когда
вектор ^ будет оканчиваться не в узле обратной решётки, а в точке,
лежащей в области значений 5, tj и С A rt: ^-, Л zt ^- и i^jf.
Мы видим, что узел обратной решётки следует рассматривать как

§ 5] РАССЕЯНИЕ РЕНТГЕНОВСКИХ ЛУЧЕЙ 239
центр эффективной в смысле рассеяния области. В данном случае
эта область — параллелепипед со сторонами -т^-, -гг- > -гг~ (в долях
-*■' 1 -"2 х * 15
ах, 6х, сх).
Можно строго доказать, что и при любой форме кристалла
•«размеры» узла обратной решётки равны обратному объёму
кристалла. Нетрудно установить тот практический предел размера
кристалла, выше которого узел обратной решётки следует апрокси-
о _
мировать точкой. Для кубического кристалла КС1 ах=о,318А V
о
для молибденового излучения радиус сферы отражения равен 1,4 А"1.
Если кристаллик имеет форму куба с ребром в Ю00-а =
= 1000 • 3,14 А = 3140 А « 3 • 10"5 см, то угловая ширина
Маконом 318
мума будет равна -щ^-: 1,4 = 2,3 • 10~4 радиан =46". Неизбежная
расходимость пучка, с которой мы имеем дело в эксперименте,
значительно превосходит эту величину; таким образом кристаллы,,
размер которых больше 10~5—Ю-4 см, обладают точечной
обратной решёткой.
Из проведённых рассуждений очевидно также, что эффективной
области, окружающей узел обратной решётки, можно приписать
не только объём, но и форму. Это будет форма области, в которой
функция L (fy£) имеет значения от максимального до половины
максимального.
И в отношении формы этой области справедливы правила «об-
ратности». Если кристалл имеет форму куба или шара, то и узел
обратной решётки имеет ту же форму. Если же одно из рёбер
кристалла, имевшего форму куба, начать увеличивать, то
соответствующее ребро эффективной области будет уменьшаться. Таким
образом кристаллу, имеющему форму диска, будет соответствовать узел
в форме стержня, и наоборот — игольчатому кристаллу
соответствует узел в форме пластинки. В предельных случаях мы перейдём
к одномерному и двумерному кристаллу и соответственно к
обратным решёткам, состоящим из сплошных плоскостей и сплошных
прямых.
Поле функции L (trfc) около каждого узла обратной решётки
имеет одинаковый вид. Более того, это распределение, т. е.
размер и форма узла, не зависит от структуры кристалла, а
определяются лишь размером и формой кристалла.
2. Структурный фактор и обратная решётка. Если
L (s) можно представить в пространстве обратной решётки
одинаковым распределением для каждого узла, то второй множитель-
в выражении для интенсивности рассеянного излучения —
структурный фактор — не является периодической функцией в пространстве
обратной решётки.

240 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСДАЛЛЕ [ГЛ. III
Формула
N
fc=t K
даёт значения структурной амплитуды для максимума. В случае
малого кристалла надо, как мы только что убедились, учитывать
рассеяние в его окрестностях. Тогда формулу для Fhkl можно
записать в виде
N
Поступая попрежнему, т. е. разлагая & на компоненть[ по осям
обратной решётки, можем выразить Fm (s) в функции
координат ;г,£
А"
J'\ui (e^) = 2 />'****+ v/fc+^) . (Ш, Щ
Разумеется, это очень медленно меняющаяся функция. Поэтому
даже для очень малых кристаллов значение F1M внутри
эффективной (в смысле рассеяния) области остаётся неизменным. Поле
функции Ь\и следует принимать во внимание лишь в том случае, когда
рассчитывается диффракционная картина от «кристалла», состоящего
из числа атомов порядка единиц.
Итак, в отношении структурного фактора каждый узел обратной
решётки можно характеризовать одним числом (в общем случае
комплексным) — значением Fhkl. Это значение называют поэтому
иногда весом узла.
Как мы увидим ниже (стр. 287), в пространстве обратной решётки
удобно изображать ещё одну функцию — интенсивность твидового
диффузного рассеяния.
§ 6. Рабочие формулы иитенсивностеи
Выведенная в предыдущем параграфе формула интенсивности
{III, 43) не служит рабочей формулой.
При проведении структурного анализа нам приходится
сравнивать интенсивности отражённых лучей, измеренных на опыте, с их
значениями, получающимися вычислением для данных структур.
Это сравнение не может быть основано на формуле (III, 43).
Действительно, измерение величины интенсивности, фигурирующей
в этой формуле, потребовало бы измерения 'интенсивности
рассеяния строго монохроматических лучей в строго определённом
направлении.
Однако в данном направлении рассеяния пойдут лучи,
отражённые под разными углами из-за расходимости пучка "и с разными
длинами волн (в методе с применением белого излучения).

§ в]
РАБОЧИЕ ФОРМУЛЫ ИНТЕНСИВНОСТЕЙ
241
Таким образом вычислять надо интегральную интенсивность,
к определению которой можно подойти следующим образом.
Предположим, что вектор s, определяющий максимум в (III, 43), имеет
зтрого определённое значение. Вычислим энергию
Г = J* IdS, (III, 49)
где суммирование происходит по площади & щели ионизационной
камеры или по площади пятна на фотопленке.
Эта величина Р опять-таки не соответствует измеряемой на
опыте величине, так как в создании диффракционпого пятна
участвуют лучи, созданные не при одном определённом значении s, а при
(в ± As), где отклонения вектора $ от среднего значения
могут иметь различный характер в зависимости от постановки
опыта. Отклонения s от среднего значения имеют следующий
смысл.
Данной отражающей плоскости в согласии с уравнением Вульфа-
Брэгга соответствует при данном угле ft вполне определённая длина
волны л и при данной л вполне определённый угол ft. Но из-за
конечной ширины диффракционного максимума в первом случае
в отражении принимают участие длины волн в интервале Х±ДХ,
а во втором случае отражение происходит в интервале углов ftztzM.
Таким образом на опыте измеряется величина К, которую принято
называть интегральной интенсивностью
E=f'pdeu (111,50)
где Sj — параметр, имеющий различный смысл в зависимости от
постановки опыта. Для метода Лауэ dev = dk> для метода вращения
оно связано с d<> и т. д.
а) Метод Лауэ. Так называется способ получения рентгенограмм
от неподвижного монокристалла, на который падает немонохромати-
зированный или белый луч, содержащий длины волн от кт1й до Хтях.
При этом условии многие системы плоскостей окажутся в
отражающем положении для различных длин волн. В пространстве
обратной решётки схема этого метода изобразится, как показано на
фиг. IV, 3 (стр. 297). Область между двумя сферами -г— и -
действенна, т. е. для любого узла, попавшего в неё, можно
построить диффракционный луч и указать его длину волны (как
это сделано на фигуре).
Измерение интегральной энергии (интенсивности) каждого
диффракционного луча производится неподвижной ионизационной
камерой с широко раскрытой щелью — весь луч входит в камеру.

242
ДИФФРЛКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. ill
Интенсивность излучения вблизи максимума определяется, как,
мы уже видели, вектором &s=ss— sn, где
s=y(t — tQ) и sH = r-(tn — t0).
а
Здесь t0—единичный вектор в направлении падающего луча, tn—
в направлении максимума интенсивности ж t — в некотором
направлении рассеяния вблизи максимума. Длины волн могут отличаться
друг от друга на небольшую
величину Sj = к — Xgr. Длина волны Х#
получится решением уравнения
Вульфа-Брэгга для точного
значения максимума.
Отклонение вектора t от tn
будем описывать двумя малыми
углами е2 и е3, как это показано на
фиг. III, 21.
Вектор As выразим через
значения трех параметров гь е2 и sft,
а также величину угла ft и длину
волны ля. Для представления
вектора воспользуемся тремя ортами
£, j> к, выбранными, как показано
на фиг. III, 21.
Имеем t0 = /
tn — / cos 2 ft ~\~j .sin 2 •).
Углы е2 и s3 весьма невелики. Поэтому
t = i cos (2 ft -f 83) + / sin (2 ft -f s3) + As2.
Пользуясь формулами cos (2 ft -|- e3) = cos 2ft — г3 sin 2ft и
sin (2ft-f-ss) = sin2ft-f-£3Cos2ft, a также имея в виду малость ег
по сравнению с л, получим:
Фиг. 1JJ, 21. К выводу формулы
интенсивности для метода Лауэ.
Д* =
2я
2п
Хд + £1
(t —*„) — ^-(tH — #о) =
чг
2т.
= Т" [(1—cos 2ft) 3j — г3 Хл sin 2ft] г 4-
хя
-f-^т-Г*яе3 cos 2& —г, sin 2ft],/-L — £0A'. (Ill, 51)
Интегральная интенсивность когерентного рассеянного излучения
есть функция вектора As, и, как мы указали (III, 49 и IH, 50),
равна
E = jjjl(As)dSdSi. (Ш, 52)
Но из фиг. III, 21 очевидно, что dS' = B2de2 de5, В,—расстояние

§ 6] Рабочие формулы иптевсивностеи 243
от кристалла до точки наблюдения. Таким образом следует вычислить
интеграл
Е= j J J* / (As) 7?2^! de2dkj. (ГТ1, 52а)
Нам известно, что вектор As может быть выражен в обратной
решётке уравнением (III, 44) и тогда As определяется тремя
параметрами pv р2, р^. Интенсивность в функции elt e2, s3 нам
неизвестна, зато мы знаем её выражение в функции параметров риР<ьР&
Чтобы интегрирование по е15 е2, е3 можно было бы заменить
интегрированием по ри j»2, Рз> наД° перейти, от dB1ds2ds^ к dptdp2dpb.
Для этого приравниваем выражение элементов объёма в
криволинейных координатах ^ХНЧ и PiPtiPs*):
dbs [dbs dbs 1 , , , дД« Г ЭД* дД* "1 , , , /ттт - л.
Wi [Ж'ЖJ di?i ^2 **» = ~^Г№' "a*JdSid*2ds*' (Ш'5Л)
Отсюда имеем множитель слева ах [Ъхсх] = у , а справа
1С *з sin2 Ь ™ -
п • Таким образом интегральная интенсивность равна
^~" 16п»Гят2»
sin2 — A xi»! sin- -5- л«р2
J J J Sitl*-^ Sill2 y-^.
X
sin--тс- -Л'зЯз
X —i dpxdp2dp.A. (ITI, 54)
sin2 — i?.5
Выбор пределов интегрирования диктуется лишь необходимостью
захватить весь максимум; т. е., как было доказано выше, интеграл
должен быть взят в таких пределах, чтобы
J
.,l,r
sin2 — Np
=- dp « 2тсЛт.
sin2 — p
Таким образом весь интеграл в (III, 54) равен -~- 8 V, где 8 V =
i=N1N2NiV есть объем кристалла (V — объём элементарной ячейки).
Окончательно получаем для интегральной интенсивности в методе
Зауэ следующее выражение:
E = l0QbV,
?де
<s*X* l + cos22& jf. mT .
*) См. В. И. Смирнов, Курс высшей математики, т. II, стр. 19], Ш8.
16*

244 ДИФФРАКЦИЙ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [гл. Ш
Е
принято называть удельной отражатель-
Е
Величину Q^Y^f 6M~1
ной способностью, величину p = QbV = -y- ем2—отражательной
способностью.
Как видно, интенсивность отражений будет, вообще говоря,
довольно быстро падать с увеличением угла &. Это'-падение
обусловливается как ходом атомного фактора, входящего в F^i, так
и ходом функции, содержащей ft в явном виде.
6)^Метод вращения
кристалла. К этому методу
относятся способы, в которых
кристалл поворачивается во время
съёмки диффракционной картины
на фотоплёнку или во время
регистрации интенсивности
ионизационной камерой.
Кристаллические плоскости по очереди
становятся в положение отражения:
иначе говоря, узлы обратной
решётки по очереди пересекаются
сферой отражения. Для работы
этим методом нужен
монохроматический луч, однако
присутствие белого спектра не является
принципиальной помехой. Белое
излучение создаёт общий фон
когерентного рассеяния, на
котором достаточно резко выделяются отражённые лучи, созданные
). — Ка и X — К'9 анода.
Нас интересует интенсивность именно такого
монохроматического рентгеновского луча. Параметр ej в этом случае — угол
вращения (фиг. 111,22).
Схема вычислений совершенно совпадает с предыдущей.
Различие в том, что вектор £0 вращается. Поэтому выражения для
вектора sh (строгое отражающее положение) и вектора .<?
(положение вблизи максимума) будут таковы:
8н — j{tn — l%)\ s = ~(t — t0).
Уравнение Вульфа-Брэгга строго выполняется при падении луча
вдоль «? и отражении вдоль £#• Интерференционное положение
вблизи максимума характеризуется вектором t0, возникающим при
повороте, и вектором £, незначительно, но произвольно смещённым
по отношению к «я. Отклонение t от *я> как и ранее, определяется
углами е2 и е8, показанными на чертеже.
Фиг. III, 22. К выводу формулы
интенсивности для метода вращения.

§ 6] РАБОЧИЕ ФОРМУЛЫ ИНТЕНСИВНОСТЕЙ 245
Выразим вектор Дв = «— «я через три параметра elt s2 и es
и через углы у, <£> ?» характеризующие ориентировку лучей по
отношению к оси вращения. Для представления вектора
воспользуемся тремя ортами i, J, к, показанными на фиг. ГП, 22,
<о =icos/
*0 = ^cosx4"^"sinsi cosx
tH = i cos <o cos ty -\-j cos cp sin <J» -J- к sin <?
« = icos (cp+e3) cos (<!>-}- s2)+./cos (<p-fa3) sin (^-|-82)-^AJsin (?+ss).
Интересующий нас вектор
^8 =2^ (*—*0) — f {tn—tf)
получим, подставив сюда написанные выражения, использовав
предварительно для упрощения малость углов е (sin в = в, cos в = 1).
Получим:
As = — у (е3 sin cp cos ф -j- H ^п 4* °os <р) г -}-
~г г (sicos У. ~\~ s2 cos ?cos Ф — es sin ? si11 W + у (8зcos ?) *• (1И>56)
Интегральная интенсивность
£ = J J J J (Д*) dtf de,. (Ill, 52)
Элемент площади поверхности интегрирования находится с помощью
той же самой фигуры dS = J?2 cos e ds2 de3. Следовательно,
/J --^ipfffl (Д*) cos ? de, de2 ds3. (Ill, 57)
По формулам (111,53) перейдём, как и ранее, к
переменным рхРъРз, по которым легко произвести интегрирование
<ЗД* Г die д^8~\ 8т:3 cos х sin 6 cos ?
El I dzi дЧ J
"^р7 L <^Г ' ^з J ~" v '
Интегральная интенсивность равна
Е-^
8г.3 У cos у. sin ty cos у
( j J I{bs)dpxdpzdpb. (Ill, 58)

246 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
Как мы уже видели, тройной интеграл равен /е^ш^я)3!^^!^.
Вводя, как прежде, объём кристалла oV и подставляя значение Jc,
получим:
E=T0QbV,
где
eW 1 + cos2 20 F'ij.,
q = . _Z_ _ ™ . (HI, 59)
c mWV* 2 cos x sin у cos у к '
Напомним, что J0 есть энергия, отнесённая к единицам времени
ц площади, следовательно Е есть энергия, отнесённая к единице
времени. Из косоугольного сферического треугольника, который
можно построить на той же фигуре, следует:
cos2& = cos^coscpcosx + sin^sin7. (Ill, 60)
Выведенная формула интегральной интенсивности справедлива
для самого общего случая «косой» съёмки в методе вращения
(см. главу IV). Если угол между лучом и осью вращения
кристалла 90э— это основной метод работы в структурном анализе,—
то / — 0, cos 2Й- = cos й cos ср. Формулу интенсивности удобно
записать для такой прямой съёмки, подставив выражение для
удельной отражательной способности в виде (исключая из (III, 59) угол ty):
eW 1 + cos2 20 F'L.j
Q= • -r- hk ^- . (Ill, 61)
m\\ yi 2 у cos2 (p — cos2 20
Таким образом, сравнивая между собой интенсивности пятел
разных слоевых линий рентгенограммы вращения, нужно учитывать
угол <р, разный для разных слоевых линий. (ср = 90°—а, где а
определяется формулой (IV, 17)). Угловой фактор —г-г=^1^°1".„ х—= надо
у cos2(p — cos220
вычислить для каждой слоевой линии в отдельности. При
помощи (IV, 14) угловой фактор можно преобразовать к виду
1 + cos2 20 cos О
sin 20 yCos20 — cos2 p '
где р — угол обратного вектора отражающей плоскости с осью
вращения.
При работе на спектрографе и при работе с нулевой линией
рентгенограммы вращения измеряют только лучи с углом © = 0
(р = 90°). Это значит, что отражённые лучп также
перпендикулярны о^и вращения. Тогда
п <№ 1 +cos2 20 „2 : „ ч

s«]
РЛ1ЮЧПЕ ФОРМУЛЫ ИПТЕНСШШОСТКЙ
247
Эта формула наиболее расиространена в структурном анализе.
Угловой фактор L = ■ . c°2So— изменяется по крнвой с минимумом
[фИ й=5
sin &
0
0,025
0,050
0,075
0,100
0,125
45°. Приводим таблицу его значений:
L
ОО
39,962
19,925
13,221
9.851
7,815
sin Ь
0,150
0,20
0,25
0,30
0,35
0,40
L
6,446
4,711
3,647
2,922
2,394
1,995
sin&
0,45
0,50
0,55
0,60
0,65
0,70
L
1,685
1,443
1,258
1,123
1,037
1,004
sin &
0,75
0,80
0,85
0,90
0,95
1,00
L
1,024
1,123
1,338
1,764
2,778
ОО
Формулы интенсивности (III, 61) и (III, 61а) непосредственно
справедливы при работе на ионизационном спектрографе или
методом качания. При расшифровке рентгенограммы полного
вращения следует учитывать наложение в одну точку отражений,
происходящих от нескольких плоскостей. Очевидно, что все векторы BL1M,
имеющие одну длину и одинаковый угол наклона с осью
вращения, будут в разные моменты вращения создавать лучи, идущие
в одну и ту же точку фотоплёнки. Число таких векторов Нпы
есть так называемый фактор повторяемости р для метода полного
вращения. Правая часть выражения (III, 61а) должна быть поэтому
умножена на р.
Интегральпая интенсивность, определённая выше формулами
(III, 01) и (Ш, 01а), измеряется фотографически как суммарное
почернение, либо но площади кривой ионизационного тока. Щель
ионизационной камеры открывается обычно достаточно широко,
чтобы поймать весь диффракционный луч. В каждое мгновение,
проходя отражающее положение, кристалл посылает в камеру
интенсивность I. Интегральная интенсивность равна по определению
Е = J 1&гх, где Sj — угол поворота. Энергия, попадающая в
ионизационную камеру Е' = f Idt. Очевидно, что Г /de1==o) J Idt,
где (о — угловая скорость вращения кристалла, a t — время.
Итак, интегральная интенсивность (эрг t сек)
Е -=-■ J Id^ = (о J Idt = £'o
(III, 616)
Этим даётся рецепт измерения Е в абсолютных единицах. Как
видно, приходится измерять энергию, падающую на единицу
площади поверхности кристалла (разумеется, надо мерить энергию

248 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
Нш
^^^
<е^
/
X
Ibkl)
Фиг. III, 23. Конус лучей,
отразившихся от беспорядочно расположенных
кристаликов порошка.
лишь характеристического излучения, участвующего в создании
интерференционного пятна) и затем соответствующую полную
энергию, отражавшуюся от кристалла при. повороте его со скоростью <ю
через отражающее положение.
в) Метод «порошка». При исследовании мелкокристаллического
агрегата (спрессованного порошка, металлической проволоки и пр.)
монохроматическим излучением, находим рентгеновскую диффракци-
онную картину, которая состоит
из серии вложенных друг в
друга конусов. Каждый конус
составлен лучами Ш,
отразившимися от беспорядочно
расположенных кристаликов.
Угол раствора конуса равен
4*>ш. Причина
происхождения такой картины вполне
очевидна. Действительно, в
силу равной вероятности
любых ориентировок
кристаллических зёрен можно
утверждать следующее: если
система плоскостей (Ш) какого-либо кристаллического зерна находится
в отражающем положении, то в образце найдётся практически
непрерывная последовательность других кристаллических .чёрен,
расположенных под тем же углом к первичному- лучу. Нормали к
плоскостям (Mel) утих кристаллов должны образовывать конус,
так же как и отраженные лучи (фиг. III, 23).
Представление этого метода в обратной решётке выглядит
следующим образом. Каждому кристаллу соответствует своя обратная
решетка, определённым образом ориентированная по отношению
к падающему лучу. Так как в образце содержатся кристалики всех
возможных ориентации, то каждый вектор Нт их обратных решёток
будет представлен сферой. Пересечение сферы отражения со сферами
Нш даёт происхождение интерференционным конусам (фиг. III, 23а).
Съёмка на плоскую плёнку приводит к созданию диффракци-
онных колец. При полной беспорядочности в распределении зёрен
интенсивность рассеянных лучей одинакова во всех точках кольца.
Для вывода выражений интенсивности рассмотрим отражение
от монокристалла объёма 8 V, вращающегося при рентгеносъёмка
таким образом, чтобы все ориентировки кристалла по отношению
к падающему лучу были равновероятны. Возникающая при таком
методе съёмки картина была бы совершенно эквивалентна
рентгенограмме мелкокристаллического агрегата того же объёма.
Для удобства вычислений рассмотрим неподвижный кристалл
и падающий луч, единичный вектор t0 которого принимает с
раиной вероятностью все положения в пространстве.

§ 6] РАБОЧИЕ ФОРМУЛЫ ИНТЕНСИВНОСТЕЙ 249
Рассмотрим отражение для определённой системы плоскостей.
При строгом выполнении условий диффракции вращающийся как
угодно луч может создать диффрагированные лучи, попадая на
плоскость под углами 05. Эти диффракционные положения t0
падающего луча образуют конус, ось которого направлена вдоль Л и
половина угла раствора которого равна —■ — ft. Из-за нестрогости
диффракционных условий отражение будет происходить и в том
Фиг. 111,2Уа. Происхождение интерференционных
конусов.
случае, если падающий луч будет являться образующей
непрерывной серии конусов, половины углов раствора которых
равны ~— Oztrs^
Величина sx (отклонение от строгого условия появления диффра-
гированного луча) есть основной параметр этого метода.
Вероятность tvds1 того, что падающий луч попадает в интервал det вблизи
угла ft, равна отношению ширины шарового пояса 2хг*со$Мг1
к поверхности шара 4~г2 (фиг. III, 24), т. е.
wds.x = — cos Hetej.
При данном г{, т. е. для копуса падающих лучей, энергия диф-
фрагированного излучения равна
y>-;//ds,
где dti = МЧе2 de.s, В — радиус сферы (фиг. III, 25).
Здесь г2 и е3 малые углы, определяющие направление t, близкое
к строгому диффракционному направлению 1н- Для подсчета
интегральной энергии надо учесть размытость в пределах =trs,,
подлежащего рассмотрению падающего конуса лучей и вероятность того

250
ДИФФРЛКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛ К [ГЛ. Ш
или иного конуса при равновероятном расположении падающего
луча. Интегральная интенсивность будет равна
wPcUi = ) ) | кк.йг.Яг.. (Ш, 02)
Дальнейший подсчёт ироизводится но прежней схеме. На фигуре
III, 25 показакы направления векторов t0, ftf, tH и t. Ось
Фиг. 111,24. К вычислению веро-
ятности происхождения луча в
интервале <lz\.
Фиг. Ill, 25. К выводу формулы
интенсивности для метода
порошка.
конусов, образованных падающими и диффракционными лучами,
обозначена через г; это направление является нормалью к
отражающей плоскости. Выражение вектора As имеет вид
А* = i у fo-j-sa) cos О -\-j ~ (2l — г2) sin П -f к -у- ая.
Переходя к переменным plt ^2 u Р-д> получим для интегральной
интенсивности формулу
E=I0QtV,
где
П ^ 1 +cos* 2ft ,,г mr «-Л
»Л*С* Г*
81П<
Это интегральная интенсивность всего диф фракционного кольца.
В методе «порошка» все отраженные лучи с одинаковым по длине
вектором Нш попадают на одно и to же кольцо. Число этих
векторов Шш одинаковой длины называется фактором
повторяемости р для метода порошка. Правая часть (111,63) должна быть
умножена на р. Величину фактора повторяемости можно без труда
найти по квадратичной форме, выяснив число различных
комбинаций h, к, I, дающих одинаковые межплоскостные расстояния.

§ 6] РАБОЧИЕ ФОРМУЛЫ ИНТВНСИВНООТЕЙ 251
Так, например, в случае кубического кристалла 1£ш = -.— ==
= --——-Hi. Дсгко видеть, что порядок следовании А, к, I u перемена
их знаков не изменяет величины Нш.
Следовательно, одному и тому л;е значению Uhkl отвечают
(семейства плоскостей {hid) и все другие, символы которых
получаются из данного переменой мест индексов и их знаков, т. е.
hllc, kid, Ihk, Ikh, hkl, hid, hid, hid, hid и т. д., всего 48 семейств
плоскостей. Итак, в данном случае фактор повторяемости равен 48.
Для каждой кристаллической системы получим свою серию
факторов повторяемости. Значения фактора повторяемости для метода
«порожка» приведены в таблице III, И.
Таблица III, II
Фактор повторяемости для метода порошка
Кубическая или
правильная система
0,„ О, Та
Th, Т
Гексагональная
система
Ромбоэдрическая
подсистема
См, С.\
Тетрагональная, или
квадратная, система
Dih, Ih, D4fc, VU
\
1 Ромбическая, или орто-
| тональная, система
1 У In У' C-2V
i Моноклинная система
j
j Триклинная система
Ci, C\
Символ семейства плоскостей
(1гШ)\ (hhl)
(Okl) | (Ofcfc)
| 1
48 : 24 j 24
24 j 24 12
(hlcit)
24
12
(hh,2h,l) (Okkl)
12
12
(hkil)\(hh,2h,l)
12
С
(hkl)
16
8
(hkl)
s
(hkl)
12
6
12
12
(Okkl)
G
G
(hhl) | (Okl)
8
8
g
8
(Okl) | (7*0/)
4
4
(АО/) ! (OfcO)
1
4 j 2 ! 2
(hkl)
2
(hhh)
(00/)
12 8 G
12 8 J 6 j
(Ш0)|(А,й,2А0»
12
G
(hkiO)
12
6
0
(J
(AA,2A,0)
G
6
(AfcO) | (hhO)
8 | 4
4 1 4
(AfcO) | (7*00)
4
2
(0Ш)| (000/)
G
G
(Ok'kO)
G
6
2
2
(ОШ)
•>
2
(OfcO) i (00/)
1
(OfcO)
2
5
(00/)
2
l
i i I i i

252 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
§ 7. Учёт поглощения
Формулы, выведенные в предыдущем параграфе, не учитывают
поглощения и экстинкции. Рассмотрим те изменения, которые
появятся в формулах, если принять во внимание поглощение.
Рассмотрим элемент объёма dVрассеивающего кристалла.
Падающий луч проходит до этого объёма путь st в веществе кристалла;
луч, рассеянный этим элементом объёма, проходит в веществе
кристалла путь s2. Если коэффициент поглощения равен ц, то, учтя
поглощение по формуле (II, 6), найдём, что интегральная
интенсивность, даваемая элементом объёма, будет равна
dE = I0Qe~*(Sl+s=)dV. (Ill, 64)
Интегральная интенсивность, даваемая всем кристаллом, будет
равна
Е = I0Q J e-^ + ЧгК. (Ill, 65)
v
Если просвечиваемый лучами объём кристалла 8 V, то пишут
обычно так:
E=l0QAoV, (III, 65а)
где
J=8-L fc-^+^dV (Ш, 60)
называется фактором поглощения. Величина А зависит от формы
образца и имеет различные значения для разных отражений.
В структурном анализе, как правило, проводят относительные
измерения интенсивностей. Поэтому наиболее существенным является
вопрос о том, в каких пределах меняется А для разных
отражений того пли иного кристалла.
Мы рассмотрим сейчас возможности оценки интеграла (III, 66)
для разных частных случаев.
а) Сечение луча меньше сечения кристалла. В ряде случаев
объектом рентгеновского исследования являются крупные
кристаллические пластинки. Сечение падающего пучка рентгеновских
лучей обычно имеет порядок 1—2 мм2. Если диффрагированный
луч возникает при таком положении кристалла, что и падающий,,
и вторичный лучи входят и выходят через широкую грань
нластинки, то вычисление фактора поглощения упрощается.
Выведем отдельно формулы для двух случаев:
1. Диффрагированный луч выходит с той же стороны пластинки,
на которую падает первичный луч (односторонний случай).
2. Диффрагированный луч выходит через грань,
противоположную той, на которую надает первичный луч (двусторонний случай).

%r
УЧЕТ ПОГЛОЩЕНИЯ
253
Односторонний случай показан на фиг. III, 26 и III, 27. Путь
падающего луча до объёма dV, находящегося на глубине у по
нормали к широкой грани пластинки, равен st = ——
путь
Фш\ III, 20.
односторонний случай.
Отраженный,
Фиг. III 27. Односторонний случай
(схр\га).
отражённого луча равен s2 =
Sdy
cos у cos p cos о
равен dV = ^~ , где S — сечение падающего пучка.
Таким образом, интегральная интенсивность
а
Е=ТпО Г е~ *У (^ + «°» /cos 6) M]L
°^ ,) COS ol'
Элемент объёма
(III, 07)
Здесь d— толщина пластинки-кристалла. Интегрирование даёт
г, п * I ./cos Зсоз 3-j coscr.
E=I0Q , Sr\C°l\ Jl-e"^^-^^^ . (111,08)
0 r' [* (COS {* COS 0 -j- COS a) L .
Рассмотрим некоторые частные случаи. При очень «толстой»
пластинке, т. е. при практическом непрохождении лучей через
пластинку (что будет при большом значении \id) имеем:
E = hQ
SCOS^COS О
0 i-i (cos p cos 5 -(- cos a)'
(III, 68a)
Очень часто встречается случай, когда, кроме того, нормаль к
пластинке лежит в одной плоскости с падающим и отражённым лучами.

254
ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЁН В КРИСТАЛЛ И flM. Ш
(Ш, 686)
Это будет при исследовании нулевой слоевой линии при вращении
кристалла около оси, параллельной широкой грани пластинки.
Тогда 8 = 0, и мм имеем:
°^ [А ((5OS [J -(- ('os °0
Наконец, следует упомянуть так называемый симметричный
односторонний случай, когда, кроме того, а = р = 90°— ft.
Отражающие плоскости параллельны внешней грани. Тогда
Е^То^ (III, 68в)
интегральное отражение обратно иропордиоиалыго коэффициенту
поглощения.
Двусторонний случай
показан на фиг. Ш, 28 и j ^Отраженный
III, 29. Путь падающего /К -h^w
луча до объРма dV равен
/fopmfi
'н машине
Падающий
луч
Фиг. III, 28. Двусторонний
случай.
Фиг. III, 29. Двусторонний случай
(схема).
s = _^— • ПуТЬ отражённого луча равен s0 = —
1 COS a ' J r J r j f,Qf
•Элемент объема d V =
Sdy
d — у d — у
os y cos p cos о
Таким образом интегральная интенсивность
d—y
Интегрирование дайт:
E — I0QSe cos p cos 6 _
cos в cos о
t*(C0S PCOSO—COS a)
X
(* — ( ?/ -I у \
ti—hQ <>< 4cosa ~™*?co»i)™JL.t (Til, 69)
.,' соя it \ » /
1-е ^U'-s »«■....?,-oe в Л (int
ГО)

§ 7] учёт поглощения 255
Здесь существенное значение имеет опять-таки случай нулевой
слоевой линии о = 0° и кроме того случай симметрии а = (И = ft.
При подстановке этих условий в (III, 70) мы получим
неопределённый результат. Поэтому подставлять о = 0° и а = ,9 = ft нужно
в интеграл (III, 69). Получим:
E==1^Soodsbr~"dSQCK (Ш,70а)
В симметричном двустороннем случае фактор поглощения
зависит от угла ft. Чем меньше ft, тем меньше поглощение. Изменение
интегральной интенсивности Е с изменением d идёт по кривой
с максимумом. При малых d интенсивность мала из-за того, что
мало рассеивающего вещества, при больших d она мала из-за
большого поглощения. Максимум функции dc-'-ut*en* находим обычным
способом
При ft = 90D оптимальная толщипа dmiJ — — .
Полученные формулы могут быть применимы и к
кристаллическому порошку, спрессованному в виде пластинки. Нужно только
учесть, что в каждом элементе объёма, поликристаллической
пластинки количество вещества в о'!р меньше, нежели в таком же объёме
монокристалла (р' — плотность образца, р— плотность вещества).
б) Сечение луча больше сечения кристалла. Наиболее
распространённым следует признать метод структурного анализа, при
котором кристалл «купается» в излучении. Сюда же относятся
случаи рентгеносъёмки удлинённых объектов, пересекающих все
сечение луча (проволока, игольчатые кристаллы). Расчёт фактора
поглощения по формулам практически возможен в двух случаях —
1) кристалл имеет форму, которую можно аппроксимировать тонкой
пластинкой, 2) кристалл имеет форму, близкую к круглому цилиндру.
Во всех остальных случаях определение фактора поглощения
происходит методом графического интегрирования.
Во всех случаях количественная оценка фактора поглощения
происходит только для пулевой слоевой линии. Эти же результаты
пригодны для рентгенограммы порошка. Фактор поглощения для
отражённых лучей, не лежащих в экваториальной плоскости, как
правило, оценивается качественно.
При желании оценить интенсивность отражения сильно
поглощающего кристалла с большой степенью точности исследователю
следует позаботиться о придании образцу такой формы, для
которой значение А может быть оценено формулами и кривыми
(цилиндрик, тонкая пластинка).
1. Цилиндрический образец. Мы будем рассматривать
отражённые лучи, лежащие только в экваториальной плоскости.

256 диффракция рентгеновских лучей в кристалле [гл. ш
В случае рентгеносъёмки порошка только эти интенсивности и имеют
практическое значение, так как фотометрирование рентгенограмм
поликристалла производится вдоль средней линии. В случае
монокристалла это значит, что- наши данные будут справедливы только
для нулевой слоевой линии. Для лучей, идущих под углом к
экваториальной плоскости, приходится ограничиться примерной оценкой
значения общей интегральной формулы (III, 66).
Весьма просто обстоит дело с учётом поглощения в сильно-
поглощающих и толстых образцах. При значениях у-В (где р —
коэффициент-поглощения, а В — радиус цилиндрического образца)
больше 50 относительные значения фактора поглощения могут быть
представлены универсальной кривой Л (&), данной на фиг. III, ВО,
фиг. Ш,30.
Фиг. III, 30. Относительные значения Фиг. III, 30а. Цилиндри-
абсорбционного фактора для цилин- ческий «непрозрачный»
дрического образца (,а R > 50). образец.
Для очень многих случаев условие <ii?>50 выполняется. Если
исследуются образцы радиуса 0,2—0,3 мм, то ход поглощения
в зависимости от угла соответствует универсальной кривой при
коэффициентах поглощения }х>2000 см-1.
Абсолютные значения фактора поглощения могут быть найдены
/?
умножением этой универсальной функции на —. Это значит, что
м-
интенсивность рассеяния, вообще говоря, падает с увеличением
коэффициента поглощения и уменьшением размера образца.
Последнее обстоятельство носит, впрочем, формальный характер, так как
указывает лишь на уменьшение поверхности образца (при
сильном поглощении отражение практически происходит с поверхности).

§ 7] учёт поглощения 257
Вид функции Л (0) может быть найден вычислением в
предположении, что отражение происходит только с поверхности.
Элементарный объём dV с поверхностью dS=Rdadh можно
рассматривать, как отражающую пластинку, совершенно не
пропускающую падающие на неб лучи.
Интегральную интенсивность элемента dS можно записать
формулой (III, 686).
E = I0QdS <™«°°°Р
°^ {A (COS 8 + COS а)
Здесь dS cos a — сечение луча, падающего на площадку dS.
Интегрируя по S, можно найти интегральную интенсивность всего образца
(Ji — «освещаемая» лучом высота)
2»
Я = /0<? * A f C0BSiC0Sa- da. (Ill, 71)
°^ fJ. J COS ft + COS a v ' '
0
Верхний предел равен 2ft, как это видно из фиг. III, ЗОа, на
которой показаны два крайних положения, при которых ещё
происходит рассеяние. Остальная часть поверхности образца не отражает.
Интеграл
2»
COS a COS ft ,
COS « + COS 8
О
берётся в квадратурах. Искомая функция равна
л /cis < I cos28 , Г cos 2& 4- sin 8 1 /ттг _rt4
А (Ъ) = 1 4* ,, . ц In тт-г -.-»wiT-n-^-ri • (HI, 72)
4 ' ' 2 sin $ [(1 + sin 0) (1-j-2sm ») J ч '
В случае малого поглощения фактором поглощения можно
пренебречь. При \>.R = 0,5 фактор поглощения колеблется в пределах
0,44—0,49, при pR — 1,0 в пределах 0,20—0,29 во всём диапазоне
углов ft.
Таким образом даже при очень точной оценке интенсивностей
при }ajR<0,5—1,0 фактором поглощения можно пренебречь.
Для органических соединений }х = 5си<-1 и обычно 72 = 0,1 см.
Таким образом, в этом случае мы имеем право пренебречь этим
фактором, хотя суммарное поглощение достигает 70—80%.
Для промежуточной области 1 < pR < 50 ход фактора
поглощения с углом Ь различен для разных значений pR и должен быть
взят из таблиц. Три типичные кривые приведены на фиг. III, 31.
В этом случае интегралы в квадратурах не берутся и интегрирование
проводится обычными методами приближённых вычислений с любой
желательной точностью.
ас
S

258 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. Ill
W)
Очень многие исследователи пренебрегают фактором поглощения
и для промежуточной области значений у-Л. Это может быть
оправдано следующим образом.
Как отмечалось на стр. 472,
при сопоставлении
вычисленных и измеренных ин-
тенсивностей в /"-кривую
вводится произвольпая
температурная поправка,
меняющая ход /"-кривой с
углом Ь. Можно полагать,,
что в эмпирической
/"-кривой учитывается также ход
фактора поглощения с
изменением угла ft (действие
температуры относительно
снижает интенсивности при
больших ft, действие
поглощения, напротив,
относительно снижает
интенсивности при малых углах ft).
Такая процедура не
оправдана, разумеется, при
стремлении к результату
большой степени точности. Строгий учёт А необходим при
определении электронных плотностей.
2. Образец в форме пластинки *). Рассмотрим
монокристалл (фиг. III, 32) в форме прямоугольного параллелепипеда аЬс.
Сечение его — прямоугольник
со сторонами а я с, причём \ к
.а>с. Отражение пусть
происходит от плоскостей,
принадлежащих зоне оси Ъ.
Для вычисления примем
систему координат такую,
чтобы ось у шла по а и ось х
по с. Направления падающего
и отражённого лучей к0 и h
могут быть, очевидно, любыми.
Однако, выбирая крест осей одним из способов, указанных на
фиг. Ш, 32, мы видим, что все возможные случаи взаимной
ориентации kQ и кристалла сводятся к первому (для этого чертежи надо
повернуть на 180° или взять их зеркальное отражение).
100 SinV
Фиг. Ill, 31. Относительные значения
абсорбционного фактора для
цилиндрического образца.
W г!/
yJ
К0-первичный луч
Фиг. III, 32. Монокристалл в форме
прямоугольного параллелепипеда.
*) А. И. Китайгородский, ЖЭТФ, 9, 1118, 1939.

<]
УЧЁТ ПОГЛОЩЕНИЯ
259
В зависимости от угла наклона (3 первичного луча к оси у все
возможные случаи ориентации кристалла по отношению к лучу
разделяются на две группы (фиг. Ш, 33):
i)tgp>£; 2)tgp<£. (Ill, 73)
Рассмотрим первый случай, который отвечает образцам в виде
пластинчатых кристаллов: — <0,1.
Если через верхний левый угол рассматриваемого сечения
провести прямую линию в направлении первичного луча, а диффраги-
рованный луч построить так, чтобы он пересекал сечение, проходя
через его угол, то сечение, естественно, разбивается на четыре или
три части. Эта разбивка происходит так, что для всех точек данной
части общее выражение для суммы путей падающего и отражённого
лучей имеет одинаковый вид.
К0-первичный пуц
Фиг. III, 33. Два вида
ориентации кристалла.
Э-любое 9*45° 9-любое 9>Ь5°
А Б В Г
Н0-первичный луя Н~ отраженный
Фиг. III, 33а. Четыре варианта
для образца в форме пластинки.
Так как направление вторичного луча и при заданном к0 может
быть любым, то, согласно вышесказанпому, рассматриваемый случай
может быть разбит на следующие четыре варианта (фиг. III, 33а):
A) угол ifx изменяется по часовой стрелке от 0 до 90°;
Б) угол 7х изменяется от 90 до 180°;
B) угол 7х изменяется от 180 до 270°;
Г) угол fx изменяется от 270 до 360°.
Эти же четыре варианта соответствуют второй группе
ориентации (tg p < - J. Таким образом все без исключения случаи взаимной
ориентации лучей и кристалла сводятся к нижеследующим восьми:
Вх: tg(l803«-гх)>-£
Вх: tg(T*-180°)>^
tg(3eo-T*)>^
А2:
Б2:
В2:
А:
tg-rx<v;
tg(180°-T*)<-£-;
tg(Tx — 180°)<^;
tg(360°-
YXj.

260 ДИФФРЛКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [гЛ. III
Для каждого из этих случаев (интервалов в значениях р и if)
выражение fo-j-sg) B формуле для А имеет один и тот же вид вне
зависимости от значений углов р и if, и интегрирование может
быть легко произведено.
Практическое значение, однако, имеют для пластинчатых
кристаллов только случаи Аь Б1 и Bv
Отражения, соответствующие случаю Г{Ь > 45°), обычно для
эксперимента роли не играют.
Рассчитанные для указанных трёх случаев факторы поглощения
имеют вид:
Случай А^*)
л_ 1 \с (tgT + tgP) .
p.(seo P + sec ч)\_ f*(sec Р + sec7)~
, (tg 7 + tg P) I _ к (sec f> 4- sec 7) \] _
"•"txlsecP + seCT) ' P\ (tgp + tgT) И
exp { ~ v[(l ~ tjT+te?) C0SGC P + tg pT tg т ] } ~ 6XP { K COgeC T>
I*1 cosec p (sec 7 — tg Y cosec
( (sec т + sec ft) )
еХР\~|А<? (tgT + tgp) ) . 1 — exp { — [*c cosec 7} ,
I** cosec P (sec 7-}- sec P) jj-^cosec p sec 7
f ., (sec P + sec i)\
1 — exp { — |ac cosec P}
f*2 cosec y sec p ^2 cosec y (sec p -\- sec y)
"'"' {-KtifrWr-K1- tjfej)cosecii1bexp{-|tcosec{'} 1
(x2 cosec Y tg P (cosec p — cosec 7)
. exp { — jj-e cosec 0} — exp { — (xc cosec 7}. , u. .
i — —, * n, — (a — с ctg p) -f-
{* (cosec 7 — cosec P) b
. exp { — |xc [cosec y + ctg 7 (sec p — tg P cosec X)]}—exp{ — y. cosec p>
I*2 (cosec 7 — cosec p)2 tg P
exp {-j, cosec 7} ( .^ , ■
^ (cosec 7 - cosec P) CtCtg ' Ctg T) ^
«-„{ Г i у «(see 3 — tg 3 cosec 7)1 r ,\
expj—^|c oosec T+(«-c) (tgp + tgfl J_ в*Р ' ^clcosec4r+ctST (sec 3—tg 3 oosec T)l>
I».3 (ooseo ^—oosec 8)? tg 3
exp{-,aC cosec 7> охр f-Лг cosec p+(a c)(sec 7~tg7 cosec P)]|
«a2 (cosec 7 — cosec p)2 tg 7
) 7 = 7х(фиг. Ill, 33a).

§ 7] учёт поглощения 261
Случай Ь\*)
_ 1 — ехр {— i>.c cosec р} _ ехр { — у- cosoc 7} — ехр{ — у-е совес р} ■
~ ja2 cosec 7 sec P |х2 cosec 7 (seep — tgPcosec7)
, 1 — ехр {—[xc cosec 7} exp {—цс cosec P} — exp {— [*c cosec 7} ,
ц.2 cosec P sec 7 f*2 cosec P (sec 7 — tg 7 cosec P)
. exp {— yc cosec ft} Г1 — exp {—ye (cosec 7 — cosec ft)} "J .
{a (cosec P~ cosec7) L ntg7(cosec7—cosec P) ~' Lg7J i"
, exp { — цс cosec P}— exp{—-|xe cosec P> . , .. , .
+ Kcosecr-cosecP) (a-cctg P),ctg7 +
, exp { — |xccosec7> Гехр { — ус cosec p — cosec 7} — 1 , t Л
,u(cosecp-cosec.7) L !*tgP(cosecP— cosec 7) "'J"
Случаи Jit**)
_ 1- exp { — ye (cosec ft 4- cosec 7)}
,a2 cosec 7 tg P (cosec P + cosec 7)
exp { — yc cosec 7} — exp { — yc (cosec ft -f- cosec ^)} ,
,u2 cosec 7 sec p ~T~
. 1 -exp{ — y.c (cosec P + cosec 7))
y* cosec P tg 7 (cosec 7 -f- cosec p)
exp { — цс cosec P) — exp { — yc (cosec p -\- cosec 7)}
(x2 cosec p sec 7
1_ exP { — t*g (cosec p + cosec 7)}., . „ , pitr M ,
^2 (cosec P +cosec T)2 (ctg l + Ug P) +
+ [g - с (ctg P + ctg 7)1* " 6XP {Г *C (ftTC P + TS6C T)> +
b ;x (cosec В 4-cosec 7)
, 2c ctg 7
ji (cosec P + cosec 7)
Из выведенных формул мы можем получить симметричное
отражение, положив в случае Ах Р —т и в случае Вх f* —180э —(2
(в первом случае отражающие плоскости параллельны малому
ребру с, во втором случае они параллельны ребру а). Предлагаемый
метод вычисления фактора абсорбции может быть применён и для
получения других формул.
Определение углов {3 и -у легко производить, пользуясь сечением
обратной решётки и подвижной сферой отражения, как это показано
на фиг. III,34.
*) 7 = 180-7* (Фиг. III, 33а).
**) 7= 7х —180(фиг. III, 33а).

262 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
3. Качественная оценка фактора поглощения.
В случае невозможности аппроксимировать кристалл простой
формой и свести имеющийся случай
Подвижная сфера отражения к разобранным выше приходится
прибегнуть к графическому
интегрированию. Интегрирование в
общей формуле заменяется
суммированием. Вычисление
-и-С^ + а.)
АЛ
Обратная решетка
Фиг. III, 34. Определение углов
Р и т.
AF
должно нроизводиться для
каждого отражения. Чем меньше
число элементов, на которые
будет разбит объект, тем грубее
результат расчёта. Пути st и s2
измеряются на чертеже,
изображающем объект от границ
образца до центров элементов объёма.
Бри проведении этого иод-
счёта следует на одном и том
же чертеже изобразить сечение
обратной решетки и ссченпе
кристалла. Устанавливая сферу
отражения в отражающее положение данного Ш, мы можем сразу
найти относительное расположение векторов к0 и к по отношению
к кристаллу.
§ 8. Учёт экстинкции (вторичной)
Наличие экстинкции должно было бы самым фундаментальным
оиразом изменить выведенные нами формулы интенсивности. Опыт
ноказывает, однако, что в подавляющем большинстве случаев
влияние экстинкции незначительно и совпадение изложенной теории
с опытом превосходное, если не говорить о нескольких самых
сильных отражениях.
Это обстоятельство приводит к представлению о мозаичной
структуре кристалла, находящему широкое подтверждение в
разнообразных фактах.
Предполагается, что кристалл не представляет собой идеальной
пространственной решётки, а состоит из весьма малых, порядка
Ю-4 см, блоков, слегка (от нескольких секунд до многих минут)
дезориентированных друг но отношению к другу. Если это так, то
становится понятной применимость теории, развитой для малого
кристалла к большому кристаллу. Отдельные блоки представляют
области когерентного рассеяния; для каждого блока строго сира-

§ 8]
УЧЁТ ЭКСТИНКЦИИ (ВТОРИЧНОЙ)
263
ведливы выведенные ранее формулы интенсивности. Излучение от
разных блоков некогерентно между собой. Это значит, что общая
интенсивность равна сумме интенсивностей, рассеянных отдельными
блоками (а не общая амплитуда поля равна сумме амплитуд волн,
идущих от отдельных блоков).
Мозаичное строение кристалла не избавляет нас, однако, от
.экстинкции полностью. Действительно, в отражающем положении
верхние блоки экранируют нижние (речь идёт об экранировании
отражением, а не поглощением). Кроме истинного поглощения
надо учесть потерю энергии на конгередтное рассеяние (отражение)
верхними блоками. Таким образом нри отражении коэффициент
поглощения заменяется суммой p-j-e, где е — коэффициент
вторичной экстинкции.
Первичной экстинкцией называют добавочное поглощение,
возникающее благодаря той же причине, но происходящее внутри
одного и того же блока. Это — явление экранирования верхпими
слоями нижних слоев того же «куска» идеальной кристаллической
решётки. При малом размере блоков первичной экстинкцией можно
пренебречь. Это обстоятельство значительно упрощает
рассмотрение интенсивности отражённых лучей, так как только вторичную
экстинкцию можно у честь коэффициентом, прибавляющимся к
коэффициенту поглощения р.. Первичная экстинкция ослабляет
амплитуду поля, вторичная—уменьшает интенсивность!
От вторичной экстинкции в монокристалле избавиться нельзя
и её учёт нри точных исследованиях неизбежен. От первичной
•экстинкции, имеющей место лишь при наличии крупных
кристаллических блоков, можно избавиться. Для этой цели либо
механическим путём (полировка), либо термическим (закалка в жидком
воздухе) добиваются «раскалывания» крупных блоков. Нам
неизвестны случаи, когда структурный анализ проводился бы с учётом
первичной экстинкции.
В этом параграфе мы рассмотрим теоретические и опытные
методы учёта вторичной экстинкции.
Вторичной экстинкцией в монокристалле можно пренебречь лишь
в том случае, если р ^> г. Опыт показывает, что вторичная
экстинкция действует в наиболее резких случаях как поглощение с
коэффициентом [а порядка 500 см-К Таким образом лишь у очень сильно
поглощающих кристаллов вторичная экстинкция не наблюдается.
Потери интенсивности луча на отражение зависят от характера
распределения мозаичных блоков, индивидуального для каждого
"кристалла, и от интенсивности надающего луча. Коэффициент
экстинкции s можно разложить в ряд по степеням интенсивности
отражения одного блока или, что ещё удобнее, по степеням
величин Q — удельной отражающей способности. Итак,
*=9Q + f<?+-~
(Ш, 74)

264 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [lVI. Ill
Нулевого члена в разложении не может быть (при Q = Oa е = о).
Опыт показывает, что достаточно ограничиться линейной
зависимостью и положить
£ = Л (III, 74а)
где д— безразмерная константа кристалла. Величина для разных
отражений одного и того же кристалла меняется обычно в
пределах 1-Т-10000. Если поэтому коэффициент экстинкции играет
существенную роль для сильных отражений, то для средних (не говоря
уже о слабых) его влияние пренебрежимо мало — здесь уже е <$С «•-
Для иллюстрации этого положения приводится таблица величин
измеренных и вычисленных интегральных интенсивностей кристалла
алюминия.
Таблица III, III
R -'106 для кристалла алюминия; односторонний случай
Х=*0,71 А, (1 в 14,35 сле-1
hkl
111
200
222
400
333
600
444
800
555

Наблюдаемое
iM0«
580
436
144
86
26.2
12,2
4,95
2,10
1,43
Рассчитанное R • 106
идеальный
кристалл
19,6
16,2
6,30
4,47
2,19
1,31
0,76
0.40
0.37
идеальный
мозаичный
кристалл
818
619
158
91
28,3
12,0
5,14
2,09
1,39
мозаичный
кристалл
р^ЗОО
547
450
144
86
27,8
11.9
5,13
2,09
1,39
0<МО«
6,1
4,4
1,3
1Д
0,3
0,11
0,04
0,02
0,01
Интегральные интенсивности рассчитаны для случая
формулы (III, 68в), т. е. с учётом экстинкции по формуле
В—безразмерная величина, характеризующая отражательную
способность бесконечной грани кристалла (коэффициент отражения).
В шестой колонке таблицы приведены значения gQ\ мы отчётливо-
видим, что экстинкция начинает сказываться лишь при
значениях gQ, сравнимых с ц, что имеет место лишь для самых
сильных отражений.

§8]
УЧЁТ ЭКСТИНКЦИИ (ВТОРИЧНОЙ)
265
Для того чтобы величина константы мозаичной структуры
кристалла стала более или менее ощутимой, достаточно указать на
простую формулу для д, имеющую место при некоторой идеальной
картине. Примем, что нормали к некоторой системе плоскостей
кристаллических блоков распределены около среднего направления
с цилиндрической симметрией и по закону Гаусса. Тогда можно-
доказать, что величина д связана со средним угловым
отклонением Д формулой
1
Например, при А = 4' д = 260, при Д = 40' д = 26.
Такой большой разброс мозаичных блоков по направлениям
означает по сути дела отсутствие экстинкции. Это и понятно,
при дезориентировке блоков луч, находящийся в отражающем
положении по отношению к нижнему блоку, не находится в
отражающем положении по отношению к верхнему блоку, и эффект
экранирования исчезает.
Для отражения (200) каменной соли на медном излучении
Q — 0,113 см~1; следовательно, при # = 26 коэффициент экстинкции
равен е = 2,94 см-1. Коэффициент поглощения каменной соли
}* = 160 см-1. Таким образом, экстинкцией можно пренебречь. При
разбросе блоков в 4' экстинкция начинает чувствоваться (е=29,4 см-1)
и при разбросе в 0,4' она начинает играть существенную роль.
(е = 294 см-1).
Какое-либо более детальное теоретическое исследование влияния
вторичной экстинкции не представляется целесообразным, так как
распределения блоков по углам и по размерам, определяющие
экстинкцию, не бывают известны исследователю.
Не представляет труда определить величину константы
кристалла д, если структура его, а следовательно, величины Q для
разных отражений известны. Если поэтому требуется доказать, что
полученные после установления кристаллической структуры
расхождения теории и опыта обязаны наличию экстинкции, то д рас-
«матривают как параметр, дают ему ряд значений, останавливаясь-
иа той цифре, при которой совпадение опыта и расчёта будет
наиболее полным.
Если структура неизвестна и мы располагаем кристаллом в форме-
Цластинки, толщину которой можно менять, то д определится из
Ферии измерений отражения для двустороннего случая от пластинки
с разными толщинами. Действительно, интегральная интенсивность.
От пластинки толщиной d
E~de~{{l+9Q)d9(!0\
Производя измерение для нескольких d и откладывая логарифм
частного от деления интенсивности на толщину по оси ординат,.

266 ДИФФРЛКЦИЯ РЕЯГГИЮВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
а толщину — по оси абсцисс, мы должны получить прямую линию,
экстраполяция которой к d = 0 даст значение Q. Зная у., нетрудно
вычислить и д.
Исключительно существенным является то обстоятельство, что
экстинкцией поликристаллического образца можно пренебречь. Это
будет в том случае, если каждый кристаллик имеет такие размеры,
что первичной экстинкцией в нём можно пренебречь, и если
кристаллики распределены совершенно беспорядочно в отношении своих
ориентировок, так что нет экранировки, а следовательно, и
вторичной экстинкцин. Изготовляя из такого порошка столбик, мы можем
с очень большой точностью совершенно строго пользоваться
формулами (III, 71) и (III, 63). Большей частью затруднительно
определять интенсивность всех отражений по рентгенограмме порошка:
для кристалла с не очень маленькой ячейкой число диффракцион-
ных конусов очень велико и они расположены очень близко друг
от друга. Однако1 первые линии — а они обычно и бывают самыми
сильными и, следовательно, подверженными экстинкции — могут
быть измерены всегда. Сравнивая эти измерения с измерениями
на монокристалле, всегда можно пайти константу вторичной
экстинкции д.
% 9. Идеальный кристалл. Первичная экстинкция
Идеальный кристалл — это блок кристаллической решётки. Как
уже отмечалось выше, реальный кристалл состоит из множества
слегка дезориентированных друг по отношению к другу блоков.
Если блоки достаточно малы (условия этой малости будут
обсуждены ниже), то интенсивность рассчитывается по формуле для
малого кристалла с поправкой на поглощение и вторичную экстинк-
цию. Если блоки велики, то надо вводить поправку на первичную
экстинкцию. Если кристалл весь представляет собой единый блок
кристаллической решётки, то формулы интенсивности меняются
самым существенным образом.
а) Интегральное отражение идеального кристалла. Ввиду
того, что обсуждаемые ниже результаты имеют лишь
принципиальное значение — объектами структурного анализа являются
мозаичные кристаллы, — то мы ограничимся лишь изложением сущности
и результатов теории. Теория, учитывающая взаимодействие между
•полями падающей и рассеянной волн, получила название
динамической, в отличие от изложенной выше кинематической теории,
-пренебрегающей этим взаимодействием.
Мы предполагали ранее, что падающая волна
пе терпит внутри кристаллического объекта каких бы то ни было
изменений и что, таким образом, нее атомы кристалла находятся

§ 9] ИДЕАЛЬНЫЙ КРИСТАЛЛ. ПЕРВИЧНАЯ ЭКСТИНКЦИЯ 267
в одинаковых условиях. Подобная точка зрения справедлива лишь
для очень малого кристалла. На самом же деле кроме падающей
волны на данный атом действуют волны, рассеянные другими
атомами. Расчёт поля диффрагированной волны исключительно
осложняется. Существуют два способа решения этой задачи: первый,
вполне строгий, заключается в решении уравнений Максвелла
с учётом граничных условий и учётом диэлектрического
коэффициента кристалла, и второй, упрощенный, в котором рассматривается
взаимодействие лучей, «отражённых» от узловых плоскостей
данного семейства
кристаллической решётки.
Идея второго решения
заключается в том, что
учитывается многократное
отражение луча. Так, например, волна,
отражённая от г-к (считая от
границы кристалла) узловой
плоскости, терпит
последовательно отражения в сторону , TTI n
тгалатши^гп пусгя пт upay «и Фиг. Ш, Зо. в — потери интенсивности
падающего Д)ча oi всех вы- отражёНного луча из-за когерентного
шележащих Плоскостей. Волна, рассеяния внутри блока (первичная
лрошедшая три плоскости и экстинкция).
отражёнпая от 4-й, 6 раз
теряет одинаковые доли от падающей амплитуды (фиг. III, 35).
Чем больше г, тем меньше доходящая до этой плоскости амплитуда
волны. Это и есть первичная экстинкция.
Рассмотрение динамического взаимодействия падающей и
отражённых волн включает в себя учёт показателя преломления рент-
теновских лучей в кристалле, который, вообще говоря, очень
близок к 1.
Динамической теорией решена до конца задача вычисления
интенсивности для плоскопараллельной пластинки как для
двустороннего, так и для одностороннего случаев. Решения сильно
отличаются для случая поглощающего и непоглощающего кристалла.
Решения сильно зависят от толщины пластинки и во всех случаях
надо различать интенсивности параллельно и перпендикулярно
поляризованных лучей.
На фиг. III, 36 и III, 37 изображены теоретические кривые
отражения от плоскости (211) кальцита для одностороннего случая
и симметричного двустороннего случая. При расчёте длина волны
о
полагалась равной 1,537 А, кристалл полагался бесконечно толстым
при расчёте одностороннего случая и толщиной 0,01 cos Ь см, т. е.
несколько меньше 0,1 мм при расчёте двустороннего случая. Как
мы видим, в двустороннем случае максимум диффракции лежит при
угле, удовлетворяющем уравнению Вульфа-Брэгга. В одностороннем

268 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. Ш
ние-тг- (Ри —энергия диф
случае максимум смещён в сторону от Ьв. Кривые
двустороннего случая совершенно симметричны как при наличии, так и
при отсутствии
поглощения. Максимальное значе-
Рн
Р»
фрагированных лучей,
Р0 — энергия падающих
лучей) равно в
двустороннем случае 0,24. В
одностороннем случае при
отсутствии поглощения в
небольшом интервале углов
происходит полное отраже-
Ря
ние -тг- = 1 • Интегральная
4 -2
2 4 6 в Ю 12
4-4$ о секундах дуги
/« /6 18
Фиг. Ill, 36. Отражение (211) от толстого
кристалла кальцита. Односторонний
случай X = 1,537 А.
Я
интенсивность равна
площади этих кривых.
Для одностороннего
случая формула безразмерной
отражательной
способности — коэффициента
отражения— имеет вид
3*
тс2
~10 -Ь
■а -2 0 2 4
д-д„ в секундах дуга
X
Д+|сов2»|
Fhkl, (111,76)
Фиг. Ill, 37. Отражение (211) от пластинки
кальцита; симметричный двусторонний
случай А = 1,537 А.
В Ю v
2 sin 2»
где N— число атомов в
единице объёма.
Наиболее существенным
обстоятельством является
то, что у идеального кристалла интегральное отражение
пропорционально первой степени, а не квадрату структурного фактора.
В таблице, которую мы приводили выше (стр. 264), для кристалла
алюминия подсчитаны интенсивности и по этой формуле. Не следует
удивляться тому, что, несмотря на полное отражение, цифры для
идеального кристалла примерно в 40 раз для сильных отражений
меньше, чем у мозаичного. Это получается из-за очень малой области
углов (несколько секунд), внутри которой отражает идеальный
кристалл. Придание кристаллу мозаичной структуры (полировка,
закалка) увеличивает угловой интервал и интегральное отражение.
Вот, например, характерные цифры для отражения 200 каменной
соли кристалла со свежесколотой поверхностью И = 10,2 • Ю-5 и
ширина максимума 45"; у полированного кристалла В = 21 • Ю-5 и
угловая ширина равна 15'.

10J
ВЛИЯНИЕ ТЕПЛОВЫХ КОЛЕБАНИЙ
269
6) Учёт первичной экстинкции. Условие идеальной
мозаичной структуры. Расчёт интенсивности кристалла, состоящего из
мозаичных блоков больших размеров, т. е. таких, внутри которых
происходит первичная экстинкция, практически невозможен.
Удаётся лишь вычислить примерную поправку на первичную
экстинкцию к величине Q для одного блока, состоящего из т слоев.
Если интегральное отражение от блока, рассчитанное без учёта,
первичной экстинкции, пропорционально Q, то с учётом первичной
экстинкции оно пропорционально
где
— Ne2Fld
^ тс2 sin Ь '
d—межплоскостное расстояние.
При wg = 0,2 #' = 0,971Q; при щ = Ь,0 Q' = 0,200Q. Таким
образом интенсивность становится меньше и тем меньше, чем.
больше щ. При щ < 0,2 поправка незначительна и это
условие можно принять, как условие идеально-мозаичной
структуры. Мы видим, что условие «малости» блока не является
абсолютным. Для разных длин волн, а также разных углов блок
может считаться малым или большим. Например, для медного
излучения отражение 200 каменной соли имеет q = 2 • Ю-4. Таким
образом кристалл, составленный из блоков размером не более
чем в 1000 слоев, можно считать идеально-мозаичным. Отсюда
следует, что размер блоков идеально-мозаичного кристалла должен
быть не более 10~4 — 10_б см. Надо думать, что эти величины и
встречаются, как правило, в исследуемых кристаллах.
Учёт первичной экстинкции для неизвестного кристалла
невозможен из-за незнания п. Удачный опыт всех произведённых до
сих пор структурных исследований является оправданием
пренебрежения первичной экстинкцией и одновременно доказательством
малости мозаичных блоков.
§ 10. Влияние тепловых колебаний
Тепловое движение атомов в кристалле заключается в
колебаниях с амплитудами, безусловно сравнимыми с межплоскостными
расстояниями. "Совершенно несомненно, что тепловое движение
должно иметь значительное влияние на картину рентгеновской диф-
фракции и притом тем большее, чем больше индексы отражения Ш.
Можно привести, например, следующие цифры. При комнатной
температуре среднее квадратичное отклонение от положения равновесия
ионов Na+ и С1~ в каменной соли равно соответственно 0,242 ж

270 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ. [ГЛ. 1ГС
0,217 А. Таким образом расстояние между соседними плоскостями
5 6 °
(155) каменной соли a155 = -pi^0,8A всего лишь в 3 раза
больше амплитуды колебания. Это уже не плоскость, а «волнистая
поверхность»; поэтому очевидно, при еще" больших индексах (Ш)
фазовые соотношения, приводящие к уравнению Вульфа-Брэгга,
сойдут на нет и диффракция исчезнет. Если бы теплового
движения не было, то переходя ко вес более коротким длинам волн, мы
могли бы безгранично увеличивать диффракционную область,
безгранично продвигаться к большим likl. Тепловое движение кладёт
границу этому продвижению и практически молибденовое
излучение является самым коротким, к которому приходится прибегать.
Это значит, что нет возможности улавливать отражения плоскостей,
у которых d < 0,4 А.
Влияние теплового движения сводится к двум явлениям:
уменьшению интенсивности отражённых лучей и созданию своей
собственной диффузной картины, накладывающейся на диффракционную
картину, рассмотренную выше. Тепловое движепие может
сказываться по-разному и для отражений от плоскостей с одинаковым d..
Действительно, на отражение от данной плоскости влияет лишь та
компонента амплитуды колебания атома, которая направлена вдоль
перпендикуляра к отражающей плоскости. Несомненно, что
тепловые колебания анизотропны; нетрудно себе представить две системы
плоскостей такие, что тепловые колебания происходят главным
образом вдоль одной и перпендикулярно другой системе плоскостей.
Тогда тепловое движение будет резко менять интенсивность лучей,
отражённых от второй и мало — от первой системы плоскостей.
Переходим к количественному рассмотрению вопроса и
поставим перед собой прежде всего задачу вывести формулу
интенсивности диффракции от кристалла, атомы которого находятся в
состоянии теплового движения.
В каждое мгновение атомы такого кристалла не находятся уже
в положениях, соответствующих идеальной решётке. Пусть атом,
находящийся в Х-й ячейке в &-м положении, сдвинулся, на
вектор Afty от положения идеальной решётки. Этот атом даёт
элементарную волну с той же амплитудой fk. Однако фаза волны
изменится по отношению к той, которая была в идеальной решетке,
на величину (7г — к0) Aj = sAj? (сравни стр. 226). Таким образом
амплитуда волны, посылаемой атомом, смещённым от положения
равновесия, дожна быть представлена величиной
й = //'4. (Ш.77,
В один и тот же момент времени смещения к-то атома в
разных ячейках могут иметь самое различное значение. Соответ-

§ \0) ВЛИЯНИЕ ТЕПЛОВЫХ КОЛЕБАНИЙ 27/
«тв&вжо и величины д\ имеют разное значение для атомов ку.
находящихся в разных ячейках. Среднее рассеяние &-го атома
будет
-г 1 VI г ■ j? 1 V^ {»LlJ г ia*i
Vi = WZirf = fkN2Ae *=/>•*• (Ш, 77а)
Итак, среднее рассеяние смещённых атомов к равно
произведению их атомного фактора на среднее значение фазового
множителя е' к. Статистическая физика утверждает, что «среднее по
совокупности равпо среднему по времени». Это значит, что
написанное выражение ~дк можно понимать не только как среднее
мгновенное излучение всех атомов 1с, но и как среднее во времени
излучение каждого из атомов ~к.
Таким образом мы приходим к заключению, что рассеяние
атома в реше'тке следует характеризовать не атомным фактором fk,
а атомно-температурным д^ Среднее значение еа к имеет
определенную величину для данного &-го атома при данной интерференции..
Как будет показано ниже, это среднее значение может быть
представлено в виде ё~м*, где Мк — действительное число.
Величину е к называют тепературным фактором.
Соответственно сказанному выше изменяется и структурная
амплитуда, дающая амплитуду волны, рассеянной элементарной
ячейкой. Мгновенное значение структурной амплитуды равно
F, = 24ei'('i+4'> "Self*4*»; (Ш. 78)
к ^к
мгновенные значения FL будут, вообще говоря, разными для
разных ячеек. Средняя структурная амплитуда
N
л« = i S Рь=2 л е"г*=S h е<!"НГк (Ш-78а)
Л = 1 к к
имеет ту же форму, что и (III, 22), только атомные факторы
заменены атомно-темнературными.
Интенсивности, определяемые на опыте, связаны, разумеется,
со средними значениями структурного фактора, так как время
измерения достаточно велико по сравнению с периодом колебания
атомов (~10-13 сек.). В то же время этот период колебания очень
велик по сравнению с периодом электромагнитной рентгеновской
волны (Ю-18 сек.). Поэтому мы действительно имеем право
рассматривать электромагнитное поле мгновенного распределения

272 ДИФФРАКЦИЯ РЕНТГЕНОИСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
вещества решётки (вещество кристалла неподвижно относительно
надающей волны).
Рассмотрим теперь рассеяние рентгеновских лучей маленьким
кристаллом, поглощением и экстиякцией в котором можно
пренебречь. Амплитуда, рассеянная мгновенным распределением вещества
в кристалле, может быть представлена формулой (сравни Ш, 31)
^мгн = Ее 2 FLeieRn,nP) (Ш, 79)
где JRmnp = Rl — радиус-вектор L-ж ячейки; сумма берётся по
всем ячейкам. Интенсивность излучения, которую мы хотим
подсчитать, равна
Для удобства вычисления среднего квадрата преобразуем
выражение для Ежи, прибавляя и вычитая к нему одно и то же число:
Ямгн = Ее 2 FLeieR^ — Ее 2 FeieRL + Ее 2 Ft*"''
L L L
ИЛИ
Л.™ = E,F 2 eiaHL + Ев 2 (/'х - F) eieR^
Обозначая два слагаемых этой суммы через Ех и Е.2, можем
записать
|^«.Н|-=Г^1"+ТЖ1М- ЦЩ\Щ. (ти, so)
Но среднее значение удвоенного произведения равно нулю, так
как д\ — 0к = О (ведь дк есть среднее значение всех д%).
Следовательно, искомая интенсивность
/=~|"^Т2 + -^1ЖТ2=/,+/2- (Ш, 81)
Так как \Е\2 равно произведению Е на комплексно сопряжённую
величину, то
А = /е1^|222^Л£^В^'.
L L'
Значение этой двойной суммы вычислено нами ранее (стр. 232),
таким образом,
_ sin2 -Ту Nxsa sin2 — К&Ъ sin2 -5- &&с
h = lA -x \ \ . (Ill, 82)
sin2 -~- sa sin2 — sb ein2 — *c
« il *2k

§ 10] ВЛИЯНИЕ 'ШИЛОВЫХ КОЛЕБАНИИ 273
Второе слагаемое в выражении интенсивности равно
т. е. *)
h = ^2 S «'*%-"** {Fl-F)(FL,-F)*. (П1,83)
При помощи (1П, 78) и (III, 78а) получаем:
/•V, - * = S f* («'*** - «***) Л*. (111,84)
Эту величину надо умножить на
(/.',,, - F)* = 2/*(<•"'***' -e""Af) .-'*r* (III,84a)
и взять среднее.__При образования среднего исчезнут два члена
из-за того, что Д7^ =0. Подставляя в Т2, имеем":
L L' ~—г Т'
1а=/е22е J'c ''22Ш« ~е fe« *')• (П1.85)
L L' к к'
Этим вычислением доказано, что интенсивность рассеянного
излучения разбивается на две части. Первая часть /, представляет
собой когерентное рассеяние и имеет такую же форму, что и (Ш, 34а).
Отличие J, от интенсивности, рассчитанной для покоящихся
атомов, заключается лишь в том, что вместо атомного фактора fk
в формуле фигурирует атомно-температурный множитель gk. Это
позволяет трактовать 1и как рассеяние от «средней решётки».
Измерение 1Л и расчёт структуры из его значении приводит нас
к средней во времени картине электронной плотности. Ещё раз
подчеркнём, что интенсивности 72 диффракции от кристалла, атомы
которого находятся в движении, эквивалентны интенсивностям,
которые возникли бы от кристалла с покоящимися атомами
рассеивающей силы дк.
Вторая часть 7а—это диффузное рассеяние. Как будет
показано ниже, эта часть суммы много меньше первой и в структурном
анализе она пока что не играет роли. Отметим, что квантовое
рассеяние не учитывается выведенной формулой.
:) Звёздочкой обозначена комплексно сопряжённая величина.

274 ДИФФРЛКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. lit
Ниже мы рассмотрим детальнее как влияние теплового
движения на когерентное рассеяние (температурный фактор), так и
подробности в отношении диффузного рассеяния (§ 12).
Несколько иной метод подсчёта значений lt и /2 был
предложен С. Г. Калашниковым и М. А. Леонтовичем *). Вычисление
теплового рассеяния было сведено к решению некоторой
статической задачи теории упругости.
Этот расчёт позволяет (в противоположность излагаемому ниже
методу анализа тепловых волн в кристалле) получить простое
выражение отношения ~ при условии, что сфера отражения проходит
через узел решётки. Приведём лишь выражение этого отношения
в максимуме диффракционного пятна
А = JL*^ 2х + ьу.
/2 Ю к р {1 (X + 2и) '
где X и [а — константы Ламэ, а о — размер кристаллического блока.
Например, для монокристалла меди Х=1,4-1012и [i=4,5«lOn абс. ед.
•шачение s— —=— возьмём для высоких порядков
(максимальное) Т = 300° К. Размер кристаллического мозаичного блока
примем «-10 см. Mbi получим для отношения— цифру 10~4. Таким
образом тепловое рассеяние в общем в 10 000 раз слабее основной
части рассеяния.
§ 11. Температурный фактор
Рассмотрим луч с длиной волны X, отразившийся под углом Я от
определённого семейства плоскостей кристалла. Атомы кристалла,
находящиеся при этом в движении, рассеивают лучи с амплитудой
а - f J** <Ш» 77а)
Ук — Тке
Выражение температурного фактора можно преобразовать
следующим образом. Скалярное произведепие яА£ можно записать
в виде
^' = 4 = ^4 №«■>
где z\ — проекция смещения на направлении нормали к отражаю-
.щей плоскости (при отражении s== 2кЦ). Таким образом
температурный фактор равен
. 4к sin 0 jt
е' l Ч (IH, 87)
*) ЖЭТФ 10, 749, 1940.

§ 11] ТЕМПЕРАТУРНЫЙ ФАКТОР 275
Обозначим через w (z) вероятность выхода атома из
отражающей плоскости на эту величину. Тогда температурный фактор
может быть записан в форме (опускаем дли краткости индексы у з)
-{-00 . 4ге sin Ь
j w(z)e* x * dz. (III, 88)
— со
Обозначим через и2г среднее квадратичное отклонение всех атомов
в данный момент времени от узловых плоскостей решётки вдоль
направления z (или, что то же самое, среднее квадратичное
отклонение одного атома во времени). Тогда распределение Гаусса
имеет вид
м; (г) = (2я«*) 2 е ~"z .
Зная w (z), мы можем вычислить написанный выше интеграл.
Переходя к действительной части, имеем*):
+ 00 о. 2 Л ' V X /
__— е cos —.- — z)dz =*e
—оо
Итак, температурный фактор, действительно, имеет форму е~ ,
где
М = ЫЧ1 {^р) . (ГП, 87а)
Величина и* есть константа определённого семейства плоскостей
,р /sin fl\2
данного кристалла. Гак как (—— J пропорционально квадрату
порядка отражения от данной плоскости, то можно утверждать
строгую экспоненциальную зависимость температурного фактора от этой
величины. Этим обстоятельством можно воспользоваться для
опытного определения v,z. He приходится объяснять, что среднее
квадратичное отклонение возрастает с увеличением температуры. «Jto
значит, что при больших температурах интенсивности отражённых
лучей быстро падают с увеличением угла скольжения Ь. Именно
это обстоятельство является решающим в ограничении числа
рентгеновских отражений, могущих быть измеренными при данной
температуре.
Величина проекции среднего квадратичного отклонения uz на
направление нормали к отражающей плоскости не будет зависеть
от индексов плоскости в случае изотропии тепловых колебаний,
*) Этот интеграл находится методом дифференцирования по параметру
в аргументе косинуса.

276 ДИФФРЛКЦИИ РЕНТГКНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. Ill
т. е. в том случае, если колебания атомов происходят с равной
амплитудой во всех возможных направлениях. Изотропия тепловых
колебаний—это идеальный случай, который будет осуществляться
лишь в простейших кубических решётках. Только в этом случае
uz не зависит от Ш и является константой кристалла как целого.
Если uz—константа, то значение температурного фактора может
быть введено в /-кривую, так как атомный фактор зависит от
того же аргумента s-^~ .
Приведём некоторые соображения о величине иг. В динамике
кристаллической * решётки доказывается (см. ниже), что вектор
смещения атома можно представить как сумму независимых
гармонических, так называемых нормальных колебаний. Каждому
колебанию соответствует, как известно, энергия е = ш2а^, где ш—
частота и «ш — амплитуда колебания. Принимая для распределения
энергии по частотам закон Планка, мы можем вычислить, сколько
каждое нормальное колебание привносит в смещение частицы вдоль
данного г.
Проще всего подсчёт производится для случая изотропии
величины иг. Так для кубической решётки, все атомы которой
колеблются изотропно, было показано, что
^=й№-*?. (Ш, 89)
А" ч А /
Функция D (ж) — монотонно убывающая функция, имеющая
значения: при х = О Z) (0) = 1; при* x = l D(l) = 0,778; при х = 10
D (ю) = о,164; при х-+ оо D(x)-+Q. Величина 6 есть константа
hv О
вещества, равная ——^ , а х = -^ . Здесь п и к — постоянные
Планка и Больцмана, a vmax — максимальная частота в спектре
колебаний атомов кристалла. Величина Ь имеет размерность
температуры и поэтому называется характеристической температурой.
Характеристическая температура связана с 4 упругими константами
кристалла. Это вполне понятно, так как частоты колебания
определяются упругими силами, возвращающими отклонившиеся атомы
в положение равновесия.
Величина М определяется, как видно из приведённой формулы,
отношением характеристической температуры к температуре опыта.
Таким образом «большая» для одного кристалла температура может
быть малой для другого.
Значения 6 находятся опытным путём из данных о теплоёмкости.
Эти значения колеблются в пределах 100 —1000°. Резкое
исключение представляет алмаз, у которого В — 2340°. Таким образом
М =
6h\
mkb
D[T
+ ■

11]
ТЕМПЕРАТУРНЫЙ ФАКТОР
277
0
комнатная температура даёт для алмаза дг = 9, а, например, для
NaCl (6 = 281°) l»l.
Значения коэффициента В при (^у—), рассчитанные из
характеристических температур для простейших кубических решёток,
колеблются от 0,1 до 2 А-2; -г, фигурирующая в выражении для М,
появилась благодаря учёту нулевой энергии. Поэтому та часть
температурного эффекта, которая заключается в падении интенсив-
ностей с возрастанием угла рассеяния, имеет место всегда. Что
же касается температурной зависимости, заключающейся в
увеличении М при возрастании Т, то для таких «жёстких» кристаллов,
как алмаз, она может отсутствовать I—— <С! -г)в большом темпе-
ратурпом интервале.
Для некоторых кристаллов гексагональной сингонии, т. е. при
анизотропии тепловых колебаний атомов, удалось рассчитать Ж.
Так, например, для цинка
3/=1,1 • КГ19(1,80cos2? +sin2?) l'(^-J.
Здесь со—угол между вектором обратной решётки данной плоскости
и осью с. В зависимости от ориентировки отражающей плоскости
(т. е. от значения ср) коэффициент при (^- ) может меняться
в пределах от 1,1 • 10м0 Т до 1,9 • 10'19'Л
Очень важно обратить внимание на то, что для разных
направлений нормали отражающей плоскости различия в М могут
достигать 200%.
Сравнение теории с опытом, т. о. вычисление по упругим
константам кристалла его температурного фактора, может быть
произведено лишь для простейших случаев, а именно таких, при
которых вполне очевиден характер тепловых колебаний или при
которых колебания изотропны. Такие измерения и вычисления были
произведены для некоторых металлов кубической и гексагональной
систем и для ряда галогенидов щелочных металлов. Было
получено удовлетворительное совпадение теории и опыта. ;
В структурпом анализе более или менее сложных соединении
исследователю ничего не известно о величине-Ж за исключением
того, что для данной системы узловых плоскостей решётки оно
/sin & у "
строго пропорционально I ——). Можно также заранее утверждать,
что для разных кристаллографических символов Ш коэффициент
/sin & \2
при г-т-j имеет различное 3Ha4f>Hne, которое может колебаться

278 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
в большинстве случаев в пределах 20%» а в редких случаях и в
пределах zt 100%-
В рентгеновском эксперименте температурный фактор е~м
выступает неотделимо от атомного фактора /", так как в структурный
фактор входит произведение fe~M — атомно-температурный фактор.
Расчёт /* может быть произведён только для свободных атомов.
Следовательно, установить расчётом значения
атомно-температурного фактора не удаётся по двум причинам—1) искажения в
распределении электронной плотности атома из-за наличия связанных
электронов, 2) искажения из-за анизотропии тепловых колебаний.
Таким образом кривая атомно-температурного фактора, которой
пользуются для сравнения FBb,4 и FH3K (сравни стр. 468), имеет
смысл лишь средней кривой, отклонения от которой могут
достигать значительных величин.
Как указывалось выше, доля внешних электронов в рассеянии
относительно мала. Поэтому искажения первого типа будут
существенны лишь для атомов с небольшим числом электронов. У более
тяжёлых элементов отклонения от средней кривой атомпо-темпе-
ратурного фактора будут определяться лишь анизотропией
тепловых колебаний.
-в (92!}±)2
Обычно пользуются /-кривой с температурной поправкой е V. х >
(А— в ангстремах). Параметр В подбирается таким, чтобы
совпадение опытной и теоретической (с поправкой) /-кривых было
наилучшим. Для органических соедииепий в большинстве случаев
хорошие результаты даёт Б = 4 А"2. Только опытом можно
подобрать среднюю /-кривую для того или иного соединения.
Если строение кристалла может быть установлено объективным
путём (методом рядов электронной плотности), то значения fe~M
для разных отражении могут быть вычислены. Этим способом можно
ставить задачу об определении искажений указанных двух типов.
Систематических исследований такого рода почти пет.
§ 12. Тепловые диффузные максимумы
а) Основные факты. Как было только что выяснено,
тепловые колебания решётки сказываются на интенсивности диффрак-
ционных максимумов: в формулы интенсивности оказывается
необходимым ввести вместо атомного фактора fk атомно-температурный
фактор fkete к , где Д£ — вектор смещения /:-го атома /,-й ячейки
от положения равновесия.
Однако этим не ограничивается действие теплового движения.
На диффракционную картину накладывается картина теплового
диффузного рассеяния. Это последнее та^же характеризуется неко-

§ 12] ТЕПЛОВЫЕ ДИФФУЗНЫЕ МАКСИМУМЫ 279
торо*й функцией I2(s) (формула 111,83) для данного кристалла.
Отличие её от основной для структурного анализа функции J, ($),
даваемой формулой (III, 82), заключается в наличии значительно
более слабых и более размытых максимумов. При абсолютном нуле
/2 (s) должно равняться нулю.
Связь J2 со структурой значительно сложнее, чем
соотношения между структурой и Iv Однако некоторые общие заключения
могут быть сделаны,
несмотря на то, что
точный расчёт 72
удаётся лишь для
простейших случаев.
Особенно важно то
обстоятельство, что
изучение теплового
диффузного рассеяния
позволяет в принципе
проводить
исследования динамики
кристаллической решётки.
Так как 12
значительно (порядка
тысячи раз) слабее, чем
соответствующее /,,
то обычно наблюдают
картину диффузного
теплового рассеяния
на
переэкспонированных лауэграммах или
рентгенограммах
качания. Диффузное
рассеяние обязано своим
происхождением
характеристическому
излучению. Для тща- , .„„от. и
тельных исследований *"г- •»• 38' ^КГимум^3"™ тяи0,ых
необходимо
фильтровать первичный пучок, чтобы отличить 12 для характеристического
излучения от I, для белого спектра.
Типичные картины диффузных тепловых максимумов показапы
на фиг. III, 38 и III, 39.
Следующие основные факты установлены экспериментально и
подлежат объяснению:
1) Дискретные диффузные максимумы возникают при
использовании монохроматического излучения иод углами скольжения,
отвечающими уравнению Вульфа-Брэгга, и под углами, отстоящими

280
ДИФФРАКДИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
от Ьв до нескольких градусов (в особых случаях до 20—30°);
максимумы могут сливаться в линии.
2) Интенсивность максимумов возрастает с увеличением
температуры.
3) Интенсивность пятен тем меньше, чем больше отвечающие им
углы скольжения
отличаются от 05. В случае
*> = »*
диффузный максимум
образует ореол около
основного диффракцион-
ного пятна.
Эти диффузные пятна
являются главным
результатом тепловых
колебаний. Фон
рентгенограммы обязан своим
происхождением
некогерентному квантовому
рассеянию (разумеется,
в случае
монохроматического луча).
С диффузными
пятнами, к теории
которых мы переходим, не
следует смешивать
эффектов белого спектра
(при специальных
исследованиях необходимо
поэтому работать с моно-
Фиг. III, 39. Картина диффузных тепловых хроматическим излуче-
максимумов (другой случай). нием). Диффузные гало,
радиальные полосы,
непрерывные кривые
постоянного р (см. стр. 334) — всё это эффекты, которые исчезают
при использовании монохроматора.
Каждый диффузный максимум можно привести в соответствие
с определённым диффракционным пятном. Интенсивность теплового
максимума составляет 0,01 — 0,0001 долю от интенсивности диф-4
фракционного пятна.
б) Тепловые волны. Колебания атомов решетки не могут
происходить независимо. Отклонившийся атом «тянет» за собой
соседний; /образуется волна — все тождественные атомы колеблются
с одинаковыми амплитудами и частотами, но с систематическим
сдвигом фазы в данном направлении,

12]
ТЕПЛОВЫЕ ДИФФУЗНЫЕ МАКСИМУМЫ
281
Упорядоченность движения атомов есть непосредственное
следствие периодического распределения массы в кристалле.
Кинетическая энергия атомов решётки равна
Потенциальная энергия есть сумма энергии взаимодействия всех пар
атомов между собой. Если энергию взаимодействия частиц Z& и Lw
LL'
обозначить ®кк, , то потенциальная энергия решётки пишется в виде
F=4£ 2?i*;- (1П'91>
L, L' к, к'
что при суммировании каждая пара
ЪЪ'
Коэффициент ~ учитывает то
и
атомов учитывается дважды. Потенциальная функция ^ш, зависящая
от координат xyz, может быть разложена в ряд Тейлора по
проекциям вектора (Ад; —Afc/). Нулевой член разложения не существен,
так как потенциальпая функция определяется с точностью до
постоянного слагаемого; первый член разложения равен нулю, так как
первые производные функции <р по смещениям, имеющие
физический смысл сил, равны нулю, если смещения равны нулю
(положение равновесия). Таким образом разложение имеет вид
+
д2ср
+
+
Af-
2—*-
дхду
w дудз
&!
\*i
А.1-
+
V * г),)/2
-А{'.'!.„
А \у
Ai-
|А<?
At-
2/1 |А{
дх дз'
-aj;
-Aj
-bV
Д* I
,3 , <Ap
I.+
,|д(;-
■д*
д£ч
-A?
(III, 92)
Все вторые производные, фигурирующие в этом выражении,
должны быть взяты для положений равновесия. Производные можно
рассматривать как компоненты симметричного тензора
д2у д3у д2у
хкк'
дх2 бх ду дх dz
<Т-у д'-ср
с/у2 ду д~
Раскрывая скобки в предыдущем выражении, замечаем
ы
?кк
(III,»3)
что
функцию ©fjjj' можно символически записать «следующим образом:
кк'
Сиг, o-i^

282 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. Ш
(так как ?^' имеет форму скалярного произведения вектора Д^Ф^.,
т. е. вектора AjE, преобразованного матрицей Ф на вектор Дь<).
Итак, потенциальная энергия кристаллической решётки равна
Г==4£ £ ****£'*£• (III, Ola)
U L,L' к, к'
В этой сумме отсутствуют слагаемые, выражающие действия
атомов самих на себя. Поэтому надо полагать
Теперь мы можем записать уравнения движения ife-ro атома
L-ii ячейки
<*3Д* д v
тк—#- + -^-£==0, (111,95)
at o^/c
т. е.
m*~d£ + 2 S **kVA*' ~ °- (Ш' 06)
I/ /с'
Каждый член двойной суммы последнего равенства есть сила,
действующая со стороны атома XV на рассматриваемый атом 7,/,.
Решение подобного уравнения приводит к следующему
заключению: динамическое состояние кристаллической решётки доллшо
рассматриваться как суперпозиция 3SN волн различной частоты,
длины волны, поляризации и направления распространения. Здес1.
Дт — число элементарных ячеек, a S — число атомов в ячейке.
Действительно, будем искать решения уравнения двилсения в форме
плоской волны
»! = ^^/". (III, 97)
Здесь со — частота, т—волновой вектор, численпо равный у, и
vu ■—радиус-вектор /с-то атома L-й ячейки. То, что это решение
удовлетворяет уравнению движения, — вполне очевидно. Мы все'
лее подставим его в уравнение для того, чтобы выяснить условия,
накладываемые на частоту и длину волны.
Получим
где тензор
V - 2 ФЙ^" йкхС'*" '■*•'), (in, 08a)

8 12] тепловые диффузные максимумы 283
Значки Jj можно опустить, так как для всех L решения получаются
одинаковые. Напротив, для каждого к, нумерующего атомы в ячейке,
будет своё уравнение. Таких векторных уравнений будет S.
Из этих уравнений можно найти <о. Вековое уравнение, которое
надо будет составить для решения системы SS уравнений, будет
иметь порядок 38 относительно ш. Все 3S корней этого уравнения
будут действительными и
положительными.
Эти 3s колебаний,
существующие для каждой возможной
длины волны, разбиваются на 2 типа:
акустические колебания и
оптические колебания. Первые — их
3 — это колебания решетки как
целого, вторые—их 3(8—1) —
это волны, образованные атомами
одного сорта
(кристаллографически эквивалентными; см. схему на
фиг. 111,40).
Рассмотрим теперь
ограничения, накладываемые на длины
волн. Так как Ф, а
следовательно и $, есть симметричный
тензор, то решения уравнения
(III, 98) будут выступать
парами— для векторов х и —х.
Это, однако, означает следующее: сумма двух бегущих волн
типа [е*2к(*гНгС—«3it(Tr)je<u»* представляет собой стоячую волну.
Каждой паре бегущих в противоположные,стороны волн х и —х
будут соответствовать 2 стоячих волны (знак :±г в квадратных
скобках).
Возможные значения волновых векторов лежат в ограниченном
объеме пространства обратной решётки, а именно, они не выходят
за пределы параллелепипеда, построенного около узла обратной
решётки так, чтобы его грани делили пополам расстояние между
соседними узлами.
Доказательство не представляет труда. Разложим вектор х но
осям обратной решётки:
Фиг. 11Т, 40. а) акустические,
б) оптические колебания.
Предположим, что имеется вектор х', который выходит за пределы
указанной зоны. Найдётся такой вектор х, который будет
заканчиваться р точке, лежащей в пределах зоны, и при этом
х'^х + Я,

284 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [ГЛ. III
где JEC—вектор обратной решётки. Из формулы волны
следует, что вектор т' не даёт вследствие- периодичности решётки
нового решения, так как
KvI = Hrk -f- HIiL - Hrk + m,
где т — целое число и
ri = Hl + А-
Таким образом х и х' дают одни и тс же волны (различающиеся
только по начальной фазе, что не существенно).
Это ограничение легко понять. Вектор х может быть как угодно
мал, т. е. длина стоячей волны может быть, вообще говоря, как
угодно велика для бесконечного кристалла, но вектор х не может
быть больше размера элементарной обратной ячейки. Это значит,
что длина волны не может быть меньше размера прямой
элементарной ячейки.
Максимальная длина определяется, очевидно, размерами всего
кристалла. Как и при любых собственных колебаниях ограниченного
тела половина максимальной длипы стоячей волны равна
размеру тела. Набор длин волн не может из-за граничных условий
быть непрерывным: границы кристалла должны быть узлами
стоячей волны.
Для одномерного кристалла (цепочки атомов) с периодом а
и длиной Nxa возможно существование N1 волн ( —■ = —^?, -j?,
^— , ..., -=£). В трёхмерном кристалле, имеющем форму
параллелепипеда со сторонами N^, N2b и IV3c, будет существовать JV^A'a
волн. Таким образом в кристалле существует столько волн,
различающихся по длине, сколько в кристалле элементарных ячеек.
Можно доказать, что у крупного кристалла внешняя форма не
сказывается на характере собственных колебаний.
Мы показали, что тепловое движение кристалла можно
представить себе как результат наложения 3SN волн. В кристалле
существует N волн разной длины и направления; при этом каждому
волновому вектору соответствует 3# частоты.
в) Геометрические условия днффракции на тепловых
волнах. Диффракция на волнообразном распределении вещества
встречается в природе для волн различных длин. Соотношение между
длиной волны излучения и длиной волны распределения вещества
определяет чёткость эффекта.

§ 12] ТЕПЛОВЫЕ ДИФФУЗНЫК МАКСИМУМЫ 285
Рассмотрим простой пример, а именно, диффракцию
рентгеновских лучей от кубического кристалла, находящегося в состоянии
стационарного поперечного колебания, распространяющегося вдоль
оси [100].
По сути дела стоячая волна тепловых колебаний накладывает
на статическую картину сверхрешётку, период которой равен длине
тепловой волны. На фиг. III, 41 длина тепловой волны около За.
Буквами отмечены узлы новой сверхрешётки. В этой решётке
будут существовать, например, семейства плоскостей типа АВ',
слегка наклонённых к основной плоскости А А' и обладающих почти
тем же самым периодом. Следует рассматривать только эти
плоскости сверхрешётки, ближайшие к основной плоскости, ибо только
они дадут отражения и притом только в первом порядке. Если так,
то основное отражение должно сопровождаться двумя «диффузными
отражениями», происходящими под углами $±<х, где а — малая
величина.
Каждая из 3sN волн, которые были рассмотрены в предыдущем
разделе, даёт свою сверхрешётку. Таким образом диффрагированный
луч будет окружён множеством «диффузных» лучей. Около диф-
фракционного пятна на плёнке возникнет размытое пятно лучей,
««отражённых от тепловых волн». Это распределение
интенсивности (диффузных лучей вокруг диффрагированного) не обязано
Ьыть симметричным. Симметрия будет достигаться в весьма ред*
ких случаях, теоретически—лишь при полной изотропии
колебаний.
i Мы рассматривали выше отражения только первого норядка и
Только от АВ'. Причины очевидны: отражения от плоскостей,
проверенных через А и В', и других подобных попадут в соседство иного
основного отражения. Что же касается отражений второго, третьего
И т. д. порядков от тепловой волны данной длины, то они
эквивалентны отражению первого порядка от тепловой волны с длиной
Ф два, три и т. д. раза меньшей.
' Условие диффракции от тепловых волн должно иметь обычный
РИД
27гД=А- — /»-0,
Где И' — вектор, имеющий направление нормали к отражающей
цлоскости и численно равный -=-. Как видно из фиг. III, 42, Н =
t= J3T-f- х,. где 1 — вектор тепловой волны. Действительно, из
фигуры очевидно, что -^ = у и, следовательно, ON = — = т. Итак,
условие диффракции имеет вид
2тг (Н + т) = к — 7.V (III, 99)

286 дйффракция рентгеновских л Учен в кристалле [гл. ill
Фиг. III, 41. Вдоль А А' распространяются тепловые колебания
с длиной волны А А'. Возникают дополнительные узловые
плоскости АВ', ВС, CD' и ВA'f CB', DC Отражение от этих
плоскостей приводит к образованию тепловых диффузных
максимумов. Отражение происходит под углами ь = Ьв гго, где
&в — угол, удовлетворяющий уравнению Вульфа-Брэгга.
W и W— лучи, отразившиеся от дополнительных плоскостей
(нижний рисунок).

§ 12] ТЕПЛОВЫЕ ДИФФУЗНЫЕ МАКСИМУМЫ ^87
На фиг. 111,43 показан геометрический смысл условия: диффрак-
ция от тепловых волн кристалла в данном направлении имеет
место в том случае, если вектор тепловой волны соединит конец
вектора к с ближайшим узлом обратной решетки. Как было
доказано в предыдущем разделе, все векторы т не выходят за
пределы параллелепипедалъной зоны, построенной вокруг узла
обратной решётки. В зону данного узла попадает, разумеется, только
по одному порядку отражения от тепловой волны.
Фиг. III, 42. Условие диф- Фнг. III, 43. Истолкование
фракции от тепловых диффракции от тепловых волн
ноли. с помощью обратной решётки.
Если условие диффракции 2-k{H-\~i) = & —&0 «перевести на
язык прямой решётки», то это будет означать следующее. Изменяя
угол падения Ь в широких пределах, мы можем получить
диффузное «отражение» от данной области Ш под углом ft + *«2^«
Угол O-j-Ф меняется всего лишь в пределах 1—2°, в то время
как угол {> может меняться в пределах 30°, а диффузное пятно
всё ещё будет видно на фотоплёнке.
Условие (III, 99) можно вывести более строго, исследуя
полуденное нами в § 10 выражение (111,85) для /2. Из этого же
уравнения вытекают также и следствия о распределении
интенсивности диффузного рассеяния.
Зона каждого из узлов обратной решётки может быть
охарактеризована интенсивностью рассеяния в функции ЛГ-j-'c.
Поверхности функции ДЯ"+т), которые называют поверхностями
равного рассеяния (изодиффузии), могут быть построены в пространстве
обратной решётки. Мы используем здесь обратную решётку как
пространство для изображения интенсивности теплового рассеяния
М«), которую так же, как Jt(s), можно представить в функции
•координат обратной решётки £т]С (сравни стр. 238). Функция 12 (а)
падает от своего максимального значения очень медленно;
соответствующие области около узлов обратной решётки имеют поэтому
Значительные размеры и даже могут сливаться.

288 ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [гл. Ш
Удобство в рассмотрении указанных явлений методом обратной
решётки можно проиллюстрировать следующим примером. На
фиг. 1П, 44а показана лауэграмма КС1. Она состоит из обычных
пятен (It (s)) и выделяющихся своим размытым видом диффузных
пятен. Часть пятен на лауэграмме может быть создана
характеристическим излучением, но основная их масса обязана своим
происхождением белому излучению. Если монохроматизировать
первичный луч, то эти пятна исчезнут и на рентгенограмме кроме
нескольких очень сильных и чётких интерференционных пятен
останется картина диффузного теплового рассеяния. Разумеется,
для чёткого воспроизведения этой картины надо резко увеличить
экспозицию.
Возникшие диффузионные пятна лежат очень близко к тем
положениям, в которых находились бы пятна от характеристического
излучения, возникающие при качании кристалла, короче—диффузные
пятна образуют рентгенограмму «качания» па характеристическом
излучении и при неподвижном кристалле.
Происхождение этих пятен нетрудно понять, сравнивая
рентгенограмму со схемой (фиг. 111,446). Около каждого узла обратной
решётки построена сферическая область; предполагается, что внутри
них функция I2 (s) имеет заметную величину. На схеме изображён
луч, падающий, как это и было в эксперименте, под углом 20°
к [010]. Круги 0, 1, 2 — это следы сечений сферы отражения
нулевой, первой и второй плоскостями обратной решётки. Все они
проходят в основном через одни и те же нормальные к плоскости
чертежа ряды узлов. При этих условиях и должна возникнуть
рентгенограмма качания (сравни § 3 гл. IV).
В этом объяснении форма области считалась сферической; это
заведомо неверно, однако большей частью сделанное приближение
оказывается достаточным для понимания характера явлений.
Разумеется, целый ряд интересных подробностей ускользает от
нашего внимания при таком рассмотрении.
Роль области /2 (s) около узла решётки иллюстрируется
примером, показанным на фиг. III, 45. На ней показана обратная решётка
ХаС1, а также отдельно увеличенное изображение области около узла
[[002]] (фиг. III,45,а,б). На фигуре показана проективная
картина. На самом же деле область диффузного рассеяния имеет 8,
а не 4 выступа. 4 выступа смотрят вверх и 4 вниз под углами 30°
к горизонтали.
На некоторых рентгенограммах, снятых и при
монохроматическом падающем луче, можно видеть диффузные линии, соединяющие
отдельные диффузные пятна. При этом линии образуют иногда
сетку, обрисовывающую сечение обратной решётки. Причина этого
обстоятельства может быть лишь одна: слияние диффузных
областей отдельных узлов. В этом случае сфера отражения будет

Фиг. Ill, 44а. Лауэграмыа КС1. Снимок КС1. Неог-
фильтрованное излучение. Первичный луч
перпендикулярен к [100] и под углом 20° к [010].
№
206
COS
Фиг. III, 446. Объяснение снимка
КС1 в обратной ячейке.
сх
«с

200 ДИфФРАКЦИЯ РКНТГВНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛ К [lYT. 1ТТ
проходить по непрерывной области и скользящий вдоль неё луч
опишет на рентгенограмме линию.
Итак, на точечную обратную решётку тепловые колебания
накладывают решётку из размытых областей. Зная величину и форму
№
i
//:/{/ (о)
Фиг. ТП, 4Г). а) Обратная решётка NaCl; б) увеличенное изображение
области около узла [(002]].
размытой области для данного Ш, мы по обычным правилам работы
с обратной решёткой находим направление и интенсивность
рассеянного диффузного излучения и, наоборот, исследуя его при
углах, близких к 9^, мы можем построить около данного узла Ш
поверхности равного рассеяния.
Мы обсудили геометрию дйффракции на тепловых волнах.
Теория, элементы которой были изложены выше, даёт возможность
определить не только геометрические условия максимумов, но л
вид функции /2(s).
Вид поверхности изодиффувии может быть связан с упругими
константами кристалла, определяющими его колебательное
состояние. Такие вычисления удаётся провести до конца лишь для
кубических кристаллов.
Поэтому вид формулы не представляет особого интереса. Один
из существенных выводов этого расчёта заключается в том, что
интенсивность диффузного рассеяния убывает медленнее с
возрастанием порядка отражения, нежели интенсивность главного
рассеяния.
Для частот колебаний с характеристической температурой
в = —g <^ T интенсивность диффузного рассеяния пропорциональна
первой степени температуры и обратно пропорциональна квадрату
частоты атомных колебаний.

§ 121
ТЕПЛОВЫЕ ДИФФУЗНЫЕ МАКСИМУМЫ
291
Теория показывает также, что интенсивность пропорциональна
cos9«, где а — угол между вектором обратной решётки и
направлением колебания атомов. Последнее условие довольно очевидно,
так как искажения решётки из-за тепловых колебаний,
происходящие в отражающей плоскости, т. е. в направлении,
перпендикулярном вектору обратной решётки, не сказываются на
рентгеновской диффракции. Амплитуда излучения, отражённого плоскостью,
определяется проекцией амплитуды колебаний атома на вектор
обратной решётки, т. е. косинусом угла а.
г) Связь между картиной диффузных максимумов и
структурой. На фиг. III, 46 изображена схематически продольная волна,
распространяющаяся вдоль направления [100] кубического
кристалла. Все узлы обратной решётки вытянуты вдоль [100]. Так
как атомы колеблются вдоль плоскостей (07;/), то диффузное
рассеяние от этих плоскостей отсутствует. Максимальным диффузным
рассеянием должна отличаться плоскость (100); плоскости (Ш).
дают промежуточные значения.
Поперечная волна, распространяющаяся в том же направлении,
приведёт к иной картине. Плоскость (100) не даст диффузного
Ш . Ш
100
Ш
(У
tiki
(6)
т
109
ш
Фнг. 111,46. а) Продольная волна, распространяющаяся вдоль [1001;
б) обратная решётка. «Растягивание» отражении.
рассеяния; плоскость (011), перпендикулярная к направлению
колебания, даст максимальное рассеяние. Все узлы обратной
решётки «вытянуты» вдоль того же направления распространения
воаны, т. е. [100].
Эти два примера положены в основу дальнейших рассуждений,
«оторыми мы хотим показать, какой вид имеет картина
диффузного рассеяния в случае слоевой и цепочечной структуры.

•292
ДИФФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ В КРИСТАЛЛЕ [lVl. Ш
Рассмотрим слоистую решётку типа графита. Пусть А (фиг. III, 47)
есть плоскость слоя. Между атомами, принадлежащими одному
слою, действуют значительно большие силы, нежели между атомами,
Д Д Д Д
в-
0
-и-
ъ
0.
/
Q}
0
Фиг. Ш, 47. Диффузное отражение от слоистой решётки: А — плоскость
слоя, В— нормаль к ней. Преимущественная поляризация волн и
максимальная амплитуда колебаний решётки вдоль В. Справа — обратная
решётка и области её узлов.
принадлежащими разным слоям. Такие слоистые структуры гораздо
легче сжимаются в направлении, перпендикулярном слою, чем
вдоль него. Поэтому мы должны предположить, что колебания
атомов будут происходить с наибольшей амплитудой в
направлениях нормали к слою. Тепловые волны, распространяющиеся
в любом направлении, будут поляризованы: максимальными явятся
амплитуды вдоль нормали к слою. Таким образом отражение от
плоскостей В не должно сопровождаться диффузным рассеянием.
Отражение от А даёт максимальное рассеяние, причём поперечные
волны, идущие вдоль Л., дают более значительную диффракцию,
нежели продольные волны, идущие вдоль В. Остальные отражения
дадут промежуточные области, максимально вытянутые вдоль
отражающей плоскости (волны, идущие вдоль отражающей плоскости,
дают максимальный эффект).
Для кристаллов с цепочечной структурой, таких, как нормальные
углеводороды, сжимаемость вдоль цепи много меньше сжимаемости
в перпендикулярных направлениях, в которых действуют лишь
межмолекулярные силы. Очевидно, что в таких кристаллах можно
пренебречь колебаниями атомов вдоль цепи. На фиг. III, 48 через В
обозначены плоскости, в которых лежат цепи. Рассмотрим
отражения от плоскостей А, перпендикулярных цепям. Эффективными

12]
ТЕПЛОВЫЕ ДИФФУЗНЫЕ МАКСИМУМЫ
293
в отношении создания теплового рассеяния будут только волны,
распространяющиеся в плоскостях А. Действительно, рассмотрим
волны, идущие в перпендикулярном направлении, т. е. в напра-
д д й д
В-
В-
В~
В
о <Э ъ
д
Запрещенное
(Колебание
Возяожвыв
колебаний
ъ О &
Фиг. III, 48. Диффузное отражение от кристалла цепочечной структуры:
В— направление цепей, А—перпендикулярные цепям плоскости.
Колебания вдоль В минимальны, вдоль А — максимальны. Справа—обратная ре-
шётка и области её узлов.
влении цепи. Продольных волн этого тила нет, а поперечные волны
создадут колебания, лежащие в отражающих плоскостях. Таким
образом точки А обратной решётки будут окружены
дискообразной, а не эллипсоидальной, диффузной областью.

ГЛАВА IV
МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА
РЕНТГЕНОГРАММ МОНОКРИСТАЛЛА
§ 1. Введение
Исследование рентгеновской диффракции от кристалла (как
геометрической картины, так и интенсивности диффрагированных
лучей) может быть произведено фотографическим и ионизационным
методами. Весьма редко исследование проводится целиком
ионизационным методом; напротив, очень часто исследователь
ограничивается на всех стадиях структурного анализа фотографическими
методами.
При решении структурной задачи исследование проходит обычно
следующие стадии: 1) определение симметрии и поиски осей
у плохо образованного кристалла *), 2) определение размера
элементарной ячейки и трансляционной группы, 3) определение
пространственной группы, 4) измерение ицтенсивностей.
Для решения каждой из этих задач большей частью лригодек
какой-либо один из методов, к описанию которых мы сейчас
переходим. Так, для рзшения первой задачи используется метод Лауэ, для
решения второй задачи нужно прибегнуть к методу вращения или
качания кристалла, третья и четвёртая задачи решаются методом
качания или одной из разновидностей метода рентгеновского
гониометра; к решению последней задачи в некоторых случаях
целесообразно привлечение ионизационного метода. Если последнее не
делается, то интенсивности определяются по почернению плёнки
рентгенограмм качания или рентгенограмм гониометра.
Если исследуется поликристаллическое вещество, то все задачи
решаются в принципе по одной рентгенограмме, полученной
методом порошка.
Существующие .методы рентгеносъёмки монокристалла могут
быть классифицированы следующим образом.
*) В случае хорошо образованного кристалла эта стадия сводится
к определению его внешней симметрии (макросимметрии), т. е.
принадлежности к тому или иному кристаллическому классу (гониометрия).

§2]
МЕТОД ЛАУЭ
295
Белый луч, неподвижный кристалл, неподвижная плёнка —
метод Лауэ.
Монохроматический луч, вращающийся кристалл, неподвижная
плёнка — методы вращения и качания.
Монохроматический луч, вращающийся кристалл, движущаяся
плёнка (или ионизационная камера) — методы рентгенгониометра
и рентгенспектрографа.
Поликристаллические объекты всегда снимаются
монохроматическим лучом. Вращения объекта и движения илёнки применяются
и здесь, но не меняют принципа получения рентгенограммы.
§ 2. Метод Лауэ
а) Идея метода. Схема установки для съёмки показана на
фиг. IV, 1. Рентгеновский луч, выходящий из рентгеновской трубки
в направлении РА, проходит через диафрагменный тубус AT).
Металлическая ширма S
экранирует кристалл С
от всех других лучей,
кроме луча, который
выходит из отверстия р
диафрагмы D. Кристалл С
укреплён на кристалло-
держателе F
(гониометрическая головка такого
же типа, как и
употребляющиеся в
кристаллографическом анализе)
при помощи воска. Надо
следить за тем, чтобы
лучок лучей не пересекал
воска, а проходил только
через кристалл. Это Фиг. IV, 1. Схема метода Лауз.
желательно потому, что
воск рассеивает рентгеновские лучи, создавая фон и кольца на
рентгенограмме. Кристаллодержатель может перемещаться по
скамье В; однако во всех случаях кристалл находится вблизи
выходного отверстия диафрагмы. Плоская фотоплёнка или
пластинка G вставляется « чёрном конверте в рамку Н и
располагается перпендикулярно к первичному лучу. Маленьким
свинцовым кружком К закрывают то место, куда попадает
первичный луч, црощедщий через кристалл. Это делается потому, что
очень сильный первичный луч создаёт около места попадания
на плёнку сильный ореол, который может сделать плохо
видимыми интерференционные пятна, лежащие вблизи центра
рентгенограмм ы,

296 МЕТОДЫ НОЛ УЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
Типичная лауэграмма показана на фиг. IV, 2. Очевидно,
вторичные лучи.исходят из кристалла во многих направлениях.
Лауэграмма всегда очень богата интерференционными пятнами.
Лауэграмма снимается без фильтра и в её создании участвует
весь спектр (белый и характеристический) рентгеновской трубки.
Чтобы понять происхождение и характер лауэграммы, обратимся
к методу трактовки рентгеновских интерференции при помощи
обратной решётки и сферы отражения, изложенному на стр. 206.
Фиг. IV, 2. Лауэграмма.
На фиг. IVr, 3 изображены (в сечении) обратная решётка
кристалла и сфера отражения. Если бы на кристалл падал
монохроматический луч, то вторичные лучи при неподвижном кристалле
возникли бы в очень малом числе, так как весьма маловероятно, чтобы
больше десятка узлов попало на поверхность сферы. Если же
на кристалл падает спектр, содержащий длины волн от Х2 до Х2,
то это значит, что имеется непрерывный ряд сфер с радиусами
от ^- до —. Поэтому все узлы, попадающие в пространство между
этими двумя граничными сферами (в сечении кругами), создают
интерференционные лучи. Числр пятен на рентгенограмме будет
весьма велико. Каждому из узлов обратной решётки, попадающему
в пространство между двумя граничными сферами, соответствует
своя длина волны, для которой выполняется условие 2dsinft = wX.
В некоторых случаях благодаря симметрии кристалла несколько

2]
МЕТОД ЛАУЭ
297
узлов может пересекаться одной сферой, т. е. несколько
интерференционных лучей создаётся одной длиной волны. Так, например,
если первичный пучок совпадает с осью симметрии порядка п,
одна и та же сфера пересекает п узлов. Поэтому, если на рентге-
м n" n' n
Фиг. IV, 3. Схема метода Лауэ и пространстве обратной
решётки. Узлы, попадающие а область между сферами отражения
с радиусами с—- и г—, дают отражения. Эта область заштрп-
max miii
ховапа. Центры сфер отражения располагаются на отрезке РР".
Так как первичный пучок направлен вдоль плоскости
симметрии (перпендикулярной плоскости чертежа и секущей её
по ОТ"), картина диффракции также обладает плоскостью
симметрии. Узлы 1, 2, 3, лежащие на одной узловой прямой,
проходящей через начальный узел О, дают отражения в одном
направлении (отражённые лучи P2V, P'N', P"N"). Это
происходит в силу подобия треугольников О IP, 02Р', 03V".
нограмме имеются пятна, симметрично расположенные относительно
первичного, они созданы одной и той же длиной волны.
Если увеличить напряжение на рентгеновской трубке, то спектр
растягивается п вместе с ним растёт толщина слоя между
сферами— число пятен на рентгенограмме возрастает.
Следует, однако, отметить, что ввиду ограниченных размеров
пластинки не все интерференционные лучи дадут на ней пятна.

298
МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ
[ГЛ. IV
Интерференционные лучи идут во всех направлениях, поэтому
пластинку можно располагать сверху, сбоку, сзади от кристалла
и т. д. Обычно, однако, её помещают за кристаллом
перпендикулярно к первичному пучку. Лучи, дающие пятна на прямоугольной
пластинке, расположенной таким образом, идут внутри
четырёхгранной пирамиды (основание — пластинка, вершина — кристалл).
Эту пирамиду с достаточной точностью можно аппроксимировать
конусом, ось которого совпадает с первичным пучком, а угол
раствора '^ определяется размерами пластинки и со расстоянием
от кристалла (при пластин-
Первичное
Плрстинка / пятно
та.
ке 9X12 см и расстоянии
от кристалла 4 см z>t ~ 120°)
(фиг. IV, 4). С другой
стороны, лучи, {[опадающие на
пленку вблизи
расходящегося первичного пучка,
должны отходить от него
на 2 — Н\ Поэтому не
будут обнаружены
интерференционные лучи,
идущие внутри конуса, ось
которого также совпадает
с иервичкым пучком, а угол
раствора ?2=70. Таким
образом практические
условия съёмки накладывают
на углы скольжения еле-
" ~ " " < "г* (половина угла раствора конуса
Фиг. IV, '1. Возникновение ноля нндексои.
дующее ограничение: -~
равна удвоенному предельному значению 1>). Предельные конусы
сужают эффективную область между граничными сферами
отражения, как это показано на фиг. IV, 4а. Эта эффективная (и притом
не только принципиально, но и практически) в смысле создания
и регистрации интерференционных лучей область обратной решётки
носит лазвание ноля индексов.
б) Геометрия интерференционной картины. Зональные
кривые. Гномоническая проекция лауэграммы. Каждое пятно
рентгенограммы есть след луча, отражённого от семейства узловых
плоскостей кристалла.
Интересной особенностью метода Лауэ является совпадение и<>
направлению лучей, отражённых в разных порядках от одного
и того же семейства узловых плоскостей. Разным порядкам
отражения от одного и того же семейства узловых плоскостей отвечают
пересечения сферами отражения узлов, лежащих на одной узловой
прямой обратной решётки, проходящей через начальный узел. Из
фиг. IV, 3 видно, что радиусы сфер отражения, пересекающих

§2]
МЕТОД ЛАУЭ
299
узлы одной и той же узловой прямой обратной решётки, относятся,
как расстояния соответствующих узлов от начального: -у-: у- =
1 . п
или
к
п
Н° *'mbl = 2d^i: Sin°- =
n\t
— ол - 9Г~, • СЗледова-
тельно, bi = bnt т. е. лучи
совпадают по направлению.
Между направлением
отражённого луча и нормалью
к плоскости (или, что то
же, её вектором обратной
решётки) имеется
однозначное соответствие. Так
как нормаль к отражающей
плоскости, луч падающий
и луч отражённый лежат
в одной плоскости, то из
фиг. IV, 5 очевидно
следующее: если луч любой
длины волны, отражённый от
какой-либо плоскости
кристалла, образует с
первичным лучом угол 2&, то угол
нормали с отражённым
лучом будет 90°— 0;
направление нормали принимается
всегда от отражающей
плоскости в сторону, обратную
отражённому лучу.
Из фиг. IV, 5 следуют
равенства
.1)—расстояние от
кристалла до фотопластинки,
ОН—расстояние между
данным пятном лауэграммы
и первичным,
ON—расстояние от первичного пятна
до точки пересечения
нормали к отражающей
плоскости с фотопластинкой.
Диффрагир
луч
Фиг. IV, 4а. Иоле индексов. Предельные
конусы ОМ и ON% сужающие
эффективную область (крупная штриховка) в
пространстве обратной решётки, имеют своей
осью первичный пучок, а вершины их
находятся в начальном узле О. Они
ограничивают угловой интервал направлений
обратных векторов Н. Ограничительные;
конусы шоричных лучей в пространстве
обратной решётки провести нельзя, ибо
неопределённой остаётся точка, в
которой должна находиться вершина конуса
(центр соответствующей сферы отражения).
Углы раствора ограничительных
конусов ОМ и ON определяются условием:
*1=180°-!1.
Поле индексов отмечено двойной
штриховкой.

300 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
Равенства (IV, 1) позволяют построить с помощью лауэграммы
гномоническую проекцию кристаллической решётки снятого
кристалла, т. е. точки пересечения нормалей к узловым плоскостям
с плоскостью проекции (фотопластинки). Для этой цели удобно
пользоваться гномо-
нической линейкой,
изображённой на фиг.
IV, 6. От начальной
точки О линейки в
одну сторону идёт
шкала Т) tg 2ft
(линейка изготовляется,
разумеется, для
данного ТУ). Эта сторона
линейки является
более короткой. В
другую сторону от О
идет шкала I) ctg ft.
Обе шкалы размечены
в градусах.
Линейка иакладывается на
лауэграмму так, чтобы
точка О совпадала
с первичным пятном.
Поворачивая линейку
вокруг этой точки, накладывают её короткую часть последовательно
на все пятна лауэграммы и по шкале отсчитывают соответствующие
углы ft. Отсчитывая по другой шкале найденный угол ft, находят
точку выхода нормали к семейству узловых плоскостей, отражением
от которого было создано данпоо пятно, ибо первичное пятно,
Фиг. IV, 5. М—кристалл; J [О — первичный луч;
MR—отражённый луч; тстс' — след отражающей
плоскости; MN—нормаль к ней;
ФФГ—-фотопластинка; В — пятно лауэграммы; О — след
первичного пучка; N—выход нормали (гномо-
ническая проекция); SS—плоскость
стереографической проекции; С и Q—стереографическая
и сферическая проекции.
I ' Г | ЦЦЧЩПИЦ-п-, -
35 й 30 25 201510'
(Оа \ ,,-!■,■■,„.,,,,
-.у-"Л 1L,353025 20
С±
Фиг. IS, 6. Гномоническая линейка.
интерференционное пятно и выход нормали лежат на одной прямой..
Способ применения гномонической линейки показан на фиг. IV, 7.
Гномоническая проекция нормалей узловых плоскостей есть,
иначе говоря, проекция обратной решётки кристалла. Именно
проекция, но не сечение обратной решётки. Все обратные узловые
прямые, лежащие в одной плоскости обратной решётки, изобразятся
в этой проекции точками, ложащимися на одну прямую
(пересечение плоскости обратной решётки с плоскостью проекции).
Совокупность узловых прямых обратной решётки, принадлежащих одной

§2)
МЕТОД ЛАУУ
8ul
плоскости обратной решётки, соответствует в прямой решётке зоне
плоскостей, ось которой перпендикулярна к данной плоскости
обратной решётки. Итак, плоскости, принадлежащие одной зоне,
дадут отражения, ложащиеся на одну прямую гпомонической
проекции лауэграммы.
В общем случае эти прямые линии могут итти как угодно.
Картина приобретает, однако, правильность, если рентгеновский
луч идёт вдоль одной
из основных
плоскостей кристалла. Тогда
один из основных
векторов обратной
решётки будет
параллелен плоскости
проекции (фотопластинка
всегда
перпендикулярна к лучу). Теперь
все плоскости обрат-
пой решётки,
принадлежащие зоне этого
обратного вектора,
будут пересекать
фотопластинку по
параллельным линиям.
Направление этих линий
совпадает с
направлением обратного
вектора,
перпендикулярного к лучу. Итак,
если одна из
основных плскостей прямой
решётки
перпендикулярна к пластинке, то на гномонической проекции лауэграммы
возникает система параллельных линий, перпендикулярных к этой
плоскости.
Если луч направлен вдоль кристаллографической оси, скажем а,
то плоскости ah, ас, а также все плоскости типа (Ш будут
перпендикулярны к плоскости проекции. В этом случае на проекции
возникнет не одна, а несколько серий параллельных линий. На
такой проекции можно непосредственно измерить углы между
обратными векторами, идущими в плоскости, параллельной плоскости
проекции; можно также получить некоторые сведения об отношении
длин этих обратных векторов.
Рассматривая внимательно характер расположения пятен
лауэграммы, мы всегда находим возможность сгруппировать пятна,
отнеся их к коническим сечениям, проходящим через центр рент-
Фиг. IV, 7. На лауэграмму L накладывают
кальку К. Гномоиическую линейку накладывают
на кальку, совмещают ее точку О с первичным
пятном лауэграммы и закрепляют булавкой.
Вращая линейку (не меняя относительного
положения К и L), совмещают её короткую часть
последовательно со всеми пятнами Р. По
длинной шкале отсчитывают соответствующий угол ft
н наносят гномоиическую проекцию пятна V.

302
МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [гЛ. JV
т
I S
!/? А
JS'
о
■т
шнограммы. На приведённой выше рентгенограмме отчётливо видны
эллипсы и гиперболы, проходящие своей вершиной через первичное
пятно, вдоль которых
располагаются диффракционные пятна.
Нетрудно видеть, что каждый
эллипс или каждая гиперболасоот-
ветствует зоне плоскостей.
Поэтому-то эти кривые на лауэграмме
называются зональными. При
помощи гномонической линейки
каждый эллипс будет развёрнут
в прямую. Действительно, пусть
А А' на фиг. IV, 8 есть ось зоны,
которой принадлежит множество
плоскостей. Крайние положения
этих плоскостей таковы: 1) под
углом 90° к плоскости чертежа
(как показано на рисунке)—в этом
положении плоскость создаёт
луч PR; 2) в плоскости чертежа—
в этом положении луч скользит
вдоль плоскости и попадает в
точку О (совпадает с первичным).
При промежуточных положениях
ЛУЧ будет описывать коническую
поверхность (одна из образующих
конуса—первичный луч),
которая при пересечении с
пластинкой даст зональную кривую
(эллипс или гиперболу, в
зависимости от наклона оси зоны).
По виду эллипса без труда
находится выход оси зоны. Он
лежит па оси симметрии этой
зональной кривой на расстоянии
■Dtgft от первичного пятна.
Здесь ft отвечает точке эллипса,
наиболее удаленной от
первичного пятна.
Чем больше отклонена ось
зоны от луча, тем больше эллипс;
при угле в 45° эллипс вырождается
в параболу, при угле более 45°
зональная кривая имеет вид гиперболы. Наконеп, при угле 90°,
т. е. если ось зоны параллельна пластинке, гипербола вырождается
в прямую. Направление этой прямой указывает на расположение
i Первичный пу^ок
Фиг. IV, 8. Зональные кривые. Л А'—
ось зоны. Крайние положения
плоскостей зоны: 1) в плоскости
чертежа— отражённый луч совпадает
с первичным, ибо § == 0°; 2)
перпендикулярно плоскости чертежа (в этом
случае А А'—след плоскости) —
отражённый луч PR. Лупи,
отражённые от промежуточных плоскостей,
образуют конус (его ось совпадает
с осью воин). В силу этого лучи,
отражённые от плоскостей зоны,
дают на лауэграмме пятна,
расположенные по коническому сечению
(зональная кривая). Гномоническая
линейка развёртывает зональную
кривую в прямую,
перпендикулярную оси симметрии кривой. S', N',
Тг — проекции пятен 8, В и Т.

§21
МЕТОД ЛАУа
308
важной оси зоны кристалла, а именно, оно перпендикулярно к одному
из основных векторов решётки, лежащих в плоскости кристалла,
параллельной плоскости пластинки.
Если перпендикулярно к фотопластинке будет расположена
плоскость решётки и, следовательно, если целая серия осей зон
попадёт в одну и ту же плоскость, перпендикулярную к пластинке,
Фиг. IV, 9. Зональные кривые. АЛ' первичный луч;
М—узловая плоскость, нормальная к фотопластинке N; OP, 00,
OR, OS и ОТ —выходы осей зон; РР', QQ', ПН'— прямые
гномонической проекции, отвечающие соответствующим
лоннльни м кривим.
то на лауэграмме возникнет серия зональных кривых, «вложенных»
одна в другую и обладающих общей линией симметрии (фиг. IV, 9).
Если перпендикулярно к пластинке расположена ось решётки- и,
следовательно, ряд плоскостей, то возникнет несколько семейств
зональных кривых.
Каждому семейству зональных кривых будет соответствовать своя
система параллельных липий на гномонической проекции.
в) Индицированис лауэграмм. Индицирование лауэграмм не
представляет в настоящее время практического интереса, поэтому
мы остановимся на нём лишь вкратце. Существуют графический и
аналитический методы индицирования. Наибольшее применение имеет
графический метод ипдицирования. Для проведения графического
индицирования необходимо прежде всего получить гномоническую
проекцию лауэграммы. Построение гномонической проекции уже

3()4 МЁГОДЫ ПОЛУЧЕНИЯ И РАСЧЕТА РЕНТГЕНОГРАММ [гЛ. IV
описывалось выше. Как указывалось, при правильной ориентации
кристалла (одна из основных плоскостей обратной решётки
параллельна пластинке) гномоническая проекция кристалла представляет
собой правильную систему пересекающихся семейств параллельных
прямых. Обычно два из этих семейств выделяются среди прочих
заполненностью своих прямых точками. Две прямые этих семейств,
проходящие через центр гпомоническои проекции, отвечают двум
основным узловым плоскостям обратной решётки, перпендикулярным
2Кй ^^ 6ИЗ
1-3
1*2
1'1
h'O h*2 Л=4 h'6
Фиг. IV, 10. Гномоническая проекция плоскости есть
точка пересечения нормали к ней с плоскостью
проекции. По нормаль совпадает по направлению
с обратным вектором плоскости. Поэтому для
получения гномоеической проекции достаточно
продолжить векторы всех узлов обратной решётки до
пересечения с плоскостью проекции. Очевидно, что
координата проекции любой плоскости
пропорциональна индексу соответствующего узла обратной
решётки по соответствующей оси. Это не относится,
конечно, к индексам по оси перпендикулярной
плоскости проекции, ибо соответствующей
координаты на двумерной проекции нет.
плоскости пластинки. Прямые этих семейств не проходят через цент})
проекции, если первичный луч не совпадает с вектором обратной
решётки (случай съёмки триклинного кристалла вдоль осей а, Ь, с
и моноклинного вдоль осей an с). В обоих случаях нара таких
прямых (проходящих через центр или пересекающихся ближе всего
к нему) принимается за проекции осей обратной решётки, скажем
ах и сх. Узлы первой плоскости обратной решётки образуют на гномо-
нической проекции основную и самую крупную сетку, как это ясно
видно из фиг. IV, 10. Узлы второй плоскости частично проекти-
Щ2 zn* опа цп^ 1ипц
1КЗ 2ИЗ JH1 3M2 2К1 5Н2
Плоскость
проекции

§ 2] МЕТОД л л у:) 305
руцтся в те же места, а частично образуют новые точки проекции,
измельчая первоначальную сетку. Наложение узлов третьей и т. д.
плоскостей ещё более усложняет проекцию. Узлы нулевой плоскости
обратной решётки не могут быть спроектированы па плоскость,
перпендикулярную пучку, ибо их нормали параллельны ей. Из
фиг^ IV, 11 легко видеть, что
к ~ qa^ ' к ss*' ~qc^ ' / —" TW* ' ' >*>
где р н у—координаты проекции пятна //7.7 и указанных осях,
Фиг. IV, 11. К — кристалл, Т — плоскость гномони-
ческой проекции (плёнка). Г — у:зел обратной
решетки. Р'— его гномоничеекая проекция.
Соотношения (IV, 2) вытекают из подобия фигур.
Первичный пучок КО направлен по оси сх.
ах,Ь* и с*—периоды обратной решётки, D—расстояние от
кристалла до плёнки. Пользуясь этими соотношениями, мы легко найдём
пятно (ill) и тем самым определим стороны ячейки основной сетки.
Дальнейшее индицирование не представляет труда, ибо очевидно,
что h: 1 =р :р0; 7с: 1 = q : q0> где р и q — координаты индицируемой
точки, р0 w.q0 — координаты точки (111). Соотношения (IV, 2)
позволяют проиндицировать гномоническую проекцию кристалла, т. е.
лауэграмму, если известна его элементарная ячейка. Однако в этом
случае удобнее, пользуясь этими соотношениями, построить
теоретическую гномоническую проекцию и, накладывая её на проекцию,
построенную по лауэграмме, проиндицировать имеющиеся пятна.
Ири индицировании лауэграмм удобно поступать следующим
образом. Определив индексы двух пятен, лежащих на одной
зональной кривой, по правилу зональности (страница 154) находят
символы оси зоны [mnp]: m=kj2—l1k2;n—llh2--hll2;p==hlk2~-1clh<i,

306 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
где (hjkj^ и (Ая&а^) — символы двух проиндицированных пя^ен.
Найдя подобным образом индексы осей нескольких зон, ищут индексы
пятен, лежащих на пересечении зональных кривых по аналогичным
формулам: fe = №^2—Pi^ti It—p^m^ — wi,^2; l = '/n1nq—wtw2, где
[ж^,^,] и [m2n^>z] — символы осей соответствующих зон. О
порядке отражения от той или иной плоскости можпо говорить только,
зная примерную длину волны, создавшей данное пятно. Для этого
необходимо по формуле Вульфа-Брэгга подсчитать соответствующие
данному пятну углы скольжения и посмотреть, какие из них
допускаются полем индексов. Если допустимы два или более углов ft,
то необходимо с помощью фильтров сузить интервал Xmin — Xmax и тем
самым уменьшить поле индексов, после чего порядок отражения
может быть определбн однозначно.
На практике индицирование лауэграмм удобнее всего
производить путём построения по лауэграмме стереографической проекции.
В случае, если размеры элементарной ячейки неизвестны, этот
способ является практически единственно возможным. Из фиг. IV, 5
очевидно, что расстояние стереографической проекции пятна лауэ-
граммы от полюса проекции равно
J-fltg(453-4). (IV, 3)
Разумеется, стереографическая проекция пятна, само пятно и
первичное пятно лежат на одной прямой. Для построения
стереографической проекции лауэграммы удобно пользоваться
стереографической линейкой со шкалами i>tg2ft и fcDtgf45°—~).
Коэффициент к подбирается в зависимости от Т) и размеров
имеющейся сетки Вульфа. Стереографическая проекция удобнее
гномонической из-за меньших размеров и большей лёгкости ииди-
цирования. Для проектирования в данном случае естественно
используется исключительно южный полюс. Индицирование
стереографической проекции производится по формуле
//. \Ь:1 = cos a : cos {3 : cos7, (IV, 4)
где а, р и •{ — углы между стереографической проекцией данного
пятна и проекциями пятен 100, 010, 001. Эти углы легко находятся
с помощью сетки Вульфа. Разумеется, и в этом случае порядок
отражения должен быть определён с помощью поля индексов.
Стереографическая проекция может принести большую пользу при
установке требуемой ориентации кристалла. По существу простое
применение сетки Вульфа указывает углы поворота, необходимые для
получения требуемой ориентации кристалла. Некоторое затруднение
здесь состоит лишь в выборе осей на стереографической проекция
произвольно ориентированного кристалла. Это применение
стереографической проекции пока ещё мало распространено.

§ 21
МЕТОД Л А У:)
307
Ироиндицировав лауэграмму и промерив по ней углы 0, можно
(зная, конечно, приблизительную длину волны) получить некоторое
представление о линейных размерах элементарной ячейки. Однако
значительно чаще лауограммы применяются для определения
угловых констант, о чём будет сказано несколько ниже.
г) Нахождение и уточнение ориентировки кристалла. Одно
из весьма существенных применений лауэграммы — это нахождение
осей решётки в таком кристаллическом образце, внешний вид кото-
Фиг. IV, 12. Лауаграмма, полученная при уточнении ориентировки.
рого не позволяет произвести ориентировку кристалла оптическим
путём—но отражению света гранями кристалла.
Мы рассмотрим ряд случаев, с которыми приходится
сталкиваться на практике.
1. Уточнение ориентировки. Очень часто кристалл
устанавливается в камере оптическим путём весьма приблизительно,
(грани кристалла плохо образованы и дают тусклые и размытые
отсветы). В этом случае производят съёмку лауэграммы так, чтобы
\уч совпадал с направлением, к которому близко расположена
кристаллографическая ось. Полученная лауаграмма позволяет поправить
ориентировку так, чтобы эта ось строго совпадала с лучом, и таким
образом ориентировка кристалла уточняется для дальнейшей съёмки.
Подобная лауэграмма показана на фиг. IV, 12. Около первичного
|№гна мы видим маленький зональный эллипс. Его происхождение

3()8 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЕТА РЕНТГЕНОГРАММ [гл. IV
очевидно—это эллипс зоны той кристаллографической оси, которую
мы ищем. Проводя 1инию симметрии эллипса и отмечая точку,
находящуюся на расстоянии DtgO, мы определяем угол и
направление, в котором должен быть сделан такой поворот, чтобы ась
зон совпала с первичным лучом (а зональный эллипс «вогнался
бы в точку»).
2. Определение угловых констант кристаллов
триклинной и моноклинной системы. К рентгеновскому
определению углов между осями элементарной ячейки трикдинных
и моноклинных кристаллов приходится также прибегать в случае
нлохообразованных кристаллов. В случае плохообразованных
кристаллов средних и кубической систем достаточно доказать
равенство углов 90° или 60°, т. е. определить симметрию, для чего также
служат лауэграммы (см. стр. 314).
Предположим, что ось Ь моноклинного кристалла установлена
вдоль первичного пучка. Если удалось найти плоскость (010), то
ее устанавливают перпендикулярно пучку. Уточнив ориентацию,
как указано выше, получают хорошую лауэграмму. В данном случае
плоскости зоны оси Ь (т. е. плоскости ДО/) перпендикулярны
плоскости пластинки. Линия нересечения любой такой плоскости с
фотопластинкой будет являться линией симметрии семейства зональных
кривых. Две наиболее отчбтливо выраженные на лауэграмме линии
этого типа перпендикулярны двум наиболее «густым» узловым
прямым обратной решётки. Эти узловые прямые принимают за оси ах и сх,
тогда угол {3х равен углу между соответствующими линиями
лауэграммы (фиг. IV, 13). В случае триклинного кристалла наиболее
отчётливо выраженную грань устанавливают перпендикулярно
первичному пучку. Параллельными пластинке оказываются основные
векторы прямой решётки (рёбра указанной грани, если они есть).
Каждому из этих векторов (являющемуся осью зоны) отвечает
зональная прямая на лауэграмме. Выбрав две наиболее отчётливые
прямые, принимаем перпендикуляры к ним за оси а и с, измеряем
угол р и продолжаем исследование (фигура IV, 14). Если у
триклинного кристалла (или у кристалла неизвестной системы)
отчётливо выражено только одно ребро, то его принимают за ось
прямой решётки, скажем а, и устанавливают вдоль первичного пучка.
В этом случае, как и в описанном случае съёмки моноклинного
кристалла вдоль оси Ь, параллельными плоскости пластинки
оказываются векторы обратной решётки. Считая две наиболее явно
выраженные линии симметрии зональных кривых перпендикулярными
осям 6х и сх, определяем угол <хх и продолжаем исследование.
Таким образом следует различать 2 случая съёмки с целью
определения углов: а) ребро кристалла направлено вдоль пучка,
В этом случае основные векторы обратной решётки параллельны
пластинке; б) грань кристалла перпендикулярна пучку. Здесь уже
основные векторы прямой решётки параллельны пластинке.. Оба

§2]
МЕТОД ЛАУЭ
309
случая, естественно, совпадают, если ребро является нормалью
к грани, т. е. луч направлен как по оси прямой, так и но оси
обратной решётки (6||6Х).
3. Нахождение осей решётки в кристаллическом
обломке. В описанных выше случаях мы предполагали, что
у кристалла отчетливо выражена либо одна грань, либо одно ребро.
Фиг. IV, 13. Определение моноклинного угла по
лауэграмме. Первичный луч идёт вдоль Ь; ах и сх
параллельны пластинке и перпендикулярны к
линиям симметрии двух наиболее богатых семейств
зональных кривых.
Возможен случай, когда и этого нет. Тогда, устанавливая кристалл
нроизволъно, мы снимаем три лауэграммы, поворачивая кристалл
последовательно два раза на углы в 60° около любой оси *)
(практически около оси гониометрической головки).
Для каждой из этих лауэграмм строится стереографическая
проекция. Если наложить (с соответствующим поворотом) эти три
*) М. М. У м а н с к и й, ЖТФ (н печати).

310 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
желаем вывести
вращал её" на
tik *Ч * > Ml
»<lf-. . . ♦ V +1
"Чк I ♦ ♦ ♦
проекции друг на друга, то получится вполне исчерпывающее
представление о комплексе нормалей кристалла.
Дальнейшая задача заключается в выборе осей, которые мы
в заданное положение. Для этой цели на проекции,
сетке Вульфа, находим наиболее заполненные
точками меридианы.
Каждый меридиан соответствует
кристаллической зоне, ось
которой легко найдётся под
углом в 90° к меридиану.
Таким образом могут
быть выбраны 3
кристаллографические оси, не
лежащие в.одной плоскости.
Эти оси по очереди
выводятся в вертикальное
положение и исследование
продолжается методом
вращения или качания.
Дальнейшее исследование ио-
кажет, образуют ли
взятые трп вектора правильно
выбранную элементарную
ячейку.
Опишем теперь более
сложный способ
нахождения ориентировки при
помощи гпомонической
проекции. Он применим тогда,
когда ориентировку хотят
найти по одной лауэграмме.
Строим гномоническую
проекцию. Рассматривая её,
мы не найдем выраженной
системы параллельных
линий, как это будет па
проекциях ориентированного
образца, но мы всегда
сможем расположить пятна на системе сходящихся прямых,
обладающей линией симметрии, проходящей через центр проекции. Смысл
этой картины очевиден. Если какой-либо обратный вектор ах
параллелен плоскости проекции, то возникает система параллельных
линий (фиг. IV, 15); если вектор а* вращать около
перпендикулярного к нему направления, то система параллельных прямых на
проекции перейдёт в систему сходящихся (фиг. IV, 15а). Линия
симметрии — это след плоскости, проходящей через ах и\цервичный луч.
t£u:
(ОЮ)
Ъ
к
Фиг. IV, 14. Определение моноклинного
угла по лауэграмме. Плоскость (010)
перпендикулярна первичному лучу. Оси
а и с нараллельпи пластинке. Им отве
чают две наиболее ярко выраженные
зональные прямые на лауэграмме.

2]
МЕГОД Л ЛУП
311
Таким образом, получив на проекции некоторую систему
сходящихся линий, мы находим направление и величину поворота
кристалла, приводящие какие-либо обратные векторы решётки в
положение, параллельное пластинке (сходящиеся линии становятся
параллельными). Для этого кристалл надо новернуть около оси,
перпендикулярной линии симметрии сходящихся прямых.
Направление поворота очевидно из чертежа. Угол поворота определяется
углом схождения прямых.
♦ у
Фиг. IV, 15. Если обратный
вектор ах параллелен плоскости
проекции, то имеются системы
параллельных линий.
Фиг. IV, 15а. Переход системы
параллельных линий в систему
сходящихся линий.
Линии, получающиеся на проекции, возникают в результате
пересечения плоскостей обратной решётки, проходящих через ах,
с плоскостью проекции. Уравнение плоскости обратной решбтки
х cos a -f- у cos р -\- s cos ?о = 0.
Углы а, J3, То суть углы нормали к этой плоскости с осями
координат. При вращении около оси z угол fo остается
неизменным. Уравнение линии пересечения этой плоскоеш о плоскостью
у — D имеет вид
х cos a -f- D cos p -j- з cos *f0 = 0
или
д. tos" jy cos?
cos t0 cos Ко
(IV, 5)
Углы «J u ]0 находим непосредственно из проекции, измеряя
тангенс угла наклона прямой к линии симметрии и отрезок,
отсекаемый ею на оси, перпендикулярной оси симметрии. Двух
уравнении для определения а, р и к0 вполне достаточно, так как они

812 МЕТОДЫ ПОЛУЧЕНИЯ Ц РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
связаны условием cos2 a -j- cos2|3 -j- cos2^0= 1. Зная а и Yo» находим
угол поворота по формуле
(IV, о)
COSa
sin (о = —.
sin To
— X
Эта формула есть решение сферического треугольника, иоказан-
пого на фиг. IV, 16.
Описанным способом можно вывести в плоскость проекции и
вторую ось кристалла, и таким образом продолжать «нащупывание»
невидных глазу
кристаллографических осей.
После того как углы
поворота найдены при
помощи проекции,
можно перейти к повороту
самого кристалла.
Один из возможных
способов нахождения
соответствия поворота на
проекции и поворота
кристалла иллюстрируется
фиг. IV, 16а. Оси, около
которых можно вращать
кристалл, помечены
цифрами 1, 2 и 3;
поворот около осей 1 и 2
осуществляется винтами
головки, ось 3 есть ось
самой головки. Оси
вращения, найденные на гномонической проекции, лежат в плоскости
фотопластинки V и 2''. Головка устанавливается во время съёмки
так, чтобы ось 1 была перпендикулярна плоскости фотопластинки.
Если найдены повороты о} и cpg около осей 1 и 2 и если угол
между осью V и горизонталью равен я, то кристалл надо
повернуть на угол а около оси 1, на угол ?| около оси 2 и на угол ».'
около оси 3.
д) Некоторые замечания о симметрии рентгенограмм.
Большим распространением пользуется метод Лауэ для определения
симметрии кристаллов. Пятна лауэграммы, снятой так, чтобы
первичный луч шёл вдоль оси симметрии или плоскости симметрии,
располагаются с соответствующей симметрией. Вообще очевидно,
что симметричному расположению узловых плоскостей
соответствует симметричное расположение отражённых лучей, однако только
рентгенограммы, снятые по методам Лауэ (см. ниже) и
фотографирования, обратной решетки, непосредственно и полностью
отображают симметрию диффракционной картины. Рентгенограммы, снятые
Фиг. IV, 16. К решению сферического
треугольника.

2]
МЕТОД ЛАУЭ
313
по методу фотографирования обратной решётки, представляют
неискажённые «фотографии» плоскостей обратной решётки и поэтому,
естественно, полиостью отражают их симметрию. Рентгенограммы,
полученные по всем другим методам, представляют искажённые
проекции обратной решётки или отдельных плоскостей её и потому
не могут отражать симметрию кристалла, по крайней мере
полностью. На рентгенограммах качания отображается лишь плоскость
симметрии, перпендикулярная оси качания, или ось симметрии
чётного порядка,
совпадающая с ней (о
причине этого сказано
несколько ниже). В обоих
случаях рентгенограмма
симметрична
относительно нулевой слоевой
линии, ибо верхняя и
нижняя «половины» диф-
фракционной картины
тождественны. Кроме
того, при наличии осп
симметрии п-то порядка,
совпадающей с осью
качания,
рентгенограммы, снятые при повороте
36(Р
кристалла на углы ,
оказываются
идентичными. Это получается
вследствие того, что при
повороте на эти углы сфера отражения пересекает симметрично
связанные области обратной решётки. Рентгенограмма полного
вращения всегда имеет вертикальную линию симметрии, проходящую
через первичный луч, независимо от симметрии кристалла. Это
происходит потому, что при полном вращении каждая плоскость
даёт отражение «вправо» и «влево» под равными углами г). Этим
обусловлено появление вертикальной (параллельной оси вращения
и проходящей через первичное пятно) линии симметрии. Наличие
плоскости симметрии, перпендикулярной оси вращения, или оси
симметрии чётного наименования (параллельной оеи) приводит
к появлению горизонтальной линии симметрии по той же
причине, что и в случае рентгенограмм качания. Таким образом
имеется лишь два типа симметрии рентгенограмм вращения: с одной
и с двумя линиями симметрии. Рентгенограммы вращения не
отражают симметрии кристалла полностью потому, что все лучи,
созданные симметрично связанными плоскостями, имеют
одинаковый угол 0 и дают только два эквивалентных пятна справа
Фиг. IV, IGa. Способ нахождения
соответствия поворота на проекции и поворота
кристалла.

314 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [гл. IV
и слева от первичного. Индивидуальные рентгенограммы качания
не могут отражать симметрии кристалла, так как они охватывают
случайную область обратной решётки, узлы которой, вообще говоря,
не связаны симметрическими операциями. В случае рентгенограмм,
снятых на цилиндрическом гониометре, ось симметрии п-то порядка,
совпадающая с осью вращения, выявляется наличием
интерференционных прямых, отстоящих друг от друга па расстояниях I, соот-
360°
ветствующих углам поворота кристалла на -=—■, за исключением
оси 3, для которой этот угол вдвое меньше и равен 30°. Для нулевой
слоевой линии эти интерференционные прямые, взятые через одну,
оказываются тождественными. В методе кругового гониометра ось
симметрии, совпадающая с осью вращения, проявляется в
тождественности интерференционных кривых', отвечающих узловым
прямым, проходящим через начало и связанным этой осью симметрии.
Угол между этими кривыми тот же, что и в методе
цилиндрического гониометра.
е) Симметрия лаузтраммы. Метод Лауэ отличается той
особенностью, что все интерференционные лучи возникают одновременно.
Лучи, созданные симметрично связанными отражающими
плоскостями, индивидуальны и связаны теми же элементами симметрии.
Плёнка неподвижна и фиксирует все лучи, отвечающие полю
индексов одновременно. В силу этого лауэграмма и отражает
симметрию диффракционной картины. Необходимо, однако, иметь в виду,
что симметрия диффракционной картины (т. е. область узлов,
эффективных для отражения) всегда выше симметрии лауэграммы,
которая снимается на плоскую пластинку.
Метод Лауэ является основным рентгеновским методом
определения симметрии кристалла.
Пятна лауэграмм, снятых так, чтобы луч шёл вдоль оси симметрии
или плоскости симметрии, расположены с соответствующей
симметрией. Это не нуждается в особом объяснении, так как, очевидно,
симметричному расположению атомных плоскостей соответствует
симметричное расположение отражённых лучей.
Необходимо, однако, иметь в виду, что симметрия пучка
отражённых лучей будет выше симметрии кристалла на центр
инверсии.
Действительно, система плоскостей (Ш) и (Ш) это одна и та
же система. Отражения ДО и Ш суть отражения с разных сторон
плоскостей этой системы. Если кристалл не обладает центром
симметрии и (ДО) не эквивалентно (ДО), то это значит лишь то, что
вид на одну и ту же систему с двух разных сторон не одинаков
(как на фиг. IV, 17). Однако вторичные лучд ДО и Ш* будут
отражаться под тем же углом Ь (d и X в уравнении Вульфа-Брэгга

§2]
МЕТОД ЛАУЭ
П15
те же) и с той же интенсивностью (тот же структурный, фактор) *),
вне зависимости от- того, эквивалентны плоскости (Mil) и (hkl) или
нет. Если, например, у кристалла имеются две эквивалентные
плоскости (hkl) и (Met) (ось второго порядка вдоль оси Ь), то от него
возникнут не два симметричных отражённых луча, а четыре: два
отражённых от «обеих сторон» плоскости hkl (и hkl) и два от
плоскости hkl (и hkl).
Кристалл с одной плоскостью симметрии, имеющий две экви-»
валентпые плоскости (hkl) и (hkl), даст четыре эквивалентных
луча hkl, hkl, hkl, hkl. Таким образом
кристаллы трёх классов симметрии С2Л =
= —, С8 = м и С2 — 2 обладают
одинаковой «рентгеновской симметрией», т. е.
относятся к одному «рентгеновскому»
или, как нринято говорить, лауэвскому
классу симметрии. Лауэвским классом
данного кристалла называется, очевидно,
совокупность' элементов симметрии дан- Фиг. IV, 17. Равенство
ного кристалла плюс, центр симметрии структурных факторо^ для
и появляющиеся при этом производные отражений (Ш) и (hkl)-
элементы симметрии. Лауэвские классы
симметрии — это, очевидно, те 11 (пз 32) кристаллических классов,
которые обладают центром инверсии. В один лауэвский класс
попадают те кристаллические клавсы, которые отличаются друг от
друга на центр инверсии. Чтобы узнать, к какому лауэвскому
классу относится данный кристаллический класс, необходимо
добавить к нему центр инверсии, см. табл. IV, I.
Симметричная лауэграмма может возникнуть лишь в том случае,
если ось симметрии или плоскость симметрии лауэвского класса
данного кристалла перпендикулярна плоскости фотопластинки. Это
*) Строго говоря', структурный фактор имеет одно и то же значение
для отражений Jikl и hkl в том случае, если атомный фактор представляет
собой действительную величину. Однако имеется возможность'встретиться
с комплексным атомным фактором. Уто будет тогда, когда падающая волна
имеет длину, близкую к границе поглощения атома (см. гл. III). В этом
случае происходит сдвиг фаз по отношению к падающей волне, а это и
значит, что амплитуда атомного рассеяния становится комплексной.
Неравенство Fflkl и F?-- повлечёт за собой различие в шпенбивностях,
отражённых от противоположных сторон одного и того же^емейства
плоскостей решётки. Несоблюдение правила F^kl — Fj-- наблюдалось на опыте-
Так, для кристалла ZnS, не обладающего центром симметрии, для длины
волны 1,2420 А отношение интегральных отражений 111 -и 111 равняется 1,12,
а для длины волны 1,2792 оно доходит до 1, 42.

316 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [г.1. IV
понятно из следующих соображений. Диффракционная картина при
съёмке по методу Лауэ всегда имеет симметрию соответствующего
лауэвского класса. Однако пластинка регистрирует лишь часть этой
картины, определяемую полем индексов. Симметрия лауэграммы
поэтому отображает только ту подгруппу симметрии диффракцион-
ной картины, которая является одновременно подгруппой симметрии
Таблица IV, I
Лауэвскне классы
Наименование |
лауэвского ; Входящие в него кристаллические классы
класса i
С« = 1
C2h — 2, т
<?,г = 3
£'«'«
DW
■Овл
Cih
1'/,
Dih
п
Oh
C1=l:
C»h = 2 m;
G&i = 3;
C«h =6/»и;
D>d = 3 m;
T)^ = Qjmmm;
С л = 4/m;
]'h = mmm;
I)4h = 4jmmm;
Th = w»3;
0;, = w3'ft;
C» = l
G',s = m;
Сг = 3
C6-0;
D, = 32;
i>0 = 622;
Q = 4;
С«г. = ш;
Л4 = 422:
Г =23
0 =43;
С* = 2
Са = 6
C-6V = 3>м
Се,, = 6ш»; Ду,
Яф=4
/)2 = V = 222
Сцг = 4>«w; X>2</
Г«/ = 43»»
поля индексов. Что касается симметрии пространства поля
индексов (безотносительно симметрия расположения узлов в этом
пространстве), то это есть симметрия круглого конуса, ось которого
совпадает с первичным пучком. Такой конус имеет любое число
плоскостей симметрии, проходящих через его ось, и в соответствии
с этим с его осью можно совместить ось симметрии любого порядка
(симметрия т • со по Шубникову). Других элементов симметрии
у этого конуса нет. На лауэграмме отображается только симметрия
плоскостей и осей симметрии, параллельных первичному пучку.
Плоскость, перпендикулярная пучку, эквивалентна оси 2 лауэвского
класса, совпадающей с пучком, и поэтому также отображается на
рентгенограмме, но уже как ось 2, а не как линия симметрии. Таким
образом триклинные кристаллы не дают симметричных рентгенограмм;
моноклинные кристаллы дают лауэграмму с линией симметрии, если
плоскость базиса (ас) перпендикулярна пластинке, * лауэграмму

§ 2]
метод лаУу
с осью симметрии (иначе говоря, — так как это то же самое для
двумерной картины, — с центром симметрии) при съёмке вдоль
оси Ь. Ромбические кристаллы при събмке вдоль любой из осей
ромбической ячейки дают лауэграммы, обладающие двумя взаимно
перпендикулярными линиями симметрии. Если одна из осей
ромбического кристалла параллельна плоскости пластинки, а в остальном
ориентировка произвольна, то возникнет лауэграмма с одной линией
симметрии. Всего может возникнуть 10 типов лауэграмм,
показанных на фиг. IV, 18. I тип — несимметричную лауэграмму может
дать любой кристалл, если он произвольно ориентирован; II тип
VI VU VIII IX
Фиг. IV, 18. 10 типов лауэграммы.
лауэграмм могут дать кристаллы всех лауэвских классов, кроме С'<
и Сы, если одна плоскость симметрии (лауэвского класса)
перпендикулярна плоскости фотопластинки; III тин дают моноклинные
кристаллы, снятые вдоль оси Ь\ IV тип нредставляют лауэграммы,
снятые вдоль тройной оси кристаллов лауэвского класса С${, а также
кубические кристаллы лауэвского класса Th, снятые вдоль
пространственных диагоналей; V тип нринадлежит только классу C\h
(съёмка вдоль оси 4); VI тин — классу С№ (съемка вдоль оси С);
VII тип дают кристаллы класса Vh , кристаллы классов DQh, Dih
и Th, снятые вдоль двойных осей; VIII тип дают кристаллы
класса Dbd, снятые вдоль гексагональной оси, и кристаллы класса Oh,
снятые вдоль пространственной диагонали; IX тип дают кристаллы
класса D4h, снятые вдоль тетрагональной оси, и кубические
кристаллы классов Oh и Th, снятые вдоль осей куба: X тип
принадлежит только классу D6h (съёмка вдоль оси 6).
Так как обычно система бывает известна до определения лау-
эвекой симметрии, то в большинстве случаев одна
лауэграмма, снятая при полной ориентировке, определяет лауэвекий класс
симметрии.

Й18 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [lYI. IV
Если система неизвестна, то она вполне уверенно может быть
установлена по одним лауэграммам. При этом следует обращать
внимание на симметрию не только геометрического расположения
пятен, но и их интенсивности (симметрично связанные пятна
обладают, естественно, одинаковой интенсивностью). Лауэграммы вообще
очень чувствительны к изменению ориентации кристалла. Это
обстоятельство позволяет осуществлять по лауэграммам весьма точную
ориентировку кристалла, но мешает определению симметрии, ибо
достаточно ничтожного отклонения плоскости или оси симметрии
лауэвского класса от перпендикуляра к пластинке, чтобы нарушить
симметрию лауэграммы.
ж) Астеризм. Любая деформация кристаллической решётки так
или иначе отражается на интерференционной картине. Особенно
чётко выявляются искажения кристалла на лауэграмме. Деформация
монокристалла приводит обычно к растяжению интерференционных
пятеп лауэграммы в радиальном направлении. Могут также
появляться повые радиальные полоски, Лауэграмма деформироваипого
кристалла получает таким образом звездчатый вид, отсюда
название этого явления — астеризм.
Упругий изгиб легко отличить от пластического, снимая
рентгенограмму от разогнутой пластинки: в первом случае восстанавливается
обычная лауэграмма, во втором — нет.
В случае произвольной деформации и любой ориентации осей
деформации по отношению к падающему лучу количественная
интерпретация лауэграммы весьма сложна. Рассмотрим явления
астеризма, происходящие при изгибе кристаллической пластинки,
превращающем её в элемент цилиндрической поверхности*).
Положим, что луч падает перпендикулярно цилиндрической поверхности.
Пятна рентгенограммы можно перенести на стереографическую
проекцию нормалей. Так как отражающие плоскости изогнуты, то
выходы нормалей изобразятся не точками, а областями (а если
пренебречь поперечными размерами пятеп, то штрихами).
Проекцию можно строить для пеекдлышх точек лауэвского пятна, а затем
очертить полученную область (если пренебречь поперечными
размерами, то строятся только концы удлиненного пятна).
Расположение нормали к отражающей плоскости, т. е. обратного
вектора, будем описывать углами », <j» и О, где »— широта
стереографической проекции, "Ь — долгота и 8—угол скольжения
рентгеновского -луча. Выберем ось у вдоль луча, ось г вдоль
образующей цилиндра. Вектор 7/ образует с лучом угол 90° — Ь.
Следовательно (см. фиг. IV, 19),
sin <р — ~-, sin 4» = г х^— , sin 0 = — *- .
н УгЪ+Ъ "
*) С. Т. К о н о б е е в с к и й и И. И. М и р е р. Сборник ^работ Гпнцвет-
мета, 1932.

§2)
МЕТОД ЛЛУЭ
31Й
Угол вектора Я ег\осыо г определится равенством
cos a —cos <p sin «1*.
Стереографическую проекцию лауэграммы строим, как обычно.
Типичная для астеризма картина для кристалла каменной
соли изображена на
фигуре IV, 20а, IV, 206.
Следует обратить
внимание на то, что штрихи не
совпадают с широтными
кругами фиг. IV, 20 в. Это
имело бы место, если бы изгиб
можно было представить, как
вращение около оси s (при
таком вращении <? = const).
Это отклонение, как
сейчас будет показано,
объясняется деформацией
решётки, сжатой на вогнутой
и растянутой на выпуклой
стороне. Благодаря этому
наклон грани по
отношению к лучу меняется по
мере прохождения луча
через кристалл.
Каждое интерференционное пятно характеризуется своей
областью на проекции. Будем характеризовать эту область занимаемыми
(мо интервалами углок
Д«, Д«!> и АО и
покажем, что эти разности
непосредственно
связаны с упругой
деформацией решетки.
Сначала проведСм
расчёт для бесконечно
тонкого луча. Тогда
угол между лучом и
какой-либо гранью
будет зависеть лишь
от состояния
напряжения в данной точке,
а интервал углов —
от разницы
напряжения па выпуклой и вогнутой части. В нашем случае
цилиндрического изгиба имеется только одно главное напряжение,
пропорциональное координате у (идущей перпендикулярно
Фиг. IV, 19. К выводу зависимости между
углами и составляющими вектора И.
Фиг. IV, 20а. Лауэ-
грамма изогнутого
кристалла каменпои
соли.
Фиг. IV, 206. Лауэ-
грамма изогнутого
кристалла каменной
соли после снятия
напряжения.

320 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
нластинке), равное ox = -—-i/t где Е—модуль Юнга и Я — радиус
кривизны. Чтобы упростить расчёт, проведём его для изотропной
Фиг. IV, 20и. Стереографическая проекция изогнутого кристалла.
среды. Тогда компоненты осей решётки а,- измепятсл и буду
иметь после деформации следующие составляющие:
ац, = а{у (l— K-^-j»
где н- — коэффициент Пуассояа.

§ 2] мИтод лауу 321
Основные векторы обратной решРтки 6; изменяются в обратном
отношении, т. е.
bum = uix ' w
h'U = /;///
/>/* = ta
1 + н
1
i'
/i
Из этих формул определятся разности компонент но осям
обратного вектора каждой грани
Здесь D — толщина пластинки. Действительно, например,
т i Urn i .'/»« Jl
где г/ш — значение у на граничных плоскостях (начало координат
предполагается в центре иластинки).
Теперь мы можем вычислить по приведённым выше формулам
интересующие нас величины изменений углов »,фи 0. Получим:
Д!> = -Ц. V 4- (^ ЬЩ = tg a cos2 а £ (1 -j- ix).
Так как изгиб иластинки не фигурировал в нашем выводе
(учитывалась лишь разность напряжении вдоль оси у, по которой шёл
бесконечно тонкий пучок), то, следовательно, тот же астеризм мы
будем наблюдать и при отсутствии изгиба, лишь бы форма ячейки
менялась в кристалле от точки к точке. Существование подобных
искажений для ряда случаев вполне вероятно. Можно представить
себе, например, кристаллит литого металла с различной по сечению
концентрацией твёрдого раствора.
Длина «хвостов» на рентгенограмме в основном зависит от Д#.
Оценка значения ДО по порядку величины приводит к значениям
1—2°, что совпадает с опытом.

322 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
Астеризм, который вычисляется для бесконечно тонкого пучка,
существенно отличается от астеризма, вычисляющегося при учёте
различных ориентировок отражающей плоскости, возникающих при
изгибе.
Положим теперь, что на изогнутый кристалл падает
параллельный пучок лучен ширины А'. Лучи отразятся от серии плоскостей,
возникающих из плоскости недеформированпого кристалла при
вращении её на угол м около оси е. Угол м образован осью у и
нормалью к основной грани пластинки. Нормаль плоскости с обратным
вектором Н будет обладать следующими угловыми координатахми:
Hz Нхсо$и— #„sinw Ну cos и — Нх sin it
sin ф' =-==. ; sin <!/ = -—r —; sin Ь = Гг .
Приращения этих углов по отношению к углам при отсутствии
изгиба равны:
А»' = -г-sin </ Aw = О.
cos у ои '
ДЛ' — . sin Л' Дад — _.
т COS О ОМ ' Е
. ,., 1 ° • a/ a COS а . COS а Л'
Д!> = jt-j- sin » Дм = <г Дм = п • -п .
COS w 0/f COS w COS W Ji
Величина Дм равна j? , хотя и приближенно, но с совершенно
достаточной точностью.
Астеризм, происходящий из-за изгиба (но без учёта
неоднородного состояния напряжения по толщине), носит иной характер.
Надо обратить внимание на то, что в этом случае Да' = 0. Это
значит, что вытягивание нятен на нроекции происходит вдоль
широтных кругов. Следовательно, отклонение направления
вытягивания пятен от кругов широт является критерием величины упругих
напряжений.
Разумеется, и значения Дф+Дф', а также Att-J-дО' тоже
зависят от состояния папрялсопия образца. Комбинируя все дагашг
лауэграммы, молено получить довольно отчётливую картину
состояния деформации образца.
з) Исследование формы узлов обратной решётки. Метод
Лауэ употребляется с успехом для изучения размеров и формы
узлов обратной решётки. В предыдущей главе были приведены
примеры использования этого метода при изучении тепловых
колебаний решётки.
Метод съёмки неподвижного кристалла представляется
целесообразным по следующим причинам. Если почему-либо узлы
решётки превратились в области, то условия диффракции
будут осуществляться для весьма многих кристаллических плоско-

§ 3] МЕТОДЫ ВРАЩЕНИЯ И КАЧАНИЯ КРИСТАЛЛА 323
стой при неподвижном кристалле. Более того, при исследовании
указанных проблем становится возможной рентгеносъёмка
монохроматическим излучением. Если бы узлы обратной решётки
были точечными, то одна сфера отражения, проходящая через
решётку, давала бы одно-два пересечения с узлами. Если же узел
превратился в область, то сфера отражения пересечёт ряд этих
областей. Некоторые из областей будут пересечены в тонких, другие
в «толстых» местах.
Следовательно, возникающие интерференционные пятна будут
в некоторых случаях малыми, в иных — большими и
расплывчатыми.
Подобные исследования приводят, как мы видели, к
установлению картины тепловых колебаний решётки, превращающих узел
решётки в область специфической формы.
Этим, однако, пе исчерпываются возможности метода. Как
показал опыт, в некоторых случаях мы сталкиваемся внутри
кристалла с двумерными 'решётками. Например, старение сплавов
алюминий-медь (4% Си) приводит к выделению атомов меди на
плоскостях- (100) кристалла. Атомы меди образуют при этом
тонкие (очевидно единицы атомных слоев) слои кристалла,
обладающего примерно тем же периодом трёхмерной решётки. Это значит,
что на обратную решётку трёхмерного кристалла надо наложить
обратные решётки двумерных образований — слоев меди.
Опыт показал, что такие слои присутствуют как в плоскостях (100),
так и в плоскостях (010) и (001). Параллельные двумерные
образования дают, разумеется, совпадающие обратные решётки.
Обратная решётка слоев параллельных, скажем, (100), представляет
собой (см. стр. 205) решётку, подобную трёхмерной, с тем отличием,
что все узлы растянуты в линейные отрезки в направлении
обратного вектора (100).
Имея в виду, что существуют слои параллельно всем граням
куба, мы ожидаем превращения каждого узла обратной решётки
в систему трёх взаимно перпендикулярных, вытянутых вдоль
основных осей обратной решётки отрезков.
Из этой картины обратной решётки рассчитывается обычными
способами вид диффракционной картины. Место попадания
соответствующего диффракционного луча на плёнку можно найти
геометрическим путём или по общим формулам для каждой точки
пересечения сферы отражения с областью около узла.
§ 3. Методы вращения и качапия кристалла
а) Идея метода. Слоевые линии. Измерение периода вдоль
оси вращения. Для применения этих методов нужно располагать
хорошо юстированным кристаллом, а именно так, чтобы какая-либо
из осей решётки совпадала с осью вращения или качания.

324 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [iVI. IV
Съёмка производится монохроматическим лучом, падающим под
прямым углом к оси вращепия. Рентгеноплёнка помещается в
цилиндрическую кассету, ось которой совпадает с осью вращения
(фиг. IV, 21). Значительно реже применяется съёмка
рентгенограмм качания и вращения на плоскую плёнку.
В методе качания кристалл поворачивается с постоянной
скоростью взад и вперёд на небольшой угол (2°, 5°, 10° или 15°).
Источник
рентгеновских
Рентгеновская / лучей
трубка
Фотографическая
пленка
_ Цилиндрическая
кассета
с пленкой
Вращающий
ся вал >чЫ
Зубчатая \j-
передача
Г
Мотор
\
1
Фиг. IV, 21. Схема метода вращения и качания.
Типичная рентгенограмма вращения показана на фиг. IV, 22.
Пятна рентгенограммы располагаются вдоль параллельных прямых,
называемых «слоевыми» линиями. Линия, проходящая через
первичное пятно, называется нулевой, следующая сверху — плюс
первой, снизу — минус первой и т. д. Слоевые линии
перпендикулярны оси вращения и расположены симметрично относительно
нулевой.
Если кристалл установлен таким образом, что некоторое
кристаллографическое направление «вертикально», то семейство плоскостей
обратной решётки будет «горизонтально».
Каждая из этих плоскостей будет при вращении кристалла
пересекаться со сферой отражения по кругу (фиг. IV, 23а). Как
нам известно, отражённые лучи имеют направления векторов,
соединяющих центр сферы с узлами, попавшими на поверхность
сферы. Отсюда следует, что каждой плоскости обратной решётки
будет соответствовать прерывистый конус вторичных лучей;
плоскости, проходящей через начало координат, будет соответствовать

} 3] МЕТОДЫ ВРАЩЕНИЯ И КАЧАНИЯ КРИСТАЛЛА 325
I
I
Фиг. IV, 22. Типичная рентгенограмма вращения.
Фиг. IV, 23а. Плоскости обратной решётки пересекают поверхность
сферы отражения но окружностям. Первичные лучи, соединяющие
Центр сферы с точками этих окружностей (узлами), образуют конусы
с осями, параллельными оси вращения.

326 МВТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
пленка
конус с углом раствора 180° (т. е. плоскость). Если ось
цилиндрической плёнки совпадает с осью вращения кристалла, то диффрак-
ционные пятна расположатся вдоль окружностей (пересечение
конуса с цилиндром), а при развёртывании цилиндрической
плёнки на плоскость — вдоль
Цилаидрачвсмая црямых ЛИНИЙ; ЭТО И
есть слоевые линии
(фиг. 236).
Получению
рентгенограммы вращения
соответствует вращение
обратной решётки около
заданного направления
при неподвижной сфере
отражения. Для
практических целей удобнее
представлять себе
решётку неподвижной, а
сферу и первичный луч
вращающимися в
сторону, обратную
истинному движению. В
отражении участвуют все те
узлы 1гЫ [и,
следовательно,
кристаллографические плоскости (Ш)],
которые при вращении
сферы пересекаются * с
ней. Таким образом при
повороте кристалла, а
следовательно, и сферы от-
Пврвичньш pv.
afuoK рент- j~- ' -
первая слоевая
Фиг. IV, 236. Пересечение
интерференционных конусов с цилиндрической плёнкой
образует интерференционные прямые на
плёнке (слоевым линиям).
ражения по отношению к обратной решётке на 360° в отражении
участвуют все узлы, заключённые внутри тороида,
изображённого на фиг. IV, 24.
Если производится качание кристалла в некотором градусном
интервале, то в отражении участвуют узлы, заключённые в
пространстве, пересекавшемся сферической поверхностью при
движении сферы отражения от начального до конечного положения.
Фиг. IV, 25 показывает, что интерференционные лучи создаются
конечным числом узловых плоскостей обратной решётки,
перпендикулярных к оси качания (вращения). Однако плёнка, имеющая
ограниченную высоту, регистрирует ограниченное число слоевых
линий. Помещая плоскую плёнку перпендикулярно оси качания,
можно зафиксировать слоевые линии, не уловленные
цилиндрической плёнкой. Этот метод съёмки находит специальное применение
(см. стр. 353).

з]
МЕТОДЫ ВРАЩЕНИЯ И КЛЧЛШ1Я КРИСТАЛЛА
327
Если расстояние между плоскостями обратной решётки,
перпендикулярными оси вращения, есть dx, радиус сферы -у, а угол
Фиг. IV, 24. Тороид, внутри которого находятся уулы
обратной решётки п отражающем положении. Л —радиус сферы
отражения, Ilb R» — радиусы сечений сферы соответственно,
первой и второй узловой плоскостями, oj и а» — углы раствора
конусов.
раствора «.-го конуса ап (фиг. IV, 236 и IV, 2Г>), то имеют мести
следующие соотношения:
cosa,t = -r (IV, i)
или
J-
cos «„'
(IV, 8)
где J = jx- -период повторяемости в направлении оси вращения.
Расстояние 1п между п-п слоевой линией и нулевой равно:
ln = Tldgant (IV, 0)
где И — радиус цилиндрической пленки («радиус камеры»).
Исключая ап из уравнении (IV, 8) и (IV, 9), находим
J= да
/"• + (?
т
(IV, 8а)
Таким образом с помощью элементарного расчёта, зная радиус
камеры В, длину волны а н измеряя на рентгенограмме величину 1п,
находят величину периода идентичности J вдоль оси вращения.

328 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
Обычпо измеряют на рентгенограмме не 1п, а 2/п, т. е.
расстояние между минус то-й и плюс w-й линиями. Вычисление должно
быть проделано для всех слоевых линий, вышедших па пленке.
Обычно на рентгенограммах вращения видны не только а-линии,
но и р-линии. В этом случае применение фильтров смысла не
имеет, так как более слабые (3-линии нельзя спутать с а-линиями;
как показывают уравнения (IV, 7) и (IV, 9), расстояния между
слоевыми линиями тем меньше, чем меньше длина волны. Поэтому
р-пятна располагаются на слоевых линиях, расположенных более
часто; таким образом каждая а-слоевая линия сопровождается
своей р-слоевой линией, лежащей от
неб в сторону нулевой слоевой. Для
слоевых линий с достаточно большим
номером р-линия может настолько
удаляться от а-линии, что между ними
окажется а-линия номера на единицу
меньше. Расположение а- и р-пятен
на разных слоевых линиях позволяет
легко отличать их друг от друга. Это
невозможно только для нулевой
слоевой (ибо здесь а- и (3-пятна,
естественно, находятся на одной линии)
и для различения а- и (3-пятен
необходимо произвести индицирование.
Следует иметь в виду, что
величины периода, полученные
вычислением из значений 1п разных слоевых
линий, обладают разной точностью. Чем выше порядок слоевой
линии, тем больше точность полученных результатов. Вместо оценки
ошибки рекомендуется следующая процедура: для каждой пары
линий многократно измеряются величины /„ и записываются
значения /„ и Мп, где Ып — среднее отклонение от среднего значения;
затем вычисляются J-\- A J и J—AJ для /„ -f- Мп и 1п — Мп.
Сравнивая эти величины, полученные для разных линий, без труда
находят значения вероятной ошибки в определении периода и Jcp«
Измерение 1п особенно просто в том случае, если
перпендикулярно оси вращения есть плоскость симметрии для диффракцион-
ных дучей (лауэвская плоскость симметрии). Тогда каждому пятну
на минус w-й линии соответствует эквивалентное на п-й линии. Поэтому
измерение величины 21п сводится к измерению расстояний между
эквивалентными пятнами. Если такой симметрии нет, то
приходится процарапывать на рентгенограмме линии, пересекающие пятна
каждой слоевой линии, и мерить расстояния между ними.
Определение периода идентичности описанным способом не
обладает большой точностью. Следует считать исключительно хорошими
результаты, полученные с ошибкой порядка 0,2*—0,3%> например
Фиг. IV, 25. Определение пара
метра вдоль оси вращения.

§ 3] МЕТОДЫ ВРАЩЕНИЯ И КАЧАНИЯ КРИСТАЛЛА 329
о о
5,02 zt 0,01 А, 20,42 =*= 0,00 А и т. д. Поэтому измерения расстояния
между нятнами при помощи линейки и измерительного циркуля
с оценкой десятых миллиметра «на-глаз» вполне достаточны.
Вид рентгенограммы качания, вообще говоря, не отличается от
вида рентгенограммы вращения. Существенно то, что на слоевых
180°
линиях возникнет число пятен, меньшее в — раз, где ш —
интервал качания. Это обстоятельство имеет некоторое отрицательное
значение при определении по рентгенограмме качания периода
вдоль оси качания (слоевые линии, разумеется, менее резко
выражены по сравнению с рентгенограммой полного вращения).
Напротив, малое число пятен является необходимым условием при инди-
цировании рентгенограммы. Все же (опричинах ниже) для
определения периодов предпочитают использовать метод качания.
Если ось кристалла отклоняется от оси вращения, то
рентгенограмма искажается — слоевые линии искривляются, а при большой
дезориентировке не выявляются вовсе. .Гегко показать, что при
деюстировке пятна, отвечающие одной слоевой линии, заполняют
полоску толщиной в М мм, причём М определяется формулой
kl = 2Rsm~ • sins,
где Л— радиус камеры, е — угол отклонения кристаллографической
оси от оси вращения, ш — интервал качания (для метода полного
вращения ш=г180°). Расчёт по этой формуле показывает, что при
обычно применяемых интервалах качания (5—15°), радиусе камеры
порядка 60 мм ив — порядка нескольких градусов Д/ незначительно
и составляет всего 0,3—0,4 мм. В случае полного вращения А/
составляет уже (при г = Зэ) 5 мм. Таким образом рентгенограммы
качания менее чувствительны к деюстировке, чем рентгенограммы
вращения. Это обстоятельство и, главное, меньшая экспозиция*)
заставляют предпочесть применение метода качания для
определения размеров элементарной ячейки.
Если угол между лучом и осью вращения отклоняется от 90°,
то картина сохраняет свою правильность в отношении расположения
пятен вдоль слоевых линий, но теряет симметрию в расположении
слоевых линий по отношению к нулевой. Поэтому в нрипципе
в методе вращения возможна так, называемая «косая съемка»: луч
образует с осью вращения угол $ -£90°.
Интерференционная картина при косой съёмке может быть
построена совершенно так же, как это было сделано на фиг. IV, 25.
Разница лишь в том, что центр сферы отражения не лежит на
*) Экспозиция, требуемая для получения рентгенограммы качания,
вообще говоря, меньше экспозиции, требуемой при методе полного вра-
180°
щения, в раз, где ш — интервал качания.

330 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [г.Г. IV
нулевой узловой плоекости. Половина угла раствора конуса,
созданного ю-й узловой плоскостью обратной решётки, будет
подчиняться уравнению
п)
cos aft = cos р-f у , (IV, Ш)
происхождение которого очевидно из фиг. IV, 20.
Косая съемка не применяется
на практике. Также не принято
вести работу при малых
отклонениях угла р от 90° и вводить
поправку по приведённой формуле.
б) Интерференционные
кривые. В предыдущем разделе мы
видели, что горизонтальные
плоскости обратной решётки
отображаются ыа рентгенограмме иптер-
ференциопными прямыми —
слоевыми линиями. Уместно поставить
вопрос о том, какими линиями
отображаются па рентгенограмме
другие геометрические образы обратной
Фиг. IV, 26. Косая съёмка, решётки. Негоризонтальные
плоскости обратной решётки не будут
отображаться линией на рентгенограмме, но зато любая узловая
прямая обратной решётки имеет соответствующую
интерференционную кривую на рентгеновской плёнке.
Найдём связь между координатами узла обратной решётки и
направлением созданного им луча. Обратим внимание на то, что
все узлы, для которых одинаковы длина обратного вектора Я и
угол его наклона к оси вращения р, дадут одинаково направленные
лучи (фиг. IV, 27). Действительно, различные узлы такого типа
будут подходить по мере вращения кристалла всегда к одному и
тому же месту сферы отражения. Таким образом направление диф-
фракционного луча однозначно определяется координатами If и р
узла обратной решётки.
Направление диффрагированного луча будем характеризовать
углом а — это угол между лучом и осью вращения —и углом х — это
угол между проекцией луча на горизонтальную плоскость и
первичным лучом. Как видно из фиг. IV, 28, между углами а, т, р и
О имеется следующая связь:
из сферического треугольника SAJJ
cos 2t> = cos ■: sin a, (IV, 11)
из сферического треугольника tfb'ilf,
cos a = sin 20 cos o} (IV, 12)

МЕТОДЫ ВРАЩЕНИЯ И КАЧАНИЯ КРИСТАЛЛА
331
Первичный
луч
Фиг. IV, 27. Направление диффрагированного луча АР
(характеризуемое углами х и а) однозначно
определяется вектором Л соответствующего узла обратной
решётки Р и его наклоном к оси вращения р.
Фиг. JV, 28. К выводу уравнений интерференционных
кривых.

332 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [гл. IV
из сферического треугольника SJ/iV
cos p = cos ft cos 8. (IV, 13)
Комбинируя две последние формулы, имеем:
COS <* /1\' 1 л\
cosр = - . п. (1\,14)
' 2 sin w v » /
Угол о имеет вспомогательный характер — это, как видно из
фигуры, угол плоскости отражения с вертикальной плоскостью.
гп г г 2 sin 8 тг
1ак как # = —=-—, то между Я и р, с одной стороны, и а, т,
с другой стороны, устанавливается однозпачное соответствие, а
именно
cos а = Ш cos р,
1-у(Щ)8 } (IV, 15)
COST =
Vl — tXtf)2eos2P
Теперь, мы можем обратиться к поставленной выше задаче —
найти уравнения интерференционных кривых.
Практическое применение имеют кривые двух типов: 1) кривые
постоянного р и 2) симметричные интерференционные кривые. Мы
остановимся только на этих двух случаях.
Рассмотрим узловую прямую обратной решетки, «проходящую
через начало координат и наклонённую к оси вращения под углом р.
Узлы, лежащие на этой прямой, соответствуют разным порядкам
отражения от одной и той же плоскости, нормаль к которой
образует угол р с осью вращения. Найдём уравнение кривой
постоянного р, т. е. такой интерференционной кривой на плёнке, на
которую ложатся отражения всех порядков от данной плоскости. Для
этого из уравнений (TV, 15) исключаем Я. Получим:
,ч о COS2 OL /т,, . ,
2COS2p== : . (1\, Ю)
Конкретный вид кривой будет зависеть от того, о какой
пленке — плоской или цилиндрической — идёт речь. Для вывода
кривых в случае цилиндрической плёнки, имеющей наибольшее
применение, надо подставить следующие выражения для а и ~
(см. фиг. IV, 29):
, г . х 180° /1ЛГ ,„ч
где z и х — ортогональные координаты интерференционного пятна
на плёнке (ось г параллельна оси вращения, ось х совпадает с
нулевой слоевой линией, начало координат — место попадания
первичного луча),

§3]
МСТОДЫ ВРАЩЕНИЯ И КАЧАНИЯ КРИСТАЛЛА
333
Кривые постоянного р для цилиндрической плёнки изображены
на фиг. IV,30. Размер, к которому пужно привести сетку для
использования при расшифровке
рентгенограмм, снятых в
данной камере, определяется
радиусом камеры. На фигуре
показано, что в
горизонтальном направлении сетка должна
иметь размер 2-й. Кроме
кривых р = const, исходящих
из' центра сетки, на графике
построены кривые 0 — const
(*>, как всегда, угол
скольжения в формуле Вульфа-Врэгга),
т. е. cos х sin a = const.
Весьма наглядное
представление о происхождении
кривых постоянного р можно
получить следующим образом. Узловая прямая обратной решётки,
наклонённая к оси вращения кристалла и проходящая .через
начальный узел, описывает конус с углом раствора 2р. Линия пере-
50 йО liO SU
Фиг. IV, 29. К выводу уравнений
интерференционных кривых.
2ТТЯ-
Фиг. IV, 30. Кривые постоянного р и кривые
постоянного 5> (овалы), р и Ь указаны в градусах.
сечения этого конуса с поверхностью сферы отражения (фиг. IV, 31)
и есть кривая постоянного р, т. е. геометрическое место точек,
где узлы дапной узловой прямой обратной решётки, проходящей

334 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЁНТГЕНОГГЛ.ММ [гл. IV
Фиг. IV, 31. Происхождение кривых постоянного о
как результат пересечения конуса со сферой.
Фиг. IV, 32. Рентгенограмма с ярко выраженными кривыми
постоянного о.

§ 3] МЕТОДЫ ВРАЩЕНИЯ И КАЧАНИЯ КРИСТАЛЛА §36
через начальный узел, приходят в отражающее положение. На
кривые постоянного о ложатся пятна hhl, созданные а- и (3-излу-
чением и «хвосты» белого излучения, отраженного данной плоскостью.
Это правило является, разумеется, общим для всех методов — на
интерференционные кривые, отвечающие узловым прямым обратной
решётки, проходящие через начальный узел, ложатся наряду с а-пят-
нами отвечающие им (3-пятна и хвосты белого излучения. Это
очевидно из того, что в уравнения этих интерференционных кривых не
Фиг. IV, 33. Кривые постоянного Н
входит X. Типичная рентгенограмма с хорошо выраженными
интерференционными линиями р = const показана па фиг. IV, 32.
Другая полезная серия интерференционных кривых, называемых
симметричными интерференционными кривыми, получится для всех
узлов, лежащих на прямой обратной решётки, параллельной оси
вращения. При вращении, скажем, вокруг оси с на эту кривую
ложатся отражения с h — const и Jc = const.
Эти кривые будут отчётливо выражены в том случае, если
перпендикулярно оси вращения имеется плоскость симметрии лауэв-
ского класса.

336 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЕТА РЕНТГЕНОГРАММ [г.1. IV
Для таких узлов
Я sin р = const = П±_ или sin о sin ft = -г- f/j, (TV, 18)
где II ^— составляющая вектора обратной решётки,
перпендикулярная оси вращения.
Эти интерференционные кривые вместе с горизонтальными
линиями — следами пересечения равноотстоящих плоскостей
обратной решётки, перпендикулярпых оси вращения, изображены на
фиг. IV, 33. Эта сетка особенно удобна, так как сразу даёт
координаты узла обратной решётки (Н^ и Н\\), соответствующего
данному интерференционному пятпу. Сетка даёт эти координаты в
масштабе — = 1 и потому применима для любой длины волны.
Необходимо только увеличить или уменьшить масштаб сетки так, чтобы
её горизонтальный размер равнялся 2ъИ. Происхождение
симметричных интерференционных кривых очевидно из фиг. IV, 34.
Узловая прямая обратной решётки, параллельная оси вращения,
при полном повороте описывает цилиндр. Линия пересечения этого
цилиндра со сферой отражения и есть кривая постоянного 7/j_.
Рентгенограмма с чётко выраженными кривыми ТТ^ = const
представлена на фиг. IV, 35.
в) Индицирование рентгенограмм качания. Рентгенограмму
полного вращения можно проиндицировать, т. е. определить индекс
интерференции каждого пятна, только в исключительно простых
случаях. Если нужно знать, какие интерференционные лучи
присутствуют, какие нет, или требуется определить интенсивность
каждого луча Ihkh то индицирование необходимо. Одним из
методов, позволяющих проводить индицирование вполне наделено,
является метод качания кристалла.
Один из индексов интерференционного пятна определяется
непосредственно из номера слоевой линии. Очевидно, например, что при
вращении вокруг оси а индекс h равен номеру слоевой линии.
В общем случае при вращении вокруг кристаллографической оси
с символом [тпр] индексы hkl пятен, лежащих на ю-й слоевой
линии, должны удовлетворять следующему условию:
hm-\-hn-\-lp = n. (IV, 10)
Это уравнение получается, если перемножить скаллрно 2 вектора
Щы = Ь(*х-\-кЬ*-]г1с*(нш=^) и q~ma-\-nb-\-pe
\ ahkl/
(q = J—период идентичности вдоль оси вращения). Имеем:
hm-j- Jen4-lp = -5— * ^cos an = nJxJ = n.

§ 3) МЕТОДЫ ВРАЩЕНИЯ И КАЧАНИЯ КРИСТАЛЛА 387
Фиг. IV, 34. Происхождение кривых
постоянного Н., какЗрезультат пересечения цилиндра
со сферой.
Фиг. IV, 35. Рентгенограмма с ярко выраженными кривыми Я,.

ззн
МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕШТЕНОГРАММ [ГЛ. IV
Вывод иллюстрируется фиг. IV, 36. Определение двух других
(скажем Id) индексов каждого пятна производится методом обратной
решётки. Каждая слоевая линия является отображением одной
плоскости обратной решетки. На фиг. IV, 37 и IV, 37а изображена
плоскость обратной решётки, перпендикулярная оси качания. На этой
же фигуре изображён также вид сверху на кристалл, расположение
осей которого, разумеется, однозначно связано с расположением
осей обратной решётки. Нам должно быть обязательно известно
взаимное расположение первичного луча и кристалла в крайнем
положении интервала качания. Кроме того, для проведения инди-
цирования необходимо знать
параметры ячейки.
На фигуре показано, что в
этом положении луч
перпендикулярен большой грани кристалла.
Зная интервал качания, мы
можем изобразить на плоскости
обратной решётки два сечения
сферы отражения. Если речь
идёт о нулевой слоевой линии,
то эти сечения будут кругами
1
Фиг. IV, 36. К выводу
hm -\- 1;н -\-1р<= п.
условия радиуса г0
проходящими
через начало координат. Следует
помнить, что направление, в котором мы отвели сферу от
начального положения, должно быть обратно тому направлению, в
котором вращается (от начального положения) кристалл. Две
заштрихованные области заняты узлами, попадающими во время
качания кристалла в отражающее положепие. Одна область отвечает
диффракционным лучам, идущим вправо, другая — идущим влево
от первичного луча. Если плёнка — полный цилиндр, то это две
половины рентгенограммы.
Остановимся сначала на нндицировании нулевой слоевой линии.
Оно Происходит следующим образом. Измеряем расстояния /
интерференционных пятен нулевой слоевой линии до первичного пятна.
По величине / находим значение утла скольжепия 0 (фиг. ]\т, 38);
ОЧеВИДНО, <)()O.JMM
*и ,мм = ft (TV, 20)
пКмм ' v
Находим далее вектор обратной решётки:
0 2 sin &
Радиусами, равными найденным значениям 7/, проводим в
плоскости обратной решётки дуги, пересекающие заштрихованные
области. Дуга должна пройти через один из узлов области, индексы
которого и присваиваются данному пятну.

§8]
МЕТОДЫ ИРАЩЕНИЯ II КАЧАНИЯ КРИСТАЛЛА
339
Фиг. IV, 37. Индицирова-
ние нулевой слоевой линии
рентгенограммы качания.
Узлы ]10, 210, 220, 230,
100, 110, 120 лежат в
эффективных областях
(заштрихованы) и поэтому дают
отражённые лучи; первым
четырём узлам
соответствуют отражённые лучи,
идущие вправо от
первичного (если смотреть вдоль
него), остальным — идущие
влево.
Фиг. IV, 37а. Для нулевой
слоевой плоскости при
полном вращении (или при охвате
последовательными
интервалами качания 360°)
эффективная область является кругом
2
радиуса -г-.

340
МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЕТА РЕНТГЕНОГРАММ [ГЛ. IV
Фиг. IV, 38. Нахождение
угла скольжения.


ференционное пятно
Первичное
пятно
Фиг. IV, 38а. АО а ВО—
направления первичного
пучка в начале и конце
интервала качания.
Правая эффективная область
(заштрихованы обе)
пересечена дугами а, Ь, с,
d, e и f, радиусы
которых отвечают
найденным значениям Н. Дуги
проходят через узлы,
символы которых (Ш)
приписываются
соответствующим
интерференционным пятнам. Дуга/*
пересекает два узла: 1
и 2; соответствующие
пятна слились или почти
слились на
рентгенограмме. Чтобы сделать индицирование более надёжным, следует
шить интервал качания. Тогда в эффективную область попадает
один из узлов (/).
умень-
только
I ' I > | ' I Ч I I I I | |
ТПГ
1,7
Т"
2,0
90°Ь
QJ Of 0,5 0,7 0.9Щ1 \£ 1,5
)Ю° \20° \30° \40° \50с
19
60° \?0С
И
\*°° I
t-
ffft
Фиг. IV, 39. Линейка для индицирования нулевой
слоевой линии (Н в масштабе 1/Х = 1). Такая линейка
универсальна (для всех А).

3] МЕТОДЫ ВРАЩЕНИЯ И КАЧАНИЯ КРИСТАЛЛА 341
Практически на миллиметровой бумаге вычерчивают в
определённом масштабе (обычно у = 125 ими узловую плоскость
обратной решётки. Из начального узла как центра проводят окружность
радиуса у, на которой отмечают направление первичного пучка
в начале интервала качания. По
этой окружности двигается центр
сечения сферы отражения
(картонный круг радиуса у J.
Накладывая центр круга на отметку,
отвечающую началу интервала
качания, и затем отводя его на
угол <о (интервал качания),
очерчивают эффективную область.
Проводя из начального узла
решётки (циркулем) дуги
радиусами, равныйи найденным
значениям Ну пересекают узлы в
эффективной области (фиг. IV, 38а).
Для того чтобы не тратить
время на расчет Я, изготовляют
показанную на фиг. IV, 39
линейку H = f (1мм) у годную для
данного радиуса камеры.
При определении значений Я
надо уметь отличить а-пятно от
Р-пятна. Если оба пятна
присутствуют на рентгенограмме, то
это легко сделать:
интенсивность (3-пятна примерно в 5 раз .
меньше, а отношение значений Я, найденных по линейке (по-
1 \
строенной для К в каком-либо масштабе, например ^—= 125 мм) равно
Дх Хр
На рентгенограмме присутствует одно л-пятно или одно (3-пятпо,
если данный узел обратной решётки попадает в диффракционную
область для Хл и лежит вне области ла (или наоборот). На фиг. IV, 40
показаны эти случаи.
Определение Я для р-пятен не имеет смысла производить при
помощи специальной линейки. Бели по линейке, построенной для ла,
найдено значение Я1э а на самом деле пятно создано Ц, то
величина его вектора обрати ой решётки будет равна Я, • г- .
Фиг. IV, 40. Эффективные области Хв
и Хр излучений. Узлы /, 2, 3
лежат вне эффективных областей Xtt
и Хр. Соответствующие плоскости
не дают отражений. Узел 4 лежит
в области Хв; на рентгенограмме
имеется а-пятно. Узел 5 лежит
в эффективных областях Xtt и Хр,
имеется и о- и (3-пятно. Узлы в и 7
лежат в эффективной области Хр,
имеются только (З-пятна.

342 МЕТОДЫ . ПОЛУЧЕНИЯ П РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
Другое затруднение при индицировании заключается в
некоторой неопределенности выбора центральной точки первичного пятна
(места, с которым должно быть совмещено начало линейки). Начало
отсчёта должно быть совмещено с центром тепи кристалла; если
кристалл установлен строго на оси диафрагмы, то начало отсчёта
совпадает с центром первичного пятна. Тень кристалла видна лишь
Фиг. IV, 41. Индицирование n-ii слоевой липни.
в том случае, если в мес,те попадания первичного луча
происходит соляризации и кроме того кристалл обладает значительным
поглощением. Если тень не видна и нет уверенности в строгой
установке кристалла, то начало отсчёта «нащупывают», проверяя
себя по совпадению экспериментальных значений Я с
теоретическими.
Если однозначного индицирования не получается, то следует
уменьшить интервал качания.
Рассмотрим теперь индицирование п-й слоевой линии. Её пятна
соответствуют узлам w-й плоскости обратной решётки, вид которой,
разумеется, ничем не отличается от вида нулевой плоскости. Зато
сечение сферы отражения имеет иной вид: яз приведённых выше
фигур (например, IV, 25) очевидно, что радиус кругового сечения
.сферы для ю-й слоевой линии будет равен

§ 3] МЕТОДЫ ВРАЩЕНИЯ И КАЧАНИЯ КРИСТАЛЛА 343
где J—период идентичности вдоль оси качания. Центры сечений
будут отстоять от центра вращения на —, т. е. сечения не
проходят через ось вращения (фиг. IV, 41).
Таким образом узлы п-k узловой плоскости, лежащие в
круге, описанном вокруг
пересекаются сферой
отражения. Это — мёрт-
иая область узлов,
№ дающих отражений
(фиг. IV, 41а).
Расстояние от центра
вращения до узла »-й
плоскости равно в
изображённом сечении
проекции вектора И узла
на эту плоскость, т. е.
равно Hj_. Значения Н±
надо уметь находить по
рентгенограммам. Для
этой цели служит
описанная выше сетка
симметричных
интерференционных кривых.
Пятна, лежащие на
одной кривой,
обладают одинаковым значением Н±, которое в единицах -j- указано иа
экваториальной линии сетки.
Накладывая сетку на рентгенограмму, находим значения Н±
для каждого пятна. Далее поступаем так же, как и при расчёте
нулевой слоевой линии, т. е. засекаем циркулем дуги, радиусы
которых равны экспериментальным значениям. Дуги должны
проходить через узлы, индексы которых и присваиваются
соответствующим пятнам.
Индицирование м-й слоевой линии проще индицирования
нулевой в том отношении, что я- и р-пятна уже не лежат па одной
слоевой линии рентгенограммы. Однако это индицирование требует
не только правильного совмещения начала отсчёта с центром
рентгенограммы, но и правильной ориентации* рентгенограммы по
отношению к сетке.
Пользоваться сетками симметричных интерференционных
кривых особенно легко в тех случаях, когда форма и ориентировки
центра вращения и имеющем радиус
Фиг. IV, 41а. Эффективная область п-й
плоскости обратной решётки, отвечающая
полному вращению или охвату качаниями 360°,
является кольцом. Ширина кольца
лл'-,/ФГ-®\

344 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
обратной решётки таковы, что имеется серия узловых прямых
обратной решётки, параллельных оси вращения. В этом случае
одной и той же интерференционной кривой на рептгенограмме
будет принадлежать множество пятен. Каждая узловая
прямая будет иметь свою кривую. Картина будет симметричной.
Такой симметричной картины не будет, если перпендикулярно
оси вращения нет плоскости лауэвской симметрии. Рентгенограммы
такого типа расшифровываются значительно труднее. Эта трудность
не сводится лишь к отсутствию выраженных на плёнке
интерференционных кривых. (Сетка симметричных интерференционных
кривых, разумеется, применима и в этом случае.) Она заключается
главным образом в правильном установлении центра вращения,
который теперь может не совпадать с начальным узлом w-й
плоскости обратной решётки. Действительно, начальный узел сечения «хсх
обратной решётки лежит на векторе Ъ*, а центр вращения лежит
на векторе Ь.
Таким образом надо вычислить угол ЬЬХ, а также найти
положение плоскости ЪЬ* по отношению к осям а* и сх (см.
фиг. IV, 42) — этим опре-
рсь вращения ^ делится расположение
точки Л (центра вращения).
Длина отрезка ОЛ равна
Сдвиге W X У' у' X ndUgW
Плоскость hn2
длина uxpct
в данном
примере dx = -А. Его расноло
жение но отношению к осям
рекомендуется определять
но' стереографической
проекции кристалла и
обратной решётки.
Если интервал качания
невелик, то индицирование
w-x слоевых линий
весьма часто происходит с
Помощью сетки симметричных
интерференционных кривых почти что «на-глаз». Это во всяком
случае относится к симметричным рентгенограммам качания.
Индицирование рентгенограмм вращения мало отличается от инди-
цирования рентгенограмм качания. Отличие состоит в том, что
эффективная область представляет собой не полумесяц, как в методе
качания, а сечение тороида, т. е. окружность (нулевая слоевая)
или кольцо (п-я сдревая линия). Радиусами, равными найденным
значениям Н±, проводят окружности, проходящие в эффективной
области. Естественно, что при сколько-нибудь больших параметрах
прямой и малых обратной решётки в эффективную область попадёт
Фиг. IV, 42. Если е осью вращения
совпадает только вектор прямой, но не
обратной решётки, то для всех слоевых линий
кроме О-й проекция оси вращения не
совпадает с начальным узлом обратной решётки.

§4]
ПРАКТИЧЕСКИЕ ЗАМЕЧАНИЯ
345
столь много узлов, что указанная окружность, воооще говоря,
пересечёт (или пройдёт очень близко, что одно и то же из-за
ошибки в определении Л) несколько узлов. В силу этого метод
вращения не допускает однозначного индицирования.
§ 4. Практические замечания
а) Камеры. Существует очень большое число конструкций
рентгеновских камер. Часть из них приспособлена для съёмки
рентгенограмм по одному из описанных выше методов, другая часть —
это универсальные камеры, позволяющие получать рентгенограммы
нескольких типов. Наиболее
распространены камеры для получения лауэ-
грамм (плоская пластинка и отсутствие
механического вращения кристалла),
камеры полного вращения с
цилиндрической кассетой, универсальные
камеры для получения рентгенограмм
вращения, качания и лауэграмм (с
плоской и цилиндрической кассетами),
камеры для съёмки рентгенограмм
качания и лауэграмм также с двумя
кассетами и рентгенгониометры —
приборы, разворачивающие каждую
слоевую линию в плоскую
рентгенограмму.
Общим элементом всех камер является диафрагма, или, вернее,
система диафрагм, служащая для получения тонкого более или
менее параллельного пучка рентгеновских лучей, направляемого
Входная
диафрагма
Выходная
диафрагма
Фиг. IV, 43. Диафрагма.
Фиг. IV, 43а. Схема устройства диафрагмы: а — входная, в —
выходная диафрагмы, б—диафрагменный тубус; ААГ — пучок,
выходящий из окошка рентгеновской трубки. Диафрагма выделяет из
него значительно менее расходящийся пучок ВВ'. Наиболее
интенсивной является строго параллельная часть этого пучка ССГ.
на кристалл. Как правило, длина диафрагменного тубуса равна
40—60 мм. В тубус вставляются (фиг. IV, 43 и IV, 43а) входная и
выходная диафрагмы. Обычно применяются диафрагмы с круглыми
отверстиями. Диафрагмы делаются сменными для того, чтобы можно
было получать пучки различных сечений (обычно диаметром от

346
МЕТОДЫ ПОЛУЧЕНИЯ U РАСЧЕТА РЕНТГЕНОГРАММ
[ГЛ. IV
0,3 до 2 мм). Наиболее употребительные размеры диафрагменных
отверстий 1 мм» Входная диафрагма имеет форму усечённого конуса
и прижимается гайкой к тубусу. Выходная диафрагма вставляется
внутрь тубуса. Это делается для того, чтобы стенки тубуса
поглощали лучи, рассеянные концом диафрагмы, которые в противном
Фиг, IV, 436. Расходимость пучка, прошедшего чере;*
диафрагму.
случае привели бы к появлению ни рентгенограмме паразитных
колец. В то же время выступающая часть тубуса не должна
задерживать лучи, пропущенные диафрагмой, ибо иначе появится
паразитное рассеяние тубусом. Сказанное иллюстрируется фигурой IV, 41.
Фиг. IV, 44. а) Диафрагменный тубус не имеет выступа за
выходную диафрагму. Часть лучей пучка рассеивается
материалом диафрагмы и создаёт паразитные кольца фона на
рентгенограмме, б) Диафрагменный тубус с выступом. Лучи,
рассеянные диафрагмой, экранируются, пучок, прошедший через
диафрагму, не задерживается, в) Длина выступа диафрагмен-
ного тубуса I слишком велика. Тубус задерживает края пучка,
прошедшего через диафрагму. В данном случае паразитное
рассеяние происходит от выступа тубуса.
Фигура IV, 436 показывает, что расходимость первичного пучка,
характеризуемая углом ч, определяется условием
Т _ di + rfa .
2 21 '
tg-J"
(TV, 22)
d{ и d2 — диаметры отверстий входной п выходной диафрагм,
I — расстояние между диафрагмами.
Если кристалл полностью омывается пучком, то размер пятна
на рентгенограмме определяется размерами кристалла и
расходимостью пучка. Если же сечение кристалла больше сечения пучка,
влияет только расходимость. Предположим для простоты, что ври-

i]
ПРАКТИЧЕСКИЕ ЗАМЕЧАНИЯ
347
сталл может быть представлен шариком диаметра 2л, тогда, если
расстояние от кристалла до плёнки равно В и кристалл полностью
омывается лучом, диаметр пятна
на плёнке равен
Плата
dn = 2Jl + 2Dtgj. (IV, 23)
Кристалл
Происхождение формулы
очевидно из фигуры IV, 45. Мы
говорим лишь о геометрических
размерах пятна, интенсивносп.
в разных точках его определяется
многими факторами и, в
частности, коэффициентом поглощения.
Кассеты для плёнки бывают
трёх типов: цилиндрические, по-
луцилиндрические и плоские
'(фиг. IV, 46). Обычно диаметр
цилиндрических и
полуцилиндрических кассет равен 57,3 мм. *) Для
специальных целей изготовляют
цилиндрические кассеты и
больших размеров. Что же касается
плоской кассеты, то при
расстояниях от кристалла до кассеты
порядка 25—45 мм её размер
может быть сделан 90 лшХ
X 120 мм.
Необходимо снабдить кассеты
приспособлением для крепления
конверта с фотоплёнкой. Эти
приспособления видны на
фотографиях. Их задача прижать конверт с плёнкой как можно плотнее
к кассете. В противном случае прп расчёте рентгенограмм
возникнут ошибки.
На фиг. IV, 47 изображена камера для исследования
монокристалла производства Института физики Московского университета **).
Эта камера позволяет снимать рентгенограммы качания и лауэ-
граммы. Основная особенность камеры заключается в том, что она
Фиг. IV, 45. АВ—диффракционное
пятно. 00'— ось первичного, 00"—
ось вторичного пучков. Ввиду
расходимости первичного пучка
плоскость hkl даёт отражение в
интервале углов 7. так как, строго говоря,
направление первичного пучка опре-
Y
делено «с точностью» ± —■.
*) Этот диаметр удобен потому, что углы скольжения 9 для пятен
нулевой слоевой линии, выраженные в градусах, численно равны
расстояниям этих пятен от первичного пятна, выраженным в миллиметрах. Дей-
90° 90° 90°
ствительно, для нулевой слоевой $ = —~-1. Условие —~- = 1 дает В = =
«= 28,65 мм. Обычная высота кассеты 80—90 мм.
**) Уманский М. М. и Вагаряцкий Ю. В.,, Зав, лаб. 14, fflo,
1948.

348 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [гл. IV
позволяет получить серию рентгенограмм при различной
ориентации кристалла по отношению к лучу и к оси вращения, не
переклеивая кристалла на гониометрической головке. Такая
возможность всегда удобна и просто необходима в том случае, если
кристалл плохо образован и при его переклеивании грозит
опасность «потерять уже снятое направление». Если исследованию
подлежит обломок
кристалла, то без
описываемой камеры нельзя
обойтись.
Гониометрическая
головка в положении,
фиксируемом срезом еб
ножки, вставляется в
держатель и закрепляется
винтом В. Вращая барабан Д
можно поворачивать
кристалл около оси головки.
Передвигая держатель
вдоль дуги, мы
поворачиваем кристалл около оси
(нормали к плоскости)
- ,,,.,. т„ дуги. Этими двумя угла-
Фиг. 1\, 46. Кассеты для рентгеновских "„ ,*.™„.™™™.i гчЛЛ„Л„Л
камер: а - полуцилиндрьческая кассета для ми фиксируется располо-
универсальной камеры (РКОП); б — большая жение кристалла ПО ОТ-
цнлиндрическая кассета для камеры полного ношению к лучу И к оси
вращения (РКВ); в —плоская кассета для вращения. Фотоплёнка в
съгмки лауэграмм £ = Р1СОП; ,) ко»- штшш КОЕверте ^ ^
ной бумаги вкладывается
в кассету, которая по направляющим нолозьям вдвигается в камеру.
Пружинящие шпильки закрепляют кассету в нужном положении
(для цилиндрической кассеты это, очевидно, то положение, при
котором ось кассеты совпадает с осью качания). Качание
производится электрическим моторчиком, который непосредственно или
через редуктор вращает «сердечко», металлическую пластинку,
имеющую (фиг. IV, 47а) форму кардиоиды. Рычаг, укреплённый
на оси качания, прижимается пружиной к сердечку. При вращении
сердечка рычаг совершает движение взад и вперёд; при этом ось
качания поворачивается на некоторый угол (зависящий от размеров
и формы сердечка) сначала в одну, а затем в другую сторону.
Форма сердечка выбрана таким образом, чтобы скорость качания
была равномерна.
Если нужно снять серию рентгенограмм качания, необходимо,
чтобы соответствующая ось совпадала с осью гониометрической
годовки, которая в этом случае совмещается с осью качания. Сняв
одну рентгенограмму качания, поворачивают барабан на определённый

м
ПРАКТИЧЕСКИЕ ЗАМЕЧАНИЯ
349
Я Й РчО В
ао°чо
я и go w
« Ч
ч 9
« » 3
а*
о
VO
ев
Й -
fa
Рч
с ч
.Ч I Ц
СО ез О
Н Ч
в о
о t->
».
О
КЗ
за2!
р О jj Я
ч I;
ев _ ©
Я2К
И
сЗ
Я ф
о р,
Ч М
>з СО
ев
Я I О ев
НЬн ф S Я g
«> Я g I t>s
я 9 ir ** &.
С ,*■ , е- к Ч
О ® -
^§5
!Ч
Он'
ев :
3i
S I
СЗ
о _
Сц ф
5 и
Я Ф
as °
0 ° л
* « "
°
1 я
О к
ев
ф
с; А
ев
О VO а
со ф
я
я
к
я >>2
р. и
л Г
о? о
S Q в 2
,^Я* «в;
« ° а
ев
» Рч© 0
3 5 ? »

H50 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
угол и снимают вторую рентгенограмму и т. д. Этот угол должен
быть несколько меньше угла качания, чтобы эффективные области
перекрывались. Если кристалл качается от исходного положении
Фиг. IV, 47а. Металлические пластинки
в форме кардиоиды.
данного интервала по часовой стрелке, то указанный поворот
производят против часовой стрелки и наоборот (фиг. IV, 48).
Фиг. IV, 48. Получение серии рентгенограмм качания. 1,11.
III—эффективные области трёх последовательных рентгенограмм; А, В —
перекрывание эффективных областей; Klt Кп, К1П — направления первичного пучка
в начале I, II и III интервалов, Кр Ки, Кш — то же в конце
интервалов, <о — величина интервала качания, е — величина поворота при переходе
от интервала к интервалу; Д — величина перекрывания интервалов.
Качание от «начала» к «концу» интервала — по часовой стрелке, поворот от
одного интервала к другому — против часовой стрелки,
б) Выбор спектра и образца. Особое внимание
исследователь должен обратить на характер спектра рентгеновской трубки.
Как ясно из предыдущего, во всех случаях, за исключением
съёмки лауэграмм, в структурном анализе пользуются монохрома-

§4]
ПРАКТИЧЕСКИЕ ЗАМЕЧАНИЯ
351
тическим излучением. Рентгеновская трубка дабт обычно белый-
спектр, на котором резко выделяется линия Ка вещества анода, а
также примерно в 5,5 раза более слабая линия Щ. В большинстве
случаев ни белый спектр, ни линия К? не мешают распознанию и оценке
интенсивностей пятен, созданных линией Ка; однако в некоторых
случаях желательно получать более строгий монохроматический спектр.
Наиболее прямой метод для этой цели — это предварительная
монохроматизация пучка отражением при нужном угле скольжения
от кристаллов каменной соли или кальцита. Монохроматоры могут
быть изготовлены из обычных крупных кристаллов, а также в виде
изогнутых кристаллов.
Более простой способ — это монохроматизация при помощи
специальных фильтров. Такие фильтры легко подбираются для
значительного ослабления Щ линии. Дело в том, что между длинами
волн Ка и jSTp линий элемента с менделеевским числом Z всегда
находится граница поглощения (на которой коэффициент
поглощения совершает резкий скачок) элемента с менделеевским числом
Z—1. Следовательно, для медного анода фильтром является никель,
для железного — марганец и для молибденового—ниобий. Так как
ниобий малодоступен, то пользуются окисью циркония. Подходящие
толщины фильтров Мп — 0,005 мм, Ш — 0,007 мм, Zr02 — 0,03 мм.
Можно пользоваться солями этих элементов в виде порошков,
нанесённых ровным слоем на бумагу. Количество порошка следует
рассчитывать, исходя из количества нужного элемента на 1 см2 (см.
также стр. 189).
Предложены также комбинированные фильтры, дающие весьма
высокую степень монохроматизации.
Подавляющее большинство структурных исследований проводится
на медном излучении. Однако в ряде случаев целесообразно
отходить от этого правила. Выбор излучения должен определяться:
1) необходимостью захватить большее число отражений, 2)
необходимостью избегнуть наложения или близости интерференции,
3) поглощающими свойствами объекта. Первый и второй факторы
противоречивы: чтобы увеличить число отражений, надо увеличить
диаметр сферы отражения, т. е. уменьшить длину волны; напротив,
для лучшего разрешения диффракционных пятен длину волны надо
увеличить. Именно поэтому среднее по длине волны излучение меди
и получило столь широкое распространение. Если температурный
фактор кристалла мал и переход на молибденовое излучение может
реально увеличить число наблюдаемых отражений, то этот переход
надо сделать, правда, лишь в том случае, если имеется в виду
довести исследование до конца, т. е. до построения рядов (см.
гл. VI). Однако большей частью температурный фактор сводит
на нет отражения, для которых ^_;>0,6 — 0,7. Ясно, что в этом
случае переход на молибденовое излучение нецелесообразен.

•{Г)2 методы получения л расчёта рентгенограмм [гл. iv
Что касается поглощающих свойств вещества, то их надо
учитывать в соответствии с кривой поглощения исследуемого вещества
в области 2Гв-излучения. Если внимательно рассмотреть кривые
поглощения элементов, то станет ясным, что кобальт сильно
поглощает Си2Га-линию, хром сильно поглощает Ре2Га-линию и т. д.
Таким образом исследование строения каких-либо соединений
кобальта при помощи трубки с медным анодом безусловно невыгодно.
Большое значение имеет выбор размера кристалла. Толщина
объекта должна быть ни слишком мала (рентгеновские лучи
к основном проходят и мало рассеиваются), пи слишком велика
(рентгеновские лучи в основном поглощаются и опять-таки мало
рассеиваются). Можно рекомендовать следующую простую формулу
оптимальной толщины:
W = 4' ([V'24)
г
где {1 — коэффициент поглощения вещества кристалла для
используемого излучения. Эта формула получается следующим образом.
Интенсивность диффрагированного луча пропорциональна прежде
всего интенсивности первичного пучка и, во-вторых, числу
рассеивающих центров (атомов). Число атомов, в свою очередь, тем
больше, чем больше линейные размеры кристалла, поэтому можно
положить I = kl0tn, где /—интенсивность диффрагированного, /0—
интенсивность первичного пучка, t — линейные размеры кристалла,
к—коэффициент пропорциональности. Учёт поглощения приводит к
выражению I = к10Р1е—^. Для нахождения оптимальной толщины
кристалла достаточно найти максимум /, т. е. приравнять нулю
производную -гг = к!01п—хе-^* (п — |г/) = 0.' Откуда п—ty. = О или <опт= — .
Обычно полагают рассеяние пропорциональным квадрату толщины
кристалла, что приводит к формуле (IV, 24). Это справедливо,
например, в случае часто встречающихся игольчатых кристаллов. В
других случаях правильнее полагать рассеяние пропорциональным t
1 3
или 23, что дабт tom, равное — или —. Во всяком случае поря-
док /опт остаётся прежним. Оптимальные толщины большей частью —
десятые доли миллиметра. Для органических веществ практически
удобна толщина 0,5—1,0 мм.
§ 5. Методы уточнённого определения периодов идентичности
по рентгенограммам качания и вращения
Определение периодов идентичности путём измерения расстояний
между слоевыми линиями не приводит к особо точным результатам.
Дифференцируя формулу (IV, 8), находим, что ошибка в
определении периода идентичности равна
*f=-tgada. (IV, 25)

§ 5] методы уточнённого определения периодов 353
Выражая а через радиус камеры Л и расстояние между слоевыми
линиями /,,, приходим к выражению
dJ
lnRbR 4- JWn
(IV, 25а)
При большом радиусе камеры (7t!~60 мм), высоте кассеты
(/„ = 60 мм) и ошибках в определении В к I (0,2 мм) находим,
что точность индивидуального определения периода идентичности
не превосходит 0,3%* Эти формулы учитывают лишь ошибку в
определении радиуса и расстояния между слоевыми линиями и не
учитывают ряда других факторов, уменьшающих точность (деюсти-
ровка кристалла, сжатие плёнки и т. д.). Практически точность
индивидуального определения периода идентичности не
превышает г+z 1°/о- Разумеется,
точность может быть
повышена за счёт
многократности измерения. Однако
существует весьма простой
способ увеличения точности
индивидуального
измерения.
Этот метод состоит в
определении периода
идентичности по высоким
слоевым линиям (с большим п).
Эти линии не фиксируются
обычными
цилиндрическими кассетами, но легко
могут быть фиксированы
на плоской плёнке,
перпендикулярной оси качания или вращения *). При этой съёмке
слоевые линии имеют вид колец. Легко видеть, что в этом случае
(фиг. IV, 49)
Фиг. IV, 49. Метод съёмки рентгенограмм
вращения и качания по Уланскому.
U
т* • л '
(IV, 26)
где В. — радиус кольца, А — расстояние от кристалла до плёнки.
. В данном случае применимы формулы (IV, 8а) и (IV, 25а):
однако /„ следует заменить на А — константу камеры (напротив Л
здесь меняется с номером слоевой линии). Этим способом можно
Иодойти к углам а, близким к 0°, и тем самым значительно
Повысить точность (по крайней мере на один порядок вели-
-*) М. М. У м а н с к и и, Зав. лаб. 14, 1343, 1948.

/{51 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЕТА РЕНТГЕНОГРАММ [ГЛ. IV
чины). Единственный недостаток этого способа состоит в том, что
при больших размерах периодов обратной решётки в
направлениях, перпендикулярных оси вращения, высокие слоевые линии
оказываются слабо выраженными. Это происходит потому, что
эффективная область обратной решётки представляет для п-й
слоевой линии кольцо с радиусами ~-±-*у- (фиг. IV, 25).
С уменьшением а ширина кольца уменьшается и, следовательно,
уменьшается заполненность слоевых линий интерференционными
пятнами, сильно снижающая точность в определении R. Указанный
способ ценен ещё и тем, что, позволяя фиксировать высоки**
слоевые линии, он тем самым увеличивает охват съёмки.
Весьма точные значения периодов идентичности (и угловых
констант ячейки) получаются путём измерения расстояний между
пятнами нулевой слоевой линии и первичным пятном. Для этого, однако,
необходимо знать индексы каждого пятна, т. е. проиндидировать
рентгенограмму. Из уравнения
где В — радиус камеры, I — расстояние данного пятна от
первичного, находят значения углов скольжения & для всех пятен.
По найденным зпачениям & находят d, а затем по квадратичным
формам и параметры ячейки. В случае, например, моноклинного
кристалла, снимаемого при вращении оноло оси Ь, получают для
определения трёх неизвестных а, с и (3 столько уравнений, сколько
пятен на рентгенограмме, т. е. обычно более 10. Решая уравнения
группами по 3, получают весьма много значений а, с и (3 и затем,
пользуясь методом средних квадратичных отклонений, находят
среднее значение.
В данном случае, дифференцируя (IV, 20) получаем:
д»« » («. + **) (IV, 27)
dg Ш - - ,-,tg 9 . ft (*L + ^ j . (IV, 27о)
Для далёких пятен (Ь близко к 90°) точность получается весьма
высокой. Практическая точность этого метода 0,1—0,2%. В случае
резких пятен правильной формы с 0, близкими к 90°, измерения I
на компараторе и точного определения В эта точность может быть
значительно повышена. Указанный метод, вообще говоря, не
требует знания Ж, ибо число неизвестных значительно меньше числа
уравнений, так что R можно исключить. Однако обычно поступают
иначе. Указанным способом определяют R, снимая стандартный
кристалл (обычно каменную соль), а затем найденное значение R
или
a

5 6] РЕНТГЕНГОНИОМЕТРЫ С ЦИЛИНДРИЧЕСКОЙ ПЛЁНКОЙ 355
аспользуют для расчёта параметров изучаемых кристаллов. В
принципе, однако, лучше исключать В из уравнений* ибо фактическое
значение В меняется от рентгенограхммы к рентгенограмме (несколько
иная закладка плёнки, другой конверт, влияние проявления и т. п.).
§ 6. Рентгенгоншшетры с цилиндрической плёнкой
а) Общие замечания. Классификация. Нужно стремиться
к получению таких рентгенограмм, которые позволяли бы
измерением на плёнке устанавливать координаты узла обратной решётки.
Если производить послойный анализ обратной решётки, то требуется
знание двух координат. Методы вращения и качания отображают
плоскость обратной решётки одной слоевой линией.
Интерференционные пятна представляют одномерное множество и из их
расположения можно найти только угол О, следовательно, только длину
вектора обратной решётки. Вторая координата узла обратной решётки
(направление вектора И) угадывается в методе качания, если
размеры элементарной ячейки известны. Действительно, зная
исходную ориентацию кристалла ц, следовательно, обратной решётки,
мы можем указать, какие узлы её попадут в эффективную область
нри данном иптервале качания. Поскольку длины векторов
обратной решётки для разных узлов, вообще говоря, различны, мы можем
при малом числе пятен однозпачно проиндицировать рентгенограмму,
т. е. приписать каждому вектору свой узел. Если асе в
эффективную область попадает много узлов, индицирование становится
ненадёжным, и приходится уменьшать интервал качания. Однозначное
индицирование рентгепограмм полного вращения возможно поэтому
только в исключительно простых случаях кристаллов с большими
периодами обратной решётки.
Вполне понятны достоинства такого метода, который позволил
бы «развернуть» слоевую линию и получить на одной
рентгенограмме двумерпое множество интерференционных пятен с тем, чтобы
измерением двух координат на плёнке можно было бы найти две
координаты узла обратной решётки. Эта задача будет решена, если
синхронно с вращением кристалла будет перемещаться плёнка.
Тогда кроме угла 0 станет известным момент времени, в который
плоскость дала отражение и, следовательно, ориентировка этой
плоскости по отношению к лучу, иначе говоря ориентировка вектора
обратной решётки.
Разумеется, при этом способе съёмки все слоевые линии, кроме
«разворачиваемой», должны быть отширмованы. Рентгенограмма
!дабт отображение лишь одной плоскости обратной решётки.
Все приборы, работающие на принципе «разворачивания»
слоеной линии, носят название рентгенгониометров. Существует
несколько разновидностей метода, которые могут быть классифицированы
следующим образом:

356 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЕТА РЕНТГЕНОГРАММ [гл. tV
А. Съёмка на плоскую фотоплёнку
1. Фотоплёнка перемещается поступательно в своей плоскости:
а) расположена параллельно оси вращения кристалла,
б) расположена перпендикулярно оси вращения кристалла.
2. Фотоплёнка вращается в своей плоскости около оси:
а) совпадающей с осью вращения кристалла,
б) параллельной оси вращения кристалла,
в) перпендикулярной оси вращения кристалла и совпадающей
с первичным лучом,
г) то же, что и в), но луч перпендикулярен оси вращения
плёнки.
Б. Цилиндрическая плёнка
1. Вращается около оси, параллельной первичному лучу.
2. Перемещается поступательно:
а) вдоль оси вращения кристалла,
б) вдоль оси вращения образца. Луч падает на образец вдоль
оси вращения.
Практическое значение имеют преасде всего цилиндрический
гониометр 2>2, а и камера для фотографирования обратной решётки
А2,б (КФОР). Значительно
меньше распространён
круговой гониометр А2, в. Для
поликристаллических образцов
представляет интерес текстур-
камера Жданова Ь'2, б (см.
стр. 587).
б) Цилиндрический
гониометр (прямая съёмка). В
цилиндрическом гониометре
плёнка движется с постоянной
скоростью взад и вперёд вдоль
оси вращения кристалла. При
этом движение плёнки
связано с вращением кристалла
(фиг. IV, 50а), который
качается в широком интервале
глгдииаииа»
Фиг. IV, 50а. Схема рентгенгониометра
с цилиндрической плёнкой: К —
цилиндрическая кассета; С—кристалл; пг,
«2» лз> па~ механизм движения плёнки
и вращения кристалла; ЕЕ' —
экваториальная линия рентгенограммы, т. е.
«след» первичного луча.
около 200° *). Внутрь цилиндрической плёнки вставлен неподвижный
латунный цилиндр с прорезью вдоль окружности. Цилиндр может быть
установлен так, чтобы через прорезь проходили лучи только одного
интерференционного конуса (одной слоевой линии (фиг. IV, 506)).
*) Все интерференции возникают при качании кристалла на 180°;
берётся несколько больший интервал для того, чтобы получить некоторые
пятна в двух местах плёнки. Это позволяет производить промер плёнки
с большей точностью

6] РЕНТГЕНГОНИОМЕТРЫ С ЦИЛИНДРИЧЕСКОЙ ПЛЁНКОЙ 357
решетки
Движущаяся плёнка будет «разворачивать» эту слоевую линию,
как это показано на рентгенограмме (фиг. IV, 51).
Если на рентгенограмме вращения можно было измерить только
значение Н данного пятна, то теперь кроме него мы можем
указать для каждого пятна мгновение, в которое оно возникло.
Если интервал качания кристалла в>, а поступательное
движение происходит на расстояние 1мм, то расстоянию в 1 мм вдоль
образующей цилиндрической
ПЛёНКИ СООТВеТСТВуеТ ПОВОрОТ Деленный Виффракцмон/л/и kohj/c
u^yj^nzi. uvuiijuiu ijju* v n-u слоевой линии, соответстоую-
крвсталла на у градусов. Или, щий п'й ^ЛОСЛоша обратной
говоря «языком обратной
решётки»: два
интерференционные пятна, находящиеся, на
рентгенограмме на расстоянии
а мм вдоль оси плёнки,
возникли при положениях сферы
отражения, ПОВёрнуТЫХ Друг Пучок рент- С>-:Цк^
ОТНОСЙТеЛЬНО Друга На УГОЛ геновских fL^-.^Ft^*
а • -у- градусов. Отношение
ш J \ Металлическая
-f~c есть константа прибора. / \ У* защита
Часто изготовляют приборы
таким образом, что вращению
на 1° соответствует сдвиг в
1 мм: с = 1°jmm. Вторая
константа прибора та же, что и фиг
в камерах вращения, — это
радиус цилиндрической
плёнки. Удобен радиус JR = 57,3, употребляются и вдвое более
широкие камеры.
Построение сечения обратной решётки и вместе с этим индици-
рование происходят следующим образом. Для каждого пятна при
помощи двух линеек находятся: 1) угол у поворота кристалла,
а следовательно, и сферы отражения по отношению к произвольно
выбранному начальному положению. Для этого изготовляется
равномерная линейка, на которой наносятся градусы в масштабе
1 мм = ~-. Этой линейкой измеряют расстояния Y всех пятен
рентгенограммы в направлении, параллельном оси вращения
(экваториальная линия рентгенограммы). За начало отсчёта берут
произвольную линию, перпендикулярную экваториальной линии
рентгенограммы; 2) вектор обратной решётки Н\ для этой цели
Ось вращения
IV, 506. Отширмовывание п-й
слоевой линии.
изготовляют линейку со шкалой ЙГ==
причём К

358 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [гл. IV
выражается в миллиметрах, а Я—в долях-у-. Измеряя расстояние
пятна от экваториальной линии по перпендикуляру к ней, находят
непосредственно Н данной плоскости. Таким образом линейки
располагаются взаимно перпендикулярно, как показано на фиг. IV, 52.
Узлы сечения решётки строят при помощи сечення сферы отраже-
Фиг. IV, 51. Гонпометрограмма.
ния, у которой на окружности нанесены значения Я, поворачивая
сферу для каждого пятна на нужный угол о от начального
положения.
Следует не забывать, что для каждой слоевой линии диаметр
сечения сферы отражения имеет свою величину; для всех слоевых
линий (кроме нулевой) моноклинных и триклинных кристаллов
следует учесть сдвиг центра вращения относительно нулевого узда
плоскости обратной решётки,

§ 6]
РЕНТГЕНГОНИОМЕТРЫ С ЦИЛИНДРИЧЕСКОЙ ПЛЁНКОЙ'
359
j*
\ i I i i i I

Интерференционное пятно
Паенка
Эта процедура построения нлоскости обратной решётки, пока
занная на фиг. IV, 53, исключительно проста и универсальна.
Из полученного сечения можно
определить как параметры
разворачиваемого сечения обратной
решётки, так и расположение ближайших
узлов сечения до центра вращения.
Последние данные определяют углы
моноклинного и триклинного
кристалла (см. стр. 344).
Можно поставить перед собой
задачу найти непосредственный (без
помощи сферы отражения)
переход от координат на плёнке к
координатам сечения обратной решетки.
Пусть кристалл вращается около
оси с; измерению, следовательно,
подлежат проекции векторов
обратной решётки Hxy. Выберем в
качестве начала отсчёта углов перпендикуляр к направлению первич
иого луча и оси вращения кристалла ОМ и будем характери
Фиг. IV, 52. Промер
рентгенограммы: ООг — экваториальная
линия рентгенограммы;
Н—линейка И=Н(Х); (f — линейка
9 = 9 (Г).
Направление первичного пучка
в момент создания пятна Р
Произвольное
начало отсчета <р
Направление первичного пучка
в момент создания пятна Р
Произвольное
начало отсчета со
Начальном/ узел-
центр вращения
Нулевая плоскость
Центр вращения
П'Я плоскость
Фиг. IV, 53. Построение плоское!и обратной решётки по
координатам (//, ср) пятен на рентгенограмме гониометра.
зовать координаты узлов я-й плоскости обратной решётки их
положением в момент начала вращения. Тогда (см. фиг. IV, 54)

360
МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ
[ГЛ. IV
узел плоскости обратной решётки однозначно характеризуется
значением П^, и углом S, образованным Нху с линией ОМ. На рисунке
изображено положение
сечения сферы отражения
в момент начала вращения.
Интересующий нас узел
обратной решётки даст
отражение после поворота
сферы отражения против
часовой стрелки на угол
X + S. Этот угол определит
координату
интерференционного пятна вдоль
направления поступательного
смещения плбнки, а именно
360
Фиг. IV, 54. К выводу уравнений
интерференционных кривых. Окружность —
сечение сферы отражения одной из
узловых плоскостей обратной решётки. КО —
первичный, KB— отражённый лучи, И—
узел обратной решётки, дающей
отражение после поворота кристалла на угол
5 + Х-
Х-М=~У,(ПГ,28)
где у — координата пятна,
а т] — длина пути, прохо-
(360° \
у] = —— у Зла
чение х находим из треугольника КВО *):
sin a sin г
cosv== . ft--~
л 2 8111 9 Sin p
(IV, 29)
Можем выразить / через координату х пятна и значение nd* вдоль
оси вращения. Получим:
х 180°
cosx
Л f , ,у.О . ■*• J.OU
j/l-M^Vsin-^
\н,
(IV, 29а)
ху
Что касается значения Нху, то оно определится так же, как и
в методе качания по уравнению (IV, 18):
2
Нху = у sin p sin г).
В последнее выражение мы можем ввести расстояние nd*
разворачиваемой плоскости обратной решётки от нулевой и координату я
интерференционного пятна. Имея в виду, что cos а = nd*\, и
используя формулы (IV, 14), (IV, 16) и (IV, 17), получим:
Н*у = l/li - £ cos I ^ У1-(я,<ГХ)2 - пЦ*\ (IV, 30)
*) Об обозначениях а,хир смотри стр. 331)

§ 6] РЕНТГЕНГОНИОМВТРЫ С ЦИЛИНДРИЧЕСКОЙ ПЛЁНКОЙ 361
Для нулевой плоскости т = 2&, а = р = 90°, тогда обе формулы
(IV, 28 и 30) сильно упрощаются и приобретают следующий вид:
Расчёт по этим -формулам весьма прост. Значения Ни
можно определять по заготовленной линейке, аналогичной линейке,
употребляющейся для расчёта рентгенограмм качания. Если
пользоваться двумя линейками, расположенными одна перпендикулярно
другой, то можно почти непосредственно отсчитывать по рентге-
У тт / - •• Ж «90° тт
нограмме значения \ и Н (одна линейка дает —=— и Н, другая
.. 360° \
линейка даёт у).
Пользуясь выведенными формулами, можно составить сетки для
расчёта рентгенограмм. Вся рентгенограмма отображает одну
плоскость обратной решётки. Очевидно, что узлам узловой прямой
обратной решётки соответствует группа интерференционных пятен,
расположенных вдоль некоторой линии. Рассмотрим сначала с этой
точки зрения рентгенограмму нулевой плоскости обратной решётки.'
Плоскость можно разбить: 1) на совокупность узловых прямых,
проходящих через начальный узел решётки, 2) на систему
параллельных узловых прямых.
В первом случае нас интересуют узды, для которых Б имеет
одно и то же значение.
Из (IV, 31) очевидно, что координаты ху соответствующих
интерференционных пятен отвечают прямым линиям с постоянным
для данного снимка углом наклона. Действительно, в этом случае
»/ = lex -\- const. Интерференционные прямые, отвечающие
узловым прямым обратной решётки, образующим между собой угол S,
будут сдвинуты параллельно друг другу на расстояние I, равное
t\ 9goo = — • Измерение расстояний I на плёнке (по оси у)
позволяет таким образом определять угловые константы в случае
моноклинных и триклинных кристаллов. Узловым прямым обратной
решётки, проходящим через начальный узел, отвечают разные
порядки отражения от одной и той же плоскости и кроме того при
немонохроматизированном излучении на прямую, проходящую через
начальный узел, ложится и узел Ш, отвечающий длине волны "klf
и узел hJcl, отвечающий длине волны Х2. Таким образом на одну
интерференционную прямую будут ложиться: 1) разные порядки
отражения от одной и той же плоскости, 2) а- и {3-пятна данного
отражения и 3) «хвост» белого излучения, особенно заметный
вблизи экваториальной линии рентгенограммы.
Из уравнения (IV, 28) следует, что каждая узловая прямая
фигурирует на рентгенограмме дважды; значения \ и 5-f-18QQ

362 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЕТА РЕНТГЕНОГРАММ [г.1. IV
соответствуют одной узловой прямой и двум линиям па плёнке
(при отом одна из линий разорвана на два куска). Это следствие
того обстоятельства, что каждый узел пересекает сферу отражения
дважды. Если учесть еще и то, что между собой тождественны
узлы Ш и ЪЫ, то станет понятной схема фиг. IV, 55. Если
перейти на «язык кристалла», то следует сказать, что каждая
плоскость даёт отражение
вправо и влево от падающего
луча и, кроме того,
отражает с обеих своих сторон.
Из этого рисунка
очевидно, что совершенно
достаточно качать кристалл
на 180°, сократив
одновременно длину плёнки
вдвое. Тогда мы получим
отражения от всех
плоскостей с «одной стороны».
Для расчёта
рентгенограмм можно заготовить
показанную на фиг. IV, 5(>
сетку. Горизонтальные
линии удобно откладывать
через равные промежутки
значений Н (на чертеже даны значения И. в единицах 10у, а £
положено равным нулю для крайнего положения кассеты).
Рассмотрим теперь отображение на рентгенограмме семейства
параллельных прямых обратной решётки (в частности, прямых
h = const или Тс = const). Пусть в начальный момент луч падает
перпендикулярно системе параллельных узловых прямых. Тогда
для узлов каждой прямой постоянно выралсение Haint При этом
#8т5 = 0,1ш, 21х, з/ш...,
где 1Х есть расстояние между ближайшими узловыми прямыми.
Таким образом интересующие нас кривые имеют вид
Фиг. IV, 55. Схема-расположения
тождественных пятен" на рентгенограмме.
. а-90° • /360° я90°\
Sin -„— • Sin I у £- ) = п
(IV, 32)
Давая \х значения через 0,1 — 0,2 в долях от —, получим
универсальную сетку, пригодную для расшифровки рентгенограмм
любых кристаллов (для данного гониометра). Подобная сетка изо*
бражена на фиг. IV, 57. Мы предполагали при выводе, что
узловые прямые ориентированы в начальный момент съёмки
определённым, образом. Это, однако, не имеет значения. Смещением

§ 6] РЕНТГЕНГОНИОМЕТРЫ С ЦИЛИНДРИЧЕСКОЙ ПЛЁНКОЙ 363
сетки вдоль оси у рентгенограммы мы можем задавать ей
расположения, соответствующие любым исходным ориентациям
параллельных прямых относительно первичного пучка. Разумеется, мы
будем искать* такое расположение сетки, при котором её кривые
будут наиболее густо покрыты интерференционными пятнами.
180 170 160 150 140 130 120 ПО 100 ,п90 80 70 60 50 40 30 20 /О О
Фиг. IV, 56. Сетка для непосредственного определения координат
Н и ф узлов обратной решётки по рентгенограмме.
В этом случае, очевидно, мы попадаем на главные системы
узловых прямых. При наложении сетки ориентируются по её прямым
линиям, соответствующим узловым прямым, проходящим через
начало обратной решётки.
Для кристаллов, с симметрией не ниже ромбической, удобно
заготовить сетку с наложенными двумя системами линии,
сдвинутыми на расстояние I, отвечающее повороту на 90°.
Расшифровка нулевой слоевой линии не представляет, как мы
видим, никакого труда. Сложнее обстоит дело с расшифровкой
других слоевых линий. Построение интерференционных кривых
как для узловых прямых, проходящих через центр вращения (ужз

364 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV

§ 6J Рентгенгониометры с цилиндрической плёнкой 365
не говоря о том, что в случае несовпадения центра вращения
с начальным узлом плоскости обратной решетки эти кривые теряют
свой смысл), так и для систем параллельных узловых прямых
не имеет смысла, так как их вид зависит от d* и, следовательно,
Фиг. IV, 58. Сетка, построенная для системы параллельных
узловых прямых, расположенных на расстоянии 0,25-г-.
различен для разных кристаллов. Для того чтобы судить о
характере распределения пятен рентгенограммы, мы приводим сетку,
построенную для системы параллельных узловых, прямых,
расположенных на расстоянии 0,25 — . Разворачивается плоскость обрат-
Вой решётки, у которой сГ = 0,34у, угол образующей
интерференционного конуса с осью вращения равен 80° (фиг. IV, 58).

366
МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [гл. IV
Что же касается индицированил, то его следует производить
наиболее общим методом при помощи подвижного сечения сферы
отражения, т. е. так, как это было рассказано в начале параграфа.
в) Получение рентгенограмм по эквинаклонному методу и
их расшифровка. Съёмка вращающегося кризталла называется
эквинаклонной, если первичный луч падает на кристалл под углом,
отличным от 9СГ, и притом так, чтобы угол первичного луча с
осью вращения был бы равен углу а интерференционного конуса.
При такой съёмке луч является образующей интерференционного
конуса. При разных углах падения луча на кристалл условия
эквинаклонной съёмки могут быть осуществлены для всех
возможных интерференционных конусов, т. е. для всех плоскостей
обратной решётки. На «языке обратной решётки» условие эквинаклонной
съёмки может быть
выражено следующим
образом: надо
наклонить луч к оси
вращения обратной
решётки таким образом,
чтобы центр сферы
отражения разделил
пополам расстояние
между нулевой
плоскостью и %-й.
Зная период J
вдоль оси вращения
кристалла, мы легко
рассчитаем угол, иод
которым должен
падать луч, для того, чтобы w-й конус попал в условие
эквинаклонной съёмки. Из фиг. IV, 59 очевидно, что [1 = «н
■л плоскость
, о-я плоскость
Фиг. TV, 59. Схема эквинаклонной съёмки.
п/.
(IV, 33)
При эквинаклонной съёмке центр вращения сечения сферы
отражения всегда находится на окружности этого сечения, что
приводит к исчезновению мёртвой круговой области вокруг оси
вращения для n-ii слоевой линии. Иначе говоря, эффективная
область имеет вид круга, а не кольца. Это обстоятельство
(очевидное из фиг. IV, 59) является важным преимуществом
эквинаклонной съёмки.
Индицирование эквинаклонной рентгенограммы можно,
разумеется, проводить общим способом, описанным на стр. 358,
изготовив сечение сферы отражения радиуса -г-sin р. Угол поворота
А,
сферы и величина проекции вектора обратной решётки каждого

Sei
РННТГКПГОНИОМЕТРЫ О ЦИЛИНДРИЧЕСКОЙ ПЛЁНКОЙ
367
узла отсчитываются непосредственно по рентгенограмме, как :vro
описывалось выше.
Связь координат узла обратной решётки Яху и $ с
координатами интерференционного пятна найдём при помощи чертежа,
вполне аналогичного тому, который мы строили для метода прямой
съёмки. Из фиг. IV, 60 следует, что для эквипаклонного метода
X = "Т (так как треугольпик KRO равнобедренный). Следовательно,
£
360°
У
ж90°
Як
(IV, 31)
1 h
\ \* /
\ \ ч /
\ \ ч /
\ fc«/,a\ ^j/fr
^4^««^___J^v'^v
* ^~-н
0
\»
м
--'
vHS
Фиг. IV, 60. К выводу
уравнений интерференционных
кривых для эквипаклонного
метода.
Такую же формулу мы получили для
нулевой плоскости при прямой съёмке.
В эквинаклонном методе это
соотношение справедливо для любой слоевой
линии. Из треугольника КОМ
получим:
Нху = -sin ц sin [j^rj . (I\, 34)
Это соотношение будет различным для
разных слоевых линий, так как углы
надения р. первичного луча различны
для каждой плоскости обратной
решётки.
Основное удобство рентгенограмм,
цолученных по эквинаклонному
методу, выяснится при рассмотрении
отображения узловых прямых
обратной решётки этими рентгенограммами.
Узловые прямые, проходящие через начало координат, т. е.
узлы, для которых £ = const, создадут на рентгенограмме прямые
линии с одним и тем же углом наклона, постоянным у данной
камеры. Эти прямые вполне совпадают с аналогичными прямыми,
показанными на приводившейся выше фиг. IV, 56 для нулевой
плоскости, развёрнутой гониометром при съёмке методом прямого пучка.
Рассмотрим теперь систему параллельных узловых прямых.
Как и ранее, примем для простоты, что луч падает в начальном
положении под прямым углом к этой системе. Пусть расстояние
между прямыми 1Х и расстояние до центра вращения t\x (эта
последняя величина появится в том случае, если с осью вращения
совпадает только прямой, но не обратный вектор (см. стр. 344)).
Для каждой узловой прямой
Нху sin & = const. (IV, 35)
На основании (IV, 31) и (IV, 34) приходим к следующему уравнению:
2 . я90° • /360° aflO°\ const ,1ЛТ (>.ч
•г- Sin-Tj— * Sin W 7Г-)~—- • (IV, 86)
А ЯГ. \ Yj '' ЯГ, / Sltl fA \ > У

368 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [гл. Itf
Для прямых одного и того же параллельного семейства
интерференционные кривые отличаются только значением копстанты,
т. е. они вполне подобны друг другу.
Мы видим, что характер кривой, отображающей одну узловую
прямую обратной решётки, не зависит от номера разворачиваемой
слоевой линии. В этом весь смысл эквинаклонного метода. Можно
изготовить одну универсальную сетку, вполне совпадающую с
сеткой для нулевой слоевой линии при прямом методе съёмки, пока-
Фиг. IV, 61. Сетка для индицирования эквинаклопных рентгенограмм.
занную на приводившейся выше фиг. IV, 57. Эта сетка будет пригодна
для расшифровки любой рентгенограммы, снятой эквинаклонным
методом на данном приборе. Наложение сетки на рентгенограмму
проводится с ориентировкой на наиболее ярко выраженные
интерференционные прямые линии. Сетка накладывается, и на
рентгенограмме вычерчивается одна серия интерференционных кривых,
соответствующих одной системе узловых прямых. Далее ищется
таким же способом другая серия наиболее ярко выраженных
интерференционных кривых. Каждое пятно становится, таким
образом, точкой пересечения двух кривых разных семейств. Работа
этим методом иллюстрируется фигурой IV, 61, где показана сетка
изготовленных кривых, сетка, наложенная на рентгенограмму
(фиг. IV, 61а), а также обработанная рентгенограмма, на которой
прочерчены два семейства кривых (фиг. IV, 616).

§ 6] РЕНТГЕНГ0НИ0МЕТРЫ С ЦИЛИНДРИЧЕСКОЙ ПЛЁНКОЙ 369
„ const n 2
Значения —— меняются от О до т.
Sin [A A
Обычно наносят на сетку цифры в долях-г-или — при принятом
масштабе изображения обратной решётки — непосредственно мм
Фиг. IV, 61а. Рентгенограмма с наложенной сеткой.
(считая, скажем, v = 125 мм или 100 мм). Определяя по сетке -—
л SID fx
и зная siny., определяем константу, которая для первой линии
будет равна A^-j-Ja?» Для второй &x-\-2lx и т. д. Далее остается
начертить обе серии узловых прямых разворачиваемой плоскости.
Угол между семействами узловых прямых решётки вычисляется
непосредственно из расстояния между основными интерференцион-
TfTt1*W 1¥Т\ЛГ*Г1Т1ГТГ ТТЛ ТТ -If К ТГТ!» Гк
ными прямыми на плёнке.

370 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЕТА РЕНТГЕНОГРАММ [г.[. IV
Следует иметь в виду, что при несовпадении центра вращения
с узлом обратной решётки интерференционные прямые отсутствуют.
В этом случае на рентгенограмме прочерчиваются основные прямые
сетки, не проходящие через интерференционные пятна. При
наложении сетки, ориентируются в этом случае по ярко выраженным
интерференционным кривым.
Фиг. IV, 616. Рентгенограмма с прочерчопными
кривыми постоянных h и /.-.
Остановимся теперь на практическом осуществлении метода.
Для того чтобы было возможно устанавливать ось вращения
кристалла под любым углом к падающему лучу, связывают диафраг-
менную систему жёстко с основанием камеры. Остальные части
гониометра, т. е. головка с приспособлением для её вращения и
движущаяся кассета, монтируются па отдельном основании,
которое может поворачиваться около вертикальной оси, проходящей

§ 7] ГЕНТГЕНГОНДОМЕТРЫ С ПЛОСКОЙ ПЛЁНКОЙ 371
через кристалл (см. фиг. IV, 62). Следует предусмотреть сдвиг
всей системы вдоль стержня 11 для того, чтобы можно было
рассмотрением через диафрагму проверять центрировку кристалла,
Фиг. ТУ, 62. Схема устройства камеры для
эквинаклонной съёмки.
устанавливать кристалл в заданное начальное положение и пр.
Оказывается вполне достаточным менять угол падения луча всего
лишь от 90 до 60°.
§ 7. Рентгенгониометры с плоской плёнкой
а) Метод фотографирования обратной решётки. Все
рассмотренные выше гониометрические методы рентгеносъёмки
позволяют «разворачивать» на плоскости интерференционные пятна,
принадлежащие одному конусу. Каждый интерференционный конус,
возникающий при действии рентгеновских лучей на кристалл,
вращающийся около кристаллографической оси, соответствует
плоскости обратной решётки. Рентгенограммы, полученные при
помощи гониометров всех типов, можно рассматривать как
искажённые проекции этих плоскостей обратной решётки. Представляет
значительный интерес получение неискажённых проекций обратной
решётки. Подобного типа рентгенограммы будут обладать
значительным достоинством, освобождая нас от процесса индицирования.
Задача получения рентгенограммы, интерференционные пятна
которой были бы расположены так же, как узлы плоскости
обратной решётки, решается следующим образом. Расположим плоскость
проекции, т. е. рентгеноплёнку, параллельно плоскости обратной
решётки, создавшей интерференционный конус, иначе говоря,
перпендикулярно оси вращения кристалла (фиг. IV, 63). Если луч
падает под прямым углом к оси вращения, то рассматриваемый
конус принадлежит п-ж плоскости обратной решётки; если луч
падает под другим углом, то наши рассуждения будут относиться
к любой плоскости обратной решётки, в том числе и к нулевой.
Допустим, что в некотором положении кристалла сечение сферы
отражения проходит через несколько узлов рассматриваемой

372 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [гл* IV
плоскости обратной решётки. Вполне очевидно, что взаимное
расположение соответствующих интерференционных пятен, возникающих
па плёнке, перпендикулярной оси вращения, в точности повторит
расположение создавших их • узлов обратной решётки. Допустим
теперь, что кристалл повернулся на некоторый угол. Тогда на
Фиг. IV, 63. Метод фотографирования обратной решётки.
окружность сечения сферы отражения пришли новые узлы. Если
мы хотим, чтобы новые узлы создали интерференционные пятна,
расположенные по отношению к ранее созданным пятнам так же,
как новые узлы расположены до отношению к прежним, то мы
должны повернуть плавкость проекции в том же направлении и на
тот же угол, что и обратную решётку. При этом поворот плоскости
проекции должен быть сделан около той точки, которая
представляет собой проекцию точки плоскости обратной решётки,
находящейся на оси вращения. Меняя угол, образованный лучом с осью
вращения, можно получать интерференционный конус со
стандартным углом раствора от любой плоскости обратной решётки. Помещая
плёнку на определённом расстоянии от кристалла и отширмовывая
конус с выбранным углом раствора, мы будем получать фотогафип
обратной решётки, вращая плёнку в том же направлении и с той же
скоростью, что и кристалл около центра вращения, имеющего так же,
как и угол падения луча на кристалл, индивидуальное значение
для каждой съёмки.
Пусть Соображения конструктивного и экспериментального
характера заставили нас остановиться на работе с конусом,
имеющим угол раствора 180—2v(v — угол образующей конуса с
плоскостью обратной решётки). Фотоплёнка расположена на
расстоянии D от центра кристалла. Требуется сфотографировать w-ю
плоскость обратной решётки кристалла с периодом идентичности вдоль

§ 7]
РЕНТГЕНГОПИОМЕТРЫ С ПЛОСКОЙ ПЛЁНКОЙ
373
направления оси вращения, равным J. Выбор параметров съёмки
определяется, по сути дела, одной величиной — расстоянием nd* as ~~
исследуемой плоскости обратной решётки до нулевой.
Ось вращения прямой
решетки (кристалла)
Пяенно S"
Ось вращения
пленни
Отраженный
луч
/1-я
плоскость
Нулевая
плоскость
Экватор
Первичный пучок
рентгеновских лучей
Ось вращения
обратной решетки
Фиг. IV, 64. Геометрия метода.
Из фиг. IV, 64 следует, что угол первичного луча с осью
вращения ц определяется формулой
nd* —{— у- sin ja = у- sin v. (IV, 37)
(Действительно О0О' + О0О = ОО'.)
Из этой л;е фигуры видим, что центр вращения фотоплёнки
должен быть сдвинут от оси вращения кристалла на величину
Д = J)ctg4» = D ^ (из ASH'А).
от Sin N v J
(IV, 38)
Мы получаем на рентгенограмме неискажённую проекцию
плоскости обратной решётки, увеличенную, как легко видеть из того же
рисунка, в -~7тр раз. Таким образом измеренные координаты
интерференционных пятен S"H" следует перечислять в координаты узлов
обратной регабтки S'Hf по формуле
S'H:
X D
Ъ"Н".
(IV, 39)
На фиг. IV, 65 изображена камера для фотографирования
обратной решётки производства НИИФ МГУ (КФОР) *). Камера
") М, М, У минский, -'5ав. либ. (в печати).

Фиг. IV, 65. Камера для фотографирования обратной решётки (НИИФ МГУ): Д—диафрагма;
Э — экран для отширмовывания диффракционного конуса; Щ—щель экрана; М—мотор,
вращающий кристалл и кассету; О.Тер. — ось вращения кристалла; В^— винт для установки требуемого р;
В*—винт для установки требуемой Д; О. кас. — ось вращения круглой кассеты с плёнкой; ИГ —
шкала отсчёта Д; Г—гониометрическая головка.

§ 7] РЕНТГЕНГ0НИ0МЕТРЫ С ПЛОСКОЙ ПЛЁНКОЙ 375
приспособлена для отщирмовки конусов с углами v, равными 45 и
37 градусам. Установка камеры для данной съёмки осуществляется
двумя винтами: 1) поворачивающим корпус камеры вместе с кри-
сталлодержателем относительно оси диафрагмы,—таким способом
устанавливается нужный угол jx и 2) сдвигающим в своей
плоскости кассету вместе с её осью вращения — установка нужного
значепия А. Камера достаточно компактна и превосходит лишь
незначительно по размерам камеру качапия НИИФ.
На фиг. IV,.66 приведены типичные снимки. На каждом снимке
можно отметить выход оси вращения, ибо на плёнке имеются
обычно кольца фона, центр которых совпадает с выходом оси
вращения. Таким образом, измеряя смещение первых узлов ю-й
плоскости обратной решётки от этой отметки, можно найти углы
между осями ячейки в случае моноклинного и триклинного
кристалла.
Все пятна рентгенограммы двойные и имеют вид уголков или
крестиков. Это объясняется тем, что каждый узел пересекает круг
отражения дважды (сравни фиг. IV, 63). Причём в этих двух
отражающих положениях кристалл находится в разных ориентациях
по отношению к плёнке. Пятна наиболее точной рентгенограммы
должны были бы в идеале быть крестообразными.
Основной недостаток метода фотографирования обратной
решётки по сравнению с методом цилиндрического гониометра — это
отсутствие на рентгенограмме пятен с углами &, близкими к 90°.
Следует, однако, заметить, что различие не столь уж велико и
имеет место только для нулевой слоевой линии. Чем выше номер
линии (плоскости обратной решётки), тем метод фотографирования
обратной решётки становится выгоднее.
На фиг. IV, 67 схематически изображены изменения в
эффективной для отражения области, происходящие при переходе от
съёмки нулевой к съёмке %-й слоевой линии. При съёмке нулевой
линии эффективная область представляет собой круг радиуса
1,414 -г (будем вести рассуждения для угла v, равного 45°). При
съёмке нулевой слоевой линии угол jx равен углу v. По мере
уменьшения угла р мы получаем возможность снимать первую,
кторую п т. д. слоевые линии (до nd* = 0,707 у). Эффективная
для отражения область превращается в кольцо. А именно, как это
видно из чертежа, образуется «мёртвый» участок радиуса
у (cosja — cosv). (IV, 40)
На этот же кусочек увеличивается внешний радиус
эффективной области («толщина» кольца сохраняется). При
перпендикулярном падении лучей радиус «мёртвой» области становится

a) 6)
Фиг. IV, 66. Типичные рентгенограммы КФОР. а) Рентгенограмма NaCl; о — слоевая линия, ось враще
ния [100], излучение» Си К. б) Рентгенограмма кристалла органического вещества. Симметрия C2v.

§ n
РБНТГЕНГОНИОМЕТРЫ С ПЛОСКОЙ ПЛЁНКОЙ
а 77
а) О-я слоевая
максимальным и равным у (1—cosv) (IV, 67). Из этих
рассуждений и фигуры очевидно, что мы находимся лишь в
незначительно менее выгодных условиях по сравнению с
методом цилиндрического
гониометра.
Метод
фотографирования обратной решётки столь
же пригоден для
определения интенсивности диф-
фракпионных лучей, что и
метод цилиндрического
гониометра. Способы
определения интенсивности по
почернению пятен,
изложенные на стр. 193,
применимы и здесь. Однако при
расчёте структурного
фактора из интенсивностей
должен быть учтён
специфический для этого метода
фактор.
Как было показано на
стр. 252, интегральная
интенсивность луча,
возникающего при вращении
кристалла, связана со
структурной амплитудой
формулой
где Q должно быть взято
из (III, 61, а); со — угловая
скорость вращения
кристалла и Л — фактор
поглощения. В таком виде формула
справедлива в том случае, если ось вращения кристалла
перпендикулярна плоскости отражения (иод плоскостью отражения
понимается, как обычно, плоскость, проходящая через падающий и
отражённый лучи). В противном случае для Q справедлива общая
формула (III, 59). Для интересующего нас случая удобно всё же
всходить из написанной частной формулы. При вращении плоскости
кристалла в камере для фотографирования обратной решётки ось
вращения образует угол в с нормалью к плоскости отражения.
ЗРазложим вектор угловой скорости на две составляющие вдоль
# нормально к плоскости отражения. Первая составляющая,
б) п-я слоевая
Фиг. IV, 67. Изменение э<)
области.
эективнои

378 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
равная о) sin e, даёт вращение отражающей плоскости в собственной
плоскости и, следовательно, не сказывается на интегральном
отражении; вторая составляющая определяет интегральное отражение.
Таким образом в написанную выше формулу вместо <о надо
подставить со cos е. Определение структурного фактора из интенсивностей
пятен на плёнке должно происходить по формуле
F2^E-r-^ , (IV, 41)
LA cos £ v '
1 4- cos2 2ft
где L = . 2^—, A — фактор поглощения.
Эта формула вытекает, разумеется, также из общей формулы
(111, 59), так как можно доказать, что
• . , л sin 2ft
cos у sin & cos о = .
л ' ' COSE
Значение coss легко оценить по рентгенограмме. На фиг. IV, 68
OS— ось вращения плёнки, JM — ось вращения кристалла. Кристалл
находится в J. Проведём из J сферу радиуса JO. Точка О есть
Фиг. IV, 68. К пыводу формулы интенсивности
для КФОР.
точка пересечения первичного луча с осью вращения плёнки.
Проведём экваториальную плоскость и плоскость фотоплёнки. Пусть
точка F—возникающее интерференционное пятно, а М—точка,
В которую в это время проектируется ось вращения кристалла.

7] РЕШТЕНГОНИОМЕТРЫ С ПЛОСКОЙ Ш1ЁНКОЙ 379
расстояние центра окружности от оси вращения А — SM = D ^-^ .
Радиус R окружности с центром в М определяется лишь
значениями Т) и v, а именно равен .R = i)ctgv. В случае развёртки
нулевой слоевой линии SM = lt.
Переходим к способу решения поставленной задачи —
определению cos s для данного пятна Р. Из фиг. IV, 68 следует
(отношение площадей равно косинусу угла между нормалями)
1
нлощ. ДЛ/&Р
р • MS
COS г
где р высота /\MSP.
площ. AJOP
Но JO = -¥—
COS \х
~ (JO)2 sin 2ft
Следовательно,
coss =
р
sin 20
cos н- sin v
D
(IV, 42)
т> cos ix sin
Величина (~—
житель
v
sin 2ft
постоянна для данной рептгенограммы, мно-
меняется от пятна к пятну.
Для определения р следует поступить так: на прозрачной
бумаге чертится круг радиуса R на расстоянии А от центра плёнки;
вычерчивается диаметр,
проходящий через S. Круг
накладывается на пленку и
производятся отсчеты р для тех
пятен, которые попадают на
окружность; значение j? равно
длине перпендикуляра,
опущенного из нятпа на диаметр
круга (фиг. IV, 69). Из этого
чертежа следует, что пятна
у самых краёв рентгенограммы
(малые р) находятся в особо
благоприятных условиях. Это
важное достоинство метода:
слабые далёкие пятна
выявляются на рентгенограмме
при нормальной экспозиции.
Для нулевой слоевой
линии может быть дан
универсальный график фактора р.
В этом случае _p = rcosct,
sin а = -J-; r—радиальное
расстояние интерференционного
Фиг. IV, 69. Графическое
определение фактора интенсивности КФОР;
М — проекция оси вращения
кристалла; S— проекция оси вращения
плёнки; Pj, Р2 и Pg— пятна
рентгенограммы.
пятна, пропорциональное, sin D;

380
МЕТОДЫ ПОЛУЧЕНИЯ П РАСЧЁТА РЕНТГЕНОГРАММ
[гл. iv
г==^— sin 0 (из IV, 39). На фиг. IV, 70 изображены фактор
интенсивности для КФОР (1 + cos2 2d) • - ; фактор —g.^Q уже
входит в это выражение.
6) Круговой гониометр. Этот прибор является простейшим
по- конструкции, по все же применяется относительно редко, так
как обладает некоторыми
I*
30,0
28,0
26,0
24,0
22.0
20,0
18,0
16.0
14,0
12,0
10,0
8,0
6,0
4,0
2,0
0° 5" 10° 15° 20° 25° 30° 35° 40° 45° 50° 55° #
Фиг. IV, 70. Фактор интенсивности для КФОР
(нулевая слоевая).
иедостатками.
Фотография кругового
гониометра дана на
фиг. IV, 71. Схема
действия изображена на
фиг. IV, 72. Плёнка
вращается около оси,
параллельной первичному лучу
и перпендикулярной к
оси вращения кристалла.
Таким образом
первичный луч падает на плёнку
под прямым углом.
Слоевая линия вырезается
экраном таким же
способом, как и на
цилиндрическом гониометре с
той разницей, что в
круговом гониометре
ширмой выпускается только
половина слоевой линии
(это делается для того,
чтобы две половины
одной и той же линии
не наложились на этой
рентгенограмме друг на друга, что излишне усложнило бы
рентгенограмму). В гониометре ЛИТМО*) предусмотрена возможность
съёмки рентгенограммы вращения или качания. Это позволяет
наряду с «развёртыванием» плоскости обратной решётки
определять период идентичности в направлении оси вращения.
Разумеется, снимается «половина» рентгенограммы вращения
(если, скажем, лучи развертываемой линии идут вправо, то можно
получить левую часть рентгенограммы вращения).
При съёмке нулевой линии ось вращения плёнки проходит
через кристалл. При съёмке w-й линии ось вращения плёнки
следует сдвинуть так, чтобы центр слоевой линии (разумеется, такое
•) Д. Б. Гогоберидзе и Б. М. Я в о р с к и и, ЖТФ, 18, 707 (1948).

§ 7) ЯЕНТГЕНГОНИОМЕТРЫ С ПЛОСКОЙ ЦЛЁНКОЙ Ш1
Фиг. IV, 71. Круговой рентгенгониометр:
К—круглая кассета с плёнкой, Д—диафрагма;
Г— гониометрическая головка с кристаллом;
М—мотор, вращающий плёнку и кристалл.
Тип Л 2, г (стр. 35(5).
Фиг. IV, 72. Схема устройства кругового
гониометра. Тип А 2, в (стр. 356).

38'2
МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ
[гл. tv
интерференционное пятно не существует) получался бы в центре
вращения (мы описываем тип А2,в).
Плёнка вращается синхронно с кристаллом: поэтому угловая
координата интерференционного пятна сразу же указывает, при
каком положении кристалла к первичному лучу возникло то или
иное отражение. Если расстояние от кристалла до плёнки D, а
полярные координаты пятна на плёнке обозначить через г и <р> то
из нулевой слоевой линии получим координаты узла обратной
решётки по формулам
ff=.^* и ««?-», rAetg2ft = -£. (IV, 43)
Последнее равенство следует из такого соображения: если
узловая прямая обратной решётки образует с первичным лучом угол
90° — £, то узел этой
прямой пересечёт сферу,
будучи повёрнут на угол
S-j-ft (фиг. IV,73). При
этом, так как плёнка
вращается с той же
скоростью, что и
кристалл, соответствующий
луч появится тогда, когда
плёнка повернётся на
тот же угол.
Из написанных
равенств получим сразу
уравнения
интерференционных кривых,
отображающих узловые
прямые разворачиваемой
Первичный
луч
Фиг. IV, 73. 1С пыводу формулы (IV, 43).
плоскости. Для узловых прямых, проходящих через центр решётки,
имеем условие
в —ft =! const, т. о. ф —-^ arctg-jy = const. (IV, 44)
Для параллельного семейства узловых прямых получим:
/TsinE== const; т. е.
SH1&
sin (<р — ft) = const, (1V,45)
где вместо ft надо подставить -^-arctg-^. Полученные таким
образом кривые /"(?, г)— const изображены на фигуре IV, 74 через
значения константы 0,25 в долях -г-. Как видно из этой сетки,

§ 8)
РЕНТГЕНСПЕКТРОГРА Ф
383
сечение обратной решётки искажается в незначительной степени.
Типичная рентгенограмма показана на фиг. IV, 75.
Это обстоятельство позволяет индицировать рентгенограмму
«на-глаз», не прибегая ни к расчёту, пи к графикам, ник сеткам. Это
крупное достоинство метода. Недостаток метода, как и любого
способа съёмки на плоскую
плёнку, — это невозможность
охвата всех узлов обратной
решётки, дающих (в принципе)
отражения.
Гони ометр прои зводства
ЛИТМО целесообразно также
применять в том случае, когда
исследователь решил при
помощи метода качания оценвть
интенсивности всех отражений
кристалла и гониометрограмма
используется как
вспомогательное средство для индици-
рования. В подобном случае
можно снимать качания в
большом градусном интервале, не
боясь запутаться в
приписывании пятнам индексов, ибо го-
ниометрограмма, отвечающая
тому же интервалу качания,
облегчает индицирование
рентгенограммы качания.
Преимущество кругового гониометра перед камерой для
фотографирования обратной решётки — это простота конструкции.
Недостаток— искажённость сечения обратной решётки и почтив 1,5 раза
меньший охват отражений.
§ 8. Рентгепснектрограф
Если элементарная ячейка кристалла известна, то остальные
стадии исследования весьма удобно производить при помощи рентген-
спектрографа, позволяющего определять направление и измерять
ионизационным способом интенсивность каждого
интерференционного лучач в отдельности. Можно и весь структурный анализ
произвести на рентгенспектрографе с самого начала; в этом случае
придётся искать размеры элементарной ячейки, так сказать, наощупь.
Рентгенспектрограф напоминает рентгенгониометры тем, что
позволяет определять обе координаты узла обратной решётки.
Отличие состоит в том, что интерференционные лучи регистрируются
ионизационным, а не фотографическим способом. Для регистрации
Фиг. IV, 74. Изображение
параллельных линий обратной решётки для
рентгенограммы кругового гониометра.
Развёртка нулевой слоевой линии.
Цифры на кривых дают расстояния
dx между узловыми прямыми обратной
решётки в единицах 1/Х.

384 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [ГЛ. IV
Фиг. IV, 75. Типичная рентгенограмма, полученная на круговом
гониометре с наложенной сеткой, описанной выше.

§ 8] РКПТГЕНСИЬЖТРОГРАФ 385
интерференционных лучей применяется пропорциональный усилитель,
описанный в главе И. Рентгенспектрограф изображён на фиг. IV, 76,
его схематическое устройство — на фиг. IV, 77. На массивной
металлической плите расположен столик с двумя лимбами и
диафрагма. Ионизационная камера и усилитель укреплены на
кронштейне, который может поворачиваться вокруг оси столика. Угол
поворота камеры отсчитывается по нижнему лимбу. Ось камеры
проходит через ось вращения кристалла; по высоте она расположена
на уровне диафрагмы, так что регистрируются интерференционные
Фиг. IV, 7G. Рентгенспектрограф.
лучи, отвечающие только нулевой слоевой линии. Кристалл
юстируется на обычной гониометрической головке, которая вставляется
в держатель в центре столика. Угол поворота кристалла
отсчитывается по верхнему лимбу. Кристалл и камера могут поворачиваться
от руки или электромотором, раздельно или одновременно. При
одновременном повороте скорость вращения камеры вдвое больше
скорости вращения кристалла.
Если известна ориентация осей кристалла по отношению к
первичному пучку, то обычным способом с помощью сечения обратной
решётки и сферы отражения можно найти угол, на который
необходимо повернуть кристалл, чтобы возник данный
интерференционный луч Ш. В случае хорошо образованного кристалла ориентация

386
МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЕТА РКШТКНОГРАММ [ГЛ. IV
его осей относительно первичного пучка определяется обычным
способом (зайчик, отражённый от какой-либо грани кристалла при
пропускании луча света через диафрагму, вводят в диафрагму; при
этом нормаль к этой грани совмещается с первичным пучком).
Поворачивая камеру на угол 2Ь из исходного (совпадающего с
направлением первичного пучка) положения, регистрируют ионизационный
ток, созданный интерференционным лучом. Таким же образом,
поочерёдно приводят
кристалл во все
отражающие положения и,
повернув соответствующим
образом камеру,
измеряют интенсивности всех
интерференционных
лучей. Отсутствие тех или
иных лучей при
правильной ориентации
кристалла и камеры указывает
на систематические
погашения. Если исходная
ориентация осей
кристалла или даже размеры
его элементарной ячейки
неизвестны, то,
устанавливая камеру в
положения, отвечающие углам
й =2,5°; 5°; 7,5°; 10° и
т. д.*), и поворачивал
кристалл на 360°,
находят ряд
интерференционных лучей. Зная отвечающие им ориентации кристалла и камеры,
строят примерное сечение обратной решётки. После этого
исследование производится так же, как и в случае кристалла с известной
ориентацией осей и элементарной ячейкой.
Установив кристалл и камеру в положение, отвечающее какому-
либо отражению, и пустив затем мотор, вращающий кристалл со
скоростью со и камеру со скоростью 2ю в одном и том же
направлении, мы регистрируем максимумы ионизационного тока,
отвечающие отражениям от той же плоскости, но с большими (если
камера и кристалл вращаются в сторону больших 0) или с меньшими
(вращение в сторону меньших Ь) индексами. Иначе говоря, мы
проходим всю узловую прямую. Такое соотношение скоростей вращения
Фиг. IV, 77. Схематическое устройство рент-
генспектрографа: Д— диафрагма; М—мотор;
Ж\ — лимб (отсчёт поворота камеры);
Жъ — лимб (отсчёт поворота кристалла); щ и
Н2—нониусы; Ер.— кронштейн;
ЯК—ионизационная камера; У— ламповый усилитель;
Г—гониометрическая головка; Е—
кристалл.
*) Входное окошко камеры, имеющее форму вертикальной щели,
достаточно широко для регистрации (при данном положении камеры) лучей,
авляющих с осью камеры угол, не превышающий 2,5°.

8]
Рептгенсиектрограф
387
кристалла и камеры непосредственно следует из того, что угол
между интерференционным и первичным пучками вдвое больше
утла скольжения. Применение самопишущего гальванометра и
указанного способа прохождения по узловым прямым позволяет
автоматизировать работу рентгенспектрографа.
Рентгенспектрограф позволяет весьма точно измерять углы
скольжения, а следовательно, межплоскостные расстояния и параметры
решётки. Для этого данное отражение с большими 0 (ошибка
в определении 0 пропорциональна ctg Ь) измеряют при положении
камеры слева и справа от первичного луча. Разность
соответствующих отсчбтов лимба, фиксирующего положение кристалла, равна 2&.
Точность в определении Ь составляет обычно 5—10'.
Как уже говорилось выше, величины Ъч, установление которых
есть цель измерения, пропорциональны интегральной интенсивности
диффракционного луча. Строго говоря, на плбпке надо измерять
интегральное почернение пятна, а в ионизационном методе —
площадь максимумов кривой интенсивности в функции угла *).
Отражение не наступает, разумеется, при каком-либо математически
определбнном значении угла, а возрастает от фона к максимуму
и затем опять падает в угловом интервале порядка 10—40'. Именно
площадь этого максимума, а не высота его пропорциональна
интенсивности отражбнного луча. Наиболее правильные (сравни стр. 247)
результаты получаются при одновременном (механическом) повороте
через отражающее положение кристалла со скоростью <о, а
камеры— 2ю. Однако при широком входном окне в камеру вполне
достаточно поворачивать один кристалл. Если падающий на
кристалл луч сильно расходится, то высота максимума
интерференционной кривой и его площадь должны быть пропорциональны.
Необходимо проверять
для конкретного случая
наличие такой
пропорциональности, и при
положительном результате
вести веб исследование,
измеряя высоты
максимумов кривой, а не
площади (при отсутствии
автоматизации измерение
ВЫСОТЫ максимумов ЗНа- Фиг. IV, 78. Максимумы /(»).
чительно проще).
Типичные максимумы 1(Ь) показаны на фиг. IV, 78. Измерения
производились при обычных размерах диафрагмы (диаметр отверстий
1 мм, длина 40 мм), ширина щели камеры 4 мм, расстояние щели
от кристалла 100 мм.
Для измерения такого максимума поступают следующим образом.
Установив кристалл и камеру в такое положение, чтобы иониза-

388 МЕТОДЫ ПОЛУЧЕНИЯ И РАСЧЁТА РЕНТГЕНОГРАММ [гл. IV
ционный ток, создаваемый данным интерференционным лучом, был
максимален, закрепляют камеру. Кристалл поворачивают из этого
положения последовательно на углы ср = 10', 20', 30', 40' в ту и
другую сторону, записывая каждый раз показание гальванометра.
Достаточно повернуть кристалл на такой угол, чтобы два-три
последовательные показания гальванометра совпадали. Это указывает,
что кристалл уже вышел из отражающего положения и
ионизационный ток создаётся фоном. Таким образом мы измеряем интенсивность
только интерференционных максимумов. Отойдя от максимума на
50'—1°, можно измерить и интенсивность фона при данном угле 0.
По найденным парам значений гион и © строят кривую зависимости
ионизационного тока от угла поворота кристалла относительно
отражающего положения, которая при пропорциональности работы
ионизационного прибора и усилителя совпадает с кривой интенсивность —
угол поворота. Площадь максимума измеряется планиметром или
находится путём взвешивания максимума, вырезанного из бумаги,
на точных весах.
Пропорциональный усилитель позволяет измерять интенсивности
в интервале 1 :10 000 с точностью до 2—5%. Рентгенспектрограф
может быть снабжён также счётчиком Гейгера или ионизационной
камерой.

ГЛАВА V
СТРУКТУРНЫЙ АНАЛИЗ ВЕЗ ОЦЕНКИ ИНТЕНСИВНОСТЕЙ
А. ТЕОРИЯ ПЛОТНОЙ УПАКОВКИ
§ 1. Введение
Полные рентгеноструктурные исследования проводятся методом
анализа интенсивностей диффрагированных кристаллами
рентгеновских лучей. Интенсивности определяют структурные факторы, а они,
в свою очередь,—координаты атомов в ячейке. Б простейших случаях
достаточно констатировать отсутствие или наличие того или иного
диффрагпрованного луча (отражения), в обычных случаях надо
оценивать интенсивности диффрагированных кристаллами лучей.
В результате более чем 30-летних исследований кристаллов
методом рентгеноструктурного анализа были определены тысячи структур,
чем и был заложен фундамент кристаллохимии — учения о строении
кристалла из атомов, ионов и молекул. Эти исследования показали,
что в первой степени приближения атому или иону могут быть
приписаны определенные размеры и форма. Атомам и ионам,
входящим в состав комплекса или молекулы, соподчинено пространство
в виде шарового среза, в прочих случаях атом или ион могут быть
аппроксимированы шарами (фиг. V, 1). Рядом исследований было
показано наличие определённых атомных групп в том или ином
■классе соединений, например, тетраэдрических групп Si04 в
силикатах. Стали известными также средние значения валентных углов,
относительно мало изменяющиеся при переходе от одной молекулы
к другой.
Нельзя сказать, что уровень современной кристаллохимии
достаточен для объяснения строения кристаллов. Однако некоторые общие
идеи были установлены для кристаллов ряда классов химических
соединений. К ним молено отнести, например, нравила Паулинга
и схемы Белова*) для ионных кристаллов, а также правила
автора **) для кристаллов органических соединений.
*) II. В. Белов, Структура ионных кристаллов и металлических фаз,
Академиздат. 1948.
**) А. К. Китайгородский, ИОХН, стр. 278, 1948,

390 СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦЕНКИ ИНТЕЯСИВНОСТЕЙ [ГЛ. V
В настоящее время, приступая к структурному исследованию
неизвестного соединения, мы имеем возможность пользоваться всеми
данпыми кристаллохимии и зачастую способны решить структуру
в общих чертах только на основании аналогии с уже известными
структурами или пользуясь общими правилами кристаллохимии.
Метод иптенсивностей может в этих случаях не применяться или
применяться только как способ независимой проверки полученных
а) б)
Фиг. V, 1. а) Атомы, входящие в состав комплекса или
молекулы, аппроксимируются шаровыми срезами. Показано
расположение линейных молекул HgC^ в кристалле, б) В
случае координационных кристаллов атомы и ионы
аппроксимируются шарами. Показано расположение атомов в бинарном
кристалле типа NaCl.
результатов. Как бы то ни было, но и при решении сложных
структур мы большей частью не можем обойтись без данных
кристаллохимии (за исключением случаев полной объективности метода интен-
сивностей—см. стр. 546). Сводку этих данных мы и хотим привести.
§ 2. Топологическая характеристика кристаллов
а) Классификация. Рассмотрим кристаллическую решетку, для
которой известно расположение центров атомов. Возможны
следующие случаи:
1) В элементарной ячейке решётки можно выделить группу Мточек,
такую, что любая точка этой группы имеет внутри группы более
близких соседей, чем вне группы. Назовём такую группу динадой.
Если динада М точек охватывает все симметрически не связанные
точен, то динада М представляет собой молекулу, и притом молекул у.
лишённую симметрии.

§ 2] ТОПОЛОГИЧЕСКАЯ ХАРАКТЕРИСТИКА КРИСТАЛЛОВ 391
Если динада М охватывает точки, принадлежащие острову
симметрии S, то динада М представляет собой молекулу этой симметрии.
Если динада М не охватывает всех симметрически не
связанных точек и остальные точки решётки образуют одну (или несколько)
динад N, то кристалл построен из молекул двух (или нескольких)
сортов М и /V (случаи молекулярного соединения). Если две динады
одинаковы, то имеет место случай ассоциации молекул.
Геометрически эквивалентно этому случаю сложное комплексное соединение,
состоящее из многоатомных
анионов и катионов. ж^^И^^^ШШ^^^^Мш^^^^^
Фиг. V, 2. Цепочечная
структура. Бесконеч- 0 12 3 4 5 /•<?
ные спиральные цепи i i 1 1 . i ■ , i
— Se — Se — тянутся
вдоль оси с гексаго- Фиг. V, 3. Графит. Пример кристалла, по-
нальной ячейки. строенного из сетчатых динад.
плексное соединение, в котором «отдельные точки» представляют
собой одноатомные ионы и вообще ионное соединение, в котором
один из ионов является одпоатомным, а другой многоатомным
(например, соль органической кислоты с простым катионом).
2) 13 решётке можно выделить бесконечную линейную
последовательность точек — цепь или цепочечную динаду. Точки этой динады
связаны трансляцией или открытой симметрической операцией.
Каждая точка цепочечной динады имеет внутри неё более близких
соседей, чем вне её. Примером таких кристаллов может служить
решётка селена, показанная на фиг. V, 2.
3) В решётке можно выделить бесконечную сетку, точки
которой связаны открытыми симметрическими операциями. Если
каждая точка не имеет вне сетки соседей, более близких, чем внутри
сетки, то мы имеем дело с сетчатой динадой. Пример кристалла,
построенного из сетчатых динад, показан на фиг. V, 3 — это

392 СТРУКТУРНЫЙ АНАЛИЗ ВЕЗ ОЦЕНКИ ИНТШОИВНОСТЕИ [ГЛ. V
графит. Возможны и многоатомные слоистые решётки, например
йодистый кадмий.
4) Выделить в решётке динаду нельзя. Этот случай будет иметь
место в ионных (не комплексных) кристаллах, в гомеополярных
кристаллах типа ZnS и алмаза, в кристаллах с металлической
связью. Здесь пет возможности выделить какую бы то ни было группу
атомов, так как каждая точка имеет по крайней мере четырёх
(некомпланарных) соседей на одинаковых расстояниях.
Кристаллы такого типа построены не из каких-либо более илп
менее обособленных «кирпичей» (молекул, многоатомных ионов),
а представляют в сущности одно единое целое. Нельзя, например,
выделить в решётке хлористого натрия молекулы NnCl, ибо
каждый ион Na+ в равной степени принадлежит 6 ионам С1~, точно
так же как и каждый ион С1~ принадлежит G иопам Na+. Это не
означает, конечно, существования молекул (NaCl)6, ибо ионы,
например Na+, других таких «молекул» в той лее мере принадлежат
ионам С1" данной молекулы, как и ионы Na+ её самой.
Итак, все кристаллические структуры разделяются на 2 типа:
1) Динадного типа с полной возможностью выделения «кирпичей»
структуры — небольших трёхмерных, длинных цепочечных или
плоских молекул или соответствующих ионов. К этому типу относятся
кристаллы всех органических соединений и кристаллы других
соединений с молекулярными решётками, а также кристаллы всех
комплексных соединений.
2) Нединадного (координационного) типа с полной
невозможностью выделения обособленных в решётке комплексов атомов. Это
кристаллы ионного типа, гомеополярные кристаллы типа ZnS и алмаза,
металлы и т. п.
б) Атомные и межмолекулярные радиусы. Осповное различие
описанных типов с тонологической точки зрения заключается в тОхМ,
что атомам, образующим кристаллы динадного типа, нужно
соподчинить пространство в виде срезанного шара (как оно образуется,
ясно из фиг. V, 4 а) и б), в то время как атомы и ионы кристаллов
нединадного типа могут рассматриваться как шары определённого
радиуса. Таким образом атом- или ион в последнем случае
характеризуется одной константой—атомным или ионным радиусом, а во
втором двумя — атомным (валентным) радиусом, определяющим
межатомные расстояния, и межмолекулярньш радиусом.
Атомный (или ионный) радиус есть попросту радиус шара,
которым всегда можно аппроксимировать атом (или ион) в кристаллах
нединадного типа (в кристаллах динадного типа, например
комплексных соединений, отдельные одноатомные иопы также
аппроксимируются шарами соответствующих ионных радиусов). Понятие
атомного (валентного) радиуса нриложимо и к атомам в кристаллах
динадного типа. Однако в этом случае атомные радиусы определяют
расстояние между атомами, связанными валентно. Расстояния жо

§ 2] 'ГОМОЛОГИЧЕСКАЯ ХАРАКТЕРИСТИКА КРИСТАЛЛОВ 398
между атомами, валентно не связанными, определяются межмоле-
вудярными радиусами. Так как эти радиусы определяют возможное
сближение молекул в кристалле, они и называются
межмолекулярными. Итак, расстояние cIab между атомами (ионами) А и В с
атомными (ионными) радиусами гл и гв равно dAB = rA-\-rB во всех
координационных кристаллах и в динадных кристаллах, если А и В
связаны валентно. Напротив, если атомы А и В в динадном
кристалле не связаны
валентно, то <1ав = На-{-Ив, где
В л и В в —
соответствующие межмолекулярные
радиусы. В подавляющем
большинстве случаев 7?д>
> га. Сказанное
иллюстрируется фиг. V, 4 в) и г).
Оыыт показывает, что
в первом приближении
удаётся разработать такую
схему атомных и
межмолекулярных радиусов, что
все существующие
структуры могут быть
представлены в виде упаковок
шаров (структуры нединад-
ного типа) или упаковок
молекул, которым
приписана определённая форма
межмолекулярными
радиусами (структуры динадного
типа). Это значит, что,
получив сведения о новой
структуре, а именно о
расположении центров атомов
в элементарной ячейке, мы
можем, помещая в
соответствующие точки центры шаров (радиусы которых берутся из
литературных данных), более или менее плотно заполнить
пространство. Шары не будут «висеть в воздухе» и не будут проникать
друг в друга. Это относится, конечно, к кристаллам нединадного
типа (атомы — шары).
В случае кристаллов динадного типа пространство аналогичным
образом заполняется трехмерными телами более или менее сложной
формы (молекулы, «построенные» с помощью межмолекулярных
радиусов), причём заполнение оказывается не менее, а зачастую
более плотным, чем в случае заполнения тарами. В этом, собственно,
и заключается так называемый «принцип плотнейшей упаковки»,
Фиг. V, 4. о) Атомный кристалл.
Атомный радиус Вгв равен половине
расстояния между двумя атомами dBB. б)
Бинарный координационный кристалл.
Атомы А и В находятся на расстоянии dAB,
равном сумме их атомных радиусов.

394 СТРУКТУРНЫЙ АНАЛИЗ ББ5 ОЦЕНКИ ИНТШСИВНОСТШ [ГЛ. V
составляющий, пожалуй, основу всей кристаллохимии. Итак, в любой
кристаллической структуре составляющие еб частицы (атомы, ионы,
молекулы) при аппроксимации их шарами или телами более
сложной формы (молекулы) с помощью атомных, ионных и
межмолекулярных радиусов заполняют пространство кристалла плотно, т. е.
касаются друг друга в возможно большем числе точек.
Разумеется, универсальность межатомных к* межмолекулярных
радиусов может быть рассматриваема только кик правило первого
и довольно грубого приближения. Однако выполнение этого правила
даже в пределах ±0,05—ОДА оказывает неоценимые услуги при
структурном анализе, позволяя применять результаты кюрии
плотной упаковки атомов и молекул в кристаллах.
Фиг. V, 4. в) Двуатомная молекула А%. Ковалентный (атомный) радиус гА
равен половине расстояния dAA. Межмолекулярный радиус ЛА равен
половине минимального расстояния между атомами разных молекул, строящих
кристалл. ») Двуатомная молекула ЛВ. Расстояние dAB равно сумме кова-
лентных радиусов гА и гв. Внешний контур молекулы определяется
межмолекулярными радиусами ВА и Л^-
Значения атомных, ионных и межмолекулярных радиусов,
которыми пользуются на предварительных стадиях структурного анализа,
приведены в таблице V, 1.
в) Координационное число. Под координационным числом
данной частицы (атома, иона, молекулы) понимают число частиц
(атомов, ионов, молекул), непосредственно её окружающих. Цри
этом в случае атомов и ионов соприкосновение данного атома или
иона с окружающими его другими атомами и ионами необязательно.
В случае же кристалла, построенного из молекул, под
координационным числом понимается число молекул, не только непосредственно
окружающих данную молекулу, но и обязательно касающихся еб.
Молекулы в отличие от шарообразных ионов и атомов могут касаться
не в одной, а в нескольких точках (касаются нескольких атомок

§ 2] ТОПОЛОГИЧЕСКАЯ ХАРАКТЕРИСТИКА КРИСТАЛЛОВ 395
Таблица V, I
о
А) Иоииыс и атомные радпусы в А
Z
2
3
4
Г)
0
7
8
9
10
11
12
13
J4.
15
16
17
18
19
20
21
22
23
24
Элемент
Н*
Li
Be
В
С
N
О
Р
Nc
Na
Mr
Al
Si
P (чёрный)
S (ромбическая)
CI
А г
К
Ca
Sc j
Ti
V
a-Cr
P-Cr
Y-Cr
Атомный
радиус
1,50
1,112
0,77
0,53
0,68
1,60
1,80
1,51)5
1,18
1,172
1,08
1,06
0,97
1,91
2,27
1,97
1,45
1,313
1,210
1,35
1 22
Ион
Li+
Be + +
; в+«
c+i
N+5
O"1'
p->
Nu + 1
1 Mg + '
Al+;J
Si'*
sr4
p-3
iS-2
Cl+7
CI"1
K+1
Ca+2
Sc+3
Ti+2
Ti+J
,n+4
v r°
Cr+3
C.H5
Ионный
радиус
0,78
0,34
0,24 (тсор.)
0,20
0,15
1,32
1,33
0,98
0,78
0,57
0,39
1,98
0,35
2,12 (теор.)
0,34 !
1,74
0,26 (теор.)
1,81
1,33
1,06
0,83
0,76 (теор.)
0,70 (теор.)
0,64
0,75 (теор.)
0,61
0,40
0,65
0,37

396 СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦЕНКИ ИНТВНСИВНОСТЕЙ [ГЛ. V
Продолжение
Z
25
20
27
28
29
30
3L
32
33
34
35
36
37
3S
39
40
41
42
43
44
45
46
Элемент
а-Мп
£-Мп
Т-Мп
a-Fv
Со
Ni
Си
Zn
Ga
Gc
As
Se
Br
Кг
Rb
Sr
Y
Zr
Nb
Mo
Tc
Ru
Rh
P.l
Атомный
радиус
1.24
1,26
1,29
1,238
1,26
1,25
1,243
1,275
1,329
1,22
1,22
1,25
1,16
1,13
2,0
2,43
2,14
1,79
1,58
1.43
1,36
1,322
1,342
1,372
Ион
Ми+?
Mn+4
Mn+7
Feb2
Feb3
Соьз
Ni+2
Cu+1
Zn+2
Ga+3
Gcf4
Ge~4
As+r>
As"3
Se ifi
Se"2
Br+6
Br"1
Rb + 1
Sr + 2
Y+3
Zr+4
Nb+4
Mo+4
Mo+6
Ru+4
Rh+3
Rh+4
Pd+2
Ионный
радиус
0,91
0,52
0,46 (тсор.)
0,83
0,67
0,82
0,65 (тсор.)
0,78
0,96 (теор.)
0,83
0,62
0,44
2,72 (тсор.)
0,69 (теор.)
0,47 (теор.)
2,22 (теор.)
0,35
1,91
0,39 (теор.)
1,96
1,49
1,27
1,06
0,87
0,69
0,68
0,62 (теор.)
0,65
0,69
0,65 (тсор.)
0,50 (тсор.)

§ 2] ТОПОЛОГИЧЕСКАЯ ХАРАКТЕРИСТИКА КРИСТАЛЛОВ 397
Продолжение
Z
47
48
49
50
51
52
53
54
55
56
57
58
59
60
63
64
68
69
70
71
72
73
74
Элемент
Ag
Cd
In
Sn
Sb
Те
J
X
Cs
В а
Lu
Co
aPr
aNd
Eu
Gd
Ei-
Tu
Yb
Lu
Hf
Та
W
Атомный
радиус
1,441
1,486
1,62
1,40 (серое)
1,508 (белое)
1,439
1,44
1,35
2,2
2,62
2,17
1,86
1,81
1,82
1,81
1,87
1,57
1,427
Pl,37
al,26
Ион
Ag+1
Cd42
ln^}
Sn+2
Sn + 4
Sn-4
Sb+3
Sb+5
Sb"J
Te+*
Te+6
Те"2
J+5
J+7
J"1
Cs+1
Ba+S
La+'{
Ce+3
Ce+4
Pr+:{
Nd+3
Eu+2
Gd+3
Ег+3
Tu+3
уьи-з
Lu+:J
W+4
W+«
Ионный
радиус
1,13
1,03
0,92
1,02 (теор.)
0,74
2,94 (теор.)
0,90 (теор.)
0,62 (теор.)
2,45 (теор.)
0,89
0,56 (теор.)
2,11
0,94
0,50 (теор.)
2,20
1,65
1,43
1,22
1,18
1,02
1,16
1,00
1,08 (теор.)
1,17 (теор.)
1,11
1,04
1,0.4
1,00
0,99
0,68
0,65 (теор.)

3ftft структурный анализ бВз оценки интенсивностей [гл. ^
Продолжение
1
i
75
76
77
78
79
80
81
82
83
88
90
92
Элемент
Re
Os
Ir
Pt
Ли
Hg
Tl
Pb
Bi
Ra
Th
a-U
Атомный
радиус
1,367
1,335
1.354
J.384
1,43!)
1,50
P1.71
al,70
1,740
1,55
1,79
1,48
1,41
Ион
Os+4
Ir+4
Pt+2
Pt+4
Au + 1
Hg+2
T, + i
Tl + J
Pb+2
Pb+4
Bi+S
Bi+*
Ra+2
Th+4
u+4
Ионный
радиус
I
0,67
0,66
0,52 (теор.)
0,55 (теор.)
1,37 (теор.)
1,12
1,49
1,05
1,32
0,84
1,20 (теор.)
0,74 (теор.)
1,52 (теор.)
1,10
1,05
1
1
о
В) Ковалентные и межмолекулярные радиусы и А
Z
1
3
5
6
Элемент
Н
Li
В
С
Ковалентный радиус
0,30
1,34
0,88 (одинарная связь)
0,76 (двойная связь)
0,68 (тройная связь)
0,771 ^одинарная связь)
0,665 (двойная связь)
0,602 (тройная связь)

Межмолекулярный радиус
1,17
1,72 *)
*) В крупных ароматических молекулах; в алифатических соединениях
и системах с одним-двумя циклами — 1,8.

§ 2] ТИПОЛОГИЧЕСКАЯ ХАРАКТЕРИСТИКА КРИСТАЛЛОВ 3§0
Продолжение
1 •
Z
7
Н
9
11
14
15
16
17
1!)
32
33
34
35
50
51
52
53
80
Элемент
N
0
F
Na
Si
р
S
01
к
Ge
As
Se
Br
Sn
Sb
Те
J
Hg
Ковалентный радиус
0,70 (одинарная связь)
0,60 (двойная связь)
0,547 (тройная связь)
0,66 (одинарная связь)
0,55 (двойная связь)
0,50 (тройная связь)
0,64 (одинарная связь)
0,54 (двойная связь)
1,54
1,17 (одинарная связь)
1,07 (двойная связь)
1,00 (тройная связь)
1,10 (одинарная связь)
1,0) (двойная связь)
0,93 (тройная связь)
1,04 (одинарная связь)
0,94 (двойная связь)
0,87 (тройная связь)
0,99 (одинарная связь)
0,89 (двойная связь)
1,96
1,22 (одинарная связь)
1,12 (двойная связь)
1,21 (одинарная связь)
1,11 (двойная связь)
1,17 (одинарная связь)
1,07 (двойная связь)
1Д4 (одинарная связь)
• ,04 (двойная связь)
1,40 (одинарная связь)
1,30 (двойная связь)
1,41 (одинарная связь)
1,31 (двойная связь)
1,37 (одинарная связь)
1,27 (двойная связь)
1,33 (одинарная связь)
1,23 (двойная связь)
1,30 (одинарная связь)

Межмолекулярный радиус
1,57
1,38
1,35
j
1.9
1,85
1,80
2,0
2,00
1,95
2,2
2,20
2,10
1,50
i
I

400 СТРУКТУРНЫЙ АНАЛИЗ ЕЁЗ ОЦЕНКИ ИНТВНСИВНОСТЕЙ [РЛ. V
двух молекул). Однако независимо от числа касаний данной
молекулы с окружающими её непосредственно молекулами
координационное число равно именно числу касающих молекул, а не числу
касаний. О координационных числах в молекулярных кристаллах
будет сказано ниже. Здесь мы остановимся на координационных
числах атомарных и ионных кристаллов.
Отметим, прежде всего, что для кристалла, в котором атомы
располагаются в узлах примитивной кубической ячейки,
координационное число равно 6. Если атомы располагаются в узлах
кубической объёмно- или гранецентрированной решётки, то
координационное число равно соответственно 8 и 12. В плотных шаровых
упаковках координационное число равно 12. Указанными решётками
обладает большинство металлов. Интересно отметить, что плотность
упаковки (об этом несколько ниже) растёт в этом случае с ростом
координационного числа. Это правило применимо не только в этом
простейшем случае высокосимметричных решёток элементарных
металлов, а имеет значительно большую общность.
В случае структур элементов, естественно, можно говорить
только о координационном числе атомов одного сорта. Для структур
бинарных соединений А^В^ нужно различать 2 координационных
числа: координационное число атомов А и координационное число
атомов В. В решётках тройных соединений необходимо различать
координационные числа трёх разных атомов и т. д. Естественно,
что в структурах бинарных соединений формулы АВ
координационные числа обоих атомов (ионов) должны быть одинаковы. В случае
бинарного соединения формулы А2В, координационное число атома
(иона) А должно быть вдвое меньше координационного числа атома
(иона) В. Действительно, пусть координационное число А равно пх,
координационное число В равно щи Это значит, что каждый из
атомов А, окружающих атом В, принадлежит ему на — . Всего лее
МА
на долю атома В приходится пв — атомов А. Следовательно,
пв
— = 2 или пн — 2п\. В общем случае для бинарного сосдипс-
"а
ния А^Вр с координационными числами п.\ и пв координационные
числа обратно пропорциональны соответствующим стехиометриче-
ским коэффициентам: пАх — пву.
Структуры простейших бинарных соединении и
координационные числа приведены в таблице V, II.
Для ионных кристаллов координационные числа зависят от
соотношения ионных радиусов. Действительно, стремление к минимуму
потенциальной энергии требует отсутствия соприкосновения
одноимённых ионов, и напротив — наличия соприкосновения
разноимённых ионов. Рассмотрим, например, каково должно быть соотношение

§ 21
ТОПОЛОГИЧЕСКАЯ ХАРАКТЕРИСТИКА КРИСТАЛЛОМ
А()\
Таблица V,H
Наиболее распространённые типы структур бинарных соединений
1)' Хлористый ни
рин
rf=&=3\
ш
NaCl
Координационным ионный кристалл.
Кубическая система. Параметр ячейки а = 5,628 кХ.
Ионы Na+ находятся в узлах_ всестороннецентри-
рованной решётки, ноны С1 находятся в узлах
другой такой же решётки, сдвинутой на ~ ребра
первой. Координаты атомов:
Na+ (000;
tr 0;
l> 2 ' -2 2;
CI"
~ 00; 0 -~ 0; 00-i
11
2 2
Число «молекул» в ячейке 4. Координационное
число Na+ относительно С1 и наоборот равно 6,
координационное число Na+ относительно Na+ и
С1 относительно С1 равно 12. Структура может
рассматриваться_как плотнейшая кубическая
упаковка ионов 01 , все октаэдрические пустоты
которой засолены ионами Na+.
I) Цинковая
манка
2пЗ
Координационный гомеополярний кристалл.
Кубическая система. Параметр решётки: а = 5,12 kX.
Атомы Za находятся в узлах всестороннецентри-
роваиной решётки; в узлах такой же решётки
находятся атомы S. Вторая решётка сдвинута
относительно первой на 1ji пространственной
диагонали. Координаты атомов:
ZnfoOO; ~ io; 4 ° J"; TT0/
<, / 1 1_ }
1 4 4 4
3 8 1
4 4 4
JL i_ J*.
4 4 4
1 3 1
4 4 4
у
Число «молекул» в ячейке равно 4.
Координационное 4HMoZnотносительно S инаоборотравно4;
координационное число Zn относительно Zn и S
относительно S равно 12. Структура может
рассматриваться и иначе, — как плотнейшая
кубическая упаковка атомов S, половина тетраэдрических
пустот которой заселена атомами Zn. Если
подобная структура образована атомами одного сорта,
получаем структуру типа алмаза (алмаз, кремний,
германий, олово).

№
СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦЕНКИ ИНТЕНСИППОСТЕЙ [тЛ. У
Цродолжепи<
3) Хлористый
цезий
Л~^Т
CsCl
Координационный ионный кристалл.
Кубическая система. Параметр ячейки а = 4Д10 кХ.
Ионы Сз+ находятся в узлах примитивной
кубической решётки, ионы С1 находятся в узлох
такой же решётки, сдвинутой относительно иер-
1
вой на — пространственной диагонали. Коорди-
2
паты атомов: Cs+ (000), Cl (— —
1 JL A
2 2 2
Число «молекул» в ячейке равно 1
национное число Cs+
рот равно 8.
относительно СТ
Коорди-
и наобо-
4) Вюрцит
Координационный гомеополярный кристалл.
Гексагональная система. Параметры ячейки а =
= 3,8П кХ, с = 6,234 кХ. Атомы ZnnS находятся
в узлах непримитивных гексагональных
решёток Гл, сдвинутых друг относительно друга на3/8 с.
' 12 1 2 12
Базис решётки Гл : 000; —-^-—; — ~ —.Это-
О О О О О О
координаты атомов Zn. Координаты атомов
s-ool- г- I1-?-2 И
8 ' 3 3 24' 3 3 24 *
Число «молекул» в ячейке равно 3.
Координационное число атомов Zn относительно S и
наоборот равно 4 (тетраэдрическое окружение).
Координационное число атомов S относительно S и
Zn относительно Zn равно 12. Структура может
рассматриваться как плотнейшая гексагональная
упаковка атомов S, половипа тетраэдрических
пустот которой заполнена атомами Zn.
Координационный кристалл с металлической
связью. Гексагональная система. Параметры
ячейки а = 3,602; с — 5,000. Коордппати атомов:
Ni(00O;0oi);As(A|i;|i4j.
Число «молекул» в ячейке равно 2.
Координационное число As относительно Ni и наоборот
равно 6. Координационное число атомов As
относительно As равно 12. Структура может
рассматриваться как плотнейшая гексагональная
упаковка атомов As, все октаэдрические пустоты
которой засолены атомами Ni. Атомы Ni,
окружающие атом As, располагаются в вершинах три-
гональной призмы.

fj 2] ТОПОЛОГИЧЕСКАЯ ХАРАКТЕРИСТИКА КРИСТАЛЛОМ 403
Продолжение
6) Нитрид бора
1
B.N
Динадный кристалл, построенный из слоев.
Внутри слоя связь гомеополярная, между слоями
вандерваальсовская. Каждый слой может
рассматриваться как бесконечная плоская молекула (BN)„.
Гексагональный кристалл с параметрами « =
= 2,51 кХ; с = 6,69 кХ. Расстояние между слоями
равно -^ = 3,35 кХ.
Расстояния В — N внутри
слоя равны 1,65 кХ. Подобную структуру,
построенную из атомов одного сорта, имеет графит.
7) Флюорит
8) Крнетобалит
5к^
\р*°^-р*
SIO,
Координационный ионный кристалл.
Кубическая система. Параметр ячейки а — 5,451 кХ.
Ионы Са+2 расположены в узлах всесторонне-
центрированной кубической решётки, ионы F
расположены в узлах двух^ таких же решёток.
Решётки, занятые ионами F , сдвинуты
относительно решётки Са+2 соответственно на *Д и %
пространственной диагонали. Координаты атомов:
л-/1 1 1 .
Са'"
3 ^
4 4
1 3
000; i- }о;
1 • {i 1 1
4 ' 4 4 4 '
13 11
i'f»1-
4 4~
2
2 2
i- _3
4 ' <Г
F
1 1
4 4
4 4 4'
111-
4 4 4'
4 4 4 4 4 4
Число «молекул» в ячейке равно 4.
Координационное число ионов Са+ относительно ионов F-
равно 8 (окружение по кубу), координационное
число F- относительно Са+2 равно 4 (окружение
по тетраэдру), центры ионов Са+ занимают
положение центров шаров плотнейшей кубической
упаковки, центры ионов F занимают центры
всех тетраэдрических пустот.
Координационная гомеополярная структура.
Атомы кремния располагаются подобно атомам
углерода в алмазе (ср. 3), т. е. занимают узлы
кубических всестороннецентрированных решёток
с координатами начальных узлов 000 и — — - .
Посредине между двумя соседними атомами Si
находится атом кислорода. Каждый атом Si
окружён четырьмя атомами О по тетраэдру, напротив,
координационное число О относительно Si равно 2.
Число «молекул» в ячейке равно 8. Структура
может также рассматриваться как плотнейшая
(кубическая трёхслойная) упаковка атомов
кислорода, четверть тетраэдрических пустот которой
занята атомами кремния.

404 СТРУКТУРНЫЙ АНАЛИЗ ВЕЗ ОЦЕНКИ ИНТЕНСИВНООТЕН [гл. V
Продолжение
9) Рутил
Координационный ионный кристалл.
Тетрагональная система. Параметры ячейки а — 4,492 кХ;
с = 2,893 кХ. Координаты атомов: Ti+^OOO; 4 Ц);
0,31).
О"2Ггш0;
1 . 1
«;
гдем
Число «молекул» в ячейке равно 2.
Координационное число ионов Ti+4 относительно О-"
равно 6 (координационный полиэдр — слегка
искажённый октаэдр); координационное число О""'
относительно Ti+4 равно 3 (координационный
«полиэдр» — треугольник). Структура может
рассматриваться как плотная упаковка нонов О
стотами, заселёнными ионами Ti+4.
-2
с пу-
10) Углекислота
а
Динадный молекулярный кристалл. В узлах
веестороннецентрированной кубической ячейки
находятся атомы С молекул С02. Число молекул
в ячейке 4. Параметр ячейки а = 5,60 кХ.
«Координационное число» атома С равно 2, атома О
равно 1. Правильнее говорить о координационном
числе молекулы, которое равно 12. Структура
может рассматриваться как плотная кубическая
упаковка молекул СОг.
Совершенно аналогичную структуру имеет
пирит (FeS^) с параметром а = 5,404 кХ.
Фиг. V,6. Связь размеров
ионов с координационным
числом.
между ионными радиусами при
координационном числе 8 (фиг. V, 5).
(катион радиуса гк находится в
центре куба, анионы радиуса га в
вершинах). Пространственная диагональ
куба равна 2ra-\-2rh. Ребро куба
2
равно —==. {га~\~гк). Чтобы анионы
не соприкасались, сумма их ионных
радиусов должна быть меньше ребра
куба, т. е. 2ra<y= (ra+rk) или
— >V1J—1 = 0,73.
Га
анионов
При перемене
и катионов местами полу-
г*
чаем — < 0,73. Это так называемые

§3]
ТЕОРИЯ ПЛОТНЕЙШЕЙ ШАРОВОЙ УПАКОВКИ
405
верхний и нижний пределы устойчивости данного
координационного числа.
Приведём границы устойчивости для наиболее распространённых
координационных чисел:
К. ч.
2
3
4
4
6
8
12
Конфигурация
расположения ионов
Равносторонний тре-
Куб
Плотная упаковка . . .
Критическое
значение
rklra
0,00
0,15
0.22
0,41
0.41
0,73
1,00
§ 3. Теория плотневшей шаровой упаковки
а) Симметрия упаковки. Плотнейшая упаковка шаров в
плоском слое показана на фиг. V, 6. Следующий слой может
накладываться на данный двумя способами, а именно, можно заполнить
шарами лунки В или лунки С. Если обозначить центры шаров
первого слоя через А,
то становится
очевидным, что центры шаров
последующих слоев
могут приходиться либо
над точками А
(начиная с третьего слоя),
либо над точками Б,
либо над точками С.
Таким образом возникает
бесконечное число
плотных упаковок, примеры
которых даны на фиг.
V, 7. Отметим, что
координационное число любого шара такой шаровой упаковки равно 12.
Все эти упаковки обладают, разумеется, одной и той же
плотностью упаковки. Эти упаковки являются плотными в том смысле,
что 1) шары в сдой не могут быть уложены более плотно,чем это
показано на фиг. V, 6,2) слои шаров накладываются друг на друга
также с максимально возможной плотностью, ибо шары верхнего
слоя ложатся во впадины между шарами нижнего слоя. Плотность
Фиг. V, 6. Плотнейшая упаковка шаров
в плоском слое. Два последовательных плотно
упакованных плоских слоя в
пространственной плотнейшей шаровой упаковке.

406
СТРУКТУРНЫЙ АНАЛИЗ ВЕЗ ОЦЕНКИ ИНТЕНСИВНОСТЕИ [ГЛ.
упаковки принято характеризовать коэффициентом упаковки, т. е.
отношением собственного объёма частицы (атома, иопа, молекулы)
к приходящемуся на её долю объёму кристалла. Таким образом
коэффициент упаковки есть та часть общего объёма кристалла, которая
заполнена строящими его частицами. Остальная часть объёма при-
Фиг. V, 7. Примеры плотней-
тих шаровых упаковок; а, о,
в — гексагональная
двуслойная в трёх аспектах — ...
ABAB...f ...ACAG..., ...
ВСВС...\ %, д — кубическая
трехслойная в двух
аспектах — ... ABGABG ... и ...
АСВАСВ...; е—четырёх -
слойная упаковка; ж — шести-
слойная упаковка.
Фиг. V, 8. Подсчёт
коэффициента
упаковки шаров.
ходится на пустоты. Практически полезна следующая формула: если
в элементарной ячейке кристалла объёмом V находится пх частиц
объёма V^l, w2 частиц объёма V{? и т. д., то коэффициент упаковки
к равен:
«— у •
Подсчитаем коэффициент упаковки для одной из этих шаровых
упаковок. Это удобно сделать для простой гексагональной призмы,
в которой третий слой находится над первым (шары 2 на фиг. V, 8).
Объём такой призмы равен произведению площади основания
3
4pUa на высоту 2а]Д|*),т. е. F=3a3|/"2.
Ha призму приходится 6 шаров объёма V0 = -^tz(^
довательно, коэффициент упаковки равен '
jb«eia« * «0,7405.
V 3 /2
~6~
Сле-
•У\
есть высота тетраэдра со стороной а.

§ 3] ТЕОРИЯ ПЛОТНЕЙШЕЙ ШАРОВОЙ УПАКОВКИ 4()7
Перейдём теперь к вопросу о симметрии упаковок. Вообще
говоря, слои могут упаковываться совершенно беспорядочно (в
отношении следования А, В, С) и тогда кристалла не возникает. Если
же, начиная со слоя п, порядок наложения слоев начинает
повторяться, то возникает %-слойная упаковка, решётка которой обладает
определённой симметрией, зависящей от характера чередования
слоив А, В и С.
Через точку А проходит ось 6 и шесть вертикальпых
плоскостей симметрии. Через точки В л С проходит ось 3 и три
вертикальных плоскости симметрии. Вполне очевидно, что как бы ни
накладывались слои, тройную ось и вертикальные плоскости
симметрии через точки В и С провести можно всегда. Поэтому: 1)
минимальная симметрия любой шаровой упаковки это симметрия
пространственной группы C]v = Сдт (фиг. V, 9); 2) характер взаимного
Фиг. V, 9. Фёдоровская группа С^.
расположения вертикальных плоскостей симметрии любой из шаровых
упаковок должен быть таким же, как в C3t>.
Этому условию удовлетворяют следующие 8 пространственных
трупп: <7i, = C3m; Cje = .R3m; Пм = СЯт: Вьм = ВЯт: D\h =
= Сбт2; Civ = СЬтс; Dtn = CQlmmc; 0\ — FmZm.
Простейшими упаковками являются двуслойная обычная
гексагональная упаковка, слои которой чередуются по закону
\АВ\ АВ\АВ\... (симметрия этой упаковки Dth) и плотнейшая
кубическая упаковка симметрии 0\. В этой упаковке слои
(параллельные плоскости (111)) чередуются по закону \ABC\ABC\...
Эти 2 простейшие шаровые упаковки показаны на фиг. V, 9а,
Беловым *) были выведены все возможные шаровые упаковки
с числом слоев до 30. Для данного п указывается порядок наложе-
*) Цит. на стр. 389.

408 СТРУКТУРНЫЙ АНАЛИЗ ВВЗ ОЦЕНКИ ИНТЕНСИВНОСТИ [г."1. V
ния слоев и возникающая пространственная группа. Число
возможных упаковок для некоторых п весьма велико, например,
существует 43 12-слойных плотных упаковки.
Рассматривая произвольную плотную упаковку шаров, мы можем
встретиться, как уже было сказано выше, со слоями трёх типов:
если один слой обозначить А, то другие слои, связанные с исходным
трансляцией, перпендикулярной слою (т. е. находящейся по вертикали
над исходным), будем называть также слоями А; по отношению
к слою А другие слои могут быть сдвинуты двумя способами —
слои В расположены так,
что их шары приходятся
над одной системой
лунок слоя А и слои С
расположены так, что их
шары приходятся над
другой системой лунок.
Чередованием трёх букв А, В
и С можно
характеризовать любую упаковку.
Существует три вида
Фиг. V, 9а, а) Плотнейшая кубическая уна- символов плотной
упаковка; симметрия 0£. б) Плотнейшая гекса- КОВКИ шаров, включая
тональная упаковка; симметрия J)L. упомянутую. Второй
способ заключается в том,
что каждая из букв А, В, С заменяется одной из букв г или к.
При этом буква г пишется взамен буквы А или В или С в то.м
случае, если эта буква стоит между двумя одинаковыми, скажем,
вместо В в ряду . .. С ВС.. • или .. .ABA...
Таким образом получим, например, символ
...\А ВС А С В |... = ...! гШгШ |...
Удобство символа второго типа заключается в том, что по этому
символу легче различить элементы симметрии.
Третий вид символа носит название числового *) и получается
по следующему правилу: в серии букв г и к вместо нескольких
идущих подряд букв г ставятся единицы в количестве на 1 меньшем,
т. е. вместо .. .ггъг.. .ставится... ill... Одна буква г пропускается.
Вместо нескольких идущих подряд букв к ставится число на 1
большее, т. е. вместо.. .ккк... ставится .. .4... Таким образом
получаем, например, символы:
... \гккгкк\... = ...|3, 3|...
•..! гШгггкггк | ... = ... 13112121. • . и т. д.
*) Г. С. Ж д а н о в, ДАН, 40, 1945.

§ 3] ТЕОРИЯ ПЛОТНЕЙШЕЙ ШАРОВОЙ УПАКОВКИ 409
Числовой символ имеет также ряд достоинств. Сумма чисел даёт
период упаковки, выраженный в числе слоев. Число членов символа
должно быть чётным. Линия симметрии, проходящая через цифру,
соответствует центру симметрии, проходящая между цифрами —
плоскости симметрии.
По символу можно судить, к какой пространственной группе
принадлежит соответствующая упаковка. Если числовой символ
разделяется на два одинаковых полупериода (с нечётным числом
членов в каждом), то имеем пространственную группу С&>. Если оба
полупериода отделяются, кроме того, плоскостью симметрии, то
имеем группу В\п или D3h. Эти две группы легко различаем, так
как в первом случае есть, а во втором нет центра симметрии между
плоскостями симметрии. Отсутствие элементов симметрии говорит
о группах Civ и CL и, наконец, наличие одних лишь центров
симметрии говорит о группах В\а и В\а. Ромбоэдрические группы в\#
и Ctv определяются условием:
величина А не делится на 3.
Эта величина равна разности цифр, стоящих на чётных и стоящих
на нечётных местах. Вот, например, символы ромбоэдрических
упаковок:
. ..|4, С|..., ... 1121111121...; ... |283333 |...
6—4=2 6—4=2 9—8=1 и т. д.
6) Пустоты в шаровых упаковках. В рассмотренных шаровых
упаковках существует два типа пустот. Если треугольная лунка
одного слоя прикрывается сверху шаром, то мы имеем пустоту,
окружённую четырьмя шарами. Имеются в структуре и другие лунки,
Фиг. V, Ю. Тетраэдриче- Фиг. V, 10а. Октаэдрическая
пуская пустота плотнейшей стота плотнейшей шаровой упа-
шаровой упаковки. ковки.
которые закрыты сверху не одним шаром, а другим треугольником
шаров, повёрнутым на 60°. Образующиеся пустоты окружены
6 шарами. Пустоты первого типа (точка А на фиг. V, 6) называются
тетраэдрическими (фиг. V, 10), пустоты второго типа (точка В на
фиг. V, 6)—октаэдрическими (фиг. V, Юа).

410 СТРУКТУРНЫЙ АНАЛИЗ ВЕЗ ОЦЕНКИ ИНТЕНСИВН0С1 ЕЙ [г.1. V
Каждый шар в слое окружён шестью лунками. При
накладывании слоя сверху данного образуются 3 тетраэдрические и 3 окта-
эдрические пустоты. То же самое имеет место при наложении
нижнего слоя. Кроме того сам рассматриваемый шар закроет ещё
две лунки — по одной в каждом из соседних слоев; образуются ещё
две тетраэдрические пустоты. Итак, каждый шар окружён 6 окта-
эдрическими и 8 тетраэдрическими пустотами.
Каждая октаэдрическая пустота окружена 6 шарами и каждый
шар окружен 6 октаэдрическими пустотами. Следовательно, в
бесконечной структуре на 1 шар приходится 1 октаэдрическая пустота.
Каждая тетраэдрическая пустота окружена 4 шарами, каждый шар
окружён 8 тетраэдрическими пустотами. Каждая пустота
принадлежит шару на 1/i, следовательно, на один шар приходится 2
тетраэдрические пустоты.
Совершенно очевидно значение проведённых рассуждений. Если
многоатомное соединение строит кристалл по принципу плотной
упаковки и частицы можно аппроксимировать сферами разных
радиусов, то решётка должна представлять собой плотную шаровую
упаковку самых крупных частиц с пустотами, запятыми более
мелкими частицами.
Для ионных кристаллов роль шаров играют анионы, имеющие,
как правило, размер, значительно больший размера катиона. Катионы
же заполняют нустоты в плотной упаковке апионов.
Итак, каждый анион может быть окружён 8 маленькими
(«тетраэдрическими») и 6 большими («октаэдрическими») катионами.
Легко подсчитать возможные размеры катионов, т. е. шаров, которые
могут быть вписаны в пустоты.
Маленький шар, помещённый в пустоте между основными шарами
упаковки, не будет «болтаться» в ней, если он будет касаться всех
основных шаров, окружающих данную пустоту. При этом центр
этого шара будет равно удалён от центров всех соседних основных
шаров, т. е. будет находиться в центре тетраэдра или октаэдра
(с ребром а), образующихся соединением прямыми центров
основных шаров, окружающих пустоту. Условие касания имеет вид
r-\-R = dr в, где г—радиус шара, помещённого в пустоту,
R—радиус основного шара упаковки, с1г—в — расстояние от центра
тетраэдра или октаэдра до его вершины.
Для шара, помещённого в октаэдрическую пустоту, имеем г^=
a Y% a _ ... а
=—g q — 0,414тг > для шара, помещённого в тетраэдрическую
пустоту г =з ± xoqo^— Т == °»225 |" • 3Десь а — расстояние
sin —s—
/а
между центрами основных шаров упаковки I-g- = И — радиус
основного шара), 109° 28' —угол между высотами правильного тетраэдра-

3] ТЕОРИЯ ПЛОТНЕЙШВЙ ШАРОВОЙ УПАКОВКИ 11 1
Мы вычислили, естественно, максимальные возможные радиусы
помещённых в пустоты шаров. Если радиус шара, помещаемого
в пустоту, оказывается большим найденного значения, упаковка
искажается, если же меньшим — шар «болтается» в пустоте.
Интересно, что объём шаров, заполняющих пустоты, весьма невелик.
На рассмотренную выше гексагональную призму объёма За3К2
приходится 6 основных шаров, т. е. 6X1 «октаэдрических» и 6X2
«тетраэдрических» пустот. Объёмы соответствующих шаров равны:
6* з"7С(0,414т) и 12 *-т~(0»2254) • Следовательно, шары,
заполняющие (без «болтания») все октаэдрические пустоты, занимают
всего лишь ——у—— • 100 = 5,255% пространства, приходящегося
на упаковку, а шары, занимающие все тетраэдрические пустоты —
'(МуУ?. 100,1,0870/,.
О
Большинство минералов, как показал Белов, может быть описано
исчерпывающим образом, как плотные упаковки шаров-анионов
с пустотами, заполненными катионами. Каждый минерал
характеризуется типом плотнейшей упаковки, сортностью и числом
заселённых катионами пустот, а также
«узором» заселения пустот.
Наиболее прост случай, когда
заселены все пустоты данного сорта.
Большинство соединений типа MeHal (NaCl,
КВг и пр.) даёт плотную упаковку,
построенную ионами галогена, в которой
все октаэдрические пустоты заселены
катионами щелочных металлов. В
структуре Li20 ионы Li+, которых в два раза
больше, чем ионов О-2, заполняют все
тетраэдрические пустоты в плотнейшей
упаковке ионов кислорода.
Если в упаковке заселены не все
пустоты, то описание и в особенности
модельное представление структуры в
виде шаров становится очень
затруднительным и не наглядным. Крупные
анионы, заполняющие 74% объёма
кристаллического пространства, «заслоняют» расположение катионов, т. е.
именно ту часть картины, которая обусловливает разнообразие
минерального мира.
Прекрасным выходом из положения является изображение
структуры координационными полиэдрами так, как это показано на
фиг. V, 11. От каждого шара — аниона оставляется лишь одна
Фиг. V, 11. Представление
структуры
координационными полиэдрами.
Структура NaCl как плотная
упаковка .октаэдров. Между
октаэдрами остаются
тетраэдрические пустоты.

412 СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦЕНКИ ИНТЕНСИВНОСТЕЙ [ГЛ. V
точка — центр; весь материал распределяется по 14 (6 октаэдриче-
ских, 8 тетраэдрических) пустотам следующим способом. Проводятся
линии, соединяющие данный шар с его 12 соседями. Через каждые
две линии проводятся плоскости, которые разобьют пространство
на октаэдрические и тетраэдрические ячейки так, как это показано
на фигуре.
Удобство этого метода для модельного изображения структуры
заключается в том, что «пустые», т. е. незаселённые катионами
тетраэдры мы можем либо не помещать в модель, либо делать их
из стекла или прозрачной пластмассы.
в) Правила строения ионных кристаллов. Представление
о координационных полиэдрах служит основой для некоторых общих
правил строения ионных кристаллов.
1) Каждый катион окружён анионным полиэдром, причём
расстояние катион — анион определяется суммой соответствующих
ионных радиусов, а координационное число катиона—отношением
ионных радиусов. Первое утверждение, представляющееся на
первый взгляд тривиальным, весьма полезно при расшифровке
новых сложных структур. Второе утверждение уже иллюстрировалось
выше.
2) Стремление структуры к минимуму потенциальной энергии
приводит к тому, что каждый анион (катион) стремится
непосредственно окружить себя таким числом катионов (анионов), которое
уравновесило бы его электростатический заряд. В некоторых
случаях этому стремлепию препятствует соотношение размеров катиона
и аниона. Так, например, маленький многозарядный катион но
может быть непосредственно окружён крупными анионами в числе,
достаточном для нейтрализации его заряда. Однако в простейших
случаях это правило соблюдается. Если координационное число
аниона па, его заряд za, то на каждый из окружающих его п
катионов приходится заряд —. С другой стороны, при
координата
ционном числе катиона пк и заряда зк на каждый из окружающих
z.
его пк анионов приходится заряд -. Условие минимума
потений
Z Z,
циальной энергии требует, чтобы —£=—£-. Эта запись правила при-
менима, естественно, к бинарным соединениям АХВГ Более общая
VI nkZn ' VI naZk
запись V -~ = zk или V —s— = га применима в случае наличия
катионов и анионов разных сортов. Итак, правило гласит:
координационное число иона прямо пропорционально его заряду, если
это допускают относительные размеры катиона н аниона.
Примерами, иллюстрирующими это правило, могут служить структуры
куприта Си80, а также рутила ТЮ2, и флюорита CaF2, приведён-

§ 3] ТЕОРИЯ ПЛОТНЕЙШЕЙ ШАРОВОЙ УПАКОВКИ 41.1
ные в таблице V, П. Основное применение правила —
определение одного из координационных чисел (например катиона), если
известно другое координационное число.
3) Наличие общих рёбер и, в особенности, граней у
координационных полиэдров понижает устойчивость структуры. Действительно,
такое «срастание» полиэдров по рёбрам и граням означает
значительное сближение находящихся в их центрах катионов. При этом
должно возрастать кулоновское отталкивание катионов, т. е.
возрастать потенциальная энергия системы. Естественно, что чем выше
заряд катиона и чем ниже его координационное число, тем резче
возрастание потенциальной энергии, т. е. падение устойчивости
структуры.
4) Если в структуре имеются катионы нескольких сортов, то
катионы с большей валентностью и меньшим • координационным
числом располагаются так, чтобы их полиэдры имели между собой
возможно меньшее число общих анионов (т. е. граней, рёбер,
вершин). Это правило следует из тех же энергетических соображений,
что и предыдущее.
5) Число кристаллохимически различных составных частей
в кристалле стремится быть небольшим.
Так, например, если катионы могут располагаться вокруг
анионов различными (но равно приемлемыми с точки зрения энергетики
и геометрии структуры) способами, то в действительности
осуществляется только один из типов расположения и притом для всех
катионов.
г) Область применения. Принципы плотной упаковки имеют
широчайшее применение не только при исследовании структуры
ионных кристаллов. Они оказываются приложимыми и к
металлическим фазам. Плотнейшую упаковку в этих фазах составляют
атомы металлов, в пустотах между которыми могут располагаться
разные неметаллические атомы, например В, Si, С, Н, N и даже
кислорода, которые в ионных кристаллах играли роль
«основы упаковки». В некоторых случаях плотнейшую упаковку
образуют более крупные металлические атомы, а в пустотах
размещаются также металлические атомы, но меньшего размера
(сплавы).
В ионных кристаллах возможны случаи, когда крупный катион
замещает шар основной упаковки. Это будет тогда, когда катион
требует координационного числа 12 или 8. Примером первого
случая является СаТЮ3 (кальций замещает кислород).
При отступлении от законов плотнейшей упаковки удаётся всё же
сохранить представление пространства при помощи
координационных полиэдров, вводя трёхгранные призмы, кубы и пр. Однако
при этом метод теряет своё предсказательное значение и
должен рассматриваться лишь как удобный способ изображения
структуры.

414 СТРУКТУРНЫЙ АНАЛИЗ ВЕЗ ОЦЕНКИ ИНТЕНСИВНОСТЕЙ [гл. V
§ 4. Теория плотной упаковки молекул *)
Остановимся прежде всего на правилах «построения молекулы»
с помощью атомных и межмолекулярных радиусов. Для такого
построения нам должна быть известна структура молекулы (т. е.
её состав и порядок связи атомов друг с другом) и валентные
углы (примерные величины которых берутся из таблиц). Если
структура молекулы точно не известна, то её можно строить несколькими
наиболее вероятными способами и затем с помощью геометрического
анализа (смотри ниже) выбрать способ, отвечающий
действительности. Прежде всего находят межатомные расстояния в молекуле,
суммируя соответствующие атомные радиусы. Затем располагают
центры атомов на найденных расстояниях друг от друга и притом
так, чтобы линии,»соединяющие центры атомов, образовывали
соответствующие валентные углы. Полученное трёхмерное (в общем
случае) расположение центров атомов образует скелет молекулы.
Описывая из центра каждого атома шар радиусом, равным
межмолекулярному радиусу этого атома, получают объёмное тело,
поверхность которого состоит из участков шаровых поверхностей разных
радиусов. Это и есть молекула в том виде, как она существует
в кристалле. Её сложная поверхность является «непроницаемой»
для посторопних атомов, с физической точки зрения это есть весьма
высокий потенциальный барьер. В результате многочисленных
пересечений шаров, описанных межмолекулярными радиусами, на
долю каждого атома молекулы приходится не полный шар, а
шаровой срез, т. е. то, что осталось от шара в результате отсечения
от него нескольких (от 1 до
4) сегментов. Число сегментов
равно, естественно,
валентности данного атома. Принцип
построения молекулы можно
пояснить на примере 2,6-ди-
хлорнафталина.
Этот случай особенно прост,
ибо молекула является
плоской. Известно, что
валентные углы углерода в
нафталине равны 120°. Найдя кроме
того расстояния dc—с, ^с—н
и dc-ci суммированием
атомных радиусов, получаем скелет молекулы (фиг. Y, 12). Проведя
шары межмолекулярными радиусами (фиг. V, 12а), получим
молекулу (фиг. Y, 126). Подобным же образом строятся бесконечные
«молекулы» в кристаллах с сетчатыми и цепочечными динадами.
Фиг. V, 12. Расположение атомных
центров — скелет молекулы.
*) Китайгородский А. И., цит. на стр. 389.

§ 4] ТЕОРИЯ ПЛОТНОЙ УПАКОВКИ МОЛЕКУЛ 415
Если «построить молекулу» по этим правилам, то
возникнет объёмная фигура весьма сложной и, вообще говоря,
неправильной формы. Примеры объёмных моделей молекулы
показаны на фиг. V, 13. Исходя из идеи плотной упаковки, молено от-
Фиг. V, 12а. Из точек — центров атомов проводятся
сферы соответствующими межмолекулярными
радиусами.
вергнуть ряд способов размещения молекул в кристалле. Можно
утверждать, что «выступы» одной молекулы приходятся во «впадины»
другой. Таким образом, очевидно, в молекулярных кристаллах мы
не должны встречаться с
плоскостью зеркальной
симметрии, проходящей между
двумя соседними
молекулами. Можпо, однако, в
значительно большей степени
уточнить те требования,
которые накладываются на
симметрию кристалла
принципом плотной упаковки.
Принцип плотной
упаковки в применении к
молекулярным кристаллам
гласит следующее:
молекулярный кристалл всегда можно
рассматривать как систему
плотно упакованных слоев; молекулы слоя обладают координацией 6
и расположены так, что не существует полярности
перпендикулярно слою. Под координацией или координационным числом
молекулы понимается число соприкасающихся с ней молекул (это, так
Фиг. V, 126. Пересечение
межмолекулярных сфер образует тело весьма сложной
формы. Это — молекула, как она
существует в кристалле.

4i() структурный лиллиз вез оценки интенсивностеи |гл. v
сказать, молекулярная координация). Слой молекул с
координацией 6 показан схематически на фиг. V, 14. При плотнейшем
наложении слоев чаще всего (но не обязательно, как показывает опыт)
возникает пространственная координация 12. Можно сказать, что
сформулированный выше принцип — это та же идея плотной
упаковки шаров, но только «искажённых». Для того чтобы стал
очевидным генезис принципа, а также существенные его следствия,
рассмотрим сначала упаковку в слое фигур произвольной формы.
Из теории пространственных групп следует, что существует 80
типов слоев. Элементарные ячейки слобв могут быть квадратными,
а)
6) в)
Фиг. V, 13. а) Молекула нормального додекана
СН3 — (СН2)ю—СН3; б) молекула дихлорантрацена;
в) молекула гекеаметилентётрамина.
тригональными, прямоугольными и косоугольными. Первые две из
них не разрешают, естественно, упаковку фигур произвольной
формы. Следовательно, пригодными оказываются лишь те типы
слоев, элементарные ячейки которых являются прямоугольными и
косоугольными. Число этих слоев равно 48. Далее, для того чтобы
при произвольной форме фигуры было возможно образование
максимально плотного слоя, необходимо, чтобы оси фигуры можно
было располагать под любыми углами к осям ячейки слоя. Это
может иметь место для фигуры, занимающей в слое общее
положение, положение с центром симметрии, а также положения с сим-

§ 4] ТЕОРИЯ ПЛОТНОЙ УПАКОВКИ МОЛЕКУЛ 417
метрией 2 или т или 2/т; последние три — при условии, что ось
симметрии перпендикулярна к плоскости слоя, а плоскость
симметрии совпадает с плоскостью слоя. Условие
произвольности ориентировки по
отношению к осям ячейки слоя заставляет
исключить из рассмотрения те группы, в
которых двойные оси лежат в плоскости слоя,
плоскости симметрии перпендикулярны
к слою, а также такие слои, плоскость
которых совпадает с плоскостью скольжения.
Анализ показывает, что плотная
упаковка в слой молекул произвольной
формы достигается только в двух типах
слоев: а) в слоях с косоугольной
ячейкой, в) в слоях, построенных осью 21 и
перпендикулярной к ней трансляцией \.
Характер упаковки в этих двух весьма
распространённых слоях показан на фиг.
V, 15 и V, 16.
Вполне очевидно, что для создания плотной упаковки слоев
в кристалл необходимо наложить запрет на некоторые симметри-
Фиг. V, 14. Слой
молекул с координацией 6
(схема).
Фиг. V, 15. Упаковка
в косоугольной ячейке.
Фиг. V, 16. Упаковка
в прямоугольной ячейке.
ческие операции, посредством которых кристалл строится из слобв.
В частности наложение слоев не может происходить при* помощи
зеркальной плоскости симметрии.

418 СТРУКТУРНЫЙ АНАЛИЗ ВЁЗ ОЦЕНКИ ИНТЁНСИВНОСТЕЙ [гл. V
Учитывая подробные запреты, удаётся составить таблицу (V, III),
в которой указывается, в каких пространственных группах будут
кристаллизоваться молекулы, собственная симметрия которых 1, го,
mm, 2, 1, 2/m, 222 и чптт.
Рассмотрим подробно каждую графу таблицы. В первой графе
даны пространственные группы для несимметричных молекул.
В первой колонке приведены символы групп; далее указано число
молекул в ячейке (Z).
Наиболее удобной для органических молекул является группа С?л;
это совершенно понятно с изложенной точки зрения, так как
группа С\ъ позволяет разбить кристалл на все возможные типы
плотных слоев с координацией 6 по всем трём координатным
плоскостям. Неудивительно, что половина всех органических
соединений кристаллизуется в этой группе. В группе С^Л при Z= 4
заняты оба слоя двойных винтовых осей, при этом слои
симметрически связаны.
В группе 0\ возможны случаи, когда:
1) Z = 2: тогда один из слоСв двойных винтовых осей свободен, и
наложение слое'в трансляцией эквивалентно наложению винтовой осью;
2) Z=4: оба слоя осей заняты и не связаны симметрической
операцией.В группе d при Z=2 занята одна из двух плоскостей,
проходящих через центры симметрии; при Z=4 заняты оба слоя.
В таблице приведено разделение пространственных групп на
вероятные и возможные. Мы называем вероятными те случаи, при
которых на ориентировку молекулы по отношению к нормали слоя
не наложено каких-либо ограничений (напомним, что ориентировка
по отношению к осям слоя произвольна во всех плотных
упаковках). В случае молекул симметрии 1 и 1 такое ограничение будет
иметь место при наложении слоев двойными осями (молекулы,
связанные двойными осями, не соприкасаются или, во всяком случае,
упаковка определяется не этим соприкосновением). Поэтому
группы F3, CI, C\h и V™ должны встречаться реже — они возможны,
хотя и менее вероятны.
Если молекула занимает в кристалле положение с симметрией 2
или т, то ось молекулы совпадает с нормалью слоя. Поэтому,
с точки зрения плотности упаковки, более вероятно, что молекула
симметрии т или 2 займёт в кристалле общее положение. Из всех
элементов симметрии молекулы без противоречия с требованиями
плотной упаковки в кристалле сохраняется центр симметрии.
Из теории плотной упаковки следует:
1. Молекула симметрии ттт и 2/т всегда сохраняет в
кристалле центр симметрии, и только центр симметрии.
2. Молекула симметрии mm либо «теряет» все свои элементы
симметрии, либо сохраняет в кристалле симметрию т или 2.

Таблица V, III
Проетранственные групаы, разрешённые принципом плотной упаковки для молекулярных кристаллов
Вероятные
пространственные
группы
Возможные
пространственные
группы
Симметрия молекулы
1

Пространственные группы
C'ih = P2Je
С) = P2i
VA = Р2Д2,
ct = I
C)v = Pea
C',v = Pnm
l"3 = P2,2i2i
С] = Л2
Z
4
2.4
4
2.4
4
4
4
4
m, mm
Пространствен-1 у
ные группы j
С] = P2i
С, = 1
C*t, = Pea
C\v = Рюп
V™ = Pnma
C22v = Рте
Cg = Cm
4
2,4
4
2.4-
4
4
4
4
4
2, mm

Пространственные группы
C% = P2lC
С] = P2!
1'4 = P212l2l
G; = i
G]v = Pea
Clv = Pnm
l^4 = Pnca
V3 = P2&{1
Z
4
2,4
4
2,4
4
4
4
2
i, 2jm шю»г

Пространственные группы
<4 = P2!/C
C]h = 42/a
z
2.4
4
1.2
4
4

420 структурный анализ вёз оценки интенсивностей [гл. v
3. Молекулы симметрии т чаще «теряют» в кристалле свою
симметрию, иногда сохраняют еб *). Весьма показательно, что
плоские молекулы, обладающие плоскостью симметрии, проходящей
через все атомы молекулы, всегда теряют эту симметрию в
кристалле.
На основе табл. V, III можно ввести определение «ассоциации
молекул». А именно, число молекул Z в ячейке, большее, чем
приведено в таблице, указывает на ассоциацию и, более того,
на симметрию возникающего острова. Так, например, при Z=8 —
в группе V™ имеется ассоциация в центросимметричные острова;
при Z—8 в группе Pj,6 имеется ассоциация в зеркальносимме-
тричные острова.
В. 011РЕДЕЛЕНИЕ РАЗМЕРА И СИММЕТРИИ ЯЧЕЙКИ КРИСТАЛЛ!
И ЗАКЛЮЧЕНИЯ, КОТОРЫЕ МОГУТ БЫТЬ СДЕЛАНЫ
ИЗ ЭТИХ ДАННЫХ
§ 1. Определение размеров элементарной ячейки кристалла
и трансляционной группы
В некоторых случаях эта задача исключительно проста, однако
иногда и опытный исследователь может затратить на еб решение
много дней.
Если кристалл хорошо образован и система его очевидна, то
работа сводится к събмке рентгенограмм вращения (или качания)
около основных осей. По расстояниям между слоевыми линиями
(стр. 327) вычисляются значения периодов.
Особенно удобной для этой цели является описанная выше
камера НИЙФ МГУ. Кристалл устанавливается своей основной
осью вдоль оси гониометрической головки. Первый снимок делается
при вертикальном положении оси головки; для получения других
снимков кристалл поворачивается по кругу и по дуге на углы,
вычисленные из гониометрических исследований или из съёмки
лауэграмм. В сложных случаях для нахождения пужиых углов
поворота (т. е. таких, при которых интересующее нас
направление кристалла совпадает с осью качания) следует пользоваться
стереографической проекцией.
В качестве примера рассмотрим определение параметров
элементарной ячейки и трансляционной группы кристалла одного
органического соединения формулы НООС — СН2—N = (СН2—СН2—ОН)2.
Кристаллы этого соединения имеют форму длинных пластинок.
Гониометрическое измерение указывает на принадлежность их
*) Подчеркнём, что речь идёт не об искажении формы молекулы, а о том
что еб элементы симметрии не принадлежат кристаллу.

8 1] опредЕлянйЕ размеров ячвйки кристалла 421
в моноклинной системе, причём ось Ь совпадает с нормалью
к широкой грани пластинки, а моноклинный угол Р (угол между
длинным и коротким ребром пластинки) равен 76°32' (фиг. V, 17).
Кристалл был съюстирован так, чтобы длинное ребро пластинки
(ось а) совпало с осью гониометрической головки. После этого
головка была аеренесеиа на камеру НИИФ МГУ и установлена
вертикально (положение на дуге 0°). Пользуясь камерой как одно-
кружным отражательным гониометром (пуская пучок света в
диафрагму), головку повернули так, чтобы широкая грань пластинки
была перпендикулярна оси диафрагмы, т. е. совпадала с плоскостью
дуги (при нулевом положении дуги). При этом лимб, фиксирующий
(010)
(011)
Фиг. V, 17. Кристалл (НОСН2СН2)2 NCHgCOOH.
поворот гониометрической головки вокруг собственной оси,
находился в положении 70°. При такой ориентации кристалла была
снята рентгенограмма качания с интервалом 15° (вообще для
определения параметра рекомендуется снимать рентгенограммы качания
с возможно большим интервалом качания, ибо при этом слоевые
линии выражены особенно четко). Путбм измерения расстояний
между слоевыми линиями (см. стр. 327), был определён период
вдоль выбранной оси а: а = 10,25 ±0,05 А. Поворотом головки по
дуге на величину моноклинного угла с осью качания была
совмещена ось с (ориентация: дуга 76°30', круг 70э). Рентгенограмма,
снятая при этой ориентации, дала величину параметра с=13,99±0,07А.
Повороты гониометрической головки вокруг её оси на 90° и по дуге
в положение, перпендикулярное оси вращения (ориентация: лимб
160°, дуга 90°) привели ось Ь в совмещение с осью качания.
Полученная рентгенограмма, как и следовало ожидать, обладала
горизонтальной плоскостью симметрии и позволила определить

422 структурный анализ без оцвнки интенсивности [гл. v
параметр Ь: 6 = 11,08 zt 0,03 А. Для определения наличия или
отсутствия центрировки выбранной ячейки необходимо было
определить экспериментально величины периодов вдоль трех плоских
(dab, dbc, dca) и пространственной (dabc) диагонали и сравнить их
с вычисленными. Решением прямоугольных треугольников со
сторонами 1) а и Ъ и 2) Ъ и с были вычислены величины периодов
о
вдоль диагоналей (dab= 15,10 A; dbc = 17,85A) и углы этих
плоских диагоналей с осями (a> = dab, а = 47°14'; ? = dbc, Ь = 51° 37').
Для определения периода вдоль диагонали dab кристалл должен быть
ориентирован так, чтобы 1) плоскость аЪ совпадала с плоскостью
дуги (лимб 160°), 2) ось головки отклонялась от оси качания
(первоначально совпадавшей с осью а) на угол <о дуга яь 47°. Для
определения периода вдоль диагонали dbc: 1) плоскость be должна
совпадать с плоскостью дуги (лимб 70°), 2) ось головки должна быть
отведена по дуге от положения, соответствующего вертикальности
оси Ь на угол 51,5° (дуга 38,5°). Рентгенограммы, снятые при этих
о
ориентациях кристалла, дали величины da6— 15,05 и df;c = 17,86A.
Следовательно, выбранная ячейка нецентрирована в гранях ah и Ьс.
Аналогичным образом была найдена ориентация кристалла,
необходимая для определения величин периодов вдоль диагоналей dac и dahp,
а также вычислены величины этих периодов (dac = 15,20 А, диаго-
о
наль, лежащая против острого угла (з; dabe== 18,81 А лежит в одной
плоскости с предыдущей). Экспериментальные же значения
периодов вдоль этих диагоналей таковы: dac = 7,62 =t0,08 A; dalc==
о
= 18,88 =t 0,10 А. Следовательно, выбранная ячейка центрирована
в грани ас. Поскольку кристалл моноклинный, возможен (и
необходим) переход к примитивной ячейке по формулам
Ъ' = Ъ,
, а — с
Параметры этой новой ячейки (элементарной согласно правилам,
излагавшимся в гл. I) таковы:
a = 9,44 А; Ь = 11,08 А; с = 7,62 А; р = 108°.
В большинстве случаев наличие или отсутствие центрировки
ячейки очевидно из наблюдения рентгенограмм качания, снятых
по основным осям. Для этого надо, чтобы на рентгенограмме были
чётко выявлены хотя бы 2—3 интерференционные кривые, изобра-

§ 1] ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ЯЧЕЙКИ КРИСТАЛЛА 423
жбнные на сетке симметричных интерференционных кривых. Как
уже говорилось выше, пятна, попавшие на одну симметричную
интерференционную кривую, соответствуют одной узловой прямой
обратной решётки, параллельной оси вращения. Это означает, что из трёх
индексов Ш, характеризующих каждое пятно, два (скажем, huh)
одинаковы для всех пятен, попадающих на одну кривую, а третий
получает значение 0 для пятна на нулевой слоевой линии, 1—для
пятна на первой линии, 2— для пятна на второй линии и т. д.
Если интерференционная кривая сплошь занята пятнами, то, значит,
присутствуют отражения с индексами, hkO, hkl, hk2 и т. д. Может
быть и такой случай, когда пятна присутствуют на симметричной
интерференционной кривой через одну линию, т. е. либо имеются
ftjbo, Кк2, ЬЫ и т. д., либо hkl, hkb, hkb в т. д. Нетрудно видеть,
что кривые, заполненные пятнами через одну слоевую линию,
указывают на центрировку ячейки в вертикальной плоскости (плоскости,
проходящей через ось вращения), тем более справедливо обратное
заключение — центрировка отсутствует, если кривые заполнены
пятнами сплошь.
Это положение следует непосредственно из выражения для
структурной амплитуды
1 hkl — jLI I re
г
Наличие центрировки в вертикальной плоскости означает, что, каждой
точке xry1zr имеется эквивалентная либо в центре грани хз, либо
в центре грани уз, либо, наконец, в центре объёма элементарной
ячейки (качание происходит вокруг оси з). Координаты этих точек
соответственно будут:
,1 ,2.- ■ « А - л- i -ul -J-.1 - _l L
xrl~2 > Ur> zr\ g' xr> Уг~Т~ 2 ' *r ' 2 ' ^T j > Уг\ 2 ' sr\ 2 "
Всю сумму в выражении F можно разбить на пары слагаемых:
•ir.i(hx + ку +1г ) . 2Ki(ha>r+kyr + te,Л^~-)
Центрировка хз: е r rr/-j-evr r ' г ',
lj3. е8-* (Ч-+k,Jr+иг) _|_ е^ ('">+кУг+V-Ч1 )f
<■ « 2Bi(toг + кУг+1гг) I *r-*(b*r+*Vr+l*r+ — %±L)
» по ооъбму: с у r r -\-e v r r r 2/.
Сумма будет обращаться в нуль при условии
центрировка хз: к~\-1ф2п,
» уз: к~\-1ф2п,
» цо объёму; Н-\-Ь-\-1ф2ц,

424 СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦЕНКИ ПНТЕНСИВНОСТЕЙ [ГЛ. V
Следовательно, при наличии одной из этих центр ировок слоевые
линии, полученные при качании кристалла около оси г, будут
заполнены пятнами через одну на каждой симметричной
интерференционной кривой.
При рассмотрении трёх рентгенограмм, снятых при качании около
трёх осей ячейки, мы можем столкнуться со следующими тремя
случаями: а), ни одна из рентгенограмм не указывает на
центрировку—трансляционная группа простая; выбранная ячейка
примитивна; б) две из трёх рентгенограмм указывают на центрировку —
ячейка центрирована по одной грани, причём по той, которая
перпендикулярна к оси вращения «нецентрированной» рентгенограммы;
в) все три рентгенограммы указывают на центрировку — ячейка
либо центрирована по всем граням, либо по объёму.
В последнем случае, а также, если симметричные
интерференционные кривые выражены нечётко, устанавливают центрировку
съёмкой рентгенограмм качания около диагоналей (плоскостных
или пространственной). Ясно, что в случае центрировки период
должен быть в два раза меньше, чем это следует по расчбту длины
диагонали в предположении простой ячейки. Если кристалл плохо
образован, то оси его приходится «нащупывать» при помощи лауэ-
граммы так, как это описано выше (стр. 307). Итак, мы показали,
что систематические погашения отражений общего типа НЫ
однозначно определяют трансляционную группу. Эти систематические
погашения сведены в таблицу V, V (стр. 441).
Следует помнить, что в таких случаях одновременно с ячейкой
мы определяем и систему кристалла. Найденная «вслепую» ячейка
может быть не элементарной, а также и преуменьшенной. В
заблуждение могут ввести случайные значения моноклинных или триклин-
ных углов, близкие к 90°.
Преувеличение размера ячейки обнаружится по наличию такой
центрировки граней, которая не приводит к новой трансляционной
группе (например, центрировка базиса моноклинной ячейки). При
полном индицировании рентгенограммы такая ошибка всегда
обнаружится по погашениям интерференции общего типа Ш. Съёмка
рентгенограмм качания вдоль диагоналей также докажет
центрированность ячейки, принятой за элементарную.
Преуменьшение размера ячейки может произойти при
одновременном неправильном определении системы. Представим себе
например, что в ромбической объбмноцентрированной ячейке мы нашли
периоды вдоль пространственной диагонали и вдоль двух основных
осей. Можно сделать ошибочное заключение, что мы имеем дело
с триклинным кристаллом. Эту ошибку можно обнаружить,
внимательно рассматривая соотношения между углами и длинами рёбер
полученной ячейки. Б. Н. Делоне предложил общий метод, который
позволяет производить так называемую однозначную установку
кристалла, если известна одна из его элементарных ячеек. Обоснование

§ 1] ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ЯЧЕЙКИ КРИСТАЛЛА 425
этого способа дано в специальной книге*). Мы приведём здесь лишь
рецепт. Пусть найдена ячейка, длины осей которой a, b и с и углы
между этими осями а, р и f (угол а = &, с, {3 = с, а, тг = а, &)• П°
этим шести числам находим значения следующих шести величин:
д = Ъс cos а; 1=~а2 — h — h;
h — са cos (3; m =— б2 — # — Л;
& —a&cos?; w = — с2 — g — h.
Эти шесть величин располагают в пространстве, приписывая
каждое число стороне изображённого на фиг. V, 18 тетраэдра. Если
все шесть величин отрицательны, то nqeflKa выбрана правильно и
изображённый тетраэдр даёт символ кристалла,
по которому, как мы увидим ниже, находят
систему и трансляционную группу. Если
среди этих величин встречаются
положительные, то символ нужно преобразовать но
следующему рецепту.
Выбирают любой положительный параметр
символа и вычитают его из параметра,
стоящего на противоположном ребре; прибавляют
его к параметрам, стоящим на остальных
четырёх рёбрах, меняют между собой местами
полученные параметры на двух из этих
четырёх рёбер, сходящихся в одном из концов
исходного ребра (всё равно каком) и, наконец, меняют знак самого
рассматриваемого параметра.
Если, например, #>(), то нереход выглядит так:
Фиг. V, 18. К
правилу рациональной
установки.
Исходное ребро выделено жирной линией.
Эту операцию повторяют до тех пор, пока все шесть величин
не станут отрицательными.
Пример
*) АдександровДЦелоне, Падуров, Математические основы
структурного анализа, 1936,

42(3 СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦВНКИ ИНТЁНСИВПОСТЬШ [г.1. V
Жирная черта указывает ребро, соответствующее параметру,
исходному в данной операции; жирной точкой отмечен тот конец, около
которого мы хотим менять параметры местами.
Пространственный тетраэдрический символ, полученный в
результате такого преобразования, даёт знание сингоний и
трансляционной группы. Числовые значения шести величин не существенны,
важно лишь знать, какие из них равны нулю и какие равны или
не равны между собой. Для отыскания сингоний и трансляционной
группы служит следующая таблица.
а) Ни одно из чисел символа не равно нулю
А~г; А-ч А-г- А~г;
А~г* А-?- А-* А-?»
б) Одно из чисел символа равно нулю
в) Два числа па противолежащих рёбрах равны пулю
Д-* &-* Д-r А~г» Д-*
г) Два числа на сходящихся рббрах равны нулю
д) Три числа равны нулю
Д-* Д-* Д-с
Если на ребре нет отметки, то это значит, что соответствующее
число может быть любым, не равным остальным числам. Рёбра,
отмеченные одинаковым числом штрихов, имеют одинаковые числа.
(Об обозначениях трансляционных групп смотри стр. 75.)

§ 1] ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ЯЧЕЙКИ КРИСТАЛЛА 427
Если нас не удовлетворяет одно лишь указание на то, что
выбранная элементарная ячейка не дабт правильной установки кристалла
и что на самом деле кристалл обладает такой-то системой и такой-то
трансляционной группой, а мы хотим кроме того знать, как перейти
от начальных осей а, Ь и с к новым А, В, С, в которых кристалл
получает правильную установку, то надо действовать по следующему
рецепту: вершины начального тетраэдра отмечаем буквами а, 6, с и d.
ъ
Параллельно с описанными преобразованиями чисел д, /*, k,
I, m, n проделываем преобразование векторов а, Ь, с и d
следующим образом.
Вектор, стоящий у жирно отмеченной вершины, прибавляют
к векторам, стоящим у вершин, не принадлежащих жирному ребру,
и меняют его знак на обратный. Вектор d — а-\-Ъ-\-с.
В приведённом выше примере преобразование векторов
выглядит так:
ъ ~ь ъ
Проиллюстрируем применение метода на примере (фиг. V, 19).
1 V-
10
- /
оу
/
/
/
/
/
/CSfl
С--64
Д=74
Фиг. V, 19. Пример перехода к правильной установке.
Предположим, что в ромбическом кристалле трансляционной группы Г'

428 СТРУКТУРНЫЙ АНАЛИЗ ВЕЗ ОЦЕНКИ ИНТЕНОИВЯОСТЕЙ [гл. V
была найдена триклинная ячейка:
а=10,63А; 6 = 8А; с = 5А;
cos а = 0,8; cos 8
^_М. ,
10,63 '
COSf =
10,63
11окажем, что описанным выше способом можно найти «правильную»
систему и трансляционную группу кристалла.
Вычисляем шесть параметров:
0 = 8-5- 0,8 = 32,
/i = 5- 10,63
6,4
= 32, h = 8 • 10,63
6J,
10,63 ""' "'"" 10,63
Z = — 113 — 32 — 64 = — 209, t» = —64—32 —64 = —100,
п = — 25 — 32 — 32 = — 89.
Выписываем исходный символ и приступаем к его приведению:
+32
+ 64,
-§2
+32
то-есть
или, так как символ надо мыслить пространственно,
Цо приведённой выше таблице находим правильный символ Г'

§2]
Размеры ячейки
Ш
§ 2. Размеры ячейки и заключения о структуре кристалла
а) Вычисление коэффициента упаковки. Если объём ячейки V
вычислен, то при известной плотности и молекулярном весе может
быть найдено число молекул в элементарной ячейке. Масса,
приходящаяся на ячейку, равна pV=nMmH; отсюда
где V—объём элементарной ячейки в кубических ангстремах;
р— плотность вещества в г/см3; »»я= 1,66 • 10~24г — вес атома
водорода; М — молекулярный вес. На одну молекулу приходится
у
объём —; обозначая собственный объём молекулы через V0, получим
следующее выражение для коэффициента упаковки
*-^- (V.8)
В случае не молекулярного кристалла, а кристалла
координационного (например, ионного) типа понятие молекулы, как'
известно, не -имеет смысла. По существу весь кристалл хлористого
натрия, например, представляет собой гигантскую молекулу (Na0l)n,
где п -► со. Однако и в этом случае можно подсчитать объём
«молекулы» NaCl, который попросту равен сумме объёмов шаровых
ионов Na+ и С1~, и подсчитать по формуле (V, 3) коэффициент
упаковки. Можно пользоваться и видоизменённой формулой
коэффициента упаковки (формула (V, 1), которая удобна именно для ионных,
атомарных и вообще координационных кристаллов.
Для плотной упаковки одинаковых шаров любого размера в лю^бой
ячейке к = 74,05%. Для ионных кристаллов, состоящих из плотной
упаковки анионов, в пустоты которой входят катионы, коэффициент
упаковки может возрасти примерно до 81,5%« Если коэффициент
упаковки становится много меньше 70%» то эт0 следует
рассматривать как прямое указание наличия гомеополярной связи.
Представление атомов шарами в этом случае имеет чисто формальный
характер. Так, например, представляя шарами атомы углерода
в структуре алмаза, атомы Zn и S в структуре цинковой обманки,
мы получим к =34 — 35%* Это — прямое доказательство наличия
обменной связи между атомами*).
*) Гомеополярные кристаллы относятся к нединадным кристаллам,
ибо в них нельзя выделить молекулы. Однако в этих кристаллах имеет
место направленная связь между атомами и в силу этого можно различить
2 расстояния: 1) меньшее между атомами, связанными валентно
(характеризуется атомным радиусом); 2) большее между атомами, валентно не
связанными. Наличие расстояний двух типов и обусловливает «рыхлость»
структуры при аппроксимации атомов шарами с атомными радиусами.

ЫО СТРУКТУРНЫЙ АНАЛИЗ ВЕЗ ОЦЕНКИ ИНТЕНСИВНОСТЕЙ [гл. V
В органических кристаллах представление атомов шарами
привело бы к коэффициентам упаковки порядка 15—20%, что
показывает также совершенную неприменимость этих представлений. Как
мы указывали уже ранее, в случае гомеополярпой связи следует
характеризовать структуру двумя радиусами — атомными (сумма
которых даёт межатомное расстояние химически связанных атомов)
и межмолекулярными (сумма которых дабт межатомное расстояние
химически не связанных атомов).
Если имеет место гомеополярная структура, в которой нельзя
выделить молекулу, то атом будет представлен почти полным
многогранником, стороны которого суть плоскости,
перпендикулярные связям. Этот многогранник есть остаток от шара, описанного
межмолекулярным радиусом. На фиг. V, 20 изображен такой
«остаток» от углеродного атома алмаза.
Из вычислений коэффициента упаковки можно сделать ряд
существенных следствий. Аппроксимируя атомы шарами атомных или
Фиг. V, 20. Слева «остаток» углеродного атома алмаза; справа
«остаток» атома азота аммиака.
ионных радиусов и определяя к, мы можем судить о «степени
атомарности или ионности» кристалла. Малые (меньшие 0,6—0,7)
значения к указывают па невозможность такой
аппроксимации н, следовательно, на наличие в структуре гомеополярнов
связи.
Как это следует из приводимой таблицы V, IV, коэффициенты
упаковки молекулярных кристаллов колеблются в незначительных
пределах (собственные объёмы вычислены при помощи двух
радиусов) н близки к коэффициенту плотной упаковки шаров.
Выпадающие значения к указывают на какую-либо ошибку (в определении
плотности, молекулярного веса, размера ячейки).

РАЗМЕРЫ ЯЧКИКЦ
4:41
Табл ица V, IV
Коэффициенты упаковки (&)
Соединение
Л. Д и н а д н ы е
к р и с т а л л ы
Бензол
р-дибромбензол
Формула
н
1
II 1
• ?г
и с
J '
Br
• со
■*« я
о о Я
Ой ч
83
126
122
170
i
: А-
i
0,681
0,740
/>-бромхлорбен-
зо л
jo-дихлорбоньол
^гЛ^с^г
a-CV»
I I
120
114
168
0,714
166
0,681
Дифенил
Парадифенилбеи
зол
и
н н и
V-/ х '
с=с с—с
/ \ // \\
и—с с—с с
W W
сн
||СЧ>^СН
сн
сн
1Г>3
223
207
306
0,740
0,730

432 СТРУКТУРНЫЙ АНАЛИЗ ВИЗ ОЦЕНКИ ИНТЕНСЙВНОСТЕЙ [ГЛ. V
Продолжение
2
7
8
9
10
11
12
13
14
1£
16
П
18
Соединение
Тетрафенил
Нафталин
Антрацен
Графит
Диоктилиафта-
лин
Б. Координа-
ционные
кристаллы
Алюминий
Медь
Т-жедезо
а-железо
Магний
Хлористый литий
Хлористый
натрий
Формула
ск
НсЦ^СН
СП
v i
и i T
I 1
н и
н н н
"n/VAcAc^
J ¥ i JL
■»' VCWV"
1 1 f
H II II
1
i
Al
Cu
T-Fe
o-Fe
Mg
LiCI
NaCl
Объём

молекулы в A8
293
127
171
15,82
402
12,3
8,8
8,6
8,0
17.2
25,8
29,0
I
l
l
i
392
181
237
17,83
675
16,5
11,76
12,0
11.7
23,0
34,0
44,6
1:
0,746
0,702
0,722
0.887
0,595
0,74
0,74
0,73
0,69
0,74
0,76
0,65

2] РАЗМЕРЫ ЯЧЕЙКИ 433
Продолжение
"в"
2
19
20
21
22
23
24
25
Соединение
Хлористый калий
Хлористый
рубидий
Хлористый цезий
Йодистый натрий
Рутил
Цинковая
обманка
Алмаз
Формула
КС1
КЬСЛ
CsCl
NaJ
тю2
ZnS
С
Объём

молекулы в А3
34,7
38,5
43,6
48,3
21
4,28
61,8
70,0
69,4
67,5
30,9
39,8
5,514
к
0.56
0,55
0,63
0,72
0,68
0,776
Примечание к таблице V, IV. В качестве динадных
кристаллов выбраны кристаллы ароматических соединений. Коэффициенты упаковки
весьма высоки и в большинстве случаев превосходят коэффициент плот-
нейших шаровых упаковок (0,74). Коэффициент упаковки закономерно
растёт с укрупнением молекулы (например ряды 1, 8, 9 и 1, 5, 6, 7);
максимально плотной, естественно, является упаковка графита. Малой плотностью
упаковки отличается диоктилнафталин. Это обстоятельство объясняется
«неудобной» формой молекул, которым трудно упаковаться в кристалл.
Это вещество кристаллизуется с очень большим трудом. Повидимому,
органические вещества не могут кристаллизоваться, если Тс оказывается
меньше £ts 0,60.
Координационные кристаллы 12, 13,14,15,16 представляют собой плот-
нейшие шаровые упаковки атомов (первые — плотнейшую кубическую,
последний — гексагональную). В силу этого для них fc = 0,74. а-железо
кристаллизуется в объёмноцентрированной кубической решётке; эта
упаковка является менее плотной, чем упаковка в кубической всесторонне
центрированной решётке кристалла у-железа. Поэтому а- и f-Fe имеют
разные коэффициенты упаковки (0,69 и 0,73).
Для бинарных ионных кристаллов коэффициенты упаковки закономерно
изменяются в ряду 17—22. Маленькие ионы Li+ свободно входят в окта-
эдрические пустоты плотнейшей упаковки ионов С1~. Поэтому fc
оказывается ббльшим. чем fc плотнейшей упаковки шаров. При увеличении
размера катиона (Li+ -*Na+ -»-K+ -»-Rb+) упаковка ионов С1"" перестаёт
быть плотнейшей, ибо катионы, не умещаясь в пустотах, раздвигают
анионы. Коэффициент упаковки закономерно падает, но способ упаковки
остаётся прежним (тип NaCl). Наконец, кристалл «предпочитает» изменить
способ упаковки, чтобы сделать её более плотной (структура CsCl). По сути
дела упаковку анионов в кристаллах, подобных NaCl, KC1, RbCl нельзя
считать плотнейшей (шары основной упаковки не соприкасаются). Поэтому-
то структуры таких кристаллов с полным правом можно сопоставлять
с различными типами плотнейших шаровых упаковок. Интересно отметить,
что, оставляя катион прежним и заменяя анион на более крупный, мы
приближаем структуру к истинной плотнейшей упаковке анионов (сравни
NaCl и NaJ).
Кристаллы алмаза и цинковой обманки являются гомеополярными. Поэто*
му для подсчёта к необходимо пользоваться межмолекулярными радиусами.

4:34 СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦЕНКИ ИНТЕНСИВНОСТЕИ [гл. V
Доля объёма Va, приходящегося на тот или иной атом
молекулы А, может быть вычислена, если известны межмолекулярный
радиус RA, расстояния dAl,dAV dAydA4,.. . до химически связанных
с ним атомов, имеющих межмолекулярные радиусы Ви В2, />'а и
Rt, ... по формуле
4
^ = ^-2i*/^8*4--A,), (V,4)
где
есть высота сегмента сферы радиуса Л а, отсекаемая сферой
радиуса Bi (фиг. V, 21).
Кроме вспомогательного значения при структурпом анализе
вычисление коэффициента упаковки органических молекул в кристалле
имеет и самостоятельный
интерес.
Наименьшие из
наблюдавшихся
коэффициентов упаковки
принадлежат легко
переохлаждающимся
веществам, дающим
«охотнее» аморфные тела,
нежели кристаллы. В
качестве примера можно
привести 2,6 диоктил-
нафталин, имеющий
коэффициент упаковки,
Фиг. V, 21. К вычислению доли объёма, при- равный О 595
холящегося на атом в молекуле. Чем слоящее форма
молекулы, тем, вообще
говоря, меньше её коэффициент упаковки. У молекул, обладающих
формой, близкой к эллипсоиду (нафталин, антрацен), коэффициент
упаковки близок к 0,74.
Заслуживает упоминания и то обстоятельство, что
коэффициенты упаковки полиморфных модификаций одинаковы. Это
несомненно указывает на существенное значение коэффициента
упаковки, как одного из энергетических факторов образования
кристаллической решётки.
В этой связи можно также отметить, что при потере симметрии
в решётке (в смысле, указанном на стр. 419) коэффициент
упаковки при прочих равных условиях возрастает. Так, коэффициент
упаковки перилена, кристаллизующегося с двумя кристаллографи-

и
РАЗМЕРЫ ЯЧЕЙКИ
435
чески неэквивалентными молекулами в ячейке, равен 0,805. Может
быть стремление к максимальной симметрии и к максимально
плотной упаковке являются двумя важнейшими конкурирующими
факторами в образовании кристаллической решётки.
Примером этой конкуренции является, например, ряд тетра-
фенйлстаннатов Sn (C6H4R)4:
Формула
1) Sn (С6НБ)4
2) Sn (p C6H4CH3)4
3) Sn(^C6II4OCH3)4
4) Sn(/>C6H4OC2H5)4
Симметрия кристалла
Тетрагональная . . .
Тетрагональная . . .
Тетрагональная . . .
Симметрия
молекулы
в кристалле
4
4
4
1

Коэффициент
упаковки
0,70
0,68
0,62
0,67
При переходе от соединения 1) к 3) усложняется арильный
радикал, форма молекулы становится «мало удобной» и
коэффициент упаковки падает. Однако симметрия молекулы в кристалле
пока ещб сохраняется. Переход от 3) к 4) привёл бы при
сохранении прелшей симметрии к ещё меньшему коэффициенту упаковки
(<0,6). Это, однако, уже недопустимо малый коэффициент
упаковки, и соедипение 4) «предпочитает» кристаллизоваться с мепь-
шей симметрией, но с большей плотностью.
б) Тождественные и подобные ячейки. Изоморфизм, хорошо
известный кристаллографам, находит, разумеется, своё объяснение
в тождественпости или подобии элементарных ячеек. Из
тождественности элементарных ячеек могут быть сделаны выводы о.
возможности образования твёрдых растворов," предсказания об
аналогии свойств и т. д.
К важным выводам приводит сравнение ячеек химически
родственных органических соединений.
Одним из первых наблюдений, сделанных в этом отношении,
было измерение элементарных ячеек нафталина и антрацена.
Оказалось, что моноклинные ячейки кристаллов этих двух соединений
очень схожи: два основных периода и «моноклинный» угол очень
близки друг к другу, а третий период у антрацена больше на
2,50 А. Все первоначальные выводы в отношении строения молекул
ароматических соединений основывались на структуре графита.
Известно, что основная сетка графита построена из правильных
шестиугольников, сторона которых равна 1,42 А. Ширина такого
шестиугольника равна 2,44 А. Таким образом, из сравнения
размеров ячеек нафталина и антрацена можно вывести ряд следствий,
28*

436 СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦЕНКИ ИНТЕНСИВНОСТЕЙ [гЛ. V
а именно, естественно предположить, что молекулы нафталина и
антрацена построены из таких же шестиугольников, что и графит,
и далее, что оси молекул нафталина и антрацена примерно
совпадают с той осью .кристалла, вдоль которой изменяется период
(фиг. V, 22).
Позднее были получены аналогичные данные в отношении
полифенилов. Ячейки дифенила, терфенила и кватерфенила отли-
о) Нафталин 6)антрацен
Фиг. V, 22. Ячейки нафталина и антрацена. Центры
молекул занимают вершины и центры граней Ъс
элементарных ячеек. На фигуре показана проекция на
плоскость Ъс. Ячейки отличаются размером лишь по одной
оси с: нафталин—а = 8,34; b = 5,98; с = 8,68 А; р = 122°44';
антрацен—а=8,58; Ь = 6,02; с —11,18; р = 125°. Разность
^антр ~ снафт = ^50 А весьма ,близка к ширине
бензольного кольца. Это указывает, что ось молекулы
ориентирована почти параллельно оси с.
чаются только длиной одпой из осей, причём эта длина возрастает
на величину 4,2 А при добавлении к молекуле одного бензольного
ядра. Вполне очевидно, что эта величина представляет собой сумму
диаметра ядра 2,8А и длины С — С — связи между ядрами,
которая, следовательно, должна равняться 1,5 А (фиг. V, 23).

§2]
РАЗМЕРЫ ЯЧЕЙКИ
437
Парадифенилбензол
Такие же сходные друг с другом ячейки можно наблюдать
у производных названных выше соединений. Например,
исследованные недавно 1,5-дихлорнафталин и 1,5-дихлорантрацен,
кристаллы которых образуют подобные
ячейки, отличающиеся друг от
друга лишь длиной одной из осей
о
на ту же величину 2,45 А.
Разумеется, заключения о
строении молекулы, делаемые из
измерения ячеек, могут носить
лишь самый общий характер,
а цифры, аналогичные
упомянутым выше, не могут
претендовать на большую точность. И все
же значение подобных
заключений (в особенности, принимая
во внимание лёгкость получения
экспериментальных результатов)
не следует недооценивать.
Суждения об аналогии в
строении легко и уверенно
делаются по измерениям
элементарной ячейки. Например,
кристаллы jp-дихлорбензола, .р-ди-
бромбензола и jp-хлорбромбен-
зола обладают почти
одинаковыми ячейками. Очень большое
число 2,6 и ^-производных
нафталина обладает ячейкой, одна
сторона которой имеет всегда
о
размеры 8 X 6 А. Число
примеров можно было бы умножить.
Таким образом несомненно, что
если измерение ячейки одного
соединения не даёт, вообще
говоря, сведений о строении
молекулы, то сопоставление таких
измерений для какого-либо ряда
соединений может дать ценные
сведения о структурных
различиях или сходстве молекул.
в) Определение
молекулярного веса и плотности. Хотя
число молекул в ячейке не
определяется измерением размера
Фиг. V, 23. Ячейка гюлифенилов.
Центры молекул находятся в
вершинах и центрах граней Ъс ячейки.
На фигуре показана проекция на
грань Ъс. Ячейки бифенила а) и
парадифенилбензола (терфенила) б)
отличаются лишь размером вдоль
оси с; а): а = 8,11; Ь = 5,67°; с=9,47 А;
Р = 93,3Э б): а = 8,08; Ь = 5,60°; с =
= 13,59 А; р = 91°55'. Разность длин
осей г. 4Д2 А близка к сумме длин
диагонали бензольного кольца
(2,8 А) и связи между кольцами
(1,5 А) —4,3 А. Это указывает на то,
что длинные оси молекул
ориентированы примерно параллельно оси с.
Совершенно аналогична ячейка
следующего члена ряда кватерфенила:
/—\_/—\_/~~\_/~~\
а = 8,05; 6=5,55; с=17,81 А; р=95,К"\
Разность гкв — гтор «4,22 А,

438 СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦЕНКИ ИНТЕНСИВНОСТЕЙ [г.1. V
элементарной ячейки, но всё же о нём можно сделать
определённые предположения.
Число несимметричных молекул не может быть меньше
кратности общего положения пространственной группы. Если нам
известна система или класс симметрии, то и в этом случае на
число молекул может быть наложено ограничение. Так, например,
в моноклинных решётках число несимметричных молекул не может
быть меньше 2, в классе С2Л оно не может быть уже меньше 4,
в пространственной группе С%ъ оно не меньше 8. Следует
отметить, что случаи ассоциации молекул (см. стр. 420) встречаются
весьма редко. Поэтому с большой вероятностью можно утверждать,
что число несимметричных молекул равно кратности общего
положения. В этом числе мы не будем сомневаться, если имеется
возможность примерной оценки собственного объёма молекулы VQ.
Выбрать один из двух возможных вариантов, скажем 8 или 16
молекул в ячейке, не представит труда, если подсчитать на
основании V0 коэффициент упаковки, который должен оказаться
близким к 0,70—0,75.
Молекулярный вес будет определяться по формуле (V, 2),
куда входит плотность. Различают рентгенографическую плотность
ррентг, т. е. вычисленную из размера ячейки, числа молекул и
молекулярного веса, и непосредственно измеренную рИЗм.
Эти величины могут довольно сильно различаться, так как
Рронтг это плотность идеальной решётки, а ризм — плотность
реального кристалла. Наличие невидимых микротрещин и пор скажется,
разумеется, в определённую сторону. При измерениях плотности
фактический объём кристаллической массы преувеличивается, т. е.
рИ:ш имеет заниженные значения. В эту же сторону уменьшения
Ризм при измерении могут подействовать пузырьки воздуха,
цепляющиеся за кристалл. Таким образом, рЯЗм < Рронтг- Как правило,
наблюдаются отклонения на 2—3% в указанную сторону.
§ 8. Определение пространственной группы
Наличие среди элементов симметрии кристалла плоскостей
скольжения и винтовых осей может быть наидепо по систематическим
погашениям определённых диффрагированных лучей.
Пусть, например, у кристалла) имеется плоскость со
скольжением вдоль оси а, перпендикулярная оси Ь. Таким образом, любой
точке xryf2r внутри элементарной ячейки соответствует
эквивалентная xr-\-~, {3— yr, zr, где р зависит от выбора начала
координат (см. выше табл. I,VII). В этом случае сумма в
выражении структурной амплитуды
Ящ = 2 fr ехР 2™ (hxr + ,СУГ "Н Ц-)

§ 3] ОПРЕДЕЛЕНИЕ ПРОСТРАНСТВЕННОЙ ГРУППЫ -130
разобьётся па пары слагаемых
Dxp 2гл (krr-f hjr-j- Ьг) + ехр 2тЛ(кгг — кцг -f Ur -}- T-j- ,3/,
Проанализируем эту сумму. Если индекс к отличен от нуля, то
никаких закономерных
обращений в нуль написанное вы-
еажение иметь не будет, но
рели к = 0, то получаем
выражение
ехр 2ы (кгг -\- ter) -\-
-}- ехр 2га hxr -j- lzr -j- — ) ,
которое будет обещаться
в нуль при нечётном h.
Отсюда вытекает правило:
наличие плоскости со
скольжением вдоль а (Ь, с),
перпендикулярной оси Ь (с, а), влечёт
за собой исчезновение
интерференционных лучей,
отражённых от плоскостей зоны оси
Ь (с, а), у которых индекс,
соответствующий линии
скольжения, нечётный.
Нетрудно образно
представить себе причины этих
погасаний. Наличие скольжения
по-разному сказывается на
плоскостях, скажем, 101 и 201.
На фиг. V, 24 показано,
что плоскость со скольжением
вдоль а образует вставные
плоскости между плоскостями
системы (АО/) при h ф 2» и не
образует их у систем (До/)
при h = 2n.
И ещё один способ
наглядного представления причин
погасаний. Пусть построена
проекция распределения
электронной плотности на
плоскость xOz. Эта функция
представляется рядом (см. стр.
474), коэффициентами кото*
4EZ^
2^
6)
Фиг. V, 24. о) А, А'— плоскости
семейства (101). Плоскости скольжения
а (010) с компонентой скольжения
я/2— С, С, С" — образуют вставные
плоскости В, расположенные между
плоскостями семейства (101). б) А, А',
А" — плоскости семейства (201). В этом
случае плоскости скольжения С, G'JG"
не образуют вставных плоскостей
(вернее, они совпадают с основными
плоскостями А, А'у А"\

440 СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦЕНКИ ИНТЕНСИВНОСТЕЦ [ГЛ. V
рого являются F,,0j. Так как все h—четные, то, очевидно, ту же
проекцию можно получить, уменьшая все /*, а вместе с ними и
длину оси а вдвое (сравни формулу структурного фактора). Таким
образом наличие плоскости скольжения, перпендикулярного некоторой
оси, уменьшает вдвое величину независимой площади
соответствующей проекции.
Таким же способом нетрудно убедиться, что наличие
диагональной плоскости скольжения п, перпендикулярной, скажем,
оси а, влечёт за собой погашение интерференции типа (Ш при к -\~ I
нечётном.
d£
Г"
/
/В
г
Л '
/-1
/
/
V-S \ \
ь/2
1--/Л ь
/ ■'
L/
tb
о)
V
б)
Фиг. V, 24а. а) А, А'— плоскости семейства ((J10).
Винтовая ось 2j [010] с компонентой скольжения Ь/2
образует вставные плоскости В. б) А, А', А"—плоскости
семейства (020). Вставные плоскости не образуются.
Рассмотрим теперь кристалл, у которого имеется винтовая ось
второго порядка 2V направленная вдоль оси Ъ (фиг. V, 24а).
Тогда каждой точке хГ1 уг, гг соответствует эквивалентная а — хг,
уг-\--г, у — zr, где а и -у зависят от выбора начала координат.
Структурная амплитуда и в этом случае разбивается на пары
слагаемых:
ехр2iti{hxr-\- kyr-f- lzr)-f exp 2ra(—hxr-j-kyr—lzT-\- ha-\-у -J- l-Л .
Эта сумма будет закономерно обращаться в нуль при нечётных
значениях к, причём это будет возможным лишь для тех лучей,
у которых индексы h ж I равны нулю. Иначе говоря, будут
погашены нечётные порядки отражения от плоскости (010)»

§ 3] ОПРЕДЕЛЕНИЕ ПРОСТРАНСТВЕННОЙ ГРУППЫ 441
Итак, наблюдение погашений среди отражений общего тина Ш
позволяет (как мы видели ранее, на стр. 423) выносить суждение
о трансляционной группе, наблюдение погашений среди отражений
от плоскостей зоны позволяет определить наличие плоскости
скольжения, перпендикулярной оси зоны, и, наконец, наблюдение
погашений отражений от одной плоскости позволяет установить
наличие винтовой оси, перпендикулярной этой плоскости.
Определение открытых элементов симметрии по погашениям легко
осуществляется при помощи таблицы V, V.
Таблица V, V
Определение трансляционной группы и открытых элементов симметрии
по систематическим погашениям
Класс
отражений
Ш
(Ш
лог
Условие
систематического
погашения
отражений
Н + 1с-\-1ф2п
П + кф2п
к + 1ф2п
к + 1ф 2»
h + k \
h + 1 \ф2п
fc-H J
— h -f к +1 = Ы
h + k-\-l = 3n
кф2п
1 ф 2w
1с + 1ф2п
к + 1ф4п
Пф2п
1ф2п
к + 1ф2п
Н + 1ф4п
Причина погашений
Объёмно-центрированная
решётка
С-центрированная решётка
В-центрированная решётка
Л-центрированная решётка
Гранецентрированная
решётка
Ромбоэдрическая решётка в
гексагональной установке
Гексагональная решётка в
ромбоэдрической
установке
Плоскость скольжения (100)
компонента Ь/2
с/2
Ь/2 -f с/2
» ft/4 -f c/4
Плоскость скольжения (010)
компонента а/2
с/2
» я/2 + с/2
» я/4 + с/4
Символ соот-
ветств.
трансляционной группы
или открытого
элемента
симметрии
J
а
и
л
F
Д
Н
Ь (Р, В, С)
c(P,G,J)
п(Р)
d(F)
а (Р, A, J)
с(Р, Л, С)
п(Р)
d(F),(B)

442 структурный лпа.ш;? без оценки шгшюшшостей [гл. v
Продолжение
Класс
отражений
hhl
hOO
ОкО
001
hhO
Условие i
систематического! ,, „„.„••
погашения | Причина погашении
отражений
i
1ф2ч
НфЫ
Ь-\-1ф2п
2Ь-\-1ф±п
кф2п
h фАп
кф2п
кф±п
1ф2п
1фЫ
1фЫ
1фЪп
Ъ,ф 2п
Плоскость скольжения (НО)
компонента с/2
» а/2 + Ь/2
а/4 4- Ь/4 4- с/4
а/2 4-Ь/4 + с/4
Винтовая ось [100]
компонента Ь/2
» «/4
Винтовая ось [010]
компонента Ь/2
» Ь/4
Винтовая ось [001]
компонента с/2
» с'З
» с 4
» с, 6
Винтовая ось [110]
компонента я/2 -f- Ь/2
Символ соот-
ветств.
трансляционной группы
или открытого
элемента
симметрии
с (/\ 0, F)
Ь(С)
п(С)
d(J)
2i, 42
4ь 43
-ь 4,
4ь 43
2l. 42, 6;{
Зь Зг, 6г, 64
4i, 4г
fil, 02
2!
На основании этой таблицы можно составить список
систематических погашений, характерных для того или иного сочетания
элементов симметрии (открытых и закрытых), т. е. для той или
иной пространственной группы. Таким образом возникает таблица
для определения пространственных групп по погасаниям,
предложенная Ждановым (таблица V, VI), .

Таблица V, VI
Таблица погасаний для определения 120 рентгеновских rpyuu *)
I. Триклинная система Лауэ-класс С; — 1
с/у>
п/п
Диффракционный
символ
1 1рГ
Погасания
Пространственные группы
6\ = Р1; Сг = Р1
II. Моноклинная система Лауэ-класс Cyt — 2/w
№
п/п
2
3
4
5
6
7
Диффракционный
символ
2/мР —/—
2/i»P2i/—
2/mP —/>«
2/wP2i/c
2jmC —/—
2/mC —jc
Погасания
hkl
—
—
—
—
\h + k\
\h+k\
m
—
—
M
MM
h
h\T\
ОАО
—
ill
—
\±\
к
к
Пространственные группы
C\h = Р2/т- С] = Р2; С] = Рт
C]h = Р21,'т; С- = P2t
<4 = Р2/с; С] = Рс
Cb2h = P2l!c
C\h = 02/w; С* = С2; Oj = Cm
C%h = С2/с; Cj = С*с
о
с
•ч
и
>-
к
Еч
к
в
и
к
►о
о
о
*) Г. С. Жд анов и В. А. Поспелов, ЖЭТФ 15, 709, 1945.
со

Ш. Ромбическая система Лауэ-класс Vh — D^—ттт
Продолжение
1
i №
, п/п
8
9
10
И
12
13
14
15
16
17
18
19
Днффрак-
ционный
символ
тпгтР
mmmP2i
тттР2\2\—
mm7nP2\2i2i
тттРс
тттРч
тттРЬа —
тттРса —
тттРсс —
тттРпа—
тттРпс
тттРпп
Погасания
Ш
—
—
—
—
—
оы
—
—
—
—
И
|* + ?|
Щ
Ш
и
|*-и|
•* + '|
\к + г{
hOl
—
—
—
—
—
В
и
hkO
—
—
—
—
—
\h\
Li.
\h + 7\
—
A00
—
\h\
1*1
N
—
n
h
n
h
OkO
—
—
m
s
к
к
к
к
к
001
—
—
—
а
г
i
г
г
i
Пространственные группы
D\h = Рттт; В\ = Р222;
C\v = Ртт2
D* = P2j22
Z)| = P212J2
Я* = Р2&&
Щп = Pcmm; C\v = Pcm2\;
Cl = Pc2m
ВЦ = Рптт; C72v = Pnm2
Dlh = Pbam; G\v^Pba2
Dx^ = Pcam; Clv = Pca2
Dlh = Реем; C.J, — Pcc2
D\l = Pnam; C^ = Px«2
J}\b = Pncm; G\v = Pnc2
D^i = Pnnm; СЦ = Рпп2

Продолжение со>
со
Х«
п/п
20
21
22
23
24
25
26
27
28
29
Днффрак-
ционный
символ
ттмРЬса
тттРсса
тттР Ьоп
тттРЬсп
тттРссп
тттРппа,
тттРтпп
тттА
тттА 2\
mnimA — а —
Ш
U- + M
fc-H
I* + *
Погасания
Old
Т|
!* + *!
йог
"Л
11
Гл+П
д|;
/)fc0
|л|
1 д + fc 1
Ift + fcl
|л + ь|
д + &|
доо
OfcO
ooz
Пространственные группы
А I к
ПЦ = РЬса
Т&п = Рсса
D*h = Pban
D\b = РЬсн
D1,?, = Рссп
D?,b = Рипа
)6
'2ft
Z>2ft = P»WMl
2>5ft = 4ww>n; Г>6 = Л222;
GJJ, = Л2ши
C*J, = Amm2
B\ = Л2Х22
D^ss Amam; С** = Am*2;
Gfv = Л2ши

Продолжение
м
п/п
30
81
32
33
34
35
36
37
38
39
40
Диффрак-
ционный
сектор
тттАЪ
mmmAba —
тттА - аи
тттАЬаа
mmmj
it.mmJb
mmmJba —
mmmJbca
mmmF
mmniFdd —
mmmFddd
Погасания
hkl
\b+l\
\k-{-l\
Ll+lI
EH
| h + k +?|
IA +fc + Z,
1 h + к + I1
jI+T+Tl
ow
jTl?
k + l
\k\l
Vk~\l
k + {
Jfc + 7 = 4»i|
|&+? = 4n|
лог
[h\i
\h\i
h -f;
л -'- /
A|7j
h + l
А + 7 = 4и'
|ft + I=4n|
Ш
&
_1_Л_| А-
Л-i-fc
A + A:
h + k
Yh\k
h + k
h -j- к
\h + k =4n |
Ш
h
h
h
h
h
h
h
h
A = 4n
A = 4n
OfeO
к
к
к
к
к
к
к
к
к
ft = 4n
fc = 4n
оог
/
i
i
i
'
i
i
i
f
I = 4:11
I = 4u
Пространственные группы
Dll = Abaw; СЦ = АЪа2
ВЦ = А таа; СЦ - А 2а а
D?h= Abaa
П\ = J222;
DtX = Jmmm;
Cg° = Jmm2
Dfn = Jbmm; Gfv = Jbm2
ПЦ = Jbam; Cf0 = Jba2
Dr^ = Jbca
D?2l = Fmmm; B\ = F222;
СЦ == Fw///2
G^ = Fdd2

3]
ОПРЕДЕЛЕНИЕ ПРОСТРАНСТВЕННОЙ ГРУППЫ
447
о
Пространственные группы
Погасания
8
©
-г?
г*:
Диффракционный
символ
-^ А, ->
II II II
rJ -f -* >* ч' "*
тН -Ф "*■ -т ч* -т
Рц Сц A, ^ i-s *-s
li II II 11 II II
17 Ъ" *Г t? о* «^
S" Д. S -?_ а
^ -ф "^ **+• ^1
1! II II II II
О О О о w
,Е,
! 1
-5
il
>
5 4i
1 |~| - ll ll
1313
+
r-5;
й « Й
r«j r«e '—1
; i I
+
as
+
r-S;
+
+
1—1
rid
+
l~
■^i^ тН " "^ "Ф "^ "Ф ■*+* "^t1
,о, И пН 54 СО -* Ю О С- 00
i
s
1
3
Ю
о
о
rrt
4
«
Лауэ
■я
53
о
£->
О
S
<У
и
•
ч
ев
о
и
Pi
V. ТвТ
3
с
Pi
и
ные
»
нств
ев
Рч
о
Про
«
к
огасан
С
о
о
8
»«
►с
о
о
•ее
г«
*е
«3
3
я
я
2 ч
S3 о
я" за
« Я
се я
Pi О
>9<
>е*
S3
Ч
*f
а
g
■ф
Он
11
р
о"
s
Сч Рц
И II
J
Ps
II
Q
1
1
.„
CO
Рч
II
•в
to ы
I
|
I
1
I
t
1
1
1
1
Г
1
►ч
I
^

Продолжение
№
п/п
50
51
52
53
54
55
56
57
58
59
60
61
62
63
Диффракционный
символ
ijmrnmP —,'— 2i —
4/w»w?P42/
4/»m»?P4i/
4/ш>шР42/— 2t —
4jmmmP4.il— 2j —
4jmmmP —/— b —
4\mmmP —/— с —
4/ш>шР —/— n —
4/ш>шР —jn
4jmmmP —/ с
4/ш/шР —/— 2iC
4jmmmP —/— be
AlrnmmP —/— cc
4lmmmP —/—не
Погасания
hkl
—
—
Ш
—
—
—
—
~~" i ~
- \h+k]
— —
— —
_ _
— —
—
—
Okl
—
. ..
1*1
Ш
IM-'I
—
—
—
щ-
M
1 k+l |
hhl
—
*
—
—
—
H
Ш
Ш
Ш
ill
MX)
1*1
—
1*1
1*1
h
h
h
—
\h\
h
h
00?
—
Hi
|?=4w|
Ul
|/ = 4»|
—
1
I
—
1
1
I
I
I
Пространственные группы
1)\а~Р42хт; Dj = P421
D* = P4a2
Dl = P4t2
PJ = P432]
^ = P4121[Z)« = P4321]
nlh = P4imbm; D7M = P4&2; 0^ = PAbm
D\l = P4jmcm; B\d = P4c2; C\v = Picm
D^ = Pijmnm; D\d = P4n2) C*v = P4nm
D\h = P4\nmm
n\h = P\:mmc; Dld = Pl2e; C'47v = P4>wc
/)24d = P42lC
J>S = P4/«be; &*,=P4bc
J)*ft « P4/wcc; <&, = P4cc
Djh = P4/wnc; Cj„ = P4wc

№
п/п
Диффракционный
символ
Погасания
hkt.
МО
(Ш
hhl
64
65
66
67
68
69
70
71
72
73
74
75
76
77
4\тттР —'nb —
IjtnmmP —[пс —
^jmmmP —jnn —
ijmmmP — jn — с
ijwmmP —!nbc
4.[mmmP —/ncc
4jmtnmP —Innc
4\mmmJ—/
4/mmmJ4i/
4jmmmJ —/— с —
4/mmntJ — / d
4jmmmJ —/— cd
ijmmwJ —/a — d
4lmmmJ —jacd
—
—
—
—
—
—
—
\h+k+l\
\h+k+l\
lA-ffc-Hl
\h+k+l\
\h+k+l\
|A+Jc+?|
~h+k+i\
U+fc|
\h+k\
|A+fc|
1 h+h |
|A+ft|
\h+k{
I h+k |
h+k
h+k
h+k
h+k
h+k
Щк
\h\k
E
ill
[k+l\
—
E
EO
\k+l\
k+l
k+l
k\T\
k+l
k\l\
k+l
k\T\
ш
ill
2A+?
2Л+/
2h+l
|2A+Z=4w|
|2A+Z=4h|
\2h+l=4n\
\2k+l—4n\
11родолжение СОй
— _-_ со
Пространственные группы
*>а
»S = J4/
^
J74?l —
D16 —
7)12 _
J^47»
7)11 -
J^4ft —
ns —
ubh —
P4jnbm
P4jncm
P4jnnm
P4jnmc
P4inbe
P4jncc
P4jnnc
= Jijmmm; ^
D2d~
Glv = J4mm; Z)J =
D\°
ncm; D2°c
I = J42d
Cil =
D™ -
П20 i
=/4^
= J4c:;
Jlm2;
J4~2m;
= /42
CjJ = J4cm
СЦ = Mm-l
= J4cd
= J\\amd
— J4jacd

\ТГ. Ромбоэдрическая система Лауэ-класс С3/ — 3
Продолжение
№
п/п
78
79
80
Диффракционный
символ
Зс-
3c3t
ЗД —
Погасания
hkil
—
\ii— fc-f l=3n\
hhOl
2h -f / = 3n
000Z
—
| / = 3n |
1 = Sn
Пространственные группы
G3} = (73; (73 = (73
C* = C3j; [Oj = (732]
Gj,- = .КЗ; С .j = Mo
VII. Ромбоэдрическая система Лауэ-класс I^ — 3m
п/п
81
82
83
Диффракционный
символ
ВмО
3/мОЗ!
a»wO —с —
Погасания
hkil
hhQil 000?
—
(
1 1 = 3n | |
и
Пространственные группы
•
D\d = C3~lm; Dj = 0312; С'^ = C3wl
D\d = Cbml; Dl = (7321; C|„ = C?31w
1)3 = c-3^2; [D^=C3212]
DjeOe^l; [D^= 03^21]
Z)*d = 03c; C*,= 08e

Продолжение ^
№
п/п
84
85
86
Диффракционный
метод
ЗтН с
ЗшЕ
3/»JR — с
Погасания
hkil
\h—~k = Зи |
\h — k-{-l=3n\
\h — k-\-l=3n\
hhOl
| /, h = 3n 1
|2Д+г=зп|
|2/*+/ = 3n|
000/
/
I — 3n
| I = 6n |
Пространственные группы
Dld = R3c; G\v=EZc
VIII. Гексагональная система Лауэ-класс G'e/t—6/m
с
a
w
fa
п/п
87
88
89
90
Диффракционный
символ
6>C—/ —
6/*iC6a/—
6//«C62/-
. 6/i»C6i/—
Погасания
000/
Ш
| г = зп |
| г = en |
Пространственные группы
(4 = C6/m; Cj-Св; <4=C6
<4=C63/w; C« = C63

Продолжение
IX. Гексагональная система Лауэ-класс D^.— (jjmmm
П;'П
91
92
93
94
95
96
97
i
Диффракционнын
символ
QjmmmG —/
QjmmmCQ2l
6/»»»mC6i/
6'mmmC—/ с
QjmmmG—/—с —
(jt'mmmC—/— rr
Погасания
hl)2bl
—
—
Ш
—
и
hhQl
—
—
—
ш
и
000^
—
и
| 1 = Зн |
| Г = вп\
1
I.
1
Пространственные группы
В4 -
if —
D\h = Cfymmm; D\ = 062;
D\h = C6///2
С(1.у = CQmm;
Dlh=Cb2m
J>J = C632
^ = C'6,2; [Z>5=Oe42]
^6=^2; [Z>i?=C652]
GQImmc; C^ = C6wc; Л}й = C62c
C6>cw; 6*^ = C6c/w; D'lh = CGc2
^eft = Сб/'wcc; C^ - C6cc

X. Кубическая система Лауэ-класс 1),, — шЗ
Продолжение °Оо
со
п/п
98
99
100
101
102
103
104
105
Днффракционный
символ
тЗР
тВР21 —
тЗР — а
шЗР — п
тЗ,1
m3Ja —
m'SF
m'SFd —
Погасания
hid
—
—
Ih+k+i i
1 h+k + l \
LsJ
Ш
hl-0
—
m
|A-bfr|
A-f к
\h\k
h к
| h 4- к = 4н 1
Л00
ш
Л
A
Л •= An
Пространственные группы
2t;, = Pw3; Тх = Р23
Т* = Р2{3
К = РаЗ
T'i = J23
Tj] - JihB;
TJ = J2V3
Г* = Z-w3; Г- = /'23

XL Кубическая система Лауэ-класе Oh — m3»i
Продолжение
№
п/п
106
107
108
109
НО
111
112
113
114
115
116
117
118
119
120
Диффракцион-
ный
символ
тдтР
w3w»P42
w8wP4i
mZmPn
тВтР п
тВшРп — п
mB>nJ
mdmMi
mSmJ d
mZmJa — d
mBmF
m3mFii
mdmF с
mSmFd
mBmFd — с
Погасания
Ш
_
i й+fc+d
I A + fc-f l\
\h-\-k~\-l\
1 h'+ k-\-l\
ГЁ1
ls"r
AfcO
—
\_h±kj
1 h + k\
h + k
A-ffc
h + k
Yh\ к
h к
h к
h k
|ft + fc=4«|-
\h + k=4n\
hhl
и
2h + l
2h + l
|2A + ? = 4n|
\2h + 1=*in\
h + f
h + l
h\T\
h+1
А И
A00
Щ
| h = 4n |
A
A
A
| A = 4h 1
h
h
h
| A = 4»? |
A
A = 4«
A = 4»
Пространственные группы
Oj = P»i3w; O1 = P43; T\ = P43w
O- = P423
07 = P413; [0(1 = P4y3]
Oxh = Pn3w»
O-; = Pmdn; T\ = Р43я
O^ = pndn
Ol=J>nBm; 05 = ЛЗ; Гj = J43w
O8 = J4X3
Tj = J4.U
O™ = J«3d
O* = Fw3>«; O3 = F43; Tj = F43m
0* = F4t3
Oj = Fw3c; T^ = F-i3c
О), = Fd3/«
Ol = Fd3c

§ 3] ОПРЕДЕЛЕНИЕ ПРОСТРАНСТВЕННОЙ ГРУППЫ 455
В первом столбце приведён диффракционный символ. Он
составлен следующим образом: на первом месте указывается символ
лауэвского класса, далее трансляционная группа. Далее, в
моноклинной, тетрагональной и гексагональной системах указывается
характер главной оси; если эта ось простая, то ставится тире.
После дробной черты в этих системах и непосредственно за
символом трансляционной группы в остальных системах
указываются элементы симметрии в обычной последовательности, т. е.
плоскости, перпендикулярные осям а, Ь и с, и оси, параллельные
осям а, 6, е. В тетрагональной системе на первых двух местах
ставятся элементы симметрии, перпендикулярные осям а и Ь, на
последнем месте стоят диагональпые плоскости симметрии. Простые
элементы симметрии не проставляются — вместо их символов
ставится тире — так как они не дают погашений.
В следующем столбце приведены погасания общего типа. В
случае отсутствия погасаний ставится тире. Далее идут погасания
зон и, наконец, погасание отражений разных порядков от
координатных плоскостей. В последнем столбце приведены символы
пространственных групп, входящих в данную «рентгеновскую группу».
Смысл квадратных рамок, которыми обведены некоторые
индексы, следующий: эти погасания определяют пространственную
группу. Если же погасания ЫЛ являются следствием из
погасаний Ш, то они не обведены квадратными рамками. Например,
в группе С1ь. погасания hoi при 1ф2п определяют наличие
плоскости скольжения, а погасания при Ь,ф2п являются следствием
условия появления Ш только при чётном h-{~Jc.
Следует помнить, что условия погашения составлены для
определённого выбора осей. Поэтому при сравнении опытных
результатов с таблицей следует перепробовать все перестановки в
наименованиях осей.
Знак £ означает закон погасания гранецентрированной решётки,
т. е. Ъ,-\-~кф2п, к-\-1фп и h-\-1фп. Индексы в графе
«погасания» указывают, что отражения присутствуют на
рентгенограмме, если индексы равны чётному числу. Иные условия
присутствия отражений написаны в явной форме, например I = Вп.
Во многих случаях рентгеновское исследование не позволяет
определить пространственную группу однозначно. Несколько
пространственных групп оказываются неразличимыми при
рентгеновском исследовапии. С точки зрения диффракции рентгеновских
лучей они совершенно эквивалентны и поэтому объединяются в одну
так называемую рентгеновскую группу. Число пространственных
групп равно 230, а число рентгеновских 120*).
Возьмём, например, 18-ю строку таблицы. Указанным в
таблице погасаниям могут соответствовать группы Рпст в Рпс2. Мы
*) Г. С. Ж л а н о в, ЖЭТФ 15, 1945.

456 СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦЕНКИ ИНТЕНСИВНОСТЕЙ [ГЛ. V
не можем только по симметрии рентгенограмм и закономерностям
в погасаниях отличить простую двойную ось от перпендикулярной
к ней зеркальной плоскости симметрии. Первая группа отличается
от второй лишним цептром симметрии. Можно указать такое
правило: если две пространственные группы различаются друг от друга
в отношении комплекса элементов симметрии на центр симметрии
и если этот центр симметрии не создает новых плоскостей
скольжения и винтовых осей, то такие группы не различимы.
Вывод погасаний, характерных для пространственной группы,
может быть сделан при помощи выражения для структурной
амплитуды, которое, в свою очередь, вычисляется из координат общего
положения атомов, как это было показано на стр. 228.
Приведём пример: структурная амплитуда группы /Лл имеет
следующий вид:
*ш = 28/;cos2*k[cos2r(/^^
г
+ coS2,(tx, + *i|±-')coS2x(fo/r + i±l±i)] .
Мм видим, что это выражение не упрощается для индексов
типа hid и hko. Напротив, для индексов ОМ структурная
амплитуда имеет вид
Fou — У\Sfr cos2,idz cos2*^-~- cos2^(ky 4--~) +
r
+ cos 2* (lex + ^J cos 2тг *ii]
и обращается в нуль при к-\-1ф2п. Аналогично находИхМ, что для
индексов типа hhl имеют место погашения при I ф 2и.
Следует иметь в виду, что совокупность погасаний, даже и
в том случае, когда в последнем столбце стоит один символ, лишь
характерна для данной пространственной группы и делает ее в
высшей степени вероятной, но не доказывает её. Действительно,
система закономерных погасаний может существовать и не будучи
связанной с наличием плоскости или оси скольжения. Вот простой
пример, иллюстрирующий сказанное. В элементарной ячейке
моноклинной системы имеются 4 атома с координатами хх, уи гх\
Первая и вторая, а также третья и четвёртая точки связаны
винтовой осью вдоль Ь; других симметрических связей между
точками нет. Поэтому пространственная группа будет 2%. Но
благодаря связц между х и з координатами первой и третьей, а также

§ 4]
ПРОСТРАНСТВЕННАЯ ГРУППА
457
второй и четвёртой точек возникнут погасания hoi при h
нечётном, т. е. погасания, характерные для группы P2ja. Случаи
такой псевдосимметрии хотя и относительно редки, но встречаются.
Только чутьё исследователя поможет здесь избежать ошибки.
Иногда псевдосимметрия может быть явной; например, в
моноклинной решётке обнаруживаются ногасания типа hkO при Ъ,ф2п
или в ромбической решётке класса C2v обнаруживаются погасания
О&О при расположении оси класса вдоль а или вдоль с. Наличие
таких исевдоосей и псевдоплоскостей симметрии приносит большую
пользу в структурном апализе, указывая па сверхспммстрическую
закономерность в расположении частиц.
Особо осторожно следует относиться к заключениям, делаемым
но погасаниям о пространственной группе при наличии в ячейке
очень тяжёлых (по сравнению с остальными) атомов.
В кристалле дифенилртути атом ртути занимает центр
симметрии в группе С|л; в ячейке 2 молекулы. Так как атом ртути
рассеивает в Zug: Zq раз больше, чем атом углерода, то картина диф-
фракции в первом приближении указывает на более высокую
симметрию, а именно, на наличие центрировки. Это получается по той
причине, что для отражений типа Ш при 7ь-\-7сф2п волны,
идущие от двух атомов ртути, взаимно уничтожаются; напротив,
при h-\-U~ 2n эти волны усиливаются (атомы Hg центрируют
плоскость аЬ).
Для того чтобы в аналогичных случаях можно было бы сделать
быстрые заключения о структуре по погасаниям, в существующих
таблицах пространственных групп указывают обычно «особые
погасания» для специальных положений атомов в решётке. Эти
«особые погасания» указывают, какие отражения отсутствовали бы,
если бы кроме атомов, находящихся в данном специальном
положении, не было бы других атомов.
§ 4. Пространственная группа, симметрия расположения атомов
и молекул в ячейке и химическая формула
Пространственная группа, число молекул в ячейке и
химическая формула молекулы находятся в определённой связи.
Действительно, в данной нространственной группе каждый из атомов может
быть размещён в общем положении—тогда ему соответствует
максимальная кратность, или на элементах симметрии с кратностью
меньшей максимальной. Зная символ пространственной группы, мы
можем составить список возможных в ней частных положений и
указать их кратность и кратность общего положения.
Рассмотрим в виде примера группу 1)\ь — 14jnmm. В
специальных справочных изданиях найдём, что в этой группе имеются

458 СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦЕНКИ ИНТЕНСИВНОСТКЙ [ГЛ. V
следующие положения:
Кратность
Число стопе-
ней свободы
Число
положений
2
0 12 3
2 1 — -^
* 1 «
0 12 3
2 1 — —
0 12 3
— 2 2 —
16
0 12 3
1
В нашей пространственной группе всего 4 положения без
степеней свободы, 4 симметрически независимые линии и 2
симметрически независимые плоскости, в которых можно
расположить, вообще говоря, сколько угодно атомов. Общее положение,
разумеется, только одно.
Пусть в ячейке находятся 2 атома А; тогда рассмотрению
подлежат только двукратные положения; все три заранее возможны.
В нашей ячейке не может находиться нечётное число атомов одного
сорта, ибо все положения обладают чётной кратностью. Если
в ячейке находятся 4 атома А, то возможно следующее. Либо все
атомы кристаллографически эквивалентны и, следовательно,
занимают одно из трех четырёхкратных положений. Либо атомы должны
быть разбиты на две группы по два и занимают любые два из
трёх двукратных положений. 6 атомов могут в принципе занять
три двукратных или одно четырёхкратное и одно двукратное
положения. 8 атомов могут занять либо одно из восьмикратных
положений, либо два четырёхкратных, либо одно четырёхкратное и
два двукратных и т. д.
В зависимости от того, имеем ли мы дело с ионным или
молекулярным кристаллом, анализ возможных размещений в ячейке
производится по-разному. В случае ионных кристаллов
рассматриваются возможности размещения ионов каждого сорта в
отдельности; в случае молекулярных кристаллов такой способ не имел
бы смысла, так как атомы, принадлежащие одной молекуле,
составляют • «одно целое». В этом последнем случае надо ставить
вопрос не о возможных точечных расположениях в данной
пространственной группе, а о возможной симметрии и числе
островов, существующих в данной пространственной группе. Точка хуг
находится либо в общем положении, либо на элементах симметрии
(или в пересечении элементов симметрии); в последних случаях
ей может быть приписана симметрия определённого класса. Это и
будет симметрия острова, «центр» которого попадёт на
соответствующий элемент симметрии. Так, в нашем случае в положениях
с кратностью 2 без степеней свободы пересекаются оси 4, 2 и
зеркальные плоскости т. Таким образом в рассматриваемой группе можно
разместить две молекулы симметрии 42m = D2d. В двукратном
положении с одной степенью свободы точка имеет симметрию

§4]
ПРОСТРАНСТВЕННАЯ ГРУППА
459
Civ = 4:mm; в четырёхкратных положениях без степеней свободы—
симметрию C2ft = —, в четырёхкратных положениях с одной
степенью свободы — симметрию C2v = 2mm. В нашей ячейке могут
быть размещены 8 молекул, обладающих симметрией С2 = 2, и 8
молекул, обладающих симметрией С8 = т. Число несимметричных
молекул в рассматриваемой ячейке должно быть 16 или кратно 16.
Наиболее просто размещение частиц в низкосимметричных
ячейках. Например, в группе C\h возможны лишь острова 1 или 1.
Центросимметричных молекул, связанных между собой операцией
симметрии, имеется 2. Таких двукратных положений имеется,
однако, 4. Число несимметричных молекул при этой симметрии
должно быть равно или кратно 1.
Случаи, когда число молекул в ячейке больше кратности общего
положения, означают ассоциацию молекул. Так, в ячейке
тринитротолуола находится 16 молекул при кратности общего положения 4.
В общем положении находятся четырёхкратные ассоциаты молекул.
Приведённые примеры охватываются общим нравилом:
произведение из относительного числа точек данного сорта на их
кратность есть величина постоянная для данной пространственной
грунпы (закон А. В. Шубникова).
Как для неорганических, так и для органических кристаллов
могут быть сделаны определённые выводы в отношении химической
формулы уже по определению общего характера структуры (размер
элементарной ячейки, пространственная группа). Вот один из
многочисленных примеров. Минералу гемиморфиту на основании
химических анализов присваивали формулу H2ZnSi05. Однако
структурный анализ показал, что ионы кислорода занимают в решётке
три типа неэквивалентных положений. Это объясняется, если
формулу минерала записать в виде (НО)2 Zn2Si207 • Н20.
В случае органических кристаллов определение элементов
симметрии молекулы (происходящее на основе определения
пространственной группы) в ряде случаев решает вопрос о строении.
Исследуя, например, пространственную группу диоктил-нафталина
неизвестного строения, удалось установить, что его пространственная
группа C*h и число молекул в ячейке равно 2. Это возможно,
если молекула обладает центром симметрии. Следовательно, объект
имеет формулу
с8п17
ила
СоН
8П17

460 СТРУКТУРНЫЙ АНАЛИЗ БЕЗ ОЦЕНКИ ИНТЕНСИВНОСТИ [гл. V
Геометрические соображения (см. ниже) помогли произвести
выбор и между этими двумя возможностями.
Иногда встречаются такие случаи, когда молекула (или
многоатомный ион) занимает частное положение, требующее от неб
определённой симметрии и притом не совпадающей с собственной
симметрией молекулы. Так, например, молекула jo-хлорбромбензола
С1—<^ Ъ—Вг занимает положение с симметрией центра
инверсии, а сама им не обладает. Другой пример: молекула C2H6HgCI,
имеющая собственную симметрию С8, находится на оси 4. Эти
отступления от общего правила (собственная симметрия молекулы !>
>- симметрии занимаемого ею положения в кристалле) объясняются
одной из двух причин. Во-первых, статистическим распределением
молекул. Это случай jp-хлорбромбензола. Грубо говоря, дело обстоит
так, что половина молекул ориентирована атомом Вг в одну
сторону, другая половина ориентирована атомом Вг в сторону прямо
противоположную. Поскольку рентгеновское исследование фиксирует
лишь среднюю для громадного числа элементарных ячеек картину,
мы не можем различить оба конца молекулы (С1 и Вг), т. е.
молекула приобретает «статистический» центр инверсии.
Гораздо чаще указанное отступление объясняется свободным
вращением. Молекулы в кристалле испытывают тепловые
колебания, а при благоприятных (в смысле наличия достаточного для этого
пространства) условиях могут притти и во вращательное движение
вокруг какого-либо направления (вообще говоря, момент инерции
молекулы относительно этого направления должен быть минимален).
При этом молекула приобретает симметрию тела вращения и может
занимать положение на оси любого порядка, если она совпадает
с осью вращения. Так, молекула C2H6HgCl вращается вокруг линии
CI — Hg — С, и эта ось вращения совпадает с осью 4. Особенно
часты случаи свободного вращения для кристаллов, построенных
из некрупных молекул (многоатомных ионов), которые, вращаясь
вокруг нескольких осей, приобретают симметрию шара. При этом
кристалл может приобрести весьма высокую симметрию.
В. ГКОМЕТРИЧЕСКИЙ АНАЛИЗ
§ 1. Учёт конечного размера атомов при размещении
их в ячейке
Геометрическим анализом называется рассмотрение возможностей
размещения частиц (атомов и ионов для неорганических и
молекул для органических соединений) в кристалле на основе данных
о симметрии и размере ячейки, с одной стороны, и о форме и
размерах частиц, с другой стороны.

§1)
УЧЁТ КОНЕЧНОГО РАЗМЕРА АТОМЯЁ
461
Рассмотрим совокупность элементов симметрии ячейки кристалла.
Через неб проходят плоскости и оси симметрии. Если в этой ячейке
требуется разместить какое-то количество атомов радиуса М, то
сразу же в ячейке могут быть выделены некоторые запрещённые
области, внутри которых наверняка не может находиться центр
а)
б)
в)
г) _ д)
Фиг. V, 25. а) Запрещённая область оси 2 (т, 1). б) Запрещённая область
оси 3. в) Запрещённая область оси 4. *) Запрещённая область оси 6.
д) Попадание центра атома в запрещённую область привело бы к
пересечению его с симметрично связанным, что противоречит установленному
на опыте постоянству атомных радиусов.
атома. Этими областями будут, очевидно, являться для простых
осей симметрии цилиндрические области радиуса R для оси 2,
njf 9 7?
радиуса —=. для оси 3, радиуса --==. для оси 4 и радиуса 2И для
У 3 V 2
оси 6 (см. фиг. V, 25, а, б, в, г).
Действительно, если центр атома находился бы от оси 2 на
расстоянии, меньшем радиуса атома В, то симметрическая операция

462 СТРУКТУРНОЙ АНАЛИЗ БЕЗ ОЦЕНКИ ИНТЕНСИВНОСТЕЙ [г.1. V
оси 2 «создала» бы из этого атома другой. Этот второй атом
«прорезал» бы первый, как это показано на фиг. V, 25 д, что
противоречило бы твёрдо установленному правилу постоянства атомных
(ионных и межмолекулярных) радиусов. Подобные соображения
заставляют принять существование запрещённых областей и для
других осей симметрии.
Аналогичные области охватывают и плоскости симметрии — их
толщина равна 2Е. Наконец, центр атома может приблизиться
к центру симметрии не ближе, чем на В,\ следовательно, центр
симметрии окружён сферической запрещённой областью этого радиуса.
Необходимо отметить, что положение центра атома на самой
оси симметрии (плоскости симметрии или в центре симметрии),
вообще говоря, не является запрещённым, если атом обладает
соответствующей собственной симметрией. Действительно, в этом
случае атом преобразуется симметрической операцией в самого
себя. Центр сферического атома или иона может находиться поэтому
на любом элементе симметрии. Если же атом входит в молекулу,
то центр его может занять положение на элементе симметрии лишь
в том случае, если через него проходит соответствующий
собственный элемент симметрии молекулы.
К винтовым осям и плоскостям скольжения атомы могут
подходить, вообще говоря, как угодно близко, если только величины
соответствующих трансляций имеют значение, большее 2Е.
Прекрасным примером применения геометрического анализа
этого типа является исследование карбида бора Ждановым и
Севастьяновым (см. стр. 625).
§ 2. Геометрический анализ ионных кристаллов
на основе теории плотной упаковки
Теория плотной шаровой упаковки позволяет, исходя из чисто
геометрических соображений, предсказать относительно небольшое
число возможных размещений ионов. Общие принципы
геометрического анализа ионных кристаллов по сути дела были изложены
выше. Самые крупные ионы определяют основную упаковку, и их
координаты могут быть вычислены, если имеются основания для
выбора типа упаковки. Другие ионы располагаются в пустотах,
координаты центров которых также можно вычислить. Заселяя ионами
те или иные пустоты, мы учитываем присущие им координации и
размеры пустот. Множество вариантов размещения ионов отпадёт
по этим признакам.
Приведём пример такого анализа, а именно, определение
структуры рамзаита, проведённое Беловым и Беляевым.
Рамзаит—сложный хибинский силикат Na3Ti3Si209. В элементарной ячейке
находится 4 молекулы. Пространственная группа F". Всего в ячейке

§ 3] геометрический апализ молекулярных кристаллов tG3
36 атомов кислорода. Крупные ионы кислорода в силикатах, окислах
и т. д. образуют всегда основную плотнейшую шаровую упаковку.
Разложение 36 на множители 6X3X2 очень хорошо соответствует
размерам элементарного параллелепипеда, если в основу положить
упаковку с тройной осью, иараллельнои наибольшему размеру
ячейки. Теория плотной упаковки показывает (см. стр. 407), что
период из 6 слоев может возникнуть в удвоенной кубической
упаковке, утроеппой гексагональной и единственной шестислойной
упаковке с символом ... | АВСАСВ |...
Удвоенная кубическая упаковка исключается, так как в группе Vh
имеются взаимно перпендикулярные плоскости симметрии,
невозможные в кубической упаковке с вертикальной тройной осью.
Должны быть рассмотрены две другие возможности.
Разбив формулу соединения на три части, можно исходить
из Na20 • 2ТЮа •' 2Si02. Известно, что кремний в силикатах всегда
занимает тетраэдрические, а титан — октаэдрические пустоты.
Шестерная координация вероятна и для натрия.
Сходство в размерах ячейки рамзаита и иироксена позволило
принять, что размещение атомов кремния в октаэдрических
пустотах у них одинаково. Сходство в размерах ячейки рамзаита и бру-
кита (ромбическая форма ТЮ2) позволило выбрать «узор», по
которому размещены в структуре рамзаита атомы титана. Для
размещения атомов натрия оказались возможными два варианта — один
из них приводил к утроенной гексагональной, а другой — к
шестислойной упаковке. Методом интенсивностей оставалось лишь выбрать
между двумя возможностями. Расчёты для шестислойной упаковки
совпали с опытом.
§ 3. Геометрический анализ молекулярных кристаллов
Опыт показывает, что геометрическое исследование при
известной форме молекулы приводит к единственной или во всяком случае
к небольшому числу возможностей размещения молекул в кристалле.
Поэтому геометрический анализ является средством нахождения
ориентировки молекул по отношению к основным осям ячейки.
Кроме того, геометрическим анализом можно в ряде случаев
установить и форму молекулы, пробуя поочерёдно размещать в
найденной ячейке возможные модели.
Идеи, делающие возможным проведение геометрического анализа,
сводятся к следующему: 1) молекула ограничена межмолекулярными
радиусами, остающимися неизменными во всех соединениях с
достаточной точностью (скажем, ztO,05A); 2) молекулы должны быть
уложены в элементарной ячейке с максимальной плотностью, т. с.
так, чтобы осуществлялось наибольшее число касаний между
атомами разных молекул*).
*) Китайгородский А. И., ИОХН, 587, 1946.

464 СТРУКТУРНЫЙ АНАЛИЗ ВЕЗ ОЦЕНКИ ИНТЕНСИВНОСТИ [ГЛ. V
Для проведения геометрического анализа нужно, изготовить
модели исследуемой молекулы и нужно располагать специальным
прибором — «структуроиска-
телем». В каждой
модели молекулы
просверливается три взаимно
перпендикулярных
отверстия — это собственные
оси молекулы X0YqZ0.
Четыре модели надевают-
ся на четыре стержня
и закрепляются винтами,
входящими в канавки,
прорезанные на
стержнях «структуроискате-
ля» (фиг. V, 26). Каждой
модели может быть
придан любой поворот по
отношению к основным осям
х, у, г прибора.
Основные оси прибора
пересекаются в том месте
стержня, где прорезана
канавка («центр стерзк-
ня»). Таким образом
становится попятным, что
начало собственной
системы коюрдинат
молекулы выгодно выбирать
именно в «центре
стержня». Три эйлеровых угла
Фиг. V, 2G. Структуроискатель. На стержни его
надеты три модели молекулы хлорбензола.
?i> ?2 и ?з>
определяющие взаимное расиолозкение систем координат хуг и X0Y0Z0,
отсчитываются но градуированным кругам, видным на фотографии.
Направление и начало отсчёта углов и начальное положение
систем координат должны быть ириняты раз и навсегда, например
так, как показано на фигуре V, 27. Соотношения между
координатами точки X0Y0Z0 и хуг будут иметь следующий вид:
х = У0 (sin срз cos в, -j- cos cpg sin <?2 sin ot) — ZQ cos ?2 sin <plf
У = Y0 cos cp3 cos cp2 + Z0 sin e2, (V, 5)
г = Y0 (sin o3 sin ot — cos сра sin ©2 cos ® t) -f- Z0 cos <pj cos cp2.
Написанные формулы пригодны для плоской молекулы Уо^о-
Не представляет труда добавить ко всем трём строчкам слагаемое

§ 3]
ГЕОМЕТРИЧЕСКИЙ АНАЛИЗ МОЛЕКУЛЯРНЫХ КРИСТАЛЛОМ
465
с множителем Аг0. Квадрат коэффициента при Аг0 легко находится
как дополнение до единицы квадратов двух других коэффициентов.
Каждая модель может линейно перемещаться. Две модели,
расположенные слева, могут перемещаться только вверх и вниз, модель
справа может перемещаться вдоль всей вертикальной плоскости и,
наконец, модель, находящаяся на переднем плане, имеет все
возможные степени свободы.
Рассмотрения соприкосновений четырёх молекул в подавляющем
большинстве случаев вполне достаточно. Для конкретности
предположим, что mf.i хотим провести геометрический анализ органиче-
'П
=4=W
f
~-~ф
Фиг. V, 27. Системы координат
молекулы и структуроискателя.
Ccosfi
Фиг. V, 28. Расположение центров
молекул.
ского кристалла, у которого пространственная группа i'2, а и ячейка
содержит 2 молекулы. Это значит, что центры молекул
фиксированы— в этом случае геометрический анализ особенно лёгок и
удобен.
Прежде всего центры стержпей располагаются так, чтобы
образовать узлы элементарной ячейки. Центр нижней левой молекулы
будем полагать в начале координат, центр верхней левой будет
расположен в точке .>' = 0, ц = Ь, 2 = 0; центр правой модели в точке
х—-о* ?/ = "о > ^ = ^ и, наконец, центр модели на переднем плане
в точке х = — с cos Р, у = О и z = с sin (3. Расположение центров
молекул показано на схеме (фиг. Y, 28).
Начинаем теперь поворачивать молекулы так, чтобы они могли
уложиться при нужных расстояниях между центрами. Сначала
удобнее всего установить две молекулы, связанные трансляцией
вдоль оси Ь. Разумеется, таких возможных расположений будет
множество. Но третья молекула разрешит из всей этой серии
расположений одно или незначительное число (падо помнить, что третья

4G0 СТРУКТУРНЫЙ АНАЛИЗ ВЕЗ ОЦЕНКИ IIHTEHCHBUOCTEii [ГЛ. V
молекула также симметрически связана с первой). При помощи
четвёртой молекулы, расположение которой также определяется
эйлеровыми углами первой молекулы, можно произвести проверку или
окончательно выбрать возможное решение.
Фиг. V, 29. Плотная упаковка молекул на
структуроискатолс. 1,5-дихлорантрацен.
Если углы, определяющие ориентировку основной молекулы,
суть <р„ ©2 и <е3, то молекула транслированная имеет углы ©,, ср2, ©а,
связанная с первой центром инверсии —о1} —?2, —©з
» » » осью 2 или 2j || а: —©j, cpQ —|- 180°,—?3
» » » » 2 » 2j ||?/ 9i -+-180°,—<р2, —«р3
» » » » 2 » 2j |J£ —»lf —©2, ©34-180°
» » » плоскостью симметрии J_ х — &и ©2, —<р3
(любой)
?/ ?1» — ?2
2»
»«
?1» — ?2» ?8

§ 3] геометрический лнллиз молекулярных кристаллов 407
В случае цептросимметричных молекул преобразования оси
и перпендикулярной к ней плоскости симметрии совпадают.
На фиг. V, 29 показано в виде примера найденное прибором
расположение молекул дихлорантрацена. Если мы хотим уточнить
полученные результаты, то можем поступить следующим образом.
Записываем, между какими атомами осуществляются касания.
Зная координаты Х0, У0, Z0 каждого атома (если считать
межатомные расстояния известными) и примерные значения эйлеровых
углов, полученных на приборе, можем рассчитать по обычным
формулам, приводимым в любом математическом справочнике,
значения координат х,у,з и далее найти расстояние между атомами
*» = VC'i -*а)» + (>Ji — ?/2)2 + (*i -*£*•
Для этой цели надо пользоваться приведенными выше
формулами координат. Однако следует помнить, что формулы резко
упрощаются для частных случаев. Например, формула расстояния между
атомом Уо1,^!1) основпой молекулы и Y^zlP молекулы,
транслированной вдоль оси //, имеет вид:
d\-> = Д Го + ^& + />2 — 2Ь (Д )'0 cos <?;J cos ср., -]- AZ0 sin cp2),
где ДУ0=Уо,)—УГ; Д^о = 4,) —^о2) и 6 —период вдоль этой
оси.
При таком уточнении можно ставить перед собой самые
различные задачи. Число касаний в обычном случае будет 5—6; таково
будет и число уравнений. Мы можем поэтому найти 5—6 величин,
т. е. три эйлеровых угла и два межатомных или межмолекулярнт.тх
расстояния и т. д.
В настояние время ещё трудна сказать, с какой точностью
сохраняются межмолекулярные радиусы в различных структурах.
Когда это станет известным, возможности геометрического анализа,
выходящие за рамки определения ориентировки молекул известной
формы и выбора из нескольких возможных моделей какой-либо
одной, станут также очевидными. Сейчас еще трудно сказать, можно
ли геометрическим анализом определять межатомные расстояния,
однако значение этого метода для нахождения ориентировки
молекул в кристалле трудно переоценить. Также большое применение
имеет геометрический анализ для выбора одной из возможных
пространственных конфигураций молекулы.

ГЛАВА VI
СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ
§ 1. Сравнение с опытом возможных моделей структуры
а) Измерение интегрального отражения и вычисление F,I3m.
Мы показали в главе III, какими формулами связывается
интегральное отражение Е{ЬЫ) с соответствующим структурным фактором.
Для определения F в абсолютных единицах надо знать, кроме
значения всех факторов интенсивности, величину интенсивности
первичного луча 70. Для измерения /0 необходимо прежде всего
монохроматизировать излучение рентгеновской трубки при помощи
отражения от кристалла (каменная соль, кальцит).
Монохроматический луч мы можем пустить в ионизационную камеру и, учитывая
площадь щели, найти /0.
Таким способом может быть найдено абсолютное значение Fwiiii.
Нет необходимости прибегать к этому измерению каждый раз.
Достаточно провести его один раз для какого-либо отражения hid
кристалла, выбранного в качестве эталона, а затем сравнивать с
величиной интегрального отражения этого кристалла значения интенсив-
ностей исследуемого объекта. Этот способ сравнения также даёт
возможность определить абсолютные значения F.
В таких измерениях (если это возможно) удобнее всего
пользоваться кристаллом, размеры которого меньше сечения первичного
луча (метод купающегося кристалла) и поглощением которого можно
пренебречь. Тогда для сравнения значений F эталона и
исследуемого объекта достаточно зпать объбмы образцов.
Измерения абсолютных значений F удобнее всего производить
при помощи рентгенспектрографа. Характеристикой интегрального
отражения, как это явствует из вывода формулы интенсивности для
метода вращения кристалла (стр. 244), является площадь кривой
силы ионизационного тока в функции угла поворота кристалла.
Если пучок падающих лучей был бы строго параллельным, то
интегральную интенсивность следовало бы измерять, не меняя
направления к — к0, а меняя только его величину. Это значит, что, найдя
точное значение угла Ьв (при этом ионизационная камера должна
находиться под углом 2ЬВ к первичному лучу), надо было бы
измерить интенсивность, поворачивая одновременно кристалл на угол Д&

§ 1] СРАВНЕНИЕ С ОПЫТОМ ВОЗМОЖНЫХ МОДЕЛЕЙ СТРУКТУРЫ 469
и камеру на удвоенный угол. Площадь возникающей таким образом
кривой ионизационного тока в функции \к—А?0| пропорциональна
интегральному отражению.
По этой причине наиболее строгим способом является
измерение интегральной энергии Е', попадающей в ионизационную камеру
при вращении камеры и кристалла со скоростями <а и 2<о. В этом
случае интегральное отражение равно Е'<а.
Интегральное отражение можно с успехом измерять,
поворачивая кристалл и оставляя неподвижной ионизационную ка меру с
широкой щелью.
При расходящемся пучке отношение площадей кривых отражения
(т. е. кривых зависимости ионизационного тока от угла поворота)
весьма близко к отношению максимальных значений
ионизационного тока. Для измерений с точностью ± 10—20% такая процедура
вполне удовлетворительна.
Если измерения эталона не проводились, то полученные цифры
дают относительные значения интенсивностей и, следовательно,
относительные значения F.
При определении интенсивностей фотографическим методом, как
правило, ограничиваются определениями относительных значений F.
В большинстве случаев удаётся без особого труда найти
коэффициент перехода к шкале абсолютных значений.
Дело заключается в том, что отражения с малыми индексами,
как правило, мало чувствительны к тонким изменениям в
структуре. Это нструдпо понять, если вспомнить, что плоскостям с
малым значением Ш соответствуют большие межплоскостные
расстояния. Если в грубых чертах структура решена, то значения FBU4,
вычисленные по формуле
N
*\ш = 2 fr еХР * 27Г Ои'г П - *//r + kr).
г=1
нс могут сколько-нибудь значительно отличаться от У,тизм. Следует
рекомендовать делать переход к абсолютным значениям F по
значениям средних по силе отражений. Иначе при наличии вторичной
экстинкции коэффициент перехода может быть выбран неверным.
Не следует, однако, недооценивать значения абсолютных
измерений /*', в особенности в тех случаях, когда в первой стадии
анализа— нахождения грубой модели структуры, приходится
сталкиваться со значительными затруднениями. Действительно, зная,
например, что какое-либо значение F1M близко к 2/г» мы заключаем
сразу, что все атомы расположены вблизи данной плоскости (hid).
Всё же большей частью перед тем, как приступить к анализу
интенсивностей, исследователь обладает таблицей относительных
величин У'изм в некотором неизвестном ему масштабе. Обычно самое

470 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ. VI
сильное отражение принимают равным 100. Величины Fastt
определяются по формуле
где 2 — относительные числа, измеряющие интегральное отражение,
a L и А — факторы угловой и поглощения, определяемые так, как
это было изложено в §§ С, 7 гл. III.
Как только что указывалось, в ряде случаев структурный анализ
значительно облегчается при знании абсолютных значений F. Это
имеет место тогда, когда метод 7^-рядов неприменим и
исследователю необходимо получить грубые представления о расположении
молекулы по отношению к осям ячейки. Зная абсолютные
значения Fmit и вычислив единичные структурные амплитуды F, можно
определить, к каким из плоскостей кристалла ближе всего
расположены атомы. Если, например, Fqq^^O,!—0,8, то это означает,
что практически все атомы лежат в этой плоскости. Разумеется,
абсолютные измерения необходимы, если исследователь желает
воспользоваться неравенствами для определения знаков F (стр. 549).
6) «Испытание» модели. Метод проб. Полученная таблица Fmtt
может послужить для сравнения с опытом грубой модели структуры,
найденной на основании геометрического анализа или иных
соображений. Структурные факторы вычисляются но формуле,
приведенной на стр. 469. Атомные факторы берутся из таблиц для
свободных атомов. Значения v выч сравниваются с tBSM. Для этой цели
часто прибегают к наглядным графикам, откладывая по оси абсцисс
^—, а по оси ординат F%™ и Рш-
Если кристалл не обладает центром симметрии, то методом проб
должны быть найдены не знаки, а фазы а структурных амплитуд.
Если обозначить через А действительную, а через В мнимую часть
структурной амплитуды, то F= A ±iB и tg а = —. Опыт дает
знание модуля \F\, т. е. У А*-{-В*. Подсчёт FBU4 становится гораздо
более громоздким, так как А и В это суммы, взятые по координатам
отдельных атомов. Более существенным является то обстоятельство,
что изменения в значениях координат менее резко сказываются на
величинах модулей 7*"Выч, чем изменения знаков в центросимметрич-
ных структурах.
Мы полагаем, что находимся близко к правильному решению,
если общий вид опытной и рассчитанной картин совпадают.
Отдельные расхождения могут достигать 500—600%. но важно, чтобы
«сильные отражения были сильными, а слабые слабыми». Если
такого общего согласия опыта с расчётом нет, то модель можно
отвергнуть. Иногда модель можно отбросить по двум-трем цифрам:

§ 1] СРАВНЕНИЕ С ОПЫТОМ ВОЗМОЖНЫХ МОДЕЛЕЙ СТРУКТУРЫ 471
например, если расчёт приводит к тому, что /'^ должно быть больше
FQiQ в 10 раз, а опыт показывает, что отношение равно 0,1.
Пробуя различные модели, можно добиться совпадения общего
характера для Гизм и /Лш,- Число испробованных моделей должно
быть ограниченным, так как, пропесс расчёта F довольно
громоздкий (о технике расчёта см. стр. 556).
Метод проб начинает играть решающую роль лишь в том
случае, если структура не содержит тяжёлых атомоп и геометрический
анализ приводит к широкому спектру решений. Одпако
систематическое применение метода проб практически осуществимо лишь в том
случае, если число неизвестных параметров структуры относительно
невелико. В качестве общих приёмов метода проб можно указать на
следующие. Прежде всего пытаются подобрать одни #-ые, одни у-ые
и одни ^-ыс координаты атомов, сравнивая с опытом рассчитанные
значения Fh00, F0li0 и Гш. Затем привлекают для уточнения отражений
одной зоны, затем следующей и т. д. Большую пользу приносит
в этой работе привлечение сильных F плоскостей с большими
индексами. При исследовании коронена было тгайдено, что отражений
16.00, 16.61, 14.08, 10.03, 602, J05, 207 исключительно сильны. На
фиг. III. 17 прочерчены эти плоскости. Нахождение расположений
молекулы коронена не представляет труда. Правда в этом случае
анализ в высшей степени облегчается симметричным и правильным
расположением атомов внутри молекулы.
Исследуя строение молекулярных кристаллов или комплексных
соединений, принимают некоторую модель молекулы или комплекса.
Положение такой группы атомов характеризуется 6 степенями
свободы. Структурный фактор выражают через 3 координаты центра
тяжести и три эйлеровых угла, определяющих наклон осей
молекулы к осям решётки. Для этой цели нужно заменить xyz каждого
атома по формулам (V, 5), вводя туда *0у0з0 — координаты центра
тяжести группы; XQY0Z0—координаты атома внутри группы.
Если мы находимся вблизи правильпого решения, то можем
встретиться с двумя систематическими отклонениями 2<тИЗм от FBbl4,
причипа которых очевидна. Это: 1) заншкенные в 2—10 раз
значения 2'изм самых сильных отражений, 2) заниженные значения
/»зм отражений при больших углах (больших -^J, притом
занижение систематически увеличивается с увеличением -^-J.
Первое обстоятельство указывает на необходимость учесть экстинк-
цшо, второе на необходимость введения среднетемпературной
поправки. Как мы видели на стр. 264, экстинкция сказывается на
сильных отражениях. Можно подобрать эту поправку так, чтобы
7'изм совпали с FKU.,. Сам факт возможности подбора такой поправки
свидетельствует о её правильности. При желании можно прибегнуть
к способам опытного измерения экстинкции. Средний температур-

472 структурный лнллнз с оцкнкой инткнсивностей [гл. vi
ный множитель можно только подобрать. Ищется такой коэффи-
циент В, при котором замена атомных факторов f ко. fe ^ k '
привела бы к наилучшему совпадению рассчитанных и измеренных
величин.
После того, как это сделано, можно перейти к уточнению
модели, добиваясь все лучшего совпадения путём небольших
изменений координат отдельных атомов или ориентировки молекулы
в целом.
Следует отметить, что пи при каких обстоятельствах не удаётся
привести /<7ВЫ,, и /-7,ш, к полному совпадению. Улучшая схождение
с опытом одних FBU4, мы
ухудшим это совпадение для
других. Структуры, у которых
средпее расхождение в FH3M и
Рвыч равно 20—30% и имеется
5—10% цифр с расхождением
до 200—300%, считаются
«хорошими». На фиг. VI, 1
приводится типичная кривая рас-
!?ПТ Т ! ТТТ пределения ошибок для двух
'«"''' * ' №• • независимых исследований
ро чо иа о
с' °' _ ' кристаллической структуры
Гчам'Грасч нафталина.
ивм Более того, стремление при-
Фиг. Vf, 1. Вертикальные чёрточки вести к полному совпадению
означают единичные измерения. ртч и /,^м ошибочно.
Анизотропия тепловых колебаний и
отклонение распределения электронов от того, которое имеется в
свободном атоме, не учитываются при расчёте значений F. Следовательно,
даже в том случае, если средние положения центров атомов
реальной структуры совпадали бы точно с центрами атомов модели, то
всё равно структурные амплитуды FBbJ., и FmH не совпадали бы
из-за различия в значениях f.
Поэтому следует признать нецелесообразными разработанные
американскими авторами методы нахождения структуры путём ми-
нимализации значения | /»'„,,,., —Fn3M j.
Интересно прикинуть порядок величины возможных
расхождений FBu4 и F„3m, происходящих из-за незнания f (для связанных
атомов и при анизотропии тепловых колебаний).
Если бы атомные факторы всех одинаковых атомов в молекуле
были бы одинаковыми, то ответ на этот вопрос был бы
элементарным: очевидно, относительные ошибки в /' и F были бы равны
друг другу.
Заранее очевидно, что этого нет: анизотропия тепловых
колебаний и влияние химической связи будет различно сказываться на

§ 1] СРАВНЕНИЕ С ОПЫТОМ ВОЗМОЖНЫХ МОДЕЛЕЙ СТРУКТУРЫ 473
разных атомах одного сорта (скажем, на разных атомах С большой
углеводородной молекулы), если связи этих атомов различно
ориентированы но отношению к падающему лучу.
Допустим, что в ячейке находится п «кристаллографических
молекул» — микродинад, каждая из которых содержит Na атомов
с рассеивающей способностью fa, Nb атомов — fh и т. д. Допустим,
что значения атомных факторов / колеблются около среднего
значения f в пределах =*=Д/*.
Выражение структурной амплитуды запишем в виде
«Иг) Ь к,(г)
*т=< s 0 --/С")008 *гН~ *?* 2 (*+7r)cos *'•+ • • • (VI»1}
г—\ г=\
Ошибка в F, совершаемая из-за незнания атомно-темиератур-
поГо фактора, равна
Д/«' = »2± Д/fcos ar i- » 2 zt Д/f cos ar + ... (VI, 2)
r—l r=l
Для примерной оценки AF примем, что все значения |Д/(г>|
равномерно распределены ме;кду О и Д/"тах, т. е. что среднее
значение |Д/'И| = ^.
Тогда вероятное значение сумм таково:
VI
N
0.707
(Д/ И cos a,.)2 = ^ Д/шах \ГУ (VI, 3)
и, следовательно, вероятная ошибка
Д/«'вср = =£ 0,35nV.\aA/S + -VbA/g + . .. (VI, 4)
13 случае атомов одного сорта
AFBep = ±: 0,35 Д/wJAV. (VI, 4а)
Характерна ошибка в единичной структурной амплитуде
д//,ер = ^£^=±". (VI, 46)
niVf У> /
Как бы то ли было, но -= есть величина порядка десятков
процентов *). Для У =10 вероятная ошибка в Д/<т имеет порядок
*) Расчёт и опыт показывают, что анизотропия тепловых колебаний
может привести к значениям /', отличающимся в 2 — 3 раза для двух
отражений, происходящих под примерно одинаковыми углами Ь,

474 структурный анализ с оценкой интенсивностей [гл. yi
нескольких сотых. Таким образом схождения /<7„ыч и /*ТИ8М более
чем на 0,01—0,02, безусловно, фиктивны. Кроме того, у тех
отражений, для которых 7<т<0,02, знак не может быть определен
вычислением из гипотетической структуры, так как вполне
возможно, что истинный знак структурной амплитуды обратен
вычисленному даже и в том случае, если для вычисления были взяты
истинные «центры» атомов. Структурные амплитуды, вычисленные
для этих отражений, можно назвать «антагонистическими» или
« противоречивыми ».
§ 2. Метод рядов электронной плотности
а) Формула ряда для общего случая. Область ырикененкн
метода. Напомним, что рентгеновские лучи рассеиваются
электронами. Таким образом картина рассеяния рентгеновских лучей
непосредственно связана с характером распределения электронов
в кристалле.
Обозначим среднее число электронов, приходящихся на единицу
объёма, через р. Эта величина есть, разумеется, функция координат
и притом периодическая с периодами, равными основным периодам
идентичности решётки. Как известно, всякую периодическую
функцию можно разложить в ряд Фурье и представить в виде:
РМ = 22 2 Q,lW,ae-*s"*t«+w+w>. (VI, 5)
Pi, Р*,Рл=-оо
Коэффициенты разложения 2 могут быть-, как известно,
записаны в виде
1 1 1
QPlp,Pj = f f j p (хуз) ei2* (pi»+p*v+p*)dx dy ds. (VI, 6)
0 0 0
Интеграл должен быть взять по периодам. В нашем случае
пределы интегрирования равны 1, так как подразумевается, что х, //, z
суть координаты в долях периодов элементарной ячейки. Элемент
.объёма элементарной ячейки dV= Vdxdydz, где V—объем
элементарной ячейки. Таким образом
2;wa= у I Р (ж^) с*'г*<Р0+Р*У+РЛйУ. (VI, ба)
v
Нетрудно видеть, что полученный интеграл равеп структурной
амплитуде отражения PiP^Jh- Действительно, структурная амплитуда
отражения ЬМ есть, по определению, амплитуда волны, рассеянной
веществом элементарной ячейки. Если плотность электронов р {%yz),
то амплитуда волны, рассеянной элементом dV элементарной ячейки,
будет равна (сравни стр. 224)

§ 2] метод рядов электронной плотнобти 475
где И—радиус-вектор узла Ш обратной решётки, а г — радиус-
вектор элемента объема dV. Таким образом
I\ki = fpe2Kl{Ur)dV (VI, 7)
v
Fm == J p e2™ V™ + ки+'*> d V. (VI, 7а)
v
®1>&гРл — ~у I'PiPPr ( VI, 8 )
Нулевой член разложения
^ooo=r f ?(хуг)<1У = у, (VI, 8а)
v
где Z—число электронов в элементарной ячейке. Таким образом
V<m = Z. (VI, 86)
Итак, разложение в ряд электронной плотности р {хуг) имеет
вид:
р {хуз) = у S S S ^wiC"^ (»*+*!'+'■> (VI, 9)
А к I
—со
или, короче,
Р (г) = т 2 7'™ с "2" (Г"Ш • (VI' 9a)
Этим вычислением распределение электронной плотности в
кристалле связывается с экспериментом. Связь p(xyz) и Fm не является
однозначной, так как опыт даёт лишь значение модулей F и не
определяет их фаз, а в случае центроеимметричных кристаллов
даёт лишь абсолютное значение 1,у и не определяет его знака.
Поэтому определение электронной плотности кристалла пе является
тривиальной задачей и становится возможным после
предварительного анализа, цель которого есть установление знаков или, в общем
случае, фаз структурной амплитуды.
Определение электронной плотности в большинстве случаев
преследует цель нахождения межатомных расстояний. Максимумы
электронной плотности должны, вообще говоря, совпадать со
средними положениями центров атомов. В редких случаях определение
электронной плотности было самоцелью; обычно ищутся лишь
координаты максимумов функции р(хуг).
или
Таким образом

476 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ. VI
Несмотря на сказанное, не следует рассматривать метод
построения рядов электронной плотности лишь как завершение метода проб
даже и в том случае, если из рядов определяются только
координаты максимумов. Этот метод является прежде всего объективной
проверкой грубой структуры. Метод проб никогда не дает
результатов, которые могли бы рассматриваться как однозначные.- Если
же на основании предварительного исследования удалось построить
ряд, подтверждающий грубую модель, положенную в основание
расчёта, то это можно рассматривать как безусловное
доказательство правильности выбранной модели.
Второе достоинство метода рядов заключается в возможности
оценки точности результата. Действительно, в случае метода проб
весьма трудно, а в подавляющем числе случаев невозможно
установить, какое же отклонение того или иного атома от положения,
признанного за окончательное, следует считать предельно
возможным. В методе рядов, как мы увидим ниже, существует
возможность определить ошибку любой координаты атома.
Наконец, третье, исключительно важное обстоятельство, то, что
результат, полученный методом рядов, вообще говоря, не требует
знания величин атомных факторов, так как коэффициенты ряда
вычисляются непосредственно из экспериментальных данных. Таким
образом результат исследования, в отличие от метода проб, не
зависит от предположений, сделанных в отношении f.
Построение рядов электронной плотности не избавляет нас,
к солсалению, от обязанности неоднократно пересчитывать
структурные факторы. Необходимо из построенного ряда найти координаты
атомов и пересчитать значения структурных амнлитуд. Правда, этот
расчет можно производить грубо, так как цель его — убедиться
в том, что структурные амплитуды не переменили знак. Обычно
лишь небольшое число Fhkl меняет знак. Тогда необходимо внести
соответствующие исправления в ряд и продолжать эту процедуру
до тех пор, пока принятые знаки не сохранятся. Привлекать к этой
процедуре антагонистические структурные амплитуды нельзя.
Описанный метод есть основной метод работы, который
можно назвать методом постепенного приближения к правильной
структуре.
Отсутствие у кристалла центра симметрии усложняет не только
подсчёт ряда (об этом ниже), по, что гораздо важнее, делает очень
медленной и не вполне определенной процедуру приближения к
правильному решению. Знаки FhM в центросимметричных
структурах, естественно, меняются скачком, а величины фаз (нецентро-
симметричные структуры) непрерывно. Если в случае центросим-
метричной структуры приходится изменить знак F незначительного
числа отражений, то, при отсутствии центра симметрии, фазы,
вычисленные из ряда, будут отличаться от фаз, принятых при
построении ряда почти для всех коэффициентов ряда. Только

§ 2] Л1ЕТ0Д РЯДОВ ЭЛЕКТРОННОЙ ПЛОТНОСТИ 477
в простых случаях можно ожидать, что процедура постепенного
приближения приведет к однозначному решению, не говоря уже
о том, что быстрота приближения будет много меньшей. Незнание
точного значения атомного фактора, о котором говорилось выше,
играет здесь более существенную роль.
б) Трёхмерные ряды и их сечения. Для того чтобы
определить значение электронной плотности р (хуг) в любой точке
элементарной ячейки, надо измерить амплитуды всех отражений,
даваемых кристаллом. Как нам уже известно, с возрастанием угла
рассеяния интенсивность, а вместе с ней и значения F, быстро
падают. Это обстоятельство весьма важно, так как при подсчетах
должна быть обеспечена сходимость ряда. Принципиальных
затруднений здесь нет (сравни стр. 515), так как переходя от
длинноволнового излучения к коротковолновому (т. е. увеличивая диаметр
сферы отражения), мы всегда сможем привлечь к построению ряда
все отражения, выделяющиеся над фоном. Для разных кристаллов
и разных температур число членов ряда будет различным, так как
величина самых малых межплоскостных расстояний d, дающих ещё
заметное отражение, определяется размахом тепловых колебаний
атомов.
Расчет трёхмерного ряда для случая кристалла без центра
симметрии исключительпо громоздок. Из-за отсутствия центра симметрии
работа удваивается, так как плотность представляется суммой
двух рядов:
-|_0О
Р С'' V ~) = ~222 А cos 2lt </w' + hJ + '*> +
h к I
—оо
-f- В sin 2u (h.r -f kif 4- fe), (VI, 10)
где Л и В—действительная и комплексная части F= А-\- Вг.
Справедливо также представление
Р (■* V *) = -у22Ц1Ъш!со* 2* (fcr + *?' + U + *ш)- (VT, 1 «а)
При наличии центра симметрии ряд имеет вид:
+00 СО
p(;r^^)=i^000 + A2]22/,^cos2x(/A,;-[-/^^/z), (VI, 11)
А к 1=0
—оо
где Fh]a может быть положительным и отрицательньш.
При подсчёте трёхмерных рядов можно рекомендовать
следующую процедуру. Распределение электронной плотности записываем

478 СТРУКТУРНЫЙ АНАЛИЗ О ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ. VI
в виде (случай центросимметричного кристалла)
Р & У 2) =
оо оо оо
Ь=0А:=0 l=>0
— [Fhki — *W№*i — * a*i) sin 2* hx cos 2irfo/sin 2ic U —
— {^*w + Fhn — FhU—Fhid) cos 2ic hx sin 2ic fcy sin 2тг te —
— {*»« — Ны—Fhki-\-Fhili} sin 2ти hx . sin 2*fa/ cos 2r /0. (VI, 12)
За направление с принимают направление в решётке с
минимальным периодом. Очевидно
оо
Р (х у z) = у 2][Р (V, у, 0 cos 2* U + Q (•«, ?/, 0 sin 2* fe], (VI, 12а)
1=0
где Р и Q определяются сравнением этой формулы с предыдущей.
Функции Р и Q рассчитываются обычным способом — это
двумерные ряды—для всех значений I (см. ниже). После этого
определение электронной плотности в любой точке пространства ячейки
сводится к подсчету одномерных рядов. При оси с = 4—5 А
придётся вычислить всего лишь по 3—4 функции Р и Q. Как видим,
в этом случае подсчёт трёхмерного ряда займёт времени не более
чем в 10 раз больше но сравнению с двумерным рядом.
При высокой симметрии формула (VI, 12) может упроститься.
Если
•^'ш == ^*ш = Рта = ^'ш,
оо
Р (■>' V s) = -у 2^ £i ^ Fhki cos 2* hx cos 2я h/ cos 2ъ h.
Напротив, формула становится очень громоздкой, если к решётке;
нет центра симметрии.
Исходя из (VI, 10а), получим:
р(хуз) =
-f-oo
= т2 Ad ^jl-^fcwl (cosfcj?cos*t/cosfecosa-|-siii Aa?sinA;i/ sin 1^ sin a—
—00
— cos hx cos ky sin Iz sin a — sin hx sin ky cos Is cos a —
— sin hx cos ky sin fer cos a—sin fear cos ky cos te sin a —
— cos Л# sin ky cos Ijst sin a — cos /&# sin ky sin fe cos a).
Упрощения будут иметь место при наличии соотношения между
фазами и амплитудами (см. стр 230).

§ 2] МЕТОД РЯДОВ ЭЛЕКТРОННОЙ ПЛОТНОСТИ 479
Если измерены все Fhkl, то их можно с успехом использовать
для построения различных «сечений» электронной плотности.
Расчётная часть работы в этом случае не больше труда,
затрачиваемого на построение проекций электронной плотности, а
результаты представляют, несомненно, значительно больший интерес.
Прежде всего, располагая указанным экспериментальным
материалом, можно построить распределение электронной плотности
вдоль заданной линии. Рассмотрим линию, параллельную узловой
прямой Itmnp и нроходящую через заданную точку я = st a-\-s2b-\-s3c.
В качестве точки s удобнее всего выбирать точку пересечения
интересующей нас прямой с координатной плоскостью (тогда su
или s2, или % равны нулю). Если iv есть координата, отсчитываемая
вдоль прямой, то любая еб точка может быть представлена в виде
Подставляя это значение в выражение ряда электронной плотности
(VT,Oa), получим:
Р(г)г=^^гше-^с"пе-^>г('т (VI, 13)
или, так как НП — Ьт-\-Ьп-\-1р равно целому числу (сравни
стр. 337),
Р(»-) = 2Л^-^'Г, (УГ, 13а)
j
т. е. одномерный ряд с коэффициентами
"j-t 2 2 2 *»« <'-'2"""+*- <■"■■> • (VM4)
ft к I
Коэффициенты Ли JB2, />3 и т. д. получаются из
условия hm-\-kn-\-lp=j, т. е. Bt суммирует все 1гиы> Для
которых j= 1, V>2 — для которых i=2 и т. д.
Пусть, например, мы хотим найти распределение электронной
плотности вдоль пространственной диагонали; тогда последняя
формула предельно упрощается (s1 = s2 = .93 = ()j и получает вид:
^-tSSS^w (VI'l4a)
ft к I
причём j=h-\-Tc-\-l.
При составлении подобных сумм следует учитывать фактор
повторяемости. Одно и то же отражение в зависимости от знака
может входить в разные коэффициенты Bj. Например, в случае
составления ряда вдоль диагонали кубического кристалла
отражение 532 войдет в Bj для i = 0, 532 в Bj для; = 4, 532 в В) для
) = 6и 532 в Bj для i= 10.

480 С1ТУ1ПУМШЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕИ [ГЛ. VI
Фактор повторяемости {532} равен 24 (отбрасываем центросим-
метричные отражения). 24 отражения распределятся равномерно по
всем четырем коэффициентам Bj. Это, однако, будет не всегда.
Например, отражение от {633} с фактором повторяемости 12
распределится следующим образом. 3 отражения типа 633 войдут
в В0, 3—типа 633 в В12 и 6 — типа 633 в JB6._B случае отражений
{hhh} из общего количества 4 три отражения hhh, hhh и hhh
войдут в коэффициент Bh и одно отражение hhh войдёт слагаемым в B%h.
Большей частью исследователь, измеривший все Рш кристалла,
строит распределение электронной плотности в нескольких сечениях
ячейки.
Допустим, что нас интересует распределение электронов в
плоскости, параллельной узловым плоскостям (hkl) и отсекающей на
одной из осей координат отрезок s, равный stat или s2b, или s%c.
Выберем в узловой плоскости (hkl) два направления Итпр и
Ит'п'р'. Тогда любая точка интересующей нас плоскости может
быть задана так:
r = s -\-иКтщ, -\- ivlim>„<p<,
где и и w — относительные координаты, отсчитываемые вдоль
соответствующих узловых прямых. Подставляя это значение у
в (VT, 9а), имеем:
р (г) = ~ >] Fm e-i-^u ,,- tir. („nnMVp ^ >ritnm,H.y) (yif j 5)
Ho HRwnp = hm -j- kn -{- lp =j\ и HBm>H>p> — hm' -{- kn' -j- 1р'=%,
где jt и j2 — целые числа. Таким образом получаем двумерный
ряд:
рИ= 2BJt,Jte-W+J»0 . (у[) 15а)
Ум J-.
Коэффициенты ряда имеют вид:
4],= у^^_ЙМЦ''^+",; <у1.156)
hkl
при этом для Bjlt jt индексы hkl должны удовлетворять двум
равенствам: hm-\-kn-\-lp=j1 и hm' -\-kn' -j- lp' =j2.
В качестве примера выберем плоскость (ПО), проходящую через
начало координат ячейки.
Тогда
п. . _L V // p—r>-(h ;-/.•)
т. е.

§ 2] МЕТОД РЯДОВ ЭЛЕКТРОННОЙ ПЛОТНОСТИ 481
причём hkl должны удовлетворять следующим условиям: если мы
будем отсчитывать координаты вдоль с и [110], то
l=jx и h — h=j2.
Таким образом, в сумму Вп будут входить индексы 101, 211, 321,
431 и т. д« В самом простейшем случае сечения, совпадающего
с плоскостью решётки, например ху, jx = h, j2 = h,.u = x, w — y и
i
В случае, если B^ ^ комплексно — а это может быть не только
при комплексной структурной амплитуде, но и при комплексном
экспоненциальном члене в (W, 156)—расчёт усложняется, так как
приходится подсчитывать два ряда. Если
Bh л = Т 2 FhM cos 2* (hSl + Ь2 +ls^' I
| (VI, 16а)
Bj\ h = -у 2d FM Sin 2X №1 + ks* + fes). {
то (VI, 15a) принимает вид:
P И = 2 B'h h cos 2тг (;> -f J» -f 2 #1 ^ sin 2* (j> +,;». (VI, 16)
Ji> h ji, j«.
Если, кроме того, структурные амплитуды комплексны, то
обозначая Fm=\Fh]c1\eiafiMJ можем ввести фазу структурной
амплитуды в скобку (sJH"). Таким образом лишь несколько усложняется
подсчёт коэффициентов В, суммирование рядов остаётся прежним.
в) Проекции ряда электронной плотности. Измерение ивтен-
сивностей всех возможных для данной длины волны отражений и
пересчёт значений интенсивностей в Fhld, наконец, нахождение
знаков этих Fhkt методом проб является исключительно большой
работой, требующей для изучения одного кристаллического объекта
многомесячной затраты времени.
Поэтому в большинстве случаев удовлетворяются изучением
проекций электронного распределения на две координатные плоскости.
По этим проекциям удаётся восстановить пространственное
расположение атомов и получить некоторые, хотя и значительно более
скудные, данные о распределении электронной плотности.
Как мы сейчас покажем, для построения проекции электронной
плотности вдоль некоторого направления достаточно измерить
интенсивности отражений рентгеновского луча от зоны плоскостей, для
которой это направление служит осью.

482 структурный анализ с оценкой интЕНСпвностЕй [гл. vi
Проекция электронной плотности вдоль оси z равна, очевидно,
°И/)= fpixye)^, (VI, 17)
где с — период вдоль оси г. В предыдущем мы пользовались
относительными (безразмерными) координатами. Переходя к ним по
формуле ds — —-, получим:
^о(ху) = J ${xyz)dz.
о
Запишем теперь выражение структурной амплитуды для
плоскостей зоны оси г:
1
Fm = V J р (хуз) еш <*»+*»> dx dy ds
о
или, воспользовавшись предыдущей формулой,
1
I\uo=^xy^^y)eiiK(hx+Jiy)dxdyt (VI, 17а)
о
где Sxy есть площадь сечения ячейки, перпендикулярного оси с.
На основании последней формулы заключаем, что существует
следующее разложение в ряд:
°(-™/) = -Г- 22^в"Л(1кя+,|,)' (VI'18)
ху ь к
т. е. действительно, для построения проекции достаточно знать
интенсивности отражений от плоскостей одной зоны. Если нужно
определить проекцию вдоль иного направления, отличного от оси
ячейки, то следует произвести преобразование координат так,
чтобы ось проекции стала осью координат.
В ряде случаев имеет смысл расчёт особой «поясной»
проекции. Очень часто при построении проекции одни молекулы
накладываются иа другие. Было бы желательно при построении проекции,
скажем вдоль оси у, иметь возможность выделения пояса между
высотами yt и г/2 и построения проекции электронного облака,
заключённого только в этом поясе. Плотность распределепия
электронов в такой проекции будет, очевидно, равна
v*
#eJp(*y*)«V. (VI, 19)
ш

§ 2] МЕТОД РЯДОВ ЭЛЕКТРОННОЙ ПЛОТНОСТИ 483
Подставляя значение р(хуе) и интегрируя, получим:
+ 00
#=т%111!1£кр™^^и+™—е~^{*+,а+Ш]'(VI'20>
А к I
—оо
Подсчёт этого двумерного ряда, разумеется, значительно сложнее
подсчёта для проекции, ибо требуется знание знаков всех Fhkl.
В этом случае, пожалуй,
целесообразнее строить
трёхмерные сечения, хотя и
несомненно, что построение поясной
проекции проще построения
сечений трёхмерного ряда, а
результаты, которые даёт ajj,
не уступают при подходящем
выборе ух и у2 результатам,
получаемым с трёхмерным
рядом.
Фиг. VI, 2 хорошо
иллюстрирует сказанное сравнение
поясной проекции и обычной
проекции распределения
электронной плотности для
кристалла дибензила.
Весьма мало опытных
данных требуется для построения
проекции электронной
плотности на некоторое
направление. Для этого достаточно знать
интенсивности всех порядков
отражений от системы
плоскостей, перпендикулярных
этому направлению.
Выберем за ось г
интересующее нас направление.
Оно будет нормально к
некоторой системе плоскостей.
В одной из них выберем оси х и у. Проекция электронной
плотности на ось z равна
] 1
1>(г) —S^J J?(*y8)dxdy, (VI, 21)
о о
где £L, — площадь сечения ячейки координатной плоскостью хОу,
Фиг. VI, 2.
СН,
Ди бензил
<^ у вверху поясная, внизу
обычная проекция электронной плот
ности. Очевидна большая чёткость
первой. Например, атом углерода 2,
сливавшийся с атомом углерода/ в
обычной проекции, прекрасно выявлен
в поясной.

484 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСГЕЙ [ГЛ. VI
а х и у— относительные координаты. Запишем теперь выраженже
структурного фактора отражения от плоскости, нормальной к оси г.
Получим:
1 1 1
Fooi = V j J j p (xyz) ei2«ls dx dy dz, (VI, 21a)
0 0 0
т. e.
i
Fm = с j p (г) ei2*l* dz, (VI, 216)
о
где с — период вдоль оси z. Опять-таки общая теория
тригонометрических рядов позволяет заключить, исходя из последней
формулы, что существует разложение в ряд
*(*)в7 2 *«*-'**. (VI'22)
1=х ОО
Итак, действительно, для построения линейной проекции
достаточно знать все порядки отражения от одной системы плоскостей.
§ 3. Техника подсчёта двумерных рядов Фурье
В подавляющем большинстве случаев в структурном анализе
приходится прибегать к подсчёту двумерных рядов Фурье. Либо
исследование состоит в построении нескольких сечений
трёхмерных рядов электронной плотности, либо в изучении
двумерных проекций. Столь же, если не более часто, приходится
прибегать к построению двумерных рядов Фурье для межатомных
векторов (см. ниже).
Еассмотрим двумерный ряд Фурье с комплексными
коэффициентами
+ оо
Ь (ху) =s22**.*e-*2'c(fta:+*!'). (VI, 23)
к h
—с»
Частными случаями этой формулы являются формула сечения
объёмного электронного распределения (VI, 15а), формула проекции
электронного распределения (VI, 18) и аналогичные формулы (VI, 63)
и (VI, 65) для межатомных векторов (см. дальше).

3]
ТЕХНИКА ПОДСЧЁТА ДВУМЕРНЫХ РЯДОВ ФУРЬЕ
485
Если коэффициенты ряда комплексны*), то Ь(ту) разбивается
на две части:
8с (ху) = 22 *й cos 2* (hx + ку),
к h
—оо
8в {.щ) = 22 ФЙ sin 2я (Ал; + ty),
— оо
(«)
(«)
.ML
(VI, 24)
(8)
где Фй, fc = Фл, л + *Ф*. а-- При этом, так как всегда Фп, к —- — ф£, g и
Ф^)А. = Ф^д, то каждую из двойных сумм можно записать так:
+оо
8С (ху) = Фоо + 2 2 *£о cos 2- for +
Л=1
+ оо
+ 2 2' 2 *М cos 2тг(кс+ &?/), (VI, 24а)
8S (хг/) = 22 Ф# о sin 2* for -f
Л = 1
+ оо
+ 222 **fi sin 2* (for -|- %). (VI, 246)
Л= —оо ft=l
Двойные суммы разбиваем каждую на две, преобразовывая
косинус и синус суммы:
2 2 ФЙ cos 2х (hx + fa/) =
Л=—даfc=l
+ 00
= 22 Фл, л cos 2тг A.r cos 2тсАя/ —
ft = — no ft—1
+ оэ
— 2 2 Фл? ft sin 2тг foe sin 2тг А;?/, (VI, 25)
Л = —ooft = l
*) Коэффициенты Фл к будут комплексны в следующих случаях: 1) для
сечений рядов межатомных векторов и электронной плотности, если
е—i2K(h<sl+Ju,+idi) не 0бращается в действительное число, 2) для сечений
и проекций рядов электронной плотности, если структурная амплитуда
комплексна, т. е. если кристалл (или соответственно проекция) не
содержит центра симметрии. Коэффициенты Ф^ъ всегда действительны
для проекций рядов межатомных векторов и для проекций рядов
электронной плотности вдоль оси симметрии чётного наименования.

486 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕИ [ГЛ. VI
+ оо
2 2 *£* sin 2тг (Лж -f *!/) =
й=—оо h - t
= 22 ФЙ sin 2« й# cos 2w &?/ 4-
+ <ю
+ 2 2^i*Uos2icAa;8in2ic*v. (VI, 25a)
A = — oofc = l
Теперь внутри каждой суммы можно произвести суммирование
одномерных рядов Фурье. Как для ф£й, так и для ФД- имеем:
+ 0О -f-OO
2 *л, * cos 2* Ля = 2 (Ф*. ft Н- ф», ft) cos 2л Лж + Ф0, *, (VI, 26а)
Л=—оо й=1
и аналогично
+ 00 4-СЮ
2 Фа, к sin 2* hx = 2 (ФЛ к — Ф^, fe) sin 2« fca\ (VI, 266)
Этими преобразованиями задача подсчёта ряда сведена к
последовательной серии подсчётов одномерных рядов Фурье.
Рассмотрим дальнейший ход суммирования на примере Ье (scy)
(в большинстве случаев приходится иметь дело с центросимме-
тричньши рядами и Ья(ху) отсутствует).
От построения нецентросимметричных рядов электронной
плотности отказываются, как было сказано выше, не потому, что
работа по построению рядов возрастает в два раза, а из-за
исключительной громоздкости метода проб, которым в этом
случае приходится подбирать не только знаки, но и фазы
структурных факторов. Что же касается рядов межатомных векторов,
о которых пойдёт речь ниже, что они всегда центросим-
метричны.
Итак, рассмотрим дальнейший ход суммирования. Запишем
функцию Ьс (ху) в следующей форме (в дальнейшем откидываем
значки с)
оо оо
& (ху) — Фад -\- 2 2Фл,о cos 27Г ^ + 2 2 Фо ft cos 27r *?/ 4~
А=1 ' ft=l '
оо
-|~22 2 (Фл,л+Фл",л)С08 2т/ал;с08 2тг^//—
оо
— 2 2 2 (Фй, к — Ф£ ft) sin 2ir hx sin 2тг ley. (VI, 27)

§3]
ТЕХНИКА ПОДСЧЁТА ДВУМЕРНЫХ РЯДОВ ФУРЬЕ
487
Теперь мы можем произвести суммирование в два этапа.
Сначала нужно рассчитать величины
ПО
А0х=2 2*v>eos2,:fcr> (^ = 0), ■
со
а затем найти 5 (ж?/) по формуле
(VI, 27а)
'ху
S.
ху>
где
С*» = ^Лкхсов2т,ку,
к —О
Зову = 2 Вкх sin 2тс %.
fc=l
(VI, 276)
(VI, 27в)
Указанным преобразованием суммирование разбивается на два
этапа. Каждая из этих двух операций производится обычно при
помощи так называемых «штрипсов», представляющих собой
линейную табличку выражения типа Л cos 2тг ку (или Л sin 2т: ку),
составленную для данных значений Л и к для значений у, скажем О,
12 12 л
48' 48''' * '48' Ввиду периодичности косинуса продолжать «штрипс»
далее не нужно. В общем случае нужны такие таблички для
косинусов и для синусов. Для многих работ достаточно изготовить
таблички до к = 20 для пятидесяти значений амплитуд (от 0 до
100 через 2 единицы). Таким образом должно быть изготовлено по
крайней мере 2000 «штрипсов».
Не нуждается в комментариях подсчёт 8 (ху) для первой
шестнадцатой доли сечения ячейки (значения х и у до — J. При
подсчёте для остальных частей ячейки используется связь между
значениями тригонометрических функций первой четверти с
остальными четвертями.
Каждую из подлежащих вычислению сумм можно разбить на
две части: 2i — сУмму по нечётным индексам и 2г — СУММУ п0
чётным индексам. Нетрудно видеть, что если значения всех сумм А,
-В, С и S равны 2i + 22 ДДя точки ^ первой четверти, то для

488 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТИ! [ГЛ. VI
точки ~— второй четверти для А и С они равны 2г— Si» a
для В и S, 2i ~~ 2з- Например, для суммирования второго этапа
5 " 19
для точек у = ^ и у = ^8 '
64 = А0Х + 4te cos 2* (2 • ^) Н- Акх cos-2- (4 • ^) -\ - . . . +
4- A.lxcos 2тг (l • jg) + A3acos2ic (з • ^)+ • • .,
С? = 4*4-4*cos 2* (2 • |) + -*4.cos2* (4 • А)4- •. • -
— 4*cos2*(l ' ^) —^з«С082«(з-jg)—...,
так как
cos 2,(2-1) = cos 2. (2-|);
cos 2тг (з • £) = — cos 2тг (з • Ц) и т. д. (IV, 28)
Сделанные замечания приводят нас к правилам работы, ясным
из приводимых таблиц. Первое суммирование рекомендуется
производить по тем индексам, которые изменяются до меньшей
величины. В принципе же различия нет.
В таблице первого суммирования (стр. 489) приведена одна
строка для некоторого значения /.-. Вообще же число строк
определяется объемом эксперимента. Суммирование косинусов
происходит с амплитудами, взятыми из третьего столбца, синусов—из
четвёртого.
Как это следует из общей формулы, коэффициенты ряда для
членов, у которых один из индексов (h или к) равен нулю, должны
быть взяты в формулу с коэффициентом 2; таким образом там,
где в общем случае выставляется коэффициент 2(Фъ>к-\-Фк,к),
в случае таких индексов ставится 2ФЛ>0 (или 2Ф0д). Таким
образом, если ФЬ)Л = ФЬ-Л, то коэффициент для индекса общего типа
будет в два раза больше коэффициента индекса с одним нулём.
На стол выкладываются штрипсы для чётных и нечётных
значений h и вычисляются 13 значений £j и -2 (см. фиг. VI, 3). Эти
значения подписываются одно под другим; затем, складывая эти
цифры, мы получим строку от А°к до А™, а вычитая из верхних
нижние — от Ак" до Агк. Суммирование пгтрипсов удобно
производить на счётах и на счётных машинах. Положительные и
отрицательные числа штрипсов выписываются разными по цвету
чернилами. Слева указывается, синусная или косинусная данная
таблица, величина амплитуды и порядок (т. е. к или h).

к
к
h
0
1
2
3
4
2 (*»* + ***)
2(*J№-
Таблица первого суммирования (по
-фм)
ft)
Суммирование косинусов
0
24
1
2
23 | 22
4
4?
А
11
... 1 13
значения^»
значения^
А1
12
12
4"
Суммирование синусов
0
1
24 | 23
0
0
в\
в?
•)
22
в\
в?
значения^
значения^
11
12
13 | 12
*?
*?
и12
п12
соо
со
Таблица второго суммирования
X
л;
\
к
0
\
2
3
А
Ч
Суммирование косинусов
0
24
1
23
<£
|«
2
22
<!1
С??
vx
Значения 2-
Значения ^i
11
13
«
с™
12
12
oS
cl2
Суммирование синусов
0
24
0
0
1
23
4
2
22
4
У-3 1 s2~
^х
Значения 2i
Значения 22
11
13
X
гг13
6Х
12
12
$х
€

490
СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНООТЕП [ГЛ. VI
Рассмотрим теперь таблицу второго суммирования. Число строк
в таблице будет 24 для значений х от нуля до 23/48.
Суммирование косинусов происходит с амплитудами, взятыми
из третьего столбца, а синусов — из четвёртого. С и S
вычисляются
совершенно так же, как А
и В. Значения
функции 8 (ху)
рассчитываются для каждой
точки сечения по
формуле
8(ху) =
= Сху-8ху (VI, 29)
для четверти ячейки,
лежащей в первом
(положительном)
квадранте, и по формуле
8(ху) =
— C^ + fl^ (VI,29a)
40
54
12
22
78
92
С
С
0
С
С
С
0
2
4
6
8
Ю
40
54
/5
22
78
92
60
52
Л
16
39
24
40
47
6
0
39
во
40
38
0
16
78
65
40
27
6
22
39
46
40
Ц
11
16
39
89
40
0
12
0
78
0
40
/4
V
16
39
89
40
Z7
6
22
39
46
40
38
0
16
78
65
40
47
6
0
39
80
40
52
Л
К
39
Я
40
54
12
22
Т8
92
£,=118
О)
42
20
64
38
18
4
С
С
С
С
С
С
1
3
5
7
9
11
42
20
64
36
18
4
42
18
50
22
7
1
41
/4
17
9
13
4
39
8
24
33
17
2
36
0
55
31
0
3
33
8
бЪ
5
Г7
2
30
14
45
25
13
з
26
18
8
36
7
3
21
20
32
18
18
2
16
18
59
14
7
4
//
/4
62
35
13
1
5
8
39
28
17
4
0
0
0
0
0
0
2,-24
б)
•Фиг. VI, 3. а) Выложены штрипсы для чётных
порядков. В первом столбце указывается
амплитуда, во втором функция, на которую она
умножается (в данном случае с — косинус); в
остальных столбцах указаны значения F^i cos 2яйа?
<или Fhkl sin 2яй<в) для х = О, i, ^, ..., Ц.
б) Серия штрипсов для нечётных порядков.
Суммирование ведётся по вертикальным столбцам.
для четверти ячейки,
лежащей во втором
квадранте (х или у
отрицателен). Третий и
четвёртый квадранты
связаны с первым и
вторым центром
симметрии в начале
координат (только в этом
случае и возможно
построение ряда).
Если 8 (ху) = 8С (ху) -\- 88 (ху) (нет центра симметрии), то работа
удваивается. Так как 8С (ху) = 8С (ху), а 88 (ху) = — 88 (ху), то при
К (ХУ) = С3ху — Зву Для положительного квадранта получим для
четырёх четвертей ячейки значения:
I 8(^) = C^-^ + Ci,-$*,
П b(xy) = (fxy-^Sxy-\-Caxy-Saxy,
III b(xy)=,<fxy — ^xy~C%y^rgxyi
IV b(xy) = CcXy-^Scxy— C%y — Si,.
В результате описанного вычисления, занимающего обычно
у одного человека время от двух-трёх дней до одной-двух не-
(VI, 30)

§ 3] ТЕХНИКА ПОДСЧЁТА ДВУМЕРНЫХ РЯДОВ ФУРЬЕ 491
Ооо
°и
а02
^03
О,о
°п
Оп
Ozo
021
4»
Фиг. VI, 4.
Интерполяционный
квадрат.
дель*), мы получаем проекцию Ъ(ху) на координатную плоскость
ячейки в виде двумерной таблицы цифр. Эту таблицу необходимо
обработать следующим образом: во-первых, для
представления характера функции, в особенности
электронной плотности, можно построить
графическую картину линий, равной электронной
плотности, во-вторых (это важнее), следует уточнить
положение максимумов. Линии равной плотности,
например для органических соединений, следует
о
строить через 1 эл./А2. Строят полученную
таблицу в абсолютном масштабе и затем
соединяют линией центры элементарных площадок,
значения о {ху) для которых одинаковы. Большей
частью приходится производить примерное
интерполирование.
Точное интерполирование имеет смысл производить только для
главной цели — для определения точных положений максимумов
ряда. Для этой цели можно
воспользоваться распространением
интерполяционной формулы
Грегори-Ньютона на двумерный
случай **>.
На фиг. VI, 4 выделена часть
двумерной функции —
«интерполяционный квадрат»,
составленный 17 цифрами. Самое большое
значение о находится в центре
фигуры. Координаты % = 0, у = 0
приписываются точке, в которой
о(ху) обозначено через о^.
Этот интерполяционный
квадрат дабт возможность произвести
4 интерполирования, захватывая
в каждое вычисление 10
разных цифр, как это показано
на фиг. VI, 5. Десятью цифрами
•
•
•
•
®
•
•
•
•
•
•
•
•
•
•
ф
•
•
•
•
•
•
•
•
•
®
•
•
•
•
•
•
•
•
<§>
•
•
•
•
•
■Фиг. VI, 5. Интерполирование при
помощи интерполяционного квадрата.
*) Трудоёмкость вычисления зависит, как мы увидим ниже, от
симметрии проекции. Мы рассмотрели самый общий случай, когда кроме
центра симметрии других элементов симметрии в сечении нет. При более
богатой симметрии независимой областью может явиться
■5- и даже
о
уг ячейки. Если Fhk = — Fh^ или Fhk = Fhk, то пропадут суммы
косинусов или синусов; могут отсутствовать Fjijc с нечётным h или fc, благодаря
чему пропадет ^1 и т- Д»
*•) А. И. Китайгородский, ЖТФ. 17, 1003, 1947.

492
СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ. VI
характеризуется кривая третьего порядка. Интерполирование в
большем приближении смысла не имеет. Из 10 цифр каждого из
треугольников можем получить искомую функцию в виде полинома
третьего порядка по х и у.
Так как нас интересуют максимумы функции, то надо решить
совместно два уравнения
дх
О и
г-*
дУ
(VI, 31)
Исследование второй производной не нужно, так как примерный
ход функции очевиден. Выведенные таким способом уравнения
максимума имеют вид:
ЗА^-f 2A%xy -{- AKt + 2*6* + АчУ +А = 0,
ЪА^ -\- 2А±ху + Аъх* + 2Алу + Ачх -\- AQ = О,
(VI, 32)
где
2^i = -g К°зо — °2о) — 2 (°20 — бю) + (°ю — °oo)L
2х12 = з~ [(а03 — Ом) — 2 (а02 — а01) + (а01 — а^)],
2^s= [(°21 — б20)-Ко01— °00) — 2(0ц — «to)],
2^4 = [(^2 — °02) + (°ю — °оо) — 2 0»ц — o0i)]»
2iiB = [-(o80 —6ao) + 3(oao —°ю) —2(о,о —ew)]. > (VI,32a>
24 6 =: [— (а03 — а02) -f- 3 («02—aoi) — 2 (% — °oo)I,
2^7 = [—2А — (°i2 — а02) — 3 (о10 — °оо) + 4(о„ — с01)],
2J.8 = з" 12 (^зо — °2о) — 7 (^20 — °ю) Н- 11 (°ю — °оо)Ь
2 J9 = з" [2 (о03 — Оо2) _ 7 (ам — о01) + 11 (а01 — 0(Ю)].
За единицу j> и г/ в этом расчёте следует выбирать величину
интервалов (т. е- То и ^r)-
Решая уравнения (VI, 31) для четырёх «треугольников»
(фиг. VI, 5), мы получим четыре пары значений а?тах, утл%,
которые в идеале должны были бы совпадать, а на самом деле будут
несколько отличаться друг от друга. Разброс значений даёт
точность интерполирования.
Точность самого интерполирования (т. е. та точность, которая
имела бы место, если бы значения о (ху) были известны абсолютно
точно) может быть' представлена в долях интервалов Д# и Дг/.
Она будет зависеть от характера функции (острота максимума и

§ 4] СИММЕТРИЯ ДВУМЕРНОГО РЯДА ЭЛЕКТРОННОЙ ПЛОТНОСТИ 493
проч.). В каждом отдельном случае эта точность найдётся по
разбросу значений при 4-х интерполированиях.
На ряде типичных примеров можно установить следующие
цифры:
Величина _ „ Вероятная
Разброс; -
интервала ^ ошибка
ОД А ±0,004 A =£0,002 А
0,2 A rt 0,016 А ±0,008 А
0,3 А ±0,035 А ±0,017 А
Очевидно, в практически обычных случаях ошибка
интерполирования не превышает 0,01 А.
При больших требованиях к точности, нежели приведенные
в таблице, следует прибегнуть к непосредственному вычислению
по точкам в районе максимума.
Рекомендуется определить графическим построением примерную
координату вдоль одной из осевых линий, скажем х; затем
рассчитать электронную плотность в функции от у для данного х для
точек в районе максимума; построить кривую распределения
плотности вдоль у, найти максимальное значение плотности, а затем
вычислить кривую распределения вдоль х при У = Утах* Далее эта
процедура повторяется любое число раз.
Можно методом последовательных приближений находить
производные по двум координатам и последовательными вычислениями
искать точку одновременного обращения в нуль этих двух
производных. Для одномерных рядов эта процедура является наиболее
рациональной.
§ 4. Симметрия двумерного ряда электронной плотности
а) Центросииметричные плоские группы. Для двумерного
случая существует 17 комбинаций элементов симметрии,
называемых плоскими группами (аналог пространственной группы).
Симметрия двумерного ряда может принадлежать к одной из этих
17 групп.
Эти 1*7 групп (данные о них см. в табл. VI, 1) можно вывести
различными способами; в частности, можно рассмотреть проекции
пространственных групп.
Из 17 плоских групп 7 групп являются центросимметричными.
Именно эти 7 групп имеют значение для практики структурного
анализа, ибо до сих пор лишь в единичных случаях прибегали
к построению нецентросимметричных проекций: ряды межатомных
векторов всегда центросимметричны, а для построения нецентро-
•симметричных рядов электронной плотности надо «угадать» фазы
структурных факторов.

494 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТВНСВВНОСТВЙ [ГЛ. VI
Таб
Данные о 17 плоских группах и
№
\А
1В
2Л
2В
3
4
Плоская
группа
и соот-
'ветств.
трансля-
цион. гр.
Тот
1
с\а
Тот
с\в
4
То
То
Число
эквивалентных
точек
1
2
1
2
2
4
1
2
2
Координаты эквивалентных
точек
(а) ху
(а)ж. у; «+ "2". » + -2-
(в)00;(Ь)-|о;(в)0^-;(й)-2-у
(е) asy; 7y
(а) 00; \ \\ (Ь)-^О; 0~
,,1133
(С)4 4:ТТ;
•л* 8 Х • Х 3
(е)ху;х + -—, У + Y
- - 1 ,1
(«)0у; (6) у у
(с) ху; ху
(а)ху;х, J/+Y
Данные для F-рядов
(соотношения между
(hk) = 0 при
к-\-кф2п
(hk) = fhk)
(hk) = (hk)
(hk) = 0 при
h 4- к ф 2п
(hk) = (hk)
(hk) = (— l)k (hk)
(Ofc) = 0 при кф2»

§ 4] СИММЕТРИЯ ДВУМЕРНОГО РЯДА ЭЛЕКТРОННОЙ ПЛОТНОСТИ 495 <
лица VI, I
двумерных проекциях F я F* рядов
Данные для F2 рядов
плоская
группа
0\А
с\в
С\А
0'Б
G2v
G2v
«веса»

максимумов
ZfZg
ZrZg
4
17,J,,
к
2ZrZg
z%
ZfZg
zl
ZfZg
координаты максимумов
xr x*i Уг У»
Xr Xgy yr 1/g
2xr, 2yr
xr ^e» Уг У#»
ХГ + *«' У Г + У8
2xr2yr
Xr — Xg', yr ■— ya
xr + xs> yr-\-y8
2av0
xr — x»> Уг — У»'
xr -j- ха, yr ys
2xy-
xr — x»> Уг — Уа'>
«r + ^e» Уг — Уа + Y
Тип
положения
максимума
e
e
e
e
e
e
e
i
f
i
Изображение
плоской
группы
F-ряда
\-\
u
\
■r^
<
\ ®c 0<A \
о b i
i
о
•
6
•
Г !
i
1 ! •
1 I
1 |
1 |
|
j

496 структурный анализ о оценкой интенсивностеи [гл. vi
1
I
№
5
6
7
Пдосвая
группа
и соот-
ветств.

трансляцией, гр.
То
G2v
То
То
Число
эквивалентных
точек
Координаты эквивалентных
точек
i
2 I И0>;|-,?/+1
4
1
2
4
2
4
1
(Ъ) ху; х-\-—у + — \
-- - . 1 - , 1
С«)00.(Ь)-|-0, (с) оф, (<*)----
(е) жО, «0;
(f)*~2>^-2 (9) ty; Oy;
,u l 1
(г) ху; ху; ху; ху
(a)00;i-i-; (*) ]-0; 0-|
(с) жу; ж7г/ 4- —
-- . 1 - , 1
«у. я + тру + у
Данные для .F-рядов
(соотношение между
Fft*o)
{hk) = (-l)h + k(hk)
(hk) — 0 при
(к-\-к)ф 2п
(hk) = (hk) =
(й&) = (-1)л+*да =
= (hie) =
= (-1)л+*да
(Л0) = 0 при hzfi2n
(Ok) = 0 при к ф 2и
8
лШ
b2v
То
2
4
(а) 00; 0-Ь (b)~ol
/ ч 1-3
'1 I
'2 2
((*) жу; ж, у + — ;
— - , 1
«у; ху + —
(ftfc) = (— 1)* (A*)
= (hk) =
= (-l)fc(*fc)
(Ofc) = 0 при к ф

§ 4] СН.\[.\1ЙШ1Я ДВУМЕРНОГО РЯДА .UEKTPOIIH01I ПЛОТНОСТИ 497
Продолжение
Данные для F~ рядов
плоская
группа
«веса»

максимумов
координаты максимумов
<х>
%
о
о
с
с
2
^
К
V
и
а
Я
«
я
ев
>,
>>
55
Изображение
плоской
группы
i''-ряда
zi
2.т.г{)
GYv
,1Г J:$< .'/'»• ,'/s>
«r-f-^e. Уг + Ун
_f...-
1
1
' 1-
1
<-!
j
о i
•
i •
...i
ct
2£
v2
2.r,.0; 02?/,.
<2; g
Zl
2:vr2yr
2/r/u
Xr 3.'s, Vr Уд,
•'V + ^'s. Уг—Vs
Xr X»i Vr ~T У8'
aV-f-Je. Уг + Ув
Щ !
V + T' Y; 2"' //r
/': Л
_.
2*r2yr
MS,
xr os, у у — уя\
•*v — »•« + v • •''• + •"»
xr 4- ■''*- ?/r + ;'/«•.
.• <
- -1- 4 •
о '-Ь
2*\ | 2.<>1; 0,2?/,.-h-j
/': fJ
z:
2^,-2»/,.
<4
2ZrZs
я-у — х,, ur — y9;
л ] ■
xr ж8» ?/r "Г У 8 ~\' 1J '
aV-r-^a' ?/r~ 2/s + ^"
f-r9—t
I—I""
>.,.
I •
ф* Ф

•198 структурный анллил с одкнкои иптецсивностеи [г.т. vi
№
Плоская
группа
и соот-
ветств.
трансля-
цион. гр.
|
9
То
i
!
i
i
, с\л
10.1 ! 4
! 7/
1
107*
11Л
0\VA
Число
эквивалентных
точек
2
4
Координаты эквивалентных
точек
(«)00;1А; (Ь)1о,о1
{е) 1 1 3 1 13 3 3
^ 4 4 ' 4 4 ' 4 4 ' 4 4
(d)xQ;xQ;x + ^, -i-;
- , 1 !
i - - __ /11
8 \ ху; л у; ху; ху и эти -\Л-^ -%> '
! 1 1
1 («) 00; (6)^-4
2
4
2
4
8
1
2
И у 0,0-1-
(Й) Ж</, J/Я1, Ж1/, у/Ж
С) 00. ±±; (6)lofoI
11 31 13 33
U4 4'4 4'44'44
(d) ху, ух, ху, ух
иэти+(|у)
(«) 00; (6) 1 I
1
Данные для .F-рядов
(соотношения между
^ftfco)
(hk) = (hk) = (hk) ^
= (Щ
(hk) = 0 при ]
h +1 :£ 2w ;
(A/.-) - (kh) « (At) =
= (WO
(ЛА-) = (frAj = (/7/7) =
= (Щ
(hk) = 0 при
h + Pjz 2n
(hk) = (hk) = (hk) =
= fhk) = (kh) =
= (fc/») = (fc/7) =
= (kh)

§ 4] СИММЕТРИЯ ДВУМЕРНОГО РЯДА ЭЛЕКТРОННОЙ ПЛОТНОСТИ 499
Продолжение
Данные для F2 рядов
плоская
группа
«веса»

максимумов
координаты максимумов
о о
ч «
О ев
Е « *
Н К 2
Изображение
плоской
группы
F-ряда
AV
с[л
с\в
<V*
2Z:
2.тго; 02 ?/,
2Zr | -г,. + ?/г, Уг — *г
Z'i
2хг2у,
2ZrZs
ХГ ^8* У Г l's>
'Г — У8, Уг + Х8\
Xr-\"*v Уг+'У»
хг-^-У8> Уг — Х*
2Zr
Хг + Уг> Уг~хг
2хг2уг
ii/J *•/-* С
xr— xs, yr— ys\
■(Г — У8> Уг + *%\
ХГ + Х8> Уг + 1'S,
Хг + У& У г —«я
2Z.
2тг0; 2}/г0
*г+Уг> жг+у,-;
хг уг, хг уг
ХГ "Г У Г' ХГ У Г
d, e
К
2ZrZs
2тг2цг
ХГ Х8> У Г
xr -j- xg, yr
хг •'"в» У г
xr -J- х§) уг
—
—
+
+
У»
Уа
?/в;
У/в
/•
/'
#-т-<>
• !
е
rtf-tlt-
,<s^^>

500
СТРУКТУРНЫЙ ЛНЛЛЮ С ОЦЕНКОЙ ТПТТЕНСНШЮСГКЙ [ГЛ. VI
х°
1Ы
пи
■
:
!
12Л
Плоская
группа
и соот-
ветств.

трансляцией, гр.
5 и
и Я
§g £
4
V\vA i
1U |
'it : 8
i
о
л
1
1
С] Б I S
41*
9
'it
j
If)
C" 4
4гл
7«
2
4
i
Координаты эквивалентных
!
точек i
(d) xO; Or; xO; Ox
/ s 1 1 -11-
(«)*y; 2-я?; я'у; -^
(f) j-af; aw?; xx; xx.
{(,) xy; yx; xy; yx
yx; xy; yx\ xy
11 ,1 1
<") 00; -i-i; (b) -OjOy
.. 1 1 . 1 3,31,33
^' 4 ~4 ' 4 4 ' 4 4 ' 4 4
(d) xx; xx; xx; x.t
, /1 1'»
И ЭТИ + (-^ —j
1 1
(f) a?, .r + — ; x, x -f — ;
" . 1 • 77 '■ *
Л t Л —т~ — Л- уЛ^ " ' J
.J w
.'11
11 ЭТ1,_:"'\1Г "а.
(/') а-0; .тО; Ох; Ох
. /1 1'.
Ul)xVt ?/'т> •*'?'> .'Аг< /Аг» •'.'/' .
ух, ху и этн-4-f— — J
11 11
С) 00. Т ~; <Ь) 4°'°4
1 -j
(С) цг, х -}- — ; 7г. -f — , х;
. 1 , !
Данные для Т^-рядов i
(соотношения между
^ш)
j
i
I
i
что и для С4,..1
и, кроме того,
(hk) = 0 при
(Ь + 1с)ф2п
{Ьк) ={-!?+* (Щ=*
= (-i)fc+*(w~) =
= (_!)* + * (*:/*) =
=*(JtA)

§ 4] СИММЕТРИЯ ДВУМЕРНОГО РЯДА ЭЛЕКТРОННОЙ ПЛОТНОСТИ 501
Продолжение
Данные для F2 рядов
плоская
группа
j
1
1
i
clvr>
<
1—
«веса»

максимумов
4
1У,Г7,,
■г/;-;
К
2/.,.г,
■>у}г
координаты максимумов
2хг2уг
•*'r ^S' У Г ~~~ ?',S>
хг — *«*' У г "1 Us
orr-\ xs> !>r—yS>
■»/• — Ун- Уг — •**;
'*V II в' У >•' г *'s
•'v +.'/«. ."»• — v.
■'V 4-."«. //,- -f #*
2a;r, 0; 2?/r, 0
rr — .'/r. Vr—Ur
■'■>■ ~\- 11 r, rr — Уг
2x/2fjr
x.r -£s ?/r - - i/s;
•'V -Ь «s> nr — ,vs;
*«■»• — ."*• !/>• — 'V
! ^- + 2/.s. //,•—•'•.,;
2*r + -2 , y; 2i/r+—, —
Тип иоложе- 1
ния
максимума
»
Я
/'
rf
ft
с,
И
г
,1 , . 1 I
i Li I ! '"
I •*■,. — Уг "Г -«-. ■>> — .'//• -г "о 1
! ■*> + .">. *,-—Яг
! •'/
Изображение
ПЛОСКОЙ
группы
F-ряда
4
К ~ ' О. ! 1^
'Mi
А \ 1
ро 4Л
1
f
г г >
• 'ix
го Ь-
•Ж-
*ХёУ\
i ' 1"
X ' • -

502 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТИ [ГЛ. VI
№
12 Л
12В
Плоская
группа
и соот-
ветств.

трансляцией, гр.
§
'it
Число
эквивалентных
точек
8
4
8
16
Координаты эквивалентных
точек
(d) ху; ух; ху; ух;
,1 - , 1
х А . у А ;
-г 2 ' J ~ 2
У + -2' х + ~2 ''
- , 1 - , 1
У+2". «-'-b-g*
(а) 00; у у;у0;0-1
м 1 1.13 3 1.33
U 4 4 ' 4 4 ' 4 4 ' 4 4
п1 ,1-31
1,1 ,31
НЭГ»Чт-2)
- — - - 1
ж*/; уж; a?i/; jar, ж + у, у;
,1 . , 1 -
Данные для F-рядов
(соотношения между
Fhko)
(ДО) = 0 при A qt 2н
(0/.-) = 0 » /.• ф 2н
{hi) = (-1)к (Ък) =
=:(АА) =
= (- l)fc (Afc) =
= (-l)ft(fcA) =
= (fcA) =
= (-1)л(ЛЛ) =
= (*А~)
(At) = 0 при
А + fc ^ 2п

§ 4] СИММЕТРИЯ ДВУМЕРНОГО РЯДА ЭЛЕКТРОННОЙ ПЛОТНОСТИ 503
Продолжение
1
Данные для F2 рядов
плоская
группа
ci.--i
С.."
«веса»

максимумов
z-
2ZrZ,
2Х;
К
2ZrZ8
координаты максимумов
I
2хг2уг
хг ха> Уг 2/в'
xr _j_ ла _|_ _. > уг _ уь _|_ -}-
*г г ««е. .'/г + У8'»
«V — xs -г у» •'/'• + У я ' г -^
1 1 1 I 1 1
•'V + !/s+Y' •'//• ■*-''s + Т
^V Ув> Уг i '''в»
•'> — У* + "2"' ///'~~■''« "т" ~T
1 • ., х
, 1
*r + Уп «V -h Vr + Y ' '
( , 1 i
xr Уг> ,lr b'r\ ./ !
Хг+Уг> «r—Vr
&Ху&Уу
■*> + *•*» У/- — Ув-г-у
■*v + *'«» УгЛ~ tig*
*r — x* Уг+УвЛ- -.7
•*V "T" Уз» Уг жв>
*V -f У8. Уг + *« 4- т,-
»>—Уа. Уг +-*';,;
хг~Уа> Уг — г*+^
ложе-
кси-
Тип пс
пил ма
мума
V
.'/
/'
с
<1
(1
!/
Изображение
плоской
группы
.F-ряда
HUc»! X-j
ГГу6 •! I-1
0] 'С
k 1 «_Л< '
1-Т- '• T6#i'

504 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТКЙ [ГЛ. VI
№
Плоская
группа
и еоот-
ввтетв.

трансляцией, гр.
и-
« У,
и 3
Л а
§ и к
§ 2 Q
g Ч й"
СГ ffl Е-
Координаты эквивалентных
точек
Данные для /''-рядов
(соотношения между
*Wko)
13
с;
7/j
WOO; <6>if; (с,I |
(й) ж*/; у, а: — у; iy—х, х
(hk) = {—h — k, h) =
= (&, —h — k)
ниже это условие
называется 2'-условие
14 I
01.
1 _ (аИ)0; ^1|;(,)|1
id) r, '!■'■; 2х, х; хх
(е) х/, у, х — у; у — х, ;»•; ху;
х, х — у; у— х, у
/'•условие;
{1,1с) = (Щ
b3v
'th
1 J (»)Ш; ,/,)||: (с, |1
(d) .их; хО; Ох
(е) ху; У, х — у; у — х, х;
ух; х, у — х; х — //, у
Т-условие;
(hk) = (kh)

1] СИММЕТРИЯ ДВУМЕРНОГО РЯДА ЭЛЕКТРОННОЙ ПЛОТНОСТИ 505
Продолжение
Данные для ¥г рядов
плоская
группа
! г1
i
i
i
«веса»

максимумов
хгх8
координаты максимумов
ХГ i V Гу "У Г ХГ
xr xs> У г Уа>
хг + У»> У г — хг "Г .'/«I
хг !'* ~Г л\, У г ~\~ xs
1
Тип
положения
максимума
Изображение
плоской
группы
F-ряда
Л
1
i
1 / °ь \
1 Ч * *
: \ ®- /
\ У
i
С:,.
! /:
it г ~\-У гу Ху-Т-Уп
Zi'r — у,., 2d у — //,.;
хг—'±цг\ Хг — 'Ач,-
d |
.»/,., 2Ху — )/у
■rr — .rs, ur—ys;
•'7 + Ув. .'//• -I- х,
■*> + //*, у,-— •■»«--.'/«;
-'> 4- •'•» — Ун, у г -\- •<■*
■«г — *«. .'/г - «« + ?/*;
•'V -г 'я — ?/8« .'/а- — .'/*
/f-
хг~Уп — * г ТУ г
Хг + Уг, 2хг—Уг
/<г/<ь
*г — »**, Уг — Уа''
Хг — Уа> Уг — **
■»V+Ks. Уг + Ха — Уа\
xr~xs — Уз' У г •''*■
'г + у*. .'/г- х8-\■//>;
ау -f .тч — f/s, »/,. -J- а-и

500
СТРУКТУРНЫ!! АНАЛИЗ С ОЦЕНК011 ИНТЕНСИВНОСТЕН
ГЛ. VI
к»
Плоская
группа
и соот-
ветств.
трансля-
цион. гр.
Я
ffl *
Л д
1СЛО
лент
чек
У аз н
Координаты эквивалентных
точек
Данные для F-рядов
(соотношения между
Fhko)
16
Ч
тл
(о) 00
12 2 1
">Г7:7Т
(с)
(d)
1
Y
а?у-
1
2
_
?/.
1
' 2
X —
0;
-?/
1
0Т
. у—
X,
—
х;
"•*.'/;
Т-уеловие;
(hk) = (hk)
У, У — *', *' — .'/, ж
17
(а) 00
^
Tft
2
3
«
12
1
1 2 *" 1
^ 1 ! • п Х • l n
(с)Т¥,0-2-,-0
(d) a;j-; лО; Ckr; ла; *0; Or
(е) #,2ж; 2л,а-; -см-; х,2х\
2х,х; хх
(/') «-у; у, л— у; у —-г, л-,
*у; у, у — х\ х — у, х;
ух; х, у — х; х — у, //;
I
ух, х; х — у; у — х, у
\
Т-условие;
(hk) = fhlc) = (kh)
= (kh)
Примечания к таблице. 1) Число групп в таблице больше 17.
Это происходит из-за того, что «моноклинные» и «тетрагональные»
плоские группы иногда бывает удобно представлять в одном из двух
аспектов (центрированная и примитивная ячейка). Поэтому эти группы
фигурируют в таблице дважды. 2) На изображениях плоских групп различные
кружки обозначают оси симметрии разных порядков, перпендикулярные
плоскости чертежа. Порядок оси легко распознать HQ расположению ма-

§ 4] симметрия двумерного ряда электронной плотности 507
Продолжение
Данные для -F2 рядов
плоская
группа
С1
«веса»

максимумов
2Z;
z;
2ZrZs
2Z;
координаты максимумов
хгУ n '^riMr» ^xr У у
2xr2yr
xr x8> Уг 2/s>
•rr + xa* УгЛ-Уа
■r>r — ys, УгЛ-Ха — Уь!
xr — x8 -\- ys, yr л'й
J> + ys. Уг— *а-гУн>
xr -p x8 ys, yr -\- xs
aV + Vr> xr + Уп
2хг — цг, 2xr — yr\
U^y "" uVai<» bba* " iuJJy
тГуХу") УуУг> XY— yr, у у ,lr
xryr; xr-\-yr, %vr — yr
2x 2«
Я'Г XS' У Г У8'
*г+ж«. Уг + Уь
J'r Ув> Уг xsi
^ + 2/s. Уг + Х*
ХГ Х8> Уг aS + •'/«>
xr ^sr Уз> Уг ' s
•'V + «s, Уг + Я8 — У в,
u'r ~t_ ^8 ' Уs> !Jr "t~ ,l's
xr+y» Уг—-чЛ-у»
'r + x8 — 2/s> Уг — Ун
Лг — У» Уг+*а — Уя\
Xr — J,s+Vs> Уг + Ув
ложе-
кси-
Гип по
ния ма
мума
(1
d
d
d
е
г
/'
1
i
1
/*
Изображение
плоской
группы
i-'-ряда
/ ° \
ч' <$• »*Ь
\ Се/
л. J® '
\7 !|
•
131
^sfi ^ТтС- **sf*
-3®c
леньких чёрных точек, изображающих точки общего положения. Линии
симметрии изображены жирными линиями, линия скольжения — пунктиром.
Латинские буквы указывают тип положения (общее, на оси или линии
симметрии). Описание типов положения максимумов, указанных буквами,
надо искать в строке таблицы, где описывается группа ^2-ряда.
Например, -F'-рядам, описываемым в строках 3, 4, 6, 7 и 8, соответствует рисунок
и описание положений строки 6, См. также фиг. VI, 13 н стр. 539.

508 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ. VI
Существует 5 трансляционных групп плоской решётки:
косоугольная, прямоугольная центрированная, квадратная и
гексагональная (фиг. VI, 6). Первым трём трансляционным группам
соответствует по одной центросимметричнои группе симметрии,. последним
двум по две. Итого 7 плоских групп симметрии, показанных на
фиг. VI, 7; смысл штриховки будет очевиден из дальнейшего.
Центросимметричные проекции электронной плотности возникают
у кристаллов, обладающих центром инверсии, а также у всех
других кристаллов при подходящем проектировании элементов
симметрии (если, например, параллельно оси проекции имеются оси
т • т • • • • •
UU!_! Ы
V1". Тт УогТг Y^T2
Фиг. VI, 6. Пять плоских трансляционных групп; косоугольную
(«моноклинную») и квадратную («тетрагональную») группы
бывает удобным изображать двояко: центрированной и примитивной.
чётного порядка). Таким образом к плоской группе Си приводят
группа С,- и проекции вдоль моноклинной оси всех групп
классов С2 и C2h.
Проекции групп класса C2h перпендикулярно моноклинной оси
приводят к плоской группе CV
Ромбические кристаллы классов V и \\ дают центросимметричные
проекции на все грани ячейки. Если проекция получится нецен-
трированной, то плоской группой будет Со», в противном случае
приходим к группе С2.
То же самое справедливо для центросимметричных проекций
групп класса С2„ — к ним относятся только проекции вдоль
полярной осп (ось 2).
Проекции civ и Й будут возникать для центросимметричных
(в проекции) тетрагональных и гексагональных кристаллов при
проектировании перпендикулярно оси с.

§ 4] СИММЕТРИЯ ДВУМЕРНОГО РЯДА .'МЁКТРОПНОЙ ПЛОТНОСТИ 5(>0
Фиг. VI, 7. Цеитросимметричные плоские
группы: = зеркальная линия симметрии,
линия симметрии со скольжением.
Показано симметрическое преобразование
точки общего положения. Штриховкой
помечены симметрически независимые
области.

510 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕИСИВПОСТЕИ [ГЛ. VI
Квадратные плоские группы 6* и Civ возникнут у
тетрагональных кристаллов первые — без вертикальных плоскостей симметрии,
вторые — с вертикальными плоскостями. Аналогичная ситуация
имеет место для гексагональных плоских групп.
Следует отчётливо представлять себе, что размер элементарной
ячейки проекции может быть долей соответствующего размера
грани (сечения) ячейки. Например, проектирование перпендикулярно
плоскости скольжения приводит к проекции вдвое меньшей размера
грани элементарной ячейки.
6) Симметрия ряда. Симметрия ряда электронной плотности
(или ряда межатомных векторов, о котором ниже) определяется
соотношениями, существующими между коэффициентами ряда Ф7ьЛ.
Действительно, если Ф,,к = Ф^к, то это значит, что проекция цен-
тросимметрична. Если в ряд входят коэффициенты ФАд,
удовлетворяющие условию h = 2w, то это значит, что проекция будет
повторяться по оси а (или ос) с периодом -х. В этом случае не надо
загромождать вычисление ячейкой удвоенного размера, а следует
перейти к вдвое меньшим осям и к другим индексам. Удвоенные
ячейки будут возникать в том случае, если в расчет входят Фй)/,.,
удовлетворяющие условию Ф;,,а=0 при 1ь^2п или при Ьф2п.
Для косоугольных и квадратных ячеек удвоенная ячейка получится,
кроме того, если Фь>к = 0 при k-\-Jcdr.2n. Действительно,
переходом от осей а к у и от с к -$ в первом случае и переходом
к новой ячейке «'= — («-|-с), я' = я во втором случае, мы пе-
рейдём к новым индексам, свободным от ограничения.
В дальнейшем мы будем считать, что это уже сделано; в
практической работе такой переход всегда должен быть совершён.
Если Флй —Ф&й> то, как нетрудно проследить по характеру
вычислений, это приводит к линии симметрии в проекции. Вообще
говоря, можно было бы вывести все возможные плоские группы
чисто алгебраическим путём, как все возможный случаи
взаимосвязи между коэффициентами Фпк.
Соответствие между наличием той или иной плоской группы и
соотношениями между Ф]1к даются условиями погашения; вывод
делается при помощи таблицы VI, I. Приводим данные для 7 центро-
симметричных групп (^hk = ^hk)-
Группа С>. Соотношений между Фьк нет. Первая и вторая
таблицы суммирований выполняются полностью.
Вычисление приходится проводить для у ячейки
(сравни фиг. VI, 7).

§ 4] СИММКТРИЯ ДВУМЕРНОГО РИДА ИЛККТРОННОЙ ПЛОТНОСТИ 511
Группа civ ФЛЙ = ФАЬ- Коэффициенты В — 0. В первой и,
следовательно, во второй таблице пропадает
суммирование синусов. Вычисление приходится
производить для — ячейки. Остальная часть ячейки
заполняется симметрическими операциями, как
это, впрочем, очевидно и из рисунка группы.
Группа C\l ®hk = {&hk и *лл —° ПРИ й + £ нечётном.
Коэффициенты Б = (). Кроме того, в таблице первого
суммирования для к чётных 2i = 0, а для 1:
нечётных 2а — 0- Поэтому вторьте 12 значений Л
повторяют первые 12 значений. Следовательно,
вычисление приходится производить для ■=■ ячейки,
о
что также следует из рисунка группы.
Группа d ^пк^^кК' В этом случае ни в первой, ни во
второй таблице суммирования упрощений нет.
Независимой будет •-- ячейки.
Группа C\v ФАЛ = ФАЛ - Ф*Л - Ф*А. Здесь В = 0 и
суммирование синусов отпадает. Вычисление проводится
1 \, ., г 1
для — ячейки, но независимой будет — ячейки
(сравни фиг. УГ, G) *).
Г ]) у п и а Со Фм = ФА^А>А = Ф;,.,А }_А. Упрощений пет ни в
первой, нп во второй таблице. Вычисление
достаточно произвести для — ячейки, но независимой
будет -«- ячейки. *)
Г р у п и а С«г то же, что и для Со и кроме того Фкк = Ф*.А«
Упрощений в обеих таблицах нет. Вычисление
достаточно произвести для — ячейки. Незавиеи-
о
мой будет -рс ячейки"-).
Последние две группы имеет смысл описывать в ортогексаго-
нальных осях. Так как ортогексагональная ячейка центрирована,
то Фль = о при h-^-k нечётном. В этих осях линии симметрии
совпадают с осями и поэтому ФАЙ. = ФАЙ;-
*) Независимая область имеет форму, не соответствующую
суммированию по столбцам и строкам. Поэтому приходится считать для большей
части ячейки, чем та. которая является независимой.

Г)12 СТРУКТУРНЬШ АНАЛИЗ С ОЦЕНКОЙ ШГТКИСИВНОСТКЙ [ГЛ. VI
Таким образом коэффициенты J3 = 0 и кроме того в таблице
первого суммирования для к чётных 2i = ^» а Для ^ нечётных- ^2
равно нулю. Поэтому так же, как и в плоской группе С™,
приходится производить суммирование для — ортогексагональной ячейки.
о
Разумеется, описанное вычисление много проще вычислений в
гексагональных осях. Оно, однако, обладает и недостатком: ячейка
укрупнена, и поэтому вычисление менее точно при разбиении
периодов для суммирования на одинаковое число частей.
Следует подчеркнуть, что все вычисления в группах Се, и CV
(как это, вирочем, непосредственно следует из определения этих
плоских групп) производятся для сокращённой элементарной ячейки
(сравни гл. Т, § 7).
§ 5. Точность ^-рядов и возможности их применения
Вопрос о точности и возможностях применения рядов электронной
плотности — это вопрос о точности и возможностях структурного
анализа, так как знание функции о (.-г//,?) является копечным
результатом исследования.
Функция р {xyz) (или о {ху), если речь идёт о проекции) известна
нам на основании опыта с определённой точностью. Поэтому
довольно легко установить для каждого конкретного случая величины
вероятных ошибок в определении значений функции, расстоянии
.между её максимумами и прочее. Несколько труднее ответить на
вопрос о точности наших суждений в отношении строения
молекулы на основании анализа этих функций, так как они являютен
средними распределениями электронной нлотности во времени и,
таким образом, характеризуют не покоящуюся молекулу, а
колеблющуюся. Коли бы колебания атомов молекулы были изотропными,
то введение поправки на колебания не представляло бы затруднения.
Нахождение этой поправки для реального случая, т. е. анизотропии
колебаний молекулы, как целого, и внутримолекулярных, возможно
лишь единственным способом — исследованием распределения
электронов при разных температурах.
Таким образом вопрос, поставленный в этом параграфе,
разбивается па две части: 1) какова точность функции электронного
распределения, находимого на опыте, 2) какие заключения можно
сделать о строении молекулы, зная вид этой функции.
а) Заключения о строении молекулы. Можно следующим
образом сформулировать задачу определения строения молекулы и
кристалла. Требуется определить расстояния между центрами
атомов и найти отклонения от распределения электронов в свободном
атоме, образовавшиеся благодаря связям между ними.
Допустим, что нам вполне точно известно расположение центров
атомов в кристаллической решётке. Пусть в этих точках находятся

>j 5] точность /'-Рядов п возможности их ш'имкнкнин 5Ь'5
ядра соответствующих свободных атомов. Электронное распределение
каждого из них может быть представлено сферической функцией
где гк— радиус-вектор ядра атома. Тогда распределение электронов
в решётке равно
Р И = 2 ?*(**— гк).
к
Функция р;,. меняется, но не теряет своей симметрии, если атом
находится в изотропном колебании. Как мы видели ранее (стр. 276),
увеличение температуры сводится в этом случае к размытию
функции— величина ее' в максимуме уменьшается, «хвост» растёт.
Функцию р(г) такого гипотетического распределения электронов
для свободных и изотропно-колеблющихся атомов можно подсчитать
и сравнить с опытной; теоретические атомные функции о (г — гк)
определяются по формулам, приводимым ниже.
Если центры атомов расположены на расстоянии, половина
которого меньше области, на которую простираются атомные
функции, то последние будут перекрываться и между атомами возникнут
«мостики», тем более высокие, чем ближе друг к другу находятся
атомы. Наличие или отсутствие этих мостиков не является, как
мы видим, чем-то характерным для связанных атомов, а есть
результат чисто геометрический. Более того, перекрывание атомных
функций приводит к смещению (сближению) их максимумов.
Максимумы г* (г) не будут удовлетворять условию г = )гк.
Как нетрудно видеть из расчёта, складывая две атомные
функции (о виде атомных функций см. ниже), центры которых
находятся на расстоянии s, например
е-*»л_|_е--*(>-+.-)-
или (см. VI, 37)
о i a
(а2 -|- г2)2 "Г" (а* + (/• -М2)- '
мы получим функцию, максимумы которой будут уже находиться
па расстоянии s — d, а вс .? (цифровые данные см. табл. VI, II).
Сказанное иллюстрируется фигурой VI, 8.
Таким образом результат исследования — функция р (готлгн) —
должен быть обработан следующим образом. Строится функция
р (Угипот) для структуры, состоящей из свободных изотропно
колеблющихся атомов, центры которых совпадают с максимумами
функции рк(г — гк). Вполне вероятно, что максимумы этих двух
функций не совпадут. Если это несовпадение находится вне пределов
ошибок, то можно найти максимумы функций рк(г— гк) следующим
рассуждением. Если максимум рГИпот(**) сдвинулся на вектор 2 по
отношению к максимуму р (^0Пытн)> то максимум
соответствующей функции рк(г—гк), т. е. вектор rki найдётся сдвигом от

*)14 игруктУйши лттлли:; <j оцьШкоп HHTiiHOiiimodTriH [r.i. vi.
максимума р(/'опытн) на вектор 2 (т- е- сдвигом на ту лее
величину, но в обратную сторону).
Действительно, перекрывание атомных функций сближает атомы,
следовательно, центры атомов должны находиться в направлении,
обратном
произошедшему сдвигу.
Разумеется,
указанная процедура может
рассматриваться лишь как
приблизительная.
Впрочем, она была бы точ-
пой, если бы
аппроксимация атомов
сферической функцией была бы
справедлива. В не очень
точных исследованиях и
при плоской проекции
атомных связей эта
поправка на перекрывание
максимумов бывает
обычно меньше ошибки
измерения.
Порядок величины
искажения межатомного
расстояния',"двух близко
лежащих атомов,
происходящего из-за
наложения атомных ■
функций, нетрудно
подсчитать, представив атомную
функцию согласно
вышеприведенным формулам.
Если подсчитать, на
какой отрезок d сместится
атом от своего
истинного положения благодаря перекрыванию атомных функции, то
получим, например, следующие цифры для атомных кривых типа Ае-аГ*
(табл. VI, II), где s — расстояние между атомами в исследуемой
проекции.
Т а б л н ц а VI, II
«(A)
0,7
0,8
0,9
1.0
d(k)
0,16
0,066
0,026
0.010
s(k)
l.l
1,2
1,3
1.4
d(k)
0,004
0,001
0,0005
0,0001
Фиг. VI, 8. Искажения электронной плоскости
в результате перекрывания атомных функций.
а) Расстояние d^ достаточно велико.
Искажается лишь ход р (г) между максимумами.
б) Расстояние d^ меньше, чем в случае а).
Налоясение максимумов даёт картину со
сближенными максимумами, которые значительно
менее остры, чем исходные. «) Максимумы
слились. с?12 меньше разрешающей
способности ряда. *) При малом расстоянии между
атомами с сильно разнящимися
менделеевскими числами могут выявиться лишь
максимумы р (»•), отвечающие более тяжёлым
атомам. Они несколько смещены от положения
центра атома.

$ oj точность /-'-Рядов и возможности их иримкнения 515
Отклонение атомных функций от сферической симметрии,
обязанное, как уже неоднократно указывалось, химической связи и
главным образом анизотропии тепловых колебаний, может быть
найдено следующим образом.
По найденным значениям rft строим ещё один гипотетический
ряд (но теперь уже его максимумы совпадают или почти совпадают
с истинными): рГип<»т(?*). Разпость
ггипот^ ' r v опытн'
может быть приписана искажениям в распределении электронной
плотности, происходящим из-за анизотропии колебаний и
химической связи. Различить эти два последние фактора можно только
сравнением нескольких р(г), построенных для разных температур.
б) /-кривая и атомная функция. Влияние обрыва ряда на
вит; атомной функции. Как известно (см. стр. 216), электронное
распределение в свободном атоме (атомная функция) связано со
значением амплитуды атомного рассеяния /' следующей формулой
со
>у w=d* Jsf(s) sil1 sr d8> (VI> 33)
0
2 sin <)
где r — расстояние от центра атома, a s = 2тсЛГ = 2~ , к —
длина волны рентгеновского луча и 2Н — угол рассеяния. Аналогичным
интегралом мы можем выразить атомную амплитуду через атомную
функцию:
со
f(8)=][v(r)^dr, (VI, 34)
о
где 4~r2p (г) — U (г).
Во всех работах английских авторов принимается, что атомную
функцию можно аппроксимировать выражением] р (г) = Jce-(,r'J.
Нетрудно видеть, производя интегрирование (VI, 34), что при этом
з
— SJ
f(s)— &(~J e 4a- Эта функция убывает с увеличением s очень
быстро; поэтому создаётся впечатление, что обрыв ряда
электронной плотности не играет роли и не скажется на ошибке
определения функции р {хуг) в кристалле. Подобная процедура, однако,
совершенно не верна. Очевидно, что законной аппроксимацией р(г)
будет служить такая функция, которая может быть получена на
опыте вычислением интеграла (VI, 33) из кривой рассеяния f(s),
представляющей собой результат эксперимента. Эта кривая
устанавливается измерением па кристаллах, в которых анизотропия
тепловых колебаний и химическая связь делают, строго говоря,

516
СТРУКТУРНЫЙ АИА.ШЛ С 0ЦКНК0Н HHTEHCHBHOCTEliT
I гл. vi
неверной аппроксимацию атома какой бы то ни было сферической
функцией. Однако для ряда целей подобное приближенное
представление вполне допустимо, и мы им будем пользоваться в
дальнейшем. Электронную плотность в кристалле мы представляем, таким
образом, в виде
р(.п/0 = 2Ра.(г--Ы (VF, 35)
А-
где *•/,.— координата центра сферического атома. Суммирование
производится но всем атомам кристалла.
Итак, поставим перед собой задачу нахождения выражения
атомной функции через опытную f-кривую.
Опыт показывает, что в большинстве случаев практическая
/'-кривая — средний результат большого числа измерений — аппрок-
е аппроксимация А И ЛитайаороОского
• опытная лрава»
• теоретическая кривая (метод Фока-лартри)
теоретические значения f умтошены »о
температурную поправку
j ааарвшшмация 6 уса
4-х
0.1 02 QJ 0.4 ДО
Фиг. VI, 9. Атомные кривые углерода
0.6 0.7 Q.H QJ
SMI? дЛМКьЛ,!
L0
симируется очень точно для всех значений s (кроме значепий $,
близких к нулю) кривой типа ке~а-\ где h и <х— параметры, смысл
которых будет пояснен ниже*).
Для атомов углерода многочисленными исследованиями была
найдена /"-кривая (средний результат по крайней мере 20
структурных работ), показанная на фиг. VI, 9. Заметим, что эта же
кривая будет получена из теоретической /"-кривой, рассчитанной,
по Хартри, с изотропной «температурной» поправкой е
*) Китайгородский А. И., ЖТФ, 1950 г.

§ 5] ТОЧНОСТЬ /''-РЯДОВ И ВОЗМОЖНОСТИ ИХ ПРИМЕНЕНИЯ 517
Как это видно из фигуры, опытная кривая весьма точно
(расхождение много меньше ошибок опыта) аппроксимируется кривой
. . /'sin Ь\
_ — >,2Н - — М(-г— ) 7.л —«
где Ш—вектор обратной решётки выражен в обратных ангстремах.
На этой же фигуре показана кривая типа ке-*8* (Бус), резко
расходящаяся с опытом.
Аппроксимация ке~** несправедлива только в области s (или Я),
близких к нулю. Это не имеет никакого значения, так как
отражения начинаются при значениях Н, лежащих в области
совпадения кривых.
Радиальное распределение электронной плотности сферически
симметричного атома (VI, 34) преобразуется к виду
Р (г) =* .Jrr J «"-" siu sr ds. (VI, 36)
0
Коэффициент к определится нормировкой из условия
lnfp(r)r*dr=zZ,
о
он равен к = — Z, т. е. 7,06 для атома углерода; для него же
о
« ==~ = 0,35.
Исходя из табличного интеграла
J (a) = c~y'*in.sr ds = -,
о
получим дифференцированием но параметру:
00
I 5е " аа sin sr ds = ryr
г
О
Следовательно,
Р<г>- *(Л.-У (V1'37)
Таким образом, например, для атома углерода

518 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕИ [ГЛ. VI
Ниже будут приведены график и таблица значений этой
важной функции.
Однако вполне очевидно, что найденная функция не
соответствует той, которая может быть установлена на опыте. В любом
опыте мы измеряем отражения до некоторого предельного
значения sraax. Желая получить результат, сравнимый с экспериментом,
мы должны в формуле (VI, 36) заменить интегрирование до
бесконечности интегрированием в конечных пределах. Интеграл
р (г) = -^7 sc-™ sin sr ds
о
берётся по частям и приводит к следующей формуле:
Р \г) = о/ ■> 1—Т~« + о ■» # о ,—2-v {(— Я Bill .ST—Г COS 6Г) S -4- -„—.—,- -
1 v ' л2 (a- -J- r2)~ ' 2n?r (a3 -f- rz) \v ' \ l a2 -j- r2 J
-f ( —acosw + rsiiisr)(-^^)}. (VI, 38)
Цри б- = сю дополнительный t член пропадает, и мы возвращаемся
к уравнению (VI, 37)- При конечных значениях s это выражении
Т а б л и ц а VI, III
г В А
0
од
0,2
0,3
0,4
0,5
0,6
0,7
П,«
6,9
1,0
1Д
1,2
1.3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
? (г) 13 Эл/А*
(S = 'ТО)
lfi.fi
14,3
9,52
5,53
3,01
1,80
1,06
0,66
0,43
0,28
0,20
0,14
0,102
0,075
0,058
0,045
0,035
0,027
0.022
0,018
0,014
Волны обрыва .
-8,25
-6,05
-2,99
-0,15
0,86"
0,65
0,18
—0,15
—0,25
-0,19
—0,035
0,117
0,123
0,180
0,014
—0,068
—0,070
—0,039
—0,007
0,030
0,046
р(/') 1! ИЛ/А'
(s = 7.85)
8,35
8,25
6,55
5,37
3,87
2,45
1.25
0,51
0,18
0,11
i 0,06
0,26
0,22
0,15
' 0,07
i —о,02
! -0,03
—0,01
i 0,01
0,05
0,06

§ 5] ТОЧНОСТЬ F- РЯДОВ И ВОЗМОЖНОСТИ ИХ ПРИМЕНЕНИЯ 519
даёт так называемые волны обрыва — шаровые волны, длина
которых равна d^j, = -^— , а амплитуда убывает обратно пропорцио-
-"тах
нально квадрату расстояния от центра атома.
В вышестоящей таблице (VI, III) приводятся значения р (г) в
отсутствие обрыва и при обрыве на значении s = 7,85, что соответствует
/5
10
-5
о р(г) при S=°*>
• волны обрыва-
а р(г) при S = 785
\<
Л
ч
-*—i Г-v^ г^
0,2 i
I
I
i
I
t
0.4
T
0.6
0.8
"" L0 12 1.4 1.6 L8 ?J
I
Фиг. VI, 10. Кривые ио данным таблицы VI, III.
//==1,25, т. е. sin fr = 0,96 для медного излучения. Это — случай,
наверное, 95% структурных исследований. Подсчбт проведбн для
значения а=0,35 и Z—6 (т. е. А; = 7,06). На фиг. VI, 10
изображены кривые, построенные на основании данных таблицы.
Как видно из этих данных, влияние обрыва сводится к резкому
занижению максимума, к, «расплывашш» всей атомной функции и
к образованию шаровых волн, окружающих атом.

520 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТВЙ [ГЛ. VI
Обрыв интеграла (или ряда) при конечных значениях s резко
искажает значение электронной плотности. Абсолютные измерения р
при этих условиях невозможны, да и об относительных величинах
может быть получено лишь самое общее суждение.
Воспользоваться приведённой выше таблицей для пересчёта
полученных на опыте значений р в правильные значения р[<* = оо],
конечно, можно, но трудно сказать, будет ли такое исправление
целесообразно, имея в виду, что расчёт произведён для
сферических изотропно колеблющихся атомов. При этом пересчёте
искажения, которые вносятся обрывом несимметричных (истинных)
атомных функций, не будут учтены.
Вычитание из полученного ряда волн обрыва в общем
эквивалентно получившей распространение процедуре умножения опытной
/-кривой на некоторый множитель е-Р*. Физический смысл
подобной операции это «повышение температуры опыта» в
предположении, что это повышение температуры приводит атомы в
состояние изотропного колебания.
Дополнительный член в точке максимума (здесь наиболее резко
отличие р^коисчн] от p[*«v.,|) равен
ке-
2*-<х2
as
+ *+■=-].
при а = 0,35 и s = 7,85 он даёт, как мы видели, 8 г>л А3. Для того
чтобы электронная плотность могла быть измерена с точностью
порядка одного процента, надо чтобы эта величина равнялась 0,01
от ^з", т. е.
0,02 = ,-»* ГА ctV 4- as -f J1 . (VI, 38a)
Если обрыв произошел при « = 7,85, то для а получаем
значение, близкое к 1 (вместо нормального 0,35).
При таком значении <х /"-кривая медного излучения спускается
при sin0=1 (место обрыва) до значения 0,0005 (вместо 0,06).
Вполне очевидно, что эта процедура ни в какой степени не
отвечает требованиям изучения распределения электронной
плотности. При увеличении а происходит резкое размытие картины,
детали исчезают и результат подобного исследования будет
тривиальным. Это очевидно хотя бы из следующего подсчёта. Значение
второй производной в вершине максимума пропорционально, как
известно, кривизне кривой.
Из формулы (VI, 38) находим:
[ °У-' =.._ JL.L Г_8. 4- ^- 4- -1 — <'—==
| дг- |r-=o t;V>^ [ <*•• ' а* Г а4 J 2--
;= Ь и. г) =-- ijp- Z? (*, а). (VI, 30)
о

§ 5] точность F-рядов и возможности их применения 521
Мы видим, как резко расплывается максимум: при переходе от
а = 0,35 к а = 1 кривизна уменьшается примерно в 200 раз. Легко
подсчитать, что обрыв ряда влияет много меньше. При а = 0,35
и s = 7,85 получаем изменение кривизны вдвое по сравнению со
значением при s — со.
Совершенно ясно, что единственным путе\и к исследованию
электронной плотности является сдвиг обрыва ряда к возможно
большему значению s. Уравнение (VI, 38а) симметрично по отношению
к а и 5. Если условие точного измерения электронной плотности
требует а = 1 при s = 7,85, то то же самое будет достигнуто при
а = 0,35 и s по крайней мере 20. Это значит, что эксперимент
должен охватывать по крайней мере все отражения, которые можно
получить на молибденовом излучении.
Итак мы видим, что влияние обрыва уничтожается лишь в том
случае, если /-кривая может быть доведена до тысячной доли
максимального значения. Искусственное доведение (умножением
на фактор e-$s, где р—порядка 0,6, если а = 0,35) приносит мало
пользы, так как точность определения координат атомов падает;
расширение предела измерений является единственным правильным
решением проблемы.
Более мягкие требования к измерениям могут быть предъявлены
в том случае, если желают определить плотность в промежутке
между атомами (а не в максимуме). Во всяком случае сглаживание
о
«фона» до 0,02—0,03 эл. А3 не говорит ещё, как иоказывает наша
таблица, о правильности определения электронной плотности ближе
к максимуму. Мы обращаем на это внимание, так как иногда
ошибочно считают эффектом обрыва лишь колебания «фона», в то
время как на самом деле наиболее существенным действием обрыва
является искажение хода электронной плотности вблизи максимума.
Выведенные выше формулы, таблица и кривые имеют целью
помочь в нахождении условий, при которых уничтожается влияние
обрыва, так как без этого исследователь не может приступить
к измерению электронной плотности.
Определение объёмного распределения электронной плотности —
будущее структурного анализа. До сих пор главным образом
производились измерения в проекции электронного распределения на
плоскость. Поэтому нам надо остановиться на вычислении
соответствующей атомной функции. Проектируя электронную плотность
вдоль прямой линии, проходящей на расстоянии а от центра атома,
получим:
со
з (i7) =2 Г ,Г 1 р (г) dr. (VI, 40)
.! у >•'- — о-
Подставляя значение j>(r) и преобразовывая интеграл
подстановкой .»•■ = г2 — а2, мы сводим интеграл к табличному. Результат

522 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ. VI
имеет вид:
*(«)= ^—j. (VI, 41)
2г(а2 + а2)а
или для атома углерода в нормальных условиях (а = 0,35)
(0,123 +а2)"
Приводим таблицу значений о (а) для двух очень близких зна^
чений а (таблица VI, IV), а именно, а = 0,35 — опытная кривая
и а = 0,37—/"-кривая, отличающаяся от нее крайне незначительно.
Таблица VI, IV
а
в А
0
0.25
0.5
0.75
ио
1,25
1,5
1,75
2,0
2,5
3
s (а) в эл./А2
при а = 0,35
9,17
5,4
1,73
0,69
0,33
0,17
0,10
0,07
0,05
0,02
0,01
при а = 0,37
8,4
4,65
L,73
0.71
0,35
0,18
0,11
0,07
0,05
0.02
0.02
Весьма интересно подчеркнуть большую чувствительность а (а)
(в сравнении с р (г)) и нритом только в центральной части к
значению а. При возрастании а кривая плотности размывается,
снижаясь весьма заметным образом в центре и чуть возвышаясь на
«окраинах».
Влияние обрыва учитывается в принципе таким же способом —
в формулу (VI, 40) надо подставить значение а (а) вместо а(д).
[j конечн] [«=ooj
Здесь приходится прибегнуть к графическому интегрированию,
которое и было проделано для случая а = 0,35 и s = 7,85. Эффект
обрыва качественно носит тот же, характер; он приводит к
значительному снижению центральной части кривой, общему размытию
электронного распределения и круговым волнам, амплитуда которых
будет убывать уже несколько медленнее, чем в трехмерном случае,
я именно кал; а'\ '.\-лто, правда, значение амплитуд волн обрыва

§6]
ОШИБКА РЯДА ЭЛЕКТРОННОЙ ПЛОТНОСТИ
523
но отношению к основной функции меньше, чем для трёхмерного
случая. В следующей таблице (VI, V) приводятся значения а (а)
о
только до 1 А; в первой графе приведено о(а), во второй значе-
ние волн обрыва и в третьей <з(а). Таблицы (VI, IV) и (VI, V)
[аконечи]
рассчитаны для одних и тех же условий, т. е. для одних и тех
же значений а и s.
а
о
в А
0
од
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
Таблица VI, V
а (а) в эл./А2
[* = .х-]
9,2
8,3
6,0
4,02
2,62
1,73
1Д7
0,81
0,59
0.45
Волны обрыва
-3,18
-2,35
—1.61
—0,35
+0,47
10,47
+0,18
-0,09
-0,20
—0,1«
0,33 j —0,01
!
з(а) в эл./А2
[.s коыечн]
6,0
5,9
4,4
3,7
ад
2,2
1,35
0,7
0,4
0,3
0,3
§ 6. Ошибка рядя электронной, плотности
а) Значения электронной илотносш. Средняя ошибка определении
электронной плотности в какой-либо точке ячейки равна
Др
0,707
1/ 2Д//Ш (.V—объём элементарной ячейки); (\'Г, 42)
h, к, 1
если ряд оборван, то
-Ь
0/707
\
Ш
hkl»
(Vi, 42а)
где вторая сумма берётся по отброшенным членам. Если полагать
процентную ошибку Ь в измерении Fhki одинаковой для всех hkl, то
ар=0'3°7К ^S^ + 2'^ш.
V
(VI, 426)
hkl
Вычисление средней ошибки с учётом обрыва ряда не представляет
труда (оно проводится в полной аналогии с вычислением приращения
производной электронной плотности (см. ниже)), однако эта цифра вряд,
ли представляет интерес ввиду систематического, а не случайного
влияния волн обрыва на картину электронного распределения. Как мы видели

524 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТКНСИВНОСТЕН [ГЛ. VI
выше, различия р(й коиечН] и p(8 = 00j в максимуме доходят до
нескольких эл./А3; в то же время различие «фона» хотя может быть большим
в процентном отношении, но в абсолютном выражении есть величина
порядка 0,01 эл./А8.
Как подчёркивалось выше, оценка электронной плотности может быть
проведена лишь в том случае, если измерениями или искусственно
достигнута вполне совершенная сходимость. Как было показано, это требование
осуществляется при условии обрыва /"-кривой на значении по крайней
мере в тысячу меньше максимального:
При выполнении этого требования безошибочные измерения интенспв-
ноетей будут приводить к точным значениям электронной плотности.
Найдём*) ереднюю ошибку в определении объёмного'распределения
электронной плотности Др и его проекции Да. Если решётка состоит из одного
сорта атомов, то
где и — число атомов в ячейке. Если решотка состоит из q сортов
атомов, то
ч
*%=/'2 Ъ "<^'=Г"Г, (VI, 43)
где Z{ — менделеевское число атомов сорта *, а /'—единичная атомная
кривая (в дальнейшем всюду предполагается, что /'-кривые разных
элементов параллельны друг другу: это достаточно точное предположение, чтобы
исходя из него подсчитывать ошибки опыта). Выражения средних ошибок
могут быть теперь записаны в виде
\Ъ'{ш =™-1-Y%i
ар=Щ1 ь v 2d?1'"»« =олотsv V Zfw- <v'• *4)
ш ш
Да- 0.707 4* У^Ц Гш- {VI Ш)
Суммы под корнем берутся по всем узлам обратной решётки. Заменим
суммы под корнем интегралами. Очевидно, что на единицу объёма
обратной решётки приходится V узлов, а на единицу плошали сечения — S узлов.
Следовательно.
2/ш= (f*(H)wr-vdir.
hkl J
2>\w= (f'UH)2*HSdH.
hk-П J
hkO
Подставляя / =-— о~'2я:*н и интегрируя от нуля до бесконечно-
о
7
сти (верхний предел по условию равен Нтлх = —— и обращает в нуль
*) Китайгородский Л. П.. пит. на стр. 516.

§ б] иШИБК.1 РЯДА ЛТЕКТРОННОИ ПЛОТНОСТИ 525
значение интеграла), имеем:
о / J
I V 8У U™ ' (4тш)^ (4-а)» J4'' () ~ 8«2аЗ U / '
00
/Зг.\« 4KgHr // 1 К .Г .v /уп\з
V 8 У L **« (4«a)*J -"Л |0 ~ '8ла2" VirJ '
Для соединения, состоящего из одного сорта атомов.
„ Г~л 2.1''
v,/""'*" 2.1'' /~п
As = /l/ —Ц-. (Vf.4',a)
' .V aK | 8
Как мы видим, ошибка в определении электронной плотности
пропорциональна менделеевскому числу, числу атомов в единице объёма, и соот-
л
ветственио площади, и обратно пропорциональна в2 в случае объёмной н a
в случае двумерной задачи. Как мы видим, Др и Дз сравнительно медленно
изменяются с а, самое небольшое изменение которого означает (ем. выше)
значительное изменение условий эксперимента. Разумеется, стремление провести
исследование при минимальных значениях а является совершенно верным:
значительно интереснее получить всего лишь с вдвое худшей точностью
распределения электронной плотности при вдвое меньшем значении а, так
как при этом выявятся подробности, исчезающие при введении фиктивного
изотропного движения атомов. Так как а будет колебаться для
подавляющего большинства экспериментов в пределах 0,5—1, то для Да и Др в
типичных органических соединениях (например, нафталин п = 5. Z = 6
»V = yoA-) получим:
0,56 < Да < Ь, о,1Ь < Др < 0,ЗЬ,
т. е. при хорошем эксперименте (6 = 0,1) проекция электронной плотности
определяется с точностью порядка ОД эл./А2. а объёмная плотность с
точностью порядка 0,02 эл./А3.
б) Значения координат максимумов. Почти во всех структурных
исследованиях, проводившихся до сих пор, авторы ставили перед собой
задачу определения лишь межатомных расстояний.
Как будет видно, условия, при которых надо производить подобное
исследование, будут значительно отличаться от обсуждённой выше
методики определения электронной плотности.

Г)2(> СТРУКТУРНЫЙ ЛЙЛ.Ш:* С ОЦКЙКОИ ИЙТЕНСИВКОСТЕИ [ГД. VI
Ошибка в определении координаты максимума (мы пишем формулу
для ортогональной системы координат) равна
*т . *ш
Дж=_^ или ДЖ = -^— (VI, 46)
в зависимости от того, производим ли мы определение #гаах, исходя из
трёхмерного или двумерного ряда. Прежде всего следует подчеркнуть, что
стремление сделать ряд сходящимся связано с расплыванием максимума и, сло-
довательно, с увеличением j-4f . С другой стороны, влияние волн обрыва на
величину первой производной не обладает систематичностью, отмеченной
в отношении величин Др. Волны обрыва могут одинаково исказить знн-
чение — как вблизи, так и вдали от максимума. Следовательно, заранее
не очевидно, что выгоднее свести к нулю волны обрыва- и зато увеличить
вторую производную или учесть волны обрыва, не уменьшая остроту
максимума.
Подсчитаем сначала среднюю ошибку в величине — . По определению,
hkl
hk
Для ошибки производной в произвольном направлении г имеем:
К£)^2А'«ф(2)]'-^2
hkl • hk
rr~ >.S-M<
hk-
Положим, что все измеренные значения /•' определены с процентной
ошибкой Ъ; тогда
LWW J ~ 2v- \" ы ш ' 2d " ш\-
hkl hkl
hk hk
где первая сумма берётся по всем узлам обратной решётки внутри сферы
радиуса Нт&%> а вторая сумма по остальным узлам.
Значение F* в вычислениях средней величины можно заменить
по (VI, 43) на

i? ()j ОШИВЙА РИДА ОЛТ.КТРоПНОИ НЛОТЙООТИ 527
Таким образом:
hkl
Л A- hk
Сумму можно заменить интегралом, имея в виду, что в единице объёма
пространства обратной решётки имеется V узлов, а на единицу площади
узловой плоскости приходится S узлов. Тогда можем написать, нод-
етавляя /' = -^— е-*8:
' 8
2*-(f)1 £/->**
hid
ffle-2"* ds.
Эти интегралы берутся без труда, и мы имеем:
-J ' 2я2 V 8 J U« (2a)2 Г (2a)8 ^ (2a)« ^ (2a)5 / L'
hkl
л%
«У /3t:\2
3*2
2л: V 8 У ^""'42» ' (2а)2 ' (2а)
Г^ + 6
(2а)*
где а и Ь — пределы интегрирования. Искомое выражение ошибки состоит
из двух сумм; для первой пределы интегрирования — от нуля до s, а для
второй от s до оо, где $ — место обрыва ряда.
Таким образом имеем:
'(ЯГ-^^^-^х
*4 I & 12*2 24,
1 2с ~ (2а)2 ' (2а)3 ~ (2а)4
(2а)5) Г
Ч^Г-Ф^Мт+*-'■>•-■•><
х
2а
3s2 , es 6 \\
(2.)2"1" (га^ + сга^Л*
Ошибка в определении координаты-максимума для пространственного слу*
чая (делим на вторую производную р в точке максимума) равна (см. VI, 39)
й
(Лг)2 в 5?Г S "* (W{ф1 (s'a) + **(*' а'Ь)>' (VI' 47)
г'=--1

528 структурный uca.ih:* с оцкнкои инткисивносткй. [гл; vi
где ZQ—менделеевское число атома, ошибка в определении максимума
которого вычисляется
ф1 (s, „. ' IV + wf+q.y + g.yTd.,.; _ 47a)
«,(.. »,(,) = -И*£ L* + «У + W + <*>* + <»W» . (VI. «6)
'*"(*• <*)
Эта формула позволяет самым детальным образом исследовать влияние
различных факторов на точность определения межатомного расстояния.
Все величины, входящие в формулу, должны быть взяты непосредственно
из опыта для данной структуры. Таким образом, установлен объективный
критерий точности результатов структурного анализа.
Если ряд сходится, т. е. s можно считать равным бесконечности,
то «Г»! (а, а) = О, Ф2 и ? упрощаются, и
<1
/ = i
(VI, 48а)
Как мы видели выше, ряд всегда может быть сделан сходящимся за
счёт увеличения «. Нормальное значение для а это 0,35, значение, при
котором ряд можно считать сходящимся для медного излучения — t = 1.
Возьмём для конкретности органическую структуру. Тогда ~ — 1, а число
, .. п
атомов на единицу объема — есть величина довольно постоянная и рав-
о-з
ная, примерно, для ароматических углеролов 0,05 А. Таким образом
5
Аг = 0,08Ь 2 .
При съёмке на меди ряд делается сходящимся при а = 1 и,
следовательно, при точности измерения Ь = 0,1 трёхмерный ряд позволяет находить
межатомные расстояния с точностью до 0,01 А.
Посмотрим теперь, не выгоднее ли не вводить искусственное
схождение ряда и работать с оборванным на медном излучении ряде, но зато
при а = 0,35.
Для а = 0,35 и s = 8 получим
** <*' *> " (-77 + 39,5)* ~ °'М; ** "■ " " ~ (-7?+^)' * * а063бЬ''
Аг = 0.04 У (0,04 + 0,063562) ,
при Ь = 0 Дг = 0,008 А. Это предел точности. При Ь = 0,1 получаем
практически ту же величину. При грубой работе (Ъ — 1) получаем Дг = 0,01 А.

§ 6] ОШИБКА РЯДА ЭЛЕКТРОННОЙ ПЛОТНОСТИ 520
Таким образом мы приходим к важному выводу: при определении
координат максимумов ряда не имеет смысла прибегать к улучшению сходимости
ряда. Это приобрело бы смысл в практически неосуществимом случае —
работе с точностью, например, Ь = 0,01-
Весьма интересным является также заключение о влиянии ошибок
в определении F на точность определения координат. Для рассмотренного
примера можно составить следующую табличку:
Ъ \ О ОД 0,5 1,0 1,5 2,0 5,0 10,0
Д г 0,008 0,008 0,0095 0,012 0,017 0,022 0,05 ОД
(А)1
Таким образом при средней ошибке в F па один порядок величины
получаем всё же точность до ОД А. Этот расчёт делает понятными
результаты вычислений некоторых исследователей, которые показали, что даже
при разбиении всех пятен рентгенограммы по интенсивноетям на 3 группы
можно получить в грубых чертах правильную (в отношении распределения
максимумов) картину распределения электронной плотности.
Следует также остановиться на другом своеобразном моменте, а именно
пропорциональности Дг величине
Здесь интересно обсудить взаимное влияние атомов разных менделеевских
чисел, входящих в состав исследуемого кристалла.
Сравним, например, точность определения атома углерода в
изоморфных структурах, в которых на 5 лёгких атомов приходится один тяжёлый,
а именно CI, Br и J. Получим, что ошибка пропорциональна в первом
случае
во втором случае
и в третьем
Как известно, в настоящее время широко распространено введение
тяжёлых атомов в молекулу как метод структурного анализа. Однако
введение атома хлора в 1,5 раза увеличивает ошибку в определении
координат атомов углерода, атома брома в 2,5 раза и атома иода более,
чем в 4 раза. Это — отрицательная сторона метода. К сожалению, меньшее
значение имеет то обстоятельство, что определение «тяжёлых» атомов
в подобных структурах происходит весьма точно и тем лучше, чем
тяжелее атом.
Ввиду большой распространённости исследования структуры методом
проекции произведём анализ формулы ошибки в определении координаты
максимума ряда а (г).
В наиболее часто встречающемся случае а = 0,35 и .«= 8 получим:
К£)Г=(т-Т^2+5>- («.«)

530 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ. VI
К сожалению, не удаётся простой функцией выразить вторую
производную о (г) в случае обрыва ряда. При отсутствии обрыва значение второй
производной легко вычисляется из (VI, 41). Оно равно
a2ci _ зь
Г <?2СТ "I
т. е. при а = 0,35 — -т-% — — 32fc. По аналогии с трёхмерным рядом
можем утверждать, что обрыв уменьшит эту величину по крайней мере
вдвое. Таким образом для проекции ряда в указанных условиях
■'О
г = 1
(п
— ^0,2 для плоской
ароматической молекулы]
0,2-20 fM , „ос1 л„ 1
(ДГ)2 = ">*'' грч -f 0,25}; Дг = —^-= V^ + 0,25 « 0,04 VV -f- 0,25.
1024-ic Ч 16^
Мы видим, что предельной точностью определения координаты атома но
проекции электронной плотности является 0,02 А при обрыве ряда на меди.
Так же, как и в объёмном случае, не приходится рекомендовать
введение искусственного схождения ряда. Как указывалось выше, для этой
цели следует положить а = 1, тогда s можно положить равным оо. При
этих условиях Дг — 0,16 Ь. Следовательно, только при очень точной работе
(6 = 0,1) будут получены результаты, не' худшие тех,, которые даёт
«естественный» ряд.
И здесь интересно привести табличку, показывающую возможность
грубых измерений при работе с оборванным рядом. Для взятого примера
получим:
Ь
дг
(А)
О ОД 0,5 1,0 1,5 2,0 5,0 10,0
0,02 0,02 0,028 0,04 0,06 0,08 0,2 0,4
Мы видим, что ухудшение точности определения структурных
амплитуд до 50% (а это зпачит ннтспсивпостсй до 100"/п) мало сказывается па
результатах анализа. Дальнейшее нарастание Дг при увеличении ошибки F
происходит для проекции с (г) значительно быстрее, чем для
трёхмерного ряда.
в) Разрешающая способность ряда электронной плотности. Для
выяснения этого существенного вопроса рассмотрим идеальную картину—
рассеяние рентгеновских лучей кристаллической решёткой, построенной
из атомов одного сорта. Мы предполагаем далее, что атомы образуют
простую решётку (узлы-атомы) и рассеивают, как точки. В этом случае
проекция плотности рассеивающего вещества на плоскость представится
в виде
°(ЖУ) = ^- ^ У cos 2тг (Ля + fry). (VI, 50)
ху h к

§6]
ОШИБКА РЯДА ЭЛЕКТРОННОЙ ПЛОТНОСТИ
531
Структурные амплитуды для рассматриваемой идеальной модели будут
иметь одинаковые значения для всех ЪЫ. Если г — вектор узла ячейки,
а Н—вектор обратной решётки, то
3 (r) e s~ 2 2cos 2тс (г/г)-
(VI, 50а)
Пусть узлы обратной решётки, привлечённые для построения ряда
ограничены кругом радиуса В*. Узлы обратной решётки распределены
равномерно внутри этой площади. Предположим, что вектор Н меняется
непрерывно. Элемент площади <25для точки с полярными координатами Я, Ф
равен ВйКйФ и содержит Sxy IIdHd<& узяоъ (фиг. VI, 11). Удобно записать
сразу число узлов, содержащихся в двух
элементах площади — в точке Я, Ф и
в центроеимметрично связанной с ней Н,
тс + Ф. Заменяя теперь суммирование
интегрированием, получим:
о (г) = 2F J* Г Я cos 2т: (гЯ cos Ф) dHd<t>.
о о
Как известно,
г
t„Jn (0 dt = zJx (?),
если
!
I COS (t COS Ф) d<b = lzJQt,
Фиг. VJ,11. Элемент площади
dS для точки с полярными
координатами Н, Ф.
где «То (О И Л О суть функции Бесселя нулевого и первого порядков.
При помощи этих формул а (г) можно представить через функцию Бесселя:
R*
(г) - 2*F f Я/„(2гсгЯ) <*Я,
т. е.
c(r)=:2FnR**-
Jt (2rcrB*)
2ягЛ*
(VI, 51)
(VI, 51а)
Изменение этой функции с г весьма похоже на ход известной
функции -, где х = 2пгН. Кривая —1-^ (множитель FitR** не играет роли)
изображена на фигуре VI, 12. Кривая имеет главный максимум при х — О,
превращается в первый раз в нуль при х = 3,832 и дальше спадает к нулю,
проходя через ряд максимумов и минимумов.
Итак, проекция точечных рассеивающих центров не даёт точек. Этот
эффект полностью аналогичен эффектам диффракции Френеля на
отверстии. Он ограничивает разрешающую способность ряда электронной
плотности совершенно так же, как диаметр объектива ограничивает разре-
3,832
тающую способность телескопа. Точка размывается в круг радиуса —ш ;

532 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ. VI
кроме того появляются ложные кольцевые максимумы, окружающие
рассеивающую точку. При увеличении В*, т. е. числа отражений,
привлекаемых для построения ряда, разрешающая способность растёт, — главный
максимум сужается и ложные
максимумы уменьшаются.
Как мы видим, разрешающая
способность ряда невелика:
3,832 0,61 _
2kR* ~ R* ""
0,61Х
2J, (х)/х
г =
2 sin 0„
0,61 dn
Фиг. VI, 12. Кривая 2Jl^
она определяется минимальным
межплоскостным расстоянием. Если,
например, экспериментальный мате-
i 2
,ь У риал ограничен В* = -г- для медного
излучения, то г = 0,47 А. Поэтому
лишь в специальных случаях можно
надеяться построением ряда
электронной плотности обнаружить
слоистую электронную структуру атома.
То обстоятельство, что
рассеивающие атомы не являются
точечными и, самое главное, что они находятся в состоянии теплового движения —
делает ряд электронной плотности сходящимся. Это избавляет нас от
ложных максимумов, но, разумеется, не может увеличить разрешающей
способности. Если, благодаря тепловому движению, плоскостей с
межплоскостным расстоянием меньшим d^ не существует (колебания имею? этот
порядок величины), то среднее во времени распределение рассеивающего
вещества можно представить себе в виде наложения картин, подобных
показанной на фиг. VI, 12, сдвинутых по г друг по отношению к другу*
Если узел есть среднее положение колебания, то функцию для точки надо
проинтегрировать в пределах :ic а, где a — амплитуда колебания. Как было
указано выше, эта величина имеет при комнатной температуре порядок
0,2 — 0,3 А. Если учесть ещё и объёмное распределение внешних
электронов (внутренние сосредоточены в весьма малой области), то станет
очевидно, что интегрирование функции
JA*)
по х уничтожит ложные
максимумы и даст главный максимум, полуширина которого будет иметь
порядок 0,6 dmin.
Если ряд не сходится, т. и. за пределами суммирования остались
значительные Ь'лиь T°i разумеется, возможно возникновение ложных
максимумов.
Низкая разрешающая способность ряда электронной плотности не
противоречит обсуждённой выше возможности достижения значительной
точности в локализации максимумов и измерении величин средней во
времени электронной плотности.
Действительно, спектрограф может не разрешить двух близких линий,
но определение средней длины волны двух слившихся линий равной
интенсивности может быть сделано со значительной точностью, намного
превышающей разрешающую способность спектрографа.
Низкая разрешающая способность оправдывает рассмотренный выше
метод суммирования рядов по точкам с разбиением периодов решётки
на довольно крупные отрезки.

§7] РЯДЫ МЕЖАТОМНЫХ ВЕКТОРОВ — /^-РЯДЫ 533
§ 7. Ряды межатомных векторов—Т^-ряды
а) Основная формула. Обозначим через р (г) электронную
плотность и подсчитаем интеграл
M*)*=yfp(r)p(r+ и)dv, (VI, 52)
7
помня, что р(г) можно представить рядом Фурье (коэффициент у.
отбрасываем)
+^
Р Ь %
ft, ft, 1=— оо
При подстановке в (VI, 52) образуется интеграл вида
\ е «<и- = < пи ш — целые числа. (VI, 53)
о *
Следовательно,
+ 0О
А (ад) = 2л * те —
ft, к, Z=—оо
-f-oo
= Ь%ю + 2 2 F\n cos 2тс (иН). (VI, 54)
ft, к, 1 = 1
Функцию А (и) можно назвать /^-рядом. Этот ряд Л (ад) может
быть построен на основании опыта (не требуется знания знаков
или фаз членов ряда). Поэтому следует поинтересоваться данными
о структуре, которые можно извлечь из функции Л (и).
Воспользуемся обсуждённым выше представлением электронной
ллотности, как суммы N атомных функций
дг
p(r)= ^Eippir — Vp).
р=1
Каждую из атомных функций можно разложить в ряд Фурье:
(•,(1—г,)- "2 /уГ*""—»1', (VI. 66)
ft, ft, 1=—оо
где fp—атомный фактор р-то атома, и таким образом представить
электронную плотность в виде
N +оо
РИ=2 2 fpe-'lrA{r-rP)H. (VI, 56)
pi=l ft, ft, l = — 00

534 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕН [ГЛ. VI
Подставляя эту формулу р (г) в интересующий нас интеграл
А (и)у получим:
# +00
Х£ У />-2,ci(r-r«+u)ffdF. (VI, 57)
8=1 ft.fc.Z — — со
Интеграл Л (и) разбивается на отдельные слагаемые, которые из-за
условия (VI, 53) ортогональности экспоненциальных функций будут
равны нулю во всех случаях, когда перемножаться будут
функции с разными Н. В остальных случаях интеграл приведёт к
выражению
ДГ N + со
2 2 2 fpf8e-M[u-(r*-rP)]H , (VI, 58)
з=1 р = Х h,lc,l=—со
которое остаётся просуммировать по р и $. Выделяя из этой суммы
выражения p = s, получим:
-*<«)-2 2 *-**"+
j» = l ft, ft, Z=—00
ДГ N +co
+ 2 2 2 ///-2rtt'[M-(r*-V)fi. (vi, 59)
p —1 8 = 1 ft,fc,l=— 00
Каждая сумма (VI, 58) по своей структуре похожа на атомную
функцию, формально совпадая с ней, если «атом» рассеивающей
силы VfpfH находится в точке (г8-—гр) пространства и.
Функцию (VI, 58) можно назвать функцией межатомного вектора, так
как её вид определяется атомными факторами двух атомов s ж р
и векторным расстоянием г8 — гр между ними.
Этим обстоятельством определяются интересующие нас свойства
функции Л (и), т. е. F2-ряда. Очевидно, что 7^-ряд может быть
представлен как сумма межатомных функций для всех возможных
пар атомов в элементарной ячейке кристалла. Это значит, что
максимумы /^-ряда должны образовываться для таких значений
вектора и, которые встречаются в кристалле как межатомные
векторы.
Как следует из последней формы ряда А (и) для кристалла,
в ячейке которого содержится N атомов, он состоит из
^-максимумов, из которых N тривиальных (расстояния атома с самим
собой, т. е. межатомный вектор равен нулю). Этот максимум
в точке [[000]] мы будем называть нулевым. Остальные максимумы
/^-ряда должны в принципе позволить в какой-то степени облегчить
решение, а иногда и полностью решить структурную задачу.
Если в ячейке содержится 20 атомов, то i^-ряд состоит из
380 нетривиальных межатомных функций. Очевидно, что в сложных

§ 7] РЯДЫ МЕЖАТОМНЫХ ВЕКТОРОВ — Т^-РЯДЫ 535
структурах будет происходить перекрывапие этих максимумов, и
анализ i^-ряда вряд ли принесет какую-либо пользу.
Однако иначе обстоит дело, если среди 20 атомов один тяжёлый
(скажем, С1, Вг или J в органической молекуле). Так как
межатомные функции имеют высоту, пропорциональную произведению
атомных номеров, то 19 межатомных векторов, соединяющих лёгкие
атомы с тяжёлым, резко выделятся среди прочих.
Как мы видим, в случае структур с тяжёлыми атомами намечается
возможность проведения при помощи 7^-рядов объективного
структурного анализа. Как мы увидим ниже, такая возможность
действительно может быть осуществлена в некоторых случаях. Однако,
црежде чем обсуждать работу методом 7^-рядов, надо рассмотреть
несколько частных случаев.
б) Частные случаи /^-рядов. ^-ряды всегда обладают центром
симметрии, и самой общей формулой трёхмерного ряда является
следующая:
-!-оо
A(uvw)= 2 2 2 **hKlisos2v(h» + hv-\-lw). (VI, 60)
й=о fc=o г =о
Мы отбрасываем постоянный член 7<ооо и коэффициент 2 при
сумме, так как абсолютное значение А никакой роли не играет.
В рассмотрении частных случаев мы можем следовать § 3, в.
Однако смысл сечений и проекций функции A (uvw) будет обладать
специфическими особенностями. Так же, как и ранее, мы можем
рассмотреть распределение функции A (uvtv) вдоль линии и вдоль
плоскости, а также проекции A (uvw) на линию и на плоскость.
1) Сечения. Рассмотрим значения функции Л (uvw) на
некоторой ПРЯМОЙ Г = 8 -{- tUmnp-
Пусть на прямой этого направления в пространстве функции
A (uvw) возникло несколько максимумов. Мы обнаружили несколько
межатомных векторов, концы которых лежат на этой прямой.
Итак, распределение функции A (uvw) вдоль некоторой прямой
позволяет найти межатомные векторы, концы которых лежат на
этой прямой, или, иначе говоря, позволяет найти все межатомные
векторы, проекции которых на плоскость, перпендикулярную
этой прямой, одинаковы для всех векторов. (Начало всех векторов
в начале координат.) Повторяя преобразования, проделанные на
стр. 477, получим одномерный F^-ряд следующего вида:
А (8 + tBmnp) = J Bje ~**ij\ (VI, 61)
i
где
В* = 2 /4ie-2^+*s°+z4 (VI, 61a)
hkl
для Ш, удовлетворяющих условию hm-^-kn~\-lj}—j.

530 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТКЙ [ГЛ. VI
Применение этого ряда для исследования расположения атомов
вдоль какого-либо кристаллографического направления (для которого
можно положить 8 = 0) приносит значительную пользу. Например,
если атомы расположены вдоль пространственной диагонали, их
межатомные расстояния обнаружит функция Л вдоль этой прямой:
л{1)= S *lBcos2ir(fc+fc+g<. (vi, 616)
h + k+l
Последний ряд обладает, однако, одним недостатком: в нТ'м
присутствует сильный нулевой максимум, не дающий каких бы то
ни было полезных сведений о структуре и в то же время могущий
повлиять на точность в определении других максимумов.
Следует помнить, что эта функция (VI, 616) обнаружит
межатомные расстояния не только между атомами, лежащими на [111],
но и расстояния между атомами, соединительные линии которых
параллельны этому направлению.
Рассмотрим кристалл, в котором имеется плоскость симметрии
или плоскость скользящего отражения. Пусть эта плоскость
перпендикулярна оси у. Тогда каждый атом подвергается следующим
операциям. В случае
зеркальной плоскости симметрии:
плоскости скольжения а:
плоскости скольжения п:
В цервом случае эквивалентные атомы соединены межатомными
векторами 0, 2у, О; во втором -^, 2у, О и третьем -«г, 2у, ■=■. Если
мы рассмотрим распределение Л (uvw) вдоль этих прямых, то найдем
значение межатомных векторов, связывающих эквивалентные атомы
и тем самым координаты атомов в направлении, перпендикулярном
к плоскости симметрии или скольжения.
В этом случае составляются следующие ряды:
т А(ОгЮ) = 2Bkcos2nJcv, Bk = 2*"ш, (VJ, 02)
к П,1
xyz -*
xip ->
xyz—>
XIJ3,
1 , -
"2+^
■j+ хги
>
*+
а Л (j«о) = ^ Вхcos 2nhv* B* = S (—1)Л/*«» <VI' 62a)
к л, г
П A(jvj) = ^^os2rJcvf Bk^\(~l)h+kFlki. (VI, 626)
к ft, I
Первый ряд дает указание на те векторы, у которых проекции на
оси и и w равны нулю, второй — -^ по и и 0 по w и т. д. Воз-

§ 7J РЯДЫ МЕЖАТОМНЫХ ВЕКТОРОВ — ^-РЯДЫ 537
можность построения таких рядов является одним из примеров
полностью объективного рентгеновского структурного анализа.
Разумеется, на указанные сечения могут попасть и «случайные»
максимумы от таких же векторов, соединяющих атомы, не
связанные элементами симметрии: равные по величине параллельные
векторы всегда дают совпадающие максимумы. Однако вероятность
этого обстоятельства довольно мала и только в очень сложных
случаях помешает объективному определению координат атомов.
Рассмотрим теперь сечение A (uvw) какой-либо плоскостью.
Опять-таки, повторяя рассуждения стр. 480, получим для
произвольной плоскости
А (в + ^Вмпр + /2bV,lV) = 2 Вце-*«имш, (VI, 03)
KJiJt = 2^е-2-<Л*. + ^+'Ч (VI, 63а)
Сечения плоскостью функции А (*«) имеют следующий смысл:
максимумы межатомных векторов, лежащие в данном сечении А (и),
соответствуют межатомным векторам, заканчивающимся на этой
плоскости, т. е., иначе говоря, таким векторам, у которых
проекция на нормаль к этой плоскости одинакова.
Практическое значение имеют сечения плоскостью,
перпендикулярной оси симметрии. Если плоскость сечения перпендикулярна
оси Ь ячейки, то
■fb-mnp== *^> -Ч'т'п'р' — с» Ч== и> 1%=М
И
A {us2w) = 2j -bfo, j e ; bht г =- 2j * мае ~, (VI, 64)
а, г к
т. е.
A (ws2w) = 2 (2 ^ш cos 2яЛ»2) с°ч 2R Um "T lv) 4-
h, l к
-}- 2 (2 Кы sin 2ir^2) sin 2ic (/гад -f to)- (VI, 64a)
л, г ft
Если ось Ь параллельна какой-либо оси симметрии, то при
определённых значениях s2 для каждого отдельного случая можно
получить ряды межатомных векторов, соединяющих эквивалентные атомы,
связанные этой осью.
Действительно, в случае простых осей симметрии межатомные
векторы перпендикулярны этой оси (за которую мы выбрали ось Ъ)
и, следовательно, s2 = 0. В случае винтовых осей симметрии
межатомные векторы, соединяющие эквивалентные атомы, имеют
проекцию s2t равную трансляции этой оси, т. е. для осей 2lt 42 и 63
$2 —-о-; Для осей 4t и 43 s2 = ~; для осей 31; 32, 6j и 64 «2:5=*з

538 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [CI. VI
и, наконец, для 6Х и 6- s2 = -^ . Для всех этих случаев мы получим
различные выражения для коэффициентов ряда. Ряды по синусам
пропадут при s2 = О и -^ .
2) Проекции. В полной аналогии с § 2, в), исходя из
формулы проекции электронной плотности на грань ячейки о (ху) или
на ребро ячейки р(%), мы придём к соответствующим /^-рядам,
которые будут представлять собой проекцию функции A (uvw) на
соответствующую плоскость или прямую:
A (uv) = S F2hk0 cos 2* (hx -I-fc//), (VI, 65)
л, л
A («•) e 2 ^ftoo cos 2* /w;. (VI, 66)
ft
Максимумы этих рядов указывают величины проепгщй
межатомных векторов на плоскость ху или ребро х ячейки.
В большинстве случаев рентгеновские измерения ограничиваются
определением F\ki для двух или трёх зон рёбер ячейки. Поэтому
ряды проекций межатомной функции имеют преимущественное
применение.*
Проекции функции А на ребро ячейки не дают обычно каких-
либо ценных сведений о структуре. Все максимумы сливаются
в нер-асшифровывасмую картину.
Весьма целесообразно построение одномерных рядов — сечении
двумерной проекции. Такой ряд будет построен по всем индексам hko,
но расчётная работа займёт несколько минут. Например, ряд
А (и, О) = 2Вь cos 2^Ь;, где Bh = 2 &ш (VI, 67)
ft к
имеет следующий смысл: его максимумы соответствуют межатомным
векторам, проекции которых на ось у равны нулю, причём этот
ряд учитывает лишь расстояния между атомами, лежащими в
плоскостях, перпендикулярных оси у.
Расчёт всех рассмотренных рядов происходит так, как это
описано в § 3, в котором под величиной Ф можно понимать как F,
так и F2, а также и все производные коэффициенты Вы и пр.
§ 8. Анализ проекций 1^-рядов
Так как ^2-ряд центросимметричен *), то существует всего
лишь 7 групп симметрии для плоских проекций /^-рядов,
показанных на фиг. VI, 7 и описанных на стр. 493.
*) По определению, -Р3-ряд является рядом, коэффициенты которого —
действительные величины. Так как косинус есть чётная функция, то ряд
по косинусам, в виде которого всегда можно представить ^'-ряд, всегда
будет центросимметричным. С другой стороны» совершенно очевидно, если

§8]
АНАЛИЗ ПРОЕКЦИЙ — F2-ГЯДОВ
539
Однако симметрия проекции F2-paAa не определяет ещё его
особенностей, при помощи которых делают выводы о структуре.
В таблице VI, I приведены данные о характере распределения
межатомных векторов атомов, находящихся в решётке кристалла
в общем положении. Возникающие межатомные векторы могут быть
двух типов: векторы, соединяющие атомы, связанные
симметрической операцией в кристалле, и векторы, соединяющие
кристаллографически неэквивалентные атомы. В таблице указан вес максимума;
иногда вес удвоенный—два межатомных вектора совпали в проекции.
В таблице приведены независимые (симметрически) максимумы;
остальные получаются без труда применением симметрических
операций плоской группы ^-ряда. Самый сильный максимум нулевой,
который присутствует, разумеется, в любом случае.
Рассмотрение таблицы показывает, что распределение максимумов
характерно для каждой из 17 плоских групп. При небольшом числе
атомов все плоские группы могут быть отличены друг от друга
довольно легко. На фиг. VI, 13 *) мы изображаем схему
расположения максимумов для всех плоских групп, считая, что в ячейке
находится один атом в общем положении. При одинаковой
симметрии возникают характерные легко различимые комбинации.
Вывод данных таблицы весьма прост и заключается в
комбинировании между собой координат атомов. Максимумы, которые
указаны в табл. VI, I, попадут лишь в независимую область.
Рассмотрим один пример, а именно проекцию вдоль моноклинной
оси FS-ряда кристалла, имеющего пространственную группу Р 2Ja
и две молекулы формулы АВ2 в ячейке. Таким образом атом А
находится в центре симметрии. В проекции атомы расположатся
в плоской группе С\ с одной молекулой в плоской ячейке (ось а
проекции в два раза меньше действительной). Таким образом имеем
исходить из свойств F-'ряда, что максимуму в точке uvw должен
соответствовать максимум в точке uvw, так как если первый вектор означает,
скажем, расстояние от атома В до атома А, то второй означает
расстояние от Л до В.
*) Рисунки VI, 13 построены в согласии с таблицей. Чёрными кружками
отмечены точки общего положения .F-ряда, остальные кружки относятся
к возникающим из этого общего положения максимумам F2-pflfla.
Максимумы двойной силы отмечены двойными кружками.
В таблице VI, I заданы независимые максимумы -Z^-ряда. На
рисунках эти максимумы «размножены» операциями симметрии. Заштрихована
независимая часть плоской ячейки. Эти риеунки подчёркивают в
особенности то обстоятельство, что разные F-ряды, хотя и приводят к .Р'-рядам
одинаковой симметрии, различимы друг от друга по характеру
расположения максимумов.
Стрелки на рисунках помогают отождествить кружок с данными
таблицы. Даны стрелки только для независимых максимумов, приведенных
в таблице. В некоторых случаях максимумы F и ^2-рядов совпадают.
В этих случаях чёрные кружки попадают внутрь больших белых.

Фиг. VI, 13а. Плоская группа С\.
Симметрия .Р^ряда С\ (однако при
наличии в общем положении лишь
одного атома имеется лишь
тривиальный максимум 00).
Фиг. VI, 136. Плоская группа
Симметрия .Р^-ряда С\.
О*.
-~2х
Фиг. VI, 13в. Плоская группа С\.
Симметрия .Р^-ряда CL.
Фиг. VI, 13г. Плоская группа С9
(скольжение вдоль у). Симметрия
-F^-ряда C\v, т. е. .Р^-ряд имеет
ту же симметрию, что и Р^-ряд
группы С\. Однако иное
расположение максимумов позволяет
различить эти группы.
ру у ■■^гО-;,т,- \
1
! •
1|Г"~
s *-«^=f '
• 1
>
1 П ' ■ 1 '
■2л
III
Фиг. VI, 13д. Плоская группа С
(скольжение вдоль у). Симметрия
jf^-ряда С^. Напоминаем, что
чёрные кружки это максимумы F-pn-
да, а белые — -Р^-ряда для
случая одного атома в ячейке.

2и*Уг
2у
И
о о
•
>
ь Ч
-—2г
Фиг. VI, 13е. Плоская группа С^.
Симметрия Т^-ряда C\v, т. е. та
же, что и для плоских групп
I ТТ
Са и Cs, иное расположение и
число максимумов позволяет
различать все три группы по F^-рядам.
— 2х
2х*Уг
Фиг. VI, 13ж. Плоская группа G\v
Симметрия jF'-ряда Gl,v, однако
/,2-ряд отличен от Л^рядов групп
pl рП р\
°й» °«' Ц»'
Фиг. VI, 13з. Плоская группа С1^1.
Симметрия Л^-ряда c\v. Однако
/,2-ряд отличен от i^-рядов групп
pl pU pl rrll
°s» Ч>» °2г» b-lv-
Фиг. VI, 13и. Плоская группа CifJ
Симметрия ^2-ряда С^, ^2-ряд
отличен от i^-ряда группы С*11
~2х
х,у
Фиг. VI, 13к. Плоская группа С4.
Симметрия Т^-ряда С4.

542 структурный анализ с оценкой интенсивностей. [гл. vl
-•- 2х
— х-у
х+у
Фнг. VI, 13л. Плоская группа G\v. Симметрия ^-ряда C\v.
-0-Zx*1/2
-~- х*у
— х-у*Уг
-2у+Чг
х+у+Уг
2х
Фиг. VI, 13м. Плоская группа CJJ,. Симметрия Т^-ряда G\v. Р2-ряд позво-
ляет, однако, отличить эту группу от группы Civ.

§ 8] АНАЛИЗ ПРОЕКЦИЙ—jf^-РЯДОВ 543
1-1 9
1-1 СП
о
ев
Г!
С
>,
Pi
t,
w
ев
И
О
о
ч
К
в'
i-t
>
(-,
Я
•У
и
о
№
»
-.«а
О
ев
П
«
Pi
«
fc»
W
Я
Pi
н
ф
я
СЕ]
О
?>
— те
О
К
>-««а
О
с
с
>>
Pi
(-
«
§
Pi
н
ts
р*
Я
и
»
О
ев
Е
с:
>>
Р,
в!
Св
ЛОСК
Зо. П
i-t
,_^
>
U
я
е
и
о
и
«
0*
*5»
О
•ряда
еч
«
К
Pi
н
ф
Я
я
я
и
м Р
о
я
»
сГ
с
с
>>
Pi
а
о
ряд
Е-
о
ш
V
я
РЗ
с «
>; Р,
P-ei
МСЦ
в;
ев
И «
о я
О Pi
m я
со *
■-( О
»
>н(0
и
s ^
е §
efl
>=(

544 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ. VI
координаты: А:(00), В:(хз) и {хз). Получим всего G межатомных
максимумов, из которых половина независима:
^(00) В(хз) В(хз)
^(00)
В(хз)
В (хз)
00
хз
хз
хз
00
£0Су Ci&
ХЗ
2х, 2з
00
Представим теперь себе, что атом_ А_много тяжелее атома В,
тогда из трёх максимумов #*, vz и 2х, 2з остапутся только первые
мов с координатами одного из удвоенных максимумов со-
атомов. впадают с координатами атомов.
два {^а^в 1Э>^в). Таким образом 2'72-ряд даст непосредственно
картину распределения атомов в решётке. Это будет во всех
аналогичных случаях.
Как это следует из рассмотрения табл. VI, I, в ряде случаев
атомы, находящиеся в общем положении, дают межатомные векторы,

§8]
АНАЛИЗ ПРОЕКЦИЙ У^-РЯДОВ
545
непосредственно определяющие координаты атомов. Например,
в группе Сы атом хгуг даст в ^-ряде максимумы xri уг и 2жг, 2уг.
На подобные закономерности необходимо обращать внимание при
проведении структурного анализа *).
Если в структуре имеются тяжёлые атомы, то в 2^2-ряде
выявятся прежде всего межатомные векторы, соединяющие эти атомы,
и во вторую очередь векторы, указывающие расстояния лёгких
атомов до тяжёлого. Если в структуре содержится один тяжёлый
атом, то проекция .Р2-ряда даёт непосредственно координаты атомов
по отношению к этому тяжёлому атому. Практически подобный
случай может осуществиться в триклинном кристалле с одной
молекулой в ячейке и в кристалле, где тяжёлые атомы занимают центры
симметрии.
Мы говорили до сих пор о том, как должен выглядеть Т^-ряд
для заданного расположения атомов. Однако на самом деле
приходится решать обратную задачу, и она далеко не всегда решается
однозначно, так как приходится гадать, чему соответствует тот или
иной максимум.
В несложных случаях выбор между возможностями,
представляемыми Т^-рядом, осуществляется при помощи кристаллохимических
соображений. Допустим, что исследованию подлежит кристалл
группы C\h~P2ja, в ячейке которого содержится 4 структурно
эквивалентных атома брома с координатами хуз; хуз\ — -\-х, -х—у, z\
— — ос, -- -]-у, г. ^2-ряд подобного кристалла даст один независимый
максимум (не считая нулевого), соответствующий межатомному
вектору Вг — Вг; если другие атомы лёгкие, то остальные векторы
не выявляются в ^т2-ряде или выявляются слабо. Составим таблицу
межатомных векторов
xyz
jy z
1 , 1
-4-х, у, г
2 ^ ' 2 9
1 1 , „ -
xvz 1 ООО 1 2х, 2«. 2г 1 _ , — Л- 2«/, 0 1 — 4- 2ж. - -. 2г
xyz
1 , 1
1 1 , ~
~-X,-+y,z
2х, 2]!, 2г
■у.-£--*. о
ooo (A—a* i 2*
"£ + 2ar*T'2z
i , i -h 22/, 0
000
1 1 •> л
— , - - — 2w, 0
2 ' 2
2x, 2y, 2z
2.T, 2y, iz 1 000
i
i
*) См., например, Белов Н. В. и Бутузов В. П. ДАН, 1943.

546 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ..У1
Таким образом имеем максимумы:
одинарные двойные одинарные двойные
2х, 2у, 2з, J—2X, -|, 2з, 2х, 2^, 2з, -|, \~\-2y, О,
2х, 2у, 2~з, -|—f-2ar, | , 2з, 2х, 2у, 2~з, j, -| — 2у, О.
Четыре максимума в общем положении, два в положении с двумя
степенями свободы и два с одной степенью свободы.
Как видим, наиболее целесообразным было бы построение
сечений ^Р2-ряда через плоскость г/ = — и вдоль линии х — —, г = О.
Величины х, у, з определяются из двукратных максимумов
однозначно по величине. В отношении их знака можно различить
следующие возможности: х и г имеют одинаковые знаки, х и г имеют
разные знаки. Если бы речь шла об установлении #£-проекции, то
задача решалась бы полностью, так как в проекции точки хз и хз
структурно эквивалентны. Что же касается пространственного
размещения, то его мы не узнаем однозначно. Действительно, из
положений с одной степенью свободы мы можем узнать лишь =t у. Таким
образом, ^т2-ряд приводит к двум возможным вариантам хуз и хуз.
Нетрудно видеть, что одинарные максимумы не помогут в
различении указанных двух возможностей. Итак, даже при исчерпывающем
исследовании, в самом простом случае и в предположении, что нет
слияния максимумов, мы всё же не получаем из ^'2-ряда вполне
однозначного ответа. Здесь мы опять-таки сталкиваемся с принципиальной
невозможностью определить однозначно структуру объекта по его
диффракционной картине. Выбор между двумя возможностями
(помещением атома в точку хуз или хуз) должен решаться на основе
иных соображений. Может, например, оказаться, что в одном из
возможных расположений атомы находятся недопустимо близко друг
к другу.
Зачастую по ходу структурного анализа приходится ограничиться
какой-либо одной проекцией //2-ряда. В этом случае число
возможных решений возрастает. Рассмотрим, например, проекцию хз.
В ней мы получим кроме тривиальных максимумов 00, — 0, — у
следующие (все двойной силы):
1
UV -к V>, V,
— 1 1
uv — -J-t*, г'.
Любой из четырёх наблюдаемых в проекции максимумов может
быть максимумом 2л? 2гг. Таким образом возможны 4 решения для
трбхмерной и 2 решения для двумерной задачи (так как в послед-

9]
МЕТОДЫ УТОЧНЕНИЯ СТРУКТУРЫ
5П
нем случае каждая пара, связанная центром симметрии, даёт одно
решение). Выбор между различными возможностями опять-таки
должен основываться на химических или кристаллохимических
данных.
Итак, полная расшифровка Т^-ряда удаётся лишь в
отношении 2 — 3 тяжёлых атомов. В многоатомных структурах, без
выделяющихся по менделеевскому числу атомов, 7^-ряд приносит мало
пользы. Действительно, если в кристалле 24 атома, то Т^-ряд
будет содержать (N2—N), т. е. 552 максимума. Вполне понятно,
что максимумы сольются, и даже если бы этого не было задача
отождествления данного максимума с конкретным межатомным
вектором была бы безнадёжной.
Вряд ли можно дать какой-либо рецепт наилучшего пути
расшифровки 7^2-ряда. В последней главе мы приведём несколько
примеров этой расшифровки.
§ 9. Методы уточнения структуры, основывающиеся
на идее максимального сближения 7^,абл и /^выч
Как неоднократно отмечалось, вычисление структурных
амплитуд возможно для идеальных свободных атомов, обладающих
сферической симметрией теоретического распределения электронной
плотности и колеблющихся изотропно. Следовательно, ни одна
реальная молекула не может быть представлена системой таких
атомов. Различия ^7набл и F\U4 должны и могут достигать больших
значений. Поэтому совершенно не очевидно, что структура, для
которой /<лопыт и FBH4 наиболее близки, является оптимальной, т. е.
наиболее близкой к действительности. Описываемые ниже методы
уточнения структуры основываются на произвольном допущении,
что наиболее близкой к истине является система атомных центров,
для которой минимально одно из следующих выражепий:
*1 = 2 (I ^набя ! — I /<выч |), (VI, 68)
hkl
Л* = 2 (/4бл — /1ыч), (VI, 68а)
hkl
<Р = 2i 0 '-бл ! - ! /'«и|)2. (VI, 686)
hklt
В последнем выражении J—средний атомный фактор.
Если мы располагаем примерным решением, т. е. знаем грубо
координаты хГУ yr, zr всех атомов, то можно доказать, что мини-
мализация выражений Rt или Е2 будет заключаться во введении
к первоначально выбранным координатам поправок, вычисляемых

548 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ.. VI
по формулам Поправка к хг)
V —2Д.-^/2(^)1 (VI.69)
Г
ЫИ
г г, г'
Аналогичные уравнения могут быть получены, если за основу
берётся выражение, обозначенное через ©. Уточнение координат
должно производиться последовательно: поэтому метод получил
название последовательных приближений. Первое уточнение должно
быть проделано при помощи первого из двух уравнений (VI, 69) :
оно более грубо, но зато менее громоздко. Вычисляются поправки
ег для всех координат и затем новые координаты подставляются
во второе уравнение (VI, 69а); процедура (при помощи второго
уравнения) повторяется, очевидно, до тех пор, пока уравнение не
даст все ег — 0.
Как видно, расчёт довольно громоздок, так как в формулы
входят суммы производных структурных амплитуд всех отражений,
записанных в общем виде.
Сомнительно, чтобы этот расчёт отнимал меньше времени, чем
подсчёт двух-трёх рядов электронной плотности, которые
приходится строить при работе методом постепенного приближения,
описанным на стр. 476.
Мы видим смысл в этом методе в единственном случае, именно
тогда, когда ряд не разрешает атомы.
Некоторый интерес представляет следующее пока что ещё
неопробованное предложение. Построим следующий ряд:
(Рпабл — Рвыч ) = 2 (I ^набл | — | ^выч |) COS (& ССВЫЧ ), (yj^ 7O)
hkl
где & = 2я (кх-\-ку-\-1г), а авыч есть фаза 1\ыч- Для построения
такого ряда должна быть, разумеется, известна грубая структура,
более или менее близкая к истинной. На картине, изображающей
этот ряд, отметим координаты хг уг гг, которые послужили для
вычисления ГВЫч. Тогда направления, в которых от этих точек
идёт наиболее крутой подъём, т. е. направления максимального
градиента функции (рнабл— рВЫч) в данной точке, показывают
направление сдвига атома с принятого положения в истинное.
Величины градиентов будут пропорциональны величинам нужных
сдвигов.
Это правило есть результат общей идеи описываемого метода.
Сдвигая атом согласно указанному правилу, мы будем стремить
к нулю величину © уравнения (VI, 686).

§10]
ОПРЕДЕЛЕНИЕ ЗНАКОВ
549
Действительно, сдвиг не нужен лишь в том случае, если
максимумы рНабл и рвыч совпадают между собой, а координаты их
совпадают с xr yr zr (что, строго говоря, неверно, см. стр. 513).
Условие оптимального решения запишется так:
| grad (pH — рв)| =0.
У=УГ
(VI. 71)
А это условие совпадает с условием минимума величины <?, как
показывает следующее вычисление (пишем формулы только для
одной проекции градиента):
<>(Рн — Рв)
дх
= Х(1*н| — №|){— 2^sin(0r — авыч)},
hkl
НО
*\F,
дх.
{2nh) • fr sin {Ьг — авы,)#
откуда
Рв)
дх
= 2(1^н|-|*Тв|)т
e*r hkl ,r
dl-F.I
дх.
=-t|k2№I-i^D*7;L--- <У1л2)
Последнее выражение равно нулю в случае максимума. Значение
<р при этом минимально, что мы и хотели доказать.
В заключение ещё раз подчеркнём, что изложенные в этом
параграфе методы построены на допущении, которое имеет
приближённый характер (сферическая симметрия атома). Степень
точности, достигаемая в этом приближении, опытом не установлена.
§ 10. Определение знаков Fm по далным об их величине
Основная трудность структурного анализа заключается, как мы
указывали, в невозможности определения знаков структурных
амплитуд из рентгеновского эксперимента. Однако недавно было
указано, что это положение не вполне справедливо и что ряд
сведений о знаках Fhkl может быть получен, если известны их
абсолютные величины.
Принципиальная возможность определения знаков Fhkl, хотя
опыт даёт лишь значение \FhM\, следует из факта взаимосвязи
структурных факторов. Например, очевидно, что Fhkl-факторы
отражений разных порядков связаны между собой. Если, скажем,
отражение первого порядка максимально (все атомы отражают
в одной фазе), то отражения следующих порядков также должны

550 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНОИВНОСТЕЙ [ГЛ. VI
быть максимальными *). Подобные, но менее тривиальные
соотношения могут быть получены между различными Fhkl при помощи
одного общего приема, к рассмотрению которого мы переходим.
Одним из простейших соотношений 2У-мерной геометрии
является неравенство Коши
I 2 afy |* < (21 aj |») (21 bj |«). (VI, 73)
Это неравенство утверждает, что квадрат скалярного
произведения векторов меньше произведения квадратов их длин.
Придавая а}- и bj различный смысл, мы можем получить серию
неравенств для структурных факторов.
Докажем основную теорему, что при наличии в ячейке центра
симметрии имеет место следующее неравенство:
Нм < у -f у ***. 2*, si. (VI, 74)
Единичная структурная амплитуда
*ш= UH.e^^V-*/4-11^ (VI, 75)
в случае центра симметрии имеет вид
JL
2
Fhki = 2 2 nj cos 2u (hxj -f- Щ -f Uj). (VI, 75a)
,7 = 1
Напомним, что п$ = -^, где Z, — число электронов в атоме j,
a Z—число электронов в ячейке. Рассмотрим два — JV-мерных
вектора, один с компонентами о,- = (2nJ)1/» и другой с компонентами
bj = (2n^)"* cos 2:r (foa^- -|- kifj -j- Щ). Между составляющими этих
векторов имеется связь, даваемая неравенством Коши. Имеем:
N_
2
12 2n, cos 2z (A^ -j- % -J- Щ Y <
< (2 2»,) (2 2^-cos2 2* (/^-f Icyj-i-tej)). (VI, 76)
В левой части мы получили Fm- Правую часть преобразуем,
пользуясь равенством 2 cos8 а = 1 -j- cos 2a.
*) Структурные факторы для отражений разных порядков
отличаются в этом случае лишь величиной атомного фактора, который при данном
sin #
—г— одинаков для всех отражений.

§ 10] ОПРЕДЕЛЕНИЕ ЗНАКОВ 551
Получим
2 2
4 2 пз 2 */ COS8 2т: (fe^- -f- fci^ -J- fy) =
J=l .7=1
= 2 ^ -\~ 2 2 wj ™s 2* (2ta^- + 2%,- + 2%). (VI, 76a)
Но первое слагаемое в правой части равно -к-, а второе -тг .Рал, 2Л, 2?.
Таким образом неравенство (VI, 74) доказано. Если, скажем, опыт
даёт, что |Fioo | = 0,6, a |2'?2ool =°»8, то полученное неравенство
может быть выполнено лишь при i^oo= Н~ 0» 8. Очевидно, что
далеко не во всех случаях неравенство (VI, 74) определяет знак
F2h,2k,2u Если p2h%2k,2i отрицательно, то неравенство не приведёт
к определённому результату, так как оно будет подавно
удовлетворяться положительным F2h,2k,2i. Неравенство тем «сильнее»,
чем больше Fm. При | Fm I=1 Ал, зл, 2i = 4-11 при Ны =
уполучим — F2h, 2fe, a > 0. Таким образом, при. — < Fhki < 1 F<>h, 2*, 21
всегда положительно. При F'iki = -г имеем т Н~ т ^чн,<ik< -l^ °- ^сли
,| F2h, 2fe, 21 I < -5- > то неравенство не даёт определённого результата.
Значения F2h,2k,-a большие —, требуют для него положитель-
лого знака-
Таким образом неравенство применимо лишь в том случае, если
хотя бы один из сравниваемых факторов \F\~> —■ . Следует тут
Li
же отметить, что в более или менее сложных структурах
мы редко-встречаемся со столь сильными отражениями (скажем, —
атомов действуют в одной и ——в противоположной фазах!;
поэтому возможность применения данного неравенства сильно
ограничена.
Однако приведенное неравенство является простейшим, но далеко
не единственно возможным. Выбирая а, и 6^- иным образом, можно
получить другие неравенства. Положим, например,
ау-=(2^-)2;
Ъ.} = (2м3)a [cos 2-й (hxj-j-hi/j ~\- Is) A- cos 2:r (h'xj-j-fc't/ •-j- I'zj)]

552 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ. VI
и подставим в неравенство Коши. Имеем в левой части неравенства
N_
2
12 2 »j [cos 2тг (hxj + Щ + les) 4" cos 2ic (/*'#>• -j- k% 4 J'^) ] |2 =
В правой части получим:
N_ _£
2 а
2 2WjS 2w, [cos2 2ic (Ля,- 4 kyj -f Ц) + cos8 2ic (fc's,. 4 *'#,• + J'*,) 4~
-j- 2 cos 2тс (b?,- -J- Щ 4 Ц) cos 2<:r (^j + *'% ~f~ *4)1 -
При помощи тригонометрических формул cos2 a 4- cos2 p = 1 4
4 cos (а + р) cos (а — (3) и 2 cos а cos р = (cos а -j-p) 4 cos (а — (3)
преобразовываем правую часть к виду
(1 -{-Fh + h', к + к', i+v){l-\-Fh—hf, к—к', l—i')-
Таким образом имеем:
(Ам+ &'*!')•<
<(4FH»',i+t',i+i')(4A-h'j-i',w'). (VI, 77>
Справедливо также аналогичное уравнение, в котором
положительные знаки заменены отрицательными.
Полученное неравенство связывает структурные факторы
четырёх отражений, например 309, 202, 50.11 и 107. Успех в
применении этого неравенства также зависит от величины привлечённых
значений F. Чем они больше, тем «сильнее» неравенство. Нетрудно
видеть, что в этом случае неравенство не приводит к какому бы
то ни было результату, если все структурные амплитуды меньше -$.
о
Таким образом это неравенство «сильнее» предыдущего.
Можно вывести множество таких неравенств, которые будут
охватывать большее или меньшее число отражений. Например,
< -| (1 4- F2h, а», п) (3 4 4/< а*, з*. 2? + В\н. **. и?. (VI, 78)
Неравенства, о которых говорилось до сих пор, справедливы для
любого центросимметричного кристалла. Специальные соотношения
возникнут при наличии дополнительных элементов симметрии.

§ 10] ОПРЕДЕЛЕНИЕ ЗНАКОВ 553>
Рассмотрим в качестве примера кристалл, обладающий
симметрией P2j. Для него
N
Fhkl
2 », [e*™V>*j+kyj+l*j> +.**(-^+ъмг1*3+Щ
(предполагаем, что ось 2г совпадает с осью у). Или, иначе,
К.
2
FMl - 2 2 е3" ^ cos 2* [&в, + fy Н- (~l)fc f J •
i
Для подстановки в неравенство Коши полояшм а^=(2^) 3 вг
bj = (2Wy)"2 е * у* cos 2тс &a^ -j- tej -f- (—l)fc y • Получим в левой
части неравенства Fjm, а в правой, заменяя cos2 а на -=• (1 + cos 2<х)>
N N
2 % | е***"* I 2 + 2 2 w, J /*'' |2 cos 2я [2Лл, + 2L- + (— 1)» л].
•inky. a
Выражение \е 3\* может только уменьшить обе суммы. Поэтому
мы имеем право отбросить его в неравенстве; получим:
Рш < у + ~2— Afc.o.«. (VI, 79)
Мы не будем останавливаться на выводе других неравенств.
Как мы уже отмечали выше, успех в применении этого метода
зависит от наличия для исследуемой структуры большого числа
сильных отражений. Кристалл дигидрата щавелевой кислоты даёт
50% отражений с |F|>~, из них половина с /?> — • К этому
кристаллу метод был применён с достаточным успехом. Обычно
в более сложных структурах отралсения с |F|>- присутствуют
1
как исключения, а отражения с \F\>-r составляют 10 —15% от
общего числа отражений. Вполне очевидно, что к таким
структурам метод совершенно не применим.
Не следует думать, что даже и в таком случае, который имеет
место для дигидрата щавелевой кислоты, описанный метод даёт
однозначные результаты. Мы уже указывали, что из диффракци-
онной картины не могут быть в принципе сделаны однозначные
выводы о строении объекта. Описываемым методом в лучшем
случае удаётся, обозначив знаки двух — пяти структурных амплитуд
через а, Ъ, с,. .. выразить знаки остальных F как аб, cd, аЪс и т. д

"554 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНООТЕЙ [ГЛ. VI
Таким образом возникнет ограниченное число возможностей,
для которых могут быть построены ряды электронной плотности.
Справедливым будет тот вариант, который приведёт к разумным
результатам (с химической, или с какой-либо иной, точки зрения).
Необходимо также обратить внимание, что, несмотря на
кажущуюся простоту, метод требует большого труда и выдумки в
поисках целесообразных неравенств. Поэтому кроме всего прочего
метод надо применять лишь в структурах с атомами одинаковой
рассеивающей способности, т. е. там, где 7^-ряды приносят мало
пользы.
Существует особый случай, когда по величинам F можно уверенно
•судить об их знаках.
Допустим, что получены все опытные данные о двух изоморфных
структурах, отличающихся лишь тем, что атом А молекулы замещён
на атом В. Предполагая, что координаты атомов в обоих
структурах одинаковы, получим:
FL ~ 2^А C0S 27t (hXA + кУА Н~ **а) +
N—1
+ 22 /г cos 2я (hxr + kyr + Ьг), (VI, 80)
r = l
Fn = 2/"B cos 2ic (forB + kyB + teB) +
»—i
+ 2 2 /rcos2Tt(kcT + fo/r + ter). (Vl,81)
Опыт дает |Fi| и |Fn|. Если известны (из F-'-ряда) #А*/А*А, то
можно определить знаки F* и Fn. С другой стороны, если считать,
что знаки Fi и Fn должны быть одинаковыми, то по опытным
данным можно построить ряд с коэффициентами F\ — Fu и найти из
этого ряда значения #А?/А<г?А.
Существует ещё один более старый и, пожалуй, более мощный
метод, позволяющий находить знаки структурных амплитуд.
Пусть найдены абсолютные значения единичных структурных
амплитуд
* #
,\ v* 2гЛ (hx >+k,J 1+и 1-)
^Aw=i"»/ J J 3
3 = 1
rij—доля j -го атома, равная-^-. Обозначим
ZrJx. 2гЛу. 2nis.
Тогда 3' 3 iJ
/>ш=2^РМ (VI, 82)

§10] ОПРЕДЕЛЕНИЕ ЗНАКОВ 555
Составим теперь такой многочлен, корнями которого были бы
величины <xv а2, а3 ... а.... а^. Это будет многочлен степени N,
имеющий вид
un + ay-i + ау-ъ + ... + aNiU 4- aN. (VI, 83)
Если кристалл центросимметричен, то независимыми корнями
будут лишь -g- значений ajt так как at = ai-1, a3 = a^1 и т. д.
Если так, то aN=l, aN_x==alf aN_2 = a2 и т. д.*) Таким
образом этот же многочлен можно записать в виде
(«*+!) + «, О»»"1+«) +
N—l N+l К
+ а2 (uN~2 + ц2) + ♦.. + ay-i (« а +» 2 ) + а*_«а. (VI, 83а)
Если JV—нечётное, то последний член будет отсутствовать.
Подставляя в этот многочлен любой из его корней ар мы
обратим его в нуль. Сделаем эту подстановку и умножим многочлен
на MjCijfijtj. Имеем:
«Д«Т+*1»»г}+«ЙМ>+«!», (*J+k-Yd+«Г'РМ) + • • • +
—
+ «£tyV+ P*TJ = 0. (VI, 84)
Составим iV таких равенств для всех о,- и сложим их. Тогда
получим интересующее нас соотношение между структурными
амплитудами
Fs + h, к, г + *ш + «1 ( FN-i + h, M + ^M-i. *.i) + ' • • +
+ а*^+л>м==0. (VI, 85)
2V
Значения — коэффициентов a^- нам неизвестны. Но они не зависят
от выбранных значений hkl. Другие равенства с -=- неизвестными
коэффициентами bj и Cj для серий отражений с индексами,
отличающимися значениями к и /, записываются по аналогии.
Ограничение этого метода заключается в следующем. Уравнение
может быть составлено лишь в том случае, если среди
измеренных отражений имеется серия /'TftW, в которой один индекс
(например h) последовательно меняется от 0 до N. Скажем, при 10
атомах надо иметь серии (Ш, Ш, 2kl, ЗЫ, Ш, Ьк1...Ш, 10Ы.
*) Например, при Л" = 3, и3-)-a, «2-f- «2и ~Ь аз = ^> гДе м== а1 — "Т*'
Тогда «J + а^ -fa/, -f- a;J = 0, и 1 -f a1a1 + a,a2 -f a3a3 — О- Следовательно,
<J3 = 1 Hfl]= 02-

556 СТРУКТУРНЫЙ АНАЛИЗ С ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ. VI
Так как N есть полное число атомов в ячейке, то случаи, когда
нужно будет иметь 20 — 30 отражений в таком ряду, будет
встречаться часто. А подобное число отражений найти, как правило,
не удаётся.
Этим методом не было сделано, повидимому ни одного
структурного исследования. Поэтому трудно сказать, в чём должен
заключаться наиболее целесообразный путь работы этим методом.
Очевидно, прежде всего надо составить как можно большее число
подобных уравнений и исключить из них коэффициенты а^ далее
из полученных уравнений определять знаки FhJd (хотя бы
некоторых). Если удастся затем найти числовое значение
коэффициентов ар то, несомненно, удастся найти знаки амплитуд всех
измеренных отражений.
Более того, зная коэффициенты aj, можно, решив многочлен
(VI, 84), определить ajf а следовательно, координаты атомов.
§ 11. Автоматизация расчётов в структурной анализе
Исключительная громоздкость расчётов, которые приходится
производить по ходу структурного анализа, делает жизненно важной
проблему автоматизации некоторых серийных расчётов. Рядом
авторов были предложены самые различные образцы счётных машин,
пригодных для двух целей: во-первых, для подсчёта структурной ампли-
N
туды Fhkl по формуле Fhkl= 2frcos2те(hxr-f lcyr-\-lzr) и, во-вто-
r=l
рых, для подсчёта рядов.
Первая задача весьма трудоёмка. Подсчёт, скажем, 100 — 200
значений Fhki при IV = 15 — 20 — громоздкая работа. Так,
пользуясь номограммой Белова, а также счётами или счётной
машиной, мы затратим на подсчёт каждого значения Fhkl не менее
10 —15 минут. Вероятно, что одна рабочая неделя является тем
средним временем, которое затрачивается на подсчёт Fhkt для
структуры средней сложности.
В случае работы методом проб и ошибок интенсивностей
подсчёты серий значений Fhla производятся многократно и машина
для расчёта FhM становится весьма необходимой. Как мы видели
выше, правила кристаллохимии, с одной стороны, и метод
^-рядов, с другой, позволяют в очень многих случаях определить
грубую структуру, не прибегая к методу проб и ошибок. Тогда
и машина для расчёта Fhkl становится излишней, так как
значения Ръш рассчитываются один-два раза для окончательно
установленной структуры. Этот способ работы, схема которого была
намечена на стр. 476, по всей вероятности, является наиболее
идеальным. В тех случаях, когда он недостижим, структурный
анализ становится исключительно громоздким и нуждается в
помощи машины для подсчёта Fhki.

11
АВТОМАТИЗАЦИЯ РАСЧЁТОВ
557
В большинстве случаев приборы, подсчитывающие ряды,
приспособлены также и для вычислений сумм типа 2 frcos 2* (hxr -j-
r
-\-куг-\-1зг)\ об этих машинах мы скажем ниже. Из
приспособлений, пригодных только для подсчёта структурных факторов,
упомянем только одну довольно простую машину, работающую ручным
способом и подсчитывающую /'cos2tc (hx-j-ky), при заданных х, у
и h, к и /". Эта машина собирается из частей мекано; специально
изготовляются лишь два диска и планиметровые колеса. Другие
машины либо не имеют
смысла, как,
например, простая ручная
машина,
подсчитывающая 2/rC0S^"r (если
все атомы обладают
одинаковой
рассеивающей способностью,
то гораздо быстрее
проделать
суммирование на счётах), либо
слишком сложны и
дороги. Схема машины,
конструкция которой
нам кажется
целесообразной, показана на
фигуре VI, 14. Два
колеса П1 и Л"2С011Рика"
«аются с металлическими дисками Т)^ и D2- Колёса могут вращаться
около неподвижной (горизонтальной на чертеже) оси, приходя в
движение от вращения (около вертикальных осей) дисков D1 и 1)2.
Механизм конструируется так, чтобы можно было ручками Сг и С2
осуществить вполне точно полный оборот дисков Т)1 и D2.
Помещая колёса планиметров П1 и П2 на расстояниях х и у от осей
вращения дисков, мы передадим этим колёсам вращения,
пропорциональные hx и ку, поворачивая С± и Со на h и к полных
оборотов. Дифференциал М суммирует вращения П1 и //а и передаёт
их через стержень АХА^ коленчатому валу К. Возникает линейное
движение скользящей системы Т вдоль рельсов Р. Смещение будет
пропорционально cos 2тс (hx -j- ку). Со скользящей системой Г
соединена шарниром длинная стрелка Е. Укрепляя стрелку в точке ./>'
и изменяя положение этой точки перемещением вдоль рельсов Н,
мы производим операцию умножения косинуса на произвольный
фактор. Таким образом показания стрелки на шкале Ш дают
значение f cos 2~ {hx -j- ky).
Столь же большое значение имеет для структурного анализа
машина для подсчёта рядов. Подсчёт двумерного ряда, произво-
Фиг. VI, 14. Принцип устройства машины для
расчёта структурных факторов.

558 структурный анализ с оценкой интенсивностей [гл. vi
димый при помощи штрипсов, занимает в зависимости от вида
проекции примерно от 2 до 7 дней. Это, конечно, не так много,
но дело в том, что, желая получить удовлетворительные
результаты, приходится строить далеко не одну проекцию. Прежде всего,
в ряд может входить 10 — 20 антагонистических членов (см. стр. 474),
т. е. таких, знак которых не может быть определён. Кроме того,
предварительное, грубое определение структуры (геометрическим
методом, или методом Т^-ряда) не даёт знаков всех
коэффициентов. Наконец, если есть возможность работать методом неравенств,
то однозначного решения не получается и метод приводит к
значительному числу возможностей.
Таким образом один и тот же ряд должен быть «испробован»
с различными знаками. Изменение знака хотя бы одного члена
ряда сказывается, разумеется, на всей картине ряда. Поэтому
пробы в количестве нескольких десятков связаны с очень большой
вычислительной работой. Если меняется знак одного из слагаемых,,
то быстрее всего построить его двумерную таблицу (с удвоенной
амплитудой, так как этот член, скажем, вычитался, а его нужно
прибавить) и затем эту двумерную таблицу сложить с таблицей
ряда. Такая работа займёт ио крайней мере 3 — 4 часа. 100 проб —
это почти 2 месяца работы.
Это, однако, не всё. Последние исследования показывают всю
важность пользования в структурном анализе сечениями
трёхмерных рядов. 20 — 30 таких сечений должны быть построены для
уточнения координат атомов и- (что особенно важно) для
установления распределения электронной плотности в пространстве. Это ещё
во много раз увеличивает длительность исследования.
Применение вычислительных машин для подсчёта рядов в корне
меняет возможности структурного анализа. При этом
целесообразной является лишь такая машина, которая позволяет в
кратчайший срок видеть результаты изменения того или иного знака ряда.
Этим условиям удовлетворяет электронный вычислитель, который
будет описан ниже. До этого предлагался ряд машин, как чисто
механических, так и электромеханических. Предлагалось также
производить суммирование рядов методом оптической аналогии,
создавая для калсдой волны ряда Фурье соответствующую световую
волну. Было также показано недавно, что для целей структурного
анализа могут быть с успехом применены счётные коммерческие
машины, работающие с перфорированными картами. Нет сомнений,
что все эти методы уступают электронно-оптическому прибору
и будущее структурного анализа находится в прямой зависимости
от его развития.
Электронно-оптическая счётная машина предназначена для
суммирования двумерных рядов типа 2 2 Fhk0 cos 2ъ (hx -f- ky}
h к
(проекция электронной плотности), причём результат подсчёта

§ И] АВТОМАТИЗАЦИЯ РАСЧЁТОВ S59-
представляется на экране катодного осциллографа в виде картины
распределения интенсивности, пропорциональной величинам
электронных плотностей. Этот счётный прибор основан на том же
принципе, что и следующий оптический метод суммирования.
Каждое слагаемое ряда представляет собой, как нам известно, плоскую
волну, идущую под
некоторым наклоном к
выбранным осям координат
и обладающую
определённым периодом. И то и
другое определяется
аргументом косинуса (hx-\-
+ &у)> Можно
приготовить на плёнке такие фиг- VI»15- пРимеРы эталонов,
эталоны, распределение
почернения которых будет пропорционально cos 2к(Ь,х -\-Jcy).
Примеры таких эталонов показаны на фиг. VI, 15. Накладывая эти
эталоны на фотографическую бумагу и пропуская свет через эталон
с экспозицией, пропорциональной FM0, мы можем произвести
оптическое суммирование, результат которого показан на фиг. VI, 16.
Сравнение нескольких подобных картин и выбор из них
картины, совместимой с химическими
и кристаллохимическими данными,
вполне возможен.
Электронно-оптический прибор и позволяет нам
производить такое сравнение.
Перемена каких-либо знаков и
получение новой проекции занимает
30 секунд! При этих условиях
становится возможным находить
правильный результат систематической
переменой знаков ряда. Подобную
возможность трудно переоценить.
Отдельное слагаемое ряда типа
эталона на фиг. VI, 15 создаётся
в электронном приборе на экране
осциллографа модулированием ин-
Фиг. VI, 16. Результат опти- тенсивности электронного луча пу-
ческого суммирования Для пен- TgM нал(щешм J сетку ькштй
трубки синусоидального
напряжения с амплитудой, пропорциональной Fh1{0 и с частотой
ш
hkO
— ЛШ„ерТ —|— ЙШГ0рИ3.
Луч катодного осциллографа колеблется с постоянными частотами
<»верт и <огориз. Частоты сильно разнятся. Скажем, шверт=1000

560 СТРУКТУРНЫЙ АНАЛИЗ О ОЦЕНКОЙ ИНТЕНСИВНОСТЕЙ [ГЛ. VI
циклов в секунду, а <огориз = 1 циклу в секунду.
Смодулированный луч вычерчивал бы на экране при таких условиях сплошную
полосу.
Если теперь модулировать луч при помощи сетки, то получится
-следующее. Если, например, (ohk0 будет целым кратным от шгориз,
то на экране осциллографа возникнут вертикальные полосы, при
этом повторяемость полос будет соответствовать числу 7с, т. е.
отношению (ohjc0 к <агориз. Если <юЛЛо будет кратно о>верт, то ввзник-
нут горизонтальные полосы:
в промежуточных случаях
возникнут наклонные полосы. Так,
например, чтобы создать член ряда
^y70cos 2тс (\х -\- 1у) требуется
модулировать луч осциллографа с
частотой a>j70 = 1 • h~\~ 1000 • к =
= 1 • 14- 1000 • 7 =6999 циклов
в секунду. Возникает картина,
показанная на фигуре VI, 17.
На сетку осциллографа подается
напряжение, соответствующее
сумме ряда. Напряжение,
отвечающее каждой структурной
амплитуде, устанавливается
потенциометром.
Возможно, что применение
в структурном анализе
электронного счётчика позволит несколько пересмотреть методику и сделает
возможным систематический подбор комбинаций знаков в ряде
электронной плотности.
Фиг. VI, 17. Осциллографическая
картина при модулировании
катодного луча.

ГЛАВА Vlt
ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ
§ 1. Сущность и цели исследования
Диффракционная картина, создаваемая при встрече
монохроматического луча с иоликристаллом, представляет собой систему
коаксиальных конусов. Осью диффракции является направление
первичного луча. Каждый из конусов соответствует лучам,
отраженным от одних и тех же
плоскостей беспорядочно
ориентированных
кристалликов.
Происхождение
рентгенограммы поликристал- ^
да нетрудно понять из
фиг. VII, 1. Если плоскость Петчтй |
одного из кристалликов,
пучок
дающая отражение Ш,
находится в нужном
положении к лучу, то, в силу
беспорядочности
распределения кристалликов,
найдётся ряд таких же
плоскостей других
кристалликов, дающих также
отражения hkl. Эти отражения
будут созданы всеми
кристалликами,
соответствующие плоскости которых
имеют нормали, лежащие на конусе с углом раствора 2(90°—0).
Этому конусу нормалей соответствует конус отражённых лучей
с углом раствора 40.
Для того чтобы получить изображение всех возможных
конусов, следует снимать рентгепограмму поликристалла на
цилиндрическую плёнку, пуская луч но радиусу цилиндра. Схема такой
съемки показана иа фиг. VII, 2.
Фиг. VII, 1. Картина диффракции от
поликристалла К обладает симметрией тела
вращения (ось вращения — первичный
пучок).

Г)62 ИССЛЕДОВАНИЕ НОЛИКРИСТЛЛЛИЧЕСКИХ ВКЩЕСТВ [ГЛ. VII
Какие данные можно получить из рентгенограммы
поликристаллического вещества? Прежде всего это значения углов i\w и интен-
сивностей 1Ш возникших отражений. В этом отношении методы
поликристалла и монокристалла совпадают. Кроме того из
рентгенограммы поликристалла можно получить некоторые специфические
сведения; это структура линии (точечная, сплошная), распределение
интенсивности вдоль линии и ширина линии. Очевидно, что
последние сведения находятся в связи со свойствами поликристаллического
объекта и не определяются
строением кристалла исследуемого
вещества.
На первый взгляд может
показаться, что метод исследования
поликристаллических веществ
богаче, так как дает нужные для опреде-
i ления структуры величины Ьш и 1Ш
• и кроме того позволяет изучать осо-
i бенности строения поликристалла.
Однако это не вполне так, потому
что рентгенограмма должна быть
проиндицирована, а нахождение
индексов по значению угла 0Ш
является задачей, которая решается
без труда для кубических
кристаллов, с трудом для тетрагональных
и гексагональных и не решается
для кристаллов низших сипгонии.
Применение рентгенограмм
порошков в целях определения
расположения атомов в кристалле с каждым годом уменьшается, так
как число неисследованных веществ, принадлежащих к
кубической системе, падает. В некоторых случаях имеет смысл
получение рентгенограммы порошка наряду с исследованием
монокристалла. Если размеры ячейки кристалла известны и линий на
рентгенограмме порошка не очень много (а это будет зависеть от объема
ячейки, которому прямо пропорционально число линий), то
рентгенограмма может быть проиндицирована, и все данные об
интенсивностях могут быть получены из одной рентгенограммы.
Это тем более удобно, что, как отмечалось на стр. 256, в
случае съёмки порошка очень прост учет поглощения и отсутствует
экстинкция.
Не представляет, однако, сомнения, что применения метода
порошка при определении структуры кристалла составляют лишь
небольшую часть применений этого метода к специальным
проблемам строения поликристаллических тел, а также к вопросам,
связанным с уточнением размеров ячейки. Именно это направление
Фиг. VII, 2. Схема съёмки
рентгенограммы поликристалла. DKO—
первичный пучок. I) — диафрагма,
К — образец, Д —
цилиндрическая плёнка, О — прорез в плёнке
для выпуска первичного пучка.
/, //, III — диффрагированные
лучи. Картина симметрична
относительно первичного пучка.

§21
ОБЫЧНЫЙ МЕТОД ИССЛЕДОВАНИЯ
563
работ продиктовало разработку множества типов камер и типов
съёмок поликристаллических веществ.
К основным применениям рентгеновского исследования
поликристаллических веществ относятся:
1) идентификация вещества;
2) качественный и количественный анализ фазового состава;
3) прецизионное определение размеров ячейки;
4) определение размеров кристаллитов;
5) исследование внутренних напряжений и искажений решётки;
6) исследование текстур.
Съёмки различных типов применяются иногда одновременно для
нескольких целей. Поэтому классификация по методам
рентгеносъёмки не связана непосредственно с перечислением возможностей
рентгеновского метода.
Основные типы съёмок суть следующие:
а) Съёмка образца на цилиндрическую плёнку; образец—на оси
цилиндра, луч — вдоль радиуса цилиндра.
б) Съёмка образца на плоскую пластинку, находящуюся за
объектом (по ходу луча); нормаль к пластинке совпадает с лучом.
в) Съёмка образца на плоскую пластинку, находящуюся перед
объектом.
г) Съёмка на цилиндрическую плёнку, ось которой совпадает
с лучом.
д) Съёмка на цилиндрическую пленку при расположении объекта
на поверхности цилиндра.
Для идентификации вещества и фазового анализа применяется
съёмка по типу а); для определения размеров кристаллитов — а) и
б); для прецизионных определений используют метод а), в) и
в особенности д); для исследований внутренних напряжений
применяется нормальная съёмка а) и в особенности в); для текстурных
исследований разработан метод съёмки по г) и кроме того
применяется метод б).
Для целей структурного анализа употребляется (если метод
поликристалла оказывается пригодным) обычная съёмка а).
§ 2. Обычный метод исследования поликри,сталлических
веществ
а) Вид рентгенограммы. На фиг. VII, За и б изображена
простейшая цилиндрическая камера, употребляемая для съёмок
этого типа. Снимаются образцы либо в виде цилиндриков диаметра
0,1—0,7 мм *), либо в виде пластинок для шлифов. В последнем
*) Столбики из порошка могут быть выпреесованы из капилляра.
Можно также производить съёмку тонкого капилляра из лёгкого стекла,
набитого порошком, или, наконец, можно наклеить порошок на тонкую
стеклянную нить.

504 ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [гл. VII
случае сам образец мешает образоваться полному
интерференционному конусу—на пленку попадают лишь лучи, идущие от (а не
в глубь) образца, возникает часть рентгенограммы. Цилиндрическая
кассета прикреплена к крышке камеры. В цилиндрической плёнке
должно быть сделано две прорези—одна для луча, входящего
в камеру, и вторая для уходящего. Так как закладываемая плёнка
имеет вид полоски, то возможны различные способы расположения
Фиг. VII, За. Камера для съёмки Фиг. VII, 36. Крышка-кассета ка-
ноликристалла. меры для съёмки поликристалла.
прорезей по отношению к сошедшимся концам плёнки. Могут быть
применены три способа. Обычным способом называется способ, при
котором через концы плёнки проходит входящий луч. Обратным
способом назовём способ, при котором через концы плёнки
проходит выходящий луч. Наконец, способом с двумя прорезями пазовё'м
способ, при котором в плёнке пробиваются два отверстия как для
входящего, так и для уходящего луча; концы пленки сходятся
посредине камеры. Последний способ, как будет показано ниже,
уменьшает погрешность измерения, связанную с сокращением длины плёнки
при проявлении. Схемы рентгенограмм, снятых при различных
креплениях плёнки, показаны на фиг. VII, 4.
Как видно из фигуры в камеру закладывается узкая полоска плёнки.
Пересечение с ней интерференционных конусов оставляет следы в виде
линий. Интерференционный конус с углом раствора 180° (т. е. круг)
создаёт на плёнке прямые линии, при меньших углах мы будем
получать кривые линии с вогнутостью, обращенной к первичному
лучу. При углах раствора, больших 180°, получится вогнутость
и обратном направлении. Вогнутость возрастает по мере отдаления
от центральных прямых линий. Конусы пересекаются с цилиндри-

§2]
ОБЫЧНЫЙ МЕТОД ИССЛЕДОВАНИЯ
565
ческой пленкой по линиям четвёртого порядка,Впрочем, форма этих
кривых не играет роли, так как с углом ft непосредственно связант.у
расстояния между «средними» точками (т. е. лежащими на экваторе,
проходящем через луч) линий. Иначе говоря, для определения
угла 0 надо промерить расстояния между симметричными частями
а) Д
«) fl
а) Я
п~п
I ■ * - * I
ш
гтт>
МЧЗ,
т
о
-я-
гтт?
в
Л Г^\Первичный
~c\ZJB Пуч
V/
АС
Фиг. VIT, 4:. Три способа крепления плёнки: а — обычный;
б—обратный, в — асимметричный.
интерференционного кольца, взятые вдоль экваториальной линии.
Измеряя эти расстояния 21, мы находим углы ft по формуле
0 =
5ТГ в радианах.
Очень часто диаметр камеры берут равпым 57,3, и тогда
расстояние линии от места попадания первичного луча I даёт значение
угла ft в градусах.
6) Индицировали е. Индицирование рентгенограммы
поликристалла, безусловно, возможно, как мы уже указывали, лишь в
случае кубического кристалла, и с некоторым трудом, и не всегда
достоверно в случае тетрагональных и гексагональных кристаллов.
Для тетрагональных и гексагональных кристаллов, а также для
кристаллов низших систем в случав значительного объёма ячейки,
расшифровка рентгенограммы невозможна. Действительно,
представим себе, что исследованию подлежит ромбический кристалл, объём
ячейки которого есть величина порядка 1000 А3, и рентгенограмма
получается на медном излучении. Независимый объём обратной
решётки, узлы которого участвуют в отражении, можно принять
равным 1/8 части сферы радиуса у (сравни ехр, 206), т. о.
1 4 /2 у тг ... „
■Б-'тг л(г) • При указанном выше ооъеме элементарной ячейки
о
число узлов ооратной решётки на 1 А~,! равно 1000; следовательно,
число узлов, которое примет участие в отражении, равно

566 ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
1000 • -Q- • -в *(ttz) * чт0 Давт ДИФРУ порядка 1000. Итак,
рентгенограмма подобного поликристалла должна содержать 1000 линий.
Разумеемся, даже при длине половины плёнки, равной 200 мм
(а это вдвое больше, чем обычно), число линий будет столь велико,
что анализ рентгенограммы станет невозможным.
Если число линий не очень велико, то рентгенограмму можно
расшифровать. Для этой цели из значений 0 вычисляют sin2 0 и
подбирают в квадратичной форме -^ значения основных параметров
ячейки так, чтобы все вычисленные значения sin2& совпали
с измеренными. Для кубической решётки эта работа не
представляет затруднения, так как из квадратичной формы
*-№ + » + *
следует, что отношения sin2i> равны отношению целых чисел и
притом вполне определённых целых чисел. Так, для простой
кубической ячейки эти отношения должны иметь вид 1:2:3:4:5:6 :
:8 : 9 ..., для объёмноцентрированной 1:2:3:4:5:6 : 7:8:9...;
для гранецентрированной 3:4:8:11 ... Различие отношений для
разных трансляционных групп определяется законами погашения,
о которых мы говорили на стр. 441.
[Тля того чтобы отличить кубическую простую решётку от
объёмноцентрированной, надо иметь на рентгенограмме ив крайней
мере 7 линий. Однако простые кубические решётки практически не
встречаются. Отличие же объёмно- и гранецентрированной решёток
очень резко. В первой отношение sin2 8 второй линии к первой
равно 2, а во второй — 4/3. После того, как тип решётки
установлен, всем линиям могут быть приписаны индексы, и по
квадратичной форме определяется размер ячейки а.
При индицировании рентгенограммы следует помнить о том,
что характеристическое излучение, кроме сильнейшей линии 1а,
содержит всего лишь примерно в 5—6 раз более слабую липпю Хр.
Поэтому, если фильтры не применялись (см. стр. 188) и излучение не
монохроматизировалось от кристалла, то надо выделить и не
вводить в расчёт (3-линии. Это обычно нетрудно сделать, зная, что
sin&«:sinftp для одного и того -же отражения Ш равно K'-h-
Шзшшы, правда* усложнения, так как, вообще говоря, Р-линия
может совпасть со слабой а-линией другого отражения.
Для тетрагональных и гексагональных кристаллов sin ft каждого
отражения зависит от а и от —. При этом, так как а входит
множителем при всей квадратичной форме, то lgsinft с точностью
до достоянного слагаемого (конечно, разного для разных объектов)

§2)
ОБЫЧНЫЙ МЕТОД ИССЛЕДОВАНИЯ
567
будет функцией одного лишь —. Л именно для тетрагонального
кристалла
lg sin Ьм = const + ± lg [ Л» + fc* + (j)* *2]»
для гексагонального-кристалла
lg sin Ьш = const -f1 lg [| (Л» + Л» -f Ли) + (^)2 J»] .
Таким образом, опуская константу, можем построить кривые lg sin Ь
в функции от — для любого Ш. Это будут универсальные
кривые, справедливые для любого кристалла. Значение lgsinft для
данных Ш и — не определяется этими кривыми, так как начало
отсчёта lg sin 0 не установлено. Однако для всех Ш данного
кристалла это начало отсчёта одно и то же. Если поэтому мы нанесли
бы на полоску бумаги значения IgsinO всех hkl и эту полоску
наложили бы на график при нужном значении —, то общее начало
отсчёта нашлось бы при горизонтальном перемещений полоски,
производимом до тех пор, пока все линии полоски не совпадут
с какими-либо кривыми графика. При неизвестном значении —
такие перемещения надо проделать для всех значений —. Обычно,
несмотря на свободу как горизонтального, так и вертикального
смещения полоски, находится лишь единственное её расположение,
совместимое с данными опыта. После того как такое положение
найдено, значения периодов ячейки найдутся по квадратичным
формулам. Пример такой сетки показан на фиг. VII, 5.
В случае кристаллов ромбической системы, обладающих
ячейкой относительно небольшого размера, индицирование также удаётся
провести. Для этой цели было предложено весьма много
несовершенных способов, излагать которые не имеет смысла. Практически
работа происходит путём подбора тех линий, которым можно
приписать индексы с двумя нулями.
Что касается кристаллов моноклинной и триклинной системы,
то определение их элементарной ячейки но рентгенограмме
порошка следует признать безнадёжным.
в) Точность определения межплоскостных расстоянии и
меры к её увеличению. Из уравнения Вульфа-Брэгга следует:
^в —ctgOA». (VH, 1)
Относительная ошибка в определении межплоскостного
расстояния пропорциональна ошибке в определении угла отражения в и

568 ИССЛЕДОВАНИЕ ИОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
тем меньше, чем более.далёкие интерференции мы измеряем. Как
упоминалось выше, в наиболее часто употребляющихся камерах
угод 0 численно равен I—расстоянию линии от места попадания
первичного луча. Без принятия особых мер I может быть
измерено с точностью±0,1 мм. Таким образом иАО = it 0,1° «0,5%.
Решающим для получения точных результатов является измерение
s Лэ «гг§э e
8 8:11 ? §и1М§1е!_!_!
150 200 300 Л00 500 Ш 700 600 9001000 1600
1 !■■■>'■• ■ I ■ . J . I . . . . I .. ■ ■ll.ltll...lt4llllHlmilll..lllllllllllmllllllLl.l—l ■ \tJ J Дд| ) f^-ддЦ
Фиг. VII, 5. Сетка для индицирования рентгенограмм порошка
(тетрагональная система); на бумажной полоске Л нанесены значения Ig sin v для
окиси магния.
при больших углах *>. Действительно, в средних частях
рентгенограммы ctgd^l и точность достигает 0,5%- При больших
углах, например при угле около 80°, точность равна уже 0,1%
(ctgft«0,2). Значения периодов решетки можно, вообще говоря,
уточнить до 0,001%- Ещё большая точность в обычных опытах
теряет смысл, так как такого порядка будут изменения периодов
благодаря тепловому расширению при изменении температуры па
1—2°, что может произойти во время опыта. Увеличения точности
на два порядка величины добиться нелегко и сделать это уже можно
лишь за счёт уменьшения ошибки в определении АО.

§2]
ОБЫЧНЫЙ МЕТОД ИССЛЕДОВАНИЯ
569
Угол О вычисляется из непосредственно измеряемого
расстояния между симметричными (принадлежащими одному конусу)
линиями. Если 21 — расстояние между ними, то
0 =
2Н
и ДО
М ■ I AB
2R ' В 2R
(VII, 2)
ЛЩРСфр+т20
где М — ошибка в измерении расстояния, а А7? — в значении
радиуса камеры.
Для того чтобы эти формулы были вполне точны, необходимо,
чтобы цилиндрический образец был установлен строго в центре
камеры. Нетрудно показать, что
имеет значение только сдвиг
образца 8 в сторону от первичного
луча. Это смещение даёт ошибку
в угле, равную ДО = ztz-^ sin20.
Как видим, при 0 -> 90° эта ошибка
приближается к нулю.
Если луч отклоняется от
экваториальной плоскости цилиндра, то
также возникнет ошибка в угле.
При отклонении в 3° может
возникнуть ошибка ДО = 0,004°.
Ошибочные результаты будет давать также
камера с сечением, отличающимся
от кругового. Две последние ошибки
должны быть устранены;
установление их возможно лишь при
помощи тарировки камеры известным
веществом.
Надо обратить внимание также
на то, чтобы измерение плёнки
производилось точно вдоль
экваториальной линии. Рекомендуется измерять
расстояние между линиями при
четырёх положениях плёнки, меняя
верх, низ, а также правую и левую
части.
Все перечисленные ошибки могут
быть практически устранены.
Нужно учитывать две причины
ошибок, играющие решающую роль: это
поправка на поглощение образца и
учёт эффективного радиуса камеры.
Необходимость в поправке на поглощение вытекает из фиг. VII, С
Если лучи падают снизу вверх и отклоняются вправо, то у погло-
Фиг. VJI, 6. Если образец не
поглощает, середина линии на
плёнке определяется прямой АР,
проходящей через ось образца.
Если образец отражает лишь
участком поверхности ВС (концы
его определяются касательной
к образцу, параллельной
направлению первичного пучка, и ка-
сатсльпой, параллельной
направлению диффрагированного луча),
то середина линии определяется
центральной линией
диффрагированного пучка (точка Р'\
смещение
А = Р1>' = -* (РМ -f PN) =
= 1(Л/;+/;с).

570 ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
щающего образца в отражении участвует лишь зачерченная часть
его (разумеется, такое выделение отражающей области носит
лишь условный характер, так как. доля участия в отражении
данного элемента объема постепенно уменьшается с его «глубиной»).
На рисунке показан возникший луч и место его попадания на
плёнку. Если бы образец не поглощал рентгеновские лучи, то 21
было бы меньше на некоторую величину Д, которую нам надо
вычесть из 21. Правильное вычисление угла 0 требует знания
1 = 1пш——. Величина этой поправки максимальна для образца,
отражающего лишь поверхностью. В этом случае, как видно из
рисунка,
д == р (1 + cos 20),
где р— радиус цилиндрического образца. Как видим, эта поправка
весьма значительна (так как обычно р = 0,2—0,7 мм). Когда же
можно пользоваться приведенной формулой? По формуле
половинного ослабления Л= -1— (см. стр. 186) находим, что лучи мед-
ного анода поглощаются на 50% при прохождении через 1,4 мм
органического вещества, 0,07 мм алюминия и 0,03 мм железа.
Таким образом цилиндрики из органических материалов можно
полагать (для наиболее употребительного излучения Ка меди)
прозрачными, а металлические тела отражающими лишь с
поверхности. В этом последнем случае и применима приведённая
формула. Поправку к промежуточным по поглощению случаям лучше
всего подбирать на основании опыта.
Радиус кассеты рентгеновской камеры можно было бы измерить
с большой точностью, однако не этот радиус должен войти в
расчет угла 0. Пленка обладает конечной толщиной, она завёрнута
в черную бумагу, кроме того плёнка несколько сокращается при
проявлении. Если учесть все эти поправки, то мы найдём нужный
для расчёта «эффективный радиус».
Целесообразно не вносить эти поправки, а устранять их опытом.
Для этой цели употребляется способ установки плёнки с двумя
отверстиями, показанный выше на рисунке VII, 4. Так как на
нлёнке мы видим линии симметричные как в отношении входящего,
так и в отношении выходящего луча, а точки входа и выхода
расположены точно под углом 180°, то, следовательно, мы на самой
плёнке находим длину, равную ъВЭф. Если расстояния одной иары
линий до произвольного начала отсчёта (где-либо между В и В\
фиг. VII, 4в) суть 1Х и Z2, а другой пары 1[ и V& то координаты
входа луча равны —х—, а выхода —>— . Следовательно,

§2]
ОБЫЧНЫЙ МЕГГОД ИССЛЕДОВАНИЯ
571
Подставляя в (VII,2), находим ошибку в определении угла
Это — максимальная ошибка, так как мы положили 1 = кИ.
При работе этим способом можно стремиться к более точному
измерению расстояния между линиями (пользоваться
компаратором); таким образом можно добиться при А£ = 0,01 мм для
далёких линий точности в 0,03—0,04% в Д&, а это уже позволяет
получать межплоскостпые расстояния с точностью до тысячных
долей процента. Для d = 1А это означает измерение с точностью до
стотысячных долей ангстрема. Во всяком случае четвёртую цифру
за запятой можно получать вполне уверенно.
Если по значениям d вычисляются размеры элементарной ячейки,
то нельзя производить усреднение по данным, полученным из всех
линий, помня, что точность возрастает с углом. Вполне
целесообразно определять среднее, приписывая каждому измерению
определённый вес. Весовую функцию не так легко найти для общего
случая. Если полагать точность в измерении взятых в расчёт линий
одинаковой, то весовая функция для линий с ft> 45° равна . 29ft.
Для получения точного значения межплоскостного расстояния
из данных измерения можно предложить ряд способов.
Из формулы -т = — ctg &Д& следует, что погрешность стремится
к нулю при 0 -> 90°. Поэтому можно построить диаграмму,
откладывая значения постоянной решётки (скажем, для кубического
кристалла) для каждой линии рентгенограммы в функции утла Ь,
а затем провести через полученные точки плавную кривую,
экстраполируя её к углу {> = 90°.
Было показано, что вблизи 0 = 90° кривая измеренных
значений а, отложенных для разных cos2 Ь *), должна иметь вид прямой
линии. Это обстоятельство, разумеется, в сильной степени
упрощает экстраполирование.
Предложен также аналитический экстраполяционный метод,
особо ценный для некубических кристаллов.
Можно показать, что наиболее существенная систематическая
погрешность, а именно, ошибка в значении sin2&, равна
A(sin20) = jDsin22»,
*) Другие авторы рекомендуют откладывать для этой цели а в
функции etgo cos2 ft.

572 ИССЛЕДОВАНИЕ ЛОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
D — величина, постоянная в пределах одной рентгенограммы. Если
так, то для каждой линии можно составить уравнение:
sin2 {>=£+# sin2 2&,
где L — соответствующая квадратичная форма. Таким образом для
кубических кристаллов, у которых L есть фунция одного пара-
X.2
метра т^2 (^2 + ^2 + ^2), достаточно два уравнения, для
гексагональных и для тетрагональных — три и т. д., для того, чтобы найти
средние квадратичные значения параметров.
Вид поправки может быть различным для разных камер.
Как было показано выше, наиболее точные результаты при
измерении d получаются в том случае, если величина d вычисляется
из расположения так называемых задних линий, т. е. тех, для
которых 2&>90°. Чем ближе значение 2& к 180°, тем точнее будет
результат вычисления.
Так как прецизионные измерения проводятся улге после того,
как структура выяснена, то каждой линии можно присвоить индексы Ш
на основании
предыдущих исследований.
Поэтому нет нужды
иметь на пленке все
линии, которые
вещество может создать.
Это обстоятельство
определяет характер
конструкции камер
для прецизионных
измерений — они
фиксируют только задние
линии.
На фиг. VII, 7 изображены схематически два типа камер задней
съёмки с пол у цилиндрической и с плоской кассетами. Через кассету
проходит диафрагма. Камеры особо удобны ещё и потому, что
образец находится вне камеры п размеры и форма его не играют
роли. Как угол 0 связан с параметрами камеры, видно из чертежа.
АВ=2йЦ(Л-2Э)
AB=2R(7l-2&)
Фиг. VII, 7. Схема камер задней съёмки.
§ 3. Фазовый анализ
а) Общие замечания. Каждое кристаллическое вещество даёт
специфическую рентгенограмму с характерными значениями межплоскостных
расстояний и интенсивностей линий. Полиморфные модификации одного и
того же вещества дают различные рентгенограммы. Поэтому рентгеновская
картина есть сумма рентгенограмм всех фаз, содержащихся в образце.
Рентгеновский метод является основным способом проведения фазового
анализа. Применение его очень широко. Совершенно незаменимым является
рентгеновский фазовый анализ при анализе смесей модификаций одного

§з]
Фазовый анализ
573
и того же вещества. Мы можем встретиться, например, с необходимостью
определить процентное содержание каждой из возможных модификаций
в карбиде кремния, каждой из 6 модификаций в Si02. Можно обнаружить,
в какой форме (брукита, анатаза или рутила) существует в данном образце
двуокись титана ТЮ2. Такие же ценные сведения получаются при анализе
смесей, состоящих из фаз разного химического состава, например Fe и
Fe3C, MgO и Zr02 и т. д.
Обычно фазы, присутствующие в смеси в количестве порядка 1%,
уже не могут быть обнаружены рентгеновским методом. Обнаруживаемость
одной фазы в другой зависит от множества обстоятельств: от атомных
номеров элементов примеси (вообще говоря, интенсивность линий
возрастает с атомным номером), от размеров и симметрии ячейки кристалла
и пр. Чем выше симметрия, тем меньше будет число линий на
рентгенограмме и тем интенсивнее будут эти линии. Причины этого обстоятельства
станут понятными, если вспомнить, что плоскость hkl повторяется в
кубическом кристалле 48 раз, а в триклинном попадают на одну линию лишь
отражения hkl и hkl. Следует также иметь в виду возможность совпадения
линий. Иногда для уверенности в результатах анализа идут на
увеличение экспозиции и ведут съемки на длинноволновом излучении в камере
большого радиуса. В литературе можно найти следующие указания об
обнаруживаемости отдельных фаз.
Серое олово в белом олове обнаруживается при количестве от 10%
Ni в NiO — от 2%,
NaCl в СаС03 и наоборот — от 8%,
Sb в Си —от 1%,
2СаО • Si02 в ЗСаО • Si02 — от 30%,
W в Ni — от 0,1%.
Для проведения количественного анализа большей частью
производится съёмка с эталоном. Если исследуется порошок, то эталонное
вещество подмешивается к исследуемому. Например для определения
количества муллита в изучаемом веществе подмешивался порошок поваренной
соли. Опыт показал, что отношение интенсивностей линий (220) NaCl и (401)
муллита (эти две линии располагаются рядом) пропорционально
отношению содержания NaCl к количеству муллита. Построив градуировоч-
ную кривую при помощи образцов с известным содержанием муллита, мы
сможем определять по отношению интенсивностей указанных линий
процент муллита в исследуемом образце, подмешивая к нему известное
количество поваренной соли.
Таким образом, приступая к фазовому анализу смесей, надо прежде
всего выбрать эталонное вещество (его коэффициент поглощения должен
быть близок к коэффициенту поглощения изучаемого вещества); затем
приготовить ряд смесей известного состава; выбрать на рентгенограмме
подходящие пары линий и построить градуировочный график.
В случае, когда вещество нельзя истереть в порошок, прикрепляют
к цилиндрическому образцу вдоль его образующей узкую полоску фольги.
Образец приводят во вращение, благодаря чему доля участия эталонной
фольги в рассеянии будет пропорциональна доле её поверхности от всей
боковой поверхности цилиндра.
При анализе двухфазных систем можно при близости коэффициентов
поглощения этих фаз полагать интенсивность линии нропорциопальнон
процентному содержанию фазы.
Если на рентгенограмме обнаружена пара линий, принадлежащих
двум фазам и имеющих равное почернение, то отношение процентных содер-

571 исследовании поликристаллических веществ [гл. vjT
жаний ЭТИХ двух фаз х :(100—-х) будет равно отношению v.j>x Fj: v^F^. Здесь
t;—объём ячейки, р—фактор повторяемости, F2—структурый фактор.
Остальные факторы интенсивности, зависящие от угла &, сокращаются, если
вЗяты две близкие линии. В обратном случае эти коэффициенты войдут
в приведённое отношение. И здесь необходимо предварительное
исследование смесей известного состава. Устанавливается *), например, что
интенсивности линий (220) Y-Fe и a-Fe равны при 35% содержания y Fe, при
равенстве интенсивности (220) 7-Fe и (211) a Fe имеем 6870 7-Fe.
Практически удаётся найти достаточное число таких пар линий, чтобы
производить анализ в любом желательном интервале концентраций.
б) Химический анализ по рентгенограммам. Каждое вещество даёт
на рентгенограмме свою систему линий, характеризующуюся значениями
межплоскостпых расстояний и интенсивностей диффракционных линий.
Разумеется, найти химический состав вещества, рассчитывая
кристаллическую структуру по этим данным, задача практически невыполнимая.
Напротив, химический анализ становится вполне реальным, если имеются
стандартизованные данные о виде рентгенограмм большого числа
веществ. В этом случае задача исследователя — получить рентгенограмму
исследуемого вещества в тех же стандартных условиях и сравнить свои
данные с табличными.
Опубликованы данные в отношении более чем 1000 веществ **). Если
среди них не найдётся нужных, то придётся получать эталонные
рентгенограммы. Рекомендуется следующая практика получения эталонных
рентгенограмм. Образец должен быть размельчён в агатовой ступке до
200 меш. Если образец недостаточно хрупок для того, чтобы его истолочь,
то прибегают к напильнику. Порошок помещается в стеклянный капилляр
внутренним диаметром 0,4—0,6 мм с толщиной стенок, меньшей ОД мм.
В случае длинноволнового излучения вместо съёмки в капилляре следует
прибегать к изготовлению столбика 0,5 мм диаметром, подмешиванием
10% коллодия; в случае графита, слюды и пр. — прибегать к вращению
образца, так как возможная предпочтительная ориентация зёрен исказит
отношения интенсивностей. Материалы с большим атомным номером
рекомендуется разбавлять. При работе, с молибденовым фильтром нужно
пользоваться цирконовым фильтром (Zr02) и работать на 42 киловольтах.
Полученные рентгенограммы измеряются следующим образом. При
помощи линейки (см. стр. 341) определяются значения d для каждой лини»
и далее методом шкал почернения оцениваются относительные
интенсивности линий.
Для целей быстрого химического анализа можно предложить систему
классификации химических соединений по трём наиболее сильным линиям.
Вся шкала межплоскостных расстояний от 20 до 0,5 А разбивается на
77 групп. Каждая группа на 77 подгрупп. К разным группам принадлежат
соединения, у которых самая сильная линия имеет d от 3,00 до 2,95 А,
от 2,95 до 2,90 А и т. д. В разные подгруппы попадут соединения, у
которых вторая по силе линия попадает в разные интервалы межплоскостных
расстояний. Далее подгруппы разбиваются таким же образом при помощи
третьей по силе линии. Если 2 линии одинаково сильны, то «первой»
считается та, у которой d больше.
Ниже приводится таблица VII, I для анализа. Соединения, которые
фигурируют в этой таблице, имеют самую сильную линию с d между
2,90 и 2,95 А. Вторая по силе линия, например олова Sn, имеет d между
*) Нечволодов, в сборнике «Рентгенография в применении к
исследованию материалов», 1936.
**) Ind. and Eng. Chera. Anal. Ed., 10, 457—512, 1938; 16, 209—17, 1944.

§ 3| ФАЗОВЫЙ АНАЛИЗ 575
Т а б л и ц а VII, I
2-я липия
20,00—15,00
15,00—12,00
12,00—10,00
10,00— 9,00
9,00— 8,50
8,50- 8,00
8,00— 7,50
7,50- 7,00
7,00- 6,50
0.50— 6,00
6,00— 5,75
5,75— 5,50
5.50— 5,25
5,25— 5,00
5,00- 4,90
4,90- 4,80
4,80— 4,70
4,70— 4,60
4,60— 4,50
4.50— 4,40
4,40— 4,30
4,30— 4,20
4,20— 4,10
4,10— 4,00
4.00— 3,90
3,90— 3,80
3,80— 3,70
3,70— 3,00
3,60— 3,50
3,50— 3,40
#,40— 3,30
3,30— 3,20
3,20— 3,10
3,10- 3,00
3,00— 2,95
2,95— 2,90
2,90— 2,85
2,85— 2,80
Вещество
3-я и 4-я
линии
i
P2S5
HgS04. 2Hg0
Na2S203 • 51I20
(C6H4C02)o BONa
Nn.T03
Pb3(P04)2
CdC03
Ba(CJ04)2-3H20
C16H802N2(S03K)2
NaCI03
4,90; 4,05
5,5; 3,33
2.84; 2,76
3.45; 2,18
.4.19: 1.60
3.61; 3,31
1.83; 2.46
2,14; 1,92
3,00; 2,22
1,76; 2,68
2-я линия
2,80—2,75
2,75—2,70
2,70—2,65
2,65—2,60
2,60—2,55
2,55—2,50
2,50—2,45
2,45—2,40
2,40 -2,35
2,35—2,30
2,30-2,25
2,25-2,20
2,20—2,15
2.15-2,10
2,10-2,05
2.05—2.00
2.00—1,95
1,95—1,90
1.90—1.85
1,85—1,81)
1,80—1,75
1,75—1,70
1,70—1,65
1,65-1,60
1Д)—1,55
1,55-1,50
1,50—1,45
1,45—1.40
1,40—1,35
1,35—1,30
1,30-1,25
1,25—1,20
1,20-1,15
1,15—1,10
1,10—1,05
1,05-1,00
1,00—0,90
0,90-0,80
Вещество
I Sn
1 СаС2 II
Na2Cr04
NaHCOs
Tli
к2с2о4
Na-I3407 • 5II20
NaN3
ln203
CaCl
1
3-я и 4-я
линии
2,01; 2,05
1,95; 2,09
4,09; 3,88
3,48; 3,04
1.79; 1,52
2,32; 2,62
4.40; 3,44
2,42; 2,18
1,52; 2,52
4,11; 2,05

576 ИССЛЕДОВЛПИЕ ИОЛИКРИСТАЛЛИЧЕСКИК ВЕЩЕСТВ [ГЛ. VII
Таблица YIT, la
Вещестпо
P2S5
HgS04 • 2HgO
Na2S203-5tl<>0
(C6H4C04),BONa
NaJ03
Pb3(P04)2
CdC03
Ba(C104)2 • 3IIoO
C16H802N2(S03K),
NaC103
Sii
CaC2H
Na2O04
NaHC03
Th
K2C204
Na2B407 • 5HoO
NaN3
Mg3(P04)2 • 8H20
MnCl2 • HoO
BaCl2 • 2H20
Mg(N03)2.6lbO
MgS04 • 6II0O
K1I2P04
a-ZnS
PbO
GaC2III
UgsPO,
C6H4(CO)oNK
Bi(C2H302)3
AgC2H302
tta(CN)2
SnCl4 • 5H20
CoCl2 • 6II20
CuOH•CuP04
MgNH4P04-OHoO
HgCl2.3HgO
PbHAs04
K2S207
Ag2Cr04
K2Se03
(NH4)IIC204 • 11,0
Li2C03
Na2Si03 • 9H20
1-Я ЛИПИЯ
2,90
2,92
2,93
2,94
2,93
2,91
2,94
2,90
2,90
2,94
2,91
2,93
2,91
2,94
2,92
2,92
2,94
2,91
6,7
5,7
4,48
4,42
4,40
3,72
3,29
3,06
2,86
2,60
14,5
13,5
10,0
9Д
6,2
0,6
4,81
4,28
3,95
3,39
3,23
3,14
3,08
3,00
2,80
2,79
2-я линия
6,7
6,2
5,4
4,40
4,25
4,03
3,77
3,65
3,35
3,28
2,79
2,79
2,73
2,58
2,53
2,46
2,19
1.82
2,94
2,93
2,91
2,93
2,92
2,90
2,91
2,93
2,92
2,94
6,4
3,35
3,04
3,37
5,3
4,85
2,63
2,69
2,70
3,17
3,07
3,02
4,35
6,2
4,16
3,83
3-я линия
4,90
5,5
2,84
3,45
3,19
3,61
1,83
2,14
3,00
1,76
2,01
1,96
4,09
3,49
1,79
2,32
4,40
2,42
2,69
2,55
2,54
3,29
4,04
1,95
1,76
2,72
2,05
3,09
2,90
2,90
2,91
2,94
2,94
2,94
2,91
2,93
2,92
2,93
2,90
2,92
2,94
2,90
2,91
2,92

§ 4]
СЪЁМКА В ФОКУСИРУЮЩИХ КАМЕРАХ
577
2.80 и 2,75 А. Тут же приведены данные о величинах межплоскостных
расстояний для третьей и, на всякий случай, для четвёртой линия.
В таблице пока что больше пустых мест, чем заполненных. Во всяком
случае приведённая форма достаточно удобна.
Для каждой группы даётся ещё одна дополнительная табличка (VII, 1а),
полезная при анализе смесей. В верхней части таблицы ещё раз повторены
основные данные, в других двух частях приводятся соединения, не
относящиеся к данной группе, которые, однако, можно спутать с основными
данными. Это те соединения, у которых вторая по силе линия попадает
в интервал 2,90—2,95 н третья по силе линия попадает в интервал 2,90—
2.95. Бели учесть возможность наложения линий при фазовом анализе
подобных смесей, то ценность дополнительной таблицы станет понятной.
Подобным методом удавалось производить анализ смесей с числом
компонент вплоть до пяти.
Следует подчеркнуть, что подобный химический анализ пригоден
лишь для кристаллических веществ.
Преимущества рентгеновского химического анализа следующие: 1)
анализируемые вещества не меняют своего состояния при анализе, 2) для
анализа нужно ничтожное количество вещества, 3) химический
рентгеновский анализ одновременно является фазовым, 4) документация анализа
сохраняется в виде рентгенограммы, 5) дешевизна и простота.
§ 4. Съёмка в фокусирующих камерах:
а) Принципы фокусировки и схемы камер. Если источник излучения и
образец расположены на той же цилиндрической поверхности, что и
плёнка, то имеет место идеальная фокусировка всех отражённых от
цилиндрической поверхности лучей. Это совершенно очевидно ввиду
равенства углов между падающим и отражённым лучами: эти углы опираются
на одну хорду. Идеальная фокусировка имеет место лишь в плоскости,
перпендикулярной оси цилиндра.
Менее совершенна, но имеет большое практическое значение
фокусировка от плоского образца.
Нетрудно показать, что эта фокусировка возможна лишь для пучка
лучей, лежащих на конической поверхности (вырезаны прн помощи
конической диафрагмы) и притом лишь при определённом угле наклона о
поверхности образца к лучу.
При заданном расстоянии а от точечного источника до центра образца
и угла раствора 2{3 конической поверхности лучей нетрудно построить
точку пересечения лучей, идущих от краёв отражающей пластинки. Угол
наклона а должен быть таким, чтобы углы между падающим и
отражённым лучами для обоих краев пластинки были равны одной и той же
величине 2&. Геометрический расчёт приводит к несколько громоздкой
формуле. Однако, расчёт сильно упрощается в том случае, если угол
раствора конуса не более 15—20°, что соответствует экспериментальным
условиям. В этом случае исчезает зависимость от угла и лучшее положение
образца определяется формулой Курдюмова *):
, sin 20 /лгттяч
tg « = -ц , (VII.3)
Ь сов 2Ь
а
где В — расстояние от образца до интерференционной линии. Разумеется,
возможность пренебрежения углом р в формуле для tga ещё не означает
того, что все конусы лучей проектируются в одну точку. Если не ставить
*) К у р д ю м о в Г. В., ЖФХО, 1926 г., стр. 43.

578 ИССЛЕДОВАНИЕ ПОЛИЕРИСТАЛЛИЧЕСКИХ ВЕ1ЦКСПЗ [гД. VII
конической диафрагмы и использовать полный конус лучей, то и прк
оптимальном угле а интерференционная линия получит ширину,
пропорциональную tg2 p. Её значение для точечного анода
вычисляется из общей формулы *).
Наиболее распространённой является такая фокусировка, при которой
«точечным» источником служит щель камеры. Этот случай будет
осуществляться тогда, когда диафрагма мала по сравнению с фокусным пятном.
Практически это условие выполняется в кратко описанных ниже
фокусирующих камерах.
Если фокусное пятно меньше размеров диафрагмы, то фокусировка
может быть осуществлена лишь в том случае, если роль «точечного»
источника будет играть фокусное пятно. Диафрагма может тогда практически
отсутствовать. Для расположения на одной окружности фокуса трубки*
образца и плёнки требуется специальная конструкция откачиваемой
камеры-трубки. Это, однако, имеет большой практический смысл, так как
в камерах-трубках этого типа из-за возможности использования широкого-
пучка лучей и из-за приближения образца к истинному источнику
лучей можно достигнуть секундных экспозиций. Указанный метод
позволяет, следовательно, осуществлять быстрый контроль образцов и
даже рентгенокиносъёмку. Кон-
г, ^^. — -^^^ струкции камер-трубок этого-
^ -""' ч ^ типа были разработаны Геллером,
а также Цукерманом и Альтшу-
лером **).
Приведём схемы устройств
часто применяемых камер с
фокусировкой. Употребляются камеры
как с плоской, так и с
цилиндрической кассетой.
Цилиндрические
фокусирующие камеры могут быть разбиты
на два типа: I — такие камеры,
в которых каждый из диффрак-
ционных конусов даёт одно
пересечение с плёнкой — одну линию,
II — камеры, в которых это
пересечение осуществляется в двух
местах.
Схема камеры второго типа
дана на фиг. VII, 8. Очевидно,
что в камерах II типа мы
получаем только задние линии с
углами Ь, начиная от 50—60°. Таким • образом такая камера специально
пригодна для прецизионных исследований, в которых по одной-двум линиям
судят о точном значении параметра кристаллической решётки.
Образцы для съёмки в камере этого типа приготовляют чаще всего
втиранием исследуемого порошка в цилиндрическую пробку, вырезанную
по радиусу камеры. Расчётная формула этой камеры такова:
АО_пло L 180°
Фиг. VII, 8. Фокусирующая
цилиндрическая камера II типа: 1 —
источник рентгеновских лучей, 2 — плёнка,
3— щель, 4 — камера, 5—образец.
*) Г е л л е р Г. Б., ЖТФ, VIII, стр. 1690, 1938.
**) Альтшулеьр Л. В. и Цукерман В. Я., Заводская лаборатория»
VIII, 449, 1939.

§ 4^ СЪЁМКА В ФОКУСИРУЮЩИХ КАМЕРАХ 579
где L — расстояние между линиями одного конца и В — радиус камеры.
Ошибка в определении межплоскоетного расстояния выражается формулой:
Д<2 + . ДЬ 180°
Камеры I типа изготовлялись на интервал углов скольжения 15—80э.
Положение диффракционной линии в этих камерах определяется
расстоянием от тени, создаваемой пластинкой, расположенной на конце плёнки.
Поэтому камера должна быть проградуирована съёмкой эталона.
В случае съёмки на подобной камере плоского образца условие
фокусировки будет соблюдаться лишь для определённого интервала углов,
определяющегося уравнением (VII, 3) и зависящего от параметров камеры,
и угла, под которым образец устанавливается к лучу. Таким образом можно
предусмотреть поворот образца, позволяющий поочереди создавать
оптимальные условия съёмки для того или иного интервала углов. Можно
также пользоваться серией камер, каждая из которых даёт хорошие
условия фокусировки для данного интервала углов.
Также распространены фокусирующие камеры с плоской кассетой.
В этих случаях так же, как и в цилиндрических камерах II типа,
пользуются обратной съёмкой, ограничиваясь фиксированием одних лишь
задних линий. Держатель образца
может перемещаться так, чтобы
изменением а в формуле (VII, 3) ..-.,.•..
можно было бы изменить условия
фокусировки. Можно также
изменить условия фокусировки
изменением наклона образца.
При наличии крупнозернистого
препарата в обычных камерах для
съёмки поликристалла вращают
образец, если хотят избавиться от
точечных диффракционных линий.
В камерах для обратной съёмки на
плоскую кассету также можно
избегнуть точечных линий, вращая около
луча плоскую кассету. Ещё одно
удобство камеры с плоской кассетой
заключается в следующем. Можно,
изготовляя круглую кассету,
открывать для лучей отдельный её
сектор и получать, таким образом, - - - - *■*■-'- —"-*
на одной плёнке несколько
снимков, сравнение которых между собой фиг. VII, 9. Серия порошковых рент-
представляет интерес. Серия та- генограмм, снятых на одной плёнке,
ких рентгенограмм показана на
фиг. VII, 9.
Описанные камеры фокусируют лучи, исходящие из «точечной»
диафрагмы камеры. Опишем конструкции камер-трубок Альтшулера и Цукер-
мана, использующих фокус анода в качестве «точечного» источника лучей.
Схема съёмки изображена на фиг. VII, 10. В камеру вставлен
ограничитель в виде трубочки диаметром 5 Мм. Выпускаемый широкий конус лучей
встречает плоский образец под нужным для фокусировки углом а к
первичному лучу. Образец расположен, как и в других фокусирующих
камерах, так, чтобы его плоскость была касательна к фокусирующей
окружности. Интенсивность сфокусированной линии, получаемой по этому
методу, настолько велика, что её можно видеть на флуоресцирующем экране.

580 ИССЛЕДОВАНИЕ ПОЛИКРИОГАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
Фиг. VII, 10. Схема фокусировка
широкого пучка: 1 — анод, 2 —
катод, 3—ограничитель пучка лучей,
4—плёнка, 5 — образец.
Поворачивая шлиф, можно последовательно фокусировать различные участки
рентгенограммы. Нормально экспонированные рентгенограммы отдельных
линий получаются при этих
условиях за время 3—5 секунд!
На фиг. VII, 11 показана
цилиндрическая камера I типа,
использующая фокус трубки в
качестве точечного источника. И эта
камера выполнена как одно
конструктивное целое с мощной
рентгеновской трубкой.
Цитируемые авторы употребляли
вращающийся анод, что позволяло
резко увеличить ток в трубке.
б) Определение диаграмм
состояния. Каждая фаза сплава
характеризуется своей системой
линий на рентгенограмме. Бели
фаза представляет собой твёрдый
раствор, то она обладает
размерами ячейки, изменяющимися
в зависимости от концентрации
твёрдого раствора. Таким
образом рентгенограмма однозначно
характеризует состояние сплава.
Если требуется охарактеризовать состояние сплава при высокой
температуре, то можно прибегнуть либо к рентгеносъёмке при нужной температуре
(что требует
применения специальных камер,
термопар, газовой
камеры для защиты от
окисления), либо к
закалке сплавов до
комнатной температуры, если
эта закалка фиксирует
структуру, устойчивую
при высокой
температуре.
Определение
диаграммы состояния можно
в принципе
производить путём фазового
анализа. Интенсивность
линий рентгенограммы,
принадлежащих данной
фазе, пропорциональна
количеству этой фазы
в f плаве. Следовательно,
по мере приближения
к границе двухфазной
области интенсив ность
линий,
характеризующих исчезающую фа-
ву, постепенно
уменьшается. Граница двух
Фиг. VII, 11. Цилиндрическая камера I типа:
/—-корпус, 2—вращающийся анод,
3—направляющие кассеты, 4-— кассета, 5 — плёнка, 6 —
исследуемый образец, 7 —окно для выпуска лучей
в камеру, Л — рабочая поверхность анода.
фазной области может быть установлена экстраполяцией До точки
исчезновения фазы на графике, изображающем интенсивность в функции состава.

§ 4]. СЪЁМКА Б ФОКУСИРУЮЩИХ КАМЕРАХ 581
Однако точные определения границы фаз требуют измерения периодов
кристаллической решётки. Внутри однофазной области периоды
кристаллической решётки плавно, а весьма часто и линейно» изменяются в функции
состава. Например, постоянная кубической решётки сплава Си — Zn может
быть представлена формулой о = 3,608 ■+- 0,00226 cZa, а для сплава медь-
олово о = 3,608 4- 0,0100 cSa; здесь с — концентрация.
Если кривая (прямая) такого типа известна, то состав сплава
определяется измерением периода решётки.
371
3.70
3.69
3.68
3JS7
° 3.65
^ З.бй
3,63
3.62
3.61
123456789 ЮН
»- Am%Sn
Фиг. VII, 12. Изменение постоянной решётки для
сплавов Си— Sn.
После того как кривая построена, можно приступить к построению
кривой растворимости. На фиг. VII, 12 изображена прямая изменения
постоянной решётки для сплавов Си—Sn, построенная С. Т. Конобеевским и
В. Л. Тарасовой*).
Возьмём сплав, содержащий около 11°/0 олова, и проведём отпуск
сплава с температуры 500° с последующей закалкой. При 500° в меди
растворится не всё олово, а часть его. Определяя по рентгенограмме
параметр решётки, находим, что при температуре 500° растворяется 8,7°/cSn.
Аналогичным путём получаются другие точки кривой растворимости.
Всё исследование производится на одном сплаве, заведомо пересыщенном
оловом.
Этот метод может оказаться негодным в тех случаях, когда параметр
решётки слабо меняется с концентрацией. Не всегда удаётся резким
охлаждением сохранять высокотемпературное состояние.
Приготовление образцов требует большой тщательности. Сплав
предварительно гомогенизируется, превращается в порошок напильником и
запаивается в стеклянную капсюлю. Происходит отжиг при нужной
температуре в течение времени, достаточного для установления равновесия.
После этого капсюли погружаются в воду и тут же разбиваются для
380°-3.6797хЮ'?- 7,16%
350е- 3.6691x10 ~8-6,1 %
3,6№*Ю-6р%
-о
400-3,8835*10-7.54%
&-:
вЮ°-3,6478хЮ -3.96%^
218°-3,6J90xlO -V%
1б7°-3,6120хЮ~8-0А%
*) ЖФХ 2, 681, 1937.

582 ИССЛЕДОВАНИЕ ПОЛИКРИС ГАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
того, чтобы каждая частица порошка пришла в контакт с охлаждающей
средой и резко охладилась.
Порошок собирается, сушится и снимается в фокусирующей камере.
Если съёмка происходит в цилиндрической камере, то относительная
ошибка в измерении параметра
Да Д (2L) , .
где В — радиус камеры a 2L — расстояние между линиями одного диффрак-
ционного конуса.
Удаётся достигнуть точности определения олова в меди 0,07
весовых %, меди в серебре 0,03%, кремния в алюминии 0,09%. Точность в
определении концентрации зависит в основном от хода кривой a = f(c), так
как точность в определении а при одном и том же угле 0 одинакова для
всех сплавов.
Измерение периодов решётки применяется также и при построении
тройных диаграмм.
в) Контроль термической обработки стали *). Рентгенограммы
характеризуют состояние стали после различных видов термической обработки.
Состояние аустенита и мартенсита закалённой стали определяется
содержанием углерода в этих фазах и степенью неоднородности твёрдого
раствора. Содержание углерода определяется, в свою очередь, размером
элементарной ячейки. О степени неоднородности можно судить по размытию
линий.
Мартенсит обладает тетрагональной ячейкой с отношением осей,
близким к единице. Его рентгенограммы состоят поэтому из пар близких
линий 011 и 101, 002 и 200, 112 и 211. Чем больше процент углерода в этой
фазе, тем дальше отстоят друг от друга линии каждой пары. При
содержании углерода менее чем 0,6% раздвоения линий практически нет.
При отпуске закалённой стали происходит распад мартенсита.
Вследствие выделения из твёрдого раствора углерода отношение осей
постепенно приближается к единице. Процесс распада протекает по-разному
в различных кристаллитах. Сталь приобретает неоднородную тетрагональную
структуру. При увеличении времени и температуры отпуска постепенно
уменьшается число кристаллов с большим отношением осей, и решётка
постепенно приближается к кубической объёмноцентрированной решётке
альфа-железа. Чем выше температура отпуска, тем более резки линии
рентгенограммы. Из сказанного очевидно, что состояние мартенсита в стали
действительно характеризуется шириной линии рентгенограммы
неоднородной тетрагональной структуры. Изменение ширины линий альфа-железа
позволяет давать характеристику и других фаз, входящих в состав стали.
Для того чтобы подобные методы могли быть использованы как
заводские методы контроля, необходимо производить точную и быструю
рентгеносъёмку. Так как в большинстве случаев состояние фазы может
быть охарактеризовано одной или несколькими линиями рентгенограммы,
лежащими в небольшом угловом интервале, метод фокусировки линии
оказывается исключительно подходящим для решения этой задачи. При
определении степени неоднородности отпущенного мартенсита наиболее
удобной для исследователя является первая пара линий, у которой более
интенсивная линия 011 имеет и большее смещение. Благодаря этому она
остаётся хорошо видимой даже и в том случае, когда в решётках
кристаллитов имеется полный набор отношений осей от максимального до 1.
Большую точность измерений можно получить, увеличивая до 120 **
расстояние от образца до плёнки и применяя хромовое излучение. Экспо-
*) Каминский Э. и Курдюмов Г. В., Заводская лаборатория, VII,
1150, 1938.

§5]
ИССЛЕДОВАНИЯ ТЕКСТУРЫ
583
зиция может быть сделана ничтожно малой (несколько секунд) за счёт
применения фокусирующей съёмки в описанной выше камере, составляющей
«одно целое с корпусом трубки и использующей анод в качестве
«точечного» источника.
Путём сравнения стандартных снимков, полученных в описанной
камере, можно определять содержание углерода в стали или содержание
углерода в тетрагональном мартенсите с точностью до 0,05%. Точность
/Определения температуры отпуска 15—20 градусов.
§ 5. Исследования текстуры
а) Сущность метода исследования. Образец обладает текстурой, если
кристаллиты расположены не вполне беспорядочно и имеются направления
или плоскости, вдоль которых преимущественно располагаются те или
иные узловые прямые или узловые плоскости кристаллитов. Текстурой
обладают деформированные металлы*) и деформированные полимеры.
Представляет интерес нахождение «параметров текстуры», т, е. определение
индексов [тпр] и (Kkl) тех прямых и плоскостей, которыми кристаллиты
устанавливаются по отношению к направлениям деформации. Требуется
также определять «степень текстуры», т. е. находить примерное
распределение направлений [тпр] и Нш около направлений деформации. Эти
задачи хорошо решаются рентгеновским методом.
Описание текстуры проводится при помощи стереографической проекции
обратных векторов И кристаллитов. Вообще говоря, для описания может
■быть выбрана любая плоскость Kkl кристаллитов. Разумеется, целесообразно
выбрать плоскость с малыми индексами и характеризовать текстуры
распределением в пространстве
обратных векторов таких плоскостей,
как (100), (НО), (111) и т. д.
Стереографическую проекцию
обратных векторов кристаллитов
текстурированного поликристалла
называют полюсной фигурой.
Пусть, например, все
кристаллиты вытянулись ребром [1111 вдоль П1П
направления растяжения. Если в '" ' \ЮО)
остальном расположение кристаллы- Ось проекции [111]
тов беспорядочно, то имеет место
аксиальная текстура. Полюсная фи- Фиг- VII, 13. Полюсные фигуры ку-
гура (Ш) изобразится одной точкой бического кристалла.
б центре проекции (для кубического
кристалла); ось проекции принимают за ось текстуры. Полюсная
фигура (100) кубического кристалла для той же текстуры будет
кольцеобразной (100) (фиг. VII, 13). Изображённые полюсные фигуры характеризуют
идеальную текстуру. В реальном случае будет иметь место значительное
рассеяние ориентировок около указанных точек.
Полюсные фигуры строятся экспериментально либо на основании
ряда снимков, сделанных на плоскую кассету, либо на основании одного
снимка, полученного в специальной камере — рентгеновском гониометре —
для определения текстур (текстургониометр).
Из фиг. VII, 14 видно, что интерференционное кольцо даёт нам сведения
об одном срезе сферической проекции обратных векторов и, следовательно,
определяет некоторую часть полюсной фигуры. Два конуса — конус
*) Успенский Н. Е. и К о н о б е е в с к и й С. Т., Zs. f.
Phys. 1в, 215, 1923.

584 ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
обратных векторов и конус отражённых лучей — однозначно ввязаны.
Распределение интенсивности вдоль интерференционного кольца в точности
повторяет распределение обратных Викторов соответствующей плоскости
всех кристаллитов. Изображённая на рисунке картина возникнет, например,
в случав аксиальной текстуры (111). Тогда 4 сгущения на
интерференционном кольце и соответственно на сферической проекции будут
характерны для отражения 100 или 200 или 300... Одна рентгенограмма даёт
лишь один срез на полюсной сфере. Однако мы можем «прощупать» всю
сферу проекции, если будем изменять угол наклона оси текстуры к лучу.
Этим способом можно покрыть сферу любым числом срезов и получить
полную полюсную фигуру.
Значительно удобнее вместо серии. рентгенограмм получить один
снимок в текстургониометре. Текстургониометр аналогичен рентгенгонио-
метру для монокристалла. Образец
устанавливается на вращающемся
держателе, и во время съёмки ось текстуры
проходит все углы с падающим лучом.
Один из интерференционных конусов
(разумеется, конус коаксиаден
цилиндрической кассете камеры) выпускается
через диафрагму, остальные
экранируются. Плёнка движется
поступательно синхронно с вращением образца.
Следовательно, на плёнке получится
как бы непрерывная серия
рентгенограмм, снятых на плоскую плёнку.
При развёртывании цилиндрической
плёнки интерференционное кольцо
развернётся в линейную полоску. Понятно, что по такой рентгенограмме
можно установить полную картину распределения обратных векторов на
сфере проекции.
б) Построение полюсных фигур но рентгенограммам. Универсальный
способ построения полюсных фигур, состоящий в непосредственном
использовании сетки Вульфа, заключается в
следующем. На фиг. VII, 15 XX есть направ-
Фиг. VII, 14. Картина в случае
аксиальной текстуры.
Фиг. VII, 15. К объяснению способа
построения полюсных фигур.
Фиг. VII, 16. К построению
полюсной фигуры
прокатанной пластинки.
ление первичного луча. Цифрой 1 обозначен интерференционный конус,,
цифрой И—конус отражающих плоскостей; образующие конуса III—
это нормали к отражающим плоскостям. Половина утла раствора этого»

§ 5] ИССЛЕДОВАНИЯ ТЕКСТУРЫ 585«
конуса -JJ- — Ь. Сфера SS' есть сфера проекции, жёстко скреплённая
с образцом.
Максимумы на кольце, создаваемом интерференционным конусом
на плёнке, соответствуют «сгущениям» отражающих плоскостей на конусе II,.
а следовательно, и областям плотного заполнения нормалей на сфере SS'
в точках её пересечения конусом /77.
Рассмотрим построение полюсной фигуры прокатанной пластинки
металла. Распределение кристаллитов в таком образце целесообразно'
рассматривать по отношению к системе координат, построенной на
осях Rw, Bq и Bjj, где Bw—направление
проката, Вп — поперечное направление и
BN—нормаль к плоскости проката (фиг. VII, 16).
Плоскость стереографической проекции
совмещают с плоскостью проката.
Допустим, что луч перпендикулярен оси
Вур и составляет угол а с В^. Для
выбранного кольца hkl находим угол Ь по формуле
Вульфа-Брэгга и с помощью сетки Вульфа
строим на стереографической проекции
кольцо 1 с радиусом —— Ь (фиг. VII, 17). На
этом кольце отмечаем расположение
максимумов рентгенограммы и затем производим
при помощи сетки поворот кольца с макси- фиг. VII, 17. Построение
мумами на угол а около Bw. При этом ма- кольца 1.
ксимумы АА\ и ВВ\ перейдут в положения,
отмеченные буквами со штрихом. Эти последние соответствуют
максимумам на полюсной фигуре с указанной выше ориентировкой. Таким
образом полюсная фигура строится шаг за шагом на основании рентгенограмм,,
снятых при различных углах падения первичного луча по отношению-
к осям текстуры.
в) Плоская и аксиальная камеры. Исследование текстур производится
либо при помощи рентгенограмм, снимаемых на плоскую фотопластинку,,
либо при помощи специальных аксиальных камер, в которых ось
цилиндрической фотоплёнки совпадает с первичным лучом.
Выбор метода в конечном счёте определяется значением угла раствора
интересующего нас конуса. Однако этот угол зависит от применённого
излучения, выбор которого делается на основании соображений, изложенных
на стр. 351.
Если найденный угол 28<45°, то более пригодной является плоская
камера. При этих условиях угол встречи интерференционных лучей,
с плоскостью фотопластинки близок к прямому, н линия рентгенограммы
размывается лишь незначительно. По этим причинам невыгодно
применение при 29<45° аксиальной камеры. Соотношения будут обратными для
углов 20>45°. В этих условиях аксиальная камера выгодней (см.
фиг. VII, 18); при малых углах АВ<^А'В', при больших углах А'В'<^АВ.
Размытость интерференционной линии вследствие косого падения
лучей на плёнку или пластинку приводит, во-первых, к увеличению
экспозиции и, во-вторых, размывает текстурные максимумы.
При равных условиях аксиальная камера обладает дополнительным»'
преимуществами. В ней сглаживаются неравномерности в интенсивностях.
разных конусов вследствие того, что более сильные (передние) конуеьь
пересекаются с фотоплёнкой на больших расстояниях, чем менее
интенсивные конусы, у которых 2Ь близко к 90°. После выпрямления цилиндри-

~)86 ИССЛЕДОВАНИЕ ПОЛИКРЙСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
«Фиг. VII, 18. Иллюстрация более
выгодного применения
аксиальной камеры при 2# > 45°.
ческой плёнки интерференционные кольца разворачиваются в прямые
линии. Количественное исследование текстуры требует микрофотометри-
рования вдоль кольца — разумеется,
работа с прямой линией является
значительным упрощением.
Аксиальная камера обладает весьма
простой конструкцией. В одно дно
цилиндра вставляется диафрагма:
кассета вставляется через
противоположное дно камеры. Держатель образца
вставляется в центре камеры вдоль
радиуса. Должна быть предусмотрена
возможность поворота образца.
г) Текстуркамера. Основной
недостаток метода полюсных фигур
заключается в его «ступенчатом»
построении. Большое число снимков, которое
нужно сделать при желании уменьшить
величину «ступеньки», делает этот
метод громоздким.
Прилагая к съёмке
ориентированных поликристаллов принципы
рентгеновской гониометрии, удаётся
разработать специальную текстуркаме-
РУ*)> один снимок на которой
эквивалентен построению всей полюсной
фигуры.
Сущность метода состоит в съёмке непрерывно вращающегося образца
на плёнку, движущуюся вдоль оси аксиальной камеры.
На фиг. VII, 19 F—фотоплёнка, XX—первичный пучок лучей,
О — обрзец, SS' — сфера проекции. Рассмотрим один интерференционный
конус АОВ и соответствующий ему конус нормалей А'ОЪ'. Если во
время съёмки сфера
проекции будет равномерно
вращаться около SS', то через
неподвижный конус А'ОВг
пройдут все точки сферы
проекции, лежащие на
широком сферическом поясе
(Аг и В' ограничивают его
ширину). Если
цилиндрическая плёнка находится
в движении вдоль XX, то
точки сферического пояса
будут однозначно
воспроизведены на
прямоугольнике развёрнутой
рентгенограммы.
Схема текстуркамеры
Жданова показана на
фигуре VII, 20. Здесь А — диафрагма. О —образец, укрепляемый в
держателе В, который может вращаться в шайбе С, К—цилиндрическая
кассета и F — плёнка. На кассете укреплена рейка Е, имеющая зубчатую
насечку. С помощью шестерни D осуществляется согласованное вращение
Фиг. VII, 19. Принцип метода текстуркамеры.
*) Жданов Г. С, Сборник работ рентгенографической лаборатории
Гинцветмета, 1932 г.

£5]
ИССЛЕДОВАНИЯ ТЕКСТУРЫ
587
■объекта и перемещение плёнки. Экранирование всех интерференционных
конусов, кроме одного, осуществляется при помощи двух трубок ГГ.
Таким образом, круговая щель РР может быть установлена в любом
лесте цилиндра.
Текстуррентгенограмма, получающаяся в такой камере, имеет две
эквивалентные половины. Это обстоятельство есть следствие того, что при
вращении сферы проекции две половины интерференционного кольца
пересекают одни и те же точки сферы.
От текстуррентгенограммы можно перейти к полюсной фигуре. Если
описывать распределение интенсивности на плёнке в системе координат
ж, у, где х— направлено вдоль, а у — поперёк перемещения плёнки, то
каждой точке ху плёнки
соответствует опреде- С D
ленная точка на
стереографической проекции.
Нетрудно показать, что
кристаллические
плоскости, нормали
которых ложатся на одну
параллель сетки Вульфа,
дают отражения,
которые лягут на
рентгенограмме на прямую,
параллельную оси х.
Меридиан стереографической
проекции отображается
ла плёнке следующей
жривой:
cos -^ = tg Ь • tg
У,
Фиг. VII, 20. Схема текстуркамеры.
где Л — радиус кассеты, ш — угловая скорость вращения образца,
a v—линейная скорость перемещения кассеты. Действительно, приведённый
выше рисунок показывает, что при вращении сферы проекции точки А'
•описывают круг широт, а соответствующий рентгеновский
интерференционный луч создаёт точки А, лежащие на прямой. Масштаб в проведении
широт будет равномерным. Значение 2яВ развёрнутой плёнки
соответствует удвоенному углу раствора интерференционного конуса. Если,
например, Ь =s 20° и плёнка вставлена так, что её края и средняя линия лежат
в вертикальной плоскости (проходящей через луч и ось вращения), то
«рая и середина плёнки будут соответствовать широтам 70°, а эквато-
риальная широта придется на у = -j и -г- от 2к1{,
Все меридиональные кривые имеют одинаковый вид и сдвинуты друг по
отношению к другу вдоль оси х. Возникающая сетка показана на фиг. VII, 21.
При помощи этой сетки текстуррентгенограмма может быть пересчитана
в полюсную фигуру.
При расшифровке текстуррентгенограммы надо иметь в виду то
обстоятельство, что неоднородность почернения плёнки может быть вызвана не
только наличием текстуры у образца, но и фактором поглощения. Таким
образом образец с идеально беспорядочным расположением кристаллитов
не даст равномерно зачернённой плёнки. Это обстоятельство сильно
усложняет количественный анализ текстур. Наименьшее значение и наибольшую
простоту имеют поправки на фактор поглощения в случае съёмки
цилиндрических образцов оптимальной толщины.

588 ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
При выборе интерференционного кольца для исследования текстуры
следует останавливаться на плоскости с наименьшим фактором
повторяемости (в случае кубического кристалла на грани куба). Действительно,
Фиг. VII, 21. Сетка для пересчёта текетуррентгенограммы
в полюсную фигуру.
если полюсная фигура {100} вычерчиваетвя 6 нормалями, то полюсная
фигура, скажем {113}, будет образована 24 нормалями. Такое большое
число нормалей весьма густо заполняет поверхность сферы проекций, и
анализ кристаллических ориентировок затрудняется.
§ 6. Определение размера частиц по рентгенограммам
Как было показано в гл. III, из самых общих соображений
следует, что у малых кристаллов точечные узлы обратной решётки
превращаются в заметные области и соответственно с этим
отражение лучей от кристалла происходит в более широком интервале
углов. Интерференционный конус возникает как результат
пересечения сферы отражения сферой обратных векторов. Если узды
обратной решётки превратились в области, то возникающие
интерференционные конусы будут обладать конечной шириной — на рент-

§6].
ОПРЕДЕЛЕНИЕ РАЗМЕРА ЧАСТИЦ
589
генограмме мы обнаружим линии, расширенные в более
значительной степени, чем это следовало бы из таких геометрических
условий, как, например, расходимость пучка.
В этом параграфе мы рассмотрим, каким способом измеряется
это специфическое расширение интерференционной линии и каким
образом по этим измерениям устанавливается размер кристалликов
исследуемого мелкокристаллического образца.
Как указывалось в гл. III, расширение линии имеет порядок
величины отношения длины волны к линейному размеру кристал-
диков. Впервые это расширение наблюдалось, повидимому, у
коллоидального золота. Частички размером более Ю-4 см уже велики
в диффракционном отношении, и сказанное ниже имеет основное
значение для размеров частиц Ю-6—10~4 см (от нескольких
десятков до тысяч ангстрем).
В подобных экспериментах исследуется порошок или иное
мелкокристаллическое тело, содержащее большое количество частиц самого
различного размера. Если не проводятся специальные исследования
распределения частиц по размерам (см. ниже), то расчёт ведётся
на некоторую среднюю частицу. Поэтому в расчётах величины
частиц грубые приближения, делающиеся в отношении формы
частиц, обычно не сказываются сильно на результате.
В качестве экспериментальной меры ширины линий принимается
некоторая условная величина [3, определяемая равенством
T/(e)de
^ = " /(да) '
где /(e) — распределение интенсивности по углам (т. е. профото-
метрированная линия), интеграл—это площадь кривой
интенсивности, а 1(т)—величина максимума кривой. Таким образом под
шириной линии понимается ширина прямоугольника, высота
которого равна высоте максимума кривой интенсивности, а площадь —
площади, охватываемой кривой интенсивности. Если бы
распределение интенсивности имело форму треугольника, то {3 являлось бы
полушириной линии.
Идея вычисления величины {3 для кристаллика данного размера
и формы очень проста, но практическое выполнение расчёта
несколько громоздко. Как было выяснено в гл. III, в случае малого
кристалла узел обратной решётки «размазывается» в область, форма
которой, так сказать, обратяа форме кристалла; при этом форма
области не зависит от типа решётки. Точнее это значит, что
интерференционная функция L (S, ч\, С) имеет периодический характер
и распределена одинаковым образом около каждого узла.
Мы рассматриваем множество беспорядочно ориентированных
кристалликов. Поэтому диффракция определяется средним
значением интерференционной функции, которая возникает вращением

590 ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VIL
обратной решётки около её начала во всех направлениях. Среднее
значение X есть функция только абсолютной величины вектора
^ Х( h5: )* т-е- будет иметь одно и то же значение на всех
точках сферы, проведённой радиусом ^ из начала координат
обратной решётки. Максимальные значения L лежат на сфере,
описанной радиусом Н. Величина L для данного радиуса равна
£(*) = £ J Z (6, i|, QdS,
4я sin j с ,
где s = —£-—e a dS — элемент площади в пространстве обратной
решётки. Искомая величина р в функции s имеет вид
Р\2я-/ L{m)
Значение структурного фактора вводить в эти вычисления нет
необходимости, так как он очень мало меняется с координатами S,
1), С. Поэтому значение F2 будет входить как в числитель, так и
в знаменатель выражения для (3 и, следовательно, сократится.
Так как на практике мы измеряем р в функции от угла
рассеяния, то от р (s) следует перейти к р (20). Так как
то
P<2»>-5ilP(s)'
Р^)—со.» ЬЫ
Интегрирование величины L \-£~)> усреднённой только вдоль
сферы, происходит вдоль радиуса-вектора -^ обратной решётки.
Можно утверждать, что
№№) ,„.
-—— = /с • Д$'
L(m) '
As—«размеры» области около узла в радиальном направлении,
где функция L Г~ J отлична от нуля, а к — коэффициент, зави-

§6]
ОПРЕДЕЛЕНИЕ РАЗМЕРА ЧАСТИЦ
mi
сящий от характера распределения функции L (-^А, т. е. константа
для кристалла данной формы. Размер кристаллика в направлении
обратного вектора (т. е. нормали к отражающей плоскости):.
2) = -д^*). Следовательно,
Значение константы к вычислялось разными авторами. Для
сферических частиц к =1,075. Ряд авторов приводит значения к для
кристаллов кубической, формы порядка 0,9. При больших
требованиях к результату измерений следует стремиться к опытному
определению к на порошках, значения I) для которых установлены
независимым путём. Так как измерения D не могут претендовать
на большую точность хотя бы уже потому, что расчёты не
учитывают неоднородности в форме и размерах зёрен, то для большинства
опытов бывает достаточно принять к = 1 и полагаться в основном
на результаты относительных, но не абсолютных измерений.
Следует также иметь в виду затруднения, связанные с оценкой
полуширины линии. Порошок, который состоит из зёрен с бесконечно
малыми диффракционными .областями (размер зерна > Ю-4 см)%
всегда даст линии конечной ширины, значительно большей, чем
ширина из-за диффракции. В этом случае наблюдаемая ширина
линий зависит от геометрических условий съёмки — ширины щели,
расходимости первичного луча, величины поглощения. Все эти
факторы не учитывались при выводе формулы для* $(2&). Наконец
на ширине линии сказывается спектральная неоднородность луча,
например дублетность линии Ка.
Таким образом прежде всего надо уметь перейти от наблюдае^
мой ширины линии к значению (3 (20).
Был предложен .рад способов устранения этих эффектов, а также
их расчёта. Мы не будем останавливаться на всех них, а опишем
лишь один, наиболее точный.
Если к исследуемому порошку подмешать некоторое количество
эталонного вещества, размеры зёрен которого достаточно велики,,
то по ширине линий этого вещества можно судить о влиянии всех
геометрических факторов.
*) Максимум интерференционной функции расположен в простейшем
случае (сравни стр. 238) в пределах £ = h rt -—, -ц = fc ±-tjt-,; = I± —. Mo*
JS\ iV2 IV3
жно принять за размеры узла ребра -ят" > дГ > ■ят" • Пусть As — —; тогда
размеры кристалла в соответствующем направлении ща =-— =-пг •
**) Селяков Н. Я., Zs. f. Phys., 31, 439, 1924.

592
ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
Фиг. VII, 22. Диффракционное расширение.
Предположим, что измерены две близко расположенные линии—
одна эталонного, а другая исследуемого вещества, и определены их
полуширины Ъ и В.
Искомая величина (3, характеризующая диффракционное
расширение, лежит между этими двумя величинами. Найдём связь
между (3 и
непосредственно измеряемыми
Ъ и В.
На фиг. VII, 22
сплошной линией (с)
изображена
стандартная (не расширенная)
линия. При наличии
диффракционного
расширения каждый
элемент этой линии, соответствующий dx, расплывётся в пунктирную
кривую (d). Ширина этой последней кривой равна (3. Если записать
кривую эталонной линии в виде I™**f(x), то
p/mai = .#"/(*) <**;
здесь Гпах — высота кривой (d).
Реальная линия возникает в результате подобного расширения
всех участков dx кривой эталона. Если 1(1) — интенсивность,
создаваемая элементом dx в точке, находящейся на расстоянии $ от
середины линии, то суммарная интенсивность в точке $ будет равна
Im(t) = fl(l)dx.
Если принять для кривой (d) запись
Ia = F&xF(Jcx),
где к — параметр, зависящий от размера зёрен, то
jJF(hx — J£)f(z)dz.
'®-J
lm&*F(kx — U)dx = ll
Теперь мы можем записать выражение для полуширины
исследуемой линии
В
jlm(Z)d- (* j F(kx — khs)f(x)dxds
С(0) =
но
Г F(lcx)f(x)dx
+ 00
J F(kx — Щ d% = J F(kl) d% = J F(kx) dx.
-f-oo

б]
ОПРЕДЕЛЕНИЕ РАЗМЕРА ЧАСТИЦ
>93
Следовательно,
J /<' (/.#) dx Г /' (х)
doll = -х .
J F(1cx)f(x)dx
Для ширины эталонной линии имеем:
b = ff(x)<Lr,
искомая ширина также равна, по определению,
р = j F(kx)dr.
Таким образом
f F(kx)f(x)d*
Г F {кх) dx
Кривая /(,/) известна из опыта, кривая F{bx) может быть взята
в форме в **>__.f 1_ит> д>
Таким образом можно получить кривую
По опытному значению -=т- определяют к и зате.\г но формуле
Г F(kx)dx находят значение (3.
Как видно, при определении ширины линии приходится делать
предположения относительно характера распределения частиц по
размерам (вид F(kx)). Это, однако, неизбежно в описываемом
методе.
Для того чтобы читатель мог получить представление о
величинах, с которыми приходится иметь дело» приведём таблицу
полуширины (в мм) линий коллоидального золота, рентгенограмма
которого была получепа в камере с радиусом 45,3 мм (табл. VII, П).
Таблиц а- VII, II
Символ
111
200
220
311
222
331
422
В
0,45
0,59
0,54
0,56
0,49
0,75
1,22
Ь
\ в
0,58
0,42
0,48
0,48
0,55
0.41
0,28
Р
0,24
0,42
0,35
0,36
0,28
0.54
1,02
Размер частиц
в А
310
180
240
250
340
230
180

*)94 ИССЛЕДОВАНИЕ П0ЛИК1*ИСТЛЛЛИЧЕб1ШХ ВЕЩЕСТВ [lVI. Vlt
То, что размер частиц, вычисляемый из разных интерференционных
линий, сильно различен, можно использовать для определения
средней формы частицы — следует помнить, что из данного отражения
определяется размер в направлении нормали к отражающей
плоскости.
Остановимся теперь на методике исследования распределения
зёрен по величине. Как это следует из предыдущего, зерну данной
формы соответствует специфическое распределение функции I(t, t\,V)
около узла обратной решётки. При большом числе беспорядочно
ориентированных зёрен диффракция определяется средним значением
этой функции. И всё же возникающая интерференционная кривая
может быть связана интегральным равенством с кривой
распределения зёрен но размерам. Можно пытаться связать различные
распределения—гауссово, максвеллово, прямоугольное и т. д.—с
видом профотометрированяой кривой рентгенограммы порошка.
Есть и другой путь, заключающийся в измерении распределения
интенсивности, рассеянной под углами порядка 0,2—2'' к
первичному лучу.
Принципиальной разницы между этими исследованиями и
изучением формы интерференционной кривой, по сути дела, нет. Если
в последнем случае речь идёт об установлении характера
распределения усреднённой интерференционной функции около узлов
обратной решётки, то и в первом случае решается та же задача, только
изучается интерференционная функция в области нулевого узла
обратной решётки.
Распределение интерференционной функции определяется, как
указывалось выше, только размером и формой частицы, но не
структурой её решётки. Поэтому мы вправе написать для интенсивности
рассеяния лучей от малой частицы под малыми углами:
/(20)=/ePe2{/2-#(Z?, »),
где /е — интенсивность рассеяния одного электрона, р — средняя
плотность электронов, V — объём частицы, a S(B, S)—фактор формы
частицы, вполне аналогичный ахомиому фактору.
Если N (R) dll — общее число частиц, имеющих размер между Л
и B-\-dF, то интенсивность, рассеянная веществом
оо
I(2&) = Je?l JN(E) V2 (R) S {В, ft) dlt.
0
Вид кривой интенсивности определяется распределением частиц но
размерам. Для сфероидальных частиц значение S (Ry &) может быть
вычислено. Тогда, задаваясь распределениями по размерам
разных типов, можно вычислить J(20) и сравнить вычисление
с опытом.

§ б] ОПРЕДЕЛЕНИЕ РАЗМЕРА ЧАСТИЦ 595
Исследования рассеяния при малых углах технически не просты.
Прежде всего излучение должно быть монохроматизировано
отражением от кристалла; съёмка должна проводиться в вакууме. Окошко
камеры следует сделать из бериллия. Полуширина пучка не должна
превышать 0,1—0,15 мм. Образец берут в виде пластинки,
спрессованной из порошка. Расстояние образец — плёнка колеблется в
разных опытах от СО до 400 мм. Разумеется, метод требует больших
экспозиций, доходящих до 100 часов.
Результаты, полученные исследованием рассеяния под малыми
углами, определяют кривую распределения частиц по размерам.
Разумеется, из такой кривой может быть вычислен средний размер
частиц. Таким образом, исследования расширения диффракцион-
ных линий целесообразно вести вместе с описанными
исследованиями.
Сопоставление результатов измерения средней величины частиц,
проведенное в некоторых работах, приводит к удовлетворительным
результатам. В худших случаях расхождение достигает 40%, среднее
расхождение 10—15%-
Следует рекомендовать не зависимый от рентгеновских
измерений снособ определения размера частиц вычислением из значений
удельной поверхности мелкокристаллического порошка, которая
может измеряться адсорбционными методами. Этим способом можпо
воспользоваться для тарировки рентгеновских измерений.
Остановимся на определении величины кристаллитов «большого»
размера. В случае достаточно больших размеров кристаллических
зёрен диффракционное кольцо рентгенограммы поликристалла
перестаёт быть сплошным. Отдельные точки кольца представляют собой
отражения от отдельных зёрен.
Г. С. Ждановым был предложен метод *) определения числа
кристаллитов N в единице объёма. Очевидно, что N пропорционально -«-,
где I—линейный размер кристаллита. Поэтому способ суждения
о величине зёрен по их числу будет обладать большой
чувствительностью.
Можно предположить, что число интерференционных пятен п
на диффракционном кольце hid будет пропорционально N, а именно
п = У j pdV=Nj)V,
где р — вероятность отражения от одного кристаллита, находящегося
под данным углом О к лучу, а V—просвечиваемый объём.
Коэффициент пропорциональностиpV онределяется размерами диафрагм
и фокального пятна рентгеновской трубки, формой и размерами
*) Г. г. Ж д anon и И. И. Иверонова, Зав. лаб., стр. 1235, 1935-

596 ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VH
объекта, а также углом скольжения 0. Этот коэффициент, вообще
говоря, можно вычислить, однако несомненное его постоянство для
данной методики съёмки позволяет применять написанную выше
формулу для относительного измерения числа, а следовательно, и
размера кристаллитов.
Подсчеты интерференционных пятен производятся под
микроскопом.
При рекристаллизации металла число кристалликов спачала
возрастает, достигает максимума, а затем падает. Очевидно, что
нахождение этого максимума позволяет судить о начале процесса
поверхностной рекристаллизации, т. е. «поедании» одних кристаллических
зёрен другими.
Этот способ исследования и контроля отжига успешно
применяется в том случае, если размеры зёрен колеблются в пределах
от 0,1 до 0,001 мм.
§ 7. Измерение напряжений
Следует различать микронапряжения или напряжения 2-го рода от
макронапряжений или напряжений 1-го рода. Микронапряжения могут быть
определены как напряжения, варьирующие в широких пределах и притом
беспорядочно как в отношении величины, так и в отношении направления,
от зерна к зерну. Они возникают тогда, когда перейдён предел упругости
при холодной обработке. Под макронапряжениями понимаются упругие
напряжения. Очевидно, что в этом случае напряжения меняются
закономерно от кристалла к кристаллу и от точки к точке внутри данного
кристалла.
Рентгеновские методы измерения напряжений имеют свои достоинства
и недостатки. К первым принадлежат возможность абсолютного измерения
напряжения (без сравнения с ненапряжённым образцом) и возможность
измерения напряжения на малом участке (порядка квадратного миллиметра)
без необходимости интерполирования или экстраполирования на соседние
участки. К недостаткам относится невозможность измерения напряжений
первого рода при наличии значительных напряжений второго рода. Метод
требует значительной затраты времени, специального оборудования и
опытного исследователя. Рентгеновским методом нельзя исследовать
переменные напряжения.
Напряжения обоих родов сказываются на изменении межплоскоетных
расстояний. Вариации в значениях межплоскоетных расстояний, связанные
с. микронапряжениями, сказываются на расширении диффракциошшх линии.
Необходимость в таком расширении следует непосредственно из закона
Вульфа-Брегга, так как небольшие изменения в величинах d причиняют
небольшие изменепия в значениях угла & для данной длины волны
рентгеновского излучения.
Следует отметить трудность различения между расширением линий,
происходящим из-за малости размера зерна и из-за микронапряжений.
Возможный путь заключается в измерении зависимости полуширины линии
от угла скольжения. Как мы видели выше, в случае малых зёрен
расширение пропорционально X sec ft. С другой стороны, полуширина линии,
расширенной из-за микронапряжений, пропорциональна изменению угла %,
вычисляемому дифференцированием уравнения Вульфа-Брегга. Имеем:
A9 = -^tg&s=_etg&,

§7]
ИЗМЕРЕНИЕ НАПРЯЖЕНИЙ
597
где е — напряжение. Таким образом в этом случае полуширина
пропорциональна tgd, а не sec$ и кроме того не зависит от длины волны
рентгеновского излучения.
Что касается напряжений 1-го рода, то их наличие скажется лишь на
сдвиге диффракционных линий*), т. е. на уменьшении или увеличении
некоторых межплоскостных расстояний. Изменение величин d зависит от
направления первичного луча, падающего на образец, так как не у всех
зёрен одинаково изменяются данные межплоскостные расстояния. В этом
отличие этого сдвига линий от аналогичных сдвигов, происходящих из-за
теплового расширения или тех изменений параметра, которые имеют место
в сплавах (твёрдых растворах) с разной концентрацией одной из компонент.
Исследование обоих видов напряжений происходит методом задней
съёмки. Линии при углах &, близких к 90°, будут сдвигаться на большую
величину в случае напряжений 1-го рода и более значительно расширяться
в случае напряжений 2-го рода.
Существенную пользу в наблюдении напряжений 2-го рода оказывает
дублет ifa.ov Этот дублет разрешается только при достаточно больших
углах 9. При большой (более 10 ~4 мм) величине зёрен и отсутствии
микронапряжений ширина линии рентгенограммы равна 0,5°. Следовательно,
дублет начинает расщепляться лишь при значениях #, вычисляемых из
дифференцированного уравнения Вульфа-Брогга dX = 2d cos & db. d\ для
дублета равно 0,006 А. Если ширина линии из-за микронапряжений или
из-за малого размера зёрен начинает превышать 1°, то линии дублета
начинают перекрываться и дают нам чёткое указание на
соответствующий эффект. Чем ближе длина волны рентгеновского излучения к
удвоенному межплоскостному расстоянию, тем точнее можно производить
исследования этого типа. В идеале длина волны должна быть немного меньше
и как можно ближе к 2d. В соответствии с этим правилом исследователь
выбирает материал анода. Именно поэтому при изучении напряжений обычно
работают иа разборной трубке со сменными анодами.
При съёмке рентгенограмм на неотфильтровапном излучении
напряжённые образцы, в соответствии с теорией, развитой иа стр. 318, дают
астеризм. Последние исследования показывают, что явления астеризма
содержат в себе ещё целый ряд неясностей и могут быть использованы
при изучении напряжений лишь как качественная характеристика.
Количественная оценка микронапряжений, т. е. вычисление е, сводится,
как мы уже указывали, к измерению полуширины линии, так каке=—ctg $dft.
Способ измерения расширения диффракционной линии мы рассмотрели
в § VII, 6. Можно, кроме того, указать на иную процедуру, применявшуюся
специально для измерения напряжений. В случае, когда Ка-дублет
расщеплён, мы пользуемся тем обстоятельством, что Ка -линия в два раза
сильнее Ка -линии. На кривой изображающей результат фотометрирова-
ния рентгенограммы, проводится линия, параллельная фону через вершину
более слабого пика а%. Эта линия пересекает более сильный пик oj и
позволяет измерить таким образом его полуширину. За показатель
микронапряжений принимается величина — ctg &, где В— измеренная указанным
образом полуширина.
В случае неразрешённого дублета полуширина линии определяется как
ширина в том месте линии, где интенсивность равна среднему
геометрическому значению, из максимальной интенсивности и интенсивности фона.
Полуширина линии, определяющаяся напряжениями, вычисляется по
формуле:
В* = Ядам — В12 + Sv
*) А к с е н о в Г. И., ЖЭТФ 4, 627, 1934,

508 ИССЛЕДОВАНИЕ ИОЛИКРИСТАЛЛИЧЕСКИХ ШНЦЕСТИ [ГЛ. VII
где инзм есть измеренная величина, В12—поправка на присутствие линии
«о в неразрешённом дублете и Jis— поправка на конечную ширину щели.
Для этих поправок применяются следующие формулы:
В,, 2 = (2.45-^-tg»)'; В] = 0,4Ъи>1,
гдо А/"- — ширина дублета и ws — угловая ширина щели. Следует
напомнить, что угловая ширина линии 2Д9- равна линейной ширине, делённой
на радиус камеры в случае обычной съёмки и на диаметр камеры в
случае фокусирующей съёмки.
Переходим к методу измерения упругих напряжений на поверхности
образца. Рентгеновским методом может быть определена величина
напряжения в данной точке и в данном направлении. Для этого необходимо
лишь иметь возможность установки поверхности образца под разными
углами к падающему лучу. При этом ещё раз надо подчеркнуть, что
рентгеновский метод и только этот метод не требует сравнения с состоянием,
при котором напряжения отсутствуют. Это существенно, так как задача—
установить, какое именно состояние является ненапряжённым, весьма
трудна.
Для полной характеристики напряжений в образце достаточно,
разумеется, измерить главные напряжения.
Данный днффракционный луч, составляющий интерференционный конус,
отражён каким-либо определённым зерном. Угол, под которым он отразился,
даёг нам значение межплоекостного расстояния в направлении нормали
к отражающим плоскостям. Эти плоскости упругим растяжением или
сжатием приведены на расстояние, отличное от обычного на величину Ad.
Таким образом каждый днффракционный луч кольца приносит сведения
о линейной деформации е = -г-. Днффракцнонное кольцо, полученное при
данном расположении образца по отношению к лучу дает сведения о
деформациях в целом конусе направлений. Поворачивая образец к
лучу и повторяя съёмку, мы получим сведения о другом «конусе
деформаций» и т. д.
Итак, проблема измерения напряжений сводится к установлению связи
деформаций с напряжениями.
Если t есть произвольное направление, не лежащее в плоскости
образца, х и у — две оси, лежащие на поверхности, угол $— угол между
направлением t и нормалью к поверхности образца и угол ф — угол
проекции t с осью х (азимут), то
Щ = 6" (1 + v) sin2 i> - v (Sx + Sy),
где v — коэффициент Пуассона. Е — модуль Юнга, Sr = Sx cos2 ф 4- Sy sin2*
и Sx, Sy—напряжения в направлениях Sx и Sy.
Измеряя разность двух tt для одинаковых ср и разных «|\ мы можем
определить значение напряжения в данном направлении Sx, так как второй
член в написанном выше выражении сохранит своё значение для второго
измерения при другом угле.
Для случая 6 = 0 уравнение получает вид:
т. е. одним измерением zt в направлении нормали к поверхности мы
определяем сумму главных напряжений. Из такого измерения мы не можем,
конечно, определить направления главных напряжений.
Можно предложить различные методы рентгеновского измерения
напряжения.

§ 7|
ЖШКРЕНИК НА IT РЯЖЕНИЙ
599
Прежде всего следует отметить возможность определения величины Л"
из одной рентгенограммы. Как это следует из сказанного выше, при съёмке
образца под углом при наложении напряжений интерференционное кольцо
искажается. Действительно, каждому лучу, образующему конус,
соответствует своё направление t, своё значение tt и, следовательно,
межплоскостного расстояния (а значит, и угла 9).
Допустим, мы хотим определить напряжение Sr в заданном
направлении. Проведём через центр диффракцнонного кольца линию, параллельную
этому направлению. Образовавшиеся два радиуса кольца rt и г2 не будут
одинаковы. Нетрудно показать, что разность г\ — г2 определяет величину S'
следующей формулой:
S'
i'i — r2 = 4D —~г (1 -\- <) sec5 2v) cos8 f\ sin 2a,
где r, = 90° — &, a — угол луча с нормалью к пластинке, 1) — расстояние
объект — пластинка.
Эта формула получится из приведённой выше общей записи для ц,
если её записать дважды для обоих рассматриваемых лучей (для одного
Ф = а+к], а для другого <Ь=.а — Y]) и вычесть одну формулу из другой.
Значение е* —st можно преобразовать к виду
_ ?i — r2 sin т; cos22r\
ч\. Hi ~~ 2D cos fj '"
В случае железа намерение производится обычно для кольца iilO.
Угол а выбирают равным 20°. Ввиду важности точного значения D
рекомендуется съёмка с эталоном; для этого тонкий слой золота, серебра или
вольфрама наносится (напыляется) на исследуемую поверхность.
Особые усилия приходится прилагать для точного фиксирования центра
рентгенограммы (от которого отсчптываются ?\ и *2). Так как эта
процедура не слишком проста, то нужно описать другой метод, не нуждающийся
в этом.
Произведём два снимка — один луч под углом otj к нормали, другой
иод углом а2 к пормали. Тогда
E*tx = S' (1 + v) sin* a2 - v (Sx -f Sy),
Л% = <?''(! + v) sin" at - v (Sx -I- Sy).
Откуда
E (£tt — %) = & (1 + v) (Sin- a2 — sin2 0l).
»4 — r2 sin ri' cos2 2ti
ef — zt нопрежнему равно ——~ ■ — .
1 - 2D cos ([
Однако под величинами г теперь понимаются средние радиусы колец.
Это значит, что для каждой съёмки мы определяем среднее значение е
для плоскостей, перпендикулярных падающему лучу. Это приближение
должно выполняться достаточно хорошо, имея в виду небольшой угол
раствора конуса лучей. Очевидно, что азимут, для которого определено S',
определяется плоскостью, проходящей через два положения первичного луча.
Несомненным является факт, что напряжения 1-го и 2-го рода не
исчерпывают характеристику состояния тела, подвергающегося деформации.
Известно, что в металле, разрушившемся при знакопеременной нагрузке
много ниже предела прочности, нет напряжения 2-го рода — линии
рентгенограммы такого тела не являются размытыми. В то же время эти снимки
Указывают на наличие некоторых изменений в металле, выражающихся
Я изменении интенсивности диффракционных линий,

000 ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛЫЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
Это изменение, как показывает опыт, можно учесть, вводя в формулу
интенсивности дополнительный множитель вида
Константы С я В характеризуют это новое состояние металла, которое
называют напряжением 3-го рода.
Вид написанного фактора подсказывает трактовку явления. Если
принять, что деформированные кристаллики представляют собой искажённую
решётку, причём таким образом, что большинство атомов выведено из
плоскости hkl решётки в среднем на величину U, то
В = 8*2 U*
в полном соответствии с аналогичной формулой для теплового фактора
(сравни стр. 275). Действительно, вычисление остаётся тем же, так
как и при расчёте температурного фактора рассматривается неподвижная
решётка.
Методика измерения констант С и В сводится к построению кривой
атомно-температурного фактора. Можно также определять В по отношению
интенсивности линии до и после деформации. Значения U, находимые
таким образом, довольно велики (порядка 0,2 А), значения С близки
к единице.
Исследования напряжений 3-го рода имеют большое значение при
изучении усталости металлов. Так, Иверонова и Костецкая, исследуя ширину
линий и их интенсивность в зависимости от числа циклов нагрузки на
рельсовой стали, установили, что ширина линии не меняется до момента
излома, а отношение интенснвностей линии 310 и 220 падает с увеличением
числа циклов. Рентгеновский метод позволяет, таким образом, предвидеть
усталостное разрушение.
§ 8. Определение радиального распределения плотности
вещества в кристалле
Хорошая профотометрированная рентгенограмма порошка
кристаллического, а также аморфного, позволяет решить интересную, и иногда
определяющую структуру задачу — нахождение среднего радиального
распределения плотности вещества около данного атома.
Решение этой задачи требует знания лишь интенсивности в функции
угла рассеяния. Подобный метод исследования позволяет обходиться без
каких бы то ни было допущений о структуре и является совершенно
незаменимым, когда речь идёт об установлении строения аморфных тел или
таких кристаллических порошков, которые не дают монокристаллов.
Как сейчас будет показано, можно получить формулу, связывающую
функцию интенсивности I(s), где s = —г , и функцию р (г),
определяющуюся условием: на расстоянии между г и г -f dr от данного атома
находится 4я2р (г) dr атомов. Разумеется, далеко не во всех случаях знание р (г)
эквивалентно знанию структуры, но, безусловно, ценные сведения о
строении вещества эта величина даст всегда. Метод, к изложению которого мы
переходим, аналогичен в некоторой степени методу i^-рядов. В обоих
случаях мы получаем сведения об имеющихся в структуре межатомных
расстояниях.
Диффракционную картину, созданную кристаллическим порошком, зёрна
которого расположены беспорядочно, можно рассматривать как картину
усреднённой интенсивности, возникающей от одного кристаллика, прини-

8] ОПРЕДЕЛЕНИЕ РАДИАЛЬНОГО РАСПРЕДЕЛЕНИЯ ПЛОТНОСТИ 601
мавшего во время съёмки все возможные положения в пространстве. Это
допущение вполне законно, так как каждое зерно рассеивает независимо
и не существует интерференции между лучами, идущими от соседних
кристалликов. Такое рассмотрение аналогично постановке задачи о
рассеянии лучей независимыми молекулами. В этом случае роль «молекулы»
играет кристаллическое зерно.
Рассмотрим сначала наиболее простой случай — вещество, состоящее
из атомов одного сорта с атомным фактором f. Каждая частица
(кристаллик) содержит N атомов. Задача заключается в нахождении
радиального распределения р (г) плотности вещества около произвольного атома.
Если кристаллик содержит достаточно много атомов, то для каждого из
них р (г) одинаково.
Как показано в § VII, 9, интенсивность рассеяния одной молекулой
в электронных единицах равна
'W-S/J + aSS^
sin slpq
slpq
p V 4
lpq — расстояние между двумя атомами. Учитывая, что все атомы
одинаковы (fp = fq), заменяя суммирование интегрированием по г (на
расстоянии г находится 4тсг2р (г) dr атомов), получим искомое выражение для
интенсивности в виде:
I(.у) = NP Г1 + 4я Г г2р(/•) -5!HiL dr\
Обозначим через р0 среднюю плотность атомов в кристалле; прибавляя
и вычитая одно и то же выражение к правой части равенства, можем
записать предыдущую формулу в виде:
I (.) - W [l + 4* J г» {р (г) - Ро} Ц£ dr + 4*р0 J г* ^ dr] .
При больших г рО')->р0; поэтому в первом интеграле интегрирование по
размеру кристалла можно заменить интегрированием от 0 до оо. Последний
интеграл берётся в квадратурах (интегрированием по частям); после
интегрирования s войдёт во второй степени в знаменатель, а размер кристалла
в первой степени в числитель. Если размеры кристалла много больше
длины волны (а это условие выполняется всегда), то этот интеграл будет
иметь значение, отличное от нуля лишь при малых s (в
непосредственной близости к первичному лучу). Поэтому второй интеграл можно отбросить.
Рассеянная интенсивность может быть представлена в виде
оо
б
Применяя теорему об интеграле Фурье, получим:
ОО
4*г'р (/•) = 4itr*p0 + —■ | s\ ^ — llshia-rff.,

602 ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛЫЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
Таким образом численным или графическим интегрированием для
разных значений г можно получить радиальную плотность, зная на основании
, опыта интенсивность рассеян-
ипг2р(г\
18
I
/
10
2.0
3.0
и.о
50
6.0
re A
Фиг. VII, 23
электронной
Радиальное распределение
плотности в ромбической
сере.
ного излучения I(s)
Этот вывод можно
распространить и на случай
вещества, содержащего несколько
сортов атомов.
На фиг. VII, 23 показано
найденное таким способом
радиальное распределение
атомов в ромбической сере. Как
видно из рисунка, особенно
чётко выделяется пик при
2,3 А, указывающий на
расстояние между ближайшими
атомами серы.
Следует помнить, имея
в виду пренебрежения,
сделанные при выводе, что метод
неприменим для кристаллов
малого размера. Для
получения правильных результатов
необходимо иметь основание
для проведения
интегрирования от 0 до со, не принимая во
внимание формуй размер кристалла. Описанный метод с большим успехом
применялся при исследовании строения стекла.
§ 9. Структурный анализ газов, жидкостей и аморфных тел
а) Введение. Рентгенограммы вещества, не находящегося в
кристаллическом состоянии, обладают круговой симметрией. Их снимают
монохроматическим излучением на плоскую пластинку, которую фотометриругот
в радиальном направлении. В большинстве случаев на рентгенограмме
отчётливо видно одно диффузное кольцо (гало), редко два-три. Таким
образом экспериментальный результат это — кривая 1(2%), обладающая
одннм иди несколькими максимумами.
С первого взгляда не очевидно, почему на рентгенограмме должны
появиться максимумы даже в небольшом числе. Ведь молекулы
расположены по отношению к лучу и друг к другу беспорядочным образом (в
аморфном теле), а в газах принимают за время съемки все возможные ориентации.
Если бы мы наблюдали рассеяние от одной неподвижной молекулы,
то интерференционные эффекты, разумеется, существовали бы. Однако
опыт даёт среднее значение интерференционной функции; при этом
усреднение должно произойти по всем возможным ориентациям молекулы. Как
мы сейчас увидим, несмотря на полное отсутствие предпочтительной
ориентировки рассеивающей молекулы, возникающее распределение
интенсивности 7(2&) даёт интерференционную картину. Кривая 1(2&) связана
со значениями часто встречающихся в рассеивающем образце расстояний
между рассеивающими центрами. Если исследованию подлежит газообраз-
вое вещество, то все осуществляющиеся межмолекулярные расстояния
более или менее равноправны. Напротив, в жидкости, где молекулы
находятся в состоянии соприкосновения, будут особенно часто встречаться
расстояния между атомами, равные сумме межмолекулярных радиусов.
Однако, прежде всего, для возникновения рентгенограммы существенны
межатомные внутримолекулярные расстояния; эти расстояния будут
встречаться во всех случаях в любом мгновенном расположении молекул,

§ 9] СТРУКТУРНЫ!! АНАЛИЗ ГАЗОВ, ЖИДКОСТЕЙ 603
6) Структурный анализ газообразного вещества. Рассмотрим
молекулу, состоящую ив N атомов, с атомными факторами fy ... fy. Центры
атомов определяются векторами гр в системе координат, связанной с
молекулой. Так как колебания атомов происходят огромное число раз за время
съёмки, то молекулу можно рассматривать как жёсткую. Влияние
внутримолекулярных колебаний может быть в принципе учтено атомным
фактором. Напишем выражение рассеяния интенсивности для некоторой
произвольной ориентации молекулы к лучу. В единицах рассеяния электрона
амплитуда волны для данного вектора s (как и ранее я = к — К'0):
К
а= j/у*0'"**>".
Интенсивность излучения получим, как обычно, помножая на
комплексно-сопряжённую величину
р а
В сумму входит N членов p = q; для каждого из них
экспоненциальная функция равна 1. Поэтому
1= 2*5 + 2 22 /■/,'■<* (v>-
р = 1 р q
В таком написании предполагается, что каждое межатомное расстояние
учитывается один раз.
Написанное выражение имеет довольно универсальный характер.
Чтобы перейти к наблюдаемой интенсивности / (29), последнюю формулу
надо усреднить, учитывая вероятность того или иного взаимного
расположения частиц. Мы вели рассуждение относительно абстрактной
молекулы; поэтому полученный результат применим для любого количества
атомов, интерференционные эффекты между которыми нужно учитывать.
Если происходит рассеяние газа, находящегося не под очень
большим давлением, то интерференционными эффектами между атомами разных
молекул можно пренебречь (все rpq одинаково возможны). Интенсивность
рассеяния газа можно рассматривать как сумму интенсивностей
рассеяния отдельными молекулами. При этом все ориентации можно полагать
равно вероятными. Последнюю формулу требуется, таким образом,
усреднить и помножить на число молекул п. Среднее значение косинуса (грдя)
найдётся по формуле:
т.
1 /* s\ns/p(]
cos(rpqs) — — cos (s7pq cos a) sin a dt = — ,
2 .
о
pq
где ?»g = ! »>д I. а a — угол между направлениями s и rpq. Вероятность
того, что rpq лежит иод углом между а и a -f da к я равна sin a d*.
Итак, для газа
ж-Ц'Я'Я'лЗД
р<1
pq

604 ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛА ЧЕСКИХ" ВЕЩЕСТВ fl'.l. VII
Следует иметь в виду, что эта формула не должна применяться для
направлений, непосредственно примыкающих к первичному лучу. Дело в том,
Yi sin slpq
что в предельном случае (s = 0) нельзя пренебрегать V fpfq —- ,
взятой по атомам разных молекул по сравнению с такой лес суммой,
взятой по атомам одной молекулы. Это замечание, однако, носит скорее
принципиальный характер, так как написанная формула становится
справедливой уже при самых малых s.
Рассмотрим несколько подробнее рассеяние двухатомной молекулой.
Его можно представить в виде
I о > Sin slPQ )
или, если молекула состоит из двух одинаковых атомов,
( sin sln„ \
Первый член этого выражения представляет собой сумму интенсивностей,
рассеянных каждым атомом независимо от другого. Второе слагаемое
учитывает интерференцию от
нары атомов.
Выражение для I(s) есть
произведение двух факторов,
каждый из которых зависит от &.
Зависимость от угла
рассеяния атомного фактора
обсуждалась нами достаточно пбдробно
(стр. 220). Что же касается
второго слагаемого, то оно имеет
главный максимум при « = 0 и
ряд следующих постепенно
убывающих по высоте максимумов
при si = 2,459я, 4,477я и т. д. Если
бы атомы рассеивали, как точки,
то Р было бы постоянной
величиной и распределение
интенсивности давало бы весьма
отчётливую систему колец. Однако
j sln& быстрое уменьшение f, с возра-
05 j0 *. стаписм s размазывает картину,
и её периодический характер
Фиг. VII, 24. Рассеяние хлором: /— обнаруживается с некоторым
теоретическая кривая для точечной трудом.
модели; 2 — теоретическая кривая, Типичная картина предста-
расечитанная по f-кривой Фока-Хартри; влеиа на фиг. VII, 24, .где изо-
3— опытная кривая (X Си /С«); 4— опыт- бражено распределение интен-
ная кривая (ХМо К). сивностей для молекул С1*
" которое имело бы место в том
случае, если бы атомы рассеивали, как точки. В нижней части
рисунка сплошная кривая вычислена при помощи значений Фока-Хартри
для Л кривой. Расстояние С1—С1 положено равным 2,0 А. Рисунок
показывает хорошее совпадение расчёта с опытом, который был проделан
как на медном (кружки), так и на молибденовом излучении (крестики).
2
:ивность
,
^
1 /ч С'2
-Да
V
«. д 3 оооо
\ 4 хххх
.li.iii
/\х
1 In 1 1

§ 0] СТРУКТУРНЫЙ АНАЛИЗ ГАЗОВ, ЖИДКОСТЕЙ g()5
Уравнение рассеяния для газов показывает, что каждой паре атомов
в молекуле соответствует свой интерференционный член и то, что этот
член привносит в рассеяние, не зависит от ориентации линии,
соединяющей эти два атома, а только от длины связи.
Если молекула обладает неправильной формой, то в всей имеется
большое число различных межатомных расстояний; все они дают
различные кривые, каждая из которых уже сама достаточно диффузиа. Понятно,
Фиг. VII, 25. Рассеяние QC14: 1— Фиг. VII, 26. Схема эконери-
опытная кривая; 2 — теоретиче- ' мепта.
екая кривая (жёсткая модель).
что наложение таких несовпадающих в отношении расположения
максимумов диффузпых кривых даёт очень нечёткую интерференционную
картину.
Напротив, чёткие картины получаются для правильных молекул,
например СС14. Интерференционная функция имеет в этом случае вид
где / — ребро, а г —радиус тетраэдра. На фиг. VII, 25 сравниваются
результаты вычислений по этой формуле и наблюдений; совпадение
превосходное.
При изучении строения газов описанным методом обычно отдаётся
предпочтение электронным лучам. Основная причина заключается в
уменьшении времени съёмки.
Схема прибора изображена на фиг. VII, 26: узкий и почти
параллельный пучок лучей XX проходит через газ или пар,
содержащийся в подходящем сосуде С. Сосуд имеет плоское окошко О,
заклеенное целлофаном, слюдой, алюминиевой фольгой или бериллием.
Луч проходит параллельно окошку и как можно ближе к нему. Окошко
ограничено щелью FJ3 2—3 мм ширины. Плёнка находится в
полуцилиндрической камере D, ось которой параллельна щели и лежит в
плоскости окошка. Рассеянное излучение, приходящее в точку В плёнки,
приходит из примерно одинаковых объемов рассеивающего газа, вне
зависимости от угла рассеяния. Луч должен быть строго
монохроматическим, должны быть введены поправки на поглощение луча, которое будет
меняться с углом рассеяния.
в) Структурный анализ одноатомной жидкости. Как указывалось
выше, интерференционную функцию жидкости трудно, если не
невозможно, оценить из-за неравной вероятности осуществления тех яле иных
межатомиых расстояний. Даже для самых простых по строению молекул

006 исследование поликристалл и ческих веществ [гл. vit
решение этой задачи наталкивается на большие трудности. В
интерпретации рентгенограмм, состоящих из одного-двух размытых колец, столь
много произвола, что применение метода рассеяния рентгеновских лучен
к изучению строения молекул жидкостей или характера расположения
молекул в жидкостях следует признать целесообразными лишь в
исключительно редких случаях. К последним относится изучение одноатомных
жидкостей. Мы остановимся на идее этого исследования достаточно
подробно для того, чтобы выяснились принципы метода.
Рассмотрим жидкость, состоящую из шарообразных атомов диаметра d.
Расстояние между атомами р и q не может быть меньшим d, да и другие
расстояния будут осуществляться с разной вероятностью. Введём
вероятностную функцию W{rpq), одинаковую для любой пары атомов и
обладающую шаровой симметрией. Вероятность того, что атом q находится
в объёме dvq, в то время как атом р находится в объёме dvp, равна
"J72 ^ (rpg) dvp dvq, где V—объём рассеивающего газа. Амплитуду
рассеяния пары атомов надо помножить на эту величину и заменить в
формуле (VIJ, 4) суммирование интегрированием. Получим:
Л' — число молекул газа. Удобно вместо Ж.ввести под знак интеграла
I — (1 — W). Тогда двойной интеграл разобьётся на два. Первый
будет равен нулю дди всех значений s, кроме непосредственно
прилегающих к первичному лучу. Действительно, интеграл разбивается па
произведение двух схожих интегралов типа
f e~ierdv.
Рассматривая объём газа как сферу радиуса Я и вводя угол а между
векторами * и г (последний имеет начало в центре сферы), мы можем
взять в квадратурах написанный интеграл.
Получим:
г. R
Г -isrdv =^ jj J* r3e-<rfrco8«sinarfadr==
о о
47:
— v 3 {sin {sli) — sli cos (sH)}.
Нетрудно подсчитать, что, например, для медиого излучения (/. = 1,54 А)
и радиуса сферы рассеивающей жидкости в 1 мм при значениях &>0,02"
произведением N(N—1) на этот интеграл можно пренебречь но
сравнению с АГ.
Второй интеграл
Лdv„ dva Iff
(1— \V)etarP<i^^- = y- I J 2r.(l- IF) rV!rcos* sin arfadr.^
Для a пределы интегрирования от 0 до я, а для г !можно провести
интегрирование от 0 до бесконечности, так как при увеличении г (1 — W)
стремится к нулю.

§ 0] етУктурнын анализ газон, жидкостей 607
Итак,
оо
цв) =Р[м- *«*(*-В J (1 _ w) ,*^Z.dr].
о
Функция вероятности, которой мы пользовались, предполагается
функцией с шаровой симметрией; она зависит только от величины г
расстояния между двумя атомами, но не от ориентации вектора rpq в
пространстве. Числовое значение W(r) выбирается так, чтобы W=l, если
все расстояния между центрами атомов равновероятны.
Удобно ввести в рассмотрение функцию радиального распределения
плотности р (г), которая определяется условием: на расстоянии между г
и г -j- dr от данного атома в сферическом слое находится 4яг2р (г) dr
атомов. В однородной среде р (г) будет одним и тем же, из какого бы атома
мы ни исходили. Между ?(г) и W(r) имеется простая связь. Положим,
что распределение атомов совершенно беспорядочно. Тогда р {г) есть сред-
N
нее число атомов, в единице объёма р0 = -—. Функции р (»•) и W (г) должны
быть прямо пропорциональны, так как вероятность того, чтобы атом q
лежал на расстоянии г от атома р, пропорциональна среднему числу
атомов, находящихся от атома р на этом расстоянии. Следовательно,
так как при р = р0
?{r) = ~.W(r),
1Г(г) = 1.
Заменяя W(r) в полученных выше формулах функцией радиальной
плотности, получим:
оо
(■уг -]) *= i7Z / ^(г) ~ •о}'"sin sy dr-
о
При помощи теоремы об интеграле Фурье получим:
оо
4гг2 {? (»')—Ро> = "7" I * (-тг — lj sin *r «fo.
о
Таким образом из рентгеновского эксперимента можно числовым или
графическим интегрированием находить радиальную плотность или
вероятность распределения частиц.
Если жидкость не обладала никаким порядком на близких
расстояниях, то W{r) = l для г>тг и W{r) = 0 для »"<— (требование взаим-
а и
ного непроникновения атомов). Опыт показывает, однако, что существует
порядок расположения на близких расстояниях. Объяснение этого порядка
для одноатомных жидкостей заключается в следующем. Рассмотрим плот-
нейшую шаровую упаковку; в ней осуществляется дискретный набор
межатомных расстояний d, У 2d, V^d> Y^d и т.д. Функции p(r)nW{r)
будут в этом случае прерывными. Представим себе, теперь некоторую
расстройку упаковки. Резкость кривых р (г) и W(r) исчезнет — они
станут непрерывными. Однако максимумы должны сохраниться на своём
месте, или, точнее, несколько сдвинуться к большим г, так как в общем
расположение стало менее плотным. Следует ожидать особенно сильного

60S ЙССЛЕДОВАЙИЕ ПОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [iVf. VII
25
20
10
максимума для наименьшего г, затем максимумы должны уменьшаться и
стремиться к р0 'фн больших г. Результаты подобного характера были
получены для жидкого натрия,
жидкой ртути и пр.
Одноатомные жидкости дают
более четкие, чем газ, диффрак-
ционные картины, состоящие из
нескольких чётких колец. Вид
кривой распределения плотности
показан на фиг. VII, 27 для
натрия. Чёрточками показано
распределение соседей в
кристаллическом натрии. Это соответствие
позволяет говорить о наличии
в небольшом объёме жидкостей
такого расположения атомов,
которое в среднем соответствует
упаковке в кристаллах.
Опыты с жидкостями и
стёклами следует проводить на
монохроматическом излучении.
Прибегают к съёмке цилиндрического
образца (в упаковке или без неё,
в зависимости от вязкости) или
текущей струи на плоскую
пластинку или фиксируют
рассеянное излучение ионизационной
камерой.
Исследования структур жидких металлов применялись с большим
успехом для изучения процессов кристаллизации В. И. Даниловым и его
сотрудниками *).
tnrfyr
■
_~—-Лв<0
)
si
1/
* 1
I
У**? р
6 1
ги
\
ЧА
С
1, .
ю
гвА
Фиг. VII, 27. Радиальное
распределение плотности в жидком натрии.
§ 10. Исследования строения решёток с элементами беспорядка
и сверхструктурой
Гораздо более часто, чем это кажется с первого взгляда, мы
сталкиваемся с веществами, строение которых может быть представлено
правильной решёткой, имеющей не вполне тоясдеетвенные друг другу ячейки.
Строго говоря, в этом случае решётка вообще отсутствует, так как нет
периодичности, распределения всего вещества. Однако вполне
целесообразно рассматривать подобные объекты как кристаллы, так как либо
имеется строгая периодичность в отношении каких-либо сортов атомов,
либо имеется периодичность средней в объёме ячейки плотности вещества,
либо, наконец, имеется периодичность в следовании центров атомов.
Ярким примером веществ этого тина является сплав Cu3Au. Сплав,
закалённый с достаточно высокой температуры, даёт линии гранецентри-
рованной ячейки, в которой можно разместить 3 атома Си и один атом Аи.
Единственное объяснение этого результата таково: все 4 атома занимают
центры граней кубической ячейки. Так как атомы не тождественны,
а занимают структурно-эквивалентные места, то это значит, что атомы
распределены в веществе беспорядочно. Мы имеем правильную решётку
в отношении распределения центров атомов, но, строго говоря, отсутствие
решётки в отношении распределения между собой атомов Аи и Си.
*) Д а н и л о в В. И., Сборник научных работ лаборатории
металлофизики, АН УССР, 1948.

§ 10] ИССЛЕДОВАНИЯ СТРОЕНИЯ РЕШЁТОК fiOO
При отжиге этого сплава рентгенограмма совершенно меняет свой вид:
последовательные стадии показаны на фиг. VII, 28. Это значит, что
происходит перегруппировка атомов, направленная к упорядочению структуры.
Действительно, на рентгенограмме появились лишние линии, указывающие,
что решётка превратилась в простую кубическую с теми же размерами
ячейки. Таким образом, выявилась истинная ячейка, содержащая
3 атома Си и один Аи. Это могло произойти лить потому, что атомы Аи
стали занимать в ячейках одинаковые места. Появление дополнительных
линий, связанное с упорядочением структуры, называют образованием
Фиг. VII, 28. Рентгенограммы упорядоченных
твёрдых растворов Cu3Au: a — неупорядоченное
состояние, С> — частично упорядоченное состояние,
е — высокая степень упорядоченности.
сверхструктуры. При отжиге сверхетруктура начинает расти из
многочисленных центров. Сначала линии сверхструктуры размыты, затем они
становятся веб резче и, наконец, перестают отличаться от обычных.
Уменьшение расширения линий иллюстрирует рост сверхструктурных
областей.
Элементы беспорядка в структуре происходят часто благодаря
ошибкам в наложении слоев плотной упаковки. Как известно, гексагональная
решётка строится по принципу АВАВ... Если через некоторое случайное
число слоев происходит «ошибка» и следующий слой становится в
положение С, а затем опять нарастает гексагональная структура, то возникает
непериодическая структура, хотя и плотно упакованная. Если же
подобные «ошибки», будут происходить через строго определённое число слоев,
то они перестанут быть ошибками — возникнет сверхструктура и на
рентгенограмме появятся новые линии, соответствующие истинной
укрупнённой ячейке.
Исследуя интенсивности линий рентгенограммы, мы можем получить
некоторое суяедение о характере беспорядка в подобных структурах.
Рассмотрим решётку с элементами беспорядка, полагая, что каждая
ячейка находится в правильном положении, но структурные факторы
ячеек различны. Обозначим через г и гп, векторы, идущие из начала
координат к началам п-й и w'-й ячеек. Их структурные амплитуды пусть
будут Fn и Fn,. Тогда интенсивность рассеяния получим, как обычно,
умножая суммарную амплитуду всего объекта на комплексно сопряжённую

610 ИССЛЕДОВАНИЕ ПОЛИКРИСТАЛЛИЧЕСКИХ ВЕЩЕСТВ [ГЛ. VII
величину (объект представляет собой «молекулу» и поэтому справедлива
формула (VII, 4)):
п п'
Вектор ~ s = $«х -f- 4&х + Ссх (сравни стр. 238), а
гн, — тп = тха + 1пф -f- »«зс = rw.
Следовательно,
i се, ть о = 2 2 вд:+„«■* <»*+»*+»,:>.
Здесь индексы и и w-f-»& символизируют тройки чисел щп^щ и (»i-bw'i)>
(«2 + '^2)5 (% 4~ отз); каждая из сумм тройная. Если М есть фактор_ повто-
ряемости вектора rm, a Jm есть среднее значение произведения FnFn + M
(структурных амплитуд ячеек, разделённых этим вектором, то
м
Мы получили выражение интерференционной функции в обратной
ячейке. Характер беспорядка будет определять как интенсивность диф-
фракционной линии (вес узла), так и её ширину (размер области около
узла).
Величину Jm можно выразить через вероятность «ошибки». Расчёты
показывают, что для сверхетруктурных линий расширение тем больше,
чем больше вероятность ошибки. В предельном случае полного
беспорядка линии исчезают, а в случае идеальной сверхструктуры расширение
исчезает.
Исследование идеальной сверхструктуры ничем не отличается от
изучения обычного кристалла. То, что сверхструктура связана по своему
происхождению с более простыми структурами, является облегчающим
моментом при расшифровке структуры.
К решёткам с элементами беспорядка относятся также решётки с
периодическим изменением межплоекостных расстояний. В этом случае на
рентгенограмму от решётки со средними размерами накладываются
добавочные линии — сателлиты основных.
Предположим, что при среднем межплоекостном расстоянии d р-я
плоскость, считая от выбранной за начальную, отстоит от неё не на pd,
а сдвинута со своего правильного положения на В cos 2щ> dg. Таким
образом максимальное смещение от правильного положения равно Б. Период
повторяемости максимального смещения определяется величиной д.
Суммарная амплитуда отражения от семейства из N таких плоскостей равна
Л =s V4 e*'tf (pd + B cos 2irp dg)
p = 0
Как известно, функцию e%VG0SX можно разложить в ряд по функции
Вееселя *):
-f-oo
t = . £л l Jm \v> cos mr-
m= —00
*) См. Смирнов В. И., Курс высшей математики, т. III,
стр. 633, 1939 г.

§11] ИССЛЕДОВАНИЕ ОТРОЕНИЯ ВОЛОКНИСТЫХ ВЕЩЕСТВ 611
Здесь Jm (v) — функция Бесселя m-го порядка. Если v = sB и х = 2пр йд,
то амплитуда Л представится в следующем виде (cos тх заменены экспо*
ненциальными функциями):
+ оо N — I
«1 =— оо р=0
Рассматривая внутреннюю сумму как прогрессию и помножая на
комплексно сопряжённое выражение, получим формулу для интенсивности
л-* Zl J\f»\{8D) sin*iwl(*+2n»i^) •
»t = — оо
При »» = 0 возникает главный спектр от средней правильной решетки,
но кроме него появляются дополнительные спектры при т = 1, 2 и т. д.
Они возникают в виде сателлитов главных линий, так как условие
максимумов имеет вид:
* rt 2я тд « 27t/f или 5 = 2л (II ± тд),
где ЙГ—вектор обратной решётки. Мы видим, что в пространстве обратной
решётки появляются дополнительные узлы, окружающие каждый
основной узел обратной решётки. Интенсивность еателлитных линий
возрастает с увеличением порядка спектра. Самыми сильными являются линии
т — 1. Известно несколько случаев, когда наблюдались липии и с т = 2.
§ 11. Исследование строения волокнистых веществ
Определённой спецификой обладает методика исследования
волокнистых веществ, полимеров, вообще всех соединений, построенных из
длинных цепевидных молекул, более или менее упорядоченно ориентированных
друг по отношению к другу.
Монокристаллы таких веществ, как, например, целлюлоза, кератин,
полиэтилен и пр., не могут быть выделены. Большей частью подобные
соединения представляют собой своеобразную комбинацию аморфной и
кристаллической фаз. Мы сталкиваемся в этих веществах как с
совершенно беспорядочным расположением материи, так и с частично
упорядоченным. Возможны случаи одномерного, двумерного и трёхмерного
(кристаллического) порядка. У некоторых соединений кристаллическая
структура появляется лишь при растяжении. В этом случае возникает
обязательно текстура — кристаллические участки ориентировали так,
чтобы цепи молекул стали параллельными оси растяжения. Иногда
текстура обладает высокой степенью совершенства. Рентгенограмма подобного
образца вполне подобна снимку с вращающегося монокристалла.
Упорядоченность строения волокнистых веществ даже и в этом
предельном случае много менее совершенна, чем у обычного кристалла. Поэтому
интенсивности быстро уменьшаются с возрастанием угла рассеяния.
Методика съёмки универсальна и состоит в получении рентгенограмм при
помощи монохроматического излучения на плоскую пластинку. Если
текстура совершенна, т. е. все кристаллические области имеют строго
одинаковое расположение по отношению к оси волокна и совершенно
беспорядочное расположение около этой оси, то полную характеристику
строения даёт одна рентгенограмма. То же справедливо и для аморфного
вещества. В случае неполной текстуры целесообразно построение полюсной
фигуры методами, обсуждавшимися в § VII, 5.

012 ИССЛЕДОВАНИЕ ПОДПКРИСТАЛЛИЧЕСКПХ ВЕЩЕСТВ [ГЛ. VII
О соотношении аморфной и кристаллической фаз можно судить по
отношению интенсивностей диффузного гало и интерференционных пятен.
Разработана методика количественного суждения. Относительная оценка
может быть легко сделана при наличии серии рентгенограмм, снятых
с веществ, процент аморфной фазы в которых различен.
При исследовании волокнистых веществ большей частью удаётся
решить качественные вопросы, касающиеся степени текстуры, степени
аморфности данного вещества. К определению атомной структуры молекул
Фиг. VIT, 29. Рентгепограммы волокнистых веществ.
удается приступить лить в случае совершенных текстур. Как отмечалось
в главе, посвященной методу вращения, индицирование рентгенограммы
полного вращения представляет собой очень сложную задачу. Не зная
системы, к которой принадлежит кристаллит, приходится испробовать
возможность истолкования интерференционных пятен при помощи различных
квадратичных форм. Не всегда имеется уверенность в однозначности решения
подобной задачи. Если индицирование удалось произвести, то дальнейший
ход структурного анализа обычен.
Исходя из общей теории диффракции рентгеновских лучей, можно
пытаться судить по виду рентгенограммы о характере упорядоченности.
Мы дадим лишь самые общие указания. Если вещество состоит из
параллельных цепей и если эти цепи можно рассматривать как одномерные
решётки, то рентгенограмма должна состоять из сплошных слоевых линий
без каких бы то ни было выраженных точечных максимумов. Слабые

§11] ИССЛЕДОВАНИЕ СТРОЕНИЯ ВОЛОКНИСТЫХ ВЕЩЕСТВ 613
максимумы на таких линиях могут возникнуть из-за структурного
фактора одномерной решётки. Надо, следовательно, различать рассеяние
ряда атомов от рассеяния правильного одномерного ряда некоторых
сложных структурных единиц.
Если между соседними цепями имеются фазовые соотношения, т. е.
существует некоторый порядок в расположении цепей, на близких
расстояниях, то возникают диффузные максимумы на нулевой слоевой линии.
Возникновение интерференционных пятен не только на нулевой липии
указывает с определённостью на наличие кристаллических областей.
Несовершенство текстуры оценивается известными нам способами;
в этом случае максимумы растягиваются вдоль колец.
Типичные рентгенограммы волокнистых веществ приведены на фиг.
VII, 29.

ГЛАВА VIII
ПРИМЕРЫ РЕНТГЕНОСТРУКТУРНОГО АНАЛИЗА
КРИСТАЛЛОВ
Нельзя предложить общего рецепта решения структурной задачи.
В каждом случае квалификация и чутьё исследователя определят
наиболее простой и надёжный путь нахождения тех или иных подробностей
строения кристалла.
В то же время несомненно, что есть некоторые общие правила,
некоторые характерные черты, которыми можно руководствоваться в этой
работе.
Первая стадия исследования в значительной степени зависит от того,
имеем ли мы объект в форме порошка, в форме плохо образованного или
хорошего кристалла. Как уже указывалось выше, в первом случае
исследование структуры оказывается не всегда возможным, так как
рентгенограмма порошка может быть проиндицирована лишь в случае кристаллов
нысокой системы и с небольшими размерами ячейки.
В случае плохо образованного кристалла или бесформенного обломка
все без исключения данные получаются рентгеновским способом. Хороший
кристалл целесообразно (хотя и не обязательно) исследовать на
отражательном гониометре.
Первый шаг анализа — это определение системы, элементарной ячейки
и числа атомов (молекул) в ячейке. Второй шаг—определение
пространственной группы симметрии молекулы в ячейке или нахождение^ратности
и симметрии положений, занимаемых в решётке атомами. Третий шаг —
определение интенсивностей отражений и пересчёт их в значения \F2\,
Далее требуется найти знаки структурных факторов. Для этого
приходится найти грубую модель структуры. Это может быть достигнуто либо
геометрическим анализом, либо методом построения рядов межатомных
векторов, либо, наконец, методом проб и ошибок. Зачастую приходится
прибегать к нескольким методам.
Нахождение грубой структуры является самым сложным этапом
анализа, требующим от исследователя больше всего труда, умения и
сообразительности. Если модель найдена, то остаётся вычислить знаки
структурных факторов и построить ряд электронной плотности.
Мы схематически описали ход полного структурного анализа. Весьма
часто не доходят до конца исследования и останавливаются на
промежуточной стадии. Во многих случаях, когда расположение атомов очевидно
на основании геометрического анализа, метода проб или рядов межатомных
векторов, останавливаются на этом этапе и не строят ряд электронной
плотности. На нескольких примерах мц покажем разные подходы к регае»
нию структурной задачи,

§ 1]
ИССЛЕДОВАНИЕ СТРУКТУРЫ
615
§ 1. Исследование структуры по рентгенограмме порошка.
Кубический кристалл Zn(CN)2*)
В нижеследующей таблице приведены опытные данные, а именно
межплоскостные расстояния для некоторых линий и интенсивности
линий рентгенограммы, полученной на молибденовом аноде с цирконовым
фильтром.
Таблица VIII, 1
№
п/п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Ш
100
110
111
200
210
211
220
300
221
310
311
222
320
321
400
410
322
411
330
331
420
421
332
422
500
430
510
d
4,19
3,40
2,95
2,40
2,08
1,86
1,70
1,57
1,47
, 1,39
I
1,315
1,256
1,202
1Д57
i
i
Г
выч
0
100
10
4,2
0
33
21
0
0,6
11
1.0
2,0
0
19
2Д
0
0
5
4,4
ОД
2,8
0,5
1,5
зд
0
0
2,8
/ ,
*изм
0
100
13
4
0
40
27
} «
U
0
1
0
20
1
} -
1 7
1 '
0
3
0
1
1
1 »
3
J
Для того чтобы выяснить систему вещества, составляем -^ для всех
линий. Получим следующие цифры: 0,0569; 0,0864; 0,115; 0,174; 0,231 и т. д.
Примем первое число за 1. Тогда отношение второго числа к первому
будет равно 1,51. Очевидно, что первой линии следует приписать Ш + fc2 -\- *2>
равное не 1, а 2. И действительно, в этом предположении все линии
расшифровываются так, как это указано в таблице.
Этим доказывается, во-первых, принадлежность кристалла к кубической
решётке, во-вторых, так как на рентгенограмме присутствуют
отражения 110 и 111, то очевидно, решётка простая. Ио так как все линии
кроме 111 удовлетворяют требования h-\-k-\-l = 2n, то отсюда следует,
что тяжёлые атомы цинка выполняют объёмно-центрированную решётку,
#) Жданов Г. С.. С. К. 31, 352, Ш1,

616 ПРИМЕРЫ РЕНТГЕНОСТРУКТУРНОГО АНАЛИЗА КРИСТАЛЛОВ [ГЛ. V11I
Размер элементарного куба найдём по формуле а = d Yh* -J- fc2 -}- P из
каждой линии. Среднее значение равно 5,89 А.
По формуле (V.2) находим, что число молекул в ячейке равно двум.
Итак, мы имеем дело с кубической решёткой, в ячейке которой размещены
два атома Zn, 4 атома С и 4 атома N. Среди пространственных групп
кубической системы с простой решёткой находим по таблицам следующие
возможные Т1 и Txd. В этих группах имеются два однократных
положения 000 и — — —, в которые можно поместить атомы цинка (мы
£ а 6
упоминали выше, что решётка квазиобъёмноцентрированная), а атомы С
и N получают четырёхкратные положения ххх, ххх, я.хх, ххх. Группы О2, О*
OZn++
Фиг. VIII, 1. К
изображению структуры
цианида цинка.
OZn
QcuN
Фиг. VIII, 2. Структура,
принятая для Zn (CN)2.
и Т^, содержащие одно двукратное и два четырёхкратных положения, всё
же отпадают, так как четырёхкратные положения цишены степеней
свободы, и если одно из них занять атомами С, а другое атомами N, то
группа CN не будет составлять одного целого. Правда есть ендё одна
заманчивая возможность, а именно — занять в этих группах для CN одно
четырёхкратное положение. Это, разумеется, возможно лишь в том случае,
если группа CN вращается. Тогда ячейка Zn (CNb представляет
совокупность объёмноцентрнровашюй ячейки атомов Zn и всестороннецен-
трированной ячейки групп CN (ем. фиг. VIII, I), сдвинутых друг
относительно друга. В этом случае и геометрическая трактовка очень
легка, так как структуру можно рассматривать как плотнейшую
упаковку «шаров» CN, в */4 тетраэдрических пустот которой находятся
атомы цинка.
Однако вращение групп CN маловероятно, и исследования других
цианидов показывают, что этой группе нельзя приписать шарообразную
форму. Поэтому для Zn (CN)? была принята структура, показанная на
фиг. Vni, 2. Параметр хс = 0,20 и a?N = 0,30, т. е. центр группы находится
всё же в положении узла гранецентрнрованной решётки, изображённой на
предыдущей фигуре.
Данные о значении параметров были получены в этой работе
сравнением вычисленных и найденных на опыте величин интенсивностей.

2J
ОПРЕДЕЛЕНИЕ СТРУКТУРЫ
617
Схождение вычисленных и найденных на опыте величин весьма
удовлетворительное. Интенсивности вычислялись по формуле
, 1 +cos2 28 f1.,-B(-l—)
S1I1'J 6 COS V
R /Sinft\2
(~T~) •• v
Здесь p — фактор повторяемости, ас v ' — температурный фактор,
выводимый из структуры. Значение В бралось равным 4. Атомные факторы
азота и кислорода полагались одинаковыми, а вместо кривой атомного
фактора двузарядного иона Zn++ бралась кривая для атома никеля.
Следует подчеркнуть, что хотя структура обладает всего лишь двумя
параметрами (% и а?с), нахождение их не может быть проведено очень
уверенно, так как в основном рассеяние обусловлено цинком: как уже
упоминалось, из отражений h -f- к -f-1 ф 2м возникает только 111.
§ 2. Определение структуры метил- и ли л хлор ид он ртути
CHeHgCl и C2H5HgCl*)
Эти вещества возгоняются при комнатной температуре. Для того чтобы
достигнуть достаточно долгой жизни объекта, ориентированный на головке
кристалл заключался в цилиндрик из целлофана. Внутри цилиндрика
помещалось ещё несколько кристаллических обломков того же вещества.
Таким способом обеспечивается насыщение пространства, в котором
находится объект, его собственными парами.
Кристаллы имеют форму тончайших пластинок (0,002 см, площадь
до 2 ем2) и обладают спайностью, аналогичной слюде. Отдельные слои
пластинок повёрнуты друг относительно друга, поэтому объекты дают
рентгенограммы с размытыми пятнами. Этим затрудняется выбор объекта
для съёмки.
Исследование в поляризационном микроскопе показало, что кристаллы
одноосные. Лауэграмма, снятая лучом, перпендикулярным к плоскости
пластинки, указала на лауэвекий класс D^. Тетрагональная ось
перпендикулярна плоскости спайности. Ось а, лежащую в плоскости пластинки,
пришлось устанавливать для съёмки рентгенограмм качания при помощи
лауэграммы.
В основу дальнейшего исследования были положены результаты,
полученные съёмкой серии рентгенограмм качания (около оси а) и точные
измерения отражений 0Ы на рентгенспектрографе. Размеры ячейки
определялись сначала не очень точно из рентгенограмм качания, а затем были
уточнены измерением на рентгенспектрографе.
Были получены следующие данные:
CH3HgCl C2II5IIgCi,
а = 4,62 А, а — 4,65 А,
с = 9,59 А, с = 10,82 А
(направление оси с перпендикулярно к плоскости пластинки). Так как
для CH3HgCl плотность р = 3,83 и для C2H5HgCl p — 3,482, то в ячейке
этих соединений имеется по две молекулы.
Методом обратной решётки была проиндицирована серия
рентгенограмм качания и найдено, что присутствуют все отражения с индексами Ш,
*) Гр д е н и ч Д. Р. и К и т а й г о р о д с к и i\ A. II., ЖФХ, 1161, 1949.

618 ПРИМЕРЫ РЕНТГВЫОСТРУКТУРНОГО АНАЛИЗА КРИСТАЛЛОВ [ГЛ. VIII
все 001, а погашены все ftfcO с нечётной суммой h -f- fc. Таким законом
погашения обладает группа C\h = P^fn, но она отпадает, так как лауэ-
грамма показывает более высокую симметрию. Группы класса C4v также
отпадают, так как доказано, что существует ось 4-го порядка и
перпендикулярная к ней плоскость скольжения.
Остаются группы класса D4h. Найденным законам погасания
удовлетворяет группа D74h = Pijnmm с частным положением для атомов ртути,
хлора и углерода (ООг) и -~- -~ г.
Из размеров ячеек и расположения элементов симметрии видно, что
атомы могут размещаться только на оси с, т. е. на оси 4-го порядка.
Так как сама молекула этой симметрией не обладает, то надо
предположить, что алкильная группа свободно вращается в решётке вокруг связи
ртуть — углерод.
Найденная кристаллическая структура объясняет физические
свойства кристаллов этих соединений, как, например, спайность вдоль
пластинки, летучесть, форму кристалла.
Итак, все атомы находятся в полоясении с одной степенью свободы.
Неизвестны только их ^-координаты.
Структурная амплитуда имеет для исследуемых структур
следующий вид:
^ш = з2]Л-eos 2*(Щ+/.,).
г
Сумма состоит из трёх членов для CH3HgCl и из четырёх для CjHeHgCl.
При этом для групп СНз и СНз следует брать координаты zr их «центров
тяжести». Считая в первом приближении, что рассеяние определяется
в основном атомами ртути, мы можем без труда определить координату zHp .
Для этого можно воспользоваться хорошо измеренными отражениями (ХК
от плоскости спайности.
Структурная амплитуда имеет вид
■*001 = 2fHg C0B 2к1г-
Построив косипусоиды для всех измеренных 001, мы сразу находим
единственное значение г, при котором ординаты косинусоид относятся друг
к другу так, как измеренные на опыте значения F. Таким способом были
найдены цифры
для CH8HgCL ^llg = l,30A,
» C2H5HgCl ^Hg = l,31A.
Начало отсчёта в центре симметрии ячейки.
Эти цифры были положены в основу вычисления знаков всех F^i-
Определение координат атомов ртути, хлора и углерода в изучаемых
кристаллах значительно облегчается тем, что все атомы находятся на
одной прямой. Целесообразно построение проекции электронной плотности
на плоскость (010):
h I
Знаки F определяются координатой ртутного атома, которая нам уже
известна, Измерение отражений было проведено на ионизационном

§ 2] ОПРЕДЕЛЕНИЕ СТРУКТУРЫ 619
спектрографе. У CH3HgCl измерено всего 40 отражений (из 55 возможных
з условиях опыта, применяя излучение Си Кл). Отношение самой меньшей
к самой большой измеренной интенсивности равно 1:260.
Фактор поглощения играет большую роль, так как коэффициент
поглощения [х = 800 для CH3HgCl (экспериментально определён), м- = 590 для
C2H5HgCl. Он был вычислен для каждого отражения по формуле:
got*. ZoP-
_ S Sin (2ft + а) Г sin(» + a) siadl
2JT cos (& + <*) shift Le e J'
где S — сечение пучка, a — угол падающего луча с пластинкой, з0 —
толщина пластинки, а ft— угол скольжения.
Т а б л и ц а VIII, II
hkl
001
002
003
004
005
006
007
008
009
00.10
200
400
101
102
103
104
105
106
107
108
-L' выч
110
28
114
124
38
38
64
44
4
22
138
56
94
94
52
28
78
48
6
26
изм
76
38
96
100
38
44
68
48
10
1С
104
32
78
86
78
36
86
40
—
26
hkl
109
201
202
203
204
205
206
207
208
209
20.10
301
302
303
304
305
401
402
403
404
F
выч
30
74
17
80
94
30
32
48
38
3
20
54
54
30
и
42
32
8
38
42
•* изм
28
74
16
96
104
38
22
26
14
—
11
46
50
8
18
42
18
8
22
26
В таблице VIII, II приведены вычисленные (по окончательным данным)
и измеренные амплитуды для CH8HgCl. Некоторые значения Fmit
завышены, например, для отражений 103, 104, 105, для которых угол а мал
(~ 5°), и формула даёт неточные значения А (формула справедлива для
бесконечной пластинки).
Значительную роль играет температурный фактор. Отражения дальних
порядков 30£ и 50? не были обнаружены как на рентгенограммах, так и
на спектрографе. Температурный фактор растёт от метил- к этилхлориду,
что, возможно, находится в связи со свободным вращением алкйльных
групп. У C2H5HgCl было обнаружено ещё меньшее число отражений (35).
-в (^±)'
Температурный фактор с '■ ; был для метил-Е^-хлорида принят со
значением В = 4А"2.

620 ПРИМЕРЫ РЕНТГБНОСТРУКТУРНОГО АНАЛИЗА КРИСТАЛЛОВ [ГЛ. VIII
1
Значения функции я (хг) были вычислены для точек, взятых через -^
периода. Из кривых распределения электронов вдоль направления '1001),
т. е. вдоль оси молекул, ясно видно, что расстояния атомов можно
определить довольно точно, так как максимумы чёткие и острые (даже и
максимум, принадлежащий углероду) (фиг. VIII, 3).
' ..ii.n.1,,,.1 1....I,,,,i,,..i e
О \ 2 3 & Ь 6 7 8 9А
CjlicHqCl
i....i....i...fti...lii.li....i....;...,I ,,.i
01 23456 7 8 9 ЮА
Фиг. VIII, 3. Кривые распределении
электронной плоскости вдоль
направления [001].
*■ Ш —
Фиг. VIII, 4. Упаковка
молекул CH3HgCl:
a — вид вдоль оси с,
б — вид вдрль оси ff.
Координаты максимумов были определены аппроксимированием
полученной функции в области максимума кривой третьего порядка (не
графическим, а аналитическим путём).
Получены координаты:
CHsHgCl *Hg= 1,30 А,
зГ = 3,36 А,
C2H5HgCl з^ = 1,31 А,
еС1 = 1,21 А.
~С1
— 1,20 А,
Расстояние Hg — С (в CH3HgCl): зс—2ilg = 2,06 А, а расстояние Hg-Cl:
-Hg — *ci = 2,50 А.
Такие же цифры для Hg — С1 получаются и для C2H5HgCl.
Из полученных таким образом координат атомов были вычислены
значения ^выч, фигурирующие в табл. VIII, II. Ни одно значение Ъ
не изменило своего знака. Поэтому первый ряд электронной плотиости
является одновременно и окончательным.
Переходим к анализу межмолекулярного расположения. Модели
структур показаны на фиг. VIII, 4 (метил) и VIII, 5 (этил).

§ 2] Определение Структуры 621
Данное исследование показало наличие свободного вращения алкиль-
ных групп в кристалле. Это доказано как тем обстоятельством, что
молекула занимает ось симметрии, так и рассмотрением межмолекулярного
расположения.
Молекулы в решётке касаются следующим образом. Алкильные группы
молекул, связанных трансляцией по оси а, касаются благодаря вращению.
Затем касаются алкильные группы, связанные симметрической операцией,
а именно, касается алкильпая группа в положении (ООз) с алкильной
группой в( — , -~, с — г). Касаются
атом хлора с атомом ртути, но нет
касания между хлорными атомами.
Следовательно, мы имеем, с одной
стороны, возможность определить
эффективный радиус вращающихся
алкильных групп, а с другой
стороны,— проверить значения
межмолекулярного радиуса ртутного
атома, принимая межмолекулярный
радиус хлора 1,8 А.
Расстояние, на котором
находятся атом ртути и атом хлора
соседних молекул, равняется:
'01
+ r"g=|/ (4fe--ci)2+"i-
Для га получены следующие япачо-
ння и кристаллах:
OHsHgCl rHg=l,48A.
CoHBHgCl r% = l,52A.
Для вращающейся метильнон
группы получаем меясмолекулярный
радиус:
гоня- 2 У (г— 2гс)2-Ь
для CH3HgCl
о ii А Фиг. VIIT, 5. Модель структуры
гсна = 4"А- C4H6HgCl.
Эта цифра на ОДА меньше
обыкновенно принятой. Для оправдания
этих заниженных значений как здесь, так и у этильнон группы, мы должны
принять предположение о согласованном вращении. Например, в решётке
CHgHgCl одновременный поворот двух касающихся метильных групп
водородными атомами навстречу Друг другу невозможен без значительного
искажения межмолекулярных расстояний.
По той же причине этильные группы соседних молекул этилхлорида
ртути не могут одновременно находиться в плоскости (110), так как в этом
случае углеродные атомы находились бы на расстоянии 3,10 А, а это
меньше межмолекулярного диаметра углерода 3,4 А. Следовательно,
этильные группы обходят друг друга. Согласованно вращаются и их метилыше
группы.

622 ПРИМЕРЫ РЕНТГЕНОСТРУКТУРНОГО АНАЛИЗА КРИСТАЛЛОВ [ГЛ. VIII
Этильные группы молекул, связанных трансляцией а, также могут
вращаться только согласованно. В этом случае их эффективный радиус
равен —, т. е. 2,35 А.
а
Остановимся на точности эксперимента и расчёта. Так как молекулы
исследуемых соединений расположены на одной прямой, а именно вдоль [001],
то точность определения межатомных расстояний в первую очередь
зависит от точности определения периода вдоль оси с. Этот период
определялся многократно измерением у нескольких образцов углов скольжения
для далёких отражений 001 (до 008). Он был определён для CH3HgCl
с помощью спектрографа (на трёх объектах) и из 25 значений было взято
среднее 9,39 А с вероятной квадратичной ошибкой 0,013 А. В отношении
предельной ошибки можно утверждать, что она пи в коем случае не
превышает ±0,04А. Такое же среднее значение было получено методом
порошка (радиус камеры 43 мм).
Период с был с такой же точностью определён для Cs^HgCl. Вероятная
квадратичная ошибка при среднем значении периода 10,87 А равна 0,01 А.
Период идентичности а в плоскости пластинки определён с несколько
меньшей точностью, так как могли быть найдены только отражения 200
и 400. Этот период в случае CH3HgCl был определён по рентгенограммам
качания, на спектрографе и методом порошка. Получен результат 4,62 А
с максимальным разбросом rt 0,08 А.
. Переходим к точности определения координат атомов. Как было уже
сказано выше, координаты атомов были определены из ^'-ряда
интерполированием. Ошибка интерполирования незначительная, ибо разброс
полученных значений не превышал ± 0,01 А.
Значения FhQi, взятые для построения ряда (в произвольных
единицах), определены в среднем с ошибкой 10%. Следовательно, из формулы
Д<* = 0,707-0,1 УИ-F2 ошибка суммы ряда Дз = 61 (в тех же единицах, что
и значения о в табл. VIII, II). Ошибка определения координаты максимума
Дя связана со значением Ди, с остротой максимума и величиной интервала
периода, через который были вычислены значения функции а (хг) (в йагаем
случае 0Д955 А для CH3HgCl). Для координаты ртути (для CH3HgCl)
Д* = 0,005А, для углерода Д* = 0,02 А и для хлора Иг = 0,01 А. В соответствии
е формулой точности (сравни стр.529) Иг для Hg, C1 и С должны относиться
друг к другу, как 1,2:2,4:4,1. Значения ошибок также совпадают с
предсказанием формулы (VI, 47).
Принимая во внимание ошибку в определении периода, можно
полагать, что полученные межатомные расстояния определены с точностью, не
меньшей ±0,03 А.
§ 3. Исследование структуры карбида кремния на основе
теории плотной упаковки *)
Карбид кремния встречается в многочисленных модификациях. Одна
из ннх, весьма редкая, это SiC V, кристаллы которого отличаются особо
большим периодом вдоль гексагональной оси. Размеры элементарной ячейки
таковы: а = 3,08 А и с = 128 А.
Индицирование рентгенограммы показывает, что присутствуют лишь
индексы, удовлетворяющие условию — h + fc Ц-1 = Зи. Таким образом
примитивная ячейка имеет в три раза меньший объём, чем ячейка в
гексагональных осях, и возможными пространственными группами являются
либо CL, либо DL.
*) Жданов Г. С. и Минерв и н а 3. В., С. R. 48, 182,1945.

§ 3] ИССЛЕДОВАНИЕ СТРУКТУРЫ КАРВИДА КРЕМНИЯ 623
Более простые модификации SiC были описаны как плотнейшие
упаковки атомов Si, половина тетраэдрических пустот которых заполнена
атомами углерода.
Допустим, что рассматриваемая структура представляет собой
многослойную упаковку такого же типа.
Если высоту слоя обозначить через h, то
-/г
h и с = nh,
где п — число слоев вдоль оси с. Отсюда— = 0,817«.В исследуемом
с
случае — = 41,6, откуда п = 51. Итак, если основное предположение спра-
а
ведливо, то мы имеем 51-елойную упаковку. Уверенность в справедливости
основного предположения мы черпаем из того обстоятельства, что более
простые модификации SiC имеют то же значение а и дают для п различные
целые числа.
Какие же упаковки возможны в 17-елойной ромбоэдрической
структуре?
Так как числовой символ упаковки (см. стр. 409) должен содержать
чётное число членов и сумма его должна равняться п (в данном случае 17),
то возможные упаковки получатся сразу. Однако их будет очень много.
Поэтому, авторы для начала допустили, что по аналогии с другими
модификациями числовой символ плотной упаковки состоит только из цифр 2 и цифр 3
(структура SiC II (3 3), SiC 111 (2*2), SiC I (2 3 3), SiC VI (2 3 3 3). Число 17
можно только двумя способами разложить на чётное число слагаемых 2 и 3.
Таким образом подлежат рассмотрению: две возможные структуры
2 3 3 3 3 3 и 2 2 2 2 2 2 2 3.
Остаётся произвести вычисление структурных факторов из
гипотетических структур и сравнить результаты вычисления с опытом.
Вполне очевидно, что структурный фактор решётки, состоящей из
нескольких вставленных друг в друга решёток, может быть представлен
в виде произведения соответствующих факторов (§ III, 4). В нашем случае
имеются две вполне тождественные решётки атомов Si и атомов С.
Поэтому структурная амплитуда равна 7*'= FaFM, где
FM= U\ + ftf
a Fn — структурная амплитуда плотной упаковки. Если шары типа А (см.
Р
стр. 405) имеют координаты 00—, где пс — число слоев в ячейке и
пс
р — номер слоя, то шарам типа В и хина С придётся приниеахь координаты
2 1 q 1 2 г
—- — — и -й--;■ —» где q и г —также номера слоев.
3 3 "г « о *ifj
В ячейке содержится, вообще говоря, по нескольку шаров каягдого
типа. Необходимо для расчёта структурного фактора, исходя из числового
символа, выяснить, какие значения р, q и г встречаются в ячейке.
Если упаковка ромбоэдрическая, то гексагональная ячейка не
примитивна и каждая точка разрешается в три прибавлением одной из троек
12 1 2 1 2\
000, 'Т'Т'о*» ТТ'ч']' координаты атомов всех трёх типов можно в этом
случае выразить в функции только г, а именно для атома типа А
7> 2 (I 1 *'
взять 00—, атома типа В—00, -к -+- — и атома типа С —00, т + ;Г-

624 ПРИМЕРЫ РЕЙТГЕНОСТРУКТУРНОГО ЛЙЛЛИЗЛ КРИСТАЛЛОМ [ГЛ. VIII
В элементарной ячейке исследуемого соединения находится 51
молекула. Если считать условие ромбоэдра выполненным, то структурный
фактор плотной упаковки будет состоять из 17 слагаемых. Как
указывалось выше, подлежат рассмотрению два варианта структуры. Пользуясь
правилами, указанными на стр. 409, переходим от числового символа
упаковки к буквенному. Получим:
2 3 3 3 3 3 = ifc tfcfc \кк %kk Orfc ikk = AB CBA CAB GBA CAB С В A,
т. е. р = 0, 4, 6, 10, 12, 16; q = 1, 3, 7, 9, 13, 15; г = 2, 5, 8, 11, 14.
Аналогично, для второго варианта р — 0, 4, 8, Д2, 16; q = \, 3, 5, 7, 9, 11, 13, 15
и г = 2. 6, 10. 14.
Остаётся подсчитать структурный фактор плотной упаковки по фор-
2,iJLi _ m(1 + !L)i o™(A_;.JL),
и сравнить два возможных варианта с тем, что даёт опыт.
Эти расчёты сведены в табл. VIII, III.
Таблица VII], III
Третий
индекс
'i
1
2
4
5
7
8
10
11
13
14
16
17
19
20
22
23
25
и
50
49
47
46
44
43
41
40
38
37
35
34
32
31
29
28
26
К
Вариант i Вариант
1 | 11
0,3
0,3
0,6
0,5
7,4
22.3
14.7
0,9
5,8
0,2
51,7
64,0
14,5
0,4
7Д
2,2
98
10
5,1
0,3
1.9
0
2,6
од
14,7
59,3
31,5
1,2
4,0
16,2
3,1
2,9
7.7
143,1
экои
символ 21/
к
0
0
0. 0. СЛ.
0. 0. СЛ.
ср.
с.
ср. с.
о. о. ел.
с.
0
0. С.
0. С.
ср. с.
0. 0. СЛ.
СЛ.
0
0. С.
/2
0
0
0
0
СЛ.
с.
СЛ.
0
0. 0. СЛ.
0
с.
0. С.
0. СЛ.
0
0. 0. СЛ.
0
0. С.
символ 10?
h
0. СЛ.
0. СЛ.
0. СЛ.
СЛ.
ср.
с.
ср. с.
с л.
ср.
0. 0. СЛ.
с.
0. С.
ср. с.
0. СЛ.
ср.
ср. с.
о. с.
h
0
0
0
о,
0
0
0
0
0
0
о. с.
о. с.
с.
0
ср. с.
СЛ.
0. С.
Примечание. Величины F„ одинаковы для ИШ^ и Ш.„ если l{ -f- l.z = 51
(числу слоев); напротив, ТЭКС11 для этих отражений несколько разнятся
из-за различия в FM,
Как видим, опыт отвергает второй вариант и подтверждает первый.
Для выбора между этими двумя вариантами достаточно было провести
весьма грубое сопоставление: интенсивность — квадрат F для плотной

§ 4] ИССЛЕДОВАНИЕ СТРУКТУРЫ КАРЁИДА ЁОРА g^5
упаковки» Монотонно изменяющиеся факторы интенсивности, в том числе
и FM, не учитывались.
Настоящее исследование является характерным случаем решения
структурной задачи при помощи геометрических соображений и законов
кристаллохимии. Интенсивности отражений используются лишь для
окончательной проверки и выбора между малым Числом (в этом примере лишь
двумя) возможных вариантов.
§ 4. Исследование структуры карбида бора *)
Кристаллы карбида бора В4С3 обнаруживают рентгеновскую симметрию
'6т — DM. Рентгенограммы вращения дали значения периодов а = 5,60 А»
с = 12,1 А. Индицирование рентгенограмм вращения и качания по оси (100)
показало, что индексы интерференции удовлетворяют только условию
ромбоэдра h — к+ 31 = 71. Возможны пространственные группы 1>\а,
*>! и с*.
Интенсивности были определены визуально с помощью шкал с марками
почернения (см. стр. 194) на большом числе рентгенограмм, снятых на
излучениях Си и Мо (Ка). Структурные амплитуды определялись по
формуле на стр. 470. Фактор поглощения учитывать не надо, так как даже для
медного излучения ц = 6 с*-1. Для образца, но форме близкого к цилиндру,
фактор поглощения будет колебаться в пределах ±10% от среднего
значения. Визуальная оценка интенсивностей приводит к значительно более
грубым ошибкам.
Прежде всего была построена проекция межатомной функции вдоль
главной оси. Для группы D\d эта проекция должна иметь симметрию
плоской группы C\v.
На фиг. VIII, 6 изображен вид вдоль оси с на картину расположения
элементов симметрии в группе D^. Показана гексагональная ячейка
с тройным базисом.
В случае проекции горизонтальные оси 2-го порядка дают линию
симметрии так же, как и плоскости зеркальной симметрии, перпендикулярные
плоскости проекции или плоскости скольжения при линии скольжения
вдоль нормали к плоскости проекции. Соответствующая картина изображена
на фиг. VIII, 7. Возникшая симметрия соответствует симметрии плоской
группы Cl6v (см. стр. 509). Элементарная ячейка этой плоской группы
выделена жирными чертами. Приведём в соответствие возможные
расположения точек в группе D^ с возможными расположениями точек
в группе Cgw. При этом в первом случае пользуемся утроенной ячейкой и
соответствующей системой координат, а во втором случае примитивной
ячейкой и системой координат, повёрнутой на 90э. Соответствие между
координатами легко читается из приведённого чертежа. Для примера
отмечены положения (А) группы JD^, соответствующие, как это
непосредственно очевидно, положениям (d) группы C\v (ем. табл. VI, I).
На фиг. VIII, 8 изображена ячейка проекции ряда межатомных
векторов. На проекции имеются один трёхкратный максимум типа (с) высо-
12 2 1
той 950 и один двукратный максимум типа (о) с координатами -^-s*; *з*"з**
*) Жданов Г. С. и Севастьянов Н. Г., ЖФХ, 326, 1941.

626 ПРИМЕРЫ РЕНТГЕНОСТРУКТУРПОГО АНАЛИЗА КРИСТАЛЛОВ [ГЛ. Vllt
Фиг. VIII, 6. Вид вдоль оси с на картину расположения
элементов симметрии в группе D^.
Фиг. VIII, 7. Переход от пространственной
группы JDj^ к плоской группе GGv.

§ iJ ИССЛЕДОВАНИЕ СТРУКТУРЫ КАРБИДА БОРА 62?
Высокая симметрия проекции позволяет прежде всего предположить,
что общее положение (12-кратное в ромбоэдрической ячейке) не занято*).
?
Xxv. /Д ;-vn ;' Ах4-; £
,<$
аж>^Ш^
Фиг. VIII, 8. Ячейка проекции ряда межатомных векторов.
*) Выборка из описания группы T>\d.
Гегсагонадьная установка
12 1 2 12
Ромбоэдрическая установка
1
/м 1 1 х
(Ь) 7-?
2 2 2
2: (с) жжж; жжж
6: (Л) xxz; xzx; zxx
3: (Ь) 00~
6: {с) 00* 00^
18: (u) xxz, x,2x,z, 2x% xz,
xxz, x, 2x, z, 2xxz.

628 ПРИМЕРЫ РЕНТГЕНОСТРУКТУРНОГО АНАЛИЗА КРИСТАЛЛОВ [ГЛ. VIII
Вероятнее всего, в ячейке осуществляются шестикратные положения.
Выбор среди (f), (g) и (й) также очевиден. Мы видим, что в 1^-ряде
самые сильные максимумы резко вытянуты вдоль координатных линий
ячейки C6v. Следовательно, в этих вертикальных плоскостях симметрии
лежат межатомные векторы, т. е. можно предположить, что атомы занимают
в ячейке кристалла также положения (d) (для Gl6v), т. е. положения (h)
(для D^).
В элементарной ромбоэдрической ячейке надо разместить 12 атомов
бора и 3 атома углерода. Из сказанного следует, что бор вероятнее всего
занимает два независимых (h) —
положения X\xxz± и х^с^гг. Атомы
углерода могут занимать либо
одно трёхкратное положение, либо
одно двукратное и одно
однократное.
Выбор параметров, а также
выбор между двумя последними
возможностями может быть
произведен частично геометрическим
анализом.
Действительно, если
вспомнить, что центры атомов, не
лежащих на данной плоскости
симметрии, не могут
приблизиться к ней на расстояние, большее
радиуса атома, то станет
очевидным, что около плоскостей
симметрии образуются непроницае-
Фиг. VIII, 9. Области возможных мые слои толщиной 211в = 1,8к.
значений х. Прежде всего мы можем
выделить области возможных
значений х, рассматривая находящиеся на одной высоте (одинаковые Z) атомы
бора одного и того же комплекса. Стороны отмеченного на фиг. VIII, 9
пунктирного равностороннего треугольника не могут быть меньше 1.8 А.
Проводя круги соответствующего радиуса (он равен 1,04 А), без труда найдём,
что возможные значения х лежат в пределах ЛВ, т. е. 0,107 < х <0,226.
Имея в виду относительно небольшой интервал в изменениях
параметров, можно провести анализ проекции структуры на плоскость базиса
методом проб и ошибок. Для этой цели достаточно для разных значений
параметров — а их будет лишь два для проекции — сравнивать опытные
и рассчитанные значения структурных амплитуд -Fftfro» Подобная работа
позволила подобрать значения х\ ъ хъ а именно оказалось, что
а?! = — и х% = ОД06.
о
Координаты z атомов, занимающих положения (К), можно определить
геометрическим анализом. Мы должны рассмотреть возможности в
изменении з\ координаты первого комплекса (пусть это будет тот, для
которого a?i = -jH. При некоторых значениях г± атомы этого комплекса будут
подходить друг к другу на расстояние, меньшее 1,8 А. То же надо сделать
для атомов второго комплекса. Кроме того, атомы двух комплексов могут
мешать друг другу. Таким образом должны возникнуть три системы
запретов: запрет по sit запрет по ?2 и запрет для гх при данном г^

§4]
ИССЛЕДОВАНИЕ СТРУКТУРЫ КАРБИДА ВОРА
629
ML N
J"
н к
Тз
Рассмотрим сначала взаимное расположение атомов одного комлекса
Связь атомов тройной осью даёт только рассмотренный выше запрет
некоторых значений х. Запрет по г может произойти благодаря наличию
центров симметрии. Атом не может приблизиться к ним ближе, чем на 0,9 А.
На фиг. VIII, 10 изображена часть сечения
плоскости симметрии, в которой лежат два атома
одного комплекса (т. е. 6 атомов гексагональной
утроенной ячейки). Рассмотрим один из них; так
как его координата ж определена, то он находится
где-то на линии KL, проведенной на рисунке
пунктиром. Линии ON и PR совпадают с тройными
осями; на них лежат центры симметрии (о) и (Ь)
в точках (000), (оО-|) + f 000, J 4у)• Первые два
обозначены цифрами / и 2. На линии МП
лежат центры симметрии типа (d) и (е), а именно
/1 1 п 1 1 1\ . 1 1 2 0 _.
{1 ¥ °' Т "2 27+¥ Т Т Эти цен1ТЫ еимме" ^
трии обозначены Цифрами 3 и 4. Линия KL для
комплекса с ж< = — совпадает с МИ, а для комп-
b
лекеа с #2 = 0,106 проходит от Л/iT на расстоянии
НК — 0,59 А, следовательно, КО = 1,03 А (период
в направлении ОР равен 3X3,23 А).
Полосы запрета координат гх и я^ для атомов,
лежащих в одной и той же плоскости симметрии,
возникают благодаря центрам симметрии 3 и 4.
Получим около этих точек полосы шириной для первого комплекса
1,8 А, т. е. 0,148 в долях периода, а для второго комплекса 2 У 0,92— 0,592=
=2X0,63 А, т. е. 0,112 в долях периода.
Кроме этих полое запрета возникнут ещё и другие запрещения, не
позволяющие приблизить друг к другу атомы, лежащие на соседних
плоскостях симметрии. Действительно, в проекции вдоль с два таких атома
вместе с центрами 1 и 2 (проектирующимися в одну точку) образуют
равносторонний треугольник- Следовательно, проекция их межатомного
вектора будет равна -^ • 9,69 А = 1,61 А для первого и 0,106 • 9.69 А = 1,03 А
для второго комплекса. Центр симметрии в 1 или в 2 связывает плоские
тройки атомов. Расстояние ьг между этими плоскостями равно для
первого комплекса У"1,82 —1,61- = 0,82 А, т. е. 0,068 в долях периода, а для
второго Vl,82—1,032=1,48 А, т. е. 0,122 в долях периода. Итак, возникают 4
полосы запрета для ги а именно: 1) от ( 0,167 ~- ) = 0,С93 до (о,167 + ^|"~)~
= 0.241; 2) от 0,593 до 0.741; 3) от —0,034 до -f 0,034; 4) от 0,466 до 0,534.
Для г? получим: 1) от 0,111 до 0,223; 2) от 0,611 до 0,773; 3) от —0,061 до
+ 0,0Я1; 4) от 0,439 до 0.:61.
Нам остаётся рассмотреть запреты, возникающие благодаря
сближению атомов первого комплекса с атомами второго. Рассмотрим сначала
атомы, лежащие в одной плоскости симметрии. Так как расстояние между
линиями KL и МН равно 0.59 А, то. очевидно, разность гх — г2 не может
быть меньше 1,7 А (У" 1,8s — 0,59°). Эта полоса 8апрета может быть
изображена на графике *\z%, приведенном на фиг. VIII, 11, в виде
Фиг. VIII, 10. Часть
плоскости симметрии,
в которой лежат два
атома одного
комплекса.

СЗО ПРИМЕРЫ РКШТЕНОСТРУКТУРНОГО АНАЛИЗА КРИСТЛЛЛОИ [ГЛ. V1I1
полосы около линип з1 = г2; ширина полосы вдоль z равна 1,7 А. На эту
же диаграмму нанесены полосы запрета, возникающие благодаря
сближению атома, лежащего на линии МП с атомами, находящимися на двух
соседних плоскостях симметрии. Вывод этих частей диаграммы мы
предоставляем читателю.
В результате взаимного наложения запретных зон на диаграмме
остаётся 20 свободных участков, причём только два из них имеют
значительные размеры. Дальнейшее исследование структуры было проведено
путём расчёта структурных амплитуд для различных возможных значений
«1 и «2 и сравнением расчёта с опытом.
Фиг. VIII, 11. Изображение полос запрета
В ОСЯХ 2\S<i.
Фиг. VIII, 12.
Расположение атомов в кристалле
карбида бора.
При этом одновременно испытывались различные возможности
размещения в ячейке трёх атомов углерода.
В результате подобных проб было установлено, что атомы находятся
в ячейке в следующих положениях:
В : 6/*i (a?ia,'i-i),
В : 6Л2 (aW2)>
2с (00с3),
1ь(оо|),
?! = 0,36, хг — 0,106, *, = 0,110 и -г3 = 0,38.
причем лг
_1
6 '
Расположение атомов в кристалле карбида бора изображено на
фиг. VIII, 12 отдельно — в проекциях на плоскость симметрии (снизу) и
на плоскость базиса (сверху). Изображена только часть атомов,
находящихся в ячейке (косой штриховкой показаны атомы, не лежащие в рас-

§ 5] СТРУКТУРНЫЙ АНЛЛИ:* ОРГАНИЧЕСКОГО СОЕДИНЕНИЯ G31
сматриваемой плоскости симметрии). Атомы образуют компактные группы;
при этом координационные соотношения характеризуются следующим
образом:
3BXI -f- 2Bj[ -f- lCjj,
13 jt в 6Ai
В jj В 6/«2
Сп в 2с
С{ в 16
ЗВ, + ЗВП>
2С,
§ 5. Структурный анализ органического соединения,
проведённыЁ количественно геометрическим методой
(2,6-дифенилнафталин *)
Исследуемое вещество было получено в виде ромбовидных пластинок
размером порядка 0,5 мм (толщина 0.1 мм). Рентгенограммы качания,
снятые около трёх взаимно-перпендикулярных осей, подтвердили результат
гониометрического исследования, позволившего отнести кристаллы к
ромбической системе. Размеры ячейки: а = 8,24 А, Ь — 6,28 А, с = 31,4 А. При
таком выборе осей имеют место погашения ОЫ при I ф 2п, hOl при кф2п
и hkO при 1;ф2п, что приводит к пространственной группе v]^ в
установке РсаЬ. Плотность кристалла
указывает на Z = 4, следовательно,
центры молекулы 2,6-дифенилнафта-
лина расположены в центрах
инверсии ячейки.
Как известно из литературы,
нафталин кристаллизуется в
моноклинной ячейке, образуя плотные слои
типа 2-[а (1) (см. стр. 418) в плоскости
аЪ. При этом размеры а и Ь ячейки
нафталина таковы: — о = 8,34 А, Ъ =
= 5,98 А. Так как в 'группе РсаЬ в
плоскости аЪ молекулы 2,6-дифенил-
нафталина образуют тот же слой
2\а (1), то не представляет никакого
сомнения то обстоятельство, что
в сечении аЬ ячейки исследуемого
соединения имеет место плотная упаковка нафталиновых ядер молекул
2.6-дифенилнафталина.
Таким образом геометрический анализ должен строиться по
следующему плану. Сначала надо рассмотреть возможные упаковки
нафталиновых ядер в сечении аЪ ячейки. Затем определить расположение осей
фенильных колец и, наконец, рассмотреть упаковку фенильных ядер, имея
в виду возможность любого наклона плоскости фенильного ядра к
плоскости нафталинового ядра.
Пусть начальное положение нафталинового ядра будет таково, что
собственные оси молекулы У0 и Z0 (фиг, VIII, 13) совпадают с осями h
и с ячейки, нормаль к плоскости нафталинового ядра совпадает с «.
Ориентировку ядра по отношению к осям ячейки будем характеризовать
углами поворота ср^ около оси Ъ, <р2 около нормали к плоскости молекулы
и <f з около оси Zq (фиг. V, 27).
Фиг.
V1IT, 13. Начальное положение
нафталинового ядра.
*) Китайгородский А- И., Известия Хим. Отд. АН СССР, 507, 1947.

632 ПРИМЕРЫ РЕНТГЕНОСТРУКТУРНОГО АНАЛИЗА КРИСТАЛЛОВ [гл. VIII
Углы (pi, ?2 и ^з связаны с направляющими косинусами осей
молекулы равенствами:
, COS а31 . COS ctoo
tg <Pl = 1 Sin f 2 = COS Oao, COS Ф3 = — " .
&T1 COS a33 T" *-' Td Sin a32
Рассмотрим атомы с координатами Y\Z\ и Y^Z^ пусть первый из них
принадлежит молекуле, центр которой находится в начале координат, а
второй — молекуле, связанной с начальной трансляцией по оси Ъ. Обозначая
Y-s ~ Yi = A Y и Z^ — Z^ — &Z, найдём расстояние между этими двумя
атомами по формуле
Я* з = Д Г8 -f AZ2 -f &2 _ 2Ъ (Д Tcos <р3 cos <p2 4- &Zq sin <р2).
Касание нафталиновых ядер может происходить в зависимости от
величины Ь и ориентировки соприкосновением атомов водорода, водорода и
углерода, и, наконец, атомов углерода. Значения Щ 2 равны соответственно
1Д7 +1,17 = 2,34 А; 1,17 +1,78 = 2,90 А; 1,73 + 1,73 = 3,46 А. Таким образом,
прослеживая, какие атомы находятся в состоянии касания для данного
значения Ъ, можно определить угол <р3, как функцию утла ?2- Так, для
Ь = 6,оА при ср2 до 14° касаются атомы Cj и Щ, при <р2 до 38° атомы Cj
и С5 и т. д. Для интересующего нас значения 6 = 6,28 А найдём,
например, следующие значения <рз по заданному <f>2
ср2 15° 20° 25° 30°
ср3 13° 22° 29° 32°3(У
Для каждой пары значений ?о, ср3 нужно подбирать значение угла ср,
(грубо на етруктуроиекателе, а затем точнее расчётом межмолекулярных
расстояний), рассматривая соприкосновение нафталинового ядра с
центром в (000) и связанного с ним плоскостью скольжения с центром
Таким образом возникает ряд решений <рг, ?з> Ti» из которых правильное
должно быть выбрано рассмотрением касаний между молекулами, лежа-
щими в соседних слоях, сдвинутых на —. Координата крайнего (9-го)
атома фенильного кольца не зависит от предположений об угле между
фенильиым и нафталиновым ядрами. Упаковка слоев осуществляется
соответствующими водородными атомами Н* Расстояние от центра всей
молекулы до Но несколько больше 8,0 А, а расстояние между центрами
слоев равно 15,65 А. Рассмотрение упаковки моделей на етруктуроиекателе
показывает, что плотная упаковка водородных атомов Н$ возникнет в том
случав, когда центры атомов Нд соприкасающихся молекул будут лежать
примерно в одной плоскости. Если так, то угол а наклона
радиус-вектора Н9 к оси с не должен быть меньше 16° и более 22°. Для углов а,
лежащих в этих пределах, мы можем рассчитать значения <pi« Серии этих
значений будут мало отличаться друг от друга. В частности, для а = 19
расчёт даёт значения ?2 (для данных ?з и ?3):
<Р2 15 20 25 30
% 13 22 29 32°30'
f 1 Ц°30/ 8°30/ 7° 4С30/

§ 5] СТРУКТУРНЫЙ АНАЛИЗ ОРГАНИЧЕСКОГО СОЕДИНЕНИЯ 633
Сравнивая эти тройки углов с аналогичными данными, полученными
для нафталиновых ядер, мы устанавливаем наличие единственного
решения при
<р2 = 24—25°, ?з = 27—28°, сР1=7°30/.
Итак, ориентировка нафталинового ядра найдена. Этих данных
достаточно для того, чтобы определить углы '?х и <р2 фенильного кольца, а если
ГфИНЯТЬ ВСЮ МОЛеКулу ПЛОСКОЙ, ТО И ('т'з)пл.
Таким образом, надо решить геометрическую задачу: при заданном
расположении начала и осей системы координат X0YQZQ по отношению
к XqYqZq найти эйлеровы углы yv ?2><Рз системы XQYQZ0 по отношению
к системе осей аЪс, если заданы эйлеровы углы cpi?2'f3 системы XqYqZq
но отношению к аЪс. Расчёт приводит нас к следующим цифрам для
плоской молекулы:
?;=2i°, ?;=2л (ср;)пл=з7°.
Центр фенильного кольца имеет но оси у координату 0,37 А. Этих
данных достаточно для рассмотрения касаний фенильных ядер.
Оказывается, что в случае плоской молекулы у фенилов, связанных трансляцией
по ft, касаний нет, а у колец, связанных плоскостью скольжения вдоль
оси а, атом углерода находится на расстоянии 2,48 А от атома водорода.
Это намного меньше суммы межмолекулярных радиусов; поэтому следует
утверждать невозможность нахождения фенильного кольца в плоскости
нафталинового ядра.
Переходим к поискам этого угла поворота. Для того чтобы
установилось нормальное расстояние (2,90 А вместо 2,48 А) между кольцами,
связанными плоскостью скольжения, угол <р3 должен быть равен 13э, в то
же время прн угле ?3 = 13°15' начинает осуществляться касание
фенильных колец, связанных трансляцией по оси Ъ. Таким образом одни лишь
геометрические соображения приводят к необходимости поворота
фенильного ядра по отношению к нафталиновому на угол 23—24°.
Совершенно независимо можно подтвердить правильность
установленных фактов, оставаясь в рамках геометрического анализа. Надо проверить
касания между водородными атомами бензольных ядер. Оказывается, что
при найденном расположении осуществляется весьма плотный контакт
между водородными атомами. Атом Нд касается одновременно атомов JEf8
одной и Ню другой молекулы, связанных с первой скольжением вдоль
оси Ь перпендикулярно оен с. Расчёт этих расстояний показывает точное
совпадение с обычными межмолекулярными расстояниями. Если принять
все С — С расстояния внутри ядра за 1,4 А (так это и предполагалось
выше), а расстояние С — С связи между нафталиновым н фенильными
ядрами считать неизвестным, то для расстояния Н — Н 2,34 А мы
найдём расстояние С3 — Св = 1,53 А.
Структуру, решённую геометрическим анализом, имеет смысл в общих
чертах проверить методом ннтенеивностей, рассчитав ^-значения для
20—30 отражений и сравнивай их с опытными цифрами. При наличии
богатого экспериментального материала (200—300 отражений) можно
рассчитать знаки F и строить ряды электронной плотности в целях уточне*
ния межатомных расстояний.

634 ПРИМЕРЫ РЕНТГЕНОСТРУКТУРНОГО АНАЛИЗА КРИСТАЛЛОВ [ГЛ. \'Ш
§ 6. Исследование структуры (J2H2HgClBr методом ^-рядов *)
fi-хлорвинилмеркур бромид С1 — СН = СН — HgBr получен из транс-
3-хлорвинилмеркурхлорида. Продукт перекриеталлизован из спирта л
плавится с разложением при 121—122°.
Кристаллы, имеющие форму тонких пластинок (0,002x0,064X0,4 см),
были исследованы на рентгеноспектрографе. Предварительно
рентгенограммами вращения, снятыми на плёнку, была установлена ромбическая
система и простая трансляционная группа. Для анализа интенснвноетей и
точного измерения размеров ячейки были проверены на медном
излучении все отражения типа МО, Qkl и АО?.
Размеры ячейки кристалла исследуемого вещества:
а = 6,84; 6 = 18,42 и с = 4,17 А.
Имеют место следующие погашения: hkO при Л = 2л + 1 и Шири
h -f-1 — 2п -f-1. Таким образом, кристалл обладает плоскостью скольжения
Ъ _1_ с и плоскостью скольжения п ±_ Ь. Перпендикулярно оси а возможна
плоскость зеркальной симметрии. Таким образом, возможными
пространственными группами являются G\v и У},6. При этом, так как в ячейке
находятся 4 молекулы (плотность 4,3), то в группе V^ молекула может
лежать только на плоскости симметрии.
Для определения структуры были построены два Г'2-ряда A (у, z)
и А (х, у), i
Ряд А (.г, у) обладает максимумами только при х = 0 и ^ = -~.
Следовательно, тяжелые атомы располагаются в плоскостях Ъс, отстоящих
друг от друга на расстоянии—. Если бы и углеродные атомы лежали в этой
а
лее плоскости, то кристалл принадлежал бы к группе V™. Как мы увидим
ниже, это не так: симметрия Vff имеет место только по отношению к
тяжёлым атомам; истинной же пространственной группой исследуемого
вещества является G\v.
Локализация атомов Hg;, Br, CI была произведена при помощи
составленных рядов. На фиг. VIII, 14 и 15 приведены сечения двумерного
ряда:
МО*. 2/)1ж=о и [А(.*,у)[х^_;
на фиг. VIII, 16 изображён двумерный ряд.
Величины F2 пересчитывалиеь из непосредственно измеренных
ионизационным способом ннтеноивностей при помощи углового фактора и
фактора поглощения. Последний имеет существенное значение, так как
коэффициент поглощения |х = 700.
Проекции межатомных векторов одной и той же молекулы на ось г
дают максимумы у ряда [А (х, у)\т==0, то же для разных молекул даёт ряд
[А (х, у)\ j. Поэтому использование нзобралеённых на фиг. VIII, 14 и 15
сечений позволяет безошибочно расшифровать ряд Л (у, г). На всех
фигурах указано, каким атомам принадлежат те или иные максимумы.
Обратим внимание на то, что даже атомы С1 только слабо выделяются построен'
*; Китайгородский А, И., ИиХН, № 3, 1947 г., стр. 259,

Фиг. VIII, 14. Сечение двумерного
ряда [А (ж, у))х-0.
,
1
1
р
2
(
Y
<м
МО
76
ю
-8
/2
«6
НЮ
122
I/O
102
40
104
82
66
50
HL
62
-:»
Г
щ
3»
w
72
32
18
аз
м
и
-6
■1
16
48
101
122
но
102
110
105
04
69
52
S1
84
'<
^
я
■/
158
„7
п
4,
31
393
297
67
9
16
29
ss
юг
121
109
100
№
т
89
23
56
S7
89
т
158
(39
100
74
66
65
/^^^
300
\
233
60
31
40
50
65
102
IIS
Ж
96
104
/06
96,
У
63
66
97
137
№2
1'2
77
75
99
45
208129
-м
1?
58
Л
67
S3
75
99
III
4
1,0
62
76
90
89
Ъ
87
SS
m
100^9/
92
100
106
102
86
70
77
Щ
^g
(f
^
Of
f&f
53
77
т
165
87
es
104
>oy
90
78
89
1,9
Щ
HI
4
US
63
Lw
//
163
207
72
*»
w
72
92
110
Щ
4Л
102
92
86
80
82
90
/00
106
94
86
,00
m
ut
Ц
m
so
24
78
ЙО
,lf
234
\
С
2
0
^H
If
84
,00
122
*m
«Sfc
123
97
7i
69
79
87
96
105
96
92
l09
133
05
99
47
\2*
73
/85
Щ
243
32
39
94
98
,27
as
Л
IS,
/03
65
62
78
86
92
100
96
98
113-
/30
125
93
49
3,
в.
182
^
237
JS
39
100
89
m
m
es
at
62
58
80
88
90
96
97
/Of
m
/23
,09
86
56
43
65
,73
221
42
41
101
79
ES
203
2/S
V*
/37
63
57
82
00
88
93
97
104
1,3
1,3
97
78
63
56
88
/62
4
4S
a
too
70
as
f/
*§
a'
64
58
84
92
67
90
97
106
II,
M»
86
73
68
65
91
155
<C(
V
я
a
m
66
124
^
&
66
66
58
86
9*
№
90
®
106
110
102
82
70
70
68
92
152
s
ft
К
Фиг. VII], 15. Сечение двумерного Фиг. VIII, 1С. Двумерный ряд А (у,г).
ряда [А(х,у)]г= 1

636 ПРИМЕРЫ РЕНТГЕНОСТРУКТУРНОГО АНАЛИЗА КРИСТАЛЛОВ [ГЛ. VIII
ними рядами, что же касается атомов углерода, то их локализация при
том объёме эксперимента, который возможен на медном излучении, является
совершенно невыполнимой.
Найденные при помощи -Р2-рядов, т. е. вполне объективным способом,
координаты (в долях осей) тяжёлых атомов, имеют следующие значения:
S/Hg = 0,191; *Hg = 0,10;
yBr = 0,300; гБт = 0,415;
ycl =-0,025; *cl = — 0,415.
Точность определения координат атомов Вг и Hg порядка 0,02 А,
атома С1—значительно меньше. Однако произведенное уточнение координат
этого атома вполне реально, если
принять во внимание плотную
упаковку атомов хлора и брома в слое.
На фиг. VIII, 17 изображено
размещение тяжёлых атомов в ячейке
исследуемого вещества. Рядом
показана кристаллическая структура
HgCl2 (сулема), обладающая большим
сходством с кристаллом
исследуемого металлоорганического
соединения.
Найденные координаты тяжёлых
атомов приводят к
межмолекулярным радиусам для брома 2,07 А и
для хлора 1,80 А.
Для ртути можно указать лишь
вероятную границу, рассматривая
соприкосновения атомов Вг и Hg в
двух слоях Ъс, а именно 1,48 А.
Расстояния между атомами,
принадлежащими одной молекуле,
оказываются следующими:
Hg—Вг = 2,4зА;
Hg-C1=4,54A.
HgCtBrСгНг
Фиг. VIII, 17. Размещение тяжёлых
атомов в ячейке.
При этом все три атома лежат
на одной прямой'яинии с точностью
до 1—2\ Совершенно ясно, что
исследуемое соедипспие принадлежат
к транеформе.
Переходим к вопросу о локализации углеродных и водородных атомов.
Так как анализ интенсивностей не позволяет делать в этом отношении
каких-либо заключений, то единственным способом исследования является
геометрический анализл При этом мы опираемся на исследования,
показавшие на большом материале, что во всех органических соединениях
межмолекулярный контакт определяется радиусом 1,17 А у водорода и
1,73 А у углерода.
Прн заданном расположении атомов Hg, Br и С1 при известных
расстояниях С1—С, Hg—С и С—С координаты атомов С определяются
однозначно. Если положить С1—С = 1,70 A, Hg—С = 2,25 А, то валентные углы
Hg —С — С и С — С — С1 (если считать их одинаковыми) должны быть
равны 108° при С-С = 1,34А и 112° при С—С в 1,19 А,

§ 7] КРИСТАЛЛЙЧЁСКАЙ СТРУКТУРА «ГЛОЁУЛЯЙЫХ ПРОТйЙЙОЙ* <Ш
Если положить расстояние С—С неизвестным и принять указанные
валентные углы равными 120°, то расстояние С—С должно быть равно 1,0а.
Это мало, так что, если справедливы значения межатомных расстояний
С—-Hg и С—С1, то валентные углы ртути и хлора с углеродной линией
имеют указанный выше интервал 103—112°.
Если полагать эти углы неодинаковыми, то приближение одного угла
к 120° будет отклонять другой угол от этого значения. Правда, если
положить угол С — С — С1 равным 120°, то угол С — С — Hg будет незначительно
меньше 110°.
На фиг. VIII, 18 изображены
молекулы исследуемого вещества,
связанный трансляцией по оси с в
предположении, что атомы углерода
лежат в плоскости be. Фигура
показывает, что такое предположение
не соответствует истине; при любом
расстоянии С—С имеет место
перекрывание областей, принадлежащих
разным молекулам.
Для того чтобы избежать этого
перекрывания, мы можем вращать
молекулу около линии Hg—С1; при
этом сохраняются валентные углы
Hg —С —С и (Л — С — С.
Это вращение выведет молекулу
из плоскости Ъс и нарушит симме-
г!6
Фиг. VIII, 18. Молекулы
исследуемого вещества, связанные
трансляцией по оси с.
трню группы Т^. Именно поэтому
мы и должны принять, как это
указывалось выше, группу C|v.
Поворачивая молекулу (собственно говоря, группу С2Н2), находим, что
перекрывание молекул не будет иметь места лишь при выводе из
плоскости Ъс на угол 12Ь° для всех возможных моделей. Координаты атомов
углерода равны: хх = 0Д7 A; ух — — 0,35 А; гх — 1,47 А; а?2 = W А; у2 = —1,13 А;
г2 = 1,09 А. Вероятные координаты водорода: сс3 = —1,3 А; Уз = — 0,15 А;
зг = 0,8 А; ж4 = 1,2 A; t/4 = —1,35 А; г4 = 1,65 А.
Угол поворота найден, разумеется, весьма приближённо с точностью
не более ± 5—7Э. Действительно, при размещении группы С2Н2 у нас
слишком много неизвестных (валентные углы) и известных неточно
величин, чтобы это вычисление можно было произвести с ббльшей точностью.
§ 7. Кристаллическая структура «глобулярных» протеинов
Уже давно известно, что ряд протеинов образует хорошие
монокристаллы, размеры которых вполне достаточны для производства полного
рентгеноструктурного исследования. Задача эта, однако, весьма сложна.
Монокристаллы трудно поддерживать во время всего исследования в
неизменном состоянии.
Особые трудности возникают также из-за того, что элементарные
ячейки кристаллов исключительно велики, и поэтому интерференционные
пятна на рентгенограмме при обычной съёмке расположились бы
исключительно тесно н в близости первичного пятна.
Несмотря на указанные трудности, число исследованных протеинов
достаточно велико. Среди этих объектов особенно подробно были изучены
инсулин, лактоглобулин и гемоглобин. Для этих соединений кроме
измерений элементарной ячейки и пространственной группы был проведён
анализ внтеисивностей рентгеновских отражений.

ft:i8 примеры РЕнтгЕноструктурного анализа кристаллов [гл. vm
Для большинства веществ измерения проведены для влажных и сухих
кристаллов. Существование кристаллов протеинов в этих двух формах —
с кристаллизационной жидкостью и без неё — является интересной
особенностью этих веществ. Это же обстоятельство, как будет видно ниже,
оказывает важную услугу в решении основных вопросов структуры
протеинов.
Исследование влажных кристаллов производится в специальных
капиллярных трубках, изготовляемых из проницаемого для рентгеновских лучей
боросиликатного стекла. Толщина стенок капилляра должна быть около
0,01 мм, сечение 1 мм, длина 30 мм. Кристалл протеина вводится в
капилляр вместе с каплей маточного раствора. При помощи тоненькой
шерстяной нитки в оба конца капилляра вводится жидкость. Кристалл остается
посредине между двумя 10-миллиметровыми столбиками жидкости, и так
как он влажный, то прилипает к стенке. С обоих концов капилляр
заклеивается пицеином. Таким образом, кристалл остается в равновесии с
раствором и в то же время рентгеновские лучи проходят только через
кристалл. Если эти предосторожности не будут приняты, то кристалл будет
разрушаться во время съёмки.
Гораздо труднее приготовлять сухие кристаллы. Они трескаются из-за
того, что между мозаичными блоками выкристаллизовываются соли.
Хорошие образцы получали, погружая свободные от соли влажные кристаллы
в чистый ксилол, который гигроскопичен, поглощает кристаллизационную
воду, а сам не проникает в кристалл. Сухие кристаллы являются
значительно худшими объектами для физического исследования. В то время как
влажные кристаллы позволяют провести полное оптическое исследование,
измерить их двойное лучепреломление и плеохроизм, сухие кристаллы
всегда имеют трещины и непрозрачны. Рентгеновское рассеяние сухих
кристаллов очень слабо по интенсивности, так что получению хороших
рентгенограмм мешает даже рассеяние воздуха.
Удовлетворительные результаты были получены только при съёмке
в вакууме.
Для получения рентгенограммы капилляр с кристаллом монтировался
на гониометрической головке и помещался в камере качания. Съёмка
производилась на плоскую пластинку, находящуюся на расстоянии 50—60 мм
от объекта. Съёмка на цилиндрическую камеру не имеет смысла, так как
наблюдаемые интерференции расположены вблизи первичного пятна.
Рентгенограммы снимались большей частью фильтрованным медным
излучением: снималась серия рентгенограмм качания около основных осей
кристалла, причём интервал качания был 3—5°. Типичные рентгенограммы
показаны на рис. VIII, 19. Чтобы судить о максимальных отклонениях
интерференционных лучей от первичного направления, приведены данные
о наименьших наблюдавшихся межплоскостных расстояниях:
Влажный гемоглобин 2,4 А
Влажный инсулин 4,5 «
Влажный лактоглобулип .... 5,5 «
Сухой инсулин 7,5 «
Сухой гемоглобин 13 «
На приведенных рентгенограммах пятна расположены вдоль обычных
слоевых линий. Обращает внимание своеобразное расположение отражений
кольцами. Это расположение становится понятным из рассмотрения
рис. VIII, 20. В верхней части рисунка показана серия плоскостей
обратной решётки кристалла, перпендикулярных первичному лучу. Ввиду
близости этих плоскостей друг к другу, а также из-за густоты узлов
обратной решётки на этих плоскостях, эффективными для отражения областями
в обратной решётке будут кольца (составленные из двух серпов),
показанные в нижней части рисунка. Эти кольца суть сечения отражающей

S 7J КРИСТАЛЛИЧЕСКАЯ СТРУКТУРА «ГЛОБУЛЯРНЫХ ПРОТЕИНОВ» 639
Фиг. VIII, 19. Две типичные рентгенограммы качания кристаллов
глобулярных белков.
Фото- 5 9 3 2 7 1-0 / 2 3 Ч
пленкой
Плоскости
обратной
решетки
Фотопленка
0J
Фиг. VIII, 20. Расположение отражений.

B40 ПРИМЕРЫ РЕНТГЕЙОСТРЯГГУРНОГО АЙАЛИЗА КРИСТАЛЛОВ [гл. VIII
области, т. е. области между двумя положениями сфер отражения в начале
и конце интервала качания, плоскостями обратной решётки,
перпендикулярными к лучу. Это обстоятельство облегчает расшифровку
рентгенограмм— пятна, лежащие в одной области, имеют один общий индекс
интерференции. Второй индекс определяется номером слоевой линии
данного пятна. Следовательно, расшифровка сводится к нахождению одного
лишь третьего индекса.
Следует учесть, что расстояние между слоевыми линиями равно
большей частью 0,5—1,0мм. Это налагает требование очень точной
юстировки кристалла; необходимо также пользоваться достаточно тонкими
диафрагмами.
Мы остановимся на изучении структуры гемоглобина. Объектом
исследования являлся гемоглобин лошади. Кристаллы этого вещества удалось
получить размерами до 1—1,5 мм. Влажный гемоглобин даёт отражения
вплоть до межплоекостных расстояний, 2,4 А, это — предельная величина
для всех исследовавшихся до сих пор протеинов. Наконец особенно
существенно для точного анализа то обстоятельство, что молекула
гемоглобина занимает в кристалле специальное, а не общее положение, а именно
находится на простой двойной оси. Это следует совершенно строго из
следующих соображений. Все 62 700 отражений, которые могли бы
наблюдаться при предельном значении угла скольжения (соответствующего
межплоскостному расстоянию 2,8 А; от 2,8 до 2,4 А наблюдались лишь
единичные слабые отражения), указывают на равенство интенсивностей hkl и hkl,
а также на отсутствие всех индексов hkl, для которых h + к нечётно.
Таким образом, исследуемые кристаллы принадлежат к моноклинной
системе и образуют элементарную ячейку, центрированную по грани ab. Три
пространственные группы удовлетворяют этому условию: (72, Cm и
2
С — *). Однако установлено, что гемоглобин обладает оптической
активностью; поэтому из указанных трёх групп возможна лишь группа,
содержащая только оси симметрии, т. е. 02. В этой группе имеется четыре
общих положения. Химическим способом можно получить данные о
молекулярном весе гемоглобина: из предположения, что в одной молекуле нахог
дится 4 атома железа, с точностью порядка 5% получается цифра 67000.
Исходя из размера элементарной ячейки сухих кристаллов, находим, что
число молекул в ячейке равно двум (следует тут же подчеркнуть, что
симметрия влажных и сухих кристаллов одна и та же). Таким образом,
молекулы гемоглобина занимают в кристалле частное положение, а именно
находятся на двойной оси, идущей вдоль оси b кристалла.
На основании данных о симметрии и размерах элементарной ячейки
из чисто геометрических соображений можно сделать ряд выводов о форме
и объёме молекулы. Рассматривая форму ячейки сухих кристаллов,
обращаем внимание на то, что центры молекул в плоскости аЬ образуют почти
идеальную гексагональную картину. На фиг. VIII, 21 кружками трёх типов
показано расположение центров молекул в трёх последовательных слоях.
Плоскость аЬ можно было бы плотно заполнить сферами диаметра Ь, т. е.
радиуса, примерно равного 30 ангстремам. Однако в этом случав следующий
слой не может подойти на расстояние, более близкое, чем d cos 30э к
первому слою. Это даёт цифру около 50 А, в то время как наблюдаемое
межплоскостное расстояние 36 А. Отсюда следует, что сферическую форму
молекулам гемоглобина приписать, безусловно, нельзя.
*) Размеры ячейки влажного объекта оказались равными а = 109 А,
Ь = 63,2 А с = 54,4 А, р — 112° при двух молекулах в ячейке.

§ 7] КРИСТАЛЛИЧЕСКАЯ СТРУКТУРА «ГЛОБУЛЯРНЫХ ПРОТЕИНОВ» 641
Из геометрических, соображений, основывающихся на размерах
элементарной ячейки, можно аппроксимировать молекулу гемоглобина
эллипсоидом, близким к эллипсоиду вращения, с размерами полуосей 30X30X16 А.
Коэффициент упаковки должен со-
о
7
it
о
бе'
-©—о.
XX
"9
■й
Фиг. VIII, 21. Расположение
центров молекул гемоглобина.
ставлять 0,73. Оси эллипсоидов
наклонены к плоскости аЬ.
Необходимость в таком наклоне вполне
очевидна из фиг. VIII, 21. Мы
видим, что шестиугольник центров
каждого последующего слоя
сдвинут по отношению к предыдущему
вдоль оси а на небольшую
величину от симметричного
расположения. Эта величина, указанная
стрелками, определяет наклон оси
эллипсоида от нормали к
плоскости аЬ. Таким образом все
экспериментальные данные хорошо
объясняются при аппроксимировании
молекул гемоглобина трёхосными
эллипсоидами размера 30X30X16 А,
наклонёнными своей малой осью к
плоскости аЬ на небольшой угол.
Примерный объём и форма молекулы гемоглобина совершенно очевидны.
На них основывается дальнейшее исследование — самая интересная часть
работы, касающаяся влажных кристаллов. Экспериментальным материалом
для этой части работы служат оценённые на рентгенограммах качания
интенсивности 7840 отражений. На основании этих измерений для всех
исследованных кристаллов можно построить Т^-ряд межатомных
векторов.
С первого взгляда может показаться неясным смысл построения
F2-pflfla. Совершенно понятно, что при числе атомов в молекуле
гемоглобина порядка 5000 и соответственном числе пиков в Т^-ряде порядка 108
не приходится и мечтать о расшифровке ряда, т. е. об отнесении того или
иного пика к конкретному межатомному расстоянию. Более того, можно
подумать, что при таком большом числе максимумов ряд будет размазан
и не будет вообще обладать характерными чертами. Последнее, однако,
наверно. Действительно, если имеется известная правильность в строении
самой молекулы, и при наличии, безусловно, имеющейся правильности
в расположении молекул по отношению друг к другу, должны существовать
межатомные векторы, которые будут встречаться особенно часто.
При этом мы вправе полагать, что в ряде обнаружат себя межатомные
векторы двух типов — внутримолекулярные (их пики должны бить вблизи
начала координат ряда — маленькие расстояния) и межмолекулярные,
соответствующие значительно большим расстояниям. Перекрывание
максимумов двух типов должно быть небольшим, так как расстояние между
молекулами велико по сравнению с важными межатомными векторами.
Вполне понятно, что рассмотрение одного ^"2-ряда не может принести
какой бы то ни было пользы, и анализ интенсивноетей приобретает смысл
благодаря исключительному свойству кристаллов глобулярных протеинов
давать серию объектов, содержащих разный процент влаги. Особенно
интересны опыты по замене кристаллизационной жидкости. Ионы
диффундируют в кристалл протеина. Поэтому удалось получить объекты, в которых
электронная плотность кристаллизационной жидкости колебалась от 0,33
до 0,45 электрона на кубический ангстрем. Исследование двух объектов,
различающихся лишь концентрацией электронов в кристаллизационной
жидкости, имеет следующий смысл. Молекула протеина моясет быть губ-

012 ПРИМЕРЫ РЕ1ПТЕНОСТРУКТУРНОГО АНАЛИЗА КРИСТАЛЛОВ [ГЛ. VIII
чатой и впитывать в себя кристаллизационную жидкость; возможно и
другое — кристаллизационная жидкость размещается в промежутках между
молекулами. Если тяжелые ионы проникнут внутрь молекул, то должна
измениться вся картина рассеяния. Если, напротив, молекула не позволяет
кристаллизационной жидкости проникнуть внутрь ее, то тяжёлые ионы
только окантуют молекулу. В этом случае картина внутримолекулярного
рассеяния должна остаться неизменной, а это значит, что от введения
тяжёлых ионов может меняться интенсивность отражений низкого порядка.
Общий характер распределения интенсивиоетей должен остаться
неизменным. Тщательное исследование, произведенное для гемоглобина, доказывает
этим путём, что кристаллизационная жидкость расположена между
молекулами. Интересно также и то, что имеются отражения низкого порядка —
одни мало, другие особо чувствительные к замене лёгкой
кристаллизационной жидкости на тяжёлую. Скажем, интенсивность отражения 110
меняется резко, а 200 почти не меняется. Эти данные можно использовать
для того, чтобы локализовать кристаллизационную жидкость в кристалле
и, следовательно, уточнить контуры молекул.
Прекрасным доказательством структуры влажных кристаллов, как
системы, состоящей из «твердых» молекул, окружённых кристаллизационной
жидкостью,, является сравнение аналогичных А'2-рядов для кристаллов на
разной степени набухания или сокращения.
Набухание кристаллов вызывалось подвешиванием их в некоторой
определённой среде (например, ненейтрализованный раствор сульфата
аммония). Сокращение вызывалось искусственным высушиванием раствора,
с которым кристалл находился в равновесии. Проще всего это достигается,
если в описанной выше капиллярной трубке, заклеенной пицеином, сделать
маленькое отверстие.
У гемоглобина удалось наблюдать пять различных ячеек па различных
стадиях сокращения кристалла. Можно считать доказанным, что процессы
набухания и сокращения происходят ступенчато, так как при
многократном повторении наблюдений получаются только эти пять вполне
определённых ячеек. Процесс обратим, так что можно заставить появиться эти
пять ячеек в порядке от большей к меньшей и наоборот. Если не
рассматривать полностью высушенного кристалла, то оказывается, что все
изменения сводятся к вариации моноклинного угла от 127,5° до 84,5°. Величина
периода с в пределах ошибок остаётся неизменной. Значения периодов а
и Ъ весьма строго остаются постоянными. Таким образбм, изменение
решётки, происходящее при набухании кристалла, сводится к возрастанию
межплоскоетного расстояния 001 от 42 до 55 А. Таким образом, характер
распределения жидкости в кристалле становится очевидным: жидкость
должна быть распределена слоем вдоль плоскости ab; лишь совсем
небольшое её количество может участвовать в образовании слоя аЪ. Следовательно,
слрй оЪ — это слой молекул протеина. Ещё более определённые суждения
в этом же направлении могут быть вынесены из рассмотрения 7*'2-рялов.
построенных для кристаллов, находящихся на разной степени набухания.
Собственпо говоря, только это рассмотрение и должно считаться за
непосредственное доказательство существования неизменного на разных
стадиях сокращения или набухания молекул протеина. В проекциях .Р2-ряда
как для влажного, так и для сухого инсулина была найдена группа
в 18 максимумов, находящихся около начала координат проекции и
имеющих друг по отношению к другу одинаковое расположение в обеих
проекциях. На рис. VIII, 22 показаны эти две проекции для инсулина; для
ясности под этими проекциями приведены их схематические представления.
Разница в двух проекциях в основном сводится к ориентировке всей
группы 18 максимумов — она различается на 6 градусов. Тот же эффект
был показан серией рядов для гемоглобина и для лактоглобулина. На
рис. VIII, 23 показаны две проекции Р*2-ряда этого последнего вещества на

§ 71 кристаллическая структура «гловулярных протеинов» 643
двух стадиях сокращения. Во всех случаях удаётся подметить постоянство
группы пиков, располагающихся около начала координат проекции (т. е.
постоянство некоторой системы малых' межатомных расстояний). Именно
так должна вести себя проекция ^-ряда, если представлять себе процесс
набухания или сокращения как процесс взаимного перемещения «твёрдых»
молекул.
Фиг. VIII, 22. Две проекции для инсулина.
Как мы говорили, для гемоглобина измерения ячеек на разной степени
сокращения делают вероятным расположение молекул слоями аЪ. Ряды
для гемоглобина позволяют подтвердить и уточнить эту картину. При
набухании и сокращении слои ab протеиновых молекул приближаются и
удаляются друг от друга, а также сдвигаются. Наблюдая те пики, которые
меняются от проекции к проекции, мы находим пики, соответствующие
важным межмолекулярным расстояниям. У гемоглобина такие пики
соответствуют расстоянию 18—20 А. Таким способом определяется расстояние
между «поверхностями» молекул, т. е. толщина слоя жидкости. На
основании сказанного кристаллическую структуру гемоглобина можно
иллюстрировать фиг. VIII, 24*).
Рентгеновское исследование позволяет решить интересный вопрос
о гидратации протеинов. Известно, что концентрация подвижных ионов
в кристаллизационной жидкости всегда меньше, чем в среде, с которой
кристалл находится в равновесии. Таким образом кристалл содержит
избыток воды, не зависящий в широких пределах от концентрации соли.
*) Молекулы для простоты представлены в виде цилиндров, а
эллипсоидов.

644 ПРИМЕРЫ РЕНТГВНОСТРУКТУРНОГО АНАЛИЗА КРИСТАЛЛОВ [гл.- \Ш
Можно сделать две гипотезы о местонахождении этой «добавочной» воды.
Во-первых, можно предположить, что воду надо разделить на два сорта:
«связанную», непосредственно соединяющуюся с молекулой протеина, и
Фиг. VIII, 23. Две проекции 1''2-ряда лактоглобулина.
«свободную», которая разрешает диффузию ионов и находится в
динамическом равновесии со средой. Разумеется, состав «свободной» жидкости буд«т
такой же, как и у окружающей среды. Другое предположение будет обратно
первому: мы можем дЬпустить, что «добавочная» вода равномерно
распределяется вдоль всей кристаллизационной жидкости. щ
У нормального влажного кристалла расстояние между слоями равно
50,7 ангстрема. Если справедливо второе предположение, то исследуемый
кристалл надо рассматривать как слой протеина толщиной 34 ангстрема

§ 7] КРИСТАЛЛИЧЕСКАЯ СТРУКТУРА «ГЛОБУЛЯРНЫХ ПРОТЕИНОВ» 645
и слой жидкости однородной концентрации толщины 16,7 ангстрема. Если
верно первое предположение, то мы имеем слой гидратированного протеина
толщиной 40,1 ангстрема и слой свободной жидкости толщиной 10,6ангстрема.
Фиг. VIII, 24. Кристаллическая структура гемоглобина.
Последняя цифра вычислена умножением 16,7 на отношение «свободной«
воды ко всему её количеству. При наличии в жидкости тяжёлых ионов
средняя электронная концентрация слоя кристаллизационной жидкости
значительно больше этой величины для воды. Для обеих указанных
моделей можно подсчитать интенсивности отражений типа 00]. Сравнение
с опытом приводит к доказательству гидратации протеина. Каждая
молекула белка гидратирована, т. е. окружена слоем воды.
Дальнейшее исследование строения молекулы проведено в отношении
гемоглобина. Целый ряд косвенных соображений помогает установить знаки
структурных амплитуд отражений от основной плоскости аЬ кристалла
(плоскость молекулярного слоя). Таким образом, оказалось возможным
построение одномерного ряда электронной плотности. Так как в ячейке
один слой молекул, то полученный ряд позволяет непосредственно
определить общий характер распределения электронной плотности вдоль короткой
оси (равной 32—36 А) молекулы. Были найдены четыре максимума
электронной плотности на расстоянии около 9 А друг от друга. Смысл этих
скоплений плотности остаётся неясным. Опыт не может в настоящее время
проверить такие теории строения белка, как, например, циклольную гипотезу.
Оставаясь в рамках рентгеноструктурного анализа, мы можем надеяться
на получение новых результатов, только применив трёхмерный ^-синтез.
Эта исключительно громоздкая работа, очевидно, будет скоро проведена
и. надо надеяться, даст новые данные о строении глобулярных протеинов.

алфавитный указатель
Анизотропия кристаллов 12(5
тепловых колебаний 472, 512
Аппарат рентгеновский 164
Астеризм 318
—, связь с деформацией кристалла
319
Атомно-температурнын фактор 271,
273
Атомный фактор 214
— — единичный 225
- - • , расчет для свободных атомов
219
, расчёт по Фоку-Хартрн 221
--, универсальная функция 220
Базис 22
Белов Н. В. 231, 389, 407, 462
Вектор обратной решетки 205
Векторы волновые 204
обратные 16, 204
- основные 17
, преобразование 27
- узловых плоскостей 18
- основные 14
, способы выбора 22
Винтовые оси 87, 441
, номенклатура 88
Волны обрыва 519
Вращения и качания метод 323
- • , определение периода
идентичности 327, 353
, трактовка и обратной
решётке 326
- — , формулы
интенсивности 246
Вульф Ю. В. 138, 139, 169, 208, 584
Гексагональная система 63
—, выбор осей 82
---. трансляционные группы 71
, четьбртый индекс 80
координат 72
- , связь с ромбоэдрической 84
Генерирование элементов симметрии
62, 93, 99
Геометрический анализ 460. 031
— - ионных кристаллов 462
— молекулярных кристаллов 403
Голоэдрические точечные группы 67
Гониометр отражательный 147
-——, установка кристалла 149
Фёдорова 152
Гониометрическая головка 149, 34^
Гониометрия кристаллов 147, 152
Грань единичная, выбор 123
Двусторонний случаи 254
Диафрагма 345
Дннада 390
сетчатая 391
— цепочечная 391
Динамическая теория 267
Диффракция, условия 204, 235
—, — на тепловых волнах 284
Дуга большого круга 137
-- малого круга 143
Жданов Г. С. 194, 408, 442, 586, 59."»,
615, 622, 625
На кон зон 20, 125, 305
кристаллографических пределов
158
Шубникова 457
Законы кристаллогпа&ии опытные
121, 122, 123, 125
Запрещённые области 461, 630
Зональные кривые 302
Идеальная форма роста 126
Инверсия 31
, преобразование точки 98
Индексы диффракции 204
интерференции 204
кристаллографических
плоскостей 123
узловой плоскости 15
- - —, преобразование 28

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
647
Индексы узловой прямой 15, 27
-, преобразование 28
Инднцирование лауэграмм 303
— рентгенограмм вращения 344
— качания 336
- порошка 567
рентгенгониометров 358, 363,
368. 383
Интегральная интенсивность 241
— —. измерение в абсолютных
единицах 247
Интегральное отражение, идеальный
кристалл 266
—, измерение' и определение F
468
Интенсивность, визуальная оценка
193
, ионизационное измерение 196
— , определение методом шкал 194
Интерференционные кривые 330,361,
367, 382
— постоянного р 332
симметричные 332
Ионизационная камера 197, 199
Камеры аксиальные 585
— для монокристалла 345, 375
— для поликристалла 564
— задней съёмки 572
— фокусирующие 577
Кассеты 347
Кенотрон 164
Килоикс 171, 172
Класс симметрии 91
лауэвский 315
Комплекс кристалла 135
-- полярный 135
Комплексное представление волны
210
Координационное число 394
Косая съёмка 246, 329
Коэффициент вторичной лксгиикцни
263
— ослабления 183, 185
- отражения 264
— поглощения 183
атомный 184
— и длина волны 180
— - — - менделеевское число 186
- —- массовый 184
- рассеяния 183, 214
упаковки 406, 429, 431
Кристалл идеальный 121. 266
— - , интегральное отражение 266
реальный 121
Кристаллические структуры
бинарных соединений 401
Кристаллические структуры динад-
ные 392
— • --■ координационные 392
Кристаллохимический анализ 160
Кристаллы, внешний облик 120
, вычисление 153
— -, гониометрическое изучение 147
Кристаллы ионные 412
—, топологическая характеристика
390
■--. черчение 156
Круговой рентгенгониометр 380
Кубическая система 67
, трансляционные группы Ш
Лауу метод 295
. определение угловых
констант 308
, ориентировка кристалла 307
—. трактовка в обратной
решётке 296
— - , формула интенсивности 241,
244
Линейка гиомоническая 300
— для индицирования
рентгенограмм качания 341
Лучи вторичные 203
— рассеянные 180
Максимум интенсивности, главный
и побочные 232
- , условие 231
— —, ширина 236
Межилоскостное расстояние 18
— и обратный вектор 20
— —, экспериментальное
определение 171, 387, 567
Межплоскостные расстояния
стандартные 170
Метод «купающегося» кристалла 255
468
— последовательных приближений
476
проб и ошибок 470, 556
Уманского 353
фотографирования обратной
решётки 371
- - • — — и определение интененп-
ностей 377
— __ ._. —? угловой фактор 379
Мозаичная структура 121, 262
, условие идеальной 269
Моноклинная система 63
— , трансляционные группы
68
Монохроматоры 351

648
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Напряжение возбуждения 173, 178
Напряжения второго рода 596
— первого рода 596
— третьего — 600
Номограмма Белова 281
Обратная решётка 205, 238
, вектор узла 205
, зона —287
и интерференционная функция
238
структурный фактор 239
, форма узлов 322
Обрыв ряда 515, 528
Однозначная установка по Долоно 424
Односторонний случай 253
Оптимальная толщина образца 255,
352
Оси симметрии, возможные углы
поворота 39
— — инверсионные 38, 40. 42, 43
поворотные 38, 39, 42, 43
полярные 46
, преобразования 95
Остров 43, 48, 459
—, кратность 62
Острова, расположение и симметрия
120
Нараллелоэдры 158
Параметры грани 123
Периоды идентичности, основные 14
, формула 15
, экспериментальное
определение 327
, , точность 329, 353
Плёнка рентгеновская 190
, контрастность 192
, почернение 191, 192
, широта эмульсии 191
Плоские группы 493
Плоскость симметрии зеркальная 42,
95, 145
, преобразование 97
— скольжения 88, 90, 441
, преобразование 97
Плотная упаковка молекул 414
Плотнейшая шаровая упаковка 405,
413
, пустоты 409
Плотнейшне шаровые упаковки, вы?
вод возможных 407
, символы 408
, симметрия 405
Плотность рентгеновская 438
Погашения 443
— и определение пространственной
группы 443
Поглощение 183, 237, 252
—, края полос 187
Поле индексов 298
Положение общее 62, 119
— частное 62, 119
Положения точек 119
Полюсные фигуры 138, 583
Порошка метод 562
, определение размера частиц
588
, основные типы съёмок 563
, способы крепления плёнки 564
, трактовка в обратной решётке
248
, формула интенсивности 250
Порядок отражения 208
Почернение 191, 192
Преобразование линейное 28, 33, 35
— идентичности 38
-- осей ячейки 25
Преобразования симметрические
закрытые 37, 97
открытые 87, 97
Принцип плотнейшей упаковки 393
Проекция гномоническая 136, 300
— гномостереографическая 138
— линейная 135
— стереографическая 41, 136, 306
— -, свойства 138
— сферическая 136
Пропорциональный усилитель 200,
385
Пространственные группы 38, 108
, выбор начала координат 95
, вывод 92, 100
— - - и химическая формула 457
— — молекулярных кристаллов 418
— -, номенклатура 106, 118
, определение но погасаниям 443
, положения точек 119, 457
.^симметрия «н расположенно
остр*овов 120
Прямая съёмка 246, Злб
Радиус атомный 392, 414
- ионный 392
— ковалентный 392
— межмолекулярный 393, 414
Рассеяние диффузное 273
— квантовое 180, 182
— классическое 180,182
— малым кристаллом 231
— молекулой 601, 604
— электроном 209, 213
Расходимость пучка 346
и размер пятна 347
Рентгенгониометры 355

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
(Ш
Рентгенгониометры с плоской
пленкой 371
'цилиндрической — 355
„ , прямая съёмка 356, 358,
361
, эквинаклонная —366
Рентгеновская симметрия 315 .
Рентгеновские группы 455
— лучи, длины волн 168, 179
— —, ионизующее действие 196
, коэффициент преломления 168
, фотографическое действие 190
Рентгенспектрограф 383
Ромбическая система 63
, трансляционные группы 69
Ромбоэдр 63
—, условие 622, 625
Ромбоэдрическая подсистема 63, 71
Ряды межатомных векторов 494, 533,
634
, проекции 538
— • , сечения 535
— - —, симметрия 539
—• электронной плотности 474, 494
— , влияние обрыва 515, 528
— — - -, машина для подсчёта 557
— — - , оптическое суммирование
559
•-- -. ошибка 523, 525
-- ■ , проекции 481, 483
— ■ - - • , — «поясные» 482
, - , техника подсчёта 484
, разрешающая способность
531
—, сечения трёхмерных 477
— — —, симметрия проекций 493,
510
—, точность 512
, уточнение координат
максимумов 491
С-верхструктура 608
Свободное вращение 460, 621
Селективное отражение 209
Сетка Вульфа 138, 584
Символ грани 123
— международный 61, 106
- плоскости 16
-- простой формы 134
Симметрия рентгенограмм 312, 314
Системы кристаллические 62, 424
-- —, специализированные формулы
64
Скорость роста граней 126^
Слоевые линии 324, 326
Слои 416, 417
Соляризация 191
Спектр рентгеновских лучей 167
— непрерывный (белый) 168,
172, 173, 175
характеристический 168,177,
179
Структурная амплитуда 224, 472
единичная 225
, измерение абсолютного
значения 468
, машина для расчёта 556
, ошибка расчёта 473
, фаза 230, 470
Структурный фактор 223, 228
— — для центроеимметричных
отражений 315
и обратная решётка 239
Структуроискатель 464
Сфера отражения 206, 326
Сферический атом 216, 514
Текстура 583
Текстургониометр Жданова 586
Температурная поправка 218, 222,
278, 471, 516
Температурный фактор 271, 274
кубической решётки 276
Тепловые волны 279
— диффузные максимумы 278. 291
- колебания решётки 269, 283
Тетрагональная система 63
— • ---, трансляционные группы 70
Точечная группа 42, 49
-- -, кратность 43, 62
— —. общее положение 43
, центр 43, 61
Точечные группы голоэдрические
67
, символы 49
, с поворотными осями 46
циклические 48
Точки гомологические 38
-- эквивалентные 38
Трансляция 14, 29
—, вектор 29
Трансляционные группы 67
двумерные 493
■ и расположение элементов
симметрии 99
, определение по погашениям
420, 422, 424
Тригональная подсистема 63
Триклинная система 63, 68
Трубка рентгеновская 161
, коэффициент полезного
действия 175
разборная 163

()oO
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Угловой фактор 246, 379, 470
Угол скольжения 208
— тетраэдричеекий 48
Углы между кристаллографическим и
направлениями 21, 22
Удельная отражательная
способность 244
Узел 13
—, вес 240
Уравнение Вульфа-Врагга 169. 208
— Курдюмова 577
Установка гексагональная 65, 87
— ромбоэдрическая 65. 87
- С 82
-- Я 82
Фазы отражений 230, 470
Фактор повторяемости 250
поглощения 252
— - — пластинки 258
цилиндрического образца 255
Фёдоров Е. С. 38, 106, 148, 158, 159,
160
Фильтры 188, 351
Фокус рентгеновской трубки 157
Формулы интенсивности 240
Формы простые 127
, комбинации 127
-, символы 134
Фотометрнровапие рентгенограмм
194
Фотоэлектроны 181
Функция распределения электронов
215. 219
/'-кривая 218
— , аппроксимации 541
и атомная функция 515
опытная для углерода 516
F-ряды 474
/*2-ряды 533
Характеристическая температура 276
Центр инверсии 31, 40
— симметрии 31, 40
, преобразование 08
Число молекул в ячейке 429
НГтрипсы 487
Эквинаклонный метод 366
Экраны светящиеся 196
Экспозиция 191
Экстинкция 237, 471
--- вторичная 262, 263
первичная 263, 266, 269
Электронная плотность 215, 474
, проекция 217, 218
Электроны отдачи 181
Электронный счбтчик для рядов
559
Элементы симметрии 38
— • и трансляционная группа 90
, преобразования 95
Эффективный радиус 570
Ячейка примитивная 22
сложная 22
— - ■-, базис 22
элементарная 11
обратная 19
--, объём 19
—, правило выбора 07
Ячейки обозначения 24
тождественные и подобные 435
центрированные 22. 23
, экспериментальное определение
размеров 420

Опечатки
Стр.
17
95
200
211
344
452
625
Строка
9 св.
2 сн.
14 св.
11 св.
pnc.IV,42
Головка
таблицы
9 св.
Напечатано
ах антипараллельны
3i
в НГ3_10~6 раз.
(Aitt) + iAM (А(9))-
-iA{m))
вместо hk% hk\,
быть h?l, h\l,
hhlhl, hhOl
B4C3
Должно быть
ax параллельны
32
в 103 — 10° раз.
{А(в) + Ж")) (А(в) ^
- -iA(m))
hkO должно
ЛО/
hhlhl, ЛШ
Н4С
По чьей
вине
Ред.
„
„
-
Авт.
Ред.
Авт.