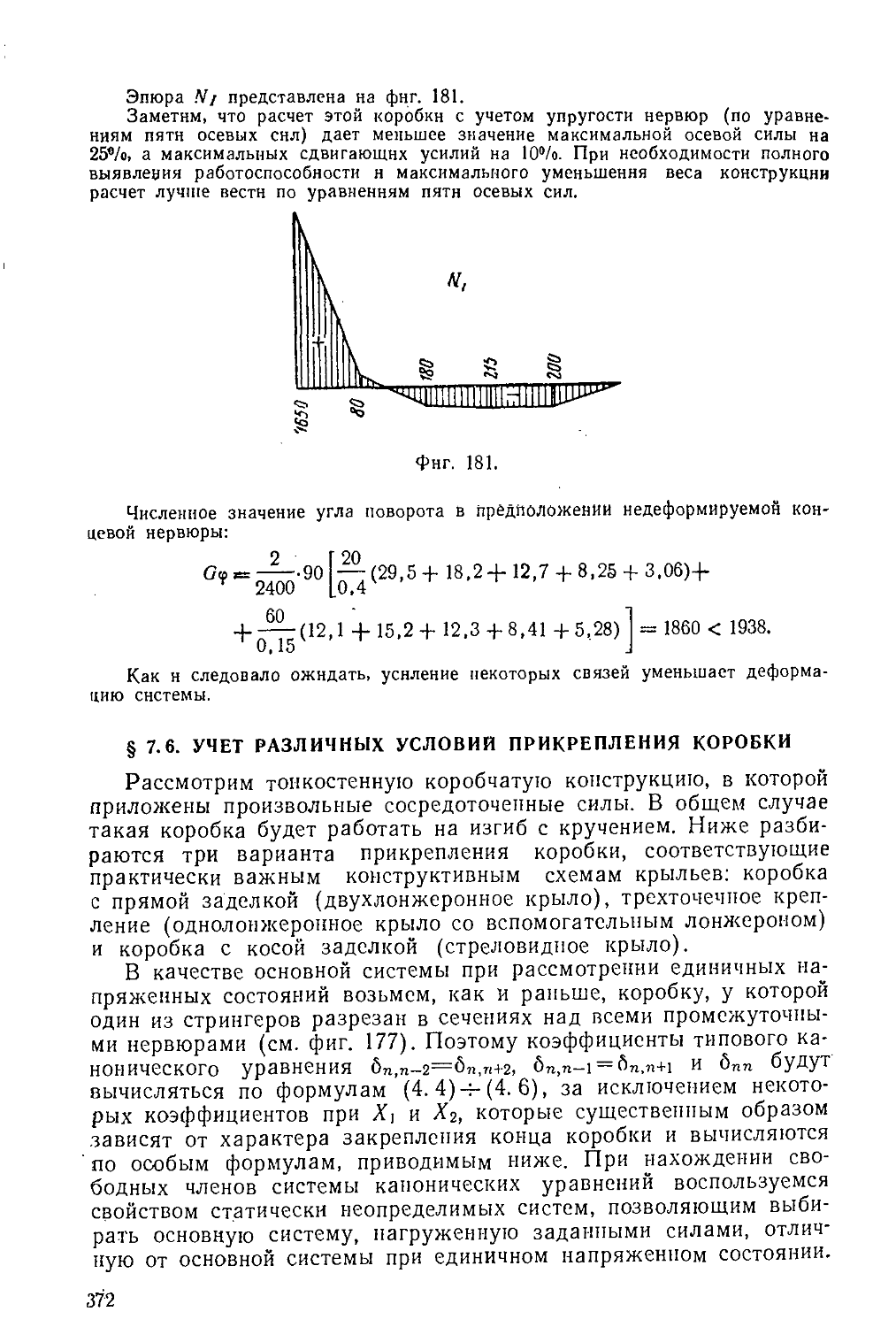
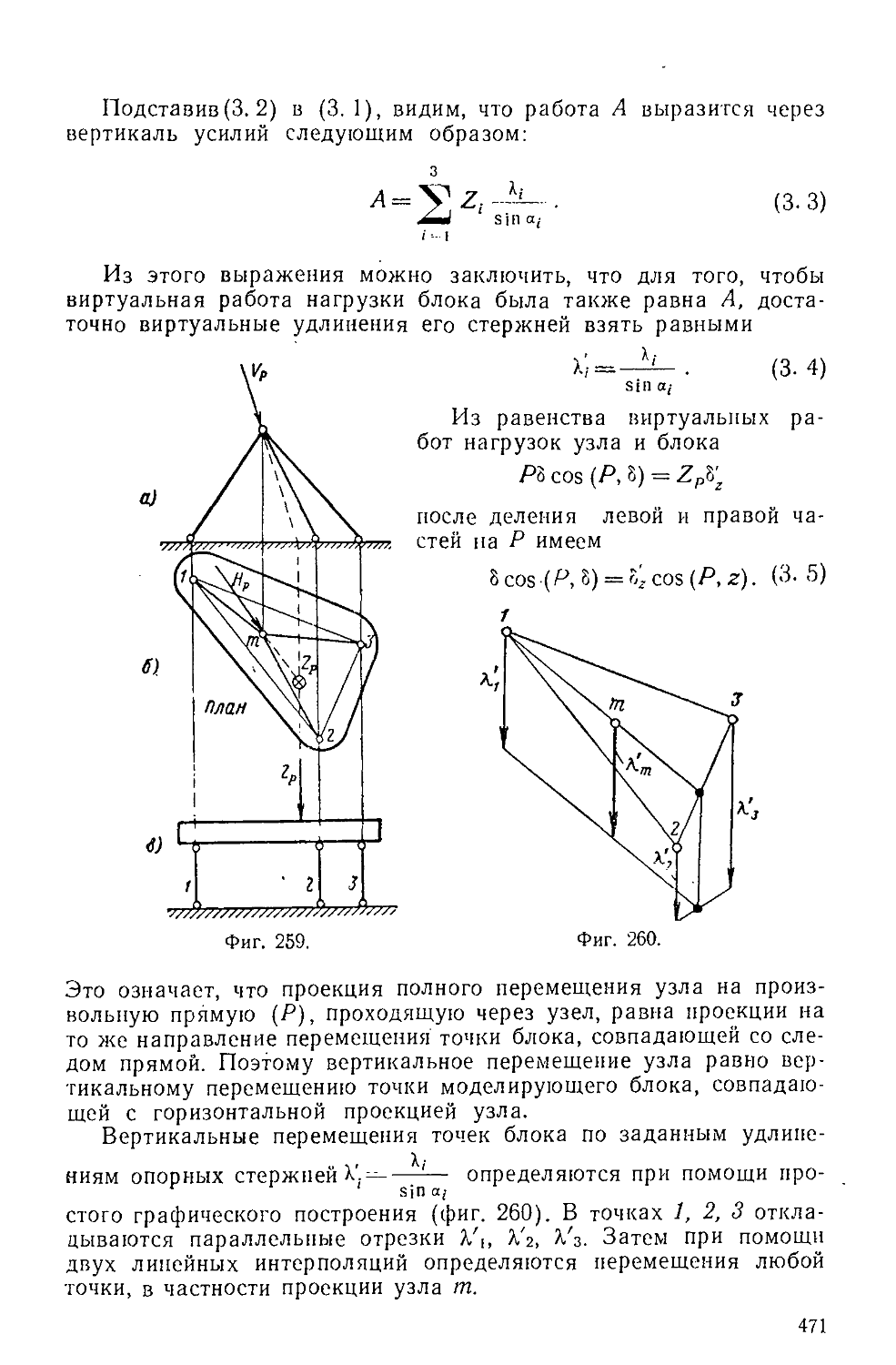
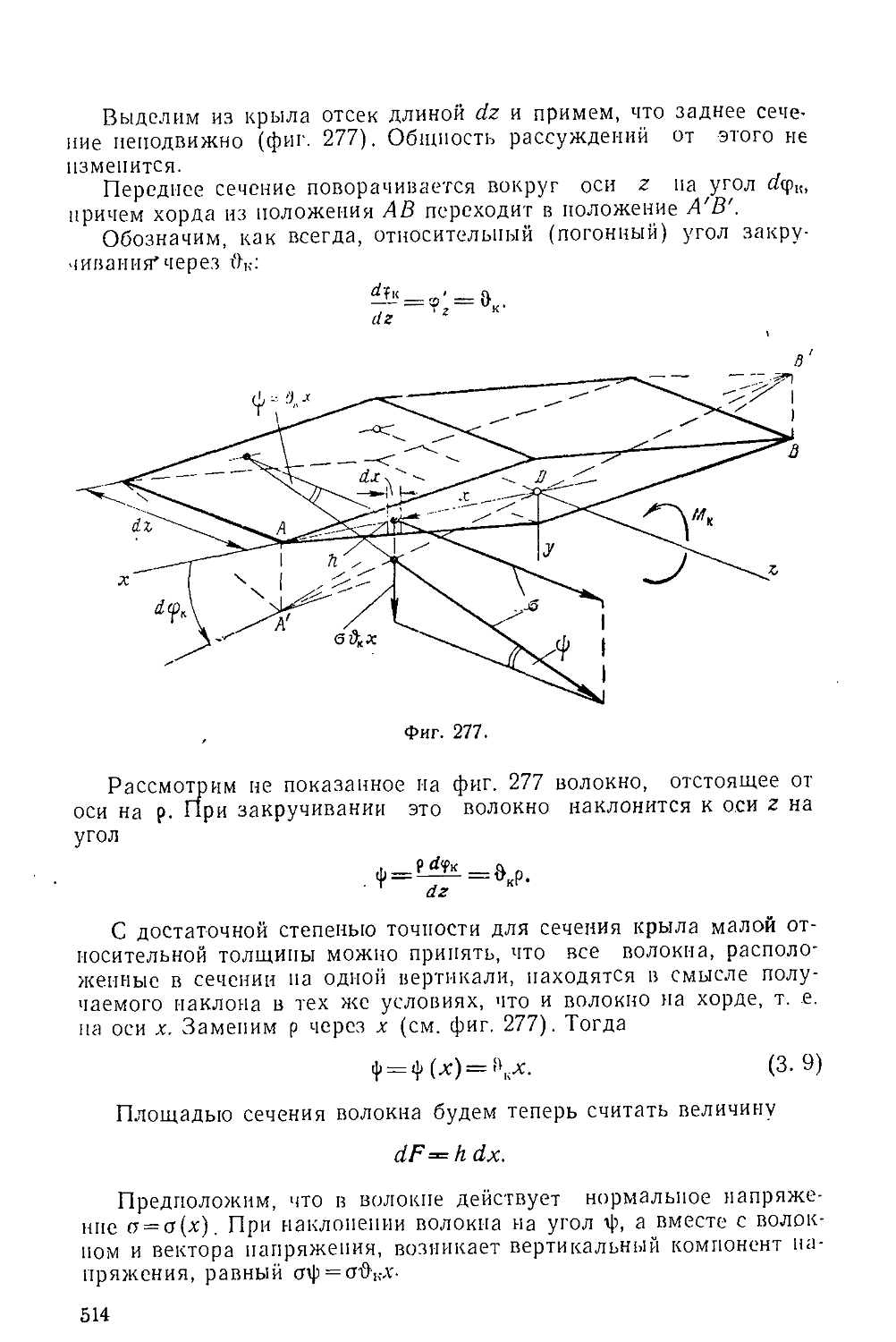
Text
А. А. УМАНСКИЙ
СТРОИТЕЛЬНАЯ МЕХАНИКА САМОЛЕТА
Допущено Министерством высшего и среднего специального образования РСФСР в качестве учебника для авиационных вузов и факультетов
ГОСУДАРСТВЕННОЕ
ТЕХНИЧЕСКОЕ ИЗДАТЕЛЬСТВО ОБОРОНГИЗ
Москва 1961
Книга является учебником для авиационных вузов по дисциплине «Строительная механика самолета», содержащей основную теоретическую базу статических расчетов, излагаемых в дисциплине «Расчет самолета на прочность».
В ней излагаются вопросы сложного изгиба брусьев, прочности и устойчивости пластинок и оболочек, расчет прочности и несущей способности конструкций типа крыла и фюзеляжа, расчет плоских и пространственных ферм и ряд дополнительных вопросов с соответствующим математическим аппаратом.
Книга отражает современный уровень теоретических знаний в области строительной механики авиационных конструкций и может быть использована инженерами промышленности в практической работе.
Рецензенты: Кафедра строительной механики самолета Московского авиационного института им. Серго Орджош'
кидзе,
докт. техн, наук проф. Г. Г. Ростовцев
Редактор канд. техн, наук Б. В. Засл?
вскии
Зав. редакцией инж. С. Д. Край
льников
ПРЕДИСЛОВИЕ
Предметом дисциплины «Строительная механика самолета» являются теоретические основы расчетов на прочность несущих, иначе силовых, конструкций самолета под действием различных нагрузок, рассматриваемых в качестве статических. Определение самих нагрузок выполняется по нормам прочности, в основе которых лежат данные аэродинамики, динамики полета и летных испытаний. Изучение нагрузок входит в программу дисциплины «Расчет самолета на прочность». К этой дисциплине относят также упрощенные методы предварительного (проектировочного) расчета на прочность, вопросы весовой отдачи различных конструктивных форм, расчеты шасси, вопросы колебании самолета в воз душном потоке (аэроупругость) и др.
Содержание курса «Строительная механика самолета» обусловлено особенностями конструкции современного цельнометаллического самолета распространенного типа. Основные конструктивные агрегаты — крыло, фюзеляж, оперение представляют собой удлиненные подкрепленные оболочки цилиндрической, или близкой к цилиндрической, формы (тонкостенные брусья). Приближенная схема работы такой конструкции заключается в еле дующем.
Обшивка и подкрепления работают солидарно, воспринимая все нагрузки. Панель (Клетка) обшивки работает как пластинка на изгиб от местной аэродинамической нагрузки и одновременно испытывает растяжение или сжатие в сочетании с касательными усилиями, возника’ющими при работе тонкостенного бруса на из гиб и кручение. Сказанное о работе обшивки относится также к стрингерам (продольным связям), для которых можно в первом приближении установить местные нагрузки, передаваемые обшив кой и вызывающие изгиб, и продольные усилия от общего изгиба конструкции. При определении усилий от местной нагрузки стрингеры считаются опертыми па сравнительно редко расставленные поперечные связи — силовые шпангоуты или переборки.
Важнейшее требование к конструкции состоит в том, чтобы для наиболее напряженных элементов были соблюдены условия прочности и устойчивости. Это безусловно необходимое требование в целях снижения веса можно, однако, несколько ослабить, до пуская при упругих деформациях превышение критических напря
425 3
жений в обшивке, при условии, что устойчивость стрингеров обеспечена.
Этому кругу вопросов посвящены первые три главы книги.
Первая глава содержит теорию сложного изгиба балок, в частности сжатой и растянутой гибких балок и балки на упругом основании, включая температурные задачи. В пей уделено особое внимание различным методам интегрирования дифференциальных
уравнений сложного изгиба, в частности, методу начальных параметров (Н.П. Пузыревского —А. Н. Крылова), играющему видную роль в задачах строительной механики. Читатель знакомится с вариационными методами-—приложением принципов Лагранжа и Кастильяно, прямыми методами Бубнова-—Галеркина и Ритца — Тимошенко.
Вторая и третья главы содержат классические задачи, относящиеся к прочности и устойчивости гладких прямоугольных пластинок при различных нагрузках и граничных условиях и рассмотрена работа подкрепленных стрингерами пластинок после потери ими устойчивости от сжатия. Тут же даются основы метода редукционных коэффициентов, позволяющего о-пределить несущую способность (предельную нагрузку) сжатого перекрытия. Следует отметить, что метод редукционных коэффициентов, сводящий расчет подкрепленной оболочки к расчету «эквивалентного бруса», составляет важное, достижение пауки о прочности и связан с именем выдающегося ученого и инженера-кораблестроителя И. Г. Бубнова (1884—1919). Метод получил дальнейшее развитие в трудах П. Ф. Папковича, П. А. Соколова, Ю. А. Шиманского, а применительно к самолетостроению — в трудах Г. Г. Ростовцева, И. А. Свердлова, Кармана, Маргерра и др. Способ последовательных приближений, лежащий в основе метода редукционных коэффициентов, используется также при определении несущей способности конструкций за пределом упругости (работы В. Н. Беляева, А. Ю. Ромашевского) и в более широкой постановке, при объемном напряженном состоянии, — в методе упругих решений А. А. Ильюшина. В главе III рассматривается также работа тонкостенной балки после потери устойчивости стенкой от действия поперечной силы (поле диагональных растяжений).
Четвертая глава посвящена вопросам прочности и устойчивости гладких оболочек. Дается вывод дифференциального уравнения изгиба и растяжения—-сжатия тонкой оболочки, рассматриваются простые, но важные случаи осесимметричного нагружения круговой цилиндрической оболочки. Как известно, решение задач устойчивости оболочек в предположении весьма малых деформаций приводит к линейным дифференциальным уравнениям безразличного равновесия, а эти уравнения во многих случаях дают завышенные, по сравнению с экспериментальными, значения критической нагрузки. Сложность нелинейной теории не позволяет изложить ее в учебнике, поэтому автор ограничился коррективами к результатам линейной теории, которые вносятся экспериментами и исследованиями в нелинейной постановке. Для ознакомления с теорией оболочек, построенной на базе нелинейной теории упругости, интенсивно развивающейся последнее десятилетие, рекомендуем читателю обратиться к монографии А. С. Вольмира и монографии X. М. Муштари и К. 3. Галимова.
Пятая глава посвящена теории прямых брусьев с тонкостенным открытым замкнутым или многосвязным профилем поперечного сечения, созданной трудами С. П. Тимошенко, Г. Ваг
нера, В. 3. Власова, В. Н. Беляева, Р. Каппуса и других ученых. Особенно велики заслуги советского ученого В. 3. Власова (1906—1958 гг.), обогатившего науку фундаментальными трудами — «Тонкостенные упругие стержни», «Строительная механика тонкостенных пространственных систем» и «Общая теория оболочек».
Элементы теории стержней с открытым профилем теперь излагаются во многих учебниках по сопротивлению материалов. В настоящей книге эта теория связана с исследованием брусьев и цилиндрических оболочек с неизменяемым в своей плоскости замкнутым или мпогосвязным поперечным сечением, к которым с известными допущениями могут быть отнесены также крыло и фюзеляж. Достаточно подробно освещен вопрос о нагрузках и расчете поперечных подкреплений (шпангоутов) в виде рам и колец. Изложенная в конце главы теория общей устойчивости стержня с открытым профилем при центральном сжатии вместе с § 2. 13, посвященным местной устойчивости, дает читателю достаточное представление о существе проблемы.
Глава шестая содержит вопросы расчета балок с топкой стенкой как плоской, так и искривленной по цилиндрической поверхности, а также более сложных двухпоясных систем, носящих общее название бикопструкций. Уяснение напряженного состояния биконструкций весьма важно для более глубокого понимания работы оболочек с замкнутым и открытым поперечным сечением (оболочек с вырезами), а также роли подкреплений при различных силовых воздействиях.
Глава седьмая посвящена определению перемещений и расчету статически неопределимых тонкостенных балок, коробок и подкрепленных оболочек (при определенных упрощающих допущениях) по методу сил. Основы метода сил в применении к статически неопределимым стержневым системам-—-балкам, рамам, фермам и комбинированным системам—достаточно подробно излагаются в курсе сопротивления материалов. Здесь этот метод распространяется на системы, состоящие из стержней и тонких плоских или цилиндрических стенок. Этим создается возможность изучения напряженного состояния основных силовых агрегатов сложных авиационных конструкций. Роль метода сил в связи с развитием машинной вычислительной техники должна возрастать, так как решение большой системы линейных алгебраических уравнений уже не представляет больших трудностей, ранее заставлявших инженеров идти па различные, часто необоснованные, упрощения. В конце главы дается ряд примеров анализа практически важных систем по методу сил (корневая часть крыла и фюзеляж на участке выреза, треугольное крыло).
Главы восьмую и девятую следует рассматривать как необходимое дополнение к элементам теории ферм, изучаемых в разделах «Статика» и «Графостатика» дисциплины «Теоретическая механика». Основное внимание в гл. VIII уделено вопросам образования ферм и практическим приемам расчета простраист-6
венных ферм. В гл. IX рассматриваются вопросы статически неопределимого прикрепления отдельных узлов и твердых тел (блоков двигателей). Показано применение метода перемещений, дающего в ряде случаев существенное упрощение расчета.
Глава десятая содержит три перспективных специальных вопроса: расчет консольных пластинок переменного сечения, элементы расчета трехслойных конструкций и некоторые температурные задачи. Этот материал может быть использован читателями книги для дальнейших самостоятельных разработок.
Настоящий курс опирается на достижения отечественной школы строительной механики и является одним из результатов длительной коллективной научной и методической разработки теоретических вопросов прочности летательных аппаратов кафедрой, руководимой автором книги.
Ряд товарищей оказал автору непосредственную помощь в написании книги. Гл. III и § 6. 8—6. 10 написаны канд. техн, наук доцентом Ю. П. Григорьевым. Материалы в § 4. 5 по устойчивости оболочек в нелинейной постановке предоставлены докт. техн, наук проф. А. С. Вольмиром. В разработке отдельных вопросов и примеров приняли участие кандидаты техн, наук доценты А. М. Афанасьев, А. И. Макаров, В. А. Марьин, В. В. Новицкий и А. И. Тюленев.
Автор выражает глубокую благодарность рецензентам книги — коллективу кафедры строительной механики самолета Московского авиационного института им. Серго Орджоникидзе и доктору техн, наук проф. Г. Г. Ростовцеву за ценные замечания, а также канд. техн, наук доценту Б. В. Заславскому, тщательно отредактировавшему книгу.
Просьба все замечания и пожелания присылать по адресу: Москва, И-51, Петровка, 24, Оборонгиз.
Москва 1960 г.
Глава I
КЛАССИЧЕСКИЕ И ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ СЛОЖНОГО ИЗГИБА БАЛОК
Изгиб балки называется сложным, когда усилия в ней существенно зависят от деформации самой балки. В отличие от обыкновенных статически неопределимых балок, у которых лишними неизвестными являются сосредоточенные силы, моменты или перемещения в'Определенных сечениях, здесь неизвестными являются прогибы или моменты во всех сечениях, другими словами,— некоторые функции. Поэтому расчет балки на сложный изгиб связан с составлением и интегрированием дифференциальных уравнений или с другими методами, позволяющими определить искомые функции.
Примером сложного изгиба является так называемый продольно-поперечный изгиб. При достаточно гибкой балке приходится учитывать те дополнительные изгибающие моменты, которые создает продольная сила в изогнутом стержне, причем самый изгиб в свою очередь зависит от этих моментов. Работа балки на упругом основании, несущей поперечную нагрузку, также должна быть отнесена к сложному изгибу независимо от того, действует ли одновременно продольная, сила или нет.
Выдвигая на первый план теорию сложного изгиба балок, руководствуются значением этой теории для понимания работы стержней, входящих в состав тонкостенных конструкций в качестве подкрепляющих элементов, а также для понимания работы отдельных волокон (балок-полосок), мысленно выделенных из пластин и оболочек.
При интегрировании дифференциальных уравнений сложного изгиба используются как классические (строгие), так и вариационные (в большинстве случаев приближенные) методы. Последние играют большую роль в современной технике вообще, в теории пластин и оболочек в частности. Первоначальное ознакомление с ними на примерах задач сложного изгиба является особенно наглядным.
9
§ 1.1. ЭПЮРЫ УСИЛИИ В СЕЧЕНИЯХ БРУСА И ИХ ПРИЛОЖЕНИЯ К РАЗЛИЧНЫМ ЗАДАЧАМ
Эпюры N, Q, М
Предположим, что на балку или иной прямой бурс действуют распределенные нагрузки с переменной по1 длине погонной интенсивностью — продольная с интенсивностью д кг/см, мо-
ментная с интенсивностью т кгсм/см и поперечная р кг)см (фиг. 1,а).
Составим аналитические выражения усилий N, Q, М в сечении х. С этой целью возьмем начало отсчета в произвольном сечении О и направим ось х, а также совпадающую с ней вспомогательную ось § — вправо. В дальнейшем будем отмечать аргумент (абсциссу) различных усилий не как обычно в скобках, а ниж
10
ним индексом. Аналогичное обозначение обычно принимается в •теории пластинок и оболочек.
Интересующие нас выражения усилий известны из курса сопротивления материалов и легко могут быть получены читателем из уравнений равновесия 2А—О, 27=0, 2Л1 —О отрезка балки длиной х (фиг. 1,6). Усилия запишутся следующим образом:
Nx=N0-^qdt, о
Qx=Q0-$p^ 1 (1.1)
о
Мх = Af04-Q0^+ f mdi. — Ср (x — I)di. о 6 ;
.Здесь знак аргумента £ при переменных интенсивностях нагрузок q, ,р, т опущен как самоочевидный.
Величины No, Qo, АД представляют собой усилия в сечении О, принятом за начальное или, так называемые, начальные параметры.
Равенства (1.1) можно рассматривать как уравнения э п ю р N, Q, М и использовать их для построения эпюр по точкам. При этом начальные параметры (начальные ординаты эпюр) должны быть определены заранее. Построение эпюр сводится к вычислению интегралов с переменным верхним пределом х.
С другой стороны равенства (1.1) можно рассматривать как общее решение (общий интеграл) системы дифференциальных уравнений равновесия балки, часто называемых дифференциальными зависимостями растяжения — сжатия и изгиба.
Дифференциальные уравнения равновесия—это уравнения равновесия элемента балки. На фиг. 1,в показан элемент длиной rfg с действующими на него нагрузками и усилиями по торцам. Из уравнений равновесия 2М=0, 27=0, 2М —0 после замены на dx получаем
d.N__ . dQ
dx dx
dM ,
(1-2)
Первое из этих уравнений независимо от двух других. Исключив из двух последних уравнений Q, получим дифференциальное уравнение второго порядка для изгибающего момента М:
d^M . dm ,,
—г = ~Р~\ (1- 3)
dx^ dx 7
Третья строка группы формул (1. 1) представляет собой общий интеграл этого уравнения, содержащий две произвольные постоянные. В данном случае эти постоянные — начальные параметры АД и Qo-
11
Практически важный для нас вывод состоит в следующем: для решения дифференциального уравнения вида
d^y __
dx^
/w
(1.4}
аналогичного (1.3) могут быть использованы как формулы (1. 1), так и все хорошо известные способы и приемы построения эпюр изгибающих моментов обыкновенных балок.
Эпюры углов поворота сечений (ср) и прогибов (п)
Обратимся к геометрической задаче — определению малых, углов поворота сечений ф и перемещений по вертикали (прогибов) и по заданным во всех сечениях величинам относительного угла поворота '& еж-1 и величинам относительного сдвига сечений 7.
Сама формулировка задачи предполагает, что сечения остаются плоскими и жесткими в своей плоскости или, что то же, размеры сечения бесконечно малы по сравнению с размерами балки по длине.
Малый угол поворота сечения ф=1§ф считается положительным при повороте сечения по часовой стрелке (фиг. 2,а). Относительный (погонный) угол поворота О считается положительным, когда соответствует отрицательному приращению угла ф. Следовательно,
&=-^. (1.5)
dx
При малом искривлении, о котором здесь идет речь,
dx~ds, dx ds
где z—кривизна деформированной оси бруса. Поэтому относительный угол '& при расчете балок часто называют приближенным значением кривизны или просто кривизной. Для О находят применение также термины «интенсивность угловой деформации» и «интенсивность фиктивной нагрузки».
Относительный сдвиг 7 (подразумевается общий по высоте сечения относительный сдвиг) считается положительным, когда он создает положительное (т. е. направленное вниз) приращение прогиба (фиг. 2,6).
Полное приращение прогиба
откуда
dv — у dx-}-~[ dx,
dv
dx
= <?+?•
(1-5')
12
Система (1-5), (1. 5') эквивалентна одному уравнению второго порядка:
Отметим, что благодаря учету сдвига, угол наклона искривленной оси к горизонту
не равен углу поворота сечения ф и, в свою очередь, относительный (погонный) угол наклона оси cftvldx2 не равен величине—
Полная аналогия статического уравнения (1.3) и геометриче-
ского (кинематического) уравнения (1.6) позволяет использовать
13
вторую и третью строки (1.1) и записать решение уравнени (1.6) так:
г
0 л .V ! (L7
6 О )
Формулы (1.7) позволяют построить эпюры углов поворот, сечений ф и прогибов v по заданным эпюрам кривизны О и отно сительных сдвигов -( и могут быть использованы при изучение влияния начальных, температурных, пластических и упругих де формаций на перемещения (форму оси) балки.
Определим относительный угол поворота сечений ft1 от действия неравномерного по высоте балки изменения температуры Ограничимся случаем линейного закона изменения температурь по высоте. Пусть t°„ увеличение температуры нижнего волокна в данном сечении балки, — увеличение температуры верхнего волокна, а—коэффициент линейного расширения, h—высота сечения.
Обращаясь к фиг. 2, в, легко находим
= (1.8)
h '
Величины , отложенные в виде ординат вдоль пролета балки, дают эпюру О'.
Температурный сдвиг считается равным пулю.
Подставив значения (1.8) в (1.7) и выполнив интегрирование, мы можем определить ординаты эпюры углов поворота ф и прогибов V.
Практически наиболее важным остается определение упругих перемещений балок.
Относительный угол поворота сечения при изгибе в упругой стадии пропорционален изгибающему моменту в сечении:
Осредпенный относительный сдвиг пропорционален поперечной силе и равен
7УП=~. (1-Ю)
GFy
Здесь Fy — эффективная площадь сечения при определении деформации сдвига в вертикальной плоскости, учитывающая неравномерность распределения касательных напряжений изгиба по высоте сечения.
Для двухпоясной тонкостенной балки касательные напряжения в поясах близки к нулю, а в стенке почти постоянны по высоте. Поэтому эффективная площадь Fy принимается равной площади поперечного сечения стенки ht.
Формулы (1.7) для определения упругих перемещений принимают вид
(1-11)
Эти формулы известны из курса сопротивления материалов и представляют собой общий интеграл системы дефференциальных уравнений изгиба
df ___ М
dx EI ’
dv , Q
---= ® ~— dx ‘ GFy
ИЛИ
(1.12) dx- EI GFy
Последний член выражает влияние упругой деформации сдвига, которым часто пренебрегают.
Предлагаем самостоятельно доказать, что прогиб простой балки постоянного сечения от сдвига равен изгибающему моменту в том же сечении, деленному на жесткость GFy.
Гибкая нить
Рассмотрим теперь задачу о форме провисания тонкой и гибкой нити под действием вертикальной нагрузки (фиг. 3, а).
Гибкая нить представляет собой систему с бесконечно большим числом степеней свободы. Форма нити зависит от нагрузки. Усилия в сечениях сводятся к продольной силе N, н а -правление которой совпадает с касательной к линии провисания (фиг. 3,6).
Обозначим ординаты линии провисания через у, угол наклона касательной к оси х через ф. Усилие N раскладываем на горизонтальную составляющую Н и вертикальную составляющую Q.
По сказанному выше
^-=tg<p = ^. (а).
Н dx 1
Обозначим интенсивность вертикальной нагрузки, отнесенную к горизонтальной проекции нити, через р кг/см.
15
Рассмотрим условия равновесия элемента нити с проекцией dx. Уравнение проекций 2Х = 0 дает
Н= const. (б)
Уравнение проекций SK=0 дает
Фиг. 3.
Соотношение (в) показывает, что вертикальная составляющая может быть найдена по правилам определения балочной поперечной силы Q.
Учитывая (б), дифференцируем левую и правые части (а) по х и подставляем значение dQjdx из (в). Получаем дифференциаль-
ное уравнение линии провисания нити
d'-y р
d^~ ’
(1.13)
Сопоставляя полученное уравнение с (1.3) (при т = 0), заключаем, что линия провисания гибкой нити под вертикальной' нагрузкой р кг/см совпадает с эпюрой моментов балки под той же нагрузкой с ординатами, уменьшенными в Н раз, при условии, что граничные условия нити и балки э кв и-
16
валентны. Это значит, что если точки подвеса нити лежат на одном уровне на взаимном расстоянии I, то балка должна иметь две шарнирные опоры и пролет I. И тогда
(1.14)
Эпюра тангенсов углов наклона нити к гори-зонтусовпадает с эпюрой поперечныхсил балки с ординатами, уменьшенными в Я раз:
tg(p=y==^-. (1.14')
/7
Продольные усилия в нити определяются по формуле
N=\Q2-\-H\ (1.15)
где Q — балочная поперечная сила.
Отсюда видно, что основным параметром работы нити является распор Н.
Распор легко определяется, если, кроме концевых, известна еще одна ордината ус кривой провисания, например, в сечении С
Н= — . (1.16)
Ус
Здесь Мс — ордината эпюры моментов в сечении С.
Пусть, например, нить несет равномерно распределенную по проекции нагрузку р== const (фиг. 3, в). Кривая провисания представляет собой параболу второй степени. Если f — стрелка провисания по середине пролета, то
у— — х (I — х); — = —(Z —2х);
Г- v dx lz v
(1.17)
УИп>ах = /Иср= —: Я = — •
max ср g ’ gy
При пологой нити (Z//>10) приведенные формулы могут применяться для расчета нити постоянного сечения от действия собственного веса. Кроме того, для пологой нити можно принимать
N Н— const.
При очень пологой нити необходимо учитывать влияние упругого удлинения на стрелку провисания.
Решим следующую задачу. Дана нить, первоначальная длина которой равна пролету I. Определим распор Н и стрелку провисания f под действием равномерно распределенной нагрузки.
Для решения этой и аналогичных задач необходимо иметь выражение длины нити в зависимости от пролета и стрелки провисания.
17
Общее выражение длины дуги
(1. 18)
заменяется приближенным, тем более точным, чем более полога кривая:
i
[' Г, । 1 /й'у \2] j ,1 1С,'\
s= 1 -------(--) \dx. (1.18)
J L 2 \dx / J v .
о
Подставив сюда значение dyjdx, из (1. 17) и интегрируя, находим
\ 1 3 /? / 1 3 /
(П 19)
Отметим также формулу, принадлежащую к классу приближенных формул Чебышева, отличающихся весьма большой точностью:
/2-р^-/2. (1.20)
Если первоначальная длина нити равна длине хорды (пролету) I, то приращение длины вследствие искривления на основании формулы (1. 19) равно 8/2/3/. Приравниваем эту величину приближенному значению упругого удлинения HI/EF, предварительно выразив f через Н. Пользуясь последней формулой (1. 17), находим
/У= |7 (1.21)
24 ’ 4 |/ EF V
Таким образом, распор Н и стрела провисания f нелинейно связаны с нагрузкой р.
Большинство задач, относящихся к провисанию упругих нитей, носит нелинейный характер.
Мы рассмотрели три задачи, решение которых приводится к интегрированию простейшего дифференциального уравнения второго порядка:
Из широко известных задач сюда можно- было бы присоединить задачу о прямолинейном ускоренном движении тяжелой точки
18
под действием переменной силы постоянного направления, сводящуюся к уравнению
rfjx __ Р
dtP т
Интегрирование этих уравнений эквивалентно построению эпюры изгибающих моментов некоторой балки.
Математическая аналогия позволяет использовать расчетные приемы, разработанные в одной области, к проблемам другой области. Еще большее значение имеет возможность моделирования одних процессов другими, более удобными для экспериментального изучения.
Широкое развитие здесь в первую очередь получил метод электромоделирования.
§ 1.2. СЖАТАЯ И РАСТЯНУТАЯ БАЛКИ
Дифференциальные уравнения продольно-поперечного изгиба
Рассмотрим балку, шарнирно опертую по концам, несущую поперечную нагрузку и сжатую или растянутую постоянным усилием N (фиг. 4, а, б). При не очень жесткой балке возникает задача учесть влияние деформации балки на усилия в пей. Речь в
первую очередь идет о дополнительных моментах в сечениях, равных произведениям продольной силы на прогиб в данном сечении. Легко видеть, что в рассматриваемом случае сжимающая сила увеличивает прогиб, а растягивающая — его уменьшает. Поэтому ограничиться определением прогиба только от поперечной нагрузки
2 й
19
значит вести расчет не в запас прочности при сжатии и в запас прочности при растяжении. Следовательно, возникает задача определения прогиба от одновременного действия поперечных нагрузок и продольной силы, что достигается интегрированием дифференциального уравнения продольно-поперечного изгиб а.
При выводе уравнений мы будем пользоваться гипотезами простого изгиба балок и, в частности, приближенным выражением кривизны, вытекающим из допущения ds = dx. Поэтому получаемые результаты будут тем точнее, чем прогибы меньше. Для растянутой балки теория точнее, чем для сжатой. Теория стержней большой гибкости, основанная на точном выражении кривизны, имеет применение главным образом в приборостроении и здесь, не рассматривается.
Предположим, что простая балка имеет малую технологическую погибь, характеризуемую начальным искривлением •0'° и начальными прогибами v°. В отдельных случаях под О0 и v° можно подразумевать также температурную кривизну и прогибы от действия переменного по высоте балки стационарного нагрева или охлаждения.
Пусть балка несет некоторую вертикальную нагрузку, от действия которой в ней возникают изгибающие моменты Л1° и соответствующая им упругая кривизна М°1Е1.
Дифференциальное уравнение для полных вертикальных перемещений и, включающих как начальный прогиб, так и упругие прогибы, будет
(а) dx* EI
Если балка нагружена также продольной силой N, то изгибающие моменты получают добавку +Nv, где знак «+» относится к случаю сжимающей силы N, а «—»—к случаю растягивающей силы N.
Заменив в уравнении (а) величину Л4° на M°+Nv и перенеся неизвестный член в левую часть, получим дифференциальное уравнение для полного прогиба при продольно-поперечном изгибе:
_,')о . (2.1)
dx- ~ EI El
Представим полный прогиб как сумму начального и упругого прогибов
'П = 'П°-(-'Пуп. (б)
Подставляя (б) в (2. 1) и учитывая, что
= — &о,
dx^
20
получим дифференциальное уравнение для упругой части полного прогиба:
__L(Afo±^O). (2.1')
dx2 El El
Часто бывает полезно представить полный прогиб как сумму элементарного прогиба, удовлетворяющего уравнению (а) и, следовательно, не учитывающего наличия продольной силы, — и дополнительного прогиба
-l-f®0”. (в)
Подставляя (в) в (2. 1) с учетом уравнения (а), написанного для v эл, получим
+ ТУ ^доп ZjT . (2.1")
El El v
Таким образом, для v, пуп, -пд0П получили уравнения, имеющие одну и ту же структуру левой части, но отличающиеся правыми частями.
Интегрированием уравнений получают уравнение прогибов в конечном виде, иначе— уравнение эпюры прогибов или уравнение изогнутой оси.
Уравнение углов поворота получается дифференцированием уравнения для прогибов:
Ду ,п rft,yn non rfC1011 / \
Ф = . , ИЛИ = -----, ИЛИ <рдоп =- . (г)
dx dx dx
Уравнение полных изгибающих моментов получается через уравйения моментов от вертикальных нагрузок и уравнение полных прогибов:
M==M9+Nd. (д)
Кроме того, изгибающие моменты могут быть получены путем двукратного дифференцирования уравнения упругих прогибов:
-E/f—(е) dxi \ах2 ) v
Поперечные силы получаются дифференцированием одного из выражений для изгибающих моментов, так как соотношение O^dMddx, получаемое из уравнения моментов для элемента балки, имеет место и при наличии продольной силы:
Q = Q = Q°±^; . (ж)
dx dxs
Соотношение dQJdx =—p также остается в силе, если под р подразумевать полную погонную интенсивность нормальных к оси балки распределенных нагрузок элемента, складывающихся в данном случае из заданной нагрузки р°, приложенной вдоль
21
верхней или нижней поверхностей балки, и дополнительных сил, приложенных в сечениях. Дифференцируя среднее выражение (ж), принимая для заданной вертикальной нагрузки обозначение р° и по-прежнему обозначая полную кривизну &= — у- = — >
получим
^-=-р=~(Р*±№). (3)
dx
Отсюда легко перейти к дифференциальному уравнению изги-_ „ dQ dPM a Qn । М
бающих моментов. Достаточно подставить ——-----; = ---.
dx dx2 EI
Тогда после переноса неизвестных в левую часть, будем иметь
— ± — М= -(/?°±Ж°). (2.2)
EI
Снова получилось уравнение с прежней структурой левой части.
Если представить полный момент в виде суммы момента от вертикальных нагрузок и дополнительного момента от силы N
+ /Илоп,
то для последнего получим дифференциальное уравнение
dx” — EI \ 1 EI ) v
Разумеется, это уравнение можно было бы написать сразу по уравнению (2. 1), так как Л4д0П=+7Уц.
Отметим еше, что уравнение (2. 2) тесно связано с дважды продифференцированным уравнением (2. 1). Учитывая соотношение (е) между М и vyn, можем переписать (2. 2) следующим образом:
rf4-yn N d<vy" рЭ±ДГ8О ,2 3)
dx* ~ EI dx'2 ~~ EI
Ценность этого уравнения состоит в том, что оно связывает прогибы непосредственно с нагрузкой, минуя изгибающие моменты. Кроме того, общее решение уравнения (2.3) содержит четыре произвольных постоянных и обобщает решения уравнений (2. 1) и (2.2), содержащие по две произвольные постоянные.
В заключение наших выводов отметим, что, пользуясь для рас-суждений балкой на. двух опорах, мы нисколько не уменьшили общности полученных дифференциальных уравнений. Существенным является тот факт, что изгибающий момент имеет слагаемое, пропорциональное прогибу в том же сечении. При этом роль коэффициента пропорциональности играет сила N. В то же время приложение силы N в вертикально подвижной точке, например, на конце консоли, с заданным или наперед неизвестным эксцентриситетом имеет некоторые особенности, которые отра
92
жаются не на уравнениях, а на граничных условиях. Эти вопросы будут рассмотрены ниже на примерах.
Особенность полученных выше простейших уравнений, как и всяких линейных уравнений с постоянными или переменными коэффициентами, состоит в том, что при определении неизвестной функции (в данном случае v=vx либо М=МХ) при заданных граничных условиях сумма нескольких решений одного и того же уравнения равна решению уравнения с суммарной правой частью. Отсюда вытекает принцип сложения действий поперечных нагрузок, а также начальных и температурных искривлений: при неизменной продольной силе действие различных поперечных факторов суммируется.
Приближенные формулы для прогиба
Прежде чем перейти к строгому интегрированию полученных уравнений, остановимся на выводе важных приближенных формул.
Во многих случаях эпюра прогибов и эпюра начальной погиби простой шарнирно опертой балки с достаточной степенью, точности могут быть представлены синусоидой с одной полуволной.
Уравнение синусоиды, когда начало взято на левом конце балки, имеет вид
‘Цэ;1 = ^ sin—— . (и)
Здесь V3*— средняя ордината, определяемая элементарно и равная сумме упругого прогиба и начального прогиба посередине.
При равномерно распределенной нагрузке
Т1ЭЛ = -5- -1- Т>° .
ср 384 EI ср
При нагрузке сосредоточенной силой по середине пролета
Р 78
<уэл __-----L <у0
ср 48.57 ср
При сосредоточенной силе на расстоянии | от левой или правой опоры
или приближенно
-----Sin----Р'Ц® .
ср 48/3/ I ' ср
Последняя формула получена на основании теоремы о взаимности упругих перемещений, которая в данном случае показывает, что прогиб по середине пролета от силы на расстоянии g от левой
23
опоры равен прогибу в сечении g от силы, приложенной по середине пролета.
При нагрузке системой сосредоточенных сил
Z3 ---------- ср 48£/
При произвольной распределенной нагрузке p=p(g) = р i.
fASin Т^₽’
r 4qZJZ J I к
О
При нагрузке моментами МА и Мв по концам пролета
М. + М„ Р фэл . А В с₽ 2EI 8
Синусоидальный начальный прогиб должен быть задан средней ординатой v°cp.
При постоянной температурной кривизне
средняя ордината будет
Обратимся теперь к уравнению (2. 1").
Вспоминая правила дифференцирования тригонометрических функций (вторая производная пропорциональна самой функции), заключаем, что если правая часть уравнения выражается синусоидой, то частное решение уравнения также может быть представлено синусоидой. Это значит, что синусоидальной форме -оэл отвечает синусоидальная же форма 'оАОП:
= ®Jpnsin у- (к)
СР Z dx2 I2 р I
Подставляя это выражение в (2. 1"), после приведения подоб-пх
ных членов и сокращения на sin у, находим среднюю, ординату дополнительного прогиба
NP
ч------
-ГТ 2 р J , «
(л )
ср ср1-
т.2£/
24
Знак «+», как и всюду в § 1.2, относится к сжатию, знак «—» — к растяжению, сила N вводится по абсолютной величине.
В случае сжатия знаменатель может обратиться в нуль, ЭТО' происходит, когда
8
Если знаменатель равен нулю, то величина о"11 может быть отличной от нуля и конечной и в том случае, когда v™ ->0. Это значит, что найденное значение N равно эйлеровой критической силе в плоскости изгиба, что, впрочем, сразу видно, поскольку речь идет б шарнирно опертом стержне.
Хотя в формулу (л) входит точное значение эйлеровой силы, однако при больших значениях N, приближающихся к N3, она дает при конечном V™ крайне преувеличенное и даже абсурдное значение щ°п, в пределе обращающееся в бесконечность. Это объясняется использованием дифференциального1 уравнения изгиба,, основанного на приближенном значении кривизны, приемлемом лишь при малых прогибах. Практически формула (л) может быть использована при сжатии, когда N не превосходит 254-30% от Na.
При растяжении такого ограничения разумеется нет. Но надо-следить за тем, чтобы получаемое значение бСр = Уср + ‘исрП было-не больше 5-4-10% от пролета.
Для практического пользования перепишем формулу (л) так:
N
тДОП--- тЭ Л
ср ср
1 =F -— N»
или (2.4)
<7}Д0П-±2____
ср ср } т %2 ’
где
Кроме того, имеем простую формулу для полного прогиба:
„эл
<2-4‘
Заметим, что выведенные формулы становятся совершенно точными, если эпюра прогибов пэл является точной синусоидой, что-имеет место при нагрузке, также распределенной по закону синуса. Однако неточность в прогибах и в моментах намного ниже неточности в распределении нагрузок.
Случай неподвижных опор
Воспользуемся формулами (2.4) для определения продольной силы, возникающей в балке, шарнирно опертой на две неподвижные опоры под действием поперечной нагрузки и неравномерного нагрева. Для решения этой статически неопределимой задачи, найдем сначала сокращение пролета сжатой или растянутой балки с одной неподвижной и другой подвижной опорами под влиянием искривления. Это сокращение с точностью до малых высшего порядка можно вычислить как разность между длиной дуги и стягивающей ее хорды.
На основании формулы (1. 18') при у = и имеем
/
u = s — I =—- С(~\dx. ' (2.5)
2 ,) \iix /
о
Имеем
(2. 5")
Сокращение пролета балки от нагрева оси на f равно uf = ~ — й/Н. Сокращение пролета от неизвестной продольной силы равно = NlfEF. Напомним, что верхний знак относится к сжимающей силе. Выражение и х преобразуем, умножив числитель на ^2£7 Л 7 rV
----, а знаменатель на АЗ. Тогда
ujV
Х21С2/
IF
Здесь v — полное перемещение (прогиб), суммирующее упругий прогиб от всех факторов, температурное и начальное искривление:
= дуп Д ф-тЛ
Однако обычно надо Иметь сокращение пролета уже искривленной начальной погибью балки,тогда
и =
(2. 5')
26
При неподвижных опорах сумма трех сокращений, пролета равна нулю:
zt + «щЬ = О-
После несложных преобразований получаем кубическое уравнение для х2:
(2.6)
Возможен случай, когда расстояние между опорами получает наперед заданное или упругое увеличение А/. Тогда в уравнении (2.6) правой частью вместо нуля будет величина (—А/). При упругом приращении соответственно +W6, (б — податливость опорного устройства, иначе говоря, приращение пролета при Af=l).
Уравнение (2.6) решается путем проб с введением верхнего или нижнего знака. Единственное пригодное значение х2 должно быть положительным и в случае верхнего знака, когда сила сжимающая, должно быть меньше единицы. Имея %2, находим У = Уэх2.
При отсутствии начального прогиба и изменения температуры оси, а также наперед заданного приращения пролета сила N получается заведомо растягивающей. Кубическое уравнение принимает вид
+ Сгщ.)2, (2. 6')
Это уравнение легко решается несколькими попытками при помощи логарифмической линейки.
При начальной погиби, обращенной навстречу поперечной нагрузке, возможна потеря устойчивости путем прощелкиваиия. Этот и аналогичные вопросы рассматриваются в трудах, посвященных теории гибких стержней, пластинок и оболочек, к которым и отсылаем читателя *.
Интегрирование уравнений для случаев равномерной нагрузки постоянной начальной или температурной кривизны
Примем за исходное дифференциальное уравнение изгибающих моментов (2.2). В случае сжимающей силы N введем обозначения
P°-F^’)0 = /’*-= const.
В случае растягивающей силы N
— я= | — = const.
El [ El ' ‘ "
* См., например, E. П. Попо в, ней. ГТТИ, 1948, А. С. В о л ь м и р,
Нелинейные задачи статики топких стерж-Гибкие пластинки и оболочки, ГТТИ, 1956,
27
N
Различные обозначения для одной и той же величины -------
ЕГ
(поскольку мы пользуемся абсолютным значением У) мотивируются структурой справочной табл. 1 на стр. 57, которой будем пользоваться в дальнейшем.
Уравнения (2. 2) принимают вид
1) ^Д82Л7=-р*; 2)^-а2Л7=-Л.
' dx~ Г dx2
Общие интегралы подобных уравнений хорошо известны из курса высшей математики.
Общее решение для сжатой балки
7Wx=CJcospjc4-C2sin₽%—. (2.7)
Общее решение для растянутой балки
Mx=Clchax-}-C2sh ах — ~ . (2.8)
Произвольные постоянные определяются из граничных условий.
Предположим, что изгибающие моменты на концах пролета (опорные моменты) известны. Обозначим их соответственно Мд и Мв.
Если взять начало отсчета на левом конце, граничные условия формулируются так:
а) MQ=MA, б)
Для сжатой балки
а) С1-^-=Л/А, б) C1CoS^ + C2Sm^-^=MB.
Решая эти уравнения, находим
=мА+^. с2= - МА cos (1 - cos ].
Для эпюры М эти значения следует подставить в (2. 7).
Если взять начало отсчета по середине пролета, граничные условия формулируются следующим образом:
a) M__i_=MA, б) M_L = MB, 2 2
. „ pz п . pz р*
а) Ct cos —C2sin^—
б) Cj cos —-j-C2sin ^~-р~ = Мв.
Отсюда
28
Уравнение изгибающих моментов (уравнение эпюры Мх)
М ,+ Ма
Мх— —------ cos Sx
2 cos —
Mb~Ma -o , I cos ₽x — — sin Bx 4- —’ i —
2 sin— I cos —
1
Изгибающий момент
по середине пролета (х = 0)
Чр
Ма+Мв , 4 /.__L_
₽/ И У
2 cos— I cos —
(2- 9)
Если речь идет о растянутой балке, то соответственно будем иметь
М.+ Мп МО~М. п /гь „х
М ~ 5 ch ах -I---- sh ах — — /---1
„ , al 1 „ al «2 ai
2ch— 2sh —— \ cn.—
2 2 \ 2
_мА+мв р.*
с₽_ al
2chT
а2 а/
VhT
(2. 10)
Имея изгибающие моменты, нетрудно перейти к прогибам. Так ка к /И — JMQ+Nv, то v — + М~М° .
N
Для сжатой балки прогиб по середине пролета
ср N L К 2 8 /]
Упругий прогиб равен полному прогибу минус стрелка начального прогиба:
C = ^p“^p = ^p-g
Рассмотренная задача принадлежит к числу наиболее важных. Поэтому дадим также ее графическое решение, предложенное Н. Г. Ченцовым в 1929 г., относящееся только к сжатой балке.
Круговая диаграмма Н. Г. Ченцова
Представим общий интеграл дифференциального уравнения моментов сжатой балки (2.7) в следующем виде:
Afx = Z)sin(₽x + (p)-^-. р2
(м)
1
29
Поставленные выше граничные условия при х = 0 и х = 1 выражаются так:
а) Л1Л = £> sin ф-^-; б) Мв = D sin (р/+ф) — р-~- (п)
р2 pz
Эпюра моментов, удовлетворяющих уравнению (м), и константы D и ф, удовлетворяющие зависимостям (н), могут быть получены следующим графическим построением (фиг. 5). Вычерчиваем окружность радиусом р*1$2 кгсм и на ней откладываем дугу ЛВ = -у-кащи, отвечающую центральному углу pt. При р = 0> окружность обращается в точку. От точек А и В вдоль радиусов
Фиг. 5.
ОА и ОВ откладываем опорные моменты МА и Мв (положительные моменты снаружи окружности). Через точки А' и В' проводим перпендикуляры к радиусам до пересечения в точке С. На ОС, как на диаметре, строим вторую окружность, которая, очевидно, проходит через точки А' и В'. Заключенные между двумя окружностями отрезки лучей, проведенных из центра первой окружности, дают ординаты эпюры моментов. Перенося их на чертеж балки, получаем эпюру моментов в обычном виде.
В самом деле, если положить отрезок ОС равным D, угол А'От' равным рх, угол ОСА' равным ф, то отрезок тт' выразится через D, рх, ф в точном соответствии с величиной Мх по уравнению (м). Остается показать, что величины D и ф удовлетворяют уравнениям (а), (б). В том, что это, действительно, так, убеждают самые простые геометрические соображения. Это можно проверить по чертежу.
Дифференцируя Мх по х находим
Q,v=pZ?cos(px+'p). (о)
30
Обращаясь к фиг. 5, видим, что
Qx=-pCm'.
Следовательно, ординаты эпюры Qx представляются умноженными на р хордами второй окружности, выходящими из точки С. Максимальные значения поперечной силы равны, очевидно QA № QB. Поперечная сила равна нулю в сечении балки, отвечающем лучу ОС. Поэтому максимальный изгибающий момент равен отрезку КС.
Слабое искривление эпюры Q является типичным: продольная: сила значительно менее влияет на поперечные силы, чем на изгибающие моменты. Поэтому для определения касательных напряжений часто пользуются эпюрой Q°.
При отрицательных опорных моментах эпюра М имеет участки разного знака. Характер эпюры Q не изменяется.
Ординаты эпюры прогибов сжатой балки получаются как ординаты эпюры моментов, отсчитанные от пунктирной прямо» А'В' и разделенные на продольную силу N. Для получения эпюры ф надо из эпюры Q вычесть эпюру Q0 и разность разделить на' N. Так как результаты получаются из разности, то построение следует вести в достаточно большом масштабе, либо, пользуясь чертежом, находить искомые величины аналитически.
При угле р/=л: точки А и В на первом круге располагаются по концам диаметра и точка С стремится в бесконечность. Соотношение p/=jt отвечает соотношению sin р/ = 0 в задаче Эйлера, когда продольная сила N становится критической, равной Л/э=-------- -
Но и при сжимающей силе, не намного меньшей эйлеровой в плоскости изгиба, когда точки А и В близки к концам диаметра, построение теряет смысл, так как в основе его лежит линейная теория деформации балок (ds^dx), пригодная только при относительно малых прогибах. По исследованиям Е. П. Попова пользование выводами линейной теории еще допустимо, если получаемый по этой теории прогиб не превосходит достаточно большой величины //10, где / — пролет балки. При этом погрешность в определении прогиба не превосходит 5% в сторону преувеличения фактического прогиба, получаемого по нелинейной теории стержней большой, гибкости.
Динамическая модель сжатой балки
Обратим внимание на аналогию (2.1) и (2.2) для случая' сжатой балки с уравнением малых вынужденных колебаний упругой системы с одной степенью свободы:
Здесь у — перемещение, с-—жесткость (отпорность) упругой связи или ее реакция при перемещении у=1; т — масса системы;. P—P{t)—возмущающая сила.
31
Общее решение уравнения (м) или выражение для перемещения у в функции времени t обычно дается в курсах механики в •следующем виде:
^=_V0COSarf + ^sinw/+J_ f^sinw(z„T)6/T (р) со J т
о
Дифференцированием по времени получают выражение для •скорости
С Л
yt — — ®у0 sin cos <о/-ф I — cos ® (/ —т) dx. (р')
J т 'г /
о
Здесь Уо и Уо — начальные параметры, или перемещение и скорость в начальный момент времени, т. е. при /=0. Через т обозначен момент времени в интервале от 0 до /:
0<t<t
Через со2 обозначен множитель при неизвестной функции в уравнении (п), так называемая круговая частота
Важно отметить, что вид функции P—P(t) (в интеграле взято Р(т), обозначенное РД является практически произвольным, функция Р может быть непрерывной и разрывной, может иметь разрывы (скачки). Допустимы также мгновенные импульсы силы, которые трактуются как действие бесконечно большой силы .Р->оо в течение бесконечно малого промежутка времени т->0, причем произведение Pdx имеет конечное значение *. Отсюда ясно большое практическое значение решения в форме (м) и (м') для изучения вынужденных колебаний.
На основании отмеченной аналогии записываем решение уравнений сжатой балки в виде, соответствующем (р) и (р').
Уравнение моментов сжатой балки
Мх—Мй cos fix-]-— sin рл-— f р* sin р (х —;) di. (2. 11)
о
Уравнение поперечных сил
'Qx —“.M0₽sinpx-{-Q0cospx — j /»jcos^(x —S) di. (2. 11') о
* С математической точки зрения такое расширенное толкование подынтегральной функции связано с понятием интеграла Стилтьеса. Вообще же интеграл рассматриваемого вида носит название интеграла Дюамеля.
32
Здесь обозначено: £ —вспомогательная абсцисса, аналогичная т в уравнениях (р), (р'); 0<T<x; где ^ — начальная или
температурная кривизна от неравномерного по высоте нагрева балки в сечении В.
Уравнение прогибов
X
vx— cos sin Вх—— S &* sin 8 (х-Д) dt. (2. 12)
о
Уравнение углов поворота
=s — -рорsin px-ф %cos рл — j ftjcosp (х —(2.12') о
Здесь &*
м9
~ЕЛ
Но если подразумевать под v не полный про-
гиб, а упругий прогиб v^n, то
5 EI 1 EI
— см. уравнение (2. 1').
Напомним, что. нулем в верхнем индексе отмечены момент от вертикальных сил, начальный прогиб и начальная кривизна. Нуль в нижнем индексе, как здесь принято, отмечает аргумент (абсциссу), в данном случае — начало отсчета.
Использование решения в форме (2.11) — (2.12) имеет часто определенные преимущества. Во-первых, установлен механический смысл произвольных постоянных как величин начальных параметров или величин, пропорциональных начальным параметрам, что облегчает постановку граничных условий. Во-вторых, частное решение неоднородного уравнения, входящее в общее решение, выражено в виде интеграла с переменным верхним пределом для произвольной нагрузки и наперед заданной деформации, снято ограничение p*=const или ft*=const. Тем самым даны общие уравнения эпюр Мх, Qx, vx, <рж.
Пример. Балка АВ с пролетом /, шарнирно опертая по концам, нагружена продольной сжимающей силой N, опорными момёнта-ми МА и Мв, равномерно распределенной нагрузкой на всем пролете, и сосредоточенной силой Р на расстоянии а от левой опоры. Определим изгибающий момент под силой Р. Рекомендуем читателю сделать соответствующий рисунок.
Поместим начало на левом конце. Тогда начальный параметр Мо заранее известен: Мп = МА. Другой начальный параметр Qo определим из условия на правом конце, Мг =МВ. Выражаем это условие при помощи строки (2. 11), принимая p*=p°=const. Для
S3
учета сосредоточенной силы Р полагаем pt dt = P, Ъ,=а, а знак интеграла отбрасываем. Граничное условие запишется в виде
z
МВ—МА cos U — sin р/ — f sin р (/ — £) —— sin р (/— а).
о
Выполняя интегрирование, находим
(Мв - МА cos ₽/) (1 - cos р/)-|-Р sin ₽(/-«)].
Для Qo получается конечное значение, если sin р/ =/= 0. Равенство sin.pZ = O отвечает случаю, когда N~N3.
Изгибающий момент в сечении а
Мп = МА cos ра 4- — sin Ва — — а Л Г р Г ^2
(1 — cos ра).
При МА = Мв=р=0 имеем Ма
— s‘n s<n Р — а) ₽ sin ₽/
Статическая модель сжатой балки
Рассмотрим плоский кривой брус с круговой осью, нагруженный перпендикулярно плоскости кривизны распределенной нагрузкой интенсивностью р кг)см (фиг. 6, снизу). Обозначим попе
речную силу в сечении, принятом за начальное, через Qo. Вектор Qo изображен кружком с точкой. Изгибающий момент в начальном сечении обозначим Л1° и изобразим по правилам механи-
34
ки вектором с волнистой стрелкой, направленным вдоль начального радиуса. Нагрузка изображена системой кружков с крестиками.
Положение сечений определяем дуговой координатой х.
Изгибающий момент в сечении х равен
—7W0cosy~4-Qorsin ~ — ^Arsin (с)
6
Здесь г — радиус круговой оси бруса.
Если принять
г=Т=|/д <т)
то уравнение (с) обращается в (2. 11).
Таким образом, брус с круговой осью можно рассматривать как модель сжатой б'алки в том смысле, что при тождественной нагрузке, изгибающие моменты модели и балки одинаковы. Это заключение относится не только к силам и силовой распределенной нагрузке, но и к парам и моментной нагрузке.
Использование круговой модели сообщает определению изгибающих моментов сжатой балки большую наглядность.
Предлагаем в качестве упражнения рассмотреть решение предыдущего буквенного примера с помощью модели, а также показать, что при р/=л, т. е. когда модель обращается в полуокружность, усилия приобретают- бесконечные значения. Чему равна сила N при р/=л?
Развернутые уравнения эпюр перемещений и усилий сжатой балки
Для определения величины v, ср, М, Q и расчета статически неопределимых сжатых балок при произвольной нагрузке целесообразно пользоваться развернутыми уравнениями перемещений и усилий — уравнениями эпюр.
Предположим сначала, что на участке балки от сечения О до сечения х нагрузка и другие местные деформирующие факторы (-б0) отсутствуют. Очевидно, эпюра А1° на этом участке будет прямолинейной и может быть выражена уравнением
+ (2.13)
Подставим в уравнение (2. 12) вместо -0-* величину NT^jEI, выраженную через (2. 13). В результате получим уравнение эпюры vx на незагруженном участке. Если на участке О—х нагрузка и другие факторы имеются, то к правой части полученного уравнения следует добавить дополнительное слагаемое, в общем случае довольно сложное, которое мы пока обозначим через [oj. Проделав
35
интегрирование, упрощая постоянные множитель при помощи равенства fi2=N/EJ и вынося АД и 0° за скобки, получим
1^=-Поcos ₽х Ц-~- sin ^х —Л4д-^- (1 — cos рх) —
-Qo-^r^-siHW + K]- (2.14)
Дифференцируя эту строку по х, получаем
dv г '0 й
—^ = <РЛ= — ^opsinpA -t-TocosH-Mo-^sinpx —
-Pg~(l--cosPxHW- (2.14')
Аналогично поступаем с (2.11), подставив в это уравнение Af0—Л/о-ДМ/д. С другой стороны, учитывая, что при сделанных допущениях цуп отличается от v на линейную функцию Д-Дс^х, можно найти Мх дифференцированием:
х dx*
Mr=t’0Wcos₽x + ?0-^sinpx-|-MoCOs₽x-|-
+ QoASinpx+[Mj. (2,14*)
Дифференцируем еще раз:
Qx — — v^Nfi sin —)-*^Pg^\^ cos px —/Ио p sin px-(-
+ Q®cospx + [QJ. (2. 14'")
Мы получили уравнения эпюр перемещений и усилий. Множители, стоящие при начальных параметрах, называются функциями влияния (иначе — функциональными плечами),
В написанном выше простейшем уравнении эпюры моментов от вертикальных нагрузок на незагруженном участке—(2.13) — функциями влияния являются постоянное число 1 и плечо х В уравнениях (2. 14) — (2. 14"') в эти функции входят синусы и косинусы приведенных (безразмерных) величин fix.
Функции влияния начальных параметров на те перемещения или усилия, к которым принадлежит и сам начальный параметр, называются главными. В данном случае все четыре главные функции влияния равны cos fix. Главные функции влияния ’ при х=0 обращаются в единицу.
Перейдем к составлению готовых формул для грузовых и деформационных членов, взятых в квадратные скобки. Эту операцию будем называть развертыванием грузовых чле-н о в.
•36
Начнем-с выяснения действия сосредоточенных факторов или импульсов. К ним прежде всего принадлежат сосредоточенные силы Р и сосредоточенные моменты L. Силу Р можно рассматривать как наперед заданный скачок в эпюре Q0, численно равный —Р, или такой же величины скачок в эпюре Q. Сосредоточенный момент — это наперед заданный скачок в эпюре М°, численно равный -[L или такой же скачок в эпюре М. Напомним, что сила Р
Фиг. 7.
положительна, если она, как и распределенная нагрузка р, направлена сверху вниз. Момент L условимся считать положительным, если он вращает по часовой стрелке. Помимо привычных силовых импульсов Р и L, целесообразно ввести в рассмотрение два деформационных импульса (иначе — дислокации) — малый излом оси 0 и малый сдвиг Г (фиг. 7). Положительный излом 0 создает выпуклость снизу и отрицательный скачок в эпюре ср, положительный сдвиг Г создает положительный скачок в эпюре V.
На фиг. 7 показаны импульсы всех четырех типов:
Р=-Дф; £=Д/И; 0=-Д?; Г-ДТ>. (2.15)
Существенное свойство любого линейного дифференциального уравнения балки состоит в том, что действие начальных параметров и импульсов подчинено принципу сложения. Это значит, что изучая действие какого-либо импульса, можно предварительно считать начальные параметры равными нулю. В таком случае каждый отдельно взятый импульс выступает в качестве соответствующего начального параметра, но только не в нулевом сечении, а в том сечении, где он приложен. Поэтому, например, импульс Г
37
в сечении g (0<g<x) влияет на ординаты эпюр в сечении х точно так же, как и начальный параметр Vq, с той разницей, что вместо аргумента (плеча) х следует взять аргумент (плечо) х—g.
Сказанное дает возможность записать развернутые выражения грузовых членов для случая сосредоточенных воздействий Г, &, L, Р:
[iJ=rcosp(x-Sr)-jSinp(x-S())-Zy [1 -cosp(x-SJ] +
+ [? (х - SP) - sin р (х - SP) ], (2- 16)
[<pj = — гр sin р (х — Sr) — 0 cos р (х — Se) — Z ~ sin р (х — SJ +
+ ^y [l~cosp(x-SP)],
(2. 16')
[MJ = ПУ cos (р - Sr) - 0 у sin р (х - So) +
J-Zcos Р(х — S£) — Ру sinp (х — SP), (2. 16")
[QJ = — ГТУр sin p (x~Sr) -~QNcos p (x — So) —
— Zp sin p (x —SJ — Pcos p (x —SP). (2. 16'")
Формула (2.14) в сочетании с формулой (2.16) иллюстрируется фиг. 8. Формулы. (2. 16) — (2. 16'") даны для одного импульса каждого из четырех типов. В конкретных задачах некоторые импульсы могут отсутствовать, других может быть несколько. Тогда перед слагаемыми в (2. 16) — (2. 16'") появятся знаки сумм. Важно отметить, что в суммах учитываются только те импульсы, которые приложены между начальным сечением О и исследуемым сечением х.
Соответственно четырем типам импульсов Г, 0, L, Р рассматриваются четыре типа распределенных воздействий: 1) распределенный сдвиг интенсивностью см/см (относительный сдвиг), 2) распределенный излом оси 0° IIсм (искривление), 3) распределенная моментная нагрузка т° кгсм/см, 4) распределенная силовая поперечная нагрузка р° кг/см. Речь идет от активных наперед заданных факторах, потому они отмечены нулем в верхнем индексе.
Воздействие распределенных факторов рассматривается как суммарное воздействие элементарных импульсов Y O'Y/g, m°rfg, p°dg. Соответственно формула .(2. 16) принимает вид
[‘г’л-]== Ji°cos р (х—-S) ^S — у sin Р (х — S) di, — о о
j^Jm.°[l — cosp (x — S)]dS + -y-Jp°[P(x — S) — sinp(x — S)]^S. о о
38
Аналогично записываются и грузовые члены [<px], [Мж], [QJ.
Как уже отмечалось, в авиационных конструкциях приходится иметь дело почти исключительно с равномерно распределенной нагрузкой p° = const и с равномерно распределенным искривлением 6° = const. Последнее отвечает нагреву с постоянной разностью температур нижнего и верхнего волокон, а также начальной погиби по параболе второй степени Для балки на двух опорах
параболическая погибь выражается уравнением
-z)0.= —j-x(/ —х).
Здесь -цОр —стрелка начального прогиба по середине пролета. В этом случае
а<1_ dW 8< dX> /2
Выполняя интегрирование в строке [аж] и ей аналогичных для воздействий p°=const и б10 = const, находим
•/V Z р J г
sinpx, (у')
[ЛЦ = — р° ~ (1 — COS рх) — а0 ~ ( 1 — cos рх), (у")
р* р*
[Q J= —sinBx — ft0^ sin Вх. (у” )
* Напомним, что пользуемся приближенным выражением кривизны, основанным на допущении ds=dx. Поэтому постоянному искривлению отвечает не окружность, а парабола.
39
Когда равномерно распределенная нагрузка расположена на отрезке от £ = с до %, — d (фиг. 9), то грузовые члены могут быть получены по тем же формулам (у) — (у"'), причем с ними необходимо проделать операции, коротко записываемые так:
К]=№35; t Ы=[?е
IQJHQJ.^-
Это означает, что в правые части выражений (у) — (у'") следует вместо х подставить сначала (х—с), затем (х—d) и вычесть из первого результата второй.
Фиг. 9.
Например:
Ы.^.d)2.-|__L [COS р (л - с) - cos р (х - с?)]} +
[cos р (х — с) — cos р (х — d)].
Эти же формулы применяются при c<x<d.
Если х<с, то [fJ = [?J==[MJ = [QJ=0.
Другая форма развернутых уравнений для сжатой балки
Подставляя в уравнения (2. 14) — (2. 14'") Л4° =Л40—Nv&; Q° = Qo—Wo и делая приведение, получим
^х=^о + ?о* ~ ^о (1 ~ cos И ~ Qo ~ SM*) + Ы> (2. 17)
<Рх = ?о-Л40^-sinpx -Q0^(l-cospx) + [?J. (2. 17')
По-прежнему —см. (2.14"), (2.14'") —
Мх — 2W0cospx 'hQo^y sin Px-J-fM,.] (2.17")
Qx — — AfoPsinpx 4-QqCOs Px4-[Qx]- (2. 17”)
Сопоставляя эту форму решения с (2. 14) — (2.14'"), видим существенное отличие в функциях влияния, стоящих множителями
40
при начальных параметрах и ф0, в то время как функции влияния при ЛГо и Qo остались такими же, как и при и Q°. Это приводит к различию в процессе развертывания грузовых членов на действие внешних сосредоточенных факторов (импульсов) 0, Г. Следует учитывать, что в связи с наличием продольной силы N излом 0 и сдвиг Г сопровождаются силой P = N® и соответственно моментом. L = Nr и эти импульсы следует учитывать особо. Но в результате формулы развертывания оказываются тождественными с (2. 16) —(2. 16'").
Важно также отметить, что форма решения (2. 17) — (2. 17'") может быть получена путем интегрирования дифференциального уравнения четвертого, порядка:
(2.18) dxA EI dx2
получаемого двукратным дифференцированием уравнения (2. 1), взятого без правой части.
Общий интеграл однородного уравнения
vx — Cj cosPx4~C2sinpx + C3x + C4 (2.,19)
преобразуется так, что в качестве постоянных интегрирования выступают величины начальных параметров v0, <р0, ЛТ0, Qo, что и приводит к форме (2. 17). Процесс преобразования для уравнения четвертого порядка самого общего вида подробно описан в 1.3.
Развернутые уравнения для растянутой балки
Для получения общего интеграла дифференциальных уравнений (2.1) и (2. 2) при знаке «—» в левой части в форме, аналогичной (2.11) — (2. 12), достаточно заменить тригонометрические функции на гиперболические:
= 7Wochax -[
.Г
— sh ах—- Сщ sh а (х—$) dl, a а ,) 5
О
X
= Q = Моа sh ах Qochax — f р, ch а (х —5) dt, dx J s
о
(2. 20)
(2. 20')
x м®
<vx = ЦосЬах — shax----------— C—-Sh a (x—c) ^,(2.20")
a a J EI
0
X M
—= -шх sh ax‘ 4-% ch ax ~~ f—-cha(x —(2.20") dx ,) EI
о
41
Развернутые уравнения в форме, аналогичной (2. 14) — (2. 14'"), 'будут
Q°
<VX= 4»ochax Ц- — sh ах+-^(1 —-ch ах) Ц--^.(ах—sh ах) ЦД'нД,
(2.21)
a Q°
•<?_,.= <ноа sh ах Ц- <pochax —- /Ио-^-shax -ф ~ (1 — ch ах) -ф [<рж],
(2. 21')
N О Qo
Мх= — цф/сЬах + <р0— shax 4- ЛфсЬах -j--------зЬах-ф[Лф],
а а
(2.21")
•Qx— —‘Ид./УазЬ ах — ^0Л^сЬах-ф Л/oashax -ф Q° ch ax~HQJ.
(2. 2Г")
Развернутые уравнения в форме, аналогичной (2. 17) — (2. 17"'), будут
Дк==®о + !Рол: + фф' О — ch ах)-ф—-(ах —shax) ф [фх], (2. 22)
<Рх:= ?о~ Ч — shax + -^(l-chax) + [?J, (2.22'
MQ ch ax -j—— sh ax a + ВД,(2. 22"
Qx= MQu. sh ax —Qg ch ccjc
(2.22”)
Развертывание грузовых членов в обоих случаях выполняется по правилам, подробно изложенным выше при • выводе формул (2. 16)—(2.16'"). Дадим соответствующие формулы, полагая р° = const, 6-°=const,
[^1-- p° Г -^2 j L(i У [ 2 a2 ' — ch ax) + — (1-chax), a2 (Ф)
[<Px] — - - (ax — Sh ax) Na 9° , Sh ax, a (Ф')
(1 — ch ax) fl" — 8° — (1 —ch ax), a2 (Ф")
[QJ = —— sh ax a — fto 2У_ sh ax. a (Ф'")
В случае частичной равномерно распределенной нагрузки применяются операции [nJ = [®е]ФД и т- Л-
42
Практические указания. Определение критической силы. Примеры применения развернутых уравнений
Исчерпывающий статический расчет балки сводится к построению четырех эпюр vx, <рж, Мх, Qx. Практически бывает достаточно определить только небольшое число усилий и перемещений в определенных сечениях.
Расчет при помощи уравнений (2. 14) или (2. 17) для сжатой и (2. 21) или (2. 22) для растянутой балки начинается с выбора начала отсчета и определения четырех начальных параметров — перемещений и усилий в сечении, принятом за начальное.
Начало выбирают в сечении, в котором наибольшее число из четырех величин v0, <ро, Мо, Qo известно заранее или определяется из условий равновесия.
Для однопролетных балок начало берут, как правило, на левом конце. Неизвестный начальный параметр (или начальные параметры) определяют из условий на другом конце.
В случае балки с симметричными граничными условиями целесообразно взять начало по середине пролета и заменить нагрузку симметричной и антисимметричной силовыми группами. Это в первую очередь относится к балкам с жестко или упруго защемленными концами. При симметричной нагрузке имеем Qo=<po = 0, при антисимметричной — vo = M(,=O.
При статически неопределимом опирании однопролетных балок процесс определения начальных параметров по характеру операций не отличается от случая статической определимости. При многопролетной балке появляются дополнительные неизвестные в виде реакций промежуточных опор, изгибающих моментов над опорами и т. и. Для составления дополнительных уравнений используются снова уравнения (2. 14) и (2. 17). То же следует сказать о балках с промежуточными шарнирами, в том числе статически определимых. Дополнительными неизвестными здесь являются углы взаимного поворота в шарнирах.
Во всех наших выводах внешняя продольная сила N, приложенная к торцу балки, считается действующей центрально вдоль недеформированной оси балки, которая принимается за ось абсцисс.
Продольная (нормальная) сила N в поперечных сечениях деформированной балки отождествляется по величине с внешней продольной силой, так как принимается ds=dx, cos<p=l. По той же причине при составлении уравнений моментов полная поперечная сила Q, как и поперечная сила Q0, считаются перпендикулярными к недеформированной оси (вертикальными).
Если внешняя сила, параллельная недеформированной оси (условно горизонтальная) приложена с эксцентриситетом е, то она переносится на ось оалки с добавлением момента L=±Ne. Можно также рассматривать эксцентриситет как начальную ординату эпюры начального прогиба vQ, совместив ось абсцисс с линией действия силы N.
43
Если внешняя сила 2V приложена к свободному концу консоли и перемещается поступательно вместе с концом, то момент в защемлении консоли заранее неизвестен и определяется из условия, что на свободном конце момент равен нулю или наперед заданной величине. Последнее имеет место при приложении силы jV к торцу консоли с эксцентриситетом или при заданном моменте на торце консоли.
Учитывая эти замечания, обычно нетрудно составить систему линейных уравнений, из которых получаются начальные и -граничные параметры (реакции промежуточных опор и т. п.).
В случае сжатия эта система уравнений имеет смысл только, при условии, что сила 2V значительно меньше NKV, так как при jV=jVkp, как мы уже знаем, для перемещений и усилий получаются бесконечные значения.
Величина NKP получается из соотношения, выражающего, что знаменатель буквенной формулы для одного из неизвестных начальных параметров равен нулю.
Если имеется только один неизвестный начальный параметр, то интересующее нас соотношение получаем просто, приравнивая нулю коэффициент при начальном параметре в том единственном уравнении, выражающем некоторое граничное условие, из. которого этот неизвестный начальный параметр может быть определен.
При нескольких начальных параметрах и, следовательно, нескольких граничных условиях, выражаемых уравнениями, нужно приравнять нулю детерминант из коэффициентов системы уравнений. Практически, однако, путем последовательного исключения неизвестных составляют формулу для последнего начального параметра и приравнивают знаменатель этой формулы нулю.
Таким образом получаем уравнение потери устойчивости прямолинейной формы в виде некоторого тригонометрического соот-
/" N
ношения с неизвестной величиной Р = ]/ —под знаком тригоно-у EI
метрических функций — часто в комбинации с линейной функцией. Подобные уравнения называются трансцендентными. Они имеют бесконечное количество корней (Bi, 02, Рз, --, из которых практический интерес представляет наименьший ненулевой корень, дающий критическое значение
minTVKp = E7Bmin.
Простейшим примером является соответствующее уравнение в задаче Эйлера для стержня, шарнирно опертого по концам:
Откуда
sinpZ = O или sin
EI
Чр
т?Е1
Р
44
Это один из немногих случаен элементарного решения трансцендентного уравнения потери устойчивости прямолинейной формы сжатого стержня. Если стержень оперт па одном конце шарнирно, а на другом жестко защемлен, то соответствующее уравнение будет (см. ниже пример 3)
jJZ = tg fZ.
Подобные уравнения решаются подбором при помощи тригонометрических функций либо графически. В данном аргумент р/ = х получается как абсцисса точки пересечения прямой у = х и тангенсоиды y~tgx. Это дает
таблиц случае
4,49.
2п?£/
/2
на
в)
V
Фиг. 10.
л==4,49; ₽Z = 4,49;
/2
^кр
Пример 1. Стойка несет свободном конце груз и нагружена поперечной сосредоточенной силой на расстоянии а от защемленного конца. Чтобы не изменять направления координатных осей в расчетных формулах, на фиг. 10, а стойка повернута в горизонтальное положение. Определим прогиб свободного конца. Начало поместим на левом конце. Тогда фо=О; Qo = P. Единственное неизвестное— начальный параметр /Ио. Определим его, воспользовавшись условием на правом конце Л1; = 0. При помощи равенства (2. 17") записываем
Отсюда
Л40 cos ₽Z + — sin pZ —— sin = 0.
>И0= —(sin — sin fZ). p COS p/
Имея Mv, можно определить vt при помощи равенства (2. 17). Но проще воспользоваться равенством, вытекающим из условия равновесия консоли:
45
откуда
Л10- Mqq
Vl~ N
Здесь, очевидно,
М°=-Ра.
Критическое значение сжимающей силы получаем из простейшего трансцендентного уравнения cos |3/ = 0, откуда легко находим общеизвестную величину
N
КР 4/2
Пример 2. Сжатая балка с консолью (фиг. 10,6). Начало возьмем на левом конце. Имеем Уо = О; Л1о=О; Qo-Л 0; сро-^О. В данном случае можно определить Qo независимо от ср0, используя уравнения равновесия и опять равенство (2. 17).
Полная поперечная сила Qo равна полной реакции левой опоры. Полная реакция правой опоры равна Р—-Qo. Выражаем условие Л'1/_|_с=0 при помощи (2. 17):
-у- Sin Р (Z с) ~ sin Рс-------у Sin Р& = 0.
Отсюда
__ P(sinpc— sin pi)
0 sin p (Z + c) — sin pc
Имея Qo, можно найти <p0 и vt из очевидных соотношений: Q0-Q° + 2V%; A^;=(Q°-QO)Z,
где Q° =----— .
Значение jVkp найдем при помощи трансцендентного уравнения: sin Ркр (Z-|-c) — sin ркрс—0.
Графическое решение этого уравнения сводится к нахождению абсциссы х точки пересечения двух синусоид с общим началом и различной длиной полуволны — соответственно с и 1+с.
0. пх . т.х
_y = sin— ; 2) у = sin ------.
с 14- с
Здесь
Ркр (Z + С) с X —----------- .
Следовательно, найдя х, получим
46
Пример. 3. Сжатая балка с одним защемленным и другим шарнирно опертым концом. Неизвестные начальные параметры Мо и Qo найдем из условий на правом конце щ=0, Л1г=0 (фиг. 10, в):
1) =
2) M^--Q^-P^=0.
Исключая из этих двух уравнений Мо, найдем
_ Р (pi cos ₽/— sin рб)
0 р/cos р/ — sin pZ
Затем из второго уравнения получим
ypj _ Р sin $b sin !il — sjn 36
°“ {Й pZ cos pZ — sin р/
Критическое значение параметра найдем из трансцендентного уравнения
Mcos M~sin М=о-иначе
M=W-
Пример 4. В качестве более сложного примера (фиг. 11) рассмотрим двухпролетную неразрезную балку со средней упруго оседающей опорой с отпорностыо х кг/см. Отпорпостыо опоры называется ее реакция, соответствующая осадке на 1 см. Если прогиб /над опорой и одновременно осадка опоры равна щ, то реакция опоры, эквивалентная сосредоточенной силе в сечении 1 , равна
Р — — Х'О].
Начало поместим на левом конце. Неизвестными начальными параметрами являются ср0 и Qo. Кроме того, в число неизвестных входит также граничный параметр vt. Для определения неизвестных составляются уравнения 1) М2 = 0, 2) р2=0. Сюда надо
47
присоединить третье уравнение, выражающее щ через фо> Qo. Итак:
1) /И2=0,
Q SM(ZI + Z2) р Sinp(b| +/9) . sin p/? p sin^2_g.
Vo p 1 3 ^ 1 p 2 p '
2) ^ = 0
?o(Л+ ^) ~ Qo^7 IP (Л + ^)~ sin ₽(/, + /,)]-p/V
- (^2 - Sin p/2) + P1 I P (6! + Q - Sin P (Й1 + ] +
+ ^2^-(₽62-Sin₽&2) = °:
3) = 7o/, - Qo (p/, - sin ₽/,) + Pt - sin ₽£,).
Решив совместно полученные уравнения, найдем неизвестные
•То, Qo,
§ 1.3. СЖАТАЯ И РАСТЯНУТАЯ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
Сплошным упругим основанием называется конструкция, поддерживающая балку по всей длине, или на отдельных участках •большего или меньшего протяжения, создающая в отличие от отдельных опор распределенную поперечную реакцию. При этом погонная интенсивность реакции в каждом сечении пропорциональна прогибу (осадке) в этом сечении.
Обозначим через рРеакт интенсивность реакции основания. Тогда
Л>еакт--= (3-0
Здесь k — так называемая отпорность упругого основания, или погонная интенсивность реакции, соответствующая осадке в 1 см. Отпорность измеряется в кг!см2.
Примером балки на упругом основании, в полном объеме отвечающей расчетным предпосылкам, является плавающая балка прямоугольного сечения. В этом случае на основании закона Архимеда
k — \b кг)см2. (3- 2)
.Здесь f — удельный вес жидкости (воды), b — ширина сечения балки.
Часто в качестве сплошного упругого основания рассматривают систему сближенных поперечных балок, на которую оперта
48
исследуемая балка. Упругое основание представляет собой расчетную модель большого числа отдельных упругих опор.
Пусть 6 — податливость одной поперечной балки или прогиб ее от силы 1 кг, приложенной непосредственно к ней, а — расстояние между отдельными поперечными балками. Тогда
Л=—- кг/см2. Za
(3.3)
Помимо упругого основания, балка может иметь также отдельные жесткие или упругие опоры, а также защемления. На фиг. 12 показана сжатая балка на упругом основании, шарнирно опертая по концам на жесткие опоры.
Фиг. 12.
Балка несет поперечную нагрузку и может иметь начальную (производственную) погибь, к которой может быть отнесено также температурное искривление, подсчитанное для основной системы, т. е. без учета продольной силы, упругого основания и лишних неизвестных.
Наиболее важны случаи, когда упругое основание реагирует только на упругую и температурную части полного прогиба балки. Примером может служить основание, собираемое без натяга, после того как установлена предварительно искривленная балка.
Иногда рассматриваются также другие виды упругих оснований, например, создающие распределенную моментную реакцию, пропорциональную углу поворота сечения балки или создающие продольную распределенную реакцию (тангенциальные силы), пропорциональную продольным перемещениям сечений. Подобные основания объединяются общим названием упругой среды.
Вывод дифференциальных уравнений
В основу вывода положим дифференциальное уравнение упругого прогиба сжатой и растянутой балок без упругого основания (2.3). Достаточно в правой части уравнения (2.3) заменить р° на р°—kvvn . После переноса неизвестного члена в левую часть получим
й?4ууп . W Д2^УП k ро ± М)0
----------------------------^уп _. >--±------
dx* Е/ dx2 1 EI EI
(3 4)
49
Это уравнение и отвечает случаю, когда начальная погиб! балки непосредственно на реакцию основания не влияет, хотя косвенное влияние (через моменты от продольной силы) и оказывает. Если считать, что реакция основания пропорциональна полному прогибу ц = Р°4-Ууп, то правая часть (3.4) примет вид
(^°-^°±W).
Уравнение для полного прогиба при первой предпосылке получим, подставив в (3.4) значение vy“ = v—v°. После сокращений это дает
d*v , N d2v , k d*v® , po + kvo . ,
dx* ~ El dx’'- 1 El dx* ' El
При второй предпосылке правая часть упрощается: в ней исчезает слагаемое ku®.
Проинтегрировав уравнение для руп, последовательным дифференцированием получаем
Q = (3.5)
dx dx1 dx3
Можно составить и проинтегрировать уравнение непосредственно для изгибающего момента. Продифференцировав (3.4) дважды по х и сделав подстановку в соответствии со второй формулой (3.5), после сокращения получим
(з.б) dx* — El dx* El \dx* dx* )
Структура левой части дифференциальных уравнений для и, цуп , <р, М, Q одинакова. Отличаются уравнения только структурой правой части.
Интегрирование уравнений
Уравнения (3. 4) и (3. 4') запишем обобщенно в виде
T)IV ± 2aV' -ф b*<u = . (3.7)
Здесь введены обозначения
2а2=—; М = —-. (3-8)
El EI
Обозначение р * ясно из формул (3.4) и (3.4х).
Напомним без доказательств, но с некоторыми дополнениями известный из курса высшей математики классический порядок интегрирования подобных уравнений.
Общее решение (иначе — общий интеграл) линейного дифференциального уравнения равно сумме общего решения однородного уравнения (содержащего в данном случае 4 произвольных
50
постоянных) и частного решения неоднородного уравнения, удовлетворяющего произвольным граничным условиям.
Для отыскания общего решения однородного дифференциального уравнения надо составить алгебраическое характеристическое уравнение, заменив производные на г , где п — порядок производной, и определить его корни г,, г2, Гз.-•, '"«•
Всякому вещественному корню г—г' кратности k' соответствует решение вида
ег'хРк’-\ (х),
где —полином степени k'—1 с произвольными коэффи-
циентами.
Всякой паре комплексных сопряженных корней г = а+0г кратности k' соответствует решение вида
eax[Uk’-\ (х) cos рх+ И/у_| (х) sin рх], где U и V — полиномы степени k' — 1 с произвольными^ коэффициентами.
Общее решение есть сумма указанных решений. В случае простых корней полиномы обращаются в произвольные постоянные *.
Для рассматриваемого дифференциального уравнения характеристическое уравнение получается биквадратным:
r4±2a2r2 + &4 = 0. (3.Q)
Для сжатой балки на упругом основании (знак «+») находим
'1.2,з,4i я4 — &4.
Для растянутой балки
(3. Ю)
г1,2,з,4= + «2 .г Va*-b*. (3.-10')
Рассмотрим подробно практически наиболее важный случай, когда &4>а4, что отвечает сравнительно небольшой величине продольной силы В этом случае для обоих вариантов про-
дольной нагрузки балки получаем две пары простых (некратных) сопряженных комплексных корней:
Г l,2,3,4=iacbi₽>
Значения а и р для" сжатой балки (индекс с):
(зло
То же для растянутой балки (индекс р)
(3.11')
♦ В. И. Смирнов, Курс высшей математики, т. II, ГТТИ, 1940, § 41.
4»
51
Отметим, что ар = рс; рр = 9с. Предлагаем самостоятельно проверить формулы (3. И) и (3. 1Г).
Общий интеграл однородного уравнения или уравнение прогибов для незагруженного участка как сжатой, так и растянутой балки имеет один и тот же вид:
y=Cl<?a-rcospx-}-C’2<?“-rsinpA:4_
-\-С3е~ах cos р*-]-С4<?-“х sin $х. (3.12)
Отличие сосредоточено в коэффициентах аир.
Введем обозначения
Хх ~ е™ cos Зх; A'2 = eaxsin рх; )
Х3 = <?-ях cos рх; Х4 = е~ах sin рх. J (3.13)
Решение (3. 12) коротко перепишется так:
с{х} + С2У2+С3Х3+С4Х4. (3.13')
Как видно, четыре функции X представляют собой гармоники с одной и той же длиной волны Л=л/р, но с возрастающей или с затухающей амплитудой. При этом длина волны для растянутой и для сжатой балок оказывается различной: для растянутой она больше, чем для сжатой.
При х— 0, имеем:
Л’1==А'3=1; Xs=X4=0. (3.14)
Формулы дифференцирования для функций X получаются элементарно и легко приводятся к виду
X'\~a.Xi-~^X2,
Х’2=аХ2-]^Х1,
(3. 15)
Аз= —ф-p.¥.|,
Х4 = -аХ4 + $Х3.
Таким образом, первые производные X'. (/=1, 2, 3, 4) представляют собой простейшие линейные комбинации функции X,. Поэтому и старшие производные выражаются через те же функции, что существенно облегчает вычисление М, Q.
Решение в функциях X наиболее удобно при Ь4 для расчета весьма длинных балок, загруженных вблизи середины или на одном конце, когда балку приближенно можно рассматривать как бесконечно длинную. Дело в том, что по мере удаления сечения от области приложения нагрузки перемещения и усилия длинной балки затухают все сильнее и сильнее и на удаленном; конце могут считаться пренебрежимо малыми. Напряженное состояние достаточно длинной балки в области нагрузки практиче-;
52
ски ничем не будет отличаться от напряженного состояния бесконечно длинной балки. А для такой балки условие на бесконечности требует, чтобы решение выражалось только затухающими функциями. Поэтому должно быть С( = С2=0 и решение для незагруженного участка принимает вид
v—C3X3-}-C4X4. (3.16)
Недостаток функций Ль Х2, Х3, Х4 при расчете коротких балок состоит в том, что они не обладают свойствами четности или нечетности (симметрии или антисимметрии относительно начала отсчета абсцисс).
Функции X представляют собой, как известно, линейно независимые частные решения однородного дифференциального уравнения. Линейные комбинации этих функций также представляют собой решения.
Новое решение образуем, беря полусуммы и полуразности функций X] и Х3, Х2 и Х4.
Решение имеет вид
v = DiY^-D.1Y^DJ^DiYi. (3.17)
Здесь
Pj _ ch ал-cos рл; K2 = ch ах-sin fix, lZ3 = sha%-sinpx;: K4 = sh ax-cos fix.
Очевидно, функции У] п Уз — четные, функции У2 и У4— нечетные.
Решение (3.17), (3.18) особенно удобно при расчете симметричных балок. Возьмем начало отсчета по середине пролета балки. При симметричной нагрузке эпюра прогибов также должна быть симметричной. Поэтому O2 = Z)4 = 0. При антисимметричной нагрузке соответственно Di = D3 = 0.
Следовательно, разложив любую нагрузку на симметричные и антисимметричные составляющие, сводим число неизвестных постоянных для каждой из этих нагрузок к двум, вместо четырех.
(3. 19)
(3. 18
Значения функций У при х = 0:
/, = 1; Y2=Y3=Y4 = Q.
Формулы дифференцирования функций У:
Y \ = ^ = aY4-fiY2, иХ
У '2 = ^=аГ3 + рГ1, dx
Y 3=^ = aY2 + fiY4, ах
Г ; = -^- = аГ,-ВУ3. dx 1 г 3 )
(3. 20)
53
Вторая и третья производные функций Y также выражаютс? через две функции Y, но с более сложными коэффициентами. Например,
+ (3. 21'
При детальных расчетах формулы дифференцирования составляются заранее. Для их проверки используется подстановка функций Л, У’ , У?у(/=1, 2, 3, 4) в исходное дифференциальное уравнение (однородное). Результаты подстановок должны быть тождественно равны нулю.
Имея общее решение однородного уравнения можно получить частное решение неоднородного уравнения подбором или в квадратурах при помощи метода вариации произвольных постоянных.
Формулы общего решения однородного уравнения (3. 13х) и (3. 17) удобны в том случае, когда правая часть уравнения (3. 7) представляет собой постоянную или непрерывную функцию абсциссы. При сложной и прерывной нагрузке правая часть R также является сложной функцией абсциссы. Наиболее рациональный путь при сложной нагрузке основан на использовании общего интеграла однородного уравнения, написанного по методу начальных параметров. Развертывание этого решения, выполненное по самым простым правилам, сразу дает решение не только при произвольной непрерывной правой части уравнения (3.7). но и при любых силовых и деформационных воздействиях на балку, например сосредоточенных силах и моментах, начальной погиби по ломаной или ступенчатой линии, воздействии температуры, не отражаемых непосредственно в правой части. Эти преимущества метода, о которых говорилось в § 1.2, требуют, однако, предварительной затраты труда на построение функций Z, заменяющих здесь функции X или Y. Рассмотрим процесс получения функций Z для уравнения четвертого порядка самого общего вида.
Произвольными постоянными по этому методу является прогиб v и три его производные в сечении, принятом за начальное или начальные параметры v0, г1” .
Общее решение однородного уравнения имеет вид
у=^1 + 'Оо^2-]--По^з + г'о ^4- . (3.22)
Учитывая, что
y = M=-EIv"-, Q=-EIv”, (3.23)
можно записать (3. 22) также в виде
+ %Z2- (3. 24)
Для получения функций Z, представляющих собой некоторые линейные комбинации функций Y, поступаем следующим образом. 54
Сначала выписыв нем полное решение в функциях У в виде четырех строк:
vx= ^d^x^d2y2x + d3y^d^x,
dx— ’DxY\x-\- D2Y,X + ^з^зх-ф DiYtx, г. } (З-о)
d^L^Y]x + D2Y2x + D^ -\-D^x,
d"x = г»/!.'"- ф£>2Кх+ d,y;x-\-dj\x.
Производные функций Y доля^.чы быть выражеш заранее.
Затем в (3.25) полагаем x=tг>. Это дает сисему четырех линейных алгебраических уравнении ч.относително констант D:
v0 = OtYw-[-D2Y20 + D3Y30 + D4Y40, j Do = D^Yy)-^ D2Y2o-\-&зУзо-{-D4Y40, I
г'о = DiYto-Y YYYw-\-D3Yzo-^-DtYiO'
Do =DiY\o-\-D2Y2o-\-^^Y3o-\-D4Y4o-
Решение этой системы записывается так:
Dx = Dod1 -|- v’od\ -ф 1 -|- of 1 , ] D2 — v0d2 да/2 ф D0d2 D0d2 , I
D3 — Dod3 фvod’3-p D0d3-va d3,
D4 D3d4 4- ш/4 4- 1/0^4 4- Do d4 .
Г(3. 25')
(3. 25")
Шестнадцать множителей d\ носят название чисел влияния или коэффициентов обратной матрицы уравнений (3.25').
Числа влияния получаются путем четырехкратного решения системы уравнений (3.25') при следующих комбинациях значений свободных членов: 1) По=1; н0 = ^о=т/” =0; 2) v0 = l; Oo = ^q=: = -ц”=0; 3) р,; = 1; vo=v’=Vo=O; 4) < = 1; vo=v3-d\ -0.
Эта трудоемкая в общем случае операция чрезвычайно облегчается для рассматриваемого нами уравнения (3.7) благодаря тому, что многие коэффициенты системы (3. 25') равны нулю и отдельные уравнения содержат не более двух неизвестных. Например, первое уравнение, учитывая, что Ую=1, У2о = Узо = Кю==0 сразу сводится к уравнению с одним неизвестным. В результате и многие числа влияния оказываются равными нулю.
55
Подставляя полученные выражения для D в (3. 25) и вынося затем Уо, о0, v"Q, за скобки, приводим (3. 25) в к следующему виду: „
Vx ~ X 4~ VQZ?X + V0 ^Зх + ^4; г, |
'Vr—'Vn^\x-!lr'^0^2x-\~'^0'Z3x-\~'v0 Z' ,х> ! „ , „ . „ } (3.26)
Vx '= vaZu + 'Уо-^г.г 4~ г'о^з.г+fo ’^.г, |
= vnZ" v + v0Z2x + v’^Zlx 4'[- г'о Z\x, ]
ОчевиднЦзнаки аргумента х в индексах опущены): Z^r^+Г^+У d3+Y4d4, ]
Z4 — Y,di -|- Y2d2 -j- У3(Уз~|- )
Производные функций Z записываются аналогично. Например, вторые производные:
\z\ = Y\d} + Y2d2+Y3d^Y’4d4, |
! (3.26")
............................I
z;=K^+E^ + r;rf:+rX.)
Таким образом, получаем не только выражения функций Z через функции Y, но и формулы дифференцирования. Достаточно, впрочем, выписать формулы для Z], Z2, Z3, Z4, так как процесс дифференцирования элементарен.
Не приводя выкладок, дадим окончательный вид функций Z для рассматриваемого здесь случая растянутой и сжатой балок, когда &4>й4:
:4= -1—_Ly\
4 + Р2 2fi 2 2а У
Мы довольно подробно рассмотрели интегрирование однородного уравнения при £>4>я4. Случай 64<д4 для растянутой балки дает действительные корни характеристического уравнения (3.9), а для сжатой балки — мнимые.
56
Таблица
Виды общего решения однородного дифференциального уравнения yiv± 2а2у ± Ь4у = 0:
1) y=CJXJ(x) + С2Х2 (х) + С3Х3 (х) 4-С4Х4 (х); .. 2) у = D.Y, (х) + D2Y2 (х) + D3Y3 (х) + D4Y4 (х); 3) у = у (0) Z, (х) + у' (0) Z2(х) + у" (0) Z3 (х) + у'" (0) Z4 (х)
№ по пор. Вид уравнения Корпи характеристического уравнения ц [см-1] Л< X} A, x3 z4 у i y2 Y3 Y< Yi Zi
Zi Zy z2 Z3 z,
1 ylv=0 ri = г, = г3 = г4 = 0 Х< — — — — 1 X X2 X3 Yi Zi
Zi Y, Y2 -1- r3 2 3 Tr<
2 yv + 2а2ун=0 ° п « 11 1сЧ 1 li 1 СО Ч Xi — — — — 1 X COS px sin px Yi
Zi Zi Y2 p2 4 Zi
3 /V — 2д2у" = 0 Г, = гг = 0 г3 = — г4 = а а = 2 а xt 1 X eaX e 1 A ch ax sh ax Yi
z, z. y2 -V (Гз — Г1) Q Z -b(K4-aK2) a6 Zi
4 ylv + My==0 7 7 -о + I I е в 1сч II II ~ к е с и 1 1 - 1! II |! С ” н Xl eax cos ax ea v sin ax e ax cos ax e аЛ8|пах ch ax QOS ax ch ax cos ax sh ax Sin aX sh ax cos ax Yi
ZL z. ^(Yi+YJ za Y3 2a2 3 Т7<Г2-Г4) Zi
5 у v — ь«у = 0 Г] = — Г2 = а Г3 == — г4 = «7 а = р = Ь Xi e°x e-ax COS aX sin ax Ch ax sh ax COS ax мН ax Yi
Zi ~ (Zi 4- Y3) 7Т(У'-/з) -Уу*~У2> Zi
6 y’V 4- 2ц2у" + Ь*у = 0 С4 Л сч Г\ = — Г2 =-- а /р Г3 = — Гц = а — гр , / /,2 _ а2 / //2 + Xi eax cos px e,x sin px e rJX cos px e a v sin px chax cos px ch ax sin px sh aX sin Px sh ax COS px Yi
Zi 62 — a2 Г1+~¥ГГз 1 /3f 2 —a2 2p Yi + r\ zap 1 / 1У Yi~ /4) Zi
-У 2 a2 + p2 \ 3a5- + 2a a2 + p2 к 1 2a
7 С4 <3 II сч Л = г3 = -г2 = -г4-=/р ₽ = а Xi — — — — cos px sin px x sin px X cos px Yi
Zi Zi+-~$z3 ^-(3K2-pr4) Y -Y 2p2 \ p 2 Yi) Z-i
8 CS <3 V о» И = — г2 = ; г3 == - г4 = 1?2 р, ,.= У а2 + - Ь* ₽> = У а'2 — \/ а> — № Xi — — — — cos px sin p:x cos p2X sin p2x Yi
Zi 1 /o2 Y^-ftY^ 1 I 5? - V2- 1 Yi - Y3) 1 / - Zi
o2 о 2 (P2 P2 — h _ -- q2 p2 >*2 ~ P| ft-ft J
Продолжение табл. 1
№ по пор. Вид уравнения Кории характеристического уравнения п [см—Ц Х( Xi *2 хй X4 У ^2 Y3 У 1
zt Zi Zz z3 Z4
9 О 11 "Г е-’T4 <3 СМ 'г'* Ь- > а- Г! = — /*2 “ ® ~Ь <3 = — Г4 = а — Z8 Xt Zi Вид функции Xj, Yj, Z> см. строку 6 У zt
10 Ь- = Я2 Г\ = Г3 = ~ Г2 = — = а а ~ а Xi eax 1 > xe e-"x хе лх ch ax sh ax X sh ax I .V ch ax Yi Zi
Zi Г1-уаГ3 ‘ (ЗГ2 -*У) 2a 1 ’Jr,-.-' r,) la- \ a /
11 Ь- < а- О г - ^ = аЬ /3 = — <4 = “2 о. [/д2 — |/а4 _ /;4 а -- л1 — Ijl Xi Z-i e«;.v e-’M- x ch a, X sh a|X ch a>X sh a*X Yi
“7^r3-«22^i) а^ао £ ' 1 °’ — I S’ 1 CM CM 1 W О I G 1 1 ~ 1 * G —2J - 2- (Г, - r3) al -“2 a-’ a2 \ «1 1 \ «2 / Zi
12 >lv +2д2у" - А'у = О г{ — — г2 = а; г3 — - Г4 = ZB а = ]/ 1 л'1 У — а2 fi = V У <Г* У -|- а'2 X, e*x f-a.v cos fix 1 / а'2 + У k a- + '3 sin ch aX sh ax COS $X sin $x Yi
Zi /09 a2 _i_ p2 I7! : а2Г.,) 32 а ’r'*) t Ч2 (Г,- r3) a- -|- ,12 -yy J — V; -a -•J Zi
13 y1V — 2д2у" -- =. 0 = ’ Г-> = а; /-3 = — г4 — /р а = У У cY -j- й4 + Л2 S = У Уа4 '+1У~ а2 Вид функций Xh Yi, Zi см. строку 12
Зак. 425
Случаю а4—Ь4 отвечают двукратные действительные или соответственно мнимые корни.
Вид функций X, Y, Z для различных вариантов однородного дифференциального уравнения четвертого порядка, содержащего только четные производные, приведен в табл. 1. Этими уравнениями в одних случаях описываются статические, в других — динамические задачи. Так, например, изученное выше уравнение сжатой или растянутой балки на упругом основании (см. табл. 1, строки 6 и 9) после замены k на (—- со2) переходит в уравнение форм собственных колебаний весомой балки без упругого основания (см. табл. 1, строки 12 и 13).
Строка 1 таблицы относится к однородному уравнению, описывающему простой изгиб балки. Интегрирование этого уравнения подробно излагается в курсе сопротивления материалов. Напомним известные формулы:
или
vx = С, -|- с. ._х С х2 С4х3 -|- ['Пд.]
, . " X2 . ” Л-3 .
Чг = Vo* + -1’0 — -Но --- 4- ['‘'J
(3. 28}
или
Строки 2 и 3 таблицы относятся к неполным однородным уравнениям четвертого порядка, представляющим собой дважды продифференцированные уравнения второго порядка типа сжатой и растянутой балок. Их общее решение в функциях Z совпадает с полученными выше уравнениями (2. 17) и (2.22).
Строки 4 и 5 относятся к уравнениям балок на упругом основании без продольной силы соответственно с положительной и отрицательной отпорностыо основания /г. Функции Z в первом случае совпадают с точностью до постоянного множителя с так называемыми функциями Пузыревского — Крылова А, В, С, D:
Av = ch ах cos ах
Вх = — (ch ах sin ax-|-sh ах cos ах)
п ’ и
С, = — sh ах Sin ах
х 2
Dx= Y (ch'ax sin ах —sh ах COS ах)
Z, = AX, Z2 = —Bx, а
-4аГ)д В'х = а.Ах
Сх=аВх
В)'х~аСх
z.=~-cx, z4=±dx;
(3. 29)
(3. 30)
(3.31)
57
Второй случай дает общее решение для форм собственных колебаний весомой балки без продольной силы и без упругого основания.
Остальные строки 6—13 относятся к уравнениям сжатых и растянутых балок на упругом основании с положительной и отрицательной отпорностями оснований при различных соотношениях величин и знаков коэффициентов а и Ь, характеризующих продольную силу и отпорность основания. Отметим здесь, что учет деформации сдвига, моментного упругого основания, инерции вращения не изменяют структуры уравнений четвертого порядка с четными производными. Это позволяет считать данное уравнение одним из основных дифференциальных уравнений строительной механики.
Частное решение неоднородного уравнения. Действие нагрузки, начального прогиба и температуры
Частное решение уравнения (3. 7) обозначим через [о].
Пусть р* подчинено закону прямой линии:
p>p* + xtga*. (3.32)
Тогда частное решение можно представить также в виде линейной функции, отличающейся от (3.32) постоянным множителем:
«
1 _ Рх bA k
Рх
EI
(3. 32')
В этом легко убедиться, подставив р* по формуле (3.32) в уравнение (3. 7) и учитывая, что EIb*=k.
Напомним, что частное решение должно удовлетворять дифференциальному уравнению и произвольным граничным условиям.
Предлагаем самостоятельно, не производя вычислений, подобрать такие граничные условия балки на упругом основании без продольной силы и с продольной силой, при которых (3. 32') становится общим решением.
Пусть теперь р* подчинено параболическому закону:
+ ' (3.33)
Частное решение можно получить в виде
^4-2Д^
k ~ £2
(3. 33')
Предлагаем самостоятельно убедиться в этом подстановкой в уравнение (3.7).
Если р* подчинено закону произвольной целой алгебраической функции *
+ + ” (3-34)
58
то частное решение разыскивается в виде
♦
k
(3. 34')
Множители А, В, С... определяются путем подстановки (3.34) в (3.7) и сравнения коэффициентов при одинаковых степенях х.
Если в уравнении (3. 7) Ь* = 0, то при нагрузке, подчиненной закону прямой линии (3. 37), имеем
Рх 1 _________ />*
£? 2а2
(3. 35)
Отсюда после интегрирования
2^
Нёа*-^-+^+^2-
(3. 35')
Постоянные интегрирования Hi и Н2 несущественны и могут быть положены равными нулю.
Получив частное решение, записываем общее решение в виде
=ад, +с2х2+с2х3+cixi+м или
Обратимся к случаю произвольной поперечной нагрузки и наперед заданных деформаций (технологической погиби, температурной кривизны). Для этого используем общее решение однородного уравнения (3.24), дополнив его частным решением в виде [о], которое затем развернем аналогично тому, как это было показано для сжатой балки без упругого основания — см. (2.16). Итак:
^=^nZIX4-<f>0Z2x---2-Z3x--%Z4x4-[^]. (3.36)
Сначала рассматриваем действие импульсов Р и L в произвольных сечениях и ^L. Исходя из уже известной качественной и количественной связи сосредоточенной силы Р с начальным параметром Qo и сосредоточенного момента с начальным параметром Л4о, записываем
= (3.360
Затем рассматриваем действие импульсов I) и Г, учитывая, что продольная сила N порождает также дополнительную (поперечную) силу в месте излома Po=+Nf) и момент Lt=±NI\ Здесь,
59
как и всюду, знак «+» относится к сжимающей силе N, а знак «—» — к растягивающей:
[ЧгЬ = — °^2,.r-'o ±-^-Z4^-5o^,
«г — ~р7 ^З.л—Ег . \ Е1 /
(3.36")
В случае распределенных воздействий р°, т, О0, 7 имеем *
[Чг! = -77~ Р° Ах-6 # — f /Пл23,л-; di — EI J EI J
о о
X
— f i Z^x-(, di. -f-
J \ El /
о
(3.36")
Совершенно аналогично записываем и развертываем решение для других перемещений и усилий:
<9х = + ?оZ'3,x - Z\,x + [ТJ,
Мх~ —EIv0Z}.x — -MyZs'X-j- QgZ.-t.x[ATJ,
Qx~ ~ Zl'VgZi^ — EI'f0Z2,x-\- M0Z3ix-\~QaZitX-\-[Qx].
(3.37)
Начальные параметры v0, <p0, Mo, Qo, как всегда, определяются из граничных условий или условий опирания. Выбирая начало координат в сечении, где два из четырех начальных параметров известны, сводим задачу (для одпопролетной балки) к решению двух алгебраических уравнений с двумя неизвестными.
Важное и интересное, отличие представляет собой двусторонняя бесконечная балка (Ь4>. а4).
Поместим мысленно начало на левом бесконечно удаленном конце. Тогда все начальные параметры от действия нагрузки в конечной области равны нулю. Наряду с этим каждый импульс является источником затухающего возмущения, распространяющегося вправо и влево от импульса.
Сосредоточенная сила Р дает симметричные относительно сечения, где действует Р, эпюры перемещений v и усилий М и антисимметричные эпюры перемещений <р и усилий Q. Характер эпюр
* р и О отмечены нулем, чтобы отличить их от полной нагрузки р = ро—kv М
и полной кривизны О='О0+ .
60
для сжатой балки в районе силы Р показан в первом столбце фиг. 13. Эпюры от действия сосредоточенного момента L даны во втором столбце, от излома 6 —в третьем и от сдвига Г — в четвертом. Эпюры расположены в столбцах в таком порядке, что каждая последующая эпюра является интегральной кривой от предыдущей, причем на первое место поставлена эпюра, соответствующая (по размерности) данному импульсу. Эти первые эпюры будем называть главными. Скачки в главных эпюрах равны импульсу, а ордината в начальном сечении, где приложен импульс, — половине импульса. Положительные ординаты эпюр v и М отложены вниз от оси, положительные ординаты эпюр <р и Q — вверх от оси. Первый и второй столбцы эпюр особых пояснений не требуют. В третьем и четвертом столбцах вверху пунктиром показаны дополнительные нагрузки, сопутствующие импульсам 0 и Г. Пунктиром показан характер эпюр при условии М = 0. В этом случае имеем всего четыре типа эпюр, идентичных с точностью до постоянного множителя эпюрам первого столбца.
Отмстим, что для каждого импульса, приложенного в сечении, принятом за начальное, две из четырех начальных ординат заранее известны: они принадлежат эпюрам первой и третьей строк. Это дает возможность без труда определить произвольные постоянные Ci и С2 в уравнении (3. 16) от действия любого импульса.
Выписываем уравнение эпюры прогибов (3. 16) и дифференцируем его три раза. Находим
v = C3X3 + C4X4,
= С3Хз C4Xi,
(3-38)
М = -Е/С3Хз-Е1С4Х4. ।
Q = - Е1С3X - Е1С4Х\. I
Пусть действует одна сила Р в начальном сечении. Имеем
1) 2) <?о=о.
Полагаем в (3.38) х=0 и записываем:
1) -С3Хз,о~С4Х1о^ 2) C3Y3,o + C4^,o=O. (3.39)
Выражения для Х3 и Х< даются формулами (3. 13). Находя первую и третью производные от них и полагая х = 0, определяем коэффициенты уравнений 1) и 2). Наконец, находим величины С3 и С4. Подстановкой найденных значений в (3.38) завершаем составление уравнений эпюр и, ср, М, Q.
Указанные операции настолько просты, что для читателя нс представит затруднений самостоятельно вывести готовые формулы для С\, Сч, С3, Ci в зависимости от импульсов Р, L, 0, Г.
61
Отметим, что бесконечная балка может быть использована в качестве основной системы при расчете балок любой длины, в том числе и коротких. С этой целью балка сначала рассматривается как продленная в обе стороны до бесконечности и определяются перемещения и усилия в левом и правом сечениях, соответствующих концам действительной балки, противоречащие ее истинным граничным условиям. Таких факторов будет по два с каждого конца.
Затем берем по два неизвестных импульса в этих сечениях и величины их подбираются так, чтобы в итоге были удовлетворены действительные граничные условия. Это требует составления и решения четырех уравнений с четырьмя неизвестными. Разложение нагрузки на симметричную и антисимметричную позволяет свести эти уравнения к двум парам независимых уравнений с двумя неизвестными.
В задачу интегрирования уравнений сложного изгиба балки на упругом основании входит также определение критических сжимающих сил Мф. Этот вопрос, однако, целесообразно рассмотреть в связи с такими методами интегрирования уравнений и решения задач сложного изгиба, при которых граничные условия балки удовлетворяются заранее. К этим методам и перейдем.
§ 1.4. МЕТОД ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ И МЕТОД БУБНОВА—ГАЛ ЕРКИНА
Интегрирование при помощи разложения решения в тригонометрический ряд
Остановимся на важнейшем примере балки, шарнирно опертой по концам. Граничные условия такой балки сводятся к следующим требованиям:
•ц = 0 при х — 0, х = 1, d^v п а /
---=0 при х=0, л — I. dx2
Вторая строка вытекает из условия М = 0 в шарнире.
Изогнутая ось представляет собой плавную кривую с нулевыми ординатами и нулевыми кривизнами по концам. Этим условиям удовлетворяет разложение прогиба в ряд по синусам на интервале, равном пролету балки:
« . их , . . 2т-.л
V=A, sin----Г Л,sin --н
1 I 1 2 I 1
+ Asin-^- + ... = V^sin-^. (4.1)
п = I
Здесь I—.пролет балки, п — число полуволн, укладывающихся в пролете.
63
Упругая линия представляется наложенными друг на друга синусоидами с возрастающим числом полуволн п. При п нечетном имеет симметричные формы эпюры прогибов, при п четном — антисимметричные (фиг. 14).
Задача состоит в разыскании коэффициентов ряда А], А2, А3.., при которых представление (4.1) удовлетворяет изученному выше дифференциальному уравнению
rf4?? , W d-v , k р*
--------1---------------------v —— dx^ ~ EI dx2 1 EI-------------EI
(4- 2)
С этой целью необходимо все члены уравнения (4.2) разложить в ряд по синусам, привести подобные члены, содержащие синусы
Фиг. 14.
одного и того же аргумента, и приравнять коэффициенты приведенных членов нулю.
Напомним, что вычисление коэффициентов ра и жшия задан-нои функции f (х) в ряд a, sin—--(-a2sin-
J У ся следующим образом.
Записывается тождество
. осуществляет-
/ (%) — (at sin ——Р a., sin —— -1-.. J=0.
п~.х , Оое части этого тождества умножаются ;на sin _ -ах и
грируются в пределах от 0 до Г.
I I оо
р , , , . , С 'mtx"', хл • пт-х ,
j /(%) sin—ах — I sm —-— ап sin ~—dx=Q.
О 0 zi = Ij
инте-
64
Учитывая функций
затем свойство ортогональности тригонометрических
Г . пкх . тпх , п
1 sin-----sin------ax = 0
J i /
при m ф п.
получают формулу для коэффициента n-го члена разложения:
i г . п~х j/(x)sin—— dx t
an^~l-------------=-y-j/(x)sin-^afx. (*)
Полагая последовательно n—l, 2, 3..., находят коэффициенты an.
С точки зрения механики последний интеграл выражает работу «погонной нагрузки» f(x) на перемещениях sin Это очень важное представление во многих случаях облегчает разложение функций в тригонометрические ряды.
Возвратимся к нашему уравнению (4.2). Вычислим при помощи (4. 1) вторую и четвертую производные от у:
(4.3)
Видим, что первые три слагаемых в (4. 2) уже разложены в ряд по синусам. Что касается нагрузки р*, то ее необходимо предварительно разложить, определив по указанному правилу коэффициенты разложения.
Пусть
р* = ^ ^„sin-^. (4-4)
1
Внося значения производных и нагрузки в уравнение (4. 2) и делая приведение, получаем
65
Приравнивая нулю множители, заключенные в фигурные скобки, получаем формулу, выражающую коэффициент разложения прогиба Ап через коэффициент разложения нагрузки Вп:
‘4Вп__________
N12 „ Pk
rP Т -----п2 4- —--
т$Е/ тВЕ1
Выражение в скобках представляет собой безразмерную величину, зависящую от номера члена разложения. Обозначим ее Сп. Имея в виду дальнейшие приложения, целесообразно также входящие в Сп величины обозначить следующим образом:
*2Е1 1&EI А
-----= JV q, -----— 1^.
I2 9 k
Здесь Л^э, очевидно, представляет собой эйлерову критическую силу простой балки без упругого основания. Как будет показано ниже, величина 4 представляет собой длину волн бесконечной балки на упругом основании, теряющей устойчивость от сжатия.
Итак,
(4-5)
(4. 6)
С. = п4 -+- ----------= п4 +
" -K.2EI rPEJ
Выражение коэффициентов разложения прогиба в ряд (4. 1) принимает вид
(4.7)
А= ———п~. (4.5')
" тРЕ1 Сп Окончательно для произвольной нагрузки уравнение эпюры прогибов (4. 1) записываются так:
v=
В тВЕ/
V —— sin .
£ 1
(4- 1')
В табл. 2 приведено общее выражение Вп для нескольких типов нагрузки. В случае сосредоточенной силы Р, приложенной в сечеции с абсциссой £, коэффициент Вп вычисляется как умноженная на 2/Z величина работы силы Р на перемещении (прогибе) sin , Заменяя Р на p°dc, и интегрируя Вп в пределах от 0 до /, получают новые значения Вп для случаев сплошной равномерно распределенной нагрузки и нагрузки на участке от %=с до % = d. В случае сосредоточенного момента L коэффициент Вп вычисляется как умноженная па 2/1 работа момента на угле поворота, равном производной от прогиба sin7—.
d . птР. пк n-r.Z
<?_ = — sin - — =-------------------cos-----------.
T" II i
66
В общем случае учета влияния нагрузки и погиби производится разложение функции
р* = ра в- Д/ 8° -j- kv.
Предлагаем в виде упражнения проверить выражения общего члена разложения нагрузки р°.
Ряд для произвольной нагрузки (4.4) сходится обычно довольно медленно и даже может быть расходящимся, но ряд для прогиба (4. 1) сходится быстро и при приближенном решении можно ограничиться небольшим числом членов этого ряда, иногда только одним.
Таблица 2
Разложение нагрузки шарнирно опертой балки в ряд по синусам
Схема нагрузки В„
4 рО пя (d -I- с) -------sin — /гл
' ггк (Ц — с)
21
' 2 пк
— L — cos
I I I
ММпк -z
Важно отметить, что при симметричной нагрузке обращаются в нуль коэффициенты Вп (а значит и Ап} с четным номером. При антисимметричной нагрузке — наоборот, с нечетным номером.
Так как ряды для производных сходятся значительно медленнее, чем ряд для прогиба, то вычисление ординат эпюры М лучше производить, непосредственно суммируя эпюру Л4°, построенную Для простой балки, с эпюрой Я- от действия продольной силы и
эпюрой
v(x—
от реакции упругого основания.
67
Определение критической силы
Критическая сжимающая сила получается из условия, что в отсутствии активной поперечной нагрузки прогибы не равны нулю. Из формулы (4. 5) заключаем, что если коэффициенты разложения нагрузки Вп=0, то коэффициенты разложения прогиба Ап не равны нулю только при условии, что стоящее в знаменателе выражение в скобках, обозначенное Сп, равно нулю.
При нижнем знаке «-)-», соответствующем растягивающей силе, это выражение, состоящее из существенно положительных слагаемых, естественно, не может обратиться в пуль. Пользуясь соответствующим знаку «—» видом выражения Сп в (4.7), записываем, полагая, N=NKP:
Отсюда
^=Ч,,!+(ШЬ <4-8>
Очевидно, что упругое основание увеличивает критическую силу шарнирно опертой балки. Практический интерес представляет наименьшее значение критической силы. Следует найти число п=п0, обращающее в минимум выражение в квадратных скобках, а затем подставить в (4. 8) ближайшее меньшее целое
Приравнивая по правилам определения экстремума производную пулю, получаем уравнение
число п. первую
(4-9)
против-
Отсюда
Это решение имеет смысл, если п0^> 1, т. е. при 1>1к- В ном случае ближайшее меньшее целое число равно нулю и из (4. 8) найдем Л4р=0. Этот вопрос рассмотрим ниже, а сейчас доведем до конца решение, полагая п0>\.
Если окажется, что п0 — целое число, то его и подставим в. (4.8). Получим
ЛГкр=^э.2^= 2/Ш (4.Ю)
При нецелом п0 надо, как указано выше, взять ближайшее меньшее целое число. •
Из приведенных выкладок видно, что введенная формулой (4. 6) величина 4 представляет собой длину полуволны при выпучивании балки на упругом основании при условии, что шарнирные опоры совпадают с узлами изогнутой оси и, следовательно, не оказывают влияния на форму искривления. Можно сказать, что 4 — длина полуволны выпучивания бесконечно длинной сжатой балки на упругом основании.
68
Малое значение /г0< 1 получается при большой величине 4, отвечающей малой величине отпорности k. Приближенное значение критической силы для этого случая получим, положив в (4.7) fe==0, т. е. рассматривая балку на двух опорах без упругого основания; min Л1кр соответствует выпучиванию по одной полуволне (я0=1), что непосредственно дает
TV, N (4.11)
С? X f
Решение дифференциального уравнения сложного изгиба в тригонометрических рядах в случае шарнирно опертой балки дает достаточно быстро и просто ответ на существенные вопросы расчета прочности и устойчивости. Простота в первую очередь связана с ортогональностью тех функций, в которых было представ^ лено решение, в данном случае функции sin —- .
Аналогичное решение при других граничных условиях оказывается более сложным. В общем случае оно основано па разложении в ряд по так называемым фундаментальным функциям, представляющим собой частные решения однородного уравнения, удовлетворяющие граничным условиям.
Метод Бубнова—Галеркина
Сущность метода, являющегося приближенным, проиллюстрируем на примере сжатой балки на упругом основании.
Дифференциальное уравнение изогнутой оси (прогибов, осадок) запишем в виде
г,, d^v , ., dAu El-----\-N----
dxA dx'-
Решение этого уравнения, удовлетворяющее граничным условиям, иначе говоря, частное решение, не содержащее классических произвольных постоянных, ищем в виде ряда (обычно конечного)
т
‘y = A1‘z?1-|-A2T>2 + A3T>3-!- . ... +Amvm= Aivi
Ь 1
(г= 1,2,3, . . . ,/n). (4. 13)
Здесь vi—vi(x) (i=l, 2, 3,... m) так называемые аппроксимирующие (иначе—подходящие) функции, подобранные так, чтобы каждая в отдельности удовлетворяла по возможности всем граничным условиям балки, как геометрическим (относящимся к перемещениям), так и статическим (относящимся к усилиям). Удовлетворение граничным условиям выражается в том, что на границах функции Vi и их производные тождественно равны наперед заданным величинам, например нулю.
Функции V{ в совокупности должны отражать характер изогнутой оси. Так, было бы неправильным ври симметричных гра
4- kv— р* — 0.
(4- 12)
69
ничных условиях и симметричной нагрузке задавать только антисимметричные функции V;, например, синусоиды с четным числом полуволн. Чем больше число аппроксимирующих функций, тем точнее может быть решена задача.
Множители представляют собой неизвестные, подлежащие определению, или коэффициенты разложения решения в ряд по функциям Vi. Множители Л, — это постоянные, назначение которых создать такую линейную комбинацию функций v{, которая в известном смысле была бы наиболее близкой к точному решению уравнения на протяжении между границами, в то время как на самих границах решение, в смысле выполнения заранее известных условий, является совершенно точным.
Рассмотрим последовательность операций в методе Бубнова — Галеркина. Для конкретности положим т = 3, следовательно, прогиб аппроксимируем тремя функциями щ, v2, v3.
Первая операция. Подставляем выражение (4. 13) . в уравнение (4. 12), для чего сначала выразим вторые и четвертые производные функции щ, v2, v3. Результат подстановки имеет вид
д/(А<+д2^+д3^) +
-|-/?(Л^1 + Л2^2 + А^з)-Р*==0. (4.14)
Вторая операция. Умножаем левую часть уравнения (4. 14) на dx и затем на t»i и интегрируем в пределах балки. Результат приравниваем нулю. Это дает первое уравнение, связывающее неизвестные Ль А2, А3.
Уравнение имеет вид
i I i \
Ах[Е1 С •o’v vx dx~\-N f v''vx dx k C vxvx dx ) + \ 6 0 6 '
it I I
Л3( EI § i>3v dx-\-N J v’3vx dx-\-k^ dx \ о о о
t
— j p*vx dx=Q о
или в сокращенной записи
АП1 ^4 2^ i 2 ^3^13 ' Д1р = 0>
где коэффициенты г равны выражениям в скобках.
(4. 15)
(4- 15')
70
Аналогично, умножая уравнение (4. 14) на dx, на v%, интегрируя и приравнивая результат нулю, получаем второе уравнение для определения неизвестных Аь Аг, А3.
Наконец, умножая уравнение (4. 14) па dx, на v3, интегрируя и приравнивая результат нулю, получаем третье уравнение.
Все три уравнения представляются в виде
1) ^)г11 1 Лг1зН
2) H_^2r22“l~^3,’23'i'^2p = 0>
3) АГЗз + ^Зр = 0-
(4- 16)
Коэффициенты двух последних уравнений могут быть получены круговой перестановкой индексов 1, 2, 3 в уравнении (4.15).
Вычисление коэффициентов упрощается, так как при функциях Vi, ^2, Уз, удовлетворяющих одним и тем же граничным условиям, имеет место взаимность коэффициентов
rjk = rkj. (4.17)
Так, путем интегрирования по частям с учетом граничных условий при х = 0 и х=1 легко показать, что, например, ri3 приобретает симметричную форму относительно функций щ и и3 и потому г13=г31. Проделаем преобразование:
i i i
rl3 — EI J •zi}vi’3Jx-(-.V J v\v3dxф-k v,v3dx— О 0 0
— v\v3dx-\-N\ v'3 dx-f~k j vtv3dx —
ooo
i i t
— El £ dx-\-N j v'3<v\ dx-\-k j •нун, dx = r31.
0 0 0
Третья операция—• решение уравнений. Осуществляется наиболее просто, если побочные коэффициенты обращаются в нуль и, следовательно, каждое уравнение содержит только одну неизвестную. Важнейший пример функций, удовлетворяющих для самих функций и их производных условиям ортогональности — тригонометрические функции. Если для случая шарнирно опертых концов задать: u^sin ~, U2=sin-J- и т. д., то решение по методу Бубнова—Галеркина ничем не отличается от рассмотренного выше решения уравнения в тригонометрических рядах, и притом для произвольного числа сохраняемых членов.
Обоснование метода Бубнова — Галеркина для задач сложного изгиба балок состоит в следующем. Левая часть уравнения (4. 12) после умножения на dx представляет собой по своему механическому смыслу сумму проекций на вертикаль внутренних и внешних сил, действующих на элемент, длиной dx. Поскольку балка находится в равновесии, то па основании начала возможных перемещений сумма работ всех сил па всякой системе одно
71
временно возможных бесконечно малых перемещений должна был равна нулю. В качестве возможных перемещений (прогибов) здесь берутся выбранные функции vlt v2, v3,..., линейная комбинация которых рассматривается как приближенная эпюра прогибов.
Операции метода Галеркина имеют целью удовлетворить интегральным условиям равновесия балки в форме начала возможных перемещений, оставляя в стороне дифференциальные условия равновесия, которые могут и не удовлетворяться. Последние удовлетворяются только в том случае, если функции иь v2, v3,„. представляют собой точные частные решения уравнения (4. 12), определенные с точностью до постоянного множителя.
Представление операций метода Бубнова — Галеркина как составление уравнений возможных работ очень важно в случае, когда на балку действуют нс только силы, но и пары (моменты). Их следует умножать не на v{, а на ср, = у'., так как работа момента равна его произведению на угол поворота сечения, а не на прогиб.
Критическую сжимающую силу определяем из тех же уравнений (4. 16), положив свободные члены, зависящие от поперечной нагрузки, равными нулю. Условие того, что неизвестные А2, А3 отличны от нуля (а значит и прогибы v2, v3 отличны от нуля) при нулевых свободных членах состоит, как известно, в обращении в нуль определителя из коэффициентов г:
Hi
Г21
Г31
Ги Г13
Г22 Г33
Г32 Г33
(4. 18)
Коэффициенты г, как видно из (4. 15), содержат слагаемое, пропорциональное M = jVkp. Развертывая определитель третьего порядка и приравнивая его нулю, получаем уравнение третьей степени относительно NKP:
ANsKp-\-BN^-CNKp-\-IJ = & (4.18')
Решая это кубическое уравнение, получаем три значения jVkp. Практический интерес представляет наименьший корень, который и принимается за приближенное значение критической силы.
Если прогиб аппроксимируется одной функцией то условие для определения jVI(P записывается в виде Гц = 0 или
I I i
v\'Jvl dx-\-NKp J v’Vj dx-\-k^ rv2dx = 0. (4. 18")
о oo
Для кривой, обращенной выпуклостью вниз, коэффициент при. М<Р получается отрицательным. Из (4. 18") сразу находим /VKp. Для шарнирно опертой балки без упругого основания, пола-
72
^ая Oi = sin-- , получаем Лгкр=Лгэ. Для балки на упругом основами получаем (4. 8).
При неортогональпых аппроксимирующих функциях порядок определителя и степень уравнения, из которого находят А/’кр, равна числу аппроксимирующих функций.
Точность решения по методу Бубнова — Галеркина зависит от удачного выбора аппроксимирующих функций, а также от их числа. Для суждения о точности решения аппроксимируют неизвестную последовательно одной, двумя, тремя функциями. Малое отличие последующих приближений от предыдущего служит показателем хорошей точности решения по крайней мере при определении наименьшей критической силы. Важное значение имеет также возможность сравнения приближенного и точного решения в частном случае.
Примеры применения метода Бубнова—Галеркина
На фиг. 15 показаны балки с характерными геометрическими условиями на концах: а—шарнирно опертая балка, б — консоль, в— балка, жестко защемленная на левом конце и шарнирно опер-
1
t
тая на правом, г — балка с обоими жестко защемленными концами.
Жесткой (неоседающей) шарнирной опоре отвечает геометрическое условие у = 0 и, если момейтная нагрузка отсутствует,— статическое условие у"=0.
Защемлению отвечают геометрические условия у = 0, у' = 0.
Свободному концу отвечают статические условия у" = 0, v'"=0.
Предлагаем самостоятельно проверить, что следующие выражения для аппроксимирующих функций vn, представляющих прогиб в виде бесконечного ряда
= (4.19)
п= 1
73
удовлетворяют геометрическим и статическим граничным условиям ^алок, представленных на фиг 15.
a) vn=s\ntvtz ,
б) v„ = 1 — cos п — — ,
’ п 2 2
в) ^ = cos(2n-l)-|-y-cos(2n+l)y-у-, .
г) vn — 1 — cos 2п.к ~ ,
•on = cos ПК -у- — COS (n-j-2) к -у- .
(4. 20)
Если взять начало координат по середине пролета, то в качестве аппроксимирующих функций в симметричных случаях можно принять
a) vn = cos (2п -1) *у ,
г) vn = 1 — (—-1 )л cos 2/гк -у- .
(4. 21)
Если взять начало на свободном конце консоли, то возможна •форма
б) 4,= sin(2n-l)-|- -у-.
(4. 22)
Рассмотрим изгиб обыкновенной балки с защемленными концами. Дифференциальное уравнение изгиба EIvw = p проинтегрируем, принимая в соответствии с (4. 21, г)
•п = 2 А р — ( — 0" c0S 2пк Су j .
Подставляя этот ряд в уравнение изгиба, найдем
- 2Ап (~1 >"п*cos 2п~у^р-
Умножаем обе части этого равенства на
р — (— 1)л cos 2 дк у-1dx
и интегрируем в пределах от х = —1/2 до х=4-//2.
74
Учитывая ортогональность тригонометрических функций, получим бесконечную систему уравнений для Ап (лг= 1, 2, 3...), каждое лз которых содержит одну неизвестную и имеет вид
+ ~
16H£Zn4 I я С Г, , , о х I ,
-----------А„ — п 1 — (— 1 )л cos 2 п~ — dx.
Р 2 п J v ’ I J
В случае равномерно распределенной нагрузки на всем пролете правая часть этого равенства равна pl.
Тогда
А п 8пШЕ/
В случае нагрузки сосредоточенной силой Р по середине пролета (при х = 0) правая часть равна Р[1 — (— 1) л]. Отсюда
А Р(1-(-1)я]/3 п 8пЫЕ1
Здесь при четных значениях п имеем Лп=0. При нечетных значениях n = 2k—1 имеем
п 4(2А —
Таким образом, уравнение эпюры прогибов в случае равномерной нагрузки и сосредоточенной силы представится в виде
рР X? 1 Г, / 2/гкх']
•»(„)==—-— V— 1 —(—Ineos---------------- ,
{р) 8тАЕ1 tP [, I J
Р/3 х? 1 Г, । 2 (2Л — 1) лл-'|
•О(Р) =---> ----------- 1 4- COS -3----— .
1 ' 4H£Z (2/? — !)•> L I 1
Найдем прогиб по середине пролета. Если ограничиться первым членом ряда, будем иметь при распределенной нагрузке
/ \ рр О рр va(p)=~-—'2~ ---------
81PEI 396£7
Точное значение равно ; разница составляет 0,3%. В слу-
Р/з "РР
чае сосредоточенной силы v0(P) — ——«----------при точном значе-
2т& EI ¥№Е1
Р13
нии Отметим, что в данном случае точные значения, известные из курса сопротивления материалов, могут быть получены путем суммирования бесконечных рядов.
В качестве другого примера рассмотрим определение критической сжимающей нагрузки шарнирно опертого бруса ступенчато
75
переменного сечения (фиг. 16). Продольная нагрузка состоит и; двух сил: силы N на конце А и силы Т в среднем сечении С.
Дифференциальные уравнения продольного изгиба па участках АС и СВ будут
1) + Nv" = 0; 2) EI2v™ + (2V Т) v" = 0.
Если задаться прогибом (формой выпучивания) в виде суммь: синусоид
^Sin— ’
Фиг. 16.
то коэффициенты Ап будут связаны между собой п однородными уравнениями вида
о
I
ппх \ . ппх , .
--) sin.— ах +
1 / HI
V Л , n~X\ . П~Х , .
4-/V I -> Л„sin------ sin-• dx-\-
1 J \ Цд-2 « i j i 1 0
+<Л'+7'Ш^2л-5!"'т£)5|"5г‘,-'=°-
4'
Ограничимся первым членом разложения. Выполняя дифференцирования и интегрирования и сокращая на Дь получим
-Р
С • 9 КЛ' .1 I Е1? (* . 9 ^х ,
----- sin2 — ах-\-----I sin2 — ах —
В J / ' В J I
° 4-'
Т /
— N J sin2 ‘^-dx— (Л^-|- 7) у2~ J siп2dx—0.
76
Сокращая также на интегралы, каждый из которых равен Z/4, й на *2//2, найдем
= N + ~2~ Т' 23)
Этому соотношению должны удовлетворять силы N и Т, если нагрузка является критической.
Введем обозначения
Тогда (4. 23) приводится к виду
(№ + Лкр (L+lLL. (4. 24)
k 1 'ир I1 (\+k) i
При k='[ = \ получается формула Эйлера. * * *
Мы рассмотрели метод Бубнова — Галеркина в приложении к задачам сложного изгиба и устойчивости балок, сводящихся к линейным обыкновенным дифференциальным уравнениям. Основное значение этот метод имеет, однако, в применении к исследованию пластинок и оболочек и вообще к уравнениям в частных производных и притом, нс только к линейных, но и к нелинейным уравнениям. Широко этот метод применяется также в задачах аэро- и гидродинамики, теории колебаний, чисто физических проблемах. В последние десятилетия наряду с математическим обоснованием метода получили развитие вопросы его сходимости, иначе говоря, точности получаемых этим методом результатов. К сожалению, важный вопрос сходимости удалось решить только для частных случаев, а в общей постановке он в настоящее время еще,остается открытым.
§ 1.5. ЭНЕРГЕТИЧЕСКИЕ (ВАРИАЦИОННЫЕ) МЕТОДЫ ИССЛЕДОВАНИЯ СЛОЖНОГО ИЗГИБА
Основные положения. Применение принципа Лагранжа
Рассматриваемые здесь методы основаны на интегральных принципах механики, в первую очередь, на начале возможных перемещений. Как известно, это начало формулируется следующим образом: система находится в равновесии, если сумма работ всех сил на любой совокупности одновременно возможных бесконечно малых перемещений равна нулю. При вычислении работы сил деформируемой системы следует учесть как работу внешних, так и работу внутренних сил.
Предположим, что балка на упругом основании нагружена поперечной нагрузкой р° = р°(х), продольной нагрузкой q — q(x) и сосредоточенной продольной растягивающей силой №. Предположим также, что ось балки искривляется по закону v = v(x). Оче
77
видно, кривая v(x) будет представлять собой действительную эпюру прогибов при соблюдении двух условий:
1) геометрические условия по концам кривой и(х) должны совпадать с геометрическими условиями рассматриваемой балки, т. е. на опертом конце и = 0, а на защемленном конце о = 0 и о' = 0 и т. д.;
2) каждый малый элемент балки (отрезок балки длиной dx) должен находиться в равновесии под действием приложенной к нему внешней нагрузки и усилий в его торцовых сечениях без участия каких-либо дополнительных сил.
Для определения истинной кривой: v = v(x) поступим следующим образом. Составим выражение суммарной работы внешней нагрузки на перемещениях v = v(x) и работы внутренних усилий на перемещениях, связанных с искривлением оси по закону v = v(x), предполагая заранее, что эта кривая удовлетворяет геометрическим граничным условиям. Работа должна быть выражена в функции абсциссы х, ординат кривой о и ее производных v', v". Далее варьируем кривую и(х), давая каждой ее ординате произвольное бесконечно малое приращение бо(х). Приращение или вариация действительной работы вследствие варьирования кривой и(х) и дает искомую работу на произвольных бесконечно малых перемещениях, называемую обычно элементарной работой. Приравнивая элементарную работу нулю, получаем! условие истинности кривой v = v(x).
Введем некоторые обозначения. Работу нагрузки обозначим Aiarp, работу усилий Лус.
Полная работа
Д = Днагр+Лус.. (5.1)
Обычно оперируют величиной 3 =—А, называемой полной энергией системы. Для иллюстрации этого термина заметим,, что если речь идет о вертикальной нагрузке, то Дпагр можно рассматривать как отрицательное приращение потенциальной энергии положения нагрузки. С другой стороны, как известно из курса сопротивления материалов, работа усилий в упругой системе равна потенциальной энергии деформации с обратным знаком. Таким образом,
3== К (5.2)
Здесь U — потенциальная энергия упругой деформации,
V = — Д1агр— потенциал нагрузки, равный работе нагрузки с обратным знаком.
Условие истинности кривой v = v(x) записывается так:
83 = 0. (5. 3)
Это равенство можно трактовать как условие экстремума величины 3. Та форма кривой и = о(х) является истинной, которая дает экстремум полной энергии 3. В этом и состоит п р и н-
78
,дИп Лагранжа в применении к упруго деформируемой системе. Как видим, принцип Лагранжа является одной из форм ;начала возможных перемещений,'именно той формой, которая связана с понятием энергии.
Переходим к использованию этого принципа.
Потенциальная энергия упругой деформации балки равна !Сумме интегралов:
Здесь F&— эффективная площадь сечения при сдвиге в вертикальном направлении. В случае тонкостенного двутавра принимают FV=FCT (площадь стенки).
Фиг. 17.
Энергию сдвига отбрасываем по малости, энергия растяжения— сжатия в задаче изгиба роли нс играет и также отбрасывается.
Подставляем
M^-EIv"-, PpeaKT=-kv. (5.5)
Получаем выражение энергии через прогибы v = v(x) и вторую производную v" = v"(x):
f l - . Е I
dx-\- — f EI (v"Y dx.
2 1J 2 U V
0 0
(5. 6)
79
Работа поперечной нагрузки
i
Ар° = ^ pGvdx. (5.7)
6
Работа продольной нагрузки (фиг. 17, а)
i
Aq= —Nouo— qudx. (5. 8)
d
Здесь «о — перемещение точки приложения силы Л/о, и — текущее перемещение сечения балки под влиянием искривления. Пере,, мещения и считаются положительными, если они направлены вправо. Поэтому работа растягивающей силы, направленной’ влево, имеет знак минус.
Подсчитаем интеграл по частям, воспользовавшись тем, что продольная сила в сечении х равна N=No+qx, следовательно, q dx = dN. i i i
j' qu dx = ^ udN = (m7V)|' — Ndu.
6o 6
Учитывая, что мг = 0, имеем (m7V)|'= - — Nouo. В результате i
Aq — f Ndu. b
Отметим, что выражение Aq можно получить и непосредственно на основании начала возможных перемещений, учитывая, что N представляет собою усилие, a du — элементарное удлинение; Короче говоря, работа нагрузок вычисляется как работа усилий с •обратным знаком.
Выразим теперь du. Из фиг. 17,6 видно, что du (сокращение; проекции dx в результате искривления) с точностью до малых; высшего порядка равно
du= — dx v' —-- (v')2dx. (5.9)
Окончательно
i
Aq=-----^-^N(v')2dX. (5.10)
b
Когда распределенная нагрузка q отсутствует, имеем
7V=--7VO = const,
i
Aq = —~- j (v'ydx. (5. 10')
b
При сжимающей силе знак «—» изменяется на «+».
80
Итак, работа нагрузок
i /
A,arp= [p°vdx- у j N (v')2dx.
О 6
Полная энергия
z
Э=и -Л„агр = С [— (^")2 + — )2 + — -P°v\ dx = нагр S * I
6
I
— F (x,v,v‘ ,v")dx. (5-H)
6
Подобные выражения называются функционалами или функциями от линий. В данном случае речь идет об упругой линии балки о = о(х).
Составим выражение вариации функционала полной энергии *, когда v, о', о" переходит соответственно в оВо, о’4-So', о"-|-Во" при условии, что o-f-So, 'и'-|-So' . . . удовлетворяют тем же .геометрическим условиям, что и о, о', о".
По определению
/
оЭ — рЛ (х, v 4-So, v' 4- So', о" 4-So") —
6
' i I
— F(x, v, v', о")] dx — ~ Во 4- ~~ So'-|- у^Во". (5. 12) 0 0 6
Вид первого из интегралов сохраняем без изменения. Учитывая, что 6о' = —Во; Во"=—Во и пользуясь формулой интегрирования dx dx2
по частям, преобразуем второй и третий интегралы:
f ~ г »' dx=1^- Р Г - Г — (2^) dXi
,} dv' \dv’ / Io ,) dx \dv' /
о о
I I
f dF > „ , / dF . , \p I’ d / dF \ г ,
I- oo dx = \-------oo ] — —I------)Bo dx.
J dv" \dv" /Io J dx \dv“ )
о о
Снова пользуясь формулой интегрирования по частям, приводим последнее равенство к виду
! . I
f dF „ „ , / dF Г d / dF \1 Л |! . f* d2 j dF \ * ,
---co dx=--------oo — —(--------) oo 4~ I--------poax.
J dv" \dv' /Io [dx \dv" |o .) dx2 \dv" /
о о
* Точнее следует сказать первой вариации, составляющей главную часть приращения функционала.
81
Собирая отдельно интегральные и неинтегральные слагаемые и приравнивая результат нулю, представим (5. 3) в виде вари а-ционного уравнения
Ввиду произвольности вариации би между границами (внутри пролета) подынтегральное выражение в (5. 13) должно быть равно нулю:
(5.14) до dx \dv' / dx- \dv" /
Полагая теперь би^-0, находим, что вторая строка в (5.13) самостоятельно должна быть равна нулю:
Уравнение (5. 14) носит название дифференциального уравнения Эйлера для задачи минимизации функционала Э. Уравнение (5. 15) представляет собой вариационное уравнение для так называемых естественных граничных условий.
Конкретизируем уравнения (5.14) и (5.15) для случая балки. Выполняя дифференцирование функции F(x, v, v', v”) —см. формулу (5. 11), получим
EIE’ -d-NE -ф Ev - - z>° = 0. (5.14ф
d.x- dx
Мы пришли к дифференциальному уравнению равновесия растянутой балки на упругом основании. Для случая £7=const, /V== const, k = const это уравнение было детально изучено выше. Отмстим, что после умножения па dx каждое слагаемое выражает приращение поперечной силы на длине dx, а уравнение в целом представляет собой уравнение равновесия 2Д = 0 элемента балки.
Из (5. 15) получаем
(NE - EIE") dv |;+ EIE’ ЕЕ |; - 0. (5. 15')
Выполняя подстановку пределов и учитывая произвольность вариаций, записываем
ЙД=О; (Л>;~ Д/Дф) 0;
ЕI fl’ ZEt = 0; El<E"oiV'o °-
Пользуясь (5. 15"), можно сформулировать две пары зависимостей между перемещениями v и и' па левом и правом концах 82
(5. 15")
балки, выражающих граничные условия и необходимых для определения четырех произвольных постоянных, входящих в общий интеграл дифференциального уравнения (5. 14').
Прежде всего заметим, что геометрические граничные условия, например, условия отсутствия прогиба и угла поворота на левом конце, ой= 0, v =0 не требуют применения уравнения (5.15").
Но если бы мы хотели применить уравнения (5. 15"), то должны были бы записать бдо = О, 6^ = 0 (неварьируемость заданных перемещений су и о0) и тогда уравнения (5. 15") для левого конца удовлетворяются тождественно.
Наоборот, в случае свободного левого конца, вариации дсу и б'Цц произвольны. Поэтому необходимо, чтобы было
Механический смысл этих равенств, выражающих статические граничные условия, в данном случае очевиден, так как для растянутой балки
Nv-EIE"=Q: -EW'=M.
Здесь естественные граничные условия непосредственно приводят к равенству нулю усилий Q и 7И на свободном торце.
Если левый конец имеет шарнирную опору, то
-ь'о==О; % = 0.
Аналогичные пары равенств имеем и для правого конца (с заменой индекса 0 на 1}.
Таким образом, последовательное применение вариационного принципа Лагранжа приводит к дифференциальному уравнению равновесия и к формулировке граничных условий задачи.
Метод Ритца—Тимошенко
Ценность вариационны?; методов состоит отнюдь но в возможности составления дифференциальных уравнений и формулировки граничных условий, что может быть достигнуто и непосредственно из рассмотрения условий равновесия и условий совместности деформаций. Гораздо важнее то, что вариационные уравнения допускают их п р я м о с решение, основанное на аппроксимации реформированного или напряженного состояния '. Прямым методом, основанным на принципе Лагранжа, является метод Ритца — Тимошенко.
Сущность метода состоит в следующем. Неизвестную функцию прогиба и = о(х) представляем в виде ряда — см. формулу (4.13).
т
д-А1ц1 + Лц2+ . . (/=1, 2, 3, ...,т). (5.16)
j „ 1
Отсюда название — прямые методы вариационного исчисления.
6*
83
Аппроксимирующие функции щ, v2, о3>... выбираются так, чтобы были удовлетворены геометрические граничные условия. А\, А2... Ат — неизвестные постоянные коэффициенты.
Коэффициенты A (i=l, 2, 3,..., т) определяются из условия экстремума полной энергии Э — см. формулу (5. 11). С этой целью выражение (5.16) подставляется в (5.11). После интегрирования полная энергия Э представляется в виде квадратичной функции от коэффициентов А^:
Э=Ф(А1, А, . . . , Ат). (5.17)
Условие экстремума требует, чтобы
-^-=0; — = 0; . . . ; —=0
дЛ, дА2 дАт
(5. 18)
Это дает систему т линейных алгебраических уравнений. Решая уравнения, определяем неизвестные коэффициенты Аь А2,...Ат.
Уравнения можно выписать в форме, аналогичной уравнениям метода Бубнова — Галеркипа (4. 16). Однако в этом случае коэффициенты при неизвестных Ah А2, А3,.„ имеют вид, отличный от показанного в формуле (4. 15), а именно:
1 1 1 1
riK — EI J v^dx-^N v/o^dx-^k J v^dx-, | °; 0 0 j (5. 19)
RiP= - [p^idx. |
о J
Коэффициенты г обладают свойством взаимности, т. е.
rik = rki-
Если аппроксимирующие функции ортогональны, то побочные коэффициенты (z^£) обращаются в нуль и неизвестные А, определяются из независимых уравнений.
Критическое значение силы N в случае сжатой балки определяется из условия обращения в нуль детерминанта системы уравнений (5. 18).
Расчет растянутой и сжатой балок по методу Ритца—Тимошенко
Рассмотрим балку постоянного сечения, шарнирно опертую по концам и имеющую начальную технологическую погибь, обращенную выпуклостью вниз. Балка растянута силой N, приложенной над подвижной опорой и несет поперечную нагрузку (фиг. 18).
Упругий прогиб естественно аппроксимировать в виде бесконечного тригонометрического ряда:
со
^0= 2 A„sin^(/I=l, 2, 3. . . ). (5.20)
П — I
84
Коэффициенты Ап подлежат определению.
Ординаты начальной погиби представим в виде другого ряда:
(5.21)
л = 1
Коэффициенты Вп должны быть определены заранее.
Сокращение пролета, вызванное упругим искривлением, найдем как разность между воображаемым полным сокращением,
обусловленным погибыо v° и упругим прогибом ыу", и сокращением от одной только погиби v°. Учитывая (5. 9), получим
1 Г/Л>уп\г. , frfwyn
о о
----ах. dx
(5. 22)
Подставив сюда ряды (5.20) и (5.21), найдем
Составим выражение полной энергии, считая, что балка нагружена одной сосредоточенной силой Р в сечении
Э= — _р^уп.
2 J ( dx- ) Г 5
• о
Подстановка рядов дает
э=ттг2 ”,л"+Л'тг(2,1М"+2 2
-PV.4,sln“S. (5.23)
85
Условие минимума полной энергии запишется так:
(п=1, 2, 3. . .
и Ап
Пользуясь частной производной от (5. 23), получаем
^»4A+^(^+5Zi)-psin^=o.
Отсюда
А 2РР 8'П ~ (5.24)
п Е1тА П~ (п2 -Р 7.2) ' п2-\--/Л
Здесь введено обозначение
о NP N
* EhP~^э :
(5.25)
При наличии распределенной нагрузки р—р(х) следует в последних выражениях заметить Psin ~ интегралом
I
| р (?) sin <Д. о
При равномерно распределенной нагрузке p = const на всем пролете первое слагаемое (5. 24) запишется так:
у|ЛОП_ 4/?/^ 1
£7х5 П3 (д2 7,2)
Ряд для прогиба (5. 20) обычно сходится очень быстро, и в отдельных случаях можно ограничиться первым членом разложения, полагая, что изгиб происходит по синусоиде с одной полуволной. При этом упругий прогиб по середине пролета равен
• 51
^сп А mi _j___________в,.
СР 1 £/.1-1 14-х2 1 Е1л5 l-Hx.2 Ц- 7.2 1
(5. 26)
При х = 0 получаем приближенное решение для простой балки, весьма мало отличающееся от известных решений сопротивления материалов. Действительно,
_2____1_. _4
48 ’ 384‘
Если известен прогиб для простой балки, то для учета про-
дольной растягивающей силы достаточно умножить этот прогиб
на
1
1 + 7.2’
Дополнительный упругий
прогиб от начальной поги-
86
би равен этой погиби, умноженной на
. Полная стрелка
прогиба
(5. 27)
где оэсЛр — стрелка прогиба или погиби, определенная элементарно без учета продольной силы.
При сжимающей продольной силе знак перед х2 всюду изменится на обратный:
„ Sin---
. 2PZ3 I
" = А, =--------------
ср 1 £7*4 1—7.2
Elrfi 1 — х2 1 1—7.2 1
(5. 28)
Критическое значение сжимающей силы получаем из условия обращения в нуль знаменателя дробей (5.24), причем предварительно следует заменить х2 на (—х2), так как речь идет о.сжимающей силе.
Получаем
п2-х2 = 0.
Отсюда следует известный результат
NKp — nN3 (п— 1, 2, 3 . . . ), min NKp = N3.
Применение принципа Кастильяно
Из курса сопротивления материалов известна теорема о минимуме потенциальной энергии, основанная на теореме Кастильяно о частных производных потенциальной энергии упругой деформации. Теорема о минимуме утверждает, что если выразить энергию упругой статически неопределимой системы в функции заданных нагрузок и лишних неизвестных, приложенных к неизменяемой основной системе, то действительные величины лишних неизвестных тс, при которых энергия приобретает минимальное значение.
Теорема обобщается на случай, когда точки приложения лишних неизвестных получают наперед заданные перемещения или когда вообще система подвергается наперед заданной, в частности, температурной деформации. В этом случае к потенциальной энергии упругой деформации должна быть добавлена работа усилий на независящих от них дополнительных деформациях, взятая с обратным знаком и притом без множителя 1/2, характерного для вычисления работы сил на вызванных ими же упругих перемещениях.
Балки в условиях сложного изгиба принадлежат к числу статически неопределимых систем по с сосредоточенными, а с распределенными (функциональными) лишними неизвестными. Для таких
87
систем теорема о минимуме энергии обобщается в том смысле, что напряженное состояние, заведомо удовлетворяющее условиям равновесия, удовлетворяет также условиям совместности деформации; если энергия принимает минимальное значение. Это значит, что вариация энергии’ при варьировании неизвестной функции, характеризующей напряженное состояние, должна быть равна нулю. Следовательно, здесь снова находят применение элементы вариационного исчисления, коротко затронутые выше при рассмотрении метода Лагранжа.
Рассмотрим балку на упругом основании, несущую поперечную нагрузку р° и подвергающуюся неравномерному нагреву, дающему кривизну 0°. Возьмем в качестве неизвестной функции, подлежащей определению, изгибающий момент М = М(х). Потенциальная энергия балки и ее основания с добавкой, выражающей работу усилий на заданном искривлении, взятую с обратным знаком, запишется так:
(— м"~ роу , .„1 , ------4- Mb dx—
2k 1
I
-J F(x,M, M")dx. о
(5. 29)
Составляем условие экстремума энергии U как уравнение Эйлера:
dF____d dF , d* dF __g
dA4 dx dM’ ' dx* dM"
Выполняя эту операцию, получаем дифференциальное уравнение изгибающих моментов балки на упругом основании:
Aflv + — Л? =.-• - (р°)" - №. (5. 30)
По аналогии с (5. 15) можно получить и вариационное уравнение для граничных условий.
Задаваясь уравнением моментов в виде ряда из аппроксимирующих функций, удовлетворяющих статическим граничным условиям, можно приближенно свести задачу интегрирования уравнения (5. 30) к решению системы линейных алгебраических уравнений
=-0; . . . : ^-0.
о/ll dA? dAm
Особенности применения метода Кастильяно при расчете нелинейно деформируемых систем
Теорема Кастильяно и теорема о минимуме потенциальной энергии деформации, изучаемые в курсе сопротивления материалов, как извест1Ю, применимы только при расчете линейно деформируемых
88
достаточно жестких упругих систем, для которых потенциальная' энергия выражается в виде функции второй степени от нагрузок,, прикладываемых к основной системе. Не только материал системы,, но и система в целом должны подчиняться закону.Гука в обобщен-
ном смысле: должна существовать пропорциональность между нагрузками и перемещениями. При увеличении всех нагрузок в оди-
наковое число раз все перемещения должны возрасти в том же отношении. Этому требованию не удовлетворяют прежде всего системы, сильно деформирующиеся от нагрузки, например, пологие-.
гибкие нити. Балки в условиях сложного изгиба являются линейно деформируемыми от поперечных нагрузок при постоянной продольной силе, причем в случае сжатия, продольная сила должна быть значительно меньше эйлеровой. Весьма гибкие балки с закрепленными концами, сочетающие свойства гибкой нити и балки, принадлежат к числу нелинейно деформируемых систем также и при чисто поперечной нагрузке.
Рассмотрим нелинейную систему в случае нагрузки одной силой. Предположим, что зависимость между перемещением и изображается кривой
Фиг. 19.
силой Р и соответствующим АтВ (фиг. 19).
Под потенциальной энергией деформации принято
вать интеграл:
подразуме-
U = Р dv.
6
(5.31)-
Этот интеграл равен вертикально заштрихованной площади на фиг. 19. Он выражает работу упругих сил на малых приращениях перемещений, иначе говоря, при варьировании перемещений. Дифференцируя обе части (5.31) по верхнему пределу интеграла, находим
dv
(5.32)
что отвечает принципу Лагранжа.
Однако при криволинейной зависимости между Р и v равенства, эквивалентного теореме Кастильяно, не получается, так как
dU , — -PV. dP r
89
Формулировка теоремы Кастильяно остается в силе, если вместо U взять так называемую дополнительную энергию (иначе — энергию напряжений), выражаемую интегралом
р
R=--^v dP = Pv — U. (5,33)
6
Данный интеграл равен горизонтально заштрихованной площади на фиг. 19.
По расширенной теореме Кастильяно
(5.34) dP ’
При линейной зависимости между Р и v потенциальная и дополнительная энергия численно равны друг другу, теоремы Кастильяно в обычном и расширенном смысле — эквивалентны.
При нескольких силах Р\, Ръ,--. полные производные заменяются частными производными
= (5.35)
В качестве примера решения нелинейной статически неопределимой задачи на основе принципа Кастильяно рассмотрим гибкую балку, прикрепленную по концам к шарнирно неподвижным опорам. Балка нагружена равномерно распределенной нагрузкой ;/? кг/см.
Расчленяем мысленно балку с неподвижными концами на простую балку и гибкую пить (фиг. 20, а и б). Первая работает на изгиб, вторая — на растяжение. Каждая из этих конструкций способна воспринять заданную нагрузку.
В качестве функциональной лишней неизвестной выбираем погонную интенсивность вертикальных сил взаимодействия между балкой и цепью, обозначаемую рп=р„(х), или, что то же, — интенсивность нагрузки, передаваемой на пить.
Для уточненного расчета следовало бы представить рп = Рп(х) в виде ряда аппроксимирующих функций с неизвестными коэффициентами. Ограничимся одним членом этого ряда, полагая рп постоянной. В такой постановке задача сводится к определению числа а, характеризующего распределения полной нагрузки p = const между .балкой и нитью:
А>=ар; р„=(’-а)р-
Найдем дополнительную энергию системы. Балка представляет «обою линейно деформируемую систему. Для нее потенциальная энергия деформации и дополнительная энергия численно равны
I
„__ц___ 1 (‘M2dx
~ 2 J EI
о
90
Подставляя сюда
найдем
М — ар Л ~
2
о «2Р2/5
Хб 240£/ ’
Нить — нелинейно деформируемая система. Предварительно найдем зависимость между нагрузкой рп и провисаниями отдель
ных точек нити. Известно, что нить под равномерной нагрузкой провисает по параболе, ординаты которой совпадают с ординатами эпюры моментов простой балки, деленными на распор Я:
_ РнХ (I — х)
У ' 2Н
Средняя ордината (стрелка провисания) , Р12
Oil
Другое уравнение, связывающее распор и стрелку провисания, найдем, приравняв разность между длиной дуги параболы и первоначальной длиной нити (пролетом /) упругому удлинению нити.
91
При этом усилие во всех сечениях нити с достаточной точностью можно считать равным распору:
у 1 3 /2
Заменяя радикал приближенным значением
8 /2 = /у ,
3 Г- ~ EF
получим
Из двух уравнений получим
(5. 36)
Уравнение кривой провисания
jy = y^x(Z-x), или у=^^-^х(1-х). (5.37)
Найдем дополнительную энергию нити как разность между работой нагрузки и потенциальной энергией деформации. Последняя выражается через продольные усилия, принимаемые равными распору Н:
п С 1 с № dx
Rv=\PKydx- — \—-— =
J J
о о
I ________
Г /1 \ ,3 f д (1 — «) F Е ,. . ,
== I (1 — а)р 1/ —-—— х (1 — х) ах —
о
__i_ ГЛ3/^а-^^.у^=
2EF J \ У 24 /
о
_ 3 Z 3 / /Н(1 —а)4£2/72/4
” 2 EF у 576
Дополнительная энергия системы, равная сумме дополнительных энергий балки и нити, будет
d_d ±р _ I JL 1_ */~
*' 240£/ I" 2 EF У 576
Условие минимума для
±1 = 0- ap?Z5 2 1
да 120Е/ EF У 576
92
После простых преобразований для определения а получаем кубическое уравнение
а3= 4,069 (1 - а). (5.38)
___ \wcp/
Здесь г— радиус инерции балки,
8®р== — ^- —прогиб по середине простой балки от заданной нагрузки р.
Значения величины а в зависимости от аргумента г/п°р представлены на фиг. 20.
Данный пример носит иллюстративный характер. Для практических целей было бы достаточно определить а, приравнивая прогиб балки и провисание нити по середине пролета.
Предлагаем проделать это самостоятельно.
* *
*
Проблемы сложного изгиба и связанные с ними математические, в частности, вариационные методы служили предметом фундаментальных исследований выдающихся отечественных ученых И. Г. Бубнова, Б. Г. Галеркина, А. И. Крылова, Л. С. Лейбензопа, П. Ф. Пап-ковича, С. П. Тимошенко. Эти исследования сыграли большую роль в развитии современной строительной механики и прикладной теории упругости. Творческое овладение этими дисциплинами требует глубокого изучения оригинальных трудов названных ученых-
Глава II
ПРОЧНОСТЬ И УСТОЙЧИВОСТЬ прямоугольных ПЛАСТИНОК
В настоящей главе рассматривается теория работы тонких пластинок, являющаяся развитием теории балок, находящихся под действием поперечных и продольных нагрузок.
Плоскость, делящую пополам толщину недеформированной плоской пластинки, называют срединной плоскостью.
Напряженное и деформированное состояние пластинки, сопровождаемое искривлением срединной плоскости, называют изгибом п л а с т и и к и.
Нагрузки, приложенные по краям пластинки в срединной плоскости, вызывают плоское напряженное состояние пластинки, при котором срединная плоскость остается плоскостью. Изгиб вызывается нагрузками, перпендикулярными срединной плоскости.
Однако, если учесть влияние прогибов на плечи нагрузки, лежащей в срединной плоскости, то она вызывает дополнительный изгиб, аналогично сжатой или растянутой балке, работающей в условиях сложного изгиба.
При значительных прогибах усилия в срединной плоскости возникают и от действия одной только поперечной нагрузки.
Нагрузки, действующие в срединной плоскости пластинки, могут вызвать потерю устойчивости. С этой точки зрения наибольшую опасность, разумеется, представляют сжимающие нагрузки по контуру пластинки.
Пластинка может иметь начальную ногибь и тогда следует говорить ие о срединной плоскости, а о с р е д и и п о й поверхности пластинки. Впрочем, чтобы отличать пластинки от оболочек, часто во всех случаях пластинок применяют термин срединная плоскость.
Толщина пластинок в авиационных конструкциях (стенки и полки балок, обшивка несущих поверхностей) в десятки и сотни раз меньше остальных размеров (длины, ширины опорного контура).
Очень тонкие пластинки способны эффективно воспринять поперечную нагрузку (давление) только при условии, что их контур будет закреплен как перпендикулярно плоскости пластинки, таки
94
в плоскости пластинки (аналогично шарнирно неподвижной опоре-балки). При этом наряду с изгибными напряжениями, изменяющимися по толщине пластинки по линейному закону, возникают растягивающие напряжения, распределенные по толщине равномерно—-так называемые цепные, или мембранные напряжения. Если при этом изгибине напряжения пренебрежимо-малы по сравнению с мембранными, пластинку называют абсолютно гибкой, или мембраной. Такая пластинка имеет много общего с пологой гибкой нитью. Если, наоборот, мембранные напряжения оказываются весьма малыми, пластинку называют жесткой (в судостроении — абсолютно жесткой). Жесткая пластинка может работать и без контурных закреплений в своей плоскости. Она аналогична обыкновенной балке. В случае,, когда величины изгибных и цепных напряжений получаются одного порядка, пластинка называется гибкой.
Иногда неподвижное контурное закрепление в плоскости гибкой пластинки заменяется достаточно жестким кольцом, работающим на сжатие. В таких условиях работают круглые плоские днища цилиндрических резервуаров, подвергающихся внутреннему или внешнему давлению. При больших прогибах свободно опертой неподвижной круглой пластинки «кольцо жесткости» как бьг возникает автоматически — в виде края пластинки. В этом случае возникает опасность потери устойчивости сжатого края.
Подобно тому, как расчет балок на сложный изгиб труднее расчета гибкой нити и обыкновенной балки, так и расчет гибкой пластинки труднее расчета мембраны и жесткой пластинки. Пластинку можно считать жесткой и игнорировать влияние закрепления контура -в плоскости пластинки, если рассчитанный в этом предположении максимальный прогиб не превосходит ‘/з—’А се-толщипы. При большем значении прогиба и неподвижном контуре рекомендуется перейти к расчету пластинки как гибкой. Если при расчете гибкой пластины с неподвижным контуром прогиб превосходит 5—6 толщин, то одновременно и влияние изгибных напряжений оказывается небольшим п пластинку практически можно-рассчитывать как мембрану.
Жесткие пластинки часто называют пластинками малого прогиба, а гибкие — пластинка м и большого пр о-гиба. Для первых характерна линейная зависимость между поперечной нагрузкой и прогибами; для вторых — нелинейная зависимость. При не очень больших прогибах нелинейность практически проявляется только в пластинках с неподвижно закрепленным контуром.
§ 2. 1. ИЗГИБ ПЛАСТИНОК ПО ЦИЛИНДРИЧЕСКОЙ ПОВЕРХНОСТИ И ЦИЛИНДРИЧЕСКАЯ ЖЕСТКОСТЬ
Представим себе весьма длинную прямоугольную пластинку,, шарнирно опертую вдоль длинных сторон на неподвижные опоры (фиг. 21).
Срединную плоскость будем считать плоскостью ху.
95-
Возьмем в произвольной точке срединной плоскости начало координат и направим ось х перпендикулярно длинным сторонам, •ось у — параллельно им, а ось z и ось прогибов w — перпендикулярно срединной плоскости.
Предположим, что пластинка нагружена нормальным давлением, изменяющимся только вдоль оси х и неизменным вдоль оси#. Это значит, что все эпюры давления, построенные вдоль оси х,
тождественны, эпюры, построенные вдоль оси у, имеют постоянные ординаты.
Такая пластинка будет изгибаться по цилиндрической поверхности с образующими, параллельными оси у, и это заключение будет тем точнее, чем пластинка длиннее. Отступления от цилиндрической формы имеют место только вблизи коротких сторон.
Разрежем мысленно пластинку на параллельные оси х полоски шириной 1 см. Все полоски (за исключением расположенных вблизи коротких сторон) будут находиться практически в одинаковых условиях и их можно рассматривать как элементарные балочки, иначе балки-полоски с прямоугольным сечением, шириной 1 см и высотой t см ((— толщина пластинки).
Есть, однако, и отличие в работе обыкновенной балки и балки-полоски: поперечная деформация волокон каждой балки-полоски в горизонтальном направлении стеснена соседними балками-по лосками; если нарушить связь между балками-полосками, то по; перечные сечения балок-полосок представились бы в виде 1'2'3'4', показанном на фиг. 21, в. В действительности же боковые грани
•96
балок-полосок остаются вертикальными, кривизна вдоль оси у рав-ц.а нулю, и сечения имеют вид 1234,
Отсюда следует, что наряду с напряжениями <тх в пластинке возникают напряжения а,,. Что касается напряжений сг2, имеющих адин порядок с нагрузкой р, то их влиянием в теории тонких пластинок пренебрегают.
Напряжения ov выразим через напряжения од-, записывая условие стеснения еу = 0 на основании закона Гука при плоском напряженном состоянии:
(°v — Г=л-) = 0.
Отсюда
S = !-r- (1-D I
Напряжения <7У. равны напряжениям <тх, умноженным на коэффициент Пуассона, т. е. составляют около одной трети — одной четверти напряжений <тх.
Найдем теперь деформацию волокон вдоль оси х:
(З.г-И°у) = у (3x-r2ax)=--£'J:-sx- (h 2)
Полученную зависимость можно сформулировать так: волокна балки-полоски деформируются так, как если бы они находились в одноосном напряженном состоянии, но модуль упругости был бы равен £/(1—и.2), вместо Е.
Деформация изгиба балки-полоски в плоскости xz также описывается как деформация балки из материала с модулем упругости £/(1—ц2).
Жесткость балки-полоски при изгибе поэтому равна
гл £-Г*з
D -------• -------- \кгсм .
1—Д 12(1—Д) 1
Здесь момент инерции / отнесен к ширине балки полоски в 1 см.
Величина D, выраженная в кгсм, называется ц и л и н д р и ч е-ской жесткостью пластинки-. Происхождение этого термина понятно из предыдущего.
При исследовании пластинок целесообразно оперировать с погонными, или отнесенными к 1 см ширины или 1 см длины, величинами. Примером может служить цилиндрическая жесткость D, момент инерции Р/12. В первую очередь это относится к распределенной нагрузке и усилиям. Заметим, что давление р кг/см2 по отношению к балке-полоске шириной 1 см является погонной нагрузкой. Изгибающие моменты также относят к ширине балки-полоски шириной 1 см, сохраняя для них обозначение М с индексом оси балки полоски. Таким образом, балка-полоска изгибается моментом Мх (вместо Му по обычным балочным обозначениям).
97
При равномерном давлении р кг/см2 максимальный момент при шарнирном опирании длинных краев равен
,, ра- кгсм
max Mt~---------.
х 8 см
Полоски шириной 1 см, выделенные параллельно длинной стороне пластинки, работают на чистый изгиб каждая со своим постоянным изгибающим моментом
= (1.4)
пропорциональным изгибающему моменту в сечении балки-полоски, параллельной короткой стороне. Если рассматривать напряженное состояние длинной балки-полоски как одноосное, то модуль упругости и изгибная жесткость условно могут быть приняты равными бесконечности, так как удлинения волокон такой полоски при цилиндрическом изгибе пластинки не происходит.
Нормальные напряжения в пластинке при цилиндрическом изгибе
Мх 12ЛДг 6Л/д.
а=~ z—--------— , тахо =-------;
х I t2 х ft '
12н-М.гг /з
°у=Иол =
д-
max а„=---------
у ti
Потенциальная энергия деформации пластинки при цилиндрическом изгибе на 1 см длины пластинки
U=— СМ2 = {M*dx. (1.5)
2D J х J 2
о о
Поскольку расчет пластинки при цилиндрическом изгибе сводится к расчету балки-полоски с измененным модулем упругости (или с измененной изгибной жесткостью, что в данном случае одно и то же), здесь могут быть использованы все приемы расчета балок, в том числе и методы, изложенные в гл. I. Большое практическое значение имеют пластинки, опертые на ребра, расстояние между которыми не изменяется или изменяется на наперед заданную величину. Тут возникает задача определения цепной силы балки при шарнирно-неподвижных опорах. Пластинка может быть изогнута по цилиндрической поверхности (начальный или температурный прогиб). Это обстоятельство также легко учитывается методами, изложенными выше.
Пример. Длинная прямоугольная пластинка с короткой стороной а = 60 см шарнирно оперта на неподвижные длинные ребра. Толщина пластинки ^ = 0,5 см. Материал пластинки — сталь, £ = 2,1 • 108 кг/см2. Пластинка нагружена равномерно распределенной нагрузкой р=0,7 кг/см*. Определить расчетное нормальное напряжение, считая пластинку гибкой, т. е. с учетом цепных напряжений. Начальная погибь отсутствует.
98
Воспользуемся формулой (2.6') гл. I, которая после подстановки
/ _ _1/з ___/£
F ~ 12-1-/- 12 принимает вид
(1+z2)2z2==A(^)2. (!.6)
Прогиб по середине пролета без учета распора (цепной силы) вычисляется по известной формуле сопротивления материалов
41 Фо/-»
и" — —-— . С'Р 384£/
В данном случае следует заменить Е1 на D; I па a; v на w. Обо-. значая w9c” через fcp, получим
f _ 5 Pai _ 5 £а4<1 ~р2) л 7\
Jcp 384 D ’ 32 £/з ’ ' ’ ’
При ц=0,3 правая часть уравнения (1.6) принимает вид
Подставляя сюда а — 60 см; t = 0,5 см, р = ®,7 кг/см2,
£=2,1 • Ю6 кг/см2, находим
з/2
-—^-’ — 290.
/2
Кубическое относительно х2 уравнение (1.6) записывается в виде
(1 -1-х2)2х2== 290-
Пользуясь логарифмической линейкой, после двух-трех попыток подбором находим
х2=5,97.
Для нахождения цепной силы определяем сначала эйлерову силу. Для балки она равна
N3=^.
э Г,
В данном случае
л7 %2£> ^£/3 л2.2,1-106.0,53 — ,
= —— =-----------=-----------= 66 кг см.
а2 12(1-ц2)а2 602-12 (1—0,32) 1
Так как
NIN3==^-см. (5. 25), то N = *2N3.
Получаем
?V=5,97 • 66 = 395 кг/см.
7*
99
Имея поперечную нагрузку и продольную растягивающую силу балки-полоски, можно воспользоваться теорией и формулами растянутой балки — см. (1.2). Обычно точность приближенной формулы (2. 4) гл. I оказывается достаточной.
Прогиб пластинки но продольной оси будет
/ср wrn =------.
tp 1 -f- 7.2
Прогиб /Ср> подсчитанный по формуле (1.7), равен 4,9 см. Поэтому
Максимальный изгибающий момент
ла J. Л ~ t 0,7* GO* с\ ^7 л /л Kzr м
•М.... =----AzwCI,=--------395-0,7 = 40 -------.
",dX н ср 8 см
Точная формула,, вытекающая из рассмотрения общего интеграла уравнения растянутой балки, гласит
Пренебрегая вторым слагаемым в скобках, получим другую, приближенную формулу:
1пах х2г2
В данном случае это дает 0.7-602 ., - кгсм кгсм
Л/ =----------= 41,о------вместо 40----.
п,',х 5,97-it2 см см
Максимальное напряжение
Л7п.ах I N й'40 , .395 |7-„ , 2
3,пах~-~------=-----------=17о0 кгсм2.
,nd W F 0,52 0,5
§ 2.2. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИЗОГНУТОЙ ПОВЕРХНОСТИ ПЛАСТИНКИ
Так же как и техническая теория изгиба балок, теория изгиба пластинок строится на определенных гипотезах, являющихся расширением гипотез, известных из курса сопротивления материалов.
Вместо закона плоских сечений, нормальных к изогнутой оси бруса, принимают гипотезу прямых нормале й к и з о-гнутой поверхности пластинки. Это значит, что точки, лежащие на нормали к срединной плоскости до деформации, остаются на нормали к изогнутой срединной поверхности в после деформации.
100
Гипотеза прямых нормалей эквивалентна гипотезе плоских сечений для брусочков с сечением dx I и dy • t при их ч п ст о м и з-. гибе, т. е. при условии игнорирования деформации сдвига.
Вместо гипотезы об одноосном напряженном состоянии волокон бруса принимается г и п о т с з а о и л о с к о м и а и р я ж е и и о м состоянии слоев и л а с т и и к и, параллельных срединной п л о с к о с т и. Это значит, что слои пластинки друг па друга ис надавливают. В действительности напряжения между слоями пластинки будут одного порядка с внешней распределенной по площади нагрузкой. Но интенсивность нагрузки всегда мала по сравнению с напряжениями изгиба в поперечном сечении пластинки. Касательные напряжения между слоями будут меньшего порядка малости, чем нагрузка, по также незначительные.
Не будем переходить от этих гипотез к вычислению напряжений на основании закона Гука и условий равновесия, как это делалось в случае балки в курсе сопротивления материалов, а введем сразу некоторые гипотезы, относящиеся к напряжениям. Исследование показывает, что при изотропном упругом материале и при постоянной толщине пластинки обе группы гипотез эквивалентны.
Подобно тому, как мы переносим всякую нагрузку на ось балки, будем так же поступать с нагрузкой пластинки, перенося каждую силу, если нужно, с добавлением пары, в срединную плоскость пластинки. Затем раскладываем каждую силу на два компонента— лежащий в срединной плоскости и к ней перпендикулярный. Так же поступаем с реакциями.
В результате нагрузка пластинки представится суммой двух нагрузок — лежащей в срединной плоскости (или более общо-— симметричной относительно срединной плоскости) и антисимметричной относительно срединной плоскости, в частности, перпендикулярной к пей.
Ввиду малой толщины пластинки можно принять, что в первом случае имеем одно и то же плоское напряженное состояние по всей толщине пластинки. Для панели обшивки крыла, являющейся жесткой пластинкой, это состояние определяется нормальными и касательными напряжениями общей прочности конструкции, которые определяются из рассмотрения крыла как тонкостенного бруса. Вместо нормальных и касательных напряжений
о а т == т = т
Л* у’ ху ух
удобно пользоваться и о г о и и ы мп усилиями
Nx=axt, = <7 = тЛ
Во втором случае напряженное состояние будет антисимметричным относительно срединной плоскости, и мы считаем его переменным по толщине плоским напряженным состоянием, причем срединная плоскость должна быть своего рода нейтральным слоем.
Учитывая снова малую толщину пластинки, примем, что напряжения, характеризующие состояние отдельных слоев, следуют по
101
толщине пластинки линейному закону. Аналогия с балко в отношении нормальных напряжений тут очевидна, но разниц состоит в том, что вместо линейного закона изменения по высот балки одноосного состояния имеем линейное изменение всех ком понептов плоского напряженного состояния, в том числе и каса тельных напряжений.
Отметим, что можно было бы ввести гипотезу о линейном рас пределепии по толщине только нормальных напряжений, а линей ное распределение горизонтальных касательных получить Kai
следствие па основании теории плоского напряженного состояния, исходя из пропорциональности т в отдельных слоях величинам о в тех же слоях. Напомним, что
(’•«— М та =-------sm 2а.
Перейдем к установлению связи между напряжениями и моментами.
Координатную плоскость ху совместим со срединной плоскостью пластинки, ось z направим вниз.
На фиг. 22, а показан вырезанный из пластинки элементарный параллелепипед с ребрами dx, dy, t, ориентированными параллельно принятым координатным осям (коротко — элемент пластинки). Его можно рассматривать также как общий элемент двух ' балок-полосок — балки шириной dy, вырезанной параллельно оси х, и балки шириной dx, вырезанной параллельно оси у. Напряжения по боковым граням параллелепипеда показаны в виде эпюр.
Нормальные напряжения (точнее, совокупность элементарных нормальных усилий) статически эквивалентны изгибающим моментам, касательные напряжения — крутящим моментам (фиг. 22, б) *.
* На фиг. 22 показаны эпюры напряжений и моменты па передней и правой боковых гранях. По двум другим боковым граням дейетвуют уравновешивающие напряжения и моменты того же знака, равные моментам Мх, Mv, К или отличающиеся от них на бесконечно малые величины.
102
Моменты подсчитываются на единицу ширины грани в кг • см]см. Моменты обозначаются
мх, му, кух=кху=к.
В отличие от принятого в сопротивлении материалов правила здесь индексы при изгибающих моментах соответствуют не оси, относительно которой берется момент, а направлению вектора напряжения, отвечающего данному моменту. Можно также сказать, что Мх — это изгибающий момент в балке-полоске, ось которой параллельна оси х. Этим правилом мы уже пользовались в гл. I.
Учитывая вид эпюр напряжений, легко установить, что связь между напряжениями и всеми тремя моментами такая же, как и для нормальных напряжений и изгибающего момента обыкновенной балки:
Так как моменты взяты на единицу ширины грани, то и момент инерции следует взять на единицу ширины грани:
г I3 4/
/= — см4 см.
12 '
Так же и момент сопротивления берется на единицу ширины:
W= — см31см.
6 '
Перейдем к деформациям. Найдем относительные удлинения и относительный сдвиг в слое па расстоянии z от нейтрального слоя (срединной плоскости):
1 М х — и.Му 1
е — — (о — ра ) —--------------------г,
Л Zi Л у Е/
1 . . Л4У —|хЛ1Л-
= ------й------г,
I
zxy К I
ь-у— g~mz- I
(2. 2)
Свяжем теперь деформации с перемещениями — вертикальными прогибами пластинки w. Прогибы пластинки отождествляем с прогибами срединной поверхности. Прогибы считаются положительными, если они направлены вниз.
Предположим, что весьма пологая изогнутая срединная поверхность пластинки дана в виде функции двух переменных х, у: w — w(x,y).
103
Нанесем мысленно па срединной плоскости до дсформацщ сетку прямых, параллельных осям х, у.
Приближенное значение кривизны линий сетки, параллельны; оси х, после деформации выразится второй частной производно! 0 d2W
V'x = — ——, а для линии сетки, параллельных оси у — соответствен дх%
но &у =--. Рассматривая линии сетки как оси балок-полосок i
ду2
учитывая, что кривизна равна относительному удлинению во
локпа е, деленному на его расстояние z от нейтрального слоя, из (2. 2) находим
d^w гх Мх — ртМу
дл2 ~ г ~ EI ’ (2. 3)
02w гу Л1у — h-M х
dy2 z EI
Кроме того, определим меру кручения срединной поверхности
о <flw к~дх()у
По своему геометрическому смыслу мера кручения (или просто кручение) представляет собой относительный угол закручивания волокна, выделенного параллельно оси х или параллельно оси у:
<~flw д dw д dw дх ду дх ду ду дх
Кручение тесно связано с интенсивностью роста сдвига в слоях, параллельных срединной плоскости.
Выделим элементарный параллелепипед, верхняя грань которого лежит в срединной плоскости, а нижняя отстоит от нее на z (фиг. 23).
101
Чтобы связать кручение со сдвигом, поступим следующим образом. Будем считать отрезок 00' неподвижным, верхнюю грань и четыре боковые грани недеформируемыми в своих плоскостях. Допустим, что точка А получает малое перемещение Awa. Одновременно грани ОАА'О' и СВВ'С' повернутся на угол —— , а точ-дх
ка С' сместится вдоль прямой В'С' на г--. Это обусловливает при-дх
ращение прямого утла А'О'С', равное
<7 dw d2w — z ----= z-----.
ду дх дх ду
Совершенно аналогично, когда точка В получает малое перемещение AwB, тот же прямой угол вследствие поворота другой его стороны получает малое приращение той же величины д dw - d2w
— z-----— z------.
дх ду дх ду
Полное приращение прямого угла, равное относительному сдвигу в плоскости О'А'В'С' составляет 2z & w . Приравнивая эту дхду
величину сдвигу согласно формуле (2.2), получаем
(2.4) дхду ‘2.GI
Таким образом выражаются деформации элемента пластинки (иначе деформации пластинки в данной точке) через моменты
Мл, Му, К.
Вообразим прямоугольную пластинку, не несущую поперечной нагрузки и нагруженную по краям моментами постоянной величины
М,.= const, М,—const, const.
Тогда напряженное состояние конечной пластинки будет тождественно с рассмотренным выше состоянием элемента со сторонами dx, dy. Нагружение 44r = const, My='const по аналогии с балкой называют чистым изгибом пластинки. Нагружение моментами Кху = Кцх = К = const — кручением пластинки. Наряду с цилиндрическим изгибом чистый изгиб прямоугольных пластинок в практике встречается довольно часто.
Выразим теперь изгибающие моменты через деформации (кривизны), решая совместно два уравнения (2.3) относительно ЛД и Му. Получаем
My——D
d2w , d2w \ дх2 1 11 ду2)’
[d2w
\с)у2
, d2w
-Ц-----
дх2
(2-5)
105
Здесь через D обозначена введенная выше величина цилиндрической жесткости пластинки (1.3).
Выразим также крутящий момент через меру кручения при помощи (2.4). Предварительно подставляем
2 (1 4- (*)
После этого найдем
А7 = £)(1—И) (2.6)
дх ду
Рассмотрим теперь условия равновесия элемента пластинки, несущей поперечную нагрузку р=р(х, у) кг/см*. В этом случае
р dx dy
Фиг. ‘24.
придется учесть вертикальные касательные напряжения по граням и соответствующие поперечные силы.
Элементарный параллелепипед нагружен силой pdxdy, которая уравновешивается приращениями вертикальных поперечных сил по боковым граням.
Вертикальные поперечные силы по четырем граням элемента пластинки, а также моменты, показанные в виде векторов с волнистой стрелкой, даны на фиг. 24. Направления векторов-моментов отвечают правилу правого винта: если смотреть от острия стрелки к перу, то увидим вращение против хода часовой стрелки. Интенсивность роста усилий вдоль оси х или оси у выражается их частными производными вдоль этих осей.
Усилия, приходящиеся на грани шириной dx и dy, с соответствующими приращениями, выраженными через частные производные, выписаны на фиг. 24.
Уравнение проекций на ось z дает
р dx dy - Q v dy -| - dx) dy — Q^dx-y-
-I- “ у dy) dx=0.
106
После сокращений находим
dQx । ()Q> _ дх ' ду
(2- 7)
Соотношение (2. 7) является очевидным обобщением известной зависимости теории балок
dQ
_р,
dx
Из уравнения моментов относительно 'малых величин высшего порядка малости
дМх дК
дх ду
оси у с отбрасыванием находим
(2.8)
Соответственно из уравнения моментов относительно оси х
дМу дК п ду ~ дх
(2. 9)
Отметим, что касательные напряжения, обусловленные поперечными силами Qx и Qy, распределены по толщине .пластинки по параболическому закону и имеют максимум по середине толщины пластинки
3 Q т =------- .
шах 2
По величине эти напряжения всегда пренебрежимо малы и никакой роли в расчете на прочность не играют.
Соотношения (2. 8) и (2.9) повторяют известную зависимость теории балок
для балок-полосок, вырезанных из пластинки. Роль погонной интенсивности распределенной изгибающей моментной нагрузки в пластинке играют приращения крутящих моментов в направлении, перпендикулярном оси полоски, или величины дК1ду и дК/дх.
Пользуясь (2.8) и (2.9), а также (2.5) и (2.6), выразим поперечные силы через прогибы:
дК г, Г 03и> > d*w , ,, ч д$ш ] = — и\--Н р-------------------------- (1 — р)-, ду----------------------------------------------------[_ дхл г дх ду--дх ду2\
ЩИ.
дх
(2.8')
(2.9')
107
Подставим теперь в уравнение (2. 7) значения поперечных сид из (2.8) и (2.9). Получим дифференциальное уравнение равновесия, выраженное в моментах:
+ (2-Ю)
дх2 их ду ду- '
Если подставить в (2. 7) значения поперечных сил из (2. 8') и (2.9'), то получим дифференциальное уравнение равновесия в перемещениях:
d4w , d4w । d4w р
----—1_ /--------(------= — .
дх* дх2ду2 ду* D
(2. 11)
Это д и ф ф е р е и ц и а л ь и о с уравнение в частных производных четвертого порядка впервые было получено французским математиком Софией Жермен (1815 г.). Оно обобщает уравнение изгиба балки
d4w р
дх4 ~ EI ’
дифференциальным уравнени-
являющееся о б ы к н о в е и и ы м ем четвертого порядка.
Обратим внимание на то, что
можно представить как результат двукратно проведенной опера-
<92 <92
ции-----, проделанной над функцией двух переменных
дхг ду2
w = w(x, у).
левую часть уравнения (2. 11)
В самом деле
d4w
, g d4w । d4w дх4 1 дх2 ду2 ду4
д2 / d"w . d2w \ j д'1 / d"w , d2w \ дх2 \ дх2 ду2 ) ду2 \ дх2 ' ду2 )
Операцию-------1----р..., обозначают символом V (так пазы-
дх2 ду-
ваемый оператор Лапласа). Двукратное применение оператора Лапласа обозначается V2?2.
Сокращенная запись уравнения изгиба пластинки будет
V2v2ay = -|“ • (2- 11')
Уравнения, по структуре совпадающие с (2.11), называют б и г а р м о н и ч е с к и м и.
§ 2.3. ГРАНИЧНЫЕ УСЛОВИЯ ПРЯМОУГОЛЬНОЙ ПЛАСТИНКИ
При интегрировании дифференциального уравнения для прогибов граничные (краевые) условия также желательно представить в виде зависимостей, связывающих прогибы па границах.
Координатные осн х, у считаем параллельными краями пластинки. Рассмотрим практически наиболее важные случаи геометрических и статических краевых условий.
108
1. Край, параллельный оси у, жестко защемлен. Это означает, ;что торцы всех балок-полосок, параллельных оси х, жестко защемлены. Поэтому для всех точек края имеем
1) да = 0; 2) --- = 0. (3.1)
дх
Аналогично при жестком защемлении края, параллельного „ л
оси х, имеем на этом крае да —0, -— = U.
Срединная плоскость пластинки вблизи жестко защемленного края остается плоскостью. Поэтому кручение равно нулю, и одно-временпо н крутящие моменты на крае обращаются в нуль. Реакция жесткого защемления сводится к изгибающему моменту и поперечной силе вдоль края. Разумеется, речь идет о погонных величинах.
Жесткое защемление является частным случаем наперед заданных прогибов и углов поворота па крае. Граничные условия заданных перемещений па крае отличаются от (3. 1) тем, что в правых частях этих равенств вместо пуля стоят известные функции от координаты у точки на крае.
2. Край, параллельный оси у, шарнирно оперт. Для общности будем считать заданными прогиб и изгибающий момент на крае. Граничные условия имеют вид
1) w = w*-, 2) -d(— -р ——) = М*. (3.2)
\ дх- ду2 /
Звездочкой отмечены известные (наперед заданные) функции координаты у точки на рассматриваемом крае, параллельном оси у. Если край шарнирно оперт на неподвижную опору, то
* А d‘!w* п да-т- = 0; ----= 0.
дх2
Тогда
1) да = 0; 2) =0. (3.2')
дх2
В противоположность жесткому защемлению шарнирно неподвижное опирание не приводит к аннулированию крутящих моментов вблизи края. В то же время очевидно, что крутящие моменты здесь не могут быть реализованы системой горизонтальных касательных усилий на крае. Они реализуются вертикальными касательными усилиями, что сопровождается изменением величины распределенных вертикальных реакций па шарнирном крае, а также появлением сосредоточенных реакций в углах, обусловленных неуравновешенными составляющими крутящих моментов у угла.
3. Край, параллельный оси у, свободен или нагружен наперед заданными силами и парами (погонными).
Начнем со случая иена груженного края. На первый взгляд кажется, что следует удовлетворить трем граничным условиям
Afv —0; Qv = 0; /< = 0.
109
Первое граничное условие принимает вид
д-w , 0-w
------- U.-----
дх-
0.
(3. 3)
рому и третьему условиям. Приходится
Фиг. 25.
Анализ показывает, что допущения теории топких пластинок, в частности игнорирование деформации сдвига при постановке кинематических гипотез, не позволяет удовлетворить порознь вто-* скомбинировать погонные факторы Q.v и А в статически эквивалентную группу (обобщенную сщ лу) и приравнять ее нулю. На основании принципа Сеи-Веиана это вызовет заметное изменение напряженного состояния лишь в весьма узкой об-' ласти пластинки вблизи ее края, что никакого практического значения не имеет.
Преобразование состоит в том, что крутящие' моменты А заменяются-системой пар с вертикальными компонентами и эти компоненты добавляют к поперечным силам Q*.
На фиг. 25 показан с торца край, параллельный оси у, изображены моменты А н заменяющие их пары сил с вертикальными компонентами.
Ось х направлена к наблюдателю. Погонная интенсивность результирующих вертикальных компонент получается равной дК/ду.
Учитывая направление поперечных сил, действующих на край (вниз), и указанных компонент (вверх), запишем обобщенное граничное условие в виде
Qx
ду
(3.4)
Подставляя сюда значение Qx из (2.8х) получим
и значение А из (2. 6),
_D(1 _ ) дх3 1 дхдуУ V
д3ш q
0.x Оу2
110
или
^ + (2-К)^=0. дх3 ' дх ду2
(3. 4')
Таким образом, в случае свободного края два граничных условия даются уравнениями (3.3) и (3.4'). Граничные условия для свободного края, параллельного оси х, записываются по аналогии.
Пусть теперь на крае заданы изгибающие моменты М* , поперечные силы Q* и крутящие моменты К*. Граничные условия имеют вид
-D f—-+н —) = (3.5)
\ дх2 ду2 )
_ r_№L.(2 - р.)| = Q*. -. (3.6)
[ дх3 дхду2] ду
Теоретическая замена крутящих моментов вдоль края вертикальными силами, хотя и позволяет корректно поставить граничные условия в перемещениях, приводит к ряду следствий, которые требуют критического разбора в каждом отдельном случае. Например, получается, что при нагрузке двух смежных свободных краев крутящими моментами угол пластинки нагружен сосредоточенной вертикальной силой, численно равной 2 К кгсм/см. Такая сила, действительно, возникает, но не при свободных, а при шарнирно опертых краях. Подробнее эти вопросы рассматриваются в специальных курсах теории пластинок и курсах теории упругости.
Расчет пластинок при распределенной нагрузке, как правило, ведется методами, требующими предварительной аппроксимации вида изогнутой поверхности, удовлетворяющей граничным условиям. Отметим несколько частных случаев.
Пластинка, защемленная по четырем краям при симметричной нагрузке. Координатные оси совпадают с осями симметрии. Длины сторон обозначим 2а, 2Ь.
. Для аппроксимации симметрично изогнутой поверхности применяются преимущественно двойные ряды алгебраических и тригонометрических функций.
Двойной алгебраический ряд
W==2 ^Атп{а2-х2Г{Ь2-у2у. (3.-7)
т-2 п=2
При четырех членах аппроксимирующая функция имеет вид
w = А22 (а2 — х2)2 (Ь2—у2)2 -j- Аз (а2~ х2)2 (Ь2~у2)з:\-
+ Л32 («2 - X2)3 (Ь2 —у2)2 + Л33 («2 - -Г2)3 (Ь2-_у2)3. (3. 7')
Двойной тригонометрический ряд:
w — Ai cos2—— cos2 —-^-"а Acos2-^- cos2 ^-A • • • (3. 8) 2a 2b 1 3 2a 2b 1 v 7
111
Предлагаем читателю убедиться в том, что при х=±а имеем да = 0, dw/dx=0\ при у=±Ь соответственно io = 0, dw[dy=Q. Следовательно, функции (3. 7) и (3. 8) удовлетворяют условиям полного защемления всех четырех краев.
Функцию можно образовать также, комбинируя отдельные члены рядов (3.7) и (3.8).
Пластинка, шарнирно опертая по четырем сторонам при произвольной нагрузке. Координатные оси совпадают со сторонами пластинки. Длины сторон обозначены а, Ь.
Фиг. 26.
Аппроксимирующий двойной тригонометрический ряд
V. х"1 л . тт.х . пг.у
w~ у У A sm-----------sm—— . (3.9)
а b т 1 п -1
Первые четыре члена имеют вид
Т0=/1П sin----sin A., sin--------sm-------
a b a b
-4-A,, sin--sin - --i A„,sin----sin— —. (3. 9 )
a b ~ a b
Нечетные номера отвечают симметричным волнам, четные — не--симметричным.
При х = 0 или х = а имеем пу = 0, d2wfdx2 = 0. Аналогично при у = 0 или у = Ь имеем w=0, d2w/dy2=0. Условия шарнирного опирания удовлетворены на всех четырех краях.
Пластинка, шарнирно опертая по трем сторонам со свободным четвертым краем (фиг. 26). Аппроксимирующая поверхность должна удовлетворять следующим условиям па краях:
1) при у — 0 и у-- b w = 0, ---------------------------= О
ду-
2) при х = 0
И) = 0,-----— 0;
дхУ-
112
3) при х = а d‘w , d’w d3w , ч d3w
дх2 1 г ду2 дх3 1 v г' дх ду2
Лервая пара условий требует введения в качестве множителя Синусоиды вдоль оси у. Вторая пара указывает, что вдоль оси х ряд также должен состоять из синусов, чтобы обеспечить обращение в нуль функции и ее второй производной при х=0.
Выбираем аппроксимирующую функцию в виде
7C) = y^sin^(sin^ + #,,sin-^4-C/sin—). (3. 10) Ь \ 4а 2а а /
Множители Вп и Сп определяются из третьей пары граничных условий. Полагаем ц=0,25. Тогда из условия
находим
Из условия
Г d3w . . „г d3w 1 „
Р-1,75 - =0 [ дх3-------------дхду2]х~а
находим
С — 62 + 28пУ
" 128 &2-|- l,75n2<?2 ’
©тот пример иллюстрирует те соображения, которые приходится использовать при подборе аппроксимирующих функций.
§ 2.4. ГИБКАЯ ПЛАСТИНКА И МЕМБРАНА
Выше неоднократно подчеркивалось соответствие жесткой пла-Фгинки и обыкновенной балки. Подобно балке, подвергающейся действию поперечных и продольных сил, и в случае пластинки возникает вопрос об учете влияния напряжений в срединной плоскости на изгибающие и крутящие моменты, когда прогибы пластинки не очень малы.
На фиг. 27 показана пластинка, находившаяся до изгиба поперечной нагрузкой в плоском напряженном состоянии от действия равномерно распределенных продольных растягивающих сил №х и Ny и касательных сил q. Предполагается, что окончательные углы поворота балок-полосок настолько малы (coscp^l), что компоненты плоского напряженного состояния в элементах пластинки сохраняются без заметного изменения.
113
Рассматривая балки-полоски шириной 1 см, вырезанные параллельно осям х, у, устанавливаем, что изгибающие и крутящие моменты в них равны
Mx=M°t-Nxw, Му — — Njw,
Здесь нулем отмечены усилия от действия одной только поперечной нагрузки.
Фиг. 27.
Выразим вертикальные поперечные силы элемента пластинки, пользуясь формулами (2.8) и (2. 9). Получим
z-Ф лг "w dw Qx^Qx-Nx-~q—, дх ду
Qy=Qy~N ' 3 ду дх
(4-2)
Подставив эти значения в уравнение равновесия элемента (2. 7) и учитывая при этом, что члены, зависящие от Q°v и дают умноженную па D левую часть уравнения (2. 11), найдем
+ (4.3),
дх* дх^ду1 ду* / дх2 у дуъ 1 дхду
Уравнение (4. 3) будем называть уравнением сложного или про-; дольно-поперечного изгиба пластинки.
Соответствие с уравнением изгиба растянутой балки
EI^L=p + H^L dx* dx*
здесь совершенно очевидно.
114
Следует подчеркнуть, что хотя использовалось при выводе .предположение о равномерном плоском напряженном состоянии пластинки от действия краевых сил Nx, Ny, q, но пришли мы к .дифференциальному уравнению, имеющему общее значение и охватывающему случай переменных на контуре усилий Nx, Ny, q. По существу такой же прием применялся и при рассмотрении балок. В некоторых случаях этот прием ведет к цели быстрее, чем изучение равновесия элемента.
При сжимающих силах Nx или 2VW знак перед соответствующим слагаемым в уравнении (4.3) должен быть изменен на обратный.
При весьма гибкой пластинке и опорах, закрепленных в горизонтальном направлении, поперечная нагрузка может быть воспринята одними мембранными напряжениями. Полагая в (4.3) цилиндрическую жесткость исчезающе малой
D >0,
получим в пределе дифференциальное уравнение провисания абсолютно гибкой пластинки:
N^+N^+Ъ-^-р. (4.4)
дх- ' ду2 дх ду
Отметим, что всегда можно, так повернуть координатные оси ху, чтобы третий член в правой части обратился в нуль.
От абсолютно гибкой пластинки следует отличать мембрану, не оказывающую сопротивления сдвигу и потому не воспринимающую касательных усилий. Примером такой мембраны может служить мыльная пленка, поэтому будем употреблять термин плен к а.
Так как касательные напряжения в любом сечении пленки равны нулю, то из теории плоского напряженного состояния следует, что нормальные напряжения по всем направлениям одинаковы. Для пленки имеем
Nx —- Nv — const.
Малые провисания сильно растянутой пленки под действием небольшой распределенной нагрузки р=р(х, у) происходят без изменения ее первоначального натяжения M = const. Соответствующее дифференциальное уравнение равновесия получим из (4.4), положив q~0, Nx=и заменив обозначение w на да",
дх- ' ду? N { ‘ ’
или в сокращенной записи
— (4.5')
Здесь мы имеем гармоническое уравнение.
Покажем теперь, что бигармоническое уравнение изгиба жесткой пластинки (2,11') может быть заменено двумя гармоническими уравнениями вида (4. 5').
S* 115
Обратимся к равенствам (2.5), связывающим моменты и прогибы. Сложим левые и правые части этих равенств. Разделив обе' части на (Н~н)> получим
Мх + Му_______и / d2w
1 + |л ~ \ дх?
d-w ду2
(4- 6)
Левую часть (4. 6) примем за новое обобщенное усилие, которое будем называть приведенной суммой моментов и обозначать буквой М. Равенство (4. 6) перепишем в виде
V2®=--j. (4.6')
Проделаем теперь операцию V2 над обеими частями уравнения (4.6'). Приняв во внимание (2. 11'), получим
V27W=-p. (4.7)
Уравнения (4. 6') и (4. 7) и представляют собой те два гармонических уравнения, которые заменяют бигармоническое уравнение (2. 11').
Через вспомогательное усилие М весьма просто выражаются поперечные силы и формулируются граничные условия.
Предлагаем читателю показать, что дМ . дЛ1
дх у ду
(4. 8)
Условия шарнирного опирания края пластинки имеют вид
I) ау=О; 2) М=0. (4.9)
Отсюда следует, что шарнирно опертая пластинка является статически определимой в том смысле, что усилия М в ней могут быть определены интегрированием гармонического уравнения (4.7) независимо от прогибов. Определив функцию М=М(х, у) и подставив ее в уравнение (4.6'), можем определить прогибы w—w(x, у).
Определение моментов Мх, Му, К требует интегрирования гармонических уравнений:
V2t4x=-/7x; v2/Hy=—AV<=pvy, (4. 10;
здесь
/ . д2М \ [ д2М , д?М X
+ ',’=-(^г+и‘Лг)’
/>«=('-и) <4-Ч)
л дх ду
Следовательно, расчет жесткой пластинки на всех стадиях приводится к последовательному интегрированию уравнений того же типа, каким определится провисание пленки (4.5'). Автор основанной на этом теории Г. Маркус формулирует все расчетные операции как определение провисаний пленки с контуром, совпадающим с контуром пластинки при тех или иных действительных или фиктивных нагрузках и развивает численный метод расчета, основанный па замене пленки сеткой из гибких нитей.
116
V
В связи с этим папомним, что дифференциальные уравнения провисания гибкой нити, эпюры моментов и эпюры прогибов простой балки однотипны (см. § 1. 1, гл. I):
y"---J--t м"=-р-, z" М .
у Н 1 EI
Напомним также известное из курса сопротивления материалов построение эпюры моментов простой балки как веревочной кривой (веревочного многоугольника) и аналогичное построение -эпюры прогибов как веревочного многоугольника от фиктивной нагрузки. Таким образом, между работой пленки и пластинки имеются такие же соотношения и аналогии, какие существуют между работой гибкой нити и обыкновенной балки.
§2.5. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИ ИЗГИБА ПЛАСТИНКИ
Потенциальная энергия изгиба выражается двойным интегралом, распространенным на площадь пластинки:
U=T [[ Wx + M^ + 2/<bK)dxdy. (5.1)
Подставляя известные выражения усилий и деформаций через прогибы, получим
, п ,, . <92w d2W 1 , , /с ч\
+ 2(1-р) ТТ-—— \dxdy. (5.1)
дх ду дх ду J
Эта форма энергии путем несложных алгебраических преобразований приводится к виду
г г В СС(/д2ю । д2® \2 о/1 .Г d2w d2w
2 J J (\ дх2 ду2 / [ дх2 ду2
Ч-йгУ]}^- <51">
Подсчитаем энергию для случая, когда прогибы даются двойным тригонометрическим рядом (3.9).
Находим
дУи
дх2
m2Tt2
‘mn 7,
tn
nir.x . nr.y
Sin ------Sin —-
a1 a b
d2w
ду2
'тп
Ь2
mr.x . n~y Sin------sin----— ,
b
(5.2)
д2ш
дх ду
т- 1 л = 1
mn
tn~\ n - 1
тп~2
---- пяу
cos-------cos ——
ab a b
а
117
Подстановка в (5. 1") дает _ (I Ь 00 00 „ -10
z г ® С Г V V .1 / '”2~2 I Я2л2 \ . тт.х . пг.у | ,
114^Ms,nvs'nv у~
о 0 т-\ л-1 v )
Q Z? по со
r~i/i \ffv V'1 л 2 т2п2л* / . , т~х . 2' ппу
~D (1-р) У У Атп ——- sin2-------sin2—-
J J “ \ а о
О 0 т --1 л--1
о тт.х 9 п~.у \ , ,
— cos2-cos2 —— ) ах ay.
a d )
Изменив последовательность интегрирования и суммирования, запишем
IT D ЖП Л.1 Л2 / ОТ2-2 | П2л2 \2 г г ,9 ППХ . о ялу ,
Hsin —sin ь dxdy~
т=^\ п- 1 О О
е° « п е, . / Q Ь
— V Уд’й^ ffsin2^sin2^^ a2b2 \J J a b
m - 1 n 1 '0 0
a I) x
f f о mr.X « nrvV , , \
— I 1 COS2 — - COS2- - ax dy .
0 0й /
Каждый из двойных интегралов, как легко убедиться, равен ab/^. Поэтому вторая строка тождественно обращается в нуль й энергия полностью определяется первой строкой:
<53>
т=^ 1 п = \
Выпишем еще развернутое выражение энергии, ограничиваясь членами с индексами т=1; 2 и п— 1; 2:
Отметим, что нечетные индексы характеризуют симметричные] синусоиды, а четные индексы— антисимметричные синусоиды.
§2.6. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ СЛОЖНОГО ИЗГИБА ПРЯМОУГОЛЬНОЙ ПЛАСТИНКИ, ШАРНИРНО ОПЕРТОЙ ПО ЧЕТЫРЕМ КРАЯМ
Рассмотрим прямоугольную пластинку, нагруженную поперечь ной нагрузкой р кг!см2, а также растягиваемую в двух направлениях равномерно распределенными силами ;Vx = const и Ду const. Нагрузки jV.v, Ny, q выражены в кг/см. Дифференциальное уравнен
118
ние изгиба пластинки получим из (4.3), полагая в нем /Vx = const, const, <7=0.
Учтем также начальный прогиб да0. Для этого, считая да упругим прогибом, заменим в правой части уравнения (4. 3) да на да + да°- Перепишем уравнение (4. 3) в виде
U / д*гг> , 2 ^4® । д4® \ _
\ дх* дх2 ду2 ду* /
.r d2w ,T d2w * — ЛД---------Nv------— p*,
x дх2 y ду2 r
Где
* ... г)2ау0 . dhifi
p*=p-\-N------------------- .
Н H 1 x dx2 J dy2
(6-2)
Решение будем искать в виде двойного тригонометрического ряда (3.9), удовлетворяющего условиям шарнирного опирания на всех четырех краях. С этой целью приведенную поперечную нагрузку раскладываем в аналогичный ряд:
т — 1 л=-1
Втп
sin
т~х . пну -----sin —— .
а b
(6.3)
В дополнение к (5.2) находим
д*ш дх*
т ™ 1
. г тт_х
'тп— — SIH-------
а* а
п 1
ппу
sin-----
ь
d*w ду*
т- 1
Vi л п*к* . тих . пну
7 Лтп----sm------sin—- ,
тп b* а Ь
п — ]
(6.4)
d*w чк-ч
дх2ду2
J т-1
л.-, . п*т2п2 . mttx
7 Атп--------SIB ------
тп а2Ь2 а
П = 1
. пг.у sin—— .
ъ
Внося (6.4), (5.2) и (6.3) в уравнение (6.1) и приравнивая множители при одинаковых произведениях тригонометрических функций, легко получим
(6- 5)
Эта простая формула охватывает большинство практически важных задач расчета прямоугольных пластин со свободно опертыми краями. При Nx=Ny = Q имеем решение задачи о поперечном изгибе жесткой пластинки. ЕслиТУ^О, Ny -^0—решение задачи о продольно-поперечном изгибе, причем может быть учтена начальная погибь пластинки. Забегая несколько вперед, формулируем задачу устойчивости пластинки от продольных сил как отыскание
119
таких сил Nx и Ny, при которых возможны отличные от нуля прогибы и в отсутствии поперечной нагрузки; если речь идет о пластинке с начальной погибыо, то разыскиваются силы Nx и Ny, дающие прогиб более высокого порядка, чем аппликаты поверхности начальной погиби. И в том и в другом случае критические значения Nx и Ny подчинены уравнению, которое получается, если приравнять нулю знаменатель дроби (6. 5).
Обозначая через Nx и Ny краевые сжимающие силы, получим уравнение устойчивости в виде
<6-6)
\ а2 Ь2 } а2 Ь2
Применение этого уравнения рассматривается ниже (см.
§ 2.9). Возвратимся к задачам прочности. Первоочередным вопросом является разложение приведенной нагрузки р*~р*(х, у) в тригонометрический ряд.
С этой целью левая и правая части равенства (6. 3) умножаются на sin r^-dx и интегрируются, затем полученное равенство умно-а
жается на sin dy и интегрируется. Опуская несложные вы-ft
кладки и упрощения, основанные на свойствах ортогональности тригонометрических функций, запишем окончательный результат*:
. ah
^mn~~ f fp*sin — sin-^-dxdy. (6.7)
ab J a b
о о
Случай равномерно распределенной силовой нагрузки р — const (без учета начальной погиби)
Равенство (6. 7) принимает вид
° 0
Отсюда
Втп~-^~. — (1 —cos/nir)-^-(l —cosnw). ab пт пп
При нечетных значениях тип выражения в скобках равны соответственно 2«/тл и 2Ь1пл. При четных значениях т, п они равны нулю.
Следовательно,
Вт — при ГП=\, 3, 5,.., со; п— 1, 3, 5, - • • . °0.' тп ifirnn •
Втп~0 при /г= 2, 4, 6, ..., со; т— 2, 4, 6,..оо.
* Рекомендуем проделать эти преобразования самостоятельно.
120
Остается подставить значение Втп в (6.5):
л Г гч о / ,п2 , Л2 \ т2 п2 1
Лт Dr2 I —— ~— + Nx----+ Nv —
L \ а2 b2 j а2 у *2 J
Прогиб в точке с координатами х, у выражается рядом (3.9).
После подстановки (6. 8) имеем
" " Е Е
т 1 л -1 (т= 1, 3,
т~х пт.у
sin ------sin ------
а b
тп D~2
п2 \ т2 п2 3
+ 77/ + Nx~T + ^77 о* J а,* о* J
п — 1, 3, 5,..., сю).
(6.9).
Максимальный прогиб — в центре пластинки при х = 0,5а, j/ = 0,5&.
При Nx — Ny=Q'.
Ряд для максимального прогиба сходится быстро, и практически достаточно ограничиться одним членом ряда, полагая-т—п-- 1:
Дп — max -------------------. (6. 10).
J_\2
Кд2 + Tv
Для квадратной
пластинки при Ь—а\ ц = 0,3 . ^7,
л ики Ра* хЛ.0 0 1 ,R in
тахте; = 0,454-—. ' (6.11).
Имея ряд (6.9) для прогибов, можем найти изгибающие моменты Мх и Му и крутящий момент К по формулам (2. 5), (2. 6).
Приближенное значение максимальных изгибающих моментов, Отвечающее одному члену ряда (6.9), дается формулами
max Мх —
16р а2Ь2 (Ь2 + у.а2)
к4 (а2 Щ />2)2
max Му
16р аЧ2 (а2 + р.Ь2) (а2 + Ь2)2
Для максимальных нормальных напряжений :мулы
„ / 1 \2 1
max ох= 6 (max Мг) (—) ,
max зу= 6 (max Му) (—
(6. 12).
получаются фор-
(6. 13).
121:
Более точные значения, полученные с удержанием трех членов ряда для прогибов, вычисляются по формулам
maxw = C, ; шах ау= ; max ах= С3р . (6.14)
Здесь а — короткая, b — длинная сторона пластинки.
Коэффициенты С в зависимости от отношения b/а приведены в табл. 3.
Таблица 3
bja Cl c2 C3
1,0 0,0443 0,287 0,287
1,2 0,0616 0,376 0,301
1,4 0,0770 0,452 0,304
1,6 0,0906 0,517 0,296
1,8 0,1017 0,569 0,287
2,0 0,1106 0,610 0,278
3,0 0,1336 0,713 0,242
4,0 0,1400 0,741 0,230
CO 0,1422 0,750 0,225
При Ь/о>Зн-4 изгиб пластинки равномерно распределенной нагрузкой практически можно рассматривать как цилиндрический и вести расчет для изолированной балки-полоски с пролетом Ь.
Случай сосредоточенной силы Р в точке с координатами х=с, y = d
Силу Р заменим распределенной нагрузкой на бесконечно малой площадке dxdy. Интенсивность распределенной нагрузки
(6. 15)
р=^-----
dx dy
В выражении для коэффициента разложения нагрузки (6.7) следует считать р*=0 всюду, кроме точки х = с, y = d, где она равна величине (6. 15). Поэтому
Втп
4 Р , тт.с . n-d , , 4Р . тт.с . nnd
--------sin sin dxdy>= sin - — sin - - (6. 16) ab dx dy a-----------------------b-ab a b
и далее
A„n ntn
mr.c nnd
4Psin------sin------
a b
(6. 17)’
Dr^ab
122
Прогиб дается рядом
Вычисление усилий делается по общим правилам.
(6. 18)
Случай начальной погиби
Начальная погибь обычно задается в виде
Л . м , СТ
= 7°sin-----sin -2—,
а b
(6. 19)
другими словами, в виде одного члена разложения функции w° = w°(x, у) в двойной тригонометрический ряд.
Следовательно, при q = 0
* Л, <92®о . Л, d^w° / j-пм 1 712 \ • г-х Т--У
-------сдг--------= — — ----f0Nv] sin — sin —.
f x dx2 1 v ду9 \a? x b9- 4 a b
Отсюда
(6. 20)
(6-21)
(6. 22)
Знак минус, разумеется, объясняется тем, что при положительной (направленной вниз) погиби и растягивающих силах Nx и Nv упругий прогиб направлен вверх.
§ 2.7. ПРИМЕНЕНИЕ МЕТОДА РИТЦА — ТИМОШЕНКО
Аппроксимируя изогнутую поверхность прямоугольной пластинки, свободно опертой по четырем краям, двойным тригонометрическим рядом, составим выражение полной энергии как раз-
123
ности между потенциальной энергией упругой деформации и ра-ботой нагрузки. Пользуясь выражением (5. 3), получим
Q Ь со оо
-JP7 2 sindxdy. (7.1}
О 0 m-Н л=1
Совершенно аналогично рассуждениям, приведенным в§ 1.5, гл. I, на примере балки заключаем, что для определения коэффициентов Атп служат условия экстремума полной энергии Э;
83=0,
откуда
= 0 (/«=1,2,3,...; п= I, 2, 3. . . .).
дАтп
Выполнение этой операции над (7. 1) дает
~~ DAtnn (,-4 + тг)2 - f J (psin sin-^-)^J> = 0. (7. 2)
4 \ a/- J J и \ а о ]
' 0 0
В случае постоянной нагрузки p = const двойной интеграл обра: щается в нуль для всех четных значений! т, п, а для нечетных он 4аЬ г-.
равен ----. Поэтому
rdnm
А 16р
1
(7. 3)
что совпадает с результатом (6.8), если положить в нем Nx= = /Vw = 0.
Если пластинка нагружена сосредоточенной силой Р в точке х — с, y = d, то вместо уравнения (7.2) будем иметь
г, . /' пР , п2 \ п . тт.с . n~d
DAm„ (------11-) —Psin------sin-----= 0. (7.4)
\ а~ Ь* / а b
Отсюда найдем
Атп
, тт.с пт-d
4/Jsin------sin------
a b
а1
гр \2
62 )
(7.5)
Исследование шарнирно опертой прямоугольной пластинки по методу Ритца—Тимошенко приводит в данном случае к тем же результатам, что и применение метода рядов.
124
§2.8. ЧАСТНЫЕ СЛУЧАИ НАГРУЗКИ И ГРАНИЧНЫХ УСЛОВИЙ
Формулы, полученные для прямоугольной пластинки, шарнирно опертой по краям и нагруженной равномерно распределенной или сосредоточенной нагрузкой, обычно кладутся в основу расчета па прочность и при другом распределении нагрузки и других
граничных условиях.
Подсчеты показывают, что при распределенной нагрузке, не слишком сильно изменяющейся по площади пластинки (фиг.
28, а), расчет прогибов и моментов практически можно вести по среднему значению интенсивности нагрузки:
y)dxdy _р dx dy ~~F'
(8-1)
Здесь Р— равнодействующая нагрузки, p — ab — площадь пластинки.
Оказывается, что если нагрузку, распределенную вдоль короткой сто
Фиг. 28.
роны по закону треугольника и постоянной вдоль
длинной стороны (фиг. 28,6), заменить статически эквивалентной постоянной нагрузкой рСр=Ртах/2, то ошибка в максимальном прогибе не превзойдет 1,5%, а в максимальном изгибающем моменте— 9% в сторону преуменьшения действительного момента.
Между прочим, следует отметить, что ошибка в моменте всегда превосходит ошибку в прогибе, если заменить данную нагрузку любой статически ей эквивалентной.
Нагрузку, распределенную на небольшой части площади, обычно заменяют сосредоточенной нагрузкой. Как прогиб, так и моменты при этом получаются преувеличенными. Если же заменить такую нагрузку равномерно распределенной, то прогибы и моменты получаются меньше действительных. Поэтому иногда расчет ведут дважды: один раз, считая нагрузку распределенной равномерно по всей площади, и другой раз, считая ее сосредоточенной. В качестве расчетных величин берут средние значения.
Граничные условия в реальных конструкциях более или менее сильно отличаются от идеального свободного опирания, жесткой заделки и т. п„ как, например, условия опирания клеток обшивки крыла (фиг. 29).
Очень часто клетка обшивки рассматривается как свободно (шарнирно) опертая по контуру пластинка (фиг. 30, а). Однако
125
при малой толщине обшивки, большой жесткости продольного и поперечного силового набора и наличии двухрядного заклепочногс
шва более правильно считать края пластинки жестко защемленными (фиг. 30,6). Неразрезность пластины при равномерной на-
фиг. 30.
грузке и при однорядном шве приводит к условиям, близким к защемлению (фиг. 30, в). Наличие жесткого защемления уменьшает
126
наибольший прогиб пластинки в 3—4 раза по сравнению со свободно опертыми краями, а изгибающий момент в центре пластинки в | 5—2 раза. Зато в середине каждого защемленного края пластины появляются изгибающие моменты, которые более чем в два раза превышают момент в центре пластины и имеют противоположный ему знак. Величины наибольших изгибающих моментов на защемленном краю оказываются в несколько раз больше максимального момента для аналогичной пластины, свободно опертой по контуру.
Нервюры, как правило, имеют большую жесткость па изгиб и могут рассматриваться как абсолютно жесткие опоры. Стрингеры обладают большей гибкостью и в некоторых случаях приходится
Таблица 4
х
№
я <11 а
по
Условия опирания пластинки
Схема
:Х а
:Х X а
пор.
'О
3
2
X
2
3
4
г
8
и
X
Все четыре края шарнирно оперты па жесткие ребра
Все четыре края жестко защемлены
Два противоположных края жестко защемлены, остальные шариирио оперты
Два противоположных края шарнирно оперты на жесткие ребра, остальные оперты па упругие ребра 1
1
0,31
0,47
1,07
0,5
0,69
1,05
—1,07
-1,46,
1
О
О
1 Изгибпая жесткость ребер £т = lOzzD, где D-.— цилиндрическая жест* кость пластинки. Упругая заделка краев пластинки изображена волнистыми линиями.
127
считаться с их податливостью, принимая их в качестве упруги: опор. Наличие упругих опор несколько увеличивает прогиб и мак симальпый изгибающий момент.
Для сравнения в табл. 4 приведены относительные величннь ютах И Мтах для равномерно нагруженной квадратной пластин ки с различными условиями опирания по краям.
Прогиб и изгибающий момент в середине шарнирно оперто? пластинки приняты за единицу. Данные этой таблицы можно применять по соображению и для учета различных условий опирания прямоугольных пластин с неравными сторонами.
§ 2.9. УСТОЙЧИВОСТЬ ПЛАСТИНОК ПРИ СЖАТИИ В ОДНОМ НАПРАВЛЕНИИ
Исследование устойчивости прямоугольных пластинок имеет первостепенное значение для расчета самолетных конструкций. Сжимающие напряжения, возникающие в обшивке при изгибе крыла, могут привести к выпучиванию обшивки, после чего опа ________________________ почти целиком выключается из работы.
* Это может повести к катастрофе; если только соседние элементы не воспри-N* мут па себя нагрузку пластинки.
Предположим, что прямоугольная пластинка шарнирно оперта по четырем краям и подвергается действию сжимающих усилий Nx, равномерно распределенных вдоль двух противоположных краев (фиг. 31). Нагрузка,
перпендикулярная плоскости пластинки, отсутствует. Будем считать, что края пластинки могут свободно перемещаться в плоскости пластинки.
Будем постепенно увеличивать погонную сжимающую силу Nx. При малых значениях Nx пластинка устойчиво сохраняет свою плоскую форму- Это значит, что она противодействует всяким внешним факторам, вызывающим отклонение от плоской формы. Если, например, изогнуть пластинку, приложив нормально к ее поверхности какую-либо силу, то с удалением этой силы исчезает и прогиб. По мере возрастания сжимающей продольной силы сопротивление пластинки поперечному изгибу несколько падает, но качественно картина остается без изменения до того момента, когда сила подойдет к своему критическому значению АД = Дкр- В этот момент пластинка практически теряет сопротивление изгибу, и достаточно минимальной поперечной нагрузки, чтобы произошло выпучивание в ту или другую сторону. Выпучивание в состоянии безразличного равновесия может произойти и без видимой причины. После выпучивания форма пластинки становится устойчивой и пластинка вновь оказывает сопротивление поперечному изгибу. Дальнейшее возрастание сжимающей силы, как правило, вызывает разрушение пластинки
128
,в процессе нарастания выпучин, иначе говоря,—-от продольного изгиба. Картина будет иной, если пластинка оперта на достаточно мощные продольные ребра, способные воспринять не только приходящуюся па них нагрузку, но и часть нагрузки пластинки и этим воспрепятствовать прогрессированию деформации пластинки.
Займемся теперь вопросом определения критической силы, оставив пока в стороне явления, происходящие после потери устойчивости.
Будем определять критическую силу Nx=Nl<p как наименьшую силу, при которой возможно упругое искривление срединной поверхности сжатой пластинки несмотря на отсутствие поперечной нагрузки. Речь идет о возможности при определенной силе УУЖ = МФ другой формы равновесия пластинки, помимо плоской формы. Сила 2VX = A/Kp должна быть способна удержать искривленную форму пластинки, если таковая наступила.
Вся подготовительная работа для решения поставленной задачи была выполнена в § 2.6, и можно непосредственно использовать уравнение устойчивости (6.6). Оно было получено в предположении, что упругая поверхность пластинки представлена двойным тригонометрическим рядом. Следует заметить, что чередование прямоугольных выпучин и впадин, отвечающее этому ряду, очень точно характеризует действительную картину, наблюдаемую при опытах.
Положив в уравнении (6.6) Nv = 0, получаем
N ^(пгЬ п^\2. (9.1)
№ \ a mb]
Задача сводится к определению числа полуволн т и п, при котором АС принимает наименьшее значение Nx = NKp- Очевидно, при прочих равных условиях следует взять
л= 1, другими словами, перпендикулярно направлению сжатия образуется только одна полуволна.
Число полуволн в направлении сжатия т зависит от отношения размеров а и b и определяется из условия минимума выражения tmb j а \ ( a mb /
Легко сообразить и не делая выкладок, что минимум имеет место при
mb а ।
a mb
или, иначе говоря, при
Следовательно, минимальное значение N„p соответствует таким размерам пластинки, когда ее ширина целое число раз укладывается в ее длине. Изогнутая поверхность при этом разбивается
129
на квадратные участки впадины..
Критическая сила
(фиг. 32) — чередующиеся выпучины i
4-ЗД
*2
(9.2
Критическое напряжение
^кр 4n2Z)
В общем случае, когда а/b не является целым числом, критическое напряжение выражается формулой
где
(9.4)
(9-5)
На фиг. 33 показаны кривые коэффициента ka в зависимости от отношения а/b для различных значений числа продольных полуволн т. Минимумы всех этих кривых соответствуют a/Z> = l, 2, 3, ... и дают значение /?3 =4.
Анализ кривых показывает, что для коротких и широких пластин, когда а/Ь — малая величина, минимальное значение отвечает т= 1, т. е. потере устойчивости по одной полуволне в направлении действия сжимающей силы. При а/6<<С 1, т. е. для очень широких коротких пластин, величиной а/b можно пренебречь ио сравнению с b/а и принять ki^b^/ci2, а критическое напряжение
_ r^D
°к₽~ аЧ •
(9-6)
В этом случае критическое напряжение Не зависит от ширины пластины, а зависит лишь от ее длины. Формула получается аналогичной формуле Эйлера для сжатого стержня длиною а с наименьшей изгибной жесткостью, равной цилиндрической жесткости пластинки. Это объясняется тем, что с увеличением ширины пластинки ослабляется влияние опор по коротким сторонам и она ведет себя почти как стержень, шарнирно опертый по концам.
130
По мере приближения формы пластинки к квадратной величина Аа'"] уменьшается и достигает минимума /?а =4 при a/b — 1. Затем при дальнейшем увеличении длины пластинки (по сравнению с шириной) kc снова возрастает и становится большим, чем значение k„, соответствующее т = 2. Это означает, что при данной величине а/b пластинка потеряет устойчивость, выпучившись не по одной, а по двум полуволнам, так как последней форме изогнутой поверхности соответствует меньшее критическое напряжение. Точ-
ка пересечения кривых k„ при /п=1 и /<а при т=2 соответствует такому значению а/b, при котором одинакова возможность потери устойчивости как по одной полуволне, вытянутой в направлении длины пластинки, так и по двум полуволнам, вытянутым в направлении ширины (фиг. 34). Продолжая увеличивать длину пластинки, найдем, что минимальное значение k, получается при все возрастающих величинах tn. Нижние части кривых, изображенные на фиг. 33 жирными линиями, определяют наименьшую величину ka при данных размерах пластинки. Точки' пересечения кривых соответствуют переходу формы потери устойчивости по т полуволнам к новой форме с /п+1 полуволной. Абсциссы этих точек определяются из условия равенства ординат
k, (/n) = /?o (/«-|- 1) или из условия
/ mb , а \2__/(т -р 1) b , а _\2
\ a mb ) \ а (т +1) b)
откуда получим
—=//п(/п-|-1) , (9.7)
ь
Подставляя в (9.5) последовательно значения /п=1, 2, 3, ... , находим числовые значения абсцисс точек пересечения кривых ]/2Г УбГ /12, /20...
9*
131
По мере увеличения длины пластинки отклонение k° от минимума становится все меньше и меньше. Наибольшее значение k, для удлиненной пластинки, соответствующее —=4^2, оказывается ь
равным 4,5, т. е. отличается от min ka =4 только на 12,5%. Поэтому критическое напряжение для пластинок со сторонами а^- ь можно вычислять по формуле для квадратной пластинки (9.3). Изогнутая поверхность при выпучивании длинных пластинок разбивается на квадратные, или близкие к квадратным, полуволны, и величина критического напряжения будет зависеть от ширины b пластины, а не от ее длины.
Формулу (9.4) часто применяют несколько видоизмененной, подставляя значение цилиндрической жесткости при pi = 0,3, что приводит к выражению
0,9*о£
(9 8)
или для удлиненной пластинки при ka = 4
(9. 8')
Пределы применимости формул критического напряжения
Критическое напряжение, получаемое по выведенным выше формулам, должно быть ниже предела пропорциональности.
Для удлиненной пластинки это условие дает
Для дуралюминовых пластинок при £=7,2-10s кг/см2 и о'пц= = 28004-2900 кг!см2 предельное отношение будет
Таким образом, при толщине обшивки t=2 мм ширина пластины, т. е. расстояние между смежными стрингерами, должна биты не менее 60 мм для того, чтобы критические напряжения можно было определять по выведенным выше формулам.
В конструкциях современных летательных аппаратов часто встречаются пластинки значительной толщины, а стрингерный на,-бор ставится настолько часто, что отношение b/t оказывается меньше предельного значения. В этом случае сжатые пластинки теряют устойчивость при напряжениях, превышающих предел пропорциональности, так что применение формулы (9. 8) дает завышенные: значения критических напряжений и приводит к неправильному представлению о действительном запасе прочности.
132
Устойчивость пластинок за пределом пропорциональности
Теоретическое исследование вопросов устойчивости пластинок за пределом пропорциональности представляет большой интерес и большие трудности.
Точное решение задачи об устойчивости сжатой пластинки за пределом пропорциональности получено А. А. Ильюшиным на основании теории малых упруго пластических деформаций. Он показал, что критическое напряжение зависит от свойств материала в пластической области, характеризуемых не одним модулем упру-
гости Е, а двумя модулями: секущим Ес и касательным Ек. Для вычисления этих модулей необходимо иметь диаграмму зависимости между сжимающим напряжением ст и соответствующей ему 'относительной деформацией в. Примерный вид диаграммы ст, в для дуралюмина показан на фиг. 35, а. Касательный и секущий модули определяются как тангенсы углов наклона касательной и секущей, проведенных в точке М диаграммы
£,K=tgaK; £'c=tgac-
Таким образом, каждому напряжению ст соответствуют свои значения Е,, и Ес. Очевидно, на линейном участке кривой оба модуля становятся равными модулю упругости Е. Если материал имеет площадку текучести (фиг. 35,6), то при о==от касательный модуль обращается в нуль, а секущий уменьшается по мере увеличения деформации.
Приведем приближенную формулу, дающую величину критического напряжения, полученную на основании точного решения
а (2-1-1/ Н-З— И—f, (9.10)
кр 12(1 — и)\ У 1 Ес J\ b ) v 7
где Ек и Ес определяются по диаграмме ст, в для данного материала, коэффициент Пуассона ц до предела упругости равен 0,3, а за пределом упругости возрастает до 0,5.
Эта формула для материалов без площадки текучести (легированные стали, дуралюмин) по сравнению с точным решением дает
133
-ошибку не больше 4,5%. При напряжениях, меньших предела упругости, ЕК=ЕС = Е и формула (9. 10) при ц = 0,3 переходит в формулу (9.8).
В случае материала с ясно выраженной площадкой текучести на диаграмме растяжения в формуле (9. 10) следует положить £'к = 0, а р. = 0,5. В результате имеем
°кр= 3,3£с^—. (9. 11)
Из этой формулы видно, что критические напряжения в пластической области существенно зависят от величины секущего мо-
Фиг. 36.
дуля и при нарастании пластических деформаций постепенно уменьшаются.
Для ряда материалов, в том числе для дуралюмина, критические напряжения за пределом пропорциональности могут быть вычислены по приближенной линейной формуле, сходной с эмпирической формулой Тетмайера — Ясинского для устойчивости стержней:
(9-12)
Величины Оо и с для различных материалов имеют разные значения, которые могут быть вычислены теоретически или получены экспериментально.
Для дуралюмина Д16 можно принять о0 = 4880 кг/см? и с = = 80 кг/см2 в случае шарнирного опирания кромок и а/Ь^>3. Однако применение формулы (9. 12) возможно лишь в пределах
16 < — <36.
t
Зависимость между окр и b/t можно изобразить в виде графика (фиг. 36), линейный участок II которого соответствует потере устойчивости за пределом пропорциональности.
При больших толщинах разрушение пластин происходит при напряжениях, близких к оь материала пластинки. Поэтому при 6Д<16 наблюдается резкое отклонение величины оКр от линейного закона (участок III на фиг. 36).
Влияние граничных условий
На величину о1(р сильно влияют условия закрепления краев пластины. Жесткое защемление повышает устойчивость, наличие свободных краев резко уменьшает величину критического напряжения. Общий ход вычисления окр для пластин с различно закреп-
134
ценными краями ничем не отличается от 'проведенного выше Исследования уе^рйчивости пластины с шарнирно опертыми кромками. Только выражение для w приходится выбирать отличным от (3.9) с тем, чтобы удовлетворить новым граничным условиям. В результате получается формула того же вида, что и формула (9.8), но ka имеет различные значения в зависимости от харак-
Фиг. 37.
гера закрепления краев пластинки. На фиг. 37 приведены графики коэффициента k<, (обозначения краев, соответствуют фиг. 30). Графики показывают, что при увеличении длины пластины в направлении сжатия влияние условий опирания по коротким сторонам становится несущественным и критические напряжения стремятся к значениям, определяемым характером закрепления длинных сторон и шириной пластинки.
Для удлиненной пластинки (а/6>3), защемленной по боковым сторонам, можно принять k„ =7 независимо от условий закрепления ее торцов.
135
При желании более точно учесть реальные условия прикрепления листа к другим конструктивным элементам приходится принимать во внимание упругие свойства опор пластинки. Подкрепляющие ребра под действием реакций со стороны пластинки могут изгибаться и закручиваться, что создает условия, отличные от тех, которые соответствуют жестко защемленному краю. Реальные условия часто бывают также далеки и от условий шарнирного закрепления, так как опорные стержни, к которым приклепывается пластинка, обладают значительной жесткостью па кручение.
Теоретическое решение задачи об устойчивости упруго опертой пластинки достаточно сложно. Приведем кратко результаты для одного практически важного случая, когда пластинка подкрепляется жесткими на изгиб ребрами, причем края х = 0, х = а, к которым приложена нагрузка, оперты шарнирно, а края г/ = 0, у = Ь упруго закреплены от поворота вокруг оси х.
Этот случай соответствует Опиранию ненагружепных краев на стрингеры, имеющие сравнительно большую жесткость па изгиб и малую жесткость на кручение- Критические напряжения стк вычисляются также по формуле типа (9.8), однако коэффициент ко здесь зависит не только от величины а/b, но и от соотношения жесткости опорных ребер на кручение GIk и цилиндрической жесткости пластинки D.
Значения коэффициента ko приведены на фиг. 38, где каждая кривая соответствует определенной величине параметра a = bDIGIk. При нулевой жесткости кручения получим случай пластинки, шарнирно опертой по всему контуру (кривая 4, см. фиг. 37), а при бесконечно большой жесткости кручения — случай пластинки, шарнирно опертой по нагруженным краям и жестко защемленной по двум другим (кривая 2, см. фиг. 37)-
Пример 1. Вычислить критические напряжения для клетки обшивки верхней части крыла самолета, работающей на сжатие, считая ее шарнирно опертой на жесткий контур, образованный смежными стрингерами и поясами
136
нервюр (фиг. 39), какую силу сможет воспринять обшивка до потери устойчивости. Дано: а = 350 лмц />==100 мм; 1 = 2 мм, материал обшивки — дуралюмин 016 (£=0,72 • 10е кг/см2, аПц = 2800 кг/см2).
Отношение 6// = 100/2 = 50>30, следовательно, можно пользоваться формулой (9.8). Так как а/6=350/100 = 3,5, то =4 и нормальное напряжение
_ 3,6-0,72-106
ОкР /1ПП\2
1040 кг [см2.
Наибольшая сила, воспринимаемая пластинкой до потери устойчивости, Nup = OKpbt= 1040 • 10-0,2 = 2080 кг.
Пример 2. Вычислить наибольшую сжимающую силу, которую может выдержать до потери устойчивости пластинка толщиной / = 4 мм со сторонами а =
= 600 31Л1 и 6 = 180 мм, сжимаемая вдоль длинных сторон. Пластинка оперта на жесткие ребра и защемлена по длинным сторонам,, а по коротким сторонам— свободно оперта. Определить, на сколько изменится величина критической силы, если учесть деформацию кручения продольных ребер, выполненных из прессованных угольников Пр 100—10 размером 35X35X4 льи. Материал пластинки дуралюмин Д16 (£ = 0.72-102 кг/см2, н = 0,34, а,щ = 2800 кг/см2), материал ребер дуралюмин Д6 (0 = 0,25-10° кг/см2).
Коэффициент /го для а/6 = 600/180=3,33 берем по графику 2 фиг. 37. Принимаем 6О=_7 и подставляем в формулу (9.8):
0.9-7-0,72-1Q6 а'<р = 7w?\2
W )
= 2240
Kzj см2.
Полученные напряжения менние Опц, следовательно, формула (9.8) для данной пластинки применима. Наибольшая сжимающая сила
£i ~0:<pbt = 2240 • 18 • 0,4= 16 100 кг.
Для того чтобы учесть влияние деформации кручения продольных ребер, вычислим их жесткость GIfl = Gst2/3 по известной формуле для открытого тонкостенного профиля, принимая длину средней линии полки угольника $ = 33 мм,
GIk = 0,25-106-— -2-3,3-0,43=: 0,352-105 кг]см2
3
137
Цилиндрическая жесткость пластинки
0,72-106-0,43
D — ---------——-----= 0,435-104 кгем.
12(1 — 0,342)
bD 18-0,435-104
G/k ~ 0,352-105 -2’22-
По графику фиг. 38 находим ka при а/й=3,33 и а=2,22. Получаем /го-«5,3 и вычисляем о кр по формуле (9.8):
0,9-5,3-0,72-106
°кр= --------;Тй,к2------= 1700 кг/сл/2.
Максимальная сжимающая сила с учетом упругости продольных ребер оказывается равной
/>2=1700-0,4- 18 = 12200.
Таким образом, благодаря малой жесткости продольных ребер на кручение критическая сила оказывается меньше на
ДР= 16 100—12 200 = 3 900 кг.
§ 2.10. УСТОЙЧИВОСТЬ ПЛАСТИНОК ПРИ СЖАТИИ В ДВУХ ВЗАИМНО-ПЕРПЕНДИКУЛЯРНЫХ НАПРАВЛЕНИЯХ
Рассматривая пластинку, свободно опертую по четырем краям (фиг. 40), используем вновь уравнение (6.6). Записываем его в виде
Nxm2-\-Nn2 — = — V. (10.1)
х 1 у Ь* аг \ 1 *2/
Здесь т и п-—числа полуволн в направлениях х и у. Величины тип следует выбрать таким образом, чтобы критическая нагрузка на пластину была минимальной. Для решения этой задачи необходимо знать отношение
нагрузок Nx н Ntl. При Ny = 0 имеем случай сжатия в одном направлении. Сравнивая (9. 1) и (10. 1), видим, что наличие постоянной сжимающей силы Ny уменьшает критическую величину силы Nx. Наоборот, растяжение пластинки в направлении оси у способствует увеличению критической силы Nx.
Если силы Nx и Nv возрастают, оставаясь в постоянном отношении Nx/Ny=a, то установить
минимальное значение критической комбинации нагрузок не представляет особых трудностей. Пусть, например, а= 1, Nx=Ny; тогда
минимальное значение сжимающих нагрузок достигается при
138
rn=n=l (пластинка теряет устойчивость по одной полуволне в обоих направлениях):
minTV— min N (1 -ф—Y
х у а2 \ ' b2J
Для квадратной пластинки при а~Ь имеем
min Nx =
а2
Сравнивая это выражение с (9.2), видим, что критическая сила равномерно сжатой по двум направлениям квадратной пластинки вдвое меньше критической силы для такой же пластинки, сжатой в одном направлении.
Для квадратной пластинки со всеми жестко заделанными краями, сжимаемой в двух направлениях равными силами, критические напряжения можно вычислять по формуле (9.8), принимая ka =5,33.
Представляет интерес случай а =—1, когда пластинка сжимается в одном и растягивается в другом (перпендикулярном первому) направлении. Растягивающие напряжения в обшивке могут появиться в результате действия поперечной нагрузки, вызывающей цепные напряжения в срединной поверхности гибкой пластинки. Таким образом, формула (10. 1) при (Vx>0 и Nv<0 учитывает влияние цепных напряжений на устойчивость пластинки (напомним, что в задачах устойчивости сжимающая сила считается положительной) .
Положим для простоты анализа силы Nx и Nv равными по абсолютной величине:
ЛЛ.= ЛГ; M=-N. л У
Тогда критическое значение силы N найдется из уравнения (10. 1):
К₽
' \2
ОТ2 4-Л2_—-)
Ь2 )
(10. 2)
а2 т2 — п2 — —
Очевидно, минимальное значение (VKp соответствует п=\, так как уменьшение п увеличивает знаменатель и уменьшает числитель. Принимая п=\ и вынося в числителе за скобки величину at/b2, получим
/ Ь а \2 (т2 — 4“ ~7~ )
n = v?---------------b_L . (Ю.з)
"Р ь2 а2
т2 — —
Ь2
Второй множитель этой формулы зависит от т. Для выяснения характера этой зависимости можно было бы построить серию кривых, подобно кривым ka на фиг. 33. Ограничимся аналитическим определением минимального значения (VKp.
139
Беря производную dNKVldm и приравнивая ее нулю, получаем
п b q а р т2------3 — = 0.
а b
Таким образом, минимум критической силы имеет место при соотношении сторон пластины
В случае потери устойчивости пластинки по одной полуволне в продольном направлении (/?z= 1) минимальная сила будет при соотношении сторон —=—» 0,577. При т — 2, — = -Л= = 1,15 и т. д.
Ь уз Ь уз А
Подставляя значение а/Ь (10.4) в (10.3), вычислим минимум критической силы:
N =^Р-. (10.5)
Сравнивая это значение 7VKp с критической силой для случая одностороннего сжатия длинной пластинки (9.2), видим, что наличие растягивающих напряжений ЛД, равных сжимающим Nx, увеличивает критическую силу в два раза. Заметим, что в этом случае наименьшей критической силе соответствует форма потери устойчивости с образованием выпучин, удлиненных в направлении растягивающей силы (а = 0,5776), а не квадратных, как в случае одностороннего сжатия.
Для определения соотношения сторон пластинки z^a/b, при котором происходит переход от формы потери устойчивости с т полуволнами к форме с т+1 полуволной, надо решить биквадратное уравнение
3z4~y {//г2-|- (/иI)2] z2— т2 (/п Д-1 )2 = 0.
Так, например, переход от /и=1 к т = 2 происходит при alb-z~ =0,77, а переход от т = 2 к т = 3 имеет место при
-—=2=1,38.
ь
Следовательно, квадратная пластинка будет терять устойчивость с образованием двух полуволн в направлении сжатия.
§ 2.11. УСТОЙЧИВОСТЬ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ПРИ СДВИГЕ
Тонкая прямоугольная стенка, нагруженная по краям касательными усилиями, теряет устойчивость, покрываясь волнами, гребни которых составляют с осью х угол а, близкий к 45° (фиг. 41). Как известно, при чистом сдвиге возникают главные растягивающие напряжения си и сжимающие напряжения си, численно равные т и наклонные под углом 45° к направлению касательных напряже-
но
ний. Наличие сжимающих напряжений сг2 объясняет характер
(выпучивания пластинки.
Дифференциальное уравнение равновесия элемента пластинки (4.3) в рассматриваемом случае (р = 0, ЛД=0, Ny = 0) принимает вид
дх*
д*ш дх2 ду2
, d*w \ q d2w ~Г ду* ? ^дхду
0.
(Н-1)
Для шарнирно опертой по всем краям пластинки можно задаться функцией прогибов в форме, удовлетворяющей граничным усло-
Фиг. 42.
виям, и для нахождения величины критического сдвигающего усилия 9кр воспользоваться методом Бубнова—Галеркина или Ритца—Тимошенко. Отметим, что в данном случае непосредственное использование двойного тригонометрического ряда для прямого интегрирования уравнения (11.1) не достигает цели, так смешанная- производная выражается не через синусы, а через косинусы. Ограничимся сводкой некоторых результатов.
Формула для критического напряжения имеет вид
укр 0,9/г.£
(11.2)
Формула (11.2) верна при тКр<тПц. Она внешне совершенно идентична формуле (9.8), но коэффициент k разумеется, вычисляется иным способом, чем в случае потери устойчивости при сжатии.
141
Для шарнирно опертых кромок величину k-. можно подсчитывать по следующей приближенной формуле, удовлетворительно подтверждающейся экспериментально:
^ = 5,35 + 4^у, (Н.З)
причем всегда а^Ь.
Формула (11.3) показывает, что наиболее устойчивой будет квадратная пластинка (k-.— 9,4). По мере удлинения пластинки величина критической силы довольно быстро падает, приближаясь к значению для бесконечно длинной пластинки (/г^— 5,35).
Болес точные значения коэффициента /г- для различных способов закрепления краев приведены в табл. 5 и на графиках фиг. 42.
Сравнение приведенных данных показывает, что защемление краев пластинки увеличивает ее устойчивость на сдвиг примерно па 7%.
§ 2.12. УСТОЙЧИВОСТЬ ПЛАСТИНКИ ПРИ СОВМЕСТНОМ ДЕЙСТВИИ СЖАТИЯ И СДВИГА
Работа пластин при совместном действии сдвига и сжатия (растяжения) в одном направлении характерна для авиационных конструкций. В качестве примера приведем работу обшивки крыла или фюзеляжа самолета при одновременном действии изгибающего и крутящего моментов. Изгибающий момент при нормальном полете вызывает сжатие обшивки верхней части крыла, в то время как крутящий момент заставляет обшивку работать па сдвиг.
Величины а и т, вызывающие при совместном действии потерю устойчивости пластинки (фиг. 43), приближенно определяются из соотношения
+ (12.1)
сткр \ткр /
142
где oI(p и тКр—критические напряжения для пластинки при действии только сжатия или только сдвига, вычисляемые по формулам (9.8) и (11.2).
Показатель степени п по различным опытам колеблется от 1,5 до 2. Обычно принимают п=1,7, хотя без большой ошибки можно брать п = 2 в запас устойчивости по нормальным напряжениям. Пользуясь формулой (12.1), можно вычислить величину ст при
Фиг. 44.
Фиг. 4.3.
фиксированном т (или, наоборот, т при определенном ст). Если же Стит возрастают одновременно и пропорционально, то их критические значения находим, вводя в (12. 1) параметр а = ст/т.
Наличие сдвига понижает величину сжимающих критических напряжений. Так, например, при т = 0,5тКр пластинка потеряет
устойчивость при сжимающих напряжениях ст=(1—0,52)сткр = = 0,75сткр. Наличие нормальных напряжений также сказывается на величине критических напряжений сдвига. Сжимающие напряжения уменьшают ткр, а растягивающие — увеличивают, так как затрудняют волнообразование при потере устойчивости от сдвига.
При определении критической нагрузки стенки тонкостенной балки приходится иметь дело с пластинкой, по краям которой действуют касательные напряжения т, вызываемые поперечной силой, и нормальные напряжения ст, вызываемые изгибающим моментом
143
(фиг. 44). Нормальные напряжения распределены по ширине пластинки по линейному закону, касательные напряжения можно считать постоянными.
Критические значения наибольших нормальных напряжений вычисляются по формуле, аналогичной формуле (9.8), где коэффициент k, зависящий от величины отношений b/а и т/ткр, определяется по графику фиг. 45. Критические значения касательных напряжений тКр вычисляются по формуле (Н.2) для данного отношения сторон пластинки Ь/а.
Как видно из фиг. 45, коэффициент /г при изменении соотношения длин сторон пластинки меняется незначительно, особенно при значениях т/ткр, близких к 1. Поэтому при расчетах допустимо пользоваться кривой k для квадратной пластинки (при />/а = 1).
§ 2.13. МЕСТНАЯ УСТОЙЧИВОСТЬ ТОНКОСТЕННЫХ ПРОФИЛЕЙ
Применяемые в конструкциях летательных аппаратов стержни представляют собой либо тонкостенные трубы, либо профили, согнутые из тонкого листового материала или изготовленные прессованием (прокаткой, штамповкой). Профиль можно рассматривать как систему узких пластинок (полок, стенок), жестко соединенных вдоль ребер (фиг. 46).
При сжатии длинных профилей происходит общая потеря устойчивости, сопровождаемая изгибом или закручиванием оси профиля, причем поперечные сечения не искривляются, а смещаются в процессе потери устойчивости, сохраняя свою форму.
Для коротких профилей более характерна местная потеря устойчивости, когда ось профиля
и его ребра остаются прямолинейными, а отдельные пластинки выпучиваются, в связи с чем поперечные сечения теряют свою первоначальную форму, искривляются.
В практике расчетов широко применяются экспериментальные кривые, построенные для профилей определенного типа. Эти кривые получаются путем испытания на сжатие тонкостенных стержней различной длины и определяют предельную нагрузку независимо от характера потери устойчивости стержня. Стержни большой гибкости (длинные) разрушаются от общей потери устойчивости, стержни малой гибкости (короткие)—от местной потери устойчивости.
На фиг. 47 изображены кривые предельной нагрузки для трех шарнирно опертых равнобоких угольников из дуралюмина Д16 с шириной полки 15, 18 и 45 л<лс при различной толщине стенки.
144
Криволинейные участки соответствуют общей потере устойчивости, прямолинейные горизонтальные участки — потере устойчивости в пластической области или местной потере устойчивости. Анало-
гичные кривые имеются и для других условий закрепления концов. Очень часто пользуются графиками для стержней с приторцованными концами,так как притор-цовка дает условия опирания промежуточные между шарнирным прикреплением и жесткой заделкой и поэтому ближе всего подходит к реальным условиям работы стержня в авиационной конструкции.
Приближенный теоретический подход к исследованию местной устойчивости основан на рассмотрении тонкостенного профиля как системы соединенных под углом пластинок. Определяют критические напряжения для каждой пластинки в отдельности с учетом условий закрепления се краев. Наи
меньшее критическое напряжение принимается в качестве критического напряжения местной потери устойчивости стержня. Расчет ведется по формуле (9. 8)
0,9*а£
где Ь — ширина полки (пластинки), устойчивость которой проверяется;
kc — коэффициент, зависящий от условий опирания краев полки профиля.
Обычно стенку, к краям которой примыкают две полки (например, стейка швеллера), считают в запас устойчивости, пластинкой с шарнирно опертыми краями и берут /г, =4, так как длина ее всегда намного больше ширины. Полку, имеющую свободный край (полка швеллера, угольника и т. п.), считают пластинкой, шарнирно опертой по остальным трем краям, принимая /?а ^0,45. Для половины полки таврового профиля (заштрихована на фиг. 48) или для его ножки можно принять один край защемленным, другой край свободным, а остальные два края, к которым
145
приложены сжимающие напряжения,— шарнирно опертыми. Коэффициент йа в этом случае равен 1,33. Реальные условия взаимного опирания стенок профиля весьма сложны и не могут быть сведены только к указанным выше условным схемам. На жесткость закрепления каждого элемента тонкостенного стержня сильно влияет не только его расположение относительно остальных элементов, но и ширина (а следовательно, жесткость) примыкающих элементов. Более точное значение коэффициента k-. можно получить, пользуясь графиком фиг. 49 в зависимости от отношения Ь/а смежных элементов и от расположе-
Фиг. 48.
Фиг. 49.
сторон элементами а, не имеющими свободных краев (остальная часть профиля дана пунктиром). Из кривой видно, что малая ширина поддерживающих элементов способствует более жесткому защемлению элемента Ь; при больших значениях а условия опирания приближаются к шарнирному. Вторая кривая дает значения /ы для элемента Ь, поддерживаемого с одного конца элементом а, имеющим свободный край. При очень малых значениях а элемент Ь работает как пластинка со свободным краем; этому случаю соответствует кривая 3. Заштрихованная область вокруг кривой дает практический разброс значений ka.
Анализируя кривую 2, можно попять значение небольших отгибов, тлеющихся на концах целого ряда авиационных профилей (фиг. 50, а). Наличие отгиба а значительно повышает устойчивость смежной стенки Ь. Наивыгоднейшая ширина отгиба а = (0,25-э-0,3)Ь. Уменьшение а ведет к резкому падению устойчивости поддерживаемой стенки, а увеличение, не оказывая сколько-нибудь заметного влияния на устойчивость стенки Ь, приводит к значительному ухудшению устойчивости самого отгиба, работающего как пластинка с одним свободным краем. Очень часто для подкрепления стенок профиля вдоль свободных краев делают утолщения — «бульбы», выполняющие ту же роль, что и отгибы. Прессованные бульб-профили широко применяются в авиастрое-146
нии. Некоторые типы таких профилей показаны на фиг. 50, б. Все стенки бульб-профиля можно считать шарнирно опертыми по контуру и при определении критического напряжения принимать £0=4.
Пример. Определить критическую силу для шарнирно опертой по концам тонкостенной дуралюмиповой стойки длиной / = 70 с.-и. Сечение стойки и основные размеры показаны на фиг. 51. Для дуралюмина принимаем £ = 0,72-10е кг/см2: , с
ппр = 2400 кг. см2. Площадь сечения /•'= —
= 1,3 см'2. Минимальный радиус инерции 1 v -jg
сечения 1х = 1,16 см. (—--—
Фиг. 50.
Все стенки стержня, кроме отгибов, можно считать как пластинки, шарнирно опертые по контуру (/г, =4). Наименьшее критическое напряжение будет иметь самая широкая пластинка. Вычисляем критическое напряжение местной устойчивости для пластинки шириной 6==40 мм:
0,9-4-0,72-103 а,,,-, --------------= 16'20 кг/см-.
/40 уз
\ 1 /
Для вычисления критического напряжения отгибов надо принять наименьшие значения /г_, =0,5 и 6 = 5 мм.
0,9-0,5-0,72- Юз
°кр,2 ==------Дг~7---------= 13 000 K/jcM1-.
( 1 )
Следовательно, местная потеря устойчивости произойдет при о,,Р11 = 1620 кг!см-. Вычислим напряжения общей потери устойчивости при
Т 1 70 ГС .
А = —.----~~ -—- — 60
*min 1
д ---“’= 1950 кг!см
VV ,
Таким образом, предельная сила должна определяться по напряжениям местной потери устойчивости:
Д1|£р — скрд-А = 1620-1,3 = 2100 кг.
Для того чтобы сделать стержень равноустойчивым, надо несколько уменьшить ширину самой широкой стенки. Тогда критиче
10*
147
ские напряжения местной потери устойчивости возрастут, а момент инерции и вместе с ним критические напряжения общей потери устойчивости уменьшатся. Равенство г>кр,1 = сгэ соответствует наиболее выгодным размерам поперечного сечения. Если местная потеря устойчивости происходит при напряжениях, превышающих о’пц, то определение, критических напряжений по формуле (9. 8) недопустимо. В этом случае предельные напряжения определяются по эмпирической формуле типа (9.12).
Фиг. 52.
Приведенные способы оценки местной устойчивости тонкостенных профилей следует рассматривать как весьма приближенные, могущие давать ошибку в ту и другую сторону. Основной источник ошибок состоит в допущении об изолированной работе полок, в то время как в действительности потеря устойчивости всех полок происходит совместно.
На фиг. 52, а показана картина деформации полок и стенки швеллера, шарнирно опертого по торцам, при местной потере устойчивости от центрального сжатия. Так как ребра остаются прямыми, то для теоретического изучения вопроса швеллер можно заменить пластинкой с двумя свесами, опертой на два промежуточных ребра (фиг. 52,6).
Изогнутая поверхность аппроксимируется в виде двойного тригонометрического ряда;
л • тт-х Г (2/г—Чг.у (2л—1)г.Л I ,
w = Атп sin — -- cos ----------— -— cos — ------— • (13. 1)
Второе слагаемое в квадратных скобках (постоянное) введено затем, чтобы удовлетворить условию опирания ® = 0 при y — h (па ребрах). .
148
Ф1 г. 5?.
1 \ Д' / т-1 т-2 у/ r=J
\ ' 277=4
. х*’г - —" 777=5
1 ~~т I
1 1 1 I I
1 Л* Л» I
О 123456789
Фиг. 54.
149
.Достаточно ограничиться двумя членами разложения, положив тих Г / ку кА \ ,
W = Sin----- С, COS —-----COS----- -
I [_ \ с 2с j
-j-C/cos 3------cos 3. (13.2
С с /I
Косинусоиды показаны па фиг. 53.
Решение задачи методом Ритца—Тимошенко при постоянной и одинаковой толщине стенки и полок и ц = 0,3 приводит к формуле для критического напряжения местной потери устойчивости. Данное выражение соответствует числу полуволн т, обращающему аКр.м в минимум:
= (13-3)
Коэффициент k см зависит от соотношения размеров поперечно' То сечения. При b/h=Q,5, kw ^2,7 (фиг. 54).
Для другйх соотношений b/h коэффициент Лом берется из графика фиг. 55.
Глава III
РАБОТА ПОДКРЕПЛЕННЫХ ПЛАСТИНОК ПОСЛЕ ПОТЕРИ УСТОЙЧИВОСТИ И НЕСУЩАЯ СПОСОБНОСТЬ КОНСТРУКЦИЙ
Тонкие листы, входящие в состав авиационных конструкций, как правило, подкрепляются стержнями, образующими каркас, на который опираются пластинки (обшивка крыла или фюзеляжа, стенка лонжерона или нервюры и т. д.). Поэтому потеря устойчивости отдельной пластинки еще не означает выхода из строя всей конструкции в целом. Разрушение конструкции произойдет только в том случае, когда напряжения в основных силовых элементах каркаса достигнут предельной величины. Предельные напряжения рассматриваются здесь в самом широком смысле слова. Это могут быть напряжения, равные временному сопротивлению <тв материала и вызывающие разрушение в буквальном смысле, но могут быть и напряжения, равные пределу текучести от материала или критические напряжения оКр для подкрепляющего стержня. Подкрепляющие ребра поддерживают выпучившуюся обшивку, и благодаря этому несмотря на потерю устойчивости она оказывается в состоянии воспринимать нагрузку, большую критической, до тех пор, пока не разрушатся поддерживающие ее стержни.
В ряде случаев оказывается возможным допустить в конструкции упругую (обратимую) потерю устойчивости обшивки без вреда для се нормальной эксплуатации *. Тогда несущая способность конструкции определяется не по критическим напряжениям обшивки, имеющим небольшую величину, а по напряжениям, вызывающим разрушение конструкции в целом. Необходимость максимальной экономии веса требует от авиационного конструктора тщательного учета всех возможностей увеличения несущей способности конструкции. При таких условиях большое значение приобретает определение той дополнительной нагрузки, которую может воспринять подкрепленная пластинка, потерявшая устойчивость.
* В особенности это относится к элементам, не подвергающимся непосредственному действию потока.
151
§ 3. 1. НЕСУЩАЯ СПОСОБНОСТЬ ПОДКРЕПЛЕННЫХ ПАНЕЛЕЙ ПРИ СЖАТИИ
Рассмотрим плоскую прямоугольную панель, состоящую из тонкой пластинки, подкрепленной продольными ребрами (стрингерами). Панель подвергается сжатию (фиг. 56). Часть пластинки, заключенная между двумя соседними стрингерами, теряет устойчивость при напряжении
3,6£ а“р~/ М2 \ t I
(1-1)
см. формулу (9.8х) гл. II для длинной пластинки, шарнирно опертой по четырем сторонам.
Вплоть до критической нагрузки напряжения сжатия по нагруженным краям пластинки распределены равномерно. После потери устойчивости наиболее искривленная средняя часть пластинки сказывается не в состоянии выдержать сжимающих напряжений, больших окр. Однако края пластинки, связанные со стрингерами, остаются прямыми и могут воспринимать значительную дополнительную нагрузку. Можно считать, что напряжение обшивки в зоне, прилегающей к стрингеру, равно напряжениям в стрингере. Действительное распределение напряжений в пластинке, хорошо согла
152
сующееся с результатами экспериментов, может быть представлено формулой
°сж=Т [(Лтр+~ ^стр “ a><p)cos 'Дг] ’ (1 •2)
где а — максимальное сжимающее напряжение в пластинке, равное напряжению в стрингере;
акр—критическое напряжение пластинки.
Эпюра сжимающих напряжений в пластинке после потери устойчивости дана на фиг. 56, а сплошной линией, пунктиром указаны средние напряжения.
Суммируя сжимающие напряжения по ширине пластинки и учитывая, что площадь, ограниченная косинусоидой и пунктирной линией, равна нулю, получим, что среднее напряжение в пластинке после потери устойчивости равно полусумме напряжения в стрингере и критического напряжения пластинки
°стр + акр °ср=-------- • (1-
Полная нагрузка, воспринимаемая панелью в целом, может быть вычислена путем суммирования напряжений в пластинке и в стрингерах.,
Иная трактовка работы пластинки после потери устойчивости была дана Карманом. Он предложил считать, что средняя часть потерявшей устойчивость пластинки не работает вовсе, зато в части пластинки шириной 26Пр, непосредственно примыкающей к стрингеру, действует напряжение <гта№С>стр. Получающаяся при этом условная эпюра напряжений показана на фиг. 56,6. Величина 26пр, называемая приведенной шириной пластинки, определяется из условия, что усилие, воспринимаемое пластинкой шириной 2оИр, равно действительной нагрузке Л^пл, выдерживаемой пластинкой после потери устойчивости:
^пЛ=2М°п,аХ-
Площадь сечения панели, воспринимающая сжатие, определяется как сумма площадей стрингеров и примыкающих к каждому пз них участков обшивки приведенной ширины 26пр. Для сплошной панели с равномерным размещением и одинаковыми размерами стрингеров, крепящихся к обшивке однорядным заклепочным швом, имеем
Д=---/г (/•'стр-|-2Z?lip/), где /г —число стрингеров в панели.
Полное усилие, воспринимаемое панелью, будет
Чум = ’стр/?=«3стр (Дстр-!- 261|р/).
(1-4)
(1-5)
153
Часто вместо понятия приведенной ширины вводят понятие редукционного коэффициента обшивки
2^пр
? = _г
(1-6)
где b — ширина между осями крепления смежных стрингеров.
Редукционный коэффициент ср показывает долю участия потерявшей устойчивость обшивки в работе всей панели или, иначе говоря, какая часть площади обшивки может считаться работающей с тем же напряжением, что и стрингер. Выражение для полной нагрузки па панель может быть записано в следующем виде:
сум ( В стр Н- ?Зстр’ (1.7)
где /70бщ = Bt — площадь сечения пластинки, входящей в панель.
Площадь сечения панели, воспринимающая сжимающую силу после потери устойчивости обшивкой, показана на фиг. 56, где прилегающие к стрингеру участки обшивки шириной 2ЬП[> заштри
хованы.
Увеличение сжимающей нагрузки на панель приводит к уменьшению приведенной ширины пластинки, так как при возрастании напряжений выпучивание охватывает все большую часть пластинки. Приведенная ширина пластинки зависит от величины сжимающих напряжений в стрингере. Поэтому можно считать, что критическое напряжение длинной пластинки шириной 2ЬПр, примыкающей к стрингеру и сохраняющей при данных напряжениях прямолинейную форму, равно напряжению, действующему в стрингере (остр). Считая эту пластинку шарнирно опертой и пользуясь формулой (1.1), получим условие для определения приведенной ширины:
_ 3,62? _
Oft „ \2~~а<:тр’
\ t /
откуда ___
26-=1'9'iAfr (L8)
или
Подсчитаем среднее напряжение, действующее в пластинке, исходя из закона распределения о согласно фиг. 56, б:
2^прсстр
Зср ~ ь
или, используя (1.6), имеем
а = сро ср т стр’
154
откуда
ср
°ср
?=-------
сстр
(1.10)
Редукционный коэффициент ср можно рассматривать как отношение среднего напряжения в пластинке к максимальному.
Подставив (1.9) в (1. 10) и учитывая, что критическое напряжение пластинки (обшивки) оКр следует вычислять по формуле (9.8), получим
°ср = V 3кр3стр • . (1-И)
Отсюда видно, что принятый Карманом закон распределения напряжений приводит к вычислению среднего напряжения в пластинке как среднего геометрического из напряжений (Ткр и Остр, в то время как закон распределения <т (1.2) приводит переднему напряжению, вычисляемому по (1.3) как среднее арифметическое. Если напряжения, действующие в стрингере, не на много превосходят окр пластинки, то различие между (1.3) и (1.11) невелико.
Выразим редукционный коэффициент <р через напряжения в стрингере и критические напряжения обшивки, пользуясь формулами (1.10) и (1.11):
? = ]/—• (112)
V Остр
Определение приведенной ширины илй редукционного коэффициента пластинки по формулам (1. 10) или (1. 12) возможно только путем последовательных приближений, так как напряжение в стрингере аСТр в свою очередь зависит от приведенной ширины пластинки. Для панели, подкрепленной п стрингерами, площадью ЕСТр, можно предложить следующую схему вычисления ср и напряжений, возникающих в панели от действия сжимающего усилия N.
1. Вычисляем напряжения в стрингерах в первом приближении, считая, что усилие N совершенно не воспринимается пластинкой, т. е. полагая редукционный коэффициент обшивки равным пулю:
С’стр’1 ~ «Л '
111 стр
При наличии некоторого опыта можно назначить редукционный коэффициент обшивки исходя из размеров стрингера и толщины пластинки, ориентировочно гр-^0,5.
2. По формуле (1.9) вычисляем редукционный коэффициент пластинки в первом приближении
155
3. Вычисляем, пользуясь формулой (1.4), рабочую площадь сечения панели с учетом редуцированной площади пластинки и находим Остр,2 во втором приближении:
__ N стр’2 Л+ Vibt
Если значения oCTPi2 и <гСтр,1 будут отличаться не более чем на 5%, то величину оСТР12 можно принять за истинные напряжения, действующие в панели, а в качестве редукционного коэффициента пластинки взять значение фь В случае большого различия остр,2 и cfCTp,i следует описанный выше процесс повторить, взяв ггстр,2 за исходное для вычисления редукционного коэффициента второго приближения ф2. При необходимости расчет проводят несколько раз, добиваясь совпадения напряжений остр в двух последовательных приближениях с точностью до 5%,
При определении несущей способности панели (максимальной нагрузки, которую панель способна выдержать до разрушения) для вычисления редукционного коэффициента панели в формулу (1.9) подставляют Остр = Щред. Под Щтред стрингера может пониматься предел текучести, критическое напряжение местной устойчивости или, наконец, критические напряжения общей устойчивости стрингера с присоединенной к нему приведенной обшивкой.
Если панель рассчитывается так, чтобы стрингеры при нормальной работе конструкции не испытывали значительных остаточных деформаций, то в качестве разрушающей нагрузки следует принять (Тсл.?-~Од. При расчете панели на полное разрушение напряжение в стрингере часто берут равным критическому напряжению местной ПОТСрИ УСТОЙЧИВОСТИ Остр ~ О'ц'р. местгг. Тогда редукционный коэффициент пластинки
, ~ t Е . Г пкр.оГ>|11
ф ----- 1,9------- или <р=1/ ------------,
Ь Окр мести 1 скр.мести
а разрушающая нагрузка
(ЫЗ)
Этот случай не требует применения метода последовательных приближений, так как разрушающие напряжения в стрингере можно вычислить независимо от напряжений, действующих в обшивке, Однако в большинстве случаев разрушение панели связано не с текучестью и не с потерей местной устойчивости стрингера, а с потерей общей устойчивости. Критические напряжения общей устойчивости стрингера следует определять с учетом поддерживающего влияния обшивки, С этой целью в сечение каждого стрингера засчитывается обшивка приведенной ширины 2Ьпр, зависящей от напряжений в стрингере. Поэтому для определения несущей способности панели приходится прибегать к методу последовательных приближений. Критические напряжения общей устойчивости 156
стрингера с присоединенной обшивкой находятся как для стержней соответствующей длины, причем момент инерции сечения вычисляется относительно центральной оси, параллельной краю панели, так как стрингер может выпучиться только в направлении, перпендикулярном поверхности пластинки. Иногда момент инерции приближенно вычисляют относительно средней линии пластинки.
Пример 1. Дуралюминовая панель 600X400X3 мм подкреплена в направлении сжатия четырьмя стрингерами типа Пр 106-9. Определить величину нормальных напряжений, возникающих в обшивке и стрингерах при сжатии ианелп силой Л' = .ЗО 000 кг. Дано £ = 0.7 - 10е кг/см2-, ч = 0,3; £(;Тр=-3,33 см-.
Средние напряжения в панели
_____30 000____
4-3,33 + 60-0,3
Критические напряжения для участка обшивки между смежными стрингерами
3,6-0,7-Ю6 ХР.об|и=
<>65 кг^см-.
Следовательно, обшивка потеряет устойчивость и только часть се будет работать со стрингерами.
30 000
Примем в первом приближении астр ==—= 2260 кг/см-. 1огда по формуле (1.9)
ш 1 9 -----
П
/ 0,7-106
2260
Напряжения во втором приближении
30 000
- == 1330 кг1см-‘.
0,3
-----=0,66.
1330
Напряжения в третьем приближении
30 000
1190 KzjcM-
0,3 0,7-106
= 1 g ._т----= 0,69.
20 1190
Расхождение между аСТр,2 и астр,з порядка 10^6. Сделаем четвертое приближение 30 000
астр,4
1160 Kijc.u'.
Расхождение между четвертым и третьим приближением всего около 2,5,s,’«. Принимаем <т(;Тр311 i60 кг/см-. При этом в работе панели принимают участи? около 70(,/о обшивки, потерявшей устойчивость.
Пример 2. Определить предельную нагрузку дуралюминовой панели длиной /-=450 мм. шириной /> = 480 мм и толщиной 1 — 2 мм. Панель подкреплена пятью стрингерами. Сечение стрингеров — равнобокий угольник 30X30X2 мм. Панель шарнирно оперта по краям, к которым приложена сжимающая сила; края,
157
параллельные стрингерам, свободны (фиг. 57, а). Принять f^OJ-lO® кг/см2 и=0Д
а) Вычислим предельную нагрузку AIMCCth исходя из местной устойчивости стрингера. Для полки уголка, не приклепанной к обшивке, находим По кривой 3 фиг. 49. Учитывая сильный разброс значений k, принимаем /го=0,5.
Критические напряжения местной устойчивости вычисляем но форму, ле (9. 8) — гл. II — при ширине полки угольника & = 30 мм:
0.9-0,50-0,7-106
ок„ мести ~-----------------= 1400 кг!см?.
/ Зо\2
Q)
Фиг. 57.
Для вычисления редукционного коэффициента в формуле (1.9) полагаем 6--12 см (расстояние между стрингерами)
°стр “ акр.мсстн = 1400
1,9-0,2 , /0,7-10в
¥ = —2— V П?оГ = 0-708-
Площадь стрингера
Лс.,.р = 2-30-2 = 120 лгл/2 =1,2 см-.
Предельная нагрузка на панель
Mice™ = 1400(1,2-5 + 0,708-48-0,2) = 17900 кг.
б) Определим разрушающую нагрузку тУосш, вызывающую общую потерю устойчивости стрингеров с присоединенной обшивкой.
В качестве первого приближения примем напряжения в стрингере, равные напряжениям местной устойчивости
астр,1 ~ °Кр.местп ~ 1400 кг1см-,
тогда (pi = 0,708 и приведенная ширина обшивки
2й11р.1 = <f+ = 0,708-12 = 8,5 см.
Вычислим положение центра тяжести сечения, образованного стрингером с присоединенной к нему обшивкой (фиг. 57,6):
3,0-0,2-0,2 + 3,0-0,2-1,6
•Уо~ 2-3,0-0,2 + 8,5-0,2 ~ °- 7 с-«-
158
Потеря устойчивости панели будет происходить в направлении, перпендикулярном плоскости панели. При выпучивании сечения будут поворачиваться относительно оси хй—х$. Момент инерции панели относительно этой оси равен
0 2 3-2 \
= — + 0,2-3-1,232 + 0,2-3 - 0,172-]-0,2-8,5-0,372) = 8 см*.
\ 12 /
Критическая сила при общей потере устойчивости вычисляется по формуле Эйлера
Л'общ —
я2.о,7-106-8 ------------= 27 400 кг.
Критическое
напряжение
°стр,'
27 400
= 2140 кг ':СМ-5-1,2 ф-0,708-48-0,2
существенно
отличается от
Остри, поэтому берем второе приближение
„0.2
= 1,9 —
'-----= 0.574,
2140
2йПрд =-' <Р2- = 0,574-12 6,9 см.
Вычисляем положение центра тяжести во втором приближении: 3-0,24-3-0,2-16 у о =--------------------------------=0,42 см.
У 2-3-0,2 4-6,9-0,2
Момент инерции сечения панели относительно оси х0—х<,:
/0 2-33
До = 5|—^-4-0,2-3-1,182 4-0,2-3-0,222 д
= 7.8 слН.
Критическая сила во втором приближении
Л^общ
:2.0,7-106-7,8
---- ---- - - 25 900 кг.
452
Второе приближение отличается от первого менее чем па 6%. Для более точного определения ЛД.-.щ требуется еще одно приближение. Однако делать его не следует, так как ясно, что разрушающая нагрузка для панели определяется не обшей, а местной потерей устойчивости. Поэгому ЛДа;|ри = 17 900 кг.
Рассмотренные выше формулы для определения приведенной ширины пластинки получены в предположении, что стрингер и пластинка соединены непрерывным швом. Это допущение справедливо для случая сплошного сварного шва или для заклепочного соединения при очень частом размещении заклепок. Если заклепки (или сварные точки) имеют большой шаг, то необходимо ввести поправку в подсчет приведенной ширины для того, чтобы учесть влияние выпучивания обшивки пластинки между точками крепления.
Участок обшивки между заклепками можно рассматривать как стержень, защемленный двумя концами, работающий па продольный изгиб. Длина стержня равна шагу заклепок 1Ш (фиг. 58). В момент выпучивания обшивки между заклепками напряжения в стрингере и в обшивке будут одинаковые в том случае, если вся панель выполнена из одного материала. Если материал обшивки
159
имеет модуль foOm, а материал стрингера — модуль ЕСтр, то в силу равенства укорочения всех элементов сжатой панели имеем
Остр •
—• (1.14)
^стр ^обш
Напряжение стрингера, при котором наступит потеря устойчивости обшивки между заклепками, найдем, подставляя в (1.14) вместо Ообш критическое напряжение при продольном изгибе пластинки, две стороны которой защемлены, а две свободны. Получим
° стр
При р-==0,3 имеем
.<2£>цДц, СстР _______ г~~^стр
(0.51,,^ "~ з'(1 - р.2) /2, ‘
с
стр
(I. 15)
Для дуралюмииовых соответствующее
пряжение,
панелей £,обш = Дстр = 0,72 • 106 кг/см2 и па-началу выпучивания обшивки между заклепками, равно
о стр
in
Разумеется, эти результаты применимы для напряжений сгстр, не превышающих предела пропорциональности.
Выпучивание обшивки между заклепками резко ослабляет несущую способность пластинки, что выражается в уменьшении приведенной ширины. Предполагая (в запас прочности), что выпучившаяся между заклепками обшивка не в состоянии воспринимать
критических, вычислим приведенную ширину
больше чиваиия:
напряжении, после выпу-
откуда
(2йпр)о(Дтр)о/ = (2^,р)|(д.тр)1 ^ = const,
(2й11р)1 = (2&11Р)о^С-у >
1-стр} 1
где индекс «0» относится к моменту выпучивания, а индекс «I» соответствует нагрузке после выпучивания.
Потеря устойчивости обшивки между заклепками не только уменьшает несущую способность пластинки, по и вызывает дополнительные вредные нагрузки на стрингер в точках крепления. Выпучившаяся обшивка растягивает заклепки и может вызвать
160
отрыв головок или преждевременное местное разрушение стрингера.
Более детально эти вопросы рассматриваются в курсе «Расчет самолета на прочность».
§ 3.2. РАБОТА ТОНКОСТЕННОЙ БАЛКИ ПОСЛЕ ПОТЕРИ УСТОЙЧИВОСТИ ЕЕ СТЕНКИ
Тонкостенную балку можно рассматривать как удлиненную пластинку, окаймленную поясными стержнями. Обычно поясные стержни соединяются между собой стойками, приклепанными к стенке. Назначение стоек двоякое. Во-первых, стойки уменьшают длину панели стенки и тем самым повышают ее устойчивость на сдвиг (см. § 2. 11). Во-вторых, стойки улучшают условия работы поясов при . действии сосредоточенных поперечных нагрузок.
По условиям весовой отдачи желательно делать стенку по возможности более тонкой. При этом выясняется, что по прочности стенка легко может воспринять поперечные силы балки и соответствующие касательные напряжения оказываются в допустимых пределах. Значительно труднее удовлетворить условиям устойчивости — см. формулу (11.2) в § 2. 11 гл. II.
Как уже было отмечено, прямоугольная пластинка, теряя устойчивость от сдвига, покрывается волнами (складками), образующими со сторонами прямо
угольника угол, близкий к 45° (см. фиг. 41). Вдоль волн действуют главные растягивающие напряжения, а перпендикулярно к волнам — главные сжимающие. По мере дальнейшего роста нагрузки главные сжимающие напряжения, численно равные ткр, не возрастают; что касается главных растягивающих напряжений, то возрастание их ограничено практически лишь прочностью стенки на растяжение. Если пояса балки способны воспринять распределенную нагрузку, создаваемую напряжениями в стенке, действующими вдоль волн, то несущая способность балки не только не исчерпывается при достижении напряжениями в стейке величины ткр, по может и значительно возрасти.
Таким образом, характер работы стенки балки в закритиче-. ской области существенно изменяется: вместо напряженного состояния, близкого к чистому сдвигу, возникает напряженное состояние, близкое к одноосному растяжению по направлению биссектрисы прямого угла панели (фиг. 59). Практически использование этих свойств тонкостенной балки ограничивается стремле
161
нием не допустить остаточных (пластических) деформаций. Поэтому, важно проследить, чтобы напряжения ткр не превосходили ту. Растягивающие напряжения в стенке при эксплуатационной нагрузке не должны превосходить оу и, тем более, от. При этих условиях в стенке не образуется остаточных складок и со снятием нагрузки исчезают и складки. Для определения усилий, возникающих в элементах балки, проведем сквозное зигзагообразное сечение на расстоянии х от конца балки и рассмотрим равновесие отсеченной части, учитывая, что при произвольной' нагрузке в сечении действует поперечная сила Q и изгибающий момент М. Форма сечения выбрана таким образом, чтобы выявить напряжения О[, действующие в площадках под углом 45° к оси балки.
Составляя уравнения равновесия, имеем
।
Л^4-^н + а/ясо5а=0; j
Q — 0,/asina — O; (
(2.1)
Учитывая, что а = /г cos а, получим
2Q 1
1 ht sin 2i ’ I
/И Q . !
4------^Ctga, } (2.2)
n 2 j
Л, M Q ,
N„ =-------- ctga.
h 2 ° '
Пояса и стойки балки оказываются нагруженными распределительными наклонными силами од (фиг. 60), вызывающими в окаймляющих стержнях изгибающие моменты, продольные и поперечные силы.
Проанализируем распределение усилий в тонкостенной бал к после потери устойчивости стенки на простом примере окаймленной четырехугольной панели фиг. 60, а. На фиг. 60, б показаны элементы, окаймляющие стенку, со всеми нагрузками на них. Погонная нагрузка на пояса равна р ==arsina =—“— (как это следует из h COS а
фиг. 60, в). Па единицу длины стойки действует сила/?ст = a/cos a =
= ——, Эти нагрузки вызывают сложную деформацию (изгиб с h. Sin а
растяжением или сжатием) стержней тонкостенной балки. Проектируя погонные силы р„ на нормаль к оси пояса, получаем изгибающую равномерно распределенную нагрузку на пояса, равную /?„ sin a= — tg а. Аналогично находим изгибающую нагрузку для
162
стоек дт cos a =-y-ctg а. Эти нагрузки вместе с уравновешивающими их реакциями изображены на фиг. 60, г, где также даны эпюры изгибающих моментов для поясов и стоек, рассматриваемых как балки на двух опорах под равномерной нагрузкой.
Фиг. 60.
Наибольшие изгибающие моменты оказываются равными
в поясе:
., Q/2 tg а
шах М— ——-— ,
8Л (2.3)
в стоике: |
шах М — ctg а. |
Для построения эпюры продольных сил в каждом стержне спроектируем погонные силы рп и рст соответственно на направления осей поясов и стоек. Получающиеся погонные продольные силы оказываются одинаковыми для всех стержней и равными Q/h. Нагрузки, вызывающие продольную деформацию поясов и стоек, и соответствующие им эпюры продольных сил, изображены на фиг. 60, д.
Действительное распределение усилий будет несколько отличаться от полученного выше, хотя бы за счет упругой податливости
И* 163
поясов и стоек, которые выше рассматривались как абсолютно жесткие опоры.
Угол наклона волны а с учетом деформации поясов и стоек в продольном направлении определяется следующей формулой:
tg«=
ht
9Р F
___/£__
^EZ1F с-
(2.4)
определения поясах:
1
где I, h, t — длина, высота и толщина панели балки;
EnFn и ECTFCT — жесткость па растяжение поясов и стоек.
При обычных соотношениях элементов балки угол а колеблется от 40 до 50°. Принимая в среднем а = 45° и подставив в формулы (2.2), имеем следующие зависимости для усилий в стенке и 20 о а. — —- = 2т, 1 ht
в Л 2 |
н h 2 j
Таким образом, растягивающие усилия в стенке после потери устойчивости оказываются вдвое больше касательных усилий, которые действовали бы в стенке, если бы она не выпучивалась.
Полученные формулы справедливы в-предположении, что большую изгибную жесткость, поля диагонального растяжения
(2.5)
пояса и стойки имеют бесконечно В действительности при появлении стержни, окаймляющие стенку, прогибаются, что приводит к некоторой разгрузке стенки. Эффект разгрузки учитывается поправочным коэффициентом k, зависимость которого от расстояния между стойками I и от величины со, определяемой ио формуле
w == 1,25 sin а 1 /-------, (2. 6)
И (Л,-4) Л
где /в и /н —моменты инерции сечений верхнего и нижнего пояса, представлена на фиг. 61.
Наибольшие растягивающие напряжения в стенке равны
164
где сп—средние напряжения, вычисляемые по формуле (2.5) в предположении равномерного нагружения стенки, потерявшей устойчивость.
Эту же поправку следует ввести и в ту часть нагрузки на пояс, которая возникает от растяжения обшивки. Для узловой нагрузки в стойках, которая не зависит от распределения растягивающего напряжения между участками обшивки, поправка не вводится.
Приведенные формулы хорошо подтверждаются экспериментом для балок с очень тонкой стенкой (<0,8 мм. В случае более толстых стенок расчет приводит к конструкциям с завышенной прочностью и поэтому чрезмерно тяжелым. Это объясняется тем, что при более толстых стенках уже нельзя пренебрегать сжимающими напряжениями сг2 = ткр, имеющими значительную величину. Таким образом, сдвигающая сила, воспринимаемая балкой, должна рассматриваться как сила, состоящая из трех частей: 1) сдвигающей силы, воспринимаемой стенкой как элементом, сопротивляющимся сдвигу (до потери устойчивости), 2) сдвигающей силы, воспринимаемой поясами, имеющими, хотя и малую, но не бесконечно малую жесткость на сдвиг и 3) сдвигающей силы, воспринимаемой стенкой после потери устойчивости благодаря полю диагонального растяжения.
В этом случае поле диагонального, растяжения потерявшей устойчивость стенки воспринимает не всю поперечную силу Q, а избыток силы Q—QKp, где QKp—-величина поперечной силы, при которой теряет устойчивость стенка.
§ 3.3. НЕСУЩАЯ СПОСОБНОСТЬ ПОДКРЕПЛЕННОЙ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ ПРИ ИЗГИБЕ
Расчет на прочность крыла, фюзеляжа и оперения требует определения несущей способности цилиндрических или слабоконических подкрепленных оболочек, рассматриваемых как составные брусья, отдельные волокна которых обладают различными упругими, или точнее, различными деформационными свойствами. Решающее значение при такой расчетной • схеме имеют нормальные напряжения, возникающие в обшивке и в продольных подкреплениях (стрингерах, поясах лонжеронов) от общего изгиба.
Как известно из курса сопротивления материалов, трехчленная формула для нормального напряжения в z-м волокне упругого составного бруса гласит:|
„ / N Мх , му \ /о п
а. = Е.----------у.-)--------хi . (3.1)
\DAT ЪЕ1х ЪЕ'у /
Здесь модули упругости Е отдельных волокон считаются различными. Площади F, моменты инерции 1Х и /и отдельных волокон вводятся умноженными па свои модули. Центр тяжести и главные оси определяются для площадей, предварительно умноженных на свои значения Е.
165
Формула (3.1) выведена на основе закона плоских сечений при чистом изгибе, являющегося следствием тождества всех поперечных сечений бруса в смысле геометрии и распределения модулей. Формула (3. 1) действительна и в неупругой области, когда модули Е нельзя рассматривать как постоянные, не зависящие от напряжения величины (фиг. 62). В этом случае упругий модуль
6?яупр Сущ, Е =------—-------—const
^гупр еупр должен быть заменен величиной
Гс==?плзст^СОП81 епласт
Величина Ес, как известно, носит название секущего модуля. Он может рассматриваться либо как функция относительного
удлинения, либо как функция напряжения:
Секущий модуль при напряжениях, не превосходящих <тШ1, совпадает с модулем упругости Е.
При пластических деформациях, когда материал не подчиняется закону Гука, формула (3. 1), как уже сказано, внешне сохраняет свой вид. Однако пользование ею затруднено тем, что величины £с, входящие в
нее вместо Е, зависят от щ. Следовательно, сг< непосредственно вычислено быть не может.
Приходится прибегнуть к методу последовательных приближений. Сначала задаются значениями £'c = ^ = const и подсчитывают величины Si в отдельных волокнах. Для тех волокон, для которых окажется модуль остается без изменений. Для тех же
волокон, для которых сг,\>сгпи, по диаграмме определяется значение сг<>сгпц, площади этих волокон умножаются на свои Ес, а затем определяется положение центра тяжести, находятся главные оси, моменты инерции сечения и снова определяются напряжения о,- в отдельных волокнах. Далее процедура повторяется сначала. При этом напряжения изменяются, по, как правило, новые значения Ес будут меньше отличаться от предыдущих, чем предыдущие отличаются от Е= const.
Приближения обычно достаточно быстро сходятся, и в результате нескольких приближений значения о, и Ес в последовательных приближениях перестают заметно отличаться. На этом расчет заканчивается, если речь идет о проверке заданного сечения при
16G
в пределах упругости,
заданных усилиях Ni, Мх, Му: достижение в основных продольных подкреплениях предельного напряжения является признаком исчерпания несущей способности- Соответствующая группа величин (Vi, Л1х, рассматривается как характеристика предельной нагрузки.
Здесь важно подчеркнуть, что второстепенные связи могут исчерпать свою несущую способность без существенного ущерба для общей прочности, которая определяется прочностью основных связей. Если деформация второстепенных связей ограничена прочными основными связями, то переход второстепенных связей в состояние текучести не вызывает разрушения конструкции. ЛАало того, эти связи продолжают нести усилия, соответ- . ствующие состоянию текучести.
Аналогично рассматривается явление потери устойчивости обшивкой при стрингерах, не потерявших устойчивости и прочности: обшивка несет свою критическую нагрузку, равную критическому напряжению, умноженному па площадь сечения обшивки.
Секция обшивки или стержень, теряющий устойчивость, могут характеризоваться диаграммой сжа
тия (фиг. 63). Если устойчивость теряется диаграмма состоит из двух ветвей — наклонной (tga = E) и горизонтальной (Е = 0).
Практически удобнее иметь дело не модулями Е и Ес, а с безразмерными редукционными коэффициентами.
Умножим и разделим все слагаемые правой части равенства (3. 1) па произвольную величину Ер, выраженную в кг/см2. Обычно в качестве Ео берется модуль упругости основного материала.
Условимся называть редукционным коэффициентом Его волокна величину
Ei
(3. 2)
Введем обозначения
сечени я. Редукция (приведе-очевидно, в том, что площадь сечения
Эти величины будем называть геометрическими характеристиками редуцированного ние) сечения состоит,
167
каждой продольной связи умножается на свой редукционный коэффициент, а затем производится вычисление суммарных геометрических характеристик.
Формула (3.1) перепишется следующим образом:
/ N Мх . Му \
—у?ред урод । уред Xij ‘ (3-4)
Выражение в скобках можно истолковать как напряжение в z-м элементе цельного бруса с редуцированным поперечным сечением. Обозначим это выражение сгРел. Тогда
и, следовательно, = №
Редукционный коэффициент равен, таким образом, отношению, фактического напряжения в элементе к напряжению в соответствующем элементе редуцированного сечения.
Расчет при помощи редукционных коэффициентов также сводится к ряду последовательных приближений. Приближения повторяются до тех пор, пока редукционные коэффициенты двух последовательных приближений не сделаются достаточно близкими друг другу.
Покажем использование метода редукционных коэффициентов на примере определения нормальных напряжений в подкрепленной цилиндрической оболочке типа крыла самолета. Обычно в такого рода конструкциях приходится сталкиваться с тремя видами продольных элементов, работающих на нормальные напряжения. Это пояса лонжеронов, стрингеры и обшивка. Пояса лонжеронов часто делаются из высокопрочной легированной стали. Обшивка, так же как и стрингеры, выполняется из дуралюмина, Она теряет устойчивость и частично выпучивается задолго до полного разрушения крыла. Поэтому степень участия обшивки в восприятии нормальных напряжений оценивается приведенной шириной, присоединяемой к стрингерам. Редукционный коэффициент обшивки по отношению к стрингерам вычисляется в зависимости от напряжения стрингера на основании формулы (1.9) для подкрепленной панели. Очевидно, что по отношению к идеальному материалу с модулем Ес редукционный коэффициент обшивки выразится следующим образом:
?обш= — W
ь У Остр
Таким образом, расчет несущей . способности подкрепленной оболочки требует предварительного построения диаграмм (сг, е) только для поясов лонжеронов и стрингеров. Диаграммы (сг, е) для элементов оболочки в области растяжения полностью совпа-
168
дают с соответствующими диаграммами для материалов, получаемых из стандартных механических испытаний, В области
сжатия диаграммы для лонжеронов и стрингеров существенно
отличаются от диаграмм для материалов благодаря тому, что при напряжениях больше критических деформация потерявшего устойчивость элемента возрастает без существенного увеличения сжимающей силы (горизонтальные участки на фиг. 63).
Построение диаграмм сг, е для сжатых элементов подкрепленной оболочки требует проведения большого числа экспериментов
при различных гибкостях стержней и для .каждого типа профиля в отдельности. Однако практически можно ограничиться приближенной диаграммой сг, е при сжатии, состоящей из двух прямолинейных участков, соединяемых кривой линией 2 (фиг. 64)-. Наклонная прямая 1 соответствует упругой работе материала и строится исходя из величины модуля упругости £ = tga = cr/8. Горизонтальная прямая 3 при сг = (Тк характеризует поведение стержня после потери устойчиво
сти. Промежуточная кривая 2 проводится на глаз через точки сгПц и сто,2 таким образом, чтобы плавно соединить наклонную прямую 1
с горизонталью, проходящей через точку сг = сгб (временное сопротивление материала).
С помощью диаграмм сг, е, можно определить редукционные коэффициенты по методу последовательных приближений. Приве-
дем примерную схему расчета.
1. Описанным выше методом строятся диаграммы растяжения— сжатия для поясов лонжеронов и стрингеров оболочки. Примерный вид этих диаграмм дан на фиг. 63. Кривая 1 относится к стальным элементам (поясам лонжерона), кривая 2 — к дур-алюминовым (стрингеры с присоединенной обшивкой).
2. Оболочка предполагается состоящей из однородного идеально упругого материала с модулем Ей (диаграмма этого материала на фиг. 63 изображена пунктиром). Чаще всего в качестве Ео выбирают модуль стали.
3. Приведение поперечного сечения к модулю Ео производится путем выбора редукционных коэффициентов для каждого продольного элемента оболочки. В первом приближении величины совершенно произвольны. Однако от удачного выбора <ргд зависит быстрота сходимости процесса последовательных приближений. Если ср,-д оказываются близкими к их действительным значениям, то весь расчет потребует не больше двух-трех приближений. При наличии некоторого опыта расчетчик может с большой точ
169
ностью назначать редукционные коэффициенты «на глаз» и лишь слегка корректировать их во втором приближении. Можно рекомендовать для поясов лонжеронов принимать редукционный коэффициент равным 1, а для стрингеров в зоне сжатия равным отношению критического напряжения стрингера к критическому напряжению пояса лонжерона. Редукционный коэффициент обшивки вычисляется в зависимости от фстр по формуле (3.6). В растянутой зоне оболочки редукционные коэффициенты сечений поясов лонжеронов и стрингеров, определяемые по диаграмме, уменьшают на 10%, чтобы учесть ослабление отверстиями под заклепки. Редукционный коэффициент растянутой обшивки принимают равным фобщ0,7<рСтр, чтобы учесть различие в диаграммах растяжения листов и профилей за пределом упругости и влияние несовершенства натяжения обшивки при клепке.
4. После выбора редукционных коэффициентов вычисляются приведенные площади первого приближения
определяется положение центра тяжести приведенного сечения г главные моменты инерции /^елж
5. Вычисляются нормальные напряжения стР]ед по формуле (3.4).
6. По найденным значениям ст?,0,1 определяются истинные напряжения ст/1 в элементах оболочки. Для этого на диаграмме идеального материала с модулем Ео откладываются найденные значения стлл (отрезок КА на фиг. 63). Пересечение вертикали КА с диаграммой (ст, е) для с-го элемента определяет напряжения щ i (отрезок КА).
7. Вычисляются редукционные коэффициенты во втором приближении
°<i 'f'2 рея ‘ °il
Если ф,2 сильно отличается от фл, то расчет производится сначала, причем в качестве исходных коэффициентов берутся ср/2-Вычисления повторяются до тех пор, пока редукционные коэффициенты в двух последних приближениях не окажутся достаточно близкими друг к другу. Редукционные коэффициенты последнего приближения кладутся в основу окончательного вычисления истинных напряжений. Точность расчета можно считать удовлетворительной, если окончательные величины нормальных напряжений отличаются от предыдущего приближения не более чем на +5%.
Напряжения в элементах подкрепленной оболочки вычисляются от действия увеличенных в f раз эксплуатационных нагрузок (/ — коэффициент запаса). Наибольшее напряжение сравнивается с временным сопротивлением материала.
При необходимости вычислить касательные напряжения при изгибе подкрепленной оболочки за пределом пропорциональности
ПО
ее материала можно воспользоваться методом и формулами, изложенными в гл. V, только геометрические характеристики брать не для заданного, а для приведенного сечения. Тогда погонные касательные усилия, вызываемые в стенках оболочки вертикальной поперечной силой QXJ, определятся по формуле
QySp™
<7(s)=—/Т^-+/?о-
где S^;l и /^ел — статический момент и момент инерции площади приведенного сечения относительно его нейтральной оси.
Приведенное сечение представляется как совокупность площадей ==<Р>^1, сосредоточенных в центрах тяжести соответствую
щих элементов. Площадь обшивки приведенной ширины 2ЬПр включается в площадь примыкающего к ней стрингера, остальная
Фиг. 66.
Фиг. 65.
часть обшивки считается не работающей на нормальные напряжения и не учитывается при вычислении SpQ11 и /₽ся . Примерный вид действительного сечения и соответствующего ему приведенного сечения показаны на фиг. 65, а и б. Обшивка, не воспринимающая нормальных напряжений, на фиг. 65, б обозначена пунктиром, а приведенные площади—жирными точками.
Определив <?(s), можно вычислить касательные напряжения, разделив погонное касательное усилие на истинную толщину соответствующей стенки или обшивки.
Пример 1. Вычислить нормальные напряжения в сечении прямоугольной коробки, изгибаемой в вертикальной плоскости моментом М=65 000 кгм. Верхняя панель коробки сжата, нижняя — растянута. Пояса коробки — профили таврового сечения из стали ЗОХГСА площадью /'П=Ю см2, стрингеры — дуралюминовые угольники, площадь сечения которых /?стР=2 см2. Толщина обшивки /=1,5 мм. Нормальными напряжениями в вертикальных стенках коробки пренебречь. Принять: временное сопротивление материала поясов сы.п = 12 000 кг/cjtt2; для остальных элементов <тв = 4000 м!см2, критические напряжения сжатых поясов <Тпрп = И 000 кг/см2, стрингеров — <ткр.стр = 2700 кг!см2, предел текучести мате
171
риала поясов сгт.п—10 000 кг/см2, остальных элементов сгт = 3000 кг/см2. Размеры сечения коробки взять с фиг. 66, а. Для дуралюмина £д = 0,7 106 кг/cTt2, |х=0,3, для стали £'ст=2,1 • 10» кг/см2.
По данным для стали ЗОХГСА и дуралюмина строим диаграммы сг, е для поясов и стрингеров коробки. Приближенно предел пропорциональности можно определить так:
Для стали ЗОХГСА опц = 0,7ай = 8400 кг/см-;
?для дюралюмипа я„ц = 0,6од = 2400 лгг/слА
Схематизированные диаграммы для сжатых элементов показаны на фиг. 67. Точки Ci и Cs определяют условный предел текучести материала сго-а и соответствуют уклонению диаграммы от линейного закона на 0,2% I, т. е. Д/=0,002.
Задаемся редукционными коэффициентами сжатых элементов в первом приближении. Для поясов лонжеронов примем <pni = l, для стрингеров <pCTpi = °кр.стр 2700 1,5.. А,7-106
=-------~ -- — 0,25, для обшивки о0бi = 1,9 — I / ----- 0,25 = 0,06 .
°кр.п И 000 Y 1 175 у 2700
172
Редуцируя растянутые элементы, надо иметь в виду, что пояса сделаны из стали, а остальная часть коробки из дуралюмина. Кроме того, надо учесть ослабление заклепочными отверстиями. Поэтому выбираем <pni=0,9; <pcrpi=
= 0,9—"Р- =0,3; (роб-=0,7, (Ретт ~ 0,2. °в.п
Вычислим положение центра тяжести приведенного сечения (см. фиг. 66). в первом приближении.
_________________(2-10-1 4- 3.2.0,25 + 70-0,15-0,06)30______________
У0- 2-10+ 2-10-0,9 + 3-2-0,25+ 3-2-0.3 + 70-0,15-0,06+ 70-0,15-0,2 “
= 15,1 см.
Момент инерции относительно оси равен
/х1=(2-10-1+3-2-0,25+7,0-0,15-0,06)14,92+(2-10-0,9+3-2-0,3+
+ 70-0,15-0,2)15,12=9900 см4.
Напряжения в
сжатых элементах по
формуле (3. 4)
оред = 65 000-100
0,1 9900
14,9 = 9770 кг{см2.
Напряжения в
Исходя из
15,1 =9900 кг/см2.
растянутых элементах
ред = 65000-100
9900
этих напряжений, на диаграмме <т, е идеально-упругого мате-
риала получаем точки А (для растянутой зоны) и В (для сжатой зоны). Проводим вертикали АК. и BL и вычисляем редукционные коэффициенты второго приближения.
Сжатые элементы
9000
<рП9= =—•=--------= 0,92,
Vn2 BL 9770
B.,L 2700 n OQ 0,2о, ,стр- BL 9770
?об2 —
< 1,5
’9 175
0,7-106
2700
•0,28 = 0,07.
Растянутые элементы
А+
<РстР2- -Лк
8920 ----= 0,9, 9900
2780 ----== 0,28, 9900
?об2 = 0,7<рстр’ = 0,196.
Редукционные коэффициенты второго приближения отличаются от соответствующих коэффициентов первого приближения примерно иа 1О°/о. Ограничимся полученной точностью и дальнейших расчетов производить не будем.
Итак, принимаем напряжения:
в растянутых поясах лонжеронов ап = А{К = 8920 кг/см2,
в растянутых стрингерах н обшивке астр = = 2780 кг/см2,
в сжатых поясах лонжеронов ап = В}К — 9000 кг/см2,
в сжатых стрингерах и обшивке астр = В^К — 2700 кг[см2.
173
Для более точного определения а нужно проделать следующее приближение на основе редукционных коэффициентов второго приближения.
Следует обратить внимание на сравнительно малую долю участия обшивки и стрингеров в работе коробки, что объясняется наличием мощных поясов, воспринимающих основную нагрузку (в данном примере около 80%).
Пример 2. Вычислить предельный изгибающий момент для коробки, рассмотренной в предыдущем примере (см. фиг. 66).
Предельное состояние коробки будет достигнуто в момент потери устойчивости продольными ребрами сжатой панели. Напряжения в растянутых элементах в этот момент будут близки к временному сопротивлению материала.
Редукционные коэффициенты следует взять равными редукционным коэффициентам первого приближения в предыдущем примере. Редуцированное сечение и момент инерции будут те же, что и в этом примере.
Из условия прочности для верхней (сжатой) панели имеем
•^пред 9900
14,9= акр.п = 11000,
откуда 9900-11000 МПред— Л - 7,3-106 кг-см. 14,9
Условие прочности для нижней (растянутой) панели имеет вид •Мдред 9900 15J 120°°-
откуда получим 9900-12000 ЛГпред- . - 7,9-10<> кг-см2. 10,1
Окончательно предельное значение изгибающего момента оказывается равным Л411ред=73 000 кгм из условия прочности сжатой панели. Ввиду большой мощности поясов по сравнению с остальными элементами коробки растянутая и сжатая панели оказываются примерно равнопрочными. Несколько меньшая прочность сжатой панели объясняется потерей устойчивости поясов лонжеронов.
Глава IV
ПРОЧНОСТЬ И УСТОЙЧИВОСТЬ ГЛАДКИХ КРУГОВЫХ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
§ 4.1. ОСНОВНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
Наряду с пластинками оболочки играют первостепенную роль в авиационных конструкциях.
Из курса сопротивления материалов известно уравнение равновесия тонкой «безмоментной» оболочки:
(i.i)
Pi Р‘> t
Здесь р, и р2 — радиусы кривизны главных нормальных сечений.
Если срединная поверхность оболочки имеет форму тела вращения, то Pj — радиус кривизны нормального сечения, касательного к параллельному кругу, р2 — радиус кривизны меридиана (фиг. 68).
Известно, что р, равен отрезку нормали между исследуемой точкой оболочки и осью вращения; Р р2 определяют по уравнению меридиана, пользуясь правилами дифференциального исчисления.
Возьмем начало координат в исследуемой точ
ке т, ось х совместим
с касательной к меридиану, ось у — с касательной Мальному сечению, совпадающей с касательной к кругу. Ось z направим вдоль внешней нормали.
к другому нор-параллелыюму
175
Обозначая
Pi = Ру!
°i =
Р2 = Рх!
(1.2)
а/ = P = P'J\ напишем уравнение (4. 1) в виде
Рх Ру
С другой стороны, можем рассматривать элемент оболочки dxdy как элемент гибкой пластинки, обладающей цилиндрической жесткостью D.
Дифференциальное уравнение равновесия гибкой пластинки было получено выше — см. (4.3) гл. II:
ZV Nx^L _ N (1.3)
\ дх- ду2 / дх2 y ду2 “ dxdy
Складывая почленно уравнения (1.2) и (1.3) и обозначая РобН_Рпл— Р<
получим
/ДтД. д_ d2w \ дх2 ' (д>2
^у • уу d2w ру х дх2
у ду2
„ d2w
2а-----= Р-
дхду
(1-4)
внешняя на-изгиба и co-
очевиден: усилиями
Механический смысл этого уравнения грузка р уравновешивается поперечными ставляющими усилий в срединной поверхности.
„ d2w d2w д-w
Величины ------, ---,-----здесь представляют собою не при-
_дх2 ду2 дхду
ближенные значения упругих или полных кривизн, как в случае пластинки, а приращения кривизн оболочки. Величины -уу d2w
и ----, стоящие-.под знаком оператора V2 и имеющие множителем
ду2
цилиндрическую жесткость D — это упругие приращения кривизн, , - , „ d2w d2w d2w
обусловленные изгибом. Величины --------, ----,-----, имеющие
J дх2 ду2 дхду
множителями Nx, Nv, q— это полные приращения кривизн, заключающие прежде всего часть, зависящую от изгиба, ио в отдельных случаях учитывающие также и другие факторы, в частности, упругие и температурные удлинения срединной поверхности, неправильности формы оболочки, температурное искривление от неравномерного нагрева. Для оболочек характерно вторичное влияние прогибов на приращение кривизны. Это значит, что при-
176
ращение кривизны содержит слагаемое, зависящее непосредственно от прогиба w в данной точке. В самом деле, дифференциал
1
величины — равен
<<^щ/ ₽с Рх
Аналогично
d [ 1 \ , rfPy w
1 ' I «Ру —*“ —~ ' 2~ 2~ *
Ру \ Ру / ?у ?у
(1.5)
(1-5')
Таким образом, приращение кривизны, зависящее от прогиба
в данной точке оболочки, обпатно начального радиуса кривизны. Ясно, что для пластинки эта величина равна нулю. Чем более полога оболочка, тем меньше значение добавки (1-5).
В случае осесимметричной нагрузки оболочки вращения все факторы становятся функциями одной координаты х, отсчитываемой по меридиану. Деформированная срединная поверхность также представляет собой поверхность вращения. Здесь имеется аналогия с изгибом пластинки по цилиндрической поверхности. Подобно тому как цилиндрический изгиб пластинки сводится к изгибу балки-полоски, выделенной вдоль короткого измерения пластинки, так и осесимметричная деформация оболочки вращения может быть
пропорционально квадрату
Фиг. 69.
изучена путем рассмотрения кривого бруса-полоски, выделенного вдоль какой-либо образующей (меридиана).
Если оболочка вращения имеет прямолинейные образующие (цилиндр, конус), то снова приходим к балке-нолоске постоянной
или переменной ширины, но в отличие от цилиндрического изгиба
пластинки здесь получаем балку-полоску на сплошном упругом
основании.
Рассмотрим круговую цилиндрическую оболочку постоянной толщины, нагруженную осесимметричной нагрузкой (фиг. 69).
В данном случае p.v=oo; py = const = r, где г—радиус цилиндра.
Уравнение (1.4) принимает вид
+(Л). г \ t/л2 dx'2 I
(1.6)
Здесь w — упругий прогиб, — начальный прогиб.
177
Выразим Ny через w. Относительное удлинение срединной поверхности вдоль окружности поперечного сечения равно относительному удлинению радиуса кольца:
С другой стороны, учитывая, что срединная поверхность находится в плоском напряженном состоянии, имеем
еу=-у О-Г)
Приравнивая правые части (1.7) и (1.7'), найдем
Л7у=^4-иД7х. (1.8)
Подстановка в (1.6) дает
n d*w .. rf2w , Et ... / d?wO и \ ,, _
D-------Nr----------------------------. (1.9)
dx* x x \ r I '
Обычно Nx = const, так как оболочка нагружается продольными силами только по торцам. Поэтому уравнение (1.9) представляет собою обыкновенное дифференциальное уравнение четвертого порядка с постоянными коэффициентами, детально изученное в гл. 1 в связи с расчетом растянутой балки на упругом основании.
Изгибная жесткость балки-полоски шириной 1 см
EI=D=>———. (1.10)
12(1 —р.2)
Отпорность упругого основания
k^. (1.11)
Погонная нагрузка
(1.12) \ djfl г )
В случае сжимающей силы следует переменить знак перед Nx на обратный.
Сказанное позволяет изучить прочность цилиндрической оболочки при осесимметричной деформации, опираясь на аппарат расчета растянутой или сжатой балки -па упругом основании или балки, не несущей продольной нагрузки.
§ 4.2. РАЗЛИЧНЫЕ СЛУЧАИ ОСЕСИММЕТРИЧНОЙ НАГРУЗКИ
Рассмотрим цилиндрическую оболочку без начального прогиба- Найдем нагрузку, при которой прогиб изменяется по линейному закону:
w = ®»04-?x. (2.1)
178
Здесь Wo — прогиб в сечении, принятом за начальное, ср — постоянный по длине оболочки угол поворота сечений балки-полоски.
Подставляя (2.1) в (1.9), находим
^(w0 + ?z)=^-^. (2.2)
г
Продольную силу Nx считаем постоянной и заданной. Тогда
Прогибу, изменяющемуся по линейному закону, отвечает нагрузка, также изменяющаяся по линейному закону, а постоянному прогибу отвечает постоянная нагрузка.
Если задано уравнение поперечной нагрузки в виде
Р = Ро + х[ёл'
а также величина Nx, то легко найти значения w0 и <р0:
г2 , ? = — tga'
(2-3)
(2-4)
Обратимся к случаю несвободных, например, шарнирно опертых или защемленных концов.
Общее решение уравнения четвертого порядка (1.9) можно представить как сумму общего решения однородного уравнения, содержащего четыре произвольных постоянных, и частного решения, отвечающего произвольно взятым граничным условиям. Таким частным решением при нагрузке, следующей линейному закону, и является равенство (2. 1) с учетом (2.3) и (2.4). При достаточно длинной оболочке число произвольных постоянных сокращается с четырех до двух. Эти вопросы были подробно обсуждены в гл. I. Ограничимся поэтому двумя примерами.
На фиг. 70, а показан характер деформации достаточно длинной цилиндрической оболочки, находящейся под внутренним давлением р в предположении шарнирного опирания левого конца.
12* 179
Окончательное выражение для прогиба в предположении 74 = 0 получается в виде
w = w0 —®>0<?-a'cosax, (2.5)
где
/2 у r2D У rt
Второй член в (2.5), как правило, быстро затухает по мере удаления от опертого конца и остается постоянный прогиб w0, отвечающий свободному концу.
На фиг. 70, б показана оболочка под той же нагрузкой, но с жестким защемлением левого конца.
В этом случае уравнение прогибов получается в виде
w = п>0 — woe~aj: (cos ах У sin ах). (2.7)
Как в том, так и в другом случае полное деформированное (а значит и напряженное) состояние можно представить как сумму безмоментного состояния, характеризуемого постоянным прогибом wq и краевого эффекта, характеризуемого затухающей волнообразной эпюрой прогибов и аналогичной эпюрой продольных изгибающих моментов.
Практически влияние краевого эффекта существенно в пределах довольно узкой зоны. Ширину зоны (интервал затухания) можно оценить, подсчитав длину полуволны периодических множителей, входящих во вторые слагаемые выражений (2.5) и (2.7):
= - (2.8)
/3(1-/)
Принимая ft х= 0,3, получим
X —2,5 /г/.
(2. 8')
Чем меньше зона краевого эффекта, тем больше оснований отнести его к местным перенапряжениям, влияние которых при пластическом материале и статической нагрузке несущественно. Наряду с этим при переменных нагрузках краевой эффект должен быть учтен, так как нередко может явиться причиной преждевременного разрушения конструкции, рассчитанной исходя из бе'»-моментного напряженного состояния.
Неприятная особенность краевого эффекта состоит в том, что увеличением толщины оболочки не всегда удается существенно снизить наибольшие изгибные напряжения. В этом случае снижение жесткости опор может дать лучшие результаты.
180
Допустим, что в некотором сечении длинной оболочки к ней приложена радиальная нагрузка, равномерно распределенная по окружности (фиг. 71, а).
По отношению к продольным волокнам (балкам-полоскам) эта нагрузка играет роль сосредоточенной силы. Обозначим через Р силу, приходящуюся на единицу длины дуги. На фиг. 71,6 показаны эпюры прогибов, углов поворота, изгибающих моментов и
Фиг. 71.
поперечных сил для участка вблизи нагруженного сечения. Этот участок представляет собою зону краевого эффекта. При малой толщине оболочки приложение сколько-нибудь значительной нагрузки, хотя бы и равномерно распределенной вдоль окружности, нежелательно, так как всякое отступление от правильной геометрической формы и равномерности распределения ведет к появлению поперечных изгибающих моментов Му. Местная нагрузка указанного типа часто приводит к образованию глубокой поперечной вмятины. Поэтому оболочку вдоль линии нагрузки следует подкреплять достаточно жесткой диафрагмой или шпангоутом. Последнее особенно необходимо по соображениям устойчивости, когда нагрузка направлена внутрь оболочки,
181
§ 4.3. ОБОЛОЧКА ПОД САМОУРАВНОВЕШЕННОЙ ПОПЕРЕЧНОЙ НАГРУЗКОЙ, ПОСТОЯННОЙ ВДОЛЬ ОБРАЗУЮЩЕЙ
Пример подобной нагрузки показан на фиг. 72, а. К чей прежде всего относится равномерное внутреннее или внешнее давление, линейная постоянная нагрузка вдоль двух диаметрально противоположных образующих и др. Если длина оболочки значительно превосходит ее радиус, то можно пренебречь искривлением образующих вблизи краев и свести задачу к расчету элементарного кольца шириной 1 см, вырезанного из оболочки. Подвешенная
вдоль образующей по всей длине оболочка (фиг. 72, б) также относится к рассматриваемому случаю.
Дифференциальное уравнение равновесия оболочки, как и в случае осесимметричной нагрузки, получим из (1.4).
Подставим
d2w п d^w п ,
Рх=°°; Py=r; дг7 = 0: тт=0;
' ал2 дх ду
Кроме того, введем уточнение, даваемое формулой (1.5').
В результате получим уравнение в обыкновенных производных:
\ dy'< г2 dy2 Jr 3 dy2 или
D + f _ N Ad*™ (3. !)
dy* 1 \r2. У] dy?1 v
Это уравнение используется в дальнейшем для определения критй-ческого внешнего давления, при котором происходит потеря устойчивости круговой формы поперечного сечения оболочки.
§ 4.4. УСТОЙЧИВОСТЬ ОБОЛОЧЕК В ЛИНЕЙНОЙ ПОСТАНОВКЕ
Потеря устойчивости оболочек связана в первую очередь с возникновением сжимающих напряжений в срединной поверхности. Перпендикулярно к траекториям сжимающих напряжений можно ожидать образования волн (выпучин и впадин).
182
Начнем со случая цилиндрической оболочки, равномерно сжатой вдоль образующих. Случай общей потери устойчивости как трубчатого стержня может иметь практическое значение
только при сравнительно толстой стенке и здесь им заниматься не
будем. Речь, таким образом, будет идти о выпучивании стенки, иначе о местной потере устойчивости оболочки.
Сделаем допущение, что волнообразование носит осесимметричный характер (фиг. 73). В таком случае можно использовать дифференциальное уравнение (1.9), изменив знак перед Nx на обратный и поло, жив правую часть равной нулю. Величину Nx—^кр определяем из условия существования прогибов w и при условии отсутствия поперечной нагрузки р. Так как мы отбро-снли также член Nx-----------в правой
\дх2 г '
части, то это означает, что под w подразумевается дополнительный прогиб, отсчитываемый от первоначально деформированной срединной поверхности оболочки. Итак, уравнение для определения iVx = yVKp имеет вид
гл rf’w , ,r tflw . Et _
D---------/V..n------------w~0-
dxt 1 Kp dx2 1 r2
(4-1)
Как и следовало ожидать, мы пришли к уравнению устойчивости сжатой балки с изгибной жесткостью El^D, опертой на
, Et п .
к = —. Вдоль обра-
упругое сплошное
основание с отпорностыо
зующих возникают синусоидальные волны. Длина волны, если пренебречь влиянием граничных условий на концах, или что то же, считать оболочку при исследовании ее местной устойчивости бесконечно длинной, определится из формулы (4.6) в гл. I:
, , / Dr2 / г2/'2
к — ^ |/ Et ~~ 4________
Г К12(1-нД
при р = 0,3 получаем
ZK= 1,75/77.
Критическая сила по формуле (4.10) гл. Г / Л/ F&
NK = 2 1 / D ~ .
кр I Z-2 г /3(1 — |л2)
Полагая р = 0,3, получим приближенно
окг=.Д21=0,6^. ' t г
(4- 2)
(4. 2')
(4.3)
(4.4)
183
В случае короткой оболочки должны быть учтены положения § 1.4.
Рассмотрим теперь длинную оболочку под равномерным внешним давлением (фиг. 74), используя для этой цели полученное выше уравнение (3. I).
Будем приписывать знак «плюс» внешнему давлению p = const и отвечающей ему сжимающей силе Nv=pr. При нарастании дав-
ления р круговая форма поперечного сечения оболочки первоначально сокращается, но при достаточно большом р = Рь-р возможно образование продольных складок, характеризуемых переменной по окружности величиной радиального прогиба w=w(y). В критическом состоянии Nу-N к? — Ркр • f.
«Уравнение устойчивости» (по существу —• уравнение безразличного равновесия) получим, положив правую часть уравнения (3.1) равной нулю. Физически это означает, что
мы ищем такое значение Mtp=pitpr, при котором прогибы w, определяемые из уравнения с правой частью, перестают быть пропорциональными правой нагрузочной части. Итак, имеем
rf4w । / 1 I ^крг \ _л
rfy4 \ f2 D / dy2
Общий интеграл этого уравнения, очевидно, будет
w = С. cos 0_у-ф С2 sin р_у-ф С3у -ф С4.
Здесь
е!=-ф+фф. г2 и
(4. 5)
(4.6)
(4. 7)
Начало отсчета дуг у может быть выбрано- произвольным. Граничные условия сводятся к требованию периодичности функции w и ее производных. Период равен 2-ггг.
Постоянную С4 полагаем равной нулю, ведя отсчет радиальных прогибов w от равномерно деформированной окружности.
Слагаемое С3у нарушает периодичность. Поэтому Сз = 0.
Беря начало отсчета в точке, где прогиб равен пулю, из условия ш(0)=0 получаем Ci = 0. Уравнение радиальных прогибов принимает вид
w = С2 sin 9_у.
Постоянная С’2 = щтах, равная амплитуде прогибов, остается неопределенной. Для нахождения [3 служит уравнение
C2sin (р«2яг) = 0>
184
откуда
2~гй п*к.
Здесь /г* — число полуволн. Это число может быть только четным. Если предположить, что на окружности укладывается нечетное число полуволн, то будет нарушена периодичность углов поворота dw/dy.
Обозначим через п число волн:
где п, вообще говоря, может быть любым целым числом.
Тогда
₽2=~ (л = 0, 1, 2, 3. . . ). (4.8)
Сразу видно, что при /г = 0 отсутствует искривление. При п=\ имеем перемещение кольца как твердого тела. В самом деле, при п= 1
w sin — = ®тах sin О,
г
где 0-—центральный угол (см. фиг. 74).
Таким образом, п в условиях дайной задачи может принимать значения 2, 3, 4 . . .
Подставляя (4.8) в (4.7), после небольших преобразований находим
Лр-^^(« = 2.3, 4. . .). F Г3
Практический интерес представляет наименьшая величина критического давления. Полагая п = 2, имеем
Эта же формула используется для изолированного кольца, а также шпангоута круговой оболочки в виде
кг1см- (4-10>
F г3
Здесь под р подразумевается погонная нагрузка кольца, EI — изгибная жесткость кольца.
Итак, мы рассмотрели вопрос об устойчивости круговой цилиндрической оболочки при осевом сжатии и при поперечном давлении, задаваясь характером деформации — в первом случае осесимметричной деформацией, во втором случае деформацией по цилиндрической поверхности. В действительности, благодаря влиянию концевых закреплений в обоих случаях появляются как поперечные, так и продольные волны.
185
С. П. Тимошенко исследовал случай осевого сжатия, задаваясь деформацией срединной поверхности, при которой перемещения и, v, w следуют зависимостям
и = A sin /гО cos —,
v— В cos «О sin } (4.11)
. л . т-х w= С sin /гО sin-----.
Этим вводится допущение, что по длине при выпучивании образуется т продольных полуволн, а по окружности п поперечных волн, или 2п полуволн. Допущения (4. 11) отвечают условиям
w — Q и
Дл-2
при х=0, х=1, т. е. шарнирному опиранию стенки на торцах.
Оказалось, что при сжатии достаточно длинной оболочки образуется большое число (несколько десятков) продольных волн и критическое напряжение теоретически снова определяется формулой (4.4) независимо от длины оболочки.
При очень короткой оболочке по длине образуется одна полуволна, и критическое напряжение сжатия определяется формулой Эйлера для волокна:
В случае поперечной нагрузки формула для критического давления, учитывающая шарнирное опирание краев, была дана Мизесом в предположении, что по длине оболочки образуется одна полуволна. Формула имеет вид
(1 — м2)гдКр
Е/
] — р.2
/ «2/2 \
2п2 — 1 — |Л
(4. 13)
Здесь Z — длина оболочки, п —число поперечных волн, подлежащих определению из условия рк — min. Это может быть выполнено рядом попыток.
При длинной оболочке, когда 1/г большое число, можно пренебречь членами, содержащими в знаменателе квадрат этого отношения. Тогда
£<3(П2_1)
ЛР 12гЗ(1 _р2)
(4. 14)
Положив п = 2, получаем для min ркр формулу (4.9).
186
В случае совместного действия осевого сжатия и поперечного давления критическая комбинация их значений определяется из уравнения
Cl — С3? 1 F ^4?2-Здесь приняты обозначения
(4. 15)
12 г2
Обозначая, кроме того, Х = -~—, имеем
С'1 = (1 — ;л2) )<,
с2 = (,.2 + /г2)4 - 2 [рк6 -|- Зк4/г2 + (4 - у.) ).2/г4 + /г6] +
+ 2(2-р))Лг2+/г4,
(4.16)
С3 = п2 (Х2 + /г2)2- (ЗХ2/г2+/г4), С4 = л2(А2 + /г2)2 + 2Х2/г2.
Здесь т— число продольных полуволн, п — число поперечных воли, которыми следует задаваться при определении коэффициентов Ci, С2, Сз, С4.
Для частного случая замкнутой цилиндрической оболочки, испытывающей всестороннее равномерное давление или имеющей внутри вакуум, имеем постоянное соотношение коэффициентов <р:
В этом предположении для рКр получается приближенная формула
Г л2_|_о,5
(4. 17)
Теория устойчивости оболочек при совместном действии сжатия и поперечного давления была разработана ЛАизесом.
Можно привести ряд рекомендаций, облегчающих подбор числа полуволн т и волн п, а также графиков, позволяющих в известном диапазоне размеров находить нужные параметры. Обширный материал имеется в книге С. П. Тимошенко «Устойчивость упругих систем». Не будем останавливаться на этих практически важных вопросах, так как многочисленными эксперимен
ту
тами установлено, что в теоретические формулы, полученные на основе интегрирования линейных дифференциальных уравнений следует ввести весьма существенные коррективы. Критические напряжения, получаемые по линейной теории, оказываются всегда завышенными.
Удовлетворительное совпадение теоретических и 'экспериментальных результатов получается лишь в случае применения н е-линейной теории оболочек.
Главное отличие этой теории состоит в введении уточненных зависимостей между перемещениями и деформациями срединной поверхности. Вместо известных соотношений
(4-18)
в нелинейной теории имеем соотношения
ди . 1 / dw \2
х дх 2 \ дх ) ’
__ ди , 1 / dw \2 w
у ду 2 \ ду ) г '
____ ди , ди . dw dw ху~~ду '~~~дх' ~д7~ду'’
1
(4. 19)
J
Первая строка равенств (4. 19) уже встречалась при изучении работы балок с неподвижно закрепленными концами. Из (4. 19) видно, что действительные упругие удлинения волокон срединной поверхности ех и еу и сдвиги больше их проекций па координатную плоскость ху, между тем как в линейной теории эти величины отождествляются. К применению нелинейной теории имеется тем больше оснований, чем ближе порядок величин прогибов к толщине оболочки h. Поэтому нелинейную теорию оболочек часто называют теорией оболочек при больших прогибах.
Решение нелинейных дифференциальных уравнений приводит к большим вычислительным трудностям, даже при использовании прямых вариационных методов, приводящих задачу к решению системы нелинейных (обычно кубических) алгебраических уравнений. Кроме того, экспериментальные данные по определению критических напряжений дают значительный разброс результатов. Поэтому ниже дадим только качественное рассмотрение работы оболочек в нелинейной постановке и результаты некоторых опытов.
188
§ 4.5. ДАННЫЕ ОПЫТОВ И НЕЛИНЕЙНОЙ ТЕОРИИ. ПРАКТИЧЕСКИЕ УКАЗАНИЯ
Осевое сжатие
Наибольшее расхождение опытных данных по устойчивости оболочек с данными линейной теории наблюдается при осевом сжатии. Даже при соблюдении особой тщательности изготовления
образцов и их испытания'реальные значения критических напряжений, как правило, оказываются в два-три раза ниже тех, которые вычислены по формуле (4.4). Если же
оболочка, как это часто имеет место в реальных конструкциях, имеет ощутимые начальные неправильности формы, то выпучивание оболочки будет происходить при еще более низких напряжениях. Такая «чувствительность» оболочек к начальным неправильностям формы является их особенностью, которая не согласуется с данными, относящимися к другим упругим системам; например, в случае стержня или пластинки данные экспериментов лежат очень близко от теоретических.
Другая, качественная особенность состоит в том, что самый процесс выпучивания обо
лочки на практике происходит совершенно
иначе, чем в случае пластинки; выпучивание ф11Г. 75.
оболочки происходит внезапно с ярко выра-
женным хлопком. Во время хлопка образуются глубокие ромбические вмятины, обращенные главным образом к центру кривизны (фиг. 75). Поэтому предположение о малости прогибов, возникающих при потере устойчивости оболочки и использование соответствующих этому линейных уравнений, не является оправданным при исследовании устойчивости оболочек. Необходимо сопоставить с начальной равновесной формой оболочки не только соседние бесконечно близкие формы, но и формы, характеризующиеся большими прогибами; последние должны считаться сравнимыми с толщиной оболочки. Но при этом надо исходить из нелинейных уравнений теории гибких оболочек *.
Надо, таким образом, различать верхнее критическое н а п р я ж е н и е, при достижении которого оболочка безусловно должна потерять устойчивость, и нижнее к р и т и ч е
* Более подробное исследование показывает, что в известном интервале нагрузок, лежащих ниже «линейной» критической величины, можно найти равновесные формы оболочки, сильно удаленные от начальной формы, ио обладающие значительно меньшей полной потенциальной энергией. Поэтому скачок оболочки к такой изогнутой форме вполне вероятен; должен быть лишь преодолен больший или меньший энергетический «барьер», чтобы оболочка прошла через область «соседних» равновесных состояний и совершила скачок к «отдаленному» состоянию. Если оболочка изготовлена с некоторыми начальными погрешностями формы или нагрузка приложена при испытании не вполне центрально, уровень энергетического барьера резко снижается.
189
с кое на п р я ж е н и е, при котором возможен перескок к изогнутой равновесной форме. Практически всегда находятся факторы, помогающие оболочке совершить скачок, так что реальные критические напряжения находятся в области, лежащей между нижним и верхним теоретическими значениями.
В практических расчетах уместно ориентироваться, идя на заведомое увеличение запаса прочности, на нижнее критическое напряжение, в то время как формулы линейной теории (4.4) — (4. 13) дают верхние значения напряжений. Опыты и нелинейная теория приводят при осевом сжатии к формулам для <ткр того же тина, что и линейная теория, но с другим численным коэффициентом
а”р=0,18£^-. (5.1>
Эта формула применима при условии, что критическое напряжение не превышает предела пропорциональности материала оболочки. Более подробное исследование показывает, что формулу типа (5. 1) можно с известным приближением распространить на область, лежащую за пределами пропорциональности, если вести определение не критического напряжения, а критической деформации:
£кр=0,18^-. (5.2>
Напряжение же, соответствующее деформации (5.2), находится по диаграмме а, е; последняя должна быть получена при испытаниях на сжатие коротких образцов, изготовленных из того же материала.
Поперечное давление
В случае внешнего поперечного давления результаты линейной теории значительно лучше сходятся с экспериментальными данными и тем точнее, чем оболочка длиннее. При 1/г)>5ч-6 можно непосредственно пользоваться формулой (4.9).
Опыты показывают, что для оболочек средней длины (когда г<7<3г) с закрепленными при помощи колец торцами потеря устойчивости оболочки сопровождается образованием ряда вмятин по окружности цилиндра, причем эти вмятины суживаются к торцам. Выпучивание сопровождается, как и в случае осевого сжатия, резким хлопком. Таким образом, и здесь имеет место потеря устойчивости «в большом», т. е. с образованием значительных прогибов; процесс выпучивания оболочки, описываемый линейной теорией, можно было бы назвать потерей устойчивости «в малом».
Решение линейной и нелинейной задач для оболочек средней длины показывает, что число выпучип, располагающихся по окружности, должно возрастать с уменьшением длины оболочки. Это можно видеть по фотографии фиг. 76; здесь показаны две оболочки разной длины, изготовленные из фотопленки, и испыты-190
вающис выпучивание под действием внешнего давления (в действительности внутри оболочек создается вакуум). В случае более короткого образца число вмятин заметно увеличивается.
Верхнее критическое давление для случая шарнирно опертых торцов можно определить по приближенной формуле
„ _ /2 к F f t (1-Д)0'75 RL |/ R
или при (1 = 0,3
где А — длина оболочки.
Н и ж и е е значение р”р здесь лежит гораздо ближе к верхнему, чем в случае осевого сжатия, и составляет 70% и более от верхнего в зависимости от соотношения между размерами обо-
Фиг. 76.
лочки. Так, при г//=180 было получено, что для //г=1 нижнее критическое давление равно 77% от ркр, для //г=1,2 составляет 78%, для Z/r=2,2— около 79% и при 1/г=^ — около 86%.
Как видим, по мере увеличения длины оболочки различие между р” и рЕр сглаживается; и, как указано, для весьма длинных оболочек формулы линейной теории можно считать окончательными.
Данные опытов подтверждают эти заключения. Рассеяние этих данных оказывается значительно меньшим, чем при осевом сжатии; реальные значения критических напряжений составляют примерно 70% от вычисленных по линейной теории. Правда, при наличии больших начальных неправильностей формы, когда первоначальные прогибы превышают толщину оболочки, отношение это снижается до 45—65%.
В практических расчетах оболочек средней длины следует определить ркр по формуле (5. 3'), а затем умножить эту величину на коэффициент, лежащий в пределах от 0,5 до 0,8; коэффициент выбирается в зависимости от условий изготовления и характера возможных начальных неправильностей.
191
Кручение оболочки
Выпучивание оболочки может происходить под действием скручивающих пар, как показано па фиг. 77. Обозначим через Л)кр момент пары; тогда средние касательные напряжения в топкой стенке оболочки могут быть найдены по формуле
Мкр
(5.4)
Как показывают опыты, при потере устойчивости оболочки
здесь образуются наклонные выпучины, располагающиеся по вин-
товым линиям; подобно предыдущим случаям, и здесь обычно происходит внезапное скачкообразное продавливание вмятин.
Рассматривая устойчивость оболочки «в малом» и решая линейную задачу, можно прийти для весьма длинной оболочки к следующей формуле для критиче-
ского напряжения:
__ Е / i \П5
Т|(Р Т/3 (1 — ku.2)(>,75 R )
(5. 5)
(5.5')
или при р. = 0,3
4=0,29f(<)l'S.
Для критической величины крутящего момента получаем выражение
7Икр=1,84£72]/Д/. (5 6)
При расчете оболочек средней длины верхние критические напряжения можно вычислить по приближенным формулам. Приведем такую формулу для случая шарнирного опирания торцов (при |н = 0,3):
ткр
5+/9'4+0'67О"У(Я-
(5. 7)
Решение задачи в нелинейной постановке указывает на то, что для длинных оболочек верхнее критическое напряжение надо считать совпадающим с нижним значением. Между тем, в случае оболочек средней длины нижнее критическое напряжение отличается от верхнего, причем т"р составляет 804-85% т;;р. Данные опытов указывают па то, что реальные критические напряжения составляют при кручении в среднем 70—75% от значений, вычисленных по линейной теории. Таким образом, здесь эффект нелинейности оказывается примерно таким же, как при внешнем давлении, и далеко не так велик, как при осевом сжатии. Это
192
объясняется тем, что в первых двух случаях вмятины охватывают всю длину оболочки и их образование затрудняется вследствие закрепления торцовых сечений. Между тем, при сжатии выпучины получаются мелкими во всех направлениях и «продавливание» их происходит более свободно.
Для практических расчетов оболочек средней длины можно использовать формулу (5.7) с поправочным коэффициентом 0,7-т-0,8.
При совместном действии осевого сжатия и кручения критические напряжения могут быть определены из следующей приближенной зависимости:
(5.8
Здесь под Окр и ткр понимаются критические напряжения при одновременном приложении нагрузок, причем (Ткр отвечает сжимающей силе, а ткр — крутящему моменту. Через (То и То обозначены критические напряжения, найденные для раздельного действия усилий сжатия и кручения с учетом поправочных коэффициентов. Задаваясь одной из величин (Ткр или ткр, находим вторую по уравнению (5.8).
Устойчивость цилиндрических панелей
На фиг. 78 представлен отрезок круговой цилиндрической оболочки, ограниченный двумя образующими и двумя дугами поперечных сечений; будем называть этот отрезок цилиндрической панелью. Обозначим длину панели через а, ширину, измеренную вдоль дуги, через Ь, охватываемый панелью центральный угол, измеряемый в радианах, через 0. Допустим, что по краям панель закреплена шарнирно.,
При действии осевых сжимающих усилий, равномерно распределенных вдоль дуговых кромок (фиг. 78), может происходить выпучивание панели. Расчетные формулы будут иметь различную структуру в зависимости от того, является ли панель пологой или имеет значительную кривизну. Для отнесения панели к одной или другой категории может служить «параметр кривизны»
k~ — . (5.9)
rt
Если &'<12, то панель можно считать пологой. При этом она рассчитывается на устойчивость по формулам, близким к тем формулам, которые относятся к плоским пластинкам. Решение задачи в линейной постановке приводит к следующей формуле для критических напряжений (при условии а>Ь)-.
. 1&D , „ 02
°"Р — 4 *2Г Е 4Л2 ’
(5. 10)
193
Как легко видеть, первый член представляет собой критическое напряжение для плоской пластинки шириной Ь, второй же член учитывает влияние кривизны. При ц = 0,3 формулу (5. 10) можно представить в виде
0 =3,6£'Л-У + —^02. (5.11)
кр \ b J ' 39,5 '
Опыты показывают, что в действительности выпучивание цилиндрических панелей происходит хлопком, с продавливанием
вмятин, обращенных преимущественно к центру кривизны. Исследование нелинейной задачи показывает, что при k< 12 нижнее критическое напряжение для цилиндрической панели можно считать равным критическому напряжению для плоской пластинки тех же размеров (при а>Ь):
°:»=3’6£(т)!- ,5-12)
Здесь, таким образом, эффектом кривизны вообще можно пренебречь.
В случае панели значительной кривизны, когда /<>12, для определения верхнего критического напряжения может быть использована та же формула (4.4), что и для замкнутой цилиндрической оболочки (при а>Ь):
Вместе с тем на случай такой панели можно с известным приближением распространить и формулу (5.2), относящуюся к нижнему критическому напряжению:
<’"р=0,18£'у . (5.13)
194
Данные опытов указывают на весьма большой разброс критических напряжений для сжатых вдоль оси цилиндрических панелей. Реальные критические напряжения лежат во всей области, заключенной между верхним и нижним теоретическими значениями. Поэтому практические расчеты рекомендуется вести по формулам (5. 12) и (5. 13).
Приведем также данные для расчета слабо искривленных цилиндрических панелей, подвергающихся действию сдвига (фиг. 79). Для квадратной панели (а = Ь) нижнее значение критического касательного напряжения можно определить по следующим формулам:
при 0<£<10 8,5Д > (5.14)
при 10<А<25 т»р=7,5Д(“-)2 + 0>1^-4' • (5.15) \ 0 / к
Выражение (5. 14) отвечает критическому напряжению для квадратной плоской пластинки тех же размеров.
* * *
Проблемы прочности тонких оболочек относятся к числу наиболее сложных задач прикладной теории упругости. Крупнейшие заслуги в развитии теории оболочек принадлежат английскому ученому А. Ляву и советским ученым В. 3. Власову, Б. Г. Галер-кину, А. Л. Гольденвейзеру, А. И. Лурье, X. М. Муштари, В. В. Новожилову, И. Я. Штаерману и др. В последние два десятилетия быстро развивается нелинейная теория оболочек, позволившая решить ряд важных для теории и практики вопросов устойчивости. В этой области необходимо отметить заслуги Т. Кармана, Цянь Сюэ-сэпя, X. М. Муштари, В. И. Феодосьева, С. А. Алексеева, Н. А. Алумяэ, А. С. Вольмира. Из исследований последних лет в области прочности и устойчивости авиационных оболочек отметим работы В. М. Даревского, С. Н. Кана, И. И. Трапезипа.
13*
Глава V
ПРЯМЫЕ ТОНКОСТЕННЫЕ БРУСЬЯ
§ 5.1. КАЧЕСТВЕННАЯ ХАРАКТЕРИСТИКА ТОНКОСТЕННЫХ БРУСЬЕВ
Подавляющее большинство металлических брусьев, применяемых в авиации, имеет тонкостенный профиль. Работа тонкостенных брусьев обладает значительными особенностями, отличающими их от массивных брусьев. С другой стороны, многие сложные конструкции (например, крыло, фюзеляж), представляющие собою подкрепленные оболочки с достаточно жестким поперечным сечением, могут рассматриваться как тонкостенные брусья. Отсюда ясна важность изучения теории тонкостенных брусьев.
Основное отличие тонкостенного бруса от удлиненной цилиндрической или призматической оболочки (складки) состоит в жесткости поперечного сечения. В одних случаях, например, при прокатных профилях, жесткость поперечного сечения достигается автоматически, за счет достаточной толщины стенок, препятствующей разгибанию поперечного сечения. В других случаях жесткость должна быть обеспечена специально поставленными поперечными подкреплениями — ребрами, шпангоутами, нервюрами. Чем больше габариты поперечного сечения по сравнению с толщиной стенок, тем большее значение имеет обеспечение поперечной жесткости для того, чтобы конструкция работала в соответствии с теорией тонкостенного бруса. При недостаточной поперечной жесткости степка сильно прогибается под действием нагрузки, нормальной к ее поверхности, и на первый план выступают напряжения изгиба стенки вместо нормальных и касательных напряжений, зависящих от усилий, подсчитанных для сечения в целом.
Линия, делящая пополам толщину стенки в поперечном сечении, называется средней линией профиля. По виду средней линии профили делятся на открытые и замкнутые.
Открытые профили могут быть простые (например, корытный профиль) и разветвленные (например, тавр, двутавр). Замкнутые профили могут иметь одну или несколько ячеек. В последнем случае профиль называется многосвязным.
Среди открытых профилей должны быть выделены профили с прямолинейными средними линиями стенок, пересекающимися
196
в одной точке, иначе говоря,— образующими пучок. Примерами могут служить уголковый, крестовый и тавровый профили.
На фиг. 80 представлены открытые и замкнутые тонкостенные профили. Первые два ряда относятся к строительным и авиационным прокатным профилям. В третьем и пятом ряду даны авиапрофили, согнутые из листового дуралюмина. В четвертом ряду — трубы и профили замкнутых подкрепленных оболочек крыла,
фюзеляжа, летающей лодки, судна. Следует заметить, что брусья с открытыми авиапрофилями применяются главным образом для подкрепления обшивки более сложных тонкостенных конструкций и в качестве самостоятельно работающих деталей встречаются очень редко.
Основное свойство тонкостенных брусьев с открытым профилем— слабое сопротивление свободному кручению. Свободным называется скручивание прямолинейного бруса двумя равными и противоположными парами, когда депланация торцов ничем не стеснена. С явлением депланации — искажения плоскости поперечного сечения — читатель познакомился при изучении кручения брусьев с пекруглым профилем. Это явление наиболее ярко проявляется именно в тонкостенных брусьях. В случае тонкостенных брусьев деплапация профиля определяется выходом из плоскости сечения точек средней линии, так как близко расположенные смежные точки относительно средней линии перемещаются незна
197
чительно. Поэтому, говоря о депланации профиля, будем иметь в виду депланацию средней линии стенки в поперечном сечении.
Слабое сопротивление свободному кручению и явление депланации известно всякому, кто держал в руках стержень, согнутый из листового материала, и пытался его скрутить. При таком простейшем опыте особенно отчетливой становится разница между сопротивле-пнем изгибу и скручиванию. По отно- , /
шению ко всем видам деформации стержень ведет себя как массивный, ( f 'v
но закручивается на заметный угол \ j ’
усилием рук, а средняя линия торцов ' /
при этом из плоской ломаной или кри- /
вой линии превращается в пространст- ^**,**»J 1 венную.
Фиг. 81.
На фиг. 81 показан характер деформации при свободном кручении двутавра и кругового цилиндра, разрезанного вдоль образующей.
Деформация двутавра может быть представлена как скручивание относительно продольных осей двух его полок и стенки, причем плоскости этих пластин превращаются в косые плоскости; одновременно полки вращаются в разные стороны относительно поперечной оси, проходящей через точку А, чем и обусловливается депланация торцов. Взаимное вращение полок принуждается неизменяемостью поперечных сечений, которые поворачиваются, как диски. Если бы поперечное сечение могло перекашиваться, то закручивание полок и стенки могло бы осуществляться и без взаимного вращения полок. Явление может быть наглядно изучено при помощи простейшей модели, склеенной из ватманской бумаги.
Деформация при кручении цилиндра, разрезанного вдоль
198
образующей, иллюстрируется прямоугольным листом бумаги, свернутым в трубку: смещая один относительно другого продольные края листа, получаем взаимное вращение торцов и депланацию поперечных сечений.
Отметим, что не все открытые профили депланируют: поперечные сечения профилей-пучков при кручении остаются плоскими.
Брусья с замкнутым профилем несравненно лучше сопротивляются скручиванию, чем открытые. Сопротивление скручиванию тонкостенной трубы, разрезанной вдоль образующей, можно считать исчезающе малым по сравнению с сопротивлением скручиванию цельной трубы.
Замкнутые профили обладают всеми свойствами массивных. Депланация замкнутых профилей значительно меньше депланации открытых профилей. Из замкнутых тонкостенных профилей не депланируют такие профили, как круг, квадрат, и вообще все профили со стенкой постоянной толщины, у которых средняя линия представляет собой многоугольник, описанный около круга.
Сопротивление скручиванию брусьев с открытым профилем повышается в тех случаях, когда имеются препятствия для депланации поперечных сечений.
Так, например, если заделать один из торцов двутавра, то характер деформации существенно изменяется и кручение сопровождается изгибом полок в своих плоскостях, но в разные стороны (фиг. 82). При этом, очевидно, в поперечных сечениях возникают не только касательные, но и нормальные напряжения изгиба.
Такое осложненное изгибом кручение называется и з г и б н ы м или стесненным кручение м.
Заделывая торец или создавая другим способом препятствия для депланации (например, путем приварки планок, соединяющих две полки), можно заставить воспринимать крутящие моменты при сравнительно небольших деформациях и такие профили, жесткость которых при свободном кручении следует считать практически исчезающей.
Стесненное кручение имеет место не только при внешних препятствиях для депланащит, но и при внутренних. Например, если крутящий момент изменяется по длине бруса, то и относительный угол закручивания становится переменным, а значит и депланация смежных сечений не будет одинаковой и сечения будут нажимать одно на другое.
Аналогичное явление наблюдается и при замкнутом профиле, но в меньшей степени, в связи с меньшей депланацией замкнутых профилей.
При недепланирующем профиле (открытом или замкнутом) нормальные напряжения от кручения отсутствуют.
Важная особенность тонкостенных брусьев состоит в том, что при действии изгибающих сил в одной из главных плоскостей инерции сечения возникает не только изгиб, но и закручивание. Такое явление наблюдается в случае, когда плоскость действия сил не является плоскостью симметрии (фиг. 83, а).
199
Можно указать точку в поперечном сечении, называемую центром изгиба, через которую должна проходить сила, чтобы изгиб не сопровождался закручиванием (фиг. 83,6).
Тонкостенные брусья закручиваются и от действия продольных сил.
Потеря устойчивости тонкостенными брусьями также отличается большим своеобразием. Сжатые стержни открытого профи-
Фиг. 83.
ля могут потерять устойчивость, не только изгибаясь, но и закручиваясь. В отдельных случаях крутильная форма потери устойчивости возникает при растяжении.
§ 5.2. СВОБОДНОЕ КРУЧЕНИЕ БРУСА С ОТКРЫТЫМ ПРОФИЛЕМ
Принято говорить, что прямой брус работает на свободное кручение (иначе — чистое кручение), если он нагружен в плоскостях торцов парами сил с одинаковыми по величине, но противоположными по направлению моментами, причем плоскости торцов не стеснены, а отдельные точки обоих торцов могут беспрепятственно получать перемещения, выходя из своих плоскостей.
Практически свободное кручение может быть осуществлено путем передачи нагрузки при помощи двух весьма тонких жестких только в своих плоскостях торцовых диафрагм (фиг. 84).
Приведем без доказательства некоторые результаты, получаемые методами теории упругости и относящиеся к кручению бруса с сечением в виде узкого прямоугольника.
Нормальные напряжения в поперечных сечениях отсутствуют.
Напряженное состояние во всех поперечных сечениях одинако вое и определяется одними касательными напряжениями. '
Траектории касательных напряжений имеют вид, показанный на фиг. 85. По траектории видно, что па значительном протяжении профиля полные напряжения т параллельны длинным сторонам прямоугольника. Максимальные касательные напряжения действуют у края, по середине длинных сторон. По толщине (меньшему
200
измерению прямоугольника) напряжения т2у распределены по' закону, весьма близкому к линейному. Отступления от линейного закона заметны только вблизи коротких сторон прямоугольника, где напряжения т2Х имеют свое наибольшее значение.
Отметим, что хотя напряжения т2Х значительно меньше, чем напряжения xzy, но в общем балансе касательных усилий те и другие играют одинаковую роль: половина крутящего момента вос
принимается касательными усилиями т2Х dF, другая половина — усилиями т2у dF. Объясняется это различием в величине плеч при попарной группировке усилий в симметричных точках: пары усилий т2у dF имеют значительно меньшие плечи, чем пары усилий Т2Х dF.
Характер траекторий касательных напряжений показывает также, что в силу закона парности касательных напряжений, сре-
Фиг. 85.
динная плоскость бруса, параллельная длинному измерению прямоугольника, на значительном протяжении свободна от касательных напряжений, другими словами, является нейтральной. Касательные напряжения в срединной плоскости появляются лишь вблизи краев. Так как относительный сдвиг пропорционален касательному напряжению, то срединная плоскость не испытывает деформации сдвига. Если предположить, что на ней нанесена система квадратных клеток, то при закручивании клетки остаются квадратными. Наоборот, клетки, нанесенные на наружных поверхностях бруса — перекашиваются, превращаются в ромбы.
Основные зависимости, даваемые теорией упругости, таковы. Относительный угол закручивания
d'fK ' AfK
dz к (7/к
201
Здесь /к — так называемый момент инерции сечения бруса при 'кручении. С достаточной для практики точностью при s> 1О/ можно пользоваться приближенной формулой:
/к = — st3. к 3
Более точная формула
о
(2.1)
(2. 1')
Максимальное сторон):
касательное
напряжение (по середине длинных
Фиг. 87.
sfl
Момент кручении в .вен
ттах
WK сопротивления при данном случае ра-
W
Фиг. 86.
Данные формулы выведены в предположении, что угол закручивания мал. При значительных углах закручивания в поперечных сечениях бруса возникают нормальные напряжения, существенно изменяющие всю картину напряженного состояния. Однако в практике приходится иметь дело, главным образом, с малыми перемещениями.
Исследования показали, что картина напряженного состояния и приведенные формулы без всяких изменений переносятся на случай профиля в виде узкой полоски постоянной ширины t с криволинейной или ломаной средней линией (фиг. 86). Под s следует подразумевать длину средней линии. Этим самым решаются основные задачи, относящиеся к свободному кручению прямого тонкостенного бруса открытого профиля со стенками постоянной толщины t.
Формулы с известным приближением применяются также для профиля переменной толщины. Тогда
— \t3ds, x =
3 J /,<
5
‘202
Профиль, состоящий из нескольких прямоугольников различной толщины (фиг. 87), рассматривается как совокупность отдельных прямоугольных профилей. Наибольшее касательное напряжение действует по середине наиболее толстой стенки. Расчетные формулы будут
4 = 4-УМ; = (2.2)
О 1К и/к
i
Пользуясь этими формулами, можно вести приближенный расчет на свободное кручение прокатных профилей, причем вместо t вводится средняя толщина полки или толщина стенки по данным сортамента *. Более точные данные, подсчитанные с учетом закруглений и переменной толщины полок, см. в «Справочнике машиностроителя», т. III.
§5.3 ДЕПЛАНАЦИЯ ПОПЕРЕЧНОГО СЕЧЕНИЯ ТОНКОСТЕННОГО БРУСА ПРИ СВОБОДНОМ КРУЧЕНИИ
Известно, что кручение бруса с некруглым профилем сопровождается искажением плоскостей поперечных сечений, иначе называемым депл аиацией этих сечений. .
Депланация в данной точке поперечного сечения характеризуется величиной проекции полного перемещения этой точки на нормаль к поперечному сечению, т. е. на ось бруса.
Важно отметить, что при свободном кручении депланации всех поперечных сечений бруса одинаковы, Деплапация в каждой точке зависит от крутящего момента (предполагаемого постоянным по длине бруса), по не зависит от длины закручиваемого бруса. Если бы поперечные сечения депланировали по разному, то волокна между ними получали бы удлинения или укорочения и одновременно возникали бы нормальные напряжения. Кручение, при котором создаются условия для неодинаковой депланации поперечных сечений, называется стесненным, В дальнейшем мы еще к нему возвратимся, а сейчас займемся численным определением депланации при свободном кручении.
Нижеследующие рассуждения действительны как для массивных брусьев, так и для тонкостенных с открытым или с замкнутым профилем.
Поставим себе задачей установить деплапацию в точках поперечного сечения, лежащих па какой-либо из траекторий касательных напряжений, и допустим, что напряжения т вдоль траектории нам известны.
Выделим цилиндрическую поверхность, направляющей которой является рассматриваемая траектория, и возьмем па этой поверх
* При подсчете <рк рекомендуется умножать ZK на коэффициент 1,2 для двутавров и 1,12 для швеллеров. В формуле для Ттах поправочный коэффициент при /,< не вводится.
203
ности прямоугольный элемент ds dz, находящийся, очевидно, в плоском напряженном состоянии — в условиях чистого сдвига.
На фиг. 88 ось z совпадает с образующей взятой нами цилиндрической поверхности и параллельна оси бруса.;
Подвижная ось s совпадает с касательной к траектории и является продолжением элемента дуги ds. Одновременно под s будем
подразумевать дуговую координату точки на траектории, измеренную от какого-либо начала.
Проекции полного перемещения точки С на оси z и s обозначены соответственно w и и. Величина w и представляет собою депланацию в точке С.
После деформации элемент сместится и примет форму параллелограмма.
Относительный сдвиг-— приращение прямого угла элемента — легко выражается как сумма двух малых углов, равных интенсивностям роста перемещений w и и вдоль осей s и z. Из фиг. 88, а видно, что
•<=tl+4l- <з-'> ds дг
Обратимся к плану на фиг. 88, б. Буквой Р обо-
значен след оси, вокруг которой происходит закручивание. Величина « есть проекция полного перемещения точки С на ось В свою очередь и равна проекции на ось s вектора v, являющегося горизонтальной проекцией полного перемещения. Очевидно, v перпендикулярен к радиусу-вектору РС=р и равен
'У = рсрк.
где фн — угол закручивания.
Обозначим через г длину перпендикуляра из Р на ось s. Из подобия треугольников со сторонами р и г соответственно и и и тотчас устанавливаем
— = г?к.
Р
20-1
Дифференцируя обе части по г, находим интересующее нас значение производной:'
ди d<e
dz dz
Здесь срк — относительный угол закручивания, равный, в данном случае постоянной величине MK/GIK.
На основании закона Гука при сдвиге имеем
t="g ’
где т — касательное напряжение в данной точке траектории.
Подставляя эти значения в первое уравнение и заменяя обозначение частной производной обозначением полной (поскольку в данном случае w зависит только от s— дуговой координаты — и не зависит от z), получим
dw , I х /о о-.
(3'2)
Мы получили дифференциальное уравнение депланации вдоль траектории касательного напряжения. Заметим, что в правой части гит — функции дуговой координаты s, измеренной вдоль траектории.
Интегрируя это уравнение, найдем депланацию вдоль траектории.
Умножим обе части последнего уравнения на ds и проинтегрируем в пределах от 0 до s. Находим
w (s) — — <?(. j г ds 4* j т ds 4* iv (0). (3-3)
о о
Последнее слагаемое представляет собою постоянную интегрирования, зависящую от того, в какой точке траектории взято начало пути интегрирования.
Первый из интегралов имеет простой геометрический смысл. В самом деле, г ds есть удвоенная плошадь элементарного сектора с дугой ds и полюсом Р. Поэтому
j гds=<s> (3. 4)
о
равен удвоенной площади сектора с дугой s и полюсом Р.
Обозначение со постоянно будем применять для удвоенной сеК-ториальной площади, играющей большую роль в теории тонкостенных брусьев.
Второй интеграл представляет собой площадь эпюры т на отрезке s дуги траектории.
205
Таким образом получаем
w (s) — w (0) = — + -±- [т ds. (3.5)
4 о J
о
Следовательно, приращение депланации в некоторой точке дуги траектории по отношению к депланации в точке, принятой за начальную, равно взятому с обратным знаком произведению относительного угла закручивания срк на удвоенную площадь сектора с полюсом Р и дугой s плюс деленная на G величина площади эпюры % на отрезке s дуги траектории.
Заметим, что депланацию необязательно вычислять вдоль траектории касательного напряжения. Можно вести вычисление и вдоль любой кривой в плоскости поперечного сечения. Но тогда интеграл f т ds придется заменить интегралом б
J г cos (т, ds) ds, (3. 6)
о
где т — полное касательное напряжение в данной точке взятого нами пути интегрирования. Этот интеграл носит название циркуляции касательного напряжения.
Наибольшее практическое значение для тонкостенных стержней имеет депланация не вдоль той или иной траектории касательного напряжения, а вдоль средней линии профиля, в точках которой в случае открытого профиля, как известно, составляющая т. параллельная самой средней линии, равна нулю на всем протяжении профиля.
Поэтому для депланации вдоль средней линии открытого тонкостенного профиля при свободном кручении имеем в высшей степени простую зависимость:
w (s) — w (0)= — %'®. (3-7)
Величину с» удвоенной площади сектора иногда называют ед и-ничной дсила нацией при свободном кручении.
Изменение величины со вдоль дуги средней линии изображается графически в виде эпюры. Ординаты эпюры со откладываются перпендикулярно к средней линии. Для Построения эпюры необходимо иметь полюс Р (след оси закручивания) и начальную точку II, где значение со равно нулю или другой наперед задаваемой величине. Если в точке Н имеем со=0, то прямая PH определяет неподвижный радиус-вектор. Приращение с/со (удвоенную площадь элементарного сектора) считаем положительным при движении подвижного радиуса-вектора против часовой стрелки и отрицательным при движении по часовой стрелке. Этим определяется знак векториальных площадей со и знаки отдельных участков эпюры со,
206
На фиг. 89 дано построение эпюры со для разветвленного профиля при полюсе Р и нулевой точке Н.
Фиг. 89.
Предлагаем читателю повторить вычисление всех ординат эпюры со, пользуясь приведенными на фиг. 89 размерами профиля.
§ 5.4. СВОБОДНОЕ КРУЧЕНИЕ БРУСА С ЗАМКНУТЫМ ТОНКОСТЕННЫМ ПРОФИЛЕМ
Задача о кручении круглой трубы очень часто рассматривается' как частный случай задачи о кручении полого вала. Чем меньше толщина стенки трубы по сравнению с ее диаметром, тем с большим основанием можно считать, что по толщине стенки касательные напряжения распределены не по закону трапеции, а по закону прямоугольника, т. е. равиоме р н о.
Это положение в качестве естественной гипотезы переносим и на случай трубы с весьма тонкой стенкой и некруглой формой средней линии в поперечном сечении.
Таким образом, эпюра т по толщине стенки представляет собою прямоугольник. Векторы т направлены параллельно краям и при постоянной толщине стенки параллельны средней линии. При изменяющейся толщине стенки будем считать, что векторы т также параллельны средней линии, что не приводит к заметной погрешности, поскольку стенка тонкая. Итак, средняя линия является траекторией равномерного по толщине стенки касательного напряжения.
При этих условиях целесообразно оперировать не с касательными напряжениями, а с погонным касательным уси-д и е м — равнодействующей элементарных касательных усилий, отнесенной к единице длины стенки:
q=xt.
Размерность q, очевидно, кг!см. Погонное касательное усилие есть вектор, лежащий па касательной к средней линии и направленный в ту же сторону, что и касательное напряжение в данной точке средней линии (фиг. 90)*.
* На фиг. 90 толщина стенки показана в увеличенном масштабе.
20"
Так же как и касательные напряжения, погонные касательные усилия подчиняются закону парности: если зафиксировать какую-либо точку средней линии, то погонное касательное усилие
в поперечном сечении численно равно погонному касательно-
му усилию в продольном сечении, проходящем через ту же точку.
Докажем теперь очень простую, но вместе с тем важную теорему: при свободном кручении тонкостенной трубы погонное касательное усилие во всех точках средней линии поперечного сечения имеет постоянное численное значение.
Для доказательства вырежем из закручиваемой тонкостенной трубы кольцо шириной 1 см. Рассечем кольцо вдоль двух образующих А и В и рассмотрим условия равновесия одной из двух частей кольца (фиг. 91).
Обозначим погонные касательные усилия вдоль прямолинейных
•сторон через qA и qB. Так как ширина кольца равна 1 см, то ре-
зультирующие силы вдоль прямых краев отсеченной части численно также равны qA и qB. Вдоль криволинейных краев действуют только касательные усилия. Нормальные на-г пряжения при свободном ’ кручении отсутствуют. Из условия равновесия про- 1 екций всех сил па продольную ось (т. е. па образующую) сразу находим
Qa Q 13-
Так как сечения А и В были взяты в произвольных точках средней линии, то отсюда следует
<? = const.
(4. 1)
Теорема доказана. Погонное усилие q можно'уподобить постоянному расходу жидкости, циркулирующей без притока извне и без потерь вдоль замкнутой (кольцевой) трубки, ось которой имеет форму средней линии поперечного сечения нашего тонкостенного бруса. При этом касательное напряжение уподобляется скорости жидкости.
208
Покажем, что средняя линия в поперечном сечении в некотором масштабе представляет силовой многоугольник (точнее — силовую кривую) касательных усилий (фиг. 92).
В самом деле, элементарные усилия q ds при q = const пропорциональны элементам ds средней линии и направлены вдоль ds. Следовательно, цепочка отрезков ds, умноженная на масштабное число q кг/см, изображает силовой многоугольник для сил q ds. Но цепочка отрезков ds и есть контур средней линии.
Известно, что если силовой многоугольник замкнутый, то система сил эквивалентна паре. Величина моТиепта пары не зависит от полюса, взятого в плоскости пары для вычисления момента.
Найдем момент усилий q ds относительно произвольной точки О в плоскости поперечного сечения. Имеем:
M = (pqds-r=q(j)rds = qwK. (4.2)
В соответствии с геометрическим смыслом произведения rds, как удвоенной площади элементарного сектора, величина интеграла равна удвоенной площади, охватываемой средней линией в поперечном сечении. Она обозначена сок.
Приравнивая момент касательных усилий в поперечном сечении внешнему крутящему моменту, имеем
Откуда
<7шк = Л1к-
"к
(4-3)
И, следовательно, на участке стенки с толщиной t касательное напряжение равно:
t=jWk
(4. 4)
209
Сопоставим касательное напряжение в тонкостенном брусе в виде круглой трубы, разрезанной вдоль образующей, и в той же трубе, но без продольного разреза:
тахт0ТКр = ЗЛ4К _ . ЗЛ4,<
2лг/2
Л4К _ . мк
замки тоткр “к* 3 г
тзамкн 2 t
(4.5)
При r!t = <2.Q имеем Тоткр/Тзамкп — 30, т. е. напряжение при открытом профиле превосходит напряжение при замкнутом профиле той же конфигурации в 30 раз.
Этот пример показывает, что в случае кручения замкнутый профиль несравненно рациональнее открытого. Поэтому в практике ответственные конструкции удлиненной формы, работающие на кручение, всегда (если это возможно) выполняются с замкнутым профилем.
Выведем формулу для относительного угла закручивания бруса с тонкостенным замкнутым профилем при свободном кручении.
Мы уже установили, что средняя линия является траекторией равномерного по толщине стенки касательного напряжения.
Воспользуемся формулой (3.5) для приращения депланации траектории касательного напряжения:
5
w (s) - zv (0) = - -г-J ' ds.
о
При обходе вдоль замкнутого контура средней линии и возвращении в исходную точку будем иметь w(sK) =оу(0). Следовательно, левая часть написанного равенства обращается в нуль.
Обозначая через сок удвоенную площадь, охватываемую средней линией, и вводя знак интегрирования по замкнутому контуру, получим
Отсюда
В рассматриваемом
Поэтому
г Ч' т а:
и“к
случае
q __ Мк
t
, Мк Г ds
(4- 6)
(4. 7)
(4. 8)
(4. 9)
210
Полученное соотношение можно записать в виде стандартной формулы деформации при кручении:
(4.10)
где
“?•
I =----
' " Фт
/к — так называемый момент инерции при кручении.
г, , . Г ds sK
Пели t = const, то (V)—= —,
J t i
где sK— периметр средней липни, и мы имеем
Г!
Л--—- (4. И)
SK-
Сопоставим моменты инерции, при кручении для случаев разрезанной вдоль образующей и цельной круглой трубы:
_ sK/^’ 2кгЛ3 А
‘ ~ р ~ "7 -" “ >
о о
, -кгЪ
/Щза-мкн)-- -- -у , j (/j. 12)
_{к Ыамкн)_ 3 / г \ 2
Ацо1кр) 4 \ t /
При /',7 = 20 имеем
Ас (замки) _ ^qq
Ас(откр)
Этот результат еще резче подчеркивает нерациональность открытых профилей при работе на свободное кручение. Жесткость открытого профиля оказывается в сотни раз меньше жесткости замкнутого профиля той же конфигурации. Объясняется это, конечно, тем, что плечи внутренних пар касательных усилий в замкнутом профиле значительно больше, чем плечи в открытом профиле. Если в первом случае они одного порядка с г, то во втором они одного порядка с t.
Рассмотрим теперь вопрос о построении эпюры дспланации замкнутого профиля.
Выражение для денлапации в точках средней линии открытого профиля согласно (3.7) имеет вид
w (s) — w (0) — — (s).
Оказывается, что к аналогичному виду приводится и выражение для депланации в точках средней липин замкнутого профиля.
14* 211
Выразим касательное напряжение (4.4) через погонный угол
закручивания (4.9). Имеем
___Мк_____-f к I ds zcb—
(4. 13)
мк‘
В этом произведении все множители, за исключением t в знаменателе, постоянные.
Подстановка (4. 13) в формулу (3. 5) для депланации даст
w (s) — w (0) = — <P,'C
или
w (s) — w (0)= — (s). (4.15)
Здесь через w(s) обозначено выражение в квадратных скобках.
Величина ы(з), имеющая, как и о> (s) размерность см2, называется единичной депланацией при свободном кручении замкнутого профиля.
При постоянной толщине стенки выражение <о упрощается:
ш (s) = co(s)-^.s. (4.16)
•Гк
Отметим некоторые частные случаи. Легко установить, что единичная депланация яри кручении круглой трубы около центральной оси тождественно равна нулю, иначе говоря, профиль остается плоским, не деплапируег. Действительно, o) = rx; <i!K-=2nr2, sK = 2n.r; отсюда
® = rs — rs — 0.
Не приводя здесь доказательства, отметим, что профили, не депланирующие при закручивании около определенной оси, остаются плоскими и при закручивании около любой другой продольной оси.
К педеплапирующим профилям принадлежат все профили постоянной толщины с контуром средней линии в виде многоугольника, описанного около круга.
Треугольные профили при переменной толщине стенок не депла-нируют в том смысле, что вершины треугольника всегда лежат в одной плоскости, но на протяжении сторон депланация имеет место. Если же каждая стенка имеет постоянную толщину, то депланация отсутствует.
Вытянутые профили декламируют более сильно, чем близкие к окружности. При всех обстоятельствах депланация замкнутых про-
212
филей значительно меньше, чем депланация открытых .профилей той же конфигурации.
Придадим теперь другой вид формуле для единичной деплана-
ЦИИ 0).
Условимся называть приведенным элементом дуги величину
ds'~ds~. (4.17)
Здесь tc — вводимая для удобства расчетов произвольная толщина, обычно равная средней толщине профиля или близкая к ней.
Умножив н разделив выражение единичной деплапации на tc, получим
(4.18)
,?
Здесь sK = (j)ds'; Очевидно, s* можно назвать приве-
6
денным периметром, a s' — приведенной длиной дуги.
, Полученное выражение для со по структуре аналогично с со в случае стенки постоянной толщины. Разница состоит в замене действительных длин — приведенными.
Определение со сводится к вычитанию из со некоторой величины, пропорциональной приведенной длине дуги. Вычитание может быть выполнено графически (фиг. 93).
Начиная от нулевой точки Н вдоль горизонтальной прямой чертится развертка приведенного периметра. Величины со откладываются в виде вертикальных ординат в соответствующих точках. Вершина последней ординаты со соединяется прямой линией с точкой Н. Ординаты о отсчитываются от этой прямой.
Построение на фиг. 93 относится к коробчатому профилю с двумя осями симметрии. Полюс взят в центре тяжести, начальная точка Н — воображаемый разрез при построении эпюры со — на оси симметрии.
В данном случае принято, что приведенная длина горизонтальных стенок больше, чем приведенная длина вертикальных стенок, т. е. b'^>h'.
При обратном соотношении b'<Ji' знаки отдельных участков эпюры со изменяются на противоположные.
При b'—h' эпюра со имеет нулевые ординаты, т. е. профиль не депланирует.
213
Итак, если толщины стенок симметричной прямоугольной коробки пропорциональны их ширинам, профиль не депланирует. В авиационных конструкциях обычно встречается обратное соотно-
шение широкие стенки коробок тоньше узких. Поэтому с депланацией коробок приходится считаться.
§ 5.5. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ ТОНКОСТЕННЫХ БРУСЬЕВ С ОТКРЫТЫМ ПРОФИЛЕМ
Определение касательных напряжений при изгибе брусьев с массивным профиле м основано на двух гипотезах;
1) векторы касательных напряжений считаются параллельными поперечной силе Q*;
2) касательные напряжения считаются распределенными равномерно по ширине бруса Ь.
Эти гипотезы могут считаться вполне оправданными лишь для профилей, близких к прямоугольнику. Для профилей, состоящих из нескольких прямоугольников разной ширины, получаются значительные противоречия с законом парности касательных напряжении в местах уступов. Сюда относятся и многие тонкостенные профили.
Для тонкостенных п р о ф и л е й опыты и теоретические соображения приводят к двум другим гипотезам, переходящим в приведенные выше для случая прямоугольника:
* В случае круглого сечения векторы т принимаются пересекающимися в конечной точке.
214
Г) векторы касательных напряжений считаются направленными параллельно средней линии стенок профиля1
2) касательные напряжения считаются распределенными равномерно по толщине стенок.
Очевидно, что при прямоугольном профиле, расположенном длинным измерением параллельно поперечной силе Q, допущения
теории массивных профилей и теории тонкостенных профилей совпадают.
Поскольку т = const по толщине стенки, можно пользоваться погонным касательным усилием q—xi аналогично случаю кручения брусьев с замкнутым профилем. Однако здесь, как мы увидим ниже, q не является постоянным вдоль средней линии пи при открытом, пи при замкнутом профиле.
Погонные касательные усилия определяются из условия равновесия проекций на продольную ось бруса, составленного для сил, действующих на отрезок бруса длиной dz и размером по дуге средней линии, определяемым дуговыми координатами Ohs.
Рассмотрим равновесие элемента ds dz (фиг. 94).
Составим уравнение проекций всех сил, действующих на вырезанный элемент, на ось z. В это уравнение войдут нормальные
215
силы, приложенные к криволинейным краям элемента, и касательные силы, приложенные к прямолинейным краям.
Нормальные силы по криволинейным краям равны соответственно
atds и dz\tds.
\ dz )
„ da
Здесь------интенсивность изменения а вдоль оси 2; произведе-
dz
ние dz — приращение величины а на длине dz. dz
Касательные силы по прямолинейным краям будут qds и
ds\dz. Механический смысл частной производной оче-ds / ds
виден: это интенсивность изменения погонного касательного усилия по дуге s.
Уравнение равновесия запишется так:
(a-\--^-dz\tds — at ds + lq —ds\dz—-qdz— 0. (5. 1)
\ dz / \ ds J
Делая приведение подобных и сокращая на ds dz, получим
(5.2) ds dz
Это дифференциальное уравнение равновесия играет большую роль в теории тонкостенных стержней. Знаки частного дифференцирования (д вместо d) мы применяем в связи с тем, что как q, так и о следует рассматривать как функции двух переменных: положения сечения по оси бруса (координата z) и положения исследуемой точки на средней линии профиля (дуговая координата s), т. е.
q = q (s, г); а = а (s, г).
Переходя к конкретному сечению z = const, будем применять для дифференцирования по s знаки полного дифференцирования.
Из дифференциального уравнения равновесия для зафиксированного сечения z имеем
dq=-----d-^tds' (5.3)
Интегрируя обе части по дуге s от точки, обозначаемой дуговой координатой О до точки, обозначаемой дуговой координатой s, получаем интегральное уравнение равновесия:
<7(5)-7(0)=-f4°-^’ (5-4)
J dz о где dF = tds — элемент площади.
То же уравнение мы получили бы, непосредственно составляя уравнение равновесия цилиндрического элемента длиной s по криволинейному- краю и dz вдоль оси бруса.
216
Очевидно, q (s) ~q (0) представляет собой конечное приращение погонного касательного усилия на длине s, или разность, погонных касательных усилий в точках s и О.
При обычном расположении координатных осей имеем
Отсюда
Здесь для интеграла применено обозначение ^(s), учитывая, что интеграл выражает статический момент относительно оси х для части профиля между дуговыми координатами Ohs.
Интегральное уравнение равновесия принимает вид
’ 7(S) = ^-5Js) + <7(0). (5.7)
* X
Целесообразно взять начальную О точку средней линии на крае сечения, тогда, очевидно, <7(О)=0, и мы получаем
Q(s) = -^-5x(s). (5.8>
*х
Отсюда переходим к постоянному по толщине, но переменному по дуге средней линии касательному напряжению:
т(з) = -^- = —(5.9> t(s) Ix t v
Получилась формула, отличающаяся от формулы Д. И. Журав- • ского для массивных профилей только тем, что в знаменателе вместо ширины Ь, измеренной параллельно нейтральной оси х, стоит толщина стенки I, измеренная перпендикулярно к средней линии в исследуемой точке. Следует помнить также, что векторы т параллельны средней линии, а не поперечной силе Qv.
Обычно при ‘исследовании изгиба тонкостенных профилей оперируют не касательным напряжением т, а погонным касательным-усилием q, переходя в случае необходимости к т.
Так как Q.vlIх в каждом заданном сечении есть величина постоянная, то построение эпюры q(s) сводится к построению, эпюры статических моментов Sx(s) вдоль средней линии профиля. Для перехода к q следует ординаты эпюры Sx умножить на О.у/1Х. Эпюра q совпадает с эпюрой Sx, если положить-Qy/7X=1-
217
Для практического построения эпюры q рекомендуется сначала построить эпюру Sx(s), а затем умножить все ординаты на Qy/Zx и поставить стрелочки в соответствии с направлением поперечной силы.
Эпюра Sx(s) строится по точкам, начиная от свободного края, путем вычисления последовательных значений статического момента относительно главной оси х для части профиля, лежащего по одну сторону от исследуемой точки, определяемой координатой s.
На фиг. 95 а, б показаны швеллерный (корытный) профиль и эпюра Sx(s) для него. Выражения для Sx(s) в точках полки и стенки имеют вид
(*,) = «Л 4; Р + = bt^+
4)- (5-10)
Первое уравнение даст треугольную эпюру для полки с максимальной ординатой ЬЦ—. На стенке эпюра представляется в виде суммы прямоугольника с ординатами Ы} ~ и параболического сегмента с максимальной . ординатой при s2 = h/2, равной t2h2/8. На фиг. 95, б к характерным ординатам эпюры Sx приписаны множители Qy/Iy. Поставлены стрелочки, изображающие поток q по обращенному к наблюдателю торцу в предположении, что поперечная сила действует на этот торец снизу вверх.
Другой способ построения эпюры Sx(s) вытекает из анализа формулы
= (5.11)
о 6
Последний интеграл выражает последовательные площади эпюры с ординатами yt, иначе говоря, эпюра 5x(s) может быть по-
218
строена как интегральная эпюра от эпюры yt. На фиг. 96 а, б показаны эпюры у и yt. Легко убедиться, что инте-
Фпг. 96.
тральная эпюра от эпюры yt дает эпюру Sx(s), изображенную на фиг. 95, б. Предлагаем читателю проделать это построение.
Второму способу можно придать следующее простое и наглядное истолкование: эпюра Sx(s) строится как эпюра поперечных сил
Фиг. 97.
для ломаной в плане балки со свободными концами, нагруженной распределенной нагрузкой интенсивностью yt на 1 пог. см. Ось балки в плане совпадает со средней линией исследуемого профиля. В перспективе эта балка изображена на фиг. 96, в.
На фиг. 97 показаны эпюры qx для различных профилей. Здесь усилия q отнесены к отсекаемой части стержня и поэтому показаны уравновешивающими силу Qy.
219
Для быстрого построения этих эпюр целесообразно придерживаться следующих правил. Положив Q/I=\ и, следовательно, q~S, определяем значения q в углах профиля. Затем сосредоточиваем площади всех полосок в их центрах тяжести в виде сил, перпендикулярных к плоскости чертежа. Сумма моментов сил, расположенных по одну сторону от угловой точки, и дает искомые ординаты в углах. Соединяем концы этих ординат прямыми линиями. После этого следует «пристроить» к каждой трапеции соответст-
<0 Уп-г < Уп S) ул_, > ул
Фиг. 98.
вуюший (положительный или отрицательный) параболический сегмент. Для этого находим уклон (полный) концевых касательных каждого такого сегмента к оси полоски. Так как
<7 = 5= j.у/ ds-\-q0,
О искомый уклон будет tg а== ds
Имея концевые касательные, легко построить и кривую. Заметим, что концевые касательные пересекаются против центра тяжести (середины) полоски, причем ордината f параболы (фиг. 98), отсчитанная от хорды перпендикулярно к оси полоски, равна половине ординаты треугольника, образованного касательными и хордой. На фиг. 98 показаны два случая построения эпюры q на протяжении полоски между углами п—1 и п. На фиг. 98, а
tg%_,.n=Tn-iZ/i и tgan л_1-=Л/л, то
tg«„ -,.„<^„-1
220
и кривая получается вогнутой. На фиг. 98, б, наоборот: уп-\У>уп-Соответственно меняется и соотношение тангенсов концевых касательных, поэтому эпюра будет выпуклой.
В дальнейшем нам придется вычислять величину равнодействующих касательных усилий, приложенных к отдельным полоскам. Очевидно, такая равнодействующая равна пощади эпюры q. Поэтому дадим еще формулы для стрелки f и площади й параболического сегмента.
Из фиг. 98 видно, что отрезок
отрезок
отрезок
— о/ Щ 4. Уп+Уп-\ sntnyn-\ Рп(Уп — Уп-\>
ас = 2 f= ad — cd = s„t„-------—•-------------=-----------------
п п 4 2 4
откуда
Площадь сегмента
2 = V s»fn = ту (Уи ~Уп-1) sn о 1Z
Заметим,что величинам f и.й следует приписать знак плюс в случае выпуклой кривой и знак минус в случае вогнутой.
Таким образом, величина результирующей касательных сил при единичном потоке будет
77 '/л-1 + <7л /> , .
и =----------s„ 3—— ( — V ,) S
2 — 12 п—I' '
Для получения действительной силы эта величина умножается на Q//.
Установим теперь величину и положение равнодействующей всех касательных усилий, распределенных вдоль средней линии. Начнем с корытного профиля, рассмотренного выше.
Равнодействующие усилий вдоль полок (см. фиг. 95, б) равны
Tn= — b-btx — ^-=^^.— . (5.12)
2 1 2 1Х 4 1Х
При этом сила Гп для верхней полки направлена влево, для нижней полки — вправо.
221
Равнодействующая усилий вдоль средней линии стенки как сумма площадей прямоугольника и параболы равна
Л-ЛИ.А —+ —(5. 13}
’ 2 1Х ' 3 8 1Х [ Ч 2 ) 1 12 J Ix V ;
Легко установить, что выражение в квадратных скобках есть не что иное, как момент инерции 1Х, подсчитанный при условии, что площадь полок сосредоточена на их средней линии, т. е. без учета собственного момента инерции полок. Действительно, первое слагаемое равно удвоенной площади одной полки, умноженной на квадрат расстояния ее центра тяжести до оси х. Второе слагаемое, очевидно, есть момент инерции стенки.
Таким образом, после сокращения имеем
Равнодействующая силы Тс и пары сил с компонентами Тп численно равна и параллельна силе Qy, по отстоит от нее на расстоянии, равном частному от деления момента пары на силу Тс:
(5.14)
Очевидно, плечо d следует отложить вправо от стенки. Таким образом, равнодействующая касательных усилий при поперечном изгибе бруса корытного профиля, равная Qy, не проходит через центр тяжести профиля, а расположена па расстоянии d от средней линии стенки с закрытой стороны корыта:
§ 5. G. ЦЕНТР ИЗГИБА
Полученный результат очень важен. Он показывает, что поперечная сила Qy только в том случае может быть реализована касательными усилиями изгиба в плоскости у, если она совпадает по липин действия с найденной нами равнодействующей касательных усилий. Если же внешняя поперечная сила Q;/ не лежит па указанной прямой, то к изгибу присоединяется кручение моментом
/Ик = + Qytz, где а — расстояние между внешней поперечной силой и равнодействующей касательных усилий изгиба.
В этом случае поперечная сила реализуется касательными напряжениями изгиба и касательными напряжениями кручения, действующими совместно.
Иллюстрируем эти заключения примером. Брус корытного профиля защемлен одним концом и нагружен на свободном конце силой Р, действующей вдоль главной оси у (фиг. 99). Рассмотрим равновесие отрезка бруса длиной г.
Условия равновесия 2г=0; 2х=0; 2Му=0 удовлетворяются тождественно: в эти уравнения входят только нормальные и каса-222
тельные усилия, распределенные по поперечному сечению, которые этим требованиям, очевидно, удовлетворяют. Условие SAfx = 0 также удовлетворяется: момент Р-г уравновешивается моментом нормальных усилий. То же следует сказать об уравнении £У = 0: равнодействующая касательных усилий в сечении, равная Qv, равна в данном случае—Р, так что P + Qy = 0.
Остается уравнение 2/Иг = 0, которое не удовлетворяется, так как остается неуравновешенная пара P(c-\-d), вращающаяся про-
Фиг. 99. Фиг. 100.
тив часовой стрелки. Поэтому в сечении возникают касательные-напряжения кручения, уравновешивающие крутящий момент
МК=Р(С-Н).
Конечно, брус закручивается по часовой стрелке. Этот теоретический вывод прекрасно подтверждается экспериментом. Собственно говоря, явление закручивания брусьев корытного профиля при изгибе и явилось основным толчком, побудившим детально' исследовать вопрос о касательных напряжениях тонкостенных брусьев.
Явление закручивания тесно связано с асимметрией профиля. Нагружая брус корытного профиля поперечной силой вдоль главной оси (ось симметрии сечения), никакого закручивания не наблюдаем.
На фиг. 100 построена эпюра q при изгибе в горизонтальной главной плоскости х, т. е. когда нейтральной является ось у. Равнодействующая касательных усилий, очевидно, совпадает с осью симметрии х. Поэтому поперечная нагрузка в плоскости оси х уравновешивается без закручивания.
Точка пересечения двух равнодействующих касательных усилий — точка D на фиг. 95 и 99 — носит название центра изгиба профиля. При расчете тонкостенных профилей центр изгиба играет не меньшую роль, чем центр тяжести.
Если поперечная сила проходит через центр изгиба, то она всегда может быть разложена на две составляющие Qy и Qx, каждая
22.5
из которых вызывает изгиб, но не вызывает кручения, следовательно, и их геометрическая сумма дает косой изгиб, но не закручивает брус.
В общем случае профиля, не имеющего осей симметрии, центр изгиба определяется как точка пересечения равнодействующих касательных усилий, соответствующих двум случаям прямого изгиба.
Центр изгиба принимается за начало второй системы координатных осей х' и у', параллельных главным центральным осям х, у. Ось Z, перпендикулярная плоскости сечения, называется осью центров изгиба.
Введение второй системы осей имеет серьезное основание: к первой системе Oxyz следует приводить усилия, связанные с нормальными напряжениями — продольную силу N и изгибающие моменты Мх и Му. Ко второй системе Dx'y'z' — усилия, связанные с касательными напряжениями: поперечные силы Qv и Qx и крутящий момент Мк=М'г.
Практически это означает, что изгибающие моменты, как всегда, подсчитываются относительно главных центральных осей х, у поперечного сечения. Крутящий же момент подсчитывается относительно продольной оси центров изгиба z', параллельной оси бруса z.
Существуют профили, для которых центр тяжести и центр изгиба совпадают. Сюда относятся сечения с двумя осями симметрии (например, двутавр) и антисимметричные-сечения (например, зетовый профиль).
Важной особенностью обладают профили-пучки, состоящие из плоских полок, у которых средние линии всех полок пересекаются в одной точке. Примерами могут служить уголковый, тавровый и крестовый профили. Центр изгиба подобных профилей-пучков совпадает с точкой пересечения средних линий полок—центром пучка. Это свойство является очевидным, так как каждая из частных равнодействующих касательных усилий изгиба в полках обязательно проходит через эту точку, а следовательно, точкой пересечения двух равнодействующих Qv и Qx никакая другая точка быть не может.
Другой способ определения положения центра изгиба
Выше определен центр изгиба как точка пересечения равнодействующих Qy и Qx- Однако координаты центра изгиба относительно осей О'х'у', параллельных главным центральным осям, можно определить по готовым формулам.
На фиг. 101 оси Ох, Оу — главные центральные, а О'х', О'у' — •им параллельные; Оу — равнодействующая касательных усилий изгиба в плоскости Оу, т. е. при нейтральной оси Ox; Qx— равнодействующая касательных усилий изгиба в плоскости Ох, т. е. при нейтральной оси Оу.
Составим условие эквивалентности распределенных касательных усилий qy и qx и их равнодействующих Qv и Qx, приравняв моменты относительно точки О'. Имеем
При взятом па фиг. 101 направлении обхода и положительном
направлении q, получим
6 qx=—~= —^{xdF.
у Jy J
Учтем, что rds=d(<> выражает площадь элементарного с полюсом О' и дугой ds.
Интегралы принимают вид
Jqyds>r*= ^qy(fa = — ~~^dw^y (IF,
5 Л' 5 0 ।
С с о с с I
\qxds-r’=\qrdu>=——^clw^xdF. ।
« s у i о I
(6.2)
сектора
(6.3)
225
Двойные интегралы можно привести к однократным, воспользовавшись формулой интегрирования по частям
и dv — uv~ vdu
и полагая u = ^ydF, du*=ydF или u = J xdF, du —xdF ^ dv= — dw.
Тогда •s
J dw § у dF= w § у dF — J <uy dF, s 0 л 5
J rf® J xdF — <u J xdF — J wx dF. s 0 s s J
(6. 4)
Таким образом, в выражениях моментов усилий qy и qx относительно полюса О' стали фигурировать величины w (ординаты эпюры единичной депланации при свободном кручении). Полученные выражения упрощаются, так как jc/a'/7=0 и Jxc//7=0, как статиче-ские моменты полной площади профиля относительно центральных осей х, у. Принимая это во внимание из первых уравнений моментов после сокращения па Qy и Qx окончательно найдем
| о>у dF J <лх dF
XD=J~.-----; Уо^-~---------• (6-5)
‘X
Числители этих формул обладают важным свойством: они инвариантны относительно начала отсчета секториальной площади со, т. е. начальная точка при построении эпюры <о может быть взята произвольно. В самом деле, изменение начальной точки эквивалентно добавлению к ординатам некоторой константы соо. Но, очевидно,
(О) а>0) у dF=^wydF + ®0
5 5 5
\ydF. (6.6)
Второй интеграл равен нулю, что и доказывает требуемое.
Возможность выбрать произвольно полюс О', а также начальную точку И при построении эпюры со в отдельных случаях чрезвычайно облегчает вычисление координат центра изгиба.
Остановимся на вопросе вычисления интегралов, входящих в формулы для координат центра изгиба.
Прежде всего представим эти интегралы в соответствии с их математическим смыслом не как интегралы по площади, а как интегралы по дуге, положив
dF=t(s} ds.
226-
Вместо области интегрирования F мы и раньше писали 5. Перепишем интегралы числителей в таком виде:
J wy dF= J w (s)y (s) t (s) ds =y w (s) t (s) ds-y (s), 5 5 5
У wxdF=^ w (s) x (s) t (s) ds = y io (s) t (s) ds-x (s). 5 5 5
(6.7)
Построим эпюру co = co(s) и умножим ее ординаты в каждом сечении на соответствующую толщину стенки / = /(s). Получим эпюру co(s) Z(s). Очевидно, первый из интегралов выражает статический момент площади эпюры co(s)/(s) относительно о с и х; второй интеграл выражает статический момент площади той же эпюры относительно оси у.
Статические моменты эпюр вычисляются без затруднений; эту операцию мы постоянно применяем при определении прогибов балок графоаналитическим методом. Следует только помнить, что ординаты эпюр в действительности должны считаться отложенными перпендикулярно плоскости чертежа и лишь для удобства совмещаются с плоскостью чертежа. Это обстоятельство важно учесть, когда статический момент вычисляется как произведение площади на плечо ее центра тяжести относительно оси.
Таким же образом можно (и следует) трактовать моменты инерции тонкостенных профилей 1Х и 1У:
Ix— ^y'1dF=<^yi (s)t (s) ds = у у (s) t (s) ds-y (s), F s s
7,= j* a2dF = y x2(s) t (s) ds = у x (s) t (s) ds-x(s]. F 5 5
Первый интеграл вычисляется как статический момент эпюры y(s]t(s] относительно оси х; второй — как статический момент эпюры x(s)t(s) относительно оси у.
Итак, абсцисса центра изгибав системе осей х', у', параллельных главным, осям х, у, вычисляется как отношение двух статических моментов: площади эпюры (at и площади эпюры yt относительно оси х. Ордината вычисляется как взятое с обратным знаком отношение статических моментов площадей эпюры at и xt относительно оси у.
В качестве иллюстрации определим абсциссу центра изгиба швеллера. Полюс О' выбираем на пересечении оси стенки с осью симметрии (фиг. 102). Эпюра со при этом получается простейшей в виде двух треугольников в пределах полок. В данном случае /=const, и поэтому эпюра и в другом масштабе дает и эпюру со/, так что отдельной эпюры со/ строить не нужно.
Интересующий нас интеграл числителя
С Jc ъ/ 1 «. bhtx \ Л 62Л2/]
I toy dF— 2(— b---Ч — =--------.
J \ 2 2/2 4
5
227
Подсчитываем аналогичным способом 1Х. На фиг. 102 показаны также эпюры у и yt.
I —2(b— —4- — — h 2 W|A2 I /,ЛЗ х \ 2’2'2 2 2 3 2 2 12 '
Итак,
__
D~ 41 *~й ~ i f2bt1/^ + — F/F C! 3 -
Результат совпадает с полученным выше.
Фиг. 102.
Пример. Па фиг. 103 показан корытный профиль с осью симметрии, содержащий наклонные элементы. Выбирая полюс О', как показано на фигуре, построим эпюру <о, которая, как и в предыдущем случае, может служить в дру
гом масштабе эпюрой <а/. Вычисляем интеграл J ту dF как статический момент площади эпюры mt относительно оси симметрии профиля х:
= 2-0,2(37|52+ 1 ~-5-5,54-"~-4,5^ =306,5 см5.
Далее вычисляем момент инерции сечения 1Х:
/х = 2-0,2 [б-5,5-5,5 ф-5-2,5-4-р-4,5 + 2’5~2 ’ • 2,51 === 96,1 сл<.
L 2 2 о J
Следовательно, 1 f 306,5 „
Хо = _^г = __= 3,19 см.
228
§ 5.7. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ ТОНКОСТЕННЫХ БРУСЬЕВ С ЗАМКНУТЫМ ПРОФИЛЕМ. ЦЕНТР ИЗГИБА
Определение нормальных напряжений изгиба в брусе с замкнутым тонкостенным профилем каких-либо особенностей не представляет. Нормальные напряжения будут такими же, как и при открытом профиле, полученном из замкнутого путем разреза в какой-либо точке средней линии. Брус с открытым профилем, полученный из замкнутого разрезом вдоль образующей, будем называть основным брусом (фиг. 104, а). Для основного бруса всегда можно определить не только нормальные, но и касательные напря-
Фиг. 104.
жепия (усилия), а также центр изгиба по правилам, указанным в § 5.6.
Действительный брус отличается от основного тем, что в нем вдоль разреза, следовательно, также в поперечном сечении, имеется дополнительное постоянное усилие qo. Это усилие легко определяется из условий равновесия (или эквивалентности) внешних сил и усилий в сечении.
На фиг. 104, б точка D — центр изгиба основного бруса, Qy— заданная поперечная сила. Перенесем ее параллельно так, чтобы опа проходила через точку D, добавив момент
MK = Qy(xQ~xDY (7.1)
Тогда сила Qy будет уравновешена касательными усилиями основного бруса
^±y-Sx(s), (7-2)
‘X
а момент вызовет постоянное вдоль средней линии усилие ?о, равное усилию в разрезе
%== (73)
<ок
Суммируя оба усилия — переменное qy и постоянное q0, получим окончательную эпюру q^ для замкнутого профиля.
229
Имея эпюру qy, можем определить относительный угол закру-
чивания <рй по формуле (4.7):
Подставляем сюда
Имеем
1
1
GwK
У У , .
у ds + %
(7. 4)
Видно, что изгиб сопровождается закручиванием. Существуют, однако, такие положения сил Qy и Qx, при которых <p'K=0.
Если определить положения каждой из сил Qv и Qx из условий ф/к = 0, то пересечение этих двух сил даст центр изгиба замкнутого профи л я. Эту точку будем обозначать буквой /<.
Чтобы найти положение Qv, соответствующее изгибу без кручения (поступательному перемещению сечения), полагаем в написанном выше равенстве <р'к=0. Найденное при этом условии значение л
<7о обозначим q<j
л Ф / cls
?0 = -2г4“ СЭ
ф—rfs
или
Jo==_±6l£sL. (7.6)
Д
Равенства (7. 5) и (7. 6) дают два равноценных варианта вы-л
числения величины qo. В первом числителе подсчитывается площадь приведеннойэпюры qvlt вдоль периметра, во втором— площадь эпюры qy — вдоль приведенного периметра.
Определив положение равнодействующей усилий qv и <70 = const, найдем прямую, параллельную оси у, на которой лежит центр изгиба К.
Другая прямая, параллельная оси х, определяется аналогичным путем при помощи касательных усилий от Q,>
Дадим теперь аналитическое выражение координат центра изгиба К. Поступим точно таким же образом, как при выводе формул для х'о и у'о в случае открытого профиля (см. § 5. 6).
Проведем оси х' и у', параллельные главным осям х и у, и составим условие эквивалентности касательных усилий изгиба замк-л л
нутого профиля qy и qx и их равнодействующих Qy и Qx, приравняв моменты относительно точки О'.
230
Имеем
§ qyda = Qyx'K-, $ Чх^=-^хУ'к- (7.7)
Здесь, как и выше, cZ<o = rcZs.
Ограничимся подробной выкладкой для первого равенства. Подставляем
находим
Л 1 X j ,
9у=9у------(A)^yds •
SK J
(7.8)
л
Выражение в скобках обозначим с?со. Очевидно, это не что иное, как дифференциал единичной депланации бруса с замкнутым профилем при свободном кручении — см. (4.18).
Л °’к t
и; = <в--s .
Таким образом, получаем интересное равенство сЛ»=$ qyd»>.
Поступая как и в случае открытого профиля, получаем Г Л' О. Р Л (Г) qy -----------------------(Г) <оу dF.
Это приводит сразу к абсциссе центра изгиба:
Ф ыу dF хк = - - .
(7-10)
(7. 11)
Аналогично получается ордината:
Ф шх dF
УК— .--------
* у
Видно, что положение центра изгиба замкнутого профиля определяется теми же формулами, что и открытого, с той разницей, что вместо эпюры единичной депланации со следует пользоваться эпю-л рой со.
Центр изгиба К профиля с двумя осями симметрии совпадает с центром тяжести.
Центр изгиба профиля с одной осью симметрии лежит вблизи центра тяжести, но с ним не совпадает. При изгибе силой Q вдоль оси симметрии касательное усилие на оси симметрии заведомо рав
231
но нулю, так что окончательная эпюра q строится сразу для левой и правой половин, как и для открытых профилей (фиг, 105).
Подчеркнем, что для определения касательных усилий в замкнутом профиле нет необходимости разыскивать его центр изгиба К. Достаточно иметь положение равнодействующей касательных усилий в сечении основного бруса. Центр изгиба приобретает существенное значение при исследовании перемещений. Заменяя нагрузку силами, проходящими через ось центров изгиба, и крутя-
Фиг. 105.
щими парами, можно отделить кручение бруса от его изгиба. Этот вопрос играет большую роль при исследовании вибрации таких конструкций, как крыло, фюзеляж, оперение самолета.
Пример. На фиг. 106 показан замкнутый квадратный профиль с вертикальными стенками неравной толщины и с одинаковыми горизонтальными стенками. Ось х совпадает с осью симметрии.
Приняв в угловой точке А разрез, строим эпюру Sx, или, что то же, эпюру q при <2V/Zx=l. Находим площадг отдельных участков эпюры Sx, что дает касательные силы вдоль стенок. Сумма вертикальных сил равна поперечной силе Qy Находим
/х = 433,3+ 133,3=566,7 см\
Целесообразно определить положение центра изгиба D основного бруса Л
(разрезанного). Это даст возможность найти <7о от любым образом расположенной силы Q:
133,3-20 —200-20
XD —--------------------= — 2,35 см.
Для лой (7. 5):
566,7 л
нахождения центра изгиба К определяем qА, пользуясь форму-
133,3
433,3 „ 200
---- + 2---
Л _ °-05 °>1 °-2
дА~~ 20 „20 20
-----+ 2 - — + —' 0,05-0,1 0,2
^ = -17,1.
700
232
Расстояние между точками К, и D хк—xd=18,8 ель
Это дает положение точки К, .показанной на фиг. 106.
Разумеется, определив qл, можно найти положение К, не разыскивая предварительно положение D. Для этого достаточно найти равнодействующую Л
усилий q в основной системе и qА-
§ 5.8. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ ТЕОРИИ ДЕПЛАНАЦИИ
До сих пор при построении эпюры единичной депланации ш-л
или и мы предполагали, что полюс задан, известна также начальная точка Н (конец неподвижного радиуса вектора). Однако действительное положение оси закручивания нами не определялось. Оказывается, что для определения его при свободном кручении необходимы дополнительные данные, относящиеся к закреплению одного из сечений. Так, например, если потребовать, чтобы три. точки торца, закрепленного в своей плоскости для передачи крутящего момента, были неподвижны, т. е. депланации торца в этих точках равны пулю, то ось закручивания может быть определена, однозначно.
Для решения подобных и других, более важных, задач необходимо вывести формулы, позволяющие найти изменение единичной деплапации при изменении координат полюса и начальной точки Н.
233
Задача ставится так. Подсчитана единичная депланация в точке А (фиг. 107) при полюсе Р и в начальной точке Н, в которой деплапация равна
А ma = u>h-v [ rds. н
(8.1)
Требуется определить величину единичной депланации при переносе полюса в Р' и изменении депланации в начальной точке с
Фиг. 107.
Имеем .
"л = “я + J r'cis' (8'2) И'
Из чертежа видно, что
г' = r — a sin а — b cos а;
dv dx
sina=----; cos а—-----
ds ds
Поэтому
H A
== <o'' f Г ds + f rds — {cLy]y*
H ] 1 I 1 ^‘y=yHt 1 1 x~x,,
. »' *} 11 Ji
H' H
или
“л = “и + “л - а (Уа-Ун-) + Ь(хА-хн.). (8.3)
Собирая все постоянные с индексами Н и Н' в одно слагаемое k, окончательно получим
^АяшША~аУА + ^А + /г-
(8.4)
Таким образом, при изменении, положения полюса к ординатам эпюры ® добавляется линейная функция координат исследуемой точки средней линии профиля.
Иначе говоря, депланация изменяется так, как если бы к аппликатам депланировавшей средней линии добавили бы аппликаты некоторой плоскости.
Угловые коэффициенты этой плоскости равны умноженным на разностям координат а и Ь нового и старого полюсов. Постоянная k характеризует аппликату плоскости в начале координат.
234
Покажем, как использовать полученный результат для нахождения полюса и начальной точки Н из условия равенства нулю со. в трех точках А, В, С.
Выбираем произвольный полюс и произвольную начальную точку Н и по общим правилам находим величины <ол, . Берем
произвольные ортогональные оси и находим хА, уА, хд, v)S хс, ус.
Далее составляем три уравнения:
0 = <ол-аЛ4 + йхл + ^-
0=о)в — ауд 4- Ьхв 4- k,
0=о)с — аус4-йхс4-Л.
Вычитаем из первого уравнения второе и затем из первого — третье. Получаем два уравнения, из которых определяем а и Ь, что сразу дает положение нового полюса. Постоянную k определясь не нужно, так как при построении эпюры (o' достаточно за начальную точку взять одну из точек А, В или С.
Подобные задачи легко также решаются графически по правилам начертательной геометрии: ординаты эпюры <ч при произвольном полюсе поворачиваются перпендикулярно плоскости чертежа, а затем пространственная эпюра срезаете,.- плоскостью так, чтобы ординаты в точках А, В, С были равны пулю.
Практически большую пользу оказывает также следующее простое правило: уклон эпюры и к средней линии сменки равен длине перпендикуляра, опущенного из полюса на касательную к средней линии.
Действительно, так как
d<£>~rds, то г= ——.
,1s
Этим правилом удобно пользоваться для проверки готовых эпюр.
Рассмотрим теперь одну задачу, которая непосредственно подводит к проблеме стесненного кручения. Рассмотрим брус, Закрепленный по отношению к углу закручивания на одном коние и свободный на другом. К свободному концу приложен сосредоточенный крутящий момент, следовательно, брус работает на свободное кручение, причем все его сечения депланируют по известному нам закону (3. 7)
®(s)= — <f>(s) . (8.5)
Однако положение полюса и начальной точки неизвестно и, вообще говоря, может быть произвольным. Определяется оно при наличии дополнительных данных.
Допустим теперь, что закрепленный на кручение конец заделан •в стену так, что депланации торца'стеснены. Естественно предположить, что па торце разовьются нормальные напряжения.
235
Можно утверждать, что элементарные нормальные усилия adF в совокупности эквивалентны нулю, так как при кручении имеем
N = 0, Л1ж=0, Му = 0.
Что касается закона распределения нормальных напряжений на торце, то весьма естественно считать их п р о п о р ц и о п а л ь н ьь м и д е п л а н а ц и я м т о р ц а в о т д е л ьн ы х точках, или что то же — единичным депланациям со.
Построим эпюру со при произвольном полюсе Р и произвольной начальной точке Н. Перейдем к другому полюсу Р' и другой начальной точке И', т. е. положим
— ay-\-bx-\-k. (8.6)
По вышесказанному нормальное напряжение
о = Ли' = Л(о) — ay-^-bx-Pk), (8-7)
где А — коэффициент пропорциональности.
Поставим требование равенства нулю главного вектора и главного момента:
N=^dF=p-, Мх —<зу dFMy = ^xdF=Q.
Начнем именно с составляющих Мх и Му главного момента. Подставляя в них значение о, после приведения и сокращения па А легко находим
coy dF — a ^y^dF-}- b ху dF-[- 1г у dF-О, F F F F
j" uxdF—a j xy dF-\-b x2 dF-\-k x dF= 0.
F F F F
Интегралы, за исключением стоящих вначале, представляют собой величины хорошо известные из теории моментов инерции площадей. Что касается интегралов, стоящих первыми, то они уже встречались при определении координат центра изгиба.
Сразу видно, что если взять в качестве исходных осей х, у глав ные центральные оси, то ряд интегралов обращается в пуль и мы получаем
j' шу dF — al х — 0; F
F
откуда
j* ш_у dF , j1 ax dF
a = A-----t &==_Z_-------. (8.8
lx ly
236
Сопоставляя 'полученный результат с формулами (6.5) для х'о и yD, видим, что новый полюс есть не что иное, как центр изгиба профиля D.
Построим при этом полюсе новую эпюру со, взяв произвольную начальную точку 1~Г. Подберем Н' так, чтобы удовлетворить также условию равенства нулю главного вектора. Изменение начальной точки эквивалентно добавлению ко всем ординатам эпюры некоторой константы. Обозначим ее ®о.
Фиг. 103.
Имеем
j(a/ + <o0)c//n=0. (8.9)
F
Отсюда
J ш' dF
Прибавив к ординатам со найденную постоянную ©о, автоматически получим и новую нулевую точку.
Если заранее удается подобрать точку И так, чтобы было J(oEF=-0, то определение со0 отпадает. На практике при симметричных профилях так и бывает.
На фиг. 108 показаны эпюры со для двутавра и швеллера при полюсе в центре изгиба D и при нулевой точке Н, удовлетворяющие поставленным требованиям. Легко видеть, что нормальные напряжения, пропорциональные величинам ординат со, образуют самоуравповешенную систему сил.
237
Так, в случае двутавра усилия adF приводятся к двум моментам, вращающим в противоположные стороны в плоскостях полок.
В случае швеллера также имеем два уравновешенных момента в вертикальных плоскостях. Самоуравновешенная эпюра обязательно имеет не менее чем две пары участков разного знака.
Выяснив на основе сделанных допущений характер нормальных напряжений в плоскости торца, мы, однако, пока ничего не можем сказать относительно величины этих напряжений. Из условия равновесия их определить невозможно. Здесь приходится привлечь условия деформации. К этому мы и переходим.
§ 5.9. ТЕОРИЯ СТЕСНЕННОГО КРУЧЕНИЯ ТОНКОСТЕННЫХ БРУСЬЕВ С ОТКРЫТЫМ ПРОФИЛЕМ
Предположим, что брус работает на свободное кручение. Де-планации одноименных точек средней линии различных поперечных сечений будут одинаковы и подчинены общей зависимости (3.7):
w(s)= —
При свободном кручении крутящий момент на протяжении длины бруса не изменяется, поэтому и относительный угол закручивания ф'к остается постоянным. В результате смежные сечения друг другу не препятствуют в их депланации. В качестве иллюстрации можно привести горку из одинаковых тарелок, вложенных одна в другую.
Допустим далее, что относительный угол закручивания становится переменным, например, в результате нагружения бруса внешними сосредоточенными или распределенными по длине крутящими моментами. Так, если крутящий момент изменяется по длине одним скачком, то будем иметь как бы два бруса, работающих с постоянными моментами. Если рассмотреть эти брусья отдельно в качестве работающих на свободное кручение, а затем сложить их торцами, то окажется, что плотного совпадения торцов уже не будет, так как депланации их будут различными. Но в действительности брус остается непрерывным, поэтому между соединяемыми торцами неизбежно возникновение нормальных напряжений.
Наиболее яркий пример стеснения—полная заделка одного из торцов бруса, препятствующая как повороту вокруг продольной осн, так и искажению плоскости—деплапации торца. Можно представить себе и различные другие виды стеснения, например, неполную— упругую заделку торца против депланации и т. п.
Характерным для всех этих стеснений является появление продольных, параллельных оси бруса нормальных напряжений в поперечных сечениях. Эти напряжения больше в сечениях с наибольшим стеснением, например, у заделки, или в местах приложения внешних сосредоточенных крутящих моментов, где имеется тенденция к резкому изменению относительного угла закручивания. Нор
288
мальные напряжения уменьшаются, рассасываются по мере удаления от места резкого стеснения. Так как нормальные напряжения изменяются по длине бруса, то им сопутствуют касательные напряжения в продольных сечениях, а в силу закона парности также и в поперечных сечениях бруса. Здесь имеет место соотношение, аналогичное известному из теории поперечного изгиба балки: касательные напряжения пропорциональны производной от изгибающего момента, т. е. от того фактора, которому пропорциональны нормальные напряжения. Вспомним известную формулу (5.8):
Таким образом, при стесненном кручении в поперечных сечениях появляется новая, дополнительная система касательных напряжений, сопутствующих нормальным и отличным от напряжений свободного кручения. Эти новые напряжения воспринимают часть крутящего момента в сечении. В случае очень тонких стенок, когда жесткость свободного кручения GIK весьма мала, новые напряжения воспринимают большую часть крутящего момента в сечении, иногда практически даже весь крутящий момент. Отсюда следует, что создавая стеснение, например, заделывая один торец против депланации, можно повысить сопротивление бруса скручиванию.
Новые касательные напряжения будем называть касательными напряжениями стесненного кручения. В отличие от напряжений свободного кручения эти напряжения распределены равномерно по толщине стенки подобно касательным напряжениям изгиба тонкостенного бруса.
Также как и касательные напряжения изгиба, касательные напряжения стесненного кручения играют большую роль в силовом балансе в сечении бруса, однако роль их в перемещениях бруса с открытым профилем невелика. Напомним, что при исследовании деформации балок обычно пренебрегают влиянием касательных напряжений.
Основная кинематическая гипотеза, лежащая в основе технической теории стесненного кручения тонкостенного стержня с открытым профилем, состоит в том, что связь между депланацией точек средней линии каждого поперечного сечения и относительным углом закручивания та же, что и при свободном кручении*. Так как относительный угол закручивания в этом случае изменяется подлине бруса, то запись данной гипотезы будет такой:
w(z, s) — — <»(s). (9.1)
Эта гипотеза основана на допущении, что влиянием касательных напряжений стесненного кручения на депланацию можно пренебречь.
* Заметим, что эта гипотеза эквивалентна гипотезе о иедеформируемости поперечного сечения в своей плоскости.
239
Вторая гипотеза статического характера состоит в том, что в продольных сечениях бруса нормальных напряжений не возникает. Такое же допущение принимается в технической теории изгиба балок. Она дает возможность выразить связь между нормальным напряжением в поперечном сечении и продольной деформацией, следуя закону Гука при одноосном напряженном состоянии.
Приведенных двух гипотез достаточно для построения теории, охватывающей определение напряжений и деформаций тонкостенного бруса с открытым профилем, работающего в условиях стесненного кручения.
Перейдем к выводу дифференциального уравнения, связывающего усилия и перемещения и заменяющего известное соотношение (2.2)
__ G/к ’ которое также можно рассматривать как дифференциальное уравнение свободного кручения или как приближенное уравнение для общего случая, когда эффектом стеснения мы пренебрегаем.
Дифференцируем уравнение (9. 1) по z. Тогда слева будет стоять относительное удлинение, так как
Будем писать е без индекса. Имеем, следовательно, e(z, s)= — <р" (z)w(s).
Умножаем это уравнение на Е. Согласно второй гипотезе Де2 = ст2. Записывая результат без индекса, но с показанием функциональной зависимости, имеем
° (z, s) <= (г) ю (s). (9. 2)
Так как по предположению нагрузками бруса являются только крутящие моменты, то совокупность нормальных усилий odF в любом сечении должна быть с а м о у р а в и о в е ш е н и о й. Математически это выражается равенством пулю двух изгибающих моментов и нормальной силы, выраженных через нормальные напряжения:
aydF— 0; J ах dF = 0; J a dF— 0. F F г
Подставляя значение ст, получаем три зависимости для величины (o(s), дающие возможность определить полюс и начальную точку для построения эпюры со. Эта задача со всеми подробностями решена в § 5. 8, где найдено, что полюс совпадает с ц е н т р о м изгиба профиля.
Итак, при стесненном кручении ось кручения имеет вполне определенное положение: ее след на плоскости сечения совпадает с центром изгиба.
2-10
Что касается нулевой точки Н, то, как показано в § 5.8, положение ее также определяется без всяких затруднений на основании условия (8.9).
Показанные на фиг. 108 эцюры депланации и есть те эпюры, ординатам которых пропорциональны нормальные напряжения при стесненном кручении.
Следовательно, если будет из1вестна величина q>u"(z), то тем самым определятся и напряжения в сечении z.
Продолжим вывод дифференциального уравнения для <pK(z).
От нормальных напряжений переходим к касательным усилиям q в продольных и поперечных сечениях. Из условия равновесия элемента (5.2) следует, что
q (z, s) = —- ( — dF, (9.3)
J о
где
dF—t(s) ds.
При этом предполагается, что начало отсчета дуги взято на свободном крае профиля — </(0)=0.
Подставляем сюда значение
-^-=-^(г)Ш(5). (9.4)
Получаем
7 (г, s) = £t"(z) JwrfF. (9.5)
О
Интеграл
о о
л
по аналогии с ydF называется секториальным статическим и
моментом части площади профиля или статическим б и момент о м. Размерность этого интеграла, см4.
Формула для q принимает вид
<7 (г, s) = (г) S„> (s). (9.7)
Для построения эпюры S .,(s), дающей закон распределения погонного касательного усилия стесненного кручения вдоль средней линии, поступаем следующим образом. Очевидно эпюра S<a (5) есть интегральная эпюра от эпюры u)(s)t(s). Поэтому сначала строим эпюру co(5)/(s), умножив все ординаты эпюры ы на соответствующие толщины стенки t. Затем, двигаясь вдоль s, подсчитываем 1! л о щ а д и позади лежащих частей эпюры м/. Последовательные величины площадей и дают ординаты эпюры S<„(s).
J ш (s) t (s) ds = Sa (s) (9.6)
241
Эпюры S.o (s) для двутавра и швеллера показаны на фиг. 109.
Выразим теперь крутящий момент, создаваемый касательными усилиями стесненного кручения. Этот момент обозначим ЛД.
Имеем
(г) J d&
s s 0
Двойной интеграл возьмем по частям
J rfo) J wdF=<s> у &dF—у v^dF.
s 0 $
Ч(^)=У^=^
\<x>dF. (9.8)
Первый из интегралов равен нулю в силу специального выбора начальной точки при построении эпюры со, удовлетворяющего именно требованию j (odF=0. Второй интеграл обозначим и будем называть векториальным моментом инерции профиля или б и м о-
Фиг. 109.
ментом инерции профиля. Размерность его см6.
о>2dF = у «>2 (s) t (s') ds. s s
(9- 9)
Способ вычисления его точно такой же, как для момента инерции 1Х, если приписать ординатам эпюры со значение у.
/т=у <u (s) t (s) dsu> (s).
Строим эпюру (o(s)Z(s), подсчитываем площади отдельных прямолинейных участков этой эпюры, а затем умножаем их на ординаты той же эпюры co(s), измеренные против центров тяжести площадей участков, и произведения суммируем.
Для двутавра получаем
г __ hWtb
t Ц) -- •
24
Для швеллера
г h-ii- Г,., , с, ,, . Ч(Ь —rf)3 j 1 z“>=—Ц
Окончательное выражение для ~MK(z) принимает вид
7Ик(г)= — Д/Ш<рк (г).
(9. 10)
242
Крутящий момент, воспринимаемый напряжениями свободного кручения, обозначим Л4к(г). Через <pK(z) он выражается следующим образом (2.2):
Я(г) = О/кТ' (г). (9.11)
Сумма моментов (9. 10) и (9. И) должна быть равна крутящему моменту внешних сил в сечении М:
- Е/^’к (г) + С/к?' (г) = Мк (z). (9.12)
Это и есть дифференциальное уравнение стесненного кручения.
Определив путем интегрирования уравнения с учетом граничных условий значения угла закручивания <рк и его производных в интересующих нас сечениях, можем затем по формуле (9. 11) найти Ми, а следовательно, касательные напряжения свободного кручения; по формулам (9.2) и (9.7) и эпюрам w(s) и S» (s) — нормальные и касательные напряжения стесненного кручения.
Если профиль недепланирующий (угольник, крест, тавр), то вопрос о стесненном кручении не возникает, так как Е1<о = 0 и уравнение (9. 12) переходит в уравнение свободного кручения. В отдельных случаях ЕЛ. — малая величина, и первый член также можно отбросить. При очень тонких стенках G/It->0, и отпадает наоборот второе слагаемое. Внешний момент уравновешивается только касательными усилиями стесненного кручения. Уравнение (9. 12) охватывает таким образом разнообразные случаи соотношения жесткостей стесненного и свободного кручения.
Прежде чем перейти к интегрированию уравнения, введем одно новое понятие.
Выпишем вновь формулы (9.2) и (9. 10):
a (z, s) = — Е<р"к(г)а) (s),
Мк (г) = — Е1а (г).
Умножим левую и правую части (9.2) на /ш/со(5). Так как при этом справа будет стоять функция только от z, то и выражение слева не будет зависеть от s и будет функцией от z. Обозначим его В (г).
Итак,
B(z) = --'S~a. (9.13)
“ (s)
Равенство (9. 13) запишется теперь так:
(9.14)
Выясним теперь свойство введенной нами функции В (г).
16* 243
Эту функцию можно рассматривать, как усилие в сечении, которому пропорциональны нормальные напряжения а. В самом деле, из (9. 13) находим
,(г.5)_Ж^. (9.15)
*0)
Формула (9. 15) имеет такую же структуру, как и известная •формула для нормальных напряжений при изгибе. При обычно .принимаемом нами расположении координатных осей (ось у — вверх), имеем
а (г,
Для полной аналогии (вплоть до знака) достаточно строить эпюру со не для позади лежащего сечения, а для впереди лежащего. Тогда в формуле (9. 15) также будет стоять знак минус *.
Функция В (г) называется изгиб но крутящим бимоментом или просто б и мо ментом. Размерность ее кгсм2.
Для выяснения распределения напряжений о по длине бруса строится эпюра бимомснта.
Сопоставляя формулы (9. 10) и (9. 14), видим, что
В'(г)-Я (г). (28)
Между бимоментом и крутящим моментом стесненного кручения имеется такая же зависимость, как между изгибающим моментом и поперечной силой, выражаемая теоремой Журавского:
М' (z)=Q(z).
Эпюра бимоментов может быть получена как интегральная кривая от эпюры моментов стесненного кручения.
в (г) = в (0) 4-J Мк (г) о
Это значит, что любая ордината эпюры В равна ординате в каком-либо сечении, принятом за начальное, плюс площадь эпюры Мк на участке от начального до исследуемого сечения.
§ 5.10. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ СТЕСНЕННОГО КРУЧЕНИЯ
Переходим к интегрированию дифференциального уравнения (9. 12).
Это обыкновенное линейное дифференциальное уравнение третьего (или второго относительно <рк) порядка с постоянными коэффициентами.
* Такое правило и принято в «Справочнике машиностроителя», т. Ill, В главе «Расчет тонкостенных стержней».
244
В общем интеграле удобнее иметь не три, а четыре произвольных постоянных, поэтому дифференцируем (9. 12) один раз по г, обращая его в уравнение четвертого порядка. После простых преобразований уравнение принимает вид
U0-1')
Здесь /ик= — ——есть погонная интенсивность внешней крутящее dz
моментной нагрузки, считаемая положительной, если она при движении вдоль оси z уменьшает положительный крутящий момент:
О
Правило знаков принято по аналогии с изгибом
Q (z) = Q (0)-^pdz. о
В уравнении (10. 1) введено обозначение
(10.2)
^4
Корень квадратный из этой величины носит название характеристики стесненного кручения или и з г и б н о-крутильной характеристики:
к-А <£-. (10.3)
Выпишем выражения усилий через производные угла <рк.
Крутящий момент свободного кручения (9. 11)
^k=G/k?'k-
Бимомент (9. 14)
В=-Е1^’к.
Крутящий момент стесненного кручения (9. 10)
ЛГК= -Efa<?’K.
Отметим другую форму дифференциального уравнения задачи. Подставляя (9. 14) в (10. 1), получим
B"-k2B=-mK. (10.4)
245
При пользовании этим уравнением усилия и перемещения выражаются следующим образом:
м=м-в>,
<Рк(^) = ?к(0)--~(/Йк^- (10.5)
о
Интегрирование уравнения (10. 1) начинаем с того, что выписываем общий интеграл уравнения без правой части:
^к(г) = С] 8h te4-C2ch/s2:4-C3z-|-C4. (10.6)
Дифференцируя последовательно три раза и принимая во внимание (9.10), (9.11) и (9.14), получим
Мк (г) = GIK (kCt ch kz 4- kC2 sh kz-f- C3); В (z) = — EIJPlCi sh kz-\- C2 ch kz)\ MK (z) = — EIJ? (Cjch kz C2 sh kz).
Преобразуем полученные выражения по методу ных параметров.
Полагаем z—О. Имеем ?к(0)=с24-с4, j
мк(0) = о/к(^с,4-с3), Д(0)= -Е1„ФСг, I
Жк(0)= - ДЛ,A3 Cr I
Величины фк(0), Л4к(0), В(0), Л4к(0) носят название ных параметров.
Рассматривая Ci, Сч, С3, С4 в качестве неизвестных, их через начальные параметры:
С ^к(О) 1 £ДЛ3 ’
С в (0)
2 EIJ& ’
с _= л7к (0) . мк (0)
3 G/K EIwk^ ’
(Ю.7)
н а ч а л ь-
(10.8)
н а ч а л ь-выражаем
246
Подставляя эти значения в (10.8) и делая приведение подобных членов, получаем четыре строки общего интеграла с начальными параметрами в качестве четырех произвольных постоянных:
, . . Л4к(0) В(0) , . , ,,
(г) = <Рк ОН—Z-- —A-MchAz-l)-
---мк (0) (sh
yWK (2) = yWK (0) — В (0) A sh г-|-шГк (0) (1 — ch Аг);
В (г) = В (0) ch Агф-Ж (0) — sh kz; k
Мк (г) = AfK (0) ch kz 4~ В (0) Ash kz.
(Ю.П)
J
__ В отдельных случаях вместо одного из уравнений MK(z) или Л4к(г) удобно пользоваться уравнением полных крутящих моментов. Очевидно
Ж (г) = Л4к (г)4-Мк (г).
Таким образом получена удобная форма уравнений <рк, Мк, В, Мк на н е з а г р у ж е н п о м участке бруса. Однако для определения этих величин необходимо иметь начальные параметры <рк(0), Л4к(0), В(0), Л4к(0) в каком-либо сечении, принятом за начальное.
Начальные параметры определяются из условий на концах бруса. Как это выполняется, рассмотрим ниже, а сейчас разрешим вопрос, какой вид принимают уравнения эпюр, если между началом 0 и исследуемым сечением z приложен внешний сосредоточенный крутящий момент Абсциссу сечения, в котором приложен момент, обозначим zL.
Итак:
0<гЛ<г.
Условимся считать момент положительным, если он вызывает отрицательное приращение крутящего момента Мк. Если смотреть по направлению оси z (слева направо), то Е1( вращается по часовой стрелке. При взгляде против оси z увидим наоборот вращение против часовой стрелки (фиг. ИО,а).
Подобно тому как тк аналогично р, момент — аналогичен Р (см. фиг. 110, б).
На первый взгляд может показаться, что момент LK в каких-то долях воспринимается и крутящим моментом стесненного крученая и крутящим моментом свободного кручения, так что в эпюрах М1( и Мк в сечении zL должны появиться скачки, сумма которых равна LK.
247
Легко, однако, установить, что скачок может появиться только в эпюре Л1К. В самом деле, допустив, что в эпюре Л4К имеется скачок, одновременно должны принять, что и в эпюре относительных углов закручивания возникает скачок, поскольку <р« =G/lt7WK, а значит в депланациях точек средней линии сечений слева и справа от скачка появляется разрыв в силу (10. 11). Так как разрыв исключается, то наше предположение отпадает, откуда следует,
Фиг. ПО.
венно по тем же уравнениям с на (z—zL}.
Итак, в уравнение <pIt(z)
что сосредоточенный момент вызывает скачок, равный Ll( только в эпюре ~МК.
Скачок в эпюре Мк влияет на впереди лежащие ординаты всех jnnop, как начальный параметр Мк(0) с той разницей, что начало переносится в сечение zL. Окончательное значение ординаты эпюры в сечении z>?A складывается из двух частей: одна зависит от начальных параметров и выражается уже написанными уравнениями (10.11), другая часть -Составляется непосредст-заменой М<(0) на LK и аргумента z
при z^>zL добавляется
-j^\shk(z-zL}-k{z-zL)]. (10.12)
К уравнению MIt(z) добавляется
-ZK[(1 - ch k (z- zL)\. (Ю.12')
К уравнению B{z) добавляется
-I±shk(z-zL). (10.12")
k
К уравнению Mlt(z) добавляется
—ZKch k(z-zL).
(10. 12'")
В уравнении A4K(z) интересующая нас добавка очевидно равна —Лк.
Подчеркнем, что при z<zL никаких добавок к уравнениям (10. 11) делать не нужно. Эти выражения для любого незагруженного участка являются окончательными, если начальное сечение принадлежит к этому участку.
248
Формулы для добавок написаны нами в предположении положительного сосредоточенного момента, вызывающего отрицательный скачок в эпюре Мк.
При нескольких сосредоточенных внешних моментах добавки получаются в виде сумм. Например, (10. 12) принимает вид
(10.13)
Здесь индекс k опущен, а i выражает номер сосредоточенного момента.
Если задана распределенная крутящая моментная нагрузка переменной интенсивности /пк(£), то добавка (10. 12) будет
2
~{niK^[shk{z^)-k(z-^]dZ. (10.14)
Аналогично можно получить выражения добавок для других эпюр в случаях нескольких сосредоточенных моментов и распределенной моментной нагрузки.
Таким образом, нами составлены развернутые уравнения эпюр, учитывающие как начальные параметры, так и действие местных крутящих моментов.
Остается только показать, как определяются начальные параметры, так как, имея их, можно подсчитать любую ординату каждой из четырех эпюр.
Начало координат обычно помещают на конце, чаще всего на левом. В случае симметрии или антисимметрии нагрузки берут начало по средине длины бруса. И в том и в другом случаях два из четырех начальных параметров определяются сразу или определяется один начальный параметр и устанавливается простая зависимость, связывающая другие два. Две недостающие зависимости для определения двух неизвестных начальных параметров дают условия на правом (свободном) конце.
Рассмотрим различные условия закрепления.
Заделка, препятствующая повороту, дает
<Рк=О-
Заделка, препятствующая депланации (например, приваренная концевая планка, плоскость которой параллельна оси бруса), дает
?к = 0
или, что то же, _
я=о.
Возможность свободного поворота дает Л4к = 0 или, что то же,
мк4-Жк=о.
249
Возможность свободной депланации торца дает
В = 0.
Если левый конец свободен в смысле депланации, но нагружен моментом LK, то для этого конца
Ч -j- /И1( = — LK.
Если правый конец свободен в смысле депланации и нагружен моментом LK, то для этого конца
Мк 4” -Мк — LK.
Фиг. 111.
Для левого (правого) конца с полностью стесненной депланацией при нагрузке моментом LK имеем
Л7К=— LK (соответственно MK = LK).
Рассмотрим несколько примеров определения начальных параметров.
Пример 1. Брус длиной / полностью защемлен на левом конце, а на правом свободном конце нагружен моментом Ек (фиг. 111).
Начало поместим на левом конце. Известные начальные параметры
<р(0) = 0; Ж(0) = 0.
Неизвестные начальные параметры:
Д(0), Я(о).
250
Для их определения имеем условия на правом конце:
B(Z) —0; 1к(0 + Я(0 = ^.
В данном случае задачу можно упростить, так как /Ик(0) определяется сразу из условий статики. Очевидно, Л4к(0)=£к. Поэтому, учитывая, что /Ик(0)=0, имеем
Д(0) = 4.
Остается определить только В(0). Составляем по (10. И) выражение для В(1) и приравниваем его нулю:
B(O)chkl + LK±-shkl=O,
откуда
5(0) = —^-th kl. k
Подставляя эти значения в (10.11), получаем
?к И = Ith kl (ch kz -1) “ sh kz + kz\'
MK (z) = £K[th kl sh kz-\-1 —ch kz\,
В (z) — (th kl ch kz — sh kz), k
2ИК (г) —LK (ch kz — th kl sh kz).
Вид эпюр показан на фиг. Ill: а — при большом значении 1//г. соизмеримом с длиной бруса, б — при малом значении \)k^,l. Чем больше жесткость свободного кручения G/I{, тем меньшее значение имеют нормальные и касательные напряжения стесненного кручения, тем быстрее они затухают по мере удаления от места наибольшего стеснения, в данном случае — от заделки. Вообще с этими напряжениями на расстоянии от стеснения, равном 1//г, можно уже не считаться.
Пример 2. Та же задача, но момент LK приложен на расстоянии zL от левого конца.
По-прежнему имеем <р|( (0) = 0, /Ик (0)--0, /Ик(0) = LK. Уравнение для определения В(0) будет
5(0) ch— sh kl-LK — shk(l-zL) = Q. k k
Отсюда
5(0)= -~~h7[sh kl-shk(l-zL)].
251
Пример 3 (фиг. 112). Брус на двух опорах закручивается сосре- . доточенным моментом Lu, приложенным на расстояниях и и и' от опор. Предполагается, что опоры препятствуют повороту торцов, пене препятствуют депланации.
Начало поместим на левом конце. По условиям закрепления
<Рк(0) = 0, 5(0) = 0.
Неизвестные начальные параметры Мк (0) и 7Ик(0) найдем из условий на правом конце:
Выразим эти условия
1 - (sh kl - kl) Н------(sh ku’ - ku') = 0,
G/K £/шйз EImk3 v
2) MK (0) — sh kl — LK — sh ku! — 0. k k
Отсюда находим
УИК(О)=АК^^ , K v к Sil kl
v K( I sh H
Отметим, что полный момент на левой опоре
M(0)=zK-7-.
т. е. он может быть получен аналогично реакции простой балки, нагруженной сосредоточенной силой, численно равной Бк.
252
эльшом значении 1//г, справа — при
•ф \ х К А' К А А \\\
К Эпюра В
Фиг. 113.
Это одно из проявлений формальной аналогии, существующей между стесненным кручением и изгибом.
По соображениям симметрии находим
Тт / . bsh ku
Мк (I) = — ------ >
к 7 к sh kl
I и sh ku \ \ I sh kl )
Интересная формула получается для бимомента В в сечении под нагрузкой:
с , х , sh ku sh ku' b{tl)=LK ——— k sh kl
Дальнейший расчет не представляет никаких затруднений.
На фиг. 112 показан вид эпюр <рк, тИк, В, М1{ для двух случаев— слева при сравнительно малом.
Пример. 4. Случай равномерно распределенной крутящей нагрузки т1; нгсм/см. Левый торец полностью защемлен, правый свободен (фиг. 113).
Уравнение эпюр может быть получено путем интегрирования добавок, зависящих от элементарного сосредоточенного момента dLK~mKdz. Однако при равмиомерно распределенной по всей длине
бруса крутящей нагрузке проще непосредственно проинтегрировать уравнение с правой частью (10. 1) или (10.4), не пользуясь методом начальных параметров.
Общий интеграл уравнения (10.4), как можно убедиться дифференцированием, будет
В (z) = С, sh kz -ф С2 ch kz~[- ,
№
В' (г) = М.. (г) — kCx ch kzф- /гС2 sh kz.
Произвольные постоянные определим из условий на концах
1) жк(о)=тик(о)=«к/; 2) #Ю--=о-
Имеем
1) Сг = -^-
К
2) J^Lsh^4-C2ch^4-^ = 0 с =- + —1— \
й № 2 k \ ch AZ kchklj
Следовательно,
B(z)=^!-shkz—^<Zth^ + ^_\chte + —, k k \ k ch kl) №
M (г) — ch kz — m (l th kl -j--—sh kz.
\ 1 kchkl)
Вид эпюры В показан на фиг. ИЗ. Характерно то, что эпюра В меняет знак па протяжении длины бруса.
Предлагаем читателю показать, что в случае исчезающе-малой жесткости свободного кручения G/K->0, эпюры В и Л1К от нагрузок Дк и тк могут быть построены как эпюры М и Q от нагрузок ^=^кир = тк (фиг. 110, а, б).
§ 5-J’-JSACATEJlbHb,E НАПРЯЖЕНИЯ ПРИ СВОБОДНОМ КРУЧЕНИИ
И ПОПЕРЕЧНОМ ИЗГИБЕ ПОДКРЕПЛЕННЫХ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК С МНОГОСВЯЗНЫМ ПРОФИЛЕМ
Рассматривается оболочка достаточно жестко подкрепленная в поперечном направлении.
Примером^ подобной оболочки может служить крыло самолета с рабо1ающеи обшивкой, подкрепленное нервюрами и одной, двумя или тремя продольными стенками. Обычно вдоль границы обшивки и стенок располагаются более мощные стрингеры, так что стенки вместе с этими стрингерами-поясами можно приближенно рассматривать как балки-лонжероны
Для предварительного расчета крыла на изгиб изгибающие моменты передают этим условным лонжеронам, присоединяя к поясам некоторые полосы прилегающей обшивки. Крутящие моменты передают наружной обшивке. При уточнении расчета производится редуцирование площадей сечений обшивки, определяется центр тяжести и главные оси сечения крыла. Определение нормальных напряжении существенных особенностей не представляет и делается по общим правилам.
Здесь мы рассмотрим задачу определения касательных напряжении от деишвия произвольной системы поперечных нагрузок в предположении, что поперечные сечения оболочки являются жесткими. Ото значит, что в каждом поперечном сечении нагрузка может быть заменена статически эквивалентной системой сил. ечь, таким образом, идет об определении общих касательных напряжении, и мы используем все положения, на которые опирается расчет тонкостенных брусьев с замкнутым профилем поперечного сечения. 1 асчет поперечных прикреплений (диафрагм, нервюр или шпангоутов), обеспечивающих жесткость поперечного сечения, рассматривается ниже.
254
Все рассуждения проведем на примере профиля с четырьмя ячейками (фиг, 114).
Чтобы превратить профиль в открытый (односвязный), необ-
ходимо провести четыре разреза так, чтобы не оставалось замкнутых полей. Проводим по разрезу в каждой ячейке (фиг. 114,6) и
строим эпюру погонных касательных усилий qv при изгибе в глав-
ной плоскости yOz. Если положить Оу!1х = = 1, то ординаты этой епюры будут равны величинам статических моментов части сечения по одну сторону от исследуемой точ-' ки. Равнодействующая усилий qyds = S/ds равна 1Х и проходит через центр изгиба открытого профиля D параллельно оси у. Аналогично можно построить эпюру погонных касательных усилий qx при изгибе в главной плоскости xOz. Соответст-
вующая равнодейст- Фиг. 114.
вующая при Qx/Iy —
= 1 равна 1у. Она параллельна оси Ох и пересекает первую равнодействующую в точке D — центре изгиба открытого профиля (см. фиг. 114, а).
Предположим, что фактическая поперечная сила Q с компонентами Qv и Qx проходит не через точку D, а через некоторую другую точку с координатами xQ и yQ. Пусть, кроме того, действует крутящий момент М. Переносим силу Q параллельно в точку D с добавлением момента. Полный крутящий момент
= м + Qy (*q-xD)-Qx(yQ-yD).
Этот момент должен быть воспринят четырьмя неизвестными погонными касательными усилиями в разрезах. Обозначим их <?i, <?2, 7з, <7-1. Каждое из этих усилий является постоянным па протяжении ячейки (фиг. 114, в). Кроме того, не известен угол закручивания <рк .
Необходимые пять уравнений получим, выразив, что четыре ячейки поворачиваются па один и тот. же угол и, кроме того, что момент неизвестных касательных усилий эквивалентен моменту внешних сил относительно точки D. Напомним, что момент
255
известных касательных усилий qy и qx относительно этой точки равен нулю.
Воспользуемся уравнением (4.7) для угла закручивания. Учитывая, что модуль G и толщина t могут быть переменными, представим уравнение (4.7) следующим образом:
— i^ds==v4—§Qds'
(11.1)
Здесь Gctc — произвольная величина, выраженная в кг/см и вводимая для удобства вычислений. Обычно это произведение некоторого среднего модуля на среднюю толщину стенки.
Величина
ds' — ds Gt
— представляет собой приведенный элемент дуги профиля.
Составляя для каждой ячейки уравнение типа (1 Г. 1), следует учесть, что q — это суммарное погонное касательное усилие. Оно складывается из известных усилий qy и qx и неизвестных постоянных усилий </1, <72, <7з,
Заметим, что на каждую ячейку (например, на ячейку 2) действуют только усилия <71, <?2, <7з, причем <71 действует па стенку 1—2, <?2 — па все четыре стенки ячейки и q3 — на стенку 2—3. Для этой ячейки интеграл в формуле (11.1) принимает вид
<7^+Q^ — 71S;-2 + <72S2 — 73S 2-3. (и- 2)
Здесь
Q2y Qx ds ,
•$ i-2 — « dsr’, s2 —</s'; s2-3 = J2_3<7s'.
Аналогично получается интеграл для стенок ячейки 3. Что касается стенок ячеек 1 н 4, то в них входят соответственно усилия <71, <7г и <73, <74.
В итоге четыре уравнения типа (11. 1) и уравнение эквивалентности крутящих моментов представятся в виде
<7,s । — q2s 1-2 + Qiy + Qix = ;
- qxs 'i-2 + <72s j - q3S 2-3 + Q2y + Q?x = (И. 3)
QiS 2-3 "i- Qzs 3 '?4S 3—4 ~r Qtly “l~ Qsx ~ ^£ i'c'?Ku,3’
-- q3S 3-4 -|“ <?4s4 <?4У + Qax —
Qiwi ‘I 9Л "г <7зшз “b 74U)4==: А/ф- Qy (Xq xd) Qx (yQ yD).
2,56
Система уравнений (11.3) замечательна в том отношении, что дает ответ на все вопросы, относящиеся к определению касательных напряжений и центра изгиба. Отметим, что благодаря удачному выбору основной системы (разрезы проведены в наружных стенках профиля) первые четыре уравнения получились трехчлен-н ы м и относительно неизвестных q-it q2, q2, q\. Это существенно облегчает решение системы уравнений.
Рассмотрим три расчетных случая.,
1. Общий случай расчета без отделения изгиба от кручения. Неизвестные qx, q2, q-s, q>. и X = Gc,tc^ получаются непосредственно нз решения системы уравнений. При этом рекомендуется такой порядок расчета. Сначала неизвестные qx, q2, q-л q-t при помощи первых четырех уравнений выражаются через X, а затем найденные значения подставляются в пятое уравнение, что дает величину А7.
2. Расчет на кручение без изгиба. В системе уравнений полагаем все Q = 0 и проводим решение в указанном выше порядке. Примем Х=1 и найдем из первых четырех уравнений величины q, которые обозначим соответственно 'q^, q2<f, q^, q^. Действительные значения равны найденным, умноженным на X. Подставляя их в пятое уравнение, получаем
v М М
Л —--------------------------== -----.
<71<>а)1 + + <7з?“з 2j У-.'рН
Отсюда следует общая формула для погонного усилия в i-i: ячейке при кручении:
vz Mq i ср 11
Д = = (П-5)
2 7,у"/
/=1
Формула для утла закручивания будет
X м
(О =--------------------.
к (If п
с'с СС1с% /-1
(11.4)
(П-6)
3. Расчет на изгиб без кручения и определение положения центра изгиба. В этом случае в уравнениях (11.3) надо положить «/ = Х — 0, М = 0. .Первые четыре уравнения решаются дважды. Сначала полагаем Qy = 1, Q.v = 0. Тогда свободные члены Qix обращаются в нуль и остаются только члены Qiy. Пусть результат решения будет qty, q2v, q3y, q.\y. Подставляя эти значения в пятое уравнение (предварительно положив в нем Qx=0, Л1=0, Qy = 1). решаем уравнение относительно xQ. Этим самым определим плечо силы Qy, которая вызывает изгиб без кручения, т. е. найдем
257
абсциссу центра изгиба, которую обозначим вместо xQ: п
ХК ~ (11-7)
I - t
Затем проделываем решение, полагая Qx=l, Qy = 0, 7И=0, X=Q. Результат решения первых четырех (трехчленных) уравнений пусть будет <71Х, q2x, q2x, <?4х. Подставив эти значения в пятое уравнение, получим
п
1=1
(П-8)
Имея центр изгиба /<, можно привести к нему любую систему внешних касательных сил в виде силы и пары (момента). Пара даст усилия q, найденные выше в расчетном случае 2. Сила дает две группы усилий, равных соответственно qiV и qix, умноженных на величины компонентов силы по осям у и- х. Таким образом, решив систему уравнений (11.3) три раза на единичные факторы Л4=1, Qv=l, Qx=1 и найдя центр изгиба, можно обследовать действие любой нагрузки.
Варианты решения. Можно указать несколько вариантов решения задачи. Мы фактически пользовались изменяемой основной системой, благодаря чему, кроме неизвестных q, в уравнениях фигурировал угол (р« . Если разрезать не все четыре ячейки, а только три, то основная система получается неизменяемой и решение ничем не отличается от обычного применения м е-т о д а с и л.
Если требуется определить центр изгиба К, а определение усилий не является необходимым, можно рекомендовать такой порядок расчета. Нет необходимости находить координаты центра изгиба открытого профиля xD и yD, а можно сразу, установив полные касательные усилия от Qy=l, Qx = 0, М = 0 и соответственно от Qx=l, Qy = 0, /И = 0 найти положение равнодействующих касательных усилий. Точка пересечения их и даст центр изгиба К мпогосвязного профиля.
Существенно отличный способ определения центра изгиба основан па пользовании эпюрой единичной деплана-А
ции co. Здесь, как и в случае простого замкнутого (двухсвязного) профиля координаты центра изгиба вычисляются по Формулам (7. 11).
Доказательство этого положения основано на рассуждениях, совпадающих с приведенными в § 5.7.
Пример. Определить положение центра изгиба подкрепленной цилиндрической оболочки (фиг. 115, а), построить эпюру погонных касательных усилий и вычислить относительный угол закручивания. Действие внешних сил на оболочку приводится к силе Q,, = 2200 кг. Модуль сдвига материала, постоянный и для всех частей оболочки, (7 — 0,27 • 10“ кг;см~. Размеры оболочки даны на чертеже.
258
Поскольку уравнение контура оболочки не задано, решаем задачу прибли жснно, рассматривая полигональный вписанный контур ABHCNRFR'N'C'H'B'A (фиг. 115,6).
Выбираем основную систему, разрезан оболочку в точках А и F. Нензвест ные касательные усилия <?i и </2 в местах разрезов (фиг. 115, о, г) определяются
Фиг. 115.
из системы уравнений (11.3), которая для двухконтурной оболочки при заданной нагрузке имеет вид
(Н.9)
где л — абсцисса точки приложения силы Qy, а xD — абсцисса центра изгиба основной системы.
17*
259
Поместим начало координат в точку Д (см. фиг. 115,6), тогда Xq~—30 см, a xD требуется определить. Построим эпюру qv (s) ==SX для основной системы, полагая QV=IX.
Для контура /: SA = 0;
$в = — 17-0,12-6,75 = - 13,8;
SH= — 15-0,16 ——- — 13,8 — — 52,2;
18,54-20 S„=— 15-0,16-------- - -52,2 = - 98,4.
2
Для контура 2: SF — 0;
=47-0,12 ~ = 32,4;
18.5Ч-И-5
5^ = 45.0,12—-----------32,4= 113,4;
20 + 18,5
S =30-0,16—----------+ 113,4 = 206.
2
Для стенки СС имеем
Sc = 2 • 2 • 20 4- 206 4- 98,4 = 384;
SE = 20-0,16-10 4- 384 = 417.
Эпюра показана на фиг. 116, о.
Определяем касательные усилия в стенках Тц,, численно равные площадям соответствующих эпюр погонных касательных усилий:
Titi = 7у ds.
i
Тц, вычисляем по абсолютной величине, а направление их определяется по направлению усилий qy=Sx на соответствующей стенке (грани):
172-0.12
Г = АВ 6 13,5 = 78 кг.
Т = вн 13,8-15,5 15,5-0,16 + (27 + 18,5)— 505 кг.
Т -- 1 НС 52,2-154- 152-0,16 . (37 + 20) = 6 1120 кг.
т = CN 113,4-30 - 302-0,16 (- (37 + 20)- О = 4770 кг.
т = NR 32,4-45 4 452-0,12 (23+18,5) О = 3140 кг.
Т RF “ 472-0,12 6 -11,5 = 508 кг.
ТСС = 384-40 4- 402-0,16 G [40 - 20} - 16 260 кг.
260
Далее определяем момент инерции сечения относительно оси х:
-1 * *-7 *'0,12 13,52 + (13,52-4- 13,5-18,5+ 18,52) +
3 3
15-0,16 20-0,16 „ о
---------(18,52 + 18,5-20 + 202) _ь 4.202 +------2--- 202 +
О о
30'^16 (202 + 20-18,5+ 18,52) -|- 45'°'12-(18,52 + 18,5-11,5 + 11,52) + О о
47-0,12 1
+--------:-- 11,52 = 13 800 сщ4 * *.
3 I
Ту же величину найдем, спроектировав на вертикаль силы Т. Вычисляем координату центра изгиба:
1 ягт 2
х п ~~ — У ---— [78-31 + 505-22,5 + 1120-20 —
D / ‘ ‘ 13 800 1
— 47^0-20 — 3140-22,5 — 503-29,5] = —21 см.
Это значит, что точка D лежит левее точки Е на 21 см (см. фиг. 115,6).
При вычислении суммы плечи измеряются по чертежу, а знаки слагаемых
определяются ио знаку момента, создаваемого силой 7+ относительно точки Е
(момент, вращающий против часовой стрелки, положителен).
261
Вычислим коэффициенты при неизвестных в системе (11.3). Удвоенные площади, ограниченные контурами, будут
Определяем приведенные длины контуров ячеек (периметры, приведенные к толщине Л "0,12 щн). Gc принимаем равным заданному G, постоянному для всех стенок оболочки:
/ 0,12 „ 0,12\ 0,12
s, — 2( 17—2-15-—) + 40—109 см,
1 \ 0,12 0,16/ 0,16
0,12 Г 0,12 0,121
s = 40----4- 2 30---+ (45 + 47) = 259 см,
2 0,16^ L 0,16 k 0,12.|
, 0,12
Sl9 = 40 --— 30 см.
12 0,16
Подсчитываем §qyds по контурам / и 2. Очевидно, для этого необходимо просуммировать силы 1\и, действующие на каждом контуре, предварительно приведя их к толщине 0,12 см, т. е. умножив каждую силу на отношение /<://,. Полученную сумму надо умножить на отношение <2,,//, —2200/13 800, так как Тц, вычислялись как равнодействующие потока qu — Sx, а не действительного Qy
потока -—ду Слагаемые берутся со знаком плюс, если соответствующая
сила Tik но направлению совпадает с положительным обходом контура при интегрировании (против часовой стрелки).
Итак, имеем
С 2200 Г / 0,12 0,12 0,12\ 0,121
CD q v ds' =---- 2 78----505 —— -|- 1120---- + 16 260 --= 2360 кг,
у 13 800 [ 0,12 0,16 0,16/ 0.16J
с 2200 Г / 0,12 0,12 0,12\ 0,121
^’>-^'~!-1Т8-со1Чма^+зм0д.75+47то^б/ + 16260^=-4250«г-
Находим ?уК,не разделяя изгиба от кручения, т. е. не определяя предварительно положения центра изгиба /(. Подставляя найденные величины в уравнения (11.9), получим
109с/] — 30^2 — 2350% -|- 2360 = 0, — 30^2 Н- 259^2 -I- 5990ЛГ — 1250 = 0, 23507] "I- 599072 = 2200 ( — 30 -]- 21). Решение этой системы дает
q°K ——25,6 кг)см; 7“ = 7,1 кг1см.
X = Gctc<?'K = ~ 0,282,
откуда находим относительный угол закручивания
0,282_____
0,27-106.0,12
— 0,87-10-5 см-Т
262
Эпюру погонных касательных усилий для оболочки получим алгебраически,
2200
13 800
о Qy
суммируя ординаты эпюры умноженные на -------
0,16, с уси-
лиями <7, и <79.
Окончательная эпюра q°yK показана на фиг. 116,6.
Для определения положения центра изгиба многоснязного профиля также воспользуемся системен уравнений (11.9) при х^=х Подставив вычисленные значения коэффициентов и свободных членов, получим
109?”31' — 30?2,зг + 2360 = 0;
— ЗОг?*’3'' + 259^,зг — 4250 = 0;
2350<7”зг -]- 5990^3’' = 2200 (^ + 21).
Отсюда находим
<7i'31 =—17,5 кг/см; ^ЗГ = 14,6 кг/см; х^~0,1 см.
В данном случае центр изгиба профиля К расположен очень близко к промежуточной стенке, разделяющей контуры 1 и 2 (см фиг. 116, а).
§ 5.12. РАСЧЕТ ПОПЕРЕЧНЫХ ПОДКРЕПЛЕНИЙ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Элементы каркаса цилиндрической оболочки выполняют разнообразные функции. Продольные элементы (стрингеры) служат опорами обшивки и участвуют в восприятии нормальных усилий при общем изгибе оболочки. Поперечные подкрепления служат опорами стрингеров и воспринимают непосредственно приложенные сосредоточенные поперечные нагрузки, которые передаются оболочке. Функцию поперечных подкреплений можно охарактеризовать как обеспечение неизменяемости п о п е р е ч-ных сечений, лежащей в основе расчета оболочки как т о н-кост е н и о г о б руса.
На фиг. 117, а показана прямоугольная замкнутая оболочка. Если нагрузка распределена по площади или вдоль образующей, то часто можно обойтись без специальных поперечных подкреплений, ограничившись проверкой прочности элементарной рамы, выделенной из оболочки двумя сечениями, отстоящими одно от другого на 1 см.
При действии сосредоточенной силы Р приходится ввести в конструкцию специальную поперечную связь в виде рамы, фермы пли комбинированной системы — так называемый силовой шпангоут. Если рама зашита сплошным листом, то шпангоут называют диафрагмой.
Нагрузка шпангоута уравновешивается разностью (перепадом) касательных усилий в поперечных сечениях оболочки, проведенных непосредственно перед шпангоутом и за шпангоутом. На фиг. 117,6 показана часть эпюры Q на участке, где расположен
263
шпангоут. Указанная разность усилий, равная погонной реакции оболочки, действующей вдоль края шпангоута, выразится так:
+ Q е _ Ps.<-
Ч ш j j Лх j
(12.1)
Таким образом, распределенная реакция оболочки выражается той же формулой, что погонное касательное усилие при изгибе оболочки с заменой Q на Р, где Р — нагрузка на шпангоут.
Если нагрузка шпангоута приводится к паре LK (сосредоточенному крутящему моменту по отношению к оболочке), то реакция
Р х?.
Фиг. 117.
оболочки представится в виде постоянного погонного касательного усилия
7„, = — > (12-2)
где сок — удвоенная площадь, охватываемая средней линией поперечного сечения оболочки.
И здесь мы имеем формулу погонного касательного усилия при кручении оболочки с заменой Мк па LK.
Видно, что уравновешивание шпангоута при заданной нагрузке не представляет затруднений. Следует заметить, что учет деформации шпангоута приводит к некоторому перераспределению сил взаимодействия между шпангоутом и оболочкой, причем существенной становится конфигурация нагрузок шпангоута, а не только ее равнодействующая Р или Л1:. Обычно, однако, ограничиваются элементарным решением, приводящим к формулам (12. 1) и (12.2).
264
Поскольку нагрузка шпангоута уравновешена, расчет его сводится к простой задаче строительной механики стержневых систем, изучаемой в курсе сопротивления материалов.
На фиг. 118, а помазано сечение оболочки. Жирной линией отмечена обшивка, пунктиром — ось рамного шпангоута. На фиг. 118,6 стрелками показана распределенная реакция шпангоута 7Ш, на фиг. 118, в дана эпюра qm. Ось рамы совмещена со средней линией обшивки, что обычно лишь незначительно влияет на результаты расчета. Впрочем, учет эксцентриситета между распределенной реакцией и осями брусьев рамы никаких затруднений не представляет.
Пренебрегая, как обычно, продольной упругой деформацией брусьев, приводим задачу к расчету самой обычной замкнутой рамы, показанной на фиг. 118, в. Ввиду симметрии число лишних неизвестных равно двум.
В качестве неизвестных берем изгибающие моменты в углах М\ = М\> и Л12 = Л42'.
Благодаря тому, что узлы рамы остаются неподвижными, можем воспользоваться теоремой о трех опорных моментах неразрезной балки па жестких опорах.
Уравнение для узла /:
М,— + 27и7— + — Нти, — =
2 /Л lb) h
Уравнение для узла 2:
6Р&з
167*
Л4 Л + + Л = о.
2 h \!b Ьг) ' 1 /Л
Решая эти уравнения, находим и М2. Эпюра моментов показана па фиг. 118, г.
При криволинейном поперечном сечении оболочки и, следовательно, криволинейной оси кольцевого шпангоута (фиг. 119), целесообразно вести расчет но м е т о д у с т а т и к о-к и н е м а т и ч е с-кой аналогии. Сначала, как всегда, определяется распределенная реакция шпангоута — погонные касательные усилия q (фиг. 119, 6).
265-
Далее выбирается основная система, например, путем разреза кольца по оси симметрии, и строится эпюра изгибающих моментов от известных нагрузок основной системы М° (см. фиг. 119,6).
Ось шпангоута принимается за среднюю линию тонкостенного фиктивного профиля с толщиной
(12. з)
Фиг. 119.
где EI—изгибиая жесткость шпангоута в данном сечении. Определяются площадь фиктивного профиля
= (р‘” ds, (12.4)
положение его центра тяжести Оф и главные центральные оси х‘” и у'". Для этих осей находятся главные моменты инерции:
^х = ^)У2^' ds; Гу = фх2^ dx. (12. 5)
Наконец, определяются величина и положение результирующего фиктивного груза. Величина его равна площади приведенной эпюры моментов М°:
причем самый груз рассматривается как вектор, перпендикулярный плоскости фиктивного профиля.
Положение его определяется так же, как положение равнодействующей параллельных сил, равных приведенным площадям отдельных эпюр, составляющих эпюру Л4°. При симметричной раме и симметричной эпюре /И0 он, очевидно, находится на оси симмет
266
рии и х'р =0. Вообще же положение фиктивного груза определяется двумя координатами х'р и у'р.
После этой подготовительной работы определяем полный изгибающий момент в любом сечении хф, _уф кольцевого шпангоута по общей формуле
ф ф ф ф \
М=--М°- Р* - (12.6)
\ ’ X У )
Подставляя вместо хф, _уф координаты последовательных точек осн шпангоута, получаем ординаты эпюры М.
Итак, статически неопределенная часть изгибающего момента в любой точке замкнутого кольцевого шпангоута определяется по формуле, имеющей ту же структуру, что и формула нормальных напряжений при внецеитрепном растяжении — сжатии фиктивного профиля фиктивным грузом.
В этом состоит использование метода аналогии, который нан-лучшим образом приспособлен для расчета кольцевых шпангоутов.
При постоянной толщине обшивки и постоянном сечении кольцевого шпангоута все расчеты существенно упрощаются. Если пренебречь небольшим расстоянием между средней линией сечения оболочки и осью шпангоута, то центры тяжести действительного профиля оболочки и фиктивного профиля, используемого в расчете шпангоута, совпадают. Совпадают также главные оси, а геометрические характеристики — пропорциональны. Достаточно вычислить один раз величины §ds, у2 ds, <|5 х2 ds, тогда
F'P==^F5; /' = ^7^-y2flrs: ry-^ijx2ds- О2-7')
Таким образом, одни и те же геометрические характеристики используются и при расчете нормальных напряжений в сечениях оболочки и изгибающих моментов в кольцевом шпангоуте. Нагрузка шпангоута определяется по данным касательных усилий в оболочке.
Дополнительная затрата труда но расчету шпангоута сводится главным образом к построению эпюры М° и к вычислению фиктивного груза
(12.8)
В рассматриваемом случае E7 = const, фиктивный груз равен площади эпюры /И0, деленной па Е1.
Воздействие температуры также легко учитывается по этому методу. Если на протяжении ds имеем нагрев оси кольца на Р, то
267
это создает элементарный фиктивный момент с вектором, направленным вдоль ds и равным
dL^^ds. (12.9)
Здесь а—коэффициент температурного расширения.
Равномерный нагрев с одной и той же температурой Р на протяжении дуги s дает фиктивный момент с вектором, параллельным хорде, стягивающей дугу, и равным
АФ = а/°я, (12.10)
где а — длина хорды, стягивающей дугу s.
Если обозначить угол между указанной хордой и главной осью через ф, то изгибающий момент в любой точке кольца выразится формулой
М= _ (1Ф. c°s_l уф + £ * s‘n ф \ . (12.11)
\ X У '
Неравномерный нагрев, вызывающий температурную кривизну fy, дает фиктивный груз
P?=(ptds. (12.12)
Изгибающий момент в любой точке от неравномерного нагрева равен
. ф ф ф ф
м= . (12.13)
\ * X у /
Напомним, что изгибающие моменты- М° в основной статически определимой системе от действия равномерного или неравномерного нагрева не возникают.
§ 5.13. КРУГОВАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА И ЕЕ КОЛЬЦЕВОЙ ШПАНГОУТ
Ввиду большой практической важности круговых цилиндрических оболочек рассмотрим задачу их расчета более подробно.
Начнем с определения нормальных напряжений и погонных касательных усилий в поперечном сечении исходя из элементарной теории.
Как нормальные, так и касательные напряжения считаются распределенными равномерно по толщине стенки. Векторы касательного напряжения т параллельны, и вектор погонного касательного усилия q=xt в поперечном сечении направлен по касательной к средней линии стенки. Положение точки срединной поверхности в поперечном сечении будем характеризовать угловой координатой р, отсчитанной от плоскости изгиба, условно считаемой вертикальной (плоскость у). Нейтральная линия при изгибе совпадает с осью х.
268
Момент инерции сечения оболочки относительно любой центральной оси
2 гс
<г=/у = = (Г COS р)2 /гd/р = ~гЧ. (13. 1)
/•' о
Момент сопротивления
Wx=Wy = -r2t.
Нормальные напряжения в точке с угловой координатой £
М М
= ^c°sp. (13.2)
i X W
При р = -л: и р=0 напряжение достигает максимума (минимума)
• 3 max mm
ч-^t.
— т.гЧ
Погонное касательное усилие
о
= -£-sinp. (13.3) КГ
Касательное усилие достигает к з ральной линии при Р = у и р = —
максимума (минимума)
на нейт
На фиг. 120, а, бив показаны различные по внешнему виду эпюры, иллюстрирующие изменение ст и q от точки к точке в функции угла р.
При кручении погонное касательное усилие имеет постоянное значение и равно
Мк q = —— 2лГ2
(13.4)
Перейдем к расчету шпангоута (фиг. 121). Предположим, что шпангоут нагружен тремя сосредоточенными силовыми факторами— радиальной силой Р, сосредоточенным моментом L и тангенциальной силой Т на уровне оси шпангоута. Определим реакцию оболочки, уравновешивающую нагрузки шпангоута. Как известно, реакция оболочки реализуется в виде погонных касательных усилий, действующих по краю шпангоута. От силы Р согласно (13.3) имеем
Р qp =-----sin (3.
269
От момента L согласно (13-4)
Для получения реакции qT, отвечающей тангенциальной силе Т, переносим силу параллельно иа ось х с добавлением момента Л = 7гш. На основании формул (13.3) и (13.4) находим
или
(13.5)
Фиг. 120.
Основную систему выбираем, проведя разрез вдоль оси у в нижней части шпангоута. Общее выражение для изгибающего момента в основной системе на участке от (3 = 0 до |3 = л будет
- j'6/(Р,) rfw.
6
(13. 6)
Здесь dw— удвоенная площадь элементарного сектора, заштрихованного на фиг. 121:
= tZ[3z.
270
Плечо с равно
с —г — rni cos (₽ — ₽,) = г — гш (cos р cos ₽,• — sin £ sin pj.
Подставляя в (13.6) значение qP при |3=|3г, а также значение dw и интегрируя, найдем уравнение М°:
Мр — — fr cos р -1- гш у sin р — . (13.7)
Дальнейший расчет замкнутого трехкратно статически неопределимого кольца выполняется методом сил (неизвестные—момент, поперечная и продольная сила в разрезе) или методом аналогии.
В результате получаем уравнения полных величин М, N, Q в сечениях кольца в функции угловой координаты |3. Приведем эти уравнения:
M^^^sinpH-^cosP-l^Pr,-^, (13.8)
ЛД = — (cos(3 —- cos 8—8 cos $\ — P-KNP, (13. 8')
2- \ Гп1 2 j
= (cosP+ — -sin p —-5-sinp^ = P-/CQP. (13. 8")
Графики коэффициентов К для случая гш=г приведены на фиг. 122. Очевидно, эти графики КМР совпадают с эпюрой Мр при Р=1, /'=!, графики Кмр и Kqp с эпюрами N и Q при Р=1. Интересно отметить, что значение коэффициента Кмр не зависит от отношения г//’ш.
271
Уравнения эпюр от действия L и Т имеют вид
= (13.9)
Nl = - -±- = --L- -KNL, (13. 9')
Г ш р г ш
/Л=Рг^Км\ N-РКцр
Мп„-0^Ргш; qma=fl,5P; К,„.-О,25Р Нш-СМР
Фиг. 122.
Соответственно
М (1 sin ?._ р cos р - = Тгш • Кмт, (13. 10)
2~ \ 2 /
272
^=~frcos₽+ — sin?+|sinpW-/<A,r, (13. 10') 2л \ Гщ 2 J
Q7=^-(>Sinp---^COSPH^COS?-—W-'V (13-10")
2л \ riu 2 r /
Графики коэффициентов К приводятся в справочной литературе.
Имея формулы (13.9) — (13. 10), для сосредоточенных факторов можно скомбинировать любую нагрузку, действующую в различных точках в плоскости кольца. Путем интегрирования легко также определить усилия от распределенных нагрузок. Эти формулы с успехом применяются также и в том случае, когда изолированное кольцо находится под действием уравновешенной системы нагрузок и, следовательно, распределенные реакции не возникают: окончательный результат подучается путем суммирования действия отдельных сил, влияние реакции при суммировании автоматически аннулируется.
§ 5.14. РАСЧЕТ БАЛОЧНЫХ НЕРВЮР КРЫЛА
Уравновешивание нагрузок нервюры крыла распределенными касательными усилиями в обшивке ничем не отличается от рассмотренного выше определения сил, действующих па шпангоут.
На фиг. 123, а показана нервюра, нагрузка которой состоит из пары сил, и, следовательно, реакция обшивки, уравновешивающая пару, будет постоянным погонным касательным усилием
q = = const. (14.1)
“А
Изгибающий момент в сечении нервюры под первой силой М = qo>, (14-2) где со — удвоенная площадь
фигуры, заштрихованной на фиг. 123, а.
Если нагрузка нервюры представлена одной сосредоточенной силой, то уравновешивающее усилие q не будет постоянным (фиг. 123,6).
Как известно, при условии, что сила Р параллельна главной оси у сечения крыла,
q=-^-Sx. (14.3)
h
В этом случае изгибающий момент в сечении нервюры левее силы Р равен
M — ^qdw. (14.4)
273
Здесь dw— удвоенная площадь элементарного сектора, заштрихованного на фиг. 123,6, со— удвоенная площадь фигуры левее исследуемого нами сечения нервюры.
Имея нагрузку и реакцию обшивки, не представляет никаких затруднений построить эпюру изгибающих моментов нервюры.
§ 5.15. ПОНЯТИЕ О СТЕСНЕННОМ КРУЧЕНИИ ЗАМКНУТЫХ ПОДКРЕПЛЕННЫХ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК*
Как было установлено выше, при одном и том же угле свободного закручивания депланация замкнутого профиля значительно меньше, чем депланация открытого профиля той же конфигурации.
л
Эпюра единичной депланапии ы имеет существенно меньшие ординаты, чем эпюра со того же профиля с продольным разрезом. Соответственно снижается практическое значение учета стеснения, поскольку нормальные напряжения стесненного кручения замкнутого профиля, как правило, невелики. Все же при вытянутых профилях (крыло) напряжения стесненного кручения могут быть существенны и с ними приходится считаться. Ограничимся здесь кратким изложением механической картины явления, опираясь на теорию открытого профиля, и дадим окончательные результаты без вывода**.
Рассмотрим сначала брус с открытым профилем, работающий в условиях стесненного кручения, например, полностью защемленный одним концом. Если предположить, что его продольные волокна имеют модуль упругости Е= оо , то такой брус закручиваться не будет, поскольку мы исходим из соотношения
w (г, s) = — (г) u> (s). (15. 1}
Действительно, при w= 0 имеем ср' = 0. Это связано с игнорированием деформации сдвига в срединной поверхности тонкостенного бруса.
Иначе обстоит дело с брусом, имеющим замкнутый профиль, в деформированном состоянии которого сдвиг в срединной поверхности играет самую существенную роль. Если положить £ = 0, Сф 0 и тем самым навязать брусу закон плоских сечений, закручивание в этих условиях абсолютного стеснения депланации все же будет иметь место, причем связь между крутящим моментом и относительным углом закручивания получается аналогичной случаю круглого вала или сростка Шухова
* Л. А. Уманский, О нормальных напряжениях при кручении крыла самолета, ТВФ, 1940, № 12.
** Более детальное освещение вопроса см. в работах Л. Л. Уманского, а также Л. И. Балабуха, Г. Ю. Джанелидзе и Я. Г. Пановко, В. В. Новицкого и др.
274
Отличие здесь состоит в том, что в формулу для вместо по-лярного момента инерции IP~~§p4ds входит так называемый направленный полярный момент инерции
/С=<Р2 tds. (15.3)
Здесь иод г подразумеваются не радиусы-векторы элементарных дуг р, а их плечи г, перпендикулярные к ds и проведенные из центра закручивания.
Заметим, что использование формулы (15.2) в плоскости полного защемления является вполне обоснованным. Ка-
(15. 4)
сательные напряжения при этом выражаются формулой
_= Мк_г ~fc
Из сказанного ясно, что при построении теории стесненного кручения бруса с замкнутым профилем непосредственная л
замена (o(s) на (o(s) является слишком грубым допущением. Между тем, закон распределения перемещений w по сечению экспериментально всегда ока-д
зывается близким кис полюсом в центре изгиба К. Необходимое уточнение состоит в том, что вместо функции ср* (г)
в зависимость (15. 1) вводится другая функция /(z), называемая' мерой депланации, и тогда
л
w (г, s) — — f (г) • со ($).
(1о. о)
Оказывается, что функции /(z) и ср’( (z) связаны линейной зависимостью, графически проиллюстрированной па фиг. 124, где по оси абсцисс отложены значения f, ио оси ординат значения ср’ .
При /=0 имеем ср'. = , при /=ср'( значение ср* равно углу
_ с , мк
закручивания при свооодиом кручении, т. е. ср.=—— , где к О/к
“г г К
К “ ,
(15. 6)
18*
275
Для промежуточных значений f величина дф ординатами точек прямой О'В'. Аналитически
Мк
GIK 1
Мк GlK
выражается
Вводя обозначение
Мк
G/r
(15.7)
,г==1-^
получим простую зависимость
'?к(г)==Нт7± +н/ (г).
(/ [£
(15. 8)
Величина ц называется коэффициентом де план а-ц и и.
При /1; = /с имеем ц = 0, сечение не депланирует, стеснение отсутствует и равенство (15.7) переходит в основную зависимость свободного кручения:
При /к-> 0 имеем ц.->1 и тогда <рк определяется формулой (15. 2).
Считая, что продольные волокна при стесненном кручении находятся в одноосном напряженном состоянии, на основании закона Гука из (15.5) найдем
о (г, s)=—£/'(z) w (s). (15.9)
Это равенство запишем в виде . . В (г) л ,
a (z, «) = —;— <0 (s), 7 л
ш
(15. 10
где B(z) — функция, называемая бимоментом, равная
В (z) - — El^f (z). ш
(15.11)
Здесь через /д обозначен так называемый бимомент инерции — интеграл, равный
/л =Л) odtds. (15. 12)
Удобство этих обозначений состоит в полной аналогии формулы (15. 10) с формулой нормальных напряжений при изгибе. Кроме
276
того, что особенно важно, производная от бимомента равна крутящему моменту стесненного кручения:
B'(z)=M(z). (15.13)
Остается составить уравнение равновесия внутренних и внешних крутящих моментов:
< + Д = ' (15. 14)
или
О4?к4-^'=^к- (15.14')
Подставляем сюда ф'( из (15.8), затем дифференцируем обе части один раз по z и используем формулу (15. 11) для выражения f через В. Обозначая через тк погонную интенсивность внешнего крутящего момента, окончательно получим
В"-у.~^В. = ^тк. (15.15)
ш
Это и есть дифференциальное уравнение стесненного кручения бруса с замкнутым тонкостенным профилем. По своей структуре оно совпадает с уравнением (10.4) для открытого профиля.
л
На фиг. 125 приведены эпюры со и rt для сечения симметричной прямоугольной коробки с угловыми стрингерами. Там же выписаны готовые формулы для геометрических характеристик и усилий.
Уравнение (15.15) может быть уточнено путем учета деформации (искривления) поперечного сечения в своей плоскости. В этом случае
= (15.16)
где g — множитель, зависящий от деформации поперечного сечения.
Кроме того, путем аппроксимации продольных перемещений при помощи двух функций fi(z) и /г(г):
^(2)5) = /! (z)^(s) + /2(2)w2(s) (15. 17)
можно уточнить форму осн центров вращения отдельных сечений, которая в рассмотренном нами решении предполагалась совпадающей с осью центров изгиба К.
Расчет на стесненное кручение тонкостенных брусьев с топким (удлиненным) замкнутым или многосвязным профилем может быть значительно упрощен, так как в этом случае можно положить ц=1 и тогда уравнение (15. 15) в точности совпадет с уравнением (10.4). Ввиду большой практической важности тонких крыльев этот вопрос самостоятельно рассмотрен в § 10. 2.
277
Приведенные здесь результаты относятся также к мпогосвяз-л
ному профилю. Достаточно под эпюрой депланации (о понимать эпюру депланации миогосвязного профиля.
Эпюра й
2 bth t
b2h2 ,
= ^+/>Гви>л2
fCT = 2(fctl,+Atft)
_ ( bth-htb\2
> ' 6£.Л + Л£.Д фиг. 125.
Проблеме работы замкнутых и многосвязных оболочек типа крыла посвящена обширная литература. Отметим здесь капитальные работы Г. С. Елеиевского, С. Н. Кана, В. Ф. Киселева, И. Ф. Образцова, Г. Ю. Одипокова.
§ 5.16. ОБЩАЯ УСТОЙЧИВОСТЬ ОТКРЫТЫХ ТОНКОСТЕННЫХ ПРОФИЛЕЙ ПРИ ЦЕНТРАЛЬНОМ СЖАТИИ
При изучении вопросов устойчивости профилен принято отличать местную потерю устойчивости от общей потери устойчивости. Местная потеря устойчивости (фиг. 126, а) была рассмотрена в §2. 13 гл. 11.
Общая потеря устойчивости связана с перемещением отдельных сечений, причем каждое сечение не искривляется и перемещается как диск. Хорошо известным примером является изгибиая (Эйлерова) потеря устойчивости, когда сечения перемещаются в плоскости наименьшей жесткости (фиг. 126,6). Долгое время считали, что Эйлерова форма потери устойчивости сжатого стержня является единственной. Это, однако, оказалось справедливым только для сплошных и толстостенных сечений. В дальнейшем была обнару-
278
жена изгибно-крутильпая форма потери устойчивости авиапрофилей, характеризуемая одновременным поступательным и вращательным перемещением отдельных сечрний (фиг. 126, в). Эта форма потерн упругой устойчивости при весьма малой толщине стенок может наступить и после местной потери устойчивости:
<0
Фиг. 126.
здесь происходит явление, аналогичное работе подкрепленной па-
нели на сжатие, когда несущая способность определяется не
устойчивостью пластинки, а устойчивостью окаймляющих стринге-
ров. Роль стрингеров здесь играют ребра, остающиеся прямолинейными при местной потере устойчивости (фиг. 126, г). Указанное явление можно назвать вторичной общей потерей устойчивости.
Перейдем к рассмотрению теории общей потери устойчивости.
В самом общем случае перемещение какого-либо сечения в его плоскости при потере устойчивости можно охарактеризовать тремя малыми перемеще-
ниями:
1) перемещением | вдоль оси х,
2) перемещением ц вдоль оси у,
3) углом закручивания <рк.
Оси х, у в плоскости сечения могут быть выбраны произвольно. Если бы заранее была известна та точка, вокруг которой происходит вращение, то, поместив в эту точку начало координат, мы свели бы вопрос к задаче с одной переменной <р. В некоторых случаях ось вращения фиксирована, и тогда задача упрощается. Здесь этого предполагать не
будем. Проведем оси х, у через центр тяжести сечения, не совмещая их с главными осями.
Напомним вкратце вывод уравнения Эйлера. Это уравнение выражает равновесие между моментом
нормальных сил, распределенных .ио сечению, и мо-
ментом внешней силы jV1[P == Фиг. 127.
Если ось х — главная, то имеем (фиг. 127)
но
о.-рЛ? - - М = 0,
М=
279
Следовательно,
£-//' + акр^ = 0. (а)
Аналогично для второй главной оси находим
f4V' + ci<p/?Tl=O. (б)
Заметим, что знак плюс здесь приписывается сжимающим напряжениям. Уравнения (а) и (б) совершенно независимы. Написав общий интеграл каждого из них и удовлетворив граничным условиям, получим два значения сгКр, из которых расчетным, очевидно, будет меньшее.
Если оси х, у центральные, ио не главные, то уравнения равновесия будут иметь дополнительный член, так как момент нормальных напряжений от изгиба вокруг оси х, взятый относительно оси у, не равен нулю; также и наоборот. Легко сообразить, что при кривизне, равной единице, эти моменты обладают свойством взаимности и каждый из них численно равен Е1ху.
Уравнения Эйлеровой задачи представятся в виде двух совместных линейных дифференциальных уравнений:
£Z/+£ZxX+«kp^=0; (16.1)
EZX-H£Zvyr + %^ = 0. (16.2)
Решение этих уравнений приводит к тем же значениям критических напряжений, что и в предыдущем случае.
Если, кроме поступательных перемещений центра тяжести, происходит еще закручивание, то этой деформации сопутствуют добавочные нормальные напряжения, определяемые формулой (9. 2)
а = E'Fyx
Знак мы изменили в связи с тем, что здесь положительными считаются сжимающие напряжения.
Дополнительные моменты от этих напряжений относительно осей х и у, очевидно, будут
Мх=Е<$к \uydF; (16.3)
M^E^uxdF. (16.4)
/=•
С интегралами подобного вида мы встретились уже выше при вычислении крутящих моментов, сопровождающих изгиб.
Обозначим
^ydF=Fx; (16.5)
F
^xdF=Ry. (16.6)
280
Введя дополнительные моменты в уравнения равновесия (16. 1) и (16.2), получим
+ Е1ХЛ' E^Ry + акрЛ = О, (16.7)
Е/Л’ + Е1хуС +£-<?Х-Накр5т) = 0. (16. 8)
К этим двум уравнениям равновесия моментов относительно осей х и у надо присоединить третье уравнение, выражающее равновесие моментов относительно оси z или крутящих моментов. Уравнение имеет вид, аналогичный (9. 12):
(16.9)
Здесь Мк —-крутящий момент внешних сил, !ы —бимомент инер
ции относительно центра тяжести величины, а также Rx и Ry мы дальше скажем подробнее.
Подсчитаем крутящий момент нормальных усилий aKpdF, возникающий при закручивании профиля в результате потери устойчивости. При кручении продольные волокна наклоняются к оси г на угол ф = <р/р, где р — радиус-вектор, проведенный к волокну из центра тяжести.
В этом легко убедиться из следующих рассуждений. Прове
сечепия. О вычислениях этой
дем два параллельных сечения, отстоящих на dz (фиг. 128), и отметим две точки т и п, принадлежащие одному волокну. При повороте одного сечения относительно другого на с/(рк точка п сместится на nn'=pd<pK. Отсюда
Prf<P><_ 'п
Ф
В каждом сечении нормальное усилие волокна oi(PdF теперь можно разложить па два компонента — вдоль оси z и перпендикулярно к ней. Последняя составляющая, равная
°кр^Ф==°1<р<РкР^>
дает элементарный крутящий момент
3кР<Р2^-
Полный крутящий момент будет
??кР |р2«'^=?>кр/Р:=сРЛр(;л + ^)- (16. Ю)
281
Учтем теперь крутящие моменты, сопутствующие перемещениям £
И Т),
Mt=^qd<b —
(Ъ jr
----dF. дг
то
Так
как относительное удлинение dr^
s =-----х,
dzt
а = — Е—- х; dz'i
да dz
-Е—х=-Е?х-, dz3
М’.=Е^" ^d^\ xdF=E^" <о \xdF~ &xdF =
F 6 L F F
= - Ei" f ax dFa= - Ek"'Ry. (16. 11)
F
С другой стороны,
Mr,= ~E-q'Rx. (16.12)
Внося моменты (16.10) — (16.12) в уравнение (16.9), получим третье недостающее уравнение, связывющеае т), <рк:
+ ERxr“ + ERfK -I- т- (Окр/Р - GfK) = 0. (16. 13)
Уравнения (16.7) и (16.8) продифференцируем два раза, а уравнение (16. 13) один раз. В таком виде системой удобнее пользоваться, если приходится удовлетворить более или менее сложным условиям на концах стержня:
f//,v -|-Е/ху1]™ + ERy-?™ + о,(рЛГ = (); (16. 14)
Е1ху^ +ЕГутГ + ERX^’ -I-Okp^V' = 0; (16. 15)
ERy^ -I-ERX^ -k ER*™ i- (5кр/р- G/K) ?|>0. (16. 1.6)
Остановимся здесь более детально на вопросе о вычислении коэффициентов системы (16. 14) — (16. 16). Коэффициенты Iy, R, Ixy, I P = R + R, /к= специальных пояснений не требуют.
Оси х, у—-произвольные ортогональные оси, проходящие через центр тяжести сечения. Удвоенная секториальная площадь <о берется относительно ц. т. сечения. При вычислении Rx и 7?;, можно взять совершенно произвольный начальный радиус-вектор, так как при центральных осях величины Rx и Ry не изменяются, если к о)
282
прибавить постоянную величину. Что касается /„,, то оно вычисляется по формуле
= J ^dF. г
При этом должно удовлетворяться требование
J ^dF^=Q, (в)
F
что может быть, как известно, достигнуто надлежащим выбором начального радиуса-вектора.
Условие (в) имеет определенный механический смысл. Так как
а-Е®’®, ' к ’
то из (в) следует, что
^adF—Q- (г)
F
Равенство (г) выражает неизменность силы Р в процессе деформации (т. е. равенство нулю ее вариации).
Величину /ш вычисляют, помещая полюс в центре тяжести сечения и принимая за начальный радиус вектор, удовлетворяющий условию (д). Если не хотят связывать себя начальным радиусом-вектором, то для вычисления 'пользуются формулой
/ц,= ^(о2йг/?—i- KwdF^. (д)
? 'к /
Эта формула выводится следующим образом. Пусть <о=ш-|-ш0. Тогда
/ш = [ (ф-|- wtfdF— f dF-Р 2<о0 j* w dF-\- w^F. (е) f f F
С другой стороны, необходимо, чтобы
<о dF— (ш -|- ф0) dF == О
F F
или
[ ф dF-\- woF=O-F Отсюда
0>n=-----I <0 dr.
F J
F
Подставив это значение в формулу (е), найдем выражение (д).
Займемся теперь определением критического напряжения из системы совместных однородных дифференциальных уравнений (16. 14) —(16. 16).
283
В простейшем случае двух осей симметрии /.Yy=0; Rx=0't Ry = Q, и система распадается на три независимых уравнения:
Ч^+°кЛ'==о; О6-14')
^lv+aKpFV'=0; (16.15')
^Mv + (VP-G/K)< = 0. (16.16')
В этом случае получается три независимых минимальных значения сгкр, из которых практическое значение имеет наименьшее.
Будем считать концы стержня шарнирно неподвижными, причем предположим, что на концах не имеется препятствий к депланации поперечных сечений. Эти граничные условия выражаются так: при г=0 и z=l
i = q" = Т| = 7]" = ?|. = <?’ = 0.
Мы можем удовлетворить уравнениям (16. 14') — (16. 16') и указанным граничным условиям, полагая
S = «1sin-^; 7] = «2sin-y-; <рк = а3sin , (16.17)
что соответствует деформации с одной полуволной. Подставляя эти значения в (16.14') — (16.16'), получим после сокращения общих множителей в левой и правой части
Г^Г/у о ==----•
у l^F
^-Е1Х \ lip л2 G/r + —
(16. 18)
(16. 19)
(16.20)
Первые два критических напряжения, очевидно, совпадают с эйлеровыми для выпучивания стержня в плоскостях симметрии. Последнее соответствует закручиванию стержня вокруг оси z.
Для двутавра закручивание может наступить ранее выпучивания только при весьма малой толщине профиля и когда ширина полок немала по сравнению с высотой стенки. При антисимметричном профиле (зетовом) уравнения (16. 14) 4-(16. 16) также разделяются. Этот вид профилей тоже теряет устойчивость путем выпучивания или закручивания вокруг центральной оси *.
Пусть профиль имеет только одну ось симметрии (ось х). В этом случае /Ху = 0, Rv = 0, а первое уравнение системы (16. 14) —
* Как установил проф. В. 3. Власов, зетовый профиль может потерять устойчивость путем закручивания также при растяжении.
284
(16. 16) становится независимым от двух остальных и принимает вид:
Д//У+%А'=0. (16.14")
Отсюда, полагая при шарнирно опертых концах
f . яг
k = a1 sin —,
находим
Л2
F
Два других уравнения образуют совместную систему:
(16. 15„}
ERx^ + ^KpIp-GIT)^0. (16. 16")
Полагая снова
. ~z .яг
7] = tz2 sin — и <f>K = tz3sin-y- , получим после подстановки этих форм в (16. 15") и (16. 16") два однородных линейных уравнения:,
(тгEI* ~ i °^F) а*+тг ER*a*=0; (16-21 >
-^Д/?А + (Д1д/<в+^-О/к-^-а1(р/р)а3=0. (16.22)
Эти уравнения могут дать отличные от нуля решения для и йз только при условии, что определитель из коэффициентов этих уравнений равен нулю. В этом случае аг и а3 могут быть определены с точностью до произвольного постоянного множителя.
. Я2
Итак, после сокращения на —
(у^/х-окрД)
— Д/?г
Z2
Вводя обозначение
_ я2 ERX Рх~ Z2 уЕгГр
(16. 23)
и принимая во внимание обозначения (16. 18) — (16.20), перепишем определитель ‘следующим образом:
о — а
X кр
Рх
= 0.
285
Раскрывая определитель, находим
(°х — °кР) (°? — °кр) - Рл = О
°кР - °кР (°<г + ° J + (°Л- Р2г) =0-
Отсюда получаем два значения для а
°..f=24iL + |/(AV;-)2+^- (|6-24>
Из формулы (16.24) следует, что с1<р2 всегда меньше ах и аг, а акр3 всегда больше ах и с,.
Фиг. 129.
Решение (16.24) можно получить графически при помощи круга Мора (фиг. 129). На прямой Ах откладываем отрезки АВ = <5? и А С = щ, затем отрезок СС = ВВ' —^х. Соединив В' с С', найдем центр О. Проведя окружность радиусом ОВ' = ОС', получим точки Е и F; легко видеть, что Л£=оКр2 и Л^ = сгкр?.
Определим теперь абсциссы центров вращения D? и D3> соответствующих найденным нами критическим напряжениям (ТКР2 и бкрз. Обозначим абсциссу Z)2 или D?, через xD. Тогда абсцисса центра тяжести, отсчитанная от D, будет — xD. Из кинематических соображений следует, что
7)= —xDvK или
С другой Vk стороны, v]=tz2sin-y, <pK=a3sin-y-,
поэтому V 21 Лр а3
286
Из уравнений (16.21) и (16.22) следует, что отношение--
аз можно выразить через цкр следующим образом:
D —
кр
(ж)
Подставив вместо с найденные выше два значения акр2 и окр3> получим два значения для xD. Так как акр =£ ох и акр ф ov, то для xD получаем всегда два конечных значения. Другими словами, открытый профиль, симметричный относительно оси х, подвергающийся центральному сжатию при выпучивании не в плоскости х, всегда закручивается. При толстостенном сечении сгкг>2 приближается к сгх, а Щфз приближается к о? . Одновременно Ь2 удалится на значительное расстояние, так что практически выпучивание вдоль оси у можно считать совершающимся без закручивания.
При полной заделке концов, препятствующей как повороту, так и депланации сечений, при z = 0 и z = l, имеем т)=т)/ = 0 и. фк=ф/к=0. Этим граничным условиям и уравнениям (16. 15") — (16. 16") можно удовлетворить, полагая
V]—а2^1 —-cos ; (16.25)
<Рк=«з(1 — cos^. (16. 26>
Здесь имеется полная аналогия с решением эйлеровой задачи для случая заделанных концов. Формула для сгкр совпадает с (16. 24), но вместо / в выражения для сгх, о¥ , (>х следует подставить //2. Для всех промежуточных случаев между шарнирной и полной заделкой свободная длина колеблется в пределах от I до Z/2.
Рассмотрим в заключение другой метод решения задачи об-устойчивости профиля, имеющего одну ось симметрии. Предположим, что центр вращения нами фиксирован. Будем относить перемещения к центру вращения. В таком случае т) = £ = 0 и перемещения определяются углом <рк. Дифференциальное уравнение задачи будет аналогично (16. 16):
Д7^ + (Окр7р-С//,()<р"=0. (16.27).
Решение этого уравнения для простейшего случая граничных условий будет в соответствии с (16.20) иметь вид
я2 —
О/к+ —£/ш
oD-------, (16.28)
‘ р
287'
причем /«, и !р должны быть отнесены к оси вращения. Обозначим абсциссу оси вращения через xD(yD =0). Выберем ось симметрии за неподвижный радиус-вектор. Тогда
<о — <й — xDy\
/«>=J u?dF— J (о>2 — + dF=R~ 2xDRx-]-x~Dlx. (16. 29)
F F
бкр
Фиг. 130.
Далее имеем
Ip = Ix -}- -}- -XdF У 0 — Ip XqF. (16.30)
Подставив эти значения в (16.28), получим
7t2 9
GIK + — Е (1Ш - 2xdRx + хух)
288
На фиг. 130 показан график изменения сго при различных положениях оси вращения для корытного профиля. Мы видим, что по мере удаления центра вращения влево (так же как и вправо) ординаты кривой асимптотически приближаются к Эйлерову критическому напряжению сгх. Имеются, кроме того, ясно выраженный минимум и максимум. Можем найти соответствующие абсциссы из уравнения
^_ = 0- (16.32)
dxp
Продифференцируем (16.31) по xD и приравняем результат
нулю. Получим квадратное уравнение х° Xd rx F (16.33)
Легко убедиться, что корни этого уравнения дают найденные нами выше значения xD. Подстановка их в уравнение (16.31) приводит к величинам сгкР2 и сгКрз- Таким образом сгкР2 и Ццрз представляют собой экстремальные значения сжимающего критического напряжения, соответствующие принятым формам равновесия •— синусоидам с одной полуволной *.
Устойчивость коротких профилей
Все полученные нами выводы, разумеется, сохраняют силу лишь при условии, что найденные значения сгкр ниже предела пропорциональности материала профиля. В противном случае, например, при малой длине I, модуль Е уже невозможно рассматривать как величину постоянную, а его приходится в каждой точке считать функцией относительного удлинения волокна. Приближенно задача решается путем введения приведенных модулей Е' и G' по аналогии с модулем Энгессера-Кармана. Этот вопрос находится в стадии интенсивной разработки рядом исследователей на базе теории А. А. Ильюшина, но своего окончательного решения еще не получил.
Следует помнить, что с уменьшением длины профиля на первый план может выступить местная потеря устойчивости.
На фиг. 131 дан график для швеллеров, согнутых из листового материала постоянной толщины I; ширина стоики /?, ширина полок Ъ. Через I обозначено расстояние между шарнирами пли вообще длина полуволны выпучивания. Подсчитываются координаты точки — абсцисса bjh и ордината b(.{h2. Если точка попадает выше наклонной линии графика, происходит общая потеря устойчивости, если ниже — местная потеря устойчивости.
" Этот факт, разумеется, вытекает н из общей теории нахождения собственных чисел системы однородных линейных дифференциальных уравнений.
19 425 289
Для подсчета критического напряжения вторичной потери устойчивости можно пользоваться приближенной формулой (16. 34).
„ Р /3
акр.вт=С--т, (16.34)
Коэффициент С берется из графика, данного па фиг. 132.
Напряжения сТнр.вт, вычисленные по этой формуле, не должны превосходить предела пропорциональности материала. В противном случае.получится завышенным.
290
Практические указания. Пример
При вычислении геометрических характеристик 1Х, ly, I , 1Р, относящихся к центральным (необязательно главным) осям х, у, очень часто пользуются величинами /Л, Iy, 1 ху, Iр, подсчитанными для параллельных осей Л', у, а затем переходят к осям х, у, пользуясь известными формулами перехода Ix — lx — b2F; — — a2F; /ху = lxy — Fab; /P — JP — F (a2 + &2). Точно так же при вычислении величин /ш, Лф, Д’у для центральных осей иногда целесообразнее брать за исходные величины /ш, Rx, Ry, подсчитанные для осей, параллельных центральным. Выше мы уже приводили некоторые формулы для перехода от центральных осей к параллельным. Соберем здесь формулы для перехода от произвольных осей х, у к параллельным им_ центральным осям х, у. Пусть а, b — координаты начала осей х, у в осях х, у. Тогда
— ау -ф Ьх ф- К.
Отсюда
и — ю-^ау — Ьх — К;
Rx—\ ^ydF= \ w(bA-y)dF-\-a J y2dF — b\ xy dF-К J у dF= F F F F F
=Kx+aIx-b(lxv-\»dFy, (16.35)
Ry = J wxdF = [&(a-}-x) dF-\-a^ xy dF — b J x2dF — K J xdF— F 'p F F F
= Ry + a(lxy + ^dF}-bIy; (16.36)
/«,= f =.
F YF ’
= 7m 4- a2lx - 2ablxy 4- b2iy 4- 2a~<x - 2bRy. (16. 37)
В этих формулах
Rx=^7ydF; Ry^^xdF; 7 = J ш2 dF-у (16.38)
F F F 'F '
Таким образом Rx, Ry, Д выражаются через те же величины для осей х, у, что и моменты инерции 1Х, /у, 1ху.
Рассмотрим пример определения критического напряжения швеллерного профиля (фиг. 133). Вследствие симметрии относительно оси х, Ry'-=O- Для вычисления Rx и 1т воспользуемся осями х~х и у=у с началом в О'.
19* 291
При обходе контура в положительном направлении (против часовой стрелки), от точки 2' к точке 2, перпендикуляр г (или г) равен для полок Л/2, для стенки же г=0. Принимая неподвижный радиус-вектор совпадающим с осью х, получим следующие значения m в угловых точках:
6Л »2' — > ш1' =0;
- п - , bh
“>j=0; w2=-]-—.
При этом $<n>dF=0. _ _
Теперь легко определить по правилу Верещагина Rx и 1
— __ , bh b h . , bh b /___Л\__ __ th2b2 .
^х~~ ~Т~2~~' 2~Т\ 2/ 4 ’
Далее определяем:
абсциссу начала О, равную яо абсолютной величине расстоя нию центра тяжести сечения от оси стенки:
t (h + 2b)
__ b2 h~j-2b
момент инерции:
-1- th2-}- 2tb -- = -—th2 (Zt + 6b);
величины:
b2 1 j, 9/, । th2b2 h-f-3b
th2 (h 4- 6b) —-----— —-~ < h~)-2b 12-------------------------' 3 h+2b
Jm^=Tm + a2Ix-]-2aRx
_ thW 2ft2 + + 26&2
~ 12 (ft-(-2&)2
592
Найдем также
у 12 (6 4-26)2 3 (Л 4-26)
iP=ix+iy\ . (6 4- 26)<з к 3
Теперь можно определить — 712 £/х № (h + 66) .
х— /2 F = /2 12 (6 4-26) ’
Ъ2Е b3(2h+b)
y /2Д fl 3 (A 4-26)2 Tt2 G/K+ — В1ш I *•
4 G
„„ 6263 (262 4- 1566 4-2662)4--------(6 4- 26)3^2/2
1&E Tt2 £
/2 (Il 4- 26) [62 (6 4- 66) (6 4- 26) 4- 463 (26 4- 6)] ’
_ tc2 ERx _ ifiE ______________________26262 (6 4- 36)______________
Px— /2 YWP~ P (h + ЧЬ) /3[h2(h 4- 66) (6-f-26) 4- 463 (26 4- 6)]
E
В частном случае при h = b и — = 2,6 имеем
т$Е
0,1944
Дальнейшее определение акр2 по формуле
не представляет затруднений. Остается сопоставить с акр2 и взять меньшее значение.
293
Глава VI
ПРЯМЫЕ И КРИВОЛИНЕЙНЫЕ БАЛКИ СО СТЕНКОЙ, РАБОТАЮЩЕЙ только НА СДВИГ. БИКОНСТРУКЦИИ
§6.1. БАЛКИ С ПАРАЛЛЕЛЬНЫМИ ПОЯСАМИ
счет балок, составленных из различных материалов, делается 6 иным правилам, основанным на гипотезе плоских сечений, а по°бЫна гипотезе, что продольные волокна друг на друга не на-ТаКЖеот Если проследить вывод известных формул для прибли-Н<ИМа'го'значения кривизны балки, а также для нормального на-же11Н°иия но при этом отказаться от предположения £ = const, то
El '
, м О —+-у,
полУчиМ М
дх2 j £у2 dF •’
М
Е.У>
(1-1)
а
отдельных воло-
постоянный для
(1-2)
причем Е уже является величиной, различной для Кон (площадок dF).
Обозначим через Ео произвольно взятый, но
данного расчета модуль упругости, например, модуль упругости какого-либо одного волокна. Условимся называть редукционным коэффициентом для z-ro волокна отношение
Z?o fi'
где Ei — модуль упругости /-го волокна.
разделив и умножив правые части формул для d^v/dx2 и о на g придадим им следующий вид:
d2v __ м
^рГд
„ , м с — -4—--
/ред
(1.4)
294
Здесь через /ред обозначен так называемый редуцированный момент инерции поперечного сечения, иначе—момент инерции редуцированных площадок:
J ^0
y2dF^-
Таким образом, формула для кривизны имеет теперь тот же вид, что в случае £ —const, с той разницей, что вместо Е взята произвольная величина Ео, по площадки при вычислении / изменены умножением на редукционные коэффициенты (1.2). Формула для нормальных напряжений (1.4) отличается наличием множителя <р, в числителе.
Фиг. 131.
Само собою разумеется, что при определении положения нейтральной линии поперечного сечения приходится пользоваться не истинными площадями, а редуцированными, т. е. умноженными на редукционные коэ ф ф и ц и е пты.
Остановимся на случае двухпоясной балки с топкой стенкой, выполненной из материала, отличного от материала поясов. Собственными моментами инерции поясов пренебрегаем; высоту стенки будем считать равной расстоянию h между центрами тяжести поясов (фиг. 134, а). Обозначим через FB и Лп — площади верхнего и нижнего поясов, через I — толщину стенки. Модули упругости материала поясов и стенки обозначим соответственно через Е и С(.
Примем Ео = Е, тогда редукционные коэффициенты для поясов будут равны единице, а для стенки ф;=-- -У-.
h
Нейтральная ось (н. о.) проходит через центр тяжести суммарной редуцированной площади. Расстояние между нейтральной осью и серединой высоты стенки
j/o = O,5 Л--(1.6)
FB -I- /;„ + М -~
295
Редуцированный момент инерции относительно нейтральной оси
/ред = (/Г8 + Л.)7- + ^-^-(Ь7) где
^рел^Л. + ^н + А^ • (1.8)
Нормальное напряжение в поясах
п
м
Г~у"
'ред
где уп — расстояние между н. о. и осью соответствующего пояса. Нормальное напряжение в волокнах стенки
. М Et
* ред
На границе поясов и стенок эпюра нормальных напряжений, очевидно, имеет перепад, и отношение напряжений в стенке и поясе
, , F,
как раз равно редукционному коэффициенту стенки <pt=——
Если пояса стальные, а стенка дуралюминовая, то
Et 0,7-106
Е — 2,1-106
0.33-
Так как сечение стенки, как правило, меньше сечения поясов, то нормальные усилия в стенке в общем балансе сил играют подчиненную роль и в первом приближении для предварительных расчетов можно принять Е;/Е = 0, т. е. считать стенку не воспринимающей нормальных напряжений в поперечном сечении. Расчетные формулы при этом чрезвычайно упрощаются.
Расстояния от осей поясов до нейтральной оси, очевидно,
равны:
Л8=Л
F,. + Fa ’
F в + Fn
(1-9)
Момент инерции относительно нейтральной оси
Ев + 6Й Моменты сопротивления
W= — = FJi, WH = -^——Fnh.
Напряжения в поясах
М М
а„ =------: °.,— — •
в FJi “ FKh
(1-Ю)
(l.H)
(1.12)
296
Усилия в поясам
NB=—— ; л^н= —• (1.13)
Л Л v
Тот же результат получим из условий равновесия моментов для отсеченной части балки аналогично определению усилий в поясах фермы. Вообще, приняв Et = Q, можно получить усилия из условий статики, не вводя гипотезы плоских сечений.
Определим по общим правилам касательные усилия в горизонтальных и вертикальных сечениях стенки. Как известно, в силу закона парности касательных напряжений пропорциональные им касательные погонные усилия
q=tt
в вертикальных и горизонтальных сечениях (и вообще во взаимно-перпендикулярных сечениях), проведенных через одну точку, будут по абсолютной величине одинаковы. Они равны
QS q = ~ '
Статический момент S вышележащей части относительно нейтральной оси при сделанных допущениях (ф; = 0) оказывается величиной постоянной и не зависящей от положения рассматриваемой точки по высоте:
5 = 5 А А =__£Л_ h.
88 н " ав + ан
Подставив значение I, найдем
q =—= const. (1.14)
h
Усилие q в данном поперечном сечении есть величина постоянная, равная поперечной силе, деленной на высоту h. Если по высоте стенки толщина t не изменяется, то и т есть величина постоянная в данном сечении:
По длине балки величины q и т изменяются по тому же закону, что и поперечная сила Q. При сосредоточенных нагрузках q остается постоянным на участке между нагрузками. На фиг. 134, б показаны два (заштрихованных) элемента, вместе с действующими на них сдвигающими усилиями q\. Обратим внимание на принятые нами обозначения: касательные, сдвигающие усилия обозначаются стрелками с полуостриями, обращенными гладкой стороной к той полуплоскости, к которой относится сдвигающая сила. Если представить себе элемент удаленным, то для изображения действующих вдоль края прямоугольного отверстия касательных сил следует повернуть стрелки в противополжную сторону (действие
297
равно противодействию), а полуострие нарисовать со стороны отверстия (см. на фиг. 134,6 в левом нижнем углу фасада балки).
В дальнейшем, часто будем пользоваться этим способом обозначения сдвигающих усилий. Преимущество его в том, что поло-
жение полуострия сразу отмечает тело, к которому приложено усилие.
При равномерно распределенной на балку нагрузке погонное
усилие q изменяется вдоль балки по закону прямой.
Сдвигающее усилие q связано простой зависимостью с усилиями в поясах N.
Так как
то
dx h
dN
(1. 15)
V’
т. е. производная от нормального усилия в поясе по его длине равна погонному касательному усилию в степи е. Эта зависимость легко выводятся также из рассмотрения равновесия элемента пояса, выделенного двумя близкими поперечными сечениями и продольным сечением между поясом и стенкой.
Указанный упрощенный метод расчета, основанный на допущении, что модуль упругости первого рода продольных волокон стенки равен пулю н стейка не воспринимает нормальных напряжений в поперечном сечении, применяется в самолетостроении очень часто в связи с особенностями конструктивного выполнения балок. Так, например, в случае шарнирного крепления поясов лонжерона (см. фиг. 134,6) нет оснований считать, что в последней панели стенка воспримет нормальные напряжения. Наличие погиби стенки (вмятины) сильно снижает ее сопротивление нормальным усилиям. Наконец, в отдельных случаях стенка выполняется из гофра с вертикальными волнами, и тогда упрощение Д/ = 0 наиболее точно отмечает действительности.
§ 6.2. БАЛКИ С НЕПАРАЛЛЕЛЬНЫМИ ПОЯСАМИ
Для приближенного расчета балок со сходящимися поясами прежде всего надо условиться о понятии поперечного сечения. Обычно так называют сечения, перпендикулярные к биссектрисе угла, образуемого поясами. Иногда поперечные сечения считают параллельными стойками жесткости. Существует метод расчета, когда сечение берется но дуге окружности с центром в точке схода поясов.
Балку можно трактовать как брус переменного сечения по правилам сопротивления материалов, определяя нормальные, а также касательные напряжения по известным формулам.
Другой прием, аналогичный описанному в § 6. 1 для балок с параллельными поясами, основан на двух допущениях: 1) считают,
298
'что стенка в поперечных сечениях не воспринимает нормальных напряжений; 2) предполагают, что силы взаимодействия между поясами и стенкой направлены параллельно осям поясов, т. е. являются исключительно с д в и г а ю щ и м и (касательными). При этом в поясах возникают только продольные усилия. Поперечное касательное усилие в стенке не равно поперечной силе балки.
Определим усилия Л/в, Mt и Т в сечении п'п трапецеидальной балки из условий статики (фиг. 135). Пусть R— равнодействую-
ф|,г. 135.
щая нагрузок левой отсеченной части балки. Задача сводится к уравновешиванию силы R тремя силами Л/п, N„ и 7’, не пересекающимися в одной точке (см. фиг. 135). Графическое построение показано на фиг. 135, в. Аналитически Т, /VB, /V„ определяются из уравнений равновесия моментов относительно точек k, п и п' соответственно. Целесообразно заменить R двумя компонентами: V, параллельным поперечному сечению, и Н, направленным вдоль одного из поясов, например, верхнего (см. фиг. 135). Тогда
Т = V У-У- ; j kn' hr ’ ।
N-H-V—-, } (2-0
Г“ I
TV, I
r» j
299
Касательное усилие Т обычно принимается распределенным равномерно по ширине стенки в сечении пп'. Погонное усилие в сечении пп'
Т
hT
Погонное касательное усилие между поясом и стенкой может быть найдено дифференцированием усилия в поясе, выраженного
в виде функции длины пояса. Так, из равновесия элемента пояса (фиг. 135, г) следует
N„ + dNn — N„—qndx=Q,
откуда
_ _у rf д(х) н dx dx rsi (х)
Отрезки а(х) и гн(х) — линейные функции от х:
а^^ад + ^х; гн (х) = г0 + £2х.
Поэтому
_ у (го + Ъ-*)^ — (Дд + ktx)ks = у rokt-a-)^ (Гр + ^2^)2 (Го + 'М)2
Расчеты несколько упрощаются, если балка симметрична относительно горизонтальной оси или если поперечные сечения принимаются перпендикулярными к одному из поясов балки.
В случае симметрии и при вертикальной нагрузке (фиг. 136) усилия в сечении пп' легко выражаются через изгибающий момент М и поперечную силу Q в этом сечении:
ДГ =_/V =21.= г h cos a
(2.2)
T—Q — 2--sin <х = Q — 2 —tga=Q — —
г h х
Здесь х отсчитывается от точки пересечения поясов.
300
§ 6.3. ПЕРЕМЕЩЕНИЯ ТОНКОСТЕННЫХ БАЛОК С ПАРАЛЛЕЛЬНЫМИ ПОЯСАМИ
При вычислении перемещений тонкостенных конструкций обыч-
но приходится учитывать не только деформацию удлинения, но и
деформацию сдвига. Так, в случае высокой и сравнительно корот-
кой тонкостенной балки прогиб от изгиба (удлинений поясов —
см. фиг. 137, а) и прогиб •от сдвига стенки (фиг. 137,6) будут величинами одного порядка па расстоянии до ЗАч-4/i от заделки, где h — высота балки.
Изгиб обусловливает как поворот поперечных сечений, так и их перемещение; сдвиг прямоугольной стенки — только поступательное перемещение. При учете сдвига угол наклона касательной {dvldx = v') уже не равен углу поворота поперечного сечения <р.
Составим дифференциальное уравнение изогнутой оси балки переменного сечения с учетом деформации сдвига. Компоненты дефор-
Фиг. 137.
маций и перемещений, зависящие- от изгиба, отме-
чаем индексом «из», Полный прогиб
зависящие от сдвша — индексом «сд».
<V==fV -4- <V
и VM3 ' сд
(3.1)
Дифференцируем это
равенство один раз:
(3.1')
Первое слагаемое есть угол поворота от изгиба, второе — не что иное, как относительный сдвиг па уровне оси балки:
О
(3. 2)
В некоторых случаях величине v'cn приписывается значение среднего по высоте балки относительного сдвига или осереднен-ного но площади, исходя из величины потенциальной энергии сдвига *.
* Н. М. Беляев, Сопротивление материалов, гл. XXI, Гостехиздат, 1949. § 132.
301
Для тонкостенной балки вычисление и'сл значительно упрощается и различные трактовки дают совпадающие результаты.
Если пренебречь нормальными напряжениями в поперечных сечениях стенки, погонное касательное усилие по высоте стенки будет иметь постоянное значение:
При постоянной по высоте толщине стенки t = t(x) касательное напряжение также будет постоянным по высоте и равным
X==JL= Л.
t th
Следовательно,
Дифференцируя равенство (3. Г) и принимая во внимание значения вторых производных, получаем
„ М . d Q /г> ,\
V ---------_ J-------------. (3. 4),
El (х) dx Ght(x)
Учитывая, что dQ/dx — ~р (интенсивности распределенной нагрузки), при Gh.t — const получаем
Такой вид имеет дифференциальное уравнение изогнутой оси балки при учете деформации сдвига.
Общий интеграл уравнения (3.4) или уравнения прогибов и углов наклона касательной легко представить в аналитической форме, аналогичной даваемой так называемым графоаналитическим методом, но с добавлением членов, выражающих влияние деформации сдвига:
v' (л) = v' (0) - f di 4- —; (3. 5)
v v .) /?/($) Ght(x) •
о
/ \ , t irw ( M(i)(x—£)di , Q (6) di
•у(л) = г>(0) + т/ (O)x-j + j • (3'6>
Прогиб (3.6) можно трактовать как фиктивный изгибающий момент от двух фиктивных нагрузок: обычной «силовой» фиктивной нагрузки интенсивностью/?ф-~ — и дополнитель-
ной «моментной» фиктивной нагрузки интенсивностью
302
Выражение тангенса угла наклона (3.5) можно истолковать как сумму фиктивной поперечной силы и интенсивности фиктивной моментной нагрузки.
Итак, эпюра v строится как эпюра изгибающих моментов от двух фиктивных нагрузок рф нт'".
Эпюра и' строится, как эпюра поперечных сил от фиктивной нагрузки ординаты которой затем увеличиваются на величину ти.
т
Фиг. 138.
Заметим, что считаем распределенную силовую нагрузку положительной, если она направлена в сторону оси V, т. е. сверху вниз, а моментную считаем положительной, если элементарные внешние моменты тс!^ вращают по часовой стрелке.
Само собою разумеется, что построение эпюр ведется с соблюдением граничных условий для перемещений, т. е: для соответствующим образом закрепленных фиктивных балок, как это подробно излагается в курсах сопротивления материалов. Для простой шариирноопертой) балки опорные условия действительной и фиктивной балок совпадают.
Для иллюстрации на фиг 138 показаны две балки, нагруженные сосредоточенной силой, фиктивные балки с соответствующими фиктивными нагрузками рф и тф и отдельно эпюры прогибов от изгиба и от сдвига. Предлагаем читателю проверить значения прогибов в характерных точках, вычисляя их как изгибающие моменты от фиктивных нагрузок.
303
§ 6.4. КРИВОЛИНЕЙНАЯ БАЛКА С ЦИЛИНДРИЧЕСКОЙ СТЕНКОЙ
Представим себе тонкостенную балку с параллельными поясами, но не с плоской, а с цилиндрической стенкой и соответственно криволинейными поясами (фиг. 139). Стенка и пояса могут быть не криволинейными, а ломаными. Пояса не обязательно должны иметь центр тяжести сечения на средней линии поперечного сечения
костенных сосудов, имеющих
щих давление газа
стенки.
Полученную таким образом конструкцию можно рассматривать с разных точек зрения—как цилиндрическую или призматическую оболочку (панель), подкрепленную шпангоутами (поясами); как два параллельных плоских бруса, соединенных тонкой стенкой, поверхность которой представляет собою боковую поверхность цилиндра или призмы; наконец, как плоский тонкостенный брус, в частности тонкостенный двутавр или швеллер с криволинейной или ломаной осью. В последнем случае роль поясов или шпангоутов играют полки профиля.
Основная гипотеза о работе тонкой, не теряющей устойчивости цилиндрической стенки состоит в том, что напряжения а и т распределены по толщине стенки равномерно. Эта же гипотеза о плоском или безмо-ментном напряженном состоянии принимается в сопротивлении материалов при изучении прочности тон-форму тела вращения и испытываю
и, в частности, цилиндрических котлов. Здесь
задача осложняется тем, что, кроме нормальных' напряжений по площадкам, параллельным образующим и параллельным к касательным к направляющим цилиндра (см. фиг. 139), приходится
иметь дело также с касательными напряжениями.
Вместо касательных напряжений будем оперировать п о г о н-н ы м и касательными у с и л и я м и
q — x-t.
Погонные касательные усилия q, так же как и напряжения т, подчинены закону парности: величины q, действующие в одной точке по взаимно-перпендикулярным площадкам, равны по абсолютной величине. Векторы q направлены либо оба к вершине угла, либо оба от вершины.
304
Из теории тонкостенных сосудов, изучаемой в курсе сопротивления материалов, известно уравнение (1.1), приведенное в гл. IV, которое запишем здесь в следующем виде:*
"ч । °? Р*
Pi Р2
Отсюда можно получить важный вывод для цилиндрической стенки. Учитывая, что р2 = сю, и принимая, что разность давлений р* по обе стороны стенки равна нулю, находим
о„=--0.
Следовательно, нормальные напряжения в сечениях, параллельных образующим, равны пулю. Цилиндрическая стенка криволинейной балки, показанной на фиг. 139, не воспринимает в поперечных сечениях нормальных напряжений. Видно, что гипотеза о работе плоской стенки, которой мы пользовались в гл. II, в случае цилиндрической стенки является следствием допущения о равномерности распределения напряжений по толщине стенки.
Составим теперь два условия равновесия элемента стенки, учитывая малые приращения напряжений (фиг. 139,6).
Результат проектирования на ось и очевиден: параллельное оси и погонное касательное усилие сохраняет постоянное значение вдоль оси z (образующей цилиндра). Учитывая парность погонных касательных усилий, можно сказать, не отмечая направлений, что вдоль одной и той же образующей величины q остаются постоянными. Математически этот результат формулируется так: х
q=q(uY (4.1)
q есть функция только дуговой координаты и и пе зависит от координаты Z.
Составим уравнение £z = 0. Пусть интенсивность роста нормального напряжения равна dcz/dz. Толщину стенки будем считать переменной по направляющей и постоянной вдоль образующей, т. е.
/ = £(«).
Интенсивность роста погонного касательного усилия вдоль оси и пусть будет dqldu.
Уравнение проекций па ось г:
{oz-\---—-dz\-tdu — c tdu -(q-[- — du\dz + qdz = 0, (4. 2)
\ dz j \ du /
откуда
(4.2) dz du
* Отметим, что ио характеру вывода этого уравнения касательные напряжения, по граням элемента с точностью до малых высшего порядка не влияют на его формулировку.
20 425 305
Так как в силу (4. I) dqldu = dqjdu есть величина постоянная для всех точек, принадлежащих одной образующей, то из (4. 2) следует, что и daz/dz есть величина постоянная для всех точек одной образующей. Поэтому и о р м а л ь н о е напряжение сг2 изменяется вдоль образующей по линейному закон у. Следовательно, если известны два значения аг для двух
площадок, расположенных вдоль одной образующей, то эпюра сг2 может быть построена путем прочерчивания прямой По двум орди
натам.
Отсюда, между прочим, следует вывод, что сосредоточенная сила, приложенная к краю цилиндрической стенки вдоль образующей, в поперечном направлении почти не распределяется, а
вызывает значительные напряжения в том волокне, вдоль которо-' го опа действует. Сосредоточенные силы, как правило, должны передаваться через стрингеры, идущие от пояса до пояса (фиг. .140, а), либо при помощи поперечного подкрепления (фиг. 140, б). Конструкция, показанная на фиг. 140, в, не освобождает от перенапряжений и является нерациональной.
Предположим, что цилиндрическая полоса высотой h загруже-
Фиг. 141.
на вдоль криволинейного края распределенной нагрузкой интенсивности р(«) кг/см и сосредоточенными силами Р (фиг. 141).
Примем одно из вертикальных сечений за начальное н обозна-
чим погонное касательное усилие в этом сечении через <?(0). Проектируя на вертикаль (ось z) все силы, действующие на отрезок полосы длиной и, находим
q (0)Рф- jp (it) du — q (и)-h = Q, t*) и О
306
откуда
Lu U
(4.3)
Определение погонного касательного усилия q(u) сводится к нахождению поперечной силы в этом сечении полосы и делению ее на h.
По закону парности вдоль криволинейных краев должны действовать касательные усилия той же погонной интенсивности, как и в вертикальных сечениях.
Фиг. 142.
Если местная нагрузка отсутствует, то
7 (и)— 7(0) = const. (4-3')
Полоса работает в условиях, которые можно назвать обобщенным чистым сдвигом. В этом случае не только вдоль образующих цилиндрической поверхности, но и вдоль направляющих (криволинейных краев) погонное касательное усилие q сохраняет постоянное значение. Постоянное q будет и в том случае, когда вдоль обоих криволинейных краев приложены одинаковые по величине, но противоположные по направлению нагрузки. ,
Состояние обобщенного чистого сдвига цилиндрической стенки делается особенно отчетливым, если представить себе предварительно плоскую стенку, нагруженную постоянным касательным усилием q, а затем стенку перегнуть по прямым, параллельным одному из краев (фиг. 142). Условия равновесия, очевидно, останутся удовлетворенными, так как по линиям перегиба нормальные напряжения отсутствуют. Увеличивая число перегибов, в пределе придем к цилиндрической стенке, работающей на чистый сдвиг.
§ 6.5. ОБРАЗОВАНИЕ БИКОНСТРУКЦИЙ
Перейдем теперь к конструкциям, в которых, с точки зрения статики, может быть реализовано рассмотренное выше напряженное состояние стенки. Простейший пример дает упомянутая выше плоская тонкостенная балка (консоль), нагруженная в плоскости стенки, и затем искривленная но цилиндрической поверхности так, что пояса превращаются в плоские кривые . брусья, заделанные
2С* 307-
одним концом. Очевидно, на пояса передаются сдвигающие усилия от стенки, причем усилия действуют вдоль кривой, совпадающей с осью стенки (средней линией толщины) в плане. Ясно, что пояса должны быть приспособлены к восприятию не только нормальных сил, но и поперечных сил и изгибающих моментов в плоскостях криволинейных краев стенки. На фиг. 143, а показана криволинейная балка, нагруженная силой на свободном конце.
Примем, что пояса оказывают сопротивление изгибу и сдвигу только в горизонтальных плоскостях; тогда поперечная сила будет целиком воспринята стенкой. Погонное касательное усилие в стенке при данной нагрузке будет постоянным:
Пояса нагружаются усилиями, противоположными усилиям криволинейных краев стенки (фиг. 143,6). Определение усилий N, Q, М в поясах, нагруженных сдвигающими усилиями, распределенными вдоль линии, затруднений нс г4редставляет и будет подробно рассмотрено ниже.
Очевидно, для нагрузок, действующих вдоль образующих стенки, а также лежащих в плоскостях обоих поясов, данная конструкция является статически определимой и геометрически неизмсняе-
308
мой. Если необходимо передать силу, нс совпадающую с какой-либо образующей стенки, то стенку и пояса необходимо продолжить в виде отростка или диафрагмы (фиг. 144). То же относится к горизонтальным нагрузкам, не лежащим в плоскости одного из
поясов.
Общее число реакций в заделке равно семи: по три реакции каждого из двух плоских брусьев-поясов и погонное касательное усилие (или поперечная сила) в сечении стенки. Точно так же напряженное состояние • конструкции в любом промежуточном сече-
нии характеризуется семью усилиями.
Криволинейная тонкостенная балка (см. фиг. 143) является представителем обширного класса конструкций, для которых характерно наличие двух расположенных в параллельных плоскостях неизменяемых систем, соединенных тонкой цилиндрической стенкой. Такие системы условимся называть т о н к о-стенными б и к о н с т р у к ц н я-м и. С этой точки зрения рассмотренную выше балку назовем б и консолью.
Из предыдущего ясно, что напряже-
ния в тонкой стенке могут быть опре- . фИг. 144.
делены, если будет известно погонное
касательное усилие в каком-либо одном сечении. Стенка входит в состав биконструкции в качестве элемента, усилия которого в каждом сечении определяются одним параметром. Если на одном прямом крае стенки нет нагрузки вдоль образующей, то на этом крас <7 = 0 и величина </(«) зависит исключительно от местной нагрузки. Второй прямолинейный край обязательно должен быть закреплен опорным стержнем вдоль образующей.
Если оба прямых края стенки не нагружены, то в каком-либо промежуточном сечении должен иметься опорный стержень вдоль образующей, в противном случае нагрузки, параллельные образующим стенки, пс могут быть восприняты.
Как правило, каждая стенка должна быть окаймлена вдоль всех четырех краев. Стержни вдоль прямолинейных краев должны воспринимать нагрузки или реакции, брусья вдоль криволинейных краев (пояса, штангоуты) должны воспринимать касательные усилия,' передаваемые стенкой.
Перейдем к конкретным примерам образования бикопструкций.
На фиг. 145 показана биконструкция в виде двух плоских кривых брусьев с балочным опиранием в своих плоскостях. Брусья соединены тонкой стенкой, идущей непрерывно между краевыми стрингерами. Вдоль одной из образующих стенки расположена подвеска (стенка в этом месте усиливается стрингером). Легко видеть, что вертикальные нагрузки, расположенные по одну сторону от
309
подвески, вызывают усилия в стенке только на участке от нагруженного сечения до подвески. На той же фиг. 145 изображен план биконструкции, причем ось поясов показана сплошной линией, а стенка отмечена пунктиром; подвеска показана кружком на осп стенки. Как и в случае биконсоли, число неизвестных опорных ре-
акций равно семи. Конструкция статически определима.
Тонкая стенка должна быть непрерывной на всем протяжении поясов. Разрез (щель) в стенке допустима, но должна компенсироваться дополнительным опорным стержнем вдоль образующей (подвеской).
Симметричная трехшарнирная биарка (фиг. 146) имеет тонкую ци
линдрическую стенку, прерванную в среднем сечении, зато каждая из половин стенки имеет самостоятельный опорный стержень вдоль крайних образующих (кружки рядом с шарнирами на фасаде биконструкции). Конструкция статически определима. Если уничтожить щель в стенке, сделав ее непрерывной между опорными стержнями АА' и В В',
система становится однажды статически неопределимой.
Пользуясь принципом замены связей (в частности — стенок, стержней), можно, приняв какую-либо из рассмотренных статически определимых биконструкций за исходную, образовывать новые
статически определимые системы. Однако здесь надо соблюдать осторожность.
На фиг. 147 показана бнконструкцня с четырьмя опорными стержнями 1, 2, 3, 4, параллельными образующим стенки, и тремя стержнями I, II, III, не пересекающимися в одной точке и расположенными в плоскости одного из поясов. Если поставить три стержня параллельно образующим стенки и четыре стержня в плоскости пояса, система в целом окажется подвижной (геометрически изме
310
няемой), а закрепленный пояс будет в своей плоскости статически неопределимым.
Важное практическое значение имеют бикопструкции с замкнутой стенкой (тонкостенные кольца). Замыкая стенку, вводим дополнительную связь. /Для сохранения статической определимости следует удалить один из четырех стержней, параллельных образующим стенки. К тому же результату придем, не замыкая стенки, а мысленно сближая ее края и сливая концевые стержни (например, / и 4 — см. фиг. 147) в один стержень.
Фиг. 147.
Итак, для прикрепления биконструкции с замкнутой стенкой необходимо шесть опорных стержней. Пояса должны представлять собою жесткие в своей плоскости системы, например трехшарнирные кольца или рамы.
Схематическое изображение биконструкций. Большинство биконструкций достаточно наглядно изображается в одной плоскости проекций, параллельной плоскостям поясов или основной плоскости. Оси поясов условимся показывать сплошными линиями. Если они не сливаются, то для пояса, ближайшего к наблюдателю, — более жирной линией. Проекцию срединной поверхности стенки (среднюю линию) будем изображать пунктиром. В случае совпадения оси поясов и средней линии они изображаются весьма близкими параллельными линиями.
Если оси поясов совпадают, условия закрепления их, а также нагрузки в своих плоскостях одинаковы, то можно ограничиться вычерчиванием одной оси (см. фиг. 145, 146). В других случаях приходится показывать оба пояса (см. фиг. 147). Шарнир в поясе показывается кружком на оси пояса. Опорная стойка вдоль образующей стенки — кружком на оси стенки или се отростка.
Силы, перпендикулярные к основной плоскости, показываются кружком с точкой или кружком с крестиком — в зависимости от направления силы (к наблюдателю или от наблюдателя). По направлению силы стенка предполагается усиленной стрингером.
311
В случае необходимости стрингеры показываются черными (жирными) точками или профилями.
На чертеже биконструкции указывается- ширина стенки h.
§ 6.6. ОПРЕДЕЛЕНИЕ УСИЛИЙ В БИКОНСТРУКЦИИ
Степка нагружает пояса распределенными вдоль линии касательными усилиями q кГ/см, являющимися для поясов продольной нагрузкой.
Остановимся на случае постоянной интенсивности сдвигающего усилия 7 = const, соответствующем нагружению сосредоточенной силой (см., например, фиг. 143). Покажем, каким образом определяется равнодействующая и момент системы элементарных сил qdu, действующих вдоль кривой и имеющих в каждой точке кривой направление элемента дуги (фиг. 148).
Кривая, вдоль которой действуют силы qdu, представляет собод» в некотором масштабе силовой многоугольник, причем масштаб сил будет: 1 CM = q • т, где т — мае-. штаб длин. Если чертеж сделан в натуральную величину или снабжен размерами, то непосредственно 1 CM = q кГ/см.
Имеем здесь случай плоской системы сил, когда план сил и силовой многоугольник совпадают. Будем называть такую систему сил силовой цепочкой. Силовая цепочка может быть не кривой, а ломаной.
Равнодействующая силовой цепочки АВ, очевидно, параллельна хорде АВ и равна
T = qa,
(6.1)
где а — длина хорды.
Проекция равнодействующей па любую ось х равна умноженной на q проекции хорды на ось:
Т— q-a -cos (a,x) = qa
(6- 2)
Составим выражение момента М силовой цепочки относительно произвольного полюса О. Обозначим перпендикуляр, опущенный из: полюса на касательную к дуге в точке, определяемой дуговой координатой и, через г(и). Тогда
М= j qdu-r(ti) =q [ г (и) du.
АВ АВ
312
Подынтегральное выражение r(u)du есть не что иное, как удвоенная площадь элементарного сектора с вершиной О и дугой du. Обозначим
г (и) du — dQ.
Тогда
M = q\ dQ = qQ. (6.3)
АВ
Здесь Q— удвоенная площадь сектора АОВ.
Зависимость (6. 3) играет исключительно важную роль в теории биконструкций.
Определим положение равнодействующей Т, приравняв момент равнодействующей относительно полюса найденному значению М. Обозначим через d плечо равнодействующей относительно полюса.
Имеем
Td = M.
Принимая во внимание (6.1) и (6.3), найдем
Определение d несколько упрощается, если взять полюс на хорде АВ. Расстояние равнодействующей Т от хорды оказывается равным удвоенной площади сегмента, стягиваемого хордой, деленной на длину хорды, иначе говоря, удвоенному значению средней высоты сегмента. При параболическом сегменте (симметричная парабола второй степени) получаем
d= — f,
3 J
где —стрелка параболы. От вершины параболы равнодействующая отстоит на расстоянии
d— f=—f.
J 3 7
Линия действия равнодействующей заданной силовой цепочки является геометрическим местом точек, относительно которых момент цепочки равен нулю (линия нулевого момента). Площадь сектора с дугой А В и вершиной на этой прямой равна нулю (фиг. 149). При этом участки площади, лежащие по разные стороны дуги, вводятся с разными знаками.
Полезно вспомнить выражение удвоенной площади сектора в полярных координатах
2=|р2(ф)дГф. (6.5)
о
313
Площадь* Й интерпретируется как сумма последовательных площадей элементарных секторов, ометаемых подвижным радиусом-вектором при вращении вокруг полюса. Элементарный угол dip условимся считать положительным при вращении подвижного радиуса-вектора против часовой стрелки и отрицательным — при вращении по часовой стрелке. Примем ОА (фиг. 149) за неподвижный начальный радиус-вектор. Тогда от А цо М приращения площадей будут положительные, на участке rnCDn — отрицательные, на участке пВ снова положительные. В соответствии с этим на фиг. 149 поставлены знаки отдельных участков площади.
Фиг. 149.
Если алгебраическая сумма площадей, заключенных между цепочкой и ее хордой, равна нулю (S-образная цепочка), то линия действия равнодействующей совпадает с хордой.
Особый интерес представляет случай замкнутой силовой цепочки (фиг. 150). Очевидно,
Т=0.
Момент относительно любого полюса имеет постоянное значение, равное
Л4 = <72к> где йк удвоенная площадь, охватываемая замкнутым контуром цепочки.
Таким образом, замкнутая силовая цепочка, как и всякий замкнутый силовой многоугольник, приводит к системе сил, эквивалентной паре. Замкнутая цепочка в виде восьмерки с одинаковыми площадями обоих половиц статически эквивалентна нулю; Т=М = 0.
Полученные результаты можно тотчас же использовать для определения усилий Q, N, М в сечениях поясов биконструкции, а также для определения реакций опор. Заметим, что статика дает
* Речь всюду идет об удвоенных площадях.
314
семь независимых уравнений равновесия биконструкции в целом или ее части. Это будут: три уравнения равновесия одного пояса в его плоскости, три уравнения равновесия другого пояса в его плоскости и уравнение равновесия проекций всех сил на ось, перпендикулярную основной плоскости. В отдельных случаях целесообразно пользоваться и эквивалентной системой шести обычных уравнений равновесия твердого тела и одним дополнительным уравнением равновесия одного из поясов в его плоскости, например уравнением ЕЛ4^=0. Перейдем к конкретным примерам.
Биконсоль. Биконсоль (фиг. 151, а) нагружена сосредоточенной силой Р = 25 кг на свободном конце В. Определим погонные касательные усилия в стенке и усилия N, Q, М в сечениях заделки обоих поясов.
Уравнение £z = 0 дает
Р 9^
а — —= const =— = 2,5 кг/см.
' h Ю
Вертикальная реакция в заделке
VА — —Р= 25 кг.
На фиг. 151,6 стрелками показано направление цепочки сил, передающихся на верхний пояс. Погонная интенсивность цепочки сил 7 = 2,5 кг/см. Нижний пояс нагружен такой же цепочкой, но обратного направления.
Анализируя соотношение между направлениями элементарных сил gdu цепочки верхнего пояса и направления сосредоточенных вертикальных сил Р и V А =—Р по концам, видим, что сила V, направленная в точке А вверх (реакции заделки), эквивалентна источнику, а нагрузка Р на свободном конце, направленная вниз, — эквивалентна стоку, если мысленно уподобить цепочку потоку жидкости, текущему от А к В.
Проекции хорды цепочки сил на направления нормали и касательной к сечению заделки соответственно равны 45 и 60 см. Нормальная и поперечная силы в сечении заделки поэтому равны
N=qax= 2,5-45= 112,5 кг,
Q = ^ = 2,5-60=150 кг.
Изгибающий момент в сечении заделки как момент от цепочки сил равен
/И == 2,5^Д~~ 60-45^ = 7400 кГсм.
Чтобы установить направление вращения момента, проще всего представить себе равнодействующую Т цепочки. Она проходит, очевидно, справа от заделки и направлена параллельно хорде АВ и, следовательно, вращает против часовой стрелки. Следовательно,
315
реактивный опорный момент МА вращает биконсоль по часовой стрелке.
Для нижнего пояса получим те же числовые величины усилий, ио направление их будет противоположное.
Фиг. 151.
Ординаты эпюры М в сечениях верхнего пояса равны (фиг. 151, в).
(и.'), (6.6)
где и' — дуговая координата сечения, считая от точки В,
316
й(м')—значение удвоенной площади сегмента, хорда которого соединяет точку приложения силы Р с исследуемым сечением.
Приблизительный вид эпюры, ординаты которой отложены от общей оси стенки и пояса (полки) со стороны растянутого волокна, показана на фиг. 151, в пунктиром. Эпюры QmN можно построить, проектируя радиусы-векторы из точки В на направления сечения и нормаль к нему..
Предположим, что пас интересует значение опорного момента пояса при различных положениях сил Р вдоль дуги. Исчерпывающий ответ на этот вопрос дается построением и нфл юенты (иначе инфлюептной линии, линии влияния), Инфлюеита представляет собою диаграмму, ординаты которой равны интересующему нас усилию (или другому фактору в зафиксированном сечении), от действия силы Р=1, передвигающейся вдоль определенной линии —• в данном случае вдоль средней линии стенки. Ординаты инфлюенты опорного момента
MA=1-Q(u). (6.7)
Здесь й(и)— удвоенная площадь сегмента с дугой «. Инфлю-ента изображена на фиг. 151, в тонкой сплошной линией.
Итак, эпюра моментов в поясе от действия одной сосредоточенной силы, перпендикулярной основной плоскости, и инфлюенты изгибающего момента в определенном сечении биконсоли, строятся как диаграммы, ординаты которых равны последовательным значениям удвоенных площадей сегментов. В первом случае полюс сегментов совпадает с точкой приложения силы Р, во втором случае он совпадает с центром тяжести исследуемого сечения пояса.
Пусть ось пояса не совпадает со средней линией стенки (фиг. 152). Расчет по существу остается прежним. При определении опорного момента Мл в качестве Й берется удвоенная площадь сектора с полюсом В', заштрихованная на рисунке. При определении NA и QA надо исходить из хорды А'В', соединяющей крайние точки А' (источник VA) и В' (источник Р) силовой цепочки.
Действие местной нагрузки. Сосредоточенные силы, приложенные в различных сечениях биконсоли, вызывают усилия только на участке между точкой приложения силы и заделкой. Коротко можно сказать, что нагрузки действуют на биконсоль только в сторону заделки. Каждая сосредоточенная сила, перпендикулярная основной плоскости, дает начало распределенному сдвигающему усилию интенсивности P/h, создающему нагрузку пояса в виде силовой цепочки между Р и заделкой.
На фиг. 153 показана разветвленная бикопсоль, нагруженная тремя сосредоточенными силами, перпендикулярными основной
317
плоскости. Работа пояса наглядно интерпретируется при помощи гидравлической модели — трубопровода. Сосредоточенные нагрузки можно мысленно представить как два источника с расходами жидкости qi = PJh и q^ — Pilh и один сток с расходом q^P^h. Сосредоточенная реакция в заделке дает сток с расходом —Рз/h. От источников идут потоки по направлению к заделке, от стоков—в обратном направлении (фиг. 153, б, в, г).
При определении усилий разветвленную биконсоль можно заменить тремя биконсолями, имеющими свободные концы в местах приложения сил Р. Разветвленная труба как бы заменяется тремя
г)
Фиг. 153.
трубами без промежуточных источников и стоков, и, следовательно, с постоянными расходами жидкости.
Изгибающие моменты считаем положительными, если растянуты волокна, отмеченные пунктиром. Изгибающий момент в сечении т верхнего пояса
М = — У±Р2. (6.8)
h
В данном случае
(6.9)
Здесь знаки поставлены в соответствии с направлением вращения.
Усилия Q и N также определяются путем суммирования усилий, соответствующих отдельным цепочкам. С этой целью хорды цепочки проектируются на сечение и нормаль к нему, а проекции умножаются на q-
Если биконсоль нагружена распределенной нагрузкой р(и), перпендикулярной основной плоскости, то изгибающий момент в сечении пояса получится путем суммирования действий отдельных элементарных нагрузок р(и) и па основании (6.8) представится интегралом
М= ± — Ср (и) 2 (и) du. h J
(6.10)
318
При равномерно распределенной нагрузке имеем
Ж=-^-js(w) du.
(6.10')
Определение усилий от нагрузки в плоскости пояса делается по правилам статики плоских систем.
Биконструкции с балочным креплением поясов (фиг. 154). От действия сосредоточенной силы Р, приложенной к отростку перпендикулярно основной плоскости, передний пояс нагружается силовой
цепочкой, идущей от Р к опорному стержню С, являющемуся продолжением образующей стенки. Усилие Рс в стержне С равно Р и направлено к наблюдателю. Реакция VА определится из уравнения моментов относительно опорного шарнира В.
~QB+V А1 = (У,
til
Реакция VA логично
действует на пояс в направлении снизу вверх. Ана-
^3=77(сверху вниз).
Горизонтальная реакция согласно уравнению 2Х = 0;
//л= — -ах (слева направо). h
Имея реакции в плоскости пояса и распределенную реакцию
стенки \ q =
•^на участке РС, нетрудно построить эпюры М, N, Q.
Эпюры для заднего пояса получаются такими же, как и для перед-
него, но с измененным знаком.
Биконструкция, прикрепленная четырьмя стержнями 1, 2, 3, 4, перпендикулярными основной плоскости, и тремя стержнями /, II, III, параллельными ей (фиг. 155).
Расчет начинается с определения усилий в стержнях I, 11, III, параллельных основной плоскости. Для этого служат три уравнения моментов относительно трех осей, перпендикулярных основной плоскости и пересекающих каждый раз по два из трех стержней. Если какие-либо два стержня параллельны, то уравнение моментов для определения усилия в третьем стержне заменяется уравнением проекций на ось, лежащую в основной плоскости и перпендикуляр-
319
ную двум параллельным стержням. При нагрузке, перпендикулярной основной плоскости, усилия в стержнях I, II, III равны нулю.
Для определения усилий Vj, V2, V3, в нашем распоряжении имеются три условия равновесия пояса (верхнего) в своей плоскости и уравнение проекций всех сил на ось z, перпендикулярную основной плоскости. '
Чтобы избежать совместного решения уравнений равновесия, поступаем следующим образом. Разрежем три опорных стержня,
например 1, 2, 4, и возместим разрез неизвестными усилиями Vi, V2, 1Д. Так как стержень 3 не разрезан, то пояс оказывается нагруженным тремя силовыми цепочками с неизвестными иптен-сивностями —— и — , h h h
идущими от точек 1, 2, 4 к точке 3, и, кроме того, силовой цепочкой с известной,интенсивностью Р/й от то’\чки приложения силы Р до точки 3. Определяем три равнодействующие силовых цепочек Тп, Т'гз, Т43 по положению, а равнодействующую силовой цепочки Тт3—и по положению и по величине.
Фиг. 155.
Далее определяем Т13, Т23, Т34 по величине. Это можно сделать, например, графически, разложив Ттз по линиям действия указанных трех сил, либо из уравнений моментов относительно точек попарного пересечения сил. Так из уравнения моментов относительно точки С24
находим
откуда
7 13 + ^24 —О,
7- __
13~ ~dx ’
й13 al3d
Здесь под М24 подразумевается момент горизонтальных сил, действующих на верхний пояс, в которые, кроме силы Тт3, могут войти еще и горизонтальные нагрузки пояса, если они имеются. Имея Vi, V2, V4, находим V3, воспользовавшись уравнением проекции на ось Z-.
1Л + и2 + Уз+и4+р-о.
320
Решение допускает различные варианты. В качестве опоры, реакция которой определяется в последнюю очередь, можно взять любую из четырех опор 1, 2, 3, 4. Форма решения получается более симметричной, если за неизвестные принять поперечные силы в стенках Qi2=Vi; Q23=Vi + V2; <3з4 = Pi-j-V2+P3 или пропорциональные им значения погонных касательных усилий 7i2 = Qi2/A; 42 3 = Q2 3/h; qt = Q.3t/h. Эти неизвестные дают три цепочки сил на участках 1—2, 2—3, 3—4.
'4
Фиг. 156. Фиг. 157.
На фиг. 156 показана схема четырехопорпой биконструкции. F12, Т2з, Т34— линии, действия равнодействующих цепочек 1—2, 2—3, 3—4. Чтобы получить линию действия равнодействующей цепочки Тц от Vi при сохранении опоры 3 или 4, достаточно через точку С2 прочертить прямую, параллельную хорде 1—3. Линия действия 7’14 проходит через Ct параллельно хорде 7—4. Прямая С4С3 должна быть параллельной хорде 2—4, что может служить поверкой правильности построения. Отметим, что четырехугольники 1 2 3 4 и Ci С2 С4 представляют собою так называемые взаимные фигуры, известные из графостатики.
Пояс бикоиструкции можно рассматривать как неизменяемый диск, закрепленный в своей плоскости тремя стержнями, не пересекающимися в одной точке. В качестве направлений этих стержней можно Припять любые три непересекающиеся в одной точке прямые, входящие в полный шестистороииик С1С2С3С4. Можно представить себе ряд примеров, когда линии действия трех равнодействующих проходят через одну точку (фиг. 157). Это является признаком мгновенной изменяемости бикоиструкции, делающей ее непригодной для практического применения. Подобные вопросы рассматриваются в теории ферм (см. гл. VIII).
21 425
321
Пример. Построить эпюры усилий в поясах и в стенке для топкостей и ой балки (биконструкции) (фиг. 158).
Усилия в горизонтальных стержнях I, II, III равны нулю.
Ввиду полигонального очертания осн стенки в плане построение равнодействующих цепочек, а также точек моментов для независимого определения реакций опор А, В, С, D очень упрощается. Закрепим опору В.
Чтобы найти- линию действия Т Ав , достаточно через точку Е провести прямую, параллельную Ат (фиг. 159), продолжить прямую Вт до пересечения с предыдущей в точке т'; через точку т' пронести прямую, параллельную хорде АВ. Это и будет линия действия Тлв- Действительно, иаино,и.нс1 чующая цепочка Ат проходит через точку Е параллельно Ат; равнодействующая прямолинейной цепочки тВ сливается с тВ. Поэтому равнодействующая всей цепочки АВ проходит через точку т' пересечения частных равнодействующих.
Фнг. 158.
Равнодействующая цепочки ВС совпадает с прямой ВС. Равнодействующая цепочки CD проходит через точку G параллельно CD.
Определяем точки попарного пересечения равнодействующих ТАВ и Тдс, Твс и TCD’ Тав и 1 CD' Это бУдУт точк» с' и Н- Уравнения моментов, относительно этих точек дают погонные касательные усилия QCD< qAB И qBC' а также реакции D, А, С.
Достаточно найти одну реакцию, например D. Зададимся направлением реакции D к наблюдателю. Тогда силовая цепочка будет направлена от D (источник) к В (сток). Силовая цепочка от силы Р в точке m будет направлена от В (источник) к m (сток).
Уравнение моментов сил, действующих па отрезанный верхний пояс, относительно точки В'
— Q" _ - -Q" -О, h Вт h DB
откуда
Находим
о"'
_ "'Вт
D=P —77Г-
<>К
-DB
= 43-40 = 1720 слР;
Q$B = 143-100 —40-40 = 12 700 см";
D = — — = 0,1352Р.
12 700
322
Реакцию А найдем из уравнения моментов сил, действующих ла- всю биконструкцию, отрезанную от опор, относительно оси ВС.
Л-140 — Р-40 4-0,1352Р-100 = 0, откуда
А = 0,1802В.
Реакцию С определим из уравнения моментов всех сил относительно вертикальной (в плане) оси, проходящей через точку В.
Л-20 —Р-40—С-60—0-100 = 0;
С = — — (0-40 — Л-20 + 0-100)=-------- (Р-40 — 0,1892P-20-f-0,1352Р-100) =
60 60
49 716
—-— = — 0.829Р (вниз).
60
?св
Фиг. 159.
Уравнение проекций на ось, перпендикулярную основной, плоскости, дает В—Р — А—С — D = 1,505Р (вверх).
Три реакции можно также легко определить графически. Для этого достаточно равнодействующую нагрузку пояса, зависящую от заданной нагрузки, т. е. Твгп— -56,6 разложить на три направления Тан, Тсв и ?Db, не пересекающиеся в одной точке. Соответствующее построение показано на фиг. 159, 21* 323
Находим (по масштабу)
^=49,7—; Где =27—; Tdb = 19 —. п п п
Отсюда реакции ,
С = — —- h ------ Р =. — 0.829Р; ас в 60
А = -~ h = ~Р = 0,1891й;
адв 144
п _ Тов . _ 19
аов 140
Р~ 0.135Л
Фиг. 160.
Последняя реакция В определится из уравнения^] 7 = 0.
Эпюра погонных касательных усилии q в стенке строится как эпюра поперечных сил от нагрузок, уменьшенных в h раз. На фиг. 160 нагрузками являются сила Р=1 и четыре реакции А, В, С, D. Принято Л=1. Для получения действительных значений q следует все ординаты эпюры Q = qh умножить на P/h.
Я Am = 0,1892-4;
Л
Л Р Р Р
^8 =0.1892 —-—=-0.8108 —;
Л Л Л
324
O' =—0,8108—' 4- 1,505—= 0,6912 -4- ;
* h h h
<7_n = 0,6942 —-0,829-^-= -0,1348-^ = 0,135-^- .
CD h h h h.
Ординаты эпюры Мл изгибающих моментов верхнего пояса
Л4"=0; МпЕ = 0; Л4" = -ф йАт = 0,1892 41200 = 227 4 ; А ь т h h h
Мпв = 4 Qab - 4QmB = 0,1892 4 6000 - 0 = 1136 4;
D h h h h
APB P „ P
M"c = S,tc - — 2 лс + — Qec = (0,1892-14 400 - 1-2400) — = 324 —.
c h h h h h
Идя от точки D в обратном направлении, убеждаемся в том, что
Mq = -Л4/) = 0,
Полученные ординаты отложены от сжатого волокна.
Ординаты эпюры поперечных сил Qn в плоскости верхнего пояса можно найти как тангенсы углов наклона эпюры М на отдельных участках:
М"-Л4"
QAE — °- QEm — — =-- = 3,78— ; lEm GO h h
MnR~Mnm ОП = —®™ ЧтВ j „ LmB n 324 — 1136 Qbc~ 60 = 1136-227 = 4±, 56,6 h h P P — = — 13,52——; h h
„ 0 — 324 Р
Qcg = —-7Т" = -5 -73 Qod = °-
□0,0 Л
Другой способ определения ординат эпюры Q состоит в проектировании равнодействующей односторонней сдвигающей нагрузки на нормаль к осн пояса. Например, Qbc равна вертикальной (.в плайе) проекции вектора ТВВ (см. фиг. 159)
Ординаты эпюры Af п легко получаются из эпюры q. В угловых точках значения N изменяются скачкообразно. На прямых участках ординаты эпюры .V подчиняются закону прямой. Ординаты обозначаем двумя индексами. Первый индекс показывает угловую точку, второй индекс—.противоположный конец того стержня, к которому относится нормальное усилие:
Л^я = 0; NaFA = - q lAE = -0,18924 ’44,7 =-8,45; fl fl
~Я aJae cos (1Ae> ^Em) — — 0,1892 —-40 = — 7,58— ; fi fi
= -0,1892 4-* 100 = - 18,92“4- ;
h h
NnmB = - 0,1892 4 -56,6 = — 10,7
325
В последнем выражении множитель 56,6 представляет величину проекции ломаной Ат на ось стержня тВ. Определение этой проекции показано на фиг. 159.
Р Р Р
N* = ^"я— ,-56,6-у- 0,1892 -56,6 = 35,2—- ;
та h h h
„ Р Р Р
№г ==—0,1892 —-20+— -40 = 36,22—-;
и h h h
Р Р Р Р
N1' = —0,1892 — -80 + — -100— 1,505 —-60 = — 5,42 — . h h h h
Далее идем от точки D к точке А:
Луф-О; Л/“о = -0,1352-^--60 = -8,11
/V" =—0,1352 — -60-0,707 = -5,74^-; h h
N" = - 0, 1352 (42,4 + 56,6) = — 13,39 — ;
h h
Р Р
N£r = 0,1352 —-40 = — 5,42 — (проверка).
h /г
Эпюры для нижнего пояса будут иметь ординаты той же величины, но обратного знака.
Обратим внимание на то, что при вертикальной нагрузке ординаты всех эпюр, в том числе Qn и М11, обратно пропорциональны высоте конструкции Л. ‘ Умножив все ординаты на h, получаем основные усилия для всего сечения:
Q qh, М — N"h; MK = Qnh.
Естественно ввести в рассмотрение также величину
В = M"h кг см1,
так называемый б и м о м е н т, известную из гл. V.
Эпюры усилий Q, М, Мк, В могут быть при желании построены и независимо от усилий в поясе.
§ 6.7. КОЛЬЦЕВАЯ БИКОНСТРУКЦИЯ
Наметим ход расчета биконструкции с замкнутой (кольцевой) стенкой, прикрепленной тремя стержнями I, II, III, параллельными основной плоскости, и тремя стержнями А, В, С, перпендикулярными к ней (фиг. 161). В данном случае шести стержней для прикрепления достаточно, так как кольцевая биконструкция, отделенная от опор, является неизменяемой системой.
Усилия в стержнях 1, II, III определяются при помощи уравнений моментов относительно вертикальных осей. Усилия в стержнях А, В, С также могут быть найдены независимо при помощи уравнений моментов относительно горизонтальных осей, пересекающих два из трех стержней.
326
Погонные касательные усилия в стенках определяются независимо от реакций А, В, С при помощи условий равновесия пояса, отделенного разрезом, проведенным через стенку. Для этого необходимо построить треугольник линий действия равнодействующих силовых цепочек на участках АВ, ВС, CD. Вершины треугольника обозначены буквами А', В', С'. Пусть, например, верхний пояс загружен парой Лк, силой Т, лежащей в основной плоскости, и силой Р, перпендикулярной основной плоскости в точке пт. Напряженное состояние пояса, помимо нагрузок £к и Т, обусловлено сдвигающи-
Фиг. 161.
ми усилиями, передаваемыми стенками. Эти усилия можно представить как сумму усилия q=P/h на участке Ст и усилий q Ав, qBC, Уса-
Погонное касательное усилие оАВ в стенке АВ определяется из уравнения моментов относительно точки С'. Аналогично из уравнений моментов относительно точек А' и В' найдутся усилия q вс и qCA.
Очевидно, усилия qBC и qCA дают относительно точки С' момент, равный нулю. Поэтому момент усилия qAB относительно С' не изменится, если считать, что !/ля распространяется вдоль всего замкнутого контура, а не только на участке АВ. Но момент постоянного касательного усилия относительно любой точки равен где QK—удвоенная площадь замкнутого контура.
Будем считать момент, вращающий пояс п.р отив часовой стрелки, положительным, а усилие q будем считать положительным, когда оно уравновешивает положительный момент, т. е.
327
создает вращение пояса почасовой стрелке. Уравнение моментов относительно точки С' гласит
4 + ^ ~ &тС Ялв®к~®- (7-1)
Здесь &С'С —удвоенная площадь сектора с дугой тС и вершиной (полюсом) С'.
Аналогичные выражения получим и для qBC и qCA. Если действует только пара LK, то, очевидно, ,
Яав~Явс — Яса ~Я = • (7.2)
Это известная формула (Бредта), играющая большую роль в расчетах авиационных оболочек.
Фиг. 162.
От погонных усилий q легко перейти к поперечным силам в стенках Q = qh. Разности поперечных сил слева и справа от опор А, В, С дают реакции этих опор. В случае одной пары Мк эти реакции, очевидно, равны нулю.
Имея заданную нагрузку пояса и сдвигающие усилия, передаваемые стенкой, нетрудно рассчитать пояс как плоский кривой брус, статически определимый (разрезанный или трехшарнирный) или статически неопределимый (бесшариирный), нагруженный в своей плоскости.
Выведем формулы для кольца, нагруженного четырьмя уравновешенными силами, перпендикулярными основной плоскости (фиг. 162).
Такая система сил, очевидно, получается при нагружении кольца на трех вертикальных опорах сосредоточенной силой. Для получения наиболее симметричных формул обозначим равнодействующие двух сил, направленных в одну сторону, буквой V. Равнодействующая двух сил Vp-f-Vg — V проходит через точку О пересечения диагоналей и направлена вверх; равнодействующая
328
VA-\-Vc —У проходит через ту же точку и направлена вниз. Четыре силы Vд, Vв, Vс, VD выражаются в симметричной форме через обобщенную силу V. По правилу рычага находим
d
Выразим погонные касательные усилия через одно из них, например qDA :
_ , VA V с
Я ав—Я вал — Ява ' >
Л Л а -|- с
, VA , Ув V I с
Явс—Ява^ —Ява~ h i
Л Л п \a-\- с
__ К /. a d \ .
~~У°А Л \ а + с b + d/'
Ясв~Ява + Л + л + л ~
__ V / с d . а \ V b
~ Л \ а + с b+d ‘ а+с J~^DA л ’ b + d '
Приравняем нулю момент усилий, действующих на верхний «-пояс, отсеченный горизонтальной плоскостью относительно точки О:
Ялв^лв “F Явс^вс + Ясв^св + Ява-вл — 0.
(7. 4)
замкнутого
(7-5)
Подставляя сюда значения Яав'Явс* Ясв> выписанные выше, и решая уравнение относительно qDA, получим п V QB'c
где 2K = 2XB-]-2fiC4-2СО 4-—удвоенная площадь контура;
п о । с^лв — а~вс । bQCp~ dQBC иВ’С’ = UBC 4-----ГТТ~..--------’
CL С О "р и
Если стенки АВ, ВС, CD, DA плоские и без отростков (этот случай практически важен в связи с часто встречающимся расчетом прямоугольной коробки с четырьмя стрингерами), то числители дробей в формуле (7. 5) обращаются в нуль, так как ®ав __ ®вс с
и тогда
Sco d
'--вс &
Sb- с
Явл
— ®ВС’ V У-вс Л 2К
(7. 6)
329
•— погонное касательное усилие в стенке пропорционально площади противоположного сектора.
Если точки А, В, С, D расположены в вершинах прямоугольника, т. е. a = b = c = d, то независимо от очертания стенок в плане
2в'С' =-^-(2лв + 2со);
„ _ Е -лв + ‘-'со qDA~ 2Л ~ йк " •
Погонное усилие в стенке пропорционально суммарной площади двух секторов, прилегающих к стенке с боков.
Зная qDA, можно определить Ялв'Явс' Ясо 110 написанным выше формулам. Но можно также непосредственно по формулам (7. 4) и (7.5) найти любое из погонных усилий круговой подстановкой с чередованием знака (так как знаки 1/D, VA, V п, Vc чередуются). Усилия q дают взаимно уравновешивающуюся систему нагрузок пояса, характера двух противоположных пар. Деформация кольцевого пояса в своей плоскости напоминает деформацию сдвига, хотя и реализуется изгибом.
Покажем применение так называемого метода замены связей к расчету четырехопорной открытой биконструкции. '
Предположим, что в кольцевой биконструкции на трех опорах (фиг. 161) введен опорный стержень D, но зато вырезана стенка DA. После того как подробно изучена работа кольцевой системы на действие четырех*сил (фиг. 162), не представляет никаких затруднений определить напряженное состояние открытой системы как суммы двух напряженных состояний:
1) от действия заданной нагрузки,
2) от действия сосредоточенной вертикальной силы Vп, подобранной так, чтобы суммарное погонное касательное усилие в фактически отсутствующей панели стенки было равно нулю. Вместо того чтобы искать силу VD, можно взять за неизвестную величину обобщенной силы V, характеризующей в симметричной форме все компоненты напряженного состояния, в том числе и силу (реакцию) V D.
Пусть, например, биконструкция нагружена парой с моментом Лк в плоскости верхнего пояса, как на фиг. 161. Тогда погонное касательное усилие во всех стенках, в том числе и в стенке DA, будет
От обобщенной силы V имеем
п _ V й^с-qDA h йк
Уравнение^для определения У:
LK V ^-в’с
QK A
азо
откуда
(7. 7)
В'с
Теперь можно найти VA, VB, Vc, qDA. Аналогично решается задача и нагрузке биконструкции.
VD, а также qAB, qBC, qCD, при любой другой заданной
§ 6.8. КРИВОЛИНЕЙНЫЙ ДВУТАВР С ИСЧ ЕЗАЮЩЕ-МАЛ ОЙ ЖЕСТКОСТЬЮ СВОБОДНОГО КРУЧЕНИЯ
Рассмотрим брус малой кривизны с двутавровым профилем, нагруженный перпендикулярно плоскости кривизны. Никаких специальных допущений о работе стенки не вводим. При толщине полок и стенки менее '/го их ширины сопротивление кручению становится
ничтожным, а вместе с тем теряется возможность использования бруса в качестве составной части пространственно нагруженной конструкции при обычных способах опирания. Однако при некоторых условиях крутящий момент может быть целиком воспринят направленными в разные стороны поперечными силами полок в их плоскостях. Этот вид нагружения полок вызывает их изгиб в разные стороны в своих плоскостях. •
Простейший способ прикрепления двутавра, позволяющий реализовать
восприятие крутящего момента изгибом
полок,—полное защемление одного торца, несколько отличающееся от обычного защемления, воспринимающего шесть усилий N, Mz, Му и Qx, Qy, Мк. Чтобы воспринять шесть усилий, достаточно закрепить одну полку тремя связями (стержнями), другую полку двумя связями и стенку — одной связью (фнг. 163,6). Теперь же необходимо и вторую полку закрепить тремя стержнями с тем, чтобы она могла самостоятельно воспринять изгибающий момент в своей плоскости.
Рассматриваемый здесь способ восприятия крутящих пар носит название изгиб и о го или стесненного кручения. В более широкой постановке этот вопрос рассматривался в гл. V. Здесь же мы ставим лишь задачу по-другому осветить полученные выше результаты для биконструкций.
331
Обозначим поперечную силу изгиба верхнего пояса в своей плоскости через Q11 (см. фиг. 163, а). При вертикальной нагрузке поперечная сила нижнего пояса равна —Qn. Пусть h есть плечо пары, образуемой силами Q11 и —Qn (высота балки между осями полок). Эквивалентность крутящего момента и момента пары поперечных сил выражается равенством
MK=Q"h. (8.1)
Определим изгибающие моменты в плоскостях поясов. Обозначим момент в верхнем поясе через Л4". При вертикальной нагрузке общий момент в горизонтальной плоскости Мг = 0, поэтому изгибающий момент нижнего пояса равен —Мц.
По известной из курса сопротивления материалов теореме имеем-
=Qn(H). (8.2)
du
Через и обозначена дуговая координата, измеряемая по оси пояса балки в плане. Отметим, что в рассматриваемом случае ось балки в плане, ось пояса и ось, относительно которой вычисляются крутящие моменты, совпадают.
Из (8.2) следует известная интегральная зависимость, позволяющая определить изгибающий момент как сумму момента в начальном сечении и площади эпюры поперечных сил на участке между начальным и исследуемым сечением:
Мп (a1) = Afn(O) + j’Q"(«)rf«- (8.3)
В этом выражении достаточно заменить Qn (и) на -у-714к(и), чтобы получить интересующее нас значение изгибающего момента в поясе, выраженное через крутящие моменты.
Умножим величину изгибающего момента на h и назовем полученную величину бимоментом. Бимомент можно рассматривать как некоторый аналог пары, но не сил, а моментов. Бимомепт обозначается буквой В и выражается, очевидно, в кг • см2.
Итак,
5(w) = W(w). (8.4)
Учитывая равенства (8. 1), (8. 2), (8. 3), отсюда находим
^-^=Л4К(М); (8.5)
В (и{) *= В (0) 4- j2WK(w) du. (8.6)
о
Очевидно, что соотношение между бимоментом и крутящим моментом такое же, как между изгибающим моментом и поперечной 332
силой. Крутящий момент равен производной от бимомента, эпюра бимоментов есть интегральная кривая от эпюры крутящих моментов. Равенство (8. 6) позволяет в каждом отдельном случае определить бимомепт, а следовательно, и изгибающий момент пояса, если предварительно найдены крутящие моменты.
Бимомент можно рассматривать как обобщенную внутреннюю силу или усилие, характеризующее наряду с шестью обычными усилиями напряженное состояние в сечении тонкостенного двухпоясного бруса с исчезающе малой жесткостью свободного кручения. Таким образом, общее число усилий в сечении'данного своеобразного бруса равно семи. Конструкции этого рода называем б и к о н с т р у к ц и я м и. Тонкостенная консоль, иначе б и к о и с о л ь, должна быть закреплена так, чтобы могли развиться семь опорных реакций. Поэтому обязательно оба пояса в концевом сечении должны быть защемлены и стенка должна быть закреплена против сдвига.
Отметим, что величины крутящих моментов, а следовательно, и бимоментов не изменятся, если все поперечные сечения балки повернуть на некоторые (одинаковые или неодинаковые — безразлично) углы вокруг продольной оси. Балка может иметь естественно завитую ось. Кроме того, величина бимомента не зависит от размеров поперечного сечения, балка может иметь переменное по длине сечение.
Рассмотрим случай нагрузки биконсоли одной сосредоточенной силой (фиг. 163). Пусть требуется определить бимомент в сечении т. Проведем в сечении и между I и т подвижные оси: ось касательную к оси балки, и ось т], перпендикулярную ей. Крутящий момент в сечении и от силы Рг- равен
Мк(и) = Р^(и). (8.7)
Здесь через т](и) обозначена длина перпендикуляра из точки I на ось £.
Подставляя значение Л4к(ц) в интегральное выражение бимомента (8. 6) и принимая во внимание, что левее сечения I бикоп-соль не нагружена, найдем
“я.
вт = р1 (8.8)
Но Y[(u)du есть не что иное, как удвоенная площадь элементарного сектора, показанного черным на фиг. 163. Поэтому интеграл равен удвоенной площади сегмента с дугой 1т. Обозначим эту удвоенную площадь через Q,m.
Итак,
Вт==Р£1т, (8.8')
следовательно, бимомент равен вертикальной силе, умноженной на удвоенную площадь сегмента, образованного дугой между точкой i
333
приложения силы и точкой т, принадлежащей исследуемому сучению, и хордой im.
Бимоменту условимся приписывать тот же знак, что щ изгибающему моменту верхнего пояса, если рассматривать пояс сверху как обыкновенный плоский кривой брус и пользоваться балочным правилом знаков. Запомним, что бимомент получается положительным, если сила направлена вверх и площадь сегмента при движении от силы к сечению лежит слева от хорды (как на фиг. 163).
Фиг. 164.
На фиг. 164, а показана эпюра бимоментов консоли от действия силы Р=1, направленной вверх. Последовательные ординаты эпюры равны удвоенным площадям сегментов, стягиваемых хордами, соединяющими точку приложения силы с исследуемой точкой. Ординаты й вычисляются путем суммирования удвоенных площадей элементарных секторов шаг за шагом от точки i к заделке.
На фиг. 164,6 построена инфлюента (линия влияния) бимомента в сечении т от движущегося вертикального единичного груза, направленного вверх. Очевидно, ординаты инфлюенты также равны удвоенным площадям сегментов. Здесь целесообразно двигаться от сечения т к свободному концу консоли и суммировать элементарные секторы с полюсом в точке т. Ординаты инфлюенты получаются положительными, если площади сегментов лежат справа от хорды.
При вычислении бимомента по формуле (8. 8') можно рассматривать величину Qfm как «координату» или «плечо» исследуемой точки т по отношению к точке приложения силы i. В этом случае площадь считается положительной, если дуга лежит левее хорды, идущей от I к т.
334
С другой стороны, Q можно считать «координатой» или «плечом» точки I приложения вертикальной силы по отношению к исследуемой точке т. Тогда площадь придется считать положительной, если она лежит справа от хорды, идущей от т к I.
Заметим, что эпюра и иифлюента на фиг. 164 показаны в известной мере условно: каждая из них является разверткой боковой поверхности прямого вертикального цилиндра, образующие которого (аппликаты) равны значениям Q. Поэтому точная форма состоит из ряда трапеций с криволинейными боками.
Pj
Фиг. 165.
В случае нескольких вертикальных сил бимомент вычисляется как сумма бимоментов, обусловленных каждой силой в отдельности.
На фиг. 165, а показана разветвленная биконсоль, нагруженная силами в точках j и I. Площадь, заключенная между хордой itn и осью балки, имеет участки двух знаков. Приписывая положительный знак площадям, лежащим слева от хорды, при движении от силы к заделке, получим
im hm im
Здесь Qitm — удвоенная площадь криволинейного сегмента; Пип — удвоенная площадь треугольника ikin.
Бимомент в сечении заделки равен
В — PQ. — PQ .
Отрицательный знак перед вторым членом взят в соответствии с направлением силы Pt вниз.
Перейдем к другим случаям закрепления.
Предположим, что балка имеет три вертикальные опоры и нагружена вертикальной силой. В таком случае горизонтальные реакции равны нулю, а три вертикальные реакции легко определяются из уравнений моментов относительно горизонтальных осей,
335
пересекающих каждый раз два опорных стержня. Однако система, вообще говоря,* не будет находиться в равновесии, так как бимомент в торцовом сечении только в частном случае окажется равным нулю. Необходимо обеспечить восприятие бимомента либо на одном из двух торцов, либо на торце произвольного отростка, примыкающего в любом сечении к нашей балке. Имея опорные реакции, нетрудно определить и реактивный бимомент как сумму произведений сил и реакций на соответствующие удвоенные площади сегментов. Защемление, воспринимающее бимомент, является седьмой связью, необходимой для закрепления биконструкции.
Бимоментное защемление можно заменить четвертой вертикальной опорой. Дополнительное уравнение равновесия, дающее возможность определить четвертую реакцию, напишем как условие равенства нулю бимомента на торце отростка с произвольной формой оси в плане, примыкающего в произвольном сечении к нашей балке. Само собой разумеется, что для составления этого уравнения приходится дополнительный отросток изобразить, так как без этого невозможно вычислить удвоенные площади Q. Указанное равенство нулю бимомента иа торце отростка можно интерпретировать как седьмое условие равновесия биконструкции—.условие равновесия бимоментов относительно произвольного полюса т:
или при вертикальных силах
М=°. (8.9)
i
Здесь бимомепты выступают в качестве внешних силовых факторов. Удвоенные площади сегментов Q играют роль плеч при вычислении моментов.
Произвольно выбирая полюс бимомснтов, можно существенно упростить определение реакций.
В дальнейшем будем считать отросток, на котором выбирается полюс, прямолинейным.
Введем понятие о прямой нулевого бимомента. Предположим, что биконсоль, состоящая из криволинейной
336
части АВ и прямолинейной Вт, защемлена в точке т (фиг. 166). Если точка т взята на таком расстоянии гАВ от хорды АВ, что площадь сегмента АВ равна площади треугольника тАВ, или, иначе говоря, площадь сектора тАВ равна нулю, то бимомент Вт от нагрузки в точке А обращается в нуль. Кроме того, он равен нулю и от нагрузки в точке В.
Очевидно, расстояние гАВ равно
= (8.10)
алв
где Q—удвоенная площадь сегмента АВ-, аАВ— длина хорды АВ.
Прямая, параллельная хорде АВ и отстоящая от нее со стороны сегмента на расстоянии гАВ, является герметическим местом полюсов, относительно которых бимоменты от РА и Рв равны нулю. Эту прямую и будем называть прямой нулевого б и-мо мента для дуги АВ. Она обозначена (А—В). Очевидно, прямая нулевого бимомента представляет собой линию действия равнодействующей ТАВ касательных усилий q вдоль дуги АВ.
Когда построена прямая нулевого бимомента, то упрощается определение бимомента относительно полюса п, лежащего на любом прямолинейном отростке, например Вп:
Bn~PAaABd. (8.11)
Здесь d — длина перпендикуляра из полюса п на прямую нулевого бимомента. В самом деле,
Вп—РА (2Лд4-2 пл. ДЛВ/г).
Но
®АВ ~ аАВГАВ1 2 пл. /\АВп = aAB(d ГАВ).
Отсюда находим выражение (8.11).
Повторим решение задачи определения четырех реакций вертикальных опор тонкостенной балки со свободными концами, пользуясь понятием бимомента (фиг. 167).
План оси криволинейной балки показан на фиг. 167. Опоры, вынесенные на отростках, отмечены кружками 1, 2, 3, 4. Сила Р действует в точке I. Прежде всего определяем положение -прямых нулевого бимомента для дуг 1—2, 2—3, 3—4. Эти прямые параллельны хордам 1—2, 2—3, 3—4 и отстоят от них на расстояниях ri2 = HI2/ai2, <23 = ^23/023, /'34 = ^34/034, где знаменатели равны хордам, а числители — удвоенным площадям сегментов, стягиваемых одноименными хордами.
Пусть требуется определить реакцию Z4. Выберем за полюс при составлении уравнения равновесия бимомеитов точку т4 пересечения прямых нулевого бимомента для дуг 1—2 и 2—3. В качестве оси отростка, которому должна принадлежать точка т4, возьмем прямую т42.
337
Очевидно, бимоменты в точке т4 от реакций Z2 и Z3 равны нулю. I
В уравнение равновесия бимоментов войдут только бимоменты от силы Р и от реакции Z4.
Бимомент от силы Р равен PQim4, где Qim4 — удвоенная величина площади левого заштрихованного сегмента с хордой 1т4. Этот сегмент можно трактовать и как сектор с дугой 12 и полюсом т4.
Фиг. 167.
Бимомент от силы Р имеет знак «Н-», так как площадь сегмента, хотя и лежит справа от хорды, но сила направлена вниз. Следовательно, (—)•(—) = ( + )•
Бимомент от реакции равен по абсолютной величине
^4^4т< -^4а34^34-
Для определения знака заметим, что удвоенная площадь S4,Zi< сегмента с хордой 4/и4 и дугой 42т4 равна удвоенной площади сегмента с той же хордой, но с дугой 43т4, так как разность между этими двумя площадями (сегмент с хордой Зт4) равна нулю по свойству прямой нулевого бимомента, на которой лежит полюс т.
Предположим, что сила Z4 направлена вверх. Площадь лежит правее хорды 4нг, следовательно, бимомент от Z4 имеет знак «—».
Уравнение равновесия бимоментов гласит
PQlm,-Z,a3td3i=0, (8.12)
откуда
Z4=P-^- . (8. 13)
азД.34
338
Аналогично из независимых уравнений определяются и другие реакции, нужно лишь в каждом отдельном случае правильно назначить полюс. и отросток.
Так, для нахождения Z2 следует взять полюс в точке пересечения прямых нулевого бимомента для дуг 3—4 и 1—3. Первая прямая уже построена. Легко видеть, что вторая прямая, параллельная хорде 1—3, проходит через точку т4. Искомый полюс обо-
значен ш2.
Следует заметить, что можно ограничиться определением одной реакции из уравнения бимоментов. Остальные могут быть найдены из уравнений моментов. После того
как найдены три реакции, можно определить четвертую из уравнения проекций на вертикальную ось.
После того как подсчитаны реакции, определение усилий в любом сечении не представляет затруднений.
Другие случаи нагружения. Мы рассмотрели случай нагрузки вертикальными силами. Остановимся коротко на вычислении бимоментов от нагрузки сосредоточенной парой в вертикальной плоскости и сосредоточенным бимоментом.
Пара L в вертикальной плоскости может быть передана тонкостенной балке при помощи диафрагмы или тонкостенного отростка. В плане отросток изобразится отрезком, примыкающим под тем или иным углом к оси балки (фиг. 168).
Заменим пару двумя вертикальными, равными по величине, ио противоположными но направлению силами. Если расстояние между силами обозначить через с, то каждая сила должна быть взята равной Lie. Бимомент в сечении т
вп-~ С
(8. 14)
где Ай — удвоенная площадь треугольника, заштрихованного на фиг. 168.
Так как &Q — cr, то
Bm = Lr. (8. 15)
Бимомент определяется как изгибающий момент от силы, численно равной внешнему сосредоточенному моменту. Сила эта имеет направление, изображенное пунктирной стрелкой L на фиЕ 168.
Под нагружением тонкостенной балки сосредоточенным бимоментом подразумевается нагружение двумя равными и противоположными парами в одном сечении. Пары могут действовать каждая в плоскости одного из поясов. Если величина сосредото-
22* 339
ценного бимомента равна В, то каждая из пар равна BJh, где Л — расстояние между осями поясов (полок).
Пары можно считать действующими в плоскостях двух бесконечно близких параллельных диафрагм. В этом случае каждой из пар следует приписать бесконечно большую величину, произведение которой на бесконечно малое расстояние равно заданной величине В.
Если бимомент от действия сосредоточенного момента в плоскости вертикальной диафрагмы определяется как момент от силы, численно равной моменту, то бимомент от действия сосредоточенного бимомента определяется как момент от сосредоточенной пары (см. дуговую пунктирную стрелку В на фиг. 168).
Итак, мы убедились, что путь, основанный на рассмотрении касательных усилий в стенке, не воспринимающей нормальных напряжений, и непосредственное изучение работы двутаврового профиля с исчезающе малой жесткостью кручения, приводит К одинаковым результатам. Оказывается, что биконструкция и тонкостенный двутавр в известном смысле моделируют криволинейный брус с любым открытым тонкостенным профилем. Этот вопрос рассмотрен в книге автора «Пространственные системы».
Глава VII
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ И РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ТОНКОСТЕННЫХ КОНСТРУКЦИЙ ПО МЕТОДУ СИЛ
В настоящей главе рассматриваются статически определимые и неопределимые конструкции, состоящие из стержней и тонких стенок, причем для упрощения расчета принимается, что стенки работают «только па сдвиг» (см. конец § 6. 1 и § 6. 2). Для определения перемещений целесообразно пользоваться методом, основанным на начале возможных перемещений, учитывая при этом как растяжение и сжатие поясов, так и сдвиг стенки, а в отдельных случаях также изгиб поясов. Для определения лишних неизвестных статически неопределимых систем пользуемся методом сил.
§ 7.1. ПЕРЕМЕЩЕНИЯ (ПРОГИБЫ, УГЛЫ ПОВОРОТА) ТОНКОСТЕННЫХ БАЛОК С НЕПАРАЛЛЕЛЬНЫМИ ПОЯСАМИ
В дальнейшем через Т будем обозначать сдвигающее усилие стенки и считать, что оно по высоте распределяется равномерно, так что при толщине стенки, постоянной для данного сечения х, имеем постоянное по высоте касательное напряжение
--JL м’
Интеграл, дающий составляющую перемещения, зависящую от касательных напряжений, имеет вид
СТТ dx _ С ТТ dx
J GACT J Ght
i
Для перемещений тонкостенной балки или системы балок получаем формулу
, С NN dx , С ТТ dx ,, ,,
Д = 1 —:------ | . (1. 1)
J EF 1 J GM
341
В случае, когда тонкостенная конструкция составлена из элементов, имеющих постоянную жесткость (Е»Гг- = const; G,7,- = const), формула (1.1) принимает вид
<ь2)
i i
Определим угол поворота и прогиб на конце симметричной по форме консоли переменной высоты, загруженной одной силой Р (фиг. 169). Толщину стенки принимаем постоянной. Площади верхнего и нижнего поясов соответственно Fa и FH.
Начало координат поместим в точке О пересечения' поясов. Плечо усилия пояса
/г' (л) = 2 х tg a COS а.— 2 X Sin а.
Усилия в поясах в функции расстояния х (уравнения эпюры N):
/Ув (Л) = Р(х~д); N„ (х) = -.
2 X sin а 2 X sin а
Сдвигающее усилие в стенке находим из уравнения моментов относительно точки О:
Т(х)=-^.
Высота стенки в сечении х\
А (л) = 2х tga.
Усилия от нагрузки силой Р=1 (уравнение эпюры N):
ЛГ(х) = -2^; Т(х)=-^.
2х sin а 2х sm а -X
342
Прогиб по формуле перемещений (1. 1):
= •—? ...(— 4- -Л‘dx4
E-4sin2a \ЛВ /•'„ / J Л2
Ра?
2Gt tg
l + a
_ С dx_ а J X3 а
Отсюда
, Р / 1 . 1 \/, / + 2а , п . а \ .
ДаР =-----------------Z---------к 2а In---- 4-
аР 4£sin2a \ЛВ Лн /\ /4-« 1 + а) '
। Рд2 I 1+2а
1 2Gttg а 2 а2 (/ + а)2
(1.3)
Усилия от нагрузки парой М = 1 на конце, вращающейся против часовой стрелки:
(V,W=-^ ; /v;i(x)=-v4— ; .
2xsina zxsina X
Наклон касательной к упругой линии на свободном конце:
Р
^аР -----------
4£sin2 а
- р
4£sin2 а \ЛВ Лн / \ а
1+а
Ра Р dx 2Gt tg a J Л3 а
Отсюда
I
1-\-а
Ра 1(1 +2а)
2Gitga 2(/ + а)2а2
(1-4)
Входящие сюда натуральные логарифмы берутся из таблиц, либо вычисляются суммированием достаточного числа членов одного из следующих бесконечных рядов:
,. . ZZ2 , и3 и4 .
1) п х — и------------------р • . . ,
’ 2 3 4 1
где u = x— 1, причем —
2) 1пх = 2Г.у4-4 + т+т4- ’ • ]’ 3 5 / J
где у —
причем х>0.
Дйр
а
г2 гЗ z4
3) 1пх=г-)---------•-(——+ . . . ,
2 3 4
где г —
. 1
, причем х —
343
§ 7.2. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ТОНКОСТЕННОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ С ПРЯМОУГОЛЬНЫМИ ГРАНЯМИ
Показанная на фиг. 170, а ферма с одной открытой гранью геометрически неизменяема и статически определима. Заменим раскосы тонкими стенками и будем считать, что между стенками
Фиг. 170.
ниях диска эта замена не отражается.
и стержнями возникают только сдвигающие силы взаимодействия. Полученная система при узловой нагрузке также будет геометрически неизменяемой и статически определимой в отношении нормальных усилий в стержнях вблизи узлов и результирующих сдвигающих усилий (фиг. 170,6).
Приняв допущение, что нормальные напряжения в поперечных сечениях боковых стенок отсутствуют, заключим, что стенки работают в условиях чистого сдвига, причем от стенок на пояса передаются равномерии распределенные сдвигающие усилия q постоянной величины для каждой отдельной стенки.
Введем следующие упрощения: 1) систему будем считать симметричной относительно горизонтальной плоскости, 2) торцовый диск (нервюру) А В А'В' будем считать недеформируе-мым в своей плоскости.
Поставим себе зада-
чей изучить перемещения торцовой нервюры от действия сил, приложенных в ее же плоскости. Так как нервюра в своей плоскости эквивалентна твердому телу, то любую систему сил можно заменить статнчески-эквивалентной системой— двумя составляющими по произвольным координатным осям и моментом относительно начала координат. На перемеще-
344
Начнем с выяснения действия пары в плоскости нервюры. Момент пары М\ примем равным единице и направим пару против часовой-СТрелки. Пара вызывает в горизонтальных стенках АВАВ и А'В'А'В' поперечные усилия 7'i=±l//i; в вертикальной стенке ВВ'ВВ' поперечное усилие равно нулю. Погонные касательные усилия в полках равны
b ~ bh
Нормальные усилия в стержнях нарастают по линейному закону от ^=0 в сечении нервюры до = = ±— в сечении за-
bh
дел ки.
По формуле (1.1) для .перемещений угол поворота нервюры от единичного момента в своей плоскости
°п
о
2
2_/_1_ , Д_
ЗЕ \Fa Ад
/з
/?2/г2
о
2/
GtfltBb
(2. 1>
Определим теперь поступательные перемещения в плоскости нервюры.
Горизонтальную ось х в плоскости нервюры совместим с осью симметрии- Вертикальную ось у направим вдоль стенки ВВ' (вверх).
Для отыскания перемещений точки, совпадающей с началом координат О вдоль оси х (перемещение 32i) и вдоль оси у (перемещение 831), нагрузим систему единичной силой Р2=1 вдоль оси х, затем силой Р3— 1 вдоль оси у.
Напряженное состояние от Р2=1 является симметричным, а от пары — антисимметричным. Поэтому сразу можно написать
иначе говоря, точки, лежащие на оси симметрии х, от действия пары перемещаются только перпендикулярно оси.
От силы Рз=1 работает только вертикальная стенка и пояса ВВ и В'В'. Поперечная сила (сдвигающее усилие) в стенке Гз=1-Усилия в поясах изменяются по линейному закону от А/3 = 0 у нервюры до W3 = ^l/h. у заделки.
Найдем вертикальное перемещение 8-31 точки О от пары:
s + =_____(2. 2)
J1 J EF 'J Ghth 3EF3b№
Знак минус показывает, что точка О от действия пары, вращающей нервюру против часовой стрелки, смещается вниз.
345-
Нетрудно определить положение мгновенного центра С упругого поворота нервюры, нагруженной парой. Очевидно, точка С лежит на оси Ох.
Составим уравнение, выражающее, что вертикальное перемещение точки С равно нулю. Пусть хс— абсцисса точки С.
Простые геометрические соображения дают
oCI = S11xc-|-oJ3=0. (2.3)
Отсюда, принимая во внимание (2. 1) и (2.2), получаем
2 /з
в13 __________3£АД __________
8,1 2 / 1 1 \ /3 21
ЗЕ \Ад +Лд/&2Л2+ Gft2&ZB
=ь_______1_____
1 + ^. + 3A^_2i
A G Иа Р
(2. 4)
При возрастании отношения l/Ь абсцисса хс быстро стремится к пределу
limxc = Z>——. (2.5)
С Fa + Fb
Наоборот, если отношение l/Ь уменьшается, то хс стремится к нулю.
Таким образом, центр вращения нервюры от действия пары всегда лежит между вертикальной стенкой и точкой справа от стенки, абсцисса которой определяется формулой (2.5).
Найдем угол поворота нервюры от вертикальной силы Р = \, проходящей через произвольную точку т на оси Ох. На основании теоремы взаимности перемещений искомая величина 0 =6im равна прогибу (вертикальному перемещению) точки т от пары L= 1;
— ^тГ
Но диаграмма прогибов от Т=1, очевидно, представляет собою прямую, проходящую через точку С и наклоненную к оси х на угол, тангенс которого равен 6ц. Таким образом, линия влияния угла поворота нервюры от действия единичной вертикальной силы получается также в виде прямой, пересекающей ось х в точке С. Вертикальная сила в точке С не вызывает вращения нервюры в своей плоскости. Так как сила, направленная вдоль оси Ох, также не вызывает вращения нервюры, то ясно, что и всякая наклонная сила, проходящая через С, вызовет только поступательное перемещение.
34(5
Перейдем к определению вертикальных перемещений нервюры от вертикальных же сил. Сила, приложенная в точке О, вызывает вертикальный прогиб в том же месте, равный
^зз
k-F в J о
1___(
Ghth J о
2 /з .____I
3EFB /fi ' GMk
l^dz =
(2. 6)
Обозначим через 8СС прогиб точки С от единичной силы, приложенной в той же точке. Легко сообразить, что между 833, 8И и Зсс существует следующая зависи-
мость:
^33=^cc + ^nxc' (^’
Для этого достаточно учесть, что сила Р=1 в точке О эквивалентна силе Р=1 в точке С и паре с моментом L = = 1 -хс. Из (2.7) находим
^сс = ^зз °11-лсс* (2- 8)
Точка С обладает тем свойством, что прогиб по направлению вертикальной силы, приложенной в той же точке, имеет минимальное значение.
Эпюра прогибов от силы Р= 1 в точке С, очевидно, представляет собою прямую, параллельную оси. С этой эпюрой совпадает линия влияния прогиба для вертикальных единичных сил в произвольной точке оси
Фиг. 171.
(фиг. 171).
Имея положение точки С и зная величины Зсс и 3ц, можно определить прогиб в любой точке К от произвольной нагрузки нервюры. Достаточно нагрузку заменить статически эквивалентными силой в точке С и парой (моментом относительно точки С). Сила вызывает поступательное перемещение нервюры; пара — вращение. Пусть £—плечо интересующей нас точки, отсчитанное от С. Тогда прогиб в этой точке получится как сумма поступатель-
ного перемещения и перемещения от поворота:
o=P8cc-|-£8nt
(2.9)
Пользуясь выражением (2.9), нетрудно построить ипфлюенту (линию влияния) прогиба любой точки К нервюры при перемещении единичной вертикальной силы вдоль оси х. Все линии влияния имеют вид прямых, различным образом наклоненных к оси Ох. Ордината каждой линии влияния в точке С одна и та же, равная Зсс.
347
Мы рассмотрели вопрос о перемещениях нервюры в своей плоскости. Необходимо обратить внимание на то, что в результате удлинений и укорочений поясных стержней плоскость нервюры несколько искажается, или, как говорят, происходит депланация нервюры. Депланация характеризуется выходом одной точки, например А, из плоскости трех остальных (А', В, В').
§ 7.3. ПРОСТЕЙШИЕ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
Ограничимся здесь рассмотрением статически неопределимых тонкостенных конструкций с прямоугольными стенками, и стерж
нями, соединенными в углах при помощи шарниров.
Можно считать, что при узловой нагрузке стенки в такой коист-х рукции работают в условиях чис-
Фиг. 172.
того сдвига, причем погонное касательное усилие в продольных и поперечных сечениях каждого отдельного прямоугольника сохраняет постоянное значение. Стержни испытывают растяжение или сжатие нормальными силами, изменяющимися по линейному закону. Эпюрой N является трапеция (фиг. 172).
Составим для этого случая выражение перемещения, воспользовавшись правилом перемноже-
ния эпюр. __
Разбив каждую из трапецеидальных эпюр N и N на два тре
угольника, находим
[ NNdx=( \nb=
= [(2/Ул + NB) Na + (2NBNa) Nb].
Величины N и N можно при желании поменять местами.
Перемножаем эпюры сдвигающих сил, являющихся, очевидно, прямоугольными:
J TTdx — ^qh-qh dx=h?lqq = qqfli, i i
где f — площадь стенки длиной I и высотой h.
Учитывая, что площадь сечения стенки равна ht, получаем общую формулу для перемещения, зависящего от деформаций т стержней и п стенок:
т п
348
При более сложных эпюрах N и q приходится пользоваться формулой в общем виде:
д pWrfx.fitf (3.2)
х J ЕР 1 J Gt '
‘ /
Здесь / — площадь стенки,
df — элемент площади стенки.
Расчет по методу сил статически неопределимых систем из стержней и пластин, работающих в условиях чистого сдвига, как всегда, сводится к выбору основной системы и неизвестных, а затем составлению и решению системы канонических уравнений.
Степень статической неопределимости проще всего устанавливается путем сравнения с пространственной фермой, которая получается, если все четырехугольные стенки заменить раскосами.
В качестве неизвестных могут быть взяты погонные касательные усилия в отдельных стенках, нормальные усилия в поперечных сечениях стержней, а также линейные комбинации усилий — групповые силы. Неизвестные находятся из системы канонических уравнений.
Свободные члены и коэффициенты канонических уравнений вычисляются по формулам (3.1) или (3.2).
Пример комбинированной системы
Па фиг. 173 показана пространственная система, состоящая из двух параллельных тонкостенных консолей, соединенных продольными и поперечными связями из стержней. Конструкция дважды статически неопределима. В качестве неизвестных выбираем усилия внутренних раскосов Xi и Х2.
От заданной нагрузки в основной системе работает только передняя балка. Эпюра NP строится без затруднений.
От действия усилия Л) = 1 работает первый (корневой) отсек пространственной фермы. На балки передаются вертикальные силы +'l sin а. Соответствующие эпюры даны на фиг. 173. На верхнюю и нижнюю стержневые фермы передаются горизонтальные силы H_cos а. От этих нагрузок общие пояса вертикальных и горизонтальных ферм получают дополнительные нормальные усилия, которые должны быть алгебраически просуммированы с усилиями N\. Аналогично выясняется работа системы от сил Х2=1.
Дальнейшее вычисление коэффициентов канонических уравнений делается по известным правилам. Заметим, что интегралы для стержней, к которым не примыкает стенка, заменяются суммами
ЕЁ'
Рассмотрим еще три примера, на которых выясним типичный для многих авиационных конструкций метод выбора лишних неизвестных.
349
Замкнутый тонкостенный параллелепипед (неизменяемая система), прикрепленный семью опорными стержнями (фиг. 174).
Данная система однократно статически неопределима.
Не фиксируя пока определенной основной системы, заметим, что сила Pi может быть уравновешена усилиями опорных стержней Л^з, Л^, N6 и усилиями Аид задней вертикальной тонкостенной фермы.
Фиг. 173.
Аналогично, силу Р2 можно уравновесить усилиями опорных стержней Ni, Nt, N7 и усилиями N и q верхней подкрепленной пластины. Что касается силы Рз, то она уравновешивается усилиями стержней As. Ae, N7 совместно с N2 и N3 либо Aj и N4. При этом работает левая торцовая вертикальная тонкостенная ферма совместно с нижней либо с верхней горизонтальной фермой.
350
Выберем в качестве неизвестной Aj усилие в опорном стержне 1. При %! = 1 имеем = Ne = N7 = 0, Д/з = 1; N2=Nt——1- Параллелепипед оказывается нагруженным системой четырех параллельных статически уравновешенных единичных сил. Нормальные усилия возникают только в четырех продольных стержнях. Эти усилия следуют закону прямой, изменяясь от +1 до нуля.
Покажем, что погонные касательные усилия во всех шести величине и равны |<7|= — , где ‘2d
сил Xi = l. Действительно, так вдоль стержня AD отсутствует усилия в обеих примыкающих быть одинаковы, иначе нару-" ' I последова-ребрах AD, ВС, В'С', A'D', усилия всех этих стенок
стенках одинаковы по абсолютной d—размер вдоль линии действия как нарастание продольной силы (N' =0), то погонные касательные стенках ADA'D' и ADBC должны шится условие равновесия элемента стержня. Обходя тельно грани, пересекающиеся на заключаем, что погонные касательные одинаковы. Итак,
Qarcd—Qbcb’C —Чв’с'а’О' ::~Чл'В'ad-
351
С другой стороны, ребра АВ, DC, D'C', А'В' также имеют нулевые нормальные усилия. Поэтому
(]А' В' =(] ABCD —ClCDCD' — Q С D'А'В'•
•Отсюда следует, что
|71| = const
для всех шести стенок.
Величину 71 найдем, составив условие равновесия стержня АА'
1—27,4/ —0, откуда <7i=~-
Так как читатель знаком с формулой кручения тонкостенного цилиндра или призмы
то для него не представит затруднений получить тот же результат, рассматривая четверку единичных сил как две равные и взаимно противоположные пары, производящие закручивание призматической оболочки вокруг оси, параллельной АВ, либо как две пары, закручивающие систему вокруг оси, параллельной AD. Интересно отметить, что в первом случае величина крутящего момента равна 1 • Ь, а расстояние между плоскостями действия пар равно h. Во втором случае момент равен 1 • h, а расстояние между плоскостями равно Ь. Произведение крутящего момента на расстояние между плоскостями действия пар сохраняет постоянное значение.
Каноническое уравнение для определения Xi имеет вид
Х13ц-|-Д1р=0.
Составим выражение для 8ц. Деформацией опорных стержней пренебрегаем:
, 1 ,2 d bh hd Ц- db _
О«j —— • • 1 * I” I I ~—
з \2d/ Gt
l\d । bh hd -|- db
~3£Щ 2O7d2
При этом предполагается, что стержни АА', ВВ', СС, DD' имеют одинаковое поперечное сечение F, а все стенки — одинаковую толщину t.
Заметим, что величина может получиться значительной только в случае нагрузки, вызывающей скручивание системы (см. § 7.4).
,352
Подкрепленная в продольном и поперечном направлениях симметричная пластина (фиг. 175, а).
Основную систему образуем, удалив стенку в двух полях. Неизвестными являются попарно одинаковые погонные касательные усилия Xi и Х2. Система канонических уравнений будет
+ ^2^12 + д.р = 0; + ^4^22 0- (3-4)
Nl>4z
Фиг. 175.
Строим эпюры нормальных усилий N и определяем погонные касательные усилия q для трех случаев загружения основной системы (фиг. 175, б, в, г): 1) силами Р; 2), 3) усилиями А'|-1, Х,= 1.
Нормальные силы стержней во всех узловых точках наружного контура известны •— равны заданным нагрузкам или пулю. В двух нижних панелях стенка отсутствует, поэтому сила 2Р без изменения передается в верхний внутренний узел. Отделим сквозным сечением вертикальный стержень. Проектируя силы в сечениях на
353
вертикальную ось, находим, что вертикальное касательное усилие в верхнем поле стенки равно Р, поэтому погонные касательные усилия в вертикальных и горизонтальных сечениях этого поля численно равны P/h. Зная касательные усилия в горизонтальных сечениях, тотчас определяем нормальные усилия в горизонтальных стержнях:
Л/ГОр = ±-“- • ь.
Касательные усилия Xi = l в двух средних полях дают вертикальные касательные силы 1 •/г, которые должны быть уравновешены такими же касательными силами в верхних полях (см. сквозное сечение па фиг. 175, в). Следовательно, погонное касательное усилие в верхних полях равно (по абсолютной величине)
h
Нормальные усилия в стержнях вблизи наружных узловых точек соответственно равны
2Vrop=-b&; 2VBepT=-bA.
То же вблизи внутреннего узла:
МоР=2Д; 2VBepT = 2.A.
Знаки нормальных сил легко определяются по направлению касательных усилий, нагружающих стержни. _
Аналогично выясняются усилия N-г и qz. Отметим, что если уменьшить высоту средней панели до нуля и слить внутренние горизонтальные стержни, то эпюра Уг ничем не будет отличаться от эпюры N\.
Та же конструкция п. 2 при большом числе панелей.
При большом числе панелей более удобен другой выбор лишних неизвестных, при котором в каждое из канонических уравнений входит меньшее число неизвестных. Расслоим мысленно горизонтальные стержни (фиг. 176), раздвинем несколько отдельные панели и введем в узлах вертикальные стерженьки, соединяющие отдельные панели. Эти стерженьки будем считать бесконечно жесткими или, что эквивалентно, длину их будем считать бесконечно малой.
Полученная конструкция в статическом отношении ничем не будет отличаться от исследуемой. Для образования основной системы перережем или удалим стерженьки, расположенные на оси симметрии. Усилия этих стерженьков и примем за лишние неизвестные Xi, Х2,. .., Хп. __
На фиг. 176 показаны эпюры N и направления касательных усилий от Хп-2=1, Xn-i = l и Хп=1. Можно показать, что при 354
указанном выборе основной системы в n-е каноническое уравнение войдут только пять неизвестных и оно будет иметь вид
Х1-2^п,п-2-j-A'n-i + +
+ Хп + 1 8,^-ф хп +2 8„7+'Я- Дщ -0. (3. 5)
В этом состоит преимущество данного выбора лишних неизвестных: независимо от общего числа неизвестных, которое может быть очень большим, уравнения получаются пятичленные.
Фиг. 176.
Составим буквенные выражения для коэффициентов типового уравнения в предположении, что конструкция является регулярной, т. е. что все панели тождественны. При вычислении слагаемых, относящихся к расслоенным стержням, их частичные усилия
355
следует суммировать и вводить площади сечений цельных стержней.
Площади сечений крайних продольных стержней обозначим Ftl, среднего стержня F'h, горизонтальных стержней Fb.
Перемножая эпюры, находим
j. Л Г) 1 b Ь b
йл,л-2 = йл,л+2=
/>3 .
3 2Л 2 Л EFb &EFbh2 ’
Чл.л—1 = ^л, л +1--
. 1 l> b b 4 . ;
3 h 2Л EFb
, 2>_1_ J___1______Л . _1_ j । /г 2 1 1 М
' ’ 6 ’ 2 ’ 2 EFh "Г 6 EFh ' 2h 2h ОТ
3 EFblF Г \2EFb' QEFh 2Ght
8 4._L.2_A_^ + 2._LAA_L +
, n,n '3 2h 2h EFb 3 h h EFb
|_4\±..±.Х.^ + 2.^.1.1.2Ц + 4.Х-^
3 2 2 EFh 3 EFh 2h 2h Gt
— Z’3 I h I 2/г h
~EFbh.2' 3EFb 3EFb Ght '
Остальные коэффициенты канонических уравнений равны пулю, так как действие каждого единичного усилия распространяется только на две смежные панели и три нервюры.
Частный случай. Пусть h=b, Fh=F’h =Fb = F, тогда
j h х 5Л 1
On п О1.—— ——— On п — 1 ~“* _ »
6EF 12EF 2Gt
п,п EF~ Gt
Типовое пятичленное уравнение принимает вид
хп_2-(^+з^\хп-а(\^^\хп-
\ 2 Ght / \ Ght /
&EF h
&пр'
(3.4')'
Иногда первый и последний члены отбрасывают, так как коэффициенты при Хп-2 и Хп+2 малы по сравнению с остальными.
В системе канонических уравнений первое и второе, а также последнее и предпоследнее уравнения содержат соответственно по три и четыре неизвестных (при п=1 имеем Х\=Р, JYo = JY-i = O), а остальные по пять.
356
При вычислении свободных членов нет необходимости строить эпюры Nv и <7Р для той же основной системы, которую мы нагружали единичными силами Л\=1. Как известно, можно воспользоваться любым «статически возможным» напряженным состоянием, т. е. находящимся в равновесии с заданными нагрузками.*
Из различных статически возможных напряженных состояний преимуществом часто обладает то, по которому производился предварительный расчет на прочность (подбор сечений), так как этим достигается экономия счетной работы и неизвестные X играют роль поправок к предварительному напряженному состоянию, поправок тем меньших, чем удачнее были в самом начале определены расчетные усилия.
В данном случае достаточно хорошее предварительное суждение о распределении усилий от нагрузки силами 2Р, Р и Р (см. фиг. 175) можно получить, отбросив промежуточные горизонтальные стержни. Получается как бы двухпояспая «балка» пролетом 2Ь и высотою ЗЛ, нагруженная силой 2Р посредине- Усилия в крайних стоиках убывают сверху вниз от Р до нуля по линейному закону, усилие средней стойки убывает снизу вверх также по линейному закону.
Погонные касательные усилия в левом и правом полях стенки одинаковы по абсолютной величине и равны P/Sh. Усилия в поясах следуют закону треугольника.
§ 7.4. КОРОБЧАТЫЕ ТОНКОСТЕННЫЕ КОНСТРУКЦИИ. ПЯТИЧЛЕННЫЕ УРАВНЕНИЯ
Основные положения. Вывод канонических уравнений
Несущая конструкция крыла весьма часто представляет собою тонкостенную коробку в виде параллелепипеда или усеченной пирамиды с небольшим углом схождения ребер, разделенную на отдельные отсеки (фиг. 177, а).
Свободная коробка с двумя торцовыми нервюрами представ-тяет собою неизменяемую систему. При стенках, работающих «только на сдвиг», коробка статически определима. Подразделение коробки на s отсеков установкой s—1 нервюр делает конструкцию (s—1) раз внутренне статически неопределимой.
При консольном креплении, подобном показанному на фиг. 177, а и типичном для крыла, обычно имеется закрепление корневой нервюры 1 в ее плоскости тремя стержнями //', IIP н четырьмя опорными стержнями I, II, III, IV, являющимися про
* Доказательство этого положения приведено, например, в книге И. М. Рабиновича «Курс строительной механики стержневых систем», ч. II, 1954. Ограничимся следующей ссылкой на аналогию: подобно тому как общий интеграл линейного дифференциального уравнения складывается из общего интеграла однородного уравнения и частного интеграла неоднородного уравнения, удовлетворяющего любым граничным условиям, так и в канонических урав нениях допустимо пользоваться свободными членами, отвечающими другой основной системе.
357
должением стрингеров. 1акое крепление содержит одну дополнительную лишнюю связь (один из параллельных стержней) так, что полная степень статической неопределимости в этом, практически наиболее важном, случае равна $—1 + 1=5, т. е. совпадает с чис-
Фиг. 177.
лом отсеков, или равна общему числу нервюр, не считая торцовой на свободном конце. Разберемся сначала в роли лишних связей.
Вообразим коробку с двумя плоскостями симметрии. Вырежем 5 нервюр и заменим их действие на основную систему сдвигающими усилиями. Очевидно, это будут антисимметричные относительно обеих плоскостей симметрии силовые группы. Отсюда следует, что при симметричной нагрузке коробки,
358
например, при изгибающей вертикальной нагрузке, лишние неизвестные равны нулю, система работает как статически определимая, не имеющая промежуточных нервюр. Наоборот, при нагрузке антисимметричной, типа кручения, роль нервюр может оказаться существенной. Практически и при неполной симметрии расчет па изгиб в вертикальной плоскости обычно делается без учета статической неопределимости — как для коробчатой балки. Поэтому займемся случаем кручения.
Прежде всего постараемся выбрать основную систему так, чтобы напряженное состояние от действия крутящих пар, приложенных в плоскостях нервюр, определялось как можно проще.
Известно, что в поперечном сечении трубчатого тонкостенного стержня (цилиндрической или призматической оболочки) можно уравновесить крутящие моменты постоянными по периметру средней линии стенки касательными усилиями:
Здесь Мк— крутящий (односторонний) момент в данном сечении; й1:— удвоенная площадь, охватываемая периметром средней линии стенки в поперечном сечении.
Если остановиться на этом статически возможном напряженном •состоянии, когда продольные силы отсутствуют, то для образования основной системы следует разрезать один нз стрингеров в s сечениях над нервюрами, начиная от корневой, а в качестве лишних неизвестных принять попарно равные и противоположные силы X, приложенные к отделенным разрезами торцам стрингера. Другими словами, принимаем за неизвестные усилия в стрингере в сечениях нервюр. Число неизвестных s.
Может оказаться, что указанный выбор основной системы при другой нагрузке является неудобным. Однако и здесь приходит на помощь положение, согласно которому основная система, нагруженная лишними неизвестными, н основная система, нагруженная заданными силами, не обязательно должны быть тождественными. Окончательное напряженное состояние (после определения неизвестных из канонических уравнений) получается путем суммирования напряженных состояний двух основных систем и является инвариантным.
Чтобы более отчетливо представить себе напряженные состояния от неизвестных, расслоим мысленно каждую нервюру и несколько отодвинем друг от друга смежные отсеки, вставив в местах стрингеров короткие стерженьки. Стерженьки вдоль одного ребра разрежем, и усилия в них примем за неизвестные Xi, Х2, Л3,, . ., Хп,, , ., Xs (фиг. 177,6). Остальные связи, и в частности обшивка коробки над нервюрами, считаются ненарушенными.
Напряженное состояние от Хп = 1 устанавливается без затруднений.
359
На фиг. 177, в стрелками с половиной острия, обращенной гладкой стороной к окаймляющим стенки стержням, показаны касательные усилия, передающиеся от стенок на стержни. Если стержни не нагружены, то касательные усилия по одну и другую сторону стержня одинаковы и их векторы равны по величине и противоположны по направлению, как в случае отсутствия стержня.
В примере на фиг. 177, в касательные усилия уравновешивают силы Хп = 1, направленные вдоль стрингеров.
Легко видеть, что в неперерезанных стерженьках в том же сечении п усилия (V= + l, а в других сечениях (п—1, п+1 и т. д.) усилия в стерженьках равны нулю. Следовательно, от двух сил А'„ = 1 работают только два смежных отсека (п—1, п.) и (п, п+1). Усилия в их элементах определяются без затруднений (аналогичная задача решена в § 7.3).
Погонные касательные усилия во всех стенках отсека по абсолютной величине одинаковы и равны
Их направления указаны на фиг. 177, в. Длина панели d берется соответствующая отсеку, т. е. Уп-! — для левого отсека и dn — для правого. Заметим, что мы нумеруем отсеки по номеру левой нервюры.
Окончательная величина погонного касательного усилия в расслоенной нервюре п получается суммированием усилий, подсчитанных для левого и правого «слоя», т. е.
1----------। 1 q == ---------,
2йл_, 2d„
что при
dn—i = dn — d
дает
В нервюрах же п — 1 и п-)-1 окончательные усилия от Хп—\ 1 1 равны соответственно------- и — .
2 6Л_! 2d„
Нормальные усилия в стрингерах убывают на протяжении панели от +1 до нуля по закону треугольника (см. эпюры на фиг. 177, в). В других окаймляющих стенки стержнях нормальные усилия отсутствуют.
От /-„^1 = 1 и от Хп+1 = 1 картина напряженного состояния будет такая же, как от Хп = 1 (см. фиг. 177, в), но соответственно смещенная на один отсек влево и на один отсек вправо. Рекомендуем читателю сделать рисунок, на котором изобразить три пары смежных отсеков.
360
Одновременно от Хп и Хп-\ напряжены элементы отсека п—1.. От Хп и Xn+i одновременно напряжены элементы отсека п+1.
Если рассмотреть последовательно напряженные состояния от А'п-2 до Хп+2, то окажется, что напряженными все они имеют общие с состоянием от Хп элементы. Следующие неизвестные Хп-з и Хп+3. уже не имеют общих с Хп напряженных частей конструкции. Следовательно,- отличными от нуля коэффициентами дп,< канонического уравнения будут только коэффициенты bn,n-2', 6п,п-ь бп,п;. бп,п+1> &п,п+2-
Это показывает, что n-е типовое каноническое уравнение содержит пять неизвестных
Х„-2, А4-1, Х„, Х„.,„ Хп |2
и имеет, следовательно, вид
Хп -2Ч«,л-2 -|- Хп-} ^п,п- \ 4~ хп^пп 4“ Хпл I ?>п,п + I -J-
4" Хп+2 ^л,лт2-|-Д,(р = 0. (4. 1 )>
Счет п ведется от сечения корневой нервюры, которой приписывается номер 1 (фиг. 177, а). Так как, очевидно, влево от первой нервюры стенки отсутствуют, то можем положить Х0 = Х\, кроме того, благодаря наличию жестких опор в плоскости О имеем Х_! = 0. Поэтому первое уравнение содержит не пять, а всего три неизвестных: X}, Х2, Х3, второе — четыре неизвестных: Аф, Х2, Х3, Х4 и только начиная с третьего — идут пятичленные уравнения вида (4. 1). То же и на другом конце системы уравнений: Xs+i = Х.,+2==0.. Поэтому последнее s-е уравнение содержит 3 неизвестных, предпоследнее — 4 неизвестных,.
В целом система канонических уравнений будет
1) А^ + ^Лг + ^.з + Д^О,
2) А\82, -р X.J>22 -ф- .X3823 + А"4824 Д2р — О,
3) AriS3, + X2832 +^33+^4 +^5835+Д3р =0,
П) ХП -2 8л,л-2-(- Xn-i ^л,л-1 -ф-Х„8,1Л~| Хп-} &Л,Л41 4 ' | ’ Хп +2 ^л,л 1-2 4- Длр = 0’
s 2) Аф_48б._2> s_4 4- Xs_3<>s_2 5-з•AC6._.2oj._2> ^_2 |-
- i Л-2, ,s_, - i - *a_2> , -I- д,_2> p=0,
•s—1) X!_3oi_I i_34 Ari_28d_]^_2-j-A4-i55-i.3-i4_ |
+^Д-1,,4-Д.-1,р = 0. I
s) ф Аф_|4( ,5-1 + Д5Р — 0- i
361
Коэффициенты и свободные члены системы уравнений вычисляются по формуле
+ (4.3)
I
Интегралы могут быть взяты по правилу Верещагина; / — означает площадь прямоугольной стенки, t — ее толщину.
Отметим две формулы для интегралов. Когда эпюры N и N — треугольные с вершинами^ обращенными в одну сторону, и концевыми ординатами и NA , то из (3. 1) получаем
^NNdx = -^- .
Когда эпюры N и N— треугольные, но с вершинами, обращенными в разные стороны, и концевыми ординатами NA и NB, то имеем
§NNdx = — i
Этих формул достаточно для вычисления величин А и 3 при постоянной на протяжении отсека жесткости стрингеров.
Составим выражения для коэффициентов, принимая длины отсеков d и площади всех стрингеров F одинаковыми, модули сдвига G и толщины одноименных стенок t— также одинаковыми.
Индексами а и b отмечены горизонтальные и вертикальные стенки (в соответствии с нх ширинами а и Ь). Нервюры отмечаются звездочкой.
8 —. 8fif । Л.(— I — ^_|_________—• (4 4)
пп ЗЕГ d \Guta 1 Gbtb j ’
. ___1 / д I____6 \ a,} . /4 co
п.л+1-3£Л yQata ~FQbt~) d2G*t*
* ab
Коэффициенты первого уравнения
4d ! 1 ( a । b । ab
°“ 2d\G^ ' Gbh>] 2d2G*t*
। di । d"i । rfiv
EE^EEn £A,„ 1 EEIV-
(4. 6)
(4. 7)
362
Вторая строчка в (4. 7) выражает влияние упругости стержней I, II, III, IV. Они могут быть неодинаковыми по жесткости и по длине:
й X \ { а . b \ ЗаЬ
12 21 ЗЕЕ 2d \Gata~Gbtb) 4rf2O,/,, ’ )
Если корневая нервюра 1 считается абсолютно жесткой, то в формулах (4.7) и (4.8) слагаемые, зависящие от заменяются соответственно через
ab ab
и 4rf2O;^;..--2rf2G*^
и, кроме того, 522 вычисляется не по общей формуле (4.4), а по следующей:
s 3d . 1 / а , b \ , 5 ab
3EF d\ Gata Gbtb )V 4 d*G*t* 1
Коэффициенты усеченных уравнений s—1 и s вычисляются по общим формулам (4. 4) -4- (4. 6).
Перейдем к составлению выражений для свободных членов. Ограничимся случаем крутящих пар (Lj, L2, . . . ., L6), образованных вертикальными силами, приложенными по краям нервюр в плоскостях вертикальных стенок (фиг. 178, а).
На фиг. 178,6 построена эпюра крутящих моментов М.
Фиг. 178, в иллюстрирует вычисление одинакового во всех четырех степках погонного касательного усилия четвертого отсека (между нервюрами 4 и 5):
„о__ 444 М4
U ЧаЬ '
Сопоставим направление касательных усилий в стенках на фиг. 177, в и 178, в. Будем считать нервюру 5 па фиг. 178, в эквивалентной «-Й нервюре па фиг. 177, в. Легко убедиться в том, что в верхней и нижней горизонтальных стенках .(и—1)-го отсека направления усилий q будут одинаковы, в боковых степках — противоположны- В n-м отсеке — наоборот: в горизонтальных стенках направление касательных усилий противоположное, в вертикальных — одинаковое. Эти данные надо иметь в виду при определении знака отдельных слагаемых ДЛр-
Рассмотрим напряженное состояние нервюры 4 (фиг. 178, а). Вырежем нервюру вместе с окаймляющими стержнями. Слева па нее действует постоянное по периметру касательное усилие =М3/2аЬ, справа — усилие q°— M4/2ab в противоположном направлении.
Результирующее погонное касательное усилие
Лз__ = 1.4
2ab 2ab 2аЬ
;63
Это усилие эквивалентно моменту L4 и уравновешивается двумя силами вдоль стоек, образующих пару с моментом, противоположным моменту L4.
Степка нервюры нагружена уравновешенными касательными усилиями q°f=L4/2ab, направленными, как показано на фиг. 178, г, справа (вид от правого конца коробки к левому). Интересно отме-
<Риг. 178.
тить, что если пара Ь4 имеет не вертикальные составляющие, а горизонтальные (при том же направлении вращения), то касательные усилия по краю стенки нервюры изменяют свое направление на противоположное.
Направление усилий в стенке нервюры совпадает с направлением усилий от неизвестной Х4, направленной, как Хп на фиг. 177, в: и противоположно направлениям усилий от неизвестных Х3 и Аг, (Хп-1 и An+i).
Выразим свободный член n-го канонического уравнения, пользуясь вторым членом формулы (3. 1). В одних и тех же стержнях
364
нормальные усилия от Хп=\ и от заданной нагрузки, как мы видели, не возникают:
д — 2Л4'1~1 1 da 2Мп-\ 1 db
пр 2аЬ 2d Qata 2ab 2d Qbtb
_ 2 1 I 2 Мп 1 db I
2ab 2d Gata 2аЬ 2d Qbtb
, 1 1^-1 J 1^n + i 1 1
2ab d Gt* ' 2ab 2d Gt* 2ab 2d Gt*
I-п f a____\ i — Ln—\ + 2^/i — Ln+\ ,л ]j|
2ab \Gata Gbtb/‘ 4dGt*
При этом принято во внимание, что Mn-]—Mn = Ln. Такую же структуру имеют все свободные члены, за исключением AiP. Если корневая нервюра (/) имеет такую же стенку, как и все остальные, то
д = а_______ь \ 2Л4| — Д2 (4.12)
,р 2ab \Gata Gbtb )' 4dGt*
Если корневая нервюра абсолютно жесткая, то
д -------------------М--------(4.13)
ip 2ab \Gata Gbtb) 4dGt*
В этом последнем случае и ДзР имеет несколько отличное от .(4.11) выражение:
Д2о=-----------------—) + ^=-Л_з . (4. 14)
2р 2ab \Gata Gbtb ) 4dGt*
Пример. Коробка образована четырьмя стальными трубами с поперечным сечением F— 8 см2, £=2,1-10° кг/см2. Обшивка и нервюры (стенки) — дуралю-миновые:
(а=0,15 см, г‘ь=0,40 cm, t* =0,1 см, G=0,28-103 кг/см2.
Размеры коробки: а=60 см, Ь = 20 см, d=9Q см. Число отсеков s = 5 (фиг. 178, а).
Определить осевые силы, полагая
L\— L2 — L3 = L4 — L5 = L6 = L = 10 000 кгсм.
Система 5 раз статически неопределима. Вычисляем коэффициенты системы пяти канонических уравнений, пользуясь выведенными формулами. Закрепление в плоскости первой нервюры считаем абсолютно жестким (Gt\*—oo). Все коэффициенты увеличиваем в G раз. Для этого вводим
2,1-10°
0=1; Е=--------------= 7,5;
’ 0,28-106
4-90 1 ! 60 20 \
3-7,5-8 +2-9оЬ-О,15+1-0,4 / +
+ —--------= 2,0 + 2,5 + 0,37 = 4,87;
4-902-0,1
365
2-90 1 / 60 '20 \
3-7,5-8 ~2-90 \1-0,15+14М/
60-20 2-902-0,1
1,0 — 2,5 — 0,74 = —2,24;
60-20
б 13 — Во I = = 0,37
13 31 4-902 - 0,1
8-90 1 / 60 20 \
22~ 3-7,5-8 + 90 \1-0,15 + 1-0,4 / +
5-60-20
+Т^П=4’° + 5-° + 1’85-10-85:
2-90 1 / 60 20 \
2з- з2- 3.7>5.8 ~2-90\1-0,15 1-0,4/
60-20
~ 902^0?Г = 1’° ~ 2’5~ 1,48 ~ ~_Г;2’98’
»24 = В42 = 0,37;
Г8-90 1/60 20 \
•3 3-7,5-8 90 \1-0,15 1-0,4 )
3-60-20
+ —------; =4,0 + 5,0 + 2,22= 11,22.
2-902-0,1
Остальные коэффициенты равны найденным выше:
^44 = ®55 — ®331 ®34 = ®45 = ^2з! ®35 = ®24 = ®13-
1сСодные члены:
- 5L ( 60 20 L
1р~ 2-60-20 \1-0,15 ~1-0,4/~ 4-90-1-0,1 °’ 4Л’
L / 60 20 \ L
^ip~ 2-60-20 \1-0,15 ~ 1-0,4/"*' 4-90-1-0,1 _°1174Л’
L Ч 60 20 \
Лзр~ 2-60-20 Д1-0,15~ 1-0,4/ °’146
^4р = = Дзр = 0,146 L.
Система уравнений будет:
1) 4,.87А'1 —2,24^2 + 0,37X3 —5840 = 0;
2) — 2,24Х] + 10,85Х2 — 2,98Х3 +0,37Х4 + 1740 = 0;
3) 0,37^! — 2,98Х2 + 11,22X3 — 2,98X4+ 0,37Х5 + 1460 = 0;
4) 0,37X2 — 2,98X3 + П.22Х4 — 2,98Х5 + 1460 = 0;
5) 0,37X3—2,98X4 +11,22X5+ 1460 = 0.
Решение уравнений дает:
Xi=1230 кг; Х2 = 36,5 кг; Х3=—215 кг; Х4 =—250 кг; Х5=—187 кг.
На фит. 179, а показана эпюра крутящих моментов; если ординаты этой эпюры разделить на 2аЬ=2400, то получим эпюру cf.
366
Условимся усилия считать положительными, когда опи по направлению совпадают с усилиями, вызываемыми положительными крутящими моментами. Ординаты эпюры <?° будут
о 50 000 п 40 000
71 = ~24(Ю = 20,8 KZ,CM; 1)2 ~ 1400 = 1617 Кг,СМ;
4® ~ 12,5 кг/см; q° = 833 кг)см; у® = 4,17 кг/см.
На фиг. 179,6 построена эпюра продольных сил в верхнем переднем стрингере. Ординаты ее в узловых точках равны неизвестным X,. Если принять обыч-
ное правило знаков, считая продольные силы положительными при растяжении, то эпюра A hi совпадает с Ni, эпюры -Уц и Niv совпадают по величине ординат, ио обратны по знаку.
На фиг. 179, в дана эпюра погонных касательных усилий в передней вертикальной стенке от действия неизвестных Х,, построенная в соответствии с правилом знаком, которое принять при расчете для q«. Ординаты ее равны половинам тангенсов углов наклона эпюры .V; к оси абсцисс, взятым с обратным знаком:
=1-^(36,5-1230) =
= 6,13 кг[см;
^=-^(-215-36,5) =
а)
6)
.10*
Мп
ТПм*
Ni
§
.10*
шпшп^
— 1,40 кг/см;
— 0,19 Kz'jCM;
:<74i’=—[0,35 кг)см;^
187
ai i = — —— = — 1,04 кг1см.
511 2-90
Чтобы получить ординаты окончательной эпюры q в передней стенке, необходимо просуммировать q'J и q(X):
41,1 — 20,8 + 6,13 = 26,93 кг1см;
?1,2 = 16,7 + 1,40 = 18,10 кг]см;
<7|,з = 12,5 0,19 12,69 кг)см;
<71Л = 8,33 — 0,35= 7,98 кг/см;
<7!,5 = 4,17—1,04= 3,13 кг1см.
Фиг. 179.
Эпюра дана на фиг. 179, г. Аналогичная эпюра будет и для другой вертикальной стеики.
Для верхней и нижней горизонтальных стенок имеем:
<7IV l = 20,8 — 6,13=14,67 кг[см\
qiv 2 = 16,7 — 1,4 = 15,3 кг/см;
7|V 3 = 12,31 кг/см; <?1у 4 = 8,08 кг/см; <?1у 5 = 5,21 кг/сл.
367
Так как нагрузка состоит из вертикальных сил в узлах, то касательные усилия в стенках нервюр равны разностям касательных усилий в горизонтальных «стенках:
< 72< = 14,67 — 15,3 = 0,63 кг/см;
< l3t. = 15,3 — 12,31 = 3,0 кг)см;
< 74* = 12,31 —-8,68 — 3,63 кг/см;
75* = 8,68 — 5,21=3,41 kzIcju;
qe* = 5,21 кг)см.
Положительный знак соответствует направлению, показанному на фиг. 178. г справа.
Определение угла закручивания
Перемещение статически неопределимой системы можно вычислить как перемещение основной системы, нагруженной заданными силами и предварительно найденными лишними неизвестными.
Поставим себе задачей определить углы поворота стержней, окаймляющих, нервюру на свободном конце, в плоскости самой нервюры. Эти углы обозначим:
для верхнего горизонтального стержня <рг, для правою вертикального cpD. Единичные силы для нахождения двух этих углов показаны па фиг. 180. Они образуют пары с моментами, равными единице, причем компоненты пар равны соот ветственио I/а или \/Ь.
Погонное касательное усилие во всех степках обшивки равно
- 1 1 _2
q =----=------СМ .
2аЬ 2400
В стенке торцовой нервюры q имеет ту же величину, но направление уси лий неодинаково и зависит от характера приложения единичного момента (см фиг. 180).
368
Очевидно, углы поворота <рг и (рв также неодинаковы, причем разница зависит от деформации стенки нервюры и окаймляющих стержней. Однако эта разница незначительна и обычно ею пренебрегают, считая торцовую нервюру абсолютно жесткой. В этом случае можно говорить об угле закручивания нервюры. Общая формула будет:
— d-b —d-а
’=2’й72^+2’й72Х«- (4-15)
П=1 Л-=1
Подстановка численных значений дает:
1 I 20
G<? = 2^90 <77<26>93 + 18>10 * + 12>69 + 7>98 + 3’13> +
60
+ т—; (14,67+ 15,30 4- 12,31 + 8,63 4-5,21) = 1938. 0,15
Если не учитывать влияния лишних неизвестных на величину угла поворота, то: . „..x/j'jsS
1 /20 60 \ 2110
= 2 24Оо's * * * 9° fa + БТ5)(20’80+16’70 + 12-50+8’33 + 4’
Как и следовало ожидать, Добавление лишних связей делает систему более жесткой.
§ 7.5. ТРЕХЧЛЕННЫЕ УРАВНЕНИЯ
Очень часто довольствуются точностью расчета, получаемой в предположении, что все нервюры недеформируемые (&*^* = оо), т. е. отбрасывая в (4. 4)4-(4. 6) слагаемые, зависящие от деформации нервюр. Поэтому
8/|,л-2= ^л.л + 2^0.
Канонические уравнения получаются трехчленными следующего вида:
1) Х,В,1 + Х2812+Д^=0>
2) A’+jj-}-zV2o22 4"42р= 0,
п) '’Ci-A.n-i + A’,JB„n4-А'п+18п,л+1 4-Ь„р--0, (5.1)
s 1) j-z4--Уг-i^-i,j-i 4~ЛА-i.s4-— 0»
s) 1Ч- ‘‘VAfj-!- 'sp== 0‘
Коэффициенты этой системы:
g _ 8_________________d_ 1 / a . b \
nn~ 3 EF ~'~d \Gata ' Obtb ) ’
g __ g _ 2rf___________1_ / a b \
л,л-1 л,л+1 3EP 2d \Gata + )'
(5. 2)
(5. 3)
24 4 2 5
369
8П=— + — + +
11 3EF 2d \Gala Gbtb / rf. d d d
+—+—+——н—~ EFi EFn EFm EFw
(5: 4)
Все остальные коэффициенты вычисляются по общим формулам (5.2) и (5.3).
Свободные члены вычисляются по общей формуле
(5-5> 2лу \Gata Obtb / t
за исключением свободного члена первого уравнения, который равен:
— ------—V (5.6)
'р 2аЬ \Gata Gbtb]
Мы видим, что при
а ___ Ь
Gala Gbib
т. е. когда жесткости сдвига горизонтальных и вертикальных стенок одинаковы, все свободные члены обращаются в нуль, а, значит, и все усилия X также равны нулю.
В общем случае для определения усилий необходимо вычислить коэффициенты 8„,, и свободные члены Ап, р, составить и решить систему трехчленных уравнений (5. 1), а затем найти погонные касательные усилия в стенках и продольные силы в поясах по формулам
^ = 9°-7Лл + 7л+Лл+1=9°+^-(А'я+1-Х„),
где q°p и Д7° —усилия в основной системе; q„=qn+i — ^- согласно фиг. 177, в;
Хп и Хп+\ — осевые силы, определяемые из системы (5.1).
Для приближенной оценки величины усилия в стрингере в корневом отсеке (при консольном креплении и крутящей нагрузке оно имеет максимальное значение) следует в первом уравнении системы (5. 1) положить Л2 = 0. Тогда
Оказывается, что при положительном крутящем моменте в корневом отсеке знак усилия в стрингере 1 зависит от знака величины
а
Ра^-а
_Ь \
Gb4 /
370
Если жесткость сдвига горизонтальных стенок больше, чем: вертикальных, то стрингер 1 оказывается растянутым. В противном случае он сжат.
Лятичленные и трехчленные уравнения очень часто встречаются при расчете мпогопролетпых и многопанельных конструкций. Так, неразрезная балка на упруго оседающих опорах приводит к типовому уравнению пяти опорных моментов, неразрезная балка на жестких опорах — к уравнению трех опорных моментов, рамная балка — к уравнению трех усилий в затяжках. Типовое пятичленное уравнение для расчета коробчатой конструкции обычно называют уравнением пяти осевых с и л, а типовое трехчленное уравнение— уравнением трех осевых сил.
Следует заметить, что уравнение трех осевых сил по своей структуре близко именно к уравнению для рамной балки, так как побочные коэффициенты, как правило, получаются отрицательными. Уравнение же трех моментов перазрезной балки имеет положительные побочные коэффициенты.
Уравнение трех осевых сил впервые дано В. Н. Беляевым в 1932 г.
Пример. Решим пример из § 7.4. Вычисляем коэффициенты системы пяти трехчленных уравнений, пользуясь выведенными формулами. Все коэффициенты подсчитываем увеличенными в G раз. Для этого вводим
2,1-106
G = l; Е=—------------= 7,5;
0,28-106
4-90 1 / 60
1 3-7,5-8 2
„ „ 2-90
О «о == Sol я 3-7,5-8 8-90 б22 =
20 \ 1-0,4 Д
20 \
1-0,4 )
<1,5;
20
<1-0,15 1 1-0,4 1 / 60 1
2-90\1 -0,15 + 1 / 60 3-7,5-8 г 90\1-0,15 +
Остальные коэффициенты равны найденным выше:
Сз.З ®44 = ^55 ~ ®22 = 9,0; 0;3, = Ь34 = 645 = = — 1,5.
Свободные члены
20
Д.р = —---—— —гг-1= —0,730К= —7300,
1Р 2-60-20 \1-0,15 1-0,4 /
/< / 60 20 \
Д2р - Дзр - Д4р - Д5р = 2 60 20 ^.0 55-1,0)4 ) = °- У
Система уравнений имеет вид:
4,5 X,— 1,5Х2 —7300 = 0,
— 1,5 А'1 4- 9 АС — 1,5 А'3 + 1460 = 0, — 1,5 А2 + 9 Х3 — 1,5 *4 + 1460 = 0, — 1,5 *з +„9 А4 —, 1,5 Х5 + 1460 = 0, — 1,5*4 4-9-А5 + 1460.= 0.
Решение системы дает
Xi=1650 кг; Х2—80 кг; Х3=—180 кг; Xt ——215 кг; Аз=—200 кг.
= 1460.
371
Эпюра .V/ представлена на фнг. 181.
Заметим, что расчет этой коробки с учетом упругости нервюр (по уравнениям пяти осевых снл) дает меньшее значение максимальной осевой силы на 25”/о, а максимальных сдвигающих усилий на 1О°/о. При необходимости полного выявления работоспособности н максимального уменьшения веса конструкции расчет лучше вести по уравнениям пяти осевых сил.
Численное значение девой нервюры:
угла поворота в предположении недеформируемой кон-
20
•90 — (29,5 + 18,24- 12,7 4-8,25 + 3,06)4-
„ 2
Go -----•
Y 2400
60
4- — (12,1 4- 15,2+ 12,3 + 8,41 +5,28) = 1860 < 1938. 0,15
Как и следовало ожидать, усиление некоторых связей уменьшает деформацию системы.
§ 7.6. УЧЕТ РАЗЛИЧНЫХ УСЛОВИЙ ПРИКРЕПЛЕНИЯ КОРОБКИ
Рассмотрим тонкостенную коробчатую конструкцию, в которой приложены произвольные сосредоточенные силы. В общем случае такая коробка будет работать на изгиб с кручением. Ниже разбираются три варианта прикрепления коробки, соответствующие практически важным конструктивным схемам крыльев: коробка с прямой заделкой (двухлонжеронное крыло), трехточечпое крепление (однолонжеронное крыло со вспомогательным лонжероном) и коробка с косой заделкой (стреловидное крыло).
В качестве основной системы при рассмотрении единичных напряженных состояний возьмем, как и раньше, коробку, у которой один из стрингеров разрезан в сечениях над всеми промежуточными нервюрами (см. фиг. 177). Поэтому коэффициенты типового канонического уравнения бп,п-2=дп,п-<-2, 6n,n-i = 6n,n+i и дПп будут вычисляться по формулам (4. 4) -+ (4. 6), за исключением некоторых коэффициентов при X] и Х2, которые существенным образом зависят от характера закрепления конца коробки и вычисляются по особым формулам, приводимым ниже. При нахождении свободных членов системы канонических уравнений воспользуемся свойством статически неопределимых систем, позволяющим выбирать основную систему, нагруженную заданными силами, отличную от основной системы при единичном напряженном состоянии.
372
Коробка с прямой заделкой. Будем считать, что коробка в сечениях, где поставлены нервюры, нагружена вертикальными силами Р{ и Si. Положительное направление сил указано на фиг. 182, а. Закрепление коробки ничем не отличается от случая, разобранного в § 7. 4, а поэтому все коэффициенты в системе канонических уравнений следует вычислять по формулам (4. 4) 4- (4. 10).
Для вычисления свободных членов в качестве основной системы возьмем коробку, у которой вырезаны все нервюры, кроме корневой (нервюра 1). В такой основной системе от заданной нагрузки будут работать только передняя и задняя тонкостенные балки, нагруженные каждая в своей плоскости (фиг. 182,6). Остальные элементы оказываются ненапряженными. Величину усилий в каждом элементе основной системы легко подсчитать, если построить эпюры изгибающих моментов и поперечных сил, возникающих в сечениях передней и задней балок. Обозначая изгибающие моменты у n-й нервюры через Msn, М? и поперечные силы слева от n-й нервюры через Q„, соответственно для задней и передней балок
коробки, легко найдем, что продольные усилия в стрингерах равны*.
NPn — ±—r~ и Nn=±~ b ь
* Передней называем здесь балку, обращенную в сторону полета, т. е. удаленную от наблюдателя.
373
а погонные касательные усилия в стенках
Qn 0s
= ~ и qs = —
Чп ь п ь
Свободный член Дпр вычисляется по следующей формуле*:
4.,=^<Л.-.+Ж+Л1.«)+^~. (6.1)
оЬЕг
здесь введено обозначение
(6.2)
Особенности прикрепления влияют только на величину первого свободного члена Д1р, который имеет вид
д . М ^fCu, , М <
" Ь \efJefJ b\EFjEF^r
, Qf-Qf , d
Т” 2Gbtb "Г 3b EF
(2М, + Л42).
(6.3)
После решения системы канонических уравнений и определения окончательные значения усилий в элементах коробки находятся путем алгебраического суммирования усилий, вызываемых силами Xi в первой основной системе, с усилиями от сил Pi и S, во второй основной системе. Когда все Pi = Sj, коробка работает только на изгиб. Если передняя и задняя балки ее (включая прикрепляющие стержни I, II, III, IV) одинаковы, то верхняя и нижняя стенки не напряжены, а балки (лонжероны) работают только от нагрузок, лежащих в их плоскостях. В этом случае напряженное состояние коробки совпадает с напряженным состоянием второй основной системы — коробки с вырезанными нервюрами. Расчет можно производить, не прибегая к решению статически неопределимой задачи. Поскольку Mi = M? — М? = 0, то Д1Р и все Дпр обращаются в нуль. Система канонических уравнений будет однородной, а, следовательно, все Хг = 0. Однако, если жесткости передней и задней стенок различны, задача расчета на изгиб является статически неопределимой, поскольку промежуточные нервюры включаются в работу.
Трехточечное крепление. В случае трехточечного крепления (фиг. 183) изгибающий момент может быть воспринят только стержнями В и С, прикрепляющим'!! переднюю стенку. Изгибающий момент с задней стенки передается через нервюры па переднюю стенку коробки. Таким образом, продольные усилия в стрин-
* Можно вывести эту формулу самостоятельно, пользуясь методом, изложенным в § 7.4.
374
repax задней стенки в сечении над корневой нервюрой должны обратиться в нуль. Используя это уравнение, получаем
< 5
1 1 ь
или
(6. 4)
Таким образом, усилие Xi известно заранее, и число неизвестных продольных усилий уменьшается на единицу. Система канони
Фиг. 183.
ческих уравнений начинается сразу со второго уравнения, которое имеет вид
А'А2+А723++д Л Y 321 = 0. (6.5)
Третье уравнение также несколько изменится:
= «з + АС4о34 ^35 М- у- 8з> = 0. (6.5')
Остальные уравнения имеют обычный вид. Все коэффициенты и свободные члены вычисляются так же, как и в случае коробки с прямой заделкой.
На фиг. 183 изображен примерный вид эпюры продольных сил в стрингерах для коробки с трехточечпым креплением.
Коробка с косым прикреплением. На фиг. 184 показана схема коробки с косым прикреплением. Корневая нервюра ABCD распо
375
ложена под углом а к оси коробки, остальные нервюры перпендикулярны оси. Корневая нервюра считается закрепленной в своей плоскости четырьмя абсолютно жесткими стержнями Г, II', ///', IV, являющимися продолжением стержней, окаймляющих нервю-
ру. Это дает возможность в последующих расчетах считать корневую нервюру абсолютно жесткой. Коробка в точках А, В, С, D прикреплена четырьмя упругими горизонтальными стержнями /, II, II1, IV, перпендикулярными плоскости корневой нервюры. Особенность данной схемы по сравнению с предыдущими заключается в пали-
376
чии треугольного в плане корневого отсека. При рассмотрении этого отсека будем считать, что обшивка треугольных полей не работает, а все усилия в горизонтальной плоскости передаются достаточно жестким стержневым треугольником. Коробка нагружена по передней и задней стенкам вертикальными сосредоточенными силами Pi и S/. Как и в предыдущих случаях, при подсчете коэф-
Фиг. 185.
фициентов и свободных членов канонических уравнений пользуемся двумя различными основными системами. Для вычисления дгл основная система получается после перерезания одного из стрингеров над каждой нервюрой. В месте каждого n-го разреза прикладывается продольная сила Хп = 1. Поскольку в точке С сходятся две нервюры, то приходится делать два разреза справа и слева от точки С. Вторая основная система, используемая для вычисления Д/р, получается удалением стенок нервюр, кроме корневой, в. силу чего нагруженными оказываются только элементы задней и передней балок. Усилия в поясах и стойках второй основной системы без труда определяются после построения эпюр N„3 и Q для этих, балок. На фиг. 185 балки показаны в аксонометрии соответственно фиг. 184, а.
377
Легко установить почти полное совпадение напряженного состояния с напряженным состоянием для случая коробки с прямой заделкой. Различие касается лишь небольшого участка вблизи заделки (треугольный отсек ABCDEF). Поэтому вычисление большинства коэффициентов и свободных членов следует вести но формулам (4.4)—-(4.6) и (6.1). Изменяются лишь выражения для $и, 612, 6]з, 622, 623, Aip и Агр. Чтобы получить эти выражения, рассмотрим первую основную систему, нагруженную силами Х[ — 1 (фиг. 184, б), Х2=1 (фиг. 184, s)*, и вторую основную систему под действием заданных сил Л и S (см. фиг. 184, а).
Определив усилия в основных системах, вычисляем 3 и А, пользуясь формулой (4.3). После ряда упрощений получим
8 - 2 f 2 | М । ь ( а___I--1M-4.
" 3EF \ COS2 а ' sin2 а) a2 cos2 а \О,,У* G bt ь }
1 ^1 [ Сп j £ш । £гу. E/F ЕЕ^'
S22 = — (t/„ + 2y + fltg2a)+— (Л + — 1 +
22 ЗЕр V О Т -Г S ) I d2 2rf2y I
1 __a___I b .
+ 2dGuta + Gbtb I d0 J '
812= — ------
SCPlsina dp COS a /
------[i + a2A/_L+_Ln.
acasaGbtb G^t* \d0 2d /]
g ______.
13 2rfG,/s,cosa ’
<s __ 2d 1 / a , b \ ab / 1 j 1 \
°23-3£Л 2d \Gata ' Gbtb) 2dG*l:i,\do d )'
j С. C \ zWfsin a
Д - + —IL _!---------
'p \EFl EFj b
Cw A 2MP+MP Qf
EF^ 3b EF sina Gbtbs\na
=+ 2<} (2уИ2+Мз) ~
_ 2Qf - Q.f + Ql
2gFi,
(6- 6)
(6- 7)
'* Напряженное состояние от силы A3~l, L^l, . . . будет точно таким же, как и в случае коробки с прямой заделкой.
378
Составление и решение системы канонических уравнений, а также нахождение окончательных величин усилий в элементах коробки производится обычным порядком.
Пример. Определить продольные усилия, возникающие г стрингерах коробки с косой заделкой, нагруженной по пеоедней балке в сечениях над нервюрами вертикальными силами P-2=Ps—P.f—Ps=l00 кг (фиг. 186). Стрингерами служат четыре стальных трубы одинакового поперечного сечения А=10 см2, £=2,1 ' 106 кг/см2. Обшивка и стенки нервюр дуралюминовые, одинаковой толщины ta~tb = /*. = 0,2 см; G' = G,3- 10“ кг/см*.
Размеры коробки: а=100 см; 6 = 20 см; d = do=l00 см; С\ = Сц = =гСщ=С\у=50 см.
Фиг. 186.
Число отсеков 4 (в том числе один косой отсек). Угол наклона корневой нервюры к оси коробки а = 45°.
Система четыре раза статически неопределима. Вычисляем коэффициенты и свободные члены четырех канонических уравнений, используя формулы (6. 1), (6.6), (6.8), (4. 4)-: (4. 6).
Коэффициенты подсчитываем увеличенными в G раз, введя 6=1, Р=7.
4-50 2 /100 , 1004 , 20 /100 100\ ггг
й 11 ----4- 1 -4- > г -р ) —10,671
11 7-10 3-7-10\0,5 0,5- 1002-0,5 \О,2 0,2/
2 100-20/ 1 , 1 \
- ПТ."” + 200 + 1”-1’+ТГ (1№ +Нй) +
+ JL.+ »(l+“k э.з,;
2-100-и,2 1 0,2\100 2Ю/
8-100 1 /100 200\ 3-100-20 ,,
= блл - --+ — I---4- — ч----------~ = 11,31;
33 443-7-10 100\0,2 0,2/ 2-1002-0,2
_ _ _1____/ 100 2-10Q2 \
,2~ 21 = 3-7-10 (д 707 ~ 100-0,7о7,/
20 Г /1 1 \|
—------------=— 1 4- 1С0 ( — -р — = —4,21,
100-0,707-0,2 \Ю0 200/J
379
20
& i о == Sot = =0,707;
13 31 2-100-0,2-0,707 ’ ’
, 200 1 /100 20 'I
Boq = Soo = ЬоЛ = b.q - | -4- I —
3 3- 34 13 3-7-10 200 \0,2 0,2/
100-20 /1 1 \ „ nr.
2-100-0,2X100 100/
100-20
В 94 == Ьдо = — 0,25.
24 42 4-1002 - 0,2
Свободные члены. Для заданных размеров коробки и нагрузок /’, = 100 кг, 5i=0 имеем следующие значения изгибающих моментов и поперечных сил в сечениях над нервюрами (см. фиг. 186).
Передняя балка (по полету):
44f=10-10*; 44f = 6-10*; 44f = 3-10*; 44f = 1 • 10*; Л-lf = 0?2
Qf= 0,4-103; Q^ = 0,3-103; Qf = 0,2-103; Qf = 0,1-103.
Задняя балка:
М* = М* = М34 =0; Q3 = Qf=Qf=-0.
Следовательно, согласно (6. 2)
44, = 10-10*; 442 = 6-10*; 443 = 3-10*; 44 4 = 1 • 10*.
Вычисляем свободные члены:
_ 2-50 10-10*-0,707 , 100 2-10-10* + 6-10* , 0,4-10-3
Д1р ~ 7-10
100
= 1,664-10*;
0,2-0,707
3-20 7-10-0,707
(10-10* + 12-10*) (12-10* + 3-10*) -
и • ZU•/• 1 v
20
Лг/,== 3-20-7-10
2-0,4-103 —0,3-103
= 0,756-10*;
2-0,2 100-10* 100
Д3р =--------- (6 + 4-3 4-1)—-----= 0,427-10*;
Зр 3-20-7-10v 2-0,2
100-10* 100
Д4Р = ------—(3 + 4-1)—---------= 0,142-10*.
4₽ 3-2017-104 2-0,2
Система уравнений получается следующей:
10.67Х,—4,21Х2+0,707Х3+1,664 • 10*=0;
—4,21 Хх+9,31 Хг—3,05Хз+0,25Х.,+0,756 • 10*=0;
0,707Х!—3,05X2+11,31X3—3,05X4+0,427 • 10* = 0.
0,25X2—3,05X3+11,31X4+0,1-11 10*=0.
Решение системы уравнений дает: Х,=—2350 кг; Х2 =—2160 кг; Х3 = —900 кг, Х4=—320 кг.
Окончательные значения продольных сил в стрингерах получаются путем алгебраического суммирования X, с фиг. 185). Таким образом продольные дует вычислять по формуле р О
усилиями второй основной системы (см. силы в передних стрингерах (/ и //) сле-
для i = 2, 3, 4 . .
380
Как видно из фиг. 184, б и фиг. 185, усилие над корневой нервюрой для передних стрингеров вычисляется так:
n
A'f = —-
1 b
sin a
а) изгиб
4
560
3860
IIIIHf"!
Эпюра N^kz)
1805
1550
Эпюра Мш{кг)
570
800 in
6100 б) Кручение
75 106
ТТЛ! IIII111 rrm
3
11Г1ТТПI ITTnrrr^-.
4
e Эпюра Ni(kz)
~5
г'
• inn hlll
110 15 106
4'
- Эпюра Ы]ц{кг)
1
^ul
в) Нагрузка по задней, стенке
113 6
Эпюра М:{кг)
630 ~7
810
1500
1'
3'
6f
110
830
Фиг. 187.
эпюра Мш(кг)
1050
а усилия в прикрепляющих стержнях / и // равны:
Alf sin a
Nj '== — ] = - + Xj.
b
Суммарная эпюра продольных сил показана на фиг. 186. Из этой эпюры видно, что вблизи косого отсека интенсивность возрастания уменьшается,
381
зато резко увеличиваются усилия в заднем стрингере (TVhj). Наличие косой заделки приводит к значительной перегрузке задней балки (лонжерона). При прочих равных условиях задний лонжерон всегда короче переднего, а следовательно, более жесткий на изгиб и воспринимает большую долю нагрузки, чем передний.
Определение касательных усилий в стенках можно проделать самостоятельно, руководствуясь фиг. 184 и 185, а также § 7.4.
Для более полного выяснения особенностей работы коробки с косой заделкой рассмотрим конструкцию из предыдущего примера при различных случаях нагружения.
1. Pi—Sj—100 кг (коробка работает только на изгиб).
Коэффициенты канонических уравнений остаются без изменения. Свободные члены
Д1р= 1,361-104; Д2р = 0,324-104; д,р = д1р = 0.
После составлении и решения уравнений получаем
Х4=—1735 кг-, Х2 — —1200 кг; Х3 =—230 кг; Х4 =—40 кг.
Эпюра продольных сил в стрингерах I и III показана на фиг. 187, а (/, 2, 3, 4, 5-—точки приложения сил на передней балке, 2', S', 4', 5'-—точки приложения сил на задней балке).
2. Р\=—5,-100 кг (случай кручения).
Вычисляем свободные члены:
Д|р = 1,967 - 104; д2р= 1,188 • 104; Д3р = 0,855 • 104; Д4р = 0,283 • 104.
Решение системы уравнений дает: АД = —2970 кг; Х.,=—3120 кг; Xs= 1575 кг; Х4 = —606 кг.
Эпюра продольных сил для стрингеров / и III показана на фиг. 187,6. Точно* такой же результат можно получить и без решения системы уравнений, если воспользоваться принципом независимости действия сил и представить крутящую нагрузку в виде суммы двух нагрузок, решение, для которых уже имеется: нагрузка силами 2Р;=200 кг по переднему лонжерону (см. фиг. 186) н изгиб силами —Р,= — 5,=—100 кг (см фиг. 187. а).
3. Р,=0, Si=100 кг (нагрузка по задней стенке).
Не прибегая к решению системы уравнений, получим эпюры N\ и Л^шкак сумму соответствующих эпюр продольных сил от изгиба силами Р,——100 кг, приложенными по переднему лонжерону (см. фиг. 186), и изгиба силами P=S,= 100 кг (см. фиг. 187, а). Суммарная эпюра изображена па фиг 187, в.
Заключение. Все изображенные на фиг. 187 эпюры показывают, что вдали от прикрепления обе балки (лонжероны) работают примерно одинаково, а наличие косого отсека приводит к значительной перегрузке заднего лонжерона вблизи второй нервюры (точка 2')-
§ 7.7. ЭНЕРГЕТИЧЕСКИ ЭКВИВАЛЕНТНЫЕ СТЕНКИ
Очень часто по конструктивным соображениям стенку в отдельных панелях коробок и других тонкостенных балок и ферм заменяют раскосом (расчалкой или парой расчалок), либо выполняют в виде замкнутой жесткой рамы. Чтобы не перестраивать формулы для вычисления перемещений или расчета статически неопределимых величин, выведенных для систем со стопками, удобно пользоваться понятием об энергетически эквивалентной стенке. Так называют стенку, у которой накапливаемая потенциальная энергия одинакова с энергией растяжения раскоса или изгиба рамы при одной и той же нагрузке. На фиг. 188 показана простейшая однопанельная плоская конструкция в трех вариантах— со стенкой, с раскосом и в виде жесткой рамы. Наружные
382
габариты и нагрузка одинаковы. Предполагается, что рама обладает упругой симметрией относительно горизонтальной и вертикальной осей.
Составим выражения потенциальной энергии стенки, раскоса и рамы. Энергию удобно выражать не через Р, а через
Р q=-T-Энергия стенки
, , 1 nab
U, =— q2—.
1 2 Gt
Энергия раскоса
П 1 Л72 1 1 2 Р
О, = — N2 —=— q2 — .
2 2 ЕР 2 ЕР
Энергия рамы
и=-Ly-L Сл/2^л=4 — м2
3 2 J 6 \ 2 EaIa
+
4-----------= — q*—— .
2 EbfbJ 2 24 \ E0Ia Eb!b /
Условие эквивалентности ' UX = U2=:U3 после сокращения па <?2/2 представится в виде
Фиг. 188.
Следовательно, стенка, эквивалентная раскосу, должна иметь
жесткость
(О/э),=
EFab
(7- 2)
Стенка, эквивалентная раме,
должна иметь жесткость
(О/э)2
24
ab
b
Еа^а
В случае Eala = Eblb=^EI
24Е/
а!> (а ф b)
(7.3)
(7. 4)
Задавшись модулем сдвига G, можно заменить раскос или раму стенкой определенной толщины /э. Определив в результате полного расчета коробки погонное касательное усилие q в эквивалентной стенке, найдем и усилие в раскосе или угловой момент в раме по формулам
N-=ql\ M = q~.
383
Возникает вопрос, дает ли пользование понятием эквивалентной стенки совершенно точное решение при замене одной конструкции другой? На этот вопрос приходится ответить отрицательно. Решение получается с некоторым приближением благодаря тому, что не учитывается специфика напряженного состояния окаймляющих стержней. Так, например, окаймляющие стержни в случае раскоса имеют постоянное продольное усилие, а в случае стенки — переменное по длине.
§ 7.8. ВЛИЯНИЕ ИЗМЕНЕНИЯ ЖЕСТКОСТИ ОДНОГО ИЗ ЭЛЕМЕНТОВ КОРОБКИ НА РАСПРЕДЕЛЕНИЕ УСИЛИЙ ПРИ КРУЧЕНИИ
0 )( ———— —
(ъ h
/•2 о-------------------
а
Фиг. 189.
В процессе конструирования нередко приходится сталкиваться с необходимостью изменения сечения какого-либо элемента, что приводит к перераспределению усилий во всех (или во многих) элементах данной статически неопределимой системы. Так, напри-* мер, в результате поверочного
Z) /г расчета может оказаться, что ка-
Г сательные напряжения в одной из панелей тонкостенной коробки будут выше допускаемых. Попи-___; жая эти напряжения за счет
з утолщения данной стенки, конструктор должен учесть, как
это повлияет иа усилия в остальных частях коробки. 4
Предположим, что имеется тонкостенная коробка с т отсеками и т+1 жесткими нервюрами. Для определения лишних неизвестных следует использовать систему т уравнений трех осевых сил (5.1).
Вычислив коэффициенты и свободные члены по формулам (5.2) и (5.5) и решив систему (5.4), получим осевые силы для случая, когда сечения всех элементов по длине коробки постоянны. Решение системы (5.1) обозначим ЛУ (г=1, 2, 3... т). Изменение толщины какой-либо стенки в одном из отсеков приведет к изменению коэффициентов и свободных членов двух уравнений системы (5.1). Определение новых величин усилий требует повторного составления и решения системы уравнений. Этот путь нерационален. Его можно значительно упростить, если рассматривать окончательные усилия как сумму усилий в первоначальной коробке и дополнительных усилий, вызываемых изменением толщины одной из стенок.
Пусть в отсеке п толщина какой-либо стенки (например, верхней) изменилась с tn до = Сечения остальных элементов остались неизменными (фиг. 189). Изменение толщины пластины вызовет изменение величины сдвига данной панели. Точно такой же результат получим, если, оставив толщину пластины неизменной, дадим ей некоторый (пока не известный) угол сдвига уп. Пол-
384
пый угол сдвига пластины первоначальной толщины будет равен Yn+ , в то время как угол сдвига утолщенной панели равен
—7 . Приравнивая эти выражения, получим зависимость между & п начальным углом сдвига усилием в панели и изменением толщины пластины:
(8-1)
1 С int'n kt
Gt„f'a
где kt~—, причем Д/ считается положительным, если
т. е. при увеличении толщины пластины.
Теперь толщины всех, элементов коробки можно считать прежними, по, кроме заданной внешней нагрузки, приложить в верхней панели n-го отсека сосредоточенный сдвиг уп.
Усилия от нагрузок, приложенных к такой коробке, уже известны в результате решения системы (5. 1). Остается добавить к ним усилия, возникающие от сдвига 7 п. Коэффициенты при неизвестных Х‘, выражающих влияние у71, остаются те же, что и в системе (5. 1), так как основная система не изменяется. Свободные члены /г-го и п-\-1 -го уравнений будут равны соответственно Л*„ = а7 г. и —-Д*п=—a'in. Это — перемещения точек приложения сил У*п и X*n+i от сдвига панели на угол '(п (фиг. 190). Остальные свободные члены равны нулю, так как внешняя нагрузка отсутствует. Система уравнений для определения дополнительных осевых сил запишется так:
^21^1 + ^22^2== 0,
°2i Xt +о22/У2 + 823А'з = 0,
1
I (8. 2)
)
25 425
385
S, л-1^’л-1 + *Л, и*" + S„, n + i-Vn., 1 — Д/i,
2/i r 1 ,nXti ~h 0л i I,n i-1zk n i-1 “1“ O/i । 1, л i 2^ л i-2 ~ Д/i ’
Vl, m-1^ m-z + O/n-i, m-r^ '«-> H' 1. mz^m~“0, %, m-lzY'«-l + ~ 0-
(8. 2)
Систему (8. 2) удобно решать в такой последовательности: сначала положить Д*п = 1 и вычислить значения неизвестных Х{ при единичных свободных членах, затем уже умножить полученные величины неизвестных па Д%. Таким образом, Х*,= Д*ПХ1-. Окончательные величины осевых сил, возникающих в поясах коробки после изменения толщины стенки, найдутся суммированием решений систем (5. 1) и (8. 2):
A’I = ДлА’р
^Л = ^° + ДХ- ,й
2Гот = ^-|-дХ- J
Остается определить величину множителя Д*. Используя первое уравнение (5.7) и зависимость (8.4), получим
(8-4)
откуда
где 7^ = 7р + ^- (А’л-м — -¥°) — сдвигающее усилие в стенке /г-го отсека до изменения ее толщины.
Выражения (8.3) совместно с (8.4) дают решение поставленной задачи. Ясно, что этот же путь решения задачи следует избрать и в том случае, когда приходится изменить нс только толщину стенки, во и материал, из которого она сделана. Только при этом надо вместо изменения толщины рассматривать изменение жесткости сдвига Gt.
Рассмотренный способ расиста нетрудно распространить и на случай изменения сечения какого-либо пояса (стрингера) в любом
386
отсеке коробки. Введя удлинение пояса, эквивалентное изменению его жесткости, придем к системе уравнений, аналогичной системе (8.2), только свободные члены n-го и n+il-ro уравнений будут равны половине упомянутого выше удлинения.
§ 7.9. ВЛИЯНИЕ УДАЛЕНИЯ СТЕНКИ В ОДНОЙ ПАНЕЛИ
Расчетной схемой двухлонжеронного крыла, имеющего большой вырез в обшивке, является тонкостенная прямоугольная коробка, в одном из отсеков которой удалена стенка. Вырез в крыле делается из конструктивных соображений (люк для крыльевого бака, уборки шасси и т. п.) и коренным образом изменяет распределение усилий в элементах конструкции.
Расчет коробки в области выреза является важной самостоятельной задачей. Приводимый ниже расчет имеет лишь целью иллюстрировать прием, изложенный в предыдущем параграфе.
Удаление одной стенки можно рассматривать как переход к стенке бесконечно малой толщины (или бесконечно малой жесткости), причем касательные усилия в этой стенке равны нулю. Поэтому расчет коробки с вырезом может быть выполнен как предельный случай расчета, разобранного в предыдущем параграфе, когда толщина одной из стенок /*п->0, т. е. при /г(->0.
Допустим, что решена система (5. 1) и найдены все усилия в коробке без выреза (в том числе и продольные силы в поясах). Тогда дополнительные осевые силы, возникающие в поясах коробки при вырезании одной из дтенок n-го отсека, будут равны
Х = (/==1,2,3.......т),
где — решение системы (8.2) при Д* =1, а Д* вычисляется по формуле, вытекающей из формулы (8.4) при
Продольные силы в поясах коробки с вырезом получаются как сумма сил первого и второго расчета:
= + Х (t-1,2,3- . . . ,т).
Контролем правильности решения должно служить обращение в нуль погонного касательного усилия в вырезанной стенке 7п = 0.
Напомним, что 7° — касательное усилие от внешней нагрузки, действующее в той стенке основной системы, которая в действительной конструкции отсутствует. В случае нагружения коробки крутящими моментами
п 2аЬ
где Мк — крутящий момент, действующий па протяжении отсека с вырезом.
25*
387
Примеры. Вычислим осевые усилия в одном из поясов прямоугольной коробки с шестью отсеками, нагруженной па свободном конце парой сил с моментом М Другой конец коробки жестко защемлен, жесткости стенок нервюр па сдвиг и прикрепляющих стержней на растяжение считаем бесконечно большими. Размеры коробки показаны на фиг. 191 (а= 150 см, 5^50 см). Все пояса имеют одинаковые площади сечений F,=10 см2, толщины стенок лонжеронов и обшивки коробки 0,2 см, расстояния между соседними нервюрами длина отсека— d=100 см. Модуль упругости материала стержней Ё=2- 10° кг/см2, модуль сдвига материала стенок G--2,5 105 кг/см2.
Сначала определим осевые силы для коробки без выреза, затем проведем ряд расчетов, предполагая, что вырезается верхняя стенка одного из отсеков.
1. Коробка без выреза. По формулам (5.2)-:-(5. 5) вычисляем 6# И hip'-
4-100 2 (150 + 50)
-----------+-----------!-------= 2 67- 10-ь-
3-2-10е-10 4-100-2,5-105.0,2
2-100-4 2(150 + 50)
3-2-106-ю’1' 2-100-2,5-105~0,2 =5’33’10 ° G = 2, 3, 4, 5, 6);
4-100 2 (150 -1-50)
Ъ,к = „----—------.............= 1,67-10-5 (i < k)-
1 6-2-106-10 4-100-2,5-105.0,2 1 ’’
Л —2(150+50) Мк
Д, „ =-----------!-----—— =-1,33-10-7 мк.
р 4-150-50-2,5-105-О,2
+ р=0 ((=2, 3, 4, 5, 6), так как крутящие пары Ki на промежуточных нервюра^' отсутствуют.
Составляем систему уравнении трех осевых сил (5. 1). После сокращения на Ю-5 получим
2,67 +“- 1,67+!? — 1,33-10+Ик = 0,
— 1,67 -)- 5,33 +!? - 1,67 +° = 0,
- 1,67+!?+ 5,33 А'!? —1,67+!? = 0,
— 1,67+“ + 5,3,3+!.’— 1,67+9 = 0,
— l,C)7+g + 5,33+g-l,67+? = 0,
— 1.67+“ + 5,33+5 = 0.
383
Решая систему, находим осевые силы X? в коробке без вырезов:
X? = 640- 10-АИк, X* = 27,6- 10-5Л/к,
X!? = 225-10-SM1<( =9,6-10-5Л4к,
*£== 78,9.10-5Л4|(, Л^ = 3,0-10-5Л(К.
Эпюра осевых сил изображена пунктиром на фиг. 192.
Фиг. 192,
2. Вырез в отсеке I (у корня). Единичные дополнительные усилия X,-.вычисляем, решая систему (8. 2), причем свободные члены 1 и —1 будут и первом Иво втором уравнениях, так как вырез сделан па первом участке (п=1):
389
2,67*, - 1,67*г = 1,
- 1,67 *,4-5,33*,— 1,67*3 = — 1,
—' 1,67 *, + 5,33 *3 — 1,67 *4 = О,
— 1,67Х3 + 5,33 ХА — 1,67*5 = 0,
— 1,67 *4 + 5,33 *5 — 1,67*67 =0,
— 1,67*5 4-5,33*6 = О.
Решение этой системы дает:
*1 = 312-10-я, *4 = —12,4-Ю-з.
. *2 = —101-10-3, *5 = -4,31-10-3,
*3 = —35-Ю-з, *6 = —1,35-Ю-з.
Вычисляем погонное касательное усилие, действующее в верхней стенке первого отсека коробки без выреза (осевые силы нам известны из предыдущего-расчета):
л XI к 1 Л Л Л4If
?-=^ + 2Т(^-Л-) = 2Ч5^ +
+ (225-10-5 — 640-10-5) Мк = 4,59-10-8 мк.
Далее по формуле (8.5) вычисляем
. ' 200-4,592-10-5 мк
Д,=--------'------------ = 2,22-10-2 м
312-10-3+101-10-3
Окончательные значения осевых сил в коробке с вырезом находим ио формуле (8.3), используя величины сил Х!-, найденные при расчете коробки без выреза.
*! = 640-10-5 Мк 4-312- Ю-з-2,22-10-2мк = 1330-10—5 Мк,
Х2 = 225-10-5 Мк — 102-10-3-2,22-10-2 Мк = — 2-10-5 Мк,
*3 = 78,9-10-5 Мк — 35,5-10-3-2,22-10-2Мк = 0,
*4 = 27,6-10-5Л4К _ 12,4- Ю-з-2,22-10-2Л4к = 0,
*5 =9,6 -10-5 Мк — 4,31-10-3-2,22-10-2Мк = 0,
*6 = 3,0 • 10-5 Мк - 1,35-Ю-з.2,22-10-2Мк = 0.
3. В ы р е з в о т с е к е II (фиг. 191, б). Составляя систему (8.2), надо считать
п=2.
Решаем коробки
2,67*, + 1,67*2 = 0, — 1,67*| + 5,33*2 — 1,67*з 1.
— 1,67*2-|-5,33*з—1,67*4 = - 1, — 1,67*3 + 5,33*4— 1,67*5 = 0, — 1,67*4 4-5,33*5 — 1,67*6 = 0, - 1,67*5 + 5,33*6 = 0.
систему, а затем вычисляем касательное усилие в стенке второго отсека без выреза для того, чтобы иметь возможность определить Л2 •
*,= 100-10-3, *4 = —52-Ю-з,
*2 = 175-10-3, *5 = -18,1-10-3,
390
Л3 = — 150-10 3; zfi=_5,7-10--’;
= 2?^' + 2^6 С8'9' 10~8 ~ 225' 10’5) Мк “ 5’93- 10"5Мк:
*2 =
200-5,93-10-54+
175-Ю-з 4- 150-Ю-з
= 3,65-10-24+.
р^числяем осевые силы в поясе коробки:
Xt =640-10-5Л1к+ 110-Ю-з.з,б5-10-2Д+ = 10-10-10—з/Ик, Х2 = 225- 10-5Мк +175-10-3-3,65- 10-24+ = 863-10 '5/1+, Х3 = 78,9- 10~54+ — 150- Ю-з.3,65- 10-2Мк = - 470- 10-54+, Х, = 27,6 • 10 -5М,< — 52.10-3-3,65-10-2Д+ = — 165 • 10-544к, Х5 = 9,6- 10-5А+ — 18,1 • Ю-з.3,65- 10-2Л4к = - 57- 10 -5/Мк, Х6 = 3,0- 10-54+ - 5,7- Ю-з.3,65- Ю-2Д1К - — 18-10-54+.
д. Вырез в отсеке 111, Система уравнений (8.2) при п = 3 имеет вид 2,67Х| — 1,67Лг 0,
— 1.67 Х\ -р 5,33%2 — 1.67 Х3 = 0,
- -1,67 X., 5, -ЗЗЛ3 1,67Х| = 1,
--1,67 Л3 +5,33л.!— 1,67Л5 = —1,
— 1,67 Л4 5,3.ЗХ5 — 1,67 Х6 = 0,
- 1,67Л5+5,33X(i-0.
X оказываются равными
Xj =60-10-3, Л4 150-Ю-з, х2 = 100-10-3. Л5 = -52,4-10-3, Л3 = 172-Ю-з, Х6 = - 16,4- Ю-з.
Находим величину касательного усилия в верхней стейке коробки без выреза: ’3" + 2тЬб <27 6' “78-9' * » мь io-»,.
Определяем величину Д3. Согласно (8. 5)
, 200-6,41-10-5Мк
А, =-----------------2— =3 98- 10-2/U,.
3 172-10-з + 150-Ю-з ’
Вычисляем величины осевых сил в поясе коробки с вырезом:
X, = 640- 10-5Л4к + 60- Ю-З-3,98• 10—2Д4К 880-10~5Л4К,
Х-2 = 225- 10-5Мк 100- Ю-З-3,98- 10~2/Ик = 623- 10-5Мк,
Х3 = 78,9.10-5Л4к + 172 • Ю-з - 3,98 • 10-2Л4к = 764 • 10-5Д1к, Х4 = 27,6- 10-5Л4к..150- Ю-з.3,98- 10-2Л4к = -570- 10-5Мк,
Л5 = 9,6-10-54-+ —52,4-10-3-3,98-10-?Л4к = — 200 • 10-5Д/к, Л6 = 3,0-10-54+ - 16,4-10-3.3,98-10 -244к = -62-10 -5Д+.
Заключение. Эпюры продольных сил в поясе коробки для рассмотренных выше четырех случаев приведены на фиг. 192. По виду
391
эпюр можно судить о влиянии выреза на распределение усилий в коробке. Так, например, при вырезании стенки в первом отсеке продольные силы в остальной части коробки практически отсутствуют. Это объясняется тем, что вырез в корневой части крыла превращает жесткую заделку в упругую и тем самым резко уменьшает эффект стесненного кручения. В то же время очень сильно возрастают осевые силы на протяжении первого отсека, поскольку крутящий момент на этом участке воспринимается только за счет изгиба вертикальных стенок в противоположные стороны, т. е. за счет растяжения и сжатия поясов.
При вырезании стенок в других отсеках (четвертом, пятом и шестом) задача решается аналогично, но практический интерес представляют именно рассмотренные выше варианты, так как наличие большого выреза в крыле вдали от корня мало вероятно.
§ 7.10. РАСЧЕТ КОРОБКИ С ВЫРЕЗОМ, ОКАЙМЛЕННЫМ ЖЕСТКОЙ РАМОЙ
Коробчатые конструкции обычно рассчитываются в предположении, что входящие в их состав стержни работают только на растяжение или сжатие. Это эквивалентно представлению о шарнирном соединении стержней. В действительности же пояса коробки выполняются неразрезными, а стойки соединяются с поясами лонжеронов и нервюр жестко. Стержни коробки образуют миогопро-лстную раму, зашитую тонкой стенкой. До наступления потеря устойчивости стенки нормальные напряжения от изгиба стержней невелики. Обычно этими напряжениями можно пренебречь. Иная картина имеет место при наличии выреза. Пренебрежение изгибом стержней окаймляющих вырез, может привести к весьма большим погрешностям и существенно исказить истинный характер работы участка коробки вблизи выреза. Иногда вырез компенсируется установкой съемного раскоса или даже съемной панели, кренящейся по контуру большим числом силовых шурупов.
Расчет коробки с компенсированным вырезом можно свести к обычному расчету коробки без выреза, если воспользоваться понятием энергетически эквивалентной стенки (§ 7.7). Жесткость, а следовательно и толщину /э стенки, эквивалентной раме или раскосу, определяют по формулам (7.2) и (7.3).
Поставив в месте выреза эквивалентную стенку, приходим к расчету коробки, у которой одна из стенок имеет измененную толщину (см. § 7.8). Произведя расчет эквивалентной короб-
ки (коробки с эквивалентной стенкой), следует ввести коррективы, учитывающие перераспределение усилий, возникающее при замене рамы или раскоса эквивалентной стенкой. Для этого из эпюр усилий в элементах коробки, окаймляющих эквивалентную стенку, нужно вычесть усилия, вызываемые погонными касательными усилиями в эквивалентной стейке, и добавить вместо них соответствующие изгибающие моменты или продольные силы, имеющие место в аналогично нагруженной раме или ферме.
392
Пример. Для коробки, рассмотренной в § 7.9, имеющей вырез но втором отсеке (случай 3), вычислить осевые усилия в поясах и изгибающие моменты в стержнях, окаймляющих вырез.
Принять осевой момент инерции каждого пояса коробки /а=5 см*, а момент инерции поясов нервюр /п = 0,5 слЛ Модули упругости Еа~ E,t = 2 • 10° кг/с л2. Стержни, окаймляющие вырез, жестко связаны друг с другом, образуя раму.
Прежде всего по формуле (7. 3) вычисляем толщину эквивалентной стенки, считая, что она, как и все остальные стенки коробки, выполнена из материала с модулем сдвига G=2,5- 103 кг/см2:
Величины X®, Xi и будут те же, что и для коробки с некомпенсированным вырезом (см. § 7.9, пункт 3), но теперь значение Д2 нужно вычислять но формуле (8.4), полагая в ней п—2, a t*=t^ и предварительно определив k,:
2,5-105-0,2-4-10- 5
5,93-10-5Л4к
, = 0,868- 1О-ЗЛ4К.
1 10
-----(175-10-3 + 150-10-3)4- —
2-100' ’ 150
Далее находим усилия в поясах коробки с эквивалентной стенкой:
Xi = 640-10-5Мк -|- 110-10 -3-0,868- 10-зуик = 650- 10-5Л?к, ' Л2 -- 225-10—5Л4К + 175-10-3-0,868-10-змк = 240- 10-5Мк, Х-t = 78,9-10-5Л4к- 150-10--3.0,868-10-з.Мк = 65-10-5JWIt, Ал4 = 27,6 • 10-f’+lк — 52 • 10- з - 0,868 • 10--!Л4К - 23 • 10- %1К, Л5 = 9,6- 10-5Мк — 18,1 • 10-3-0,868- 1О-ЗМК = 8- 10-5Л4к, Л6 = 3,0 • 10-5Л4к — 5 • 7 -10-3.0,868 • 10-3/Мк = 2,5 • 10-5Л1к-
Эпюра продольных сил приведена на фиг. 193 сплошной линией. Пунктиром дана эпюра при одинаковой толщине стенок. Хотя стенка, эквивалентная раме имеет очень малую толщину (С —4-Ю-3 см при 1 = 0,2 слс), ординаты эпюр отличаются незначительно (в пределах 10%).
393-
Чтобы перейти к напряженному состоянию рамы, отделим верхнюю панель второго отсека вместе с окаймляющими ее стержнями. Панель с нагрузками изображена на фиг. 194, а. Вырезав эквивалентную стенку, ио считая все узлы жесткими, получим раму, окаймляющую вырез, которая должна воспринимать Те же силы, что и панель с эквивалентной стенкой (фиг. 194,6).
Эпюры Л!Цаг и N и буквенное значение их ординат для рамы показаны иа фиг. 194, в и г. Вычислим значения максимальных ординат этих эпюр, принимая п=2, поскольку вырез во втором отсеке):
65-10-5 — 240-10-5 щах Л4ИЗГ =
100 .И к
150 =°’217м«;
8-50
8
65-10-5 -240-10-5
^1 =
4
394
3-240-10-S —65-10-5 100Л4к
No = '---------------------Л4К +----------
2 л 4-150-50
100
495-10-5 Л/к;
4
, 3-65-10—s 4-240-10-s
№> = -------------------- Мк
3 л 4-150-50
= - 190-10-5Af„.
4
Эпюра .V на участке с вырезом изображена на фиг. 194, <9. Там же дана исходная эпюра N в коробке с эквивалентной стенкой.
Расчет коробки без вырезов или с компенсированным вырезом значительно упрощается, если пренебречь осевыми силами в консольной части коробки, имеющими незначительную величину (см. фиг. 193, а). В рассмотренном примере без большой потери точности можно положить Л4 = Л5 = Лб=0, уменьшая число неизвестных и уравнений до трех.
§ 7.11. ПРИМЕРЫ ВЫБОРА ОСНОВНОЙ СИСТЕМЫ ПРИ РАСЧЕТЕ КОНСТРУКЦИЙ ПО МЕТОДУ СИЛ
На фиг. 195, а изображена корневая часть крыла. Осевые силы передаются четырьмя параллельными опорными стержнями /, II, III, IV. Кроме того, обеспечивается передача сил в плоскости корневого сечения, что схематически показано тремя опорными стержнями.
От прямоугольной коробки, подробно рассмотренной выше, конструкция отличается двумя дополнительными боковыми отсеками, так что миогосвязпый контур поперечного сечения имеет три ячейки.
В целом система три раза статически неопределима. Основную систему получим, перерезав один из опорных стержней, например, стержень 1, и разрезав боковые ячейки продольными разрезами. Лишними неизвестными являются?
1) усилия Xt в опорном стержне 1 или, что то же, — групповая сила, состоящая из четырех попеременно растягивающих одинаковых сил в стержнях I, II, III, IV;
2) погонные касательные усилия Xi и Х3 в продольных разрезах боковых ячеек.
Система канонических уравнений имеет вид
1) + ЛЛг + ^3°1з +— О’
2) 2Ci821-|-2C23.,2 + 2C3S32 + Д>р—0, 3) X-|- 21^32 + 2С3833 + ^зр — 0-
(И- 1)
Для вычисления свободных членов и коэффициентов определяем усилия в основной системе от заданной нагрузки и единичных лишних неизвестных. Пусть, например, заданная нагрузка сводится к крутящему моменту /Ик. В стенках средней ячейки, имеющей форму, близкую к прямоугольной коробке, возникают погонные касательные усилия q — MK!2ab = const (фиг. 195,6). От неизвестной ^1 = 1 в стенках-поясах коробки возникают нормальные усилия, следующие закону прямой с ординатами, изменяющимися от +1 У корня до нуля у передней нервюры, и касательные усилия в сред-
395
пей ячейке, равные \/2d (фиг. 195, в). От Х2=1 (фиг. 195, г) нормальных усилий не возникает, а крутящий момент, равный 1 • Q2 и создаваемый касательными усилиями ячейки 1, уравновешивается касательными усилиями, второй ячейки, равными, очевидно, 1 • Q2/2ab. Сказанное относится также к действию Х3=1. В средней ячейке получаем погонное касательной усилие Qd2ab (фиг 195, д).
Решая систему (11. 1), целесообразно сначала выразить Х2 и -Уз через Xt, пользуясь вторым и третьим уравнениями, а затем подставить результат в первое уравнение. В результате'первое уравнение принимает вид XiSjf’=0. Свободный член и коэффициент бц<2> имеют определенный механический смысл: это перемещения двукратно статически неопределимой основной системы», не имеющей разрезов в ячейках 2, 3. Отсюда видно, что процесс: решения уравнений можно интерпретировать как переход к стати--чески неопределимым основным системам. Эти соображения часто бывают полезны при анализе различных систем.
395
Рассмотрим другой пример. На фиг. 196 изображен участок фюзеляжа с вырезом, подкрепленный четырьмя шпангоутами А, А' й В, В'. Предполагается, что левее шпангоута В и правее шпангоута В' возмущение напряженного состояния, вызванное вырезом, практически не существенно и, например, кручение моментами Л4,( реализуется постоянным погонным касательным усилием 7 = Л1К/ПК.
Конструкция, состоящая из двух замкнутых цилиндрических оболочек АВ и А'В' и открытой оболочки АА', при условии, что обшивка работает только па сдвиг, а четыре стрингера — только на продольные силы, рассматривается как два твердых тела, соединенных семью связями (четыре стержня и три стенки) и нагружеп-
Поперечные сечения
Фиг. 196.
ные уравновешенной системой сил, на фиг. 196 — равными и противоположными моментами /Ик. Система однократно статически неопределима, так как для неизменяемого соединения двух тел достаточно шести связей. Лишним неизвестным является усилие в каком-либо сечении одного из стрингеров. Усилия q в трех стенках открытого отсека всегда определяются из уравнений равновесия, но если конструкция имеет поперечную плоскость симметрии, то при кручении можно заранее сказать, что в среднем сечении всех стрингеров усилия N ,равны нулю >и раскрытие статической неопределимости отпадает: после определения усилий q в стенках сразу определяются и усилия N в стрингерах, следующие линейному закону. Усилия в сечениях А и А' открытого отсека являются нагрузками замкнутых отсеков АВ и А’В’. Имея нагрузки по торцам замкнутых отсеков, нетрудно определить усилия q и N, а затем и нагрузки шпангоутов или нервюр.
Конструкцию фюзеляжа с четырьмя мощными стрингерами иногда называют «нолумонокок». Количество стрингеров часто превышает четыре. Добавление каждого стрингера в открытом отсеке (фиг. 197, а) повышает степень статической неопределимости на два: одно неизвестное усилие в каком-либо сечении стрингера и одно неизвестное усилие в повой панели стенки. Симметрия конструкции относительно поперечной и продольной плоскости позволяет снизить число совместно решаемых уравнений.
397
При раскрытии статической неопределимости приходится учитывать деформацию шпангоутов, каждый из которых в замкнутых отсеках представляет статически неопределимую систему — кольцо или раму (фиг. 197,6). Целесообразно заранее рассчитать усилия в шпангоутах от единичных неизвестных с тем, чтобы в системе канонических уравнений фигурировали только основные неизвестные— усилия в стрингерах.
Промежуточные шпангоуты также повышают степень статической неопределимости.
Ю. Г. Одиноковым и его сотрудниками разработан метод рас-».-'та мпогострипгерной конструкции («монокок») при помощи си-
а) S)
Фиг. 197.
стемы дифференциальных в стрингерах в качестве
уравнении второго порядка с усилиями функциональных неизвестных. Метод Ю. Г. Одинокова является одним из вариантов дискретно-континуального метода расчета призматических оболочек, развитого В. 3. Власовым. Термин «дискретно-континуальный» отмечает наличие сосредоточенных (дискретных) неизвестных в поперечном сечении оболочки и континуальных (т. е. функциональных, непрерывных) неизвестных по длине оболочки. Применительно к задачам авиационных оболочек, в том числе и многосвязных, метод Власова в его общей форме развит И. Ф. Образцовым.
При большом числе стрингеров решение при помощи системы алгебраических уравнений как методом сил, так и дискретно-континуальным методом становится весьма кропотливым. Целесообразно использовать ту или иную гипотезу о распределении напряжений по сечению оболочки, сводя ее, таким образом, к брусу.
В случае кручения фюзеляжа на участке выреза часто ограничиваются учетом работы двух боковин, игнорируя работу части сечения вблизи оси симметрии. Крутящий момент Мк воспринимается парой поперечных сил Та в боковинах, где а—расстояние между центрами изгиба боковин (фиг. 198). Если / — длина выреза, то каждая боковина работает на изгиб, причем наибольший изгибающий момент (в защемлении) равен
М + Т — = 4-^ —.
п,ах -- 2 — а 2
.398
Более обоснованное решение получается, если рассматривать
фюзеляж на участке выреза как защемленный по концам открытый
тонкостенный профиль (корытный) с исчезающе малой жесткостью свободного кручения и использовать теорию стесненного кручения,
изложенную в гл. V. Расчетные формулы для о и t=q!i написаны на фиг. 199.
Бимомент в сечении защемленного торца равен
Вт.,= --- •
ш«х — к 2
Этот прием детально разработан Г. Н. Рудых.
Используется также метод, основанный на гипотезе плоских сечений при сдвиге и кручении. Для открытого тонкостенного профиля, окаймленно
го вдоль краев стрингерами, эта гипотеза оказывается достаточно-обоснованной. Получаемые в этом случае расчетные формулы имеются на фиг. 200. Через С обозначен так называемый центр сдвига, совпадающий с центром кручения, г — перпендикуляр из центра
Фиг. 199.
сдвига на касательную к средней линии. /<•. — так называемый направленный полярный момент инерции площади сечения обшивки (без учета площадей стрингеров) относительно центра сдвига:
/с = J гЧ ds.
Положение центра сдвига определяется из условия аннулирования равнодействующей касательных усилий в обшивке при кручении или, что то же, из условий аннулирования крутящего момента при поступательном перемещении (сдвиге). Формулы для коор
399
динат центра сдвига аналогичны формулам (2. 13) и (2. 14) § 9.2.
Бимомент имеет прежнее значение. Производная dr Ids выражает интенсивность роста плеча г по дуге средней линии.
Отдельные элементы этого метода разрабатывались В. Н. Беляевым, Р. А. Ададуровым, В. Л. Марьиным.
Существует метод, основанный на комбинировании напряженных состояний, отвечающих двум последним способам, исходя из требования минимума потенциальной энергии деформации. Этот метод разработан В. Л. Марьиным.
Эпюра г, Г Эпюра ff
Фиг. 200.
Расчеты показывают, что результаты, даваемые двумя гипотезами и их комбинацией, отличаются не очень сильно.
В заключение рассмотрим две расчетные схемы тонкостенных крыльев малого удлинения, предложенные И. А. Свердловым.
На фиг. 201, а показано крыло в форме прямой призмы, основания которой образуют два лонжерона треугольной формы, а боковую поверхность — обшивка. Один лонжерон защемлен, другой— имеет левый шарнирно опертый конец. Нагрузка считается приложенной в плоскости лонжеронов, либо в плоскости грани обшивки.
Погонные касательные усилия в обшивке найдем из условия равновесия переднего лонжерона. Из уравнения моментов относительно шарнира В имеем
Здесь Пк —• площадь сечения профиля призмы, в данном случае — площадь треугольника. В этом примере крутящий момент в сечении замкнутой оболочки заменяет момент защемления консоли (фиг. 201,6). На фиг. 201,0 показана аналогичная четырехлонжеропная конструкция. Система также статически определима.
Предлагаем в виде упражнения наметить порядок расчета системы и указать наиболее выгодное положение защемленного лонжерона.
-400
Треугольное крыло с защемленными лонжеронами, высота которых условно принята постоянной (фиг. 202, а). Выбираем основную систему в виде пяти консолей, приняв за лишние неизвестные крутящие моменты Xi касательных усилий в четырех трубчатых панелях между лонжеронами. Для упрощения заменяем пирамидаль-
Фиг. 201.
ные отсеки обшивки призматическими (фиг. 202,6). Уравнения получаются трехчленными:
^1§11 + ^2812 4"Д1р==0> ।
^1821+^2822 + ^382з + Д2р —0- ! (112)
^2^32 4"^з"зз + у’(,4®34 + Д3р~ 0. I
-^3843 + -^4844 + Д4р == 0- |
Каждый лонжерон нагружен равномерно распределенной нагрузкой интенсивностью pi—pa и разностью потоков касательных усилий
_ 1 _ 1 __ 1 _ 1
q‘~ Q. 2Л/-Р И ^'+! й/+1 2Л/?Р,
(фиг. 202,в). Эпюры изгибающих моментов от заданной нагрузки и
единичных неизвестных Xt и X+i изображены на фиг. 202, г.
Коэффициенты и свободные члены уравнений (11.2) равны
8 _ Z'CP , 4A + z/₽)
!i " 2G/A2 ( / 2*
401
Решая систему, получим искомые величины крутящих моментов в обшивке, а затем построим окончательно эпюры изгибающих моментов в каждом лонжероне. В рассматриваемой схеме распреде-
Фиг. 202.
ление нагрузок по лонжеронам будет более равномерным, так как наиболее нагруженные длинные лонжероны будут через обшивку передавать часть своей нагрузки на менее нагруженные передние лонжероны, обладающие большей жесткостью.
Глава V111
ОБРАЗОВАНИЕ И РАСЧЕТ ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ ФЕРМ
§ 8. 1. ОБЩИЕ ПОЛОЖЕНИЯ
Фермой принято называть неизменяемую систему прямых стержней, соединенных тем или иным способом в узловых точках и обладающую той особенностью, что при замене всех узловых соединений шаровыми шарнирами, работающими без трения, система остается неизменяемой. Ферма с шаровыми шарнирами во всех узлах и является той расчетной схемой, с которой мы в дальнейшем будем иметь дело. Вместо термина «расчетная схема фермы» будем говорить «шарнирная ферма» или, чаще всего, — просто ферма. Обоснованность замены реальной фермы, например, со сварными узлами, шарнирно стержневой фермой тесно связана с характером нагрузки: если не будет специальных оговорок, речь будет идти только об узловой нагрузке. При узловой нагрузке основную роль в напряженном состоянии фермы играют продольные усилия в стержнях. Моменты же и поперечные силы, возникающие вследствие жесткости узлов, создают напряжения, играющие подчиненную роль. Оказывается, что продольные усилия в стержнях фермы с жесткими узлами и шарнирной фермы разнятся весьма мало. Узловые нагрузки создают в стержнях шарнирной фермы только продольные усилия, направленные по прямым, соединяющие центры узловых шарниров.
Отметим, что шарнирная ферма является неизменяемой не при всех нагрузках: нагрузки должны быть приложены в узлах или должны пересекать оси стержней. Крутящих моментов стержни фермы с шаровыми шарнирами передавать не могут.
Фермы всегда рекомендуется конструировать так, чтобы стержни были центрированы, т. е. оси стержней (линии центров тяжести поперечных сечений) пересекались бы в точках — центрах узлов. Другими словами—-оси стержней должны совпадать с прямыми, образующими геометрическую схему фермы. В противном случае стержни будут работать на внецентренное растяжение или сжатие, что крайне невыгодно в смысле прочности и жесткости.
26*
403
С образованием и расчетом простейших плоских ферм детально знакомит курс теоретической механики. Ряд задач, относящихся к статически неопределенным фермам, рассматривается также в курсе сопротивления материалов. Поэтому в следующих параграфах лишь напоминаются основные правила расчета плоских фер;и и более подробно рассматриваются вопросы их образования и далее изучаются пространственные фермы.
§ 8.2. ПЛОСКИЕ ФЕРМЫ
Плоская ферма называется простейшей, если она образована последовательным прикреплением узлов каждый раз двумя стержнями.
На фиг. 203, а показаны простейшие прикрепленные фермы, а па фиг. 203,6 — простейшие свободные фермы или неизменяемые ферменные диски. Предлагаем самостоятельно наметить порядок прикрепляемых узлов при анализе каждой фермы.
Для прикрепления свободной плоской фермы к опорному диску необходимо три стержня, не пересекающихся в одной точке (фиг. 204).
Количество стержней (s) простейшей прикрепленной фермы, очевидно, равно удвоенному числу узлов (п):
2л. (2.1)
Количество стержней свободной фермы равно удвоенному числу узлов при условии, что опорные стержни также засчитываются, в число стержней. В противном случае, если опорные стержни не засчитываются, то:
s = 2п-3. (2-2)
404
Простейшие плоские фермы, очевидно, являются статически определимыми, так как число уравнений равновесия узлов в точности равно числу неизвестных усилий в стержнях. Вырезая все узлы и составляя для каждого из узлов два уравнения равновесия,
£г=о.
(2. 3)
получаем возможность определить усилия во всех стержнях, в том числе и в опорных.
Решение задачи существенно упрощается, если составлять и решать уравнения в определенной последовательности. Именно ре-
шение надо производить в г------
порядке, обратном об- / \ / \
разованию фермы, начиная у \
'от того узла, в котором схо- ?
дятся всего два стержня с ' неизвестными усилиями. я
В том же порядке, как Г
ИЗВеСТНО, ПРОИЗВОДИТСЯ И графический расчет усилий— построение диаграммы Мак- % свелла—Кремоны. 4 J
Если следовать этому по-рядку,то аналитический расчет сведется к решению си- ‘ и1,
стемы уравнений, состоящей из пар уравнений с двумя неизвестными, так как предыдущие усилия в каждую новую пару уравнений войдут в качестве известных сил. Мало того, пользуясь удобно взятыми осями проекций или уравнениями моментов вместо уравнений (2. 3) для произвольных осей можно определить каждое усилие из одного уравнения с одним неизвестным.
На фиг. 205 показана прикрепленная ферма простейшего образования. Расчет следует вести, переходя от узла 5 к узлу 2 и затем к узлу 1.
Если удается провести разрез, пересекающий одновременно только три стержня, то усилия в трех перерезанных стержнях, как известно, могут быть определены независимо от усилий во всех остальных стержнях. Так, усилие М[_2 определяется из уравнения моментов относительно точки С, усилие А^с-з—из уравнения моментов относительно точки С, усилиеЛ^с_2—из уравнения проекций на ось, перпендикулярную направлению параллельных стержней 1—2 и С—3.
При расчете ферменных лонжеронов (удлиненных ферм, заменяющих балки со сплошной стенкой), нагруженных параллельными силами, при составлении уравнений проекций и моментов целесообразно использовать эпюру поперечных сил в сечениях, парал-
405
лельных силам, и эпюры изгибающих моментов в сечениях обоих поясов. На фиг. 206 силы имеют вертикальное направление. Балка, для которой строят эпюры Q и М, горизонтальна.
На протяжении первых трех отсеков поясд параллельны. Поэтому усилия в стойках и раскосах получаются из уравнений проек-
ций. Учитывая, что сумма проекций односторонних внешних сил на вертикаль равна Q, находим
-'Vl-I'— Ql-2; Д^1'-2= ———-.
Sin а
406
В данном случае стойка 1—Г— сжата, раскос Г—2 — растянут.
Принимая во внимание, что момент односторонних внешних сил равен изгибающему моменту, получаем усилия в стержнях поясов:
Nv_2, = h а
Стержень верхнего пояса сжат, стержень нижнего пояса — растянут.
Усилия всех стержней других отсеков определяются из уравнений моментов. Для., поясов можно непосредственно использовать ординаты эпюры изгибающих моментов:
М_5==—ЛГ4,_5, =-^5-.
А4 г5
Усилия в стойках и раскосах получаются из уравнений моментов относительно точки С:
9
2 МОМ„Р/
di di
э
Г4'-5 г4'-5
Вычисление моментов односторонних сил (в данном случае сил ^5,- • •, относительно точки С можно упростить, воспользовавшись ординатами эпюр Q и М. Действительно, учитывая, что совокупность сил Ps,..., Pg статически эквивалентна <?4прав и Mi, находим
Q inpae d*-
Здесь С?4прав ордината эпюры Q правее сечения 4.
§ 8.3. ПРЕОБРАЗОВАННЫЕ ПЛОСКИЕ ФЕРМЫ И ИССЛЕДОВАНИЕ ИХ ГЕОМЕТРИЧЕСКОЙ НЕИЗМЕНЯЕМОСТИ
Геометрическая неизменяемость (жесткость) простейших плоских ферм, образованных последовательным прикреплением узлов двумя стержнями является очевидной. В то же время такие фермы статически определимы, другими словами, при заданных узловых нагрузках во всех стержнях возникают конечные усилия, которые могут быть однозначно определены из условий равновесия.
Оказывается, однако, что не все прикрепления узла двумя стержнями являются равноценными.
Если прикрепляющие стержни образуют «очень острый» или «очень тупой» угол, то от нагрузки, близкой к перпендикулярной направлению стержней, в стержнях возникают усилия, которые во много раз превосходят нагрузку.
407
В пределе, предполагая оси стержней сливающимися, приходим к бесконечным усилиям в стержнях АС и ВС. Одновременно можно установить, что прикрепление шарнирного узла в предельном случае не является жестким: узел может получить малое смещение без заметного удлинения стержней. Объясняется это тем, что каждый из стержней ограничивает свободу перемещения узла, заставляя его находиться на окружности; в предельном случае малые участки круговых траекторий сливаются и, следовательно, стержни не препятствуют движению узла в пределах этого участка (фиг. 208). Только при более значительном смещении возникает препят
Фиг. 208.
ствие к дальнейшему движению, система как бы «заклинивается». Отметим еще, что в конструкциях такого типа при узловой нагрузке, направленной вдоль стержней, усилия в стержнях получаются конечные, но статически неопределимые: чтобы распределить силу Р между стержнями АС и ВС, пришлось бы использовать условия деформации.
Описанные конструкции носят название м гиовен но из м е-н яемых. Их следует считать практически непригодными во всех случаях, когда конструкция должна быть жесткой и особенно когда нагрузка может иметь произвольное направление.
Таким образом, давая правило образования простейших ферм, надо оговориться, что пары прикрепляющих новый узел стержней не должны быть вытянуты в одну прямую. Впрочем, эта оговорка является настолько очевидной, что обычно она не упоминается.
Рассмотрим теперь преобразованную ферму, полученную из простейшей путем (фиг. 209, а) перестановки одного стержня (фиг. 209, б). Переставляя стержень А—1 в положение 1—4, получаем систему с тем же количеством узлов и стержней и, следовательно, можем составить столько уравнений равновесия узлов, сколько имеется неизвестных усилий в стержнях. На первый взгляд ферма статически определима. Легко, однако, убедиться, что мы можем задаться одним из усилий по произволу и получить для
408
некоторых видов нагрузки уравновешенную систему. Зато для других видов нагрузки равновесие оказывается невозможным, что яри: аналитическом расчете выражается в том, что усилия получаются бесконечными.
Пусть, например, в узлах 2 и 3 приложены две одинаковые силы Р. Зададимся произвольно усилием ТУг-з- Производя последовательное разложение от узла 2 влево и от узла 3 вправо, определим все усилия, причем для усилия N\-4 получим два значения, которые
в силу симметрии системы оказываются одинаковыми. Таким образом, система может воспринять симметричную нагрузку, причем-одним из усилий можно задаться. Другими словами, усилия определяются неоднозначно. Это означает, что для симметричной нагрузки система является статически неопределимой. Раскрытие статической неопределимости требует, как известно,, привлечения условий деформации.
Пусть теперь система нагружена несимметрично. Выполняя указанные выше операции, получим из равновесия узлов 1 и 4 два разных значения одного и того же усилия TVi-4, причем независимо от величины произвольно взятого усилия Л^2-з. Значит, при несимметричной нагрузке равновесие невозможно, а это исключает практическое использование системы, если нагрузка может иметь произвольное направление.
Покажем, хотя и нестрого, что данная система допускает малую подвижность при практически неизменной длине стержней. Сме
4091
стим стержень 1—4 поступательно в горизонтальном направлении. Тогда узлы 2 и 3 займут положение 2' и 3'. При малой величине векторов 2—2' и 3—3' длину 2'—3' можно считать равной длине 2—3. Значит, стержень 2—3 не создает в начале препятствий для перемещения точки 1, т. е. допускает мгновенную изменяемость системы.
Указанные свойства системы всегда сопутствуют друг другу. Так, если система с минимальны,м числом стержней для плоской фермы (s = 2n или s = 2n—3) допускает самонапряженпое состояние, т. е. одним из усилий можно задаться и получить равновесное состояние, то можно утверждать, что существуют нагрузки, при которых равновесие невозможно и, кроме того, система допускает малую подвижность, т. е. является мгновенно изменяемой. И наоборот, малая подвижность системы сопровождается возможностью самонапряженпого состояния и невозможностью уравновесить некоторые виды нагрузки.
Доказательство этого общего положения, которое весьма просто получается на основании начала возможных перемещений, опускаем. Достаточно иметь в виду следующие соображения. Если в системе можно задаться одним усилием и получить равновесное состояние, то это значит, что при некоторых нагрузках система статически неопределима, иначе говоря, имеет в этом случае лишний стержень. Но так как общее число стержней является минимальным, то при другой нагрузке, наоборот, должно не хватать одного стержня, и эта нагрузка не может быть воспринята. Следовательно, подобная система практически непригодна.
Отсюда вытекает основной статический способ анализа практической пригодности преобразованной системы: надо убедиться, что задаваясь усилием в одном стержне (в отсутствии нагрузки), нельзя получить равновесного состояния.
Так, если систему на фиг. 209, б сделать несимметричной, то, задаваясь усилием в стержне 2—3, вообще говоря, не получим одного и того же значения для усилия Ni-*, идя влево от узла 2 и вправо от узла 3. Однако в частных случаях такое совпадение возможно. Практическая непригодность системы в данном случае связана с ее симметрией и с соотношением размеров при асимметрии*.
Общий метод расчета преобразованных систем основан на замене преобразованной системы простейшей путем перестановки стержней. Первый этап расчета дает и ответ на вопрос, является ли система практически пригодной.
Этот метод принято коротко называть методом замены стержней. Сущность его поясним на примере рассмотренной выше системы, но при несимметричной конфигурации (фиг. 210, а).
* Подобно тому, как следует избегать «очень острых» или «очень тупых» углов прикрепляющих стержней, следует избегать и малых отступлений от симметрии, так как это не избавляет от весьма больших усилий. Точно так же надо избегать малых отступлений от мгновенно изменяемых несимметричных схем.
410
В системе нет ни одного узла, в котором бы сходились только два стержня с неизвестными усилиями. Поэтому начать расчет и провести его методом последовательного разложения сил (иа два направления) не представляется возможным. В этом — основная черта преобразованной системы и ее отличие от простейшей системы.
Перережем одни из стержней, например стержень 1—4, и введем вместо него стержень 1—А (фиг. 210, б). Полученная система является простейшей. Будем называть ее основной систе-
Фиг. 210.
мой. Действительное напряженное состояние представим как сумму двух напряженных состояний основной системы: 1) от совместного действия заданных нагрузок Pi, Рг\ усилия от всех нагрузок Р будем называть NiP', 2) усилия от двух равных и противоположных сил Xi, приложенных в разрезе стержня 1—4. Если обозначить усилия от сил %i = l через Nn, то от Л) будем иметь усилия XiNu. Таким образом, усилие в Том стержне выразится суммой __
+ (3. 1)
В действительном состоянии системы стержень А—1, обозначаемый индексом k, отсутствует. Это значит
7Vft=0.
411
Иначе говоря,
Отсюда находим
Мр+ ^1^1 = 0-
Nkp Nki '
(3. 2)
с определения усилия Nki i сил Х1=1. Если бы оказалось, что это
Р
Фиг. 211.
Имея X., получаем из (3. 1) усилия во всех стержнях.
Рекомендуется начинать расчет именно । заменяющем стержне от усилие равно нулю, то из (3. 2) получили бы бесконечно большое значение усилия Хг и, следовательно, бесконечно большие усилия во всех стержнях системы. Обращение в нуль усилия Л ,_л>1 свидетельствует о возможности самонапряженно-го состояния заданной системы, а это, как известно, является признаком практической непригодности системы.
Таким образом, пользуясь методом замены стержней, на первом этапе расчета устанавливаем практическую пригодность или непригодность системы и фактически избавляемся от специального рассмотрения этого вопроса.
Существуют, очевидно, фермы, которые могут быть сведены к простей
шим только при условии замены более чем одного стержня. Расчет подобных конструкций требует решения системы линейных уравнений, каждое из которых выражает мысль, что усилие в заменяющем стержне от действия заданных нагрузок и неизвестных усилий Хь Х2, ... заменяемых стержней равно нулю.
Отметим вариант метода замены стержней, который рекомендуется в случае нагрузки фермы одной силой Р (фиг. 211, а).
В этом случае целесообразно ввести заменяющий стержень по направлению силы (фиг. 211,6). Тогда усилие в нем от нагрузки непосредственно равно силе со знаком «+.» или «—»:
412
Определив усилие Nhi в заменяющем стержне от Xi = l, находим
Этот прием можно трактовать, и не прибегая к представлениям метода замены стержней. Речь идет о нахождении усилия в одном из стержней фермы из условия, что усилие в опорном стержне, направленном вдоль силы Р, равно ±Р.
Метод замены стержней практически дает ответ на все вопросы, относящиеся к определению усилий в статически определимых фермах.
§ 8.4. ПЛОСКИЕ ДИСКОВЫЕ СИСТЕМЫ
При расчете ферм отдельные неизменяемые части постоянно рассматриваются как- диски и к ним применяются условия равновесия твердого тела, нагруженного плоской системой сил:
j
Jr=0, (4.1)
Ум=о.
Под дисковой системой подразумеваются конструкция, элементами которой являются плоские диски, стержни и шарнирные узлы.
К числу дисковых систем относятся не только фермы. Диски могут иметь разнообразную конструкцию, в частности представлять собой прямые или ломаные брусья, работающие в основном на изгиб и продольную силу. К дисковым конструкциям относятся, например, фермы, у которых отдельные стержни подвергаются местной нагрузке. Эти стержни правильнее называть дисками или брусьями. Подобные системы обычно называют комбинированными, или рамно-ферменными системами.
Для расчета дисков (или брусьев комбинированных систем) прежде всего должны быть определены усилия в соединительных стержнях и реакции шарниров.
Остановимся на основных правилах образования, проверки практической пригодности и определении усилий и реакций в соединительных элементах дисковых систем. Имея эти усилия, можно рассчитать ферменные диски по общим правилам расчета ферм. Вопрос о построении эпюр усилий в рамных брусьях рассматривается з курсе сопротивления материалов.
Диск в плоскости обладает тремя степенями свободы. Для неподвижного прикрепления диска к другому диску необходимо и достаточно трех независимых связей, например трех стержней (фиг. 212, а) или шарнира и стержня (фиг. 212, б).
Точки 1,2, 2,3, 1,3 попарного пересечения стержней иногда называют фиктивными шарнирами. Относительно этих
413
точек составляют уравнения моментов при определении усилии
в соединительных стержнях. Та фиг. 212, а) следует составить сил, действующих на один из диск II) относительно точки 23.
Для определения усилия стержня АВ (см. фиг. 212, б) составляется уравнение моментов относительно центра шарнира С. Для нахождения реакции шарнира С следует выделить один из дисков и геометрически просуммировать найденное усилие Nab с нагрузкой диска. Равнодействующая дает искомую реакцию шарнира С. Можно также заменить шарнир двумя стержнями, определить в них усилия, а затем их геометрически просуммировать.
к, для определения усилия N\ (см. уравнение равновесия моментов дисков (безразлично диск I или
Фиг. 212.
Фиг. 213.
Три стержня, соединяющие должны пересекаться в одной параллельными). В противном случае
два диска, не точке (или быть соединение получает-
414
ся практически непригодным — мгновенно изменяемым, а в отдельных случаях — и конечно изменяемым.*
Жесткое соединение трех дисков в неизменяемое кольцо осуществляется при помощи трех пар' стержней (фиг. 213, а) или трех шарниров (фиг. 213,6). Подобные системы часто называют трехшарнирными арками. На фиг. 213, б и в показаны две реальные конструктивные схемы — трехшарнирной арочной несущей конструкции ангара и силового, шпангоута фюзеляжа крупного самолета.
Фиг. 214.
Реакции шарниров для схемы 213, б определяются в следующем порядке.
Реакция VA находится из уравнения моментов всех сил, действующих на обе полуарки, относительно шарнира отделенные от опор А и В, В. Реакция Vb определяется из уравнения моментов относительно шарнира А или из уравнения проекций 2У=0, пользуясь тем, что сила Vв уже определена.
Для определения реакции На составляется уравнение моментов сил, действующих па левую полуарку, относительно шарнира С. При этом VA выступает как известная сила. Диалогично определится Н в, но можно воспользоваться уравнением 2Х=0, имея в виду, что НА уже определено. Обратим внимание на то,, что при вертикальной нагрузке НА=НВ. В этом случае величину НА = НВ — Н называют распором арки. Имея реакции шар
* Конечная изменяемость имеет место, если три стержня пересекаются в реальном шарнире либо имеют одинаковую длину и параллельны.
415
нира А, нетрудно определить реакции шарнира С, пользуясь уравнениями равновесия 2А=0 и 2У = 0 для полуарки //.
Для определения реакций шарниров трехшарнирной системы пользуются также графическим методом (фиг. 214). Допустим, что равнодействующие нагрузок дисков // и ///, обозначенные на фиг. 214, а через Рц и Рш,заранее найдены. Равнодействующая нагрузки диска I, обозначенная Рр проходит через точку F пересечения Рц и РП1, а по величине определится как замыкающая 31 силового треугольника 123, построенного по силам Рц и Рin на фиг. 214,6. Силу Рп раскладываем по направлениям
BCD и DA. Это дает реакции в шарнирах С и А от действия силы Рц. Реакция в шарнире В, очевидно, равна и противоположна реакции в шарнире С. Аналогично раскладываем силу Рщ по направлениям АСЕ и ЕВ. Это дает реакции в шарнирах С, В и А от действия силы Рш. Полные реакции получаются геометрическим суммированием найденных частных реакций. Задача сводится к построению параллелограмма 2456. Искомые реакции (силы взаимодействия в шарнирах) показаны штрих-пунктирными стрелками. Направление острия стрелки зависит от того, к какому из двух дисков, соединенных шарниром, отнесена реакция. Направления реакций РА, Rc, RB перенесены на фиг. 214, а.
Условие практической пригодности трехшарнирпой дисковой системы состоит в том, что три шарнира (действительных или фиктивных) не должны лежать па одной прямой. ‘Системы, показанные на фиг. 215, а и б, являются мгновенно изменяемыми.
Пользуясь правилами соединения двух и трех дисков, можно образовывать и более сложные системы, в состав которых входит
416
большее число дисков. Существуют формулы, устанавливающие соотношение между числом дисков, числом шарниров и числом стержней статически определимой дисковой системы. Подсчет по ©тим формулам не освобождает, однако, от структурного анализа для выяснения практической приемлемости системы. В процессе этого анализа выясняется и вопрос, обладает ли система необходимым и достаточным числом элементов.
Помимо простых систем, встречаются и разнообразные преобразованные дисковые системы. Расчет их в ряде случаев требует применения метода замены связей (стержней или шарниров).
Фиг. 217.
Дальнейшее развитие теории дисковых систем приводит к рассмотрению связей других типов, в первую очередь моментных связей, передающих момент, по не передающих силу. Пример конструкции такой связи показан на фиг. 216, а. Важнее, однако, воображаемые моментные, связи*.
Сформулируем несколько простых правил, относящихся к соединению дисков при наличии моментной связи.
Если один из трех стержней, соединяющих два диска, заменяется моментной связью, то два других с т е р ж и я не должны быть н а ра лл сльн ы. В противном случае невозможно уравновесить нагрузку, перпендикулярную параллельным стержням. Положение моментной связи в плоскости дисков безразлично, так как усилие связи (пара сил, момент) может быть произвольно перенесено в плоскости диска. Среди трех связей, соединяющих два диска, не должно быть более одной моментной связи.
Моментная связь показывается дугой (фиг. 216,6).
На фиг. 217 показан ряд дисковых систем. Предлагаем в виде упражнения проанализировать системы с точки зрения практиче-
* Воображаемыми моментными связями постоянно пользуются при расчетах статически неопределимых рамных систем: жесткое соединение заменяете;! двумя силовыми и одной моментной связью, а усилия в этих связях (/V, Q, М) принимаются за лишние неизвестные.
27 425
417
ской пригодности и наметить порядок их расчета от произвольной нагрузки, которой следует задаться. Последовательность вырезания отдельных дисков отмечена римскими цифрами.
§ 8.5. ПОЛЯРНАЯ ДИАГРАММА ПЕРЕМЕЩЕНИЙ УЗЛОВ ПРОСТЕЙШЕЙ ПРИКРЕПЛЕННОЙ ПЛОСКОЙ ФЕРМЫ
Очень часто возникает необходимость решить следующую задачу: известны малые удлинения всех стержней фермы; требуется
определить векторы перемещений всех узлов.
которые
назовем
С' '
В
Ас
Ал
Графическое решение этой задачи основано на следующих соображениях.
Рассмотрим узел С, прикрепленный стержнями к узлам А и В, исходными (фиг. 218, а). Предположим, что исходные узлы А и В получают малые перемещения, векторы которых АЛ и АВ отложены в точках А и В. Пусть стержень АС получает удлинение 7.лв , а стержень ВС—удлинение ьвс.
Допустим, что перемещение узла С найдено и отложено в узле С в виде вектора Лс.
Проекция геометрической разности А с —Ал на направление стержня АС должна быть равна удлинению Хлс.Точно так же проекция геометрической разности А с — &в на направление стержня ВС должна быть равна ?• вс.
Перемещения считаются в е с ь-м а м а л ы м и по сравнению с длинами стержней. Практически они со-
,• ставляют доли процента от длин.
°"г' |Ь' стержней. 11ри этих условиях можно
пренебречь поворотом стержней и при проектировании брать направления стержней недеформнрован-ной фермы и, кроме того, можно откладывать векторы в собственном масштабе, не зависящем от масштаба фермы.
Высказанное положение о геометрических разностях реализуется следующим построением (фнг. 218,6). От произвольного полюса О откладываем векторы перемещений исходных узлов Оа — Дл и О[, = Вв и к концам их пристраиваем векторы клс и 7.вс , параллельные стержням АС и ВС. Направление их берется в соответствии с тем, удлиняются или укорачиваются ли стержни АС и ВС и соответственно удаляется ли узел С от узла А (В) или он приближается к узлу Л (В). Через концы векторов 7„лс и 7. вс к ним проводим перпендикуляры. Пересечение их дает точку С — конец искомого вектора Ос- перемещения узла С.
418
).вс; при этом кон
а)
Фиг. 219.
Обоснование этого построения можно дать непосредственно при помощи кинематических соображений: сначала в узле С стержни АС и ВС разъединяются; стержню АС дается поступательное перемещение Ал и затем удлинение Хлс; стержню ВС дается поступательное перемещение Ад и удлинение цы С стержней АС и ВС расходятся. Для их соединения надо дать стержням поворот до соединения их в точке С. Заменяя по малости поворотов круговые траектории перпендикулярами к радиусам АС и ВС и продолжая эти перпендикуляры до пересечения, находим точку С—конец вектора Ас.
Перемещения трех узлов — двух исходных и прикрепленного к ним оказываются отложенными от одного полюса О. Теперь узел С может рассматриваться в качестве одного из двух исходных узлов для следующего прикрепленного узла, и построение может быть продолжено.
На фиг. 219, а показана ферма типа консоли (лонжерон крыла), характерная тем, что имеются два смежных узла, перемещения которых известны заранее, в частности, равны пулю. Здесь это будут опорные узлы А и В, которые мы считаем неподвижными. Сначал вычисляются малые удлинения стержней, являющиеся результатом упругой деформации от действия нагрузки, температурной деформации и неточности изготовления. Знаки удлинений выписаны около стержней на фиг. 219, о. Построение диаграммы дано на фиг. 219, б. Выбран полюс О, концы а и b нулевых векторов перемещений узлов А и В совпадают с полюсом. Вправо—вниз от точки а отложено удлинение стержня АС, влево — укорочение стержня ВС. Пересечение перпендикуляров к этим отрезкам, восстановленных в концах векторов — удлинений дает точку с. Перемещение узла С равно вектору Ос. Переходим к узлу D. Вправо от точки а откладываем удлинение стержня AD. Вниз от точки с откладываем укорочение стержня CD. Пересечение перпендикуляров дает точку d. Дальнейшее построение предлагаем проследить самостоятельно. Перемещение последнего узла II дается вектором Oh, показанным пунктирной стрелкой.
Построение диаграмм в более сложных случаях можно найти в курсе строительной механики стержневых систем. И. М. Рабинови-27’
419
ча и в книге автора «Статика и кинематика ферм». Преимущество графического метода состоит в том, что он дает сразу полные перемещения всех узлов фермы. Если же достаточно выяснить перемещение одного узла по определенному направлению, то проще всего это достигается аналитически — вычислением по формуле, известной из курса сопротивления материалов:
§ 8.6. ПРИКРЕПЛЕНИЕ ШАРНИРНОГО УЗЛА В ПРОСТРАНСТВЕ. УСИЛИЯ в ТРЕХ СТЕРЖНЯХ, ПРИКРЕПЛЯЮЩИХ УЗЕЛ
Для прикрепления шарнирного узла (точки) в пространстве к некоторому твердому телу (опорной поверхности) достаточно трех стержней, не лежащих в одной плоско-с т и. Двумя стержнями узел закрепляется от перемещений
в плоскости этих стержней, третьим стержнем он закрепляется от перемещений из плоскости двух стержней и в результате оказывается лишенным возможности перемещения в пространстве.
Три стержня в одной плоскости дают мгновенно изменяемое, а иногда и вполне изменяемое прикрепление.
Усилия в трех правильно расположенных стержнях от действия любой силы, приложенной к у!лу, могут быть однозначно определены из трех уравнений проекций сил, действующих на узел. Вырезая узел (фиг. 220), считаем предварительно три неизвестных усилия Уц N2, N3 р а с т я г и в а ю щ и м и, т. е. направленными от узла. В этом предположении составляем три уравнения проекций, пользуясь произвольно выбранными ортогональными осями х, у, г-
420
1) О, или Pcos (Р, •*)+ Ад cos (1, х) Д Афсоэ (2, х) Д-Д А’3 cos (3, х)~0;
2) V}'=o, или Pcos(^,y) + A^1cos(l,j/) + Ar2cos(2,j/) + + N3 cos (3, j/) = 0;
3) y'Z — tj, или P cos (P, z} + ;¥[ cos (1, z} +N2 cos (2, z) 4-&ssi
+ Лфсоз (3, z) = 0.
Решив уравнения, находим Nu N2, Ns-
При подсчете косинусов следует иметь в виду, что знак их совпадает со знаком проекции на ось положительного, т. с . растягивающего, направленного от узла, усилия. Можно также всегда считать косинусы положительными (беря острые углы между силами и осями), но тогда знаки проекций Ntcos(j, х) и т. д. придется брать по смыслу.
Неудобство данного способа состоит в необходимости решать три уравнения с тремя неизвестными. Каждое из трех усилий можно получить из независимого уравнения проекций, если выбрать ось проекций так, чтобы она была нормальной к плоскости двух других стержней. Этот способ удобен лишь в частных случаях расположения стержней, например, когда два стержня лежат в вертикально или горизонтально проектирующей плоскости.
Другой способ независимого получения усилий основан на применении уравнений моментов. Для нахождения усилия, папршиер АД следует взять ось моментов, пересекающую стержни 2 и 3. В качестве такой оси можно взять прямую, соединяющую следы стержней 2 и 3 на горизонтальной плоскости проекции (фиг. 221). Силу Р и усилие АС надо продолжить до пересечения с плоскостью проекции и разложить на составляющие— в плоскости проекций Нр и Нг и перпендикулярные к пей
Xp — Psin ар и
421
Уравнение моментов гласит
урГр + Г1Г1 = 0.
Откуда
Гр Р Sin арГр
Y^-Yp-P-; N{ =--------
Г\ Г\ sin Я]
Плоскость, па которой берутся следы, называется основной плоскостью. Если она горизонтальна, то составляющие И называются горизонтальными проекциями, а составляющие Y—
(?)
Фиг. 222.
в е р т и кала м и. Если основная плоскость вертикальна, то составляющие сил, взятые в этой плоскости, будем называть вертикальными проекциями сил , а составляющие нормальные к основной плоскости — го р и зон та л а-м и. При пользовании уравнениями моментов па первый план выдвигаются вертикалы или горизонталь!, горизонтальные и вертикальные проекции роли не играют.
На фиг. 222, а основная плоскость, как и на фиг. 221, горизонтальна. Следы стержней и силы Р обозначим соответственно А, В, С, D. На рисунке следы, А, В, С показаны в виде шарниров, однако совпадение следов с шарнирами необязательно. Проекции сил на вертикальную ось будем называть в е р т и к а л а м и и обозначать буквой Y с соответствующим индексом.
Пусть следы остаются неизменными, а узел К переходит в положение К'. Если при этом вертикал силы Р не изменяется, то и
вертикалы усилий также ие изменяются. Это непосредственно следует из уравнений моментов относительно осей ВС, АС, АВ, служащих для определения величины YА, Yu, Yc. Легко видеть, что определение вертикалов Yл, YB, Yc совпадает с нахождением реакций или усилий в вертикальных опорных стержнях блока, нагруженного вертикальной силой YP (фиг. 222, б).
Определив вертикалы Y, находим усилия N путем деления вертикала на синус угла стержня с основной плоскостью.
На фиг. 223 приведен пример использования в качестве основной плоскости — вертикальной плоскости проекций и определения
422
трех горизонтален 7-\, Z2, Z3 усилий в стержнях некоторого узла по горизонталу силы ZP .
Вместо составления уравнений моментов относительно осей, попарно соединяющих следы, можно дважды применить «правило рычага». Это дает
с d
с
£ __ с d b . £ _____________ с d л
1 1 с а b “ Р с а -\- b
Знаком минус здесь отмечено, что в системе четырех уравновешенных сил силы 2'| и Z2 направлены противоположно Z р н Z3. Вооб-
У
Z — Z
с
Z1 + Z2=-(ZP + Z3)=-ZP
Фит. 223.
ще возможны два случая: 1) один из следов занимает внешнее положение по отношению к треугольнику следов трех остальных сил (фиг. 223, а, б)-, 2) один из следов занимает-внутреннее положение в треугольнике трех остальных следов (фиг. 223, а). В первом случае силы попарно направлены в противоположные стороны; во втором — внутренняя сила противоположна по направлению трем остальным.
Остановимся на случае, когда сила Р пересекает основную плоскость за пределами чертежа. Целесообразно разложить ее в
423
узле на две составляющие: перпендикулярно основной плоскости и параллельно ей. Первая составляющая раскладывается ио указанным выше правилам. Вторая — Н переносится в вертикальной плоскости параллельно Самой себе в основную плоскость с добавлением нары с моментом Hh (фиг. 224), пара заменяется двумя составляющими +Hhla-, одна из этих составляющих дает непосредственно вертикал Уд> другая, приложенная в точке Е, раскла-п, дывается на Y# и Ус по пра-
вилу рычага;
Фиг. 224.
lz Hh с . v Hh b 1 n-- ' i c-- •
a c + b a b + c
Имея вертикалы, определяем истинные величины усилий в стержнях, разделив вертикалы на синусы углов стержней с основной плоскостью.
Графический способ. Идея чисто графического способа разложения силы на три направления в пространстве состоит в следующем. Четыре силы Р, Ni, Nz, находятся в
равновесии; поэтому равнодействующая сил Р и Д3 должна быть по величине равна, по направлению — противоположна равнодействующей сил и Nz и, очевидно, должна лежать на прямой пересечения двух плоскостей; одной, содержащей
силу Р и стержень 3, и другой, содержащей стержни 1 и 2. Построение начинается с. нахождения указанной прямой пересечения. Затем сила Р раскладывается по направлениям найденной прямой н стержня 3. Направление составляющей вдоль прямой пересече
ния изменяется на противоположное и полученная сила раскладывается по направлениям стержней 1 и 2. Все построение осуществляется в двух проекциях. По проекциям усилий находятся их истинные величины, пользуясь правилами начертательной геометрии.
Построение упрощается, если два из трех стержней лежат в одной вертикально или горизонтально проектирующей плоскости, т. е. когда вертикальные или горизонтальные проекции двух стержней лежат на одной прямой. Такой случай показан па фиг. 225.-Проекции стержней 1 и 2 в фасадной плоскости сливаются. Раскладываем в фасадной плоскости проекций силу Р по направлениям 3' и 1'2'. Для простоты построение силового треугольника частично совмещено с чертежом узла, что, разумеется, необязательно. Имея фасадную проекцию усилия ЛД (отрезок D'm'), находим профильную проекцию этого усилия (отре
зок D"m"), далее через конец силы Р" и точку т" проводим прямые соответственно параллельные 2" и 1". Точку п проектируем обратно в п.
Обходя один из силовых многоугольников по течению проекций Р' или Р" известной силы Р, устанавливаем знаки усилий: Ni и N2 — растяжение, N3—-сжатие. Для получения истинной величины усилия, например Ntt пристраиваем к отрезку п'т' катет m'q'=m"q" и измеряем гипотенузу n'q'=Ni.
ч
Фиг. 225.
Если вертикальные или горизонтальные проекции никаких двух стержней не лежат на одной прямой, то следует предварительно повернуть одну из плоскостей проекций так, чтобы достигнуть требуемого совпадения. Таким образом, способ, указанный на фиг. 225, является достаточно' общим.
§8.7. ПРИКРЕПЛЕНИЕ БЛОКА. УСИЛИЯ В ШЕСТИ СТЕРЖНЯХ, ПРИКРЕПЛЯЮЩИХ БЛОК
Для прикрепления блока (твердого тела) к другому твердому телу (опорной поверхности) достаточно ш с с т и стержней. Отрежем блок сквозным сечением, пересекающим все шесть стержней. Неизвестные усилия .. . , NC1 в стержнях могут быть теперь определены из шести уравнений равновесия блока:
2Z==0;
^<=0; = ^Д = °-
Задача имеет единственное решение при условии, что определитель системы уравнений равновесия не обращается в нуль. В противном случае возможны бесконечные (а/0) и неопределенные решения (0/0), что указывает на мгновенную изменяемость системы. Таким образом, анализ геометрической неизменяемости
425
прикрепления осуществляется одновременно с решением системы уравнений равновесия (как известно, решение системы линейных уравнений начинается с вычисления определителя из коэффициентов) .
Указанный общий метод применяется только в случае совершенно произвольного расположения стержней, не подчиненного определенным условиям. Подобный случай является крайне редким. Практически отдельные группы стержней пересекаются в некоторых точках, другие лежат в общих плоскостях. Это дает возможность, выбирая надлежащим образом оси проекций и оси моментов
Фиг. 226.
(необязательно в виде трех ортогональных прямых), получить шесть уравнений равновесия с частично пли полностью разделенными неизвестными. Разделение неизвестных важно потому, что избавляет от необходимости решать систему шести уравнений, каждое из которых содержит все 6 неизвестных. Впрочем, с развитием машинной вычислительной техники эти затруднения отпадают.
Для быстрой ориентировки в выборе рационального порядка расчета целесообразно рассмотреть важнейшие частные случаи расположения стержней.
П е р в ы и с л у ч а й, называемый нами основы ы м, когда три стержня (/, 2, 3) лежат в одной плоскости Q, но не пересекаются в одной точке, три других (4, 5, 6) — пересекаются в одной точке q, но не лежат в одной плоскости. Кроме того, точка q не должна лежать в плоскости Q.
На фиг. 226 показаны три примера, относящиеся к этому случаю. На фиг. 226, а точка q совпадает с шарниром, па фиг. 226, б— точка q удаляется в бесконечность (стержни 4, 5, 6 — параллельны), на фиг. 226,в — точка q занимает произвольное положение.
426
Легко убедиться, что усилия во всех стержнях определяются из независимых уравнений моментов, так как всегда можно провести ось, относительно которой моменты пяти из шести усилий равны пулю. Если ищется усилйе одного из трех стержней первой группы, то за ось моментов выбирается прямая, соединяющая точку q с точкой пересечения двух других стержней первой группы. Если ищется усилие в стержне второй группы, за ось моментов берется прямая пересечения плоскости Q с плоскостью остальных двух стержней второй группы.
Фиг. 227.
Основной случай можно охарактеризовать как такое закрепление блока, при котором обеспечивается фиксация одной плоскости (Q) и одной точки (</) блока. Поэтому блок можно закрепить, соединив его с опорной плоскостью балкой или ломаным брусом, жестким только в своей плоскости, и неподвижным шаровым шарниром.
Второ й с л у ч а й (фиг. 227) можно представить и двух модификациях: один стержень (/)—изолированный, два стержня (2, 3) — пересекаются, три остальных стержня (4, 5, 6) — лежат в одной плоскости Q (фиг. 227, а), либо пересекаются в одной точке q (фиг. 227, б). Расчет начинается с определения усилия N\. ria фиг. 227, а для этого служит уравнение моментов относительно осп, являющейся ребром пересечения плоскости 2—3 и Q; на фиг. 227, б берем ось моментов, соединяющую точку пересечения стержней 2 и 3 с точкой q. Для определения N2 (фиг. 227, а) продолжаем ось стержня 3 до пересечения с плоскостью Q. Ось моментов проводим через точку пересечения так, чтобы эта ось лежала в плоскости Q. Так как N{ уже известно, то величина N2 определится сразу. Аналогично может быть найдено усилие А3. Наконец, усилия Na, As, Ng определяются из уравнений моментов относительно осей, соединяющих точку пересечения стержней 2 и 3 с одной из точек пересечения стержней 5 и 6, 4- и 6 или 4 и 5. При этом Ni выступает по-прежнему в качестве известной силы. Таким же путеги могут быть определены усилия в случае фиг. 227, б.
427
Но здесь осями моментов служат прямые пересечения соответствующих плоскостей. Например, для определения надо в качестве оси моментов взять прямую пересечения плоскости 4—5 и 2—3. Следует заметить, что вообще, когда три из шести прикрепляющих стержней проходят через одну точку или лежат в одной плоскости, определение всех усилий возможно без совместного решения уравнений равновесия при условии соблюдения определенной последовательности в нахождении усилий из уравнений моментов. Таким образом, стержни, отмеченные номерами 2 и 3 на фиг. 227, необязательно должны пересекаться.
Фиг. 228.
Третий случай (фиг. 228, а, б)— шесть стержней попарно расположены в трех плоскостях, иначе говоря, попарно пересекаются. На фиг. 228, а и б точки пересечения обозначены А, В, С. Покажем, что третий случай с точки зрения расчета легко приводится к первому, когда три стержня лежат в одной плоскости, а три других — пересекаются в одной точке. Продолжим плоскости 1Л2, 354, 5С6 пересекающихся пар стержней до пересечения в точке q (см. фиг. 228, а). Точку q соединим с точками А, В, С (пря-' мые qAa, qBb, qCc). Проведем плоскость через точки А, В, С и найдем ребра пересечения этой плоскости с плоскостями пересекающихся пар стержней. Очевидно, условия закрепления блока не изменятся, если вместо стержней /11 и /12, 53 п 54, С5 и С6 введем стержни, попарно лежащие в тех же плоскостях, что и указанные, а именно Ла и Ла', ВЬ и ВЬ', Сс и Сс'. Расположение новых стержней удовлетворяет требованиям основного случая: стержни Ла, ВЬ, Сс проходят через точку q, стержни Аа', ВЬ', Сс лежат в одной плоскости АВС. Определив усилия новых стержней и найдя равнодействующие этих усилий, взятых попарно, можно легко определить усилия заданных стержней. На фиг. 228, б показано расположение стержней, когда плоскости 1/12, 354, 5С6 параллельны одной и той же прямой. Точка пересечения q в этом..
428
случае удаляется на бесконечность. Закрепление блока при переходе к заменяющим стержням становится эквивалентным показанному на фиг. 226, б.
Перечислим правила, позволяющие судить о мгновенной изменяемости шестистержневого прикрепления блока. Мгновенная изменяемость имеет место, если:
1) можно провести прямую, пересекающую все шесть стержней. Взяв момент произвольной нагрузки относительно этой прямой, убеждаемся, что уравновесить его невозможно;
а)
Фиг. 229.
б)
2) если четыре из шести стержней пересекаются в одной точке либо параллельны. Проведя плоскости через указанную точку и каждый из остальных двух стержней, убеждаемся, что существует прямая, пересекающая все шесть стержней (ребро пересечения двух плоскостей)
3) если четыре из шести стержней лежат в одной плоскости. Прямая, соединяющая две точки встречи остальных двух стержней с указанной плоскостью, пересекает все шесть стержней;
4) самый общий признак был указан в начале настоящего параграфа.
Переходим к конкретному определению усилия в стержне, для которого найдена ось моментов. Проекция искомого усилия на плоскость, перпендикулярную к оси моментов, равна моменту нагрузок блока относительно заданной оси, деленному на кратчайшее расстояние между осью и стержнем. Знак усилия находится из условия, чтобы нагрузка блока и усилие перерезанного стержня, приложенное к блоку, вращали бы в противоположные стороны.
Простейший случай — когда ось моментов перпендикулярна одной из плоскостей проекций или, наоборот, параллельна плоскости проекций.
429
Рассмотрим пример (фиг. 229, а) Блок прикреплен стержнями 1, 2, 3, лежащими в одной (вертикальной) плоскости (но не пересекающимися в одной точке) и стержнями 4, 5, 6, параллельными одной прямой, иначе говоря, пересекающимися в одной бесконечно удаленной точке. Усилие в стержне 1 определяется из уравнения моментов относительно оси /, параллельной стержням 4, 5, 6 и проходящей через точку пересечения стержней 2 и 3:
7У,=
«1
Фиг. 230.
Усилие в стержне 5 определяется из уравнения моментов относительно оси 1Г, пересекающей стержни 4 и 6 и лежащей в плоскости стержней 1, 2, 3:
N _ —Pi sin(P|,/Z')с, + Р2Ь2 5 а5
здесь «5 — длина перпендикуляра из 5' на 1Г (на фиг. 229 не показано).
Шестистержневая мотоустановка, обладающая плоскостью симметрии (фиг. 230). Систему стержней можно двумя различными способами отнести к третьему случаю — один раз, объединив стержни 1 и Г, 2 и 3, 2' и 3', и другой раз, объединив симметричные стержни 1 и 1', 2 и 2', 3 и 3'. Второй прием представляется более наглядным и мы на нем останавливаемся, тем более, что стержни 2 и 3, 2' и 3' в отдельных вариантах могут и не пересекаться.
Целесообразно придерживаться следующего порядка расчета, типичного для пространственных систем, обладающих плоскостью 430
симметрии. Все нагрузки заменяются симметричными (относительно плоскости) и антисимметричными силовыми группами. Первые дают в симметричных стержнях одинаковые и по величине и по знаку усилия; вторые дают в симметричных стержнях усилия, одинаковые по величине, но противоположные по знаку..
Симметричные нагрузки, приложенные к блоку, имеют равнодействующую Rc, лежащую в плоскости симметрии. В частном случае это может быть пара. Антисимметричные нагрузки, приложенные к блоку, имеют равнодействующую 7?а, перпендикулярную плоскости симметрии. Для получения равнодействующих проще всего каждую силу, приложенную к блоку, продолжить до плоскости симметрии и здесь разложить па две составляющие: одну — в плоскости симметрии и другую — перпендикулярную плоскости симметрии. Сложив затем отдельно все составляющие в плоскости симметрии и все составляющие, перпендикулярные плоскости симметрии, получим две равнодействующие в наиболее удобном для дальнейшего расчета виде.
Два одинаковых и по величине и по знаку усилия в симметричных стержнях дают приложенную к блоку равнодействующую в плоскости симметрии, направленную вдоль биссектрисы угла между стержнями. Эту равнодействующую можно, в свою очередь, рассматривать как усилие одного стержня, расположенного в плоскости симметрии и совпадающего с биссектрисой. Можно высказать следующее положение.
При симметричной нагрузке равнодействующие одинаковых усилий в симметричных стержнях получаются как усилия трех стержней, прикрепляющих диск в плоскости симметрии.
Рассматривая проекцию блока на фиг. 230, а как диск, прикрепленный стержнями, отмеченными 1, Г; 2, 2'\ 3, 3', сводим определение равнодействующих усилий стержней 1 и Г, 2 и 2', 3 и Зг к разложению силы /?Сим на три направления в плоскости, не пересекающиеся в одной точке. Это простейшая задача строительной механики плоских систем, рассмотренных выше.
Имея равнодействующие усилий N\,v, , Л/з.з', определим и
истинные величины усилий:
JV. ,, М ,,
N^NV =-------; N2=N’ =--------,
„ а2
2 cos — 2 cos ——
2 2
Ct о 2 cos —— 2
Здесь ctj, ct2, «з — истинные углы между симметричными стержня-Ми 1 и Г, 2 и 2', 3 и 3'.
Одинаковые по величине, но обратные по знаку усилия в симметричных стержнях при антисимметричной нагрузке имеют равнодействующие, перпендикулярные к плоскости симметрии и прило
431
женные в точках пересечения симметричных стержней. Эти точки на левой проекции блока (фиг. 230, а) обозначены цифрами I, II, III. Равнодействующие можно рассматривать как усилия трех стержней, перпендикулярных плоскости симметрии и высказать следующее положение./
При антисимметричной нагрузке равнодействующие одинаковых по величине, но обратных по знаку усилий в симметричных стержнях получаются как усилия трех стержней, перпендикулярных плоскости симметрии.
Задача сводится к разложению силы Ra на три параллельные ей составляющие (или к уравновешиванию силы Ra тремя силами). Обозначим уравновешивающие блок силы через Nlt Nu.
----, Тогда определится из уравне
ния моментов относительно оси //—III, взятой в плоскости симметрии,и^ ш определяются соответственно из уравнений моментов относительно осей /—/// и /—II. Имея jVp Nw NiU, находим истинные величины усилий в симметричных стержнях при антисимметричной нагрузке:
2 sin ——
2
2 sin ~
JV3
Мы видим, что все расчетные операции производятся на плоскости проекций, совпадающей с плоскостью симметрии. Вторая проекция (фиг. 230, б) имеет вспомогательное значение для определения точек 1, 11, Ill. По расположению «стержней» 1, Г; 2, 2'; 3, 3' и I, II, III на фиг. 230, а можно судить о рациональности прикрепления блока: плечи усилий всех стержней относительно соответствующих моментных осей должны иметь достаточную величину.
О составлении уравнений моментов в общем случае. Общий прием вычисления момента силы относительно прямой известен из курса теоретической механики.
Остановимся па графоаналитическом способе, основанном ла пользовании ортогональными проекциями и следами.
Пусть на эпюре Н, V сила Р\ (скользящий вектор) лежит на прямой 1, 1' и требуется вычислить момент этой силы относительно
432
прямой 2,2' (фиг. 231). Обозначения 1, Г и 2, 2' будем относить также к горизонтальным следам указанных прямых.
Обозначим горизонтальную проекцию силы Р\ через Hi, а проекцию на вертикальную ось через /ц Выберем на прямой 1, 2 совершенно произвольный вектор Рг, горизонтальную проекцию которого обозначим через Н2, а вертикал — через У2.
Для вычисления искомого момента учтем, что он равен сумме проекций на ось 2, 2' вектор-моментов, найденных относительно трех ортогональных осей, имеющих начало в какой-либо точке оси 2, 2'.
В качестве начала возьмем след 2, 2', в качестве осей — векторы (точнее линии их действия) Н2, У2, а также перпендикуляр к Н2 в плоскости Н (см. пунктир на фиг. 231). Сразу видно, что момента относительно этой последней оси составлять не нужно, так как проекция его вектора на ось 2, 2' равна нулю.
Момент относительно оси У2
±Н1Г2Г
Момент относительно оси 772
“Ь ^1г12-
Сумма проекций моментов на ось 2,2'
^4 = 4-77^, ^-±Г,г12^-. ~ 1 21 р2 1 12 р2
Знак выбирается в зависимости от направления вращения и принятого правила знаков. При правиле правого винта для случая, показанного на фиг. 231, будем иметь
2W=-//1r21^ + r2r12^.
Практически на чертеже задаются величиной Н, получают У2 и вычисляют Т/|4~/22.
Пользуясь выражением для момента, можно найти кратчайшее расстояние между прямыми 1, Г и 2,2'-.
=1А | = —1(4-.77,Г2г21 4-7/2Г,г12)|.
Приведенных данных достаточно для определения усилия в произвольно наклоненном прикрепляющем стержне, когда задана нагрузка блока и найдена моментная ось.
Обратим внимание па чисто графический прием определения усилия в стержне, для которого найдена моментная ось. Предварительно рассмотрим аналогичную задачу в плоскости. Пусть А (фиг. 232, а) есть точка моментов для стержня а. Усилие Na можно определить двукратным разложением силы на два н а п р а в л е н и я, иначе говоря, построением диаграммы усилий для фермочки, один из узлов которой взят в точке А, другой на силе Р, третий на стержне а. Совершенно аналогично, если
28 425
433
АА' ось моментов для стержня а в пространстве (фиг. 232,6), то усилие Na определяется двукратным разложением силы на три направления'—графическим расчетом
Фиг. 232.
пространственной фермочки, два узла которой взяты на оси А, третий узел на силе Р и четвертый — на стержне а.
§ 8.8. ПРОСТЕЙШИЕ ПРИКРЕПЛЕННЫЕ ПРОСТРАНСТВЕННЫЕ ФЕРМЫ
Так называют фермы, образованные путем последовательного прикрепления узлов каждый раз тремя стержнями, не лежащими в одной плоскости (фиг. 233, а).
Если обозначить число узлов (не считая опорных) через п, полное число стержней через s, то, очевидно,
s = 3n.
Вырезая п узлов, можем составить Зп уравнений статики вида \X = 0; р=0; 2Z = 0, из которых определяются усилия во всех Зп стержнях. Таким образом, простейшая прикрепленная пространственная ферма статически определима. Ее геометрическая неизменяемость (жесткость) следует из самого способа ее образования.
Анализ всякой пространственной фермы начинается с попытки ее р а с ф о р м и р о в а н и я *, т. е. последовательного отбрасывания узлов, прикрепленных тремя стержнями. Прежде всего надо отыскать узлы, в которых сходятся по три стержня, отбросить их,
* Термин «расформирование» предложен доцентом Д. В. Ангельским. По мнению автора, он удачнее, чем часто применяемый термин «разрушение». Проф. С. А. Бернштейн указал на возможность использования термина «разборка».
434
затем продолжить эту операцию дальше. Возможность расформировать (разрушить) таким путем ферму до конца говорит о том, что перед нами простейшая прикрепленная ферма.
В том же порядке расформирования производится расчет фермы. В большинстве случаев пользуются методом узловых сечений, рассматривая узел за узлом в порядке, обратном образованию фермы, причем ранее определенные усилия являются нагрузками следующих в порядке расформирования узлов.
Фиг. 233.
Здесь находят применение как чисто аналитический метод (составление системы троек уравнений проекций для всех узлов), так и графоаналитический метод (составление уравнения равновесия моментов с определением усилий из независимых уравнений) и, наконец, графический метод — последовательное разложение сил па три направления во всех узлах в порядке расформирования фермы.
На фиг. 233 показан ряд простейших прикрепленных ферм, причем номера узлов поставлены в порядке образования системы. Опорные узлы оставлены без номеров. Рекомендуем самостоятельно проследить образование этих систем, начиная от опорных узлов.
Анализируя ферму, следует обратить внимание не только на трехстержневые узлы, от которых начинается расчет, но и на еще одну важную категорию узлов — именно, на многостержневые узлы, все стержни которых, за исключением одного, лежат в одной плоскости.
Из условия равновесия проекций на нормаль к указанной плоскости можно определить усилие в выходящем из плоскости стержне 28* 435
независимо от усилий во всех остальных стержнях пространственной фермы,
К таким узлам принадлежат узлы: 2— на фиг. 233, а, 1, 2 и 3— на фиг. 233, б, 8 — на фиг. 233, д. Узел 2 на фиг. 233, а характерен также тем. что разность усилий в стержнях 1—2 и 2—3 также может быть определена независимо от усилий в других стержнях.
Усилие в стержне, выходящем из плоскости остальных стержней, можно определить и графически. Достаточно группу стержней, лежащих в одной плоскости, заменить какими-либо двумя стержнями, лежащими в той же плоскости, и произвести разложение нагрузки на три направления. Проводя плоскость (Q) через нагрузку и выходящий стержень и определяем линию ее пересечения с плоскостью остальных стержней. Приняв эту линию за стержень, раскладываем нагрузку на два направления в одной плоскости (Q). Получается усилие в выходящем стержне и уравновешивающая усилий во всех стержнях, лежащих в общей плоскости.
Если нагрузка подобного узла лежит в общей плоскости группы стержней, то усилие в выходящем стержне равно пулю. Точно так же, если такой узел не нагружен, то усилие в выходящем стержне равно нулю. Усилия же в остальных стержнях, вообще говоря, не равны пулю; они равны нулю только в том случае, если этих стержней два, т. е. узел — трехстержневой.
Приступая к расчету пространственной фермы, следует сразу определить нулевые стержни и перечеркнуть их на чертеже фермы. При малом числе нагруженных узлов число работающих стержней обычно значительно сокращается.
Обратим внимание на то обстоятельство, что расформирование простейшей прикрепленной фермы и последовательное отбрасывание пулевых стержней фермы, не несущей нагрузку, представляет собою по сути одну и ту же операцию. Между прочим, проверка факта, что у ненагруженной фермы все стержни нулевые, есть не что иное как контроль невозможности само напряженного состояния (см. § 83).
Существуют фермы, не являющиеся простейшими по образованию, но могущие быть расформированными, пользуясь принципом' отбрасывания стержня, выходящего из плоскости всех остальных. Такие фермы (будем называть их п о ч т и простейшими) могут быть рассчитаны как простейшие, если все или некоторые усилия в выходящих стержнях будут определены заранее.
На фиг. 234, а к б показаны два варианта двухъярусной шестигранной фермы купольного вида. Ферма на фиг. 234, а является простейшей. Образование ее легко проследить, начиная от опорных узлов. Точно так же нетрудно расформировать, начиная от трехстержневых узлов верхнего кольца. Ферма на фиг. 234,6 — почти простейшая: она может быть расформирована, начиная со всех узлов верхнего кольца, путем отбрасывания в первую очередь стержней кольца, выходящих из плоскости остальных трех стержней узла, а затем «зубцов», состоящих из раскоса и ребра, и т. Д. Возникает вопрос, каким способом образована ферма на
436
фиг. 234, б Метод образования может быть представлен следующим образом: взята ферма по фиг. 234, а и произведена замена части раскосов, расположенных в плоских гранях, на раскосы обратного направления (накрест). Таким образом, ферма по фиг. 234, б является преобразованной, но особенности расположения стержней в плоскостях граней делают ее, по нашей термино-
Фиг. 234.
логии, почти простейшей.
На фиг. 234 жирной линией отмечены стержни, работающие от нагрузки в узле верхнего яруса. Легко видеть, что работающая часть фермы на фиг. 234, б яв"' ляется простейшей.
Графический расчет при действии одной силы как в том, так и в другом варианте’фермы выпол
4
Фиг. 235.
няется без всяких затруднений. Последовательность разложений сил на три направления при некотором опыте приводит к диаграмме усилий, не содержащей повторений.
Пример 1. Определить усилия в стержнях фермы (фиг. 2.35). Число стержней (12) и узлов (4) удовлетворяет условию статической определимости. Ферма принадлежит к числу простейших, в чем легко убедиться, проследив ее образование, начиная с опорных узлов.
Длина стержней: ЛВ=100 см; AC=AD = 80 см; BC=BD=CD — 30 см, высота нижнего яруса 30 см; верхнего — 50 см. Сила Р^ЗОО «г.
Расчет начинаем с узла А, в котором сходятся три стержня и приложена известная сила Р. Уравнения равновесия узла А будут
УЛ =0,
jVi cos (1, х) + Л2 cos (2, х) Л3 cos (3, х) -фР cos (Р, х) = 0;
У Г=0,
Л| cos (1, у) 4- Л2 cos (2, у) 4- N-s cos (3, у) 4- Р cos (Р, у) = 0;
У Z = 0,
Ni cos (1, г) 4- yV2 cos (2, г) 4“ Л^з cos (3, z) 4- P cos (P, z) = 0.
437
. Неизвестные усилия считаем растягивающими, т. е. направле..ями от выре, занного узла к середине стержня. Косинусы углов подсчитываем по абсолютной величине как отношение длины проекции стержня па ось к длине самого стержня
Составляя уравнения проекций, нам придется вводить отдельные слагаемые со знаком плюс или минус в зависимости от того, в какую сторону осн наврав-лена проекция усилия.
Находим
ViOQZ—50а _ / 3
”100 ~ ч '
cos (1, х) =
cos (2, х) = cos (3, х) ==
~ 2 ’
100 /з 30/3
2 ~ 2 _ 7 /3
80 ~ 16 '
cos (Р, х) = 0;
1 5
. cos (1, _)/) = —; cos (2, у) = cos (3, у) = -— ; cos {Р, у) = 1;
3 3
cos(l, г) = 0, cos(2, у) = cos(3, z) = — = —;
Z • о 10
cos (Р, г) = 0.
Записываем уравнения в числовом виде, принимая во внимание направление проекций сил по отношению к выбранному направлению осей координат:
2х = о,
/3 7 /.3 7 /3 л
— N, -— — n2 —----------N3 = °;
1 2 16 16
2 Y = 0,
1 5 5
2) — ЛГ3 V -300 = 0;
Zoo
2 z == о,
з з 3) ~N2 — + N3 — =0. ' 2 16 16
Решая уравнения, находим
T/j = 140 кг, N2 = N2,~—80 кг.
Знак минус перед усилиями Ns и Ns показывает, что стержни 2 и 3 сжаты.
Переходим к узлу С, к которому приложена известная теперь сила .V2 и три неизвестных усилия Ns, Nr„ Nn.
Определяем косинусы углов неизвестных сил с осями координат:
//
cos (5, л) = ; cos (6, х) = 0; cos (11, х) = 0;
cos (5, у) = cos(6,у) = 0; cos(ll,у) = 1;
cos (5, z) —- ; cos (6, z) = 1; cos (11, z) — 0,
438
Уравнения равновесия сил, действующих на вырезанный узел С, будут
Х-У=0,
Уз 1 уз
4)- ~N5 = -— — 80 —-— = 0;
’ 5 2 16
2г = о,
5) _W„_8oA_„;0] о
У г = о,
6) n5 — + Ne ~80 -j? = °’
При составлении этих уравнений мы поступали-с N% как с известной силой, принимая во внимание ее направление по отношению к вырезанному узлу С. Из уравнений 4, 5, 6 находим
N5 = — 70 кг, N6 — 50 кг, Nn = — 50 кг.
Далее переходим к узлу В, в котором сходятся три стержня (4, 9, 10) с неизвестными усилиями, и два стержня (/ и 5) —с известными. Уравнения равновесия для этого узла будут
2Л=0,
Уз У& Уз Уз
7) A^-y-H-^o-^+UO — -70 -~- = 0;
2г=о.
8) -Л^1-ЛГ10 £^+14oJ-=O;
У z = о,
9) 4'-лГ1°1?+70‘т==0:
Отсюда
ЛГ4= —70 кг, N5 = 70 кг, 7У,0 = 0.
Условия равновесия последнего узла D (известные силы
77 4 = — 70 кг, N6 = + 50 кг, N3 = — 80 кг):
2Л=0,
Уб 7 Уз Уз
10) -Л^8—• + 80 —^-+70 -у--0;
2г = о,
' У 2 У 2 5
П) -80-— = 0;
2 2 о
У Z = 0;
/2 У2 1 3
12) _ЛГ8 Х-j—— ЛЛ12 —50-1 Д-70-—4- 80-—= 0.
439
Последние неизвестные усилия
ЛГ7 = — 50 л г; = 0; ДГ12 = 0.
Мы составляли уравнения равновесия узлов, придерживаясь одной и той же заранее выбранной системы координатных осей. Заметим, что постоянство осей нельзя считать обязательным и отдельные уравнения часто можно упростить, выбирая для различных узлов различные (в том числе и косоугольные) системы осей. Впрочем, преимущество постоянных осей состоит в том, что для каждою стержня косинусы углов наклона стержней к осям координат приходится определять только один раз, н то время как при различных системах координат для отдельных стержней необходимо несколько раз находить косинусы.
Пример 2. (фиг. 2.36). Этот пример иллюстрирует последовательное разложение сил на три направления с использованием симметрии.
Прежде всего устанавливаются нулевые стержни. Они показаны тонкими линиями. Расчет начинается с нагруженного узла н разложения силы Р' на два направления Г и 2' (сливающееся с 2 в вертикальной плоскости проекции). Горизонтальная проекция треугольника равновесия строится путем разложения проекции / на направления 2 и 2Л Далее в вертикальной плоскости проекций усилие 2' раскладывается по общему направлению 3' и -5' и направлению 4'. Проектируя 4', находим 4. Суммируем 2 и 4 и раскладываем на 3 и 5, после чего определяем 3' и 5'. Обращаясь снова к вертикальной плоскости проекций и учитывая, что усилие 3' равно усилию 3, раскладываем геометрическую сумму Д-|-3'-|-3' по общему направлению 6' и 6' и направлению 7'. Дальнейший расчет предоставляем читателю.
440
Заметим, что, как правило, для пространственных ферм не удается построить взаимную, т. е. не содержащую повторений диаграмму усилий; точно так же порядок следования усилий иа диаграмме не отвечает часто обходу узла. Имеются, однако, и случаи, когда диаграмма получается в классическом виде.
§ 8.9. ПРОСТЕЙШИЕ БИКОНСТРУКЦИИ
При конструировании часто возникает задача связать два плоских диска (т. е. две балки, две фермы и т. п.) в одно пространственное целое так, чтобы в определенных точках данная спаренная конструкция могла воспринимать сосредоточенные силы, не лежа-
щие в плоскостях дисков. Заметим, что считаем диски жесткими и закрепленными только в своей плоскости.
Поставленная задача проще всего решается устройством зигзага стержневых связей и введением дополнительного опорного стержня в одном из узлов зигзага; этот стержень, который в дальнейшем будем называть упорным стержнем, должен, естественно, выходить из плоскости диска, к которому он примыкает.
Полученную систему (фиг. 237, а) будем называть простейшей спаренной конструкцией или простейшей биконструкцией. Итак, простейшая биконструкция состоит из двух плоских дисков, закрепленных в своих плоскостях каждый тремя стержнями (или иным статически определимым способом) и соединенных зигза
441
гом стержней, в одном из узлов которого помещен упорный стержень,
В случае необходимости пространственно подкрепить большое число точек нет необходимости развивать зигзаг так, чтобы он охватил все точки: можно применить вспомогательные распорки и подкосы или дополнительные зигзаги, передающие местную нагрузку в узлы основного зигзага. На фиг. 237, б показан пример двух спаренных лонжеронов; основной зигзаг связей расположен в плоскости верхних поясов, образуя так называемые продольные связи; дополнительные зигзаги из двух стержней образуют поперечные связи или нервюры. Упорный стержень помещен в плоскости нервюры.
Простейшая биконструкция представляет собою статически' определимую систему. Действительно, усилие в упорном стержне, а также усилие в любом стержне основного зигзага (например, Л^з-4, на фиг. 237, а) определяется методом сквозных сечений из уравнения равновесия моментов сил, действующих на отсеченную часть относительно прямой пересечения плоскостей дисков *. Напомним, что диски считаем жесткими только в своей плоскости; поэтому составляющие усилий в сечениях, перпендикулярные плоскостям дисков, равны нулю. Получив усилия в раскосах связей, следует в каждом узле связей просуммировать усилия двух примыкающих раскосов и внешнюю нагрузку. Результирующая, которая автоматически должна получиться лежащей в плоскости диска, дает нагрузку диска в данном узле. Имея все узловые нагрузки дисков, рассчитываем их по правилам строительной механики плоских систем
Практически более эффективным оказывается метод расчета, основанный на последовательном разложении сил в узлах основного зигзага связей, начиная от крайнего узла, к которому примыкает один раскос связей. При этом одновременно получаются как усилия в раскосах связей, так и нагрузки (реакции) дисков в узлах.
В каждом узле производится разложение результирующей известных сил на два направления: на направление раскоса связей с еще неизвестным усилием и на направление прямой пересечения двух плоскостей — плоскости, объединяющей результирующую известных сил с упомянутым раскосом, и плоскости диска.
Обратимся к фиг. 237, а. В узле О раскладываем силу Ро по направлению стержня О—1 и прямой пересечения плоскости переднего диска с плоскостью Р и О—1. Переходим к узлу /; внешней нагрузки здесь пет; раскладываем найденное усилие №~‘ по направлению 7—2 и прямой пересечения плоскости О—1—2 с плоскостью заднего диска. Переходим к узлу 2. Прежде всего складываем силу Р2 и найденное усилие Л^_2. Результирующую раскла
* Отсюда следует, что если нагрузка лежит в плоскостях дисков, то связи не работают. Если плоскости дисков параллельны, то уравнение моментов заменяется уравнением равновесия проекций на ось, перпендикулярную плоскостям обоих дисков. Этот случай рассмотрен ниже более подробно.
442
дываем по направлению стержня 2—3 и прямой пересечения плоскости, объединяющей результирующую и TVi-2 и плоскости переднего диска, и т. д. Составляющие, получаемые на прямых пересечения плоскостей, и представляют собою не что иное, как нагрузки дисков.
Заметим, что усилия стержней, примыкающих к узлам и принадлежащих дополнительным зигзагам, должны быть определены заранее. Они входят в геометрическую сумму известных нагрузок узла, которая затем раскладывается на два направления.
Расчет чрезвычайно упрощается, если выбрать плоскости ортогональных проекций так, чтобы одна из них, например горизон-
тальная, была перпендикулярна плоскостям обоих дисков. В этом случае плоскости дисков проектируются на Н в виде двух прямых; горизонтальные проекции прямых пересечения любых плоскостей с плоскостями дисков лежат па этих прямых.
В горизонтальной плоскости.проекций операции последовательного разложения сил па два направления приводятся к построению диаграммы усилий для весьма элементарной плоской ферменной конструкции (см. фиг. 238 — план). Чтобы изобразить эту конструкцию, следует взять имеющий вид плоской фермы план биконструкции, сохранив из связей только основной зигзаг, затем заменить все поясные стержни короткими опорными стерженьками. К узловым нагрузкам должны быть присоединены горизонтальные проекции усилий второстепенных стержней, примыкающих к узлам. Усилия в раскосах плоской системы дают горизонтальные проекции усилий в раскосах связей. Усилия в опорных стерженьках плоской системы дают горизонтальные проекции узловых реакций дисков или, что то же (с переменой направления),-—узловых нагрузок дисков.
Далее следует найти вертикальные проекции тех же сил. Поскольку вертикальные проекции стержней связей имеются на чертеже, достаточно спроектировать концы векторов усилий из плана на вертикальные проекции прямых.
443
Что касается вертикальных проекций нагрузок дисков, то определение их также не сложно: в каждом узле нужно геометрически просуммировать известные силы—-две вертикальные проекции усилий раскосов и внешнюю нагрузку. Для контроля служит величина горизонтальной проекции, которая должна совпадать с найденной при построении диаграммы для плана.
Имея горизонтальные и вертикальные проекции, определяют истинные величины усилий в стержнях связей и узловых нагрузок дисков.
Заслуживает внимания способ расчета, при котором как усилия основного зигзага связей, так и узловые реакции (нагрузки) дисков сразу получаются в истинную величину. Вообразим, что прямые действия реакций дисков в каждом узле известны. Тогда достаточно было бы развернуть на плоскость основной зигзаг связей вместе с указанными прямыми в виде стерженьков и нагрузок; усилия в элементах плоской системы (развертки) были бы равны истинным величинам усилий. В каких же случаях указанные прямые пересечения можно определить заранее, не проделывая всей цепи расчета? Ответить на этот вопрос очень легко: в тех случаях, когда узловые нагрузки лежат в плоскостях раскосов основного зигзага связей, примыкающих к данному узлу.
В тех же плоскостях должны лежать стержни, принадлежащие второстепенным зигзагам. Произвольную узловую нагрузку (или усилие второстепенного стержня) всегда можно, и притом различными способами, разложить на две составляющие, из которых одна лежит в плоскости диска (и ие оказывает влияния на работу связей), другая не лежит в указанной плоскости. Таким образом, поставленному требованию можно удовлетворить всегда. Следовательно, прочертив в каждом узле прямую пересечения плоскости диска с плоскостью двух примыкающих раскосов (зубца зигзага), можем применить метод развертки. Особенно просто эти прямые определяются при так называемой раскосной системе решетки (зигзага) связей, состоящих из раскосов одного направления и параллельных распорок. В этом случае искомые прямые, очевидно, соединяют последовательные узлы связей каждого диска, совпадая с осями поясных стержней при ферменной конструкции (фиг. 239). Если, кроме того, нагрузки направлены вдоль распорок, а следовательно, лежат и в плоскостях примыкающих раскосов, то пользование разверткой, безусловно, представляет собой самый короткий путь решения задачи. Подчеркнем еще раз, что развертка делается для основного зигзага связей, второстепенные стержни могут быть включены в развертку, если они лежат в плоскостях, образованных смежными стержнями основного зигзага. '
Простейшая биконструкция с параллельными дисками. Выделяем этот случай как практически важный, а также потому, что определение усилий в стержнях связей и нагрузок (реакций) дисков сводится к простым и изящным операциям, имеющим много точек соприкосновения с расчетом тонкостенных цилиндрических оболочек.
444
Определим усилие в стержне зигзага связей методом сквозного сечения (см. фиг. 237, а и б).
Проектируя силы, действующие на отсеченную часть, на перпендикуляр Р к плоскостям дисков, находим
Здесь Qi — сумма проекций нагрузок, действующих на отсеченную часть, па перпендикуляр к плоскостям дисков; h — расстояние
между плоскостями дисков; It — истинная длина i-ro раскоса связей.
Остановимся на случае нагрузки одной силой Р, перпендикулярной к плоскостям дисков. Тогда для всех раскосов, расположенных левее Р, имеем Q = P=const. Для левых раскосов
Ni=±— I. h '
Абсолютная величина усилий левых раскосов пропорциональна их истинным длинам. Знак, очевидно,зависит от уклона раскосов. Растянутыми оказываются раскосы, имеющие в плане' нисхо
дящее направление, если
двигаться слева направо. фиг 239.
Знак всегда может быть
легко определен из соображений уравновешивания отсеченной части биконструкции.
Перейдем к отысканию узловых нагрузок (реакций) дисков для того же случая действия одной силы Р, перпендикулярной к плоскости дисков. Прежде всего замечаем, что горизонтальные проекции усилий раскосов связей пропорциональны длинам горизонтальных проекций раскосов:
~~ h 1
а следовательно, и вертикальные проекции усилий раскосов пропорциональны длинам вертикальных проекций:
N(iV} = ±—
h ‘
445
Эти заключения непосредственно вытекают из основной формулы, устанавливающей пропорциональность истинного усилия истинной длине раскоса. Можем прибегнуть также к ферменной конструкции в плане (фиг. 240, в) и определить усилия графически. Оказывается, что диаграмма усилий имеет вид фиг. 240, б, причем усилия раскосов совпадают с самими раскосами, а усилия
коротких стерженьков (горизонтальные проекции реакций дисков) равны длинам противоположных «стержней», так что, например, усилие стерженька в узле на фиг. 240 изобразится отрезком Ьс на фиг. 240, б.
В вертикальной проекции усилие стерженька в узле а' изобразится отрезком Ь'с', а самый стерженек параллелен Ь'с' (фиг. 240, а).
Мы видим, что реакции (нагрузки) дисков без затруднений определяются на фасаде дисков непосредственно по чертежу зигзага связей. Остается внести четкость в вопрос о направлении нагрузок дисков.
Изобразим отдельно вертикальные проекции усилий, передающихся на передний диск (фиг. 240, г) и задний диск (фиг. 240,5). Геометри
ческая сумма двух усилий, передающаяся на передний диск в узле,
должна лежать в плоскости диска; следовательно, составляющие усилий, нормальные к плоскости диска, взаимно уничтожаются. Отсюда следует, что вертикальные проекции усилий, передающихся на диск, можно рассматривать как лежащие в плоскости диска нагрузки. Итак, снабженные стрелками зигзаги связей в вертикальной проекции непосредственно дают нагрузки узлов диска, разумеется, после умножения на общий множитель P/h.
Для переднего диска сила Р, обращенная к наблюдателю,
играет роль источника, а для заднего диска — роль стока.
Оба диска нагружены плоскими силовыми цепочками одинаковой конфигурации, но противоположного направления. Они отличаются также точками приложения отдельных сил (узлы перед-
446
него диска отмечены светлыми кружками, узлы заднего — черными).
Мы рассмотрели случай одной силы Р. При нескольких силах диски будут нагружены соответствующим количеством цепочек.
При аналитическом расчете дисков целесообразно оперировать цепочками в их натуральном виде. При графическом расчете ферменных дисков следует геометрически просуммировать нагрузки отдельных узлов, заменив зубцы цепочки отдельными силами в узлах. В случае необходимости суммируют и несколько «звеньев»
цепочки. Приведем несколько простых правил, облегчающих операции с силовыми цепочками.
На фиг. 241 показана цепочка из четырех сил. Обозначим величину силового масштаба, т. е. множителя, на который следует умножить отрезки на чертеже, чтобы получить силы, через q:
Равнодействующая всей цепочки равна и параллельна вектору АЕ, умноженному на q. Положение равнодействующей определится графически последовательным суммированием звеньев: равнодействующая АС=АВ-\-ВС проходит через точку В параллельно АС. Равнодействующая AD = AB + BCA-CD проходит через точку пересечения АС и CD. Наконец, равнодействующая AE==AB + BC + CD-\-DE проходит через точку пересечения A~D и DE.
Момент цепочки относительно, полюса О равен сумме моментов отдельных сил цепочки, которые обозначим
Г. = ql., М = V 7г, = q = qQ.
Величина й есть, очевидно, не что иное, как удвоенная площадь полигонального сектора с полюсом О и дугой, совпадающей с цепочкой.
447
Проекция цепочки на какую-либо ось равна проекции на ту же ось замыкающей АЕ, умноженной па q.
Замкнутая цепочка имеет равнодействующую, равную нулю; она эквивалентна паре с моментом
где йк — удвоенная площадь, охватываемая замкнутым контуром цепочки.
Эти правила значительно облегчают определение опорных реакций, изгибающих моментов, продольных и поперечных сил сплошных дисков, а также усилий в стержнях ферменных дисков, нагруженных силовыми цепоч
ками.
Изображение биконструкций с параллельными дисками. Биконструкцию достаточно изобразить фасадом переднего диска
и, предположив этот диск прозрачным, показать просвечивающие через него связи в их вертикальной проекции. Выше мы изображали узлы переднего диска светлыми кружками, а узлы заднего диска — черными.
Это не всегда удобно, особенно когда нужно от
метить (точкой или крестиком) силы (нагрузки), перпендикулярные плоскости диска. Поэтому узлы заднего диска лучше показывать светлыми квадратиками (фиг. 242, а). Распорка изобра-
жается двумя рядом поставленными узлами — кружком и квадратиком, упорный стержень—концентрическим кружком, внешним по отношению к кружку или квадратику. На фиг. 242, а показана нагружающая передний диск цепочка сил от действия силы Р, приложенной от наблюдателя к узлу заднего диска. Составляющие цепочки приложены к диску в кружках.
В вертикальных проекциях ферменных бикопструкций стержни связей обычно сливаются со стержнями дисков — ферм. Целесообразно изображать стержни связей несколько отодвинутыми прямыми, отличая короткой черточкой конец, примыкающий к переднему диску (см. фиг. 239 и 242,6). Распорки можно вовсе не показывать, подразумевая их наличие в каждом узле.
На фиг. 242, б показана силовая цепочка PFECDA от силы Р. Упорный стержень предполагается в А. При графическом расчете
448
фермы следует определить результирующие узловые нагрузки. В узле F это будет вектор PF; в узле Е—вектор, равный FC. В узле D — вектор, равный СА.
§ 8. 10. СВОБОДНЫЕ ПРОСТРАНСТВЕННЫЕ ФЕРМЫ
Свободная пространственная ферма, иначе ферменный блок, представляет собою систему, геометрически неизменяемую в отношении своей формы; при узловых нагрузках, удовлетворяющих условиям равновесия твердого тела, система находится в равновесии.
Установим зависимость между числом узлов и числом стержней свободной фермы. Для прикрепления свободной фермы к другому твердому телу (опорной поверхности) необходимо и достаточно шести стержней. Как известно, прикрепленная ферма простейшего образования должна иметь при п узлах s = 3n стержней. Отсюда следует, что всякая геометрически неизменяемая статически определимая прикрепленная ферма должна иметь Зм стержней, где п число узлов, не считая опорных: действительно, перестановка стержней, не делающая систему изменяемой, не отражается па числе независимых уравнений равновесия. Поэтому свободная ферма должна иметь стержней
s = 3n—6.
Этому условию можно удовлетворить разнообразными вариантами стержневых систем. Особый интерес представляют так называемые сетчатые оболочки системы, не содержащие внутренних стержней: все стержни сетчатой оболочки лежат на поверхности некоторого многогранника. Оказывается, что всякая замкнутая сетчатая оболочка, имеющая треугольные поля, удовлетворяет требованию S=3n—6. Проверим это правило на простейших примерах (фиг. 243).
Стержневой тетраэдр: п=4, 5 = 6, 3-4—6 = 6.
Параллелепипед с «гранями», дополненными диагоналями: п = 8, 5=18, 3-8—6=18.
Октаэдр: м = 6, 5=12, 3-6—6=12.
Докажем высказанное положение в общем виде. По известной теореме Эйлера между числом вершин (п), числам областей (/), числом границ (5) сети, изображенной па поверхности шара или другой «одиозамкпутой» поверхности, существует соотношение
5 + 2=n+f.
Применим эту теорему к сетчатой оболочке.
При треугольных областях на каждую область (поле) прихо-9 2
дится 3/2 границ (стержней), т. е. f=-|-s, поэтому s + 2 = n-|-yS, откуда s = 3zi—6.
Таким образом, любая замкнутая сетчатая оболочка с треугольными полями ’ обладает необходимым и достаточным
29 425 449
для геометрической неизменяемости и статической определимости числом стержней. Возникает вопрос, при каких условиях расположение стержней является правильным, т. е. исключает возможность малой подвижности (мгновенной изменяемости) сочленения.
Прежде всего, необходимо потребовать выполнения очевидного условия: в системе не должно быть узлов, все стер».
Фиг. 243.
ни которых лежат в одной плоскости. Это требование аналогично известному условию образования плоских ферм — не должно быть узлов, прикрепленных двумя стержнями, вытянутыми в одну прямую.
Второе условие носит весьма общий характер. Оно вытекает из теоремы Коши о жесткости выпуклого многогранника. Именно многогранник, образованный полями сетчатой оболочки, должен
Фиг. 244.
быть выпуклым. Отсюда не следует, что невыпуклый многогранник обязательно дает мгновенно изменяемую систему: последний случай является исключением, а не правилом. Но среди выпуклых многогранников не существует мгновенно изменяемых, а среди невыпуклых — они существуют.
Пример мгновенно изменяемой сетчатой оболочки показан на фиг. 244. Квадратная горловина может принять форму ромба с углами, мало отличающимися от прямого при практически неиз
450
менных длинах стержней. Одновременно искажаются плоскости верхнего и нижнего оснований.
В дальнейшем ограничимся рассмотрением нескольких основных типов сетчатых оболочек.
Простейшими будем называть такие сетчатые оболочки, которые могут быть образованы последовательным присоединением узлов тремя стержнями, начиная от вершин исходного тре-
Фиг. 245.
угольника (или исходного тетраэдра). Простейшие оболочки могут быть и расформированы в порядке, обратном их образованию.
На фиг. 245, а показан пример простейшей шестнузловон оболочки. При изменении направления раскоса (фиг. 245, б) получаем преобразованную систему. Однако, если боковые поля — пло-
с) б)
Фиг, 216.
ские четырехугольники с диагоналями (фиг. 245, в), то система всегда может быть расформирована (а значит и рассчитана), пользуясь правилом об узле, все стержни которого, за исключением одного, лежат в одной плоскости (см. § 8. 8). Такие системы называем почти простейшими.
На фиг. 246 приведены различные варианты восьмиузловой сетчатой оболочки: фиг. 246, а — простейшая система, фиг. 246,6 — преобразованная, она же с плоскими гранями — почти простейшая.
29*
451
Общий метод расчета простейших и почти простейших систем— составление уравнений равновесия узлов или графическое разложение сил в порядке расформирования системы.
Для систем, составленных из ряда трехгранных секций пирамидального или призматического типа (фиг. 247) с успехом приме-
няется метод сквозных сечений. В этом случае сквозным сечением удается пересечь шесть стержней; отсеченная часть является блоком, и усилия в перерезанных стержнях рассчитываются, следуя указаниям § 8.7.
На фиг. 248 изображена сетчатая оболочка в виде октаэдра. Очевидно, это преобразованная система,
Фиг. 248.
Общий метод расчета преобразованных систем — метод замены стержней, принципиальная сторона которого изложена в § 8. 3 применительно к плоской преобразованной системе. Руководящей идеей разнообразных методов расчета статически определимых систем является принцип единственности решений статики, согласно которому решение, полученное любым способом, например суммированием двух напряженных состояний (как в методе замены стержней), но удовлетворяющее условиям
452
равновесия всех элементов, есть правильное, единственное решение. Большую роль при выборе рационального решения
играет характер нагрузки.
На фиг. 248 показана классическая схема применения метода замены стержней. Один стержень разрезается и заменяется другим
стержнем. Истинное напряженное состояние рассматривается как сумма напряженных состоянии: 1) от заданной нагрузки и 2) от действия сил Х\ в перерезанном стержне. Второе состояние подсчитывается от%1=1 с последующим умножением всех усилий на величину Хх. Неизвестное Х1 определяется из условия, что истинное усилие в дополнительно введенном стержне i равно нулю, что дает линейное уравнение
Nip-\-X\Nn = Q.
При замене нескольких стержней получается система линейных уравнений.
Рассмотрим один важ- • дый прием, носящий название метода разложения на плоские фер-м ы.
На фиг. 249, а показана сетчатая оболочка с плоскими решетчатыми гранями. Геометрическая неизменяемость системы вытекает
хотя бы из приведенной выше теоремы Коши *. Если имеется нагрузка только в узлах,
Фг,г. 249. образующих вершины
.много-
гранника, то первый этап расчета состоит в том, что решетка граней заменяется минимальным количеством раскосов (при четырехугольной грани — одним раскосом) и определяются усилия полученной упрощенной системы от заданных нагрузок (фиг. 249, б)-Второй этап расчета: введенные раскосы каждой грани мысленно разрезаются и вместо них в свободное поле грани вставляется пло
* Отметим здесь, что решетка граней может быть произвольной, лишь бы была соблюдена неизменяемость плоских ферм в своей плоскости. Допустимы также плоские узлы, однако при условии, что отсутствует нагрузка узла, перпендикулярная плоскости.
453
ская ферма, имеющая форму грани с фактической решеткой; определяются усилия всех плоских ферм-граней от действия равных и противоположных сил, эквивалентных усилиям перерезанных раскосов (см. фиг. 249, в). Полученные усилия во внутренних стержнях решетки ферм-граней являются окончательными. Усилия же поясных стержней должны быть просуммированы с усилиями в ребрах упрощенной фермы, полученными на первом этапе расчета.
Указанный прием с успехом применяется и в элементарных случаях и, прежде всего, для расчета очень распространенных коробчатых ферм с плоскими четырехугольными гранями, когда переменой направления раскосов в одной или нескольких гранях систему удается превратить в простейшую. Впрочем, в этом случае можно пользоваться и методом замены стержней в его классической форме: задача сводится к системе уравнений, каждое из которых содержит одно неизвестное усилие раскоса фактического направления.
§ 8.11. СВОБОДНЫЕ БИКОНСТРУКЦИИ
Мы видели (§ 8.9), что простейшая прикрепленная биконструкция имеет семь опорных стержней. Следовательно, если перерезать (или отбросить) опорные стержни, то отделенная система не будет представлять собою жесткого целого, а будет обладать свойствами механизма — системы с одной степенью свободы деформации. Эту степень свободы можно устранить, выполнив зигзаг связей замкнутым. Если диски биконструкции представляют собою плоские фермы, а связи расположены по контуру, то мы приходим к свободной пространственной ферме в виде сетчатой оболочки *.
Остановимся на интересном частном случае нагрузки свободной биконструкции. Допустим, что биконструкция нагружена силами, лежащими в плоскостях основных дисков. Так как система нагрузок должна находиться в равновесии, то равнодействующая сил, приложенных к одному диску, должна быть равна и противоположна равнодействующей сил, приложенных к другому диску. Ясно, что обе равнодействующие могут быть направлены только по прямой пересечения обоих дисков. Итак, не всякую систему сил, приложенную в плоскости одного диска, можно уравновесить силами, приложенными в плоскости другого. Наоборот нагрузка диска весьма ограничена — ее равнодействующая должна лежать на определенной прямой — ребре пересечения плоскостей дисков.
Перережем, зигзаг связей продольным сквозным сечением, нс задевающим диски. Усилия в стержнях связей, обнаженные в сечении, должны, очевидно, уравновешивать нагрузку одного диска, а следовательно, их равнодействующая также направлена по прямой пересечения плоскостей обоих дисков.
* Для прикрепления свободной биконструкции с замкнутым зигзагом связей необходимы шесть стержней, однако их нельзя расположить в плоскостях обоих дисков: один из стержней обязательно не должен принадлежать плоскостям дисков, т. е. упорный стержень должен быть сохранен.
451
С другой стороны, усилия всех стержней замкнутого зигзага могут быть выражены через усилие одного из стержней. Действительно, перерезав только один раскос и приложив к торцам его, отделенным разрезом, две равные и противоположные силы, эквивалентные усилию, можем шаг за шагом определить усилия во всех стержнях зигзага. Задача ничем не отличается от нахождения усилий в связях простейшей (открытой) биконструкции, нагруженной силой, не лежащей в плоскости диска: роль внешней нагрузки на этот раз играет сила, приложенная к одному из торцов разрезанного стержня. Одновременно с усилиями в стержнях связей получаем и нагрузки (реакции) дисков, пропорциональные взятому нами усилию в одном из раскосов. ,
Задача теперь состоит в подборе усилия в этом раскосе с таким расчетом, чтобы равнодействующая нагрузок диска со стороны связей была равна и противоположна равнодействующей заданных нагрузок диска. Это достигается нахождением первой равнодействующей сперва в неопределенном масштабе (т. е. единичного усилия в разрезанном раскосе), а затем пропорциональным увеличением всех усилий раскосов в число раз, равное отношению равнодействующей заданных нагрузок к равнодействующей от усилия в раскосе (с обратным знаком).
Ход расчета проследим на примере. На фиг. 250, а показана биконструкция в аксонометрии. Система нагружена на торцах парами сил с одинаковыми, но противоположными по знаку моментами. Компоненты Pi и Р? пар, отнесенные к дискам, имеют равнодействующие (равные Р?—Pi) вдоль прямой пересечения плоскостей дисков, в чем легко убедиться, проделав элементарный расчет, основанный на правиле рычага.
На фиг. 250,6 дана развертка связей, а на фиг. 250, в построена диаграмма усилий для развертки. При построении диаграммы в произвольном масштабе отложено усилие распорки 0—1 и последовательным разложением сил получены все усилия, а также нагрузки дисков, равные усилиям в опорных стерженьках развертки. Из диаграммы видно, что усилия распорки, повторенные дважды на обоих концах развертки, получились, как и следовало ожидать, одинаковыми.
На фиг. 250, г построен фасад переднего диска, на фиг. 250, д— многоугольник нагрузок диска от связей. Он оказался незамкнутым, а замыкающая—’Вертикальной (в соответствии с прямой пересечения плоскостей основных дисков). Равенство замыкающей (пунктир на фиг. 250, д) равнодействующей Р?—Pi заданных нагрузок одного диска и дает масштаб как диаграммы усилий в стержнях связей, так и многоугольника нагрузок переднего диска. После этого остается рассчитать диск по правилам строительной механики плоских систем. Нагрузки заднего диска численно равны и по направлению противоположны нагрузкам переднего.
Задача расчета свободной биконструкции чрезвычайно упрощается, если плоскости основных дисков параллельны. В этом слу
455
чае нагрузки, если они расположены в плоскостях дисков, могут быть только эквивалентны парам с численно равными, но противо-’ положно вращающими моментами. Биконструкция подвергается закручиванию аналогично короткой тонкостенной оболочке замкнутого профиля. Если задаться усилием какого-либо раскоса и по-
‘Расад переднего диска. Многоугольник сил Т и определение масштаба сил
' д)
Фиг. z50.
строить диаграмму усилий для развертки, то немедленно обнаруживается, что усилия остальных раскосов, чередуясь по знакам, численно пропорциональны их длинам, а нагрузки каждого из дисков пропорциональны длинам фасадных проекций раскосов связей, образуя в плоскости диска замкнутую силовую цепочку.'
Интенсивность (силовой масштаб) цепочки q получается из условия равновесия момента М* пары, создаваемого заданной нагрузкой диска, и момента пары, создаваемого реакциями связей:
М*- qQ; q--~ .
ч 1 й
456
Здесь Й—удвоенная площадь многоугольника, образуемого раскосами связей в фасадной проекции.
На фиг. 251 показан пример биконструкции, нагруженной аналогично рассмотренной выше конструкции (см. фиг. 250).
Две равные и противоположные пары M = P-h по торцам экви-валентны двум равным и противоположным парам /И = —Zc другим направлением вращения в плоскостях дисков.
Интенсивность силовой цепочки
Ml
Таким образом, выяснение системы нагрузок диска выполняется без труда.
* *
*
В заключение отметим, что рассмотренные выше статически определимые фермы имеют не только самостоятельное значение, но часто выступают в качестве основных систем статически неопределимых конструкций.
Теория ферм тесно связана с теорией тонкостенных конструкций со стенками, работающими «только на сдвиг». В последние годы развивается теория тонкостенных пространственных ферм. С элементами ее читатель может познакомиться по книге автора «Статика и кинематика ферм».
Глава IX
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИКРЕПЛЕНИЯ ТВЕРДОГО ТЕЛА
В настоящей главе рассматриваются задачи определения усилий в упругих связях, прикрепляющих твердое тело — блок авиадвигателя (или короче — блок) к неподвижной опорной поверхности. Подобные задачи могут быть во всех случаях решены методом сил. Основное внимание уделяем, однако, методу перемещений, который приводит к цели особенно быстро, если деформациями блока и опорной поверхности можно пренебречь по сравнению с деформациями упругих связей. Начнем с рассмотрения двух основных задач.
§9.1. ПРИКРЕПЛЕНИЕ БЛОКА ПАРАЛЛЕЛЬНЫМИ
УПРУГОСМЕЩАЮЩИМИСЯ ОПОРАМИ И ПЕРПЕНДИКУЛЯРНЫМИ К НИМ УПРУГОВРАЩАЮЩИМИСЯ
На фиг. 252 показан блок, прикрепленный связями, упругосме-щающимися в вертикальном направлении, и связями, упруговра-щающимися вокруг горизонтальных осей. Связи не оказывают сопротивления горизонтальному смещению блока и его вращению вокруг вертикальных осей. Очевидно, блок может быть нагружен только вертикальными силами и парами, вектор-моменты которых параллельны горизонтальной плоскости.
Упругосмещающимся опорам присваиваем индекс I, упруговра-щающимся — индекс j. Податливость и жесткость (отпорность) первых обозначаем соответственно |Зг- и /гг-, податливость и жёсткость вторых ej и Cj. Если упругосмещающаяся опора представляет собой стержень постоянного сечения, то податливость и жестокость ее выражается следующим образом:
I FiFt I кг/см.
В этом случае жесткость опоры равна силе, вызывающей удлинение стержня на 1 см.
-158
Упруговращающаяся опора в виде работающего на кручение стержня с круглым сечением обладает податливостью и жесткостью, соответственно равными
I, tj =-- \/кгсм,
GI р
Gjlpj
кгслф.
Жесткость такой опоры равна моменту, который развивается стержнем при принудительном закручивании его на малый угол,
принимаемый равным единице.
Упругосмещающуюся опору будем сокращенно называть силовой, упруго-вращающуюся — моментной, так как реакция первой представляет собой силу, а реакция второй — момент. В некоторых случаях оба типа опор могут быть конструктивно совмещены и могут представлять собой не стержни, а сложные системы.
В дальнейшем будем считать блок абсолютно жестким, другими словами, будем пренебрегать его деформациями по сравнению с перемещениями как твердого тела. Эти перемещения и будем определять в первую очередь, ведя, таким образом, расчет п о м е-тоду перемещений.
Перемещения рассматриваемого блока могут быть охарактеризованы тремя величинами — вертикальным перемещением 8Z начала ко-
Фиг. 252.
ординат и двумя углами <рх и <ру поворота тела вокруг координатных осей Ох и Оу.
Систему координат принимаем правую и вектор-момент откладываем в такую сторону, чтобы при взгляде от острия стрелки к перу получить вращение против часовой стрелки. Углы поворота фх, Фу считаются положительными при вращении вокруг осей Ох и Оу против часовой стрелки (при взгляде от острия оси к началу
459
координат). Перемещение блока по направлению оси силовой опоры I выражается через бг, <рх, фу следующим образом (перемещения считаются малыми):
= + О-1)
где yt и Хг — координаты следа оси силовой опоры (см. фиг. 252, б).
Закручивание (угол поворота) моментной опоры равно проекции на ее ось углов фх и фу:
= Ъ c°s *j + <?y sin <zy. (1.2)
Реакция силовой опоры по абсолютной величине равна перемещению опорной точки, умноженному на жесткость опоры:
^ = ^==М8г + ‘Р.гЛО-3)
Реактивный момент, развиваемый моментной опорой, по абсолютной величине равен
Л4у.= сду=с7(©Лсо8ау.-|-<ру81пау). . (1.4)
Задача сводится, таким образом, к определению перемещений дг, фх, фу- Обратим внимание на то, что перемещения 6г- подчиняются закон уплоскост и. Это позволяет написать решение, исходя из очевидной аналогии с перемещениями и напряжениями при растяжении — сжатии и изгибе или при внецентренном растяжении — сжатии:
Здесь Р2, Мх, Му — вертикальная нагрузка на блок и ее моменты относительно главных центральных осей жесткости хг.а>уг.ч Последние определяются по правилам, аналогичным правилам геометрии сечения: центр жесткости О совпадает с центром тяжести системы сосредоточенных площадок, величина которых принимается равной 2, 3,....). Координаты центра
жесткости относительно исходных осей Оху (фиг. 252, б) равны
Ikiyi (! 6)
Суммирование распространяется на все точечные жесткости ki-Числители аналогичны статическим моментам, знаменатели — площади сечения. Для знаменателя вводится обозначение
(1.7)
Перенесенные параллельно в центр жесткости оси х и у затем поворачиваются на угол ао, определяемый тангенсом двойного угла:
tg2«, = ^. (1.8)
Су-
460
Здесь Сх, Су, Сху — величины, в общем аналогичные моментам инерции площади, но с учетом членов, зависящих от моментных реакций, входящих в уравнения равновесия моментов:
сх=2 +2С>cos2 а'; (1 9)
=2 +2 cj sin2 aj: (i •1 °)
Cxy — '^ikixiyl — 2 е/ sin gy cos <zy. (1-П)
После поворота осей вычисляются значения Сх и Су, главных центральных моментов инерции жесткостей, причем могут быть
Фиг. 253.
использованы обычные формулы перехода при параллельном переносе и повороте осей.
Проделанные операции позволяют, привести (редуцировать) систему всех опор к трем опорам: силовой вертикальной опоре с жесткостью Kz и двум моментным опорам, параллельным главным центральным осям, с жесткостями Сх и Су. Редуцированная конструкция, являющаяся статически определимой, показана на фиг. 253. Представив себе мысленно произвольную нагрузку и заменив ее компонентами Pz, Мх, Му, тотчас придем к формулам (1-5).
Подстановка выражений (1.5) в (1-3) и (1.4) даст абсолютные значения реакций:
X y‘~wxi) Му \
+ — sin а/ Су /
(1. 12)
(1-13)
461
Указанная редуцированная система не является единственной, а существует бесконечно большое число вариантов. Так, например, всю совокупность опор всегда можно заменить тремя вертикальными силовыми опорами, причем положение одной из них можно задать произвольно; можно пользоваться неортогональными осями, взяв одну из них произвольной, и т. п. При решении большую помощь оказывают различные графические приемы, например веревочный многоугольник или метод Мемке для определения центра тяжести и круг Мора для опреде-
ления положения главных центральных осей и главных центральных моментов инерции.
Прием Мемке состоит в следующем (фиг. 254). Из произвольной точки С'проводятся радиусы-векторы pi к точечным массам Шг (площадкам, жесткостям). Вычисляются произведения rn^i, которые затем откладываются, начиная от произвольного полюса А, одно за другим в виде силового многоугольника со сторонами, параллельными радиусам-векторам Pi. Прямая, соеди-
няющая последнюю точку В силового многоугольника с полюсом А, параллельна радиусу-вектору центра тяжести. Величина радиуса-вектора центра тяжести
АВ
Метод легко обосновать, учитывая, что момент системы масс относительно точки С должен быть равен моменту равнодействующей
§ 9.2. АБСОЛЮТНО ЖЕСТКИЙ ДИСК, ЗАКРЕПЛЕННЫЙ
В СВОЕЙ ПЛОСКОСТИ УПРУГИМИ СИЛОВЫМИ И УПРУГИМИ МОМЕНТНЫМИ ОПОРАМИ
Схема конструкции представлена на фиг. 255, а. Очевидно, диск может быть нагружен только в своей плоскости силами (Р) и парами (М). Перемещения всех точек диска определяются тремя параметрами, например двумя линейными перемещениями дх, точки, в которой взято начало координат, по направлениям осей х и у и углом поворота диска tpz.
Обозначим угол наклона стержня / к оси х через а,, длину перпендикуляра из начала координат па ось стержня (плечо) —через г,, точку пересечения плеча и стержня, так же как и стержень, буквой j. Координаты точки / обозначим Xj и у, (см. фиг. 255,6).
462
(2. 1>
Связь между плечом г,- и координатами Xj и у, устанавливается следующими формулами:
Xj — Г] sinay, у,——rjCosay,
г, — Xj sin a-j—yj cos
Перемещение опорной точки m по направлению опоры j (осадка упругой опоры /) равно
8У = 8Х cos а, + sin a.t + = (С — <P^/) c°s «/ ~|-
+ (8v + <p?c) sinay. (2. 2>
z
-У
Фиг. 255.
Угол закручивания всех моментных опор одинаков и равен углу поворота диска <р2:
<^ = «^(/==1,2,3. . . ). (2. 3>
Реакции опор (по абсолютной величине):
Nj—kyy = kj (о, cos sin a./ + vyy) =
= kj [oxcos a,- -f-8ysin «/ + {Xj sin а,— у,-cos a/)]; (2. 4)
(2.5)
463
Обозначим проекции равнодействующей внешних нагрузок на координатные оси через Рх и Ру, момент нагрузки относительно оси z (начала координат О) — через Mz. Составим три уравнения равновесия диска:
1)VJC=O или c°s «/ = Рх'>
2) ^К=0 или sin а/ = Ру;
3)^/И = 0 или =
Подставляй сюда значения Nj и Mi из (2. 4) и (2. 5) и делая приведение, получим уравнения равновесия в таком виде:
оДлу + 5 A.V + fz^y — Ру' -<>xHx-\-\Hy + vzCz = Mz. Здесь введены следующие обозначения: главные коэффициенты
Кх— V kj cos2а?-; Ку-= V kj sin2a/;
(2.6)
(2._7)
(2-8)
побочные коэффициенты
Кх/= kj cos а/ sin a.j = -^- kj sin 2а/;
Нх = - kiricos «/ = 2 kj УУ
Hy=Y kir> sin а/ = У kjXj.
(2. 10)
При повороте координатных осей на угол ао аргумент а/ заме- пяется аргументом а,- — ао. Определим а0 из условия аннулирования коэффициента Кху'
^Pkj sin (а/ — а0) cos (а; — а0) = 0
или
kj sin 2 (а/ — а0) = V kj (sin 2а/ cos 2а0 — cos 2а/ sin 2а0) = 0,
откуда
! у kj sin 2а/ 2/Gy 1ц2ап=-----------=---------.
6 0 £ kj cos 2 а/ Кх — Ку
Новые оси будем называть главными и отмечать индексом г. Их наклон не зависит от выбора начала координат. Коэффи
-464
циент Cz при изменении наклона осей не изменяется. Формулы перехода к главным осям для коэффициентов /<х и приведем в двух формах:
Кх — Кх cos2 я0 4- Ку sin2 я0-ф Кху2ай=
=Y+ /(^-^)2+4№vJ;
КГу = Кх Si П2 я0 4- Ку cos2 я0 — Кху S i n 2я0 =
=~ [ {кх+ку~} -•
(2. 12)
Вторая форма не требует предварительного вычисления аргумента сю. Однако практически а0 вычислить нужно, так как коэффициенты Н'х и Н‘у лучше определять по координатам х) и у) относительно главных осей. Путем параллельного переноса главных осей достигается аннулирование коэффициентов Н\ и Нт. Обозначим координаты нового начала относительно главных осей через Xq и Уд. Проектируя замкнутый пятиугольник со сторонами г,-, yj, xj, г“ и //“ на направление г,-, получим
r'i =o+j/ocosao“-xosinar (2.13)
Приравниваем нулю значение Н'х — — V kjr'f cos я/:.
2 (О + X cos — х^ sin яр cos a'j — 0.
Раскрывая скобки под знаком суммы и учитывая, что
= kj sin я' cos «у = 0, получим
V kjrjcos я1; -f- v;; V k, cos2 ai; =- о, откуда
-Уо =
Аналогично получим
xQ =
(2. 14)
Определив положение центра жесткости О, проводим главные центральные оси хг.ц и уг.ц параллельно главным осям хг и у' . В каждом из уравнений равновесия остается по одному неизвестному.
30 425
465
Система уравнений (2.6) принимает вид
^Ку=Ру; (2.16)
Коэффициенты K’v и K'v вычислялись в процессе определения Ло и Уг0, и пересчитывать их не нужно. Коэффициент следует определить, исходя из положения центра жесткости, по формуле (2. 21). При желании С" можно найти путем перехода от С2 по известным координатам центра жесткости относительно главных осей и величинам Кх и /(у:
Cz = Сг —Кх (уг0)2 —К'у (л'^2=С2 —(2. 17)
Последняя формула показывает, что коэффициент С", подсчи-
жесткости, имеет минимальное значе-
танный относительно центра
ние.
Из (2.29), опуская индексы, получаем
. Р-г , Ру ™z ьг —----; о„ —-----; <₽, ——.
• Кх у Ку cz
(2. 18)
Можно сказать, что совокупность упругих опор приведена к двум силовым опорам-—двум стержням, направленным вдоль главных центральных осей жесткости, и вертикальной моментной опоре. Жесткости этих опор равны соответственно Кх, Ку, Cz. Соответствующая модель показана
на фиг. 256.
Подставляя значения, найденных перемещений (2.31) в равенства (2. 17) и (2.18), получим расчетные формулы для определения реакций:
xr I' Р* Ру мг 1
Nj = kj-------cosa,-]--sin а,- -)--(х,- sin a,-—_ycos а;) : (2. 19)
I Кх Ку Cz J
1 г
(2. 20)
Имея величины Ъх, бу, ф?, можно определить положение центра вращения D диска — при заданной нагрузке. Координаты центра будут
2 у.
У о —
XD —
(2. 21).
466
Из этих соотношений видно, что когда к диску приложена пара (компоненты силы Рх и Ру равны нулю), малое вращение диска происходит вокруг центра жесткости. В свою очередь сила, проходящая через центр жесткости, вызывает только поступательное перемещение диска.
Некоторые аналогии в задаче о диске и задаче о твердом теле $ параллельных упругих опорных стержнях. Расчетные операции ожно сделать более наглядными, если установить некоторые ана-огии в коэффициентах, относящихся к случаям § 9. 1 и § 9.2.
На фиг. 257 показан диск, закрепленный в своей плоскости, |ругими стержнями. Из произвольно взятого начала координат О сведены перпендикуляры к стержням. Точки встречи рпендикуляров с осями стержней отмечены черными кружками и означены теми же номерами, что и стержни (аналогично [г. 255,6).
Проведена окружность произвольным радиусом а с центром в Точки встречи с перпендикулярами отмечены светлыми кружка-и обозначены номерами со штрихом.
Отметим, что углы плеч с осью Оу равны углам а, образуемым фжнями с осью Ох.
467
Поэтому можно легко установить, что
/<Л=2 ^cos2a/=^ у;
= = (2<22)
K™ = V ^sin a/Cosa/= — 4- V kjXjy,=------\cxy. j
J z -* /74 /- — -I f) l i
Итак, коэффициенты ЛТ, Ку, Кху равны «моментам инерции» жесткостей kj, сосредоточенных на окружности радиуса а, относительно тех же осей, которые отмечаются индексами при К, деленным на квадрат радиуса а. Отсюда следует, что главные оси могут быть определены по обычным правилам в применении к системе расположенных па окружности точечных жесткостей, равных жесткостям стержней в плоскости диска. Вполне уместно применить круг Мора, который даст не только положение главных осей хг, уг, но и величины коэффициентов Кгг = С';.', С,,'.
Что касается коэффициентов
то они, очевидно, равны статическим моментам жесткостей, сосредоточенных в черных кружках / (/=1, 2, . . . , 6) относительно главных осей Охг и Оуг. Определив эти статические моменты и разделив их на величины k\. и krv, получаем координаты центра жесткости у? и xj.
Графический способ определения главных осей и главных жесткостей смещения. Покажем, что формулы (2. 11) и (2. 12) допускают графическую интерпретацию, близкую к кругу Мора.
Рассмотрим пятистержневой узел (фиг. 258, а). Проведем из вершины узла С произвольные ортогональные оси х' и у’ и окружность радиуса О'С с центром О', взятым в произвольной точке на оси х'.
Обозначим стержни номерами 7=1, 2, . . ., 5, а точки встреча стержней с окружностью Г, 2',..5'. Радиусы, проведенные к этим точкам, образуют с осью х углы, равные удвоенным углам образованным стержнями с той же осью, например Z.x'0'3'= = 2Zx'C3.
Из произвольного начала О проведем оси х и у, параллельные осям х', у’ (см. фиг. 258, б).
Начиная от точки О, построим многоугольник жестко стен ki, откладывая векторы k, параллельно радиусам (см. фиг 258, а). Таким образом эти векторы образуют с осью х углы 2од Конец многоугольника жесткостей обозначим буквой М. Вырази?-тангенс угла DOM и сопоставим его с формулой (2. 11):
i%DOM =
DM
Ob
kt sin 2<ц ki cos 2*/
= tg2a0-
468
Мы видим, что угол DOM равен удвоенному углу наклона давной оси х' к исходной оси х. Отсюда легко получить, что ось г параллельна прямой СМ, а ось уг — прямой СМ', перпендикулярной первой. Очевидно, точки М и М' совпадают с концами диаметра круга, очерченного из точки О, как из центра, радиусом ОМ.
Остается показать, как определить главные жесткости смеще-яия К/ и Ку. Влево от точки О откладываем в виде отрезка сумму жесткостей ££, = ^1 + ^24-. . •. +kt>. Конец этого отрезка обозначим
Фиг. 258.
буквой А. Составим выражения отрезков АВ и АС — от точки А до концов диаметра, совпадающего с осью х.
Радиус круга равен
ОМ = У OD2 4- DM2— j/Щ k{ cos 2az)2 + (2 Ь sin 2 a J2. Но
cos 2а~^/г; (cos2az —sin2^i')=Kx~ Ky\
V k, sin 2а,- = V k, sin a,- cosaz= 2Л"
л У
Поэтому
ОЛГ= |/(Мл-Лу)2 + 4Л27-
Далее
до —• fez ==/<л. +/cv
4ЛЙ>
и окончательно
АВ = АО 4- ОМ = Кх + Ку + /K-\v)2-t-47(^;
ДС= АО - ОМ= Кх + Ку - |/Х-Ку)2 + 4/<А.у .
Сопоставляя эти выражения с формулами (2. 12), мы видим что они равны удвоенным величинам жесткостей К/ и Луг.
Итак,
Кх' = — АВ; К•/' = -- АС. 2 v 2
Отличие данного построения от так называемой обратной задачи, решаемой при помощи круга Мора, состоит в том, что угол щ отсчитывается от оси Ох до прямой ОМ, а не до ее зеркального изображения.
§ 9.3. МЕТОД МОДЕЛЕЙ И ЭКВИВАЛЕНТНЫХ ЖЕСТКОСТЕЙ ДЛЯ МНОГОСТЕРЖНЕВОГО ШАРНИРНОГО УЗЛА
Многостержневой узел. Рассмотрим параллельно трехстержневой узел (фиг. 259, а и б) и блок (фиг. 259, в), опертый на три вертикальных стержня. Следы последних стержней на горизонтальной плоскости проекций совпадают со следами стержней узла. Узел нагружен произвольной силой Р, блок нагружен вертикальной силой, равной вертикалу Zр силы* Р и приложенной к точке, совпадающей со следом силы.
Как известно, усилия в опорных стержнях блока равны вертикалам усилий в стержнях узла. Блок как бы моделирует узел в смысле величин вертикальных составляющих усилий в стержнях (§ 8.6).
Предположим, что стержни узла получают малые удлинения М, А.2, Хз. Составим выражение для виртуальной работы внешней силы Р на перемещении узла 6, обусловленном указанными удлинениями стержней.
Очевидно,
з
.4=P3coS(P,8)=^ArA- (3-1)
t ।
Здесь Ni — усилия в стержнях, обусловленные силой Р.
Обозначим через а, угол стержня I с горизонтальной плоскостью проекций.
Тогда усилие А4 выражается через его вертикаль Z, так:
Nt = . (3. 2).
sin а/
* То есть проекции силы Р на вертикальную ось г (см. гл. I).
4ТО
Подставив(3. 2) в (3. 1), видим, что работа А выразится через вертикаль усилий следующим образом:
з
л = Vz.-Al.. . (3.3)
Sin Ct;
i -1
Из этого выражения можно заключить, что для того, чтобы виртуальная работа нагрузки блока была также равна А, достаточно виртуальные удлинения его стержней взять равными
(3.4) sin а/
Из равенства виртуальных работ нагрузок узла и блока
Р8 cos (Р, 8) = Zpb'z после деления левой и правой частей на Р имеем
8 cos •(Р, 8) = 8- cos (Р, z). (3. 5)
Это означает, что проекция полного перемещения узла на произвольную прямую (Р), проходящую через узел, равна проекции на то же направление перемещения точки блока, совпадающей со следом прямой. Поэтому вертикальное перемещение узла равно вертикальному перемещению точки моделирующего блока, совпадающей с горизонтальной проекцией узла.
Вертикальные перемещения точек блока по заданным удлипе-
ниям опорных стержней X, —------ определяются при помощи про-
sin а/
стого графического построения (фиг. 260). В точках 7, 2, 3 откладываются параллельные отрезки Х'2, Х'з. Затем при помощи двух линейных интерполяций определяются перемещения любой точки, в частности проекции узла т.
471
Что касается проекции, перемещения узла иа горизонтальную ось, то она равна углу поворота блока вокруг оси, перпендикулярной к данной, умноженному на высоту Л узла над горизонтальной плоскостью проекций. Угол поворота блока определится как разность вертикальных перемещений двух точек, деленная на расстояние между точками. Точки должны быть взяты па прямой, параллельной заданной горизонтальной оси*.
Рассмотрим, при каких условиях потенциальная энергия стержней узла совпадает с энергией моделирующих стержней.
Имеем
1 3 № 1 3 z2
и=± у у (3.6)
2 Лл ki 2 Лл ^sin2a; v ’
i-I 1=1
Отсюда видно, что энергия стержней блока совпадает с энергией стержней узла при условии, что жесткость стержней блока будет
sin2 af. (3-6)
Горизонтальные стержни / узла моделируются горизонтальными же моментными опорами блока, оси которых перпендикулярны .моделируемым стержням, а моментная жесткость '
с) = А/А2. (3. 8)
Выполнение равенств (3.7) и (3.8) позволяет моделировать при помощи блока не только статические и кинематические особенности узла, но и его упругие свойства.
Переходим к многостержйевому узлу. Перережем п—3 стержня (из общего числа п стержней) и примем вертикалы перерезанных стержней за лишние неизвестные Zi, Z2, Z3,. .., Zn_3. Неизвестные определяются из системы канонических уравнений, причем т-е уравнение имеет вид
+Л>8тг + •' +^т°тт+ • •
• • • + Zn-4°m, л-4 + ^л-3°т. л-3 + Лтр = 0', (3-9)
коэффициенты и свободные члены вычисляются по формулам
з ___ _ з . _ з__
5 = "V NimNir = V ZjmZir = V' ZimZlr . -
mr k-t £fSin2a; k-
i — l i-l ' i-1
mm ~/ ! b b _;n2 / 1 b' b’ ’ } (3- 10
kl ^Sin2om k-t km I
i • • I i — 1 *
3 3 _
y4 NipNim VI ZipZlm
ml' ~ kl Zj k't
* Различные методы статического моделирования пространственных систем рассмотрены в книге автора «Статика и кинематик.а ферм».
472
Мы видим, что каноническое уравнение для неизвестных вертикалов узла вместе с тем является уравнением для неизвестных усилий блока при условии, что жесткости стержней блока взяты эквивалентные, т. е. связаны с жесткостями стержней узла зависимости (7.7) или (7.8).
Отсюда следует, что вертикалы усилий стержней узла равны усилиям стержней моделирующего? блока также и в статически неопределимом случае.
На фиг. 261 показаны многостержневой узел и соответствующий моделирующий блок. При большом числе стержней расчет целесообразно вести по методу перемещений, как указано в § 7. 1. На фиг. 261 отмечены центр жесткости и главные центральные оси жесткости. Вертикалы усилий в стержнях получаются по формуле-(1.12) с заменой k( на Л'г-=Л,-sin2»-/.
Полное усилие z-ro стержня узла будет
Z; /Zp Мх Л4у \
N, =------= k: sin а,1—г + — у,-----Лл:'). (3.11)
\Кг с/1 Cv
473'.
Усилие горизонтального стержня./
Л 7 I. I, ( . ^У . \
М = kjti I —COS а; -|- — SinаД . (3. ] 2)
Штрихами отмечено, что коэффициенты относятся к моделирующему блоку. Зная перемещения блока 6'z, <р'ж, q'y— см. формулы (1.5),-—тотчас определим и проекции перемещений узла на вертикальную и две горизонтальные оси:
5y=/!?>'l.. (3.13)
Отметим, что центр жесткости блока представляет собой одновременно след прямой, обладающей тем свойством, что сила, на
правленная вдоль этой прямой, вызывает упругое перемещение узла, вектор которого вертикален.
Изучив работу блока, диска и узла, можно без затруднений рассчитать усилия в прикрепляющих стержнях для систем, показанных на фиг. 262 и 263, в предположении, что прикрепляемые тела являются абсолютно жесткими. В обоих случаях нагрузка раскладывается на две составляющих, из которых одна лежит в плоскости .диска, а другая проходит через центр узла (см. фиг. 262) или параллельна опорным стержням блока (см. фиг. 263).
§ 9.4. ПРИКРЕПЛЕНИЕ БЛОКА, ОБЛАДАЮЩЕГО ПЛОСКОСТЬЮ СИММЕТРИИ
Этот случай прикрепления является практически весьма важным. На фиг. 264 показан пример прикрепления десятью попарно одинаковыми стержнями, расположенными симметрично относительно плоскости хОу, параллельной вертикальной плоскости проекций (на фиг. 264 шарниры по концам стержней не отмечены).
Идея расчета состоит в разложении заданной нагрузки на две 'составляющие—одну Vр, лежащую в плоскости симметрии, и другую Zp, к ней перпендикулярную, и в раздельном расчете усилий на оба вида нагрузки.
-474
В случае нагрузки, действующей в плоскости симметрии, усилия в симметричных стержнях * равны и но величине, и по знаку, и равнодействующие каждой пары стержней лежат в плоскости симметрии, причем фасадные проекции равнодействующих совпадают с фасадами стержней.
При нагрузке, перпендикулярной плоскости симметрии, усилия в симметричных стержнях равны по величине, ио обратны по зна-
Фиг. 264.
ку. Равнодействующая каждой пары усилий проходит через точку пересечения стержней и перпендикулярна плоскости симметрии. Точки пересечения стержней легко определяются в плане и затем проектируются на фасаде стержней. Они отмечены светлыми кружками с номерами соответствующих стержней.
Определение равнодействующих в плоскости симметрии, очевидно, эквивалентно решению задачи о диске, прикрепленном стержнями к- своей плоскости.
Расчет на нагрузку, перпендикулярную плоскости симметрии, эквивалентен задаче о блоке, прикрепленном параллельными стержнями.
* В статически неопределимых схемах имеется в виду ие только геометрическая, но и упругая симметрия — равенство жесткостей.
475
При общем числе стержней, равном шести, расчет сводится к разложению силы Vp на три компонента в плоскости симметрии и к разложению силы Zp на три компонента, перпендикулярные плоскости симметрии.
При большем числе стержней речь идет о статически неопределимом закреплении диска и блока.
^Установим эквивалентные жесткости стержней, закрепляющих диски и блок. Они будут различными. На фиг. 264, б показана развертка пары симметричных стержней. Угол «-—истинный угол, образуемый стержнем с. плоскостью симметрии, k—жесткость каждого из симметричных стержней.,
Податливость, или перемещение по направлению силы V от нагрузки У=1 по оси симметрии пары стержней определяется при помощи общей формулы перемещения:
п 5 V 1 у ' 3 ______1__. (4п
Рг» vv ЕР \2cosa/ EF 2 COS2 а , 2Й Cos’a
Отсюда следует, что эквивалентная жесткость стержня в плоскости симметрии
=2£cos2a. (4.2).
v
Податливость, или перемещение по направлению Z от силы Z—1 получается аналогично:
В2=—?--------. (4.3)
12 2 sin2 а 2Й Sin2 a
Жесткость эквивалентного стержня, перпендикулярного плоскости симметрии, равна
£2=2£sin2a. (4.4)
Некоторые особенности представляет случай симметричных параллельных стержней (фиг. 265, а).
Эквивалентный стержень, направленный вдоль оси v в плоскости симметрии, имеет податливость и жесткость соответственно:
= ^ = 2й. (4.5)
Что касается стержня, направленного перпендикулярно плоскости симметрии вдоль оси г, то он вырождается в моментную связь в плоскости vz (на фиг. 265, б эта связь изображена условно в виде дугового стержня), реализующую пару сил, а не одну силу.
Податливость е моментной связи определяется как угол поворота тела (см. фиг. 265) от действия единичного момента. По общей формуле перемещения имеем
S = (1.6)
476
так как в данном случае N = ±A/d, где d — расстояние между параллельными стержнями.
Соответственно жесткость моментной связи или момент, развиваемый при принудительном повороте на единичный угол, равна
е = (4.7)
Отметим, что с равна моменту инерции жесткостей k относительно оси симметрии:
Пользуясь этими данными, можно построить две модели, упрощающие расчет симметричного статически неопределимого при-
• Фиг. 265.
крепления. Первая модель — плоский диск, прикрепленный в своей плоскости упругими стержнями с известными податливостями 0,, или жесткостями kv. Вторая модель — тело, прикрепленное параллельными упругими стержнями или моментными связями в пространстве с известными податливостями е или жесткостями kz, с.
Диск и тело, как и прикрепляемый блок, считаются для упрощения расчета абсолютно жесткими.
Расчет усилий в стержнях может быть выполнен как по методу сил, так и по методу перемещений.
Решение по методу сил не нуждается в особых пояснениях, так как основная система представляет собою шестистержневое статически определимое прикрепление, рассмотренное выше.
Отметим, что через податливости и жесткости общая формула перемещения выразится так:
4 = + = + (4.8)
477
Что касается изложенного выше расчета по методу перемещений, то он допускает вычисление усилий в стержнях, независимо от числа стержней по готовым формулам.
При малом числе стержней расчет ведется по методу сил. При большом числе — по методу перемещений. В плоскости симметрии (т. е. па фасадной проекции) будем иметь два центра жесткости и две системы главных центральных осей.
Определив равнодействующие пар усилий V, и Zf, получим истинные величины усилий:
lv 2 COS Я; ’ iz 2 sin а;
Полные величины усилий от заданной нагрузки составят
Д/. = Д/. + Д/. .
1 ’ I 1 т IV — 1 т iz
Указанный способ дает возможность составить себе еще до расчета отчетливое представление о рациональности намеченной конфигурации опорных стержней с точки зрения восприятия заданных нагрузок. Так, например, схема на фиг. 264 имеет тот большой недостаток, что точки 1, 2, . .., 5 близки к одной прямой, поэтому жесткость при действии нагрузок, перпендикулярных плоскости симметрии, мала.
Метод легко обобщается на тот случай, когда, кроме стержней, работающих на растяжение, сжатие или кручение, имеются стержни, работающие па изгиб. В общем случае упругий стержень, прикрепляющий тело и жестко с ним соединенный, может быть заменен тремя силовыми и тремя моментными связями.
Пример. Вычислить усилия в стержнях, прикрепляющих реактивный двигатель к фюзеляжу самолета, считая, что тяга /’=2500 кг, вес двигателя с учетом перегрузки 6=2000 кг, боковая сила инерции /=1000 кг. Все силы действуют одновременно. Необходимые размеры указаны на фиг. 266 а, б. Площади сечений стержней /:'i = /7]=l,5 см2; — см; ~2 см2. Все
стержни рыполнены из стали ЗОХГСА, модуль упругости Е=2,1 • 106 кг/см2.
По величинам проекций, данным на фиг. 266, определяем истинные длины I стержней, вычисляем их жесткости и, зная углы а наклона стержней к плоскости симметрии, вычисляем по формулам (4.1)—(4.5) жесткости эквивалентных стержней. Последними формулами приходится пользоваться при вычислении жесткостей эквивалентных стержней для пар 1,1; 3,3; 4,4 парал-лельных стержней. Результаты вычислений следующие:_________________
№ стержня 1,1’ 2,2’ 3,3' 4,4’
1 см 72,8 89,6 92,2 80,6
F см- 1,5 1 2 2
kv 1,84 *2 *2 1,94 *2 2,22 *г
а 0 38°40' 0 0
sill а 0 0,624 0 0
COS а 1 0,781 1 1
3,68 *2 1,22 *, 3,88 *2 4,44 *2
Кг или С 6-11 100 *2 *г=0,78 *2 6=11 700 *2 С=13 400й2.
478
Все эквивалентные жесткости выражены через жесткость второго прикреп-EF<2
«яющего стержня k2—~—, значение которой вычислять нет необходимости.
<2
а) Расчет на симметричную нагрузку. Прикрепляющие-эквивалентные стержни ас, ak, be, bd имеют податливость kv. Диск нагружен.' силами Р и G (фиг. 267), действующими в плоскости симметрии прикрепления.
Система один раз статически неопределима, так как для прикрепления диска» 8 плоскости достаточно трех стержней. Воспользуемся методом сил. Выбираем основную систему, перерезав стержень Ьс. Усилие X, в перерезанном стержне определяем из канонического уравнения:
^18П + = О,
479'
где
NpN_
Ку ky
Нагружаем основную систему заданными силами и вычисляем усилия .Vр в не-перерезанных стержнях.
Из
суммы моментов относительно точки а имеем Л^2, lab 4- Р-ат — G От ~ 0,
откуда,
подставив величины сил и плеч ab, ат, От, взятые с чертежа, получим р —2500-11,5 + 2000-31
Л';,, =-------------------------= 830 кг.
2.2 40
Из
уравнения моментов относительно точки </, имеем
•Wf 4 ’ qi + Р - Ое G qe ~ 0,
„ -2500-28,5 -2000-77,5
7V£4, = --------------------= — 3870 кг-
58,5
Последнее усилие определим из уравнения проекций сил на ось ab: N??i, cos -%: cab -|- Х44, cos + kab — G = 0, 3870-cos 60° + 2000 ------------------------------------------= 100 кг. cos 50°
Затем нагружаем основную систему силой Xi = l и определяем усилия W и том же порядке:
Е Ма = 0:
N,
• ab + 1 • ап — 0,
откуда
^2,2' —
36.4
—- = _ 0,96.
40
»ito дает
Сумма
проекций
N-, ,, - cos
2Ж = 0:
ап ab
^1,4’^— 1'р7=°.
Г, Pl
N/i-v ql
на ось ab:
—— = 0,23.
58.5
4 cab -|- Л/4 4, - cos 4 kab — I-cos 4 abc -= 0, 0,23.cos 60° — 1-cos 73° =--------------------------= — 0,28.
cos 50°
В перерезанном стержне, очевидно, будет действовать усилие Л'ы'^1. 12-5, 0,96'25о 0,282б2 0,23’6.
3,68 1,22 3,88 4,44
д _ 830•(— 096) ЮО(— 0,28) — 3870-0.23
>р~ 1,22 + 3,88 + 4,44
= 1,065;
860;
Разумеется, при вычислении коэффициентов вместо жесткостей в знаменателе можно пользоваться податливостями в виде множителей.
860
X, ,, =----------= 810 кг.
1 '-1 1,06
480
Теперь определяются усилия в остальных стержнях по формуле
W = Np^.XN,
М,.2, ^N2,2’ + ^1-^2,2-=83°+ 810(-0,96) = 50 кг,
N33, = ЮО 4-810-(— 0,28) = — 130 кг,
Ni4, = -3870 + 810-0,23 = —3680 кг.
Фиг. 267.
б) Расчет на антисимметричную нагрузку. Эквивалентная схема изображена на фиг. 267, б. Стержни 2 и 2' заменяются стержнем с жесткостью kz, перпендикулярным плоскости симметрии и прикрепленным в точке d пересечения реальных стержней. Каждая пара параллельных стержней заменяется моментной связью с жесткостью с, перпендикулярной плоскости,
31 425 481
проходящей через соответствующую пару стержней. Реактивные моменты М, возникающие в связях, изображены векторами с волнистой стрелкой.
Основную систему получим, удалив моментную связь, эквивалентную паре стержней 1 и Г. Усилие (момент), действующее в этой связи, обозначим Х2.
Каноническое уравнение для определения Х2 имеет вид
2f2822 “ О*
Вычисляем усилия в стержнях (связях) основной системы от действия заданной силы Т.
Из уравнения проекций всех сил на нормаль к плоскости диска имеем
2, + Т — 0 или Л^2 2' ~ — Ю00 кг-
Составим уравнение моментов относительно осн ас, перпендикулярной вектору реактивного момента Мз,2:
Мт4 4, cos р4 — • md -f- Т -pq = 0.
Величины плеч и углов определим по фиг. 267. — 1000-16.,7— 1000-28,4 ЛД4, = — =-48 000 кг-см.
Уравнение моментов относительно оси ak дает Л43_3, cos ₽з — v nd + Т Op — 0,
откуда т —1000-70— 1000-4 МГ ,, — — — 78 600 кг • см. з.з 094
Прикладываем к основной системе единичный момент Х2 и определяем усилия в связях.
Из уравнения проекций на ось, перпендикулярную плоскости симметрии, следует, что
Уравнение М2,2- = 0. моментов относительно оси ас дает .414 4, = cos р4 — 1 • cos Р] = 0
или — cospi 0,41 М, ., ^1_ г ’ ., 0>435 4,4 cos р4 0,94
Проектируя вектор-моменты на ось ak, получим
М3 3, • cos р3 — 1 cos р2 = 0,
откуда — cosp2 0,76 Л4, — = 0,81. 3,3 cos р3 0,94
Момент в перерезанной связи М। = 1.
822 = (М2Л, )2 8 + (М,,,, У г + (Л43>3, )2 е + (М4>4, )2г = 1'25 (0,81)28 (0,435)28 _ 1,68 - 11100 + 11700 4 13 400 105 ’
. Доу = Л0>,2> ’ ^2,2' 5 + 1,| ’ 8 "Ь ^з",3' ^3,3+ ^4,4' ^4,4' ®
482
-78600-0,818 -48000-0,4358
= 04-0+ --------------4--------------
г 11 700 13400
— 76;
Дог 7 •10®
Хг — М, ,, = ——— = —-—— = 437000 кг-см. ’ °22 1,6
Вычислим усилия в остальных связях от антисимметричной нагрузки Г:
N =N% 9, + -¥2-N9 9, = — 1000 кг, Ав f X* Ав 1 X* Ав ) Ав
2И3>3, = 7И[3, +-¥г-Л4313, = -78 600 +437 000-0,81 =275 000 кгсм,
М4>4, = 2И4Г4, + Х2.Л/4(4, =-48 000 + 437 000-0,435= 142 000 кг-см.
Суммарные усилия в прикрепляющих стержнях при совместном действии всех трех сил Р, G, Т определяются путем разложения равнодействующих усилий в эквивалентных стержнях по направлениям стержней соответствующей пары.
Следует иметь в виду, что реактивный момент в эквивалентной моментной связи реализуется парой сил в реальных стержнях.
Общая формула для вычисления усилий в стержнях имеет вид
TV™" N^, ЛI ~ ~ ~
2cosa{ 2 Sinai
или для случая параллельных стержней
ДИ™
где a; — угол наклона стержня к плоскости симметрии; d — расстояние между параллельными стержнями.
Переходим к вычислению окончательных усилий в стержнях:
437000
—;-----=4370 кг,
НО
437 000
-------= — 3560 кг, 110
1000
+ 2-0,624
1000
810 ^"2
810
2
50 М> =
= 830 кг,
N4 =
2-0,781 50
---------— = — 770 кг, 2-0,781--2-0,624
— 130 275 000
------—----------= — 2560 кг, 2 ПО
— 130 275000
2 +
— 3680
2
— 3680
2
= 2440 кг , 110
142 000
110
142 000
ПО
= —3130 кг,
550 кг.
< =
Наиболее нагруженными оказываются стержни 1 и 1'.
Глава X
НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ВОПРОСЫ РАСЧЕТА ПЛАСТИНОК
§ 10.1. ДВУХСЛОЙНЫЕ ПЛАСТИНКИ С ЗАПОЛНИТЕЛЕМ
В качестве обшивки современных скоростных самолетов широко используются двухслойные пластинки с промежуточным заполнителем (иначе — трсхслойные пластинки).
Идея конструкции пластинки из двух раздвинутых слоев й заполнителя из менее прочного, но более легкого материала эквивалентна идее двухпоясной топкостенной балки (лонжерона) со
стальными поясами и ду-ралюминовой стенкой: при достаточной строительной высоте легко достигнуть увеличения прочности и жесткости па изгиб при
одновременном уменьшении веса по сравнению с балкой из одного материала. Для обшивки важно также повышение устойчивости на сжатие и па сдвиг.
Наружные слои изготовляются из того же материала, что и однослойная обшивка, чаще всего из дуралюмина. В качестве за-
полнителя применяются пористые пластмассы (пенопласты) с весьма малым объемным весом — от 0,05 до Q,2^-
(фиг. 268, а). Соединение несущих слоев и заполнителя достигается склейкой. Другой вид заполнителя — с о т ы из металлической фольги толщиной 0,05—0,2 мм, изготовляемые из гофрированных лепт, имеющих ширину, равную расстоянию в свету между несущими слоями. Ленты спаиваются между собой и припаиваются к несущим слоям, образуя призматические соты различ
484
ной формы. На фиг. 268, б показан горизонтальный разрез по сотовому заполнителю.
Кроме сот, применяется также гофр с волнами, параллельными наружным слоям. Гофр укладывается в один или несколько слоев. Применяется конструкция с промежуточными стенками, пространство между которыми заполняется легким материалом.
Двухслойная обшивка обладает многими преимуществами, позволяющими упростить конструкцию самолета. Сюда относится, например, возможность обойтись бе.з стрингеров. Немаловажное значение имеют также теплоизолирующие свойства легкого заполнителя. В отдельных случаях трехслойиые пластинки применяются в качестве несущих конструкций (крыло, оперение, лопасти ротора вертолета). Основной недостаток рассматриваемых конструкций — технологические трудности изготовления.
Двухпоясная тонкостенная балка
Для уяснения работы двухслойной пластинки с заполнителем целесообразно исходить из двухпоясной тонкостенной балки с поясами и стенкой из различных материалов. Подобно тому как обыкновенная балка служит элементарной моделью пластинки, так и двухпоясная балка может служить моделью (балкой-полоской) для двухслойной пластинки. В отличие от балки, изученной в § 7. 1, здесь мы не будем пренебрегать собственной изгиб-
Фиг. 269.
ной жесткостью поясов, полагая, что пояса работают не только на продольные силы ±N, по и воспринимают некоторую часть полного изгибающего момента.
На фпг. 269 показана балка, симметричная относительно горизонтальной оси.
Нагрузку и реакции раскладываем на две составляющие — симметричную и антисимметричную. На фиг. 269 разложение нагрузки изображено условно в виде равенства.
При симметричной нагрузке балка испытывает сжатие или растяжение в поперечном направлении. Простейшую расчетную схему получим, мысленно разрезая стенку на бесконечно узкие вертикальные волокна и предполагая, что силы взаимодействия между волокнами отсутствуют. При этих допущениях пояса ра
485
ботают, как балки на упругом основании. Отгюрность основания каждого пояса равна
/г = Ест~-т-, (1.1)
“СТ
Здесь Ест —модуль упругости материала стенки в‘ вертикальном направлении; Лот'— высота стенки в свету между'" поясами; /ст — толщина стенки.
При антисимметричной нагрузке конструкцию (фиг. 270, а) можно рассматривать как совокупность двух конструкций, работающих в вертикальном направлении совместно, т. е. имеющих одинаковые вертикальные прогибы: первая конструкция (см. раз-
рез на фиг. 270, б) представляет собой две балки — пояса, работающие на поперечный изгиб; вторая (см. фиг. 270, в) — тонкостенную балку с поясами, работающими только на продольную силу, и стенкой, работающей только на сдвиг в поперечных и продольных сечениях.
Величины, относящиеся к каждому из поясов, обозначим индексом 1; относящиеся к тонкостенной балке — индексом 2. Соответственно, Л4, — изгибающие моменты в поясах, M-, = N\h — изгибающий момент в тонкостенной балке.
Пусть М — полный изгибающий момент в произвольном сечении (см. фиг. 270, а, слева).
Условие равновесия отсеченной части балки дает
7И = 2/14, Н-ТИ2. (1.2)
Дифференциальное уравнение прогибов каждого из поясов
(1.3)
м Ely 1 '
Дифференциальное уравнение прогибов тонкостенной балки с учетом деформации сдвига в стенке и температурного искрив-
ления . dQ? 1 dx2 EJ2 dx <3E„ 2‘ 7
Здесь /2=Е, Л2 x ——момент инерции сечения тонкостенной балки в предположении, что площадь сечения F=2FX сосредоточена в центрах тяжести сечений поясов, расстояние между которыми равно h.
486
/г<.т = йст/ст —площадь сечения стенки;
$2—наперед заданная температурная кривизна тонкостенной балки. При равномерном нагреве нижнего пояса на tu и верхнего на /в имеем
f a \ и
Уравнения (1.2), (1.3), (1.4) сводим к трем уравнениям, каждое из которых содержит одну неизвестную. С этой целью в уравнении (1.4) заменяем dQ2/dx через dlM/dx2; далее, учитывая, что = приравниваем правые части (1.3) и (1.4) и используем (1.2). Наконец, из (1.4) исключаем Л42. Результат имеет вид двух однотипных уравнений второго порядка и третьего уравнения четвертого порядка типа, отвечающего первым двум:
7Wi-a2M-=-a2-i-(]. 5) 1 /22 ’
М'2 - АИ, = - а2 М + аЛст&2; (1.6)
^'V_a2^" = a2 —+- /’--4-а2А ^2. (1.7)
£/T2E/i 1 I У '
Здесь приняты обозначения:
/=2Л + /2 — полный момент инерции сечения тонкостенной балки с учетом собственных моментов инерции поясов;
Интегрирование уравнений, подобных (1.5) —(1.7), детально рассмотрено в гл. I.
При решении уравнений нет необходимости интегрировать все три. Достаточно проинтегрировать одно уравнение, например (1. 7). Другие неизвестные легко выразить через v.
Рассмотрим предельные
При стенке, абсолютно
из (1.5) — (1.7) получаем
случаи.
податливой на сдвиг (G/?Ct = 0, a2 = 0),
X = 0: =
Пояса работают на изгиб как две самостоятельные балки, каждая под нагрузкой р/2. Закон плоских сечений удовлетворяется в пределах каждого из поясов, по высоте всей балки этот закон, разумеется, не имеет места. При стенке, абсолютно жесткой на
487
СДВИГ (GFCT = OO, а2=оо), после деления уравнений (1.5) — (1.7)
на а2, получаем
М + ft', 1 1 I 2
мг = ^-м-2-^^> 2 I I (1.10)
„Л М Л
EI I
Балка в этом случае работает как монолитная, закон плоских
сечений соблюдается по всей высоте балки. Нормальные напряжения от нагрузки определяются при помощи классической формулы:
Вторые слагаемые формул (1.9) позволяют определить температурные напряжения от неодинакового, по равномерного нагрева или охлаждения каждого из поясов.
При конечной жесткости стенки на сдвиг напряженное состояние в сечении является промежуточным по отношению к двум предельным случаям. Закон плоских сечений по высоте балки не соблюдается.
Обратим внимание па практически важный случай небольшой высоты поясов, когда их собственным моментом инерции Д можно пренебречь по сравнению с h, следовательно:
/1==0; Z2=/; ^ = 0; Л!2 = Л!.
Работа тонкостенной балки в этом предположении рассмотрена в гл. V.
Дифференциальное уравнение прогибов здесь имеет вид
—----------ft'. (1.11)
EI GF„
v
Итак, приближенный расчет на симметричную нагрузку привел к балке на упругом основании, расчет на антисимметричную нагрузку к уравнениям, аналогичным уравнениям для растянутой балки.• Отметим, что если считать стенку абсолютно жесткой на растяжение — сжатие в вертикальном направлении (Дст = оо), то безразлично, к какому из двух поясов приложена нагрузка, разложение нагрузки на симметричную и антисимметричную можно не производить и пользоваться непосредственно .уравнениями для антисимметричной нагрузки.
Устойчивость при сжатии
Допустим, что балка на двух опорах сжимается силой N, поровну передающейся на оба пояса. Возможны две формы потери устойчивости в вертикальной плоскости-—симметричная и анти
488
симметричная относительно продольной оси. Обе формы показаны на фиг. 271.
Интуиция подсказывает и подсчеты это подтверждают, что, как правило, симметричной форме отвечает большая величина критической силы и поэтому внимание должно быть сосредоточено на антисимметричной форме.
Обратимся к дифференциальному уравнению для прогиба (1.7). Дифференциальное уравнение сложного изгиба сжатой балки получим, подставив в правую часть значения
p = pQ — Nv", (1.12)
где Л1° и р° — изгибающий момент и интенсивность нагрузки, определенные без учета продольной силы.
Фиг. 271.
Задача нахождения приводит к интегрированию однородного уравнения сложного изгиба.
Полагая 7И°—0; /?° = 0; &о=О, подставляем в (1.10) значения M = NKjr, p=-NK^'-, ^ = 0.
После приведения получаем уравнение на устойчивости (уравнение безразличного равновесия):
Ограничимся случаем обычно:
шарнирно опертых концов и примем, как
и = T\.psin -— («=1,2,3,. . . ). (1.14)
Тогда
„ Л2 К2 . П~Х
v = — ---- sin — ;
СР /2 / ’
,v ТриА . ПТ.Х
-р„----sin----.
СР Z4 I
Подстановка [в (1.12) после сокращения па vCf sin дает
П4*4 П2к2 / NKp \ a2JVKp
-----------а2----------------= U.
/4 /2 ( 2Е1] J Е1
Отсюда
^-2+а2
N =......../2..-____.
КР 1 а2‘2
2Elt + ElnW
489
Очевидно, 2Vl(p принимает наименьшее значение при п=1:
-- 4- q2
/2
min Лф„ =-------------. (i 1
кР j а2/2 (. * • Ю)
25Д + Е№
Легко убедиться, что NKp лежит между эплеровыми критическими силами
о я2£/, rfEI
2------ и ---,
/2 /2
отвечающими GF„ -Ди GFCT -> оо.
В случае малой высоты поясов можно упростить выражение для А^кр, проделав указанные операции с уравнением (1. 11), вместо уравнения (1.7). Предлагаем проверить окончательный результат:
1 gf„
iflEI
Здесь N3 —-------эплерова критическая сила в плоскости изгиба
/2 балки.
/ = /2= 4^-—момент инерции сечения балки, воспринимаю 2 щий нормальные напряжения.
Формула (1. 16) справедлива также в случае жестко защем-' ленных концов. В этом случае Na возрастает в 4 раза.
Устойчивость двухслойной пластинки
Чтобы перейти от балки к пластинке, изгибаемой по цилиндрической поверхности, достаточно подразумевать под Е приведенное значение модуля упругости:
Е* = £/(1-р2).
Под усилиями N, Q, М следует понимать их погонные величины. Момент инерции и площадь сечения вычисляются на 1 см ширины сечения пластинки. Вместо /=’ст=ЛСт^ст имеем FMn= =Лзап- 1 = (/г—I) • 1, где t — толщина наружного слоя.
Для использования формулы (1. 16) заменяем EI цилиндрической жесткостью D:
EI Eth2
' 2(1—ц2)'
Тогда
д/ — д2Д _ *2Eth2 э— й2 ~2(1 — ф2) л2
Здесь t — толщина внешнего слоя, а—пролет пластинки.
490
В случае весьма длинной пластинки шириной в шарнирно (свободно) опертой вдоль длинных сторон и сжатой в продольном направлении, критическое усилие будет
Здесь
_ 4_________ifiEth?
кр~ (1 + Л)2 2(1 — н2) *2
, iflEth k =-----------------.
2(1 -р.2) О
(1-17)
Приведем также, следуя А. П. Вороновичу, окончательные результаты для прямоугольной пластинки с конечным отношением сторон alb = \, шарнирно опертой по четырем сторонам и сжатой силами, распределенными вдоль сторон b и направленными параллельно сторонам а.
NK? JEIfi
3-------— А*-----------.
Ч> b 4(1—р.2)*2
Здесь коэффициент
Im X \2 + I /,* _ —,n-L.
1+Ф+хТ
где т— число полуволн в продольном направлении; (в поперечном направлении — одна полуволна);
__ Азап
ЧЬЮ ’
Отношение 7.1т, при котором k* приобретает наименьшее значение, найдется из условия аннулированной производной от k* по Х/m. Это отношение равно
А = |/1£1. т V 1 + £
Наименьшее значение
k*. = --------.
mm (1+5)2
Формула (1. 18) по виду тождественна с формулой критического напряжения однослойной пластинки, причем &*)in <4.
Пример. Заданы размеры пластинки 6 = 50 см, (=0,05 см, Л.зап=1,0 см, Е=7- 105 кг/см2, G = 350 кг1см2.
Находим
с_ -.2£(йзап _ it2-7-105-0,05-0,5 _д о.
ЧЬЮ ~ 2,502-350 ’ ’
Сп
4
(1 + 0,2)2
= 2,8.
491
Отношение сторон, при котором /?* = /e*)jn , определится из формулы
1 а , / 1 —0,2 „ о
ь = ------— 0,8т.
Ь у 1+0,2
Формулой для £*1п следует пользоваться, когда Х>1. В противном случае, когда Х<1, следует пользоваться формулой для k*, куда следует подставить /п=1.
Проблеме прочности и устойчивости трехслойных пластинок и оболочек посвящена обширная литература, в которой подвергнуты детальному изучению все обстоятельства работы этих конструкций. Крупные исследования принадлежат А. Я. Александрову, Л. Э. Брюкнеру, А. П. Вороновичу, Э. И. Григолюку, Л. М. Куршипу, А. П. Прусакову, А. Л. Рабиновичу.
§ 10.2. ИЗГИБ И КРУЧЕНИЕ КОНСОЛЬНЫХ ПЛАСТИНОК ПЕРЕМЕННОГО СЕЧЕНИЯ (ТОНКИХ КРЫЛЬЕВ)
Крыло современного сверхзвукового самолета имеет . шую относительную толщину и нередко малое удлинение, няют прямые и стреловидные крылья разнообразной в плане — треугольные, четырехугольные, эллиптические. Пару крыльев, образующих в плане равнобедренный треугольник, часто называют дельтовидным крылом.
Конструктивно тонкие крылья бывают монолитные, двухслойные с заполнителем, лонжеронные, а также смешанной конструк- ции. Делались и продолжаются попытки применения армированных материалов—стеклопластиков и даже железобетона.
Картина работы крыльев различного конструктивного оформления имеет многие общие черты и целесообразно начать с рассмотрения простейшей конструкции—прямого многолонжеронного крыла. Один из вариантов расчета такого крыла приведен в качестве примера применения метода сил в § 7. 1. В этом примере связь между лонжеронами осуществляется обшивкой, нервюры же считаются отсутствующими. Здесь мы также рассмотрим многолонжеронное крыло, но с жесткими в своей плоскости нервюрами, без учета и с учетом наружной обшивки. Хотя окончательные расчетные формулы могут быть получены непосредственно на основании теории тонкостенных стержней (гл. V), выводы настолько элементарны, что целесообразно привести их тут же. От многолонжеронного крыла мы перейдем к массивному крылу (консольной пластинке) *.
неболь--Приме-формы
* Многолонжеронное крыло является частным случаем так называемой многорядной биконструкции, расчет которых рассмотрен в книге автора «Пространственные системы», 1948, гл. 3 § 13.
492
Общий изгиб и изгибное кручение многолонжеронного крыла
Будем считать лонжероны параллельными, а нервюры—-перпендикулярными к лонжеронам.
Основное упрощающее допущение состоит в недеформируемо-сти поперечных сечений в своей плоскости, что предполагает наличие достаточно жестких поперечных связей (нервюр, шпангоутов). Наряду с этим следует подчеркнуть, что гипотеза плоских сечений для крыла не вводится. Закон плоскости соблюдается только в пределах сечения отдельного лонжерона.
Остановимся на случае крыла, симметричного относительно горизонтальной плоскости. На фиг. 272, а показан отрезок крыла, состоящий из нервюры и примыкающих к ней лонжеронов. В произвольной точке па оси нервюры выбираем начало координат О, Ось z направляем параллельно лонжеронам (от заделки к свободному концу), ось х — вдоль оси симметрии нервюры, ось у — вертикально вниз.
Вертикальное перемещение нервюры в начале координат обозначаем Ко, угол поворота нервюры в своей плоскости обозначаем <рк. Индексом к отмечаем тот факт, что угол поворота нервюры совпадает с углом закручивания крыла. Угол срк считается положитель
493
ным, если поворот нервюры при взгляде с конца оси z происходит против часовой стрелки.
Вертикальный прогиб z-ro лонжерона в сечении рассматриваемой нервюры запишется так:
+ ?><*/• (2.1)
Изгибающий момент в z-м лонжероне
M^-El^'^-El^-Elx^. (2.2)
Штрихами отмечено дифференцирование по z. Найдем суммарный изгибающий момент во всех лонжеронах Л4 = 2Л4г-:
M--=-EIv\~ES^. (2.3)
Здесь
/=£ Л 1см41 (а)
— суммарный момент инерции всех лонжеронов относительно
оси симметрии у.
[СМ5] (б)
— так называемый статический бимомент сечения всех лон-
жеронов, геометрическая характеристика типа статического момента, но не от площадей, а от моментов инерции лонжеронов.
Умножим далее все члены равенства (2. 2) на х, и просуммируем по всем индексам z. Результат этой операции запишем в виде
В=-ESav"0-Е/^'к. (2. 4)
Здесь появились две новые величины.
Статический фактор (обобщенное усилие)
В = У [кгсм2], (в)
или так называемый из гиб но-крутящий бимомент — своеобразный крутящий момент, но не от сил, а от изгибающих моментов.
Геометрическая характеристика сечения
[см11], (г)
или так называемый бимомент инерции сечения всех лонжеронов—своеобразный момент инерции, но нс от площадей, а от моментов инерции. Отметим, что обшивку мы пока во внимание не принимаем.
Систему уравнений (2. 3), (2. 4) легко упростить, выбрав начало координат D (положение оси х) так, чтобы было =0. Обозначим абсциссу нового начала через уо и поставим требование
У (х,-ло) = 0.
494
Отсюда
следовательно,
U А по-
Структура формул (а), (б), (2. 5) показывает, что повое начало можно уподобить центру тяжести моментов инерции лонжеронов. Эту точку называют центром изгиба системы лонжеронов в данном сечении, иногда центром жесткости.
Для подсчета бимомента инерции относительно центра изгиба нет необходимости наново производить суммирование по формуле (г). Можно воспользоваться формулой
/«"-Д-Лтд. (е)
Предлагаем получить эту формулу самостоятельно.
При начале координат в центре изгиба D система уравнений (2.3) и (2.4) принимает вид
. (2.4')
Первое из этих уравнений — дифференциальное уравнение общего изгиба крыла. Второе — дифференциальное уравнение пзгибного (стесненного) кручения.
Для вычисления М и В в данном сечении следует предположить, что нервюры не создают связи между лонжеронами и каждый из них работает как балка, защемленная одним концом в корне крыла. Определив затем изгибающие моменты М° каждого лонжерона в исследуемом сечении, находим
М = ^М°-,
Если, например, z-й лонжерон изгибается направленной вниз вертикальной силой Ру, приложенной на расстоянии z(>0 от исследуемого сечения крыла, то имеем
М = M°i = - Pyz- В= M°iXi = - Pyzxt.
От действия горизонтальной растягивающей силы Рх, приложенной между исследуемым сечением крыла и его свободным концом с эксцентриситетом z, имеем
М—Рху\ В = РРУХ1-
495
Рассматривая совместное действие двух равных и противоположно направленных вертикальных сил в плоскости нервюры, заключаем, что они порождают бимомент
B = ±LKz,
где LK — сосредоточенный крутящий момент пары сил. Знак определяется путем сопоставления с действием компонентов пары.
Таким образом, сосредоточенный крутящий момент по отношению к бимоменту играет такую же роль, какую поперечная сила играет по отношению к изгибающему моменту.
Сосредоточенный изгибающий момент в плоскости лонжерона Т,- даст изгибающий момент М — Li и бимомент B = Lxi. Момент L играет по отношению к бимоменту такую же роль, как сила по отношению к крутящему моменту.
Отмстим, что две равные и противоположные пары с моментами ±LK пли ±L в параллельных плоскостях, отстоящих на расстоянии а, создают сосредоточенный бимомент La, передающийся без изменения вдоль оси г: M = Q; B = La.
Этих правил достаточно для определения общих усилий М и В как от сосредоточенных, так и от распределенных нагрузок. Подчеркнем, что местной прочности элементов мы здесь не касались.
Найдем выражение для изгибающего момента в г-м лонжероне. С этой целью подставим значения v'g и ср’ из (2.3') и (2.4х) в (2.2). Получим
(2.5)
Дифференцируя (2. 5) по z, найдем поперечную силу*. При этом учтем, что
в'=± 2 м‘х‘ = 2 (2-6)
— производная от б и м о м е н т а равна крутящему моменту. Поэтому
= (2.7)
1 10)
Имея изгибающий момент и поперечную силу в лонжероне, можно проверить его прочность.
Выпишем еще формулу для нормального напряжения в лонжероне:
Af/ М j В /п q\
°, =-J- X-= — х 4- - - СО. (2.8)
// J
Здесь
or— xty (2.9)
* Следует помнить, что M'=Q+m, где т — погонная интенсивность изгибающей моментной нагрузки. В данном случае мы принимаем т=0.
496
— удвоенная площадь треугольника, заштрихованного на фиг. 272, б.
Формула (2.7), как, впрочем, и большинство предыдущих, хорошо известна из теории тонкостенных стержней. В частном случае двутавра или многотавра (многорядпой биконструкции) теория стесненного кручения может быть получена без предварительного введения понятая о депланации.
Определение перемещений-—прогибов «о и углов закручивания фк требует интегрирования дифференциальных уравнений (2. 3') и (2. 4'). Полная аналогия структуры этих уравнений позволяет применить при построении эпюры углов закручивания все приемы, известные из теории изгиба балок постоянного либо переменного сечения, в частности, графоаналитический метод, метод начальных параметров и др.
Общее уравнение углов закручивания при начале в произвольном сечении имеет вид
Z
(*) = ?к (0) + (0) z- [ (С) {z- С) Л, (2.10)
о
где
0<C<z.
Если начало взято в сечении заделки, то фк(0)=0, а также 0к(0) =фк'(0) =0, так как относительный угол закручивания 'О'ц(О) пропорционален углу поворота при изгибе лонжеронов, равный, очевидно, нулю при полном защемлении.
Учет работы обшивки
Выше мы не принимали во внимание работы обшивки па нормальные и касательные напряжения. Это оправдано лишь в сечениях больших вырезов, а также при слабом обеспечении передачи усилий обшивки в корневом сечении.
Для учета работы обшивки на нормальные напряжения к поясам лонжеронов присоединяют полосы обшивки с приведенной шириной
^пр~ ' ^ТреЛ’
где фред — редукционный коэффициент.
При этом моменты инерции лонжеронов увеличиваются на величину
Л?
(ж)
Увеличенные значения Ц вводятся при вычислении полного момента инерции / = S/j и бимомента инерции .
Так как каждый лонжерон с присоединенной обшивкой приобретает вид широкополочного двутавра, то он теперь обладает собст
497
венным бимоментом инерции относительно своего центра изгиба — центра симметрии:
гсоб п /(/>П₽ИВ)3 /й,\2 ,
К величине Д, определенной, как указано выше, добавляется 2/“-б • Последняя добавка имеет подчиненное значение и ею можно пренебречь.
Для учета восприятия обшивкой касательных напряжений кручения, сечение обшивки приближенно рассматривается как один замкнутый контур без подразделения па ячейки. Этот контур берет на себя крутящий момент, пропорциональный погонному углу закручивания (так называемый момент свободного кручения):
(2. 11)
MK = G/K& = GZK?,
где
«2/
к
«к
ИЛИ
при переменной толщине стенки.
Другая часть крутящего момента — так называемый крутящий момент изгибного кручения — выразится при помощи зависимостей (2.6) и (2. 4'). Обозначим теперь этот момент через Мк:
МК = В'=-(Е/Л)'. (2.12)
Сумма моментов Мк и Мк должна быть равна полному крутящему моменту в сечении крыла
Я+Д=мк-
Подстановка значений (2.11) и (2.12) дает дифференциальное уравнение стесненного кручения с учетом работы обшивки на свободное кручение:
(Е/Л)'-О/КЬК=~МК. (2.13)
Это уравнение при EIm =const, G/K = const совпадает с полученным в гл. V для тонкостенных стержней открытого профиля и отличается от уравнения для стержней с замкнутым профилем.
Однако предварительное исследование показало, что для замкнутых профилей, сильно вытянутых в одном направлении, отличие в коэффициентах по сравнению с уравнением для открытых
498
профилей незначительно *. Поэтому приближенное уравнение (2. 13), полученное весьма элементарным путем, заслуживает полного внимания.
Крыло-пластинка
В приближенном расчете консольной пластинки она уподобляется конструкции рассмотренного выше вида, но с бесконечным числом прилегающих друг к другу бесконечно узких лонжеронов**.
Поперечное сечение пластинки показано на фиг. 272, в.
Поперечные сечения выбираются параллельными плоскости заделки. Допущение о недоформируемости нервюр в своей плоскости эквивалентно допущению об отсутствии искривления пластинки в направлении осн х;
Уравнения (2.3) и (2.4), соответственно (2.3'), (2. 4') остаются в силе. Для сплошного профиля часто вместо модуля Е берется модуль пластинки:
Впрочем, ввиду наличия свободных продольных краев полного стеснения, приводящего .к модулю Е*, не возникает. Поэтому вместо Е* иногда берут среднее значение 0,5 (Е+Е*). Вместо величин Mi, /i, относящихся к отдельным лонжеронам, вводятся погонные величины М* кгсм1см и /* смЬсм, а суммирование заменяется интегрированием
M=^M*dx; I—^I*dx-, S«--\I*xdx-, (а*,б:1:)
b b b
B—^M*xdy, /„= j” /*x2dx. (в*,г*)
l> b
Координата центра изгиба определяется по-прежнему формулой (д).
Для сплошного профиля имеется более строгое решение теории упругости, дающее значение Xq, отличное от (д). При отсчете координаты х от центра тяжести профиля уточненное значение xj y лежит между двумя пределами *** .
* См. А. А. Умански й, О нормальных напряжениях при кручении крыла самолета, ТВФ, 1940, № 12;
А. М. Афанасьев, В. Т. В а й ков и др. под ред. Л. Л. Уманского «Сборник задач по расчету тонкостенных конструкций», 1941, гл. VIII.
” Этому вопросу посвящены работы Я. Г. П а п о в к о (1953), В. В. Но-в и ц кого (1957), М. Б. В а х н то в а (1958).
*** См., например, «Справочник авиаконструктора ЦАГИ», т. Ill, «Прочность самолета», 1939.
32* 499
Чем меньше относительная толщина профиля, тем ближе уточненное значение к верхнему пределу. Нижпий предел отвечает формуле (д).
Далее вместо (2. 5) имеем
М -М /*-(- — /*л.
(2.5*)
Зависимость (2.6), разумеется, остается в силе.
Зависимость (2. 7) принимает вид
Q*=
I I...
(2.7*)
Формула (2. 8) для нормального напряжения не изменяется.
При учете сопротивления профиля свободному кручению применяется уравнение (2.13).
О вычислении ЕЕ было сказано выше. Момент инерции при свободном кручении вытянутого массивного профиля равен
1 = — f h3c/x = 4I, (и)
3 J v ’
ь
Аналогичную формулу можно применить и для немассивных профилей, например трубчатых, вытянутых в одном направлении, двухслойных с заполнителем и др.
/к 4 J/* dx = 41. (и')
ь
Проиллюстрируем это на примере тонкостенной коробки при «6.
Как известно,
Тот же результат дает формула (и'):
/ -=4-2Wf—V--2WA2.
\ 2 /
Напомним, что максимальное касательное напряжение на контуре вытянутого профиля равно
тп>ах — An>ix=2G9Kyrnax.
Для коробки имеем также
Мк т :=-------
max . wK*min
Рассмотрим частные случаи.
500
Прямоугольная пластинка постоянной толщины, защемленная вдоль одного края (фиг. 273, а). Дифференциальное уравнение (2. 13) принимает вид
где
(2. 13')
/t2 — 48(' 24 (1 — В)
‘ ~Ь^Е0~ *2
Интегрирование уравнения по методу начальных параметров, в том числе и для случая сосредоточенного крутящего момента на конце, приведено в § 5. 10.
501
Симметричное крыло с ромбовидным сечением (фиг. 273,6)
Ширина и толщина крыла изменяются по длине, следуя линейному закону. Размеры в корне обозначены соответственно Ьо и h0.
Отсчет целесообразно вести от свободного конца D'. Обозначим относительную абсциссу через ц:
1—2 2’
71 =--- = -- .
I I
Момент инерции корневого сечения крыла
. Mg
°' ' 48
Геометрические характеристики сечения ц выражаются следующим образом:
7 = -,(4/о; 7К-Ш.
Дифференциальное уравнение стесненного кручения (2. 13) принимает вид
1__d / 6 . _ 6ОЛ4К (т,)
I4 dt] \ Цт] / 11 ^ElQbQ
Здесь
^=240-— £й02
Интегрирование этого линейного уравнения с переменными коэффициентами, принадлежащего к классу эйлеровых, не представляет затруднений. Произвольные постоянные определяются из граничных условий
= =0.
Цт] |т]-0
Стреловидное крыло малого удлинения
Если центры изгиба в отдельных сечениях не лежат на одной прямой, перпендикулярной сечению заделки, то крыло называется стреловидным. Линию, соединяющую центры изгиба, в отдельных сечениях будем называть линией центров изгиба. Эта линия обычно достаточно близка к прямой. Угол а этой прямой с нормалью к сечению заделки назовем углом стреловидности (см. фиг. 273, в, г).
Стреловидное крыло малого удлинения может быть приближенно рассчитано как прямое, у которого отдельные сечения, параллельные плоскости заделки, сдвинуты поступательно вдоль оси х. Условно понимаемый «относительный сдвиг» или погонная интенсивность сдвига измеряется тангенсом угла стреловидности
tga = ^- = x'( (2.14)
502
Покажем, что дифференциальное уравнение стесненного кручения стреловидного крыла совпадает (2.13), если в правой части вместо полного крутящего момента Мк взять приведенный крутящий момент
м"рив=мк + Мх', (2.15)
где М — изгибающий момент в рассматриваемом сечении.
В самом деле, при выводе уравнения (2. 13) мы исходили из зависимостей
x = =Я-
При этом существенным было то, что плечи лонжеронов Хг при переходе к сечению, отстоящему на dz, не изменялись. Теперь же плечи лонжеронов при переходе к сечению, отстоящему на dz, изменяются на одну и ту же величину dx.
Поэтому, пользуясь формулой дифференцирования произведения двух функций, для стреловидного крыла получаем
= x+YiMx'. =Мк + Мх'.
Здесь 7И==£ •— полный изгибающий момент в рассматриваемом
сечении.
Но
Я'=-(£АЛк)'.
Следовательно,
Д = -(fZ^D' )' -Мх'.
Из уравнения равновесия
МК+МК=Л1К или GIK§K + MK=.MK окончательно получаем
(£7Ш О'к)' - G/Лк = - (Ч + Мх'). (2.16)
Сопоставляя это уравнение с (2. 13), мы видим, что выдвинутое предложение доказано: уравнение стесненного кручения стреловидного крыла отличается от уравнения прямого крыла только правой частью. Что касается изгиба, то уравнение и расчетные формулы для прямого и стреловидного крыльев совпадают.
Найдем изгибающий и крутящий моменты от направленной вверх равномерно распределенной нагрузки р кг/м2 в сечении z крыла, имеющего в плане форму параллелограмма (см. фиг. 273, а).
503
Равнодействующая нагрузки, приложенной правее сечения 2; P—-pb (l — z).
Плечо
AB^l-^-iga.
2 s
Плечо АС —- -—
2
Изгибающий момент в сечении z
М = Р-АС = ~pb (I - z)z.
Крутящий момент
Жк = — РАВ = —-—рЬ (В — zz) tg а.
Приведенный крутящий момент
Ж"гив = Ж к + Af tg'a = -pbz (I-z)tg а.
Отметим интересное обстоятельство: при нагрузке только изгибающими парами (векторы моменты параллельны осям х) стреловидное крыло работает не только на изгиб, ио и на кручение, поскольку приведенные крутящие моменты не равны нулю.
Обратим внимание также на определение абсолютных углов закручивания. Интегрируя дифференциальное уравнение стесненного кручения, получаем эпюру относительных (погонных) углов Интегрируя эту эпюру, т. е. вычисляя площади позади лежащих частей эпюры -&к, получаем эпюру абсолютных углов срк:
<?к(г)-?к(0) + /»к(С)Л (0<С<г).
6
Можно сказать, что величина абсолютного угла закручивания равна сумме предшествующих элементарных углов закручивания ^к(О^. Положение вектора (pK(z), иначе говоря, положение центра вращения сечения z определится как положение следа равнодействующей элементарных векторов каждый из которых при-
ложен в центре изгиба соответствующего сечения.
Дополнительные замечания
Изложенный метод расчета, при котором пластинка, защемленная вдоль одного края, уподобляется тонкостенному стержню с не-доформируемым в своей плоскости поперечным сечением, в общем удовлетворительно подтверждается более строгим решением методом сеток, или конечных разностей, а также экспериментами, в особенности для случая распределенной нагрузки. Последнее вполне 501
естественно: распределенная нагрузка почти не вызывает искривления пластинки вдоль оси х, что и положено в основу расчета. На-
ряду с этим, экспериментирование с моделями консольных пластинок часто дает значительный разброс данных в области заделки, что отчасти объясняется неучитываемой элементарным решением концентрацией напряжений у входящих углов модели, выполненной вместе с корневым блоком из одного куска металла.
Наконец, заметим, что идея выделения в профиле крыла части, работающей на изгиб и изгибное кручение (лонжероны), и части, работающей на свободное кручение, важна не только для тонких
крыльев, ио и для обычных крыльев, содержащих небольшое число лонжеронов. При этом на первый план выдвигается метод сил или вариационный метод Кастильяно.
На фиг. 274 показан профиль ф 274
двухлонжерониого крыла. Примем, что каждый из лонжеронов работает на изгиб, обшивка же работает на сдвиг, воспринимая крутящий момент. В поперечном направлении крыло подкреплено
жесткими в своих плоскостях нервюрами.
Отбросим временно второй лонжерон. При сделанных допущениях полученная основная система является статически определимой. Перенеся все нагрузки между свободным концом и исследуемым сечением в центр изгиба лонжерона Dlt являющийся центром изгиба всего сечения основной системы, мы определяем изгибающий момент в лонжероне М° и крутящий момент в обшивке М”’ для основной системы.
Восстановим второй лонжерон. Изгибающий момент, приходящийся на его долю, обозначим X. Тогда полный момент в первом лонжероне будет Л41=Му—X. Крутящий момент в обшивке будет МК=М°—Х'а, где X' = Q2 — поперечная сила во втором лонжеро
не, а — расстояние между плоскостями лонжеронов.
Составим выражение потенциальной энергии упругой деформации крыла на единицу длины:
- _ «-*)2 (Л4°-Л'«)2
2EIt ' 2EI2 2GlK
(2.17)
Полная энергия упругой деформации крыла U— f U dz
‘i
В соответствии с принципом Кастильяно составляем условие минимума энергии в виде уравнения Эйлера:
дХ dz дХ’ ~
505
Это дает дифференциальное уравнение для функции Х~Х(z)
___Л4| , X / 1 1 \ Х"д2 0 ЕЦ E\li 12Г GlK GfK
ИЛИ
_Ца'=—(2.
Еа2 \ /, /2 / а. ЕЦсР- 1
Уравнения для получения произвольных постоянных получим, используя два из четырех граничных условий:
v (0) = # (0) = 0; X(Z) = X'(Z)=0.
§ 10.3. НЕКОТОРЫЕ ТЕМПЕРАТУРНЫЕ ЗАДАЧИ
Общие положения. Температурные напряжения в упругом брусе
Причиной возникновения температурных напряжений в конструкциях является стеснение температурной деформации.
Свободное упругое тело из однородного изотропного материала, в частном случае самолет, находящийся в воздухе, при равномерном нагреве или охлаждении не испытывает температурных напряжений. При наличии в конструкции элементов с различными коэффициентами линейного расширения или при неравномерном изменении температуры напряжения, как правило, возникают. Важное правило здесь состоит в том, что те усилия (изгибающие и крутящие моменты, продольные и поперечные силы), которые могут быть определены из одних только уравнений равновесия, иначе говоря, статически определимые внутренние силы от действия температуры, произвольным образом распределенной, равны нулю.
Таким образом, в статически определимой стержневой системе температурные усилия отсутствуют. Подчеркнем, что речь идет именно об усилиях, а пе о напряжениях. В сечениях любого бруса могут действовать самоуравповешенные системы напряжений, не обнаруживаемые статическим анализом. Эти так называемые самонапряжения могут быть обусловлены предварительной обработкой, связанной с пластическим деформированием и возникновением остаточных деформаций. Здесь нас будут интересовать те самоуравновешепные напряжения, которые возникают в упругом брусе под влиянием температурных удлинений продольных волокон.
Прежде всего заметим, что если между двумя поперечными сечениями бруса одно из волокон получит температурное удлинение, то исследование распределения напряжений в брусе, вообще говоря, представляет собой весьма сложную задачу теории упругости. В то же время ясно, что действие удлинения волокна от температуры эквивалентно действию некоторой сосредоточенной продольной силы внутри бруса. При расчете на действие сил, в том числе сосредоточенных, довольствуются точностью, даваемой г и п о т е-.506
зой плоских сечений. Естественно вести расчет температурных напряжений в предположении, что сечения остаются плоскими, а продольные волокна в поперечном направлении друг на друга не нажимают. Расчетную модель бруса можно представить в виде системы абсолютно жестких поперечных пластинок, соединенных упругими продольными стерженьками.
Будем рассматривать свободный или закрепленный статически •определимым способом брус. Сразу отметим, что если нестесненные температурные удлинения волокон между двумя смежными пластинками подчинены закону плоскости, то стеснения температурной деформации не возникает и температурные напряжения отсутствуют. Следовательно, нас будет интересовать случай, когда температурные удлинения не подчинены закону плоскости. Если брус сделан из однородного изотропного материала, вместо температурных удлинений можно говорить просто о температуре. Для однородного бруса температура, распределенная по закону плоскости, при элементарном расчете не является источником напряжений. Для неоднородного бруса этого сказать нельзя.
Перейдем к составлению расчетных формул.
Образуем основную систему, на этот раз не устраняя связи, а, наоборот, введя между смежными пластинками три абсолютно недеформируемые связи — продольную силовую связь в центре тяжести сечения бруса и две моментные связи, параллельные главным центральным осям х, у.
Выбор основной системы с дополнительными связями характерен для так называемого метода перемещений, в котором в качестве неизвестных определяемых в первую очередь, выступают не силы, а перемещения. Мы уже пользовались этим методом при решении задач, относящихся к статически неопределимому прикреплению твердого тела упругими стержнями. Рассматриваемая здесь задача очень близка к задаче § 9. 10.
Пусть между двумя смежными пластинками, расстояние между которыми примем равным 1 см, происходит неравномерный по площади сечения нагрев, другими словами, различные волокна получают неодинаковое приращение температуры/°. В основной системе продольные удлинения волокон абсолютно стеснены. Поэтому для отдельных волокон имеем
а/° 4- у = 0; а»' = - ЕъГ. (3.1)
При нагреве всех волокон каждое волокно в основной системе оказывается сжатым.
Одновременно во введенных связях возникают усилия. Три связи можно для наглядности уподобить абсолютно жесткому брусочку, в котором возникает продольная растягивающая сила
Nr'‘ЕаЕ dF (3.2)
1'
507
и изгибающие моменты
М"‘ = + [ Ev.fy dF-, М‘‘ — ± Eo.t°x dF. (3.3)
? г
Знак следует выбирать в соответствии с правилом знаков, принятым при расчете бруса.
Если теперь устранить введенные абсолютно жесткие связи (перерезать брусочек), то усилия №(, М°£ будут восприняты
упругими волокнами, которые получат удлинения, следующие закону плоскости.
Обозначим дополнительные напряжения в волокнах через а*1. Они определяются по элементарной формуле сопротивления материалов. Окончательные напряжения
N"1 М"‘ М?
= + -)---У±-^-х. (3.4)
Л Ijc /у
При переменном по сечению бруса модуле упругости отдельных волокон Е — Е (х, у) вводят редукционные коэффициенты
где Ес — модуль, принятый за постоянный при расчетах.
Тогда
/ №)М Л4рел Л1рсл \
о1 — — E.at° -j----1—-— у -4-----— X I ср. (3. 4')
I с 1 угрел — урод j — уред I 1 ' '
\ х У /
Здесь
Npen=Ec$at°<fdF-, (3.2')
Г
±Ec\aFy<?dF-, MpQ^^±Ec\at°xVdF; (3.3')
F F
F=^<?dF; Ix-=§ у2 <fdF; Iy = $x2<fdF. (3.5)
F F F
Центр тяжести и главные центральные оси определяются для редуцированного сечения.
Особенность полученного элементарного решения состоит в том, что температурные напряжения в каждом сечении свободного или внешне статически определимого бруса зависят только от распределения температуры в этом же сечении и, следовательно, не зависят от граничных условий.
Обратим внимание па то, что окончательные величины температурных деформаций бруса, сечения которого считаются остающимися плоскими, получаются через усилия в основной системе по формулам для упругих деформаций.
508
Относительное удлинение центрального волокна
г1 = = ЕЕ £г./7₽ел ‘ (3.6)
Кривизны
л/рел
(3. 7)
t _ М°у _
У~Е1У Ес1^'
Эти формулы охватывают и тот случаи, когда температурные удлинения волокон распределены по сечению по закону плоскости и в действительной системе температурные напряжения отсутствуют.
Пластина, окаймленная стрингерами из другого материала
Допустим, что удлиненная пластинка шириной b и толщиной h окаймлена вдоль длинных сторон стрингерами с площадями сечения Fj из другого материала. Температура повышается равномерно на t°.
Обозначим модули упругости стрингеров и пластинки соответственно через £] и £2, коэффициенты линейного расширения через О] И 02-
Используем решение для бруса. В качестве основного при расчетах берем модуль £1. Тогда редукционный коэффициент для , , е2
стрингеров будет cpi = 1, для пластинки ф2 = ~ - •
£i
Определяем редуцированную площадь сечения и усилия в связях основной системы
£>>ejl = 2£j.l +bh®2-,
NpQI1 ~ EJ° (а. • 2£ • 1 + v.2bh <₽,);
Напряжение в стрингерах
Напряжение в пластинке , ( р , А,ред \
°2~ I ~^2а2( +-/гред1?2-
5Э9
Рассмотрим числовой пример, относящийся к лонжерону с дур-алюминовой стенкой и стальными поясами при ^=100° (условно).
b — 60 см; А = 0,05 см; F\=-2 см2-, кг1см2; £'2 = 0,72-10с /сг/сщ2;
04--11,3-10~6; «2=22,6-]0~6;
71 = 1; <р2~0>33.
Вычисляем
5рел=2-2-|- 60-0,05-0,33=4+ 1 =5 см2;
7VpM = 2,2-106-100 (11,3-10_М+ 22,6-10-6-1) 15 000 кг
Напряжения в поясах лонжерона
о' = - 2,2 • 10° • 11,3 • 10-6 • 100 + —5- = - 2500 + 3000 = 500 кг) с м2.
Напряжения в стенке
^ISOOO \ о зз = _660 кг1см2.
5 /
о'=( — 2,2-106-22,6-10~6-100
Как и следовало ожидать, при нагреве пояса испытывают растяжение, стенка — сжатие. Объясняется это меньшей податливостью поясов сравнительно со стенкой.
Проверим равенство растягивающих и сжимающих сил по сечению.
500 • 2 • 2—660 • 3^0.
Небольшая погрешность (около 1%) обусловлена применением логарифмической линейки.
То обстоятельство, что стенка является сжатой, ставит задачу проверки ее устойчивости. При охлаждении знаки напряжений изменяются на обратные.
Элементарный расчет тем более точен, чем пластинка более вытянута в длину. При бесконечно длинной пластинке полученные результаты не отличаются от решения теории упругости.
Для более строгого подхода при конечном отношении сторон может быть использовано решение плоской задачи теории упругости в гиперболотригонометрических рядах *.
На фиг. 275 показан вид эпюр о'х, и для квадратной пластинки, окаймленной стержнями вдоль четырех краев **. Параметры конструкции соответствуют случаю, рассмотренному выше. Вдоль краев нормальные напряжения, перпендикулярные стержням, равны нулю, так как принято, что стержни не обладают
* А. А. Уманский и Б. С. Б л я х е р, О совместной работе стрингеров и обшивки, Техн, заметки ЦАГИ, № 125, 1936.
** И. И. Меерович, Температурные напряжения в листе, подкрепленном стрингерами из другого материала, Техн, заметки ЦАГИ, № 162, 1938.
510
изгибной жесткостью. Характерным является падение нормальных напряжений от краев к середине и наличие больших касательных напряжений вдоль краев, теоретически стремящихся к бесконечности вблизи угловой точки. Здесь можно ожидать появления пластической деформации, нс представляющей особой опасности при отсутствии вибрационной нагрузки. Впрочем, фактически имеющаяся изгибпая жесткость стрингеров существенно искажает картину напряженного состояния в углах.
Фиг. 275.
Отметим, что напряжения max<Jx=inax^ ^700 кг/см? получились близкими к найденному элементарно значению =660 кг/см2. Напряжение в стержне erf =357 кг!см2 ниже полученного элементарно erf =500 кг/см2. Касательное напряжение по соседству с небольшой областью интенсивного возрастания в углах оказалось равным +670 кг/см2.
Эти данные показывают, что следует тщательно взвешивать возможность применения конструкций из разных материалов в условиях их работы при повышении или понижении температуры.
Температурные напряжения в тонком крыле
Крыло в сверхзвуковом потоке воздуха испытывает сильный нагрев от трения, называемый аэродинамическим, иначе кинетическим нагревом. Нагрев достигает наибольшей интенсивности вдоль передней и задней заостренных кромок крыла, имеющего обычно ромбовидный или аналогичный профиль. Перегрев кромок происходит в процессе набора скорости и объясняется тем, что утолщен-
511
пая часть крыла нагревается медленнее, чем кромки. В дальнейшем при установившейся скорости происходит почти полное выравнивание температуры по хорде крыла с одновременным уменьшением средней температуры. С точки зрения величины возникающих напряжений опасным является распределение температуры с наибольшим градиентом вдоль хорды, отвечающее концу периода набора скорости.
Построение температурного поля крыла выполняется по методам, изучаемым в курсах газовой динамики и теории теплопередачи. Температурное поле зависит от многих факторов — ускорения, конечной скорости и высоты полета, температуры и плотности воздуха, гладкости поверхности крыла, характеристик теплопередачи — коэффициента теплового расширения, удельной теплоемкости, теплопроводности и температуропроводности.
Крыло постоянного сечения считается бесконечно длинным, температура постоянной по размаху и по толщине. Поэтому температурное поле в каждый момент исчерпывающим образом характеризуется эпюрой распределения температуры вдоль хорды крыла.
При симметричном профиле крыла эта эпюра всегда обладает небольшой асимметрией, связанной с направлением полета. Асимметрию устраняют, попарно осредняя соответствующие ординаты эпюры. Существуют также упрощенные нормативные способы построения эпюры распределения температуры.
На фиг. 27'6, а сплошной линией показана эпюра температуры в конце двухминутного периода разгона до скорости 2М, т. е. удвоенной скорости звука для стального крыла с относительной толщиной 5%. Пунктиром даны эпюры к концу четвертой и восьмой минуты полета. При дальнейшем продолжении полета температура крыла вдоль хорды почти полностью выравнивается. Соответственно температурные напряжения достигают своего максимума в течение первых двух минут полета, а затем убывают до нуля.
Таким образом, задача сводится к построению эпюр ы и а-п р я ж е н и й а1 по хорде крыла в конце периода набора скорости. Это выполняется по формуле (3.4'), причем в рассматриваемом случае симметрии Л4',~л = М Д = 0. Особенность определения редукционных коэффициентов состоит здесь в том, что модуль упругости материала Е при температуре выше 150° существенно снижается. Так, например, модуль упругости стали при 300° уменьшается на 10-4-15%, а алюминиевых сплавов—на 40%. Изменяются также все другие физико-механические характеристики.
Вид эпюры oz показан на фиг. 276, б. Практически достаточно найти наибольшее сжимающее напряжение Ю,.». Порядок этой величины определяется простой формулой, дающей верхний предел ° max
«пах
max Anin) (''max)-
(3. 8)
Например, для крыла из специальной стали при /Шах — = 300°—0° = 300° и коэффициенте снижения модуля =0,85, имеем
I Отах 1 = 2,2-106• 11,3-10-6.300.0,85 = 6200 кг^см?.
Действительное напряжение на 10—25% меньше этой величины.
При проверке прочности учитывается снижение предела прочности материала в зависимости от температуры.
В качестве благоприятного фактора следует отметить сравнительную кратковременность действия наиболее высоких температур и напряжений.
Кручение крыла при одновременном действии температурных напряжений
Предположим, что прямой брус (крыло) работает на кручение и крутящий момент равен Л4К- Покажем, что кинематический нагрев крыла вызывает увеличение угла закручивания срк> независимо от того, что этот угол возрастает в связи с уменьшением модуля G.
33 425
513
Выделим из крыла отсек длиной dz и примем, что заднее сечение неподвижно (фиг. 277), Общность рассуждений от этого не изменится.
Переднее сечение поворачивается вокруг оси z на угол dqK, причем хорда из положения АВ переходит в положение А'В'.
Обозначим, как всегда, относительный (погонный) угол закручивания'через dK:
Фиг. 277.
Рассмотрим не показанное на оси на р. При закручивании это угол
фиг. 277 волокно, отстоящее от волокно наклонится к оси z на
Л = ^=«.Р. az
С достаточной степенью точности для сечения крыла малой относительной толщины можно принять, что все волокна, расположенные в сечении на одной вертикали, находятся в смысле получаемого наклона в тех же условиях, что и волокно на хорде, т. е. на оси х. Заменим р через х (см. фиг. 277). Тогда
ф = ф (х) = Н,.х.
(3. 9)
Площадью сечения волокна будем теперь считать величину dF=h dx.
Предположим, что в волокне действует нормальное напряжение о = а(х). При наклонении волокна на угол ф, а вместе с волокном и вектора напряжения, возникает вертикальный компонент напряжения, равный аф = аО'кл'.
514
Составим теперь условие эквивалентности крутящего момента внешних сил М,( и момента, издаваемого касательными и наклоненными нормальными напряжениями, в сечении. Получим
/И,. = Н/Д. 4- [ dF х
i-или
Мк (G/l( + J айл2 dx j &|(. (3.10)
Нормальные напряжения как бы повышают жесткость кручения. При a — const, что отвечает растяжению центральной силой, это увеличение жесткости составляет
д(0/к)=’^-
Более точное значение, не предполагающее замены р=х, равно
Д(О/к) = о/^о(/у+/,).
При аэродинамическом нагреве крыла в сверхзвуковом потоке преобладают сжимающие напряжения. Приращение величины GIK получается отрицательным. Условившись теперь приписывать температурным сжимающим напряжениям знак ( + ), получим фор-мулу для э ф ф е к т и в п о й жесткости кручения
<7/> = G/K- Г Fhx^dx. (3.11)
ь J
Задача о снижении жесткости крыла в результате аэродинамического нагрева представляет собой один из простейших вопросов, служащих предметом исследования теории аэротермоупругости, методы которой выходят за пределы программы курса строительной механики самолета.
§ 10.4. ЗАКЛЮЧЕНИЕ
Непрерывный рост летных данных современных самолетов и повышение требований к их эксплуатационным качествам неизбежно приводит к поискам новых аэродинамических форм, к изменению размеров н действующих нагрузок, а отсюда и к изменению конструктивных форм и материалов. Массовое производство самолетов требует использования в них стандартных конструктивных элементов. В качестве типичных примеров, иллюстрирующих эти положения, отметим широкое применение двухслойной обшивки с заполнителем, тонких крыльев малого удлинения, новых сплавов на основе титана и других редких металлов, армированных пластмасс, цельноштампованных оребренных панелей. Новые условия полета и новые конструкции стимулируют развитие строительной механики самолета.
Некоторые из разрешенных новых задач были рассмотрены в настоящей главе.
33*
515
Большое влияние на дальнейшее развитие строительной механики, несомненно, окажет современная вычислительная техника — электронные счетные машины непрерывного действия и цифровые электронные машины. Применение таких машин расширяет возможности практического использования часто весьма сложных решений, получаемых методами теории упругости и пластичности. Благодаря ©тому значимость строгого аналитического подхода к решению задач прочности возрастет.
На очереди также широкое внедрение статистических методов при определении расчетных нагрузок и реальных свойств конструкционных материалов.
П риложение
ФУНКЦИИ
sin $, cos $, ,е-£, ch $, sh £
e COS $ sin $ e $ ch $ sh $
0 1 0 1 1 1 0
0,01 0,99995 0,01000 1,01005 0,99005 1.00005 0,01000
0,02 0,99980 0,02000 1,02020 0,98020 1,00020 0,02000
0,03 0,99955 0,03000 1,03015 0,97045 1,00045 0,03000
0,04 0,99920 0,03999 1,04081 0,96079 1,00080 0,04001
0,05 0,99875 0,04998 1,05127 0,95123 1,00125 0,05002
0,06 0,99820 0,05996 1,06184 0,94176 1,00180 0,06004
0,07 0,99755 0,06994 1,07251 0,93239 1,00245 0,07006
0,08 0,99680 0,07991 1,08329 0,92312 1,00320 0,08009
0,09 0,99595 0,08988 1,09417 0,91393 1,00405 0,09012
0,1 0,99500 0,00983 1,10517 0,90484 0,00500 0,10017
0,2 0,98007 0,19867 1,22140 0,81873 1,02007 0,20134
0,3 0,95534 0,29552 1,34986 0,74082 1,04534 0,30452
0,4 0,92106 0,38942 1,49182 0,67032 1,08107 0,41075
0,5 0,87758 0,47943 1,64872 0,60653 1,12763 0,52110
0,6 0,82534 0,56464 1,82212 0,54881 1,18547 0,63665
0,7 0,76484 0,64422 2,01375 0,49659 1,25517 0,75858
0,8 0,69671 0,71736 2,22554 0,44933 1,33743 0,88811
0,-9 0,62161 0,78333 2,45960 0,40657 1,43309 1,02652
1,0 0,54030 0,84147 2,71828 0,36788 1,54308 1,17520
1,1 0,45360 0,89121 3,00417 0,33287 1,66852 1,33565
1,2 0,36236 0,93204 3,32012 0,30199 1,81066 1,50946
1,3 0,26750 0,96356 3,23930 0,27253 1,97091 1,69838
1,4 0,16997 0,98545 4,05520 0,24660 2,15090 1,90430
1,5 0,07074 0,99749 4,48169 0,22313 2,35241 2,12928
425 517
Продолжение
е COS 5 sin £ е £ сП £ sh 6
7з 0 1 4,81049 0,20788 2,50918 2,30130
1,6 —0,02920 0,99957 4,95303 0,20190 2,57746 2,37557
1,7 —0,12884 0,99166 5,47395 0,18268 2,82832 2,64563
1,8 —0,22720 0,97385 6,04965 0,16530 3,10747 2,94217
1,9 -0,32329 0,94630 6,68589 0,14957 3,41773 3,26816
2,0 —0,41615 0,90930 7,38906 0,13534 3,76220 3,62686
2,1 —0,50485 0,86321 8,16617 0,12246 4,14431 4,02186
2,2 -0,58850 0,80850 9,0250'1 0,11080 4,56791 4,45711
2,3 —0,66628 0,74571 9,97418 0,10026 5,03722 4,03696
2,4 —0,73739 0,67548 11,02318 0,09072 5,55695 5,46623
2,5 —0,80114 0,59847 12,18249 0,08208 6,13229 6,05020
2,6 -0,85689 0,51550 13,46374 0.07427 6,76901 6,69473
2,7 —0,90407 0,42738 14,87973 0,06721 7,47347 7,40626
2,8 —0,94222 0,33499 16,44465 0,06081 8,25273 8,19192
2,9 —0,97096 0,23925 18,17415 0,05502 9,11458 9,05956
3,0 —0,98999 0,14112 20,08554 0,04979 10,06766 10,01787
3,1 —0,99914 0,04158 22,19795 0,04505 11,12150 11,07645
К —1 0 23,14069 0,04321 11,59195 11,54874
3,2 —0,99829 —0,05837 24,53253 0,04076 12,28665 12,24588
3,3 —0,98748 —0,15775 27,11264 0,03688 13,57476 13,53788
3,4 —0,96680 -0,25554 29,96410 0,03337 14,99874 14,96536
3,5 —0,93646 —0,35078 .33,11545 0,03020 16,57282 16,54263
3,6 —0,89676 —0,44252 36,59823 0,02732 18,31278 18,28546
3,7 —0,84810 —0,52984 40,44730 0,02472 20,23601 20,21129
3,8 —0,79097 —0,61186 44,70118 0,02237 22,36178 22,33941
3,9 —0,72593 -0,68777 49,40245 0,02024 24,71135 24,69110
4,0 -0,65364 -0,75680 54,59815 0,01832 27,30823 27,28992
4,1 —0,57482 -0,81828 60,34029 0,01657 30,17843 30,16186
4,2 —0,49026 -0,87158 66,68633 0,01500 33,35066 33,33567
4,3 —0,40080 -0,91617 73,69979 0,01357 36,85668 36,84311
4,4 -0,30733 —0,95160 81,45087 0,01228 40,73157 40,71930
4,5 —0,21080 —0,97753 90,01713 0,01111 45,01412 45,00301
4,6 -0,11215 —0,99369 99,48432 0,010052 49,74718 49,73713
4,7 —0,01239 —0,99992 109,94717 0,009095 54,97813 54,96904
з/2 л 0 1 111,31778 0,008983 55,66338 55,65440-
518
Продолжение
•э COS $ е" ch g sh g
4,8 0,08750 —0,99616 121,51042 0,008230 60,75932 60,75109
4,9 0,18651 —0,98245 134,28978 0,007447 67,14^61 67,14117
5,0 0,28366 —0,95892 148,41316 0,006738 74,20995 74,20321
5,1 0,37798 -0,92581 164,02191 0,006097 82,01400 82,00791
5,2 0,46852 -0,88345 181,27224 0,005517 90,63888 90,63336
5,3 0,55437 —0,83227 200,33681 0,004992 100,17090 100,16591
5,4 0,63469 —0,77276 221,40642 0,004517 110,70547 110,70095
5,5 0,70867 -0,70554 244,69193 0,004087 122,34801 122,34392
5,6 0,77557 -0,63127 270,42641 0,003698 135,21505 135,21135
5,7 0,83471 —0,55069 298,86740 0,003346 149,43537 149,43203
5,8 0,88552 —0,46460 330,29956 0,003028 165,15129 165,14827
5,9 0,92748 —0,37388 365,03747 0,002739 182,52010 182,51736
6,0 0,96017 —0,27942 403,42879 0,002479 201,71564 201,71316
6,1 0,98327 —0,18216 445,85777 0,002243 222,93001 222,92776
6,2 0,99654 -0,08369 492,74904 0,002029 246,37554 246,37351
2л 0 1 535,49166 0,001867 267,74676 267,74489
6,3 0,99986 0,01681 544,57191 0,001836 272,28687 272,28503
6,4 0,99318 0,11655 601,84504 0,001662 300,94335 300,82169
6,5 0,97659 0,21512 665,14163 0,001503 332,57157 332,57006
6,6 0,95023 0,31154 735,09519 0,001360 367,54827 367,54691
6,7 0,91438 0,40485 812,40583 0,001231 406,20353 406,20230
6,8 0,86940. 0,49411 897,84729 0,001114 448,92420 448,92309
6,9 0,81573 0,57844 992,27472 0,001008 496,13786 496,13685
7,0 0,75390 0,65699 1 096,63316 0,0009119 548,31704 548,31612
7,1 '0,68455 0,72897 1 211,96707 0,0008251 605,98395 605,98312
7,2 0,60835 0,79367 1 339,43076 0,0007466 669,71576 669,71501
7.3 0,52608 0,85044 1 480,29993 0,0006755 740,15030 740,14963
7,4 0,43855 0,89871 1 635,98443 0,0006113 817,99252 817,99191
7,5 0,34664 0,93800 1 808,04241 0,0005531 904,02148 904,02093
7,6 0,25126 0,96792 1 998,19590 0,0005005 999,09820 999,09770
7,7 0,15337 0,98817 2 208,34799 0,0004528 1 104,17422 1 104,17377
7,8 0,05396 0,99854 2 440,60198 0,0004097 1 220,30119 1 220,30078
г’/2 л 0 1 2 575,97050 0,0003882 1 287,98544 1 287,98505
7,9 —0,04600 0,99894 2 697,28233 0,0003707 1 348,64135 1 342,64098
8,0 -0,14550 0,98936 2 980,95799 0,0003355 1 490,47916 1490,47883
8,1 -0,24354 0,96989 3 294,46808 0,0003035 1 647,23419 1 647,23389
34*
519
Продолжение
6 cos $ Sin g e £ Cll J sh $
8,2 -0,33915 0,94073 3 640,95031 0,0002747 1 820,47529 1 820,47502
8,3 —0,43138 0,90217 4 023,87239 0,0002485 2011,93632 2 011,93607
8,4 —0,51929 0,85460 4 447,06675 0,0002249 2223,53349 2 223,53326
8,5 —0,60201 0,79849 4 914,76884 0,0002035 2 457,38452 2 457,38432
8,6 —0,67872 0,73440 5 431,65959 0,0001841 2 715,82989 2 715,82970
8,7 —0,74865 0,66297 6 002,91222 0,0001666 3 001,45619 3 001,45603
8,8 -0,81109 0,58492 6 634,24401 0,0001507 3 317,12208 3 317,12193
8,9 —0,86544 0,50102 7 331,97354 0,0001364 3 665,98684 3 665,98670
9,0 —0,91113 0,41212 8 103,08393 0,0001234 4 051,54203 4 051,54190
9,1 —0,94772 0,31910 8 955,29270 0,0001117 4 477,64641 4 477,64630
9,2 —0,97484 0,22289 9 897,12906 0,0001010 . 4 948,56458 4 948,56448
9,3 —0,99223 0.12445 10 938,01921 0,00009142 5 469,00965 5 469,00956
9.4 —0,99969 0,02478 12 088,38073 0,00008272 6044,19041 6 0'14,19032
3 Л — 1 0 12 391,64781 0,00008070 6 195,82394 6 195,82386
9,5 —0,99717 -0,07515 13359,72683 0,00007485 6 679,86345 6679,86338
9,6 —0,98469 —0,16433 14 764,78157 0,00006773 7 382,39082 7 382,39075
9,7 —0,96236 —0,27176 16 317,60720 0,00006128 8 158,80363 8 158,80357
9,8 —0,93043 —0,36648 18 033,74493 0,00005545 9 016,87249 9 016,87244
9,9 —0,88919 —0,45754 19 930,37044 0,00005018 9 965,18524 9 965,18519
10,0 —0,83907 —0,54402 22 026,46579 0,00004540 11 013,23292 11 013,23287
ЛИТЕРАТУРА
Абрамов Г. Д., Черемухин А. М., Строительная механика. Статически определимые системы, СИТИ, 1937.
Ад ад у ров Р. А., Определение касательных напряжений в тонкостенных конструкциях вблизи заделки, Труды ЦАГИ, вып. 164, 1947.
А д а д у р о в Р. А., Напряженное состояние в четырехпоясной призматической коробке, загруженной на торцах, ДАН СССР, т. XXIX, 1951, № 3.
Александров А. Я., Брюк к ер Л. Э., Куршин Л. М., Прусаков А. П., Расчет трехслойных панелей, Оборонгиз, 1960.
Александровский С. В., Об устойчивости цилиндрической оболочки ..при больших прогибах, Сб. «Расчет пространственных конструкций», вын. Ill, Госстройиздат, 1955.
Алексеев С. А., К теории мягких оболочек вращения, Сб. «Расчет пространственных конструкций», вып. III, Госстройиздат, 1955.
А м б а р ц у м я н С. А., Анизотропные оболочки, Физматгиз, 1961.
Астахов М. Ф., К а р а в а е в А. В., М а к а р о в С. Я., Суздаль-пев Я. Я., Справочная книга по расчету самолета на прочность. Оборонгиз, 1954.
Афанасьев А. М., Кал инин Н. Г., Марь и и В. А., Основы строительной механики, Оборонгиз, 1951.
Афанасьев А. М., Байков В. Т., Г е м м е р л и н г А. В., М а р ь и п В. А. и др., под редакцией А. А. Уманского, Сб. задач по расчету тонкостенных конструкций, Оборонгиз, 1941.
Байков В. Т., Строительная механика самолета, ч. I, изд. МАИ, 1950.
Б а й к о в В. Т., Л о п о в о к Б. Н., Т р а п е з и н И.И., Об изгибе косоугольной пластины, Труды МАИ, вып. 69, Оборонгиз, 1956.
Б а л а б у х Л. И. и Г е м м е р л и и г А. В., О редукционном коэффициенте обшивки крыла, ТВФ, 1937, № 5.
Бал абу х Л. И., Изгиб тонкостенной коробчатой балки, Труды МАТИ, вып. 1, 1940.
Б а л а б у х Л. И., Изгиб и кручение конических оболочек, Труды ЦАГИ, вып. 577, 1946.
Б а л а б у х Л. И., Расчет на прочность конических кессонов, Труды ЦАГИ, вып. 640, 1947.
Б а л а б у х Л. И. Прочность и устойчивость шпангоутов, связанных тонкой обшивкой, Труды ЦАГИ, вып. 681, 1949.
Б е л о у с А. А., Устойчивость овальных и рамных шпангоутов, Труды ЦАГИ вып. 334, 1937.
Белоус А. А., Колебания и статическая устойчивость плоских и пространственных рам, Сб. «Расчет пространственных конструкций, вып. III, Госстройиздат, 1955.
Беляев В. Н., О центре жесткости замкнутых контуров, Технический бюллетень ЦАГИ, 1933, № 4.
Беляев В. И., К расчету пространственной коробчатой системы при действии закручивающих сил, ТВФ, 1932, № 4.
Беляев В. И., Испытание и расчет крыльев с различной обшивкой, ТВФ 1935, № 5, 10, 12.
Беляев В. II., Расчет свободно несущих крыльев, ТВФ, 1932, № 7, 8, 9.
521
Беляев В. Н и Юхарин В. И., Расчет моноблочного крыла па изгиб, 'Груды ЦАГИ, вып. 428, 1939.
Биргер И. А., Вариационные методы в строительной механике турбомашин, Оборонгиз, 1957.
Блейх Ф.. Устойчивость металлических конструкций, Физматгиз, 1959.
Богданов А. П., В и н о г р а д о в Р. И., М и р т о в К. Д., Сборник задач по конструкции и прочности самолетов, Оборонгиз, 1959.
Бро уде Б. М., Об устойчивости стержней, сжатых с двухосным эксцентриситетом Сб. «Расчет лрострапствениых конструкций», вып. V, Госстройиздат, 1959.
Б р о у д е Б. М„ Устойчивость пластинок в элементах стальных конструкций, Машстройиздат, 1949.
Бубнов И. Г., Труды по теории пластин, ГТТИ, 1953.
В а р в а к П. М., Развитие и приложение метода сеток к расчету пластинок изд. АН УССР, Ч. I, 1949; ч. II, 1952.
Вахитов М. Б., Статьи по расчету монолитного крыла, Труды КАИ, т. XLV1, 1959; Изв. высш. уч. завед., серия «Авиационная техника», 1958, № 1; 1959, № 3; 1960, № 4.
Власов В. 3., Тонкостенные упругие стержни, Госстройиздат, 1940, 1959.
Власов В. 3., Строительная механика тонкостенных пространственных систем, Госстройиздат, 1949, 1958.
В л а со в В. 3., Общая теория оболочек, ГТТИ, 1949.
В о л ь м и р А. С., Теория устойчивости н больших деформаций цилиндрической оболочки при сжатии и сдвиге, Сб. «Расчет пространственных конструкций, вып. 1, Машстройиздат, 1950.
В о л ь м п р А. С., Гибкие пластинки и оболочки, ГТТИ, 1956.
Воль мир А. С., Обзор исследований по теории гибких пластинок и оболочек за периоде 1941 но 1957 гг., Сб. «Расчет пространственных конструкций», вып. IV, Босстронизцат, 1958.
Вол ьмпр А. С., Об устойчивости пластинок при пластических деформациях, Сб. «Расчет пространственных конструкций», вып. VI, 1961.
Вопросы прочности цилиндрических оболочек, Сб. переводов под ред. В. М. Даревского, Оборонгиз, 1960.
Вопросы расчета элементов авиационных конструкций, Сб. статен 75 1,2 под ред. А. Я. Александрова и Л. М. Куртина, Оборонгиз, 1960.
Галерки н Б. Г., Стержни и пластинки, Собр. соч., Изд. АН СССР, т. I, с гр. 168—195.
Г а л е р к и н Б. Г., Упругие тонкие плиты, там же, т. 11.
Гейтвуд Б. Е., Температурные напряжения, ИЛ, 1959.
Гем мер л инг А. В., Несущая способность стальных стержневых систем, Госстройиздат, 1958.
Гениев Г. А., Чаусов Н. С., Некоторые вопросы нелинейной теории устойчивости пологих металлических оболочек, Госстройиздат, 1954.
Г и л ь м а н Л. С., Расчет тонкостенных трубопроводов, Сб. «Расчет пространственных конструкций», вып. 1, Машстройиздат, 1950.
Гольденвейзер А. Л., Температурные напряжения в тонких оболочках, Труды ЦАГИ, вып. 618, 1947.
Гольденвейзер А. Л., Теория упругих топких оболочек, ГТТИ, 1950.
Горбунов Б. Н. и С т р е л ь б и ц к а я А. И., Расчет прочности тонкостенных стержневых систем, Сб. «Расчет пространственных конструкций», вып. I, Машстройиздат, 1950.
Гр иго люк Э. И., Упругая устойчивость ортотропных и слоистых конических и цилиндрических оболочек, Сб. «Расчет пространственных конструкций», вып. Ill, Госстройиздат, 1955.
Григорьев Ю. П., К расчету кривых тонкостенных брусьеи, Сб. «Расчет пространственных конструкций», вып. I, Машстройиздат, 1950.
Григорьев Ю. П., Формулы и таблицы для расчета тонкостенных круговых колец, Сб. «Расчет пространственных конструкций», вып. II, Госстройиздат, 1951.
Даревскнн В. М., Устойчивость консольной цилиндрической оболочки, Сб. «Расчет пространственных конструкций», Госстройиздат, 1959.
522
Джанелидзе Г. Ю. и Пановко Я- Г., Статика упругих тонкостенных стержней, ГТТИ, 1948.
Е л е н е в с к в й Г. С., Работа Двухлонжерониого трапецеидального крыла на кручение, Труды ЦАГИ, вып. 208, 1935.
Е л е и е в с к и й Г. С. и Д а р е в с к и й В. М., Кручение двухлонжеронного пирамидального крыла с непрерывно расположенными жесткими на изгиб нервюрами, Труды ЦАГИ, вып. 292, 1937.
Еленевский Г. С., Строительная механика крыла переменного сечения, Оборонгиз, 1954.
3 воли некий И. В., Приближенное решение некоторых задач устойчивости цилиндрической оболочки, Труды ЦАГИ, вып. 246, 1936.
Зе х л ер Е. и Нью вел л Ж., Современные методы расчета монококовых авиационных конструкций, ВНТИ ЦАГИ, 1946.
3 и а м е н с к в й И. М., Общая устойчивость длинных открытых профилей при продольном сжатии, ТВФ, 1934, № 12.
3 и а м е и с к и п П. М., Схема расчета и работа элементов фюзеляжа монокок, ТВФ, 1935, № 7, 8.
Илью ш и и А. А., Теория пластичности, ГТТИ, 1948.
И м м е р м а н А. Г., Расчет ортотропной круговой цилиндрической оболочки на поперечную нагрузку, Сб. «Расчет пространственных конструкций», вып. 111, Госстрой нзд ат, 1955.
И м м е р м а н А. Г., О проверке устойчивости круговых цилиндрических оболочек при совместном действии продольной и поперечной нагрузки, Сб. «Расчет пространственных конструкций», вып. IV, Госстройиздат, 1958.
Исследования прочности тонкостенных конструкций крыла и фюзеляжа. Сб. переводов под род. А. А. Уманского, Оборонгиз, 1938.
К а н С. И. и Свердлов И. А., Расчет самолета на прочность, Оборонгиз, 1940, 1945, 1957.
К а н С. И., Прочность самолета, Оборонгиз, 1953.
К а н С. Н., Прочность замкнутых и открытых тонкостенных оболочек, Сб. «Расчет пространственных конструкций», вып. VI, Госстройиздат, 1961.
К а и С. Н. и И а н о в к о Я. Г., Элементы строительной механики тонкостенных конструкций, Оборонгиз, 1952.
К а н С. 11., О работе цилиндрических оболочек с большими вырезами, серия «Авиационная техника», 1959, № 1.
Кар яки и Н. И., Основы расчета тонкостенных конструкций, Изд. «Высшая школа», I960.
Киселев В. Ф., Методы расчетов па прочность лонжеронных и кессонных крыльев, Труды ЦАГИ, вып. 738, Оборонгиз, 1959.
К о р н о у х о в И. В., Прочность и устойчивость стержневых систем, Госстройиздат, 1949.
Кузьмин 11. Л., Рекач В. Г. и др. иод редакцией И. М. Рабиновича. Сб. задач по теории сооружений (строительной механике), Стройиздат, 1950.
Л с и б е н з о и Л. С., Вариационные методы решения задач теории упругости. Собр. трудов, т. I, изд. АН СССР, 1951, стр. 177—463.
Л с и ь к о О. И., Устойчивость ортотропных цилиндрических оболочек. Сб. «Расчет пространственных конструкций», вып. IV, Госстройиздат, 1958.
Л е и ь к о О. И., Об устойчивости ортотропной цилиндрической оболочки, нагруженной осевыми силами и внешним давлением, Сб. «Расчет пространственных конструкций», вып. V, Госстройиздат, 1959.
Л е х и и ц к и й С. Г., Анизотропные пластинки, ГТТИ, 1947.
Лившиц Я. Д., Строительная механика самолета, Оборонгиз, 1946.
Л о п о в о к Б. II., Т р а п е з и и И. И., Устойчивость пластины, очерченной по параллелограмму, Труды МАИ, вып. 69, Оборонгиз, 1956.
Макаров А. И., О расчете тонкостенных многогранных куполов, Сб. «Расчет пространственных конструкций», вып. 11, Госстройиздат, 1951.
Марьин В. А., Приближенный расчет коротких открытых цилиндрических оболочек, Сб. «Расчет пространственных конструкций», вып. I, Машстройиздат, 1950.
523
Марьин В. А., К расчету общей прочности корпуса цельнометаллического вагона, Сб. «Расчет пространственных конструкций», вып. IV, Госстройиздат, 1958.
Марьин В. А., Устойчивость цилиндрической оболочки при кручении и внутреннем давлении, Сб. «Расчет пространственных конструкций», вып. V, 1959.
Марьин В. А.,. Устойчивость цилиндрической панели при сдвиге, Сб. «Расчет пространственных конструкций», вып. V, 1959.
Марченко В. М., Безмоментиая сферическая оболочка при больших смещениях, Труды ЦАГИ, вып. 630, 1947.
Меерович И. И., Температурные напряжения в листе, подкрепленном стрингерами из другого материала, Техн, заметки ЦАГИ, вып. 162, 1938.
Минаев К. А., Исследование работы стальных профилей на сжатие, Труды ЦАГИ, вын. 521, 1940.
Муш та риХ. М., Об устойчивости круглой тонкой цилиндрической оболочки при кручении, Сб. трудов КАИ, 1934.
Му ш тар и X. М. и Г а л и м о в К. 3., Нелинейная теория упругих оболочек, Таткннгоиздат, 1957.
М у ш т а р и X. М. и др., Труды физ.-техн. института Казанского филиала АН СССР по проблемам теории оболочек, вын. 1 —10.
11 е в с к а я Т. В., Влияние внутреннего давления на устойчивость цилиндрической панели при сдвиге и комбинированном действии сдвигаюшнх и нормальных сил, Сб. «Расчет пространственных конструкций», вып. 111, Госстройиздат, 1955.
Новицкий В. В., О прикреплении твердого тела, шестью стержнями. Сб. «Расчет пространственных конструкций», вып. 11, Госстройиздат, 1951.
Новицкий В. В., Приближенные методы расчета на прочность замкнутых цилиндрических оболочек, Сб. «Расчет пространственных конструкций», вып. IV, Госстройиздат, 1958.
Новицкий В. В., Расчет скошенных конических оболочек, Сб. «Расчет пространственных конструкций», вып. IV, Госстройиздат, 1958.
Новожилов В. В., Теория тонких упругих оболочек, Судпромгиз, 1951.
Образцов И. Ф„ К расчету тонкостенных стержней на устойчивость при изгибе, Труды МАИ, вып. 26, Оборонгиз, 1953.
Образцов И. Ф., /Методы .расчета на прочность кессонных конструкций типа крыла, Оборонгиз, I960.
О ди но ков 1О. Г„ Расчет тонкостенных конструкций типа крыла, фюзеляжа и оперения самолета, Труды КАИ, т. XVII, 1946.
Оги балов П. М., Изгиб, устойчивость и колебания пластинок, Изд. МГУ, 1958.
Олейников Г. А., Исследование работы подкрепленных и иеподкреплен-ных обшивок на сжатие, Труды ЦАГИ, вып. 370, 1938.
П а н о в к о Я. Г., О предельных состояниях цилиндрических тонкостенных конструкций, Сб. «Расчет пространственных конструкций», вып. 11, Госстройиздат, 1951.
И а и о в к о Я. Г., Изгиб и кручение полосы. Изв. АН Латв. ССР, № 8, 1953.
Папкович П. Ф., Строительная механика коробля, ч. 1 и II, Судпромгиз, 1941- -1947.
Пиковский А. А., Статика стержневых систем со сжатыми элементами, Физматгпз, 1961.
Пономарев С. Л., Б и дерм ан В. Л. Лихарев К. К-, М а к у-HI и и В. М., М а л и н и н 11. Н., Феодосьев В. И., Расчеты па прочность в машиностроении, тт. 1, 11, 111, Машгиз, 1956—1959.
Прочность и устойчивость тонкостенных конструкций в самолетостроении, Сб. переводов и рефератов под ред. А. А. Уманского и П. М. Знаменского, ЦАГИ, 1937.
Рабинович И. М., Курс строительной механики стержневых систем, ч. 1 и 11, Госстройиздат, 1950, 1954.
Ржаницин А. Р., Устойчивость равновесия упругих систем, ГТТИ, 1951..
Ржаницып А. Р., Безмоментная теория пологих оболочек, Сб. «Расчет пространственных конструкций», вып. Ill, Госстройиздат, 1955.
524
Ромашевский А. Ю., Исследование работы балочных систем с тонкой стенкой, Труды ЦАГИ, вып. 203 и 206, 1935.
Ромашевский A. IO., Упруго-пластический изгиб, балочных конструкций при произвольной зависимости между напряжением и деформацией, Труды ЦАГИ, вып. 624, 1947; Труды МАИ, 1954.
Ростовцев Г. Г., Строительная механика самолета, ч. I, И, ОИТИ НКТП, 1936.
Сегаль А. И., Итоги решения циклических задач, Сб. «Расчет пространственных конструкций», вып. 3, Госстройиздат, 1955.
Сегаль А. И., Практические методы расчета тонкостенных конических оболочек, Сб. «Расчет пространственных конструкций», вып. II, Госстройизда", 1951.
Сегаль А. И., Прочность и устойчивость судовых перекрытий, Изд. «Речной транспорт», 1955.
Справочник авиаконструктора, ч. Ill, «Прочность самолета», ЦАГИ, 1939.
Справочник по строительной механике корабля под ред. А. 10. Шиманского, 1957—1960.
Стрельбицкая А. И., Исследование прочности тонкостенных стержней за пределом упругости, Изд. АН УССР, 1958.
Строительная механика в СССР в 1917—1957 гг. под ред. И. М. Рабиновича. Госстройиздат, 1957.
Стригунов В. М., К расчету на прочность стреловидных крыльев и оперения самолета, Оборонгиз, 1955.
Т е р е б у ш к о О. И., Расчет несущей способности круговой цилиндрической панели, подкрепленной ребрами Сб. «Расчет пространственных конструкций», вып. IV, Госстройиздат, 1958.
Т е р е б у ш к о О. И., Устойчивость цилиндрической оболочки при кручении, внешнем давлении и сжатии, Сб. «Расчет пространственных конструкций», вып. V, Госстройиздат, 1959.
Т и м о ш е н к о С. П., Пластинки и оболочки, ГТТИ, 1948.
Тимошенко С. II., Устойчивость упругих систем, ГТТИ, 1955.
Т р а и е з и н И. И., Статьи по устойчивости тонкостенной конической оболочки, Труды МАИ, вып. 17, 69, Оборонгиз, 1952, 1956. Сб. «Расчеты па прочность», вып. 1, 3, 5, Машгиз, 1955, 1958, 1959.
Туркин К. Д.. Статьи по расчету цилиндрической оболочки. Сб. «Расчет пространственных конструкций», вып. III, 1955, вып. IV, 1958, вып. V, 1959.
Тюленев А. И., Расчет цилиндрической оболочки п шпангоута на сосредоточенную нагрузку, Сб. «Расчет пространственных конструкций», вып. V, Госстройиздат, 1959.
Уманский А. А., О расчете мпогопролетных упруго опертых балок, Труды ЦАГИ, вып. 247, 1936.
Уманский А. А., Б л я х е р Б. С., О совместной работе стрингеров и обшивки, ЦАГИ, 1937.
У м а п с к и й А. А., Кручение и изгиб тонкостенных авиаконструкций, Оборонгиз, 1939.
У м а н с к и п А. А., О нормальных напряжениях при кручении крыла самолета, ТВФ, 1940, № 12.
Уманский А. А., Специальный курс строительной механики, Госстройиздат, ч. 1, 1935; ч. II, 1940.
У м а н с к и й А. А., Пространственные системы, Стройиздат, 1948.
Уманский А. А., Строительная механика бруса и систем брусьев, Статья в расчетно-теоретическом справочнике проектировщика, Госстройиздат, 1960.
У м а н с к и й А. А., Статика и кинематика ферм, ГТТИ, 1957.
Цибуля Б. II., Изгиб и кручение тонкостенных конических оболочек, Сб. «Расчет пространственных конструкций», вып. 1» Машстройиздат, 1950.
Ч у д п о в с к и н В. Г., Методы расчета колебаний и устойчивости стержневых систем, Изд. ATI УССР, 1952.
Argyris, Energy Theorems and Structural Analysis Aircraft Engenecring, 1954, No. 308—315.
Biirgermeister— Steup, Stabilitatstheorie, Tell I, Akademie—Verlag, Berlin, 1957.
525
Hertel, Leichtbau, Springer, Berlin, 1960.
Hoff, The Analysis of Structures based on the minimal principles and the principle of virtual displacements, Wiley, N. J., 1956.
Кар pus Drillknicken Zentrisch gedriickter Stabe, Luftfahrtforschung, 1937, № 9.
К i m m, Bauelemente des Flugzeuges, Oldenburg, Munchen und Berlin, 1940.
К i m m, Beitrag zUr Stabiiitat diinnwandiger U—Profile im elastischtn Bereich, Luftfahrtforschung, № 5, 1941.
Kochansky, Argyris, Some Effects of Kinetic Heating on the Stiffness of Thin Wings, Aircraft Eng., 1957, № 344, 1958, № 348.
Kuhn, Stresses in Aircraft and Shell Structures, Mc-Graw— Hill Book C°, N. J., 1956.
Rudnai, Theorie des Leichtbaues, Periodica—Polytechnica, vol. 2, № 4, Budapest. 1958.
Rutecki, Wytrimalosc konstrukcyi cienkosciennych, Panstwowe wydawnictwo naykowe, Warscawa, 1957.
Sechler, Dunn, Airplane structural Analysis and Design, Wiley, N. J., 1942.
Wagner—P r e t s c h n e r, Verdrehung und Knickung von offenen Profilen, Luftfahrtforschung, № fl, 1934.
ОГЛАВЛЕНИЕ
Стр.
Предисловие . ........................................................ 3
Глава I. Классические и вариационные методы решения задач сложного изгиба балок.......................................:................ 9
§ 1.1. Эпюры усилий в сечениях бруса и их приложения к различным задачам . . ................................ 10
§ 1.2. Сжатая и растянутая балки............................................................................ 19
§ 1, 3. Сжатая п растянутая балки на упругом основании.................................. 48
§ 1.4. Метод тригонометрических рядов и метод Бубнова -Галеркина 63
§ 1.5. Энергетические (вариационные) методы исследования сложного изгиба 77
Глава 1.1. Прочность и устойчивость прямоугольных пластинок.......... 94
§ 2. 1. Изгиб пластинок по цилиндрической поверхности и цилиндрическая жесткость ................................................. 95
§ 2. 2. Дифференциальное уравнение изогнутой поверхности пластинки . . . . .................................................. 100
§ 2.3. Граничные условия прямоугольной пластинки ................ 108
§ 2.4. Гибкая пластинка и мембрана............................... 113
§ 2.5. Потенциальная энергия упруой деформации изгиба пластинки 117
§ •2.6. Интегрирование уравнения сложного изгиба прямоугольной пластинки, шарнирно опертой по четырем краям..................... 118
§ 2.7. Применение метода Ритца—Тимошенко . . ;.................. 123
§ 2. 8. Частные случаи нагрузки и граничных условий............. 125
§ 2.9. Устойчивость пластинок при сжатии в одном направлении . . 128
§ 2. 10. Устойчивость пластинок при сжатии в двух взаимно-перпендикулярных направлениях......................................... 138
§ 2. 11. Устойчивость прямоугольных пластинок при сдвиге .... 140
§ 2. 12. Устойчивость пластинки при совместном действии сжатия п сдвига ........................................••................ 142
§ 2. 13. Местная устойчивость тонкостенных профилей.............. 144
Глава III. Работа подкрепленных пластинок после потери устойчивости и несущая способность конструкций................................. 151
§ 3. 1. Несущая способность подкрепленных панелей при сжатии 152
§ 3.2. Работа тонкостенной балки после потери устойчивости ее стенки . . ..................................................... 161
§ 3.3. Несущая способность подкрепленной цилиндрической оболочки при изгибе ......................................... 165
Глава IV. Прочность и устойчивость гладких круговых цилиндрических оболочек.......................................................... 175
§ 4. 1. Основное дифференциальное уравнение.................... 175
§ 4.2. Различные случаи осесимметричной нагрузки................ 178
527
Стр.
§ 4. 3. Оболочка под самоуравновешенной поперечной нагрузкой, постоянной вдоль образующей........................................ 182
§ 4.4, Устойчивость оболочек в линейной постановке.............. 182
§ 4.5. Данные опытов и нелинейной теории. Практические указания 189
Глава V. Прямые тонкостенные брусья.................................. 195
§ 5. 1. Качественная характеристика тонкостенных брусьев .... 196
§ 5.2. Свободное кручение бруса с открытым профилем ..... 200
§ 5.3. Депланация поперечного сечения тонкостенного бруса при свободном кручении.............................................. 203
§ 5.4. Свободное кручение бруса с замкнутым тонкостенным профилем . ......................................................... 207
§ 5.5. Касательные напряжения при изгибе тонкостенных брусьев с открытым профилем............................................ 214
§ 5.6. Центр изгиба . . ........................................ 222
§ 5. 7. Касательные напряжения при изгибе тонкостенных брусьев с замкнутым профилем. Центр изгиба............................... 229
§ 5. 8. Дальнейшее развитие теории депланации .................. 233
§ 5. 9. Теория стесненного кручения тонкостенных брусьев с открытым профилем..................................................... 238
§ 5. 10. Интегрирование дифференциального уравнения стесненного кручения ........................................................ 244
§ 5. И. Касательные напряжения при свободном кручении и поперечном изгибе подкрепленных цилиндрических оболочек с миого-связным профилем................................................. 254
§ 5. 12. Расчет поперечных подкреплений цилиндрических оболочек 263
§ 5. 13. Круговая цилиндрическая оболочка и ее кольцевой шпангоут 268
§ 5. 14. Расчет балочных нервюр крыла............................ 273
§ 5. 15. Понятие о стесненном кручении замкнутых подкрепленных цилиндрических оболочек . . . ................................... 274
§ 5. 16. Общая устойчивость открытых тонкостенных Профилей при центральном сжатии . . . . ...................................... 278
Глава VI. Прямые и криволинейные балки со стенкой, работающей только на сдвиг. Биконструкции....................................... 294
§ 6. 1. Балки с параллельными поясами . . ..................... 294
§ 6, 2. Балкн с непараллельными поясами......................... 298
§ 6.3 . Перемещения тонкостенных балок с параллельными поясами 301
§ 6.4 . Криволинейная балка с цилиндрической стенкой............ 304
§ 6.5 . Образование биконструкций .............................. 307
§ 6.6 . Определение усилий в бикоиструкции ..................... 312
§ 6.7 . Кольцевая биконструкция................................. 326
§ 6.8 . Криволинейный двутавр с исчезающе-малой жесткостьго свободного кручения................................................. 331
Глава VII. Определение перемещений и расчет статически неопределимых тонкостенных конструкций по методу сил.................. 341
§ 7. 1. Перемещения (прогибы, углы поворота) тонкостенных балок с непараллельными поясами........................................ 341
528
Стр.
§ 7.2 . Определение перемещений тонкостенной пространственной системы с прямоугольными гранями................................ 344
§ 7.3 . Простейшие статически неопределимые системы................ 348
§ 7. 4. Коробчатые тонкостенные конструкции. Пятичленные уравнения .......................................................... 357
§ 7,5 . Трехчленные уравнения...................................... 369
§ 7. 6. Учет различных условий прикрепления коробки................ 372
§ 7.7 . Энергетически эквивалентные стенки......................... 382
§ 7. 8. Влияние изменения жесткости одного из элементов коробки на распределение усилий при кручении .............................. 384
§ 7. 9. Влияние удаления стенки в одной панели..................... 387
§ 7. 10. Расчет коробки с вырезом, окаймленным жесткой рамой . . 392
§ 7. 11. Примеры выбора основной системы при расчете конструкций по методу сил .................................................. 395
Г лава VIII. Образование и расчет плоских и пространственных ферм . . ,. 403
§ 8. 1. Общие положения............................................ 403
§ 8.2 . Плоские фермы.............................................. 404
§ 8. 3. Преобразованные плоские фермы и исследование их геометрической неизменяемости .......................................... 407
§ 8.4 . Плоские дисковые системы .................................. 413
§ 8.5 . Полярная диаграмма перемещений узлов простейшей прикрепленной плоской фермы ....................................... 418
§ 8. 6. Прикрепление шарнирного узла в пространстве. Усилия в трех стержнях, прикрепляющих узел ................................... 420
§ 8.7 . Прикрепление блока. Усилия в шести стержнях, прикрепляющих блок..................................................... 425
§ 8.8 . Простейшие прикрепленные пространственные фермы . . . 434
§ 8.9 . Простейшие бикоиструкции................................... 441
§ Ю. 1. Двухслойные пластинки с заполнителем...............449
§ 8. 11. Свободные биконструкции.................................... 454
Глава IX. Статически неопределимые задачи прикрепления твердого тела 458
§ 9. 1. Прикрепление блока параллельными упругосмещающимнся опорами и перпендикулярными к иим унруговращающимися 458
§ 9.2. Абсолютно жесткий диск, закрепленный в своей плоскости -упругими силовыми и упругими моментными опорами . . . 462
§ 9.3. Метод моделей и эквивалентных жесткостей для многостерж-невого шарнирного узла......................................... 470
§ 9.4. Прикрепление блока, обладающего плоскостью симметрии . . 474
Глава X. Некоторые специальные вопросы расчета пластинок................ 484
§ 10. 1 Двухслойные пластинки с заполнителем...................... 484
§ 10. 2. Изгиб и кручение консольных пластинок переменного сечения (тонких крыльев).......................................... 492
§ 10. 3. Некоторые температурные задачи........................... 506
§ 10. 4. Заключение............................................... 515
Приложение.............................................................. 517
Литература . . . . ..................................................... 521
Александр Азаръевия Уманский
СТРОИТЕЛЬНАЯ МЕХАНИКА САМОЛЕТА
Издательский редактор А. Г. Белевцева Техн. ред. В. П. Рожин
Т-07748. Подписано в печать 21/VIII 1961 г. Учетно-изд. л. 31,16.
Формат бумаги 60X921/is= 16,87 бум. л.—33,75 печ. л., в т. ч. I вкл.
Цена 1 р. 24 к Тираж 10 000 экз Заказ 119/1565
Типография Оборопгиза
Отпечатано в московской типографии Госгортехиздата. Москва, Ж-88, Южно-портовый 1-й пр., 17. Зак. 425
Замеченные опечатки
Стр. Строка Напечатано Следует читать
25 формула (2. 4') „ЭЛ ср
1 Jx2 1 т
32 11 снизу (м) и (м') (Р) и (р')
56-57 4, столбец У а ch а X COS а х Ch ах sin ах
вклейка табл. 1 8, столбец У1 COS р X COS р, X
11, столбец ' а = . ., t а — . . . а, = .. . , а, = .. . .
И, столбец 1 / 1 (
2 „2 I 2 «2 1
а1 а2 \ а1 ~ а2 \
2 \ 2 \
11, столбец Zj а2 1
а, / а1 /
68 20 сверху! 8 снизу J меньшее меньшее или большее ,
68 13—16 снизу строки 13—16 не читать.
131 3 снизу (9.5) (9.7)
134 На фиг. 36 а акрит
161 На фиг. 59 По оси зигзагообразного сечения должна быть
буква С.
211 Формула (4. 12) 1 4с(откр)
сверху
290 На фиг. 132 м ь ч = h
404 3 сверху неопределенным неопределимым
Заказ 119/1565