Функции и графики. Библиотечка физико-математической школы - Гельфанд И.М., Глаголева Е.Г., Шноль Э.Э.

Author: Гельфанд И.М. Глаголева Е.Г. Шноль Э.Э.
Tags: алгебра математика функции
Year: 1968
Similar
Функции и графики (основные приемы). Библиотечка физико-математической школы
Задачи по элементарной математике. Последовательности. Комбинаторика. Пределы. Библиотечка физико-математической школы
Метод координат. Библиотечка физико-математической школы
Целые функции.
Text
                    mu
л
u
ч
м m
И.М.Гельфанд
Е.Г.Глаголева
Э.Э.Шноль
ни,
иг
ш
А
i L
V

Математика	Библиотечка
физико-математической школы
Выпуск 2
П.Ф.
И. М. Гельфанд фуНКТТИИ
Е. Г. Глаголева Ч^ J ПЛЦПП
и графики
Э. Э. Шноль
(основные приемы)
Издание третье,
исправленное и
дополненное
.\Д]ГМДТИ-,'ЕСКОГО
Колледжа НМУ
Издательство «Наука»
Главная редакция
физико-математической
литературы
Москва 1968

512
Г32
УДК 512 2/512.3
Математика	Библиотечка
физико-математической школы
Редактор cepjuii
И. М. Гельфанд
2-2-2
53- 68

Содержание
Предисловие 		4
Вступление		5
§ 1. Некоторые примеры		11
§ 2. Линейная функция		24
§ 3. Функция у = | х |		27
§ 4. Квадратный трехчлен		38
§ 5. Дробно-линейная функция		52
§ 6. Степенные функции		63
§ 7. Рациональные функции		77
Задачи для самостоятельного решения		85
Ответы и указания к задачам и упражнениям,
отмеченным значком ©	 ....	94

Предисловие
Эта брошюра посвящена разбору основных приемов
построения графиков на примерах простейших функций.
Книга рассчитана на учащихся 9-х классов.
Научиться строить графики по книге нелегко: читателю
не хватает доски, на которой во время урока или лекции
преподаватель постепенно строит график. Поэтому авторы
отказались от чертежей, на которых дается обычно только
окончательный вид графика, и попросили художников
выпуска В. В. Смолянинова и В. Б. Янкилевского превра-
превратить поля брошюры в некоторое подобие доски. Следя за
рисунками на полях, Вам нетрудно будет воспроизвести шаг
за шагом весь процесс построения графика.
Часть теоретического материала изложена в виде задач.
Для понимания текста необходимо внимательно разбирать
все задачи и примеры, помещенные в тексте.
При подготовке книги авторы пользовались помощью
и советами своих товарищей по работе: В. М. Алексеева,
В. И. Кейлис-Борока, А. А. Кириллова, И. X. Сивашин-
ского, С. В. Фомина, |М. Л. Цетлина |. Авторы благодарят
их за помощь. Особенно благодарны авторы редактору выпу-
выпуска Б. В. Шабату, чья работа существенно улучшила книгу.
Авторы благодарят учащихся Заочной математической
школы при МГУ, приславших свои замечания о книге, а
также Н. Б. Васильева и В. Л. Гутенмахера, оказавших боль-
большую помощь при подготовке этого издания.
Все замечания и пожелания по улучшению книги про-
просим направлять по адресу: Москва, В-234, МГУ, механико-
математический факультет, Заочная математическая школа.
Авторы

Вступление
Рис 1
На рис. 1 Вы видите две кривые, начерченные сейсмо-
сейсмографом — прибором, записывающим колебания земной коры.
Верхняя кривая получена, когда земная кора спокойна,
на нижней видны сигналы землетрясения.
На рис. 2 — две кардиограммы. Верхняя показывает
нормальную работу сердца, нижняя снята у больного.

Волыч -О--Ч терне
I ТСХ, JUOL
\т - наприокенце
¦¦ 1
1
ко э
е
0
-г
У
f
у
/
o,s
1
/
/
/
и
Рмс.З
На рис. 3 показана
так называемая характе-
характеристика полупроводнико-
полупроводникового элемента — кривая
зависимости силы тока от
напряжения.
Сейсмолог, анализи-
анализируя сейсмограмму, узна-
узнает, когда было землетря-
землетрясение, где оно произошло,
определяет силу и харак-
характер толчков. Врач, иссле-
исследующий больного, может
по кардиограмме судить
о нарушениях сердечной деятельности; изучение кардио-
кардиограммы помогает правильно поставить диагноз заболевания.
Инженер-радиоэлектроник по характеристике полупроводни-
полупроводникового элемента выбирает наиболее подходящий режим его
работы. Все эти люди изучают некоторые функции по графи-
графикам этих функций.
Что же такое функция и что же такое график функции!
Прежде чем дать точное определение функции, пого-
поговорим немного об этом понятии. Описательно говоря, функ-
функция— это когда каждому значению некоторой величины,
которую математики называют аргументом и обозначают
обычно буквой х, отвечает значение другой величины у,
называемой функцией.
Так, например, величина смещения земной поверхности
при землетрясении в каждый момент времени имеет опре-
определенное значение — величина смещения есть функция вре-
времени. Сила тока в полупроводниковом элементе есть функ-
функция напряжения, так как каждому значению напряжения
соответствует определенное значение силы тока.
Таких примеров можно привести очень много: объем
шара есть функция его радиуса, высота, на которую под-
поднимается брошенный вертикально вверх камень, есть функ-
функция его начальной скорости и т. д.
Перейдем теперь к точным определениям. Когда говорят,
что величина у есть функция величины х, то прежде всего
указывают, какие значения может принимать х. Эти «раз-
«разрешенные» значения аргумента х называются допустимыми
значениями, а множество всех допустимых значений вели-
величины х называется областью определения функции у.

Например, если мы говорим, что объем V шара есть функ-
функция его радиуса R. то областью определения функции
V — 5- ftRs будут все числа, большие нуля, поскольку вели-
О
чина Я радиуса шара может быть только положительным
числом.
Всегда, когда задается функция, необходимо указывать
ее область определения.
Определение I
Мы говорим, что у есть функция величины х,
если: 1) указано, какие значения х являются допусти-
допустимыми, т. е. задана область определения функции,
и 2) каждому допустимому значению х соответ-
соответствует в точности одно значение величины у.
Коротко вместо слов «величина у есть функция величи-
величины х» записывают:
у = /(*)•
(Читается: «игрек равно эф от икс».)
Запись / (а) означает численное значение функции f(x),
соответствующее значению х, равному а.
Например, если
то
=1 И Т- Д"
Правило, с помощью которого по значению х находят
соответствующее значение у, можно задавать различными
способами, и никаких ограничений на форму, в которой оно
выражается, не накладывается. Если сказано, что у есть
функция от х, то Вы должны проверить только, что 1) задана
область определения, т. е. указано, какие значения может
принимать х, и 2) дано правило, по которому каждому до-
допустимому значению х Вы можете поставить в ссогветствие
единственное значение у.
Каким может быть это правило.''

Приведем несколько примеров.
1.	Пусть сказано, что х — это любое действительное,
число и у находится по формуле
У = х2.	<
Функция у = х2 задана формулой.	(
Правило может быть и словесным.
2.	Функция!/ задается следующим образом: если х —
положительное число, то у равно 1, если х — отрицательное
число, то у равно —1, если х равно нулю, то у равно 0. ',
Приведем еще один пример функции, задаваемой сло-(
весным правилом.
3.	Каждое число х можно записать в виде
где а — неотрицательное число, меньшее единицы, ay —
целое число. Ясно, что каждому числу х соответствует
единственное число у, т. е. у есть функция от х. Область
определения этой функции — вся числовая ось. Эта функция
называется «целая часть х» и обозначается так:
у = М-
Например,	(
[3,53] = 3, [4] = 4, [0,3] = 0, [—0,3] = — 1.
Ниже мы используем эту функцию в наших упражнениях. ,
4. Рассмотрим функцию у = / (х), заданную формулой
_ УГ+з
tJ~ х-ъ-
(
Что разумно считать ее областью определения?
Если функция задана формулой, то рассматривается
обычно ее так называемая естественная область опреде- (
ления, т. е. множество всех чисел, для которых можно вы-
выполнить действия, указанные формулой. Значит, в область
определения нашей функции не входит число 5 (так как
при х = 5 знаменатель дроби обращается в нуль) и значе-
значения х, меньшие чем —3 (так как при х < — 3 подкоренное
выражение отрицательно). Итак, естественная область опре-
определения функции у =	— это все числа, удовлетво-
X — о
ряющие соотношениям:
х> — 3,

ч
-2 -\ О
-1
Функцию можно изображать гео-
3метрически с помощью графика.
Чтобы построить график некоторой
функции, рассмотрим некоторое до-
допустимое значение х и отвечающее
ему значение у. Например, пусть
значение х — это число а, а соот-
соответствующее ему значение у — чис-
'ло b = f (а). Эту пару чисел а и
Ъ изобразим на плоскости точкой
'с координатами (а, Ь). Построим та-
такие точки для всех допустимых
значений х. Набор получивших-	РисЛ
ся точек и есть график функции.
Определение II
График функции — это множество точек, у которых
абсциссы являются допустимыми значениями аргумен-
аргумента х, а ординаты — соответствующими значениями
функции у.
Например, на рис. 4 изображен график функции
У= М-
Он состоит из бесконечного множества горизонтальных от-
отрезков. Стрелочки означают, что правые концы этих отрез-
отрезков не принадлежат графику (левые же концы принадлежат
ему и поэтому обозначены жирной точкой).
График может служить правилом, задающим функцию.
Например, по характеристике полупроводникового элемента
можно определить (см. рис. 5), что если аргумент U равен
0,6 (вольт), то функция / равна 1,3 (миллиампер).
Изображать функции графиками очень удобно, потому что,
поглядев на графики, можно сразу отличить одну функцию
от другой. Посмотрите еще раз на нижнюю кривую рисун-
рисунка 1. На этом графике самый неопытный человек сразу
увидит сигналы землетрясения (участки
В и С). Присмотревшись, он, безусловно,
заметит и разницу в характере волн на
участках В и С (сейсмолог мог бы объяс-
объяснить Вам, что на участке В записана так
называемая волна Р — волна, идущая в
глубине земной коры, а на участке С вол-
волна S, идущая по поверхности).
Попробуйте, удастся ли Вам отличить
эти два участка по помещенным рядом

Во
(ша
0,1
0,1
-1,6
-1,7
—2,4
—3,0
-4,5
-3,8
—2,9
—1,1
0,8
3,3
5,1
3,7
0,0
-2,0
-4,4
-5,8
—3,8
—1,6
0,2
0,5
2,5
4,9
7,1
6,1
3,8
0,4
0,2
0,7
1,5
2.5
3,2
2,8
0,4
-2,2
-3,3
-4,5
—4,8
-4,8
—4,8
—3,7
-3,5
—4,4
—6.6
таблицам. (Мы не смогли привести здесь
таблицы для всей кривой: она заняла бы
всю страницу. На полях Вы видите таб-
таблицы для небольших кусков участков
В и С.) .
На рис. 6 показаны графики двух
функций, которые задаются очень похо-
похожими формулами:
1	1
и«=-
+ 2х — 3 '
Разницу в поведении этих двух функ-
функций можно, конечно, обнаружить и по
формулам. Но если посмотреть на их гра-
графики, эта разница сразу бросается в
глаза.
Всегда, когда нужно выяснить общий
характер поведения функции, обнаружить
ее особенности, график в силу своей на-
наглядности является незаменимым. Поэто-
Поэтому инженер или ученый, получив инте-
интересующую его функцию в виде формулы
или таблицы, обычно берется за каран-
карандаш, набрасывает эскиз графика и смот-
смотрит, как ведет себя функция, как она
«выглядит».
г-

X
§ 1. Некоторые примеры
1. Если буквально следовать опре-
определению, то для построения графика не-
некоторой функции нужно найти все пары
соответствующих значений аргумента и
функции и построить все точки с этими
координатами. В большинстве случаев это
сделать практически невозможно, так как
таких точек бесконечно много. Поэтому
обычно находят несколько точек, принад-
принадлежащих графику, и соединяют их плав-
плавной кривой.
Попробуем построить таким способом
график функции
» = -*—	(Ь
Ч	л i о •	\
J 1 + х-	х
Выберем несколько значений аргу-
аргумента, найдем соответствующие значения
функции и запишем их в таблицу (см.
табл. 1). По полученным координатам
построим точки и соединим их пока пунк-
пунктирной линией (рис. 1).
Проверим теперь, правильно ли мы
провели кривую между найденными точ-
точками графика. Для этого возьмем какое-
•
1
ъ
\
ч -
1 о
Фо
1
11

тс.
.с г
нибудь промежуточное значение аргумен-
аргумента, например х — 3/2, и вычислим соответ-
соответствующее значение функции у = 4/13-
Полученная точка C/„, 4/13) хорошо «ло-
«ложится» на нашу кривую (рис. 2), так что
мы провели ее вроде бы правильно.
Однако возьмем еще х = 1/2. Тогда
у = 4/5 и соответствующая точка ложится
выше нарисованной нами кривой (рис. 2).
Значит, между х = 0 и х = 1 график идет
не так, как мы думали. Возьмем на этом
«сомнительном» участке еще значения х —
= V4 и х = 3/4. Соединив все полученные
точки, мы получим более правильную
кривую, изображенную на рис. 3. Взя-
тые для контроля точки (Vs, 9/]0) и B/.з. "Лз)
хорошо «ложатся» на эту кривую.
к
1
2.
г
э
к
2. Чтобы построить левую половину
графика, нужно заполнить еще одну таб-
таблицу для отрицательных значений аргу-
аргумента. Это сделать просто.
Например,
при х = 2 имеем у = .,, , . = =- ,
1	1
при х = — 2 имеем # = ¦).,., = г ¦
(—ZJ -г х °
Значит, вместе с точкой B, 1/5) на гра-
графике лежит точка (—2, V5), симметрич-
симметричная первой относительно оси ординат.
Вообще, если точка (а, Ь) лежит на
правой половине нашего графика, то на
левой его половине будет лежать точка
(—а, Ь), симметричная (а, Ь) относительно
оси ординат (рис. 4). Поэтому, чтобы
получить левую часть графика функции
A), соответствующую отрицательным зна-
значениям х, нужно зеркально отразить от-
относительно оси Оу правую половину это-
этого графика.
12

(-CL.8)
h
\
*)
Если <^
слот?е/гст6
ОСЛОЖИЫ-Д [
го такй# Ц
cujuj4erpu"!tH
van
,И.О
а
на
b(U
ЛС+
Ц
4 <
е-
и^ келсоторвй <|>i
е "d&jju jifoSw-A» «j
-а),рабиы метки
р^нчцм^ цлаящ
~кос4лтепьно оси
(w.e.
ZCTHOCj.
JL
L
I
^=V/*'-i|;-

»
Общий вид графика — на рис. 5.
Если бы мы поторопились и достроили
для отрицательных х наш первоначаль-
* ный набросок (рис. 1 и 2), то на нем при
i°-He.»w<Mc/ v; = 0 получился бы «излом» (уголок).
Этого излома нет на правильном графике:
вместо него здесь плавный «купол».
X
Упражнения
1. График функции
+ 1
похож на график функции у = _2
ла
1
B)
Построи-
Построите его.
2. Какие из следующих функций являются чет-
четными (определение и график четной функции, а
также некоторые примеры см. на стр. 13):
а)у=1—
х;
X
0
1
г
-1
-2
У
-1
Vz
V<
Vi
4Л,
-О.
О
•1
1
О
,i
. О
Рмс 6
3. Возьмем теперь функцию
1
2/ =
Зд:2 — 1
C)
По виду эта формула мало отличается
от формулы B). Однако при построении
этого графика по точкам сразу же начи-
начинаются неприятности.
Составим снова таблицу и нанесем на
чертеж полученные точки. Как соединять
эти точки — неясно: создается впечатле-
впечатление, что точка @, •— 1) «выпадает» (рис. 6).
Попытайтесь сами построить график
этой функции. Не огорчайтесь, если для
того, чтобы понять, как идет эта кривая,
Вам понадобится найти больше точек,
чем Вы ожидали.
После этого обязательно прочитайте
на стр. 16—18 как у нас строится этот
график и какие полезные выводы делают-
делаются из построения.
14

14.1 График многочлена
y=xi — 2х3 — х2
D)
мы тоже начнем строить по точкам.
Взяв для аргумента значения, равные
О, 1, 2, мы получим значения функции,
равные нулю. Возьмем еще значение
х — — 1. Снова получим, что у равно
нулю. Соответствующие точки графика
(О, 0), A, 0), B,0), (—1, 0) лежат на оси
Ох (рис. 7).
Если ограничиться этими четырьмя
значениями аргумента, то «плавной» кри-
кривой, соединяющей полученные точки,
будет ось абсцисс. Однако ясно, что ось
абсцисс не яйляется графиком нашей
функции: ведь многочлен х4 — 2л;3— х2 +
+ 2х не может быть равен нулю при всех
значениях х.
Возьмем еще два значения аргумента
х = — 2 и х = 3. Соответствующие точки
(—2, 24) и C, 24) уже не лежат на оси Ох,
а, напротив, расположены очень далеко
от нее (рис. 8).
Как выглядит график, остается по-
прежнему неясным. Можно, конечно, как
мы делали раньше, найти достаточное ко-
количество промежуточных, точек и при-
приблизительно построить график, но этот
способ не очень надежен.
Попробуем поступить иначе.
Выясним, где функция положительна
(и, значит, график лежит выше оси Ох)
и где отрицательна (т. е. график лежит
ниже оси Ох).
Разложим для этого многочлен, задаю-
задающий функцию, на множители:
х4 — 2х3 — х2 + 2х = х3 (л: — 2)—х (х—2) =
= (х3 — х) {х — 2) = х(х2 — \)(х — 2) =
Рис.7
15

Э-х'-У
Рис.
Теперь видно, что наша функция рав-
равна нулю только в тех четырех точках, ко-
которые мы уже нанесли на график. Левее
точки х = — I все четыре сомножителя
отрицательны — функция положитель-
положительна. Между точками х — — 1 и х — О (т. е.
на промежутке —1 <^ х <^ 0) множитель
х + I становится положительным, а ос-
остальные остаются отрицательными —
функция отрицательна. На участке 0 <^
<^ х <i I имеем два отрицательных сом-
сомножителя и два положительных — функ-
функция положительна. На следующем уча-
участке функция снова отрицательна. Нако-
Наконец, при переходе через точку х = 2
последний из сомножителей становится по-
положительным — функция становится по-
положительной.
График функции представляется нам
теперь примерно в таком виде, как на
рис. 9.
15.1 Перейдем к построению графика
функции
_ 1
lJ~~ 3** — 1 •
о котором мы уже говорили на стр. 14.
Отметим на рисунке точки графика,
отвечающие значениям х = —1, 0, 1, 2,
и соединим их линией. Получится при-
примерно так, как на рис. 10.
Возьмем теперь х = V2. Мы получим
у — — 4, и точка G2, —4) лежит гораздо
ниже нашей кривой. Значит, между х = 0
и х = 1 график идет совсем по-другому!
Более точный ход графика мы изобра-
изобразим на рис. 11. Возьмем еще х — 3/2 и
х = 8/2. Соответствующие точки довольно
хорошо ложатся на нашу кривую.
Но как же проходит график между точ-
точками х = 0 и х = I?
Возьмем х — 1/4 и х = 3/4. Получим
соответственно у = — 1в/13 яг — 6/4 и у —
— le/xi ~ 34- Ход графика между точками
16

х — 0 и х = 1/2 несколько прояснился
(рис. 12), но, как ведет себя функция ме-
между х = 1/2 и л: = 3/4, по-прежнему не-
непонятно.
Если мы возьмем еще несколько про-
промежуточных значений между х = V2 и
X — 3/4, то увидим, что соответствующие
точки графика ложатся яа не одну, а на
две плавные кривые, и график приобре-
приобретает примерно такой вид, как на рис. 13.
Вы теперь хорошо понимаете, что по-
построение графика по точкам — это риско-
рискованный и длинный путь. Если взять мало
точек, то может оказаться, что мы получим
совсем неверное представление о функции.
Если же брать точки чаще, то будет мно-
много лишней работы и все равно останется
сомнение, не пропустили ли мы чего-ни-
чего-нибудь, существенного. Как же быть?
Вспомним, что при построении графи-
графика У = —2 , , на участках 2 < х < 3 и
1 < х < 2 никаких дополнительных то-
точек не потребовалось, а на участке 0 <^
<^ х < 1 пришлось найти еще 5 точек. Так
графика у = 3x2_t
же при построении	3x_t
основной работы потребовал участок
0<л: < I, где кривая разрывается на две
ветви.
Нельзя ли заранее
«опасные» участки?
выделить такие
16. | Вернемся в третий раз к графику
1
У =
Зх2
Если посмотреть на выражение, за-
задающее функцию, то сразу видно, что
при двух значениях х знаменатель'этого
выражения обращается в нуль. Эти зна-
значения равны + Vll* и — JЛ/з, т. е. при-
примерно + 0,58. Одно из них лежит в про-
промежутке Vg <С х < 3/4, т. е. как раз там,
^Фесечжо П.Ф.|
17
г\

где функция ведет себя необычно, график
идет неплавно. Теперь понятно, почему
это происходит.
Действительно, при значениях х =
= + У1/* функция не определена (деле-
(деление на нуль невозможно); значит, на гра-
графике не может быть точки с такими абс-
абсциссами — график не пересекает прямых
а = У~Ча и х — — \/rJs. Поэтому гра-
график распадается на три отдельные вет-
ези. Если х приближается к одному из «за-
«запрещенных» значений, например к л =
= У1/3, то дробь 3.x2 —1 неогРаниченно
растет по абсолютной величине — две вет-
ветви графика приближаются к вертикальной
прямой х = У1/3-
Аналогично ведет себя наша (четная!)
функция вблизи точки х = — У1/3.
Общий вид графика
1
У
У~~ Зх2—1
показан на рис. 14.
Мы понимаем теперь, что всегда, когда
функция задана формулой, которая предс-
представляет собой дробь, необходимо обращать
внимание на те значения аргумента, при
которых знаменатель обращается в нуль.
17.1 Какой же урок можно извлечь из
рассмотренных примеров? При изучении
поведения функции и построении ее гра-
графика не все значения аргумента одина-
одинаково важны.
На примере функции
У= 3x2 — 1
мы видели, насколько важными являют-
являются те «особые» точки, в которых функция
не определена. Характер графика
у = xi — 2jcs — х2 + 2х
18

\??
2*

нам стал понятен тогда, когда мы нашли
точки пересечения графика с осью абс-
абсцисс, т. е. корни многочлена.
В большинстве случаев основная ра-
работа при построении графиков состоит
как раз в том, чтобы найти существенные
для данной функции значения аргумента
и изучить ее поведение вблизи этих зна-
значений. После такого исследования для
полного построения графика достаточно
бывает найти несколько промежуточных
значений функции между этими харак-
характерными точками.
Упражнения
1.	Постройте график функции у = Зх — 1—
В каких точках график пересекает оси коор-
координат?
Представьте себе, что мы поместили начало ко-
координат в самой середине тетрадного листа и взяли
за единицу масштаба 1 см (для опррделенности будем
считать тетрадный лист прямоугольником размером
16 еж X 20 см). Найдите координаты точек, в кото-
которых график уходит за пределы тетрадного листа.
2.	Постройте графики многочленов*)
а)	у = хэ — х2 — 2х -f 2;
б)	у = х3 — 2а:2 + х. ©
(обратите внимание на то, что в случае б) при раз-
разложении многочлена на множители получается два
одинаковых сомножителя).
8. | Построив график какой-либо функ-
функции, с помощью разных приемов можно
легко построить графики некоторых дру-
других «родственных» с первой функций**).
*) Знак ® стоит около задач и упражнений, к ко-
которым имеются ответы в конце книги (см.
стр. 94).
**) С приемом такого рода мы уже встречались на
1
стр. 12 при построении графика у = Х2 i \ ¦ По-
Построив график этой функции для положительных
значений х, мы смогли сразу построить график
и для отрицательных х.
20

Vsr
Puc./S"
О 'А.
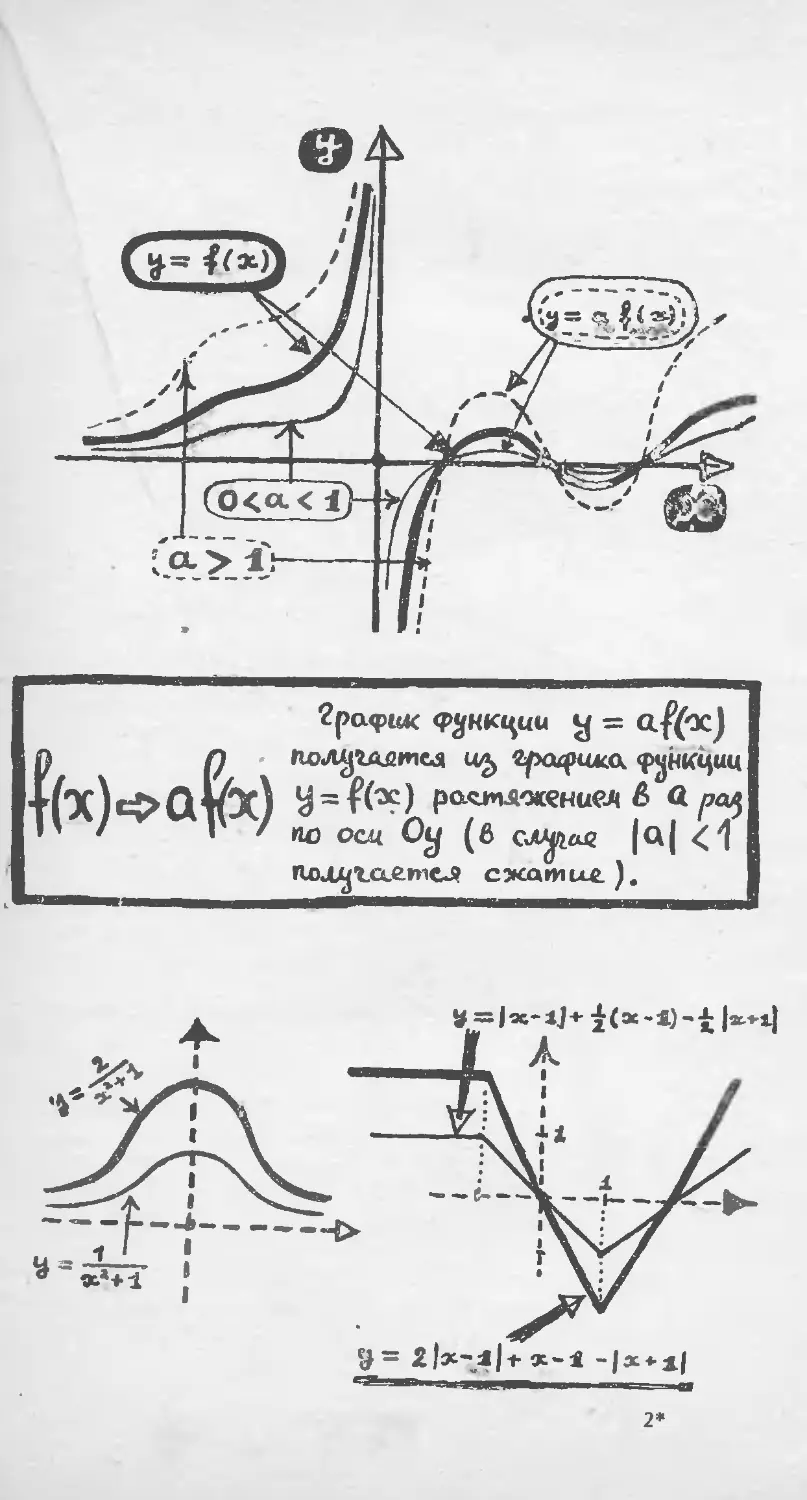
Один из простейших таких приемов —
это так называемое растяжение по оси Оу.
Мы построили уже график функции
у= х2 +1
(см- Рис- 5 на СТР- 14)-
Построим теперь график функции
3
Возьмем какую-нибудь точку первого
графика, например х = V2, # = 4/5, т. е.
точку Мг (У2, 4/5). Ясно, что мы можем
получить точку второго графика, оставив
х тем же (т. е. х = V2) и увеличив у в три
раза. Получится точка М2 (V2,12/5). Ее мож-
можно получить прямо на чертеже (рис. 15).
Для этого нужно увеличить ординату точ-
точки Мх (V2, 4/5) в три раза.
Если мы проделаем такое преобразо-
преобразование с каждой точкой графика у —	,
х -f- 1
то точка М (а, Ь) перейдет в точку М' (а,
ЗЬ) графика у =	, а весь график,
х -\-1
растянувшись втрое по оси Оу, превратит-
g
ся в график функции у = - ¦ ¦ (рис. 16).
Итак, график у = ¦ представляет
х -j-1
* собой график у = ¦ 2 . , растянутый
Pu.cJfi втрое по оси Оу.
19. Еще проще получить из графика
У= v2-L.i график функции
У = — х2 + 1 .
Чтобы получить из таблицы 1 на стр. 11
для функции у = х2,1 таблицу для функ-
22

ции у = —
нужно просто по-
менять знак у каждого из чисел второго
столбца.
Тогда из каждой точки графика у =
=¦ 2 , например, из точки М с абсциссой
2 и ординатой 'Д. получится точка ЛГ гра-
графика у =		с той же абсциссой 2
и противоположной ординатой (—1/ь).
Очевидно, точка М' B, —1/ъ) симметрич-
симметрична точке М B, V6) относительно оси Ох.
Вообще всякой точке ./V (а, Ь) графика
у — . соответствует точка N' (а, —Ь)
графика у = — ^ +1 .
Итак, график функции у =
tf-г 1
1
можно получить из графика у =
зеркальным отражением относительно оси
Ох (рис. 17).
Упражнения
1. Имея график у = л4 — 2л3 — л^2 + 2х
(рис. 9, на стр. 16), постройте графики функций
у = Зл-4 — 6л-3 — Зл-2 + 6х и {/ = — х* + 2г> +
+ х2 — 2х.
\ ^ '
2.	Постройте график у =
график у = х2 + 1 .
3.	Постройте графики *):
а) у = ~y [х] J
б)у=х-[х] и г/=-2 («-[«]);
ИСПОЛЬЗУЯ
*) Смысл символа [х] — целой част числа х —
объяснен на стр. 8.

/
I/
0
<
/
-x
§ 2. Линейная функция
11.1 Приступим теперь к систематичес-
систематическому изучению поведения различных
функций и построению их графиков. При
этом с характерными чертами поведения
функций и особенностями их графиков
мы будем знакомиться на простейших
примерах. При построении более слож-
сложных графиков будем стараться найти в них
знакомые элементы.
Самая простая функция — это функ-
функция у = х. Графиком этой функции яв-
является прямая — биссектриса первого и
третьего координатных углов (рис. 1).
Вообще, как Вы знаете, графиком лю-
любой линейной функции у = kx + Ъ яв-
является некоторая прямая. Обратно, лю-
любая прямая, не параллельная оси Оу,
является графиком некоторой линейной
функции.
Положение прямой вполне определяет-
определяется заданием двух ее точек. В соответствии
с этим линейная функция вполне опреде-
определяется заданием ее значений для двух
значений аргумента,
24

Упражнения
1.	Найдите линейную функцию у = kx + Ь,
которая принимает при х = —10 значение у = 41,
а при х = 6 значение у = 9.
2.	Прямая проходит через точки А @, 0) и
В (а, с). Найдите линейную функцию, графиком ко-
которой является эта прямая.
3.	Проведите через начало координат прямую
под углом 60° к оси ординат. Графиком какой функ-
функции она является?
4.	а) В таблице 1 значений некоторой линейной
функции два из пяти ее значений записаны неверно.
Найдите их и исправьте.
б) Тот же вопрос для таблицы 2.
5.	Найдите функцию у = kx + Ь, если ее гра-
график параллелен графику у = х и проходит через
точку C,—5).
6.	Найти линейную функцию, график'которой со-
составляет угол в 60° с осью абсцисс и проходит через
точку C, —5).
7.	Угловой коэффициент прямой*) равен а.
Прямая проходит через точку C, —5). Найдите
линейную фугкцию, графиком которой является
эта прямая.
I 2.1 Характерным свойством линейной
функции является то, что когда х увели-
увеличивается равномерно, т. е. на одно и
то же число, у меняется тоже равномерно.
Возьмем, например, функцию у = Зх — 2.
Пусть х принимает значения 1, 3, 5, 7,...,
каждое из которых больше предыдущего
на одно и то же число 2. Соответствующие
значения у будут: 1,7, 13, 19,... Вы видите,
что каждое из значений у больше предыду-
предыдущего тоже на одно и то же число — на 6.
Ряд чисел, который получается из ка-
какого-нибудь числа прибавлением одного
и того же числа, образует так называемую
арифметическую прогрессию. Таким обра-
образам, характерное свойство, о котором мы
говорили, можно выразить так: линейная
функция переводит одну арифметическую
прогрессию в другую арифметическую
прогрессию (рис. 2). В нашем примере
*) Угловым коэффициентом прямой у = kx + Ь
называется коэффициент k.
-2
-1
о
ОС
— —
чо
о
io
-г
-3
-зз
+2?
ь
. А
/1
/
г
1
•х.
о\/1 2 Ъ Ц
25

функция у = 3-v — 2 переводит арифме-
арифметическую прогрессию 1, 3, 5, 7,... в ариф-
арифметическую прогрессию 1, 7, 13, 19,...,
а на рисунке 2 показано, как функция
у = 2х — 1 переводит арифметическую
прогрессию 0, 1, 2, 3,... в арифметическую
прогрессию— 1, 1, 3, 5, 7,...
Упражнения
1.	Придумайте линейную функцию, которая
переводила бы арифметическую прогрессию —3,
—1, 1, 3,... в арифметическую прогрессию —2, —12,
—22,...
Какая линейная функция переведет вторую про-
прогрессию в первую?
2.	Пусть даны две арифметические прогрессии:
а, а + h, а + 2А,„. и с, с + I, с + 21,... Всегда
ли можно найти линейную функцию у = kx + Ь,
которая переводит первую прогрессию во вторую?
3.	а) Прямая у = -tf- х + -д— проходит через
две точки с целыми координатами: А A0,5) и
В (—20,—9). Есть ли на этой прямой еще «целочис-
«целочисленные точки» (т. е. точки с целыми координатами)?
б)	Известно, что прямая у = kx + b проходит
через две целочисленные точки. Есть ли на этой
прямой еще целочисленные точки?
в)	Легко построить прямую, не проходящую ни
через одну целочисленную точку. Например, у =
= х + У2-
Может ли какая-нибудь прямая у — kx + Ь
проходить только через одну целочисленную точку?*)
*) Если Вы не сможете найти ответа на этот воп-
вопрос, посмотрите на стр. 86 — 87 задачу 4.

§ 3. Функция у =\х\
Jl.J Рассмотрим теперь функцию
У = 1*1.
где \х\ означает абсолютную величину*),
или модуль, числа х.
Построим ее график, пользуясь опре-
определением абсолютной величины. При по-
положительных х имеем | х | = х, т. е. этот
график совпадает с графиком у = х и яв-
является лучом, выходящим из начала ко-
координат под углом 45° к оси абсцисс
(рис. 1). При х < 0 имеем | х\ = — х; зна-
значит, для отрицательных х график у = \х\
совпадает с биссектрисой второго коорди-
координатного угла (рис. 2).
Впрочем, вторую половину графика
(для отрицательных х) легко получить
из первой, если заметить, что функция
у = \х\ — четная, так как | — а\ = |а|
¦Ри-с
*) Напоминаем: абсолютная величина положитель-
положительного числа равна этому числу (если х > 0, то
\х\ = х); абсолютная величина отрицательного
числа равна противоположному числу (если
х <0, то |jr| = — х), абсолютная величина нуля
равна нулю (|0| = 0).
27

(см. определение четной функции на
стр. 13). Значит, график функции у= \х\
симметричен относительно оси Оу, и вто-
вторую половину графика можно получить,
отразив относительно оси ординат часть,
начерченную для положительных х. По-
Получается график, изображенный на рис. 3.
|2.| Построим график функции
~~	у = \х\+\.
Этот график легко построить непо-
непосредственно. Однако мы его получим из
графика функции у=\х\. Составим таб-
таблицу значений функции у= \х\ + 1 и
сравним ее с такой же таблицей, состав-
составленной для у — | х\, выписав эти таблицы
рядом (табл. а, б). Ясно, что из каждой
точки первого графика у = | х\ можно по-
получить точку второго графика у = | х | + 1,
увеличив у на единицу. (Например, точка
(—2, 2) графика у = \ х | переходит в точ-
точку (—2,3) графика у=\х\-\-\, лежащую
на 1 выше первой — рис. 4.) Значит, что-
чтобы получить точки второго графика, нуж-
^ но каждую точку первого графика сдви-
сдвинуть на 1 вверх, т. е. весь второй график
получается из первого сдвигом вверх на
1 (см. рис. 4).
Задача. Постройте график функции
у = \х\ — \.
Решение. Сравним этот график с
графиком у = | х \. Если точка х — а, у =
= |о| лежит на первом графике, то точка
х = а, у = \а\ — 1 будет лежать на вто-
втором графике. Поэтому каждая точка
(а, \а\ — 1) второго графика может быть
получена из точки (а, \ а |) первого графика
сдвигом вниз на 1 единицу, и весь график
получается, если график у = | х\ сдвинуть
вниз на 1 (рис. 5).
Такой сдвиг вдоль оси Оу полезен при
построении многих графиков (см. стр. 29).
28

р
р ... v
2pc,(pi
лол^гав!
<и)8игол
«к
сд
Вк
На
0
Фчнкции ч-
ЗОИ» ОСМ 0^
«•раблениа с
НА
jhakoju гисла. <Х
ик сйёихсигтс
- ЬииЪ).
4 бб<
а.
к. ОП-
S=-3x-3

Пусть надо построить график функции
Представим эту функцию в виде
X2 + 1 + 1
Теперь ясно, что ее график может быть
получен из графика у= 2 , (см. рис. 5
на стр. 28) сдвигом вдоль оси Оу на 1
вверх.
Put. С1
3. | Возьмем теперь функцию
~~	у = \х+\\.
График этой функции мы тоже полу-
получим из графика у = \х\. Напишем опять
рядом две таблицы: для у = |х| и для
у = \х + 1| (табл. с, б). Если сравни-
сравнивать значения этих функций при одина-
одинаковых х, то окажется, что для некоторых х
ордината первого графика больше, чем
второго, а для некоторых — наоборот.
Однако, если внимательно посмотреть
на правые столбцы этих двух таблиц, связь
между таблицами можно установить.
Именно, вторая функция принимает те же
самые значения, что и первая, только
принимает их на единицу раньше, при
меньших значениях х. (Почему?) Значит,
из каждой точки первого графика у =
= |*| получается точка второго графи-
графика у = | х + 1 |, сдвинутая на 1 влево; на-
например, из точки (—1, 1) получается точка
с координатами (—2,1) (рис. 6). Поэтому
и весь график у = | х + 11 получится,
если сдвинуть график у = \х\ на 1 влево
вдоль оси абсцисс.
Задача. Построить график функ-
функции у — | х — 11.
Решение. Сравним его с графиком
у = \х\. Если А—точка графика у —
30

= |х| с координатами (а, \а\), то точкой
графика у = \х — 1 | с тем же значением
ординаты у будет точка А' (а + 1, \а\).
(Почему?) Эту точку второго графика
можно получить из точки Л (с,| с |) перво-
первого графика сдвигом вдоль оси Ох вправо.
Значит, и весь график у = | х — 11
получается из графика у = \ х | сдвигом
вдоль оси Ох вправо на 1 (рис. 7).
Мы можем сказать, что функция
у—\х— 1 | принимает те же значения, что
и функция у — \х\, только с некоторым
запозданием (а именно, на 1).
Такой сдвиг вдоль оси Ох полезен при
построении многих графиков (см. стр. 33).
Упражнения
1.	Постройте график функции
	1
у== *2-2*+2 •
(Указание. Представьте знаменатель дроби
	J	_ в виде (л- — IJ + 1.)
X 	 ?Х ~~у~ С*
2.	Сформулируйте правила, по которым из
графика функции у = f (х) можно получить гра-
графики функций у = / (х + 5) и у = / (л- — 3).
3.	Постройте графики у = \х\ + 3 и у=
4.	Найдите все линейные функции, которые
при х = 3 принимают значение у = — 5.
Решение. Геометрически условие форму-
формулируется так: найти все прямые, проходящие через
точку C, —5). Любая (невертикальная) прямая,
проходящая через начало координат, является гра-
графиком некоторой функции у = kx. Сдвинем эту
прямую так, чтобы она проходила через нужную
точку C, —5), т. е. на 3 единицы вправо и на 5
единиц вниз (рис. 8). После первого сдвига мы
получим уравнение у = k (х — 3), после второго
Ответ. Все линейные функции, которые при
х = 3 принимают значение у = — 5, выражаются
формулой у = k(x — 3) — 5, где k — любое .дейст-
.действительное число. (Сравните эту задачу с задачей 7 на
стр. 25.).
|4.1 Задача. Построить график
у= \х+ 1 |-г \х— 1|.
Г1Л.С. t

Рис. 10
Решение. Построим сначала на
одном чертеже графики каждого из сла-
слагаемых: у = |л;+1|иу = |л; — 1 |. Орди-
Ордината у искомого графика получается
сложением ординат двух построенных гра-
графиков в этой же точке. Так, например,
если х = 3, то ордината yv первого гра-
графика равна 4, ордината у2 второго графи-
графика равна 2, а ордината у графика у =
= \х + 1\ + \х — 11 равна 6.
Попробуем получить искомый график,
складывая в каждой точке (т. е. при каж-
каждом х) ординаты обоих графиков. Полу-
Получим чертеж, данный на рис. 9.
Мы видим, что графиком у = | х + 1 | +
+ \х — 11 является ломаная, составлен-
составленная из кусков трех прямых. Значит, на
каждом из трех участков функция меняет-
меняется линейно.
Упражнен и я
1.	Напишите уравнения для каждого из звеньев
ломаной
у = \х+1\ + \х-1\.
(Ответ: для д;< — 1 у = . . . х-\-. . .,
для — 1 <л:< 1 у = . . .,
для х > 1	у = . . .)
2.	В каких точках имеются изломы у лома-
ломаной, являющейся графиком функции у= \ х | -f-
-j— | jc -f— 1 I -f- I jc -j— 2 |r* Найдите уравнения каж-
каждого из звеньев.
3.	а) Функцию, график которой изображен
на рисунке 10, можно задать следующими усло-
условиями:
при лс<0 # = 0,
при х > 0 у = 2х.
Попробуйте задать эту функцию одной фор-
формулой.
б) Напишите формулы для функций, графики
которых изображены соответственно иа рис. 11
и 12. ©
4.	Постройте график функции
у=\-Ах-2\.
Указание. Получите этот график из графика
у = \х\ двумя преобразованиями: сдвигом по оси
Ох и растяжением по оси Оу. Чтобы правильно
определить величину сдвига, нужно вынести коэф-
коэффициент при х за знак модуля: | Зл: — 2| =
= 3 | лг — 2/31.
32

II
2,-рафик фя/н&и,ии-
лолу —
А -	3 "~ Т v /
оси их ил. -а е^икиц.
s" оэкагаё/Wi, тлпо если Ц>0,
1иеЬо, если а<0,
й>пр<хе>о.
2 ИМ. Гельфанд и др.

OCl
15. | Задача. Построить график
y = \2x-\\.
Решение. Получим этот график из
прямой у = 2х—1 (рис. 13). Там, где
прямая идет выше оси абсцисс, у положи-
положительно, т. е. 2х — 1 ^> 0. Значит, на этом
участке 12х — 11 = 2х — 1 и искомый
график у = 12х — 11 совпадает с графи-
графиком у = 2х — 1. Там, где 2х — 1 ¦< 0
(т. е. прямая у = 2х — 1 идет ниже
оси Ох), \2х—1 |=—Bх—1). Значит,
чтобы на этом участке из графика у =•
— 2х — 1 получить график у = | 2х— 11,
нужно у каждой точки прямой у = 2х — 1
поменять знак ординаты, т. е. отразить
эту прямую относительно оси абсцисс.
Получаем рис. 14.
Упражнение
Зная график
у = х* — 2х3 — х°- ^ 2х
(рис. 9, стр. 16), постройте график
у = | х4 — 2х3 — х* + 2х |.
A)
B)
6. Задача. Зная график
1
(рис. 15), построить график
1
а л:2-2 |л:|+2*
Решение. Так как для положи-
положительных значений аргумента \х\ = х, то
Значит, справа от нуля график B)
совпадает с графиком A) (рис. 16). Что-
Чтобы получить левую половину искомого
графика B), заметим, что функция у =»
= тг—о, 1 , о четная. Значит, левая
34

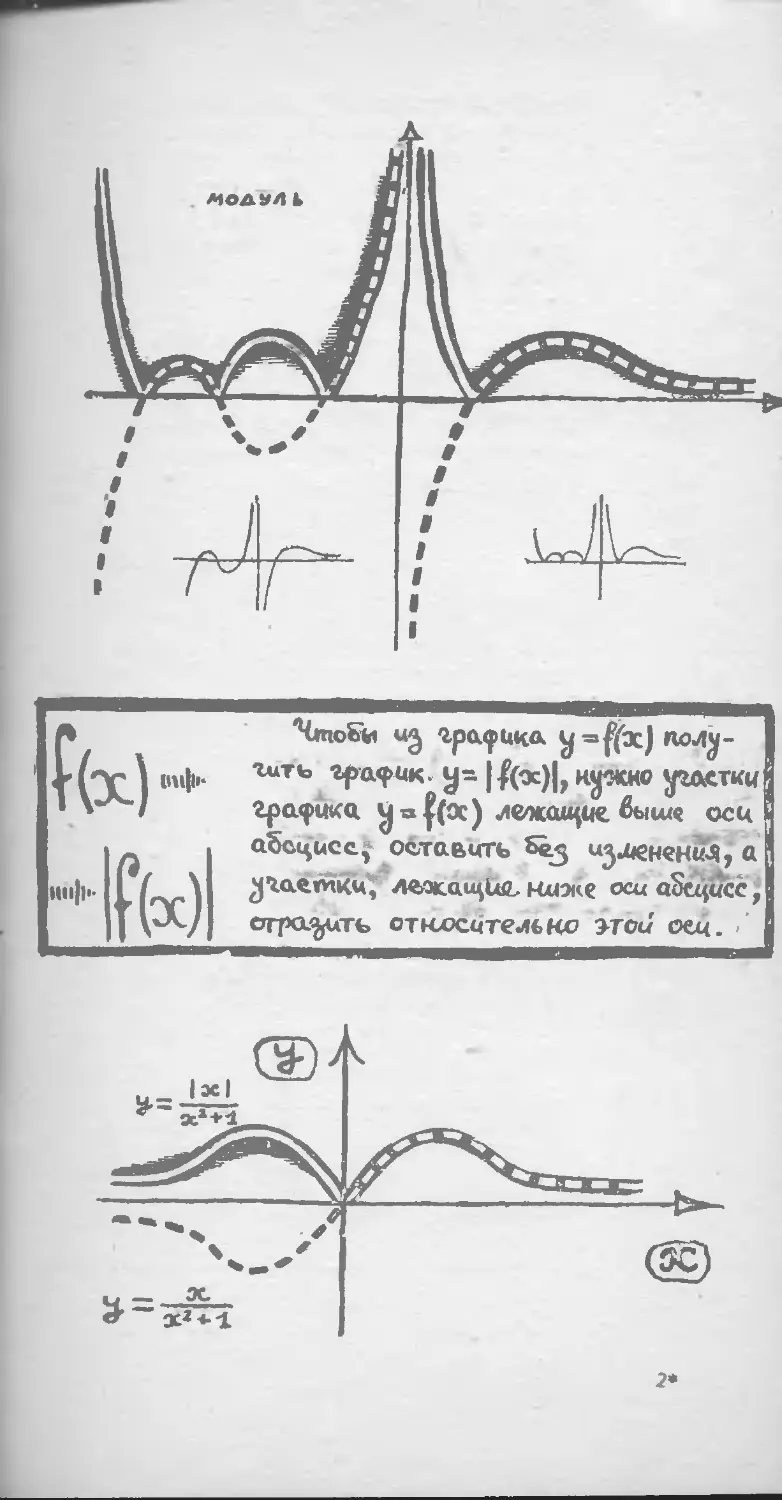
Л	"Члюйп ug графика Jf=f(bcJruMy-
U'X] im|i- гить «pa^iK. y= |#oc)|,крсно
'^/	графика ^| = f(oc) л
абсцисс* оставить
Hll||>-
wl
оси
а
оси aSti\ucc,
отюоеи'теибмо этой сек. -

- - -/
17
половина графика B) получается из его
правой половины зеркальным отражением
относительно оси ординат (рис. 17). То
же самое верно и в общем случае: чтобы
получить из графика у = / (х) график
У — f (I x\)> нужно половину первого гра-
графика, лежащую справа от оси ординат,
отразить зеркально относительно оси ор-
ординат (см. стр. 35).
Упражнения
1.	Постройте график у = 2\х] — 1.
2.	Постройте графики:
а) у = 4 — 2х\ б) у = | 4 — 2х |;
в) {, = 4-21*1; г)у = \4-2\х\\.
3.	Найдите наименьшее значение функции
В заключение этого параграфа пред-
предлагаем Вам решить несколько задач. На
первый взгляд кажется, что они совер-
совершенно не имеют никакого отношения к то-
тому, чем мы занимались в этом параграфе,
но, подумав, Вы увидите, что это не так.
Задачи*)
1. Семь спичечных коробок расположены в ряд.
В первой лежит 19 спичек, во второй 9 спичек,
в следующих соответственно 26, 8, 18, 11 п 14
спичек (рис. 18). Спички можно перекладывать
пз любой коробки в любую соседнюю с ней. Нуж-
Нужно переложить спички так, чтобы во всех короб-
коробках их стало поровну. Как это сделать, пере-
перекладывая как можно меньше спичек?
Решение. Всего во всех коробках содержит-
содержится 105 спичек. Значит, если спичек в коробках
было бы поровну, то в каждой коробке лежало
бы по 15 спичек. При таком расположении коро-
коробок задача имеет всего одно решение. Именно,
из первой коробки во вторую нужно переложить
четыре спички. После этого в первой коробке
*) Задачи 1—4 и способ их решения предложены
М. Л. Цетлиным.
36

будет 15, а во второй 13 спичек. Добавим недостаю- („.
шие две спички из третьей коробки во вторую, |г
тогда в третьей останется 24 спички. Лишние
спички из этой коробки переложим в четвертую
и т. д.
Задачи 2 и 3 несколько более трудные. Воп-
Вопрос в них ставится тот же, что и в задаче 1.
2.	На прямой расположены по-прежнему 7 ко-
коробок со спичками, но количество спичек в ко-
коробках другое. Именно, в первой лежит 1 спичка,
во второй 2, в следующих 3, 72, 32, 20, 10.
3.	Коробки со спичками расположены «со-
«собачкой» (рис. 19). Спички можно перекладывать
только по линиям (маршрутам), соединяющим
коробки.
Для следующей задачи уже полезно приме-
применить графики.
4.	На окружности расположено 7 коробок
со спичками. В первой лежит 19 спичек, во вто-
второй 9, в остальных соответственно: 26, 8,18, И, 14
спичек (рис. 20). Разрешается перекладывать
спички из любой коробки в любую из соседних
с ней. Требуется переложить спички так, чтобы
во всех коробках их стало поровну. Как это
сделать, перекладывая как можно меньше спи-
спичек? ©
C0 1/, 10 20
Рмс. TS
Рис, 2.0

§ 4. Квадратный трехчлен
11. Перейдем теперь к функции
fltt.l
Вы, конечно, строили ее график и знае-
знаете, что у этой кривой есть специальное
название — парабола. Графики функций
у = ах2 получаются из графика у = х2
растяжением и тоже называются парабо-
параболами*).
Упражнение
На рис. 1 изображена парабола, а) Известно,
что это — график функции у = х2. Определите
масштаб (масштаб по обеим осям одинаков),
б) Какую надо взять единицу масштаба по осям,
чтобы та же кривая рис. 1 служила графиком
функции у = 5л:2?
I2. Посмотрим, как будут меняться
значения функции у = л:2, если значения
аргумента меняются на одну и ту же вели-
величину, т. е. составляют арифметическую
*) Интересно, что все параболы подобны друг другу
(см. стр. 41, а также 90, задача 16 г).
38

прогрессию. Для простоты рассмотрим
положительные значения х. Например,
пусть х принимает значения:
1,2,3,4,...
Тогда у будет принимать значения
1,4,9,16,...
Вы видите, что значения у уже не об-
образуют арифметической прогрессии.
Добавим к таблице значений аргу-
аргумента и функции еще один столбец (рис. 2).
В этом столбце мы будем записывать,
на сколько меняется значение у, когда
аргумент х переходит от своего значения
к следующему. Например, пусть аргу-
аргумент меняется от значения х = 2 до зна-
значения х = 3. Тогда функция меняется
от значения у = 4 до значения у = 9.
Изменение или, как говорят, приращение
функции*) равно разности нового иста- ..
рого значения функции, т. е. 9—4 = 5.
Итак, в третьем столбце нашей табли-
таблицы мы запишем приращения функции
у = х2. Теперь ясно видно, что функция
у — х2 изменяется так, что при возра-
возрастании х возрастает не только сама функ-
функция, но и ее приращения. На графике этот
факт тоже виден: кривая у = х2 все круче 9
и круче идет вверх, в то время как гра-
график линейной функции, которая изменяет-
изменяется равномерно, идет все время под одним
и тем же углом к оси Ох (рис. 3).
Интересно заметить, что приращения ^
функции у = г2 составляет арифмети- п,
ческую прогрессию! Попробуйте доказать 2
этот факт в общем виде: если значения *
аргумента х образуют арифметическую
прогрессию
а, а + d, a + 2d,. .., а + nd,...,
то значения соответствующих приращений
*) Приращение функции у = f (х) обозначается
обычно греческой буквой А (дельта):
Ау, или Д/ (х).
•х.
А
к
f
V
i
ss
/J
ис
.3.
Oc
з Ч
39

о
У?
квадратичной функции у = х2 также
образуют арифметическую прогрессию.
Если аргумент t есть время, а функция s —
пройденный путь (мы меняем обозначения х на t и
{/ на s в соответствии с тем, как это принято в физи-
физике), то зависимость s = /2 соответствует равноуско-
равноускоренному движению (с ускорением, равным 2), а
формула s = *г + b — равномерному движению со
скоростью k. При равномерном движении за равные
промежутки времени тело проходит равные отрезки
пути, т. е. равным приращениям аргумента соответ-
соответствуют равные приращения функции (линейная
функция переводит каждую арифметическую прогрес-
прогрессию в арифметическую прогрессию). При равноуско-
равноускоренном движении отрезки пути, пройденные за рав-
равные промежутки времени, равномерно возрастают.
Соответственно этому для квадратичной функции
(кстати, не только для у = дг2, но и для любой функ-
функции у = ах2 + Ьх + с) равным приращениям ар-
аргумента соответствуют равномерно возрастающие
приращения функции.
1
О i
ис.
Упражнения
1.	Составьте таблицу с тремя столбцами (зна-
(значения аргумента, значения функции и значения
приращений функции) для трехчлена у = х2 + х —
— 3, взяв для х значения 1, 0, —1, — 2, —3. Добавь-
Добавьте к таблице еще один столбец и запишите в него
разности двух последовательных приращений.
Возьмите теперь другой трехчлен: х* + Зх + 5.
Составьте и для него такую же таблицу. Сравните
1 последние столбцы этих двух таблиц. А что получит-
получится, если взять трехчлен у = 2х2 + 3* + 5?
2.	Из рисунка 4 видно, что если взять на по-
положительной половине оси абсцисс равномерную
шкалу, то график у = дг2 переведет ее в шкалу
О, Av A2, А3 и т. д., расположенную на оси ординат,
которая уже не будет равномерной. Этой шкалой
ось ординат разбилась на отрезки OAlt -Л,^, А2А3 и
т. д. Представьте себе, что вы разрезали ось орди-
ординат на эти отрезки и поставили их вертикально один
за другим вдоль оси Ох на равных расстояниях друг
от друга (основаниями в точки 1, 2, 3 и т. д.) (рис. 5).
Как расположатся концы этих отрезков? Объясните
результат.
3.	Рассмотрим график у = дг3 для положи-
положительных значений х (рис. 6). Проделайте с ним то же
самое, что и с графиком у = х2 в упражнении 2. На-
Нарисуйте, как расположатся концы отрезков в этом
случае. Более трудный вопрос: ие можете ли Вы
подобрать уравнение кривой, на которой лежат
концы отрезков?
40

Задача. Постройте график у = х2.
Масштаб возьмите покрупней: 1 = 2 см
D клетки). Отметьте на оси Оу точку F (О,
1/4). Полоской бумаги измерьте расстояние
от точки F до какой-нибудь точки М пара-
параболы. Затем приколите полоску в точке М
и поверните ее вокруг этой точки так,
чтобы она стала вертикальной. Конец
полоски опустится немного ниже оси
абсцисс. Отметьте на полоске, насколько
она выйдет за ось абсцисс (рис. 7). Возь-
Возьмите теперь другую точку на параболе и
повторите измерение еще раз. Насколько
теперь опустился край полоски за ось
абсцисс? Результат мы вам сможем ска-
сказать заранее: какую бы точку на параболе
у = х2 Вы ни взяли, расстояние этой точки
до точки (О, V4) будет больше расстояния
от той же точки до оси абсцисс всегда на
одно и то же число — на V4.
Можно сказать иначе: расстояние от
любой точки параболы до точки (О, V4)
равно расстоянию от той же точки пара-
параболы до прямой у = — V4, параллельной
оси Ох.
Эта замечательная точка F (О, V4) на-
называется фокусом параболы у = х2, а пря-
прямая у = — V4 — директрисой этой пара-
параболы.
Директриса и фокус есть у всякой
параболы. (См. также рис. 1 на стр. 44).
13. | Рассмотрим графики квадратных
трехчленов вида
у = х% + рх + q.
Покажем, что они по форме ничем не от-
отличаются от параболы у = хг и занимают
лишь другое положение относительно ко-
координатных осей.
41

Put. 8
Рассмотрим сначала численный при-
пример. Возьмем трехчлен
3.
Чтобы получить его график, представим
его в виде у = (х + 1) 2 + 2, выделив
?», полный квадрат.
График у = (х + IJ получается из
параболы у = х2 сдвигом вдоль оси Ох.
(Объясните, почему кривая у = (х + IJ
получается из у = х2 сдвигом влево.)
Из графика у = (х + 1)г график у =
= (х + IJ + 2 получается совсем про-
просто (рис. 8).
Итак, график трехчлена у = (х+ IJ +
+ 2 = х2 + 2х + 3 получается из пара-
параболы у — х2 сдвигом влево на 1 единицу
и вверх на 2 единицы. При таком преобразо-
преобразовании вершина параболы, помещавшаяся
в точке @, 0) — начале координат, пере-
переходит в точку М с координатами (—1, 2).
Упражнение
1. Нарисуйте графики функций:
a) {/ = (x+
в) 1/ = (л:-
, б) {/ =
; г) у = (х- 2J-3.
Задача, а) Найдите наименьшее зна-
значение функции
Решение. Наименьшее значение
указанной функции — это ордината вер-
вершины параболы у = х2 + 6х + 5. Чтобы
определить координаты вершины, выде-
выделим полный квадрат:
х2 + 6х+5 = (х+3J—4.
Таким образом, наша парабола получилась
из у = хг сдвигом по Ох на —3 единицы
и на —4 по оси Оу, т. е. наименьшее зна-
значение функции равно —4.
42

б) Вершина параболы у = х2 + рх + q
лежит в точке (—1, 2). Найти р и q.
Докажем теперь," что, сдвигая пара-
параболу у = л:2, можно получить график лю-
любого квадратного трехчлена вида
у = х- + рх + q.
Для этого, как и выше, выделим полный
квадрат, т. е. представим наш. трехчлен
в виде у = (х + ...J + ..., где второе
слагаемое в скобках и свободный член
нужно подобрать не зависящими от х.
После раскрытия скобок член с первой
степенью х получается лишь в удвоенном
произведении, и так как этот член должен
быть равен рх, то второе слагаемое в скоб-
скобках нужно взять равным -|-. Таким об-
образом, мы имеем
Так как свободный член трехчлена дол-
должен быть равен q, то вместо многоточия
нужно написать q — /?2/4.
Итак, трехчлен у = х2 + рх + q мож-
можно переписать в виде
Мы видим (рис. 9), что график
представляет собой параболу у = х2, сдвину-
сдвинутую*) на — р/2 по оси Ох и на q —/?2/4 по
оси Оу.
Вершина М этой параболы имеет абс-
абсциссу хм = —р12 и ординату ум = q — /?2/4.
-\%\ о III -x
*) Сдвиг на—р/2 по оси Ov означает сдвиг вправо,
если — р/2 > 0, и сдвиг влево, если — р/2 < 0.
43

Интересные свойства параболы
1.	Любая точка параболы равноудалена от некоторой точки, назы-
называемой фокусом параболы, и некоторой прямой, называемой ее директри-
директрисой.
2.	Если вращать параболу вокруг оси ее симметрии (например, пара-
параболу у — хг вокруг оси Оу), то получается очень интересная поверхность,
которая называется параболоидом вращения.
Поверхность жидкости во вращающемся сосуде имеет форму пара-
параболоида вращения. Вы можете увидеть эту поверхность, если сильно поме-
помешаете ложечкой в неполном стакане чая, а потом вынете ложечку.
3.	Если в пустоте бросить камень под некоторым углом к горизонту,
то он полетит по параболе.
4.	Если пересечь поверхность конуса плоскостью, параллельной ка-
какой-либо одной его образующей, то в сечении получится парабола.
5.	В парках культуры устраивают иногда забавный аттракцион «Па-
«Параболоид чудес». Каждому из стоящих внутри вращающегося парабо-

\^ "**¦ ^ jjf ^
лоида кажется, что он стоит на полу, а остальные люди каким-то чудом
держатся на стенках*).
6.	В зеркальных телескопах тоже применяют параболические зер-
зеркала: свет далекой звезды, идущий параллельным пучком, упав на зеркало
телескопа, собирается в фокусе.
7.	У прожекторов зеркало обычно делается в форме параболоида.
Если поместить источник света в фокусе параболоида, то лучи, отразившись
от параболического зеркала, образуют параллельный пучок.
*) Опыты, описанные в пунктах 4 и 5, основаны на одном и том же
свойстве параболоида: если вращать параболоид с подходящей скоростью
вокруг его оси, расположенной вертикально, то равнодействующая цен-
центробежной силы и силы тяготения в любой точке параболоида направлена
перпендикулярно к его поверхности.

|4.| Взяв «за основу» график у = ах\
можно таким же образом получить график
квадратного трехчлена более общего вида
у = ахг + Ьх + с.
Разберем это на примере. Возьмем трех-
А
член у = -д- х2— Зх -\- 6. Вынесем коэффи-
коэффициент при хг за скобки:
= 4г(х* — 6х+ 12).
В выражении, стоящем в скобках,
выделим полный квадрат:
1
\
г
2
\./
-2 О
Рис '
Итак, окончательно
1	Я
Мы видим, что график у = у (х — ЗJ + -г-
получается из параболы у = -=- х2 сдвигом
Li
по оси Ох на 3 единицы вправо и по оси
Оу на 3/2 единицы вверх.
Задачи
1.	Сдвинуть параболу у = а*2 по оси Ох и
по оси О# так, чтобы поЛучить график трехчлена
у = ах% + Ьх + с.
(Ответ. Парабола у = ах2 + Ьх + с полу-
чается из параболы у == ахг сдвигом по оси абсцисс
Ь 4ас — № \
на ~~ 2а и по оси °РДинат на	4<z	' /
2.	Найти наименьшее значение функции у ¦¦
= 2х2 — 4^ + 5 на участках:
¦а) от х = 0 до х = 5 @ < х < 5),
б) от * = — 5 до х = 0 ( — 5<*<0).
Решение. Воспользуемся результатом пре-
предыдущей задачи и построим график функции у =
= 2л2 —4л- + 5 (рис. 10).
46

По рисунку видно, что при изменении х от
значения х = 0 до значения х = 5 функция у =
= 2х2 — 4л- + 5 сначала убывает (до х = 1), затем
возрастает. Таким образом, наименьшее значение
функции у = 2а-2 — 4л- + 5 на участке а) есть ее
значение при х = 1 (рис. 10, а). При изменении
х от —5 до 0 функция у = 2л-2 — 4л- + 5 все время
убывает. Значит, наименьшее значение функции
на участке б)-есть ее значение при х = 0 (рис. 10, б).
(Ответ. Наименьшее значение на участке а)
равно 3, на участке б) равно 5.)
Упражнения
1.	Нарисуйте графики следующих функций,
указав точные координаты вершины каждой из па-
парабол и координаты точек пересечения графиков
с осями координат:
а) у = х — х* — 1;
б)(/ = — За:2 — 2а-+ 1;
в) у =-- 10а-2 — 10а- + 3;
2.	График какой функции получится, если па-
параболу у = хг сначала растянуть по оси ординат в
два раза, а потом сдвинуть по той же оси на три еди-
единицы вниз? График какой функции получится,
если эти даа преобразования проделать в обрат-
обратном порядке: сначала сдвинуть параболу у = х2
на три единицы вниз, а Потом полученную кривую
растянуть в два раза вдоль оси Оу? (См. рис. 11).
3.	Насколько нужно сдвинуть параболу у —
= х2 — Зл- + 2 по оси Ох и по оси Оу так, чтобы
получилась парабола у = х2 + х + 1?
4.	Сдвиньте параболу у = л-2 вдоль оси Ох
так, чтобы она прошла через точку C,2). График
какой функции Вы при этом получите? (См. рис. 12.)
15.1 Посмотрим теперь, что можно ска-
сказать по графику функции у = х2 + рх +
+ q о решении квадратного уравнения
х2 + РХ + q = 0.
Корни этого уравнения — это те значе-
значения х, при которых значение функции
у = х2 + рх + q равно нулю. На гра-
графике эти точки имеют ординаты, равные
нулю, т. е. лежат на оси абсцисс.
Рис
47

Из графика квадратного трехчлена
у = х2 + рх + q сразу видно, что квадрат-
х ное уравнение х2 + рх + q — 0 имеет два
действительных корня, если ^- — q^>0,
и не имеет корней, если -|	q <[0.
(Вспомните, что парабола# = х2 сдвигает-
.ся вниз, если q	^-<^U, и вверх, если
д — -j->0; см. рис. 13.)
Если же -|	д = 0, то квадратное
уравнение х2 + рх + g = 0 превращает-
превращается в уравнение (х + -|г) =0. Этот случай
особенно интересен. Рассмотрим его под-
_?. робно.	«
Уравнение х — 2 = 0 имеет одно ре-
решение х = 2. Уравнение (х — 2J = О
тоже имеет лишь решение х = 2 — ведь
никакое другое число не удовлетворяет
этому уравнению.
Однако в первом случае мы говорим,
_?. что уравнение х — 2 = 0 имеет один ко-
= 0	рень, а во втором случае мы говорим, что
уравнение (х -•- 2J = 0 имеет кратный ко-
корень, или два равных корня: хг = 2 и
х2 = 2.
Рис. /3	Как же объяснить это различие?
Есть несколько способов это сделать.
Мы приведем один из них. Изменим не-
немного первое уравнение: заменим нуль в
правой части каким-нибудь маленьким
числом. Корень, конечно, изменится, но
он по-прежнему останется единственным:
уравнению по-прежнему будет удовлет-
Iворять только одно число. Например,
<х —2 = 0,01, х = 2,01.
Изменим теперь таким же образом вто-
второе уравнение:
(х— 2J = 0,01, х2 — 4х + 3,99 = 0.
Полученное уравнение теперь будет
иметь два корня: хх «2,1и х2 д& 1,9. Бу-
48

дем теперь в уравнении (х — 2J = 0,01
опять менять правую часть, заменяя ее
все меньшими и меньшими числами. До
тех пор, пока эта правая часть не будет
равна нулю, уравнение будет иметь два
различных корня. С уменьшением правой
части корни будут «сближаться», так что
их значения будут отличаться друг от
друга на все меньшую и меньшую вели-
величину. Наконец, когда правая часть станет
равной нулю, два корня «сольются» в
один — значения двух корней станут рав-
равными друг другу. Поэтому говорят, что
уравнение (х — 2J = 0 имеет два корня,
слившихся в один двукратный корень.
Геометрически случай слившихся кор-
корней соответствует касанию параболы у =
= (х — 2J с осью Ох.
Разберем теперь геометрически общий
случай квадратного трехчлена. Пусть сна-
сначала свободный член q меньше /?2/4 (т. е.
д — /?2/4 <^ 0), так что парабола у = х2 +
+ рх + q имеет две точки пересечения
с осью абсцисс (рис. 14). Будем увеличи-
увеличивать свободный член: первое время пара-
парабола, двигаясь вверх, все еще будет иметь
две точки пересечения с осью Ох (урав-
(уравнение х2 + рх + q тогда имеет два раз-
различных корня), затем эти точки пересече-
пересечения, сближаясь, в некоторый момент (ког-
(когда q — р21А = 0) сливаются в одну. В
этот момент парабола у = х2 + рх + q =|
= (х + р/2J касается оси, а уравнение .
х2 + рх + р2/4 = 0 имеет один двукрат- *'
ный корень. При дальнейшем увеличении _
свободного члена парабола перестает пе-
пересекать ось Ох, и уравнение х2 + рх +
+ q = 0 не будет иметь действительных
корней.
Упражнения
1. Найти параболу у = ахг + Ъх -\- с, которая
пересекает ось абсцисс в точках х=3 и х = — 5,
а ось Оу — в точке у = 30.
49
-з

V-Г
2) -A" "yi
а=-у
.(«.-*)!
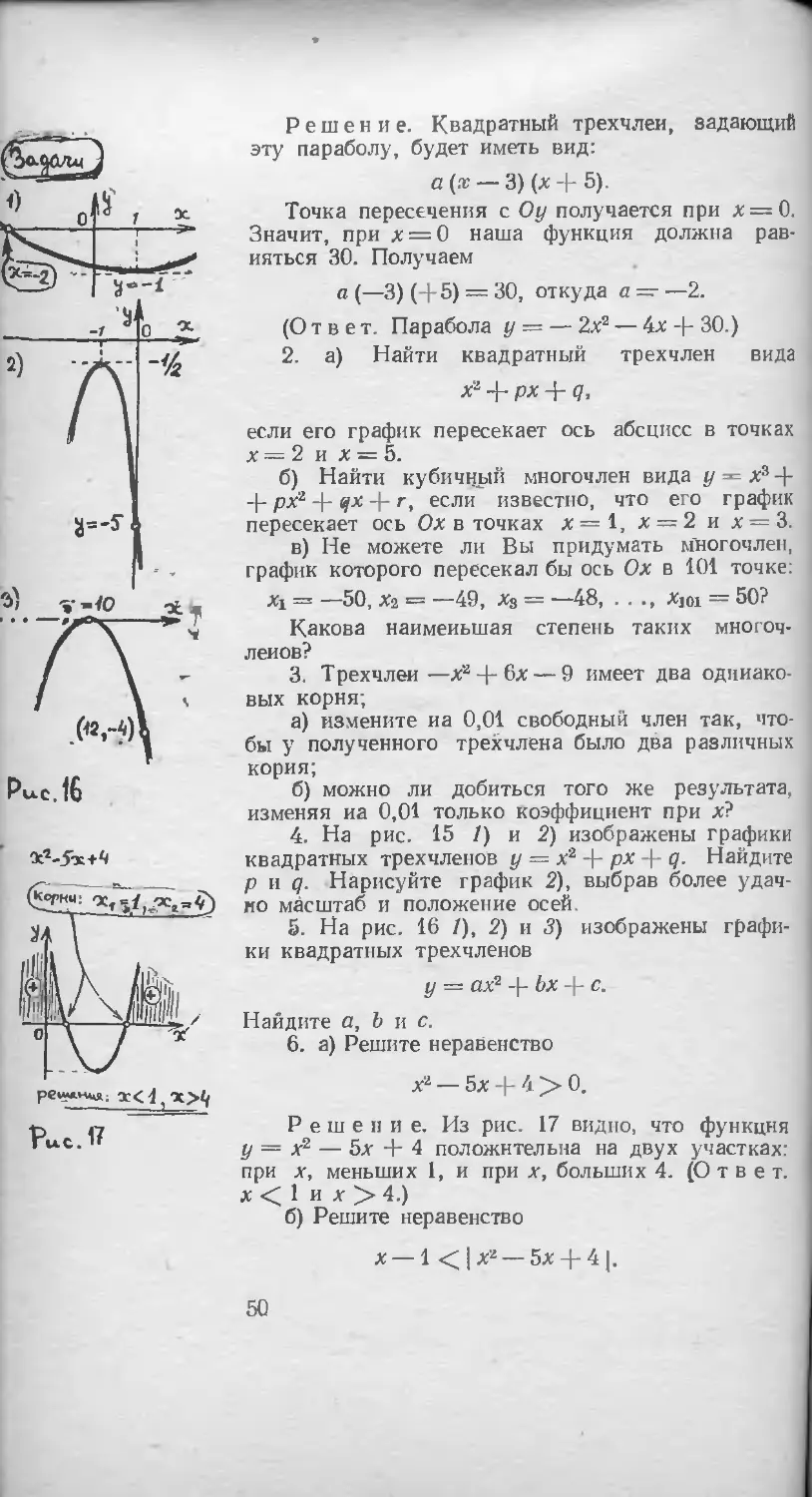
Решение. Квадратный трехчлен, задающий
эту параболу, будет иметь вид:
а(.т-3)(*+5).
Точка пересечения с Оу получается при х = 0.
Значит, при х = 0 наша функция должна рав-
равняться 30. Получаем
а(—3)(+5) = 30, откуда а ——2.
(Ответ. Парабола у = — 2х2 — 4х + 30.)
2. а) Найти квадратный трехчлен вида
если его график пересекает ось абсцисс в точках
х = 2 и х = 5.
б) Найти кубичный многочлен вида у = х3-}-
+ рх2 -\- qx-\- г, если известно, что его график
пересекает ось О* в точках # = 1, я = 2 и д;=3.
в) Не можете ли Вы придумать многочлен,
график которого пересекал бы ось Ох в 101 точке:
хх = —50, х2 = —49, л;3 = —48	хт = 50?
Какова наименьшая степень таких многоч-
многочленов?
3.	Трехчле-и —х'1 + 6х — 9 имеет два одинако-
одинаковых корня;
а)	измените иа 0,01 свободный член так, что-
чтобы у полученного трехчлена было два различных
кория;
б)	можно ли добиться того же результата,
изменяя иа 0,01 только коэффициент при х?
4.	На рис. 15 /) и 2) изображены графики
квадратных трехчленов у = х2 + рх + q. Найдите
р и q. Нарисуйте график 2), выбрав более удач-
ио масштаб и положение осей.
5.	На рис. 16 /), 2) и 3) изображены графи-
графики квадратных трехчленов
у = ах2 + Ьх + с.
Найдите а, Ъ и с.
6.	а) Решите неравенство
х2 — 5х + 4 > 0.
Решение. Из рис. 17 видно, что функция
у = хг — 5х + 4 положительна на двух участках:
при х, меньших 1, и при х, больших 4. (Ответ.
х < 1 и х > 4.)
б) Решите неравенство
х — 1<|*2
5Q

Решение. Нарисуем на одном чертеже
графики функций, стоящих в правой и левой части.
По рис. 18 видно, что прямая у = х — 1 имеет с
графиком у = \х2 — 5л- + 4| три общих точки:
A (*i, yi), В (х2, у-2.) и С (Лз, ys). Условие х — 1 <
< |лг2 — 5л- + 4| выполняется на трех участках:
х < xlt xt < х < х2, х > л-g. Значения лгг и л-3 на-
находятся из уравнения х — 1 = х2 — 5л- + 4. Зна-
Значение х2 находится из уравнения
х— 1 = — (х2 — Ьх + 4).
(Ответ, х < 1, 1 < х < 3 и х > 5, т. е.
все л-, кроме л- = 1 и 3 ^ х ^ 5.)
в) Напишите ответ для неравенств
х —
7. Найдите наибольшее значение функции
у = х2 — 5|л-| + 4 на участке от —2 до 2.
6.1 График у = х* можно также на-
нарисовать, «возводя в квадрат» график Kf
у = х, т. е. мысленно возведя в квадрат У°
значение каждой ординаты (рис. 19).
Упражнения
1. Нарисован график (рис. 20)
1	"X
put. 1Э
Нарисовать на этом же чертеже график
«/ = (х-1J.
2.	Нарисован график ^рис. 21)
У = / (*)•
Нарисовать на том же чертеже график
У = (Кх)J.
3.	Воспользовавшись графиком
y=x(x+l)(x—i)(x — 2).
(см: рис. 9 на стр. 16), нарисовать график
4.	Нарисовать графики:
:/
л
Рис'^
Mfcj
Рис.2Т

§ 5. Дробно-линейная функция
Рнс.1
¦х >о
>о
1.1 На рис. 1 изображен» «график»
функции у = \1х в том виде, как его ча-
часто рисуют люди, не искушенные в по-
построении графиков. Они рассуждают так:
«При х = 1, у = 1. При х — 2, у = 1/2.
При х = 3, у = 1/3. При х = — 1, у =
= •— 1. При х — 0,...? Неясно... Что
значит 1/0 — неизвестно, поэтому х = О
пропустим...»
Вы уже знаете из предыдущего тек-
текста, что так рисовать графики нельзя.
Чтобы представить себе правильную кар-
картину, заметим сначала, что при х = О
функция не определена. В таких случаях
интересно посмотреть, как ведет себя
функция около этой точки. Когда х,
уменьшаясь по абсолютной величине, под-
подходит к 0, то у становится по абсолютной
величине как угодно большим. При этом,
если х приближается к нулю справа
(х > 0), то у = 1/х тоже положителен.
Поэтому при приближении к нулю спра-
справа кривая графика поднимается вверх
(рис. 2, а). Если же х приближается к ну-
52

лю слева (х <^ 0), то у отрицателен, поэто-
поэтому слева график спускается вниз (рис. 2,6).
Теперь ясно, что около «запрещенного»
значения х = О график, разорвавшись на
две ветви, расходится вдоль оси Оу:
правая ветвь идет вверх, а левая вниз
(рис. 3).
Посмотрим теперь, как ведет себя функ-
функция, если х увеличивается по абсолютной
величине. Сначала рассмотрим правую
ветвь, т. е. значения х ^> 0. При положи-
положительном х значения функции у тоже поло-
положительны. Значит, вся правая ветвь рас-
расположена выше оси абсцисс. При увели-
увеличении х дробь 1/х уменьшается. Поэтому
при движении от нуля вправо кривая
у = 1/х опускается все ниже и ниже,
причем она может подойти к оси Ох на
как угодно маленькое расстояние (рис.
4, а). Для х <[ 0 получается- аналогичная
картина (рис. 4, б).
Таким образом, при неограниченном
увеличении х по абсолютной величине
функция у = 1/х неограниченно умень-
уменьшается по абсолютной величине и обе ветви
^*7/S)
графика приближаются к оси абсцисс:
правая сверху, левая снизу (рис. 5).
Кривая, являющаяся графиком у =
= 1/х, называется гиперболой. Прямые, к
з тс
Рис. 5
53

A
i
i
i
i
i
i
i
i
i
i
I
I
I
I
r
I
I
I
I
4
i
i *>
I
I
I

II
-i- .
fl
I
I
I
I
-i
в
II
Л
ЭС

/
¦и I
'1 i
* J
} »
которым приближаются ветви гиперболы,
называются ее асимптотами.
12. | Можно построить график у = 1/х
несколько иначе.
Нарисуем график функции у ~ х
(рис. 6, с). Заменим каждую ординату ве-
величиной, ей обратной, и нарисуем соот-
соответствующие точ"ки на рис. 6, б. Полу-
Получим график у = 1/х.
Нарисованная картина наглядно пока-
показывает, как маленькие ординаты первого
графика превращаются в большие орди-
ординаты второго и, наоборот, — большие ор-
ординаты первого в маленькие ординаты
второго.
Этот прием «деления» графиков бывает
полезен всегда, когда мы умеем строить
график у = f (x), а нам нужно построить
график функции у = ,. (см. стр. 54—55).
Упражнения
1.	Зная график у = )Р, построить график у =
= 1/х\ (Решение на рис. 7.)
2.	Построить графики:
(Вы увидите, что эти два графика выглядят со-
совершенно по-разному).
3. Зиая графики у = [х] (см. стр. 9)яу = х —
— [х], построить графики:
1
[*]
б) v= -jzr
13. Кривые, которые Вы будете строить
в следующих упражнениях, получаются
из гиперболы у = \'х известными Вам пре-
преобразованиями. Все они тоже называют-
называются гиперболами.
56

Упражнения
1. Нарисуйте графики функций:
Укажите, какие асимптоты имеет каждая из
этих гипербол.
2. а) Докажите, что прямые у = х и у = — х
являются осями симметрии гиперболы у = 1/х.
б) Имеет ли ось симметрии правая ветвь
графика у = 1/х2? ф
3. Зная график у = 1/х, постройте график
у = 4/jc. Имеет ли эта кривая оси симметрии?
Графики функций вида
0
получаются из графика у = 1/х сдвигом по
оси Ох и растяжением по оси Оу. Чтобы
правильно определить величину сдвига и
коэффициент растяжения, нужно числи-
числитель и знаменатель дроби поделить на
с— коэффициент при х\
Ъ	Цс
cx + d
+ d/c'
1
Зх + 2 "
Проделаем это на примере у ¦¦
Имеем:
1 _ 1/3
Зх + 2 ~~ х + 2/3 '
Теперь видно, что график нашей функции
и = ———=- это график — , сдвинутый по
си Ол; на (—2/з)*) и сжатый по оси Оу
i грое (рис. 8).
у J_
')А не иа (—2), как часто необдуманно говорят
ученики!
57

Интересные 'свойства гиперболы
1.	Гипербола есть геометрическое место точек М, разность расстоя-
расстояний кото'рых до двух заданных точек Fx и Fit называемых фокусами, по
абсолютной величине равна заданному числу.
2.	Комета или метеорит, залетевшие издалека в солнечную систему,
движутся по ветви гиперболы. В фокусе находится Солнце. Одна асимп-
асимптота*) дает направление, в котором комета прилетает, вторая — направ-
направление, в котором она покидает солнечную систему.
3.	При бомбардировке атомного ядра а-частица, пролетающая мимо
ядра, движется по гиперболе.
*) У всякой гиперболы есть две асимптоты. У гипербол, являющихся
графиками дробно-линейных функций у = —'	, асимптоты взаимно
перпендикулярны. У других гипербол асимптоты бывают расположены
под ApyrviM углом.

JAMU	Ш
me. xmtefa A?n
../^//¦*ii
4.	Если вращать гиперболу вокруг ее оси симметрии, не пересекаю-
пересекающей ее ветвей, то получится поверхность, называемая однополостным ги-
гиперболоидом. Эта поверхность обладает удивительным свойством; она «со-
«соткана» из прямых линий. Ажурная мачта московского телецентра составле-
составлена из «кусков» таких гиперболоидов, целиком сделанных из прямых сталь-
стальных стержней.
5.	Если вращать гиперболу вокруг другой оси симметрии, то полу-
получается поверхность, состоящая из двух «кусков» — двуполоспгный гипер-
гиперболоид. Именно его имел в виду А. Толстой в своем романе «Гиперболоид
инженера Гарина». Впрочем, нужным инженеру Гарину свойством — со-
собирать лучи в параллельный пучок — обладает на самом деле не гипер-
гиперболоид, а параболоид. Так что правильней было бы назвать книгу «Пара-
«Параболоид инженера Гарина».
6.	Если подходящим образом пересечь бесконечный конус плоскостью,
то в сечении получится гипербола. Если у Вас есть лампа с круглым аба-
абажуром, Вы можете в этом убедиться. Лампа освещает часть стены, ограни-
ограниченную куском гиперболы.

Упражнение
Нарисуйте график
1
(Указание. Дробь ^ZTx преобразуйте, как ска
заио выше: поделите числитель и знаменатель
на коэффициент при х, т. е. на (—1). Получится
4. | Графики функций вида
^= cx + d '
называемых дробно-линейными, по форме
не отличаются от графика у = Их. Мы
предполагаем, конечно, что с =(= О (иначе
получится линейная функция у = ~ х -f- ~
и что ale =f= bid, т. е. числитель не есть
кратное знаменателя (как у функции
4х + 6 \	, v
у = 2 4-з ) ' иначе функция постоянна
Докажем это. Рассмотрим сначала при-
2х I I
мер: у = ^_ 3 . Выделим «целую часть»
у
'"j t-з дроби, разделив числитель на знаменатель
SjyH. 2"} (Рис- 9). Мы получим
9 _
х — 3 —J+ jc_3 "
Теперь видно, что график этой функ
ции получается из графика у = 1/х сле>
дующими преобразованиями: сдвигом на
3 единицы вправо, растяжением в 7 раз
вдоль оси Оу и сдвигом на 2 единицы вверх.
Любую дробь у = aX]~d- можно запи-
записать аналогичным образом, выделив
60

«целую часть». Следовательно, графики
всех дробно-линейных функций
У~ cx + d
есть гиперболы (различным образом сдви-
сдвинутые вдоль координатных осей и растя-
растянутые по оси Оу).
Замечание. Для построения гра-
графика какой-нибудь дробно-линейной
функции не обязательно преобразовывать
дробь, задающую эту функцию. Посколь-
Поскольку мы знаем, что график есть гипербола,
достаточно найти прямые, к которым при-
приближаются ее ветви (асимптоты гипербо-
гиперболы), и еще несколько точек.
Пример. Построим график функции
_ 3* + 5	У
у- 2*+2 •	•
и
Найдем сначала асимптоты этой ги-
гиперболы. Функция не определена там,
где2х Ч- 2 = 0, т. е. при х = —1 (рис.10).
Стало быть, вертикальной асимптотой слу- ^~i'°); ° <х
жит прямая х = — 1.	р .«
Чтобы найти горизонтальную асимпто-	ис'
ту, посмотрим, к чему приближаются зна-
значения функции, когда аргумент возра-
возрастает по абсолютной величине. Для боль- "
ших (по абсолютной величине) значений х
_ Зх + 5 _ 3* _ _3_	ft v
У ~ 2х + 2 ~ 2х ~ 2 "	| I
Стало быть, горизонтальная асимптота —	''
прямая у — 3/2.	__ . ,'
Определим точки пересечения нашей
гиперболы с осями координат. При х — О
имеем у = 6/2. Функция равна нулю,
когда Зх + 5 = 0, т. е. при х = —6/3.
Отметив на чертеже точки (—6/3, 0)
И @| %). построим график (рис. И).
61
^

Упражнения
1. Постройте графики функций:
Л	О I
2*+ 11
х+1\
2. На рис. 12, а и б изображены графики
дробно-линейных функций
px+q
у— х+г •
Найдите эти функции (т. е. определите р, q и г).
3. а) Сколько решений имеет уравнение
1-х л '
Решение. Построим на одном чертеже
графики функций
У= tlx и у = х*
На рис. 13 видны две точки пересечения этих
графиков. Ясно, что есть и третья точка, так как
парабола пересекает асимптоту гиперболы. Абс-
Абсциссы точек пересечения графиков и являются ре-
решениями уравнения.
(Ответ. Три решения.)

§ 6. Степенные функции
11.1 Степенные функции — это функ-
функции вида у = х". Графики степенных
функций для первых двух натуральных
значений.показателя п (п = 1 и п = 2) мы
уже строили. При п = 1 получаем функ-
функцию у = х; график этой функции — пря-
прямая (рис. 1, а). При п = 2 получается
функция у = х2; график этой функции — г
парабола (рис. 1, б).
График функции у — х3 (п = 3) тоже .
называется параболой — параболой тре- „
тьего порядка, или кубической параболой.. ^\
Для положительных значений аргумента Ъ)
кубическая парабола у = х3 похожа на
параболу второго порядка у = х2. Дейст-
Действительно, при х = 0 функция у = х2 рав-
равна нулю, и функция у = л;3 тоже равна
нулю — оба графика проходят через нача-
начало координат; при х = 1 значение х1 равно
1 и х3 тоже равен 1 — оба графика про-,
ходят через точку A,1).
С увеличением х (если х положителен)
увеличиваются и значения функции у =¦
= х2 и значения функции у = х9, куби-
кубическая парабола у = х3, как и обычная
63
Рис 1

парабола у = х2, справа от начала коор-
координат все время поднимается вверх (рис. 2).
Для отрицательных значений х кри-
кривая у = xs ведет себя иначе, чем кривая
у = х2: при отрицательных х значе-
значения х3 тоже отрицательны, поэтому кри-
кривая уходит вниз (см. рис. 2). Таким обра-
образом, в целом кубическая парабола совсем
непохожа на квадратную.
Левую половину графика у = х3 мож-
можно получить из правой его половины с
помощью симметрии, правда, другого ро-
рода, чем та, которую мы рассматривали
на стр. 12—14. Возьмем какую-нибудь
точку М на правой половине графика
у = х3 (рис. 3). Если а — абсцисса этой
точки, то ее ордината Ь равна as (b =
— f (a) = as). Найдем теперь точку гра-
= - Ч(а) фика, соответствующую противополож-
противоположному значению абсциссы, х — — а. Ор-
Ордината такой точки равна (—аK, т. е.— а3,
или —Ъ. Итак, для каждой точки
М (а, Ь) на правой половине графика у=х*
на левой его половине найдется точка М'
(—а, —Ь). Очевидно (см. рис. 3), точка М'
симметрична точке М относительно на-
начала координат. Значит, всю'левую поло-
половину графика можно получить из правой
симметричным отражением относительно
начала координат.
рис. 2
Рис 3
Упражнения
1.	Какие из графиков следующих функций
имеют центр симметрии, какие ось симметрии:
у = я4; у = хъ\ у = х7; у = я16?
2.	Докажите, что график функции у = 1/д5
симметричен относительно начала координат.
Решение. Рассмотрим две точки кривой
у = 1/х3 с абсциссами х = а к х = — а. Ордината
первой равна 1/а3, ордината второй 1/(—аK = —1/а3.
Значит, для каждой точки М (а, 1/а3) нашей
кривой найдется точка Mi (—а, —1/а3), симметрич-
симметричная первой относительно начала координат. Следо-
Следовательно, вся кривая у = 1/л-3 симметрична отно-
относительно начала координат.
64

3. Какие из следующих функций являются чет-
четными и какие нечетными*):
X
у = х3 | х |; у = | х31 + х; j/ = у^
{/ = | х — х-1; у = Bа; + 1)' + Bх —
I 2x + x21
1
1
J/ =
12. | Посмотрим теперь, чем отличаются
друг от друга графики у = хъ и у = х2
для положительных значений х. Для этого
представим х3 как х2-х и получим гра-
график у = х3, «умножая» график у = х2
на график у = х (рис. 4).
При х = 1 значение х3 равно значе-
значению х2: точка A,1) — общая для обоих
графиков. Пойдем теперь от этой точки
направо и налево.
Справа от точки A,1) значения функ-
функции у = х3 получаются из значений
функции у == х2 умножением на числа,
большие единицы. Поэтому для х ]> 1
значения х3 больше, чем х2 — справа от
точки A,1) кубическая парабола у = х3
идет выше параболы у = х2, все больше
и больше ее обгоняя (так как приходится
умножать х2 на все большие и большие
числа).
Если пойти от точки A,1) налево, к
х — 0, то значения х3 будут получаться
из значений х2 умножением на число,
меньшее единицы. Поэтому слева от точ-
ки A,1) кубическая парабола лежит ниже
параболы у — х2, еще более тесно приле-
гая в начале координат к оси абсцисс
(рис. 5).
*) Определение четной функции — на стр. 13, опре-
определение нечетной — на стр. 71.
3 И. М Гельфанд и др.	^
\
4,1)
	^м.

Вопросы
= X3- ЭС2
I ¦
I-
I-
При каком х значение х3 будет больше, чем
значение х2 в 100 раз? в 1000 раз? На сколько выше
окажется при этих х кубическая парабола, чем квад-
квадратная? Поднимется ли при каком-нибудь х ку-
кубическая парабола выше, чем квадратная на 100
единиц? на 1 000 000?
Если считать, что толщина карандашной линии
равна 0,1 мм и принять за единицу масштаба 1 см,
то при х = 0,1 парабола у — х2 на глаз сливается
с осью Ох. Во сколько раз ближе к оси Ох находится
при этом значении х кубическая парабола?
-1
(ос>д)
<X
13.1 Получая x3 из х2 умножением на
x, мы видим, во сколько раз ордината
у •= х3 больше (или меньше), чем ордината
у — х2. Постараемся теперь наглядно
изобразить, на сколько значения функции
у = х3 больше (или меньше), чем значе-
значения у =* х2. Для этого нарисуем график
функции у — х3 — х2, ординаты которого
можно получить, вычитая из ординат
^Г графика у = х3 ординаты графика у = хг
(рис. 6).
При х = 0 и х3 и х2 обращаются в
нуль, значит, график функции у = х3 —хг
проходит через начало координат. Сле-
Слева от начала координат из отрицательного
^ х3 вычитается положительный х2; раз-
гщ.7 ность х3 — х2 отрицательна, так что гра-
график у = х3 — х2 идет ниже оси Ох
(и даже ниже, чем график у = Xs; см.
рис. 7).
Справа от начала координат дело
.;"	сложнее: обе функции положительны, и
результат зависит от того, что больше по
* абсолютной величине: х3 или х2. Сначала
х2 больше, чем х3; поэтому кривая у =
= л:3 — х2 около начала координат рас-
расположена ниже оси Ох (рис. 8). Посте-
Постепенно х3 начинает расти все быстрее и к
х =* 1 догоняет по своему значению функ-
функцию у = х2. Поэтому кривая у = х3 — х2,
где-то между х = 0 и х = 1 начинает
рис.
66

подниматься и при х — 1 пересекает ось
абсцисс (рис. 9).
В дальнейшем, после х = 1 значения
функции у — х3 — х2 увеличиваются, гра-
график идет вверх и для больших х, когда х2
по сравнению с х3 мал, по форме почти не
отличается от графика у — х3 (рис. 10).
Упражнения
1.	Рассматривая значения функции у — х3 —х2,
можно приблизительно определить, при каком х эти
значения начинают увеличиваться. Попробуйте
найти это значение, хотя бы с точностью до 0,1
(т. е. один знак после запятой). Мы потом сможем
найти это значение точно. Как раз на этом месте и
находится нижнят точка «впадины» графика.
2.	Решите неравенства:
х3 — л:2>0, х3 — *2<0.
Сравним теперь поведение функции
у — х3 и у = сх2 и построим график
функции у = Xs — сх2. Возьмем сначала
маленькое значение с, например, с = 0,3.
Вид графика зависит от того, как распо-
расположены друг относительно друга два гра-
графика у = х3 и у = 0,3л:2. На рис. 11 легко
понять, что построение графика вдали от
начала координат, т. е. для значений х,
больших по абсолютной величине, не вы-
вызовет затруднений. Однако на рисунке не
разглядишь, как расположены графики
у = х3 и у = 0,Зх2 вблизи начала коор-
координат: какая из этих парабол лежит ни-
ниже, а ведь от этого зависит, будет ли на
результирующем графике впадина или
не будет.
Чтобы уточнить этот вопрос, решим
неравенство:
х3 > 0,3л:2, или х2(х — 0,3) >0.
Теперь ясно, что вблизи начала коор-
координат, а именно для положительных
значений х, меньших 0,3, кубическая
рис. 9
-1
Рис
Pvt.11
»• 67

парабола лежит ниже параболы t/ = 0,3 л:2
(см. рис. 12, а). Поэтому мы можем теперь
нарисовать неясное нам ранее место
рис. 11 в увеличенном виде и построить
график разности у = х3 — 0,Зх2.
На этом графике, как и на графике у —
= х3 — х2, будет впадина, только более
узкая (рис. 12, б).
Упражнения
1) Найдите ширину «впадины» для графиков
функции:
Рис. М
РИС13 а,
# a) j/ = x3 —
б) у = х3 — ЮООх2.
2)	Будет ли впадина на графике
у = х3 + 0,001л;2?
3)	Укажите, после какого х парабола у = х2 бу-
будет лежать выше параболы у = 5Qv2; параболы
у = 10 000 л-2.
Проделав эти упражнения, Вы пой-
поймете, что графики функций у = х3 — схг
при любом с ^> 0 имеют один и тот же
характер, одну и ту же форму: слева от
начала координат график идет вниз, в
начале координат касается оси абсцисс,
далее заворачивает опять вниз, а потом
вверх; впадина, получающаяся при этом
на графике, тем больше, чем больше с
(рис. 13, а).
Если мы будем постепенно уменьшать
с, то впадина постепенно заравнивается
и в конце концов, когда с станет равным
нулю, заровняется совсем, и график пре-
превратится в обычную кубическую параболу
у = х3 (рис. 13, б).
4. Теперь мы можем сделать общий
вывод относительно того, как ведет себя
функция у = х3 для положительных зна-
значений х по сравнению с любой функцией
вида у =* сх2. Для х, близких к нулю,
68

функция у = хэ будет меньше любой
функции у = сх2, даже если коэффициент
с будет очень мал. Для больших значе-
значений х, напротив, функция у = Xs будет
больше, чем всякая функция вида у = сх2,
даже если коэффициент с очень велик.
Можно сказать иначе: парабола третье-
третьего порядка в начале координат прилегает
к оси абсцисс настолько тесно, что между
параболой и осью не может пройти не
только ни одна прямая, но и ни одна пара-
парабола' у = сх2, каким бы малым ни был
коэффициент с. Наоборот, при больших
значениях х (для х > 0) парабола у =
= х3 «перегоняет» любую параболу у =
= сх2 с любым (даже очень большим)
коэффициентом с.
Упражнения
1. Нарисуйте графики функций:
у — 1 4- х3;
у = х3 + Зх2 + Зх.
2. На рис. 14 изображены параболы у = 5дг8 и
у = л-2; из-за небольшого масштаба рисунка не
ясно взаимное расположение графиков около нуля.
Посмотрите на этот чертеж под «микроскопом»
и нарисуйте, что Вы там увидите: область, отмечен-
отмеченную маленьким кружочком, нарисуйте в увеличе i-
ном масштабе.
3. Докажите, что график функции у = х3 +
+ ах2 + Ьх + с всегда имеет центр -симметрии.
|5.1 Функции у = хп прил^>3 мы не
будем разбирать столь подробно, как
у = х3. Графики этих функций по внешне-
внешнему виду напоминают либо параболу
у = х2 (при п четном), либо параболу
у = х3 (при п нечетном).
¦х
ь_
РИС. 13
\ 31
4'

рис. is
16
Понятно, что функция у =¦ х* для
больших (по абсолютной величине) зна-
;Эс» чений х растет еще быстрей, чем у = х3,
хг а функция у =* хъ — быстрей, чем у = х4.
Вообще, чем больше п, тем быстрее растет
степенная функция у = х" для больших
значений х (рис. 15).
Когда х приближается к нулю, значе-
значения всех степенных функций у = хп тоже
приближаются к нулю, причем тем бы-
быстрее, чем больше п. Графики всех сте-
степенных функций у — хп (начиная с п = 2)
касаются в начале координат оси абс-
абсцисс, прилегая к ней тем тесней, чем боль-
больше п (рис. 16).
При большом п график функции у = хп нари-
нарисовать с соблюдением масштаба практически не-
невозможно. Почти на всем отрезке от 0 до 1 зна-
значения функции очень малы и график у = хп сольет-
сольется с осью Ох. На маленьком участке около х = 1
функция подрастает до 1 и затем быстро вырас-
¦** тает настолько, что график выходит за пределы
любого листа бумаги *). Пусть, например, п = 100.
Попробуем нарисовать график у = я100, начиная
от х = 1. При л; = 2 получим у = 2100. Это слиш-
слишком много! Возьмем ж = 1,1. Тогда у = A,1I™.
Это все еще большое число. В самом деле: A,1I00 =
= ИМI0]10.
Воспользуемся теперь неравенством A + а)п >
> 1 + па (справедливым при а>0)**). Мы полу-
получим A,1I0 > 1 + 10 • 0,1 = 2. Итак, A,1 )и» >
>210>1000.
Таким образом, участок от 1 до 1,1 все еще слиш-
слишком велик для построения графика у = х1т. Только
на участке длиной в одну-две сотых значения функ-
функции отличаются друг от друга не слишком сильно.
Выберем теперь масштаб по оси Ох в 100 раз
больше, чем по оси Оу. График у = дг100 растянется
*) Для отрицательных значений х все обстоит анало-
аналогично.
¦*) A + а)" = A + а) A + а). . .A + а) =-
= 1-1. ..1+1-1. ..1-а + 1 - 1 . . . 1 ¦ а +
п	Я—1	п—1
+ . .. -J- 1 ¦ 1. .. 1 ¦ а +...= 1+па + .
П— 1
Обозначенные через ... невыписанные члены все по-
положительны.
70

= - f (а). Zpcxpuu нечеткой

0,999
р*...
при этом в горизонтальном направлении в 100 раз
и будет иметь вид, изображенный на рис. 17,а.
Если п еще больше, то участок для аккуратного
построения графика придется выбирать еще мень-
меньшим. На рис. 17, б Вы видите графику = д1иои, рас-
растянутый в 1000 раз по оси Ох. Замечательно, что
получились две одинаковые кривые! *).
Упражнения
1.	Постройте график функции
у = х2 — х*
двумя способами:
а} вычитанием графиков у = х'2 и у = х*\
б) разложив многочлен jfl — *4 на множители.
2.	а) Даны две возрастающие последователь-
последовательности
ап: 0,001; 0,004; 0,009; .
Ьп: 100; 300; 500; . . .
Может ли первая последовательность перегнать вто-
вторую (т. е. может ли при каком-нибудь п выполняться
неравенство ап > Ьп)?
б) Ответьте на этот же вопрос для последова-
последовательностей
ап; 0,001; 0,008; 0,027; ....
Ьп: 100; 400; 900; ...
3.	Определите, сколько решений имеют следую-
следующие уравнения:
а) Xs = хг + 1; б) Xs = х + 1;
в) Xs + 0,1 = Юх; г) хь — х — 1 =i 0.
4.	а) Нарисуйте графики функций
у = Xs — х; у = х3 + х.
б) Подберите а и Ъ так, чтобы на графике функ-
функции ;/ = ах3 + Ъх была впадина шириной в 10 и
глубиной не меньше 100.
|б. I Говоря о поведении степенных
функций у = хп для малых значений ар-
аргумента х, мы отмечали, что графики этих
функций в начале координат касаются оси
Ох. Остановимся на этом вопросе, чтобы
уточнить смысл выражения: прямая ка-
касается кривой.
В самом деле, почему мы говорим, что
ось Ох касается и параболы у = х2 и
*) Разница между кривыми, конечно, есть, но она
слишком мала, чтобы ее можно было заметить на
графике.
72

кубической параболы у =х3 (хотя пара-
параболу у =х3 ось Ох «протыкает насквозь»
(см. рис. 18)?
Все зависит от того, какой смысл при-
придать выражению «прямая касается кри-
кривой», что считать основным, определяю-
определяющим свойством касательной, какое дать
определение этому понятию. До сих пор
в курсе школьной геометрии мы знакоми-
знакомились только с одной-единственной кривой
— с окружностью и знали только опре-
определение касательной к окружности.
Попробуем понять, чем отличается ка-
касательная к окружности от секущей. Нам
сразу бросаются в глаза два следующих
обстоятельства: 1) касательная имеет с ок-
окружностью только одну общую точку,
а секущая—две (рис. 19); 2) касатель-
касательная около точки касания М «прилегает»
к кривой ближе, чем секущая. (Поэтому
даже если на чертеже поместилась не вся
окружность, и мы не видим, есть ли на
самом деле вторая общая точка, мы можем
отличить касательную от секущей; рис. 20.)
Какое же из этих двух обстоятельств
считать более важным (главным), какое
следует положить в основу определения
касательной к кривой вообще (а не только
к окружности)?
Более простым является первое. Мож-
Можно попробовать назвать касательной ¦ пря-
прямую, имеющую с кривой только одну об-
общую точку. Однако, приняв такое опре-
определение, мы будем часто приходить в про-
противоречие со здравым смыслом и с нашим
наглядным представлением о касательной.
Например, через вершину параболы
у = х2, кроме оси абсцисс, проходит еще
одна прямая, имеющая с параболой толь-
только одну общую точку — это ось Оу; одна-
однако ось Оу не называется касательной к
параболе у =xz (см. рис. 18).
На рис. 21 положение еще хуже: все
прямые, лежащие внутри угла АОВ,
Рис. 20
Put. 41
73

Рис.23
• рис.25"
пересекают кривую только один раз! С дру-
другой стороны, на рис. 22 прямая АВ имеет
с кривой две общие точки, но, очевидно,
в имеет полное право называться каса-
касательной. Действительно, если «обрезав»
чертеж, посмотреть, на участок кривой
вблизи точки касания О, то расположение
кривой и прямой будет по своему харак-
характеру совершенно таким, как расположение
параболы относительно оси Ох (рис. 23).
Значит, в качестве основного, опреде-
определяющего свойства разумно выбрать то, что
касательная тесно прилегает к кривой.
Так, например, естественно считать, чт(
кубическая парабола у = Xs касается в на-
начале координат оси Ох: парабола у =xs в
начале координат тесно прилегает к оси
Ох (еще тесней, чем парабола у =хг).
Чтобы дать определение касательной,
нам осталось сформулировать, что зна-
значит прямая «тесно прилегает» к кри-
кривой. Рассмотрим снова параболу у =х2.
Между осью Ох (прямой у =0) и пара-
параболой не может пройти ни одна прямая:
всякая прямая у —kx (при /г>0) на не-
некотором участке идет выше параболы и
пересекает ее еще один раз.
Если, поворачивая прямую, умень-
уменьшать k, то вторая точка (точка М на
рис. 24) приближается к первой (к точ-
точке О) и в конце концов сливается с ней.
В этот момент прямая из секущей пре-
превращается в касательную.
То же самое можно увидеть в любом
случае касания. На рис. 25 через точку
М окружности проведена секущая МК-
Если точку К приближать к М, то секу-
секущая поворачивается вокруг точки М и,
в конце концов, когда точка К сольется с
точкой М, превращается в касательную
к окружности в точке М. При этом она
других общих точек с окружностью иметь
не будет. Но это обстоятельство явля-
является несущественным, второстепенным.
74

Итак, мы примем следующее опреде-
определение касательной.
Определение. Пусть имеется
некоторая кривая (L) и точка М на этой
кривой (рис. 26). Проведем через точку
М и еще какую-нибудь точку К кривой
(L) прямую МК (такая прямая, прохо-
проходящая через какие-нибудь две точки кри-
кривой, называется секущей; она может пере-
пересечь кривую и еще в каких-нибудь точ-
точках). Если теперь двигать точку К по
кривой (L) так, чтобы она приближалась
к точке М, то секущая МК будет повора-
поворачиваться вокруг точки М. Если в конце
концов, когда точка К сольется с точкой
М, прямая совпадает с некоторой опре-
определенной прямой MN (см. рис. 26), то
эта прямая MN и называется касательной
к. кривой (L) в точке М.
Итак, существенным отличием прямой,
касающейся некоторой кривой в точке
М, от других прямых, проходящих через
ту же точку, является то, что для каса-
касательной общая ее точка с кривой —
точка касания является двойной, полу-
получается как результат слияния двух сбли- о
жающихся точек пересечения.
Иногда в точке касания сливаются не
две точки, а три (рис. 27).
Замечание 1. В определении ни-
ничего не говорится о числе общих точек кри-
кривой и касательной к ней. Это число мо-
может быть любым. На рис. 28, а вы вндите
прямую, касающуюся кривой (Г) в точ-
точке М и пересекающую ее еще в двух точ-
точках, а на рис. 28, б прямую MN, которая
касается кривой сразу в нескольких
точках.
Замечание 2. В определении ка-
касательной предполагается, что точка К
может приближаться к точке М лю-
любым способом. Во всех случаях секущая
должна стремиться к одной и той же пря-
прямой, которая и называется касательной.
TS
рис.

Если при различных способах приближе-
приближения К к М секущая стремится к разным
прямым, то говорят, что кривая в этой
точке не имеет касательной (например,
график функции у — \х\ в точке @, 0)
не имеет касательной; см. рис. 29).
Упражнения
РИГ 9 Я
rnv,.,cj	| Найти касательную в точке О @, 0) к пара
боле у = х2 + х.
Решение. Возьмем на параболе некоторую
точку М с координатами (а, Ь). Очевидно, Ъ = а2 +
+ а. Проведем прямую через точки О и М.
Уравнение этой прямой имеет вид у = kx.
При х = а имеем у = а2 + а, значит, k = а + 1, и
уравнение секущей есть у = (а + 1) х. Будем теперь
приближать точку М (а, Ь) к точке О @, 0). Когда
точка М сольется с точкой О, ее абсцисса а обратится
в нуль, а секущая у = A + а) х превратится в каса-
касательную у = х.
Ответ. Уравнение касательной у = х.
2.	Найдите касательную к параболе у = дг2 +
+ х в точке А A, 2). ф
3.	Какая из прямых, параллельных прямой # =
= х, касается параболы у = — х2 + 1? ©
4.	а) Докажите, что прямая у = 0 есть каса-
касательная к кривой у = х3 + х2 в начале координат.
б) Найти касательную в точке О @, 0) к кривой
у = х9 — 2х.
5.	Для каких кубических многочленов у =
= ах3 + fcjr3 + сх ось Ох служит касательной в
начале координат?

§ 7. Рациональные функции
1 1. (Рациональныефункции—это функ-
функции, которые можно представить в виде
частного двух многочленов.
Примеры рациональных функций:
у—
у—
(х—
*).
Разобранная в § 5 дробно-линейная
а*
функция у — а* J. является рациональной.
Она представляет собой частное двух ли-
линейных функций — многочленов первой
степени.
Если функция у — f (х) представляет
собой частное двух многочленов степени
выше первой, то график ее будет, как
*)у = л-2 + 3 — —зт — рациональная функция,
так как ее можно записать в виде отношения
двух многочленов:
х1 + 3 —
х— 1
х-1
77

I
правило, более сложен, и построить его
точно, со всеми деталями бывает иногда
трудно. Однако часто достаточно приме-
применить приемы, аналогичные тем, с которы-
которыми мы уже знакомились.
|2.1 Разберем несколько примеров. По-
Построим график функции у = х2 ^ 2х ^_ 1 .
Обратим прежде всего внимание на то,
что при х = — 1 функция не определена
(так как знаменатель дроби х2 + 2х + 1
при х = — 1 равен нулю). При х, близких
к —1, числитель дроби х — 1 приблизи-
приблизительно равен —2, а знаменатель (х + IJ
положителен и мал по абсолютной вели-
у 	 Л
чине. Значит, вся дробь ¦ ,2 будет от-
(л -f- 1)
рицательна и велика по абсолютной вели-
величине (и тем больше, чем ближе х к зна-
значению х = — 1). Вывод: график распа-
i дается на две ветви (поскольку на нем нет
точки с абсциссой, равной — 1); обе ветви
ч	уходят вниз, когда х приближается к —1
	- (рис. 1).
Обратим внимание на числитель. Он
А обращается в нуль при х = 1. Значит,
<*i0 •&?* в точке х — 1 график пересекает ось абс-
«^з цисс. Нарисовав еще точку пересечения с
р	осью Оу (при х = 0,у = —1), мы можем при-
ис мерно представить себе ход графика в
средней его части (рис. 2).
Остается посмотреть, что делается с
функцией при больших по абсолютной ве-
величине значениях х.
Если х положительно и увеличивает-
увеличивается, то числитель и знаменатель дроби уве-
увеличиваются. Но так как в числителе стоит
х в первой степени, а в знаменателе есть
член х2, то знаменатель при больших х
увеличивается гораздо быстрей, чем числи-
числитель. Поэтому при неограниченном увели-
увеличении х функция у= „._?7>!i-« бУдет все
78

больше и больше приближаться к нулю.
Таким образом, правая ветвь графика4
правее точки х = 1 немного поднимется
над осью абсцисс (рис. 3), а потом опять
начнет опускаться и будет приближаться
к оси Ох.
Аналогичные соображения покажут
нам, что левая ветвь кривой при увели-
увеличении х по абсолютной величине тоже
приближается к оси абсцисс, только не
сверху, а снизу (рис. 3). Позже мы пока-
покажем (см. стр. 81), как можно точно найти
место наивысшего подъема правой ветви
графика.
По отмеченным деталям можно найти
общий вид графика (рис. 4).
|3.| Построим график функции
Для удобства начертим сначала графики
числителя у — х и знаменателя у = х2 +
+ 1 (рис. 5). Для построения графика
нашей функции нужно значения числите-
числителя делить на значения знаменателя.
При х = 0 числитель равен нулю —
график проходит через начало координат.
Пойдем теперь направо (т. е. рассмотрим
положительные значения аргумента). Так
как величина х2 много меньше х при
очень маленьких х, то при выходе из на-
начала координат знаменатель будет не--
которое время почти равен единице (не-
(немного больше, чем единица); поэтому вся
функция будет примерно равна числителю
х (чуть-чуть меньше числителя) — график
пойдет рядом с прямой у = х, постепенно
от нее отставая (рис. 6).
Вскоре, однако, х2 + 1 начинает ра-
расти быстрее, чем х, знаменатель обгоняет
числитель и дробь начинает уменьшать-
уменьшаться — график заворачивает вниз (рис. 7).
РисЗ,
79

Так как в числителе стоит х в первой
степени, а в знаменателе есть член с х2,
то при больших х знаменатель растет
быстрее числителя. Поэтому дробь с уве-
увеличением х становится все более малень-
маленькой — график приближается к оси абс-
абсцисс (рис. 8).
Левую половину графика можно по-
получить, заметив, что данная функция —
нечетная. Общий вид графика показан
на рис. 9.
4. Вернемся снова к построенному на-
нами графику функции у = * и разберем
х ~\-1
на этом примере еще один интересный во-
вопрос. Попробуем точно найти самую вы-
высокую точку правой половины графика (а
значит, конечно, и самую низкую точку
левой половины).
Очевидно, что наша кривая не может
подняться очень высоко, так как знаме-
знаменатель х2 + 1 довольно быстро начи-
начинает обгонять числитель х. Посмотрим,
может ли она подняться на высоту, рав-
равную 1, т. е. может ли при каком-нибудь х
значение у быть равным 1.
Так как#= . , то для этого нужно
решить уравнение ¦ 2 . = 1 или уравне-
ние х2 — х + 1 = 0. Это уравнение не име-
имеет действительных корней. (Проверьте!)
Значит, на графике нет точек с ордина-
80

той у = 1 — график не пересекает пря-
прямой у = 1 (рис. 10).
Посмотрим, поднимается ли кривая на
высоту, равную 1/3. Для этого нужно, что-
X	1
бы было , , = -^- или х2 — Зх + 1 = 0.
х- -|- 1 о
Это уравнение имеет два действительных
корня (проверьте!), и, значит, наш график
имеет две точки с ординатами, равными
V3) т. е. пересекает прямую у — V3 в двух
точках (рис. 11).
Чтобы найти самую высокую точку,
надо узнать, при каком самом большом
h уравнение ., = h будет иметь решение
(рис. 12). Уравнение 2 ,.= h заменим
квадратным:/ix2 — х + h = 0. Это уравне-
уравнение имеет решение, когда 1—4/i2 ^> 0.
Отсюда находим самую большую вы-
высоту, на которую поднимается график:
h = Va.
Найдем, при каком х это большое
значение у достигается. Так как у = * ,
ф
х = 1.
Итак, самая высокая точка графика —
это точка A, V2).
Упражнение
Найдите самую большую ординату графика
У=	<	2)
Рис.10
г 1и с .11
|5. j Построим график функции
Общий вид его легко нарисовать, если
заметить, что
л? + 1 _ 1
х — л/(де» + 1) •
•) Случайно ли получился полный квадрат?
81

43 I
Рис.4*
и, следовательно, мы пришли к задаче,
которую уже решали: зная график у =
= / (х), построить график у — f. . (см.
стр. 54—55).
Получаем примерно такую картину
'рис. 13).
Построим этот график другим спосо-
¦х бом. При этом выяснится еще одна его
интересная особенность.
Поделим числитель на знаменатель:
Теперь построим график у = х + Их
«сложением» известных нам графиков у =
= х и у = Их (рис. 14).
Мы видели, что график у ———— имеет
вертикальную асимптоту — ось Оу, к ко-
которой график приближается, когда х
уменьшается по абсолютной величине.
Теперь видно, что этот график имеет
еще наклонную асимптоту — прямую у =
= х (к этой прямой он приближается, ког-
когда х неограниченно возрастает).
Упражнения
у9. I Л
1.	Проверьте, что график у = 	21	 сим-
х
метричен относительно начала координат.
2.	Найдите координаты самой низкой точки
х1 -А- 1
правой ветви графика у =	21
х
Ответ на второе упражнение ясен из
первого способа построения этого графика
(см. рис. 13): самая низкая точка графика
х2 -4-1
г/=—¦— получается при том х, при ко-
котором на графике у=	получается са-
х -р 1
мая высокая, т. е. при х = 1. Наимень-
х24- 1
шее значение ординаты графика у —
равно, таким образом, 2.
82

Мы получили интересное неравенство:
для положительных х (речь шла о пра-
правой части графика) всегда х + Мх > 2.
Задачи
1. Докажите неравенство
—>2 для х>0
непосредственно.
2. Докажите неравенство
A)
B)
Оио выражает такой факт: «среднее арифметическое
двух положительных чисел а и b всегда больше или
равно среднему геометрическому этих же чисел».
Неравенство A) есть частный случай неравен-
неравенства B). При каких а и 6?
3. Неравенство х + \/х ]> 2 используется при
решении известной задачи о «честном купце». Один
честный купец знал, что весы, на которых он взве-
взвешивает товар, неточны, потому что одно коромысло
немного длиннее другого (в то время еще пользова-
пользовались весами с двумя чашками, см. рис. 15). Что де-
делать? Обвешивать покупателей — грех, но и себя
обижать не хочется. Купец решил, что половину
товара каждому покупателю ои будет взвешивать
на одной чашке, а вторую половину — на другой
чашке.
Спрашивается, что при этом получилось: ока-
оказался ли купец в выигрыше или в проигрыше?
|б.| В следующем примере возьмем
ФУНКЦИЮ у = —-T-j- Н	^j .
Она представлена в виде суммы двух
функций, и, конечно, можно строить ее
график сложением графиков у = , и
х -\- i
у= _ . Но здесь, пожалуй, можно и
сразу выяснить общий вид графика из та-
таких соображений:
а)	функция не определена при х = 1
и х — — 1, значит, кривая распадается
на три ветви (рис. 16);
б)	при приближении к х = 1 второе
слагаемое, а значит, и вся функция растет
Рис.IS
Т<Л
1
1
1
1
1
-1
1
0
1
i
1 *
|
Л
83

Рис.17
по абсолютной величине — значит, ветви
графика удаляются от оси абсцисс, при-
приближаясь к прямой х — 1. При этом спра-
справа от х = 1 кривая идет вверх, а слева —
вниз (рис. 17).
Аналогичная картина получается око-
около прямой х = — 1;
в)	у = 0 при х = 0; кривая проходит
через начало координат (рис. 18);
г)	для больших по "абсолютной величи-
величине значений х оба слагаемых малы по аб-
абсолютной величине — обе крайние ветви
графика приближаются к оси абсцисс:
правая сверху, а левая снизу (рис. 19).
Объединив все эти сведения, получим
общий вид графика (рис. 20).
Покажите, что этот график симметри-
симметричен относительно начала координат.
| 7. | Разобранные примеры показывают,
что даже при построении одного и того
же графика можно пользоваться различ-
различными приемами. Поэтому сейчас мы да-
дадим еще несколько примеров на построе-
построение графиков и не будем лишать Вас удо-
удовольствия самим подобрать подходящие
приемы для их построения.
Упражнения
1. Постройте график
X
х + 2 *
х + 1
На сколько «кусков» распадается кривая?
2. а) Постройте график
1	1
РисЛО
х+1 "
1
б) Постройте график у = —
А
жите ось симметрии этой кривой.
3. Постройте графики:
1
б)У = (х_1)(х_|
1
Ука-

Задачи для самостоятельного решения
1. Постройте графики функций:
a) y = x{i — x) — 2; б) у = х{1—х){х — 2);
4-х .
)
2|х| —3 .
3|х| — 2 '
1
1
и) {/ =
— 4х2 — 8х — 5 ' е) ^
1	11
: 3) У = -хг + -хТ
х2—2х+4
;
н) у = (х— 3)|х+1|; о) {/=|х-2| + 2|
Г 1 1	U + 1I— х
т) Постройте графики дробно-линейных функций вида
_Зх + Д
для различных значений а.
2. Функция у = f (x) определена следующим правилом:
f(*)=-
1 ири х > О,
О при х = О,
— 1 при х < 0.
•5

Эта функция часто встречается, и потому
для нее есть специальное обозначение у =
= sgn х (читается «сигнум икс»— по-латыни
signum — это «знак»). График этой функции
изображен на рис. 1. Функцию sign х можно
х *)
для х Ф О задать формулой у = | х^ '•
Нарисуйте графики функций:
3. Общий вид графика функции, являющейся частным от деления од-
одного квадратного трехчлена на другой:
ах2 + Ьх + с
у== x2 + px + q •
зависит от того, сколько корней и какие корни будут иметь числитель и
знаменатель.
а) Постройте графики функций:
4х2 — 8х + 3	ха— 2х + 1	Зх2— Юх+3
б)	Какой вид имеет график функции w	„ 	^- , если оба кор-
» х2 + рх + q
ня числителя меньше корней знаменателя? ф
в)	Разберите все возможные случаи и нарисуйте возможные типы гра-
графиков у функций вида ,, = ах ~*~ ~*~ с .
J/ х2 + рх + 9
Постарайтесь не пропустить ни одного случая и приведите по примеру
на каждый тип.
4. Постройте график функции у = V^3 x.
а)	Докажите; что он не может пройти ни через одну точку, координаты
которой — целые числа, кроме точки @, 0).
Если Вы возьмете за единицу масштаба одну клеточку, то такими
«целочисленными» точками будут вершины клеток. Возьмите начало ко-
координат поближе к левому нижнему углу тетради и проведите аккуратно
прямую у = \^3 х. (Под каким углом к оси Ох ее надо провести?) Некото-
Некоторые из целочисленных точек окажутся очень близко от этой прямой. Поль-
Пользуясь этим, найдите приближенные значения для|^3 в виде обыкновенных
дробей. Сравните полученные значения с табличным: "^3 ж 1,7321.
б)	Трудная задача: докажите, что найдется целочисленная точка,
_	1 **\
отстоящая от прямой у = \ 3 х на расстоянии, меньшем чем	/ .
1000
•) Почему только для х ф 0?
**) Число "TTjnjT можно заменить любым другим числом. Тогда будет дока-
доказано, что какое бы малое число ни взять, найдется точка с целыми
координатами, отстоящая от прямой у = |^3 х на расстояние, меньшее
этого числа.
86

При решении задачи 5—9 используйте графики подходящим образом
подобранных функций.
5.	Сколько решений имеют уравнения:
а) — х2 + х — 1 = | х |; б) | Зх2 + 12х + 9 | + х = 0;
в) X2-X+1 =*¦• г) U-l| + |x-2| + |x+l|+|x+2|=6;
д) х(х+1)(х+2) = 0,01; е) | х+ 3 | = | х + 2 \ (#- 1);
11	1
ж) [х] = х на участке |х|<3; з) — + x,i + х , 2~ = 100?
6.	Решите уравнения:
а) 2х2 — х— 1 = |*|; б) |2х2 —х—1 | — х = 0;
в) |*| = |*-1| + |*—2|.
7.	а) Определите, сколько решений может иметь уравнение ] 1 — | х \\=а
при различных значениях а.
б) Тот же вопрос для уравнения х2+	= а ).
X
8.	Решите неравенства:
9. Найдите наибольшее значение функции и определите, при каких
значениях х оно достигается:
а) у=х{а-х); б) у=\х\{а—\х\)\ в) у = хЦа-х>);
Х2 I 4	_
г) У^'дД-^х^! » Д) {/=1—1^2х на участке |х|
е) {/ = — х2 + 2х — 2 на участке — 5 ^ х
х+3
ш) у—	г на участке х^2.
10.	Две дороги пересекаются под прямым углом. По направлению к
перекрестку движутся две автомашины: по первой дороге — со скоростью
60 км/час, по второй — со скоростью 80 км/час. В 12 час. обе машины на-
находились за 10 км от перекрестка.
В какой момент расстояние между машинами будет наименьшим? Где
будут находиться машины в этот момент?
11.	Среди всех прямоугольных треугольников с даниым периметром р
найти треугольник, имеющий наибольшую площадь.
12.	Пусть у = f (х) — четная функция, а у = g (x) — нечетная функ-
функция. Что можно сказать о четности или нечетности функций:
: y = f(x)-g(x)\ S/=lg(x)|;
» = f (*)-*(*): y = f(\x\)-g(x); j/ = f(x)-
13. Найдите все четные и все нечетные функции вида:
рх + q	а& + Ьх + с
a){/ = *x + b; Oy ^T; в)у
14. Функция у = х4—х не является ни четной, ни нечетной функ-
функцией. Однако эту функцию легко представить в виде суммы четной функ-
функции у = xi и нечетной функции у = — х (рис. 2).
*) Значение а, разделяющееразныеслучаи, найдитеприближеннопографнку.
87

\:

а) Представьте функцию у = -
• в виде
.¦:¦ v»v*'i
X4 — X
суммы четной и нечетной функций.
б) Докажите, что любую функцию f (x) мож-
можно представить в виде суммы четной и нечетной
функций, ф
15.	Через каждые две точки с разными абс-
абсциссами проходит прямая — график линейной
функции у = kx + 6. Аналогично, через каждые
три точки с разными абсциссами, не лежащие
на одной прямой, можно провести параболу —
график функции у = ах2 + Ьх + с.
Найдите коэффициенты квадратного трех-
трехчлена ах2 + Ьх + с, график которого проходит
через точки:
а)	(-1, 0); @, 2); A, 0);
б)	A, 0); D, 0); E, 6);
в)(-6, 7); (-4, -1); (-2, 7);
г)	@, -4); A, -3); B, -1);
д)	(-Ц9); C, 1); F, 16).
16.	а) Совершите подобное преобразование
параболы у = х2, выбрав центр подобия в начале
координат и коэффициент подобия, равный 2.
Какая кривая получится?
б)	Какое подобное преобразование переводит
кривую у = х2 в кривую у = 5л-2?
в)	Воспользовавшись результатом задачи
166, найдите фокус и директрису параболы
у = 4л4*. (Определение директрисы и фокуса —
на стр. 41.)
г)	Докажите, что все параболы у = ах2 +
+ Ьх + с геометрически подобны.
17.	Докажите, что точка F @, V4) есть фо-
фокус, а прямая у = — V4 — директриса параболы
у — х2, т. е. что любая точка этой параболы рав-
равноудалена от точки F @, VJ и прямой у = — V4.
Указание. Возьмите на параболе некоторую точку М с коорди-
координатами (а, а2). Запишите расстояние от этой точки до точки F @, V4) по фор-
формуле расстояния между двумя точками *). Запишите затем расстояние от
точки М (а, а2) до прямой у = — V4 **).
Докажите равенство полученных выражений.
18. Докажите, что точки
Ft (/27 /2) и F% (- /27- /2)"
являются фокусами гиперболы у = 1/л-, т. е. что разность расстояний любой
точки этой гиперболы до точек Fx и F2 по абсолютной величине есть величи-
величина постоянная.
Указание. Возьмите на гиперболе у = l/х произвольную точку
М (а, \1а). Выразите через а расстояния этой точки от точки Fj (/2, /2
*) Расстояние между двумя точками A (xlt yj и В (х2, {/2) йает,ся форму-
формулой р (Л, В) = /(л-j — лт2J + (г/i — {/аJ.
**) Расстояние от точки А (х^ уг) до прямой у = с равно| ух —с(.
ВО,
М
наллгнаА.

2 (
Найдите разность этих рас-
расстояний. Покажите, что абсо-
абсолютная величина этой разно-
разности при всех значениях а оди-
одинакова (и, значит, не зави-
зависит от выбора точки на ги-
гиперболе).
19.	На стр. 88—89 даны
17 графиков и столько же
формул. Ваша задача — оп-
определить, какая формул а
относится к какому номеру
графика. Среди этих графиков вы найдете ответы к упражнениям.
20.	На рис. 3 изображен график функции у = f (х).
Нарисуйте эскизы графиков следующих функций:
ОС
Ркс.З
a) y = f(x)-2; б) y =
в) y=\f(x)\
); д) у = -
1
f(x)
и) у*шx+f(x); к) У=~~-
21.	На плоскости нарисован квадрат со сторо-
стороной а (рис. 4). Кривая L$ есть геометрическое место
точек, наименьшее расстояние которых до какой-ни-
какой-нибудь точки квадрата равно S. Обозначим площадь
фигуры, ограниченной кривой Ls> через Р (S).
а)	Найдите Р (S) как функцию S.
б)	Решите задачу, аналогичную задаче 21а, взяв
вместо квадрата прямоугольник со сторонами а и Ь.
в)	Та же задача для треугольника со сторонами
а, Ь и с.
г)	Та же задача для круга радиуса г.
22.	Не можете ли Вы заметить закономерность
в получающихся выражениях для Р (S)? Напишите
общую формулу для любой выпуклой фигуры. Вер-
Верна ли эта формула для невыпуклых фигур?
23.	Будем рассматривать квадратные уравне-
уравнения вида х2 + рх + q— 0; каждое такое уравнение
задается двумя числами р и q. Условимся изображать
sto уравнение точкой на плоскости с координатами
(р, q). Например, уравнение х2 — 2х + 3 = 0 изоб-
изобразится точкой А (—2; 3); уравнение дг2 — 1 = 0 —
точкой В @, —1).
а)	Какое уравнение соответствует началу коор-
координат?
б)	Нарисуйте множество точек, соответствую-
соответствующих тем уравнениям, у которых сумма корней рав-
равна 0.
в)	Возьмите наугад точку на плоскости. Если
уравнение, соответствующее Вашей точке, имеет два
вещественных корня, • отметьте эту точку зеленым
91

19 +¦ 9 1- 26
t18 +ц + щ
8 +
105:7 =15-
ос-Э
ьССИ
карандашом. Если же уравнение не имеет веществен-
вещественных корней, то отметьте точку красным карандашом.
Возьмите еще несколько точек и сделайте с ними
то же самое. Не можете ли Высказать, какую часть
плоскости занимают «зеленые» точки и какую —
«красные»? Какая линия отделяет «зеленые» точки
от «красных»? Сколько корней имеют уравнения,
соответствующие точкам этой линии?
г)	Какое множество точек соответствует тем
уравнениям, у которых корни вещественны и поло-
положительны?
д)	Какой точкой может изображаться уравне-
уравнение, если известно, что один из его корней равен 1?
24. Автомобиль двигался равноускоренно до
некоторого момента и затем стал двигаться равно-
равномерно (с достигнутой им скоростью). График дви-
движения этого автомобиля изображен на рис. 5. До-
Докажите, что прямая АВ есть касательная к пара-
параболе ОКМ.
25.	а) Воспользовавшись графиками, определи-
определите число решений следующих кубичных уравнений:
1)	0,01 ж8 = л? —1,
2)	0,001 Xs = х2 — 3* + 2.
б) Найдите приближенные значения корней
этих уравнений.
26.	а) На стр. 33 есть рисунок, показывающий,
что график многочлена у = х* — _— Х2 _j_ _— полу-
получается из графика многочлена у = л — 2*3 —
—*2 + 2х сдвигом вдоль оси Ох. Найдите величину
этого сдвига.
б)	Решите уравнение 4-й степени
х4 — 6xs + 7х2 + &х — 8 = 0.
Указание. Сдвиньте график многочлена
л? — 6л;3 4- 7х2 -\- %х вдоль оси Ох так, чтобы он
стал графиком некоторого биквадратного много-
многочлена.
в)	При каких условиях кривая у = х4 -f- bxs +
+ ex"-1 + d имеет ось симметрии? ©
27.	Решим задачу 4, стр. 37. Всего спичек
19+9 + 26 + 8+18+11+14 = 105. Поэтому
нам нужно добиться, чтобы в каждой коробке бы-
было 105:7=15 спичек.
Обозначим буквой х число спичек, кото-
которые нужно переложить из первой коробки во
вторую. (Может быть, конечно, что спички при-
дртся перекладывать из второй коробки в первую—
тогда х будет отрицательным.) После того как
мы переложим х спичек из первой коробки во
вторую, во второй коробке будет х + 9 спичек.
Значит, из второй коробки в третью нужно
переложить х — 6 спичек, из третьей в четвертую
х + 5 спичек. Аналогично из четвертой коробки в
пятую перекладывается х — 2, из пятой в шестую

+, из шестой в седьмую х— 3, наконец, из 0тёр г
седьмой в первую х— 4 спичек (рис. 6).
Обозначим теперь через S общее число перело-
переложенных спичек:
В этой формуле знаки абсолютной величины
использованы потому, что нам важно лишь число
переложенных спичек, а не то, в каком направле-
направлении их перекладывали.
Нам теперь нужно выбрать х так, чтобы S
имело наименьшую величину. Здесь нам может по-
помочь график функции S = /(ж) (рис. 7). Самая низ-	+25оо
кая точка графика есть вершина At, значит, функ-	+
ция S = / (х) принимает свое наименьшее значе- -50/'ч\^ -7оо
ние при х = 2. Таким образом, х найден, и мы Г	Д
можем сказать, сколько и куда спичек нужно перек- ф-Ш 1+1500
ладывать (рис. 8). Этим способом задачу можно ре- /
шить, конечно, и для произвольного числа (п) коро- 1-^со 1-K00
бок. Для этого нужно так же , как в нашем приме- Nv J
ре, написать выражение для S. Оно будет иметь »—¦•-fioo
вид: +5™
S=|*| + |* — ai| + |x —Оз1 + ... +\х — ап_1\. Pvl.4. 3
Для того чтобы найти нужное значение X в случае нечетного числа п,
можно воспользоваться следующим простым правилом: числа 0, а1у а2>...
..., an-i нужно выписать в возрастающем порядке. После этого х выбирается
равным числу, стоящему ровно в середине этой последовательности чисел
(если п нечетно, такое число всегда найдется). Подумайте, как выглядит
график в случае четного п.
Попробуйте затем сформулировать правило для нахождения х в этом
случае.
С этой похожей на игру задачей связана практически важная задача
о перевозках по кольцевым маршрутам. Представьте себе кольцевую же-
железную дорогу с равноотстоящими станциями. На некоторых станциях на-
находятся склады угля, на других — потребители, которым нужно доста-
доставить весь этот уголь. На рис. 9 указаны запасы угля на складах и (со зна-
знаком —) потребность в нем.
Воспользовавшись решением предыдущей задачи, составьте наиболее
экономный план перевозок.

Ответы и указания к задачам и упражнениям, отмеченным
Значком ffi
Упр. 26, стр. 20. Ответ ищите среди графиков на стр. 88—89.
Упр. 36 на стр. 32, график рис. 12. Ответ ищите среди графиков на
стр. 88—89.
Упр. 3, стр. 36. Указание. Эта функция принимает наименьшее
значение на целом отрезке.
Задача 4 на стр. 37. Решение см. в задаче 27 на стр. 92.
Упр. 26 на стр. 57. Нет, не имеет. Строгое доказательство этого факта
не очень просто, и мы его здесь не приводим. Однако ясно, что так как и
ось Ох и ось Оу являются асимптотами этой кривой, то осью симметрии
могла бы быть только прямая у = х. То, что эта прямая не является осью
симметрии, легко проверяется.
Упр. 2 на стр. 76. Уравнение касательной у = Зл: — 1.
Упр. 3 на стр. 76. Указание. Система у = х + а, у = — х2 — 1
должна иметь два.слившихся решения.
Задачи 1з и 1с, стр. 85. Ответ ищите среди графиков на стр. 88—89.
Задача 36, стр. 86. Возьмем числовой пример. Пусть корни числителя
будут —5 и 0, а корни знаменателя +2 и +4. Тогда наша функция имеет
ах (х + 5)
вид«= -,	577	7\' Выберем какое-нибудь конкретное значение а,
(X — <SJ (X—4J
2х (х + 5)
например а = 2. Функция у = ,х	^\ <х	4) не 0ПРеДелена ПРИ * = 2 и
х = 4. При приближении х к этим значениям знаменатель уменьшается,
приближаясь к нулю; значит, функция неограниченно растет по абсолют-
абсолютной величине — прямые х = 2 и х = 4 являются вертикальными асимпто-
асимптотами графика.
Функция равна нулю при х = Ои г= —5. Отметим на оси Ох две точ-
точки графика: @, 0) и (—5, 0).
Четыре «особых» значения аргумента: х = —5, 0, 2, 4 делят ось Ох
на 5 участков. При переходе через границу любого участка функция ме-
меняет знак (обращаясь в нуль или «уходя в бесконечность») (рис. 10).
Осталось выяснить поведение функции, когда аргумент неограниченно
растет по абсолютной величине. Попробуем вместо х подставлять большие
числа (например, х = 10 000, х = 1 000 000 и т. д.). Так как 2х2 будет
гораздо больше, чем Юл-, а х2 гораздо больше, чем —6л- + 8, то дробь
2х (х + 5)	2л? + Ю*
(х—2)(х—4)— л? — 6л:+8
будет примерно равна отношению старших членов числителя и знаменателя
2л:2 + 10л: 2л:2
д== х2 — 6л: + 8 ~1? = 2'
причем тем ближе к 2, чем больше |лг|. Значит, при удалении от начала ко-
координат график будет приближаться к горизонтальной прямой у = 2.
Общий вид графика — на рис. 11. Во всех случаях, когда оба корня
знаменателя больше корней числителя, график будет примерно такой.
94

Задача 14, стр. 87. Как это часто бывает в
математике, задачу легче решить в общем виде,
чем для заданной конкретной функции. Поэтому
мы сначала решим задачу б), а решение а) по-
получим как частный случай.
Итак, пусть дана некоторая функция / (дг).
Предположим, что задача решена, т. е. / (х)
представлена в виде суммы четной функции g (x)
и нечетной h (x):
g(x) + h(x).	(*)
Так как это равенство верно для всех значений
х, то в него можно подставить —х вместо х, и
мы получим
f(-x)=g(-x) + h(~x). (**)
Так как функция g (х) четная, a h (x) нечетная, то
g (—х) = g (х) и h (—х)= — h (x). Пользуясь
этим, мы сначала сложим (*) и (**), а затем выч-
вычтем одно из другого; найдем:
f (*) + f (- x) = 2g (x), f(x)-f (- x) = Щх).
Отсюда находятся функции g (x) и h (x) и полу-
получается искомое разложение функции / (х) на
сумму четной и нечетной функций:
A)
': \
Рис.10
11
2
Заметьте, что формальное доказательство полученного результата еще
проще: напишите сразу разложение A), проверьте, что оно выполняется
тождественно для всех х и что первое слагаемое в правой части — четная
функция, а второе — нечетная.
Решение задачи а) получается непосредственно по формуле A):
Jл?	1

— х — л*—
х7—
Замечание. Если функция у = f (х) не определена для некото-
некоторых значений х, то и функции g (x) и h (x) тоже будут определены не для
всех значенил х. При этом может оказаться, что для некоторых х функция
/ (х) определена, a g (x) и h (x) не определены.
Упр. 26в, стр. 92. Ad = в3 + 26с.

Израиль
Моисеевич
Гельфанд
Елена
Георгиевна
Глаголева
Эммануил
Эльевич
Шноль
Функции и графики
(основные приемы)
М., 1968, 96 стр. с илл
Редактор
Художники
Техн. редакторы
Корректор
И. М. Овчинникова
В. В. Смолянинов, В. Б. Янкилевский
В. С. Никифорова, С. Я- Шклчр
Л. Н. Боровина
Сдано в набор
Подп. к печати
Бумага
Фив. печ. л.
Усл. печ. л.
Уч.-изд. л.
Т- 03844
Тираж
Цена книги
Заказ №
5/Ш 1968 г.
22/VII 1968 г,
84X108V32
3.
5,04.
4,74.
220 000 экз.
13 коп.
232
Издательство «Наука»
Главная редакция
физико-математической литературы
Москва В-71, Ленинский проспект, 15
2-я типография издательства «Наука».
Москва Г-99, ШубинскиЛ пер., 10

Математика	Библиотечка
физико-математической школы
Серия основная
Выпуск 1	И. М. Гельфанд, Е. Г. Глаголева, А. А. Кирил-
Кириллов, Метод координат.
Выпуск 2	И. М. Гельфанд, Е. Г. Глаголева, Э. Э. Шноль,
Функции и графики (основные приемы).
Выпуск 3	С. И. Гельфанд, М. Л. Гервер, А. А. Кириллов,
Н. Н. Константинов, А. Г. Кушниренко, Задачи
по элементарной математике (последовательности,
комбинаторика, пределы).
Серия вспомогательная
Выпуск I *	Е. Б. Дынклн, С. А. Молчанов, А. Л. Рогенталь,
А. К. 1олпыго, Математические задачи.
Выпуск 2 *	А. А. Кириллов, Пределы.