Text
MOLEKULE
UND
KRISTALLE
VOb.
Professor
ENRICO FERMI
19 3 8
ЭНРИКО ФЕРМИ
МОЛЕКУЛЫ
КРИСТАЛЛЫ
Перевод с немецкого
м. и. певзньр
Под редакцией
В. Б. БЕРЕСТЕЦКОГО
Государственное издательство
ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва
1947
О Г Л А В Л Е Н И Е
От редакция , . . 4
Часть I. Молекулы
Глава 1. химическая связь
1. Полярные и го ме о полярные молекулы ..... 5
2. Полярная связь 6
3. Гомеополярное соединение. Молекула водорода 9
4. Распространение на другие молекулы ..... .15
5. Силы притяжения Ван-дер-Ваальса 17
Глава II. спектры двухатомных молекул
6. Общая слема термов молекулы 20
7. Правила отбора для / и v 26
8. Вращательно-кслебательные полосы 27
9. Электронные полосы . . 32
10. Ангармоничность колебаний и диссоциация ... ЗУ
1 i. Предиссоциация 4 L
12. Отклонения от свойств жесткого ротатора ... 42
13. Электронные термы „ . . , 43
14. Квантовомезаническое исследование электронных
термов 44
15. Влияние спина .......... 46
1.6. Молекулы с несколькими валентными электро-
электронами ". 50
17. Случаи связи по Гунду 51
IS. А-удвоенне * . • . . 54
19. Сопоставление молекулярных термов с атомными
термами ................... '5
20. Четные и нечетные термы 62
21. Симметричные и антисимметричные термы ... 67
264 ОГЛАВЛЕНИЕ
22. Спин ядра 69
23. Чередование интенсивности 72
24. Пара- и орто-водород 74
25. Изотопические эффекты в полосатых спектрах , 76
26. Эффекты Зеемана и Штарка в полосатых спек-
спектрах 78
27. Флуоресценция двухатомных молекул 82
28. Эффект Рамана у двухатомных молекул .... 83
Глаза III. тепловые сеойства двухатомных молекул
29. Теплоемкость 87
30. Распределение интенсивностей в полосах ... 91
31. Постоянная энтропии 93
Глава IV. многоатомные молекулы
32. Структура многоатомных молекул , . 97
33. Рассеяние молекулами рентгеновских луче? , . 98
34. Электрическая поляризуемость молекул .... i 00
35. Электрический момент молекул 103
36. Вращательные термы многоатомных молекул . . 105
37. Колебания дмногоатомных молекул . 107
38. Инфракрасные спектры многоатомных молекул . 112
39. Раман-эффект многоатомных молекул 115
40. Правила отбора в колебательном эффекте Рамана 119
41. Особенности колебательных термов многоатом-
многоатомных молекул 121
Часть II. Кристаллы
Г ласа I. геометрия кристаллической решетки
1. Простые и сложные решетки . 125
2. Симметрия решеток 128
3. Определение структуры кристаллической решетки 131
4. Определение структуры для сложных решеток . 133
5. Примеры кристаллической структуры 137
ОГЛАВЛЕНИЕ 265
Г.адва II физические свойства кристаллической
РЕШЕТКИ ,
6. Теплоемкость кристалла 140
7. Теория теплоемкости Дебая 143
8. Упругие ствойства одномерной решетки .... 147
9. Колебания простых и сложных решеток .... 151
10. Инфракрасные частоты и остаточные лучи . . . 153
11. Раман-эффект в кристаллах 157
12. Тепловое расширение н теплопроводность кри-
кристаллов 160
13. Ионная решетка 165
14. Электростатическая энергия ионной решетки . . 169
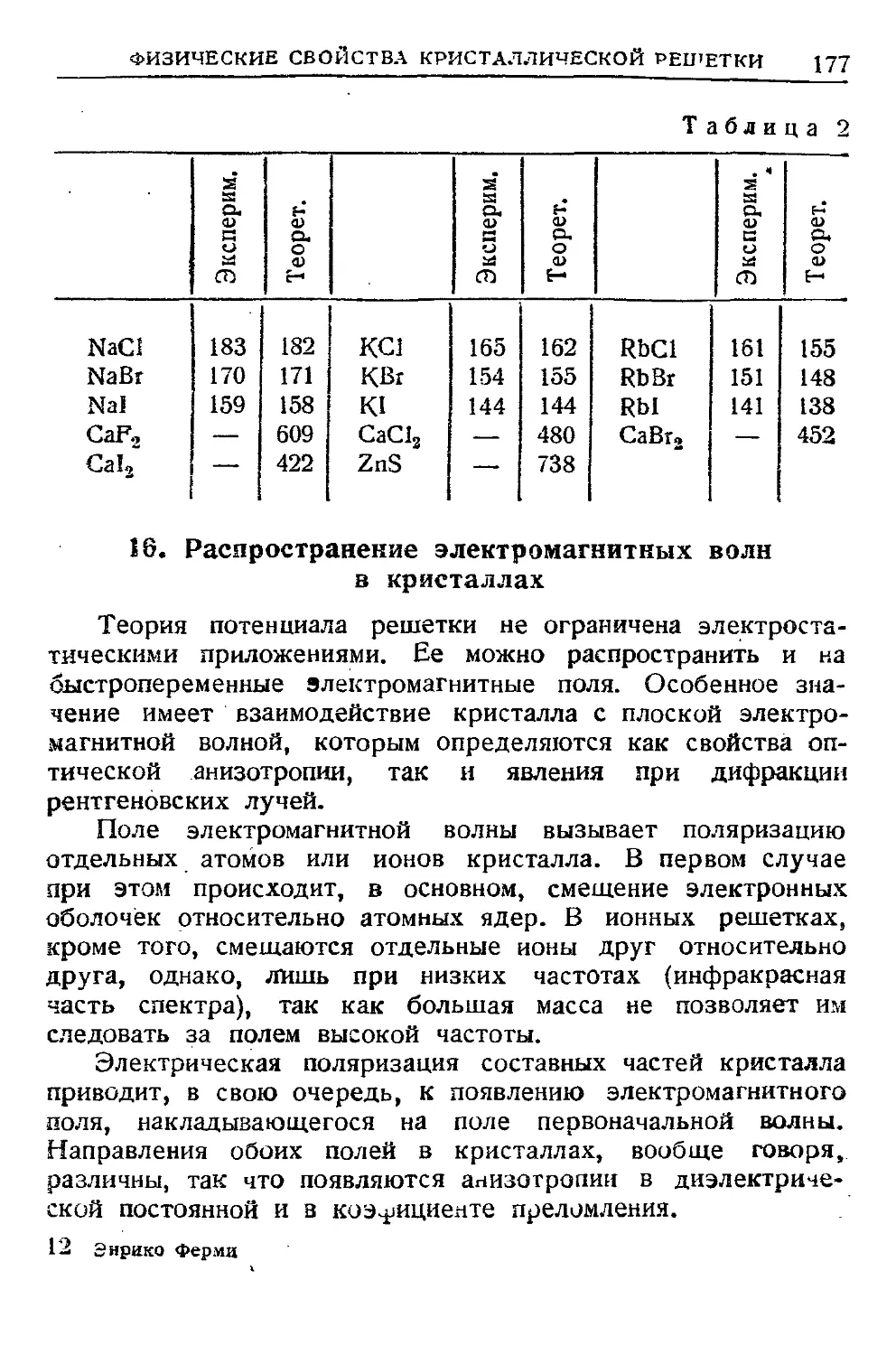
15. Силы отталкивания. Сравнение с экспериментом . 173
16. Распространение электромагнитных волн в кри-
кристаллах 177
17. Поглощение света в кристаллах 179
Часть III. Статистика и квантозая теория
Глава I. СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ
СОСТОЯНИЙ
1. Обобщение принципа Больцмана ....... 185
2. Тепловое равновесие и вероятность заполнения
квантовых состояний атома или молекулы ... 189
3. Антистоксовы линии флуоресценции и раманов-
ские линии 193
4. Средняя энергия осциллятора . 194
5. Спектр черного тела 196
6. Формула Планка 201
7. Статистическое равновесие между атомами и из-
излучением полости 205
8. Квантовая теория парамагнитного газа 208
' 9. Статистическое толкование термодинамических
величин ....... 212
10. Принцип Нернста 214
Глава II. квантовая статистика глЗА
11. Фазовое пространство идеального газа .... 218
12. Постоянная энтропии 222
ОГЛАВЛЕНИЕ
13. Тепловое ионизационное равновесие и тепловая
электронная эмиссия 227
14. Новая статистика 232
15. Статистика Бозе-Эйнштейна . 237
16. Эйнштейновское вырождение raja 241
17. Бозевский газ световых квантов 244
18. Статистика Ферми 246
19. Статистические свойства газа Фер:»ш 250
20. Свойства сильно вырожденного газа ...... 256
21. Статистическое распределение электронов а а юме 259
Редактор К. Гуров
Технический редактор Б. Корнилов
Корректор Б. Ерусалимский
*
Сдано в производство 23/VII 1947 г.
Подписано к печати 15/Х 1947 г.
А 10393, Объем 16 Н п. л. Уч.-издат. л. 14
Формат 82х1087з, Издат. *& 2/8Э.
ОПЕЧАТКИ
Стр, Строка
12 8 снизу
Следует читать
член 2W
света.
39 формула B9) '
83 6 свеРхУ
82 15 сверху
107 формула F9) Wtot= ~{~ J (/+1)
174 формул» F8) £=[ig
225 формула F5)
Ферми. Зак. 355
v -jr)
ОТ РЕДАКЦИИ
Предлагаемая читателю книга Ферми содержит обстоятель-
обстоятельный обзор современного учения о строении и свойствах моле-
молекул и кристаллов. Кроме того, в третьей части рассматривается
квантовая статистика. На первый план автор ставит изложе-
изложение физической сущности вопросов, оставляя в стороне матема-
математические методы решения. Автор подразумевает, что читатель
знаком с квантовой механикой и применяемым в ней математи-
математическим аппаратом.
Интересующимся более полным освещением рассмотренных
в книге вопросов можно рекомендовать следующие книги:
М. А. Л е о и т о в и ч, Статистическая физика, М.—Л., 1943;
Я. К. Сыркин и М. Е. Дяткина, Химическая связь и
строение молекул, М,. —: Л., 1.94.6; М. Борн и М. Мейер,
Теория твердого тела, М. — Л., 1938; К. В. Никольский,
Квантовая механика молекулы, М. — Л., 1934.
Книга рассчитана, главным образом, на физиков — научных
работников, аспирантов и студентов старших курсов.
Ч А С Т Ь I
МОЛЕКУЛЫ
ГЛАВА Г
ХИМИЧЕСКАЯ СВЯЗЬ
1. Полярные и гомеополярные молекулы
Нейтральные атомы не взаимодействуют друг с другом
до тех пор, пока расстояние между ними велико по срав-
сравнению с их диаметрами. Если вследствие теплового движе-
движения атомы случайно сближаются, то появляются силы взаимо-
взаимодействия, величина которых быстро возрастает с уменьшением
расстояния, а знак зависит от природы атомов. Если эти
силы являются силами притяжения, то атомы в определенных
условиях могут соединяться в молекулы. Тогда говорят о
„химической связи".
Силы, вызываюшие образование этой „химической связи",
имеют электрическое происхождение; другие явления, на-
например, i равитационные, здесь не играют никакой роли.
Несмотря на это, факт образования молекул невозможно
объяснить „классически", т. е. только на основе чисто элек-
электростатического взаимодействия ядер и электронов. В дан-
данном случае, как и для всей атомной физики в целом, ис-
исчерпывающее понимание стало возможным лишь с появлением
квантовой теории.
Для упрощения * мы рассмотрим сначала двухатомные
молекулы, т. е. системы, состоящие из двух положительно
заряженных ядер и электронов в количестве, соответствую-
соответствующем суммарному заряду обоих ядер. Исследуя, на какие
составь ые части распадается молекула при постепенном уве-
увеличении расстояния между ядрами, можно установить нали-
наличие существенно отличающихся между собой видов связи.
Изменение расстояния между ядрами должно при этом про-
производиться „адиабатически", т. е, настолько медленно, чтобы
распределение электронов при каждом расстоянии между
jVIARA I
ядрами устанавливалось таким же, каким оно было бы, если
бы ядра постоянно имели это расстояние. При этом элек-
электроны, в конечном итоге, распределяются на две группы,
каждая из которых окружает одно из ядер, причем так,
что образуются два совершенно самостоятельных комплекса.
Существуют две возможности:
a) Оба комплекса представляют собой нейтральные атомы;
так как последние электрически равноценны, то в этом слу-
случае говорят о гомеополярной связи.
b) Оба комплекса не являются нейтральными. Один из
них обладает количеством электронов, большим, чем заряд
соответствующего ядра, — это отрицательный ион.
Количество электронов во втором меньше на величину,
равную избытку электронов в первом,—это положи-
положительный ион. В этом случае химическая связь называется
полярной или гетерополярной. Связь может быть
однократной, двух- или трехкратной, в зависимости от за-
заряда образующихся ионов, т. е. от числа изоытичных или
недостающих электронов.
2. Голяряая связь
Типичными примерами полярных связей являются моле-
молекулы солей Например, молекула NaCJ при увеличении рас-
расстояния между ядрами распадается не на два нейтральных
атома, а на положительно заряженный ион натрия (Na + ) и
отрицательно заряженный ион хлора (С1~). Недостающий
у натрия электрон присоединен к хлору.
Подобный вид связи характерен, "главным образом, для
соединений металлов с металлоидами или с соответствую-
соответствующими радикалами. Для металлов величины потенциалов
иопизаиии незначительны, т. е. количество энергии (измеряе-
(измеряемое в eV), требующееся для отделения электрона от атома
металла, — невелико. С другой стороны, металлоиды харак-
характеризуются относительно большим электронным сродством.
Это значит, что при присоединении электрона к нейтраль-
нейтральному атому металлоида выделился значительное количество
энергии.
ХИМИЧЕСКАЯ СВЯЗЬ
Схематически образование молекулы соли, например,
NaCl, можно представить следуюишм образом^ Атом натрия
отдает электрон атому хлора. Возникшие при этом ионы
Ка+ и С1~, обладающие противоположными зарядами, со-
согласно закону Кулона, притягиваются. Однако расстояние
между ними не может стать произвольно малым, так как
при малых расстояниях, когда ионы, так сказать, приходят
в соприкосновение друг с другом, возьикают силы оттал-
отталкивания, препятствующие дальнейшему сближению. Ионы
остаются на таком расстоянии друг от друга, при котором
силы притяжения и отталкивания уравновешиваются: они
образуют молекулу NaCl.
Такое описание процесса образования соли, однако, еще
является весьма неточным и неполным. Почти во всех слу-
случаях потенциал ионизации металлов несколько больше, чем
электронное сродство металлоидов, так что для образования
ионов, т. е. для перехода электронов с одного атома на
другой, требуется небольшая затрата энергии. Самопроиз-
Самопроизвольно это явление происходить не может. Недостаток энер-
энергии должен быть восполнен из освобождающейся при сбли-
сближении иинов электростатической энергии. Поэтому образо-
образование ионов и сближение ье могут следовать друг за
другом, а образуют единый процесс. Это значит, что пе-
переход электронов происходит лишь после т^го, как атомы
сблизились настолько, что параллельно с образованием ионов
выделяется необходимое для этого количество электроста-
электростатической энергии.
Приведем численные значения для случая NaCl: по-
потенциал ионизации IMa— 5,1V; электронное сродство
С1 — 3,8 V.
Для образования ионов Na+ и С1 из атомов, следова-
следовательно, требуется 5,1 —3,8 = 1,3 eV. С другой стороны,
электростатическая энер| ия двух ионов, находящихся на
расстоянии / друг от друга, равна —е^г;=—300 ejr eV.
Так как элементарный заряд е = 4,8 • 10~10 Е^Е, то раз-
разность между потенциалами ионизации и электронным срод-
сродством восполняется электростатической энергией, когда
расстояние г=11»10~8 см. Следовательно, переход
8 ГЛАВА I
электрона от Na к С1 может иметь место лишь тогда, когда
расстояние между атомами меньше, чем 11 АA А= 10"8 см).
Равновесное расстояние атомов в молекуле значительно
меньше и приблизительно равно 1,4 А. Вычисленная отсюда
электростатическая энергия в 10,2 eV превышает энергию,
необходимую для образования ионов, на 8,9 eV. Этому со-
соответствует величина 205 ккал для теплоты образования
1 моля NaCl из свободных атомов Na и С1. В действитель-
действительности эта величина несколько меньше, так как и а*ла от-
отталкивания влияет на потенциальную энергию, несколько
уменьшая последнюю. Число отданных или присоединенных
электронов зависит от природы металлов и металлоидов.
У одновалентных металлов (например, щелочных) первый
электрон отщепляется очень легко, второй же — только при
затрате большого количества энергии. При присоединении
одного электрона к атому галоида выделяется большое ко-
количество энергии; присоединение второго выделением энер-
энергии не сопровождается. Это связано с расположением элек-
электронов в атоме. Атомы щелочных металлов имеют на один
электрон больше, а атомы галоидов — на один электрон
меньше, чем соответствующие благородные газы. При от-
отделении или присоединении электрона образуется весьма
стабильная конфигурация благородного газа, для разрушения
которой необходимо большое количество энергии. Щелоч-
Щелочноземельные металлы имеют на два электрона больше, чем
соответствующие благородные газы; поэтому они легко от-
отдают два электрона и образуют в подавляющем большин-
большинстве случаев двухвалентные ионы. В других случаях, как
например, для металлов группы меди, могут образовываться
как одновалентные, так и двухвалентные ионы, потому что
разница между „первым" и „вторым" потенциалом ионизации
не так велика, как у щелочных металлов, но и не так мала,
как у щелочноземельных. У этих элементов имеется два
ряда солей — например, медные и медистые.
Ионы полярной молекулы связываются электростатиче-
электростатическими силами, поэтому они легко диссоциируют в водных
растворах, поскольку высокая диэлектрическая постоянная
воды (около 80) сильно снижает действие кулоновских
ХИМИЧЕСКАЯ СВЯЗЬ
притяжения. Подобная диссоциация имеет место и в других
растворителях (например, в спирте), но в меньшей степени
из-за меньшей величины диэлектрической постоянной.
3. Гомеополярное соединение. Молекула водорода
Мы попытаемся здесь дать представление об образова-
образовании гомеополярных соединений.
Примерами этого типа соединений являются молекулы
с двумя одинаковыми ядрами, как Н2, О,, N2. Прежде всего
рассмотрим Н2. В связи с этим мы коснемся также вопроса
0 природе сил отталкивания, обусловливающих состояние
равновесия полярных молекул. По сути дела и в гомеопо-
гомеополярных молекулах взаимодействие между ядрами и электро-
электронами — электростатического происхождения. Однако решаю-
решающее значение для механизма соединения имеют явления ре-
резонанса между электронами обоих исходных атомов. Так
как электроны совершенно одинаковы, то при обмене двух
из них местами состояние системы не меняется. Чем сильнее
взаимодействие между двумя электронами, т. е- чем больше
взаимное проникновение их облаков заряда, тем чаще в дей-
действительности происходит этот „обмен". Соответствующая
энергия, величина которой возрастает с частотой обмена,
обусловливает существование так называемых „обменных"
сил, являющихся основой гомеополярной связи.
Мы разъясним это на примере молекулы водорода (те-
(теория Гайтлера и Лондона). Рассмотрим систему из двух
электронов и двух протонов и проследим, как зависят силы
между этими частицами от расстояния между обоими про-
протонами.
Обозначим оба протона через а и Ь, оба электрона —
1 и 2. Безразлично, отнесем ли мы 1 к а, а 2 к b или
1 к b, a 2 к а. Обоим случаям соответствует та же вели-
величина анергии. Когда два состояния одной системы обладают
одинаковой энергией, говорят о „вырождении". В нашем
случае имеет место „обменное вырождение".
Масса протонов относительно велика. Мы момсем поэтому
пренебречь их собственным движением и считать расстояние
10 ГЛАВА I
между ними г постоянным. Расстояния между электронами
и протонами обозначим через гд1, гд?, гй1 и rs2. Точное
решение залачи определения сил, действующих гежду че-
четырьмя частипами, — невозможно. Мы будем считать, что
вначале расстояние между атомами настолько велико, что
воздействие частиц друг на друга исключается. Взаимодей-
стние частиц при постепенном сближении будем рассматри-
рассматривать, как малое возмущение, учитываемое с помощью осо-
особого математического метода теории возмущений и дающее
поправку к основному решению.
В волновой механике каждое состояние системы описы-
описывается собственной функцией. Если оба атома не зависят
дру1 от друга, то собственная 4Ункчия системы равна про-
произведению собственных функций атомов. Пусть вначале
электрон 1 относится к протону а и электрон 2 к протону
Ь. Тшда собственная функция системы равна:
^ = f9(ra-l)-^(rM), A)
где со — собственная функция основного состояния водорода.
Она содержит, если не учитывать спина, только одну пе-
переменную— радиус-вектор электрона. Пусть теперь элек-
электрон 1 относится к протону Ь% а электрон 2 к протону а;
тогда получается система с той же энергией, собственная
функция которой равна
Функции ф, и ф2 только тогда являются собственными
функциями, описывающими определенные квантовые состоя-
состояния системы, когда расстояние между ядрами велико в срав-
сравнении с диаметром атома.
Поскольку функциям ф, и ф2 соответствуют одинаковые
значения энергии, любая линейная комбинация их также
отвечает состоянию с той же энергией. Мы должны с по-
помощью теории возмущений исследовать, какие из этих ли-
линейных комбинаций следует избрать в качестве нулевых
приближений при учете взаимного влияния атомов. Первое
приближение даст тогда энергию этого взаимодействия, за-
висящую, конечно, от расстояния между атомами. Можно
ХИМИЧЕСКАЯ СВЯЗЬ Ц
рзссматрирать эту энергию, как потенциал, определяющий
силу взаимодейстния двух атомов.
Потенциальная энер!ия всей системы равна
е2(Х<± 1 L ! !Л C)
а полная энергия
V^ ' ^12 ^i Пл гса гь-i- 2т '
где рл и ро — величины импульсов обоих электронов.
В уравнении Шредижера квадратам этих импульсов соответ-
соответствуют операторы —- т-^А, и —г~2^ъ (*^i и \ — опера-
операторы Лапласа, относящиеся к координатам первого и вто-
второго электронов).
ср(/;я,) удовлетворяет уравнению Шредингера для атома
водорода
E)
(W— энергия основного состояния водорода).
Ч>1гьО> Ч(гаъ) и *Р (г*г) удовлетворяют аналогичным урав-
уравнениям.
Подставляя уравнения E) в D), получим
Из совокупности всех линейных комбинаций ф, и ф2
выбираем в качестве собственных функций нулевого при-
приближения такие две функции, которые обладают теми же
свойствами симметрии, что и возмущенные собственные функ-
функции, и которые, подобно последним, взаимно ортогональны.
Этим условиям удовлетворяет сумма и разность ф, и ф2„
Действительно, ф-, —j— <1>2 является симметричной функцией
координат электронов, т. е. функцией, не изменяющейся
при оомене местами двух электронов. При этом фх — ф2
12 ГЛАВА I
меняет знак, т. е. является антисимметричной. Так как опе-
оператор1 D) симметричен по отношению к координатам элек-
электронов, то имеет место равенство:
Таким образом, ф, -{- ф2 и ф, — ф2 являются собственными
функциями нулевого приближения, из которых должна
исходить теория возмущений. Предполагая собственные функ-
функции атомов нормированными и обозначая для сокращения:
Р = С <Р (raJ <Р Kl) dh = U (^2) <Р (ГИ) йГта, G)
окончательно получим в нормированном виде:
фсим-~ У2ТГТК -
*"• ГШ^гщ •
Из (8) можно получить значение энергии U в первом при-
приближении. Двум невозмущенным собственным функциям со-
соответствуют и два значения энергии:
(9)
которые "вычисляются с помощью F). Отбрасывая постоян-
постоянный член 2, соответствующий невозмущенной энергии уда-
удаленных друг от друга атомов водорода, окончательно на-
находим :
А~В пп\
П
где положено:
й2'dz{dT
ХИМИЧЕСКАЯ СВЯЗЬ
13
Физическое значение интеграла А совершенно ясно: он вы-
выражает электростатическую энергию взаимодействия обоих
атомов в предположении, что каждое из ядер, независимо от
другого, окружено определенным количеством отрицательного
электричества (заряженные облака). Последние жестко свя-
связаны с ядрами и имеют плотность зарядов е<р2(га) и ец>2(гь),
(
соответственно (через га и гь обозначены расстояния от
^
^
1
\
\\
ft
V
\
\
г
\
\
\
\
\
\
\
\
4 ■
\
_———
Фиг. 1. Зависимость энер-
а ь
ядер а и Ъ соответствующих электронных облаков; распре-
распределение отрицательного заряда,
следовательно, считается сфе-
рически симметричным).
Смысл интеграла В, „обмен-
ной энергии", не так прост,
так как он основан на специ-
фически квантовом эффекте,
неизвестном в классической тео-
рии. Именно: оба электрона
совершенно одинаковы. Они мо-
гут, следовательно, обмени-
ваться местами, не вызывая из-
изменений в состоянии системы.
В есть энергия этого „обме-
на". В\h можно рассматривать
как частоту обмена местами
обоих электронов. Вследствие
обменного вырождения энергия взаимодействия U обоих
атомов расщепляется на два терма, среднее значение кото-
которых при больших расстояниях от ядра достаточно точно
совпадает с электростатической энергией А; при этом зна-
знаменатель в формуле A0) приблизительно равен I.
На фиг. I графически представлена зависимость энергий
^сим. и ^аит.. соответствующих симметричному и антисим-
антисимметричному состояниям системы, от расстояния между яд-
ядрами. Так как В отрицательно, то кривая £/С!Ш. проходит
ниже кривой £/ант>
До сих пор в наших выводах не принимались во внима-
внимание спины электронов и принцип Паули. В обычной кван-
говомеханической форме принцип Паули утверждает, что
от расстояния до ядра (по
Гайтлеру и Лондону).
14 ГЛЛЧА I
в системе с многими электронами собственная функция всегда
алтисимметрична, т. е. что она меняет свой знак при вза-
и.\:1гом обмене координат каких-либо двух электронов (вклю-
(включая и „спиновую координату").
Это не значит, конечно, что из наших собственных
функций (8) вj3Mo/KHa только антисим утетричная, так как в
(8) мы не учитывали спин и, следовательно, использовали
неполную собственную функиию. Принцип Паули применим,
конечно, только для полных собственных функций. Спин
электрона может быть легко учтен, если спиновое состояние
не зависит от орбитального. Тогда полная собственная функ-
функция р;вна произведению функции, содержащей только про-
страмстиениые координаты, и функции спина. Последняя мо-
может быть симметричной или антисимметричной, в зависи-
зависимости от того, параллельно или антипараллельно расположены
векторы спилов оооих электронов. Отсюда следует, что при
симметричной собственной функции (8) векторы спипов
должны быть антипараллельны, и наоборот. Тогда, в соот^
вет^твии с принципом Паули, полная собственная функция
будет алтиелмметрична.
Таким образом, в нашем случае обе собственные функ-
функции представляют физически возможные состояния. Но
поскольку только потенциальная кривая £/сим- имеет минимум,
то лишь фСим. ведет к соединению оооих атомов. Следова-
Следовательно, в невозбужденной молекуле водорода спины обоих
электронов антипараллельны. Состояние с потенциальной
кривой UaiT, (с параллельными спинами), наоборот, не при-
приводит к образованию молекулы: атомы отталкиваются при
любых расстояниях между ядрами.
Потенциальные кривые фиг. 1 стремятся к бесконечности,
когда г приближается к нулю. Следовательно, во всех слу-
случаях в действие вступают силы отталкивания, препятствую-
препятствующие дальнейшему сближению. Причину этого нужно искать
в кулоновском отталкиьапии обоих ядер, перевешивающем
все остальные силы, как только расстояние между ядрами
становится меньше определенной величины.
Количественный расчет молекулы водорода был произ-
произведен, помимо Гайглеиа и Лондона, также а Сигиура.
ХИМИ"ЕСКАЯ СВЯЗЬ
Полученное равновесное( расстояние между атомами находится
в хорошем согласии с экспериментом. Возможно, что это
совпадение случайно, так как нулевое приближение, приня-
принятое Гайтлером и Лондоном за исходную точку теории воз-
возмущений, достаточно точно только для больших расстояний
между ядрами. При малых г оно заведомо непригодно.
Следовательно, этот метод применим только для качест-
качественного рассмотрения вопроса и ьеюден для количественных
расчетов.
Лучшее приближение получил Ванг с собственными функ-
функциями вида:
— (rai+n>,) —
а -\-е а
-\-е
тле а — радиус первой круговой орбиты Бора, т. е. „тра-
ектори i* электрона в основном состояпии атома водорода,
г — параметр, .зависящий or расстояния между ядрами. Ванг
определяет этот параметр ни методу Ритма для каждого
значения г таким ооразом, чтобы собственная функция ф
соответствовала минимуму среднего значения энергии D).
Для равновесною расстояния Ванг находит z =1,66, в
то время как из предпосылок Гайтлера-Лондона люоому
значению г соответствует постоянное значение z=l.
Сопоставим для наглядности результаты Ванта с изме-
измеренными значениями. Дат.ые соответствуют равновесному
расстоянию.
По Вангу Измерено
Энергия молекулы
в единицах Ридоерга .... — 2,278 — 2,326
Момент инерции 0,45d-lu—*° 0,467-Ю»
Частота колеоапий ядра в см . 4 900 4 360
4. Распространение на другие молекулы
Ограничиваясь качественной стороной вопроса, рассмот-
рассмотрим еод.е коротко результаты применения метода Гайтлера-
Лондона к более сложным типам связи. Гомеополярная связь
между двумя атомами всегда основана ьа и^меньом взаимо-
16 ГЛАВА I
действии между двумя электронами. Каждой валентности
■соответствует пара электронов, один из которых принадле-
принадлежит одному из атомов, а второй — другому. Когда два та-
таких валентных электрона имеют параллельные спины, взаи-
взаимодействие приводит к отталкиванию атомов. Потенциальная
кривая имеет вид, подобный £/ант# на фиг. 1.
Когда спины антипараллельны, появляются силы притя-
притяжения. Потенциальная кривая имеет, как и £/сим. на фиг. 1,
явно выраженный минимум, соответствующий равновесному
расстоянию между атомами.
Вообще, в каждом атоме часть электронов образует либо
замкнутую оболочку с исчезающим суммарным моментом
(К-, L-,. .. оболочки), либо пары электронов с равной нулю
суммой спинов (например, два s-электрона с одинаковым
главным квантовым числом). Такие замкнутые оболочки* или
пары создают силы отталкивания между атомами. Гомеопо-
лярная сила притяжения может возникнуть только в резуль-
результате взаимодействия электронов, спины которых еще не
насыщены в атоме. Поэтому два атома щелочных металлов
с одним валентным электроном образуют молекулу, правда,
не очень стабильную. Наоборот, между двумя атомами бла-
благородных газов, обладающих лишь замкнутыми электроннымг
орбитами, действуют силы отталкивания.
Существование молекулы Не2, казалось бы, противоречит
этому утверждению. Доказано, однако, что эта молекула
никогда не образуется при соединении двух нормальных
атомов, а только тогда, когда в результате электрического
разряда имеются возбужденные атомы гелия. Возбуждение
разрушает замкнутую оболочку, и в результате взаимодействия
возбужденных электронов с электронами невозбужденного
атома образуется (правда, очень слабое) химическое соединение.
Подобные „гомеополярные" силы действуют и в поляр-
полярных молекулах. Например, в молекуле NaCl оба иона Na +
и С1~ обладают электронной конфигурацией атомов благо-
благородных газов. Вследствие этого между ними действует го-
меополярная сила отталкивания, которая при малом расстоя-
расстоянии между ионами превосходит полярную силу притяжения
а препятствует дальнейшему сближению.
ХИМИЧЕСКАЯ СВЯЗЬ 17
Все эти рассуждения о механизме гомеополярных связей
имеют, конечно, 'лишь качественное значение. Они служат
для беглого рассмотрения природы сил, действующих в мо-
молекулах. При более точных исследованиях они неприменимы
даже для приближенных расчетов. Кроме того, во многих
случаях невозможно различить, имеет ли место полярная
связь, при которой каждый электрон принадлежит какому-
либо одному ядру, или гомеополярная связь, когда одна или
несколько пар электронов принадлежат одновременно обоим
атомам.
б. Силы притяжения Ван-дер-Ваальса
Гайтлер и Лондон сводят силы, действующие между
двумя атомами, к обменной энергии пар электронов, при-
принадлежащих одновременно обоим атомам. Так как собствен-
собственные функции, а следовательно, и плотность зарядов элек-
электронных „облаков" экспоненциально падают но мере удале-
удаления от ядра, то и величина обменного интеграла обоих
атомов, по крайней мере для больших расстояний, умень-
уменьшается по тому же закону. Поэтому соответствующие силы
притяжения и отталкивания имеют сравнительно маленький
радиус действия и практически исчезают при расстоянии от
ядра, равном нескольким А.
Но, кроме них, между атомами действуют и другие силы,
величина которых при увеличении расстояния падает более
медленно, благодаря чему на больших расстояниях их дей-
действие преобладает по сравнению с действием обменных сил.
Силы эти — результат электрической поляризации обоих
атомов. Такие же силы притяжения входят в уравнение со-
состояния газа Ван-дер-Ваальса. Мы будем называть их по-
поэтому силами Ван-дер-Ваальса.
Квантовомеханическая теория этих сил была создана Лон-
Лондоном и Эйзеншитцем. Ниже мы изложим коротко основное
содержание этой теории.
Оба атома А и В настолько удалены друг от друга,
что их собственные функции не перекрываются. Тогда можно
пренебречь обменными силами между атомами и невозмущен-
2 Эирико Ферми
\S ГЛАВА I
ную собственную функцию нашей системы записать в виде
Фп^/я — произведения собственных функций первого атома <ЬЯ
и второго шт. Невозмущенное собственное значение будет
следующим:
Еат === Аа ~Т~ Вт>
где через Аа и Вт обозначены энергии л-го состояния А
и /га-го состояния В. Предположим теперь, что расстояние г
между обоими атомами остается неизменным. Построим пря-
прямоугольную систему координат xyz, ось z которой совпа-
совпадает с прямой, соединяющей оба атома. Пусть X, Y, Z и
£, rj и £ означают компоненты электрических дипольных мо-
моментов атомов. Тогда, как известно, потенциал взаимодей-
взаимодействия будет равен:
X< — Yi\
Эта энергия связи между обоими атомами, которую мы
рассматриваем теперь как энергию возмущения, является
причиной сил Ван-дер-Ваальса.
Рассмотрим сначала возмущение основного состояния
системы под действием энергии связи. В первом приближе-
приближении возмущение определяется средним значением энергии
возмущения Н, вычисляемым с помощью невозмущенной
собственной функции фо'-ро:
0,00==
где для сокращения обозначено:
и т. д.
Все эти величины равны нулю, так как 'невозмущенный
атом в основном состоянии не имеет электрического момента.
Вследствие этого в первом приближении возмущение соб-
собственного значения энергии отсутствует.
ХИМИЧЕСКАЯ СВЯЗЬ
Второе приближение для энергии возмущения будет
согласно теории возмущений, выражаться формулой:
Д W= —
причем матричные элементы энергии возмущения Ноо,
определяются следующими выражениями:
Здесь ХОт и соответствующие величины являются матрич-
матричными элементами электрических моментов обоих атомов.:
Они определяют также и вероятности оптического перехода.'
Подставляя их в уравнение для AWn одновременно учитывая
значения Ета и £"„, получим
—
г6
где
Z A
Так как и числитель и знаменатель правой части этого
выражения положительны (Ао и Во — энергии атомов в ос-
основном состоянии всегда меньше Ат и Ва), то постоянная
К положительна.
Следовательно, силы Ван-дер-Ваальса, действующие
между атомами в основном состоянии, являются силами при-
притяжения. Определяющий их потенциал обратно пропорцио-*
нален шестой степени расстояния между ядрами.
Можно легко оценить порядок величины К. Например,
для двух щелочных металлов, в предположении, что
a) спин можно не учитывать;
b) следует принимать во внимание только переход} со».
ответствующий резонансному излучению;
20 ГЛАВА II
с) так же, как в классической теории, этому переходу
соответствует один дисперсионный электрон (сила осцилля-
осциллятора /= 1), получим
She*
64гЛт2сЗ Ао-
где лA — длина волны резонансной линии. Отсюда для нат-
натрия АГ= 1,5.10-".
Для других атомов, поляризующихся менее сильно, чем
атомы щелочных металлов, получаются значительно меньшие
значения. Например, для водорода (по Эйзеншитцу и Лон-
Лондону) Л"=6-10-60'
ГЛАВА II
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
6. Общая схема термов молекулы
По обилию линий и характерной их группировке спек-
спектры молекул уже на первый взгляд можно отличить от спектров
атомов. Большое количество линий объясняется большим
числом возможных колебаний и вращений ядер. Так как
масса ядер много больше массы электронов, то разности
энергии вращательных и колебательных термов, в общем
случае, значительно меньше изменения энергии при переходе
между различными электронными состояниями.
Согласно квантовому условию Бора, небольшой разности
энергии соответствует и небольшая разница длин волн. Этим
объясняется своеобразная группировка линий, из-за которой
полосатые спектры получили свое название.
В то время как спектры двухатомных молекул могут
быть истолкованы с помощью простейших представлений,
законы спектров многоатомных молекул настолько сложны,
что до сих пор не получили исчерпывающего объяснения.
Поэтому мы будем рассматривать сначала только спектры
двухатомных молекул.
При исследовании структуры термов двухатомной моле-
молекулы целесообразно исходить из упрощенной модели. Раз-
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 21
ность энергий двух состояний молекулы, отличающихся
только вращением, невелика в сравнении с разностью энер-
энергий двух различных колебательных состояний; последняя,
в свою очередь, мала по сравнению с расстояниями между
двумя квантовыми состояниями с различным движением элек-
электронов. Поэтому в первом приближении мы можем рас-
рассматривать вращение, колебание и движение электронов
как независимые друг от друга явления. Позже, во втором
приближении, мы рассмотрим их влияние друг на друга.
Рассмотрим прежде всего движение электронов, считая
ядра неподвижными. Действительно, вращение и колебание
ядер происходят настолько медленно, что частотой этих
движений, по сравнению с частотами движений электронов,
можно пренебречь. Система электронов может находиться
в различных квантовых состояниях, которым соответствуют
значения энергии U . В U входит и электростатическая
энергия ZZ' — обоих ядер с порядковыми номерами Z и Z',
которая постоянна при неизменном г. Тогда U действительно
выражает полную энергию молекул при неподвижных
ядрах. Очевидно, U зависит от расстояния между
ядрами.
На фиг. 2 представлена эта зависимость для различных
электронных состояний. Все кривые („потенциальные кри-
кривые") имеют общее свойство: при г—*0 они стремятся
к бесконечности. Следовательно, при небольшом расстоянии
г между атомами действуют силы отталкивания, превосхо-
превосходящие все остальные силы.
Кривые фиг. 2 имеют еще одно общее свойство. Вез
они обладают асимптотой, параллельной оси г. Следовательно,
для больших расстояний между ядрами энергия системы
в каждом электронном состоянии имеет определенное пре-
предельное значение, вообще говоря, разное для различных
электронных состояний. Когда ядра удаляются друг от
друга, электроны молекул разделяются на две группы,
распределяющиеся вокруг обоих ядер. Наконец, при большом
расстоянии между ядрами из полярной молекулы возника-
возникают два отдельных иона, из гомеополярной — два атома.
20 ГЛАВА II
с) так же, как в классической теории, этому переходу
соответствует один дисперсионный электрон (сила осцилля-
осциллятора /= 1), получим
где лA — длина волны резонансной линии. Отсюда для нат-
натрия АГ=1,5.10-67.
Для других атомов, поляризующихся менее сильно, чем
атомы щелочных металлов, получаются значительно меньшие
значения. Например, для водорода (по Эйзеншитцу и Лон-
Лондону) АГ=6.10-60-
ГЛАВА II
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
6. Общая схема термов молекулы
По обилию линий и характерной их группировке спек-
спектры молекул уже на первый взгляд можно отличить от спектров
атомов. Большое количество линий объясняется большим
числом возможных колебаний и вращений ядер. Так как
масса ядер много больше массы электронов, то разности
энергии вращательных и колебательных термов, в общем
случае, значительно меньше изменения энергии при переходе
между различными электронными состояниями.
Согласно квантовому условию Бора, небольшой разности
энергии соответствует и небольшая разница длин волн. Этим
объясняется своеобразная группировка линий, из-за которой
полосатые спектры получили свое название.
В то время как спектры двухатомных молекул могут
быть истолкованы с помощью простейших представлений,
законы спектров многоатомных молекул настолько сложны,
что до сих пор не получили исчерпывающего объяснения.
Поэтому мы будем рассматривать сначала только спектры
двухатомных молекул.
При исследовании структуры термов двухатомной моле-
молекулы целесообразно исходить из упрощенной модели. Раз-
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 21
ность энергий двух состояний молекулы, отличающихся
только вращением, невелика в сравнении с разностью энер-
энергий двух различных колебательных состояний; последняя,
в свою очередь, мала по сравнению с расстояниями между
двумя квантовыми состояниями с различным движением элек-
электронов. Поэтому в первом приближении мы моясем рас-
рассматривать вращение, колебание и движение электронов
как независимые друг от друга явления. Позже, во втором
приближении, мы рассмотрим их влияние друг на друга.
Рассмотрим прежде всего движение электронов, считая
ядра неподвижными. Действительно, вращение и колебание
ядер происходят настолько медленно, что частотой этих
движений, по сравнению с частотами движений электронов,
можно пренебречь. Система электронов может находиться
в различных квантовых состояниях, которым соответствуют
значения энергии U . В U входит и электростатическая
энергия ZZ' — обоих ядер с порядковыми номерами Z и Z',
которая постоянна при неизменном г. Тогда U действительно
выражает полную энергию молекул при неподвижных
ядрах. Очевидно, U зависит от расстояния между
ядрами.
На фиг. 2 представлена эта зависимость для различных
электронных состояний. Все кривые („потенциальные кри-
кривые") имеют общее свойство: при г—*0 они стремятся
к бесконечности. Следовательно, при небольшом расстоянии
г между атомами действуют силы отталкивания, превосхо-
превосходящие все остальные силы.
Кривые фиг. 2 имеют еще одно общее свойство. Все
они обладают асимптотой, параллельной оси г. Следовательно,
для больших расстояний между ядрами энергия системы
в каждом электронном состоянии имеет определенное пре-
предельное значение, вообще говоря, разное для различных
электронных состояний. Когда ядра удаляются друг от
друга, электроны молекул разделяются на две группы,
распределяющиеся вокруг обоих ядер. Наконец, при большом
расстоянии между ядрами из полярной молекулы возника-
возникают два отдельных иона, из гомеополярной — два атома.
22
ГЛАВА II
Предельное значение полной энергии, к которому приближа-
приближаются потенциальные кривые при г—>оо, равно сумме энергий
обеих отдельных частиц. В зависимости от исходного состоя-
состояния молекулы, частицы, образовавшиеся при ее расщеплении,
могут, конечно, находиться и в возбужденном состоянии.
Таким образом, предельные значения энергии для различных
квантовых состояний могут быть различными. Они склады-
складываются из энергий каких-
либо двух квантовых состоя-
состояний разделенных атомов или
ионов.
Например, кривая с фиг. 2
снижается с увеличением г;
кривые а, Ь и d, напротив,
проходят через минимум.
Этот факт имеет решающее
значение, так как минимум
потенциальной кривой соот-
соответствует положению равно-
равновесия, наличие которого
необходимо для образования
молекулы. В случае с подоб-
подобного состояния равновесия
нет; образование молекулы,
следовательно, невозможно,
так как ядра отталкиваются
при любых расстояниях.
Кривые подобного типа
встречались уже при рассмот-
Ф и г. 2. Зависимость энергии
Uq двухатомной молекулы от
расстояния между ядрами г для
различных электронных состоя-
состояний (потенциальная кривая).
рении молекулы водорода (фиг. 1). Также и там к образо-
образованию молекул водорода ведет только симметричное со-
состояние, потенциальная кривая которого имеет минимум.
В антисимметричном состоянии оба атома отталкиваются
при любых расстояниях. Мы рассматривали там только слу-
случай, когда при разделении молекулы возникают два невоз-
невозбужденных атома. Обе кривые £/с,.ш. и £/аНт. имеют, следо-
следовательно, одно и то же асимптотическое предельное значение.
Конечно, и в случае молекулы водорода имеются состояния,
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
из которых возникают возбужденные атомы. Они будут
рассмотрены пбзже.
Когда для определенного электронного состояния мо-
молекулы энергия О (г) имеет минимум, ядра находятся на
равновесном расстоянии г0. Мы можем разложить U(г)
в ряд по степеням х = г — г0. Разумеется, в этом раз-
разложении отсутствует член первой степени, так как в ми-
минимуме первая производная равна нулю и разложение
имеет вид:
t/(r)=fl-fJ.jc2-fc-^ + ... A2)
Коэфициенты а, Ь, с... различны для различных элек-
электронных состояний. В случае необходимости мы будем от-
отмечать их индексом q.
В первом приближении мы обрываем разложение на вто-
втором члене, пренебрегая, следовательно, членами более вы-
высоких степеней, чем хг. Тогда энергия, с точностью до
постоянного члена, пропорциональна квадрату расстояния
х от положения равновесия г0. Это означает, что на ядра
действует квазиупругая сила, стремящаяся вернуть их к по-
положению равновесия. Вследствие этого они колеблются
вокруг положения равновесия, периодически сближаясь
и удаляясь друг от друга. Обозначим частоту этих коле-
колебаний через cv (v — волновое число — обратная длина волны).
Энергия различных колебательных состояний выразится
уравнением:
(i) A3)
где v — колебательное квантовое число, могущее принимать
значения 0, 1,2,...
Это уравнение также справедливо только в первом
приближении, т. е. для малых значений v. Для больших
v амплитуда колебаний настолько значительна, что в фор-
формуле A2) необходимо принимать во внимание члены более
высоких степеней. Тем самым колебание становится ангар-
ангармоническим, и выражение A3) должно быть, как мы увидим
впоследствии, дополнено еще одним членом.
24
ГЛАВА II
Рассмотрим еще коротко вращательное движение. При
этом в первом приближении пренебрежем колебаниями,
считая ядра жестко связанными между собой. Массой элек-
электронов мы также можем пренебречь, тем не менее, их дви-
движение может оказывать существенное влияние на вращение.
В соответствии с нашим полуклассическим способом
рассмотрения, это следует представить себе так: если не
учитывать вращения прямой, связывающей ядра, -— „ моле-
молекулярной оси", то момент силы,
действующей на электроны,
относительно этой прямой
равен нулю, а составляющая
момента количества движения
электронов в направлении этой
оси постоянна.
Согласно квантовой теории,
величина этой составляющей
момента может быть целой или
полуцелой кратной величины
— . В нашем случае она равна
Q • —, где Q принимает целые
^5 ТС
или полуцелые значения. Если
теперь оба ядра вращаются
вокруг центра тяжести .моле-
.молекулы, то соответствующий
Фиг. 3. Векторная сумма
момента количества движе-
движения электронов в направле-
направлении молекулярной оси S и
момеьта количества движе-
движения молекулы R, образую-
образующая полный момент J[ из-
h
\
мерено в единицах —
момент количества движения /<тг перпендикулярен линии,
соединяющей ядра. Он складывается векторно с Q ^ , об-
разуя полный момент 7^- (фиг. 3). J — постоянно по вели-
чине и направлению, R и й совершают тогда регулярную
процессию вокруг неизменного направления /, подобно оси
волчка, подвешенного в центре тяжести. Только при равен-
равенстве момента Q нулю движение молекулы упрощается и сво-
сводится к вращению вокруг прямой, перпендикулярной к мо-
молекулярной оси. Обозначая через / момент инерции молекулы,
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 25
получим следующее классическое выражение для энергии
вращения обоих ядер Ег:
где для сокращения положено
С другой стороны, из фиг. 3 следует:
Поэтому A4) принимает вид:
Квантовая механика частично подтверждает, частично ви-
видоизменяет эти результаты. Для энергии вращения полу-
получается следующее квантовомеханическое выражение:
) — Q2}. A6).
Q и У принимают целые значения @, 1, 2, 3 .. .) при четном.
/13 5 \
числе электронов и полуцелые значения —, к-, -к-. . . nptt
\ Л л 2 /
нечетном числе электронов в молекуле.
В имеет разные значения для различных электронных
состояний, так как зависит от момента инерции и, тем самым,
от равновесного расстояния между ядрами, изменяющегося,
вообще говоря, с изменением электронного расстояния.
В случае необходимости, мы можем отмечать В индексом
q. В небольшой степени В зависит и от колебательного-
и вращательного состояний, так как и они оказывают опре-
определенное влияние на среднее расстояние между ядрами.
Мы получаем, наконец, полную энергию молекулы Е как
сумму электронной энергии G(го) = Я0, энергии колебаний
и энергии вращения:
Й21.
26 - ГЛАВА II
Из этого упрощенного выражения энергии, с помощью
некоторых правил отбора, которые мы рассмотрим ниже,
можно получить общее строение полосатых спектров.
7. Правила отбора для J и v
Важнейшее правило отбора, распространяющееся как на
•молекулы, так и на атомы, гласит, что при каждом кванто-
квантовом переходе квантовое число J может измениться не больше,
чем на единицу. Имеются, следовательно, три возможности
перехода:
J$J . A8)
У—1
Кроме того, запрещен переход У=0—>J=0. Это
правило справедливо для любых систем (атомы, двух- или
многоатомные молекулы).
Правило отбора для колебательного квантового числа
гармонического осциллятора, v —* v -±z 1» не распространяется
на полосатые спектры, главным образом, по двум причинам.
Первая причина состоит в том, что, в общем случае, при
переходе в молекуле одновременно изменяются колебатель-
.ное, вращательное и электронное состояния. А с каждым
электронным переходом связано изменение частоты колеба-
колебаний и равновесного расстояния ядер. Естественно, что на
такой переход правило отбора, пригодное для неизменного
м неподвижного осциллятора, не распространяется.
Вторая же причина та, что, даже для перехода в молекуле
без изменения электронного состояния, правило v—*-vA- I
пригодно только в первом приближении, так как, с одной
стороны, колебания всегда несколько ангармоничны, в то
время как правило отбора в точности справедливо только
для гармонического осциллятора, и, с другой стороны,
электрический момент молекулы изменяется не строго ли-
линейно по отношению к изменению расстояния ядер от по-
положения равновесия.
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 27
8. Вращательно-колебательные полосы
Частоты излучения молекулы можно определить, составив
разность энергий двух уравнений и разделив ее на h (или
на /г-с, если нужно выразить частоты'в волновых числах).
При этом нужно различать два случая, в зависимости
от того, связан ли переход с электронным переходом или
нет. В первом случае разность энергий обоих состояний
и, соответственно, излучаемая при переходе частота много
больше, чем во втором. Причина этого, как уже было упо-
упомянуто, заключается в том, что разница в энергии между
двумя электронными состояниями, в общем случае, много
больше, чем расстояние между смежными вращательными
и колебательными термами. Испускаемые при электроннол!
переходе полосы обыкновенно располагаются в видимой или
ультрафиолетовой части спектра. Наоборот, полосы, при
испускании которых изменяются только вращательная и ко-
колебательная энергии, расположены в инфракрасной части
спектра. В этом смысле не вполне правильно различаются
видимые и инфракрасные полосы. Правильнее называть их
электронными полосами и вращательно-колебательными поло-
полосами или, соответственно, вращательными полосами.
В инфракрасных полосах почти всегда имеем дело с ко-
колебательными и вращательными переходами в основном
электронном состоянии. Обычно они наблюдаются при по-
поглощении у газов и паров при температурах, недостаточных
для возбуждения более высоких электронных состояний.
Инфракрасные полосы наблюдаются далеко не у всех
молекул. Например, они отсутствуют у симметричных двух-
двухатомных молекул Н2, N2, О2... . Действительно, испуска-
испускание (или поглощение) излучения есть электромагнитный
процесс, который может иметь место, только если молекула
обладает электрическим моментом, направленным, в случае
излучения колебательной энергии, параллельно молекулярной
оси.
Когда ядра молекулы колеблются друг относительно
друга, происходит периодическое изменение величины этого
момента, и при этом происходит излучение, „классическое"
28 ГЛАВА II
излучение, при котором частота излучаемой электромагнит-
электромагнитной радиации соответствует частоте колебания ядер. При
вращении молекулы подобным же образом изменяется на-
направление электрического момента, и этому изменению со-
соответствует испускание вращательной линии. Следовательно,
вращательные и колебательные полосы могут появляться,
только если молекула имеет постоянный электрический мо-
момент, т. е. состоит из разнородных атомов. Молекулы, со-
состоящие из одинаковых атомов, вследствие симметрии не
обладают подобным моментом, поэтому ни в спектрах ис-
испускания, ни в спектрах поглощения они не имеют инфра-
инфракрасных полос.
При рассмотрении строения вращательно-колебательной
полосы мы исходим из выражения A7) для энергии моле-
молекулярного состояния. Так как электронное состояние ос-
остается неизменным, величины £0, v и В для начального
и конечного состояний имеют одно и то же значение. Кроме
того, мы можем принять, что 0 = 0, так как это почти
всегда имеет место для основного состояния молекул,
у которых наблюдаются вращательно-колебательные полосы.
Для этих полос справедливо уточненное, по сравнению
с A8), правило отбора, запрещающее переходы, при кото-
которых J остается постоянным. Действительно, при ii = O R
всегда равно J, поэтому проекция электрического момента
(имеющего направление молекулярной оси) на ось J исчезает.
Таким образом, полагаем, что Q = 0. Обозначим кван-
квантовые числа колебательного движения для начального и ко-
конечного состояний через v' и v". Соответствующие значе-
значения J (которые при й = 0 равны значениям вращательного
квантового числа) обозначим У и J". Полная энергия на-
начального и конечного состояний тогда будет иметь вед:
V + ±) + ( +), )
1A9}
Для частоты перехода между этими термами (выраженной
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 29
з волновых числах) получим:
c*=^- = v(xr' —г/'0 + Я[У (У+1) —/'(/'+1)]. B0)
На основании нашего правила отбора, имеем I' = У -4- 1.
При J" = У -(- 1 получается ряд частот:
«, = v(V — г/") — 25 (У+ 1) У = 0, 1, 2, 3, . .. B1)
А при У' = У —1:
ш = v {V — */') -f 2ЯУ У =1,2,3,... B2)
Во втором случае значение У = 0 исключается, так как
зто соответствовало бы отрицательному значению J". Для
определенной пары значений v' и v" при различных значе-
значениях У из формул B1) и B2) получатся два ряда линий,
совместно образующих вращательно-колебательную полосу.
Оба ряда называют „ветвями". Ряд, частоты которого
меньше, чем v(v' — if), т. е. соответствующий формуле B1),
называется Р-ветвью. Ряд, соответствующий формуле B2),
называется R-ветвыо. Его частоты больше, чем v (г»' — if).
В обеих ветвях разность частот Av между двумя последо-
последовательными линиями равна:
£A_cm-i. B3)
Первые линии обеих ветвей отстоят на расстоянии 43
друг от друга. На фиг. 4 схематически изображена подоб-
подобная полоса. Она состоит из непрерывной последовательности
равноотстоящих друг от друга линий, из которых выпадает
одна — нулевая линия на границе Р- и R-ветвей. Позже,
при обсуждении соотношения интенсивностей различных ли-
линий, мы увидим, что интенсивность линий, примыкающих
к нулевой линии, в обеих ветвях мала. С удалением от
нулевой линии она сначала достигает максимума, а затем
снова падает. На фиг. 4 это изображено толщиной линий.
На фиг. 5 и 6 показаны две экспериментально наблюдав-
наблюдавшиеся инфракрасные полосы, в которых изменение интен-
интенсивности вращательных линий следует этому правилу.
so
ГЛАВА И
Из формулы B3) следует, что разность частот соседних
линий вращательно-колебательной полосы обратно пропор-
пропорциональна моменту инерции молекулы. Вследствие малых
моментов инерции ли-
р ''—"i-?<9 p—ft- *.. нии двухатомных гид-
гидридов особенно далеко
отстоят друг от друга.
Наоборот, линии в по-
полосах тяжелых молекул
лежат очень близко
друг к другу и, вслед-
вследствие малой разрешаю-
разрешающей силы спектромет-
спектрометров в инфракрасной об-
Л
Фиг. 4. Схематическое изображение
вращательно-колебательной полосы в
масштабе частоты. Полоса соответ-
соответствует единственному колебательному
переходу v' — v". Толщина штрихов
характеризует интенсивность враща-
вращательных линий.
всегда могут быть раз-
разделены. В немногих случаях, когда линии наблюдаются раз-
раздельно, можно, с помощью уравнения B3), из разности частот
ласти спектра,
не
I
Ф и г. 5. Фотографическое изображение инфракрасной
вращательно-колебательной полосы в поглощении
(по Герцбергу).
довольно точно определить момент инерции, и отсюда — рас-
расстояние между ядрами. Например, разность частот двух
соседних линий в полосе хлористого водорода (фиг. 8}
равна 20,9 см-1. Отсюда получается значение для момента
инерции /;
/=
=2.6
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
31
Если обозначить массу атома водорода тн, массу атома
хлора mcv то по правилам механики момент инерции выра-
выражается формулой:
'= тнГПс1 г2.
т
н
■2.3?
3,3р
•SO
\ю
га
t
JLil
1
It
1
1
1
Ч
4' 3
У
-1
A Л Л
...,, ,, ^
и
-!-■ - -А
/дг iar
100' 93'
Ф и г. 6. Кривая поглощения хлористого водорода
в инфракрасных лучах.
Масса атома водорода равна 1,66-10~24, масса атома
хлора в среднем в 35,5 раза больше. Отсюда:
7=1,61- 10-24. Г2.
А подставляя полученное значение 7, находим расстояние
между ядрами г0:
го = 1,27.1О-6 см.
Обычно инфракрасные полосы наблюдаются при. погло-
поглощении. Поэтому в них имеют место только такие переходы,
нижний терм которых лежит вблизи основного состояния.
На фиг. 7 приведена общая схема колебательных и вра-
вращательных термов молекулы. Каждый терм обозначен двумя
цифрами, колебательным и вращательным квантовыми чис-
числами v и J. При температуре абсолютного нуля все моле-
молекулы находятся в состоянии 00. При комнатной температуре
они распределяются, соответственно тепловой энергии kT, по
оазличным вращательным уровням (см. раздел 30). Разность
ГЛАВА II
энергии между высшими колебательными состояниями и ос-
основным состоянием в большинстве случаев больше, чем kT,
так что преобладающая часть молекул на-
ходится в основном колебательном состоя-
нии. Поэтому в поглощении появляются
^^^^ только линии, исходящие из основного
колебательного состояния, нижний
терм которых, следовательно, имеет кван-
товое число v" = 0. Наиболее сильная
полоса оответствует переходу; v'=.l,
^ v" = 0, так называемому основному ко-
колебанию. Переходы 2,0 и 3,0 значи-
значительно слабее. Кроме этих полос, су-
ществует чистая вращательная полоса
v' = •»"= 0. Она лежит далеко в глу-
———— бине инфракрасной области.
гз-
22-
21 -
2О~
13 ■
/2 .
/7 .
а*-
оз -
02-
01 -
СО'
•Фиг. 7. Схема
вращательно -коле-
-колебательных термов
двухатомной моле-
молекулы. Первая из
двух цифр, кото-
которыми обозначен
каждый терм, яв-
является колебатель-
колебательным квантовым чис-
числом v, вторая — вра-
вращательным кван-
квантовым числом J.
9. Электронные полосы
Когда, кроме вращательного и коле-
колебательного состояний, изменяется и
электронное состояние, полоса приоб-
приобретает совершенно другую структуру.
Чтобы вычислить расстояние между ли-
линиями такой электронной полосы,
необходимо снова, с помощью A7),
найти разность энергий начального и
конечного состояний и разделить ее
на he:
' = Е'0 + hey
' (V + 4, ) + hcB' [У (У + 1) — Q'2},
E" = £J -f- Асу" ( г>" + ^ ) + /гс5" [У (/'
B4)
Однако в этом случае, вследствие изменения электрон-
электронного состояния, v' и В' ые равны соответственно у" и В'.
Мы получаем поэтому:
о = А + vV — vV-f B'J' {J' + 1) — B"J" (f -|- 1), B5)
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 33
где только величина
А = 1 {Е'о — Е"о) + 1 (v' — v") + В»®'* — B'&'t B6)
1
не зависит больше от вращательных и колебательных кван-
квантовых чисел и, следовательно, имеет одинаковое значение
для всех линий, соответствующих одинаковым электронным
переходам. Совокупность этих линий называется системой
полос, в то время как часть этих линий, соответствующая
определенной паре квантовых чисел v'—v", называют по-
полосой. Частоты линий отдельных полос можно получить из
B5), подставив для v' и v" два определенных значения.
По правилам отбора A8) J" может принимать значения
/'-|~1, J' и J' — 1. Соответственно этому, в общем случае
полоса состоит из трех ветвей Р, Q и R. Из B5) частоты
линий трех ветвей определяются следующими выражениями:
Р-вгтвь {Vf )
+ (В" — В') У'2 — (ЗЯ' — В') J' — 2В",
Q-ветвь <o — A-\-y'V—v'V \ !
+ (
R-зетвь (о = А -\- v'v' — v'V
+ (В' — в") J'2 -f- J' {В' -н в"). )
При этом необходимо учитывать, что J' и J" должны
быть, по крайней мере, не меньше Q' и й". Например,
когда Q' = Q" = Q, J' в ветвях Р и Q может принимать
значения Q, Q —|— 1 т Q-{-2, ...,а в ветви R — только
%-\-\, Q-f-2,..., так как при J' = Q в R-ветви
(/'■ = J' — 1) имели бы для I' значение /' = 2 — 1.
На фиг. 8 графически представлены величины частот
различных линий полосы, в зависимости от вращательного
квантового числа J'. Частоты отложены по оси абсцисс,
зращательные квантовые числа — по оси ординат. Три кривые
соответствуют трем уравнениям B7) для случая, когда
2' = Q" = 0 и В' ^> В". Легко видеть, что полоса резко
отделена со стороны малых частот. В этом месте линии
сгущаются и образуют так называемую голову (кант) полосы.
С ростом частоты расстояние между линиями возрастаем
J Энрико Фепми
ГЛАВА II
а их интенсивность постепенно уменьшается. Полоса к фио-
фиолетовой части спектра стушевывается. Когда В' <^ В",
наблюдается обратное явление — полоса стушевывается
в сторону длинных волн, а ее кант находится в коротко-
коротковолновой части спектра. Как видно из B7), три кривые
фиг. 8 являются параболами. На фиг. 9 приведен практи-
практический припер.
4
Фиг. 8. Графическое определение положения линий полосы
с помощью уравнений B7) (диаграмма Фортра). В качестве
абсцисс нанесены частоты <о, в качестве ординат—вращательные
квантовые числа J. Показанные параболы соответствуют трем
уравнениям. Линии лежат при значениях частот, соответствую-
соответствующих целочисленным J.
Здесь следует указать, что имеется много полос, струк-
структура которых отклоняется от этой схемы. Например, част»
наблюдаются случаи, когда, вследствие особых соотношений
симметрии электронных термов, отсутствует Q-ветвь, как
это всегда имеет место в инфракрасных полосах. Часто,
когда электронные состояния расщеплены или вырождены,
лолосы имеют больше трех ветвей.
Случаи, в которых оба электронных терма — простые,
т, с. не расщеплены и не вырождены, встречаются соав-
СПЕКТРЫ ДВУХАТОМНЫХ .МОЛЕКУЛ
нительно редко. Возьмем в качестве примера полосу гид-
гидрида алюминия А1Н, для которой А =44597 cm~j,
:/= I 326, у"= 1 625, В' — 6,37 и Б" = 6,30. С помощью
уравнения A5} мы можем вычислить отсюда моменты инер-
инерции для начального и конечного состояний. Получаем
/' = 4,33 • 10~40 и /" = 4,38 • Ю-40. Поскольку массы обоих
Фиг. 9. Диаграмма Фор-.-ра полосы 4 241А
гидрида алю линия по Бенгтсону.
атомов известны, то из этих величин могут быть опреде*
лены равновесные расстояния для обоих квантовых состоя-
состояний. Они оказываются равными Гд=1,65 А и Гд=1,6бА.
Мы уже указывали, что правило отбора для гармони-
гармонического осциллятора (v" -ф' + 1) непригодно даже в пер-
зом приближении для электродных полос. На основании
установленного Франком и К^д^илм при i4>nici &ю„- -4
36
ГЛАВА II
однако, хотя бы приблизительно, оценить относительные ин-
интенсивности отдельных полос системы. Для этой цели на
фиг. 10 изображена зависимость энергии U (г) от расстоя-
расстояния между ядрами. Верхняя потенциальная кривая соответ-
соответствует начальному состоянию системы полос, а нижняя
кривая — конечному. Допустим, что молекула находится в
верхнем состоянии на уровне
АВ, которому соответствует
квантовое число v1. Расстояние
между колеблющимися друг
относительно друга атомами ме-
меняется от А до В. В этих по-
поворотных пунктах колебания
относительная скорость атомоз
равна нулю. За полупериод
колебаний она возрастает до
максимума и к достижению
следующего поеоротного пункта
снова падает до нуля. Поэтом}
не все расстояния равновероят-
Ф и г. 10. Потенциальные
кривые U(r) для двух элек- ны Величины, которым соот-
тронных состояний двух- _ ' F
атомной молекулы. Поясне- ветствует большая относитель-
ние принципа Франка-Кон- пая скорость, пробегаются бы-
дона. стро. Чаще всего атомы нахо-
находятся друг от друга на расстоя-
расстоянии А или В. Но когда в определенный момент происходит
квантовый переход, вместе с электронным „«стоянием изме-
изменяется и взаимная энергия атомов, которая теперь будет изоб-
изображаться -нижней потенциальной кривой фиг. 10. Переход
происходит так быстро, что расстояние между ядрами при
этом заметно не изменяется. Чаще всего переходы проис-
происходят в точках А и В, так как последние соответствуют
наиболее вероятным положениям атомов. Во время элек-
электронного перехода кинетическая энергия колебания не может
существенно измениться, так что новое колебание начи-
начинается также в поворотном пункте, но уже на новой по-
потенциальной кривой.
Когда электронный переход происходит при расстоянии
СПЕКТРЫ ДБУХАТО.МНЫХ МОЛЕКУЛ
между ядрами А, молекула переходит на новую потенци-
потенциальную кривую в точке А и продолжает колебание с
квантовым числом v±. Наоборот, при переходе с точки В
О
®<л © @© ©©®
Фиг. П. Интенсивность полос системы полос молекулы
(по де Кронигу).
молекула попадает в колебательное состояние В' с кван-
квантовым числом v'i. Если потенциальные кривые известны, мы
можем найти оба значения v\ и х>2, отвечающие определен-
определенному v', при помощи графического построения, приведен-
приведенного на фиг. 10. Конечно, из состояния v\ при расстоянии
между ядрами в пределах от А до В, могут быть полу-
получены и другие колебательные уровни конечного состояния.
Как мы видели, это происходит, однако, значительно реже,
и саответствующие полосы имеют меньшую интенсивность.
Мы рассмотрим это более подробно на приведенном
Кронкгом примере (фиг. 11, система полос молекулы Na2).
38
ГЛАВА И
По оси абсцисс отложены квантовые числа v', по оси ор-
ординат— квантовые числа v". Каждой точке (v'v'') соответ-
соответствует определенный переход. Интенсивность всех наблю-
наблюдавшихся полос нанесена в соответствующем месте диаграммы
Точки, соответствующие, по принципу Франка-Кондона,
наиболее частым переходам, лежат на кривой — параболе
Кондона.
10. Ангармоничность колебаний я диссоциация
Мы уже отмечали, что сила, стремящаяся вернуть ядра
положение равновесия, только в первом приближении
и пропорциональна их уда-
удалению от этого положе-
положения. Вследствие этого ко-
колебания вокруг положения
равновесия могут рассмат-
рассматриваться как гармониче-
гармонические тоже только в первом
приближении. Это озна-
означает, что формула A3)
справедлива только для
малых значений кванто-
квантового числа v. Для боль-
Фег. 1j. Потенциальная кривая
двухатомной молекулы с нарисо-
нарисованными колебательными уровня-
уровнями. Заштрихованная часть соот-
соответствует области диссоциации, в
которой амплитуда колебаний
бесконечна.
ших значений энергия с
хорошим приближением
может быть представлена
квадратичным выраже-
выражением:
О-Л-f-v. B8)
Ev={a-v~-bv2)-/i-c-v.
Для простоты здесь опущен член с у/2— энергия ос-
осциллятора для v = 0 (нулевая энергия).
Ангармоничность колебаний тесно связана с диссоциа-
диссоциацией молекулы. Для гармонического осциллятора рассто-
расстояние между последовательными колебательными термами
одинаково. В реальной молекуле, напротив, с ростом кван-
квантовых чисел термы располагаются все ближе друг к другу
• СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 39
пока, наконец, расстояние между ними не становится ис-
чезающе малым. На фиг. 12 это изображено для типичной
потенциальной кривой. Горизонтальные прямые соответст-
соответствуют колебательным уровням. Дискретные термы выше
места сгущения отсутствуют. Как видно из cj.nr. 12, в
месте сгущения один из поворотных ■ пунктов колебаний
отодвигается в бесконечность, т. е. „амплитуда" колебаний
становится бесконечно большой: молекула диссоциируется.
Необходимая для диссоциации энергия равна, следовательно,
разности между самым низким колебательным термом и ве-
величиной U {г) для г=оо, к которой сходятся термы с
возрастанием квантового числа v. По Франку, энергия
диссоциации гложет быть поэтому определена с помощью
полосатого спектра, если из распределения колебательных
термов основного электронного состояния удается найти
положение места схождения.
Если последовательность колебательных термов молекулы
может быть представлена квадратичной формулой B8) и
для больших значений v, то приближенное выражение для
расстояния между соседними термами получается диффе-
дифференцированием Ev no v\
В месте сходимости, в котором происходит диссоциа-
диссоциация. Д£^ = 0 и отсюда v = сц2Ь. Подставляя это выраже-
выражение в B8), получаем значение энергии диссоциации:
WW = /^. B9)
Конечно, эта формула является только грубым прибли-
приближением, так как для очень больших v уравнение B8) те-
теряет свою применимость.
Очень надежные результаты получаются, если известны
высшие колебательные термы и возможно непосредственно
определить место их сходимости.
Этим путем для молекулы водорода определено:
W,rcc. = 4,34 eV, в то время как из B9) с а = 4247 и
£=114,4 для Wjwzc. следует значение 4,86 eV. Это
40 ГЛАВА II
отклонение объясняется; ограниченной применимостью урав-
уравнения B8). '
Во многих случаях этот метод неприменим, так как
известно слишком мало колебательных термов основного
состояния. В этих случаях можно исходить из более высо-
высоких электронных состояний, если для них известно больше
термов. Например, для молекулы водорода из наблюдений
поглощения достаточно точно известна общая точка сходи-
сходимости двух возбужденных электронных состояний. Она
лежит приблизительно при 118 000 см~!, что соответствует
14,6, считая от основного состояния. При диссоциации в
этих электронных состояниях молекула распадается на воз-
возбужденный и невозбужденный атом. Энергия возбужден-
возбужденного атома составляет 3/4 единицы Ридберга = 10,2 eV,
которые должны быть вычтены из наблюдаемой энергии
диссоциации. Энергия, необходимая для расщепления мо-
молекулы водорода на два невозбужденных атома, составляет,
таким образом, 14,6—10,2 = 4,4 eV, что согласуется с
вышеприведенным значением.
В качестве другого примера рассмотрим молекулу
хлора С12. Спектр поглощения его хорошо известен. Ко-
Колебательные полосы сходятся при длине волны 4785 А» что
соответствует 2,58 eV. Известно, однако, что один из двух
образующихся атомов находится в зр^-состоянии, лежа-
лежащем на 0,11 eV выше основного состояния. Энергия, необ-
необходимая для диссоциации молекулы хлора на два невоз-
невозбужденных атома, равна, следовательно, не 2,58, а только
2,58 — 0,11=2,47 eV. В хорошем соответствии с этим
находится химическое значение — 57 кал.
Диссоциация может быть вызвана различными причинами:
постепенным возрастанием колебательной энергии при
столкновении с другими молекулами, поглощением светового
кванта или электронным ударом. В обоих последних случаях
имеются различные возможности. Если молекула переходит
непосредственно в терм отталкивания (потенциальные кри-
кривые типа с, фиг. 2), то она диссоциирует немедленно, так
как атомы в этом электронном состоянии отталкиваются
при любом расстоянии между ними. Но даже если возбуж-
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
дение привело к стабильному состоянию (потенциальные
кривые с минимумом типа a, b или d, фиг. 2), молекула
все же может распасться. Это произойдет, например, если
молекула при излучении перейдет в состояние отталкивания:
или достигнет другого стабильного состояния с колебатель»
ной энергией, превосходящей границу диссоциации.
11. Предиссоциация
Коснемся коротко явления предиссоциации, впервые на-
наблюдавшегося на полосатых спектрах S2 Генри и теоре-
теоретически объясненного Бонхоффером и
Фаркасом. На фиг. 13 изображены дис-
дискретные колебательные уровни двух
электронных состояний а и Ь, к которым
в области больших энергий примыкают
сплошные спектры уровней энергии
диссоциировавших молекул (заштрихо-
(заштрихованные области).
Пусть молекула находится в элек-
электронном состоянии Ь, колебателььые
термы которого расположены частично
под границей диссоциации а @,1,2),
а частично над ней C, 4, 5...)..Термам
О, 1, 2 состояния Ъ фиг. 13 в общем
случае не соответствуют собственные
значения равной энергии электронного
состояния а, так что между ними, вообще
говоря, нет никакого взаимодействия.
(Если случайно два дискретных терма
обеих систем имеют одинаковую энер-
энергию, они рассматриваются как возму-
возмущенные, но это возмущение приводит
снова к двум дискретным термам.)
Другие условия существуют для колебательных термов
3, 4, 5... электронного состояния Ь, энергия которых за-
заходит в сплошной спектр а. Для этих термов существует,
возможность самопроизвольного перехода без излучения в !
Фиг. 13. Колеба-
Колебательные уровни:
двух электронных1
состояний, а и Ьп
двзгхатомной моле-;
кулы для поясне-;
ния предиссоциа-
предиссоциации. Заштрихован-
Заштрихованные поверхности'
изображают дне-'
социационные кон- :
тинуумы.
42 ГЛАВА II
эту область сплошного спектра, т. е. в состояние, в кото-
котором молекула диссоциирована. Переходы из колебательных
состояний 3, 4, 5 возможны не только с излучением, но и
описанным выше способом. Поэтому среднее время их жиз-
жизни мало и им соответствуют линии не резкие, а расплывча-
расплывчатые, так называемые диффузные. Крониг показал, что по-
порядок величины наблюдающегося расширения линий совпа-
совпадает с вычисленным на основании приведенных рассуждений.
12, Отклонения от свойств жесткого ротатора
Подобно тому, как энергия колебаний может быть
только в первом приближении вычислена по формулам гар-
.монического осциллятора, модель жесткого ротатора не дает
полного представления о явлениях при вращении молекул.
Уже согласно классическим представлениям, расстояние
между ядрами, а следовательно, и момент инерции молекулы
увеличиваются под действием центробежной силы, возни-
возникающей при быстром вращении. Колебательное движение
тоже действует на вращение, так как с ростом квантового
колебательного числа, вследствие асимметричности потен-
потенциальной кривой, возрастает среднее расстояние между
ядрами. Поэтому величина момента инерции, а следовательно,
и расстояние между вращательными линиями зависят и от
колебательного состояния.
Кроме этих отклонений, возрастающих равномерно с
ростом колебательных и вращательных квантовых чисел,
имеются еще и нерегулярные возмущения отдельных вра-
вращательных термов. Возмущения эти проявляются в том,
что отдельные линии полосы лежат не в местах, опреде-
определяемых интерполяцией между соседними линиями, а оказы-
оказываются более или менее сильно сдвинутыми. Причина этого
заключается в случайном совпадении одного из соответ-
соответствующих термов с каким-либо вращательным термом дру-
другого электронного состояния. Это происходит нередко при
наличии большого числа уровней энергии молекулы. Как-
известно из теории возмущений, такие термы воздействуют
друг на друга и расщепляются так, что линии сдвигаются.
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 43
Эти возмущения часто оказываются весьма полезными
для анализа25полосатых спектров, так как линии, Имеющие
общий возмущенный терм, можно легко определить по од-
н ор од.и ости в оз мущен ия.
13. Электронные термы
До сих пор мы не занимались детально вопросом о
структуре электронных состояний, но предполагали все
время, что разницы в их энергии велики по сравнению с
колебательными и вращательными термами. Однако это не
всегда имеет место, особенно в тех случаях, когда электронные
состояния многократно вырождены. Поэтому электронные
термы мы рассмотрим теперь несколько подробнее.
Электронные термы молекулы могут быть подразделены
согласно тем же принципам, что и термы атомов. В частно-
частности, различают так же, как и там, термы различных муль-
тнплетностей, в соответствии с возможностями расположения
электронного спина. Электроны молекулы связаны друг с
другом своими спинами. Так же, как и для атомов, эта
связь основывается не на магнитном взаимодействии момен-
моментов спинов, а, в основном, на явлениях резонанса электри-
электрического происхождения. В общем случае и для молекулы
достаточно рассматривать наиболее слабо связанные валент-
валентные электроны, так как суммарный спин замкнутых орбит
равен нулю.
Спины валентных электронов располагаются относительно
друг друга параллельно или антипараллельно; в сумме они
дают результирующий спин S. При четном числе атомов
в молекуле результирующий спин равен целому кратному
/г/2тт, а при нечетном — полуцелому. Максимально возмож-
возможная мультиплетность терма равна 2S-\~\, соответственно
числу возможных расположений 5 по отношению к опреде-
определенному направлению.
Классификация термов по величине результирующей L
орбитальных моментов всех электронов не может быть не-
непосредственно перенесена с атомных на молекулярные спек-
спектры, так как результирующие орбитальных моментов явля-
44 ГЛАВА II
Ются интегралами движения только в центральном поле, а
в молекулах поля не обладают центральной симметрией, так
как всегда имеется несколько силовых центров. Если пре-
пренебречь вращением всей молекулы, то для двухатомных
молекул сохраняется центральная симметрия, по крайней
мере в плоскости, перпендикулярной линии, соединяющей
ядра. Поэтому для этих молекул проекция момента на мо-
молекулярную ось приближенно является интегралом движения.
Она является квантованной величиной и, измеренная в еди-
единицах й/2тт, может принимать только целые значения А.
Электронный терм молекулы обозначается как 2-, II- или
Д-... терм, если А равно 0,1 или 2... К каждому такому
символу вида терма так же, как и для атомов, вверху
слева приписывается индекс, показывающий мультиплетность
терма. Например, 811 — триплетный терм (результирующий
спин S = 1) с А=1.
2-термы (А = 0) отличаются от других (А ^> 0) тем.
что они „простые". Если изменить направление движения
электрона вокруг оси, а следовательно, и знак момента, то
мы получим во всех случаях, кроме А = 0, новое состояние,
имеющее, однако, то же собственное значение, т. е. ту
же энергию, так что П-, Д-... состояния являются, следо-
следовательно, „двойными", или „дважды вырожденными". Только
для А = 0 B-терм) при этом получается то же состояние
и, соответственно, та же собственная функция. Таким об-
образом, 2-термы являются простыми.
14. Квантовомеханическое исследование электронных
термов
Рассмотрим сначала одноэлектронную систему. Другие
электроны должны либо совершенно отсутствовать, как для
молекулярного иона водорода Н2, либо схематически учи-
учитываться аксиально симметричным дополнительным членом
в поле ядер. Мы идем, следовательно, по тому же пути,
что и в атомной теории при исследовании спектров щелоч-
щелочных металлов. Влияние электронных оболочек на валентный
ьлектрон рассматривается просто как экранирование заряда
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 45
ядра, которое, не нарушая шаровой симметрии поля, ведет
к отступлению от закона Кулона. Мы пренебрегаем вра-
вращением и колебаниями ядер, т. е. считаем, что они нахо-
находятся в состоянии покоя.
Примем прямую, соединяющую ядра, за ось z. Вместо
декартовых координат х, у, z введем систему цилиндриче-
цилиндрических координат z, p (расстояние от оси z) и ф (азимут в
плоскости, перпендикулярной к оси z). При пренебрежении
спином уравнение Шредингера гласит:
дФ + ^Ф
Д — оператор Лапласа — в цилиндрических координатах
имеет вид:
д ' Х *
— J*. ' & Л- Х
— дг* ~Г др "Г J
V — электрический потенциал, по нашим предположе-
предположениям, аксиально симметричен и поэтому независим от <р,
т. е. V= V(z, p). Окончательно уравнение Шредингера
принимает вид:
df- ' р dp ' р2 <Э<
, р)ф. C2)
Легко видеть, что переменные z и р отделяются от <р
подстановкой
ф = Х(*. Р)Ф(<Р)- C3)
Подстановка в C2) дает для % и Ф два уравнения:
'Ф=0, C4)
г.™е Л — постоянная.
Уравнение C4) имеет два решения:
46 ГЛАВА II
Очевидно, они должны быть периодическими функциям:!
с периодом 2тт.
Из этого следует, что А может принимать только дей-
действительные целые значения:
А = 0, 1, 2,...
Л в единицах Л/2тг — величина орбитального момента
электрона относительно молекулярной оси.
Так что собственная функция C3) имеет вид:
<b = %-e-iA?, C7)
где "/ — интеграл уравнения C5). ^ и собственное значение
W из C5) зависят от Л.
Из C7) непосредственно вытекает доказательство ут-
утверждения предыдущего раздела о том, что II-, Д-,... со-
состояния— двойные, а 2 — простые. Действительно, для
А =^= 0 формула C7) дает две вырожденные собственные
функции, соответствующие обоим знакам А, в то время как
для А = 0 имеется только одно решение ш = у.
15. Влияние сяина
Исследуем теперь влияние спина, ограничиваясь при
этом только качественным рассмотрением и используя те-
теорию Паули вместо теории Дирака.
При учете спина, вследствие двоякой возможности его
ориентации, все термы молекул удваивают свою степень
вырождения, т. е. считавшиеся до сих пор простыми 2>
термы являются теперь двойными, II-, Д-, ... термы — четы-
четырежды вырожденными. Исследуем теперь в первом прибли-
приближении возмущение вследствие взаимодействия между
спином и орбитальным движением. Оно возникает благодаря
тому, что образующееся при движении электрона в элек-
электрическом поле виртуальное магнитное поле воздействует,
обратно на собственный момент электрона. Выражение для
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 47
взаимодействия (с учетом томасовского ^множителя -к- i —
такое же, как и для атома:
^}^), C8)
01
1 0
[0
— i
0
• аг
|1
- o-
0
-1
где Z:—электрическое поле, /? — импульс электрона, ко-
которому соответствует оператор:
h
p=-^-:grad, C9)
и о — вектор Паули, компонентами которого являются опе-
операторы:
Л 1 ( А I 1 Г\ I
D0)
По теории Паули, каждая собственная функция пред-
представляется парой функций только от пространственных ко-
координат, на которые операторы D0) влияют как линейные
подстановки. Можко показать, что скалярное произведение
в энергии возмущения C8) сводится к произведению гг-ком-
понент, так как компоненты х и у в первом приближении;
не приводят к возмущению. Функция возмущения имеет,
следовательно, форму:
Вследствие аксиальной симметрии вектор Е лежит в пло-
плоскости меридиана, поэтому мы можем написать:
с- ,, f п F п h F и^А
1 Множитель -к- необходим, чтобы учесть релятивистскую
поправку, поскольку фактически вывод этой формулы произво-
производился в системе координат, связанной с электроном. Укажем
также, что, независимо от Томаса, вывод этой формулы дал
Я. А. Френкель. (Прим. ред.)
4S
ГЛАВА П
dv
■ компонента электрического поля
к 1 д
в на-
направлении р; оператор р9 = 2^7— •— соответствует пер-
перпендикулярной к z и р составляющей величины импульса.
В качестве невозмущенной собственной функции выбираем
следующие пары функций:
D3)
При Л = 0 они, конечно, попарно идентичны.
Из D0) и D2) следует, что четыре невозмущенные соб-
собственные функции D3) при применении оператора D1) пре-
преобразуются в
0
0
0
о
о
ekz\F9
1ЬгЯт'*с2р
Iе
0
0
J
?
D4)
Теперь легко может быть образована часть матрицы
возмущения, соответствующая четырем вырожденным соб-
собственным функциям D3). В D4) А входит в качестве со-
сомножителя, поэтому при А = 0 матричные элементы D4}
равны нулю, т. е. в 2-термах возмущение электронного
терма спином, в первом приближении, равно нулю.
Для А ^> 0 получается следующая матрица возмущения:
1 0 0 Of
О —1 О О
О 0 —1 О
О 0 0 1
Поскольку это диагональная матрица, то возмущения соб-
собственных значений четырех собственных функций D3) пред-
представляются непосредственно диагональными элементами:
D5)
6r.2/n2ff2 J 7
СПЕКТРЫ ДВУХАТОМНЫХ .МОЛЕКУЛ
49
Положительный знак относится к первой н четвертой; от-
отрицательный— к© второй и третьей из собственных функ-
функций D3).
Таким образом, видим, что при одном валентном элек-
электроне I1-, А-, ... термы расщепляются на два, в соот-
соответствии с двумя знаками D5). Каждый из этих двух терми«
дважды вырожден.
Эти результаты легко подтверждаются с помощью на-
наглядного представления. Взаимодействие между спином п
орбитальным движением при одном валентном электроне
может быть представлено как связь между спином и орби-
орбитальным моментом. Так как в двухатомной молекуле- орби~
тальный момент Л имеет направление молекулярной оси, то
для спина имеются только две возможности. Он устанавли-
устанавливается параллельно или антнпараллельно к А. Образуются
два терма (дублетная система), суммарный момент которых
Q равен:
о— i _!_ I
Каждый из этих двух термов Дважды вырожден, так как
изменение направления вращения, и тем самым направле
ния А и спина, приводит к другому состоянию с той же
энергией. Исключение представляют только 2-термы с
А = 0, так как при отсутствии орбитального момента нет
никакого преимущественного направления для установления
спина и связь между спином и орбитальным движением ис-
исчезает. Поэтому 2-термы не обнаруживают расщепления
за счет спина.
Для различения термов к символам 22, а11, 2Д, ...,
характеризующим род терма и его мультиплетность. справа
внизу приписывают в качестве дополнительного индекса ве-
величину Й, например:
Все эти термы дважды вырождены.
4 Эпгтко Ферми
30 ГЛАВА II
16. Молекулы с несколькими валентными
электронами
Эти рассуждения легко могут быть перенесены на мо-
молекулы с несколькими валентными электронами. Мы огра-
ограничимся качественными рассуждениями и рассмотрим для
простоты случай двух электронов. Пренебрегая сначала
спином, мы найдем так же, как в разделе 14, что компо-
компонента А орбитального момента в -направлении оси может
принимать только целые значения 0, 1, 2, ... B-, 11-,
Д-, ... термы). Как и для всех систем с двумя электро-
электронами, в зависимости от их поведения при обмене электрон-
электронных координат, различают симметричные и антисимметрич-
антисимметричные термы.
Согласно принципу Паули, полные собственные функции
(включая спиновую часть) должны быть антисимметричными
по отношению к перестановке электронов. Поэтому сим-
симметричным по отношению к пространственным координа-
координатам неполным собственным функциям соответствуют
антисимметричные спиновые собственные функции и
наоборот. В си .метричном состоянии спины, таким
образом, антипараллельны (суммарный спин 5 = 0),
а в антисимметричном, наоборот, параллельны (суммар-
(суммарный спин 5=1). Первому случаю соответствуют синг-
лентные термы B5 -f-1 = 1), второму — триплетные термы
B5-1-1 = 3).
Для синглетных термов сумма спинов равна нулю; по-
поэтому было бы бессмысленным говорить об установлении
спина в направлении орбитального момента. Для триплетных
термов (суммарный спин 5 = 1) имеется различие между 1-
и U-, Д-, ... состояниями. В нервом случае, в первом при-
приближении также нет связи между спином и орбитальным дви-
движением, так как орбитальный момент Д отсутствует. В 11-,
Д-, ... состояниях, напротив, действует связь между спином
и орбитальным движением. Компонента вектора спина в на-
направлении А, т. е. в направлении молекулярной оси, может
иметь значения: — 1, 0 или -j- 1. В соответствии с этим
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ JJS
■имеются тон терма с
A-i-i
А —1.
Синглетные термк обозначаются следующим образом:
причем индекс справа внизу снова показывает величину;
полного момента Q в направлении молекулярной оси. По-
Поскольку S = О, то последний в этом случае совпадает с А.
Аналогично, триплетные термы обозначаются символами:
ЗУ 31Т 8П ЗП ЗА ЗА ЗА
—1» и2» Ul* U0» *%> ^З» а1*
Таким же образом в молекулах с числом электронов, боль-*
шим двух, суммарный спин S и орбитальный момент А скла-;
дываются в полный момент 9, который может принимать
значения:
A-f-S, A-j-S—l, ..., A — S. . .
И здесь в 2-термах в первом приближении нет связи между
спином и орбитальным движением.
Как и для атомов, величина мультиплетного расщепления
сильно возрастает с ростом порядкового номера ядер. В об-
общем случае для молекул оно имеет тот же порядок вели-
величины, что и для составляющих молекуйу атомов.
17. Случаи связи по Гунду
При анализе электронных термов до сих пор мы считали
направление молекулярной оси постоянным и, следовательно,
не учитывали вращения молекул. Однако вращение оказы- ■
вает значительное влияние на связь между спином и орби-
орбитальным моментом электронов. Поэтому необходимо различать
два крайних случая, которые, по Гунду, обозначаются как
случаи связи а к ,b. ; .
4*
ГЛАВА П
Н
Случай а. Энергия связи между спином и орбиталь-
орбитальным моментом велика по сравнению с разностью энергий
вращательных термов.
Случай Ь. Энергия связи адла по сравнению с раз-
разностью энергий вращательных термов.
Для легких молекул обычно имеет место случай Ъ; дей-
действительно, слабое мультиплетное расщепление показывает,
что энергия связи между спином и орбитальным движением
электронов мала, а расстоя-
расстояние между вращательными
термами, вследствие малых
моментов инерции, велико.
Наоборот, для тяжелых мо-
молекул чаще всего имеет
место случай а. Исключением
являются 2-термы, у которых
в первом приближении отсут-
отсутствует какая бы то ни было
связь между спином к орби-
орбитальным моментом.
Фиг. 14. Полный момент/как Для одного и того же
векторная сумма Д-=У? + Л и электронного состояния воз-
S (случай связи b по Гунду). можен также непрерывный
переход от случая а к слу-
случаю Ь. Действительно, с возрастанием вращательного кванто-
квантового числа R растет и расстояние между вращательными тер-
термами. Энергия связи между спином и орбитальным моментом
может быть больше расстояний между вращательными тер-
термами для малых R (случай а) ип наоборот, меньше для
больших R (случай Ь).
В случае а спин устанавливается параллельно молеку-
молекулярной оси и образует с составляющей А орбитального
момента суммарный момент п. Последний складывается
векторно с моментом вращения ядра R, согласно схеме фиг. 3.
и образует полный момент молекулы J,
Случай b имеет.место тогда, когда взаимодействие между
спином и орбитальным моментом так мало, что./? и Л сначала
складываются в целочисленную результирующую /С.(фиг. 14),
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
затем уже последняя складывается со спином 5 в полный
момент молекулы J, так что J, в зависимости от величины
S. принимает только целые или полуцелые значения.
На основании полуклассических соображений можно
сделать заключения относительно расположения вращатель-
вращательных термов в случае Ъ. Вращательная энергия Ег равна:
С другой стороны, из фиг. 14 следует, что
#2=а*-а3, „:
и потому:
Er = ckBK3 — chBA2.
Более точный квантовомеханический расчет дает:
D6)
В первом приближении положение вращательных термов
определяется квантовым числом К, а не У. Как следует
из фиг. 14, всегда АГ^А и
равна A, A-f-1, A-f-2, — К j
Каждому значению К, соот- • а_. '" '""~€1.
ветственно различным возмож- т/г
ностям ориентации 5, сопо- 3 =-~ —s/г-
ставляются различные значения г —=г ■■#£■-
полного момента У, лежа-
лежащие между K-\-S и \К—S\y Фиг. 15. Положеш!е вра«
причем, при отсутствии вся- шательных термов в случае
кой связи между спином и связи » ди А = 2 и S = i/s.
электронным движением, этим значениям принадлежит* оди-
одинаковая величина энергии. Однако в действительности
всегда существует слабая связь, поэтому термы с одина-
одинаковым К расщепляются иа несколько отдельных термоз
с различным У. (Расщепление основано на том, что, в за-
зависимости от величины У, проекция S на молекулярную ось,
а следовательно, -и энергия связи между А и S имеют раз?
личные значения.) На фиг. 15 схематически представлен©
положение вращательных термов в случае b
54 ГЛАВА П
К имеет значения 2, 3, 4 ..,, и каждому значению К
соответствует вращательный терм, который при 5=1/2
расщепляется в дублет J=K-¥-1/2.
Соответствующие соотношения при а-связи представлены
на фиг. 16 (для А = 2 и .5== 1/2). Вследствие сильной
связи между спином S и орбитальным моментом А послед-
последние образуют прежде всего результирующую Q, которая
в нашем случае также имеет зяаче-
2^h 1/2. Каждому Q принадлежит
и/г 1_ ,л свой ряд вращательных термов с
1
Л
>
Кроме этих двух случаев, име-
имеются три других случая связи, о ко-
торых мы здесь только упомянем.
Случай с. .В некоторых слу-
чаях связь между суммарным орби-
тальным моментом L и спином S так
Фиг. 16. Положение сильна> ™ S и ,L самй
вращательных термов результирующую Ja со значениями,
а случае связи а для лежащими между .S-J-Z, и \S — L\.
А=2 и S==i/'s- Проекция ее Q на молекулярную ось
принимает роль А и образует с мо-
моментом вращения ядра R полный момент J.
Случай d. Сильная связь между вращением молекулы
я электронным движением, т. е. между R и L соответ-
соответственно S; средней силы связь между L и молекулярной
осью; слабая связь между L и S.
Случай е. Подобен случаю d, с той разницей, что
L сильнее связан с S, чем с молекулярной осью.
18. А-удвоение
Мы упоминали, что электронные термы с А=^0, з том
числе и синглетные термы, дважды вырождены, так как
при изменении электронного движения вокруг молекуляр-
молекулярной оси на обратное образуется новое состояние с тем же
собственным значением, т. е. с той же энергией. Если пре-
яебречь вращением молекулы, т, е, если считать молеку-
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 55
лярную ось неподвижной, то имеет место полное вырожде-
вырождение. Но под влиянием вращательного движения термы рас-
расщепляются на два отдельных терма (А-удвоенне).
В синглетных термах и в рядах термов с 6-связью»
у которых спин может ориентироваться независимо от мо-
молекулярной оси, расщепление быстро возрастает с ростом J.
Для П-термов, например, расщепление пропорционально
J(J-\-l) и соответственно, в случае связи Ь, пропорцио-
пропорционально К(К-\-1). Множитель пропорциональности имеет
величину порядка
где v—-электронная частота, а В—:константа вращения A5).
Поэтому этот эффект особенно заметен у молекул с не-
небольшим моментом инерции. Он изучался наиболее детально
на полосах гидридов. Для Д-термов расщепление значи-
значительно меньше, и его до сих пор не наблюдали, несмотря
на то, что с ростом J оно должно было бы возрастать еще
быстрее, чем у П-термов.
Для S=^=0 и при а-связи соотношения сложнее. Однако
н для этого случая теория возмущений дает формулы рас-
расщепления, находящиеся в соответствии с результатами экс-
экспериментов (Мэллнкен).
При S =^= 0, 2-термы, имеющие всегда связь Ь, также
обнаруживают расщепление, основанное на взаимодействии
между спином и вращением молекулы. По расчетам Ван
Флека, при 6=1/2 оно пропорционально AT-f-1/2.
19. Сопоставление молекулярных термов
с атомными термами
Между электронными термами двухатомной молекулы
и термами соответствующих атомов имеются, как впервые
показал Гунд, взаимозависимости, позволяющие в некото-
некоторых случаях определять приблизительное положение моле-
молекулярных термов по положению соответствующих атомных
термсш. . ...
56 ГЛАВА II
Это сопоставление производится следующим, образом:
расстояние между ядрами адиабатически произвольно варьи-
варьируется, причем, с одной стороны, следуют до объединения
ядер (/-=0), с другой — доводят до их полного разъеди-
разъединения (г=оо). Если обозначить через Z и Z' порядковые
номера обоих ядер, то из молекулы образуется в одном
случае атом с порядковым номером Z-j-Z', а в другом —
два раздельных атома или иона с зарядами ядер Z и Z'.
Таким образом, определенный электронный терм молекулы
переходит в одном случае в терм атома [Z-j-Z'], а в дру-
другом — в терм, равный сумме двух отдельных термов разде-
разделенных атомов или ионов [Z] и [Z']. Между этой суммой
и термом [Z-\-Zr] должен быть возможен непрерывный
переход, ведущий через электронные термы молекулы и
позволяющий отиосить их к термам атома [Z-j-Z'].
Мы покажем сначала, что это сопоставление дает воз-
возможность (часто, впрочем, практически неосуществимую)
описывать состояние отдельного электрона в молекуле
точно так же, как и в атоме, определенными квантовыми
числами (я, /, /., . ..). (Как и для атомов, квантовые числа
отдельных электронов обозначаются малыми буквами, а кван-
квантовые числа электронных оболочек—большими.) Мы пре-
пренебрегаем сначала спином и учитываем влияние остальных
электронов введением соответствующего экранирующего
потенциала, так что поле, в котором движется электрон,
может рассматриваться как аксиально симметричное. Тогда,
как указывалось раньше, проекция импульса орбитального
момента электрона / на молекулярную ось постоянна. Она
имеет значение
а(гЬ0» 1» 2 ...) является одним из квантовых чисел на-
нашего электрона. Если оба ядра сближаются, то при их
объединении состояние молекулы непрерывно переходит
а состояние атома [Z-j-Z'l с квантовыми числами ли/
(главное квантовое число и азимутальное квантовое число).
Оба эти квантовые числа мы припишем нашему электрону
и в молекуле. Таким образом, в нашем распоряжении
СПЕКТРЫ ДВУХАТОМНЬГХ^МОЛСКУЛ 5Т
гмеются: три квантовых числа (п, /, \], с помощью которых
ш можем определять состояние нашего электрона. Значе-
Значения I или X, равные 0, 1, 2 ..., мы обозначим буквами s^
р, d, или, соответственно, а, щ 8, .... Символ З^тг, на-
например, обозначает электрон, у которого аксиальная со-
составляющая X импульса орбитального момента равна 1, пе-
переходящей при адиабатическом соединении ядер в. 3d-
электрон (« = 3, 1 = 2) атома [Z-j-Z']- Все эти термы
(за исключением соответствующего Х = 0) и без учета
спинового расщепления — двойные. Учет спина еще раз.
удваивает каждый из них, так что окончательно осостояник.
становятся двойными, а остальные — четырехкратными.
S/2 S/2 * ■ "
S/2 / 3/г
<С 1/2
-^ - S/2
3/2
1/2
Фиг. 17. Связь между термами молекулы с одним
валентным электроном и термами атома, получающе-
получающегося в результате объединения обоих ядер. Средняя
часть фигуры — молекулярные термы, левая часть —
сильно дублетное расщепление атома, правая часть —
пренебрежимо малое дублетное расщепление атома.
Исследуем теперь зависимость между термами атомэ
[Z-j-Z'] и термами молекулы, спином которой пренебречь.
нельзя. Для упрощения рассмотрим случай, когда выделяют-
только один оптический электрон, а влияние остальных
электронов учитывается введением экранирующего потен-
потенциала.
До тех пор, пока ядра объединены, состояние электрона
определяется величинами его квантовых чисел п, I и f
(внутреннее квантовое число = /Чз 1/2). Вследствие двух,
значений j в атоме [Z-j-Z'] имеет место дублетное рас-
расщепление (левая сторона фиг. 17). Ориентировка j в от-
-D8 • ГЛАВА II
■яошении преимущественного направления или его проекция
на эта направление будет определяться четвертым кванто-
квантовым числом т (магнитное квантовое число =/, /—1»
j— 2, ... —J). Пока отсутствует возмущение, это число
не влияет на энергию состояния. Поэтому вначале все тер-
термы Bj-\~ 1)-кратно вырождены. Когда ядра постепенно
удаляются одно от другого, это вырождение частично
снимается, и возникают j-\-1/2 различных термов. Так
«ак энергия расщепления не зависит от знака магнитного
■квантового числа т, то каждый из термов еще дважды
вырожден, т. е. состоит из двух отдельных термов, разли-
различающихся только знаком т. Расщепление увеличивается
■с ростом расстояния между ядрами и становится, наконец,
■больше, чем дублетное расщепление исходного атома (сред-
(средняя часть фиг. 17).
Если, с другой стороны, с самого начала пренебречь
дублетным расстоянием атома \Z~^-Z'^ по сравнению
с этим расщеплением (правая часть фиг, 17), то положе-
положение термов при разделенных ядрах может быть оценено
следующим образом: так как связь между спином и орби-
орбитальным моментом / мала, то результирующей j не обра-
образуется,- а / ориентируется по отношению к молекулярной
■оси так, что его проекция \ на последнюю определяет
расщепление X=db/» ziz(l—1)» •••, rb ls Q- (X соот-
соответствует квантовому числу. т1 атомной теории.) Поскольку
расщепление не зависит от знака X,- то образуется / -f-1
различных термов. Параллельное или антипараллельное рас-
расположение спина по отношению к X, т. е. к молекулярной
оси, расщепляет эти термы в дублеты. Простыми остаются
только 2-термы с Х = 0.
На фиг. 17 представлены эти соотношения для валент-
валентного электрона с /==2. В первом случае (сильное взаимо-
взаимодействие между спином и орбитальным моментом I) при
очень малом расстоянии между ядрами существуют только
лва терма (/=5/2, 3/2 — левая часть фигуры). С ростом,
расстояния между ядрами они расщепляются на три или
два отдельных терма с приведенными на фигуре зьаче-
от. В противоположность этому правая часть фигуры
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
59
представляет второй случай, когда в атоме [Z. 4- Z'] взаимо-
взаимодействие между спином и моментом орбитального импульса /
мало. Тогда при разведении ядер, т. е. при снятии вырож-
вырождения направлений, терм с / = 2 переходит сначала в три
отдельных терма с Х==0, ±2 B-, П-, Д-термы). Термы
с X = ifcl и X = rfc2 под влиянием спина снова расщеп-
расщепляются. Следовательно, в обоих случаях образуется всего
пять термов, которые на фи- -
гуре связаны между собой
соединительными линиями.
Особый интерес пред-
представляют молекулы с двумя
одинаковыми ядрами: На,
2М2, О2, С12 и другие, так
как для них обнаруживаются
некоторые особенности, су-
существенные, между прочим,
и для ядерной физики.
В общих чертах струк-
структура термов этих молекул . ,„;>*■
может быть изучена на очень Фиг' !8' Собственные функ-
простой модели. С этой
целью рассмотрим точку,
движущуюся вдоль прямой
под действием зависящей от
ции точки, движущейся вдоль
прямой под воздействием силы,
потенциал которой изображает-
изображается кривой pp. Функции а и Ь
соответствуют очень высокому
_ потенциальному барьеру А:
координат силы. Сила опре- с ий-низкому потенциаль-
деляется потенциалом, ход . ному барьеру А.
изменения которого пред-
представлен кривой рр на фиг. 18. Кривая, состоит, в основном,
из двух одинаковых потенциальных „ям", разделенных по-
потенциальным „барьером", Ямы соответствуют обоим
атомам, а передвигающаяся вдоль прямой точка — элек-
электрону.
Допустим, что потенциальный барьер очень высок и очень
широк. Вероятность перехода электрона из одной ямы в
другую очень мала: он находится в течение долгого вре-
времени только в одной из ям, которые поэтому независимы
одна от другой. .:•■:.
60 . ГЛАВА II
. Когда точка находится в левой яме, энергия ее имеет,
определенные значения wv w2, ... с соответствующими
собственными функциями ах> а?, ...., например, значение т
с собственной функцией а (фиг.. 18). Вследствие тожде-
тождественности обеих ям то же собственное значение получается,
когда точка находится в правой яме, где собственная функ-
функция представляется кривой Ъ. Собственное значение w,
следовательно, вырождено, так как ему соответствуют две
собственные функции.
При уменьшении потенциального барьера вырождение
уничтожается, так как появляется конечная вероятность пе-
перехода электрона из одной ямы в другую. Этот „обмен"
дает дополнительную энергию (см. раздел 3), и значение
энергии w расщепляется на два отдельных терма, расстоя-
расстояние между которыми тем больше, чем ниже и уже потен-
потенциальный барьер. Этим термам, соответствуют две новые
собственные функции end, которые приближенно пред-
представляются суммой и разностью а и Ь. Собственная функ-
функция с, которая не имеет узлов и поэтому соответствует
более низкому собственному значению, симметрична по от-
отношению к точке симметрии потенциала; напротив, d анти^
симметрична.
Эта модель легко может быть перенесена на соотноше-
соотношения в симметричных двухатомных молекулах.
В качестве примера рассмотрим систему, состоящую из
двух водородных ядер и одного электрона (ионизованная
молекула водорода Нз ).
Пока ядра сильно удалены друг от друга, электрон
находится в состоянии Is и связан с одним из двух ядер.
Вследствие большого расстояния протоны практически не
воздействуют друг на друга, поэтому соответствующие
собственные функции имеют одинаковые собственные значе-
значения. При сближении ядер вырождение снимается, и обра-
образуются два разделенных уровня. Более низкому уровню со-
соответствует симметричная по отношению к центру тяжести
ядер собственная функция, более высокому — антисиммет-
антисимметричная.
Первая собственная функция, очевидно, не имеет узло-
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
вых поверхностей и при соединении ядер переходит в соб-
собственную функцию \s иона гелия Не+,-также не имеющую
узлов. Она обозначается поэтому lsj. Напротив, антисим-
антисимметричная функция имеет узловую поверхность, лежащую
в экваториальной плоскости молекулы. При соединении ядер
она переходит в собственную функцию иона Не+, но имею-
имеющую узловую поверхность, следовательно, в 2р-функцик>
с т = О. Соответствующий молекулярный терм обозначаете*
символом 2ра. Это наглядно изображается при помощи
следующей схемы:
Не" Не+ Н + Н +
Благодаря наличию спина оба состояния дважды вырож-
вырождены. \sa—более низкое состояние.
Если оба протона удерживаются на определенном рас-
расстоянии одно от другого и им придаются последовательно
два электрона, то образуется молекула водорода. При этом
оба электрона связываются в lsa-состоянии. Спины их
должны установиться антипараллельно один к другому, так
как, по принципу Паули, они оба не могут находиться
в одном квантовом состоянии. Образовавшееся таким обра-
образом состояние является основным состоянием молекулы во-
водорода. Так как сумма спинов 5 = 0, оно относится, в со-
соответствии с теорией Гайтлера-Лондона, к синглетной
системе (см. раздел 3). Полный символ терма:
Таким образом, мы имеем синглетный . 2-терм, обра-
образуемый двумя 153-электронами.
Высшие электронные термы образуются, когда один
электрон остается в основном состоянии, а другой возбуж-
возбуждается до более высокого квантового состояния. Поэтому
высшие термы можно обозначать просто квантовыми числами
возбужденного электрона. :
62 ГЛАВА II
В высших состояниях наряду с синглетными имеются
и» триплетные термы, в зависимости от параллельности или
антипараллельностн спинов друг к другу.
Ниже приведены величины (в волновых числах см}
синглетных термов Н2, по данным Вейцеля;
1 5<т=128 525 2 рс = 37 371 2 ртг=2
2 sa= 29 340 3 />а = 13 742 3 ртг=12
4 рп= 7 067
5 ртг= 4 493
3rfa=.15 77i 3</тг=15 541 6 рп= 3107
Особенно характерна здесь последовательность пяти
_рте-термов. По Ричардсону, они могут быть расположены
в серии Ридберга, так что из них может быть подсчитана
абсолютная высота терма.
20. Четные и нечетные термы
Собственная функция молекулярного терма зависит от
координат электронов и ядер. Пусть ф является такой
функцией и пусть она невырождена и сначала независима
от спина. Возьмем за основу декартову систему координат
с началом в центре тяжести молекулы. Если мы ф отражаем
в начале координат, т. е. изменяем знаки всех электронных
и ядерных координат, то получается новая собственная
функция ф', также удовлетворяющая. уравнению Шредин-
?ера и соответствующая тому же собственному значению,
что и ф. Так как мы исключили всякое вырождение, то ф
и ф' могут различаться только на постоянный коэфициент;
Так как после повторного такого отображения снова
должна получиться первоначальная функция ф, то ф = А^-ф,
а отсюда: К2=\, K = zkz^- Следовательно, имеются две
возможности; собственная функция после пространственного
отражения остается неизменной или изменяет свой знак.
В первом случае говорят о четной функции, во вто-
втором — о нечетной. :
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
Эти рассуждения могут быть легко распространены is
па вырожденные собственные функции и на функции, вклю-
включающие спины. Если мы отнесем и часть собственной функ-
функции, зависящую от спина, к системе координат х, у, г„
то она не будет меняться при отражении в нулевой точке,,
поскольку спин изменяется как момент вращения, т. е. как
выражения вида
х ду У дх' • ' • '
которые, очевидно, не изменяются от перемены знаков.
Различие между четными и нечетными термами приво-
приводит к важнейшему правилу отбора, которое гласит, что
переходы с излучением возможны только между четными
и нечетными термами, а между одинаковыми термами-—за-
термами-—запрещены.
Это правило основано на том, что два терма могут ком-
комбинировать друг с другом, только если соответствующий
матричный элемент электрического момента, т. ё. вели-
величина
!Цг, = 3№ D7>
отлична от нуля (ei — заряд /-той частш'ы, а г( — ее радиус-
вектор). Суммирование должно быть распространено на все
частицы молекулы. Из D7) следует, что электрический мо-
момент 931 — нечетная величина; при отражении в начале ко-
координат она изменяет свой знак.
Рассмотрим теперь два различных терма нашей молекулы*
с собственными функциями <Ьа и фй. Они комбинируют, еслиь
соответствующий переходу а —*■ Ь матричный элемент
- D8>
(проинтегрированный по всему конфигурационному прост-
пространству) отличен от нуля.
В D8) мы можем также произвести отражение в начале
координат, т. е. поменять знаки координат всех частиц»
Если <ha и Фь — обе четные или обе нечетные, произведе-
64 -■■• :■ ■■ ГЛАВА II.
чне их при этом не изменяется. Но так как Ш — нечетное,
то знак интеграла изменяется:
Следовательно, ШаЬ равно нулю, т. е. переходы между
двумя четными или двумя нечетными состояниями невоз-
невозможны. Этим доказывается наше правило отбора. (Оно
справедливо строго, только если мы пренебрегаем квадру-
польньш излучением. Однако
Jcf т последнее имеет интенсивность
в 106 раз меньшую.)
Особенно важно различие
между четными и нечетными
Фиг. 19. Последователь- термами при вращательных пе-
ность четных (X) и нечет- „еходах которых мы кпатко
ных (О) вращательных тер- Рех°Дах, которых мы кратко
мов в случае связи а: а) для коснемся.
Q=0, b) для а Ф 0. В случае связи а враща-
вращательные термы для Q = 0 бу-
будут простыми и попеременно четными и нечетными (фиг. 19, а).
Для Й=^0 — они двойные. На фиг. 19, Ь изображена после-
Ф«.г, 20. Последовательность четных
(X) и нечетных (О) вращательных термов
в случае связи b для 5 = г/з-
ловательность четных и нечетных термов при Q==0. Чет-
яые и нечетные термы расположены попарно вместе, причем
верхними в каждой паре являются четные и нечетные по-
леременно.
Вышесказанное применимо к случаю Ь, если заменить
J через К, a Q — через А, с той разницей, что каждый
терм, как показано на фиг. 20 для 5= 1/2, состоит из
2S-\- 1 отдельных термов.
У молекул с двумя одинаковыми ядрами разделение на
четные и нечетные термы .следует распространить и на
СП£КТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 65
электронные состояния. Будем считать, что ядра находятся
в состоянии покоя. Собственная функция ф определенного
электронного состояния зависит тогда только от координат
ьлектронов. Можно показать, что и в этом случае отражение
в средней точке прямой, связывающей ядра, не меняет соб-
собственной функции или преобразует ее в ф. Поэтому и
для члектронного состояния различают четные и нечетные тер-
термы Кечи бы ядра действительно не имели собственного дви-
движения, го и в этом случае было бы строго применимо пра-
правило отбора о невозможности комбинирования одинаковых
терчив. Но так как ядра вращаются, это правило приме-
применимо лишь приближенно. Оно приводит к тому, что пере-
переходы между одинаковыми термами происходят с пониженной
пшене явностью.
Четные гермы обозначаются индексом g, нечетные —
индексом и. Например, 3П —четный триплетный терм
с Л = 1. В молекуле с одним оптическим электроном элек-
электронные термы могут быть четными или нечетными, в за-
зависимости от четности или нечетности квантового числа /
электрона. Это видно из того, что при объединении ядер
в одно ядро с зарядом 2Z собственная функция с кванто-
квантовым числом ./ переходит в произведение функции радиуса
вектора и шаровой функции /-того порядка. При отражении
в нулевой точке последняя остается неизменной или изме-
изменяет знак, в зависимости от того, является ли / четным или
нечетным. Когда мы затем адиабатически разводим ядра,
характер функции и ее зависимость от /, из соображений
непрерывности, сохраняются.
Когда молекула содержит несколько электронов с кван-
квантовыми числами /х, /2, /8, . .., электронный терм является
четным или нечетным, в зависимости от того, четной или
нечетной является алгебраическая сумма /:
Это объясняется тем, что суммарная собственная функция
может быть представлена как произведение собственных
функций отдельных электронов с квантовыми числами lv
1%, 'з> • • • Последние приобретают при отражении в нуле-
5 Эярико Ферми
66 ГЛАВА II
вой точке коэфициенты (—I)'1, (—1)?», (—1)'», так что
суммарная функция получает коэ4иииент (—1 )*!+*»+'»•••..
Следовательно, терм двух электронов с одинаковыми кван-
квантовыми числами (я, /, X) всегда четный.
В качестве примера рассмотрим полосы атмосферного
кислорода, истолкованные Мэлликеном. Как известно, боль-
большинство фраунгоферовых линий возникает при поглощении
в солнечной атмосфере. Однако некоторые фраунгоферовы
линии образуются при поглощении в атмосфере земли. К их
числу относится протяженная система полос в красной
части спектра, принадлежащая кислороду. Поглощение на-
настолько слабо, что эти полосы, несмотря на большую тол-
толщину слоя атмосферы, не очень интенсивны. По этой при-
причине в лаборатории их можно наблюдать только при
применении очень больших давлений.
Наиболее низкие термы молекул кислорода содержат
два равноценных тт-электрона; остальные четырнадцать
электронов молекулы образуют замкнутые оболочки. Можно
легко убедиться в том, что оба эти электрона могут обра-
образовать три различные терма Ч, 41 и 32. Именно, когда
оба электрона вращаются в одном направлении вокруг мо-
молекулярной оси, их результирующий орбитальный момент
в каправлении оси A=l-j-l=2, так что мы получаем
1-терм. Так как все три квантовых числа одинаковы, то,
по принципу Паули, спины должны быть антипараллельны
{$ = 0). Поэтому Д-терм относится к синглетной системе.
Напротив, когда направления вращения различны, орбиталь-
орбитальный момент А = 1 — 1=0, что соответствует 2-состоянию.
'Так как в этом случае оба электрона имеют одинаковые а
и I, но различные М-j-l или —1), то и их спины могут
установиться различным образом, т. е. параллельно или
антипараллельно. В первом случае возникает а2-терм, так
как 5=1, во втором случае C = 0) возьикает 12-терм.
Таким образом, наиболее ьизкими электронными тер-
термами молекулы кислорода будут:
!2, 32 и 1Д.
Самый низкий из них 32 является, следовательно, основным
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ <JJ
состоянием. Это вытекает, между прочим, и из того, что
кислород — парамагнитен. Действительно, как показал
Ван Флек, парамагнитизм кислорода определяется действием
результирующего спина 5=1.
Наблюдавшееся в сол1 ечном спектре поглощение моле-
молекулы О2 соответствует переходу из основного терма 32.
Так как полосы лежат в красной области спектра, то раз-
разность энергий, т. е. расстояние между термами, не очень
велика. Следовательно, переход должен происходить в терм,
близко расположенный от основного состояния. По Мэлли-
кену, это >2-терм.
Поглощение слабо по двум причинам: во-первых, это
синглетно-триплетный переход. Как и для атомов, пере-
переходы между термами различной мультиплетности, особенно
у легких элементов, очень маловероятны. Во-вторых, оба
терма — четнье, так как отдельные электроны в обоих
состояниях имеют одинаковые квантовые числа / (=■ 0).
21. Симметричные и антисимметричные термы
У молекул с двумя одинаковыми ядрами нужно также
учитывать взаимозаменяемость ядер и различать термы сим-
симметричные или антисимметричные относительно координат.
При перемене ядер местами из каждой собственной
функции ф возникает новая собственная функция ф', имею-
имеющая, вследствие тождественности ядер, то же собственное
значение и могущая отличаться от <J> только на постоянный
множитель. Для козфициента пропорциональности из сооб-
соображений, аналогичных приведенным в разделе 20, полу-
получаются значения -j- 1 и —,1. Для молекул с двумя одинако-
одинаковыми ядрами имеем, таким образом, два класса собственных
функций: симметричные, не изменяющиеся при обмене ядер-
ядерных координат, и антисимметричные, знак которых при этом
изменяется.
Из этого различия также вытекает важное правило от-
отбора: переходы между состояниями различной симметрии
строго запрещены, независимо от того, происходит ли пе-
переход за счет излучения, за счет удара или любым дру-
другим способом.
Л*
68 глава а
Это прапи.'Ю отбора может быть доказано совершенно
так же, как и соответствующее запрещение перехода между
двумя четными или нечетными термами. Мы представляем
лнюое возмущение системы, например, взаимодействие с по-
полем излучения посредством оператора Р. Так как ядра
одинаковы, то Р должен симметрично зависеть от их коор-
координат. Обозначим через 'bv и !/п собственные функции мо-
молекулы 1< —функции, CHviweTpH жая по отношению к ядер-
ядерным киординагач, Ьп— антисимметричная. Вероятность
перехода определяется магри шым
Тек кач Р и ф5 симметричны, а 'Ь^ антисимметрична,
то этот иагеграл меняет знак при обмене коирдинат обоих
ядер. Но поскольку при эгом вероятность перехода не мо-
может изменяться, то Рач = — Pas, поэтому Pas должно
быть равно нулю (Pas = 0).
Следовательно, переходы между симметричными и анти-
антисимметричными состояниями происходить не могут.
Из волномеханического истолкования принципа Паули
известно, что для частиц одного и того же рода из двух
математических возможных классов собственных функций
(симметричных и антисимметричных) в действительности
всегда реализуется лишь один. Для частиц, которые, по-
подобно электронам, подчиняются принципу Паули и на которые,
следовательно, как мы позже увидим, распространяется
статистика Ферми, возможны только асимметричные собствен-
собственные функции. Напротив, частицы, для которых принцип
Паули несправедлив и которые, следовательно, подчиняются
статистике Бозе-Эйнштейна, возможны только симметричные
собственные функции.
Рассмотрим систему из двух электронов, в которой
взаимодействие между спином и орбитальным движением
мало. Тогда в первом приближении мы можем ограничиться
пространственными координатами электронов и представить
полную собственную функцию <Ь как произведение функции
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
Ф (лг), зависящей только от пространственных координат,
на и (о) — функцию координат спинж
ф==ф(л:).д(а). D9)
По принципу Паули, (]> по отношению к координатам элек-
электронов должна быть антисимметрична. Вследствие этого
при симметричном Ф множитель а (в) антисимметричен, т. е.
направление спинов противоположно, а их результирующая
5 равна нулю. Напротив, когда Ф антисимметрично, а (з)
будет симметрично, т. е. спины параллельны и сложатся в
суммарный спин 5=1. Таким образом, если рассматривать
только ту часть собственной функции ф, которая зависит
от пространственных координат, т. е. функцию Ф, то, на-
наряду с симметричными термами, встречаются и антисиммет-
антисимметричные; однако эти термы различаются своими статисти-
статистическими весами. Для антисимметричного терма суммарный
спин имеет три возможных ориентации B5-f-l); вес этого
состояния равен трем. Статистический вес симметричного
терма вследствие того, что 5 = 0, равен единице. Когда
принцип Паули неприменим и, следовательно, частицы под-
подчиняются статистике Бозе-Эйнштейна, имеет место обратное
явление. Для симметричных собственных функций Ф, со-
состоящих из двух частиц, система и (с) должна быть симмет-
симметричной, а, следовательно» <S=1. Их статистический вес,
следоватечьно, равен трем. Для антисимметричных собст-
собственных функций и (а) также должно быть антисимметрично,
т, е. 5 = 0; следовательно, они имели бы вес, равный
единице.
22. Спин ядра
Все то, что мы установили в предыдущее разделе для
двух электронов, справедливо также и для двух одинако-
одинаковых ядер. Действительно, многие ядра, подобно электронам,
обладают спиновым моментом, всегда равным целому крат-
кратному величины h; 4л. Так, спиновый момент ядра водорода
равен А/4л, а момент ядра азота й/2тг = 2-А/4тт. Встре-
Встречаются и более высокие значения, например, у ядра вис-
висмута 9А/4п. Напротив, другие адра (гелий и кислород) не
70 ГЛАВА II
имеют спинового момента. Следовательно, измеренный в
обычных единицах hj2u, спин ядра / может принимать
значения: О, 1/2, 1, 3/2,...
Существуют различные методы определения спина ядра.
Например, он может быть определен по сверхтонкой струк-
структуре атомных ли 1ИЙ. Как мы увидим в дальнейшем, он
проявляется в полосатых спектрах, так как структура
системы вращательных термов зависит от собственных
функций ядра. "**
Спин ядра связан с магнитным моментом, который, од-
однако, значительно меньше, чем спин электрона. Из иссле-
исследований сверхтонкой структуры для ядерного магнитного
момента получается значение, приблизительно равное 1/1 000
боровского магнетона.
Многие явления в спектрах молекул, состоящих из двух
одинаковых атомов, могут быть объяснены предположением
о существовании двух видов ядер. К первому виду отно-
относятся ядра, удовлетворяющие статистике Бозе-Эйнштейна,
для которых, следовательно, неприменим принцип Паули;
ко второму виду — ядра, подчиняющиеся принципу Паули,
или, что то же самое, статистике Ферми. Их полные соб-
собственные функции симметричны или антисимметричны отно-
относительно осей координат, в зависимости от применимости
той или иной статистики.
Конечно, и для ядер влияние спина в первом приближении
можно не учитывать. Для ядер это даже более возможно,
чем для электронов, так как магнитный момент их много
меньше. Как и в D9), полная собственная функция <|> при
этом разложится на функцию Ф координат положения и на
зависящий от спина множитель и.
Когда для обоих ядер справедлива статистика Бозе-
Эйнштейна, Ф и а — о-5а симметричные или антисимметрич-
антисимметричные, поскольку произведение Ф-и должно быть симметрич-
симметричным. Если, чапро.ив, справедлива статистика Ферми, то,
для того чтобы произведение было антисимметричным, Ф
должна быть симметрична, а и — антисимметрична, или
наоборот.
В дальнейшем под выражениями симметричный или
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
антисимметричный будет подразумеваться только поведение
србственной функции ядра по отношению к обмену про-
пространственных координат. Иными словами, мы относим обоз-
обозначение только к множителю Ф и не рассматриваем свойств
симметрии функции спина а. Обоснованное в разделе 21
запрещение перехода для термов различной симметрии
применимо с хорошим приближением и к переходу между
термами, обладающими различной симметрией только по
отношению к обмену пространственными координатами ядер.
Так как магнитный момент спина ядра очень мал, то его
взаимодействием с внешним возмущением можно пренебречь.
Следовательно, оператор Р предыдущего раздела действует
лишь незначительно на зависящую от спина часть и собст-
собственной функции. Несмотря на это, функция а играет
важную роль. Если / — измеренный в единицах А/2 те спин
отдельного ядра, то имеется всего B'-f-lJ линейно не-
независимых функций координат спина обоих ядер, из кото-
которых /B/ -{-!) антисимметричных и (/ -+-1) B1 -\- 1) симмет-
ричных. Отношение р числа симметричных функций и к
числу антисимметричных функций равно:
. E0)
Если ядра подчиняются статистике Бозе-Эйнштейна, то
симметричному Ф соответствуют (/—|— 1) B/—|— 1) симмет-
симметричных а, а антисимметричному Ф соответствуют /B/-J-1)
антисимметрич ых и. Статистический вес симметричных
состояний, следовательно, равен (/-{- 1) B/-J-1), а анти-
антисимметричных— составляет только I B1 -j- 1). Для ядер, под-
подчиняющихся статистике Ферми, — наоборот. Следовательно,
для ядер со статистикой Бозе-Эйнштейна р есть отно-
отношение весов симметричных и антисимметричных состояний,
а для ядер со статистикой Ферми — отношение весов анти-
антисимметричных состояний к весам состояьий симметричных.
В частности, у ядер без спина (/ = 0) при статистике
Бозе-Эйнштейна симметричные состояния имеют вес, равный
единице, а антисимметричные— вес, равный нулю; напротив,.
при статистике Ферми симметричные состояния имеют весг
72
ГЛАВА {I
равный нулю, а антисимметричные — вес, равный единице.
Таким образом, в колекуле с двумя одинаковыми ядрами,
когда 1=0, гри статистике Бозе-Эйнштейна выпадают
все антисимметричные термы (например, у О2и Неа), а при
статистике Ферми — все симметричные термы.
Для ядер с /=1,2 имеем р = 3, а отсюда отношение
весов симметричных и антисимметричных состояний равно
3:1 или 1:3. Например, для ядер водорода /=1/2, атак
как они подчиняются статистике Ферми, то для молекулы
Н2 антисимметричные термы имеют вес в три раза больший,
чем симметричные.
Для ядер с /=1 имеем р = 2, и соотношение стати-
статистических весов равно 6:3 или 3:6.
23. Чередование интенсивности
Эти соображения прекрасно подтверждаются на опыте.
В полосах многих молекул с одинаковыми ядрами, напри-
например, Н2, N?, Li2, интен-
интенсивности следующих друг
за другом линий изменя-
изменяются неравномерно. Чаще
наблюдается поразитель-
поразительная смена сильных и
слабых линий, как пока-
показано на фиг. 21 для по-
полосы N2. Это своеобраз-
своеобразное явление носит название
чередования интенсивно-
стей. Гейзенберг дал ему
. „, „ следующее объяснение.
Фиг. 21. Чередование интенсив- ц. J
ностей в полосе молекулы азота. Как мы видели в разделе
22, в молекуле возмож-
возможны только переходы между состояниями, с одинаковой
симметрией пространственных координат относительно
положения ядер. Если /=0, то, в зависимости от
статистики, которой подчиняются ядра, в молекуле
имеются только симметричные или только антисимметричные
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 75
термы. Всем наблюдаемым линиям соответствуют, следова-
следовательно, по статистике Бозе-Эйнштейна, переходы между
симметричными термами, а по статистике Ферми — переходы
между антисимметричными термами. Чередование интенсив-
ностей отсутствует.
Но если имеется ядерный спин, то в молекуле, наряду
с симметричными, имеются и антисимметричные термы, а в-
полосатых спектрах появляются два рода линий, соответ-
соответствующих переходам между симметричными или антисим-
антисимметричными термами {„симметричные" или «антисимметрич-
«антисимметричные* линии). Так как обоим классам термов соответствуют
различные веса, то симметричные и антисимметричные
линии обладают различной интенсивностью. При статистике
Бозе-Эйнштейна более интенсивны симметричные линии, а
ери статистике Ферми — антисимметричные. Так как сим-
симметричные и антисимметричные состояния чередуются, то-
внутри полосы сильная линия следует за слабой и наобо-
наоборот.
Рассмотрим эти соотношения более детально. Сначала
пренебрежем электронным состоянием и будем рассматривать
молекулу как совокупность двух жестко связанных ядер..
Если пренебречь еще jl спином, то положение молекуль*
может характеризоваться направлением прямой, связывающей
ядра, например, углами д и ср (широтой и долготой)-
Тогда собственные функции являются шаровыми функциями
Pj*{&, <p)- Обмену обоих ядер соответствует перемена
направлений прямой, связывающей ядра, т. е. замена ft на
я — д и <р — на TT-j-cp, Шаровые функции четного порядка
при этом не изменяются, а нечетные меняют знак на об-
обратный. Отсюда мы заключаем, что в этом случае термы
с четным J симметричны, а с нечетным J — антисиммет-
антисимметричны.
Электронное состояние не оказывает существенного
влияния на эти соотношения. Оказывается, что в опреде-
определенном электронном состоянии либо симметричные термы
имеют четное J, а несимметричные — нечетное J (тогда,
состояние симметрично по отношению к электронам), либо
термы с четным J антисимметричны, а с нечетным J сим-
74 ГЛА°А Н
^етричны (тогда состояние антисимметрично по отношению
к электронам). Для многократных или вырожденных состо-
состояний термы различной симметрии распределяются так же,
как четные и нечетные термы на фиг. 19 и 20.
Спин ядра / может быть определен с помощью измере-
измерения отношения интенсивностей последовательных линий.
Отношение интенсивностей двух соседних линий определяет
отношение статистических весов симметричных и антисим-
антисимметричных термов, т. е. ~у . Отношению интенсивностей
3:1 соответствует, следовательно, спин ядра /=1/2
^например, водород); отношение интенсивностей 2:1 озна-
означает / = 1 и т. д.
Если возможна классификация электронных термов по-
полосатого спектра, то из чередования интенсивностей можно
сделать вывод о статистике ядер. Например, если при
симметричном электронном терме линии с четным J слабее,
то ядра подчиняются статистике Ферми. Это имеет место,
например, для молекулы Н.г, т. е. протоны удовлетворяют
принципу Паули. Напротив, Разетти по вращательному
спектру Рамана установил, что ядро азота подчиняется
статистике Бозе-Эйнштейна.
Когда спин ядра равен нулю (как у молекул О2 и Не2),
чередования интенсивностей не происходит, а каждая вторая
.лииия полностью выпадает (как для О2, так и для Не2
отсутствуют все антисимметричные линии). Для этих ядер
справедлива, следовательно, статистика Бозе-Эйнштейна.
24, Пара- и орто-водород
Интересное подтверждение этого толкования чередовании
интенсивностей было получено из теплового поведения мо-
молекулы водорода. Основным термом Н2 является»12-терм,
Этот терм симметричен по отношению к электронам, в силу
«чего вращательные уровни с четным J симметричны, а уровни
с нечетным J антисимметричны по отношению к ядрам
<фйг. 22),
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 75
Вследствие малого момента инерции расстояние между
вращательными состояниями довольно велики. Поэтому при
очень низких температурах, например, при точке кипения
водорода, все молекулы должны были бы находиться на
самом низком вращательном терме (У=0), Тем не менее,
это не всегда так. Так как переходы между симметричными
и антисимметричными состояниями чрезвычайно маловероятны,
то все симметричные молекулы при
охлаждении попадают в состояние / = 0, * а
а те молекулы, которые до охлаждения
были антисимметричными, могут пе- s 5
рейти только в самое низкое антисим- 2 а
метричное состояние, т. е. на второй / : s
вращательный уровень (У=1). Но
теперь все же переход между симме- Фн г- 22- После-
тричными и антисимметричными состоя- метоичныТ^Г*"
ниями хотя и очень маловероятен, но антисимметричных
не совершенно невозможен. Вследствие (я) ротадионных
этого, если выдерживать водород в уровней в основ-
течение нескольких дней при низкой ^^"
температуре, равновесие все же на-
наступит, и, таким образом, все молекулы, в конце
концов, оказываются в симметричном состоянии с 7=0.
Если затем водород нагревается, то будут заниматься к
более высокие вращательные уровни, сначала, однако, толь-
только симметричные, так как переход в антисимметричные
состояния снова требует достаточного количества дней.
Когда подготовленный таким образом водород возбуждается
до свечения в разрядной трубке, он испускает спектр, в.
котором отсутствует половина линий, наблюдающихся у
нормального водорода. Появляются только симметричные
линии, обладающие в нормальном спектре меньшей интен-
интенсивностью. Но когда затем часть молекул с течением вре-
времени медленно перейдет в антисимметричные состояния,
снова выступят антисимметричные линии. Своей нормальной
л интенсивности они достигают лишь с установлением полного
равновесия. Так же, как для атома гелия, более распро-
распространенные антисимметричные состояния называют орто-.
76 ГЛАВА И
менее распространенные симметричные — пара-состояниями
(орто- и пара-водород). В то' время как для гелия это
различие относится к поведению собственных функций
электронов при обмене координат обоих электронов, орто-
и пара-водород различаются свойствами симметрии их соб-
собственных функций при обмене обоих ядер. Так как маг-
магнитный момент ядер значительно меньше, чем момент
электронов, то, вследствие меньшей энергии взаимодей-
взаимодействия, переход между пара- и орто-состояниями у молекулы
водорода еще менее вероятен, чем у атома гелия.
Разумеется, у молекулы водорода, как и у гелия,
следует различать электронно симметричные (синглетные)
и электронно антисимметричные (триплетные) термы или
собственные функции. Они рассматривались подробнее в
разделе 3 при изложении образования молекулы водорода.
Вероятности перехода между этими термами малы, но все
же существенно больше, чем между орто- и пара-водо-
пара-водородом.
Чистый пара-водород, получающийся из обычного водо-
водорода (путем длительного выдерживания при очень низкой
температуре), отличается от последнего не только спектром,
но и другими свойствами (прежде всего изменением тепло-
теплоемкости при низких температурах). К этому мы вернемся
позднее.
25. Изотопические эффекты в полосатых спектрах
Влияние изотопии в атомных спектрах невелико. Рас-
Расстояние между линиями, испускаемыми атомами с одинаковым
зарядом ядра, но с различной массой так мало, что рас-
расщепление может наблюдаться только с помощью особенно
сильных приборов. Наоборот, в спектрах двух молекул,
различающихся между собой только массами ядер, обнару-
обнаруживаются характерные различия. Это объясняется тем, что
ядро в атоме практически находится в состоянии покоя,
в то время как в молекуле ядра совершают колебательные
и вращательные движения, частота которых находится в
прямой зависимости от их масс.
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 77
Рассмотрим две молекулы АВ и АВ'. Пусть В' означает
более тяжелый изотоп атома В. При замене В на В' поло-
положение электронных термов остается практически неизменным,
так как оно не зависит от массы ядра. По той же причине
остаются неизменными равновесное расстояние между ядрами
и квазиупругая сила, удерживающая их в положении равно-
равновесия. Следовательно, изменение массы ядра не влияет на
силовое поле. Но в то же время частота колебаний, как
следует из элементарной формулы
2г. V МАМВ '
существенно изменится. Постоянная К одинакова в обоих
случаях, но масса Мв должна быть заменена массой /Ив»
при переходе от молекулы АВ к АВ'. Отношение обеих
молекулярных частот будет равно:
мв
Например, литий, имеющий два изотопа с массами 6и7,
образует три различные вида молекул: Li6 Lie, Li6 Li7 и
Li7 Li7. Частоты колебаний этих трех молекул относятся
между собой, по нашей формуле, как
1:0,96:0,93.
Различие между ними достигает, следовательно, 7%.
Для молекул с тяжелыми ядрами относительные разности
масс, а следовательно, и смещение частот, естественно,
меньше.
Особенно большие смещения получаются при сравнении
гидридов и дейтридов, так как массы изотопов водорода
относятся друг к другу, как 2:1. Влияние такого же ха-
характера, но меньшее по величине, оказывается на враща-
вращательные термы. Как уже упоминалось, равновесное расстоя-
расстояние остается практически постоянным. Поэтому момент
инерции АВ' больше, чем АВ, и вращательные термы или
линии молекулы АВ' расположены на меньших расстояниях
78 ГЛАВА ii
друг от друга, чем соответствующие термы или линии мо-
молекулы АВ. Изотопический эффект в полосах является
ценным вспомогательным средством при поисках новых
изотопов. Например, оба изотопа кислорода с атомными
весами 17 и 18 были открыты при наблюдении очень слабых
полос О16 0» и 01в 018.
У молекул с двумя одинаковыми ядрами влияние изото-
изотопии еще сильнее. Из трех молекул АА, АА' и А'А',
образованных из двух изотопов А и Аг, только АА и А'А'
имеют одинаковые ядра, и только для них имеет место
чередование интенсивьостей или исчезновение линий. На-
Напротив, у молекулы АА' все линии обладают полной интен-
интенсивностью, так как ядра не одинаковы. Таким образом,
в спектре наиболее распространенной молекулы кислорода
0ie Qie появляются, например, только симметричные лш.ии,
поскольку ядро О16 не имеет спина и подчиняется статистике
Бозе-Эйнштейна. В спектрах молекул О16 О17 и 01в О18
выступают также и антисимметричные линии, т. е. в сумме
имеется двойное количество линий.
26, Эффекты Зеемана и Штарка в полосатых спектрах
Подобно атомным спектрам, молекулярные спектры также
реагируют на присутствие магнитного и электрического
полей.
Рассмотрим сначала влияние электрического поля. Для
атомов водорода характерен линейный Штарк-эффект, т. е.
прямая пропорциональность между силой поля и смещением
терма. У всех остальных атомов смещение зависит квадра-
квадратично от силы поля (квадратичный эффект Штарка). Это
различие объясняется тем, что у водорода имеются кван-
квантовые состояния, средний электрический момент Ш которых
отличен от нуля. (В полуклассической модели Бора им
соответствуют эллиптические электронные орбиты.) В элек-
электрическом поле Е возникает поэтому электрическая энергия
взаимодействия — Ш'Е, средняя величина которой пропор-
пропорциональна Е. Напротив, у других атомов средний электри-
электрический момент всегда равен нулю. Поэтому эта энергия
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ 79
взаимодействия исчезает, и остается только возмущение,,
пропорциональное Е2.
Возможность линейного эффекта Штарка у молекул
также связана с существованием отличного от нуля среднего-
электрического момента Ш. Если пренебречь движением
ядра, то в двухатомной молекуле этот эффект может иметь
только направление вдоль оси молекулы. Когда оба ядра
одинаковы, он, по соображениям симметрии, очевидно, равен
нулю. Линейного Штарк-эффекта можно поэтому ожидать
только у молекул с различными ядрами. Этим случаем мы
и ограничимся.
Пусть jUi — среднее значение электрического момента^
параллельного оси молекулы. Примем сначала, что имеется
случай а связи по Гунду (см. раздел 17). Тогда мы можем
придерживаться следующего полуклассического рассуждения:
при вращении ось молекулы прецессирует вокруг неизменного
направления полного момента У и образует с У угол, коси-
косинус которого равен Й/У (см. фиг. 3). В этом прецессионном
движении, конечно, принимает участие и электрический
момент il)t. Его среднее значение равно проекции на на-
направление У;
Если молекула находится в электрическом поле, У устанав-
устанавливается так по отношению к направлению поля, что его
проекция М принимает целые или полуцелые зиачеиия, ш
зависимости от того, является ли У целым или полуцелым,
Следовательно, У образует с направлением поля угол, ко-
косинус которого равен /И/У. Средьий электрический момент
в направлении поля поэтому равен:
а определяемая нолем средняя электростатическая энергия,,
т. е, смещеьие терма, имеет вид:
80 ГЛАВА II
Этот результат подтверждается точным квантовомехани-
ческим расчетом. Следует только заменить У3 выражением
J(J-\-l), Сдвиг значений термов, таким образом, следую-
следующий:
В случае связи Ь соотношения совершенно аналогичны. Так
как спин 5 не связан с молекулярной осью, его можно
совершенно не учитывать. Он не обладает электрическим
моментом, поэтому его дополнительная связь с К (раздел 17)
не ведет к Штарк-эффекту. Поэтому в уравнении E1)
достаточно заменить J на К, М на Мк и И на Л, чтобы
■получить выражение для смещения терма в ел} чае Ь:
E2)
Из этой формулы видно, например, что 2-термы не могут
иметь линейного Штарк-эффекта, потому что для них А
равно нулю, и, кроме того, в D-термах имеет место связь 6,
что всегда обеспечивает справедливость именно уравне-
уравнения E2).
К сожалению, имеется мало экспериментальных данных
о Штарк-эффекте в линиях полос.
Подобным же образом об ьясняется . в молекулярных
спектрах и эффект Зеемана. В случае связи а магнитный
момент вдоль молекулярной оси равен (A -f- 2 2) магнетонов
Бора, если через 2 обозначать проекцию на ось суммарного
спина 5. Коэфиииент 2 об ьясняется тем, что каждому
электрону с механическим моментом 1/2 (в единицах Л/2тт)
соответствует Mai нитпый момент, равный целому магнетону
Бора. Возмущение эиер! етических термов магнитным нолем И
может быть, следовательно, вычислено непосредственно из
уравнения E1) при замене Е на И и Ш на (Л 4-2 2)-^—
(eh ' с \
(где j- величина магнетона Ьора):
eh И , 1 , Л ^ч SM ,,-Qi
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
В случае связи b магнитный момент в направлении мо-
молекулярной оси равен А магнетонов, так как магнитный
момент 2S спина не связан с молекулярной осью. Эти Л
магнетонов создают дополнительную энергию возмущения,
определяемую уравнением E2) при замене Е на Н и Si на
eh
А -: . Магнитный момент спина учитывается особо. Он
4 тс
устанавливается по направлению поля таким образом, что
проекция Ms вектора спина принимает значения, лежащие
между -j- S и — S и отличающиеся одно от другого на
единицу. Определяемая спином составляющая магнитного
момента в направлении поля содержит, следовательно, 2М3
магнетонов Бора, а соответствующая энергия возмущения
равна:
Отсюда получается суммарное смещение термов под влиянием
внешнего магнитного поля при наличии связи Ь:
\ ivr т-j eh Г A3 Me- , „„
Д W = -Н — [щщ^ + 2MS
\. @4;
Конечно, выражения E3) и E4) строго справедливы
только дли граничных случаев связи а или Ь. Кроме того,
расщепление должно быть всегда мало по сравнению с рас-
расстоянием между вращательными термами. В случае Ъ оно
должно быть- одновременно велико по сравнению с энергией
взаимодействия между спином и молекулярной осью, для
того чтобы спин действительно мог рассматриваться несвя-
несвязанным. Если эти условия не выполняются, то и у молекул
так же, как и у атомов, появляются сложные соотношения
при переходе от нормального эффекта Зеемана к эффекту
Пашек-Бака.
Теория эффекта Зеемана для линий полосатого спектра
была проверена и полностью подтверждена на примере пе-
перехода 12 — Ш в СО.
82
ГЛАВА II
27. Флуоресценция двухатомных молекул
Обычно молекулярные спектры получаются в разрядных
трубках при столкновениях молекул с электронами или иона-
ионами. Но так же, как и атомные спектры,
они могут быть получены и с помощью
флуоресценции, при облучении молекулы
светом, длина волны которого соответ-
соответствует одной из ее линий поглощения.
Поглощая лучистую энергию, молекула
переходит в возбужденное квантовое
состояние, из которого может снова воз-
возвратиться в основное состояние путем
одного или нескольких квантовых пере-
переходов, сопровождающихся испусканием
свиста.
Особенно подробно полосатая флу-
флуоресценция излучалась на полосах иода.
При этом наблюдались некоторые при-
примечательные явления. В то время как
при электрическом возбуждении с боль-
большей или меньшей интенсивностью воз-
возбуждаются все возможные термы моле-
молекулы и, соответственно, излучаются пол-
полные системы полос, при облучении мо-
молекулы соответствующей узкой спек-
спектральной линией она попадает на
совершенно определенный уровень энер-
энергии и может испускать только линии,
исходящие из этого терма (резонансная
флуоресценция).
Рассмотрим пример, изображенный
на фиг. 23. Пусть молекула при
поглощении соответствующего монохроматического излу-
излучения попала на вращательный уровень 2 состояния
р, из которого может перейти с излучением в со-
состояние а. Однако квантовое число J при переходе может
изменяться только на —|— 1,0 или — 1, поэтому будет
Фиг. 23. Схема-
Схематическое изобра-
изображение врашатель-
ных термов @, 1,
2) в двух различных
колебательных со-
состояниях аир двух-
двухатомной молекулы.
К пояснению поло-
полосатой флуоресцен-
флуоресценции.
СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
83
излучена не вся полоса [5—у а, а только те три линии,
которые соответствуют /—*J переходам 2—3, 2—2, 2—1.
Так как переход J—*-У очень часто запрещен, то вместо
трех линий обычно проявляются только две линии каждой
полосы. Типичный спектр флуоресценции состоит поэтому
кз групп по три или по
две линии. Каждая группа
соответствует своему ко-
колебательному или элек-
электронному переходу.
При повышении дав-
давления или добавлении по-
посторонних газов спектры
флуоресценции изменяются
весьма характерным обра-
образом. Молекулы, возбуж-
возбужденные поглощением излуче-
излучения до определенного вра-
вращательного состояния одного
из высших электронных или
колебательных термов, успе-
Фиг. 24. Превращение резо-
резонансного спектра паров иода в
нормальный полосатый спектр
путем прибавления гелия: 1 —
чистые пары иода, 2 — 2-мм Не,
5— 10-мм Не.
вают столкнуться с други-
другими молекулами, прежде чем
излучать свою энергию. При этом изменяется их враща-
вращательная энергия, и в спектре флуоресценции появляются и
другие вращательные линии, отсутствующие при низком
давлении. На фиг. 24 ясно видно это изменение спектра
флуоресценции в спектре паров иода.
28. Эффект Рамана у двухатомных молекул
Наблюдение эффекта Рамана двухатомных молекул имеет
большое значение потому, что позволяет осуществить ис-
исследование основного электронного состояния, которое ины-
иными путями может быть произведено лишь с очень большим
трудом.
Строение спектра Рамана определяется следующим ос-
основным правилом отбора. Переход между двумя термами в
6*
84
ГЛАВА II
эффекте Рамана возможен лишь при наличии третьего терма,
с которым оба могут комбинировать. Рассмотрим, например,
вращательные термы двухатомной молекулы в основном
электронном состоянии (фиг. 25). Переход
между двумя термами У и У только тогда
„активен" (в смысле Рам аи-эффекта), когда,
согласно основным правилам отбора, воз-
возможны переходы между У и У и третьим
термом, например, вращательным уровнем
У возбужденного электронного состояния.
Согласно правилу отбора для У (У—*У— 1,
У, У-1-1), отсюда непосредственно следует,
что У и У могут отличаться друг от друга
не больше, чем на две единицы.
Если, как это часто случается, пере-
переход У— У запрещен, в Раман-эффекте
имеют место только три перехода:
Фиг. 25. Схема
термов для по-
пояснения правил
отбора для ра-
мановских пе-
переходов.
ь -
3 -
1 -
о -
/1 .
Z1
/
!
У—2.
Для случая, когда в основном состоя-
состоянии Q = 0, вращательная эьергия равна
chBJ{J-{-\).
Тогда в Раман-эффекте трем переходам
соответствуют следующие частоты:
2?ГУ(У+1)_ (У+2)(/+3)] = — 5D,7+6), j
) — (У_ 2) (У— 1)] = ДDУ — 2), |E5)
J
Последнему из трех уравнений соответствует нулевая ветвь,
совпадающая в этом случае с возбуждающей спектральной
линией. Два других выражения соответствуют стоксовым
и антистоксовым вращательным рамановским линиям. Первый
ряд начинается с У=0, 1, 2, второй — с У =2, 3, 4... (так
СПЕКТРЫ ДВУХАТОЛШЫХ -МОЛЕКУЛ
85
как при J=0 и 1 получались бы отрицательные зна-
значения У). *
Эти рамановские линии располагаются точно так же, как
и вращательные линии полосы, с той только разницей, что
расстояния в эффекте Рамана в два раза больше, чем
в полосах, т. е. 4В вместо 2В. На фиг. 26 и 27 приведены
такие вращательно-рамановские спектры, снятые Разетти
для азота и кислорода. На фиг. 26 можно видеть также
Ф и г. 26. Вращательный ракановский
спектр азота по Разетти.
чередование интенсивностей, характерное для молекул
с одинаковыми атомами. Из распределения слабых и силь-
сильных линий этого рамановского спектра по четным и нечет-
нечетным квантовым числам J выяснилось, между прочим, что
ядро азота подчиняется статистике Бозе-Эйнштейна. Этот
факт имеет большое значение для ядерной физики.
Кроме вращательных частот, в Раман-эффекте проявля-
проявляются колебательные частоты. По причинам, которые будут
рассматриваться при изучении многоатомных молекул, на-
наблюдается только основное колебание, т. е. частота, соот-
соответствующая переходу из основного состояния в первое
возбужденное колебательное состояние. Переходы на высшие
колебательные уровни очень слабы и совсем не обнаружи-
86
ГЛАВА II
ваются для двухатомных молекул. Обычно у двухатомных
молекул наблюдается простая колебательная линия. Только
для Н2 Разетти получил несколько линий рамановской по-
полосы, соответствующих одновременному изменению колеба-
колебательного и вращательного состояний. Они представляют
собой менее интенсивное отображение вышеописанного вра-
Ф и г. 27. Вращательный рамановский
спектр кислорода по Разетти. Верхняя
часть снимка является сравнительным
спектром.
;дательного рамановского спектра, расположенное по обе
стороны от первичной линии. Раздельные вращательно-коле-
бательные линии у других молекул до сих пор не наблю-
наблюдались.
Разности частот основного терма и высших электронных
состояний обычно так велики, что не проявляются в рама-
новских спектрах. Единственное, известьое до сих пор, на-
наблюдение электронного перехода в эффекте Рамана при-
принадлежит Разетти. Оно сделано на NO, основной терм
которого — дублетный BIIita и 2П»/„), с незначительной раз-
разницей частот.
ТЕПЛОВЫЕ СВОЙСТВА ДВУХАТОМНЫХ МОЛЕКУЛ 87
ГЛАВА III
ТЕПЛОВЫЕ СВОЙСТВА ДВУХАТОМНЫХ МОЛЕКУЛ *>
29. Теплоемкость
Когда говорят, что при определенной температуре Т
газ находится в состоянии теплового равновесия, то под
этим подразумевается, что вся совокупность молекул этого
газа, каждая из которых может обладать рядом непрерыв-
непрерывных или квантованных значений энергии, распределена
между этими значениями энергии таким образом, что каж-
каждое из них заполнено характерной для температуры долей
от общего числа молекул. Распределение осуществляется
независимо для отдельных видов энергии (поступательная,
вращательная, колебательная и электронная энергии/.
Для энергии поступательного движения, т. е. для ско-
скоростей, всегда справедлив закон распределения Максвелла.
(Отклонения, обусловленные тем, что вместо классической
статистики Больцмана действует статистика Бозе-Эйнштейна
или Ферми, для обычных газов в общем случае пренебре-
пренебрежимо малы.) На каждую из трех поступательных степеней
свободы молекулы приходится в среднем энергии kT\2
{к—постоянная Больцмана, Т—; абсолютная температура).
Поступательная энергия одной молекулы, таким образом,
в среднем равна Ъ\2лТ, а для N молекул:
Wiaml = ^NkT. E6)
Для внутренней энергии (вращательная, колебательная
и электронная энергии) справедлив закон распределения
Больцмана. В тепловом равновесии вероятность нахождения
молекулы в квантовом состоянии с энергией wt пропорцио-
пропорциональна:
в~Шш E7)
!) В этой главе используются понятия и результаты, которые
будут обоснованы только в III части книги.
86
ГЛАВА II
ваются для двухатомных молекул. Обычно у двухатомных
молекул наблюдается простая колебательная линия. Только
для Н2 Разетти получил несколько линий рамановской по-
полосы, соответствующих одновременному изменению колеба-
колебательного и вращательного состояний. Они представляют
собой менее интенсивное отображение вышеописанного вра-
!; ЙЙШ
Ф и г. 27. Вращательный рамановский
спектр кислорода по Разетти. Верхняя
часть снимка является сравнительным
спектром.
гдательного рамановского спектра, расположенное по обе
стороны от первичной линии. Раздельные вращательно-коле-
бательные лимии у других молекул до сих пор не наблю-
наблюдались.
Разности частот основного терма и высших электронных
состояний обычно так велики, что не проявляются в рама-
новских спектрах. Единственное, известьое до сих пор, на-
наблюдение электронного перехода в эффекте Рамана при-
принадлежит Разетти. Оно сделано на NO, основной терм
которого—дублетный BII»ta и 2П<%), с незначительной раэ-
няцей частот.
ТЕПЛОВЫЕ СВОЙСТВА ДВУХАТОМНЫХ МОЛЕКУЛ g7
ГЛАВА III
ТЕПЛОВЫЕ СВОЙСТВА ДВУХАТОМНЫХ МОЛЕКУЛ1)
29. Теплоемкость
Когда говорят, что при определенной температуре Т
газ находится в состоянии теплового равновесия, то под
этим подразумевается, что вся совокупность молекул этого
газа, каждая из которых может обладать рядом непрерыв-
непрерывных или квантованных значений энергии, распределена
между этими значениями энергии таким образом, что каж-
каждое из них заполнено характерной для температуры долей
от общего числа молекул. Распределение осуществляется
независимо для отдельных видов энергии (поступательная,
вращательная, колебательная и электронная энергии).
Для энергии поступательного движения, т. е. для ско-
скоростей, всегда справедлив закон распределения Максвелла.
(Отклонения, обусловленные тем, что вместо классической
статистики Больцмана действует статистика Бозе-Эйнштейна
или Ферми, для обычных газов в общем случае пренебре-
пренебрежимо малы.) На каждую из трех поступательных степеней
свободы молекулы прихлдится в среднем энергии kT\2
{k—постоянная Больцмана, Т—-"абсолютная температура).
Поступательная энергия одной молекулы, таким образом,
в среднем равна 3J2^T, а для N молекул:
WUaasl = ^NkT. E6)
Для внутренней энергии (вращательная, колебательная
и электронная энергии) справедлив закон распределения
Больцмана. В тепловом равновесии вероятность нахождения
молекулы в квантовом состоянии с энергией wl пропорцио-
пропорциональна:
■ац
-йг E7)
г) В этой главе используются понятия и результаты, которые
будут обоснованы только в III част книги.
ГЛАВА III
Если состояние /?г--кратно вырождено, то эта вероятность
должна быть умножена на pt.
Если значения энергии wt не квантованы, а распреде-
распределены непрерывно, то при каждой температуре устанавли-
устанавливается такое больцмановское распределение. Соответствую-
Соответствующая степень свободы тогда „возбуждена" уже при самых
низких температурах. Если же, напротив, возможны только
дискретные значения W-, то из уравнения E7) для состоя-
состояний, энергия wt которых существенно больше kT, следует
очень малая вероятность заполнения. Степень свободы, при
которой это имеет место для всех wt, остается при соот-
соответствующей температуре „невозбужденной", т. е. все
молекулы находятся в основном состоянии. При обычных
температурах это имеет место, например, для всех высших
электронных состояний. У многих, особенно у легких, мо-
молекул энергия первого колебательного состояния так велика,
что при обычной температуре оно термически не возбуж-
возбуждается. В этом случае двухатомная молекула в теплозом
отношении ведет себя как система, состоящая из двух точек,
жестко связанных между собой осью. Помимо поступатель-
поступательного, возбуждено только вращательное движение, все осталь-
остальные степени свободы „заморожены". Сначала не будем рас-
рассматривать квантования вращательного движения и применим
к этой „молекуле-гантели" классическую статистику. Вра-
Вращение вокруг центра тяжести имеет две степени свободы.
На каждую приходится средняя энергия kTj2, а на обе
вместе, следовательно, kT. Вместе с кинетической энергией
поступательного движения 3&F/2 тепловая- энергия такой
молекулы составляет ЪкТ\2, а для N молекул:
■| NkT.
Отсюда теплоемкость /V молекул при постоянном объеме
равна:
Если отнести это к одной грамм-молекуле, то А/—число
Лошмидта, a Nk — газовая постоянная R. Теплоемкость
ТЕПЛОВЫЕ СВОЙСТВА ДВУХАТОМНЫХ МОЛЕКУЛ 89
(на моль) двухатомной молекулы при постоянном объеме
равна, следовательно: ,
evz= — R. E8)
. Это выражение справедливо, однако, только в области
средних температур. Если температура слишком высока,
заметно возбуждаются и высшие колебательные и электрон-
электронные состояния, так что повышается и теплоемкость. При
слишком низкой температуре величина kT становится
порядка расстояний между вращательными термами. При
этом нельзя более пренебрегать квантованием вращатель-
вращательного движения, и cv становится меньше, чем 5/?/2. Враща-
Вращательная часть теплоемкости исчезает полностью, когда
разность энергий между первым вращательным термом и
основным состоянием существенно больше, чем kT. Это
явление особенно ярко выраже Н2, вращательные термы
которого далеко отстоят друг _. друга вследствие малого
момента инерции молекулы.
С другой стороны, при высоких температурах cv пре-
превосходит значение 5kT/2, так как постепенно возбуждаются
колебательные состояния, а при определенных условиях —
и высшие электронные состояния.
Чтобы составить себе представление о вращательном
движении при' низкой температуре, примем, что основное
состояние молекулы является х^-термом, так что враща-
вращательная энергия выражается формулой:
Если сначала пренебречь влиянием ядерного спина, имею-
имеющего значение только для молекул, состоящих из одинако-
одинаковых атомов, статистический вес состояния J оказывается
равным 2J-\- 1 (соответственно 2J-\- 1 возможным ориента-
циям вектора импульса вращения). Вероятность состояния^.,
будет равна:
90 ГЛАВА Ш
и средняя энергия вращения молекулы имеет вид:
• F0)
Можно показать, что при более высокой температуре
эта формула дает для WIot значение k Т. Напротив, при
низких температурах не только WI0t, но и ее производная
по Т, т. е. вращательная часть теплоемкости, очень малы.
При Г = 0 они равны нулю. Для средних температур паде-
падение теплоемкости может быть численно определено из F0).
При сравнении с экспериментом обнаруживаются сущест-
существенные расхождения между расчетными и опытными вели-
величинами. Можно было бы попытаться объяснить эти рас-
расхождения тем, что основной терм Х2 У Н2 симметричен
по отношению к электронам и поэтому вращательные со-
состояния с четным У симметричны, а с нечетным J — анти-
антисимметричны. Так как ядро водорода обладает спином 1/2
и подчиняется принципу Паули, то симметричные состояния
(пара-водород) имеют суммарный спин ядра, равный нулю,
т. е. статистический вес 2У —j— 1. Антисимметричные состоя-
состояния (орто-водород), напротив, имеют суммарный спин ядра,
равный 1, и, соответственно его трем возможным ориента-
циям, статистический вес 3B/-|-1). При учетэ спинаядра
формула F0) должна быть изменена в соотоетствин с раз-
различными вероятностями:
B7-|-1)й ~кг при четном J
3 BУ -j- 1) г kT при нечетном J.
Но и этой поправкой не достигается совпадения между
теорией и экспериментом. По Деннисону, это объясняется
тем, что при изменении температуры равновесие между
ТЕПЛОВЫЕ СВОЙСТВА ДВУХАТОМНЫХ МОЛЕКУЛ 91
различными квантовыми состояниями устанавливается не
сразу. Скорость установления зависит от вероятности пере-
перехода. Так как переходы между симметричными и антисим-
антисимметричными состояниями маловероятны, то до установления
равновесия между пара- и орто-водородом проходит не-
несколько дней. В продолжение короткого периода изменений
соотношение в смеси пара- и орто-водорода остается практи-
практически постоянным и не изменяется, когда при определении
теплоемкости температура сильно понижается. Можно рас-
рассматривать водород как смесь двух газов, один из которых
обладает только симметричными (пара-водород), а другой —
только антисимметричными (орто-водород) вращательными
состояниями. Их количества в смеси относятся, как 1:3.
Формула, правильно отображающая изменение тепло-
теплоемкости, получается, если написать выражение F0) отдельно
для этих двух „газов", а затем выражение с нечетным /
умножить на 3 и сложить с выражением с четным J.
SO. Распределение интенсивностей в полосах
Интенсивность спектральной линии пропорциональна за-
заполнению исходного состояния и вероятности перехода.
Заполнение вращательных термов в тепловом равновесии
определяется законом распределения E9), которое, правда,
строго применимо только к электронным и колебательным
состояниям. Если, например, газ возбужден электрическим
разрядом, часть молекул попадает в высшие электронные
и колебательные состояния, для которых вероятность за-
заполнения вращательных термов сначала неизвестна. Именно
эти высшие электронные термы являются исходными уров-
уровнями электронных полос.
Однако путем простого рассуждения можно показать,
что и для вращательных термов возбужденных состояний
приближенно применимо уравнение E9). Возбуждение моле-
молекул в разряде происходит при столкновении с ионами или
электронами, причем J редко изменяется больше, чем на
единицу. Так как, кроме того, продолжительность жизни
возбужденной молекулы очень мала и за это время враща-
92 ГЛАВА III
тельное состояние нэ может претерпеть никаких сущест-
существенных изменений, то относительная вероятность различных
вращательных термов в возбужденном состоянии почти
та же, что и в основном.
Интенсивность линии полосы определяется не только
заполнением исходного терма, но и вероятностью соответ-
соответствующего ей перехода. Например, для перехода между
двумя з-^-термами, разность частот которых велика по
сравнению с таковой для вращательных термов, вероятность
для переходов J—>J-~~\ (Р-ветвь) пропорциональна У—{— 1,
для переходов У—*J—1 (Q-ветвь) пропорциональна /. Про-
Произведение заполнения исходного терма и вероятности пере-
перехода, определяющее интенсивность, таким образом, равно;
(/+1)е кТ (Р-ветвь)
Js kl (Q-ветвь/.
Отсюда видно, что интенсивность для перехода J •—±J— 1
вблизи нз'левой линии очень мала, затем, с ростом /, растет,
достигает максимума, после чего снова падает, причем;
у ;
-' kT
2hcB '
С помощью этого соотношения может быть приближенно
определен момент инерции молекулы по неразрешенной вра-
щателько-колебательной полосе. Так как обе ветви враща-
тельно-колебательной полосы расположены симметрично по
отношению к нулевой линии (фиг. 5), а расстояние между
линиями постоянно и равно 2В, то расстояние между макси-
максимумами интенсивности равно:
д.. _4R/ 1
"'mas rti-'~'max у ис >
из которого при известной температуре можно определить В.
В частности, для тяжелых молекул, у которых из-за боль-
ТЕПЛОРЫЕ СВОЙСТВА ДВУХАТОМНЫХ МОЛЕКУЛ 93
того момента инерции линии расположены очень густо и
поэтому трудно разделимы, это уравнение делает возможным
определение момента инерции по расположению максимумов
интенсивности.
31. Постоянная энтропии
Для расчета химического равновесия между различными
газами недостаточно знать только связанные с реакциями
теплоты образования. В условия равновесия входят постоян-
постоянные, которые должны быть определены термодинамическим
путем из абсолютных постоянных энтропии, участвующих
в реакции газов.
В III части книги мы увидим, что вопрос постоянных
энтропии тесно связан с вырождением газов, которым объ-
объясняется исчезновение теплоемкости одноатомных газов при
абсолютном нуле. Для энтропии газов, атомы которых имеют
простой, т. е. невырожденный, основной терм, мы получим
(ч. 111, раздел 12) следующее выражение:
+ log V — log N + log Bm"*fe%\, F1)
где /V—число атомов, т—их масса, V — объем газа и
г — основание натуральных логарифмов.
Формула \Ь\) не справедлива для очень низких темпера-
температур, при которых проявляются явления вырождения, и для
очень высоких температур, при которых имеют значение
возбужденные атомнье состояния.
Энтропия газовой смеси равна сумме отдельных энтро-
энтропии, если можно рассматривать газ как идеальный.
Рассмотрим газ, состоящий из атомов или молекул с раз-
различными уровнями энергии wo = O, wx, гг>2, ..., где wQ —
основное состояние, от которого отсчитываются все осталь-
остальные состояния, /г-кратно вырожденное состояние счи-
считается п. раз, так что все энергетические уровни wl явля-
являются простыми. До тех пор, пока не возбуждены высшие
состояния w£, справедлива формула F1). Для одноатомных
газов с простым невырожденным основным состоянием это
94 ГЛАВА III
имеет место еще при относительно высоких температурах.
У молекул, напротив, уже при достаточно низких темпера-
температурах происходит тепловое возбуждение высших вращатель-
вращательных состояний.
Если термически возбуждены высшие состояния, то при
температуре Т число молекул в состоянии wc, по закону
оольцмана, равно:
m
kT
Чтобы вычислить постоянную энтропии этого возбужденного
газа, будем рассматривать его как смесь, число компонент
которой равно числу возбужденных состояний, /-тая компо-
компонента состоит из Nt молекул, с энергией w.t. Суммарная
энтропия равна тогда сумме отдельных энтропии компонент,
которые могут быть вычислены так же, как для обыкновен-
обыкновенных газов, по формуле F1). Уравнение справедливо не
только для одноатомных газов. Оно предполагает лишь, что
все частицы находятся в одинаковом (простом) квантовом
состоянии, так что для полного описания последнего доста-
достаточно дать распределение энергии поступательного движе-
движения. Для Nt молекул в /-том состоянии это условие выпол-
выполнено, и, следовательно, применима формула F1).
Суммарная энтропия нашего газа равна:
Х {4
Так как 2 ^i — J*^> то эта формула переходит в следую-
следующую:
ТЕПЛОВЫЕ СВОЙСТВА ДВУХАТОМНЫХ МОЛЕКУЛ 95
Из F2) рледует:
kT
2 ще~^
kT
N log N — 1уш5^^ — kT
где w — среднее значение внутренней энергии молекул.
Суммарная энтропия оказывается, наконец, равной
F3)
Это выражение отличается от F1) только последним
членом, содержащим долю в энтропии, за счет термически
возбужденных состояний.
В качестве примера вычислим энтропию двухатомного
газа с основным электронным термом J2- Значения энергии
вращательных термов тогда равны:
chBJ(J-{-l).
Спином ядра сначала пренебрегаем. Считаем, что темпера-
температура настолько высока, что kT велико по сравнению с рас-
расстояниями между вращательными термами, но мало по сравне-
сравнению с энергией возбуждения колебательных и электронных
термов. Тогда мы можем ограничиться влиянием вращатель-
вращательных термов.
_ з
Вычислим сначала величину 2 е кТ, в которой также
следует учитывать только вращательные термы. Состояние
96 ГЛАЗА III
chB ,,,,,.
с квантовым числом J имеет вероятность е kT ' ' ' и вес
2J-{-\, т. е. оно должно считаться B/-J-1) раз. Отсюда:
chBJtj ■ 11
Так как Й7" очень велико, то мы можем заменить эту сумму
интегралом и, кроме того, пренебречь 1 по сравнению с J,
Тогда получим:
kT= f 2Je~ *T~J dJ=-§o . F4)
_ * о
•w (в нашем случае—средняя вращательная энергия), со-
согласно формуле F0), имеет значение kT. Отсюда F3) пре-
преобразуется к следующему'виду:
{65}
где, по формуле A5), В зависит от момента инерции.
При выводе F5) мы не учитывали спин ядра. Если ядра
имеют спин, необходимо различать молекулы с одинаковыми
и разными ядрами. Если оба ядра различны и обладают
спином /2 и, соответственно, /2, веса отдельных состояний
должны быть просто помножены на B/j-j-l) B12-{-1),
соответственно {21 х ~\- 1) возможностям ориентировки одного
я B/2-[-1) возможностям ориентировки второго ядра. На
такую же величину умножается поэтому F4), вследствие
чего в выражении для энергии F5) появляется новый член;
В случае молекулы, состоящей из одинаковых атолюв с ядер-
ядерным спином /, состояния с четными или нечетными J, в
зависимости от статистики, которой подчиняются ядра
(раздел 22), имеют статистические веса A-\-1) B/—|— 1) и,
МНОГОАТОМНЫЕ МОЛЕКУЛЫ 97
соответственно, /B/-f-l), или наоборот. Так как, заменив
суммирование интегрированием, мы пренебрегли расстоя-
расстояниями между отдельными вращательными термами, то мы
можем просто умножить F4) на среднее значение обоих
коэфициентов:
B/-Г- 1;-
Доио/шительный член в выражении энтропии запишется
тогда в виде:
kN [ 2 log B/ -f-1) — log 2 }.
Вследствие наших упрощений эти уравнения справед-
справедливы только в температурном интервале, в котором тепло-
теплоемкость двухатомных газов равна 5R/2.
ГЛАВА IV
МНОГОАТОМНЫЕ МОЛЕКУЛЫ
32, Структура многоатомных молекул
Как мы уже видели, двухатомные молекулы и их спек-
спектры исследованы весьма детально. Наоборот, свойства мно-
многоатомных молекул как экспериментально, так и теоретически
до сих пор изучены значительно меньше.
В то время как для выяснения структуры двухатомной
молекулы достаточно определить равновесное расстояние
между атомами, в многоатомной молекуле нужно еще знагь
взаимное расположение атомов, что представляет большие
дополнительные трудности. Поэтому для изучения структуры
многоатомных молекул необходимо одновременно пользоваться
различными, частично косвенными методами. Важнейшие из
них мы далее коротко изложим,
Первой существенной отправной точкой является хими-
химическая структурная формула. Она особенно помогает при
изучении структуры органических молекул. Так, представ-
представление о равноценности четырех валентностей атома углерода,
расположенных по углам тетраэдра, дает в большинстве
/ Энрпко Ферми
96 ГЛАЗА III
chB
с квантовым числом J имеет вероятность е kT " ' и вес
2J-\~\, т. е. оно должно считаться B/-J-1) раз. Отсюда:
Так как kT очень велико, то мы можем заменить эту сумму
интегралом и, кроме того, пренебречь 1 по сравнению с /.
Тогда получим:
J
£
kT
w (в нашем случае — средняя вращательная энергия), со-
согласно формуле F0), имеет значение kT. Отсюда F3) пре-
преобразуется к следующему "виду:
«S = AN|-| log T -f log V — log N— log(hcB) -f
F3)
Jh
где, по формуле A5), В зависит от момента инерции.
При выводе F5) мы не учитывали спин ядра. Если ядра
имеют спин, необходимо различать молекулы с одинаковыми
и разными ядрами. Если оба ядра различны и обладают
спином /j и, соответственно, /2, веса отдельных состояний
должны быть просто помножены на B/j-j-l) B/2-{-l),
соответственно B/1-{- 1) возможностям ориентировки одного
и B/2-[-1) возможностям ориентировки второго ядра. На
такую же величину умножается поэтому F4), вследствие
чего в выражении для энергии F5) появляется новый член:
В случае молекулы, состоящей из одинаковых атомов с ядер-
ядерным спином /, состояния с четными или нечетными У, в
зависимости от статистики, которой подчиняются ядра
(раздел 22), имеют статистические веса (/-{-!) B/—[— 1) и,
МНОГОАТОМНЫЕ МОЛЕКУЛЫ 97
соответственно, /B/4-1), или наоборот. Так как, заменив
суммирование интегрированием, мы пренебрегли расстоя-
расстояниями между отдельными вращательными термами, то мы
можем просто умножить F4) на среднее значение обоих
коэфициентов:
Дополнительный член в выражении энтропии запишется
тогда в виде:
kN {2 log B/ 4- Ц ~ log 2}.
Вследствие наших упрощений эти уравнения справед-
справедливы только в температурном интервале, в котором тепло-
теплоемкость двухатомных газов равна 5R/2.
ГЛАВА IV
МНОГОАТОМНЫЕ МОЛЕКУЛЫ
32» Структура многоатомных молекул
Как мы уже видели, двухатомные молекулы и их спек-
спектры исследованы весьма детально. Наоборот, свойства мно-
многоатомных молекул как экспериментально, так и теоретически
до сих пор изучены значительно меньше.
В то время как для выяснения структуры двухатомной
молекулы достаточно определить равновесное расстояние
между атомами, в многоатомной молекуле нужно еще знать
взаимное расположение атомов, что представляет большие
дополнительные трудности. Поэтому для изучения структуры
многоатомных молекул необходимо одновременно пользоваться
различными, частично косвенными методами. Важнейшие из
них мы далее коротко изложим.
Первой существенной отправной точкой является хими-
химическая структурная формула. Она особенно помогает при
изучении структуры органических молекул. Так, представ-
представление о равноценности четырех валентностей атома углерода,
расположенных по углам тетраэдра, дает в большинстве
/ Экрпко Ферми
98 ГЛАВА IV
случаев ясную картину расположения атомор. Эта картина
подтверждается и дополняется другими методами, которые
позволяют определить также расстояния между атомами.
Молекулы метана СН4, а также CCL, СВг4 и др., согласно
структурной теории, состоят из атома углерода, располо-
расположенного в центре тетраэдра, по углам которого находятся
атомы Н, С1 или Вг. Эта структура подтверждается физи-
физическими методами, которые, кроме того, позволяют опреде-
определить длину ребра тетраэдра. Для простых замещенных про-
производных метана, как, например, для СН3С1, химики при-
принимают аналогичную структуру с несколько искаженным
тетраэдром. Из соображений симметрии три атома водорода
образуют равносторонний треугольник, центр которого лежит
на прямой, проходящей через оба других атома. Расстояния
трех атомов водорода от атома хлора равны между собой,
но отличны от длины стороны основного треугольника.
Для сложных молекул структурная формула оставляет
открытыми несколько возможностей строения. Часто выбор
между ними не может быть сделан и с помощью других
методов. Если представить себе, например, оба атома угле-
углерода этана Н3С — СН3 лежащими на прямой линии, то
каждые три атома водорода расположены в плоскости, перпен-
перпендикулярной к этой прямой. Они образуют углы двух рав-
равносторонних треугольников и находятся на одинаковом рас-
расстоянии от соответствующего атома углерода. Формула,
однако, не дает данных о взаимном расположении обоих
треугольников.
Из структурной формулы следует шестиугольное строение
молекулы бензола С6Д6. Однако взаимное расположение
атомов углерода и атомов водорода структурной формулой
не выясняется.
33. Рассеяние молекулами рентгеновских лучей
Другой метод определения структуры молекулы, дающий,
по крайней мере в простейших случаях, хорошие результаты,
состоит в применении рентгеновских лучей, с помощью ко-
которых, как известно, может быть точно определена струк-
структура кристаллов.
МНОГОАТОМНЫЕ МОЛЕКУЛЫ gc,
Если пучок рентгеновских лучей падает на молекулу,
то лучи, падающие на отдельные атомы, интерферируют
между собой; при исследовании рассеянных лучей,, в зави-
зависимости от угла рассеяния, наблюдаются максимумы и ми-
минимумы интенсивности.
Эксперимент производится следующим образом. Пучок
рентгеновских лучей направляется на сосуд, содержащий
пары исследуемого вещества. На своем пути через сосуд
рентгеновские лучи встречают молекулы со всевозможными
орнентациями. Таким образом, наблюдаемое в одном опре-
определенном направлении рассеянное излучение фактически яв-
является средним значением интенсивности рассеянного излучения.
Если перпендикулярно к направлению первичного пучка лучей
поставить фотографическую пластинку, то на ней будет видно
изображение прямого луча, окруженное концентрическими
кольцами. По положению и интенсивности этих колец можно
сделать вывод о расположении атомов в молекуле. Конечно,
этот способ применим только в простейших случаях, так
как истолкование картин рассеяния затрудняется побочными
явлениями.
Атомы не являются рассеивающими точками. Их протя-
протяженность имеет величину того же порядка, что и расстояния
между ними в молекуле и длина волны рентгеновских лучей.
Поэтому кольца оказываются размытыми, и детали их струк-
структуры легко теряются. Это влияние может быть учтено, если
известно распределение электронов в атоме.. Далее, некоге-
некогерентное рассеянное излучение за счет эффекта Комптона,
создающее сплошной-фон, также ведет к возмущению пер-
первоначальной картины.
Кроме того, необходимо учесть, что легкими атомами,
в частности водородом, рентгеновские лучи рассеиваются
очень- слабо. Поэтому расположение легких атомов этим
способом, вообще не может быть определено. Тепловое дви-
движение молекул также уменьшает резкость интерференционных
колец.
Особенно неприятно то обстоятельство,, что эти наблю-
наблюдения не могут быть произведены над жидкостями, а только
над газами и парами, хотя рассеивающая способность по-
100 ГЛАВА iV
следних значительно меньше. При рассеянии рентгеновских
лучей в жидкостях, даже в одноатомных (например, в ртути),
появляются диффузионные кольца, похожие на „молекулярные
кольца8. Появление этих колец объясняется тем, что благо-
благодаря своей протяженности частицы жидкости распределяются
в пространстве не хаотически, а в известной степени упоря-
упорядочение», поскольку расстояние между двумя частицами ич
может быть меньше суммы их радиусов. Это расстояние,
при котором частицы соприкасаются, встречается тем чаще,
чем плотнее расположены частицы, и дает в картинах рас-
рассеяния жидкостей диффузионное кольцо. Это „кольцо жидкос-
жидкости" исчезает, как только среднее расстояние между частицами
становится ббльшим по сравнению с их диаметром. Поэтому
структура молекулы может быть определена только по на-
наблюдениям над газами и парами.
Вместо рентгеновских лучей могут употребляться и элек-
электронные лучи, для которых имеют место те же явления.
Они дают даже значительно более интенсивные картины
рассеяния. Однако разрешающая способность в случае рент-
рентгеновских лучей больше.
34. Электрическая поляризуемость молекул
Одним нз важнейших методов молекулярной физики яв-
является определение электрического момента отдельных мо-
молекул путем измерения электрической поляризуемости.
В молекуле, находящейся в электрическом поле, инду-
индуцируется электрический момент, в первом приближении про-
пропорциональный напряженности поля Е. Коэфициент пропор-
пропорциональности а называют электрической поляризуемостью.
Поляризуемость молекулы составляется обычно.из двух
частей. Первая образуется вследствие того, что молекула
состоит из отрицательных электронов и положительных ядер,
на которые в поле действуют противоположно направленные
силы. Центры тяжести положительных и отрицательных за-
зарядов смещаются полем друг относительно друга; молекула
поляризуется, Поляризационным силам противодействуют
внутренние силы между электронами и ядрами, стремящиеся
МНОГОАТОМНЫЕ МОЛЕКУЛЫ
сохранить первоначальную структуру молекулы. Под вли-
влиянием этих двух противоположных сил молекула получает
пропорциональный электрическому полю момент аЕ. Вели-
Величина этого момента зависит в общем случае от ориентации
молекулы в направлении поля. В молекуле имеются направ-
направления более сильной и более слабой поляризуемости. Так-
как в газе молекулы имеют всевозможные направления, то
наблюдается только среднее значение, которое мы обозначим
через ап. Величина а0 представляет собой независящее от
температуры свойство молекулы. Этот вид поляризуемости
называется „деформационной поляризацией *, так как она
соответствует частичному изменению структуры молекулы,
именно — сдвигу положительных ядер по отношению к от-
отрицательным электронам.
Кроме того, во многих молекулах существует второй
вид поляризуемости, так называемая „поляризация ориента-
ориентации*. Многие молекулы и в отсутствии электрического поля
обладают постоянным электрическим моментом р.. Например,
все молекулы, состоящие, подобно NaCl, из ионов противо-
противоположных знаков, обладают моментом, равным просто про-
произведению заряда на расстояние между ионами. Но и гомео-
полярные двухатомные молекулы обычно имеют электриче-
электрический момент. Исключение составляют, конечно, молекулы
с. одинаковыми атомами, у которых из. соображений симмет-
симметрии он отсутствует. Многоатомные молекулы также обладают
постоянным электрическим моментом, когда это совме-
совместимо с условиями симметрии. Молекулы, обладающие таким
моментом, называются полярными.
Когда такая молекула находится в электрическом поле,
постияньый момент стремится установиться в направлении
поля. Этим ориентирующим силам противодействует тепловое
движение, стремящееся создать беспорядочное распределение
молекул по всем возможным направлениям, В тепловом рав-
равновесии электрический момент jx чаще принимает направление
поля, чем противоположное. Средняя величина проекции
момента на направление поля поэтому отлична от нуля, т. е.
газ поляризован.
В то время как поляризация деформации независима от
102 ГЛАВА IV
температуры, поляризация ориентации, при неизменной силе
поля, с повышением температуры падает. Это происходит
потому, что с повышением температуры усиливается тепловое
движение, противодействующее установлению для моментов
определенной ориентации.
Теория поляризации ориентации очень сходна с ланжеве-
новской теорией парамагнетизма. Она дает для температур,
при которых можно не учитывать квантование вращательного
движения, величин}' поляризации, равную:
ЗлГ
т. е. поляризация ориентации обратно пропорциональна аб-
абсолютной температуре. К аналогичному результату приводит
и квантово-механический расчет.
Суммарная поляризуемость а равна сумме деформационной
и ориентационной частей:
Для газа можно пренебречь взаимным влиянием молекул.
Отсюда диэлектрическая восприимчивость равна произведению
поляризуемости а отдельной молекулы на число п молекул,
содержащихся в единице объема. Поэтому диэлектрическая
постоянная равна:
г = 1 -|— 4тгязе- F7)
В случае жидкости взаимным возмущением молекул пре-
пренебречь нельзя. Однако во многих случаях можно учесть
влияние соседних молекул упрощенным способом и получить,
таким образом, для поляризуемости отдельной молекулы
формулу Клаузиуса-Мозотти:
3 г —1
s -f- 2
МНОГОАТОМНЫЕ МОЛЕКУЛЫ
: 35. Электрический момент молекул
Из описанных в предыдущем параграфе закономерностей
вытекает простая возможность выяснения наличия у молекулы
постоянного электрического момента (дипольного момента)
и измерения этого момента. Поляризуемость молекулы и,
следовательно, диэлектрическая постоянная (отнесенная к рав-
равной плотности, т. е. к одинаковому числу частиц) не зависит
от температуры, если молекула не имеет постоянного элек-
электрического момента. Когда, напротив, имеется постоянный
момент, поляризуемость, а следовательно, и диэлектрическая
постоянная уменьшаются при повышении температуры.
Следовательно, по независимости диэлектрической посто-
постоянной от температуры можно непосредственно судить об от-
отсутствии постоянного момента. Если, с другой стороны,
диэлектрическая постоянная зависит от температуры, то по фор-
формуле F7) или F8) вычисляется молекулярная поляризуемость а.
Нанесенная как функция i IT, последняя, по формуле F6),
должна дать прямую, из наклона которой может быть по-
получена величина р. постоянного момента.
Знание электрического момента молекулы дает важные
сведения о ее структуре. В частности, когда электрический
момент равен нулю, можно притти к общему выводу о том,
что отсутствие постоянного момента связано с симметрией
5,юлекулы. Почти невероятно, что момент только случайно
неизмеримо мал. Например, фактом отсутствия постоянного
момента у молекул СН4 и СС14 подтверждается принятая
по стехиометрическим соображениям тетраэдрическая струк-
iypa этих молекул. Наоборот, следует ожидать электриче-
электрического момента, если, например, в метане симметрия нару-
нарушается частичным замещением атомов водорода. Центральная
симметрия тогда уничтожается, и, действительно, у молекул
CHgC^, CHCL и др. наблюдается электрический мо-
момент.
В этом отношении особый интерес представляет молекула
бензола. В соответствии со структурной формулой она не
имеет электрического момента. Но все ее простые замещенные
104
ГЛАВА iV
производные, как, например, СвН5С!, обладают дипольнь»
моментом, что понятно из структурной формулы:
Из трех двукратно замещенных хлорбензолов: орте
мета- и парздихлорбензола
С1
С1
Cl Cl
ci
ва основании соотношений симметрии, только два первых,
должны являться электрическими диполями. Представим себе,
что каждому атому хлора, расположенному в бензольном
кольце, соответствует направленный к центру колы.а элек-
электрический момент, величина которого совпадает с величиной
дипольного момента монохлорбензола A,5-10 1S ESE). Тогда
полный момент ортодихлорбензола является результирующей
двух таких моментов, образующих друг с другом угол в 60°.
Его величина равна, следовательно, 1,5-10 18 ^/~3 =
= 2,6-1O~1S ЕСЕ. У метадихлорбензола направления обоих
составляющих моментов образуют угол в 120°. Величина
полного момента поэтому равна величине единичного момента
—-1,5 • 10~18 ESE. У парадихлорбензола, в котором атомы
хлора расположены симметрично, нельзя ожидать наличия
электрического момента, так как оба вектора имеют прота-
МНОГОАТОМНЫЕ МОЛЕКУЛЫ
воположиые направления. Эти
результатами эксперимента:
СвН6С1
о-СвН,С12
m-CeHjCl2
о-ан.с1„
данные
Вычислено
1,5-
2,6-
1,5.
0
. 10-18
10-18
,10-18
сопоставлены ниже с
Наблюдено
1,6 -10-18
2,25-10-is
1,4 • 10-18
0
Совпадение — весьма хорошее. Отклонения объясняются
тем, что в действительности углы не полностью соответствуют
принятым нами упрощениям.
В некоторых простых случаях по отсутствию дипольного
момента можно непосредственно определить структуру моле-
молекулы. Так, молекула
двуокиси углерода СО2, ' Q.
не имеющая момента, о с О
может иметь только С- ° С'
линейную форму, изоб-
изображенную на фиг. 28, ф и г> 28^ структура молекул СО2 к
так как для любой дру- . н„О.
гой формы момент
будет отличен от нуля. Такую же симметричную структуру,
подтвержденную, впрочем, другими методами, имеет также
неполярная молекула сероуглерода CS2. Наоборот, в Н..О,
а также в SO2 и HaS атомы образуют равнобедренный тре-
треугольник (фиг. 28). Все эти молекулы обладают большими
дипольными моментами. У молекулы аммиака равноценность
трех атомов водорода и существование электрического мо-
момента заставляет предположить пирамидальное расположение, в
котором атомы водорода образуют лежащий в основании рав-
равносторонний треугольник, а равноотстоящий от всех трех ато-
атомов водорода а, ом азота располагается на вершине пирамиды.
36. Врашательные термы многоатомных молекул
В многоатомных молекулах так же, как и в двухатомных,
можно в первом приближении колебания ядер относительно
положения равновесия и вращение всей молекулы, рассмат-
Юб ГЛАВА IV
риваемой в качестве жесткой, считать независимыми друг
от друга. Но, в то время как в двухатомных молекулах си-
система электронных термов хорошо известна и во многих
случаях теоретически объяснена, в многоатомных молекулах
она известна очень мало. Исследование частот колебаний
поэтому ограничивается почти исключительно основным элек-
электронным состоянием. Вращение многоатомных молекул также
изучено лишь в самых простых случаях.
Вращательное движение линейных многоатомных молекул,
например, молекулы СО3 или ацетилена НС — СН, четыре
атома которого в состоянии равновесия также лежат на одной
прямой, можно рассматривать так же, как для двухатомных
молекул. Если принять, что момент количества движении
электронов в направлении молекулярной оси равен нулю
(это допущение возможно только для простейших молекул
в основном состоянии), то можно использовать формулу для
жесткого ротатора. Энергия У-ro вращательного уровня будет
тогда равна:
chBJ(J-\-\)
с константой В, которая, согласно A5), обратно пропорцио-
пропорциональна моменту инерции молекулы. Такая молекула будет,
следовательно, обладать вращательными или вращательно-
колебательными полосами и вращательными линиями Рамана,
подобными тем, которые мы изучали у двухатомных молекул.
По расстояниям между вращательными линиями здесь также
может быть определен момент инерции. Так, из вращатель-
вращательного спектра Рамана получается момент инерции молекулы СО2.
Он оказывается равным приблизительно 70-10~40 г/см2. Так
как структура молекулы симметрична, то отсюда следует,
что расстояние С — О равно 1,16 А.
Сложнее соотношения в молекулах, атомы которых не лежат
на одной прямой. Они имеют три (в общем случае различ-
различных) главных момента инерции. И ведут себя, следовательно,
так, как произвольное жесткое тело при вращении вокруг
своего центра тяжести (волчок). Однако применение кванто-
квантовых законов к этому случаю довольно сложно, особенно когда
зсе три главных момента инерции /„, /„ и /„ различны. В этом
МНОГОАТОМНЫЕ МОЛЕКУЛЫ ]Q7
случае невозможно дать точную формулу для вращательных
термов. Когда два из моментов инерции, например 1Ж и /
равны по величине, а следовательно, эллипсоид инерции об-
обладает вращательной симметрией, для энергии вращательных
состояний получается выражение:
F9)
может принимать значения 0, +1, + 2 . .. , a J — значения
Q |Q Q|+
j | + |+
Формула F9) проверена и подтверждена на спектре мо-
молекулы NH3.
37. Колебания многоатомных молекул
Молекула, находящаяся в определенном электронном
состоянии, например, в основном состоянии, ведет себя так,
как будто ядра связаны квазиупругими силами, в первом
приближении пропорциональными расстояниям удаления ядер
от их положения равновесия. Если мы выведем ядра из этого
положения и затем предоставим их самим себе, то они будут
совершать упругие колебания относительно этого положения
равновесия. До тех пор, пока амплитуда этих колебаний
мала, их можно разложить в ряд гармонических колебаний,
частоты которых — нормальные частоты колебаний моле-
молекулы— зависят от массы ядер и сил, действующих между
ними.
Если молекула состоит из N атомов, она представляет
собой систему, обладающую ЗЛГ степенями свободы. Но три
степени свободы соответствуют перемещению и три — вра-
вращению молекулы как целого, так что на долн> деформации,
т. е. на движение атомов друг относительно друга, прихо-
приходится ЗЛГ — 6 степеней свободы. Этим ЗЛГ — 6 степеням
свободы соответствуют ЗЛГ — б нормальных колебаний, ко-
которые могут быть не все различными. Нормальные колебания,
лмеющие одинаковую частоту, называют вырожденными.
Линейные молекулы обладают только двумя вращательными
степенями свободы, так как вращение вокруг молекулярной
108 ГЛАВА IV
иси при подсчете степеней свободы не учитывается. Такая
молекула имеет, следовательно, 3/V—о нормальных коле-
колебаний.
Общий метод определения нормальных колебаний и соот-
соответствующих форм, колебания состоит в следующем. Обо-
Обозначаем через 5ls S2» ^з'"'*' Чм компоненты смещения
Л/ядер, а через £,, 52, £3, ..., S3jV—их производные по време-
времени. Кинетическая энергия Т является квадратичной ортого-
ортогональной функцией £.:
До тех пор, пока амплитуды малы, а колебания, следова-
следовательно, гармонические, потенциальная энергия V представляет
собой квадратичную функцию £f:
Заменим теперь £.- новой переменной
так что Т выразится в виде:
а V:
Дальнейшей заменой координат V также переводится
в ортогональную квадратичную форму от новых перемен-
переменных и;:
174}
Известно, что это преобразование всегда возможно путем
решения секулярного уравнения вида G3), корни которого
непосредственно дают коэфициенты vt уравнения G4). Так
МНОГОАТОМНЫЕ МОЛЕКУЛЫ 109
как ьто преобразование ортогонально, то кинетическая энер-
энергия и в новых переменных сохраняет вид:
Для полной энергии молекулы окончательно получаем вы-
выражение:
^=Ц|Н+^?Ь 175)
в котором переменные разделены. Отдельные члены, соот-
соответствующие различным переменным и;, представляют собой
энергию гармонического осциллятора. Его частота v,- задается
через значения коэфипиента v. с помощью соотношения:
±Tt*;*t = vr Gt>)
Решением секулярного уравнения и определением коэфици-
ентов v{ можно, следовательно, найти частоты нормальных
колебаний из G0) и G1). Из ЗЛ/ частот, которые могуч4
частично совпадать, б соответствуют степеням свободы без
деформации и поэтому равны нулю. Остальные ЗЛГ— 6 ча-
частот являются характеристическими частотами молекул, каж-
каждая из которых соответствует определенной форме колеба-
колебаний. Если две или более из них совпадают, то форма
колебаний неопределенна, так как она может быть представ-
представлена любой линейной комбинацией соответствующих от-
отдельных колебаний.
Для простых молекул с особыми свойствами симметрии
можно избежать полного решения секулярного уравнения
и вывести характеристические формы колебаний из нагляд-
наглядных соображений.
Наиболее удобным является следующий метод. Сначала
сопоставляются все элементы симметрии молекулы и подби-
подбираются формы колебаний, при которых молекула и ао время
деформации' сохраняет полную симметрию. Такие колебания
называются полностью симметричными. Если далее постепенно
отбрасывать отдельные условия симметрии и отмечать коле-
колебания, удовлетворяющие уменьшенным условиям симметрии.
ГЛАВА IV
получаются последовательно все остальные колебания моле-
молекулы.
На фиг. 29 сопоставлены нормальные колебания для не-
некоторых важных типов молекул.
Ф и г. 29. Нормальные колебания некоторых важ-
важных типов молекул.
Видно, что молекулы типа СО2 обладают тремя нормаль-
нормальными колебаниями v]} v2 и v3, причем v: и v3 — простые
«хлебания, a v3 — двойное колебание, которое всегда можно
МНОГОАТОМНЫЕ МОЛЕКУЛЫ
ill
разложить на два независимых колебания, происходящих во
взаимно перпендикулярных плоскостях.
На этом простом примере мы применим упомянутые выше
соображения симметрии. В состоянии равновесия молекула
СО3 обладает т^емя взаимно перпендикулярными плоскостями
симметрии (а), ([J), (у). Плоскости ($) и (у) пересекаются
по молекулярной оси, в то время как плоскость (я) образз/ет
с ней угол в 90° и проходит через атом С. На фиг. 29
Q) расположена, например, в плоскости фигуры, а (у)—
перпендикулярно к ней. Положение атомов определяется
тогда одним параметром, а именно — расстоянием С — О,
В ' соответствии с этим имеется только одно совершенно
симметричное нормальное колебание (Vj). Все остальные ко-
колебания изменяют симметрию молекулы. Если молекула во
время колебания должна сохранять только плоскости сим-
симметрии (а) и (J3), то атом углерода должен перемещаться
вдоль линии пересечения обеих этих плоскостей, принимаемой
нами за ось х. Оба атома кислорода должны колебаться
симметрично по отношению к (а) в плоскости фигуры (^»).
Пусть их координатами будут 5 и Н^ Z. Колебания будут пол-
полностью описываться значениями х, S, £. Создается впечат-
впечатление, что имеется 3 нормальных колебания с рассматриваемым
свойством симметрии. Одно из них, однако, соответствует
полностью симметричному колебанию vls в то время как дру-
другое представляет собой просто перемещение молекулы как
целого в направлении оси х. Остается, следовательно, только
одно нормальное колебание, оставляющее неизменными эле-
элементы симметрии (а) и (|j) (v2 на фиг. 29). С (а) и (у)
вместо (а) и ([$) также получается нормальное колебание
с той же частотой V.,. Эти колебания, следовательно, выро-
вырождены.
Если сохраняются только плоскости симметрии ($) и (у),
то все три атома колеблются вдоль молекулярной оси, по
которой пересекаются обе эти плоскости. Колебательное
состояние молекулы описывается тогда одной координатой
каждого из трех- атомов. Снова существует видимость того,
что три параметра указывают на три нормальных колебании
молекулы. Однако, одно из них снова нилностыо симметрн .-
H2 ГЛАВА IV
ное колебание, другое является перемещением молекулы как
целого в направлении оси, и только третье представляет
собой новое нормальное колебание. На фиг. 29 оно обозна-
обозначено через vs. Этим исчерпываются все 3N — 5 колебаний
молекулы С09. Молекулы типа Н2О имеют вследствие своей
структуры только три нормальных колебания vlt v3 и v3,
которые изображены на фиг. 29. Колебания с частотами
v, и v3 имеют ту же симметрию, что и сама молекула,
следовательно, являются полностью симметричными. В уа со-
сохраняется только одна из плоскостей симметрии.
Молекулы типа NH4 обладают четырьмя различными
нормальными колебаниями v]s v2, v3 и v4. Полностью симмет-
симметричные колебания Vj и v2 имеют, как и сама молекула, ось
симметрии, совпадающую с высотой пирамиды, и три плос-
плоскости симметрии, каждая из которых проходит через атом
водорода. Эти оба колебания — простые. Колебания v3 и v4,
напротив,—дважды вырожденные.
Тетраэдрические молекулы (СН4 и др.) также имеют че-
четыре различных нормальных колебания vt, v9, v3 и у4. Ко-
Колебанию Vj соответствуют сжатие и расширение тетраэдра,
причем центральный атом находится в состоянии покоя. Оно,
следовательно, является простым и полностью симметричным.
Колебания v2 и v3 — трижды вырожденные. Соответствующие
формы колебания имеют тройную симметрию. Наконец, v4 —
дважды вырожденное колебание, при котором центральный
атом находится в покое, а атомы тетраэдра колеблются по-
попарно друг относительно друга на шаровой поверхности
вокруг центрального атома.
38. Инфракрасные спектры многоатомных
молекул
До тех пор, пока смещения атомов молекулы очень малы,
можно считать колебания гармоническими. При больших
амплитудах появляются отклонения от пропорциональности
между противодействующей силой и расстоянием удаления
от положения покоя, т, е, колебания становятся ангармони-
ангармоническими
МНОГОАТОМНЫЕ МОЛЕКУЛЫ
Для гармонических колебаний легко получить уровни
энергии, соответствующие отдельным квантовым состояниям,
так как молекулу можно заменить системой из 3N — б осцил-
осцилляторов, частоты которых соответствуют нормальным часто-
частотам Vj, v£, v8,. . . Каждый осциллятор обладает энергией
~2 Щ -j-vfiVi, где vt — целое число.
Если пренебречь нулевой энергией £^~о ^V> T0
этой системы осцилляторов, или колебательная энергия всей
молекулы, равна
Околев. =2 Л V^. G7)
Молекула может излучать или поглощать только частоты,
соответствующие разностям между двумя различными зна-
значениями ^колеб.. Это могут быть не только нормальные
частоты v,-, но и высшие гармонические и комбинационные
частоты. Так же, как и для двухатомных молекул, и по
той же причине нормальные колебания проявляются, в об-
общем, наиболее интенсивно. Интенсивность перехода опреде-
определяется величиной соответствующих матричных элементов
9Л;д электрического момента 3Jt. Этот момент 9J£ может
быть разложен в ряд по степеням координат uv #2, «8,...
отдельных нормальных колебаний:
2
ik
Первый член 9Л0 постоянен и представляет собой постоян-
постоянный электрический момент молекулы и может быть равен
нулю. На излучении он не сказывается. Если ограничиться
линейными членами 2 ЗК,-«/, т. е. гармоническим случаем,
то матричный элемент будет отличен от нуля, только если
одно из квантовых чисел изменяется на единицу. Следова-
Следовательно, в первом приближении появляются только основные
колебания. Высшие гармоники и комбинационные частоты
появляются тогда, когда нельзя пренебречь членами второй
и высших степеней в разложении G8), т. е. ангармонич-
ангармоничностью. Поэтому они вообще менее интенсивны.
8 Энрнко Ферми
Ц1 ГЛАрА IV
Естественно, обычно проявляются не только чистые
колебательные линии, но и врашательно-колебательные по-
полосы, возникающие при одновременном изменении враща-
вращательного состояния. По строению и внешнему виду они
очень похожи на вращательно-колебательные полосы двух-
двухатомных молекул. Однако у нелинейных молекул вращатель-
вращательная структура значительно оижнее.
Обычно инфракрасные спектры многоатомных молекул
исследуются в поглощении с помощью инфракра.ного спек-
спектрографа. Так как разрешающая способность атих приборов
не очень велика, то в большинстве случаев вместо враща-
вращательной структуры наблюдаются два абсорэц.-юнных макси-
максимума, разделенных минимумом (см. раздел 30).
Чаще всего в спектрах поглощения обнаруживаются
только переходы, исходящие из основного колебательного
состояния, поскольку при температуре, при которой обычно
производятся исследования (комнатная температура), более
высокие колебатеаьные состояния заметно возбуждаются
только у молекул с малыми частотами колебаний. Такими
малыми частотами (около 200 см~' и меньше) обладают
только молекулы с тяжелыми ядрами. Молекулы, содержа-
содержащие водород, вследствие малой массы атома Н обладают
в большинстве случаев группой колебательных частот в об-
области 3000 см—1, которая, естественно, не возбуждается
при комнатной температуре. Как мы видели, нормальные
к^л^бавия молекулы обычно являются наиболее интенсив-
интенсивными. При наблюдениях над парами большой плотности
и при наличии Сольшой толщины слоя, получается трудно
расшифровываемое смешение высших гармоник и комбиьа-
ционных частот, в которых зачастую очень трудно различить
нормальные колебания. При работе с меньшими плитностями
и при меньшей толщине слоя нормальные колебания легко
различимы по своей интенсивности. Об интенсивности погло-
поглощения в нормальных колебаниях можно с>дить уже по-
потому факту, что даже самое ничтожное содержание СО2
в атмосферном виздухе при малых толщинах слоев может
быть обнаружено по поглоще ию в инфракрасной области.
В то ирсыя как большинство нормальных колебаний
МНОГОАТОМНЫЕ МОЛЕКУЛЫ Ц5
отличается своей большой интенсивностью, в некоторых мо-
молекулах часть этих колебаний иногда не проявляется вообще.
Это имеет место всегда, когда, вследствие симметрии моле-
молекулы, при колебаниях не образуется электрического момента.
Мы поясним это на примерах фиг. 29. Для линейных
молекул типа СО2 в поглощении появляются частоты v2
и v3. Как видно, свойства симметрии, вызывающие исчез-
исчезновение электрического момента в состоянии равновесия,
снимаются колебаниями у2 и v3. Поэтому с ними обоими
связан электрический момент, и они проявляются при по-
поглощении. Полностью симметричное основное колебание v15
напротив, ничего не изменяет в общей симметрии моле-
молекулы; электрический момент не появляется, так что частота
V, отсутствует в спектре поглощения и оптически неактивна.
В действительности в инфракрасном спектре СО2 наблю-
наблюдаются только две сильные полосы при 15 и 4,3 jt, соот-
соответствующие нормальным колебаниям v2 и v3. Более слабые
полосы приписываются высшим гармоникам и комбинацион-
комбинационным частотам.
У Н2О все основные колебания инфракрасно-активны.
То же имеет место для NH2. У тетраэдрических молекул
типа СН4 частоты v2 и v3 активны, полностью симметричное
колебание Vj, разумеется, неактивно. Колебание v4, не даю-
дающее момента, также неактивно.
39. Раман-эффект многоатомных молекул
Важнейшим методом определения нормальных колебаний
многоатомных молекул является исследование эффекта Ра-
мана. Спектры Рамана превосходят инфракрасные спектры
поглощения во многих отношениях. Линии Рама.,а, в особен-
особенности для газов, очень резки, так что их частота может
быть измерена с большой точностью. Кроме того, в Раман-
эффекте проявляются почти исключительно нормальные
колебания.
Теоретическое обьяснение эффекта Рамана производится
с помощью теории дисперсии Кракерса и Гейзеноерга. Но,
8*
116 ГЛАВА IV
поскольку при этом должны быть учтены, помимо началь-
начального и конечного термов, линии Рамана и остальные кван-
квантовые состояния системы, этот метод неприменим для
многоатомных молекул, электронные термы которых неиз-
неизвестны.
Поэтому ограничиваются приближенным методом, при-
пригодным всегда, если только рамановская частота мала по
сравнению с частотой возбуждающего света и с электрон-
электронными частотами молекулы. В большинстве случаез эти
предпосылки выполняются.
Когда возбуждающий свет попадает на молекулу^ по-
последняя окажется в очень быстро изменяющемся электри-
электрическом поле, именно, в электрическом поле Е световой
волны. В молекуле индуцируется электрический момент,
пропорциональный напряженности поля Е; молекула поля-
поляризуется. Коэфициеит пропорциональности между полем
и поляризацией а, само собой разумеется, устанавливает
только чистую деформационную поляризацию. Он не содер-
содержит ориентационной части, так как колебания Е происходят
так быстро, что постоянный момент не может следовать за
полем. Правда, а не в точности соответствует деформацион-
деформационной поляризации в статическом поле, но несколько от нее
отклоняется. Это отклонение тем сильнее, чем ближе ча-
частота возбуждающего света подходит к резонансной частоте
(частоте аномальной дисперсии) молекулы.
Когда молекула изотропна, индуцированный электри-
электрический момент М имеет то же направление, что Е. В общем
же случае этому нет места, и а является тензором. Его
составляющая, например, аху представляет коэфициент про-
пропорциональности между индуцированной в направлении у
составляющей Му момента Ш и силой поля Ех в направ-
направлении х (х и у — два произвольных направления, которые
могут и совпадать). Если молекула деформируется, то по-
положение ядер изменяется, а тем самым и поляризуемость.
Поэтому, когда молекула колеблется, а меняется между
двумя величинами, среднее значение которых равно поля-
поляризуемости в состоянии покоя. Следовательно, а является
функцией координат иг, и%,... отдельных нормальных коле.
МНОГОАТОМНЫЕ МОЛЕКУЛЫ JJ7
баний молекулы, и мы можем разложить ее в ряд по сте-
сте= ахуо + 2 «,,/*у + S «^*«у«* + • ■ • G9)
пеням и,:
Влияние вращения мы для простоты учтем только под самый
конец.
Эффект Рамана может быть истолкован на основании этих
предпосылок при помощи простых классических соображений.
Электрический момент М связан с силой поля Е соотно-
соотношением:
Му = ахуЕх. (80)
Е изменяется периодически с частотой v возбуждающего
света:
Е = Ео cos 2itvf.
Для axV мы берем значение, получающееся из G9),
если опустить члены второй и высших степеней. Координата
и, изменяется периодически с частотой v, соответствующего
нормального колебания. Мы можем, следовательно, написать:
и] = и/о + cos
и получим
+ 2 W*yo cos B^ + Ы ■ Ео cos 2m»^
+ cos{2rr(v —vy)^-gy}]. J
Таким образом, Му содержит составляющую с частотой v
возбуждающего света и две модифицированные составляющие
с частотами (v-f-Vy) и (v — Vj). Каждой из этих составляю-
составляющих соответствует, согласно электромагнитной теории, излу-
излучение света соответствующей частоты, наблюдаемое как
118 ГЛАВА IV
рассеянное излучение. Последнее состоит, следовательно,
из излучения неизменной частоты (эффект Тиндаля) и рама-
рамановских линий с частотами
симметрично смещенных в обе стороны от первичной линии.
Различие в частоте рамановского излучения и возбуждающего
света совпадает с соответствующей частотой нормальных
колебаний. Составляющая v-j- v, называется антистоксовой,
а составляющая v — vy- стоксовой.
Теперь необходимо исследовать влияние допущенных
при этих рассуждениях приближений и упрощений.
Если заменить классическое рассмотрение квантовомеха-
ническ ни расчетом, мы получим те же значения частот, но
интенсивности окажутся иными. По классической теории
стоксовы и антистоксовы линии должны были бы иметь
одинаковые интенсивности. По квантовой же теории, в со-
согласии с опытом, получается, что стоксовы линии значительно
интенсивнее, чем антистоксовы. Это различие тем больше,
чем ниже температура и чем больше разница в частотах.
Далее, мы не учитывали влияния вращения. Оно сказы-
сказывается для всех трех составляющих в появлении расщепле-
расщепления, подобного расщеплению, имеющему место в Раман-эф-
фекте двухатомных молекул. Оно наблюдается обычно
только на первичной линии, так как интенсивность колеба-
колебательных рамановских линий значительно меньше.
Наконец, мы опустили высшие члены разложения G9).
Члены второго порядка соответствуют рамановским линиям,
расстояние которых от первичной линии равно удзоеьной
частоте нормальных колебаний или сумме частот двух раз-
различных нормальных колебаний. Высшим членам соответствуют
линейные комбинации этих частот. Такие гармоники и ком-
комбинационные линии в некоторых отдельных случаях наблю-
наблюдаются в виде очень слабых рамановских линий. Соотношение
интеисивностей этих линий и линий нормальных колебаний —
того же порядка величины, как между нормальным эффек-
эффектом Рамана и тиндалевским рассеянием, т. е. очень мало.
МНОГОАТОМНЫЕ МОЛЕКУЛЫ Цд
40. Рравила отбора в колебательном эффекте Рамана
Из сказанного в предыдущем разделе следует, что
с заметной интенсивностью наблюдаются только переходы,
в которых одно из колебательных квантовых чисел изме-
изменяется на единицу, а остальные остаются неизменными.
Другими словами, в эффекте Рамана проявляются нормаль-
нормальные колебания; по сравнению с ними интенсивности гармоник
и комбинационных частот исчезающе малы.
И в Раман-эффекте часть нормальных колебаний из
соображений симметрии запрещена. Так как появлению нор-
нормального колебания в эффекте Рамана сопутствует изменение
поляризуемости за счет этого колебания уже в первом при-
приближении, что означает aXslJ.=^0, то можно следующим
образом сформулировать правило отбора:
Основная частота в Раман-эффекте появляется только
тогда, когда поляризуемость молекулы в противоположных
фазах соответствующего нормального колебания -различна.
Если этого нет, то поляризуемость должна зависеть, хотя
бы квадратично, от расстояния удаления атомов из положе-
положения покоя. В этом смысле различаются четные и нечетные
колебания.
Рассмотрим определенное нормальное колебание молекулы
в два момента времени, соответствующих противоположным
фазам. Когда молекула в оба момента времени одинакова
или зеркально подобна и когда она в состоянии колебанит
сохраняет элементы симметрии, параллельные друг другу
в оба момента времени и достаточные для фиксирования
направления оси эллипсоида (т. е. две плоскости или, в худ-
худшем случае, трехкратную ось), то колебание четное. Если
хотя бы одно из этих условий не выполняется, колебание
нечетное.
В Раман-эффекте с большой интенсивностью проявляются
только нечетные основные колебаьия.
Поясним это на примерах <^иг. 29. Тип СО2: колебание
vx — нечетное, так как если в одной фазе молекула вытя-
вытянута, то в противоположной — сжата. Наоборот, v2 — коле-
колебание четное: противоположные (^азы можно перевести одну
120 . глава rv
в другую полуповоротом вокруг молекулярной оси. В обоих
случаях плоскости и оси симметрии одни и те же. Колеба-
Колебание v3 также четное: два состояния противоположной фазы
симметричны по отношению к плоскости, проходящей через
атом углерода перпендикулярно молекулярной оси. Кроме
того, в течение всего колебания атомы расположены на
одной прямой. Поэтому v2 и v3 рамановски неактивны.
У Н„О, NH3 и СН4 все колебания нечетные и поэтому
раманозски активны.
Строение рамановских спектров очень часто нарушается
вырождением или квазивырождением, т. е. случайным ра-
равенством частот различных колебаний. Благодаря большому
числу колебательных частот, которые существуют в много-
многоатомной молекуле, это случается очень часто.
Примером этого является спектр молекулы СО3. По-
Поскольку она обладает только одним нечетным нормальным
колебанием, спектр Рамана должен был бы состоять из
одной единственной линии. В действительности же наблю-
наблюдаются две интенсивные и две довольно слабые линии.
Появление двух первых можно объяснить следующим об-
образом.
Обе основные частоты v2 и v3 молекулы СО2, определен-
определенные из инфракрасного спектра, равны 670 и 2 350 см*
Для рамановски активной, но инфракрасно-неактивной частоты
va из модельных представлений получается величина около
1 300 см. Две наблюдаемые линии имеют частоты 1 285
и 1 388 см. Как мы видим, Vj случайно в два раза
больше, чем v2, и в этом „ квазивырождении" можно искать
причину удвоения линии. Так как оба энергетических уровня
с колебательными квантовыми числами A00) и @20) (три
числа соответствуют трем квантовым числам vv v.2, v3
отдельных основных колебаний) приблизительно равны, ан-
ангармоничность, т. е. асимметрия потенциальной кривой,
приводит к сильному возмущению. Возмущенные собственные
функции являются линейными комбинациями собственных
функций A00) и @20). Так как состояние A00) в Раман-
эффекте комбинирует с основным состоянием @00), то оба
состояния с возмущенными собственными функциями, содер-
МНОГОАТОМНЫЕ МОЛЕКУЛЫ
жащими рамановски активную собственную функцию A00),,
также комбинируют.
Еще две слабые рамановские линии можно объяснить как
эффект Рамана на молекулах, термически возбужденных до=
первого уровня основного колебания v2. Интенсивность и по-
положение этих линий подтверждают наше толкование про-
происхождения интенсивного дублета.
41. Особенности колебательных термов
многоатомных молекул
В структуре колебательных термов многоатомных моле-
молекул иногда обнаруживаются особенности, не наблюдающиеся
у двухатомных молекул. Некоторые из этих особенностей-
здесь будут кратко описаны.
Колебательное состояние молекулы только при достаточно-
малых амплитудах может быть представлено как наложение
отдельных нормальных колебаний. В классической теории
возможны сколь угодно малые амплитуды. Напротив, в кван-
квантовой механике может случиться, что уже энергия самого
низкого состояния, так называемая нулевая энергия, так
велика, что движение происходит негармонично или теряет
колебательный характер.
Примером этого является так называемая „свободная
вращаемость " определенных радикалов, например, метиловой*
группы этана. Химические данные говорят о том, что обе группы^,
связанные простой С — С связью, могут вращаться вокруг
прямой, соединяющей атомы углерода. Для радикалов, свя-
связанных между собой двойной связью, это не имеет места.
Это видно, например, из того, что имеется только один>
дважды замещенный этан CHjCl — СН2С1, но две соответ-
соответствующие производные этилена
С1 Г^С1 Cl H
с с< >с с<
Существование и химическое различие этих обоих продук-
продуктов показывают, что при натичии двойной связи требуется
значительная энергия, для того чтобы повернуть радикалы?
122
ГЛАВА IV
на 180° по отношению друг к другу. Напротив, для СН2С1 —
— СН.С1 из отсутствия изомерных форм можно сделать вывод,
что необходимая для поворота радикалов энергия довольно
мала. Она, повидимому, меньше, чем нулевая энергия
соответствующей степени свободы, так что никакое коле-
колебание не может возникнуть и уровни энергии распределя-
.ются так же, как при вращательном движении. Правда, до
сих пор положение
этих уровней энергии
еще не удалось точно
установить.
Другая особенность,
экспериментально под-
подробно изученная, со-
состоит в следующем
явлении, проязля ощем-
ся, например, у аммиа-
аммиака: как известно, мо-
молекула NH3 имеет фор-
форму трехгранной пира-
пирамиды, на вершине
которой находится атом
N. Потенциальная энер-
энергия U молекулы рас-
рассматривается как функция расстояния х между атомом азота и
плоскостью расположения трех атомов водорода, которые мы
предполагаем покоящимися. Следовательно, х — высота пира-
пирамиды. Последняя в состоянии равновесия имеет величину х0,
а потенциальная энергия U(x) минимальна. Кроме того, потен-
потенциальная кривая симметрична по отношению к точке лг = О
и имеет ориентировочно -вид, представленный на фиг. 30.
Можно сравнить колебание v2 молекулы (фиг. 29) с дви-
движением вдоль оси х точки, на которую действует сила,
о ис лваемая потенциалом (J(x) и масса которой равна
•сумме приведенных масс отдельных атомов.
Свойства собственных функций и уровней энергии такого
.движения описывались в разделе 19. Если потенциальный
«барьер достаточно широк, то точка находится в одной или
"Ф и г. 30. Потенциальная энергия
-U(x) молекулы NH3 в зависимости
от расстояния х атома азота от плос-
плоскости атомов водорода.
МНОГОАТОМНЫЕ МОЛЕКУЛЫ 123
в другой яме. Все собственные величины поэтому дважды
вырождены. В действительности, однако, возможны переходы
кежду обеими ямами, и тем легче, чем ниже и уже потен-
потенциальный барьер. Тем самым вырождение снимается, и двой-
двойное собственное значение распадается на более низкое
с симметричной по отношению к х = 0 собственной функ-
функцией, и более высокое с антисимметричной собственной
функцией. Деление этой разности энергий на h дает частоту
Фиг. 31. Рамановский спектр аммиака по
Амальди и Плячеку. Обе линии, 933,8 см~й и
964,3 см, являются компонентами колебания v2,
которое расщепилось в дублет вследствие
двух положений равновесия атома азота.
с которой происходит переход точки из одной ямы в дру-
другую и обратно. Для различных колебательных уровней
разность имеет различную величину. Для высоких колеба-
колебательных термов она имеет наибольшую величину, так как
с приближением к потенциальному барьеру частота перехо-
переходов увеличивается. Это расщепление колебательных термов
исследовалось особенно тщательно на примере нормальных
колебаний v2 аммиака. В соответствующей полосе поглоще-
поглощения все линии — двойные. Дублетное расстояние составляет
30 см-1. В Раман-эффекте также набюдалось это явление
(фиг. 31). Такое же расщепление проявляется в основном
колебании v1} но там оно, в соответствии с теорией, зна-
значительно меньше и равно приблизительно 0,9 см—1. Соот-
Соответствующая этой разности частот длина вольы 1,1 см на-
124 ГЛАВА IV
блюдалась и непосредственно в поглощении электрических
волн.
Аналогичные явления характерны и для многих других
молекул, и притом всегда, когда ядра имеют два различных
стабильных положения равновесия. По классической теории
для перехода молекулы из одного положения равновесия
в другое необходима определенная минимальная энергия.
Согласно квантовой механике, при сколь угодно малой
энергии все же существует конечная вероятность перехода
между обоими уровнями, но которая при определенных
условиях очень мала.
В частности, для всех оптически активных веществ су-
существует конечная вероятность перехода из одной изомер-
изомерной формы в другую. Если конечная вероятность мала, эти
формы относительно устойчивы и могут длительное время
существовать в чистом состоянии. При больших вероятностях
перехода оптически изомерные формы настолько быстро
переходят одна в другую, что часто получается только
рацемат.
ЧАСТЬ II
КРИСТАЛЛЫ
ГЛАВА 1
ГЕОМЕТРИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
1. Простые и сложные решетки
Исследование кристаллического состояния материи всту-
вступило в совершенно новую стадию, после того как Лауе
с сотрудниками в 1912 г. удалось наблюдать отражение
рентгеновских лучей на „атомной решетке" кристаллов.
Это открытие имело фундаментальное значение как для
физики рентгеновских лучей, которой оно дало удобный
и надежный метод спектрального разложения, так и для
исследования структуры кристаллов, которая даже в сложных
случаях могла быть выяснена достаточно полно с помощью
рентгеновских лучей.
Предположение, что кристаллы состоят из правильно
размещенных атомов или молекул, было высказано в конце
XVIII столетия кристаллографом Гайи, а за 60 лет до
открытия Лауе повторено Браве. Открытие отражения
рентгеновских лучей окончательно подтвердило это пред-
предположение.
Мы обсудим сначала некоторые основные понятия теории
решетки.
Рассмотрим три группы параллельных и равноудаленных
друг от друга плоскостей. Множество точек пересечения
каждых трех плоскостей образует простую объемную
точечную решетку. Каждая из этих плоскостей содержит
тогда плоскую точечную решетку, которая соответственно
образована двумя семействами равноотстоящих параллельных
прямых (фиг. 32).
Простую объемную решетку можно образовать также
следующим образом. Выберем три вектора а, Ь, с, имеющие
различные направления и не лежащие в одной плоскости
124 ГЛАВА IV
блюдалась и непосредственно в поглощении электрических
волн.
Аналогичные явления характерны и для многих других
молекул, и притом всегда, когда ядра имеют два различных
стабильных положения равновесия. По классической теории
для перехода молекулы из одного положения равновесия
в другое необходима определенная минимальная энергия.
Согласно квантовой механике, при сколь угодно малой
энергии все же существует конечная вероятность перехода
между обоими уровнями, но которая при определенных
условиях очень мала.
В частности, для всех оптически активных веществ су-
существует конечная вероятность перехода из одной изомер-
изомерной формы в другую. Если конечная вероятность мала, эти
формы относительно устойчивы и могут длительное время
существовать в чистом состоянии. При больших вероятностях
перехода оптически изомерные формы настолько быстро
переходят одна в другую, что часто получается только
рацемат.
Ч А С Т Ь II
КРИСТАЛЛЫ
ГЛАВА I
ГЕОМЕТРИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
1. Простые и сложные решетки
Исследование кристаллического состояния материи всту-
вступило в совершенно новую стадию, после того как Лауе
с сотрудниками в 1912 г. удалось наблюдать отражение
рентгеновских лучей на „атомной решетке" кристаллов.
Это открытие имело фундаментальное значение как для
физики рентгеновских лучей, которой оно дало удобный
и надежный метод спектрального разложения, так и для
исследования структуры кристаллов, которая даже в сложных
случаях могла быть выяснена достаточно полно с помощью
рентгеновских лучей.
Предположение, что кристаллы состоят из правильно
размещенных атомов или молекул, было высказано в конце
XVIII столетия кристаллографом Гайи, а за 60 лет до
открытия Лауе повторено Браве. Открытие отражения
рентгеновских лучей окончательно подтвердило это пред-
предположение.
Мы обсудим сначала некоторые основные понятия теории
решетки.
Рассмотрим три группы параллельных и равноудаленных
друг от друга плоскостей. Множество точек пересечения
каждых трех плоскостей образует простую объемную
точечную решетку. Каждая из этих плоскостей содержит
тогда плоскую точечную решетку, которая соответственно
образована двумя семействами равноотстоящих параллельных
прямых (фиг. 32).
Простую объемную решетку можно образовать также
следующим образом. Выберем три вектора а, Ь, с, имеющие
различные направления и не лежащие в одной плоскости
126
ГЛА^А I
Из фиксированной точки Ро с помощью вектора
/а -(- тЪ -\- пс A)
мы приходим в точку Р,.иа. Когда /, т и п проходят все
положительные и отрицательные целочисленные значения,
включая нуль, точки /\яя образуют простую об ьемную
решетку.
Наконец, такую решетку можно представить себе третьим
спосооом с помощью прямоугольной или остроугольной
декартовой системы кооряинат с раз-
различными масштабами по трем осям.
Тогда точки с целочисленными значе-
значениями координат являются узлами ре-
решетки.
В простой решетке все точки равно-
равноценны, так как каждая одинаковым об-
образом окружена соседними точками и
может быть в них переведена с по-
помощью одной и той же операции.
Параллелепипед, образованный тремя
исходящими из одной точки основными
векторами а, Ь, с, называется элементар-
элементарной ячейкой. В плоском изображении
фиг. 32 заштрихованный параллелограм
является такой элементарной ячейкой.
Нужно учесть, что выбор основных векторов, а следова-
следовательно, и установление элементарной ячейки в простой
решетке являются весьма произвольными. Для случая двух
измерений это видно из фиг. 33. Изображенную здесь
плоскую решетку можно описать с помощью вьктороз а, Ъ
так же хорошо, как с помощью векторов а', Ь'.
В обоих случаях элементарная ячейка различна. В одном
случае она дается изображенной на фиг. 33 сеткой прямых,
в другом заштрихованным параллелограмом.
Сложные решетки образуются при вдвижеьии одна в дру-
другую двух или нескольких простых решеток, смещенных на
определенную величину одна относительно другой. Для этого
Фиг. 32. Плоская
точечная решетка.
Заштрихована эле-
элементарная ячейка
З решетки.
ГЕОМЕТРИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
12Г
выбирается столько исходных точек PQ, Pq, Р'о, сколько
имеется простых решеток, и три основных вектора а, Ь, с.
Вектор (I) переводит эти фиксированные точки в новые точки
Pfmni P'tmm Р'ым- • -, которые соответствуют узлам сложной
решетки, когда I, т и п снова проходят все положительные
и отрицательные целые значения, включая нуль.
В сложной решетке не все точки равноценны. Вообще-
говоря, друг другу соответствуют только точки, принадле-
принадлежащие одной простой решетке. Для
плоского случая это наглядно пока-
показано на фиг. 34, изображающей слож-
сложную решетку, состоящую из двух
простых. Узлы одной решетки изо 5-
ражены большими кружками, узлы
другой — малыми. Все маленькие и
все большие кружки соответственно
равноценны друг другу.
Сложную решетку часто описы-
описывают с помощью ячейки простой ре-
решетки, в которой находятся, по
меньшей мере, по одной узловой
точке от всех других простых реше-
решеток. Если помещается только один узел, то он находится вну-
внутри ячейки. Узел, лежащий на одной из граней, должен быть-
обязательно повторен на противолежащей грани; узел на
одном из ребер должен встретиться на параллельных ребрах,,
следовательно, по меньшей мере, четыре раза в одной ячейке.
Сложная решетка полностью описана, если известны элемен-
элементарная ячейка и координаты остальных точек по отношению
к этой ячейке.
На фиг. 34, например, было бы достаточно определить
координаты больших кружков относительно нарисованной
элементарной ячейки.
Атомы кристалла расположены совершенно так же, как
узлы простой или слож! ой решетки. По сути дела, узлы
решетки фактически соответствуют только равновесным по-
положениям атомов. Вокруг этих положений атомы, благодаря
наличию у пих тепловой энергии, совершают большие или
Фиг. 33. Плоская
точечная решетка с
различно выбранными
элементарными ячей-
ячейками (а, Ь) и (а', Ь')„
123
ГЛАВА I
меньшие колебания. Если кристалл состоит из однородных
атомов, образующих простую решетку, его называют одно-
атомным. Если же атомы образуют сложную решетку, то
кристалл называют многоатомным и притом двух-, трех-,
о о о о о четырех-...атомным, в зависимости от
числа простых решеток, из которых он
о оо о о построен.
Решетка кристалла, состоящего из
разнородных атомов, построена из не-
О/ О/ О О скольких простых решеток, так что каж-
каждая содержит только атомы одного сорта.
Атомы одного сорта могут, однако, обра-
образовывать и несколько простых решеток.
Кристаллическая молекула содержит
наясложная решет- по одному атому от каждой простой ре-
река, состоящая из щетки. Это понятие молекулы, однако,
сильно разнится от понятия молекулы
газа или жидкости. В жидкости или газе
молекула как целое участвует в тепловом
движении, так что все части молекулы
вместе меняют свое положение. Такое
понятие молекулы теряет в кристалле
смысл, так как здесь тепловое движение
состоит только в колебаниях отдельных атомов вокруг
своих положений равновесия, поэтому скорее весь кристалл
следует рассматривать как одну большую молекулу. Кри-
Кристаллической молекулой в узком смысле слова мы назы-
называем тогда совокупность отдельных атомов от каждой про-
простой решетки. Эти атомы следует выбирать так, чтобы в
решетке они были по отношению друг к другу самыми
ближайшими соседями. Это требование часто осуществимо
различными равноправными способами, так что оно остав-
оставляет известный произвол.
2. Симметрия решеток
Симметрия кристалла тесно связана с симметрией решетки.
Браве и Шенфлис показали, что различные симметрии кри-
кристаллических систем уже полностью содержатся в немногих
О О О О
© О—Q О О
О О О О
о о о о о
Фиг. 34. Двухмер-
двух простых.
Однородные точки
обозначены О и
соответственно о.
Параллелограм изо-
изображает элемен-
элементарную ячейку дан-
данной решетки.
ГЕОМЕТРИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
J29
аростых типах решеток. Эти четырнадцать решеток Браве
сведены в следующую таблицу. _
I ЗОЛ И Ц a S"
Тип решетки
Кристалли-
Кристаллическая
система
Общий тип объемной решетки
/\ у\ /\
афЬФС, аЬфЬс&са ,.,....,.
a-=b; ac = bc
аЬ=ас=-^-, . , , . . . .
а =1к ас-=-Ъс= - . • . . . , . . , , .-
То же. что и 4, с узлом в центре каждой элемен-
элементарной ячейки ..... о. .......
1 Л "^ я
ab—bC=Ca——4
Го же, что и 6, с узлом в центре каждой эле-
меитарной ячейки ......
/\ /\ /\
a=zb—c% ab—bc — са
а=д; ай = -т-; ае= ое = — .......
•ч /\ /\ ж
й = й; ab=bc=ca=—
То же. что я 10, с узлом в центре каждой эле-
мен гарной ячейки
Простая кубическая решетка .
Объемно-центрнрованная кубическая решетка,
как 12, с узлом в центре ка.кдоа элементар-
элементарной ячейка •
Решетка с центрированными гранями, как 12,
с vr;»o4« в середине каждой грани . , . ■> -.
Триклиннаа
Моноклин-
Моноклинная
Моноклин-
Моноклинная
Ромбическая
Ромбическая
Ромбическая
Ромбическая
Тригональ-
ная
Гексаго-
наль ная
Тетрагоиалев-
ная
Тетраго-
Тетрагональная
\ Кубическая
Кубическая
Кубическая
130
ГЛАВА i
Через a, b ы с обозначены длины основных векторов,
s\ У\ У\
в-b, be и со. — углы между ними,
Все четырнадцать решеток являются простыми объемными
решетками. Это откосится и к типам 5, 7, 11, 13 и 14,
Напри»4ер, объемно-центрированную кубическую решетку и
решетку с центрированными гранями можно изобразить основ-
основными векторами следующим образом:
Ф я г. 35. Элементарные ячейки кубической, кубиче-
кубической объемно-центрированной и кубической гргне-
центрированыог! решеток.
Кубическая объемно-центрированная решетка:
а;
' — "о"! ас=Ьс;
/"Т
ГО
Кубическая решетка с центрированными гранями:
a
—;
- Однако обычно предпочитается более простое представ-
представление с помощью регулярной ячейки, как показано на фиг. 35.
Симметрия кристаллов со сложными решетками определяет-
определяется симметрией соответствующих простых решеток, Они могут
ГЕОМЕТРИЯ КРИСТАЛЛИЧЕСКОЙ "ЕШЕТКИ 13j
быть расположены таким образом, что общая симметрия
кристалла окажется меньше симметрии отдельных простых
решеток.
3. Определение структуры кристаллической
В этом разделе мы кратко рассмотрим основы методов,
Фпределения стр ктуры.
Как известно, кристалл, на который падает пучок рент-
рентгеновских лучей, ведет себя так, как будто лучи отражаются
от параллельных заполненных атома vи плоскостей. Отра-
Отражающиеся от различных параллельных плоскостей лучи
интерферируют ajyr с другом, так что появляются мак-
максимумы интенсивности под углами, определяемыми заколом
Брегга,
n\-=2d cos&, B)
где:Х — длина волны рентгеновских лучей,
п — целое число, порядок отражения,
$ — угол падения,
d — расстояние между отражающими плоскостями,
В общем случае определение структуры производится
двумя этапами.
a) Определение вида простой решетки (или простых редпе-
ток), из которых построен кристалл.
b) Определение взаимного расположения отдельных реше-
решеток.
Первая задача решается сравнительно легко. Если кри-
кристаллическая система известна, то нужно только выбрать
между немногими и.шестныАЫ типами ^табл. 1} и определить
величину основных векторов. То и другое возможно посред-
посредством наблюдение уииа отражения рент! еновских лучей
определенной длины во.иы or мпо(их, кристаллографически
различных (ьискостей и примепепин уравнения Брегга B),
Измеряя углы г, Слогвегсгау.о.ди^: \.аксим^мам отражения
различных nojjrtAKJB, и иоАСшалян £илуче.1пые зпачепия вместе
с длиной волны Ич:пол...з.^апг1ого и^лучепия в B/, мо/КНО
вычислить расеголпия те/п.д^ ujijwKjv»>imh и различных крисгал-
а*
132 ГЛАЗА I
яических поверхностей и. отсюда, при учете угловых за-
зависимостей, размеры элементарной ячейки.
Рассмотрим простой случай правильного кристалла. Из
табл. 1 следуют три возможности для формы элеиентарной
ячейки простая кубическая, кубическая обьемно-центрирован-
ная и кубическая с центрированными гранями (фиг. 35).
Чтобы выбрать между этими тремя возможностями, мы
измеряем рассюнния »ежду плоскостями для грех поверхно-
поверхностей A00), (ПО) и AП), т. е. для поверхности грани и
для поверхностей, перпендикулярных диагоналям граней и
Объемным диагоналям. Из фиг. 35 видно, что ати три рас-
расстоянии дли грех различных типов решетки имеют разные
значения и при длине ребра куба а равны соответственно;
в простой кубической решетке
а. а
loo * ii© ~в/ гт** iii ■»/""„ 1 •
в объемно-центрированной кубической решетке
а
в кубической решетке с центрированными гранями
Отношение расстояний между плоскостями rf,00: duozdntt
таким образом, для' трех случаев соответственно равно:
простая кубическая 1 s —?-=: -у^.1
I
кубическая объемно-центрированная i: j/ s -*=■ %
кубическая сцентрированными гранями 1:—=:—s ..
ГЕОМЕТРИЯ КРИСТАЛЛИЧЕСКОЙ РЕГГЕТУИ 133
Поэтому легко выбрать между тремя возможностями и-
нз значений d в каждом случае непосредственно? вычислить
длину ребра а элементарного куба.
4„ Определение структуры для сложных решеток
Когда исследуемое вещество имеет простую решетку,
gro структура полностью определяется измерение™ элемен-
элементарной ячейки. Значительно сложнее определение структуры,
когда решетка состоит из нескольких простых. Если размеры
простых основных решеток известны, то прежде всего вычис-
вычисляем объем элементарной ячейки и, отсюда, с учетом плотно-
плотности,— общую массу входящих в ячейку атомов. Затем, с
помощью химической формулы вещества учитывая атомные
веса, получают число атомов в элементарной ячейке, т. е.
число простых решеток, из которых построена кристалли-
кристаллическая решетка.
Для определения взаимного расположения этик решеток
не существует общего правила. Иногда достаточно уже
знания числа атомов в ячейке и симметрии кристалла зля
определения положения атомов. В других случаях некоторые
отправные точки получаются из сравнения интенсивности
максимумов отражения различных порядков. Когда кристалл
состоит только из одной простой решетки, все параллельные
плоскости решетки равноценны и отражают рентгеновские лучи
с одинаковой интенсивностью. Интенсивность максимумов
отражения тогда закономерно уменьшается с увеличением
порядка 'атомный фактор}. Напротив, в сложных решетках
рядом с густо заполненными плоскостями расположены плос-
плоскости менее плотные или заполненные атомами другого рода.
Тогда это чередование повторяется периодически с периодом
d пр«»стой решетки. В этом случае интенсикность отражения
зависит от угла сложным образом и, поиидимому, незаконо-
незакономерно распределена по порядкам. Это явление можно сравнить
С отражением от обыкновенной штриховой решетки И там
положение отражений занисит только о» постоянной решетки,
т. е. от расстояния аде*ду штрихами, в ти время как рас-
распределение интенсивности но различным порядкам опреде-
134
ГЛА°А
ляется формой бороздок таким образом, что при некоторых
условиях второй порядок, [например, может быть интенсивнее
первого.
Поэтому рассмотрим отражение пучка рентгеновских лучей
от кристалла несколько подробнее. Пусть имеются две раз-
различные системы плоскостей, параллельных одной из плоскостей
кристалла и имеющих коэфициенты отражения К и К'. Пусть
поверхность кристалла является ^"-плоскостью. Расстояния
/^-плоскостей от поверхности кристалла равны m-d {tn целое
число). ""*"
Ф и г, 36. Разность хода лучей, отраженных
■от поверхности и от плоскости, лежащей ни
расстоянии р от поверхности.
Обозначим через § расстояние перкой верхней /с"-шгос-
кости от поверхности кристалла, т. е. от первой Л"-гогоскостн,
Тогда расстояние любой АГ'-плоскости от поверхности кристал-
кристалла будет равно m-d-\-$.
Пусть на кристалл падает !тучок параллельных рентгенов-
рентгеновских лучей. Оптическая разность хода между лучами, от-
отражающимися от поверхности и на глубине р, согласно
фиг. 36, равна .4О-|- QB—2p-cos §. Две волны, первона-
первоначально когерентные, имеют поэтому после отражения разность
Амплитуда аодкы, отраженной от /Г~пдоекости нз расстоя-
расстоянии wid от поверхности, пропорциональна действительной
чрсти выражения:
/ 2ttl<tfCQSU\
ГЕОМЕТРИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ {3=
Соответствующее выражение для /С'-плосксстей имеет вид,
Если в отражении участвует N пар плоскостей, суммарная
амллитуда имеет вел'{чину:
и;т, если просуммировать геометрическую прогрессию:
,v 2 d cos 'i
Чтобы получить интенсивность J, умножим это выра.ке-
н«е на комплексно-сопряженное число. Следовательно, J про-
пропорционально Бели чине '! •
о._.2 2n:,¥f cos 9
sin2
Поскольку /V очень большое число, йтарей множитель в C)
только тогда заметно больше единицы, когда знаменатель
равен нулю, т. е, когда
Это увдвненне идентично условию Брегга дли отражения й-го
яоряд-ка:
;гХ = 2rf соз Ь,
Соотношение кнтенсивностей различных порядков дается
первым множителем выражения C), которое с помощью B)
преобразуется в
К-;- лГ -{- 2 у кгГ cos -Jrai - • ГН
136 глддд i
Подстановкой в это выражение измеренных величин интен-
К' &
сивностей можно вычислить значения -^- и — . При этом не
учитываются такие факторы, как конечные размеры атомов,
нарушения и тепловое дви-кение кристаллической решетки,
вызывающие и для простых решеток спадание интенсивности
при переходе к высшим порядкам. Однако мы их здесь не
рассматриваем.
Так как нтенсивность отражения рентгеновских лучей
от коисталлической плоскости пропорциональна плотности
К'
заполнения ее электронами, то-гг есть просто отношение этих
плотностей заполнения. Зная его, мы можем сделать заключе-
заключения относительно рода и числа атомов, лежащих в рааличныж
плоскостях.
В частности, из выражения D) следует, что, например,,
S „ о,
ори —=1/2 четные порядки интенсивнее, чем нечетные, в то
время как при -? = 1/4 и К'=К интенсивности последова-
последовательных ворядков относятся друг к другу как
Теоретически этот метол применим и и большему, чем
2, числу периодически повторяющихся плоскиетей. На прак»
тике, однако, неточность в измерении интенсивности и влияние
«естественного спадания интенсивности при возрастании порядка
отражения (вследствие конечных размеров атомов и теплового
дви-кения) так велики, что вычисленш! приводят к цели шльаш
э простейших случаях.
Когда удалось установить структуру различных групп
плоскостей в кристалле, следует подбором выяснить, какое
расположение атомов обьясниет наблюдаемые соотношения
Интенсивностей. При этом важные отправные точки могут
дать химические ссх*бражения |например, существование
определенных групп атомов; и кристаллографические условия
симметрии. Общих праьил здесь привести нельзя.
В своей первоначальной форме этот способ определения
структуры применим голыш к кристаллам совершенной формы,
137
для которых, по , методу Брегга, возможно раздельное
наблюдение отражений от различных плоскостей, Для
мелкокристаллических или порошкообразных веществ
Дебаем и Шерёром разработан способ, очень часто при-
применяющийся на практике. При этом получаются отраженна
всех поверхностей на одном снимке. Первоначальный метод
Лауе, в котором также одновременно фотографируются
see отражения, тоже часто исшльзуется для определения
структуры»
5. Примеры кристаллической структуры
Рассмотрим теперь некоторые- примеры известных типов
решеток.
Среди однозтомных кристаллов регулярных систем мы
упомянем прежде всего металлические медь и серебро, которые
сравнительно легко кристалли-
кристаллизуются в больших монокристал*
яах. Они имеют кубическую
объемно-пентрированную решет-
решетку (фиг. 35) с длиной ребра
3,597 А (медь) и 4,079 А (се-
(серебро).
Другим правильно кристал-
кристаллизующимся одноатомным веще-
веществом является алмаз. В его ре-
решетке каждый атом окружен
четырьмя другими, так что об-
образуется правильный тетраэдр
(фиг. 37). Решетка алмаза не
является простой, а может рас-
рассматриваться как сочетание двух
■кубический решеток с центри-
центрированными гранями, сдвинутых
друг относительн > друга а на-
направлении об ьемной диагонали
яа четверть ее длины.
Решетка поваренной соли и решетка плавикового шпата
Фиг-. 37. Решетка алмата.
образованная явумя яубиче-
екпмп гранецентрированны-
ми решетками, сдвинутыми
по отношению яруг к apvry
в направлении яиагонаяя
куба на четверть ее длины,
138
ГЛАВА I
также регулярны. Решетку поваренной соли (фиг. 88} проще
всего изобразить как простую кубическую решетку, з узлах
которой чередуются ионы натрия и хлора, так что каждый
ион С1 окружен шестью ионами Na, и наоборот. Однако
решетку NaCi нельзя счигать простой, так как оба рода
ионов неравноценны. Эту решетку следует счигать сложной^
образованной двумя простыми решетками с центрированными
гранями, состоящими соответственно из ионов хлора и натрия,.
Ф и г. 38. Решетка NaCl,
состоящая нз двуя про-
простых кубических гране-
центрированных решеток
натрия (О) и хлора (О),
вдвинутых аруг относи-
относительно друга на половину
ддзны pe-''ра элементар-
элементарного куба.
граяенентрирсваа-
решеток. Решетки,
Фиг. 39. Решетка плави-
плавикового шпата, состоящая
нз трех простых кубиче-
кубических
ных
заполненные ионами фто-
фтора, сдвинуты на поло-
половину длины ребра аруг
относительно друга,.
Третья решетка, запол-
заполненная ионами кальция,
сдвинута на четверть
объемной диагонали по
отношению а первым
двум.
сдвинутыми на половину длины реора друг относительно
друга.
Решетка плавикового шпата CaFo (фиг. 39) является про-
простой кубической решеткой, состоящей из атомов фтора, внут-
внутри которой —~ з центре каждой второй ячейки — расположены
геометрия кристаллической ре;г£тки
139
алжы кальция. Атомы кальция сами образуют кубическую
решетку с центрированными гранями, длина ребра которой
вдвое больше длины ребра простой решетки фтора. Решетку
плавикового шпата следует поэтому рассматривать как соче-
сочетание трех простых граиецентрированных решеток, две нз
которых, заполненные ато-
атомами фтора, сдвинуты на
половину длины ребра
друг относительно друга,
а третья, •образованная
■хтомамн кальция, сдвинута
на четверть объемной диа-
диагонали.
Примером несколько
более сложной кристалли-
кристаллический структуры является
изображенная на фиг. 40
решетка известкового шпа-
шпата СаСОд. Она относится к
тригональной системе и со-
стоит из простых решеток
типа 8 Браве (см, табл. 1).
Ее строение легко себе
нредставнть, если рассма-
рассматривать сначала комплекс
СОЯ как целое. Тогда ее
можно себе представить
образованной из решетки
типа поваренной соли, в
которой ионы No, и С! заменены путем деформации в на-
направлении объемной диагонали соответственно кочаыи Са
и COg.
Три атома кислорода группы СО« образуют равносторон-
ййй треугольник с атомом С в середине, расположенный
перпендикулярно тройной оси симметрии. Биссектрисы тре-
треугольников параллельны граням ромбоэдрической ячейкн.
Здесь можно определить две различные элементарные ячейки
( раздел 1), которые обе изображены на фиг, 40,
шпата, состоящая
известкового
из простых:
Б
р
решеток S типа Бреве.
340 ГЛАВА II
ГЛАВА II
ФИЗИЧЕСКИЕ СВОЙСТВ * КРИСТАЛЛИЧЕСКОЙ
РЕШЕТКИ
6. Теплоемкость кристалла
Динамика кристаллической решетки, в особенности
колебаний решетки, тесно связана с вопросом теплоемкости
твердых тел. Поэтому обе проблемы всегда изучались н связи
друг с другом, и здесь мы будем их рассматривать совместно-
Основным положением относительно теплоемкости ткерльгк
тел является закон Дюлонга и Пти. Он гласит, что атомная
теплоемкость, т. е. теплоемкость, отнесенная на один грамм-
атом для всех твердых элементов, равна одной и той же
величине }~*-6 кал град.). При обычных температурах этот
закон, за малым числом исключений (например, углерод и
бор), является всеобщим. Однако при достаточно нн.шик
температурах он гериеч свою применимость ко всем элементам,
именно величина 6 кал град, оказывается слишком завышен-
завышенной. При высоких температурах наблюдаются отклонения
з другую сторону.
На основании классической статистики закон Дюлокга
я Пти не должен был бы иметь исключений. Действительно,
по закону равномерного распределения энергии, в состоянии
теплового равновесия каждой ctcbichh свободы системы соот-
соответствует Средняя кинетическая энергия 5,2 кТ, а слежмга-
тельно, каждому атому твердого тела в общей сложно-
сложности— 3>2 кТ. С другой стороны, в системе, совершающей
колебания под действие упругих сил, средняя кинетическая
энергия равна средней потенциальной. Так как атомы твер-
твердого тела могут, по крайней мере в первом приближенеда,.
рассматриваться как материальные точки, удерживаемые около
своего положения покоя упругими силами, то на каждый
атом прихотится еще потенциальная энергия той »ке величины»
Средняя полная энергии атома поэтому равиа '6 кТ„ а гиа
атома
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ i4l
Теплоемкость получается отсюда дифференцированием по
температуре: >dW
Газовая постоянная R равна приблизительно 2 кал/град.>
поэтому дла с действительно получаем значение Дюлонга
и Ити 6 кал/град.
Из отклонений от закона Дюлонга и Пти в рамках клас-
классической теории понятно только возрастание атомной тепло-
0,9
0,8
0,7
0.6
€,3
0,2
f)
у
1
1
1
I
f
/
—■—*
——
Серебро
I.
100
20О
ЗОО
Фиг. 41. Теплоемкость серебра в зави-
зависимости от температуры. Кривая по-
построена согласно теории Дебая
(см. раздел 7).
емкости при переходе к высоким температурам. По Берну
и Броди это возрастание можно объяснить не вполне упругим
характером сил между атомами. Отступления от пропорцио-
пропорциональности между расстоянием удаления от нейтральной точки
т величиной восстанавливающей силы особенно заметны при
больших амплитудах колебания, т. е„ при высоких темпера-
температурах. Так как при этом колебания становятся негармони-
негармоническими, средняя потенциальная энергия не равна больше
средней кинетической, а в случае кристаллической связи —
больше этой последней, так что полная энергия превосходит
&RT и теплоемкость превосходит ЗЯ. При средних темпера-
ГЛАВА U
турах амплитуды колебаний в общем настолько малы, что
эти отклонения незаметны.
Значительно большие отклонения от закона Дюлонга и Пти
наступают, однако, при низких температурах. Показано, чта
теплоемкость всех находящихся в твердом состоянии элемен-
элементов зависит от температуры так, как изображено на фиг. 41 „
От величины 3R при средних температурах кривая падает
сначала медленно, затем круто, и при Т = 0 достигает оси
абсцисс. Температура, при которой начинается спадание,,
различна для различных элементов. Обычно она лежит значи-
значительно ниже комнатной температуры. Только у немногих элемен-
элементов, например, у бора и углерода, спадание начинается при
сравнительно высоких температурах, так что уже при комнат-
комнатных температурах атомная теплоемкость меньше 6 кал, град,
Первое объяснение этого явления дал в 1905 г. Эйнштейн
с помощью квантовой теории, которая нашла здесь одно из
своих первых применений. В основу своих соображений он
положил очень грубую модель твердого тела, приняв, чт©
атомы совершают, независимо друг от друга, упругие коле-
колебания. Колебаниям в трех различных осевых направлениях
для каждого атома соответствуют три гармонических осцил-
осциллятора, т. е. телу из N атомов соответствуют ЗЛ/ осциллятора,,
для которых Эйнштейн принял одинаковую частоту v. Со-
Согласно классической теории, каждый из осцилляторов обладает
энергией kT (no kTj2 для кинетической и потенциальной
энергии),, ЗЛ/ осцилляторов вместе — 3NkT, откуда для
теплоемкости получается значение Дюлонга и Пти. Но, соглас-
согласно квантовой теории (см. Ш часть), средняя энергия осциллято-
осциллятора зависит от температуры по другому закону. Именно:
Л*
Таким образом, при низких температурах средняя энергия
эсциллитира, по квантовой теории, значительно ниже, чем
согласно классической статистике. Для высоких температур,
когда /гу<^/еГ, выражение G) асимптотически переходит
в классическую величину kT.
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕ1Н2ТХИ 143
Итак, полная энергия твердого тела с N атомами, по
Эйнштейну, равна:
!?£. (8)
e kl — i
Отсюда для темплоемкости получается:
с== ~аг ~ 7 Тг, Га Тгз • (9)
Можно легко видеть, что в общем ход кривой фиг- 4*
правильно передается этим уравнеьием Кроме того, получен-
полученная с помощью этого уравнении из эмпирического изменениа
теплоемкости величина частоты v совпадает по порядку вели-
величины с инфракрасными частотами, наблюдаемыми у твердых
тел. Если учесть грубость предпосылок, положенных в основу
теории Эйнштейна, последнюю следует считать весьма удо-
удовлетворительным приближением. Однако при очень низких
температурах наблюдаются большие отклонения. Спадание
в этой области происходит значительно более плавно,, чем
следует из уравнения 5,9).
7. Теория теплоемкости Дебая
Это несогласие было устранено Дебаем, который исходил
из того, что не все атомы в твердом геле колеблются с оди-
одинаковой частотой, как это предполагается в теории Эйнштей-
Эйнштейна, но что тело обладает больашм числом, целым „спектром"
собственных частот, ото оостомтельство Дебай учел схема-
схематически следующим образом.
Сначала пренебрегав гея атомной структурой твердого
тела, и оно рассматривается так же, каь в классической
теории ynpyiос 1 и, как упругий континуум. Гак^е iело колеб-
колеблется с бесконечным числом частот, которые могут быть
вычислены, при известных форме и величине тела, из его
модуля упругости и плотности, подобно гому, как собственные
колебания (т. е. исноыиые килс^а^ин и оъхкопечпое число
!44 гланд и
обертонов) струны могут быть вычислены из ее длины и упругих
свойств.
Можно показать, что в изотропном теле, со скоростью
распространения с, и с2 для поперечных и продольных упру-
упруги* волн и с об ьемом V, число йп собственных частот, лежа-
лежащих в пределах v и v ~\- dfv, для достаточно больших у равно
dn = 4тгС ~ + -1- ) V"v2 dv. A0)
Общее число собственных частот континуума, таким обра-
образом, оесконечно велико, как этого следует ожидать дли системы
с бесконечно большим числом степеней сво юды. В действи-
действительности наше тело состоит только из N атомов, оно имеет
поэтому только 3 V степеней свободы, и число собственных
части г поэтому не больше 3/V. Мы заключаем отсюда, что
часть содержащихся в A0) собственных частот, а именно
высоких, в реальном теле, вследствие ею атомной структуры,
выиадаь-т. Для упругих волн, длина волны которых сравнима
с расстояниями между атомами, справедлив другой закон
распространения, так что уравнение A0) теряет свою при-
применимость. ДеОай предположил просто, что для каждого
тела существует максимальная частота vmax, до которой
справедливо уравнение A0/, и что частот больших, чем vmass
souome не имеется.
Частоту vma!t можно вычислить из A0), если учесть, что
■общее число частот точно равно 3N:
"max
Мы увидим, что, несмотря на большие упрощения, тем-
температурная зависимость теплоемкости предсказывается этим
путем весьма точно.
Тепловая энергия /V-атомного тела объема V, по Дебаю,
получается приписыванием каждой из ал их собственных частот
доли энергии, следующей из G), согласно квантовой теории,
гармоническому осциллятору той же частоты, и суммированием
ФИЗИЧЕСКИЕ СВОЙСТВА КРЯСТАЛЛЯЧЕСКОЙ. РЕШЁТКИ 145
по всем частотам меньшим, чем утах. Так как в интервале
частот йч лежит dn частот, величина полной энергии равна
vmas
f 2
В связи с A1) мы получаем отсюда, вводя новую перемен-
ную x = jy:
в/г
T~-li A2)
где
e=^i|sa A3)
9 имеет размерность температуры и является характери-
характеристичной материальной константой, которая вычисляется из
упругих постоянных соответствующего вещества с помощью
A1) и A3).
Продифференцировав A2) по Т, для теплоемкости нашего
тела получим выражение:
""•) , (Н)
через D здесь для сокращения обозначена величина дебаев-
фунхции:
4- з
D (S) совершенно не зависит от специальных свойств
рассматриваемого вещества. Они проявляются только з вели-
величине ^характеристической температуры" У.
146 ГЛАВА II
Особенный интерес представляют предельные случаи
Г> в и Т< в. Для £_> оо A5) дает lim D (£) = 1; для £ < 1
с помощью интегральной формулы
J г*-1-15
о
мы получаем асимптотическое приближение:
Поскольку для грамматома Nk = R, атомная теплота при
высоких температурах {Т^>®), ъ согласии с законом Дю-
лонга и Пти, равна:
Для достаточно низких температур G<^6) мы находим,
напротив:
Сяедовательио, вблизи абсолютного нуля теплоемкости всея
элементов пропорциональны третьей степени температуры.
Дебаевсхая теория теплоемкости элементов в твердой
состоянии прекрасно совпадает с опытом (фиг. 41). Это
особенно замечательно в связи с тем, что константа в вы-
выражения A4) вычисляется непосредственно из упругих кон-
констант соответствующих элементов без привлечения каких-
либо тепловых величин.
Опыт подтверждает также и возрастание теплоемкости
пропорционально Г8 ири очень анзких температурах, как к
следующий S3 A4) факт, что кривые температурных зави-
зависимостей для всех элементов могут быть совмещены по-
посредством соответствующего выбора масштаба ио. оси теи-
йеоатто.
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТК И 147
8. Упругие свойства одномерной решетки
В дебаевской теории теплоемкости атомная кристалли-
кристаллическая структура твердого тела учитывается очень схема-
схематически, введением граничной частоты vmax упругих волн.
В этом разделе будет подробнее исследовано влияние атом-
атомной структуры на распространение упругих волн.
Вначале мы и здесь рассмотрим упрощенный случай —
именно цепочку однородных атомов, находящихся на одной
прямой на равных расстояниях а друг от друга. Между
соседними атомами действуют упругие силы, стремящиеся
сохранить равновесное расстояние а. Таким образом, мы
имеем простую одномерную кристаллическую решетку, упру-
упругие свойства которой будем исследовать.
Предположим, что атомы могут двигаться только вдоль
упомянутой прямой. Расстояние я-ro атома от положения
равновесия мы обозначим через £а. На я-й атом действуют
силы со стороны (п -\~ 1) и (п — 1) атомов. Если три атома
удалены на расстояния ^я_1, £а £а+1 от своих положений
равновесия, то расстояние между соседями равны £я+1 — £я
и £а_1 — йа, а соответствующие силы имеют значения
£(£а+1 — £„) и k(%a_l — $а) (k — константа упругой связи
между атомами). В результате, на л-й атом действует сила
k(£a+i-\-Za-i—'2Se)- Если масса атома равна т, уравне-
уравнение движения будет иметь вид:
™'ia = k (Se+1 + £я_! — 25.). A7)
Если атомную цепочку продлить безгранично в обе сто-
стороны, то ее возможные движения описываются бесконечно
большим числом уравнений типа A7), в которых п прохо-
проходит все отрицательные и положительные целые значения,
включая нуль.
Решение этой системы уравнений, изображающее упру-
упругие волны вдоль цепочки атомов, получается без труда.
Ищем решение в виде: —-
£я = Acos 2тг (v* — gn). A8)
trie
148 глава а
Подставляя в A7), получаем, что A8) действительно
представляет решение нашего уравнения4 движения, есла
соблюдается условяе:
v = — l/~— shirrs A9)
tC * fit
Уравнение A8) описывает упругую волну вдоль линей-
линейной решетки, причем длина волны X определяется расстоя-
расстоянием между я-й точкой и ближайшей точкой решетки,
находящейся в той же фазе колебания:
Х = ~, B0)
где а равновесное расстояние между двумя соседними ато-
атомами.
G помощью B0) мы получаем из A9)
Отсюда находится верхняя граница для у:
т
т. е. вдоль рассматриваемой прямой могут распространяться
только упругие волны с частотами, не превышающими
1 Г~к
— 1/ —. Этим требованием известным образом оправды-
оправдывается и дебаевское допущение максимальной частоты vmax.
Умножая теперь B1) на X, получим скорость распро-
распространения v нашей волны:
1 / к . . TZIX
Скорость распространения зависит, таким образом, от
длины волны. Это является специфическим свойством упру-
упругих волы в среде с атомной структурой. В упругом кои-
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ 149
тинууме скорость распространения не зависит от длины
волны.
Для достаточно больших Х(Х^>я) можно в B2) заме-
заменить sin его аргументом и получить тогда постоянную ско-
скорость распространения
Этот предельный случай соответствует, следовательно,
обычной теории упругости. Если, однако, X становится по-
порядка расстояния между атомами, скорость распространения
уменьшается, и для X = о- имеем v = 0.
Для динамики кристаллической решетки особенно важно
определение собственных частот для случая конечной про-
протяженности тела. В качестве одномерной модели рассмотрим
заполненую N атомами линейную цепочку конечной длины.
В качестве граничных условий мы можем установить, что
конечные точки цепочки не принимают участия в колеба-
колебаниях. Однако это условие усложняет решение. Поэтому мы
заменяем его, как это делается и в других подобных слу-
случаях, физически равноценным условием, что в бесконечно
протяженной цепочке 2 атома, номера которых различаются
на N, всегда должны находиться на одном расстоянии друг
от друга. Свойства бесконечной цепочки с этим условием
периодичности те же, что и у конечной цепочки с N ато-
атомами, конечные точки которой находятся в покое.
Чтобы найти собственные частоты нашей одномерной
решетки, ищем решение системы уравнений A7) в виде:
Se=i]ecosBirttf + P). B3)
Здесь v — одна из собственных частот, а т]я — независящая
от времени величина, удовлетворяющая условию периодич-
периодичности
Подставляя B3) в A7), получаем уравнение
= к (Чв + 1 + i)a_! — 2Г|Я), B5)
150 ГЛАВА II
решениями которого являются выражения вида
ria = cos izgn или 7)я = siu тгgn, B6)
если одновременно удовлетворяется, аналогичное A9), соот-
соотношение
4 Г^ siting. B7)
Так как уравнение B5) линейно относительно 7], любая ли-
линейная комбинация обеих функций B6) также представляет
собой решение B5).
Чтобы выполнялось условие периодичности B4), необ-
необходимо и достаточно, чтобы
2f, B8)
где /—целое число. Оба решения B6) принимают тогда
вид:
т]3 = cos -~ п, соответственно, т\а = sin ~ п. B9)
Для каждого значения / существуют, следовательно,
2 линейно независимых решения. Двум значениям /, сумма
или разность которых равна целому кратному N, соответ-
соответствуют, однако, равные или противоположно равные решения.
Следовательно, чтобы получить все решения B9), нужно
использовать значения /, лежащие между 0 и iV/2, т. е.
при четном N—значения
1
a
при
нечетном -
f=0, 1,
— значения
/=0, 1,
2,
2,
дг
Для /=0 и /=— существует только одно решение, дру-
другое пропадает. Любому другому значению / соответствуют
2 независимых решения, так что общее число решений все-
всегда равно N.
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ 151
Соответствующие частоты получаются, если подставить
в B7) величину g из B8):
C0)
/у
Каждому значению / между 0 и ~ соответствует одна
собственная частота, которая в общем случае дважды вы-
вырождена. Только частоты с /=0 и /=-4} простые.
9. Колебания простых и сложных решеток
Развитые в разделе 8 представления о распространении
упругих волн вдоль прямолинейной цепочки однородных ато-
атомов легко распространяются на трехмерный кристалл, атомы
которого образуют простую объемную решетку. Для упру-
упругих волн, образующихся в таком кристалле, также суще-
существует закономерная связь между длиной волны и частотой,
однако, благодаря анизотропии кристалла, она з общем слу-
случае зависит еще от направления распространения, при
заданных направлениях и частоте скорость распростра*
нения также является функцией длины волны, которая, прав-
правда, для больших X, почти постоянна, но резко спадает,
как только X становится сравнимой с расстоянием между
атомами. Таким образом, для достаточно больших длин
волн и трехмерная решетка ведет себя как упругий
континуум.
Соотношения в кристаллах со сложной решеткой совер-
совершенно иные. Мы это увидим, как только рассмотрим коле-
колебания с «бесконечно большой длиной волны", т. е. коле-
колебания, в которых все атомы решетки двигаются в одной
фазе. В кристалле с простой решеткой это колебание со-
соответствует перемещению всего кристалла, которое, есте-
естественно, имеет нулевую частоту. В кристалле, состоящем,
например, из двух простых решеток, колебания с бесконеч-
бесконечно большой длиной волны не обязательно являются про-
стыми трансляционными движениями, поскольку, при этом,
152 ГЛАВА II
одна решетка может как целое колебаться относительно
другой. Тогда бесконечной длине волны соответствует не-
неравная нулю частота этих колебаний решеток друг относи-
относительно друга. То же самое относится и к кристаллам, по-
построенным из большего, чем два, числа простых решеток.
Эти колебания называются .оптическими колебаниями" и
соответствующие частоты—«оптическими частотами".
Можно показать, что кристалл, состоящий из г простых
решеток для каждой длины волны и направления распро-
распространения, обладает з общем случае Зг частотами, которые
при некоторых обстоятель-
т.чтмтмтмтл} ствах могут совпадать.
<>Ч1)-<>~0-<>-0~<>~0~0~" Когда длина волны стано-
т-г п-г w a-i * в w «v о-з »*2 вится бесконечно большой,
3 из этих частот, так на-
Фиг. 42. Одномерная сложная зываемые акустические
цепочка, состоящая из двух про- стоемятся к '„ Им '
стых. Атомы Мит расположены стремятся к нулю, им со-
друг от друга на одинаковых рас- ответствуют, пока длина
стояниях. волны велика в сравнении
с атомными расстояния-
расстояниями, 3 упругих волны обыкновенной теории упругости,
в которой кристалл рассматривается как упругий конти-
континуум. Частоты в анизотропном теле в общем случае
различны. В изотропном теле же 2 из них (обе поперечные
волны) обладают одинаковой частотой, а продольная волна
имеет ту же длину волны, но другую частоту.
Остальные Зг — 3 частот при увеличении длин волн до
бесконечности не обращаются в нуль. Оии носят название
оптических частот. При некоторых обстоятельствах многие
из них могут совпасть.
Поясним это снова на одномерном примере. Линейная
цепочка составлена попеременно из атомов массы т и мас-
массы М таким образом, что расстояние между двумя после-
последовательными атомами равна а. Как и в примере раздела 8,
каждый атом связан упругими силами с обоими своими со-
соседями. Исследуем распространение упругих волн на этой
одномерной модели сложной решетки.
Будем обозначать атомы индексами п таким образом, что
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ 153
л-й атом массы т лежит между л —1 и я-атомами мас-
массы М (фиг. 42). %п есть перемещение д-го атома т и
j)a — перемещение л-ro атома М. Сила действия соседних
атомов на л-й атом т равна
*(Ч«+Ч«-1 —25.)
(А — константа упругой связи). Соответствующая сила на
й-й атом Ж равна
*E«+, + 5. —2ч.).
Таким образом, уравнения движения обоих атомов запишут-
запишутся в следующем виде:
3
Если л принимает все положительные и отрицательные
целые значения, то получается система уравнений, описыва-
описывающая движение атомной цепочки.
Мы ищем решения, соответствующие распространению
упругих волн вдоль линейной решетки, в виде:
j
C2)
Здесь sin и cos ради простоты заменены экспоненциальными
функциями. Так как период решетки не а, а 2а, то длины
упругих волн равны:
■k=j- C3)
Подставляя C2) в C1), после простых преобразований
получим: _
= k [{ 4 е
re™g) — 2A] \
!54
ГЛАВА II
= 0.
Эти линейные "относительно Л и В однородные уравне-
уравнения только тогда имеют неравные нулю решения, когда их
детерминант равен нулю:
ir2v2m — 2k k(l-\- е**в)
k A -f- e~™e) 4tt2vVW — 2k
Из этого условия, с учетом C3), получаем зависимость
между v и \, которую можно разрешить относительно v;
C5)
cos
Каждому значению к соответствуют два значения v3 и,
так как отрицательные значения не имеют смысла, два зна-
значения v, в то время как для
простой одномерной решетки
каждому значению v соответ-
соответствовало только одно значе-
значение частоты.
Зависимость частоты от
длины волны изображена на
фиг. 43. По оси абсцисс
отложены обратные длины
волн, волновые числа, по
оси ординат — частоты. . В
предельном случае X = «з,
т. е. 1/Х = 0, из C5) полу-
получаются две возможности:
Фиг. 43. Зависимость частоты
собственных колебаний линей-
линейной цепочки, состоящей из двух
простых, от длины волны.
= <( тМ
C6)
Одна из двух частот, акустическая, в этом предельном
случае равна нулю, в то время как другая стремится к пре-
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ [55
дельной величине, отличной от нуля. Она является един-
единственной оптической частотой нашей модели. Она соответ-
соответствует колебанию /я-решетки относительно /И-решетки при
неизменности расстояний между однородными атомами.
10. Инфракрасные частоты и остаточные лучи
Положение оптических колебаний кристалла может быть
установлено наблюдением инфракрасного поглощения и при-
притом либо путем прямого измерения поглощения тонких слоев
кристалла, либо с помощью более удобного, однако, менее
точного метода остаточных лучей. Последний состоит в том,
что инфракрасное излучение источника с непрерывным спек-
спектром заставляют несколько раз отражаться от поверхности
кристалла и затем, с помощью решетки или призмы и
термопары, исследуют спектральный состав отраженного
света. Так как вблизи оптических частот спектральная от-
отражательная способность особенно велика, то оптические
частоты можно приравнять к частотам наблюдаемых макси-
максимумов отражения.
Следующие соображения показывают, почему в инфра-
инфракрасном спектре могут возникнуть только оптические коле-
колебания и отсутствуют остальные собственные колебания.
Так как длина волны инфракрасных лучей приблизительно
в 104-105 раз больше атомных расстояний, то мы можем
ограничить наше рассмотрение кристаллическим куском, со-
содержащим достаточно большое число атомов, но малым по
сравнению с длиной волны излучения. Испускание и погло-
поглощение такой кристаллической области будут определяться
изменениями ее электрического момента. Колебания, дефор-
деформирующие кристалл, вызывают и изменение этого момента.
Но, в то время как при обыкновенных собственных коле-
колебаниях фаза в различных частях нашей кристаллической
области различна, так что образующиеся частичные момен-
моменты в среднем взаимно уничтожаются, оптические колебания,
при которых одна простая решетка как целое колеблется
относительно другой, имеют во всей области одинаковую
фазу. При этом, вследствие смещения электрических заря-
зарядов в атомах или непосредственно ионов з ионной решетке.
156 ГЛАВА II
меняется электрический момент всего кристалла с периодом
оптических колебаний. Поэтому последние заметны в ин-
инфракрасной части спектра, в то время как собственные ко-
колебания, при которых суммарный момент не меняется, не
вызывают поглощения.
Конечно, вследствие особых условий симметрии отдель-
отдельные оптические колебания могут происходить и без изме-
изменения электрического момента. Тогда они инфракрасно не-
неактивны. Это имеет место, например, у плавикового шпата
CaF2 (фиг. 39).
Эта решетка состоит из трех гранецентрированных ку-
кубических решеток. Одна из них заполнена атомами Са, а
две другие, образующие в сумме простую кубическую ре-
решетку с половинной длиной ребра, — атомами F. Вследствие
симметрии эта решетка имеет только две различные опти-
оптические частоты. Частота Уг соответствует движению решет-
решетки Са относительно обеих решеток F, взаимное положение
которых при этом не меняется. Так как решетка плавико-
плавикового шпата является ионной, т. е. в действительности со-
состоит не из атомов Са и F, а из ионов Са+ + и F~~, то при
этом смещении решеток возникает большой электрический
момент, периодически меняющийся с оптической частотой vr
Поэтому частота Vj активна в инфракрасной части спектра.
Наоборот, частота v2 соответствует колебаниям, при кото-
которых меняется только взаимное расположение обеих решеток
фтора, а решетка Са остается в покое. Из соображений
симметрии при этом не возникает электрический момент, и
колебание является неактивным.
Решетка каменной соли (фиг. 38) имеет только одно
оптическое колебание. Решетка ионов Na+ колеблется как
целое относительно решетки О. При этом, естественно,
возникает большой электрический момент, так что колеба-
колебание активно.
В решетке алмаза (фиг. 37) единственное имеющееся
оптическое колебание состоит в смещении обеих простых
гранецентированных решеток друг относительно друга. Из
соображений симметрии при этом, естественно, не обра-
образуется момента, и колебание является неактивным.
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ 157
11. Рамая-эффект S кристаллах
Точность измерений в инфракрасной области вследствие
ограниченной разрешающей способности аппаратов большей
частью не очень велика. Более точное определение опти-
оптических колебаний кристалла чаще возможно с помощью
Раман-эффекта.
Рамановский спектр кристалла в общем случае состоит
из одной или нескольких достаточно хорошо определенных
линий, расстояния которых от возбуждающей линии обычно
соответствуют оптическим колебаниям кристалла, Так же,
как при Раман-эффекте на молекулах, при этом появляются
поляризационные явления, зависящие как от угла наблюде-
наблюдения и направления поляризации первичного пучка, так и от
ориентации кристалла.
Толкование рамановских спектров кристаллов аналогично
объяснению рамановских спектров многоатомных молекул
(ч. I, раздел 39). И здесь появление смещенных линий объя-
объясняется периодическим изменением поляризуемости кристал-
кристалла, вызванной колебаниями.
Можно показать, что при Раман-эффекте в кристаллах
появляются только такие частоты, упругие длины волн ко-
которых соответствуют по порядку величин световым длинам
волн. Но, поскольку последние очень велики в сравнении с
атомными расстояниями, необходимо обсудить (исключая аку-
акустические частоты с v '-V- 0) только оптические частоты.
Рассмотрим снова кристаллический кусок, содержащий
большое число атомов, но размеры которого малы по срав-
сравнению с длиной волны света. Для рассеяния света суще-
существенен электрический момент М, образуемый полем Е пер-
первичного света. Величина М определяется поляризуемостью а:
М = аЕ. C7)
В определенных случаях а может иметь тензорный ха-
характер. Здесь она отнесена к единице объема.
В общем случае колебания деформируют кристалл в
различных точках, а так как при деформации меняется и
поляризуемость, то это приводит к местным колебания*/.
158 ГЛАВА II
величины а. Тогда, в первом приближении, изменение по-
поляризуемости в точках, находящихся в противоположной
фазе колебаний, равно и противоположно, так что для
упругих волн малой длины средняя величина а по кристал-
кристаллической области остается постоянной. Изменения в средней
поляризуемости появляются только тогда, когда весь кри-
кристалл колеблется с одной фазой, т. е. длина волны упру-
упругих колебаний практически бесконечно велика по сравнению
с расстояниями между атомами, что осуществляется только
для оптических колебаний. Поляризуемость а меняется с ча-
частотой, равной оптической частоте v, и, так как сила по-
поля Е колеблется с частотой v0 возбуждающего света, гар-
гармоническое разложение момента М [уравнение C7)] даст
частоты vorbv, соответствующие стоксовым и, соответ-
соответственно, антистоксовым рамановским линиям. Теоретическое
рассмотрение проблемы на основе квантовой механики в
первом приближении приводит также к результату, что в
Раман-эффекте проявляются только оптические частоты.
Так же, как и многоатомные молекулы, в кристаллах
могут существовать рамановски-неактивные оптические коле-
колебания. Это происходит тогда, когда вследствие симметрии
поляризуемость кристалла во время колебания в первом
приближении не меняется. Например, из двух рассмотрен-
рассмотренных в разделе 10 оптических частот плавикового шпата vt
и v2 инфракрасно-активная частота vx рамановски неактивна.
Вследствие симметрии этого колебания поляризуемость в
положениях с противоположной фазой одинакова. Зависи-
Зависимость поляризуемости от расстояния удаления из положения
равновесия не ниже квадратичной, и поэтому в первом при-
приближении поляризуемость исчезает. Наоборот, инфракрасно-
неактивное колебание v2 является рамановски-активным.
Действительно, Раман-спектр CaF2 состоит только из одной
линии с расстоянием удаления по частоте 321 см—1.
Существуют кристаллы, которые (по крайней мере в
первом приближении) вообще не имеют рамановски-активных
частот, например, кристаллы с простыми решетками, у ко-
которых нет оптических частот. Однако это может иметь ме-
место и для сложных решеток. Так, решетка поваренной соли.
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ 159
(фиг. 38) имеет только одну оптическую частоту, которая
соответствует колебанию обеих простых решеток друг от-
относительно друга. Эта частота инфракрасно-активна, но ра-
Фиг. 44. Раман-эффект второго порядка на
каменной соли (по Ферми и Разетти).
мановсхн неактивна, так как поляризуемость кристалла в
противоположных фазах колебания имеет одинаковое значе-
значение. Соответственно этому для каменной соли рамановские
линии не наблюдались.
Только благодаря применению особенно большой свето-
светосилы Разетти все же удалось обнаружить Раман-эффект на
каменной соли (фиг. 44). Спектр состоит, однако, не из
дискретных линий, как у других кристаллов, а из протя-
протяженного до 365 см" континуума с довольно нерегулярным
150 ГЛАВА II
распределением интенсивности. Этот чрезвычайке слабый
Раман-эффект является эффектом второго порядка. В то
время как в первом приближении, учитывающем только ли-
линейную часть зависимости поляризуемости от деформации
решетки, изменения поляризуемости в областях с противо-
противоположной фазой колебаний взаимно уничтожаются для всех
собственных частот, кроме оптических, во втором прибли-
приближении среднее значение поляризуемости зависит от всех
собственных частот, ибо в квадратичных членах знак изме-
изменения поляризуемости не зависит уже от направления коле-
колебаний. Поэтому во втором приближении в рамановском
спектре выступают, хотя и с очень малыми интенсивностями,
все собственные частоты. Более точное рассмотрение пока-
показывает, что образующийся таким образом континуум прости-
простирается до точки спектра, соответствующей удвоенной наи-
наибольшей частоте кристаллической решетки. Качественно
удается также объяснить наблюдаемое, кажущееся нерегу-
нерегулярным, распределение интенсивности.
12. Тепловое расширение и теплопроводность
кристаллов
Теория теплового расширения и процессы теплопровод-
теплопроводности в кристаллах будут рассмотрены лишь в общих чер-
чертах. При рассмотрении теплопроводности мы ограничимся,
кроме того, изолирующими кристаллами, так как в элек-
электрических проводниках теплопроводность тесно связана с
электропроводностью, которой мы здесь заниматься не бу-
будем.
Тепловое расширение и теплопроводность в изоляторах
находятся в тесной связи с тем, что силы в решетке не
совершенно упругие, т. е. зависят от расстояния удаления
из положения равновесия не линейно, а содержат члены
второй и более высоких степеней, влияние которых возра-
возрастает с ростом амплитуды колебаний.
В случае теплового расширения можем ограничить наше
рассмотрение простой моделью двух атомов, расположенных
по соседству. Мы увидим, что точно так же, как среднее
ФР13ИЧ£СКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ \ft\
расстояние между ними растет с температурой, повышение
температуры кристалла ведет к увеличению» среднего рас-
расстояния между атомами, которое проявляется в расширении
всего кристалла. Для двух атомов А и В (у которых рав-
равновесное расстояние равно а), совершающих колебания
вдоль своей соединительной линии, расстояние между ними
в некоторый момент времени пусть будет равно а-\-й.
Если учитывать только член второго порядка, то эти атомы
возвращаются в положение равновесия силой
/= —oS + PS1- C8)
Первый член с постоянной а пропорционален смещению
и представляет упругую силу. Отклонения от закона упру-
упругого взаимодействия содержатся во втором члене, обычно
значительно меньшем, к которому в некоторых случаях
нужно добавлять члены высших порядков. Так как мы рас-
рассматриваем проблему только качественно, то мы ограничим-
ограничимся классическим рассмотрением. Для малых амплитуд киле-
бания достаточно первое приближение, т. е. достаточно
учитывать упругий член а£. Соответствующая потенциаль-
потенциальная Анергия равна
Поскольку колебательное движение, которое наша система
совершает под влиянием теплового движения, должно все
время иметь направления соединительной линии, то ему со-
соответствует только одна степень свободы. При температу-
температуре Т, согласно принципу равномерного распределения, на
это движение приходится средняя кинетическая энергия
l].7kT. С другой стороны, раз мы ограничиваемся только
упругой частью силы, эта энергия равна средней потенци-
потенциальной энергии, т. е.
или
1» = ^ C9)
где $2 есть среднее значение S2.
11 Знрико Ферми
162 ГЛАВА II
Среднее значение / силы / должно быть, конечно, рав-
равно н>лю (условие равновесия). Поэтому из C8) находим:
1=4-*. D0)
Подставляя вместо I2 приближенное значение C9), мы
пол.) чим с ошиокой ьеличины порядка В2:
Из этого уравнения следует, что среднее расстояние £
двух атомов друг от друга вследствие теплового движения
меняется на величину, пропорциональную абсолютной тем-
температуре.
Ко^ициент удлинения х (удлинение, отнесенное к еди-
единице длж.ы и градуса), согласно D0), равен:
v—JL ii /4п
" "г п • \ ^ * /
tXl Q.0A
Подсавляя разумные величины для констант аир, по-
получаем для х. числа, совпадающие по порядку величины с
наблюдаемыми.
В качестве практического примера рассмотрим случай,
к 1гда А и В противоположно заряжены однократными ио-
иона..; и. Сила взаимодействия А и В складывается из куло-
новской силы притяжения f ^) и силы отталкивания,
описываемой потенциалом, обратно пропорциональным при-
приблизительно девятой степени расстояния удаления, так что
сила отталкивания пропорцисальна Y/r'u-
Величина коэаициента пропорциональности у опреде-
определяется из условия, что при равновесном расстоянии и обе
силы равны и противоположны:
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ "Е'Г'ЕТКМ J 53
Поэтому сила / равна:
f= _£?_L —
Подставив r = a -j- S, мы можем разложить / по сте-
степеням S:
, . 8fe2f 52 ?а t,
Постоянные а и ft в [38] имеют, следовательно, значе-
значения:
Подставляя в D1), получаем:
__ 52-тА
С учетом, что &=1,36-10~16 (постоянная Больцмана) и
е= 4, О-10~10 (эле енгарный электрический заряд в
электростатических единицах), получи , беря для с значе-
значение 3 - 10—8 см: х — 1,4- 10~5. Это значеьие по порядку
величины согласуется с наблюдае ыми у ионных рь.летик
коэфициентами удлинения
Обратимся теперь к теплопроводности. Как л ы ьидели,
в кристалли шской решетке могут беспрепятственно распро-
распространяться упругие волны, т. е. зз_уковые волны с длипа и
волн до атомных размеров. Тепловое движение атомов можно
тоже рассматривать как наложение таких упругих вслм
с амплитудами, возрастающими с температурой. На основании
этих представлений след,ет ожидать, что теплопроводность
кристаллов должна Сыто необы айно велика. Если, напри-
например, одна часть кристал ia находилась бы при температуре Т,
а другая - при температуре 0, то упругие волны распро-
распространились бы из первой части кристалла во втор., ю со ско-
скоростью звука, так что равенство температур устанавлива-
устанавливалось бы в доли секунды.
В действительности же теплопроводность изолирующих
кристаллов весьма л.ала и, кроме того, сильно за^и.ит от
11*
164 ГЛАВА II
температуры. Это тоже происходит вследствие того, что
силы в решетке не являются чисто упругими, а содержат
квадратичные члены и члены более высоких степеней. При
анализе распространения упругих волн мы пренебрегали
этим обстоятельством и считали движение атома кристалла
чисто гармоническим. Если закон упругого взаимодействия
выполняется не строго, то отдельные волны уже не смогут
больше накладываться без возмущений и будут ослабляться
за счет процесса рассеяния. Их амплитуда будет умень-
уменьшаться, а соответствующая энергия перейдет в новые
упругие волны с измененной длиной волны, распространяю-
распространяющиеся по всем направлениям Это рассеяние тем сильнее, чем
меньше разнится длина волны от атомного расстояния. Кроме
того, оно возрастает с ростом амплитуды колебания.
Чтобы учесть это рассеяние, можно определенным об-
образом ввести среднюю длину свободного пробега упругих
волн в кристалле. При этом мы схематизируем процесс так,
как будто волна после пробега определенного пути внезапно
обрывается и на ее месте возникает новая, с другим на-
направлением и частотой. Распространение теплового движения
от теплой к холодной области кристалла сильно затрудняется
этим механизмом, так как волна должна распространяться не
по прямому, а, так сказать, по зигзагообразному пути.
Рассмотренный процесс имеет известное сходство с теп-
теплопроводностью в газе. Пока средняя длина свободного
пробега велика в сравнении с размерами сосуда, отдельные
молекулы могут без столкновений проходить от горячей к
холодной стенке и за весьма короткий промежуток времени
переносить энергию. Когда же между молекулами происходят
частые столкновения, так что длина свободного пробега
мала по сравнению с размерами сосуда, атомы газа диффун-
диффундируют от одной стенки до другой лишь очень медленно,
поскольку они движутся теперь не прямолинейно, а зигзаго-
зигзагообразно. Вследствие этого и установление температурного
равновесия требует значительно большего времени. Однако
точная количественная оценка этих соображений о тепло-
теплопроводности кристаллов весьма затруднительна и до сих
иор удовлетворительно никем еще не выполнена.
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ ОЕШЕТКИ 165
ДЗ. Ионная решетка
Мы различали полярную и гомеополярную связи между
атома:..и молекулы. Полярную молекулу можно рассматривать
как соединение двух ионов противоположных знаков, удер-
удерживаемых электростатическими силами. Гомеополярные мо-
молекулы, наоборот, состоят из нейтральных атомов, между
которыми действуют силы притяжения резонансного харак-
характера, подобные введенным Гейтлером и Лондоном в теории
молекулы водорода.
Силы, действующие в кристалле, можно классифицировать
подобным же образом. Конечно, механизм гомеополярной
кристаллической связи еше не очень ясен и менее точно
изучен, чем более простой случай связи в полярных кристал-
кристаллах. Типичными полярными кристаллами являются кристаллы
соли, состоящие так же, как и молекулы соли, из поло-
положительных металлических ионов и отрицательных неметал-
неметаллических. Как и у полярных молекул, кроме электростати-
электростатических сил притяжения, в полярной решетке между ионами
возникают такие же силы отталкивания. Мы их учитывали
в предыдущем разделе при расчете коэфициента теплового
расширения. Пока ионы подходят не слишком близко друг
к другу, эти силы очень малы и и .и можно пренебречь по
сравнению с кулоновскими силами притяжения. Однако,
когда ионы, в известном смысле, соприкасаются, т. е. вза-
взаимное проникновение зарядных облаков становится сущест-
существенным, силы достигают очень больших величин. В теории
полярных кристаллов, в согласии с опытом, обыкновенно
принимается, что силы отталкивания описываются потенциа-
потенциалом, приблизительно пропорциональным девятой степени
расстояния между ядрами. Поэтому эти силы действуют
только между ближайшими друг к другу ионами, в то
время как радиус действия кулоновских сил значительно
больше.
Основной проблемой в исследовании ионных решеток
является определение потенциала решетки. Если узлы беско-
бесконечно протяженной простой решетки заполнены однородными
чонами, потенциал повсюд} равен бесконечности. Это видно
166 ...■■■■ ■ ГЛАВА II
из того, что он изображается суммой
е-
(г—заряд иона, rt—расстояние / иона от исходной точ-
точки), которая при /—5-cso, очевидно, расходится.
' Однако ионные кристаллы не могут иметь простой ре-
решетки, поскольку они электрически нейтральны и, следо-
следовательно, должны состоять, по крайней мере, из двух сор-
сортов ионов различного знака. Отдельные простые решетки
обозначаются индексом к. Узлы к-решетки заполнены ионами
с зарядом в]ц. Отдельные ячейки решетки мы будем обозна-
обозначать векторным индексом 1 с композитами /,, /,, /3.
Пусть тк1 означает расстояние от к иона 1 ячейки исход-
исходной точки Р, т. е. точки, потенциал которой требуется
вычислить. Тогда потенциал в точке Р имеет вид:
причем первое суммирование производится по бесконечно
большому числу ячеек 1, второе — по конечному числу раз-
различных простых решеток.
Сумма D2) также сходится только условно. Можно,
однако, с помощью искусственного приема однозначно
определить потенциал решетки, если вместо D2) рассмот-
рассмотреть сходящееся выражение
(с положительной постоянной а), которое при а = 0 пере-
переходит в D2). Тогда потенциал Vр равен
Vp= lim I pa. D4)
а->0
Другой путь для определения потенциала решетки со-
состоит з-применении уравнения Лапласа
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ г>Е1РЕТ"И 167
Это уравнение должно выполняться во всем объеме, за
исключением »узлов решетки. При приближении к точкам
(Ik), занятым ионами, V должно приближаться к бесконеч-
бесконечности, как ek//"ik- Если, кроме того, учесть, что потенциал
должен иметь ту же периодичность, что'и решетка, т. е.
в соответствующих точках каждой ячейки он должен иметь
одинаковое значение, то V определяется с точностью до
аддитивной постоянной. Последняя выбирается так, чтобы
среднее значение равнялось нулю. Таким образом прихо-
приходят к той же величине, что и в D4).
Мы разложим прежде всего потенциал V в ряд Фурье,
в предположении, что решетка состоит только из простых
кубических решеток с постоянными а. Так можно предста-
представить все правильные решетки. Обобщение на другие кри-
кристаллические системы не представляет трудностей. Разложим
с этой целью плотность электрического заряда р, имеющую,
конечно, также период а, в тройной ряд Фурье:
^AГ). D6)
где г — радиус-вектор точки, в которой рассматривается
плотность заряда; A-г) = /1гд.-|-/2гу -+- /Згг — скалярное
произведение г на вектор 1 с целочисленными компонентами
llt /2, /3. Компоненты разложения D6) вычисляются обычным
способом. Если учесть, что заряды имеют точечный хаоак-
тер (заряд е<л в точке Гк), то получим:
?1И, D7)
где сумма 2Li распространяется на отдельные атомы элемен-
к
тарной ячейки.
Для потенциала V справедливо подобное же разложе-
разложение:
168 ГЛАВА II
козфициенты которого с1 определяются с помощью уравне-
уравнения Пуассона:
№ = — 4тгр.
Подставив D8) в D6), найдем:
и отсюда
с» = 7^ + /1+<§' D9>
Учитывая это равенство и равенство D7), мы аайдем
для потенциала в точке с радиус-вектором г:
V(r)={ekB(r — rk), E0)
где
« — (И
1У' g E1)
1
Штрих у знака суммы означает, что точка /1 = /2 = /3 = О
исключается, так как средний заряд Bек) и средний по-
тенциал решетки, которые в ряде представлены членами
с 1 = 0, равны нулю.
Следовательно, пользуясь E1), можно вычислить энер-
энергию решетки для всех правильных решеток, при произволь-
произвольном числе и расположении ионов в элементарной ячейке.
Если вычисление нужно обобщить на другие кристалличе-
кристаллические системы, следует вместо В(г) подставить новую, по-
подобную В (г), функцию, соответствующую соотношению
осей и углов в кристаллической системе.
Легко понять физический смысл В. Будем рассматривать В
как потенциал распределения заряда с плотностью р*, тогда
сравнение Пуассона запишется в виде:
-«п 1
, » _ -L . E2)
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ 169'
Первый член
представляет собой разложение в ряд Фурье несобственной,
функции, принимающей отличные от нуля значения только^
в узловых точках простой кубической решетки с ребром а..
Интеграл от этой функции по длине периода равен еди-
единице. Таким образом E3) представляет распределение за-
зарядов, при котором в каждом узле решетки сосредоточен:
заряд -\- 1. Второй член
соответствует равномерному распределению отрицательного
электричества с плотностью—1/а8 таким образом, что
в каждой элементарной ячейке находится заряд — 1, кото-
который компенсирует положительный заряд узлов решётки.
14. Электростатическая энергия ионной решетки
Содержащаяся в ионной решетке электростатическая
энергия имеет большое значение для многих химических и.г
физических приложений, так как, прибавляя к ней в боль-
большинстве случаев очень малую часть, соответствующую силе
отталкивания, мы получим полную энергию, т. е. сможем*
прямым путем вычислить энергию образования кристалла
из свободных ионов.
Электростатическая энергия опэеделяется, в основном,
одной единственной функцией, характерной для кристалло-
кристаллографической системы рассматриваемого кристалла. Поскольку
эта функция зависит только от углов и от соотношения"
осей и не зависит от распределения иоков в элементарной
ячейке, то она имеет одинаковую форму для всех правиль-
правильных кристаллов, которыми мы ограничим наше рассмот-
рассмотрение.
Для вычисления электростатической энергии решетки
мы используем борновский мет.^д .^повноги потенциала,.
170 ГЛАЗА II
Пусть длина ребра кубической элементарной ячейки снова
равна а. Разделим ребро а на л равных частей (п — целое
положительное число) и введем новую решетку таким об-
образам, что элементарная ячейка исходной решетки будет
содержать л3 ячеек с ребром а/п. Тогда, при л достаточно
•большом, все ионы кристалла будут лежать в узлах новой
решетки. В большинстве случаев, в частности всегда, когда
координаты ионов находятся в простом рациональном отно-
отношении к а, достаточно небольших значений л. Для описа-
описания узлов второй решетки служат тогда тройные индексы
/,, /.,, /3 и ku k2, kz (сокращенно, 1 и к). Соответствую-
Соответствующие 1, как и раньше, могут принимать все положительные
я отрипательные целые значения, включая нуль, и служат
для обозначения ячеек главной решетки с постоянной а,
,а составляющие к могут принимать значения, лежащие
.между 0 и л— 1, и показывают положение точки внутри
гячейки. Соответствующий радиус-вектор составляется таким
образом из векторов 1 и к:
г№ = £(л1 + к). E4)
Пусть #к означает электрический заряд иона в точке
'A, к). Он не зависит от индекса 1, так кзк распределение
зарядов в элементарной ячейке периодически повторяется.
Для точек (I, к), в которых заряда нет, еь равно нулю.
С помощью разложения в ряд ек можно представить сле-
следующим образом:
2-i
(hk! F5)
Компоненты кл, л2, я3 вектора h определены с точностью
до целого кратього п. (h • к) представляет собой скалярное
произведение и равно л,А1 -t- h^,k2-\-hbk3. Величины £ь , об-
общее число которых п3, определяются подобно коэфициентам
разложения Фурье:
^^(Ьк) E6)
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ 171
Для вычисления электростатической энергии решетки
мы определим сначала потенциал, создаваемый в месте рас-
расположения иона к' ячейки с индексами 1Х = /2 = /а = О
всеми остальными ионами.
Он равен, очевидно:
Штрих у знака суммы снова означает, что член с
1Х = 10 = 1г = 0 и k = k' при суммировании исключается.
Учитывая E4) и E6), получим:
kh ~\Г.
E8)
-к'| • j
Следует заметить, что компонентами вектора п\ -j- k — к*
может быть любая тройка целых чисел, за исключением
(О, О, 0). Поэтому обе суммы по 1 и к можно объединить
в одну сумму по I, распространенную на все целые компо-
компоненты вектора I, именно:
2-1
I k
где для упрощения введено обозначение:
П ы\ V' gfa'(pl) _ ^' cos 2* (prj
и(р) = 2м i/| —2- —ПТ~ ' ( э)
|
1 1
И в этой сумме I === @, 0, 0) исключается, что отмс-
чрчо ьитрих iM у знака суммы. Ряды, определяемые функ-
иие£ Д* с.\Ч)дят.^я лиль условно, т. е. только тогда, когда
172 ГЛАВА II
члены имеют определенную последовательность, например,
расположены по возрастающим значениям вектора 1,
Функция основного потенциала II вычислена Эмерслебе-
ном. Она, очевидно, симметрична по отношению к компо-
компонентам ри р2, р3 вектора р и имеет период 1. Так как
аргументы рг, р0, рь можно произвольно заменять один дру-
другим, то ее достаточно вычислить для области
Тогда E8) запишется как сумма конечного числа чле-
членов:
^^„Д'""'!!^). F0)
h
Для электростатической энергии на ячейку решетки
F1)
к'
мы получаем, наконец, из уравнений E5) и F0) значение
hn'It'
Суммирование по к' можно произвести сразу. Сумма
отлична от нуля, только если й' = —й. так что
С помощью E6) последнее выражение приводится к-
форме:
■ \ п
kk'h
содержащей только конечное число членов. Эту
можно использовать для численных расчетов.
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕП'ЕТКИ 173
Этим путем получается для кристаллов типа NaCI
(фиг. 38) с четырьмя молекулами в ячейке решетки:
Wel =—10,17- (NaCI), F4>
а для решетки плавикового шпата (фиг. 39) — с четырьмя
молекулами в ячейке:
е1= — 46,5 J2 (CaFa). F5)
Вообще выражение для электростатической энергии
оешетки имеет вид
W* = — p~\ F6)
где р — безразмерная постоянная, вычисляемая из потенциала
решетки.
15. Силы отталкивания. Сравнение
с экспериментом
Мы уже несколько раз указывали, что два атома или
иона в кристалле не могут подходить друг к другу сколь
угодно близко, так как между ними возникают силы оттал-
отталкивания, быстро принимающие большие значения, когда
расстояние становится меньше равновесного. Как мы видели
в I части, существуют две причины этих сил: электроста-
электростатическое отталкивание и явление квантовомеханического
резонанса. Непосредственное получение закона отталкивания
из этих явлений почти бесперспективно. Поэтому для чис-
численного определения мы пойдем по более удобному экспе-
экспериментальному пути, т. е. примем, что сила убывает с ка-
какой-то степенью расстояния. Показатель степени мы опре-
определим по Борну из сжимаемости кристалла.
Как и прежде, обозначим через а длину ребра элемен-
элементарной ячейки в состоянии равновесия. Под действием внеш-
внешнего давления р она уменьшается равномерно по всему
кристаллу на величину г-а. Объем кубического кристалла,
174 ГЛАВА II
состоящего из N ячеек VQ = Na3, становится тогда рав-
равным '
V = Na3 (\ ~ £K = Nas (\ — 3s + ...)■ F7)
Сжимаемость % равна отношению между относительным
изменением объема и давлением р, так что с точностью
до членов высших порядков имеем:
1 р'
Электростатическая энергия деформироваиного кристалла
получается, если подставить в F6) вместо и, выражение
а{\ — s) и умножить получившуюся величину на число яче-
ячеек N:
Если сила отталкивания може" быть представлена сте-
степенной функцией ог расстояния между атомами, то и по-
потенциал, которым она определяется, должен иметь вид:
N. А
ап A — г;« '
который, помимо числа элементарных ячеек N и констан-
константы 4, содержит в знаменателе расстояние между атомами
в неизвестной пока степени п. Полная энергия равна сумме
этой энергии отталкивания и электростатической энер-
энергии, т. е.
F8)
Обе постоянные Лил определяются следующим обра-
образом. Когда наружное давление равно нулю (кристалл в ва-
вакууме), в состоянии равновесия длина ребра равна #. По-
Поэтому F8) должно для s - 0 иметь минимум:
e=o
ФИЗИЧЕСКИЕ СВОЙСТВА К^ИСТАЛЛИ"ЕСКОЙ РЕГТ'ЕТКИ 175-
Из этого условия следует:
п '
и после подстановки в F8):
а \\ — s n(l — up)
Разлагая это выражение в ряд по степеням е и прене-
пренебрегая членами порядка выше второго, получаем:
'^ е». F9)-
Если кристалл находится под воздействием внешнего
давления /?, то при изменении параметра е на ое совершается
работа
вызывающая равное по величине изменение энергии решетки..
Приравнивая последние выражения друг другу, получим
для сжимаемости следующую формулу:
Зг9а*
* р
откуда можно вычислить показатель степени потенциала:
отталкивания:
Этот расчет был произведен для различных кубических
кристаллов и дал для п довольно олизкую во всех случаях,
величину, равную приблизительно 9. Поэтому она оудет
обычно лежать в основе па ии.< дальнейших рассуждений..
.176 ГЛАВА II
С помощью этого значения мы можем из F9) вычис-
вычислить энергию нашего кристалла в нормальном состоянии
Полная энергия ионной решетки составляет, таким образом,
-приблизительно 8/9 величины ее электростатической энергии.
Прямое экспериментальное определение теплоты обра-
образования ионной решетки из свободных ионов невозможно.
Однако ее можно определить обходным путем из экспери-
экспериментальных данных, с помощью так называемого кругового
.процесса Борна.
Например, для NaCl из термохимических измерений
.известна энергия образования кристалла из металлического
_кагрия и газообразного двухатомного хлора. Этот процесс
образования можно разложить следующим образом на после-
последовательные частичные процессы:
a) Испарение металлического натрия в одноатомный пар
натрия. П^и этом расходуется энергия, равная энергии
сублимации натрия.
b) Разложение CL, на атомы. Для этого необходима
энергия диссоциации С12.
c) Образование положительных ионов натрия и отрица-
отрицательных ионов хлора, при котором у каждого атома натрия
отбывается электрон и передается атому хлора. Необходи-
Необходимая для этого процесса энергия равна разности работы
.ионизации Na и электронного сродства О.
d) Образование кристалла из ионов Na+ и С1~. Осво-
Освобождающаяся при этом энергия должна быть равна полной
знергии ионной решетки, даваемой формулой G2). Так как
остальные величины известны, эта энергия может быть вы-
вычислена из этого кругового процесса как разность между
-упомянутой выше термохимической теплотой образования
и суммой энергий, израсходованных в процессах.
В следующей таблице (по Борну) сопоставлены полу-
полученные таким образом энергии решеток в кал/моль с энер-
энергиями, вычисленными из выражения G2) для различных крис-
кристаллических решеток. Видно, что числа хорошо согласуются.
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ 177
Таблица 2
NaCl
NaBr
Nal
CaF2
Cal3
хсперим.
m
183
170
159
—
—
;орет.
r
182
171
158
609
422
KCJ
KBr
KI
CaCl2
ZnS
icnepHM.
m
165
154
144
—
—
горет.
E-
162
155
144
480
738
RbCl
RbBr
Rbl
CaBr2
ссперим.
m
161
151
141
—
горет.
E-
155
148
138
452
16. Распространение электромагнитных волн
в кристаллах
Теория потенциала решетки не ограничена электроста-
электростатическими приложениями. Ее можно распространить и на
быстропеременные электромагнитные поля. Особенное зна-
значение имеет взаимодействие кристалла с плоской электро-
электромагнитной волной, которым определяются как свойства оп-
оптической анизотропии, так и явления при дифракции
рентгеновских лучей.
Поле электромагнитной волны вызывает поляризацию
отдельных атомов или ионов кристалла. В первом случае
при этом происходит, в основном, смещение электронных
оболочек относительно атомных ядер. В ионных решетках,
кроме того, смещаются отдельные ионы друг относительно
друга, однако, лишь при низких частотах (инфракрасная
часть спектра), так как большая масса не позволяет им
следовать за полем высокой частоты.
Электрическая поляризация составных частей кристалла
приводит, в свою очередь, к появлению электромагнитного
поля, накладывающегося на поле первоначальной волны.
Направления обоих полей в кристаллах, вообще говоря,
различны, так что появляются анизотропии в диэлектриче-
диэлектрической постоянной и в коэффициенте преломления.
12 Эирико Ферма
178 ГЛАВА II
Если сначала рассматривать только диэлектрическую
постоянную, то за основу рассмотрения можно взять стати-
статическое поле. Если внешнее поле равно Еа, то на каждую
частицу в кристалле действует сила поля Е = Еа -\- Et,
причем „внутреннее" поле Е{ учитывает действие соседних
поляризованных частиц. Поле индуцирует в частице момент
который мы, ради простоты, будем считать пропорциональ-
пропорциональным Е и направленным в ту же сторону (изотропный слу-
случай). Кроме того, ограничимся рассмотрением решетки,
состоящей из нейтральных атомов. Смещение частиц, по-
появляющееся в ионных кристаллах, остается, таким образом,
неучтенным.
Внутреннее поле Е{, создаваемое в месте расположения
атома его соседями, можно представить потенциалом:
V = V ti cos Э
Сумма распространена на все атомы, за исключением
рассматриваемого, причем г означает расстояние от них до
рассматриваемой точки, $• — угол между направлениями г
и ja. Сумма V. вычисляется совершенно одинаково с суммой
встречавшейся в потенциале ионной решетки. После того,
как найдено Vit тем самым и непосредственно получается
зависимость между р. и внешним полем Еа.
При этом, для неправильных кристаллов в общем слу-
случае получается тензорная зависимость, т. е. анизотропия
поляризуемости, а следовательно, и диэлектрической по-
постоянной.
Анизотропии диэлектрической постоянной соответствует,
естественно, анизотропия в оптических свойствах и, осо-
особенно, в козфициенте преломления, что приводит к двой-
двойному преломлению.
При точном вычислении следует учесть, что при рас-
распространении электромагнитных волн от атома к атому
появляются запаздывающие потенциалы, значение которых
возрастает с уменьшением длины волны. Их влияние (по
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ 179
Эвальду) объясняет небольшие отклонения от закона Брегга
при отражении рентгеновских лучей.
С помощью теории электромагнитного потенциала ре-
решетки был, наконец, объяснен тот факт, что в некоторых
кристаллах с особыми соотношениями симметрии плоскость
поляризации падающей световой волны при прохождении
через кристалл испытывает поворот (вращение плоскости
поляризации).
17. Поглощение света в кристаллах
Если кристалл поглощает свет различного цвета с неоди-
неодинаковой силой, то в белом свете он кажется окрашенным.
Его спектр поглощения состоит из полос, число, положение
и форма которых различны для различных веществ. Инте-
Интересным примером являются редкие земли, дающие большое
число особенно узких, почти линейных полос. Соли хрома
и марганца имеют узкие полосы, которые так же, как
у редких земель, становятся уже с понижением темпера-
температуры.
Поглощение света кристаллами основано на квантовых
переходах внутренних электронов. Чтобы составить себе
представление об энергетических состояниях электронов
в кристалле, мы в качестве упрощенной модели рассмотрим
электрон, движущийся в трижды периодическом потенци-
потенциальном поле. Следовательно, мы не изучаем в отдельности
его взаимодействия с каждым электроном, а учитываем
влияние всех взаимодействий как поправку к потенциалу,
т. е. как экранирование зарядов ядра. Кроме того, в нашей
модели мы пренебрегаем неоднородностями решетки, воз-
возникающими вследствие теплового движения или деформа-
деформации.
Это потенциальное поле, в котором движется электрон,
изображается системой потенциальных ям, расположенных
друг подле друга, подобно ячейкам кристалла, и разделен-
разделенных потенциальными барьерами. Фиг. 45 дает одномерное
изображение такого поля.
12*
|80 ГЛАВА II
При исследовании квантовых состояний электрона в по-
подобном потенциальном поле обыкновенно исходят из двух
предельных случаев.
Случай а, особенно детально изученный Блохом, имеет
место тогда, когда энергия электрона заметно меньше вы-
высоты потенциального барьера (состояние а на фиг. 45).
Тогда, согласно классической механике, электрон не может
покинуть потенциальную яму, в которой он находится.
Согласно же квантовой механике, даже если энергия элек-
II II II II I! I
Ф и г. 45. Периодическое потенциальное
поле одномерной решетки.
трона недостаточна для перехода через потенциальный
барьер, существует конечная вероятность перехода в со-
соседнюю потенциальную яму. Эта вероятность возрастает
с ростом средней энергии электрона. В первом приближе-
приближении потенциальные ямы могут рассматриваться, как и
в классической теории, независящими друг от друга. Это
соответствует расчету с изолированными атомами. Только
во втором приближении учитывается возмущение за счет
переходов электронов.
Случай b (по Пайерлсу) имеет место тогда, когда
энергия электрона существенно больше максимума потен-
потенциала (состояние b на фиг. 45). В этом случае в основу
кладут состояние свободного электрона, а периодическое
изменение потенциала рассматривают как возмущение.
Мы ограничимся опять одномерным случаем (коорди-
(координата х). Если потенциал является периодической функцией
от х (с периодом а), то собственные функции имеют вид:
2irf
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ 181
где v {х) функция с периодом а. Для постоянной q можно
всегда считать выполняющимся соотношение \q\*SL1\v
В случае а можно, по Блоху, в первом приближении
положить:
+ 00
v(x)=2.a(x — па), G3)
— со
причем и (х) — собственная функция электрона в случае,
когда она находится в потенциальной яме, далеко располо-
расположенной от соседей и лежащей в точке х=0 (собственная
функция изолированного атома). Собственное значение энер-
энергии, соответствующее функции с|> (х), в этом случае в пер-
первом приближении равно:
Е = А-\-$ cos 2nq. G4)
Постоянная А равна собственному значению энергии
отдельного атома, а [} тем больше, чем меньше разность
между энергией электрона и высотой потенциального барь-
барьера, разделяющего две соседние ямы.
Так как q может принимать любые значения между
— !/2 и -j- 1/2, то G4) представляет собой непрерывную
полосу собственных значений, простирающихся от А — ($
до A -j- p. Ширина полосы равна, таким образом, 2р.
У состоянии с малой энергией, которым в отдельном
атоме соответствуют быстро спадающие собственные функ-
функции, оказываются очень узкие полосы. Когда, с возра-
возрастанием энергии, связь электрона с атомом слабеет, полосы
становятся шире. Это изображено на фиг. 46, на которой
сопоставлены энергетические ступени изолированного атома
с полосами энергии кристалла различной ширины.
Соответствующие соотношения для случая Ъ показаны
на фиг. 47. Так как в этом случае мы исходим из свобод-
свободного электрона, то в основу положены его собственные
функции. Невозмущенная собственная функция имеет тогда
вид:
2itf
— qs
еа
132
ГЛАВА II
Этой собственной функции з незозмущенном случае,
г. при пренебрежении потенциальным полем, соответ-
соответствует энергия:
Е =
2ma2
G5)
где т — масса электрона. Таким образом,
Е зависит квадратично от q (парабола на
фиг. 47). Возмущение изменяет ее указан-
указанным на фигуре образом; разрывы находятся
в точках # = ±1/2, ±1, ±3/2,...
Правая часть фигуры показывает соот-
соответствующий энергетический спектр, кото-
который также состоит из непрерывных полос,
разделенных, однако, более узкими интер-
интервалами, чем в случае а.
Одномерный способ рассмотрения легко
переносится на объемную решетку. Спектр
собственных значений и в трехмерном слу-
случае состоит из непрерывных полос, ширина
которых возрастает с энергией электрона,
и которые, по крайней мере в случае а,
довольно точно соответствуют собственным
значениям отдельного атома. В противо-
противоположность линейной модели, полосы в
объемной решетке могут частично пере-
перекрываться.
Возвратимся теперь к исходному пункту
нашего рассмотрения — к поглощению света
твердыми телами. Поглощение света со-
состоит, в основном, в возбуждении электро-
электронов, т. е. переходе их состояний в более
энергетически высокие. Так как электроны
не могут обладать любой энергией,
а только соответствующей определенным полосам, то погло-
поглощаемый световой квант должен обладать энергией, соответ-
соответствующей возможным в кристалле энергетическим разнос-
разностям. Поэтому, в общем случае, спектр поглощения будет
Фиг. 46. Срав-
Сравнение уровней
энергии для
изолированного
атома с энерге-
энергетическими по-
полосами кристал-
кристалла в случае а
(энергия элек-
электрона меньше
максимума
потенциальной
энергии). Слева
изображены раз-
различные атомные
термы, которым
снизу вверх со-
соответствуют во-
возрастающие зна-
значения потен-
потенциальной энер-
энергии, а справа —
соответствую-
соответствующие энергетиче-
энергетические полосы.
ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
183
V
-3/2 -I -I/2
J
//г
3/2'
состоять из отдельных полос, ширина которых зависит от ши-
ширины энергетических полос и иногда кзожет быть еще уве-
увеличена за счет теплового движения атомов в кристалле.
Причину аномального поведения солей редких земель
следует искать в особой структуре этих ионов, имеющих
неполную внутреннюю
электронную оболочку
D/). Именно содержа-
содержащиеся в этой оболочке
электроны могут быть
легко, т. е. с малой
затратой энергии, пе-
переведены в другое неза-
незанятое состояние обо-
оболочки. Состояния эти
лежат так глубоко вну-
внутри атома, что их тер-
термы в кристалле замет-
заметно не расширяются.
Поэтому ионы редких
земель поглощают не
широкими полосами, а почти линиями. Большое число
внутренних энергетических уровней, а, тем самым, и линий
поглощения, объясняется частично различными возможными
ориентациями электронных орбит друг относительно друга,
а частично и их различной ориентацией по отношению
к кристаллографическим осям. Каждый ион находится в элек-
электрическом поле, создаваемом соседними ионами, а симмет-
симметрия этого поля зависит от симметрии кристалла. Это поле
приводит к заметным расщеплениям, подобным эффекту
Штарка, которые были подробно исследованы Бете. При
этом не только увеличивается число термов, но и возни-
возникают различия в спектрах солей с различными анионами.
Эти различия обыкновенно весьма малы.
В изолированном атоме переходы между энергетическими
уровнями, различающимися между собой только ориента-
ориентацией орбитальных моментов 4/ электронов, запрещены.
Электрическое поле кристалла снимает этот запрет. Однако,
Фиг. 47. Энергия электрона в кри-
кристалле в случае Ъ (энергия элект-
электрона больше максимума потенциаль-
потенциальной энергии) в зависимости от q (век-
(вектор распространения). Справа даны
соответствующие энергетические пот
лосы (заштрихованы).
184 глава п
согласно результатам наблюдений магнитного вращения
вблизи линий, число дисперсионных электронов, т. е. сила
осциллятора /, очень мало, порядка 10~8. Следует еще
упомянуть, что исследовался также эффект Зеемана для
этих линий поглощений. Картины расщеплений, однако,
весьма сложны и соответствуют аномальному эффекту Зее-
Зеемана.
Представление об энергетических полосах электронов
в кристалле подтверждается, по Кронигу, также тонкой
структурой границ поглощения рентгеновских лучей. При
поглощении рентгеновских лучей электрон из внутренней
оболочки переходит на один из более высоких незанятых
уровней кристалла. Так как эти уровни не распределены
равномерно, спектр поглощения не имеет равномерного хода.
На его границе, т. е. при малых избытках энергии, обна-
обнаруживается тонкая структура, отображающая строение энер-
энергетических полос. Эта тонкая структура поэтому различна
для различных соединений одного и того же элемента.
ЧАСТЬ III
СТАТИСТИКА И КВАНТОВАЯ ТЕОРИЯ
ГЛАВА I
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ
СОСТОЯНИЙ
1. Обобщение принципа Больцмана
Характерная трудность классической статистики заклю-
заключается в том, что для определения вероятностей необхо-
необходимо производить произвольное деление пространства ско-
скоростей или фазового пространства на ячейки конечных
размеров, не имеющих, однако, никакого физического
смысла. В этом смысле статистика квантованных систем го-
гораздо лучше согласуется с вероятностными представлениями.
Она с самого начала содержит прерывность, предполагаю-
предполагающую существование ячеек: отдельные ячейки фазового
пространства соответствуют просто различным квантовым
состояниям системы.
Основная проблема статистики квантованных систем та
же, что и в классической статистике.
Пусть система (атом, молекула,...), имеющая квантовые
состояния с энергиями ©,, w%, ws..., при абсолютной тем-
температуре Т находится в тепловом равновесии с окружаю-
окружающей средой. Какова вероятность найти ее в состоянии
с энергией wtt Этот вопрос может быть заменен другим:
дано большое число равноценных и независимых друг от
друга систем, могущих иметь энергии wu w.2, ws. Какое
количество из этих систем в состоянии теплового равнове-
равновесия при температуре Т будет обладать энергией w^
Проблема может быть решена тем же путем, что и за-
задача классической статистики о нахождении распределения
большого числа отдельных систем по всем возможным со-
состояниям. Как мы увидим ниже, получается следующий
результат.
184 ГЛАВХ II
согласно результатам наблюдений магнитного вращения
вблизи линий, число дисперсионных электронов, т. е. сила
осциллятора /, очень мало, порядка 10~8. Следует еще
упомянуть, что исследовался также эффект Зеемана для
этих линий поглощений. Картины расщеплений, однако,
весьма сложны и соответствуют аномальному эффекту Зее-
Зеемана.
Представление об энергетических полосах электронов
в кристалле подтверждается, по Кронигу, также тонкой
структурой границ поглощения рентгеновских лучей. При
поглощении рентгеновских лучей электрон из внутренней
оболочки переходит на один из более высоких незанятых
уровней кристалла. Так как эти уровни не распределены
равномерно, спектр поглощения не имеет равномерного хода.
На его границе, т. е. при малых избытках энергии, обна-
обнаруживается тонкая структура, отображающая строение энер-
энергетических полос. Эта тонкая структура поэтому различна
для различных соединений одного и того же элемента.
ЧАСТЬ III
СТАТИСТИКА И КВАНТОВАЯ ТЕОРИЯ
ГЛАВА I
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ
СОСТОЯНИЙ
1. Обобщение принципа Больцмана
Характерная трудность классической статистики заклю-
заключается в том, что для определения вероятностей необхо-
необходимо производить произвольное деление пространства ско-
скоростей или фазового пространства на ячейки конечных
размеров, не имеющих, однако, никакого физического
смысла. В этом смысле статистика квантованных систем го-
гораздо лучше согласуется с вероятностными представлениями.
Она с самого начала содержит прерывность, предполагаю-
предполагающую существование ячеек: отдельные ячейки фазового
пространства соответствуют просто различным квантовым
состояниям системы.
Основная проблема статистики квантованных систем та
же, что и в классической статистике.
Пусть система (атом, молекула,...), имеющая квантовые
состояния с энергиями wv w2, w3..., при абсолютной тем-
температуре Т находится в тепловом равновесии с окружаю-
окружающей средой. Какова вероятность найти ее в состоянии
с энергией w/? Этот вопрос может быть заменен другим:
дано большое число равноценных и независимых друг от
друга систем, могущих иметь энергии wu w2, wv Какое
количество из этих систем в состоянии теплового равнове-
равновесия при температуре Т будет обладать энергией wt"i
Проблема может быть решена тем же путем, что и за-
задача классической статистики о нахождении распределения
большого числа отдельных систем по всем возможным со-
состояниям. Как мы увидим ниже, получается следующий
результат.
186 ГЛАВА I
Если предположить, что все состояния со значениями
энергии
являются простыми, т. е. что вырожденные состояния
считаются столько раз, сколько соответствует их пара-
параметру вырождения, то вероятность того, что система на-
находится в г-том состоянии, пропорциональна
Больцмановский закон распределения классической ста-
статистики может быть, таким образом, формально распро-
распространен на квантованные системы.
Вывод закона распределения B) для квантового случая
также совершенно аналогичен классическому выводу.
Пусть большое число N однородных систем находится
между собой в тепловом равновесии. Отдельные состояния
с энергиями wu w?, w3 заняты
Nlt N2, N,, ... C)
системами, т. е. мы принимаем, что Л^ систем имеет энер-
энергию Wj, Л/2 — энергию w2, и т. д. Совокупность чисел C)
представляет собой, таким образом, распределение N систем
по энергетическим состояниям wt. Мы должны теперь ис-
исследовать, сколькими способами может быть осуществлено
это распределение C). Вероятнейшим распределением будет
тогда такое, для которого число возможных осуществлений
наибольшее. Как и в классической статистике, здесь при-
принято, что отдельные квантовые состояния a priori ■ равно-
равновероятны.
Число II способов осуществления для C) вычисляется
следующим образом. Сначала мы рассматриваем N, систем
в состоянии wv Имеется { .. ) возможностей выбрать их
из общего числа N. Из оставшихся М—Л/, систем, N2 при-
приписывается состоянию wz, Что может быть осуществлено
(' 77 О способами. Чтобы из оставшихся N — Na — No
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ 187
систем выбрать Л/3 систем в состоянии wB, существует
I1 , J 2) различных возможностей. Таким образом,
мы распределяем все системы. Общее число возможностей
для осуществления распределения C) равно поэтому произ-
произведению:
\(N — Nx\lN—Ny—N%\ _
ад ш-w ш
У (ЛГ — Яг)! N2l (N — JVX —
/V!
А Na\ {N — Nx — N2 — N3)l ' '' Ni\ ЛГ2! Л'3!...
Кроме того, справедливо равенство:
т. е. общее число систем равно N, а таже равенство
2 Nlwi = NlWl + Nawa + Л^з +. .. = IF,
утверждающее, что полная энергия N систем равна W.
Определение вероятнейшего распределения является те-
теперь только математической проблемой, состоящей в нахож-
нахождении системы чисел N^IS/2NB ..., удовлетворяющей (о) и F)
и делающей Е [формула D)] максимальным. Мы можем
поставить требование максимума для log II вместо П. С по-
помощью формулы Стерлинга, справедливой для больших зна-
значений аргумента N,
= N{logN—\)
мы приходим при учете E) к уравнению:
log И = N (log N — 1) — Sty fM ty — 1) =
= N log N — 5 ty bg ty.
188ГЛАВА 1
Чтобы найти максимум для logll, мы используем метод
неопределенных коэфициентов, т. е. будем искать абсолют-
абсолютный максимум выражения:
N log N — 2 Nt log N, — a 2 Nt — 0 2
i i i
i
где аир параметры, не зависящие от Л^, а 2^л соответ-
соответственно, 2 N/Wg, на основании E) и F), — постоянные. Так
как оба дополнительных члена не зависят от N{, это вы-
выражение имеет те же экстремальные свойства, что и log П.
В месте максимума все частные производные по А/| в от-
отдельности равны нулю, и мы получаем
— log TV,— 1 —а — Р^=0,
Вводя вместо а. новую постоянную
мы получим отсюда:
причем константы А и {} следует определить таким образом,
чтобы удовлетворялись E) и F).
Величина р так же, как и в классической статистике, свя-
связана с абсолютной температурой соотношением:
P = -Jp (8)
где k — постоянная Болышана (k = 1,36 • 10"6 эрг/град).
Справедливость соотношения (8) в квантовой теории сле-
следует непосредственно из его справедливости в классической
статистике, если учесть, что, на основании принципа соот-
соответствия, при больших квантовых числах квантово-теорети-
ческое описание системы переходит в классическое. Так как
Р не зависит от квантового числа, уравнение (8), справед-
справедливое в предельном случае больших квантовых чисел, дол-
исно быть справедливо и при переходе к малым.
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ 189
Поэтому можно написать:
(9)
- - c
Для определения А производим суммирование
состояниям и, согласно E), получаем;
по всем
получаем;
А =
/
N
2е kT
j
{10}
Подстановка в {9) дает для числа систем в /-том состоя-
состоянии:
(И)
Вероятность нахождения одной из N систем в i-том со-
состоянии равна поэтому:
A2)
2, Тепловое равновесие и вероятность заполнения
квантовых состояний атома или молекулы
Применим боль цмановский закон распределения к рав-
равновесию между квантовыми состояниями атома.
Рассмотрим два квантовых состояния атома 1 и 2
с энергиями w) и w2 и внутренними квантовыми числами
/j и Jo. Тогда состояние 1 вырождено Byj-|-l) раз, а со-
состояние 2 вырождено {2J2-\-l) раз.
190 ГЛАВА I
При температуре Т в тепловом равновесии Nt атомов
находится в состоянии с энергией wx, и N2 атомов — в со-
состоянии с энергией w2. Так как уровни wx и w2 состоят из
B7а-I-1) и, соответственно, из BУ3-{-1) совпадающих от-
отдельных уровней, то iVj и /V2 пропорциональны величинам
откуда следует:
W
Применим это уравнение к парообразному натрию -и вы-
вычислим относительные заполнения основного состояния 325i/a
и состояния 32Рз/а атома натрия. Переход между этими
состояниями соответствует D^-линии натрия с длиной волны
5890 А и частотой v = 5,10 -1014. Отсюда разность энер-
энергий между обоими состояниями оказывается равной
А так как J1==lj2 и /2 = 3/2, то из уравнения A3) сле-
следует:
4 • 3,34-10—12 _ 24500 —10630 ,
В частности, отношение имеет следующие значения: при
комнатной температуре Г=273°К имеем ^ = 2 • 10~3S;
при 7 = 1 000° К будет ^? = 4,7-101; в пламени горелки
достигается температура в. 2 000° К, которой соответствует
xj? = 9,7'\0 , при температуре кратера вольтовой дуги
7=4 000° К получается JJ? = 0,0044; при Т= 10 000° К
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ
найдем -^ = 0,173; наконец, для 7~ = собыло бы ^ = 2.
При не слишком высоких температурах число атомов в со-
состоянии 32Si,, значительно больше числа 32А,5 атомов; таким
образом оправдывается название основного терма для самого
низкого состояния. Само собой разумеется, что эти величины
справедливы только для теплового равновесия. Если равновесие
нарушено, например, электрическим разрядом, заполнение
высших состояний может заметно возрасти, вследствие воз-
возбуждения, производимого ускоренными в поле электронами.
И у многих других элементов большинство атомов
остается в основном состоянии вплоть до довольно высоких
температур. Но у нескольких других, наоборот, второй
терм лежит очень близко к основному состоянию, напри-
например, 2Pa/s — терм металлов третьей группы —■ расположен
близко над основным состоянием %Р%. Расстояние между
обоими термами составляет у алюминия только 15 см, что
соответствует w2 — w} = he • 15 = 2,95 • 10~16 эрг. Поэтому
в данном слз'чае и при обычных температурах показатель
степени (w2— w^jkT в A3) очень мал, так что экспонен-
экспоненциальный фактор близок к 1, и отношение заполнений при-
приближается к предельному значению, даваемому отношением
статистических весов. Промежуточное место занимает таллий,
имеющий аналогичное строение термов, т. е. основное со-
состояние 2А(„ и лежащий над ним 2А/а-терм, но разность
энергий между ними составляет около 8 000 волновых чисел.
Поэтому при низких температурах только небольшая часть
атомов таллия находится в состоянии гА,5, а при 1 200° К—
в этом состоянии находится уже заметная доля. Это изме-
изменение соотношений заполнения проявляется в спектрах по-
поглощения таллия. При низких температурах в поглощении
видны только линии, исходящие из основного терма аА,„.
С возрастанием температуры постепенно появляются линии
с исходным уровнем 2Ps,s. Наблюдение температурной зави-
зависимости заполнения с помощью аномальной дисперсии двух
абсорбционных линий с исходными термами 2А/, и 2Р% экс-
экспериментально подтвердило справедливость закона распре
деления Больцмана для обоих квантовых состояний.
192 ГЛАВА I
Мы должны, впрочем, еще указать на одну принци-
принципиальную трудность в нашем выводе. Она состоит в том,
что число квантовых состояний атома бесконечно велико
и поэтому сумма в знаменателе выражений A1) и A2)
состоит из бесконечно большого числа членов, которые
для достаточно больших j приблизительно равны по ве-
величине. Большие значения j соответствуют границе серии,
у которой термы лежат бесконечно густо, так что w{
стремится к предельному значению (энергия ионизации).
Однако в таком случае знаменатель становился бы
бесконечно большим, и абсолютные величины опреде-
определяемых A1) и A2) заполнений и вероятностей равнялись
бы нулю.
Это противоречие основано на том, что больцмановский
закон распределения может применяться только к невозму-
невозмущенным состояниям. Высшие квантовые состояния атома,
которым соответствуют очень далеко вытянутые электрон-
электронные орбиты, всегда существенно возмущены вследствие
столкновений с другими атомами. Поэтому сумму следует
распространять не на все квантовые состояния, а только на
невозмущенные, т. е. на такие, для которых диаметр ор-
орбиты меньше, чем среднее расстояние между атомами в газе.
Кроме того, следует учитывать, что в тепловом равновесии
более или менее значительное число атомов ионизовано и
что эти последние так же, как и атомы в возмущенных со-
состояниях, не следует учитывать при определении абсолютных
заполнений.
Больцмановский закон распределения применим, есте-
естественно, и к квантовым состояниям молекул. Однако, в то
время как в атомах основное состояние обычно отделено от
более высоких состояний значительным интервалом энергии
и поэтому преобладает при низких температурах, в моле-
молекулах всегда имеется большое число близких к самому
низкому состоянию вращательных уровней. По закону Боль-
цмяна, эти уровни уже при низких температурах заметно
заь оляены. У более тяжелых молекул при обычных температу-
температурах и высшие колебательные состояния часто бывают терми-
термически возбуждены.
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ 193
3. Анткетоксозы линии флуоресценции и рамановекяе
линии
Тепловое возбуждение более высоких кзантовых состоя-
состояний является также причиной некоторых прежде необъяс-
необъяснимых явлений при флуоресценции и при эффекте Рамана.
Частота света, испускаемого при флуоресценции, как
правило, меньше частоты падающего света (закон Стокса)
по следующей причине: ббльшая часть флуоресцирующих
атомов находится в основном состоянии (состояние а на
фиг. 48). При облучении светом
соответствующей частоты v атомы
могут путем поглощения светового
кванта hv переходить в состоя-
состояние Ь, а оттуда, за счет испуска-
испускания кванта hv (флуоресценция),
попасть в состояние с. Как видно
из фиг. 48, в согласии с законом
Стокса, v' ^ v. Однако часто на-
наблюдаются линии флуоресценции Фиг. 48. Схема термов,
и рамановские линии, частота ко- К истолкованию закона
торых несколько больше частоты Стокс^ н объяснению
к антистоксовых линии,
падающего света, так назыяаемые
антистоксовы линии. Такие линии
появляются, если флуоресцирующие атом или молекула
имеют энергетический уровень с, настолько близкий к ос-
основному состоянию а, что в тепловом равновесии заметная
часть атомов или молекул находится в состоянии с. Эти
атомы или молекулы могут тогда возбуждаться до состоя-
состояния b путем поглощения кванта света hv', а оттуда возвра-
возвращаться в основное состояние с испусканием кванта флуо-
флуоресценции /zv. Так как v' меньше, чем V, излучение флуо-
флуоресценции оказывается более коротковолновым, чем падающий
свет, что противоречит закону Стокса. Существование ан-
антистоксовых рамановских линий объясняется таким же об-
образом.
Термически возбуждены могут быть только уровни, энер-
энергия которых отличается от энергии основного состояния на
13 Эирико Ферми
194 ГЛАВА I
величину порядка тепловой энергии kT. Поэтому и смеще-
смещения частоты антистоксовых линий могут быть порядка н^
больше kTjh и при обычных температурах не должны пре-
превосходить -V, Ю13 сек~!. В действительности, фиолетовые
смешения, ббльшие, чем 500 — 600 см—1, почти не наблю-
наблюдались.
4. Средняя энергия осциллятора
Теперь с помощью закона распределения Болышана
вычислим среднюю энергию гармонического осциллятора при
температуре Т.
Энергетические уровни осциллятора, как известно, да-
даются cojTHomeHHeM iva= fn(n -J-1^), где v — собственная
частота осциллятора, а п может принимать значения 0, 1, 2 ..,
При статистическом и термодинамическом рассмотрениях
постоянный член /rv/2 может быть опущен, т. е. энергия
может отсчитываться от основного состояния. Значения
энергии различных квантовых состояний будут тогда целыми
кратными:
wa=hvn п==0, 1, 2,... A4)
Вероятность того, что осциллятор в тепловом равнове-
равновесии при температуре Т находится в /z-том состоянии, со-
согласно A3), равна:
—Av
П_=-
2- кТ
/=0
Стоящая в знаменателе этого выражения сумма, так назы-
называемая сумма состояний, в этом случае легко определяется,
так как ее члены образуют геометрическую прогрессию:
/=0 l_v kT
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ 195
Таким образом, находим:
' ' Пя = 1^1— е кТ)е kT . A6)
Отсюда средняя энергия осциллятора да равна:
оо / —Ам\ оо —Av
£ П ( ~^J £ "?7 "
л=0 л=0
Для вычисления суммы продифференцируем A5) по v:
—hi
h ~W
со — h->, —= e
Откуда получаем:
e
. A7)
Если / заменить через п, то это выражение оказывается
идентичным искомой сумме. По подстановке получаем со-
соотношение:
ekT -
A8)
Это уравнение, полученное впервые Планком в своих зна-
знаменитых исследованиях по спектру абсолютно черного тела,
явилось началом квантовой теории.
Для сравнения напомним, что, согласно классической
статистике, средняя энергия гармонического осциллятора
равна
A9)
При очень высоких температурах, когда hy/kT<^\, вы-
выражения A8; и A9; практически совпадают. Знамена гель
13*
196
ГЛАВА I
в A8) разлагается тогда в ряд по степеням kvjkT, который
можно оборвать на втором члене: *
/zv Лу _
При низких температурах, особенно для
B0)
наблюдаются значительные расхождения между обеими ве-
величинами (фиг. 49). Для макроскопических осцилляторов
эти расхождения лежат при недостижимо низких темпера-
температурах; напротив, для атомных
осцилляторов они играют суще-
существенную роль уже при обычны»
температурах.
Интересное применение фор-
формула A8) находит при вычислении
теплоемкости твердых тел {ом. ч. 11,
разделы 6 и 7). По Дебаю, темпе-
температурная зависимость теплоемко-
теплоемкости полностью объясняется пред-
предположением, что колебания атомов
вокруг положений равновесия сле-
следует рассматривать как колебания
гармонического осциллятора.
Ф я г. 49. Зависимость
средней энергии w гар-
гармонического осциллятора
от температуры по клас-
классической %<(гг>кл.) и кван-
квантовой теории (w).
Другим приложением является планковский расчет рас-
распределения энергии в излучении абсолютно черного тела.
Именно здесь впервые было введено в физику понятие кванта
действия.
5. Спектр черного тела
При достаточно высокой температуре все тела накали-
накаливаются, т. е. начинают испускать видимое излучение. Спо-
Способность излучать не связана, однако, с высокой темпера-
температурой. Все тела излучают заметные количества энергии н
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ 197
при обычной температуре. Когда тело имеет ту же темпе-
температуру, что и окружающая среда, излучаемая энергия пол-
полностью компенсируется. Тело поглотает из излучения окру-
окружающих тел ровно столько, сколько оно само испускает.
Излучение, испускаемое телом при определенной темпе-
температуре 7, имеет, вообще говоря, непрерывное по спектру
распределение энергии. Обозначим через e(v)u"v количество
энергии, испускаемое с единицы поверхности гела в единицу
времени в интервале частот между v и v-j-fifv. Функцию
е iv) dv назовем излучательной способностью тела при тем-
температуре 7 и частоте v. Так как кзлучательная способность
зависит не только от свойств тела, но и от температуры,
то, для общности, обозначим ее через е (v, T) d?v.
Общая излучательная способность е^, т. е. количество
энергии, испускаемое с единицы поверхности в единицу
времени по всему спектру, равна, очевидно:
ea(T)=\e(v,T)dv. B1)
Функция B1) очень сильно возрастает с температурой.
Когда определенное количество энергии излучения па-
падает на тело, часть ее поглощается, а остаток отражается
от поверхности тела или, если последнее прозрачно, про-
проходит насквозь.
Отношение поглощенной энергии к падающей называется
коэфицнентом поглощения а. Этот коэфициеат зависит от
многих факторов: в первую очередь,-—от состояния тела,
особенно его поверхности. Некоторые тела, например сажа,,
почтя полностью поглощают падающую на них энергию
излучения. Другие, наоборот, почти полностью отражают,,
например, металлы, подобные серебру. Кроме того, коэфи-
циент поглощения зависит от частоты падающего излучения.
У некоторых материалов он имеет ясно выраженные макси»
мумы для определенны» частот, между которыми лежат
области большой прозрачности или высокой отражательной
способности. Например, все поверхностные дзета являются
198 ГЛАВА I
результатом того, что кажущиеся окрашенными тела нерав-
неравномерно отражают излучение различных частот. Темпера-
Температура также оказывает известное влияние на коэфициент
поглощения. Наконец, он зависит и от угла падения излу-
излучения. Поэтому мы будем все наши рассуждения всегда
относить к изотропному полю излучения (одинаковая интен-
интенсивность излучения для всех направлений в пространстве).
Тогда коэфициент поглощения а для данного тела зависит
только от v и Т:
а = а {v, T).
По нашему определению, наибольшее возможное значе-
значение для коэфициента поглощения равно единице. Тело
с а = 1 поглощает все излучение, падающее на его поверх-
поверхность. Такое тело носит название „абсолютно черного
тела". Применяемые в технике измерения излучения „чер-
„черные тела" представляют собой только более или менее хо-
хорошие приближения к этому идеальному случаю.
В термодинамике процессов излучения показывается, что
коэфициент поглощения любого тела находится в тесной
связи с его излучательной способностью. По Кирхгофу, от-
отношение Е излучательной способности е к коэфициенту
поглощения а зависит только от частоты и от температуры
и не зависит от свойств тела:
~=Е(у,Т). B2)
Физический смысл универсальной функции Е (у, 7") ясен
из предельного случая а=\. В этом случае e = E{v, T).
Функция E(v,T) представляет собой, таким образом, излу-
излучательную способность абсолютно черного тела. Из этого
факта ясно, насколько важно знать излучательную способ-
способность или распределение энергии по спектру в зависимости
от температуры для абсолютно черного тела, так как
она равна универсальной функции Е{у,Т).
Наилучшим приближением к абсолютно черному телу
является малое отверстие в стенке протяженной полости.
Луч света, попавший через это отверстие внутрь полости,
должен подвергнуться весьма многим отражениям от стенок,
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ 199
раньше чем он сможет снова через отверстие покинуть
полость. При многократном отражении луч практически
полностью поглотится, так что коэфициент поглощения от-
отверстия можно считать равным единице. Это предположение
выполняется тем лучше, чем меньше отверстие по сравне-
сравнению с протяженностью полости. По этой же причине зра-
зрачок глаза, отверстия в залах без окон или входы в пещеру
кажутся нам черными поверхностями.
Внутри полости существует определенная плотность
энергии излучения, которая зависит только от температуры
стенки Т. Излучение, испус-
испускаемое стенкой, ею же и по-
глощается. При этом влиянием
отверстия можно пренебречь,
поскольку его площадь мала
по сравнению с общей внут-
внутренней площадью. Если коэ-
коэфициент поглощения стенки
меньше единицы, то, по за-
закону Кирхгофа B2), стенка ф
будет испускать меньше излу-
излучения, чем черная поверх-
поверхность. Несмотря на это, плотность излучения в полости та-
такая же, как ив полости с „черными" стенками, так как луч до
полного поглощения может пройти соответственно больший
путь.
Небольшая часть излучения покидает полость через
отверстие, которое, таким образом, будет испускать излу-
излучение. Так как отверстие ведет себя как черная поверх-
поверхность, то это излучение по интенсивности и спектральному
составу должно быть идентично излучению абсолютно чер-
черного тела температуры Т.
Вычислим, сколько излучения испустит полость через от-
отверстие АВ с поверхностью 5 (фиг. 50) в единицу времени.
Плотность излучения полости в интервале частот между
у и v -j- dv равна и (v, T) dv. Излучение в интервале частот dv,
испускаемое в единицу времени поверхностно 5 под углом О
с нормалью к S в телесном угле а?о), очевидно, равно ко-
200 ГЛАВА Е
лнчеству энергии, содержащемуся в косом цилиндре ABCD
с основанием S и длиной AD = c (скорость света) и рас-
распространяющейся в направлении da). Объем этого цилиндра
равен S.с- cos 6. Искомое количество энергии определится
как часть полной энергии излучения, содержащейся в ци-
цилиндре,
и (у, T)-S- с -cosOrfv,
направление движения которой лежит в телесном угле da).
-хг и (у, Т) -S-с-cos 6• d'K
Общее количество энергии в интервале частот dv, ис-
исходящее в единицу времени из отверстия, определится
интегрированием последнего выражения по полусфере. Вы-
Выразив элемент телесного угла через б, получим:
IT
2
Г d® cos G = 2тг С cos () sin QafO = тт,
. полусс)
и для искомой полусферы энергии мы находим выражение
—■ a (v( T) rfv. B3)
С другой стороны, наше отверстие должно иметь ту же
излучательную способность, что и черная поверхность той
же величины, именно:
Приравнивая оба выражения, получаем соотношение
Е (v, T) dv = ~u (у, Т) aTv (- 4)
между излучательной способностью черного тела к плотно-
плотностью излучения внутри полости с той же температурой.
Плотность энергии а (у, Т) зависит от v и Т таким же
образом, как и £{v, Ту, это означает, однаю^ что плотность
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ 20*
и спектральное распределение излучения, образующегося
при тепловом равновесии внутри полости, зависят только
от температуры, а не от состояния стенки. Это заключение
можно сделать и непосредственно из термодинамических
соображений.
6. Формула Планка
С помощью формулы B4) определение распределения
энергии в излучении черного тела сводится к исследованию
соотношений в излучении внутри полости, иначе говоря,
к определению функции и (v, T).
Мы не приходим, однако, к цели при более точном
изучении хода этой функции с помощью чисто термодина-
термодинамических соображений. Этим путем можно вывести закон
Стефана-Болышана и закон смещения Вина, в которых
выражаются некоторые важные свойства функции a(v, T),.
Однако чисто термодинамическим путем не удается опре-
определить самую функцию. Это возможно только с помощью
статистических методов. Попытка решить эту проблему с
помощью классической статистики привела к закону излу~
чения Релея-Джинса, который находится в согласии с опытом
только в области малых частот, но, в то же время, для
плотности суммарного излучения он дает при любой тем-
температуре бесконечность.
Непригодность классической статистики побудила Планка
искать решение этой проблемы совершенно новым путем.
Он предположил, что энергия осциллятора не может прини-
принимать любое значение, а должна составлять целое кратное
определенного кванта энергии. Это предположение, поло-
положившее основу квантовой теории, привело к закону излу-
излучения Планка, полностью объяснившему наблюдаемое
распределение энергии в излучении полости.
Выведем формулу Планка наиболее простым путем:
заполненная излучением полость с полностью отражающими
стенками имеет свойства, во многих отношениях совершенно
аналогичные упругому телу. В частности, она обладает
собственными колебаниями, зависящими от ее формы и ве-
величины, причем, как и в упругом континууме, распределение
202 ГЛАВА I
собственных частот в достаточно большой полости не зависит
от ее формы, и их число пропорционально объему Q. Интер-
Интервал частот между v и у -{- dv содержит в последнем случае
Q^v»rfv B5)
собственных частот1). Каждая из них ведет себя.
*) Приведем простое, хотя не вполне строгое доказательство
этой формулы. Каждой собственной частоте v соответствует
система стоячих волн с длиной волны X. Если полость имеет,
например, форму куба с длиной ребра а, стоячая волна должна
удовлетворять трем условиям:
X Пх X я2 А п%
а~1Г' Y~T if ^T"^'
где «1, щ, щ — целые числа, а а, р, -у—косинусы направления
волны. Так как <x2-f-Pa + 72= 1, то отсюда следует:
«?+«»+«»=*£. (а,
Каждой тройке целых положительных чисел пх, щ, щ соот-
соответствует одно собственное колебание. Число собственных
колебаний в интервале частот dv получится из геометрического
представления уравнения (а). Будем считать п\, щ, п$ декартовыми
координатами точки, расстояние которой от начала координат
равно:
А С
Собственным колебаниям, лежащим в интервале частот от v до
v-J-dv, соответствуют все точки с целочисленными значениями
координат, содержащиеся в положительном октанте между ша-
шаровыми поверхностями с радиусами 2я»/с и 2д (>-j-dv)jc. Так
как в каждой ячейке с объемом 1 лежит одна точка, то их число,
в среднем, равно объему, ограниченному этими шаровыми по-
поверхностями, т. е.
1 /
— 4я (
8 \
2e 4ra*
) — dv = —в- 'Adv . (с)
с / с сг
Каждое собственное колебание обладает двумя направлениями
поляризации. Мы должны поэтому ввести множитель 2 и, заме-
заменяя яЗ через 2, получаем число собственных колебаний полости
з интервале частот от v до ff
СТАТИСГйЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ 203
з основном, как гармонический осциллятор той же частоты.
Мы можем поэтом}' поле излучения в полости рассматривать
как множество гармонических осцилляторов, частоты кото-
которых совпадают с частотами собственных колебаний. Средняя
энергия этих осцилляторов в тепловом равновесии при тем-
температуре Т дается формулой A8). Полная энергия dN
осцилляторов в интервале частот dv по B5) равна
С другой стороны, эта энергия равна Q • и (v, T) dv. От-
Отсюда и получаем для и (v, T) формулу Планка:
*ЬТ) =%-£*-. B6)
На основании уравнения B4), связывающего плотность
излучения в полости с излучательной спосооностью абсо-
абсолютно черного тела, получим далее:
B7)
Ход этой функции для различных температур приведен
ва фиг. 51, (На фигуре в качестве аргумента взята длина
волны )., а ке частота v.)
Излучательная способность имеет максимум при частоте
'Vmais которая может быть вычислена из условия, что произ-
производная от E(yt T) по v при этой частоте должна обращаться
в нуль:
VmaX = a-/- Т. B8)
Здесь a — корень уравнения
C — a)-ea = 3
и равен приблизительно 2,77. Представляя в B8) числен-
численные значения, получаем закон смещения Вина;
J B9)
Черте тело
Фиг. 51. Спектральное распределение энергии «ер
ного тела при различных температурах.
СТАТИСТИЧЕСКОЕ РАВНОЕЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ 205
который получается и непосредственно из термодинамических
соображений. Таким образом, частота vmax пропорциональна
абсолютной температуре.
С помощью B9) можно, например, определять темпера-
температуру звезд. Большинство звезд излучает, примерно, как
черное тело. Из наблюдаемого максимума интенсивности
можно тогда по формуле B9) вычислить температуру звезды.
В формуле Планка содержится и другой выведенный
ранее на основе чисто термодинамических соображений
закон излучения, именно закон Стефана-Больцмана. Он
утверждает, что полное излучение абсолютно черного тела
растет пропорционально четвертой степени температуры.
Интегрируя B6) по всем частотам, получим:
ос оо со
Г 8it Г hy3dv to**T* Г х* dx
о ekT — 1 о
и, так как последний интеграл равен тг4/15,
Излучательная способность абсолютно черного тела по-
получается отсюда умножением на с/4 и оказывается равной:
что находится в прекрасном согласии с опытом.
7. Статистическое равновесие между атомами
и излучением полости
Пусть при температуре Т внутри полости в равновесии
с черным излучением находится атом, имеющий энергети-
энергетические уровни wx и S2>2 (для определенности пусть <wx <^w2).
Тогда возможны следующие два процесса:
а) Если атом находится в состоянии w2, он может ис-
испустить квант с частотой
206 ГЛАВА 1
b) Если атом находится в состоянии wu он может пе-
перейти в состояние тр2 с поглощением кванта Av.
В тепловом равновесии оба эти процесса должны
происходить одинаково часто. Обозначая через рл и р%
вероятности нахождения атома в состоянии w, и, соответ-
соответственно, w2, согласно закону Больцмана, будем иметь:
ТО; WX fit
Вероятность того, что атом из состояния чол перейдет
за единицу времени в состояние w2 за счет поглощения
кванта hv, пропорциональна плотности в полости излучения
с частотой v, т. е. равна B-u(v, T), где В — пока неиз-
неизвестный множитель пропорциональности. Вероятность про-
процесса Ь) равна произведению вероятности перехода на
вероятность нахождения атома в состоянии тг, т. е. равна:
/>,£-a(v, T).
Если атом находится в состоянии w%, он может перейта
в состояние w, как самопроизвольно, так и под воздей-
воздействием излучения. Вероятность этого перехода мы полагаем
равной поэтому выражению:
Л + С-я(у, Т). C3)
Второй член представляет собой вероятность „вынужденного
излучения", наличие которого нужно предположить, так
как иначе было бы невозможно установление равновесия.
Вероятность процесса а)-равна произведению C3) на веро-
вероятность нахождения атома в состоянии w2t т. е. имеет вид:
p,H4-C.e(v, Г)).
В статистическом равновесии вероятность процесса Ь) дол-
должна быть равна вероятности обратного ему процесса а):
р,И+ C-a(v, T))=pl-B-u(v, T).
Используя C2), отсюда получаем:
е — В-щт,, Т)^ В'
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КРАНТОВЫХ СОСТОЯНИЙ 207
Если в этом соотношении для и (v, T) подставим план-
ковское выражение, то найдем:
h— л ( Av \ г
^ = 85^7^-0+f
Это соотношение должно быть справедливо для любой
температуры, что возможно только в том случае, если
между постоянными существуют следующие соотношения:
£, C5)
В = С. C6
Эти важные соотношения между величинами А, В и С,
впервые полученные Эйнштейном, дают сведения относительно
связи между вероятностью А спонтанных переходов w2 —»• wt
и коэфициентом поглощения В атома в состоянии wu необ-
необходимого для излучения с частотой v = w* ~ Wl-. .
Эти соотношения показывают, кроме того, что действие
излучения состоит не только в поглощении с i ереходом
в высшее состояние. Как указано выше, под его воздей-
воздействием может также произойти „вынужденное" испускание,
при котором атом переходит из состояния чю„ в состояние
тл. Вероятности перехода для этих двух процессов равны.
Вместо вывода этих соотношений из формулы Планка
можно было бы итти обратным путем. Именно, можно вы-
вывести C5) и C6) непосредственно из квантовой теории
излучения Дирака, без применения статистических сообра-
соображений, и таким образом притти к C4), которое после под-
подстановки значений А, В и С переходит в
e L_-i
Ж и (*, Г) ' *
Решая это соотношение относительно a (v, T), получим фор-
формулу Планка B6).
208 ГЛАВА I
8. Квантовал теория парамагнитного газа
Развитие классической теории парамагнетизма связано
с именем Ланжевена. Он предположил, что молекулы или
атомы парамагнитного газа обладают собственным магнитным
моментом, который стремится установиться параллельно
направлению внешнего поля. Этому установлению противо-
противодействует тепловое движение, которое стремится создать
равномерное в пространстве распределение направлений мо-
моментов. При статистическом равновесии между этими двумя
воздействиями, хотя моменты и распределены по всем воз-
возможным направлениям, моменты, имеющие составляющие
з направлении поля, преобладают. Таким образом, в сред-
среднем, имеется намагничивание в направлении поля, соответ-
соответствующее наблюдаемому парамагнетизму.
Рассмотрение проблемы на основе квантовой теории
отличается от классического рассмотрения только учетом
квантования направлений. Магнитный момент атома или
молекулы во внешнем поле может устанавливаться только
таким образом, что его составляющая в направлении поля
принимает определенные значения, равномерно распределен-
распределенные между крайними величинами (соответствующими парал-
параллельной и антипараллельной ориентации по отношению к
полю). Проекция внутреннего квантового числа J на на-
направление поля, т. е. магнитное квантовое число т, может
принимать только значения, равные
J, У—1, У — 2,... —(у_1), —J.
Таким образом, составляющая магнитного момента р. з
направлении поля равна (так как *jl имеет направление У):
а соответствующая магнитная энергия:
— Hix^r, C8)
де Н—напряженность внешнего магнитного поля.
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ- КВАНТОВЫХ СОСТОЯНИЙ 209
Положим для простоты, что. высшие квантовые состояния
очень удалены от основного состояния. В таком случае их
влияния можно не учитывать; в тепловом равновесии атомы
будут распределяться, по закону Больцмана, только по
уровням, возникающим во внешнем поле C8). Вероятность
того, что атом находится в состоянии с магнитным кванто-
квантовым числом mt согласно A2), равна:
г? __
ln~ m=J
Среднее значение магнитного момента в направлении поля,
при учете C7), равно:
Ь V
m=J J Ь
Р _. IT т — — ],
«И "-» ==::
т j
Обе суммы легко вычисляются. Знаменатель является ко-
конечной геометрической прогрессией, сумма которой равна:
Дифференцируя это выражение по If., получаем также
и сумму в числителе:
m=J t
Ферми
'210 ГЛАВА I
'Таким образом, среднее значение момента jjl равно;
Это выражение можно разложить по степеням Н в ряд,
который при не слишк^ больших полях можно оборвать
на первом члене. Тогда для среднего значения момента н^а
малых нолях получается выражение:
>-&-?"■ <«>
Магнитная восприимчивость •£, рассчитанная на атом„
отсюда равной:
Следовательно, магнитная восприимчивость, как и в тео-
теории Ланжевена, обратно пропорциональна абсолютной тем-
температуре (закон Кюри)„ В предельно случае оч^нь б >льшиж
квантовых чисел J формула D1) совпадает с классической
формулой Ланжевена:
так как в этом случае крантование направлений несуше=-
ственьо. Эта формула обычно служит дли определения маг-
магнитного момента ji* (при 1ем даже тогда, когда она не
вполне строго выполняется):
p*-=Va%kT; D3)
Обозначаем эту величину через р.* вместо \l, чтобы
подчеркнуть, что она не представляет собственно магнитного
момента атома, а является лишь весьма произвольной мерой
его наблюдаемых магнитных свойств. С истинной величиной
ji она, согласно D1) и D3), связана соотношением:
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ 231
Магнитный момент }i* часто измеряется в „магнетонах Вейса*
* I
(один магнетон Вейса ->—=• магнетона Бора), поскольку и
до сих пор подчас считают, что значение ji* будет оста-
ваться кратным магнетона Вейса также в твердых телах
и в растворах. Однако это предположение теоретически
совершенно не обосновано и не очень оправдывается на
опыте.
:, Формула: D1) была провеяна и подтверждена только
в одном случае, именно для паров натрия, магнитный мо-
момент которых равен магнетону Бора (J = у). Применяется
эта формула для вычисления магнитных моментов раство-
растворенных ионов. Однако при эт»м нужно учитывать, что
условия, при которых выведена формула D1), выполняются
в растворе лишь очень приблизительно. Только в единичных
случаях, например, для рехкратных ионов редких земель,
магнитные свойства, определенные из спектроскопических
наблюдений,,в паре, совпадают с таковы и для ионов в pac-
хворе. Для ионов редки v земель это основано на следующем.
Электронная оболочка этих ионов состоит, в основном, из
замкнутых, оболочек, не имеющих "магнитного момеьтз.
Электроны, ответственные за создание магнитнаго момента
(их число возрастает от 1 для церия и 2 — для празеодимия
до S4 для кассиопея), прш.адлежат к единственной неза-
незаполненной оболочке 4 /, т. е. находятся глубоко внутри
зтома и поэтому не подвержены внешним воздействиям. На
поведение этих электроноз практически не оказывают влия-
влияния молекулы растворителя. Поэтому свойства ионов в рас-
teope очень близки к чх свойствам в газовом состоянии,
Парамагнетизм ионов редких земель теоретически изу^-
тлея, в частности, сомме эфельдом и ван-Флеком. При такой
исследовании следует в D1) подставить теоретические зна-
значения для р. и J n затем учесть возмущение, вносимое
энергетическими уровнями, близко расположенными к основ-
основному состоянию. В нашем выводе мы их влиянием прене-
пренебрегли. Насколько хорошо здесь согласуются теория и опыт,,
доказывает фиг, 52, на которой представлен эффективны = 5
2\2
ГЛАВА I
магнитный момент jji* в зависимости от порядкового номера.
При попытке перенести эти соображения на другие
группы периодической системы, в первую очередь на группу
железа, ни в одном случае не было получено столь хоро-
хорошего согласия. Основной причиной этого следует считать
то обстоятельство, что электрон-
ные орбиты, создающие магнитные
моменты, лежат не столь глубоко
в электронной оболочке, как в
случае редких земель, так что силь-
сильно сказывается влияние молекул
растворителя.
Если известны энергетические
уровни системы, то с помощью за-
захарактеризует пределы
ошибки.
57 ?!z 9. Статистическое толкование
Ф и г. 52. Эффективный термодинамических величин
магнитный момент ред-
редких земель в зависимости
от атомного номера. Кри-
Кривая вычислена теорети- ,,
чески. Измеренные зна- кона Больцмана, распространенного
чения нанесены в виде на квантованные системы, можно
штрихов. Длина штрихов вычислить и термодинамические
свойства этой системы. В дальней-
дальнейшем мы вычислим, в зависимости
от положения энергетических уровней, энтропию S и свобод-
свободную энергию F газа, состоящего из независящих друг от
друга одинаковых атомов или молекул с энергетическими
уровнями w0, w^ w%,.... Будем отсчитывать энергию от
основного состояния, т. е. будем считать, что
wo = O. D5)
Пусть термы расположены в порядке возрастания их энер-
энергии. Будем считать, что взаимным возмущением атомов
можно пренебречь, так что заполнение уровней может вы-
вычисляться с помощью закона Больцмана.
При рассмотрении нашего газа будем исходить из ста-
статистической суммы:
D6)
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ 21
которую можно вычислить, если известны значения w •.
производная по JJ равна:
Число iVy систем в состоянии/, согласно A1), равно:
■ ' -■ — WJ
Поскольку каждая из этих систем имеет энергию w-, го
суммарная энергия состояния j равна N.Wj. Полная энер-
энергия газа из N атомов, таким образом, имеет вид:
ОО —W]
= Y^JNi = N S
Подставив
учитывая D7), получим соотношение
выражающее тепловую энергию нашего газа как функцию
величины рэ а следовательно, температуры 7",
Вычислим энтропию газа 5- Так как газ не совершает
внешней работы, то
С помощью соотношений D8) и D9) получим:
214 ГЛАВА S
Наконец, находим:
Мы получили выражение для энтропии из ее термоди-
термодинамического определения E0)= Мы могли бы также положить
е основу больцмановское соотношение между энтропией к
вероятностью:
Тогда нужно было бы с помощью формулы Стирлинга вы-
вычислить логарифм выражения D) для вероятности и подста-
подставить Nj, согласно A1). Однако здесь это вычисление мы
не будем проводить.
Свободная энергия^ выводится из D9) и E1):
F=W— TS= — NkTlogZ($), E2)
Аналогично, с помощью статистической суммы Z(jJ) мож»
ао выразить и другие термодинамические величины.
10, Принцип Нернста
Обычное определение энтропми с помощью термодина-
термодинамического равенства E0) устанавливается только с точностью
до аддитивной постоянной. Поэтому при термодинамическом
расчете состояний равновесия, напри ер, между насыщенными
паром и жидкостью, появляются постоянные, зависящие от
аддитивных констант отдельных энтроиий8 которые должны
определяться экспериментально.
Эта неопределенность устраняется высказанной Нернстом
теоремой, так называемым третьим началом термодинамики,,
гласящим, что энтропия всех веществ при абсолютном нуле
равна нулю.
Таким образом, интеграл, определяющий энтропию, пе-
перестает быть неопределенным. В качестве нижней граница
следует подставить 7*='0: •
]ф. ■ E3)
СТАТИ0ТИ"ЕСКОЕ "АВЧОЧЕСИЕ КИАЧТОЧЫХ СОСТОЯНИЙ 215
Здесь dQ подразумевает дифференциал количества теплоты,
яодводимой к телу обратимым образам.
Между принципом Нернста и статистикой квантовых ск?>
стем существуют некоторые интересные соотношения, кото-
которые мы коротко рассмотрим, не касаясь их применения к
химическому равновесию. В статистическом определенна
энтропии ,
S = klogH E4)_
П является, собственно говоря, не вероятностью, а числом-
возможных сгюсооов осуществления (статистическим весом)
рассматриваемого состояния. Вероятность получается отсюда^
после деления 11 на число возможных случаев. Она про-
пропорциональна 11.
Определекие статистического веса некоторого состояния
в классической статистике возможно только при помощи
произвольных допущений. Именно, необходимо разделить
фазовый об ьем частиц, составляющих систе >у, на произ-
произвольное число ячеек равной величины, заполнение которых
однозначно описывает состояние. Естественно,: число воз-
возможностей осуществления состояния зависит от величины
этих ячеек. Оно с ановится тем меньше, чем меньше ячейки.
Можно показать, что 11 содержит множитель, зависящий от
объема ячеек. Этому множителю в выражении log 11, а пЫ
E4) и в энтропии, соответствует аддитивны.* член. О.сюда
следует, что в классическом случае, при статистическом
определении, так же, как и при термодинамическом, энтро-
энтропия может бы ь определена только с точностью до аддитив-
аддитивной постоянной. , ' .,
Но всякая произвольность исчезает, если в основу ста!-
тистикц положить квантованные системы. Действшельно,'
вместо произвольного числа ячеек рассматривается точно
определяемое число квантовых состояний. Число возможно-
возможностей осуществления состояния системы становится тогда со-
совершенно определенным. Оно вычисляется по формуле D).,
Выражение E4) тогда однозначио "определяет соответствую-;
jm.ee значение энтропии. ..:!:;•
216 ГЛАВА I
Если прежде всего предположить, что самое низкое
товое состояние системы является простым, то связь с прин-
принципом Нернста заключается в следующем положении: при
абсолютном нуле все атомы находятся в основном состоянии
Это „распределение" осуществимо только одним способом.
При этом, как следует и из D), II равно единице и, в со-
согласи с принципом Нернста, из E4) получаем 5=0. .
Если основное состояние г—кратко вырождено, то та-
такого согласия с принципом Нернста не получается: N атомов
распределяются по г отдельным состояниям основного терма.
Вероятнейшим распределением является такое, при котором
каждое из них заполнено Njf атомами. По D) число воз=
нежностей реализации этого распределения равно
гт N Г • - •
По формуле Стерлинга
log п ! = п (log1 // — I)
отсюда получаем:
• log И == N(log N— 1) — г £ (lug £ — ! ) = Nlog r.
(То E4) энтропия имеет вид;
S—kNlogr,
так что для г^> 1 она не равна нулю.
Против этого результата, противоречащего принципу
Нернста, можно возразить, что полная независимость атомов
друг от друга является неосуществимым идеальным случаем
и что в действительности всегда будет существовать хотя
бы слабое взаимодействие, снимающее вырождение основного
состояния. Тогда нижний терм был бы простым, и энтропия к
8 этом случае равнялась бы нулю. Вообще же мы увидим
а дальнейшем, что атомы газа при очень низких темпера-
температурах подвергаются и другим явлениям вырождения, увели-
увеличивающим энтропию. Все же нельзя полностью исключить.
СТАТИСТИЧЕСКОЕ РАВНОВЕСИЕ КВАНТОВЫХ СОСТОЯНИЙ 217
возможность существования систем, в противоречие с прин-
принципом Нернста, обладающих при абсолютном нуле конечной,
энтропией, хотя до сих пор такие системы неизвестны.
Согласно классической статистике, теплоемкость любой
системы вплоть до абсолютного нуля должна сохранять от-
отличную от нуля величину. Действительно, средняя кинети-
кинетическая энергия, согласно классической теории, пропорцио-
пропорциональна Т, а ее производная по Т, т. е. кинетическая часть
теплоемкости, постоянна. Отсюда также видно, что принцип
Нернста противоречит классической теории. Именно, инте-
интеграл, определяющий энтропию, можно с помощью введения
теплоемкости системы с преобразовать к выражению:
которое при с, все время неравном нулю, обращается в бес-
бесконечность для 7*= 0, так что интеграл не может быть
распространен до нижней границы Г = 0.
На основании принципа Нернста, теплоемкость всех ве-
веществ при абсолютном нуле также должна исчезать. Это,
действительно, имеет место для квантованных систем, как
мы8 например, видели для вращательной части теплоемкости
в ч„ I, раздел 29, и для твердых тел в ч. 11, разделы 6 и 7,
Это следует также из того, что при низких температурах
тепловой энергии, имеющей величину порядка kT,. недоста-
недостаточно для возбуждения высших состояний. Если, однако,
все составные части системы находятся в основном состоянии,
■то ее энергия не зависит от температуры, и теплоемкость
равна нулю, Следует поэтому ожидать, что теплоемкость
при уменьшении температуры тем медленнее приближается
к нулю, чем меньше расстояние между основным термом и
более высокими. Классической статистике соответствует пре»
дельный случай бесконечно близко расположенных термов,
благодаря чему уже небольшого изменения температуры до-
достаточно для возбуждения более высоких состояний, так что
теплоемкость при абсолютном нуле будет сохранять конечное
значение.
2\Яглд°А ft
ГЛ4ВА 11 ;;
КВАНТОВАЯ СТАТИСТИКА ГАЗА
11. Фазовое пространство идеального газа
Рассмотрим теперь квантование движения молекул газа.
,Поа движением мы подразумеваем только поступательное
движение, так как со статистической точки зрения вращение
и внутренние колебания не обладают никакими особенностями.
Мы ограничимся простейшим случаем, считая, что молекуль»
ведут себя как материальные точки, не обладающие вну-
внутренней структурой (идеальный газ). Примем далее, что вли-
влиянием столкновений молекул друг с другом можно прене-
пренебречь и что при соударении со стенками сосуда они
отражаются упругим образом.
Пусть N таких атомов находятся в сосуде с объемом V.
Система имеет 3/V степеней свободы. По закону равномер-
равномерного распределения,, ее средняя кинетическая эьергии равна:
1ГЙЛ=^. E6)
Так как потенциальная энергия отсут'-твует, то E6)
выражает полную энергию газа. Тенлоемксдль а см ом случае
не 4<шисит от температуры
что, как уже было сказано, противоречит принципу Нернста^
Но если, как того требует принцип, теплоемкость при аб-
абсолютном нуле должна исчезать, то классическая предпо-
предпосылка о равномерности распределения энергии неприменима
для достаточно низких температур. Попытаемся поэтому ирий
менить законы квантования и к поступательному движению
молекул.
Первая попытка в этом направлении была сделана в
1913 г. Тетроде. Он принял, что рбьем ячейки фазового
пространства постоянен и равен hs {й — постояаная Планка).
КВАНТОВАЯ СТАТИСТИКА ГАЗА 219
При помощи условий квантования можно дополнительно
обосновать это предположение. Если счи.ать сосуд ^кубом.
е длиной ребра а, то, поскольку мы пренебрегаем соударе-
соударениями, движение молекул состоит в их непрерывном полете
между стенками туда и обратно. Это движение квантуется,
согласно волновой механике, таким образом, что энергия
(кинетическая энергия, так как потенциальная равна нулю)
может принимать только значения:
1И + 4+'Ф. <58>
где л,, л2, п% — «елые положительные (включая нуль) числа.
Если а представляет собой микроскопическую велич ну,
энергетические уровни следуют друг за другом так близко,
что практически образуют непрерывный спектр. Число энер-
энергетических термов между L и L +- dL вычисляется, если
каждому из этих состояний сопоставить в декартовой системе
координат точку с целыми положительными координатами
л1 по п.А. Эти точки образуют простую куби 1ескую решетку
с длиной реб а 1. Все они лежат в положительном октанте.
Для состояний с энергией между £ и L-\- dL спраьедливы
неравенства:
т. е. они помешаются в объеме между двумя шаровым»
поверхностями с радиусами:
2VIJ
При достаточно большом L их число dQ численно равно
объему, лежащему между шаровыми поверхностями в поло-
положительном октанте:
,L.
220 ГЛАВА И
Так как а3= V, то число состояний, кинетическая энер-
энергия которых лежит в пределах dL, равно: t
E9)
С другой стороны:
%п (Р'импУЛьС =
а, следовательно, состояниям с кинетической энергией меж-
между L и L-\-dL соответствуют величины импульсов между
р = КЗ/пГ и
р -f- dp = J/2/ra (L 4- ^^) = K^raZ -f |/^
Они содержатся в части пространства импульсов, ограни-"
ченной двумя шаровыми поверхностями с радиусами р к
p-\-dp, объем которой da равен;
Использовав это соотношение и соотношение E9), по-
получим для плотности распределения состояний в простран-
пространстве импульсов выражение:
dQ__V ;
Так как элементу dw пространства импульсов соответствует
элемент объема dx= Vd<a в фазовом пространстве, то каж-
каждому состоянию в фазовом пространстве соответствует зле-
мент объема, равный h3, Действительно,
dQ dQ
Следует отметить связь этого обстоятельства с принца-
лом неопределенности Гейзенберга. Ради простоты, покажем
ее на примере системы с одной степенью свободы (напри-
(например, для движения материальной точки вдоль прямой). Со-
Согласно Гейзенбергу, между достижимой точностью Л<7 и ^Р
КВАНТОВАЯ СТАТИСТИКА ГАЗА 221
в определении координат и импульса точки существует со-
соотношение:
Точка в фазовом пространстве, изображающая состояние
этой системы, имеет, следовательно, область неопределен-
неопределенности порядка h. В трехмерном случае этому соответствует
область с объемом порядка /г3. Наше разделение фазового
пространства на ячейки сделано, следовательно, таким обра-
образом, что каждой изображающей точке, несмотря на неопре-
неопределенность ее координат, соответствует совершенно опреде-
определенная ячейка. Дальнейшее деление фазового пространства,
или, что то же самое, задание положения изображающей
точки внутри ячейки, не имело бы никакого смысла. Про-
Простое сопоставление изображающей точки с определенной
ячейкой фазового пространства содержит все, что может
быть высказано, согласно квантовой статистике, относительно-
состояния системы.
Благодаря постоянному установлению объема ячейки фа-
фазового пространства, число II возможностей осуществления
данного состояния также становится однозначной величиной.
Следовательно, энтропия идеального газа может быть вы-
вычислена из соотношения Больцмана S = klogH без неопре-
неопределенной постоянной. Однако мы не получим удовлетвори-
удовлетворительного результата при последовательном проведении этого
расчета. Окажется, что энтропия газа при заданных темпе-
температуре и давлении не пропорциональна количеству газа, а
очень быстро возрастает с ростом числа молекул. Благодаря
аестрогости своего вывода Тетроде все же получил правиль-
правильное выражение для энтропии, подтвгржденное позднейшими
теоретическими и экспериментальными исследованиями.
Было сделано немало попыток точно обосновать резуль-
результат Тетроде. Однако почти все они содержат более или
менее ясно выраженные соображения, находящиеся в проти-
противоречии с основными предпосылками статистики Больцмана.
Теперь мы знаем, что иначе и быть не могло, так как ста-
статистика Больцмана неприменима к молекулам газа и должна
г'ыть заменена одной из новых статистик (Возе-Эйнштейна
222 • ГЛАЕА .II
или Ферми). При высокой температуре и малой плотности
газа они приводят к тем же результатам, что и статистика
Болышана. Но наблюдаемые при низких температурах и
больших плотностях „явления вырождения" могут быть объ-
объяснены голько новыми статистиками.
12. ^озтолнная энтропия
Постоянную энтропии газа можно вычислять по способу,
предложенному Штерном, без использования новой стати-
статистики, а исходя из термодинамических соображений. Термо-
Термодинамика позволяет вычислить давление насыщенного пара,
т. е. термодинамическое равновесие между паром и твердой
фазой, с точностью до неопределенной величины, зависящей
©т константы энтропии пара. С другой стороны, равновесие
между паром и твердой фазой можно при известных пред-
предположениях исследовать с помощью статистических еообра-
жеьиЯ и из них определить давление наеы ценного пара. Из
сравнения обоих результатов можно тогда определить посто-
постоянную энтропии.
Сначала мы исследуем статистически равновесие между
парообразной и твердой разами. Предположим, что в объ-
объеме V находится N молекул, внутренние структуры которых
мы здесь не рассматриваем (материальные точки), причем п
из них существуют в виде па^а, а остальные {N— п) обра-
образуют твердую фазу.
Чтобы напрасно не усложнять задачу, введем еще неко-
некоторые упрощения. Положим:
a) Обьемом твердой фазы можно пренебречь по срав-
сравнению с V.
b) Молекулы в твердой фазе так жестко связаны друг
с другом, что тепловые колебания при рассматриваемой тем»
яературе ие возбуждаются, вследствие чего тепловой энер-
энергией и теплоемкостью твердой фазы можно пренебречь.
c) Для отрыва молекулы от твердой фазы необходимо
определенное количество энергии.
; Для определения статистического равновесия между
обеими фазами нужно вычислить вероятность того, что
КВАНТОВАЯ СТАТИСТИКА ГАЧА 223
я молекул находится в виде пара и (М — п) в твердом состоя-
состоянии. Затем следует найти значение п, для которого эта
вероятность имеет максимум.
Существует большое количество состояний системы, в
которых п. молекул находится в паре и (V — /г) в твердой
фазе. Они различаются способом, которым выбраны п. моле-
молекул лара из общего количества, и тем, как расположены'
остальные {N—п) молекул в решетке твердой фазы. Кроме,
того, их отличают различные возможности квантования по-
поступательного движения (раздел 11), определяющего ско-
скорости отдельных молекул.
Обозначим энергию определенного состояния нашей'
двухфазной системы, состоящей из N молекул, через
где п — число молекул пара; индекс / различает отдельные
квантовые состояния, относящиеся к распределению in, N— я),
молекул между фазами. Согласно закону Болышана, веоо-
жтность состояний с энергией и/а, пропорциональна величине
. * а/— " »
а суздмяоная веооятность всех состояний, пли котооых п мо-
яекул ийач>ди1ся в газовой фазе, проп^рциоиальма величине
^=S^y = Se «\ F0>
Необходимо вычислить величину Рп и найти, при каком
значении п она максимальна.
Для выбора /г молекул, образующих пар, из общего
числа N существует | ) равноценных возможностей. Рас-
Распределение остальных (А^— а) молекул по узлам решетки
твердой фазы возможно {N—я)! различными способами.
Согласно предположению Ь), этим (N—п)! возможностям-
соответствует одно и то же квантовое состояние твердой
фазы, так как при рассматриваемой температуре биле
224 ГЛАВА II
высокие состояния не могут быть заняты. Каждой из молекул
пара мы, на основании E8), должны приписать одно из раз-
разрешенных значений кинетической энергий поступательного
движения (на молекулу):
так что полная кинетическая энергия я молекул пара ока-
оказывается раъной
2 i-Нг
1=1
где Lrt — кинетическая энергия i-той молекулы в газовой
фазе. Прибавив к этому выражению энергию nw, необходи-
необходимую, согласно предположения с), для перевода п молекул
из твердой фазы в пар, мы получим полную энергию со-
состояния (л/) (энергия твердой фазы, согласно предположе-
предположению Ь), равна нулю):
Это состояние ln j (/v—n\! = —^-кратно вырождено, со-
ответственно f i возможностям выоора молекул в газооб-
газообразной фазе и {./V—п) I возможностям распределения молекул
а твердой фазе. Выражение F0) принимает вид:
Этот расчет вероятности справедлив, только если молекулы
пара могут независимо друг от друга распределяться по
различным квантовым состояниям поступательного движения.
Это, характерное для статистики Болыхмана, условие отсут-
отсутствует в новой статистике. Но при достаточно малой плот-
плотности пара оно, по крайней мере в первом приближении,
•шолняётся.
КВАНТОВАЯ СТАТИСТИКА ГА^А 225
Для вычисления суммы в F1) вспомним, что, согласно E9),
число квантовых состояний поступательного движения моле-
молекулы в интервале кинетической энергии от L до L-\-dL
равно
a Q = ~ Bт)*:> VI dL ,
гак что сумма в F1) может быть заменена интегралом
00 £
-^~ Bт)Ч* f ew VI dL. F2)
о
Интегрируя, получаем:
е ~#f~ == p {2nmkTyf*, F3)
а {61} переходит в
Вместо того, чтобы определять максимум Paf мы можем
искать максимум logPa. С помощью упрощенной формулы
Стерлинга
получаем:
i
logn — ^i log
В точке максимума этого выражения его производная по а
равна нулю;
1 _ log п -- — -j~ log -—р-2 1=0-
Отсюда для плотности насыщенного пара, находящегося
при температуре Т в равновесии с твердой фазой, получаем:
i5 Эирико Ферми
226 ГЛАВА II
Эта формула сама по себе мало интересна, так как она
выведена § предположениях, являющихся в действительно-
действительности несправедливыми [предположение Ь)]. Она удобна, од-
однако, для сопоставления с результатом соответствующего
термодинамического рассмотрения и получения отсюда по-
постоянной энтропии.
Выведем теперь термодинамическую формулу. По предпо-
предположению Ь), внутренняя энергия и теплоемкость твердой
фазы равны нулю. Согласно принципу Нернста, должны быть
равны нулю также ее энтропия и свободная энергия. Сум-
Суммарная свободная энергия F системы состоит тогда только
из свободной энергии газовой фазы, слагающейся из работы
выхода nw и энергии теплового движения 3j2nkT. Так как
энтропия «S является функцией V, п и T[S=S(V, n, Т)]г
то свободная энергия равна выражению:
F = n (w-\-~kT) — TS(n, V, Т).
В термодинамическом равновесии свободная энергия имеет
минимум, т. е,
дп ' 2 дп
Подставив в это равенство w из F5), получим:
dS , , I ЗА , . 1 V B%fnkTf/"
^~= klogn + Aklog
Интегрированием по п получаем энтропию. Постоянная ин-
интегрирования, зависящая от V и Т, находится из условия,
что для п = 0 (т. е. когда молекул газа вообще нет) эн-
энтропия 5 равна нулю. Окончательная формула для S примет
тогда вид:
t.1 1 ЗА , ,, V{2T.mkTp^ ,
klogn-\- T-j-/felog }0 jdn =
=== — an (log n — 1) + -7Г- -r ktl l°S ' hS—— = F6/
= кп j -j log T — log v -f- log ы>
КВАНТОВАЯ СТАТИСТИКА ГАЗА 227
Равенство F6) определяет энтропию газа, молекулы ко-
которого могут рассматриваться как материальные точки. Это
условие удовлетворительно выполняется для одноатомных
газов в случае, если температура настолько низка, что все
молекулы находятся в основном состоянии, которое не дол-
должно быть при этом вырождено. Если имеется ^-кратное
вырождение, равенство F6), как легко вычислить, перехо-
переходит в следующее:
S — nk ^—logr— logpr-flog j~z—j. F7)
• Постоянная энтропия газа, состоящего из двухатомных
молекул, была нами вычислена с помощью выведенной в
ч. I (раздел 31) формулы.
13. Тепловое ионизационное равновесие и тепловая
электронная эмиссия
Выведенное в предыдущем разделе выражение для по-
постоянной энтропии имеет фундаментальное значение для тер-
термодинамики химических реакций, процессов испарения и
многих других явлений. Мы рассмотрим два физически наи-
наиболее интересных процесса, именно, диссоциацию атомов на
ноны и электроны при высоких температурах и электронную
эмиссию накаленных металлических поверхностей.
Исследуем сначала диссоциационное равновесие одноатом-
одноатомного газа с атомами сорта А. При высокой температуре
часть атомов самопроизвольно распадается на ион А + и элек-
электрон е, Происходит своего рода химическая реакция, при-
притекающая по схеме:
Сяедует определить число таким образом диссоциирующих
атомов, в зависимости от температуры. Положим, что в со-
сосуде с объемом 1 сначала имеем п атомов. Пусть ,:степен!>
22Я ГЛАВА И
ионизации" при определенной температуре равна х. Тогда ах
есть число диссоциировавших атомов. Таким образом, всего
в сосуде находится я И—х) нейтральных атомов А, пх
ионов Д~:" и пх электронов. Следовательно, мы имеем дело
со смесью трех газов, газа нейтральных атомов, газа ионов
и электронного газа. Между этими тремя компонентами ка;
шей системы существует равновесие, когда свободная энер-
энергия F=W—TS имеет минимум.
Энергия W системы слагается из кинетической энергии
всех частиц и энергии ионизации пх диссоциировавших ато-
атомов. Каждая из п{1—х) -j- пх -j- пх = п A -j- x) частиц об-
обладает средней кинетической энергией 3/2 kT. Полная ки-
кинетическая энергия поэтому равна:
~nkT(l-\~x).
Работа ионизации атома равна w. Тогда энергия иониза-
ионизации пх частиц равна nxw, а полная энергия системы W
имеет вид:
W = | п. kT A + х) -+- max.
Энтропия газовой смеси, как известно, равна сумме от-
отдельных энтропии. Обозначим через тА массу атома, прак-
практически совпадающую с массой иона, через т массу элек-
электрона и через gA и gj статистические веса основных состоя-
состояний атомов и, соответственно, ионов. Так как статистиче-
статистический вес электронов, соответственно двум возможным ори-
ентациям спина, равен 2, то для полной энтропии получим
выражение:
= ak{l -*) {| tog7--Iog*(l -jc
КВАНТОВАЯ СТАТИСТИКА ГАЗА 229
Отсюда свободная энергия равна:
nkT (I — х) log
***£}■
Степень ионизации л; в термодинамическом равновесии
при температуре Т получается из условия, что свободная
энергия в зависимости от х имеет в равновесии .минимум,
т, е. производная от F по х равна нулю:
£=••
Отсюда
Из этого уравнения и определяется степень ионизации д;.
Уравнение F8) можно рассматривать так же, как „закон
действующих масс". Действительно, можно записать левую
пх
часть уравнения в виде пх —■. , т. е. как произведение
из концентраций ионов на концентрацию электронов, делен-
деленное на концентрацию атомов, а правую часть рассматривать
как константу равновесия.
В качестве численного примера определим тепловую
ионизацию паров натрия. Потенциал ионизации натрия равен
5,12 V, работа ионизации, следовательно, равна 8,15- Ш-
эргов. Основное состояние "Si^ у Na двукратное, £"д —2.
Основное состояние подобного благородному газу иона Na + —
простое, gj=\. Подставив в уравнение F8) эти величина
и заменив экспоненту степенью десяти, мы получим
„,-2 3, 26000
Y^~ = 2,42 • 10» • Т и. 10~г-.
При Т-.-- 4 000° (температура кратера вольтовой дуги):
= 1,94-101*.
230 ~ ••■••.' ГЛАВА II
Если принять я = 3,5.1013, что при обыкновенной тем-
пературе соответствует давлению 1 мм Hg, то -т~—==
= 5,5-10-s и х = 0,071. Степень диссоциации при данных
условиях составляет, следовательно, около 7°/0.
Индийский физик М. Н. Саха, развивший эту теорию,
применил ее, в частности, к атмосфере звезд.
Рассмотрим еще одно применение формулы F7), именно
расчет термоэлектронной эмиссии, металлов.
При повышенной температуре все металлические поверх-
поверхности испускают электроны. В полости внутри металлического
блока при температуре Т, вследствие электронной эмиссии
стенок, образуется „электронный газ*. Плотность этого газа
не может возрастать безгранично, так как, наряду с непре-
непрерывным испусканием электронов стенками, часть падающих
из объема на стенки электронов снова поглощается. В теп-
тепловом равновесии количество испускаемых в единицу времени
электронов должно быть равно количеству поглощаемых. Вы-
Вычислим соответствующую этому плотность электронного газа.
Пусть полость имеет объем 1 и в состоянии равновесия
содержит п электронов. Вычислим снова свободную энергию
нашей системы (металл -J- электронный газ) и будем искать
значение п, при котором свободная энергия F имеет мини-
минимум. Энергия F слагается из свободных энергий металла
и электронного газа. Свободная энергия металла не зависит
от п, так как, как известно, электроны в металле при обыч-
обычной температуре не влияют на теплоемкость, а следова-
следовательно, на свободную энергию и на энтропию. Потеря п.
электронов не скажется, таким образом, на свободной энер-
энергии. Поэтому мы можем не учитывать свободной энергии
металла и при определении минимума свободной энергий
ограничиваться рассмотрением электронного газа.
Энергия U электронного газа слагается из кинетической
энергии п электронов 3/2 nkT и суммы работ выхода nwt
если w означает работу, которую нужно совершить, чтобы
вырвать один электрон из металла:
КВАНТОВАЯ СТАТИСТИКА ГАЗА. 231
Энтропия электронного газа получается из F7) при V=l
я g"= 2. Окончательно свободная энергия равна: ,-,-г
F — U — TS = nw -f 4 nkT — nkT fj log T — .'■ :
Условие равновесия шэи температуре Т гласит;
откуда:
о=w+4kT—kT DIogT
В равновесии для п получаем выражение;
Единственной материальной константой в этой формуле
является работа выхода w, которая может быть определена
независимо от явления термоэмиссии из длинноволновой
границы фотоэффекта.
Большее практическое значение, чем плотность а элек-
электронного газа, находящегося в равновесии с горячей метал-
металлической поверхностью, имеет число N электронов, выходя-
выходящих из такой поверхности в единицу времени. Оно непо-
непосредственно определяет ток насыщения накаленного катода...
Порядок величины N при известном п может быть оце-
оценен следующим образом. Вследствие теплового движения
электронного газа металлическая поверхность подвергается
непрерывной бомбардировке электронами. Число таких. столк-
столкновений в единицу времени на единицу поверхности, со-
дла/^io кинетической теории газов, равно ' . ' ".
' ' til/ =— » ... г.
232 ГЛАВА 11
При ударе часть электронов отражается, другая часть
проникает в металл. Если вероятность того, что Электрой
при ударе о поверхность металла абсорбируется, равна #.
то в единицу времени через единицу поверхности в металл
проникнет
электронов. Так как в состоянии равновесия столько же элек-
электронов будет испущено металлом, то после подстановки
выше найденного значения п получим следующее выражение
„для N:
И = 2»^ Т* ■ е W = N.
Величинч О здесь еще неизвестна. Ее можно оценить только
при определенных предположениях относительно хода потен-
потенциала у njeepxHOCTH металла, но мы этим заниматься не бу-
будем. Для оценки порядка величины N можно принять д за
единицу.
14. Новая статистика
Выведенное в разделе 1 обобщение закона распределения
Больцмана на квантованные системы пригодно только для
совокупности однородных независящих друг от друга систем.
Примером может служить газ, состоящий из однородных
удаленных друг от друга атомов, распределенных по раз-
различным внутренним квантовым состояниям.
Для статистического распределения энергии поступатель-
поступательного движения по атомам газа этот закон не справедлив/
Рассмотрим, например, газ, состоящий из однородных мате-
материальных точек, между которыми не действуют никакие силы
(идеальный газ). Если в сосуде содержится только одна мо-
молекула этого газа, она .может находиться в любом квантовом
состоянии поступательного движения (раздел 11); ее энергия*
имеет одно из значений ~
Lv L2f L3, . . ., Lr F9)-
формулы E8).
КВАНТОРАЯ СТАТИСТИКА ГАЧА - . . 233
Если в сосуде содержатся две молекулы, каждая из них
может находиться в любом из энергетических уровней F9).
Однако, хотя, согласно предположению, молекулы не взаимо-
взаимодействуют друг с другом, мы не можем отсюда заключись,
что они независимы друг от друга. Если, например, на них
распространяется принцип запрета Паули, то они взаимодей-
взаимодействуют друг с другом, т. е. обе не могут находиться в одном
состоянии. Аналогично, N молекул, если бы на них распро-
распространялся принцип Паули, должны были бы занять N раз-
' личных энергетических уровней. Тот факт, что только два
электрона в атоме могут находиться в /С-оболочке, тоже
связан не с механическими силами, а просто с выполнением
принципа Паули.
Если для совокупности частиц справедлив принцип Па-
Паули, т. е., если в каждом состоянии может находиться толь-
только одна частица, больцмановская статистика должна быть
заменена новой статистикой Ферми. Мы рассмотрим позже
другого рода зависимость между состояниями движения,
требующую применения статистики, разработанной Бозе и
Эйнштейном.
Существование различных возможностей распределения
молекул газа и причины различий между классической ста-
статистикой Больцмана и новыми статистиками с точки зрения
квантовой механики было рассмотрено Дираком. Он вывел
при этом новым путем статистику Ферми.
Обозначим через лг, координаты первой молекулы (лг,
есть сокращенное обозначение х^у^), через х2 — второй
и т. д. Пусть
суть собственные функции, соответствующие энергетическим
уровням F9). Если первая молекула находится в квантовом
состоянии гг, ее собственная функция запишется как фГ| (дг,).
Если первая молекула находится в состоянии гх, вторая
в состоянии г2 и т. д., то, поскольку, согласно предполо-
предположению, между молекулами не действуют силы, полная функ-
234 ГЛАВА И
ция системы будет равна произведению собственных функций
отдельных молекул
Соответствующая полная энергия раввд
Так как все молекулы одинаковы., то в энергетических
уровнях проявляется обменное или резонансное вырождение.
Получится то же значение энергии G2), если любым другим
образом распределить N молекул по состояниям г,, г2,..., rv.
Если мы обозначим одну ; из N1 перестановок, которые можно
осуществить с индексами 1, 2,..., N, через Я и числа,
в которые переходят 1, 2,..., N с помощью перестановки Pt
через Р\, Р2,..., PN, то собственному значению G2) бу-
будет соответствовать N1 собственных функций вида
Ч'я= Фл (*jn) Фгя.(*и)• • • Фглг(*лу)- (Щ
Если все состояния rv r2..., г^ различны, то и все N1
собственных функций G3) отличны друг от друга. Следо-
Следовательно, состояние G2) также ЛП-кратно- вырождено. Если,
наоборот, мы примем, что некоторые из индексов rv г2,..., г'к
одинаковы, т. е. что принцип Паули неприменим, то неко-
некоторые из собственных функций G3) совпадут друг с другом.
Степень вырождения будет, следовательно^ меньше. В этом
случае мы можем разбить N индексов г1г г2,..., rN на
s групп равных между собой индексов Nx, N2,..., Ns, так
что A/j -j- N2 -f-. .. -j- Ns = N. Каждое из чисел Nv Д/2,
, . ., Ns может быть равно и единице. Число отличных друг
от друга собственных функций G3) равно тогда числу воз-
возможных распределений N индексов по группам Nv No,...,
Ns, т. е. хэ-авыр*
Каждая линейная комбинация вырожденных собственных
функций G3) также является собственной функцией, соответ-
соответствующей собственному значению G2). Из этих линейных
КВАНТОВАЯ СТАТИСТИКА ГАЗА
235
комбинаций, различающихся характером симметрии по отно-
отношению к перестановке координат частиц, физический смысл
лмеют симметричные и антисимметричные. Симметричная
собственная функция не меняется при любой перестановке
координат частиц; антисимметричная функция при переста-
перестановке координат частиц по абсолютной величине также ос-
остается неизменной, а знак ее зависит от числа перестановок:
если производится четное число транспозиций (четная пере-
перестановка), он остается прежним, а если число транспозиций
нечетное (нечетная перестановка), знак меняется.
Симметричная линейная комбинация просто равна сумме
.всех ЛЛ собственных функций G3);
Антисимметричная комбинация равна
G6)
иричем для четных перестановок Р следует брать знак -j-,
а для нечетных —. Можно Ф'ант написать также в форме
детерминанта:
Фл (хд Фг: (-£2). ■ . фг, (хм)
гр =
G7)
В природе встречаются частицы, собственные функции
которых всегда антисимметричны, а также частицы, соб-
собственные функции которых всегда симметричны. К первым
относятся, например, электрон и протон, ко вторым а ча-
частицы и световые кванты, поскольку их можно рассматривать
как частицы.
Частицы системы, собственная функция которой антисим-
антисимметрична, подчиняются принципу Паули. Это видно непо-
непосредственно из G7). Действительно, когда состояние запол-
заполнено дважды, два из индексов ги..., rN совпадают. Тогда
236 '■' ГЛАВА tl
две строки детерминанта G7) одинаковы, и последний равен
нулю. Когда собственная функция симметрична, справедлива
статистика Бозе-Эйнштейна.
Мы должны теперь исследовать, какие состояния возможьи
для системы, подчиняющейся статистике Ферми или стати-
статистике Бозе-Эйнштейна. Как мы увидим, если бы система
подчинялась статистике Больцмана, каждой из Nt собствен-
собственных функций G3) соответствовало бы разрешенное квантовое
состояние.
Состояние газа полностью описывается заданием чисел
заполнения отдельных энергетических уровней
Nv N9, М,,..., Nr,...; (Nt-\-Ns-\-Nt-t-...+Nr-\-
-f...=/V) G8)
ЛР, из N индексов rv r2, r3,..., rN равны 1, N2 из них
равны 2,..., Nr из них равны г и т. д.
В случаэ статистики Бозе-Эйншгейна G8) представляет
собой простое квантовое состояние, осуществимое только
одним способом, так как имеется только одна симметричная
собственная функция G5) системы из N молекул.
В случае статистики Ферми ни одно из чисел заполнения
не может быть больше 1. Действительно, если одно из чи-
чисел Nr больше единицы, антисимметричная собственная функ-
функция G7) равна нулю, так что состояние G8) не соответ-
соответствует собственной функции. Следовательно, Nr могут при-
принимать только значения 0 и 1. Таким образом G8) пред-
представляет собой простое состояние, осуществляемое только
одним способом.
Наконец, в случае, в действительности не встречающемся,
когда всем собственным функциям G3) соответствуют кван-
квантовые состояния G8), будем иметь, что, согласно G4), число
этих состояний
N\
Nil Ntl...
совпадает с числом способов осуществления этого распреде-
распределения по статистике Болышана.
Покажем различия между статистиками на простом чис-
численном примере. Примем, что система состоит из двух оди-
КВАНТОВАЯ СГАГИПГИКЛ ГАЗА
237
маковых молекул, причем каждая из них может находиться
з одном из трех квантовых состояний поступательного дви-
движения. На фиг, 53 они изображены схематически как ле-
лежащие рядом квадратные ячейки. Сумма чисел запольения
А/,, Л/2 и Ns этих квантовых состояний равна 2. Имеется
в возможностей распределить две молекулы по трем кван-
квантовым состояниям:
B00), @20), @02), @11), A01), (ПО).
Для случая статистики Больцмана молекулы ка фиг. 53
обозначены двумя различными буквами а и д, так как
два состояния, получаемые
одно из другого переста-
перестановкой местами а и Ь в
случае, когда последние
расположены в двух раз-
разных ячейках, различны.
Полная же равноценность
обеих молекул в новой
статистике, их „нераз-
личаемость" выражается
здесь тем, что обе моле-
молекулы обозначаются одним
символом а.
B00}
(ого)
@02)
(Oil)
A01)
(по)
ЭА.
15. Статистика Бозе- Фиг. 53. Возможные распределе-
Эйнштейна ния ДВУХ частиц по трел кван-
квантовым состояниям в различны*
Как мы видели, в ста- статистиках. Состояния изобра-
тистике Бозе-Эйнштейна жены квадратными клетками.
распределение молекул
полностью определяется заданием чисел заполнения от-
отдельных квантоьых состояний поступательного движения.
Действительно, так как частицы принципиально неразли-
чаемы, каждое такое распределение осуществимо един-
единственным образом. Оно представляет собой, таким об-
образом, простое состояние, имеющее статистический вес 1.
Рассчитаем закон распределения газа, состоящего из молекул,
подчиняющихся статистике Бозе-Эйнштейна,
238 ГЛАВА II
Число состояний молекулы поступательного движенияу
при которых кинетическая энергия имеет значения между
L и L-\-dL, получается из E9). Чем больше объем сосуда,,
тем гуще лежат энергетические уровни. Если сосуд имеет
микроскопические размеры, уровни лежат так густо, что их
распределение можно рассматривать как непрерывное.
Простейший способ определения статистического распре-
распределения заключается в следующем. Ряд энергетических зна-
значений L, которые может прини-
"С*)С*)Н\ I Г">О ! in мать отдельная молекула, под-
kJ kJ vj j <J О j | w разделяется на небольшие об-
Фчг 54 ласти от 0 до Lv от /., до
Z.2..., вообще от /.„_! до Lal
Отдельные области могут быть
не одинаковы по величине, однако они должны быть
малы по сравнению со средней энергией молекулы и, тем
не менее, содержать большое число квантовых состояний
Поступательного движения, которым соответствует достаточно
много молекул. Пусть область между Ьг_г и Lr содержит Qr
квантовых состояний. Так как Lr —- Lr_x можно рассматривать
как дифференциал, согласно E9), Qr с достаточной точно-
точностью определяется по формуле:
Qr = ^ B,п) 'VLr (Lr - Lr_x). G9)
Рассмотрим произвольное распределение N- молекул, при
котором п1 молекул имеют энергию в пределах между 0 и
/.,, п2 молекул — в пределах между Ьг и L2, вообще пг мо-
молекул — энергию в пределах между Lr_l и Lr, и исследуем,,
прежде всего, сколькими способами может быть осуще-
осуществлено это распределение
/VVV ••«-••• С80)
Для этого определим число возможностей распределения
пт молекул по Q, квантовым состояниям в области от Lr_l
до Lr. Для частиц со статистикой Бозе-Эйнштейна каждое
решение уравнения
■''■• х1 '~\-х., -f- . . . -j- <Qr - ", if,- = 0, 1, 2,. . . j . {81}
КВАНТОВАЯ СТАТИСТИКА ГАЗА 239
представляет такую возможность, так как мы можем рас-
рассматривать xt непосредственно как число заполнения г'-того
квантового состояния в области Lr_, до L,.
Уравнение (81) имеет
<Пг±£г-}>1 ,82)
яг!«?г-1I *° ;
решений ХК Число II возможностей осуществления распреде-
распределения (80) равно произведению отдельных вероятностей
П —
—1I {Пг-\-Ог— 1I
Распределение, для которого II имеет наибольшую величину,
является наивероятнейшим.
Числа заполнения пг зависят друг от друга, так как-
полное число N и полная энергия W молекул постоянны:
л,-Ьла+ . ..+ n,-\-...=N ■ (84)
я,/., 4" «Л + . . . + «А + . • • = W. (85)
{Вследствие малости отдельных областей Lr — £r_i, всем
содержащимся в них молекулам приписывается энергия Lr.)
Так как, согласно предположению, пг и Qr большие
числа, то мы можем снова применить приближенную формулу
Стирлинга log/г! = п (log/г—1) и пренебречь единицей по
сравнению с Qr, Таким образом, получим:
1) Это можно показать следующим образом. На фиг. 54 изо-
изображено пг кружков (яг = 6) и Qr—1 штрихов (<2г = 4)в произ-
произвольной последовательности. Каждой из (nr-\-Qr—1) перестано-
перестановок этих (nr-j-Qr—1) знаков соответствует решение уравнения
(81), если принять, что хг равно числу кружков слева от первого
штриха, х:2 равно числу кружков между первым и вторым штри-
штрихами ... и, наконец, Xq равно числу кружков справа от послед-
последнего штриха. На фигуре дг^ = 3, л-.2 —2, х$ = 0, Хл=1. Однако
не все эти (nr-j-Qr—1)! решений различны, так как перестановки,
в которых меняются местами только кружки или только штрихи,
не меняют расположения знаков. Каждое решение встречается
«сего (Qj.— 1)! пг\ раз, так что число различных возможностей
расположения определяется выражением ('82;.
240
ГЛАВА И
log 11= 2 [(«г
1
«r
— nr log nr
QrlogQr]. (86)
Так как максимум log [I лежит в том же месте, что и
максимум L1, то можем определить последний, приравнивая
нулю производную от log II по пг. Условия (84) и (85) мы
учтем вычитанием из (86) выражений а 2 пг и Р 2 пгК>
где а. и р не зависят от «г и вначале являются неопреде-
неопределенными постоянными. Получившееся выражение отличается
от log 51 только независящими от пг членами aN и [J1F
и поэтому имеет те же максимальные свойства. Положение
максимума определяется уравнением
Отсюда, после подстановки вместо а новой постоянной
.4 = еа, находим:
°г
п. =
_1
(87)
Так как обе постоянные А -и $ определяют из условий
(84) и (85), наша задача тем самым решена.
Из (87) определяется также среднее заполнение кванто-
квантового состояния Qr в области между Ьт_л и Lr (плотность
ваполнения). Мы получим, если опустим индекс г:
t
(88)
Выражения (87) и (88) отличаются от соответствуюащх
выражений статистики Больцмана только членом — 1 в зна-
знаменателе. Для очень больших L, при которых AePL очень
велико, можно пренебречь 1, так что (88) после подста-
подстановки
о— 1
kT
(89)
непосредственно иерехиднт в зикчш
КВАНТОВАЯ СТАТИСТИКА ГАЗА 241
Так как р есть константа, независящая от L, (89) должно
быть справедливо всегда и, следовательно, выражения (87)
и (88) можно записать в виде:
пг = —^—; р = _11_. (90)
^ 1
АекТ — 1 AekT— 1
Постоянная А выбирается таким образом, чтобы сумма
л (84) была равна полному числу молекул N. '
Другой путь к определению [J заключается в вычислении
энтропии S = klogll с помощью уравнений (86) и (87) и
энергии W на основе (85) и (87) и в использовании термо-
термодинамического соотношения
± — ?S- (91»
T~dW K '
что также приводит к выражению (89).
16. Эйнштейновское вырождение газа
Так как при выводе функций распределения (90) мы
совсем не использовали формул G9) и E9), то (90) спра-
справедливо независимо от них.
Исследуем свойства газа, подчиняющегося статистике
Бозе-Эйнштейна, для которого, помимо (90), справедливо
соотношение E9). Если мы в (90) вместо р напишем -т-^
и подставим dQ из E9), то для числа dn молекул с энер-
энергией между L и L-\-dL получится выражение:
, dQ '2кУ<2т)> VldL
dn = —j = p -jt
AekT — 1 AekT — 1
Это соотношение представляет собой закон распределе-
распределения скоростей в статистике Бозе-Эйнштейна. Оно соответ-
соответствует закону Максвелла в статистике Больцмана и пере-
переходит в него при высоких температурах и малых плотно-
16 Энрико Ферми
242 ГЛАВА II
стях газа, т. е. когда можно пренебречь — 1 по сравнению
с AeLlkl.
Константа А определяется таким образом, чтобы полное
число милекул равнялись N:
N\dn
\dn= -~-—z . (93)
о AkT 1
о AekT—l
Если, в частности, А^> 1, отклонения функции распределе-
распределения (92) от закона Максвелла малы, и эйнштейновский газ
ведет себя подобно идеальному. Мы можем разложить
интеграл (93) в ряд по степеням —
/л.
/V '2-т»7У'* Г 1_. 1 , "I (9^
V ля<* L 2 '"А ЫА* J
и для А ^> 1 оборвать его на втором члене. Решая полу-
получившееся уравнение относительно А и пренебрегая -^ по
сравнению с 1, получаем:
Так как каждая из dn молекул в (92) обладает энер-
энергией L, полная энергия получится интегрированием:
**, . (96)
о Л^*г—1
Этот интеграл также разложим в ряд по степеням —г :
2 Ah? L ' 21'A * 6 'M2 ^^ J 7
Подставляя Л из (95),, получаем приближенное значение W;
КВАНТОВАЯ СТАТИСТИКА ГАЗА 243
В первом приближении энергия равна 3/2 NkT, как и
в классической статистике. Отклонения от классического
закона пропорциональны второму члену в скобках выраже-
выражения (98), так называемому „параметру вырождения" £): .
Л Nh3L- (СО)
D возрастает с ростом плотности газа р- и убывает с тем-
температурой. D тем больше, чем меньше молекулярный вес
газа.
Из (98) можно с помощью общего соотношения: между
давлением Р и кинетической энергией поступательного дни-,
жепия W
\W A00)
без труда вывести уравнение состояния газа
= NkT\\ jr—N-- -4-...1. A01)
В первом приближении получается снова классическое
уравнение идеального газа PVz=.NkT. Если "имеётсй вы-!
рождение, давление падает ниже классического значения.' '
Для обычных газов рассмотренные явления выр ждения1
очень малы и заслоняются дру1ими отклонениями от газо-
газового уравнения, происходящими из-за наличия сил Ван-дер-
Ваальса и из-за коне ных размеров молекул. Наибольшего,
отклонения за счет вырождения следует ожидать у гелия,,
вследствие его малого атомного веса и низкой температуры;
кипения. Так как гелий подчиняется статистике Бозе-Эйнг
штейиа, вырождение может Сыть подсчитано по формуле
A01). Для Г = 4°К и гг = Ю21 параметр вырождения
£) = 0,С8. Соответствующее отклонение давления в/в°/в
должно было бы наблюдаться, если бы оно не маскировав
лось другими упомянутыми отклонениями. ; .
16*
244
17. Еозевский газ световых квантов
^
Гораздо показательнее, чем вырождение газа, является
применение статистики Бозе-Эйнштейна к световым квантам
(фотонам). Оно позволяет получить закон излучения Планка,
который основывается на корпускулярных свойствах свето-
световых квантов.
Энергия L и импульс р светового кванта, как известно,
определяются соотношениями:
L = hv; P = ^. A02)
Элемент объема ^rcp^dp пространства импульсов для
светового кванта с частотой между v и v -4- #у поэтому
равен:
hs
4np*dp = 4тт -j v2*/v.
Если мы примем, что наши световые кванты заключены
в полости с объемом V, то этому элементу объема простран-
пространства импульсов будет соответствовать элемент объема фа-
фазового пространства:
с*
Будем рассматривать световые кванты как молекулы газа
и разделим фазовое пространство на элементарные ячейки
величины А3. Области частот dv соответствует
—„ VWv
с*
ячеек. Так как для каждого светового кванта возможны два
направления поляризации, ячейки следует считать дважды,
и, окончательно, полное число dQ состояний в интервале
частот dyt оказывается равным величине:
Вычислим распределение этих световых квантов по воз-
возможным частотам, пользуясь методом, аналогичным приме-
примененному в разделе 15 для вывода функций распределения
КВАНТОВАЯ СТАТИСТИКА ГАЗА 245
(90). При этом примем, что наш газ световых квантов на-
находится в тепловом равновесии в объеме V и что он под-
подчиняется статистике Бозе-Эйнштейна.
Разделим весь интервал частот между 0 и оо на после-
последовательные малые части:
rfVj, dv2, ..., dvr, . .. A04)
каждая из которых заполнена количеством
пг, п2, .. ., «,, ... A05)
световых квантов. Число П, соответственно П log, возмож-
возможностей осуществления определенного распределения A05)
получается точно таким же образом, как (83), соответ-
соответственно (86), в разделе 15. Нужно, согласно A03), для
газа световых квантов
использовать выражение:
log П = § [(«г + Ф log (лг + Qr) — ■ A07)
— nrlognr— QrlogQr.]
Для наивероятнейшего распределения A05) величины П
и, соответственно, log II имеют наибольшее значение. Мы
приходим снова к условию, что производные от A07) по пг
должны в отдельности равняться нулю. Причем пг здесь
взаимно не независимы, так как они должны удовлетворять
условию, аналогичному (85), выражающему постоянство пол-
полной энергии:
fcixtix + Av8/Xa -(- • • • + h\nr -\- .. . = W. A08)
Для световых квантов не существует условия, соответ-
соответствующего (84) (постоянство числа частиц). В противополож-
противоположность атомам или электронам, число световых квантов может
увеличиваться или уменьшаться.
Чтобы найти наивероятнеишее распределение газа све-
световых квантов или, соотьстств максимум log II, нужно,
246 ГЛАИА II
следовательно, приравнять нулю производные по пг от вы-
выражения 1ое II — $W. Здесь параметр, независящий от пг,
следует определить таким образом, чтобы выполнялось
условие A08):
Отсюда следует:
. : - Яг=^г_1' A09)
• ■' 1
И, если, снова положить р = -г™ (что было обосновано в раз-
разделе 15) и подставить Qr "из A06), то окончательно полу-
получится:
Каждый из «г световых квантов имеет энергию //vr
Полная энергия dW, приходящаяся на интервал частот dv,
равна, следовательно (индекс г опусхаем), выражению:
Если учесть, что
dW= V-s h ,ьт dv.
с3 е^1кТ \
-Tr = u(v, T)dv,
то это выражение совпадает с соотношением Планка B6)
раздела 6.
18. Статистика Фер?ли
Исследуем, наконец, статистические свойства газа, моле-
молекулы которого подчиняются статистике Ферми. В то время
как статистика Бозе-Эйнштейна находит основное примене-
применение при рассмотрении фотонного газа, статистика Ферми
приобрела особенное значение для электронного газа.
В частности, она сделала возможным понимание электри-
электрических свойств металлов, определяемых поведением свобод-
свободных электронов.
КВАНТОВАЯ СТАТИСТИКА ГАЗА 247
При изучении этого вопроса мы можем очень близко
следовать выводу, проведенному в разделе 15 для стати-
статистики Бозе-Эйнштейна. Мы рассматриваем снова сосуд
с объемом V, наполненный N частицами, которые на этот
раз подчиняются статистике Ферми. Примем, что частицы
одноатомиы и, с учетом дальнейшего применения к элек-
электронному газу, что основное состояние g-кратно вырождено
{для электронов, соответственно двум возможным ориента-
циям спина, g= 2).
Снова разделим область значений кинетической энергии
О <^ L <^ оо на последовательные интервалы:
которые должны быть настолько малы, что их можно рас-
рассматривать как дифференциалы. Отдельные интервалы за-
заполнены
пи я2, .. ., пг, ... A10)
частицами. Числа «,, я2, ..., пг, ... должны быть доста-
достаточно большими. Как и раньше, обозначим через Qr число
состояний отдельной молекулы, соответствующих интер-
интервалу dLr. Этому интервалу dL , согласно E9), соответ-
соответствует
ячеек фазового пространства. Вследствие ^-кратного вы-
вырождения, каждой ячейке соответствует g состояний. Таким
образом, получаем:
Qr = ^Bmy»V^dLr. (Ill)
Мы должны прежде всего исследовать, каким образом
распределены пг частиц в интервале энергии dLr no Qr
квантовым состояниям. Так как частицы подчиняются прин-
принципу Паули, в каждом состоянии может находиться не
больше одной частицы. Число возможных распределений
определяется таким образом числом
248 _ ГЛАВА II
различных возможностей для выбора пг заполненных со-
состояний из Qr имеющихся. Число П возможностей осущест-
осуществления распределения (ПО) равно, очевидно, произведению
Н?)B)(£) ' <••*>
Состояния, получающиеся перестановкой частиц, вслед-
вследствие неразличаемости частиц, рассматриваются как тож-
тождественные. Это согласуется с тем, что антисимметричные,
согласно принципу Паули, собственные функции G7) для
двух таких состояний равны или прямо противоположны,
в зависимости от четного или нечетного числа перестановок.
Они различаются между собой не больше, чем на множи-
множитель (— 1), и, следовательно, в смысле квантовой механики,
представляют одно и то же состояние.
Наивероятнейшим распределением является снова такое,
для которого II, и, соответственно, log II имеют максимум.
Вычислив, с помощью приближенной формулы Стирлинга,
отдельные сомножители в A12), получим:
J' I = log Qr! — log nr ! — log (Qr — nr) I =
= Q, log Qr — «r log nr — (Qr — nr) log (Q, — ftr),
и отсюда.
lo^ I1 = S [ Qr 1OJ Q—n, \ognr—(Q—nr)\og{Qr—n,)\ A13)
причем rt, снова должны удовлетворять условиям постоян-
постоянства числа частиц и энергии
Максимум выражения A13) при дополнительных усло-
условиях A14) определяем снова по методу неопределенных
коэфициентов (см. раздел 15), т. е. ищем абсолютный мак-
максимум выражения:
log II — aN— $W.
КВАНТОВАЯ СТАТИСТИКА ГАЗА 249
Параметры а и [J следует определить таким образом,,
чтобы выполнялись условия A14). *
Производные этого выражения по пг должны быть в^
отдельности равны нулю:
a
а если вместо а введем новую постоянную А = е", то по-
получим выражение для пг, аналогичное выражению (87):
J^A15).
4-1
Это выражение с точностью до знака в знаменателе совпа-
совпадает с соответствующим выражением (87) для статистики1
Бозе-Эйнштейна. Так же, как и последнее, оно переходит
в классическую функцию распределения Болышана, когда,,
например, при больших значениях L, можно пренебречь 1
по сравнению с Ae^L. И здесь мы получаем значение $ из--
сравнения обоих законов распределения:
Вследствие независимости величины р от L, это соотноше-
соотношение справедливо не только для больших L, когда оба за-
закона распределения совпадают, но и для любого L. Впрочем,,
то же значение для fj можно получить и способом, изло-
изложенным в конце раздела 15, основанным на чисто термо-
термодинамических соображениях.
Можно поэтому записать A15) в виде:
п ==.—j-Ц' . A16)«
Среднее заполнение состояния — плотность заполнения —
250 плод п
-,р = уу равна (если опустить индекс г) выражению:
Р ——г*г О17)
-я, в соответствии с принципом Паули, всегда меньше
■единицы.
19. Статистические свойства газа Ферм»
Закон распределения энергии получается из A16), если
-мы вместо Q подставим его значение из A11). Число мо-
молекул dN (до сих пор обозначавшееся пг), кинетическая
энергия которых лежит в пределах между L и L -\- dL,
равно:
Этой формулой следует заменить закон распределения
Максвелла, если вместо статистики Больцмана действует
статистика Ферми. Если А очень велико, так что мо/кно
L
пренебречь 1 по сравнению с AekT (малое вырождение), то
•оба закона совпадают.
Величина А определяется из условия, что общее число
.молекул равно N:
ЛГ= dN=~
о АеЯ1 4- 1
■Введем вместо общего числа частиц N в объеме V плот-
плотность
л=^ A19)
т введем в функцию F(A), определяемую интегралом:
A20)
КВАНТОВАЯ СТАТИСТИКА ГАЗА 251
тогда;
N B-mkTI*
v p). A21)
Вычислим из A18) полную энергию W наших N мо-
молекул:
J h3 J АеикТ-\-\
о
где новая функция С? {А) определяется интегралом:
- A23)
о
Средняя кинетическая энергия молекулы L, с учетом
, равна:
Отсюда с помощью A00) можно вычислить давление:
A25)
которое после исключения А переходит в уравнение
состояния.
Раньше чем совершить это исключение, мы приведем
без доказательства некоторые математические свойства функ-
функций F(A) и G(A).
Для А^\ справедливы сходящиеся разложения в ряд:
1 lil.
£? ( Л \ . _ I _^^____ {
?-*Т. J " , "~Т ™" ~ "" i a v ф
А г. -А* о -л- A2{.
G(A}=~ ^—4-^ h...
. А 2'1-А-2 ' Я-/М3 '
252 ГЛАВА И
Малым А соответствуют разложения:
Г
I J
L '
Кроме того, справедливо соотношение:
<™j A28)
С помощью соотношений
6 е£^ 4г A29)
мы вводим третью функцию R (в), которая для О ^> 1
в <;; 1 изображается, соответственно, рядами:
оЬ /» / н9'зт/а , A30)
5-2/з J 3/s ^
Из A29) можно без труда получить, что:
в
(Q) 5 G(A) , 2
С помощью функции R (в) можно дать в другой форме
уравнение состояния газа. Исключая с помощью A29) и
A21) А из A25), получим:
\ №п'а j
Подобным же образом из A24) получается соответствующее
выражение для средней, энергии молекулы:
\ A33)
V 2t i •
КВАНТОВАЯ СТАТИСТИКА ГАЗА
553
В предельном случае малого вырождения (высокая тем-
температура и малая плотность), после подстановки вместо
/?@) первого разложения из A30), эти выражения примут
вид;
p —'
A34)
В первом приближении получается, естественно, клас-
классическое уравнение состояния p = nkT и классический
3
закон равномерного распределения энергии L = -^kT. Когда
наступает вырождение, давление и средняя энергия воз-
возрастают по сравнению с классическими значениями. Однако,
как и в случае статистики Бозе-Эйнштейна, отклонения для
обыкновенных газов очень малы.
С физической точки зрения значительно интереснее
случай сильного вырождения. Он находит себе применение
в теории электронного газа в металле.
Если в случае сильного вырождения (малая температура,
большая плотность) поставим в A32) и A33) второе раз-
разложение из A30), то получатся выражения:
±(_У% | 2%*/зmsisni40T* ■
20 V тс У mg'<* ' 35/э №■ "Т~ * • '
T'2 I A36)
L
40
Отсюда видно, что при абсолютном нуле давление и
средняя кинетическая энергия молекулы нашего газа не
равны нулю. Это не будет казаться удивительным, если мы
примем во внимание, что вообще в квантованных системах
и в состоянии с наименьшей энергией, соответствующем
абсолютному нулю, частицы не находятся в покое. Напри-
Например, электрон в атоме в основном состоянии обладает зна-
значительной скоростью. В следующем разделе мы рассмотрим
простой способ для обнаружения существования конечного
254 ГЛАВА II
давления и конечного значения кинетической энергии при.
абсолютном»нуле.
Степень вырождения здесь также характеризуется зна-
значением величины D, которую мы назовем »параметром вы-
вырождения "
£> = ^--. {137>
BkT!*
Если D<<*1, то, как следует из A34), вырождение
мало, и давление и кинетическая энергия имеют приблизи-
приблизительно классические значения. Если, наоборот, D^>\, то
газ сильно вырожден и, согласно A35) и A36), Р и L
имеют значения такие же, как при Т=0. Для обычных
газов, при практически осуществимых условиях, параметр
вы, о бдения очень мал. Однако для электронного газа,,
вследствие малой массы и высокой концентрации (например^
в металлах), параметр вырождения может достигать больших
значений.
Если число „свободных" электронов в металле порядка
числа атомов, что, например, безусловно правдоподобно для
металлов группы меди и щелочных, концентрация электрон-
электронного газа имеет величину порядка 1022—10г3. Для серебра,,
например,
Тогда из A37) (взяв g=2, вследствие двух возможных
ориентации спина), при Т = 300° К (комнатная темпера-
температура), параметр вырождения D равен:
D = 2 330.
Следовательно, D при этих условиях велико в сравне-
сравнении с еД1 ницей; электронный газ сильно вырожден.
Для вырожденного (одноа томного) газа молекулярная
теплоемкость имеет не классическое значение (cv^=-^-k ),
а меньшее. При сильном вырождении, согласно A36):
КВАНТОВАЯ СТАТИСТИКА TAcSA 2M
При абсолютном нуле она, в согласии с принципа Нернста,.
равна нулю и, в первом приближении, возрастает пропор-
пропорционально температуре. Для электронного газа, вследствие
малости массы электрона, множитель пропорциональности
в A38) очень мал. Кроме того, поскольку плотность элек-
электронов металла п очень велика, составляющей теплоемкости
металла, обязанной свободным электронам, и при обычных,
температурах можно пренебречь. Для серебра, например,
cv составляет только 1 60 классического значения 3,2 k
на электрон. Эти явления вырождения являются, следова-
следовательно, причиной того, что электроны в металле не вносят
в удельную теплоемкость доли, соответствующей закону
равномерного распределения.
С помощью принципа Нернста вычислим энтропию нашего
вырожденного газа. Допустим, что газ нагревается при.
постоянном объеме от абсолютного нуля до температуры Т..
Тогда, так как для Г = 0 энтропия, согласно принципу
Нернста, равна нулю, энтропия для температуры Т равна
о
С учетом A24), A29) и A31), отсюда получаем:
Значение А берется из A21).
В предельном случае исчезающего вырождения
согласно A26), в первом приближении:
/Л
так что из A21) получается вырах:е..ие для Л:
A= N
256 ГЛА«А 11
я по A39) энтропия равна:
-что совпадает с выражением F7).
20. Свойства сильно вырожденного газа
'Имея в виду теорию металлов, в этом разделе мы ис-
исследуем свойства сильно вырожденного газа, подчиняюще-
подчиняющегося статистике Ферми.
Мы видели, что давление и кинетическая энергия при
низких температурах стремятся не к нулю, а к конечному
предельному значению. Это можно представить себе на-
наглядно следующим образом. Если в объеме V находится
.вначяле только одна частица, то при абсолютном нуле она
будет находиться в самом низком квантовом состоянии по-
поступательного движения. Вторая появляющаяся частица,
.согласно принципу Паули, может занять только следующее,
более высокое, состояние движения. По той же причине
третья частица может занять при абсолютном нуле только
третье состояние, а N-я частица только N-e состояние.
Когда появляются новые частицы, занимаются все более и
более высокие состояния, и средняя кинетическая энергия
.вырожденного газа растет с ростом плотности. А благодаря
ударам о стенки газ поэтому оказывает отличное от нуля
давление.
При абсолютном нуле каждая молекула находится в наи-
наиболее низком возможном состоянии. Поэтому в газе с N
частицами все состояния, от состояния с нулевой кинети-
кинетической энергией . до N-ro, заполнены, а все состояния
^с более высокой энергией — свободны.
Сделаем это наглядным с помощью модели в простран-
пространстве импульсов. Ячейки пространства импульсов имеют
объем -—. Если основное состояние наших частиц ^-кратно
.вырождено, каждой ячейке соответствует g состояний.
КВАНТОВАЯ СТАТИСТИКА ГАЗА 257
Плотность состояний (число на единицу объема пространства
импульсов) поэтому равна:
При абсолютном нуле эти состояния поступательного
движения занимаются в порядке возрастания их кинетиче-
кинетической энергии. N частиц распределяются, следовательно,
в пространстве импульсов равномерно с плотностью р внутри
шара с центром в нулевой точке, содержащего как раз N
состояния. Радиус ртах этого шара в точности равен наи-
наибольшей величине импульса нашей частицы. Чтобы вы-
вычислить ртах, нужно учесть, что шар объема -о-р^ах, со-
согласно A40), содержит
If
3
состояний. Решение относительно ртах дает:
о —(±X'>JL (f
а отсюда:
_Апак_(_3_у/' Н Шу,
*W— т —\&) ^Ji\v) • <142>
N
р и v зависят, естественно, от тт, т. е. от концен-
трации частиц. В случае, например, серебра максимальная
скорость свободных электронов при абсолютном нуле равна
г>юах = 1,39 -108 см/сек = 5,5 eV.
На фиг. 55 этот закон распределения скоростей для
различных температур нанесен графически. По оси абсцисс
отложена величина импульса р, по оси ординат — плотность
заполнения в пространстве импульсов, которая, конечно,
никогда не может быть больше р. Для 7" = 0 эта плотность,
как мы видели, постоянна и равна р, вплоть до значения ртах,
где она внезапно падает до нуля. Это распределение изо-
17 Энрико Ферми
258
ГЛАВА II
Сражено на фнг. 55 прямоугольником. При несколько более
высокой температуре Т, это спадание распределения при
Ртгъ происходит более плавно, так как некоторые частицы
переходят в более высокие состояния. При дальнейшем
повышении температуры, число таких частиц возрастает,
так что функция распределения получает вид, обозначенный
на фиг. 55 индексом Т2. Наконец, при очень высоких тем-
температурах функция распределения переходит в классическое
каксвелловское распределение.
Фиг. 55. Плотность заполнения р = £
пространства импульсов в зависимости от
импульса р для вырожденного газа при
различных температурах.
Интересно рассмотреть поведение нашего газа при
Г = 0 (т. е. при полном вырождении) в том случае, когда
на частицы действует внешняя сила. Сила' описывается
меняющимся в пространстве потенциалом U. Тогда, согласно
статистике Больцмана, в областях меньшего потенциала
возникло бы уплотнение газа, причем такое, что плотность
всюду была бы пропорциональна е~ uikT. Исследуем, как
будет выглядеть этот закон для полностью вырожденного
газа.
Формула A42) дает наибольшую величину импульса ртах
для полностью вырожденного газа в зависимости от плот-
TV
ности /z==-j-r. Наибольшее значение кинетической энергии
получается отсюда равным:
5
КВАНТОВАЯ СТАТИСТИКА ГАЗА 259
Наибольшее значение w полной энергии частицы з точке
с плотностью п равно сумме кинетической энергии £*тя, и
потенциальной энергии U:
Если существует равновесие, w должно иметь одинако-
одинаковое значение во всех точках. Из A43) следует соотноше-
соотношение, определяющее искомое распределение плотности:
n = ^ff-{zv~UfU. A44)
Значение постоянной w определяется из условия, что пол-
полное число молекул должно быть равно i\<:
\ndx-N, A45)
причем интеграл распространяется на весь объем газа.
Формула A44) справедлива только для областей, в которых
(w — U) ^> 0. Для (w — U) <^ 0 выражения для п было бы
мнимым, а кинетическая энергия соответствующих частиц —
отрицательна. Так как это невозможно, то в этом случае
21, Статистическое распределение электронов в атоме
Простое применение этих соображений независимо друг
от друга нашли Томас и Ферми при исследовании распре-
распределения электронов внутри атомов.
В случае атомов с многими электронами можно, по
крайней мере в первом приближении, вместо исследования
движения отдельных электронов рассматривать электронную
оболочку как газовое облако, образованное электронами.
Это облако связано с ядром электростатическими силами.
При обычных температурах этот электронный газ практи-
практически полностью вырожден. Оценка порядка величины пара-
параметра вырождения A37). „приводит всегда к очень большим
значения:,!. Мы можем поэтому распространить на это элек-
260 ГЛАВА П
тронное облако соображения предыдущего раздела.. Вычислим
с их помощью плотность электронного облака как функцию
расстояния от ядра.
Электрический потенциал (положительного заряда ядра
и электронного заряда) обозначим через V(r). Электрон
с зарядом — е имеет в этом поле потенциальную энергию
£/= — eV. Так как для электронов g = 2, из A44) сле-
следует
*™>,, A46)
Здесь постоянная w объединена с произвольной постоянной
электрического потенциала.
Уравнение Пуассона, после подстановки плотности за-
заряда — еп, запишется в виде:
£* £=♦«•• о«>
Следовательно, потенциал V удовлетворяет дифферен-
дифференциальному уравнению:
df*^ r dr~~ 3A3 v '
Вблизи ядра с зарядом Ze (Z — порядковый номер), где
отсутствует экранирующее действие электронного облака,
V должно приближаться к граничному значению Z —. От-
Отсюда получается граничное условие:
A49)
Вторым дополнительным условием является то, что полное
число электронов» т. е. объемный интеграл электронной
плотности, равно Z:
Z = J tuft = ■■■-^ — J V'hr*dr. A50)
КВАНТОВАЯ СТАТИСТИКА ГАЗА 261
Потенциал, определяемый A48) с граничными условиями
A49) и A50), вычисляется с помощью двух подстановок:
* = |' *=~, A51)
где
Уравнение A48) переходит в новое дифференциальное
уравнение
Граничные условия A49) и A50) с помощью этих под-
подстановок преобразуются в
A54)
Можно легко показать, что это условие тождественно
условию
^@0) = 0. A55)
Дифференциальное уравнение A53) с граничными усло-
условиями A54) и A55) полностью определяет функцию Ц(х).
Она может быть численно определена. Соответствующие
значения приведены в табл. 3.
Таким образом, наша задача решена. Электрический
потенциал на расстоянии г от ядра равен:
A56)
Плотность электронов по A46) оказывается равной:
*'—*?'"* 1. ' "V A57)
262
ГЛАВА П
Таблица 3
1
X
0,00
0,01
0,02
0.03
о;о4
0,05
одо
0,15
0.20
о;25
0,30
0,35
0,40
0,5
0,6
0,7
Численные значения функций <? (х)
1,000
0,985
0,972
0,959
0,947
0,935
0,882
0,836
0,793
0,758
0,721
0,691
0,660
0,607
0,562
0,521
X
0,8
0,9
1,0
1,2
1,4
1.6
1,8
2,0
2,5
3,0
3,5
4,0
4,5
5,0
6
7
0,485
0,453
0.425
0;375
0,333
0,297
0,268
0,244
0,194
0,157
0,130
0,108
0,093
0,079
0,059
0,046
X
8
9
10
12
14
16
18
20
22
24
26
28
30
32
34
36
f(x)
0,037
0.029
0;024
0,017
0,012
0,0093
0,0072
0,0056
0,0045
X
38
40
45
50
55
60
65
70
75
0,0037 80
0,0031
0,0026
0,0022
0,0019
0,0017
0,0015
85
90
95
100
0,0013
0,0011
0.00079
0,00061
0,00049
0,00039
0,00031
0,00026
0,00022
0,00018
0,00015
0,00012
0,00011
0,00010
Итак, V и п определяются одной и той же функцией,
одинаковой для всех атомов, независимо от порядкового
номера.
Метод статистического потенциала нашел широкое при-
применение при расчете различных свойств атома. В первую
очередь, следует отметить расчет оптических и рентгенов-
рентгеновских термов, исследование образования групп в периоди-
периодической системе и т. п. Вследствие своей статистической
природы этот метод особенно пригоден для представления
атомных свойств, меняющихся непрерывно с атомным но-
номером. Свойства, меняющиеся с атомным номером скачко-
скачкообразно, этим методом передаются хуже.