Author: Пиотровский Р.Г. Бектаев К.Б. Пиотровская А.А.
Tags: анализ теория вероятностей и математическая статистика математика
Year: 1977
Text
Р, Г. ПИОТРОВСКИЙ, К. Б. БЕКТАЕВ
А. А. ПИОТРОВСКАЯ
МАТЕМАТИЧЕСКАЯ
ЛИНГВИСТИКА
Рекомендовано к изданию
Министерством просвещения СССР
в качестве пособия
для студентов
педагогических институтов
МОСКВА «ВЫСШАЯ ШКОЛА» 1977
4
П 32
УДК 517+519.2: 80@75)
ОГЛАВЛЕНИЕ
Рецензенты: кафедра русского я-шка и общего языкознания
Горьковского государственного университета и проф. А. М. Длин
Пиотровский Р. Г. и др.
П32 Математическая лингвистика. Учеб. пособие для пед.
ин-тов. М., «Высш. школа», 1977.
383 с. с ил.
Перед загл. авт.: Р. Г. Пиотровский, К. Б Бектаев, А. А. Пиотровская.
В книге рассматриваются различные вопросы языкознания, связанные с примене-
применением в нем математического анализа, теории вероятностей и математической стати-
статистики. Достаточное место уделено теоретическому обоснованию и приемам практиче»
ского применения математических методов в изучении языка.
Предназначается для студентов педагогических институтов,
60602—222
001@1)—77 37~77 А
© Издательство «Высшая школа», 1977 г.
Введение "
Часть первая. Исследование лингвистических процессов
методами квантитативной лингвистики
Глава 1. Исходные понятия квантитативной лингвистики
1. Множество лингвистических объектов 11
2. Действительные числа 16
3. Лингвистическое явление как математическая величина . . 18
4. Понятие функции 22
6, Числовые функции в лингвистике 24
6. Элементарные функции 26
7. Диахронический скачок и его моделирование с помощью эле-
элементарных функций 31
§ 8. Моделирование информационного построения речи 38
§ 9. Моделирование периодичности речи 41
Глава 2. Глоттохронология, информационная схема текста
и их моделирование с помощью аппарата бесконечно
малых величин и пределов
§ 1. Понятия бесконечно малой величины и предела в квантитативной
лингвистике . . . . 51
6 2. Число Эйлера и модель роста словаря 55
§ 3. Глоттохронология 57
§ 4. Информационные модели слова и текста 62
Глава 8. Динамика лингвистических процессов и ее описание
с помощью приемов дифференциального исчисления
§ 1. Диахроническая скорость и понятие производной 64
§ 2. Дифференциал 73
§ 3. Исследование функций, аппроксимирующих лингвистические
продессы 78
Глава 4. Суммирование и интегрирование в лингвистических
процессах
§ 1. Основные понятия теории рядов 87
§ 2. Каков максимальный объем информации в слове? . . . 91
§ 3. Лингвистические задачи, приводящие к понятию интеграла 95
§ 4. Основные понятия интегрирования и применение их к лииг-
вистическим задачам 100
Часть вторая. Вероятностно-информационные оценки нормы языка
и статистическое построение текста
Глава 5. Комбинаторика лингвистических единиц.
Вероятность и информация лингвистических событий
§ 1. Комбинаторные схемы Ц0
§ 2. Лингвистическое событие 113
| 3. Вероятность элементарного лингвистическою события . . 115
| 4. Вероятности сложных лингвистических событий 125
§ 5. Информационные измерения в тексте 133
Глава 6. Вероятностное моделирование порождения текста
и составляющих его единиц
§ 1. Повторение независимых испытаний в тексте .149
§ 2. Случайная лингвистическая величина, ее характеристики и
функция распределения 166
§ 3. Законы распределения, моделирующие образование языковых
единиц текста 183
§ 4. Понятие о законе больших чисел 205
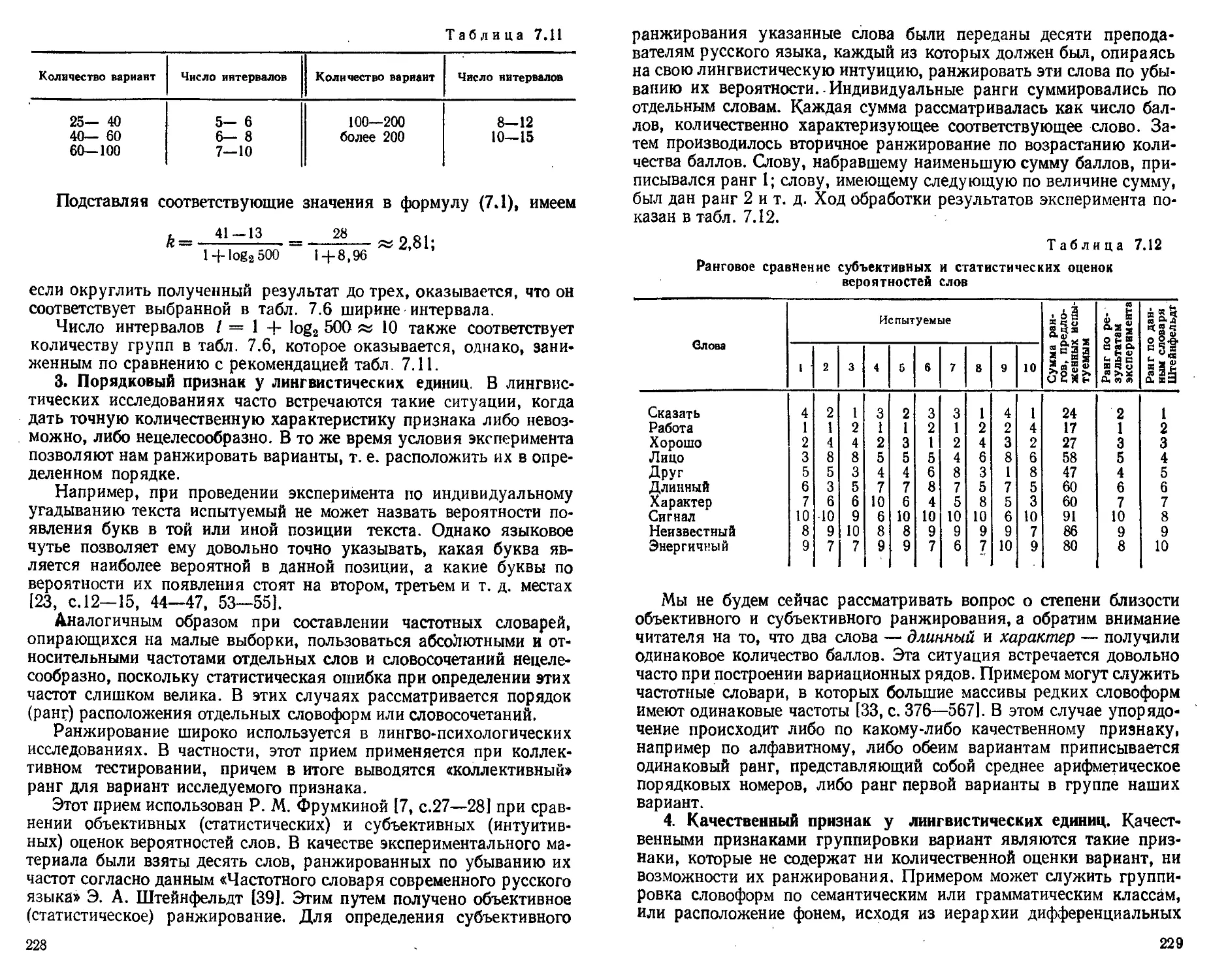
Глава 7. Первичная статистическая обработка текста
§ 1. Статистическая совокупность лингвистических объектов и ее .
организация 219
§ 2. Вариационные ряды лингвистических признаков 222
§ 3. Статистические характеристики лингвистических вариацион-
вариационных рядов 233
§ 4. Исследование лингвистических вариационных рядов с помощью
эмпирических моментов 252
Глава 8. Статистическая модель текста и вероятностные
характеристики нормы языка
§ 1. Точечная оценка параметров генеральной лингвистической
совокупности 266
§ 2. Оценка математического ожидания с помощью доверитель-
; ного интервала и статистическая параметризация стилей . . . 269
§ 3. Доверительный интервал для дисперсии н среднего квадра-
тического отклонения 278
§ 4. Доверительные интервалы для вероятности качественного лин-
лингвистического признака .....' 283
§ 5. Оценка функции генерального распределения по данным линг-
во-статистического наблюдения 289
Глава 9. Исследование вероятностных свойств языка
и статистики текста с помощью метода гипотез
§ 1. Элементы теории статистических гипотез 302
§ 2. Гипотеза о лексической нормативности текста и ее проверка
с помощью порядковых критериев 308
§ 3. Проверка гипотез о характере расхождений статистических
характеристик языков, функциональных стилей и подъязыков
с помощью параметрических критериев 316
§ 4. Проверка статистических гипотез о тождестве двух лингвисти-
лингвистических распределений 329
§ 5. Распределение средних длин словоформ в языках мира . . 333
.§ 6. Доминантные смысловые единицы и элементы заполнения
текста 351
Заключение 358
Приложение 362
Литература 375
Предметный указатель 378
ВВЕДЕНИЕ
1. Язык и математика. В эпоху научно-технической революции
математизация охватывает все сферы человеческой деятельности,
в том числе и такие, казалось бы, чисто гуманитарные науки как
языкознание. Проникновение математических методов в лингви-
лингвистику обусловлено двумя причинами.
Во-первых, развитие языковедческой теории и практики тре-
требует введения все более точных и объективных методов для анали-
анализа языка и текста. Одновременно использование математических
приемов при систематизации, измерении и обобщении лингвистиче-
лингвистического материала в сочетании с качественной интерпретацией резуль-
результатов позволяет языковедам глубже проникнуть в тайны построения
языка и образования текста.
Во-вторых, все расширяющиеся контакты языкознания с дру-
другими науками, например с акустикой, физиологией высшей нервной
деятельности, кибернетикой и вычислительной техникой, могут осу-
осуществляться только при использовании математического языка, об-
обладающего высокой степенью общности и универсальности для раз-
различных отраслей знаний. Особенно настойчиво математизируется
языкознание в связи с использованием естественного языка в инфор-
информационных и управленческих системах человек—машина—человек.
В действующих системах машинного перевода, автоматического ан-
аннотирования, человеко-машинного диалога всякое сообщение на есте-
естественном языке перекодируется в математическом языке компьютера.
Говоря об особенностях взаимодействия языкознания и матема-
математики, следует иметь в виду, что как естественный язык, так и язык
математики являются знаковыми (семиотическими) системами пере-
передачи информации.
Основные расхождения между этими языками связаны с различ-
различным построением языкового знака и знака математического.
Во-первых, лингвистический знак (слово, словосочетание, пред-
предложение) обычно включает в себя четыре компонента — имя (ма-
(материальный носитель информации), "денотат (отражение предмета
из внешнего мира), десигнат (понятие о предмете) и коннотат
(комплекс чувственно-оценочных оттенков, связанных с предметом
и понятием о нем); знак математического языка включает только
имя и десигнат (математическое понятие): сказанное иллюстрирует
рис. 1.
Во-вторых, лингвистический знак многозначен; математический
знак имеет, как правило, одно концептуальное значение.
В-третьих, лингвистический знак потенциально метафоричен,
У знака математического метафоричность полностью отсутствует.
Все эти свойства лингвистического и математического знаков
можно проследить, сравнив значения математического знака 7 и
слова семерка. Если 7 имеет единственное десигнативное матема-
математическое значение — «семь любых объектов», то слово семерка
имеет несколько значений: «цифра 7», «карта в семь очков», «груп-
«группа из семи человек» и т. п. При этом в значении слова семерка со-
содержатся не только указанные десигнативные понятия, но оно мо-
может указывать на конкретный предмет, например на вполне опре-
определенную группу в семь человек. Одновременно это слово несет до-
дополнительные коннотативные метафорические оттенки, связанные
с такими словосочетаниями как «великолепная семерка», «семь
чудес света», «семь смертных грехов», «семь дочерей Атланта (Пле-
(Плеяды)» и т. д.
Рис. 1
Из всего сказанного вытекает еще одно важное различие между
десигнативными значениями математического и лингвистического
знаков.
Значение каждого математического знака легко представить
в качестве множества элементов, причем такое множество имеет
вполне четкие границы: значение знака 7 является множеством,
охватывающим такие конкретные совокупности, которые включают
только семь (не шесть и не восемь!) предметов.
Иначе организовано десигнативное значение лингвистического
знака — оно также может рассматриваться как множество денота-
денотатов, однако это множество не всегда имеет четкие границы. Так,
например, не удается определить смысловые границы слов голубой
и синий, голубой и зеленый. Разные люди в зависимости от особен-
особенностей своего хроматического зрения будут называть показывае-
показываемые им конкретные сине-голубые оттенки то синим, то голубым
вдетом. Нельзя также указать точную временную границу, разде-
разделяющую значения слов ночь и утро. Иными словами, значения лин-
лингвистических знаков представляют собой нечеткие множества с раз-
размытыми границами [26, с. 207—214]; [65].
6
С многозначностью, метафоричностью и нечеткостью смысловых
границ лингвистического знака связана также изменчивость его
значения. В качестве примера снова возьмем русское прилагатель-
прилагательное голубой. В 50-е годы это слово, судя по 3-му изданию «Словаря
русского языка» С. И. Ожегова (М., 1957), имело в литературном
русском языке только одно толкование: «с окраской светло-синего
цвета». Однако, словарь-справочник, составленный по материалам
прессы и литературы 60-х годов «Новые слова и значения» (М.,
1971), указывает для слова голубой еще одно значение — «идеализи-
«идеализированный», отмечая одновременно такие новые метафорические упот-
употребления как «голубое топливо», «голубой экран».
Особенности построения лингвистического языка приводят к
тому, что естественный язык представляет собой нежестко органи-
организованную диффузную систему, которая воспринимается и исполь-
используется человеком в значительной мере интуитивно.
Напротив, язык математики является хорошо организованной
системой, существующей и функционирующей в виде логического
построения, каждый элемент которого имеет осознанную значимость.
Конфронтация естественного языка и языка математики требу-
требует, чтобы каждому лингвистическому объекту был поставлен в со-
соответствие некоторый математический объект. Лингвистический
знак, например, словосочетание или слово и составляющие этот
знак фигуры — фонемы, буквы, слоги — должны интерпретиро-
интерпретироваться с помощью знаков математических. Эта математическая ин-
интерпретация связана с расчленением лингвистического объекта и вы-
выделением в нем одного смыслового или сигнального компонента,
который становится предметом дальнейшего исследования. Осталь-
Остальные сигнальные и смысловые элементы лингвистического объекта,
а также разного рода метафорические коннотативные оттенки из
рассмотрения исключаются.
Применение математических методов в языкознании имеет своей
целью заменить обычно диффузную, интуитивно сформулирован-
сформулированную и не имеющую полного решения лингвистическую задачу одной
или несколькими более простыми, логически сформулированными
и имеющими алгоритмическое решение математическими задачами.
Такое расчленение сложной лингвистической проблемы на более
простые алгоритмизуемые задачи мы будем называть математи-
математической экспликацией лингвистического объекта или
явления.
Математическая экспликация интересна не только с чисто по-
познавательной и теоретической точки зрения. Она совершенно не-
необходима при решении прикладных вопросов, связанных с анали-
анализом и синтезом устной речи или информационной переработкой текс-
текста на ЭВМ. Математическая экспликация лингвистических объектов
применяется не только при решении на ЭВМ несложных, хотя и
трудоемких задач такого типа как составление частотных и алфа-
алфавитных словников [3]; [8]; [22] или пословного и пооборотного ма-
машинного перевода [32 а, с. 286 и ел.], [32 б, с. 107-130], но также при
составлении и реализации таких эвристических алгоритмов искус-
ственного интеллекта как семантический машинный перевод [32 в,
с. 128—146] или тезаурусное реферирование текста [26, с, 248—268].
2. Комбинаторная н квантитативная лингвистика. Выбор ма-
математического аппарата в лингвистических исследованиях — во-
вопрос не простой. Его решение зависит в первую очередь от того,
как определяется предмет и основные понятия языкознания и его
теоретического ядра — структурно-математической лингвистики.
Некоторые математики и лингвисты считают, что предметом
математической и структурной лингвистики должно быть изучение
грамматики, порождающей текст. При этом грамматика понимается
как конечное множество детерминированных правил, в том числе,
неграмматических, а язык рассматривается как бесконечное число
регулярных цепочек слов, порождаемых этой грамматикой. При
этом подходе экспликация лингвистических объектов должна опи-
опираться на такие разделы «неколичественной» математики как тео-
теория множеств, математическая логика (в особенности, теории ре-
рекурсивных функций и бинарных отношений), теория алгоритмов
и т. д.
Что же касается «количественных» разделов математики (мате-
(математическая статистика, теория вероятностей, теория информации,
математический анализ), то они считаются либо неприменимыми
для экспликации лингвистических явлений, либо играющими вспо-
вспомогательную роль. На основе применения «неколичественного», или
. как его иногда называют, «качественного» математического аппарата
в теоретическом языкознании сформировалось направление, услов-
условно называемое комбинаторной лингвистикой. Это
направление противопоставляется квантитативной (ко-
(количественной) лингвистике [43, с. 273].
Методы детерминистского комбинаторного языкознания интен-
интенсивно разрабатываются в теории порождающих грамматик Хомско-
го [45], в теоретико-множественных моделях Маркуса [56] и в дру-
других лингвистических направлениях.
Однако математическое языкознание не может ограничиться де-
детерминистской, неколичественной экспликацией лингвистически*
объектов.
Во-первых, это ограничение затрудняет преобразование нечетких
лингвистических множеств, элементы которых имеют вероятностные
веса принадлежности, в четкие множества искусственных языков.
Между тем указанное преобразование лежит в основе всех видов
машинной переработки текста и автоматического распознавания
смысла [26, с. 215—228].
Во-вторых, при таком ограничении вне сферы применения мате-
математических методов остается акустико-физиологическая и психо-
психолингвистическая проблематика речеобразования, а также стилисти-
стилистика и история языка, при изучении которых широко применяются
не столько комбинаторные, сколько количественные измерения [18];
[21]; [27];[32 в, с. 361—400].
Для того чтобы правильно оценить соотношение комбинаторных
и количественных математических методов при описании языка и
8
текст
ситуация
Рнс. 2
текста, рассмотрим общую схему речевой деятельности и тексто-
образования.
Порождение текста определяется, с одной стороны, системой
языка и ограничивающей ее действие нормой, а, с другой — совер-
совершенно независимой от языка внешней ситуацией (рис. 2).
Если согласиться с тем, что система языка есть механизм, по-
порождающий тексты без каких-либо вероятностных ограничений
[45]; [59], то станет ясным, что экспликация этой системы должна
осуществляться с помощью тех неколичественных разделов матема-
математики, о которых мы говорили выше.
Рассматривая язык как неколичественную систему, комбинатор-
комбинаторная лингвистика пытается описать механизм перехода от языка к
речи с помощью тех же приемов
«неколичественной» математики.
Такие описания представляют со-
собой контекстно-свободные грамма-
грамматики, т. е. грамматики, не учиты-
учитывающие контекстных ограничений
на употребление отдельных лингви-
лингвистических единиц и их сочетаний.
В связи с этим контекстно-свобод-
контекстно-свободные грамматики порождают много
цепочек, не являющихся реальны-
реальными предложениями данного языка.
Чтобы добиться порождения реаль-
реальных текстов, необходимо перейти от контекстно-свободных грамма-
грамматик к более сильным контекстно-зависимым грамматикам. Такие
грамматики можно построить при условии, что к элементам систе-
системы языка применяются вероятностные оценки, асам язык рассмат-
рассматривается как неколичественная производящая система, функцио-
функционирование которой регулируется вероятностными ограничениями,
заложенными в норме [32а, с. 5 — 46]; [47].
Что же касается текста (речи), то он представляет собой линей-
линейную цепочку отграниченных друг от друга (дискретных) символов,
(фонем, букв, слогов, слов). Каждый из символов встречается в тек-
тексте с определенной частотой и обладает особыми валентностями, т. е.
лингвистическими способностями сочетаться с другими символами.
Эти свойства лингвистических единиц в тексте эксплицируются
в терминах теории вероятностей и математической статистики. К
результатам вероятностно-статистического описания, взятым в со-
сочетании с данными лингво-психологического эксперимента, может
быть применен аппарат теории информации, с помощью которого
удается количественно оценить как структурную организацию текс-
текста, так и заключенную в нем смысловую информацию.
Из всего сказанного следует, • что математическая экспликация
центральной проблемы современного языкознания «система языка —
норма — текст» может быть осуществлена на основе применения
методов как «качественной», так и «количественной» математики.
В связи с разработкой лингвистических аспектов искусствен-
ного интеллекта возникает необходимость формального описания
внешних ситуаций, стимулирующих порождение текста. Для описа-
описания этих ситуаций используются как количественная, так и комбина-
комбинаторная методика.
Что же касается моделирования непрерывных изменений языка
во времени (диахроническая лингвистика), географическом про-
пространстве (диалектология), а также в специально-профессиональном
и художественном континууме (социолингвистика и стилистика),
то целесообразно использовать понятия бесконечного множества,
предельного перехода, непрерывности, т. е. понятия, составляю-
составляющие основу математического анализа.
В области комбинаторной лингвистики наряду с фундаменталь-
фундаментальными исследованиями появилось уже немало работ типа учебных
пособий, в которых систематизируются и популяризируются основ-
основные ее идеи [13]; [45]; [56]. В ином положении находится кванти-
квантитативная лингвистика. Здесь можно указать лишь несколько книг
и сборников, в которых исследуются или описываются отдельные
вопросы приложения математического анализа, теории вероятно-
вероятностей и статистики в языкознании — см. [4]; [61; [7]; [15].
Однако систематического изложения основных идей квантитатив-
нсй лингвистики до сих пор нет. Предлагаемая читателю книга имеет
своей целью восполнить этот пробел.
В первой части книги рассматриваются элементы математиче-
математического анализа и их лингвистические приложения. С помощью этого
аппарата строятся математические модели, описывающие: изменение
лингвистических объектов во времени (гл. 1—4); распределение
информации в письменном тексте (гл. 1, 2, 4), акустическую струк-
структуру устной речи (гл. 1).
Во второй части к лингвистическому материалу прилагается
аппарат комбинаторики, теории вероятностей и математической
статистики. Эта методика используется для: измерения смысло-
смысловой информации слов и избыточности текста (гл. 5); описания функ-
функций распределения в тексте слогов, слов, словосочетаний и грам-
грамматических классов (гл. 6); построения статистических моделей
текста и вероятностных характеристик норм языка (гл. 8, 9).
Математический аппарат, необходимый для построения всех
этих моделей, чаще всего дается в виде определений без строгих
математических доказательств, которые читатель всегда может
найти в вузовских учебниках и пособиях по математическому ана-
анализу [28], теории вероятностей [10]; [14]; математической статисти-
статистике [30]; [36] и лингво-статистике [6], [7].
Авторы приносят благодарность рецензентам проф. Б. Н. Го-
Головину и проф. А. С. Длину, а также доц. П. М. Алексееву и канд.
техн. наук К. А. Разживину, замечания которых способствовали
улучшению книги. Авторы благодарны В. В. Колесниковой, С. А.
Моисеевой, П. В. Садчиковой и коллегам по группе «Статистика
речи» за помощь при подготовке рукописи к печати. Кроме того,
авторы выражают признательность редактору А. М. Суходскому,
проделавшему большую работу по редактированию книги.
ЧАСТЬ ПЕРВАЯ
ИССЛЕДОВАНИЕ ЛИНГВИСТИЧЕСКИХ ПРОЦЕССОВ
МЕТОДАМИ КВАНТИТАТИВНОЙ ЛИНГВИСТИКИ
ГЛАВА 1
ИСХОДНЫЕ ПОНЯТИЯ КВАНТИТАТИВНОЙ ЛИНГВИСТИКИ
§ 1. Множество лингвистических объектов
1. Понятие множества. Одно из основных понятий современной
математики — понятие множества. Оно является первичным, т. е.
не поддается определению через другие, более простые понятия.
С понятием множества мы встречаемся довольно часто: буквы русско-
русского алфавита образуют множество, то же можно сказать о словоупо-
словоупотреблениях*, содержащихся в данном предложении, на данной
странице и т. д.
Приведенные примеры обладают одним существенным свойством:
все эти множества состоят из определенного конечного числа объек-
объектов, которые мы будем называть элементами множества. При этом
каждый из объектов данного вида либо принадлежит, либо не при-
принадлежит рассматриваемому множеству. Так, например, буква
ф вне всякого сомнения принадлежит множеству букв, образующих
русский алфавит, в то время как буква / этому множеству не при-
принадлежит. Множества, включающие только такие объекты, принад-
принадлежность или непринадлежность которых к тому или иному множе-
множеству не вызывает сомнения, называются четкими множествами.
Поскольку каждый рассматриваемый объект либо принадлежит, либо
не принадлежит к рассматриваемому четкому множеству, эти мно-
множества всегда имеют ясно очерченные границы.
В дальнейшем мы будем различать следующие лексикологические
понятия: словоупотребление, форма слова (слово-
(словоформа), слово, а также исходная форма слова. Под слово-
словоупотреблением понимается цепочка букв, заключенная между двумя пробела-
пробелами в тексте и имеющая одно значение (омонимические словоупотребления
рассматриваются как различные). Полностью совпадающие словоупотребле-
словоупотребления представляют одну словоформу. Слово выступает как некоторый класс
(сумма) семантически и грамматически связанных между собой с.ювоформ.
Словоупотребление является единицей текста, слово — единицей двуязыч-
двуязычного, толкового, энциклопедического и т. д. словаря. В этих словарях слово
представлено в так называемой исходной форме, в качестве которой в русском
языке выступает обычно именительный падеж единственного числа — для
•«генных форм и инфинитив — для глагольных форм. Что же касается слово-
словоформы, то она используется обычно в качестве единицы частотного словаря.
11
Четким множествам противопоставлены нечеткие или «лингви-
«лингвистические» множества, включающие такие объекты, которые могут
быть отнесены к тому или иному множеству лишь с определенной
степенью достоверности. Понятие нечеткого множества проиллю-
проиллюстрируем на примере семантических полей прилагательных младен-
младенческий, детский, отроческий, юношеский, молодой, среднего возра-
возраста, старый [26, с. 210].
Чтобы определить границы семантических полей указанных слов
и словосочетаний, произведем следующий эксперимент.
Предложим большой группе испытуемых — носителей русско-
русского языка относить к той или иной возрастной группе мужчин раз-
различного возраста. При этом выясняется, что интервал от 10 до 14 лет
Сценка дсстоберности
0,5E0%,
75 20 Ik 28 32 36 40 44 US
Рис. 3. Вероятностно-семантические поля русских
прилагательных (н адъективальных словосочетаний)
младенческий A), детский B), отроческий (<?), юно-
юношеский D), молодой E), среднего возраста F), ста-
старый (старческий) G)
одними испытуемыми будет квалифицироваться как детский, а
другими — как отроческий возраст. Аналогичным образом период
от 17 до 23 лет может считаться либо как юношеский, либо как отно-
относящийся к молодому возрасту.
Если нанести результаты этого эксперимента на график, где
на оси абсцисс отмечать конкретный возраст, а на оси ординат —
процент достоверности его отнесения к той или иной понятийной
области, то -мы получим картину распределения семантических
полей указанных терминов. При этом выясняется, что каждое из
рассмотренных семантических полей представляет собой нечеткое
подмножество с размытыми краями (рис. 3).
Объекты, попадающие на эти размытые края, относятся к ука-
указанным множествам лишь с известной долей достоверности. Так,
например, двадцатилетний мужчина может быть с достоверностью
50% отнесен к множеству юношей, и с той же достоверностью —
к множеству молодых людей.
Аппарат нечетких множеств начинает применяться для описания
процессов мышления, лингвистических явлений и вообще для моде-
моделирования человеческого поведения, при котором допускаются ча-
частичные истины, а строгий математический формализм не является
чем-то категорически необходимым [65, с. 6—12].
12
Множества, которые состоят из конечного числа элементов, на-
называются конечными множествами.
К числу конечных множеств относится также и пустое множе-
множество, т. е. множество, не содержащее ни одного элемента. Введение
понятия пустого множества связано с тем, что, определяя тем или
иным способом множество, мы не можем знать заранее, содержит
ли оно хотя бы один элемент. Например, множество двухбуквенных
комбинаций чы, бй, оъ, можно считать пустым, если иметь в виду
только русские тексты, написанные на литературном языке и не
содержащие опечаток*.
Лингвистика чаще всего имеет дело с конечными множествами
объектов. Однако приходится рассматривать и бесконечные' мно-
множества. Например, бесконечным является множество всех слово-
словоупотреблений в текстах данного языка при условии, что этот язык
беспрерывно порождает и будет порождать новые тексты без какого-
либо ограничения во времени.
2. Способы задания множества. Существуют два различных спо-
способа задания множества. Можно дать полный перечень элементов
этого множества. Этот способ называется перечислением множества.
Элементы перечисляемого множества заключают обычно в фигур-
фигурные скобки**. Например, множество Л, состоящее из букв русско-
русского алфавита, вместе с пробелом (его обозначают знаком А) запишет-
запишется так:
А = {а, б, в, ..., ю, я, Д}.
Другой способ состоит в том, что задается правило для определе-
определения того, принадлежит или не принадлежит любой данный объект
рассматриваемому множеству. Этот способ называют описанием
множества. При описании множеств используются различные сим-
символы, операции. Если А есть некоторое множество, ах — входящий
в него объект, то символическая запись х ? А означает, что х
является элементом множества Л; при этом говорят: «с входит в Л»,
*х принадлежит Л» (рис. 4, а).
Если х не принадлежит множеству Л, то пишут х ?Л (за-
(заштрихованная область на рис. 4, б). Пусть, например, Л есть мно-
множество букв русского алфавита, ал — буква этого алфавита; так
как буква I в русский алфавит не входит, то можно записать л ? Л,
II А.
Однако этого нельзя утверждать с полной уверенностью относительно
любого русского текста, поскольку этн комбинации могут появиться в запи-
записях диалектной речи, а также в результате орфографических ошибок или опе-
опечаток, например чысто вместо чисто, оъ вместо об. Кроме того, такие комби-
комбинации букв могут быть использованы в качестве каких-то условных обозна-
обозначений, например, как обозначение серии перед номерами документов или де-
денежных знаков. Поэтому множество двухбуквенных комбинаций чы, бй, оъ
применительно к любому русскому тексту целесообразно рассматривать как
нечеткое множество.
** Множества звуков, так же как н отдельные звуки, мы будемобозна-
чать квадратными скобками [ J, а множества фонем и отдельные фонемы —
косыми скобками / /. Для обозначения звуков и фонем используются знаки
международной фонетической транскрипции [5, с. 475].
13
В том случае, когда речь-идет о нечетком множестве, указывает-
указывается степень достоверности, с которой х принадлежит множеству А.
Это выражается записью Р (х ? Л). Например, пусть А — множест-
множество юношей, а х обозначает двадцатилетнего мужчину; тогда, исхо-
исходя из приведенных выше рассуждений, можно записать 0,5 (х ? А).
Если имеются два множества Л и Б, причем каждый элемент
множества А принадлежит множеству В, то множество А называет-
называется частью (или подмножеством) множества В. Записывается это так:
А а В или В zd А. Соотношение, выраженное знаком с, называет-
называется включением (рис. 4, в).
Операцию включения можно проиллюстрировать на следующем
лингвистическом примере. Русские [и] и [о], образующие множество
огубленных (лабиализованных) гласных, принадлежат множест-
W
а)
б)
в)
г)
Р)
з)
Рис. 4
ву гласных звуков. Таким образом, множество лабиализованных
гласных следует рассматривать как подмножество, включенное во
множество гласных звуков.
3. Основные операции над множествами. Основными операция-
операциями, осуществляемыми над множествами, являются сложение (объе-
(объединение), умножение (пересечение) и вычитание. Эти операции, как
мы увидим дальше, не тождественны одноименным операциям,
производимым над числами.
'Объединением (или суммой) двух множеств называется множе-
множество, содержащее все такие и только такие элементы, которые яв-
являются элементами хотя бы одного из этих множеств (сумма мно-
множеств обозначается знаком (J или +). Это определение означает, что
сложение множеств А и В есть объединение всех их элементов в од-
одно множество А -f- В или A (J В (рис. 4, г). Если одни и те же эле-
элементы содержатся в обоих множествах, то в сумму А + В эти эле-
элементы входят только по одному разу (рис. 4, д). Так, если множе-
множество губных казахских согласных [р, b, m, wl есть А, а множество
сонорных согласных [m, n, n, w, 1, г, j] есть В, то сумма А -\- В
состоит из элементов [р, b, m, n, n, w, I, r, j]. Число элементов во
множестве А + В равно 9, а не 11, как это имело бы место при сло-
сложении чисел.
Сложение множеств, как и сложение чисел, обладает свойства-
свойствами коммутативности: А + В — В + А, и ассоциа-
ассоциативности: (А -\- В) + С = А -\- (В + С), что легко проверить
на примере множества казахских согласных.
Кроме того, сложение множеств обладает еще и такими свойст-
свойствами, которые неприсущи сложению чисел; например, если А с В,
то А + В — В. Действительно, если множество всех звонких со-
согласных принять за Л, а множество шумных согласных — за В,
то сумма множеств А и Б равна В, т. е. множеству шумных соглас-
согласных. Всякое множество есть часть самого себя, т. е. А с: А. Пустое
множество есть часть всякого множества А.
Два множества А и В считаются равными (А = В), если они со-
состоят из одних и тех же элементов, т. е. каждый элемент множества
А является элементом множества В, и наоборот. Иначе говоря,
А с В и В а А (рис. 4, е). Например, сравнивая множество А,
состоящее из словоформ еы, вас, вам, вами, с множеством В, вклю-
включающим формы склонения местоимения вы, убеждаемся, что А сг В
и В zd 4, т е что оба множества равны.
Неравенство множеств А и В (А Ф В) указывает на то, что, по
крайней мере, в одном из этих множеств есть такой элемент, кото-
которого нет в другом множестве. Например, множество ударных глас-
гласных звукотипов (фонем) по классификации Л. В. Щербы [40] не
равно множеству тех же звукотипов (фонем) в классификационной
схеме Р. И. Аванесова [11; [2]. Легко заметить, что первое множе-
множество [а, е, i, о и, ы] содержит элемент [ы], которого нет вовтором
множестве [а, е, i, о, ul*.
Пересечением (или умножением) двух множеств А и В (обозна-
(обозначается А П В или А В) называется множество тех элементов, ко-
которые принадлежат и к А, и к В (заштрихованная область на
рис. 4, ж) Если мы обозначим множество ртовых чистых твердых
смычных согласных (р, b, t, d, k, g] в русском языке через В, а
множество заднеязычных твердых звуков [k, g, x] через А, то пере-
пересечение этих множеств АВ или А Г) В даст множество согласных
Ik, gl.
Операция пересечения множеств обладает свойствами:
1) коммутативности: ЛБ = ВА\
2) ассоциативности: (АВ) С = А (ВС);
3) дистрибутивности: (А + В) С = АС + ВС.
Пересечение множеств обладает также такими свойствами, каких
операция умножения чисел не имеет: например, если Л с: В, то
А В = Л (см. рис. 4, в), в частности, АА = А. Эти свойства легко
проверяются на •множестве твердых смычных согласных.
В действительности мы имеем здесь дело с разными разбиениями (груп-
(группировками) одного и того же множества конкретных звуков — разбиениями,
определяемыми разными фонологическими позициями ленинградской
(Л. в. Щерба) и московской (Р. И. Аванесов) школ. Фонологическая позиция
авторов настоящей работы изложена в [24].
J4
15
Разностью двух множеств А и В называется множество всех
таких элементов множества А, которые не содержатся во множестве
В. Разность множеств обозначается А —В или А\В (рис. 4, з).
Определение вычитания не требует, чтобы A cz В. Если жеД с
с В, то разность В — А называется дополнением к множеству А
во множестве В (см. рис. 4, в). Нетрудно видеть, что разность толь-
только что рассмотренных множеств согласных составляет
В\А = [р, b, t, d].
Более сложное применение указанных операций для определе-
определения лингвистических понятий «язык», «диалект», «поддиалект», «го-
Еор», «подговор» см. в работе [251.
4. Упорядочение множества лингвистических объектов. В пре-
предыдущем параграфе мы рассматривали множества, не задаваясь
вопросом о порядке расположения составляющих их лингвистиче-
лингвистических единиц. Однако порядок расположения единиц в том или ином
лингвистическом множестве имеет принципиальное значение. Так,
например, в толковых, энциклопедических словарях и разного вида
справочниках слова расположены по алфавиту; размещение лек-
лексических единиц в другом порядке, например по убыванию частот,
в корне меняет организацию этих множеств и их лингвистические
приложения.
Рассматривая порядок размещения элементов внутри разного
вида лингвистических множеств, мы приходим к понятию упорядо-
упорядоченного множества. Это понятие можно определить следующим обра-
образом: множество А называется упорядоченным, если для любых двух
элементов один считается предшествующим другому.
Относительно любых элементов аъ аг, а3 множества А это пра-
правило удовлетворяет следующим условиям: 1) если ах предшествует
а2, то а2 не предшествует аг (асимметричность); 2) если
Й! предшествует а2 и а2 предшествует а3, то и ах предшествует а3
(транзитивность).
Одно и то же множество можно упорядочить многими различ-
различными способами — ср. в этом смысле разные построения словарей.
Вместе с тем не для каждого множества удается задать конкрет-
конкретный и эффективный закон упорядочения. Например, неясно, как
можно упорядочить множество значений всех слов или словосоче-
словосочетаний в произведениях Шекспира или Льва Толстого.
§ 2. Действительные числа
1. Понятие числа. Квантитативная лингвистика, исследующая
количественную сторону языка и речи, постоянно оперирует не
только понятием множества, но также и другим основным понятием
математики — понятием числа.
Понятие числа выводится из понятий величины и измерения. Ос-
Основное свойство величины состоит в том, что она может быть со-
сопоставлена с другой определенной величиной того же класса, кото-
которая выступает в роли -единицы меры. Сам процесс сопоставления
первой величины с единицей меры и называется измерением. В итоге
измерения мы получаем некоторое число, которое выражает отноше-
отношение рассматриваемой величины к величине, принятой за единицу
меры.
Если измеряемая величина соизмерима с единицей меры, то от-
отношение между этой величиной и единицей меры выражается ра-
рациональным числом. К множеству рациональных чисел относятся
числа целые и дробные (и те, и другие могут быть положительными
и отрицательными), а также число нуль. Для лингвистов, разумеет-
разумеется, наиболее привычным является понятие целого положительного
(натурального) числа: в каждом слове имеется целое положитель-
положительное число букв, а в каждом предложении — целое положительное
число слов и т. п. Упорядоченное множество целых положитель-
положительных чисел 1, 2, 3, 4, ..., п составляет натуральный ряд чисел. Од-
Однако запаса одних лишь натуральных чисел оказывается недоста-
' точным для квантитативных измерений текста. Так, например, для
измерения средней встречаемости той или иной грамматической, лек-
лексической, фонологической единицы используются дробные числа.
•В некоторых зависимостях, описывающих лингвистические явления
и процессы, используются отрицательные величины.
Если квантитативное языкознание ограничивало бы свои изме-
измерения четырьмя действиями элементарной математики, то запаса
рациональных чисел было бы здесь вполне достаточно. Однако
в лингвистике приходится решать задачи, которые требуют исполь-
использования более сложных действий, например логарифмирования,
извлечения корня. Бывает, что решение таких задач оказывается
невозможным во множестве рациональных чисел. Так, например,
располагая одними рациональными числами, мы не могли бы ре-
решить такое использующееся при исследовании информационного
веса лингвистических единиц простейшее уравнение, с помощью
которого оценивается нулевая энтропия английского алфавита:
#0 = Iog2 27.
Действительно, среди рациональных чисел нельзя найти такое,
которое будучи степенью числа 2, давало бы 27. Этим числом ока-
оказывается иррациональное число, которое изображается бесконечной
десятичной дробью: loga7 = 4,7548... .
Запаса действительных (т. е. рациональных и иррациональных)
чисел вполне достаточно для решения основных задач квантитатив-
квантитативной лингвистики.
2. Множество действительных чисел. Все элементы множества
действительных чисел — положительные и отрицательные (как ра-
рациональные, так и иррациональные, равно как целые и дробные),
а также число нуль — упорядочены по величине. Это значит, что
все эти числа связаны соотношениями взаимного расположения
«равно» (==), «больше» (>), «меньше» (<). При этом для двух про-
произвольных действительных чисел а и b имеет место одно и только
17
одно из трех соотношений* й = Ь, а > Ь, a<Cb. Короче говоря,
два числа или два составленных из этих чисел выражения могут
быть связаны отношениями равенства или неравенства.
Из курса средней школы известно, что каждому действительному
числу соответствует определенная точка числовой оси, поэтому
только что указанные алгебраические отношения можно перевести
на язык геометрии. Так, например, записи а=Ь эквивалентно пред-
предложение «точка а совпадает с точкой Ь», выражению а > b соответст-
соответствует высказывание «точка а лежит правее точки Ь», а вместо а<.Ь
говорят: «а лежит левее 6». Отсюда следует, что в тех случаях,
когда между двумя лингвистическими элементами существуют от-
отношения равенства и неравенства, они могут быть представлены не
только алгебраически, но и геометрически.
§ 3. Лингвистическое явление как математическая величина
1. Математическая величина. При изучении количественных
закономерностей, языка приходится встречаться с такими лингви-
лингвистическими явлениями, как употребительность слова или словосо-
словосочетания и их порядок в частотном списке [3], длина звука, длина
буквосочетания, информационный вес слога, морфемы или слова
[23, с. 79—89], степень аналитичности языка [26, с. 1901
Если такое лингвистическое явление может быть выражено в
виде числа, то его можно рассматривать в качестве математической
величины.
2. Переменные и постоянные величины. Величина, которая при
данном исследовании принимает различные значения, называется
переменной, а величина, сохраняющая одно и то же значение,—
постоянной {константой). Величины, которые в любых условиях
сохраняют одно и то же числовое значение — так называемые аб-
* Символы «>» «<» выражают так называемые строгие, неравенства.
Кроме того, теория неравенств оперирует отношениями нестрогого неравенст-
ваа > b («а не меньше Ь», т. е. «а больше или равно 6») и а < Ь («а не больше 6»,
т. е. «а меньше или равно 6»). В дальнейшем нам придется иметь дело со сле-
следующими свойствами:
1) необратимостью неравенств — если а < Ь, го Ь > а,
если же а > Ь, то Ь < а;
2) обратимостью равенств — если а = Ь, то b — а;
3) транзитивностью неравенств и равенств —
если а < b и b < с, то а < с; аналогично, если а = Ь и b = с, то а = с,
4) монотонностью сложения неравенств и р а •
в е р с т в — если а < Ь, ас — любое действительное число, то а ¦+¦ с <
< Ь + с; аналогично, если а = Ь, то а + с = b + с. Отсюда следует, что
если к обеим частям неравенства прибавить любое действительное число, то
получится новое неравенство того же смысла, т. е. любой член неравенства
можно перенести из одной части в другую с противоположным знаком. Так,
если имеется неравенство а < Ь + с, то, прибавив к обеим его частям —с,
получим а — с < Ъ;
5) монотонностью умножения неравенств —
если а > b и с > 0, то ас > be; если о > b и с < 0, то ас < be; иными слова-
словами, при умножении ( или делении) обеих частей неравенства на отрицатель-
ную величину знак неравенства меняется на противоположный.
18
салютные постоянные (например, отношение длины круга к диамет-
диаметру, равное л = 3,14159...) —встречаются довольно редко. Чаще мы
будем иметь дело с величинами, сохраняющими одно и то же зна-
значение только при данных условиях исследования. Эти величины
называются параметрами.
Понятия постоянной и переменной величин в значительной сте-
степени условны. Одна и .та же величина может оказаться в одних
условиях переменной, а в других — постоянной, и наоборот.
Рассмотрим, например, зависимость между частотой словофор-
словоформы, которую она имеет в тексте длиной в N словоупотреблений, и ее
номером в частотном словаре, составленном на основе данного текста.
Эта зависимость выражается формулой (называемой обычно зако-
законом Эсту—Ципфа—Мандельброта), которая имеет следующий вид:
A.П
В этой зависимости Ft (частота словоформы) и i (номер ее в
частотном словаре) выступают в качестве переменных величин,
а величины N (длина иссдедованного текста), k (коэффициент от-
относительной частоты наибопее частого слова), р (поправочный ко-
коэффициент частых слов) и у (коэффициент лексического богатст-
богатства текста) выступают в качестве параметров, сохраняющих постоян-
постоянное числовое значение лишь для текста определенной длины, опре-
определенного стиля и тематики.
Зависимость Эсту—Ципфа—Мандельброта представляет собой
весьма грубое приближение к истинной статистической структуре
текста. Она более или менее удовлетворительно выполняется лишь
для двух-трех тысяч наиболее частых словоформ.
Для описания статистически редких словоформ приходится опе-
оперировать другими зависимостями, в которых величины k и у вы-
выступают уже в качестве переменных, а р может рассматриваться
в качестве некоторого параметра [3]; [26, с. 106]; [551.
Переменная величина считается заданной, если указано множест-
множество значений, которое она может принимать. Это множество назы-
называется областью изменения переменной. Например, номер слова
в списке может иметь только целочисленное значение, поэтому об-
областью изменения переменной i в зависимости A.1) является мно-
множество натуральных чисел.
Для обобщения некоторых формулировок и рассуждений бы-
бывает удобным рассматривать постоянную величину как частный
случай переменной, у которой область изменения состоит из одно-
одного единственного числа. Так, например, в отдельных участках ча-
частотного списка область изменения величин k и у можно с известным
допущением охарактеризовать одним числом Это дает нам право
считать величины k а у постоянными для определенных участков
списка.
Геометрически можно изобразить область изменения переменной
в виде некоторого множества точек числовой оси. Постоянной ве-
субстанция
дискретно-непрерывное
построение
. форма
дискретное построение
форма
дискретное построение
субстанция
дискретно-непрерывное
построение
Рис. 5
личине в этом случае соответствует множество, образованное одной
точкой числовой оси.
3. Дискретные и непрерывные величины. Лингвистические яв-
явления могут быть представлены в виде дискретных и непрерывных
переменных величин.
Область изменения дискретной величины состоит из отдельных
изолированных точек числовой оси, например, —2, —1, 0, 1, 2.
Область изменения непрерывной переменной величины состоит из
всех точек, расположенных на каком-либо участке числовой оси,
например между нулем и единицей, или из всех точек числовой оси,
которые соответствуют
всем действительным
числам. Иными словами:
между любыми двумя
сколь угодно близкими
значениями непрерыв-
непрерывной величины может
существовать любое ко-
количество ее промежу-
промежуточных значений.
4. Дискретность и
непрерывность в языке
и речи. Известно, что
речь представляет со-
собой последовательность
дискретных, т. е. от-
отграниченных друг от друга лингвистических единиц — фигур (букв,
фонем, слогов) и знаков (морфем, слов, словосочетаний и даже пред-
предложений). Система языка выступает в виде сети отношений между
единицами-инвариантами, также имеющими дискретную природу
(фонемы, морфемы, слова, грамматические схемы). Отсюда иногда
делается вывод, что в математической лингвистике, в том числе и в
квантитативном языкознании, лингвистические объекты должны
интерпретироваться с помощью дискретных величин и конечных
множеств, а понятие непрерывности и связанное с ним понятие бес-
бесконечного множества для интерпретации лингвистических явлений
малопригодны.
Чтобы оценить справедливость этого утверждения, обратимся
к схеме речевой деятельности, изображенной на рис. 5.
Субстанция содержания охватывает здесь все то, что может
быть предметом мысли. Таким образом, сюда входят как объекты,
имеющие дискретную природу, так и понятия, которым присуща
непрерывность (ср. цветовую гамму). Структура (форма) содержа-
ния представляет собой потенциально бесконечное множество идей.
Эти идеи выступают в качестве особо упорядоченных в данном
языке квазидискретных инвариантов плана содержания, образую-
образующих обычно нечеткие множества конкретных значений (см. § 1, п. 1).
Субстанция выражения представляет собой акустический, гра-
графический или иной материал, использующийся для формирования
знаков. Этот материал может иметь как дискретную природу (на-
(например, печатные буквы или импульсы тока, кодирующие эти бук-
буквы в ЭВМ), так и непрерывное строение (последовательности зву-
звуков, образующих устный текст). Структура выражения орга-
организует этот материал в систему дискретных и квазидискрет-
квазидискретных инвариантов (например, в систему фонем) плана выра-
выражения.
Если рассматривать процесс изменения языка во времени, а так-
также территориальное и социальное его варьирование, то здесь пре-
преобладают непрерывные процессы. Особенно наглядно прослежива-
прослеживается это в области субстанции выражения. Действительно, утрата
русских редуцированных гласных [ь] и [ъ] представляет собой с аку-
акустической точки зрения непрерывный процесс: их акустические
следы на конце слова обнаруживаются даже в современном произ-
произношении [18, с. 33 и ел.]. Устранение произносительно-акустиче-
ских различий между древнерусскими [<$\ и [е] (обозначавшимся
через «ять») тоже имело непрерывный характер не только в хро-
хронологическом, но и в территориальном отношении [1, с. 41
и сл.1.
Что касается количественного измерения смысловой и статисти-
статистической информации, содержащейся в тексте (субстанция плана со-
содержания), то она также осуществляется с помощью непрерывных
переменных величин (см. ниже, § 8).
Однако если аппарат непрерывной математики следует исполь-
использовать для описания явлений и процессов, происходящих в суГсган-
ции выражения и субстанции содержания, которые рассматриваются
многими лингвистами в качестве периферийных областей языка,
то можно ли применять этот аппарат для интерпретации объектов
структуры выражения и структуры содержания, составляющих
структурное ядро языка и речи (ведь все объекты структурного ядра
языка имеют дискретный характер)?
В ходе количественных группировок постоянно возникают си-
ситуации, когда разность между смежными дискретными переменны-
переменными, характеризующими эти группировки, очень мала по сравнению
с их величинами. Так, например, словарь языка состоит из многих
десятков и сотен тысяч лексических единиц. Увеличение словаря
на одно вновь образованное или заимствованное слово несуществен-
несущественно с точки зрения общего объема словаря. Поэтому постоянно уве-
увеличивающийся со временем объем словаря можно рассматривать
в качестве непрерывной переменной величины. В то же время ме-
меняющийся от варианта к варианту объем какого-либо древнего па-
памятника не может рассматриваться в качестве непрерывной величи-
величины. Объем такого памятника обычно нецелик, и его увеличение или
уменьшение даже на одно слово представляет собой заметное изме-
изменение. Таким образом, изменение объема словаря памятника вы-
выступает в качестве дискретной переменной величины.
Непрерывность возникает также при наложении диалектных
и особенно идиолектных (т. е. индивидуальных) систем в фонологии,
грамматике и лексике [24, с. 32 и ел.]; [26].
20
21
Итак, для интерпретации лингвистических явлений могут быть
использованы не только дискретные, но и непрерывные переменные
величины. Последние должны использоваться в первую очередь
при описании изменений языка во времени и пространстве, а также
при экспликации информационной структуры текста.
§ 4. Понятие функции
1. Соответствия между лингвистическими множествами и функ-
функциональные зависимости. В предыдущих разделах нам уже несколь-
несколько раз приходилось сравнивать разные лингвистические и нелинг-
нелингвистические множества. Сопоставление множеств приводит к поня-
понятию соответствия, которое подобно понятию множества является
одним из основных понятий математической лингвистики.
Рассмотрим вопрос о соответствии множеств на примере соотно-
соотношения индоевропейских и готских согласных.
Если опустить все спорные и дискуссионные вопросы, то индо-
индоевропейские звонкие смычные придыхательные согласные могут
быть традиционно [57, с. 11—116] представлены в виде множества
А, имеющего вид [bh, dh, gh], а соответствующие им готские со-
согласные объединены во множество В, имеющее вид [b, d, g]. Меж-
Между множествами А а В имеется соответствие, описываемое в герма-
германистике с помощью так называемого первого передвижения соглас-
согласных [58, с. 37 и ел.]. Сущность этого соответствия состоит в том, что
каждому звукотипу во множестве А взаимно однозначно соответст-
соответствует определенный звукотип во множестве В. При этом переход от
звукотипа множества А к звукотипу множества В совершается по
четко определенному правилу: каждый из индоевропейских звуко-
типов теряет придыхательность.
Если два множества находятся в таком соответствии, что каж-
каждому объекту х множества А ставится в соответствие некоторый опре-
определенный объект у из множества В, то говорят, что между А и В
существует функциональная зависимость. Правило /, по которому
можно перейти от объекта х ? А к соответствующему ему объекту
у ? В, называется функцией. В нашем примере правило потери
придыхательное™ у индоевропейских [bh, dh, gh] можно рассматри-
рассматривать как пример лингвистической функции.
Для обозна^лия функции используется запись у = / (х).
2. Правила задания функций. Если соответствие между двумя
множествами установлено, то принято говорить, что на множестве
А задана функция со значениями, принадлежащими множеству В.
Объекты х множества А, которым поставлены в соответствие эле-
элементы множества В, называются значениями аргумента (или зна-
значениями независимой переменной); в нашем случае в этой роли вы-
выступают индоевропейские звуки [bh, dh, gh]. Все множество А
называется множеством значений аргумента, или областью опре-
определения (существования) функции f (x).
Объекты у или f (x) множества В называются значениями функ-
функции (иля значениями зависимой переменной), соответствующими аргу-
22
менту х; в нашем примере это готские [b, d, g]. Множество В объек-
объектов, поставленных в соответствие элементам множества А, назы-
называется областью значений (изменения) функции f (x).
Вопрос о том, объекты какого множества следует считать незави-
независимыми переменными, решается обычно исходя из построения линг-
лингвистической задачи. Так, например, если первоначально заданными
считать готские смычные звонкие согласные [b, d, g], от которых
с помощью правила восстановления придыхательное™ можно ре-
реконструировать индоевропейские [bh, dh, gh], то первые можно
рассматривать как значения аргумента, а вторые — как значения
функции. Само же правило восстановления придыхательное™ вы-
выступает тогда в роли функции.
Введем еще одно важное понятие. Пусть задана функция у =
= / (х), где х — независимая, а у — зависимая переменная. Если
этого требуют интересы задачи, можно рассматривать у в качестве
независимой переменной, а х — в качестве функции. В результате
мы получаем новую функцию х = ср (у), которая называется
обратной по отношению к исходной (иначе — прямой) функции
У = f (*)•
3. Алгоритм и вычислимые функции. С понятием функции тесно
связано понятие алгоритма, которое обычно толкуется как точное
предписание о выполнении в определенной последовательности
некоторой системы операций для решения всех задач данного
типа.
Если для рассматриваемой функции задан алгоритм, с помощью
которого можно найти ее значения, то такая функция называется
вычислимой.
Однако данное в п. 2 определение функции не предусматривает
задания в правиле соответствия какого-либо алгоритма. Правило
соответствия может быть каким угодно, в том числе и таким, кото-
которое не дает реальной возможности определять по значению аргумен-
аргумента соответствующее значение функции либо в силу того, что алго-
алгоритм для решения этой задачи в данный момент не найден, либо по-
потому, что такой алгоритм не существует вовсе [38].
Таких «невычислимых» функций в лингвистике много. Рассмо-
Рассмотрим, например, в качестве области определения функции упорядо-
упорядоченное по употребительности множество словоформ. Каждая слово-
словоформа из этого множества выступает в качестве значения незави-
независимой переменной, а несомая этой словоформой статистическая
информация является значением функции. Правилом соответствия
назовем утверждение о том, что более употребительные словоформы
несут меньше информации, чем более редкие формы. Хотя функцию
можно здесь считать заданной, алгоритм для определения значений
этой функции отсутствует. Для того чтобы задать такой алгоритм,
необходимо получить для каждой словоформы количественные оцен-
оценки вероятности ее появления в тексте. Если же речь пойдет не о ста-
статистической, а о смысловой информации, то современное состояние
наших знаний вообще не позволяет нам задать алгоритм для опре-
определения значений этой функции.
23
Для математической лингвистики и особенно для ее инженерных
приложений вопрос вычислимости функции имеет принципиальное
значение. Пока для функции не получен вычисляющий ее алгоритм,
корректная переработка с ее помощью лингвистической информа-
информации, особенно на ЭВМ, практически невозможна.
§ 5. Числовые функции в лингвистике
1. Построение числовых функций. Изучение функциональных
зависимостей предусматривает сопоставление множеств, различаю-
различающихся не только по качественной природе, но и по количественной
характеристике составляющих его объектов. Так, например, фор-
формула
pt=k(i + p)-y A.2)
описывает соответствие, существующее между множеством номеров
i словоформ частотного списка и множеством их вероятностей р%.
Величина i выступает здесь в роли независимой переменной, a pt
является ее функцией. Алгоритм правила соответствия заключает-
заключается в том, что к i прибавляется величина р, затем эта сумма возво-
возводится в степень —у, а результат умножается на k. Аргумент i
выражен числами натурального ряда и практически всегда ограни-
ограничен, поскольку частотный словарь всегда содержит конечное число
лексических единиц; параметры у, р, k — действительные числа.
Поэтому и область определения функции A.2), и область ее значе-
значений являются конечными множествами. Если же представить себе
частотный список с бесконечным числом лексических единиц, то
аргумент i выражался бы числом, лежащим в промежутке A, + оо).
Тогда и область определения функции, и область значений были
бы бесконечными множествами.
В только что рассмотренной функциональной зависимости зна-
значения аргумента и значения функции—числа, а область определе-
определения и область значений функции — числовые множества. Такие за-
зависимости называются числовыми функциями числового аргумента,
или сокращенно числовыми функциями. Наряду с числовыми функ-
функциями от числового аргумента существуют функции с нечисловыми
или произвольными областями определения (а также с не-
нечисловыми областями значений). Примером таких функций служит
зависимость между индоевропейскими звонкими смычными приды-
придыхательными согласными и их готскими производными.
Квантитативная лингвистика имеет обычно дело с числовыми
функциями.
2. Способы задания числовых лингвистических функций. Чис-
Числовая функция, описывающая лингвистические процессы, может
задаваться либо таблицей, либо в виде формулы, либо с помощью
графика.
В современных эмпирических языковедческих исследованиях
численное соответствие между значениями аргумента и функции
устанавливается с помощью наблюдения. Поэтому здесь обычно ис-
используется табличный способ задания функции. Основ-
Основное достоинство таблицы состоит в том, что она непосредственно,
без всяких дополнительных измерений и вычислений соотносит
значения аргумента и отвечающие им значения функции. Однако
этот способ имеет существенный недостаток, состоящий в том, что
таблица дает лишь выборочные значения среди всех значений, при-
принимаемых аргументом и функцией. При этом в таблице может не ока-
оказаться тех значений аргумента и функций, которые для нас как раз
и представляют наибольший интерес. Кроме того, табличный спо-
способ имеет слабую наглядность: по таблице трудно бывает определить
характер изменения функции в зависимости от изменения аргумента.
Аналитический (формальный) способ дает возмож-
возможность вычислять значения функции при любом значении аргумента.
Одновременно этот способ позволяет анализировать с помощью мате-
математического аппарата различные свойства функции, в том числе
и такие, которые невозможно изучать методом прямого наблюдения.
Недостатком аналитического способа является отсутствие нагляд-
наглядности.
Наглядное представление функции дает графический
способ. Его преимущество заключается в том, что он дает воз-
возможность охватить рассматриваемую функциональную зависимость
«одним взглядом» и быстро выявить основной характер функции.
При решении практических задач квантитативной лингвистики
к этому способу представления функции обращаются в том случае,
когда в распоряжении исследователя имеются лишь ряды опытных
данных. Один из этих рядов рассматривается в качестве значений
аргумента, а другой — в качестве значений функции. Тогда по
табличным данным строится график (кривая) зависимости, а по
виду графика подбирается уравнение, соответствующее предполага-
предполагаемой природе исследуемого лингвистического явления.
Составить формулу, описывающую лингвистическое явление,
минуя табличный и графический способы представления функции,
можно лишь тогда, когда заранее известен внутренний механизм
этого явления. При моделировании диахронических процессов и
описании построения устной и письменной речи подобная ситуация
встречается сравнительно редко. Чаще приходится иметь дело с за-
задачами такого типа, когда по экспериментальным данным, обобщен-
обобщенным в таблице, строится кривая, а по виду кривой определяется со-
соответствующее ей уравнение.
Чтобы избежать ошибок при переходе от словесного лингви-
лингвистического описания явления и эмпирических табличных данных
к графику и уравнению, лингвист всегда должен иметь перед гла-
глазами набор таких числовых функций и соответствующих им графи-
графиков, с помощью которых обычно моделируются лингвистические про-
процессы и явления. Поэтому каждому разделу, посвященному опреде-
определенному виду лингвистического моделирования, предпослано крат-
краткое описание тото математического аппарата, который обычно ис-
используется в этом моделировании, а также будет необходим в по-
последующих разделах.
24
25
§ 6. Элементарные функции
Диахронические процессы, построение устной и письменной ре-
речи, а также диалектно-стилевую вариантивность можно моделиро-
моделировать в первом приближении с помощью различных элементарных
функций. Рассмотрим лекоторые из них.
1. Полиномы. Полином {многочлен) л-й степени задается
в общем виде выражением
у = аохп
ап_хх
ап,
A.3)
где п— натуральное число, а0, аъ ..., ап — постоянные дейст-
действительные числа (коэффициенты).
Рис. 6
Простейшими видами полинома являются следующие функции.
1. Двучлен первой степени (линейная функция)
у = ах + Ъ.
A.4)
График этой функции — прямая линия. Постоянная величина а
представляет угловой коэффициент прямой, равный тангенсу угла
ос, образованного ею с осью Ох, а коэффициент Ь — отрезок, от-
отсекаемый ею на оси Оу (рис. 6). Областью определения функции
является вся ось Ох (т. е. — оо < х<. °о).
2. Трехчлен второй степени (квадратичная функция)
у = ахг + Ьх + с,
A.5)
графиком которой служит парабола с вертикальной осью симметрии
х = -—ЫBа). При а>0 функция сначала убывает и, достигнув
минимума, снова возрастает; при а < 0 сначала возрастает, а до-
достигнув максимума, начинает убывать (рис. 7).
3. Степенная функция
у = ахп A.6)
представляет собой частный случай полинома п-й степени, когда
коэффициенты ах, а2, ..., ап равны нулю. При целых и положитель-
положительных значениях х функция определена на всей оси Ох. На рис. 8
26
изображены графики функций у = Xй при различных значениях
параметра п.
2. Дробно-рациональная функция. Дробно-рациональная функ-
функция, представляющая собой отношение двух многочленов, опреде-
определяется равенством
„— апхп+а1хп-1+...+ап
A.7)
Здесь п — натуральное число,
эффициенты.
Простейшим случаем
дробно-рацион а л ь н о й
функции является за-
зависимость
а0, аи
Ьо, Ьи
Ьп— ко-
= а/х.
A.8)
Эта функция * вы-
выражает закон обратной
пропорциональности ме-
между переменными х и у.
Так как аргумент
может принимать любые
значения, кроме нуля
(деление на нуль невоз-
невозможно), то значение
функции при х = 0 не
существует, и кривая
распадается на . две
не соединенные между
собой ветви и, как
говорят, терпит разрыв
(ср. гл. 3, § 3, п. 1).
Областью существования функции и областью значений функции
являются два интервала (— с», 0), @, + оо). Графиком функции
A.8) служит равносторонняя гипербола, ветви которой асимптоти-
асимптотически приближаются к осям координат. Если а > 0, то ветви ги-
гиперболы лежат в I и III четвертях; если же а < 0, то ветви распо-
расположены во II и IV четвертях (рис. 9).
3. Показательная функция. Показательная (экспоненциаль-
(экспоненциальная) функция задается равенством
Рис. 8
у = а*
A.9)
в котором основание а есть постоянное положительное число, не
равное единице. Графиком этой функции служит монотонно воз-
возрастающая или убывающая кривая (экспонента), которая асимпто-
асимптотически приближается к оси Ох (рис. 10 и 11). Область определения
Ее можно рассматривать и как степенную функцию вида у = ах'
27
функции — вся ось абсцисс, т. е. — оо < х < оо, область ее зна-
знаний 0< у < оо.
В лингвистических приложениях используется показательная
функция, где в качестве постоянной а взято число Эйлера е =
=* 2,718 ..., выступающее в качестве основания натуральных лога-
логарифмов. Функция
у = е* A.10)
называется экспоненциальной, а ее график — экспонентой.
У
Рис. 9
4. Логарифмическая функция. Логарифмической функцией на-
называется функция вида
0 = log.*, A.П)
где основание логарифма а есть положительное, отличное от едини-
единицы число. По определению логарифма, равенство у = log0 x яв-
является обратным по отношению к равенству х — ау, и, наоборот,
у — а" обратно х = log0 у. Поэтому график логарифмической функ-
функции (логарифмика) является зеркальным отображением экспоненты
относительно биссектрисы I координатного угла (см. рис. 10 и 11).
Логарифмика асимптотически приближается к оси Оу. Областью
определения функции служит правая полуось Ох, т. е. 0 < х < оо,
а областью значений функции — вся ось Оу, т. е. — оо < у < оо.
5. Периодические функции: Для ряда лингвистических яв-
явлений характерна отчетливо выраженная периодичность. Такой
периодичностью обладают не только акустическая субстанция ре-
речевого сигнала, но также и распределение информации в письмен-
письменном тексте. Явления этого типа описываются с помощью периодиче-
периодических функций.
Основная особенность периодических функций состоит в том,
что имеется такое постоянное число Т, прибавление которого к лю-
любому допустимому значению аргумента не изменяет значения функ-
функции, т. е.
= f (х + Т) = f (х).
A.12)
Наименьшее положительное число т, от прибавления которого
к любому допустимому значению аргумента значение функции не
изменяется, называют периодом. Следует иметь в виду, что f (х +
_j_ Пх) = f (х), где п — любое число.
К периодическим функциям отнрсятся тригонометрические и
обратные тригонометрические функции.
S
k
3
г
-г -1/
g=2xl
0 /1 ,2 J 4 X
Рис. 10
Рис. И
6. Тригонометрические функции. Рассмотрим следующие четы-
четыре основные тригонометрические функции.
1. Синус:
у = г sin (ax + ф); A.13)
здесь и далее х — аргумент, выраженный в радианной мере*, г,
ю, Ф — коэффициенты; если г = щ = 1 и Ф=0, то получается функ-
функция
у = sinx, A-14)
графиком которой является обыкновенная синусоида с периодом
Т = 2л (рис. 12), причем — оо < х < оо, —1<у<1.
2. Косинус:
A-15)
его графиком служит косинусоида, также имеющая период Т = 2п
и сдвинутая относительно синусоиды A.13) на л/2, причем
— оо<д:<оо, — 1<«/<1.
3. Тангенс:
A.16)
* Единицей радианного измерения служит дуговой радиан, представ-
представляющий собой отношение дуги, равной по длине радиусу, к самому радиусу.
Угол, образованный этой дугой, составляет 57°17'45*. Отсюда sinl =
= sin 57°17'45" = 0,8414.
28
29
график этой функции (тангенсоида) состоит из ряда отдельных
одинаковых бесконечных ветвей, каждая из которых размещается
в вертикальной полосе шириной (периодом) в Т = я (рис. 13);
область существования основных значений функции лежит в ин-
интервале (— я/2, л/2), а область значений функции — в интервале
(^оо, оо).
2. Арккосинус:
у = arccos х,
A.19)
4. Котангенс:
Рис. 12
у = ctg г,
A.17)
•графиком этой функции служит котангенсоида, являющаяся зер-
зеркальным отображением тангенсоиды относительно оси Оу (рис. 13).
Область существования основных значений функции лежит в ин-
интервале @, я), а область значений функции — в интервале (— оо, оо).
9
Рис. 13
7. Обратные тригонометрические функции. Если рассматривать
в качестве аргумента значения синуса, косинуса, тангенса или ко-
котангенса, а функцией считать соответствующие этим аргументам
значения угла или дуги, то мы получаем обратные тригонометри-
тригонометрические функции.
1. Арксинус:
у = arcsin х, A.18)
область определения этой функции есть интервал [— 1, 11, а об-
область ее значений лежит в интервале I— я/2, я/21.
30
эта функция определена в интервале [— 1, 1], ее значения заклю-
заключены в интервале [0, я].
3. Арктангенс:
y^arctgx, A.20)
областью существования функции A.20) является вся числовая ось,
т. е. — оо ¦< л: < оо, основные значения функции лежат в интер-
интервале (— я/2, я/2).
У.
-г -1
"/
/
Tt
2
n
2
/
1
2 x
- -2 ^-J
4
2
0
\
2
\
4
2 T
Рис. 14
4. Арккотангенс:
у = arcctg л:, A-21)
областью определения функции A.21) также является вся число-
числовая ось, т. е. — оо < х < оо, а основные значения функции ле-
лежат в интервале @, я).
Графики обратных тригонометрических функций получаются
из графиков соответствующих тригонометрических функций с по-
помощью зеркального отображения последних относительно биссек-
биссектрисы I координатного угла. Это легко можно проверить, сравнив
графики функций у = tg х и у = ctg x (рис. 13) с графиками соот-
соответствующих им обратных функций у = arctg х и у = arcctg x
фис. 14).
§ 7. Диахронический скачок и его моделирование
с помощью элементарных функций
В современных работах по диахронической лингвистике часто
приводятся таблицы, включающие количественные данные об упо-
употребительности исследуемого явления на различных этапах его
Ст°рии. Цель таких таблиц состоит в том, чтобы показать динамику
31
лингвистического процесса. Но, как уже говорилось, таблица обла-
обладает слабой наглядностью и может не включать в себя тех значе-
значений аргумента и функции, которые представляют наибольший инте-
интерес с точки зрения динамики исследуемого процесса. Поэтому для
более углубленного анализа лингвистического процесса следует,
используя табличные данные, дать графическое представление,
а затем и аналитическую модель исследуемого процесса.
1. Развитие нулевых форм родительного падежа множественного
числа у существительных—единиц измерения в русском языке
XIX—XX в. Рассмотрим в этой связи историю развития форм ро-
родительного падежа множественного числа у русских единиц изме-
измерения типа вольт, рентген, радиан. В русских научно-технических
текстах XIX в. употребля-
употреблялись регулярные образова-
образования родительного падежа
множественного числа: воль-
вольтов, рентгенов. Однако, на-
начиная с конца 80-х годов,
отмечается нарастающее упот-
употребление необычных форм:
вольт(ъ), рентген(ъ), ра-
]Щ ' J885 1890 1895 1900 1905 1910 диан{ъ), совпадающих о
именительным падежом един-
Рис 15 ственного числа. Через 20—
30 лет необычные формы
утверждаются не только в профессиональной речи, но и в литера-
литературном языке. Так сформировалась новая лексико-грамматическая
группа имен существительных, которая, наряду с существитель-
существительными I склонения типа башкир, гренадер, глаз, имеет в роди-
родительном падеже множественного числа нулевое окончание.
Статистический ход этого процесса отражен в табл. 1.1, состав-
составленный на основании данных, приводимых в работе [17].
Перенесем данные этой таблицы на график (рис. 15), отмечая
на оси абсцисс годы (t), а на оси ординат — относительную частоту
(/) нулевых форм (столбец G)]. Полученная последовательность
экспериментальных точек показывает резкое возрастание нулевых'
форм в период между 1886 и 1905 годами. Возникает вопрос: какой
из известных нам элементарных функций можно воспользоваться
для описания полученной зависимости? Обозначим иско'мую зави-
зависимость в виде
/ = Ф(/). A.22)
Линейная зависимость вида at + Ъ (см. штриховую линию на
рис. 15) здесь применена быть не может, поскольку значения такой
функции находятся в интервале от — оо до + оо, в то время как
по условию задачи область изменения нашей функции f лежит в ин-
интервале между нулем и единицей (относительные частоты не могут
быть меньше нуля и больше единицы). Значения же аргумента t
могут быть распределены по всему интервалу от — оо до оо. Если
Таблица 1.1
Вероятности и частоты употреблений нулевых форм родительного падежа
множественного числа у русских единиц измерения типа вольт
в конце XIX и начале XX в.
t
A)
1881
1882
1883
1884
1885
1886
1887
1888
1889
1890
1891
1892
1893
1894
1895
1896
1897
1898
1899
1900
1901
1902
1903
1904
1905
1906
1907
1908
1909
1910
« — 1895
B)
—14
-13
-12
—11
-10
—9
—8
—7
—6
—5
—4
—3
—2
—1
0
1
2
3
4
5
б
7
8
9
10
11
12
13
14
15
<-1896
3
C)
—4,66
—4,33
-4,00
—3,66
—3,33
—3,00
—2,66
—2,33
—2,00
-1,66
—1,33
—1
—0,66
—0,33
0,00
0,33
0,66
1,00 •
1,33
1,66
2,00
2,33
2,66
3,00
3,33
3,66
4,00
4,33
4,66
5
arctg X
D)
'
,35
,34
,32
,29
,27
,24
,20
,16
1.10
1,02
—0,92
—0,78
-0,58
—0,31
0,00
0,31
0,58
0,78
0,92
1,02
1,10
1,16
1,20
1,24
1,27
1,29
1,32
1,34
1,35
1,55
'l
я
F)
—0,43
—0,43
—0,41
—0,40
—0,40
—0,39
—0,38
—0,37
—0,35
—0,32
—0,29
—0,25
—0,18
—0,10
0,00
0,10
0,18
0,25
0,29
0,32
0,35
0,37
0,38
0,39
0,40
0,41
0,42
0,43
0,43
0,44
р
F)
0,07
0,07
0,09
0,10
0,10
0,11
0,12
0,13
0,15
0,18
' 0,21
0,25
0,32
0,40
0,50
0,60
0,68
0,75
0,78
0,82
0,85
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,93
0,94
f = Too
G)
0,06
0,06
0,01
0,00
0,01
0,01
0,03
0.09
0,11
0,00
0,57
.0,58
0,59
0,16
0,47
0,76
0,68
0,72
0,96
0,98
0,95
0,98
0,90
0,52
0,89
0,97
0,92
0,99
1,00
0,99
p-f
(8)
0,01
0,01
0,08
0,10
0,09
0,10
0,09
0,04
0,04
0,18
—0,36
—0,33
—0,27
0,24
0,03
—0,16
0,00
0,03
—0,18
—0,16
—0,10
—0,11
—0,02
0,37
0,01
—0,06
—0,00
—0,06
—0,07
0,05
провести эмпирическую кривую через отмеченные точки, то ее ле-
левая ветвь асимптотически приближается к оси Ot, а правая —
к прямой р = 1. Середина кривой показывает резкий подъем вверх.
Указанным условиям лучше всего соответствует график обратной
тригонометрической функции A.20). Однако рассматриваемая эмпи-
эмпирическая кривая имеет ряд особенностей по сравнению с теоретиче-
теоретической кривой (см. рис. 14). Во-первых, в качестве оси симметрии
наша кривая имеет вертикальную прямую, проходящую не через
точку t = 0, а через t = 1895. Во-вторых, интервал, в котором из-
изменяется значение функции /,. равен не л, а единице. В-третьих,
кривая поднята над осью Ot на половину интервала, в котором за-
заключены значения функции. Все эти особенности кривой могут быть
учтены с помощью коэффициентов, которые следует ввести в выра-
выражение A.20). Так, чтобы отразить сдвиг оси симметрии вправо на
1895 ед., мы должны от аргумента / отнять 1895; в этом случае имеем
32
Зак. 1287
33
t — 1895. В целях более компактного и наглядного построения гра-
графика величину t — 1895 нужно уменьшить в три раза. Следователь-
Следовательно, аргументом будет служить величина х = {t — 1895)/3. Чтобы
учесть различия в размерах интервала, в котором происходит из-
изменение значений функции /, выражение arctg (t — 1895)/3 следует
умножить на поправочный коэффициент 1/п. Наконец, чтобы под-
поднять интервал значений функции / над осью 0tt к выражению
A/я) arctg ((— 1895)/3 нужно прибавить 0,5, что равно половине
указанного интервала. В итоге получаем равенство
1 . / г1—1895 \ , п - /1 Оо\
р = — arctg —-— +0,5, A.23)
л \ i J
которое является аналитическим выражением, характеризующим
рост употребления нулевых форм родительного падежа множествен-
множественного числа у существительных типа вольт, рентген в русских на-
научно-технических текстах конца прошлого и начала нынешнего
века.
Кривая, описывающая отступление регулярных форм родитель-
родительного падежа множественного числа тех же существительных
(рис. 16), является зеркальным отображением только что проанали-
проанализированной кривой. Нетрудно поэтому прийти к заключению, что
аналитическое выражение зависимости между временем / и отно-
относительной частотой употребления регулярных форм
100 — F
100
имеет в этом случае вид
? = —arcctg/'-
A.24)
A.25)
Правильность этого вывода предлагается проверить читателю.
В только что приведенном примере использование математиче-
математических методов имеет больше иллюстративный, чем технологический
характер.
Однако в некоторых лингвистических задачах моделирование
диахронического процесса с помощью элементарных функций
служит средством восстановления не засвидетельствованных в па-
памятниках и диалектах этапов исследуемого процесса. Обратимся
в этой связи к истории формирования и развития определенного
артикля в старофранцузском языке.
2. Формирование определенного артикля во французском язы-
языке. Известно, что формирование французского определенного арти-
артикля, как и других новых аналитических категории, осуществлялось
в протороманскую эпоху (V—VIII в.) в народно-разговорной речи,
которая почти не отражена в дошедших до нас позднелатинских
памятниках [27]; 137].
Старофранцузские памятники IX—XIII в. фиксируют уже за-
завершение процесса формирования определенного артикля и уста-
установление современных норм его употребления при счисляемых име.
34
нах существительных. Распространение определенного артикля на
несчисляемые (абстрактные, вещественные, Singularia tantum) су-
существительные, а также на некоторые разряды имен собственных
происходит в более поздние периоды.
Восстановить начальный период формирования артикля непо-
ственно по народно-латинским текстам V—VIII в. невозможно, по-
поскольку эти памятники лишь косвенно отражают разговорную речь.
Кроме того, если говорить непосредственно б формировании норм
употребления артикля, то здесь очень трудно разграничить старые
местоименные и новые членные употребления форм латинского детер-
детерминатива ille, к которым восходят формы французского определен-
определенного артикля. Поэтому при-
приходится использовать различ-
различные приемы реконструкции,
исходя при этом из старо-
старофранцузского материала, где
артикль имеет не только чет-
четко выраженную форму (син-
(синкопированные производные
от ille), но также достаточно
ясно очерченные нормы упот-
употребления и грамматическое
значение.
В этом смысле опреде- Рис. 16
ленный интерес представ-
представляет экстраполяционная ре-
реконструкция текстовой статистики употребления артикля в те
периоды его истории, которые не имеют памятников разго-
разговорной романской речи. С этой целью была определена относитель-
относительная частота, или частость (/) употребления артикля в тех отрывках
из памятников, в которых дана прямая речь героев (предполагает-
(предполагается, что прямая речь лучше всего отражает нормы народно-разговор-
иого языка). Однако этого материала оказалось недостаточно. Пер-
Первым памятником, включающим прямую речь героев, оказалось
«Житие св. Алексиса», написанное около середины XI в., и только
в этом памятнике частость форм определенного артикля при счис-
счисляемых существительных заметно отличается от тех относительных
частот его употребления, которые дают более поздние памятники,
отражающие завершение интересующего нас процесса (см. табл., 1.2).
Иными словами, памятники не дают статистических сведений до-
достаточных для экстраполяционной реконструкции исследуемого про-
процесса. Поэтому приходится обратиться к данным старофранцузской
топонимики.
Латинские хартии Галлии VIII—X в. содержат уже большое"
число топонимов, отражающих не только фонетические, ной грамма-
грамматические черты живой народно-разговорной романской речи. Не-
Немало в этих документах таких названий, которые включают роман-
романские артикли (le, la, los): ср. Lagarda — начало IX в., los Grine-
urios — 900 г. Вообще ранние романские топонимы могли возник-
2* . 35
нуть только на почве устной народно-разговорной речи, поскольку
литературная или деловая письменная традиция в романском язы-
языке в этот период практически отсутствовала. Отдельные глоссы
и предположительно существовавшие памятники типа «Страсбург-
ских клятв» не могли образовать особого функционального стиля.
Известно, что средневековые письменные памятники с опозда-
опозданием примерно на 100 лет фиксируют явления, сформировавшиеся
и укрепившиеся в устной речи. Предположим, что эту хронологиче-
хронологическую поправку можно принять и для топонимики. Чтобы прове-
проверить все эти предположения применительно к нашей статистиче-
статистической задаче, сопоставим частости появления артикля в топонимах
определенного периода с относительными частотами употребления
артикля в разговорных фрагментах памятников, написанных при-
Таблица 1.2
600 800 wop под под t
Год bi
Рис. 17
мерно на сто лет раньше. Если частости артикля в топонимах XII в.
соответствовали бы его частостям в разговорных фрагментах XI в.,
а топонимические частости XIII в. были бы близки к разговорным
относительным частотам XII в. и т. д., то это означало бы, что наши
хронологические и стилистические поправки взяты правильно.
Это в свою очередь дало бы нам возможность использовать статисти-
статистику артикля по топонимам VIII—XI в., для которых памятники ро-
романской разговорной речи отсутствуют. Если же сопоставленные
частости давали бы заметные расхождения, то это свидетельствовало
бы о том, что наши стилистические и хронологические предположе-
предположения неверны, и мы не имеем права использовать топонимическую
статистику для экстраполяции начального этапа формирования
артикля.
Данные табл. 1.2, заимствованной из работы [32 в, с. 370—374],
показывают достаточную близость в частостях употребления арти-
артикля в соответствующих выборках топонимов и разговорных фраг-
фрагментах, что дает нам право использовать статистику топонимов для
VIII—X веков.
Нанесем на график наши табличные данные и подберем кривую,
отражающую динамику роста употребительности артикля в прото-
романский и старофранцузский периоды (рис. 17). Затем, применяя
методику, использованную при моделировании процесса образова-
образования нового лексико-морфологического разряда внутри русских су-
36
Динамика развития употребительности
Века
VIII—IX
X
XI
XII
XIII
XIV
в проторомаиский и
Памятники
Топонимы IX—X в.
Топонимы XI в.
Топонимы XII в.
«Житие св. Алексиса»
«Песня о Роланде»
(около 1100 г.)
Топонимы XIII в.
«Рауль де Камбрэ»
(конец XII века)
«Окассен и Николетта»
(начало XIII в.)
Топонимы XIII в.
«Бодуэн де Себур»,
Г. де Машо
«Взятие Александрии»,
Ж. Фруассар «Debat dou
cheval et dou levrier»
определенного
еврофранцузский период
• Учтено существительных
Всего
245
273
526
232
200
991
157
200
542
200
С определенным
артиклем
24
30
90
38
63
323
44
" 75
216
74
артикли'
Частость упот-
употребления опре-
определенного
артикля (f)
0,096
0,106
0,176
0,164
0,315
0,326
0,280
0,375
0,399
0,370
ществительных (см. п. 1 настоящего параграфа), найдем аналитиче-
аналитическое выражение нашей кривой, которое имеет вид
A.26)
Условные обозначения здесь те же, что и в зависимости A.23).
Математическое описание общей динамики развития определен-
определенного артикля имеет здесь не просто иллюстративный характер. Оно
может помочь при описании деталей формирования этой категории.
Так, например, высказывались предположения о том, что регуляр-
регулярное употребление артикля (или протоартикля) установилось в пер-
первую очередь при тех именах существительных, значение которых
предусматривало устойчивую ситуативную соотнесенность обоз-
обозначаемого ими предмета с некоторым количеством однородных пред-
предметов, а также при тех существительных, которые обозначают пред-
предметы или понятия, находящиеся в центре внимания собеседников
132 в, с. 373]. Предварительное статистическое обследование народ-
народно-латинских памятников VI—IX в. (Григорий Турский, путешест-
путешествие Этерии, книга истории Франков, Фредегарий Схоластик, Сали-
Салическая правда, Клунийские хартии) показывают, что существитель-
существительные, которые обладают только что указанными признаками и имеют
при себе детерминативы, восходящие к Ше нлн ipse, составляют от
3% до 5% всех существительных текста. Это хорошо согласуется
с реконструированной нами с помощью математической экстрапо-
экстраполяции относительной частотой употребления протороманского
артикля в эпоху раннего средневековья (рис. 17).
37
3. Диахронический скачок и сдвиги в структуре языка. Только
что построенные с помощью обратных тригонометрических функций
модели можно использовать при описании структурных сдвигов
не только в области лексики и морфологии, но также и в других
сферах языка — фонологии, синтаксисе, стилистике. Такие сдвиги
обнаруживаются либо в появлении новых элементов, либо в отступ-
отступлении старых лингвистических единиц, причем структурные из-
изменения языка происходят скачкообразно, что особенно отчетливо
прослеживается в диахронической статистике текстов. Действитель-
Действительно, образование новой структурной лингвистической единицы со-
сопровождается обычно быстрым ростом употребительности тех форм
(звуков, букв, морфем, суффиксов, слов, конструкций), которые
служат средством выражения новой фонемы, лексической или грам-
грамматической категории. При этом в сравнительно короткий промежу-
промежуток времени происходит переход от старого, более низкого уровня
употребительности соответствующих языковых форм к новому, за-
заметно более высокому уровню использования этих форм. Этот диахро-
диахронический скачок хорошо моделируется с помощью обратной триго-
тригонометрической функции A.20). Напротив, исчезновение той или
иной единицы из системы языка сопровождается обратным перепа-
перепадом частот, который описывается обычно с помощью функции A.21).
§ 8. Моделирование информационного построения речи
1. Измерение синтактической информации в речи. Количествен-
Количественные оценки построения речи опираются на квантитативный анализ
распределения в ней синтактической информации. Синтактиче-
Синтактическая информация характеризует структурную организацию текста,
через нее можно количественно оценить и смысловую информацию,
содержащуюся в словах, словосочетаниях и предложениях текста
126]. Как синтактическая, так и семантическая информация изме-
измеряется в двоичных единицах (битах) [41, с. 70]. Более строгое опре-
определение понятия «синт; ктическая информация» дано ниже (см. гл.
5, §5, п. б), там же описаны приемы ее вычисления. Сейчас наша
задача состоит в том, чтобы найти некоторую математическую мо-
модель, аппроксимирующую распределение этой информации в слове
и связном тексте.
2. Распределение информации в слове. Как показывают данные
табл. i.3, описывающей распределение синтактической информации
/ в слове, начальные буквы русского письменного слова несут за-
заметно больше информации, чем буквы, находящиеся в его середине
и на конце. Это предположение подтверждается данными экспери-
экспериментов, проведенных на материале ряда индоевропейских и тюркских
языков [23, с. 80—89]. Какой функцией можно было бы восполь-
воспользоваться для моделирования этого убывания информации при движе-
движении по слову слева направо? Если отвлечься от небольших «пиков»
и «провалов» информации в середине и конце слова, которые услов-
условно можно отнести за счет статистического разброса, а также если
считать, что теоретически длина слова в большинстве языков ничем
38
не ограничена (подробнее см. гл. 4, §2, п. 1), то распределение
информации в слове можно представить в виде пологой экспоненты,
асимптотически приближающейся к оси абсцисс (рис. 18). Ана-
Аналитическое выражение такой кривой имеет вид
/» = /ое-5". A.27)
Строгое доказательство этого утверждения приведено в гл. 2, § 4.
Выражение A.27) есть усложненный вариант экспоненциальной
функции A.10), где в качестве аргу-
аргумента выступает номер буквы и, а в
качестве функции /„ — количество
информации, которую несет буква п.
Формула A.27) содержит два параметра
/0 и s, имеющие лингвистический смысл.
Постоянная /0 (ее называют обычно
информацией алфавита) показывает
максимальную величину информации,
которую несла бы буква языка, исполь-
использующего алфавит S, если в системе и
норме этого языка не было заложено
ограничений на сочетаемость букв и
вероятности их употребления. Параметр
s показывает темп нарастания ограни-
ограничений, накладываемых системой и нор-
нормой языка на неопределенность выбора п-й буквы слова при
условии, что цепочка букв, находящаяся слева, уже известна.
Таблица 1.3
Распределение синтактической информации в обобщающих схемах
текстового русского слова и текста* no T
Буквы
Значения 7 в
Значения Т в
Буквы
Значения 7 в
Значения 7 в
слове
тексте
слове
тексте
1
3,45
4,22
9
0,17
2,05
1
2
0
1
2
,90
,85
10
,20
,65
1
3
0
2
3
.15
,16
И
,15
,35
0
2
0
2
4
,55
,45
12
,10
,07
0
2
1
6
,35
,28
15
—
,86
0
2
1
6
,28
,54
20
—
,37
0
2
1
7
,25
,12
25
—
,67
0
2
1
8
,20
,22
30
—
,05
Ниже будет показано (см. гл. 5, § Б, п. 4)," что существующие методы позволяют
определять яншь верхнюю G) и нижнюю (/) границы интервала, в котором находится
?"ииное значение информации /. Поэтому "при решении информационно-лингвистических
¦адач иепользуются либо верхние, либо нижние оценки информации.
89
3. Распределение информации в тексте. Приведенные выше рас-
рассуждения можно распространить и на связный текст (см. табл.1.3).
Тогда математической моделью распределения информации станет
показательная функция
U = (Л> - /») e-s»+ /со, A.28)
w
,i1
20 25 т п
отличающаяся от A.27) тем,
что в нее введен новый пара-
параметр /оо, указывающий на тот
предельный уровень, к которо-
которому асимптотически приближает-
приближается средняя величина информа-
информации на букву при бесконеч-
бесконечном увеличении длины текста
(рис. 19). Величина /«, указы-
указывает на то, что каждый текст в
отличие от слова может быть
продолжен и дальше и это про-
продолжение несет в себе некоторую информацию. Более строгое
обоснование для параметра 1Х приведено в гл. 2, §4 вместе с до-
доказательством равенства A.28). Значения /« для разных языков
показаны* в табл. 1.4.
Таблица 1.4
Значения 7 и / для некоторых индоевропейских и тюркских языков
Рис. 19
1
2
3
4
Язык
Русский
Польский ....
Английский . . .
Немецкий ....
7ос
1,37
1,28
1,35
1,36
Loo
0,82
0,76
0,74
0,71
5
6
7
Язык
Французский . .
Румынский . . .
Казахский ....
1,38
1,34
1,51
Loo
0,79
0,72
0,82
4. Распределение контекстной обусловленности. Выше уже гово-
говорилось, что /0 — максимальная синтактическая информация, кото-
которая может быть получена от лингвистического элемента, входящего
в алфавит (парадигму) S, при условии, что вероятностно-комбина-
вероятностно-комбинаторные ограничения здесь не учитываются. Поскольку /п — реаль-
реальная информация, извлекаемая из лингвистического элемента в участ-
участке текста п, то разность Кп этих информации будем называть кон-
контекстной обусловленностью:
Кп = 1о — 1п- . A.29)
Величину Кп можно рассматривать как меру тех структурных, нор-
нормативных ограничений,которые накладываются на букву или лю-
* См. сноску к табл. 1.3 на стр. 39.
бой другой лингвистический элемент, находящийся в л-й позиции
текста.
Подставляя в зависимость A.29) вместо /„ выражение A.28)
и производя необходимые преобразования, приходим к формуле
*» = (/„-'»)(!-<?-"), A.30)
выражающей рост контекстной обусловленности как функцию числа
п. Значения параметров здесь те же, что и в соотношениях A.27)
и A.28). На рис. 20 показаны
(дел)
( Велл.)
SO п.
кривые, характеризующие
нарастание контекстных сзя-
зей в русских беллетристи-
беллетристических и деловых текстах;
в табл. 1.5 приведены значе-
значения коэффициента s, харак-
характеризующего темп роста этих
связей в тексте. Вполне есте-
естественно, что в деловых тек-
текстах, использующих стан-
стандартизованную терминоло-
терминологию, фразеологию и синтаксис, контекстные связи растут быстрее,
чем в беллетристических текстах, пользующихся более разнообраз-
разнообразной лексикой, фразеологией и синтаксической вариативностью.
Табл и ца 1.5
Предельная информация и контекстный коэффициент для русских текстов
Разновидности русской речи
На верхней границе информации
'оо
1,19
0,83
S
0,21
0,24
40
Пределом, к которому стремится экспонента контекстной обуслов-
обусловленности, служит предельная контекстная обусловленность Кх —
== 'о 'оо.
§ 9. Моделирование периодичности речи
1. Гармоническая структура гласных. Наблюдения над распре-
распределением информации в тексте и слове (см. рис. 18 и 19), а также
изучение звуковой субстанции позволяют обнаружить в этих явле-
явлениях некоторую периодичность. Лучше всего эта периодичность
прослеживается в построении гласных звуков.
Однако гласный звук следует рассматривать не как элементар-
элементарную, а как сложную периодическую функцию. Чтобы дать мате-
математическое описание этой функции, нужно представить ее в виде
суммы простейших тригонометрических функции.
41
Рассмотрим это представление на примере искусственного слож-
сложного звука, который можно считать упрощенным аналогом глас-
гласного. Чтобы получить искусственный гласный, включим два ка-
камертона — первый с частотой F, равной 200 колебаниям в секунду
(герц, сокращенно — Гц), и второй — с частотой F = 600 Гц. Тог-
Тогда графическое изображение функции, которая характеризует слож-
сложный звук, производимый обоими камертонами вместе, будет пред-
представлять собой сложную гармоническую кривую С, показанную на
рис. 21. Такая кривая является результатом сложения двух сину-
синусоид, аргументом которых служит время (эти синусоиды называют-
Рис. 21
ся гармониками*). Синусоида А характеризует звуковые колебания,
производимые первым камертоном, а синусоида В — вторым. При
этом каждая точка С нашей сложной кривой имеет ординату ус,
представляющую собой сумму ординат у а и ув, или
ус = f (х) + Ф (х). A.31)
Мы использовали различные обозначения функций/и Ф, посколь-
поскольку синусоиды Аи В имеют разные по абсолютной величине периоды
колебаний и разные амплитуды.
Аргументы функций/ (х) и Ф (х) измеряются в единицах времени
(в мс). Переведем значения аргумента в радиан'ную (или угловую)
меру. Так как длина периода гармоники равна Т, то каждое зна-
значение аргумента х составляет некоторую долю этого периода, рав-
равную отношению х1Т. Но длина периода Т, взятая в радианной мере,
* В исследованиях по акустике речи гармониками называются обычно
только дополнительные синусоиды (частоты), накладывающиеся на так назы-
называемую несущую или основную частоту (синусоиду) голоса. Основную час-
частоту и дополнительные частоты можно представить также в виде обратной про-
пропорциональной зависимости F = 1/7', аргумент Г которой является периодом
колебания, измеряемым в единицах времени.
42
оавна 2я. Отсюда следует, что, умножив отношение х/Т на 2я, мы
получим значение аргумента в виде 2пх/Т, где частное 2п/Т = и
есть коэффициент перехода от линейного (временного) измерения
аргумента к его радианной мере.
Найдем значения коэффициентов перехода в рассматриваемом
примере. Так как ТА = \IFA, Тв = №, FA = 200 Гц, FB =
= 600 Гц, то Тв = Та/3. Следовательно, полагая Та = Т, по-
получим: ^= 2я/^ = 2я/^ ^ = бя/Тл= би/Т.
Таким образом, для гармоник А а В имеем
sin содх = sin Bпх/Т), A.32)
sin (йвх = sin (бпх/Т). A.33)
Однако эти величины еще не являются значениями у а и ув, ведь
амплитуды гА и гв обеих синусоид не равны между собой.
Амплитуды гармонических кривых измеряются и в единицах
длины, и в единицах интенсивности (для звуковой волны). Чтобы
не привязывать наши рассуждения к какой-либо узкой среде при-
приложения периодических функций, мы для сопоставительного изме-
измерения амплитуд воспользуемся относительными единицами, при
этом гА = 2,3 отн. ед., а гв — 1 отн. ед. Чтобы получить значения
интересующих функций, нужно умножить выражения A.32) и A.33)
соответственно на коэффициенты гА и Гв- При этом
У л = / С*) = гА sin
ув=
= гв sin ©в*,
откуда согласно A.31) получаем
ус — Га sin & а х + гв sin ®вХ.
A.34)
Взяв численные значения параметов га и гв, получим выраже-
выражение для ординаты любой точки сложной гармонической кривой:
ус= 2,3 sin Bлх/Т) + sin Fядг/Т).
Разложение сложной гармонической кривой на составляющие ее
синусоиды в том виде, как оно представлено на рис. 21, оказывает-
оказывается сложным и не очень наглядным даже при наложении двух гар-
гармоник. Если же сложная кривая является результатом взаимодей-
взаимодействия многих синусоид, то графическое изображение их взаимодей-
взаимодействия может оказаться совершенно лишенным наглядности. По-
Поэтому обычно используется упрощенное изображение структуры
(или, как говорят, спектра) сложной кривой. При этом на оси аб-
абсцисс откладывается частота колебания, а на оси ординат — вели-
величина амплитуды в единицах длины или интенсивности (децибелах —
сокращенно дБ) или, наконец, в относительных единицах. Эти схе-
схемы называются спектрограммами. На рис. 22 показана спектро-
спектрограмма сложного звука, полученного от наших двух камертонов: ле-
43
SI
J1
1-
0
вый столбик указывает сильную амплитуду гармоники Л, правый —
слабую амплитуду гармоники В. Что касается реальных гласных,
то характеризующие эти звуки кривые также могут быть представ-
представлены как суммы многочисленных гармоник.
Разложение сложной кривой можно произвести либо вручную
с помощью приемов гармонического анализа, о чем мы будем гово-
говорить ниже, либо автоматически — путем использования специаль-
специальных приборов, выделяющих составляющие звук гармоники (такими
приборами являются, в частности, спектрометр и спектрограф).
С помощью автоматического
разложения кривой речевого сиг-
сигнала обычно можно обнаружить
несколько десятков гармоник: одни
из них имеют более сильные, дру-
другие — более слабые амплитуды.
Усиленные гармоники расположе-
расположены компактно в нескольких об-
областях звукового спектра, кото-
f рые называются формантными об-
200 Ш 600 80Q ГЦ ластями (формантами), или об-
областями концентрации энергии
Рис. 22 в спектре звука речи. Эти форман-
форманты обозначаются обычно символа-
символами Fo, Fv F2, F3 и т. д.
При акустическом анализе речи гармоники со слабыми амплиту-
амплитудами не учитываются. Исследователь сосредоточивает свое внимание
на расположении и соотношении формантных областей, давая им
сначала физиологическую, а затем лингвистическую интерпретацию*.
В качестве примера рассмотрим спектрограммы трех видов эстон-
эстонского гласного [0] — краткого [б], долгого [0:1 и сверхдолгого
[б:':] (рис. 23, а, б и в). На фотографии видно, как гармоники (ап-
(аппарат отметил их в виде столбиков) группируются в форманты (F).
Каждая форманта имеет одну или несколько наиболее сильных гар-
гармоник (/т). Формантные области и усиленные гармоники каждой
из этих формант приведены в табл. 1.6, заимствованной из работы**
[54].
Получаемые е помощью гармонического анализа и автоматиче-
автоматической спектрографии данные о формантной структуре звуков имеют
* Форманты также описываются сложными кривыми, которые могут
быть представлены в виде суммы гармоник.
** Автор этой работы Г. Лийв следующим образом интерпретирует при-
приведенные экспериментальные данные. _
«Относительно спектрального состава вариантов гласного [0] разных сте-
степеней долготы следует отметить, что в связи с увеличением степени долготы
первая форманта понижается (вероятно, это акустический коррелат сужения
артикуляции); вторая и более высокие форманты также в общем понижаются,
причем более значительный сдвиг в сторону более низких частот вместе с по-
понижением относительного уровня высоких формант выступает при E::] тре-
третьей степени долготы (вероятно, это акустический коррелат большей велярное-
ти артикуляции)» [54, с. 97].
—1 —-L j,.
Частота /кГц/
7 Id
также большое практическое значение. Они используются при про-
проектировании автоматов, воспринимающих и воспроизводящих че-
человеческую речь.
2. Разложение сложной периодической кривой в ряд. Для вы-
выявления периодичности в информационной структуре текста необ-
необходим более сложный математический аппарат, чем тот, который
использовался при моделировании сложного звука. Рассмотрим
в этой связи выражение A.34).
Так как sin x = cos (х — л/2),
то указанное выражение мож-
можно переписать в виде
у — га cos (сод-х — я/2) +
+ тв cos (сов х — л/2).
Отсюда следует, что каждая
периодическая кривая может
быть сдвинута по отношению
к ее началу на некоторую вели-
величину ф, которая называется
сдвигом фазы (ф может быть и
меньше и больше, чем л/2).
Чтобы учесть этот сдвиг, вели-
величину ф надо ввести под знак
тригонометрической функции;
при этом получится равенство
вида
у = г sin [ах 4- ф)
или
у = г cos [ax 4- ф).
Колебания функции могут
происходить не обязательно
относительно оси абсцисс, как
это мы наблюдали до сих пор.
Периодическая функция может
быть сдвинута вверх или вниз
по отношению к оси Ох. Чтобы
отразить этот сдвиг, нужно
ввести в каждое из равенств
постоянный член г0, соответ-
соответствующий величине ординаты,
на которую поднята или опуще-
опущена ось, вокруг которой проис-
происходят колебания нашей перио-
периодической кривой. В результате
получается равенство вида "—д?—i ?—J—?—По
/ i; *
Частота, fnfu)
или
У = г0 + г sin (тх + ф)
У ~ r0 -f- r cos (юле + ф).
-1—i—г
Частота /кГц)
41
Рис. 23
44
45
Таблица 1.6
Формантные области и их усиленные гармоники для трех эстонских [б]
или в сокращенной записи
Форманты
Fi
fm-i
Fi
/ma
Ft
'm3
^4
fmi
[31
до 525 (Гц)
450
1150—1350
1250
1950-2250
2100—2250
2850-3300
3150
№\
до 525 (Гц)
450—525
975-1250
1150
2100-2400
2250
3150—3300
3300
до 525 (Гц)
375
¦ 975—1150
1150
около 2250
—
2850—3150
3000
Теперь предположим, что имеется некоторая сложная периодиче-
периодическая функция у (сложная гармоническая кривая), поднятая над
осью абсцисс на величину г0. Тогда мы можем представить эту
функцию в виде ряда слагаемых, каждое из которых имеет вид
У к = г k sin Bлкх/Т + фй).
Слагаемые представляют собой синусоидальные гармоники с ампли-
амплитудой rh и сдвигом фазы q>k (рис. 24). Частоты гармоник, из которых
составляется периодичес-
периодическая функция yh, образуют
гармоническую последова-
тельность. Это значит,
что частоты всех состав-
ляющих этой функции
кратны основной частоте
\1Т, причем синусоида ух
с частотой \1Т служит
первой гармоникой (А=1),
синусоида уг с частотой
Рис. 24 2/7" — второй гармоникой
F = 2), ... , синусоида уm
с частотой tn.IT — пг-й гармоникой (k = m). Величина г0, выража-
выражающая среднее значение функции у и равная ординате, на которую
поднята ось сложной периодической кривой и составляющих ее
гармоник, рассматривается в качестве нулевой гармоники. При
этих условиях наша сложная периодическая кривая может быть
представлена в виде суммы, называемой рядом Фурье:
sin
sin \~ 2х+W)
A.35)
3. Периодичность в информационной схеме текста. Используем
приведенные выше сведения для анализа лингвистического мате-
материала. Если побуквенно угадывать не связанные между собой
Рис. 25. Разложение сложной гармонической кривой распределения инфор-
информации на составляющие ее гармоники: 1 — кривая и эмпирические точки
нижней границы информации в 12-буквенной словоформе, взятой вне
контекста; 2 — теоретические точки; 3 — первая гармоника; 4 — вторая гар-
гармоника; 5 — третья гармоника; 6 — четвертая гармоника; 7 — пятая гармо-
гармоника
46
47
по смыслу слова определенной длины, то в результате обработки
получаемых данных по методу, описанному в гл. 5, § 5, п; 4, мы по-
получим кривую с повторяющимся распределением информации.
На основании приведенных в работе [23, табл. 20] данных о
нижней границе распределения информации в словах разной длины,
взятых вне текста, было осуществлено разложение каждой из этих
кривых в ряд. Это разложение, производившееся с помощью схем
группирования Рунге-Серебрен-
1(дб.ед) никова [32в, с. 397], удовле-
удовлетворяет следующему равенству:
1,0
0,6-
0,2
5
2
sln
A.36)
Z 3 4
Гармоники
Рис. 26
где / — информация; х — не-
непрерывный аргумент функции,
заменяющий дискретную вели-
величину п — 1; п — номер буквы
_, слова; г0 — нулевой член ряда
Фурье (соответствует среднему
арифметическому значению ин-
информации на рассматриваемом
участке); rh — амплитуда &-й
гармоники ряда Фурье (вели-
(величина информации &-й гармоники); / — длина слова в буквах, т. е.
длина участка, на котором производится разложение; qpft — сдвиг
фазы k-й гармоники в радианах. Результаты разложения кривых,
описывающих распределение информации русских слов длиной
в 5—12 букв (включая пробелы), приведены в табл. 1.7.
На рис. 25 показано разложение сложной гармонической кри-
кривой, характеризующей распределение информации (по нижней гра-
границе) в 12 буквенном слове, на составляющие ее гармоники. На
рис. 26 показана спектрограмма этого распределения.
Анализируя табл. .1.7, нетрудно заметить, что первые гармоники
дают обычно наибольшие амплитуды, которые ослабляются у гар-
гармоник более низкого порядка. Однако обращают на себя внимание
случаи усиления амплитуд у тех гармоник, период которых нахо-
находится в интервале между двумя и тремя с половиной буквами (в таб-
таблице они выделены жирным шрифтом). Если учесть, что именно в ука-
указанном интервале находятся средние длины корневых морфем рус-
русских слов* [23, с. 83—84], то это дает нам возможность предполо-
предположить, что такие усиленные гармоники являются математическими
соответствиями корневых морфем русских словоформ.
Гармонический анализ информационных схем слова и текста
имеет для языкознания большой теоретический и практический
интерес.
Амплитуды, сдвиги фаз и периоды гармоник при разложе
распределения информации русских словоформ, взятых вн
(распределение берется по>иижней границе информ
* Средняя длина морфемы в русском языке равна 2,5 буквы.
Длина слова
в буквах
A)
5
6
7
8
9
10
11
12
Номер гармо-
гармоники
k
B)
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
Амплитуда
Д-й гармоники
в дв. ед.
'ft
C)
0,84
0,78
0,52
0,33
0,36
- 0,76
0,66
0,38
0,38
0,35
1.U
0,79
0,38
0,32
0,41
1,11
0,37
0,51
0,48
0,43
1,08
0,50
0,51
0,66
0,40
0,92
0,34
0,60
0,16
0,38
0,99
0,56
0,20
0,22
0,33
1,03
0,57
0,28
0,35
0,41
Сдвиг фазы
в радианах
<Pft
D)
0,363
0,407
0,840
1,134
2,021
0,209
0,785
1,358
1,085
1,972
0,797
0,416
0,747
1,061
2,129
0,590
6,251
1,045
0,948
2,213
0,837
0,020
1,250
1,390
2,001
0,686
5,771
0,628
0,829
1,727
0,925
0,465
0,354
1,347
2,117
0,980
0,337
0,564
0,605
1,791
48
Во-первых, он еще раз показывает, что текст имеет квантовую
информационную структуру, где информационно нагруженные эле-
элементы чередуются со слабоинформативными элементами заполне-
заполнения. Такое «зернистое» строение текста связано, очевидно, с рит-
ритмом работы нейронов мозга, периодически накапливающих и отдаю-
отдающих информацию, поступающую к ним от органов чувств или из
других участков мозга.
Во-вторых, объективное выделение информационных гармоник
слов и текста позволяет поставить на твердую основу морфолого-
синтаксическую типологию языков и создать некоторые количест-
количественные эталоны. Сопоставляя с этими эталонами информационные
гармоники конкретных текстов, лингвисты получают возможность
пролить свет на типологию и происхождение таких загадочных язы-
языков, каким является, например, кетский язык.
ГЛАВА 2
ГЛОТТОХРОНОЛОГИЯ, ИНФОРМАЦИОННАЯ СХЕМА ТЕКСТА
И ИХ МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ АППАРАТА БЕСКОНЕЧНО
МАЛЫХ ВЕЛИЧИН И ПРЕДЕЛОВ
§ 1. Понятия бесконечно малой величины и предела
в квантитативной лингвистике
В предыдущей главе мы познакомились с математическими при-
приемами, позволяющими представить в виде аналитической схемы и
охарактеризовать числом различные лингвистические процессы.
При этом мы оперировали двумя основными математическими по-
понятиями: независимой переменной величиной (это понятие позво-
позволяет формализовать всякое лингвистическое изменение и эволюцию)
и функцией (это понятие дает возможность следить за количествен-
количественным и качественным изменением лингвистического явления в за-
зависимости от изменения его аргумента). Однако рассмотренные нами
элементарные функции представляют собой довольно грубые схемы-
эталоны, которых явно недостаточно, чтобы исследовать любые
малые, непрерывно текущие и изменяющиеся по своему темпу диа-
диахронические процессы, а также неустановившиеся состояния
языка и речи. Для описания этих процессов следует применять
более гибкий математический аппарат, построенный на понятиях
предела и бесконечно малой величины.
1. Бесконечно малая величина. Нам уже известно (см. гл. 1,
§3, п. 2), что переменной называется величина, принимающая раз-
различные численные значения в течение некоторого лингвистиче-
лингвистического процесса.
Переменная величина, которая изменяется таким образом, что
в процессе своего изменения становится и в дальнейшем остается
меньше сколь угодно малого наперед заданного положительного
числа е, носит название бесконечно малой. Кратко это определение
записывается в виде неравенства j а | < е, где а — бесконечно ма-
малая величина.
Например, бесконечно малая величина может быть получена
как вероятность фонологической системы принять устойчивое поло-
положение при однократном случайном изменении одного из дифферен-
дифференциальных признаков этой системы [24J. Указанная вероятность
определяется выражением
р = 1/2". B.1)
Предположим, что мы будем увеличивать число дифференциальных
признаков фонологической системы, последовательно придавая
величине п значения 0,1, 2, 3, 4, ...; тогда вероятность р принимает
соответственно значения 1, 1/2, 1/4, 1/8, 1/16, ....
Очевидно, какое бы малое положительное число е мы ни взяли,
среди значений р всегда найдется число, меньшее чем е.
Если в качестве е выбрать число 1/5000, то при п = 13 перемен-
переменная р примет значение 1/8192, меньшее чем е; если же за е взять
1/10000, то при п = 14 получим, что р = 1/16384, т. е. снова*
р< е.
В дальнейшем для нас будут важны следующие свойства
бесконечно малых величин.
1. Алгебраическая сумма конечного числа бесконечно малых ве-
величин есть также бесконечно малая величина, т. е.
В том случае, когда число слагаемых неограниченно возрастает,
такая сумма может и не быть бесконечно малой величиной.
2. Произведение бесконечно малой величины а на ограниченную
величину х есть также величина бесконечно малая, т. е.
ах
е.
Следствие 1. Произведение бесконечно малой величины а на
постоянную величину с также есть величина бесконечно малая, т. е.
е.
Следствие 2. Произведение двух или нескольких бесконечно
малых величин есть величина бесконечно малая, т. е.
2. Предел. Как было только что указано, вероятность фоноло-
фонологической системы принять устойчивое положение при однократном
случайном изменении одного из п дифференциальных признаков
определяется выражением р — 1/2".
Если аргументу п последовательно, придавать все возрастающие
целочисленные значения, то величина р будет неограниченно умень-
уменьшаться, приближаясь к нулю. Однако, последовательно уменьша-
уменьшаясь, эта величина всегда остается больше нуля. Следовательно,
всегда найдется какая-то бесконечно малая величина, которая по
абсолютной величине представляет собой разность между значением
переменной и величиной предела ее изменения — в данном случае
нулем. Все эти рассуждения приводят нас к понятию предела пере-
* В выражении
'о = log2S,
где /0 (S) — информация алфавита, состоящего из S букв, переменная вели-
величина S принимает последовательно значения натурального ряда чисел. Если
этот процесс возрастания происходит неограниченно, то какое бы большое по-
положительное число М мы ни взяли, среди значений /0 всегда найдется чис-
число, большее чем М, т. е. будет выполняться неравенство | /0 | > М. Такая
переменная величина называется бесконечно большой.
Между бесконечно большой и бесконечно малой величинами существует
связь, которая выражается следующим образом: если А — величина беско-
бесконечно большая, то обратная величина 1/Л есть бесконечно малая; наоборот,
если a — бесконечно малая величина (т. ё. a -+ 0), то I/a — бесконечно боль-
большая (I/a -*¦ оо).
52
менной величины, которое формулируется следующим образом: по-
постоянное число а называется пределом переменной величины и, если
абсолютная величина их разности есть величина бесконечно малая,
т. е. |« — а\ = а.
Символически это записывается в виде выражения lim и — а,
которое читается: «лимит и равен а».
Всякая переменная величина, имеющая предел, является огра-
ограниченной— такова, например, величина р в равенстве B.1).
Определив понятие предела переменной величины, заметим, что
обычно переменная величина выступает в виде функции. Так, в соот-
соотношении B.1) переменная величина р является, по существу, функ-
функцией, зависящей от п, т. е. р — f (n). Предел такой переменной ве-
величины правильнее записать в виде
lim р = 0,
указывая в этой записи характер изменения аргумента.
Понятие предела функции можно сформулировать следующим
образом. Если любая последовательность значений аргумента х
стремится к некоторому числу а, т. е. lim xn= а, и последователь-
последовательность значений функции при этом стремится к числу Ь, то число b
называется пределом функции у — f (х) при условии х-*- а. Это за-
записывается так:
¦\\ту = Ь.
х->а
Рассмотрим понятие предела функции на примере роста употре-
употребительности нулевых форм родительного падежа множественного
числа у существительных, обозначающих единицы измерения
(вольт — вольтов, рентген — рентгенов)—см. гл. 1, §7, п. 1.
Указанный процесс описывается зависимостью A.23):
» = — arctgf-
я \
или в общем виде р — f (t), где р — вероятность появления нуле-
нулевых форм, а t— время.
Возьмем такую последовательность значений аргумента: 1905,
1907, 1908, 1909, 1910 1920 1950
Вычислим по формуле A.23) соответствующие каждому из этих
значений t значения функции / (t):
0,906, 0,922, 0,927, 0,933, 0,937, .... 0,962, .... 0,983, ....
Очевидно, что по мере приближения t к со рассматриваемая функ-
функция стремится к единице.
Приведем теперь основные теоремы о пределах, которые понадо-
понадобятся нам впоследствии при решении лингвистических задач.
Теорема 1. Предел алгебраической суммы нескольких переменных
величин равен алгебраической сумме пределов этих переменных ве-
величин, т. е.
lim (* + у + ••• + г) = lim х + lim у + ... + Нт г.
53
Теорема 2. Предел произведения нескольких переменных величин
равен произведению пределов этих переменных величин, т. е.
lim (х • у ... z) = lim x • lim у ... lim z.
Из последней теоремы вытекают три следствия.
Следствие 1. Предел произведения постоянной на перемен-
переменную величину равен произведению постоянной на предел переменной
величины. Иными словами, постоянный множитель можно выносить
за знак предела:
lim ах = lim а • lim х = a lim x.
Следствие 2. Предел целой положительной степени пере-
переменной величины, имеющей предел, равен той же степени предела
этой переменной величины:
lim xa = (lim *)". B.2)
Следствие 3. Предел корня т-й степени из переменной
величины, имеющей предел, равен корню той же степени из предела
этой переменной величины, т. е.
У B.3)
Так как равенство B.3) можно представить в виде
то следствие 2 справедливо и для дробных положительных степеней.
Теорема 3. Предел частного двух переменных величин, имеющих
пределы, равен частному от деления этих пределов (при условии,
что предел делителя не равен нулю), т. е.
. х \\тх
У lim у *
Из теоремы 3 и следствия 2 вытекает, что
= (l'.mx) . B.4)
3. Сравнение бесконечно малых величин. Отношение двух бес-
бесконечно малых величин аир может быть либо бесконечно большой,
либо бесконечно малой, либо конечной величиной, либо величиной,
не имеющей предела. В общем виде об отношении двух бесконечно
малых величин нельзя сказать что-либо определенное. Это отно-
отношение зависит от характера изменения бесконечно малых величин.
Установить характер отношения двух бесконечно малых величин
или, как говорят, раскрыть неопределенность вида 0/0 можно путем
определения предела отношения а/р. Здесь имеют место следующие
ситуации.
1. Предположим, что имеются бесконечно малые величины
а = х3 и р = х, тогда
Величина а = х3, стремящаяся к нулю быстрее, чем р = х, высту-
выступает в качестве бесконечно малой высшего порядка малости отно-
относительно р.
2. Если, например, а = х, а р = х2, то
р *
В этом случае а является бесконечно малой низшего порядка ма-
малости относительно р.
3. Предел отношения может быть равен конечному числу, на-
например, в случае, когда а = (х + 5) х, а р = х:
lim = lim = ii
Р *~0 X *->
Здесь бесконечно малые аир являются величинами одного
и того же порядка малости.
4. Отношение а/р может вовсе не иметь предела, как, например,
в случае, если а = х sin —, a p = х. Предел
jc sin —
lim = lim sin —¦
не существует.
5. Предел отношения бесконечно малых величин аир может
быть равен единице, т. е.
Iim-5L=1.
Р
В этом случае аир называются эквивалентными бесконечно ма-
малыми величинами.
§ 2. Число Эйлера и модель роста словаря
В различных областях математики и ее приложениях часто ис-
используется функция
пределом которой при неограниченном возрастании х является уже
встречавшееся нам число Эйлера е = 2,718... (см. гл. 1, §6, п. 3).
Таким образом, можно записать, что
e=lim (l+—)*.
\ X I
B.5)
С помощью предела B.5) решаются многие задачи квантитативной
лингвистики, связанные с ростом или убыванием какой-либо вели-
величины.
Рассмотрим в этой связи некоторую идеальную модель роста
словаря.
64
55
*=¦
В результате постоянного расширения сферы деятельности че-
человека лексика каждого языка, особенно его терминологический
словарь, несмотря на выпадение некоторого количества слов, не-
неуклонно растет. Характеристикой, увеличения словаря служит ко-
коэффициент k его прироста за определенный период времени, напри-
например, за десятилетие. Этот коэффициент представляет собой отноше-
отношение количества новых слов, появившихся за десятилетие, за выче-
вычетом вышедших из употребления архаизмов (AL), к общему объему
(L) словаря в данный период, т. е.
AL_
L '
Зная начальный объем словаря L и коэффициент k, легко пока-
показать, что через 10 лет объем словаря составит
Lo +AL = Lo + Lok = Lo A + *).
Однако этот подсчет является в значительной степени прибли-
приближенным. Ведь в течение десятилетия прирост словаря происходит
не относительно исходной величины Lo, а относительно сумм
Lo + Д? (здесь величина AL указывает прирост словаря за то
количество времени — за год, месяц, неделю, — которое прошло от
момента, когда был зафиксирован начальный объем словаря L,,).
Предположим, что нам нужно учесть рост словаря по годам.
Тогда к концу первого года мы получим объем словаря, равный
к концу второго года он будет равен
а к концу десятилетия объем словаря составит
. k \ю
Если же учитывать прирост словаря не по годам, а по месяцам,
то получим еще более точный результат: к концу десятилетия
объем словаря будет равен
120
Теперь попытаемся представить процесс роста словаря в общем
виде. Для этого будем определять изменение словаря относитель-
относительно промежутка времени Т (например, тысячелетия), считая, что на-
начальный объем словаря характеризуется величиной Lo, а коэффи-
коэффициент прироста по-прежнему равен k. Разделим весь период Т на
л малых равных частей:
(я-1)Г
Гп Т] Г г -2Т] \ {i-l)Т /Г I Г(я-1)Г г]
L « J I п п J [ л я J L л J
IT /I }\f
Поскольку все промежутки 1 —
f
— малы, то в каждом
из них можно считать прирост новых слов AL постоянным и про-
пропорциональным исходному объему словаря и величине промежутка
Tin, т. е. № = kL(,T/n.
Объем словаря к концу дервого промежутка составит
к концу второго промежутка
и, наконец, к концу эпохи Т словарь будет включать
слов.
Предполагая, что число промежутков неограниченно растет
(т. е. п -*¦ оо), а длина промежутка Tin неограниченно убывает
(т. е. Tin -*- 0), являясь тем самым бесконечно малой величиной,
приходим к равенству
B.6)
Заменим частное kTIn величиной \1х, тогда п = kTx. Посколь-
Поскольку kTIn представляет собой произведение постоянной величины
k на бесконечно малую величину Tin, то Их есть тоже бесконечно
малая величина, т. е. Их = kTIn -*- 0. Учитывая все сказанное,
имеем:
Применяя следствия 1 и 2 из теоремы 2 (см. § 1, п. 2), перепишем
это выражение в виде
откуда на основании соотношения B.5) получаем формулу объема
словаря к концу периода Т в виде
55
§ 3. Глоттохронология
1. Классическая глоттохронология. На только что рассмотрен-
рассмотренный математический аппарат опирается современная глоттохроно-
глоттохронология, целью которой является приближенная абсолютная датиров-
датировка процессов расхождения диалектов и родственных языков, а так-
также количественная оценка степени их родства.
67
Исходные лингвистические предпосылки глоттохронологии [32в,
с 384] сводятся к пяти постулатам.
1°. Во всех языках мира существует некоторое множество слов,
обозначающих наиболее древние, всегда необходимые и поэтому не
изменяющиеся понятия-означаемые (например: большой, все, де-
дерево, птица и т. д.). Их можно объединить в некоторый тестовый
список (ТС).
2°. Доля означающих (слов или' эквивалентных словам устой-
устойчивых словосочетаний) из ТС, которая сохраняется за некоторый
промежуток времени Т для каждого языка, постоянна и не зависит
от способа выбора этих слов из ТС.
3°. Каждый язык и диалект имеет свой коэффициент сохранности
г относительно периода в 1000 лет. Величины г колеблются отно-
относительно периода в тысячу лет от 0,74 (для быстро развивающихся
«динамичных» языков) до 0,91 (для «стабильных» языков), средняя
величина г равна 0,81.
4°. Все означающие из ТС данного языка имеют одинаковые
шансы сохраниться на протяжении интервала Т.
5°. Если мы имеем дело с двумя потомками некоторого праязы-
праязыка, то вероятность означающего из праязыкового ТС удержаться
в ТС первого потомка не зависит от вероятности сохраниться в ТС
второго потомка.
Опираясь на эти постулаты, можно, во-первых, математически
оценить число тех означающих из ТС праязыка, которое сохраняет-
сохраняется в двух языках-потомках за период их независимого развития;
во-вторых* получить количественную оценку времени их самостоя-
самостоятельного развития.
Предположим, что Lo есть известное нам число означающих
ТС, которые характеризуют праязык в момент выделения из него
языков-потомков i и /. Зная коэффициенты сохранности лексики
для каждого из сравниваемых языков (rt и г}), легко определить
коэффициент потери общих слов в ходе дивергенции. Этот коэффи-
коэффициент равен k = 1 — ГгГ). Теперь, опираясь на рассуждения,
приведенные в § 2, легко показать, что число общих означающих,
сохранившихся в. языках-потомках за Т тысячелетий их самостоя-
самостоятельного развития, будет равно
B.8)
(напомним, что п — произвольное количество отрезков, на которое
разделено время дивергенции Т). Повторяя преобразования, ис-
пользованные в § 2, приходим к равенству
LT = Loe~
¦kT
B.9)
Зависимость B.9) показывает, сколько слов из ТС, определенного
в момент распада праязыка То, доживет до момента 7\ (здесь
Ух - То = Т).
Степень родства языков и диалектов можно оценивать через
отношение у — Lt/Lq. При y > 0,81 два «говорения» следует
считать диалектами, при 0,36< у < 0,81 «говорения» являются
родственными языками, входящими в одну семью; при 0,12 < у <
< 0,36 их следует считать принадлежащими к одной ветви.
Из соотношения B.9) легко получить значение периода дивер-
дивергенции Т. Для этого, прологарифмировав B.9), получаем
In LT = In Lo — kT,
откуда приходим к равенству
Т =
In Lo—In LT
B.Ю)
Теперь, опираясь на данные, приводимые В. Гуцу-Ромало [50,
с. 576—584], определим период дивергенции для пары романских
«говорений» — дакорумынского и арумынского языков-диалектов.
Всего сравнивается Lo = 202 латинских слова, из которых оба
языка-диалекта сохраняют только Ьт == 149 общих лексем. Ко-
Коэффициент сохранности лексики для дакорумынского языка-диа-
л^кта составляет rd = 0,81, для арумынского варианта соответствен-
соответственно имеем га = 0,88 [32в, с. 3861.
Тогда коэффициент потери общей лексики равен
Ь = 1 - V» = 1 - 0,81 • 0,88 « 0,29.
С помощью этих данных на основании формулы B.10) вычисляем
период дивергенции для обоих языков-диалектов. Этот период со-
составляет
In 202 —In 149
0,29
= 1,05 тысячелетия.
К8
Иными словами, распадение балканороманского языка-основы
относится к началу IX в., что хорошо согласуется с историко-линг-
вистическими фактами [24, с. 273—278].
2. Ранговый метод в глоттохронологии. Классическая глотто-
глоттохронология имеет ряд уязвимых пунктов.
Во-первых, критерии отбора понятий для ТС не являются про-
простыми, объективными и однозначными. Сами значения используе-
используемые в ТС, неизоморфны для разных языков. Примером может слу-
служить неконгруэнтность означаемых у прилагательных, обозначаю-
обозначающих цвета, у терминов родства, у существительных со значением
«дерево» [32 в, с. 285]; [44]. Поэтому между ТС и словарем конкрет-
конкретного языка трудно установить однозначное соответствие.
Во-вторых, нет никакой уверенности в том, что степень сохран-
сохранности лексики одинакова для всех участков ТС (ср. постулаты 2°
и 4°).
В-третьих, классическая глоттохронология не учитывает воз-
возможности вторичного сближения родственных языков, так широко
представленного в индоевропейском, тюркском и других ареалах.
59
Преодолеть некоторые из этих трудностей стремятся М. В. Ара-
Арапов и М. М. Херц 14], пытающиеся, во-первых, распространить
глоттохронологическую методику на лексику, находящуюся за
пределами ТС, а во-вторых, учесть различную скорость изменения
разных групп слов.
Отправной точкой построения авторов является идея о том, что
ранг (частота) слова в частотном словаре и его возраст коррели-
рованы: чем чаще употребляется слово и чем меньше его ранг, тем
больше вероятность того, что это слово древнего происхождения.
В связи с этим предполагается, что группы слов с близкими ранга-
рангами (частотами) в частотном словаре (ЧС) ведут себя так же, как и
слова ТС. Такое предположение дает возможность авторам отка-
отказаться от использования узкого тестового списка и осуществлять
исследование на словарном материале неограниченного объема.
Если в частотном словаре выбрать Lo лексических единиц (слов,
словоформ, основ, словосочетаний) с номерами i + Lq, to число
слов, имеющих в промежутке [t, i + Lo) возраст не менее Т лет,
вычисляется по формуле
где k* — постоянная, указывающая, в каком месте ЧС находится
отрезок It, i + Lo].
Чтобы учесть зависимость между скоростью изменения группы
И, i + Lo] и местом ЧС, авторы разбивают ЧС на последовательные
группы одинаковой длины по LQ слов, присваивая каждой группе
определенный номер. При этом выясняется, что существует зависи-
зависимость
?* = a//( B-12)
где /' — номер группы, a — параметр, характеризующийся объе-
объемом группы Lo и тем, на каких лексических единицах построен ЧС.
Подставляя в B.11) значение k* из B.12), авторы приходят к
основной зависимости их теории:
Lr., = Z.oe-«^. B.13)
Зафиксируем возраст слов Т и будем считать произведение аТ
параметром г\ формулы B.13). Тогда доля слов, употребляющихся
в языке не менее Т тысячелетий, быстро убывает с ростом ранга
группы:
Проверка зависимости B.14) на материале ЧС русского языка [391
показала хорошее схождение теоретических и опытных данных. Об
этом свидетельствует рис. 27, на котором верхняя теоретическая
прямая и эмпирические точки соответствуют синхронному срезу
1500 г., а нижняя — срезу 600 г. (праславянская эпоха). По оси
абсцисс выбран масштаб корня квадратного, по оси ординат —
логарифмический масштаб. График заимствован из работы 14].
Если фиксировать ранг / и вернуться к параметру k*, то можно
прийти к зависимости
связанной с исходными формулами глоттохронологии B.9) и B.11).
Таким образом, соотношение B.13) выступает в качестве обобще-
обобщения зависимости B.9).
Исходя из равенства B.13), можно построить формулу, оцени-
оценивающую число лексических единиц, имеющих возраст меньше Т
тысячелетий, т. е. появивишихся после некоторого момента. Это
число равно
{Vl) B.15)
21 25 j
и будет увеличиваться по мере роста ранга группы /, т. е. по мере
того как мы будем обращаться, ко все более редким словам.
Затем авторы вводят зависимость
Lt.t+ы., ^LTj-LT+&T.i = L0{e-^^T~e-^T+^^i), B.16)
оценивающую число слов, появившихся в языке в период от момен-
момента Т до момента Т + AT.
Исследование выражения B.16) показывает, что число неологиз-
неологизмов, появившихся, например, за 500 лет (AT = 0,5) при коэффи-
коэффициенте a = 0,02, по мере перехода ко все более редким словам сна-
сначала растет,, достигая максимума при /=1600, что соответствует
рангу i = 160 000 (если принять объем порции равным ста словам),
затем число неологизмов начинает падать.
Приведенный математический аппарат интересен с точки зре-
зрения перспектив математического моделирования различных диахро-
диахронических процессов. Действительно, если, например, выделить в
языке А слова, затронутые действием какого-либо фонетического,
морфологического или словообразовательного закона, то всегда
можно найти экспериментальное распределение каждого из этих
классов по ранговым группам ЧС.
Если бы удалось аппроксимировать эти распределения с помо-
помощью выражений B.13), B.15), B.16), то лингвисты получили бы
61
возможность количественно оценивать степень исходного и вторич-
вторичного лексического родства двух языков. Одновременно появилась
бы возможность получать абсолютную хронологию указанных диа-
диахронических процессов.
§ 4. Информационные модели слова и текста
Рассмотренный в § 2 и 3 математический аппарат может быть
применен для моделирования не только диахронических, но и ин-
информационных процессов в речи. В частности, с помощью вышепри-
вышеприведенных рассуждений можно получить строгое доказательство
формулы контекстной обусловленности, а также формул распреде-
распределения информации в тексте и слове.
Опыты по угадыванию букв неизвестного текста или слова по-
показывают, что энтропия (неопределенность) Н перед угадыванием
каждой последующей буквы (а, следовательно, и получаемая в ре-
результате угадывания информация /) последовательно убывает. По-
Получены экспериментальные оценки коэффициента убывания энт-
энтропии для некоторых разновидностей русского и французского язы-
языков. Предположим теперь, что, зная начальную неопределен-
неопределенность #0 и коэффициент убывания s, мы должны определить теоре-
теоретическую неопределенность буквы, стоящей в самом конце слова
длиной в | букв (| — величина непрерывная). Эту неопределен-
неопределенность мы обозначим символом Н\. Повторяя приведенные выше рас-
рассуждения, разделим весь текст на т равных участков
J-l [J-, JL] Г<Ь!>1, Щ
т } i т т ] L m m J
m
Если полученные участки ^ — *'~ '* = J достаточно малы, то
в каждом таком промежутке абсолютную величину убывания энт-
энтропии j АН | можно считать постоянной и в то же время пропор-
пропорциональной начальной энтропии Но и ширине участка |/т, т. е.
Количество энтропии в момент \1т равно
в момент 2\!т оно составляет
т
т
и, наконец, в конце текста ? энтропия будет равна
Снова предположив, что число участков неограниченно растет
(т ->¦ оо), а их длина неограниченно убывает (g/m -*¦ 0), получим
HI
Заменив величину — s\lm дробью Ух (при этом т = — xsl) и учи-
учитывая следствия 1 и 2 из теоремы 2 (см. § 1, п. 2), находим
#| = lira Л, (I + -L)- "WJlimfl + -LY]-*.
Так как предел, стоящий в квадратных скобках, есть число Эйлера,
то
НЪ = Н*-*. B.17)
Заменив непрерывную величину, характеризующую длину сло-
слова, на дискретные целочисленные значения буквенных позиций п
и учитывая, что неопределенность Н количественно равна синтак-
синтактической информации / (см. гл. 5, § 5, п. 2), приходим к выражению
h - 1Ф~$П, B-18)
характеризующему количество информации, которое несет буква,
стоящая на п-м месте в слове.
Теперь используем формулу B.17) для анализа распределения
информации в тексте. Нетрудно заметить, что при бесконечном уве-
увеличении длины текста (? -> сю) величина е~* стремится к нулю,
поэтому lim H» e~s* = 0, а следовательно, и lirn //g = 0.
Однако информационные исследования текста 123]; [26] показы-
показывают, что бесконечное увеличение его длины не приводит к полной
утрате неопределенности продолжений. Действительно, всякий текст,
будучи образован из сложных знаков (слов, словосочетаний, пред-
предложений), обладающих практически неограниченной комбинатор-
комбинаторной способностью, имеет несколько продолжений или, иначе го-
говоря, всегда обладает неопределенностью выбора следующей линг-
лингвистической единицы. Таким образом, предельная энтропия Нос всег-
всегда больше нуля. Из всего сказанного следует, что величина //<»,
определяемая обычно из опыта, должна быть исключена из нашего
расчета. Таким образом, моделируя распределение информации в
тексте с помощью выражения B.17), мы должны оперировать вместо
Hi разностью Hi — //«,, а вместо Но — разностью Но — //<». Учи-
Учитывая это, имеем
Я| — /Усе = (Яо - Я») е-%
откуда получаем
Щ = (На - //,) е~*+ Я,.
Заменив величины Н на значения / и введя вместо непрерывного I
дискретное п, приходим к формуле распределения информации
в связном тексте:
/» = (/о -'«) е~ю +'«• B-19)
Если в гл. 1 эта формула имела вид более или менее удачно подобран-
подобранной аппроксимации опытных наблюдений, то теперь, опираясь на
аппарат теории пределов и бесконечно малых величин, мы получили
строгое ее доказательство, раскрывающее внутренний процесс
построения информационной схемы слова и предложения.
62
ГЛАВА I
ДИНАМИКА ЛИНГВИСТИЧЕСКИХ ПРОЦЕССОВ И ЕЕ ОПИСАНИЕ
С ПОМОЩЬЮ ПРИЕМОВ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
§ 1. Диахроническая скорость и понятие производной
В предыдущих главах мы познакомились с простейшими мате-
математическими моделями, которые используются при описании диа-
диахронии языка и информационных процессов создания текста. Для
того чтобы перейти к построению более сложных моделей, необхо-
необходимо уметь измерять динамику лингвистического процесса на раз-
различных его этапах. При измерении этой динамики используется аппа-
аппарат дифференциального исчисления, одним из исходных понятий
которого является понятие производной. Чтобы раскрыть это по-
понятие, приведем два лингвистических примера.
1. Арабские заимствования в персидской прозе X—XII в. Фран-
Французский востоковед Г. Лазар [32 в, с. 374], исследуя арабские за-
заимствования в персидской прозе X—XII в., подсчитал число араб-
арабских слов и словоупотреблений в некоторых исторических и рели-
религиозных текстах этого периода (см. табл. 3.1).
Таблица 3.1
Доля арабизмов в персидских текстах X—XII в.
Длина текста (N)
Число арабизмов в
тексте (Na)
Объем словаря (Z.)
Число арабизмов в
словаре (La)
Процент арабизмов
в тексте /-^--100%)
Процент арабизмов
в словаре (jy- 100%]
Индексы текстов и время их написаиия-
1(ТВ)
963 —
964 г
2376
229
450
109
9,64.
24,22
2(ТТ)
конец
X в.
2302
260
477
152
11,29
31,86
3(ТС) | 4(ZA) | 5(TBq) | 6(At) |7(TAf) | 8(RS)
X—XI
в.
2165
237
494
128
10,94
25,91
1050
г.
2289
343
514
195
14,98
37,94
1060
г.
2424
390
586
224
16,09
38,22
1072 —
1073 г.
2299
296
519
183
12,87
35,26
1145
г.
2253
456
563
288
20,24
51,15
1200
г.
2259
590
694
357
26,11
51,44
Используя данные, приведенные в табл. 3.1, постараемся оце-
оценить темп проникновения арабизмов в персидскую прозу X—XII в.
64
Установим с помощью графика (рис. 28) зависимость между вре-
временем написания произведений и долей арабизмов, встречающихся
в тексте и словаре. По оси абсцисс отложим даты создания произ-
произведений, а по оси ординат — доли арабизмов в тексте (я =
= ^100%) и в словаре («'=х • 100%) каждого из них.
Как следует из графика, увеличение употребления арабизмов
в тексте и их нарастание в словаре аппроксимируется прямыми
линиями, которым соответствуют
линейные зависимости
(для арабизмов
y,%
+¦ bL C.1) 50±
в словаре) и
Номера t
памятников
Уы = aNx + bN C-2)
(для арабизмов в тексте); здесь
у—доля арабизмов; х—вре-
х—время, начало отсчета которого
соответствует началу X в. (т. е.
900 г.); а и b — параметры за-
зависимости.
Как известно, линейная
зависимость рассматриваемого
типа описывает равномерное
движение некоторой материаль-
материальной точки. Воспользовавшись
физической аналогией, условим-
условимся считать такой материальной точкой долю арабизмов.а пройденный
точкой путь у — количественным ростом этой доли в процентах.
Предположим теперь, что к моменту времени х = 0 наша точ-
точка уже прошла путь у0, а в последующий момент времени х длина
пути, пройденного точкой, равна у. Тогда расстояние, пройденное
точкой за время х, равно разности у — у о, а скорость, согласно опре-
определению равномерного движения, выразится отношением
Рис. 28
v = (у — уо)/х.
C.3)
Из равенства C.3) нетрудно получить следующее выражение:
y = vx + уй. C.4)
Соотношение C.4) описывает закон равномерного движения и пред-
представляет собой линейную зависимость относительно х. При этом
v (скорость равномерного движения) есть величина постоянная.
В нашем примере v характеризует темп диахронического процесса,
точнее, скорость увеличения доли арабизмов в персидском словаре
или тексте. В дальнейшем величину v будем называть диахрониче-
диахронической скоростью.
3 Зак. 1287- №
Возьмем теперь некоторый момент времени хх. «Путь», пройден-
пройденный долей арабизмов к моменту времени хи определим из выраже-
выражения C.4); он равен
ух = vxx + уа.
Аналогично получим «путь», пройденный арабизмами к моменту
времени х2:
Уг = vx2 + у0-
Следовательно, за отрезок времени х3 — хх «точка» пройдет «путь»
У 2 — У\ = (VX2 + У и) — (vx\ + у0),
или
Уг — У\ = v (х2 — хх),
откуда получаем
(Уг — УхI(х% — хх) = v. C.5)
Как было отмечено, «путь», пройденный лингвистической «точ-
«точкой» при равномерном диахроническом движении, есть функция от
времени, т. е. у = / (х). В нашем примере аргумент последователь-
последовательно принимает два значения: х± и х2. Разность хг — хх называется
приращением аргумента и обозначается символом Дл; (читается
«дельта *»):
Ах = хг — хх. C.6)
Разность значений функций, соответствующих значениям аргу-
аргумента хх и ха, называется приращением функции и обозначается
символом Ау.
АУ = / (*») - / (хх) = у, - Уг. C.7)
На основании введенных понятий приращения аргумента и функции
выражение C.5) может быть записано в виде
Таблица 3.2
Аи
— = «.
&
C.8)
Иными словами, скорость равномерного диахронического движения
есть отношение приращения «пути» к соответствующему прираще-
приращению времени.
Определим теперь числовые значения приращений аргумента
(времени) и функции (доли арабизмов), а также скорости проникно-
проникновения арабизмов в персидскую прозу.
На основании графика (см. рис. 28) составим таблицу теоретиче-
теоретических значений долей арабизмов в словаре персидского литератур-
литературного языка разных периодов. Условной единицей времени хусл бу-
будем считать промежуток в 50 лет, а величина у выражается в про-
процентах.
Используя данные табл. 3.2, определим по формуле C.8) сред-
среднюю скорость v в различные моменты времени х. Результаты при-
приведены в табл. 3.3.
Нетрудно видеть, что диахроническая скорость проникновения
арабизмов в персидскую прозу X—XII в. является постоянной ве-
величиной и составляет 6% за единицу времени (т. е. за 50 лет).
66
Т (годы)
.—.
"уел
у(%)
900
0
20
950
1
26
1000
2
32
1050
3
•
38
поо
4
44
1150
5
50
1200
6
56
1
2
3
4
5
Ч
0
1
3
3
4
20
26
32
38
44
1
1
1
1
1
Табли
6
6
6
6
6
ца 3.3
Ах
6
6
6
6
6
2. История употребления местоимения hie в позднелатинеких
памятниках. Мгновенная диахроническая скорость и понятие про-
производной. Может показаться, что мы слишком усложнили дело,
прибегая к сравнению приращения лингвистического «пути» с при-
приращением времени. Гораздо проще было бы, определяя диахрониче-
диахроническую скорость, поделить «путь», пройденный долей арабизмов, на
время х. Однако рассмотренная задача решается подобным образом
только в том случае, когда мы имеем дело с равномерно развиваю-
развивающимся лингвистическим процессом, который можно смоделировать
при помощи линейной функции. Между тем историческому языко-
языкознанию и лингвистике речи приходится иметь дело с такими про-
процессами, в которых лингвистическая скорость не является постоян-
постоянной величиной. Рассмотрим, в частности, историю употребления
латинского местоимения hie.
Судя по данным классической прозы и позднелатинским памят-
памятникам, латинское hie было наиболее вероятным претендентом сре-
среди других латинских местоимений на роль формировавшегося в то
время романского артикля. Латинские памятники первых веков
нашей эры показывают постепенное возрастание употребительности
форм hie. Однако примерное IV в. этот процесс прекращается и упо-
употребительность hie идет на убыль. Это отступление отмечается и в
латинских документах раннего средневековья, отражающих прото-
романскую речь. Имеющиеся статистические данные об употребле-
употреблении hie [27, с. 12—15]; [32 в, с. 377—3811 хорошо аппроксимируются
следующей формулой:
у = 23 — 0,75ха + 6х, C.9)
где у — доля употребительности hie в % среди других указатель-
указательных местоимений, ах — время, измеряемое в условных единицах
(каждая единица составляет столетие).
з* 67
Используя формулу C.9), определим теоретическую долю упо-
употребительности Ыс в самом начале нашей эры («нулевой» Год), в
100-м, 200-м и т. д. годах н: э., а также увеличение этой доли за
каждые 100 лет. Все эти данные показаны в табл. 3.4. На их основе
построен график, изображенный на рис. 29.
Таблица 3.5
Таблица 3.4
i
0
1
2
3
4
5
6
- "i
(начало н. э.)
A00 г.)
B00 г.)
C00 г.)
D00 г.)
E00 г.)
F00 г.)
у (%>
23,00
28,25
32,00
34,25
35,00
34,25
32,00
»1+Г»Гвср (еЛ вр->
5,25
3,75
2,25
0,75
—0,75
—2,25
—3,75
Из табл. 3.4 видно, что за каждую условную единицу времени
(столетие) происходит увеличение доли употребительности hie
(*/j+1 — yt), причем stot прирост осуществляется неравномерно:
10- 1 2 3 4 S 6 7 8 9 № 11
-100 0 100 200 300 400 500 600 700 800 900 1000 1100 X
Го д Ы
Рис. 29
в первую единицу времени (до 100 г. н. э) эта доля увеличилась на
,25%, между 100-м и 200-м годами уже только на 3,75% и т. д,
а после 400 г. вообще отмечается падение употребительности hie.
Прирост доли hie за 100 лет можно рассматривать как среднюю
скорость (i/op) нарастания роста его употребительности в течение
нашей условной единицы времени (т. е. в столетие). Эта скорость
не является постоянной величиной. Но если скорость роста употре-
употребительности hie, равная 5,25% в столетие в течение первого проме-
промежутка, упала до 3,75% в столетие в течение второго промежутка,
то, следовательно, она менялась и внутри этих промежутков.
Очевидно, что если брать промежутки времени все меньшей и
меньшей величины, то можно в конце концов прийти к мгновенной
скорости. Определим мгновенную скорость нарастания употреби-
2
B00 г.)
32
2,001
F.II 200 г.)
32,0030
2,01
B01 г.)
32,0299
2.1
B10 г.)
32,2925
2,3
B30 г.)
32,8625
2,5
B50 г.)
33,3125
тельности hie в самом начале 200-го г. н. э. Для этого, получив зна-
значения у для разных моментов времени в интервале от х = 2 до х =
= 2,5 (см. табл. 3.5), с помощью выражения C.9) будем вычислять
среднюю скорость для все более малых промежутков времени. В ито-
итоге получим следующие результаты:
о о о 1 ос тшят оо
от 2 до 2,5 имеем fop = —'¦ = 2,625% в столетие;
» 2 » 2,3 » ycp =
» 2 » 2.1 » Уср =
» 2 » 2,01 » yCD =
0,3
—132
0,1
32,0299—32
0,01
= 2,875% » >
= 2,925% » *
= 2,990% » >
» 2 » 2,001 » 32,0030-32 = з,000% » >
0,001
Из полученных данных видно, что чем меньше промежуток вре-
времени, тем ближе значение средней скорости к 3%. Короче говоря,
можно утверждать, что мгновенная диахроническая скорость в мо-
момент х = 2 составляет 3% в столетие.
Теперь определим мгновенную скорость в момент х = 3
(см. табл. 3.6). Характер вычислений тот же, что и в предыдущем
примере.
X
У(%)
3
34,25
3
34
,001
,2515
3,01
34,2649
3,1
34,3925
Та
3,2
34,5200
бл
1
и ца
3
34,
3.6
3
6325
Таким образом,
от 3 до 3,3 имеем t;cp = 34-6325-34'25 = 1,275% в столетие;
0,3
» 3 » 3,2
'25 =1,350% »
68
от 3 до 3,1 имеем иср= *4'3925 34'25 = 1,400% в столетие;
*
т> 3 » 3,01 »
3,001 »
34,2649—34,25
—:— р1
= 1,493%
34,2515—34,25 .
Уср = о 001 " '
Итак, можно считать, что мгновенная скорость в момент х =»
= 3 составляет 1,5% в столетие.
Рассматривая равномерный лингвистический процесс, мы при-
пришли к выводу, что его скорость есть величина постоянная и она оста-
остается неизменной при любом значении х и при любом значении Да:.
Иначе обстоит дело при неравномерном процессе. На примере раз-
развития употребительности латинского местоимения hie из произве-
произведенных нами расчетов видно, что оср зависит и от момента времени
х, и от Да:. Очевидно, что при одном и том же значении Да: различ-
Ау
ным моментам времени х соответствуют различные значения д2.
С другой стороны, при одном и том же значении х величина отноше-
отношения д| зависит от Да:, причем чем меньше промежуток Да:, тем бли_
же величина скорости к мгновенной.
Поэтому при неравномерном движении можно говорить не о ско-
скорости материальной точки вообще, а только о скорости в данный
момент или, как говорилось выше, о мгновенной скоро-
скорости. Отсюда следует, что величину v (x) мгновенной скорости можно
рассматривать как предел отношения д-- при Ах, стремящемся к
нулю, т. е.
-Mm **-
/u-o Ax '
(ЗЛО)
Вполне очевидно, что функция v (x) зависит от функции у (х):
функция у (х) как бы производит функцию v (х). Поэтому говорят,
что функция v (х) является производной функции у (х).
3. Нахождение производной. Из всего сказанного в п. 1 и 2
следует, что производной функции у = f (x) является предел от-
отношения приращения Ау этой функции к приращению независимой
переменной Ах при стремлении Ах к нулю, т. е.
,im
Ах дх-.О
Ах
C.11)
Для обозначения производной функции обычно используются
символы у' или у'х или /' (х) (читается: «игрек штрих», «игрек
штрих по икс», «эф штрих по икс»). Нахождение производной у'х.
функции у = / (х) по аргументу дс, или, иначе говоря, дифференци-
дифференцирование, можно разбить на следующие этапы:
1) нахождение приращения аргумента Ах и нового (наращен-
(наращенного) значения функции:
у + Ау = / (х + Ах);
2) определение приращения функции Ау.
Ау = / (х + Ах) - f (х);
3) нахождение отношения приращения функции к приращению
аргумента:
Ay ^f(x+Ax)-f(x)
Ах Ах '
4) определение предела этого отношения при условии Да:->0:
11т »m
Ьх->-о Ах д*-*о
Ах
Обращаем внимание читателя на то, что в рассмотренных выше
примерах вычисление производной (мгновенной скорости диахро-
диахронических процессов) осуществлялось по только что описанной схеме,
которая носит название непосредственного дифференцирования.
Однако непосредственное дифференцирование связано с громоздкими
вычислениями. Поэтому при определении производной обычно при-
применяют уже готовые стандартные правила и формулы, использова-
использование которых значительно упрощает процесс дифференцирования.
Ниже дается перечень таких правил и формул дифференцирова-
дифференцирования. Использующиеся в них символы расшифровываются следую-
следующим образом: х — аргумент; у — простая или сложная функция;
и, v, w, г — сложные функции от х; а, с, п — постоянные величины;
е — основание натуральных логарифмов.
Общие правила дифференцирования
у = с
= u±v±...±w
У =
с
с
v
= f(u), где « =
u'x-v—v'x-u
ух=
со'
70
Производные основных элементарных функций
Степенная функция
у— и"
Показательная функция
= ах
у'х = ах In a
ух = аи\па-и'х
Логарифмическая функция
1
y=logax
Ух =
и In a
Тригонометрические функции
у = sin х
= sin и
у —cos и
= tgu
= ctgu
— COSU-Ux
y'x=—smu-
, _1_
COS4 X
Ух=-
sin'u
Обратные тригонометрические функции
у = arc sin x
у = arc sin и
у — arc cos x
у — arc cos и
t/=arctgje
у = arc tg и
у — arc ctg x
t/ = arcctg«
У*
У'х
yi
Ух
t
Ух
У'*
У 1-х»
u'x
.У1—И*
1
u'x
i
"^
_ I
Строгое доказательство правил и формул дифференцирования
читатель найдет в книге [28].
§ 2. Дифференциал
1. Понятие дифференциала и дифференциалы простейших функ-
функций. В предыдущем параграфе было показано, что использование
производной связано с нахождением приращения функции Ду. Так
как последнее представляет собой довольно трудную задачу, то на
практике пользуются более простым приближенным значением
функции — ее дифференциалом. Эта идея лежит также
в основе применения дифференциала к приближенным вычисле-
вычислениям.
Для разъяснения понятия дифференциала воспользуемся сна-
сначала конкретной задачей. Пусть соотношение между количеством
терминов и терминологических словосочетаний, появляющихся
в текстах интересующей нас науки, написанных на германских,
романских и славянских языках, с одной стороны, и временем раз-
развития этой науки, с другой, описывается функцией
у = а + х3,
C.12)
где у — суммарное количество терминов в указанных языках, по-
появившихся за х лет развития данной области знания, а—число слов
и словосочетаний, использованных для обозначения исходных по-
73
нятий данной научной области. График этой функции изображен на
рис. 30.
Тогда производная функции C.12) согласно правилам дифферен-
дифференцирования равна
Ух = Зх2.
Предположим теперь, что интересующая нас наука существует
уже сто лет и мы хотим узнать, на сколько увеличится словарь этой
науки за два года. Это увеличение следует
рассматривать как приращение функции
Дг/ = (х + АхK — Xs. .
Раскрывая скобки, получаем
Ау = х3 + Зх2Дх + ЗхДх2 + Ах3 — х3,
или
Ау = Зх*Ах + ЗхДх2 + Ах3.
Три члена, составляющие правую часть
этого соотношения, не равноценны, в чем
можно убедиться, подставляя численные зна-
значения х = 100 и Ах — 2:
3*2Дх = 3 • 10000 • 2 = 60 000;
ЗхДх2 = 3 • 100 • 4 = 1 200; Ах3 = 23 = 8;
Ау = 61 208.
Второе слагаемое меньше первого в 50 раз, а третье — в 7500 раз.
Таким образом, среди слагаемых, в сумме составляющих при-
приращение Ау, величина Зл:2Дл: является главной частью прираще-
приращения функции / (х)=а-\-х3, в то время как сумма ЗхДл:2 + Ад;3 = а
составляет малозаметный вклад в величину приращения Ау. По-
Поскольку слагаемое ЗхЗДх прямо пропорционально (при постоянном х)
приращению Ах, его называют главной линейной частью приращения
функции f (x). Эта главная часть приращения, отличающаяся от
последнего на бесконечно малую величину, и есть дифференциал
функции:
dy = y'xAx. C.13)
Так как приращение Ах аргумента совпадает с его дифференциа-
дифференциалом dx, то отсюда следует, что дифференциал функции, равен ее
производной, умноженной на дифференциал аргумента, т., е.
Рис. 30
dy = y'xdx.
C.14)
Можно показать, что дифференциал функции и ее приращение
суть эквивалентные -бесконечно малые величины:
dy да Ау.
C.15)
Опираясь на равенство C.14), мы приходим к новому важному
для дальнейшего определению производной. Согласно этому опреде-
опреде_ о, производная функции есть отношение дифференциала этой
функции к дифференциалу ее аргумента:
Ух = — .
dx
Итак, для нахождения дифференциала функции следует найти
производную этой функции и умножить ее на дифференциал аргу-
аргумента, равный приращению последнего.
Применяя эту операцию, можно вывести формулы для нахожде-
нахождения дифференциалов -простейших функций. Сводка этих формул
приводится ниже (значения символов здесь те же, что и в сводхе
правил нахождения производной; см. § 1, п. 3).
d(axcs'mu) —
da
dx =
d(«d-.f) =
, ( и \
\ V )
dy = у
d(xn) =и
^ Ах;
du ± dv;
j-du + u-dv;
v-du—u-dv
•xn~ldx;
d (arc cos u) =
d (arc tg u) =
У
du
du
\+u
du
du
S
ulna '
d(sin«) = cos и du;
d (cos u) = —sin и du;
d(\gu)= ""
d(ctgu)= —
cos2 и
du
d (ax) = a* In a du\
2. Использование дифференциала для приближенных вычисле-
вычислений в лингвистических задачах. Исследуя динамику диахронических
процессов (ср. историю латинского местоимения hie в п. 2 § 1 и
рост романо-германской и славянской терминологии) с помощью
приращения функции Ау, мы видели, насколько трудоемки и.гро-
моздки вычисления этой величины, а следовательно, и самой
функции. Вычисление значений функции у можно значительно
упростить, опираясь на приближенное равенство
Ау да dy = ух Ах.
74
C.16)
7»
Для этого перепишем выражение C.16) в виде
/ (х + Ах) - / (х) « у'хАх,
откуда
/ (х + Ах) « / (х) + у'хАх,
или, учитывая C.13),
f {х + Ах) « / (х) + df (x). C.I7)
Проверим теперь на основе уже приводившихся данных о росте
терминологии (см. п. 1) эффективность приближенных вычислений
с помощью дифференциала.
Определим число терминов на 102-м году существования интере-
интересующей нас науки при условии, что на 100-м году ее развития име-
имелось уже 1001000 терминов. Из них количество исходных терминов
а = 1000, а вновь возникшие термины составляют Xs — 1000000.
Примем за начальное значение аргумента х = 100, тогда у =
= а + х3 = 1001000, у'х = Зх2 = 30000, а Ах = 2. Подставляя эти
значения в C.17), получаем
/ (х + Ах) = / A02) « 1001000 + 30000 • 2 = 1061000.
Посмотрим теперь, какую ошибку мы допускаем, взяв дифферен-
дифференциал dy вместо приращения Ау. Для этого воспользуемся точным
значением приращения нашей функции за два года:
Ау = Ъх*Ах + ЗхДх2 + Да:3 = 61208.
Точное число терминов через 102 года составит
у + Ау= 1001000 + 61208 = 1062208.
Допущенная ошибка при использовании dy вместо Ау равна
61208—60000 ^ п опт
1062208 «U.UUllcS,
т. е. всего лишь около 0,11%.
Используя равенство C.17), можно получить приближенные
формулы для вычисления значений некоторых элементарных функ-
функций. Приведем формулы, полезные в лингво-статистических и
квантитативно-лингвистических исследованиях.
хп
пх
п~1
Ах.
C.18)
C.19)
1. Если у = хп, то (х + Ах)п
При х = 1 и Длг = а получим
A + о)в « 1 + ла;
в случае Ах = — а выражение C.18) принимает вид
A — а)" « 1 — па.
Мы будем применять равенство C.19) при решении вероятност-
вероятностных и лингво-статистических задач. Пусть, например, необходимо
возвести в десятую степень вероятность q = 1 — Р (А) = 0,9901
(ср. гл. 6, § 1); тогда имеем:
9w = A _ 0.0099I0 = 1 — 10 • 0,0099 = 1 — 0,099 = 0,901.
76
Заметим, что формулой C.19) следует пользоваться при неболь-
небольших значениях л и а. Если п > 10, а а > 0,01, то получаемые с по-
помощью C.19) значения функции будут заметно отличаться от истин-
истинных.
2. Если у — е*, то, согласно C.17),
Ах.
C.20)
При определении количества информации, содержащейся в раз-
различных участках текста, возникает необходимость определить ве-
величину
/ (п) = >-«,
где s = 0,21 (см. табл. 1.5 на стр. 41), an — номер буквенной по-
позиции — аргумент функции / (п).
Тогда можно вычислить теоретическое значение информации
в каждой буквенной позиции беллетристического текста. Сделаем
это относительно первой буквенной позиции.
Пользуясь формулой C.17), имеем
т. е.
/ (я + Ая) = / (я) + Г (п) An,
g-sin+Дп) — g-sn—se~m An.
Далее, полагая s = 0,21, п = 0, a An = 1, получим
e-o.3i = ео _ о,21е° .1 = 1— 0,21 = 0,79.
Этот результат не очень сильно отличается от точного табличного
значения е~0'21 = 0,81.
Аналогичным образом, пользуясь только что описанным мето-
методом, для второй буквенной позиции получаем е~20'21 = 0,64
при табличном значении 0,65/
3. Производные и дифференциалы высших порядков. Произ-
Производную и дифференциал от данной функции у = f (x) можно рас-
рассматривать как новые функции от х. Пользуясь правилами, приве-
приведенными выше, от этих функций можно взять новую производную
и новый дифференциал.
Производная, взятая от производной у'х — f (x), называется
производной второго порядка (или второй производной) и обозна-
обозначается (у'х)'х = у'х'х или [/' (х)]' = /" (х). Дифференциал, взятый от
дифференциала dy =» ухАх, называется дифференциалом второго
порядка. Этот дифференциал обозначается символом d (dy) — d*y
или d [if (x)] = cPf (x).
Можно показать, что дифференциал второго порядка равен
а вторая производная
Ухх~
C.21)
C.22)
77
Последовательно повторяя описанные операции, можно полу-
получить производные третьего, четвертого, ..., я-го порядков и соот-
соответственно находить выражения для третьего, четвертого,..., тг-го
дифференциалов.
§ 3. Исследование функций, аппроксимирующих
лингвистические процессы
Чтобы оценить математическую модель, описывающую то или
иное лингвистическое явление, необходимо исследовать все особен-
особенности изменения функции (или, как говорят, ее поведение) при из-
изменении аргумента. Это исследование осуществляется с помощью та-
таких математических понятий, как непрерывность функции, ее воз-
возрастание и убывание, экстремальные значения, выпуклость и вог-
вогнутость, точки перегиба.
1. Непрерывность и точки разрыва функции. Функция у = f (х)
называется непрерывной в точке х0, если выполняются следующие
условия:
1) функция у = f (х) существует (определена) при х — х0;
2) предел приращения Дг/ функции у равен нулю, если Ая-»-О
при х-*- х0, т. е.
lim Aj/= lim |
Л<-*0 Дх->0
— f(x0)] = 0.
C.23)
Функция, непрерывная во всех точках некоторого отрезка, назы-
называется непрерывной на этом отрезке, а непрерывная во всей области
существования — непрерывной функцией (примерами непрерывных
функций служат линейная и показательная функции или функции
у «? sin х и у = cos х; см. гл. 1, § 6).
Если при х = х0 условия непрерывности не выполняются, то
точка х0 называется точкой разрыва, а сама функция — разрывной
в этой точке. Примерами таких функций являются гиперболиче-
гиперболическая зависимость у — а/х, которая терпит разрыв в точке * = 0
(см. рис. 9), а также тригонометрические функции у = tg x и у =
=» ctg х, являющиеся разрывными соответственно в точках х =
¦= Bk + 1) я/2 и х = kn; где k = 0, ± 1, ±2, ... (см. рис. 13).
2. Возрастание и убывание функции. Фунция у = / (х) назы-
называется возрастающей в интервале (т, п), если большему значению
аргумента в этом интервале соответствует большее значение функции
(см. рис. 10). Если же в некотором интервале большему значению
аргумента соответствует меньшее значение функции, то функция
называется убывающей в этом интервале (см. рис.11). Как воз-
возрастающие, так и убывающие функции называются монотонными,
а интервалы возрастания и убывания функции — интервалами мо-
монотонности.
Исследование функций опирается на простую связь, существую-
существующую между поведением функции в некотором интервале и свойства-
свойствами ее производной в этом же интервале. Эта связь описывается с по-
помощью трех теорем.
78
Теорема 1 (достаточный признак возраста-
возрастания функции). Если производная функции у = / (х) поло-
положительна для всех значений х в интервале (т, п), то функция в этом
интервале возрастает.
Теорема 2 (достаточный признак убывания
функции). Если производная функции у — f (x) отрицательна
для всех значений х в интервале (т, п), то функция в этом интервале
убывает.
Теорема 3 (достаточный признак постоян-
постоянства функции). Если производная функции у — f (х) равна
нулю для всех значений х в интервале (т, п), то функция в этом
интервале не изменяется, т. е. является постоянной.
Иногда эти теоремы объединяются под названием достаточ-
достаточного признака монотонности функции.
3. Экстремальные значения функций. Рассмотрим еще раз часть
графика функции
/ = 'о+ 2 rhsmBnkx/l-\-<ph),
k=i
аппроксимирующей распределение информации в 12-буквенном
русском слове (см. рис. 25).
Наблюдая за изменением функции, нетрудно заметить, что орди-
ординаты кривой возрастают на участках ВС и DE, достигая в точках
С и Е максимальной величины по сравнению с ординатами сосед-
соседних с ними точек. Значение аргумента, при котором функция имеет
наибольшую величину, называется точкой максимума, а соответст-
соответствующее значение функции — максимумом функции (точки С, Е).
Таким образом, функция у — f (х) имеет максимум в точке х — а,
если при всех х, достаточно близких к а, выполняется неравенство
/ (а) > / (х).
На участках АВ и CD ординаты точек последовательно убывают,
приншая наименьшие значения в точках В и D. Значение аргумен-
аргумента, при котором функция принимает наименьшую величину, назы-
называется точкой минимума, а соответствующее значение функции —
минимумом функции.
Иными словами, функция у = / (х) имеет минимум в точке
х = а, если для всех х, достаточно близких к а, выполняется нера-
неравенство / (а) < / (х).
Нетрудно заметить, что максимум является границей перехода
от возрастания функции к ее убыванию, а минимум — от убывания
к возрастанию функции. Понятия «максимум» и «минимум» объеди-
объединяются обычно одним термином — экстремум (или экстремальное
значение) функции. Понятие экстремума выступает в качестве ло-
локального свойства функции, характеризующего ее поведение лишь
в непосредственной близости от данной точки х = а.
При исследовании функций их экстремальные значения опреде-
определяются с помощью следующих признаков.
Необходимый признак экстремума форму-
формулируется таким образом: если функция у = / (х) имеет экстремум
79
в точке х = а, то ее производная в этой точке либо равна нулю
W («) = 0J, либо вообще не существует. Этот признак является не-
необходимым, но не достаточным признаком экстремума:
из того, что производная в данной точке обращается в нуль или вовсе
не существует, еще не следует, что эта точка обязательно будет
точкой экстремума. Поэтому при выявлении экстремальных зна-
значений приходится оперировать двумя более сильными — так назы-
называемыми достаточными признаками экстремума.
Первый достаточный признак экстрем у-
м а формулируется так: точка х = а служит точкой экстремума
функции y=f (х), если производная f (х) при переходе х через а ме-
меняет знак', при перемене знака с «+» на «—» точка а является точ-
точкой максимума, при перемене знака с «—» на «+» — точкой мини-
минимума (в самой точке а производная либо равна нулю, либо не су-
существует).
V. Исходя из необходимого и первого достаточного признака экст-
экстремума, получаем следующее правило исследования функции
у = f (x) на максимум и минимум с помощью первой производной:
1) найти первую производную у'х = /' (х); . *
2) найти точки, в которых f (х) = 0 или f (x) не существует;
эти точки называются критическими точками I рода (если таких
точек не существует, то функция экстремумов не имеет);
3). исследовать изменение знака производной при переходе сле-
слева направо через каждую критическую точку х—а, для чего следует
дать х значение несколько меньшее, чем а (т. е. х = а — К), а за-
затем несколько большее, чем а (т. е. х = а + h), причем под h под-
подразумевается произвольное достаточно малое положительное число
(возникающие здесь варианты представлены в табл. 3.6);
4) вычислить экстремальные значения функции в точке а.
f'(e-A)
+ 1 + 1
OOOO
f (o)
или
или
или
или
8 8 8 8
t
Характер (
максимум
минимум
экстремума нет
экстремума нет,
Таблица 3.6
сритической точки
функция возрастает
функция убывает
Иногда для установления максимумов и минимумов функции
бывает удобнее и проще воспользоваться вторым достаточ-
достаточным признаком экстремума, который формулирует-
формулируется так: точка х — а есть точка экстремума функции у = / (х),
если f (а) = 0, a f (а) Ф О, причем в том случае, когда f" (a) > О,
точка а является точкой минимума, а когда f (а) ¦< 0 — точкой
максимума.
Исходя из второго достаточного признака сформулируем сле-
следующее правило исследования функции на экстремум:
1) найти первую и вторую производные;
2) найти критические точки функции;
3) определить знак второй производной: если вторая производ-
производная в критической точке положительна, то эта точка является точ-
точкой минимума; если вторая производная отрицательна, то рассма-
рассматриваемая точка есть точка максимума; если же вторая производная
в критической точке равна нулю, то следует возвратиться к исследо-
исследованию функции с помощью первой производной (см. табл. 3.7);
4) вычислить экстремальные значения функции в точке а.
а
С (X!
0
П*)>о
Таблица 3.7
Характер критической точк>
максимум
минимум
неизвестен
(правило неприменимо)
С X
Рис. 31
4. Выпуклость, вогнутость и точка перегиба кривой. Для опре-
определения понятий выпуклости и вогнутости рассмотрим кривую
у = f (х), изображенную на рис. 31. В промежутке (а, Ь) выберем
несколько точек и прове-
проведем в них касательные, у
Из графика видно, что все
точки кривой в промежут-
промежутке (а, в) лежат ниже
любой ее касательной в
этом промежутке. В таком
случае говорят, что кривая
выпукла вверх в интервале
(о, Ь) или просто выпукла.
Рассмотрим теперь дру-
другой промежуток F, с) той
же кривой и проведем несколько касательных в точках этого про-
промежутка. Здесь все точки кривой лежат выше любой ее касатель-
касательной в промежутке (Ь, с). В таком случае говорят, что кривая вы-
выпукла вниз в интервале (Ь, с) или просто вогнута.
Вогнутость и выпуклость кривой может быть определена с по-
помощью одного из следующих признаков.
Признак 1. Интервалу убывания первой производной f (х)
соответствует участок выпуклости (а, о) кривой, а интервалу воз-
возрастания f {х) — участок вогнутости (Ь, с).
Признак 2. Если вторая производная функции у =» / (х)
во всех точках интервалами, Ь) отрицательна, т. е. f (х) < 0, то
кривая у = / (х) выпукла в этом интервале и, наоборот, если вторая
производная во всех точках интервала (а, Ь) положительна, т. е.
f" (х) > 0, то кривая у = f {x) вогнута в указанном интервале,
81
Если кривая у — f (х) имеет участки выпуклости и вогнутости,
то между ними, очевидно, будет существовать какая-то точка, ко-
которая не обладает свойствами соседних промежутков. Такая точка
называется точкой перегиба (точка В на рис. 31). Поскольку по обе
стороны от точки перегиба направления выпуклости различны, зна-
знаки второй производной /" (х) в соседних точках также различны,
а сама производная должна быть равна нулю.
Для нахождения точек перегиба, а также участков выпуклости
и вогнутости кривой у = f (х) рекомендуется пользоваться следую-
следующим правилом:
1) найти вторую производную у" = /" (х);
2) найти точки, в которых /" (х) = 0 или /" (х) не существует, —
критические точки II рода;
3) исследовать изменение знака второй производной при пере-
переходе слева направо через каждую критическую точку II рода х — Ь,
для чего следует определить знаки /" (х) в точках х = Ъ — h и
х = Ъ + h, где h — произвольное достаточно малое положитель-
положительное число; если /" (х) меняет знак при переходе через точку х = Ь,
то график функции имеет точку перегиба; если же знак /" (х) не
меняется, то точки перегиба нет — при /" (х) << 0 кривая в рассма-
рассматриваемом интервале выпукла, а при /" (х) >» 0 — вогнута;
4) вычислить ординаты точек перегиба.
5. Асимптоты. Прямая линия А называется асимптотой кри-
кривой, если расстояние точки М от прямой А стремится к нулю при
неограниченном удалении этой точки по кривой от начала коорди-
координат. Примером горизонтальной асимптоты может служить
ось Ох на рис. 9, примером вертикальной асимптоты являет-
является ось Оу на том же-рисунке. Кроме того, могут существовать и н а-
к л о н н ы е асимптоты.
Для выявления вертикальных асимптот необходимо найти точки
бесконечных разрывов, т. е. точки, в которых / (х)-> оо. Взаимное
расположение бесконечной ветви кривой и асимптоты определяется
в ходе исследования «знака бесконечности» при стремлении х к х0
слева и справа. Так, например, для функции y = tgx значения
tgx-> + оо, когда х-+ я/2, оставаясь меньше чем л/2, и tgx->
-> — оо, когда х-> я/2, оставаясь больше чем л/2 (см. рис. 13).
Если же / (х) ни при каком значении х не стремится к бесконечно-
бесконечности, то вертикальных асимптот нет.
Чтобы найти "наклонную асимптоту кривой у — f (x), нужно
выразить расстояние между точкой М (х; у) и точкой М' (х; у') пря-
прямой А через разность ординат этих точек при одной и той же абсцис-
абсциссе х:
у-у' =f{x)-(kx+b).
По определению, прямая у' = kx + b служит асимптотой кри-
кривой у = / (х) в том случае, если расстояние между ними (разность
ординат у — у') стремится к нулю при бесконечном возрастании
X Т С
lim [/(*) — {kx-\-b)} = 0. C.24)
Х-+0О
82
Определим величины k и Ь. Для нахождения k представим вы-
выражение C.24) в следующем виде:
Так как первый множитель этого произведения стремится к беско-
бесконечности, то второй множитель должен стремиться к нулю. Отсюда
или
Х-*х X х->оо X
но lim — = 0, поэтому
х-юо X
C.25)
Ж->оо Л"
Найдя величину k, теперь из равенства C.24) определим Ь:
b = lim[f(x) — kx]. C.26)
Для установления взаимного расположения кривой и асимптоты
следует выяснить знак разности / (х) — (kx + b) как при х-*- + оо,
так и при х-*- — оо. Если эта разность положительна, то кривая
расположена над асимптотой; если же она отрицательна, то кри-
кривая лежит под асимптотой.
6. Общая схема исследования функции и построение ее графика.
Как уже говорилось, при математической экспликации того или
иного лингвистического процесса представляют интерес не отдель-
отдельные численные значения моделирующей его функции, а существен-
существенные особенности этой функции, например: возрастание и убывание,
максимум и минимум, выпуклость и вогнутость ее графика. Все
эти свойства функции хорошо прослеживаются на графике. Однако
построение графика, так же как и выбор аналитической формы
функции по некоторому (пусть даже очень большому) количеству
точек, взятых наудачу, всегда связано с опасностью упустить не-
некоторые существенные особенности функции. Напротив, предвари-
предварительное аналитическое исследование, выявляя ее существенные осо-
особенности, позволяет определить положение характерных точек.
Исследование функции, а затем построение графика осущест-
осуществляется обычно по схеме, включающей следующие этапы.
1. Определение области существования и промежутков непре-
непрерывности функции.
2. Установление области возрастания и убывания функции;
нахождение точек экстремума и выяснение их характера.
3. Установление промежутков выпуклости и вогнутости кривой;
нахождение ее точек перегиба.
4. Отыскание асимптот.
5. Сведение результатов исследования в таблицу.
Эта таблица должна включать значения функции в ее характер-
характерных точках, к которым относятся точки экстремума, точки переги-
перегиба и точки пересечения функции с осями координат, точки разрыва
(если они существуют), а также границы области существования
функции. Кроме того, в таблицу вносятся и некоторые дополни-
дополнительные значения функции. Перенеся найденные точки на чертеж
и соединив их плавной кривой, мы получим график исследуемой
лингвистической функции.
Проведя исследование функции и представив его результаты в
легко обозримой графической форме, мы получаем возможность
объективно решить вопрос о соответствии математической модели
ее лингвистическому оригиналу.
7. Исследование двух функций, аппроксимирующих распреде-
распределение информации в тексте. Моделирование распределения инфор-
информации в тексте осуществляется с помощью двух функций: выражения
C.27)
где. п — номер буквы в тексте, Ях — энтропия первой буквы текс-
текста, а — коэффициент [23, с. 67], а также показательной функции
/„ = (/0 -
+ 1а
C.28)
Необходимо выяснить, какая из этих зависимостей лучше модели-
моделирует распределение информации в тексте. Чтобы сделать возможным
использование аппарата исследования функций, будем считать ар-
аргумент п в обоих случаях непрерывной величиной.
1) Приведем правую часть соотношения C.27) к общему знаме-
знаменателю:
гт Н\п—аН\п+аН\
1п ¦ •
п
Из полученного равенства видно, что функция /„" = у = f (я)
существует и непрерывна при всех значениях аргумента я, кроме
я = 0, т. е. в интервалах (— оо, 0), @, + оо).
2) Установим теперь характер поведения функции в интервале
@, + оо). Для этого найдем первую производную
C.29)
Это соотношение показывает, что при любом значении аргумента
п в интервале @, + оо) первая производная является отрицатель-
отрицательной величиной, откуда следует, что данная функция убывает
в указанном интервале.
Так как среди возможных значений аргумента нельзя найти та-
такое, при котором производная /' (я) обращалась бы в нуль, то функ-
функция C.27) не имеет точек экстремума.
84
3) Для установления характера кривой в интервале @, + оо)
(выпуклости или вогнутости) найдем вторую производную. Имеем
Очевидно, что при всех положительных значениях я вторая произ-
производная данной функции положительна. Значит, график распреде-
распределения информации в тексте представляет собой вогнутую линию
и не имеет в интервале @, + оо) точек перегиба.
4) Определим асимптоты кривой распределения информации.
Так как при я->0
lim
л-»-0
Шп
я-»-0
=+оо,
то прямая п = 0 (т. е. ось ординат) есть вертикальная асимптота.
Для определения положения наклонной асимптоты нужно вос-
воспользоваться формулами C.25) и C.26). Угловой коэффициент
равен
Начальная ордината асимптоты
b = \\m [f{n)-kn] = \\
Поскольку угловой коэффициент асимптоты равен нулю, эта
асимптота имеет горизонтальное положение, а ее уравнение при-
принимает вид
у = Н1 A — а). C.30)
Для установления взаимного расположения кривой распреде-
распределения информации и горизонтальной асимптоты определим разность
ординат этой кривой и асимптоты при одном и том же значении п:
Так как полученная разность положительна (величины а, Нх и я
положительны), то горизонтальная асимптота C.30) расположена
под кривой C.27).
Перенеся все результаты исследования на чертеж, мы получаем
график функции C.27) в том виде, как он изображен на рис. 32.
Используя ту же схему, исследуем функцию C.28), представляю-
представляющую собой второй вариант описания распределения информации
в тексте. Здесь мы получаем следующие результаты.
1) Функция /„ = у — ф (п) существует и непрерывна на всей
числовой оси: — оо < п < + оо.
85
2) Вид первой производной
Ф' (л) = - s (/0 - /J е~™
показывает, что функция является убывающей, так как первая
производная всегда отрицательна, и экстремальных значений не
имеет.
3) Вторая производная
положительна, поэтому кривая C.28) вогнута и не имеет точек пе-
перегиба.
4) График функции имеет только одну горизонтальную асимпто-
асимптоту у = 1Х. При п = О кривая пересекает ось Оу в точке у = 10.
Всем этим условиям
соответствует уже знако-
знакомый нам график, изоб-
изображенный на рис. 19.
Результаты исследо-
исследования показывают, что
зависимость
моделирует распределе-
ние информации в тек-
сте при 0<я<оо, вто
время как зависимость
Рис 32
описывает распределение информации при 0 <^ я< оо.
При информационных измерениях языка широко используется
величина /0 (информация алфавита). Эта величина характеризует
количество информации (неопределенности), возникающее в том
случае, когда совершенно не учитываются дистрибутивно-вероят-
дистрибутивно-вероятностные ограничения на употребление лингвистических единиц,
причем п здесь считается равным нулю. Эта ситуация учтена в за-
зависимости C.28), но не предусмотрена в функции C.27), которая при
п = 0 не существует.
Из всего сказанного следует, что для моделирования распределе-
распределения информации в тексте следует выбрать функцию C.28).
ГЛАВА 4
СУММИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
В ЛИНГВИСТИЧЕСКИХ ПРОЦЕССАХ
Многие задачи квантитативной лингвистики возникают как за-
задачи вычисления сумм языковых величин, характеризующих тот
или иной речевой или диахронический процесс в целом или в его
части. Эти задачи решаются с помощью аппарата теории рядов и ин-
интегрирования.
§ 1. Основные понятия теории рядов
1. Числовой ряд. Если взять множество значений величин ин-
информации, приходящихся на первую, вторую и т. д. буквы слова или
множество относительных или абсолютных частот, характеризую-
характеризующих употребительность данного лингвистического явления в опре-
определенные периоды истории языка, то видно, что из этих множеств
можно образовать числовые последовательности, подчиняющиеся
определенному правилу. Бесконечная числовая последователь-
последовательность имеет следующий вид:
«!, Ы2, .... Un
где ип — общий член последовательности.
Члены последовательности можно суммировать. Тогда алгебра-
алгебраическая сумма членов последовательности
ut + и2 + и3 + ... + ии 4- ... D.1)
образует бесконечный числовой ряд, или просто ряд. Иногда для
оо
обозначения ряда применяют запись S ип. Выражение для «-го
п= 1
члена ряда при произвольном п называется общиц членом ряда.
Обычно общий член ряда задается формулой ип = / (и), пользуясь
которой, можно сразу написать любой член ряда. Например, в ря-
ряде, характеризующем сумму информации, приходящихся на пер-
первую, вторую, ..., п-ю, ... буквы слова, общий член имеет вид
Составим из первых членов ряда D.1) суммы
S2 = «! 4- «2.
n = «1 + «2 + «3 "Г- •-• + «nr
которые называются частичными суммами данного ряда.
87
Если при бесконечном возрастании номера п частичная сумма
ряда Sn стремится к конечному пределу S, т. е.
lim Sn = S, D.2)
то в этом случае ряд называется сходящимся, а число S — его
суммой.
Если же величина Sn неограниченно возрастает, т. е. lim Sn =
Л-»оо
= оо, или Sn хотя и не возрастает неограниченно, но ни к какому
конкретному пределу не стремится, то мы имеем дело с расходя-
расходящимся рядом.
Ряды могут быть либо знакоположительными (все члены такого
ряда положительны, т. е. ип > 0), либо знакоотрицательными
(все члены такого ряда отрицательны, т. е. ип <С 0), либо знакопере-
знакопеременными (члены такого ряда могут быть как положительными, так
и отрицательными).
Членами ряда могут служить не только числа, но и функции не-
некоторого аргумента х. В этом случае мы имеем дело с так называе-
называемым функциональным рядом, который имеет вид
А (х) + U (х) + /3 (х) + - + /„ (х) + .... D.3)
где функции /х (х), /2 (х) /„ (х), ... определены в некоторой
области изменения аргумента х. Придавая х какое-либо значение
х0 из области определения функций /„ (х), получим числовой ряд
Л(*о)+М*о) + ...'+fn (х0) + ... .
Этот ряд может сходиться или расходиться. Если он сходится, то
точка х0 называется точкой сходимости функционального ряда
D.3). Совокупность всех точек сходимости функционально о ряда
называется областью его сходимости.
Важным случаем функциональных рядов являются степенные
ряды. Степенной ряд имеет вид
а9 + alX + а^х2 + ... + апхп + ..., D.4)
где х — аргумент, а а0, ах, а2, ..., ап — постоянные числа, называе-
называемые коэффициентами.
Степенной ряд можно почленно дифференцировать сколько угод-
угодно раз, причем полученные при этом ряды будут иметь ту же об-
область сходимости.
Пусть функция f (х) является суммой степенного ряда:
/ (х) = а0 + ахх + а2х2 + ... + апхп + ... . D.5)
Последовательно дифференцируя п раз степенной ряд D.5)
и полагая в полученных равенствах х = 0, найдем следующие зна-
значения коэффициентов:
4^
1-2
•@)
Подставив значения коэффициентов в степенной ряд D.5), полу-
получим ряд
/'"@)
1-2.3
@)
п\
D.6)
который называется рядом Маклорена. С помощью ряда Маклорена
любую функцию / (х) можно разложить в ряд по степеням х.
Например, разложение для функции / (х) = е* получается
следующим образом. Сначала определим значения производных
f (х) = ех, Г (х) = ех, /"' (х) = ех, ... Полагая х = 0, найдем
/ @) = 1, f @) = 1, /" @) =1, /'" @)= 1, .... Подставив значения
производных в р'яд Маклорена, имеем
ек
п\
¦+....
D.7)
Если в равенстве D.7) положить х = 1, то получим значение
«числа Эйлера» в виде суммы числового ряда:
Представление числа е в виде суммы числового ряда дает воз-
возможность вычислять эту величину с любой степенью точности.
2. Признаки сходимости ряда. Важнейший вопрос исследова-
исследования ряда состоит в определении его сходимости или расходимости.
Поэтому рассмотрим те необходимые и достаточные признаки, с по-
помощью которых по общему члену ряда можно определять его схо-
сходимость или расходимость.
Необходимый признак сходимости ряда
формулируется следующим образом: если ряд
«i + + — + «п + —
сходится, то неообходимо, чтобы общий член ряда ип при неогра-
неограниченном возрастании п стремился к нулю:
lim ып = 0.
п-*ао
Из необходимого условия сходимости ряда вытекает доста-
достаточный признак расходимости ряда: если общий
член ряда ип не стремится к нулю, то ряд является расходящимся.
Из достаточных признаков сходимости ряда мы будем применять
следующие три признака.
Первый признак сходимости (признак сравне-
сравнения). Пусть даны два знакоположительных ряда:
D.8)
л=1
D.9)
= Г'@)
1 1-2-3
причем каждый член ряда D.8) не больше соответстеующего члена
ряда D.9), т. е. ип ^ vn (п = 1, 2, ...). Тогда если сходится рядD.9),
то сходится и ряд D.8).
Легко показать, что из этого достаточного признака сходи-
сходимости ряда вытекает достаточный признак расхо-
расходимости: если ряд D.8) расходится, то расходится и ряд D.9).
При использовании только что описанного признака об одном
из сравниваемых рядов должно быть заранее известно, что он яв-
является сходящимся или расходящимся.
Чаще всего в качестве эталона сходящегося ряда принимается
геометрическая прогрессия
alql+ a
D.10)
при условии, что знаменатель |<7|< 1.
Эталоном расходящегося ряда часто служит гармонический ряд
В лингвистической практике часто встречаются такие ряды,
которые невозможно сопоставить с каким-либо уже изученным о
точки зрения признака сходимости рядом. В этом случае приходит-
приходится использовать другие достаточные признаки сходимости.
Второй признак сходимости (признак Далам-
бера). Если для знакоположительного ряда
D.12)
выполняется условие
-*оо Un
то при k < 1 ряд сходится, при k > 1 — расходится, а при k = 1
вопрос о сходимости ряда неопределен: в одних случаях ряд сходится,
в других — расходится.
Третий признак сходимости (признак Коши).
Если для знакоположительного ряда D.12) выполняется условие
lim
то при k < I ряд сходится, при k > 1 — расходится, при k = 1
вопрос о сходимости ряда остается неопределенным.
3. Абсолютно сходящиеся ряды. До сих пор мы говорили о при-
признаках сходимости знакоположительных рядов. Этими признаками
можно воспользоваться при определении условий сходимости зна-
знакопеременных рядов.
90
Пусть дан ряд, содержащий как положительные, так и отрица-
отрицательные члены:
«!+ и2+ м3+ ...4- «» + ... • D.13)
Очевидно, что такой ряд можно сделать знакоположительным.
Так, заменив члены ряда D.13) их абсолютными величинами, полу-
получим
Поскольку сумма членов знакопеременного ряда всегда меньше
суммы абсолютных величин этих членов, можно утверждать, что
знакопеременный ряд D.13) сходится, если сходится ряд D.14),
составленный из абсолютных величин его членов. В описанном
случае сходящийся^ знакопеременный ряд называют абсолютно
сходящимся.
§ 2. Каков максимальный объем информации в слове?
1. Можно ли рассматривать слово в качестве ряда? Прежде чем
ставить задачу, связанную с оценкой той максимальной информа-
информации, которую может нести слово, необходимо решить вопрос о том,
вправе ли мы рассматривать связный текст и слово в качестве ряда
и что это будет за ряд. Что касается текста, то здесь особых труд-
трудностей не возникает: каждый текст практически может быть продол-
продолжен до бесконечности (см. гл. 1, §8, п. 3). и существует функция
In = / (п), позволяющая определять количество информации, при-
приходящееся на каждую его букву при условии, что п-*- оо.
Сложнее обстоит дело со словом. Действительно, может ли слово
быть представлено в виде бесконечного ряда величин информации?
Ведь каждое слово состоит обычно из конечного и сравнительно не-
небольшого числа дискретных единиц (букв, слогов, морфем, фонем),
и трудно себе представить слово какого-либо конкретного языка,
состоящее, например, из двухсот букв.
Разумеется, каждая конкретная словоформа представляет собой
конечную последовательность букв или фонем, обычно не сильно
отклоняющуюся от средней длины слова, характеризующей данный
язык (об этом будет подробнее сказано в гл.7).
Вместе с тем, даже если следовать критерию графической цель-
нооформленности, трудно указать конкретный предел длины сло-
словоформы. Это касается не только языка вообще, но и конкретных
языков. Даже в тех индоевропейских языках, в которых флективно-
аналитическая морфология и слабые возможности словообразова-
словообразования и словосложения накладывают ограничения на образование
слишком длинных слов, мы постоянно встречаемся с такими много-
многобуквенными словоформами, как англ. transsubstantiation' возмож-
возможность переноса доказательства', или нем. Kesselsteinverhinderungs-
mittelerzeugungsgesellschaft', компания но изготовлению растворите-
растворителей для котельной накипи, или русск. двустороннесимметричный,
информационно-статистический, невосстанавливаемость. При этом
для каждой длинной словоформы можно теоретически образовать еще
более длиную ее производную —ср. transsubstantiation — intrans-
91
substantiation, двустороннесимметричный — двусШроннесиметрич-
нообразный и т. п.
Что же касается инкорпорирующих и агглютинирующих язы-
языков*, то сказать, на каком максимальном удалении от начала слова
должен находиться его конец, в этом случае еще труднее. Ср. в этом
смысле такие цельнооформленные образования, как кабард.
шыжъыф1ытхъуэр' старая хорошая буланная лошадь', чукот. мы-
трэлгитэкупрэныскивыскычетгъэ'очень стремительно] направимся
изготавливать сети', турецк. turklastiramadiklarimizdanmisiniz'He
из тех ли вы, кого мы не могли отуречить', от которых также могут
быть образованы еще более длинные производные слова. Так, на-
например, приведенная турецкая словоформа теоретически может
быть удлинена путем циклического повторения цепочки аффиксов
lastiramadik (правда, такое удлинение допустимо с грамматиче-
грамматической, но не смысловой точки зрения)**.
Отсюда можно предположить^ что длина орфографического слова
(во всяком случае в языках определенного типа) является потен-
потенциально бесконечной' величиной.
Это предположение станет еще более очевидным, если отнести
к словам стилевые образования типа «Нехочунебунехочунебуду»
(газ. «Известия», 29. III 73, с. 6).
Теперь попробуем отказаться 162, с. 89] от критерия орфографи-
орфографической цельнооформленности и будем исходить из принципа семанти-
ческо-грамматической цельности. В этом случае в категорию слов
попадут такие цепочки орфографических слов, как фр. je ne 1е
lui ai pas explique'n это ему не объяснил'; англ. (the) Prime Minister
of Britain's (residence)' (резиденция) премьер-министра Англии', где
присоединение форманта 's к словоформе Englang вм. Minister
указывает на то, что цепочка Prime Minis+er of Britain's восприни-
воспринимается как слово; русск. кое в чем и т. п. При этом подходе словами
должны считаться и китайские «цы» — комбинации иероглифов,
каждый из которых изображает слог-слово B9, с. 115—116].
Отказ от принципа графической цельнооформленности и включе-
включение в состав слов аналитических цепочек и образований типа китай-
китайских «цы» делает еще менее фиксированной правую границу слова.
Все это позволяет предположить, что длина абстрактного
слова-модели является величиной потенциально бесконечной и об-
образует ряд вычислимых величин информации
А+ /,+ -..+ /„ + .... D.15)
* В инкорпорирующих языках (в первую очередь, палеоазиатских, неко-
некоторых иберо-кавказских и индейских) широко применяется сочетание примы-
примыкающих друг к другу корней, совокупность которых оформляется служеб-
служебными элементами. Этим путем образуются слова или особого рода синтагмы
(ср. приводимые в тексте кабардинский и чукотский примеры). Агглютини-
Агглютинирующие языки (в первую очередь, тюркские и финноугорские) широко исполь-
используют присоединение стандартных аффиксов к неизменяемым основам. Приме-'
ром агглютинативного слова является приводимый в тексте турецкий пример,
в котором к основе turk-присоединена цепочка аффиксов [5, с. 31, 177].
** Турецкий пример сообщен нам А. М. Щербаком.
92
2. Оценка максимального объема информации, содержащегося
в слове. Прежде чем перейти к вычислению общей суммы информа-
информации, содержащейся в ряде D.15), необходимо выяснить, является
ли этот ряд сходящимся.
Проверим, выполняется ли необходимое условие сходимости ряда
D.15). Так как его общий член
при неограниченном возрастании п стремится к нулю, то необхо-
необходимое условие сходимости выполнено. Воспользовавшись числен-
численными значениями параметров для русского слова, взятого вне текс-
текста (/0= 5, s = 0,25) и в тексте (/0 = 5, s = 0,40), применим для
проверки сходимости ряда достаточный признак Коши. Тогда полу-
получаем для обоих случаев:
lim y/loe~sn = Ит у/г5е-°'2Ъп = 0,7788< 1
я-*оо гг-*оо
И
lim уЛ>е-°-40л = 0,6703 < 1.
Как в одном, так и в другом случае ряды являются сходящимися
и можно вычислить их сумму. Чтобы получить теоретическую оцен-
оценку того количества информации, которое может нести слово макси-
максимальной длины, взятое вне текста и в контексте, представим предел
частичной суммы ряда D.15) в следующем виде:
lim Sn =
D.16)
Сумма в квадратных скобках представляет собой сумму членов бес-
бесконечно убывающей геометрической прогрессии, знаменатель кото-
которой равен 1/е*. Следовательно, эта сумма равна
lim
1 — l/es
—l/es
Подставляя последнее выражение в D.16), получаем формулу,
оценивающую максимальное количество информации, которое мо-
может содержаться в слове:
1—1/е8
D.17)
Заменив коэффициент s численными значениями, получим тео-
теоретические оценки максимального количества синтактической ин-
информации, которое может быть передано словом, взятым в контексте
и вне контекста. Эти оценки относительно некоторых европейских
языков приведены в табл. 4.1.
Таблица 4.1
Языки
Русский
Болгарский
Английский
'max вне
текста
(дв. ед.)
22,5
22,0
21,1
'таХвтексте
(дв. ед.)
15,0
14,8
14,1
Языки
Немецкий
Французск.
Румынский
'max юе
текста
(дв. ед.)
ЧЛ
21.2
21.6
'max8 текств
(дв. ед.)
14,3
14,1
14,4
Данные табл. 4.1 говорят о том, что максимальные информацион-
информационные нагрузки текстового и словарного слова в индоевропейских язы-
языках примерно одинаковы. Возникает вопрос, сохраняют ли эти ко-
количественные оценки свою силу для агглютинирующих и инкорпо-
инкорпорирующих языков? Если да, то мы, очевидно, имеем дело с кванти-
квантитативными свойствами оперативной памяти человека, если нет, то
речь идет о новых квантитативных признаках типологии языков.
Что касается применения аппарата теории рядов к вычислению
информации, содержащейся в тексте, то этот аппарат может быть
применен к участкам текста конечной длины. Если же речь идет о
тексте неопределенной длины, то он формализуется с помощью ряда
/i+ /u+ .-+ /„+..., D.18)
общим членом которого служит выражение
U = (/о - /J е-*п + /«. D.19)
При бесконечном возрастании п выражение D.19) стремится к
/„, (см. гл. 1, §8, п. 3), что говорит о расходимости ряда. Поэтому
сумма членов ряда D.18) предела не имеет.
3. Ряд и диахронический процесс. Диахронические процессы
также могут быть исследованы с помощью рядов. Так, например,
при статистическом анализе старо- и средне-французских текстов
разных эпох выяснилось, что сумма долей употребления форм име-
именительного падежа единственного числа существительных мужского
рода, восходящих к латинским существительным II, III и IV скло-
склонения (ср. murus> murs> mur, tempus> temps), для различных
8пох истории французского языка может быть представлена в сле-
следующем виде:
1 + 0,25 + 0,036 + 0,015 + ... .
Перепишем этот ряд таким образом:
или
li ' 2» З3 44 ^""
D.20)
Сравнивая полученный ряд с бесконечно убывающей геоме-
геометрической прогрессией D.10), где аг = 1, q =* 1/2, мы убеждаемся,
что все члены ряда D.20), начиная со второго, меньше соответствую--
щих членов убывающей геометрической прогрессии. Но ряд D.10)
является сходящимся, поэтому сходится и ряд D.20). Иными сло-
словами, можно ожидать, что в какой-то период развития французского
языка именные формы единственного числа мужского рода с окон-
окончанием s полностью выйдут из употребления, и мы будем иметь ко
нечную и поэтому вычислимую сумму долей этих форм для всех пе-
периодов развития французского языка.
§ 3. Лингвистические задачи, приводящие
к понятию интеграла
1. Прогнозирование развития терминологии. Среди задач диа-
диахронического суммирования, которые не могут быть решены с по-
помощью аппарата теории рядов, рассмотрим задачу прогнозирования
роста научно-технической терминологии.
Для лексикографической практики и особенно при построении
действующих систем машинного перевода и реферирования важно
иметь прогноз количественного роста терминологии в различных
областях знаний. Такое прогнозирование давало бы возможность
сознательно планировать выпуск двуязычных и одноязычных поли-
политехнических, а также отраслевых словарей и справочников. Этот
прогноз позволил бы строить достаточно эффективные алгоритмы
пополнения машинных словарей.
Будем строить этот прогноз относительно некоторого идеализи-
идеализированного процесса развития терминологии, при котором прирост
новых терминов на протяжении равных отрезков времени последо-
последовательно увеличивается.
Задача такого прогнозирования решалась бы просто, если бы
все новые слова и выражения, появляющиеся в научно-технической
литературе за определенный промежуток времени (например, деся-
десятилетие) фиксировались и подсчитывались лексикографической
службой в конце этого периода. Тогда в течение каждого деся-
десятилетия количество узаконенных в словарях терминов оставалось
бы неизменным.. Зная число новых радиотехнических, кибернетиче-
кибернетических, ракетостроительных и т. п. терминов, вошедших в обиход в
начале 50-х, 60-х, 70-х годов нашего столетия, мы могли 6а пред-
предсказать, сколько новых слов и выражений из соответствующих
отраслей науки и техники будет введено в научный обиход в начале
80-х, 90-х годов, а также в начале первого, второго и т. д. десятиле-
десятилетий следующего века.
В действительности же развитие терминологии представляет со-
собой непрерывный процесс: статьи и книги, содержащие но-
новые термины, появляются в период всего десятилетия. Поэтому в те-
течение семидесятых годов терминология не остается неизменной по
сравнению с 1 января 1970 г., а непрерывно растет. Следовательно,
потребность в словарях и справочниках, например в 1977 или 1978 г.,
выше, чем в 1970 г. Эту потребность нельзя определить ретроспек-
ретроспективно и по прогнозу 1980 г., поскольку здесь темп роста терминоло-
терминологии будет заведомо выше уровня 1977-го или 1978-го годов.
Такие затруднения возникают всегда, когда, осуществляя кван-
квантитативное описание того или иного диахронического процесса, мы
пользуемся лингво-статистическими данными, относящимися к боль-
большим хронологическим интервалам (столетие, десятилетие), взятым
целиком. Поскольку эти интервалы выступают в виде дискретных
отрезков, динамика непрерывного лингвистического процесса внутри
этих отрезков ускользает из. поля зрения исследователя.
Как же преодолеть это противоречие между «порционным» ди-
дискретным характером результатов количественного эксперимента
в языкознании и непрерывностью лингвистического процесса?
Очевидно, что точнее описать динамику лингвистического" про-
процесса можно было бы с помощью количественных сведений, взятых
относительно более мелких хронологических отрезков. Скажем,
"при прогнозировании развития терминологии вместо десятилетия
можно было бы использовать статистику употребления новых тер-
терминов за пять лет или за год.
Рассмотрим этот вопрос более подробно.
Пусть в момент х темп роста терминологии составляет f (x)
новых лексических единиц в десять лет. Это значит, что если ука-
указанный темп развития сохранится, то в течение десятилетия, к ко-
которому принадлежит момент х, прирост новых терминов составит
f(x). В действительности же через год может появиться фундамен-
фундаментальное исследование в данной области, и скорость развития тер-
терминологии f(x) изменится. Чтобы более точно оценить ход нашего
процесса, уменьшим интервал и определим с помощью величины
f(x) увеличение числа терминов в конце первого года десятилетия
до выхода новой книги. Очевидно, что приращение будет равно
tq f(x), поскольку f(x) указывает количество новых терминов
в десятилетие.
Но и в течение года также могут произойти события, ускоряю-
ускоряющие развитие терминологии: отдельные научные открытия, созда-
создание принципиально новых технических устройств и т. п. Поэтому
в течение года появится не jr. / (х) терминов, а больше. Это количе-
количество можно оценить на основе того темпа роста, который будет
достигнут через год. Поскольку эта новая скорость развития терми-
терминологии измеряется величиной f (х + уА количество терминов,
появившихся за год, составляло бы j» f (x + уА
Однако на самом деле за первый год рассматриваемого десятиле-
десятилетия появится меньше новых терминов: ведь скорость будет достиг-
достигнута лишь в самом конце года.
Итак, истинное количество новых терминов, которое появилось
за рассматриваемый год, остается неизвестным; известно лишь, что
оно больше -jQ / (х) и меньше ^ f (x + jg).
Еще раз уменьшив величину временного интервала, попробуем
определить прирост новых терминов за месяц, т. е. в промежутке от
W
х до х +J20- Здесь снова выясняется, что хотя их число точно опре-
определить нельзя, можно утверждать, что оно лежит в интервале между
120 ^ и Гго Кх "^ 120^' ^то послеД°вательное уменьшение ин-
интервала показано на рис. 33.
Повторяя все эти рассуждения и считая f (x) непрерывной функ-
функцией*, снова уменьшим величину интервала. Обозначим этот ин-
интервал через Ах; тогда можно сказать, что в период от х до х + Ах
количество новых терминов колеблется of f (х) Ах до / (х + Ах) Ах.
Теперь возьмем Ах настолько малым, что в этом промежутке
темп появления новых терминов будет отличаться от скорости f(x)
на величину, меньшую, чем любая наперед заданная бесконечно
fix)
1980
X
Рис. 33
малая величина а. Иными словами, темп появления новых терминов
лежит в промежутке (f (х) — а, / (х) + а). Обозначим прирост тер-
терминов за сколь угодно малый промежуток времени Ах через Ау\
тогда
At/ = [f (х) ± а) Ах = f (*) Ах ± аАх D.21)
при условии, что f(x) непрерывна в интервале А*.
Таким образом, если за период Ах приращение новых терминов
составляет Ау, то общее количество терминов, накопленных в подъя-
подъязыке к моменту времени х, равняется величине у.
В правой части равенства D.21) два слагаемых, из которых пер-
первое представляет собой произведение известной функции f(x)
на сколь угодно малое приращение аргумента Ах, а второе является
* Само собой разумеется, что число новых терминов, появившихся в оп-
определенном временном срезе, величина дискретная, однако с точки зрения
диахронии ее следует рассматривать как непрерывную величину (см. гл. 1,
§ 3, п 3).
Зак. 1287
97
произведением сколь угодно малой величины Дл: на бесконечно ма-
малую величину а.
Тогда при условии, что Дя -> 0, оба слагаемых правой части
равенства будут бесконечно малыми величинами. В гл. 2 § 1, п. 3
было показано, что бесконечно малые величины могут обладать
разной степенью малости. Выясним, обладают ли одинаковой сте-
степенью малости величины f(x)Ax и аДдг. Для этого определим пре-
предел отношения этих величин к величине Дл: при условии Ах -> 0:
lim
lim
Из этого следует, что второе слагаемое аДя является величиной
бесконечно малой более высокого порядка по срав-
сравнению с Дд;, и поэтому им можно пренебречь. Что же касается пер-
первого слагаемого /(х)Дх, то оно является главной частью
приращения величины у, или ее дифференциалом. Тогда, согласно
C.13), можно записать
dy = / (х) dx.
Отсюда
dy
dx
= /(*)•
D 22)
Равенство D.22) представляет собой известное выражение про-
производной ^ = Ух. Поэтому можно сказать, что f(x) есть про-
производная некоторой функции у = F (х).
Итак, если раньше, дифференцируя функцию у = F (х), мы
находили ее производную ух = F' (х) — }(х) или дифференциал
dy = F' (x) dx = / (я) dx, то теперь, как показывает только что
рассмотренный пример, возникает обратная задача: для данной
функции / (х) требуется найти первообразную, т. е. такую функцию
F (х), производная которой равнялась бы заданной функции f(x),
или, что то же, дифференциал которой равнялся бы заданному вы-
выражению / (х) dx. Операция отыскания первообразной называется
интегрированием. Если рассматривать дифференцирование в ка-
качестве прямого действия, то интегрирование выступает в качестве
обратного действия.
Интегрирование может быть применено не только в диахронии,
но и при изучении распределения информации в тексте.
2. Прирост и накопление информации в тексте. Выше уже гово-
говорилось (См. § 2, п. 1), что распределение информации в тексте
характеризуется функцией In — f (n). Запишем ее в виде
А/* = / (п),
где Д/* — прирост информации на лингвистическую единицу
(букву, слог, морфему, слово и т. п.) в л-м участке текста. Сопос-
Сопоставляя эту зависимость с зависимостью изменения темпа развития
терминологии от времени, легко заметить, что величина /„ также
указывает на изменение величины информации, извлекаемой
S8
из разных участков текста, по мере удаления соответствующего
участка от начала высказывания. Правда, в отличие от воз-
возрастающего темпа развития терминологии для динамики ин-
информационного рисунка речи более характерно последовательное
убывание того количества информации, которое несет каждая линг-
лингвистическая единица. Это различие, разумеется, не отражается на
математической стороне наших рассуждений.
Чтобы исследовать изменения в количестве извлекаемой инфор-
информации, мы можем разбить текст на равные отрезки, соответствую-
соответствующие, скажем, средней длине абзаца, и делать информационные за-
замеры (например, методом угадывания; ср. [23]) в конце каждого
сегмента. Но тогда от нас ускользнет динамика изменения инфор-
информации внутри отрезка. Чтобы сделать наши измерения более точ-
точными, будем последовательно уменьшать интервалы измерения*,
как это мы делали, рассматривая прирост терминологии**; в ре-
результате получим выражение
Д/* = [/ (л) ± а] Ал = / (п) Дл ±
аналогичное выражению D.21).
Рассуждая так же, как и в п. 1, приходим к выводу, что / (п)
есть производная некоторой функции F(n), которая указывает общзе
количество информации Гп, извлеченной из текста к моменту п.
Таким образом, задача снова сводится к нахождению первообраз-
первообразной функции In = F (п) по заданной производной /„ = f{n).
В будущем мы будем довольно часто встречаться с лингвисти-
лингвистическими и лингво-статистическими зависимостями, которые, как и
только что рассмотренные зависимости, могут иметь интегральную
и дифференциальную формы выражения. Если для математики без-
безразлично, определяется ли интегральная первообразная функция
^(л:) по производной F'(x)=f(x) [по дифференциалу f(x)dx\
или наоборот, то для лингвистики обычно одна из этих функций
является исходной. Так, в п. 1 мы исходили из статистики прироста
новых терминов за единицу времени, чтобы затем, определив ин-
интегральную функцию накопления терминов, указать нужный объем
соответствующего отраслевого словаря или машинного словника.
* Этот прием издавна используется в неявном виде и лингвистами. Так,
например, чтобы преодолеть лингво-географическую непрерывность, диалек-
диалектологи делят язык на наречия, наречия подразделяют на диалекты, диалекты
дробят на поддиалекты, поддиалекты — на говоры и т. д. Сходным образом
звуки (звукотипы) делятся на произносительные варианты, в которых выде-
выделяются оттенки, и т. п.
** Если речь идет о буквенном тексте или о его фонематической транскрип-
транскрипции, то осуществить операцию бесконечного уменьшения интервала нельзя
из-за линейной (синтагматической) веделимости буквы & фонемы. Однако если
речь идет об инструментальной (спектрографической, осцнллографической,
кпмографической и т. п.) записи устной речи, то эта запись, имея непрерывный
характер, допускает бесконечное уменьшение интервала (величина 1п будет
в этом случае непрерывной). Разумеется, для осуществления описанного экс-
эксперимента нужно располагать некоторой процедурой измерения информация
относительно непрерывного речевого процесса.
4* 99
Напротив, при информационном измерении устной речи целесооб-
целесообразно исходить из величины накопленной информации, т. е. из ин-
интегральной функции, дифференцируя которую, можно определить
темп прироста информации в тексте.
§ 4. Основные понятия интегрирования и применение
их к лингвистическим задачам
1. Неопределенный интеграл. Мы только что выяснили, что
функцию f{x) можно рассматривать в качестве производной неко-
некоторой первообразной функции F (х). При этом возникает вопрос:
сколько первообразных может иметь функция f(x)?
Так как производная постоянной величины С равна нулю, то
функции, отличающиеся друг от друга постоянными слагаемыми,
имеют одну и ту же производную или один и тот же дифференциал.
Так, например, функции
F (х) = х\ Fx (х) =х3+ 10, Ft (х) = х3 - 5, Fn (х) = х3 + а
имеют одну и ту же производную, равную / (х) = Зхг.
Обозначим постоянное слагаемое в вышеприведенных равенст-
равенствах буквой С (С = const). Тогда получаем равенство
IF (х) + CYX = F'(x) = / (*),
из которого следует, что функция / (х) имеет бесчисленное коли-
количество первообразных функций, отличающихся друг от друга
на постоянное слагаемое С. Это множество всех первообразных
функций F (х) + С называется неопределенным интегралом и
обозначается в виде
lf(x)dx = F (x) + С. D.23)
Символ J называется знаком интеграла, f(x)dx — подынтеграль-
подынтегральным выражением, f(x) — подынтегральной функцией, ах —
переменной интегрирования. Левая часть равенств D.23) читается:
«неопределенный интеграл эф от икс де икс» и является общим
выражением первообразной функции, в то время как правая часть
этого равенства представляет собой уже найденный интеграл, где
F (х) — одна из первообразных функций по отношению к / (х),
а С — произвольная постоянная.
Так как неопределенный интеграл содержит произвольную
постоянную, то он может определяться с точностью до этого про-
произвольного слагаемого.
Пусть темп количественного роста терминологии в некоторой
отрасли знаний определяется функцией / (х), где х — время су-
существования этой отрасли науки. Тогда общее количество терми-
терминов, накопленное к моменту х, выражается неопределенным интег-
интегралом:
у = U (х) dx = F (х) + С.
100
Величину С можно интерпретировать как некоторое количество
терминологических слов и выражений, использованных данной от-
отраслью знаний при ее возникновении из других подъязыков (на-
(например, подъязык авиации использовал при своем формировании
в качестве исходного материала некоторое количество морских
терминов).
При нахождении интеграла D.23) мы получаем бесконечное
множество ответов, отличающихся друг от друга на постоянное
слагаемое. Неоднозначность ре-
решения можно проиллюстриро-
проиллюстрировать геометрически. Для этого
построим кривую, представляю-
представляющую график одной первообраз-
первообразной функции у — F{x) (при С =
= 0). Тогда остальные кривые
накопления терминологии полу-
получаются в результате смещения
по оси ординат этой кривой на
произвольную постоянную ве-
величину С, характеризующую
количество исходных терминов
(рис. 34).
Неопределенный интеграл
обладает следующими свой-
свойствами.
1. Производная от неопреде-
неопределенного интеграла равна подын- р
тегральной функции: ._ ИС-
2. Дифференциал неопределенного интеграла равен подынтег-
подынтегральному выражению:
здесь символы d и j взаимно уничтожают друг друга.
3. Неопределенный интеграл от дифференциала функции равен
этой функции плюс произвольная постоянная:
J dF (х) =» F (х) + О,
4. Постоянный множитель подынтегрального выражения можно
вынести за знак интеграла:
5. Неопределенный интеграл от алгебраической суммы двух или
нескольких функций равен сумме их интегралов:
J l/i (*) + /, (*) - /, (х)] dx = fcix) dx + #,(*) dx — Ць{х) dx.
101
2. Таблица простейших интегралов. Из определения неопреде-
неопределенного интеграла D.23) следует, что под знаком интеграла стоит
производная первообразной функции, т. е.
Исходя из этого равенства, с помощью известных формул диффе-
дифференцирования можно найти интегралы некоторых элементарных
функций, так называемые табличные интегралы.
Ниже приводится таблица простейших интегралов, наиболее
часто используемых в квантитативной лингвистике.
Таблица простейших интегралов
$dx = х + С,
(I)
х" dx ¦¦
л+1
¦+с;
In a
¦ = ех А- С
I
1
sin* dx-
dx
=
cos'jb
dx _
sin3*
dx
—cos x + С,
(III)
(IV)
(V)
(VI)
(VII)
(VIII)
(IX)
(X)
Справедливость формул интегрирования легко проверяется
с помощью обратного действия — дифференцирования. При этом
оказывается, что дифференциал от правой части формулы равен
подынтегральному выражению.
3. Приемы интегрирования и их применение в лингвистических
задачах. Нахождение интегралов, опирающееся на использование
приведенных выше формул и свойств неопределенного интеграла,
называется непосредственным интегрированием. Этот способ вклю-
включает следующие случаи:
1) интеграл берется по одной из вышеприведенных формул;
* Формула II справедлива при условии, что п ф —1, в противном слу-
чае знаменатель дроби в этом выражении обращается в нуль и формула
теряет смысл.
2) путем использования свойств 4 или 5 неопределенный инте-
интеграл приводится к одному или нескольким табличным интегралам;
3) в результате тождественного преобразования подынтеграль-
подынтегральной функции и использования свойств неопределенного интеграла
данный интеграл приводится к одному из табличных интегралов.
Чаще всего здесь применяются такие преобразования:
а) введение под знак дифференциала постоянного слагаемого
dx = d (x + С),
б) введение под знак дифференциала постоянного множителя:
dx — — d (mx),
в) введение под знак дифференциала постоянного множителя и
слагаемого:
dx = id {mx + С).
В лингвистике интегрирование используется обычно при реше-
решении диахронических и информационных задач.
Рассмотрим следующий диахронический пример. Пусть скорость
прироста новых терминов и терминологических словосочетаний в оп-
определенной области знаний для германских, романских и славян-
славянских языков характеризуется равенством
/ (х) = Ъх\
Количество новых терминов в момент х можно определить, про-
проинтегрировав правую часть этого равенства. Используя свойство
4 и интеграл II таблицы, находим
здесь постоянная интегрирования С заменена на а (ср. с примером
в гл. 3, § 2, п. 1).
Рассмотрим теперь информационный пример. Как известно,
скорость изменения величины информации, извлекаемой из раз-
разных участков текста, определяется равенством
In = (/о - /•) e~sn + /со.
Определим объем информации, извлеченной из текста к моменту
п (п — непрерывная величина). Для этого проинтегрируем правую
часть последнего равенства:
-/. J e-S"dJ-sn)-
n —e— (/„—/«) + C.
102
103
Если заданный интеграл нельзя или трудно привести к таблич-
табличному с помощью непосредственного интегрирования, то для оты-
отыскания этого интеграла применяются специальные приемы.
Рассмотрим два из них — интегрирование способом под-
подстановки (или замены переменной) и интег-
интегрирование по частям.
Начнем с интегрирования способом подстановки. Сущность
этого приема состоит в том, что в интеграле вида J" f(x) dx перемен-
переменная интегрирования заменяется другой переменной и, являющейся
также функцией от х. При этом данный интеграл преобразуется
в новый интеграл j cp (и) du, который можно вычислить с помощью
одного из табличных интегралов. После того как новый интеграл
взят, следует вернуться к исходной переменной х с помощью равен-
равенства и = f(x).
Для иллюстрации этого метода рассмотрим интеграл
J (a + x^fx'dx,
который методом непосредственного интегрирования найти нель-
нельзя. Обозначим выражение, стоящее в скобках, через и, т. е.
(а + х3) = иъ; следовательно, d (а + я3) = du, откуда
= du, или xidx —
du
3
Разбив наш интеграл на два множителя, из которых один
(а+*3M=м6, а другой Л=у, мы приходим к новому интегралу:
18
3 5+1
После того как новый интеграл найден, следует вернуться к перво-
первоначальной переменной. Для этого в полученный результат вместо
и подставим его значение; окончательно имеем
f
18 +
18
Если интеграл нельзя найти ни путем непосредственного инте-
интегрирования, ни с помощью замены переменной, то применяется
метод интегрирования по частям. Пусть и и v — функции от х,
т. в. a ¦» <р (х), а v = Ф (х). Согласно общим правилам дифферен-
дифференцирования (с**, гл. 3, § 2, п. 1) дифференциал произведения этих
функций равен
d (uv) = udv + vdu.
Интегрируя обе части этого соотношения, получаем равенство
Jd (uv) = J udv + $vdu,
которое, в силу свойств 3 и 5 интеграла принимает вид
uv+C =*ludv-\- jvdu.
104
Отсюда мы приходим к формуле интегрирования по частям:
J udv = uv—$vdu + С. D.24)
Левая часть этой формулы представляет собой исходный интег-
интеграл, подынтегральное выражение которого должно быть представ-
представлено в виде двух сомножителей. Подбор сомножителей и и dv следует
производить таким образом, чтобы дифференцирование функции
v и вычисление интеграла j v du представляло собой более прос-
простую задачу, чем непосредственное вычисление иитеграла j и dv.
Упрощение рассматриваемого интеграла может быть достигнуто
за счет дифференцирования множителя и. Поэтому ту часть подын-
подынтегрального выражения, которая упрощается при дифференциро-
дифференцировании, следует принять за и, а все остальные сомножители подын-
подынтегрального выражения, включая dx, — за dv.
Для иллюстрации этого приема найдем интеграл jxe'dx.
Полагая
и — х, е* dx — dv,
имеем
du — dx, J dv = J e'dx, т. е. v = ex.
Отсюда по формуле D 24) получаем
| xe* dx = xe? — \ex dx = xe* — e* + C.
4. Определенный интеграл и его свойства. Выше было показа-
показано, что неопределенный интеграл представляет собой бесчисленное
множество тервообразных функций, отличающихся друг от друга
произвольным постоянным слагаемым:
\f{x)dx = F (x) + С
(см. равенство D.23)]. Поэтому неопределенный интеграл не мо-
может быть выражен определенным числом: он всегда вычисляется
с точностью до произвольного слагаемого С.
Однако при решении конкретных задач бывает необходимо
точно фиксировать величину С и таким образом определить начало
того интервала, в котором находится переменная хив котором осу-
осуществляется интегрирование. Предположим, что нам известен та-
такой хронологический момент х — а, когда число терминов данной
области знаний (как исходных, так и вновь образованных) равно
нулю (этот момент существовал, очевидно, до возникновения инте-
интересующей нас отрасли знаний). Это положение можно выразить так:
F (а) + С = 0.
Следовательно, фиксированное значение С составляет
С = -F (а).
105
Подставив найденное значение величины С в правую часть ра-
равенства D.23), получаем первообразную функцию в виде Fix)—
— F (а). Тогда равенство D.23) можно записать таким образом:
D.25)
Здесь а — нижний предел интеграла (постоянный), b — его
верхний предел (переменный), а сам интеграл D.25) называ-
называется определенным интегралом с переменным верхним пределом.
В том случае, когда верхний предел интеграла есть постоянное число
Ь, выражение D.25) принимает вид
D.26)
и называется формулой Ньютона—Лейбница (или определенным
интегралом с постоянными пределами). Это читается так: «опре-
«определенный интеграл от а до Ь эф от икс де икс».
Если неопределенный интеграл является функцией, вычисляе-
вычисляемой с точностью до произвольного слагаемого С, то определенный
интеграл есть число, указывающее на приращение первообразной
функции F (х) + С (т. е. неопределенного интеграла) при изме-
изменении аргумента х в интервале от а до Ь. Эта связь определенного
и неопределенного интегралов выражена в самой формуле Ньюто-
Ньютона—Лейбница.
Для нас в дальнейшем будут важны следующие четыре свойства
определенного интеграла.
1. При перемене местами пределов интегрирования определенный
.интеграл меняет свой знак на противоположный:
\f(x)dx=-\f(x)dx.
2. Постоянный множитель можно выносить за знак определен'
ного интеграла:
ь ь
3. Определенный интеграл от алгебраической суммы двух или
нескольких функций равен алгебраической сумме их интегралов:
4. Промежуток интегрирования (а, Ь) можно разбить на не-
несколько частичных промежутков; в этом случае интеграл, вычислен'
106
ный по целому промежутку, равен сумме интегралов, вычисленных
по частичным промежуткам, т. е.
где а < с < Ъ.
5. Вычисление определенного интеграла и численная оценка
накопления новых терминов. Основным способом вычисления опре-
определенных интегралов является применение формулы D.26). При
этом здесь используются те приемы, которые применялись для вы-
вычисления неопределенных интегралов — в частности, непосредст-
непосредственное интегрирование и интегрирование по частям. Следует иметь
в виду также, что равенство D.26) применимо только тогда, когда
промежуток интегрирования конечен, а подынтегральная функция
в этом промежутке непрерывна.
Для непосредственного вычисления определенного интеграла
ь «
If (x) dx по формуле D.26) нужно найти какую-либо первообраз-
а
ную F (х) подынтегральной функции / (х) и взять разность значе-
значений .этой первообразной, вычисленных для значений х, равны!
верхней и нижним границам интегрирования.
Разность F(Ь) — F(р) символически обозначают F (х)\ьа. Исполь-
Используя это обозначение, запишем формулу Ньютона — Лейбница ¦
таком виде:
ь
= F{b)-F(a).
D.27)
Выше (см. п. 3) мы рассматривали вопрос об определении в не-
некоторый момент времени х количества новых терминов, скорость при-
прироста которых характеризуется равенством / (х) = Зх2. Оценим
с помощью формулы Ньютона —Лейбница число новых терминов
во втором десятилетии существования интересующей нас отрасли
знания.
Для этого нужно найти определенный интеграл J3**dx. Так как
одной из первообразных для / (х) = Ъхг является функция F (х) =*
== х3, то на основании формулы D.27) получаем
20
J Зх2dx = х
10
:203 —103 =
—1 000 = 7000.
Таким образом, за второе десятилетие существования некоторой
области знаний в европейских языках может появиться оком
7 тыс. новых терминов.
6. Несобственный интеграл. До сих пор мы имели дело с опре-
определенным интегралом от непрерывной функции, причем пределы
интегрирования представляли собой конечные величины. Однако
107
могут встретиться такие определенные интегралы, у которых один
или оба предела интегрирования бесконечны, или же такие, у кото-
которых подынтегральная функция имеет точки разрыва в промежутке
интегрирования. Эти интегралы называются несобственными.
В дальнейшем нам придется иметь дело только с несобственны-
несобственными интегралами, имеющими бесконечные пределы интегрирования.
Поэтому мы ограничимся рассмотрением именно этих интегралов,
выделяя здесь три случая:
а) областью задания подынтегральной функции служит ин-
интервал [а, +оо), при этом имеет место равенство
+ 00
\ f (x) dx = lim \ f {x) dx
V Ь -> + OO «-'
D.28)
(рис. 35, а);
Ж
J
a) Sj B)
Рис. 35
б) областью задания подынтегральной функции служит интер-
интервал (—оо, Ь], тогда
ь ь
\ f(x)dx= lim \f(x)dx D.29)
J a-*—оо J
— оо а
(рис. 35, 6);
в) областью задания подынтегральной функции является вся
числовая ось, тогда несобственный интеграл имеет вид
+ 00
\ f(x)dx= lim U{x)dx
а
D.30)
(рис. 35, в).
В том случае, если существует предел соответствующего опре-
определенного интеграла, несобственный интеграл называется сходя-
сходящимся, если же этот предел не существует, — расходящимся.
Можно показать [28], что основные свойства определенных ин-
интегралов обобщаются и на несобственные интегралы.
7. Неберущиеся интегралы. Интеграл вероятностей. Не всякий
неопределенный интеграл может быть выражен через элементарные
функции описанными выше способами. Среди этих неберущихся
интегралов особый интерес для нас представляет интеграл вероят-
108
ностей, который в зависимости от указанных пределов принимает
вид либо определенного интеграла:
либо несобственных интегралов:
-*>/2 dz
(вместо переменной х здесь и в гл. 6 используется переменная г).
Проведенное с помощью понятий математического анализа моде-
моделирование лингвистических процессов показало, что такая конф-
конфронтация языка и математики служит эффективным средством вы-
выявления скрытых от прямого лингвистического наблюдения свойств
языка и речи.
Так, применение производной позволяет сформулировать и ввес-
ввести в лингвистический обиход новое понятие скорости изменения
в языке и речи, а также осуществлять количественные оценки этих
изменений. С помощью тригонометрических функций и понятия
предела моделируется циклический и ступенчатый характер линг-
лингвистических процессов (ср. понятие диахронического сначка).
Ступенчатый характер диахронических и информационно-текстовых
процессов, очевидно, имеет ту Же природу, что и большинство ки-
кибернетических процессов. Для их описания в будущем найдут
применение разделы теории обобщенных функций (например функ-
функция-ступенька). Одновременно обнаруживается необходимость опи-
описывать процессы приращения и накопления новых лингвистических
элементов (диахрония) и синтактико-смысловой информации (текст),
а эти процессы моделируются с помощью аппарата теории рядов и
интегрирования.
Следует обратить внимание на тот факт, что как диахронические,
так и текстовые информационные процессы часто аппроксимиру-
аппроксимируются одними и теми же функциональными зависимостями. '
Эта общность диахронических и текстовых моделей могла бы
служить подтверждением гипотезы Г. Хердана [51, с. 173] о единст-
единстве лингвистического онтогенеза (информационной структуры речи)
и филогенеза (формирования современного состояния языка).
ЧАСТЬ ВТОРАЯ
ВЕРОЯТНОСТНО-ИНФОРМАЦИОННЫЕ ОЦЕНКИ
НОРМЫ ЯЗЫКА И СТАТИСТИЧЕСКОЕ
ПОСТРОЕНИЕ ТЕКСТА
ГЛАВА 5
КОМБИНАТОРИКА ЛИНГВИСТИЧЕСКИХ ЕДИНИЦ.
ВЕРОЯТНОСТЬ И ИНФОРМАЦИЯ ЛИНГВИСТИЧЕСКИХ
СОБЫТИЙ
§ 1. Комбинаторные схемы
1. Измерение комбинаторики внутри лингвистических множеств.
Языковеду постоянно приходится решать задачи, в которых рассмат-
рассматриваются комбинации и расположения элементов, принадлежащих
определенному лингвистическому множеству. Так, например, син-
синтаксисту важно знать, сколько позиционных вариантов может да-
давать в устно-разговорной речи предложение сегодня идет дождь.
Фонетисту, специалисту в области кодирования текста, а также
работнику Госавтоинспекции, занимающемуся распределением бук-
буквенных серий автомобильных знаков на территории страны, нужно
знать, сколько двух- и трехбуквенных комбинаций может дать рус-
русский алфавит. Иногда при этом нужно выяснить, какая часть этих
комбинаций образует слова и их формы, использующиеся в совре-
современном русском языке. Задачи, в которых требуется ответить на воп-
вопрос «сколько?» или «сколькими способами?», называются ком-
комбинаторными, а раздел математики, занимающийся реше-
решением подобных задач, именуется комбинаторикой.
Простейшие задачи комбинаторики можно решать перебором всех
возможных вариантов. Так, например, путем перебора нетрудно
установить, что предложение сегодня идет дождь имеет в русской
разговорной речи 6 вариантов:
сегодня идет дождь; сегодня дождь идет; дождь сегодня идет;
дождь идет сегодня; идет сегодня дождь; идет дождь сегодня.
Однако число комбинаций быстро растет с увеличением числа
составляющих их элементов. Так, например, четыре слова (увы,
сегодня, дождь, идет) дают 24, пять слов — 120, шесть — 720 по-
позиционных вариантов и т. д. Не все из этих вариантов допустимы
с точки зрения норм современного литературного языка. Опреде-
Определить допустимые варианты путем простого перебора оказывается
невозможным.
ПО
Поэтому, сталкиваясь с такими комбинаторными задачами,
прибегают к типовым схемам решения, учитывающим лингвисти-
лингвистические или какие-либо другие ограничения.
2. Размещения. Предположим, что имеется алфавит, включаю-
включающий я элементов. Из этих элементов составляются /п-членные
комбинации (соединения), причем каждый из п элементов может
входить в соединение не более одного раза.
Такой тип комбинаций называется размещением. Число разме-
размещений из п элементов по т определяется по формуле
= п(п—'!)... (ft — /
п\
{п—т)\
E.1)
Например, из 32 букв русского алфавита можно составить
32!
C0—2)!
= 32-31 =992
двухбуквенные комбинации, не содержащие повторений букв.
По данным четырехтомного «Словаря русского языка» (М.,
1957—1961), из этих сочетаний только 114 выступает в качестве само-
самостоятельных слов (имена собственные, сокращения, архаизмы и
диалектные слова при этом не учитываются).
3. Размещения с повторениями. Снова возьмем алфавит из п
элементов и будем составлять m-членные соединения, допуская
повторения каждого элемента от 0 до т раз. Тогда общее число
соединений, называемых размещениями с повторениями, находится
по формуле
A7=n». E.2)
Так, например, из 30 букв русского алфавита (исключая ь и ъ)
можно составить 302 = 900 двухбу квенных серий для денежных
знаков и 303 = 27 000 трехбуквенн ых серий для автомобильных
номеров.
4. Перестановки. Пусть размещения из п разных элементов
взяты по и элементов, т. е. каждое размещение содержит все п
элементов алфавита и отличается от других лишь порядком этих
элементов. Такие размещения называются перестановками. Тогда
из формулы E.1) можно получить формулу для нахождения числа
перестановок, заменив т на п и учитывая, что 01—1. Действи-
Действительно,
"! ¦• E.3)
(л-л)!
¦¦п\.
Определим, например, сколько трехсловных предложений мож-
можно построить из трех слов: сегодня, идет, дождь. Число предложений
равно здесь числу перестановок из трех элементов: Р3 = 2 • 3 = 6.
К этому же результату мы пришли в п. 1, используя метод про-
простого перебора.
5. Перестановки с повторениями. В тех случаях, когда среди
образующих перестановки элементов имеются одинаковые, полу-
111
чаются соединения, называемые перестановками с повторениями.
Число этих перестановок вычисляется по формуле
л!
E.4)
'2,2.3=-
10!
2! 31 2!
где л — общее количество элементов, входящих в перестановку,
а пи пг, ..., «ft — количество одинаковых элементов в первой, вто-
второй, ..., k-й груштах.
Определим, например, число перестановок с повторениями,
которое можно получить из букв, составляющих словоформу мате-
математика. Всего в перестановках участвует десять букв, т. е.
п = 10; буква м повторяется два раза, поэтому если бы все ос-
остальные буквы были различными, то искомое число перестановок,
было бы равно Р\° = 10!/2!. На самом деле, кроме двух одинако-
одинаковых м в нашем слове имеются три а и два т. Поэтому общее число
перестановок, полученных из букв, входящих в словоформу мате-
математика, равно
"•3-4.S.6.7-8.9-10 ^5.6.7.8-9-10^ 151 200.
1-2-1-2-3-1-2
Кстати говоря, среди более чем ста пятидесяти тысяч десяти-
буквенных комбинаций, составленных из двух м, трех а, двух т
и е, к, и, только одна — математика — является «отмеченной»
в системе русского языка. Остальные оказываются лишенными
смысла, избыточными с точки зрения современного русского языка
последовательностями букв.
6. Сочетания. В размещениях из п эламентов по т соединения
отличаются друг от друга либо элементами, либо их порядком, либо
и элементами и их порядком. Объединим в отдельные группы та-
такие комбинации, которые содержат т одинаковых элементов и отли-
отличаются друг от друга только порядком этих элементов. Нетрудно
заметить, что в каждой группе будет ровно Рт элементов. Группы
комбинаций, различающиеся только элементами, называются соче-
сочетаниями из п элементов по т. Их число равно
п!
пЛ (п—т)\
?п __ Гп — т
Р Р п '
E.5)
Например, если имеются три согласных и две гласных фонемы,
то, исходя из равенства E.5), можно построить
Cg_
J-2-3-4-5_ 1-2-3-4-5 _ 1Q
1.2-1.2-3 1-2-3-1-2
пятифонемных «слов», отличающихся друг от друга только располо-
расположением гласных и согласных фонем.
7, Сочетания с повторениями. Сочетаниями из п элементов по т
с повторениями- называются такие соединения, которые включают
т из п различающихся между собой элементов при усло-
условии, что один и тот же элемент может включаться в комбинацию
112 .
несколько раз. Два соединения считаются различными, если они
отличаются хотя бы одним элементом, и одинаковыми, если они сос-
состоят из одних и тех же элементов. Число сочетаний из п элементов
по m с повторениями определяется по формуле
7>ffl f~*tn /С С\
Рассмотрим в связи с этим следующий пример. В некотором языке
имеются два типа фонем: гласные и согласные, причем слово может
быть образовано из .одних гласных, из одних согласных, а также
из гласных и согласных (таким образом, согласные, так же как и
гласные, являются слогообразующими). Необходимо определить,
сколькими способами можно образовать трехфонемное «слово».
Поскольку здесь п = 2, а т = 3, то на основании соотношения
E.6) искомое число равно
ты ^з 4-3-2
1-2-3
= 4.
Действительно, при построении трехфонемного слова возможны два
случая: а) «слово» составлено из фонем одного типа; б) в «слово»
входят и гласные, и согласные. В первом случае могут быть два
способа образования «слова»: оно состоит либо из гласных, либо
из согласных. Во втором случае также имеются два способа: либо
«слово» образовано из одной гласной и двух согласных, либо из двух
гласных и одной согласной. Итак, существуют только четыре способа
образования трехфонемных слов.
В только что рассмотренном примере мы имеем дело с сочетания-
сочетаниями из двух элементов по три с повторениями.
§ 2. Лингвистическое событие
1. Наблюдение, испытание и событие в индуктивных исследова-
исследованиях языка и речи. Основой всех индуктивных исследований в язы-
языкознании является наблюдение за поведением и признаками изучае-
изучаемых лингвистических объектов. Это наблюдение может осуществ-
осуществляться также путем опыта, эксперимента или количественного изме-
измерения, Осуществление каждого такого наблюдения (опыта или изме-
измерения) называется испытанием. Совокупность условий, при которых
осуществляется данное испытание, называют комплексом условий (а).
Результатом лингвистического испытания является лингвисти-
лингвистическое событие.
Проведем опыт (испытание), состоящий в угадывании буквы
при следующем комплексе условий (о^): угадываемой букве пред-
предшествует цепочка ккоторо, текст русский без ошибок н опеча-
опечаток. Это испытание может дать события Alt Bu Clt Dlt состоящие
соответственно в появлении следующих букв: г {которого), е (кото-
(которое), й (которой), м (котором, которому).
Каждое событие, которое здесь может произойти, а может и
не произойти, называется случайным событием (ср. события Alt
Blt Cv Dj). Если результат лингвистического испытания полностью
113
исчерпывается каким-либо одним (и только одним) событием, то мы
имеем дело с элементарным случайным событием. Событие, состоя-
состоящее из нескольких элементарных событий, определяется как сложное
случайное событие. Появления букв г, е, й, м после цепочки Акоторо
являются элементарными случайными событиями, появления после
этой же цепочки диграмм го, му следует рассматривать как слож-
сложные, случайные события.
2. Соотношения между лингвистическими событиями. Поскольку
между алгеброй событий и теорией множеств существует тесная связь,
мы будем пользоваться, рассматривая операции над событиями, тео-
теоретико-множественными аналогиями. Соотношения между события-
событиями будут иллюстрироваться часто теми же рисунками, с помощью
которых эксплицировались операции над множествами (см. рис. 4
на стр. 14).
1. Сложное событие, заключающееся в наступлении хотя бы
одного из событий Л и В, называется суммой этих событий и
обозначается А + В или А [] В (читается: «Л или В»). Теоретико-
множественным аналогом суммы событий является объедине-
объединение множеств (см. рис. 4, д). Появление буквы г (событие
Ах) пли буквы е (событие Bt) после цепочки Акоторо является сум-
суммой Аг + В,.
2. Сложное событие, состоящее в одновременном на-
наступлении А к В, называется их произведением и обозначается А В
угли А П В (читается: «Л и В»). В качестве аналога слож-
сложного события можно рассматривать пересечение мно-
множеств (см. рис. 4, ж). Пусть, например, используется комплекс
условий (а2), заключающийся в том, что русский алфавит считается
состоящим из гласных и согласных. При этом буква й считается
принадлежащей одновременно и к классу гласных, и к классу со-
согласных. Будем считать появление гласной после цепочки Акоторо
событием <Dlt а появление согласной — событием Hv Тогда появ-
появление буквы й после цепочки Акоторо следует рассматривать как
произведение ФгН1 (или CDj П Нх) данных лингвистических событий.
3. Событие, заключающееся в том, что событие А имеет место,
а В не имеет места, называется разностью событий Л и В и обозна-
обозначается А—В. Разности событий соответствует разность
множеств (см. рис. 4, з). Появление всех согласных, кроме й,
после цепочки Акоторо можно представить как разность Ht — Фх.
4. Если событие Л, происходящее при реализации комплекса
(а), влечет за собой каждый раз событие В, то говорят, что Л явля-
является частным случаем В, и записывают Ас В (или В zd А). Этому
соотношению в теории множеств соответствует включение
(см. рис. 4, в). Так, например, появление буквы г после цепочки
Акоторо одновременно означает (влечет за собой) появление соглас-
согласной, иными словами, здесь Лх с: Нх (или Нх =э Л^.
5. Если событие А при комплексе условий (а) влечет за собой со-
событие В и, наоборот, при этом же комплексе условий В влечет Л,
то события Л и В называют равносильными и записывают А — В (см.
рис. 4, е). Так, например, условившись считать появление четвер-
114
той буквы русского алфавита событием А[ и сохраняя комплекс
условий (aj, мы можем считать события Ах и А\ равносильными,
записав при этом, что Л2 = Л1 (это соответствует равенству: г = чет-
четвертая буква русского алфавита).
6. Если некоторое событие при данном комплексе условий долж-
должно непременно произойти, то такое событие называется достоверным..
Событие, которое при комплексе условий (а) произойти не может, на-
называется невозможным. Поскольку все достоверные события равно-
равносильны между собой, их принято обозначать буквой U, невозмож-
невозможные события в силу этих же соображений обозначаются буквой
V; V = U. Проведей снова опыт по угадыванию буквы. Комплекс
условий (аз) отличается от комплекса условий (ах) только тем, что
угадываемой букве предшествует цепочка Акоторог. Испытание дает
здесь только одно событие, заключающееся в появлении буквы о.
Это событие является достоверным. Появление любой другой буквы
после цепочки Акоторог представляет собой невозможное событие.
7. Два события называются несовместимыми, если появление
одного из них при данном испытании Исключает возможность появ-
появления другого. События, состоящие в появлении после цепочки
Акоторо букв г я е, являются несовместимыми.
8. Два события являются совместимыми, если появление одного
из них при данном испытании не исключает появление другого.
Так, например, события Фх и Нх (см выше) являются совместимыми.
9. События Л, В, С, .. , Z образуют полную систему событий,
если при осуществлении испытания при комплексе условий (а)
хотя бы одно из них должно произойти. События, состоящие в появ-
появлении после цепочки Акоторо букв г, е, й, м, образуют полную
систему событий.
10. Два несовместимых события Л и Л" (Л читается: «не Л»), сос-
составляющих полную систему событий, называются противополож-
противоположными. Угадывая букву после цепочки Акотором, имеем два противо-
противоположных события, образующих полную систему. Первое из них
состоит в появлении буквы у (которому), второе заключается в
появлении пробела Д (котором А)
Система, включающая простые события А, В, С,..., а также слож-
сложные события, представляющие суммы, произведения, разности,
отрицания и т. п., называется полем событий.
§ 3. Вероятность элементарного лингвистического события
Простое перечисление и классификация лингвистических собы-
событий, которые образуют поле событий, принадлежащее данному опы-
опыту, имеет сравнительно ограниченный познавательный интерес.
Гораздо важнее оценить степень возможности того или иного собы-
события.
Мерой возможности появления лингвистического события Л при
осуществлении комплекса условий (а) является вероятность Р (А)
этого события. Большинство определений вероятности носит в боль-
115
шей или меньшей степени операционный характер, т. е. опирается
на конкретный прием оценки вероятности того или иного события.
Для языкознания интерес представляют три определения вероят-
вероятности: а) определение вероятности, исходящее из субъективной
количественной оценки возможности события; б) «классическое»
определение вероятности; в) «статистическое» определение вероят-
вероятности.
1. Субъективное определение вероятности и его использование
в лингвистике. Если человек решается интуитивно оценить вероят-
вероятность события Л, то он опирается на совокупность знаний (тезау-
(тезаурус) в относительно тех возможностей, которые могут способство-
способствовать или не благоприятствовать осуществлению события А.
Эта вероятность может быть представлена как Р (А, 6), т. е.
как вероятность события А при заключенном в мозгу данного чело-
человека тезаурусе в. Если два человека имеют относительно события
А одинаковый тезаурус б, то значения вероятностей события А
для этих людей будут одни и те же [14, с. 13]. Однако такая ситуа-
ситуация встречается редко. Чаще вероятность одного и того же события
оценивается разными людьми, исходя из разных величин в, 9'.
Даже у одного и того же познающего субъекта со временем вели-
величина в изменяется и превращается в 6', следовательно, и его
оценки вероятности события А в разные периоды его жизни являются
различными: Р (A, 6) ф Р (А, в').
Так, например, человек, недостаточно знающий русский язык,
может предполагать, что вероятности появлений букв г, е, й, м
после цепочки Акоторо равны. Напротив, человек, хорошо знаю-
знающий русский язык и ориентирующийся на художественную прозу и
разговорную речь, скажет, что вероятность появления е или й после
указанной цепочки выше, чем появление г или м. Наконец, инфор-
информант, языковое чутье которого сформировалось на основе газетной
речи, будет утверждать, что наиболее вероятной в данной ситуации
является* буква г [6, с. 46].
Часто говорят, что оценка вероятности того или иного события
имеет отношение только к состоянию познающего субъекта, и по-
поэтому все выводы из вероятностных суждений лишаются объективно-
объективного, не зависящего от познающего субъекта содержания [14, с. 18].
Вместе с тем нельзя забывать, что многие исследования в области
экспериментальной психологии и языкознания строятся на основе
* На использовании субъективных вероятностей строятся многие языко-
языковедческие исследования, а различия в субъективных вероятностях становятся
часто источником разного вида лингвистических дискуссий.
Так, например, А. Вайан считал, что русский именной суффикс-яга
(ср. бродяга, работяга, стиляга) продуктивен [60, с. 77—791, т. е. вероят-
вероятность образования с ним новых слов достаточно велика; В. В. Виноградов,
наоборот, утверждает, что этот суффикс малопродуктивен, т. е. вероятность
появления с ним новых слов очень мала [11, с. 75]. А. Н. Гвоздев считал, что
образования с приставкой раз-(разудалый, развеселый) вероятнее всего встре-
встречаются в разговорном языке и просторечии [6, с. 46, прим.], а Академичес-
Академическая Грамматика утверждает, что эти слова вероятнее всего можно встретить
в диалектах [16, с. 358].
116
обработки именно субъективных вероятностных оценок, получаемых
исследователем от информанта [21]; [23]. С помощью субъективных
вероятностей оценивается достоверность вхождения объектов в не-
нечеткие множества (см. гл. 1, § 1, п. 1). На этой же основ* делаются
попытки измерения семантической информации (см. ниже § 5,
п. 7).
2. Классическое определение вероятности (схема случаев)
и построение частотного словаря целостного текста. Существуют ис-
испытания, для которых вероятности их исходов можно оценить не-
непосредственно из условий самого опыта. Для этого необходимо, чтобы
различные исходы иопытаний обладали симметрией и в силу этого
были бы равновозможными.
Для иллюстрации симметрии и равновозможности опытов (схемы
случаев) рассмотрим слово кот, составленное из букв разрезной аз-
азбуки. Карточки с буквами тщательно перемешивают и кладут в ур-
урну. Производится испытание, состоящее в извлечении карточки
с буквой. Появления любой из букв, образующих слово кот, в силу
правила симметрии, являются равновозможными и попарно несо-
несовместимыми событиями.
Теперь обратимся к некоторому множеству S попарно несовмес-
несовместимых равновозможных лингвистических событий Аи Аг, ..., An,
которые составляют полную систему событий. Образуем систему Q,
состоящую из невозможного события V, всех событий At множества
S, а также всех комбинаций событий Ait входящих в это множество.
Если, к примеру, множество S состоит из трех событий Alt A2, А3
(ср. слово кот), то система Q включает события: V, Аъ А%, А3,
А\ ~г~ А%, А% т Aat Ai -р Аз* АуА^, А%А3, А^А^, А^А^А^, а так-
также Ау + Л2 + А3 = U.
Нетрудно видеть, исходя из определения, данного в п. 2 § 2,
что Q есть поле событий. Действительно, невозможное событие V
входит в Q по определению, комбинации событий At входят в Q
также по определению, достоверное событие U входит сюда, посколь-
поскольку U = А, + Аг + ... + AN.
Для событий системы Q может быть дано так называемое клас-
классическое определение вероятности, которое формули-
формулируется следующим образом.
Если результаты испытания можно представить в виде полной
системы /V равновозможных и попарно несовместимых событий и
если случайное событие появляется только в F случаях, то веро-
вероятность события А равна
Р (А) = FIN,
E.7)
т. е. отношению количества случаев, благоприятствующих данному
событию, к общему числу всех случаев.
В нашем примере вероятность появления согласной составляет
Р (согл.) = 2/3.
Из классического определения вероятности вытекают такие
следствия.
117
1. Вероятность достоверного события равна единице:
2. Вероятность невозможного события равна нулю'.
Р (V) = 0.
3. Вероятность появления случайного события А при N испыта-
испытаниях есть положительное число, заключенное между нулем и едини-
единицей:
0 < /> (Л) < 1.
В некоторых лингвистических работах, использующих элементы
теории вероятностей, величина вероятности выражается в процентах.
Исходя из классического определения вероятности,.осуществля-
вероятности,.осуществляется вероятностная обработка частотных словарей отдельных про-
произведений или всего творчества писателя. В этих случаях все слово-
словоупотребления, составляющие текст всех произведений или отдель-
отдельного произведения, подчиняются правилу симметрии и образуют
полную систему равновозможных и попарно несовместимых собы-
событий. Некоторое интересующее нас слово (или словоформа) А появ-
появляется в исследуемом тексте в виде словоупотреблений. Отсюда ве-
вероятность того, что наугад взятое слово из нашего текста окажется
именно словом (словоформой) А, согласно E.7), равна Р {А) = FIN.
Например, текст «Капитанской дочки» А. С. Пушкина состоит
из 29343 словоупотреблений. Формы слова быть встречаются здесь
430 раз. Отсюда следует, что вероятность появления в тексте «Ка-
«Капитанской дочки» форм слова быть такова:
Рг {быть) = FJNX = 430/29343 ~ 0,0147 = 1,47°/0.
Что касается всего корпуса текстов А. С. Пушкина, который
состоит из 544777 словоупотреблений, то здесь формы слова быть
употреблены автором 8771 раз. Вероятность того, что наугад взятое
слово окажется словом быть в любом произведении Пушкина, сос-
составит [6, с. 51—52]
Рг (быть) = FJN% = 8771/544777 ~ 0,0161 = 1,6170.
3. Статистическое определение вероятности. Выборочное час-
частотное описание текста. Классическое определение вероятности ока-
оказывается весьма удобным применительно к таким опытам, которые
заведомо дают симметрию конечного числа равновероятных исходов.
Однако при переходе от этих простых примеров к решению более
сложных вероятностно-лингвистических задач это определение на-
наталкивается на непреодолимые трудности.
Во-первых, число возможных результатов может и не быть конеч-
конечным. Так, например, определяя вероятности появления в языке
слов, словоформ или сочетаний, мы должны согласиться с тем, что
практически число этих лингвистических единиц стремится к беско-
бесконечности.
Во-вторых, утверждать о равновероятности исходов лингвисти-
лингвистического опыта обычно бывает весьма затруднительно.
118
К опытам, которые не могут быть исследованы на основе системы
случаев, применяется так называемое статистическое
определение вероятности.
Прежде чем давать статистическое определение вероятности,
введем некоторые определения и рассмотрим конкретный лингвис-
лингвистический пример.
Пусть произведена серия из N испытаний, в каждом из которых
могло появиться или не появиться событие А. Тогда абсолютной час-
частотой (или частотой) F называется число появлений события А,
а относительной частотой (или частостью) f(A) — отношение
абсолютной частоты к общему числу испытаний:
/ {А) = FIN.
E.8)
При небольшом числе опытов частоты события носят непостоян-
непостоянный и случайный характер и могут изменяться от одной группы собы-
событий к другой. Например, в одном взятом наугад тексте из произве-
произведений Пушкина длиной в 100 слов формы глагола быть не появи-
появились ни разу, зато в другом отрывке той же длины этот глагол по-
появился три раза и его относительная частота возросла до 0,03.
Однако при последовательном увеличении объема выборки относи-
относительная частота глагола быть приобретает определенную устойчи-
устойчивость, приближаясь к величине 0,01 (см. табл. 5.1). Аналогичным
образом получены относительные частоты (статистические вероят-
вероятности) русских букв, показанные в табл 5.2.
Таблица 5.1
Относительная частота глагола быть в русской художественной
прозе (Пушкин, Тургенев, Бунин)
Объемы
выборок
F
t
10
0
0,000
100
3
0,030
1000
15
0,015
2000
17
0,008
3000
31
0,010
4000
33
0,008
5000
47
0,009
Продолжение табл. 5.1
Объемы
выборок
F
1
6000
57
0,010
7000
71
0,010
8000
74
0,009
9000
88
0,010
10000
95
0,010
15000
153
0,010
400000
4186
0,011
119
Таблица 5.2
Распределение вероятностей букв в русских литературных текстах
Буква
Пробел (Д)
О
е,ё
а
и
н
т
с
Р
в
л
р
0,174
0.090
0,072
0,062
0,062
0,053
0,063
0,045
0,040
0,038
0,035
Буква
К
м
д
п
у
я
в
ы
б
ь,ъ
г
р
0.128
0 0§6
0,085
0,023
0,021
0,018
0.016.
0,016
0,014
0,014
0,013
Буква
Ч
й
X
ж
их
ю
ц
щ
9
Ф
Р
0,012
0,010
0,009
0,007
0,006
0,006
0,004
0,003
0,003
0,002
Опыт многих наук, да м вся практическая-деятельность человека
показывают, что результаты отдельных статистических испытаний
могут давать заметные флуктуации. Однако при большом числе ис-
испытаний N статистические флуктуации начинают сглаживаться,
а относительная частота / обнаруживает все большую устойчивость.
Иными словами, в случайных явлениях имеется некоторое объек-
объективно существующее свойство, которое имеет тенденцию оставать-
оставаться постоянным и проявляется все яснее при увеличении объема иссле-
исследуемого материала. Указанное свойство измеряется некоторой по-
постоянной величиной, которая является количественной объективной
числовой характеристикой изучаемого явления. Эта постоянная
величина и называется вероятностью случайного события А [будем
по-прежнему обозначать ее символом Р (А)]. Экспериментальными
значениями вероятности являются относительные частоты интере-
интересующего нас события / (А) в определенных сериях наблюдений.
Определенная таким образом вероятность случайного события носит
название статистической вероятности.
Следует обратить внимание читателя на то, что точное численное
значение статистической вероятности остается, вообще говоря, не-
неизвестным. За численное значение вероятности обычно принимается
при большом количестве испытаний либо сама частость события А,
либо некоторое число, близкое к этой частости, например некоторое
среднее арифметическое относительных частот, полученных из не-
нескольких достаточно больших серий испытаний*.
Оставляя в стороне методологические дискуссии, связанные со
статистическим определением вероятности [14, с. 17 исл.1, необходи-
мо подчеркнуть, что этот подход имеет принципиальное значение для
* Разумеется, это не значит, что вероятность события вообще не может
быть точно определена. Если мы имеем дело со схемой случаев, то вероят-
вероятность вычисляется по формуле E.7). Кстати, если нас интересует вероятность
появления глагола быть только в произведениях Пушкина, то, используя
классическое определение вероятности, нетрудно показать, что она равна
120
прикладных исследований, в том числе и лингвистических, например
при составлении частотных словарей. Не имея обычно возможности
обследовать всю генеральную совокупность возможных исходов
(например, всю совокупность словоупотреблений, составляющих
все когда-либо написанные русские тексты), мы вынуждены произ-
производить серию наблюдений, охватывающих некоторую частную сово-
совокупность (например, определенную выборку из русских текстов).
В результате таких исследований мы получаем относительные час-
частоты для случайных событий (в нашем случае —словоформ или слов).
По этим относительным частотам необходимо оценить численные
значения вероятностей, которые, как уже указывалось, являются
числовой характеристикой изучаемых явлений Эта оценка сводится
к выяснению того, насколько далеко отклоняются эксперименталь-
экспериментальные частоты от вероятности. Решение такой задачи является по су-
существу узловым вопросом всех статистических исследований.
4. Аксиоматическое построение теории вероятностей. Все только
что рассмотренные определения вероятности имеют существенные
недостатки и ограничения
Интуитивная оценка вероятности зависит от тезауруса Опознаю-
Опознающего субъекта, который обычно не поддается измерению. Схема
случаев применима лишь к таким опытам, которые заведомо дают
симметрию конечного числа равновероятных исходов. При статис-
статистическом подходе понятие вероятности вообще остается в тени.
Широкое проникновение вероятностно-статистических исследо-
исследований в естественные и гуманитарные исследования потребовало соз-
создания формально-логического обоснования всего аппарата теории
вероятностей; это обоснование дано в аксиоматическом построении
теории вероятностей, предложенном А Н Колмогоровым [19].
Поскольку аксиоматика Колмогорова позволяет преодолеть ряд
трудностей, возникающих при использовании теории вероятностей
в языкознании, мы рассмотрим ее основные идеи и положения.
В аксиоматике Колмогорова случайное событие не рассматри-
рассматривается как исходное первичное понятие, но образуется на основе
других элементарных понятий. Чтобы пояснить это положение,
рассмотрим два примера.
Пусть имеется некоторое пространство U (прямая, площадь
и т. д.). В этом пространстве содержатся подобласти А, В, ..., Z.
В пространстве U «наудачу» берется точка с. Попадания точки а
в те или иные подобласти точек и являются случайными событиями.
Одновременно каждое случайное событие выступает в качестве не-
некоторого подмножества множества точек U (рис. 36)
Возьмем другой пример Пусть имеется текст, написанный на
некотором естественном языке. Этот текст можно рассматривать
как некоторое лингвистическое пространство (множество словоупот-
словоупотреблений) U. Подобластями (подмножествами) А, В, ..., Z этого
пространства являются группы словоупотреблений, имеющие аб-
абсолютно одинаковое написание (т. е. словоупотребления, реализую-
ющие одну и ту же словоформу), например: а, абажур, абажу-
абажура, абажуру ,..., наука, науки, науке, .... '
121
ф под-
подU Эле-
ЭлеИз словаря берется некоторая словоформа, например науке, и
накладывается наугад на одно из словоупотреблений текста. Словар-
Словарная единица науке может совпасть с текстовым словоупотреблением
науке (в этом случае мы имеем дело с попаданием словарной едини-
единицы в подмножество науке), а может и не совпасть с указанным тек-
текстовым словоупотреблением. Попадание или непопадание словарной
единицы в то или иное подмножество является случайным событием.
При этом каждое случайное событие является некоторым подмноже-
подмножеством нашего лингвистического множества.
Иными словами, аксиоматика Колмогорова исходит из множества
U элементарных событий (в наших примерах — геометрических
точек или словоупотребле-
словоупотреблений), которые в данной си-
ситуации можно рассматривать
как возможные события. Да-
Далее вводится система
множеств множества
менты этой системы называ-
называются случайными событиями.
Построение системы % долж-
должно отвечать следующим тре-
требованиям:
1) g содержит в качестве
элементов Множество U, а
также пустое множество V =
Рис. зб *= У;
2)если Аи В, являющиеся
подмножествами множества U,
входят в <j как его элементы, то множества А -f В, АВ, А — В,
А и В, составленные из элементов U, также будут элементами
системы <j- В этом случае ф называется телом событий.
Нетрудно, заметить, что представленные здесь требования ана-
аналогичны условиям, на которых строилось поле событий Q в клас"
сическом определении вероятности, сводящемся к схеме случаев.
Однако к полю событий в аксиоматике Колмогорова предъявляется
еще одно требование, позволяющее применять ее к речевым ситуа-
ситуациям, в которых число исходов опыта не является конечным. Это
требование можно сформулировать так:
Если подмножества Ах, А2, ..., Ап, ..., принадлежащие мно-
множеству U, суть элементы системы $, то их сумма Аг + Аг + ... ¦>
+ Ап + ••¦ и произведение /4ХЛ2 ... Ап... также являются элемен-
элементами $.
Изложив основную идею аксиоматики Колмогорова, перечислим
теперь основные аксиомы, определяющие вероятность.
1°. Каждому случайному событию А из поля событий 5 можно
поставить в соответствие неотрицательное число Р (А) ^ 0, на'
зываемое его вероятностью.
2°. U является событием с вероятностью Р (U) = 1.
122
3°. (Аксиома сложения.) Если события А и В несовмес-
несовместимы, то
Р (А + В) = Р (А) + Р (В). E.9)
Аналогично, если события Аи А2, ..., Ап попарно несовместимы, то
Р (А, + Аг + ... + Ап) - Р (А,) + Р (А2) + ... + Р (Ап).
E.10)
4°. (Аксиома непрерывности.) Если имеется по-
последовательность событий Аъ А2, ..., Ап и эти события не могут
осуществляться одновременно, то
5°. (Расширенная аксиома вложения.) Аксиома
еложения справедлива для бесконечного количества событий. Иными
словами, если
А -— А^ -у- А$ -у" ••¦ "F Ап -р ..•
является событием, то
Р (А) - Р (А,) + Р (Аг) + ... -г Р (Ап) * ... . E.11)
Приведенные аксиомы дают ряд важных для лингвистических
приложений следствий.
1. Если несовместимые события Аи Аг, .. , Ап образуют полную
группу событий, то согласно аксиомам 2° и 3°, сумма вероятностей
этих событий равна единице т е.
Р (А,) + Р (А,)
(Ап) = 1.
E.12)
2. Сумма вероятностей двух противоположных событий равна
единице, т. е.
Р(А) + Р (А) =. 1. E.13)
3. Из формулы E.13) следует, что
Р {А) = 1 _ Р (А),
или
. р (А) = 1 — Р (А).
4. Вероятность невозможного события равна нулю'.
Р (V) = 0.
5. Каково бы ни было случайное событие А, его вероятность заклю-
заключена между нулем и единицей:
0 < Р (А) < 1.
6. Если А с В, то Р (Л)< Р (В).
E.14)
123
7. Если А и В — совместимые события, то в суммах А ¦{- В =*
*= А + (В — АВ) и В =» АВ + (В — ЛВ) слагаемые правых
частей — несовместимые события.
8. Если А и В — произвольные события (т. е. такие события, ко-
которые могут быть и совместимыми, и несовместимыми), то имеет
место неравенство
Р(А + В) ^ Р (А) + Р (В). E.15)
По индукции следует, что если Аи Аг, 0.., Ап — произвольные собы-
события, то
Р (А, + А,+ ... + Л„)< Р (Аг) + Р (As) 4- „. + Р (Ап).
Приведенные аксиомы и следствия мы проиллюстрируем в даль-
дальнейшем по ходу описания Лингвистических приложении теории ве-
вероятностей.
Аксиоматическое построение основ теории вероятностей харак-
характеризуется следующими особенностями:
I. Вероятностные понятия получают здесь теоретико-множест-
теоретико-множественную интерпретацию. Сущность ее состоит в том, что вес возмож-
возможные для данного опыта элементарные события, их суммы к произве-
произведения, а также невозможные события рассматриваются как элемен-
элементарные множества S, причем каждому элементу этого множества
ставится в соответствие некоторое число (норма), являющееся его
счетно-аддитивной (т. е. способной к арифметическому сложению),
неотрицательной мерой. Такая интерпретация вероятностных по-
понятий принципиально важна для лингвистического приложения
теории вероятностей: она позволяет перебросить естественный мост
между алгебраическим (по своей природе теоретико-множествен-
теоретико-множественным) языкознанием, квантитативной (по своему существу—вероят-
существу—вероятностной) лингвистикой и нечетко-множественным языкознанием
[26, с. 207—269]; 165].
II. Аксиоматика Колмогорова исходит из свойств и понятий ве-
вероятности, сформулированных уже в классическом и статистиче-
статистическом ее определениях. Эти последние целиком включаются в акси-
аксиоматическое определение вероятности как ее частные случаи. Вместе
с тем аксиоматика Колмогорова преодолевает ограниченность как
классического, так и статистического определений. С одной сторо-
стороны, удается избежать тех логических трудностей, которые связаны.
с несовместимостью понятий иррегулярности и требования о сущест-
существовании предела, — понятий, постулируемых в статистическом опре-
определении вероятности. С другой "стороны, преодолевается ограничен-
ограниченность схемы случаев, оперирующей лишь о конечным числом ре-
результатов. Введение А. Н. Колмогоровым в определение вероят-
вероятности аксиомы непрерывности, а также расширенной аксиомы
сложения позволяет рассматривать события, подразделяющиеся
на бесконечное число частных случаев. Этот факт имеет принципи-
принципиальное значение для языкознания, которое постоянно имеет дело
с речевыми процессами, охватывающими бесконечное число слово-
словоформ, словосочетаний и предложений.
124
§ 4. Вероятности сложных лингвистических событий
1. Сложение вероятностей. Языковеда редко интересуют элемен-
элементарные события, чаще всего ему приходится иметь дело со сложными
лингвистическими событиями, например с суммой элементарных со-
событий. Выбор правил, с помощью которых вычисляется вероятность
сложного события, определяется тем, являются ли составляющие
его элементарные события несовместимыми или совместимыми.
Согласно правилам 3° (аксиома сложения) и 5° (расширенная
аксиома сложения), вероятность наступления одного из попарно
независимых событий {Ах + Аг + ... + Ап + •••) равна сумме ве-
вероятностей этих событий:
= Р(Л1)+ Р(Аг) + ... +Р(Ап)+ ....
Однако если два события совместимы, то их вероятность опреде-
определяется как сумма вероятностей этих событий минус произведение
вероятностей этих событий:
Р (А + В) = Р (А) + Р (В) — Р (А) Р (В)
F.16)
При вычислении вероятности суммы нескольких совместимых
событий обычно, пользуются правилом, согласно которому вероят-
вероятность появления хотя, бы одного из нескольких совместимых событий
Аъ Аг, ..., Ап равна разности между единицей и вероятностью
совместного наступления (умножения) всех противоположных
событий. Иными словами,
Р{А,+ Аг + ... + Ап) = 1-Р(А,Аг...Ап) = 1- ft Q-P(At)).
E.17)
2. Прогнозирование вероятностей лингвистических событий при
повторении опытов. Рассмотренные правила широко используются
при прогнозировании событий в разного рода вероятностно-лингви-
вероятностно-лингвистических, инженерно-лингвистических и информационных задачах.
Рассмотрим в этой связи следующий пример.
Для расчета памяти вероятностного автомата, распознающего
устную речь, и построения алгоритма его работы приходится вычис-
вычислять вероятность совпадения хотя бы одной из словоформ обрабаты-
обрабатываемого текста с соответствующей лексемой, заданной в словаре
автомата.
Предположим, что нужно определить вероятность того, что хотя
бы одно из двух выбранных слов текста будет местоимением он.
Обозначим через А первое появление местоимения он, а через
В — второе появление этого же местоимения. События А и В сов-
совместимы, поскольку можно извлечь одновременно слово он как из
первого, так и из второго отрывков. Поэтому при решении нашей за-
задачи необходимо воспользоваться формулой E.16). Значение ста-
125
тистической вероятности согласно данным частотного словаря [39]
равно 0,0099. Учитывая это, получаем
Р (А + В) = 0,0099 + 0,0099 — 0,0099 • 0,0099 « 0,020.
Теперь предположим, что распознающий автомат анализирует
десять взятых наугад словоформ, и попробуем определить вероят-
вероятность того, что хотя бы одна из этих словоформ окажется местоиме-
местоимением он. Для этого воспользуемся формулой E.17), обозначив через
А совпадение текстовой словоформы с местоимением он, а через С —
появление в нашем опыте хотя бы одного он. Поскольку вероят-
вероятность Р (А) для всех отрывков одинакова, на основании равенства
E.17) найдем
р (С) = 1 — A — 0.0099I0 ~ 0,095.
Таким образом, вероятность получить хотя бы одно местоимение
он при десятикратном извлечении словоформы из текста заметно вы-
выше вероятности получить его при однократном или двукратном
извлечении.
3. Зависимые лингвистические события и условные вероятности.
До сих пор мы имели дело с независимыми событиями, т. е. с такими
событиями, вероятность появления которых не зависела от вероят-
вероятности -появления другого лингвистического события — эти вероят-
вероятности называются безусловными. Однако языкознание сравнительно
редко имеет дело с независимыми событиями. Обычно речь идет
о зависимых событиях и условных вероятностях: даже вероятности
появления букв, фонем, слогов, морфем и т. д. являются условными,
так как зависят от позиции этих лингвистических объектов в слове,
словосочетании и предложении. Например, как показывают табл. 5.3
и 5.4, буква п в начале русского слова имеет вероятность 0,207,
а после начального я вероятность ее появления составляет всего
0,001.
Т а б л и ца 5.3
Распределение вероятностей первых букв русского слова
Таблица 5.4
Распределение вероятностей русских букв после цепочки Дя*
Буква
п
н
и
с
о
в
к
м
д
а
Р
0,207
0,085
0,070
0,064
0,052
0,051
0,040
0,038
0,037
0,036
Буква
Я
3
т
ш
Ф
Р
б
у
г
р
0,035
0,032
0,031
0,030
0,029
0,021
0,020
0,020
0,016
0,015
Буква
е
9
Л
X
Ц
ж
щ
ю
й
р
0,014
0,014
0,012
0,010
0,008
0,007
0,003
0,002
0,001
Буква
Пробел (А)
в
3
Р
щ
б
р
0,701
0,157
0,036
0,031
0,016
0,009
Буква
г
й
д
к
л
м
р
0,004
0,003
0,002
0,002
0,001
0,001
Буква
Я
и
X
ш
р
0,001
0,001
0,001
0,001
126
* Таблицы 5.3 и 5.4 составлены путем обследования разговорных, беллетристичес-
беллетристических, научно-технических и публицистических текстов длиной примерно в 500 cip.
(ок. 200 тыс. словоформ). Возможное е точки зрения лексических норм сов[еменного
русского языка начальное двухбуквениое сочетание яф (ср. яфетический, Яффа)
не встретилось и поэтому не учтено в таблице.
Рассмотрим соотношение независимых и зависимых событий,
а также безусловных и условных вероятностей на примере искусст-
искусственного лингвистического опыта.
Словоформа мамам (дательный падеж множественного числа
от мама) составлена из букв разрезной азбуки. Карточки с буквами
этого слова положены в урну. Производится испытание, состоящее
в последовательном извлечении карточки с буквой и возвращении ее
обратно в урну. Событием В считается извлечение буквы м в первом
испытании (тогда В будет извлечение из урны не м, т. е. буквы а),
событием А — извлечение буквы а во втором опыте (тогда А будет
извлечение из урны не а, т. е. буквы м). В силу того, что вынутая
в первый раз буква возвращается обратно в урну, перед вторым
опытом количество букв в урне не изменяется. Поэтому вероятность
события А является безусловной, поскольку она не зависит
от того, была ли извлечена до этого из урны буква м (событие В) или
буква а (событие В), и остается равной 2/5. Безусловной является
и вероятность события В. Если изменить условия опыта и не
возвращать извлеченную букву обратно в урну, то вероятности
получить при втором, третьем и т. д., извлечениях букву а или м
будут существенно зависеть от того, какие буквы были извлечены
перед этим из урны.
Пусть исходом первого извлечения была буква м; тогда вероят-
вероятность вытащить при втором извлечении букву а составит 2/4 = 1/2.
В том же случае, когда в результате первого опыта получена буква
а (событие В), вероятность вытащить второй раз букву а равна 1/4.
Сходное положение возникает при определении вероятности появле-
появления буквы м (событие А) во втором извлечении при условии, что
в первый раз была получена буква м (событие В) или а (событие В).
Иными словами, события А и В являются зависимыми,
а их вероятности — условными.
127
Условная вероятность события А при условии, что произошло
событие В, обозначается Р (А/В). Так, в рассмотренном выше
примере
Р (А/В) = 1/2, Р (А/В) = 1/2, Р (А/В) = 1/4, Р (А/В) = 3/4.
Условная вероятность события А, вычисленная при условии,
что осуществилось несколько событий Вх, В2, В3, ..., обозначается
Р(А/В1В2В3...).
Величина условной вероятности всегда заключена в том же от-
отрезке, что и величина абсолютной вероятности, т. е.
0<Р
...)< 1.
4. Правило умножения вероятностей и вычисление вероятностей
цепочек языковых элементов. Каждый текст или его часть можно
рассматривать как совместное наступление некоторой линейной по-
последовательности лингвистических событий—совместное появление
цепочки словоформ, последовательности слогов, цепочек фонем или
букв. Определение вероятностей появления этих цепочек опирается
на теорему умножения вероятностей, согласно
которой вероятность совместного наступления двух событий равна
произведению вероятности первого события на условную вероятность
второго, вычисленную при условии, что первое событие имело место'.
Р (АВ) = Р (А)Р (В/А) или Р (АВ) = Р (В) Р (А/В). E.18)
Из этой теоремы вытекают три важных следствия.
Следствие 1. Если событие А независимо от В, то и со-
событие В независимо от А.
Для независимых событий теорема умножения вероятностей
упрощается и принимает следующий вид: вероятность произведения
двух независимых случайных событий равна произведению их безуслов-
безусловных вероятностей:
Р (АВ) = Р (А) Р (В). E.19)
Следствие 2. Если события А и В независимы, то незави-
независимы также и пары событий (А, В), (А, Ъ), (А, В).
Следствие 3. Вероятность произведения зависимых собы-
событий А, В, С равна произведению вероятности одного из них на услов-
условную вероятность второго и на условную вероятность .третьего, вы-
вычисленную при условии, что предыдущие оба события произошли:
Р (ABC) = Р (А) Р (В/А) Р (С/АВ). E.20)
Обобщая это следствие на п зависимых событий Alt Аг, ..., АП1
получаем
П Ai)=P(A1)P(A2/Ai)P(As/A1A2)...p(Anin A,\ E.21)
Выше в табл. 5.2—5.4 были приведены значения для условных
и безусловных статистических вероятностей отдельных букв в тек-
123
стах современного русского литературного языка. Используя эти
таблицы и соотношения E.18), E.20), E.21), можно рассчитать ве-
вероятности появления в письменных текстах современного русского
языка различных двухбуквенных сочетаний.
Так, например, вероятность появления группы Дя равна
Р (Ля) = Р (А) Р (я/А) = 0,174 • 0,035 = 0,006 = 0,6°/в.
Чтобы определить вероятность появления слова я, образуем
трехслойное сочетание ДяД, для которого
Р (АяА) = Р (А) Р (я/А) Р (А/Ая) =
= 0,174 • 0,035 • 0,701 = 0,00427 = 0,4°/0.
Для расчета вероятности появления морфемы япон формируем
цепочку Аяпон; тогда
Р (Аяпон) = Р (А) Р {я/А) Р (п/Ая) Р (о/Аяп) Р (н/Аяпо).
«Словарь русского языка» под ред. С. И. Ожегова показывает,
что после цепочки Аяп единственно возможным продолжением бу-
будет диграмма он*. Отсюда следует, что появления здесь букв о и н
являются достоверными Событиями, условная вероятность которых
равна единице. Таким образом,
Р (Аяпон) = 0,174 ¦ 0,035 • 0,001 • 1 • 1 = 0,00006 = 0,006°/0.
5. Определение общей вероятности лингвистического события
с помощью формулы полной вероятности. Если лингвистическое
событие А может осуществиться вместе с одним и только одним из rt
несовместимых событий Hlt Н2, .... Нп, называемых гипотезами
и образующих полную группу событий, то для определения вероят-
вероятности этого события используется формула полной ве-
вероятности:
Р(А)=
E.22)
Таким образом, вероятность события А равна сумме произведений
вероятности каокдой гипотезы на вероятность события при осу-
осуществлении этой гипотезы.
Формула полной вероятности используется для вычисления об-
общей вероятности лингвистического события при условии, что из-
известны его вероятности в узко-тематических выборках.
Пусть, например, имеется английский научно-технический текст
общей длиной в 400 тыс. словоупотреблений (около тысячи стан-
стандартных страниц). По тематике этот текст распадается на следующие
четыре выборки разной длины:
Мы опускаем в данном случае продолжение япош(ка), вероятность
рения норм русского литературного языка
появления которого с точки зрения
близка к нулю.
5 Зак. 1287
129
1) радиоэлектроника —200 тыс. словоупотреблений (ок. 500 с),
2) автомобилестроение—100 тыс. словоупотреблений (ок. 250 с),
3) судовые механизмы — 50 тыс. словоупотреблений (ок. 125 с),
4) строительные материалы — 50 тыс. словоупотреблений
(ок. 125 с),
Словоформа are — множественное число настоящего времени
глагола to be 'быть' употреблена в 1-й выборке 1610, во 2-й —
1273, в 3-й — 469 и в 4-й — 346 раз. Аналогичным образом, слово-
словоформа machine 'машина, механизм' встретилась в 1-й выборке 98,
ео 2-й — 57, в 3-й — 9 и в 4-й — 19 раз. Эти данные взяты из рабо-
работы [6, с. 80].
Необходимо определить вероятность того, что извлеченное
наугад из нашего текста словоупотребление будет: а) словоформой
are; б) словоформой machine.
Для этого будем считать появление словоформы are событием
А, а появление machine — событием В. Рассмотрим также следую-
следующие четыре гипотезы: Нг — принадлежность словоформы к текс-
текстам по радиоэлектронике, Я2 — к текстам по автомобилестрое-
автомобилестроению, Я3 — к текстам по судовым механизмам, Я4 — к текстам
по строительным материалам.
Считая доли указанных текстов в общей выборке вероятностями
наших гипотез, находим:
Р (tfj = 200000/400000 = 0,5; Р (Яг) = 100000/400000 = 0,25;
р (Я3) = Р (Я4) = 50000/400000 = 0,125.
Условные вероятности события А (появление глагола are) при
этих гипотезах соответственно равны:
Р (A/HJ = 1610/200000 = 0,008; Р (А/Нг) = 1273/100000 = 0,012;
Р (A/Hs) = 469/50000 = 0,009; Р (Л/Я4) = 346/50000 = 0,007.
Применяя формулу полной вероятности, определяем, что вероят-
вероятность извлечь наугад из данного текста словоформу are равна
Р (А) = Р (Нг) Р (А1Нг) + Р (Я8) Р (АШ2) +
+ Р (Я,) Р (А1Нг) + Р (Я4) Р (A/HJ =
= 0,5 • 0,008 + 0,25 • 0,012 + 0,125 • 0,009 + 0,125 • 0,007 =
= 0,009 = 0,9°/0.
Аналогичным образом находим условные вероятности события В:
Р (В1НХ) = 98/200000 = 0,0005; Р (В/Нг) = 57/100000 = 0,0006;
Р (В/Нд) = 9/50000 = 0,0002; Р (В/Я4) = 19/50000 = 0,0004.
По формуле полной вероятности получаем, что вероятность
извлечь из данного текста словоформу machine составляет
Р {В) = 0,5 • 0,0005 + 0,25 • 0,0006 + 0,125 • 0,0002 +
+ 0,125 • 0,0004 =¦ 0,000475 « 0,048°/0.
130
6. Априорные и апостериорные вероятности. Измерение веро-
вероятностей лингвистических гипотез. До сих пор мы имели дело с так
называемыми априорными вероятностями лингвистических событий.
Эти априорные вероятности устанавливались интуитивно-эмпири-
интуитивно-эмпирически или теоретически до осуществления опыта, исходя из наших
знаний об условиях а этого опыта. Наши сведения о всех условиях
опыта обычно неполны, поэтому априорные вероятности являются
вероятностями некоторых лингвистических гипотез Hv, H2, ..., Я„
об исходе эксперимента.
Получаемый при осуществлении этого эксперимента результат
заставляет нас обычно произвести переоценку наших гипотез и
придать им новые — апостериорные вероятности. Определение
апостериорных вероятностей осуществляется, исходя из следую-
следующих соображений.
Пусть априорные вероятности гипотез до опыта соответствен-
соответственно равны Р (Н^, Р (Я2), ..., Р (Нп), а в результате опыта отмечено
появление события А. Необходимо определить, как нужно изме-
изменить вероятности наших лингвистических гипотез в связи с осу-
осуществлением события А.
Согласно теореме умножения вероятностей для зависимых со-
событий, вероятность совместного наступления события А и гипоте-
зы Я( (i = 1, 2, ..., п) составляет
Р(АН,) = P(A) P{HJA) = P(Hi)P(A/Ht).
Отсюда следует, что
Р(А)
E.23)
E.24)
Подставляя для Р (А) его выражение из формулы полной веро-
вероятности E.22), имеем
E.25)
2 P(Hj)P(A/Hj)
Выражение E.25) носит название формулы Бейеса, или фор-
формулы вероятностей гипотез.
Чтобы показать, как с помощью формулы Бейеса измеряются
вероятности лингвистических гипотез, обратимся снова к извле-
извлечению из английского научно-технического текста словоформ are
и machine (см. п. 5).
Предположим, что первая наугад взятая из английского науч-
научно-технического текста словоформа оказалась глаголом are (собы-
(событие А). Необходимо найти вероятность того, что эта словоформа
извлечена: а) из текста по радиоэлектронике (Я^; б) из текста
по автомобилестроению (Я2); в) из текста по судовым механизмам
(На)', г) из текста по строительным материалам (Я4).
б* 131
Вероятности того, что извлеченная словоформа принадлежит
к той или иной тематической выборке, являются апостериорными
вероятностями гипотез — точнее, условными вероятностями этих
гипотез при условии, что произошло событие А. Используя соот-
соотношение E,25), получим
Р(Н1)Р(А/Н1)
Р {Hi) Р (Л/Я!) + Я {Ht) Р (А1Нг) + Р {На) Р {А/Н-л) + Р {Нк) P{AlHt)
0,5-0,008
¦ = 0,444.
0.5-0.008+ 0,25-0,012 + 0,125-0,009-fO, 125-0,007
Аналогичным образом
Р Щ%1А) = 0,333, Р {Н3/А) = 0,128, Р (HJA) = 0,095.
Нетрудно заметить, что апостериорные вероятности гипотез
о принадлежности словоформы are к определенным подъязыкам,
обусловленные появлением этой словоформы, заметно отличаются
от их априорных вероятностей, полученных в п. 5.
Используя приведенные выше данные, определим апостериор-
апостериорные вероятности гипотез Ни Я2, Я3, Я4 при условии, что из текс-
текста дважды извлекались две словоформы, причем оба раза этими
словоформами оказался глагол are. Эксперимент строился таким
образом, что обе словоформы могли быть извлечены только из од-
одной тематической выборки.
Двойное извлечение словоформы are является сложным собы-
событием, представляющим собой произведение двух независимых собы-
событий. В связи с этим формула Бейеса для расчета апостериорных
вероятностей наших гипотез принимает здесь следующий вид:
P{HJ.\A)-
_ P(Hi)\P{AlHi)\*
2
P (AIHj.A/Н,)
lp И//ОI"
Проведя несложные расчеты, получаем:
Р (НХ1АА) = 0,369, Р (HJAA) = 0,437,
Р (HJAА) = 0,126, Р (Я4 /АА) = 0,068.
Нетрудно заметить, что здесь снова имеет место перераспреде-
перераспределение вероятностей гипотез, причем на первое место выдвигается
гипотеза о том, что обе словоформы принадлежат второй выборке.
•После однократного извлечения are наибольшую вероятность име-
имела гипотеза Нг.
132
На понятиях априорной и апостериорной вероятности строится
теория решений, применение которой имеет большое будущее
в инженерной лингвистике; эти понятия используются также
при формулировке понятия логической вероятности, которая яв-
является отправным пунктом процедуры, измеряющей семантиче-
семантическую информацию в тексте 126].
§ 5. Информационные измерения в тексте
1. Энтропия как мера неопределенности лингвистического
опыта. Мы уже несколько раз встречались с количественными оцен-
оценками информации, содержащейся в тексте и слове. Однако отсутст-
отсутствие достаточных математических сведений не позволило нам дать
строгое определение количества информации и описать процедуру
ее вычисления. Теперь, когда эти необходимые сведения введены,
можно дать более или менее последовательное определение как
самого понятия количества информации, так и информационных
измерений в тексте.
Количественные измерения информации можно осуществить,
опираясь на два исходных понятия — вероятности слу-
случайного лингвистического события и неопределенности,
присутствующей перед осуществлением опыта, результатом кото-
которого является указанное событие. Понятие вероятности подробно
рассматривалось в предыдущих разделах, понятие же неопреде-
неопределенности и ее меры нуждается в специальном разъяснении.
Каждый лингвистический опыт связан с некоторой неопределен-
неопределенностью исхода. Если наш опыт состоит в последовательном угады-
угадывании букв неизвестного слова, то угадывание каждой буквы
по мере движения от начала слова имеет свою неопределенность.
Чем больше альтернатив при выборе возможного исхода опыта, тем
больше его неопределенность; чем меньше таких альтернатив,
тем меньше неопределенности в исходе опыта. Например, при после-
последовательном угадывании букв слова который наибольшая неопреде-
неопределенность имеет место при выборе первой буквы (здесь вместо к может
стоять любая буква русского алфавита, за исключением твердого и
мягкого знаков), она будет значительно меньше в случае угадывания
седьмой буквы при условии, что предыдущие шесть Акоторо нам
известны. В этой позиции возможны четыре альтернативы: либо г,
либо е, либо й, либо м. Заметим, что и в первом, и во втором
случае угадывание происходит в предположении, что все допустимые
в той или иной позиции буквы равновероятны. Если же обратиться
к угадыванию буквы, стоящей после цепочки ^которое, то исход
этого угадывания полностью определен: с точки зрения норм рус-
русской письменной речи здесь может находиться только буква о.
Неопределенность в этом случае равна нулю. Таким образом, между
неопределенностью опыта и количеством равновероятных исхо-
исходов обнаруживаются следующие две зависимости:
1) если число исходов S = 1, то неопределенность / E) = 0;
2) если имеются два опыта, причем Sx > S8, то / (Sx) > / (S2).
133
Для того чтобы окончательно определить вид функции / (S),
характеризующей меру неопределенности, рассмотрим еще один
лингвистический эксперимент.
Будем строить случайным образом трехсловное предложение.
Пусть первая позиция занята именем собственным Петр. Вторую
позицию нужно занять одной из двух глагольных словоформ видит
или слышит (St = 2), которые наугад извлекаются из урны.
Конечная позиция замещается одной из четырех словоформ —
Ивана, Лукъяна, Марка, Павла (S2 — 4), — также извлекаемых
наугад из второй урны. Это построение можно изобразить в виде
следующей схемы:
—Ивана
—Лукъяна
—Марка
— Павла
-виаит-
Петр—
-слышит -
—Ивана
—Лукъяна
—Марка
1—Павла
Неопределенность опыта, состоящего в выборе глагольной фор-
формы, равна f (Si) = f B); неопределенность испытания, представ-
представляющего собой выбор имени собственного, характеризуется вели-
величиной / E 2) =/D).
Теперь рассмотрим сложный опыт, заключающийся в комбини-
комбинированном выборе из двух урн одного из Sx • S2 = 2 • 4 = 8 двух-
двухсловных продолжений для начальной словоформы Петр.
Неопределенность этого сложного опыта, являясь суммой не-
неопределенностей двух простых опытов, характеризуется равенст-
равенством
/ (Sx ° S2) = / (Sx) + f E2).
Последнее равенство представляет собой третью зависимость,
характеризующую отношение между неопределенностью" опыта
и числом его равновероятных исходов.
Существует единственная функция аргумента S, отвечающая
трем перечисленным выше условиям: 1) / A) -=а 0; 2) если Si^Sz,
то f (Sx) > / (S2); 3) / (Si ° S,) = / (St) + f (S2). Этой функцией
является логарифмическая зависимость
Я = log S, E.27)
с помощью которой мы будем оценивать меру неопределенности,
или энтропию, опыта.,
134
В лингвистических применениях энтропии, как правило, ис-
используются логарифмы при основании 2, в связи с чем выражение
E 27) принимает вид
1 Яо = log2 S. E.28)
Отсюда следует, что единицей измерения энтропии служит неопре-
неопределенность, заключенная в опыте, содержащем два равновероятных
исхода. Эта единица называется двоичной единицей (дв. ед.), или
битом.
Вернемся к рассмотренному выше лингвистическому эксперимен-
эксперименту с выбором продолжений Для имени собственного Петр. Здесь
неопределенность выбора глагольной формы языка
log2 2 = 1 (дв. ед.),
а энтропия выбора имени собственного в третьей позиции состав-
составляет
loga 4 = 2 (дв. ед.).
Неопределенность же сложного опыта, состоящего в одновремен-
одновременном выборе сказуемого и прямого дополнения, должна составлять
log, 2 + log2 4 = 1 + 2 = 3 (дв. ед.).
Действительно,
log2 B . 4) = log2 8 = 3 (дв. ед.).
2. Комбинаторный подход к определению количества информа-
информации. Введение понятия энтропии дает возможность проводить коли-
количественное измерение информации Действительно, в результате
проведения опыта А мы получаем новые сведения, т. е. некоторую
информацию. Одновременно знание исхода опыта снимает полностью
или частично ту неопределенность, которая была до его осуществ-
осуществления. Естественно предположить, что снятая в результате опыта
А энтропия количественно равна полученной информации, т. е.
Н(А) = I (А). E.29)
Из E.28) и E.29) следует, что количество информации, полу-
получаемое от испытания с множеством S равновероятных исходов,
определяется равенством
/о = log2 5. E.30)
Применительно к языковедческим задачам множество S назы-
называется лингвистическим алфавитом, а величины /0 и Яо — соот-
соответственно информацией и энтропией алфавита.
Число равновероятных исходов 5 определяется обычно путем
исследования комбинаторики элементов и связей, характеризующих
рассматриваемое лингвистическое явление. В связи с этим вся
только что описанная методика представляет собой комбинаторный
подход к определению количества информации [23, с. 71.
3. Измерение ограничений, накладываемых на употребление
лингвистических единиц системой и нормой языка. Хотя комби-
комбинаторный подход дает, как правило, завышенные данные об энт-
энтропии и информации опыта, он может быть использован для полу-
135
чения приблизительных оценок тех ограничений, которые накла-
накладывают на употребление лингвистических единиц система и норма
языка. Рассмотрим методику получения этих оценок на примере
двухбуквенных сочетаний.
Исходя из соотношений E.2) и E.30), можно утверждать, что
информация, получаемая от выбора такого двухбуквенного соче-
сочетания, которое строится средствами русского 32-буквенного алфа-
алфавита при условии, что никаких ограничений на сочетаемость букв
не накладывается и все двухбуквенные комбинации считаются
равновероятными, составляет
log2
log2 1024 = 10 (дв. ед).
Если учесть ограничение, состоящее в том, что наши двух-
двухбуквенные сочетания не должны включать твердого и мягкого зна-
знака, то информация, содержащаяся в одной двухбуквенной комбина-
комбинации, равна
/' ~ log2 Л|о = log2 900 =- 9,81 (дв. ед.).
Если же составить двухбуквенные комбинации из всех 32 букв
русского алфавита, не допуская повторений букв, то, согласно
F.1), количество информации, получаемое от выбора одного букво-
буквосочетания, равно
Г - log2 Ah - log2 992 - 9,95 (дв. ед.).
Легко заметить, что введение тех или иных ограничений на со-
сочетаемость букв приводит к уменьшению информации,получаемой
при выборе одного двухбуквенного сочетания. Эти ограничения,
которые мы будем называть структурными контекстными огра-
ограничениями, можно количественно оценить с помощью разности
/0 -I = К, E.31)
где /0 — информация алфавита или, иными словами, количество
информации, которое извлекается из опыта при отсутствии каких-
либо ограничений в комбинаторике лингвистических элементов и
связей, / — информация, получаемая при учете интересующих нас
ограничений, а К — контекстная обусловленность
Пользуясь выражением F.31), нетрудно оценить величину
структурных ограничений, накладываемых на алфавит русских
двухбуквенных комбинаций. В первом случае эти ограничения
составляют
К* = log2 Al2- log2 Ah -¦ - 10 - 9,81 - 0,1.9 (дв. ед.),
во втором случае
/E=10 — 9,95 = 0,05 (цв ед.).
Согласно данным словарей [22]; [351; [39], в русском языке
содержится около 250 двухбуквенных слов, из которых только
136
114 допущены нормой современного литературного языка. Отсюда
следует, что лексическая система русского языка накладывает
на образование осмысленного двухбуквенного слова структурные
ограничения, равные
К (системы) = log2 A\i — log2 250 =
= 10 — 7,96 ^ 2 04 (дв. ед.).
В то же время норма литературного языка дает дополнитель-
дополнительные ограничения, составляющие
К (нормы) = log2 250—loga 114=1,73 (дв. ед.).
Комбинаторные измерения информации могут быть успешно
применены для оценки «гибкости речи» т. е. при измерении раз-
ветвленности продолжения текста при заданном словаре и за-
заданных правилах построения предложений.
4. Вероятностный подход к определению количества информа-
информации. При описании комбинаторного метода для вычисления количе-
количества информации и энтропии мы пользовались упрощающим допу-
допущением, согласно которому все исходы опыта считались равнове-
равновероятными. Между тем при исследовании текста такая ситуация
почти никогда не встречается. Норма языка и описываемая текс-
текстом ситуация приписывает каждому лингвистическому элементу
определенную вероятность. Если лингвистическое испытание пре-
предусматривает равновероятные исходы, то, очевидно, энтропия та-
такого опыта и получаемое от него количество информации будут от-
отличаться от аналогичных величин, характеризующих опыт с рав-
равновероятностными исходами. Например, неопределенность опыта,
состоящего в угадывании буквы, стоящей после цепочки Аяпо,
гораздо меньше*, чем неопределенность опыта, состоящего в вы-
выборе равновероятных глагольных форм видит и слышит.
Переход от оценки неопределенности и информации опыта
с равновероятными исходами к вычислению энтропии и информа-
информации испытания с неравновероятными исходами осуществляется
на основе следующих соображений.
Опираясь на известные правила логарифмирования, перепишем
выражение E.30) в виде
/о = —log2 A/5). E.32)
Здесь величина 1/5 есть не что иное, как вероятность р каждого
исхода опыта. Предположим теперь, что исходы опыта неравнове-
неравновероятны и каждый исход i имеет свою вероятность pt. Тогда индиви-
индивидуальное количество информации, приносимое исходом i при его
отдельном появлении, равно
/* = —loga Pi-
* Исходя из норм литературного языка, после цепочки Дяпо должна
стоять буква « (ср. японец, японка и т. п.). Вероятность же появления буквы
ш здесь очень мала (ср. редкое просторечное япошкаI, см. § 4, п. 4.
137
При многократном осуществлении опыта исход i будет проис-
происходить с вероятностью pt. Поэтому среднее количество информа-
информации, приносимое исходом i при многократном осуществлении
испытания, составит
7t = —pt log2 Pi.
Величина Tt определяет тот вклад, который вносит исход I
в общее количество информации, получаемой при многократном
проведении опыта А. Что касается общей информации, то она, пред-
представляя собой сумму вкладов всех 5 возможных исходов, опреде-
определяется равенством
/=_ 2рAо§зР/. E.33)
Это равенство является исходной формулой вероятностного
подхода к определению количества информации.
Величины I(, Ti и / имеют разную качественную интерпре-
интерпретацию и различное количественное значение. Это видно на таком
лингвистическом примере. Предположим, нам известно, что буква
н появляется после цепочки Аяпо с вероятностью рн = 0,999,
а буква ш встречается после этой цепочки один раз на тысячу
случаев (рш = 0,001). Тогда, если данный исход опыта дает после
, цепочки кяпо обычное н, мы получаем всего лишь
/„ = — log2 0,999 = 0,0014 (дв. ед.)
информации. В то же время появление редкого ш приносит
/ш = —log2 0,001 = 10 (дв. ед.)
информации, т. е. в 7 тыс. раз больше, чем появление более частого
н. Такое соотношение вполне соответствует здравому смыслу:
тривиальный исход опыта всегда малоинтересен и малоинформати-
малоинформативен, напротив, неожиданный результат всегда несет много инфор-
информации.
Однако опыт дает редко неожиданный исход, поэтому вклад
этого исхода в общую информацию опыта составляет всего лишь
1Ш = —0,001 log2 0,001 = 0,0100 (дв. ед.).
Это только в семь раз больше того вклада, который вносит
в информацию опыта частый исход, информационный вес которо-
которого равен
/н = —0,999 log2 0,99® = 0,0014 (дв. ед.).
Общее же количество информации, приносимое разновероятны-
ми исходами рассматриваемого опыта, составляет
/ = —0,001 Iog2 0,001 — 0,999 loga 0,999 = 0,0114 (дв. ед).
138
заметно меньше информации, получаемой от опыта с двумя рав-
равновероятными исходами, где
/0 = log2 2 = 1 (дв. ед.).
Информационные измерения, опирающиеся на вероятностный
подход, могут быть осуществлены при условии, что для интере-
интересующего языковеда лингвистического опыта имеется полный набор
вероятностей р (или оценивающих их частостей /) исходов этого
опыта. Например, чтобы оценить информацию, которую несет в сред-
среднем одна буква русского алфавита (так называемая информация
пербого порядка /х), необходимо обработать с помощью формулы
E.33) распределение (спектр) вероятностей букв в русских лите-
литературных текстах, показанный в табл. 5.2. Чтобы вычислить ин-
информацию, приходящуюся в среднем на одно слово или словоформу
какого-либо языка или его разновидности, необходимо также об-
обсчитать с помощью выражения E.33) соответствующий частотный
словарь [32 а, с. 179—261]; [39].
Однако информационные измерения, опирающиеся на обработ-
обработку распределений безусловных вероятностей, имеют в языкознании
ограниченное применение. Дело в том, что фонемы, графемы, слова
и другие языковые единицы выступают в тексте в качестве зависи-
зависимых лингвистических событий, обусловленных контекстом, а их
вероятности являются условными (см. § 4, п. 3). Распределение
последних вероятностей определяется тем положением, которое
занимает данная лингвистическая единица в тексте. Так, напри-
например, распределение вероятностей русских букв в начале слова
(см. табл. 5.3) сильно отличается от спектра из безусловных веро-
вероятностей (табл. 5.2) и совсем не похоже на распределения вероят-
вероятностей букв, стоящих после цепочек Дя (табл. 5.4), Дяя или кяпо.
Отсюда следует, что в большинстве случаев лингвистический
опыт характеризуется не безусловной, а условной энтропией, опре-
определяющейся тем контекстным окружением, в котором находится
данный участок текста. Так, например, выбор начальной буквы
в русском слове имеет иную неопределенность, чем энтропия выбо-
выбора буквы после цепочки Кяпо, т. е.
Н (буквы/Д) Ф Н (буквы/ Дя/го),
и т. п. Само собой разумеется, что распределение вероятностей ис-
исходов и неопределенность опыта могут быть обусловлены не только
предшествующим, но и последующим контекстом.
Что же касается информации, которая извлекается изданного
участка текста, то она равна энтропии, характеризующей этот
участок.
Рассмотрим теперь в деталях методику вычисления информа-
информации, получаемой от некоторого лингвистического опыта L, имею-
имеющего 5 исходов и осуществляющегося в ге-м участке текста при ус-
условии, что стоящая перед этим участком цепочка лингвистических
элементов bn~l известна. Цепочка Ьп~' рассматривается в ка-
качестве случайного события, принимающего частный вид i. Появ-
139
ление того или иного элемента в позиции п также рассматривается
в качестве случайной величины, принимающей значение jh A^
^ k ^ S). Для каждого значения i, которое может принять Ьп~]
имеется условная вероятность р (/»,*,/&?""') того, что Ln примет
значение jh.
Средняя условная энтропия Нп, количественно равная инфор-
информации /„, получается в результате осреднения энтропии, подсчи-
подсчитанной по всем значениям b"~l с весами, соответствующими ве-
вероятностям цепочки Ьп~х. Таким образом, имеем
E.34)
*•=!
Равенство E.34) показывает, какова в среднем мера неопреде-
неопределенности и количество информации от выбора лингвистического
элемента в позиции п, когда известна цепочка Ьп~1.
Если взаимосвязи элементов распространяются как угодно да-
далеко, то энтропия (информация) на один лингвистический элемент
составляет
¦¦ lim Я„ (дв. ед.).
E.35)
Так как величины средней условной энтропии зависят от распре-
распределения вероятностей элементов на л-м шаге текста и от вероят-
вероятностей появления б?", то эти величины могут быть определены
из статистики многоэлементных сочетаний. Расчетная формула
в этом случае имеет следующий вид:
Формула E.36) используется для определения информации,
которую несет буква при условиях, что: предшествующая ей буква
известна (информация второго порядка /и); известны две пред-
предшествующие буквы (информация третьего порядка /ш) и т. д. [23,
с. 10]/
Объем работы при вычислении /i, /ц, /ш, /iv для буквенного
и фонемного алфавита сравнительно велик. Существуют также реа-
реалистичные способы оценки Л для слов, словоформ и даже слово-
словосочетаний. Однако число комбинаций из пяти, шести и т. д. букв
(фонем), не говоря уже о комбинациях из четырех, пяти и т. д. слов
(слогов, морфем), растет так быстро, что для определения их услов-
условной энтропии требуется колоссальная счетная работа.
Поэтому необходимо искать косвенные методы, с помощью ко-
которых можно было бы достаточно быстро определить энтропию и
информацию в различных частях текста. Этому требованию отве-
отвечает эксперимент по предсказанию букв неизвестного текста, опи-
опирающийся на субъективные оценки условных вероятностей этих
букв (ср. § 3, п. 1) со стороны угадчика.
140
В основе этого метода лежит предположение, что в сознании
носителя языка заложены достаточно полные сведения о вероятност-
вероятностных характеристиках нормы языка. На основании его лингвисти-
лингвистического опыта в сознании угадчика формируется степень убежден-
убежденности по поводу того, какие лингвистические единицы встречаются
чаще, а какие — реже, и хотя «ранжирование» лингвистических
элементов в сознании разных носителей языка может быть неоди-
неодинаковым, оно приближается при достаточно хорошем знании язы-
языка к некоторой оптимальной схеме.
Испытуемый или коллектив испытуемых угадывает текст, опи-
опираясь каждый раз на ранжированный спектр лингвистических еди-
единиц. Поэтому всю совокупность предсказаний можно рассматри-
рассматривать как некоторую систему лингвистических реакций, более или
менее полно отражающую статистические процессы образования
текста, за которыми стоят вероятностные свойства нормы языка.
Если осуществляется коллективное угадывание, то результаты
его обрабатываются по формуле E.33), причем вероятность опреде-
определяется здесь из равенства pt = ntIN, где аргументом щ является
число угадчиков, предложивших ту или иную букву (независимо
от того, правильна она или нет), а N есть общее число угадчиков.
При индивидуальном угадывании по полной программе исполь-
используются две формулы: по одной определяется верхняя граница
интервала, в котором находится истинное значение информации:
7 = A—<7a)log(l— q0)—
i
а по другой — нижняя граница:
s
E.37)
E.38)
Величины qt указывают на вероятность правильно угадать букву
с /-и попытки, a q0 есть вероятность достоверного продолжения.
Результаты сокращенной программы угадывания обрабатывают-
обрабатываются по формуле
Т = Яш (l-q0- ft) + A - qQ) log A - ft,) -
— ftlog ft — A — ft, — ft) log A — ft, — ft), E.39)
где Нщ есть неопределенность (энтропия) третьего порядка, зна-
значения остальных символов те же, что и в выражениях E.37) и E.38).
Подробнее о психо-лингвистической стороне угадывания см.
[23, с. 12—14].
Кроме того, делаются попытки выработать новые приемы рас-
расчета информации [23, с. 53—55]; [41, с. 258], в том числе и такие,
которые не предусматривают обращения к вероятностному или тео-
теоретико-множественному подходу [53, с. 131—150].
5. Синтактическая информация и особенности ее распределе-
распределения в тексте и слове. Полученные при алгоритмическом и вероят-
141
ностном подходе иформационные величины не измеряют семантики
сообщения. Они ничего не говорят и о том, как интерпретирует
содержание текста его получатель (прагматика сообщения).
Получаемые в результате психо-лингвистического или просто
комбинаторно-статистического эксперимента величины являются
синтактической (по иной терминологии — статистической или се-
селективной) информацией и служат количественной мерой струк-
структурно-статистического разнообразия и свободы выбора лингвисти-
лингвистического варианта. Это разнообразив и свобода выбора задаются
в каждом участке текста системой и нормой языка. Вместе с тем
результаты нашего эксперимента отражают и то разнообразие,
которое существует внутри самой системы и нормы языка (ср.
в этом смысле оценки энтропии распределений длин слогов и мор-
морфем, которые будут приведены в гл. 6).
Наблюдения над распределением синтактической информации
в тексте и в отдельно взятом слове, о которых уже говорилось выше
(см. гл. 1, § 8; гл. 2, § 4; гл. 4, § 2 и 3), раскрывают некоторые
важные особенности функционирования языка в речи.
В частности, выясняется, что текст дает квантовое распределение
информации. Очевидно, письменная и устная речь воспринимается
и перерабатывается нашей памятью не непрерывно, а путем ритми-
ритмической отдачи накопленных порций информации. Периодичность
обнаруживается и в информационном построении длинных слов.
Похоже, что в качестве кванта синтактической информации высту-
выступает морфема — элементарная смыслонесущая единица текста (см.
гл. 1, § 9, п. 3).
Выше было показано, что в письменном тексте основная часть
информации размещается в начале слова. Концы слов, а у длин-
длинных слов и средние участки оказываются избыточными. Такое
распределение объясняет не только механизм аббревиации, но прояс-
проясняет также вопрос об установлении границы слова в тексте. Интер-
претант текста (читатель или слушатель), принимая решение
о правой границе слова, не опирается на граничные комбинации
графем или фонем, а прогнозирует положение конца слова, исходя
из его информационно нагруженного начала.
Неравномерностью распределения синтактической информации
в слове можно объяснить и особенности развития некоторых языков.
Сюда относится фонетическое выветривание середин и особенно кон-
концов слов, приводящее к ослаблению и разрушению флексий, а од-
одновременно значительная сопротивляемость фонетическим измене-
изменениям начал слов и препозитивных служебных форм [27]; [37]; [58].
6. Контекстная обусловленность и избыточность текста. Если
синтактическая информация выступает в качестве меры свободы вы-
выбора лингвистического варианта в данном участке текста, то кон-
контекстная обусловленность используется в качестве меры тех огра-
ограничений, которые накладывают на данный участок текста система
и норма языка.
Контекстная обусловленность задается уже известным нам вы-
142
ражением E.31), которое применительно к синтактической инфор-
информации, полученной вероятностным путем, имеет вид
К = 10-1п. E.40)
Значения синтактической информации и контекстной обуслов-
обусловленности сильно зависят от объема лингвистического алфавита
(числа букв, фонем, слогов и т. п.), использующегося в данном
языке. Поэтому при сравнении разных языков удобнее пользо-
пользоваться взвешенной величиной контекстной обусловленности, кото-
которая не зависит от длины алфавита. Эта взвешенная величина на-
называется избыточностью в данном участке текста:
Rn = (П - /п)//о- E.41)
Общая избыточность текстов данного языка или его разновид-
разновидности определяется из равенства
Я = </о-/.)//о. E-42)
Значения избыточности, полученные для семи языков и их раз-
разновидностей из экспериментальных значений /х и /м [см. формулы
E.37) и E.38)], показаны в табл. 5.5. Легко заметить, что все иссле-
исследованные языки в целом имеют близкие значения избыточности.
Вместе с гем явные расхождения обнаруживаются между'значениями
Таблица 5.5
Избыточность (в %) некоторых индоевропейских и тюркских языков н их
разновидностей по нижней (R) и верхней (R) границам
^^-^^^ Языки
Разновидности >v
Разговорная речь
Беллетристика
Деловая речь (науч-
(научно-технические и пуб-
публицистические тексты)
Язык в целом
Русский
R
72,0
76,3
83,4
72,1
R
83,4
86,0
90,1
83,6
Польский
R
76,3
74,5
83,6
74,7
R
86,3
83,6
89,5
85,0
Английский
R
69,4
77,1
82,9
71,9
R
81,2
86,5
92,1
84,5
Немецкий
R
73,9
71,4
79,6
71,4
R
84,4
82,5
88,2
85,1
^"^^^^^ Языки
Разновидности ^^
Разговорная речь-
Беллетристика
Деловая речь (науч-
(научно-технические и пуб-
публицистические тексты)
Язык в целом
Французский
R
68,5
71,0
83,9
70,6
R
82,9
83,6
90,4
83,4
Продолжение табл. 5.5
Румынский
R
74,2
73,8
74,4
72,1
R
85,4
83,8
85,7
85,0
Казахский
R_
76,5
75,0
78,5
71,9
R
85,0
85,0
88,0
85,0
143
избыточности, характеризующими отдельные разновидности языка.
В частности, высокую избыточность показывает в некоторых языках
деловая речь. Вопрос о существенности расхождений в численных
значениях избыточности по отдельным стилям мы рассмотрим в гл. 9.
7. Измерение смысловой информации в тексте. Количественные
оценки смысловой информации, содержащейся в тексте и в обра-
образующих его словах и словосочетаниях, можно получить, опираясь
на значения синтактической информации и пользуясь идеей кон-
контекстной обусловленности.
В ходе эксперимента по угадыванию букв неизвестного текста
было замечено, что свои гипотезы о наиболее вероятных продол-
продолжениях текста испытуемые строят, исходя из двух типов комбина-
комбинаторных ограничений: комбинаторики фигур (букв и слогов) и ком-
комбинаторики знаков (морфем, слов, словосочетаний).
Эксперимент показывает, что уже на 4-м или 5-м буквенных
шагах текста комбинаторика букв и слогов подавляется ограни-
ограничениями, связанными с сочетаемостью морфем и слов. Затем
по мере развертывания текста на комбинаторику слов напластовы-
напластовываются ограничения в сочетаемости словосочетаний и предложе-
предложений, затем появляются ограничения, связанные с комбинаторикой
параграфов, глав, частей книги или статьи.
Таким образом, при угадывании букв, находящихся на доста-
достаточном удалении от начала текста, испытуемый опирается не на ста-
статистическую комбинаторику букв и слогов, а на смысловое (лекси-
ко-грамматическое) построение текста. Поэтому если информация,
извлеченная из начального участка экспериментального текста,
выступает как количественная оценка дистрибуции (распределения)
и статистики букв, то синтактическая информация, которая полу-
получается с удаленных от начала текста участков, служит отражением
смысловой (семантико-прагматической) информации.
Эти соображения позволяют предложить некоторые приемы для
количественной оценки смысловой информации, содержащейся
в тексте и его сегментах.
Начнем с оценки смысловой лексико-грамматической информа-
информации, содержащейся в отдельном слове.
Пусть имеется текст, представляющий собой цепочку слов
щ,
., wk
и мы хотим оценить количество информации, содержащееся в слове
щ.
Для решения этой задачи проведем коллективное угадывание
сегмента текста 'wt^rWk.. Первый раз коллективу сообщено слово
щ, стоящее перед контрольным сегментом. Второй раз угадывание
начинается прямо со слова w2 (само собой разумеется, что между
обоими угадываниями должно пройти достаточно времени, чтобы
испытуемые забыли содержание текста; либо угадывания должны
быть проведены в двух разных, но идентичных коллективах).
Естественно, что оба угадывания дадут разные результаты.
144
Получаемая в первом случае от контрольного сегмента информа-
информация
/ (wt+wh) = Н (w2+wk) (дв. ед.) E.43)
будет больше информации
/ (и>2 -г- Wk/Wi) — Н (w2 -f- Wb/Wi) (дв. ед.), E.44)
полученной при условии, что испытуемым было известно слово wx.
Разность
= / (w2 -г- Шь) — / (м>2 ^ и^й/Шх) (дв. ед.) E.45)
И
представляет собой количественную оценку той смысловой (семан-
(семантико-прагматической) информации, которая содержится в слове
Wi. Именно эта информация уменьшила неопределенность конт-
контрольного сегмента [ср. неравенство Н (w2 -f- wJw^)<.H (w2 -г- к>ьI
и облегчила второе угадывание.
Результаты первых пробных экспериментов по количественной
оценке значений отдельных слов в четырех языках показаны
в табл. 5.6. Для того чтобы проводить строгое сравнение оценок
информации по разным словам внутри одного языка и по одному
слову для разных языков, необходимо иметь средние оценки смыс-
смысловой информации. Такие данные можно получить, усредняя оцен-
оценки, снятые с большого количества разных контекстов. Однако даже
предварительные результаты показывают, что в аналитических
языках (французском и болгарском) слово несет меньше смысловой
информации, чем это имеет место в синтетических (флективном рус-
русском и агглютинирующем эстонском) языках. Эти наблюдения со-
согласуются с традиционными предположениями об информацион-
информационной нагруженности слов в указанных языках.
Теперь попробуем оценить ту лексико-грамматическую инфор-
информацию, которую содержит контекст. Для этого с помощью прие-
приемов, описанных в работах [23, с. 69—73, 81—82] и [26], определим
количество синтактической информации, приходящееся на слово
средней длины /, взятое вне контекста, т. е. 7 (ajj), и в контексте,
т. е. 7 (одй). Кроме того, с помощью выражения
(w0)
. ед.)
определим то количество информации, которое может нести цепочка
длиной в I символов (букв) при условии, что все символы алфа-
алфавита данного языка равновероятны и обладают неограниченными
возможностями сочетаемости.
Тогда общая сумма контекстных ограничений, накладывающих-
накладывающихся на слово в контексте, для верхней границы информации сос-
составит
)— I(wh) (дв. ед.).
E.46)
145
tO
1O
га
sJ
s
4
VO
s
а:
о
<о
К
Я
н
а
а.
о
о m
•s о
ta ^
11
о
п
к*
g
О.*
¦IS
X >.
х a
it
I*
1
V
и
X
s
о
0)
3
s
i
II
X
s
4
о
s
и
а, о
—
8
IS
tl
о S,
a *
Слова
e
IS
-5
* +
лгарский|
Слова
S
IS
=33
* 1+
Слове
1
Ю
(M
to
о
to
38,
респон-
ентът-
I
ю
об
(N
Ю
to
,4
s
ечатът
O EC С
,88
ю
S3
34,
о
50,
t-
де
)респон
s
,74
12
о
со
.43
f-
<D
С
CO
>¦
S
©
to
Слов
CO to ^i" tO
00 ^* Oi
•— -^ ^-*
cc
[)CTB0
ата-
кла
госуда
аксплу
ци
*О1 СО ^1"
^ с^ ^?
• * ••
С^ 00 -^
СО О) (N
00 Г^ *О
klass
riik
cspluatee-
rimine
III
o>t-o>
lO — СЧ
CS C^ 00
0^ O5 CO
СО^Г* "^
§
classe
etat
exploit
¦0
&
v n
SB И
Ю (.
Q.
С
О
-
55,
«ft
oo
CM
^*
valitsus
1
m
35
8
lent
g
1
in ¦*
oo oo
к
ч tu
О ^1
нар
прези
—
58,
CO
CO
to
rahvas
oo
Ol
о
Ol
s
прези-
to t^
8S
с
1
t4^
to
CO
to
Ю
w
in
CO
<M
CO
дентът
редсе-
со
m
So
CS
1
о
CO
—
о
ч*
CO
§ 1
то Ф
d o.
to
to
<N
?5
Ol
¦ Ю
CO
peuple
preside
preside
regime
0)
Контекстные ограничения К (w^) включают информацию, ко-
которая характеризует вероятностную дистрибуцию букв и слогов
(см. выше), а также ту синтактическую информацию, которая оце-
оценивает среднюю величину смысловой информации, содержащейся
в лексико-грамматических связях контекста wx -i- wh-lt пред-
предшествующего слову Wk- Эта лексико-грамматическая информация,
определяющая предсказуемость слова te>ft, может быть получена
из равенства
(дв. ед.),
E.47)
поскольку, уже начиная со второго слова, угадывание текста осу-
осуществляется на основе смысловой информации.
Доля лексико-грамматических связей контекста относительно
общей суммы ограничений, накладывающихся на текстовое слово,
т. е. выражение
K(wh)
100%,
E.48)
может служить оценкой степени аналитичности языка. Значения
А и другие контекстные оценки относительно четырех европейских
языков приведены в табл. 5.7.
Таблица 5.7
Контекстные оценки и процент аналитизма в некоторых
индоевропейских языках
^^^-^^ Языки
Информацией- —>^^
ные величины ^^\^
(в дв ед ) ^\
Пщ)
7(a>i)
7(Шь)
R(wfc)
Л («/о)
Русский
31,85
13,50
8,15
5,35
23,70
22,57
Английский
25,97
12,59
5,41
7,18
20,56
35,00
Французский
25,23
10,88
6,46
4,42
18,77
23,55
Румынский
27,07
13,02
7,77
5,25
19,30
27,01
115
То, что значение коэффициента аналитичности А для англий-
английского языка. в полтора раза превосходит его значение в русском
языке, хорошо согласуется с нашими представлениями о соотно-
соотношении аналитизма и синтетизма в этих языках. Несколько неожи-
неожиданным кажется малая величина коэффициента А в аналитическом
147
французском языке. Этот парадокс следует отнести за счет флек-
тивности таких частотных служебных слов, как артикль, неудар-
. ные личные местоимения 3-го лица, притяжательные местоимения,
которые дают строю французского языка флективно-аналитический
характер.
Рассматриваемая лексико-грамматическая информация явля-
является по своей природе семантико-прагматической информацией.
При этом степень и качество прагматизма зависит от организации
эксперимента. При индивидуальном эксперименте речь идет о праг-
прагматизме угадчика, коллективное угадывание отражает прагматизм
угадывающего коллектива. Последнее обстоятельстве1 дает воз-
возможность использовать эксперимент по угадыванию для количест-
количественных оценок субъективного и коллективного (профессионального,
социального, возрастного) восприятия смысловой информации, со-
содержащейся в тексте.
ГЛАВА б
ВЕРОЯТНОСТНОЕ МОДЕЛИРОВАНИЕ ПОРОЖДЕНИЯ ТЕКСТА
И СОСТАВЛЯЮЩИХ ЕГО ЕДИНИЦ
§ 1. Повторение независимых испытаний в тексте
Как уже говорилось (см. гл. 5), при исследовании механизмов
порождения текста результаты отдельного лингвистического ис-
испытания не представляют большого интереса. Изучение взаимо-
взаимодействия системы, нормы и ситуации эксплицируется с помощью
моделей теории вероятностей, предусматривающих осуществление
массового эксперимента, при котором одно и то же лингвистическое
испытание повторяется много раз. Эти повторяющиеся испытания
образуют серии, в каждой из которых интересующее нас событие
появляется или не появляется определенное число раз.
Так, например, при вероятностном исследовании норм упот-
употребления слова море в произведениях А. С. Пушкина нас не будет
интересовать, употреблено ли это слово, скажем, в первом предло-
предложении на 100-й странице первого тома Академического издания
сочинений поэта. Зато нам важно будет дать прогноз общего числа
появлений этого слова в определенном числе (серии) предложе-
предложений, составляющих, например, текст «Евгения Онегина», либо об-
образующих некоторую выборочную последовательность из писем
поэта и т. д.
Выбор той или иной модели описания текста зависит от пост-
построения вероятностно-лингвистического,испытания и, в частности,
от того, как организовано извлечение из текста отдельных его
единиц.
1. -Повторная и бесповторная выборки. Рассмотрим следующий
элементарный пример. Пусть из текста взято N фонем, среди кото-
которых п гласных и т согласных, и каждая из фонем записана на от-
отдельную карточку; карточки положены в урну и перемешаны.
Испытания, состоящие в извлечении из урны одной карточки, мо-
могут осуществляться по двум схемам.
Согласно условиям первой схемы каждая извлеченная карточ-
карточка возвращается в урну, после того как в протоколе фик-
фиксируется результат каждого испытания. При каждом последующем
испытании вероятности появления гласной или согласной остают-
остаются неизменными. (Эти вероятности соответственно равны n/N и
mlN.) Вероятностно-лингвистический эксперимент, оперирующий
с последствиями взаимно независимых испытаний, в каждом из кото-
которых лингвистические события сохраняют свои безусловные вероят-
вероятности, называется повторной выборкой.
При реализации второй схемы извлеченные из урны карточки
не возвращаются. Вероятность появления гласной и
согласной при каждом последующем испытании зависит от резуль-
результатов предшествующих извлечений. Таким образом, мы имеем
здесь дело с зависимыми испытаниями, а вероятность исхода каж-
149
дого из испытаний является условной (ср. гл. 5, § 4, п. 3). Экспе-
Эксперимент, оперирующий с последовательностью зависимых испыта-
испытаний, в каждом из которых исходы имеют условные вероятности,
называется бесповторной (безвозвратной) выборкой.
Реальный вероятностно-лингвистический эксперимент может
быть осуществлен как с помощью повторной, так и с помощью бес-
бесповторной выборки.
При 'повторной выборке подвергшиеся испытанию лингвисти-
лингвистические единицы должны каждый раз как бы возвращаться в текст.
Рассмотрим организацию повторной выборки на следующем при-
примере.
Предположим, что необходимо определить статистическую ве-
вероятность имен существительных или отдельных словоформ (ска-
(скажем, и, при, можно, напряжение) в русских текстах по вычисли-
вычислительной технике. Для этого выберем массив текста из книг:
А. И. Китов и Н. А. Криницкий. Электронные циф-
цифровые машины и программирование (М., 1959, с. 1—566) и
А. А. П а п е р н о в. Логические основы цифровых машин и
программирование (М., 1965, с._7—440). Во второй книге страницы
перенумеруем таким образом, что они образуют последовательность
от 567-й до 1000-й страницы. Этим способом формируется массив
в 1000 страниц, содержащий около 400 тыс. словоупотреблений.
Поиск лингвистических единиц осуществляется здесь сле-
следующим образом. Из таблицы случайных чисел последователь-
последовательно выбираются шестиразрядные числа. Эти числа служат адре-
адресами тех словоупотреблений, которые мы будем сопоставлять при
каждом испытании с интересующей нас единицей. Первые три циф-
цифры указывают на страницу, следующие две — на строку, а послед-
последняя — на номер словоупотребления в строке.
В тех случаях, когда то или иное случайное число указывает
на несуществующую страницу, строку или словоупотребление, ад-
адрес считается недействительным и выборка осуществляется по сле-
следующему числу.
Если выбранное таким образом словоупотребление оказывается
интересующей нас лингвистической единицей, то мы имеем дело
с благоприятным исходом испытания. В противном случае имеет
место неблагоприятный исход. Сумма благоприятных исходов, де-
деленная на общее число испытаний, даст статистическую вероятность
интересующей нас лингвистической единицы.
Возьмем теперь первые двадцать пять чисел из таблицы случай-
случайных чисел: 857454, 457562, 499988, 762760, 431557, 698780, 038799,
558121, 653187, 573553, 609209, 179138, 974652, 011813, 098638,
805797, 516103, 296103, 149471, 815377, 070381, 692830, 696116,
203055, 350356.
При этом реальные адреса дают нам 8, 9, 11, 18, 19, 21, 23, 24
и 25-е случайные числа, по которым из текста соответственно вы-
выбираются следующие словоупотребления: таким, делению, бы,
1Ъ остается, зависимости, наименование, система, оба. Остальные
адреса являются недействительными.
150
Таким образом, нам удалось выбрать четыре существительных,
вместе с тем мы не встретили ни одной из исследуемых словоформ.
При обследовании высокочастотных единиц, требующих сравни-
сравнительно небольшой серии испытаний (к таким единицам относятся
части речи и члены предложений, знаки препинания, классы букв
и фонем), желательно в целях математической строгости применять
схему независимых испытаний (повторную выборку).
Если же речь идет об определении вероятности таких редких
единиц, как словосочетания, словоформы, фонемы и их сочетания,
то осуществление повторной выборки вручную оказывается неосу-
неосуществимой задачей из-за большого объема работы, связанного
с громоздкой процедурой извлечения этих единиц из текста*.
Поэтому здесь приходится применять бесповторную выборку. Хо-
Хотя бесповторная выборка представляет собой последовательность
вависимых испытаний, математическая обработка ее результатов
производится обычно исходя из схемы независимых испытаний.
Ниже будет показано (см. п. 6), что при большом объеме исследуе-
исследуемой лингвистической совокупности это нарушение математической
строгости не приводит к сколько-либо заметным искажениям ко-
конечных результатов.
2. Три схемы независимых лингвистических испытаний. Кван-
Квантитативное языкознание широко использует метод серийного на-
наблюдения. Сущность его заключается в том, что лингвистические
единицы выбираются из текста группами фиксированной длины:
например, по десять фонем, по сто предложений или словоформ и
т. п. Лингвистические единицы, составляющие серию, не обяза-
обязательно должны находиться в тексте рядом друг с другом, они могут
извлекаться и через определенный интервал.
При решении многих теоретических и инженерно-лингвисти-
инженерно-лингвистических задач оказывается необходимым знать вероятность появления
того или иного числа интересующих исследователя лингвистических
единиц в серии.
Если образующие серию лингвистические испытания рассмат-
рассматриваются как независимые, то мы можем осуществлять необходи-
необходимое прогнозирование с помощью разработанных в теории вероят-
вероятностей трех систем независимых испытаний: простой, по-
полиномиальной и пуассоновской.
Простая схема предусматривает только два исхода опыта:
появление или непоявление признака А. Примером этой схемы яв-
является повторная выборка из текста согласных (А) и гласных (А)
фонем (см. п. 1).
В полинокиальной схеме испытание дает не два, а несколько
исходов. По этой схеме осуществляется, например, эксперимент,
заключающийся в выборе из текста графем трех видов: букв,
знаков препинания и пробелов.
* В настоящее время рассматривается вопрос о создании машинного ал-
алгоритма повторной выборки редких лингвистических единиц из больших мас-
массивов текста. Адреса выборки генерируются случайным образом самой ЭВМ.
151
В пуассоновской схеме независимые испытания осуществляются
относительно нескольких совокупностей (подъязыков, стилей,
тематик), в каждой из которых данный признак имеет разную ве-
вероятность. Поэтому вероятность лингвистического исхода меняется
в зависимости от того, относительно какого подъязыка или тема-
тематики производится опыт.
Математическая модель, по которой осуществляется прогно-
прогнозирование результатов простой схемы испытаний, является ис-
исходной при построении других вероятностных моделей, в том чис-
числе и тех, которые широко используются в квантитативной лингвис-
лингвистике. Поэтому мы особенно детально рассмотрим математическую
модель простой схемы независимых испытании.
3. Простая схема независимых испытаний. Формула Бернулли.
Предположим, что в некотором тексте длиной в я фонем имеется
т согласных и п — т гласных. По схеме повторной выборки про-
производится N независимых испытаний, заключающихся в последо-
последовательном случайном извлечении фонемы из текста. Требуется опре-
определить вероятность события, состоящего в том, что среди извлечен-
извлеченных N фонем ровно х окажутся согласными, причем порядок следо-
следования гласной и согласной фонем безразличен
Считая появление согласной событием А, а гласной — собы-
событием А, определим вероятности появления гласной и согласной.
Согласно классическому определению вероятности, имеем
Теперь найдем вероятность того, что при JV независимых испытаниях
событие А появится. ровно х раз, если вероятность появления
этого события при каждом отдельном испытании постоянна и
равна р.
Для этого составим всевозможные схемы, которые представ-
представляют разнообразную последовательность из появления х раз собы-
события А и N — х раз его непоявления, т. е.
АА...А А... А #
х раз N—х раз
По теореме умножения вероятность появления каждой схемы
составляет pxqN~x, а число таких схем равно числу сочетаний
из N элементов по х, т. е. Cn. Отсюда следует, что вероятность
появления события А ровно х раз в серии N независимых испыта-
испытаний составляет
xl(N— х)\
¦РХГ
F.1)
где р -f q = 1. Заметим, также, что вероятности F.1) равны соот-
соответствующим членам разложения по формуле бинома выражения
<Й + P)N>
С помощью выражения F.1), носящего название формулы Бер-
Бернулли, и осуществляется вероятностное прогнозирование результа-
результатов в простой схеме независимых испытаний.
Все возможные несовместимые между собой исходы N опытов
состоят в появлении 0, 1, 2, . ., N раз события А. Поэтому сумма
величин F.1), представляющих собой отдельные значения вероят-
вероятностей при х = 0, 1, 2, ,. , N, равна единице:
1.
2
*>=0
Распределение вероятностей Pn (х) « С%рх qN~* при х ¦= 0, 1, 2,
..., N, называемое биномиальным распределением (биномиальным
законом распределения) вероятностей, можно записать в виде
табл. 6.1.
Таблица 6.1
2 *
*
C*NpxqN-x
...
N —
N(N -1)
"* 2 '
0N — 2
я2
Продолжение табл.
N — 1
Л'
ГЛ/ Л/ 0
LN P Я
6.1
=PN
152
При составлении алгоритмов пословного машинного перевода
и информационного поиска постоянно возникают задачи, связан-
связанные с прогнозированием появления в сегментах заданной длины
определенного числа словоформ, морфем или словосочетаний, при-
принадлежащих к некоторым классам. Формула Бернулли позволяет
решать задачи этого типа, разумеется, при условии, что сохраняется
принятое в п. 1 § 1 допущение о взаимной независимости образую-
образующих данный сегмент словоформ.
Рассмотрим в этой связи следующую задачу. Средняя длина
простого предложения или синтаксически оформленной части
сложного предложения в английских научно-технических текстах
лежит между 10 и 11 словоформами. Относительная частота появ-
появления существительных в подъязыке английской электроники
близка к 1/3 [6, с. 96—97]. Будем считать эту частоту априорной
153
вероятностью появления существительных в указанном подъязыке.
Примем также, что типовым синтактически оформленным сегментом
в английских научно-технических текстах является простое пред-
предложение, а также главное или придаточное предложение длиной
в 10 словоформ.
Считая появление отдельных словоформ в этих сегментах неза-
независимыми событиями текста, определим вероятность того, что из
10 словоупотреблений, составляющих типовой сегмент, ровно два
будут существительными.
Так как по условию р = 1/3, q = 1 — р = 2/3, N = 10,х== 2, то,
пользуясь формулой F.1), находим
^9_ . J!_= Ц520_ = 0,1951 = 19,51 %.
1-2 З10 59049
Сохраняя те же условия и допущения, вычислим о помощью фор-
формулы Бернулли вероятности появления существительных в нашем
типовом сегменте 0, 1, 2, ..., 10 раз. Результаты приведены в столб-
столбце. B) табл. 6.2.
Таблица 6.2
Вероятности появления существительных в английском предложении
X
A .
0
1
2
3
4
5
PN (*)
B)
0,0173
0,0867
0,1951
0,2601
0,2276
0,1366
p'Nw
C)
0,0226
0,0785
0,1894
0,2611
0,2419
0,1433
X
A)
6
7
8
9
10
PN <*
B)
0,0569
0,0163
0,0031
0,0003
0,000020
C)
0,0541
0,0130
0,0020
0,0002
0,000005
Расчеты показывают, что в 10-словном предложении (сегменте)
следует ожидать в среднем от двух до пяти форм имени существи-
существительного. Следовательно, на сегменты этого типа и должны быть
ориентированы алгоритмы автоматического анализа английского
текста. Появление сегментов с одним Существительным или во-
вообще без существительных, с одной стороны, а также с шестью,
семью, восемью именными формами, с другой, маловероятно.
И действительно, появление таких сегментов в английских научно-
технических текстах хвтя и возможно tcp. Comparing A0—13) to
A0—4) it is seen that . . или Harvey Fletcher, Speech and.Hearing
in Communication, Bell Telephone Laboratories]*, но встречается
* Оба примера взяты нз книги: Н. Fletcher. Speech and Hearing in
Communication. Toronto — New York—London, 1958, с I и 172.
151
в виде исключения. Что же касается предложений, состоящих
из девяти или десяти существительных, то такие отрывки просто
невозможны. В рассмотренном теоретическом распределении ве-
вероятность появления таких сегментов практически равна нулю.
Часто, чтобы получить достаточно достоверные результаты,
приходится производить большое число независимых испытаний.
При этом величины N и х могут быть довольно велики, что делает
вычисление по только что описанной схеме слишком трудоемким*.
В таких случаях вычисление вероятностей Ры(х) осуществляется
по приближенным формулам, которые мы рассмотрим в § 3.
Иногда для решения лингвистической или информационной за-
задачи необязательно определять все вероятности появления данного
события 0, I, 2, . ., N раз. Достаточно указать несколько наиболее
вероятных или даже одно наивероятнейшее число появлений этого
события.
Начнем о того, что опишем схему определения наивероятней-
шего события Для этого рассмотрим поведение распределения F.1).
Из табл. 6.1 и 6.2 видно, что с увеличением х величина Ры (х) воз-
возрастает и при некотором х0 (оно называется модальным значением)
достигает своего наибольшего значения Pn(x0). Затем по мере уве-
увеличения х вероятность Pn (x) последовательно убывает. Чтобы опре-
определить модальное значение х0, рассмотрим поведение функции
PN (x) путем последовательного сравнения двух соседних членов
распределения
Пусть Pn (хо) — наибольшее значение вероятности в распреде-
распределении F.1). Тогда должны выполняться следующие два неравенства:
Pn (х0 — 1) < Рдг (Хо), Pn («о) > р" (*о + 1). F.2)
Перепишем первое из неравенств F.2) в виде
PN(*o)
Cff /«/-*
4 4
F.3)
Заменив в последнем неравенстве q на I — р, получаем
х0 < Np + р. F.4)
Аналогичным образом, записав второе из неравенств F.2) в виде
PN(x0+l) _cfr + V°+V-*«-' = (дг
^
получим
Np + р — 1.
F.6)
* Например, если бы мы захотели определить вероятность появления
четырех существительных напряжение в серии из 2000 испытаний, зная, что
в текстах по радиоэлектронике указанная словоформа согласно данным рабо-
работы [6] имеет вероятность р ==> 0,0023, то эту вероятность мы должны были бы
получить из равенства Р2ооо D) = С$ооо @,0023L@,9977)шв, решение ко-
которого требует исключительно громоздких вычислений даже при условии
использования специальных таблиц факториалов
155
Объединяя неравенства F.4) и F.6), приходим к двойному нера-
неравенству
Np + р — 1 < хй < Np + р. F.7)
Левая часть неравенства F.7) всегда на единицу меньше его правой
части. Поэтому в тех случаях, когда Np + р — 1 и Np + p являют-
являются дробными величинами, в качестве ха берется находящееся между
ними целое число. Если же Np -+¦ р — 1 и Np -+¦ р — целые числа,
то х0 имеет два целочисленных значения: х0 = Np -+- р — 1 и
дго = Np + р, которые выступают в качестве наивероятнейших
значений появления данного события.
Теперь, пользуясь исходными данными об употребительности
существительных, приведенными выше, определим наивероятней-
шее число появлений существительных в английском 10-словном
предложении.
Так как N = 10, р = 1/3, то, согласно F.7), имеем
Следовательно, наивероятнейшее число появлений существительных
в 10-словном английском сегменте равно трем. Такой же результат
дает распределение вероятностей, приведенное в табл. 6.2.
Зная модальное значение х0, можно определить интересующее
нас число вероятностей биномиального распределения. Вычисле-
Вычисление их начинается обычно с определения максимальной вероятности
Pn («о):
F.8)
Вычисления остальных вероятностей производятся по следующим
рекуррентным формулам, построенным на использовании выражений
F.3) и F.5):
при х <. х0
(*mm
Pn (
~ *raln — 1 P
2),
F.9a)
при x>x0
*o + 1 Я
_ N-(xo+\) p
Я
Pn(xo+\),
PN(Xm^—\) =
N — (xmax — 2) p
'max — 1 Q
— I),
*max
F.96)
где жт1в > 0 и хшах < N.
Только что описанный прием расчета биномиальных вероятностей
можно проиллюстрировать следующим примером. В русском языке
вероятность появления гласной в начале синтагмы или предложения
составляет 23,21 %. Пусть осуществлена повторная выборка в сто от-
отдельных синтагм и предложений. Необходимо определить пять наи-
наивероятнейших частот появления начальной гласной, а также вы-
вычислить сумму их вероятностей.
Здесь N — 100, р = 0,2321, q = 0,7679; воспользовавшись
неравенством F.7), получаем
или
23,21 + 0,2321 — К х0 < 23,21 + 0,2321,
22,4421 <хо< 23,4421,
откуда х0 = 23. Далее по формуле F.8) вычисляем вероятность мо-
модального значения* х0:
1001
23! 771
• 0,232123-0,7679"» 0,0943.
Затем по рекуррентным формулам F.9) определяем значения х0 —• 1,
х0 — 2, хи + 1, х0 + 2:
100
B2) =-Л- .-^^-.0,0943 = 0,0920,
v; 100-22 0,2321
р B1) =
1001 '
-
100-21 0,2321
. 0,092 = 0,0848,
1йо
100
= 100-23 , °'2321..0,0943 = 0,0914,
23+1 0,7679
0,7679
.0,0914= 0,0840.
¦ Решение этого примера осуществляется путем логарифмирования с ис-
использованием таблиц логарифмов факториала [9, с. 456].
156
157
Сумма полученных пяти вероятностей равна 0,45. Это значит, что
при многократном извлечении из русских текстов серий синтагм и
предложений, каждая из которых содержит 100 единиц, примерно
Половина из этих серий содержала бы от 21 до 25 предложений, на-
начинающихся с гласного звука.
Только что описанный прием расчета вероятностей биномиаль-
биномиального распределения имеет значительные преимущества перед по-
последовательным вычислением, начиная с х = 0 (xmin). В последнем
случае мы должны вычислять все значения Pn (x), даже те, которые
близки к нулю. При использовании только что описанной методики
мы, получив максимальное значение Pn (x), продолжаем вычисление
вероятностей только до тех значений xt и хг (xt < х0, хг > х0),
которые предусмотрены в условии задачи.
4. Полиномиальная схема. Если лингвистическое испытание
имеет несколько исходов, то их вероятностное прогнозирование осу-
осуществляется с помощью полиномиальной схемы. Ее математическая
модель строится следующим образом.
Предположим, что результатом некоторого лингвистического
опыта может быть один из k различных попарно несовместимых
исходов Alt Аз, ..., Лft. Вероятность каждого из этих исходов обо-
обозначим соответственно через Р (Лх) = ръ Р (А2) = р2, ..., Р (Ah) =*
= pk- Так как событие Л1 + Ла+... + Лй достоверно,
то pj + р2 + ... + ph = 1. Осуществим N независимых испытаний
и определим вероятности того, что событие Лх появится х1 раз, со-
событие Л2 — х2 раз, ..., событие Ah — xh раз, где хх + х2 + ... +
+ xh = N.
Указанный результат получается различными путями, каждый
из которых соответствует различным перестановкам хх раз исхода
Аъ х2 раз исхода А2, ..., xh раз исхода Ah. Согласно теореме умно-
умножения вероятность появления каждой такой комбинации равна
р*'р*' ... p*kh- Общее число этих комбинаций равно произведению
которое приводится к выражению
\ дг2!
Отсюда получаем, что при N независимых испытаниях вероятность
получить хг раз результат Аъ х2 раз — результат Ла, ..., xh раз —
результат Ak равна
PN (X{, X2 Xk) =
N\
F.10)
В том случае, когда k — 2, имеем
Учитывая, что хх + х2 = N, a pt + Р% — 1, и обозначая хх через
х, хг — через N — х, pt — через р, а р2 — через q, приходим к вы-
выражению
N\
.pxqN-x=CxNpxqh
158
x\(N—x)l
т. е. к формуле Бернулли для простой схемы независимых испыта-
испытаний. Формула Бернулли является, таким образом, частным случаем
соотношения F.10).
Используя только что описанную модель, определим вероятность
того, что в 10-словном сегменте английского научно-технического
текста появится ровно три существительных, две глагольных формы
и пять словоформ, принадлежащих к другим классам (при этом мы
снова пренебрегаем контекстными связями между словоформами,
образующими рассматриваемый сегмент). Заданная нормой апри-
априорная вероятность появления существительных равна 0,33, вероят-
вероятность глагольных форм составляет 0,16, а априорная вероятность
остальных грамматических классов равна 0,51 [6, с. 104].
По условию задачи N = 10, рх — 0,33, ра = 0,16, ра = 0,51,
„ _ о у. _Ov К
At — *J$ ~~~ > " 3
Применяя формулу F.10), получаем
риC,2,5) = ——0,333 -0,16а-О.515 « 0,0800.
о] 2\ О;
Аналогичным образом можно рассчитать вероятность появления
всех возможных количественных комбинаций существительных,
глаголов и других классов слов в предложениях различной длины.
Как и простая схема, полиномиальная схема используется в пов-
повторных лингвистических выборках при условии, что величины N,
хъ х2, .... хк не слишком велики. При этих условиях использование
рассмотренной схемы дает ценную информацию не только для ве-
вероятностного построения алгоритмов синтаксического анализа иност-
иностранного текста при машинном переводе. Эти алгоритмы позволяют
также определять оптимальную последовательность подачи синтак-
синтаксического материала при обучении иностранному языку в средней
школе и вузе.
5. Пуассоновская схема. В лингвистической практике часто при-
приходится иметь дело с такой речевой совокупностью, в которой сос-
составляющие ее тексты принадлежат к разным подъязыкам и стилям.
Поскольку эти тексты строятся, исходя из различных норм, каждая
лингвистическая единица имеет в каждом тексте свою априорную
вероятность. В итоге вероятности появления и непоявления интере-
интересующих исследователя единиц меняются от опыта к опыту. Такая
ситуация описывается схемой Пуассона. Математическая формали-
формализация этой схемы осуществляется в результате следующих рассуж-
рассуждений.
Пусть производится N независимых испытаний, в каждом из ко-
которых может появиться или не появиться событие А. Вероятности
появления события А в 1, 2, ..., N испытаниях соответственно равны
159
Pi, p2, ..., Pn, а вероятности его непоявления равны qt — 1 — р1?
q% =1 —р2, ..., 9w = 1 —Pn- Можно показать, что вероятность
появления результата А в серии из N испытаний ровно х раз состав-
составляет
Pn (х) = pi р2 р3
••• + Pi % Рз ••• 9w-1
Таким образом, искомая вероятность представляет собой сумму
всех возможных произведений, в каждом из которых р с разными
индексами содержится х раз, a q с разными индексами входит N—х
раз.
Чтобы составить все возможные произведения из х вероятностей
pi и N — х вероятностей qt (i = 1, 2, ..., N), образуем произведе-
произведения биномов
F-12)
где / — некоторый произвольный параметр [10, с. 62].
Перемножая биномы и приводя подобные члены, приходим
к равенству
/=1
в котором коэффициент при tx есть не что иное, как выраже-
выражение F.11).
Раскрывая скобки в левой части равенства и приводя подобные
члены, получим все вероятности PN @), Pn A), Pn B), ..., Pn (N),
которые выступают в качестве коэффициентов соответственно при
t°, t1, f, ...,tN. Сумма всех вероятностей Р,ц (х) равна единице:
N
В частном случае, когда
s= q, имеем
ра=.
pN=p,
q2=...=qN
откуда следует формула Бернулли.
Используя только что описанную математическую модель, решим
следующую задачу.
Пусть производится повторная выборка именных групп из сле-
следующих четырех жанрово-тематических совокупностей русских
текстов (подъязыков): записей непринужденной разговорной речи,
поэзии, художественной прозы, научно-технических текстов.
Именной группой считается словосочетание, в котором существи-
существительное стоит на последнем месте. Так, например, в предложении
160
используя только что описанную модель, решим следующую задачу
триада решим следующую задачу будет именной группой.
Считая, что вероятность употребления существительных в раз-
разговорной речи равна 0,1, в поэзии — 0,2, в художественной прозе —
0,3, в научно-технических текстах — 0,4, найдем вероятности появ-
появления среди одновременно извлекаемых четырех словосочетаний ни
одной, одной, двух, трех, четырех именных групп.
Событие, состоящее в появлении именной группы, по существу,
соответствует событию, которое заключается в том, что из текста
случайным образом выбирается форма имени существительного
(к этой последней затем прибавляются два словоупотребления сле-
слева и тем самым формируется именная группа).
При четырех испытаниях, состоящих в извлечениях из каждого
подъязыка по одному трехсловному сочетанию для нашего события,
имеем вероятности: рх = 0,1, р2 = 0,2, р„ = 0,3, р4 = 0,4. Для
определения вероятностей Р4 @), Р4 A), Р4 B), Р4 C), Р4 D) вос-
воспользуемся формулой F.12). В результате получаем:
П (Pit + qt) = @,1 t + 0,9) @,2 t + 0,8) @,3 / + 0,7) @,4/ + 0,6) =-
= 0,302 + 0,440 t + 0,21512 + 0,04013 + 0,002 Л
Из этого равенства следует, что вероятности получить в каждой
серии 0, 1, 2, 3, 4 именных триады соответственно равны
Р4 @) = 0,302; Р4 A)=0,440; Р4 B)=0,215;
Р4 C) = 0,040; Р4 D) = 0,002.
Схему Пуассона, как и две предыдущие схемы, целесообразно
применять к лингвистическим испытаниям тогда, когда мы можем
организовать повторную выборку, а величины N и х не очень ве-
велики.
В предыдущих разделах мы научились прогнозировать исходы
массовых лингвистических испытаний. Такие прогнозы мы можем
пока осуществлять применительно к повторным выборкам, опираясь
на классическое определение вероятности, т. е. при условии, что
опыт осуществляется относительно сравнительно ограниченной
по объему конечной совокупности лингвистических объектов. Такая
ситуация встречается в лингвистике сравнительно редко. Чаще
всего языковеду приходится иметь дело с бесповторной выборкой,
исследующей редко встречающиеся лингвистические единицы.
В этих условиях распределение вероятностей появления события А
подчиняется гипергеометрическому закону [6, с. 156—162].
6. Бесповторная лингвистическая выборка и ее описание с по-
помощью формулы Бернулли. Гипергеометрический закон может при-
применяться только к конечным генеральным совокупностям, объем ко-
которых известен. Поскольку в лингвистических задачах объем гене-
Зак. 1287
161
ральной совокупности текстов, порождаемых открытой системой язы-
языка, обычно не является конечной величиной, применение указанного
закона для прогнозирования исхода лингвистических опытов в бес-
бесповторных выборках оказывается нереальным. Вместе с тем при опре-
определенных условиях гипергеометрическая вероятность хорошо ап-
аппроксимируется биномиальной вероятностью [30, кн. 1, с. 271 и
ел.]. Поэтому, не боясь нарушения математической строгости, мы
будем производить расчет вероятностей появления события А ров-
ровно х раз в нашей бесповторной выборке так, как если бы речь шла
о повторной выборке. Иными словами, мы применяем к беспо-
бесповторным выборкам биномиальный закон.
Будем рассматривать данные S текстов как S серий или выбо-
выборок, каждая из которых состоит из N независимых испытаний.
Лингвистическое событие А может появиться в каждой серии х
раз (х = 0, 1, 2, ..., N). Нетрудно заметить, что имеются группы
серий, в которых А появляется 0, 1, 2, ..., N раз. Отсюда следует,
что частость появления события А ровно х раз в одной серии опреде-
определяется отношением /д/ (х) = SJS, где Sx—количество серий, в ко-
которых событие А появится ровно х раз.
Априорная вероятность появления события А в одной наугад
взятой серии равна
Таблица 6.3
NS
и, следовательно,
>«1—
NS
В получаемом теоретическом распределении каждому значению х
соотнесена не его вероятность, а некоторое теоретически ожидаемое
число серий (выборок) Si, в которых событие А появляется ровно
х раз. Поскольку
SI — SPN (x) — SCjf px qN~x, F.13)
нетрудно заметить, что величины Sx и Pn (x) связаны коэффициентом
пропорциональности S.
Для иллюстрации вышесказанного рассмотрим следующий
пример.
При определении стилистико-статистических особенностей упо-
употребления существительных в романе М. Ауэзова «Путь Абая»
(на казахском языке) из текста романа случайным образом выбира-
выбираете* 4ID0 отрезков текста по 25 словоупотреблений каждый. Данные
о частотах употребления существительных в этих отрезках показаны
в столбцах A) и B) табл. 6.3. Необходимо вычислить теоретическое
биномиальное распределение вероятностей появления х существи-
тельньтХв одной серии.
162
Вероятностно-статистические характеристики употребления
существительных в романе М. Ауазова «Путь Ао«я»
Число появ<
нений события
X
A)
0
1
2
3
4
5
6
7
Ь
9
10
11
12
13
14
15
16
17
Эмпирические
частоты
' появления
выборок
5Я
B)
3
5
7
24
40
52
64
66
47
48
24
14
3
2
1
—
—
25ж = 400
Теореютески
ожидаемое
чвело выбо-
выборок sl
C)
0,050
0,580
2,960
9,710
22,880
41,210
58,870
68,480
66,030
53,440
36,640
21,440
10,720
4,600
1,680
0,520
0,140
0,030
399,980
s?. округ-
леиаое до
целых чявел
<¦)
\ ,
} '
1 з
10
23
41
59
68
66
53
37
21
И
5
1.
J
400
Чвот»о?ь
с
(В)
0,0075
0,0125
0,0175
0,0600
0,1000
0,1300
0,1600
0,1650
0,1175
0,1200
0,0600
0,0350
0,0075
0,0050
0,0025
—
1,0000
Вероятность
появления
события
ровно х раз
<6>
0,0001
0,0014
0,0074
0,0243
0,0572
0,1030
0,1472
0,1712
0,1651
0,1336
0,0916
0,0536
0,0268
0,0115
0,0042
0,0013
0,0004
0,0001
1,0000
Здесь S = 400, N — 25. Используя произведения величин х
н Sx, приведенных в первых двух столбцах табл. 6.3, находим
7>5в =0,3038.
N [ S J 25
0,7, согласно F.7), имеем
NS
Приняв р та 0,3 и q
25 . 0,3 — 0,7 < х0 < 25 • 0,3 + 0,3, или 6,8<*0 < 7,8,
откуда следует, что х0 = 7, Тогда
Pn (*о) = Р» G) = CJeO,3' • 0,7".
Логарифмированием находим, что Ра5 G) =* 0,17119. Следователь-
Следовательно,
Sx = SP2b G) = 400 • 0,17119 » 68,480.
Остальные значения ожидаемого числа выборок, вычисленные с по-
помощью соотношений F.9) и F.13), приведены в табл. 6.3.
7. Определение вероятности появления лингвистического собы-
события от а до Ъ раз. Определение вероятности того, что та или иная линг-
лингвистическая единица появится в данной выборке ровно х раз, пред-
б* 163
ставляет обычно небольшой интерес с точки зрения языкознания.
Гораздо важнее уметь вычислять вероятность появления лингвисти-
лингвистического события от а до b раз в заданном массиве текста.
Пусть В'х — событие, состоящее в том, что лингвистическая
единица А появится не менее а и не более b раз.Тогда вероятность
Pn (a «Si х sgC b) этого события составляет
2
Если количество членов, отвечающих значениям jc от а до Ь,
намного больше общего количества членов, соответствующих зна-
значениям л: от 0 до а — 1 и от 6 + I яо N, то удобнее проводить сумми-
суммирование вероятностей по этим двум последовательностям, получая
тем самым вероятность события В'х, противоположного событию В'х-
Искомая же вероятность равна
°2
х=0
= 1—Р(В'х) =
F.14)
Рассмотрим некоторые частные случаи. Предположим, что не-
необходимо определить вероятность того, что лингвистическая еди-
единица А встретится не менее а раз. Здесь
Если а мало, то целесообразно пользоваться выражением
являющимся частным случаем формулы F.14).
В том случае, когда а = 1, имеем
/Ml
= I — C% p° qN = 1 — q
F.15)
Пусть, например, из русских текстов по радиоэлектронике слу-
случайным образом извлечено 1000 словоупотреблений. Найдем ве-
вероятность того, что словоформа напряжение встретится хотя бы
один раз, если ее частость, согласно данным работы [6, с. 175—176],
равна 0,0023.
Здесь 7V — 1000, р = 0,0023, q = 0,9977. Пользуясь формулой
F.15), находим
PN(X >\)~ Ргооо (Кх< 1000) = 1 - 0,9977»«« **
да 1 —0,10 = 0,90.
Это означает, что если осуществить 100 выборок по 1000 слово-
словоупотреблений каждая, то появление словоформы напряжение
можно наверняка ожидать в 90 выборках.
Вероятность появления события А не более b раз также опреде-
определяется путем суммирования вероятностей, в которых событие по-
появится 0, 1, 2 b раз:
)= 2
0
2
*=0
При близком к N значении b эту вероятность следует вычис-
вычислять с помощью формулы
N
* рх qN~x, F.16)
2
также представляющей собой частный случай выражения F.14).
Чтобы проиллюстрировать описанную методику, определим
вероятность того, что в извлеченном наугад из романа М. Ауэзова
«Путь Абая» отрывке в 25 словоупотреблений будет не более шест-
шестнадцати существительных.
Здесь N = 25, р = 0,3, q = 0,7 (см. п. 6); вместо того чтобы
определять, а затем суммировать вероятности появления 0, 1, 2, ...
..., 16 существительных, определим вероятность появления семнад-
семнадцати существительных (появление более чем семнадцати существи-
существительных практически равно нулю — см. табл. 6.3):
Ра5 A7) = СЦ • 0,317 • 0,78 = 0,0004.
Тогда искомая величина, согласно формуле F.16), равна
Р (х < 16) = 1 — Р25 A7) = 1 — 0,0004 = 0,9996.
Иными словами, если взять 10000 выборок по 25 словоупотреб-
словоупотреблений, то в 9996 выборках можно ожидать появление не более
16 существительных.
8. Определение необходимого объема выборки. В лингвистиче-
лингвистических исследованиях и особенно при подготовке лингвистических
программ машинного перевода и информационного поиска постоян-
постоянно возникает потребность определять объем выборки, необходимый
для того, чтобы обеспечить с заданной вероятностью появление хо-
хотя бы один раз интересующей нас лингвистической единицы.
Для этого приведем сначала соотношение
к виду
Pn A < X < N) = 1 — qN = 1 — A - p)N
A
)N = 1 _ PN
N).
164
165
Прологарифмировав обе части равенства и произведя необходи-
необходимые преобразования, получим
1Г lg[l-PN{Kx<N)] '
lg(l-p)
F.17)
где N указывает на необходимый объем выборки.
Пусть, например, нужно определить тот объем выборки русских
текстов по радиоэлектронике, который необходим для того, чтобы
с вероятностью в 90% словоформа напряжение появилась в нем хо-
хотя бы один раз.
Здесь р = 0,0023 (см. п. 7), PN A < х < N) = 0,90. По фор-
формуле F.17) находим
_ 1g A-0,90) _
lg A — 0,0023)
lgO.10 _
lg 0,9977
—1
0,001
¦=1000.
Иными словами, для того, чтобы с уверенностью в 90% утверждать,
что словоформа напряжение встретится хотя бы один раз, нужно
просмотреть выборку длиной в тысячу словоупотреблений.
§ 2. Случайная лингвистическая величина,
ее характеристики и функция распределения
1. Дискретные и непрерывные случайные величины в речевой
деятельности. При проведении лингвистического опыта мы посто-
постоянно встречаемся с такими величинами, численные значения кото-
которых невозможно раз навсегда определить, причем эти значения ме-
меняются под влиянием случайных воздействий. Так, например,
выбирая наугад слова из текста, мы встречаем слова длиной в 1,
2, 3 й f. д. букв. Эти ёЛОЁа мбгут содержать 0, 1,2,3 и т. д. гласных
или согласных фонем. Длина слова, количество гласных или соглас-
согласных фонем выступают в качестве случайных величин, т.е. таких линг-
лингвистических величин, которые могут в результате испытаний при-
принимать различные, заранее непредсказуемые значения.
Только что рассмотренные случайные лингвистические величи-
величины принимают определенные четко отграниченные друг от друга
прерывные значения. Такие величины называются дискретными
случайными величинами.
Если же случайная величина принимает сплошь все значения
в каком-то интервале на числовой оси, то мы имеем дело с непре-
непрерывной случайной величиной. Примером непрерывной случайной ве-
величины является интенсивность звука, которая колеблется обычно
в определенных пределах (ср. ниже п. 5).
Когда фонолог, грамматист или лексиколог исследует структуру
планов содержания й Ёыраженйя, бй всегДа имеет дело с дискрет-
дискретными случайными величинами. Однако, обращаясь к фонетическим
и семантическим исследованиям — исследованиям, касающимся
субстанции планов выражения и содержания, лингвист должен
оперировать непрерывными случайными величинами.
166
Принятие случайной величиной X конкретного значения xt есть
случайное событие. Поэтому описываемые ниже свойства случай-
случайной лингвистической величины являются в какой-то степени обоб-
обобщением того, что было сказано о случайном лингвистическом со-
событии.
2. Законы распределения дискретной случайной величины.
Чтобы полностью задать случайную величину, недостаточно толь-
только указать те значения, которые она может принимать. Необходимо
еще знать для каждого значения xt ту вероятность Р (X = Xt) =¦
= pi, с которой случайная величина принимает это значение.
Если случайная величина X является дискретной и принимает
возможные значения х0, хъ х2, ..., Хы, то вероятности р,- точно соот-
соответствуют вероятностям Ры (х), с которыми мы имели дело в § 1, п. 3.
Рассматриваемые нами возможные значения случайной величи-
величины являются событиями попарно несовместимыми и образуют пол-
полную группу событий, поэтому сумма их вероятностей равна едини-
единице, т. е. 2pt = 1.
Правило, связывающее значения случайной величины и соот-
соответствующие им вероятности, носит название закона рас-
распределения дискретной случайной величины.
Простейшей формой закона является таблица распре-
распределения или, как еще называют, ряд распределе-
распределения. В этой таблице перечисляются все возможные значения слу-
случайной величины и указываются соответствующие им значения ве-
вероятностей; такова, например, табл. 6.1, в которой представлено
биномиальное распределение. Закон распределения может быть за-
задан в виде формулы: примером аналитического выражения биноми-
биномиального распределения служит формула F.1). Наконец, для пере-
передачи закона распределения можно использовать графическую ил-
иллюстрацию; соответствующие примеры будут приведены ниже.
* 3. Понятие функции распределения случайной величины. По-
Поскольку языкознание имеет дело не только с дискретными, но и
с непрерывными величинами, необходимо наряду с распределения-
распределениями дискретных величин рассмотреть также распределения непре-
непрерывных случайных величин. Это тем более необходимо потому, что
нам придется представлять распределения некоторых дискретных
величин в виде непрерывных распределений (см. ниже § 3, п. 4).
Если дискретную случайную величину характеризует таблица,
в которой указываются все значения этой величины и ее вероятнос-
вероятности, то для непрерывной случайной величины такую таблицу постро-
построить нельзя: во-первых, непрерывная случайная величина принимает
бесконечное множество значений; во-вторых, вероятность того, что
рассматриваемая непрерывная случайная величина точно примет
то или иное численное значение, равна нулю (см. ниже, п. 5).
В связи с этим встает вопрос об отыскании такой модели рас-
распределения, которая характеризовала бы как дискретную, так и
непрерывную случайную величину.
Строя такую модель, воспользуемся неравенством X < х,
где х является переменной величиной. Это неравенство означает.
167
что случайная величина X принимает всевозможные значения,
меньшие чем х. Вероятность появления такой величины равна
,Р(Х<х).
Ясно, что вероятность принимаемых значений случайной ве-
величины зависит от значений переменной х. Поэтому указанная ве-
вероятность является некоторой функцией от х. Обозначив эту функ-
функцию как
F (х) = Р (X < х),
или иначе,
F(x) = P (-оо<Х<х),
будем называть ее функцией распределения, или интегральной функ-
функцией распределения случайной величины. Ее называют также ку-
кумулятивной функцией, т. е. такой функцией, значения которой пред-
представляют собой каждый раз сумму численности данного признака
и численностей всех предшествующих ему признаков.
Функция распределения случайной величины обладает следую-
следующими свойствами:
1. Так как значение вероятности заключено между 0 и I, то
справедливо неравенство 0 ^ F (х) ^ 1.
2. Если случайная величина ограничена, т. е. принимает все
возможные значения в некотором отрезке [а, Ь], тодлявсех значений
X, меньших чем а (невозможное событие) F (д;)=0, а для всех значе-
¦ ний, больших чем b (достоверное событие) F (х) = 1.
3. Если случайная величина принимает любые значения в проме-
промежутке — оо<Х<+°°. то имеют место равенства:
lim F(x) = 0, lim F(x)=l.
4. Вероятность того, что случайная величина X примет зна-
значение, удовлетворяющее неравенству xt ^ X < хг, равна прираще-
приращению ее функции распределения F (х) на интервале от хх до xit т. е.
X<xJ = F (xj — F (xj.
F.18)
5. Функция распределения случайной величины является неотри-
неотрицательной неубывающей функцией аргумента, т. е. при хг <. хг
имеет место неравенство F (хг) <; F (х2).
Все перечисленные свойства характеризуют функцию распре-
распределения как для дискретных, так и для непрерывных случайных
величин.
4. Функция распределения для случайной лингвистической
величины дискретного типа. Используя данные о теоретическом
распределении частот существительных в английской научно-
технической речи (см. § 1, п. 3), построим функцию распределения
Р(х).
По условию случайная величина X <С х принимает все целочис-
целочисленные значения, заключенные на отрезке [0, 10]. Исходя из свой-
свойства 2, а также учитывая свойства 1, 4, 5, определяем кумулятив*
168
ную функцию F (х) как сумму вероятностей случайной величины X,
не превосходящей х:
F (х) = Р (Х< 1) = Р (X = 0) = 0,01734;
F(x) = Р(Х< 2) = Р(Х = 0) + Р(Х о, 1) =
= 0,01734+ 0,08671 = 0,10405.
Аналогичным образом имеем:
F (х) = Р (X < 3) = 0,29914;
F (х) = Р (X < 5) = 0,78686;
F (х) = Р (X < 7) = 0,98032;
F (х) = Р (X < 9) = 0,99963;
fW=P(X<4) = 0,55926;
F (х) = Р (X < 6) = 0,92342;
F(x) = Р (Х<8) = 0,99658;
F(x) = P(X< 10) = 0,99965;
1,0000.
если х > 10, то F (х) = Р (X < х)
График рассматриваемой функции показан на рис. 37. В том
случае, когда случайная величина принимает значения, меньшие
чем х — 0, функция
F (х) равна * нулю.
Этому значению соот-
соответствует линия, ле-
лежащая на оси абсцисс
левее начала коор-
координат.
Как только слу-
случайная величина X
примет значение, рав-
равное нулю (т. е. при
условии, что 0<л;^1
и X < х), функция
F (х) = Р (X <х)
получает значение
0,0173. Иными сло-
словами, в точке А о эта
функция претерпева-
претерпевает разрыв, сопровож-
сопровождающийся скачком
ее численного зна-
значения. Величина это-
этого скачка в точности
равна значению вероятности Ро = А0В0 = 0,0173. Это значение
функция F (х) = Р (X < х) сохраняет вплоть до следующего цело-
целочисленного значения случайной величины, т. е. до точки Аи
где F (х) — Р (X ¦< 2). Здесь снова происходит скачок величи-
величиной в Р, = АхВг = 0,0867, причем F(x) = Р (X < 2) = Ро +
+ Рх — 0,1040. Это значение F (х) сохраняется в полуоткрытом про-
промежутке [1, 2), после чего происходит новый скачок Л2?2 = Р2 и
т. д. В силу того что при х^Ю значение кумулятивной функции
равно единице, график ее при * ^ 10 сливается с прямой F (х) — 1.
1,0
0,8
0,6
DA
Ц2
Во
R. В„ В„ В„
51 Ац
в,
Вг
—
—ч
As
-!и Аг
/ г
5 6 7 8 3 10
Рис. 37
Приведенный пример показывает, что функция распределения
любой дискретной случайной величины всегда является разрывной
ступенчатой функцией, скачки которой происходят в точках, со-
соответствующих значениям случайной величины X. Скачок в каждой
такой точке равен вероятности Pt того, что случайная величина
примет целочисленное значение i. Сумма всех скачков равна еди-
единице.
5. Функция распределения для случайной лингвистической ве-
величины непрерывного типа. Прежде чем говорить об особенностях
описания непрерывной случайной величины, рассмотрим сле-
следующий пример. Пусть произведен статистический эксперимент,
ставивший целью измерения чувствительности слуха относительно
звукового тона в 1500 Гц [6, с. 122—123]. Испытанию было подверг-
подвергнуто две тысячи испытуемых. Измерения велись путем постепен-
постепенного повышения уровня интенсивности сигнала, начиная от «зву-
«звуков», не воспринимаемых ухом человека, к слышимым звукам.
На каждый распознанный сигнал испытуемый отвечал включением
светового сигнала. Таким образом определялся тот уровень интенсив-
интенсивности .(в децибелах, сокращенно — дБ), при котором каждый ис-
испытуемый начинает слышать звук указанного тона. Само собой
разумеется, что разные испытуемые начинают слышать звук на
разных уровнях его интенсивности. Такие разные уровни интен-
интенсивности, необходимые для того, чтобы тот или иной взрослый че-
человек услышал звук заданного тона, могут рассматриваться как
значения случайной величины X. Закон распределения этой слу-
случайной величины по интервалам, ширина которых определяется
условиями эксперимента, показан в табл. 6.4.
Таблица 6.4
Х(дБ)
Pi
Х(дБ)
Pi
х<—13,5
0,00
1,5<Х<
<4,5
0,29
— 13,5<Х<
< —10,5
0,01
4,5<Х<
<7,5
0,08
—10,5<Х<
<-7,5
0,02
7,5<Х<
<Ю,5
0,02
—7,5<Х<
<-4,5
0,08
10,5<Х<
<13,5
0,01
-4,5<Х<
<—4,5
0,25
Х>13,5
0,00
-1,5<Л<
<1,5
0,31
Только что построенный закон распределения существенно
отличается от закона распределения случайной величины дискрет-
дискретного типа. Действительно, если последняя принимала конечное или
во всяком случае счетное множество значений, то теперь наша
случайная величина — уровень интенсивности — может принимать
бесконечное множество значений.
Т(х)
0А\
-9 Я -6 -3
Один испытуемый может воспринять звук с интенсивностью
в —13,5 дБ, другой услышит звук при условии, что его сила равна
—13,49 дБ, для третьего испытуемого этот уровень будет равен
—13,489 дБ и т. д.
Указать в таблице распределения все бесконечное множество
значений случайной величины невозможно. Поэтому и приходится
говорить об интервалах, в которые могут попадать ее значеЯНЛ.
При этом отмечаются либо границы интервала, либо указывается
его середина (начало, конец). Вероятности, приписываемые кажДб-
му из интервалов, являются вероятностями того, что рассматривав»
мая непрерывная величина попадет в данный интервал.
При графическом изображении интервального ряда распределе-
распределения значений случайной лингвистической величины целесообраз-
целесообразно пользоваться гистограммой,
представляющей собой последо-
последовательность прямоугольников,
основание которых равно шири-
ширине интервала, а высота — соот-
соответствующей этому интервалу
вероятности (рис. 38). Нетрудно
заметить, что прямоугольники
гистограммы образуют фигуру,
ограниченную сверху ломаной
линией, а снизу — прямой KL.
Площадь этой фигуры, представ-
представляющая сумму площадей пря-
прямоугольников, равна единице.
Интегральный ряд распределения непрерывной случайной вели-
величины может быть представлен также в виде ступенчатого куму-
кумулятивного графика, аналогичного тому графику, который мы строи-
строили для кумулятивной функции F (х) дискретной случайной вели-
величины (см. рис. 37). Кумулятивный график закона распределения
уровней интенсивности звукового тона показан на рис. 39.
С теоретической точки зрения интервальное представление
непрерывной случайной величины не дает достаточно адекватного
ее описания. Сам выбор ширины границ интервала всегда произво-
произволен, поведение случайной величины внутри этого интервала оста-
остается неопределенным. Наконец, непрерывность рассматриваемой
величины не находит отражения в дискретном характере интер-
интервального ряда и соответствующих ему графиков.
Чтобы избежать этих затруднений, необходимо использовать
особый математический аппарат. Прежде чем вводить этот аппарат,
рассмотрим в геометрической интерпретации поведение непрерывной
случайной величины. Как уже говорилось, ширина интервалов
в распределении непрерывной случайной величины выбирается про-
произвольно. Теоретически ничто не мешает нам последовательно умень-
уменьшать эти интервалы, как это мы делали в гл. % § 2. При этом от-
отрезки ломаной линии, ограничивающей сверху фигуру, изобра-
изображенную на рис. 38, становятся все меньше, пока ломаная линия
о з
Рис. 38
170
171
не превратится в плавную кривую (рис. 40), которую называют
дифференциальной кривой распределения. При этом сумма площадей
прямоугольников, равная единице, практически не будет уже от-
Ю-
0,7.
о,в
0,5
О А
0,3
0,2
0,1
-12 -9 -6 -3
О 3 6 9 12 15
Рис. 39
X
личаться от площади фигуры, ограниченной снизу отрезком KL,
а сверху — кривой, полученной из ломаной линии.
Аналогичная картина наблюдается и в кумулятивном графике.
По мере уменьшения ширины интервала будет расти число интер-
6-3 С 3 6 9
12 X
валов и скачков между ними с одновременным уменьшением вели-
величины этих скачков до тех пор, пока ступенчатая линия не превра-
превратится в плавную кривую линию, которую принято называть интег-
ральной кривой распределения (рис. 41).
Теперь займемся аналитическим представлением поведения не-
непрерывной случайной величины.
Ранее (см. табл. 6.4) мы говорили о том, что вероятности, при-
приписываемые интервалам, указывают на ту вероятность, с которой
случайная величина X попадает в заданный интервал. Рассматри-
Рассматривая каждый интервал как полуоткрытый промежуток 1хи дг2), мы
можем считать, что попада-
попадание в него случайной величи-
величины X равносильно выполне- 1° •
нию неравенства хг ^ Х<.х%.
Согласно свойству 4 интег-
интегральной функции распреде- ?¦
ления вероятность выполне- ,
ния этого неравенства равна "
Ц9:
-J2 ~
= F (х2) - F (Xl).
Иными словами, вероят-
вероятность попадания случайной
величины в заданный интер-
интервал равна приращению функ-
функций на этом интервале.
Если неограниченно умень-
уменьшать интервал [xlt x2), как
это мы уже делали при по-
построении кривой распределе-
распределения, то вместо вероятности
того, что случайная величина попадает на этот участок, мы полу-
получаем в пределе, что величина X примет отдельно взятое значе-
значение хг:
Р(Х =**,)= l'm P(xx<X<a:2)= liml/7^) — F{xx)\. F.19)
Поскольку функция F (х) не имеет разрывов и непрерывна во всех
точках, в том числе и в точке хи предел F.19) равен нулю*.
Из всего сказанного следует, что вероятность каждого отдель-
отдельного значения непрерывной случайной величины равна нулю, т. е.
Р (X = х) = 0.
* При решении практических задач попадание непрерывной случайной
величины X в отдельную точку реального смысла не имеет. Ведь абсолютно
точное значение физической величины — в нашем случае длины, высоты,
интенсивности звука человеческой речи — является лишь математической
абстракцией. На практике в результате измерений мы получаем интервалы,
равные той наименьшей единице, которую может показать измерительный
прибор. Поэтому наблюдаемые в опыте значения случайной величины, строго
говоря, всегда дискретны. Но зная, что по своей внутренней природе рассМа-
риваемая случайная величина непрерывна, мы применяем для ее описания
непрерывное распределение.
172
173
Только что сформулированное свойство функции распределения
может показаться лингвисту парадоксальным. С одной стороны, при-
приводя классическое определение вероятности, мы говорили, что со-
события, имеющие нулевую вероятность, — это невозможные события;
с другой стороны, из всего только что сказанного вытекает, что собы-
событие, состоящее в том, что случайная величина X примет значение
х, хотя и возможно, но имеет вероятность, равную нулю.
Между тем появление событий, обладающих нулевой вероят-
вероятностью, можно представить себе при двух условиях: во-первых, эти
события должны рассматриваться вне рамок классической схемы
конечного числа случаев, во-вторых, они должны изучаться по ста-
статистической схеме или в рамках аксиоматического построения тео-
теории вероятностей (см. гл. 5, § 3).
6. Семантическая интерпретация непрерывной случайной ве-
величины. Некоторые области субстанции содержания представляют
собой непрерывный континуум 152, с. 308—318]. Это значит, что
между некоторыми родственными «универсальными» значениями
нет четких границ, и между ними всегда можно найти бесконечное
число переходных смысловых оттенков. Особенно наглядно эта си-
ситуация прослеживается в непрерывности цветового спектра. Хотя
разные языки по-своему формируют алфавиты (парадигмы) слов,
обозначающие отдельные хроматические интервалы [44], в каждом
языке можно найти средства для обозначения все более тонких
оттенков цветов, т. е. последовательно сужать эти семантические
интервалы*. Так,'например, внутри зеленого можно выделить сине-
синевато-зеленый оттенок, внутри синевато-зеленого можно найти сине-
синевато-зеленый с серым оттенком цвет, затем можно выделить синева-
синевато-зеленый с водянисто-серым оттенком цвет и т. д.
Теперь поставим опыт, состоящий в том, что из книги, в которой
дается описание разных оттенков цвета, наугад выбираются пред-
предложения и определяется, о каком цвете или оттенке в них идет речь.
Если говорить о таких занимающих широкие хроматические интер-
интервалы цветах, как зеленый, то вероятность того, что они окажутся
упомянутыми в наугад взятом предложении, является достаточно
большой. Однако по мере раздробления нашего цветового спектра
на все более частные оттенки вероятность появления обозначений
каждого из них будет уменьшаться. В конце концов мы придем к то-
тому, что хотя в каждом наугад взятом предложении и будет говорить-
говориться о каком-то цветовом оттенке, но вероятность появления конкрет-
конкретного оттенка будет равна нулю.
Таким образом, если считать непрерывной случайной величиной X
некоторое цветовое значение, то окажется, что при осуществлении
нашего опыта непрерывная случайная величина обязательно при-
примет одно из своих возможных значений, хотя до опыта вероятность
появления каждого из них была равна нулю. Иными словами,
* В одном из специальных английских словарей приводится около че-
четырех тысяч названий оттенков цвета [6, с. 130], число этих названий можно
увеличивать и дальше.
174
осуществится одно из событий, вероятность появления которого рав-
равна нулю. Поскольку частота события не равна, а лишь приближа-
приближается в большом количестве опытов к вероятности, то утверждение
согласно которому вероятность события X <=* х равна нулю, озна-
означает лишь, что при многократном повторений опыта это событие бу-
будет осуществляться сколь угодно редко.
7. Плотность распределения вероятностей. Применительно
к дискретным случайным величинам функция распределения яв-
является такой функцией, с помощью которой суммируются значения
Pi, выступающие в качестве элементов вероятности. Выясним те-
теперь, что является элементом вероятности непрерывных случайных
величин.
Для этого рассмотрим интервал [х, х + Ах] и определим вероят-
вероятность того, что случайная величина X попадет в этот интервал.
Согласно свойству 4 функции распределения имеем
Р (х < X < х + Ах) = F (х + Ах) — F (х).
Разделив вероятность Р (х ^ X < х + Ах) на длину интервала
Ах, получаем величину вероятности, приходящуюся на единицу
длины этого интервала:
Дх
Эту величину" будем называть средней плотностью вероятности
на данном интервале.
Если последовательно уменьшать интервал Ах, то в пределе
получим функцию
,. Р(л<Х<;
д*-*0 Л*
F.20)
называемую плотностью вероятности, или плотностью распреде-
распределения вероятностей.
Если в правую часть равенства F.20) вместо числителя подста-
подставить приращение функции F (х + Ах) — F (х), то получим выра-
выражение
Аде ..
из которого следует, что плотность вероятности является произ-
производной от функции распределения (см. гл. 3, § 1).
Отсюда следует, что функцию распределения можно опреде-
определить и через плотность вероятности. С одной стороны, по формуле
D.25) имеем
175
С другой стороны, в силу свойства 4 функции распределения нахо-
находим
ь
Полагая а = — оо, Ь = х, преходим к функции распределения:
F.21)
Таким образом, дифференциальная функция f (x) и интегральная
функция F (х) взаимно определяют друг друга.
Плотность распределения, так же как и функция распределе-
распределения, является одной из форм закона распределения. Однако, если
функция распределения является универсальной характеристикой
закона распределения как дискретных, так и непрерывных случай-
случайных величин, то плотность распределения характеризует только
непрерывные случайные величины.
Плотность распределения вероятностей обладает двумя основ-
основными свойствами:
1. Плотность распределения неотрицательна для всех х, т. е.
f (х) > 0.
2. Интеграл от плотности распределения f (x), взятый'по всему
интервалу возможных значений случайной величины, равен единице,
т. е.
J f{x)dx=\.
Геометрическая интерпретация свойств функций / (х) и F (х)
сводится к следующему:
а) график плотности вероятности является непрерывной кривой,
и в силу неотрицательности плотности эта кривая лежит выше
оси абсцисс;
б) полная площадь, ограниченная кривой, равна единице;
в) сама кривая асимптотически приближается к оси абсцисс
при условии, что случайная величина может принимать все значе-
значения числовой оси или все значения полупрямой.
В тех случаях, когда расстояние между значениями дискрет-
дискретной случайной величины (интервал, единица измерения) достаточно
мало по сравнению с самой наблюдаемой величиной, бывает удобно
рассматривать данную величину в качестве непрерывной случай-
случайной величины. Такой подход может заметно упростить решение не-
некоторых лингвистических задач.
Примером может служить использование непрерывной функции
Вейбулла для вычисления дискретных накопленных вероятностей
в частотном списке слов, словоформ и словосочетаний [6, с. 136,
1 о7 J.
176
Исходное выражение функции Вейбулла имеет вид
p; = l—e-rf*, F.22)
где р* — накопленная вероятность i-Pi словоформы, с и k — ко-
коэффициенты распределения. Значения этих коэффициентов для раз-
различных частотных списков показаны в табл. 6.5.
Таблица 6.5
Значения коэффициентов с и k относительно некоторых
языков и стилей
1
2
3
4
5
6
7
8
9
ю
11
12
Язык или подъязык
Русские деловые тек-
тексты
Русские деловые тек-
тексты
Английские корабель-
корабельные тексты
Английские тексты по
сельхозтехнике
Английские тексты по
электронике
Английские тексты по
электронике
Немецкие публицисти-
публицистические тексты
Немецкие публицисти-
публицистические тексты
Немецкие публицисти-
публицистические тексты
Немецкие тексты по
электронике
Румынский и молдав-
молдавский
Румынские публици-
публицистические тексты
Единицы подсчета
Словоформы
Основы
Словоформы
Именные трехсловные
сочетания
Трехсловные сочета-
сочетания
Именные трехсловные
сочетания
Словоформы
Трехсловные сочета-
сочетания
Именные трехсловные
сочетания
Трехсловные сочета-
сочетания
Слова
Трехсловные сочета-
сочетания
с
0,05357
0,07057
0,15532
0,01815
0,01244
0,01076
0,15534
0,00585
0,02813
0,01355
0,17331
0,00594
*
0,44640
0,48440
0,33040
0,41556
0,41062
0,47471
0,28850
0,45486
0,39088
0,38860
0,29540
0,55741
Используя выражение F.22), можно получить также значения
вероятностей лингвистических единиц, находящихся на t-м месте
в частотном списке. К этим значениям можно прийти либо через
плотность распределения
Х =(\—е-¦"*)' «cftt*-1 e~clk = pt,
F.23)
либо с помощью равенства
рг = /?;_! — р; = в-с (<-«*_ е-«\ F.24)
Так, например, применяя соотношение F.23) и опираясь на дан-
данные табл. 6.5, нетрудно показать, что вероятность словоформ
с t = 10 в частотном списке словоформ из русских деловых текстов
составляет
pla = 0,05357-0,4464.
0,006-
177
К аналогичному результату можно прийти, используя соотно-
соотношение F.24):
Ло = 2.7183-0'05357 •9
= 0,8670—0,8602 = 0,0068 да 0,006.
8. Характеристики распределения случайной величины, функ-
функция распределения, ряд распределения и плотность распределения
наиболее полно и исчерпывающе характеризует дискретную или не-
непрерывную случайную величину. Однако расчеты, связанные с опре-
определением этих характеристик, весьма сложны и громоздки.
Обычно масса вероятности случайной величины X сосредоточена
в большей своей части внутри относительно узкого интервала зна-
значений случайной величины (см. рис. 39 и 40). Определив положе-
положение и характер этого интервала, мы получаем достаточно точное
представление о распределении в целом. Эту задачу можно решить,
используя усредненные числовые характеристики распределения —
моменты, которые в сжатой, компактной форме указывают на
наиболее существенные свойства распределения. Начнем рассмотре-
рассмотрение этих характеристик с математического ожидания.
Математическое ожидание указывает на центр группировки
значений случайной величины. Для дискретной случай-
случайной величины математическим ожиданием называется сумма
произведений всех возможных значений случайной величины на их
вероятности:
N
2
г= о
Понятие математического ожидания распространяется и на не-
непрерывные величины: математическим ожиданием непре-
непрерывной случайной величины называется интеграл от произведения ее
значений х на плотность распределения вероятностей f (x), т. е.
M(X)= f xf(x)dx.
F.26)
Математическое ожидание обладает следующими свойствами,
имеющими принципиальное значение при решении лингвистических
и инженерно-лингвистических задач:
1. Математическое ожидание постоянной (неслучайной) вели-
величины С равно ей самой, т. е.
М (С) - С.
F.27)
2. Математическое ожидание произведения постоянной вели-
величины С на случайную величину X равно произведению постоянной
на математическое ожидание этой Случайной величины, т. е.
М (СХ) = СМ (X).
F.28)
Из свойств 1 и 2 вытекают два следствия:
а) математическое ожидание суммы постоянной величины и
случайной величины равно сумме постоянной С и математического
ожидания случайной величины М(Х), т. е.
М (С + X) = С + М (X);
F.29)
б) математическое ожидание линейной функции Y » Ь + аХ
равно сумме постоянной Ь и произведения постоянной а на математи-
математическое ожидание случайной величины X, т. е.
М (Y) ~
(X).
F.30)
3. Математическое ожидание суммы случайных величин Хх, Хг,
Хз, ..., Хп равно сумме их математических ожиданий, т. е.
М
= М
(Х2)
п). F.31)
Из этого свойства вытекает такое следствие: математи-
математическое ожидание разности случайных величин равно разности их ма-
математических ожиданий, т. е.
М (X — Y) = М (X) — М (Y).
F.32)
4. Математическое ожидание попарно независимых случайных
величин Xlt Xit ..., Хп равно произведению их математических
ожиданий, т. е.
М (Х1Хг ... Хп) = М (X,) М(Хг) ... М (Хп).
F.33)
Разброс возможных значений случайной величины вокруг ее
центра — математического ожидания — характеризуется теорети-
теоретической дисперсией (или просто дисперсией), которую можно опреде-
определить как математическое ожидание квадрата отклонения случайной
величины от ее математического ожидания:
D {Х)=М[Х — М {Х)\\
F.34)
Теоретическая дисперсия для дискретной случайной величины
вычисляется по формуле
F.35)
F.36)
Для непрерывной случайной величины дисперсия равна
+»
D(X)=o2= J [х—M(X)ff{x)dx.
178
'Теоретическая дисперсия имеет размерность квадрата случай-
случайной величины. Между тем из соображений наглядности в оценке
рассеивания удобнее пользоваться величиной, размерность которой
совпадает с размерностью случайной величины X. Это достигается
179
путем извлечения квадратного корня из дисперсии, в результате
чего получается среднее квадратическое отклонение:
о = УТ>Щ. F.37)
Величина а имеет ту же размерность, что и математическое
ожидание случайной величины. Это дает возможность оценивать
степень вариации в данном распределении с помощью коэффициен-
коэффициента вариации:
V(a) =
М(Х)
100%.
Дисперсия характеризуется следующими свойствами:
1. Дисперсия постоянной равна нулю, т. е.
D (С) = 0.
F.38)
F.39)
2. Постоянную можно вынести за знак дисперсии, возведя ее
в квадрат, т. е.
D (СХ) = C*D(X). F.40)
3. Увеличение (уменьшение) случайной величины на одну и ту
оке постоянную величину С не изменяет дисперсии, т. е.
D (X + С) = D (X). F.41)
4. Дисперсия случайной величины равна математическому ожи-
ожиданию квадрата случайной величины без квадрата ее математическо-
математического ожидания, т. е.
D (X) = М (X2) — [М (X)]2. F.42)
5. Дисперсия суммы конечного числа попарно независимых слу-
случайных величин равна сумме их дисперсий, т. е.
D (Хх + Х2 + ... + Хп) = D (XJ + D (Х2) + ... + D (Хп).
F.43)
Дисперсия и математическое ожидание, с которыми мы только
что познакомились, являются частными случаями понятия м о- „
мента, т. е. характеристики вида распределения.
Существует несколько видов моментов. .
Моментом Н-го порядка случайной величины X называется мате-
математическое ожидание h-й степени отклонений случайной величины
от постоянной а, выступающей в качестве произвольно фиксирован-
фиксированного начала отсчета, так называемого условного нуля.
При решении вероятностных лингвистических задач обычно
используются моменты первых пяти порядков (h — 0, 1, 2, 3, 4):
v'o(a) = M(X—а)°=\ (момент нулевого порядка)}
а) ( » первого » );
-аJ ( » второго » );
-аK ( » третьего » );
-яL ( » четвертого » ).
180
Если а = 0, то момент называется начальным и записывается
в общем виде так:
vh=M(Xh).
Запишем выражения для начальных моментов первых пяти по-
порядков:
v0 = М(Х°) = 1 (начальный момент нулевого порядка);
Vl = M(X) ( » » первого » );
v2 — M(X2) ( » » второго » );
v3 — M(X3) ( '¦» » третьего » );
\4 — М(Х*) ( » » четвертого » ).
Нетрудно заметить, что начальный момент первого порядка есть
не что иное, как математическое ожидание случайной величины X.
Если в качестве начала отсчета взято математическое ожидание
случайной величины, т. е. если а — М (X), то момент называется
центральным. В общем виде центральный момент записывается так:
\xh = М IX — М (Х)\н. F.44)
Между центральными и начальными моментами существует пря-
прямая связь, передаваемая следующей зависимостью:
F.45)
Из соотношения F.45) получаем выражения для первых пяти
центральных моментов:
ц0 = 1 (центральный момент нулевого порядка);
fii = 0 ( « « первого « );
\ii = vi—v? ( « « второго « );
Vb — Va—3vav1 + 2v? ( « « третьего « );
v.iv\—3vf (« « четвертого « ).
Центральный момент первого порядка, равный нулю, представ-
представляет собой математическое ожидание случайной величины X при
условии, что а = М (X).
Центральный момент второго порядка является дисперсией
случайной величины:
2 = v2 - v? = М (Хг) - Ш
= D (X) = а2. F.46)
Отношение центрального момента А-го порядка к h-Pt степени
среднего квадратического отклонения <г называется нормированным
моментом. В общем виде нормированный момент записывается
следующим образом:
AV) 6.47?
181
Для нормированных моментов первых четырех порядков имеем:
Pi = 0 (нормированный момент первого порядка);
Ра «= 1 ( « « второго « );
ps «=» ps'cr9 ( « « третьего « );
J* ( *
второго
третьего
четвертого
)
).
Нормированный момент третьего порядка, называющийся иног-
иногда коэффициентом асимметрии, характеризует «скошенность»
распределения.
Если распределение симметрично относительно а — М (X),
то центральный момент третьего порядка цз (как и вообще все
центральные моменты нечет-
нечетных порядков) равен нулю,
в связи с чем коэффициент
асимметрии р3 = цз/ст3 = 0.
Если же рз>0, то график
распределения характеризует-
характеризуется правосторонней (положи-
(положительной) скошенностью. При
, Рз < 0 имеем левостороннюю
(отрицательную) скошенность.
Четвертый нормирован-
ный момент используется
в качестве характеристики
«крутизны» (островершинно-
V ста или плосковершинности).
\ /р. Для наиболее важного с точ-
•. j \ ки зрения лингвистики рас-
_\ /r \ пределения — нормального
распределения (см. ниже, § 3,
п. 4) — выполняется равен-
равенство
зооо Гц р4 = fi4/cr* = 3. F.48)
woo
2000
,300014
о,з-
0.2-
¦0,1-
1000 2000
5)
Рис. 42
Для распределений, от-
отличающихся от нормально-
нормального более острой вершиной,
р4 > 3; напротив, распределения с более плоскими вершинами
(или имеющие «выемку» в центре) дают р4 <С 3.
Понятия «скошенности» и «крутизны» иллюстрирует рис. 42.
На рис. 42, а изображена эталонная кривая нормального распреде-
распределения, а на рис. 42, б — кривые распределения относительных
частот значений (в Гц) первых трех формант (Ft, F2, F») русских
гласных.
Наряду с четвертым нормированным моментом для измерения
крутизны распределения используется величина
?«р4—3, [F.49)
называемая эксцессом (или куртозисом).
182
Наиболее важными при описании распределений, использую-
использующихся в языкознании, являются следующие моменты: vx ==
= М (X) = а, у2 = D (X) « о\ рз, р4.
§ 3. Законы распределения, моделирующие образование
языковых единиц текста
В теории вероятностей известны десятки законов распределения
случайной величины. Задача квантитативной лингвистики состоит
в том, чтобы найти среди них такие законы, которые могли бы вы-
выступать в качестве наиболее адекватных математических моделей
порождения текста и составляющих его языковых единиц.
1. Биномиальное распределение. Исходной схемой при построе-
построении многих законов распределений является уже знакомое нам би-
биномиальное распределение
которое характеризуется следующими параметрами:
а) математическим ожиданием (начальным моментом первого
порядка)
М(Х) = Np; F.50)
. б) дисперсией (центральным моментом второго порядка)
D{X) = Npq F.51)
и средним квадратическим отклонением
a = VNpq\ F.52)
в) коэффициентом асимметрии
p3 = (q—p)lV^Npq\ F.53)
г) четвертым нормированным моментом
р4 = A—6pq + 3Npq)l(Npq) F.54)
и соответственно эксцессом
Е = р4 - 3=A — bpq)/(Npq). F.55)
Если частость f = XIN, так же как и случайная величина, рас-
распределена по биномиальному закону, то значения математического
ожидания, дисперсии и среднего квадрэтического отклонения та-
таковы:
-.A-.Np = p, F.56)
^Л-.Npq^-^-, F.57)
'*-• F.58)
183
Как уже говорилось, это распределение может быть использо-
использовано при описании употребления фонем, графем и их классов, а так-
также грамматических категорий при условии, что величины N и х
не очень велики. Однако в конкретных лингвистических задачах эти
условия обычно не соблюдаются, поэтому вместо биномиального
распределения приходится использовать другие аппроксимирующие
его распределения.
2. Распределение редких лингвистических единиц (распределе-
(распределение Пуассона). Будем рассматривать последовательные появления
интересующей нас языковой единицы А в тексте Т в качестве потока
лингвистических событий. Примерами такого потока могут слу-
служить последовательные появления в русском связном тексте слова
море в различных его формах, или словоформы моря, или словосо-
словосочетания у самого синего моря и т. п.
Поток лингвистических событий называется простейшим в том
случае, когда выполняются следующие условия:
1) если разбить текст Т на N отрезков равной длины, то вероят-
вероятность появления лингвистических событий в отрезке t = TIN за-
зависит только от длины этого отрезка (но не от начала отсчета). Это
условие позволяет оперировать вероятностью Р (х) того, что в лю-
любом отрезке t лингвистическая единица А появится ровно х раз
(х = 0, 1, 2, ...);
2) вероятность появления лингвистической единицы А практи-
практически не зависит от того, сколько раз употреблялась единица А до
этого в тексте и употреблялась ли она вообще. Такое предположение
оказывается вполне корректным для редких лингвистических еди-
единиц, поскольку валентности этих единиц распространяются не бо-
более чем на семь значащих шагов (обычно словоформ) текста [23, с.58];
3) вероятность наступления двух и более лингвистических со-
событий в бесконечно малом отрезке текста / есть бесконечно малая
величина более высокого порядка, чем величина t. Например, раз-
разбив текст тяа равные отрезки длиной в десять букв каждый, мы мо-
можем считать ничтожно малой вероятностью появление в одном от-
отрезке двух словоформ моря;
4) при дальнейшем уменьшении отрезка t вероятность наступ-
наступления одного лингвистического события убывает пропорционально
длине t. Таким образом, чем меньше интервал, тем меньше, вслед-
вследствие малости интервала, вероятность появления лингвистической
единицы А.
Из всего сказанного следует, что неограниченное уменьшение
р и t пропорционально неограниченному увеличению N. В связи
с этим произведение вероятности р и числа отрезков N (объема вы-
выборки), представляющее собой математическое ожидание случайной
величины, является постоянным:
М (X) = Np = X.
Отсюда р = %/N. Подставляя это значение в формулу биномиаль-
биномиальной вероятности [см. соотношение F.1)], получим
184
х\
N N N—l N—x+1
\ \N N N—l
NJ N N '"
N
где
lim Л — А
\ N
N-+oo
= 1,
а предел каждого члена
.. N-m .
lim —-—• = 1.
N-*oo N
В итоге получаем
N
¦ т
{т — О, 1,..., х — 1) составляет
lim
или
—e-x.
F.59)
Это и есть формула распределения Пуассона, использующаяся
для описания употребления редких лингвистических единиц. Един-
Единственным параметром этого распределения является величина К,
В лингвистических приложениях К есть среднее число употребле-
употреблений интересующего нас языкового элемента в тексте. Аргумент х —
обычно это число употреблений лингвистической единицы — при-
принимает значения 0, 1, 2, ... .
Аналитическое выражение распределения вероятностей Р (х, К)
показано в табл. 6.6.
Таблица 6.6
х\
N\
Распределение Пуассона характеризуется следующими парамет-
параметрами:
а) математическим ожиданием (начальным моментом первого
порядка), дисперсией (центральным моментом второго порядка),
а также центральным моментом третьего порядка, равными i:
М (X)=D (X) = ii3 = K, F.60)
и среднеквадратическим отклонением
F.61)
185
б) коэффициентом асимметрии
Р з ~ "' (г ™) =
в) четвертым нормированным моментом
р4 = (ЗА, + 1)А
и эксцессом, равным
Л»
F.62)
F.63)
-. F.64)
При малых значе-
значениях А, распределение
сосредоточено вблизи
начала координат. С
ростом А, оно приобре-
приобретает колоколообразную
форму с правосторонней
скошенностью (рис. 43).
При больших значениях
параметра % (А, ^ 10)
распределение Пуассо-
Пуассона приобретает форму
нормального распреде-
распределения при М (X) = А, и
D (X) = а2 = К.
Как и при биноми-
биномиальном распределении,
вычисление вероятно-
вероятностей пуассоновского
распределения удобно
начинать с определения
моды х0 и соответствующей ему модальной вероятности Р (х0, А,).
Рассмотрим в этой связи поведение аргумента х в нашем распреде-
распределении. Из равенства
0,5
ол
0,3
0,2
0,1
А-4/7
1
8
Рис. 43. Распределение Пуассона при различ-
различных значениях параметра X:
¦ кривые распределения Пуассона
при ^=0,5; 1,0; 4,0; о о о кривая
распределения вероятностей появления в не-
немецком тексте сегмента Adafl die (A,= l,17)
Р(х, X)
(к-1, X)
е~Чх\
Xх-1 е~х
¦1)!
X
F.65)
видно, что если дс> А,, то Р (х, А,)< Р (х — 1, А,); если же х < А,,
то Р (х, К) > Р (х — 1, А,); наконец, если х = А,, то Р (х, %) =
—Р (х— 1, Я). Ясно также, что Р (х, А,) возрастает при увеличении х
от нуля до х0 = Ш и* убывает при дальнейшем росте х. В том слу-
случае, когда Я является целым числом, Р (х, А,) имеет два модальных
значения: при х0 = А, и при хо = А, — 1; в том же случае, когда
% — дробное число, Р (х, К) имеет одно модальное значение при
х0 "= Ш.
Определив таким образом модальное значение х0 = Ш, найдем
его вероятность по формуле
F.66)
Вычисление остальных вероятностей осуществляется по рекур-
рекуррентным формулам, вытекающим из F.65):
при х < х0
Р(хо-\, А,) =
Р(хо-2, Я,)=
о, X),
-1, X),
F.67а)
при х > х0
Р(хо+1, %) =
Р(х0, X),
F.676)
В лингвистике, как уже говорилось, используется бесповторное
статистическое исследование, при котором текст разбивается на S
выборок (серий), каждая длиной в N лингвистических элементов.
При этом бывает необходимо определить теоретически ожидаемое
число серий STX, в которых лингвистический элемент А появится
ровно х раз.
Пользуясь рассуждениями, приведенными в п. 3 § 1 относительно
биномиального распределения, нетрудно показать, что
J
х\
F.68)
где S выступает-в качестве коэффициента пропорциональности, свя-
связывающего величины SJ и Р (х, А,), а
Символом [X] обозначена целая часть значения X.
Рассмотрим в связи с этим следующий пример. В немецких пуб-
публицистических текстах осуществлена выборка 100 серий по 1000
трехсловных сегментов. Используя данные, приведенные в табл. 6.7,
определим теоретическое пуассоновское распределение вероятностей
появления сегментов Adap der (начало дополнительного придаточ-
придаточного предложения с существительным в начальной позиции) в одной
серии и теоретическое количество серий STX, содержащих поО, 1,2,...
таких сегментов.
186
187
Таблица 6.7
Пуассоновское распределение вероятностей появления сегмента
A daE der в немецких публицистических текстах
Число появ-
появлений события
X
0
1
2
3
4
5
Эмпирические
частоты
появления
выборок Sx
32
38
19
5
4
2
Теоретически
ожидаемое
число выборок
31,04
36,28
21,24
8,28
2.42
0,57
*г
округленное
до целых
чисел
31
36
21
8
3
1
Частость
Q
fx
-S
0,32
0,38
0,19
0,05
0,04
0,02
Вероятность
Р {х, %)
-
0,3103
0,3628
0,2123
0,0828
0,0242
0,0057
Суммы | 100 |
Сначала вычислим значение
о - 1
100
1,00
0.9981
@-32+1-38 +2-19 + 3-5+ 4-4+ 5-2) =
100
1 C8 + 38+15+16+10)= Ш
100
100
1,17.
Модальное значение х0 равно целой части значения X, т. е. еди-
единице.--Значение Р (х0, X) будем искать с помощью табл. I, помещен-
помещенной в Приложении (см. стр. 362, 363). В этой таблице значения ве-
вероятности, соответствующей К = 1,17 и х = 1, нет. Поэтому, обра-
обращаемся к. интерполяции. Для этого берем значения Р A; 1,1) =
= 0,36616 и Р A; 1,2) = 0,36143; тогда искомая вероятность
РA; 1,17)^-0,36143+ °-36616-°-36143.3==
= 0 36143 +
0,00473
10
•3 = 0.3628.
После этого, используя рекуррентные формулы F.67), так, как
это показано в п. 3 § 1, находим по табл. I остальные значения
Р (х, X). Затем, с помощью выражения F.68) получаем значения ST
которые также приведены в нашей таблице.
Степень близости теоретического и эмпирического распределе-
распределений, приведенных в табл. 6.7, мы рассмотрим ниже.
В разделе, посвященном биномиальному распределению, уже
говорилось о том, что как с прикладной, так и с теоретико-языко-
теоретико-языковедческой точки зрения важно уметь определять вероятность появ-
появления лингвистического элемента от а до b раз. В этом случае имеем
А.) =
Xх
а-\
188
Весь ход решения этой задачи и ее частные случаи аналогичны
процессу решения, описанному в п. 7 § 1 с той лишь разницей, что
биномиальные вероятности заменяются пуассоновскими.
Таким же способом определяется вероятность появления редко-
редкого лингвистического события хотя бы один раз. Она равна
Р (х > 1, X) = 1 _ р (х & 0, X) = 1 — е
F.69)
Отсюда по схеме, описанной в п. 8 § 1, рассчитывается объем вы-
выборки N, необходимый для того, чтобы обеспечить с заданной ве-
вероятностью появление хотя бы один раз определенного лингвисти-
лингвистического элемента.
С этой целью приведем выражение F.69) к виду
е"р = 1 _ р
1, X),
а затем, прологарифмировав обе части и произведя необходимые
преобразования, получим
N_
F.70)
Используя приведенные выше числовые характеристики слово-
словоформы напряжение, определим объем текста, необходимый для того,
чтобы указанная словоформа с вероятностью в 90% появилась в нем
хотя бы один раз (предполагается, что в данном случае имеет место
распределение Пуассона).
Применяя соотношение F.70), находим
д,_ Ig A-0,90)
0,0023 lge
IgO.lQ
—0,0023-0,44
—0,001
= 1000.
Заметим, что объем необходимой выборки здесь тот же, что и в том
случае, когда мы предполагали, что словоформа напряжение имеет
биномиальное распределение (ср. § 1, п. 8).
3. Распределения, описывающие взаимодействие случайных и
детерминированных процессов в речи (распределения Чебанова —
Фукса и Фукса — Гачечиладзе). Применяя биномиальное и пуассо-
пуассоновское распределение для исследования поведения дискретных
лингвистических единице речи, мы исходили из предположения, что
речь представляет собой простейший поток лингвистических собы-
событий. Однако этот подход, представляющий собой очень грубую и уп-
упрощенную аппроксимацию лингвистических явлений, имеет ограни-
ограниченное применение в лингвистике. Выше уже говорилось (см. гл. 5),
что формирование слов, словосочетаний, предложений, высказы-
высказываний представляет собой взаимодействие как случайных, так и де-
детерминированных процессов. Случайными с лингвистической точки
зрения являются описываемые текстом ситуации объективной дей-
действительности, детерминированными же представляются некоторые
правила системы и нормы языка. Поэтому для описания образова-
образования лингвистических единиц и их распределения в тексте следует
189
применять такие распределения, которые учитывали бы взаимодей-
взаимодействие этих случайных процессов и детерминированных правил.
Одним из простейших распределений, описывающих лингво-
статистическую структуру, возникающую из комбинации абсолютно
случайного и абсолютно детерминированного процесса, является
распределение Чебанова — Фукса.
Это распределение строится исходя из следующих рассужде-
рассуждений. Наряду с бескомпонентными лингвистическими величинами,
т. е. с такими дискретными величинами, которые могут принимать
любое положительное целочисленное значение, а также значение
нуль [т. е. Р @) > 0], в языке в основном функционируют небесном-
понентные величины, которые согласно законам системы языка ни-
никогда не могут принять значение нуль. К таким величинам отно-
относятся, например, длины слогов (силлабографов), морфем, слов, пред-
предложений и т. п. Действительно, каждый слог состоит, по крайней
мере, из одной фонемы, а каждое слово состоит, по крайней мере,
из одного слога или морфемы [здесь Р @) Ф 0]. Таким образом,
небескомпонентная случайная лингвистическая величина может
принимать значения 1, 2, 3, ... .
Если небескомпонентная случайная величина встречается до-
достаточно редко в тексте, то распределение вероятностей ее значений
в тексте может быть описано с помощью распределения Пуассона
при условии, что заданный системой языка обязательный элемент
будет исключен из рассмотрения. Иными словами, вместо аргумен-
аргумента х следует взять разность х — 1, а вместо средней к — разность
к—1. Учитывая эти условия, получаем равенство
и средним квадратическим отклонением
Р(х, k—
*—1I
F.71)
представляющее собой формулу распределения Чебанова — Фукса.
Аналитическое выражение вероятностей Р (х, к — 1) показано
в табл. 6.8.
Таблица 6.8
X
1
«-«-„
2
?!?
3
2 Л
...
...
1
(х-1I Х
...
Л
(tf-l)l Л
...
Распределение Чебанова — Фукса характеризуется следующими
параметрами:
а) первым начальным моментом (математическим ожиданием)
Vl = М (X) = к;
б) вторым центральным моментом (дисперсией)
|ха =i D (X) «• к — 1
F.72)
F.73)
F.74)
в) коэффициентом асимметрии
г) четвертым нормированным моментом
р4 = 1/(Х - 1) + 3,
Е = 1/(К — 1).
и эксцессом
F.75)
F.76)
F.77)
Так же как и пуассоновское распределение, распределение Че-
Чебанова—Фукса определяется параметром к.
Поведение этого распределения точно соответствует поведению
распределения Пуассона с учетом сдвига на одну единицу: при ма-
малых значениях к распределение
имеет острую вершину и сосре- Р(х,Х-1)
доточено около прямой х — 1. о,7-
С ростом к оно постепенно при-
приобретает более пологую колоко- 0,6
лообразную форму с правосто-
правосторонней скошенностью, которая
уменьшается по мере роста к
(рис. 44).
С помощью распределения
Чебанова — Фукса делались по-
попытки описать вероятностный
процесс образования слов из
слогов и морфем по различным
языкам. Теоретические и эмпи-
эмпирические данные по распреде-
распределению вероятностей слоговых
длин слов показаны в табл. 6.9,
а распределение вероятностей
7 X
морфемных длин — в табл. 6.10.
Легко заметить, что экспери-
экспериментальные результаты дают
иногда отклонения от теоретичес-
190
Рис. 44. Распределение Чебанова —
Фукса при разных значениях параме-
параметра X:
А,=2,00;
А. = 1,35 (распределение
вероятностей слоговых
структур английского
слова).
ких оценок, на это указывают, Я=2,54 (распределение
в частности, высокие значения вероятностей слоговых
сумм абсолютных величин ли- структур грузинского
нейных отклонений для слоговой слова),
структуры румынского и араб-
арабского слова, а также для морфемной структуры английского слова.
Эти расхождения опытных данных и теоретической модели го-
говорят о том, что распределение Чебанова—Фукса нельзя рассматри-
рассматривать в качестве универсального закона, описывающего основные
свойства процесса образования лингвистических единиц.
191
&
а,
<
a
о
ь*
о
ч
и
в
в
о
о
S
н
к
о
о.
X
ш
ч
и
=(
V
с.
с
а
вн<3оэх
•<1»иэие
Biidoax
ООСЧ-^'СО'-'ЮСО^-*
со — ос*© —оо
C-1COCN—1ОООО
COO—<C7JC0-*O<
MONOOOOl
«o — 05 05 ч< 00 ~h
nra-oooo
о'о о*10*0 о'о*
иамюоо<
<N Ч« <N О О О <
W Ш — ^ *-< 1O N
CO CO О t^ CN О О
лпиоооо
06 cn <n t^- a> t
СО I4- ¦*? t~- CO (
OD Щ N 1O -> О
nn-ooo
to 00 ¦* со t-~ im
LO С O^ CO О Cj
1O CO О О О О
о"о"оооо
<М (О <?l СЧ rf —1
со со о см о о
юп-ооо
о'о'оооо
Ю •& 00 <О <?>
t-~i— о ОО О
ю со со ю ^^ о
с~) ^* ^j« Q СЭ Ф
NMOOOO
о о о"ооо"
0,0,0,0,0,0,0,0,
с*
о
о"
о
СО
о
S
CN
о
о
я 5
>1
00
CN
S
S
о
г-
э
¦а
3
Таблица 6.10
Распределение вероятностей морфемных структур слов
в английском и русском языках*
^\. Языки
Р(Х) \ч^^
(Ч
РA)
РB>
РC)
РD)
РФ)
РF)
РG)
Р(8)
X, (в морфемах)
Сумма абсолютных
величин линейных
отклонений
И (дв. ед.)
Английский
Теория
Распределение
Чебанова—
Фукса
B)
0,246
0,346
0,242
0,112
0,039
0,011
0,003
0,001
Распределение
Фукоа—Гаче-
чиладзе
C)
0,109
0,500
0,285
0,084
0,022
0,000
0,000
0,000
Экспери-
Эксперимент
D)
0,113
0,549
0,238
0,090
0,007
0,002
0,001
0,000
2,41 '
0 3%
0,124
1
1.71
Русский
Теория
(8)
0,272
0,357
0,230
0,100
0,032
0,009
0,003
0,001
Экспери-
Эксперимент
F)
0,260
0,417
0,165
0,118
0,032
0,006
0,002
0,000
2,30
0,160
2,04
¦ Таблица составлена по данным, взятым из работы [23].
Очевидно, при описании процессов образования лингвистических
единиц нужно учитывать несколько задаваемых системой языка
детерминированных правил. Об этом можно, в частности, судить
по данным румынского языка, в котором поэтическая речь показы-
показывает иной спектр вероятностей для слоговых длин слова, чем это
имеет место в деловом стиле (см. табл. 6.11). Этим же, вероятно, объяс-
объясняется и большое расхождение экспериментальных и теоретических
данных в арабском тексте. Иными словами, процесс образования
лингвистических единиц характеризуется более тонкой статисти-
статистической структурой, чем та, которая представлена распределением
Чебанова—Фукса. Эту структуру более точно описывает обоб-
обобщенное распределение Фукса —Г ачечилад-
зе.
Основная идея распределения Фукса—Гачечиладзе состоит
в следующем. Лингвистические единицы определенного типа могут
включать не только один, но и 2, 3, ..., v обязательных элементов.
Тогда, исключая из распределения v обязательно присутствующих
элементов, мы приходим к распределению вероятностей появления
лингвистических единиц различной длины, которое имеет следую-
следующий вид:
Р (х, K—v) =
F.78)
192
7 Зак. 1287
193
Таблица в.Н
Распределение вероятностей длин слогов в разных стилях
румынского языка*
Подъязыки
ЯA)
Я B)
ЯC)
Я D)
Я E)
Я F)
Я G)
X (в слогах)
Сумма абсолютных
величин линейных откло-
отклонений
Н (дв. ед.)
Румынская поэзия
(Eminescu, Luceafarul)
Теория
0,549
0,329
0,099
0,019
0,004
0,000
Эксперимент
0,580
0,263
0,119
0,034
0,003
0,001
1,60
0,134
1,56
Румынский деловой стил»
(«Гражданский кодекс»)
Теория
0,301
0,360
0,217
0,086
0,026
0,007
0,003
Эксперимент
0,400
0,222
0,160
0,158
0,049
0,001
0,000
2,20
0,398
2,07
• Таблица составлена по данным, взятым из работы [56].
Дальнейшее рассуждение приводит к распределению еще более
общего типа. Предположим, что в некотором лингвистическом клас-
классе имеются лингвистические единицы, которые включают 0, 1, 2, ...
..., v языковых элементов. Среди этих единиц можно выделить еди-
единицы, образованные хотя бы из одного элемента, из двух, из трех,
..., из v и т. д. элементов.
Обозначим вероятность появления лингвистических единиц,
состоящих из 0, 1, 2, 3, ... элементов, через е0, статистический вес
единиц, образованных хотя бы из одного элемента, через ех, ..., вео
единиц, состоящих хотя бы из v элементов, через ev и т. д. Совокуп-
Совокупность параметров ev называется лингвистическим спектром образо-
образования языковых единиц с суммой этих параметров
оо
V=l
Далее все множество единиц данного типа (предложений, сло-
словосочетаний, слов, морфем, слогов) разбивается соответственно осо-
особенностям их образования на классы. Статистический вес класса
v характеризуется разностью ev — ev+1, указывающей вклад каж-
каждого детерминированного правила в процесс образования данной
лингвистической единицы.
Например, русское предложение может не иметь ни одного су-
существительного (Пошли\), может включать одно {Пошли в кино\),
два (Ребята, пошли в кино\), ..., v существительных. В этом случае
194
вес предложений, не имеющих существительных, характеризуется
разностью е0 — elf вес предложений с одним существительным ра-
равен ех — е2 и т. д. (е0 > ех > еа > ... > ^ > Sy+i...).
Все эти соображения, а также математические рассуждения,
изложенные в работе [32а, с. 114—1181, и приводят к формуле обоб-
обобщенного распределения Фукса ->-Гачечиладзе, имеющей вид:
(ev-ev-ц)
FJ9)
Величина X определяется опытным путем, методика вычисле-
вычисления весовых коэффициентов ev через первые три момента распреде-
распределения F.79) — см. ниже — описана в [32а]. Расчет коэффициента
ФУ (А, К, х), учитывающего влияние контекстного окружения, дан
в работе [48]. Конкретные лингвистические задачи решаются при
допущении, что
<pv {А, К,х) « 1.
Распределение Фукса—Гачечиладзе характеризуется следую-
следующими параметрами:
а) первым начальным моментом (математическим ожиданием)
vx = М (X) = К
б) вторым центральным моментом (дисперсией)
i ОО
+ 2 S еА
и средним квадратическим отклонением
F.80)
F.81)
F.82)
в) третьим центральным моментом
-2 2 ч-
*=1
*•=!
H>-s^)+'}k
F-83)
Выше уже говорилось о том, что распределение Чебанова—Фук-
Чебанова—Фукса плохо моделирует процесс образования английских слов из мор-
7* '
195
фем. Попробуем описать этот процесс с помощью распределения
Фукса—Гачечиладзе, используя при этом следующий е-спектр:
е0 = 0, 8х = 1, еа = 0,8, е3 = е4 = ... = 0.
Р(х,К-А)
I
Разность ех — е2 = 0,2 характеризует вклад в процесс одноморфем-
ных служебных слов, а разность е2 — е3 = 0,8 указывает на вклад
знаменательных слов, состоящих
из двух и более морфем. Сред-
Средняя "К = 2,41, коэффициент
q>v (А, %, 1) « 1.
При этих условиях распре-
распределение вероятностей разных
морфемных построений англий-
английского слова описывается сле-
следующим выражением:
х
х 0,2
^
+ 0,8-
Данные табл. 6.10 [ср. столб-
столбцы B), C) и D)], а также рис. 45
показывают, что распределение
Фукса — Гачечиладзе довольно
хорошо описывает распределение
вероятностей различных мор-
морфемных структур английского
7 д. слова. Если принять во вни-
внимание большее число членов
Рис. 45. Распределение вероятностей е.спектра т0 можно, вероятно,
длин английского слова в морфемах: пп«ит.гя РГ1ТР бопыирй йттичпгты
тдппртииргкяа кпивая Дроиться еще оольшеи олизости
теоретическая кривая
распределения Чебано-
ва —Фукса (Х=2,41);
теоретическая кривая
Ф
теоретического и эмпирического
распределений.
Следует иметь в виду, что
КилаГзГ *ЗЙ4Т Распределение Фукса - Гачечи-
1, е2=0,80);
о О о О о экспериментальные
ки
рр
ладзе включает в себя в виде
частных случаев некоторые из
рассмотренных выше дискрет-
дискретных распределений. Действи-
Действительно, полагая е0 = 1, е1 = еа = ... = ev = 0, т. е. считая, что
рассматриваемый тип лингвистических единиц однороден и не рас-
распадается на классы, а также учитывая тот факт, что образующие
этот тип единицы принадлежат к бескомпонентному типу, т. е. мо-
могут включать 0, 1, 2, ... элементов, в связи с чем А = 0, v = 0,
q>v(A, %, x)-*- 1, мы приходим к распределению Пуассона F.59):
-0)*-°
(«-0I
• 1
-Р(х,к).
Если же речь идет о небескомпонентных единицах [при условии,
что е0 = 0, % = 1, е2 = е8 = ... = ev = 0, откуда А = 1, v = 1,
q>v (А, К, х)-*- 1], то F.79) превращается в распределение Чебано-
ва—Фукса F.71).
4. Распределение непрерывных случайных лингвистических ве-
величин. Нормальное распределение. До сих пор мы рассматривали
распределения, описывавшие поведение в тексте дискретных слу-
случайных величин. В том случае, когда речь идет о лингвистических
процессах и явлениях, осуществляющихся в субстанции выражения
и субстанции содержания (см. гл. 1, § 3, п. 4), приходится иметь дело
с непрерывными случайными величинами, к которым только что
рассмотренные законы применены быть не могут. Распределение
этих величин описывается специальными законами, среди которых
наиболее важным является нормальное распре д.е ле-
лени е (иначе но рмальный закон, или закон Гаусса).
Нормальное распределение выступает в качестве предельного
закона, к которому при определенных условиях приближаются дру-
другие теоретические распределения. Рассмотрим в этой связи соотно-
соотношение биномиального и нормального распределений. Выше было
показано (см. §2, п. 5), что при бесконечном уменьшении интерва-
интервалов в гистограмме, изображающей закон распределения случайных
величин " (например, высот основных формант речевого звука или
чувствительности слуха относительно разных уровней интенсивности
звука), ломаная линия, ограничивающая сверху площадь гисто-
гистограммы, постепенно превращается в плавную кривую. Аналогичным
образом полигон биномиального распределения при бесконечном
увеличении объема выборки N и числа отдельных вероятностей Pn(x)
приближается к плавной кривой.. Это геометрическое представ-
представление интерпретируется с помощью локальной теоремы Муавра—
Лапласа: если вероятность появления события А в каждом из неза-
независимых испытаний постоянна и равна р (где 0 < р ¦< 1), а N -*-оо,
то произведение Y^Npq на вероятность Pn (x) появления события в
1
этих испытаниях ровно х раз стремится к выражению .
z —
x—Np
л/т
F.84)
Эту замену производят в целях упрощения расчетов в прикладных
задачах.
Так как в реальных лингвистических задачах число N хотя
и велико, но всегда ограничено, то на основании только что сформу-
сформулированной теоремы можно записать приближенное равенство
или
VNpq PN (x)
PN(X):
F.85)
где а == VNpq [14j с.74, и ел.].
196
197
Исходя из определения предела (см, гл. 2, § 1, п. 2), можно ут-
утверждать, что погрешность этого равенства есть бесконечно малая
величина, стремящаяся к нулю при неограниченном возрастании N.
Поэтому равенство F.85) и называют асимптотической формулой би-
биномиального закона. Использование приближенной формулы F.85)
для оценки вероятности Рм (х) значительно упрощает вычисление,
которое ведется здесь по следующей схеме:
1) вычисляют значения Np — ц, ~VNpq = а, 1/ст;
2) по формуле F.84) определяют значение z;
3) с помощью табл. II, помещенной в Приложении (см. стр. 364),
по значению z находят
^"г!/2; F-86)
4) умножив полученное значение ф (г) на 1/ст, получают значение
Pn (x).
Считая вероятность появления существительных в подъязыке
английской электроники равной 1/3 (см. § 1, п. 3), вычислим вероят-
вероятности появления существительных в английском десятисловном
сегменте ровно 0, 1,2, ..., 10 раз.
Здесь N — 10, р = f = 1/3, д = 2/3. Используя только что при-
приведенную схему, находим все Р'ц (х).
Ход вычисления иллюстрируется на примере расчета Р' C).
1) Определим
г
о =
V «•f!4
= 0,671.
2) Вычислим
1,491
3) Учитывая, что <р (г) — четная функция, т. е. ф (—г) = ф (г),
по табл. II находим
Ф (—0,224) = ф @,224) = 0,3891.
4) Определяем произведение
—4^ Ф (г) = 0,3891-0,671 = 0,2611.
VNpq
Остальные значения Р[о (х), вычисленные по этой же схеме,
приведены в столбце C) табл. 6.2 (см. стр. 154). Сопоставляя эти
вероятности с биномиальными вероятностями, нетрудно заметить,
что асимптотическая формула F.85) дает сравнительно небольшую
погрешность даже при небольших значениях N.
198
Поскольку Np = (a, a VNpq = а, перепишем F.85) в виде
P'N (х) = —L— е~ (*-«¦/<»«•> = / (х). F.87)
а ^/2я
Если равенство F.87) рассматривать в качестве дифференциаль-
дифференциального закона (плотности вероятности) нормального распределения,
то ему должен соответствовать, как было сказано в § 2, п. 5, некото-
некоторый интегральный закон (функция распределения). Таким инте-
интегральным законом нормального распределения является выражение
(х) = ' Г e-^-^>^
F.88)
Нормальное распределение имеет следующие параметры:
а) первый начальный момент (математическое ожидание)
vx = М (X) = ц F.89)
для ненормированной случайной величины и
=-i-M(x-^H0 F.90)
F.91 J
для нормированной случайной величины;
б) второй центральный момент (дисперсия)
щ = D (х) = аа
для ненормированной случайной величины и
LU = DI т=~ = 1
для нормированной случайной величины;
в) третий центральный момент, как и остальные нечетные мо-
моменты, для ненормированной и нормированной случайных величии
равен нулю:
00
1=8три J {х~*
F.92)
в связи с этим третий нормированный момент (коэффициент асим-
асимметрии) также равен нулю:
р3 = щ/о-3 = 0; F.93)
г) четвертый нормированный момент и эксцесс соответственно
равны
Р4 = (V*4 = 3, Е ~ ц4/а* — 3 = 0. F.94)
Поскольку коэффициент асимметрии и эксцесс (крутизна) нор-
нормального распределения равны нулю, дифференциальная форма
199
нормального закона характеризуется идеальной по симметрии и кру-
крутизне кривой. Эта кривая имеет колоколообразную форму, располо-
расположена над осью абсцисс и симметрична относительно ординаты, от-
отвечающей значению х = ц. Если у, =» 0, то центром распределения
служит начало координат.
При изменении величины р и сохранении значения а кривая,
не меняя своей формы, передвигается вместе с точкой \i по оси Ох.
При изменении величины а и сохранении значения ц, кривая, не
меняя своего положения, меняет свою форму. При больших значе-
значениях о кривая становится пологой, а при малых а кривая, сжимаясь
с боков, вытягивается вверх (рис. 46).
.е х
Мы уже говорили (см. § 1, п. 7), что при решении лингвистичес-
лингвистических задач часто возникает необходимость определить вероятность
того, что значение лингвистической случайной величины попадает
в некоторый числовой промежуток от а до Ь, т. е. найти
Рм (В'х) = PN (а < X < Ь) =
= PN (a) + Pn (а + 1) + ... + Pn (Ь — 1) + Ры Ф).
Такая задача легко решается с помощью формулы Бернулли в тех
случаях, когда N мало, а интервал от а до Ъ не очень широк. Если
же N велико, а интервал достаточно широк, использование указан-
указанной формулы приводит к чрезмерно громоздким вычислениям.
В этих случаях используется приближенная асимптотическая фор-
формула
F.95)
получаемая из интегральной предельной теоремы Муавра—Лапла-
Муавра—Лапласа, которая формулируется следующим образом.
200
Если вероятность появления события при каждом отдельном не-
независимом испытании постоянна и равна р @<р<1) и число испы-
испытаний N -*• оо, то предел вероятности того, что число х появлений
события заключено межд'у а = Np + zx VNpq и b = Np + z2VNpq,
равен
limP(a<X< b)--
JV-»oo
Легко показать, что здесь
а — Np a—ц,
F.96)
а—(х _ b—Np _ Ь—ц
! о * Z%~ yWp~q ~'
Решать конкретные лингвистические задачи с помощью формул
F.95) и F.96) нельзя, поскольку интеграл / e-z'^2dz является небе-
рущимся. Это затруднение преодолевается путем введения- вспомо-
вспомогательного равенства
е-*"'2 йг.
F.97)
Функция Ф (х) называется функцией Лапласа. В дальнейшем нам
понадобятся следующие ее свойства:
а) нечетность, т, е.
ф (_д) = _ф (Х).
б) монотонное возрастание, т.е.
Ф (хх) < Ф (ха), если хг < ха;
в) выполнение равенств
Ф @) = 0, Ф (— оо) = —1/2, Ф (+оо) = 1/2.
Значения функции Лапласа приведены в табл. III, помещенной
в Приложении (см. стр. 365).
Если воспользоваться теперь функцией Лапласа, то выражение
F.95) примет вид
F.98)
При помощи только что описанной процедуры решим следующую
лингвистическую задачу.
Опираясь на статистические данные [6, с.208], будем считать, что
вероятность появления в русском тексте согласного звукотипа после
согласного (комбинация ОС) равна 0,26, в то время как появление
гласного после согласного (группа СГ) равняется 0,74. Группы ГС
201
и ГГ при этом в расчет не принимаются. Определим вероятность то-
того, что среди 500 случайным образом выбранных комбинаций СС
и СГ окажется: а) от 120 до 150 звукокомбинаций СС; б) не менее
121 звукокомбинаций СС; в) не более 150 звукокомбинаций СС; г) не
более 119 звукокомбинаций СС; д) не менее 151 звукокомбинаций
СС.
Прежде всего заметим, что комбинации СС и СГ составляют пол-
полную группу событий, т. е. если СС принять за событие А, то СР
будет событием А. Таким образом, по условию имеем:
Р(А) = р = 0,26; Р{А) = q = 0,74; N = 500; а = 120; b = 150.
Найдем теперь пределы интегрирования:
a—Np 120—500-0,26 —10
Z, =
Zo, — '
У 500.0,26-0,74 9,808
p __ 150—500-0,26
= -1,02,
VNpq /500-0,26-0,74
= 2,04.
Из табл. Ill находим, что Ф B,04) = 0,4793, а Ф (—1,02) =*
~ — Ф A,02) = —0,3461, откуда имеем
Р A20 С X < 150) = 0,4793 + 0,3461 = 0,8254.
Аналогичным образом получаем ответы и к п. б) — д) данной
задачи. В результате имеем:
Р (X > 121) = 0,8212; Р (X < 150) = 0,9793,
Р (X < 119) = 0,1314; Р (X > 151) = 0,0162.
Правильность полученных ответов предлагается проверить чи-
читателю.
5. Логнормальное распределение вероятностей длин текстовых
словоупотреблений. Реальные распределения случайных лингвис-
лингвистических величин, характеризующиеся обычно правосторонней
асимметрией, плохо аппроксимируются нормальным законом. В
связи с этим делаются попытки моделировать эти эмпирические рас-
распределения с помощью распределений Кэпптейна, Шарлье [30], вы-
выравнивающих кривых Пирсона и Бородачева [32в, с. 335—360].
Такое моделирование должно опираться не на внешнее сходство
опытной и теоретических кривых — его следует осуществлять,
исходя из лингвистической сущности случайного явления или про-
процесса, приводящего к тому или иному закону распределения. С этой
точки зрения наибольший интерес представляет логарифми-
логарифмически-нормальное (логнормальное) распре-
распределение.
Основная идея лингвистического приложения логнормального
распределения состоит в следующем.
Значение случайной лингвистической величины X обычно скла-
складывается не из независимых внутриязыковых и экстралингвисти-
202
ческих величин, как это имеет место в случае нормального распреде-
распределения. Чаще всего эти значения являются результатом действия
ряда причин, производящих последовательные «импульсы», причем
эффект этих импульсов зависит, с одной стороны, от интенсивности
самих импульсов, а с другой — от величины Хг созданной дейст-
действием предыдущих импульсов. В этом случае нормально распределе-
распределена не сама случайная величина X, а ее логарифм In X [42, с. 132—
133].
Дифференциальный закон логнормального распределения имеет
вид
f(x) =
ха у 2л
где величины цио соответственно оцениваются с помощью равенств
N
ц = __ (б.ЮО)
а =
_____
F.101)
Параметры этого распределения таковы:
а) первый начальный момент (математическое ожидание)
б) второй центральный момент (дисперсия)
fl'1 —1);
F.102)
F.103)
в) нормированный момент третьего порядка (коэффициент асим-
асимметрии)
р„ = А = Уе°' - 1 (е°' + 2); F.104)
г) четвертый нормированный момент и эксцесс соответственно
равны
р4 = (в"' — 1) (еза* + Зе2о! + 6е°' + 6) + 3,
F.105)
Е = {е°2 — 1) (e3(jJ + Зе20' + бе0' + 6).
Дифференциальная форма логнормального распределения ха-
характеризуется одновершинной (одномодальной) кривой и имеет пра-
правостороннюю (положительную) скошенность (рис. 47).
Теперь, опираясь на данные предварительного статистического
эксперимента, попытаемся дать вероятностный прогноз появления
в немецком тексте словоформ разной длины.
Наблюдения над текстами, а также данные интроспекции пока-
показывают, что хотя длина слова не имеет ясно выраженного предела
(см. гл. 4, § 2), выбор слова определенной длины на данном шаге
203
текста зависит не только от семантических «импульсов» окружаю-
. щего контекста, но также от длины предшествующего слова (ср. че-
чередование в тексте длинных, коротких и средних по длине слов).
Исходя из этих соображений, попробуем аппроксимировать распре-
распределение вероятностей длин словоупотреблений в немецком тексте
с помощью логнормально-
го закона.
Предварительным экс-
экспериментом был охвачен
научно-технический немец-
немецкий текст длиной в 1000
словоупотреблений; отно-
относительные частоты, полу-
полученные для словоформ
длиной в х букв показаны
в столбце C) табл. 6.12.
Опираясь на эксперимен-
экспериментальные данные, с по-
помощью выражений F.100)
и F.101) получаем оценки
ц = 2,3 и а = 0,6. Под-
Подставляя их в формулу
F.99), лолучаем вероятность появления двухбуквенных словоформ
Рис. 47. Логнормальное распределение
длин немецких словоформ:
теоретическая кривая;
о о о о опытные данные
__g—(In 2 —2,3)а/B-0,36) __;
_е-@.6931-2,3)»/0.72;
2-0,6 У 2л l 2-2 51
«0,0091.
1 Остальные вероятности, полученные аналогичным путем при-
приведены в столбце B) табл. 6.12. Теоретическая кривая распределения
длин немецких словоформ. вместе с экспериментальными данными
показана на рис. 47.
Таблица
распределение вероятностей появления слов разной длины
в немецком научно-техническом тексте
6.12
Длина слов
в буквах (х)
A)
1
2
3
4
5
6
7
8
9
10
11
Р М
B)
о.'ооо
0,009
0,031
0,099
0,120
0,124
0,116
0,096
0,082
0.068
0,054
! (х)
C)
0,000
0,031
0,098
0,101
0,113
0,108
0,099
0,090
0,079
0,071
0,060
Длина слов
в буквах (х)
A)
12
13
14
15
16
17
18
19
20
Р(х)
B)
0,042
0,031
0,021
0,012
0,006
0,003
0,002
0,002
0,001
0,001
/ (X)
C)
0,040*
0,022
0,020
0,020
0,018
0,010
0,010'
0,002
0,010
(и более)
204
Только что полученное теоретическое распределение может быть
использовано при построении вероятностных синтаксических алго-
алгоритмов и словаря немецко-русского машинного перевода.
Г. Хердан 151, с. 61—62] использует логнормальное распределе-
распределение для математической экспликации вероятностного построения
словаря языка и его реализации в тексте. По его мнению, эта логнор-
мальность словаря и текста отражает присущий естественному языку
принцип оптимального кодирования информации.
§ 4. Понятие о законе больших чисел
1. Принцип практической уверенности при лингвистическом ис-
исследовании. Сосредоточив внимание на построении вероятностных
моделей текста, мы избегали вопроса о том, насколько рассмотрен-
рассмотренная нами модельная теория сходится с результатами лингво-статис-
тического опыта. В частности, мы специально не касались вопроса
о том, насколько вычисленная по приведенным выше моделям ве-
вероятность близка к полученной в опыте частости или в какой степени
математическое ожидание соответствует средней частоте лингвисти-
лингвистического события.
Однако каждая теория, использующая метод моделей, должна
предусматривать процедуру, с помощью которой можно было бы
оценить степень близости теоретических данных и эксперименталь-
экспериментальных результатов.
Выше уже-отмечалось, что статистическое определение вероят-
вероятности опирается на предположение о том, что если при N испыта-
испытаниях событие А осуществлялось F раз, причем N очень велико, то
отношение FIN должно быть близко к вероятности р события А
, (см. гл. 5, §3, п. 3). Это общее представление в какой-то степени свя-
связывает математическую теорию с лингво-статистической практикой,
однако не дает возможности получить количественные оценки этой
, связи. Хотя мы и знаем, что частость может приближаться к вероят-
. ности, но пока не знаем, насколько именно. Задача состоит в том,
чтобы неясное интуитивное предположение заменить математичес-
математической процедурой, с помощью которой можно было бы количественно
измерять отношение вероятностных данных к лингво-статистическим
результатам.
Сформулировать такую процедуру можно, применяя понятия
практической достоверности и практической невозможности собы-
события. В нашей повседневной деятельности, равно как и в лингвисти-
лингвистическом поведении, мы постоянно опираемся на эти понятия. Садясь
в самолет или в автомобиль, мы уверены в практической достовер-
достоверности благополучного завершения нашего путешествия. Составляя
русско-иноязычный математический словарь или формируя автома-
автоматический словарь для машинного перевода русских текстов по теории
вероятностей, мы определенно не включим в русский словник су-
существительное дядя, считая его появление в математических текс-
текстах практически невозможным. Вместе с тем благополучное оконча-
окончание нашего воздушного путешествия или автомобильной прогулки
205
нельзя считать математически достоверным событием, поскольку еди-.
ничные воздушные и автомобильные катастрофы пока имеют место.
Аналогичным образом мы не гарантированы от того, что вопреки
нормам русского подъязыка математики в некотором наугад взятом
отрывке из математического сочинения не появится слово дядя;
кстати, в этом можно убедиться, обратившись к 17-й снизу строке
стр. 34 книги Е. С. Вентцель «Теории вероятностей» (изд. 3-е,
М., 1964).
Несовпадение понятий математической достоверности (соответ-
(соответственно математической невозможности) события и практической
ее достоверности (соответственно практической невозможности)
лежит в основе несоответствия, существующего между логической
структурой системы и вероятностным построением нормы языка.
С точки зрения системы русского языка мы можем допустить, что
в математических текстах возможно употребление словоформ лю-
любовь, дядя, бубновый и т. п. Вместе с тем, опираясь на норму, мы
практически уверены, что эти формы не встретятся при чтении или
машинном переводе математических текстов.
Понятия практической достоверности и невозможности, именуе-
именуемые иногда принципом практической уверенности, лежат в основе
всякого прогнозирования, в том числе прогнозирования, исполь-
используемого в инженерной и прикладной лингвистике. Принцип прак-
практической уверенности можно сформулировать следующим образом:
если вероятность события А в рассматриваемом процессе очень ма-
мала, то можно, практически быть уверенным в том, что при однократ-
однократном осуществлении опыта событие А не произойдет.
Вместе с тем следует помнить, что этот принцип не может быть
задан в единой численной форме для всех областей деятельности
человека. Дело в том, что пороги практической достоверности (не-
(невозможности) события определяются исходя из степени важности
для нас того или иного события. Например, если при анализе и пе-
переводе иностранного текста лишь в шести предложениях из ста сту-
студент неправильно опознает синтаксическую структуру фразы,
то можно быть практически уверенным, что, правильно пользуясь
двуязычным словарем, он в целом поймет наугад взятый текст. Та-
Таким образом, вероятностью синтаксической ошибки, равной здесь
0,06, можно пренебречь. Что же касается перевода текста на ЭВМ,
то такая же вероятность синтаксической ошибки не дает нам прак-
практической уверенности в правильности нашего автоматического пе-
перевода. Ведь машина не умеет, подобно человеку, пользоваться избы-
избыточностью текста и корректировать синтаксические ошибки, опи-
опираясь на лексический перевод. Верхняя граница вероятности до-
допускаемой ошибки может быть приблизительно оценена здесь в
0,01 или 0,02. Еще ниже граница допустимой вероятности ошибки
устанавливается в некоторых технических областях. Так, например,
если бы вероятность аварийной посадки самолета была равна 0,06
и даже 0,01, то пассажирские перевозки на авиалиниях были бы,
по-видимому, полностью исключены.
Итак, для каждой области применения теории вероятностей за-
206
даются свои, определяющиеся спецификой и практикой этой облас-
области принципы практической уверенности.
Одновременно вводится количественный критерий практической
невозможности маловероятных. событий, согласно которому пред-
предполагается, что случайное событие, вероятность которого ниже ука-
указанного порога, не произойдет при единичном испытании. Прак-
Практическое использование этого критерия выглядит следующим обра-
образом. Предполагается, что вероятность события А находится ниже
назначенного порога. Однако, произведя опыт, мы обнаруживаем,
что событие А осуществилось. Тогда следует усомниться в справед-
справедливости исходной гипотезы и искать особую причину для появления
события А. Например, появление в книге по теории вероятностей
слова дядя заставляет нас усомниться в том, что мы имеем здесь
место с отрывком, в котором рассматриваются чисто математические
вопросы. И действительно, 17-я снизу строка на стр. 34 «Теории ве-
вероятностей» Е. С. Вентцель, где зафиксировано это слово, оказы-
оказывается не математическим текстом, а цитатой из «Евгения Онегина»:
«Мой дядя самых честных правил...».
2. Случайные и систематические ошибки в лингвистическом
эксперименте. Отклонения опытных результатов от теоретических
данных могут быть вызваны либо существенными факторами, вво-
вводимыми в структуру изучаемого лингвистического явления (приме-
(примером может служить использование поэтической цитаты в научно-
техническом тексте), либо ошибками измерения (так называемыми
систематическими ошибками). И те и другие сравнительно легко
обнаруживаются, и после их устранения результаты опыта, как
правило, широко согласуются с данными теории.
Однако наряду с существенными отклонениями имеются такие
отклонения значений случайной величины от ее математического
ожидания, которые зависят от многих случайных, не учитываемых
наблюдателем причин. К таким факторам, если говорить о коллек-
коллективном восприятии речи, можно отнести личные стилистические
вкусы говорящего, его настроение в момент произнесения или напи-
написания текста, обстановка, в которой происходит беседа, и т. п. Эти
факторы, именуемые обычно случайными ошибками, то погашая, то
усиливая друг друга, приводят к флуктуациям значений случайной
величины относительно математического ожидания и соответственно
вызывают колебания относительных частот вокруг вероятности.
В дальнейшем мы будем считать, что наши лингво-статистические
измерения свободны от систематических ошибок: это позволит сосре-
сосредоточить внимание на колебаниях частостей и частот, вызванных
случайными ошибками.
Сама вероятность лингвистического события представляет для
нас ценность лишь тогда, когда имеется практическая уверенность
в том, что эта вероятность хорошо предсказывает и отражает резуль-
результаты лингвистического эксперимента, или иначе говоря, что она
очень близка к относительной частоте события, причем колебания
частостей по отношению к вероятности невелики. Таким образом,
основным вопросом соотношения теории вероятностей и лингво-ста-
207
тистической практики является вопрос о том, с какой вероятностью
обеспечена сходимость относительной частоты к вероятности собы-
события.
Ответ на поставленный вопроо дается с помощью совокупности
математических теорем, называемых законом больших
чисел. Эти теоремы показывают связь между абстрактными моде-
моделями теории вероятностей и опытом, они дают возможность предска-
предсказывать результаты опытов. Наиболее общей формой законе больших
чисел является теорема Чебышева.
3. Теорема Чебышева и другие формы закона больших чисел, их
значение для лингвистического эксперимента. Прежде чем сформу-
сформулировать основную теорему, рассмотрим некоторые предваритель-
предварительные понятия.
1) Пусть даны попарно независимые случайные величины Xlt
Х2, .... Хп, каждая из которых принимает свою последовательность
частных значений: например, для Хх имеем хи, х12, .... хи, для Х2
имеем х21, х2г, ..., хп, ..., для Хп имеем хп1, хп2, ..., хп1. При этом
распределение вероятностей значений для каждой из случайных ве-
величин может быть каким угодно. Найдем среднюю арифметическую
этих величин:
я
Легко показать, используя свойства математического ожидания
(см. §2, п. 8), что математическое ожидание средней арифметической
X случайных величин равно средней арифметической их математи-
ческих ожиданий:
х1+х2+...+хп
F.106)
2) Дисперсия средней арифметической X попарно независимых
случайных величин равна средней арифметической этих дисперсий,
уменьшенной в п раз:
D(X) = ,
±*zJ).
D(X1)+D(X2)+...+D(Xn)
п
F.107)
Вывод выражения F.107) опирается на свойства дисперсии
(см. §2, п.8). По мере увеличения п значения средней арифметической
X, выступающей в роли случайной величины (ср. выше), будут все
теснее группироваться вокруг математического ожидания М (X).
Уменьшение рассеивания здесь объясняется тем, что при образо-
образовании средней арифметической происходит частичное взаимное по-
погашение случайных отклонений, ,
208
3. Если дисперсия случайных величин ограничена некоторым по-
положительным числом так, чтоБ {X^)^.c,D (X2)^c, ...,D (Xn)
^ с, то средняя арифметическая дисперсий не превосходит числа
пс
я
— п
а дисперсия средней арифметической случайных величин не превы-
превышает величины - с:
D
Используя только что введенные понятия, мы можем перейти к
формулировке теоремы Чебышева, цель которой состоит в том, что-
чтобы оценить отклонение средней арифметической случайных величин
от математического ожидания, т. е. указать вероятность того, что это
отклонение по абсолютной величине не будет превосходить задан-
заданного числа е.
Теорема Чебышева. Если Х1г Х2, ..., Хп — последовательность
попарно независимых случайных величин, имеющих конечные дис-
дисперсии, ограниченные одной и той же постоянной с, т. е. D (Хх) ^
^.c,D (Х2) ^ с, ...,D (Xn) ^ с, то как бы мало ни было постоянное
положительное число г, с вероятностью, сколь угодно близкой к еди-
единице, можно утверждать, что отклонение средней арифметической
этих п величин от средней арифметической их математических ожи-
ожиданий не превосходит по абсолютной величине заданного положи-
положительного числа е, если число п достаточно велико.
Иными словами,
ПтР.
П-+оо
и одновременно
<= l
F.108)
>eU0. " F.109)
Теорема Чебышева имеет несколько важных для статистической
и лингво-статистической практики частных случаев.
1. Если все п независимых случайных величин имеют одинаковые
математические ожидания, равные а, и их дисперсии ограничены од-
одной и той же постоянной с, то как бы мало ни было положительное
постоянное число е, с вероятностью, сколь угодно близкой к единице,
можно утверждать, что при п -*• оо их средняя арифметическая
стремится по вероятности к постоянной а = М (Xt) — М (Х)
= ... = М (Хп). Иными словами, имеет место неравенство
<= 1
пг*
F.110)
209
которое при неограниченном
ство
увеличении п превращается в равен-
равен=1.
2. Если вероятность наступления события А в каоюдом отдела
ном независимом испытании постоянна и равна р, то при достаточно
большом числе испытаний (т. е. при N -*- оо) с вероятностью, сколь
угодно близкой к единице, можно утверждать, что относительная
частота FIN события А сколь угодно мало отличается от вероятнос-
вероятности р, т. е.
lim
F.111)
Этот частный случай теоремы Чебышева известен под названием
теоремы Бернулли.
Для доказательства этой теоремы используется вспомогатель-
вспомогательное неравенство, называемое неравенством Чебышева:
Р(| X—М(X)|>е)<
F.112)
Представим относительную частоту FIN в качестве случайной вели-
величины, математическим ожиданием которой служит вероятность р,
а дисперсией—величина pqlN. Подставляя эти значения в неравен-
неравенство Чебышева F.112), после преобразований получаем
~Tr P
РЯ
F.113)
Поскольку р, q, е — заданные положительные числа и при N -*- оо
дробь pql(N&2) стремится к нулю, то приходим к соотношению F.111).
Пользуясь теоремой Бернулли, можно определять объемы выборок,
необходимые для решения конкретных лингвистических задач.
Например, установлено [6, с. 238], что вероятность появления
существительного в румынских текстах по радиоэлектронике равна
0,34, а допустимое абсолютное отклонение относительной частоты
/ от вероятности р равно 0,03. Определим тот наименьший объем
исследуемого текста (наименьшую выборку), ири котором заданные
условия выполнялись бы с вероятностью 0,9545.
Здесь по условию р = 0,34; е = 0,03; Р (| FIN — р |< е) >
^ 0,9545; необходимо определить N. Подставляя эти данные в не-
неравенство F.113), имеем
0,9545-1- 0'34'0'66 , или 1-0,9545 = -0'34-0'66 ,
//•0,03* tf.0,0009 '
откуда
210
°'34-0-66
0,0455-0,0009
=5473.
Таким образом, текст, необходимый для выполнения поставленных
в задаче условий, должен содержать не менее 5473 словоупотреб-
словоупотреблений.
3. Теорема Бернулли характеризует соотношение между отно-
относительной частотой и постоянной вероятностью события. Однако ча-
часто мы имеем дело с такими лингвистическими явлениями, например
со знаменательными словоформами и словосочетаниями, которые
почти не повторяются в одних и тех же фиксированных условиях.
Они многократно встречаются в тексте, но каждый раз в новых усло-
условиях разного лексического окружения, принципиально различных
синтаксических позиций, причем вероятность интересующих нас
лингвистических событий сильно зависит от этих меняющихся усло-
условий. Иными словами, мы имеем здесь дело с разными вероятно-
вероятностями ри рг, ..., pN события А. Этот случай характеризует теоре-
теорема Пуассона.
Если вероятность события А при каждом независимом испыта-
испытании меняется, то при достаточно большом числе испытаний {т. е.
при N -*¦ оо) с вероятностью, сколь угодно близкой к единице, можно
утверждать, что относительная частота появления события А
сколь угодно мало отличается от средней арифметической вероят-
1 N
ностей Р = TV У, pi, лишь бы число испытаний было достаточно
-Х
велико, т. е.
lim Р\
N-*oo
F
F.114)
где F -г число появлений события А в N испытаниях.
В теоремах Бернулли, Пуассона и Чебышева закон больших чисел
применяется к независимым величинам. Однако на практике (и
особенно при статистическом описании текста) мы имеем дело с за-
зависимыми или слабозависимыми величинами. В связи с этим воз-
возникает необходимость распространить закон больших чисел на зави-
зависимые величины. Эта задача решается с помощью теоремы Маркова:
если последовательность случайных зависимых или независимых ве-
величин, Хи Х2, ..., Хп такова, что при л->- оо
¦0.
то при любом е > 0 справедливо равенство
lim P.
n-*oo
Доказательства всех приведенных теорем см. в работах [10,
с. 287—297] и [14, с. 199-207]. ¦ *
211
На основании теоремы Бернулли или теоремы Пуассона иногда
делается вывод, что с ростом числа испытаний частость неуклонно
стремится к вероятности, т. е. что
\\т-~ =
W-»oo N
F.116)
Такой вывод является совершенно необоснованным. Дело в том,
что сходимость относительной частоты FIN к вероятности (ее обозна-
обозначают термином «сходимость по вероятности») понимается здесь ина-
иначе, чем сходимость в математическом анализе (см. гл. 2, § 1, п. 2
и гл. 4, § 1, п.1). Различие между обоими понятиями сходимости
заключается в следующем.
Если имеет место соотношение lim -г. = р в том смысле, который
N-ytx "
вкладывает в это равенство математический анализ, то это означает,
что, начиная с некоторого N = пи для всех последующих значений,
выполняется неравенство
N
— Р
F.117)
Когда же утверждается, что частость FIN сходится по вероятности
(или стремится по вероятности) к р при N -*¦ оо, что записывается
обычно так:
N
то для отдельных значений N неравенство F.117) может и не выпол-
выполняться. Дело в том, что в теореме Бернулли речь идет о вероятности
с1
одного единственного неравенства | -^ — р |<е, которая при доста-
достаточно большом N становится больше, чем разность 1 — ~2, или,
иными словами, что при достаточно большом количестве испытаний
частость будет как угодно мало отличаться от постоянной вероят-
вероятности р.
Из сказанного видно, что теорема Чебышева, а также остальные
ее частные случаи справедливы только для фиксированного значения
п = N', например для п0 = No. В связи с этим нельзя утверждать,
что неравенство
—Р
F.118)
справедливо не только для No, но и для всех значений N > No. Од-
Однако для приложений теории вероятностей, и в частности для линг-
во-статистики, важно, чтобы теоремы закона больших чисел распро-
распространялись и на случаи N > No. Так, например, для лингво-ста-
тистики важно найти такие условия, накладываемые на неравенство
F.118), чтобы соотношение F.116) было бы справедливо не только
212
относительно объема выборки No, но и для всех объемов выборки,
где N > Ne. Чтобы достичь этого, на случайные величины Х{ на-
накладываются некоторые дополнительные условия.
Широкие услоьия для осуществления усиленного закона боль-
больших чисел определяются теоремами Колмогорова
и Ф е л л е р а [6, с. 244].
Первая из них показывает, что достаточным условием для приме-
применения указанного закона к последовательности взаимно независимых
оо
случайных величин XltXz,..., Xn является сходимость ряда^
Ni-
Вторая теорема говорит о том, что усиленный закон больших чи-
чисел справедлив для последовательностей случайных величин, имеющих
одинаковые распределения с конечным математическим ожиданием
Квантитативные исследования текста показывают, что числен-
численное значение, которое принимает та или иная случайная лингви-
лингвистическая величина (частота или частость появления определенной
фонемы, буквы, слога, словоформы, морфемы и т. д.), зависит от
многих случайных причин, учесть которые мы не в состоянии. Если
увеличить число случайных величин, то увеличится и число неучиты-
неучитываемых причин. Таким образом, становится, казалось бы, невозмож-
невозможным установить закономерности поведения суммы достаточно боль-
большого числа случайных лингвистических величин. Однако в действи-
действительности это не так: если. индивидуальные величины содержат
в себе более или менее значительный элемент случайности, то в их
средней этот элемент взаимно погашается и становится исчезающе
малым, если Только количество усредняемых величин достаточно
велико.
В итоге при некоторых сравнительно широких условиях сум-
суммарное поведение большого числа случайных лингвистических вели-
величин начинает утрачивать случайный характер и становится стати-
статистически устойчивым или, как говорят, почти закономерным. Ста-
Статистическая закономерность начинает принимать здесь характер
динамического закона.
Устойчивость средней арифметической, дающей при большом
количестве испытаний сходимость по вероятности к математическому
ожиданию, объясняет, почему и когда мы имеем право взять за ис-
истинное значение М (X) значение средней арифметической. Вместе
с тем становится ясным, почему при достаточном количестве испы-
испытаний можно с достаточной достоверностью использовать относи-
относительную частоту для оценки вероятности лингво-статистическогб
события.
Одновременно закон больших чисел предостерегает лингвистов,
пользующихся «симптоматической» статистикой, против неосмотри-
неосмотрительного приравнивания частот и математических ожиданий линг-
лингвистических случайных величин, а также отождествления частостей
и вероятностей независимо от того, имеются ли для этрго условия,
предусмотренные указанным законом.
213
На описанных свойствах средней арифметической и частости ос-
основан широко применяющийся в лингво-статистике (как, впрочем,
и в других приложениях статистики) выборочный метод, сущность
которого состоит в том, что по сравнительно небольшой случайной
выборке текстов судят о целой разновидности языка — функцио-
функциональной (стиль) или тематической (подъязык).
Сходимость средних арифметических частот, полученных по
частичным выборкам, к математическим ожиданиям слов (или слово-
словосочетаниям) при достаточном числе выборок позволяет рассматри-
рассматривать частотные словари в качестве моделей вероятностного распреде-
распределения слов и словосочетаний в норме данного подъязыка или стиля.
4. Центральная предельная теорема Ляпунова и сопоставление
результатов лингвистического эксперимента с вероятностной ре-
речевой, моделью. Теоремы, образующие первую часть закона боль-
больших чисел, давая полную степень практической уверенности о схо-
сходимости по вероятности определенных случайных величин к тем
или иным постоянным, слишком завышают вероятность выполнения
неравенства | X — М (Х)\ > е. Одновременно занижается вероят-
вероятность того, что отклонение случайной величины от ее математи-
математического ожидания будет не больше заданного порога е. В связи с
этим использование первой части закона больших чисел для нахож-
нахождения таких характеристик, как точность, надежность оценки, до-
доверительный интервал и т. д., связано с обследованием слишком
больших текстовых выборок, объемы которых превосходят реаль-
реальные возможности лингво-статистического исследования.
Поэтому возникает необходимость в такой, процедуре, которая
указывала бы более точно вероятности интересующих нас границ,
используя при этом меньшее число испытаний, чем этого требуют
теоремы закона больших чисел. Эта задача решается в цент-
центральной предельной теореме Ляпунова.
Центральная предельная теорема исходит из той же идеи, кото-
которая используется и при построении первой половины закона боль-
больших чисел. Эта идея заключается в том, что хотя исследуемое яв-
явление или процесс (в том числе и лингвистический) в ходе своей ре-
реализации подвергается действию большого числа независимых слу-
случайных воздействий, каждое из них лишь ничтожно мало изменяет
ход процесса. Исследователь, интересующийся изучением процесса
или явления в целом, а не воздействием отдельных факторов, должен
наблюдать и фиксировать суммарное действие этих факторов.
В отличие от теоремы Чебышева, для которой характер распре-
распределения случайных величин Хъ Х2,..., Xn, их сумм и средних X =
= (Хг + Х2 + ... + Xn)/N не имеет значения, теорема Ляпунова
утверждает, что каково бы ни было распределение независимых
случайных величин, при определенных условиях распределение их
средних подчиняется нормальному закону. Такой подход позволяет
распространить на случаи, рассматриваемые в законе больших чи-
чисел, теорему Муавра—Лапласа, дающую возможность оценивать
математические ожидания и вероятности появления отдельных зна-
214
чений случайной величины и таким образом бодев или менее точно
определять вероятности отклонений \Х — М (%)\ и соответственно
отклонений |— — р » |/ — р|.
Для того чтобы утверждение о нормальном распределении для
средних имело место, достаточно, как показал А. М. Ляпунов, вы-
выполнение двух условий: во-первых, все случайные слагаемые должны
иметь конечные абсолютные центральные моменты третьего по-
порядка
M\Xt - М (Л()|3, F.119)
во-вторых, отношение
2 М IX,-M(X,)\s
3/2
F.120)
должно стремиться к нулю при N -*¦ оо .
Смысл условий Ляпунова заключается в том, что ни одна из'
случайных величин, образующих среднюю, не была бы в ней преоб-
преобладающей, во всяком случае, не была бы заметно больше других
величин. Если же какая-либо величина или величины XJt Xh ока-
оказывают преобладающее влияние на формирование X, то второе ус-
условие не выполняется и утверждение о нормальном законе распре-
распределения средней не имеет места. Распределение средней здесь опре-
определяется законом распределения этих преобладающих случайных
величин.
Лингвистическим примером этого явления может служить ста-
статистическое поведение так называемых ключевых (или доминантных)
слов и словосочетаний текста, т. е. таких слов, которые передают
основные понятия, рассматривающиеся в данном сообщении
(в научно-технических текстах в качестве доминантных слов и слово-
словосочетаний выступают термины). Преобладающим фактором, влияю-
влияющим на статистику доминантных единиц текста, является ситуация,
отражаемая в содержании текста. Лингвистические, индивидуально
стилевые и прочие факторы подавляются ситуацией. Так как появле-
появление тех'или иных ситуаций не подчиняется нормальному закону*,
то этому закону не подчиняются и распределения доминантных слов.
Напротив, служебные слова, многие грамматические формы, фонемы
и буквы, поведение которых определяется суммой большого числа
случайных воздействий без преобладания в них семантики текста,
дают, как правило, распределение, близкое к нормальному. Выде-
Выделение в тексте слов, распределение которых не подчиняется нормаль-
нормальному закону, а также другим связанным с нормальным распредели-
* Во всяком случае, в рамках тех, ограниченных «выборок ситуаций»,
которые представлены в текстах, написанных на естественном языке;
215
нием законам, лежит в основе эффекта статистического опознания
терминологических единиц [32а, с. 111]; см. также гл. 9, § 6, п.2.
После этих предварительных разъяснений перейдем к изложению
центральной предельной теоремы Ляпунова и связанного с ней ма-
математического аппарата; "ее доказательство см. в [14].
Теорема Ляпунова. Пусть Хъ Х2, ..... Xn — последовательность
взаимно независимых случайных величин с конечными математичес-
математическими ожиданиями М (Х^), М (Х2), ..., М (Хп) и с конечными дш>
персиями D (XJ, D (Х2), ..., D (Хп). Тогда при выполнении условий
- . л
F.119) и F.1-20) сумма этих случайных величин X* = 2Х( с доста-
достаточной степенью точности распределена по нормальному закону
с параметрами
М (X*) = ц = М (Х2) + М (X,) + ... + М (Х„)
D (X*) = or* = D (Хх) + ... + D (Х„).
Отсюда вероятность того, что случайная величина X* примет
какое-либо значение в промежутке (хъ х2), согласно формуле F.98)
составляет
а среднее квадратическое отклонение
Т/2л J
<х,-ц)/а
Частным случаем последнего выражения служит равенство
: Р(|Х» — ц|<ят) = 2Ф(г).- F.122)
Нетрудно догадаться, что теорема Ляпунова имеет место и тогда,
когда случайная величина является суммой достаточно большого
числа одинаково распределенных независимых случайных величин,
имеющих абсолютные центральные моменты третьего порядка. При
доказательстве этого утверждения следует учитывать тот факт, что
моменты всех порядков этих случайных величин — в том числе
центральные моменты второго и третьего порядков — совпадают.
Средняя арифметическая указанных величин с учетом того,' что
п — N, равна
N
i
У
"
ее дисперсия
F.123)
F.124)
Используя в соотношении F.122) вместо а только что получен-
полученное значение а^, а вместо X* — среднюю арифметическую X, при.
ходим к равенству
которое можно переписать в виде
Pi
F.125)
Примерами таких случайных величин могут являться случайные
лингвистические величины, распределенные по простой схеме по-
повторений испытаний. Следовательно, здесь в качестве усредненной
случайной величины можно рассматривать относительную частоту
FIN = f, математическое ожидание которой есть вероятность р.
При этом нормированное отклонение примет вид
t-P
f-P
F.126)
о ypq/N
(ср. с §3, п.4).
Если Af достаточно велико, то, учитывая F.124), можно пере-
переписать выражение F.122) в виде
f-P
Vpq/N
<г =2Ф(г),
где
Отсюда
е = ;
VpqIN
N = z2pqle\
\-р)
F.127)
F.128)
F.129)
F.130)
216
При решении лингвистических задач, оперирующих нормально
распределенными случайными величинами X, X или X*, целе-
целесообразно задать такой интервал рассеяния случайной величины
вокруг ее математического ожидания (соответственно частостей
вокруг вероятности), в который попадало бы большинство значений
случайной величины.
С этой целью, записав равенство F.122) в виде
Р (|Х - ц|< га) =, 2Ф (г),
217
придадим 2 целочисленные значения 1, 2, 3. Тогда, учитывая дан-
данные табл. III (см. стр. 365), получим
при г— 1 :Р(\Х — \х\<а) = 2ФA) = 2-0,3413-0,6826; F.131)
при 2 « 2 :Р (|Х — |i| < 2а) = 2ФB) = 2-0,4772 = 0,9544; F.132)
при z =¦ 3 : Р (\X—[i\ <3ст) = 2ФC) = 2-0,49865 = 0,9973. F.133)
В лингвистических задачах обычно используется выражение
F.133), известное под названием травила трех сигм». Это правило
утверждает с вероятностью 2ФC) = 0,9973, что отклонения слу-
случайной величины X от ее математического ожидания не превосходят
величины За. Вероятность же того, что отклонение случайной вели-
величины X выйдет за пределы трехкратного среднеквадратического от-
отклонения, равно 0,0027. Иными словами, здесь имеется практи-
практическая уверенность, что погрешности лингвистического наблюде-
наблюдения не превысят заданной ошибки наблюдения е = За.
В некоторых работах используются более узкие — двухсигмо-
вый F.132) и односигмовый F.131) интервалы [34]. В этих случаях
практическая уверенность в том, что случайная величина попадет
в заданный интервал, значительно меньше.
До сих пор мы рассматривали вопрос о применимости централь-
центральной предельной теоремы к независимым величинам. Можно дока-
доказать [6, с. 251], что центральная предельная теорема может быть рас-
распространена и на зависимые случайные величины при условии,
что связь между величинами Х1г Х2,..., Xit ..., Хь., ..., Хц постепен-
постепенно ослабевает по мере удаления их друг от друга, т. е. при возраста-
возрастании разности i — k. Этот результат представляет прямой интерес для
лингвистического исследования речи, имеющей дело со слабо зави-
зависимыми величинами. В целом же на центральной предельной тео-
теореме Ляпунова и ее следствиях основываются как выборочный ме-
метод, так и сопоставление результатов лингвистического эксперимен-
эксперимента с вероятностными моделями построения текста.
Примерам этого сопоставления будут посвящены следующие
главы.
ГЛАВА 7
ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ТЕКСТА
§ 1. Статистическая совокупность лингвистических
объектов и ее организация
Исследование текста с помощью описанных выше вероятностных
моделей может быть осуществлено при том условии, что произведена
первичная статистическая обработка текста и к ее результатам при-
применены специальные критерии перехода к вероятностной модели.
Прежде всего познакомимся с приемами первичной статисти-
статистической обработки текстов.
1. Статистическая совокупность лингвистических объектов. Вся-
Всякое статистическое исследование предусматривает наблюдение над
множеством объектов. Эти объекты характеризуются многими приз-
признаками, каждый из которых варьируется при переходе от одного
объекта к другому. Все признаки одновременно рассмотреть не-
невозможно, поэтому языковед должен сосредоточить свое внимание
на одном определенном признаке, предполагая, что в отношении
остальных признаков объекты данного лингвистического множест-
множества равноправны. Используя такое допущение, мы можем считать,
что рассматриваемое множество однородно. Построенное указанным
способом множество называется статистической совокупностью,
а составляющие ее объекты — единицами совокупности.
Лингвистические объекты обладают как количественными, так
и качественными свойствами. Количественные свойства (например,
длина словоформы в буквах или фонемах, слогах, морфемах, либо
количество словоупотреблений в предложении и т. п.) постоянно
используются в качестве тех признаков, по которым лингвистиче-
лингвистические объекты выступают в качестве единиц статистической сово-
совокупности.
Однако статистика текста оперирует не только количественными,
но и качественными признаками. Например, в ходе статистико-
морфологического исследования словоупотребления текста группи-
группируются по признаку их принадлежности к той или иной части речи.
При статистико-синтаксическом исследовании таким качественным
признаком является функционирование каждого словоупотребления
в роли определенного члена предложения.
Часто бывает удобно использовать лишь два качественных при-
признака, точнее признак А и его отсутствие — не А (А). В этом случае
говорят об альтернативном качественном признаке. В только что
рассмотренном примере в качестве альтернативного признака мож-
можно рассматривать отнесение данного словоупотребления к сущест-
существительным или не-существительным (соответственно к глаголу или
не-глаголу, подлежащему или не-подлежащему и т. п.).
Отдельные лингвистические статистические совокупности могут
образовывать вместе более крупную совокупность — совокупность
совокупностей. Одновременно каждая совокупность может состоять
219
из частных совокупностей, которые в свою очередь могут рассмат-
рассматриваться как единицы совокупности.
Если статистическая совокупность объединяет все однород-
однородные лингвистические объекты, обладающие данным качественным
или количественным признаком (признаками), то такую совокуп-
совокупность называют генеральной лингвистической совокупностью. Ге-
Генеральная совокупность может содержать как конечное, так и
бесконечное количество единиц. Если генеральная совокупность
бесконечна или очень велика, то исследованию подвергается неко-
некоторая обозримая ее часть, называемая выборочной лингвистической
совокупностью (выборкой).
Например, если признаком объекта является длина словоформы
в пушкинском тексте, то в качестве генеральной совокупности вы-
выступают все тексты, написанные А. С. Пушкиным. Отдельные же
произведения, например «Капитанская дочка», являются выборка-
выборками, извлеченными из генеральной совокупности. Если.же иссле-
исследуется распределение длин словоформ в русском литературном язы-
языке, то генеральной совокупностью служит сумма всех русских ли-
литературных текстов. Заметим, что если хронологические границы
существования русского литературного языка не фиксированы, то
число словоупотреблений (однородных объектов) здесь бесконечно.
Произведения А. С. Пушкина в этом случае выступают в виде ко-
конечной выборочной лингвистической совокупности внутри беско-
бесконечной генеральной совокупности языковых объектов.
2. Методы организации статистического наблюдения над тек-
текстом. Успех каждого лингвистического исследования зависит от
организации статистического наблюдения, которая предусматри-
предусматривает, во-первых, выбор лингвистического признака и установление
единицы совокупности, во-вторых, определение способа наблюдения.
Само собой разумеется, что каждый количественный или качест-
качественный признак, применяемый для выделения единицы совокупно-
совокупности, должен иметь лингвистический смысл и отвечать задачам дан-
данного языковедческого исследования. Часто случается, что в лингво-
статистике используются такие качественные критерии, при ко-
которых граница переходов от одного состояния к другому оказы-
оказывается весьма неопределенной, например деление слов текста на
знаменательные (полнозначные) и служебные.
Однако каким бы ни было основание для группировки — ес-
естественное или искусственное, определенное или неопределенное —
конечное решение должно быть всегда строго фиксированным.
Каждый лингвистический объект должен быть признан либо обла-
обладающим, либо не обладающим данным качественным признаком.
Статистическое наблюдение предусматривает сплошное
и выборочное обследование генеральной совокупности. Сплош-
Сплошное обследование используется в лингво-статистике тогда, когда,
во-первых, генеральная совокупность хотя и велика, но все же обо-
обозрима, во-вторых, когда необходимо учесть все употребления инте-
интересующих нас языковых объектов, например слов. Такая ситуация
имеет место при статистическом описании языка писателя (частот-
220
ные словари произведений А. С. Пушкина или трудов основополож-
основоположника современной казахской литературы Абая Кунанбаева) и при
исследовании языка отдельного художественного произведения
(частотные словари романа Дж. Джойса «Уллис» или «Стихов
о прекрасной даме» А. Блока) — см. [7, с. 10).
Обычно же генеральная совокупность настолько велика, что при-
применить сплошное обследование оказывается невозможным даже при
условии использования вычислительной техники. Поэтому здесь
применяется лишь часть единиц генеральной совокупности. Такое
наблюдение может быть осуществлено с помощью либо повторной,
либо бесповторной выборки (см. гл. 6, § 1, п.1). И в том , и в другом
случае имеется в виду перенос результатов наблюдения над частот-
частотной выборкой на всю генеральную совокупность. Этот перенос мо-
может быть осуществлен в том случае, если средняя величина признака
и его относительная частота (доля) в выборочном наблюдении доста-
достаточно хорошо воспроизводит среднюю величину и долю признака
в генеральной совокупности.
Статистика предполагает следующие приемы выборочного на-
наблюдения.
1. Случайный отбор. Здесь выбор отдельных единиц
осуществляется либо по жребию, путем подбрасывания монет или
игральной кости и т. д., либо путем использования таблиц случай-
случайных чисел. При этом каждая единица совокупности имеет равную
возможность попасть в выборку. Это обеспечивает Достаточную бли-
близость средней выборочной величины к средней генеральной вели-
величине. Этот вид отбора ввиду его громоздкости сравнительно редко
используется в лингвистике. "
2. Механический отбор. Здесь единицы совокупно-
совокупности выбираются в определенном, формально установленном порядке.
Например, желая исследовать распределение гласных, мы нумеруем
все фонемы текста, после чего фиксируем присутствие или отсут-
отсутствие гласной во всех фонемных позициях, номер которых кратен
10 (или 5, 3 и т. п.).
3. Серийный отбор. В противоположность рассмотрен-
рассмотренным выше видам выборки, где отбор каждой единицы проводится
в индивидуальном порядке, серийная выборка предполагает отбор
сериями. Эти серии отбираются в случайном порядке, чаще беспо-
бесповторным способом. Отобрав таким образом серии, исследователь
проводит внутри их сплошное наблюдение (см. гл. 6, § 1).
4. Типический отбор. Общий недостаток первых трех
приемов выборочного обследования текста состоит в том, что они
не учитывают смысловых и жанрово-стилистических своеобразий
отдельных частей текста, выступающего в роли генеральной сово-
совокупности. Эти различия оказывают заметное воздействие на статис-
статистику знаков — в первую очередь слов, словоформ и словосочетаний.
Так, например, относительные частоты существительного крепость,
местоимения я и первого лица глаголов в «Капитанской дочке» зна-
значительно выше, чем во всем пушкинском тексте. Типический отбор
предполагает предварительную разбивку генеральной совокуп-
221
ности по определенному признаку на однородные тематические груп-
группы, из которых затем случайным порядком выбираются интересую-
интересующие нас лексические или грамматические единицы. При сопоставле-
сопоставлении частотных словарей типическая выборка сочетается с серийным
отбором. Количество серий, извлекаемых из каждой тематической
группы, определяется удельным весом этой группы в генеральной
совокупности.
§ 2. Вариационные ряды лингвистических признаков
1. Дискретные вариационные ряды. В ходе наблюдения мы по-
получаем сведения о количественном или качественном изменении
изучаемого признака относительно каждой единицы нашей совокуп-
совокупности. Так, например, для определения длины словоформы в казах-
казахских публицистических текстах взято подряд сто словоупотребле-
словоупотреблений из передовой статьи газеты «Казахстан мугалими» B6.Х. 1969 г.).
В результате получена следующая последовательность чисел, каж-
каждое из которых характеризует длину словоупотребления в буквах:
3, 6, 4, 7, 10, 13, 6, 8, 4, 4,
6, 9, 10, 10, 7; 6, 5,
5, 4, 8, 8, 3, 7, 8,
9, 11, 9,
3, 11, 11,
7, 9, 5, 12, 6, 11, 8, 8, 7, 8,
И, 5, 6, 5, 5, 7, 8, 8, 8, 7,
5, 7, 6, 6. 6, 5, 9, 3, 11, И,
16, 7, 11, 11, 3, 3, 9, 9, 10, 3,
5, 13, 12, 6, 8, 6, 6, 3, 7, 4,
9, 3, 12, 11, 6, 14, 6, 10, 16, 8,
9, 8, 7, 9, 4, 5, 3, 10, 8, 3.
Порядок следования чисел повторяет здесь последовательность
словоупотреблений в тексте. Рассматривая приведенную в примере
последовательность чисел, нетрудно заметить, что величина инте-
интересующего нас признака (длины словоформ) варьирует от одной
единицы совокупности (словоупотребления) к другой. Задачей ста-
статистического наблюдения, в том числе и лингво-статистического,
является изучение вариации признака (варьирующего признака)
в данной совокупности.
Вернемся к рассмотрению примера. Как уже говорилось, роль
варьирующего признака выполняет длина словоупотребления, при-
причем для каждого из ста словоупотреблений этот признак принимает
свое значение C, 6, 4 и т. д. букв). Возможные значения признака
в статистике называются вариантами. Различия между варианта-
вариантами могут быть как количественными (дискретными или непрерыв-
непрерывными), так и качественными (см. ниже).
222
Если ранжировать варианты нашего признака, расположив их
по возрастанию, то получим такую последовательность длин сло-
¦оупотреблении:
3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 4, 4, 4, 4, 4, 4, 5, 5, 5,
• 5, 5, 5, 5, 5, 5, 5, 6, 6, 6,
6, 6, 6, 6, 6, 6, 6, 6, 6, 6,
6, 7, 7, 7, 7, 7, 7, 7, 7, 7,
7, 7, 8, 8, 8, 8, 8, 8, 8, 8,
8, 8, 8, 8, 8, 8, 9, 9, 9, 9,
9, 9, 9, 9, 9, 9, 10, 10, 10, 10,
10, 10, 11, 11, 11, 11, 11, 11, 11, 11,
11, 11, 12, 12, 12, 13, 13, 14, 16, 16.
Ранжирование может быть осуществлено не только по возрастанию,
но и по убыванию значений признака.
Ранжированная запись всегда слишком длинна и громоздка.
Компактнее и нагляднее представить варьирование признака в виде
таблицы, в верхней строке которой указываются значения призна-
признака (варианты), а в нижней — число повторений данного значения.
Полученная в результате такого вторичного упорядочения таблица
называется вариационным рядом (рядом распределений или эмпи-
рическим распределением признака).
Вариационный ряд длины казахских словоформ по тексту из
газеты «Казахстан мугалими» показан в табл. 7.1.
Таблица 7.1
Длина словоформы
Число повторе-
повторений словоформы
данной длины
3
И
4
6
5
10
6
14
7
11
8
14
9
10
10
6
11
10
12
3
13
2
14
1
15
0
16
2
Всего
100
Обычно признак обозначается большими буквами латинского
алфавита X, Y, ..., а варианты — соответствующими строчными
буквамиxlt x2, ...,xh, УиУг, •¦•¦, Ун* •••'. число повторений вариант —
через пи п2, ..., nh. Сумма всех вариант N равна в этом случае
N =
nh =
Общий вид вариационного ряда показан в табл. 7.2.
Таблвиа 7.2
ч
«1
...
• • •
Всего
N
223
Таблица 7.5
Вариационные ряды, представленные в табл. 7.1 и 7.2, содержат
в нижней строке абсолютные частоты tit, однако вместо абсолютных
частот можно указывать относительные частоты (частости) ft =я
— jf или даже проценты /с 100% (табл. 7.3).
h
b-ioos
h
...
...
...
т
. xh
Ы
ffc-100%
аблица 7.3
Всего
1
100%
В только что рассмотренном примере мы имели сравнительно
небольшое варьирование признака (всего 14 вариант). Однако
часто приходится иметь дело с несколькими десятками и даже сот-
сотнями вариант. В этом случае вариационный ряд получается очень
растянутым и поэтому плохо обозримым. Чтобы избежать этого не-
неудобства, в верхней строке таблицы указываются не сами вначения
признака, а интервалы, в которых находятся эти значения. В ниж-
нижней строке указывается, сколько вариант падает на один интервал.
Например, при подсчете распределения существительных в 500
случайных выборках по 100 словоупотреблений каждая, взятых
из немецких текстов по физической химии, получен слишком длин-
длинный вариационный ряд (см. табл. 7.4).
X (количество суще-
существительных в одной
сотне словоупотреб-
словоупотреблений
N (количество со-
сотен)
13
1
14
0
15
2
16
5
17
6
18
10
19
15
20
20
21
26
22
23
Та
23
31
блица
24
41
25
33
7.
26
35
4
27
51
X (количество суще-
существительных в одной
сотне словоупотреб-
словоупотреблений
N (количество со-
сотен)
28
34
29
33
30
33
31
24
32
19
33
16
34
14
35
12
Продолжение
36
7
37
2
38
4
39
0
табл. !
40
1
41
2
'А
Всего
500
Интервалы
вариант
16—1
Частоты щ 1 2 11 25 46 54 74 86 67 57 35 26 9 4 3 500
Таблица 7.6
34—3
Интервалы
вариант
Частоты tit
12—14
1
15—17
13
18—20
45
21—23
80
24—26
109
27—29
118
30—32
76
33—35
42
36—38
13
39—41
3
Всего
500
Чтобы сделать этот ряд более компактным и обозримым, берем
интервалы, содержащие по два (табл. 7.5) и по три (табл. 7.6) зна-
значения признака. Наиболее наглядную картину распределения дает,
очевидно, вторая таблица.
2. Непрерывные вариационные ряды. В лингвистике исполь-
используются не только дискретные, но и непрерывные вариационные
ряды. Эти последние используются, как правило, при исследовании
фонетических явлений, поскольку здесь значения признака (напри-
(например длина, частота, интенсивность звука) могут отличаться друг от
друга на как угодно малую (бесконечно малую) величину. Посколь-
Поскольку различия между вариантами имеют непрерывный характер,
в этом случае используется только интервальное построение ва-
вариационного ряда.
Рассмотрим следующий пример. В ходе исследования длины
китайского слога произведено 150 замеров времени звучания слогов,
произнесенных дикторами-китайцами, причем длины слогов коле-
колеблются от 40 до .300 мс [7, с. 22]. В итоге вторичного упорядочения
этих данных получено три вариационных ряда (см. табл. 7.7—7.9).
Интервалы
вариант
(длины сло-
слогов в мс)
Частоты щ
40—50
2
50—60
0
60—70
5
70—80
2
80—90
4
90—100
3
о
100—1
16
О
13
120—1
20
Таблица
130—1
9
140—1
17
&
150—1
7
7.
160—
11
7
да
170—
6
Продолжение табл. 7.7
Интервалы
вариант
(длины сло-
слогов в мс)
Частоты
8 Зак. 1287
10
1
к
1 2
CN
0 1
о I
150
225
Таблица 7.8
Интервалы
вариант
(длины
слогов в
мс)
о
0Q
Частоты .
7 | 29 | 29 | 24 j 17 | 11 | 12
11 2| 11 I |l50
Таблица 7.9
Интервалы
вариант
(длины
слогов
в мс)
Частоты гц
Накоплен-
Накопленные часто-
частоты я*
о
о
16
49
65
о
to
33
98
22
120
8
О
18 I 7
i
138 145
148
о
со
i
150
о
а
и
CQ
150
В общем случае непрерывный интервальный ряд задается так,
как это показано в табл. 7.10.
Таблица 7.10
Значения признака X
Частоты
Частости
(*1. *г)
h
«г
h
...
...
• • ¦
(хт *m+l)
"m
tm
Здесь fo, х2), (д;2, Хз), ..., (хт, хт+1) являются интервалами, на
которые разбиты возможные значения признака. Введем понятие
интервальных разностей kx — #2 — xlt k2 = хг — х3, ..., km —
— хт+1 — хт, характеризующих ширину интервалов. Если ин-
интервалы имеют одинаковую ширину, то интервальные разности
равны, т. е. kx = k2 = ... = km.
В тех случаях, когда вариационный ряд имеет разные по вели-
величине интервалы, целесообразно пользоваться понятием плотности
распределения, представляющей собой частоту, приходящуюся на
единицу величины интервала:
Вместо плотности интервала можно пользоваться также относи'
тельной плотностью распределения
Ф» = fjki'
Желательно, чтобы длина интервала, а также его границы и се-
середины были выражены целым или округленным числом. Так как
все интервалы должны иметь одинаковую длину, то совершенно
очевидно, что начало первого интервала не обязательно долж го
совпадать со значением минимальной варианты — таков, напри-
например, вариационный ряд, описывающий распределение существи-
существительных в немецких технических текстах. Аналогичным образом,
конец последнего интервала может и не совпадать со значением мак-
максимальной варианты, как это имеет, например, место в вариацион-
вариационных рядах, описывающих распределение длин китайских слогов.
Вообще же при построении интервального ряда необходимо опреде-
определять интервал настолько ясно, чтобы не оставалось никаких сомне-
сомнений в отношении его границ и не мог бы возникнуть вопрос о том,
к какой группе принадлежит та или другая варианта.
Не менее важным является вопрос об определении величины ин-
интервала при выборе количества интервалов. При уменьшении коли-
количества интервалов (соответственно при увеличении ширины интер-
интервала) общий вид распределения становится более наглядным
(см. табл. 7.6—7.9), однако теряется информация о промежуточ-
промежуточных вариациях признака внутри большого интервала. Эту инфор-
информацию можно получить, сужая интервалы и увеличивая тем самым
их число, но при этом таблица становится громоздкой и труднообо-
труднообозримой (см. табл. 7.7).
Выбор ширины интервала и их числа должен осуществляться
таким образом, чтобы выделить характерные особенности распре-
распределения и сгладить случайные колебания. При решении этой зада-
задачи в лингво-статистике используются два приема.
Во-первых, ширина интервала может быть определена с помо-
помощью формулы Стерджесса [7, с. 24]
и __
G.1)
При этом интервальная разность k округляется до ближайшего
целого числа. Число же интервалов определяется из выражения
G-2)
Если же минимальная и максимальная варианты оказываются за
пределами полученных интервалов, то соответственно добавляются
два интервала — один слева, другой справа.
Во-вторых, при определении числа и ширины интервалов мож-
можно пользоваться эмпирическими соответствиями, приведенными
в табл. 7.11.
Используя формулы G.1) и G.2), а также данные табл. 7.11, про-
проверим корректность нашего интуитивного построения вариацион-
вариационного ряда немецких существительных (см. габл. 7.5 и 7.6).
226
227
Таблица 7.11
Количество вариант
25— 40
40— 60
60—100
Число интервалов
5— 6
6— 8
7-10
Количество вариант
100—200
более 200
Число интервалов
8—12
10-15
Подставляя соответствующие значения в формулу G.1), имеем
. 41-13 28
1 4- log2 500 1+8,96
* 2,81;
если округлить полученный результат до трех, оказывается, что он
соответствует выбранной в табл. 7.6 ширине интервала.
Число интервалов / = 1 + log2 500 « 10 также соответствует
количеству групп в табл. 7.6, которое оказывается, однако, зани-
заниженным по сравнению с рекомендацией табл. 7.11.
3. Порядковый признак у лингвистических единиц. В лингвис-
лингвистических исследованиях часто встречаются такие ситуации, когда
дать точную количественную характеристику признака либо невоз-
невозможно, либо нецелесообразно. В то же время условия эксперимента
позволяют нам ранжировать варианты, т. е. расположить их в опре-
определенном порядке.
Например, при проведении эксперимента по индивидуальному
угадыванию текста испытуемый не может назвать вероятности по-
появления букв в той или иной позиции текста. Однако языковое
чутье позволяет ему довольно точно указывать, какая буква яв-
является наиболее вероятной в данной позиции, а какие буквы по
вероятности их появления стоят на втором, третьем и т. д. местах
[23, с. 12—15, 44—47, 53—55].
Аналогичным образом при составлении частотных словарей,
опирающихся на малые выборки, пользоваться абсолютными и от-
относительными частотами отдельных слов и словосочетаний нецеле-
нецелесообразно, поскольку статистическая ошибка при определении этих
частот слишком велика. В этих случаях рассматривается порядок
(ранг) расположения отдельных словоформ или словосочетании.
Ранжирование широко используется в лингво-психологических
исследованиях. В частности, этот прием применяется при коллек-
коллективном тестировании, причем в итоге выводятся «коллективный»
ранг для вариант исследуемого признака.
Этот прием использован Р. М Фрумкиной [7, с.27—28] при срав-
сравнении объективных (статистических) и субъективных (интуитив-
(интуитивных) оценок вероятностей слов. В качестве экспериментального ма-
материала были взяты десять слов, ранжированных по убыванию их
частот согласно данным «Частотного словаря современного русского
языка» Э. А. Штейнфельдт [39]. Этим путем получено объективное
(статистическое) ранжирование. Для определения субъективного
228
ранжирования указанные слова были переданы десяти препода-
преподавателям русского языка, каждый из которых должен был, опираясь
на свою лингвистическую интуицию, ранжировать эти слова по убы-
убыванию их вероятности.. Индивидуальные ранги суммировались по
отдельным словам. Каждая сумма рассматривалась как число бал-
баллов, количественно характеризующее соответствующее слово. За-
Затем производилось вторичное ранжирование по возрастанию коли-
количества баллов. Слову, набравшему наименьшую сумму баллов, при-
приписывался ранг 1; слову, имеющему следующую по величине сумму,
был дан ранг 2 и т. д. Ход обработки результатов эксперимента по-
показан в табл. 7.12.
Таблица 7.12
Ранговое сравнение
Олова
Сказать
Работа
Хорошо
Лицо
Друг
Длинный
Характер
Сигнал
Неизвестный
Энергичный
1
4
1
2
3
5
6
7
10
8
9
2
2
1
4
8
5
3
6
10
9
7
субъективных
вероятностей
3
1
2
4
8
3
5
6
9
10
7
и статистических оценок
слов
Испытуемые
4
3
1
2
5
4
7
10
6
8
9
5
2
1
3
5
4
7
6
10
8
9
в
3
2
1
5
6
8
4
10
9
7
7
3
1
2
4
8
7
5
10
9
6
8
1
2
4
6
3
5
8
10
9
7
9
4
2
3
8
1
7
5
6
9
10
10
1
4
2
6
8
5
3
10
7
9
ан-
цло-
испы-
Сумма р
гов, пре,
женных !
туеиым
24
17
27
58
47
60
60
91
86
80
кЛ
Ранг по
зультата
эксперт
2
1
3
б
4
6
7
10
9
8
дан-
>аря
ЛЬДТ
Ранг по
ньш ело:
Штейнфе
1
2
3
4
5
6
7
8
9
10
Мы не будем сейчас рассматривать вопрос о степени близости
объективного и субъективного ранжирования, а обратим внимание
читателя на то, что два слова — длинный и характер — получили
одинаковое количество баллов. Эта ситуация встречается довольно
часто при построении вариационных рядов. Примером могут служить
частотные словари, в которых большие массивы редких словоформ
имеют одинаковые частоты [33, с. 376—567]. В этом случае упорядо-
упорядочение происходит либо по какому-либо качественному признаку,
например по алфавитному, либо обеим вариантам приписывается
одинаковый ранг, представляющий собой среднее арифметическое
порядковых номеров, либо ранг первой варианты в группе наших
вариант.
4. Качественный признак у лингвистических единиц. Качест-
Качественными признаками группировки вариант являются такие приз-
признаки, которые не содержат ни количественной оценки вариант, ни
возможности их ранжирования. Примером может служить группи-
группировка словоформ по семантическим или грамматическим классам,
или расположение фонем, исходя из иерархии дифференциальных
229
признаков 124, с.46}. В этих случаях, группировка вариант, отобран»
ных по качественному признаку, заключается в их классификации
по градации этого признака.
Например, при статистическом исследовании румынских текс-
текстов по радиоэлектронике выделены группы именных словоформ,
причем упорядочение этих групп осуществлено по убыванию их
номинативности (см. табл. 7.13).
Таблица 7.13.
Статистика-именных частей речи в румынских текстах по радиоэлектронике
Существительные (С)
Местоимения (М)
Числительные (Ч)
Прилагательные (П)
Адъектированные причастия (Ад)
. Артикли (Ар)
Всего
Количество
разных
еловоформ
в частотном
словаре
7180
117
111
2216
1262
20
10906
Количество словоупотреб-
словоупотреблений в тексте
68781
11124
2602
19654
4696
10572
И 7429
¦ 100%
59,1
9.4
2,5
16,3
4.1
8,6
100,0
Можно группировать лингвистические элементы по альтерна-
альтернативному качественному признаку, т. е. по наличию (Л) или по от-
отсутствию (Л) какого-либо признака. Например, в только что рас-
рассмотренном примере таким признаком может быть принадлежность
словоформы к именным частям речи. Таких словоформ в румынском
частотном словаре по электронике 10 906, и они дадут 117 429 слово-
словоупотреблений в общей выборке из 200 тыс. словоупотреблений.
Соответственно 3 386 словоформ словаря и 82 571 словоупотребление
текста не будут обладать этим признаком.
5. Графическое изображение лингвистических вариационных
рядов. Слабой стороной табличного описания колебания признака
является недостаточная наглядность этого описания. Гораздо боль-
большей наглядности мы можем достичь с помощью графического или
геометрического изображения интересующего нас распределения.
Ведь геометрическая интерпретация математической зависимости
не только придает им наглядность, но позволяет также анализи-
анализировать эти зависимости в простой и доступной форме. В лингвистике
чаще всего применяются такие формы графического представления,
как полигон, гистограмма, кумулятивная
кривая и огива, а также диаграмма. Все указанные
графики строятся в прямоугольной системе координат. Масштабы
на осях ординат и абсцисс могут быть произвольными: обычно их
выбирают так, чтобы соотношение ширины и высоты графика было
равно 1:2.
Теперь рассмотрим каждое из перечисленных графических пред-
представлений.
1. Многоугольником распределения признака (полигоном) на-
называют замкнутую ломаную линию, соединяющую вершины орди-
ординат, соответствующих частотам (или частостям) каждого из значений
признака. При построении полигона в начале и в конце вариацион-
ного ряда добавляются нулевые варианты (варианты, частоты кото-
которых равны нулю). Это дает возможность, соединив указанные точки,
замкнуть ломаную линию, которая и образует полигон. На рис. 48
полигон распределения построен для дискретного, не сгруппирован-
сгруппированного в интервалы значения приз-
признака. Можно построить полигон и
для сгруппированного интервала.
Для этого берется середина ин-
48
40
2
16
¦18 24 SO J6
Рис. 49
X 1
115 175 235 295 X
Рис. 50
тервалаи от нее строится ордината, соответствующая сумме вариант,
относящихся к данному интервалу (рис. 49). Если же распределение
непрерывно, то от середины интервала берется ордината, соответст-
соответствующая частоте (или частости; рис. 50). Как и в случае с дискрет-
дискретным признаком, вначале и в конце ряда добавлены нулевые ва-
варианты.
2. При графическом изображении интервальных вариационных
рядов обычно используется не полигон, а так называемая гистограм-
гистограмма. Отличие гистограммы от полигона состоит в том, что на оси аб-
230
231
сцисс откладываются не точки, а отрезки, соответствующие ширине
интервала. Полученные отрезки являются основаниями прямо-
прямоугольников, высоты которых пропорциональны частотам (или отно-
относительным частостям) соответствующих интервалов. В итоге полу-
получается ступенчатая фигура, образованная рядом сдвинутых прямо-
прямоугольников (рис. 51). " ¦*
uo
32
16
4. Если поменять ролями оси координат и откладывать на оси
абсцисс не значения признака, а накопленные частоты (или относи-
относительные частоты), а на оси ординат — варианты (значения призна-
признака) распределения, то получим так называемую огиву распределе-
распределения (рис. 53). И огива, и кумулятивная кривая используются для
графического изображения как дискретных, так и непрерывных рас-
распределений.
rf
55 85
115
по
120
100
80
— 60
Ш175 205 235265295 х
Рис. 51
/ п
I 60
'. I 50
' / 40
I 30
/ 20
1 10
100 160 220 280 X
Рис. 52
^^"^i III
С М Ч П At Ар
Рис. 54
X
2&0
Полигон и гистограмма представляют собой два крайних случая
идеализации интервальных вариационных рядов: если при построе-
построении полигона частот все значения, лежащие внутри интервала, «стя-
«стягиваются» к его середине, то при использовании гистограммы они
представляются равно-
равномерно распределенными
по всему интервалу. По-
Полигон используется тог-
тогда, когда статистичес-
статистическая совокупность суще-
существенно дискретна. Гис-
Гистограмма используется
чаще для изображения
непрерывных вариаци-
вариационных рядов.
3. Кумулятивной
кривой называется лома-
ломаная линия, которая сое-
соединяет вершины орди-
ординат, соответствующие накопленным частотам для данного значе-
значения признака (накопленной частотой называется сумма частоты
данной варианты и частот всех предыдущих вариант). На рис. 52
показана кумулятивная кривая накопленных частот длин китай-
китайских слогов, показанных в табл. 7.9.
232
160
2Q W 60 80 100 ПО ПО л/
Рис. 53
Рис. 55
5. Порядковый признак не требует графической интерпретации.
Что же касается качественных признаков, то для их графической
интерпретации используются столбиковые и круговые диаграммы.
Такие диаграммы, построенные на основании данных табл. 7.13
и характеризующие удельные веса румынских именных форм, при-
приведены на рис. 54 и 55. Графической интерпретацией вариаций ка-
качественного лингвистического признака можно считать и карту
лингвистического атласа.
§ 3. Статистические характеристики лингвистических
вариационных рядов
Для того чтобы иметь возможность сравнивать вариационные
ряды с вероятностными моделями, рассмотренными в гл. 6, необхо-
необходимо выявить набор тех характеристик (параметров), которые пред-
представляли бы в обобщенном виде основные свойства данной лингво-
статистической совокупности. Наиболее важными статистическими
характеристиками эмпирических распределений считаются сред-
средние (средняя арифметическая, средняя геометрическая, средняя
гармоническая, медиана, мода, квартили, децили и т. д.), а также
меры рассеивания (размах, абсолютное отклонение, сред-
среднее квадратическое отклонение, опытная дисперсия, коэффициент
вариации, квартильное отклонение и др.).
233
1. Средняя арифметическая. Среди разных видов средних наи-
наиболее широкое применение в лингвистических работах имеет сред-
средняя арифметическая. Она проще других и по смыслу, и_ по свойст-
свойствам, и по способу получения. Средняя арифметическая (х) признака
есть отношение суммы количественных вариант этого признака к об-
общему числу вариант, т. е.
N
N
N
<73>
Например, для исследования распределения букв, передающих
гласные, из русского газетного текста («Правда» от 29.Х.69 г.) из-
извлечено 20 порций по 10 букв в каждой. При этом получен следую-
следующий неупорядоченный ряд появления гласных в каждой порции:
5, 4, 3, 3, 4, 4, 3, 4, 4, 4,
4, 6, 5, 4, 3, 5, 3, 3, 3, 4.
Средняя арифметическая частоты появления гласной в газетном
сегменте длиной в 10 букв, вычисленная с помощью формулы G.3},
составляет
- .5+44-3 + 3+4+4+3+4+4+4+4+6+5+4+3+5+3+3+3+4
хгл _
= 4); следовательно,
_ 7-3+9-4+3-5+1-6 __ 21 + 36+15+6 _ 78 _ , Q
*гл~ 20 20 20 ~*У"
2. Свойства средней арифметической. Средняя арифметическая
характеризуется свойствами, некоторые из которых совпадают со
свойствами математического ожидания (см. гл. 6, § 2, п. 8).
1. Средняя арифметическая постоянной равна этой постоянной,
т. е. _
х — а при х1 = х2 = ... = xt = ... = xn — a.
2. Сумма отклонений вариант от среднего значения равна нулю,
т. е.
2 Я! (*!-*) = 0.
3. Если увеличить (уменьшить) значение признака на постоян-
постоянное число а, то средняя арифметическая также увеличится {умень-
{уменьшится) на это число, т.е.
—
З,9.
20
В тех случаях, когда мы имеем дело со сгруппированным вариа-
вариационным рядом (см. табл. 7.2), среднюю арифметическую можно оп-
определить как отношение сумм произведений вариант на их веса
к сумме весов:
=±2п*х' G-4)
Если учесть, что отношения jj = ft являются частостями (от-
(относительными частотами) вариант, то средняя арифметическая мо-
может быть также получена как сумма произведений вариант на их
частости:
2
/—1
G.5)
Среднюю арифметическую, выраженную формулами G.4) и G.5),
в дальнейшем будем называть средневзвешенной.
Представим данные о распределении гласных в русском газет-
газетном тексте (см. выше) в виде вариационного ряда
щ
N
20
4. Если увеличить (уменьшить) каждое значение признака в а раз,
то средняя арифметическая также увеличится (уменьшится)
в а раз, т. е.
N 2d Щ
2
5. Средняя арифметическая суммы признаков равна сумме сред-
средних арифметических, т. е. если признак X является суммой призна-
признаков Y и Z, то
Среднее количество гласных звукотипов в одной десятибуквен-
ной порции газетного текста (см. выше) можно получить, зная
среднюю арифметическую для букв, которые передают гласные,
стоящие после твердых согласных [ы], [э], [а], [о], [у], и среднюю
арифметическую для звукотипов, находящихся после мягких со-
согласных [и], [е], [а), [е], [yl. Неупорядоченный ряд для гласных
первого типа (будем считать их признаком Y) имеет вид
3
2
2
3
1
3
2
2
3
2
2
3
1
2
2
2
3
2
2
3
234
235
Неупорядоченный ряд для гласных второго типа (признак Z)
выглядит так:
2
2
2
3
2
2
1
2
1
1
2
2
2
1
2
1
1
1
2
1
Применяя формулу G.3), имеем
у = 45/20 = 2,25, z = 33/20 = 1,65,
а на основании свойства средней арифметической можно записать
~х =~у +~z = 2,25 + 1,65 = 3,9,
что соответствует результату, полученному ранее.
С помощью метода индукции это свойство распространяется и на
те случаи, когда признак X представляет сумму (или разность) трех
и более признаков.
3. Вычисление средней арифметической с помощью метода мо-
моментов. Упростить ход вычисления средней арифметической можно
с помощью метода моментов. Первая формула этого метода имеет вид
N
G.6)
Здесь а — произвольное постоянное число, подбираемое обычно так,
чтобы разности хг— а были бы возможно проще и меньше (это дости-
достигается тогда, когда величина а занимает серединное положение
в данном ряде и имеет наибольший вес).
Пользуясь соотношением G.6), произведем вычисление средней
арифметической в вариационном ряде распределения гласных в
русском газетном тексте (см. выше). Взяв а = 4, составим табл. 7.14.
Таблица 7.14
3
4
5
6
Сумма
7
9
3
1
20
*,-0
—1
0
1
2
«j(jcf—а)
—7
0
3
2
—2
Отсюда х = 4 — 2/20 = 3,9.
В тех случаях, когда либо все частоты щ, либо все разности
xt — а имеют общий множитель /, для упрощенного вычисления
средней арифметической используется формула моментов (ср. § 4),
построенная на использовании свойств 3 и 4 средней арифметиче-
G.7)
Воспользовавшись данными интервального ряда, приведенного
в табл. 7.9, вычислим среднюю арифметическую с помощью форму-
формулы моментов. В качестве xt возьмем середины интервальных рядов
(обозначим их через xi) и положим а =» 145. Поскольку разности
Xi — а всегда кратны тридцати, примем I = 30. Все эти данные при-
приведены в табл. 7.15.
Интервалы длин
слов (в ис)
40—70
70—100
100—130
130—160
160—190
190—220
220—250
250—280
280—310
Сумма
Середина интервала
*1
55
85
115
145
175
205
235
265
295
я.
i
7
9
49
аз
22
18
7
3
2
150
Та
хг~а
—90
-60
-30
0
30
60
90
120
150
блица 7.15
х1-° „
__„,
—21
—18
—49
0
22
36
21
12
10
13
Используя формулу G.7), видим, что средняя арифметическая
длин китайских слогов равна
?=145+
150
147,6 (мс).
4. Степенные средние. В статистике используются различные
виды средних, обобщаемые формулой
1/а
• G-8)
Если а — 1, то выражение G.8) превращается в формулу средней
арифметической G.4).
При а = 2 выражение G.8) становится формулой средней квад-
ратической
Хл
Аналогичным путем можно получить x3t xt и т. д.
236
237
Если взять а = —1, то получаем среднюю гармоническую, вы-
вычисляемую по формуле
N
N
2 nt/xt
5. Медиана, квартили и децили. Значение признака, относитель-
относительно которого совокупность делится пополам, называется медианой
(Me). Если имеется нечетное число значений варьирующего призна-
признака хъ х2, ..., *т_1, хт, хт+и ..., *am_i, которые расположены в воз-
возрастающем порядке, то медианой этого распределения служит ва-
варианта хт. Слева и справа от значения Me = xm расположено
по т — 1 значений признака.
Например, для анализа лингвистических терминологических си-
систем f7, с. 49] взято семь выборок из русских лингвистических текс-
текстов (объем каждой выборки 250 терминоупотреблений). После под-
подсчета в каждой выборке числа употреблений слова лицо получена
следующая упорядоченная совокупность числовых вариант употреб-
употреблений указанного слова:
Х\
1
9
10
12
Определим медиану ряда. Здесь нечетное число вариант, рав-
равное 7; поэтому 7 = 2т — 1, откуда т = 4. Таким образом, Me =
= х4 = 4.
В тех случаях, когда имеется четное число вариант хи х2, ....
..... *m_i, xm, хт+ъ ..., х2т, медиана, делящая совокупность на
две равные части по т членов, находится между признаками хт
и xm+i. Значение медианы условно определяется как средняя ариф-
арифметическая двух вариант, находящихся в середине ряда:
Me - (х
т+1
I2.
Например, при исследовании тех же лингвистических термино-
терминологических систем в русском языке получена следующая упорядо-
упорядоченная совокупность употребления термина значение в десяти вы-
выборках:
*3
«4
10
«9
10 13
16
20
10,
Найдем медиану ряда. Здесь число вариант четное: 2т
а т — 5, откуда находим Me == (8 + 10)/2 = 9.
Несколько сложнее вычисление медианы в случае интервального
вариационного ряда. Здесь сначала выявляют медианный интервал,
233
т. е. тот интервал, в котором находится медиана. Затем вычисляют
величину медианы, пользуясь формулой
"Т~~ SMe-1
G.9)
где Хме(т1п).— нижняя граница медианного интервала; SMe-i —
накопленная частота, которая соответствует интервалу, предшест-
предшествующему медианному; яМе — частота медианного интервала; k —
ширина медианного интервала (интервальная разность); W — объем
всей совокупности.
Пользуясь данными интервального вариационного ряда, приве-
приведенного в табл. 7.9, вычислим медиану распределения длин китай-
китайских слогов. Для этого перепишем сначала эту таблицу, добавив
данные о серединах интервалов, а также о накопленных частотах
и частостях (табл. 7.16).
Таблица 7.16
Номер
интервала
1
2
3
4
5
6
7
8
9
Интервалы (в мс)
40—70
70—100
100—130
130—160
160—190
190—220
220—250
250—280
280—310
Частота
7
9
49
33
22
18
7
3
2
Накопленная
частота
7
16
65
98
120
138
145
148
150
Накопленная
частость
0,047
0,107
0,433
0,653
0,800
0,920
0,967
0,987
1,000
Нетрудно заметить, что четвертый интервал является медианным,
отсюда имеем: Хме(пип) = 130, SMe-i = 65, п^ =33, k = 30,
N = 150.
Подставив эти значения в формулу G.9), получаем
Me ^130 + 30- 75~65 = 139,09.
33
Медиана делит ранжированный ряд на две равные группы. Ана-
Аналогичным образом можно найти такие значения признака, которые
делят каждую группу снова на две равные части. Эти значения
признака называются квартилями. Различают три квартили: пер-
первую (или нижнюю) квартиль (Qj), делящую пополам ту часть ранжи-
ранжированного ряда, которая находится ниже медианы; вторую квар-
квартиль, совпадающую с медианой, третью (или верхнюю) квартиль
(<3з), которая делит пополам ту часть ряда, которая расположена
выше медианы.
Те значения признака, которые делят объем исследуемой сово-
совокупности на десять равных по объему групп, называются дгцилями.
6. Мода Модой (Mo) называется наиболее часто встречающаяся
варианта данного вариационного ряда (ср. гл. 6, § 1, п. 3). Опреде-
Определение моды для дискретного распределения не представляет труд-
трудности. Модой здесь служит та варианта, которой соответствует наи-
наибольшая частота (кстати, таких вариант может быть несколько).
Несколько сложнее определить моду в интервальных непрерыв-
непрерывных распределениях. Здесь, как и при вычислении медианы, начи-
начинают с определения модального интервала, т. е. того интервала,
внутри которого находится мода (таких интервалов может быть не-
несколько). Затем численное значение моды определяют по следующей
приближенной формуле:
«Мо~ пМо-1
—пМо-1
о —«Мо+1
¦. G.10)
где Хмо(гшп) — нижняя граница модального интервала; k — длина
модального интервала; /тМо—частота модального интервала; пМо_,—
частота интервала, предшествующего модальному; п^^ — частота
интервала, следующего за модальным.
Пользуясь данными табл. 7.9, вычислим моду распределения
длин китайских слогов. Модальным здесь является третий интервал;
следовательно,
Мо= 100 + 30
D9-9)+D9—33)
=121,43.
7. Соотношение между средней арифметической, медианой и мо
дой. Соотношение между этими тремя основными параметрами
эмпирических распределений используется для оценки асимметрии
распределений. Нетрудно заметить, что в тех случаях, когда рас-
распределение симметрично, выполняется равенство х = Me = Мо.
В случае умеренной асимметрии вариационного ряда — явле-
явлении, часто встречающемся в лингвистике,— имеет место следующее
приближенное равенство: Мо л* х — 3 (х — Me), иными словами,
медиана расположена между модой и средней арифметической так,
что расстояние от нее до моды равно двум расстояниям от медианы
до средней арифметической. В случае умеренно скошенных распре,-
делений этим соотношением пользуются для грубой оценки неиз-
неизвестного параметра (скажем, моды) по двум известным характери-
характеристикам, например медианы и средней арифметической [7, с.55].
Сделаем теперь несколько замечаний об использовании указан-
указанных статистических параметров. Из всех этих параметров наиболее
простой по смыслу и по способу получения является средняя ариф-
арифметическая. В отличие от моды и медианы средняя арифметическая
легко поддается аналитическим операциям: выше уже указывалось,
что при объединении двух распределений с различными средними
средняя полученного распределения равна сумме средних из отдель-
отдельных распределений. Поэтому, если нет существенных доводов в
пользу иного вида средней, следует пользоваться средней арифме-
арифметической.
240
Вместе с тем следует помнить, что средняя арифметическая изме-
изменяется с изменением значения любого признака. Особенно она чув-
чувствительна к колебаниям крайних вариант распределений. Иначе
обстоит дело с медианой: из ее определения следует, что медиана не
зависит от значений признаков, лежащих справа и слева от нее (важ-
(важно лишь, чтобы число признаков, меньших и больших, чем медиана,
оставалось неизменным). Поэтому медиану целесообразно исполь-
использовать в качестве средней для таких распределений, концы которых
определены недостаточно надежно.
Что касается моды, то она служит средством выявления одного
или нескольких значений признака, около которых группируется
большая часть объема асимметричного лингвистического распреде-
распределения. В лингво-статистике модальные характеристики распределе-
распределения могут быть использованы для объективного выделения терми-
терминологических, ключевых и вообще доминантных слов и словосочета-
словосочетаний текста.[32а, с.47—112].
8. Рассеяние значений признака. Размах вариации. Хотя сред-
средняя арифметическая, мода, медиана и другие средние признаки дают
ориентировочную количественную характеристику лингвистической
единицы, они не учитывают степень равномерности употребления
этой единицы в текстах. Между тем учет количественной вариации
лингвистического признака в изучаемом тексте имеет принципиаль-
принципиальное значение для языковеда. Всякая вариация лингвистической слу-
случайной величины передает в конечном итоге лексические, граммати-
грамматические, стилевые и другие внутрилингвистические и экстралингви-
тические особенности текста.
Наиболее простой характеристикой рассеивания признака яв-
является размах вариации R, который определяется разностью
R =
— х
mln-
Рассмотрим'в этой связи два вариационных ряда частот немец-
немецкого существительного Kraft в двух выборках публицистических
текстов — одна из газет ГДР (табл 7.17), другая — из газет ФРГ
(табл. 7.18). Каждая выборка состоит из 20 текстов по 1000 слово-
словоупотреблений каждый [7, с. 57].
Таблица 7.17
т
0
16
1
2
2
0
3
0
4
1
5
1
6
0
7
0
0
9
1
11
2
0
3 '
0
4
0
Тг
5
0
] б л и ц г
6
6
7.18
7
0
.241
Используя формулу G.4), находим, что средние арифметические
значения для обоих, рядов вариант одинаковы!
~z _ ~Z' с\ кк
Вместе с тем эти ряды дают различный размах вариации;
R(x) = 16 — 0 = 16, R (х1) = 11—0=11.
Однако размах вариации является очень приближенной оценкой
степени рассеивания признака, так как совершенно не учитывает
положений и «весов» вариант признака, находящихся в пределах
крайних вариант. Действительно, хотя размах вариации немецкого
существительного Kraft в текстах ГДР выше, чем в западногерман-
западногерманских текстах, крайние варианты в первом случае встречаются редко
и имеют малый вес, поэтому вряд ли можно уверенно говорить о том,
что рассеяние здесь действительно выше, чем в текстах ФРГ.
9 Линейное отклонение. Более точную оценку рассеивания мож-
можно получить, учитывая абсолютные величины отклонений J аг/ — jc |
значения признака от его средней арифметической. Среднее значение
этих абсолютных величин, называемое линейным отклонением,
вычисляется для несгруппированного вариационного ряда по фор-
формуле
. n
а для сгруппированного ряда — по формулам
или
I*»—*l = S ft\*i—*!•
G.11)
G.12)
Линейные отклонения для вариационных рядов существитель-
существительного Kraft (см. табл. 7.17 и 7.18) соответственно составляют
|xi—jc | = 0,88 и \х'/— х 1 = 0,50.
Статистическая вариация в употреблении существительного
Kraft в публицистических текстах ГДР несколько выше, чем в га-
газетных текстах ФРГ, однако различия в рассеивании здесь не столь
значительны, как при оценке по размаху вариации.
Нетрудно заметить, что линейное отклонение имеет туже размер-
размерность, что и величина средней арифметической данного вариацион-
вариационного ряда. Поэтому если два вариационных ряда имеют разные зна-
значения х, то их линейные отклонения оказываются несопоставимыми
величинами. В том случае, когда возникает необходимость в числен-
численном сравнении вариаций в распределениях разных лингвистических
признаков, необходимо привести эти вариации к некоторому «обще-
242
му знаменателю». Это достигается путем применения так называемо-
называемого коэффициента вариации, представляющего собой средний процент
рассеивания значений случайной величины по отношению к средней
арифметической:
I XI —Х\
100%.
G.13)
С помощью выражения G.13) можно показать, что для существи-
существительного Kraft значения коэффициента вариации соответственно
равны Vx = 160% и VX' = 90%.
Рассмотрим еще один вариационный ряд. Этот ряд (см. табл. 7.19)
отражает распределение частот английского определенного артикля
the в десяти английских научных текстах по 1000 словоупотребле-
словоупотреблений каждый [7, с.62].
Таблица 7.19
Номера
текстов
Й
и
67
0,1
46
68
0,1
13
71
0,1
г
72
0,1
3; 25
74
0,2
47
80
0,1
43
82
0,1
9
83
0,1
1
84
0,1
С помощью формул G.5) и G.12) получаем, что средняя арифме-
тическая этого ряда составляет х = 75,5, а линейное отклонение рав-
равно \xt —*| = 5,4; следовательно, коэффициент вариации
V =-М_.юо% =7,12%.
75,5
Легко заметить, что коэффициент вариации у английского артик-
артикля заметно меньше, чем коэффициент вариации у немецкого сущест-
существительного. Это неудивительно: служебные формы обычно имеют во
всех языках менее рассеянное употребление, чем знаменательные
слова.
10. Опытная дисперсия и стандарт. Линейное отклонение не
всегда улавливает истинную закономерность вариации случайной
величины,так как результаты здесь сильно усредняются и сглажи-
сглаживаются, а большие отклонения становятся мало ощутимыми, особен-
особенно прн большом числе испытаний. Между тем при решении ряда
лингвистических и особенно инженерно-лингвистических задач
учет именно больших отклонений оказывается принципиально
важным. Чтобы учесть долю больших отклонений, рассматривают
не сами отклонения, а их квадраты.
Сумма взвешенных квадратов отклонения вариант от среднего
арифметического, называемая опытной дисперсией (или просто
дисперсией), для несгруппированного ряда подсчитывается по фор-
формуле
?> = s2 =
N
243
Для сгруппированного ряда дисперсия определяется по формуле
Axi-xf. G.14)
Размерность дисперсии равна квадрату размерности вариант.
Чтобы вернуться к мере рассеивания, имеющей тот же порядок, что
и сами варианты, а также их отклонения, вводят новую характе-
характеристику — стандарт, или выборочное среднее квадратическое от-
клонение, равное квадратному корню из дисперсии:
G15)
Если же нужно сопоставить рассеяние разных по качеству приз-
признаков, оцененное с помощью стандарта, используется коэффициент
вариации
= _L . Ю0%.
G 16)
' Для иллюстрации определим дисперсию, выборочное квадрати-
квадратическое отклонение и коэффициент вариации в распределениях частот
английского артикля the и немецкого существительного Kraft (дан-
(данные приведены в табл. 7.17—7.19). Значения коэффициента вариа-
вариации по стандарту V (s) сравним со значениями коэффициента вариа-
вариации V, полученными по абсолютному отклонению.
Найденные с помощью формул G.14) и G.16) величины приведе-
приведены в табл. 7.20.
Таблица 7.20
Словоформы
the
Kraft (тексты ГДР)
Kraft (тексты ФРГ)
39,70
1,85
' 0,25
6,30
1,36
0,50
V (s) (в %)
8,34
247,4
90,0
V (в %)
7,5
160,0
90,0
Рассеяние контрольных словоформ, оцененное с помощью сред-
среднего квадратического, в целом соответствует рассеянию, получен-
полученному по линейному отклонению. Однако поскольку стандарт учиты-
учитывает то влияние, которое оказывает на конечный результат рассея-
рассеяние крайних вариант, значение коэффициента вариации V (s) больше
значения V.
11. Свойства опытной дисперсии. Основные свойства опытной
дисперсии совпадают со свойствами теоретической дисперсии.
1. Дисперсия постоянной величины равна нулю:
D (С) = 0.
G.17)
2. Постоянную можно вынести за знак дисперсии, возведя ее в
квадрат:
D(CX)=C*DX. G.18)
3. Увеличение (уменьшение) значений признака на одну и ту же
постоянную С не изменяет дисперсии:
D (X ± С) = D,
G.19)
4. Дисперсия равна средней арифметической квадратов значений
признака без квадрата их средней арифметической'.
G.20)
N
Проиллюстрируем это свойство на примере распределения частот
английского артикля the. Для этого-воспользуемся столбцами A)—
D) табл. 7.21.
и
111
67
68
71
72
74
80
82
83
84
Суммы
"t
12)
с
г
10
ni'i
C)
67
68
71
72
148
80
82
83
84
755
ntx]
4.
4489
4624
5041
5184
10952
6400
6724
6889
7056
57359
l5)
—7
—6
—3
—2
0
6
8
9
10
Табл
«4 (Jtj—a.
;Si
—7
—6
—3
—2
0
6
8
9
10
ица 7.21
n( (Jtj—aJ
G)
49
36
9
4
0
36
64
81
100
379
Подставляя величины из нижней строки табл. 7.21 в формулы
G.4) и G.14), имеем
755
10
=75,5; (*)* = 5700,25;
N
57359
10
-5735,9;
244
Dx = 5735,9—5700,25 = 35,65, s = ]/5,65 =5,97.
5. Дисперсия признака относительно средней арифметической
равна дисперсии признака относительно произвольной величины (а)
минус квадрат разности между средней арифметической и этой
величиной:
-аJ—(x—af. G.21)
245
Обычно нахождение дисперсии и среднего квадратического от-
отклонения непосредственно с помощью выражений G.14) и G.15)
связано с трудоемкими вычислениями. Использование свойства 5
дисперсии значительно упрощает процедуру вычисления, которая
оказывается аналогичной нахождению средней арифметической по
методу моментов.
Проиллюстрируем этот прием вычисления дисперсии снова на
примере распределения частот артикля the. Используя столбцы
E)—G) табл. 7.21 и полагая а = 74, согласно формуле G.21) полу-
получаем
D = — • 379-G5,5—74J = 35,65,
откуда s =У35,65 = 5,97.
12. Средняя арифметическая и дисперсия для нескольких сово-
совокупностей. До сих пор мы имели дело со средней арифметической
и дисперсией, характеризовавшими одну совокупность. Однако на
практике постоянно встречаются случаи, когда та или иная лингвис-
лингвистическая совокупность образуется в результате соединения несколь-
нескольких частных совокупностей с одним и тем же признаком, но с раз-
разными его распределениями и, следовательно, с различными сред- -
ними арифметическими и дисперсиями.
Каждую из этих самостоятельных совокупностей мы будем на-
называть частной совокупностью. Характеризующую каждую част-
частную сорокупность среднюю арифметическую признака назовем внут-
внутренней (или групповой) средней (xt), а соответствующие частные дис-
дисперсии определим как внутренние (или групповые) дисперсии (Dr, =•
Полученная в результате объединения нескольких частных сово-
совокупностей общая совокупность имеет свою общую среднюю арифме-
арифметическую или просто общую среднюю х. Вычисление общей средней
производится согласно теореме сложения средних: если статисти-
статистическая совокупность S состоит из Slt 52, ..., Sm частных совокуп-
совокупностей объемом I каждая, то общая средняя равна средней арифме-
арифметической внутренних средних, т. е. '
/и /2> ¦¦•« 'т. то общая средняя равна средней из соответственно взве-
взвешенных частных средних. Иными словами,
_
т
G.22)
где *„ хг, ..., хт — средние арифметические частных совокупнос-
совокупностей.
Только что приведенная теорема описывает тот частный случай,
когда объемы частных совокупностей одинаковы и равны /. Эта тео-
теорема легко доказывается и в том случае, когда объемы частных со-
совокупностей различны. Если эти объемы соответственно составляют
246
G.23)
или короче
m
,5"
Например, в результате статистического описания классических
и позднелатинских текстов [27, с. 53—54] получены данные о соот-
соотношении препозитивного и постпозитивного употребления указа-
указательного местоимения ille при определяемом существительном в раз-
различных жанрах (табл. 7.22).
Таблица 7.22
Статистика пргпозитичного употребления Ше в текстах классической
и поздней латыни
Жанр
Эпистоляр-
Эпистолярные тексты
Повество-
Повествовательная
проза
Ораторский
стиль
Авторы и памятники
1. Цицерон «Письма»
2. Плиний «Письма»
3. Кассиодор «Сочинения»
Всего по жанру
1. Цезарь «Записки о галь-
сдой войне»
2. Тацит «Анналы»
3. «Путешествие Этерии»
4. «История франков»
5. «Салическая Правда»
Всего по жанру
1. Цицерон «Речи»
2. Сенека «О благодеянии»
3. Св. Августин «Исповедь»
Всего по жанру
Количество
препозитив-
препозитивных ille
47
27
18
92
23
9
74
22
32
160
1735
6
ПО
1851
Общее
число
учтенных
присуб-
стаитив-
ных Ше
50
97
21
168
25
10
108
49
56
248
2155
8
159
2322
Внутрен-
Внутренняя
средняя
*(%) пре-
позитив-
позитивных
Ше
54,8
64,5
79,7
Зео жанра
(число
тысяч
употреб-
употреблений)
Ше
0,168
0,248
2,322
247
Х~
Подставляя данные из таблицы в формулу G.23), получаем
54,8168+64,5-248 + 79,7-2322 _ 7q go/o
168+248+2322
т. е. около 77% препозитивных ille.
При исследовании рассеяния в нескольких лингвистических со*
вокупностях используются следующие понятия:
1) внутренняя дисперсия
-х,)\ G 24)
*яким образом, общая дисперсия в этом случае равна
где i — номер частной совокупности, / — число вариант признака
в этой совокупности, a k — номер признака [ср. с формулой G.14I;
2) общая дисперсия
I m
где т — число частных совокупностей признака;
3) средняя внутренних дисперсий
Ur = 5 — ¦"
G.26)
4) межгрупповая (внешняя) дисперсия Dm, представляющая оцен-
оценку рассеяния групповых средних Xt вокруг общей средней х:
'^~. G.27)
т
Общая дисперсия статистической совокупности S, состоящей из
Slt Sa, ..., Sm частных совокупностей объемом I каждая, равна сум-
сумме средней внутренних дисперсий и межгрупповой (внешней) дис-
дисперсии, т. е.
D = D, + Dm. G-28)
Нетрудно заметить, что в том случае, когда все внутренние сред-
средние равны общей средней, т. е. когда xt = х2 = ... = хт — х>
межгрупповая дисперсия Dm — 0, а общая дисперсия равна сред-
средней внутренних дисперсий, т. е. D =¦=* Dr. В остальных случаях об-
общая дисперсия больше, чем средняя внутренних дисперсий на вели-
величину, равную величине межгрупповой дисперсии.
Равенство G.28) имеет место тогда, когда объемы частных сово-
совокупностей равны /. Однако, как и правило сложения средних, прави-
правило сложения дисперсий легко распространяется на случай, когда
объемы частных совокупностей различны и равны соответственно
/ц /а, ..., 1т. В этом случае общая дисперсия также равна средней
внутренних дисперсий плюс межгрупповая дисперсия при условии,
что все значения дисперсий берутся взвешенными по объемам 1и
'г 'т-
248
...-Нт
¦
ХЛ i r\
или
13. Длина словоупотребления как статистико-стилистический
параметр. Величины средней арифметической и дисперсий исполь-
используются при выявлении статистических характеристик (параметров)
стилей [34, с.71—73, 150—164, 178—192, 231 и др.].
Рассмотрим в этом плане средние длины словоформ и рассеяние
этих длин в казахской прозе. Возьмем по десять словоупотреблений
из четырех разновидностей современного казахского литературного
языка — публицистики, художественной прозы (беллетристики),
драматургии и научного повествования — и запишем распределение
длин этих словоупотреблений в каждой из указанных разновидно-
разновидностей [длины отдельных словоупотреблений приведены в столбцах
C)—A2) табл. 7.23].
Таблица 7.23
Средние длины словоформ и их рассеяние в четырех разновидностях
современной казахской прозы
Разновидности
литературного
языка
A)
Публицистика
Беллетристика
Драматургия
Научная проза
Номера в
выборке
/
B)
1
2
3
4
1
C).
12
3
5
И
2
D)
13
6
5
5
3
E)
9
7
5
7
4
(в)
6
8
3
6
б
G)
11
5
2
17
в
(8)
6
6
6
И
7
(8)
8
3
2
4
8
A0)
8
3
2
13
9
3
3
3
4
10
A2)
6
7
6
10
*1
A3)
8,2
6.1
3.9
8,8
\
A4)
8,76
3,49
2,49
16,76
Пользуясь формулой G.4), вычисляем среднюю арифметическую
3+6-3+8-2+9+11 + 12+13 8„
_
Остальные значения средних приведены в столбце A3) табл. 7.23.
249
По формуле G.24) находим внутреннюю дисперсию:
D,, = ^[A2—8,2)* + A3-8,2L (9—8,2)а + F- 8,2J
— 8,2)г + (8—8,2J + C—8,2)
— 8,2J
+ F-8,2)г] = -1-87,6 = 8,76.
Значения Drs, Dr,, Drt помещены в столбце A4) табл. 7.23. С по-
помощью формулы G.26) находим значение средней внутренних дис-
дисперсий, которое равно
D - 8-76+3,49+2,49+16,76 = 31,50 _. g-g
г 4 4 ' '
Значение межгрупповой дисперсии Dm, вычисляемое по формуле
G.27), составляет
Dm = -~ 1 (8,2—6,5)8 +E,1- 6,5J + C,9- 6,5)* + (8,8 - 6,5J] =
= —A,72 + 142 + 2,62 + 2,32) = -^- = 4,225.
4 4
Следовательно, значение общей дисперсии согласно формуле
G.28) равно
D = s8 = 7,875 + 4,255 = 12,1,
а среднеквадратическое отклонение и коэффициент вариации для
общей совокупности соответственно составляют
«=/12,1 = 3,48; V =
3,48
100% =53,5%.
,1 + 3,9+8,8)
Значительное рассеяние средних арифметических по жанрам
казахской прозы говорит о том, что средняя длина словоупотреб-
словоупотребления выступает в каждом жанре в качестве стилистико-статис-
тического параметра.
14. Средняя арифметическая и дисперсия в совокупностях с ка-
качественным признаком. Статистическая однородность текста Рас-
Рассмотренные до сих пор статистические характеристики относились
к количественным лингвистическим признакам. Для того чтобы
применить понятия средней арифметической и дисперсии к совокуп-
совокупности, которая характеризуется качественным признаком, необхо-
необходимо эту последнюю преобразовать в совокупность с количественны-
количественными признаками.
Проще всего осуществить такое преобразование в том случае,
когда совокупность содержит объекты, характеризующиеся некото-
некоторым признаком, и объекты, не имеющие этого признака. Такую со-
совокупность мы будем называть статистической совокупностью о
альтернативным признаком.
250
Отметим наличие признака единицей, а его отсутствие — нулем.
Теперь данную качественную совокупность можно представить в
виде вариационного ряда, показанного в табл. 7.24.
Таблица 7.24
«,-1
F
N—F
Объем этой совокупности есть величина N, представляющая собой
сумму величин F (числа единиц) и N — F (числа нулей). Относи-
Р
тельная частота (доля) признака равна / = -^-, а доля его отсутст-
ВИЯ -jp- - 1 — /.
Найдем теперь среднюю арифметическую х и дисперсиюО. Поль-
Пользуясь формулой G.4), нетрудно показать, что средняя арифмети-
арифметическая равна частости:
F-\+(N-FH F r
N N
G.29)
На основании соотношения G.14) находим дисперсию данной
совокупности:
F{N-F)*+{N-F)P
№
. N
_ F(N
№
F) ^F N-F
N ' N
Дисперсия, являясь здесь мерой рассеивания вариации, характе-
характеризует совокупность с качественным признаком с точки зрения ее
однородности. Например, полная однородность текста относительно
признака А имеет место тогда, когда все его словоупотребления об-
обладают признаком А (т. е. F = N) или когда этот признак полностью
у них отсутствует (т. е. F — 0). Одновременно чем ближе значение
D = s2 к нулю, тем однороднее статистическая совокупность (в дан-
данном случае текст). Чем больше значение D, тем она разнороднее.
Рассмотрим следующий пример. В целях определения статисти-
статистической однородности английских научно-технических и разговор-
разговорных текстов с точки зрения использования в них именных форм
подверглись сравнению два отрывка текста из указанных стилей
по 1000 словоупотреблений в каждом. В научно-техническом тексте
обнаружено 300, а в разговорном — 200 именных словоформ.
251
Вычислим и сравним дисперсии для научно-технического (Dt) и
разговорного (?>а) стилей. Здесь N - 1000, Ft = 300, Fа = 200.
Следовательно,
~Xl = 300/1000 = 0,3, х2 = 200/1000 = 0,2,
?>! - C00 700)/( 1000-1000)- 0,21,
Da = B00 -800)/A000-1000) = 0,16.
Сравнив значения Dt и ?>а, убеждаемся, что разговорный текст
с точки зрения употребления именных форм более однороден, чем
английский научно-технический текст.
Если исследуемая лингвистическая совокупность является не
генеральной, а выборочной совокупностью, как это имело место в
рассматриваемых примерах, то формулы G.29) и G.30) дают лишь
выборочные характеристики х и D, но не истинные значения средней
арифметической и дисперсии, присущие всей генеральной совокуп-
совокупности. В связи с этим снова возникает уже ставившийся нами в
гл. 6 вопрос о близости этих выборочных характеристик к характе-
характеристикам генеральной совокупности Этот вопрос будет рассмотрен
подробно в гл. 8 и 9.
§ 4. Исследование лингвистических вариационных рядов
с помощью эмпирических моментов
Средняя арифметическая и дисперсия представляют собой част-
частные случаи эмпирических (статистических) моментов, являющихся
характеристиками опытного распределения (вариационного ряда)
лингвистических признаков.
Эмпирический момент h-го порядка определяется как средняя
арифметическая h-x степеней отклонений вариант признака X от
некоторой произвольно взятой постоянной а (так называемого нача-
начала отсчета или условного нуля) и выражается равенством
2
Эмпирические моменты являются аналогами теоретических мо-
моментов, рассмотренных в гл. 6, § 2, п. 8. По аналогии с теоретическими
моментами в зависимости от значения произвольной постоянной а
различаются четыре вида эмпирических моментов: моменты
относительно постоянной а (при условии, что а Ф 0,
а Ф х), начальные м о м е_н т ы (при а = 0), централь-
центральные моменты (при а =* х) и нормированные мо-
моменты.
1. Начальные эмпирические моменты для непрерывных и дискрет-
дискретных лингвистических вариационных рядов. Формулы для первых
пяти начальных моментов относительно произвольно фиксирован-
фиксированной постоянной а имеют вид
252
1=1
" N
G.32)
G.33)
G.34)
G.35)
G.36)
В том случае, когда разности xt — а имеют общий множитель /,
вычисление моментов можно упростить, если воспользоваться вы-
выражением
2
i— I
2
*
N
где
,—a \1
G.37)
G.38)
Величины {xt — a)/l = x\ выступают в качестве условных (рабо-
(рабочих) вариант случайной величины, а п'н является рабочим началь-
начальным моментом.
Если необходимо получить истинные значения начальных мо-
моментов относительно о, го правую часть равенства G.37) нужно
умножить на /i-ю степень множителя /. В итоге получаем
N
G.39)
Этим приемом мы уже пользовались при вычислении средней ариф-
арифметической (§3, п.З) и опытной дисперсии (§3, п. 11).
Теперь воспользуемся методом моментов для определения ха-
характеристик непрерывного распределения — вариационного ряда
длин китайских слогов (см. § 2, п.2).
Полагая а = 145, / = 30 и пользуясь формулами G.37) — G.39),
произведем расчеты, как это показано в табл. 7.25. В итоге получаем
величины пх, иа, пя, и4» которые показаны в нижней строке таблицы
(л- = 1).
Расчет начальных моментов из-за своей громоздкости часто со-
сопровождается ошибками в вычислениях. Для проверки расчетов
253
г
V—-X
v-tx
в-}х
1
D—lX
Ix- '
(ои) н
aojoiro ниотг
<N СП О СО (N
(М — О—> (N СО П- Ю ID
г-- ¦* en ©
со ¦* *
T
COIN — О
M - ^ N
о § л S S S
p. „ _ _ _ pq
? N О (О О 8
о о
55 со
II
о*
СО
§
S
1
en
Ti
1"
обычно пользуются формулой, выражающей связь первых пяти на-
начальных моментов для вариант xt с начальным моментом четвертого
порядка для вариант xt + 1. Эта формула имеет вид
Л4* = л6 + 4П|'+6л$ + 4яз + Я4, G.40)
где п'С — четвертый начальный момент вариант xt + 1, а правая часть
равенства включает пять начальных моментов вариант xt.
Если значение момента «4*1 вычисленное по формуле G.40), сов-
совпадает с его значением, полученным из выражения G.36), то это зна-
значит, что расчет первых пяти моментов для вариант Xi произведен
правильно.
Проверим правильность вычисления рабочих начальных момен-
моментов в вариационном ряде длин китайских слогов. Для этого, исполь-
используя данные столбца A1) табл. 7.25, находим, что лГ =8223/150.
Эта величина совпадает с величиной пХ, вычисленной с помощью
формулы G.40):
л 487 , 3655
1+4.JL + 6.-M-
150 150
150
150
150+52+2418+ 1948 + 3655 _ 8223
150 ~~ 150 '
Таким образом, рабочие начальные моменты для распределения длин
китайских слогов определены правильно.
Если вариационный ряд лингвистических признаков содержит
нулевую варианту, то целесообразно пользоваться начальными эм-
эмпирическими моментами.
Формулы для первых пяти начальных эмпирических моментов
имеют вид:
hxf =4т = 1 G-41)
G.42)
G.43)
G.44)
G.45)
G.46)
1 N ^ ' N
(средняя арифметическая),
*
А
п3 = — У л, *? =-^-= ?;
3 N j?d ' N
N
i= I
N
причем
255
Воспользуемся приведенными выше сведениями при решении
задачи автоматического устранения многозначности слова в тексте.
Это устранение осуществляется путем поиска в самом слове или в
его окружении некоторого формального признака — индикатора.
Этот индикатор в комбинации с другими индикаторами или же сам
по себе помогает машине выбрать из автоматического словаря под-
подходящее для данного контекста значение слова. Индикаторами могут
быть как морфемы, так и отдельные слова. Для унификации поиска
та позиция в предложении, которую занимает многозначное слово,
считается нулевой, позиции слева от контрольного слова помечаются
целыми отрицательными числами, а позиции справа — положитель-
положительными.
Для оптимизации поиска индикатора бывает важно иметь рас-
распределение частот индикаторов в различных позициях и получить
характеристики этого распределения.
Так, например, распределение 100 индикаторов в контрольном
отрывке немецкого научно-технического текста характеризуется
величинами, показанными в столбцах A) и B) табл. 7.26.
Таблица 7.26
Позиции
индикато-
индикаторов xt
A)
—2
—i
0
1
2
Частота
индикато-
индикаторов nt
B)
10
30
30
20
10
ni*t
C)
—20
—30
0
20
20
S1 = —10
ni—0.1
D)
40
30
0
20
40
S2=130
»;-i.3
nj xi
E)
—80
—30
0
20
80
S3=—10
ni=—0,1
nixl
F)
160
30
0
20
160
S.-370
ni-3,7
jtj+1
G)
— 1
0
1
2
3
nt 1*1+ "'
(8)
10
0
30
320
810
S| = 1170
nJ-11,7
Данный вариационный ряд содержит нулевую варианту, в ка-
качестве которой выступает позиция многозначного слова, поэтому по-
постоянное число а = 0. Отсюда следует, что характеристиками рас-
рассматриваемого ряда служат начальные моменты, расчет которых
следует вести по формулам G.41)—G.46), как это показано
в табл. 7.26.
Теперь проверим правильность расчетов при определении первых
начальных моментов в распределении частот индикаторов устране-
устранения многозначности в немецком научно-техническом тексте.
Для этого, пользуясь данными табл. 7.26, находим четвертый
начальный момент для вариант xi + 1:
па* = 1170/100 - 11,7.
Тот же результат получаем с помощью формулы G.40):
„;• = 1 + 4 (-0,1) + 6-1,3 + 4 (-0,1) + 3,7 = 11,7.
Таким образом, вычисления начальных моментов произведены пра-
правильно.
Тот факт, что первый начальный момент, совпадающий со сред-
средней арифметической, имеет близкое к нулю отрицательное значение
(п( = х — —0,1), говорит о том, что снимающий полисемию инди-
индикатор следует искать в непосредственном левом окружении много-
многозначного слова.
2. Центральные и нормированные эмпирические моменты. На-
Начальные моменты не только используются в лингвистике при опре-
определении средней арифметической, ной применяются в основном как
вспомогательные величины при вычислении центральных эмпири-
эмпирических моментов, которые дают основную характеристику рассея-
рассеяния случайных величин.
Формулы для вычисления эмпирических центральных моментов
аналогичны формулам теоретических центральных моментов
(см. гл. 6, § 2, п.8):
/По = 1?
тх = 0,
i2'— s8 = n2 — tii {опытная дисперсия),
ms = ns — Ъпгпг + 2n\,
3n\.
G.47)
G.48)
G.49)
Если квадратный корень из второго центрального момента
Ущ = s принять за стандарт, то отношение центрального момента
h-ro порядка к /i-й степени стандарта даст безразмерный нормиро-
нормированный эмпирический момент
rh = тьКУтр = tnhls\ G.50)
аналогичный теоретическому нормированному моменту рЛ.
Для первых четырех нормированных эмпирических моментов
имеем:
гх = 0,
'"з-'Пз/(К'пгK = 'п3/88. G.51)
r4 = m4/mj = mj/s4. G.52)
Третий и четвертый нормированные моменты подобно их теоретичес-
теоретическим аналогам р3 и р^. служат соответственно для количественной
оценки асимметрии (скошенности) и крутости (островершинности
или плосковершинности) эмпирического распределения.
Если г8, а также все нечетные центральные моменты тх, т», т6,...
равны нулю, то эмпирическое распределение является симметрич-
256
Зак. 1287
257
ным. При г, > 0 ряд характеризуется правосторонней (положитель-
(положительной), а при л3 < 0 — левосторонней (отрицательной) скошенностью
(ср. гл. 6, §2, п. 8).
При л4>3 эмпирическое распределение характеризуется острой
вершиной; плосковершинный или двухвершинный ряд дает rt < 3.
Для измерения крутизны распределения используется также вели-
величина опытного эксцесса
Таблица 7.27
Средние длины словоформ в некоторых языках мира
Еэ = г4 — 3,
G.53)
аналогичная теоретическому эксцессу (куртозису).
3. Использование эмпирических моментов для сравнения лингво-
статистических вариационных рядов с теоретическими распределе-
распределениями. Часто характер эмпирического распределения лингвистиче-
г
щ
""
6,00
о)
п
40
30
20
П '"'
9,00 X
Рис.
Щ
56
6,00
б)
ЯОО X
ских единиц оценивается непосредственно по виду графика, полигона
или гистограммы. При этом не учитывается тот факт, что графиче-
графический вид распределения во многом определяется выбором границ
и ширины интервала. Например, на рис. 56 показаны гистограммы
одного и того же распределения средних длин словоформ в языках
-мира (исходное распределение этих длин словоформ приведено
в табл. 7.27). Первая гистограмма (а) построена на основании данных
табл. 7.28, использующей узкий интервал. Вторая же (б) опирается
на ряд, который использует вдвое более широкий интервал и дает
смещение конца распределения вправо (табл. 7.29). При этом может
показаться, что оба распределения существенно отличаются друг от
друга, хотя в действительности мы имеем дело с одним и тем же эмпи-
эмпирическим распределением. Аналогичным образом можно получить
разные гистограммы распределения длин китайских слогов
(см. табл. 7.9 и 7.25) или индикаторов снятия многозначности в не-
немецких текстах (табл. 7.26).
Поэтому, чтобы не впасть в ошибку, предварительную оценку
характера эмпирического распределения следует производить не
визуально, а опираясь на количественные характеристики вариа-
вариационного ряда. Для описания лингвистических вариационных ря-
258
1
2
3
4
Б
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
S3
84
Языки
Русский
Украинский
Белорусский
Болгарский
Македонский
Сербохор-
Сербохорватский
Словенский
Чешский
Словацкий
Польский
Кашубский
Лужицкий
Литовский
Латышский
Шведский
Датский
Норвежский
Исландский
Фарерский
Немецкий
Голландский
Фламандский
Фризский
Английский
Французский
Провансаль-
Провансальский
Итальянский
Испанский
Каталанский
Португальский
Румынский
Молдавский
Ретороманский
Латинский
X
4,701
5,156
4,742
4,186
5,037
4,654
4,423
4,145
4,280
6,531
4,570
4,940
5,775
5,786
4,527
4,781
4,222
5,000
5,589
5,448
4,984
4,463
4,767
3,042
4,855
4,654
4,500
4,953
5,638
4,829
6,164
4,968
3,946
5,072
№
35
36
37
38
39
40
41
42
43
44
45
4С
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
Языки
бретонский
Ирландский
Уэльский
Курдский
Таджикский
Осетинский
Бенгали
Албанский
Армянский
Финский
Эстонский
К пмм
l\UMn
Коми-
Пермяцкий
Удмуртский
Марийский
(луговой)
Марийский
(горный)
Мор до во -
эрзянский
Мордово-
мокшанский
Ненецкий
Селькупский
Венгерский
Мансийский
Хантыйский
Азербайджан-
Азербайджанский
Татарский
Башкирский
Кумыкский
Каракалпак-
Каракалпакский
Ногайский
Казахский
Киргизский
X
3,904
3,673
4,450
3,811
6,205
4,784
5,360
3,776
6,512
7,382
7,754
4,766
5,493
5,299
4,710
5,117
5 356
5,477
6,217
5,326
4,841
5,753
4,126
6,308
5,929
5,507
5,474
5,589
5,584
5,216
5,800
№
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
Языке
Алтайский
Гагаузский
Карачаевский
Балкарский
Туркменский
Узбекский
Уйг урский
Якутский
Тувинский
Хакасский
Бурятский
Калмыцкий
Эвенкийский
Эвенский
Нанайский
Дунганский
Чукотский
Нивхский
Эскимосский
Кетский
Абхазский
Абазинский
Адыгейский
Кабардино-
черкесский
Чеченский
Ингушский
Аварский
Даргинский
Табаса-
Табасаранский
Лакский
Баскский
Хауса
Суахили
Вьетнамский
Индоне-
Индонезийский
к
5,750
5,069
5,415
6,023
5,753
7,471
5,556
5,764
8,776
6,340
5,952
4,614
5,778
6,140
6,571
4,613
8,441
8,340
8,296
6,109
6,406
6,016
7,565
7,156
3,424
5,022
7,300
7,194
6,500
5,520
5,800
4,720
5,209
4,979
6,253
259
Таблица 7.28
Интервалы
2,40—3,00
3,00—3,60
3,60—4,20
4,20—4,80
4,80—5,40
5,40—6,00
0
2
8
20
21
22
Интервала
6,00—6,60
6,60-7,20
7,20—7,80
7,80—8,40
8,40—9,00
16
2
5
2
2
#=100
Интервалы
2,40—3,60
3,60—4,80
4,80—6,00
2
28
43
Интервалы
6,00—7,20
7,20—8,40
8,40—9,60
Табл
ица
7.29
18
7
2
= 100
дов используются следующие четыре эмпирических момента, ана-
аналогичные тем четырем моментам, которые характеризовали теорети-
теоретические распределения (см. гл. 6, § 2, п. 8):
1) первый начальный момент nx =» x (средняя арифметическая),
2) второй центральный момент ma = s2 (опытная дисперсия),
3) третий нормированный момент r3 = ms/s8 (коэффициент ско-
скошенности ряда),
4) четвертый нормированный момент г4 — тл№ (коэффициент
крутости ряда).
Пользуясь численными значениями отдельных моментов, а также
сравнивая эти значения между собой, можно выдвигать гипотезы
о соответствии данного вариационного ряда тому или иному распре-
распределению. Выше было показано, что нормальное распределение
имеет, в частности, параметры р8 =0, р4 =¦ 3. Поэтому если тре-
третий эмпирический нормированный момент г, вариационного ряда не
сильно отличается от нуля, что указывает на симметрию ряда, а зна-
значение четвертого нормированного момента г4 близко к трем, что сви-
свидетельствует о средней крутости ряда, то можно выдвинуть гипотезу
о нормальности рассматриваемого нами распределения (о методах
проверки этой гипотезы см. в гл. 9).
Если же величина гь заметно отличается от нуля, а г4^3 или
i"i *^ 3, то предположение о нормальности лингвистического вариа-
вариационного ряда должно быть сразу же отвергнуто. Такие оценки
широко использовались, например, при определении нормальности
эмпирических распределений слов и суффиксов в различных подъ-
подъязыках и стилях современного латышского языка C1, с. 12—13).
Следует иметь в виду, что здесь не указываются те границы, которых
260
могут достигать отклонения эмпирических моментов от их теорети-
теоретических аналогов, т. е. границы, в рамках которых лингвистический
вариационный ряд сохраняет свою принадлежность к нормальному
распределению.
Эти границы могут быть определены исходя из следующих сооб-
соображений. Будем рассматривать значение третьего нормированного
момента г8 как показатель суммарного смещения кривой эмпири-
эмпирического распределения наблюдаемых погрешностей от центра кривой
нормального распределения. Это смещение можно оценить с помощью
среднего квадратического отклонения
G.54)
где N — объем выборки. Если N велико, то вместо G.54) можно
пользоваться приближенной оценкой
а(га)«КбУЖ G.55)
Мерой согласованности эмпирического распределения с нормаль-
нормальным законом служит отношение
|г8|/<х(г8)=а. G.56)
Если а < 3, то смещение эмпирической кривой относительно цент-
центра нормального распределения можно считать несущественным.
Для оценки расхождения эмпирического распределения и теоре-
теоретического нормального распределения используется среднее квад-
ратическое отклонение
G.57)
причем при больших N соотношение G.57) заменяется приближен-
приближенным равенством
а(Е) « 2J/6/W = 2а(г3). G.58)
Соответственно мерой согласованности эмпирического и теорети-
теоретического нормального распределений служит отношение эксцесса
к среднему квадратическому о(Е):
Еэ /а(Е) = р. G.59)
Если р*<3, то отличие вариационного ряда от нормального распре-
распределения несущественно.
Итак, если для рассматриваемого лингвистического вариацион-
вариационного ряда а ¦< 3 и |$ < 3, то можно предполагать, что этот ряд имеет
нормальное распределение. Подробнее о применении этой проце-
процедуры см. ниже.
Значения опытных моментов могут быть использованы также
для сравнения вариационного ряда и теоретического распределения
Пуассона. Поскольку для распределения Пуассона имеет место
равенство теоретических моментов v1 = \i2 = ц3 = % (см. гл. 6,
261
§ 3, п. 2), то лингвистический вариационный ряд, в котором значения
эмпирических моментов nlt ma и m3 мало отличаются друг от друга
по величине, может быть гипотетически отнесен к распределению
Пуассона.
В работе Т. А. Якубайтис [31, с. 7—46, 69—66] вычислены эмпи-
эмпирические моменты пъ m%, m8 для распределения 120 слов, 6 суффик-
суффиксов и класса частиц в различных подъязыках и функциональных
стилях латышского языка. Обнаружилось, что по мере уменьшения
частоты слов численные значения эмпирических моментов nlt m2, та
сближаются. Отсюда можно сделать вывод, что распределение неко-
некоторых редких слов (F > 70) в латышском языке соответствует
закону Пуассона.
4. Распределение средних длин словоупотреблений в языках
мира. В § 3, п. 13 было показано, что средняя длина словоупотреб-
словоупотребления может выступать в качестве статистического параметра сти-
стиля. В связи с этим возникает вопрос: можно ли считать среднюю
длину словоупотребления типологической характеристикой кон-
конкретного языка [8]; [51, с. 178—181]? Статистический анализ рас-
распределения средних длин словоупотреблений в языках мира помо-
помогает решению этого вопроса. Действительно, если вариационный
ряд средних длин хорошо аппроксимируется нормальной кривой,
то можно предполагать, что средние длины словоупотреблений раз-
разных языков равномерно группируются вокруг некоторой средней,
задаваемой возможностями оперативной памяти человека. Отклоне-
Отклонения от этой средней в каждом конкретном языке следует рассматри-
рассматривать как результат случайных воздействий, по всей вероятности, не
связанных с типологией языка.
Заметное отклонение вариационного ряда от нормальной кри-
есй можно рассматривать как указание на то, что распределение
средних длин словоформ определяется не только случайными, но
и детерминированными процессами. В этом случае естественно пред-
предположить, что расхождения в средних длинах словоупотреблений
связаны с типологическими особенностями конкретных языков.
* Чтобы решить, какое из этих двух предположений считать более
правдоподобным, обратимся к статистическому анализу распределе-
распределения средних длин словоупотреблений для ста языков мира, приме-
применяющих буквенную графику*. Для этого используем приведенные
выше табл. 7.27 и 7.28.
Статистический анализ ряда, проведенный строго по схеме, ко-
которая была изложена в п. 1—3, показан в табл. 7.30. Начнем с того,
что определим центральное значение xt каждого интервала [столбец
BI. Затем вычислим начальные моменты относительно а, в качестве
которого возьмем среднее значение центрального интервала (а =
= 5,70). Используя общий для разностей xt — а множитель / = 0,6
* Расчет произведен по разговорно-беллетристическим текстам этих язы-
языков, а также по отрывкам, приведенным в книге [12]. Если учитывать научно-
техническую и публицистическую прозу, то значения средних длин будут
несколько выше.
262
(?-'*) ?»
*-**) '„
t\ 0 —h )
1 +
v-h
,-h
ЙПО1
OMNtOOONOOCOSO
^f ^f — M
t"— Cjlt'-'OOOt"-*
OCOOiCO^Ol
1^1
'IV
^-^ СО 00 Ю <N ^
}•- -oo
Г\
С5(М-"О—-
OWQ0O—OCDWIONO
— ¦* in еч —соо — ю
? О ^ Ю CN
~!О<М — — COC
¦*СО(М
CO<N—<—ЮОО-> — IMCO
888S3888838
L?0'6ZQ
000*'SSI
os'o=e«
9183' 1
8
Wo—=
263
[столбцы D) и EI, определим сначала рабочие начальные моменты.
Для этого, разделив каждую из сумм столбцов F) —(9) на N = 100,
получим:
лб =» 1, п[ =—0,4, П2 = 3,56, л? = 0,2, п\ = 37,16.
Для проверки правильности вычислений определим четвертый мо-
момент для условных вариант —т^- + 1 с помощью равенства G.40):
п? = 1 + 4-(—0,4) + 6-3,56 + 4-0,2 + 37,16=58 72.
Этот результат совпадает со значением nj\ полученным путем не-
непосредственного вычисления по формуле G.36) [ход расчетов пока-
показан в столбцах A0)—A2) табл. 7.30]. Таким образом, расчет рабочих
начальных моментов получен правильно.
Теперь можно перейти к вычислению начальных моментов от-
относительно а = 5,7. Для этого каждое из значений nk нужно умно-
умножить на lh — О.б*. Тогда получим:
п0 = ЬО.б0 = 1; п2 = —0.4-0.61 = —0,24; л, = 3,56 -0,62 =
= 1,2816; п3 = 0,2-0,63 = 0,0432; /г4 = 37,16-0,64 == 4,8159.
Средняя арифметическая ряда (т. е. средняя длина словоупотреб-
словоупотребления) в языках мира равна
х = nj (а) + а = —0,24 + 5,7 = 5,46.
Затем, используя начальные моменты относительно а и формулы
G.32)—G.36), вычислим центральные моменты:
т0 =. 1;
щ = 0;
т2 = !?= 1,2816 — (-0.24J = 1,2816 — 0,0576 = 1,224;
та = 0,0432 — 3-1,2816-(—0,24) + 2(—0.24K = 0,0432 + 0,9228—
— 0,0276 = 0,9384;
т4 = 4,8159 —4-0,0432-( — 0,24) + 6-1,2816-( —0,24)а—
— 3- (-0,24)* - 4,8159 + 0,0415+0,4429 — 0,0100 = 5,2903.
Центральные моменты можно получить и с помощью формул
G.47)—G.49). Для этого каждую сумму из столбцов A6)—A8)
разделим на N = 100. Нетрудно заметить, что полученные резуль-
результаты совпадают до третьего знака после запятой со значениями цент-
центральных моментов, полученных по упрощенной процедуре. Таким
образом, расчет центральных моментов произведен правильно.
Теперь, используя значения центральных моментов, переходим
с помощью выражений G.54)—G.59) к непосредственной проверке
264
нормальности распределения средних длин словоупотреблений
в языках мира. Имеем:
г8 = 0,9384/(УП224)8 = 0,693;
Ев = 5,2903/1,224* — 3 = 3,527 — 3 = 0,527.
Далее получаем
а (гя) = /F-99)/A0Ы04)=: /0,05655 = 0,238,
или по приближенной оценке G.55),
i« 0,245,
а также
а (Е) = ]/B400-98-97)/(99M03-105) = /0.215244 = 0,464,
или по оценке G.58),
а (Е) я* 0,490.
Поскольку отношения
а = 0,693/0,238 = 2,91, а « 0,693/0,245 « 2,83,
р = 0,527/0,464 = 1,14, 0 « 0,527/0,490 « 1,08
меньше трех, то можно предположить, что распределение средних
длин словоформ в языках мира подчиняется нормальному закону.
Отсюда следует, что образование словоформ во всех языках мира
ориентировано на некоторый эталон, длина которого определена
возможностями оперативной памяти человека.
На этом мы заканчиваем описание важнейших приемов форми-
формирования вариационных рядов и методики вычисления их характе-
характеристик. Каждый вариационный ряд обобщает результаты статисти-
статистического эксперимента над текстом ограниченной длины, который
выступает в роли частной выборки, взятой из некоторой генеральной
совокупности (язык в целом, стиль, подъязык, язык писателя).
Обычно выборочная текстовая совокупность интересует лингвиста
лишь постольку, поскольку она может рассматриваться в качестве
модели, отражающей вероятностные свойства исследуемой гене-
генеральной совокупности текстов и стоящей за ней нормы языка или
его разновидности.
Г Л А В A a
СТАТИСТИЧЕСКАЯ МОДЕЛЬ ТЕКСТА И ВЕРОЯТНОСТНЫЕ
ХАРАКТЕРИСТИКИ НОРМЫ ЯЗЫКА
Переход от статистической модели выборки текста к вероятност-
вероятностным характеристикам нормы языка связан с решением трех задач.
Во-первых, по характеристикам 8* вариационного ряда необ-
необходимо численно оценить скрытые от прямого наблюдения парамет-
параметры 8 соответствующего распределения генеральной совокупности,
т. е. параметры, выступающие в качестве вероятностных характе-
характеристик нормы языка и его разновидностей.
Во-вторых, по данным вариационного ряда следует оценить ха-
характер генерального распределения.
В-третьих, имея в своем распоряжении численные оценки пара-
параметров генерального распределения, а также зная характер этого
распределения, необходимо решить важнейшую технологическую
задачу лингвистического исследования, состоящую в определении
того, какой объем обследуемого текста даст достаточно надежные
лингвистические результаты.
§ 1. Точечная оценка параметров генеральной
лингвистической совокупности
1. Понятие точечной оценки. Каждый параметр 0* вариацион-
вариационного ряда, вычисленный на основе ограниченного числа опытов,
всегда содержит элемент случайности. Поэтому его значение нельзя
отождествлять со значением параметра 0, характеризующего рас-
распределение исследуемого лингвистического явления в генеральной
совокупности. Величину 9* следует рассматривать лишь как точеч-
точечную оценку значения 0.
Что же представляет собой эта оценка 0* с вероятностно-статис-
вероятностно-статистической точки зрения? Чтобы ответить на этот вопрос, проведем
следующий мысленный эксперимент.
Предположим, что из генеральной совокупности текстов извле-
извлекаются 1-я, 2-я, ..., N-я выборки одного и того же объекта, в каждой
из которых наблюдаемая случайная величина X с параметром 0*
принимает значения хъ хъ ..., xN. Все эти значения имеют одинако-
одинаковые распределения, идентичные распределению величины X. Каж-
Каждое распределение соответственно характеризуется параметрами
01, 02, ..., Q*n, которые являются значениями параметра 0*. Этот
последний представляет собой функцию значений jq, х2, ..., xN и яв-
является случайной величиной (ведь каждая новая t-я выборка дает
новое значение 0* нашей оценки).
Так как точечная оценка 0* является случайной величиной, то
она может давать разные отклонения от значения 0, и следовательно,
давать разную по своей «доброкачественности» оценку параметра 0.
Наша задача состоит в том, чтобы найти критерии, позволяющие
выбирать из параметров 0«, Щ, ..., 0? исследованной частной вы-
266
борки такую величину 0*. которая давала бы наименьшее отклоне-
отклонение от значения 6 и выступала бы поэтому в качестве наилучшей
оценки.
Действительно, мы пока не знаем, что является наилучшей оцен-
оценкой математического ожидания М_(Х) = ц в генеральной сово-
совокупности: средняя арифметическая х, медиана Me или модаМо. Ана-
Аналогичным образом мы не можем пока сказать, что является лучшей
оценкой дисперсии D (Х) = а2: выборочная дисперсия s2, размах R
или среднее абсолютное отклонение \xt — х\.
Чтобы получить критерии выбора наилучших оценок параметров
распределений в генеральных совокупностях, необходимо, во-пер-
во-первых, определить те требования к оценкам 0*, которые давали бы хо-
хорошее приближение этих оценок к параметру 0, во-вторых, опреде-
определить методы нахождения оценок; в-третьих, выяснить возможности
использования этих оценок для получения надежных выводов от-
относительно значений параметров генеральной лингвистической со-
совокупности. Хорошее приближение характеристики 0* к теорети-
теоретическому параметру 0 должно отвечать требованию состоятель-
состоятельности, сущность которого заключается в следующем. Идеальной
оценкой для параметра 0 была бы такая величина 0*, которая в
каждом своем выборочном значении 9|, Ог, ..., Qn в точности совпа-
совпала бы с искомым параметром 0. Разумеется, что на практике такое
положение недостижимо. К идеальному положению, при котором
0* = 0, можно было бы приблизиться, постепенно усредняя зна-
значения Oj, Ог, ..., Qn при условии, что N -*¦ оо, как это предусмотре-
предусмотрено законом больших чисел (см. гл. 6, § 4).
В этом случае согласно закону больших чисел имела бы место
сходимость по вероятности величин 0* к 9, описываемая равенст-
равенством
limP{|0* —0|<е} =
N-
(8.1)
в котором е — сколь угодно малая величина.
Итак, оценка неизвестного параметра 0 в генеральной лингвис-
лингвистической совокупности отвечает требованию состоятельности, когда
она подчиняется закону больших чисел.
Нетрудно заметить, что требование состоятельности имеет два
практических недостатка. Во-первых, оно не всегда обнаруживается
в условиях малых выборок, с которыми имеет дело языковед; во-
вторых, при одной и той же функции распределения генеральной
совокупности для данного параметра 9 можно найти бесконечное
множество состоятельных оценок, сходящихся по вероятности к 0.
Поэтому требование состоятельности дополняется еще двумя требо-
требованиями: несмещенности и эффективности. Не-
Несмещенной оценкой называется такое приближение, при котором
математическое ожидание 0' равно параметру 0 генеральной сово-
к) пности, т. е.
М (д*) - 0.
267
Иными словами, несмещенность оценки означает равенство по
абсолютной величине взвешенных сумм отклонений значений 9J,
Эг, ..., 6л/ от центра, в качестве которого выступает параметре.
Вместе с тем она показывает на отсутствие систематической ошибки,
постоянно смещающей указанные значения в одну сторону от этого
центра.
2. Несмещенные и эффективные точечные оценки математическо-
математического ожидания и дисперсии. В работах по математической статистике
[10, с. 314—317] доказывается, что средняя арифметическая х выбо-
выборочной совокупности является несмещенной оценкой математичес-
математического ожидания случайной величины генеральной совокупности, т. е.
М (х)=*М (X),
и что относительная частота f есть несмещенная оценка вероятности
р. Одновременно выясняется, что в малых выборках (N ^ 50) опыт-
опытная дисперсия Dx^s* не может служить несмещенной оценкой тео-
теоретической дисперсии D (X) = а2. Несмещенной оценкой теорети-
теоретической дисперсии является величина
N
JV—1
¦sa.
(8.2)
При больших значениях N величиной смещения можно пре-
пренебречь и рассматривать s2 в качестве несмещенной оценки D (Х)=
= а2.
Возможные значения 0 могут не давать смещения, однако одно-
одновременно могут быть сильно рассеяны вокруг М (9*), что заметно
ухудшает оценку параметра 8. Поскольку наилучшей мерой среди
рассматриваемых в этой книге мер рассеяния является дисперсия,
целесообразно оценивать эффективность оценки 6/ параметра 9
с помощью величины
Г> (9/) == аа (9Г).
Таким образом, если имеется несколько состоятельных несме-
несмещенных оценок параметра 9, то наиболее эффективной служит та,
которая имеет наименьшую дисперсию и наиболее тесную концент-
концентрацию значений 8* вокруг М F*) = 8.
В качестве примера рассмотрим две оценки математического
ожидания употребления служебных слов, дающих обычно нормаль-
нормальное распределение в тексте. Этими оценками являются средняя
арифметическая х = 8J и медиана Me = 9р. В. И. Романовский
[30, кн. 1, с. 203] показал, что для средней арифметической диспер-
дисперсия составляет
D (9?) = а2 (х) = а*Ш,
а для медианы она равна
D (9p) ^ a2 (Me) = naVBN) = l,57aVN.
268
Так как концентрация значений 6« вокруг М (8*) в полтора с
лишним раза выше, чем концентрация значений 9'jJ, то средняя* ариф-
арифметическая является более эффективной оценкой математического
ожидания, чем медиана.
§ 2. Оценка математического ожидания с помощью
доверительного интервала и статистическая параметризация
стилей
1. Доверительный интервал. Отвечая требованиям состоятель-
состоятельности, несмещенности и эффективности, точечная оценка 9* имеет
один серьезный недостаток: она не дает сведений о точности и надеж-
надежности приближения к параметру 9 генеральной лингвистической
совокупности. Этот недостаток особенно ощутим тогда, когда число
наблюдений мало. Чтобы устранить этот недостаток, вводится иной
вид оценки — доверительный интервал.
Для определения доверительного интервала необходимо найти
такие случайные значения 9н, 9J, каждое из которых является функ-
функцией выборочных наблюдений хи х2, ..., xn, чтобы образуемый ими
промежуток (9J, 9?) с вероятностью не менее Р покрывал неравен-
неравенство 9в < 9 < 9в, в котором 9J выступает в роли нижней, а 9в —
верхней границы доверительного интервала.
При оценке параметра 9 с помощью доверительного интервала
учитываются две величины.
Во-первых, необходимо указать ширину доверительного интер-
интервала 9? — 9„, половину которого составляет величина погрешности
е = (9в — 9JJ/2, характеризующая точность нашей оценки. Чем
уже интервал, т. е. чем меньше разность 9J — 9н, и следовательно,
чем меньше е, тем точнее оценка параметра 9.
Во-вторых, следует учитывать с какой вероятностью интервал
(9J, 9в) покрывает параметр 9. Ведь нижняя (9Ц) и верхняя (9J)
границы интервала суть случайные величины, зависящие от опыта:
при многократном повторении опыта величина и положение интер-
интервала (9Ц, 9J) относительно 9 будут меняться. Однако доверительный
интервал должен быть построен так, чтобы доверительная вероят-
вероятность (надежность) Р захвата им параметра 9 была бы достаточно
велика, а вероятность ч, представляющая собой дополнение до еди-
единицы и указывающая на то, что 9 не будет покрыт интервалом (9J,
8В), была бы соответственно мала (мы будем впредь называть q
уровнем значимости). Чем ближе вероятность \> к единице, а вероят-
вероятность (? к нулю, тем меньше риск ошибиться в оценке параметра 9.
2. Определение доверительного интервала для математического
ожидания нормально распределенной случайной величины при из-
известном а. Пусть случайная величина X имеет нормальное распреде-
распределение в интересующей нас генеральной лингвистической совокуп-
совокупности, причем нам известно значение а, но неизвестен параметр
М (X) = |х.
Для оценки (х естественно использовать среднюю арифметическую
х, которая на основании центральной предельной теоремы (см. гл. 6,
269
§4. п. 4) распределена нормально с параметрами М (х) = ц, а
Для того чтобы определить доверительный интервал неизвест-
неизвестного нам параметра ц = 8 по оценке х = 8*, потребуем выполнения
соотношения
Я(|х —ц| <е) = Р, (8.3)
где е — допустимая погрешность, выступающая в качестве величи-
величины, обратной степени точности, а р, как уже говорилось, надежность,
которая должна быть близка к единице.
Так как по предположению случайная величина X распределена
нормально, то, на основании соотношения F.125) выражение (8.3)
можно переписать в виде
Р (| i—|х | <
= 2 Ф
Р,
или
(8.4)
(8.5)
где индекс Р при г означает, что значение г берется в соответствии
с надежностью (доверительной вероятностью) Р.
Нетрудно заметить, что
является нижней, а
=цв
(8.6)
(8.7)
верхней границей доверительного интервала (ц,*, Цв)- Этот интер-
интервал с надежностью Р и погрешностью ъ=гра/уы покрывает мате-
математическое ожидание ц = М (X) нормально распределенной слу-
случайной лингвистической величины X в генеральной совокупности.
Расчет доверительного интервала производится следующим об-
образом. Задавая определенную доверительную вероятность Р, мы
с помощью табл. III (см. стр. 365) определяем значение Zp, т. е. Zp =
= х. Подставив это значение в равенства (8.6) и (8.7), легко вычис-
вычисляем значения верхней и нижней границ доверительного интервала.
Например, задав согласно правилу «трех сигм» надежность
*> = 0,9973 (т. е. р/2 = 0,4986), для нормально распределенной
лингвистической величины получаем
и цв =
Погрешность в этом случае равна
е (Р = 0,997) = За/УЛ.
Задавая по правилу «двух сигм» надежность Р = 0,954, приходим
к доверительным границам
при величине погрешности, равной
е (»> = 0,954) = 2а/ УН.
Наконец, удовлетворяясь надежностью р — 0,683, мы получаем
еще более узкий.доверительный интервал с границами
причем погрешность равна
i (р = 0,683) = о/
= о (х).
270
Из всего сказанного становится ясным, что при одном и том же
объеме выборки N с увеличением надежности р уменьшается точность
(т. е. значение погрешности г становится большим) и, наоборот,
с уменьшением Р увеличивается точность (т. е. численное значение s
становится меньшим). Если сохранять постоянным значение надеж-
надежности Р и увеличивать объемы выборки N, то можно увеличить точ-
точность, и наоборот, при постоянном р с уменьшением N точность
уменьшить. Наконец, одновременного увеличения надежности и
точности можно достичь только путем увеличения объема выборки
Л'. Все эти соображения будут иметь принципиальное значение при
определении необходимых объемов лингвистических выборок.
3. Определение доверительного интервала для М (X) с помощью
распределения Стьюдента. В лингвистической практике редко встре-
встречаются ситуации, при которых известно численное значение сред-
среднего квадратического отклонения в генеральном распределении.
Чаще всего и математическое ожидание, и дисперсия, и среднее квад-
ратическое отклонение остаются неизвестными. Поэтому необходи-
необходимы такие процедуры поиска интервальных оценок параметров тео-
теоретического распределения, которые опирались бы только на значе-
значения средней х, опытной дисперсии s2 и стандарта s (соответственно
s2, s), получаемых из частных выборок, взятых из генеральной линг-
иистической совокупности.
При этом интервальная оценка математического ожидания
М (X) = ц достигается путем применения распределения Стью-
Стьюдента.
В гл. 6 (см. § 3, п. 4 и § 4, п. 4) было показано, что в тех случаях,
когда величина X распределена нормально с математическим ожи-
ожиданием М (X) = (х и средним квадратическим отклонением а (*) =
= а /Vn, величина
(8.8)
дает нормированное нормальное распределение со средней, равной
нулю, и дисперсией, равной единице.
271
Однако при определении доверительного интервала распределе-
распределением Z воспользоваться нельзя, поскольку величина а неизвестна.
Заменим а стандартом
f N — \
и перепишем (8.8) в виде -
t-hzJLyTR.
(8.9)
В работах по математической статистике [63, с. 198] доказывается, что
плотность вероятности распределения значений t задается выраже-
выражением
МО'
г —
(8.10)
где v = N — 1, —оо < t < оо, а Г — так называемая гамма-функ-
гамма-функции [9, с. 161 и сл.1. Из (8.10) видно, что распределение величины /
не зависит от неизвестных параметров М (X) = ц и D (X) = аа,
а зависит лишь от величины v, называемой числом степеней свободы
(см. ниже §3, п.1), которая представляет собой численность N — 1
независимых значений случайной величины X в выборке из N испы-
испытаний.
Интегрируя (8.10) в пределах от —оо до L, можно найти вероят-
вероятность Р (t< tp) случайных значений t, меньших, чем заданное зна-
значение /.
Р'
]
] h(x)dx.
(8.11)
Описанный закон распределения носит название закона распре-
распределения Стьюдента (/-р аспределения) с v степенями сво-
свободы (в литературе он иногда называется распределением
малых выборок).
Так как при больших значениях N выборочная дисперсия s2
и стандарте мало чем отличаются от теоретических параметров а2 и а,
то при больших v = N — 1 величина /, приближаясь к Z, получает
нормальное распределение. Однако когда v = N — 1 мало, то t,
сильно отличаясь от Z, не подчиняется нормальному распределению.
Эти особенности /-распределения показаны на рис. 57. Сохраняя ко-
локолообразную и симметричную относительно начала координат
форму, кривая распределения Стьюдента при малых значениях N и
v гораздо медленнее сближается с осью абсцисс, чем кривая нормаль-
272
яого распределения. Поэтому вероятность значений t, попадающих
в критическую область или, иными словами, превышающих по аб-
абсолютной величине заданный предел tp, гораздо больше, чем ве-
вероятность значений Z, превышающих установленный предел г^ =
= tp (рис. 57). Однако при N -*¦ оо кривая f (t) совпадает с кри-
кривой нормального распределения.
Учитывая равенство (8.11) и симметрию кривой /v @. можно лег-
легко прийти к вероятности того, что величина t будет находиться в за-
заданных пределах (—tp, tp). Эта доверительная вероятность (надеж-
(надежность) равна
P\\ (8.12)
Рис. 57
Аналогичным образом уровень значимости составляет
q = Р (|<| > tp). (8.13)
При решении лингвистических задач о помощью распределения
Стьюдента доверительные вероятности р определяются по табл. IV
(см. стр. 366,367), строки которой дают заданные значения t, а столб-
столбцы—заданные величины v=W—1. На пересечении строк и столбцов
находятся соответствующие значения доверительной вероятности.
Распределение Стьюдента легко может быть использовано для
интервальной оценки математического ожидания М {X) = ц лин-
лингвистической случайной величины, относительно которой наперед
известно, что она распределена нормально, но параметры которой
D (X) = а2 и а остаются неизвестными.
Действительно, подставляя значение t в неравенство—tv<.t<itp,
вероятность ьогорсго задана наперед, имеем
-'»<¦
х— I
(8.14)
273
или
Это неравенство, равносильное (8.12), имеет вероятность
(8.15)
. (8.16)
Нетрудно заметить, что вероятность Р, легко получаемая из таб-
таблицы значений Р (\t\ ^ /р) (см. табл. IV), является надежностью
нашего утверждения о том, что t не выйдет из доверительного интер-
Еала с нижней границей
и верхней границей
(8.17)
(8.18)
где член tp s/VN = tpS (x) оценивает погрешность 8.
Только что полученная интервальная оценка очень похожа на
оценку, приведенную в п. 2. Различие состоит в том, что вместо
теоретического среднего квадратического отклонения а здесь ис-
используется выборочная величина s, а вместо Zp применяются tp.
В тех случаях, когда выборка N — v + I велика (например, когда
N > 30), s « a, a tp « Zp, и поэтому доверительный интервал, по-
полеченный с помощью ^-распределения, близок к интервалу, вычис-
вычисленному в п. 2. В тех случаях, когда N = v + 1, мало, ^-интервал
заметно шире г-интервала. Разумеется, это не является недостатком
(алого распределения Стьюдента. Причина кроется в малом объеме
1ыборки: чем меньше объем выборки, тем меньше информации о ге-
генеральной совокупности, в том числе и о параметре М (X) = ц,
содержит выборочное распределение Стьюдента. Поэтому и ширина
доверительного интервала должна быть здесь больше по сравнению
с тем интервалом, который получен на основании сведений о распре-
распределении самой генеральной совокупности.
4. Математическое ожидание как статистический параметр сти-
стиля. Одним из важных вопросов квантитативной лингвистики яв-
является выявление объективных статистических признаков для от-
отдельных разновидностей языка (стилей, подъязыков, жанров, автор-
авторского стиля). Эта проблема исследовалась коллективом языковедов,
руководимым В. И. Перебейнос [34]. В частности, была сделана по-
попытка разграничить жанры и стили современного украинского язы-
языка с точки зрения частоты употребления в них глагольных слово-
словоформ.
Это исследование строилось следующим образом. Из современ-
современных художественных, общественно-политических и научно-техни-
научно-технических текстов было извлечено 280 выборок по 500 словоупотребле-
274
ч
И
I
' I
1ч
S
А
I
1
14 иойорма
оахээылгон
* 2
tt
Я
? a
o.2
V СО Ю
V-
й5 о
S 2
8 00 N
00
И?
SS2
S5
М П N
«) (О О
О) 00
8 S S
8
a
S
s
s
т
г
о
О)
I
S
S
S
S
I
1
a
ний в каждой (количество выборок по стилям и жанрам показано
в столбце B) табл. 8.П. Для каждого жанра и стиля была вычисле-
вычислена средняя частота F_== х глагольных словоупотреблений, а также
стандарты s»s hs(x) = s[}/N « s (x).
Поскольку дисперсия и среднее квадратическое генеральных
текстовых совокупностей по украинским стилям остаются неизвест-
неизвестными, вычисление доверительного интервала, в котором находятся
величины М (F), следует осуществлять с помощью распределения
Стьюдента. При этом, опираясь на данные предшественников [32а,
с. 43—45,104—1071, можно предположить, что частоты глагольных
словоупотреблений распределены нормально.
Драма-
Проза
Поэзия
00~ЩгТ1пЛ.
проза
Научна-
техн.
проза
Рис. 58. Доверительные интервалы математического ожидания
частоты глагольных словоупотреблений в украинской драме,
прозе и поэзии:
Ш1 — доверительный интервал при р = 0,95;
си — доверительный интервал при р > 0,996 (правило «трех
сигм»)
Если удовлетвориться надежностью наших утверждений, рав-
равной 95% (р = 0,95), то, согласно данным табл. 8.1, при v = 60 —
— 1 = 59 имеем t* = 2,00, a npnv = 50 — 1 = 49 получаем /„=*
= 2,01.
В этом случае величина погрешности при определении М (Р)
глагольных словоупотреблений в выборках из украинской драмы
составляет е = 2,00-1,98 = 3,96, а границы доверительного интер-
интервала, в силу равенств (8.17) и (8.18),
ц* = 90,5 — 3,96 = 86,54, |х* = 90,5 + 3,96 = 94,46.
Аналогичные значения погрешности и границ доверительных ин-
интервалов относительно других жанров показаны в столбцах F) и G).
Если положить, что среднее квадратическое отклонение а равно
полученному экспериментальным путем стандарту s, то интервал,
покрывающий с надежностью Р — 0,95 величину М (F), несколько
сузится [см. столбец (9)].
Как показывают данные табл. 8.1 и рис. 58, доверительные ин-
276
тервалы М (F) глагольных словоупотреблений в украинской драме
и прозе частично накладываются друг на друга. Что касается других
жанров и стилей, то там этих наложений нет. Отсюда можно сделать
вывод, что частота глагольных словоупотреблений является тем ста-
статистическим параметром, который обособляет украинские драмати-
драматические и прозаические тексты от поэтических, общественно-полити-
общественно-политических и научно-технических текстов, а также различает между со-
собой последние два стиля (о том, насколько точны эти заключения,
сделанные при условии точечной оценки среднего квадратического
отклонения, будет сказано в следующем параграфе).
Лингвистические выводы, к которым мы только что пришли,
имеют сравнительно малую надежность — всего 95%. Если же
необходимо увеличить надежность этих выводов, приблизив их к
100%-ному утверждению, то следует произвести расчет границ до-
доверительного интервала, опираясь на правило «трех сигм». Платой
за это увеличение надежности будет заметный рост погрешности е
[см. столбец A0) табл. 8.1] и расширение доверительного интервала
[столбец A1)]. Это расширение приводит к тому, что правый конец
доверительного интервала поэзии накладывается на левый конец
интервалов драмы и прозы. Поэтому вывод о том, что частота гла-
глагольных словоупотреблений является статистическим параметром,
отграничивающим украинскую драму и прозу от поэзии, оказывается
необоснованным. Частоту глаголов следует теперь рассматривать
в качестве параметра, различающего только научно-техническую,
общественно-политическую и художественную украинскую речь.
Пользуясь только что описанной методикой, В. И. Перебейнос
выделила 74 языковых признака (фонемы, аффиксы, морфологичес-
морфологические и синтаксические классы, длина слова и предложения и т. п.),
частота которых выступает в роли статистического параметра сти-
стилей, жанров и авторской манеры в украинском языке. Выясняется,
что количество признаков каждого уровня языковой структуры,
способных разграничивать языковые разновидности, зависит не от
уровня, к которому относится данный признак, а от сопоставляемых
разновидностей. Чем больше общих черт имеют сопоставляемые раз-
разновидности, тем меньше признаков их различает. Например,
на буквенно-фонемном уровне наименьшее количество харак-
характеристик различает общественно-политическую и научно-тех-
научно-техническую речь. Для каждой пары разновидностей су-
существует свой уровень, лингвистические признаки которого лучше
всего разграничивают сравниваемые стили и жанры. Более род-
родственные разновидности (например драма, поэзия, проза) обнару-
обнаруживают заметные расхождения на синтаксическом уровне, а менее
родстенные, кроме того, и на лексическом (ср. противопоставление
беллетристики, с одной стороны, и общественно-политической
и научно-технической прозы — с другой).
Как показывает работа [34], статистическое моделирование сти-
стилей не только хорошо согласуется с их интуитивными описаниями,
но помогает выявить недоступные для прямого лингвистического
наблюдения факты.
277
§ 3. Доверительный интервал для дисперсии
и среднего квадратического отклонения
В предыдущем параграфе мы пользовались точечной оценкой
среднего квадратического отклонения. Однако, как уже говори-
говорилось, такая оценка не дает сведений о том, насколько близок стан-
стандарт s к самому значению о.
В тех случаях, когда в генеральной лингвистической совокуп-
совокупности имеет место нормальное распределение величины X и извест-
известна выборочная дисперсия s, этого недостатка можно избежать,
используя для оценок D(X) = а2 и а доверительный интервал,
который вычисляется с помощью-распределения х8 Пирсона.
1. Распределение х2 Пирсона. Пусть имеется N независимых
нормированных случайных величин
7
Zn =
каждая из которых распределена нормально и обладает парамет-
параметрами М (Z) = 0 и a(Z) — 1. Сумму квадратов этих величин обозначим
через х2;
N
хг= S z? @<x2<°°)-
Тогда плотность вероятности ха определяется выражением
1
2v/2T(v/2)
•(X2)v/2~l -е-
где v — N — число независимых слагаемых в последовательности
(8.19), a T(v/2) — гамма-функция; см. § 2, п. 3, а также [36, с. 200
и ел.].
Интегральная функция распределения Пирсона имеет вид
При v ->¦ оо распределение величины х2 асимптотически при-
приближается к нормальному распределению с параметрами М (х2) =
=\, D (х2) = 2v, a = УЪ> [61, с. 119].
Правильность нахождения Р (х2 > Хо) зависит от корректного
определения величины v, называемой числом степеней свободы.
Число степеней свободы определяет то количество сведений, ко-
которое остается свободным после использования всей совокупности
сведений для определения некоторой статистической характери-
характеристики. Поясним это важное для лингво-статистики понятие на сле-
следующем примере.
Будем рассматривать русские прозаические тексты в качестве
генеральной совокупности, из которой последовательно выбира-
выбираются отрывки по 10 тыс. словоупотреблений. В каждом отрывке
отмечается количество употреблений слова море (частота употреб-
употреблений этого слова является случайной величиной X, принимающей
значения хъ хг, ..., хы). Пусть в результате этих наблюдений полу-
получены следующие сведения:
Xi = 2, х2 = 3, ха = 0, лг4 = 4, хъ — 5, хв = 3, ... .
Число отрывков, в которых производится наблюдение, у нас
не фиксировано (оно может быть и бесконечным). Каждая случай-
случайная величина может принимать любое значение. Таким образом,
число степеней свободы теоретически равно здесь количеству взя-
взятых нами значений случайной величины X, т. е. v = N (при этом
мы не должны забывать о том, что нами всегда могут быть взяты
и другие неучтенные значения X).
Теперь зафиксируем число интересующих нас отрывков вели-
величиной N = 6 и определим среднюю арифметическую частоты слова
море относительно этих отрывков:
лГ= Zx(/N = B + 3 + 0 + 4 + 5 + 3)/6 = 2,83.
Фиксирование числа выборок и суммирование частот появления
в них слова море накладывает на нашу совокупность сведений,
содержащуюся в таблице, одну линейную связь. Действительно,
зная сумму частот 2 xt слова море, а также частоты этого слова
в каждом из N — 1 отрывков, мы всегда можем вычислить частоту
контрольного слова в Л/-й выборке:
N N-1
Таким образом, значения частот слова море могут варьироваться
в каждом из N — 1 отрывков, но эти изменения каждый раз будут
предопределять частоту в N-й выборке, если общая сумма частот
уже известна. Иными словами, после определения величин N —
N
= 2 Xi
степеней свободы) уменьшилось при этом на единицу: v — N — \.
Эта связь учитывается и при определении других выборочных
характеристик—например при вычислении выборочной дисперсии
и стандарта s, при расчете которых сумма квадратов отклонений
делится не на N, а на N — 1 (см. § 1, п. 2). Как уже неоднократно
указывалось, при больших N (N > 30) указанной поправкой мож-
можно пренебречь.
В биномиальном распределении и в распределении Пуассона
должны быть учтены две связи: во-первых, связь, возникающая
при суммировании наблюдаемых частот, о которой мы только что
говорили, а во-вторых, связь, образующаяся при определении тео-
теоретических параметров (р — для биномиального распределения и
X — для распределения Пуассона). Таким образом, число степеней
свободы здесь равно v = N — 2.
мы наложили на нашу статистическую совокупность
., xN одну связь. Количество свободных сведений (число
278
279
В случае нормального распределения приходится учитывать
уже три связи: связь, образующуюся при суммировании наблю-
наблюдаемых частот, и связи, содержащиеся в величинах х и s, соответ-
соответственно оценивающих М (X) и а. Таким образом, в этом случав
v = N — 3.
Однако если при сопоставлении нормального распределения с вы-
выборочным величины х и s оказываются уже известными до опыта,
то тогда должна быть учтена всего лишь одна связь, образующаяся
при суммировании наблюдаемых частот. В связи с этим здесь число
степеней свободы v = N — 1.
30 X2
Итак, число степеней свободы определяется из разности
v = N — /, (8.20)
где N — число наблюдений (сведений), а / — число линейных свя-
связей, налагающихся на эти наблюдения при данной статистической
процедуре.
От числа степеней свободы зависит вид кривых %2 распределения.
Как видно из рис. 59, эти кривые асимметричны, причем степень
асимметрии уменьшается с увеличением числа степеней свободы.
При v ->- оо график х2 совпадает с кривой нормального распреде-
распределения.
При определении доверительных интервалов для величин
D [X) = а2 и а используется выборочная дисперсия s2, связанная
с величинами а2 и х2 следующей зависимостью:
причем v = N — 1.
180
(8.21)
Распределение-s8 подробно описано в работе [61, с. 139— 1441.
Отметим лишь, что оно имеет параметры
М (s2) = a2, D (?) = 2o*/v.
Поскольку при v -*- то распределение х2 асимптотически при-
приближается к нормальному, при этих условиях распределение ^
также должно приближаться к нормальному распределению.
Переходя к определению доверительного интервала для а2
и а, перепишем равенство (8.21) в виде
X2 = vs2/a2. (8.22)
Рис. 60
Теперь, задав надежность Р, найдем в таблице распределения
X* такие две численные границы х? и %1, для которых выполнялось бы
соотношение
Р Ocf < v"s2lo* < %l) = р. - (8.23)
Границы %i и Хг можно выбрать бесконечным числом способов:
они могут быть сдвинуты по оси абсцисс (рис. 60) влево или вправо
на любую величину, лишь бы число %2 — v^/a2 находилось внутри
интервала (%1, %1). и значение р оставалось бы неизменным.
Чтобы фиксировать положение границ %\ и %\, вводят односто-
односторонний критерии значимости, согласно которому
При этом условии надежность наших рассуждений остается рав-
равной р. Действительно,
Р {%{< vs2/ a2 < Xf) = 1 —Р (X2 < X?) —Р (X2 > XI)
(8.24)
281
Преобразуя выражение, стоящее в левой части равенства
(8.24), таким образом, что
мы получаем с надежностью р доверительный интервал для диспер-
дисперсии а2, имеющий нижнюю границу
ol' = v?/x\ (8.25)
и верхнюю границу
ol'-vs'/x?. (8-2б)
Границы доверительного интервала для среднего квадратиче-"
ского отклонения соответственно равны
OH = Kvs/fo (8.27)
и _
al-Kvs/Xi. (8.28)
Для нахождения значений х! и Ха следует воспользоваться
табл. V на стр. 368. Столбцы этой таблицы указывают A + рI2
и A — р)/2, а строки — число степеней свободы. Нужные значения
односторонних границ Xi и %1 находятся на пересечении строк
и столбцов. Подставив эти значения в формулы (8.25) — (8.28),
получаем верхнюю и нижнюю оценки неизвестных параметров
D(X) = а8 и YD (X) - a.
2. Определение существенности расхождения частот глагола
в украинской драме и поэзии с использованием интервальной оценки.
Решая вопрос о существенности статистических расхождений между
украинской драмой и прозой [см. столбец (9) табл. 8.1 на стр. 275],
мы пользовались точечной оценкой среднего квадратического от-
отклонения. Как уже говорилось, эта оценка не дает сведений о том,
как далеко отстоит от наблюдаемого стандарта s или s среднее квад-
ратическое а. Поэтому в тех случаях, когда сопоставляемые лингви-
лингвистические признаки дают близкие средние частоты F = х, как это
имеет место при сравнении употребительности глаголов в украин-
украинской драме и прозе, использование точечных оценок а может при-
привести к ошибочным лингвистическим выводам. В связи с этим снова
обратимся к вычислению доверительного интервала для средних
частот глагола в украинских жанрах украинской прозы, пользуясь
при этом не точечными, а интервальными оценками среднего квад-
квадратического a (х).
По условию задачи, имеем для драматических текстов v = 60 —
— 1 = 59, F = х = 90,5, s(x) = 1,98, а для поэтических v =
¦=50 — 1 = 49, F =*= х =» 82,1, s (x) = 1,48. И в том, и в другом
случае р = 0,95, откуда A — рI2 = 0,025, A + *>)/2 = 0,975.
Учитывая, что для драмы v = 59, из табл. V находим
=
5; 59
82>
Соответственно для поэзии, где v = 49, имеем
Х? = Х?,97в: 49=31'56. Х| = Х§>(ИВ; 49 = 70.22.
Таким образом, нижняя и верхняя границы доверительного
интервала для а в драматических текстах составляют
о'и = 1,98 j/59/82,18 = 1,68; о'в = 1,98 /59/39,66 = 2,43,
а для поэзии эти границы равны
а*= 1,48/49/70,22= 1,24; о'л = 1,48 /49/31,56= 1,84.
Из табл. 8.1 и рис. 58 видно, что хотя при точечной оценке a
доверительный интервал употребительности глагола в поэзии не
накладывается на доверительный интервал глагола в драме, верх-
верхняя граница первого интервала очень близко подходит к нижней
границе второго.
Теперь посмртрим, сохраняется ли этот разрыв между довери-
доверительными интервалами при использовании интервальной оценки а.
Для этого_определим нижнюю границу (Хн доверительного интер-
интервала F — х глагола в драме и верхнюю границу аналогичного ин-
интервала в поэзии. Само собой разумеется, 4TQ и в том, и в другом
случае следует пользоваться верхней границей интервальной оцен-
оценки среднего квадратического а*в. Тогда для драматических текстов
получаем _
(хн —И — гра'в = 90,5 — 1,96 • 2,43 = 85,73,
а для поэзии соответственно имеем
р; = 82,1 + 1,96 • 1,86 = 85,71.
Полученные результаты показывают, что нижняя часть дове-
доверительного интервала F = х глаголов в украинской драме по
существу соприкасается с верхней частью соответствующего до-
доверительного интервала в поэзии. Поэтому благоразумнее воздер-
воздержаться от сделанного с надежностью в 95% вывода § 2, п. 4 о том,
что частота глаголов может рассматриваться в качестве статистико-
стилистического параметра, надежно отграничивающего язык
украинской драмы от языка поэзии.
§ 4. Доверительные интервалы для вероятности
качественного лингвистического признака
В лингвистической практике постоянно приходится применять
интервальную оценку вероятности отдельных единиц — фонем,
графем, слогов, морфем, словоформ и т. д. При осуществлении этой
оценки интересующая нас лингвистическая единица, например
глагольная словоформа, рассматривается в виде качественного аль-
альтернативного признака А. Все остальные лингвистические единицы
(в нашем случае — все неглагольные словоформы) квалифицируются
здесь как качественный признак А, т. е. не А.
282
283
В гл. 6 (см. § 1, п. 3) было показано, что вероятность р альтер-
альтернативной величины А имеет биномиальное распределение. Одна-
Однако определение интервальной оценки р при биномиальном распре-
распределении этой вероятности связано с громоздкими расчетами, опи-
опирающимися на довольно сложный математический аппарат. Чтобы
обойти эти затруднения, пользуются более простыми приемами оп-
определения интервальной оценки р.
1. Интервальная оценка вероятности р с помощью нормального
распределения. Пусть вероятность р альтернативного лингвисти-
лингвистического признака А не слишком близка к нулю и к единице, а число
наблюдений N достаточно велико (такая ситуация имеет обычно ме-
место при статистических исследованиях в облаети грамматики,
фонетики и фонологии). Вероятность р неизвестна, и ее нужно оце-
оценить через получаемую в опыте частость / «=¦ F/N.
В гл. 6 (см. § 4) было показано, что распределение величины /
близко к нормальному Теоретически можно предполагать, что па-
параметрами этого распределения служат величины
а верхняя составляет
(см. гл. 6, § 3, п. 4) При бесконечном увеличении числа испытаний
(т. е. объема выборки) предельным распределением нормированной
частости
M(f)-t _ p-t
о VpA-P)JN
является нормальное распределение
;8.29)
где Zp — величина, значение которой соответствует заданной
надежности Р при v=oo (см. табл. VI на стр. 369). t
От неравенства
(8.30)
<zp
перейдем к двойному неравенству
р, или /_
где
o=Vp(l-p)/N. (8.31)
Заменив в (8.31) вероятность р на полученное из опыта значение
частости / и следуя рассуждениям п. 2, § 2, приходим к доверитель-
доверительному интервалу вероятности, который имеет вид
p-/)/#<p<f + zp
При этом нижняя оценка параметра р равна
(8.32)
(8.33)
p (8.34)
где величина е указывает на погрешность при определении дове-
доверительного интервала для р:
zpVf(l-f)/N = zpo = B. (8.35)
Применим только что описанную процедуру к конкретной линг-
лингвистической задаче.
В молдавском публицистическом тексте длиной в 200 тыс. сло-
словоупотреблений встретилось 31286 глагольных форм [7, с. 159].
Нужно с надежностью в 95% определить доверительные границы
вероятности появления во взятом тексте глагольного словоупотреб-
словоупотребления.
Здесь N = 200000, F = 31286, f = FIN = 0,1564. По табл. VI
находим, что гр — 1,96 при Р = 0,95 и при v = оо; затем по фор-
формуле (8.35) определим погрешность
е= 1,96/0.1564-0,8436/200000 «0,0016.
Подставляя все эти данные в равенства (8.33) и (8.34), получаем
значения
р'а 0 1564 - 0,0016 = 0,1548, pi = 0,1564 + 0,0016 = 0,1580
нижней и верхней границ доверительного интервала, в котором
с надежностью в 95% находится'истинна я вероятность молдавских
глагольных словоупотреблений.
Приближенная оценка вероятности р с помощью опытной час-
частости / всегда связана с ошибкой, величина которой тем больше,
чем меньше объем выборки. Более точную интервальную оценку
можно получить, решая неравенство (8.30) относительно р. Для
этого указанное неравенство запишем в виде
P-f<zpVp^-P)lN. (8.36)
Затем обе части неравенства возведем в квадрат и перенесем все
его члены в левую часть:
)() (8-з7)
Приравняв левую часть неравенства нулю и решая квадратное урав-
уравнение относительно р, получаем
Рг — Рн =
1
NF+Y
г
гР ~~
4+
-р
гр
У*
¦о-в
+
+
i
4
1
4
2
4
(8.38)
(8.39)
284
285
Используем только что описанную методику для вычисления
более точных интервальных оценок вероятности появления гла-
глагольных словоупотреблений в молдавских публицистических тек-
текстах.
Подставляя числовые значения в формулы (8.38) и (8.39), имеем
. _ 200000-0,1564 + 0,5-3,8416—1.96V200000-0,1564-0,84+0.25-3,8416
Р" ~ 200000+3,8416
31281,92—1,961/26388,77
200003,8416
31281,92-318,34
200003,8416
30963,58
200003,84
Следовательно,
31281,92+318,34 _ 31600,26 ^ Q j5g0
200003,84 "~ 200003,84 ~ '
0,1548<p< 0,1580.
Нетрудно заметить, что этот доверительный интервал несколько
шире интервала, полученного по приближенной оценке. Это про-
происходит потому, что улучшенная оценка дает меньшую погрешность
по сравнению с приближенной. Расхождение между обеими оцен-
оценками становится особенно заметным при малых выборках лингви-
лингвистических единиц.
2. Интервальная оценка вероятности р для малых выборок. При
малых N приближенные оценки вероятности р дают заметные ошиб-
ошибки, связанные с заменой неизвестного р опытным /, а также с пере-
переходом от дискретного биномиального к непрерывному нормальному
распределению. Чтобы уменьшить эти ошибки, используются раз-
различные поправочные пригмы.
Один из приемов со:тоит в том, что в левую и правую части двой-
двойного неравенства (8.32) вводят поправочный член 1/B N), в связи
с чем доверительный интервал р записывается следующим обра-
образом:
f-llBN)-zpVf{\-f)lN<p<f+l/BN)+zpVf(l-f)lN.
(8.40)
Используем указанный прием для решения следующей лингви-
лингвистической задачи. Из русского прозаического текста взята выборка
в 50 словоупотреблений, в которой обнаружено 20 именных форм.
Необходимо определить доверительные границы вероятности р
при надежности в 95%.
Здесь N = 50, f = 0,4, Р = 0,95 и zp = 1,96. Подставив эти
величины в формулу (8.40), получим
р; = 0,4 — 0,01 — 1,961/0,4A-0,4O50 = 0,2442 «0,24,
pi = 0,4 + 0,01 + 1,96 /0,4A—0,4)/50 = 0,5572 ж 0,56.
Другой прием заключается в том, что величина г„ в формуле
(8.32) заменяется на t0 в распределении Стьюдента, а вместо
286
"^7 О —f)W используют величину Vf A — f)/(N — 1). В этом
случае доверительный интервал для р принимает вид
Нижняя граница оценки равна
р;=/-
а верхняя составляет
1).
(8.41)
(8.42)
(8.43)
Используем этот прием для определения доверительного интер-
интервала вероятности именных форм в только что рассмотренном при-
примере.
Здесь / = 0,4, р = 0,95, v = 20 — 1 = 19, /o,95;i9 = 2,09.
Подставив эти значения в формулы (8.42) и (8.43), получим для ниж-
нижней границы
р- = 0,40 — 2,09 /0,4 A — 0,4)/49 = 0,40 — 0,1463 = 0,2537 «0,25,
а для верхней границы
р'в = 0,40 + 0,1463 = 0,5463
0,55.
Легко заметить, что оба приема дают практически одни и те же
оценки границ доверительного интервала.
Из сказанного не следует, что удовлетворительную интервальную
оценку вероятности р можно получить при любом значении N.
При очень малых объемах выборки даже самые сильные приемы
оценки вероятности не дают удовлетворительного1 результата.
В этом легко может убедиться читатель, взяв выборку в 5 словоупот-
словоупотреблений и задавшись целью определить при Р = 0,95 доверитель-
доверительный интервал вероятности появления существительных при усло-
условии, что их в этой выборке было всего 3 (т. е. 60%). При этом выяс-
выясняется, что доверительный интервал здесь имеет вид —0,08 < р <
< 1,28, перекрывая таким образом весь возможный диапазон рас-
расположения истинной доли именных словоупотреблений в тексте.
Это еще раз говорит о том, что построения «процентной» лингвисти-
лингвистики, не учитывающие объема выборки и других важных понятий
статистики, не всегда дают достаточное количество содержательной
информации.
Все рассмотренные приемы интервальной оценки для вероят-
вероятности р могут быть распространены и на логнормальное распре-
распределение.
3. Интервальная оценка вероятности редких лингвистических
событий. До сих пор мы рассматривали случаи, когда вероятность
лингвистической единицы достаточно велика. Такая ситуация ти-
типична для фонетико-фонологических и грамматических исследо-
исследований. Однако при лексикологических исследованиях вероятности
287
словоформ, слов и словосочетаний обычно очень малы. Распреде-
Распределения их вероятностей чаще всего подчиняются распределению Пуас-
Пуассона.
Поэтому доверительный интервал вероятности лексических еди-
единиц следует устанавливать не на основе нормального приближения,
которое может привести к значительным ошибкам, а путем приме-
применения пуассоновского приближения.
Для нахождения оценки р сначала нужно оценить параметр
% через число появлений события F = Nf, причем число всех ис-
испытаний N на оценку Я, не влияет, оно может быть неизвестно,
нужно лишь быть уверенным, что N велико. Распределение слу-
случайных величин F в распределении Пуассона оказывается тесно свя-
связанным с распределением %2 [7, с . 1641. Это и дает возмож-
возможность получить доверительную оценку для X.
Нижняя граница доверительного интервала пуассоновской ве-
вероятности задается выражением
* 1 л#
н = — A
(8.44)
где vx — число степеней свободы, равное 2 (F + 1), а верхняя гра-
граница определяется из выражения
*_ 1 у2„
(8.45)
где число степеней свободы va =» 2 F.
Решим следующую задачу. Из латышских научно-технических
текстов взята выборка в 300 тыс. словоупотреблений, в которой
слово aizgrieznis 'кран' встретилось 3 раза. Определить довери-
доверительные границы пуассоновой вероятности указанного слова при
надежности Р =• 0,95.
Здесь N = 300000, F = 3, Р = 0,95, vx = 8, v2 == 6. С помощью
табл. V (см. стр. 368) находим граничные значения:
; V, =ЭСо,975; 8 = 2,18,
; V,
5; 6
14,40.
Подставляя все необходимые значения в выражения (8.44)
и (8.45), получаем значения
Рп-
1
2-300000
•2,18 = 0,0000036, р\-.
1
2-300000
• 14,40 = 0,000024
нижней и верхней границ доверительного интервала, в котором
заключена вероятность латышского слова aizgrieznis.
Методика интервальной оценки пуассоновой вероятности может
быть применена также и к вероятностям, получаемым из лингви-
лингвистических распределений Чебанова — Фукса и Фукса — Гачечи-
ладзе.
«88
§ 5. Оценка функции генерального распределения
по данным лингво-статистического наблюдения
В предыдущих параграфах была рассмотрена первая задача,
связанная с переходом от статистической модели текста к скрытой
от прямого наблюдения вероятностной схеме его построения. Ре-
Решение указанной задачи заключалось в оценке неизвестных пара-
параметров распределения генеральной лингвистической совокупности.
Теперь обратимся ко второй задаче, состоящей в том, чтобы по
опытным данным оценить неизвестную функцию распределения не-
непрерывной случайной лингвистической величины X. Решение этой
задачи сводится к определению того доверительного интервала,
в котором находятся значения теоретической функции, соответ-
соответствующие определенным значениям аргумента. Shw доверительный
интервал определяется по отдельным опытным данным без какого
бы то ни было обращения к параметрам функции, которые остаются,
как правило, нам неизвестными.
1. Доверительный интервал функции генерального распреде-
распределения. При оценке неизвестной функции используются следующие
рассуждения. Предположим, что в результате исследования тексто-
текстовой выборки получена последовательность лингвистических единиц,
упорядоченная в порядке возрастания номеров их извлечений нз
текста:
*г, х„ .... xN. (8.46)
Величины Xi можно рассматривать в качестве значений неко-
некоторой конкретной случайной лингвистической величины X.
Последовательность (8.46) может быть описана с помощью ин-
интегральной функции эмпирического распределения накопленных
частостей, соответствующих значениям х(:
(xt)
N
-fl
Вместе с тем можно предположить, что имеется теоретический ин-
интегральный закон
F (x) = P(X< xt) = ph
описывающий распределение значений рассматриваемой непрерыв-
непрерывной случайной величины X в генеральной лингвистической сово-
совокупности. Вид этого закона нам неизвестен, и какой-либо допол-
дополнительной информацией о его свойствах, кроме свойства непрерыв-
непрерывности, мы не располагаем.
Оценка теоретического закона F (х) эмпирической функцией осу-
осуществляется, как и в случаях с неизвестными параметрами, при
заданной надежности Р и точности е. При этом доверительный ин-
интервал закона F (л;) имеет вид
FN(x) — е < F (х) < FN(x) + e.
Ю Зак. 1287
289
Задачу определения доверительного интервала неизвестной
теоретической функции F (х) можно решать, исходя из интегральной
предельной теоремы Муавра—Лапласа (см. гл. 6, § 3, п. 4).
Оценивая теоретический закон F (х) с помощью эмпирической
функции FN (х), мы будем считать, что значение FN (x) сходится
по вероятности к F (х), т. е.
Тогда отношение между накопленной частостью и накопленной
вероятностью при заданном х будет таким же, как и между отно-
относительной частотой и вероятностью в схеме Бернулли с N незави-
независимыми испытаниями. Следовательно, в качестве меры расхожде-
расхождения FN(x) — F(x) накопленной частости /* от вероятности р*
можно взять среднее квадратическое отклонение
Опираясь на указанную теорему, можно утверждать, что
1*~р* <г\ = 2Ф(г).
Иными словами, вероятность того, что абсолютная величина
отклонения эмпирического распределения накопленных частот от
теоретического интегрального закона будет меньше величины
*Vp*(l—p*)lN =*j(/*),
при достаточно большом N приближается к 2Ф (г):
lim Р{\Г—Р*\< го if*)} = 2Ф{г).
Теперь можно утверждать с вероятностью Р = 2(D(zj>), сколь
угодно близкой к единице, что относительно каждой точки из после-
последовательности (8.46) справедливо неравенство
-zpoW)<fi-p;<zpo(f*). (8.47)
Используем двойное неравенство (8.47) для построения дове-
доверительной полосы теоретической функции распределения F (х).
Для этого, задавшись вероятностью р и определив из табл. VI
на стр. 369 величину Zp, можно при известных р' = F (х) н N найти
для каждого Xt величину ZpO if*). Откладывая эту величину вверх
и вниз от точек р* = F (xt), получим доверительную полосу
(пунктирные линии на рис. 61). Если график эмпирической функ-
функции FN \х) (сплошная линия на рис. 61) всюду находится в пределах
доверительной полосы, то вероятность события, состоящего в том,
что для любого х отклонение | /* — р* \ меньше величины г^о (/*),
равна Р.
Положение доверительной полосы в значительной степени зави-
зависит от вида функции F (х). Поэтому если FN (x) оказывается за
290
пределами полосы, то это может указывать на несоответствие тео-
теоретического и эмпирического распределений. В этом случае следует
искать другую функцию F (х), соответствующую эмпирической функ-
функции FN (x).
2. Построение доверительного интервала с помощью функции
Колмогорова. Было бы неверным утверждать, исходя из всего ска-
сказанного, что выполнение неравенства
\f* - р*\ < гра (Г) (8.48)
гарантируется с той же большой вероятностью Родновремен-
н о для всех точек х-ь.
В самом деле, несмотря
на то что вероятность невы-
невыполнения неравенства (8.48)
в определенной точ-
точке хг очень мала, вероят-
вероятность нарушения его хотя
бы в одной точке х
может оказаться достаточно
большой. Отсюда следует, что
проверка соответствия пред-
предполагаемого теоретического
распределения опытному рас-
распределению на основании ин- О
тегральной предельной теоре-
теоремы не гарантирует от появ-
появления существенных откло-
отклонений FN(xi) — F (xt) для отдельных значений xi. Можно по-
показать, что при взятом нами значении ZpO (/*) > 0 максимальное
расхождение эмпирических и теоретических значений
DN = max \FN{x,) - F (xt)\
почти наверняка будет больше Zpo(f*).
Одновременно возникает вопрос: что представляет собой функ-
функция распределения величины Dn и какова ее доверительная
оценка? Ответ на этот вопрос дает предельная теорема Колмогорова,
которая формулируется так: если функция F (х) непрерывна, то
вакон распределения
F(x)
/
/
у
/
х
Рис. 61
Р {max | FN (x)-F(x) | <
= kN (X)
(8.49)
не зависит от F (х) и при N -> оо имеет пределом К (fy, представ-
представляющую собой сумму бесконечного ряда:
Значения функции Колмогорова К (Ц приведены в табл. VII на
стр. 369, 370.
10*
291
При больших N выражение (8.49) можно переписать следующим
образом:
Р {FN {x)-XlV~N <F(x)< FN (x) +
К (X),
где %fV~N = е можно считать величиной погрешности оценки закона
F (х), К (к) — Р — надежностью, а 1 — К (А.) = q — уровнем
значимости (табл. 8.2).
Таблица 8.2
Надежность К(А.) = р
Уровень значимости
h
0,50
0,50
0,828
0
1
0,90
,10
,224
0,95
0,05
1,358
0
0,
1,
,99
01
627
0,
0,
1,
999
001
950
Если обратиться к геометрической интерпретации, то теорема
Колмогорова утверждает с вероятностью К (к), что график неиз-
неизвестной теоретической функции F (х) целиком находится внутри
полосы Ск (к), ограниченной кривыми /* = FN (х{) — ей
7* = FN{Xi) + е (рис. 62).
Эти кривые получаются
путем смещения вниз и
вверх, вдоль оси ординат
эмпирических значе-
значений FN (xt) на величину
точности е.
Применение функ-
функции Колмогорова пред-
предполагает, во-первых,
что теоретическая функ-
функция F (х) непрерывна;
во-вторых, что эмпири-
эмпирическая функция FN (x)
Рис. 62
О
построена по не сгруп-
сгруппированным в интерва-
интервалы значениям случай-
случайной величины X. В практических приложениях допускается ис-
использование малых интервалов группировки, но получаемая оцен-
оценка в этом случае действует с некоторым приближением.
Построение доверительной полосы для неизвестного теорети-
теоретического закона распределения F (х) с помощью функции Колмого-
Колмогорова осуществляется по следующей схеме.
1. Вычисляют значения эмпирической функции FN(x), пред-
представляющие собой накопленные частости
fl = FUN. ( 8.50)
292
2. По заданному значению надежности /С(А.) — Р с помощью
табл. VII определяют значение Кр (обычно используют Р = 0,90,
или 0,95, или 0,99).
3. С помощью равенства
определяют величину погрешности.
4. С помощью формул
(8.51)
(8.52)
(8.53)
вычисляют границы доверительного интервала закона распреде-
распределения F (х) относительно точек xt (i = 1, 2, ..., N).
Замечание. Если окажется, что /7 < 0, а // > 1, то
следует считать f] — 0, а /7 = 1.
5. На график наносят значения f], ~f' и таким образом опреде-
определяют границы доверительной полосы (если имела место интерваль-
интервальная группировка данных, то графики f] и // носят ступенчатый
характер). Полученная полоса с вероятностью V покрывает график
теоретической функции F (х).
Теперь, пользуясь данными о распределении длин китайских
слогов (см. гл. 7, § 2, п. 2), дадим оценку неизвестного теоретического
интегрального закона этого распределения (табл. 8.3).
Таблица 8.3
Х1
A)
60
70
90
ПО
130
150
170
190
210
230
250
270
290
310
Pi
B)
2
7
7
29
29
24
17
И
12
7
1
2
1
1
#=150
*
C)
2
9
16
45
74
98
115
126
138
145
146
148
149
150
D)
0,0133
0,0600
0,1667
0,3000
0,4933
0,6533
0,7667
0,8400
0,9200
0,9667
0,9733
0,9867
0,9933
1,0000
E)
0
0
0,0554
0,1887
0,3820
0,5420
0,6554
0,7287
0,8087
0,8554
0,8620
0,8754
0,8820
0,8887
F)
0,1246
0,1713
0,2780
0,4113
0,6046
0,7646
0,8780
0,9513
1,0000
1,0000
1,0000
1,0000
1,0000
1,0000
Воспользуемся схемой построения доверительной полосы.
293
0,25'
.50 90 W 170 гп 250 №
Рис. 63
1. Приняв в качестве величин xt середины интервальных значе-
значений длин китайских слогов (ср. табл. 7.8 на стр. 226), запишем в
столбце B) табл. 8.3 количество Ft слогов, длина которых соответ-
соответствует данному интервалу, а в столбце C) — абсолютные накоплен-
накопленные частоты Ft для каждого xt. Пользуясь равенством (8.50) и учи-
учитывая, что общее число измеренных слогов N равно 150, в столбце
D) получим величины /*, высту-
выступающие в качестве значений
эмпирической функции Fn (х).
2. Пусть надежность f>=0,95,
тогда по табл. VII получаем
Яр = 1,358.
3. На основании равенства
(8.51) находим, что
ер = 1,358/УТоО=1,358/12,206«
« 0,1113.
4. Пользуясь формулами
(8.52) и (8.53), с учетом заме-
замечания, получаем значения ниж-
нижней (ft) и верхней (#) границ
доверительной полосы теорети-
теоретической функции распределения
F (х). 3>ги значения помещены
в столбцах E) и F) табл. 8.3.
5. Нанеся на график значения // и7/, получаем графическое
изображение доЕерительной полосы (рис. 63).
§ 6. Определение достаточности объема выборки
Ценность всякого лингвистического исследования измеряется
степенью достоверности его выводов. Само собой разумеется, что
лучшим средством оценки этой достоверности является проверка
полученных выводов на практике. Но такая проверка может быть
осуществлена в течение длительного времени после завершения
самого исследования. Между тем лингвисту нужны приемы, с по-
помощью которых можно было бы уже при постановке эксперимента
прогнозировать достоверность получаемых результатов. Наиболее
простым приемом такого прогнозирования является определение
того минимального объема выборки, при котором получается за-
заслуживающая доверия лингво-статистическая информация. Не-
Необходимый объем выборки можно определить, опираясь на оценку
одного из параметров распределения, которое должно быть близким
к нормальному, а также исходя из заранее установленной степени
точности или относительной ошибки и надежности наших суждений.
Рассмотрим несколько вариантов определения достаточного
объема лингвистической выборки.
294
1. Определение минимально достаточного объема выборки в
грамматических и фонетико-фонологическик исследованиях. Учи-
Учитывая соотношение F.129), можно утверждать, что величина мак-
максимально допустимой абсолютной ошибки равна
«max = Zp Vp(\ — p)lN (8.54)
ср. с формулой (8.36)] при условии, что I/—р|<е [ср. с
F.115)].
Предположим, что величина абсолютной ошибки е задана и за-
заранее определена надежность Р. Однако это не дает нам возмож-
возможности вычислить величину выборки N, поскольку неизвестна ве-
вероятность р той лингвистической единицы, относительно которой
определяется достаточность объема выборки. Чтобы оценить ве-
величину р, пользуются той частостью / лингвистической единицы,
которая либо получена ранее в аналогичных условиях, либо извле-
извлечена из небольшого предварительного выборочного наблюдения.
Заменяя р в выражении (8.54) на ее оценку Д получаем
(8.55)
откуда приходим к формуле, указывающей минимально достаточ-
достаточный в данных условиях объем выборки:
N = 4 /A — /)/еа. (8.56)
1ср. с F.130)]. В тех случаях, когда дана не абсолютная, а относи-
относительная ошибка
б = г/р « е// = zp V(\-f)l(Nf) (8.57)
выражение (8.56) принимает вид
(8.58)
Описанную процедуру целесообразно использовать при иссле-
исследовании употребительности грамматических, фонетических и фоно-
фонологических единиц, которые обычно дают нормальное распределе-
распределение и вероятность которых не очень мала.
Например, по данным предварительного эксперимента относи-
относительная частота употребления мягких согласных фонем в украин-
украинском драматургическом тексте равна 0,0828 C4, с. 51]. Необхо-
Необходимо при заранее заданных максимальной абсолютной ошибке
е = 0,0022 и надежности р = 0,95 определить минимально до-
достаточный объем выборки N для получения достоверных сведений об
употребительности мягких согласных фонем в украинских драматур-
драматургических текстах.
Здесь f = 0,0828, 1 — f = 0,9172, е = 0,0022; по заданной
величине р из табл. VI на стр. 369 находим 2р = 1,96. Подставляя
все эти данные в равенство (8.56), получаем
N = 1.962 • 0,0828 . 0,9172/0,00222 = 60284 « 60 тыс. фонем.
Если вместо е была бы задана величина б, которая в данном слу-
случае равна 0,027, то для определения W следует воспользоваться
295
равенством (8.58); в конечном итоге мы получаем аналогичный ре-
результат:
N = 1,962 • 0,9172/@,027* • 0,0828) - 58374 ж 60 тыс. фонем.
2. Определение минимально достаточного объема выборки в лек-
лексикологических исследованиях. В ходе лексикологических иссле-
исследований минимальный объем выборки вычисляется с помощью при-
приближенных равенств
е2 (8.59)
N
и
z«/F»/).
(8.60)
которые легко выводятся из выражений (8.56) и (8.58), если принять
во внимание, что частости / лексических единиц обычно очень малы
и, следовательно, разности 1 — / близки к единице.
Рассмотрим в связи с этим следующую лингвистическую задачу.
Относительная частота словосочетания split cylinder 'разрезной
цилиндр' в английских текстах по строительным материалам со-
составляет 0,000175 [33, с. 410]. Необходимо определить минимально
достаточный объем выборки, удовлетворяющей надежности 0,95
и 33%-ной относительной ошибке.
Здесь / = 0,000175, б = 0,33 и zp = 1,96 (при р = 0,95); по-
поскольку / очень мало, для расчета величины W можно использовать
формулу (8.60):
N = 1,967@,332 • 0,000175) » 200000.
Таким образом, для получения достоверных результатов при
статистическом исследовании лексических единиц, обладающих
частостью не менее 0,000175, при заданной 33%-ной относительной
ошибке и 95%-ной надежности нужна выборка объемом не менее
200 тыс. словоупотреблений.
В столбцах D) — F) табл. 8.4 показаны минимальные объемы
выборки, необходимые для того, чтобы получить с надежностью р
и относительной ошибкой б (соответственно с абсолютной ошибкой е)
достоверные данные об употребительности лингвистических единиц,
имеющих частоту выше заданного /.
Минимальные выборки, необходимые для получения достовер-
достоверных данных об употребительности лингвистических единиц, имею-
имеющих частоту выше заданного f, если / достаточно мало, показаны
в столбцах G) — (9) табл. 8.4.
3. Определение достаточности объема выборки с учетом рассея-
рассеяния лингвистического признака. В предыдущих разделах объем
выборки мы определяли, исходя из оценки только одного параметра
распределения —вероятности р. Однако в лингвистических и инже-
инженерно-лингвистических исследованиях нередко встречаются задачи,
которые требуют, чтобы при определении минимального объема
выборки были учтены средняя частота F, оценивающая матема-
296
Таблица 8.4
Необходимые объемы выборки при известных б (или е), р (г*) и I
(р оценено через /)
A)
0,0001
0,001
0,01
0,05
0,10
0,20
0,50
8
B)
0,00001
0,00002
0,00003
0,0001
0,0002
0,0003
0,001
0,002
0.003
0,005
0,010
0,015
0,01
0,02
0,03
0,02
0,04
0,06
0,05
0,10
0,15
в
C)
0,1
0,2
0,3
0.1
0,2
0,3
0,1
0,2
0,3
0,1
0.2
0,3
0,1
0,2
0,3
0,1
0,2
0,3
0,1
0,2
0,3
2
г., A—Р)
N
Рб»
<с
II
а-
N
D)
2720000
680000
300000
272000
68000
30000
27000
6700
3000
5200
1300
575
2450
610
270
1100
270
120
270
70
30
и
ы
(Б)
3840000
960000
430000
384000
96000
43000
38000
9500
4200
7300
1800
810
3460
860
380
1540
380
170
380
100
40
2
IV
ОО
<N
A
Л-
N
F)
6650000
1660000
740000
665000
166000
74000
66000
16500
7200
12600
3200
1400
6000
1500
670
2660
670
300
670
170
70
to
II
Л-
N
G)
2720000
680000
300000
272000
68000
30000
27200
6800
3000
5450
1360
600
2720
680
300
1360
340
150
540
140
60
16'
о>
II
(8)
3840000
960000
430000
384000
96000
43000
38400
9600
4300
7700
1920
850
3840
960
430
1920
480
210
770
190
80
СО
сч
A
Д-
N
(9)
6660000
1660000
740000
666000
166000
74000
66600
16600
7400
13300
3300
1580
6600
1660
740
3330
830
370
1330
330
150
OJ
!
Т
!
о, II
1а
г;
A0)
| 90000
)
\ 9000
1
1
910
1
| 190
100
J
)
60
I
)
40
1
297
тическое ожидание М (X) этого признака, и стандарт s, оцениваю-
оценивающий среднее квадратическое отклонение а = D (X) (величины б
и Р считаются при этом заданными).
Величина выборки определяется здесь исходя из следующих
соображений.
На основании центральной предельной теоремы Ляпунова
(см. гл. 6, § 4, п. 4), можно утверждать, что погрешность \ F — F \
распределена нормально. Максимальная величина этой погреш-
погрешности егаах = max \F — F\ может быть определена как
Отсюда
emax
= F6 =
(8.61)
Построение двуязычных и одноязычных машинных словарей
связано с разного вида сжатием лексической информации. При этом
важно иметь очень точные сведения о средней длине словарного
слова или словоформы. Эти сведения можно получить, обследуя
не тексты, а одноязычные или двуязычные словари разного объема.
Так, например, предварительное обследование русского тех-
технического словника показало, что средняя длина словоформы рав-
равна здесь 8,68 буквы при достаточно высоком рассеянии численных
значений ее длины: стандарт здесь составляет 3,12 буквы. Нужно
определить минимально необходимый объем словаря L, из которого
можно получить при б = 0,01 и р — 0,95 достоверные данные о
средней длине словоформы.
Здесь 7 = 8,68, s = 3,12, б = 0,01, р = 0,95 (zp = 1,96). Под-
Подставляя эти данные в формулу (8.61), получаем
L= 1,962-3,122/(8,б82-0,012) = 4970 словоформ.
В работе [7, с. 184] показано, что в тех случаях, когда дисперсия
D(X) = о2 = Np(l — р) больше или равна 9, случайная ве-
величина распределена нормально. Отсюда можно утверждать, что
величину минимально необходимой выборки для определенного
вначения р, оцениваемого частостью f, можно установить из нера-
неравенства
9 (8.62)
Ш-f)
Из столбца A0) табл. 8.4 видно, что формула (8.62) указывает
объемы выборок, в несколько раз меньшие чем минимально необ-
необходимые объемы выборок, рассчитанные по формулам (8.56) —
(8.60). Однако эта оценка выборки не гарантирует какой-либо на-
надежности р и не фиксирует какую-либо определенную величину от-
относительной ошибки б.
4. Оценка точности результатов лингво-статистических иссле»
дований. В лингвистических исследованиях нередко приходится
оценивать точность получаемых статистических результатов. Для
293
оценки точности можно использовать величины относительной ошиб-
ошибки б и погрешности (абсолютной ошибки) е, которые можно найти
по приведенным выше формулам. При этом нужно першить, что
степень точности находится в обратной зависимости по отношению
к величинам б и е: чем выше точность лингво-статистического изме-
измерения, тем меньше должны быть величины относительной ошибки
или погрешности.
Степень точности лингво-статистических измерений связана так-
также с объемом выборки и надежностью.
Например, при исследовании устного украинского драматур-
драматургического текста длиной в 60 тыс. фонем обнаружено, что относи-
относительная частота мягких согласных фонем равна 0,0828. Необхо-
Необходимо определить абсолютную ошибку е и относительную ошибку 8
при получении указанного результата, если надежность
Р = 0,95 (гр = 1,96).
Пользуясь формулами (8.54) и (8.57), получаем
е = 1,96 /0,0828- 0,9172/60000» 0,0022.
о = 1.96 J/0.9172/F0000-0,0828) да 0,027 = 2 7 %.
Из выражений (8.56) и (8.58) видно, что величины погрешности
и относительной ошибки находятся в обратной зависимости по от-
отношению к объему выборки. Чем больше объем лингво-статисти-
лингво-статистических наблюдений, тем меньше погрешность и относительная ошиб-
ошибка и тем выше точность наших лингво-статистических результатов.
В только что рассмотренном примере получена довольно высокая
точность наблюдений (всего 2,7% относительной ошибки). Однако
эта точность была оплачена довольно дорогой ценой: пришлось
просчитать текст длиной в 60 тыс. фонемоупотреблений (т. е. около
30 страниц среднего объема). Можно было бы при желании умень-
уменьшить относительную ошибку в 10 раз, доведя ее до 0,27%, но тог-
тогда выборку пришлось бы увеличить в 100 раз, просчитав 2400 стра-
страниц фонетической записи украинского текста. В связи с этим воз-
возникает вопрос: каков же разумный предел повышения точности
лингво-статистических измерений?
Выбор уровня точности, так же как и выбор надежности наших
суждений, зависит от теоретических и практических приложений
той дисциплины, которая использует описываемые статистические
приемы. Если для авиационной и ракетной техники относительная
ошибка измерения в 2,7% может рассматриваться как предельная,
то для лингвистических исследований такая точность оказывается
излишней и приводит к неразумному увеличению объема выборки
и, таким образом, к неоправданному расходованию сил исследо-
исследователя на механическую нетворческую работу. В настоящее время
принято считать, что в фонетико-фонологических и грамматических
исследованиях относительная ошибка не должна превышать 20%,
а при анализе лексики и фразеологии относительная ошибка может
достигать 33 — 35% [7, с. 189].
299
5. Определение достаточности объема выборки по заданной
покрываемости текста. Первая задача, с которой сталкивается лин-
лингвист, приступающий к составлению частотного списка букв, зву-
звуков, фонем, слогов, морфем, слов, словоформ, словосочетаний или
грамматических форм,—это, как уже говорилось, определение ми-
минимально достаточного объема текста.
Существуют различные подходы к решению этой задачи. Иногда
требование достаточности заменяется «критерием» осуществимости:
в этом случае определяется такой объем выборки, который можно
произвести в отведенный для этого срок.
При определении длины обследуемого текста можно исходить
из требования, согласно которому в частотный список попала бы
заранее заданная доля разных слов (соответственно букв, слогов
и т. д.), образующих данный текст.
Однако чаще всего объем выборки определяется исходя из тре-
требований к покрываемости наугад взятого текста наиболее частыми
единицами составляемого списка. При этом предполагается, что
частоты и частости этих единиц будут достоверными, т. е. определены
в пределах допустимой относительной ошибки и с заданной надеж-
надежностью. Чтобы решить эту задачу, необходимо сначала выяснить,
чему равна частость той единицы частотного списка, которая вы-
выступает в качестве нижней границы массива, дающего заданную
покрываемость текста. Будем обозначать эту относительную частоту
термином граничная частость (/,.р). Если в частотном списке ука-
указываются относительные накопленные частоты отдельных единиц,
то граничная частость находится на той накопленной частоте, ко-
которая соответствует заданной покрываемости текста (fc)..
При определении объема выборки, обеспечивающей заданную
покрываемость текста, кроме величин /гр и fc, приходится учи-
учитывать также относительную ощибку 6 и надежность *>. Если фикси-
фиксировать для /гр относительную ошибку бтах, то для частостей ft >
> /гр имеет место неравенство бг < бшах. Таким образом, можно
утверждать, что для массива единиц частотного списка, обладаю-
обладающего покрываемостью С, относительная ошибка частости не пре-
превосходит заданной величины бШзХ. Итак, задав относительную ошиб-
ошибку бтах, надежность Р и соответствующую ей величину Zp, а также
определив опытным путем по покрываемости C — fc' 100% гранич-
граничную частость /гр, мы можем согласно формуле (8.60) вычислить
минимально необходимый объем выборки; в тех случаях, когда /гр
очень мало, он равен
N(C)>
(8.63)
Для тех случаев когда /гр заметно отличается от нуля, исходя из
(8.58), получаем
г?A—/гр)
JLJL. (8.64)
бт„х
1. Пусть необходимо определить минимальный объем казах-
казахского текста для получения достоверных статистических данных
относительно массива наиболее частых словоформ, покрывающих
80% текста. Относительная ошибка не^ должна превышать 30%,
надежность V — 0,95.
По частотному словарю казахской публицистики находим зна-
значение накопленной частоты fc — 0,8, соответствующее заданной
покрываемости, это значение имеет словоформа с порядковым но-
номером i = 5503 и. Д,р = 0,00004. Учитывая, что бтах = 0,3, г0(Вв =
= 1,96, а /ГР достаточно мало, используем для определения мини-
минимального объема выборки выражение (8.63). Тогда получим
#с-ао% = 1,962/@,ЗЗа • 0,00004) « 880 000 словоупотреблений.
2. Пусть требуется определить минимально необходимый объем
русского разговорного текста для получения достоверных стати-
статистических данных с относительной ошибкой в 30% и надежностью
Р = 0,95 о массиве наиболее частых служебных слов. Этот массив
дает покрываемость С = 17%.
По данным пробного частотного словаря русских разговорных
текстов находим, что С = 17% соответствует Д, в 0,013; учитывая
также, что бтах = 0,3, а гр — 1,96, получаем
Nc..% = 1,92^1-0,01) в 3,84.0,99 словоупотребления.
С 17% 0,32.0,01 0,09-0,01
Проиллюстрируем описанную процедуру двумя примерами,
300
ГЛАВА 9
ИССЛЕДОВАНИЕ ВЕРОЯТНОСТНЫХ СВОЙСТВ ЯЗЫКА
И СТАТИСТИКИ ТЕКСТА С ПОМОЩЬЮ МЕТОДА ГИПОТЕЗ
§ 1. Элементы теории статистических гипотез
1. Статистические и нестатистические гипотезы в лингвистике.
Рассмотренные в предыдущей главе процедуры перехода от тек-
текстовой статистической модели (вариационного ряда) к генераль-
генеральному распределению давали возможность обнаружить количествен-
количественные параметры нормы, однако лингвистику интересуют не только
количественные характеристики языка и речи, но и в первую оче-
очередь их качественные признаки.
Среди различных научных методов, с помощью которых могут
быть обнаружены, описаны и количественно оценены качественные
лингвистические явления, важное место занимает метод статисти-
статистической проверки лингвистических гипотез.
Прогресс каждой науки, в том числе и языкознания, связан с вы-
выдвижением и проверкой гипотез. Использующиеся в науке гипотезы
очень разнообразны как по способам их формулировки, так и по
методам их проверки. Среди всего разнообразия этих гипотез особое
место занимают статистические гипотезы, т. е. такие гипотезы,
которые формулируются либо относительно вида распределения
случайной величины, либо относительно параметров распределения,
либо относительно ранговой упорядоченности значений случайной
величины. Будучи сформулированными относительно вероятност-
вероятностно-статистических и ранговых величин, эти гипотезы могут прове-
проверяться и оцениваться с помощью разного вида статистических при-
приемов и критериев. По результатам проверки и оценки статистических
гипотез мы получаем возможность делать качественные лингви-
лингвистические выводы.
Рассмотрим несколько статистических и нестатистических ги-
гипотез.
Статистическими можно считать гипотезы о том, что служебные
слова в тексте имеют нормальное (или же пуассоновское) распре-
распределение, а употребление большинства знаменательных слов, осо-
особенно слов терминологического значения, не подчиняется этим ви-
видам распределения. Действительно, обследуя выборочные значения
средних частот интересующих нас слов по различным сериям, мы
можем оценить, насколько близко рассматриваемое эмпирическое
распределение к теоретическому распределению Пуассона или же
к нормальному распределению.
К статистическим гипотезам можно отнести предположение
о том, что употребление служебных и многих знаменательных слов
в немецких публицистических текстах из ГДР и ФРГ подчиняется
одним и тем же вероятностным нормам. Это предположение можно
проверить путем сравнения частостей соответствующих слов в га-
газетных текстах ГДР и западногерманских публицистических тек-
текстах. Также статистическим может считаться предположение о том,
302
что средняя длина слова, измеренная в буквах латинского или ки-
кириллического алфавитов относительно научно-технического и де-
делового стиля, во всех языках мира равна 5,5 буквам, а дисперсия
составляет 1,2 буквы. Эти гипотезы рассматривают значения па-
параметров в генеральных лингвистических распределениях, и их
можно проверить, взяв случайные лингвистические выборки. На-
Напротив, к статистическим гипотезам нельзя отнести предположение
Тура Хейердала о южноамериканском происхождении населения
острова Пасхи, равно как и альтернативную гипотезу Те Ранги
Хироа (П. Бака) об этнической связи жителей этого острова с древ-
древним населением Юго-Восточной Азии. Нестатистическими являются
гипотезы о иберо-кавказском происхождении баскского языка
или предположение С. Девиса о том, что фестский диск написан по-
хеттски. Все эти гипотезы сформулированы и проверяются с помо-
помощью неколичественного научного аппарата, они не рассматривают ни
вид распределения, ни величины параметров, ни ранговые последо-
последовательности и поэтому не могут быть проверены статистическим
путем. С другой стороны, далеко не все оперирующие количествен-
количественными данными научные концепции могут рассматриваться в качестве
статистических гипотез. Примером могут служить глоттохроноло-
глоттохронологические гипотезы (см гл. 2, §3, п. 1 и 2), которые хотя и используют
количественные данные, но не могут быть сформулированы отно-
относительно какого-либо вида распределения, параметра или ранговой
последовательности.
2. Нулевая и альтернативная гипотезы. Ошибки первого и вто-
второго рода. Утверждение о предполагаемом виде распределения, ран-
ранговой последовательности или параметре формулируется в виде
нулевой (или основной) гипотезы Нп, которой противопоставляется
другая — альтернативная гипотеза Нх. Например, предположение
о том, что служебные слова в тексте имеют пуассоновское (или же
нормальное) распределение, можно считать нулевой гипотезой Но.
Утверждение же о том, что указанные слова не подчиняются пуас-
соновскому (или нормальному) распределению, в этом случае вы-
выступает в качестве альтернативной гипотезы Hv
Альтернативных гипотез может быть несколько. Например,
если считать предположение о том, что средняя длина слова во всех
языках мира равна 5,5 буквы, то в качестве альтернативных гипо-
гипотез #!, Н%, ..., Hi, ..., Нп, выступают предположения о том, что
средняя длина слова равна 5, 6, ..., 20 и т. д. буквам.
В дальнейшем мы будем рассматривать лишь такие случаи,
когда речь идет о нулевой гипотезе Яо и одной альтернативной ги-
гипотезе Н-у. Последняя может объединять несколько альтернативных
гипотез^ выступая в качестве отрицания нулевой гипотезы, т. е.
#! = Яо.
Проверка лингво-статистической гипотезы всегда осуществляется
на случайной выборке. Поскольку выборка конечна, она не может
идеально точно отразить распределение в генеральной лингвисти-
лингвистической совокупности. Вместе с тем всегда существует риск сфор-
сформировать такую «неудачную» выборку, которая дала бы совершенно
303
ложную информацию о положении дел в генеральной лингвисти-
лингвистической совокупности (вряд ли следовало бы проверять лингво-ста-
тистические гипотезы, относящиеся к мертвым языкам во всем их
стилевом разнообразии, на выборках, составленных из культовых
текстов или надгробных надписей). Короче говоря, при проверке
лингво-статистической гипотезы всегда есть шанс прийти к лож-
ложному решению.
В результате проверки лингвистической гипотезы с помощью
того или иного статистического критерия возникает одна из следу-
следующих четырех ситуаций:
1) нулевая гипотеза Яо принимается, и она верна (соответствен-
(соответственно отвергается ложная альтернативная гипотеза Нг);
2) нулевая гипотеза Яо отвергается, и она ложна (соответственно
принимается верная альтернативная гипотеза Ях);
3) нулевая гипотеза Яо отвергается, хотя она и верна (соответ-
(соответственно принимается ложная гипотеза Я^;
4) нулевая гипотеза Яо принимается, хотя она и ложна (соответ-
(соответственно отвергается правильная альтернативная гипотеза Ях).
Первые две ситуации представляют собой правильные решения,
а две последние — ошибочные решения. При этом третье решение,
состоящее в отвержении правильной гипотезы Яо, дает ошибку
первого рода, в то время как четвертое решение, заключающееся
в принятии нулевой гипотезы Яо, хотя она ложна, представляет
собой ошибку второго рода (табл. 9.1).
Табл ица 9.1
Гипотеза
гается
Гипотеза
мается
Но
Но
отвер-
прини-
Гипотеза Н, верна
Ошибка первого рода
Правильное решение
Гипотеза Н„ не верна
Правильное решение
Ошибка второго рода
Может показаться, что выбор одной из двух возможных гипотез
в качестве нулевой, т. е. основной, а другой — в качестве альтерна-
альтернативной является совершенно произвольным и определяется согла-
соглашением. Этим соглашением определяется и то, какое из неправиль-
неправильных решений считать ошибкой первого рода, а какое — ошибкой
второго рода.
Предположим, например, что алтайскую гипотезу о генетическом
родстве тюркских, монгольских, тунгусо-маньчжурских языков уда-
удалось сформулировать таким образом, что ее можно проверить с по-
помощью некоторого статистического критерия. В этом случае совер-
совершенно безразлично, будем ли мы считать нулевой гипотезой пред-
предположение о том, что эти языки родственны, или объявим в качестве
гипотезы Яо утверждение о том, что эти языки не имеют генетиче-
генетического родства. В первом случае ошибка первого рода состоит в от-
отрицании родства этих языков, хотя они в действительности восходят
304
к одному источнику. Во втором случае ошибкой первого рода слу-
служит утверждение о том, что алтайские языки родственны, хотя
в действительности они неродственны. Аналогичным образом в пер-
первом случае ошибкой второго рода будет утверждение о родстве ал-
алтайских языков (принятие гипотезы Яо, в то время как языки эти
не имеют генетического родства), а во втором случае ошибкой вто-
второго рода — утверждение о том, что языки не имеют генетического
родства, хотя они и восходят к одному источнику.
Из приведенного примера видно, что с точки зрения широкой
лингвистической общественности выбор нулевой гипотезы при ре-
решении алтайской проблемы является чисто .условным, а различия
между ошибками первого и второго рода не являются значимыми.
Однако встречаются ситуации, когда определение того, какую
гипотезу считать основной (нулевой), небезразлично для исследо-
исследователя, и в связи с этим ошибки первого и второго рода получают
разную значимость.
Предположим, что имеется программа машинного перевода тек-
текстов военно-оперативной тематики с одного языка (этим языком
может быть как язык противника, так и язык союзника) на другой.
Техническое исполнение программы сомнений не вызывает, необ-
необходимо оценить лингвистический алгоритм. Лингвистическое ка-
качество программы экспериментально проверяется на малых порциях
текста. Результаты эксперимента дают частные значения хи хг, ...,
xN случайной величины X, в качестве которой выступает число
неправильно переведенных фраз порции.
При такой постановке эксперимента мы можем сформулировать
две лингво-статистические гипотезы. Первая (гипотеза Аг) утверж-
утверждает, что программа пригодна и ее можно принять на вооружение.
Вторая (гипотеза Ай) состоит в том, что программа непригодна для
использования в войсках и ее следует вернуть на доработку.
Возьмем в качестве нулевой гипотезу Alt тогда ошибка первого
рода заключается в том, что пригодная программа будет направ-
направлена на доработку. Это приведет к потере времени и к дополнитель-
дополнительным затратам средств, прежде чем будет выяснено, что программа
в доработке не нуждается.
Если же лринять в качестве основной гипотезы предположение
о том, что программа непригодна (Л2), то ошибка первого рода со-
состоит в принятии негодной программы, использование которой мо-
может привести к срыву военных операций.
Нетрудно понять, что ошибка первого рода, могущая возник-
возникнуть в том случае, когда Яо = Л2, гораздо более серьезна, чем
ошибка первого рода, которая может образоваться при проверке
нулевой гипотезы Яо = Аг.
Заметим попутно, что в ситуации, при которой Яо = А2, ошиб-
ошибкой второго рода является ошибка первого рода ситуации Яо =
==» Аг (т. е. ошибка, состоящая в отвержении доброкачественной
программы), и наоборот, ошибка первого рода ситуации Яо = Аг
служит ошибкой второго рода для ситуации Яо — Av
305
Только что рассмотренный пример показывает, что при испы-
испытании гипотез часто возникают такие ситуации, при которых из-
избежать одной из двух возможных ошибок оказывается важнее,
чем допустить другую. В этом случае ошибкой первого рода счи-
считается та из возможных ошибок, которую нам важнее избежать.
Отсюда следует, что нулевой гипотезой следует считать то пред-
предположение, отвержение которого в том случае, когда оно является
истинным, приводило бы к ошибке первого рода.
Возвращаясь к примеру с машинным переводом, нетрудно по-
показать, что в качестве нулевой гипотезы следует принять предпо-
предположение Л2 о том, что программа машинного перевода военно-
оперативных текстов непригодна для использования в войсках.
В этом случае мы должны будем стараться максимально уменьшить
ошибку первого рода, состоящую в том, что в результате ошибоч-
ошибочного отвержения гипотезы Яо = А2 на вооружение поступает не-
недоброкачественная программа машинного перевода.
Разумеется, определение значимости ошибки, особенно в линг-
лингвистике, носит часто субъективный характер. Так, например, для
убежденного алтаиста наиболее опасной ошибкой (ошибкой первого
рода) служит отвержение нулевой гипотезы, состоящей в том, что
алтайские языки восходят к одному источнику. Ошибка второго
рода, состоящая в принятии алтайской гипотезы, хотя последняя
неверна, будет, разумеется, менее опасна для алтаиста.
3. Проверка статистических гипотез. Проверка статистических
гипотез опирается на такие фундаментальные понятия, как к р и-
тическая область, уровень существенности
(уровень значимости), критерий проверки,
а также мощность критерия.
Начнем с разъяснения понятия критической области, используя
при этом теоретико-множественные представления из аксиомати-
аксиоматического построения теории вероятностей А. Н Колмогорова
(см. гл. 5, § 3, п. 4). Пусть U обозначает множество (пространство)
значений случайной величины X, a W — выборочное, наблюдаемое
в опыте подмножество этих значений. Подмножество W состоит
из возможных выборочных точек ех, ег, ..., ет, каждая из которых
представляет собой определенную совокупность наблюдаемых зна-
значений хх, хг, ..., Хы случайной величины. Точки еъ ег, ..., ет, в свою
очередь, можно рассматривать как некоторые выборочные числовые
значения некоторой статистической характеристики Е, относи-
относительно которой выдвигаются гипотезы Яо и Hv Нулевая гипотеза
Яо проверяется с помощью некоторого статистического критерия С.
Гипотеза эта отвергается лишь тогда, когда наблюдаемая харак-
характеристика, т. е. выборочная точка et, попадает внутрь определенной
области подмножества W — в так называемую критическую область
We- Если эта наблюдаемая характеристика попадает внутрь об-
области W — We, называемой областью приемлемости решений,
то гипотеза Яо принимается (рис. 64).
Нетрудно понять, что выбор критерия проверки гипотезы эк-
эквивалентен выбору критической области, а задача проверки гипо-
306
Рис. 64
тезы является задачей выбора критической области. Основная цель
испытания гипотезы состоит в том, чтобы уменьшить ошибку в при-
принятии решения, причем избежать ошибки первого рода важнее,
чем допустить ошибку второго рода. Поэтому статистический кри-
критерий, а следовательно и критическая область, должны быть вы-
выбраны таким образом, чтобы в случае справедливости нулевой ги-
гипотезы Яо выборочные наблюдения ег- попадали бы в критическую
область We как можно реже. С этой целью фиксируется произволь-
произвольно малое число а, называемое уровнем существенности, и выдви-
выдвигается требование, согласно которому вероятность ошибки первого
рода при проверке истинной гипо-
гипотезы Яо не должна превосходить
этого уровня.
Итак, между понятиями кри
тической области, статистической
характеристикой гипотезы и уров-
уровнем существенности имеет место
следующее соотношение: критичес-
критическая область Wo должна быть та-
такова, что вероятность принятия
статистической характеристикой Е
числового значения, попадающего
в We, не превышает уровня сущест-
существенности а (при этом предполагается, что гипотеза Яо истинна).
Выбор уровня существенности определяется практическими
соображениями, точнее, ожидаемыми последствиями ошибки пер-
первого рода. Чем серьезнее эти последствия, тем должен быть меньше
уровень существенности. В лингвистике обычно используется
а = 0,05. Такой уровень существенности вполне приемлем, напри-
например, при статистическом испытании алтайской гипотезы. Однако
при проверке ответственных инженерно-лингвистических гипотез
этот уровень целесообразно значительно уменьшить: так, при про-
проверке нулевой гипотезы о непригодности программы машинного
перевода следовало бы взять уровень существенности, не превы-
превышающий 0,01. Здесь мы имели бы только один шанс из ста принять
на вооружение непригодную программу.
При рассмотрении проблемы выбора уровня существенности
в тех случаях, когда ответственность за ошибку первого рода доста-
достаточно велика, может возникнуть вопрос: нельзя ли настолько умень-
уменьшить уровень существенности, чтобы вероятность ошибки первого
рода была бы близка к нулю?
Чтобы ответить на этот вопрос, предположим, что мы взяли
а = 0. Тогда независимо от результатов опыта нулевая гипотеза Яо
будет приниматься и в том случае, когда она верна, и в том случае,
когда она ложна. Принимая нулевую гипотезу в тех случаях, ко-
когда она ложна, мы совершаем, как уже говорилось, ошибку второго
рода. При бесконечном уменьшении а вероятность ошибки второго
рода возрастает, что часто приводит к нежелательным резуль-
результатам.
307
Например, проверяя качество программы машинного перевода,
мы должны при любом результате испытания нулевой гипотезы,
состоящей в предположении, что программа перевода непригодна,
принимать эту гипотезу, отвергая альтернативную гипотезу о при-
пригодности программы. Цена этого скептицизма будет достаточно ве-
велика: органы управления и связи вооруженных сил не получат
ни одной программы машинного перевода военно-оперативных тек-
текстов.
Итак, стремясь к уменьшению вероятности ошибки первого
рода, мы не должны забывать о том, что оно может привести к не-
нежелательному увеличению вероятности р4 ошибки второго рода. Оп-
Оптимальное соотношение вероятностей а и $ достигается при удачном
выборе критической области. Условие такого выбора состоит в сле-
следующем: если вероятность того, что выборочное значение стати-
статистической характеристики et попадет в критическую область Wo
при справедливости гипотезы Но, составляет
P{et?Wc/H0} - а, (9.1)
то вероятность того, что это же значение et попадет в область We
при неверной гипотезе Но и истинной гипотезе Нх, должна иметь
максимальное значение, т. е.
P{eitWdHJ = max. ,9.2)
Тогда вероятность ?> ошибки второго рода, состоящей в том, что
ошибочно отбрасывается верная гипотеза Нх, является минималь-
минимальной.
Вся процедура проверки нулевой гипотезы осуществляется с по-
помощью определенного критерия С, представляющего собой правило,
которое устанавливает, при каких результатах случайной выборки
мы имеем право принять нулевую гипотезу, а при каких — отверг-
отвергнуть. Требование, выраженное равенством (9.2), называется по-
постулатом мощности критерия С, мощности, которая измеряется
вероятностью того, что не будет допущена ошибка второго рода.
§ 2. Гипотеза о лексической нормативности текста
и ее проверка с помощью порядковых критериев
1. Порядковые и статистические критерии. Метод статистиче-
статистических гипотез особенно широко используется при определении нор-
нормативности лексических и грамматических единиц, а также при
сопоставлении стилевых и жанровых разновидностей языка
[32 а, с. 16 и ел.]; [33, с. 131 и ел.]. Этот прием может быть применен
и для выявления лексико-грамматических особенностей стиля
отдельных авторов.
Исследования этого типа предполагают количественное сопо-
сопоставление двух лингвистических множеств (частотных списков,
распределений частот слова или грамматической формы и т. п.),
одно из которых может рассматриваться в качестве эталонного.
Выдвигается предположение о том, что оба множества по своей
308
лингвистической природе идентичны и статистически однородны.
Если это предположение рассматривать в качестве нулевой гипо-
гипотезы Но, то альтернативной гипотезой Яг служит утверждение,
что сравниваемые множества имеют разную лингвистическую при-
природу.
Гипотеза Яо проверяется, как уже говорилось, с помощью не-
некоторого объективного критерия С, который должен количествен-
количественно оценить степень (силу) сходства между сопоставляемыми линг-
лингвистическими множествами. Если оценка сходства попадает в об-
область приемлемости решений W — Wq (cm. выше), то гипотеза об
идентичности сравниваемых лингвистических множеств прини-
принимается.
Наиболее мощными критериями контроля лингвистических пред-
предположений являются статистические критерии, с помощью ко-
которых либо проверяется нулевая гипотеза применительно к зна-
значениям некоторых параметров распределения, либо оцениваются
гипотезы о характере самих распределений при условии, что оценка
строится на исследовании параметров распределения. Такие пра-
правила проверки называются параметрическими критериями. Бо-
Более простыми с точки зрения используемого математического ап-
аппарата являются непараметрические статистические критерии,
которые, используя лишь частости или частоты лингвистических
единиц, не требуют знания параметров распределения. Непарамет-
Непараметрические правила проверки гипотез менее эффективны, чем пара-
параметрические критерии. Бывает, что проверку предположения об
идентичности двух лингвистических множеств нельзя провести
с помощью указанных статистических критериев ввиду того, что
нет надежных оценок параметров распределения, неизвестен его
характер, а также отсутствуют достоверные значения (частоты)
лингвистических величин. В этих случаях для проверки статисти-
статистической гипотезы используются порядковые критерии, в которых
применяются не сами значения случайных величин, а ранговая упо-
упорядоченность этих значений. Использование рангов вместо частот
связано с потерей части статистической информации и влечет за
собой снижение мощности критерия, увеличивая тем самым вероят-
вероятность ошибки второго рода (ср. § 1, п. 2).
Несмотря на эти недостатки, порядковые критерии являются
наиболее простыми и универсальными приемами оценки лингви-
лингвистических гипотез.
Чаще всего эти критерии используются для проверки гипотезы
об однородности двух текстовых выборок относительно заданного
лингвистического признака или гипотезы об идентичности (норма-
(нормативности) функционирования данного лингвистического признака
в обеих выборках.
Идею проверки лингвистической гипотезы с помощью поряд-
порядкового, критерия можно сформулировать следующим образом.
Имеется лингвистический признак L, в роли которого может вы-
выступать конкретное слово, грамматическая категория и т. п. Взяты
также две текстовые выборки Wx и N2, разбитые на п порций каж-
309
дая. В выборке Nx лингвистический признак L может рассматривать-
рассматриваться в качестве случайной величины X, имеющей значения
xlt х2, ..., xit .... хп, а в выборке N2 он выступает в качестве случай-
случайной величины У, принимающей значения уи уг, ..., yt уп.
Поскольку случайные величины X и У и их значения
(*i, х2 xt, ..., хп), (уи у2, .... уи .... уп) представляют один и тот
же лингвистический признак L, для проверки той или иной гипо-
гипотезы можно использовать отношения упорядоченности типа
Xi < у и xt > yt. На анализе этих отношений строятся два поряд-
порядковых критерия — критерий знаков и критерий
Вилкоксона.
2. Критерий знаков. Подсчет появлений лингвистического при-
признака А в каждой из п порций выборок Л^ и N2 дает два ряда неза-
независимых частот:
Хх, X2, ..., Х{, ..., Хп', I/i, у2, ..., У(, .., уп*
где частоты, принадлежащие первой и второй выборкам, образуют
пары (хъ i/i), (х2, уг), ..., (xit yi), .... (*„, уп).
Далее составляются разности
= хх — yltz2 = х2 —
= хп
Уп,
которые являются случайными величинами.
Исключив из анализа возможность равенства xt — yt (т. е.
Zj = 0; обоснование этого приема см. в [61, с. 321 и ел.]), будем
рассматривать соотношение числа положительных значении г{
(суммы плюсов), равного /л, с количеством отрицательных значений
Zi (числом минусов), равным п — т. Величина /л рассматривается
в качестве численного значения критерия знаков.
Сформулируем сначала нулевую гипотезу Яо, щгорая утверж-
утверждает, что в каждой i-й паре порций величины X и Y являются не-
независимыми и одинаково распределенными, а вероятность того, что
разность z( = Xi — yt будет положительной, равна вероятности
того, что эта разность окажется отрицательной, т. е.
Р (г, > 0) = Р (zt < 0) = 1/2,
с учетом того, что Р (z( = 0) = 0. Напротив, согласно альтерна-
альтернативной гипотезе Нх различия между xt и yt являются значимыми,
или иными словами,
Р {zt > 0) Ф Р (гг < 0).
Чтобы решить, какую из двух гипотез следует принять, необ"
ходимо опытное значение критерия знаков сопоставить с грани"
цами доверительного интервала для числа плюсов. Эти границы*
характеризуемые уровнем существенности (уровнем значимости'
а = q, определяются исходя из следующих соображений.
Вероятность того, что п разностей z* дадут т плюсов, описы-
сывается биномиальным распределением вида
т\(п—т)\
Дальнейшая процедура проверки гипотезы Яо зависит от того
каким уровнем значимости — односторонним (<l/2) или
двусторонним (q) — мы будем пользоваться.
Рассмотрим сначала одностронний уровень значимости. Если
справедливо равенство (9.3), то вероятность события, состоящего
в том, что среди всех zb z2 zn количество положительных zt,
равное т, окажется больше некоторого граничного числа /л, со-
составит
п п
--ir<-r- (9-4)
Одновременно вероятность события, заключающегося в том, что
среди всех zx, z2, ..., zn число положительных zit равное т, будет
меньше граничного т, есть
«)= 2
(9.5)
310
Возьмем теперь величину т. в качестве наименьшего количества
положительных zt, т. е. числа, для которого равенство (9.4) еще не
превосходит некоторой вероятности q/2. Тогда гипотезу Яо мы будем
отвергать в тех случаях, когда число положительных zt окажется
больше, чем т. При этом вероятность отвергнуть гипотезу Яо,
когда она правильна, не превзойдет вероятности q/2.
Мы будем отвергать гипотезу Яо и тогда, когда и<га.Ив этом
случае вероятность отвергнуть гипотезу Но, когда она правильна,
не превышает вероятности <?/2.
Оба эти правила, взятые порознь, представляют собой одно-
односторонний критерий знаков.
При двустороннем критерии задаются как верхняя, так и ниж-
нижняя границы доверительного интервала. При этом гипотеза Яо от-
отвергается не только тогда, когда т — количество положительных
zt превышает границу т, нб также и тогда, когда число отрицатель-
отрицательных Zj, равное п — т, оказывается ниже границы т. Если границы
т и т остались теми же, что и при одностороннем критерии, то уро-
уровень значимости двустороннего критерия равен 2 • q/2 = q. Зна-
Значения границ для одностороннего и двустороннего критерия знаков
см. в табл. VIII на стр. 370—372.
Теперь, пользуясь описанным математическим аппаратом, про-
проверим лингвистическую гипотезу, согласно которой две достаточно
большие, взятые наугад из одной и той же разновидности языка
текстовые выборки окажутся идентичными относительно употреб-
употребляемой данной разновидности лексики. Если проверка этой гипо-
гипотезы с помощью критерия знаков дает положительный результат,
то это позволит предполагать, что в указанных выборках употреб-
употребление лексики подчиняется некоторой вероятностной норме.
311
Для проверки указанной гипотезы используем статистику
600 словоформ в двух случайно выбранных английских газетных
текстах, по 100 тыс. словоупотреблений каждый.
В качестве образца осуществим полную проверку гипотезы #„
об идентичности этих выборок относительно словоформы govern-
government 'правительство'.
Таблица 9.2
Проверка гипотезы об идентичности двух выборок
английского публицистического текста относительно существительного
government 'правительство'
Порции
I и II выборок
Частоты F] = xt
в I выборке
Частоты F" = yi
во II выборке
Разности
*!=¦*« — У1
1
1
2
—1
2
3
4
3
12
1
11
4
2
7
5
14
1
13
6
3
6
-3
7
12
3
9
8
5
10
—5
9
8
5
3
10
4
8
—4
Продолжение табл. 9.2
Порции
I и II выборок
Частоты F\ = xt
в I выборке
Частоты FJl = yi
во II выборке
Разности
Н — *i — yt
11
7
14
—7
12
3
1
2
13
6
4
2
14
10
10
0
15
5
13
—8
16
3
7
—4
17
4
8
—4
18
9
6
3
19
4
7
—3
20
8
3
5
Каждая из рассматриваемых выборок разделена на 20 порций,
в которых определены частоты употребления government (см. вто-
вторую и третью строки табл. 9.2); в четвертой строке помещены раз-
разности zt = F) — F". Всего имеем 10 плюсов, 9 минусов, а в 14-й
порции z14 = 0; исключив последний случай из рассмотрения,
получаем т *= 10, п = 19.
С помощью табл. VIII убедимся, что при уровне значимости
q = 0,05 полученное нами из опыта значение критерия знаков
т. = 10 попадает внутрь доверительного интервала (т = 5, т = 14).
Это говорит о том, что расхождения в частотах qovernment по обеим
выборкам несущественны, т. е. рассматриваемая словоформа имеет
в обеих выборках постоянную вероятность. Аналогичным образом
312
исследовано употребление остальных 588 именных, глагольных,
адвербиальных и служебных словоформ в английских публицисти-
публицистических текстах [32 а, с. 28]. Выяснилось, что только 4 словоформы —
busy 'сыщик', refused ¦отказал' сап 'могут', by 'при, около' дают
для критерия знаков такие значения, которые выходят за пределы
5%-ного доверительного интервала. Иными словами, только 0,7%
обследованных словоформ обнаруживают неустойчивость своих
вероятностей: остальные 99,3% словоформ имеют постоянные ве-
вероятности, что является косвенным указанием нормативности их
употребления.
3. {/-критерий Вилкоксона. Подобно критерию знаков, кри-
критерий Вилкоксона используется для проверки гипотез о несущест-
несущественности расхождения двух лингвистических выборок, а в нашем
случае для проверки гипотезы о нормативности. Строится этот кри-
критерий следующим образом. Пусть независимые выборки Nt и N2
разбиты соответственно на щ и на и2 порций, причем интересующий
нас лингвистический элемент встретился в i-й порции первой вы-
выборки хх раз, а в i-й порции выборки N2 он встретился yt раз. Рас-
Расположим теперь все значения хг и yt в одну строку в порядке воз-
возрастания численных значений х и у, не обращая внимания на индек-
индексы. В результате мы получаем смешанный вариационный ряд.
Инверсией называется случай, когда у располагается перед х не-
независимо от точного положения xt и yt в вариационном ряде.
Так, например, последовательность
уухухухх
содержит 13 инверсий, поскольку первый хдает 2, второй 3, третий
и четвертый по 4 инверсии. Полная сумма 0 числа инверсий в ва-
вариационном ряде есть случайная величина, численное значение
которой, установленное в результате опыта, и является критерием
Вилкоксона. Теперь попытаемся выяснить, о чем говорит численное
значение 0: когда оно требует принять, а когда отвергнуть проверя-
проверяемую нулевую гипотезу?
Согласно критерию Вилкоксона, нулевая гипотеза должна быть
отвергнута, если количество инверсий U выходит за некоторыэ
пределы и и и (где u<Zu), зависящие от уровня значимости й. При
этом оказывается, что если нулевая гипотеза верна, то случайная
величина U имеет, как показал Б. Л. ван дер Варден [61, с. 336],
распределение вероятностей с математическим ожиданием
и дисперсией
M(U) =
Z)(i/) = o*(t/) =
12
Показано F1, с. 3371, что если пг > 3 и ац + пъ > 20, то это рас-
распределение с достаточной точностью может считаться нормальным.
Последнее обстоятельство позволяет определить пределы и, и,
313
если уровень значимости <? задан. Введем нормированное укло-
уклонение
U-MjU)
u—M(U) - и—М
г= ~ ,,„ , г = -
тогда
В силу вышесказанного случайная величина Z имеет нормаль-
нормальное распределение с параметрами: математическое ожидание О
и дисперсия 1.
Уровень значимости <\ есть не что иное, как вероятность того,
что вследствие случайных колебаний величина U выйдет за пределы
ц и и, а Z — за пределы гиг. Обычно выбирают г = — г. Тогда
связь между и, и и а может быть найдена из очевидных соотношений:
= 1-2Ф(г),
(9.6)
(9.7)
где Ф (г) — известный интеграл вероятностей. Таким образом, при
заданном ч соотношение (9.7) определяет г (см. табл. III на стр. 365
и табл. VI на стр. 369).
По значениям пъ п2, z можно легко определить пределы и и ы:
(9.8)
(9.9)
Если выбрать уровень значимости <\ = 0,05 (двустороннее ог-
ограничение), то это означает, что при справедливости нулевой ги-
гипотезы из 100 значений критерия Вилкоксона в среднем лишь пять
могут выходить за пределы и и и. Если же a = 0,01, то за пределы
и и и может выходить лишь одно значение.
С помощью табл. VI мы убеждаемся, что если q = 0,05, то
z = 1,95, а если a = 0,01, тог = 2,58. Эти значения г говорят о том,
что выбранные нами уровни значимости хорошо согласуются с из-
известным правилом «трех сигм», которое утверждает, что если неко-
некоторая случайная величина уклоняется на опыте от своего матема-
математического ожидания на величину, превышающую За (при этом как
раз г ^ 3), то это происходит, как правило, за счет неслучайног0
воздействия на нее каких-то существенных факторов или за счет
изменения условий наблюдения этой величины. Последнее прин-
принципиально меняет характер распределения вероятностей случай-
случайной величины.
С помощью критерия Вилкоксона можно проверить гипотезу
об устойчивости вероятности словоформы government в английских
публицистических текстах.
Снова возьмем две выборки Nx и N2 из английских газетных тек-
текстов. Каждую выборку разобьем на 20 порций, а в каждой порции
'определим частоту употребления контрольной словоформы
(см. табл. 9.2).
Расположим теперь все значения F\ — xt и F" = yt в порядке
возрастания численных значений F, не обращая внимания на
верхние и нижние индексы. В тех случаях, когда величины
F\ = F\\ вопрос об их взаимном расположении решается путем
жеребьевки. Исходя из этих условий, получаем следующий вариа-
вариационный вид:
pn pi ри ри pi pn pi pi pu pi pi pu
' 3» ' 1" '6' '12' Г4> ' 1> Г6> ' 16' * 7' ' 2> ' 12' ' 20'
pi pi pn pi pu pi pn pi pi pu pn pn pi
10> 19' ' 2> ' 17> * 13' '8' * 9> * 15> * 13> J 6' ' 18> ' i> ' tl'
pu pn pi pn pn pi pi pi pn pu pi pi pu pn pi
1 16> * 19> * 20' ' 10' ' 17> Mi ' 18> ' 14' * 8> ' 14> ' 3) ' 7> ' 15> ' 11» ' f
В обозначениях хну этот вариационный ряд выглядит так:
у, х, у, у, х, у, х, х у, х, х, у, х, х, у, х, у, х, у, х, х, у, у, у, х,
У, У, х, у, у, х, х, х, у, у, х, х, у, у, х.
По описанной выше методике подсчитаем число инверсий:
+ 14 + 16 + 16 + 16 + 18 + 18 + 20 = 197.
В нашем эксперименте п1 = п2 = 20, поэтому условия
«! > 3 и их + п2 ^ 20 выполнены; найдем математическое ожидание
и дисперсию:
М (U) = -^- = ^^- = 200;
о (U) =
/пхп2 , . , ,ч л Г 20-20
,2 v 1-г 2 /— у 12
41=37.
В соответствии с выражениями (9.8) и (9.9) 5%-ные доверитель-
доверительные пределы для критерия Вилкоксона в нашем случае таковы:
и = 200 — 1,96 • 37 » 127;"й = 200 + 1,96 • 37 « 273.
Нетрудно заметить, что число инверсий и = 197 контрольного
слова government попадает в только что указанный доверительный
интервал. Это дает право с уверенностью в 95% утверждать, что
расхождения между распределениями в обеих выборках имеют слу-
случайный, нелингвистический характер, а само употребление этой
словоформы подчинено некоторой норме.
314
315
Исследование с помощью критерия Вилкоксона остальных 599
словоформ [32а, с. 16 — 26] показало, что только 16 слово-
словоформ (began, city, continue, economy, greater, in, tinformation,
mother, movement, outside, plans, real, that, through, whose, yet)
дают значения Вилкоксона, выходящие за 5%-ные доверительные
пределы.
Между тем нулевая гипотеза оставалась бы справедливой, если
бы таких случаев было тридцать. На основании этого можно сделать
вывод, что словоформы в английских публицистических текстах
имеют устойчивые распределения Р (F). Если в этих текстах и встре-
встречаются лингвистические единицы с неустойчивыми распределениями,
1 fi
то вклад таких единиц не превышает щ^ • 100% = 2,7%.
§ 3. Проверка гипотез о характере расхождений
статистических характеристик языков, функциональных
стилей и подъязыков с помощью параметрических критериев
При рассмотрении лексикологических, фонологических и грам-
грамматических проблем, связанных с сопоставлением различных язы-
языков, подъязыков и функциональных стилей, приходится сравни-
сравнивать абсолютные и относительные частоты употребления лингви-
лингвистических единиц в разных стилях, подъязыках, художественных
произведениях. Все эти оценки и сопоставления осуществляются
путем проверки гипотезы о существенности расхождения между
соответствующими параметрами распределении интересующей ис-
исследователя лингвистической единицы.
1. Может ли средняя длина словоформы быть статистической
характеристикой стиля и языка? Пусть имеется генеральная линг-
лингвистическая совокупность, элементы которой распределены нор-
нормально и характеризуются математическим ожиданием М (X) = ц.
На основе выборочных наблюдений внутри этой совокупности по-
получено значение средней арифметической х, не совпадающее точно
со значением ц. Необходимо решить вопрос о существенности рас-
расхождения величин х и ц..
Решение этой задачи сводится к проверке нулевой гипотезы Яо,
состоящей в допущении, что расхождения между х и ц. несуществен-
несущественны, т. е. что х = [I. В этом случае альтернативная гипотеза Нх
заключается в утверждении, что х Ф \i.
Выбор критерия и статистической характеристики для проверки
гипотез зависит от того, известно или неизвестно нам среднее квад-
ратическое отклонение а.
Чаще всего величина а остается неизвестной. В этом случае в ка-
качестве статистической характеристики выбирается не случайная
величина х, а величина
(9.10)
имеющая распределение Стьюдента cv = N — I степенями свободы
(см. гл.8, ?2, п. 3 и§3, п. 1).
Исходя из рассуждений § 1, п. 2, имеем критическую область
значений характеристики / с нижней границей t«y, где $ = а —
заданный уровень значимости*. Тогда областью' приемлемости
гипотезы #0 служат абсолютные значения |/| < fq;v, а вероят-
вероятность принятия этой гипотезы равна
<ta
Вероятность же отвержения гипотезы Яо и принятия альтернатив-
альтернативной гипотезы #j в этом случае составляет
<\; v
при двусторонней критической области и
для каждой из односторонних критических областей.
Проверка гипотезы Но о несущественности расхождения величин
х и ц. сводится к следующему:
а) определению по заданному уровню значимости и количеству
степеней свободы v = N— 1 величины L; v;
б) вычислению по формуле (9.10) статистической характеристики t;
в) сравнению величин t и /q.v.
Сам же критерий принятия или отвержения нулевой гипотезы
формулируется таким образом:
а) при | / j < tq. v гипотеза Но принимается как правдоподобная,
при этом утверждается, что опытная средняя х и математическое
ожидание ц. = М (х) статистически неразличимы (т. е. если разли-
различия между ними и наблюдаются, то они вызваны несущественными
причинами);
б) при |/| ^ .tq.y гипотеза Яо отвергается и принимается аль-
альтернативная гипотеза Hlt утверждающая, что расхождения между
х и \i = М (х) не могут рассматриваться как незначительные ста-
статистические флуктуации, а вызваны существенными лингвисти-
лингвистическими причинами.
Описанная процедура проверки нулевой гипотезы носит название
/-критерия, или критерия Стьюдента.
* Поскольку проверка статистических гипотез основывается иа выборе
критической области, определяемой уровнем существенности, при рассмотре-
рассмотрении наших гипотез мы будем исходить не из надежности р, а из уровня зна-
знаt t
чимости (\, учитывая при этом, что г = г^ и t —
^, .
316
317
Если для генеральной лингвистической совокупности известно
не только математическое ожидание М (х) — ц интересующего нас
элемента, но и среднее квадратическое отклонение а, то в качестве
статистической характеристики следует брать не /, а значение
(9.11)
Дальнейший ход решения задачи точно совпадает с операциями
сценки нулевой гипотезы с помощью ^-критерия: сначала по за-
заданному уровню значимости q с помощью табл. VI на стр. 369
определяют значение г., служащее нижней границей критической
области, после чего находят значение г. Если | z | > г^, то гипо-
гипотезу #0 о несущественности расхождений х и ц следует отвергнуть
и принять альтернативную гипотезу Яа; если же |г| < г^, то нулевая
гипотеза Но принимается и разность | х — ц\ рассматривается как
случайная статистическая флуктуация.
Описанная процедура называется Z-критерием проверки
статистических гипотез, или критерием нормального закона.
В гл. 7 (см. § 4, п. 4) была выдвинута гипотеза о нормальности
распределения средних длин словоформ в языках мира. Если эта
. гипотеза подтвердится (ср. п. 2, § 1), то можно считать, что расхож-
расхождения между средними длинами словоформ по отдельным языкам
несущественны.
Но значит ли это, что такая несущественность расхождения меж-
между языками мира будет наблюдаться и при сравнении средних длин
словоформ одного функционального стиля?
Чтс бы ответить на этот вопрос, рассмотрим расхождения между
средней длиной словоформы в научно-технической и деловой речи
шести славянских языков, равной 6,13 буквы при стандарте 0,43,
с одной стороны, и средней длиной словоформы в указанных стилях
всех языков мира, которая равна примерно 7 буквам, — с другой
[7, с. 2041.
Допустим, что средние длины словоформ в языках мира по
интересующим нас стилям распределены нормально, причем
М (х) = ц = 7, одновременно* = 6,13, as = 0,43. Пусть гипо-
гипотеза #0 состоит в том, что средняя длина славянской словоформы
практически соответствует средней длине словоформы в языках ми-
мира, т. е. хсл == ц.
Проверим нашу гипотезу с помощью ^-критерия. Для этого,
учитывая, что ч = N — 1=6— 1=5, воспользуемся табл. VI,
по которой найдем нижнюю границу критической области ^о,О5; 5 —
= 2,57. Затем определим значение t:
Неравенство |/| > /o,o5;5 свидетельствует о том, что значение
нашей статистической характеристики t, с помощью которой мы про-
Ееряем гипотезу о несущественности расхождений средних длин, по-
попадает в критическую область, в связи с чем эта гипотеза должна
быть отвергнута.
Пповерим эту гипотезу с помощью Z-критерия, полагая при
этом, что s = а = 0,43.
Для этого с помощью табл. VI находим нижнюю границу кри-
критической области, равную г0 о5 = 1,96, с которой сопоставляем
абсолютное значение г, вычисленное с помощью соотношения
(S.H):
6,13—7
0,43
= _iii2L .2,45= -4.95.
0,43
=ayN= 6-13-7-0
0,43
0,43
.2,45= -4,95.
Здесь снова имеем неравенство |г| > г005, свидетельствующее
о том, что значение статистической характеристики г опять попа-
попадает в критическую область.
Таким образом, и в том и в другом случае гипотеза Ио о несу-
несущественности различия между средней длиной словоформы в сла-
славянских деловых и научно-технических текстах и средней длиной
словоформы в аналогичных текстах языков мира должна быть от-
отвергнута. Более правдоподобной оказывается альтернативная ги-
гипотеза #!, согласно которой расхождение между хсл и (Л = М (X)
является существенным.
Это расхождение можно отнести, вероятно, за счет двух причин.
Во-первых, славянские языки используют флективно-аналитическую
технику оформления именных форм, составляющих значительную
часть деловых и научно-технических текстов во всех языках. Та-
Такая техника не дает столь значительного удлинения основы, как
агглютинация в тюркских, финноугорских и других языках, занима-
занимающих значительную статистическую долю во взятой нами выборке
языков. Во-вторых, славянские языки в отличие от немецкого и не-
некоторых финноугорских языков сравнительно мало пользуются сло-
словосложением при образовании научно-технических и администра-
административно-деловых терминов.
2. Существенны ли расхождения значений избыточности в раз-
разговорной, беллетристической и деловой речи? Избыточность является
информационной характеристикой, в которой обобщаются различные
статистико-дистрибутивные свойства текста (см. гл. 5, § 5, п. 6).
Поэтому при сопоставительном изучении стилей или других разно-
разновидностей языка важно знать, относится ли наблюдаемое расхож-
расхождение в значениях избыточности двух стилей к существенному или
несущественному. Сопоставление этих значений можно осущест-
осуществить, проверяя с помощью параметрических критериев гипотезы о не-
несущественности расхождения двух средних. Рассмотрим математи-
математическую схему проверки такой гипотезы.
Пусть имеются две нормально распределенные случайные и не-
независимые лингвистические выборки достаточно большого объема:
318
319
xu x2, ..., xN nylt y2,..., yN . Эти выборки взяты либо из одной, либо
из разных генеральных совокупностей. _
Согласно теореме Ляпунова (см. гл. 6, § 4, п. 4), средняя х пер-
первой выборки есть нормально распределенная случайная величина
с параметрами М (х) = Цх и D (х) = aj/N^ а средняя у второй вы-
выборки аналогично является нормально распределенной случайной
величиной с параметрами М Q) -= ца и D (у) = а\Шл.
_ Необходимо определить существенность расхождения средних
хну. Для этого зададим нулевую гипотезу Но, состоящую в пред-
предположении, что х и у различаются несущественным образом, т. е.
их математические ожидания равны: М (х) = М (у), или ^ — ц„.
Принятие гипотезы Но означает, что выборки Nx и Nt принадлежат
не к разным, а к одной и той же генеральной совокупности. Откло-
Отклонение этой гипотезы свидетельствует о том, что расхождение между
х и у существенно, М (х) Ф М (j/), а выборки Nx и Nt взяты из
разных генеральных совокупностей. _
Для проверки гипотезы Но введем величину б = х — у, которая
также является случайной величиной с математическим ожиданием
АГ(в) = М(х — ~у) = М(х) — М(у) - fij — щ
и дисперсией
D (б) = ol = \ \
Рассмотрим нормированную случайную величину
б—М(б)
которая также распределена по нормальному закону с математи-
математическим ожиданием 0 и дисперсией 1. В силу соотношения F.127)
можно считать, что
< г
2Ф B).
(9.12)
Выбор статистического критерия ?нова зависит от того, известны
ли нам дисперсии D (х) — erf и D (у) =• of или нет.
Пусть <rj и а| известны. Тогда в качестве статистической xapaifr-
теристики можно взять величину
х—у
о- - •
х — у
которая получается из (9.12) в предположении, что ^ = щ (ги-
(гипотеза Но). Затем назначается уровень значимости к», по которому
из табл. VI берется величина г^, выступающая в качестве границы
критической области. Если имеет место неравенство \г\ < г*,
т. е. статистическая характеристика лежит в области приемлемости
гипотезы Но, то это означает, что мы можем принять с надежностью ц
гипотезу о том, что различие между математическими ожиданиями
средних х и у имеет характер случайной статистической флуктуа-
флуктуации, откуда М (х) = М (у). Из равенства математических ожиданий
следует, что выборки, по которым получены эти средние, взяты из
одной генеральной совокупности.
В том случае, если | г | ;> z^ и значение статистической характе-
характеристики попадает в критическую область, гипотеза Яо должна
быть отвергнута в пользу альтернативной гипотезы Ни согласно
которой различия между х и у существенны» л М. (хуф М (у).
Принятие альтернативной гипотезы означает, чг& Щеявие взяты
из выборок, не принадлежащих одной генеральной совокупности.
Обычно теоретические дисперсии и| и о^ в распределениях
лингвистических объектов остаются неизвестными, а вместо них
используются выборочные дисперсии st и sf. Поэтому проверка
лиигво-статистических гипотез осуществляется не с помощью
Z-критерия, а путем применения критерия Стьюдента. Переход к
этому критерию осуществляется здесь исходя из следующих сообра-
соображений.
Сперва предполагается, что а* = сг? + сг|. Тогда для разности
х — у имеем дисперсию
а также нормально распределенную нормированную случайную
величину
(х—у)— М(х—у) _ (*—у)—(щ—ца)__ t (9.13)
Среднее квадратическое отклонение а можно заменить стандар-
стандартом Sjj.j,, полученным из величины s|-j, являющейся средневзве-
средневзвешенной выборочных дисперсий
N.
Sz =
Иными словами,
Г N, _ N.
Nx+Nt—2
320
П Зак. 1287
321
Заменяя в равенстве (9.13) а на у; -, можно прийти к величине
имеющей распределение Стьюдента с v = Л^ + N2 — 2 степенями
свободы. Проверка нулевой гипотезы Но, заключающейся в пред-
предположении, что М (х) = М (у) (т. е. цх = ц2), предусматривает
определение величины
*—у
s—
x. V
(9.14)
Если
и сравнение ее с табличным значением („;v. у
то гипотеза Но принимается и различия между х и у рас-
рассматриваются как несущественные, т. е. М (х) = М (г/), а вы-
выборки Л^ и Л/2 считаются принадлежащими одной генеральной
совокупности. Если же |/| ^ /..у, то гипотеза Яо отвергается
и принимается альтернативная гипотеза Ни согласно которой раз-
различия между х я у считаются существенными, т. е. М (х)фМ (у),
а выборки -Nt и N2 принадлежат к разным лингвистическим гене-
генеральным совокупностям. Критерий Стьюдента может быть исполь-
использован как при малых, так и при больших значениях Nt и N2.
Познакомившись со схемой сравнения двух средних, перейдем
к исследованию расхождений между средними значениями избыточ-
избыточности в разговорной, беллетристической и деловой речи шести евро-
европейских языков.
Таблица 9.3
Сравнение избыточностей стилей по шести европейским языкам
Разновидно-
Разновидности языка
A)
Разговор-
Разговорная речь(р)
Беллетрис-
Беллетристика (б)
Деловая
речь (д)
Избыточность
по языкам
B)
C)
О,
0,812 0,791
D)
777 0,813 0,753 0,7921
0,818 0,745 0,773 0,
х
E)
0,757 0,801
,788
0,868 0,866 0,875 0,835 0,872 0,802
F)
G)
(8)
0,782
0,788
0,853
0,024
0,027
0,029
s- -
*. У
A0)
0,0255
0,0290
0,0266
С згой целью возьмем средние арифметические нижних и верх-
верхних значений избыточности R"t = (Rt + Rt)l2 [столбцы B) — G)
табл. 9.3] и будем рассматривать их как случайные значения нор-
нормально распределенной величины избыточности по каждому из ука-
указанных выше стилей. Вычислив среднюю избыточность R и стан-
стандарт s для каждого стиля [столбцы (8) и (9)), попытаемся выяснить,
насколько существенны расхождения между значениями средней
избыточности по каждому из названных стилей. С этой целью будем
проверять с помощью критерия Стьюдента нулевую гипотезу Но,
согласно которой расхождения в значениях Rt и Rj являются несу-
несущественными. Уровень значимости примем равным 0,05, число сте-
степеней свободы в нашем случае составляет v==6 + 6 — 2=10.
При. этих условиях граница критической области равна
^о,О5;ю = 2,23.
Попарное сравнение средних избыточностей стилей с помощью
выражения (9.14) дает следующие результаты.
1) Для пары разговорная речь — беллетристический стиль
имеем
#Р— #б _ 0,782—0,788
б —
0,006-Уз
0,0255
0,0255 У Щ+ТЩ
°Ш .«-0,41.
0,0255
В связи с тем, что
А>
2,23,
Up. б I < А>,05; ю
нулевая гипотеза о несущественности различий средней избыточ-
избыточности разговорного и беллетристического стилей в шести европей-
европейских языках принимается как вполне правдоподобная.
2) Для пары разговорная речь— деловая речь аналогичным
образом находим
0,782-0,853
0,071-1,732
0,0266
:—4,59.
0,0266 У1/6+1/61
Полученное значение t здесь выше порога критической области,
т. е.
I 'р, б I -> го,о5; ю — А^.
Это говорит о существенности расхождений между разговорной
и деловой речью. Иными словами, гипотезу о несущественности
расхождений избыточности указанных разновидностей следует
отвергнуть.
3) Пара беллетристика — деловая речь дает
. 0,788—0,853 0,065-1,732
'б.д7"
0,0290 У1/6+1/6
Здесь снова имеем неравенство
0,0290
!—4.02.
322
5! 10»
говорящее о том, что значение / попадает в критическую область
отвержения нулевой гипотезы.
К аналогичным результатам можно прийти, используя вместо
критерия Стьюдента Z-критерий (в этом случае предполагается, что
а- = s-, a a- — sz). Итак, попарное сравнение средних избыточно-
11* 423
стей по трем стилям шести европейских языков показывает, . что
различия величин R письменной фиксации разговорной речи и
беллетристической речи несущественны*, в то время как расхож-
расхождения в значениях R для деловой речи, с одной стороны, и разговор-
разговорно-беллетристической разновидности в ее письменной форме, с дру-
другой, существенны. Причины этих существенных расхождений сле-
следует искать в статистико-дистрибутивных характеристиках дело-
деловой речи, отражающих ее качественные особенности. Среди этих
особенностей, противопоставляющих ее разговорной и беллетри-
беллетристической речи, основное место, очевидно, занимает использование
в деловой речи большого числа клише и штампов, нормированность
синтаксиса, а также более или менее фиксированный выбор лек-
лексики. Все это значительно увеличивает избыточность деловой речи.
3. Оценка лексических расхождений между публицистикой
ГДР и газетными текстами ФРГ. Использование статистических
критериев дает возможность не только исследовать нормирован-
нормированность текста или сравнивать разные функциональные стили по та-
таким усредненным характеристикам, как избыточность. Метод ста-
статистической проверки гипотез дает возможность выявлять и оце-
оценивать качественные расхождения в лексике, грамматике и фоноло-
фонологии двух разновидностей одного языка или двух близкородственных
языков.
Оценка этих расхождений осуществляется путем сравнения ча-
стостей употребления лингвистических единиц Ьъ L2, ..., Ln в двух
выборках Л/х и N2, каждая из которых представляет определенный
язык или его разновидность.
Для каждой лингвистической единицы L вычисляются две от-
относительные частоты:/! = /УЛ^ для первой и /2 = F2/N2 для вто-
второй выборки. Кроме того, предполагается, что в первом говорении
(т. е. языке, варианте или диалекте) единица L имеет вероятность
Рх, а во втором — вероятность р2.
Затем выдвигаются две гипотезы: нулевая Яо, предполагающая,
что pj = р2, и альтернативная Нъ утверждающая, что рг Ф ра.
Так как функция распределения разности Д — /2 имеет меньшие
скачки и меньшую асимметрию, чем функции распределений /х
и /2, то можно утверждать, что разность /х — /2 имеет нормальное
распределение с математическим ожиданием М (fx — /2) = Рх — Р2
и дисперсией** сТр.-р, = ст? + а|.
* Если бы в ходе эксперимента по определению энтропии и избыточности
текста можно было бы учесть такие дополнительные средства устной речи как
жест, мимика, интонация, то не исключено, что мы получили бы иные оценки
ее избыточности. В этом случае сравнение величин Rp, R& и Ra могло бы при-
привести к другим результатам.
** Хотя точные значения дисперсий нам неизвестны, но при достаточно
большом N можно заменить неизвестные величины а\, о? их эмпирическими
оценками
s2-'
N-,-1
Дисперсия же ор,—р, заменяется в этом случае оценкой s2 = sf +
324
Из рассуждений, приведенных в гл. б, § 4, п. 4, следует, что нор-
нормированное отклонение
распределено нормально. Отсюда при заданном уровне значимо-
значимости ч имеем
Если величина г такова, что
то можно считать, что вероятности рх и р% статистически неразли-
неразличимы (т. е. Рх — Ра)- Если же |г| > гч, то гипотеза Но отвергается
и принимается альтернативная гипотеза Hlt утверждающая, что
Pi Ф Рг-
С помощью описанного аппарата А. С. Ротарь [33, с. 163 — 199]
исследовала соотношение частостей у 1000 наиболее частых слово-
словоформ в двух выборках немецких публицистических текстов. Первая
выборка охватывает газетные тексты ГДР, а вторая — тексты из
газет ФРГ за 1965 — 1969 г. Каждая выборка содержит 100 тыс.
словоупотреблений. Для повышения надежности исследования взят
трехсигмовый критерий (zq = 3, Р = 0,9973, q = 0,0027).
Всю процедуру определения существенности расхождения ча-
частостей в обоих литературных вариантах рассмотрим на примере
словоформы nach 'после, через, по', которая, согласно данным ча-
частотного словаря А. С. Ротарь, имеет в выборке ГДР
р = 317 (fx = 0,00317), а в выборке ФРГ дает Ft = 538
(f2 = 0,00538).
1) После определения частостей вычисляются дисперсия и сред-
среднее квадратическое отклонение по каждой выборке в отдельности
и по обеим выборкам, взятым вместе:
а__-„_ /i(l — /i) _ 0,00317-0,99683^ 0,0032
°l~Sl~ Nx ~ 10? 105 '
2 = 52 =
0,00538-0,99462 0,0053
=
l_P7 = @,0032 + 0,0053)/10» = 0,0085/105;
^-р, = У 0,0085/10* = 0,0003.
325
2) Вычисляется абсолютная величина г:
| z j = 10,00317—0,00538 (/0,0003 ^
Таблица 9.
= 7,03.
Поскольку | г | > 3, следует отвергнуть гипотезу о том, что пред-
предлог nach имеет одинаковую вероятность употребления в публици-
публицистических текстах ГДР и ФРГ. Более правдоподобной является
гипотеза о существенном расхождении этих вероятностей, которое
следует искать в дистрибутивно-статистических особенностях упо-
употребления этого предлога в восточно- и западногерманской публи-
публицистической прозе (ср. ниже).
По только что описанной схеме были сопоставлены частости
остальных словоформ списка. Это сопоставление показало следую-
следующие результаты.
1. Более восьмисот словоформ дало либо полное совпадение
частостей в обеих выборках, либо показало несущественные рас-
расхождения величин /х и ft. В эту группу вошли такие общеупотре-
общеупотребительные существительные, прилагательные и глаголы, как
Land 'страна', Mittel 'средство', Ziel 'цель', kleinen 'малые',
letzte 'последний', brauchen 'нуждаться'. Общенемецкие дистрибу-
дистрибутивно-вероятностные нормы употребления показали также многие
артиклевые формы, предлоги, союзы и вспомогательные формы гла-
глагола.
2. Существенное расхождение частостей Д и fz обнаружено почти
у двухсот словоформ, покрывающих около 10% текста. Разные ве-
вероятности употребления в газетах ГДР и ФРГ имеют сложносокра-
сложносокращенные словоформы и буквенные аббревиатуры (см. табл. 9.4),
а также существительные и прилагательные терминологического
значения, которые обозначают общественно-политические и эконо-
экономические понятия, использующиеся преимущественно либо в ГДР,
либо в ФРГ (табл. 9.5). Разные вероятности употребления дают
географические названия (табл. 9.6), что объясняется либо распо-
расположением самих географических объектов, либо нормами геогра-
географических терминологий, используемых в ГДР и ФРГ, либо преобла-
преобладанием определенной тематики на страницах восточно- или западно-
западногерманской прессы.
Менее очевидны причины, порождающие существенные расхож-
расхождения в частостях количественных числительных и названий меся-
месяцев (табл. 9.7), а также у глаголов (табл. 9.8), личных местоимений
(табл. 9.9), предлогов и союзов (табл. 9.10). Эти вероятностные раз-
различия языка можно отнести за счет разной стилевой ориентации
норм восточно- и западногерманских газет. В газетах ГДР печа-
печатаются тексты речей, произносимых от первого лица, здесь широко
используются нормы деловой речи с ее именными конструкциями;
даты, включая названия месяцев, чаще всего записываются в циф-
цифровой форме. Газеты ФРГ больше ориентируются на беллетристи-
беллетристическую речь, поэтому в западногерманской публицистике преоб-
преобладают глагольные обороты со сложным предложным управлением,
а также широко используются сочинительные и подчинительные
конструкции.
326
N.
9
з
4
Б
6
7
Аббревиатуры и словоформы
DDR 'ГДР'
DM 'марка ГДР'
USA 'США-
NATO 'НАТО'
Prof, "проф."
SED 'СЕПГ'
FDJ 'Союз немецкой молодежи'
h (ГДР)
0,00250
0,00021
0,00093
0,00021
0,00027
0,00029
0,00032
U (ФРГ)
0,00005
0,00089
0,00039
0,00002
0,00077
0,00009
—
1*1
15,3
6,5
4,9
3,8
4,9
3,3
—
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Словоформы
Republik 'республика'
Genosse 'товарищ'
Frieden 'мир'
Einheit 'единство'
Socialismus 'социализм'
sozia Iistischen 'социалистические'
Betriebe 'предприятия'
demok га tischen 'демократические'
Friedens 'мира'
Betrieb 'предприятие'
Werktatigen 'трудящиеся'
Zone 'зона'
Staaten 'государство'
Prozente 'проценты'
Steigerung 'повышение'
Stellvertreter 'заместитель'
Polizei 'полиция'
Bundesregierung 'правительство ФРГ'
Konferenz 'конференция'
Ваи 'стройка'
Ministerrates 'Совета Министров'
. Arbeiterkiasse 'рабочий класс'
Staatsrates 'Государственного Совета'
Volkskammer 'Народная палата'
Т
h
0,00113
0,00047
0,00055
0,00038
0,00038
0,00055
0,00037
0,00042
0,00036
0,00043
0,00034
0,00001
0,00087
0,00034
0,00027
0,00027
0,00005
0,00007
0,00006
0,00004
0,00022
0,00027
0,00022
0,00022
аблица
h
0,00007
0,00001
0,00004
0,00003
0,00003
0,00008
0,00003
0,00003
0,00002
0,00005
0,00002
0,00030
0,00030
0,00005
0,00003
0,00003
0,00032
0,00038
0,00032
0,00025
0,00001
—
— ¦
—
9.5
1 г 1
9,6
6,7
6,4
5,5
5,5
5,9
5,4
5,8
5,6
5,4
5,3
5,3
5,2
4,8
4,4
4,4
4,4
4,4
4,3
4,0
4,2
—
—
—
1
2
3
4
5
6
7
8
9
10
Словоформы
Воппег 'бонский'
Westberlin 'Западный Берлин'
Westdeutschland 'Западная Германия'
Munchen 'Мюнхен'
Berlin 'Берлин'
westdeutschen 'западногерманские'
amerikanischen 'американские'
Bremen 'Бремен'
Istambul 'Стамбул'
№11 'Нил'
Таблица
/¦
0,00069
0,00073
0,00060
0,00001
0,00070
0,00054
0,00016
—
—
—
0,00009
0,00013
0,00006
0,00039
0,00152
0,00009
0,00055
0,00028
0,00021
0,00099
9.6
1*1
6,8
6,6
6,6
6,3
§,5
5,5
4,8
327
№
1
2
3
4
5
6
7
8
9
10
11
Словоформы
drei 'три'
zwei 'два'
elf 'одиннадцать'
sieben 'семь'
funf 'пять'
sechs 'шесть'
vier 'четыре'
August 'август'
Februar 'февраль'
September 'сентябрь'
Juli 'июль'
Таблица
0,00013
0,00026
0,00001
0,00002
0,00011
0,00009
0,00012
0,00011
0,00008
0,00008
0,00006
h
0,00093
0,00108
0,00032
0,00025
0,00042
0,00039
0,00035
0,00086
0,00048
0,00035
0,00023
.9.7
1*1
8,1
7,1
5,7
4,6
4,4
4,3
3,3
7.5
5,7
4,1
3,4
№
1
2
3
4
5
6
Словоформы
wird 'становится'
seien 'будьте'
sieht 'видит'
unternehmen 'предпринимать'
konnte 'мог бы'
diirlte 'мог бы'
Таблица
h
0,00356
0,00012
0,00009
0,00001
0,00018
0,00003
и
0,00487
0,00042
0,00032
0,00020
0,00045
0,00019
9.8
1*1
4,4
4,3
3,8
4,2
3.4
3,2
№
1
2
3
4
5
6
7
8
Словоформы
wir 'мы'
unserer 'наших'
ich 'я'
alle 'все'
unsere 'наши'
mir 'мне'
du 'ты'
unser 'наш'
Та бли ца
h
0,00454
0,00166
0,00271
0,00239
0,00143
0,00045
0,00057
0,00050
0,00096
0,00013
0,00067
0,00065
0,00015
0,00007
0,00009
0,00019
9.9
Ml
15,3
11,7
11,3
10,0
10,0
5,4
6,0
3,9
Nt
1
2
3
4
5
6
7
Словоформы
nach (prp) 'после, через, пу, согласно'
bis 'пока'
zuriick 'назад, обратно'
гит (zu+der) 'к, за, в'
da 'так как'
am (an-fdem) 'у, на, к'
bei 'у, при, возле, около'
Таблица
/¦
0,00317
0,00004
0,00011
0,00191
0,00009
0,00277
0,00017
и
0,00538
0,00046
0,00059
0,00312
0,00042
0,00384
0,00042
9.10
1*1
7.6
6,0
6,0
5,4
4,7
4,1
3.1
328
§ 4. Проверка статистических гипотез о тождестве
двух лингвистических распределений
1. Сравнение эмпирического и теоретического или двух эмпи-
эмпирических распределений. При решении некоторых теоретических
и прикладных вопросов, например при формальном выделении в тек-
тексте ключевых и терминологических слов, возникает необходимость
рассмотреть не только параметры, но и характер всего лингвисти-
лингвистического распределения. Эта задача также решается путем проверки
статистических гипотез о тождестве двух эмпирических распреде-
распределений (вариационных рядов) или об идентичности эмпирического и
теоретического распределения.
Схема проверки тождества эмпирического и теоретического рас-
распределений выглядит следующим образом. Пусть имеется эмпири-
эмпирическое распределение, например распределение относительных (/),
относительных накопленных (f*), абсолютных (F), абсолютных на-
накопленных (F*) частот лингвистического признака L в выборочной
совокупности текстов. Это распределение сопоставляется с соответ-
соответствующим ему гипотетическим теоретическим распределением —
с распределением вероятностей (р), накопленных вероятностей (р*),
математических ожиданий частот \М (F)], математических ожиданий
накопленных частот [М (F*)] признака L в генеральной совокуп-
совокупности текстов. Выдвигается нулевая гипотеза Но, состоящая в том,
что эмпирическое распределение выборки соответствует теорети-
теоретическому распределению генеральной совокупности. Сам закон рас-
распределения может быть задан различным образом, например в фор-
форме плотности распределения / (х), в интегральной форме распре-
распределения F (х) или каким-то другим образом.
Для того чтобы принять или отвергнуть гипотезу Но, конструи-
конструируется некоторая статистическая характеристика W, определяющая
степень расхождения эмпирического и теоретического распределе-
распределений. Величина W может быть построена различными способами:
в качестве ее рассматривается либо сумма квадратов отклонений
329
частот от их математических ожиданий W = 2 [F — М (F)]*,
либо сумма тех же квадратов с их весами W = 2 с IF — M(F)V,
либо максимальное отклонение интегральной эмпирической функ-
функции Fn (x) от интегральной теоретической функции распределения
F (х) и т. д.
Сконструированная одним из перечисленных способов стати-
статистическая характеристика W является случайной величиной,
аакон распределения которой зависит от закона распределения
случайной величины X (X = F, /, F*, /*) и от числа испытаний N.
Если гипотеза Но верна, то закон распределения выборочной харак-
характеристики W определяется законом теоретического распределения
случайной величины X и числом N.
Будем считать, что закон распределения известен. Пусть для
данной выборки с числом опытов N мера расхождения W приняла
значение w. Возникает вопрос: определяется ли то или иное числен-
численное значение величины W случайными несущественными флуктуа-
циями (в этом случае гипотеза Но принимается) или это отклонение
настолько значительно, что его следует относить за счет существен-
существенного расхождения между теоретическим и эмпирическим распре-
распределениями (в этом случае гипотеза Яо отвергается)?
Чтобы ответить на Этот вопрос, определим, предполагая, что
гипотеза Но верна, вероятность того, что опытное значение.w не
превысит некоторого численного порога w* выбранной меры рас-
расхождения — порога, выше которого расхождения между эмпириче-
эмпирическим и теоретическим распределениями следует считать существен-
существенными.
Если вероятность Р (w < w*) велика, то гипотезу Но можно
принять как вполне правдоподобную. Если же указанная вероят-
вероятность очень мала, то следует признать, что экспериментальные дан-
данные противоречат гипотезе Я0) и ее нужно отклонить. Аналогичным
образом проверяется гипотеза о тождестве двух эмпирических рас-
распределений.
Как же следует строить статистическую характеристику W7
Поскольку функции распределения / (х), F (х) чаще всего остаются
неизвестными, целесообразно выбирать величину W таким образом,
чтобы закон ее распределения не зависел бы от указанных функций
распределений и их параметров. Иными словами, для проверки
гипотез о расхождениях распределений целесообразно применять
непараметрические критерии согласия, среди которых наиболее
употребительным является критерий ха Пирсона. Кроме того, здесь
применяется критерий Колмогорова, упрощенные критерии Рома-
Романовского и Ястремского, проверка нормальности распределения
с помощью чисел Вестергарда и сетки Турбина, критерий Колмо-
Колмогорова — Смирнова.
2. Критерий ха Пирсона. Пусть в результате N выборочных на-
наблюдений исследуемая лингво-статистическая случайная величина X
принимает определенные значения (варианты), которые сгруппиро-
сгруппированы в k интервалах статистического ряда, представленного в
табл. 9.11.
330
Таблица 9.11
Интервалы вариант
Частота (число значений X, по-
попавших в интервал)
Частость ti = F/N
Математическое ожидание час-
частоты
Вероятность попадания X в дан-
данный интервал
h
Npi
Pi
/.
NP2
Pi
...
...
...
...
• • •
Fk
/ft
Nph
Ph
2
N
1
N
1
Предположим, что нам известен закон распределения случайной
величины X, который задан интегральной функцией F (х) или плот-
плотностью / (х). Зная этот закон, можно определить вероятность pt
попадания случайной величины в каждый из интервалов
(см. нижнюю строку табл. 9.11).
Задача состоит в том, чтобы проверить нулевую гипотезу #„,
утверждающую, что распределение полученных из опыта часто-
стей fi (или частот Ft) согласуется с теоретическим распределением
вероятностей pt (или соответственно математических ожиданий Npt).
Будем проверять гипотезу Но о согласованности эмпирического
и теоретического распределений, исходя из расхождений между
частостями /( и вероятностями pt. Если эти расхождения малы, то
здравый смысл подсказывает нам, что гипотезу Но можно считать
правдоподобной. Если же расхождения велики, то ее вероятно,
следует отвергнуть.
Мера расхождения эмпирического и теоретического распреде-
распределений частостей и вероятностей, известная под названием критерия
X2 (хи-квадрат) Пирсона, задается равенством
(9.15)
где частное Nlpt является весовым коэффициентом. Введение этого
коэффициента объясняется тем, что отклонения, относящиеся к
разным интервалам, нельзя считать равноправными: одна и та же
абсолютная величина отклонения /г — р,- может быть очень незна-
незначительной при большом значении рг и, наоборот, весьма заметной
при очень малом pt. Поэтому в качестве весовых коэффициентов
берут величины, обратно пропорциональные вероятностям р{.
Если оценивать соответствие эмпирического и теоретического
распределений по расхождениям частот математических ожиданий
р. _ д?рь то. легко показать, что выражение (9.15) примет вид
(9.16)
/= I
Npi
831
При построении интервальных вариационных рядов частоту
лингвистического признака в данном интервале мы обозначали сим-
символом щ, в связи с этим формула (9.16) может быть представлена
также в виде у
(9.17)
Случайная величина х2. представляющая собой сумму квадратов
величин, связанных одной линейной зависимостью (напомним, что
2/j = 1, a 2.Fj = N) имеет важное свойство, заключающееся в том,
что ее распределение не зависит от закона распределения F(x) или
f (х) и от N-, а зависит от числа интервалов k; в связи с этим при
N -*¦ оо распределение критерия х2 стремится к уже известному
распределению х2 с k — 1 степенями свободы (ср. гл. 8; § 3, п. 1).
Сходимость распределения критерия х2 к Х*-РаспРеДелению
дает возможность построить, задав определенный уровень значи-
значимости, критическую область для проверки гипотезы о соответствии
эмпирического и теоретического распределений. Действительно,
если величина х2 равна нулю, то это значит, что все квадраты раз-
разностей {Ft — Npi)* или (ft — р,)% равны нулю, т. е. опытные ча-
частоты, точно соответствуя теоретическим, дают полное совпадение
эмпирического и теоретического распределений. В остальных слу-
случаях величина х2 отлична от нуля и становится тем больше, чем
больше растут расхождения между указанными частотами и их рас-
распределениями. Когда величина, расхождения достигает определен-
определенного уровня, значение х* переходит из области принятия гипотезы Яо
в критическую область ее отвержения.
Схема проверки нулевой гипотезы Но с помощью критерия х*
выглядит следующим образом
1. На основании предшествующего опыта выбирается предпола-
предполагаемый закон распределения изучаемой лингвистической величины X
и определяются параметры этого закона.
2. Полученные из эксперимента частости (частоты) группи-
группируются в интервалы (группы), при этом малочисленные частоты объ-
объединяются в один интервал*.
• Математический смысл этого объединения состоит в следующем. При
использовании критерия %3 следует иметь в виду, что биномиальное распреде-
распределение частот Fi = П( сходится к нормальному. Этот предельный переход
происходит достаточно быстро только тогда, когда и вероятность р, и вероят-
вероятность q не слишком малы. Из этого следует, что математически корректным
является такое применение критерия х', при котором ни одна из интерваль-
интервальных частостей (соответственно вероятностей) и частот (соответственно мате-
математических ожиданий) не слишком мала. Это и заставляет нас объединять час-
частоты крайних интервалов. Обычно объединяются интервалы, имеющие Fi <
< 5, с тем чтобы иметь в новых интервалах F% > 5. Некоторые авторы тре-
требуют, чтобы теоретическая и эмпирическая частота интервала была не менее 10.
Существуют приемы, которые позволяют устранить неточности, возни-
возникающие в связи с применением непрерывного распределения Xе к дискретно-
дискретному распределению интервалов (поправка на непрерывность Йещса), а также
коррективы, связанные с завышенным значением величины х2> вычисленной
по сгруппированным данным (поправки Шеппарда). Подробнее об этом см.
[Г, о. 2321; [61, с. 284].
332
3. На основе выбранного закона распределения вычисляются
вероятности (математические ожидания).
4. По формулам (9.15) или (9.16) вычисляется значение кри-
критерия х8.
5. Определяется число степеней свободы v ¦¦ k — /, где k —
число интервалов, а / — число налагаемых связей (ср. гл. 8, §3, п. 1).
6. По заданному уровню значимости и числу степеней свободы
с помощью табл. V на стр. 368 находят пороговое значение xl,v>
отделяющее область приемлемости гипотезы Но от критической
области ее отклонения.
7. Полученное в п. 4 значение х2 сравнивается с пороговым зна-
значением Xn;v Если имеет место неравенство Xs < Xq; v> т- е> зна"
чение критерия Пирсона лежит в области приемлемости гипотезы,
то гипотеза Но о согласованности эмпирического и теоретического
распределений считается принятой, а это означает, что расхождения
в этих распределениях рассматриваются как несущественные. Если
же значение х* попадает в Критическую область, т. е. х2 ^ Xq; v
то нулевая гипотеза отвергается и расхождения в распределениях
рассматриваются как существенные.
Оценку гипотезы Но можно осуществлять не только путем срав-
сравнения величин х* и Х(|; v» н0 и чбрез определение вероятности того,
что некоторая случайная величина, имеющая х*-распределение,
примет при v степенях свободы значение, не меньшее, чем вы-
вычисленная по формуле (9.16) величина критерия х2- Если вероят-
вероятность Р (Xv ^ X) окажется ниже некоторого заданного наперед
уровня значимости, например ниже q = 0,05, то это означает, что
вероятность случайных отклонений окажется очень малой величи-
величиной. Тогда мы должны признать нашу оценку х* отклонения эм-
эмпирического распределения от теоретического закона неслучайной"
(ведь случайные явления с очень малой вероятностью следует счи-
считать практически невозможными). Это указывает на неправдоподоб-
неправдоподобность гипотезы #0 о несущественности расхождений между эмпи-
эмпирическим и теоретическим распределениями. Если же вероятность
Р (Xv ^ Xs) достаточно велика (в нашем случае больше 0,05), то
нулевую гипотезу о близости обоих распределений следует принять.
§ 5. Распределение средних длин словоформ
в языках мира
1. Проверка гипотезы о нормальности распределения средних
длин словоформ с помощью критерия ха Пирсона. Чтобы осуще-
осуществить проверку указанной гипотезы, необходимо сравнить полу-
полученные из опыта частости или частоты средних длин с их теорети-
теоретическими вероятностями или математическими ожиданиями.
Вычисление этих теоретических величин может быть осуществ-
осуществлено двумя способами: исходя или из дифференциальной формы
нормального закона (плотности вероятности), или из его интеграль-
интегральной формы,
333
Рассмотрим первый способ. Областью значений непре-
непрерывной случайной лингвистической величины X является либо вся
числовая ось, либо часть ее. Разобьем эту область на т интервалов,
соответствующих интервалам группировки выборочных измерений
величины X. Каждый интервал ограничен нижней границей at
и верхней границей Р*, причем рг = аг+1.
Будем оперировать событиями Аи А2, ..., Ат, состоящими в том,
что величина X попадает в интервалы с номерами 1, 2, ..., т. Ве-
Вероятности появления указанных событий соответственно равны
Ръ Рг> ¦••> Рт- Для выражения этих вероятностей используем зна-
значения плотности вероятности случайной величины. Используя рас-
рассуждения п. 3, 5 и 7 § 2 гл. 6, можно утверждать, что вероятность
попадания случайной величины в интервал (alt р() равна произ-
произведению длины интервала р( —aj = Axt на значение плотности
вероятности в одной из точек этого интервала. Такой точкой может
быть середина интервала (Pj — аг)/2 = Axt.
Таким образом, имеем
Pi = Р (а, < X < р,) - Ax,f (х) - (р, - о,) f (xt).
Наша случайная величина распределена по нормальному за-
закону, поэтому
/(*) = ¦
Отсюда следует, что
тУ2я
Поскольку значения ц, а8, а обычно неизвестны, они заменяются
величинами х, s*, s, полученными из эмпирического распределения.
В результате приходим к выражению
— ft e-<«,-*
(9.18)
Учитывая, что (xt — x)/s = г (см. гл. 6, § 4, п. 4), введем вспомога-
вспомогательную функцию
применение которой дает возможность пользоваться при вычисле-
вычислениях табл. II на стр. 364.
Поскольку Axt = Р< — ai( перепишем (9.18) в виде
Pi
Теперь определим, чему равно математическое ожидание частоты
М (nt) = ni появления величины X в t-м интервале.
Выбирая из непрерывной генеральной совокупности N наблю-
наблюдений, мы формируем ситуацию, аналогичную той, при которой
984
признак в генеральной совокупности принимает конечное число зна-
значений и при которой имеют место т событий Аи At, ,.., Ат, обра-
образующих полную систему. Отсюда следует, что теоретическая частота
(математическое ожидание) того, что при N испытаниях непрерыв-
непрерывная случайная величина X находится в t-м интервале, исходя из
(9.18), определяется равенством
— (Хм — х)г /B s2) /r\ * t гк\
е ' , (9.19)
где р; = n't IN. Используя вспомогательную функцию ф (г), перепишем
выражение (9.19) в виде
NAxt
«;=¦
(9.20)
Обратимся теперь ко второму способу определения
теоретических частот.
Исходя из свойства 4 интегральной функции распределения
(см. гл. 6, § 2, п. 3), вероятность попадания случайной величины,
подчиненной нормальному закону, на заданный интервал можно
определить из выражения
Заменяя неизвестные ц и а на опытные значения х и s (или s\
приходим к соотношению
(9.21)
Соответственно теоретическая частота того, что при N испыта-
испытаниях случайная величина X попадет в i-й интервал, равна
(9.22)
Применим описанную процедуру к проверке гипотезы о нор-
нормальности распределения средних длин словоупотреблений в язы-
языках мира (ср. гл. 7, § 4, п. 4). Эта проверка осуществляется по
следующей схеме.
1) Значения средних длин словоупотреблений для 100 языков
мира, использующих буквенную письменность (см. табл. 7.27
на стр. 259), сгруппированы в интервалы [столбец A) табл. 9.12],
каждый из которых имеет длину Ах = 0,6. Значения середин ин-
интервалов (Х[) указаны в столбце B). Для каждого интервала указано
число языков (щ), средние длины словоупотреблений которых по-
попадают в данный интервал [столбец CI.
2) Среднюю арифметическую х и опытную дисперсию будем вы-
вычислять по методу моментов (см. гл. 7, § 3, п. 3), принимая за про-
произвольное число а середину шестого интервала (а = 5,70).
»35
Таблица 9.12
Номер
интервала
1
2
3
4
5
6
7
8
9
10
11
Oj < X < Pj
A)
2,40—3,00
3,00—3,60
3,60—4,20
4,20—4,80
4,80—5,40
5,40—6,00
6,00-6,60
6,60—7,20
7,20—7,80
7,80—8,40
8,40—9,00
Хм
t
B)
2,70
3,30
3,90
4.50
5,10
5,70
6,30
6,90
7,50
8,10
8,70
fit
C)
0
2
8
20
21
22
16
2
5
2
2
(*)
—3,00
-2,40
—1,80
-1,20
—0,60
0
0,60
1,20
1,80
2,40
3,00
AX
F)
-5,0
—4,0
-3,0
—2,0
-1,0
0
1,0
2,0
3,0
4,0
5,0
Xi—a
' A*
F)
0
- 8,0
—24,0
—40,0
—21,0
0
16,0
4,0
15,0
8,0
10,0
\ A* )
G)
0
32
72
80
21
0
16
8
45
32
50
I I loo
I —40,0 | 356
Подставляя в формулу G.6) приведенные числовые значения
и сумму из столбца F), получаем значение средней арифметической:
6,70
1UU
(-4О) = 5,46.
Учитывая тот факт, что все значения признака xt имеют общий
множитель Ах, воспользуемся для упрощения расчетов опытной
дисперсии формулой G.21). Подставив в нее уже приводившиеся
выше числовые значения и сумму чисел столбца G), имеем
s* = ЛЁ_ 0,36—E,46—5,70)»» 1,224.
100 v
Далее определяем несмещенную оценку выборочной дисперсии:
N , 100
N- 1
99
1,224= 1,2364.
Следовательно, стандарт равен s = Vl,2364 « 1,11.
3) Используя выражение (9.20), вычислим теоретические частоты
n't для дифференциальной формы нормального закона. Расчеты
показаны в столбцах C) — G) табл. 9.13, причем следует учитывать,
что
.*?.—?~^ «0,5405.
О S 1,11
4) Получив значения п/, можно непосредственно перейти к
сравнению по критерию ха эмпирических и теоретических частот.
Результаты вычислительной работы, производимой по формуле
(9.17), показаны в столбцах (9) — A1) табл. 9.13. Обращаем вни-
внимание читателя на укрупнение малочисленных интервалов 1см.
столбцы B) и G)].
«ч
|
а*
е
с*
с
1
с
ч к
S- а_
жру
цел
сел
"" о г
сГ
S;
II
е"
-г.
CL
1
II
в*
—¦
S
S
(8)
(9)
5?
C)
S
_
о
8
о
0180
о
ш
со
СО
CN
О
g
eg
с
5225
ш
"?
1
со
2,35
3,29
Я
8
о
0608
о
о>
т?
7
СО
7
о
CN
СО
00
00
в
1497
о
7
7
00
8
СО
0100
со
о
ю
¦А
14,90
о
2756
о
СЛ
с?
00
т
S
сч
CN
О
о
2401
о
О)
о
20,51
О
3790
о
СО
С)
со
?
8
7
о
ю
со
S
о
9025
о!
&
О
21,05
О
3894
о
СО
CN
О
о
з
о
0256
о
СО
о
1
СО
16,16
СО
СО
о
2989
о
В
о
3
о
я
СО
ю
о
9,26
S
о
1714
о
СО
CN
•«И
CS
8
со
от
о
1
•ч-
СО
—
4,80
3,97
§
о
0734
о
оо
со
^^
3
«¦
щ
ю
S
1,27
о
о
0235
о
СО
(N
3
О)
О
со
СО
—
0,30,
о
8
о
9900
о
а>
on
о>
CN
СО
CN
СО
Я
со
100
II *
8>
о
100
337
В столбцах D) — F) можно брать также разность эмпирической
частоты щ и округленной до целых чисел теоретической частоты
n't [см. столбец (8)].
5) Частоты всякого нормального распределения, устанавлива-
устанавливаемого на основании наблюдаемого распределения, подчинены трем
связям (/ = 3). Во-первых, сумма наблюдаемых частот фиксиро-
фиксирована, т. е. 2 /it = N; во-вторых, теоретические частоты должны
давать среднюю х, равную средней эмпирических частот; в-треть-
в-третьих, дисперсии теоретического и эмпирического распределений долж-
должны быть также равны.
В результате укрупнения малочисленных интервалов общее
их количество вместо одиннадцати становится равным шести
(k = 6). В случае нормального распределения мы имеем дело с дву-
двумя параметрами М {X) « х и D (X) = ст2 « s2, а также с суммой
эмпирических частот N = 2л(. Таким образом, количество связей
¦ i = 1
/ = 3. Отсюда число степеней свободы составляет v = k — / =»
= 6 — 3 = 3.
6) С помощью табл. V выясняем, что пороговое значение нашего
критерия Хо,о5;з = 7,82 заметно больше только что полученной
величины х2-'Это значит, что последняя лежит в области приемле-
приемлемости нулевой гипотезы.
Проведем проверку нулевой гипотезы, исходя из интегральной
формы нормального закона. Первые два раздела этой процедуры
совпадают с первыми пунктами предыдущей проверки, поэтому
переходим сразу к п. 3.
3) С помощью выражения (9.22) вычисляем значения п\. Ход
расчета показан в столбцах A) — A1) табл. 9.14; при этом следует
помнить, что л; = 5,46, as = 1,11.
4) Сравнение эмпирических и теоретических частот по крите-
критерию х2 показано в столбцах A2) — A4) той же таблицы.
5) Как уже было показано, v = 3.
6) Пороговое значение х2 при v = 3 и q = 0,05 составляет 7,82.
Так как полученная нами величина х8 = 3,66 меньше этого порога,
то она снова находится в области приемлемости гипотезы Яо.
Оценку нашей гипотезы можно было бы провести, как уже го-
говорилось (см. § 4, п. 2), не только через сравнение величин х2 и
XqV, но также и путем определения вероятности того, что неко-
некоторая случайная величина, распределенная по ха» примет при
v = k — / степенях свободы значение, не меньшее, чем вычислен-
вычисленная по формуле (9.17) величина критерия х2. т- е- Р (Xv ^ Ха)-
Чтобы определить эту вероятность, воспользуемся табл. IX
(см. стр. 373,374), из которой находим, что полученное нами значе-
значение х2 при трех степенях свободы лежит в интервале между 3 и 4.
При этом значение х2 — 3 соответствует вероятности 0,3916, а зна-
значение х2 = 4 — вероятности 0,2615.
338
¦on
. ,х
,-»„
r-H
t-*T.
—* Tt* CSI
О} О")
OO —• oo О Сч oo
"Ч* О <N fc. О —
1Я t- О О О (М
о" -ч" о" ©" О -Г
СО Ю f-* •* N (N
~н W N Щ СО SO
О> to Ю *ф О SO
so so © —« о oo
S SO SO ^-» 00
-* Ь- <N —'
ся ю о -* о"
2
(N
* о о ю
о п" ™Г
СО N
со сч
8§
м n со ¦* со
оо ю о А со
Sg S38
©оооооо
— 00 Ю OO
(^ СО СО О
о оо
о" о" о
оо
2 8
¦ч- оо
оооо©
со В 1 2
СО
со
о
00
о о о о
СО
sO
О •" - N N
8
f
8 8
О — — (N
со t-~- см
т т ¦&
а & 2
" U «
oo oo O)
© ¦* со
- О н
О О •" - N И (О
so to
^f 00
8
f
Ю t * » t *
О III x S П 9)
^4 —. CN in CO
8 СО CN
ш
КПП
8
339
Чтобы получить точное значение вероятности, соответствующее
вычисленному значению х*. произведем интерполяцию:
Р(Х») = р C,66) = 0,3916 — @,3916 — 0,2615H,66 =
= 0,3916 -0,0859 = 0,3057.1
Эта вероятность не мала (она заметно больше ч ¦* 0,05), следова-
следовательно, расхождения между эмпирическими и теоретическими ча-
частотами можно считать случайными и несущественными. Иначе
говоря, снова оправдывается гипотеза Яо, согласно которой нор-
нормальное распределение достаточно хорошо воспроизводит рас-
распределение средних длин словоупотреблений в языках мира.
Разумеется, в тех случаях, когда вероятность Р (%* ^ ха) явн0
выше или ниже некоторого заранее заданного уровня значимости
ч = 0,10, или 0,05, или 0,01, мы можем принять или отвергнуть
гипотезу Яо без того, чтобы производить утомительные интерполя-
интерполяционные вычисления.
2. Проверка гипотезы о нормальности распределения средних
длин словоформ с помощью критерия Колмогорова. Оценка гипо-
гипотезы о близости теоретического F (х) и выборочного эмпирического
Fn (x) распределения может быть осуществлена с помощью крите-
критерия согласия Колмогорова, который использует в качестве меры
расхождения между эмпирическим и теоретическим распределе-
распределениями величину
DN - max\FN (*) — F (x)\,
с которой мы уже встречались в гл. 8, § 5, п. 2. Нулевая гипотеза
Яо состоит в предположении, что случайная величина X распре-
распределена по теоретическому закону F (х), или, иначе говоря, эмпи-
эмпирические значения Fn (х) сходятся по вероятности к теоретическим
значениям F {х). Альтернативная же гипотеза Ях утверждает, что
величина X не распределена по F (х).
Если величина X распределена по закону F (х), то можно ут-
утверждать (см. гл. 8, § 5, п. 2), что при достаточно большом N с вы-
высокой вероятностью Р = К (к) выполняется неравенство
DNVN<k,
(9.23)
которое можно рассматривать как некоторое событие.
Применение критерия согласия Колмогорова представляет на-
нахождение вероятности того, что распределенная по закону Кол-
Колмогорова случайная величина Dn ~Vn примет некоторое значение,
не меньшее, чем к. В этом случае имеет место неравенствоDn~\/~N ^
^ X, являющееся противоположным событием по отношению к не-
неравенству (9.23). По правилу нахождения вероятности противо-
противоположного события получаем в случае справедливости гипотезы Яо
следующее равенство:
(9.24)
)=\— /С (Я) = 1 — Р = ч,
где <? > 0 — достаточно малое число.
340
Итак, вероятность события, состоящего в появлении при еди-
единичном испытании неравенства (9.24), очень мала. По существу
мы имеем здесь дело с практически неосуществимым событием
(ср. гл. 6,§ 4, п. 1). Теперь проведем N независимых испытаний, ко-
которые в своей сумме можно рассматривать как единичный опыт про-
проверки расхождения распределений Fn(x) и F(x). Если полученная при
этом случайная величина X=Dn Vn окажется не меньше X, то это
будет означать, что в нашем единичном опыте осуществилось собы-
событие, имеющее малую вероятность ч. Однако мы предполагали, что
такое событие практически неосуществимо в тех случаях, когда
справедлива гипотеза Яо, согласно которой эмпирическое распре-
распределение Fn (х) сходится к F (х) при N -> оо. Поэтому расхождение
DN = max |^ (x) — F (x)\
между обоими распределениями следует считать существенным.
В итоге мы вынуждены отвергнуть нулевую гипотезу Яо о том, что
случайная величина X имеет распределение F(x).
Напротив, если наш единственный опыт показывает, что
Dn Yn <К то это означает, что маловероятное событие не осуще-
осуществилось и у нас нет пока оснований для того чтобы отвергнуть
нулевую гипотезу. Такая ситуация свойственна любой научной дис-
дисциплине. Чтобы опровергнуть некоторое теоретическое положение,
достаточно привести хотя бы один противоречащий пример, а для
того чтобы доказать его правильность, примеров уже недостаточно.
Применение критерия Колмогорова осуществляется по следую-
следующей схеме.
1. Строится эмпирическая функция FN (x) и предполагаемая
теоретическая функция распределения F(x).
2. Выдвигается гипотеза Яо, согласно которой эмпирическая
функция Fn (х) аппроксимирует закон F (х).
3. Ставится опыт, заключающийся в сравнении полученных эм-
эмпирических значений Fn (#0 == ft (i — 1, 2, .., N) с теоретическими
значениями F ixi) = p*. Выбирается наибольшая среди них раз-
разность D% и составляется произведение Dn VN — К-
4. По табл. VII (см. стр. 369, 370) находят вероятность того, что
случайная величина DA |/Л/, распределенная по закону Колмого-
Колмогорова, примет значение не меньшее, чем заданное ^0» т- е.
= \ -/((>•„)= V-
Это и есть вероятность того, что действительное максимальное
расхождение тах|^(х) — F {х)\, объясняемое случайными ста-
статистическими флуктуациями, не меньше полученной в нашем опыте
максимальной разности D&-
5. Если окажется, что вероятность у очень мала, т. е. не превы-
превышает заранее принятого порога ч (обычно берут q = 0,10; 0,05;
0,01), то исходя из принципа практической невозможности мало-
341
вероятных событий появление неравенства DnV^N ^ А,о считается
невозможным событием. Отсюда следует, что расхождение D% меж-
между эмпирическим и теоретическим распределениями нужно считать
существенным. Это в свою очередь означает, что гипотеза о близости
эмпирического и теоретического распределений неверна.
6. Если же вероятность у сравнительно велика, т. е. у > q,
то расхождение D% следует рассматривать как несущественное, а
гипотезу #0 можно считать совместимой с данными опыта.
Теперь применим критерий Колмогорова к проверке гипотезы
о нормальности распределения средних длин словоформ в языках
мира.
Интервалы
со
менее 3,00
3,00—3,60
3,60—4,20
4,20—4,80
4,80—5,40
5,40-6,00
6,00—6,60
6,60—7,20
7,20—7,80
7,80—8,40
. 8,40—9,00
а1
B)
0
2
8
20
21
22
16
2
5
2
2
100
C)
0
0,02
0,10
0,30
0,51
0,73
0,89
0,91
0,96
0,98
1,00
D)
i
3
8
15
20
21
16
10
4
1
1
100
Табл
F(x)-p'
E)
0,01
0,04
0,12
0,27
0.48
0,68
0,84
0,94
0,98
0,99
1,00
ица 9.15
\р N{x)-F{.x)\
F)
0,01
0,02
0,02
0,03
0,03
ГоЖ|
0,05
0,03
0,02
0,01
0
1) Воспользовавшись данными табл. 9.12, строим эмпирическую
функцию Fn (x), представляющую собой накопленную частость
fi = nllN, а также теоретическую функцию F (х), являющуюся
накопленной вероятностью р* = n]IN [см. столбцы A) — E)
табл. 9.15].
2) Сформулируем гипотезу Но, согласно которой функция
FN(x) аппроксимирует закон F (х), представляющий собой интег-
интегральную форму нормального распределения.
3) Сравниваем значения Fn (х) = /,* и F (х) = р\ [столбцы
C) и E)], в результате чего выбираем наибольшую разность
D°N = max\FN(x) — F(x)\ - 0,73 — 0,68 = 0,05
[столбец FI; в этом случае имеем X =0,05 ]/100 = 0,5.
4) Из табл. VII находим вероятность того, что случай-
случайная величина D100Y100, распределенная по закону Колмогорова,
примет значение, не меньшее, чем 0,5:
Р (Dloo УШ > 0,5) = 1 — К @,5) = 0,9639.
342
5) Полученная вероятность намного больше принимаемого обыч-
обычно уровня значимости q = 0,05, поэтому расхождение D% следует
считать несущественным; это дает нам право принять гипотезу о
нормальности распределения средних длин словоформ по языкам
мира.
При всей своей простоте и удобстве критерий Колмогорова
имеет свои недостатки.
Во-первых, он слабо учитывает «хвосты» распределения (малые
и большие значения х). Но именно поведение этих «хвостов» ока-
оказывается иногда решающим при определении близости эмпириче-
эмпирического и теоретического распределений [61, с. 281].
Во-вторых, критерий Колмогорова дает вполне удовлетвори-
удовлетворительные результаты, когда известен не только вид предполагаемой
теоретической функции, но и все ее параметры. Такой случай редко
встречается в лингво-статистической практике: обычно параметры
теоретического распределения неизвестны, и их приходится оцени-
оценивать с помощью опытных данных. Применяя критерий х2. мы учи-
учитывали это обстоятельство путем уменьшения числа степеней сво-
свободы. Критерий Колмогорова этой процедуры не предусматривает.
Поэтому применение его в случаях, когда параметры теоретического
распределения неизвестны, приводит обычно к завышению значения
вероятности у. Это может повлечь за собой принятие гипотезы,
плохо согласующейся с опытными данными. Чтобы избежать этой
ошибки, некоторые авторы предлагают считать несущественными
расхождения между эмпирическим и теоретическим распределением,
- параметры которого не известны, лишь в том случае, если вероят-
вероятность 7 > 0,6 [7, с. 271].
3. Проверки гипотезы о нормальности распределения средних
длин словоформ с помощью упрощенных критериев. Всякая гипо-
гипотеза о нормальности вариационного ряда может проверяться не
только с помощью таких строгих критериев, как критерий ха Пир-
Пирсона или критерий Колмогорова, но и оцениваться также с помощью
некоторых упрощенных приемов.
Рассмотрение этих приемов начнем с критерия Романовского.
Опираясь на правило «трех сигм» (см. гл. 6, § 4, п. 4), В. И. Романов-
Романовский показал, что
Р (| t - М (х2) |< За».) > 0,98, когда v < 7,
Р (IXa — М (х2)| < Зетх.) > 0,99, когда v > 7,
где v — число степеней свободы. Учитывая, что при больших v
распределение ха. асимптотически приближается к нормальному
распределению с 'параметрами М(у?) = v, D(xa) = ст?* = 2v (оу =
= |^2v) (см. гл. 8, §3, п. 1), и опираясь на принцип прак-
практической уверенности (см. гл. 6, § 4, п. 1), нетрудно прийти к просто-
простому правилу, согласно которому, если
843
то расхождение между эмпирическим и нормальным распределе-
распределениями можно считать с вероятностью 0,98 и 0,99 случайным;
если же
Таблица 9.15
то расхождение следует считать существенным.
Пользуясь этими правилами, проверим гипотезу о нормаль-
нормальности распределения средних длин словоупотреблений в языках
мира.
Так как f = 3,66 (см. табл. 9.14), a v = 3, то
_ 13,66—31
0,66
2,45
0,27.
Здесь Rm < 3, поэтому можно считать, что расхождение между
эмпирическим и теоретическим распределением случайно и нор-
нормальное распределение достаточно хорошо воспроизводит интере-
интересующее нас эмпирическое распределение.
Нормальность вариационного ряда может быть проверена с по-
помощью чисел Вестергарда. Эта проверка, опирающаяся на правила
«двух» и «трех сигм», строится по следующей схеме.
Сначала задаются четыре множителя 0,3; 0,7; 1,1; 3, затем вы-
вычисляется средняя арифметическая х = F и среднее квадратическое
отклонение ст. Гипотеза о нормальности рассматриваемого эмпи-
эмпирического распределения не отвергается, если удовлетворяются
следующие условия:
а) в промежутке от х — О.Зсг до х -f 0,3а находится не менее
0,25 всей совокупности^ _
б) в промежутке от х — 0,7ст до х + 0,7а расположено не ме-
менее 0,50 всей совокупности; _
в) в. промежутке от* — 1,1 а до * + 1,1а умещается не менее
0,75 совокупности; _
г) в промежутке от х — За до х + За находится не менее 0,998
всей совокупности.
Теперь, используя числа Вестергарда, еще раз проверим гипо-
гипотезу о нормальности распределения средних длин словоупотреб-
словоупотреблений в языках мира.
Учитывая, что х = 5,46, а а *¦= s ¦= 1,11 (эти значения были най-
найдены в п. 1 при проверке рассматриваемой гипотезы с помощью
критерия х2 Пирсона), сгруппируем данные табл. 7.28 (см. стр. 260)
так, как этого требуют условия Вестергарда (табл. 9.16).
Эта группировка показывает [см. столбец C)], что распределение
средних длин словоформ подчиняется нормальному закону.
Проверку нормальности эмпирического распределения можно
осуществить графическим путем с помощью вариационной сетки
Турбина П, с. 249], представляющей прямоугольную систему ко-
344
Интервалы
A)
5,13—5,80
4,68—6,24
4,24—6.68
2,13—8,79
Количество языков, попа-
попадающих в интервал
B)
27
58
77
100
Доля совокупности, попа-
попадающая в интервал
C)
0,27
0,58
0.77
1.00
ординат, в которой по оси абсцисс откладывается линейный мпс-
штаб*, а по оси ординат наносится логарифмическая шкала, со-
соответствующая интегральной функции
/г W=_L
х
-•'/« dz-
Шкала на оси ординат состоит из разных отрезков—циклов, каж-
каждый из которых соответствует изменению характеристики лога-
логарифма на единицу. Циклы разбиваются на части соответственно
изменению мантисс десятичных логарифмов. На логарифмической
шкале не может быть нулевой отметки, поскольку lg 0 = — оо.
Идея использования сетки Турбина заключается в следующем.
Пусть имеется система координат х, у @ ^ у ^ 1) с линейной
шкалой по оси х и нелинейной — по оси у. Путем некоторого пре-
преобразования у -> г = ф (х) получается система координат х, z
с линейной шкалой по оси ординат. Для этого функцию F (х) нор-
нормального распределения с параметрами ц и а2 можно нормировать
с помощью линейного преобразования г = (х — ц)/а (ср. гл. 8).
Интегральная кривая нормального распределения у = F (х) асимп-
асимптотически приближается к нулю и к единице (т. е. к 100%; рйс. 65).
Поэтому наша шкала по оси ординат не может достичь ни нуля,
ни единицы. При переходе к функции г — ф (х) интегральная кри-
кривая превращается в бесконечную прямую, имеющую наклон 1/а
и проходящую через точку х — ц При построении графика удобно
пользоваться характеристическими значениями, приведенными
в табл. 9.17.
Таб ли ца 9.17
X
г
{/ (в°/о)
ц—За
—3
0.14
ц—2о
2
2,28
ц — о
у .
15,87
0
50,00
1
84,13
ц + 2(т
2
97,72
|х + 3а
3
99,86
Иногда на ось абсцисс наносится логарифмическая шкала.
345
*
В
i
-
1;
J
-
-
to
j
'i
г.
И
"¦
>
•
-
¦
99,99
99,90
99,00.
95,00
90,00
щоо
70,00
60,00
50,00
ЩОО
ЩОО.
20,00
ЩОО
1,00
0,10
i i i , , i , ¦ , , . , kot
2,40 3,00 Ц0 WO 4,80 5,IM -6,00 6,60, %W 7,80 8,40 X (xL)
Рис. 65
Схема использования сетки Турбина для проверки нормальности
лингвистического распределения предусматривает следующие опе-
операции.
1. По оси абсцисс откладываются значения признака, взятые
из эмпирического лингвистического распределения (вариационного
ряда), а по оси ординат—соответствующие им накопленные часто-
частости (И-
2. Если эмпирическое распределение хорошо аппроксимируется
нормальным распределением, то его интегральная кривая образует
на «вероятностной бумаге» в интервале ординат 10 — 90% прямую
линию. Если же эмпирическое распределение не укладывается
в нормальное распределение, то точки, соответствующие накоплен-
накопленным частостям /*, заметно отходят от прямой линии.
Для оценки гипотезы о нормальности распределения средних
длин словоупотреблений в языках мира нанесем на сетку Турбина
(рис. 65) накопленные частоты п1 [см. табл. 9.14, столбец A5)|,
соответствующие серединам xt интервалов. Полученные точки в ин-
интервале 2 — 90% располагаются близко к прямой. Это снова го-
говорит о том, что распределение средних длин словоупотребления
в языках мира близко к нормальному*.
Итак, мы проверили гипотезу о нормальности распределения
средних длин словоформ в различных языках мира с помощью шести
статистических критериев. Все эти критерии подтвердили справед-
справедливость указанной гипотезы.
4. Проверка с помощью критерия Колмогорова—Смирнова ги-
гипотезы о согласии распределений средних длин словоформ в двух
языковых семьях. Используя различные статистические критерии,
мы выяснили, что средние длины словоформ в языках мира распре-
распределены нормально. Отсюда можно предположить, что распреде-
распределения средних длин словоформ в разных семьях языков идентичны.
Проверим это предположение применительно к финноугорским и
тюркским языкам с помощью критерия Колмогорова — Смирнова,
основные идеи которого сводятся к следующему. Пусть эмпири-
эмпирическая интегральная функция распределения Fn, (x) построена
по выборке хъ хъ ..., Xn,. Одновременно имеется другая интеграль-
интегральная функция Fn, (х), построенная по выборке хи xit ..., хч,. Если
объемы выборок Nx и N2 неограниченно возрастают так, что отно-
отношение N2/Nx остается постоянным, то при условии, что
NQ = NxN2/ (Nt + N2) -> с» вероятность неравенства
{DNtNl = max|FNl(x)-FN,(x)\}< XjV?0
стремится к функции Колмогорова (см. гл. 8, § 5, п. 2)
k= — со
* Ср. использование сетки Турбина в работе [33, с. 206—2431 при опреде-
определений нормальности вариационных рядов стилистических признаков, исполь-
использующихся при установлении авторства анонимного текста.
347
где Ji > 0; иными словами,
Р (DNlNl VW0
К (Я) = Р.
(9.25)
тической невозможности маловероятных событий, мы должны счи-
считать появление неравенства
Применение критерия Колмогорова — Смирнова, так же как и
использование критерия Колмогорова,_построено на нахождении
вероятности того, что величина Dn^n, V No примет некоторое значе-
значение, не меньшее, чем Я,. В этом случае имеет место неравенство
DNlN,~V~N'u>K (9.26)
которое является противоположным событием по отношению к не-
неравенству, входящему в выражение (9.25). По правилу нахождения
вероятности противоположного события получаем
р (DNtN, Vn0
1 -к (к) = i —v - •»,
(9.27)
где ч > 0 — достаточно малое число.
Выражения (9.26) и (9.27) используются для проверки нулевой
гипотезы Но, состоящей в предположении, что оба эмпирических
распределения, находясь в полном согласии [т. е. />,(#) = Fn,(x)},
представляют выборки Nx и N3, принадлежащие, одной и той же
генеральной совокупности. Весь ход рассуждений при проверке Но
аналогичен рассуждениям, на которых строилось использование
критерия Колмогорова (п. 2), поэтому повторять их здесь мы не бу-
будем, а ограничимся описанием общей схемы применения критерия
Колмогорова—Смирнова, которая включает следующие операции:
1. По наблюдаемым значениям выборок Nx и Nt составляются
эмпирические интегральные функции распределения FnM) и Fn, (х).
2. Выдвигается гипотеза Но о полном согласии функций Fn, (*)
и Fn, (*) и принадлежности выборок #х и N2 к одной генеральной
совокупности.
3. Ставится опыт по сравнению величин Fn, (xt) и Fn, (xt).
Выбирается наибольшая разность Dn,n, и составляется произве-
произведение
4. Из табл. VII на стр. 369, 370 определяется вероятность у того,
что случайная величина Dn,n, V^N0 = X, имеющая распределение
Колмогорова, примет значение, не меньшее, чем к0. Величина у есть
одновременно вероятность того, что действительное максимальное
расхождение
DNin, = max | FNl (x) —FNl (x)\,
которое можно отнести за счет случайных статистических флуктуа-
вдй, не Меньше полученной в нашем опыте максимальной разности
5. Если вероятность у очень мала, т. е. не выше заданного по-
порога ч (обычно ч = 0,10; 0,05; 0,01), то, опираясь на принцип прак-
348
{DNtN,
невозможным событием. При этом расхождение Dn,n, между на-
нашими эмпирическими расхождениями следует рассматривать как
существенное. Отсюда следует, что гипотеза Яо о согласии обоих
распределений и принадлежности выборок Nt я N2 к одной гене-
генеральной совокупности должна быть отвергнута.
6. Если же вероятность у. сравнительно велика, т. е. больше за-
заданной вероятности ч, то разность Dn^, можно считать несущест-
несущественной. Поэтому следует принять гипотезу Но о согласии распре-
распределений Fnj (х) и Fn, (x) и принадлежности выборок Ntn N2 к од-
одной генеральной совокупности.
Особенность критерия Колмогорова—Смирнова состоит в том,
что он со сколь угодно большой вероятностью позволяет обнаружи-
обнаруживать любое расхождение между двумя эмпирическими функциями
Fa/, (х) и Fn, (х) при условии, что Л/х и Л^а достаточно велики.
Этот критерий применяется тогда, когда нужно проверить полное
согласие обоих распределений на всем интервале изменения случай-
случайной величины X и когда для этой проверки имеется очень обширный
материал наблюдений.
Применяя приведенную выше схему, проверим гипотезу о согла-
согласии распределений средних длин словоформ в тюркских и финно-
угорских языках.
1) Воспользовавшись данными табл. 7.27 (см. стр. 259), составим
вспомогательную таблицу (табл. 9.18), в столбцах F) и G) которой
приведены эмпирические интегральные функции распределения
длин словоформ: Fjv, (*) для тюркских и Fn, (x) для финноугор-
ских языков.
2) Выдвигаем гипотезу Но о согласии этих функций и принадлеж-
принадлежности выборок Nt (тюркские тексты) и iV2 (финноугорские тексты)
к одной генеральной совокупности с точки зрения распределения
длин словоформ.
3) Выбираем наибольшую разность
D°Nl N, = max | FNt (x)-FNl (x) \ = ] 0,278-0,714 j = 0,436
и определяем пороговое значение
^ = 0,436 У 18-14/A8+ 14) = 0,436 УТЩ =1,223.
4) Пользуясь табл. VII, выясняем, что случайная величина %,
имеющая распределение Колмогорова, примет с вероятностью 0,10
значение, не меньшее, чем Хо = 1,223.
5) Полученная вероятность не мала, поэтому можно принять
нулевую гипотезу, которая утверждает, что с точки зрения рас-
распределения средних длин словоформ тюркские и финноугорские
тексты принадлежет к одной генеральной совокупности, в качестве
которой, как это было показано в п. 1 — 3 § 5, выступают тексты
языков мира.
349
Таблица 9.18
Длина слов
в буквах
A)
4,1
4,7
4,8
5,1
5,2
5,3
5,4
5,5
5,6
5,8
5,9
6,0
6,2
6,3
7,4
7,5
7,8
8,8
Частота слов о
данной длиной
тюркские
языки
F,
B)
0
0
0
1
1
0
1
2
3
4
1
1
0
2
0
1
0
1
финно-
угорские
языки
F.
<3)
1
1
2
1
0
2
1
2
0
1
0
0
1
0
1
0
1
0
Накопленная частота
слов с дайной длиной
тюркские
изыкн
4
D)
0
0
0
1
2
2
3
5
8
12
13
14
14
16
16
17
17
18
финне-
угорскне
языки
П
E)
1
2
4
5
5
7
8
10
10
11
11
11
12
12
13
13
14
14
Относительно накоп-
накопленная частота слов
с данной длиной
тюркские
изыкн
F)
0
0
0
0,056
0,111
0,111
0,167
0,278
0,445
0,667
0,723
0,778
0,778
0,889
0,889
0,944
0,944
1,000
финно-
угорокне
языки
G)
0,071
0,143
0,286
0,357
0,357
0,500
0,571
0,714
0,714
0,785
0,785
0,785
0,857
0,857
0,928
0,928
1,000
1,000
-Fn,W
(8)
0,071
0,143
0,286
0,301
0,246
0,389
0,404
0,436
0,269
0,118
0,062
0,007
0,079
0,032
0,039
0,061
0,056
0,000
18
14
Этот, казалось бы, скромный статистический результат может
иметь важные теоретические последствия не только в области тео-
теории языка или психолингвистики, но и в плане кибернетической
физиологии высшей нервной деятельности, а также инженерной лин-
лингвистики. Действительно, нормальность распределения длин слово-
словоформ может рассматриваться как указание на то/ что существует
некоторый общечеловеческий эталон, равный центру этого распре-
распределения. Величину этого эталона, определяющуюся, вероятно,
особенностями строения быстродействующей памяти человека
[21, с. 97], следует учитывать при расчете памяти слушающих, пере-
переводящих и обучающих автоматов.
Существование некоторого среднего общечеловеческого эталона
длины словоформы и нормального распределения средних длин
вокруг этого эталона в языках мира нисколько не противоречит
тому факту, что длина словоформы может неограниченно возрастать
и в отдельных конкретных случаях достигает нескольких десятков
букв (см. гл. 4, § 2, п. 1). Легко заметить, что искусственные слова
типа двустороннесимметричнообразный «не выговариваются» сразу,
«одним дыханием», а делятся при воспроизведении на сегменты,
включающие одну или более морфем, причем длина этих сегментов
350
приближается к средней длине словоформы. Аналогичным образом
осуществляется, очевидно, и восприятие сверхдлинных слов.
Нет ничего необычного и в том, что в некоторых стилях средняя
длина словоформы может заметно возрастать по сравнению с обще-
общечеловеческим эталоном или средней длиной, характерной для дан-
данного языка (ср. § 3, п. 1). Эти отклонения свидетельствуют лишь о
существовании у нашей быстродействующей памяти некоторых ре-
резервов, позволяющих человеку пользоваться различными функцио-
функциональными разновидностями языка.
§ 6. Доминантные смысловые единицы
и элементы заполнения текста
1. Исследование вариационных рядов словосочетаний в немец-
немецких публицистических текстах. Статистическая проверка лингви-
лингвистических гипотез используется для формально-семантического ис-
исследования текста и составляющих его единиц.
Рассмотрим в этой связи распределение трехкомпонентных не-
немецких словосочетаний, образованных от наиболее частых слово-
словоформ. Поскольку трехсловные сочетания являются редкими линг-
лингвистическими событиями, выдвигается нулевая гипотеза Но, соглас-
согласно которой их распределения подчиняются закону Пуассона.
Проверка этой гипотезы осуществляется с помощью критерия
X2 и проходит по схеме, близкой к алгоритму проверки нормаль-
нормальности вариационного ряда (ср. § 5).
1. Сначала находят вероятность появления частот F —О, 1, 2
и т. д. по известной формуле распределения Пуассона
к"
,-*.
Л
(9.28)
где к — параметр распределения. Поскольку этот параметр обыч-
обычно неизвестен, его оценивают с помощью средней х = F эмпири-
эмпирического распределения.
2. Определяют теоретические частоты Npt = Sf, которые по
формуле (9.17) сравнивают с опытными частотами nt = Sf. В тех
случаях, когда величины Sp и Sf меньше пяти, они соответственно
объединяются с соседними значениями (ср. табл. 9.13).
3. Полученную величину %2 сопоставляют с пороговым значением
5Cn-v, выбранным из табл. V (см. стр. 366), исходя из заданного
уровня значимости q и числа степеней свободы, равного v = N* — 2.
Принятие или непринятие гипотезы Но о пуассоновском характере
рассматриваемого распределения зависит от того, выполняется ли
неравенство f < y^.v или Xq;v < Xj; v-
4. Оценку гипотезы Но можно осуществить также путем опре-
определения вероятности того, что некоторая случайная величина, рас-
распределенная по х2. примет при v = N* — 2 степенях свободы зна-
значение, не меньшее, чем вычисленная по формуле (9.17) величина
критерия х2 (см. § 4, п. 2).
S51
По указанной схеме исследовались распределения у большой
группы различных по грамматической природе и семантике трех-
словных сегментов, взятых из немецких газетных текстов [33,
с. 131 — 162]. Ход исследования проследим на примере сег-
сегмента Д dap der (начало дополнительного придаточного предложения
с существительным в начальной позиции, символ А указывает здесь
на знак препинания), распределение которого уже рассматривалось
нами в гл. 6 (см. § 3, п. 2).
1) Имеется 100 серий (S), каждая из которых содержит 1000 трех-
словных сочетаний. По формуле (9.28) определяем вероятность
Pn(F) (F = 0, 1, 2 и т. д.) появления сегмента A dap der в каждой
серии [столбец C) табл. 9.19]. Вместо параметра к используем его
оценку
F = —i— @-32+ 1-38+ 2-19 +3-5 + 4-6) = — = 1,15
1U\J 1UU
[в связи с укрупнением последних частот — ср^столбцы B) и D),
полученная оценка несколько отличается от F, вычисленного иа
основании данных табл. 6.7].
2) Затем вычисляем теоретические частоты Sf [столбец DI,
которые сравниваем с эмпирическими частотами Sf [столбцы E)
и GI.
3) Полученная в столбце G) величина ха = 4,67 меньше порогового
значения х? ов; з в ?>^2 (с учетом укрупнения малых частот имеем
v =5 — 2 = 3) и лежит таким образом в области принятия нулевой
гипотезы о пуассоновском характере интересующего нас лингви-
лингвистического распределения.
4) Оценивая гипотезу Но с помощью вероятности Р(%а), мы убеж-
убеждаемся, что вероятность некоторой распределенной по ха случайной
величины принять значение, большее, чем 4,67 при v = 3, лежит
в пределах между 0,26 и 0,17 (см. табл. IX). Иными словами, эта
вероятность достаточно велика. Поэтому гипотеза о пуассоновском
характере распределения сегмента A dap der вполне правдоподобна.
Таблица 9.19
Номер
вала
1
2
3
4
5
(и
0
1
2
3
4
5
F
B)
32
38
19
5
4)
6
2]
100
C)
0,3103
0,3628
0,2123
0,0828
0,0242
0,0057
0,9981
4
D)
31,03
36,28
21,23
8,28
2,99
F F
E)
0,97
1,69
—2,24
—3,28
3,01
{SF sf)
F)
0,9216
2,8561
5,0176
10,7584
9,0601
Is -s?)*
SF
G)
0,03
0,08
0,23
1,30
3,03
X2 = 4,67
Аналогичным образом было исследовано еще 84 трехсловных
и двухсловных сегмента. Все эти 85 словосочетаний распадаются
на три группы.
В первую группу C4 сегмента) входят словосочетания, состоя-
состоящие либо из служебных слов (например, A dap ist А это есть ...'
A es ist 'А это — ...,' A dap die — начало дополнительного при-
придаточного предложения с существительным множ. числа или ед.
числа женск. рода в начальной позиции), либо представляющие
комбинацию служебных и общеупотребительных знаменательных
слов (например, in der Welt 'в мире). Вариационные ряды этих
сегментов независимо от количества микровыборок и их объема по-
показывают, подобно только что рассмотренному обороту A dap der,
хорошее согласие с законом Пуассона.
Вторая группа B2 сегмента) включает словосочетания, обозна-
обозначающие политические реалии обоих немецких государств; ср. такие
сегменты, как Deutsche Demokratische Republik 'Германская Де-
Демократическая Республика', in der Bundesrepublik в Федератив-
Федеративной Республике', beiden deutschen Staaten 'оба немецких государ-
государства*. Эмпирическое распределение этих оборотов обнаруживает
несогласие с распределением Пуассона при любых видах нормиров-
нормировки, т. е. при любых объемах серий (порций, на которые делится'вы-
борка).
Третья группа B8 сегментов) занимает промежуточное поло-
положение между первыми двумя группировками. Входящие в нее
обороты включают служебные слова, а также общеупотребительные
и терминологические лексемы. Согласие или несогласие эмпири-
эмпирических распределений этих оборотов с законом Пуассона зависит
от способа разбиения выборки на серии.
Тот факт, что триады первой группы четко противопоставлены
оборотам второй группы как с точки зрения лексико-грамматической
природы, так и в статистическом плане, подтверждает высказывав-
высказывавшееся предположение о том, что статистическое поведение лекси-
лексической единицы в тексте может служить формальным признаком для
выявления ее лексико-грамматической природы. В частности, можно
ожидать, что редкие слова и словосочетания, не подчиняющиеся
закону Пуассона, а тем более нормальному закону, имеют термино-
терминологическую или конкретную семантику, в то время как слова и
обороты, показывающие пуассоновское или нормальное распре-
распределения, несут служебные функции или представляют собой лек-
лексические единицы общего значения.
2. Статистическое опознание термина и выделение доминантных
единице тексте. Гипотеза о возможности формально-статистического
опознания термина была рассмотрена относительно пуассоновского,
нормального и логнормального распределений [32а, с. 47—112].
Исследованию подвергались вариационные ряды двух единиц искус-
искусственных языков (буквенные символы, цифры), 298 словоформ
и 300 трехсловных сегментов, взятых из английских научно-тех-
научно-технических текстов подъязыка судовых механизмов. Общий объем
352
12 Зак. 1287
353
исследованного текста составил 400 тыс. словоупотреблений
(ок. 1200 стр.).
Применяя электронно-вычислительную технику, авторы рас-
мотрели разные варианты разбивки и нормировки материала, в. ре-
результате чего для каждой словоформы и словосочетания были по-
построены до 27 вариационных рядов. Затем с помощью ЭВМ по кри-
критерию х2 ПРИ уровне значимости 0,01 проверялось согласие этих
рядов с указанными выше распределениями.
Поскольку учесть все совпадения и несовпадения эмпирических
и теоретических данных в 27 вариационных рядах каждой лекси-
лексической единицы невозможно, было введено следующее обобщаю-
ющее условие. Эмпирическое распределение считалось совпадающим
с теоретическим в том случае, если такое согласие показывал ва-
вариационный ряд, охватывающий целиком всю выборку, либо не-
несколько вариационных рядов, построенных на частных выборках,
составляющих в сумме весь выборочный текст длиной в 400 тыс.
словоупотреблений. В других случаях отмечалось несогласие эм-
эмпирического и теоретического распределений.
Исследование показало, что согласие или несогласие эмпири-
эмпирического распределения с тем или иным теоретическим законом за-
зависит, во-первых, от статистических условий эксперимента — ча-
частоты лингвистической единицы и способа построения вариацион-
вариационного ряда, а во-вторых, от семантики исследуемой словоформы или
словосочетания.
Если говорить о результатах эксперимента с точки зрения ста-
статистических условий его поведения, то здесь обнаруживаются сле-
следующие тенденции.
1. Если упорядочить лексические единицы в список, построен-
построенный по принципу убывания частот исследуемых единиц, то рас-
распределения словоформ и отчасти словосочетаний, стоящих в начале
такого списка, чаще всего подчиняются нормальному закону. Эта
тенденция прослеживается для первых 20 словоформ вне зависи-
зависимости от объема микровыборки (серии), на которые делится общая
выборка. Что касается словосочетаний, то согласие с нормальным
законом прослеживается в области первых 15 номеров частотного
списка словосочетаний в тех случаях, когда берутся микровыборкп
длиной не менее 4 тыс. словоупотреблений.
2. В зоне средних частот (номера 60 — 1500 списка) отмечается
постепенное отступление нормального закона перед законом Пуас-
Пуассона. При этом пуассоновское распределение появляется в первую
очередь в тех вариационных рядах словоформ, которые обобщают
малые микровыборки A — 2 тыс. словоупотреблений), наоборот,
нормальность удерживается в рядах, построенных из крупных се-
серий по 4,8 или 16 тыс. словоупотреблений. Расширяя сферу своего
распространения, пуассоновские распределения накладываются
на нормальные: начиная с 60-70-х номеров списка все чаще попа-
попадаются словоформы, вариационные ряды которых при микровы-
микровыборках объемом в 2 — 16 тыс. словоупотреблений подчиняются
и нормальному, и пуассоновскому законам. Сходная картина на-
354
блюдается и в частотном списке словосочетаний с той лишь разницей,
что наложение пуассоновского распределения на нормальное об-
обнаруживается в самом начале списка.
3. Распределение редких лексических единиц независимо от
разбивки и нормировки выборки подчиняется закону Пуассона,
исключая случаи, когда этому препятствует семантика словоформы
или словосочетания.
4. Логнормальный закон хорошо описывает эмпирические рас-
распределения большинства частых и среднечастотных словоформ
при условии использования достаточно больших микровыборок
(не менее 8 тыс. словоупотреблений).
Обращаясь к семантическому анализу полученных результа-
результатов, разобьем все лексические единицы на две группы. В первую
группу войдут словоформы и словосочетания, эмпирические рас-
распределения которых не показывают согласия ни с нормальным за-
законом, ни с законом Пуассона. Вторая группа будет включать лек-
лексические единицы, вариационные ряды которых подчиняются либо
нормальному, либо пуассоновскому распределению, либо одно-
одновременно обоим законам. Такая разбивка экспериментального ма-
материала оправдывается тем, что при больших значениях пара-
параметра А. распределение Пуассона приобретает форму нормального
распределения (см. гл. 6, § 3, п. 2). Это аппроксимирующее свойство
нормального закона обнаруживается, в частности, в наложении
этого распределения на закон Пуассона в зоне среднечастотных
словоформ и словосочетаний, о чем говорилось выше.
Обратимся к анализу первой группы. Просмотр приведенных
в указанной выше работе лексических списков [32а, с. 82 — 88,
92 — 97] показывает, что из 298 словоформ эмпирические распре-
распределения 66 единиц не подчиняются ни нормальному, ни пуассонов-
пуассоновскому законам, а среди 300 словосочетаний 22 не дают согласия
своих вариационных рядов с указанными теоретическими зако-
законами.
Какова же лексико-грамматическая природа этих слов и слово-
словосочетаний?
Во-первых, сюда относятся именные, глагольные, адъективные
словоформы, а также именные обороты явно терминологического
значения. Например:
bearing(s) 'прдшипник(и)'; blades 'попасть'; cylinder(s) 'ци-
линдр(ы)'; dtesel 'дизель'; exhaust 'выхлопная труба, выхлоп,
выпуск'; nozzle 'форсунка'; machinery 'машинное оборудование,
механизм'; piston 'поршень'; power 'сила, мощность'; pump 'на-
'насос'; temperature'температура'; tubes 'трубы'; turbine(s) 'турбина(ы)*;
valve 'клапан'; velocity 'скорость', и т. п.
the gas turbine 'газовая турбина', marine disel engine 'судовой
дизельный двигатель'; the water level 'уровень воды'; и др.
current 'текущий'; moving 'приводя(щий) в движение'; marine
'морской'; work 'работать' и т. п.
Во-вторых, не подчиняется нормальному и пуассоновскому
закону эмпирическое распределение вспомогательных и модельных
12*
355
глагольных форм was, would, should, must, а также распределение
глагольного оборота shown in fig ... 'показано на рис. ...'.
В-третьих, в рассматриваемую группу попадают сегменты тек-
текста, представляющие собой комбинацию словоформ и символов
искусственных языков — цифр и формул (х), а также буквенных обо-
обозначений и сокращений (z). Ср.: х and х'хи х'; is xz 'равняется xz';
figure xz 'рисунок xz'; see zx' см. zx'; valueof x'значение х', и т. п.
Вторая группа, как уже говорилось, включает текстовые еди-
единицы и словосочетания, вариационные ряды которых дают согласие
с распределением Пуассона и нормальным распределением. Сюда
•входят отдельно употребляемые единицы искусственных языков
(х, г), большинство служебных слов, все наречия, местоимения,
числительные, все существительные, прилагательные и глаголы
общеупотребительного характера, а также общеупотребительные
словосочетания. Вместе с тем здесь обнаруживается и небольшое
количество терминологических слов и словосочетаний.
Метод проверок гипотезы о согласии эмпирического и теорети-
теоретического распределения с помощью критерия %2 применялся не толь-
только к научно-техническим текстам, но и к художественной прозе,
публицистике, а также к речи душевнобольных. При этом выясни-
выяснилось, что несогласие эмпирического распределения с нормальным
и пуассоновским законами обнаруживают не только терминоло-
терминологические слова и словосочетания, а также близкие к ним по семанти-
семантической природе комбинации словоупотреблений и элементов искус-
искусственных языков, но и другие лексические единицы, обладающие
важным, с точки зрения сюжета текста, значением. В художествен-
художественной речи этим свойством обладают слова и словосочетания, выра-
выражающие основные образы произведения, в публицистике — имена
собственные и названия особо важных политических, экономико-
социальных и географических реалий (см. §3, п. 3), в речи душевно-
душевнобольных—слова и словосочетания, обозначающие объекты навяз-
навязчивого состояния. Короче говоря, несогласие эмпирических и тео-
теоретических распределений обнаруживают семантически доминант-
доминантные (ключевые) единицы текста, напротив, недоминантные единицы
текста, обладающие «стертой» семантикой, показывают хорошее
согласие своих распределений с теоретическими законами Пуас-
Пуассона и Гаусса.
Природа этого явления состоит, очевидно, в следующем.
Как уже говорилось (см. гл. 5), порождение текста определяется,
с одной стороны, системой языка и его нормой, а с другой — неза-
независимой от языка ситуацией, которую призван описывать этот текст.
Появление семантически нагруженных ключевых элементов текста
диктуется ситуацией, употребление же семантически истертых»
единиц, так называемых единиц заполнения, служащих средством
организации текста и связи ключевых единиц, подчиняется требо-
требованиям системы и нормы языка. Отсюда следует, что статистика
единиц заполнения подчиняется вероятностным законам нормы
языка, в то время как статистика ключевых элементов текстов уп-
управляется вероятностью ситуаций.
356
Статистика нормы имеет иной порядок, чем статистика ситуаций.
Текстовые выборки в несколько десятков или сотен словоупотреб-
словоупотреблений оказываются достаточными, чтобы обеспечить регулярную
повторяемость служебных слов, общеупотребительных слов и слово-
словосочетаний, не говоря уже о грамматических классах или фонемах,
в связи с чем их вариационные ряды начинают сходиться к пуас-
соновскому и нормальному распределениям. Напротив, такие вы-
выборки оказываются слишком малыми, чтобы обеспечить регулярную
повторяемость ситуаций: эти малые выборки остаются статисти-
статистически неоднородными для диктуемых ситуаций ключевых слов и сло-
словосочетаний. Вполне естественно, что эмпирические распределения
этих ключевых единиц не согласуются с теоретическими распре-
распределениями Пуассона и Гаусса, действующими только в однородных
выборках.
Согласие и несогласие вариационных рядов с тем или иным те-
теоретическим распределением зависит также от валентностных воз-
возможностей лингвистической единицы.
Нормальный закон и закон Пуассона хорошо описывают распре-
распределения служебных слов и общеупотребительных слов и словосо-
словосочетаний, в частности, потому, что этим последним присуще срав-
сравнительно независимое употребление в тексте. Напротив, лингви-
лингвистические единицы, характеризующиеся сильными валентностями,
статистико-вероятностным выражением которых являются марков-
марковские связи текста, дают, как правило, скошенные вправо эмпири-
эмпирические распределения, имеющие иногда несколько вершин. Эти ва-
вариационные ряды не подчиняются законам Пуассона и Гаусса, но
зато могут описываться логнормальным распределением (см. гл. 6,
§ 3, п. 5) или кривыми Пирсона с правой асимметрией [32 в, с. 335—
361]. Вариационные ряды, описываемые логнормальным распре-
распределением, дают уже упоминавшиеся английские вспомогательные
и модальные глаголы was, would, should, must. Хотя эти глагольные
формы не являются ключевыми единицами текста, они, очевидно, тес-
тесно св'язаны с такими знаменательными словоформами, которые несут
в тексте смысловую или эмоционально-выделительную нагрузку.
Описанные особенности распределений служебных и общеупо-
общеупотребительных лексических единиц, а также терминологических
и вообще доминантных элементов текста могут быть использованы
в качестве диагносцирующего аппарата, автоматически распозна-
распознающего в тексте ключевые слова и выражения текста. Извлечение
с помощью ЭВМ из больших массивов текста семантически нагру-
нагруженных ключевых единиц позволяет, с одной стороны, автоматизи-
автоматизировать трудоемкие процессы составления алгоритмов машинного
реферирования и семантического перевода текста. С другой стороны,
статистико-автоматическое исследование семантики текста на машине
дает богатый материал для решения таких теоретических и приклад-
прикладных задач, как исследование соотношений «смысл — текст», «нор-
«норма — речь», построение обучающих алгоритмов, лингвистическая
диагностика душевных заболеваний и других вопросов.
ЗАКЛЮЧЕНИЕ
1. Краткий обзор содержания. Конфронтация языка и матема-
математики осуществлялась нами, с одной стороны, в области количест-
количественной экспликации диахронических процессов и процессов раз-
развертывания текста, а с другой — в плане вероятностно-статисти-
вероятностно-статистического моделирования построения текста, являющегося резуль-
результатом взаимодействия системы, нормы и ситуации.
Одна из задач этой конфронтации состояла в выявлении таких
математических моделей, с помощью которых можно было бы не
только описать структуру и функционирование интересующих нас
лингвистических объектов, но и получить новую информацию о
природе языка и речи.
Экспликация синтагматического развертывания речи и диах-
диахронии языка с помощью аппарата математического анализа
(см. гл. 1 — 4) обнаружила, что лингвистические процессы имеют '
ступенчатый (скачкообразный) и циклический характер. Циклич-
Цикличное распределение информации в тексте диктуется периодическим
ритмом, в котором мозг перерабатывает поступающую в него ин-
информацию.
Ступенчатость и цикличность развития языка определяется,
очевидно, дискретно-порционным характером перестройки языко-
еой системы.
Общность математических моделей, аппроксимирующих разви-
развитие языка и информационное развертывание текста, заставляет
лингвиста задуматься над проблемой речевого онтогенеза и диахро-
диахронического филогенеза.
Экспликация построения текста с помощью аппарата теорий
вероятностей и информации, а также математической статистики
(см. гл. 5 — 9) показала, что порождение текста определяется не
только системой языка, но диктуется также, с одной стороны, ве-
вероятностными моделями, а с другой —вероятностью. Поэтому ин-
информационно-статистическая структура текста является результа-
результатом взаимодействия двух статистик. Одной из них является статисти-
статистика нормативных единиц заполнения (буквы, слоги, грамматические
морфемы, служебные слова и словосочетания, а также некоторые
синтаксические схемы). Другой статистикой является статистика
доминантных, или ключевых, единиц текста (слов, словосочетаний
и синтаксических построений), передающих основное содержание
текста. Несогласованность этих статистик может быть использована
для формального автоматического распознавания терминологических
единиц текста.
Одновременно возникает вопрос о том, как взаимодействуют
между собой элементы заполнения и ключевые единицы в рамках
циклической информационной схемы текста — схемы, навязанной
ритмом работы нашего мозга. Исследование этого вопроса является
одной из важных задач современной кибернетической лингвистики.
358
2. Перспективы развития математической лингвистики. Осу-
Осуществленная в книге конфронтация языка и математики проходила
под знаком преобладания математического подхода к отбору ма-
материала и его компоновке. Такой подход оказался целесообразным
ввиду того, что по сравнению с языкознанием математика имеет
более строгую и последовательную организацию. Однако при этом
подходе в сферу математической лингвистики включаются лишь
те явления языка и речи, которые могут быть подвергнуты экспли-
экспликации и моделированию с помощью жесткого аппарата современной
«количественной» и «качественной» математики, охватывающей
не только функции одной переменной, рассмотренные в настоящей
книге, но и функции многих переменных (случайных величин).
Вместе с тем процесс математизации лингвистики вовсе не направ-
направлен на обеднение языкознания и его подчинение математике На-
Напротив, этот процесс должен привести к усилению исследователь-
исследовательского аппарата языкознания и к обогащению наших лингвисти-
лингвистических знаний.
Поэтому вслед, за этапом конфронтации математики и языко-
языкознания—этапом, на котором математика исполняла роль «коро-
«королевы наук», должен следовать этап сближения, на котором мате-
математика выступает на службе остальных наук, создавая для языко-
языкознания и для других гуманитарных наук особый логический аппа-
аппарат.
Необходимость в создании такого аппарата объясняется тем, что
используемый в настоящее время для моделирования и эксплика-
экспликации лингвистических явлений традиционный математический аппа-
аппарат был первоначально предназначен для описания «жестких» и
сравнительно простых систем неживой природы. Поэтому он ока-
оказывается недостаточно адекватным при моделировании сложных
гуманистических, в том числе языковых систем, имеющих, как
принято сейчас говорить, «мягкую», полиморфную структуру {26,
с. 208]. Эта неадекватность перерастает иногда в несовместимость
традиционного математического аппарата и сложных гуманисти-
гуманистических систем. Суть этой несовместимости кратко определяется так:
чем сложнее система, тем менее способна традиционная математика
дать точные и одновременно имеющие практическое значение суж-
суждения о поведении этой системы [65, с. 7].
Преодолеть этот парадокс можно с помощью такого математи-
математического аппарата, который использовал бы эвристические подходы
и приемы, при помощи которых человек решает различные жиз-
жизненные и в том числе лингвистические задачи.
Создавая такой аппарат, следует иметь в виду, что оперативными
единицами человеческого мышления являются не дискретные мате-
математические объекты, а элементы некоторых нечетких множеств
(гл.. 1, § L, п. 1). При этом переход от принадлежности элементов
xv, Хъ xt нечеткому множеству А к «непринадлежности» этих
элементов тому же множеству осуществляется не скачкообразно,
а непрерывно, характеризуясь убыванием степени принадлежности
(д. элемента xt множеству А в интервале от единицы до нуля. Сим-
359
волически это записывается так:
1 ^ р. (хг
А) > 0.
Использование нечетких множеств для описания систем линг-
лингвистических объектов имеет принципиальное методологическое зна-
значение для языкознания. Задавая каждому элементу лингвистиче-
лингвистического множества коэффициент принадлежности ц, мы получаем
возможность математически описать размытость границ семанти-
семантических полей, слов, словосочетаний и предложений, акустических
признаков фонемы, границ диалектов и говоров, а также экспли-
эксплицировать парадокс между коллективным и индивидуальным вла-
владением языка (парадокс языка и идиолекта). С этим парадоксом
мы неоднократно встречались в книге, рассматривая субъективные
вероятности появления тех или иных лингвистических событий
(гл. 5, § 3, п. 1; § 5, п. 4 и др.).
В теории нечетких множеств построен разветвленный набор ло-
логических операций, частично повторяющий набор операций класси-"
ческой теории множеств (гл. 1, § 1, п. 3), но включающий и такие
специфические операции как концентрация и деконцентрация, сгу-
сгущение и размывание [26, с. 213]; [65, с. 18—19]. Однако наименее
разработанным и наиболее сложным вопросом теории нечетких
множеств является количественное определение коэффициента при-
принадлежности \i.
В настоящее время существует три подхода к определению ко-
коэффициента \х.
Во-первых, коэффициент принадлежности отождествляют с ве-
вероятностью элемента xit т. е. \i {xt ? А) = Р (xt € А); см. гл. 1,
§ 1, п. 2.
Во-вторых, количественная оценка \х выводится путем сравне-
сравнения свойств нечеткого множества с характеристиками входящих
в него элементов. В своем простейшем виде эту процедуру можно
представить себе следующим образом. Предположим, что нечеткое
лингвистическое множество А характеризуется некоторым набором
равнозначных признаков, а входящий в это нечеткое множество
лингвистический элемент xt имеет т признаков, из которых k
являются общими для А и #,-. Тогда степень принадлежности xt
к А равна
p{Xi € Л) = 1--^ @<ц<1).
Если признаки неэквивалентны, то при расчете следует учитывать
их весовые коэффициенты.
В-третьих, величина \i определяется с помощью экспертных
оценок, т. е. методом опроса (или голосования) информантов-спе-
информантов-специалистов. Этот метод, которым мы широко пользовались при из-
измерении информации текста (гл. 5, § 5), дает возможность сгруппи-
сгруппировать индивидуальные оценки степени принадлежности xi линг-
лингвистическому множеству А и сообщить этим оценкам количествен-
количественную меру.
Поскольку при всех этих подходах величина \\ нормируется
подобно вероятности в интервале от нуля до единицы, к ней могут
быть применены многиеиз тех операций теории вероятностей, мате-
математической статистики и теории информации, которые мы приме-
применяли в гл. 5—9.
Проиллюстрируем этот подход на следующем примере. Будем
рассматривать текст «Курса общей лингвистики» Ф. де Соссюра
как нечеткое множество правильных лингвистических положений
и подвергнем каждое предложение книги экспертным оценкам
с точки зрения степени его принадлежности к указанному множест-
множеству. Легко предположить, что такие утверждения Ф. де Соссюра,
как «... у речевой деятельности есть и индивидуальная и социаль-
социальная сторона, причем нельзя понять одну без другой» [59, с. 34]
или «... язык необходим, чтобы речь была понятна и производила
все свое действие» [59, с. 42], безоговорочно принимаются современ-
современными языковедами и вероятно воспринимались как «правильные»
тек.я современниками Ф. де Соссюра, которые разделяли взгляды
В« Гумбольдта, Г. Габеленца и И. А. Бодуэна де Куртене. Поэтому
величина коэффициента принадлежности этих высказываний к мно-
множеству правильных лингвистических высказываний близка к еди-
единице (ц ~ 1).
Вместе с тем в книге Ф. де Соссюра можно найти и такие положе-
положения, как «... звук, элемент материальный, не может сам по себе при-
принадлежать к языку» [59, с. 117] или «... в языке нет ничего кроме
различий» [59, с 117]. Эти положения до сих пор оспариваются
многими языковедами. Поэтому их принадлежность к рассматри-
рассматриваемому множеству значительно меньше единицы (\х <^ 1). Однако
именно эти высказывания вместе с другими не менее парадоксаль-
парадоксальными утверждениями Ф. де Соссюра составляют эвристическую
новизну его «Курса общей лингвистики».
Эвристичность (Ей) тех или иных элементов нечетких лингвис-
лингвистических множеств можно получить, применяя к коэффициенту \i
логарифмическую меру подобно тому, как это мы делали, оценивая
синтактическую и смысловую информацию, передаваемую отдель-
отдельными единицами текста (гл. 5, § 5, п. 3 и 4). Тогда получим
Ей = —log2 \i.
Если ц са 1, как это имело место для первых двух лингвистических
высказываний Ф. де Соссюра, то величина Еи будет близка к нулю.
Напротив, для последних утверждений, имеющих \i <^ 1, коли-
количественная оценка эвристичности будет достаточно велика (напри-
(например, если \\ = 1/16, то Еи = 4).
Мы воспользовались этим схематичным примером для того,
чтобы показать тесную связь и преемственность между традицион-
традиционными приемами математической лингвистики, описанными в настоя-
настоящей книге, и вновь создаваемым аппаратом теории нечетких мно-
множеств, который, как можно ожидать, даст более глубокое и адек-
адекватное описание естественного языка.
360
ПРИЛОЖЕНИЕ
Таблица I
Значения вероятностей для распределения Пуассона
Р{Х ) -%
Р(Х
0,1
0,2
0.3 0,4
0,5
0,6
0,7 0,8
0,9
0,9048 0,8187 0,7408.0,6703 0,6065
0905 1637 2222 2681 3033
0045 0164 0333' 0536 0758
0002 ООН 0033 0072 0126
0000 0001 0003i G007 0016
0000 0000 0000 0001 0002
0000 0000 0000 0000 0000
0000 0000 0000 0000 0000
0,5488 0,4966 0,4493 0,4066
3293 3476 3595 3659
0988 1217 1438 1647
0198 0284 0383 0494
¦ 0030 0050 0077 0111
0004 0007 0012 0020.
0000 0001 0002 0003
0000 0000 0000 С000
1.0
0,3679
3679
1839
0613
0153
0031
0005
0001
Р (X =
1,1
1,2
1.,».
1 .4
1,5 1,6
1 .7
1.8 1,9
2,0
3662
2014
0733
0203
0045
0008
0001
0000
0000
0,3329 0,3012 0
3614
21,69
0867
0260
0062
0012
0002
0000
0000
272510,2466 0
3543
2303
0998
0324
0084
0018
0003
0001
0000
3452
2417
1128
0395
0111
0026
0005
0001
0000
,2231
3347
2510
1255
0471
0141
0035
0008
0001
0000
0,2019 0,1827 0,1653 0,1496
3230 3106 2975 2842
2584 2640 2678 2700
1378 1496 1607 1710
0551 0636 0723 0812
0176 0216 0260 0309
0047 0061 0078 0096
ООН 0015 0020 0027
0Э02 0003 0005 0006
0000 0001 0001 0001
0,1353
2707
2707
1804
0902
0361
0120
0034
0009
0002
2.1
2,2 2,3
2,4
2,5 | 2,6 | 2,7 | 2,8 | 2,9 j 3,C
0,12250
2572
2700
1890
0992
0417
0146
0044
ООП
0003
0001
0000
0000
,11080
2438
26S1
1966
1082
0476
0174
0055
0015
0004
0001
0000
0000
|, 1003 0
2306
2652
2033
1169
0538
0206
0068
0019
0005
0001
0000
0000
,09070
2177
2613
2090
1254
0602
0241
0083
0025
0007
000.1
0000
0000
1,0821
2052
2565
2138
1336
.0668
0278
0099
0031
0009
0002
0000
0000
0,0743 0
1931
2510
2176
1414
0735
0319
0118
0038
ООП
0003
0001
0000
,06720,
1815
2450
2205
1488
0804
0362
0139
0047
0014
0004
0001
0000
0608 0,
1703
2384
2225
1557
0872
0407
0163
0057
0018
0005
0001
0000
1,0550
1596
2314
2237
1622
0940
0455
0188
0068
0022
0006
0002
0000
0,0498
1494
2240
2240
1680
1008
0504
0216
0081
0027
0008
0002
0001
\
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
3,5
0,0302
1507
1850
2158
1888
1322
0771
0385
0169
0066
0023
0007
0002
0001
0000
0000
.0000
0000
0000
0000
0000
0000
0000
0000
0000
0
'.0
,0183
0735
1465
1954
1954
1563
1042
0595
0298
0132
0053
0019
0006
0002
0001
OOOC
0000
0000
0000
OOOC
OOOC
OOOC
0000
0000
0000
0
4,5
,0111
0500
1125
1687
1898
1708
1281
0824
0463
0232
0104
0043
0016
0006
0002
0001
0000
0000
0000
0000
0000
0000
0000
0000
0000
0
5,0
,0067
0337
0842
1404
1755
1755
1462
1044
0653
0363
0181
0082
0034
0013
0005
0002
0000
0000
0000
0000
0000
0000
0000
0000
0000
0
P{X
6,0
,0025
0149
0446
0892
1339
1606
1606
1377
1033
0688
0413
0225
0113
0052
0022
0009
0003
0001
0000
0000
0000
0000
0000
0000
0000
0
= X)
7,0
,0009
0064
0223
0521
0912
1277
1490
1490
1304
1014
0710
0452
0264
0142
0071
0033
0014
0006
0002
0001
0000
0000
0000
0000
0000
Продолжение табл
8,0
0,0003
0027
0107
0286
0573
0916
1221
1396
. 1396
1241
0993
0722 :
0481
0296 '
0169
0090
0045
0021
0009
0004
0002
0001
0000 .
0000
0000
| 9,0
0,0001
ООП
0050
0150
0337
0607
0911
1171
1318
1318
1186
0970
0728
0504
0324
0194
0109
0058
0029
0014
0006
0003
0001
0000
0000
Г
10,0
0
0000
0005
0023
0076
0189
0378
0631
0901
1126
1251
1251
1137
0948
0729
0521
0347
0217
0128
0071
0037
0019
0009
0004
0002
0001
363
Таблица II
Таблица III
Значения функции
4zr
Т/2я
Значения функции Лапласа
Ф(*) = , Г е~г°/2 dz '
1/2я J
фB)
г
0,0
0,1
0,2
0,3
0,4
•0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
¦2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,5
5,0
0
,3989
3970
3910
3814
3683
3521
3332
3123
2897
2661
2420
2179
1942
1714
1497
1295
1109
0940
0790
0656
0540
0440
0355
0283
0224
0175
0136
0104
0079
0060
0044
0033
0024
0017
0012
0009
0006
0004
0003
0002
0001
0000160
0000015
1
0,3989
3965
3902
3802
3668
3503
3312
3101
2874
2637
2396
2155
1919
1691
1476
1276
1092
0925
0775
0644
0529
0431
0347
0277
0219
0171
0132
0101
0077
0058
0043
0032
0023
0017
0012
0008
0006
0004
0003
0002
000
2
0,3989
3961
3894
3790
3653
3485
3292
3079
2850
2613
2371
2131
1895
1669
1456
1257
1074
0909
0761
0632
0519
0422
0339
0270
0213
0167
0129
0099
0075
0056
0042
0031
0022
0016
0012
0008
0006
0004
0003
0002
000
3
0,3988
3956
3885
3778
3637
3467
3272
3056
2827
2589
2347
2107
1872
1647
1435
1238
1057
0893
0748
0620
0508
0413
0332
0264
0208
0163
0126
0096
0073
0055
0040
0030
0022
0016
ООП
0008
0005
0004
0003
0002
000
4
,3986
3951
3876
3765
3621
3448
3251
3034
2803
2565
2323
2083
1849
1626
1415
1219
1040
0878
0734
0608
0498
0404
0325
0258
0203
0158
0122
0093
0071
0053
0039
0029
0021
0015
001
0008
0005
0004
000
000
000
5
,3984
3945
3867
3752
3605
3429
3230
ЗОН
2780
2541
2299
2059
1826
1604
1394
1200
1023
0863
0721
0596
0488
0395
0317
0252
0198
0154
0119
0091
0069
0051
0038
0028
002(
0015
0010
0007
0005
0004
0002
0002
000
6
,3982
3939
3857
3739
3589
3410
3209
2989
2756
2516
2275
2036
1804
1582
1374
1182
1006
0848
0707
0584
0478
0387
0310
0246
0194
0151
0116
0088
0067
0050
0037
0027
0020
0014
0010
0007
0005
0003
0002
000
000
7
,3980
3932
3847
3726
3572
3391
3187
2966
2732
2492
2251
2012
1781
1561
1354
1163
0989
0833
0694
0573
0468
0379
0303
0241
0189
0147
0113
0086
0065
0048
0036
0026
0019
0014
0010
0007
0005
0003
0002
0002
000
8
,3977
3925
3836
3712
3555
3372
3166
2943
2709
2468
2227
1989
1758
1539
1334
1145
0973
0818
0681
0562
0459
0371
0297
0235
0184
0143
ОНО
0084
0063
0047
0035
0025
0018
0013
0009
0007
0005
0003
0002
000
000
9
(
0,3973
3918
3825
3697
3538
3352
3144
2920
2685
2444
2203
1965
1736
1518
1315
1127
0957
0804
0669
0551
0449
0363
0290
0229
0180
0139
0107
0081
0061
0046
0034
0025
0018
0013
0009
0006
0004
0003
0002
0001
0001
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
,0
,1
,2
,3
,4
,5
,6
J
,8
,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,00
3,20
3,40
3,60.
3,80
4,00
6,00
0,0000
0398
0793
1179
1554
1915
2257
2580
2881
3159
3413
3643
3849
4032
4192
4332
4452
4554
4641
4713
4772
4821
4861
4893
4918
4938
4953
4965
4964
4981
4986
4993
4996
4998
4999
49997
49999997
0,0040 0
0438
0832
1217
1591
1950
2291
2611
2910
3186
3438
3665
3869
4049
4207
4345
4463
4564
4649
4719
4778
4826
4864
4896
4920
4939
4955
4966
4975
4981
,0080 0
0478
0871
1255
1628
1985
2324
2642
2939
3212
3461
3686
3888
4066
4222
4357
4474
4573
4656
4726
4783
4830
4868
4898
4922
4941
4956
4967
4976
4982
1,0120
0517
0910
1293
1664
2019
2357
2673
2967
3238
3485
3708
3907
4082
4236
4370
4484
4582
4664
4732
4788
4834
4871
4901
4924
4943
4957
4968
4977
4983
0,0160
0557
0948
1331
1700
2054
2389
2703
2995
3264
3508
3729
3925
4099
4252
4382
4495
4591
4671
4738
4793
4838
4875
4904
4927
4945
4959
4969
4977
4984
0,01990
0596
0987
1368
1736
2088
2422
2734
3023
3289
3531
3749
3944
4115
4265
4394
4505
4599
4678
4744
4798
4842
4878
4906
4929
4946
4960
4970
4978
4984
,0239 0
0636
1026
1406
1772
2123
2454
2764
3051
3315
3554
3770
3962
4131
4279
4406
4515
4608
4686
4750
4803
4846
4881
4909
4931
4948
4961
4971
4979
4985
),0279 0
0675
1064
1443
1808
2157
2486
2794
3078
3340
3577
3790
3980
4147
4292
4418
4525
4616
4693
4756
4808
4850
4884
4911
4933
4949
4962
4972
4979
4985
,03190
0714
1103
1480
1844
2190
2517
282:
3106
3365
3599
3810
3997
4162
4306
4429
4535
4625
4699
4761
4812
4854
4887
4913
4934
4951
4963
4973
4980
4986
1,0359
0753
1141
1517
J879
2224
2549
2852
3133
3389
3621
3830
4015
4177
4319
4441
4545
4633
4706
4767
4817
4858
4890
4916
4936
4952
4964
4974
4980
4986
864
365
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
1
,000
0,937
874
814
758
705
656
611
570
533
500
470
442
417
395
374
356
339
323
308'
295
283
272
261
251
242
234
226
218
211
2
1,000
0,929
860
792
728
667
609
556
508
463
423
386
353
323
296
272
251
231
214
198
184
171
159
148
138
130
122
114
107
101
3
,000
0,927
854
784
716
651
591
534
482
434
391
352
316
284
256
231
208
188
170
154
139
127
115
105
096
088
080
074
068
063
А
,000
0,925
851
779
710
643
581
523
469
419
374
333
296
263
234
208
185
164
146
130
116
104
093
083
074
067
060
054
049
044
Значения вероятностей Р (| /1 > tp)
6
,000
0,924
849
776
706
638
575
515
460
409
363
321
284
250
220
194
170
150
132
116
102
090
079
070
062
054
048
043
038
034
6
1,000
0,924
848
774
703
635
570
510
454
403
356
313
275
241
211
184
161
140
122
106
092
080
070
061
053
047
041
036
031
027
г
1,000
0,923
847
773
701
632
567
507
450
398
351
3';8
269
235
204
177
154
133
115
099
086
074
064
055
047
041
035
031
027
023
8
1,000
0,923
846
772
700
631
565
504
447
394
347
303
264
230
199
172
148
128
ПО
094
081
069
,059
060
043
037
032
027
023
020
9
1,000
0,923
846
771
698
629
563
502
444
ЗУ2
343
300
261
226
195
168
144
123
105
090
077
065
055
047
040
034
029
024
021
018
для распределения ьтьюдента
Таблица IV
10 1 РЦЦ)
1,000
0,922
845
770
698
628
562
500
442
389
341
297
258
223
192
165
141
120
102
087
073
062
052
044
037
031
026
022
019
016
и
1,000
0,922
845
770
697
62/
561
498
441
387
339
295
255
220
189
162
138
117
099
084
071
060
050
042
035
030
025
021
017
014
1,000
0,922
845
769
696
626
560
497
439
385
337
293
253
218
187
159
136
115
097
082
069
058
048
040
034
028
023
019
016
013
13
1,000
0,922
845
769
696
625
559
496
438
384
336
291
252
216
185
158
134
113
095
080
067
056
046
039
032
027
022
018
015
012
14
1,000
0,922
844
769
695
625
558
495
437
383
334
290
250
215
¦ 183
156
132
111
093
078
065
054
045
037
031
025
021
017
014
012
15
1,000
0,922
844
768
695
624
557
495
436
382
333
289
249
213
182
154
130
по
092
077
064
053
044
036
030
024
020
016
013
011
16
1,000
0,922
844
768
694
624
557
494
435
381
332
288
248
212
181
153
129
108
091
076
063
052
043
035
029
024
019
016
013
010
17
1,000
0,922
844
768
694
623
556
493
435
381
331
287
247
211
180
152
128
107
090
075
062
051
042
034
028
023
019
015
012
010
18
1,000
0,921
844
768
694
623
556
493
434
380
331
286
246
210
179
151
127
106
089
074
061
050
041
034
027
022
018
015
012
010
19
1,000
0,921 '
844
767
6Э4
623
556
492
434
379
330
285
245
209
178
150
126
105
088
073
060
049
040
033
027
022
018
014
ОН
009
?о
1,000
0,921
844
767
693
623
555
492
433
379
329
284
244
208
177
149
125
105
087
072
059
049
040
032
026
021
017
014
011
009
00
1,0000
0,9203
8415
7642
6S92
6171
5485
4839
4237
3681
3173
2713
2301
1936
1615
1336
1096
0891
0719
0574
0455
0357
0278
0214
0164
0124
0093
0069
0051
0037
367
Значения Хг для фиксированных уровней
значимости и заданных степеней свободы v
Таблица V
Значения
Число
степеней
свободы
V
1
2
3
.4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
- 27
28
29
30
40
49
50
59
0,99
0,00016
0,020
0,115
0,297
0,554
0,872
1,24
1,65
2,09
2,56
3,05
3,57
4,11
4,66 .
5,23
5,81
6,41
7,01
7,63
8,26
8,90
9,54
10,20
10,86
11,52
12,20
12,88
13,57
14,27
14,95
22,16
28,94
29,71 ¦
36,70
Уровень значимости
0,975
0,00098
0,051
0,216
0,484
0,831
1,24
1,69
2,18
2,70
3,25
3,82
4,40
5,01
5,63
6,26
6,91
7,56
8,23
8,91
9,59
10,28
10,98
11,69
12,40
13,12
13,84
14,57
15,31
16,05
16,79
24,43
31,56
32,36
39,66
0,95
0,0039*
0,103
0,352
0,711
1,15
1,64
2,17
2,73
3,33
3,94
4,57
5,23
5,89
6,57
7,26
7,96
8,67
9,39
10,12
10,85
11,59
12,34
13,09
13,85
14,61
15,38
16,15
16,93
17,71
18,49
26,51
33,93
34,76
42,34
0,90
0,016
0,211
0,584
1,06
1,61
2,20
2,83
3,49
4,17
4,87
5,58
6,30
7,04
7,79
8,55
9,31
10,09
10,87
11,65
12,44
13,24
14,04
14,85
15,66
16,47
17,29
18,11
18,94
19,77
20,60
29,05
36,82
37,69
45,58
0,10
2,71
4,61
6,25
7,78
9,24
10,65
12,02
13,36
14,68
15,99
17,28
18,55
19,81
21,06
22,31
23,54
24,77
25,99
27,20
28,41
29,62
30,84
32,01
33,20
34,38
35,56
36,74
37,92
39,09
40,26
51,80
62,04
63,17
73,28
0,05
3,84
5,99
7,82
9,49
10,07
12,59
14,07
15,51
16,92
18,31
19,68
21,03
22,36
23,69
25,00
26,30
27,59
28,87
30,20
31,41
32,67
33,92
35,17
36,42
37,65
38,89
40,14
41,34
42,56
43,77
55,76
66,34
67,51
77,93
о.огб
. 5,02
7,38
9,39
11,14
12,83
14,45
16,01
17,54
19,02
20,48
21,92
23,34
24,77
26,12
27,48
28,84
30,19
31,53
32,85
34,17
35,48
36,78
38,08
39,36
40,65
41,92
43,19
44,46'
45,72
46,98
59,34
70,22
71,42
82,18
0,01
6,64
9,21
11,35
13,28
15,09
16,81
18,48
20,09
21,67
23,21
24,73
26,22
27,69
29,14
30,58
32,00
34,41
34,81
36,19
37,57
38,93
42,29
41.64
42,98
44,31
45,64
46,96
48,28
49,59
50,89
63,69
74,92
76,15
87,17
Табл ица VI
и zp.v для фиксированных уровней значимости q
и заданного числа степеней свободы v
,v
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Р
q
V
Двусторонний уровень
0,10
<
(
.
¦ с
¦
<
i
с
),90
5,31
2,92
2,35
2,13
2,01
1,94
1,89
1,86
,83
,81
,80
,78
,77
,76
,75
,75
.74
,05
Значимости л
0.06
0.95
12,70
4,30
3,18
2,78
2,57
2,45
2,36
2,31
2,26
2,23
2,20
2,18
2,16
2,14
2,13
2,12
2,11
0,025
0,02
0,98
31,82
6,97
4,54
3,75
3,37
3,14
3,10
2,90
2,82
2,76
2,72
2,68
2,65
2,62
2,60
2,58
2,57
0,01
0,01
0,99
63,70
9,92
5,84
4,60
4,03
3,71
3,50
3,36
3,25
3,17
3,11
3,05
3,01
2,98
2,95
2,92
2,90
0,005
Односторонний уровень
значимости q/2
V
18
19
0
21
22
23
24
25
26
27
28
29
30
40
60
120
ос
(
(
1
q-.v
Двусторонний уровень
) 10
),90
,73
1,73
.73
,72
,72
,71
,71
,71
¦ 71
1,71
,70
,70
,70
,68
,67
,66
,64
0,05
значимое и (
0,05
0,95
2,10
2,09
2,09
2,08
2 07
2,07
2,06
2,06
2,06
2,05
2,05
2,05
2.04
2,02
2,00
1,98
1,96
0,025
0,02
0,98
2,55
2,54
2,53
2,52
2,51
2,50
2,49
2,49
2,48
2,47
2,46
2,46
2,46
2,42
2,39
2.36
2,33
0,01
0,01
0.99
2,88
2.86
2,85
2,83
2,82
2,81
2,80
2,79
2,78
2,77
2,76
2,76
2,75'
2,70
2,66
2,62
2,58
0,005
Односторонний уровень
значимости q/2
q
р
zq BP)
Таблица VII
Значения функции
*=—00
— 1) е
X
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39.
0,40
0,99995
99991
99983
9997
9995
9992
9987
¦ 9981
9972
X
0,78
0,79
0,80
0,81
0,82
0,83
0,84
0,85
0,86
0,5770
5605
5441
5280
5120
4962
4806
4653
4503
,24
,25
,26
,27
,28
,29
,30
,31
1,32
Ptt)
0,0924
0879
0836
0794
0755
0717
0681
0646
0613
А,
,70
,71
,72
,73
,74
,75
,76
,77
,78
0,0062
0058
0054
0050
0047
0044
0041
0038
0035
36S
369
к
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,60
0,61
0,62
0,63
0,64
0,65
0,66
0,67
0,€S
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,9960
9945
9926
9903
9874
9840
9800
9753
9700
9639 .
9572
9497
9415
9325 :
9228
•91.24
9013 !
8896
8772 I
8643
8508
¦8368
8222 ,
«973 {
7920
7764
7604 ¦'
7442
7278
7112
6945
6777
660Э
6440
6202
6104
5936
X
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,38
0,99
1,00
,01
,02
,03
,04
,05
Г,да
1,07
1,08
1,09
1,М>
1,11
1,12
1,13
1,14
1,15
1,16
1,17
1,18
1,19
1,20
1,21
1,22
1,23
Р(%)
0,4355 '
4209
4067
3927
3791
3657
3527
3399
3275
3.154
3036
2921
2809
2700
2594
2492
2392
2296
2202
2111
2024
1939
1857
1777
1700
1626
1555
1486
1420
1356
1294
таз
1177
1122
1070
1019
0970
X
¦ 1,33
1,34
1,35
1,36
1,37
1,38
1,39
1,40
1,41
1,42
,43
,44
,45
,46
,47
,48
,49
,50
,51
,52
,53
,54
,55
,56
,57
1,58
1,59
1,60
1,61
1,62
1,63
1,61
1,65
1,66
1,67
1,68
1,69
Продолжение
РФ
0,0582
0551
0522
0495
0469
0444
0420
0397
0375
0354
0335
0316
0298
0282 :
0266
G250
.0236
0222
0209
0197
0185
0174
0164
0154
0145
0136
0127
0120
0112
0105
0098
0092
0086
0081
0076
0071
0066
X
1,79
1,80
1,81
,82
,83
,84
,85-
,86
,87
,88
,89
,90
,91
,92
1,93
1,94
1,95
,96
1,97
1,98
1,99
2,00
2,01
2,02
2,03
2,04
¦2,05
2,06
2,07
2,08
2,09
2.10
2,20
2,30
2,40
2.50
3,00
табл VII
P(Ki
0,0033
0031
0029
0027
0025
0023
0021
0020
0019
0017
0016
0015
0014
0013
О012
ООН.
0010
0009
0009
0008
0007
0007
0006
О006
0005
0005
0094
0004
О004
0004
0003
О003
0001
0001
00002
0000075
00000003
Таблица VIII
Границы критической области для критерия знаков
п
5
6
7
¦8
0
1
1
1
2,5%
5%
5
5
6
7
Односторонние границы
1%
0
0
1
1
5
6
6
7
2%
Двусторонние границы
0
0
0
1
0,5%
1%
5
6
7
7
п
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
89
40
41
42
43
44
45
46
47
48
49
50
51
52
S3
54
п ,
2.6%
2
2
2
3
3
3
4
4
5
5
5
6
6
6
7
7
8
8
8
9
9
10
10
10
11
11
12
12
13
13
13
14
14
15
15
16
16
16
17
17
IS
18
19
19
19
20
5%
7
&
9>
9
10
11
11
12
12
13
14 ¦
14
15
16
15
17
17
18
19
19
20
20
21
22
22
23
23
24
24
25
26
26
27
27
28
28
29
30
30
31
31
32
32
33
34
34
Односторонние
!%
1
t
2
2
2
3
3
3
4
4
5
5
5
б
6
6
7
7
8
8
8
9
9
9
10
10
11
11
11
12
12
13
13
14
14
14
15
15
16
16
16
17
17
18
18
19
2%
Двусторонние
Продолжение
границы
8
9
9
10
11
11
12
13
13
14
14
15
16
16
17
18
18
19
19
20
2.1
21
22
23
23
24
24 •
25
26
26
27
27
28
28
29
30
30
at
31
32
33
33
34
34
36
35
границы
табл VIII
0.5%
- 1
1
1
2
2
2
3
3
3
4
4
4
5
5
5
6
6
7
7
7
8
8
8
9»
9
10
10
10
И
и
12
!2
12
13
13
14
14
14
15
15
16
16
16
17
17
IS
1%
8
9
10
10
11
12
12
13
И
14
15
16
16
17
18
18
19
19
20
21
21
22
23
23
24
24
25
26
26
27
27
28
29
29
30
30
31
32
32
33
33
34
35
35
36
36
370
371
3
ta
в
a
•о
о
s
*1
•g
НИЦЫ
to
8S85Sg$SSSSS8gSS8828S2S»S^aaS«№-oS8^0.^»s3-o«oo0-a010,
ss^OT^s^^S88S8ra8,as^SBB^
wыww«иыиw«OJШCoыимшивwы^o^э^oм^з^5^5^зtoto^з^з^5K)^olo^5^o^o^э^o^э^г"-"-
СЛ СЛСЛСЛСЛСЛ СЛСПСП СЛ *¦¦**-t**-•(>¦*¦ ***¦***¦*¦¦*»-^ *» >t* **¦ CO CO CO CO CO CO
3
Ю
-
О
s
4
о
X
X
fT>
ницы
Sq
s
3
a3t^.COtOCO^JCOO>C©CQ
to CO О •--• СО (О СО •—* СО СО ОО
аэ со *¦ со со •— *-toco~4ai
ЮОООСП
ооаэюсл—заэ
4COOcO>-^0^'^
о •—
IlDO
DCOO
COCOO
СОСОО
-—coo
О ——
0 01-^00 00 CO CO CO CO CD CO Ъ>Ъ>
^^ocS~^-
b2*-cpojcor -
o>o o> со о as со
to — en о со en en
CO с
со с
ООСОСОСОСОСОСОСООС
сродслчсоос?)оо
О"- и- —
1 --q К? CO rf^- CO О С
СО .о ер <о to со с
-s,-—»& О> 00 CD
* <—' Ю ю с© СО ^sl со ¦
N0^
>ooc
)ОГ
. -Э О C_ -
;o О ос
>ООООООООООООО-'Ю03<
ОООО-Ю*С1^00ОФМ&1ЩМС
'-Ь —со(
. _ JOOO
3OOOOSOOOO
>OOOOOO —•—Ю
OOOOOO"— — ЮСОСЛОО
^^ ^«* ^-* ^^ ^^^ ^ч) ^^ ^*J ^fj С f*^ "^J f^*>
OOOOOOOOO
OOOOOO • ЬЭ
О О *—' •—•
ОЭСОСОСО
ocOSOl^
~-0)С0 —СОООО
СОО
&ОО
ООООООООООООООООООООО^— ¦— ЬООЭгЕь
ООООООООООООООО>— "MMUI^OOIMO-
ООООООООООМЛтОСПМ^СЛ
ОООО
ООО — >
^э ^э ^э ^э ^^ с? с
Ю 00 ^-СОООС
>ооооооос
эооооооос
^- "—• К> СО СЛ
ЭЭЙ^.Й«сдй555^ЕоЙсо§=}8^|§
8,
_ _ -5tO-l
Cncn>— tO'
'-ota-
о
X
о
о
3
5".
•о
s
о
S н
s
я
Продолжение табл. IX
ЛИТЕРА1УРА.
14
15
16
17
18
19
20
2.1
22
23
24
25
26
27
. 28
29
30
п.
2330
1825
1411
1079
0816
06! 1
0453
0334
0244
0177
0127
0091
0065
0046
0032
0023
0016
12
3007
2414
1912
1496
1157
0885
0671
0504
0375
0277
0203
0148
0107
0077
0055
0039
0028
13
3738
3074
2491
1993
1575
1232
0952
0729
0554
0417
0311
0231
0170
0124
0090
0065
0047
14
4497
3782
3134
2562
2068
1649
1301
1016
0786
0603
0458
0346
0259
0193
0142
0104
0076
15
5255
4514
3821
3189
2627
2137
1719
1368
1078
0841
0651
0499
0380
0287
0216
0161
0119
16
5987
5216
4530
3856
3239
2687
2202
1785
1132
1137
0895
0698
0540
0415
0316
0239
0180
17
6671
5955
5238
4544
3888
3285
2742
2263
1847
1493
1194
0947
0745
0581
0449
G345
0263
18
7291
6620
¦5925
5231
4557
3918
3328
2794
2320
1906
1550
1249
0998
0790
0621
0484
0374
19
7837
7226
6573
5899
5224
4568
3946
3368
2843
2373
1962
1605
1302
1047
0834
0660
0518
20
8305
7764
7166
6530
5874
5218
4579
3971
3405
2888
2424
2014
1658
1353
1094
0878
0699
Продолжение табл. IX
X' \/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
.25
26
27
28
29
30
1
1
1
1
0
2!
,0000
,0000
,0000
,0000
,9999
9994
9981
9951
9892
9789
9628
9396
9086
8696
8230
7696
7111
6490
5851
5213
4589
3995
3440
.29-81
2472
2064
1709
1402
1140
0920
1
1
1
1
0
22
,0000
,0000
,0000
,0000
,9999
9997
9990
9972
9933
9863
9747
9574
9332
9015
8622
8159
7634
7060
6453
5830
5207
4599
4017
3472
2971
2517
2112
1757
1449
1185
1
1
1
1
1
0
23
,0000
,0000
,0000
,0000
,0000
,9999
9995
9984
99С0
9913
9832
9705
9520
9269
8946
8553
8093
7575
7012
6419
5811
5203
4608
4038
3503
3009
2560
2158
1803
1494
1
1
1
1
1
0
24
,0000
,0000
,0000
,0000
,0000
,9999
9997
9991
9976
9945
9890
9799
9661
9466
9208
8881
8487
8080
7520
6968
6387
5793
5198
4С16
4058
3532
3045
2600
2201
1848
1
1
1
1
1
1
0
25
,0000
,0000
,0000
,0000
,0000
,0000
,9999
9995
9С86
9967
9929
9866
9765
9617
9414
9148
8818
8424
7971
7468
6926
6357
5776-
5194
4624
4076:
3559
3079'
2639
2243
26
1,0000
1,0000.
1,0000.
1,0000
1,0000
1,0000
0,9999
9997
9992
9980
9955
9912
9840
9730
9573
93С2
9091
8758
8364
7916
7420
6887
6329
5760 ¦
5190
4631
4093
3585
3111
2676
0
27
,0000
,0000
,0000
,0000
,0000
,0000
,0000
,9999
9995
9988
9972
9943
9892
9813
9G94
9529
9311
9035
8700
8308
7863
7374
6850
6303
5745'
51-8В
4638
4110
3fiO9
3142
|
1
1
0
28
,0000
,0000
,0000
,0000
,0000
,0000
,0000
,9999
9997
9993
9983
9964
9929
9872
9784
9658
9486
9261
8981
8645
8253,
7Й13-
7330
6815'
6278
5730'
5182
4644
4125
3632
29
1,0000
1,0000
1,0000
1,0000
1,0000
1,0000
1,0000
1,0000
0,9999
9996
9990
9977
9954
9914
9850
9755
9622
9443
9213
8929
8591
8202
7765
7289
6782
6255
5717
5179
4651
4140
t. Аванесов Р. И. Очерка русской диалектологии. М., Учпедгиз, 1949.
2. Аванесов Р. И. Фонетика современного русского литературного язы-
языка. М., изд-во МГУ, 1956.
3. Алексеев П. М. Статистическая лексикография. Л, изд-во ЛГПИ,
1975.
4.. А р а п о в М. В., Херц М. М. Математические методы в лингвистике.
М., «Наука», 1974.
б. Ах м а но в а О. С. Словарь лингвистических терминов. М., «Советская
анциклопедия»,. 1966,
6. Бектаев К. Б., Пиотровский Р. Г. Математические методы
в языкознании. Ч. I. Теория вероятностей и моделирование нормы языка.
Алма-Ата, изд-во КазГУ, 1973.
7. Бектаев К. Б., Пиотровский Р. Г. Математические методы
в языкознании. Ч. II. Математическая статистика и моделирование текста.
Алма-Ата, изд-во КазГУ, 1974,
8. Бектаев К. Б. Статистико-информационная типология текста. Авто-
реф. докт. дисс. Л., Лен. отд. Института языкознания АН СССР, 1975.
9. Больше» Я Н., Смирнов Н, В. Таблицы математической стати-
статистики. М., «Наука», 1965.
10. Вентцел-ь Е, С. Теория вероятностей. М., «Наука», 1964.
И. Виноградов В. В. Русский язык. М.—Л.., Учпедгиз, 1947.
12. Гиляревский Р. С, Гривнин В. С. Определитель языков мира
по письменностям. Изд. 3-е, испр. и доп. М., «Наука», 1965.
13. Гладкий А. В., Мельчук И. А. .Элементы математической линг-
лингвистики. М., «Наука», 1969.
14. Г не дек к о Б. В. Курс теории вероятностей. Изд. 3-е, перераб. М.,
Физматгнз, 1961.
16. Головин Б. Н. Язык и- статистика. М., «Просвещение»,. 1971.
16. Грамматика русского языка. Т. I. Фонетика и морфология. М., изд-во
АН СССР, 1952.
17. Граудина. Л'. К- Развитие нулевой формы родительного множест-
множественного у существительных — единиц измерения. Сб. Развитие грамматики
и лексики современного русского языка. М., «Наука», 1964.
18. Зиндер Л. Р., Бонда рко Л. В., Вербицкая Л. А. Акустиче-
Акустическая характеристика различия твердых и мягких согласных в русском языке.
Ученые записки ЛГУ (серия филологических наук), вып. 69, № 325, Л., 1964.
19. Колмогоров А. В. Основные понятия теории вероятностей. Пере-
Перевод с немецкого. М,—Л., ОНТИ, 1936.
20. Митр опольски й А. К. Техника статистических вычислений. Изд.
2-е, перераб. и доп. М., «Наука», 1971,
21. Невельский П. Б. Объем памяти и количество информации Сб.
Проблемы инженерной психологии. Психология памяти. Вып. 3. Л,, 1965.
22. Обратный словарь русского языка. №.. «Советская энциклопедия»,
1974.
23. Пиотровский Р. Г. Информационные измерения языка. Л., «Нау-
«Наука», 5-968.
24. Пиотровский Р. Г. Моделирование фонологических систем « ме-
методы их сравнения. М.—Л., «Наука», 1966.
25. Пи отраве кий Р. Г. Структурные модели территориальных и жан-
жанровых разновидностей языка. Сб. Вопросы романского языкознания. Киши-
Кишинев, «Шти-иица», 1963,
26. Пиотровский Р. Г. Текст, машина, человек. Л., «Наука», 1976.
375
27. Пиотровский Р. Г. Формирование артикля в романских языках.
М.—Л., «Наука», 1960.
28. Пискунов Н. С. Дифференциальное и интегральное исчисления.
Изд. 11-е, стереотипн. М., «Наука», 1975.
29. Рождественский Ю. В. Слово в свете данных китайского язы-
языка. Сб. Морфологическая структура слова в языках различных типов. М.—Л.,
изд-во АН СССР, 1963.
30. Романовский В. И. Математическая статистика. Кн. 1. Основы
теории вероятностей и математической статистики. Кн. 2. Операторные мето-
методы математической статистики. Ташкент, изд-во АН Узб. ССР, 1961, 1963.
31. Сб. Математические методы в языкознании. Рига, «Зинатне», 1969.
32 а, б, в. Сб. Статистика речи и автоматический анализ текста. Л., «Нау-
«Наука», 1971, 1972, 1974.
33. Сб. Статистика текста. Т. I. Лингвостатистические исследования.
Минск, изд-во БГУ, 1969.
34. Сб. Статистичш параметри стшив. КиТв, «Наукова думка», 1967.
35. Словарь современного русского литературного языка. I—XVII, М.—Л.,
«Наука», 1950—1965.
36. С м и р н о в Н. В., Дуни н-Б арковский И. В. Курс теории ве-
вероятностей и математической статистики для технических приложений. Изд.
3-е, стереотипн. М., «Наука», 1969.
37. Тройский И. М Очерки по истории латинского языка. М.—Л.,
изд-во АН СССР, 1953.
38. Трахтенбпот Б. А. Алгоритмы и вычислительные автоматы. М.,
«Советское радио», 1974.
39. Ш т е й н ф е л ь д т Э. А. Частотный словарь современного русского
литературного языка. 2500 наиболее употребительных слов. Таллин, изд-во
НИИ педагогики ЭССР, 1963.
40. Щерба Л. В. Языковая система и речевая деятельность. Л., «Нау-
«Наука», 1974
41. Яглом А. М., Я г лом И. М. Вероятность и информация. Изд. 3-е.,
перераб. и доп. М., «Наука», 1973.
42. А г I e у N., В и с h К. R. Introduction to the Theory of Probability and
Statistics. New-York, 1950. Цит. по русск. пер.: Арлей Н. и Бух К. Р. Вве-
Введение в теорию вероятностей и математическую стастистику. М., ИЛ, 1951.
43. В а г-Н i 11 е I, Y. Some Recent Results in Theoretical Linguistics. Logic,
Methodology and Philosophy of Science. Proceedings of the 1960 International
Congress. Stanford University Press, Stanford, California, 1962. Цит. по русск.
пер.: Ъар-Хиллел, Й. Некоторые результаты в теоретической лингвистике.
Сб. Математическая логика и ее применения. М., «Мнр», 1965.
44. Berlin В., К а у P. Basic Color Terms. Their Universality and Evo-
Evolution. University of California Press, Berkeley and Los Angeles, 1969.
45. Chomsky N., Miller G. A. Introduction to the Formal Analysis of
Natural Languages. «Handbook of Psychology», vol. 2, New York, 1963. Цит.
по русск. пер.: Хомский Н. и Миллер Дж. Введение в формальный ана-
анализ естественных языков. «Кибернетический сборник». Новая серия, вып. 1.
М., «Мир», 1965.
46. С h u r с h A. Introduction to Mathematical Logic. «Princeton Univer-
University Press», Princeton, New Jersey, 1956. Цит. по русск. пер.: Черч А. Введе-
Введение в математическую логику. М., ИЛ, 1960.
47. С о s e r i u E. Sistema, norma e «parola». «Studi linguistici in onore di
Vittore Pisani.» Vol. I, Brescia, Padeia editrice, 1969.
48. Fucks W. Mathematische Analyse von Sprachelementen, Sprachstil
und Sprachen. Arbeitsgemeinschaft fur Forschung des Landes Nordrhein — West-
falen. Heft 34a. Koln und Opladen, Westdeutscher Verlag, 1955.
49. G reen ber g J. H. A Quantitative Approach to the Morphological
Typology of Language. «International Journal of American Linguistics».
Vol. XXVI, 3, 1960. Цит. по русск. пер.: Гринберг Дж. Квантитативный
подход к морфологической типологии языков. Сб. Новое в лингвистике.
Вып. 3, М., ИЛ, 1963.
376
50. Gutu-Romalo V. Stabilirea datei de separate a aromfnei de dacoro-
mlna cu ajutorul glotocronologiei. Studii si cercetari lingvistice, X, 4, 1959
51. Herd an G. Quantitative Linguistics, London, Butterworths,' 1964
52. Hjelmslev L. Prolegomena to a Theory of Language. Supplement
to International Journal of American Linguistics. Vol. 19, Indiana University
Publications in Antropology and Linguistics. Indianapolis, 1953. Цит. по русск.
пер : Ельмслев Л. Пролегомены к теории языка. Сб. Новое в лингвистике
Вып. 1, М., ИЛ, 1960.
53. I n g a r d e n R. S., U г b a n i k К. Information without Probability. Col-
Colloquium mathematicum. Vol. IX, 1, 1962.
54. LI i v G. Acoustical Features of Estonian Vowels pronounced in Iso-
Isolation and in three Phonological Degrees of Length. «Eesti NSV Teaduste Aka-
deemia Toimetised». XI Koide. Uhiskonnateaduste seeria, nr. I, 1962.
55. Mandelbrot B. On the Theory of Word Frequencies and on Related
Markovian Models of Discourse. «Structure of Language and its Mathematical
Aspects». Proceedings of Symposia in Applied Mathematics. Vol. XII, Provi-
Providence. Rhode Island, 1961.
56. Ma r cus S., Ni со 1 a u Ed., Stati S. Introducere tn lingvistica ma-
tematica, Bucures4i, Editura stiintifica, 1966.
57. M e i 11 e t A. Introduction a 1'etude comparative des langues indoeuro-
peennes. VII edition refondue.. P., 1934. Цит. по русск. пер: Мейе А. Сравни-
Сравнительное изучение индоевропейских языков. М.—Л., Соцэкгиз, 1938.
58. Р г о к о s h E. A Comparative Germanic Grammar. Philadelphia, 1939.
Цит. по русск. пер.: П р о к о ш Э. Сравнительная грамматика германских язы-
языков. М., ИЛ, 1954.
59. S a u s s u г е F. de. Cours de linguistique generate. Lausanne — Paris,
1916. Цит. по русск. пер,: Соссюр Ф. де. Курс общей лингвистики. М.,
Соцэкгиз, 1933.
60. V a i 11 a n t A. Le suffixe russe — jaga, «Revue des etudes slaves»,
XVI, 1—2, 1938.
61. Van der Warden B. L. Mathematische Statistik. Berlin—Gottin-
gen—Heidelberg, Springer Verlag, 1957. Цит. по русск. пер.: Ван дер В а р-
ден Б. Л. Математическая статистика. М., ИЛ, 1960.
62. Vendryes J. Le langage. Introduction linguistique a l'histoire. Pa-
Paris, 1935. Цит. по русск пер.: Вандриес Ж. Язык. Лингвистическое вве-
введение в историю. М., Соцэкгиз, 1937.
63. Wilks S. S. 'Mathematical Statistics. New York — London, 1962.
Цит. по русск. пер.: У и л к с С. Математическая статистика. М., «Наука»,
1967.
64. Y и 1 е G. V. and К е n d а 11 М. G. An Introduction to the Theory of
Statistics, 14-th ed. London, 1950. Цит. по русск. пер.: Юл Дж. Э. и Кен-
дэл М. Дж. Теория статистики. 14-е изд., перераб. и доп. М., Госстатиздат
ЦСУ СССР, 1960.
65. Zadeh L. Outline of a New Approach to the Analysis of Complex
Systems and Decision Processes. IEEE TSMS. Vol. SMC—3. 1973. Цит. по русск.
пер.: Заде Л. А. Основы нового подхода к анализу сложных систем и про-
процессов принятия решений. Математика сегодня (серия математика, киберне-
кибернетика).^., «Знание», 1974. " .
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Агглютинация 92, 145, 319
Агглютинирующие языки 92
Алгоритм 23
Аналитизм в языках 142, 147
Аргумент 22
Арккосинус 31
Арккотангенс 31
Арксинус 30
Арктангенс 31
Асимптота вертикальная 82
— горизонтальная 82
— наклонная 82, 83
Бесконечно малые 51
, свойства 52
, сравнение 54, 55
, эквивалентные 55
Бит. 135
Варианта 222
Вариационная, сетка Турбина 344 —
347
Вариационный ряд 223.
дискретный 222—224
непрерывный 225, 226
Величина 18
— абсолютная постоянная 19
— бесконечно большая 52
— бесконечно малая, см. Бесконечно
малые
— бескомпонентная 190
— дискретная 20
— небескомпонентная 190
— непрерывная. 20
— переменная 18.
— постоянная 18
— случайная 166
дискретная 166
непрерывная 166
Вероятность алостернорная 131
— априорная 131
— безусловная 126
—, определение акиоматическое 121 —
124
—,— классическое 117, 118
—,— статистическое 119—121
—,— субъективное 116, 117
— условная 126
Включение 14
Внутренняя (групповая) средняя 246
Возрастание функции 78
, признак 79
Вогнутость (выпуклость) кривой 81
, правило исследования 82
Выборка бесповторная 150
— повторная 150
878
Гармоника 42
Геометрическая прогрессия 90
Гипотеза 129
— альтернативная 303
— нестатистическая 303
— нулевая 303
— статистическая 302, 303
Гистограмма 171, 231, 232
Глоттохронология 57—62, 303
Граничная частость 300
Двоичная единица 135
Денотат 5
Десигнат 5
Децили- 239
Диаграмма 233
Диалектология 10, 13, 16, 21, 99
Диахроническая лингвистика 1.0, 38
— скорость 65—67
мгновенная 68
Диахронический скачок 38
Дискретность и нелрерывность в язы-
языке и речи 20--22, 166, 167
Дисперсия внешняя (межгрупповая)
248
— внутренняя (групповая) 246, 248
— общая 248, 249
— опытная 243—246
— теоретическая 179, 180
Дифференциал 73, 74
— второго порядка 77
—, правила нахождения 75
—, применение в приближенных вы-
вычислениях 75—77
Дифференцирование 70, 71
Доверительный интервал 269
, его определение для вероятно-
вероятности прн малых выборках 286, 287
, редких лингвистиче-
лингвистических событий 287, 288
, с помощью нормаль-
нормального распределения 284, 285
, дисперсии и среднего
квадратического отклонения с по-
помощью распределения %2 280—282
, математического ожида-
ожидания нормально распределенной слу-
случайной величины 269—271
, — с помощью распре-
распределения Стьюдента 271—274
, с помощью функции Кол-
Колмогорова 291—293
функции генерального распреде-
распределения 289, 290
Дополнение к множеству 16
Единицы заполнения 356
Закон больших чисел 208
— Гаусса 197
— распределения Стьюдента 272
— Эсту—Ципфа—Мандельброта 19
Звонкие смычные согласные в индоев-
индоевропейских языках 22, 23
Знак лингвистический 5—7
— математический 5—7
Избыточность 143, 319, 322
— общая 143
Имя 5
Инверсия 312
Индикатор 256
. Инкорпорация 92, 319
Инкорпорирующие языки 92
Интеграл вероятностей 108, 109
— неопределенный, см. Неопределен-
Неопределенный интеграл
— несобственный 168
— определенный, см. Определенный
. интеграл
Интегрирование 98
— непосредственное 102, 103
— по частям 104, 105
— способом подстановки 104
Интервал медианный 238, 239
— модальный 240
Интервальная разность 226
Интервалы монотонности 78
Информация алфавита 39, 135
— синтактическая 21, 38, 84—86, 141,
142
— смысловая 21, 144—148
Испытание 113
Исходная форма слова 11
Квартили 239
Комбинаторный подход к определе-
определению количества информации 135
Комплекс условий 113
Коннотат 5
Контекстная обусловленность 40, 41,
142, 143
предельная 41
Косинус 29
Котангенс 30
Коэффициент асимметрии 182
— вариации 180, 243, 244
— контекстный 41, 62
— принадлежности элемента нечетко-
нечеткому множеству 359
Кривая кумулятивная 232
— распределения дифференциальная
172
интегральная 172 i
информации 40
— сложная гармоническая 42
Критерии непаряметрические 309
— параметрические 309
— порядковые 309
— статистические 309
Критерий Вилкоксона 313, 314
— знаков 310, 311
— Колмогорова 340—342
— Колмогорова—Смирнова 347—349
— нормального закона .(Z-критерин)
318
— Романовского 343, 344
— Стьюдента (/-критерий) 316, 317
— X2 Пирсона 330—333
Лингвистика квантитативная 8—10
— комбинаторная 8—10
Лингвистический алфавит 135
— спектр 194
Максимум 79
Математическая модель гармониче-
гармонической структуры гласных 41
дивергенции языков 58—62
для информационной парамет-
параметризации стиля 319—324
статистической параметриза-
параметризации стиля 274—277
информационного построения
слова 47—50, 62, 63, 91—94
текста 62, 63, 77, 84—86
истории местоимения hie в позд-
нелатинских памятниках 67—70
лексических расхождений в
двух литературных вариантах язы-
языка 324—329, 351—353
прироста и накопления инфор-
информации в тексте 98—100
проникновения арабских заим-
заимствований в персидскую прозу 64—
67
развития нулевых форм роди-
родительного падежа 32—34
терминологии 95—98
роста словаря 56, 57
статистического опознания тер-
термина 353—357
устойчивости употребления слу-
служебных н знаменательных слов
312, 313, 315, 316
формирования определенного
артикля 34—38.
Математическое ожидание 178
, свойства 178, 179
Машинный перевод 5, 7, 205, 256, 298,
305, 306, 350, 357
Медиана 238, 239
Минимальный объем выборки, опре-
определение его в грамматических и фо-
фонетических исследованиях 295—299
379
Минимальный объем выборки, опре-
определение его в лексикологических ис-
исследованиях 296
, по заданной покрывае-
мости текста 300, 301
, с учетом рассеяния при-
признака 296, 298
Минимум 79
Множество 11
— бесконечное 13
— конечное 13
—. нечеткое 6, 12, 359—361
—, основные операции над множест-
ствамн 14—16
— пустое 13
—, способы задания множеств 13, 14
— упорядоченное 16
— четкое 11
Мода 240
Модальное значение вероятности 155
Момент, см. Теоретический момент,
Эмпирический момент
Надежность 269
Неологизмы 61
Неопределенность 133
Неопределенный интеграл 100
, свойства 100
, таблица простейших интегралов
102
Неравенство 18
— Чебышева 210
Норма языка 9, 135, 136, 265, 356,
357
Область значений функции 23
— изменения переменной 19
— критическая 306
— определения функции 22
— приемлемости решений 306
— сходимости функционального ряда
88
— формантная 44
Общий член ряда 87
Объединение (сумма) множеств 14,
15
Огива 233
Определенный интеграл 106
, свойства 106, 107
Отклонение линейное 242
— среднее квадратическое 180, 244
Оценка интервальная, см. Довери-
Доверительный интервал
— несмещенная 267, 268
— точности результатов лннгво-ста-
тистического исследования 298, 299
— эффективная 268
380
Ошибка второго рода 304—306
— первого рода 304—306
Ошибки систематические 207
— случайные 207
Параметр 19
Первообразная 98
Пересечение (умножение) множеств
15
Перестановки 111
— с повторениями 111, 112
Период 29
Плотность распределения вариацион-
вариационного ряда 226
вероятностей 175, 176
Подмножество 14
Поле событий 1.15
Полигон 231
Полная система событий 115
Постулат мощности критерия 308
Правило «трех сигм» 218
Практическая достоверность 205
— невозможность 205
— уверенность 206
Предел переменной 53
— функции 53
, свойства 53, 54
Приращение аргумента 66
— функции 66
Произведение событий 114
Производная 70
— второго порядка 77
—, правила дифференцирования 71
—, формулы дифференцирования 72,
73
Психолингвистика 350
Равенство множеств 15
Размах вариации 241
Размещения 111
— с повторениями 111
Разность множеств 16
— событий 114
Распределение биномиальное 183, 184
— информации в слове 38, 39
тексте 40, 62, 63, 84—86
— контекстной обусловленности 40,
41
— лог'нормальное 202—205
— нормальное 197—201
— Пуассона 184—189
— средних длин словоформ в языках
мира 258—260, 262—265, 318, 319,
333—347
— Стьюдента 271—274
— Чебанова—Фукса 190, 191
— Фукса—Гачечиладзе 193—197
— х2 Пирсона 278—282
Ряд 87
— абсолютно сходящийся 91
— вариационный, см. Вариационный
ряд .
— гармонический 90
— знакопеременный 88
— Маклорена 89
—, признаки сходимости 89, 90
— степенной 88
— сходящийся 88
— расходящийся 88
— функциональный 88
— Фурье 46
Сдвиг фазы 45
Синус 29
Система языка 20, 136, 137, 356, 357
Слово 11,91—94
Словоупотребление 11
Словоформа 11,91—94
Событие достоверное 115
— невозможное 115
— случайное 113
сложное 113, 114
элементарное 114
События зависимые 126
— независимые 126
— несовместимые 115
— противоположные 115
— равносильные 114
— совместимые 115
Социолингвистика 10
Сочетания 112
— с повторениями 112, 113
Спектр 43
Спектрограмма 43
Средневзвешенная 234
Средняя арифметическая 234
-, вычисление с помощью метода
моментов 236, 237
— —, свойства 235
— внутренних дисперсий 248
— гармоническая 238
— квадратическая 237
Стандарт 244
Статистическая гипотеза 302, 303
— совокупность 219
— — выборочная 220
генеральная 220
с альтернативным признаком
250, 251
Стилистика 10, 160, 161, 215, 250,
274—277
Структура (форма) выражения 21
— содержания 20
Структурные кон гекстные ограниче-
ограничения 136
Субстанция выражения 20, 21
— содержания 20
Сумма ряда 88
частичная 87
— событий 114
Схема полиномиальная 151, 158, 159
— простая 151—158
— Пуассона 152, 159—161
— построения графика функции 83,
84
Таблица значений амплитуд, сдвигов
фаз и периодов гармоник при раз-
разложении кривых распределения ин-
информации 49
вероятностей для критерия Xs
Пирсона 373, 374
распределения Пуассона
362, 363
Стьюдента 366, 367
границ критической области для
критерия знаков 370—372
избыточности в некоторых язы-
языках 143
стилях европейских языков
322
контекстных оценок и процента
аналитизма в некоторых языках
147
минимальных объемов выборок
297
средних длин словоформ в не-
некоторых языках 259
функции Лапласа 365
Р(А.) = 1— К(Ь) 369, 370
Ф(г) = у= е-ггР 364
у
/оо и /«, для некоторых языков
40
<д. v и г-j для фиксированных
уровней значимости и заданных
степеней свободы 369
X2 Ддя фиксированных ч уровней
значимости и заданных степеней
свободы 368
— простейших интегралов 102 '
— распределения вероятностей букв
в русских литературных текстах
120
длин слогов в некоторых язы-
языках 192
морфемных структур слов в
английском и русском языках 193
первых букв русского слова
126
синтактической информации 39
Тангенс 29, 30
Тезаурус 116
Тело событий 122
Теорема Бернулли 210
381
Теорема Колмогорова 213 Формулы для вычисления вероятно-
¦ предельная 291, 292 стей при биномиальном распределе-
— Ляпунова 214—216 нии 156, 157
— Маркова 211 верхних и нижних границ ин-
— Муавра—Лапласа интегральная формации 141
200, 201 количества информации 138,
локальная 197 ~ 140, 141
— Пуассона 211 моментов 180—182
— Феллера 213 при биномиальном распре-
— Чебышева 209 делении 183
Теоретический момент 180 — логнормальном распре-
начальный 181 делении 203
нормированный 181 нормальном распределе-
центральный 181 нии 199
Теория порождающих грамматик 8 распределении Пуассо-
Терминология 73, 74, 76, 95—99, 103, на 185, 186
107,353—356 Чебанова—Фукса 190,
Точка критическая I рода 80 191
II рода 82 Фукса — Гачечиладзе
— максимума 79 195
¦— минимума 79 Функции распределения информации
— перегиба 82 в тексте 40, 84—86
— разрыва 78 Функциональная зависимость 22
— сходимости функционального ряда Функция 22
88 — Вейбулла 176, 177
— возрастающая 78
— вычислимая 23
Убывание функции 78 ' — дробно-рациональная 27
, признак 79 — квадратичная 26
Уровень значимости (существенно- — Лапласа 201
сти) 269, 307 — линейная 26
— логарифмическая 28
— монотонная 78
Фонема 13—16, 21 — непрерывная 78
Фонетическая транскрипция 13 — обратная 23
Форманта 44 —, общая схема исследования 83, 84
Формула асимптотическая биномиаль- — периодическая 28
ного закона 197—199 — показательная 27, 28
— Бейеса 131 — разрывная 78
— Бернулди 152, 153 — распределения случайной величи-
— для вычисления вероятностей в ны (кумулятивная функция) 168
бесповторной выборке 162 дискретного типа 168—
полиномиальной схеме 170
158 непрерывного типа 171 —
схеме Пуассона 160 176
— вероятности появления собы- —, способы задания функции 24, 25
тия от а до Ь раз 164 — степенная 26
— максимального количества — убывающая 78
информации в слове 93 — числовая 24
¦ минимального объема выбор- — экспоненциальная 28
ки 166
— контекстной'обусловленности 41
— Ньютона—Лейбница 106
— полной вероятности 129
— распределения Пуассона 185
— •— Чебанова—Фукса 190
Фукса—Гачечиладзе 195
— сложения вероятностей 126
— средней условной энтропии 140
*- Стерджесса 227
— умножения вероятностей 128
Число натуральное 17
— рациональное 17
— степеней свободы 272, 278
— Эйлера 28, 55, 89
Эвристичность 361
Экстремум функции 79
, правила нахождения 80, 81
— —, признаки 79, 80
Эксцесс 182
Элемент множества 11
Эмпирический момент 252
начальный 252, 253, 255
нормированный 257
центральный 257
Энтропия 62, 63, 134
— алфавита 135
Язык английский 17, 40, 91, 92, 94,
129—132, 143, 147, 153, 154, 159,
177, 191—193, 196, 245, 259, 296,
312—316, 322, 353—356
— арабский 64—67, 192
— баскский 303
— болгарский 94, 146, 259
— грузинский 191, 192
,— древнегреческий 192
— кабардинский (кабардино-черкес-
(кабардино-черкесский) 92, 259
— казахский 14, 40, 143, 162, 163,
165, 222, 223, 249, 259, 301
— китайский 92, 225—228, 237, 239,
255, 293, 294
Язык латинский 34—37, 59, 67—70, 95,
— латышский 259, 260, 288
— молдавский 177, 285, 286
— немецкий 40, 91, 94, 143 177 187
188, 192, 204, 241-244, 251 ' 252*
256, 259, 319, 322, 324-329,' 352,'
353 '
— персидский 64—67
— польский 40, 143, 259, 322
— румынский 40, 59, 94, 143, 147, 177,'
192, 194; 210, 230, 233, 322
— русский 14, 21, 32—34 38—41
47—49, 60, 91, 94, ПО, 111 I16-
121, 126—129, 136-138, 143 146
147, 149, 164, 165, 177, 182 192,
193, 220, 228, 229, 238, 259, 286,
287, 301, 322 i
— старофранцузский 34—37
— турецкий 92
— украинский 259, 274—277 282 283
295 ' '
— французский 40, 92, 94, 95, 143,
146—148, 259, 322
— чукотский 92, 259
— эстонский 44, 46, 146, 259
Языки алтайские 304—306
— иберо-кавказские 303
— монгольские 304
— тунгусо-маньчжурские 304
— тюркские 38, 304, 319, 349, 350
— финноугорские 92, 259, 319, 349,
350
См. также Таблица распределения
средних длин словоформ в языках
мира
Частота абсолютная 119
— накопленйая 232
— относительная (частотость) 119
Числа Вестергарда 344
Число 16, 17
— действительное 17
— иррациональное 17
— наивероятнейшев появлений собы-
события 156
382
Раймонд Генрихович Пиотровский
Калдыбай Бектаевич Бектаев
Анна Александровна Пиотровская
МАТЕМАТИЧЕСКАЯ
ЛИНГВИСТИКА
Редактор А. М. Суходский. Художник А. Е. Коленков.
Художественный редактор В. И. Пономаренко.
Технический редактор Э. М. Чижевский.
ИБ № 628
Сдано в набор 21/IX-76 г. Подп. к печати 25/11-77 г.
Формат 60X90'/i6 Бум. тип. №2 Объем 24 печ. л. Усл. п. л. 24
Уч.-изд. л. 23,74 Изд. № ФМ 527 Тираж 20 000 экз.
Зак. М> 1287 Цена I р. 19 к.
План выпуска литературы издательства
«Высшая школа> (вузы и техникумы) на 1977 г. Позиция Ш 37
Издательство «Высшая школа»,
Москва, К-51, Неглннная ул., д. 29/14,
Московская типография № 4 Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли.
Москва, И-41, Б. Переяславская, ул., дом 46