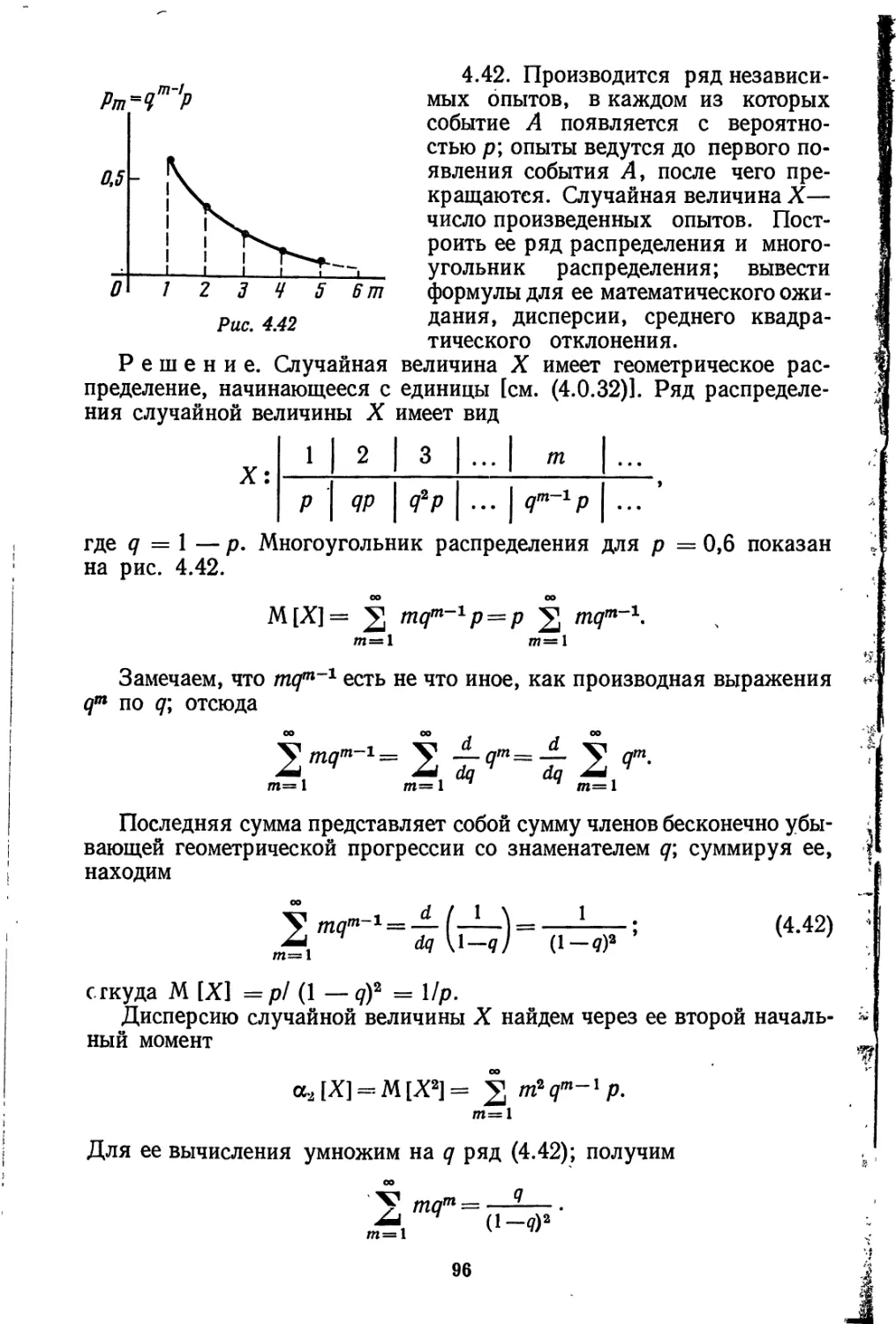
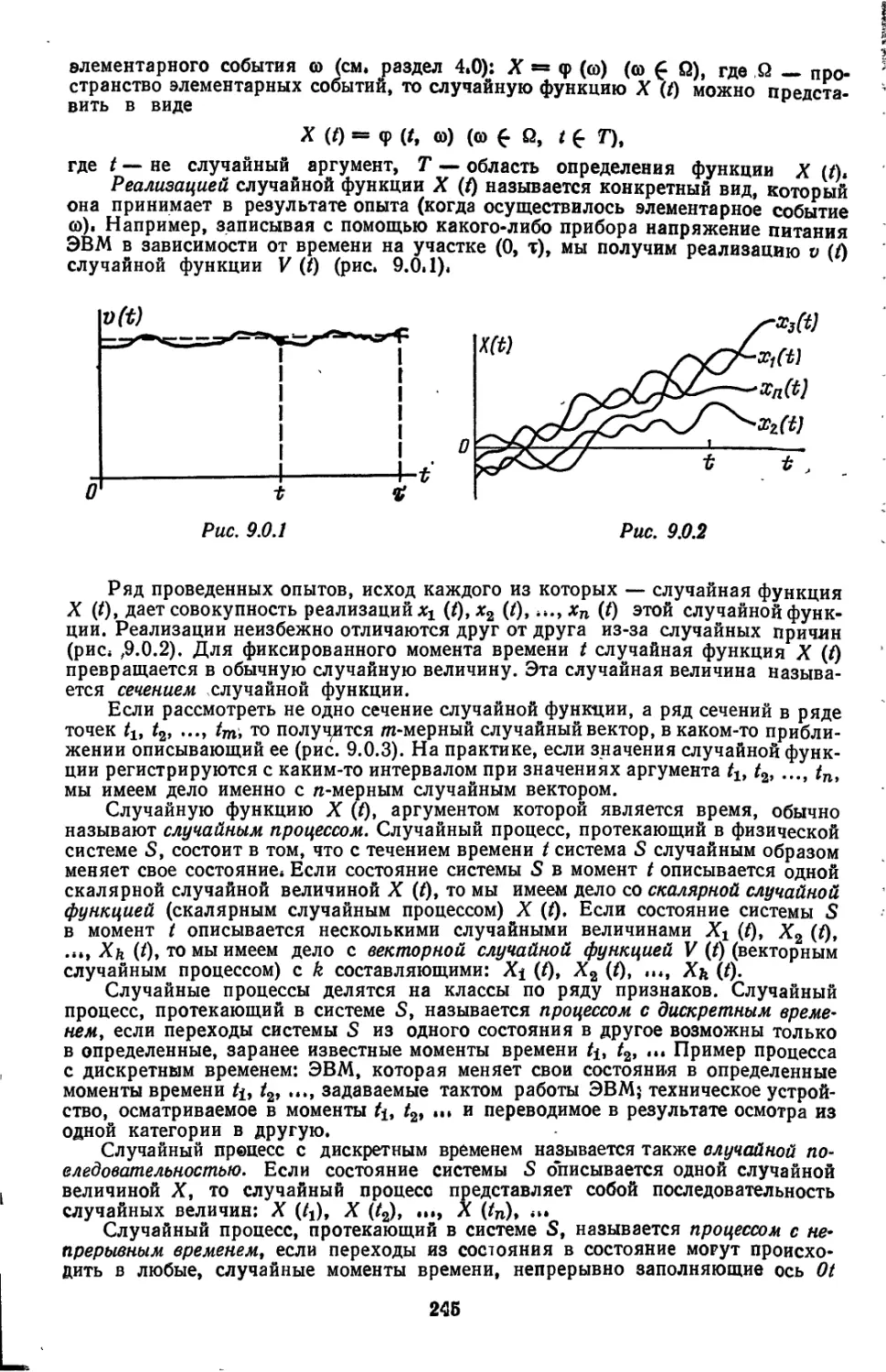
Text
Е.С.ВЕНТЦЕЛЬ, Л.А.ОВЧАРОВ
ПРИКЛАДНЫЕ
ЗАДАЧИ ТЕОРИИ
ВЕРОЯТНОСТЕЙ
МОСКВА
•РАДИО И СВЯЗЬ-
1983
ББК 22.171
В29
УДК 519.212
В29 Вентдель Е. С, Овчаров Л, А;
Прикладные задачи теории вероятностей. — М.:
Радио и связь, 1983. — 416 с, ил.
В пер.: 1 р. 60 к.
Содержится большое число задач прикладного характера,
относящихся к разным областям практики, главным образом
инженерно-техническим. В начале каждой главы приводятся краткие теоретические
сведения, необходимые для решения задач. Большинство задач
снабжено не только ответами, но и развернутыми решениями,
демонстрирующими важные методические приемы.
Для инженерно-технических работников, а также студентов и
преподавателей вузов, заинтересованных в овладении вероятностными
методами решения прикладных задач.
„ 1702060000-020 ВБК 22.171
В 107-82
[046(01)-83 517.8
Рецензент академик АН УССР Б. В: Г Н Е Д Е Н К О
Редакция литературы по кибернетике и вычислительной технике
© Издательство «Радио и связь», 1983
ПРЕДИСЛОВИЕ
Книга написана на основе многолетнего опыта преподавания
теории вероятностей и ее приложений в высших технических учебных
заведениях различных профилей. Основой для нее послужили также
многочисленные практические задачи, встречавшиеся авторам в их
научно-исследовательской и консультационной работе. Эти задачи
относятся к разным областям практики, как-то : электротехника,
радиотехника, передача сообщений; электронные вычислительные машины;
информационные системы; надежность технических устройств, их
ремонт и профилактика; точность аппаратуры; бытовое обслуживание;
транспорт, здравоохранение и др.
Книга состоит из одиннадцати глав; в начале каждой главы
приведена краткая сводка теоретических положений и основных формул,
необходимых для решения задач.
Задачи, помещенные в книге, весьма различны как по области
приложений, так и по трудности. В начале каждой главы читателю
предлагаются сравнительно простые задачи, цель которых — уяснение
основных понятий, приобретение и закрепление навыков применения
вероятностных методов. Далее приводятся более сложные задачи,
имеющие практическую направленность, решение которых становится
возможным на базе усвоенных теоретических знаний и приобретенных
навыков.
Авторы избегают стандартных, так называемых «типовых» задач,
решаемых по определенному шаблону. Многие задачи, помещенные в
книге, могут показаться трудными не только начинающему, но и
искушенному в теории вероятностей читателю (наиболее трудные, по
мнению составителей, отмечены звездочкой). В интересах читателя
большинство задач снабжено не только ответами, но и развернутыми
решениями; эти ответы и решения приводятся не в конце книги, а
непосредственно за постановкой задачи (авторы рассчитывают на
трудолюбивого и вдумчивого читателя, который прежде всего попытается
найти решение самостоятельно). Такая структура книги очень удобна
и полностью оправдала себя на примере другой книги авторов «Теория
вероятностей» (М.: Наука, 1973), многократно изданной у нас и за
рубежом (некоторые задачи этого издания повторены авторами в
настоящей книге). , ' * '
С точки зрения авторов, наибольший интерес в книге
представляют постановки и развернутые решения нетривиальных задач и
продемонстрированные в них методические приемы. Авторы ставят себе
целью не просто решить задачу, а решить ее наиболее простыми и
общими средствами. Некоторые задачи решены не одним, а разными
способами. Многие решения содержат оригинальные методические
приемы, которые имеют общее значение и могут найти применение в са-
з
мых разных областях практики. Особое значение авторы придают
аппарату числовых характеристик, позволяющему решать ряд задач с
исключительной простотой. Большое внимание уделяется прикладным
задачам теории марковских случайных процессов.
Краткие теоретические разделы, предваряющие отдельные главы
книги, в своем большинстве не конспектируют ни один из
существующих учебников по теории вероятностей, а написаны на новой
методической основе.
Таким образом, книга занимает в некотором смысле промежуточное
положение между сборником задач и учебником по теории
вероятностей. Она может быть полезна широкому кругу читателей: студентам
и преподавателям втузов, а также инженерам и научным работникам,
встречающимся на практике с задачами, требующими вероятностного
подхода. Отметим, что подробная разработанность решений и
внимание к методическим вопросам делают книгу хорошо приспособленной
к задачам самообразования.
Авторы приносят глубокую благодарность академику АН УССР
Б. В. Гнеденко, подробно ознакомившемуся с рукописью книги
и сделавшему ряд ценных замечаний, а также академику АН СССР
В. С. Пугачеву, с которым авторы многократно советовались при
работе над книгой, в значительной мере следуя методическим
принципам и системе обозначений, принятым в его монографии [12].
ГЛАВА 1
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ.
НЕПОСРЕДСТВЕННЫЙ ПОДСЧЕТ ВЕРОЯТНОСТЕЙ
В СХЕМЕ СЛУЧАЕВ
1.0. Теория вероятностей — математическая наука, изучающая
закономерности в случайных явлениях. Одним из основных понятий теории вероятностей
является понятие случайного события (или просто события). Событием
называется всякий факт, который в результате опыта (испытания, эксперимента) может
произойти или не произойти. Примеры событий: выпадение шестерки при
бросании игральной кости; отказ технического устройства за время его работы
т; искажение сообщения при передаче его по каналу связи. С событиями
связываются некоторые числа, характеризующие степень объективной возможности этих
событий, называемые вероятностями событий.
К понятию «вероятность» существует несколько подходов. Один из них
(«классический») основан на подсчете числа исходов опыта, благоприятных данному
событию, и его отношения к общему числу равновозможных исходов 1см. ниже
формулу (1.0.6) ]. Другой подход (так называемый «частотный» или
«статистический») основан на понятии частоты события в длинной серии опытов. Частотой
(или частостью) события в серии из N опытов называется отношение числа
опытов, в которых произошло данное событие, к общему числу произведенных
опытов. Существуют случайные явления, в которых наблюдается устойчивость
частот; она состоит в том, что при увеличении числа независимых опытов N
частота события стабилизируется, приближаясь к какой-то постоянной величине;
эта величина и называется вероятностью события.
Современное построение теории вероятностей как раздела математики
основывается на аксиоматическом подходе и опирается на элементарные понятия
теории множеств. Такой подход к построению теории вероятностей называется
теоретико-множественным.
Напомним основные понятия теории множеств*).
Множеством называется любая совокупность объектов произвольной
природы, каждый из которых называется элементом множества. Примеры
множеств: множество студентов, обучающихся в данном вузе; множество
натуральных чисел, не превосходящих 100; множество точек на плоскости, лежащих
внутри или на границе круга с радиусом единица и центром в начале координат.
Множество обозначается по-разному: или одной большой буквой; или
перечислением его элементов, данным в фигурных скобках; или указанием (в тех же
фигурных скобках) правила, по которому элемент относится к множеству.
Например, множество М натуральных чисел от 1 до 100 может быть записано в виде
М = {1, 2, ..., 100} = {i — целое; 1 < *' < 100}.
Множество С точек на плоскости, лежащих внутри или на границе круга с
центром в начале координат, может быть записано в виде С = {х2 + у2 ^ R2},
где х, у — декартовы координаты точки; R — радиус круга.
По числу элементов множества делятся на конечные и бесконечные.
Множество М = {1, 2, ..., 100} конечно и содержит 100 элементов (конечное множество
может, в частности, состоять из одного элемента). Множество всех натуральных
чисел N = {1, 2, ..., я, ...} бесконечно; также бесконечно и множество четных
чисел N2 = {2,4, ...,2п,...}. Бесконечное множество называется счетным, если
все его члены можно перечислить в определенной последовательности (оба выше-
В настоящее время эти понятия излагаются в средней школе.
5
приведенные бесконечные множества N к N2 являются счетными). Множество
С точек внутри и на границе круга радиуса R > О
C={x2+y2^R} (1.0.1)
является бесконечным и несчетным (его элементы нельзя перенумеровать один
за другим).
Два множества А и В совпадают (или эквивалентны), если они состоят из
одних и тех же элементов (совпадение множеств обозначается А = В).
Например, множество корней уравнения х2 — Бх + 4 = 0 совпадает с множеством
{1, 4} (а также с множеством {4, 1}).
Запись а £ А означает: объект а является элементом множества Л; или,
другими словами, а принадлежит А. Запись а ф А означает: объект а не
является элементом множества А.
Г j?^ ^^w
tnJ
Рис. 1.0.1
Пустым множеством называется множество, не содержащее ни одного
элемента; оно обозначается символом 0. Пример: множество точек плоскости,
координаты которых (xt у) удовлетворяют неравенству х2 + у2 ^ — 1, является
пустым: {х2 + у2 ^—1}=0. Все пустые множества эквивалентны друг
другу.
Множество В называется подмножеством (частью) множества Л, если все
элементы В содержатся также и в Л; обозначение В Q Л (или Л з В). Примеры:
{1, 2, .,., 100}Q {1, 2, .... 1000}; {1, 2, ..., 100}С {1, 2 100}; {** + /< 1}С
Q {** + */2<2}.
Считается, что пустое множество является частью любого множества Л:
0Я:Л.
Включение множеств можно наглядно изображать с помощью
геометрической интерпретации; в этом случае элементами множеств являются точки на
плоскости (см. рис. 1.0.1, где множество^ является частью множества Л).
Объединением (суммой) множеств Л и В называется множество С — А + В,
состоящее из всех элементов Л и всех элементов В (в том числе и тех, которые
принадлежат и Л, и В). Короче: объединение двух множеств — это совокупность
элементов, принадлежащих хотя бы одному из них. Примеры: {1, 2, ..., 100} +
+ {50, 51, ..., 200}= {1, 2, ..., 200}; {1, 2, ..., 100}+ {1, 2,..., 1000}= {1,2, ...',
1000}; {1, 2, ..., 100}+ 0 = {1, 2, ..., 100}. Изображение объединения двух
множеств А и В дано на рис. 1.0.2: вся заштрихованная область есть Л+В.
Аналогично определяется объединение любого числа множеств: Аг + Л2 +
п
+...+ Ап— 2 ^г есть множество, состоящее из всех элементов, входящих хотя
бы в одно из множеств Аъ ..., Ап. Рассматриваются также объединения беско-
со
нечного (счетного) числа множеств 2^г = Л1+Л2+... + Лп+ ... Пример:
{1, 2} + {2, 3} + {3, 4} + ...+ {пГп- 1} + ... = {1, 2, 3, ..., л, ...}.
Пересечением (произведением) множеств Л и В называется множество D =
=Л • В, состоящее из элементов, входящих одновременно и в Л, и в В. Примеры:
{1, 2, ..., 100} • {50, 51, ..., 200} = {50, 51, ..., 100}; {1, 2, ..., 100} . {1, 2, ...,
1000} = {1,2, ..., 100}; {1, 2, ..., 100} • 0— 0. Изображение пересечения двух
множеств Л и В дано на рис. 1.0.3.
6
Аналогично определяется пересечение любого числа множеств. Множество
п
А% • Л2 *- An = П А% состоит из элементов, входящих одновременно во все
А±9 А2, а., Ап. Определение распространяется и на бесконечное (счетное) число
оо
множеств: П А% есть множество, состоящее из элементов, входящих
одновременно во все множества А1з Л2, ».., Лп, ..*
Множества А и В называются непересекающимися, если их пересечение есть
пустое множество: А • В = 0, т. е. нет ни одного элемента, входящего и в Л, и
в В (рис. 1.0.4). На рис. 1.0.5 изображено несколько попарно непересекающихся
множеств.
0Q&S
Рис. 1.0.3 Рис. 1.0.4 Рис. 1.0.5
Так же как при записи обычного умножения, знак • в произведении
событий часто опускается.
Этих элементарных сведений по теории множеств достаточно для того, чтобы
пользоваться теоретико-множественной схемой построения теории вероятностей.
Пусть производится некоторый опыт (эксперимент, испытание), результат
которого заранее неизвестен, случаен. Рассмотрим множество Q всех возможных
исходов опыта: каждый его элемент ю £ Q (один отдельный исход опыта) будем
называть элементарным событием, а все множество Q — пространством
элементарных событий. Подмножества множества Q называются событиями (или
случайными событиями); любое событие А это подмножество множества Q:
A GQ,
Пример: опыт состоит в бросании игральной кости*); пространство
элементарных событий Q = {1, 2, 3, 4, 5, 6}; событие А — выпадение четного числа
очков; А = {2, 4, 6}; A G Q. В частности, можно рассматривать событие Q
(ведь каждое множество есть свое собственное подмножество); оно называется
достоверным событием (осуществляется при любом опыте, т. е. наверняка). Ко
всему пространству Q элементарных событий добавляется еще пустое множество
0; это множество тоже рассматривается как событие и называется невозможным
событием (в результате опыта оно не может произойти). Пример достоверного
события: {выпадение не более 6 очков при бросании игральной кости}; пример
невозможного события: {выпадение 7 очков при бросании игральной кости}.
Заметим, что, элементарные события в одном и том же опыте можно задавать
по-разному; например, при случайном бросании точки на плоскости положение
точки можно задавать как парой декартовых координат (х, у), так и парой
полярных (р, ф).
Непересекающиеся события Л, В (такие что А В = 0) называются
несовместными; появление [одного из них исключает появление другого. Несколько
событий Лх, Л2, ..., Лп называются попарно несовместными (или просто
несовместными), если появление^каждого из них исключает появление каждого из
остальных.
Говорят, что несколько событий А±, Л2, sii, An образуют полную группу,
если У Л $ = Q, т. е* их сумма есть достоверное событие (другими словами, в
*2 Игральной костью называется кубик, на гранях которого нанесены 1, 2, 3,
4, 5, 6 точек (или «очков»).
г
результате опыта непременно произойдет хотя бы] одно из них). Пример:
опыт— бросание игральной кости; события А = {\', 2}; В= {2, 3, 4} и С =
= {4, 5, 6} образуют полную группу: Л + В + С = {1, 2, 3, 4, 5, 6} = Q. '
Введем аксиомы теории вероятностей. Пусть каждому событию ставится в
соответствие некоторое число, называемое вероятностью события. Вероятность
события Л мы будем обозначать Р (Л)*). Потребуем, чтобы вероятности событий
удовлетворяли следующим аксиомам:
I. Вероятность любого события А заключена между нулем и единицей:
О < Р (А) < 1. (1.0.2)
II. Аксиома сложения вероятностей: если А и В несовместные события, то
Р (А ,+ В) = Р (Л) + Р (В). (1.0.3)
Аксиома (1.0.3) сразу обобщается на любое конечное число событий: если Alf
Л2, ..., Ап — несовместные события, то
У=1 / i=i
P(At). (1.0.4)
III. Аксиома сложения вероятностей для бесконечной последовательности
событий: если Ль Л2, ..., Лп, ... — несовместные события, то
(оо \ оо
P(At). (1.0.5)
Аксиомы теории вероятностей позволяют вычислять вероятности любых
событий (подмножеств пространства Q) с помощью^ вероятностей элементарных
событий (если их конечное или счетное число). Вопрос о том, как определить
вероятности элементарных событий, при этом не рассматривается. На практике
они определяются либо из соображений, связанных с симметрией опыта
(например, для симмеричной игральной кости естественно считать одинаково
вероятным выпадение каждой из граней), или же на основе опытных данных (частот).
Для опытов, обладающих симметрией возможных исходов, применяется
способ непосредственного вычисления вероятностей событий в так называемой
схеме случаев (иначе — схеме урн)/Этот способ основан на допущении о
равновероятности (равновозможности) элементарных событий. Несколько событий
Аг, Л2, ..., Ап называются равновозможными, если в силу симметрии условий
опыта относительно этих событий, вероятности их одинаковы: Р (АЛ = Р (Л2) =
... = Р (Ah).
Если в каком-то опыте пространство элементарных событий Q можно
представить в виде полной группы несовместных и равновозможных событий щ, ю2,
..., Од, то такие события называются случаями (или шансами), а про сам опыт
говорят, что он сводится к схеме случаев (схеме урн).
Случай Ю£ называется благоприятным событием Л, если он является
элементом множества Л: ю^ £ Л.
Так как случаи %, ю2, ..., ®п образуют полную группу событий, то
п
Так как элементарные события щ, ю2, ..., (йп несовместны, то по аксиоме
сложения вероятностей
pf 2o4=p(Q)=2 р(®«)=1.
*) Если событие (множество) обозначается не буквой, а словесным
описанием свойств этого множества, или же формулой типа (1.0.1), или просто
перечислением элементов множества, мы будем при записи вероятности
пользоваться не круглыми, а фигурными скобками, например Р{х2+#2<2}\
в
Так как элементарные события ©ь со2, ..., ып равновозможны, то вероятность
каждого из них одна и та же и равна \/п:
Р (©х) = Р (о)2)
Р (юп) = 1/п.
Отсюда непосредственно вытекает так называемая классическая формула
для вероятности события: если опыт сводится к схеме случаев, то вероятность
события А в этом опыте можно вычислить по формуле
РА (А) = тА/п,
(1.0.6)
a w — "М'
где тА — число случаев, благоприятных событию А; п — общее число случаев.
Формула (1.0.6), принимавшаяся когда-то за определение вероятности,
при современном аксиоматическом подходе есть следствие аксиомы сложения
вероятностей.
Рис. 1.0.6
ОС
Рис. 1.0.7
j
2
Рис. 1.0.8
Рассмотрим пример. В урне находятся 3 белых и 4 черных шара, тщательно
перемешанных. Из урны наугад выбирается один шар. Построить для этого
опыта пространство элементарных событий и найти вероятность события А = {вынут
белый шар}. Для этого перенумеруем шары в урне номерами от 1 до 7; первые
три шара — белые, последние четыре — черные:
Q= {1,2, 3,4, 5, 6, 7}; Л- {1,2,3}.
В силу симметрии условий задачи относительно всех шаров (шар выбирается
«наугад») элементарные события равновозможны. Так как они несовместны и
образуют полную группу, вероятность события А найдется по формуле (1.0.6):
Р (А) = тА/п = 3/7.
Формула (1.0.6) дает возможность в некоторых задачах, когда опыт
обладает симметрией возможных исходов, непосредственно по условиям опыта
вычислять вероятности событий.
Естественным обобщением и расширением непосредственного подсчета
вероятностей в схеме случаев является «геометрический» подход к вычислению
вероятностей событий; он применяется тогда, когда пространство элементарных
событий Q включает несчетное множество элементарных событий © £ Q, и,
по условиям симметрии опыта, никакое из них не имеет преимущества перед
другими в смысле возможности появления*). Пусть пространство элементарных
событий Q — какая-то область на плоскости (рис. 1.0.6), а элементарные
события о — отдельные точки в пределах этой области. Если опыт обладает
симметрией возможных исходов (например, какой-то «точечный» объект «наугад»
бросается в пределах области), то все элементарные события «равноправны», и ес-
*) Мы не говорим, что элементарные события ю «равновероятны»; как мы
убедимся в гл. 5, вероятность каждого из них равна нулю.
9
i
тественно предположить, что вероятности попадания элементарного события
со в две области I и II равной площади S равны, а вероятность любого события
A^Q равна отношению площади SA области А к площади всей области Q:
Р (Л) = SA/SQ. (1.0.7)
Формула (1.0.7) представляет собой обобщение классической формулы"(1.0.6)
на несчетное множество элементарных событий. Симметрия условий опыта
относительно его элементарных исходов "со формулируется обычно с помощью
слова «наугад», что, в сущности, равносильно выбору наугад одного из шаров в урне
(см. выше). Вероятности вычисляемые с помощью такого приема, в учебниках
часто называются «геометрическими вероятностями».
Пусть, например, на отрезке от 0 до 2 наугад ставятся две точки с
абсциссами х и у (рис. 1.0.7). Найти вероятность того, что расстояние L между ними
будет меньше единицы. Элементарное событие со для этого случая характеризуется
парой координат (х, у). Пространство элементарных событий — квадрат со
стороной 2 на плоскости х 0 у (рис. 1.0.8). L = \ у — х\\ событию А = {\у —
— х\ < 1} соответствует область Л, заштрихованная на рис. 1.0.8.
Р (Л) - Р { \у - х\< 1} = SA/SQ = 3/4.
Если пространство элементарных событий не плоское, а трехмерное, то в
(1.0.7) вместо площадей SA и SQ ставятся объемы VА и VQ; для одномерного
пространства элементарных событий — длины LA и LQ соответствующих участков
прямой.
ЗАДАЧИ И УПРАЖНЕНИЯ
1.1. Относительно событий, перечисленных в каждом примере,
указать, образуют ли они в данном опыте полную группу событий (да,
нет).
1) Опыт — бросание монеты; события:
Ах == {герб}; Л2 = {решка}.
2) Опыт — бросание двух монет; события:
В± = {два герба}; В2 = {две решки}.
3) Опыт — бросание двух игральных костей; события:
Сг = {на обеих костях шестерки};
С2 = {ни на одной кости нет шестерки};
С3 = {на одной из костей шестерка, на другой — нет}.
4) Опыт — передача двух сигналов по каналу связи; события:
Dt = {хотя бы один сигнал не искажен};
D2 = {хотя бы один сигнал искажен}.
5) Опыт — передача трех сообщений по каналу связи; события:
Ех = {все три сообщения переданы без ошибок};
Е2 = {все три "сообщения переданы с ошибками};
Е3 = {два сообщения переданы с ошибками, одно без ошибок}.
О т в е т.\ 1) даД2) нет, 3) да, 4) да, 5) нет.
1.2. Относительно каждой группы событий ответить на вопрос,
являются ли они в данном опыте несовместными (да, нет).
1) Опьп\—бросание монеты; события:
Ах = {герб}; Л2 = {решка}.
2) Опыт — бросание двух монет; события:
Bt = {герб на первой монете};
L L. ^а ^ {герб на второй монете}.
ю ;
3) Опыт — два выстрела по цели; события:
С0 = {ни одного попадания};
Сг = (одно попадание};
С2 = {два попадания}.
4) Тот же опыт; события:
Dx = {одно попадание}; D2 = {один промах}.
5) Опыт — вынимание двух карт из колоды; события:
Ег = {обе карты черной масти};
Е2 = {среди вынутых карт^есть дама треф};
Е3 = {среди вынутых карт есть туз пик}.
6) Опыт — передача трех сообщений по радио; события:
Fx = (в первом сообщении есть ошибка};
F2 = {во втором сообщении^есть ошибка};
F3 = {в первом сообщениигесть ошибка, во. втором — нет}.
Ответ: 1) да, 2) нет, 3) да, 4) нет, 5) нет, 6) нет.
1.3. Относительно каждой из групп событий ответить на вопрос,
равновозможны ли они в данном опыте (да, нет).
1) Опыт — бросание монеты; события:
Аг = {герб}; А2 = {решка}.
2) Опыт — бросание неправильной (погнутой) монеты; те же
события Ах\ Л2.
3) Опыт — выстрел по мишени; события:
В1 = {попадание};' В 2 = {промах}.
4) Опыт — бросание двух монет; события:
Сг = {два герба}; С2 = {две решки}; \JC3 = {один герб и одна
решка}.
5) Опыт — вынимание наугад одной карты из колоды; события:
Dr = {черва}; D2 = {бубна}; D3 = {трефа}; D4 = {пика}.
6) Опыт — бросание игральной кости; события:
Ег = {не менее трех очков};
£2 = {не более трех очков}.
7) Опыт — по каналу связи передаются ^в одинаковых условиях
три сообщения одинаковой длины; события:"
Fx = {ошибка в первом сообщении};
F2 = (ошибка во втором сообщении}; .
F3 = {ошибка в третьем сообщении}.
Ответ: 1) да, 2) нет, 3) в общем случае нет, 4) нет, 5) да, 6) нет,
7) да.
1.4. Относительно каждой из групп событий ответить на
следующие вопросы: образуют ли они полную группу; являются ли
несовместными; являются ли равновозможными; образуют ли группу случаев.
1) Опыт — бросание (правильной) монеты; события:
Аг = {герб}; А2 = {решка}.
2) Опыт — бросание двух монет; события:
В± = {два герба}; В2 = {две решки};
В3 = {один герб^и одна решка}.
3) Опыт — бросание игральной кости; события:
Сг = (1 или 2 очка}; С2 = {2 или 3 очка}; С3 = {3 или 4 очка}; х
С4 = {4 или 5 очков}; Сб =* {5 или 6 очков}.
и
-5
4) Опыт — вынимание наугад одной карты из колоды в 36 листов;
события:
£>i = {туз}; D2 = {король}; D3 = {дама}; D4 = {валет}; D5 =
= {десятка}; D6 = {девятка}; D7 = {восьмерка}; Ds =
{семерка}; D9 = {шестерка}.
5) Опыт — выстрел по мишени; события
Ег = {попадание}; Е2 = {промах}.
6) Опыт — передача (в одинаковых условиях) трех сообщений
равной длины; события:
F± = {искажено первое сообщение};
F2 = {искажено второе сообщение};
F3 = {искажено третье сообщение}.
7) Опыт — эксплуатируются два прибора в течение времени т;
события:
G0 = {ни один прибор не вышел из строя};
Gx = {один прибор вышел из строя, а другой нет};
<32 = {оба прибора вышли из строя}.
Ответ: 1) да, да, да, да; 2) да, да, нет, нет; 3) да, нет, да, нет;
4) да, да, да* да; 5) да, да, нет, нет; 6) нет, нет, да, нет; 7) да, да, нет,
нет.
1.5. Монета бросается до тех пор, пока не появится подряд два
герба или же две решки; после этого бросания прекращаются. Построить
для этого опыта пространство элементарных событий и выделить в
нем подмножество, соответствующее событию Л = {понадобится не
более трех бросаний}. Можно ли здесь найти вероятность события
как отношение числа элементарных событий, благоприятных Л, к
общему числу элементарных событий, и если нет, то почему?
Решение. Элементарные события, образующие множество Q
(герб обозначен буквой «г», решка — «р»): щ = {г, г}; со2 = {р, р};
<»з = {г, Р, р}; Щ = {р, г, г}; со5 = {г, р, г, г}; со6= {р, г, р, р}...;
число этих событий бесконечно (счетно): Q = {(о1у со2, со3, ...}.
Подмножество элементарных событий, благоприятных Л; А = {ы1у со2,
со3, со4}.
Определить вероятность события Л как отношение числа
элементарных событий, благоприятных Л, к общему числу элементарных
событий в данном случае нельзя, так как элементарные события %,
со2, (о3, ... неравновозможны: каждая последующая пара менее
вероятна, чем предыдущая [нахождение Р (Л) — см. задачу 2.19].
1.6. Многогранник, имеющий k граней (k > 3) с номерами 1,2,...
..., k, бросается наугад на плоскость; при этом он падает на ту или
другую 'грань. Построить для этого опыта пространство элементарных
событий и выделить в нем подмножество, соответствующее событию
Л = {многогранник упал на грань, номер которой не превышает
числа k/2).
Решение. Пространство Q состоит из k элементарных событий:
Q = {1, 2, ..., &}, где числа соответствуют номерам граней.
Подмножество Л состоит из элементарных событий: Л ={1,2,...., [kl2]}>
где [k/2] — целая часть, содержащаяся в k/2.
12
1.7. В условиях предыдущей задачи многогранник —
правильный; возможные значения числа граней; k = 4 (тетраэдр); k = 6 (куб);
k = 8 (октаэдр); k = 12 (додекаэдр); & = 20 (икосаэдр). Найти для
каждого из многогранников вероятность события Л.
Решение. Для правильного (симметричного) многогранника
появление каждой грани одинаково вероятно, так что можно
вычислить Р (А) по формуле (1.0.6). Так как число граней всех правильных
многогранников четно, то [k/2] = k/2 и для любого из них Р (А) =
= 1/2.
1.8. В урне а белых и Ь черных шаров. Из урны вынимают наугад
один шар. Найти вероятность того, что этот шар — белый.
Ответ, а/ (а + Ь).
1.9. В урне а белых и Ь черных шаров. Из урны вынимают один шар
и откладывают в сторожу. Этот шар оказался белым. После этого из
урны берут еще один шар. Найти вероятность того, что этот шар тоже
будет белым.
Ответ, (а — \)1{а + 6—1).
1.10. В урне а белых и Ь черных шаров. Из урны вынули один шар
и не глядя отложили в сторону. После этого из урны взяли еще один
шар. Он оказался белым. Найти вероятность того, что первый шар,
отложенный в сторону, тоже белый.
Ответ, {а — \)1 {а + Ь — 1).
1.11. Из урны, содержащей а белых и Ь черных шаров, вынимают
один за другим все шары, кроме одного. Найти вероятность того, что
последний оставшийся в урне шар будет белым.
О т в е т. а/ (а + Ъ).
1.12. Из урны, в которой а белых и Ь черных шаров, вынимают
подряд все находящиеся в ней шары. Найти вероятность того, что
вторым по порядку будет вынут белый шар.
Ответ, а/ (а + 6).
1.13. В урне а белых и Ь черных шаров (а ^ 2). Из урны вынимают
сразу два шара. Найти вероятность того, что оба шара будут белыми.
Решение. Событие А = {два белых шара}. Общее число
случаев
п = Са2+6 = (а+6)(а+6-1)/(Ь2),
где С£= : число сочетаний из k элементов по т.
т\ (k—т)\
Число благоприятных случаев
тА=С\ =а(а— 1)/(1 • 2).
Вероятность события А
Р (А) = тА/п = mAln =a(a—l)/[(a + b) (а+b — 1)].
1.14. В урне а белых и Ь черных шаров (а> 2, Ь ^ 3). Из урны вы
нимают сразу пять шаров. Найти вероятность р того, что два из них
будут белыми, а три черными.
13
Решение. Общее число случаев
„__гь _ (а+Ь)(а+Ь-1) (д+Ь-2)(а+Ь-3) (а+Ь-4)
Число благоприятных случаев
а ° Ь2 Ь2-3
^ГП_^ lQg(g_l)6(6—1) (6—2)
Р п (а + Ь)(а+Ь—\)(а+Ь—2)(а+Ь—3)(а+Ь—4)
1.15. В партии, состоящей из k изделий, имеется / дефектных. Из
партии выбирается для контроля г изделий. Найти вероятность р
того, что из них ровно s изделий будут дефектными.
Ответ. р= C'CkZ't/Ck.
1.16. Игральная кость бросается один раз. Найти вероятности
событий:
А = {четное число очков};
В = (не менее 5 очков};
С = (не более 5 очков}.
' О т в е т: Р (Л) = 1/2; PJB) = 1/3; Р (С) = 5/6.
1.17. В урне а белых и b черных шаров (а ^ 2; Ъ ^ 2). Из урны
вынимают одновременно два шара. Какое событие более вероятно:
А = {шары одного цвета}; В = {шары разных цветов}?
Решение.
Р (Л) = •С* +°1 - а(«_-!)+*(*=!)..
Р(5) =
С»+ь (а + Ь) а+Ь-1)
Са2+6 (в+*)(«+*-1)
Сравнивая числители этих дробей, находим
Р(Л)<Р(В) при а {а— 1) + Ь (Ь — 1)< 2а&,
т: е. (а — б)2 < а + 6;
Р (А) = Р (Б) при (а — Ь)2=а + Ь\
Р (Л) > Р (Я) при (а — ЬУ > а + 6.
1.18. Из ящика, содержащего п перенумерованных изделий, нау-
угад вынимают одно за другим все находящиеся в нем изделия. Найти
вероятность того,что номера вынутых изделийбудутидти по порядку:
Ответ. \1п\
1.19. Тот же ящик, что и в предудущей задаче, но каждое изделие
после вынимания вкладывается обратно и перемешивается с
другими, а его номер записывается. Найти вероятность того, что будет
записана естественная последовательность номеров: 1, 2, ..., п.
'Отвёт.-'1/лп.
1.20. В розыгрыше первенства по баскетболу участвуют 18 команд,
из которых случайным образом формируются две группы по 9 команд
14
в каждой. Среди участников соревнований имеется 5 команд
экстракласса. Найти вероятность следующих событий:
Л = {все команды экстракласса попадут в одну и ту же группу};
В = {две команды экстракласса попадут в одну из групп, а три —
в другую}.
Ответ.
Р(Л)- 2ClCU = ! ; Р(В)-с*2С1з+С|С?з_ 12
С18 34 Cf8 17
1.21. Некто купил карточку Спортлото и отметил в ней 6 из имеюг
щихся 49 номеров, после чего в тираже разыгрываются 6 «выигравших»
номеров из 49. Найти вероятности следующих событий:
Л3 = {верно угаданы 3 выигравших номера из 6};
Л4 — (верно угаданы 4 номера из 6};
Лб = (верно угаданы 5 номеров из 6};
Л6 = {верно угаданы все 6 номеров}.
Решение. Задача эквивалентна выниманию$[шаров из урны, в
которой 6 белых шаров (выигравшие номера) и 49 — 6 = 43 черных
(не выигравшие).
Р (Л3) = S£!i.« 0,01765; Р (Л4) = £Ц!а.« 0,000969;
Р(Лб) = ^^- «0,00001845; Р(Лв) = -!-«0,715-10-7.
1.22. На девяти карточках написаны цифры: 0, 1,2, 3, 4, 5, 6, 7, 8.
Две из них вынимаются наугад и укладываются на стол в порядке
появления, затем читается полученное число, например 07 (семь), 14
(четырнадцать) и т. п. Найти вероятность того, что число будет четным.
Решение. Четность числа определяется его последней цифрой,
которая должна быть четной (нуль — тоже четное число). Искомая
вероятность есть вероятность того, что на втором месте появится одно
из чисел 0, 2, 4, 6, 8, т. е. 5/9.
1.23. На пяти карточках написаны цифры: 1, 2, 3, 4, 5. Две из
них, одна за другой, вынимаются. Найти вероятность того, что число
на второй карточке будет больше, чем на первой.
Решение. Опыт имеет два возможных исхода:
Л = (второе число больше первого};
В = (второе число меньше первого}.
Так как условия опыта симметричны относительно Л и В, то Р (Л) =
-= Р (В) = 1/2.
1.24. В ящике находятся однотипные изделия, изготовленные
разными заводами; из них а изделий изготовлены заводом I, b изделий —
заводом II, с изделий — заводом III. Из ящика вынимают одно за
другим все находящиеся в нем изделия и отмечают места их
изготовления. Найти вероятность того, что при этом изделие завода I
появится раньше, чем изделие завода II.
15
Решение. В условиях задачи наличие или отсутствие в ящике
изделий завода III роли не играет; искомая вероятность равна
вероятности вынуть первым изделие завода I из ящика, где а изделий
завода I и Ъ изделий завода II, т. е. а/ (а + Ь).
1.25. Имеются два ящика, содержащих типовые элементы замены
(ТЭЗ). В первом ящике а исправных ТЭЗ и Ь неисправных; во втором —
с исправных и d неисправных. Из каждого ящика наугад вынимается
по одному ТЭЗ. Найти вероятность того, что оба ТЭЗ будут
исправными.
Решение. Каждый ТЭЗ из первого ящика может
комбинироваться с каждым ТЭЗ из второго; число случаев п = (а + Ь) (с + d).
Число благоприятных случаев т =ас, вероятность события равна
ас/ [(а + Ь) (с + d)l
1.26. В условиях задачи 1.25 найти вероятность того, что вынутые
ТЭЗ будут различными по качеству.
Ответ, (ad + be)/ [(a + b) (с + d)\.
1.27. В тех же условиях найти вероятность того, что оба вынутых
ТЭЗ будут неисправны.
Ответ. bd/[(a + b)(c + d)].
1.28. В ящике имеется k перенумерованных однотипных изделий
с номерами 1, 2, ..., k. Из ящика / раз вынимается наугад по одному
изделию, его номер записывается и изделие кладется обратно в ящик.
Найти вероятность р того, что все записанные номера будут различны.
Решение. Число случаев п = kl. Число благоприятных
случаев равно числу размещений из k элементов по /, т. е. т = k (k — 1)...
... (k — / + 1). Вероятность события
Р п kl kl(k—l)l
1.29. Из пяти букв разрезной азбуки составлено слово «книга».
Ребенок, не умеющий читать, рассыпал эти буквы и затем собрал в
произвольном порядке. Найти вероятность р того, что у него снова
получилось слово «книга».
Ответ. р= 1/5! = 1/120.
1.30. Тот же вопрос, если было составлено слово «ананас».
Решение. Число случаев п =6!; число благоприятных
случаев уже не один, как в задаче 1.29, а т =3! 2!, так как
повторяющиеся буквы «а» и «н» можно произвольным образом переставлять между
собой: р = 3! 2!/6! - 1/60.
1.31. Из полной колоды карт (52 листа, 4 масти) вынимается сразу
несколько карт. Сколько карт нужно вынуть для того, чтобы с
вероятностью, большей чем 0,50, утверждать, что среди них будут карты
одной и той же масти?
Решение. Обозначим А = {наличие среди k вынутых карт не
менее двух одной масти}.
При k = 2: п = Ch\ тА = С?3 • 4; Р (А) = 0,235 < 0,50.
При k = 3: п = Сь32; тА = С?3 • 4 + ChCh • 4; Р (А) =0,602 >
>0,50.
Итак, нужно вынуть к^Ъ карт.
16
1.32. N человек случайным образом рассаживаются за круглым
столом (N > 2). Найти вероятность р того, что два фиксированных
лица А и В окажутся рядом.
Р е ш е н и е. Общее число случаев n = N\\ подсчитываем число
благоприятных случаев т. Двух лиц А и В можно посадить рядом
двумя способами; остальных —(N — 2)! способами; тогда т =
= 2N (N — 2)!; р = 2N (N — 2)UNl = 2/ (N — 1). Эту же задачу
можно решить проще: пусть лицо А садится куда угодно; тогда для В
остается N — 1 место, из них 2 благоприятных; р = 2/ (N — 1).
1.33. Та же задача, но стол прямоугольный, и N человек
рассаживаются случайно вдоль одной из его сторон.
Р е ш е н и е. п = ЛП; благоприятные случаи делятся на две
группы: 1) А сидит с краю; 2) А сидит не с краю. Число первых тх =
= 2 (N — 2)!; число вторых т2 = 2 (N — 2) (N — 2)!; р =(тг +
+ т2)/п = 2 (N — 1) (N — 2)!/ЛМ = 2/N.
1.34. Имеется М операторов и N перенумерованных приборов,
которые они могут обслуживать. Каждый оператор выбирает случайным
образом и с одинаковой вероятностью любой прибор, но с условием,
что ни один прибор не может обслуживаться больше, чем одним
оператором. Найти вероятность того, что будут выбраны для
обслуживания приборы с номерами 1, 2, ..., М.
Решение. Число способов, которыми можно распределить М
операторов по N приборам, равно числу размещений из N элементов
по М: п = N (N — 1) ... (N — М + 1). По условиям задачи все эти
способы равновероятны, т. е. представляют собой группу случаев.
Число благоприятных случаев (при которых обслуживаются только
первые М приборов) равно т = М! Отсюда искомая вероятность
Р= м 1
N(N — 1)... (N—М + \) С%
1.35. В ящике имеется К ТЭЗ, из них Кг элементов 1-го типа, .. .
т
Kt элементов j'-го типа, ..., Кт элементов т-го типа; %Кг = К- Из
ящика выбирают наугад k ТЭЗ. Найти вероятность того, что среди них
будет kx ТЭЗ 1-го типа, ..., kt ТЭЗ i-ro типа, ..., km ТЭЗ m-го типа.
Решение. Общее число случаев п равно числу способов,
какими можно вынуть k ТЭЗ из К- п=Ск. Число благоприятных случаев
т = С^С"к\...Скк1=ПСк\,
1=1
так как k± ТЭЗ первого типа можно выбрать C^t способами, ..., km ТЭЗ
m-готипа—Скт способами, и все эти способы могут комбинироваться
между собой. Искомая вероятность
Р=ПСкк\/с1
t=i
17
1.36. В отделение связи поступило 4 телеграммы; всего имеется
четыре канала связи. Телеграммы случайным образом
распределяются по каналам; каждая телеграмма с одной и той же вероятностью
передается по любому из четырех каналов. Найти вероятность события
А = {на один из каналов попадут три телеграммы, на другой — одна
телеграмма, а два оставшихся канала будут не загружены}.
Решение. Общее число случаев -л=44. Число способов,
какими можно выбрать один канал, на который попадет три телеграммы,
CJ = 4; число способов, какими можно выбрать канал, на который
попадет одна телеграмма, Сз = 3. Число способов, какими можно выбрать
из четырех телеграмм три, чтобы направить их в один канал, С\ = 4,
Общее число благоприятных случаев ша = 4 • 3 • 4.
Р (Л) = тА1п = 4 • 3 • 4/4* = 3/16.
1.37. М телеграмм случайным образом распределяются по N
каналам связи (N > М). Найти вероятность события
А = {на каждый'канал придется не больше одной телеграммы}.
Решение. Общее число случаев NM. Число способов, какими
можно выбрать М каналов из N, чтобы направить на них по одной
телеграмме, равно С#. Число способов, какими можно выбрать из М
телеграмм одну и направить ее в первый из отмеченных каналов,
равно См = М; число способов, какими можно выбрать вторую
телеграмму из оставшихся М.— 1, равно См-\ = М — 1, и т. д. Общее число
благоприятных событию случаев будет ша =М (М — 1) ...1 =М!.
Р(Л) =С#- M\INM.
1.38*. В отделение связи поступило М телеграмм, которые
случайным образом распределяются по N каналам связи. Каналы
перенумерованы. Найти вероятность того, что на 1-й канал попадет ровно
kx телеграмм, на 2-й канал — k2 телеграмм и т. д., на N-й канал —
N
ку телеграмм, причем 2&i = М.
Решение. Число случаев п =NM. Находим число
благоприятных случаев т. Число способов, какими можно выбрать из М телеграмм
kit равно Скм\' число способов, какими можно из оставшихся М — kt
телеграмм выбрать &2, равно См-kt и т. д; Число способов, какими
можно из М — (^ + ... + ku-x) = кы телеграмм выбрать &#, равно
Ck =1. Все эти числа нужно перемножить.
гп = СмСа1—kf» См-I^-i-... +%_i)*l —
Ml (М —kt)\ [M—(kt + kt+...+kN-2)]l ^
~~ kx\(M— kj\ k2\[M—(^+£2)]! "' kN-~llkNl
_ Ml Ml
~ kx\k2\... kN\ ~~ N
П kb\
Р(Л) = т/м = Лп/ (nm ЙаД
18
1.39*. В условиях задачи 1.37 найти вероятность того, что из N
каналов] будет /0 таких, на которые не попадет ни одна телеграмма,
/х — таких, на которые попадет ровно одна телеграмма, и т.д.;
1М таких, на которые попадут все М телеграмм: /0 + 1г + ... +
+ lM = N; О • /0 + 1 • к + ... + М1М = Af.
Решение. Общее число случаев п = Л/м. Чтобы найти число
благоприятных случаев т, нужно перемножить число способов,
какими можно выбрать каналы, и число способов, какими можно выбрать
телеграммы. Число способов, какими можно выбрать каналы, равно
/ м
ЛМ/(«У»./м!) = ЛП/ П V.
/ *=о
Найдем число способов, какими можно выбрать телеграммы. Они
распадаются на группы: начальная группа (по 0 телеграмм) пустая;
первая содержит 1± телеграмм; вообще k-я —klk телеграмм (k =1,2,
..., М). Число способов, какими можно выбрать группы телеграмм,
равно
В =- т (139 1)
Теперь определим число способов, какими можно выбрать
телеграммы внутри k-й группы так, чтобы на каждый канал пришлось по k
телеграмм. Это число способов равно
(«Л)1/(И*^!) = (Ык)Щк\) \
lh раз
а число способов, какими можно выбрать все телеграммы для всех
групп, равно произведению таких чисел для разных k:
ПЩ-* (1-39.2)
Перемножая (1.39.1) и (1.39.2), получаем число способов, какими
можно выбрать телеграммы:
' м
П (Wft)!
м м ~~~ м
П (kik)\ П (*!)'* П (*!)**
£=1 k=l k=l
Умножая это на число способов, какими можно выбрать каналы,
находим число благоприятных случаев
N\ Ml
т==
м м j
П /,! П (*!)'*
/«=0 *~1
19
Отсюда вероятность интересующего нас события
Р(Л):
№М\
м м
NM П h\ П (*!) '*
/=0 *=1
(1.39.3)
1.40. На круглом экране радиолокатора радиуса г имеется
точечное изображение объекта М (рис. 1.40), занимающее случайное
положение в пределах экрана, причем ни одна область
в пределах экрана не имеет преимуществ перед
другой (изображение объекта «наугад бросается»
на экран). Рассматривается событие Л,
состоящее в том, что расстояние р от точки М до
центра экрана будет меньше, чем г/2 : А = {р < г/2}.
Найти вероятность этого события.
Решение. Пространство Q элементарных
событий — внутренность круга радиуса г. Область
А заштрихована на рис. 1.40.
Р(А) = ^=.пгЩ - '
Рис. 1.40
яг2
1.41. Имеется магнитофонная лента длины L =200 м, на обеих
сторонах которой записаны сообщения; на одной стороне сообщение
длины /х = 30 м, на другой — длины /2 = 50 м; местоположение
записей неизвестно. В связи с повреждением ленты нам пришлось удалить
ее участок длины 10 = 10 м, начинающийся на расстоянии 80 м от
начала ленты. Найти вероятности следующих событий:
А = {ни та, ни другая записи не повреждены};
В = {первая запись повреждена, вторая — нет};
С = {вторая запись повреждена, первая — нет};
D = {обе записи повреждены}.
Повреждена
1-я запись
90100
Рис. 1.41
20
Решение.Из того, что положение у
записей совершенно неизвестно, делаем д_г
вывод, что любое положение начала
каждой из них, при которое вся запись
умещается на ленте, столь же
правдоподобно, как любое другое. Абсциссу
начала первой записи обозначим х9 второй т
у. Пространство элементарных событий —
прямоугольник длины L — 1г = 170 м,
высоты L — /2 = 150 м (рис. 1.41). На 0 т /-т ""
рис. 1.41 разными видами штриховки от- . „
мечены области, соответствующие повреж- ис' '
дению первой и второй записей, буквами
Л, В, С, D — области, s соответствующие каждому из событий Л,
J5, С, D (все эти области, кроме D, состоят из частей).
SQ = 170 • 150 = 25 500 м2;
SA = 30 • 60 + 80 • 60 + 30 • 50 + 80 . 50 = 12 100 м2;
SB = 60 • 60 + 60 • 50 = 6600 м2;
Sc = 30 • 40 + 80 • 40 = 4400 м2;
SD = 60 • 40 = 2400 м2.
Р(Л) =0,474; Р(5) =0,259;
Р(С) =0,173; P(D) =0,094.
1.42. По радиоканалу в течение промежутка времени (0; 1)
передаются два сигнала длительностью т < 1/2; каждый из них с
одинаковой возможностью начинается в любой момент интервала (0; 1 —т).
Если сигналы перекроют друг друга хотя бы частично, оба они
искажаются и приняты быть не могут. Найти вероятность того, что сигналы
будут приняты без искажений.
Решение. Обозначим х момент начала первого сигнала, у —
второго. Пространство элементарных событий показано на рис. 1.42.
Заштрихованные области Л соответствуют событию:
Л = {сигналы не искажены} = {\х — #|<т}.
Р (Л) = SA/SQ = (1 — 2т)2/ (1 — т)2.
1.43. Имеются две параллельные линии телефонной связи длины
I (рис. 1.43, а), расстояние между которыми d< /. Известно, что на
каждой из линий где-то есть разрыв (неизвестно, в каком месте).
Найти вероятность того, что расстояние R между точками разрыва будет
не больше a(d<a< V/2 + d2).
Р е ш е н и е. Абсциссу первой точки разрыва обозначим х> второй
У\ R =У\х — у\2 + d2; событие, о котором идет речь, Л =
= {\х — у\2 + d2 < а2} = {\х — у\<: Va2 — d2f. Пространство
21
\У
\/
р^
\о х
1
л
\
■^ 1
У
а)
X
Уа2-а*
Рис. 1.43
элементарных событий — квадрат со стороной /; SQ = /2. Область Л
заштрихована на рис. 1.43, б.
SA = 2lV^i:rd2 + a2—cP;
cP—d*
1.44. Стержень длины 1 произвольным образом разламывается на
три части х, у, z (рис. 1.44, а). Найти вероятность того, что из
получившихся частей можно составить треугольник.
Ух У\
Рис. 1.44
Решение. Элементарное'событие о характеризуется^двумя
параметрами: х и у [так как z = 1 — (х + у)]. Будем изображать это
событие точкой на плоскости хОу (рис. 1.44, б). На величины х, у
наложены условия: х > 0, у > 0; х + у <. 1; пространство элементарных
событий есть внутренняя часть прямоугольного треугольника с
катетами, равными единице; Sq = 1/2. Условие Л, чтобы из отрезков xt
у у 1 — (х + у) можно^было составить: треугольник, сводится к двум
следующим: 1)|сумма1любых двух сторон^больше третьей; 2) разность
любых двух сторон меньше третьей. Этому условию соответствует
треугольная область Л (рис/1.44, в) с'площадью Sa== (1/2) (1/4) = 1/8;
Р (Л) — SVSe — 1/4. *
1.45. Задача Бюффона. Плоскость разграфлена параллельными
прямыми на расстоянии L друг от друга^рис. 1.45, а). На плоскость
$2
1 L ^
L
l/
L *|
a)
наугад бросается игла (отрезок) длины I <. L. Найти вероятность
того, что игла пересечет какую-нибудь&из прямых.
Решение. Будем характеризовать исход опыта (положение
иглы) двумя числами: абсциссой х центра иглы относительно ближайшей
прямой слева и углом ф, который составляет игла с направлением
прямых (рис. 1.45, б). Тот факт,^что игла бросается на плоскость наугад,
будем понимать так, что |все значения х и ф одинаково возможны.
Очевидно, можно^(не теряя общности) ограничить возможные
значения х участком от 0 [до L/2, <р*— от (Удо я/2, а возможность
пересечения рассматривать только для одной^из прямых (ближайшей левой).
Пространство элементарных [событий^ — прямоугольникТсо
сторонами L/2 и я/2д(рис. 1.45, в); Sq = LnK. Игла пересечет прямую,
если абсцисса х ее центра будет меньше, чем [ {112) sin ф; интересующее
нас событие f А = {х < {112) sin ф}. Область А заштрихована на
рис. 1.45, ft; площадь ее
О
Примечание. Эта формула, полученная Бюффоном еще в XVIII в.,
неоднократно подвергалась экспериментальной проверке, для чего подсчитыва-
лась частота пересечений в длинной серии бросаний. С помощью этой формулы
производилась даже приближенная оценка числа я и были получены вполне
удовлетворительные результаты.
ГЛАВА 2
АЛГЕБРА .СОБЫТИИ. ПРАВИЛА СЛОЖЕНИЯ
И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
2.0. Основными в теории вероятностей являются не прямые, а^косвенные
методы вычисления вероятностей, когда вероятности интересующих нас
событий выражаются через вероятности других{событий, с ними связанных. Для
этого, прежде всего, нужно Гуметь выражать интересующие нас события "черезч
другие. Этим целям служит'так называемая алгебра событий. Для событий
."вводятся понятия «сумма событий», «произведение ^событий» и "некоторые тдругие,
а также правила действий с событиями. Заметим, что все эти понятия вводятся
23
только тогда, когда события, о которых идет речь, представляют собой
подмножества одного и того же пространства элементарных событий Q.
Так как события в нашем теоретико-множественном изложении
представляют собой множества, то действия с ними (сложение, умножение) определяются
так же, как соответствующие действия с множествами (см. гл. 1).
Все же повторим некоторые определения и дадим им геометрическую
интерпретацию. Пространство элементарных событий мы будем изображать
прямоугольником, а события — частями этого прямоугольника (рис. 2.0.1). Суммой Л+
+ В двух событий А и В называется событие, состоящее в том, что произойдет
хотя бы одно из этих событий (заштрихованная область на рис. 2.0.1). Очевидно,
сумма двух событий представляет собой объединение (сумму) соответствующих
множеств. Аналогично суммой нескольких событий Аъ Л2, ..., Ап называется
п
событие S^i = Лх + Л2 + ...+ Ап, состоящее в выполнении хотя бы одного
i=i
оо
из них. Суммироваться может и бесконечное (счетное) число событий: 2 At ~
=А1 + А2+... + Лп+...
Рис. 2.0.1 Рис. 2.0.2
Произведением А • В двух событий А и В называется событие, состоящее в
совместном выполнении того и другого события (пересечение соответствующих
множеств, рис. 2.0.2). Произведением нескольких событий Аъ Л2, ..., Ап на-
п
зывается событие П At = Аг Л2 ... Ап, состоящее в совместном выполнении
i=l
всех этих событий (пересечение соответствующих множеств). Перемножаться
оо
может и бесконечное (счетное) число событий: П Л$ — АгА2 ... Ап ...
Из определения суммы и произведения событий следует, что
А + А = А; А • А = А; А + Q = Q; А • Q = Л; А + 0 = Л;
Л • 0= 0.
Если ЛСВ, тоЛ+'В=5; Л • В = Л.
Операции сложения и умножения событий обладают рядом свойств,
присущих обычным сложению и умножению.
1. Переместительное свойство:
А + В = В + А;А-В=В-А.
2. Сочетательное свойство:
(Л + В ) + С = Л + (В + С); (АВ) С=А (BQ.
3. Распределительное свойство:
А(В + С) = АВ+АС.
Все эти свойства вытекают из того, что события являются множествами (см. гл. 1).
Противоположным событием для события Л (или егр_дополнением)
называется событие Л, состоящее в непоявлении события Л : Л = {Л не появилось}*
24
Изображение противоположного события дано на рис. 2.0.3. Область Л
дополняет А до полного пространства Q.
Из определения противоположного события следует, что
(Л) = Л; "Q = 0; 0 = Q.
/ ___ ____
Легко убедиться (рис. 2.0.4), что если В Q Л, то A Q В. Также легко убедиться
(рис. 2.0.5) в следующих свойствах противоположных событий:
А+В = А-В; 17ё"=Л+5.
Рис. 2.0.3 Рис. 2.0.4
Правила алгебры событий позволяют, комбинируя между собой различные
простые события, образовывать другие, более сложные.
Вероятности сложных событий можно вычислять с помощью вероятностей
других, более простых, пользуясь двумя основными правилами теории
вероятностей: 1) правилом сложения вероятностей и 2) правилом умножения
вероятностей. Эти правила часто называют основными теоремами теории вероятностей.
На самом деле они являются теоремами только для схемы случаев, а для
опытов, не сводящихся к схеме случаев, вводятся аксиоматически.
1. Правило сложения вероятностей. Вероятность суммы двух несовместных
событий равна сумме вероятностей этих событий, т. е. если Л • В = 0, то
Р (Л + В) = Р (Л) *+ Р (В). (2.0.1)
Это правило было введено аксиоматически в гл. 1 (аксиома II).
Правило сложения вероятностей легко обобщается на случай
произвольного числа п несовместных событий: если А% • Aj = 0 при i Ф /, то
P(s^) = 2p(^)- (2-°-2>
Правило сложения обобщается и на случай бесконечного (счетного) числа
событий: если А% • Aj = 0 при i Ф /, то
= 2Р(Л*) (2-0-3)
(см. аксиому III гл. 1).
Из правила сложения вероятностей вытекает, что если события А±, Л2, ...,
Лп несовместны и образуют полную группу, то сумма их вероятностей равна
единице; т. е. если
п
2 Ai = &> Ai-Aj = 0 при 1ф]\
25
ч!/'
то
SP(i*l) = l. (2.0.4)
В частности, так как два противоположных события Л и Л несовместны и
образуют полную группу, то сумма вероятностей противоположных событий равна
единице:
Р(Л) + Р(Л) = 1. (2.0.5)
Чтобы сформулировать правило умножения вероятностей, надо ввести
понятие условной вероятности. Условной вероятностью события А при наличии
события В [обозначается Р (А \ В)] называется вероятность события Л,
вычисленная при условии, что событие В произошло.
Рис. 2.0.5 Рис. 2.0.6
Условие, состоящее в том, что событие В произошло, равносильно изменению
условий опыта, когда из всех элементарных событий остаются только те,
которые благоприятны событию В, а все остальные отбрасываются. Из этого следует,
что вместо пространства элементарных событий Q рассматривается новое
пространство йв, соответствующее событию В (рис. 2.0.6). Область А В,
соответствующая пересечению А и В, благоприятна событию А при наличии события В.
2. Правило умножения вероятностей. Вероятность произведения двух
событий А и В равна вероятности одного из них (например, Л), умноженной на
условную вероятность другого при наличии первого:
Р (АВ) = Р (Л) • Р (В | Л), (2.0.6)
или, если в качестве первого события взять В,
Р (АВ) = Р (В) • Р (Л | В). (2.0.7)
Правило умножения вероятностей обобщается на произвольное число событий:
Р 0М2 .- An) = Р (Лг) • Р (Л2 \Аг) • Р(Л3 | АгА2) ... Р (Лп | АгА2 ...Л^).
(2.0.8)
Из (2.0.6) вытекает следующее выражение для условной вероятности:
Р (В | Л) = Р (ЛВ)/Р (Л), (2.0.9)
т. е. условная вероятность одного события при наличии другого равна
вероятности произведения двух событий, деленной на вероятность того из них, которое
предполагается выполненным.
Аналогично формуле^(2.0.9) можно написать
Р (Л | В) = Р (Л В) /Р (В). (2.0.10)
Два события А и В называются независимыми, если появление одного из
них не меняет вероятности появления другого:
Р (Л | В) = Р (Л), (2.0.11)
26
или, что равносильно,
Р (В I A) = P (В). (2.0.12)
Для двух независимых событий правило умножения вероятностей
принимает вид
P (ЛВ) = Р (А) • Р (В), (2.0.13)
т. е. вероятность произведения двух независимых событий равна произведению
вероятностей этих событий.
, , Несколько событий называются независимыми в совокупности (или просто
независимыми), если появление любого числа из них не меняет вероятностей
остальных событий. Для нескольких независимых событий правило умножения
(2.0.8) принимает вид
Р (АгАг ...An) = Р (Аг) • Р (А2) ... Р (Ап), (2.0.14)
т. е. вероятность произведения независимых событий равна произведению
вероятностей этих событий. !^- м- * *
Несколько опытов называются независимыми, если вероятность того или
иного исхода каждого из них не зависит от того, какие исходы имели другие
опыты.
Следствием правил сложения и умножения вероятностей является теорема
о повторении опытов, состоящая в следующем. Если производится п независимых
опытов, в каждом из которых событие А появляется с вероятностью р, то
вероятность того, что в данной серии опытов событие А появится ровно т раз,
выражается формулой
Рт,п=С2рт(\-р)п-ту (2.0.15)
или, обозначая 1 — р = q,
Pm,n = CZpmqn-m. (2.0.16)
Вероятность того, что в серии из п независимых опытов событие А появится
не менее т раз, выражается формулой
Rm,n=% CnPk4n-k> (2.0.17)
k=l
или же
m—1
Rm.n = l- S cJpV"*« (2-0.18)
fe=0
Из двух формул (2.0.17) и (2.0.18) выбирают ту, которая содержит меньше членов.
ЗАДАЧИ И УПРАЖНЕНИЯ
2.1. Может ли сумма двух событий А и В совпадать с их
произведением?
Ответ. Да, может, если событие А ^эквивалентно событию В
(A s В и В ^ А). Например, если искажение сообщения,
передаваемого по каналу связи, может быть вызвано только наличием помех
на участке времени, занятом сообщением, и непременно происходит
при их наличии, то события
А = {сообщение искажено},
В а= {на участке времени, занятом сообщением, имелись помехи}
эквивалентны: А =£; А +В =Л *= В\ АВ = А = £.
27
2.2. Доказать, что если два события А и В совместны, то
р (А + В) = Р (А) + Р (В) - Р (АВ). (2.2.1)
Решение. Представим событие А + В как сумму трех
несовместных событий: АВ\А, но не В); АВ (В, но не А) и АВ (и А и В) (см.
рис. 2.2): _ _
А + В =АВ + АВ + АВ.
Выражаем события А и В:
А =АВ + ЛВ"; В =АВ + АВ.
Рис. 2.2
Рис. 2.3
Пользуясь правилом сложения вероятностей, находим:
Р (Л + В) = Р (АВ)_ + Р (ТВ) + Р (АВ); (2.2.2)
р (Л) = Р (АВ) + Р (АВ),
Р (В) = Р (АВ) + Р (ЛВ).
Складывая два последних выражения, получаем
Р (А) + Р (В) - Р (АВ) + Р (ТВ) + 2Р (АВ).
Вычитая отсюда (2.2.2), получаем
Р (А) + Р (В) = Р (А + В) + Р (ЛВ),
откуда и следует (2.2.1). Из (2.2.1) следует, что всегда
Р (Л + В)< Р (А) + Р (В),
и знак равенства достигается только при несовместных событиях.
2.3. Написать выражение для вероятности суммы трех совместных
событий.
Решение. Из рис. 2.3 получаем
Р (Л + В + С) = Р (А) + Р (В) + Р (С) - Р (АВ) - Р (АС) —
- Р (ВС) + Р (ABC).
2.4. Опыт состоит в бросании двух монет. Рассматриваются
следующие события:
Л = {герб на первой монете}; В = {цифра на первой монете};
С = {герб на второй монете}; £>'= {цифра на второй монете}; Е =
28
= {хотя бы один герб}; F = {хотя бы одна цифра}; G = {один герб
и одна цифра}; Н = {ни одного герба}; К = {два герба}.
Определить, каким событиям этого списка равносильны следующие
события: 1) А +С; 2) ЛС; 3) EF; 4) G + Е; 5) GE; 6) BD; 7) Е + К.
Ответ. 1) А + С = Е; 2) АС = /С; 3) £f = G; 4) G + Е =
= Е\ 5) G£ = G; 6) BD = Я; 7) £ + К = Я.
2.5. По каналу связи передаются последовательно три сообщения;
каждое из них может быть передано правильно или искажено.
Рассматриваются события:
At = {i-e сообщение передано правильно};
Ai = {i-e сообщение искажено} (i =1, 2, 3).
Выразить в виде сумм, произведений или сумм произведений событий
Ai9 ~A% следующие события:
А = {все три сообщения переданы правильно};
В = {все три сообщения искажены};
С = {хотя бы одно сообщение передано правильно};
D = {хотя бы одно сообщение искажено};
Е = {не менее двух сообщений переданы правильно};
F = {не более одного сообщения передано правильно};
G = {первое правильно переданное сообщение — третье по
порядку}.
Ответ^ А ==АхА2Аз1 В =1А1А2Аз> С =Лх^2Лз_+
"г AiA%A3 + Л1Л2Л3 + АгА2Аа + Aj_A2A3 + АгА2А3 + АХА
гЛ з>
D =_АгА2А3 + AiA2A3 + АгА2А3 + АгА2А_3 + А1А2А3 +
~г AiA2A3 + Л1Л2Л3; Б = А-±А2А3 + Л1Л2Л3 + ЛхЛ2Лз +
+ ЛхЛ2Лз; F = А±А2А3 + Ax/^Aj + АгА2А3 + АХА2А3\ G ==
= А\А2А 3.
2.6. Проводится наблюдение за группой, состоящей из четырех
однородных объектов. Каждый из них за время наблюдения может
быть обнаружен или не обнаружен. Рассматриваются события:
Л = {обнаружен ровно один из четырех объектов};
В = {обнаружен хотя бы один объект};
С = {обнаружено не менее двух объектов};
D = {обнаружено ровно два объекта};
Е = {обнаружено ровно три объекта};
F = {обнаружено все четыре объекта}.
Указать, в чем состоят события: 1) Л + В\ 2) АВ\ 3) В + С; 4) ВС;
5) D + Е + F; 6) BF. Совпадают ли события BF и CF? Совпадают
ли события ВС и D?
О т в е т. 1) Л + В = В; 2) АВ = Л; 3) В + С = В; 4) ВС = С;
5) D + Е + F = С; 6) BF = F. События ВС и CF совпадают; ВС и
D не совпадают.
2.7. Ниже указаны опыты и события, которые в них могут
произойти. Назвать противоположные для всех этих событий.
ч Передаются два сообщения по каналу связи: событие Л = {оба
сообщения переданы правильно}.
29
2) Вынимается один шар из урны» [в
которой два белых, три черных и четыре
красных шара; событие В = {появление
белого шара}.
3) Передаются пять сообщений;
событие С = {не менее трех сообщений
переданы правильно}.
4) Производятся п выстрелов" по
мишени; событиеD = {хотя бы одно попадание}.
Рис- 28 5) Производится g профилактический
осмотр технического устройства,
состоящего из k узлов; каждый узел в результате осмотра может быть либо
сразу налажен, либо отправлен в ремонт. Событие Е =i {ни один
узел не придется ремонтировать},
6) Двое игроков играют в шахматы; событие F = {выигрыш белых}.
Ответ. 1) Л = {хотя бы одно из сообщений искажено}; 2) В =
— {появление черного или красного шара}; 3) С = {не более двух
сообщений переданы правильно}; 4) D = {ни одного попадания};
5) Е = {хотя бы один узел придется ремонтировать}; 6) F =
{выигрыш черных или ничья}.
2.8. Событие В есть частный случай события А: В ^ Л, т. е. из
того, что произошло событие В следует, что событие А произошло.
Следует ли из В9 что А произошло?
Ответ. Нет, не следует. Например, опыт состоит в передаче двух
сообщений; событие А = {хотя бы одно сообщение искажено};
событие В = {оба сообщения искажены}. Если произошло событие В =
= {искажено менее двух сообщений}, то из него еще не следует, что
не искажено ни одного (событие Л). Напротив, из Л следует В (Л ^ £).
На рис. 2.8 показаны события Л и 5, причем В s А9 а также
противоположные им события А (вертикальная штриховка) и В
(горизонтальная штриховка). Непосредственно видно, что Л ^ В.
2.9. Если событие В представляет собой частный случай события
Л (В ^ Л), зависимы эти события или нет?
Ответ. Зависимы, если Р (Л) ф\> так как Р (А/В) = 1.
2.10. Зависимы или независимы: 1) несовместные события; 2)
события, образующие полную группу; 3) равновозможные события?
Ответ. 1) Зависимы, так как появление любого из них
обращает в нуль вероятности всех остальных; 2) зависимы, так как
непоявление всех, кроме одного, обращает в единицу вероятность
последнего; 3) могут быть как зависимы, так и независимы.
2.11. Опыт состоит в последовательном бросании двух монет.
Рассматриваются события:
Л = {герб на первой монете}; D = {хотя бы один герб}; Е =
= {хотя бы одна цифра}; F = {герб на второй монете}. Определить,
зависимы или независимы пары событий: 1) Л и £; 2) Л и F\ 3) D и Е\
4) D и F. Определить условные и безусловные вероятности событий в
каждой паре.
411
1II/
I
\\\\к
Li 11 I
им
TMlJi
ху^ \
у /1
{-&-( R *
г А 1 В
Ул
Л"
К., i-f|
(
/
11
30
Ответ
1) Р (Е) =3/4, Р (Е\А) = 1/2, события зависимы;
2) Р7(Л) = 1/2, Р (A \F) = 1/2, события независимы;
3) Р (D) =3/4, P(D\E) =2/3, события зависимы;
4)_PJD) =3/4, Р (D\F) =1, события зависимы.
2.12. В урне а белых, и Ъ черных шаров. Из урны вынимают
(одновременно или последовательно) два шара. Найти вероятность того,
что оба шара будут белыми*).
О т в е т. По правилу умножения вероятностей
Р {оба шара белые} = Р {66} = —- ^=1— ,
а+Ь а+Ь—1
2.13. В урне а белых и Ь черных шаров. Из урны вынимается один
шар, отмечается его цвет и шар возвращается в урну. После этого из
урны берется еще один.шар. Найти вероятность того, что оба вынутые
шара" будут белыми.
L Отвеет, [а/ (а + б)]2.
2.14. *В урне а белых и Ь черных шаров. Из урны вынимаются ера*
зу два шара. Найти вероятность того, что эти шары будут разных
цветов.
Решение. Событие может появиться в двух несовместных
вариантах: {бч} или {чб}; по правилам сложения и умножения
г» tet i а\ а b I Ь а 2аЬ
Р{бч+чб} = = - ♦
1 ' а+Ь а+Ь—l а+Ь а + Ь—1 (а+Ь) (а+Ь— 1)
2.15. Та же задача, но шары вынимаются поселедовательно и
после вынимания первый шар возвращается в урну.
Ответ. 2аЫь(а + bf.%
2.16. В урне а белых'и Ь черных шаров. Из урны в случайном
порядке, один за другим, вынимают все находящиеся в ней шары. Найти
вероятность того,1 что вторым по порядку будет вынут белый шар.
Решение. Вероятность события может быть найдена
непосредственно (см. задачу 1.12). Тот же результат может быть найден и по
правилам сложения и умножения:
Р{бб+чб}=-^ ^=J_ + -J « = _^ ,
1 ' а+Ь а+Ь— 1 а + Ь а+Ь—1 а+Ь
2.17. В урне а белых, Ъ черных и с красных шаров. Три из них вы-
нимаются7наугад/Найти вероятность того, что по крайнейjviepe два
из них будут одноцветными.
Решение. Чтобы найти вероятность события — по крайней
мере два шара будут одноцветными, перейдем к противоположному А а=
= {все шары разных цветов}.
Р(Л)=Р{бчк+бкч + кчб+...}==
6 комбинаций
*) Данная задача, как и~ряд~других в этой'главе, может быть решена'и с
помощью непосредственного подсчета числа случаев; здесь требуется решить их
с помощью правил сложения или умножения.
31
n U О С
"" а+Ь+с а+Ь+с—1 а + Ь+с—2
Отсюда
6abc
Р(Л)=1— Р(Л)=1-
(а+Ь+с)(а+Ь+с—I) (а+Ь+с—2)
2.18. Монету бросают до тех пор, пока не появятся подряд два
герба или две решки (см. задачу 1.5). Найти вероятность события Л =
= {понадобится не более трех бросаний}.
Решение. Обозначая «г» — герб, «р» — решка, запишем А
виде Л = {гг} + {рр} + {грр} + {ргг}. По правилам сложения и
умножения
Р (Л) = Р {гг}+Р {рр} + Р {грр} + Р {ргг} =
= 1/2-1/2+1/2-1/2 + 1/2-1/2-1/2 + 1/2-1/2-1/2 = 3/4.
2.19. В шкафу находятся девять однотипных приборов. В начале
опыта все они новые (ни разу не бывшие в эксплуатации)". Для
временной эксплуатации берут наугад три прибора; после эксплуатации их
возвращают в шкаф. На вид прибор, бывший в эксплуатации, не
отличается от нового. Найти вероятность события
А = {после трехкратного выбора и эксплуатации не останется
новых приборов}.
Решение. Событие Л может произойти одним-единственным
способом: и первый раз, и второй, и третий из шкафа будут взяты
новые приборы. Первый раз это обеспечено, поэтому
2.20. Условия задачи 2.19 изменены следующим образом: в
шкафу находятся N — 1М приборов; для временной эксплуатации берут
наугад М приборов. Найти вероятность р того, что после /-кратного
повторения такой процедуры в шкафу не останется новых приборов.
Ответ. (N—M)\
[N(N— l)... (N—M+l)]*-1
2.21. В шкафу стоят п новых приборов; k из них выбирается нау-
угад и в течение некоторого времени эксплуатируется {k ^Ln/2). После
этого приборы возвращаются в шкаф. Затем' снова выбираются
наугад k приборов. Найти вероятность р того, что все эти к приборов
будут новыми.
Ответ. р= —— = -^ '-l— .
n n — \ n— k + \ n\(n—2k)\
2.22. Прибор состоит из четырех узлов — первого, второго,
третьего и четвертого, которые за время т работы прибора могут
независимо друг от друга выходить из строя. Надежность (вероятность
безотказной работы) г'-го узла равна pt; вероятность отказа qt =1 —р%
(i =1, 2, 3, 4). Найти вероятности следующих событий:
32
A =, {все узлы работают безотказно};
В = (пер вый узел отказал, остальные нет};
С ^ {один из узлов отказал, другие нет};
D = {отказало ровно два узла из четырех};
Е *= {отказало не менее двух узлов};
jF = {отказал хотя бы один узел}.
Ответ. Р (А) = pip2p3p4; Р (В) = <7iP2/W> P (О = ЯгРъРзР* +
+ РхЯгРъРь + PiP2<73p4 + Р1Р2Р3&; Р (D) = ЦхЦъРъРь + РхРъЧШ +
+ РхЧгР&ь + <71р2<7зр4 + р1<72<7зР4 + ЦхРъР&ь Р(£) = Р (О) +
+ <М2<7зр4 + <7К72Рз<74 + ЯхРъЯЯь + РхЫгЧь + ЧхЯгЯ&б р (F) =
= 1-Р(Л). ,
2.23. На железнодорожную сортировочную станцию поступает
состав из k вагонов, направляемых в различные адреса; в адрес Аг
направляются kx вагонов, в адрес Л2 —k2 вагонов, в адрес А 3 — k3 ва-
гонов (кг + k2 + k3 = k). Вагоны в составе занимают то или другое
положение независимо друг от друга; все места в составе для любого
вагона равновероятны. Найти вероятность того, что все вагоны,
направляемые в один и тот же адрес, будут стоять рядом.
Ответ. Событие В, о котором идет речь, может появиться в
шести вариантах (число перестановок из трех элементов Р3 =6).
Находим вероятность одного из этих вариантов.
С = {сначала идут все kt вагонов, направляемых в Alt затем k%
вагонов — в Л2, затем k3 вагонов — в А3).
P(Q =
ki ki — 1 1 k2 k2 — 1
k k — \ k—kx + Xk—^k—ki — X
l;
J k3 k3—\
k—k\— &a 4*1 k—ki—&2 k—ki—&2 — 1
P(B), = 6P(C).
2.24. В ящике находятся однотипные изделия; среди них а изделий
завода I и & изделий завода II. Выбирается наугад 2k изделий (2k < a,
2k < &). Найти вероятность того, что среди выбранных изделий будет
больше изделий первого, чем второго завода.
Решение. Данную задачу проще решить, комбинируя метод
непосредственного подсчета вероятностей с правилом сложения.
Событие А = {больше изделий завода I, чем завода И} можно
представить в виде суммы
2k
A^Ak+x + Ak+2 + ... + A2k= 2 Аь
где At = {появление / изделий завода I}.
Непосредственным подсчетом находим
Ы C^k—l 2k ri r2k—i
Р(А1) = -Щ , откуда Р(Л)= 2
r2k J x ' jUI r2k
2 За к. 1040
33
2.25. В партии, состоящей из N изделий, имеется М дефектных.
Из партии выбирается для контроля п изделий. Если среди
контрольных окажется более'т дефектных, бракуется вся партия. Найти
вероятность того, что'партия будет забракована.
Решение. Событие Л = {партия забракована} можно
представить в виде суммы
Л=Лт+1 + Лт+2+...+Лт = ^ ЛЬ
где At = {среди контрольных изделий i дефектных}.
P(At)= См°»-М ;Р(Л)= У м N~M .
2.26. В ящике имеются однотипные изделия различных сортов;
среди них а изделий со знаком качества, Ь изделий первого сорта и с
изделий второго сорта (а ^ 4, Ь ^ 4, с ^ 4). Из ящика выбирают
одновременно и наугад четыре изделия, не обращая внимания на их ко-
чество. Рассматриваются события:
А = {среди выбранных изделий хотя бы одно со знаком качества};
В = {среди выбранных изделий хотя бы одно второго сорта}.
Найти вероятность события С t= А + В.
Решение. Переходя к противоположному событию С={нет
ни Л, ни В} = {все изделия первого сорта}, имеем
^ '~~а+Ь + с а + Ь+с—1 а+Ь+с—2 а+Ь+с—3 '
откуда Р (С) = 1 — Р (С).
2.27. При одном цикле обзора радиолокационной станции,
следящей за космическим объектом, объект обнаруживается с вероятностью
р. Обнаружение объекта в каждом цикле происходит независимо от
других . Найти вероятность того, что при п циклах объект будет
обнаружен.
Ответ, 1 — (1 — р)п.
2.28. Имеется т радиолокационных станций, каждая из которых
за один цикл обзора обнаруживает объект с вероятностью р
(независимо от других циклов и от других станций). За время Т каждая
станция успевает сделать п циклов. Найти вероятность следующих
событий:
А = {объект будет обнаружен хотя бы одной из станций};
В.= {объект будет обнаружен каждой из станций}.
Ответ. Р (Л) = 1 — (1 — р)™; Р (В) = [1 — (1 — р)«]«
2.29. Имеется группа из k космических объектов, каждой из
которых независимо от других обнаруживается радиолокационной
станцией с вероятностью р. За группой объектов ведут наблюдение
независимо друг от друга m радиолокационных станций. Найти
вероятность того, что не все объекты, входящие в группу, будут обнаружены.
Решение. Переходим к противоположному событию Л = {все
объекты будут обнаружены}:
34
р (л) = ti - (1 - p)™\K P (A) = 1 - ti - (i - pH*.
2.30. Над изготовлением изделия работают последовательно k
рабочих; качество изделия при передаче следующему рабочему не
проверяется. Первый рабочий допускает брак с вероятностью ри второй —
с вероятностью р$, и т. д. Найти вероятность того, что при
изготовлении изделия будет допущен брак.
k
Ответ. 1—П О— Pi)>
i=\
2.31. В лотерее п билетов; из которых / выигрышных. Некто
покупает k билетов. Определить вероятность того, что он выиграет хотя
бы на один билет.
Ответ.
« _ ft — / к— / — 1 ft—/ —k + l == j _ (ft—/)1 (ft—fc)!
ft n—1 "" ft—& + 1 n! (ft—/—k)\
2.32. Два шарика разбрасываются случайно и независимо друг от
друга по четырем ячейкам, расположенным одна за другой по прямой
линии. Каждый шарик с одинаковой вероятностью 1/4 попадает в
каждую ячейку. Найти вероятность того, что шарики попадут в соседние
ячейки.
Решение. Событие Л = {шарики попали в соседние ячейки}
разобьем на сумму стольких вариантов, сколько можно образовать пар
соседних ячеек; получим Л = Аг + А2 + Л3, где
Аг = {шарики попали в первую и вторую ячейки};
А2 == {шарики попали во вторую и третью ячейки};
Л3 = {шарики попали в третью и четвертую ячейки}.
Вероятность каждого варианта одна и та же и равна
V4-V2 =Х/8;Р(Л) =3/8.
2.33. k шариков разбрасываются случайным образом и независимо
друг от друга по п ячейкам, расположенным,одна за другой по
прямой линии (k < п). Найти вероятность того, что они займут k
соседних ячеек.
Решение, k соседних ячеек из п можно выбрать п —k + 1
способами. Вероятность попадания k шариков в каждую из групп
соседних ячеек равна (l/n)kk\ (так как их можно разбросать по этим
ячейкам k\ способами). Вероятность события А = {шарики попали в
k соседних ячеек} равна Р (Л) = (l/n)k k\ (n — k + 1).
2.34. На станцию связи за день поступило 20 телеграмм,
адресованных в четыре различных пункта (по пять в каждый пункт). Из всех
телеграмм выбирается наугад четыре. Найти вероятности событий:
Л = {все телеграммы адресованы в разные пункты};
В = {все телеграммы адресованы в_ один и тот же пункт}.
Решение. Чтобы выполнялось событие Л, адрес первой
телеграммы может быть совершенно произвольным; второй — не таким,
как у первой, третьей — не таким, как у первых двух, у четвертой —
не таким, как у первых трех. По правилу умножения вероятностей
2*
35
Аналогично
р(Л) = 1.-!1. Л. -А- «0,130.
v ' 19 18 17
P(5) = l._ii. J ?-« 0,00413.
19 18 17
2.35. Вычислительная машина состоит из л блоков. Надежность
(вероятность безотказной работы) в течение времени Т первого блока
равна р19 второго — р2 и т. Д- Блоки отказывают независимо друг от
друга. При отказе любого блока отказывает машина. Найти
вероятность того, что машина откажет за время Т.
п
Ответ. 1 — Ylpi-
i = i
2.36. При включении зажигания двигатель начинает работать с
вероятностью р. Найти: 1) вероятность того, что двигатель начнет
работать при втором включении зажигания; 2) вероятность того, что для
ввода двигателя в работу придется включить зажигание не более двух
раз.
Ответ. 1) (1 — р)р; 2) 1 - (1 - р)2 = (2 - р)р.
2.37. По каналу связи передаются три сообщения; каждое из них
может быть передано с различной степенью точности. Передача
одного сообщения может привести к одному из событий:
Аг = {сообщение передано правильно};
Л2 = {сообщение частично искажено};
Л3 = {сообщение полностью неразличимо}.
Вероятности событий Л1? Л2, Л3 известны и равны р1э р2, р3 (р± +
+ Ръ + Рз = !)• Считая, что сообщения искажаются (или
передаются правильно) независимо одно от другого, найти вероятности
следующих событий:
Л = {все три сообщения переданы без искажений};
В = {хотя бы одно сообщение полностью неразличимо};]
С = {не менее двух сообщений искажено полностью или частично}.
Ответ. Р(Л) -р?; Р (В) = 1 - (рг + р2)3; Р(С)=3(р2 +
+ Pz)2Pi + Pl
2.38. Две радиолокационные станции ведут наблюдение за
областью пространства, в которой перемещается объект, в течение
времени т. За это время первая станция успевает произвести 2пг циклов
обзора, вторая — 2п2 циклов. За один цикл обзора первой станции
объект обнаруживается (независимо от других) с вероятностью рь
второй — с вероятностью р2. Найти вероятности событий:
А = (объект обнаружен за время т хотя бы одной из станций};
В = {объект обнаружен первой станцией и не обнаружен второй};
С = {объект не обнаружен за первую половину времени т, но
обнаружен за вторую}.
решение. Р (А) = 1 — Р (Л).
Л = {объект не обнаружен ни одной из станций};
36
p [2)«(i -ft)84- (i -л)*1*; Р (Л)=i -(1 -A)*1* (i - л)'*; ■
P (B) = [1 -(1 -ft)2»«] (1 -ft)2*',
P (C) == (1 -ft)* (1 -pi)»- [1 -(1 —ft)* (1 -ft)"-].
2.39. Радиолокационная станция за один цикл обзора
обнаруживает объект с вероятностью р. Сколько потребуется циклов обзора для
того, чтобы объект был обнаружен с вероятностью не меньшей, чем 3й?
Решение. Обозначим N неизвестное число циклов. Должно
быть выполнено условие 1 — (1 — p)N > #>, откуда (1 — p)N < 1 —
дьа Логарифмируя, имеем
N\g(\-p)<\g{\-9)\ N^lg(l-9)/lg(l-p). (2.39)
2.40. Сообщение, передаваемое по каналу связи, состоит из п
знаков (символов). При передаче каждый знак искажается (независимо
от других) с вероятностью р. Для надежности сообщение дублируется
(повторяется k раз). Найти вероятность того, что хотя бы одно из
переданных сообщений не будет искажено ни в одном знаке.
Решение. Вероятность того, что одно отдельное сообщение не
будет искажено, равна (1 —р)п\ вероятность того, что хотя бы одно из
k сообщений не будет искажено
Р(Л) = 1 —[1 —(1—р)"]*.
2.41. В условиях задачи 2.40 сколько раз должно быть передано
сообщение для того, чтобы вероятность хотя бы одного
неискаженного сообщения стала не меньше £Р?
О т в е т. По формуле (2.39) имеем N > lg (1 —SP)! lg f 1 —(1 —р)п].
2.42. Важное сообщение передается одновременно по п каналам
связи, причем для надежности по каждому каналу оно повторяется k
раз. При одной передаче сообщение (независимо от других)
искажается с вероятностью р. Каждый канал связи (независимо от других)
«забивается» помехами с вероятностью Q; «забитый» канал не может
передавать никаких сообщений. Найти вероятность события
А = {хотя бы один раз сообщение передано без искажений}.
Решение. Обозначим
В = {по одному каналу сообщение хотя бы один раз передано без
искажений}.
Для выполнения события В канал, во-первых, не должен быть
забит помехами и, во-вторых, хотя бы одно сообщение по нему не
должно быть искажено:
Р(Б) =(l_Q)(l_p*).
Вероятность события А, состоящего в том, что хотя бы на одном
канале произойдет событие 5, равна
Р (А) = 1 - [1 - Р (В)]* = 1 — [1 — (1 — Q) (1 — pk)K
2.43. Происходит воздушный бой между двумя самолетами:
истребителем и бомбардировщиком. Стрельбу начинает истребитель: он дает
по бомбардировщику один выстрел и сбивает его с вероятностью рг.
Если бомбардировщик этим выстрелом не сбит, он стреляет по истре-
37
бителю и сбивает его с верояфностью р2. Если истребитель этим ЁысТре* 1
лом не сбит, он еще раз стреляет по бомбардировщику и сбивает его с 1
вероятностью р3> Найти вероятности следующих исходов боя: 1
А = (сбит бомбардировщик} I
В = {сбит истребитель}; 1
С = {сбит хотя бы один из самолетов}. I
Ответ. Р(Л) =р1 + (1-р1)(1-р2)р3; Р (В) -(1-Pi)p2; 1
Р(С) =Р(Л) + Р(5). I
2.44. Происходит воздушный бой между бомбардировщиком и дву- 1
мя атакующими его истребителями. Стрельбу начинает бомбардиров- 1
щик; он дает по каждому истребителю один выстрел и сбивает его с I
вероятностью рг. Если данный истребитель не сбит, то он независимо I
ит судьбы другого стреляет по бомбардировщику и сбивает его с ве- 1
роятностью р2. Определить вероятности следующих исходов боя: I
А = {сбит бомбардировщик}; Ц
В = {сбиты оба истребителя}; Ц
С = {сбит хотя бы один истребитель}; JJ
D = {сбит хотя бы один самолет}; Я
Е = {сбит ровно один истребитель}; II
F = {сбит ровно один самолет}. 1|
Решение. Вероятность того, что один истребитель собьет бом- И
бардировщик, равна (1 — Pi)p2; вероятность того, что ни один из них я
не собьет бомбардировщика, равна [(1 — Pi)p2l2; откуда 1
Р(Л) =1 — [1 — (1 — Pl)p2P; P(B)=pf; P^^l-O-px)2; 1
Р (£>) = 1 _(1 _pi)2 (1 _p2)2. p {E) =2pi (1 _pil I
Событие F представляется в виде F = F± + F2 + F3, где 1
Fi = (сбит бомбардировщик, а оба истребителя целы}; I
F2 = {первый истребитель сбит, а второй истребитель и бомбарди- I
ровщик целы}; I
F3 = {второй истребитель сбит, а первый истребитель и бомбар- 1
дировщик целы}. 1
P(fi)=(l-Pi)2[l-(l-p2)2]; 1
Р (F2) = Р (F3) = рх (1 - Рг) (1 - р2); 1
Р (F) = (1 - Р1У [1 - (1 - р2)Ч + 2Pl (1 - Pl) (1 - р2). I
2.45. Условия и вопросы те же, что в предыдущей задаче, но с тем 1
изменением, что истребители идут в атаку только попарно: если сбит В
один из них, то другой выходит из боя. я
Ответ. Р(Л) =(1-р?)[1-(1-р2)21; Р (Б) =pf; Р (С) = 1
= 1 - (1 -Pi)2; P (D) = 1 - (1 -ргУ (1 -р»; Р (Е) == I
= 2Pl (1 - Рх); Р (F) = (1 - Pl)2 [1 - (1 - р2)21 + 2Pl (1 + Pl). I
2.46. В урне а белых и Ь черных шаров. Два игрока поочередно Я
вынимают из урны по одному шару, каждый раз вкладывая его обрат- 1
но и перемешивая шары. Выигравшим считается тот, кто раньше вы- 1
38 I
нет белый шар. Найти вероятность .9г того, что выиграет первый
игрок (тот, кто вынимал шар первым).
Решение. Выигрыш первого игрока может осуществиться или
при первом же вынимании или при третьем (для чего первые два
вынимания должны дать черные шары, а третье — белый), и т. д.
а ■ / Ь у ' а ( Ь \2* а =
^1= а+Ь [а+Ь) а+Ь [а+Ь ) а + Ь
Ь \2£___ а 1 _ а+Ь
"£«U+J
а + Ь £о\а+Ь) а+Ь / Ъ у а+2Ь
(очевидно, 5й! > 1/2 при любых а и 6).
2.47. В урне два белых и три черных шара. Два игрока
поочередно вынимают из урны по "шару, не вкладывая их обратно.
Выигрывает тот, кто раньше получит белый шар. Найти вероятность З5! того,
что выиграет первый игрок.
Решение. ^_-§•+-{-■ Т ' X ""V
2.48. Производятся испытания прибора. При каждом испытании
прибор выходит из строя с вероятностью р. После первого выхода из
строя прибор ремонтируется; после второго — признается негодным.
Найти вероятность того, что прибор окончательно выйдет из строя в
точности при &-м испытании.
Решение. Для того чтобы произошло данное событие, нужно,
во-первых, чтобы прибор вышел из строя при fe-м испытании —
вероятность этого р. Кроме того, нужно, чтобы за предыдущие k — 1
испытаний прибор вышел из строя ровно один раз; вероятность этого
равна (k — \)р (1—p)k~2; Искомая [вероятность равна (k—1)Х
Хр2(1— Р)*-2.
2.49. Производится стрельба ракетами по некоторой цели.
Вероятность попадания каждой ракеты в цель равна р; попадания
отдельных ракет независимы. Каждая попавшая ракета поражает цель
с вероятностью р1и Стрельба ведется до поражения цели или до
израсходования всего боезапаса; на базе имеется боезапас п ракет (п > 2).
Найти вероятность того, что не весь этот запас будет израсходован.
Решение. Переходим к противоположному событию А = {весь
боезапас израсходован}. Чтобы произошло событие Л, первые п—1
ракет не должны поразить цель:
Р (А) = (1 -pp^-i; Р (Л) = 1 — (1 -pPlY~\
2.50. В условиях предыдущей задачи найти вероятность того, что
после поражения цели в запасе останутся неизрасходованными не
менее двух ракет.
Решение. Противоположное событие А = {останется менее
Двух ракет} равносильно тому, что первые п — 2 ракет не поразили
Р (J) = (1 - PPly-*- Р (А) = 1 - (1 - PPly-\
39
к
2.51. В условиях задачи 2.49 найти вероятность того, что будет
израсходовано не более двух ракет.
Решение. Чтобы было израсходовано не более двух ракет,
достаточно, чтобы при первых двух выстрелах цель была поражена:
вероятность этого равна 1 — (1 — ppi)2.
2.52. Радиолокационная станция ведет наблюдение за к
объектами. За время наблюдения i-й объект может быть потерян с
вероятностью pi (i = 1, 2, ..., k). Найти вероятности следующих событий:
А = {ни один объект не потерян};
В = {потеряно не менее одного объекта};
С = {потеряно не более одного объекта}.
Ответ. Р(Л)=П (1-/>0;Р(В)=1-П (1-л); P(Q =
= П(1-/7|) + Р1(1-р2)...(1-рА) + (1-Л)р2(1-Рз)...(1-Ы +
1=1
+ ... + (1— ра) (1— р2)...(1— p*-i)p*.
Последнюю вероятность можно записать в виде
Р(С)=П(1-Р|) + Ут^П (1-Л).
2.53. Техническое устройство, состоящее из k узлов, работало в
течение некоторого времени t. За это время первый узел оказывается
неисправным с вероятностью qly второй — с вероятностью q2 и т. д.
Наладчик, вызванный для осмотра устройства, обнаруживает и
устраняет неисправность каждого узла, если она имеется, с вероятностью
р, а с вероятностью q = 1 — р объявляет узел исправным. Найти
вероятность события А = {после осмотра наладчиком хотя бы один узел
устройства неисправен}.
Решение. Вероятность j'-му узлу быть неисправным после
осмотра равна вероятности того, что он стал неисправным за время t>
умноженной на вероятность того, что наладчик не обнаружит этой
неисправности: qtq. Вероятность того, что это событие случится хотя бы
с одним из узлов, равна
Р(Л)=1-П (1-<7*<7).
2.54. К условиям предыдущей задачи добавляется новое: по
истечении времени t с вероятностью Q наладчика не оказывается на
месте и устройство пускается в ход без профилактического осмотра.
Найти вероятность события А = {после пуска хотя бы один узел
устройства неисправен}.
Ответ. (l-Q)Fl- П (I-^I+qTi- ft (1-*)|.
40
2.55. Передается сообщение, состоящее из п двоичных симВблов
«О» или «1». Каждый из символов с малой вероятностью р искажается
(заменяется на противоположный). Для «перестраховки» сообщение
передается два раза; если оба сообщения совпали, информация
считается правильной. Найти вероятность того, что, несмотря на совпадение
сообщений, оба они оказались ошибочными.
Решение. Л = {оба сообщения совпадают, но искажены} ==
^= {ошибки допущены на одних и тех же местах}. Введем событие
В = {оба сообщения одинаковы}. В = А + С, где С = {оба
сообщения одинаковы и верны}.
Р (А) = Р (В) — Р (С).
п
Событие В = П Ви где pt = {на t'-м месте того и другого сообщения
стоят знаки либо оба верные, либо оба неверные}.
р (Bt) = р2 + (1 - р)2; Р (В) = [р2 + (1 - р)2]»; Р (С) =
= [(1 _ р)*]»= (1 _ Р)2*; р (Л) = [р* + (1 _ Pf\n _ (1 _ р)2п.
2.56. Железнодорожный состав состоит из п вагонов, каждый из
которых с вероятностью р имеет дефект. Все вагоны осматривают,
независимо друг от друга, два осмотрщика; первый из них обнаруживает
дефект (если он имеется) с вероятностью р1э второй — с вероятностью
р2. Если ни в одном из вагонов не обнаружено дефекта, состав
отправляется в рейс. Найти вероятность события:
А = {в рейс отправляется состав, в котором имеется хотя бы один
дефектный вагон}.
Решение. Рассмотрим один отдельно взятый вагон и событие
В = {вагон имеет необнаруженный дефект}. Р (В) =р (1 —рг) X
X (1 — Рг)- Отсюда
Р (Л)= 1- [1 -Р (В)]« = 1 - [1 -р (1 -Pl) (1 -р2)К
2.57. ЭВМ, в которой подозревается дефект, подвергается
тестированию с целью локализации дефекта. Для этого применяется
последовательно п тестов: 7\, Т2, ..., Тп. При обнаружении дефекта
тестирование прекращается. Вероятность локализации дефекта при первом
тесте равна рх\ условная вероятность локализации дефекта при втором
тесте (если при первом он не был локализован) равна р2; условная
вероятность локализации дефекта при j-м тесте (если при первых i —1
он не был локализован) равна pi (i = 1, 2, ..., п). Найти вероятности
следующих событий:
А = (проведено не менее трех тестов};
В = {проведено не более трех тестов};
С = {дефект локализован в точности при четвертом тесте};
D = {дефект не локализован после п тестов};
Е = {проведены все п тестов}.
Решение. Событие А = {проведено менее трех тестов} =
= Л + F2, где
^i = {проведен только один тест, неисправность локализована};
41
F2 = {первый тест йе дал результата, при втором йеиспраЁность
локализована}.
Р (Ft) = Pl; P (Fa) = (1 - Pl)p2; Р (А) = Л + (1 - A)Pl;
Р(4)=1-[Л + (1-й)Р|];
Событие 5 = {проведено, один, два^или три теста} = F± + F2 + F3%
где F3 = {неисправность локализована при третьем тесте}.
Р (F3) = (1 - Pi) (l-Pi)Pa; Р (В) = Pi + (1 - Pl)p2 +
+ (1 _ pi) (1 _ p2)p3; p (С) = (1 - A) (1 - p2) (1 _ p3)p4;
Рф)=(1-й)(1-А)«.(1-л)= П (1-рО; р(£)= ГП1-Л).
2.58. На железнодорожной станции пассажиру предоставляется
сейф (индивидуальная камера хранения багажа), который
открывается только при наборе определенного трехзначноппиифра (например,
253, 009, 325 и т. д.). Пассажир набрал шифр, запер сейф и ушел в
город. Посторонний человек, не знающий шифра, пытается открыть сейф,
выбирая три цифры наугад. Найти вероятности событий:
А = {сейф откроется с первой же попытки};
В = {сейф откроется после k попыток}.
Р е ш е н и е. Р (А) = 0,1 -0,1 • 0,1 =0,001. Если делается k
попыток, естественно предположить, что неудачные комбинации не
повторяются. Перейдем от В к противоположному событию В = {все k
попыток неудачны}. Тогда
Р (В) = 1 Р (В) = 1 9" "8 юоо—6+1 юоо —^ =
* '~ ^ ' ЮОО* 999 '" 1000—k+2 'lOOO — k + l
r=1_jooo-i = -^e
1000 1000 ч '
Формула (2.58), разумеется, имеет смысл только при k <C 1000; при
k^ 1000 вероятность правильного набора Р (В) ^1.
2.59. В городе Тбилиси три распространенных языка: грузинский,
армянский и русский. Берется группа жителей в составе т человек.
Из них т± знают только грузинский язык, т2 — только армянский,
т3 — только русский; т12 — грузинский и армянский; т13 —
грузинский и русский; т23 — армянский и русский; т123 — все три
языка; тх + т2 + пг3 + т12 + т13 + т23 + т123 = т. Из этой
группы случайным образом выбираются двое. Какова вероятность р того,
что они смогут разговаривать между собой без помощи переводчика
на каком-либо из трех языков?
Решение. Перенумеруем все семь групп жителей и проставим
против каждой те языки, которые знают члены группы, обозначая их
буквами «г», «а», «р».
I : г (т1 человек); II : а (т2 человек); III : рч(^з человек); IV : г,
а (т12 человек); V : г, р (т13 человек); VI : а, р (т23 человек); VII : г,
а> Р (^123 человек).
42 i
Чтобы двое могли объясниться, они должны попасть в пару групп,
имеющих между собой общий язык. В данном случае проще будет
найти вероятность того, что двое не смогут объясниться. Для этого они
должны относиться к одной из пар групп: (I, II); (I, III); (I, VI);
(II, Ш); (II, V); (III, IV). Вероятности того, что один из двух
выбранных людей относится к одной группе, а второй — к другой, равны:
Jpj^.p 1Ш J^ p(I)VI) = -^2L;
4 т (m—1) ' т (m—1) т (m—1)
р (II, III) = 2щщ ; Р (II, V) = 2m2 mi3 ; Р (III, IV) =
т (т—1) т (т—1)
2т3 т12
т (т—1)
Складывая эти вероятности и вычитая полученную сумму из
единицы, найдем искомую вероятность р:
2
/?=1 — (тг т2+т1 тв+тг т23 +
т (т—1)
+ т2 яг3 -|-m% ml3+tn3 m12).
2.60. Завод выпускает определенного вида изделия; каждое
изделие может иметь дефект; вероятность дефекта р. После изготовления
изделие осматривается последовательно k контролерами; i-й
контролер обнаруживает дефект, если он имеется, с вероятностью pt (i = 1,
2, ..., k). В случае обнаружения дефекта изделие бракуется.
Определить вероятности событий:
А = {изделие забраковано};
В = {изделие забраковано вторым контролером, но не первым};
С = {изделие забраковано всеми контролерами}.
Ответ.
рсЛ)=/7 U-• п О-Рд\; р(В)=Р(1-л)л;р(Q=pUW
2.61. Завод изготовляет определенного типа изделия; каждое
изделие имеет дефект с вероятностью р. Изделие осматривается одним
контролером; он обнаруживает имеющийся дефект с вероятностью р1э
а'если дефект не обнаружен, пропускает' изделие в готовую
продукцию. Кроме того, контролер может по ошибке забраковать изделие,
не имеющее дефекта; вероятность этого равна а. Найти вероятности
следующих событий:
А = {изделие забраковано};
В = {изделие забраковано, но по ошибке};
С = {изделие пропущено в готовую продукцию с дефектом}.
Ответ. Р(Л) =рр1 + (1-р)сс; Р (В) = (1 -р)а; Р (С) =
= Р0— Ра). , .
2.62. В условиях предыдущей задачи изделие осматривается не
одним контролером, а двумя. Вероятности забраковать дефектное
изделие для первого и второго контролеров равны соответственно ри
Рг\ вероятности по ошибке забраковать изделие, не имеющее дефекта,
43
равны соответственно а1% а2- Если хотя бы один контролер бракует
изделие, оно идет в брак. Найти вероятности тех же событий.
Ответ. Р(Л) =p[l_(l-Pl)(l_p2)]+ (1 —р) [1 —
— (1 — (Ч) (1 - сс2)]; Р (В) = (1 - р) [1 - (1 - аг) (1 - а2)];
Р(С) =p(l-Pl)(l-P2).
2.63. Прибор состоит из п блоков (рис. 2.63); выход из строя
каждого блока означает выход из строя прибора в целом. Блоки выходят
из строя независимо друг от друга. Надежность (вероятность
безотказной работы) каждого блока равна р. Найти надежность Р прибора
в целом. Какова должна быть надежность рг каждого блока для
обеспечения заданной надежности Рг прибора?
Примечание. Здесь и далее на схемах элементы, без которых работа
системы невозможна, изображаются как звенья, соединенные «последовательно»;
дублирующие друг друга элементы изображаются соединенными «параллельно».
Надежность каждого элемента записывается в соответствующем прямоугольнике.
О т в е т. Р = рп\ рх = уТ\.
-EHZHZbQ- -&1-
"V
П Р
Рис. 2.63
Рис. 2.64
2.64. Для повышения надежности прибора он дублируется
другим точно таким же прибором (рис. 2.64); надежность (вероятность
безотказной работы) каждого прибора равна р. При выходе из строя
первого прибора происходит мгновенное переключение на второй (на*
дежность переключающего устройства равна единице). Определить
надежность Р системы двух дублирующих друг друга приборов.
Решение. Отказ системы требует совместного отказа обоих
приборов; надежность системы Р = 1 — (1 — р)2.
Чл.
р
~Уу
п
Рис. 2.65
П__Л
H-Zji
I * I
I * I
I * I
Чрг
Рис. 2.66
2.65. Та же задача, но надежность переключающего устройства Я,
обеспечивающего переключение с отказавшего первого прибора на
второй, равна рх (рис. 2.65).
44
Ответ. Надежность системы Р = 1 — (1 — р) (1 — pLp).
2.66. Для повышения надежности прибора он дублируется (п—1)
другими такими же приборами (рис. 2.66)-„надежность каждого
прибора р. Найти надежность Р системы. Сколько надо взять приборов,
чтобы повысить надежность до заданной Рх?
Ответ. Р =1 — (1 — р)«; n>lg,(l — Рг)/ lg (1 — р).
2.67. Та же задача, но для включения каждого дублирующего
прибора применяется устройство с надежностью pL (рис. 2.67).
Ответ. P=\-(i-p)(l-plP)n-i; л>!&Рт^1)-Ц0-р) + 1>
lg (1 — PiP)
u
Л
Pi
Р
► •
_/7_Г
»
1 v.
Р_ h
Н Р
Р Г*
4
/7-/
Н ?
^ h~ '
Рис. 2.67
П ^ I 1^ I ""-i У5
Рис. 2.68
n_J
* •
4Z}i
2.68*. Техническая система состоит из п блоков, надежность
каждого р. Выход из строя хотя бы одного блока влечет за собой выход из
строя всей системы. С целью повышения надежности системы
производится дублирование, для чего выделено еще п таких же блоков.
Надежность переключающих устройств полная. Определить, какой
способ дублирования дает большую надежность системы: а)
дублирование каждого блока (рис. 2.68, а); б) дублирование всей системы
(рис. 2.68, б).
Решение. Надежность системы, дублированной по способу «а»,
будет ра = [1 — (1 — р)2К по способу «б» рб = 1 — (1 — рп)2.
Покажем, что ра > рб при любом п > 1 и 0 < р < 1. Так как
ра = [1 — (1 _ р)Цп = [1 _ 1 + 2р — рЦп = р« (2 — р)»,
рб = 1 — (1 — р")2 = 1 — 1 + 2р* — р2» = р" (2 — р"),
то достаточно доказать неравенство: (2 — р)п > 2 — рп. Положим
9 = 1 — р (q > 0); неравенство примет вид (2 — 1 + q)n > 2 —
— (1 — ?)*, или (1 + qY + (1 — 9)" > 2.
Применяя формулу бинома, замечаем, что все отрицательные члены
уничтожаются:
45
II I Л (^ 1) О
+ 1— к<7+ 2 92-
.. = 2 + "(«-1)<7а + ...>2,
что и доказывает требуемое неравенство.
2.69. В технической системе дублированы не все, а только
некоторые (наименее надежные) узлы. Надежности узлов проставлены на
рис. 2.69. Определить надежность Р системы.
Ответ. Р = [1 - (1 - рг)4 [1 - (1 - p2)3WJl - (1 - р5)2Ь
Pi
Pi
\Рг
[Рг
\Рг
Рз
Рч
3l
р6у
\1
ж]
ш\
Рис. 2.69
Рис. 2.70
2.70. Прибор состоит из трех узлов. В первом узле пх элементов,
во втором л2 и в третьем п3. Для работы прибора безусловно
необходим узел I; два других узла II и III дублируют друг друга (рис. 2.70).
Надежность каждого элемента одна и та же и равна р. Выход из строя
одного элемента означает выход из строя всего узла. Элементы
выходят из строя независимо друг от друга. Найти надежность прибора Р.
Решение. Надежность узла I: pi = pns надежность узла II:
рп =p>V надежность узла III: рщ = рп*\ надежность
дублированного узла (II и III): 1 — (1—рп*) (1—р"3); надежность прибора
Р = р*1 [1 —(1—p»>)(l—р*)]."
- 2.71. Имеется электроприбор, который может выходить из строя
(перегорать) только в момент включения. Если прибор включался до
сих пор k — 1 раз и еще не перегорел, то условная вероятность ему
перегореть при &-м включении равна Qfe. Найти вероятности следующих
событий:
А = {прибор выдержит не менее п включений};
В = {прибор выдержит не более п включений};
- С = {прибор перегорит точно при п-ы включении}.
Решение. Вероятность события А равна вероятности того, что
при первых п включениях прибор не перегорит:
Р(Л)« П (1-Q0-
Лг= 1
Чтобы найти вероятность события В, переходим к
противоположному: В = {прибор выдержит более п включений}. Для этого
достаточно, чтобы при первых (п + 1) включениях прибор не перегорел:
?{в)=пП (1-Q*); Р(5)=1-ЛП1(1
-Qft).
46
Чтобы прибор перегорел точно при n-м включении, надо, чтобы он
не перегорел при первых п — 1 включениях, а при п-ы перегорел:
P(fc) = Qnnn (1-Qfc).
2.72. Прибор состоит из четырех узлов; два из них (I и II)
безусловно необходимы для исправной работы прибора, а два (III и IV)
дублируют друг друга (рис. 2.72). Узлы могут выходить из строя
только при включении. Лри k-м включении
Л
Ш
исправный узел I (независимо от дру- р—| ш
гих) выходит из строя с вероятностью I T
q\ (k)> Узел И — с вероятностью q2 (&), 1
узел III и узел IV с одинаковой
вероятностью qm (k) = qiv (k) = q (k). Найти
вероятности тех же событий Л, В, С, рис. 2.72
что в задаче 2.71.
Решение. Задача сводится к предыдущей, если найти
условную вероятность Qu выхода из строя исправного прибора при
k-ы включении: Qh = 1 — [1 — qi (k)) [1 — qu (k)][l — (1 — q (k)f\ и
подставить в уже найденное решение.
2.73. Прибор состоит из трех узлов. При включении прибора с
вероятностью рх появляется неисправность в первом узле, с
вероятностью р2 — во втором узле, с вероятностью р3 — в третьем узле.
Неисправности в узлах возникают независимо друг от друга. Каждый из
трех узлов безусловно необходим для работы прибора. Для того
чтобы узел отказал, необходимо, чтобы в нем было не менее двух
неисправностей. Найти вероятность события
А = {прибор благополучно выдержал п включений}.
Решение. Для осуществления А нужно, чтобы работали все
три узла. Вероятность того, что первый узел выдержит п включений,
равна вероятности того, что при п включениях в нем окажется не
более одной неисправности (0 или 1): (1 + pt)n + прг (1 —Pi)"""1.
Вероятность того, что все три узла выдержат п включений, равна
Р И)= П [(I-Pir +nPi (\-Pi)n-ll
2.74. Прибор состоит из трех узлов; один из них безусловно
необходим для работы прибора; два других дублируют друг друга. В
результате работы устройства в нем появляются неисправности; каждая'
неисправность с одной и той же вероятностью появляется в любом из
элементов, составляющих узлы. Первый узел состоит из % элементов;
второй — из щ элементов, третий — из п3 элементов (пг + п2 + п3 =
= п). При неисправности хотя бы одного элемента узел выходит из
строя.
Известно, что в приборе имеется четыре неисправности (в четырех
разных элементах). Найти вероятность того, что наличие этих
неисправностей делает невозможной работу прибора.
47
Решен и е. Событие А = {невозможность работы прибора}
распадается на два А = А± + Л2, где
Аг = {вышел из строя первый узел};
А2 = {первый узел не вышел из строя, но второй и третий вышли}.
Чтобы произошло событие Л19 нужно/ чтобы хотя бы одна из
четырех неисправностей пришлась на первый узел:
Р(А )=1—Р (А )•=-{ п~~~щ n—ni~-{ n—ni—2 n— ni—л
к 1} v 1} п п—\ п—2 п—з
Для определения вероятности события А2 мы должны вероятность
события Аг = {первый узел не вышел из строя} умножить на
вероятность того, что второй и третий узлы вышли из строя (с учетом, того,
что все четыре неисправности приходятся на второй и третий узлы).
Последнее событие может осуществиться в трех вариантах: или одна
неисправность будет во втором, а три других — в третьем узле,"или
наоборот: три во втором и одна в третьем; или же во втором и третьем
узлах будет по две неисправности.
Вероятность первого варианта
Qi п* Щ пз—1 пз—2 __д&
л2+л3 п2+пз~-1 п2 + п3—2 п2-\-п3—3
Вероятность второго варианта
£1 п3 ^2 П2 — 1 П2—2 __ gp
п2-\~пз п2+лз—* Яг+Пз—2 я2+пз—3
Вероятность третьего варианта
= ^3
Яг+Лз «2+пз—! п2+пз—2 п2+л3—3
Отсюда
Р(^2) = [1-р (Л)] [^i+^+^sl; Р(Л)=Р(Л1)+Р(Л).
2.75. Уникальный прибор, от которого требуется очень высокая
надежность, собирается из к деталей Dlt D2, ..., Dh. Перед сборкой
каждая деталь всесторонне проверяется, и если она окажется
высококачественной, включается в прибор, а если нет — заменяется запасным
экземпляром, который тоже проверяется. В распоряжении сборщика
имеется запас деталей каждого типа: т-г экземпляров детали D% (i =
k
= 1, ..., k), всего т = 2 mt деталей. Если запасных деталей не хва-
тает, сборка откладывается. Вероятность того, что отдельный
экземпляр детали Dt окажется высококачественным, равна р% и не зависит
от качества других экземпляров. Найти вероятности следующих
событий:
А = {имеющегося запаса деталей достаточно для сборки прибора};
В = {использованы (испытаны и включены в прибор или только
испытаны) все имеющиеся детали};
С = {при данном запасе деталей сборщику удастся собрать
прибор, и хотя бы одна деталь любого типа останется в запасе}.
43
k
Решение. СобьгЬш А = П Aiy где At = {хотя бы адитг экземп-
ляр детали Dt оказался высококачественным}.
Р {At) = 1 -(1 ~Pi)\; Р (А) = П [1 -(1 - Pif11-
k
Событие В = П Вь где В* = (израсходованы все экземпляры детали?
Dis}. Чтобы имело место событие Ви нужно, чтобы первые mt — 1
экземпляров детали Dt были невысококачественными:
P(B4)=(i-Pi)W|"1; Р(В)=П(1-ргГг1.
Чтобы найти Р (С), представим событие Л в виде суммы
несовместных событий:
A =C + F, (2.75)
где F = {сборщику удается собрать прибор, но ни одной детали в за-
k
пасе не остается}; F = П Fi9 где Ft = {первые тг — 1 экземпляров
детали Dt оказались невысококачественными, а тгя —
высококачественной}.
р (^f) —О—Pi)m*_1 ft;P(f)- П [О-лГ'-'р*]-
Из формулы (2.75) имеем
р(С)=р(Л)-р(^)=п [i-(i-Pi)m*]-n Ц1-~Рдт*-1рД.
2.76. Техническое устройство S состоит из п узлов, каждый из
которых в результате эксплуатации в течение времени т может
оказаться в одном из состояний:
sL = {полностью исправен};
s2 = {требует наладки};
s3 = {требует ремонта};
s4 = {полностью непригоден}.
Р (%) = Pi. Р (s2) = Р2, Р (s3) = Рзэ Р (s4) = P4;
Р1 + Р2 + Р3 + Р4 =1.
Состояния отдельных узлов независимы. Найти вероятности
следующих событий:
А = {все узлы полностью исправны};
В = {все узлы требуют наладки};
С = {один узел требует ремонта, остальные — наладки};
D = {хотя бы один узел полностью непригоден};
Е = {два узла требуют наладки, один — ремонта, остальные
исправны}.
49-
Решение. Р (А) = р?, (В) = р£. Один узел, требующий
ремонта, можно выбрать С\ =п способами:
P(Q-nftp»-b P(D)=l/-(l-p4)*.
Два узла, требующих наладки, можно выбрать из п узлов С\ =
= п Г" способами; один узел, требующий ремонта, CJ_2 = я— 2
способами:
Р (E) = n^f^(n-2) pi pi-3-
2.77. По каналу связи передается л = 6 сообщений, каждое из
которых, независимо от других, с вероятностью р = 0,2 оказывается
искаженным. Найти вероятности следующих событий:
С = {ровно два сообщения из 6 искажены},
D = {не менее двух сообщений из 6 искажены}.
Решение. По теореме о повторении опытов [см. формулу
(2.0.15)] Р (С) = P2i6 = CI • 0,22 • 0,84 « 0,197. По формуле (2.0.18)
Р (D) = 1 - (Р0,в + Pi J = 1 - (0,86 + 6 • 0,2 • 0,85) =
= 1 — (0,262 + 0,393) = 0,345.
2.78. По каналу связи передается п сообщений. Каждое из^сооб-
щений независимо от других с вероятностью р искажается помехами.
Найти вероятности следующих событий:
А = {из п сообщений ровно т будут искажены помехами};
В = {не менее т из п сообщений будут переданы неискаженными};
С = (не более половины всех передаваемых сообщений будут
искажены};
D = {все сообщения будут приняты без искажений};
Е = {не менее двух сообщений будет искажено}.
Рг'е ш е н и е. По теореме о повторении опытов [см. формулу
(2.0.15)]
Р(А) = С?рт(\— р)п~т.
По формуле (2.0.17), заменяя р на 1 —р, получаем
п , [/г/2] .
Р(5)= 2 С*(1-/>)*/*-*; P(Q- S С*рЩ-р)Г-к9
где [я/2] — целая часть числа п/2.
P(D)=(l-p)«;
то же значение можно получить и по формуле (2,0.15):
V(D) = P0tn = C*np°(l-pr=l.\.(l-pr.
По формуле (2.0.18) находим
Р(£) = ^п=1~2^рМ1-р)^=1-[(1-рГ+пр(1~рГ-1]-
^1-(1-.ру*-1Ц+{п-1)р).
60
2.79. Техническое устройство S состоит из 5 узлов; каждый узел
за время эксплуатации отказывает (выходит из строя) с вероятностью
р = 0,4. Отдельные узлы отказывают независимо друг от друга. Если
откажет более трех узлов, устройство не может работать; если
откажет 1 узел или 2 узла, оно работает, но с пониженной эффективностью.
Найти вероятности событий:
А = {в устройстве не отказал ни один узел};
В = {устройство может работать};
*/? = {устройство работает с пониженной эффективностью}.
Решение. Р (А) = 0,6б « 0,0778;
Р(5) ^P-(A) + P(0 + P(D)t
где С= {отказал ровно^один узел}; D = {отказали ровно два узла}.
р (С) = Р1>5 = 5 ■ 0,4 • 0,6* w 0,259; Р (D) = Р2#5 = С\ • 0,42 х
X 0,63 « 0,346; Р (В) = Р (А) + Р (С) + Р (D) » 0,683; Р (F) «
= Р (С) + Р (D) » 0,605.
2.80*. Происходит соревнование между k стрелками; каждый из
них делает п выстрелов по своей мишени. Вероятность попадания в
мишень при одном выстреле для j'-ro стрелка равна pt (i = 1, ...,
^.Выигрывает соревнование тот из стрелков, который имеет больше
попаданий, чем каждый из остальных. Найти вероятность того, что среди
соревнующихся стрелков будет один (только один), выигравший
соревнование.
Решение. Таким одним может быть любой из k стрелков.
Найдем вероятность того, что *-й стрелок выиграет соревнование (событие
Аг). Это событие может произойти следующими способами: Л|ш) =
= {t-й стрелок имеет ровно т попаданий, а каждый из остальных—
не более чем т — 1} (т = 1, ..., п).
Вероятность Рт (/) того, что t-й стрелок имеет т попаданий, равна
C%p?q?~m, где qt =1 — pt. Обозначим вероятность того, что /-й
стрелок имеет не более т — 1 попаданий, через Rm (/):
т — \
Тогда вероятность того, что все остальные стрелки, кроме £-го имеют
не более т — 1 попаданий, равна
/?^_X(1)/?TO1X(2)... T?^^!^—l)/?TO^(tM-l)... /?то-х(^) = Г1 /^^^iC/).
Суммируя полученные вероятности для всех значений яг, получаем
вероятность того, что i-й стрелок в единственном числе выиграет
соревнование:
РИ|)=2 РтШ Rm-l(j) (*=1,....Л).
51
-«-.-- .
Суммируя эти вероятности для всех стрелков, получаем
Р(Л)= 2 рШ= 2 2 ^«(ОП /?m-i(/).
2.81. При въезде в новую квартиру в осветительную сеть было
включено 2k новых электролампочек. Каждая электролампочка в
течение года перегорает с вероятностью г. Найти вероятность события
А={в течение года не менее половины первоначально включенных
лампочек придется заменить новыми}.
Ответ. Р(Л)=1— 2 C?*rm(l— r)**-m#
m = 0
2.82. Завод изготовляет изделия, каждое из которых с
вероятностью г (независимо от других) оказывается дефектным. При осмотре
дефект, если он имеется обнаруживается с вероятностью р. Для
контроля из продукции завода выбирается п изделий. Найти вероятности
следующих событий:
А = {ни в одном из изделий не обнаружено дефекта};
В = {среди п изделий ровно в двух обнаружен дефект};
С = {среди п изделий не менее чем в двух обнаружен дефект}.
Решение. Вероятность того, что в одном наугад взятом
изделии имеется и обнаружен дефект, равна рг.
Р (Л) =(1 -рг)*; P (В) =СЯ (prf (1 -pry~\ P (0 = 1-
— (1 — рг)*- * [(1 — рг) + nprl
2.83. В условиях задачи 2.82 вся контролируемая партия
бракуется, если среди п изделий будет обнаружено не менее четырех
дефектных. Найти вероятность р того, что вся контролируемая партия будет
забракована.
Ответ. р=2С§(рг)'(1— ргр-1.
2.84. Первый прибор состоит из пг узлов, второй из п2 узлов.
Каждый прибор работал в течение времени t. За это время каждый узел
первого прибора выходит из строя, независимо от других, с
вероятностью qly второго — с вероятностью цг. Найти вероятность р того, что
за время t в первом приборе выйдет из строя т1 узлов, а во втором —
т2 узлов.
Ответ. р = С% q™> (1 —q±)n^^ C% q™* (l _flrJ«.-*.\
2.85. Монета бросается т раз. Найти вероятность того, что герб
появится не менее k раз и не более / раз {k^.1 ^.т).
Решение. /? = 2 *W= 2 С£,(1/2)» = (1/2)* 2 С*.
2.86. Прибор, состоящий из k узлов, работал в течение времени t.
Надежность (вероятность безотказной работы) каждого узла за вре-
52
мя t равна р. По истечении времени t прибор останавливается, техник
осматривает его и заменяет узлы, вышедшие из строя. На замену
одного узла ему требуется время т. Найти вероятность Р того, что
через время 2т после остановки прибор будет готов для нормальной
работы.
Решение. Для этого нужно, чтобы за время t вышло из строя
не более двух узлов:
P = pb + k(l-p)pk-i+ k{k~l) (l— p)V~2-
2.87. Что вероятнее, выиграть у равносильного противника: 1)
три партии из четырех или пять из восьми? 2) не менее трех партий из
четырех или не менее чпяти партий из восьми?
Решение. 1) А = {выигрыш 3 партий из 4}; В = {выигрыш
5 партий из 8}. Р (Л) = С\ (1/2)4 = 1/4; Р(В) = С| (1/2)8 = 7/32;
Р (Л) > Р (В).
2) С = {выигрыш не менее 3 партий из 4}; D = {выигрыш не
менее 5 партий из 8}. Р (С) = С\ (1/2)4 + (1/2)* = 5/16; Р (D) =
= С» (1/2)8 + С% (1/2)8 + CI (1/2)8 + (1/2)8 = 93/256; Р (D) > Р (С).
2.88. Человек, принадлежащий к определенной группе населения,
с вероятностью 0,2 оказывается брюнетом, с вероятностью'0,3 —
шатеном, с вероятностью 0,4 — блондином и с вероятностью 0,1
—рыжим. Выбирается наугад группа из шести человек. Найти вероятности
следующих событий:
А = {в составе группы не меньше четырех блондинов};
В = {в составе группы хотя бы. один рыжий};
С = {в составе группы равное ч^сло блондинов и шатенов}.
Решение. Р (Л) = 1 — [0,66 + 6 • 0,4 • 0,6б + 15 • 0,42 х
X 0,64] « 0,455; Р (В) = 1 — (1 — 0,1)6 » 0,468; С = С0 + С± +
~г ь2 + Сз> '
где С0 = {в группе нет ни блондинов, ни шатенов};
Сг = {в группе по одному блондину и шатену, а остальные —
ни то, ни другое};
С2 = {в группе по два блондина и шатена, а остальные — ни
то, ни другое};
С3 = {в группе по три блондина и шатена}.
Р(С0) = (1—0,7)6« 0,0007;
P(Cl)== 11П41 0,3-0,4 (1-0,7)* «0,0292;
P(C2H^^0,32,0>42(1~0J2)^0,1166;
Р(С3)=-^-0,33.0,43« 0,0346; Р (С) «0,181.
2.89. В течение времени t эксплуатируется N приборов. Каждый
прибор имеет надежность р и выходит из строя независимо от других.
Найти вероятность Р (А) того, что мастер, вызванный по окончании
времени t для ремонта неисправных приборов, не справится со сво-
53
ей задачей за время т, если на ремонт каждого неисправного прибора
ему требуется время т0.
Решение. Событие А равносильно тому, что число вышедших
из строя приборов больше, чем / = [т/т0], где [т/т0] — наибольшее
целое число, заключенное в т/т0.
Р(Л)= S ^(l-rtwPAr-m
2.90. Имеется N неисправных приборов, которые подвергаются
испытаниям (тестам) с целью локализации неисправности. Каждый тест
независимо' от других с вероятностью р приводит к локализации
неисправности. Если неисправность локализована, прибор передается
на ремонтную станцию, а обследованию подвергаются другие приборы.
Если во всех N приборах неисправность локализована, то тесты
прекращаются. Всего имеется возможность произвести п тестов {п> N).
Найти вероятность того, что неисправности во всех N приборах будут
локализованы.
Решение. Д = {все неисправности локализованы} =
{неисправность локализована не менее N раз}.
Р(Л)= 2 С?р»(1-р)«-«
2.91. В условиях предыдущей задачи найти вероятность того, что
в результате п тестов среди N неисправных приборов останется не
менее k приборов с нелокализованными неисправностями (k < N).
Решение. Задача равносильна следующей: найти вероятность
того, что при п тестах будут локализованы неисправности не больше,
чем в N — k приборах.
. P(A) = N%C2p>n(l-p)n-m.
m = 0
2.92*. Прибор состоит из п узлов. Вероятность безотказной работы
t-ro узла равна рг (/=1,2,..., п). Для работы прибора требуется
безотказная работа всех его узлов. При вычислении вероятности R
отказа прибора вероятности pt (i =1,2, ..., п) приближенно
заменяют их средней арифметической:
Будет ли при этом вычисленное приближенное значение R вероятности
R больше или меньше истинного R?
п
Решение. Точное значение R =1 — П qh где qt = 1 — р£.
Приближенное (по средней вероятности р)
Д4
n
n
Требуется срабйи!* ь беличины: П qt и
нее геометрическое не равных между собой положительных величин
меньше, чем их среднее арифметическое, откуда
1 п
. Известно, что сред-
п / п t п п Г п "In
Vn».<i2*"n*.<U-2«- •
следовательно, R< R.
2.93. Завод изготовляет изделия, каждое из которых должно
подвергаться четырем видам испытаний. Первое испытание изделие
проходит благополучно sc вероятностью 0,9; второе — с вероятностью
0,95; третье — с вероятностью 0,8 и четвертое — с вероятностью 0,85.
Найти вероятность того, что изделие пройдет благополучно:
А = {все четыре испытания};
В = {ровно два испытания (из четырех)};
С = {не менее двух испытаний (из четырех)};
Ответ. Р (А) » 0,581; Р (В) « 0,070; Р (С) « 0,994.
2.94. С целью повышения надежности передачи важного
сообщения, состоящего из п символов, каждый из передаваемых символов
дублируется (повторяется) т раз. В качестве воспринимаемого
символа в пункте приема воспроизводится тот, который повторен не менее
k раз из т. Если символ в пункте приема повторяется менее k раз, то
такой символ не воспроизводится, считается искаженным.
Вероятность р правильной передачи любого символа одна и та же и не
зависит от того, правильно ли переданы другие символы. Найти
вероятности следующих событий:
А = {переданный отдельный символ в сообщении будет правильно
воспринят в пункте приема};
В = {все сообщение будет правильно воспринято в пункте приема};
С = {в сообщении будет искажено не более / символов}.
Решение. Чтобы переданный символ был правильно воспринят
в пункте приема, нужно, чтобы он был передан без искажений не
менее k раз из т. Вероятность того, что символ будет передан правильно
ровно / раз из т [согласно формуле (2.0.15)1, равна
сЬрЧ^-рГ-*-
Вероятность того, чтб символ будет передан правильно не менее k раз
из т можно вычислить по формуле (2.0.17):
Р(Л)= SCLO-p)1»-'^
или, при сравнительно небольшом &<т/2, по формуле (2.0.18):
Р(А) = 1-к%с1пРЧ1-рГ-!-
55
Чтобы все сообщение было правильно воспринято в пункте приёма,
нужно, чтобы все п символов были воспроизведены правильно:
Р (В) = [Р (Л)К
Вероятность события С может быть вычислена по формуле
Р(С)=%[1-Р(А)У[Р(А)]т-'.
ГЛАВА 3
ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ
И ФОРМУЛА БЕИЕСА
'^' 3.0. Если об обстановке опыта можно сделать п исключающих друг друга
предположений (гипотез) Нг> Я2, ..., Нп и если событие Л может появиться
только вместе с одной из этих гипотез, то
Р(Л)=2Р(Я|)Р(Л|Я|), (3.0.1)
где Р (Н{) — вероятность гипотезы Я$; P (Л \ Н{) — условная вероятность
события А при этой гипотезе. Формула (3.0.1) называется формулой полной
вероятности.
Если до опыта вероятности гипотез Яь Я2, ..., Нп были равны Р (Я^,
Р (Я2), ..., Р (Яп), а в результате опыта произошло событие Л, то новые
(условные) вероятности гипотез вычисляются по формуле
Р(ЦЦ)- ?™*™В* (/-!.« и). (3.0.2)
2Р(Я,)Р(Д|Я,)
Формула (3.0.2) называется формулой Бейеса. Доопытные (первоначальные)
вероятности гипотез Р (Ях), Р (Я2), ..., Р (Яп) называются априорными, а после-
опытные Р (Ях | Л), Р (Я2 | Л), ..., Р (Яп | Л) — апостериорными. Формула
Бейеса дает возможность «пересмотреть» возможности гипотез с учетом
наблюденного результата опыта.
Если после опыта, давшего событие Л, проводится еще один опыт, в
результате которого может произойти или нет событие В, то вероятность (условная)
этого последнего события вычисляется по формуле полной вероятности, в
которую подставлены не прежние вероятности гипотез Р (Я$), а новые Р (Я$ | Л):
Р(В|Л)=2 Р(Яг|Л)Р(В|Я*Л). (3.0.3)
Формулу (3.0.3) иногда называют «формулой для вероятностей будущих событий».
ЗАДАЧИ И УПРАЖНЕНИЯ
3.1. Имеются три одинаковые с виду урны. В первой а белых
шаров и Ъ черных; во второй с белых и d черных; в третьей только белые
шары. Некто подходит наугад к одной из урн и вынимает из нее один
шар. Найти вероятность того, что этот шар белый.
56
Решение. Пусть событие А = {появление белого шара}.
Формулируем гипотезы:
#!= {выбор первой урны};
#2= {выбор второй урны};
(выбор третьей урны}.
#3 =
р(я1)=р(я2)=р(я3)=4-; РИ1#1)= а
3 а+6
Р(Л|Я2) = -^-; Р(Л|Я3)=1.
По формуле полной вероятности
v ' 3 а+6 3 c+d 3 3 \а+& c+d /
3.2. Прибор может работать в двух режимах: нормальном и
ненормальном. Нормальный режим наблюдается в 80% всех случаев
работы прибора; ненормальный — в 20%. Вероятность выхода прибора
из строя за время t в нормальном режиме равна 0,1, в ненормальном
0,7. Найти полную вероятность р выхода прибора из строя за время t.
Решение, р =0,8 • 0,1 + 0,2 • 0,7 = 0,22.
3.3. Завод изготовляет изделия, каждое из которых с вероятностью
р имеет дефект. В цехе имеются три контролера; изделие
осматривается только одним контролером (с одинаковой вероятностью первым,
вторым или третьим). Вероятность обнаружения дефекта (если он
имеется) для /-го контролера равна рг (i =1, 2, 3). Если изделие не
было забраковано в цехе, то оно попадает на ОТК завода, где дефект,
если он имеется, обнаруживается с вероятностью р0. Определить
вероятности следующих событий:
А = {изделие будет забраковано};
В = {изделие будет забраковано в цехе};
С = {изделие будет забраковано в ОТК завода}.
Решение. Так как события В и С несовместны и А = В + С,
то Р (Л) = Р (В) + Р (С). Находим Р (В). Для того чтобы изделие
было забраковано в цехе, нужно, чтобы оно, во-первых, имело] дефект
и, во-вторых, этот дефект был обнаружен. Вероятность обнаружения
имеющегося -дефекта по формуле полной вероятности равна х/3 (р± +
+ Р2 + Рз); отсюда Р (В) = V3 Р (Pi + р2 + Рз).
Аналогично Р (С)_= р [1 — V3 (Pi + Рг + РзЛРо» или,_ обозначая
V8 (Pi + р2 + Рз) = Р, _Р (В) = рр, Р (С) = рр0 (1 — р), откуда
Р(Л) =р[р+р0(1_р)].
3.4. Имеются две урны: в первой а белых шаров и Ь черных; во
второй с белых и d черных. Из первой урны во вторую перекладывают
не глядя один шар. После этого из второй урны берут один шар.
Найти вероятность того, что этот шар будет белым.
Решение. Событие А = {появление белого шара}; гипотезы:
#i = {переложен белый шар};
#2 = {переложен черный шар}.
57
a-\-b a-{-b с+«+!
Р(Л|Я2) = —4—; Р(Л)- a < + 1 '- *
c+d + l a+6 c+d + 1 a+b c+d+\
3.5. В условиях предыдущей задачи из первой урны во вторую
перекладывают не один, а три шара (предполагается, что а > 3, Ь ^
^ 3). Найти вероятность того, что из второй урны возьмут белый
шар.
Решение. Можно было бы выдвинуть четыре гипотезы:
Нг = {переложены 3 белых шара};
Я2 = {переложены 2 белых шара и 1 черный};
#3 = {переложены 1 белый шар и 2 черных};
#4 = {переложены 3 черных шара},
но проще решить задачу, имея всего две гипотезы:
Н1 = (вынутый из второй урны шар принадлежит первой урне};
Я2 = {вынутый из второй урны шар принадлежит второй урне}.
Так как во второй урне три шара принадлежат первой урне, а
с + d — второй, то Р (Нг) = 3/ (с + d + 3), Р (Я2) = (с + d)l (с +
+ d + 3).
Найдем условные вероятности события А = {появление белого
шара из второй урны} при гипотезах Нг и Я2. Вероятность появления
белого шара, принадлежащего первой урне, не зависит от того,
вынимается ли этот шар непосредственно из первой урны или после
перекладывания во вторую; поэтому
PHI^H-Ar, Р(Л|Я2) =
откуда
a + b c-{-d
7 c+d+3 a+b c+4+3 c+d
3.6. Имеется п урн, в каждой из которых а белых шаров и Ь черных.
Из первой урны во вторую перекладывают один шар; затем из второй в
третью один шар и т. д. Затем из последней урны извлекают один шар.
Найти вероятность того, что он белый.
Решение. Вероятность события Л2 = {извлечение белого шара
из второй урны после перекладывания} найдем так же, как в задаче
3.5 (при с = a, d = b):
Р(А \= а а+х I ь а = а ,
V 2/ а+b а+Ь + 1 а+Ь a + b+\ a + b'
Таким образом, вероятность извлечения белого шара из второй
урны после перекладывания будет такова же,, как и до перекладывания.
Следовательно, такова же будет и вероятность вынуть белый шар из
третьей, четвертой и т. д., /г-й урны:
Р (Ап) = а/(а + Ь).
3.7. Приборы одного наименований изготовляются двумя завода*
ми; первый завод поставляет 2/3 всех изделий, поступающих на
производство; второй 1/3. Надежность (вероятность безотказной работы)
прибора, изготовленного первым заводом, равна рг; второго р2.
Определить полную (среднюю) надежность р прибора, поступившего на
производство.
Ответ. 2/Зр! + 1/Зр2.
3.8. Имеется две партии однородных изделий; первая партия
состоит из N изделий, среди которых п дефектных; вторая партия—из
М изделий, среди которых т дефектных. Из первой партии берется
случайным образом К изделий, а из второй L изделий {K<N\ L<M)\
эти К + L изделий смешиваются и образуется новая партия. Из новой
смешанной партии берется наугад одно изделие. Найти вероятность
того, что изделие будет дефектным.
Решение. Событие А = {изделие будет дефектным}.
Гипотезы:
Н1 = {изделие принадлежит первой партии};
#2 = {изделие принадлежит второй партии}.
Р(Я1) = -^-; Р(Яв)=—!L; Р(Л) = —^_JL + _^_^L .
V v K+L V 2J K+L K+L N ^ K+L M
3.9. В условиях предыдущей задачи из новой, смешанной,
партии берется не одно изделие, а три. Найти вероятность того, что хотя
бы одно изделие из трех окажется дефектным.
Решение. Гипотезы:
#0 = {все три изделия принадлежат первой партии};
Нг = (два изделия принадлежат первой партии, а одно— второй};
Я2 = {одно изделие принадлежит первой партии, а два — второй};
Н3 = {все три изделия принадлежат второй партии}.
р/д у- Х(Х-1)(/С-2)
1 °' (K+L)(K+L—l)(K+L-2) '
Г(Н)-- 3*(X-1)L
V v (K+L)(K+L-\)(K+L-2) '
Р(Я2) =
3KL(L—1)
Р(#з) =
(K+I)(/C+I-l)(K+I-2)
1(1—1) (I—2)
(K+L)(K+L-\)(K+L-2) '
ПЛ 1 H )-: 1 W-n)(N-n-l)(N-n-2)
K { 0) N(N—\)(N—2)
(N—n)(N—n—\)(M—m)
N(N— \)M
Р(Л|//1)=1-
L
piA\H\-\ (N-n)(M-m)(M-m-l)
Г(Л\Н)-1 (М-т)(М-т-1)(М-т-2)
K ' 3' M(M—1)(<W—2)
69
Р(А) = Р(Н0)Р(А\Н0) + Р(Я1)Р(А\Н1) +
+ Р (Я2) Р (А | Я2) + Р (Я3) Р (А | Я3),
3.10. Имеется два ящика, в которых находятся однотипные
изделия; некоторые из них исправны, другие — дефектны. В первом
ящике а исправных изделий и Ъ дефектных, во втором — с исправных и d
дефектных. Из первого ящика во второй перекладывают наугад одно
изделие, его смешивают с другими, после чего из второго ящика в
первый перекладывают обратно одно наугад выбранное изделие. После
всего этого из первого ящика берут наугад одно изделие. Найти
вероятность того, что оно будет исправным.
Решение. Гипотезы:
Нг = {состав изделий в первом ящике не изменился};
Я2 = {в первом ящике одно дефектное изделие заменено
исправным};
Я3 = {в первом ящике одно исправное изделие заменено
дефектным}.
Событие А = {из первого ящика после перекладываний вынуто
исправное изделие}.
P(/yl) = _5 £±1_ + _* *±!_; Р(Я2) = «
a+b c+d + l a+b c+d + l ' a+b c+d + l
Р(#з)==_£_,_i—; pmW-^ £±L. + _*—!±!_) JL.+
4 6) a+b c+d + l * ' \a+b c+d+l a+b c+d+l ja+b
. b с a + \ , a d a —1 __
a + b c+d + \ a+b a+b c+d + l a+b
_a(a+b) (c+d + l) +bc—ad __ a . be—ad
~~ . (a+b)* (c+d + l) ~~ a+b (a + b)* (c+d + l) '
Полученное решение показывает, что вероятность вынуть
исправное изделие не изменится, если доли исправных и дефектных изделий
в обеих урнах одинаковы: с/а = d/b, т. е. be — ad = 0.
3.11. Из чисел 1,2, ..., п одно за другим выбирают наугад два
числа. Какова вероятность того, что разность между первым выбранным
числом и вторым будет не меньше т (т> 0)?
Решение. Событие А состоит в том, что разность между первым
вынутым числом k и вторым вынутым числом / будет не меньше т (т. е.
k — / ^ т). Гипотезы Hk = {первым вынуто число k) (k = m + 1, ...
..., п).
Р (Я*) = 1/л; Р (A \Hh) = (к - т)1 (п - 1);
Р(Л)= У -tl^e_J-_[l + 2+... + (n-m)] =
__ (п—т) (п—т+ 1)
"~ 2п(п—1)
60
3.12. Из N стрелков можно выделить четыре группы: аг отличнык
стрелков, а2 хороших, а3 посредственных и а4 плохих. Вероятность
попадания в мишень при одном выстреле для стрелка 1-й группы
\ равна pi (i= l, 2, 3, 4). Вызываются наугад два стрелка и стреляют
по одной и той же мишени. Найти вероятность хотя бы одного
попадания в мишень.
i -. Решение. Событие А = {хотя бы одно попадание в мишень}.
| Гипотезы Hi = {первым вызван стрелок i-и группы} (I = 1, 2, 3, 4).
Р(Я;) = 1,Р(/1)=^ P(A\Ht),
1=1
где Р (A \Hi) снова находим по формуле полной вероятности при
четырех гипотезах о том, какой стрелок был вызван вторым:
3.13. Радиолокационная станция ведет наблюдение за объектом,
} который может применять или не применять помехи. Если объект не
применяет помех, то за один цикл обзора станция обнаруживает его
с вероятностью р0; если применяет — с вероятностью рх <С р0.
Вероятность того, что во время цикла будут применены помехи, равна р и
не зависит от того, как и когда применялись помехи в остальных цик-
I лах. Найти вероятность того, что объект будет обнаружен хотя бы один
I раз за п циклов обзора.
1 Решение. Полная вероятность обнаружения за один цикл
[ (1 — р)р0 + ррг\ вероятность хотя бы одного обнаружения за п
циклов равна 1 — [1 — (1 — р)р0 — ppiK
3.14. Работает диагностическая машина, в которую вводятся ре-
[ зультаты п анализов, взятых у больного. Каждый анализ (независимо
| от других) с вероятностью р может оказаться ошибочным. Вероятность
I 3й правильного диагноза есть неубывающая функция числа т верных
I анализов: £Р = ф (т). За время т работы машины был поставлен диаг-
I ноз k больным. Найти вероятность события А = {хотя бы одному боль-
I ному поставлен ошибочный диагноз}.
| Решение. Рассмотрим событие В = {отдельному больному по-
I ставлен ошибочный диагноз}. Сделаем гипотезы о числе безошибочно
1 проведенных анализов:
I #0 = {ни одного безошибочного анализа};
I Н\ = {ровно один безошибочный анализ};
I Нт = {ровно т безошибочных анализов};
Щ • • • ;
| лп = {п безошибочных анализов}.
Я Вероятность события Нт при любом т вычисляется с помощью фор-
| мулы (2.0.15) (теорема о повторении опытов) при замене р на 1 —р:
I 61
Р(Я0) = р»;Р(Я1) = п(1-/7)/7»-«; ...;
Р (Нт) = С- (1-рГ рп~т ;...; Р (Яп) = (1 -рГ
По формуле полной вероятности
Р (Я)= 2 C^(l-p)'» р»-* Ф (от); Р (Л)= 1-11-Р (В)]*
3.15. Цех завода производит определенного вида изделия; любое
из них с вероятностью р имеет дефект. Каждое изделие осматривается
браковщиком, который обнаруживает дефект, если он имеется, с
вероятностью рг и не обнаруживает — с вероятностью 1 — рх. Кроме
того, иногда браковщик допускает ошибку, бракуя
доброкачественное изделие; это происходит с вероятностью р2- За смену браковщик
осматривает N изделий. Найти вероятность R того, что хотя бы одно
из них будет квалифицировано им неправильно: или, будучи
дефектным, отнесено к доброкачественным, или же наоборот (считается, что
результаты осмотра отдельных изделий независимы).
Решение. Гипотезы:
Н± = {изделие имеет дефект}; Н2= {изделие не имеет дефекта}.
Вероятность одному изделию быть квалифицированным неверно,
по формуле полной вероятности равна
Р =Р (1 — Pl) + О — P)Pf
Вероятность того, что хотя бы одно изделие будет
квалифицировано неправильно, равна
R = 1 — (1 — р)^-
3.16. Группа студентов состоит из а отличников, Ь хорошо
успевающих и с занимающихся слабо. Отличники на предстоящем экзамене
могут получить только отличные оценки. Хорошо успевающие
студенты могут получить с равной вероятностью хорошие и отличные
оценки. Слабо занимающиеся могут получить с равной вероятностью
хорошие, удовлетворительные и неудовлетворительные оценки. Для
сдачи экзамена вызывается наугад один студент. Найти вероятность
события А = {студент получит хорошую или отличную оценку}.
Решение. Гипотезы:
#х = (вызван отличный студент};
#2 = {вызван хороший студент};
Н3 = {вызван слабый студент}.
Р(Я^ = —^;Р(Я2) = -^—;Р(Я3) =
a+b+с а+Ь+с а+Ь+с
р(Л)=Р(я1).1+Р(я2).1+Р(я3)4-=а+6+с/3
а+Ь+с
62
3.17. В условиях предыдущей задачи вызываются наугад три
студента. Найти вероятность того, что они получат отметки отлично,
хорошо и удовлетворительно (в любом порядке).
Решение. Событие А = {получение отличной,- хорошей и
удовлетворительной отметки} возможно только при одной из следующих
гипотез:
Нг = {вызваны один слабый студент, один хороший и один
отличник};
#2 = {вызваны один слабый студент и два хороших};
#3 = {вызваны два слабых студента и один хороший};
#4 = {вызваны два слабых студента и один отличник}.
P(#l) = <М± ; Р(Я2)=, ЗН»-1)С
4 1J N (N—l)(iV—2) ч 2/ N (N—1) (tf—2)
3fc(C-l) р(Я)= &*(С-1) ^ = а + 6 + с,
v з; Л^ (ЛА— 1)(N—2) v 4/ tf(tf—l)(tf—2)
Р(Л) = Р(Я1).1.-1.. 2-+Р(я2)А. _1+
+ Р(Я3)у- |" + Р(Я4)-1~ •
3.18. В автобусе едут п пассажиров. На следующей остановке
каждый из них выходит с вероятностью р; кроме того, в автобус с
вероятностью р0 не входит ни один новый пассажир; с вероятностью
I —р0 —один новый пассажир. Найти вероятность того, что когда
автобус снова тронется в путь после следующей остановки, в нем
будет по-прежнему п пассажиров.
Решение. Событие А = {после остановки снова п пассажиров}.
Гипотезы:
#0 = {не вошел никто};
Н1 = {вошел один пассажир}.
Р (Яо) = Ро; Р (Ях) = 1 - р0; Р (А \Н0) = (1 - р)»; Р (A |#i) «
= пр (1 - р)«-*; Р (А) = ро (1 - р)« + (1 - р0)яр (1 - pY~К
3.19. Прибор состоит из двух дублирующих друг друга узлов I и
II (рис. 3.19) и может случайным образом работать в одном из двух
режимов: благоприятном и неблагоприятном. В благоприятном
режиме надежность'каждого узла равна р1э в неблагоприятном р2.
Вероятность того, что прибор будет работать в благоприятном режиме, равна
Pi, в~ неблагоприятном 1 — Рг. Найти полную (среднюю) надежность
прибора Р.
?oV*oT- Р =pi I1 — (! — Pi)2l + (1 +^i)Il — (1—Р2)21.
o.2U. В шкафу стоят однотипные приборы, из которых а новых и Ь
уже бывших в эксплуатации (а > 2, Ъ ^ 2). Выбираются наугад два
прибора и эксплуатируются в течение какого-то времени, после чего
возвращаются в шкаф. Затем вторично выбираются наугад два
прибора. Найти вероятность события А = {оба вторично выбранных при-
оора — новые}.
63
Решение. Гипотезы:
Нг = {оба выбранных первый раз прибора были новыми};
#2 = {оба выбранных первый раз прибора уже были в
эксплуатации};
Н3 = {один из выбранных первый раз приборов был новым, а
другой уже эксплуатировался}.
?(#!) = а(а-\) .р (НЛ_ *_(*-!)_
(а+Ь) (а+6-1)
;Р(я2):
(а+Ь) {а + Ь-\)
;Р(#3) =
2аЪ
Р(А)
(а+Ь,(а+Ь-\) '
_а (а—1) (а—2) (а—3)+& (6—1) а (a—l)+2ab (a—I) (а—2)
{а + ЪГ(а+Ь—1)2
j-LLh -{7}-{J|
я Н
J
if
Рмс. 5.;р
©
Рис. 3.22
©
Рис. 3.23
3.21. Сообщение может передаваться по каждому из п каналов
связи, обладающих разными свойствами (или находящимися в разных
состояниях); из них пг каналов — в отличном состоянии, п2 — в
хорошем, п3 — в посредственном и п4 — в плохом (пг + п2 + п3 + п^ —
= п). Вероятность правильной передачи сообщения для различных
видов каналов соответственно равна р19 р2, р3, р4. Для повышения его
достоверности сообщение передается два раза по двум различным
каналам, которые выбираются наугад. Найти вероятность того, что хотя
бы по одному из каналов оно будет передано правильно.
Решение. Л = {хотя бы одно из сообщений передано
правильно}. Сделаем четыре гипотезы о том, по каналу какой группы
передано первое из двух сообщений: Hlt Я2, Н3, #4, где Ht = {первое
сообщение передано по каналу *'-й группы}; Р (Ht) =tiifn (i = 1, 2,
3, 4). По формуле полной вероятности
Р(Л)=2 P(Ht)P{A\H0.
1=1
Условная вероятноть события А при гипотезе Нг равна
Р(Л|Я,) = ^4[1-(1-р02 + 2 ^
я—1
-1
П-(1-л)(1-Р/)]
3.22. Прибор состоит из двух узлов I и II (рис. 3.22),
безотказная работа которых необходима для работы прибора, и стабилизатора
напряжения S} который может быть исправен или неисправен. При
64
исправном стабилизаторе S надежности узлов I и II равны р± и р2; при
неисправном'—р[ и р'2. Стабилизатор исправен с вероятностью ps.
Найти полную надежность прибора Р.
Ответ. Р = pspip2 + (1 — Ps)p\P2-
3.23. Условия те же, что и в задаче 3.22, но узлы I и II дублируют
друг Друга (рис. 3.23).
Ответ. Р =р5 [1 - (1 -Pl) (1 _р2)] + (l-ps) [1 -(1 -
-Pl)(l-P2)l.
3.24. Имеется п экзаменационных билетов, каждый из которых
содержит два вопроса. Экзаменующийся знает ответ не на все 2п
вопросов, а только на k < 2n. Определить вероятность р того, что
экзамен будет сдан, если для этого достаточно ответить на оба вопроса
своего билета или на один вопрос из своего билета и на один (по выбору
преподавателя) вопрос из дополнительного билета.
Решение. Гипотезы:
#i = {экзаменующийся знает оба вопроса своего билета};
#2 = {экзаменующийся из двух вопросов своего билета знает
один}.
__ k (6—1) « 2k {2n—k) k—\
P~ 2n (2n—1) " 2n(2n — \) 2n—2
3.25*. Цель, по которой ведется стрельба, с вероятностью рг
находится в пункте I, а с вероятностью р2 = 1 — Pi в пункте II
(р± > 1/2). В нашем распоряжении имеется п снарядов, каждый из
которых может быть направлен в пункт I или в пункт II. Каждый
снаряд поражает цель независимо от других с вероятностью р. Какое
число снарядов пг следует направить в пункт I для того, чтобы поразить
цель с максимальной вероятностью?
Решение. Событие А = {поражение цели при направлении п±
снарядов в пункт I}. Гипотезы:
Нг = (цель в пункте I}; Р (Я2) = рх;
Н2 = {цель в пункте II}; Р (Я2) = 1 — рг.
Р(А) = р1[1-(1-рГ*] + (1-р1)[1-(1-рГ-»>].
Рассматривая Р (А) как функцию непрерывного аргумента п19
находим
dP (A)
dtii
d* P (А)
. = [_А(1_р)«, + (1_А)(1_р)»-«.]1п(1_р);
dnl = -Ift (l-P^+O-ft) О-рУ1-*'] in2 (l -p) < о,
откуда видно, что эта функция имеет единственный максимум в точке
пх =4- + ln ±=& / [2 In (1-p)], где dP(A)/dnx = 0.
2 Pi /
Заметим, что пг > л/2 при рх > 1/2.
Если полученное число %,< /i и оно целое, то это и есть искомое
число; если оно не целое (но <л), то нужно вычислить Р (Л) для двух
3 Зак. 1040 65
ближайших целых значений и выбрать то из них, для которого Р (А)
больше; если полученное число 7гх окажется больше я, то следует
направить все п снарядов в пункт I {это случится при In [ (1 — Pi)/pil ^
< л In (1 — р), т. е. Л > [1 + (1 — Ру\-\
3.26. Производится посадка самолета на аэродром. Если
позволяет погода, летчик сажает самолет, наблюдая за аэродромом визуально.
В этом случае вероятность благополучной посадки равна рг. Если
аэродром затянут низкой облачностью, летчик сажает самолет вслепую
по приборам. Надежность (вероятность безотказной работы) приборов
слепой посадки равна Р. Если приборы слепой посадки сработали,нор-
мально, то самолет садится благополучно с той же вероятностью р1э
что и при визуальной посадке. Если же приборы слепой посадки не
сработали, то летчик может благополучно посадить самолет с
вероятностью р* < Pi.
Найти полную вероятность благополучной посадки самолета, если
известно, что в k% всех случаев посадки аэродром затянут низкой
облачностью.
Решение. А = {благополучная посадка}. Гипотезы:
Нг = {низкой облачности нет};
Я2 = {низкая облачность есть}.
Р (Нг) = 1 — 6/100; Р (Я2) = А/100; Р (А \Нг) = р1.
Р (А | Я2) находим снова по формуле полной вероятности:
Р(Л|Я2) = Яр1+(1-Р)р1;Р(Л) = (1 ~5~)pi +
1 * [Ppx+(l-P)Pll
100
3.27» Имеются три урны: в первой а белых шаров и Ь черных; во
второй с белых шаров и d черных; в третьей k белых шаров (черных
нет). Некто выбирает наугад одну урну и вынимает из нее шар. Этот
шар оказался белым. Найти вероятность того, что этот шар вынут из
первой, второй или третьей урны.
Решение. Решаем задачу по формуле Бейеса (3.0.2). Гипотезы:
Нх = {выбор первой урны};
Я2 = {е
{выбор второй урны};
Hs = {выбор третьей урны}.
Априори (до опыта) все гипотезы равновероятны: Р (Нг) = Р (Я2) =
= Р (Я3) = 1/3.
Наблюдалось событие А = {появление белого шара}. Находим
условные вероятности:
Р(Л|ЯХ) =о1(а + Ь)\ Р(Л|Я2) ^c/(c + d); Р(Л|Я8) = 1.
По формуле Бейеса апостериорная вероятность того, что шар был
вынут из первой урны, равна
P(H1\A) = -Lp(A\H1)j^±fiP(A\Hi)j =
66
. [a+b)l{a+b + c+d +1J
Аналогично
P№M).(_£_ + _£_ + ,)-.
3.28. Прибор состоит из двух узлов; работа каждого узла
безусловно необходима для работы прибора в целом. Надежность (вероятность
безотказной работы в течение, времени t) первого узла равна р1э
второго р2. Прибор испытывался в течение времени t, в результате чего
обнаружено, что он вышел из строя (отказал). Найти вероятность того,
что отказал только первый узел, а второй исправен.
Решение. До опыта возможны четыре гипотезы:
Н0 = {оба узла исправны};
Нг = (первый узел отказал, а второй исправен};
Я2 = {первый узел исправен, а второй отказал};
Я3 = {оба узла отказали}.
Вероятности гипотез:
р (Но) = рл; р (tfi) = (1 - pi)p.; р (я.) = а О - р.);
Р(Я3) =0-р1)(1-р2).
Наблюдалось событие А = {прибор отказал}:
Р(Л|Я0) =0; Р(Л|ЯХ) = Р(Л|Я2) =Р(Л|Я3)' = 1.
По формуле Бейеса
Р(Я |Л) = (l—Pi)p2 = О—Pi)ft
1 (l-ft)ft+ftO-Pi) + (l-ft)(l-Pi) 1-ftPi
3.29. В условиях задачи 3.26 известно, что самолет приземлился
благополучно. Найти вероятность того, что летчик пользовался
приборами слепой посадки.
Решение. Если летчик пользовался приборами слепой посадки,
то, значит, облачность была (гипотеза Я2). По данным задачи 3.26
находим
Р(Я2|Л) =
k [Ppi + ll-P)P{]
100
(1.-1йг)л+1^1Яй+(1-,,)^
3.30. У рыбака имеется три излюбленных места для ловли рыбы,
которые он посещает с равной вероятностью каждое. Если он
закидывает удочку на первом месте, рыба клюет с вероятностью рг\ на
втором месте — с верЪятностыб ра; на третьем — с вероятностью р3.
Известно, что рыбак, выйдя на ловлю рыбы, три раза закинул удоч-
3*
67
ку и рыба клюнула только один раз. Найти вероятность того, что он
удил рыбу на первом месте.
з
О т в е т. Р (Нг | А) = [Pl (1 -Plf] / 2 Л U -Pi)2
3.31. Завод изготовляет изделия, каждое из которых с
вероятностью р имеет дефект. В цехе изделие с равной вероятностью
осматривается одним из двух контролеров. Первый контролер обнаруживает
имеющийся дефект с вероятностью р1у второй— с вероятностью р2.
Если в цехе изделие не забраковано, оно поступает на ОТК завода,
где дефект, если он имеется, обнаруживается с вероятностью р.
Известно, что изделие забраковано. Найти вероятность того, что оно
забраковано: 1) первым контролером; 2) вторым контролером; 3) ОТК
завода.
Решение. До опыта возможны четыре гипотезы:
Я0 = {изделие не забраковано};
Нг = {изделие забраковано первым контролером};
Я2 = {изделие забраковано вторым контролером};
Я3 = {изделие забраковано ОТК завода}.
Наблюдалось событие А = {изделие забраковано}. Гипотеза Я0
нам не нужна, так как Р (А |Я0) = 0;
Р (#i) =PPi/2; Р (Я2) = рр2/2; Р (#3) = Р П - (Pi + P2)/2]p3.
Вероятности гипотез после опыта:
Pi . n/tf IJ\ Pa .
Р(Нг\А) = п ,, " -;Р(Я2|Л) =
2p0+(Pi+P2) (1-Рз) 2Po + (Pi+P2) (1-Рз)
Р(Яз|Л) = р0[2~(р1 + р2)]/[2ро + (Р1 + Р2)(1-Рз)].
3.32. В группе из 10 студентов, пришедших на экзамен, 3
подготовленных отлично, 4 — хорошо, 2 — посредственно и 1 — плохо. В
экзаменационных билетах имеется 20 вопросов. Отлично
подготовленный студент может ответить на все 20 вопросов, хорошо
подготовленный . — на 16, посредственно — на 10, плохо — на 5. Вызванный
наугад студент ответил на три произвольно заданных вопроса. Найти
вероятность того, что этот студент подготовлен: 1) отлично; 2) плохо.
Решение, Гипотезы:
#! = {студент подготовлен отлично};
#2 = {студент подготовлен хорошо};
Я3 = {студент подготовлен посредственно};
Я4 = {студент подготовлен плохо}.
До опыта: Р (Нг) =0,3; Р (Я2) =0,4; Р (Я3) =0,2;. Р (Я4) =
= 0,1.
Событие А = {студент ответил на три вопроса}. Р (Л|ЯХ) = 1;
РШЯ2) = -^.-^-. il«0,491; Р (А|Я3) = —• - -«0,105;
v ' '2/ 20 19 18 V ' 3/ 20 19 18
р (А | НА = — — • — « 0,009.
4 j 4/ 20 19 18
68
После опыта:
1) Р(Н1\А) = ^^ «0,58;
4 к 1! ; 0,3.0,1+0,4.0,491 + 0,2.0,105 + 0,1.0,009
2) Р(#4|Л) =0,1-0,009/0,518^0,002.
3.33. На вход радиолокационного устройства с вероятностью р
поступает смесь полезного сигнала с помехой, а с вероятностью 1—р—
только одна помеха. Если поступает полезный сигнал с помехой,
то устройство регистрирует наличие какого-то сигнала с
вероятностью рц если только помеха — с вероятностью р2. Известно, что
устройство зарегистрировало наличие какого-то сигнала. Найти
вероятность того, что в его составе имеется полезный сигнал.
Ответ. ррх7 Ippi + (1 — p)p2L
3.34. Пассажир может обратиться за получением билета в одну из
трех касс. Вероятности обращения в каждую кассу зависят от их
местоположения и равны соответственно Pi,p2,p3- Вероятность того, что
к моменту прихода пассажира имеющиеся в кассе билеты будут
распроданы, равна для первой кассы Pl9 для второй Р2, для третьей Р3.
Пассажир направился за билетом в одну из касс и приобрел билет.
Найти вероятность того, что это была первая касса.
Решение. P(^)= pl9 Р (Я2) = р2; Р (К3) = р3\ А =
{приобрел билет}.
Р {А\Нг) = 1 - /у, Р (А\Н2) = 1 - Р2; Р (А\Н3) = 1 - Р3.
Pi О-Я1)
Р(Нг\А)=*
Pi(l-Pi)+P* 0-ЛО+Рз (1-Я,)
3.35. Производится один выстрел по плоскости, на которой
расположены две цели: I и II (рис. 3.35). Вероятность попадания в цель I
равна р1э в цель II равна р2. После выстрела получено известие, что
попадания в цель I не произошло. Какова теперь вероятность того, что
произошло попадание в цель И?
Решение. Гипотезы:
#i = {попадание в цель I};
ж
#2 = {попадание в цель II}; УУ/^Л
Н3 = {непопадание ни в одну из целей}. х^//А
Событие А = {непопадание в цель I}; У///Л
D Р(^)=Рх;Р(я2)=р2; х Рис'3'35
Р(Я|)=1-(й + р|).РИ|Я1) = 0; Р(Л|#2)=1; Р(Л|#3) = 1.
По формуле Бейеса
Р (Я,И) = р2/ [р2 + 1 - (Pi + р,)1 = pj (1 - Pi).
Эту задачу можно решить и без формулы Бейеса:
Р (#2И) = Р (Я2Л)/Р (А) = Р (#2)/Р (А) = р2/ (1 - рх).
3.36. Передача сигналов происходит с вероятностями Ql9 Q2, Q3 в
одном из трех режимов jRlf R2, R3,b каждом из трех режимов сигнал
69
доходит до адресата неискаженным помехами с вероятностями ръ р2,
р3 соответственно. Передача трех сигналов происходила в одном из
режимов (каком — неизвестно); из этих сигналов один был искажен
помехами, а два другие — нет. Найти апостериорные вероятности
того, что передача происходила в первом, втором и третьем режимах.
Решение. Гипотезы:
Нг = {режим /?х};
Я2 = {режим R2}\
Н3 = {режим R3}.
Априорные вероятности: Р (Нг) = Q±; Р (Я2) = Q2; Р (Н3) = Q3.
Событие А = .{один сигнал искажен, два другие нет}.
P(A\Ht) = 3Pi(l-Pi)* (/=1,2,3);
Р (Ht \A) = Qt Pi (l-Pif I^QtPi (1—Pi)2 ('=1. 2, 3).
3.37. Расследуются причины авиационной катастрофы, о которых
можно сделать четыре гипотезы: Нг, Я2, Я3, Я4. Согласно
статистике Р(ЯХ) =0,2; Р(Я2) =0,4; Р (Я3) =0,3; Р (Я4) =0,1.
Обнаружено, что в ходе катастрофы произошло событие А =
{воспламенение горючего}. Условные вероятности события А при гипотезах Н19
Я2, #3 и #4 согласно той же статистике равны: Р (Л|ЯХ) =0,9;
Р(Л|Я2) =0; Р(Л|Я3) =0,2; Р(Л|Я4) =0,3.' Найти
апостериорные вероятности гипотез.
Ответ. Р (Нг\А) = 2/3; Р (Я2|Л) = 0; Р (Н3\А) = 2/9;
р (Я4|Л) = 1/9.
3.38. Объект, за которым ведется наблюдение, может находиться
в одном из двух состояний: Нг и Я2; априорные вероятности этих
состояний Р (Нг) = 0,3; Р (Я2) = 0,7. Имеется два источника
информации, которые приносят разноречивые сведения о состоянии объекта:
первый источник сообщает, что объект находится в состоянии Я1э
второй — что в состоянии Я2. Первый источник вообще дает правильные
сведения о состоянии наблюдаемого объекта в 90% случаев и только
в 10% ошибается. Второй источник менее надежен: он сообщает
правильные сведения в 70% случаев, а в 30% ошибается. На основе
анализа донесений найти новые (апостериорные) вероятности состояний
Я1э Я2.
Решение. Событие А = {первый источник сообщает Н19
второй Я2}. Условные вероятности этого события при гипотезах Нг, Я2
равны:
Р (А |ЯХ) = Р {первый источник дал верное сообщение, второй
ошибся} =0,9 • 0,3 =0,27;
Р (А |Я2) = Р {первый источник ошибся, второй дал верное
сообщение} = 0,1 • 0,7 =0,07.
По формуле Бейеса
Р (Ях | А) = °'3'0'27 « 0,623;
' 0,3-0,27+0,7.0,07
Р (Я21 А) = 1 — Р (Нг | А) я* 0,377.
70
3.39. В условиях предыдущей задачи имеются три источника
информации, одинаково достойных доверия, дающих верные
сообщения в 70% случаев, а в 30% — ошибочные. Два источника
сообщили, что объект находится в состоянии Н19 а один — что он находится
в состоянии Я2. Найти апостериорные вероятности состояний Нг и
Решение. Л = {первый и второй источники сообщили Я1э
третий я2}.
р (Л \Нг) = 0,7-0,7.0,3 = 0,147; Р (Л |Я2) = 0,3-0,3-0,7 = 0,063;
Р(Я1|Л)= 0>3'0'147 = 0,5;Р(Я2|Л) = 0,5,
v ll ' 0,3.0,147+0,7-0,063 V ' '
т. е. после опыта гипотезы Н1$ Я2 одинаково вероятны.
3.40. До опыта о его условиях можно было сделать п несовместных
гипотез, образующих полную группу: Н19 Я2, ..., Нп с априорными
вероятностями: Р (Нг), Р (Я2), ..., Р (Яп). В результате опыта стало
известно, что имела место какая-то одна гипотеза из группы Я1э ..., Hk$
а остальные гипотезы невозможны: Нг + Я2 + ... + Hh = Q;
Яй + i + ... + Яп = 0. Найти апостериорные вероятности гипотез.
k
Решение. Наблюдаемое в опыте событие Л = 2 Ни По
Chopin i
муле Бейеса получим
Р(ЯНЛ) = Р(Я,)|2 p(Ht) (/=1,...,&),
т. е. если в результате опыта выяснилось, что возможна только какая-то
часть гипотез Я1э ..., Hk, а остальные невозможны, то для получения
апостериорных вероятностей нужно каждую из априорных
вероятностей Р (Нг), Р (Я2), ..., Р (Яп) разделить на их сумму.
3.41. Испытывается прибор, состоящий из двух узлов I и II.
Надежности (вероятности безотказной работы за время т) узлов I и II
известны и равны рх = 0,8; р2 = 0,9. Узлы отказывают независимо друг
от друга. По истечении времени т выяснилось, что прибор неисправен.
Найти с учетом этого вероятности гипотез:
Ях = (неисправен только первый узел};
Я2 = {неисправен только второй узел}; !
Я3 = {неисправны оба узла}.
Р е ш е н и е. До опыта возможны были не три, а четыре гипотезы*
включая Я0 = {исправны оба узла}. Опыт показал, что имеет место
одна из гипотез Я1э Я2, Я3; Л =Нг + Н2 + Я3. Априорные
вероятности этих гипотез:
Р (#i) =0,2 - 0,9 =0,18; Р (Я2) =0,8 - 0,1 =0,08;
Р (Я3) = 0,2 - 0,1 = 0,02; jj P (Я,) = 0,28.
Апостериорные вероятности гипотез:
Р (Нг\А) = 0,18/0,28 я* 0,643; Р (Я2|Л) « 0,286; Р (Я3|Л) я* 0,071.
71
3.42. Прибор, характеристики которого даны в задаче 3.41, испы-
тывается в течение времени т, причем выясняется, что он неисправен.
Для локализации неисправности прибор подвергается тестированию
с помощью трех тестов: Тг , Т2, Ту, в результате тестирования
оказалось, что первые два теста дали положительный результат, а третий —
отрицательный, т. е. произошло событие В = {-Н—}, где «+»
означает положительный результат теста, а «—» отрицательный. Известны
условные вероятности положительного результата тестов Tl9 Г2, Т3
при гипотезах #1э #2, #3; обозначаем их рц> где I — номер теста, / —
номер гипотезы; ри = 0,4; р12 = 0,6; р13 = 0,9; р21 = 0,5; р22 = 0,4;
р23 =0,6; Рз1 =0,7; р32 =0,6; р33 =0,3. Результаты тестирования
независимы.
Указать наиболее вероятное из возможных состояний прибора, для
чепГнайти апостериорные вероятности гипотез при условии, что опыт
дал события А и В (А = {прибор неисправен} = Нг + Н2 + #3).
Решение. В качестве априорных вероятностей для учета
результатов тестирования возьмем данные предыдущей задачи 3.41:
Р(ЯхИ) =0,643; Р(#2И) =0,286; Р (Н3\А) =0,071.
Вычисляем условные вероятности события В при этих гипотезах:
Р (В\НХ) = 0,4 -0,6-0,1 = 0,024; Р (В\Н2) = 0,5 • 0,6 • 0,4 =
= 0,120; Р (В|Я3) = 0,7 • 0,6 . 0,7 = 0,294.
По формуле Бейеса
Р (Нг\ А •£)= 0>643'0,024 « 0,298;
v } 0,643-0,024 + 0,286.0,120+0,071.0,294
Р (Н'2\А • В) « 0,662; Р (#зИ • В) » 0,040.
Наиболее вероятное состояние прибора Н2 = {отказал только
второй узел}.
3.43. Подбирается набор из п деталей для изготовления прибора;
из них то или другое число может оказаться дефектным. Детали
поставляются двумя заводами I и II; статистика показывает, что
вероятность дефекта в продукции завода I равна р1э завода II — р2.
Прибор собирается из деталей работы одного и того же завода; в
лаборатории, где ведется сборка, имеются три ящика с деталями, два из них
содержат изделия I, один — изделия II; ящик, из которого берутся
детали для сборки, выбирается наугад. После сборки прибор проходит
контроль; если среди п деталей обнаружено не менее m дефектных,
прибор бракуется и предъявляется рекламация заводу-изготовителю.
Оказалось, что на контроле прибор забракован. | Найти вероятность
того, что рекламация будет представлена заводу I.]
Решение. Гипотезы: > \ \ '
Нх = {прибор собран из деталей изготовления завода, I},
Н2 = {прибор собран из деталей изготовления завода II}.
Априорные вероятности: Р (#x) = 2/3; Р (Я2) = 1/3-
Появилось событие А = {прибор забракован} = {не менее m дефект
ных изделий из п).
72
p (A I ях) = 2 A (i -ft)"-'; p ИI #2) = 2 ri (i -л)"-1
По формуле Бейеса апостериорные вероятности
3
Р(Ях|ЛН
-f-2^0-Pi)""'
i = m
■f 2 ^о-л^'+тЗ ^о-л)"-1
i=m
Р(Я,^)=1-Р(Я1|А).
3.44. Имеются два ящика с однотипными деталями; в первом а
исправных деталей и Ь дефектных, во втором с исправных и d дефектных.
Выбирается наугад один ящик и из него вынимается одна деталь. Эта
деталь оказалась исправной. Найти вероятность того, что
следующая деталь, которую вынем из того же ящика, тоже будет исправной.
Решение. Гипотезы:
Нг = {выбран первый ящик};
#2 = {выбран второй ящик}.
Событие А = {исправная деталь при первом вынимании}.
Р (Ях) = Р (Я2) = 1/2;
P№M)=fe)/fe+7b);P№M)-fe)/fe+b^)-
Событие В = {исправная деталь при втором вынимании},
Р (В\А) =Р (НХ\А)Р (В\НгА) + Р (Я2|Л)Р (В\Н2А).
Условная вероятность появления второй исправной детали при
условии, что был выбран первый ящик и. из него была вынута исправная
деталь, равна
Р(В|ЯИ) =(а-1)/(а + 6-1);
аналогично Р (Б|Я2Л)= (с —l)/(c + d— 1).
Отсюда искомая вероятность
Р(В1Л) = 1^ + -£-У"!Г fl<g-!> + —£<£=П 1
' \а+Ь c+d) 1(а+Ь)(а+Ь— 1) (c+d)(c + d—\)\
3.45. Имеется три канала связи, сообщения по которым
распределяются случайным образом (с равной вероятностью). Вероятность
искажения сообщения при его передаче по первому каналу равна pl9
по второму р2, по третьему р3. Выбран какой-то канал и по нему
передано k сообщений; ни одно из них не было искажено. Найти
вероятность того, что (k + l)-e сообщение, переданное по тому же каналу,
не будет искажено.
Решение. Гипотезы:
#i = {сообщения передавались по первому каналу};
73
#2 = {соббщения передавались по второму каналу};
#3 = {сообщения передавались по третьему каналу}.
Р(Л|Яа) = (1-Л)*; Р(Л|Я2) = (1-р2)*; Р(Л|Я3) = (1-р3)*
Р(Н \Л)=- УзО-Р*)* =
" V3[(i-Pi)fe+(1-P2)4(l-P3)fe]
^~~^)- (f = 1, 2, 3).
(l-Pi)fe+(i-P2)*+(l-P3)*
Событие Л = {& сообщений не искажено}; В = {(k + l)-e
сообщение не искажено}.
, (1-Р1)*+(1-Р2)*+0-Рз)* '
3.46. Имеется т партий изделий объемом соответственно по Nlt
N2> --> Nm штук. В t'-й партии nt дефектных изделий и Ni — щ
доброкачественных (i =1, 2, ..., т). Выбирается наугад одна партия
и из нее берется для контроля k изделий; все они оказались
доброкачественными. Найти вероятность того, что следующие / изделий,
взятых из той же партии, также будут доброкачественными.
Решение. Гипотезы Н19 Я2, ..., НШ9 где Ht = {выбрана 1-я
партия} имеют равные априорные вероятности Р (Ht) = l/m(j = l,
2, ...,m).
Условная вероятность наблюденного события Л = {все k
контрольных изделий доброкачественны} при гипотезе #$ равна
Р(Л|#0 = С£_п./С&. (/ = 1,2, ...,/п). (3.46.1)
По формуле Бейеса апостериорные вероятности гипотез
P(Hi\A)^P(A\Hi)l %Р(А\Нг) (* = 1,2,...,т). (3.46.2)
/ i=\
Вероятность события В = {следующие / изделий, взятые из той
же партии, окажутся доброкачественными} вычисляется по формуле
полной вероятности с апостериорными вероятностями гипотез (3.46.2):
т
P(B)=^1P(Hi\A)P(B\HiA))
где P{B\HtA) =
Nj—nj—k Ni—nj—k— 1 Ni—tii—k—li-1'
Ni—k Ni—k—X Ni — k—l+l
(*=1,2, ..., tn). (3.46.3)
Примечание. Формулы (3.46.1) и (3.46.3) справедливы только при
условиях k < Ni — п$ I <C Ni — п% — k\ если они не выполняются,
соответствующие вероятности равны нулю.
74
ГЛАВА 4
ДИСКРЕТЛЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
4.0. Одним из важнейших понятий теории вероятностей является понятие
случайной величины. Под случайной величиной понимается величина, которая
в результате опыта со случайным исходом принимает то или иное значение.
Примеры: а) опыт — четыре выстрела по мишени; случайная величина — число
попаданий; б) опыт — эксплуатация ЭВМ; случайная величина — время
наработки ЭВМ до первого отказа.
В принятой нами теоретико-множественной трактовке основных понятий
теории вероятностей случайная величина X — это некоторая функция
элементарного события о : X = ф (ю), где ю £ Q. Значение этой функции зависит от
того, какое элементарное событие ю появилось в результате опыта.
В дальнейшем бы будем случайные величины обозначать большими буквами,
а неслучайные — маленькими.
Законом распределения случайной величины называется любое правило,
позволяющее находить вероятности всевозможных событий, связанных со
случайной величиной, например, вероятность того, что она примет какое-то значение или
попадет в какой-то промежуток. Если случайная величина X имеет данный
закон распределения, то про нее говорят, что она «распределена по этому закону»
или же «подчиняется этому закону распределения».
Наиболее общей формой закона распределения является функция
распределения, представляющая собой вероятность того, что случайная величина X примет
значение меньшее, чем заданное х:
F (*) = Р{Х<*}. (4.0.1)
Функция распределения F (х) для любой случайной величины обладает
свойствами: F ( — оо) = 0, F (+ оо) = 1, при возрастании х функция F (х) не
убывает. Наиболее простой вид имеют законы распределения у так называемых
дискретных случайных величин. Случайная величина называется дискретной,
если множество ее возможных значений конечно или счетно. Эти значения могут
быть перечислены, перенумерованы одно за другим.
В рассмотренных выше примерах случайная величина X — число
попаданий при четырех выстрелах — дискретна. Ее возможные значения: 0, 1,2, 3, 4.
Вторая случайная величина Т — время наработки ЭВМ до первого отказа —
недискретна, ее возможные значения непрерывно заполняют какой-то участок
оси абсцисс, их множество несчетно.
Простейшей формой закона распределения дискретнойслучайной величины X
является ряд распределения — таблица, в верхней строке которой перечислены
все значения случайной величины xlf x2, ..., х%, ... в порядке их возрастания, а в
нижней — соответствующие им вероятности ръ р2, ..., Ри ••••
*i I *2 I •••! *г I
Pi I Р2 I --I Pi I
(4.0.2)
гдер£ = Р{Х = ^}; Sp« = l.
Графическое изображение ряда распределений (рис. 4.0.1) называется
многоугольником распределения.
Функция распределения F (х) дискретной случайной величины X есть
разрывная, ступенчатая функция (рис. 4.0.2), скачки которой соответствуют
возможным значениям хъ х2, ... случайной величины X и равны вероятностям pl9 p2,
... этих значений; между скачками функция F (х) сохраняет постоянное значение.
В точке разрыва функция F (х) равна тому значению, с которым она подходит
к точке разрыва слева (на рис. 4.0.2 эти значения помечены точками). Функция
F (х) «непрерывна слева», т. е. при подходе к любой точке слева не терпит
разрыва, а при подходе справа может терпеть разрыв.
75
Рис. 4.0.2
Вероятность попадания случайной величины X на участок от а до р (включая
а) выражается через функцию распределения формулой
Р {a<X<P}=F(P)-F(a), (4.0.3)
или, в других обозначениях,
Р {X 6 К P)}=F(P)-F(a), (4.0.4)
где знаком [ обозначено то, что точка а включается в состав отрезка от а до Р, а
знаком) — что точка Р в него не включается.
Математическим ожиданием дискретной случайной величины X называется
сумма произведений всех ее возможных значений х% на соответствующие
вероятности pf.
M[X]=%xiPi.
(4.0.5)
Математическое ожидание случайной величины может и не существовать,
если соответствующая сумма расходится. В случае, когда надо математическое
ожидание случайной величины X обозначить одной буквой, будем писать
М [X] = тх.
Центрированной случайной величиной называется разность между
случайной величиной X и ее математическим ожиданием:
Х=Х — тх. (4.0.6)
Дисперсией случайной величины X называется математическое ожидание
квадрата соответствующей центрированной случайной величины:
D'[X] = MU4 (4.0.7)
Для дискретной случайной величины X дисперсия вычисляется по формуле
VW^^jiXi-m^pt. (4.0.8)
В случае, когда надо дисперсию случайной величины X обозначить одной буквой,
мы будем обозначать ее Dx.
Средним квадратическим отклонением (или стандартом) случайной
величины X называется корень квадратный из ее дисперсии:
а IX]-.
■УЩ
(4.0.9)
(подразумевается арифметическое или положительное значение корня).
Начальным моментом k-то порядка случайной величины X называется
математическое ожидание k-Pi степени этой случайной величины:
afe[X] = M[X*]. (4.0.10)
76
Для дискретной случайной величины X начальный момент вычисляется по
формуле
afc[X] = S*?P|. (4.0.11)
Центральным моментом k-vo порядка случайной величины называется
математическое ожидание k-и степени соответствующей центрированной
величины:
Ы*] = М[**]. (4.0.12)
Для дискретной случайной величины X центральный момент вычисляется по
формуле
Ы*1 = 2(*|-тя)*. (4.0.13)
Математическое ожидание случайной величины X есть ее первый
начальный момент, а дисперсия ^— второй центральный:
М[Х] = aJX]; D[X] = \i2[X]. (4.0.14)
Центральныг моменты выражаются через начальные моменты:
Ых\ = <*з[Х]—Зтха21Х]+2т1; \ (4.0.15)
Особенно важна первая из этих формул, выражающая дисперсию через
второй начальный момент:
D[X] = а2[Х] - ml (4.0.16)
или в другом написании
D[X] = М[Х2] — (М [X])2, (4.0.17)
т. е. дисперсия равна математическому ожиданию квадрата случайной величины
минус квадрат ее математического ожидания.
Индикатором события А называется дискретная случайная величина U,
имеющая два возможных значения: 0 и 1, равная 0, если событие А не появилось,
и единице, если появилось:
ПРИ °*Al (4.0.18)
при со £ Л.
ч:
Ряд распределения индикатора U события А имеет вид
0| 1
U:
где р — вероятность события в данном опыте; q = 1 — р.
Математическое ожидание и дисперсия величины U равны соответственно
M[U] = p\ D[U] = pq. (4.0.19)
В ряде задач теории вероятностей пользование индикаторами событий
существенно упрощает решение (см. гл. 7).
При вычислении числовых характеристик случайных величин часто бывает
Удобно пользоваться формулой полного математического ожидания: если об
условиях опыта можно сделать п несовместных гипотез Нъ #2, ..., #п, полное
математическое ожидание случайной величины X может быть вычислено по фор-
муле * *
М[Х]- 2 Р(Я|)Л*[*|Я|], (4.0.20)
т£е н- ' ^ — условное математическое ожидание величины] X при гипо-
77
Формулу полного математического ожидания можно применять при
вычислении начальных моментов любого порядка:
«*И—2 Р(1У|)М[Х*|Я|1. (4.0.21)
Пользоваться этой формулой в принципе можно и при вычислении центральных
моментов любого порядка
Ы*]=2 Р(Я1)М[**|Я,Ь (4.0.22)
но не забывать при этом, что величина X в (4.0.22) должна вычисляться как X =
= Х — тх, где тх — безусловное математическое ожидание случайной
величины X, выражаемое формулой (4.0.20), а не условное при гипотезе #*.
Существует несколько часто встречающихся типов распределений дискретных
случайных величин.
1. Биномиальное распределение. Случайная величина X называется
распределенной по биномиальному закону, если ее возможные значения 0, 1, ..., /и;...,
л, а соответствующие вероятности
Pm = p{X=m}==C™pm<7'l~m, (4.0.23)
где 0 < р < 1, q = 1 — р\ т = 0, 1, ..., п. Распределение (4.0.23) зависит от
двух параметров: р и п.
Из теоремы о повторении опытов [формула (2.0.15)] следует, что число X
появлений события при п независимых опытах имеет биномиальное
распределение. Для случайной величины X, имеющей биномиальное распределение с
параметрами рил,
MIX] = пр\ DU] = npqt (4.0.24)
где q = 1 — р.
2. Распределение Пуассона. Дискретная случайная величина X называется
распределенной по закону Пуассона, если ее возможные значения 0, 1, 2, ...,
т, ..., а вероятность события {X = т} выражается формулой
ат
Pm=P{X=m}=—-е~а (m=0, 1,2,...), (4.0.25)
ml
где а > 0. Распределение Пуассона зависит от одного параметра а. Для
случайной величины X, распределенной по закону Пуассона,
М [X] = D[X] = a, (4.0.26)
Пуассоновское распределение является предельным для биномиального
при р -*• 0, п ->- оо, если пр = а '= const. Этим распределением можно
пользоваться приближенно, если производится большое число независимых опытов,
в каждом из которых событие Л происходит с малой вероятностью.
Пуассоновскому закону распределения подчиняется также количество
точек, попадающих в] заданную область пространства (одномерного, двумерного
или трехмерного), если случайное расположение точек в этом пространстве
удовлетворяет некоторым ограничениям.
Одномерный вариант встречается при рассмотрении «потоков событий».
Потоком событий называется последовательность однородных событий,
наступающих одно- за другим в случайные моменты времени (подробнее см. гл. 10).
Среднее число событий X, приходящихся на единицу времени, называется
интенсивностью потока. Величина X может быть как постоянной, так и
переменной: X = К (/).
Поток событий называется потоком без последействия, если вероятность
попадания того или иного числа событий* на какой-то участок времени не
зависит от того, сколько событий гпоп ало на любой другой непересекающийся с
ним участок. ' ^ , ,
78
Поток событий называется ординарным, если вероятность появления на
элементарном участке At двух или более событий пренебрежимо мала по
сравнению с вероятностью появления одного события.
Ординарный поток событий без последействия называется пуассоновским.
Если события образуют пуассоновский поток, то число X событий, попадающих
на любой участок времени ( t0, t0 + т), распределено по закону Пуассона:
ат
Рт = —Г*-а (т=0, 1,2,...), (4.0.27)
т\
где а — математическое ожидание числа точек, попадающих на участок: а =
t0+x
= j X (f) dt; X ({) — интенсивность потока.
Если X = const, пуассоновский поток называется стационарным
пуассоновским или простейшим. Для простейшего потока число событий, попадающих на
любой участок времени длины т, распределено по закону Пуассона с параметром
а = Хх.
Случайным полем точек называется совокупность точек, случайным образом
разбросанных на плоскости (или в пространстве).
Интенсивностью (или плотностью) поля X называется среднее число точек,
попадающих в единицу площади (объема).
Поле точек называется пуассоновским, если оно обладает свойствами: 1)
вероятность попадания того или иного числа точек в любую область плоскости
(пространства) не зависит от того, сколько их попало в любую область, не
пересекающуюся с данной; 2) вероятность попадания в элементарную область АхАу
двух или более точек пренебрежимо мала по сравнению с вероятностью попада-^
ния одной точки (свойство ординарности).
Число X точеюпуассоновского поля, попадающих в любую область S
плоскости (пространства) распределено по закону Пуассона:
Рт~~п7*~а (т=°>{•••■>• (4-°-28>
где а — математическое ожидание ч.исла точек, попадающих в область 5. Если
интенсивность поля X (х, у) = X = const, поле называется однородным (свойство,
аналогичное стационарности потока событий). При однородном поле с
интенсивностью X имеем а = sX, где s площадь (объем) области «S. Если поле
неоднородно, то а = f f X (xt y)'dxdy (для плоскости); а = JfJ = X (х, у,z) dxdydz
(S) (S)
(для пространства).
Для вычислений, связанных с распределением Пуассона, удобно, пользовать-
ат _п
ся таблицами функции Р (т, а) = --: е а (см. приложение 1), и R (т, а) =
т k _а
= 2 —- е (см* приложение 2). Последняя функция выражает вероятность
того, что случайная величина X, имеющая распределение Пуассона с
параметром а, примет значение, не превосходящее т: R (т,а) = Р {X < /я}.
3. Геометрическое распределение. Говорят, что случайная величина X
имеет геометрическое распределение, если ее возможные значения 0, 1, 2, ..., т
а вероятности этих значений
Pm = <fn~lP ("1=0, 1,2,...), (4.0.29)
где0<р< 1, q= 1 — р.
Вероятности Рт для ряда последовательных значений т образуют
бесконечно убывающую геометрическую прогрессию со знаменателем q. На практике
геометрическое распределение встречается, когда производится ряд независимых
«попыток» достигнуть какого-то результата Л; при каждой «попытке» резуль-
79
тат достигается с вероятностью р. Случайная величина X — число
«бесполезных» попыток (до первого опыта, в котором появится событие Л).
Ряд распределения случайной величины X имеет вид
0 1 1 1 2 1 ...
р I яр \я2р I ...
т
ятр\ ...
Математическое ожидание случайной величины X, имеющей геометрическое
распределение, равно
М[Х] = q/p, (4.0.30)
а ее дисперсия
D\X] = qlp\
(4.0.31)
Нередко рассматривают случайную величину У = X + U равную числу
попыток до получения результатов Л, включая удавшуюся. Ряд
распределения случайной величины Y имеет вид
Уг
1
р
2 | 3 | ... | т 1 ...
ЯР | Я2Р | ... I Ят"хР 1 ...
(4.0.32)
Рт = Нх=т) = Са С"ь-т/(%+ь (*=0,1,...,«)•>.
М[Я = 1/р; D[K] = qlp\ (4.0.33)
Распределение случайной величины Y = X + 1 будем называть в
дальнейшем «геометрическим распределением, начинающимся с единицы».
4. Гипергеометрическое распределение. Случайная величина X с
возможными значениями 0, 1, ..., т, ..., а имеет гипергеометрическое распределение
с параметрами л, а, 6, если
(4.0.34)
Гипергеометрическое распределение возникает при следующих условиях:
имеется урна, в которой а белых и Ь черных шаров; из нее вынимается п шаров.
Случайная величина X — число белых шаров среди вынутых; ее распределение
выражается формулой (4.0.34).
Математическое ожидание случайной величины, имеющей распределение
(4.0.34), равно
М[Х] = па/ (а + b)t (4.0.35)
а ее дисперсия
D[X]-
nab
(a+b)*
4 Г а а—1 / а \*]
■"«"-"iTiTTinr-lTiTjJ- (4-0'
36)
ЗАДАЧИ И УПРАЖНЕНИЯ
4.1. Построить функцию распределения индикатора U события Л,
вероятность которого равна р.
Решение.
10 при #<0;
q при 0<х<1;
1 при х > 1,
где q = 1 — р (см. рис. 4.1).
*) При пользовании формулой (4.0.34) надо полагать С£=0, если r>k.
80
4.2. Монета бросается 3 раза. Случайная величина X — число
выпавших гербов. Построить для нее 1) ряд распределения; 2)
многоугольник распределения; 3) функцию распределения. Найти М [X],
D [XI, ох.
Решение. Величина X имеет биномиальное распределение с
параметрами п = 3 и р = 1/2. Ряд распределения
X
о | 1
1/8 3/8
3/8 I 1/8
Многоугольник распределения приведен на рис. 4.2, а, функция
распределения — на рис. 4.2, б.
F(x)
$
X
Рис. 4.1
№-
а ос
Рис. 4.3
7
о\
F(x)
i—
1
1
4
i i
F /
i
1
l
—4
i
2
-4
i
3 X
б)
Рис. 4.2
4.3. Рассматривая неслучайную величину а как частный случай
случайной, построить для нее 1) ряд распределения; 2) функцию
распределения; 3) найти ее математическое ожидание и дисперсию.
Ответ. 1) а : \~ ; 2) функция распределения приведена на
рис. 4.3; 3) М Ы = с; D [а] = 0.
4.4. К случайной величине X прибавили постоянную, неслучайную
величину а. Как от этого изменяются ее характеристики: 1)
математическое ожидание; 2) дисперсия; 3) среднее квадратическое
отклонение; 4) второй начальный момент?
„„,? Т В JJ- ^ пРибавится слагаемое а; 2) не изменится; 3) не изме-
nHrVi4 пРибавится слагаемое а2 + 2атх (так как а2 [X] =
ся if' СлУчайнУю величину X умножили на а. Как от этого изменят-
я ее характеристики: 1) математическое ожидание; 2) дисперсия;
) среднее квадратическое отклонение; 4) второй начальный момент?
81
0 | 1
(1/2)" | СА(1/2)"
• • • tn
... |c»(l/2)«
...
...
n
(1/2)"
Ответ. 1) умножится на а\ 2) умножится на а2; 3) умножится
на \а\\ 4) умножится на а2.
4.6. Монета подбрасывается п раз; рассматривается случайная
величина X — число выпавших гербов. Построить ряд распределения
этой случайной величины и найти ее характеристики: тх, DXi ох,
Ответ.
X:
тх=п/2; Dx = n/4; ox = Vn/2; |x3[X] = 0
(так как распределение симметрично относительно тх = я/2).
4.7. Производится п независимых опытов, в каждом из которых с
вероятностью р появляется событие Л. Написать ряд распределения
случайной величины X — числа появлений противоположного А
события А в п опытах—и найти ее математическое ожидание и
дисперсию.
Ответ.
X:
где q = 1 — р; тх = nq\ Dx = npq.
4.8. Производится п независимых опытов, в каждом из которых
с вероятностью р появляется событие А. Рассматривается случайная
величина R — частота появления события А в п опытах, т. е.
отношение числа появлений события А в п опытах к общему числу
произведенных [опытов п. Написать ряд распределения (этой случайной
величины; найти ее математическое ожидание и дисперсию.
Ответ:
Я:
где q = 1 — р; тх = р; Dx = pqln.
4.9*. Производится п независимых опытов. Вероятность появления
события А во всех опытах одна и та)ке и равна р. Найти наивероятней-
шее число /п* появлений события Л.
Решение. Определим, при каком условии т* = 0. Если
т* = 0, то qn>C}lpqn~1 или q>np, откуда р<1/(я+1). Если
|0| 1 |...
\-Рп \ C'nqPn-x | ••• |
т
Lnq p
... 1 п
... | qn
0 | \Щ
qn | Ckpqn-i
...
...
т/п
Qm pn qti-m
-hi
... 1 p.
rrf
*= n, то pn > C^qpn-1, p > nq, откуда p > nl (n + 1).
Рассмотрим случай, когда 0 < m* < n; при этом должны
выполняться совместно два неравенства:
Cm* m*' n—m* ^/от*-1-1 nm*-f-l „n—m* — 1.
n p q ^Cn ^ P ^ q ;
82
Cm* „m* n—m* ^> лт*-1 m*—1 jn—m* + \
Эти два неравенства эквивалентны следующим:
(m* + \)q ^ (п — т*)р\ (п — т* + 1)р > т*^,
откуда т* должно быть целым числом, удовлетворяющим неравенствам
(я + 1)р — 1 < т* < (л + 1)р.
Можно убедиться в том, что это условие выполняется и в
случае р < 1/ (п + I) (т* = 0), и в другом крайнем случае:
р> п/ (п + 1) (т* = п). Поскольку правая часть на единицу больше
левой, то между ними лежит только одно целое число т*; исключение
составляет случай, когда (п + 1)р и (я+1)р—1—целые числа.
Тогда имеется два невероятнейших значения: (п+1)р и (п + \)р — 1.
Если пр — целое число, то яг* = пр.
4.10. Два стрелка,стреляют каждый по своей мишени, делая
независимо друг от друга по одному выстрелу. Вероятность попадания в
мишень для первого стрелка р19 для второго р2. Рассматриваются две
случайные величины: Хг — число попаданий первого стрелка; Х2 —
число попаданий второго стрелка и их разность Z = Хг — Х2.
Построить ряд распределения случайной величины^ и найти ее
характеристики т% и Dz.
Решение. Случайная величина]"^ имеет^три^ возможных
значения: —1, 0 и +1.
p{z=-i} =p{x1==o} P{x2=4-i}=<7iP2;
P{Z=0} = Р{ХХ = 0}Р{Х2 =0} + Р{Х1 = 1}Р{Х2=1} =
= <7i<72 + Р1Р2'»
Р {Z = 1} =Р {Хг = 1}Р {Х2 =0} = Plq%9
где qx = 1 — Pl; q2 = 1 — р2.
Ряд распределения величины Z имеет вид
—1
4iPz
! 0 1
ЯхЧг + РхРг J Р\Яг \
mz = (— \)qlP2 + 0 (qxq2 + PlP2) + 1рхр2 = — q±p2 + Plq2 =
= Pi — Ръ-
Дисперсию находим через второй начальный момент [см. (4.0.16)]:
а2 [Z] = (-1) * . qiP2 + 0* . (Ч1д2 + Plp2) + 1« . Plq2 =
= q±p2 + Р1Я2 = Pi + Р2 — 2pip2;
Dz = a2 [Z] _ m| = Pl + p2 _ 2Plp2 — (px — p2)2 = pxqr + p2q2.
4.11. Производится 2 независимых выстрела по мишени. Вероят- .
ность попадания при каждом выстреле равна р. Рассматриваются
случайные величины: X — разность между числом попаданий и числом
83
промахов; У — сумма числа попаданий и числа промахов. Построить
для каждой из случайных величин X, Y ряд распределения. Найти их
характеристики: mxt Dx, my, Dy.
Решение. Ряд распределения величины X имеет вид
— 2 | 0 | 2
, где q=l—p.
Ф I 2pq | ?
тх = -2?2 + 2р2 = 2( р - q); а2 [X] = 4 (</2 + р2);
D* =а2 [X] — ml = 8pq.
Случайная величина Y фактически не случайна и имеет одно
значение 2; ее ряд распределения
; т„ = 2; А, = 0.
1
4.12. В нашем распоряжении имеется п лампочек; каждая из них
с вероятностью р имеет дефект. Лампочка ввинчивается в патрон и
включается ток; при включении тока дефектная лампочка сразу же
перегорает, после чего заменяется другой. Рассматривается случайная
величина X — число лампочек, которое будет испробовано.
Построить ее ряд распределения и найти математическое ожидание тх.
Решение. Ряд распределения величины X имеет вид
X:
1
4
2 | 3
РЯ | Р2Я
...
...
' 1
Р1~гЯ
...
п
Р""1
, где д=1—р. (4.12.1)
т,
=|^+^-'=,£(!j^)+V
4.13. Случайная величина X имеет распределение Пуассона с
математическим ожиданием а = 3. Построить многоугольник
распределения и функцию распределения случайной величины X. Найти:
1) вероятность того, что случайная величина X примет значение
меньшее, чем ее математическое ожидание; 2) вероятность того, что
величина X примет положительное значение.
Ответ. 1) 0,423; 2) 0,960.
4.41. При работе ЭВМ] время от времени возникают
неисправности (сбои). Поток сбоев можно считать простейшим. Среднее число
сбоев за сутки равно 1,5. Найти вероятности следующих событий:
А = {за двое суток не будет ни одного сбоя};
В = (в течение суток произойдет хотя бы один сбой};
С = {за неделю работы машины произойдет не менее трех сбоев}.
О т в е т. Р (Л) = 0,050; Р (В) = 0,777; Р (С) = 0,998.
4.15. При заданном положении точки разрыва снаряда цель
оказывается накрыта однородным пуассоновским полем осколков с интен-
84
сивностью X = 2,5 оск/м2. Площадь проекции цели на плоскость, на
которой наблюдается осколочное поле, равна S = 0,8 м2. Каждый
осколок, попавший в цель, поражает ее с полной достоверностью.
Найти вероятность того, что цель будет поражена.
Ответ. 0,865.
4.16. Та же задача, но каждый осколок, попавший в цель,
поражает ее не с полной достоверностью, а с вероятностью 0,6.
Решение. Рассмотрим вместо заданного поля осколков «поле
поражающих осколков» с плотностью Я* =0,6Я =1,5 пор. оск./м2.
Математическое ожидание числа поражающих осколков, попавших в
цель, будет а* = A,*S = 1,2 пор. оск; отсюда вероятность поражения
Rx = 1 — е-а* = 1 — 0,301 = 0,699.
4.17. Электронная лампа работает исправно в течение
случайного времени Т\ после отказа ее немедленно заменяют новой. Поток
отказов — простейший, с интенсивностью \i. Найти вероятности
следующих событий: А = {за время т лампу не придется заменять}; В =
= {лампу придется заменять ровно три раза}; С = {лампу
придется заменять не менее трех раз}.
Решение. Математическое ожидание числа отказов X за время
х равно а = [хт.
Р(Л) = Я0 = е-^; P(5) = P3 = iH)le^; P(Q« 1_(Я0 + Р1 +
+ /У = 1 —е—1**11 — цт—0,5 (И2]-
4.18. Техническое устройство состоит из трёх узлов; в первом узле
пг элементов, во втором п2 элементов, в третьем п3 элементов. Первый
узел безусловно необходим для работы устройства; второй и третий
дублируют друг друга. Потоки отказов элементов — простейшие; для
элемента, входящего в первый узел, интенсивность потока отказов
равна Xl9 во второй или третий узел Х8. Первый узел выходит из строя,
если в нем отказало не менее двух элементов. Второй узел (так же, как
и дублирующий его третий) выходит из строя при отказе хотя бы
одного элемента. Для выхода из строя устройства в целом достаточно,
чтобы отказал первый узел или второй и третий вместе. Найти
вероятность того, что за время т устройство выйдет из строя.
Решение. Вероятность выхода из строя одного элемента
первого, второго или третьего узла за время т равна соответственно
/?i=l— е-^г; р2 = р3=1— е-*»*.
Вероятность выхода из строя первого узла за время т равна
^i=l—(1-Pi)11*—/iiPiO-PiT1"1.
Вероятности выхода из строя второго и третьего узлов равны
#.= 1-(1-й)*; ^3=1-(1-/>з)Пз.
Вероятность выхода из строя всего устройства
# = #1 + 0 — #l) #2jS*8-
85
Рис. 4.20
4.19. Искусственный
спутник Земли, движущийся по
своей орбите] в течение п
суток, может случайным образом
сталкиваться с метеоритами.
Метеориты, пересекающие ор-
о— биту и сталкивающиеся со спут-
х ником, образуют стационарный
пуассоновский поток с
интенсивностью к (метеоритов в
сутки). Метеорит, попавший в
спутник, пробивает его оболочку с вероятностью р0. Метеорит,
пробивший оболочку, с вероятностью рг выводит из строя аппаратуру
спутника. Найти вероятности следующих событий:
А = {за время полета спутника его оболочка будет пробита};
В = {за время полета спутника его аппаратура будет выведена из
строя};
С = {за время полета спутника будет пробита только оболочка
спутника, а аппаратура будет действовать}.
Решение. Математическое ожидание числа метеоритов,
пробивающих оболочку, а0 = хяр0. Математическое ожидание числа
метеоритов, пробивающих оболочку и поражающих аппаратуру, ах =
= хпрхРо-
р (А) = 1 — е-°° = 1 _е-*«л; Р (В) = 1 —е-в* = 1 — е-*ял*;
р (С) = Р[(А)—Р {В) = e-*"PoPi_e-*rtPo.
4.20. Охотники, собравшиеся для охоты на волка, выстраиваются
в цепь случайным образом так, что образуют на оси Ох простейший
поток точек с интенсивностью X (X охотников на единицу длины, см.
рис. 4.20). Волк бежит перпендикулярно цепи. Любой охотник
стреляет по волку только в случае, если волк пробегает от него не дальше
чем на расстоянии R0, и, выстрелив, убивает его с вероятностью р.
Определить вероятность того, что волк будет убит, если он не знает,
где расположены охотники, и цепь достаточно длинна для того, чтобы
волк с достоверностью не пробежал за пределами цепи.
Решение. Волк, бегущий по направлению, указанному
стрелкой, обстреливается в случае, если в полосу шириной 2R0, связанную
с траекторией его перемещения, попадает хотя бы один охотник.
Каждый охотник, если ему придется стрелять по волку, с вероятностью р
оказывается «удачливым», т. е. убивает волка. Перейдем от «цепочки
охотников», имеющей интенсивность X, [к «цепочке удачливых
охотников» с интенсивностью X* = Хр. Волк будет убит в случае, если в
отрезок длиной 2R0> случайно брошенный на ось абсцисс, попадет
хотя бы один «удачливый» охотник; вероятность этого
Р(Л) = 1— е-2*оЧ
4.21. Автомашина проходит технический осмотр и обслуживание.
Число неисправностей, обнаруженных во время техосмотра,
подчинено закону Пуассона с параметром а: Если неисправностей не обнару-
86
Я
жено, техническое обслуживание машины продолжается в среднем 2 ч.
Если обнаружены одна или две неисправности, то на устранение
каждой из них тратится в среднем еще полчаса. Если обнаружено больше
двух неисправностей, то машина ставится на профилактический
ремонт, где она находится в среднем 4 ч. Определить закон
распределения среднего времени Т обслуживания и ремонта машины и его
математическое ожидание М [ТЗ.
Решение.
2
е-°
2,5
се-8
3
2
6
i_.-.(i+.+ £)
м
[T] = e-^2 + 2,5a+^a2) + 6[l-e-^l + a+|-)j =
= 6—е~« (4 + 3,5а + 1,5а2).
4.22*. Обследуется группа животных; каждое из них с
вероятностью р является больным. Обследование производится путем
анализа крови. Если смешать кровь п животных, то анализ этой смеси будет
положительным, если среди п животных будет хотя бы одно больное.
Требуется обследовать большое число N животных. Предлагается два
способа обследования:
1) обследовать всех N животных; в этом случае нужно провести N
анализов;
2) вести обследование по группам, смешав сначала кровь группы
из п животных; если анализ отрицательный, считать, что все
животные группы здоровы, и переходить к следующей группе из п животных;
если анализ положительный, обследовать каждое из п животных и
после этого переходить к следующей группе (п > 1).
Определить, какой способ обследования выгоднее — первый или
второй — в смысле минимального среднего числа анализов.
Определить, при каком п = п* для обследования группы животных
потребуется в среднем наименьшее^число анализов.
Решение. Случайная величина Хп — число анализов на
группу из п животных при втором способе — имеет ряд распределения
1
Г
л+1
1— qn
q = l—p.
Среднее число анализов на группу из п животных при втором способе
будет
М [XJ = qn + (п + 1) (1 — qn) = n (nq« — 1).
При
первом способе на группу из п животных приходится п анализов.
Очевидно, при nqn < 1 первый способ выгоднее второго, а при
Щп ^> 1 второй способ выгоднее первого.
87 ,
Установим, при каком q второй способ становится выгоднее и
каково при этом будет оптимальное значение п =п*. Из неравенства
п
nqn > 1 вытекает q > 1/Vn, а из последнего q > 0,694, так как мини-
п
мум l/Л/п для целых п достигается при п = 3. Предположим, что
q > 0,694, и найдем то значение п = п*9 которое обращает в
минимум среднее количество анализов, приходящееся на одно животное:
Rn = M[Xj/n =l-qn+ l/n.
Для этого надо найти наименьший положительный корень уравнения
dRJdn = — qn Inq— l/n2 = 0,
взять ближайшие к нему два целых числа и прямой подстановкой их
в Rn выбрать из них оптимальное п*. Уравнение —qn In q = l/n2
подстановкой — In q = a, an =x приводится к уравнению х2е~х =
= a (a = — In q < In 3/3 = 0,366). Последнее уравнение при малых
а (и, значит, малых р =1 — q) имеет решение х я^ У а, откуда я* »
« 1/Va". При не малых а непосредственное сравнение величин /?2, R3
и #4 позволяет сделать вывод, что всегда R3 < #2 и что #3 < #4 при
0,694 < ^ < 0,876; следовательно, при 0,694 < q < 0,876
оптимальное п* = 3. Можно показать, что при q> 0,889 (р < 0,111) хорошее
приближение дает формула п* ж l^Vp + 0,5.
4.23. Производится ряд попыток включить двигатель. Каждая
попытка заканчивается успехом (включением двигателя) независимо от
других с вероятностью р = 0,6. Каждая попытка занимает время т.
Найти распределение общего времени 7\ которое потребуется для
запуска двигателя, его математическое ожидание и дисперсию.
Решение. Число произведенных попыток X есть величина,
распределенная по геометрическому закону, начинающемуся с
единицы (4.0.32); Т = Хт имеет распределение
Т:
2т
ЯР
Зт
шх
фр
qm-ip
М [Г] = тМ [X] = т/р; D [Г] = t2D [X] = тУр2 (q = 1 — р).
4.24. В условиях предыдущей задачи попытки зависимы и pt —
вероятность включения двигателя после i — 1 неудачных попыток —
есть некоторая функция i : pt = cp (i). Найти распределение
случайной величины Т = тХ.
Ответ.
Pi
2т | Зт
qip2
<7i<72p3
mx
где qt = 1 — pj.
88
m-1
П <7iPn
/=1
/
4.25. При сборке прибора повышенной надежности, состоящего
из однородных деталей, каждая деталь подвергается всесторонним
испытаниям, в результате которых она либо признается
доброкачественной (с вероятностью р) либо выбраковывается (с вероятностью q =
= 1 —р). Детали оказываются принадлежащими к той или другой
категории независимо друг от друга. Запас деталей практически
неограничен. Отбор деталей и их испытания ведутся до тех пор, пока не
будет набрано k высококачественных деталей. Случайная величина
X — число выбракованных деталей. Найти распределение случайной
величины X: Рт = Р {X = т}.
Решение. Возможные значения случайной величины X : 0, 1, ...
..., т9 ... Находим их вероятности:
р0 = Р {первые k деталей доброкачественны} = рк\
рг = Р {среди первых k деталей одна выбракована, (k + 1)-я
деталь доброкачественна} = Cj^1/?* ~~ *Р =С1дгрН
рт == р {среди первых k + т — 1 деталей т выбракованы,
(т + к)-я деталь доброкачественна } = C£+m-iqmpk
(m = l,2, ...).
4.26. Две случайные величины X, Y независимо друг от друга
принимают значения 0 или 1. Их ряды распределения заданы:
0
Ях
1
Рх
• Y •
0 1
Яу | Ру\
х-<
Построить ряды распределения: 1) их суммы Z = X + Y; 2) их
разности U = X — У; 3) их произведения V = XY.
Решение. 1) Случайная величина Z имеет три возможных
значения: 0; 1 и 2.
P{Z=0} =P{X =0,7 =0} =qxqy;
Р {Z = 1} = Р {X = 1, Y. = 0} + Р {X = 0, Y = 1} =
= РхЯу + ЯхРу,
P{Z=2} =P{X =1,7=1} =рхРу;
0
ЯхЯу
1
I ^
РхЯу + ЯхРу РхРу
Аналогично находим
U:
— 1
ЯхРу
0
I i
РхРу + ЯхЯу
РхЯу
о
11
ЯхЯу + РхЧу + ЧхРу
РхРу
4.27. Случайная величина X имеет ряд распределения
89
Хг\
' I»
0,5 I 0,2
0,3
Построить ряд распределения случайной величины Y — 1/ (3 — X).
Ответ.
1
-1 0,5
0,3 0,5 0,2
4.28. Случайная величина X имеет ряд распределения
X:
Построить ряд распределения ее квадрата: Y=XZ.
Ответ:
I -2 |-1
0,2 1 0,3.
0
0,2.
1
0,2
2
0,1.
Y:
0
0,2
• 1«
0,5 0,3
4.29. При передаче сообщения по радиоканалу наблюдаются
помехи, препятствующие декодированию сообщения; с вероятностью р
сообщение не удается декодировать. Сообщение передается до тех
пор, пока оно не будет декодировано. Продолжительность передачи
сообщения равна 2 мин. Найти: 1) математическое ожидание времени
7\ которое уйдет на передачу сообщения; 2) вероятность того, что на
передачу сообщения понадобится время, большее чем /0, имеющееся
в нашем распоряжении.
Решение. 1) Случайная величина X — число «попыток»
передать сообщение — имеет геометрическое распределение,
начинающееся с единицы; Т = 2Х мин. Распределение случайной величины Т
будет
I,
|
i
2
Ц
4 | 6
РЯ | Р2<7
...
...
2т | ...
р*-1? | ...
2)Р{г>/0}= S Рт-1я=я 2 Рт~1>
m=[*0/2] + l т=[*0/2]-И
(4.29)
где [t0/2] — наибольшее целое число, содержащееся в tJ2. Суммируя^
геометрическую прогрессию (4.29), имеем
\ — q
IUI21
90
\ Xl \ X2 1 ••*
Pi | 02 J ...
Xn
Pn
z=
4.30. Дискретная случайная величина X имеет распределение
X
Случайная величина Z есть минимальное из двух чисел — значения
случайной величины X и числа а : Z = min {X, а}, где х± <! а <; лг^.
} Найти распределение случайной величины Z.
Решение. По определению
X при Х^а;
а при Х;>а.
Распределение случайной величины Z совпадает с распределением
случайной величины X для тех значений xlt x29 ..., которые меньше
или равны а\ Р {Z = а} вычисляется как единица минус сумма всех
остальных вероятностей:
P{Z = a} = \- Цр,
4.31. Распределение дискретной случайной величины X есть
„. 1 I 3 | 5 | 7 | 9
0,1 | 0,2 | 0,3 I 0,3 | 0,1
Найти распределение случайной величины Z = min {X, 4}.
Ответ. На основе решения предыдущей задачи
1 | 3 | 4
| 0,1 | 0,2 | 0,7
4.32. Две случайные величины X и У независимо друг от друга
принимают значение согласно рядам распределения:
X:
0
0,2
1
0,3
2 | 3
0,4 | 0,1
0,7
3 | 4
0,2 0,1
Построить ряд распределения случайной величины Z = min {X, Y}.
Решение. Р {Z = 0} = Р {X = 0} = 0,2;
P{Z = 1} =р {х =1} + Р {Y =1,Х> 1} =0,3 + 0,7 • 0,5 =
= 0,65;
Р {Z = 2} = Р {X = 2, Y > 2} = 0,4 • 0,3 = 0 12;
91
P {Z = 3} = P {X
0
3,Г>3}
1 I 2
0,1 • 0,3 =0,03.
1
0,49
2
0,14
3
0,27
4
0,10
0,20 J 0,65 I 0,12 0,03
4.33. В условиях предыдущей задачи найти распределение
случайной величины U = max {X, У}.
Ответ.
U:
4.34. В ячейке ЭВМ записано л-разрядное двоичное число; каждый
знак этого числа, независимо от остальных, принимает с равной
вероятностью значение 0 или 1. Случайная величина X — число знаков
«1» в записи двоичного числа. Найти вероятности событий {X = т},
{Х^т}9 {Х<т}.
Решение. Случайная величина X имеет биномиальное распре- ,
деление с параметрами п, р = 1/2. Р {X =т) =С% (1/2)л;
P{X>m} = (l/2f2C; Р{Х<т} = 1 — Р{Х^т}.
k—m
4.35. Рассматривается правильная десятичная дробь X с тремя !
знаками после запятой, причем каждый знак, независимо от других,
с одинаковой вероятностью может принимать любое значение 0, 1, ... >
..., 9. Построить ряд распределения случайной величины X и найти *
ее математическое ожидание.
Решение. Возможные значения случайной величины X : 0,000;
0,001;0,002; ...; 0,999. Вероятность каждого из них равна р = (0,1)3 =
= 0,001. Ряд распределения случайной величины X имеет вид
X:
999 999
М[Х]= 2 *i Л = 0,001 2 **. гАе ** = *-0,001.
i=0 t = 0
Числа xt образуют арифметическую прогрессию из 1000 членов с
разностью 0,001. Суммируя прогрессию, получаем
0 + 0,999
0,000
0,001
0,001
0,001
| 0,002 | .
| 0,001 1 .
.. | 0,999
.. | 0,001
М[Х] = -
1000.0,001 = 0,4995 ^ 0,5.
4.36. Случайная величина У — случайная двоичная правильная
дробь с п знаками после запятой; каждый знак, независимо от других,
с вероятностью 1/2 принимает значение «0» или «1». Найти
распределение случайной величины У и ее математическое ожидание М [У].
Решение. Аналогично предыдущей задаче, все значения
двоичного числа от 0,00...0 до 0,11 ...1 одинаково вероятны и каждое из|
92
них имеет вероятность 1/2". Математическое ожидание случайной
величины Y (в десятичной записи) М [Y] =0,5— 1/2" + 1.
4.37. Передаваемое по каналу связи в двоичном коде сообщение
состоит из последовательности знаков «0» и «1», чередующихся с
равной вероятностью и независимо друг от друга, например 0, 0, 1, 1, 1,
0, 1, 1, 1,0,0,0,0, 1,0, 1, 1, 1, ...
Рассматривается какая-то группа повторяющихся знаков,
например: 0, 0, 0 или 1,1,1,1 (или просто 0 или 1, если знаки не
повторяются). Берется какая-то из этих групп наугад. Случайная
величина X — число знаков в группе. Найти ее распределение,
математическое ожидание и дисперсию. Найти Р {X 1> к). 1
Решение. Случайная величина X имеет геометрическое
распределение, начинающееся4 с единицы: J
X:
1
0,5 0,52
т
0,5т
; М[Х] = 1/0,5 = 2;
D [X] = 0,5/0,52 = 2; Р {X > *} = 2 °>5т = °'5*-1-
m—k
4.38. В условиях предыдущей задачи Р {«0»} — 0,7; Р {«1»} =
= 0,3. Найти среднее число знаков М [X] в группе нулей, среднее
число знаков М [У] в группе единиц и полное среднее число знаков
М [Z] в наугад выбранной группе знаков. Найти дисперсия D [X],
D М, D [Z].
Решение. М [X] = 1/0,7 = 10/7; М [Y] = 1/0,3 = 10/3. По
формуле полного математического ожидания находим М [Z] =
= 0,7 • у + 0,3 • -£■ = 2, т. е. то же, что и в предыдущей задаче.
D [X] = 0,32/0,7 « 0,128; D [У] = 0,72/0,3 « 1,633.
Чтобы найти D [Z], сначала найдем а2 [Z] = М [Z2] по формуле
полного математического ожидания [см. (4.0.20)]*):
а2 [Z] = 0,7а2 [X] + 0,3 а2 [У], где а2 [X] = D [XI + (М [X])2 »
« 2,66; а2 [71 = D [Y] + (М [У])2 я? 18,9; тогда а2 [Z] « 7,53;
D [Z1 = а2 [Z] — (М [Z])2 » 3,53,
т. е. дисперсия по сравнению с предыдущей задачей увеличилась.
Вероятность Р {X ^ k) находим по формуле полной вероятности
с гипотезами: Нг = {первый знак «0»}, Н2 = {первый знак «1»}:
Р (#0) = 0,7; Р (Нг) = 0,3; Р {X > k\H0} = 0,7*"*;
Р {X^k\Hx} =0,3fe-1; тогда Р {X > k) =0,7 • 0,7*-1 +
+ 0,3 • 0,3* V =0,7* + 0,3*.
н „ ' По формуле полного математического ожидания находим второй началь-
«и момент, но не саму дисперсию (ибо условные математические ожидания при
назных гипотезах различны).
93
4.39. Техническое устройство (ТУ) состоит из т блоков типа I и
п блоков типа И. Надежность (вероятность безотказной работы в
течение заданного времени т) каждого блока типа I равна ръ каждого
блока типа II равна р2. Блоки отказывают (выходят из строя)
независимо друг от друга. Для работы ТУ достаточно, чтобы в течение
времени т работали безотказно любые два блока типа I и одновременно
с этим любые два блока типа И. Найти вероятность S5 безотказной
работы ТУ.
Решение. Событие А = {безотказная работа ТУ} есть
произведение двух событий:
Аг = {не менее двух из т блоков типа I работают безотказно};
Л2 = {не менее двух из п блоков типа II работают безотказно}.
Число Хг работающих безотказно блоков типа I есть случайная
величина, распределенная по биномиальному закону с параметрами т,
pii событие Аг состоит в том, что случайная величина Хг примет
значение не менее 2; поэтому
Р(ЛХ) = Р{ХХ>2} =1-Р{Хх<2} =1_р{х1 =0}-
- Р {Хг = 1} = 1 - (# + nuff-ip,) (Яг = 1 - Pl).
Аналогично Р (Л2) = 1 — (?2 + Щ\"1 /?2) (<7г = 1 — АО-
Вероятность безотказной работы устройства
^ = P(A) = P(A1)P(A2)^[l-(q^ + mq^p1)][l-(ql + nqn^ p2)].
4.40. Прибор применяется (приводится в действие) несколько раз
до его выхода из строя (вышедший из строя прибор не
восстанавливается). Вероятность того, что, будучи применен k раз, прибор еще не
вышел из строя, равна Р (k). Функция Р (k) задана (см. рис. 4.40).
Известно, что прибор выдержал уже п применений. Найти вероятность
Qm того, что он выдержит еще т применений, и математическое
ожидание числа X будущих применений.
1Y
Р(Ю
г з
Рис. 4.40
Решение. Qm есть условная вероятность того, что прибор не j
выйдет из строя за последующие т применений, при условии, что он!
не вышел из строя за первые п. По правилу умножения вероятностей]
Р (п + т) =Р (n)Qm\ откуда
94
4.41. Рабочий обслуживает п однотипных станков, расположенных
на одной линии с интервалами / (рис. 4.41). Время от времени станки (с
равной вероятностью и независимо друг от друга) останавливаются и
требуют наладки. Закончив наладку одного станка, рабочий остается
на месте, пока не остановится какой-либо из станков; тогда он
переходит к нему (если вышел из строя тот же станок, он остается на
месте). Случайная величина X —. расстояние, которое проходит рабочий
между двумя наладками. Найти математическое ожидание случайной
величины X.
Рис. 4А1
Решение. Применим формулу полного математического
ожидания с гипотезами Нг = {рабочий стоит у 1-го станка} (i == 1, ..., п).
По условиям задачи все гипотезы равновероятны: Р (Ях) = Р (Я2) =
= ... =Р(#П) = IIп. Найдем условное математическое ожидание
М [Х\НЦ для j'-й гипотезы. Каждый станок (включая j'-й)
останавливается с вероятностью 1/л; отсюда
+
м(Х|я,]=|-[2^1,-^+2^-о1=^-и^-1)
+ (n-i)(n-i+l)].
По формуле полного математического ожидания
М[Х] = У P(^)M[X|^] = y— т-1'('-1)+(л-0(л-/+1)] =
"^[2/ч'-1)+д(л~'+1)(п_4 (4-4i)
Пользуясь известной формулой 2 *2 = i > вычис-
ляем
У Hi n- n(n + l)(n+2j n(n + l) = я(и+1)(л-1)
Д б 2 3 " '
Применяя эту формулу для вычисления обеих сумм в (4.41), убеж-
даемсях что они равны друг другу и
MfXl = —V Щ П- 1 Я(* + Ц(*—1) __ /(и2—1)
«2 ^ * ' „2 3 Зя '
95
Pm-9""'P
4.42. Производится ряд
независимых опытов, в каждом из которых
событие А появляется с
вероятностью р; опыты ведутся до первого
появления события Л, после чего
прекращаются. Случайная величина X—
число произведенных опытов.
Построить ее ряд распределения и
многоугольник распределения; вывести
формулы для ее математического
ожидания, дисперсии, среднего квадра-
тического отклонения.
Решение. Случайная величина X имеет геометрическое
распределение, начинающееся с единицы [см. (4.0.32)1. Ряд
распределения случайной величины X имеет вид
X:
где q = 1 — р. Многоугольник распределения для р = 0,6 показан
на рис. 4.42.
М[Х] = 2 mqm^1p = p 2J nuf*-\
m=l m—1
Замечаем, что mqm~1 есть не что иное, как производная выражения
qm no q\ отсюда
Последняя сумма представляет собой сумму членов бесконечно
убывающей геометрической прогрессии со знаменателем q\ суммируя ее,
находим
1
р
2 | 3
ЯР | Я2Р
...| - |...
... | <г~хр |...
m=l
(4.42)
сгкуда М [XI =pl (1 — qf = 1/р.
Дисперсию случайной величины X найдем через ее второй
начальный момент
сс2[Х] = М[Х2] = 2 т2Ят-1Р-
Для ее вычисления умножим на q ряд (4.42); получим
Щ
mqm =
m=l
(l-?)2
96
Дифференцируя этот ряд, имеем
nrq]
т—\ ■
1+9
т=1
(1-<7)3
Умножая это выражение на р = 1 — q, получаем М [ X2] =
= (1 + q)l (1 — q)2. Дисперсия случайной величины X равна [см.
формулу (4.0.17)]
DIX] = М[Х2]-(М[Х])2 =(1 +<7)/(1-<7)2-1/(1— д)2 =
= q/p2\ Ox = VD IX] = Vq/p.
Итак, для геометрического распределения, начинающегося с
единицы,
М [X] = 1/р; D [X] = qlp2\ о = Vq/p.
Случайная величина Y = Х — 1, имеющая геометрическое
распределение, начинающееся с нуля, обладает характеристиками:
М [Y] =М М — 1 = qlp\ D [Y] = D IX] = qlp2\ ау = Vqlp.
4.43. Производится ряд попыток наладить сложную электронную
схему. Вероятность того, что схема будет налажена с первой попытки,
равна Рг\ со второй попытки Р2, ..., с &-й попытки Рк ,... Вероятности
Pi, Р29 ..., Pk> • ••> Рп заданы. После я-й безуспешной попытки
наладить схему попытки прекращаются. Найти математическое ожидание
и дисперсию случайной величины X — общего числа произведенных
попыток.
Решение. Ряд распределения случайной величины X имеет вид
X:
М[Х]-2?=1! iPi+n[l-^nkZ\Ph];
DIX^Mm-fMtX])2^^
4.44. Прибор собирается из деталей k типов; в его состав входят
trii деталей типа I (i = 1, ..., k) f 2 т-г = m; m — общее число деталей).
Вероятность того, что наугад взятая деталь t-ro типа имеет дефект,
равна qt. Прибор работает только если в составе его деталей нет ни
одной дефектной. 1) Найти вероятность Р того, что прибор будет
работать; 2) найти вероятность R2 того^что среди*деталей'будет не менее
двух дефектных. v
Решение. 1) Р есть вероятность того, что в т независимых
опытах событие А == {деталь дефекта} не произойдет ни разу: Р =
= П (1 — qt)mi = Р0; 2) R2 = 1 — (Р0 + Рг), где Р0 — вероятность
того, что среди т деталей нет ни одной дефектной; Р1 — вероятность
того, что среди них ровно одна дефектная. Рг найдем как сумму веро-
|1
{Pi
2
Рг
...
1*
Рк
...
...
п
i-^ziV
4
Зак. 1040
97
ятностёй того, что среди mt деталей /-го типа ровно одна дефектная, а
детали всех остальных типов не дефектны:
P1 = m1q1(l — ft)""-1 П q7s^l + m%q2(l— q2)m*-1 П q^"X + ...=
Ml /^2
*
m.-^-l
4.45. По каналу связи передается k сообщений, содержащих
соответственно %, я2, ..., ^А двоичных знаков («О» или «1»). Знаки
принимают значение 0 или 1 независимо друг от друга и с вероятностью 0,5.
Каждый знак искажается (заменяется противоположным) с
вероятностью р. При кодирований сообщений применяется код, исправляющий
ошибки в одном или двух знаках (практически с полной
достоверностью). Наличие ошибки хотя бы в одном знаке (после исправления)
делает ошибочным все сообщение. Найти вероятность R того, что
хотя бы одно из k сообщений будет ошибочным.
Решение. Случайная величина Xt — число ошибочных знаков
в j'-м сообщении — имеет биномиальное распределение (4.0.23) с
параметрами nif p. Вероятность того, что i-e сообщение будет ошибочным,
равна вероятности того, что в числе щ знаков этого сообщения не
менее трех будут ошибочными:
Р {Xt^3} = 1 -Р {Xt <3} = 1 - 2 CLр>(1 -/>)"*-'.
/=о
Вероятность того, что хотя бы одно из k сообщений будет
ошибочным, равна
R= n(l-ictf/i/(l-p)»-/).
4.46. Для сборки прибора требуется иметь 4 одинаковые детали;
всего в нашем распоряжении 10 деталей, из которых 6
доброкачественных и 4 негодных; на вид детали неразличимы. Из имеющихся
деталей выбирают 5 деталей (одну лишнюю — «в запас»). Найти
вероятность того, что не менее четырех из них окажутся доброкачественными.
Решение. Случайная величина X — число доброкачественных
деталей среди 5 выбранных — имеет гипергеометрическое
распределение с параметрами 5, 6, 4 [см. (4.0.34)]. Вероятность того, что среди
5 деталей т будут доброкачественными, равна Рт = С™С\-т1С\ъ\ ot-JI
сюда
Р4 = 5/21; Ръ = 1/42; Р {X > 4} = Р4 + Ръ = 14/42.
. I
4.47. Имеется 7 радиоламп, среди которых 3 неисправные, на вид
неотличимые от новых. Наугад берутся 4 радиолампы и вставляются!]
в 4 патрона Найти и построить (в виде многоугольника распределе-1
ния) ряд распределения числа радиоламп X, которые будут работать.!
Найти ее математическое ожидание, дисперсию и среднее квадратичес-1|
кое отклонение.
98
Решение. Величина X имеет гипергеометрическое
распределение с параметрами п = 4, а = 4, Ъ = 3.
Рг = CJ C8/CJ = 4/35; Р2 = С\ СЦС*7 = 18/35;
Pa = CSCi/C»= 12/35; P4-C|/Cf= 1/35.
Ряд распределения случайной величины X имеет вид
X:
Многоугольник распределения случайной величины X дан на рис. 4.47.
Пользуясь формулами (4.0.35) и (4.0.36), вычисляем: М [X] « 2,28;
D [X] « 0,38.
1
4/35
2
18/35
3 | 4 |
12/35 |1/35
4.48*. Производится ряд независимых опытов, в каждом из
которых событие А появляется с вероятностью р. Наша цель — получить
событие A k раз. Максимально возможное число опытов равно п
(причем n^2k). Опыты прекращаются либо тогда, когда событие А уже
появилось к раз, либо тогда, когда ясно, что уже нет возможности
получить его k раз, т. е. когда противоположное событие А появилось
п — k + 1 раз. Случайная величина X — число опытов, которое
будет произведено. Найти распределение случайной величины X.
Решение. Возможные значения случайной величины X : &,
k + 1, ..., п — 1, п. Найдем соответствующие вероятности Рт =
= Р {X = /72}.
При k^Ltn^n — k опыты могут прекратиться после т-то только
из-за того, что k раз произойдет событие А. Поэтому
Рт = Р {первые т — 1 опытов дали k — 1 появлений события Л,
а m-й опыт дал событие А) =
=ckm-\Pk-
.CknT-\pkqm-k.
(4.48.1)
В частности, при т = k имеем Ph = pk.
При п — k<Z.m^Ln опыты могут прекратиться после /тг-го либо
из-за того, что событие А появилось k-и раз, либо из-за того, что про-
4*
99
тивоположное событие А появилось п — k + 1 раз. Вероятность
первого варианта мы уже вычислили; вероятность второго равна
Р {первые т — 1 опытов дали п — k появлений события А, а т-й
опыт дал событие А) =
Складывая вероятности обоих вариантов, получаем
/>m = C^-,,p^m-* + d* p«-«-«+V-*+I. (4.48.2)
Итак, распределение случайной величины X при k ^ m ^ п + k
задается формулой (4.48.1), а при п — & < m < п — формулой
(4.48.2).
4.49. В условиях предыдущей задачи п = 7, k = 3; р = 0,4.
Построить ряд распределения случайной величины X.
Решение. Возможные значения случайной величины X : 3; 4;
5; 6; 7.
Р3=р3 = 0,43 = 0,064;
Pt*=ClZip*<f-9 =3 • 0.43 • 0,6 =
= 0,115;
Pb = Clz.\p3q*-* +
+CI:J,Ip5-1-'+V-3+i=6.0,43.0,62+
+ 0,6Б = 0,216;
P6 = Cl-JlP*q'-s +
+ C?Z.3ipe-1-7+3,77-3+1 =
= 10-0,43-0,63 + 5-0,4.0,65 = 0,293;
/>7=C!-\/ry-3+
= 15-0,43-0,64+15-0,42.0,68 =
= 0,312.
Pi
0,3
oft
0,1
О 1
2 J 4 5
Рис. 4.49
7 x
3
0,064
I «
0,115
1 5
! 0,216
1 e
0,293
7
0,312
Xi
^i Многоугольник распределения приведен на рис. 4.49.
глава 5
НЕПРЕРЫВНЫЕ И СМЕШАННЫЕ СЛУЧАЙНЫЕ
ВЕЛИЧИНЫ
5.0. Множество возможных значений дискретной случайной величины
конечно или счетно; не дискретные случайные величины характеризуются тем, что
множество их возможных значений несчетно. Примеры не дискретных случайных
величин: дальность обнаружения объекта радиолокатором; время опоздания
поезда; погрешность измерения угла с помощью угломера. У всех этих случайных
величин множество возможных значений несчетно, так как непрерывно
заполняет какой-то участок оси абсцисс.
100
Напомним, как определяется функция распределения случайной
величины X:
F (х) = Р {Х<х}. (5.0.1)
Функция распределения существует для любых случайных величин, как
дискретных, так и не дискретных.
Если функция распределения F {х) случайной величины X при любом х
непрерывна и, кроме того, имеет производную F' (х) везде, кроме, может быть,
отдельных точек (рис. 5.0.1), то случайная величина X называется непрерывной.
Если функция распределения F (х) на некоторых участках непрерывно
возрастает, а в отдельных точках имеет разрывы (рис. 5.0.2), то случайная величина
называется смешанной. Функция F (х) для смешанной случайной величины, как
и для дискретной, непрерывна слева.
\F(X)
1
0
i[fX)
X
Рис. 5.0.1
Xj 0 *Xh
Рис. 5.0.2
Вероятность каждого отдельного значения непрерывной случайно й2величины
равна нулю. Вероятность каждого отдельного значения смешанной случайной
величины, лежащего на участке непрерывности F (х), также равна нулю, а
вероятность каждого из тех значений хъ х2, ..., в которых функция F (х)
совершает скачки, численно равна значению соответствующего скачка.
Для любой случайной величины (дискретной, непрерывной или смешанной)
вероятность попадания случайной величины на участок оси абсцисс от а до р
(включая а и не включая р) выражается формулой
Р {а < X < р} = F ф) — F (а). (5.0.2)
Так как для непрерывной случайной величины Р{Х = а} = 0, то знак
равенства в этом случае в (5.0.2) можно отбросить:
P{a<X<p}=FA-(P)-F(a), Г (5.0.3)
или в других обозначениях
Р {X 6 (о,1Р)} = F ф) - F (а). (5.0.4)
Плотностью вероятности (или плотностью распределения или просто
плотностью) непрерывной случайной величины X называется производная
функции ^распределения:
/ (х) = F' (х). ] (5.0.5)
Элементом вероятности для непрерывной случайной величины X
называется величина / (х) dx, приближенно равная вероятности попадания
случайной величины X на элементарный отрезок dx, примыкающий к точке х:
f(x)dx^P{x<X<x+ dx}. (5.0.6)
Плотность / (х) любой случайной величины неотрицательна (/ (*) > 0)
и обладает свойством
J f(x)dx=l.
(5.0.7)
101
График плотности / (х) называется кривой распределения.
Вероятность попадания непрерывной случайной величины X на участок от
а до Р определяется выражением
P{a<*<p}=j7 (*)d*. (5.0.8)
..a
Функция распределения непрерывной случайной величины X выражается
через ее плотность:
х
F(x)= J f(x)dx. (5.0.9)
•—00
Математическим ожиданием непрерывной случайной величины X с
плотностью / (х) называется ее среднее значение, вычисляемое по формуле
ос
М[Х]= J xf{x)dx. (5.0.10)
— 00
Математическое ожидание смешанной случайной величины с функцией
распределения F (х) вычисляется по формуле
М [X]=2*iP*+ f xF\(x)dx, (5.0.11)
•I (н)
где сумма распространяется на все точки разрыва функции распределения,
а интеграл — на все участки ее непрерывности. Когда М [X] надо обозначить
одной буквой, будемjписать М [X] = тх.
Дисперсия непрерывной случайной величины X
D [X] = М [X2] = М [(X — тх)Ц
вычисляется по формуле
со
D[X] = J (x—mx)*J(x)dx. (5.0.12)
^ оо
Дисперсия смешанной случайной величины выражается формулой
D [X]«2 (*i-rnx)2Pi+ J (x-mxYF'{x)dx, (5.0.13)
i (н)
где сумма распространяется на все точки разрыва функции F (#), а интеграл —
на все участки ее непрерывности.
Корень квадратный из дисперсии называется средним квадратическим
отклонением случайной величины:
ох = ~[/Щх]. (5.0.14)
Для неотрицательной случайной величины в качестве характеристики меры
ее случайности иногда применяется коэффициент вариации
vx=ox/mx. (5.0.15)
Заметим, что коэффициент вариации зависит от «начала отсчета» случайной
величины.
Среднее квадратическое отклонение может быть применено для
ориентировочной оценки диапазона возможных значений случайной величины. При этом
пользуются так называемым правилом трех сигма, состоящим в том, что диапазон
практически возможных значений случайной величины X не выходит за пределы
тх±Зох. (5.0.16)
Это правило справедливо и для дискретной случайной величины.
Начальный момент fc-го порядка
ak [X] = М [Xk]
102
для непрерывной и смешанной случайных величин выражается соответственно
формулами:
«kW- J x*f(x)dx; (5.0.17)
—»оо
«Л [X] =2 ** P, + f xk F' (x) dx. (5.0.18)
i (н)
Центральные моменты вычисляются по аналогичным формулам:
[>ft[X] = J (*-«*)»/(*) <**; (5.0.19)
v — ОО
* (н)
Центральные моменты могут быть выражены через начальные совершенно
так же, как для дискретной случайной величины (см. гл. 4). Наибольший
практический интерес имеет выражение дисперсии через второй начальный момент:
1>Ия«|И-«1, (5.0.21)
или в другой форме
D [X] =*М [X*] —(М [X])*. (5.0.22)
Если вероятность какого либо события А зависит от того, какое значение
приняла непрерывная случайная величина X с плотностью / (*), то полная
вероятность события А вычисляется по интегральной формуле полной вероятности
00
Р(Л) = j* P(A\x)f(x)mdx9 (5.0.23)
^00
где Р (А\х) = Р {А\Х = х} — условная вероятность события А при гипотезе
{X = х).
Соответствующий аналог в схеме непрерывных случайных величин имеет
и формула Бейеса. Если в результате опыта имело место событие Л, вероятность
которого зависит от того, какое значение приняла непрерывная случайная
величина X, то условная плотность этой случайной величины с учетом появления
события А равна
fA <*) = / (*) Р (Л \х)/Р (А), (5.0.24)
или же с учетом (5.0.23)
U «*) = / С*) Р (А \х) / ? Р (А \х) f (х) dx. (5.0.25)
/ ОО
Формула (5.0.25) называется интегральной формулой Бейеса.
В схеме непрерывных случайных величин применяется также
интегральная формула полного математического ожидания
М [Х] = J M [X | у] f (у) dy, (5.0.26)
где X — любая случайная величина; Y — непрерывная случайная величина с
плотностью / (у); М [Х\у] — условное математическое ожидание случайной
величины X при условии, что случайная величина Y приняла значение у.
Перечислим некоторые часто встречающиеся на практике распределения
непрерывных случайных величин и опишем их свойства.
1. Равномерное распределение. Случайная величина X имеет равномерно
Распределение на участке от а до В, если ее плотность на этом участке постоянна:
fl/(6-a) при *£(«,*);
11 ' \ 0 при *£(<*,&). *
103
Значения / (х) в точках а и Ь никак не определены; это и несущественно, так как
вероятность попадания в любую из них равна нулю, и, значит, вероятность
любого события, связанного со случайной величиной X, не зависит от того, какое
значение имеет плотность / (х) в точках а и Ь*). График плотности вероятности
равномерного распределения показан на рис. 5.0.3.
;
ь-а
01
'№
Ш
а Ь ь
Рис. 5.0.3
Рис. 5.0.4
Математическое ожидание, дисперсия и среднее квадратическое отклонение
для случайной величины X, имеющей плотность (5.0.27), равны соответственно:
мга=
а+Ь
D[X] =
12
<** =
2 УЗ'
(5.0.28)
Равномерное распределение имеют ошибки грубых измерений при помощи
инструмента с крупными делениями, когда измеренное значение округляется
до ближайшего целого (или до ближайшего меньшего, или же до ближайшего
большего). Например, ошибка (в сантиметрах) измерения длины карандаша с
помощью линейки с сантиметровыми делениями имеет равномерное распределение
на участке ( — 1/2; 1/2), если округление производится до ближайшего целого,
и на участке (0; 1), если до ближайшего меньшего. Также равномерное
распределение имеет ошибка (в минутах) указания времени часами со скачущей
минутной стрелкой [участок (0; 1) ]. Равномерное распределение на участке (0, 2я)
имеет угол поворота Ф хорошо уравновешенного колеса (рис. 5.0.4), если оно
приводится во вращение и останавливается в результате трения. В задаче Бюф-
фона (см. задачу 1.45) угол, определяющий направление иглы, также имеет
равномерное распределение в силу того, что игла бросается наугад так, что ни одно
из значений ф не предпочитается никакому другому.
Типичные условия возникновения равномерного распределения состоят в
следующем: точка М случайным образом бросается на ось 0х9 разделенную на
равные интервалы длины / (рис. 5.0.5). Каждый из случайных отрезков X и К,
на которые делит точка М тот интервал, на который она попала, имеет
равномерное распределение на участке (0,/).
х М у
Рис. 5.0.5
В дальнейшем вместо подробной записи (5.0.27) для плотности
равномерного распределения мы часто будем пользоваться более краткой формой \
f (х) = 1/ (b — а) при х £ (а,Ь). (5.0.29)
*) В дальнейшем, задавая плотность f(x) разными формулами на разных
участках оси Ох, мы также не будем указывать значения / (х) на границах
участков.
104
/(*)■
■{*-:
[(5.0.30)
2. Показательное распределение. Случайная величина^ имеет
показательное распределение, если ее плотность выражается формулой
а—** при х>0;
при *<[0,
где X — параметр показательного распределения (рис. 5.0.6). Показательное
распределение имеет большое знечение в теории марковских случайных процессов
и теории массового обслуживания (см. гл. 10 и 11).
Если на оси времени 0t имеется простейший поток событий с интенсивностью
(см. гл. 4), то интервал времени Т между двумя соседними событиями имеет
показательное распределение с параметром X.
л<
\
0
jyW
К -
//////7
X
Рис. 5.0.6
Математическое ожидание, дисперсия и среднее квадрэтическое отклонение
величины X, имеющей показательное распределение, равны соответственно:
М[Х] = 1/Х; D[X] = 1/А2; ах = \/Х.
(5.0.31)
Коэффициент вариации показательного распределения равен единице:
Подробную запись показательного распределения (5.0.30) мы часто будем
заменять более краткой:
f(x)=Xe~u при х>0
или совсем краткой
7(д)=Хе-** (х\>0).
Таблицы функции е~х даны в приложении 3.
3. Нормальное распределение. Случайная величина X имеет нормальное
распределение (или распределена по нормальному закону*)), если ее плотность
1 (х-пр*
~ аУ 2я
2а*
(5.0.33)
(рис. 5.0.7). Математическое ожидание случайной величины, имеющей
распределение (5.0.33), равно т, дисперсия а2, среднее квадр этическое отклонение а.
Вероятность попадания случайной величины X, имеющей нормальное
распределение с параметрами m и а, на участок от а до р выражается формулой
Р{Х€(а, й)-ф(В=£)-ф(«==.). (5.0.34)
*) Этот закон также называется законом Гаусса.
105 ч
где Ф (х) — функция Лапласа:
х _^
ф(*)==171й Je 2 du (5-°-35>
о
Функция Лапласа обладает свойствами: 1) Ф (0) =0; 2) Ф (—х) = —Ф (х)
(нечетная функция); 3) Ф (оо) = 0,5. Таблицы функции Лапласа даны в
приложении 5.
Если участок (а, (^'симметричен относительно точки т, то вероятность
попадания в него
Р{ | X - т\< 1} = 2Ф (//а), (5.0.36)
где / = (Р — а) /2 — половина длины участка.
Нормальное распределение возникает тогда, когда величина X образуется
в результате суммирования большого числа независимых (или слабо зависимых)
случайных слагаемых, сравнимых по своему влиянию на рассеивание суммы
(подробнее см. гл. 8). Таблицы нормальной плотности для т = 0, о = 1 даны
в приложении 4.
ЗАДАЧИ И УПРАЖНЕНИЯ
5.1. Может ли при каком-либо значении аргумента быть: 1)
функция распределения больше единицы? 2) плотность распределения
больше единицы? 3) функция распределения отрицательной? 4) плотность
распределения отрицательной?
Рис. 5.3 ~ РиСщ 5.4
Ответ. 1) нет; 2) да; 3) нет; 4) нет.
5.2. Какова размерность: 1) функции распределения; 2)
плотности распределения; 3) математического ожидания; 4) дисперсии;
5) среднего квадратического отклонения; 6) третьего начального
момента?
Ответ. 1) безразмерна; 2) обратная размерности случайной
величины: 3) размерность случайной величины; 4) размерность
квадрата случайной величины; 5) размерность случайной величины;
6) размерность куба случайной величины.
5.3. Дан график плотности fx (x) случайной величины X (рис. 5.3).
Построить на том же графике плотность fy (х) случайной величины Y =
106
= X + a,* где а — неслучайная величина. Написать выражение для
U М-
Решение. Кривая распределения случайной величины Y
представляет собой кривую распределения7/* (#), сдвинутую вправо на а;
fy{x) =f.(x — a).
5.4. Дан график функции распределения Fx (x) случайной
величины X (рис. 5.4). Построить на том же графике функцию
распределения^/^ (х) случайной величины Y =—X.
Решение. Fy (x) =P (Y<x) = P {— Х< х} = Р {Х>—х} =
= 1 ~ Р {X < —х) = 1 - Fx (—х).
Для построения графика функции Fy (—x) нужно кривую Fx (x)
зеркально отразить в оси ординат и каждую ординату вычесть из
единицы (см. пунктирную линию на рис. 5.4).
5.5. Построить функцию распределения F (х) для случайной
величины, распределенной равномерно на участке (а, Ь).
Решение» F(x) = \ f(x)dx\
/М-
F{x) =
О при х<Са;
1/(6—а) при a<#<6;
О при х>6;
0 при #<;а; .
(х—а)1(Ь—а) при а<#<&;
1 при х > Ь
(рис. 5.5).
5.6. Случайная величина X распределена по «закону
прямоугольного треугольника» в интервале (0, а) (рис. 5.6). 1) Написать
выражение плотности / (х); 2) найти функцию распределения F (#); 3) найти
вероятность попадания случайной величины X на участок от а/2 до а;
V найти характеристики величины X: тх, Dx, ox, \i3 [XI
Ответ.
D/W-f 2*'(1-'
I о
х/а)/а при #6(0, л);
при л:"^ (0, а),
107
a x
Рис. 5.7
или, короче, f (x) =2 (1 — xla)la при х £ (0, а);
[ 0 при х^О;
2) F(*) = ] х{2—х/а)/а при 0<*<а;
( 1 при х;>а;
3) Р {X g (а/2, а)} = F (а) - F (а/2)_= 1/4;
4) тх -а/3; D* =а2/18; (7*^/(31/2); по формуле (4,0.15)
|i3 [X] «= а3 [X] — Зт^з [XI + 2т* = а3/135. •
5.7. Случайная величина X подчинена закону Симпсона («закону
равнобедренного треугольника») на участке от —а до а (рис. 5.7, а).
1) Написать выражение плотности распределения; 2) построить
график функции распределения; 3) найти числовые характеристики
случайной величины X : тх, DX9 вх, р, [XI; 4) найти вероятность
попадания случайной величины X в интервал (—а/2, а).
Ответ. 1)
/(*) =
— (l—-) при 0<х<а;
-L/l + — \ при — а<х<0;
при
при я<—а или #>-а,
или, короче,
/м=
:тг(1—т")при *6(—а,а);
2) график функции распределения при х £ (—а, а) составлен из
двух участков парабол (рис. 5.7, б);__
3) тх = 0; Dx = а2/6; а* = а/Уб; |х3 [X] = 0;
4) Р {X 6 (—а/2, а) = 7/8.
5.8. Случайная величина X распределена по закону Кош и:
/ (х) =а/ (1 +х2). 1) Найти коэффициент а; 2) найти функцию
распределения F (х); 3) найти вероятность попадания^величины^Х^ на
участок (—1, +1); 4) существуют ли для случайной величины X числовые
характеристики: математическое ожидание и дисперсия?
108
Ответ. 1) а = —; 2) F(x)=-±-arctgx+-±-■
П Я 2
3) Р {—1 < X < 1} = 1/2; 4) характеристики тх и Dx не
существуют, так как выражающие их интегралы расходятся.
5.9. Случайная величина X подчинена показательному закону
распределения с параметром р : / (х) = \ie-^x при х > 0. 1) Построить
кривую распределения; 2) найти функцию распределения F (х) и
построить ее график; 3) найти вероятность того, что случайная величина
X примет значение меньшее, чем ее математическое ожидание.
^ 14/- с л ov rw ч ( ° при *<0,
Ответ. 1) См. рис. 5.9, а; 2) F(x) = \ * ^
1 1—е-»" прн *>0
(см. рис. 5.9, б);
3) тх = 1/|х; Р {X < 1/jjl> = F (l/|i) = 1 — е-1 « 0,632,
5.10. Случайная величина X подчинена закону Лапласа.
/ (х) = ае-* Iх I, где Я — положительный параметр. 1) Найти
коэффициент а; 2) построить графики плотности и функции распределения;
3) найти тх и Dx
Ответ. 1) а = %/2; 2) F{x) =
_L е-**
при х^О;
1 е-** при #;>0,
графики плотности и функции распределения даны на рис. 5.10, а, б;
3) тх =0; D* =2/Я2.
Ffx)
5.11. Случайная величина R — расстояние от точки попадания до
центра мишени — распределена по закону Р э л ё я: / (г) =
= Are~htrt при г>0 (рис. 5.11).
Рис. 5.11
Найти: коэффициент Л; 2) моду М случайной величины /?, т. е,
абсциссу максимума ее плотности распределения; 3) тг и Dr; 4)
вероятность того, что в результате выстрела расстояние от точки
попадания до центра мишени окажется меньше, чем мода.
Ответ. 1)Л = 2А2; 2)^=1/(^^2); 3) тг = ^]/"я72 = Кя7(2А);
Ц. = (4—я)/(4А2)=.^2(4—я)/2; 4) Р{R<М) «0,393.
5.12. Случайная величина X с вероятностью рг имеет плотность
/х (#), а с вероятностью р2 — плотность /2 (л:) (рх + р2 = 1). Написать
выражение для плотности и функции распределения^величины X.
Найти ее математическое ожидание и дисперсию.
Решение. По формуле полной вероятности с гипотезами Нг =
= {величина X имеет плотность f± (x)} иЯ2= {величина X имеет
плотность /2 {х)} получаем
F (х) = Р {X < *} = PiFx (*) + p2F2 (*),
ДС Д?
где F! (х) = J /х (х) йх\ F2 (х) = J f2 (x)]dx; f (x) = F'. (x)=p^ (*) =
<— OO i»— 00
По формуле полного математического ожидания
во со
™>* = Pi J xh (*) dx + p2 j x/2 (x) dx = p! тж1+p2 m^,
где m^, mx2— математические ожидания для распределений fi(x)>
/2 (х).
Дисперсию находим через второй начальный момент:.
оо оо
Dx=-p1cc21 + p2a22—ml = p1 j x*f1{x)dx+ р2 ^ х2 f2{x)dx—ml,
.— во — оо
где а21, а22 — вторые начальные моменты для распределений f± (x)
5.13. Браковка шариков для подшипников производится
следующим образом; если шарик не проходит через отверстие диаметром dv
110
но проходит через отверстие Диаметром d2 > dlf то его размер
считается приемлемым. Если какое-нибудь из этих условий не выполняется,
то шарик бракуется. Известно, что диаметр шарика D есть нормально
распределенная случайная величина с характеристиками md =
\_ ^ _|_ d2)/2 и ad = (d2 — di)/4. Определить вероятность р того, что
шарик будет забракован.
Решение. Участок (йъ d2) симметричен относительно md. По
формуле (5.0.36), полагая / = (4 — di)/2, находим вероятность того,
что шарик не будет забракован:
Р{|о-т*К(4.-40/2}-2Ф(^).
откуда
р = 1 — 2Ф (<b^l) = 1 - 2Ф /2^-^ = 1-2Ф (2) = 0,0455.
V 2ad J \ d2— dt }
5.14. В условиях предыдущей задачи найти среднее квадратичес-
кое отклонение ad диаметра шарика, если известно, что брак
составляет 10% всей продукции.
Решение. Вероятность брака
p=l—2<b(*zzh) = 0yl; ф(£±^ = о,45.
По таблицам функции Лапласа (приложение 5) находим аргумент, при
котором функция Лапласа равна 0,45:
(d2 — dx)l (2<yd) « 1,65; ad « (d% — dJ/3,3.
5.15. При работе ЭВМ в случайные моменты возникают
неисправности. Время Т работы ЭВМ до первой неисправности распределено
по показательному закону с параметром v : q> (t) =^е-^ (*>0). При
возникновении неисправности она мгновенно обнаруживается и ЭВМ
поступает в ремонт. Ремонт продолжается время t0, после чего ЭВМ
снова включается в работу. Найти плотность / (t) и функцию
распределения F (t) промежутка времени Z между двумя соседними
неисправностями. Найти его математическое ожидание и дисперсию. Найти
вероятность того, что Z будет больше 2t0.
Решение. Z = Т + t0\
/(*) = ) ve-*«-M при t>t0; рц) = { 1— e"v('-'o) при t>t&
\ 0 при t<t0\ 1 0 при t<t0]
М \Z\< = l/v + t0; D [Z] = 1/v2; P {Z > 2t0} = 1 — F (2t0) = e-^«.
5.16. Время Т между двумя сбоями ЭВМ распределено по
показательному закону с параметром X : f (t) = Jte-м при t > 0. Решение
определенной задачи требует безотказной работы машины в течение
времени т. Если за время т произошел сбой, то задачу приходится
решать заново. Сбой обнаруживается только через время т после начала
решения задачи. Рассматривается случайная величина G — время,
и!
за которое задача будет решена. Найти ее закон распределения и
математическое ожидание (среднее время решения задачи).
Ответ. Случайная величина G дискретна и имеет ряд
распределения
' 2т
0
IX
РЧ
pqr
-к%
где р = е""ЛХ, q = 1 — р =1 — е~%г; М [6] = т/р = т/е-К
5.17. -В условиях предыдущей задачи найти вероятность того, что
за данное время t = fa будет решено не менее т задач (т < &).
• •
7.
kVJ •
Ряс. 5.79
Решение. Обозначим Рт, ft вероятность того, что за время t =
= kx будет решено ровно т задач. Pm> k есть вероятность того, что из
k промежутков времени т ровно т будет таких, в которых не будет
сбоев. Вероятность того, что за время т не будет сбоя, р = Р (Т > т) =
= е
—Ят
По теореме о повторении опытов
m,h :
: Си pm qk~m = С™ e-m^ (1 _e-^*-
Вероятность того, что будет решено не менее m задач, равна
/=от
/=т
или, если это удобнее,
/?m.»=l- S Cie-^(l~e-^)*-'.
/ = 0
5.18. Доказать, что закон распределения расстояния между
соседними событиями в простейшем потоке с интенсивностью X —
показательный, с параметром Я.
Решение. Находим сперва функцию распределения F (t)
случайной величины Т — расстояние между соседними событиями:
F (t) = Р {Т < t) = Р {за время t появится хотя бы одно событие
простейшего потока} — 1 — е~я' при t > 0; отсюда / (t) = F' (t) =
= Ле-м при />0.
5.19. Рассматривается пуассоновское поле точек на плоскости с
постоянной плотностью Я. Найти закон распределения и числовые
характеристики mry Dr расстояния R от любой точки поля до
ближайшей к ней соседней точки.
112
1
Решение. Найдем функцию распределения F (г) величины R.
Для этого проведем вокруг точки^поля окружность радиуса г (рис. 5.19)
Для того чтобы расстояние R от этой точки до ближайшей к ней
соседней было меньше г, надо, чтобы в круг попала хотя бы одна точка
(кроме данной). По свойствам пуассоновского поля вероятность этого
события не зависит от того, есть ли уже в центре круга точка или ее нет.
Поэтому
F (r)=l—e-^*(r>0),
откуда
f(r) = 2nXre-*kr* (r>0).
Такой закон распределения называется законом Рэлея] (см.
задачу 5.11).
оо
т. = f г2пХге~я^г dr = —^— :
I 21/Я*
оо
а2 [R] = Г г2 2nXre-n^a dr = — ;
J nK
о
DT = сс2 [R] — т? = 1/ (яХ) — 1/ (АХ) = (4 — п)1 (АпХ).
5.20. В пространстве трех измерений случайным образом
расположены точки. Число точек в некотором объеме v пространства есть
случайная величина, подчиненная закону Пуассона с математическим
ожиданием а = Хо, где X — среднее число точек, находящихся в
единичном объеме. Требуется найти закон распределения расстояния R
от любой точки пространства до ближайшей к ней случайной точки.
Решение. Функция распределения F (г) есть вероятность
того, что в сферу радиуса г попадет хотя бы одна точка:
F (Г) = Р (R < г) = 1 — е-*"М,
где v (г) = 'VgJtr3 — объем^сферы радиуса г; отсюда
/(г) = 4яг2Яе 3 (г>0).
5.21. В некотором звездном скоплении звезды образуют
трехмерное пуассоновское поле точек с плотностью X (среднее количество звезд
в единице объема). Фиксируется одна (произвольная) звезда и
рассматриваются: ближайшая от нее звезда, следующая (вторая) по
удаленности, третья и т. д. Найти закон распределения расстояния Rn от
данной звезды до я-й в этом ряду.
Ответ. Функция распределения Fn (г) имеет^вид
/Ъ(г)=1—"Ё -^е-а, где а = ^-яг*Х (г>0);
А=0 kX 3
113
плотйбсгь распределения
/n(r)^>=_£zLe-M^ (r>%
5.22. Деревья в лесу растут в случайных точках, которые
образуют пуассоновское поле с плотностью X (среднее число деревьев на
единицу площади). Выбирается произвольная точка О в этом лесу.
Рассматриваются случайные величины:
Rt — расстояние от точки О до ближайшего к ней дерева;
#2 — расстояние от точки.О до следующего по порядку (второго по
удаленности) дерева;
Rn—расстояние от точки О до п-го по удаленности дерева.
Найти закон распределения каждой из этих случайных величин.
Р еш е н и е. Функция распределения случайной величины
найдена нами в задаче 5.19:
fx(r) = l-e-^ (r>0).
Функция распределения F2 (г) = Р (R2 < г) равна вероятности того
что в круг радиуса г попадет не менее двух деревьев:
F2 (г) = 1 — е-*'**—яг2 X е-1** (г > 0).
Аналогично рассуждая, получаем
Fn(r) = P{/?n<r}=l-2l-fre~a (г>°)*
где а = пг2%.
Плотность fn (г) получим дифференцированием Fn (г) по г:
it*" ) о-1*1
5.23. На перекрестке стоит автоматический светофор, в котором
1 мин горит зеленый свет и 0,5 мин — красный, затем опять 1 мин
горит зеленый свет, 0,5 мин -г красный и т. д. Некто подъезжает^*;
перекрестку на машине в случайный момент, не связанный с работой
светофора. 1) Найти вероятность того, что он проедет перекресток, не
останавливаясь; 2) найти закон распределения и числовые
характеристики времени ожидания у перекрестка Тож; 3) построить функцию
распределения F (t) времени ожидания Тож.
Решение. Момент проезда автомашины через перекресток
распределен равномерно в интервале, равном периоду смены цветов в
светофоре. Этот период равен 1 + 0,5 = 1,5 мин (рис. 5.23, а).
Для^того чтобы машина проехала через перекресток, не
останавливаясь, достаточно, чтобы момент проезда перекрестка пришелся на ин-
114
тервал времени (0; 1). Для случайной величины, распределенной
равномерно в интервале (0; 1,5), вероятность того, что она попадет на
участок (0; 1), равна 2/3. Время ожидания Тож есть смешанная
случайная величина; с вероятностью 2/3 она равна нулю, а с вероятностью
1/3 принимает с одинаковой плотностью вероятности любое значение
между 0 и 0,5 мин. График функции распределения F (t) показан на
рис. 5.23, б.
Рис. 5.23
Среднее время ожидания у перекрестка
М [Тож1 = 0 • 2/3 + 0,25.. 1/3 « 0,083 мин.
Дисперсия времени ожидания
0,5
D [Тож] = а2 [Г0Ж1-(М [Гож])2 = 02.-|- + 3
31'2°'
i*.
-(0,083)2 « 0,0208 мин2; ot «0,144 мин,
ож
5.24. Нормальная функция распределения. Случайная величина
X имеет нормальное распределение с параметрами ту а. Найти ее
функцию распределения F (х).
Решение. F (х) = Р {X <х} = Р {— оо < Х< х} =
= ф/£^|_ф(_оо) = ф/^1|+0,5.
5.25*. Показать, что функция вида
f8 (х) = axs е~а*х% при х > 0
[а > 0 и а > 0 — некоторые постоянные иs — натуральное число
(s= 1, 2, 3, ...)] обладает свойствами плотности распределения.
Определить параметры а и а исходя из заданного математического
ожидания тх и найти Dx.
Решение. Параметры ц, и а находятся из условий:
^ ох» е-к***" dx=l; f^+^-W dx = mx.
о о
115
Написанные выше интегралы заменой (ах)2 = t приводятся к
гамма-функции Эйлера:
оо оо 5— 1
(V е-««>! dx = —i— f e_< t~ ^ = r(-^-)/(2as+i),
о о
оо
где Г (т) = j* егНп-Ш, (т > 0), причем Г (т + 1) = тТ (т)\ для
о
целых п = 1, 2, ..., получаем Г (п + 1) =л!, Г (я + 1/2) =
= (2п~1)П у- (2л _ 1)П = ^ 3> 5> ^ (2д _ 1}
Из заданных условий находим
w*
откуда а
га8*1
Второй начальный момент
оо
Ог [X] = Г ш?+2 е-<в*)' dx = а-
I
m
2as+3
«+1 T(s+l)
_„ 2 I 2 j= s+1
2as+1aa
= a
2a»
откуда
(s+l) Г*
2Г2(-
m
¥-)
Dx = a2[X]-m* = ^ mJ5 = mJ5
Некоторые из законов вида /s (x) имеют определенные названия:
Д (х) называется законом Рэлея, a /2 (*) — законом
Максвелла. Для закона Рэлея (s = 1) f± (x) = ахег*2**
(х>0)
а =
1 1/7Г
a=2a2=ik;Dx==ml[ir-ll
тх 2
Для закона Максвелла (s = 2) /2 (#) = ах2 е-»2*8
2 4а3 32 ~ 2 / Зя t \
'ST У1Г *2/"2 V 8 У
116
а = -
та У?
Примечание. Все законы вида
/,(*)= а* е-*'* (*>0)
при заданном s являются однопараметричными, т. е. зависят только от одного
параметра, в качестве которого можно задать, например, математическое
ожидание (или дисперсию).
5.26*. Моменты нормального закона. Имеется случайная
величина X, распределенная по нормальному закону с параметрами т и
о. Найти выражение для величины^ [X] — начального момента s-ro
порядка.
Решение. Выразим начальные моменты ав [XI = М [Xs] через
центральные моменты \i8 [XI = Ml (X — т)\:
as = M[(X-m+m)4= 2 C*|**lX]m—*; M*]=l-
Для центральных моментов при нечетном s = 2п + 1
о* _ Jl_ (х—т)*
М*] = l—r [(х-туе 2 * dx =
о У 2л J
= —l— f у*е >°%У dy=0,
о У2л J
о У2л J
а при четном s = 2n по формулам предыдущей задачи
а у 2л J
— f t/se V'Vsj ф,
2
_ 1С, _ («Ут)д,-
а"1/2я J
Tpz±L)
т /2я 2 v
Например:
2_i_ (a V2 )2n+1 =(2«+1)!! a2".
Ц2 [X] = a2; a2 [X] = m2 + a2;
a3 [X] = m3 + 3a2m;
Ц4 IX] = 3a*; a4 [X] = m4 + 6a2m2 + 3a4;
a5 [X] = mb + 10a2m3 + 5 . 15a*m;
fe [X] = 15a6; ae [X] = me + 15a2m4 + 15 • 3a4 m2 + 15a«.
5.27. Случайная величина Х имеет нормальное распределение с
параметрами яг и a. Написать выражение для ее функции
распределения F (х) = р {х < х}. Написать выражение для функции
распределения Y (у) = Р (Y<y) случайной величины Y = —X.
117
Решение. Согласно решению задачи 5.24
F(x)=®jiz£J+0,5;¥((,) = P{y<i/) = P{-X<s} =
= P(X>-0-l-f (0 = ф(£±^) = О,5.
5.28*. Функция распределения F (х) неотрицательной случайной
величины X задана графиком (рис. 5.28). Математическое ожидание
случайной величины X равно тх. Показать, что тк геометрически
может быть представлено площадью фигуры, заштрихованной на
рис. 5.28 (ограниченной кривой у = F (*), прямой у = 1 и осью
ординат).
Рис. 5.28
Решение. Имеем
0'\
Л
с*. В
Рис. 5.29
я?
'i
|
1
1
}
■ i
i
mx = ^xf(x) dx = C xFf (x)dx=~-С x [l—F (x)]' dx.
0 0 0j
Применяя интегрирование по частям, получаем
оо
тх = — х [1 — F (х)] °\ + \ [1 — F (х)] dx.
о о
Докажем, что первое слагаемое равно нулю:
х [1 + F (х)]\ = limх [1 — F (х)] = 0.
Действительно, для неотрицательной случайной величины X,
имеющей конечное математическое ожидание, из сходимости интеграла
j* xf (x)dx следует, что | xf (x)dx->■ 0 при /£-> оо, и так как
оо оо
tf$ f(x)dx^ J xf{x)dxt
к к
то М [1 — F {К)\ ->■ 0 при /С ->■ оо. Следовательно, lim х [1 —-F (#)] =
д; -»■ оо
= 0. Отсюда
118
mx = llll—F(x)]dx9
о
а это есть площадь, заштрихованная на рис. 5.28.
5.29. Случайная величина X подчинена нормальному закону~с
математическим ожиданием т=0 (рис. 5.29). Задан интервал (а, Р), не
включающий начала координат. При каком значении среднего
квадратичного отклонения с вероятность попадания случайной величины
X в интервал (а, Р) достигает максимума?
Р е ше н и е. Значение а найдем, дифференцируя по а вероятность
попадания в интервал (а, Р) и приравнивая производную нулю.
Имеем:
Р{а<Х<Р} = фШ-ф(^] =
£р.*.<*<»,■--у. -(-±)- -Н)-*
отсюда ^ j*_
ре~2а'=ае~2а'
и, следовательно,
Р 2 (In р—In а) У 2 In р—In a
Для малого интервала (а — 8, а + е)
а«а[1 — (е/а)7б] «а.
Например, при е/а<0,24 формула a « а дает погрешность менее 1%.
5.30. Имеется случайная величина X, подчиненная нормальному
закону с математическим ожиданием т и средним квадратичным
отклонением а. Требуется приближенно заменить нормальный закон
равномерным в интервале (a, P); границы a, P подобрать так, чтобы
сохранить неизменными основные характеристики случайной величины X:
математическое ожидание и дисперсию.
Решен и е. Для равномерного^распределения на участке (а,Р)
М [X] = (а + Р)/2; а [XI =* ф — а)/ (2УЗ); (а + Р)/2 = т\
(Р-а)/(2УзУ=<г.
Решая эти уравнения относительно аир, имеем
а =» т — аУЩ р = т + aV3.
5.31. Непрерывная случайная величина X имеет плотность / (х).
о результате опыта обнаружено, что появилось событие А =*
119
= {X £ (a, P)} [случайная величина X попала на участок (а, р)1.
Найти условную плотность /д (х) случайной величины X при наличии
события Л.
Э
Решение. Р (Л) = \f (x)dx. По интегральной формуле Бейе-
a
са (5.0.24) имеем
В
/ (*)/( J / (*) d*> при х^ («■ P);
/лМ =
(5.31)
при х ф (a, P).
Кривые распределения / (*) и /л (*) показаны на рис. 5.31. Орди-
ната кривой fA (x) в каждой точке равна ординате кривой / (#),
деленной на площадь S, заштрихованную на рис. 5.31. Так как
S < 1, то /л {х) > / (#) для любого х £ (а, р).
?№
А Ь0 А
Рис. 5.32
5.32. На производстве изготавливаются однородные детали,
номинальный размер которых /0, но фактически наблюдаются от этого
размера случайные отклонения, распределенные по нормальному закону
с математическим ожиданием m =0и средним квадратическим
отклонением а. При контроле бракуются все изделия, размеры которых
отличаются от номинального больше, чем на допуск Д. Найти вероятность
события А = {изделие будет забраковано}. Найти и построить
плотность вероятности для размера изделия, прошедшего контроль.
Решение. Р (Л) = Р {\Х\ > Д} = 1 —2Ф (А/а); Р (А) ».
= 2Ф (А/а).
По формуле^ (5.31)
Ыху
/(*) -
1
2а2
при \х | < Д,
Р (Л) 2а Т/2я Ф (Д/а)
Размер L изделия, прошедшего контроль, равен ошибке Х% плюс
номинал /0 и имеет условную плотность
Фл(*)= =? е 2<"
2а УШГф (Д/а)
показанную на рис. 5.32.
при х <=(/0 + Д>/о+Д),
120
5.33. Надежность р радиотехнического устройства зависит как от
общего времени т, прошедшего с момента включения устройства, так и
от того, вышел ли из строя в какой-то момент t < т стабилизатор
напряжения. Если стабилизатор напряжения не вышел из строя до
момента т, надежность задается функцией р = р0 (т); если же он вышел
из строя в момент t < т, то надежность есть функция двух аргументов;
р = рг (т, t). Время безотказной работы стабилизатора есть случайная
величина Т с плотностью / (t). Найти функцию распределения Fe (х)
времени G безотказной работы устройства и его математическое
ожидание те.
Решение. Полную надежность устройства (вероятность его
безотказной работы в течение времени т) найдем по интегральной
формуле полной вероятности:
p(x) = lp(t,T)f(t)dt + p0(T)^f(t)dt.
О Т
функция распределения времени в
Fв (х) = Р {в < х} = 1 - р (*).
Так как величина в неотрицательна, то (см. задачу 5.28)
оо оо у
те =М[в] = 5 [l—Fe(x)]dx = ^ p(x)dx.
о о
5.34. Ожидается поступление по радиоканалу какого-то сообщения
S; момент Т поступления этого сообщения случаен и имеет плотность
/ (/). В какой-то момент т обнаружено, что сообщение еше не
поступило. Найти при этом условии плотность распределения q> (/) времени
©, которое остается до поступления сообщения S.
Р е ш е н и е. По интегральной формуле Бейеса /U (t) — условная
плотность величины Т при условии, что произошло событие А = {до
момента т сообщение не поступило}, равна
JUL- Ш При;>т;
ыо=
Р(Л)
Ч
f(t)di
при t<.x.
Так как в = Т — т, то
ФОН
. У (О
1-J /(<) *
О
при />0;
при t < 0.
На рис. 5.34 изображены / (/) и ф (t)\ для закона q> (t) начало
координат совмещено с точкой т.
121
5.35. Момент Т наступления какого-то события А есть случайная
величина, распределенная по показательному закону: f (t) =Xerw
(t > 0). В момент т стало известно, что событие А еще не произошло.
Найти условную плотность ср (t) времени в, которое осталось до
наступления события. : -**}
Решение. Наблюдалось событие В = {событие А еще не
наступило до момента т}.
* Р(Б)=1—J f(t)dt=e
-Лт
/в (if) = / (0/Р (В) = ^ е-w/e-w = Яе~* ('-*> (t > т).
Случайная величина в = Т — т имеет условную плотность
/ (t) = her** при t > 0,
т. е. показательное распределение, совпадающее с / (t) (см. рис. 5.35).
Таким образом, условное распределение времени в, оставшегося до
наступления события, при показательном распределении Т не
зависит от того, сколько времени мы уже ожидали появления события.
Показательное распределение — единственное, обладающее таким
свойством. Напомним, что интервал времени между двумя соседними
событиями в простейшем потоке распределен именно по
показательному закону: время, оставшееся до наступления очередного события не
зависит от того, сколько времени мы его уже ожидаем (это следует из
отсутствия последействия в простейшем потоке).
5.36. Вероятность отказа радиолампы в момент включения
зависит от напряжения U в схеме и равна q (U). Напряжение U случайно
и имеет нормальное распределение с параметрами и0и ви. Найти
полную вероятность q отказа радиолампы в момент включения.
Решение. По интегральной формуле полной вероятности
(5.0.23)
оо оо
<7 = J ?(«)/(«)^~ J
(U-U0)*
q{u)e
2а
du.
5.37. Случайное напряжение U, имеющее плотность / (и), пропус-1
кается через ограничитель, который «срезает» все значения напряже-ill
122
ния, меньшие чем и19 и большие чем и29 в первом случае повышая его
до и19 а во втором — понижая до и2. Найти распределение случайной
величины U — напряжения, прошедшего через ограничитель, и найти
его математическое ожидание и дисперсию.
Решение.
[ иг при U <C Ui,
U при ux<.U < и2\
и2 при U > иъ
U--
Случайная величина U есть величина смешанного типа; два ее
значения иг и и2 имеют отличные от нуля вероятности р1э ра; для всех
значений и между иг и и2 функция распределения F (и) величины U
непрерывна и совпадает с -
U Ux о»
F (и) = $ / (и) du;Pl= J / («) du; рг = J / (и) du.
*—со •— о© U%
График функции F (и) показан на рис. 5.37.
\Flu),F(u)
Рис. 5.37
M[£/] = HiPi + w2p2+$ uf(u)du;
DM = a2M — (MM)2;
. a2 [(/] = u\ Pi + wi p2—^ и2 / (и) Ж*.
«i
5.38. По радиоканалу передается сообщение длительностью I
(рис. 5.38, а). Для того чтобы «забить» это сообщение,
осуществляется помеха длительностью Ь > /, рассчитанная так, чтобы центр помехи
Oi совпал с центром сообщения О.
Фактически из-за случайных ошибок центр помехи смещен
относительно центра сообщения на X. Случайная величина X распределена
нормально с параметрами т = 0, a = 1/2. Найти распределение
случайной величины U — длины части сообщения, «забитого» помехой,
123
найти математическое ожидание ти> дисперсию Du и среднее квадра-
тическое отклонение ои.
Решение. Случайная величина U — смешанная; она
принимает два значения: 0 и / с вероятностями, отличными от нуля; на участке
от 0 до / функция распределения F (и) непрерывна. Помеха Ь не
затрагивает сообщение 1(0= 0), если ее центр отстоит от 0 дальше чем
на (Ь + 1)12.
Р0 = Р{^ = 0} = Р{|Х|>^}=1-Р{|Х|<^} =
,_»(^L)-,_»(i±L).
V////W\,
ЩЩ
\\\\\\\\\\\\\\\\\\\\\\\
и ь
а)
- t
Рис. 5.38
7
о\
Fft)
Ш
}*
f ь
t
Б)
Для того чтобы помеха Ь полностью забила все сообщение
I ф — I), нужно, чтобы ее центр Ох отстоял от О меньше чем на
(6 — /)/2:
Л = Р{1/ = /} = р|,Х|<^±} = 2ф(-^±).
При (Ь — 1)12 < X < (Ь + 1)12 забитой помехами оказывается
какая-то часть U сообщения / (0 < U < /). Найдем функцию
распределения случайной величины U: P {U < и} при 0 < и < /. Чтобы
забитая помехой часть была меньше и, нужно, чтобы центр помехи 0±
отстоял от центра сообщения дальше чем на (Ь + 1)12 — и =
= (&•+/ —2и)/2:
(«) = р{|Х|
F(u) =
>
b+l— 2u
■}-1_р{|Х|.
1_2Ф( »+/-*■ у
Ь+1—2и
}-
Итак, на участке от 0 до / F (и) = 1 — 2Ф ( j—^) |
(рис. 5.38,6). '
Чтобы найти математическое ожидание и дисперсию случайной
величины U, надо будет найти F' (и) на участке (0, /). Учитывая, что
124
Ф(Х)-
1/2л
I
2л J \ I J Т/2я J
Т/25
1L
2 Л
и дифференцируя F (и) по переменной н, входящей в верхний предел,
получим:
F'{u)du = 4
-(6+/-2К)*
е 2/« du (0<и</);
/ У2я
г
М [U] = 0.p0 + lPl+ J nF' (a) da;
о
/
a2[f/] = 0.p0 + /2/7/ + 5 i*F'(u)du\
D [[/] = a2 [£/] - (M W\f\ au = YD [Ul
5.39. Случайная величина Х с вероятностью рх имеет плотность
Д (л:), с вероятностью р2 — плотность /2 (я), ..., с вероятностью ръ —.
плотность fi (x) (i = 1, ..., л)т Найти полную (среднюю) плотность
случайной величины X.
Решение. Найдем элемент
вероятности / (x)dx no f формуле
полной вероятности с гипотезами
Hi = {плотность случайной
величины есть ft (x)} (i = 1, ..., я).
По формуле полной вероятности
/(*) dx= ^Pift(x)dx9
i-i.
откуда
/w=
Рис. 5.5Р
= 2>iM*)-
В частности, если гипотезы две и их вероятности равны р± = р2 =
= 1/2, то / (#) есть полусумма плотностей Д (л:) и /2 (л:) (рис. 5.39).
Наличие двух «горбов» на кривой распределения всегда наводит на
мысль о том, что распределение получено усреднением двух
разнохарактерных распределений.
5.40. Случайная величина X с вероятностью 0,4 имеет
нормальное распределение с параметрами /п =0 и 0=2, а с вероятностью
0,6 — нормальное распределение с'параметрами т =2иа = 1.
Найти плотность распределения случайной величины X.
0,6
(X— 2)8
Ответ: f(x)=-^-e 8 +
Т/2лГ Т/2лГ
125
График / (я) показан на рис. 5.40.
5.41. Имеются две случайные величины: дискретная X с рядом
распределения
|*1 | Х2 | ... 1 *п
| А | Рг |. . -| Рп
и непрерывная Y с плотностью / (у). Величины X и У принимают свои
значения независимо друг от друга. Является ли их сумма Z =
= X + Y дискретной, непрерывной или смешанной случайной
величиной? Найти ее распределение.
-5 -Ч -3 -Z -7
J Z 3 Ц 5
Рис. 5.40
Решение. Случайная величина Z непрерывна. Ее плотность f(z)
найдем по формуле полной вероятности с гипотезами: Н± = {Х = х1};
#2 == {X =х2}> ..., Нп = {X = хп}. Условный элемент вероятности
случайной величины Z для i-й гипотезы равен
fi (z) dz = / (z — Xi)dz.
Полный элемент вероятности
откуда
/ (z) dz^^pif (z—xt) dz,
* = 1
5.42. Дискретной, непрерывной или смешанной является величина
Z= min {X, а}, где X — непрерывная случайная величина с
плотностью / {х)\ а — неслучайная величина? Найти распределение
случайной величины Z, ее математическое ожидание и дисперсию.
Решение. Случайная величина Z определяется формулой
« __ ( Ху если X < а\
\ а, если X ^ а.
126
Значение случайной величины Z = а имеет вероятность
оо
ра-Р{Х > а}==Р (X > а} = $ / (л:) dx.
а
При ра>0 случайная величина Z—смешанная, при ра =
О—непрерывная.
При z < а функция распределения F (г) случайной [величины"Z
х
совпадает с F (х) = j* / (#)d# (рис. 5.42).
»— ее
M[Z] =ape+f*/(*)dr,
D [Z] = а2 [Z1 - (М [Z])2; а2 [Z1 = а*ра + f *2/ (x)dx.
— оо
Если РЛХ^»}^0, то ^=тш2{Х,Га}^=Х-Д?(2)>,Р(г).
/1^
1УЛ^УЛУ<
а)
J( i
I
L »
Рис. 5.43
5.43. Из двух источников А и В посылаются периодические
сигналы одинаковой длительности / и с одинаковыми интервалами L между
ними (рис. 5.43, а); / < L. Моменты передачи сообщений из источников
А и В несогласованны. Сообщения, передаваемые источниками, при
наложении искажаются. Найти 1) вероятность R того, что хотя бы
одно сообщение будет искажено (полностью или частично); 2)
вероятность, того, что будет искажено не более 10 % каждого сообщения;
3) функцию распределения случайной величины Z—«доля
искаженного текста»; 4) среднюю долю искаженного текста 7.
Решение. Пусть ось В (см. рис. 5.43, а) случайно
накладывается на ось А. Так как начала и концы всех сообщений связаны
функционально, то достаточно будет рассмотреть на оси А только одну
пару соседних отрезков: / — сообщение, L — промежуток (рис. 5.43, б).
Выберем в качестве начала отсчета начало промежутка / на оси А и
обозначим X абсциссу начала ближайшего по времени промежутка /
на оси В. Величина X распределена с постоянной плотностью на
участке L + L Очевидно, неналожение сообщений будет иметь место в
случае, когда / < X < L; вероятность этого
Ро = (L - l)/(L + /); R = 1 -р0 = 1 - (L _ /)/ (L + I).
т
Для вычисления вероятности р того, что сообщения перекроются
не более чем на 10%, нужно увеличить «благоприятный»
неперекрытию отрезок L — /на два отрезка длиной 0,1/; получим L — / + 2х
X 0,1/ = L — 0,8/; р = (L — 0,8/)/ (L + /). Случайная,
величина Z — доля искаженных сообщений — есть величина смешанного
типа; ее значение z = 0 имеет отличную от нуля вероятность р0 =
= (L — /)/ (L + /); при 0< 2< 1 F (z) = [L — I (1 — 2z)]/ (L +/);
при z=l это выражение обращается в единицу: F (1) = 1, а между
2 = 0 и 2 = 1 возрастает линейно (рис. 5.43, в).
Математическое ожидание случайной величины Z равно площади,
заштрихованной на рис. 5.43, в, т. е. 7 = [1 — (L — /)/ (L + /)]/2 =
= //(L + /).
5.44. Имеется непрерывная случайная величина X с плотностью
/ (х) (рис. 5.44, а). Наблюденное значение случайной'величины
сохраняется, если оно попало в интервал (х19 х2)9 и отбрасывается, если оно
вышло зча пределы интервала (хъ х2). Получается новая случайная
величина X («урезанная» случайная величина X) с диапазоном
значений от хг до х2. Найти плотность'/ (х) случайной величины X.
Рис. 5.44
Решение. Искомая плотность / (х) есть не что иное, как
условная плотность величины X при условии, что она попала на участок.
(х19 х2). Вычислим элемент вероятности / (x)dx для участка (х, х +
+ dx) cz (xv х2) (см. рис. 5.44, а). По правилу умножения вероят-:
ностей
/ {x)dx = Р {X £ {х19 x2)}J(x)dx9
где / (x)dx — условный элемент вероятности — вероятность того, что|
величина X попала на участок (х, х + dx) при условии, что*
X £ fo, *2), и *
Р {X е= (хъ х2)} = $*/ (х) dx- J{x) = f (х) I *$/(*) dx.
Кривая f (х) подобна кривой / (х) и получается из нее делением каж*|
дой ординаты на площадь, заштрихованную на рис. 5.44, б (см. утол?|
щенную линию на рис. 5.44, б); вне участка (xlt х2) J (х) = 0.
128
5.45, Одна женщина утверждает:
«Мой муж среднего роста, а ведь
большинство мужчин ниже среднего
роста». Бессмысленно-ли это
утверждение?
Решение. Утверждение не
бессмысленно и может быть даже
справедливым, если плотность
распределения роста X мужчин
несимметрична относительно среднего значения (математического ожидания),
как, например, показано на рис. 5.45. Площадь, заштрихованная на
рис. 5.45, равна средней доле мужчин ниже среднего роста тх, и она
больше площади, оставшейся незаштрихованной.
5.46. В теории надежности технических устройств в качестве
закона распределения времени безотказной работы устройства часто
применяется закон Вейбулла о функцией распределения
F (х) - 1 _е-«" (х > 0), (5.46)
где а > 0 — некоторая константа; п — целое положительное число.
Найти 1) плотность / (х)\ 2) математическое ожидание и дисперсию
случайной величины X, распределенной по закону Вейбулла:
Решение.
1) f (x) = dF (x)/dx = naxn-1 е-"*"; 2) М [X] =С хпахп-1 е""** dx.
о
Делаем замену переменной» ах" = у, x=>a*~l/n у1'\
1«»л
dx-
JLa-i/nr »
М
У " ^у.
[XJ-f пуе—±а п у п dy =
о
«.!«» ± —L
где Г (г) = f xz**1 e^xdx—известная гамма-функция.
•i
M[X2] = \ пах»*1 e""*" dx =
1
= f «aa V a) у aQ-y±.a "у ° dy = a "[fe-prfj(=
5 Зап. 1040
129
-г('+-~)« ■=
D [XI «о-»/» IT (1 + 2/п) - {Г (1 + 1/л)}2].
5.47. Срок службы технического устройства есть случайная
величина Т с плотностью / (/) (/>0). В момент t0, если устройство до
этого момента еще не отказало, проводится его профилактический ремонт,
после чего оно работает еще время Тг с плотностью fx (t). Если
устройство отказало в какой-то момент и < t09 то немедленно производится
аварийный ремонт, после которого устройство работает еще
случайное время 7*2 с плотностью /2 (f) (второго ремонта уже на проводится).
Найти математическое ожидание времени 6, которое проработает
устройство (в него не включается время, затрачиваемое на ремонт).
Решение. Пусть Т приняло значение t <. t0; при этой гипотезе
условное математическое ожидание величины 0 будет М [в|Й =
00
= *+та, где т2=з|//2 (t)dt—математическое ожидание времени рабо-
о
ты устройства после ремонта. Если же t^t09 то естественного отказа
устройства до момента t0 не произойдет, и М [@\t]—t0+mv где ш1 =
оо
ss J tfi (t)dt. Следовательно,
{to + ntt при *>*0.
Полное (безусловное) математическое ожидание величины в
М [0] = I Q+tnJ f (ft di+j (/,+m,) /(ОЙ-
9 to
- J if tf) dt+m2 J/ (0 dt + (t9+md J / (О Л =
= Г tf (0 $+m2 ^ {T < t0} + (t0+m1) P{T> Q =*
= |V © Я + я, F (*0) + tf„ + mi) (1—P Co)),
где F (/) — функция распределения случайной величины Т:
F(t) = \f(t)dt.
О
5.48. По радиоканалу передается последовательность сообщений
одинаковой длины / (рис. 5.48, а) со случайными промежутками
7\, Т2, .... между ними. Интервалы 7\, Т2,... имеют одинаковое рас-
130
пределение. Время от времени в сообщение вмешиваются случайные
помехи (рис. 5.48, б). Моменты возникновения и прекращения помех
никак не связаны с последовательностью сообщений. Длительность D
каждой помехи случайна и распределена по показательному закону g
параметром fr, длительность интервала между помехами тоже
случайна и распределена по показательному закону с параметром v. Если
помеха захватывает все сообщение или его часть, искажается либо все
сообщение, либо соответствующая его часть. Найти среднюю долю
сообщения, которая будет искажена помехами, т. е. отношение
средней длины искажённого текста к средней длине переданного.
ivvwwvvr
WWVT
а
В)
ЧИЛЛМ'
Рис. 5.48
Решение. 1/fi — средняя продолжительность помехи; 1/v —
средняя длина интервала между ними; средняя доля времени на оси
Ot, занятого помехами, равна
1/fX-b 1/V \JL+V
Очевидно, что та же средняя доля сообщений будет искажена
помехами независимо от распределений их длительности и
продолжительности интервалов между ними, если \i = 1/M[D], v = 1/М[Л.
5.49. За время т (продолжительность наблюдения) сигнал
приходит с вероятностью р; сигнал появляется в любой точке промежутка
т с одинаковой плотностью вероятности. Известно, что в момент /< т
(рис. 5.49) сигнал еще не появился. Найти вероятность Q того, что он
появится за оставшееся время т — t. .
Решение. Q есть не что иное, как условная вероятность того,
что сигнал появится за время т — U если известно, что до момента t
r-t
Рис. 5.49
5*
131
Рис. 5.50
сигнал еще не появлялся. Полная вероятность р появления сигнала
за время т равна вероятновти tpl%9 того, что он придет за время t, плюс
вероятность 1—tpfa того, что он не придет за это время,
умноженная на Q. Отсюда
ч \ т? / \-tph
5.50. Момент прихода сигнала — случайная величина Т с
плотностью / (0. В какой-то момент t< т? сигнал еще не пришел. Найти
вероятность того, что он придет за последующий участок времени от
*до т (рис. 5.50).
Решение. Задача сходна о предыдущей. Обозначим р вероят-
ность того, что сигнал придет за время т; она равна р = j / (t)dt. Pac-
о
суждая, как в предыдущей задаче, найдем полную вероятность р
появления сигнала за время т; она равна вероятности pt того, что сигнал
t
появится до момента t г pt = f / (t)dt, плюо вероятность
противоположно
ного события 1 — pt, умноженная на условную вероятность Q того,
что сигнал придет за оставшееся время (т — t), т. е,
Ь (О Я-$ / ЮЛ + Il - J/ (0 dt\ Q,
X t X
f/ (fdt-U(t)dt \t(t)dt
q Ъ Ъ t _F(t)-f (0
откуда
'i
i 1—^(0 I—F(t)
f (t) at
где F (t) — функция распределения случайной величины Т.
Если / (t) — показательное распределение с параметром А>, то Q =
5.51. В условиях предыдущей задачи / (f) — нормальное
распределение с параметрами m, a; t = т (т. е. сигнал не пришел за
время т)*К Найти вероятность того, что он придет за промежуток
времени длиной а, непосредственно следующий за t =m.
Решение, т = /я + <т;
m-f-a
Г f(t)dt = Q> ( т+°-т \—ф (0) = Ф (1) « 0,341;
Q« 0,341/0,5 = 0,682.
*) Задача имеет смысл, только когда Т—величина практически
неотрицательная, т. е. при m — За > 0,
132
ГЛАВА 6
СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
(СЛУЧАЙНЫЕ ВЕКТОРЫ)
6.0. Система двух случайных величин (Х,К) геометрически
интерпретируется как случайная точка с координатами (Х,К) на плоскости хОд (рис. 6.0. )
или как случайный вектор, направленный из начала координат в точку (Х,К),
составляющие которого представляют собой случайные величины X и У
(рис. 6.0.2).
Система трех случайных величин (X, К, Z) изображается случайный точкой
или случайным вектором в трехмерном пространстве; система п случайных
величин (Xi, Х2, «.♦, Хп) — случайной точкой или случайным вектором в
пространстве п измерений*
\У
-1М
—-ЯМ
и
X
X
Рис. 6.0.1
Рис. 6.0.2
Совместной функцией распределения двух случайных величин (X, Y) (или
функцией распределения системы двух случайных величин) называется
вероятность совместного выполнения двух неравенств X < х и Y <3 у:
Р(х9 у)- Р{Х<х, Y <y}t
(6.0.1)
Геометрически F (х,у) интерпретируется как вероятность попадания
случайной точки (Х,К) в квадрант о вершиной (дс, у), заштрихованный на рис» 6.0.3,
Вероятность попадания случайной точки (Х,К) в прямоугольник R со сторонами,
параллельными осям координат, включающий свою нижнюю и левую границы,
но не включающий верхнюю и правую (рис. 6.0.4), выражается через функцию
распределения формулой
РЦХ.У) е Я}"- F(p, 6)-F(a,e)-F(p,v)+*(a,Y).
(6.0,2)
Функция распределения Р (х,у) обладает свойетвами: 1) Р ( — оо, —. оо) =
= Р (— оо, д) =* F (*, — оо ) = 0j 2) F ( + оо, + оо) = 1*3) Р (х, + оо) «
=F1(*)> F(+co, t/) = F2 (i/), где Ft (*), F2 (у)—функции распределения
случайных величин X и К| 4) F (*, у) — неубывающая функция аргументов х и у}
5) F (х, у) непрерывна слева по каждой координате? 6) F (р,о) — F (а, б) —
~-^ (Рэ Y) + F (a, Y) > 0 для любых а < р, Y ^ б (последнее свойство означает,
что вероятность попадания в прямоугольник неотрицательна),
&
Т
0
У
1 1
1 1
о
i p
Рис. 6.0.3
Рис. 6,0.4
133
Совместной плотностью двух непрерывных случайных величин (или плот»
ностью распределения системы) называется предел отношения вероятности
попадания случайной точки в элементарный участок плоскости Дя, Д#,
примыкающий к точке (#, у), к площади этого участка, когда его размеры Дд:, Д# стремятся
к нулю* Совместная плотность выражается через совместную функцию
распределения:
f(xty)=d*F(x>y)idxdy = F"xy(xty), (6.0.3)
т* е« представляет собой вторую смешанную частную производную функции
распределения по обоим аргументам,
Поверхность, изображающая функцию / (*, у)> называется поверхностью
распределения*
Элементом вероятности для системы двух случайных величин называется
величина / (ад) dxdy, приближенно выражающая вероятность попадания
случайной точки (X,Y) в элементарный прямоугольник со сторонами dx, dy,
примыкающий « точке (х, у)»
Вероятность попадания случайной точки (X,Y) в произвольную область D
выражается формулой
Р
Свойства совместной плотности:
{X, Y) e D}-Jf/(*, у) dxdy. (6.0.4)
1) /(*. У)>0; 2) J J f(xt y)dxdy = \.
Совместная функция распределения выражается через совместную плотность:
к у
F(x, У)** J J /(*i У) dxdy. (6.0.5)
<w»oo asg
Плотности отдельных величин, входящих в систему, выражаются через
совместную плотность:
00 О»
ftW- J fix, y)dy\ ЬОг)- J" /(*, у) dx. (6.0.6)
— 00 «wOO
Условным законом 'распределения случайной величины, входящей в систему»
называется ее закон распределения, вычисленный при условии, что другая
случайная величина приняла определенное значение»
Условные функции распределения случайных величин X и К, входящих в
систему, обозначаются Fj ix | у) и F2 (у \ х), а условные плотности
распределения — f t(x | у) и /2 (у | х).
Теорема умножения плотностей|
/ <*.*) e h W ft GM *> или f (ад) - /2 (у) /, (х I jfl. (6,0,7)
Выражения для условных плотностей через безусловные!
Л(И*)в-тт#- при м*)=£°; &(*эЛ--Чт^- при Л(й^о. (6.0.8)
/1W h \У)
Случайные величины X, Y называются независимыми, если условный закон
распределения одной из них не зависит от того, какое значение примет другая:
h (х I У) - h (х) или f% (у | х) - /, (у). (6,0,9)
Для независимых случайных величин теорема умножения плотностей
принимает вид
h(x,9)**h(x)ft(y). (6,0.10)
Начальным моментом порядка k + s системы (X,Y) называется величина
«ftst*, К]*М[Х*У»1. (6.0.11)
134
Центральным моментом порядка k + s системы (X, Y) называется величина
VhslX, У]«М [**?■]. (6.0.12)
Расчетные формулы для определения моментов:
а) для дискретных случайных величин
алв[Х.Н=22*?0?Р</; (6.0.13)
i i '
Wis]*, n = SS(^-%)M^-%)sPi;. (6.0.14)
i i
где pu = P{X = xu Y = ytyt
б) для непрерывных случайных величин
оо
a,hSlX,Y]=^^ysf(.x, y)dxdy; (6.0.15)
—оо
оо
HftJX. П-f J(*-««)* (*-%>*/(*. y)rf^f (6.0.16)
—oo
где f (xt у) — совместная плотность,
Порядком момента а&8 [X, Y] или ц&$ [X, Y] называется сумма индексов k и st
Корреляционным моментом (или коварнацией) двух случайных величин
X, Y называется смешанный центральный момент второго порядка, т. е. \\ц:
Кху = Р111Х,У]шшЩЯ?]. (6.0.17)
Величину Кху удобно вычислять через второй смешанный начальный момент:
Кху=*<х<ц[Х*У\— тх/Пу, (6.0.18)
или в других обозначениях
Кху = М[Х • Y] - М[Х] * М[К]. (6.0.19)
Для независимых случайных величин корреляционный момент равен нулю.
Коэффициентом корреляции (или нормированным корреляционным
моментом) Тху двух случайных величин X, Y называется безразмерная величина
rXy*=Kxy/(oxayh (6.0.20)
где а^У^=Уц20[Х,У]; су« Л/Щ= VW [X, Y\.
Коэффициент корреляции характеризует степень тесноты линейной
зависимости между случайными величинами,
Случайные величины X, Y называются некоррелированными, если их
корреляционный момент (или, что равносильно, коэффициент корреляции) равен
нулю*
Из независимости случайных величин следует их некоррелированность;
напротив, из некоррелированности случайных величин еще не следует их
независимость.
Если случайные величины X, Y связаны линейной функциональной
зависимостью вида Y = аХ + Ь, где а, Ь не случайны, то их коэффициент корреляции
rxy = rb 1, где знак «+» или «—» берется в соответствии со знаком коэффициента
а. Для любых двух случайных величин | гХу 1^1*
Совместной функцией распределения п случайных величин Xi, X2, 4ii, Xn
называется вероятность совместного выполнения п неравенств вида Xi < х%\
Ffa, x2i...> xn)=P{Xi<xu X2<x2,...tXn<xn}. (6.0.21)
Совместной плотностью п случайных величин называется л-я смешанная
частная производная функции распределения:
дп -
f(*i, x2,..., xn)=—z — F(xu x2,..., xn). (6.0.22)
dxidx2,..., охп
135
Функция распределения Ft (xi) одной из величин4 Х$, входящих в систему,
получается из F (xlt x2, ,.», хп), если положить в ней все аргументы, кроме *|,
равными + оо:
?l {Xi) = F ( + оо, + оо, ,.„ хь + оо, „., + о£),
(6.0.23)
Плотность отдельной величины Хи входящей в систему (Х1э Х2, ••», Хп),
выражается через совместную плотность формулой
M«i)a ] ••• J t(*u **> •»**n)dx1...dxi-1<lxi+1...dxn. (6.0.24)
Плотность отдельной подсистемы (Хь Х2, .», Х&), входящей в систему (Xif
Х2, ..«, Xft, Хй+х, ..„ ХЛ), выражается формулой
/i#...,*(*i *fe) = J ••• J /И ^..,,*п)Л;ж-Л. (6.0.25)
•» ее «*ов
Условная плотность подсистемы Xi, ,,,, Х& при фиксированных
значениях всех остальных случайных величин выражается формулой
h k(*i *nl*fc+i **)-: К*'*»'"-'*»> (6.0.26)
/ft+l, .... 71 l*fc+l» • • • t -*W
Если независимые величины (Xlf X2, «„, ХЛ) независимы, то
f (*i. x2, .,., хп) — / i(*i) /2 (*2) ••• /п (*п)< (6.0.27)
Вероятность попадания случайной точки (Хь Х2, .,,, Хп) в пределы
n-мерной области D выражается л-кратным интегралом
P{(Xi9...9Xn)eD}=^\nD\^f(xlt ...9xn)dxt.„dxn. (6.0.28)
Корреляционной матрицей системы п случайных величин (Xi, X2, .*., ХЛ)
называется таблица, составленная из корреляционных моментов всех этих
величин, взятых попарно:
ЦК|Л1 =
#11 #12 • • • %1п
^2i #*2 •»• ^2П
Kni *>П2 ••• Кпп
где Ktj e KxfXj e Ml^fjXj] — корреляционный момент случайных величин
Xi, Xj.
Корреляционная матрица симметрична AKij~Kji)* поэтому обычно
заполняется лишь половина таблицы:
Кц Ki2.**K±n
А22 • * • *>2/1
Кп
По главной диагонали корреляционной матрицы стоят дисперсии случайных
величин Xi, Х2, •*•, Хп:
Кп = D[X|]. (6.0,29)
Нормированной корреляционной матрицей системы п случайных величин
называется таблица, составленная из коэффициентов корреляции всех этих
величин, взятых попарно:
136
\Ш\*
Г12 Г13 • • • f\П
1 f"23 • • • **2П
• • •
1
где гц = Kij/(oiOj) — коэффициент корреляции величин Xj, XjA
Нормальный закон распределения для двух случайных величин X, Y
(нормальный закон на плоскости) имеет плотность вида
/(*.*)--
1
ехр
2похоуУ\—&
2г (х—тх) {у—ту)
—[■
ft— '"а)2
(У—^l
*])•
(6.0.30)
где тх> Щ — математические ожидания случайных величин X, Y; аХ1
Оц — их средние квадратические отклонения; г — их коэффициент корреляции.
Для случайных величин, распределенных по нормальному закону,
некоррелированность равносильна независимости. Если случайные величины X, Y
не коррелированы (независимы), то г = 0 и
f (*.</) = -
1
ехр
{__ * Г ft—м^;
1 2 [ а1
+
(у-щ)2
(6.0.31)
*JlUxVy к - L „x Vy
В этом случае оси Ох, Оу называются главными осями рассеивания. Если при этом
Шх = Щ — 0» то нормальный закон принимает канонический вид:
1 ( х2 Ф Л
/(*,*/)= 0 exP -1^-"^- (6.0.32)
2пох Оу
Вероятность попадания случайной точки, распределенной по нормальному
закону, в прямоугольник R со сторонами, параллельными главным осям
рассеивания (см. рис. 6.0.4), выражается формулой
(6.0.33)
Эллипсом равной плотности (эллипсом рассеивания) называется эллипс,
во всех точках которого совместная плотность нормального закона постоянна:
/ ft, У) = const* Полуоси эллипса пропорциональны ох, оу. а = kox\ Ь = koyi
Вероятность попадания случайной точки, распределенной по нормальному
закону, в область £&, ограниченную эллипсом рассеивания с полуосями а и Ь
равна
Р {(X, Y) 6 £fe> = l — e--**/2, (6.0.34)
где k — размеры полуосей эллипса в средних квадратических отклонениях:
k=a/oxz=b/Oy.
Если ах = Оу = а, рассеивание по нормальному закону называется круга»
вым. При круговом нормальном рассеивании с тх = ту = 0 расстояние R от
точки (X, Y) до начала координат (центра рассеивания) распределяется по з а-
кону Рэлея:
/М-
2о2
при г > 0,
(6.0.35)
Нормальный закон в пространстве трех измерений для независимых слу«
чайных величин (X, К, Z) выражается формулой .
137
(2пУ'гахауаг
Вероятность попадания случайной точки (X, К, Z) в область £&,
ограниченную эллипсоидом равной плотности с полуосями а = koXf Ь = koy, с = &az,
равна
Р {(X, Y, Z) 6 £ь> = 2Ф (*)-У27^^е^2/2# (6.0.37)
ЗАДАЧИ И УПРАЖНЕНИЯ
6.1. Передаются два сообщения, каждое из которых может быть
независимо от другого либо искажено, либо не искажено. Вероятность
события А = {сообщение искажено} для первого сообщения равна
р19 для второго р2. Рассматривается система двух случайных величин
. (X, У), определяемых так:
У /1, если первое сообщение искажено;
""" \0, если первое сообщение не искажено;
V — /*' еели втоРое сообщение не искажено;
-~ \0, если второе сообщение не искажено
(X и У — индикаторы события А в первом и втором опыте).
Найти совместное распределение пары случайных величин (X, У),
т. е. совокупность вероятностей ри каждой комбинации их значений.
Найти совместную функцию распределения F (х> у).
Решение. Совместное распределение определяется
вероятностями:
Роо = Р{Х =0, У =0} =^2;р10 =Р{Х = 1,У =0} =pig2;
р01 =Р {X =0, У = 1} =gip2; pu = Р {X = 1, У = 1} =Plp2,
где ?i = 1 — Pi, 92 == 1 — Р2 (см. таблицу).
Распределение на плоскости *0# сосредоточено в четырех точках с
координатами (0, 0), (0, 1), (1, 0), (1, 1) (рис. 6.1). Пользуясь
геометрической интерпретацией функции распределения как вероятности
попадания в квадрант g вершиной в точке (я, у) (см. рис. 6.0.3),
получим для F (х, у) следующую таблицу значений:
138
*\?
1 </<о
|о<у<1|
1 1<у
| *<°
0
0
0
0<*<1
0
<?1<?2
<?i
Кх
0
?2 |
1
6.2. Функция распределения системы двух случайных величин
(X, Y) равна F (х, у). Найти вероятность попадания случайной
точки (X, Y) в область D (рис. 6.2), ограниченную справа абсциссой а,
снизу и сверху ординатами 7. б.
Ответ. Р { (X, Y) € D} = F (а, б) — j? (а, у).
jfH/й
/&&
?rfe
±М*
г
1 X
щШЬ
СА US
Рис. 6.1
Рис. 6.2
6.3. Имеются две независимые случайные величины X и У,
подчиненные каждая показательному закону
М*) = Ле-** (*>0); /,(у) = |*е-^ (у>0).
Написать выражения: 1) совместной плотности; 2) функции
распределения системы (X, Y).
Ответ.
2)^Нп -*Л ПРИ,
I (1— е~я*) (1 —е1""
О при л; <С О или # < 0;
Xjx e-tt*+M0 при x > 0 и у > 0;
при х <1 0 или # <С 0;
-»**) при х > 0 и у > 0.
6.4. Система случайных величин (X, Y) распределена с
постоянной плотностью внутри квадрата R qo стороной а (ри«. 6.4, а).
Написать выражение плотности / (х, у). Построить функцию распределения
системы. Написать выражения fx (x), /2 (у). Определить, являются
ли случайные величины Х9 Y независимыми или зависимыми.
1/а2 при (х, у) е R;
при (х, у) ф R;
Ответ.
/(*■
•нт
139
F(x, 40 =
при х <; О или у < О;
при 0<х<а иО<у<о;
при х > а и 0<j/<a;
при О < х < а и t/ > a;
при х> а и j/>a,
Поверхность jF (ж, у) представлена на рис 6.4, б.
1/а при х ^ (0,a), f f 1/a при у е (0, а);
Э.а); /ia/)"\0
/iW
I 1/а
1 О
О
х#/а2
У/а
х\а
1
при л (■£ (О,
при 1/ QS (О, а).
Рыс. 6.4
Случайные величины X, Y независимы, так как
/(*.») -/i (*)/.<*)-
6.5. Поверхность распределения системы случайных величин
(X, F) представляет собой прямой круговой конус (рис. 6.5, а),
основанием конуса служит круг К с центром в начале координат и о
радиусом г0. Вне этого круга совместная плотность / (ху у) равна нулю.
1) Написать выражение / (х, у)\2) найти fx (*), /2 (t/); /2 (у\х)\)х {х\у)\
3) определить, являются ли случайные величины X, Y зависимыми;
4) определить, являются ли случайные величины X, У
коррелированными.
Решение.
1)/(*.»)=*
г* я
(г0-Ул:2+*/2) при х2+#2<г§;
при *2 + у2>г2;
2) ^(дс).
^[гвУф^-^Мп^
17| ]]при|х|<г0;
при|*|>/у,
140
hW) =
10 "пои
Далее, при \х\ < г0
Ги-У^+У2
М</1*) =
и при |*/| < г0
/i (*!#) =
,,у^_„(^£-)
' при \y\>r0.
при |у|< Vrb—x2;
при |у|> Vr§—х2
r0-T/*2+j/2
го Vrl — У2—У2 In I — 1
при \х\<1/гЬ—&1
О при \х\>УгЪ—у*;
3) так как f± (х \у)ф /i (х)9 то случайные величины X, Y зависимы;
4) находим корреляционный момент Кху\ так как тх = ту = 0, то
Кху = JJ ху/ (х, у) dxdy = у ху/ (л;, у) dxdy + J Г л#/ (х, у) dxdy,
(К) (Kt) (KJ
где /Ci — правая половина круга К\ /С2 — левая половина (рис. 6.5, б);
/ (*> У) — функция ху — нечетна относительно аргумента х, поэтому
интегралы по К\ и /С2 отличаются только знаком; в сумме интегралы
взаимно уничтожаются, значит, Кху = 0, и случайные величины X, Y
не коррелированы.
Рис. 6.5 Рис- 6.6
6.6. Пара случайных величин (X, Y) имеет совместную плотность
/ (х, у) « al(\ + х2 + хУ + у%
1) Найти коэффициент а; 2) установить, являются ли величины Л, У
зависимыми; найти fx (х); /2 (у); 3) найти вероятность попадания
случайной точки (X Y) в пределы квадрата /?, центр которого совпада-
141
ет с началом координат, а стороны параллельны осям координат и
имеют длину 6=2 (рие. 6.6).
Решение. 1) Из условия
во
J J f{x,y)dxdy=
1
находим a s= 1 / я2;
2) случайные величины X, Y независимы:
1 1
dxdy __ 1
W1*H-J J ^7T
+*2) (1 + У2)
6.7. Имеются независимые случайные величины X, К. Случайная
величина X распределена п® нормальному закону g параметрами: тх=
= 0; сх as 1/V2. Случайная величина У распределена равномерно на
интервале (0; 1). Написать выражения для совместной плотности / (х,у)
и функции распределения F (х, у) системы (X, У).
Ответ. / (х9 у)*= ——-_ е~х* при # е (0,1);
у п
( 0 при у < 0;
^ (*. #) = У № (х VT) + 0,5] при 0 < у < 1;
1ф(а:У2) + 0,5 приу>1.
6.8. Поверхность распределения / (х, у) системы случайных
величин (X, Y) представляет собой прямой круговой цилиндр, центр
основания которого совпадает б началом координат (рис. 6.8, а), а высота
irft
Ф)
-/•
0
Рио. 6.8
Р Я
равна h. Определить радиув г цилиндра, найти ft (x), f2 (у), ft (x \ у)9
Решение. Радиуо г цилиндра определяется из условия, что
объем цилиндра равен единице, откуда г ~ ТЛ/(яЛ). Совместная
плотность
142
если #2+#2>Л
«•Но;
Следовательно,
ш- f/с*.»)*-Г21Лв"~*Л при '*,<г;
J. I 0 при |х|>г.
Аналогично
Ш==( 2Кг*-»/*ft при |t/|<r;
при \у\>г.
График функции ft (х) показан на рис. 6.8, б. При \у\< г
П(х\У)
_ / (*, У) -
1
—^-/ -• при \x\<.Vrr2~y2\
О при |*|>/г^р.
Ьйг)
Аналогично при |х|< г
I 0 при \y\>V*-*-
Математические ожидания равны нулю: тх =ту = 0, так как
функция / (х,«/) четна как по х, так и по у;
г
Dx = 2h р1^*—Fdx = ftr*-^=-J; «r«.™; /C*» = 0-
6.9. Случайная точка (X, У) распределена с постоянной
плотностью внутри квадрата R9 заштрихованного на рис. 6.9, а. Написать
выражение совместной плотности / (я, у). Найти выражения
плотностей распределения /х (я), /2 (у) отдельных величин X, У, входящих в
систему. Написать выражения условных плотностей f± (х \ у) и /2 (у \ х).
Зависимы или независимы случайные величины X, У? Коррелированы
они или нет?
1
л&
^щ
У
к-
^7 X
а.)
-А
-1 0 1 X
В)
Рис. 6.9
143
_Ж
ЦЫу)
Ш
lit/ 0 1-\у\ х
В)
Hx,
Но*
Решен и е. Площадь квадрата равна двум, поэтому
f 1/2 при (x9y)eR\
при (x,y)&R.
— \ dy=*l—x при 0<я<1;
\ dy=l-{-x при -1<^<0;
/iW =
-(1-М)
о
при х<.— 1 или х>1.
или, короче,
Ы*) = {
1 —|х| при |#|<1;
О при |х|>1.
График закона f± (x) показан на рио. 6.9, б (закон Симпсона).
Аналогично
Далее, при \у\<. 1
\у\ при Ы<1;
при |#|>1.
/xCxIif)—J
h(y)
i
при |х|<1 — |у|;
О при |х|>1 — |у|.
График плотности fx (х \ у) показан на рис. 6.9, в. Аналогично при |*|<1
1
Ш\х) =
, - при |#|<1 — |jcI;
2(1—|*1)
О при \у\>1—\х\.
Случайные величины X, Y зависимы, но не коррелированы.
6.10. Совместная плотность случайных величин X, Y задана
формулой
Пх>у)=Т^ехр{—г^-К^—2>2—Ь2(х—2)(г/+з)+(г/+з)^|.
Найти коэффицент корреляции величин X, Y.
Ответ. rxy s 0,6.
6.11. Система случайных величин (X, Y) имеет распределение о
плотностью / (#, у). Выразить через плотноеть $ (х, у) вероятности
событий: 1) {X > Y } \ 2) {X > | Y | }; 3) {| X |> У };
4) {У-Х>1}.
Решение. На рив. 6.11, а — г заштрихованы области D,., D2,
D з, £>4> попадания в которые соответствуют событиям 1—4.
Вероятности попадания в эти области:
144
Рис. 6.11
1) Р{Х>У}= J | f(x,y)dxdy;
2) Р{Х>|У|} = | J f(x,y)dxdy;
О »-х
3) P{|X|>K}= J I f(x,y)dxdy;
4) Р{У-Х>1}= j j f(x,y)dxdy.
-co *+!
6.12. Система двух случайных величин X, У распределена по
нормальному закону с параметрами тх = ту = 0; (^ = 0^ = а» ^ — О-
Определить вероятности следующих событий:
[Л = {|Г |<Х};В = {у<Х};С = {7< | X | }.
Р е ш е н и е. На рис. 6.12, а — в показаны области,
соответствующие событиям Л, В и С. При круговом рассеивании вероятности
событий будут: Р (Л) = 0,25; Р (5) = 0,5; Р (С) = 0,75.
6.13. Случайная величина X имеет плотность f (х)\ случайная
величина Y связана с нею функциональной зависимостью Y = X2.
Найти функцию распределения F (х, у) системы (X, Y).
Решение. Исходим из того, что значение случайной величины
Y полностью определяется значением случайной величины X.
Случайная точка (X, Y) может находиться только на кривой у = х2.
Вероятность попадания ее в квадрант с вершиной в точке (х, у) равна
вероятности попадания случайной точки на проекцию на ось Ох участка кри-
145
вой у = х2, попадающей в квадрант (рис. 6.13). Пользуясь этой
интерпретацией, имеем
F (х,у) =
О при #<;0 или у>0 и #<—У~у\
VJ
f f(x)dx при #>0
f f(x)dx при t/>0
-V7
и х>"|/"у;
Рис. 6.13
6.14. Случайная точка (X, Y) распределена по нормальному
закону на плоскости с параметрами тх *= 1; ~ту = — 1; а, & 1; оу = 2;
гжу s= 0. Найти вероятность того, что
случайная точка попадет внутрь
области D, ограниченной эллипсом
(х-1)2 + (у+ 1)2/4 =1.
Решение. Область D
ограничена эллипсом рассеивания Ег с
полуосями aftO,sal;J= Оу 5=2;
вероятности попадания в эту область р =*
= 1 — е1/* « 0,393.
6.15. Производится стрельба( по
точечной (малоразмерной) цели-
снарядом, зона разрушительного действия которого представляет собой
круг радиуса г. Рассеивание точки попадания снаряда круговое с
параметрами тх = ту а= 0; ах г= оу = 2г (центр рассеивания
совпадает с целью). Сколько выстрелов нужно произвести для того, чтобы
разрушить цель g вероятностью Р = 0,9?
Решение. Вероятность разрушения цели при одном выстреле
р = 1 — e-(0'6>e's « 0,118. Потребное число выстрелов
п > lg (1 — P)I\g (1 — р) *= lg 0,1/lg 0,882 « 18,4, т. е. п «* 19.
6.16. Система трех случайных величин f(X, V,Z) имеет совместную
плотность / (х9 у у г). Написать выражения: 1) плотности /х (х) случайной
величины X; 2) совместной плотности /2,з(#>2) случайных величин
146
(У, Z); 3) условной плотности /2>3 (у, z I x)\ 4) условной плотности f2
(у | х, г); 5) функции распределения F (х, у, г); 6) функции
распределения Fx (x) случайной величины X; 7) функции распределения
Flt2 (х, у) подсистемы (X, У).
Ответ.
СО ОО
1) М*)= J J7(*> У. *)<№ 2) /2(8(t/, г)= j" /(x, j/, г)Лс;
fc* CO fear 00
з) ;м(у.г|*)~ , ^'г)—l
4) /,(у|*.г)- /<*'*'*> .»
J f(x,g,z)dy
fc=* 00
a: # г
5) F(x, у, г)— J J J /(*, */, z)dxdydz\
X oo oo
6) fiM = ffe oo, oo)= J J J /(x, (/, z)dxdydz;
X у oo
7) /%2 (*> y) = F(x, y, oo) = j jj j f(xtyyz)dxdydz.
6.17. Производится стрельба одним снарядом по точечной
(малоразмерной) воздушной цели. Рассеивание точки разрыва снаряда
происходит по нормальному закону; центр рассеивания совпадает с целью;
средние квадратические отклонения ох = ау = az = а. Цель
поражается, если расстояние между нею и точкой разрыва снаряда не
превышает r0 = 2а. Найти вероятность р того, что при одном выстреле
цель будет поражена.
Решение. По формуле (6.0.37) для вероятности попадания в
эллипсоид равной плотности имеем
р = р {(X, У; Z) 6 Е2} = 2Ф (2) ^ 2е~2 » 0,739.
6.18. Система трех случайных величин (X, У, Z) распределена с
постоянной плотностью внутри шара радиуса г. Найти вероятность
попадания случайной точки (X, У, Z) внутрь шара, концентричного
данному, с радиусом г/2.
Ответ, р = 1/8.
6.19. Из урны, в которой а белых, Ь черных и с красных шаров,
вынимается один шар. Случайные величины X,Y,Z определяются
следующими условиями:
У ___ (1, если появится белый шар;
10, если появится черный или красный шар;
147
У =
2 =
П,если появится черный шар;
\0, если появится белый или красный шар;
] 1, если появится красный шар;
\0, если появится белый или черный шар
(X, У, Z являются индикаторами событий: {белый шар}; {черныйшар},
{красный шар}). Построить корреляционную матрицу и
нормированную корреляционную матрицу системы случайных величин X, У, Z
Решение. Корреляционные моменты определим из таблицы
вероятностей отдельных значенй X, У и Z. Обозначим
Имеем
pXiViZh-p{X=-xuY^yJyZ = 2h}.
Р000 =Р{Х =0, У = 0,Z=0} =0;
р100 =Р{Х =1, У =0,2=0} = а/(а + Ь + с);
Р010 S=P{X =0, У =1, Z=Q}=b/(a + b + c);
Р001 =Р {X =0, У =0, Z =1} ^с/(а + Ь + с);
PllO == ^101 ^ ^011 = Pill = 0>
в Ь ... с
т~ = f
т,
K^^IW** —mx)(yj—my)PXil/iZk =
+(о-
5
а
)(о.
■)('•
+ (о-
Аналогично
+ 6 + С
6
+ Ь+с
а-\-Ь+с
)(о ь—)~
/\ a+b+c J a
—аЪ
Kxz = m
(a+b+cf
Далее находим дисперсии
Dx = a2[X] —ml = -
К
+ b+c (а+Ь+cf
—be
Уг-
(a+b+cf
j* a(b+c)
a+b+c
аналогично
Dy = b(a + c)l(a + b+cY\
Корреляционная матрица
II/С || =
(a+b+cf (a+b+c)2
D2 = c{a + b)/(a + b+c)\
J
xy
Kxz
Kyz
D,
Находим коэффициенты корреляции:
rxy —
К
ХУ
-аЬ
VDxDy l/ab{a+c)(b+c]
148
г-1^
аЬ
(а+с)(Ь+с)
Аналогично га
-vl
ас
Jvz
(a+b){c+b)'
Нормированная корреляционная матрица
--/=
be
Ф+оЩс+а)
1
\r =
1
r#2
1
6.20. Имеется система случайных величин X и Y. Случайная
величина X распределена по показательному закону в параметром X:
/й (х) = Яе~Лдг при л; > 0. Случайная величина Y при заданном
значении X =х>0 распределена также по показательному закону, но с
параметром х : /2 (у \ х) = хег*у при # > 0. Написать совместную
плотность / (#, у) величин X, Y; найти плотность /2 (у) случайной
величины У; найти условную плотность /х (х | у).
Решение.
/с
:*,#)={
tae- <*+*>* при *>0 и #>0;
0 при л; <С 0 или # <. 0;
/.ое- Г/лйл-Ьс+йг при*>0;
~~ [ 0 при у<0.
Далее, при у > 0
h (У) \ 0 при х < 0.
6.21. Даны две независимые случайные величины: непрерывная
X с плотностью /х (#) и дискретная У со значениями уъ у2У..., уп,
имеющими вероятности р1э р2> •••> /V Найти функцию распределения
системы величин X, Y.
х
О т в е т. F (х, у) п. Fx (х) F2 (у), где ^ (*) = J7 (х) rfx.
о
Р2(У) =
0 при у<^;
рх при Ух<у^у2\
J Jfe—l
2Pi при Ун~г<У<Ук (&=2,3, ..., /г);
1 при */>*/„.
6.22. Случайная величина X — дискретная величина в двумя
значениями хх и х2 (х2 > хх), имеющими вероятности рх и р2. Случайная
величина Y — непрерывная величина; ее условным распределением при
X = xi служит нормальный закон о математическим ожиданием,
равным хи и средним квадратическим отклонением, равным о (i = 1,2).
140
Найти совместную функцию распределения F (х, у) случайных
величин Х,< Y. Найти плотность /2 (у) случайной величины Y.
Решение. F (*, у) = Р{Х <х}Р {Y < у \ X < х}. Пусть
х < хг; тогда Р {X < х) = 0 и J7 (х, у) = 0; пусть ^ < х < *2;
тогда P{X<x}=Pl и F(*, у) =PlP{F< |X = хх) =
=Рх [Ф( ~) + 0,5]. При х > х2 по формуле полной вероятности
^(^^) = Р1[ф(^) + 0,5] + р2[ф(-^) + 0)5].
Следовательно,
F{x,y)=\
при а;^^;
при a;!<a;<a:2;
Л[ф(1711)+0,5]+Р2[Ф(^£2)+0'5] при x>Xi
Далее, полагая х = оо и дифференцируя по у, получаем
(У-*.)' (»-*2>2-,
2о:
Ш)=-^р^у)-
+ Р2е
2az
6.23*. Звезды на небесной сфере рассматриваются как пуассонов-
ское поле точек. Число звезд, попадающее в объектив телескопа,
является случайной величиной, распределенной по закону Пуассона с
параметром Xsy где s — площадь участка, вырезаемого на поверхности еди-
Рис. 6.23
ничной сферы полем зрения телескопа (рис 6.23, а). Поле зрения
телескопа имеет координатную сетку (рис. 6.23, б). Показать, что при
любом положении телескопа координаты (X, Y) ближайшей к
перекрестию звезды распределены по нормальному закону с параметрами
т.
,тг
= 0; ох =оу = 1/У2пХ.
Решение. В задаче 5Л9 было показано, что расстояние R от
центра перекрестия до ближайшей к нему точки пуассоновского поля
150
подчиняется закону Рэлея. Но R = Vx2 + У2, следовательно,
вероятность попадания точки (X, У) в круг D радиуса г, т. е. Р {X2 +
+ Y2 <.г2 } может быть записана в двух формах
Р {R < г} = f 2пХге**п^2 dr,
о
Р {(X, У) 6 D) = Г f / (*, jO <ОД, (6.23Л)
(О)
где / (#, у) — совместная плотность величин X, У. В силу симметрии
надо считать, что / (х, у) зависит только от расстояния: / (х, у) = g (r),
ГДе г = Ух2 + у2. Переходя к полярным координатам (г, ф),
получаем
2я т v
P{(X,y)€£>}=f d<p$g{r)dr = 2n[g(r)dr. (6,23.2)
Сравнивая выражения (6.23.1) и (6.23.2), находим: g (г) &=к~я^и,
значит, / (х, у) = X е-я*(*2+^2>, что и требовалось доказать.
6.24. В начале координат 0 сферической системы координат (г,ф, ft)
(рис. 6.24), где 0 < ф < 2 я, — я/2 < ft < я/2, находится
источник а-частиц. Частицы разлетаются равномерно по всем
направлениям. Рассматривается одна частица, полетевшая по случайному
направлению, определяемому углами Фив. Записать'совместную
плотность распределения / (ф, ft) случайных величины Ф, G.
Решение. «Равномерный во всех направлениях» разлет а-
частиц означает, что для единичного вектора е, исходящего из точки О
и определяющего направление полета частицы, все положения его
конца на сфере С единичного радиуса обладают одинаковой плотностью
вероятности. Следовательно, элемент вероятности / (ф, ft) dq> dft
должен быть пропорционален элементарной площадке ds на сфере С; эта
элементарная площадка равна dS = dtp dft cos ft, откуда
/ (ф, ft) dydft = A cos ft dydft; f (ф, ft) = A cos ft,
где А — коэффициент пропорциональности, определяемый из
условия
2я я/2
J <*Ф $ /(<р,д)Я>=1;
О —я/2
отсюда А = 1/(4 я). Таким образом,
1 a f 0 ^ ф ^ 2я и
/ (ф, ft) = — cos ft при |
4я [ _Я(
/2<ft<rc/2.
6.25.*. В условиях предыдущей задачи рассматривается плоскость
Р, параллельная экваториальной плоскости (в которой отсчитывается
угол ф) и проведенная через точку 0'J со сферическими координатами
г s= 1, ф 5=0, ft = я/2 (рис. 6.25). В этой плоскости располагается
151
декартова система координат хО'д. Все а-частицы, летящие в верхней
полусфере разлета, попадают на плоскость Р. Рассматривается одна из
таких частиц и соответствующие ей случайные величины —
координаты X, У точки попадания а-частицы на плоскость Р. Найти совместную
плотность / (х> у) этих случайных величин. Зависимы или нет случайные
величины X, У?
Решение. Найдем элемент вероятности / (х, у) dxdy,
приближенно равный вероятности попадания частицы в элементарную
площадку dxdy, примыкающую к точке (я, у). Эту вероятность
подсчитаем аналогично тому, как мы делали в предыдущей задаче. Найдем
Рис. 6М
Рис. 6.25
площадь ds участка на единичной сфере С такого, что пролетающие
через него частицы попадут в нашу элементарную площадку. Этот
участок получается центральным проектированием площадки dxdy на
сферу С. При таком проектировании площадь множится на косинус
угла Ь между направлением проектирования и плоскостью Р, а кроме
того, еще уменьшается обратно пропорционально квадрату расстояния R
от центра проектирования; элементарная площадка ds на сфере С
будет равна
dxdy
1
ds =
dxdg cos fl У\+х*+у2 __
dxdy
R*
l-|-*2+0*
(1 + Лга+^)3/2
Чтобы получить элемент вероятности, нужно величину ds разделить
на площадь всей верхней полусферы, равную 2 я. Получим:
f(x,y)dxdy =
dxdy
2я (1+*2+#2)3/2
ИЛИ f(x, у):
2л(1 + д;2 + ^2)3/2
Случайные величины Л, Y зависимы, так как их совместная плотность
не распадается на произведение двух функций, из котерых одна
зависит только от х9 а другая — только от у.
6.26. Случайная точка А9 изображающая объект на круглом экране
радиолокатора радиува 1 (рш. 6.26, а), равномерно распределена в
пределах этого круга. Найти совместную плотность / (г, ф) полярных ко-
152
ординат (/?, Ф) точки А. Зависимы или независимы случайные
величины R и Ф?
Решение. Рассмотрим в полярной системе координат
элементарный «прямоугольник», соответствующий бесконечно малым
приращениям dr, d ф полярных координат г, ф точки внутри круга (рис.
6.26, б). Площадь его (с точностью до бесконечно малых высшего
порядка) равна rdrdy. Деля ее на площадь круга, равную я, получаем
элемент вероятности
/ (Л ф) drdy = rdrdy/n,
откуда
/ (г, ф) = г/я при 0 < г < 1, 0 < ф < 2 п. (6.26.1)
Плотность распределения /х (г) найдем, интегрируя (6.26,1) во всем
диапазоне изменения ф:
2я
/х(г)=Г -L.^p = 2r При0<г<1.
Аналогично
i
/2(ф)=ГЛ dr = _L- при 0<ф<2я.
J я 2я
6
Распределение ^ (г) имеет вид прямоугольного треугольника (рив. 6.26»
в), распределение /а (ф) — равномерное в пределах участка (0, 2я).
Рис. 6.26
Перемножая ft (г) и f% (ф), получаем совместную плотность / (г, ф)
системы (R, Ф); следовательно, случайные величины R, Ф независимы.
Заметим, что для такого же равномерного распределения точки в
пределах круга ее декартовы координаты X, Y зависимы, в чем мы
убедились, решая задачу 6.8.
6.27. В условиях предыдущей задачи радиус экрана равен не
единице, а а. Написать выражение совместной плотности полярных
координат точки Л и их плотностей по отдельности.
153
Решение, Деля площадь элементарного «прямоугольника» на
площадь экрана па2 и «сокращая» на drdy, получаем
/(г,ф) = —— при 0<г<а, 0<ф<2я;
2
/i(r)==-T-/" ПРИ 0<г<а;
а2
/2(ф) = -т- при0<ф<2я.
2я
ГЛАВА 7
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
СЛУЧАЙНЫХ ВЕЛИЧИН
7*0* Одним из наиболее эффективных средств для решения вероятностных
задач является аппарат числовых характеристик, позволяющий находить
характеристики интересующих нас случайных величин помимо их законов
распределения. В частности, чтобы находить числовые характеристики функций
случайных величин, не надо знать законов распределения самих функций, а
достаточно знать закон распределения аргумента (аргументов).
Если X — дискретная случайная величина с рядом распределения
Xt
xt
Pt
Х2 1 ••• 1 *Л
Р2 • • • J Рп |
(J/-4
а величина Y связана с X функциональной зависимостью Y = ф (X), то матема*
тическое ожидание величины Y равно
ту=*М [ф (X)] »2ф (*l) Pi •
а дисперсия выражается любой из двух формул:
Dy = D[<p(X)]= 2 [ФС*!)-^]1*!.
*—1
(7.0,1)
(7.0.2)
/=1
(7.0.3)
Если (X, К) — система дискретных случайных величин, распределение
которой характеризуется вероятностями
Pij=P{X = xit Y = yt}%
a Z = ф (X, К), то математическое ожидание величины Z равно
тг=М[ф(Х,К)]=22ф(^,^)р17, (7.0.4)
* /
а дисперсия выражается любой из двух формул:
/ /
154
f
Если X — непрерывная случайная величина с плотностью/ (х), a Y = <р (X),
то математическое ожидание величины Y равно
оо
/nj,=M[(p(X)l= J <p(*)f(*)d*. (7.0.7)
«900
а дисперсия выражается любой из двух формул:
о»
Dj, = D[(p(X)]- I [<p(x)-my)4(x)dx, (7.0.8)
еэоо
00
С]у= { (ф(*)]2/(*)<*л:---т*. (7.0.9)
— 00
Если (X, У) — система непрерывных случайных величин с совместной
плотностью f (х, у), a Z = ср (X, К), то математическое ожидание величины
Z равно
00
тг = М [<р (X, К)] = Я Ф (*. У) f (*, 0) А«*, (7.0,10)
— 00
а дисперсия выражается любой из двух формул:
оо
D2=D[q> (X, Щ - Я [ф (*. y)-mz]4(x, у) dxdy, (7.0.11)
f5riOO
ОО
*>* - Я № <*» НИ* ' <*' Й rf*<*0 - «J. (7-0.12)
*-ч 00
Если (Xi, ..*, ХЛ) — система я непрерывных случайных величин с
плотностью/ fa, .,., xn)t а К=ф (Xt, «.*, ХЛ), то математическое ожидание величины
К равно
m0=*M[(p(Xlf ..., ХЛ)]= J .„ J y(xt9 ..чХп)?(хи ..9tXn), (7,0.13)
о* 00 «WOO
а дисперсия выражается любой из двух формул:
00 (я) °°
^вО|ф№» ...»ХЛ)]« J ... J [ф(*ц ...«*Л)— ту]2Х
«100 fSSOO
X/(*i, .... xn)dxi ... d*n, (7.0.14)
«> (Л) оо
D»e J ••• I №(*i» • •••*n)l*/(*it ...«XrJtfef ...d**—m», (7.0.15)
«=»O0 fee. OO
В ряде случаев, для того чтобы получать числовые характеристики
функций, не требуется даже знать законов распределения аргументов, а достаточно
знать их числовые характеристики. Ниже приводятся основные теоремы о
числовых характеристиках,
li Если с — неслучайная величина, то
ЛШ = <?| D[c] = 0. (7.0,16)
2. Если о — неслучайная величина, а X — случайная, то
М [сХ] = сМ [X] * D [сХ] = ^D [X]. (7,0,17)
3* Теорема сложения математических ожиданий.' Математическое
ожидание суммы случайных величин равно сумме их математических ожиданий:
155
M IX + Y] = М [X] + М [Y]9 (7.0.I8)
и вообще
м I 2 *i\= 2 Mf**b (7-0Л9>
lf,*'ht,
4, Математическое ожидание линейной функции нескольких случайных
величин
где ai и Ъ — неслучайные коэффициенты, равно той же линейной функции от
их математических ожиданий:
ти
пу = Щ 2 fl|X| + b|- 2 (ЧтХш+Ь, (7.0.20)
L/=l J i~\ l
где mXi = M [XJ* Короче, это правило можно записать так:
M[L(Xt,Xa, ...f XnM«L(m^f тЖ|,...,«жД (7.0.21) £|
где L — линейная функция, J ^
5. Математическое ожидание произведения двух случайных величин X, Y |
выражается формулой §
М \XY\ - М [X] М [У] + Кху, (7.0,22) |
х
где Кху — корреляционный момент величин X, К. Эту формулу в другом виде &
можно записать так: |
/C^y = M[XK]—mxmyi (7.0.23) j
или, имея в виду, что М [ХК] = од |Х, К], |
Кху=ап[Х, Y)—mxmv. (7.0.24) |
б* Теорема умножения математических ожиданий. Математическое ожи- §
данив произведения двух некоррелированных случайных величин X, У равно
произведению их математических ожиданий:
М[ХК] - М[Х] М[К]. (7.0.25)
7» Если Xj, Х2, •«•, Хп—независимые случайные величины, то математиче"
ское ожидание их произведения равно произведению математических ожиданий1
[ П хЛ= П
1/-1 J £-1
М | П X, |= П MfX«]. (7.0.26) |
8. Дисперсия суммы двух случайных величин выражается формулой
D[X+Y]=*D[X] + DlY\+2Kxg. (7.0.27) |
9, Дисперсия суммы нескольких случайных величин выражается формулой
D[ 2 Xi]= 2 Df**l+2 2 Kztz„ (7.0.28)
где KXixi — корреляционный момент случайных величин Xf, Xp
10* Теорема сложения дисперсий. Дисперсия суммы двух некоррелированных
случайных величин X, Y равна сумме их дисперсий:
D [X + У] - D [X] + D [К], (7.0.29)
и вообще, для некоррелированных случайных величин
Dl 2 Х«Н 2 °№ (7-°-30> 1
L'-l J '=l ;il
156
"11* Дисперсия линейной функции нескольких случайных величин
где ag, & — неслучайные величины, выражается формулой
Dy = D 2Ja,X,+bU S^D№] + 22Jeie/^..# (7.0.31)
В случае, когда величины Х\, Х2, .»., Xn некоррелированны,
^= D Г 2 «* *| + * U 2 fl/ D [Xil. (7.0.32)
L/= I J *= l
12. При сложении некоррелированных случайных векторов их
корреляционные моменты складываются, т. е* если
то
• **»=*»,*+***. (7-0-33)
Линеаризация функций. Функция ф (Xt, Х2, *<<, Хп) нескольких случайных
аргументов Xt, Х2, «<*, Хп называется почти линейной, если во всем диапазоне
практически возможных значений аргументов она может быть с достаточной для
практики точностью линеаризована (приближенно заменена линейной)* Это
означает, что "
<P(*ii*2« *..%Xn) ^(P(mxi*mxi* •••• тх ) +
где
аф(%>\>-.^,п)
ддс|
частная производная функции ф (х^ де2, .,,, дгп) по аргументу х^ в которую
вместо каждого аргумента подставлено его математическое ожидание.
Математическое ожидание почти линейной функции К=*ф (Хь Х2, .,♦, Хл)
приближенно вычисляется по формуле
я»у«Ф(«Ж11 «ж§» — •w*n)- (7.0.35)
Дисперсия почти линейной функции приближенно вычисляется по формуле
гдеОд; —дисперсия случайной величины X*} Кх х —корреляционный момент
величин Хи Хр ' -
В случае, когда случайные аргументы Х%, Х2, ..*, Хп некоррелированные
°-2,(^-1^, <7-°-37>
157
ЗАДАЧИ И УПРАЖНЕНИЯ
7.1. Дискретная случайная величина X имеет ряд распределения
X:
— 1
0,2
0 | 1
0,1 | 0,3
1 ^ 1
0,4 1
Найти Математическое ожидание и дисперсию случайной величины
Y = 2ХГ
Решение. ту «* 2-* • 0,2 + 2° • 0,1 + 2х • 0,3 + 22 • 0,4 »
- 2,4; Dy « at [ Y1 — ет$ - (2"1)2 ♦ 0,2 + (2°)2 « 0,1 + (21)2 • 0,3 +
+ (22)2- 0,4 — 2,42= 1,99.
7.2. Непрерывная случайная величина X распределена в интервале
(0; 1) по закону с плотностью f (х) = 2х при х £ (0; 1) (рис. 7.2). Найти
математическое ожидание и дисперсию квадрата этой случайной
величины Y = X2.
Решение.
ту = а2[Х] = 1 х2 2xdx = —$
о
i
Du = a2lY]-m*=^(xr2xdx-(±y~-±.
7.3. Случайная величина X распределена по показательному
закону с плотностью f (х) = X е~Кх при х > 0 (X > 0). Найти
математическое ожидание и дисперсию случайной величины Y = е~х.
Решение.
т.
= Ге~*Я,е~
**dx =
%+\
D9 = 4lY]-mi=§e-*kb-bdx-(-^J = -
(к+2)(к+\) 4
7.4. Случайная величина X распределена по показательному
закону о плотностью / (х) = X ех—х при х > 0. Установить, при каких
условиях существуют и чему равны математическое ожидание и
дисперсия случайной величины Y = ех.
оо оо
Решени е. ту= f е*te-**dx = X f e-fr-4*dx; при X—1>0,
т. е. при X > 1, этот интеграл существует и равен ту *=*%1(Х — 1);
fipn X < 1 он расходится.
оо оо
а2Щ = f е2* te-ь* dx = fe^-2** dx.
о о
158
При Л, > 2 этот интеграл существует и равен А7(А> — 2), а дисперсия
Dv = %1(% — 2) — [ЩХ — I)]2 « Щ% — 2) (Я — I)2!;] при % < 2
интеграл расходится, и дисперсии Dy не существует.
Рис. 7.2
7.5. Случайная величина X распределена по закону о плотностью
/ (х) = 0,5 cos х при х £ (—я/2, я/2) (рис. 7.5). Найти математическое
ожидание и дисперсию случайной величины Y = sin X.
я/2
Решение. ту =^ J sin x cos xdx « 0;
-Л/2
я/2
£>у = а2 [Y] = — V sin2 * cos яйл; = —.
2 J 3
—я/2
7.6. Случайная величина X распределена по тому же закону, что и в
предыдущей задаче. Найти математическое ©жидание и дисперсию
случайной величины Y « | sin Х|.
Решение.
ту~— 1 | sin х | cos xdx = l sin x cos xdx =—;
«Я/2 0
Я/2 л/2
a2 \Y] =; — f | sin л: I2 cos xdx =* Г sin2 * cos *d# = —;
«я/2
D, = a^n-m£=~.
12
7.7. Случайная точка (X, У) распределена равномерно внутри круга
К радиуса гь=1 (рис. 7.7). Найти математическое ожидание и
дисперсию случайной величины Z s= XY.
Решение.
/ (*. У) — 1/я при (а?, у) б /С;
159
тг =— (\xydxdy = 0\ D2 =— \\x2y2dxdy~
(К) (К)
2л 1
= — I dtp \ rb cos2 ф sin2 qpdr = .
я J J 24
о о
7.8. Случайная точка (X9Y) распределена равномерно внутри квад- |
рата R (рис. 7.8). Найти математическое ожидание и дисперсию
случайной величины Z = XY.
i Я)
Рио. 7.7
Рис. 7.8
Решение. Так как случайные величины X, Y независимы, то
тг « m^rriy « (1/2) (1/2) *= 1/4;
Dz = а2 [Z] — ml - М [(ХУ)2] — т| « М [Х21 М [Y4 - mi;
М IX2! « а21X1 = 1/3; М [Г2! - 1/3; Dt ш 7/144.
7.9. Имеются две случайные величины X и У, связанные
соотношением Y as 2 — 3 X. Числовые характеристики величины X заданы:
га* =— 1, Dx =4. Определить: 1) математичевкое ожидание и
дисперсию величины К; 2) корреляционный момент и коэффициент
корреляции величин X, Y.
Решение. 1) ту « 2—3 тх = 5; D^ = (—З)2 4 « 36;
2) /tXJ, = М1ХГ] —тхту = М[Х(2 — 3 X)] + N5 =2М[Х] —
— 3 М IX2! + 5; М [X2] =а2 [XI =Dx + m$ = 4+1 .=* 5;
отсюда ^=—2—3»5 + 5 = — 12; г^в. —12/(аяау) =
= —12/^4^36 = — 1,
что и естественно, так как X и У связаны линейной функциональней
зависимостью с отрицательным коэффициентом при X. -
7.10. Имеется система случайных величин (X, К, Z) • заданными^
характеристиками: Математическими ожиданиями тх, туу mzn кор-j
реляционной матрицей (
IA* К
XV
Кхг\
Kyz\
160
Найти математическое ожидание и дисперсию случайной величины
U = aX — bY + cZ — d.
Ответ. ти = атх — Ьту + стг — d\ Du = a2Dx + b2Dy +
+ #DZ — 2 abKxy.+ 2 oc/C^ — 2 bcKyz.
7.11. Имеется й-мерный случайный вектор X = (Xt9 X2, ..'., Хп)>
составляющими которого являются п случайных величин Xt с
математическими ожиданиями тх% (*' = 1,..., я), дисперсиями D» (*' = 1,...,
п) и нормированной корреляционной матрицей 11гЖ|х/|| (/ = 1,2,...,
/г; / > i). Случайный^ вектор X преобразуется в m-мерный случайный
вектор Y as (У1э У2,..., Ym)> причем составляющие вектора Y
получены из составляющих вектора X линейными преобразованиями:
Yk=j$aikXt + bk (fc=l,2,...,m).
Найти характеристики случайного вектора Y: математические
ожидания тУк (k ев 1, ...,/п), дисперсии DVh (k = 1,..., m) и элементы
нормированной корреляционной матрицы || гУкУ1 || (/ = 1,2,..., т\ k </).
Ответ.
Шг
Ук= 2iaiktnx. + bk (&=l,...,m);
/=.i
j= i i < /
где
7.12. Имеются две независимые случайные величины X и К. Вели-
1 -<*-')'
чина X распределена по нормальному закону ft (х) = ,_ е 8 .
Величина Y распределена равномерно в интервале (0; 2). Определить!
1) М [X + Y\\ 2) М [ХП, 3) М [X2]; 4) М [X - Га1; 5) D [X + Y);
6) D [X — Y).
Решение.
1) М[Х + У1 = М[Х1 + ММ =1 + 1 «2;
2) М1ХУ1 = М [XJ М [Y\ - Ы ■■ 1;
3) М [Х21 =а2 [XI =D [X1 + т| «4 + 1 =*5;
4) М [X - Y4 я.М [XI — М [Y4 - 1 — а2 [К] =- 1/3$
5) D [X + П =D [XI + D [71 «4 + 1/3 *= 13/3;
6) D [X — Y\ ш* D [XJ + (— 1) 2 D IYI <- 13/3.
7.13. Случайная величина X подчинена нормальному закону f (x)=
**—-— е ""***. Найти математическое ожидание случайной величины
аУ2я
Y ==1— ЗХ2 + 4 X3.
Зак. 1040 W1
/
Решение. m„ = М [1 — 3 X2 + 4 X3]-1—3 М [X2] +4М [X3].
нормального закона
Так как тх == 0, то М [X2] = а2; для нашего
М [Х31 = 0, отсюда ту = 1 — За2.
7.14. Независимые случайные величины X и К распределены по
законам ft (х), /2 (у), графики плотностей которых представлены на
рис. 7.14, а, б. Определить: 1) MIX -К И; 2) D [ЗХ — 6У + 1];
3) М [XYh 4) М [2 XY — ЗХ2 + У2 — 11.
Р е ш е н и е. М [X] = 2а/3; М [У] = 6/3; D [XI = а2/18; D [У] =»
« 62/18.
1) М [X + Y] = (2а + Ь) /3;
2) D [ЗХ — 6У + И = 9DX + 36D„ = а2/2 + 2fe2;
3) М[ХУ] = 2а&/9;
4) М [2ХУ — ЗХ2 + У2— И = 2 М [ХУ] — За2 [X] — а2 [У]—1 =
= 4 аб/9 — За2/2 + 62/6 - 1.
7.15. Ответить на вопросы 1—3 предыдущей задачи, если
величины X, У зависимы и их коэффициент корреляции гху = — 0,9.
Решение. 1)М [X + У] = (2а + 6)/3; 2) D [ЗХ — 6У + 1]=*
= а2/2 + 262 + (36afe/Vl8-18) 0,9 = а2/2 + 262 + 1,8а6;
3) М[ХУ1 =а6/9 — 0,9 аб/18 = 31а6/180.
7.16. По сторонам прямого угла хОу концами скользит линейка
АВ длины /, занимая случайное положение (рис. 7.16), причем все
значения абсциссы X ее конца А на оси Ох в пределах от 0 до / одинаково
вероятны. Найти математическое ожидание расстояния R от начала
координат до линейки.
№
01 а х- о
а)
Ь X
Рис. 7.14
Рис. 7.16
Решение. Случайная величина X распределена равномерно в
интервале (0, I): f (х) = 1// при х £ (0, /)• Случайная величина R
выражается через X (см. рис. 7.16): R = xVl — (X//)2. Ее
математическое ожидание ""
/
тг=—1*1/ 1 — 1—1 dx ='Х
W-(f/
7.17. Случайные величины V, V связаны линейно со случайными
величинами X, У: V = аХ + bY + с\ U = dX + /У + g. Известны
числовые характеристики системы случайных величин X, У : тх>
162
m , Dx, Dyy Kxw Требуется найти числовые характеристики системы
случайных величин V, U i tnvi ти, Dv> Du, Kvu> гви.
Решение.
m-n= amx + bmy + с\ Dv = аЮх + b2Dy + 2abKxyl
mu = dmx + fmy + g\ Du = d2Dx + f*Dy + 2dfKxy.
Далее, *=» aX + bY; D^dX + fX;
Kvu = M [VU] - adDx + bfDy + (af + bd) KxV\ rDU = KdJVdTd^.
7.18. Тело взвешивается на аналитических весах. Истинное
(неизвестное нам) значение массы тела равно а. Вследствие наличия
ошибок результат каждого взвешивания случаен и распределяется по
нормальному закону с параметрами а и о. Для уменьшения ошибок тело
взвешивают п раз, и в качестве приближенного значения массы берут
среднее арифметическое результатов п взвешиваний: Y (п) = JL У. Xt.
1) Найти характеристики случайной величины Y (п): математическое
ожидание и среднее квадратическое отклонение; 2) сколько нужно
сделать взвешиваний для того, чтобы уменьшить в десять раз среднюю
квадратическую ошибку массы?
1 п
Решение. 1) М [Y (n)] =_L У. М [ХЛ. Так как все взвешива-
ния производятся в одинаковых условиях, то М [Х|1 = а при любом
*; тогда
М[У(«)1 = -^=^=Й.
Считая ошибки отдельных взвешиваний независимыми, находим
дисперсию Y (п):
ovrm-±£ovct-±£*-■*--■£-.
2) Число взвешиваний п находим из условия a [Y (п)\ = VoVn =
= ъ/Уп = а/10; п = 100.
7.19. Светящаяся точка, изображающая наблюдаемый объект на
круглом экране радиолокатора, может случайным образом занимать
любое положение на экране (плотность вероятности постоянна).
Диаметр экрана равен D. Найти математическое ожидание расстояния R
от светящейся точки до центра экрана.
Решение. R = VX2+Y2, где (X, Y) — система случайных
величин, распределенная равномерно в круге Kd диаметра D;
f (x, у) = 4/(я02) при (х, у) .£ Ко;
mr = M[R] - jT V^+f-^-dxdy,
б* 163
или, переходя к полярной системе координат (г, ф),
2я D/2
тг
nD2
■w
radr =
3
0 0
7.20. Две точки X и У независимо друг от друга занимают
случайное положение на отрезке (0; 1) оси абсцисс (рис. 7.20, а), причем
плотность вероятности на этом отрезке постоянна для обеих случайных
величин. Найти математическое ожидание расстояния R между этими
точками и квадрата расстояния между ними.
Решение. Имеем R = | У—Х|; mT =M [|У — X\]. Изобразим
систему случайных величин (X, Y) как случайную точку на плоскости
хОу (рис. 7.20, б), распределенную с п@втоянной плотностью / (х, у) = 1
в квадрате со,'стороной, равной единице. В области Dx : X > У; \Y —
—Х| = Х — Y. Воблавти£2: У>Х;| Y — X \ = Y — X.
mr = ^(x—y)dxdy+U (y—x)dxdy=
(Ог)
(О*)
= fd*f(*—y)dy+ [dyUy—x)dx= -p
oo о :j
MlR2} = Ml\Y-X\2]^a2lY] + a2lX]-2tnxmy =
= 2(Dx + mx)—2mx=W.
7.21. Имеется квадрат К со стороной, равной единице (рис. 7.21).
На смежные стороны квадрата случайным образом и независимо друг
от друга падают точки X и У; каждая из них имеет в пределах
соответствующей стороны равномерное распределение. Найти математическое
ожидание квадрата расстояния между ними.
Решение. R2 = X2 + У2; MR2] =a2[X] + а2 Ш =2/3.
7.22. Условия предыдущей задачи изменены так, что точки X,
У попадают не на смежные, а на противоположные стороны квадрата
(рис. 7.22). Найти математическое ожидание квадрата расстояния
между точками X и У.
Решение. #2 = 1 + (У — X)2; М [Я21= 1 + ос2 [У] +
+ а2[Х] — 2М [X] М [У] = 1 + 2/3 — 1/2 = 7/6.
164
/
к
К
L\_
/fl
)
Y
Рис. 7.21
Рис. 732
7.23. Условия предыдущих задач (7.21 и 7,22) изменены так, что
точки X и Y случайным образом и независимо друг от друга
занимают с постоянной плотностью любое положение на периметре квадрата
/(. Найти математическое ожидание квадрата расстояния между
ними.
Решение. Выберем три гипотезы:
Ях = {точки X, Y легли на одну и ту же сторону квадрата};
Я2 == {точки X, Y легли на смежные стороны квадрата};
Я3 = {точки X, Y легли на противоположные етороны квадрата}.
Математическое ожидание величины R2 найдем по формуле полного
математического ожидания:
М [R2] = Р (Нг) М [R2 | Нг] + Р (Я2) М [R* | Я2] +
_+Р(Я3)М[#2|Я8],
где М [R2 | HJ, М [R2 | Я2], М [R2 \ Я8] — условные математические
ожидания величины R2 при соответствующих гипотезах.
Из ранее решенных задач 7.20, 7.21, 7.22 имеем
М [R2 | //J =1/6; М [R2 | Я2] - 2/3; М [R2 | Я3] = 7/6.
Находим вероятности гипотез: Р (Ях) « 1/4; Р (Я2) » 1/2; Р (Я3)=1/4;
отсюда М [Я2] = V« «% + V, • % > + V4 * */6 - 2/8.
7.24. Случайная величина X имеет плотность / (х).
Рассматривается ее функция Y = min {X, а}, где а — неслучайная величина. Найти
математическое ожидание и дисперсию случайной величины Y% не
находя ее закона распределения.
Решение. По общей формуле (7.0.7)
М[У] =Jmin {*, a)l(x)dx.
При а; < а получим min {х> а} =* х\ при х ^ а^ получим min {#, а} =
=5 а. Отсюда
165
М[У]= f xf(x)dx+a §f(x)dx= j xf(x)dx + a P {X>a} (7.24.1)
«*- oo a -~ oo
Аналогично находим второй начальный момент
«2(7]= f л;г/(л:)<*л: + а2 f /(x)d* = f x*f(x)dx + a2P{X>a} (7.24.2)
и дисперсию
DIY] = a2[K]—(М[П)2.
7.25. Тот же вопрос, что в предыдущей задаче, но случайная
величина X — дискретная, принимающая целочисленные положительные
значения о вероятностями, заданными рядом распределения
; y = min{X, a},
1 | 2
Pi | Рг
...
*i...
pk\...
n
Pn
a —не случайное целое положительное число, заключенное между
1 и п (1 < а < п).
п
Решение. М [Y] = 2 min ik> a) Pk\ ПРИ k < a получим
min {k, a} =k] при k > а получим min {ft, a) =a. Тогда
Аналогично находится второй начальный момент
*AY] = a;% k* pk + a* j$pk
и дисперсия
' ■ DIY] ==a2m — (MIY])\
7.26. Производится ряд независимых опытов, в каждом из которых
событие А происходит с вероятнготью р. Опыты прекращаются, как
только произошло событие А; общее число опытов не должно
превосходить N. Найти математическое ожидание и дисперсию числа Y опытов,
которое будет произведено.
Решение. Сначала рассмотрим случайную величину X —
число произведенных опытов, если ограничение N по общему числу
опытов снято. Случайная величина X имеет геометрическое распределение,
начинающееся с единицы; ее ряд распределения:
X:
1
Р Р9
\РЯ
А-1
(9=1-/7).
Случайная величина Y есть минимальное из X и N:Y =- min{X, N].
На основе результатов задачи 7.25 имеем (полагая п = оо)
166
{Л/—1 со Л
Вычислим первую сумму
ЛГ-l JV—I
*-i - V -1 „*-_£. g-g" - i-^-'+(^-i)y
N
k= 1
i-<7 (1~<?)3
Вторая сумма равна (NqN~{)/(l — q), откуда
7.27. В гл. 1 рассмотрена задача Бюффона: игла длины / наугад
бросается на плоскость, разграфленную параллельными прямыми,
отстоящими друг от друга на расстояние L > /, и установлено, что веро*
ятность пересечения иглой какой-нибудь из прямых равна p=2//(Lji);
так как число пересечений при / < L может быть только 0 или 1, то
математическое- ожидание числа пересечений будет равно р.
Каково будет математическое ожидание числа пересечений иглы с прямыми,
если снять ограничение / < L?
" Решение. Разобьем длину иглы / на п элементарных участков
Д/ а» Цп < L. Случайная величина X — число пересечений иглы с ли*
п
ниями — может быть представлена в виде суммы: X = У Xt, где Xt —
чибло пересечений с прямыми £-го элементарного участка. Случайная
величина Xt — индикатор пересечения /-го участка с какой-либо из
прямых — имеет математическое ожидание, равное вероятности
пересечения:
MWJ «pi =2 Д//(/,л),
откуда
п
м
1Х]=%р
2пМ 21
_ Ln Ln
7.28. На плоскость, разграфленную параллельными прямыми,
фигурирующую в предыдущей задаче, бросается случайным образом
любой контур (выпуклый или невыпуклый, замкнутый или незамкнутый)
длины /. Определить математическое ожидание числа пересечений
этого контура в прямыми.
Решение. Как и в предыдущей задаче, М [Y] = 2 ll(Ln).
Чтобы доказать это, нужно разделить контур на п элементарных,
практически прямолинейных участков длины Д/; для каждого из них
математическое ожидание числа пересечений будет 2Д//(Мгс), а для всего
контура 211 (Ln).
7.29. На плоскость, разграфленную параллельными прямыми,
отстоящими друг от друга на расстояние L, бросается случайным
образом выпуклый замкнутый контур длины /, наибольший размер кото-
167
рого а не превосходит L (рио. 7.29). Найти вероятность того, что он
пересечется с какой-либо из прямых.
Решение. Обозначим р — искомую вероятность, Y — число
точек пересечения контура с прямыми. Так как контур выпуклый и
замкнутый, а его наибольший размер меньше L, то контур может иметь
либо две точки пересечения с прямыми, либо ни одной. Ряд
распределения случайной величины Y имеет вид
0
\-р
■ 2
Р
Y:
На основании задачи 7.28 М[Г] = 0 . (1 — р) + 2р = 2р = 2l/(Ln),
откуда р = l/(Ln).
•{
м!
Л/|
1/
/
Рис. 7.29
Рис. 7.30
7.30. Плоскость разграфлена на прямоугольники со сторонами
L и М (рио. 7.30). На плоскость случайным образом бросается игла
длины /(/<£,/< М). Найти вероятность того, что игла пересечется
хотя бы g одной из линий, а также найти математическое ожидание
числа пересечений иглы в какой-либо прямой при снятых ограничениях
/<L, KM.
Решение. Рассмотрим прямые, ограничивающие
прямоугольники, как две системы линий — горизонтальных и вертикальных.
Рассмотрим события: х
А, = {игла пересечется а одной из вертикальных прямых};
В = {игла пересечется g одной из горизонтальных прямых}.
Так как положение иглы относительно вертикальных прямых
никак не влияет на ее положение относительно горизонтальных, события
А и В независимы; поэтому искомая вероятность
Р (А + В) = Р (А) + Р (В) —Р (А) Р (В).
На основания задачи Бюффона Р (А) = 2//(jtL), P (В) = 2//(яМ),
откуда
р (А + В) = 2l/(nL) +2l/(nM) — 4l2/(n2LM).
168
Снова, как и раньше, разделяя иглу произвольной длины / на
элементарные участки, имеем
М Ш = 211(пЦ + 21/(пМ) — 4/2/(п2Ш).
7.31. Прямоугольник с размерами 1г X /2 случайным образом
бросается на плоскость (рис. 7.31); все значения угла G равновероятны.
Найти математическое ожидание длины X его проекции на ось Ох.
Решение. Представим X как сумму X = Хг + Х2, где Хг —
проекция отрезка 1г\ Х2 — проекция отрезка /2. Искомое
математическое ожидание
М IX] = М IXJ + М 1Х2\ = 2/х/я + 2/2 In = 2 {1г + /2)/л,
т. е. равно периметру прямоугольника, деленному на л.
7.32. Выпуклый замкнутый контур длины / бросается случайным
образом на плоскость, причем все его ориентации одинаково вероятны
(рис. 7.32). Найти математическое ожидание длины X его проекции на
ось Ох.
Рис. 7.31
—X
Решение. Так как контур выпуклый, то каждый элемент
проекции Ал: получается проектированием двух и только двух
противолежащих элементов контура: A/Xi и Д/2 (см. рис. 7.32); значит, средняя
длина проекции контура вдвое меньше суммы средних длин проекций
элементарных отрезков А/, на которые можно разбить контур:
М
2 *d n л
7.33. Имеется случайная величина X g плотностью / (х). Найти
математическое ожидание и дисперсию случайной величины Y =
= |Х|.
Решение, Запись Y — |Х | означает, что
-г
-X при Л<0;
X при Х>0.
169
тг, = М[У1= f \x\f{x)dx*= — f xf(x)dx -; \xf(x)dx =
«_oo —c» 0
eo
= §x[f(x)+f(-x))dx;
00
Dy = a2[Y]—m\= J |лг|2/(x)^лг—m2y = a2[X]—m\ = Dx + ml—mj.
7.34. Найти математическое ожидание и дисперсию модуля
случайной величины X, распределенной по нормальному закону с
параметрами т, а.
Решение. Из предыдущей задачи
(х—т) ~ (х—т)*
_ , ... 2а* dx+——
У2я ^ aVL. 0
Делая замену переменных (х — т)1а = *, получаем
, "п {х-т) 1 г -
0V2R J а1/2я J
"1/2я J 1/2я J
— — ffX
a
"+-»(f).
V2n
где Ф — функция Лапласа,
Dy = a2 + m2—m*.
В частности, при т = О
m„ = l/—o^0,80a; Оу = а2—- о2=^1 — А\а2 ^0
J/ я я ч я /
7.35*. Независимые случайные величины X и Y имеют плотности
/i (#) и /2 (#). Найти математическое ожидание и дисперсию модуля их
разности Z *= \Х — Y\.
Решение. Имеем
оо
Щ = [ f |*—y\fi(x)f2(y)dxdy.
2 л =
-
),36о2.
4
1
I
Д
*
' 1
1
1
%
\
%
1
V,
1"
1
щ
Прямая у = х делит-плоскость хОу на две области I и II (рив. 7.35).
В области 1х>у, \х — у\ — х — у. В области II у >х, \х — у | ~ ||
*=* у — х. Отсюда
mz=\[(x—y)h(x)fAy)dxdy + [Uy—x)fx(x)f.2(y)dxdy^
(i) (П)
170
= ] Х^Щ ] Ш<т*х- J yft(y)k h (x) dx\dy +
+ 5 yh{y)\ I fi (*) dx\dy- J xh(x)\[i.Ay)dy
Введем в рассмотрение функции распределения
х у
ЛМ= j fi(x)dx\ F2(y)= J f2(y)dy.
dx.
Тогда
Щ~ J xh(x)F2(x)dx- j yh(y)[l-Fxiy)]dy+
^ОО 5ВЧ OO
OO OO
+ j yf,(y)Fi(y)dy— I xh{x)[l-Ft{x)]dx.
Рас. 7.35
Объединяя первый интеграл с четвертым, а второй с третьим; получаем
«. = 112ж/х <*) ^ (*)-*/i (*)1 <**+ I t2t//2 (у) ^ («/) -у/, (t/)] dy =*
—оо —оо
00 ОО
= 2 J */i (х) F2 (x) dx—m*+ 2 J y/2 (у) Рг {у) dy—my.
OO — OO
Так как X, Y независимы, то
a2 [Z] = M [| X — Y |2] =*M[(X — Yf] =
= M IX2] + M [У2] — 2M IX] M [Y] -
= a2 [XI + a2 [F] —2mxmy = Dx + Dy + (mx —my)\
Отсюда находим Dz = a2 [Z] — mi.
7.36. Независимые случайные величины X и К имеют плотности
/i (*) и f2 (у). Найти математичевкое ожидание и дисперсию
минимальной из этих двух величин Z — min {X, Y}.
Решение.
ztXt если Х<Г;
(к, если Х>Г.
171
Прямая у a=s х делит плоскость хОу на две области (см. рис 7.35):
I, где Z = У, и II, где Z = X (случай X = У не рассматриваем, как
имеющий нулевую вероятность).
mz=*№[Z] =\\xf1(x)f2(y)dxdy ^\[yf1(x)f2{y)dxdy^
(И) (D
- J х/хМП-/?,(х)]Лр+ J yhm\-Fx(y)\dyy
£Ё»00 М-ОО
где Т7!, F2 — функции распределения случайных величин X и У.
00 ОО
«2[2]= J x*f1(x)ll-F2(x)]dx+ J tfh{y)V-Fi(y)dy];
«-» 00 ра»00
Dz = a2[Z]—ml.
7.37. Случайное напряжение £/ распределено по нормальному
закону / (и) с параметрами т и а. Напряжение £/ поступает на
ограничитель, который оставляет его равным £/, если U ^uQl и делает равным
«0, если £/ > «о;
v • (тт \ \U ПРИ U^U0)
itt0 при (У > и0.
Найти математическое ожидание и дисперсию случайной величины
Z — напряжения, снимаемого g ограничителя.
Решение. На основании задачи 7.24 имеем:
оо * и0 оо
mz = М [Z] = I min {и, и0} f (и) du = ( uf (и) du + i "о/ («) ^и =
— оо — оо ий
«О Г -, °°
—• оо «0
-ЧфР^)+ад]-^р[-т(^)']+
+ц.[о,5- Ч>( "~mu )]-ц,-Д. Г:МФй»+0,5) +
+w-'[--!-I -«.-^,-'
Ио «>
щ [Z] = j ы2 / (и) du + J ub f (и) du =(ml + аД (Ф 0О) + 0,5) +
— оо щ
+Mo{o,5-o(^-2g»w;+q"SxPr-4-1>
V2jx L 2 J
172
Dz = a.2[Z\-ml= oS{(l + «)(<D(fe) + 0,5)+-^- exp[ 1-1-
_^o(0(Q + O,5) + 17U-exp[—f-]]*}.
Заметим, что при и0 = mU9 t0 = ,0, имеем mz = mtt — att (У2я )~x;
Dz = aj (я - 1) (2Я)"1.
7.38. По каналу связи передается N сообщений; длительность
каждого сообщения случайная, имеет одни и те же математическое
ожидание т и дисперсию D и не зависит от длительностей других сообщений.
Найти математическое ожидание и дисперсию суммарного времени 7\ '
за которое будут переданы все N сообщений. Найти Ттах —
максимальное практически возмбжное время передачи всех сообщений.
Решение. Т = 2 ^*> гДе ?\* — длительность г'-го сообщения
(i = 1,2,..., Л0.-По теореме сложения математических ожиданий
По теореме сложения дисперсий
Ь- i J *-1
По «правилу трех сигма» Ттах = iVm + 3"VND..
7.39. Решить предыдущую задачу 7.38 с тем изменением, что
длительности Tt сообщений зависимы и коэффициент корреляции
случайных величин Tt и Tj равен Гц.
Решение. Математическое ожидание по-прежнему равно
М [71 = Nm\ Для вычисления дисперсии находим корреляционный
момент величин Tiy Ту. Ktj = Гц о2 = rtj D. По формуле (7.0.28) для
дисперсии суммы
D[T]=ND + 2%ruD = D(N + 2'2>ru); Гтах = Nm + 3УЩТ].
<</ \ '<' У
\У
Рис. 7.40
7.40. Система случайных величин (X, У) распределена равномерно
в прямоугольнике^ R (рис. 7.40)^ Определить: 1) М [X + У];
2) М [X — К]; 3) М [XYh 4) D [X + У]; 6) D [Л —У]; 6) М [(X — У)2];
7) М [2Х3 + ЗУ2 + 1].
173
Ответ. 1) 3/25 2) 1/2; Зч 1/2; 4) 5/12; 5) 5/12; 6) 2/3; 7) 6.
7.41, При работе электронного прибора возникают случайные
неисправности; среднее число неисправностей, возникающих за единицу
времени работы прибора, равно Л,; число неисправностей за время х
работы прибора — случайная величина, распределенная по закону
Пуассона с параметром а = X т. Для ликвидации возникшей
неисправности (ремонта прибора) требуется случайное время 7,рем; это время
распределено по показательному закону / (/) = (ге-^ при t > 0.
Времена ликвидации неисправностей независимы. Найти: 1) среднюю долю
времени, которую прибор будет исправно работать, и среднюю долю
времени, которую он будет находиться в ремонте; 2) средний интервал
времени между двумя последовательными неисправностями.
Решение. 1) Среднее время исправной работы прибора
(математическое ожидание времени, которое проработает прибор после
пуска до остановки для ремонта) £испр = 1 А,. Среднее время ремонта 7vt,M—
= 1/[г. Средняя доля времени, которую прибор будет исправно
работать, равна
fecnp + W 1Л+1/Ц Ь + И
Аналогично средняя доля времени, которую прибор будет
ремонтироваться, равна
р = 1 _а = МЬ+ v).
2) Средний интервал времени /t между двумя последовательными
неисправностями
7* = Гиепр + Грем - \/Х + 1/у = (X +»/(X|i).
7.42. Случайная точка (X, Y) распределена на плоскости по нор^
мальному закону с круговым рассеиванием: тх = ту = 0\ ох = оу = о.
Случайная величина R — расстояние от точки (X, Y) до центра
рассеивания. Найти математическое ожидание и дисперсию величины R:
Решение.
оо
в—ОО
Переходим к полярной системе координат г, ср:
со 2Я
^Ir2i^rexK-i^)drJrf(p=°V т~l&*
0 0 r
00
Dr=*D[R] = a2[R[-m?=^ (x*+f) ^±-exp(-^£±£-\dxdy-
174
со 2Я
*'-J',-i?re'(-£-)*J *-"f -
О О
00
= 2<т2Г/е-'Л— а2 — = а2 —
J 2 2
о
7.43. Доказать, что если случайная величина X имеет
биномиальное распределение о параметрами пир, то ее математическое ожидание
М [XI = пр9 а дисперсия D [XI = npq (q s= 1 — р).
Решение. X — число появлений события А в п независимых
п
опытах — представляем в виде Х = 2 Х-ь где X* — индикатор еобы-
тия А в i-м опыте, т. ё.
X. -= ,П» есЛЙ в *""м опыте событие появилось;
1 \0, если в i-м опыте событие не появилось.
М IXt] = р\ D [X,] = pq\
М[Х]= 2 МИ = ВД °га= S W = npg.
7.44. Доказать, что для я независимых опытов, в которых событие
А происходит с вероятностями р19 р2, ..., р>г, математическое ожидание
и дисперсия числа X появлений события равны:
М[Х]=|]рг, D[X]= 2 Mi. где ^ =1—pf.
1= 1 * = l
/г
Решение. Аналогично предыдущей задаче X = 2 X*, где X* -
индикатор события А в j-м опыте;
м[Х]= 2 M^i= 2 л; °W= 2 Dt^] = is p«9i.
i= 1 /= 1 /= 1 i= 1 .
7.45. Рассматривается п независимых опытов, в каждом из которых
событие А происходит с вероятностью р. Найти математическое
ожидание и дисперсию частоты Y события А. Найти диапазон практически
возможных значений частоты.
Решение. Y = XIп, где X — число] появлений события А.
М [У ] = М [Х\1 п = —пр==р; D [Y] = яр<?/я2 = р?/п;
а1 = УгЩкГ = Кр9/л»
где q tB 1 — р. Диапазон практически возможных значений У есть
mj,±3a„=p± SVpqln.
7.46. Доказать, что математическое ожидание и дисперсия
случайной величины X, имеющей гипергеометрическое распределение (ем.
4.0.34) с параметрами а, 6, я, равны соответственно
*
175
a+b (a+b)2 la~\
nab _ ,_ 14 f a a—1
-(-
£■)"]• p-46-1»
a+fc
Решение. Рассмотрим физическую модель возникновения
гипергеометрического распределения — вынимание п шаров из урны,
где а белых и Ь черных шаров; X — число вынутых белых шаров.
Представим п выниманий шара как п опытов, в каждом из которых может
произойти событие А = {белый шар}. Представим величину X как
п
сумму величин Хг — индикаторов события А в ни опыте: X = У Хг..
Случайные величины Xt зависимы, но теорема сложения
математических ожиданий применима:
1 п
дог^ V AAiv,. iurv, a _ ккгл,, па
ЛХ]=УЩХг\; М[Х*] = —J-; М[Х1 =
a+b
Дисперсию суммы случайных величин Xt находим по формуле
(7.0.28):
Dr v , a 6 afc
2Df^l
a-j-6 a+Ь (a+&)2'
nab
(a+b)2
Найдем /G. ,. = M [X, X,]- M [X,] M [X,]. .
Произведение индикаторов XtXj события А в i-м и /-м опытах равно
единице только в случае, когда X* = 1, Xj = 1, т. е. и при t-м, и при
/-м опытах происходит событие Л. Вероятность этого равна , ?. х
(а—6) *
X 1 а_.1\> этому же значению равно математическое ожидание
М[Х,Х^З= ^=^ .
* 7 (a+b)(a+b— 1)
Отсюда
^\x§x4SSSmm~J—ГТГТ—ГТ—7^ "i , ,v, • (7.46.3)
* J (a+b) (a+b—I) (a+b)2 x '
Число слагаемых в сумме 2 Кх.х4 равно С5 «а л (л — 1)/2. Подстав-
ляя (7.46,3) в (7.46.2), получаем формулу (7.46.1).
7.47. В урне 5 белых и 7 черных шаров; из урны вынимается сразу
6 шаров. Случайная величина X — число черных шаров среди вынутых.
Найти математическое ожидание и дисперсию величины X.
О т в е т. М [X] = 3,5; D [X] = 70/33 » 2,12.
176
, , 7.48. Радиолокационная станция ведет слежение за областью
пространства, где находится N объектов. За один цикл обзора /-й объект
(независимо от других) обнаруживается с вероятностью ~рг (i = 1, ...>
//). За время наблюдения осуществляется п циклов'обзора. Найти
математическое ожидание и дисперсию числа объектов X, которые будут
обнаружены.
Решение. X = 2 %ь где Xt — индикатор события At =
/= 1
= {обнаружение /-го объекта}.
Р (At) = 1 - (1 _>,)«;
М[Х]= 2 [1-(1-рОлз = n- 2 (\-Рг)п\
D(X) = 2n-(i-Pi)tt](i-P*r.
При неограниченном увеличении числа циклов обзора п
\im Ni[X] = N\ UmD[X} = 0,
т. е. в пределе при п -> оо будут обнаружены все объекты.
7.49 *. Берется произвольная точка А внутри круга радиуса а (рис.
7.49), и через эту точку проводится хорда ВС под произвольным углом
G к радиусу, проходящему через А. Найти среднюю длину этой хорды.
Решение. Точка А берется произвольно в пределах круга,
поэтому ее полярные координаты R, Ф независимы и распределены по
законам:
2 1
fx(r) = г при 0<г<а; /2(ф)=—^ при0<ф<2я.
я2 2п
Так как средняя длина хорды, очевидно, не зависит от угла ср, возьмем
точку А на произвольном радиусе (на расстоянии R от центра) и
проведем через нее хорду ВС под случайным углом 0 к радиусу. Из
условий задачи следует, что случайная величина 0 имеет плотность /зС^) =■
= 1/2я при 0< Ф< 2я. Выразим.длину D хорды ВС через
случайные величины R и 0. Для этого опустим из центра круга
перпендикуляр на хорду и обозначим его длину Я. Очевидно,
D = 2Уа2 — Я2; Н = R sin 0; D = 2Va2 — R2 sin2 0.
Математическое ожидание случайной величины D найдется как
2зт а
MfD]^f d* f2]/a2—r2sin2fl J£-J-dr =
8
яаа
о о
я/2
Г '■С-"*») Д>—i*,» 1,70a.
J 3 sin2 # Зя
177
/
7.50 *. Найти среднее значение длины хорды ВС (рис, 7.50),
проведенной через точку А внутри круга, находящуюся на расстоянии L
от центра круга радиуса г, причем все направления этой хорды
одинаково вероятны.
Рис. 7.49
Рис. 7.50
Решение,
дующим образом:
Корда ВС выражается через величины L, Ф, г сле-
BC = 2rl/"l — ii-sin2<D.
Если длину хорды ВС считать случайной величиной X, то
я/2
та
Л/Z у- — —
= JL- Vi_ fe»sin«q>dq>,
Я/2
Ar_ С
л i
где k == Llr. Полученный интеграл представляет собой полный
эллиптический интеграл Е (k, я/2) с модулем k\ его значения можно найти в
справочниках. Например, при k = 1/2 интеграл Е (1/2, я/2) = 1,4675
и тх « 1,87г.
Так как полный эллиптический интеграл Е (k, я/2) измеряется от
я/2 (при k = 0) до 1 (при k == 1), то средняя длина хорды будет
принимать значения от 2 г (при k = 0, т. е. для точки А в центре круга)
до 4г/я (при L = г, т. е. для точек А на окружности).
7.51*. Техническое устройство состоит из п узлов. Каждый узел
может выходить из строя независимо от других. Время исправной
работы /-го узла распределено по показательному закону с
параметром %t\
M*) = fc*e~V С>0).
Каждый узел, оказавшийся неисправным, немедленно заменяется
новым и поступает в ремонт. Ремонт /-го узла продолжается случайное
время, распределенное по показательному закону с параметром р,{ г
<Р* (0 = и* е""^* if > 0). Устройство работает в течение времени %.
178
Определить: 1) математическое ожидание и дисперсию числа уз-
лов, которые придется заменить; 2) математическое ожидание еуммар-
ного времени 7\ которое будет затрачено на ремонт вышедших из етроя
узлов.
Решение. 1) Обозначим Хг число узлов t-го типа, вышедших
из строя за время т. Эта случайная величина распределена по закону
Пуассона и имеет математическое ожидание тх. = кр; и дисперсию
Dx = Я£т. Обозначим X общее число узлов, вышедших из строя за
время т. Имеем
Так как величины Xt независимы, то
2) Обозначим Tt общее время, затраченное на ремонт всех
вышедших из строя за время т узлов /-го типа. Оно представляет собой
сумму времен, затраченных на ремонт каждого из узлов. Так как число
этих узлов равно Хи то
71f = 7l1) + rii) + ... + rfJrf,= % T\k\
где Ttk)—случайная величина, распределенная по*показательному
закону с параметром [г£; величины TV \ Т/2), ... независимы.
Найдем математическое ожидание случайной величины Tt по
интегральной формуле полного математического ожидания; для этого
предположим, что случайная величина Xt приняла определенное
значение т. При этом условии математическое ожидание величины Ть
будет
tn тп л
М[Г,|т]= У М[7?>]= У -L—2L.
Умножив это условное математическое ожидание на вероятность
Рт того, что случайная величина Xt приняла значение т, и
просуммировав все эти произведения, мы найдем полное (безусловное)
математическое ожидание величины Tt
М
Применяя далее теорему сложения математических ожиданий,
получаем
Заметим, что тот же результат можно получить путем следующих
(не вполне строгих) рассуждений. Среднее числе выходов из строя уз-
179
ла /-го типа за время т равно А,*т; среднее время ремонта одного такого
узла равно l/p>f; среднее время, которое будет затрачено на ремонт
всех вышедших из строя за время т узлов г-го типа, равно M^IV,
среднее время, которое будет затрачено на ремонт узлов всех типов,
равно т 2^
7.52*Г Условия задачи 7.52 изменены таким образом, что каждый
вышедший из строя узел отправляется в ремонт, а техническое
устройство на это время прекращает работу; при неработающем
(выключенном) устройстве узлы выходить из строя не могут. Найти: 1)
математическое ожидание числа остановок устройства за время т; 2)
математическое ожидание той части времени т, в течение которой устройство
будет простаивать (оно же среднее время, затраченное на ремонт).
Ыцинд 2-й цикл 3-й и/т 4-й цикл
Рис. 7.52
Решение. 1) Обозначим X число остановок за время % и
найдем его математическое ожидание тх. Задачу будем решать с помощью
следующих не совсем строгих (но тем не менее верных) рассуждений.
Рассмотрим неограниченный во времени процесс работы устройства в
виде последовательности «циклов» (рис. 7.52), каждый из которых
состоит из периода работы системы (отмечен жирно) и периода ремонта.
Длительность каждою цикла представляет собой сумму двух
случайных величин: Траб (времени работы устройства) и 7\,ем (времени ре.
монта). Средняя длительность времени работы устройства >я*раб вы.
числяетея как среднее время между двумя последовательными отказа-
п
ми в потоке отказов интенсивности ^=2 V> оно равно
Ераб
= 1А=1 I ±
I *=1
^аб=1А=1 У\К
Находим среднее время ремонта >%ем. Будем его искать по
формуле полного математического ожидания при гипотезах Ht *=
{ремонтируется узел г'-готипа} (i = 1, 2, ..., п).
Вероятность каждой гипотезы пропорциональна параметру Я*!
Р(Я|) = Я«/2Ь, = Я,Д.
Условное математическое ожидание времени ремонта при этой
гипотезе равноЛ'/|Х|; отсюда
'рем
180
Среднее время цикла
Теперь представим себе последовательность остановок устройства
как последовательность случайных точек на ogh Ot, разделенных
интервалами, в среднем равными mt^ Среднее число остановок за время т
будет равно среднему числу таких точек на отрезке длиной т;
тх = %!т1п
2) За каждый цикл устройство будет простаивать (ремонтировать-
п
ся) в среднем время mtveu = т- 7, —; следовательно среднее время
простоя
7.53. Случайная величина X распределена по нормальному
закону с характеристиками тх и ох. Случайные величины Y и Z связаны с
X зависимостями 7 = X2; Z = X3. Найти корреляционные моменты
Решение. Для упрощения вычислений перейдем к
центрированным величинам и воспользуемся тем, что для центрированной
нормальной величины 3t=X—тх все центральные моменты нечетных по
рядков равны нулю, а М [j£2] =о2, М [X4] =3oJ (см. задачу 5.26),
Так как
Y = (X + mx)2—mX4 = X2+2Xmx + ml-Dx-m* =
= fr+2kmm—ol .
то
Кху^ЩХ¥]^М[Х(Х^ + 2Хтх-о%)]^2о1тх.
Далее
Z = (X + т.,)3—М [X3] = X8 + ЗХ*тх+ЗХтД-Ьml—0тхо2х+т%) =
^-Х3+ЗХ2тх + Зкт£—Зтхо1,
и поэтому
Кхг = ЛИ* Z] = М [X4] + Зта М [X3] + Зт2 М [X2]—
—3mxo*xM{X] = 3ox + 3mxol
181
Наконец,
Kyz = М [(Х2+ 2ктх— ol)(Х°3 + ЗХ2тх + 3Xml—3mx,ol)] =
= Ътх М1X1 + 6тх (ml- ol) М [X2] + Зтх о4х = \2тхо% + 6т3х ol.
7.54. Тело, масса которого равна а г, взвешивается на
аналитических весах четыре раза; получаются результаты Х1? Х2, Х3, Х4. В
качестве измеренного значения массы принимается их среднее
арифметическое: Y = (Хг + Х2 + Х3 + Х4)/4. Результаты взвешиваний
независимы. Весы дают систематическую ошибку тх= +0,001 г. Среднее квад-
ратическое отклонение каждого взвешивания oxt= 0,002 г. Найти
параметры: математическое ожидание и среднее квадратическое
отклонение случайной величины Y.
Ответ. ту =а + 0,001 г; оу = ох/2 = 0,001 г.
7.55. Производятся четыре независимых измерения одной и той
же величины X. Каждое измерение характеризуется одним и тем же
математическим ожиданием тх и средним квадратическим отклонением
а*. Результаты измерений: Хъ Х2, Х3, Х4. Рассматриваются разности
X
2»
между соседними измерениями: Yx *= Х2 — Хх; Y2 = Ха
Y3 = Х4 — Х3- Найти характеристики системы этих случайных
величин: математические ожидания ту„ myi, тУз; средние квадратичес-
кие отклонения оУ1, оу.гУ оУъ\ нормированную корреляционную
матрицу \\гц\\.
Решение.
тР1-тЛ = 1ЯЛ = 0; ol «<yj. = о£ = 2о|; оу, = ош = оУг = охУ2.
В силу независимости величин Хъ ^2, Х3, ^4
КУ1У2 - М К*.-*,) (X 3-Х2)] - -М [XI] - - ol;
< Kv* у*~ м tt*a—-fy(*4-*в)1 = -М [Х|] = -а|;
К* у. - М [(Х2-^)(Х4-^8)] = 0;
—а2 1
г — г — 1£ _ !_• г =0
Ч/i 02 — гУг Уг — 2а2 ~~ 2 ' У1 У
Klill-
1 —1/2 0
1 —1/2
1
7.56. Имеется кубический бак с горючим, на одной из шести стенок
которого случайным образом появляется пробоина; она оказывается с
равной вероятностью на любой из шести стенок бака и в любой точке
каждой из шести стенок. Вследствие наличия пробоины из бака
вытекает все горючее, находящееся выше пробоины. В неповрежденном
состоянии бак заполнен на 3/4 своего объема. Определить среднее
количество горючего, которое сохранится в баке после появления пробоины.
182
Решение. Для простоты будем считать ребро бака равным
единице. Высоту пробоины обозначим Х> объем оставшегося
горючего К. Так как площадь основания равна единице, то
-I х
при Х<0,75;
75 при 0,75<Х<1.
Если пробоина окажется выше чем на 0,75, от дна бака (X > 0,75),
то горючее вытекать не будет, и в баке останется, как и было,
количество горючего Y s= 0,75; вероятность этого равна доле площади
поверхности бака, находящейся выше уровня 0,75: j
Р {У = 0,75} := Р {X > 0,75} = 1/6 + (4/6) . 0,25 = 1/3.
Если пробоина окажется, в дне бака (X = 0), то вытечет все
горючее; вероятность этого равна доле площади, приходящейся на дно бака:
Р {У. = 0} =Р {X =0} *= 1/6.
Если пробоина окажется в одной из боковых стенок бака на
расстоянии X < 0,75 от дна, то в баке останется количество горючего Y = X.
Плотность вероятности в интервале (0; 0,75) постоянна и равна (1 —
— 1/3 — 1/6)/ 0,75 = 2/3. Среднее количество оставшегося в баке
горючего
0,75
my = 0J5. — + 0.—+ Г х- — dx = 0,44.
3 6 J 3
о
7.57. В интервале (0; 1) зафиксирована точка а (рис. 7.57);
Случайная точка X распределена равномерно в том же интервале. Найти
коэффициент корреляции между случайной величиной X и расстоянием R
от точки а до X (расстояние R всегда считается положительным).
Определить, при каком значении а величины X и R будут
некоррелированными.
1 * : -о 1
О Х v: Hg 1 t
R
Рис. 7.57
Решение. Определим КХг по формуле КХг *= М IXR] — тхтг.
М[Х/?] = М[Х|а—Х\] = ^х\а— x\f(x)dx = ^x\a—x\dx=^
о о
а 1
= \х(а—x)dx—{ x(a—x)dx = -^ 2- +-1-,
О а
183
Ш*= 2
1 a . 1
i-; ml.= f|a—x|dx=f(a—x)dx— f(a—x)dx = a2—а + —.
Отсюда
„ аз a i l / l \ аз a* 1
*~=— -T+T-Tr-a+TJ""i—r+ii"'
Находим
l l
D«=*—i ax= -; Dr = a2[R]—m
12 ' * 2V3'
1
a2[R]= Ua—xf dx==a2—a + — -,
о
Z)r = 2a3—a4—a2+-l-; ar=VDr.
Отсюда
.12
=-er-^+Tr)/(iAs-"-**
12 2T/3
Уравнение a3/3—a2/2 + 1/12 = 0 имеет только один корень в
интервале (0;1); а = 1/2. Поэтому случайные величины X, R становятся
некоррелированными только при а = 1/2.
7.58. Автомобиль может двигаться по шоссе с произвольной
скоростью v (0 ^ v ^ Утах)- Чем быстрее движется автомобиль, тем
больше вероятность того, что он будет задержан инспектором милиции.
Каждая задержка длится в среднем время t0. Инспекторы на пути
следования расставлены случайным образом; при этом на единицу длины
пути приходится случайное число инспекторов, распределенное по
закону Пуассона с параметром %. Зависимость вероятности задержки
от скорости машины линейная: р {v) = ко (0 ^ v <[ amax), где k =
= l/ymax. Определить рациональную скорость движения vv
автомобиля, при которой он пройдет путь s в среднем за минимальное время.
Решение. Среднее время прохождения пути s будет
t = s/u + Xsp (v) t0 s= s/v + k skvtQ.
Если минимум этой функции лежит внутри интервала (0, отах)*
то его можно найти из уравнения
0V V2
откуда
v = »р = У1/(Ш0)~ Vvm ыКЩ.
Эта формула справедлива при vv < amax, т.е. при t>max>l/(M0)
Так, например, при vmSiX = 100 км/ч, X *= 1/20 км*4 и t0 ss 20 мин
flp *= VlOO/C/ao-Vs) « 77,5 км/ч.
184
Если ©max < 1/(Ц>), то минимум функции t ь= sh + tep (v) tQ
лежит вне интервала (0, i>max), и наивыгоднейшей является скорость
vv =s агаах. Например, если при указанных выше данных время
задержки уменьшить до 10 мин, то vv = umax = 100 км/ч.
7.59. Производится ряд независимых опытов, в каждом из которых
событие А происходит с вероятностью р. Опыты проводятся до тех пор,
пока событие А не произойдет k раз, после чего они прекращаются.
Случайная величина X — число опытов, которое придется произвести.
Найти ее математическое ожидание, дисперсию и среднее квадратичес-
кое отклонение.
Решение. Представим случайную величину X в виде суммы:
X-X1 + X2 + ... + Xh^j^Xi9
где Хг — число опытов до первого появления события А; Х2— число
опытов от первого до второго появления события А; ...; Xk — число
опытов от (k — 1)-го до &-го появления события Л.
Каждая случайная величина Xt имеет геометрическое
распределение, начинающееся с единицы [gm. (4.0.32)1, и ее характеристики
М [Х*1 » \lp\ D [Xtl » q/p* (q « 1—р).
Пользуясь теоремами сложения математических ожиданий и дисперсий,
получаем
М [X] = 2 М [Xt] = kp; D [X] - 2 D l*d = W".
ох = УЩХ]=УЩ1р.
7.60. Для сборки устройства повышенной надежности необходимо
k высококачественных однородных деталей. Перед тем, как поступить
в сборку, каждая деталь разносторонне испытывается и (независимо
от других) оказывается высококачественной с вероятностью р. После
того как набралось k высококачественных деталей, испытания новых
прекращаются. Запас деталей практически неограничен. Найти
математическое ожидани^тЛ и дисперсию Dx случайной величины X (число
испытанных деталей). Найти Хтах — максимальное практически
возможное число деталей, которые будут испытаны.
Ответ. Из решения предыдущей задачи
тх a kp; Dx = kqip*\ ox = Vkq/p; Xmax = kp + 3Vkqlp.
7.61. Имеется сетевой график планирования управления (СПУ),
согласно которому момент Y начала какой-то работы представляет
собой максимальное время окончания двух ©беспечивающих работ Хх,
Х2 (моменты окончания этих работ). Случайные величины Xl9 Х2
независимы и имеют плотности fx (хг) и /2 (л:2). Найти математическое
ожидание и дисперсию влучайной величины У, ^а также диапазон ее
практически возможных значений.
Решение. Y=*max{Хъ Х2}-( Xl прИ Xi>X*>
х \ Х2 при Хх<Х2.
185 ^
Область I, где Хг > Х2, и область II, где Хг < Х2, показаны на
рис. 7.61.
^=М[Г]= J *i/i(*i)| J f2(x2)dx2\dx1 +
— oo V*-* oo J
+ J ^/2(^)1 5 f1(x1)dx1\dx2 = J ^/ах!)^*»)^^
woo [—oo J —00 t
00
+ J x2f2(x2)F1(x2)dx2,
—*oo
-Jf/=J^
Рис. 7.5i
где Fx (x) и F2 (*) — функции распределения случайных величин Хх и
и Х2 соответственно.
00 ОО
М[У2] = J xlf1(x1)F2(x1)dx1+ J xU2(x2)Fl(x2)dxz;
—.«о ■*-* oo
D M = M [ П - m*; ay = VdTFI.
Диапазон практически возможных значений Y равен ту ± 3 оу.
7.62. В условиях предыдущей задачи для начала работы (момент Y)
требуется окончание п предыдущих (обеспечивающих) работ. Моменты
их окончания Х19 Х2,..., Хп независимы и имеют плотности /х (хг)9
/* (х2),...4п (хп). Ответить на те же вопросы.
Решение.
Y = max {Xlt Х2,.„, Хп} =*'Хй при Х*>Х, (i = 1,2,..., л; / Ф /);
ту==М[К1== J агх/х(л:!) i J (/г —1) J/2 (*2)/3(*3) ^fn(xn)dx2dxs ...dxAx
-*»оо ^-e»oo *-» oo J
X dxx + J JCa/a(x2) J J (n—1) J /1 (*i)/3 (xa) ... /„ (xn) dXidxs ... d*„l x
—* 00 I en «-*oo )
°Z i ХП *П
Xdx2+... + J xnfn(xj j J' (n— 1) f/i(*i)/.(xJ..A-i(*n-i)<&iX
^°° Loo J-00
X d*2 ... dXn-! \dxn.
186
В данном случае (п — 1)-кратный интеграл распадается на
произведение п — 1 однократных, поэтому
тув2 \ *iM*i) П Fj(xt)dxi9
'-1 ^оо !</<«
где Fj (xi)— функция распределения случайной величины Xj Q'= 1, 2,
..., п) при аргументе, равном хг. Аналогично находим
МЩ=2 ftf/i(*i) П ^(xOdx,;D[r]-M[r2]-m^
Если случайные величины Xj (/ а= 1,2, ..♦, п) распределены
одинаково с плотностью f(x) и функцией распределения F(x),to
00
Шу — п f х/ (х) [F (x)]n^l dx.
Аналогично вычисляютея М [У2] и D [Yh
00
7.63. Прибор (построенный по типу максимального вольтметра)
регистрирует максимальное из двух напряжений: Ul9 £/2« Случайные
величины Ul9 U2 независимы и имеют одну и ту же плотнооть} f (и).
Найти математическое ожидание показания вольтметра, т. е.
случайной величины U = max {Ut9 U2}> если / (и) » far** (^ > 0 ) —
показательное распределение с параметром %.
Решение. В соответствии с решением предыдущей задачи
00 00
М[(/] = 2 ( u/(a)F(a)d« = 2j ^ые-^О—e-^")d« =
ОО 00
! Г Iuq-x" du—2% Г
■■ 2 1 Хиъ-%а du—2% 1 ые-2»-» du = -|— -^- = -^-
А. 2А, 2А
Отсюда видно, что М W\ больше математического ожидания* каждой
из случайных величин Ux, U2 в 1,5 раза.
7.64. Математическое ожидание и дисперсия суммы случайного
числа случайных слагаемых. Случайная величина Z представляет собой
сумму: Z = 2 Xi9 где случайные величины Xt независимы и имеют
одинаковое распределение q математическим ожиданием тх идиспереией
Dx\ число слагаемых Y есть целочисленная случайная величина, не
зависящая от слагаемых Xti имеющая математическое ожидание ту
и дисперсию Dy. Найти математическое ожидание и дисперсию
случайной величины Z.
187
1
Pi
2
Pa
....
...
*|...
Pk | ».
Решение. Пусть дискретная случайная величина У имеет ряд
распределения
У:
Сделаем гипотезу {У = &}. При этой гипотезе
M[Z|y = £]= 2 м№]=^-
По формуле полного математического ожидания
М [Z] = 2 kpk тх = та 2 kph = mx M [ У] = та ту.
Аналогично условный второй начальный момент величины Z
М[^У-*]=мГЦх* Л^
= 2 а* [Х] + 22 w* mx = te1 [X) + k (fe-l)ml =
/= i «i
=*k[Dx+ml] + k (k-l) ml = kDx + k* mi.
По формуле полного математического ожидания
aAZ) = Dx%kph + ml%k*pk = Dxmy + m*a2[Y] =
k k
^Dxmy + ml(Dy + mt,)==Dxmy + rnlDy + m2xm2y;
D [Z] = a2 \Z\—m\ m$ = Dx my + ml Dy. ч
Итак,
Если случайная величина У распределена по закону Пуассона о
параметром а, то
тг = атх\ Dz = a (Da + ml).
7.65. По каналу связи передается сообщение в двоичном коде,
состоящее из п символов «О» ил «1»; оба значения одинаково вероятны и
принимаются независимо. Найти математическое ожидание и
дисперсию числа X перемен символа в сообщении, а также максимальное
практически возможное число перемен.
Решение. Рассмотрим п — 1 переходов от предыдущего
символа к последующему как п — 1 независимых опытов, и для каждого из
них введем в рассмотрение величину Xt — индикатор перемены
символа, равную единице, если символ менялся, и нулю, если оставался
прежним.
1
188
x=°2 xA м м-'?? м[x,i = "2 />=<«-1) р.
где /? — вероятность того, что на данном (/-м) промежутке произойдет
смена символа; аналогично
D[X]^D[Xi] = {n-l)p(l-p).
В нашем случае, очевидно, р = 1/2 и М[Х] = (л — 1)/2; D [X] =
= (я — 1)/4. По правилу трех сигма Хтах = (п — 1)/2 + ЗТ/п —1/2.
7.66. Группа из четырех радиолокационных станций ведет
наблюдение за областью пространства, в которых находится три объекта: Sly
S^ S3. Наблюдение ведется в течение некоторого времени т. За эта
время каждая из станций независимо от других обнаруживает каждый
из объектов с вероятностью р1у зависящей от номера объекта, и
передает его координаты на центральный пульт управления. Найти
математическое ожидание числа объектов X, координаты которых будут
зарегистрированы на пульте.
Решение. Обозначим X* индикатор события Аг~ {/-й объект
обнаружен}:
У [ \у если 1& объект обнаружен;
1 0, если /-й объект не обнаружен (£=1, 2, 3).
Математическое ожидание случайной величины Xt равно М[Х J =
= Р {*-й объект обнаружен} =1 — (1 —рь)\
з
Так как Х= 2 Хь то
м[Х]=2[1-(1-рг)*]=з-2 0-рО4.
7.67. Условия предыдущей задачи изменены таким образом, что
вероятности обнаружения объекта разными станциями различны:
/-я станция обнаруживает 1-й объект g вероятностью ptj (i =1, 2, 3;
/-1,2,3,4).
Ответ. М[Х]-3-2 П 0-р«).
7.68. Радиолокационная станция наблюдает за областью
пространства, в которой находятся четыре объекта. Вероятность обнаружения
отдельного объекта в зависимости от времени наблюдения выражается
Функцией р (t) и не зависит от того, обнаружены ли другие объекты.
Найти: 1) математическое ожидание времени Тъ за которое будет
обнаружен хотя бы один объект; 2) математическое ожидание времени Т4>
за которое будут обнаружены все четыре объекта.
Решение. 1) Вероятность того, что ни один объект не будет
обнаружен за время t, равна [1 —р (/)14; вероятность того, то за это
время будет обнаружен хотя бы один объект, равна 1 —[1 —р (/)]4.
189
Этф есть не что иное, как функция распределения Fx (f) случайной
величины 7\. Как мы доказали в задаче 5.28, для неотрицательной елу-
чайной величины 7\ '
М [7\] -1 [1 -Fx (t)] dt = J [1 -p (W
dt.
2) Находим вероятность того, что все четыре объекта будут
обнаружены за время t; она равна [р (t)]*; это есть функция распределен
ния F4 (t) случайной величины Г4. Ее математическое ожидание
М [Г4] = J [l-F, (t)] dt = f {1 -[p (0)4} dt.
Например, еели вероятность p (t) задана формулой p (t) = 1 —e"HXt, то
M[7\] = $[l — (1— е-а')]4Л = | е~4^^ = ^-;
M
oo
.*-{*
В этом примере среднее время обнаружения всех четырех объектов
в сто раз больше среднего времени обнаружения хотя бы одного объек- |
та.
7.67. Производится п опытов, в каждом из которых может
произойти или не произойти событие Л. Случайная величина X —число
появлений события А во всей серии опытов. Найти математическое
ожидание случайной величины X.
Решение. Представляем величину X как сумму п случайных
величин Xt (i =1,..., ft), где Xt — индикатор еобытия А в /-м опыте:
если в i-м опыте событие А появится;
если в £-м опыте событие А не появится.
x=2xf,M[X]=2 м™>
М [Xi\ = pi9 где pi — вероятность появления события в г'-м опыте.
Итак,
М[Х]=2^- (7-67-1)
В частности, если рх = р2 = ... = р, то
М [X] = пр. (7.67.2
Специально подчеркнем, что для применимости формул (7.67.1) и
(7.67.2) вовсе не требуется, чтобы опыты были независимы.
7.68. Для условий предыдущей задачи 7.67 считая опыты независи- ||
мыми, найти дисперсию случайной величины X.
190
I
Решение. По теореме сложения дисперсий
D[X] = d[*J X,"L JdjX,].
Дисперсия индикатора события А в *-м опыте [ем. формулу (4.0.19)}
равна pi (1 —рг)\ тогда
DUQ* 2 Л (1-/7,), (7.68.1)
В частном случае, когда рх = р2 = ... =* рЛ = р,
D[X] =^яр(1 — р). . (7.68.2)
Специально подчеркнем, что формулы (7.68.1) и (7.68.2) применимы
только для независимых опытов.
7.69. Производится п зависимых опытов, в каждом из которых
может произойти или не произойти событие А. Случайная величина X —
число появлений события. Найти ее дисперсию.
п
Р е ш е н и е. X = 2 Хи где X, — индикатор события А в /-м
опыте. По общей формуле (7.0.28) для дивдерсии суммы случайных
величин
D[X] = 2D^i+22 * /
где Кх. х. — корреляционный момент елучайных величин Xiy X7-:
КЧ *j " М 1Х* ХА~М lXi] M lXjl
Величина Х^Х7- обращается в единицу только если X* = 1 и Xj ==1
(т. е. и в *-м, и в /-м опытах появилось шбытие Л). М [Х*Х^] = р^,
где ри — вероятность того, что и в *-м, и в /-м опытах появится событие
A- KX.XJ =* Pu—Pipj; отсюда
d [X]= 2л(!—л)+22 (р«-й РА (7-69>
*=i /</
Таким образом, для нахождения дисперсии числа появлений
события в п зависимых опытах недостаточно знать вероятность pt
появления события в каждом из опытов; надо еще знать вероятность ptj
совместного появления события в каждой паре опытов.
В частности, когда рг = р2 =* ..,=? рп = р, р^ не зависит от / и
/ и равна Р9 формула (7.69) принимает вид
D [XI = пр (1 —р) + /г (л - 1) (Р -р2),
где Р = ptj — вероятность совместного появления события в любой
паре опытов.
7.70. В урне а белых и Ь черных шаров. Из урны вынимается наугад
k шаров. Случайная величина X — число белых шаров среди вынутых.
191
[_
Не пользуясь законом распределения случайной величины X
(гипергеометрический, см. гл. 4), найти числовые характеристики случайной
величины X: ее математическое ожидание и дисперсию.
к ' '
Р е ш е н и е. X = 2 **» где
<=i
_f 1, если f-й вынутый шар белый;
** ~~ \ 0, если он черный.
М[Х]=2 М[Х!] = йр, j
где р —вероятность того, что вынутый шар —белый;* ]
р = а/(а + Ь)\ М IX] - ka/(a + b). x
Дисперсию случайной величины X находим как дисперсию числа *
появлений события в k зависимых опытах [см. задачу 7.69)]: \
D [XI - kp (1 — р) + k (k — 1) (Р — р\ (7.70) ,
Найдем Р—вероятность того, что какие-то два вынутых шара (/-й ;
и /-й) будут белыми: Р = ^-т f^l_t • Подставляя это выражение
и р = ^-2- в (7.70), получаем \
D[X] = —*2^ + *(A_i)(-^-^ <L> i
(a+&)2 \Д+*> e+b —1 (a+bf J
7.71*. На железнодорожную сортировочную станцию подается
состав, состоящий из m вагонов; из этих вагонов пг± направляется в ад- .
ресЛьт2 = вадревЛ2, ...,mft—в адрес Ak l ^пг^т). Вагоны
расположены в составе случайно безотносительно к их адресам. Если два .-
соседних вагона направляются в один и тот же адрес, расцеплять их
не нужно; если в разные —производится расцеп. Найти математичев- j
кое ожидание и дисперсию числа расцепов, которые придется произ- •)
вести, а также оценить (пользуясь правилом трех вигма) диапазон I
практически возможного числа расцепов. |
Решение. Рассмотрим т — 1 сцепок между вагонами как т —1 !
возможных позиций, на каждой из которых может произойти «рас- j
цеп» или «нерасцеп». Обозначим X случайную величину «число раеце- j
пов», a Y—«число нерасцепов»; Y = т — 1 —X. Проще будет ма- |
нипулировать с© случайной величиной У. Представим ее в виде суммы: |
Y = 2 Yu где |
У = П, если на 1-й позиции не производится расцеп;
1 ~~ [О, если производится
(индикатор нерасцепа на i-й позиции).
По теореме сложения математических ожиданий М [Y] = 23 М[У|1; I
/=i
М [Yt\ = qi9 где <ji —вероятность отсутствия расцепа на i-й позиции.
Все позиции в одинаковом положении: q± = д2 = ... = qmmul = q.
192
Вероятность q того, что на i-й позиции нет расцепа, равна вероятное™
гого, что два вагона, между которыми находится позиция,
направляются в один и тот же адрес. Складывая вероятности того, что эти
вагоны направляются в 1-, 2-, ..., &-й адрес, находим
тапц — Х) 1
/=1 /=1
Отсюда
М[Х] = т—1 -Y го,(т,—1).
т ffi
Так как величины X и V различаются на постоянную, D [X] =»
= D [УХ Дисперсию случайной величины У находим по формуле
(7.0.28) для дисперсии суммы:
Корреляционный момент случайных величин Yi% Yj находим по
формуле
K*t *,-М [У* У,]-М [Yt] M [У,] = М [У. К,]-?2.
Произведение У*К/ равно нулю, евли хотя бы на одной позиции есть
расцеп, и равно единице, если на обеих позициях нет расцепа; отсюда
Kti,rP{Yt-l,Y,-l}-f.
Находим вероятность того, что на обеих позициях (J-й и /-й) нет
расцепа. Эта вероятность различна в случае, когда позиции еаседние
(/ — / а 1) и не соседние (/ — I > 1). Обозначим эту вероятность,
когда позиции с©седние, дс, а не соседние qHG. Вероятность того, что на
двух соседних позициях нет расцепа, равна вероятности тог©, что г'-й»
(i + 1) -й и (t + 2)-й вагоны направляются в один адрес:
* «l(mi-l)(«i-2) д 1 -У m/(mr_l)(^_2).
^с ^ m<m —l):m—2) m(m—l)(m=*2) ^ ,v ' '
Для двух соседних позиций М1У^К,-1 = qG\ Ку.у. = ?0 —Я2-
Вероятность того, что на двух не соседних позициях (J —/ > 1) нет
расцепов, равна вероятности того, что каждая пара вагонов, между
которыми лежит данная позиция, направляется в один и тот же адрес.
Это может осуществиться в двух вариантах: либо все четыре вагона
направляются в один и тот же адрес (/-й), либо первая пара направляется
в/-й, а вторая —в r-й адрес. Вероятность первого варианта равна
«f(mf —l)(mi-2)(mt—3) RTnnnrn Щ (mt-\) mr (m.-1) Попняя веооят.
m(m-l)(m-2)(m-3) ' ВТ0Р0Г0m(m-1)(m-2) (m-3) ' 11олная веР0ЯТ
ность того, что на двух не соседних позициях нет расцепа, равна
7 Зак. 1040 193
*--,<«-i)<»U<m-3)[it «.(««-i)(m«-2)№_3)+
+ 2 m« (™i — 1) mr (mr — 1) .
гф1 J
Корреляционный момент /(#.*. для двух не соседних позиций равен
<?нс — Q2- С учетом количества соседних (т — 2) и не соседних (Cm_i —
— m + 2) пар позиций получим
D IX] - D 1К] = (m - 1) q (1 -9) + 2 (т —2) foe -g2) +
• +[(т-2)(т-3) -2(m-2)](qBG-q*y, ая«о,-VDIK].
Диапазон практически возможных значений X есть М IX] ± 3 ot.
Примечание: Весь расчет имеет смысл для т > 3. Если в формулах
для qG и qnc некоторые множители отрицательны, соответствующие члены
полагаются равными нулю.
Я(т)
7.72*. Производится ряд
опытов, в каждом из которых
некоторое событие А («успех») может
появиться или не появиться.
Условная вероятность того, что
событие А появится при m-м опыте,
если в предыдущих т — 1 опытах
оно не появилось, задана
неубывающей функцией R (т) (рив.
7.72)* >. Найти среднее число
опытов, которое будет произведено до
достижения успеха.
Решени е. Допустим, что опыты не прекращаются поеле
достижения успеха, а продолжаются. Каждый из них (кроме первого) может
быть «необходимым», если успех до сих пор еще не достигнут, и
«излишним», если успех уже достигнут. Свяжем е каждым (i-м) опытом
случайную величину Хь, которая равна единице, если опыт
необходим, и нулю, если он излишен.
Рассмотрим случайную величину Z —число опытов, которые
придется произвести до достижения успеха; она равна сумме всех
случайных величин Хь из которых первая Хх всегда равна единице (первый
опыт всегда необходим):
Z = Xt+2Xt.
Ряд распределения случайной величины Xt (i > 1) имеет вид
X,
О
1
R(l — l) l — R(i — l)
*) Функция R (т) задана только для целых т, но для наглядности на
рис. 7.72 точки соединены отрезками прямых*
194
(если успех уже был достигнут при предыдущих / — 1 опытах, *-й опыт
излишен; если нет —он необходим). Математическое ожидание
случайной величины Aj равно
М [X J = 0 • R И - 1) + 1 • 11 — R (i: — 1)1 - 1 —R (I — 1).
Очевидно, так же можно записать и М IXJ =М[11 = 1 — R (0);
отсюда
M\Z]=%[l-R(i-l)]= J [!—/?(*)].
7.73*. Для условий предыдущей задачи 7.72 найти дисперсию
количества опытов, достаточного для достижения успеха.
Решение. Случайные величины Хх, Х2, ..., X*, ... зависимы,
поэтому нельзя просто складывать их дисперсии. Найдем второй
начальный момент величины Z:
М[*] = мГ(;| Х£у1=м[ДхЛ+2МГ2ХгХЛ;
М[ХЛ = I2 • II —R(i — 1)1 ~ 1 -R(i —1).
Величина Х*Х^ принимает значение 1, если и Xt и X; равны
единице, т. е. оба опыта (*"-й и /-й) излишни. Для того чтобы оба опыта
(и *-й и /-й) были излишними, достаточно, чтобы излишним был более
поздний (/-й) опыт:
MWAI = Р{х* = 1, х7= 1} = 1 -/?(/'-1);
отсюда
M[Z2]=2 [i_^(/_i)] + 22[l-/? (/-!)].
Последняя сумма
у ц-д(/-1)1 = v '2 и_/?(/_i)] = 2 (/-пи-/?о-1)] =
= 2 A[l-«(ft)J;
отсюда
fe = i 6=1 U==0 J
7.74. Вероятность обнаружения объекта радиолокатором с ростом
числа циклов обзора п растет по экспоненциальному закону:
Р (п) = 1 — а» (0 < а < 1). (7.74).
Найти математическое ожидание числа циклов X, после которого
объект будет обнаружен.
7*
195
Решение; Полагая а = 1 —р, перепишем формулу (7.74)
в виде
Р(л) = 1 — (1 -р)\
из чего мы видим, что циклы независимы и вероятность обнаружения
объекта в каждом цикле равна р = 1 — а. При этих условиях
величинах имеет геометрическое распределение, начинающееся «единицы,
а ее математическое ожидание
МШ = Мр = 1/(1 — а).
Тот же результат можно получить, воспользовавшись решением
задачи 7.72:
7.75. Радиолокационная станция ведет наблюдение за областью
пространства, в которой находится п объектов. За один цикл обзора
станция обнаруживает каждый объект (независимо от других объектов
и других циклов) о вероятностью р. Сколько циклов понадобится для
того, чтобы 1) вероятность обнаружения всех объектов стала не
меньше Р и 2) среднее число обнаруженных объектов стало не меньше
данного т<Сп?
Решение. 1) Обозначим Gn (k) вероятность обнаружения всех
п объектов за k циклов; Gn (k) = [G (k)\ny где G (k) — вероятность
обнаружения одного объекта хотя бы один раз за k циклов. G (k) = 1 —
— (1 — р)\ откуда Gn (k) = 11 — (1 — р)Чп. Полагаем Gn (k) > Р\
(1 _(i —p)k]n<P; (1 _р)*<1 —VW\ k\g{\ _p)<lg(l _
n
— VP). Так как lg (1 -^p) < 0, то при делении на него знак неравен-
ства меняется на обратный:
k-v?)\
k>lg[l-VP fllgd-p).
2) Среднее число объектов М [X], обнаруженное за k циклов, по
теореме сложения математических ожиданий равно nil —(1 —р)к\.
Полагая п [1 —(1 —p)k] >/пи решая неравенство относительно
показателя k9 получаем
*>ig(i~)/ig<i-p).
7.76.*. Производится п независимых ©пытов в разных уеловиях;
вероятность появления события А в первом, втором и т. д. опытах
равна Piy Ра» •••» Рп- На© интересуют математическое ожидание и дисперсия
случайной величины X —общего числа появлений события Л. Для
упрощения вычислений вероятности pt осредняются и заменяются
одной, постоянной:
'=т!>
г 1
196
Верно ли будут вычислены М [X] и D[ X]?
Решение. М IX] будет вычислено верно:
Что касается дисперсии, то она будет завышена. Для
доказательства сравним приближенное выражение дисперсии
Dx = npq, где q=l—p «— У (l—pt)
п ы}\
с ее точным значением
п
А*= 2 Pi Яь где ?*= 1— Рг-
Преобразуем двумя способами сумму
S(Pi—Р)(<7* — <?) = 2 Pi^— 2р*?— 2 РЯ1+пРЯ=* ' '
л
2 (л~р)ta-?) = 2 (л-р)(1 -л-1 +р) = -is (/>*-р)2<о.
Отсюда
2 р* ч*—прч°-ох—Вх < о; D* > ц*
чт© и требовалось доказать. Заметим, что знак равенства в Dx ^ Dx
достигается только при рх = /?2 — ... = рп =* р.
7.77*. Доказать, что если Хх, Х2,..., Хп независимы,
положительны и одинаково распределены, то
М[14!,Х'Н
Решение. Так как все величины Х1% Х2, ..., Хп положительны,
то в знаменателе никогда не стоит нуль. По теореме сложения
математических ожиданий
М[,!Ч!Х'Ь!МК!4
Так как все величины Х19 Ха, ...» Хп распределены одинаково, то
м[х,/,1х']-мК/1х']
" 197
при любых I и т. Обозначим а их общее значение:
М[Х* /S */!-« ('=1.2 «).
Вместе с тем ясн®, что сумма всех величин вида Xt/^Xj равна единице,
следовательно, и математическое ожидание ее тоже равно единице:
м[,!Ч?,х'Ы,м[х' /,?/'] -L
Заменяя выражение, стоящее под знаком математического ожидания
п
через а, имеем %а = па = 19 откуда а = 1/л. Следовательно,
M[i, Ч! Х'Ь?, М[Ч! х'Ь!>=-ь
что и требовалось доказать.
7.78. Имеется п потребителей энергии, потребности которых за
единицу времени представляют собой независимые случайные величины
Xt, X2,..., ^п о одним и тем же (произвольным) распределением. Рас-
га
сматривается случайная величина Zt = Хг1^Хг (t = 1, ..., п)—доля
*'-го потребителя в суммарном потреблении энергии. Доказать, что при
любом i математическое ожидание случайной величины Zt равно Мп.
Решение. Ясно, что математическое ожидание величины Zt
существует, так как ее значение заключено между нулем и единицей.
Законы распределения всех случайных величин Z% (i = 1, ..., п)
одинаковы (в силу полной симметрии задачи), и их математические
ожидания равны: М [ZJ — М [Z23 = ♦.. = М fZJ. Так как сумма всех
случайных величин Zi равна единице, то сумма их математических
ожиданий также равна единице:
М Г 2 Х« 1 = 2 М Ш - *. т. е. /iM [Z,] =--1;
b=i J- *-i
M[Z,] = l//i (f = l,...fn).
7.79. Для построения равностороннего треугольника со стороной
а = 3 см пользуются следующим способом: из произвольной точки О
откладывают отрезок длины а; при нем строят угол, равный 60°;
затем на стороне этого угла онова откладывают отрезок длины а и
полученную точку соединяют g точкой О (рис. 7.79). Отрезки длины а
откладываются с помощью линейки с делениями по 1 мм; максимально
возможная при этом ошибка равна 0,5 мм. Угол откладывается с
помощью транспортира с максимально возможной ошибкой 1°. Пользуясь
методом линеаризации, найти математическое ожидание и среднее квад-
ратическое отклонение третьей стороны X.
198
Рис. 7.80
| Рис. 7.79
Решение. Обозначим фактическую длину первой стороны Хи
второй Х2, фактическое значение угла в. Эти случайные величины
можно считать независимыми. Имеем
X*=Vxt + Xi + 2XtXtco&e .
Пользуясь методом линеаризации, найдем
тх = Vml + т\% —2mXi тх, cos m® ,
где тХ{ = mXi = 30 мм, cos т$ — 0,5, откуда тх — V900 + 900—900;
= 30 мм. Далее
2£i4—*"ZX2
COS ft \ 1_
:х х2 cos О /m 2
\ d*i /т V 2 У*? + xf —2ЛЧ
/ d* \ _ / J 2х2—2xt cos ft \ 1_
\дх2 )т \2 ух2 + х2„2xtx%cos^ /т ~ 2 '
Л^Л = (-1-— 2win0 ) ^J^Z^isVSmm.
V dft Jtn \2 уХ2^Х2^2хх х2 cos ft /т 2
Вычисляем
Дисперсии аргументов нам не заданы, заданы лишь максимальные
практически возможные отклонения их от математических ожиданий:
Д*! = Д#2 = 0,5 мм; ДФ = 1° = 0,01745 рад. Полагая приближенно
оКх = ох_ = д^/3 = 0,167 мм, DXi = DXi = 0,0278 мм2, o$ =
= ДФ/3 = 0,00582 рад, D& = 3,39-10~б рад, получаем Dx = 0,25х
х0,0278-2 + 675-3,39* Ю-6 « 0,0368 мм2, ох « 0,192 мм.
7.80. Расстояние D от некоторой точки О до объекта R
определяется следующим образом: измеряется угол а, под которым виден объект
из точки О (рис. 7.80); далее, зная линейный размер объекта X и
считая угол оо малым, определяют расстояние п@ приближенной формуле:
D « X Л2 sin (а/2)] « Х/а.
Линейный размер объекта X, видимый из точки О, в зависимости ©т его
случайного пов®рота может изменяться в пределах от 8 до 12 м; угол
а определяется а точностью до 0,1 тыс. радиана. Расстояние D велико
по сравнению с размером объекта X. Найти приближенно среднее
199
квадратическое отклонение Gd ошибки в определении расстояния D,
если измеренное значение угла а равно одной тысячной радиана.
Решение. Применяя метод линеаризации, имеем
\ дх )т \ да 1т
Линейный размер X будем считать равномерно распределенным в
интервале (8; 12): ах = (12 — 8)/(2Т/3) = 2/V3 м, а\ = 4/3 м2;
т* = 10 м. Далее аа « -j 0,0001; а& = j Ю"8; та =» 0,001, откуда
oHi)>+(-f)>J-T-10,M-
aD=^lL. 10s = 1,20.10* м.
О
7.81. Имеются две почти линейные функции п случайных
аргументов: Y = ц>у (Х1э Х2,..., Xn); Z =? фа (Хх, Х2, ..., Хл). Даны
характеристики системы тх.у DXi (i ** 1,2,..., п) и корреляционная матрица
||JCfj||. Найти приближенно корреляционный момент /Cyz.
Решение. Линеаризуя функции ц>у и ф^, получаем
п
Y « фз, (т*„ тХг, ..., тХп) + ^
Z « Фг (т*,, т, /пЗСп ) + Д| ^ )m U;
отсюда
л"-"[«1-«Ц($).А|1Й1*]-
-;§(*).(a.*+2(3).&W
Последняя сумма водержит п (п — 1) членов; каждому Ки
соответствуют два члена суммы*
№.(%).*» ■ ттк»
7.82. Для определения расстояния R от точки К до начала
координат можно применить два способа: 1) определить расстояния X и Y
200
Xt;
до осей координат и. затем найти R по формуле
#х = VX2 + Y2; 2) измерить Столько расстояние
Y до оси абеиисс и угол а (рис. 7.82), затем
найти R п© формуле /?2 = Y/cos а. Нас интересует,
какой способ приведет к меньшей погрешности, е©-
ли расстояния X и У и угол а определяются с неза-.
висимыми друг от друга ошибками, причем
средние квадратические отклонения ошибок X, Y
равны ох = ау, а ошибки в угле — аа?
Привести чиеленный расчет для значений
средних квадратических ошибок ох = оу = 1 м; оа = Г = 0,0174 рад
при средних, значениях параметров, равных тх *=* 100 м; ту = 60 м;
та = arc tg (mjiriy) ж 59° « 1,03 рад.
Рис. 7.82
Решение:
D[/?JH
адх__
.^i _
1) -^1= ._
х*+у2
2)
lA2 + 02
1 . д/?2 _ у sin a #
dR2
ду
cos а
5а
cos2 а
D[tf2]=(—M og+f ^f а) (r|>0|;a2=VrD[^2]>(T1.
\cos2 a Jm \ cos2 a Jm
Для числовых данных задачи первый способ более точен:
„-о,- . »; *,=([> + (^)'] [1-+вс(^У 0,0174.])"'_3,9
м.
7.83. Система трех случайных величин X, Y9 Z имеет
математические ожидания тх = 10, ту = 5, /п2 = 3; средние квадратическиеот-
клонения ох = 0,1, ау = 0,06, а2 = 0,08 и нормированную
корреляционную матрицу
1 0,7 —0,3
1М1 = Н 1 0,6
1
Пользуясь методом линеаризации, найти математическое
ожидание и среднее квадратическое отклонение случайной величины U =
= (ЗХ2+ 1)/(У2 + 2 Z2).
Решение. ту = (3-100+1)/(25 + 2.9) = 301/43 = 7.
ди 6х
дх
ди
дг
y*+2z* '
(3*2+ 1) 4г
0/2+2z2)2
ди ^ (Зх2+1)2у m
ду т (y*+2z*)* *
\ дх )т
6-10
43
= 1 4-
201
iBu\ =_ 30Ы0 „_163/^\ в_ 30Ы2-1 _
V ty Уш (43)2 V/« (43)2
D [£/] == 1,42 • O.J2 + 1,632 • 0,06s + 1,952 0,082 +
+ 2 I—l,4«l,63.0,7*0,l-0,06 + 1,4-1,95 • 0,3 * 0,1 • 0,03 +
+ 1,63 • 1,95 • 0,6 • 0,06 . 0,08] » 0,066; ott « 0,26.
7.84. Производится параллельное соединение двух выбранных
наугад сопротивлений: R± и R2. Номинальное значение каждого
сопротивления одинаково и равно тг, = тГ2 = 900 Ом. Максимальная
ошибка в R при изготовлении сопротивлений равна 1 %
номинального значения. Определить методом линеаризации номинальное
значение сопротивления таког® соединения и его среднее квадратическое
отклонение.
Решение: /? = —* 2 = ер (Rl9 R2)\ mr = cp (тГ1. тг?) = 450 Ом;
o^-ori—LJ22-3 0m;(^) ■[ * 1 -JL;
' 3 100 Vi/m L Л+'г)2 Jm 4
2
d до = 2 ("It)* a'te т 0м2> °'«* '06 0м-
При этом максимальная ошибка будет 3,2 Ом, что составляет 0,7%
(а не 1 %, как было первоначально) номинала.
7.85. Резонансная частота колебательного контура /р определяется
из выражения /р = 1/(2 nVLC), где L — индуктивность контура,
С —емкость контура. Определить приближенно среднее значение
резонансной частоты контура и ее среднее квадратическое отклонение
если mi » 50 мкГн; тс = 200 пФ, oz = 0,5 мкГн и ос = 1,5 пФ.
Решение. mf = l/(2jiVm; mc ) = 1,59 МГц.
1 1
V *' )ш
-т*
2*m}/*mf'2 2 "Ъ 2тг '
J
2/з
mf
а'П 1 mf-±-
м*):ч*)>-^(з+4)-
-эд
«V-IO-*,
G/ =m, —.10-2= 1.0.10-2 МГц,
что составляет 0,62% номинальной частоты.
202
ГЛАВА 8
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
СЛУЧАЙНЫХ ВЕЛИЧИН. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
8.0* Если X — непрерывная случайная величина с плотностью / (ж), а
случайная величина Y связана с нею функциональной зависимостью
У = ф <*).
где ф — дифференцируемая функция, монотонная на всем участке возможных
значений аргумента X, то плотность случайной величины Y выражается
формулой
*(Ю"/(*(0Н*'«У)1. (8-0-0
где г|) — функция, обратная по отношению к ф.
Если ф — функция немонотонная, то обратная функция неоднозначна, и
плотность случайной величины Y определяется в виде суммы стольких
слагаемых, сколько значений (при данном у) имеет обратная функция:
k
§(У)= 2 f(b(y))\Vi(y)\> (8.0.2)
i= 1
где % (у), 4p2 (у)у ..., tyk (у) — значения обратной функции для данного у,
Для функции нескольких случайных величин удобнее искать не плотность
распределения, а функцию распределения. В частности, для функции двух
аргументов Z = ф (X, Y) функция распределения
G(z)= Jj* f(xfy)dxdy, (8.0.3)
D(z)
где / (*, у) — совместная плотность величин X, Y\ D (г) — область на плоскости
хОу, для которой ф (х, у) < z.
Плотность g (г) определяется дифференцированием G (z): g (z) = G' (г).
Плотность распределения суммы двух случайных величин Z = X + Y
выражается любой из формул:
ОО 00
g(z)= j f(x,z-x)dx; g(2)= J f(z-y,y)dy, (8.0.4)
— oo •—oo
где / {x, y) — совместная плотность распределения величин X, Y.
В частности, когда случайные величины X, Y независимы, / (*, у) = /i (x) X
X /2 (у) и
00
8 (г) = j" к (*) к (*-*) dx, (8.0.5)
«е— ОО
или
оо
5Г (г) = J /j (г—i/) /2 (у) dy. (8.0.6)
В этом случае закон распределения суммы g (г) называется композицией
ваконов распределения слагаемых ft (x), /2 (у),
Если случайные величины, подчиненные нормальному закону, подвергать
любому линейному преобразованию, то будут получаться снова случайные
величины, распределенные нормально* В частности, если случайная величина X
распределена нормально g параметрами mXt oXt то случайная величина Y = аХ+Ь
(где а, Ь неслучайны) распределена нормально с параметрами ту = атх + Ь\
°у = \a\aXi
203
При композиции двух нормальных ваконовх fa (x) в параметрами тх, ох и
h is) с параметрами ту, оу — получается снова нормальный закон с параметрами
тг*=тх+ту% о2=]/ <т* + а2 . (8.0.7)
При сложении двух нормально распределенных случайных величин X, У
с параметрами тх, ох> Щ, <*у и коэффициентом корреляции гху получается
случайная величина Z, также распределенная нормально, с параметрами
тг=*тх+ту; az =j/' o$ + ol+2rxyoxoy , (8.0.8)
Линейная функция от нескольких независимых нормально распределенных
случайных величин Х±, Х2, ..*, Хп
2=2 atXt + Ь,
где -Д|, b — неслучайные коэффициенты, также имеет нормальный закон
распределения с параметрами
£==1 f Г /— 1 '
где m^, аХ| — параметры случайной величины Xi (i = 1, ..,, я).
Если аргументы Xi, Х2, •••* ^ коррелированы, закон распределения
линейной функции остается нормальным, но с параметрами
mz= 2 «I «*!-+*!" a«el/ 2 «/<£+22 aiajr о g (8.0.10)
где rXixi—коэффициент корреляции величин Х^ Xj (i = 1, ,.♦,-я; (ФС).
Композицией двух нормальных законов на плоскости называют закон
распределения случайного вектора с составляющими X = Хг + Х2; Y = Yx + К2,
где (Хи Y±)t (Х2, К2) """• случайные векторы, не коррелированные между собой
Яри композиции двух нормальных законов на плоскости получают снова
нормальный закон с параметрами
°«-К^ + 0** °* = >Ч + <Ъ ; (8.0.11)
откуда
г*у в ('*, к °*. °* +г*2 a а** а*.)/<°* av>- (8-°-12>
При проектировании случайной точки (X, К), распределенной на плоскости
по нормальному закону, на ось 0zt проходящую через центр рассеивания и
составляющую угол а с осью 0х, получается случайная точка Z, распределенная по
нормальному закону с параметрами
mzt=mx cos a-{-my sin a;
ог = j/ oj cos2 а+а2 sin2 a+rxy ox oy sin 2a . (8.0.13)
Предельные теоремы теории вероятностей образуют две группы теорем:
1) закон больших чисел и 2) центральная предельная теорема. Закон больших
. чисел имеет несколько форм, каждая из которых устанавливает ту или иную
' устойчивость средних при большом числе наблюдений»
204
l.\ Теорема Я» Вернулли (простейшая форма закона больших чисел). При
неограниченном увеличении числа п независимых опытов, в каждом из которых
событие А появляется с вероятностью /?, частота Рп события А сходится по
вероятности к вероятности р этого события:
Ит
р<1^-
р|<е}= 1,
(8.0.14)
где е — сколь угодно малое положительное число*
2. Теорема Пуассона. При неограниченном увеличении числа п
независимых опытов, в которых событие А появляется с вероятностями рь р2, .„, рп,
частота Рп события А сходится по вероятности к средней вероятности события:
lim P
П-»оо
-г 2
Pi
:\
= 1.
(8.0.15)
3. Теорема Чебышева (закон больших чисел). При неограниченном
увеличении числа п независимых опытов, в каждом из которых случайная величина X
с математическим ожиданием тх принимает какое-то значение Xj, среднее
арифметическое этих значений сходится'по вероятности к математическому
ожиданию случайной величины X:
lim P
1
2
1= 1
Xi
<е\=\
(8.0.16)
4. Теорема Маркова (закон больших чисел для разных условий опыта). Если
Хп — независимые случайные величины с математическими ожида-
Xi, Х2,
ниями mv . m¥
тх и дисперсиями D
0Хг,»,Ох.
п, причем все дисперсии
ограничены сверху одним и тем же числом L: Dx. < L (i = l, ..., п), то при
неограниченном возрастании п среднее арифметическое наблюденных значений
случайных величин сходится по вероятности к среднему арифметическому их
математических ожиданий:
lim P
п
2
/=1
Хг
-^s.
<8 =1
(8.0.17)
При оценке скорости сходимости по вероятности различных средних к
постоянным величинам можно пользоваться неравенством Чебышева:
Р {| X—тх | > а} < Dx/a?9 (8.0.18)
где а > 0; тх, Dx — математическое ожидание и дисперсия случайной
величины Х4
Центральная предельная теорема имеет различные формы, из которых мы
приводим три.
1. Теорема Лапласа* Если производится п независимых опытов, в каждом
из которых событие А имеет вероятность р, то при п ->• оо закон распределения
случайной величины X — числа появлений события — неограниченно
приближается к нормальному закону с параметрами т = пр\ о = "\/npg (q = 1 — р).
На основе этого можно вычислить вероятность попадания величины X на
любой участок (а, Р): при достаточно большом п
""-•-'(-TtMiJt)-
(8.0.19)
Вместо формулы (8*0.19) часто пользуются выражением для вероятности
попадания на участок не самой случайной величины X, а нормированной велили.
ны
Z= (X—тх)/ох~ (X— np)/~]/npq\ w2=0s az = l.
205
При достаточно большом п
Р {Z е (а, р)} « Ф (Р) - Ф (а), (8.0.20)
2. Центральная предельная теорема для одинаково распределенных
слагаемых. Если Хъ Х2, ..., ^п — одинаково распределенные независимые случайные
величины с математическим ожиданием тх и средним квадратическим отклоне-
п
нием ох, то их сумма Y*= У\ Xt при достаточно большом п имеет приближенно
нормальное распределение с параметрами
ту*=птхьоу='\/п~ ох. (8.0.21)
3. Теорема Ляпунова. Если Xit Х2> *.., Хл — независимые случайные
величины, имеющие математические ожидания mXi, тх^ .*«, тХп и дисперсии DXJ
Dx9 ..., DXji причем выполняется ограничение
^[J,^/(J,s)3/2]=o. (В.0.ЭД
л
где ^j=M| | Х||3], то случайная величина К= 2 ^£ ПРИ достаточно большом
я имеет приближенно нормальное распределение с параметрами
/г / п
/ =1 1 У != 1 г
- Смысл ограничения (8.0*22) в том, чтобы случайные величины были
сравнимы по порядку своего влияния на рассеивание суммы.
ЗАДАЧИ И УПРАЖНЕНИЯ
8.1. Непрерывная случайная величина X имеет плотность / (х)
Найти плотность g (у) случайной величины Y = аХ + 6, где а и Ь
не случайны.
Решение. Так как функция ср (х) = ах + Ь монотонна,
применяем формулу (8.0.1). Обратную функцию я|э (у) находим, разрешая
относительно х уравнение у = ах + Ь\ получим г|) (у) = (у — Ь)1а.
Находим г|/ (у) = 1/д; |г|/ (*/) I = 1/ И;
8.2. Случайная величина X распределена равномерно в интервале
(—я/2; я/2). Найти закон распределения случайной величины Y =
= sin X.
Решение. Функция у = sin х в интервале (— я/2; я/2)
монотонна, поэтому плотность распределения величины Y может быть
найдена по формуле (8.0.1): g (у) = / (ф {у)) |ф' (г/) |. Решение задачи
удобно располагать в виде двух столбцов: слева писать обозначения
функций, принятые в общем случае; справа — конкретные функции,
соответствующие данному примеру:
206
/ (x) \ I 1/я при х е (—л/2; я/2)
y=(f\[x) y = sinx
x = i|>(*/) # = arcsin у
V (У) 1/УГ=?
g (У) = / (^ (if)) *' (У) I «Г (У) = 1 /(я УГ=р) n(fflj6(-1; 1).
Интервал (—1; 1), в котором лежат значения «случайной величины
У, определяется областью значений функций у = sin x для
х£ (-я/2, я/2)*>.
8.3. Случайная величина X распределена равномерно в интервале
(— я/2; я/2). Найти плотность g (у) случайной величины У = cos X.
Решение. Функция у = cos x немонотонна в интервале
(— я/2; я/2). Решение будем составлять аналогично предыдущему с той
разницей, что в данном случае для любого у обратная функция будет
иметь два значения 1см. (8.0.2)]. Решение снова оформляем в виде
двух столбцов:
1 /я при хе(—я/2; я/2)
у = ч (х)
(У)
пшикам
1ы
g(0) = 2/(4>*(y))|4>;u/)|
у = cos х
*i= —arc cos у
x2 = arccos у
1/Vl-//2
й(0) = 2/(яУГ=р)при у.
(ОД)
8.4. Случайная величина X распределена равномерно в интервале
(— я/2; я/2). Найти плотность распределения случайной величины
У = | sin X \.
О т в е т. g (у) = 2/(яУ1 — у2) при у € (0,1).
8.5. Случайная величина X имеет плотность распределения / (х).
Найти плотность распределения случайной величины У = | 1 —Х\.
Решение. Функция у = |1 —х\ —немонотонная. Решение
будем составлять так же.как в задаче 8.3:
у = <р(х)
8(У)°=2КЪ(УЩ(У)\
i=i
у = \1-х\ ч
*i=i—г/
хг^1+у
1
g (#) = / (!—{/) + /(! + У) при #>0
* В дальнейшем при решении аналогичных задач мы всюду, как и здесь,
будем писать выражение плотности только на участке, где она отлична от нуля,
подразумевая при этом, что вне этого участка она равна нулю*
207
+ exp
8.6. Непрерывная случайная величина X имеет плотность fJ (x).
Рассматривается величина Y = — X. Найти ее плотность fy (га-
Ответ. fy (у) = /*(—#). /
8.7. Непрерывная случайная величина X имеет равномернре
распределение на участке (а, Р) ф > а). Найти распределение
величины 7 = — X.
Ответ. Равномерное на участке (— р, —а).
8.8. Непрерывная случайная величина X имеет плотность /* (х).
Н айти плотность fy (у) ее модуля Y = | X |.
Ответ. /^ (у) «= /* (— у) + fx (у) при у > 0.
8.9. Случайная величина X распределена нормально а
параметрами тх, ох. Написать плотность распределения ее модуля Y = |Х|.
В частности, каков будет этот закон распределения при тх = 0?
(y-m*)2j| при у >0 Если Шзс==о, то
/v(^)=—~т=ехр [~-siiri при #>а
олТ/2л \ ^аl /
8.10. Круглое колесо, закрепленное в центре 0 (рис. 8.10),
приводится во вращение, которое затухает вследствие трения. В результате
фиксированная точка А на ободе колеса останавливается на некоторой
высоте Н (положительной или отрицательной) относительно
горизонтальной линии / — /, проходящей через центр колеса; высота Н
зависит от случайного угла 0, при котором остановилось вращение. Найти:
1) закон распределения высоты Н\ 2) закон распределения
расстояния D от точки А до прямой / — / (считая это расстояние всегда
положительным).
Решение. Н = г sin 0, где угол 0 — случайная величина,
распределенная равномерно в интервале (0; 2я). Очевидно, решение
задачи не изменится, если считать случайную величину 0 распределенной
равномерно в интервале (— я/2; л/2); тогда Н является монотонной
функцией 0.
Плотность распределения величины Н равна
g (h) = (яг}/"1 _ (т)2 ) ПрИ ~Г < h < П
Плотность распределения величины D = \Н\ равна
§1^) = 2^дгт//Г1-Ш2 У при Q<d<r.
8.11. Случайная величина X распределена по закону Рэлея с плот-
ностью / (х) = ц; exp f — ~\ при х > 0. Найти плотноеть g (у)
величины Y а е~А\
208
VeIC!>(-T5>>0)
P\e ш е н и е. На участке возможных значений аргумента функция
у = е^-х' монотонна. Применяя общее правило, получаем
fix)
У = Ч>(х)
х = Ц(у)
g(y)=f№(y))\V(y)\
х — У — In у
(2уУ=ШуГ
g(y) = -
I— 2а*
ехр
(JBJL)-
= ~^У 2°* при0<у<1
Графики g {у) при разных о приведены на ряс. 8.11.
/ У
Рис. 8.10
Рис. 8.11
8.12. Случайная величина Хг распределена по закону Коши с
плотностью f (х) = [я(1 + я2)]-1 (— оо <с х < схэ). Найти плотность g (у)
обратной величины У = 1/Х.
Решение. Учитывая, что, несмотря на разрывный характер
функции у = l/х, обратная функция х = 1/у однозначна, и решая
задачу по правилам для монотонной функции, получаем
gfr)" г ! 1 п, -т-илиз(у)=» „/Л,* (—00<У<00)>
г ' П2 |/а я(1 + #2)
■['♦тГ
т. е. величина, обратная величине, распределенной по закону Коши,
также имеет распределение Коши.
8.13. Через точку А, лежащую на оси Оу на расстоянии 1 от начала
координат, проводится прямая АВ под углом а к оси Оу (рис. 8.13)*
Все значения угла а от — я/2 до л/2 равновероятны. Найти плот*
ность распределения g (x) абсциссы X точки В пересечения прямой
е осью абсцисв.
Решение." X = tg а; эта функция монотонна на участке
— я/2 < а < я/2. Имеем g (х) « [я (1 + х2)}"1 (— оо < * < оо),
т. е. случайная величина X распределена по закону Коши.
209
2
0,1
— 1 | 0
0,2 | 0,3
1
0,3
2
0,1
8.14. Дискретная случайная величина X имеет ряд распределения
X:
Построить ряды распределения случайных величин Y — Хг 4- 1;
Z = |Х|.
Решение. Определяя для каждего X соответствующие
значения величин Y и Z и располагая их в возрастающем порядке, получаем
ряды распределения
Y:
1
0,3 0,5
0,2
Z:
0
0,3
1
0,5
2
0,2
8.15. Через точку А с координатами (0; 1) проводится прямая АВ
под случайным углом в к оси ординат (рис. 8.15). Закон
распределения угла в имеет вид / (9) = 0,5 cos Ф при — л/2 < Ф < л/2. Найти
закон распределения расстояния L от прямой АВ до начала координат.
Решение. Имеем L = | sin 9|. Функция / = | sin ftl на
интервале (— л/2, л/2) немонотонна. Применяя обычную схему для
немонотонной функции, получаем
g (/) = у—— cos (arc sin /)
или, имея в виду, что cos (arc sin /) = Vl — /2, g (I) = 1 при / g (0, 1),
т. е. расстояние L распределено равномерно в интервале (0; 1).
8.16. Радиус круга R —случайная величина, распределенная по
закону Рэлея:
/Cr)-^«p(_-£-)npiir>0.
Найти закон распределения площади круга S.
Решение. Функция S = л/?2 на участке возможных значений
i? (0, оо) монотонна, следовательно,
*(e)—^^(—sb) при8>0,
т. е. закон распределения площади круга есть показательный закон е
параметром 1/(2 ла2).
8.17. Случайная величина X имеет функцию распределения F (х);
случайная величина Y связана с нею функциональной зависимостью:
Y = 2 — ЗХ. Найти функцию распределения F(y) случайной
величины У.
Решение,
?te)=P{i'<rt-P{2-3X<»)_p{x>-2=t}=
^ 210
Если случайная величина X непрерывна, то вероятность того, что
она примет любое отдельное значение, равна нулю, и
rut-i-F(2=L).
Если величина X смешанная или дискретная, то Р\х =—«-[
может быть отлична от нуля и равна скачку функции F (х) в точке
(2 — у)/3\ таким образом, в общем случае
8.18. Имеется непрерывная елучайная величина X с функцией
распределения F (х) (рис. 8.18). Найти и построить функцию распредели
ния G (у) случайной величины У = |Х|.
Рис. 8.15 Рис. 8.18
Решение. При X > 0 получим Y = X; при X <С 0 получим
К = —X.
G(y) = P {Y<y} = P{\X\<y}.
При у < 0 получим G (у) = 0; при у > 0 получим G (#) =
= Р {—у< X < y} = F (y)—F (—у). Функция G (у) построена
пунктиром на рис. 8.18 [далее она сливается с F (х)].
8.19. Смешанная случайная величина X принимает два значения с
отличными от нуля вероятностями: отрицательное (—х±) с
вероятностью рг и положительное (х2) с вероятностью р2. В промежутке ^ежду
— хг и х2 функция распределения F (х) непрерывна (рис. 8.19, а);
x1<Z х2. Найти и построить функцию распределения G (у) случайной
величины Y = \Х\.
Решение. При у < 0 получим G (у) = 0 (рис. 8.19, б); при
у > 0 получим G (у) = Р {— у < X < у} = F (у) — F (—у).
Чтобы построить G (у)у нужно из каждого значения F (у) вычесть его
значение в зеркально отраженной от оси ординат точке —у (см.
рис. 8.19, б, где F (х) показана штрих-пунктиром, a G (у) — сплошной
линией). Функция G (у) будет иметь два скачка в точках—хг и х2,
равные соответственно рг и р2.
211
Wfi(v)
Рис. 8.19
8.20. Случайная величина X имеет нормальное распределение о
параметрами тио (рис. 8.20, а). Найти и построить плотность
распределения g (у) её модуля Y = |Х|.
Решение. Чтобы построить плотность случайной величины У,
нужно к каждой ординате кривой распределения / (х) прибавить
ординату, соответствующую значению плотности в точке — х
(см. 8.20, а). При т = 0 ординаты плотности / (я) удваиваются
(рис. 8.20, б).
\fM,ff(y)
Рис. 8.20
8.21. Случайная величина X имеет нормальное распределение с
параметрами т = 0, а. Найти и построить плотность g (у) случайной
величины Y = X2.
Решение, /(*)= *— expf—^Л У = Ф(Х) = Х2.
Обратная функция для у = х2 имеет два значения: хг = — Vy и х2=*
*= + Vyl По формуле (8.0.2)
+exp(""t)}="Wexp(~^")npHi/:>G-
812
При у = О плотность g (у) имеет точку разрыва 2-го рода (уходит на
бесконечность, см. рис. 8.21).
8.22. Имеется непрерывная случайная величина X о плотностью
/ (я). Найти закон распределения случайной величины
[+' при Х>0;
y = signX = о при Х = 0;
[— 1 при Х<0,
и ее числовые характеристики: ту и Dy.
Решение. Дискретная случайная величина У имеет всего два
значения: — 1 и +1 (вероятность того, что У = О, равна нулю).
Р{У = - 1} = Р {X < 0} = ) f (x) dx = F (0);
—-оо
Р {У = + 1} = Р{Х>0} = 1 —F(0Y,
ту - — \.F (0) + 1 * [1 — F (0)] = 1 — 2 F (0);
ос2[У) = LF(0)+ 1 . [1 -740)1 = 1;
Dy = a2 [У] — ml = 4 F (0) [1 -740)1,
где F (я) — функция распределения.
8.23. Имеется непрерывная случайная величина X с плотностью
f(x). Найти закон распределения случайной величины У = min {X9 X2},
т. е. величины, равной X, если X < X2, и X2, еслиХ2 < X.
Рис. 8.21
Рис. 8.23
Рис. 8.24
Решение. Функция у = q> (x) монотонна (показана сплошной
линией на рив. 8.23):
\х2 при х 6 (0, 1);
[х при х^(0, 1).
Так как интервал (0; 1) оси Ох отображается на интервал (0; 1) оси 0у9
то по общему правилу
Ф(х) = Г
0liA=\f(V7)№Vy) при г/ € (0,1);
BW I f(y) привад.
213
8.24. Случайная величина X имеет плотность / (я), заданную
графиком (рие. 8.24). Случайная величина Y связана с X зависимостью
у = 1 — X2. Найти плотность g (у) величины Y.
Решение. Плотность / (х) дается функцией / (х) = 0,5 (х + 1)
при х £ (— Ь + 1). Функция у = 1 —л:2 на этом участке
немонотонна; обратная функция имеет два значения: х1 = — Vl —у, хг =
= + Vl —у. Отсюда
g(y) = (4 V ь^Г1 [(1 - /T=^)+(i + уТ^")]
или
g (У) = (21/1 -г/)-1 при 0<# < 1.
8.25. Случайная величина X имеет плотность / (х). Найти
плотность g (у) обратной ей случайной величины Y = 1/Х.
Решение. Функция у = Их хотя и немонотонна в обычном
смысле слова (при х = 0 она скачком возрастает от — оо до + оо),
но обратная функция однозначна, значит, задача может быть решена
так, как она решается для монотонных функций:
*>='Ш
при тех значениях у, которые могут быть обратными заданной
совокупности возможных значений х.
8.26, Логарифмически нормальное распределение. Натуральный
логарифм некоторой случайной величины X распределен по
нормальному закону с центром рассеивания т и средним квадратическим
отклонением а. Найти плотность распределения величины X.
Решение. Обозначим нормально распределенную величину
[/. Имеем
I/-I.XS Х.е- ,,„,=-^ехр[-<^].
Функция е" монотонна;
/ ч 1 Г (1п д:— т)2 1 1
£(*)= ехр - '— — =
= ■ ехр 0 2 прих>0.
Такое распределение величины X называется логнормальным.
8.27. Пятно Я, изображающее объект на круглом экране
радиолокатора, может занимать на нем произвольное положение (рие. 8.27),
причем плотность распределения координат (X, Y) пятна в пределах
экрана постоянна. Радиус экрана равен г0. Найти плотность
распределения расстояния R от пятна до центра экрана.
Решение. Найдем функцию распределения G (г) = Р {R <г}=*
= Р { (X, Y) £ Кг}> где Кг— круг радиуса г g центром в точке 0.
214
Так как в пределах экрана плотность распределения постоянна, то
вероятность попадания в круг равна его относительной площади:
G (г) = (дг2)/(яг§) = (г/г0)2, откуда
g (г) = G' (г) = 2rlrb при О < г < г0.
8.28. Случайная величина X распределена равномерно в
интервале (0; 1). Случайная величина Y связана с X монотонно возрастающей
функциональной зависимостью Y = ф (X). Найти функцию
распределения G (у) и плотность g (у) случайной величины У\
Решение. Имеем / (х) = 1 при х £ (0; 1).
Обозначим \|) (у) функцию, обратную по
отношению к функции у = ф (х). Так как ф (х)
монотонно возрастает, то g (у) = / (ф (t/))i|/(#) = i|/ (t/),
откуда G (у) = г|) (у), т. е. искомая функция
распределения есть обратная по отношению к
функции ф (в области возможных значений величины Y).
8.29. Какому функциональному
преобразованию надо подвергнуть случайную величину X,
распределенную равномерно в интервале (0; 1), чтобы получить
случайную величину У, распределенную по показательному закону
g(f/)==^e-^ (t/>0)?
Решение. На основании решения предыдущей задачи мы
должны положить Y = G"1 (X), где G"1 — функция, обратная требуемой
функции распределения G (у) случайной величины У. Имеем
у
G (у) = С Хе-ьу dy = 1—е-** (у > 0).
о
Полагая 1 — е~х* = х и разрешая это выражение относительно у,
получаем обратную функцию у= (X)-1 In (1 — х)\ откуда искомая
зависимость будет
Y = (X)'1 In (1 — X) (0 < X < 1).
8.30. Случайная величина X распределена по показательному
закону fx (х) = X е~Кх (х > 0). Каким функциональным
преобразованием можно превратить ее в случайную величину У, распределенную
по закону Коши: /2 (у) = [п (1 + у2)]"1.
Решение.
М*)=1-е^ (*>0); F2(y) = ±\arctg у + -|-J.
1 Г л1
Полагая — are tg у + у = и и разрешая эту функцию
относительно у, найдем обратную функцию F%x (и)г
у = F~\ (и) = tg (пи •— л/2) = — etg ziu.
По решению предыдущей задачи получим
Y *= Ft» (Fx (X)) - — ctg я (1 — е-") = etg п е^Л (X > 0).
216
8.31. Двое условились встретиться в определенном месте в
промежутке времени от 12.00 до 13.00. Каждый приходит на место встречи
независимо от другого и с постоянной плотностью вероятности в любой
момент назначенного промежутка. Пришедший раньше ожидает
другого. Найти распределение вероятностей времени ожидания и вероятность
того, что ожидание продлится не менее получаса.
Решение. Обозначим моменты прихода двух лиц Тг и Т2;
за начало отсчета времени выберем 12 ч. Тогда каждая из независимых
случайных величин Ти Т2 распределена с постоянной плотностью в
промежутке (0; 1). Случайная величина Т — время ожидания: Т =
= |Ti-T,|.
Рис. 8.31 Рис. 8;32
Найдем функцию распределения G (t) этой величины. Выделим на
плоскости tx0t2 область D (t), в которой \1г— £2|< t (заштрихованная
область на рис. 8.31). Функция распределения G (t) в данном случае
равна площади этой области: G (/) = 1 — (1 — t)2 = t (2 — t)9
откуда g (t) = 2 (1 — t) при 0 < t< 1.
P {T > 1/2} = 1 — G (t/2) = 0,25. -
8.32. Случайная точка (X, Y) распределена равномерно в квадрате
К со стороной 1 (рис. 8.32, а). Найти закон распределения площади
S прямоугольника R со сторонами X, У.
Решение. Выделим на плоскости хОу область D ($), в пределах
которой xy<Ls (рис. 8.32, б). Функция распределения в данном
случае равна площади области D (s):
1 1
C(s)=l— ff dxdy=l — ^dx J d*/ = s(l —Ins).
D (s) s s/x
Отсюда g (s) = Gl (s) = — In s при 0 < s < 1.
8.33. Случайная величина Х распределена по нормальному закону
с параметрами m = 0, а. Найти закон распределения обратной ей
величины Y = XIX.
Решение. #=ф(х)= 1/х; обратная ей функция однозначна*
х *= My. По общему правилу
g(y) = expf j или g(y)~ expf :—}.
При у = 0 плотность g (у) имеет разрыв 2-го рода (см. рис. 8.33).
216
Любопытно отметить, что случайная величина Y не имеет
математического ожидания — соответствующий интеграл расходится.
8.34. Система случайных величин (X,Y) имеет совместную
плотность / (я, у). Найти плотность g (z) их отношения Z = YIX.
Решение. Зададимся некоторым значением z и построим на
плоскости хОу область D (z), где — < z (рис. 8.34 — заштрихованная
область). Функция распределения
О оо оо ZX
G(z) = Jj f(x,y)dxdy= J" dxl fix, y) dy+\dx J f(x,y)dy.
D(Z) ~ -*oo ZX 0 e»oo
Дифференцируя по z, имеем
О со
g(z) = — f xf(x, zx)dx+ [xf(xy zx)dx.
eaoo U
Если случайные величины X, Y независимы» то
О оо
g (s) = — ^ xh (х) /2 (zx) dx -f- J xft (x) /2 (z*) d*.
**» oo
№ •
Рис. 8J4
8.35. Найти закон распределения отношения Z—YIX двух
независимых нормально распределенных случайных величин X>Y g
характеристиками тх =» Шу = 0, азе, ау.
Решение. Рассмотрим сначала частный случай ax =; ay = 1.
На основании предыдущей задачи
*— оо
оо
1 2л
оо
-V<H-2*>
xdx =
1
Я (1+22)
(закон Коши).
217
В общем елучае отношение Z = XIY можно представить в виде
Z = (У^УСХха*), где величины Хг = Х1ах и Yx = Yloy имеют уже
нормальные распределения с дисперсией, равной 1; поэтому
g{z)
л[1+(ожг)аа-й] ау
В частности, если ох = оу,
g (z) - [я (1 + 22)]"1.
8.36. Случайная точка (Х,У) распределена равномерно в круге
К радиуса 1. Найти закон распределения случайной величины Z=
= Y/X.
Решение. В данном случае G (z)есть относительная площадь
области D (z) (рис. 8.36):
G(2)=JL(arotgz+ -£-),
откуда g (z) = G'J (z) = [я (1 + z2)]~l (закон Коши).
8.37. Закон Эрланга 2-го порядка. Составить композицию двух
показательных законов а параметром X, т.е. найти закон
распределения суммы двух независимых случайных величин Хг и Х2, имеющих
плотности
fi(*i) = te^** (*i > 0); h (х2) = Хе- **, (*2 > 0).
Р е ш е н и е. По общей формуле (8.0.5) для композиции
распределений имеем
оо
g(z)= I /х fo) /2 (z — xj Жсг.
— 00
Так как функции /t и /2 равны нулю при отрицательных значениях
аргументов, интеграл принимает вид
г z
g(z) ^U(x1)f2(z—x1)dx1^K^e-^e-K^^x^^xl=Vze^z (z>0).
о о
(8.37)
Закон с плотностью (8.37) называется законом Эрланга 2-го
порядка. Условия его возникновения следующие. Пусть на оси Ot имеется
простейший поток событий g интенсивностью А, и в этом потоке
сохраняется только каждая 2-я точка (событие), а промежуточные
выбрасываются. Тогда интервал между соседними событиями в разреженном
таким образом потоке есть закон Эрланга 2-го порядка.
8.38. Закон Эрланга п-го порядка. Составить композицию п
показательных законов с параметром X, т. е. закон распределения
суммы п независимых случайных величин Х1$ Х2,...,ХП, имеющих
показательное распределение с параметром X.
Решение. Можно было бы решить эту задачу, находя
последовательно композицию двух (см. задач. 8.37), трех и т. д. законов, но
218
проще решить задачу исходя из простейшего потока событий, сохраняя
в нем каждую п-ю точку и выкидывая промежуточные (рис. 8.38, а).
п
Х = 2^ь где Xt — случайная величина, имеющая показательное
распределение. Найдем плотность fn {х) случайной величины X;
сначала найдем элемент вероятности fn (x) dx. Это есть вероятность того,
что случайная величина X попадет на элементарный участок (#, х +
+ dx). Для этого нужно, чтобы на участок х (рис. 8.38, б) попало ровно
п — 1 событий, а на участок dx — одно событие; вероятность этого рав-
Рис. 8Я6 Рис, 8.38
на fn (х) dx = Рп_х X dx, где Рп_х — вероятность того, что на участок х
попало п— 1 событий. Но число событий простейшего потока,
попадающих на участок*, имеет распределение Пуассона а параметром а = Хх>
отсюда
fn(x)dx^M^Xd^dxi
- (/г—1)!
М*)- \(М"Г е-*" (х>0). (8.38.1)
(/г—1)!
Закон распределения о плотностью (8.38.1) называется законом Эрлан-
га п-го порядка-
Функцию распределения Gn (x) для закона Эрланга я-го порядка
можно было бы искать, интегрируя (8.38.1) от 0 до я, но проще вывести
ее выражение опять-таки пользуясь простейшим потоком:
Gn (х) = Р {X < х) - 1 - Р {X > х).
Для того чтобы выполнялось событие {X > *}, нужно, чтобы на
участок х попало не более п — 1 событий» т. е. 0,1,2, ...а п— 1 событий;
отсюда
Gn (х) = 1 - J -^р- е*** (*> 0). (8.38.2)
/72 = 0
Выражение (8.38.2) можно свести к табулированной функции R (т, а)
(см. приложение 2):
Gn (x)= l — R(n—UXx).
219
8.39. Обобщенный закон Эрланга. Составить композицию двух
показательных законов с разными параметрами:
fi(*i) = ^iе-** * (Хг>0); /2(х2) = \е~*. ** (х, > 0).
Решение. Обозначим X = Хг + Х2, где Xt> Xa распределены
по законам fx (хг), /2 (*2).
Согласно общей формуле для композиции законов распределения
оо
8 (*) - IЛ (*i) /2 (* — *г) dXi-
—оо
Но в нашем случае оба закона отличны от нуля только при
положительном значении аргумента; значит, fx (хх) = 0 при хх < 0 и /а (х — хх)=
= 0 при хх > х. При х > 0
* —л
Л*2 — Л» j
■J
1 » {Х>0)
(обобщенный закон Эрланга 2-го порядка). При ^ = Х2 = А,, раскрыв
неопределенность, получим закон Эрланга 2-го порядка:
g(x)=* №хе-ь* (х>0).
Примечание! Методом математической индукции можно доказать, что
закон распределения суммы п независимых случайных величин Х% Хп%
подчиненных показательным законам распределения с различными параметрами
h±t •♦*, 2tn, Ti е. обобщенный закон Эрланга я-го порядка, имеет плотность
п п —>Х. х
gn(x)=(-\)n-1 П h 2 -рг (*>0)-
п
(Запись П означает, что берется произведение всех биномов вида %j — А,& при
k = 1, 2, ..., /— 1, /+1, •«», я, т. е. кроме Xj —Xj*) В частном случае, корда
%1 = ikf
/=1
Функция распределения обобщенного закона Эрланга л-го порядка имеет
вид
п п 1 —*V. л:
o»M=-(-i)»-1 П ь* И г^ <*>о).
22Г
Если %t = (к, то
<?n(*)=S C-D7"1 С' [l-e-^*J (лг>0).
Если Af = X.2 = ••• = Xn=A,f то получаем закон Эрланра п-го порядка:
где
aw
Ш и
Р(т,а)=—— e~a; R(mfa) = 2i ТГ е^а (приложения 1,2).
8.40. Закон распределения максимальной из двух случайных
величин. Имеются две случайные величины X, У в совместной плотностью
/ (я, у). Найти функцию распределения G (г) и плотность
распределения g (z) максимальной из этих двух величин: Z = max {X, Y}.
Решение. Будем искать функцию распределения случайной*
величины Z: G (z) =* р {Z <; z}. Для того чтобы максимальная из
величин X, Y была меньше г, нужно, чтобы каждая из этих величин
была меньше z:
б(г) = Р {Х<г% Y<z}=*F(z, г),
где F (х, */)=* § J /(#, у) d*d#.
Ч-йОО <»00
Таким образом,
2 Z
G(z)= J J f(x,y)dxdy.
-WOO -ЧОО
Чтобы найти плотностьg (z), продифференцируем G (г) по величине
z, входящей в пределы двойного интеграла. Дифференцировать будем
как сложную функцию двух переменных zx и za, из которых каждая
зависит от z (zx = zt z2 =* z).
.д<3(г) dzt
6900 SSOO
В частном случае» если величины X, Y независимы, .((х, у) «*
-Л W'/а (У), то
8 (z) * /. (z) f h (У) dy + h (?) f ft (x) dx,
—00 —00
221
или, более компактно,
g (z) « f, (г) F2 (г) + ft (z) F, (г).
Если случайные величины X и Y независимы и одинаково
распределены, то Д (х) = /2 (х) = / (х) и g (г) = 2/ (z) F (г).
8.41. Закон распределения минимальной из двух случайных величин.
Система двух случайных величин (X, Y) имеет совместную плотность
/ (я, у). Найти функцию распределения G (м) и
плотность распределения g (и) минимальной из
этих двух величин: U = min {X, Y}.
Решение. Будем искать дополнение до
единицы функции распределения
1 _ Q (и) = Р (U > и) =
= Р {Х>и, Y>u}.
Это есть вероятность попадания случайной точки
Рис. 8.4! (X, К) в область D (и), заштрихованную на рис.
8.41. Очевидно, 1 — G (и) =* 1 — F (й, со)—
— У7 (оо, и) + F (и9 и), откуда G (и) = F (и, оо,) + F (оо, и) —
— F (и, и) = Т7! (м) + F2 (и) — F (и, и). Дифференцируя по ц, имеем
{см. задачу 8.40).
и и
g (и) = ft (и) + /а (и) — { / (и, y)dy— j* / (x, ы) d*.
—оо —оо
В случае, когда величины X и Y независимы,
g (и) = h (и) [1 - F2 (и)} + h (и) 11 - Л (и)].
Если случайные величины X и К независимы и одинаково
распределены, f± (х) = /2 (х) = /W и^ (и) = 2/ (ы) [1 - F (и)}.
8.42. Закон распределения максимальной и минимальной из
нескольких случайных величин. Имеется п независимых случайных величин
Х1э Х2, ..., Хп, распределенных по законам с плотностями fit(xi)9
/2 (^г)»*"» /п (хп)< Найти плотность распределения максимальной из них:
Z = max {Хъ Х2,..., Хп} и минимальной: U = min {Х1? Х2, ..., Хп}9
т. е. той случайной величины, которая в результате опыта примет
максимальное (минимальное) значение.
Решение. Обозначим Gz (z) функцию распределения величины
Z. Имеем
Gz(z) = P{Z<z}=fc(z),
/=1
где Ft (z) = f /, (д:^) dxt (i = 1,2, ..., n).
Дифференцируя, получаем сумму произведений производных
отдельных функций распределения Fx (x±)y F2 (x2),..., Fn (xn) на
произведения всех остальных функций, кроме той, которая
продифференцирована. Результат можно записать в виде
222
J
Аналогично, обозначая Gu (и) функцию распределения величины
[/, получаем
Gu(u) = l-Tl ll—Fi(u)}.
Дифференцируя, находим
8.43. Имеется а независимых случайных величин Xlf Х2, ..., ХЛ>
распределенных одинаково с плотностью/ (х). Найти закон
распределения максимальной из них: Z = max {Xlf X2,..., Xn} и минимальной:
£/ = min { Xlf X2, ..., Xn}.
Решение. На основании решения предыдущей задачи
Gz (г) = (F (г))-, £г (г) = п (F (г))-1 / (г);
Gu (и) = 1 - 11 - F (a)h £„ (и) = /г [1 - F (н)]*-1 / (a).
8.44. Производится три независимых выстрела по плоскости хОу;
центр рассеивания совпадает с началом координат, рассеивание
нормальное, круговое, ох= а у = а. Из трех точек попадания выбирается
та, которая оказалась ближе всех к центру рассеивания. Найти
плотность распределения g (r) расстояния R от ближайшей точки
попадания до центра.
Решение. Имеем R = min {Rl9 R2, R3}> Из решения
предыдущей задачи g (г) = 3 [1 — F (г)]2 / (г), где F (г), / (г) — функция
распределения и плотность распределения расстояния R от точки
попадания любого выстрела до центра рассеивания;
F(r) = P{tf<r} = l-exp[-Jl-];
/(г)=^ехр[-^] (г>0).
Отсюда
g(r)==^exp [--£■] (г>0),
т. е. плотность распределения расстояния от ближайшей из трех точек
до центра рассеивания имеет тот же вид, что и для каждой из них, но
при условии, что параметр а уменьшен в V3 раз, т. е. заменен
значением о' = а/"1/3.
8.45. Найти закон распределения gu (и) минимальной из двух
независимых случайных величин Ти Т2, распределенных по
показательным законам: Л
h Vi) ^h е-** '* & > 0); /2 (4) = ^ е-*-'. (t% > 0).
223
Решение. На основании решения задачи 8.42
gu W) = /i(«)tl—^2(")] + /1(")Г1-Л(")]в*1^»е-^в +
т. е. закон распределения минимальной из двух независимых
случайных величин, распределенных по показательным законам, есть тоже
показательный закон, параметр которого равен сумме параметров
исходных законов.
Этот вывод можно получить значительно проще, если
воспользоваться понятием потока событий. Пусть на оси 0tx имеется простейший
поток событий о интенсивностью Xi, на оси 0t2 — простейший поток с
интенсивностью к2. Сведем эти два потока воедино на оси Ot или, как-
это называется, произведем «суперпозицию» этих потоков. Нетрудно
убедиться, что результат суперпозиции двух простейших потоков
также будет простейшим (свойства стационарности, ординарности и
отсутствия последействия сохраняются). Интенсивность объединенного
потока равна'^ + А,2- Закон распределения расстояния от данной точки
до ближайшего события потока — показательный с параметром
Очевидно, то же справедливо и для минимальной из любого числа
п независимых случайных величин, распределенных по показательным
законам с параметрами Хг, А,2,..., Кп — он будет показательным с пара-
п
метром 2 ^t-
8.46. В условиях предыдущей задачи найти закон распределения
gz (z) максимальной из величин 7\, Т2.
Решение.
gz (*)=/i (г) F2 (*) + /4 (z) Рг (z) = ^ е-*--* [1 -е-И + ^2 е"^211 -
_е-М] = ^ е-^' + А, е-^—(К + Ю е-<*«+*«>7 (г > 0).
Этот закон показательным не является. При Я, = Х2 = X
gz (z) « 2 X е-** (1 — er**) (z > 0).
8.47*. Над случайной величиной X, имеющей плотность f (x),
производится п независимых опытов; наблюденные значения
располагаются в порядке возрастания; получается ряд случайных величин Zl9
22,..., Zfe,..., Zn. Рассматривается k-я из них Zk. Найти ее функцию
распределения Gk (г) и плотность gk (z).
Решение. Gh (z) = Р {Zh < z}. Для того чтобы &-я (в порядке
возрастания) из случайных величин Zlt Z2,..., Zk> ...,Zn была меньше
г, нужно, чтобы не менее k из них были меньше z:
Gh(z)=%Pm,
где Pm — вероятность того, что ровно m из наблюденных в п опытах
значений случайной величины X будут меньше z. По теореме о
повторении опытов
Рт = С? IF (z)]«ll — F (г)]«-
*m
224
J
откуда
Gk (г) = 2 Сп lp (г)Г П—Р (г)]"-т,
m=k
где F (г) = J / (х) dr.
—•00
Плотность gk (z) можно найти, дифференцируя это выражение и
учитывая, что
п (т—1)! (л—т)\ пв"х
С%(п-т) = пС^1 {т<п).
После простых преобразований получим
gk (z) = nC*z\ f (*> [F (г)]*-x [1 -F (z)]«~K
Однако гораздо проще получить gk (z) непосредственно, о помощью
следующего простого рассуждения. Элемент вероятности gk (z) dz
приближенно представляет собой вероятность попадания случайной
величины Zh (k-ro в порядке возрастания значения случайной
величины X) на участок (z, z + dz). Для того чтобы это произошло, нужно,
чтобы совместились следующие события:
1) какое-то из значений случайной величины X попало на
интервал (z, z + dz);
2) (k — 1) других каких-то значений оказались меньше z\
3) (п — k) остальных значений оказались больше z
[вероятностью попадания более чем одного значения на элементарный участок
(z, z + dz) пренебрегаем].
Вероятность каждой такой комбинации событий равна / (z) dzx
X IF (z)]*-1 [1—F (z)]n~k. Число комбинаций равно произведению числа
п способов, какими можно выбрать одно значение из я, чтобы
поместить его на интервал (z, z + dz), на число C%Z\ способов, какими
из оставшихся п — 1 значений можно выбрать k — 1, чтобы поместить
их левее z. Следовательно,
gk (z) dz - nCknZ\ f (г) [F (z)]*-1 [1 - F (z)!"-* dz,
откуда
gh (z) - n(%Z\ t (*) [F (z)]*-4l - F (г)!»-».
8.48. В электропечи установлено четыре регулятора (термопары),
каждый из которых показывает температуру с некоторой ошибкой,
распределенной по нормальному закону с нулевым математическим
ожиданием и средним квадратическим отклонением ot. Происходит
нагревание печи. В момент, когда две из четырех термопар покажут
температуру не ниже критической т0, печь автоматически отключается.
Найти плотность распределения температуры Z, при которой будет
происходить отключение печи.
Решение. Температура Z, при которой происходит отключение
печи, представляет собой второе в порядке убывания (т. е. третье в
Зак. 1040
225
порядке возрастания) из четырех значений случайной величины Г,
распределенной по нормальному закону с центром рассеивания т0 и
средним квадратическим отклонением at:
/© —
i
exp —
(t—hP
Соответствующая функция распределения
2o?
F(f) = otl=*±\+0%59
Пользуясь результатами предыдущей задачи при п = 4, k — 3,
получаем
+0,5]'[0.5_Ф(^)].
8.49, Имеется п независимых случайных величин Хг, Х2, ..., Хп,
функции распределения которых имеют вид степенной зависимости
О при xt < 0;
Л(**) =
х? при 0<*£< 1 (/ = 1,2, ...,я);
1 ПРИ Х|> 1,
где kt — целое положительное число. Наблюдается значение каждой
случайной величины и из них выбирается максимальное Z. Найти
функцию распределения G (г) этой случайной величины.
Решение. На основании решения задачи 8.42
G (*)= П Рг(г)= П г1 при 0 < * < 1,
п
или, если обозначить & = 2 ku
( 0 при 2^0;
G(z)=| zk при 0<z< lj
[ 1 при г > 1,
т. е. максимум нескольких случайных величин, распределенных по
степенному закону в интервале (0;1), также распределен по степенному
закону g показателем степени, равным сумме показателей степеней
отдельных законов.
8.50. Дискретные случайные величины Х19 Х2,..., Хп независимы и
распределены по законам Пуассона с параметрами аи а29 ..., а^.
п
Показать, что их сумма Y = 2 %t также распределена по закону
п
Пуассона с параметром а = 2 я*-
226
Решение. Докажем сначала, что сумма двух случайных
величин Хг и Х2 распределена по закону Пуассона, для чего найдем
вероятность того, что Хг + Х2 = т (т = 0, 1, 2,,..).
т
Р {Хх + Х2 = т}= 2 Р {*1=Щ Р {Х2 = /п-£} =
™ a\ am-*
= У -i- e-ai —2 е~а*.
s>k ml
Учитывая, что Ст = .^ <m__k)l » представим это выражение в виде
1 У Ct a* a™~k= (ai+€t2) e-^+oi),
ml ^d™12 ml
а это есть распределение Пуассона с параметром а± + а2.
Таким образом доказано, что сумма двух независимых случайных
величин, распределенных по законам Пуассона, тоже имеет
распределение Пуассона. Распространение этого результата на любое число
слагаемых производится по индукции.
8.51. Система случайных величин (X, Y) распределена по
нормальному закону g характеристиками тх, myi ох, оу и zxy. Случайные
величины ((/, V) связаны с (X, Y) зависимостью и = аХ + bY + о\ V =
= kX + IY + m. Найти закон распределения системы случайных
величин ((/, V).
Ответ. Система (U, V) распределена нормально о
характеристиками:
ти = атх + Ъту + с; mv = ktnx + lmy + т;
ои = Т/а2 а? + Ь2 о* + 2abox ау гху ;
o0 = Vk?o* + l*o* + 2kloxoy rxy ;
_ aka% + Ыо* +(bk+al) oxOy rxy
8.52. Составить композицию двух биномиальных распределений
g параметрами (я, р) и (£, р).
Решение. Пусть X—число появлений события А в п
независимых опытах, в каждом из которых оно появляется о вероятностью р;
X имеет биномиальное распределение с параметрами (л, р). Аналогично
У есть число появлений события А и k независимых опытах в тех же
условиях; оно имеет биномиальное распределение g параметрами (k, р).
Z = X + Y — число появлений события А в серии из п + k опытов
с вероятностью р события А в каждом опыте; величина z имеет тоже
биномиальное распределение с параметрами (п + k, p).
Заметим, что если вероятности р в разных сериях различны, то в
результате композиции двух биномиальных законов получится уже
не биномиальный закон.
8.53. Пользуясь неравенством Чебышева, оценить сверху
вероятность того, что случайная величина X, имеющая математическое ожи-
8* 227
дание m и среднее квадратическое отклонение <т, отклонится от т
меньше, чем на 3 а.
Решение. Неравенство Чебышева (8.0.18) дает
Р{|Х-т| ^ Зсг} ^2-Ш- = —Z!_ = -i-; р {| х—/п|<С Зсг> ^ -|-.
11 ' ' ^ (За)2 (За)2 9 и ' ' 9
Итак, любая случайная величина отходит от своего
математического ожидания меньше, чем на За, с вероятностью, не меньшей чем
8/9*>.
8.54. Производится большое число п независимых опытов, в каждом
из которых случайная величина X имеет равномерное распределение
на участке (1; 2). Рассматривается среднее арифметическое наблюден-
ных значений случайной величины X: Y = — \ Xt. На основе за-
г =1
кона больших чисел выяснить, к какому числу а будет приближаться
(сходиться по вероятности) величина Y при л-*- оо. Оценить
максимальную практически возможную ошибку равенства У » а.
Решение.
а = М[У] = — у М[ХЛ = — -/г-1,5-1,5;
П J*d П
1
D[Y)^—y DIX£] = — — = —; оу = УЩ7Т = —
1 * п* Ml n* 12 12/1 У 2 Т/З^Г
*) Это — крайний, самый неблагоприятный случай. На практике для
обычно встречающихся случайных величин эта вероятность гораздо ближе к единице:
например, для нормального закона она равна 0,997; для равномерного
распределения — единице; для показательного 0,982.
22S
£<i
1=\
Максимальное практически возможное значение ошибки 3<ту. |
8.55. Рассматривается последовательность п случайных величин I
Х1э Х2,...а Хп имеющих равномерное распределение соответственно на |
участках: (0; 1), (0; 2), ..., (0; п). Что будет делаться с их средним
п
арифметическим Y = — 2 %t ПРИ увеличении п?
Решение. При заданном п
м[п=1|м№1 = 1(у+т + Т+-+ т)~
__ 1 п (п + 1) __ п + \
~~ п 9 "" 4
При п -^ со эта величина неограниченно возрастает, устойчивости
среднего не наблюдается.
8.56. Случайные величины Хг, Х2,..., Хп распределены
равномерно на участках (— 1; 1), (—2; 2), ..., (—/г; /г). Будет ли среднее арифме-
1
тическое случайных величин Xt: Y = — £ Xt при увеличении п
сходиться по вероятности к нулю?
Решение. М [У] = — J^M [Хг] =0, но сходиться по
вероятности к нулю случайная величина Y не будет, так как условия теоремы
Маркова нарушены; дисперсии случайных величин Xt не ограничены
одним и тем же числом L, а неограниченно растут с увеличением п.
8.57. ЭВМ вырабатывает случайные двоичные числа так, что знаки
0 и 1 на каждой позиции появляются с одинаковой вероятностью и
независимо от других позиций. Последовательность знаков делится на
группы, состоящие из одинаковых знаков, например 000 111 0 1 00
1111 00 11 0000 1 0 ... Подсчитывается число знаков в каждой группе и
делится на число групп. Как будет себя вести эта средняя величина при
неограниченном увеличении числа групп я?
Решение. Случайная величина Xt — число знаков в *-й
группе — имеет геометрическое распределение, начинающееся с единицы
(см. гл. 4). М [Хг] =* lip =* 2; D [Xt] = q /p2 =* 0,5/0,52 =* 2.
1 n
Если Frt = — У Хь то
n ffx
M [Уп] = ±п2 = 2^[Уп] = ±п2 = ±-о„п «j/jL.
На основании закона больших чисел величина Yn при п ->• оо
сходится по вероятности к М [Yn] =^ 2: lim Р{|УЛ — 2|<С в} = 1. Ошибка
приближенного равенства Yn « 2 (по правилу трех сигма) не
превосходит 3 V2//1.
8.58. Цех завода выпускает шарики для подшипников. За смену
производится п = 10 000 шариков. Вероятность того, что один шарик
окажется дефектным, равна 0,05. Причины дефектов для отдельных
шариков независимы. Продукция проходит контроль сразу после
изготовления, причем дефектные шарики бракуются и ссыпаются в бункер, а
небракованные отправляются в цех сборки. Определить, на какое
количество шариков должен быть рассчитан бункер, чтобы о вероятностью
0,99 после смены он не оказался переполненным.
Решение, Число забракованных шариков X имеет
биномиальное распределение; так как п велико, то на основании предельной
теоремы Лапласа можно считать распределение приблизительно
нормальным с характеристиками: тх = пр =* 10 000*0,05 = 500; Dx = npq=
= 500-0,95 = 475; ох « 21,8.
Находим такое значение /, для которого Р {X < /} =* 0,99 или
229
По таблицам функции Ф (х) определяем (/ — 500)/21,8 ж 2,33, откуда
/«551, т.е. бункер, рассчитанный примерно на 550 шариков, g
вероятностью 0,99 за смену переполняться не будет.
8.59. В очереди на получение денег в кассу стоит п = 60 человек;
размер выплаты каждому из них случаен. Средняя выплата тх =
= 50 руб., среднее квадратическое отклонение выплаты ах = 20 руб.
Выплаты отдельным получателям независимы. Г) Сколько должно быть
денег в классе, чтобы их о вероятностью 0,95 хватило на выплату всем
60 получателям; 2) каков будет гарантированный с той же
вероятностью 0,95 остаток денег Ь в кассе после выплаты всем 60 получателям,
если в начале выплаты в кассе было 3500 руб?
60
Решение. 1) Суммарная выплата Y = У Xh где Xt — вы-
плата 1-му получателю. На основании центральной предельной
теоремы для одинаково распределенных слагаемых Y имеет приближенно
нормальное распределение о параметрами ту = 60, тх = 3000 руб.,
(7^,=V60.20 « 154,8 руб. Необходимый запас денег / найдем из
условия Ф [(/ — my)hy] + 0,5 = 0,95. По таблицам функции Лапласа
(приложение 5) (/ — ту)1$у « 1,65; I = ту + 1,65 ау « 3256 руб.
2) Гарантированный о вероятностью 0,95 остаток денег Ь получим,
вычитая из3500 сумму /, полученнуювп. 1:6 = 3500—3256 = 244 руб.
8.60*. Лотерея организована следующим образом. Участникам
продаются билеты, на каждом из которых имеется таблица q номерами:
1, 2,..., 90. Участник должен выбрать произвольным образом пять
различных номеров, отметить эти номера и послать билет
организаторам лотереи, которые хранят все присланные билеты в запечатанном
виде до дня розыгрыша. Розыгрыш лотереи состоит в том, что
случайным образом выбираются (разыгрываются) пять различных номеров
из девяноста; выпавшие номера сообщаются участникам. Если у
игрока совпали о объявленными менее двух номеров (0 или 1), он никакого
выигрыша не получает. Если совпали с объявленными два номера, он
выигрывает 1 руб.; если три номера— 100 руб., если четыре —
10 000 руб.; если все пять— 1000 000руб. Определить: 1) нижнюю
границу цены билета, при котором лотерея в среднем еще не приносит
убытка ее организаторам; 2) средний доход М, который приносит
лотерея организаторам, если в ней участвуют 1 000 000 человек,
назначающих свои номера независимо один от другого; каждый покупает один
билет, а цена билета 30 коп; 3) пользуясь правилом трех сигма,
найти границы практически возможных выплат по лотерее; можно ли
считать суммарную выплуту по лотерее распределенной приблизительно
по нормальному закону?
Решение. П Обозначим pt вероятность того, что из пяти
названных игроком номеров ровно / совпадут о выпавшими. Находим
Р*= CLCU «2,25.10-»; Ръ = Ц^ « 8,12.10~4;
Р*= C*f" & 0,67-10-6; л = > » 2,28.10-е.
230
Минимальная цена билета должна быть равна математическому
ожиданию выигрыша игрока, купившего этот билет: т = 2,25»10~2+
+ 8,12 . Ю-4 . 102 + 9,67 . 10-в • 104 + 2,28 • 10~8 . 10е = 22,3 X
X 10~2 руб., т. е. минимальная цена билета около 23 коп.
2) М = (0,30—0,223). 10е » 77-103 руб.
3) Общая сумма выигрышей X, которая подлежит выплате по
лотерее, представляет собой сумму выигрышей отдельных игроков: X =
i ооо ооо
= 2 Хь где Xt — выигрыш *-го игрока.
Считается, что игроки называют свои номера независимо друг от
друга, так что величины Xt (i = 1, 2, ..., 1000 000) независимы. Из
центральной предельной теоремы извести®, что сумма достаточно
большого числа назависимых одинаково распределенных случайных
величин приближенно распределена по нормальному закону.
Требуется выяснить, достаточно ли в данном случае числа слагаемых
п = 1000 000 для того, чтобы величину X можно было считать
распределенной нормально?
Находим математическое ожидание пгх и среднее квадратическое
отклонение ох случайной величины X. Для любого I = 1, 2, ...*
1 000 000 получим тх% =* 22,3* 10~2 =* 0,223; а2 [Х*1 = 2,25-10"2 +
+ 8,12 + 9,67<102 + 2,28-Ю4 = 2,38* 104; D*. = 2,38.104 — 0,22* «
» 2,38* 104. Отсюда
тх « Ю6./?г*£ =* 2,23* 105; Dx = 106*О*. - 2,38-1010; ах =
» 106V2^8« 1,54*105.
Мы знаем, что для случайной величины X, распределенной по
нормальному закону, границы практически возможных значений
заключены между тх ± 3 ах. В нашем случае нижняя граница возможных
значений случайной величины X, если бы она была распределена по
нормальному закону, была бы тх — Зох = — 2,39* 10~б.
Отрицательное значение этой границы говорит © том, что случайная величина X
не может считаться распределенной нормально.
а
—г е-*, где а — целое положительное
число.
а
—г ег0 есть вероятность того, что слу-
чайная величина X, распределенная по закону Пуассона, не
превзойдет своего математического ожидания а. Но при неограниченном
увеличении параметра а закон Пуасвона приближается к нормальному. Для
нормального закона вероятность того, что случайная величина не
превзойдет бвоего математического ожидания, равна 1/2, значит,
1™ jU m\Q 2 '
я-*» ш=о
8.62. Независимые случайные величины Х1э Х2, ... распределены
одинаково по показательному закону с параметром X: f (х) = % еги.
231
Рассматривается еумма случайного числа таких величин
у
Z = 21 Xt> гАе случайная величина Y имеет геометрическое
распределение, начинающееся е единицы:
Рп = Р {Y = п) = р^"1 (0 < р < 1; л = 1, 2,...).
Найти закон распределения и числовые характеристики случайной
величины Z.
Решение. Сумма фиксированного числа п случайных величин
п
2 Я* подчинена закону Эрланга п-го порядка (см. задачу 8.38) с плот-
ностью
% (1х)п-* *
/nM=-^zTF"e (x>0)-
Плотновть ф (г) елучайной величины Z находим по формуле полной
вероятности о гипотезами Рп = {Y = п}:
Ф (2)= 2 /л (2) Рл =2 J:j^^e^W»-i=pXe--^x
х у (М epj, е-хг e^z e ряе^2 (г > 0),
т. е. случайная величина Z будет также подчинена показательному
закону, но « параметром %р. Следовательно,
mz « 1/(Яр)1 D* =* 1/(Х2р2).
8.63. Закон распределения суммы случайного числа случайных
слагаемых. Рассматривается сумма случайного числа случайных
слагаемых Z = 2 Xf, где Х1э Х2, ... — последовательность независимых
/=i
одинаково распределенных случайных величин о плотностью / (х);
Y — положительная, не зависящая от них целочисленная
случайная величина о законом распределения Р{У = п} =* Рп (п =* 1,2,...,
N).Найти закон распределения и числовые характеристики случайной
величины Z.
Решение. Допустим, что случайная величина Y приняла
значение п (п = 1,2,..., N). Вероятность этого равна Рл. При этой гипотезе
п
Z = 2 Xt- Обозначим плотность распределения суммы п
независимых одинаково распределенных величин Х19 Х2,...ХЛ через
/W (#). Плотности /<"> (x) можно найти последовательно: сначала
/*2> (х) — композицию двух одинаковых законов / (х) и / (х), затем
/(3> (х) — композицию /(2) (х) и / (х) и т. д.
По формуле полной вероятности плотность ф (г) случайной
величины Z будет ,
232
cp(z)= 2 f(n)Mpn- (8.63)
Числовые характеристики случайной величины 2 найдены нами в
задаче 7.64:
М [Zl = tnxmy\ D [Z] «= Dxmy + mj£>y)
где тХ9 tny\ Dx, Dy — математические ожидания и дисперсии
случайных величин X и Y.
При выполнении определенных условий можно с достаточной для
практики точностью полагать, что случайная величина Z подчинена
нормальному закону с указанными параметрами М [Z], D [Z]. Покажем
это. Не нарушая общности расвуждений для простоты положим тх=0.
На основании центральной предельной теоремы для одинаково
распределенных слагаемых (см. раздел 8.0) можно приближенно полагать,
что при п> ту — Зву > 20 плотность /<л) (г) в формуле (8.63)
представляет собой нормальный закон g параметрами m<n) = 0; D^n) =nDx
[см. (5.0.33)]:
/(«) (2)=— * exp ( —).
У 2nnDx \ 2nDx)
Формула (8.63) выражает математическое ожидание функции
случайного аргумента Y:
ф(*)-2 f{n)(z)Pn=^lf{Y)(z)l
Для функций, достаточно близких к линейным в области
практически возможных значений случайного аргумента, можно приближенно
полагать математическое ожидание функции равным той же функции от
математического ожидания случайного аргумента:
М [/<» (г)] « !(тУ] (г) или ф (г) » _L^ exp ( -*_),
Y2nmy Dx \ 2myDx J
что является нормальным законом. Приближенное равенство
выполняется тем точнее, чем ближе к линейной функция /<у> (г) случайного
аргумента Y в области его практически возможных значений: ту ± 3 оу.
Расчеты показывают, что эту функцию можно считать приближенно
линейной при условии, что ту — Зоу > 20. Например, если
случайная величина У распределена по закону Пуассона с параметром а
1см. (4.0.26)1, то это условие будет выполняться при а > 40; если по
биномиальному закону с параметрами я, р [см. (4.0.24)] (и малом
параметре р < 0,1), то пр > 40. Заметим, что в обоих случаях случайная
величина Y (число случайных слагаемых) будет подчинена
приближенно нормальному закону с параметрами ту = Dy = а (для закона
Пуассона) и ту = пр ; Dy = npq (для биномиального закона).
8.64*. Независимые случайные величины Хъ Х2,..., Хп,...
распределены одинаково по показательному закону с параметром X. Случайная
233
величина Y = U + 1, где случайная величина U расспределена по
закону Пуассона о параметром а. Найти закон распределения и
числовые характеристики случайной величины Z= 2 Xt-
п
Решение. Закон распределения суммы 2 Xt представляет собой
закон Эрланга n-го порядка (см. задачу 8.38) с параметром h
L(x)
X (Xxf
(я-1)!
е-*' {х > 0).
По формуле полной вероятности плотность распределения
случайной величины Z будет
л=1 п = \
пп—\
1)! (л—1)!
*=Хе~^* у (-^£ при 2>0.
*=о
Эту плотность можно выразить через модифицированную
цилиндрическую функцию
fc=0
(*l)2
Ф (г)=Х е^2-* /0 (2 V %za ) при г > 0.
Далее на основании решения задачи 8.66
М [Z] *= mxmv = (а + 1)/Я; D [Z] = D*/?^ + m2xDy =
= (а + 1)/Я2 + аД2 - (2а + 1)/АЛ
8.65. Рассматривается система случайных величин Xt (i = 1, 2,
..., п), которая связана с дискретной случайной величиной Y
следующим образом:
Х,=
10.
1, если /^F;
если />F;
Известна функция распределения F (у) случайной величины К.
Найти закон распределения каждой случайной величины Хг и числовые
характеристики системы случайных величин (Xl9 Х2, ..., Хп).
Решение. Ряд распределения случайной величины У имеет
вид
Y •
0
Р {Y < /}
1
Р{У>1)\
§1
234
Так как Р {Y < 1} = F (0, то ряд распределения имеет вид
О I 1
откуда тх% = 1 - F (*); Dx% « F(Q [1 - F (i)l
Найдем корреляционные моменты случайных величин X* и Xjt
для чего определим М [Х*Х,-]. Произведение XtXj при * < / может
принимать только два значения: 1, если Xj = 1, и 0, если X; = 0.
Следовательно, М IXtXj) « mXj = 1 — F (j) (i < /), откуда
Ku e M 1ВД>1 - /тц/n*. *= 1 — F (J) - [1 - F (i)] [1 - F (/)]=
e F (i) [1 — F (/)] (i < /), а коэффициент корреляции
__JUl__ F(/)fl—F (/)j , - f F(/)fl — F(/)]
w a*£o*. VF (i) F 0)11 —/? (/)] [I—F 0)J V F(j)\\-F(i)]'
8.66. Производится ряд независимых опытов, в каждом из которых
событие Л появляется в вероятностью р. Опыты прекращаются, как
только событие А появилось п раз (п > 1). Найти закон распределения
и числовые характеристики числа X «неудачных» опытов, в которых
событие А не произошло.
Решение. Найдем вероятность того, что случайная величина
X примет значение k. Для этого нужно, чтобы общее число
произведенных опытов было равно п + k (kопытов кончились «неудачно», an —
«удачно»). Последний опыт по условию должен быть «удачным», а в
предыдущих п + k — 1 опытах должны произвольным образом
распределиться п— 1 «удачных» и k «неудачных» опытов. Вероятность этого
Y>{X = k) = Ckn+k^ipnq\ где<7 = 1-р(£ = 0, 1,...).
Полученное распределение является естественным обобщением
геометрического; назовем его обобщенным геометрическим
распределением П'То порядка. Оно представляет собой композицию п геометри-
п
ческих распределений с одинаковым параметром р: X = 2 XSj где
каждая случайная величина Xs имеет геометрическое распределение
Р {Х8 = k) = pqk (k = 0, 1, ....).
Действительно, общее число «неудачных» опытов складывается из:
1) числа «неудачных» опытов до первого появления события Л; 2)
числа «неудачных» опытов от первого до второго появления события
Л и т. д. Отсюда получаем числовые характеристики величины X:
пгх = nq/p; Dx — nq/p2.
8.67. Условия задачи те же, что и в задаче 8.66, но случайная
величина Y представляет собой общее число опытов (как
удачных, так и не удачных), произведенных до n-кратного появления
события Л. Найти закон распределения и числовые характеристики
случайной величины Y.
Решение. У *= X + я, где X — случайная величина,
фигурирующая в предыдущей задаче. Отсюда
235
= CnkZ\pnqk~n (k = nfn+l,...).
Числовые характеристики величины Yi
™у = тх + п = nqlp + п = n/p; Dy = Dx = я<7/р2.
8.68. Имеется случайная величина У, распределенная по
показательному закону е параметром h f (у) = Хе-^ (г/ > 0). Случайная
величина X при заданном значении случайной величины У = у
распределена по закону Пуассона с параметром у:
P{X = k\Y = y} = j£-e~y (k =0,1,2,...).
Найти безусловный закон распределения случайной величины X.
Решение. Полная вероятность события X = k
оо . оо
о о
*=±-k\(\ +Ь)-(*-М>= *^ (£ = 0, 1,2,...).
Если ввести обозначения к /(1 + %) = р; 1/(1 + %) = # = 1 — р,
получим Р {X = &} = p</fe (k = 0,1, 2,...), т. е. случайная величина
X имеет геометрическое распределение с параметром р = К/(] + А,).
8.69. На космическом корабле установлен счетчик Гейгера для
определения числа космических частиц, попадающих в него за
некоторый интервал времени Т. Поток космических частиц — пуассоновс-
кий с интенсивностьюД; каждая частица регистрируется счетчиком с
вероятностью р. Счетчик включается на случайное время Т,
распределенное по показательному закону с параметром ц,. Случайная величина
X — число зарегистрированных частиц. Найти закон распределения и
характеристики mXy Dx случайной величины X.
Решение. Предположим, что Т = t и найдем условную
вероятность того, что X = m (m = 0,1, 2,...).
P{X = m|/} = (-^e-^<.
ml
Тогда полная вероятность события {X — пг)
оо
P{X = m}=f{^e~^[xe^'^ =
J m\
о
^ JL npr f tm e- (Кр+м ,dt = ll №m . —t— /—Xp_y»
ml " j - (V+n)m+1 **»+!* V **+И /
(m = 0, 1,2,...).
236
m
Это есть геометрическое распределение с параметром \il(Xp + ц) (см.
предыдущую задачу), поэтому [см. формулы (4.0.30), (4.0.31)]:
/ %р \,1 » \_%Р. D I Ъ )1( * У =
* \ *Р + И //V ^ + И) / - и ' * \ \р+\1 )1\ Хр + Ц )
у? \ \i J и
8.70.Решить задачу 8.69 при условии, что счетчик включается на
случайное время Т с плотностью / (/) (/ > 0).
Решение. Так же, как и в предыдущей задаче, условный закон
распределения величины X при Т = t будет
P{X = m|/} = ^^e^< (m = 0, 1,2...)-
Безусловный закон распределения
оо
р {X = т} = Г i^^ е*М /(/) dt (т = 0, 1, 2,...).
J /и!
о
Находим числовые характеристики случайной величины X.
Условное математическое ожидание mx\t = Xpt\ безусловное математическое
оо оо
ожидание тх = j* Xptf (t) dt = Xp j* // (/)Л = A,pmb где mt =
== M [71. Аналогично находим второй начальный момент случайной
величины X (заметим, что так можно находить только начальные
безусловные моменты, а не центральные):
сс2 [X \t] = Xpt + (Xpt)2;
оо оо
а2 [XI = Xp j* tf (t) dt + (Xp)2112 f (t) dt =
о о
= Xpmt + (Xp)2 a2 IT] = Xpmt + (Xp)2 (Dt + ml),
где Di — дисперсия случайной величины Т. Отсюда
Dx = cca IX] - ml = Xpmt + (Хр)2 Dt.
8.71. Решить предыдущую задачу для конкретного случая, когда
/ (t) есть закон Эрланга (k + 1) -го порядка с параметром у,:
f(i) = h,i(t)=^t'^ (*>0).
оо ,
Решение. Р(Х = /я)= Г M!e-w!iM.e-w^ =
m! AI
"J
237
-С!
\ Ьр + V J V ty+V J
Итак, величина Х имеет обобщенное геометрическое распределение
(k +1)-го порядка (см. задачу 8.66) с параметром
Pi-
^р+ц
Математическое ожидание случайной величины 7\ распределенной
по закону Эрланга (k + 1)-го порядка, будет mt = (k + 1) /ц,, а
дисперсия Dt ~ (& + 1) /|jl2. Следовательно, по формулам, полученным в
предыдущей задаче,
m,-2£-<*+l); Dm = ±B-(k+l)(l+&-)9
что, как и в задаче 8.66, можно представить в виде
(k+l) n (k+\) ч
Pi Pi
8.72. При измерении физических величин результат измерения
неизбежно округляется в соответствии с минимальной ценой деления
прибора. При этом непрерывная случайная величина превращается в
дискретную, возможные значения которой отделены друг от друга
интервалами, равными цене деления. В связи с этим возникает следующая
задача. Непрерывная случайная величина X, распределенная по
закону с плотностью / (х), округляется до ближайшего целого числа;
получается дискретная случайная величина Y = Ц (Х)9 где под Ц (X)
подразумевается целое число, ближайшее к X. Найти ряд распределения
случайной величины У и ее числовые характеристики.
Решение. График функции Ц (X) представлен на рис. 8.72.
Правило округления в случае, когда расстояния от значения х до двух
соседних целых значений равны, несущественно, так как для
непрерывной случайной величины вероятность попадания в любую точку
равна нулю.
Вероятность того, что случайная величина Y примет целое значение
k, равна
Р{У = £} = Г f(X)dx (ft = 0; ±1; ±2,...),
fe^-0,5
откуда
* + 0,6 со ft + 0.6 '
Щ= S k \ f(x)dx; Dy= 2 fe2 J f(x)dx—mf\
fe= — oo fe_0,5 *=— °° fe^0.5
*> Если единица измерения (цена деления прибора) мала по сравнению с
диапазоном возможных значений случайной величины X, то ту « тх\ Dy « Dx*
238
Ц№ f
0,5 1,5 2,5 3,5
X
8.73. Случайные величины X и
Y независимы и распределены по
законам Пуассона о параметрами а
и 6. Найти закон распределения их 2
разности Z = X — Y и модуля
их разности U = | X — Y |=|Z|.
Решение. Случайная ве- 7
личина Z может принимать как ~*s ~z*5 ~w~Ofi
положительные, так и отрицатель- f L^
ные значения. Вероятность того, , i «^
что Z примет значение k > 0, i
равна сумме вероятностей того, что « ' -Jj-
X и Y примут два значения, раз- ' I
личающиеся на k (причем X боль- , pUc. 8.72
ше или равно Y):
Вероятность того, что Z примет отрицательное значение — k, будет
ат b{m+k)
л ml (m-\-k)\
m=0 v ' '
Для случайной величины £/
(ft>0).
Эти вероятности могут быть записаны с помощью модифицированных
цилиндрических функций 1-го рода:
7.И-7..И-£^5-^)'+'" №=0, ,, 2,...)«.
При этом
P{Z = k} = Ik{2V3)U-y,2e^°+b4k=0, ±1, ±2,...);
Р {г/ = 0} = /о (2 Vab) е- <"+*>;
P{f/ = ^ = /ft(2K^)[(-f-)ft/2+(-^-)"'*/2]e»(a+6>^>0).
8.74. Известна совместная плотность / (х, у) системы случайных
величин (X, Y). Найти плотность g (г) разности 2«=Х — Y.
p<z—*>= 2 in^r*-""'<*><»•
*ч Таблицы цилиндрических функций 1-го рода (функций Бесселя) можно
найти, например, в книге: Кузьмин Pi О. Бесселевы функции» — М«—Л»: ОНТИ,
1935.
239
Решение. Для системы (X, — Y) плотность распределения есть
/ (#> — у)у поэтому из равенства X — У = X + (— Y) находим
оо
g (2) = Ql (г) - J / (х, х-г) dx.
Если случайные величины (X, Y) независимы, то
00
g (2) = J /l (Ж) /г (* — 2) dx —
*— оо
00
= I fi(y — z)f2(y) dy.
—оо
8.75. Найти плотность распределения разности двух независимых
показательно распределенных случайных величин с параметрами X и
(г: Z^X — Y; /х (*) = te~** (*> 0); /2 (у) = р ел* (у>0).
00
Решение, g (г) = J /х (х) /2 (# — z) dx; fx (x) отлична от нуля
— оо
при х > 0; f2(x — г) отлична от нуля при х — z > 0.
а) г > 0; g (г) = f Яе-** fie»» <*^2> d* = Jjf£Zl,
J b+|i
г
оо
б) 2 < 0; g (г) = f Яе-Л* це-» <*&2> dx = №L
о
Следовательно,
fc+H
g{z)=i ^-^(Л. + И)"1 при 2>0;
1 Яце»^г (А,+ц)-1 при г < 0.
Параметры этого закона:
_L J и-* .
/7Z*
X\l
D*
1 _ X2+^2
X2
(W
Кривая распределения будет иметь вид, изображенный на рис. 8.75,
а. При к = \i получаем g (г) = -^ ет*1*1 (рио. 8.75, б). Такое рас-
пределение называется распределением Лапласа.
8.76. Композиция законов распределения двух неотрицательных
случайных величин. Имеются две неотрицательные случайные
величины X и У с плотностями /х (х) (х > 0) и /2 (у) (у > 0). Составить
композицию их законов распределения.
Решение. Пусть Z = X + У; найдем плотность g (z)
случайной величины Z. По общей формуле (8.0.5)
g (г) = J h (х) /2 (z — х) dx.
—'ОО
Учитывая, что ft (х) = 0 при х < 0, а /2 (г — х) = 0 при # > г,
получаем
8®-]fib)hb-x)dx. (8.76)
8.77. Имеются две независимые случайные величины X и У,
распределенные по одному и тому же нормальному закону с
параметрами тх = ту = 0; аж; с^. Найти плотность распределения суммы их
модулей Z = \Х\ + |У|.
Решение. Обозначим U = \Х\\ V = |У|. Их плотности Д (м)
и /2 (у) равны соответственно:
М"Н
2
— ехр/ —\ при ы>0;
О при и<0;
_2
о при и<:о,
=—ехр(—^г) пр* »>о;
Учитывая формулу (8.76) для композиции законов распределения
неотрицательных случайных величин, имеем
2
£ (2) = J /i («) /2 (2 - и) d« (z > 0)
или
Этот интеграл выражается через функцию Лапласа Ф (х), для чего
нужно в показателе степени выражения (8.77) выделить полный
квадрат. После преобразований получаем
Ш<А-?
\ о
241
8,78. По радиоканалу передается ряд сообщений.
Продолжительность одного сообщения X — случайная величина, имеющая
показательное распределение с параметром Я (рис. 8.78). Интервал L между
сообщениями—случайная величина, имеющая показательное
распределение с параметром \i. Длины отдельных сообщений и интервалов
между ними не коррелированы. Найти вероятность того, что за время t
будет передан© не менее т сообщений (т > 1).
Рис. 8.78
Решение. Общая продолжительность Т m сообщений плюо
перерывы между ними представляет собой случайную величину,
распределенную по обобщенному закону Эрланга порядка 2 m — 1 g
параметрами
траз (т«1) раз
Вероятность того, что за время t будет передано не менее m
сообщений есть не что иное, как функция распределения случайной
величины Г:
Р> {не менее m сообщений за время t) =P{T<.t} = G(t).
Случайная величина Т представляет собой сумму двух независимых
случайных величин: Т = Тх + Г2, где 1\ — распределена по закону
Эрланга m-го порядка g параметром %\
Т2 — по закону Эрланга (пг — 1)-го порядка g параметром у,:
Следовательно, для случая к > у,
е о
(m—2)1 (m_l)!(m_2)!
х I е*ттт%цп-*-ц-.\у («-i+oi x
242
m— I-И
X
(Л^р,)/ e**n* ^
>0).
Для случая |х>Я,
«*1 „m*»2 '"J"1
0 '«=1
X
(m + /)l Г^'У
(|l-XJ»+1+l [ 4fJ
№-*)'J* c-.,.
ft!
-M' e-^ (*
>0).
Для случая А, = [х ч
8.79. Маятник совершает свободные
незатухающие колебания, причем угол <р (рис 8.79)
изменяется в зависимости от времени / по
гармоническому закону: q> = a sin (©/ + 6), где а —
амплитуда, со — частота, G — фаза колебания.
В некоторый момент t = О, совершенно не
связанный с положением маятника,
производится его фотографирование. Найти закон
распределения угла Ф, который в момент съемки
будет составлять ось маятника с вертикалью.
Найти математическое ожидание и дисперсию угла Ф.
Решение. Ф = a sin в, где фаза в распределена равномерно
в интервале (0; 2 я); на этом участке функция q> = a sin ft
немонотонна. Очевидно, решение задачи не изменится, если считать величину 0
распределенной равномерно в интервале (— я/2; я/2), где функция q>
монотонна. Плотность распределения угла Ф будет *
Рис. 8.79
1
■(Ф) = -т
1
1
1
V-(i)'
л ~]/сР—ф2
при |ф|<а.
Так как закон g (q>) симметричен, то его математическое ожидание
w<p = 0. Дисперсия угла Ф
8.80. Рассматривается п независимых случайных величин Tt
(i = 1,2,..., п), каждая из которых распределена равномерно на
участке (0; с). Найти закон распределения числа Y случайных величин
(точек) 7$, попадающих на участок (а, Ь) с: (0, с). Каково будет
предельное распределение случайной величины Y в елучае, когда я->оо,
е-* оо, а вреднее число точек на участке (а, Ь) остается постоянным?
243
Решение. Введем в рассмотрение случайную величину Yt —
индикатор события Т% £ (я, Ь)\
у f *• если Tt б ia9b);
[ 0, если Tt €fc (а, Ь).
Очевидно,
Обозначим
Р{У|в1}врв±=1; P{y. = 0}=l-P=g^ + fl .
Рассматривая п значений Т1э ..., Тп как /г независимых опытов, в
каждом из которых может произойти или нет событие Тг £ (а, 6), видим,
что случайная величина Y имеет биномиальное распределение с
параметрами п и р и с математическим ожиданием М [У] = яр:
Р{У ^ £},= с^ (1 - р)*~* (ft = 0, ..., л).
Рассмотрим случай, когда с->оо,я-^оо, я/с = А, = const. При
этом р->0, но среднее число точек, попадающих на участок (а, 6),
постоянно: М [Y] = Я (6 — а) = const. Известно (см. раздел 4.0),
что в этом случае предельное распределение случайной величины Y
будет пуассоновским g параметром d = X (b — a):
P{Y = k) = ^e-d (k = 0,1,2,...).
Таким же распределением обладает число событий стационарного
пуассоновского потока g интенсивностью К попадающих на участок
(а, Ь).
Отсюда следует вывод: стационарный поток событий g
интенсивностью X можно рассматривать как предельный случай совокупности п
независимых случайных точек на участке (0,с),каждая из которых
имеет на этом участке равномерное распределение, при условии, чтоп-^оо,
с-> оо, но п/с = X = const. Такая модель простейшего
(стационарного пуассоновского) потока понадобится нам в дальнейшем.
ГЛАВА 9
СЛУЧАЙНЫЕ ФУНКЦИИ
9.0* Функция X (t) называется случайной функцией, если ее значение при
любом аргументе t является случайной величиной. Примеры случайных функций:
V (t) — напряжение электропитания ЭВМ в зависимости от времени t\ T (h) —
температура воздуха в данном пункте в данный момент в зависимости от высоты
h над землей; Q (t) — число отказов ЭВМ, происшедших за время от 0 до *.
Понятие случайной функции является обобщением понятия случайной
величины. Так как случайную величину X можно рассматривать как функцию
244
элементарного события со (см» раздел 4.0): X «= q> (со) (со £ Q), где Q —
пространство элементарных событий, то случайную функцию X (t) можно
представить в виде
X (0 - Ф V, ©) (со f Q, * е П,
где f — не случайный аргумент, Т — область определения функции X (*)*
Реализацией случайной функции X (/) называется конкретный вид, который
она принимает в результате опыта (когда осуществилось элементарное событие
со). Например, записывая с помощью какого-либо прибора напряжение питания
ЭВМ в зависимости от времени на участке (0, т), мы получим реализацию v (/)
случайной функции V (t) (рис. 9.0.1),
Рис. 9.0.1 Рис. 9.0.2
Ряд проведенных опытов, исход каждого из которых —- случайная функция
X (0, дает совокупность реализаций хг (t), х2 (t), >.., хп (t) этой случайной
функции. Реализации неизбежно отличаются друг от друга из-за случайных причин
(рис. ,9.0.2). Для фиксированного момента времени t случайная функция X (i)
превращается в обычную случайную величину. Эта случайная величина
называется сечением случайной функции.
Если рассмотреть не одно сечение случайной функции, а ряд сечений в ряде
точек tlf t2> ..., 6п, то получатся m-мерный случайный вектор, в каком-то
приближении описывающий ее (рис. 9.0.3). На практике, если значения случайной
функции регистрируются с каким-то интервалом при значениях аргумента tl9t2i ..., tn,
мы имеем дело именно с n-мерным случайным вектором.
Случайную функцию X (Q, аргументом которой является время, обычно
называют случайным процессом. Случайный процесс, протекающий в физической
системе 5, состоит в том, что с течением времени t система S случайным образом
меняет свое состояние. Если состояние системы 5 в момент t описывается одной
скалярной случайной величиной X (t)t то мы имеем дело со скалярной случайной
функцией (скалярным случайным процессом) X (f). Если состояние системы 5
в момент t описывается несколькими случайными величинами Хг (f), Х2 (f)t
..», Xh (0» то мы имеем дело с векторной случайной функцией V (t) (векторным
случайным процессом) с k составляющими: Х± (t), Х2 (0> «««i Xh (t).
Случайные процессы делятся на классы по ряду признаков. Случайный
процесс, протекающий в системе 5, называется процессом с дискретным
временем, если переходы системы S из одного состояния в другое возможны только
в определенные, заранее известные моменты времени t±, t2, ... Пример процесса
с дискретным временем: ЭВМ, которая меняет свои состояния в определенные
моменты времени t±, t2, *.., задаваемые тактом работы ЭВМ; техническое
устройство, осматриваемое в моменты t±, t29 ... и переводимое в результате осмотра из
одной категории в другую.
Случайный процесс с дискретным временем называется также случайной по-
еледовательностью. Если состояние системы S описывается одной случайной
величиной X, то случайный процесс представляет собой последовательность
случайных величин: X (/j), X (t2), •»., X (tn)> *»•
Случайный процесс, протекающий в системе S, называется процессом с не*
прерывным временем, если переходы из состояния в состояние морут
происходить в любые, случайные моменты времени, непрерывно заполняющие ось Ot
245
(или ее участок). Примеры случайного процесса с непрерывным временем—из-
менение напряжения электропитания ЭВМ V (f) (см. рис, 9.0.1) или
функционирование технического устройства, которое в случайные моменты времени
выходит из строя и восстанавливается.
Случайный процесс, протекающий в системе 5, называется процессом с
дискретными состояниями, если число возможных состояний системы S конечно
или счетно. Пример: техническое устройство состоит из двух узлов; возможные
состояния системы: s% — оба узла исправны; % — неисправен первый узел,
исправен второй* s8 — исправен первый узел, неисправен второй; s4 —
неисправны оба узла. Другой пример: передача сообщения по радио; случайный процесс
X (0 — количество неправильно переданных символов до момента L Этот
случайный процесс принимает, только счетное множество состояний {0, 1, ...,
л, ».»} и «подскакивает» на единицу в момент приема очередного неправильно
переданного символа (рис» 9.0.4).
BY
В
Ш1
Рис. 9.0.3
Рис. 9.0.4
Случайный процесс, протекающий в системе S, называется процессом с
непрерывными состояниями, если множество возможных состояний системы S
несчетно. Пример: процесс вывода космического корабля в заданное положение
относительно Земли. Другой пример — напряжение электропитания ЭВМ V (/).
По вышеуказанным признакам случайные процессы делятся на следующие,
1а. Процессы с дискретными состояниями и дискретным временем.
16* Процессы с дискретными состояниями и непрерывным временем.
2а. Процессы с непрерывными состояниями и дискретным временем.
26. Процессы с непрерывными состояниями и непрерывным временем.
Примеры процесса типа 1а. Некто купил т билетов выигрышного займа,
которые могут выигрывать и погашаться в известные моменты времени (тиражи) tlf
t2, ...; случайный процесс X (t) — количество билетов, выигрывших до момента
t (включая f). Другой пример — состояние оперативной памяти ЭВМ; все
возможные состояния оперативной памяти могут быть перечислены и изменения
состояний оперативной памяти могут происходить в дискретные моменты времени
в соответствии с тактом работы ЭВМ.
Пример процесса типа 16. Прибор может находиться в четырех состояниях:
sQ—не включен и исправен; st—включен и исправен;^ — не включен и
неисправен; s3 — включён и неисправен. Многочисленные примеры процессов типа 16
встретятся нам в гл. 10 и 11.
Пример процесса типа 2а. В моменты tf9 f2» *>» наблюдаются значения X (ф,
X (/2), ••• непрерывной случайной величины X. Последовательность значений этой
величины — процесс X (t) с непрерывными состояниями и дискретным
временем. Например, если температура воздуха Т измеряется дважды в сутки, то
последовательность зарегистрированных значений Т представляет собой
случайный процесс с непрерывными состояниями и дискретным временем.
Пример процесса типа 26 — процесс V (t) изменения напряжения в
электросети питания ЭВМ в любой момент времени t или уровня помех при передаче
сообщения.
Рассмотрим ряд характеристик скалярной случайной функции X (/).
Одномерным законом распределения случайной функции X (0 называется
закон распределения сечения X (t) этой случайной функции для любого значе-
246
ния аргумента L Если случайная величина X (0 непрерывна, то этот закон
представляет собой плотность, распределения сечения X (f) и обозначается / (*, 0*
Если случайная величина X (t) дискретна, то одномерный закон распределения
случайной функции X (t) представляет собой ряд вероятностей Р (*j, Q того, что
в момент t случайная величина X (t) приняла значение Х|» Для смешанной
случайной величины X (t) одномерный закон распределения задается функцией
распределения F (*, f) = Р {X (t) < #}. Так как функция распределения
является наиболее общей формой закона распределения, пригодной для любых
случайных величин, можно и для одномерного закона распределения пользоваться
общей записью F (х> t)»
Двумерным законом распределения случайной функции X (f) называется
совместный закон распределения двух ее сечений [X ft) и X ft) для любых
значений t± и *2], представляющий собой функцию четырех аргументов: хъ х2, tlt t2.
Соответственно можно рассмотреть /i-м ерный 8 а к о н
распределения, зависящий от 2я аргументов.
Случайная функция X (/) называется нормальной, если совместное
распределение любого числа п ее сечений, взятых в произвольные моменты времени
h < h < h < ш.ь <. tnt есть n-мерный нормальный закон,
Математическим ожиданием случайной функции X (t) называется
неслучайная функция тх (0, которая при каждом значении аргумента /представляет
собой математическое ожидание соответствующего сечения случайной функции:
m*(0-M[X(fl]. (9.0.1)
Корреляционной (или «автокорреляционной») функцией случайной функции
X (t) называется неслучайная функция двух аргументов Кх ft О» которая при
каждой паре значений аргументов t, t' равна корреляционному моменту
соответствующих сечений случайной функции:
Кх (ty V) = М [k (t) X (/')!. (9.0.2)
где X (0 = X (t) — тх (t) —- центрированная случайная функция.
При V = t корреляционная функция превращается в дисперсию случайной
функции:
Кх ft 0 = Dx (0 = D [X ft] = [ox (t)}\ (9.0.3)
Основные свойства корреляционной функции:
1) Кх ft ?) = KXl(t', t), т. е. функция Кх ft ?) не меняется при замене t
на V (симметричность);
2) \Kx(U?)\<Ox®*xV)\
3) функция /С* ft V)—положительно определенная, т. е. J J Kx(U ?) ф (OX
(В) (В)
X ф (?) dtdt' > 0, где ф (t) — любая функция, (В) — любая область
интегрирования, одинаковая для обоих аргументов.
Для нормальной случайной функции характеристики тх (0> Кх ft f)
являются исчерпывающими и определяют собой закон распределения любого числа
сечений.
Нормированной корреляционной функцией случайной функции X (t)
называется функция
Г*«' П ~ ох (I) ах (П УВХ(1)ВХ(П ' ( • >
т. е. коэффициент корреляции сечений X (0 и X {t')\ при t= V rx ft t') = Ь
Случайный процесс КХ (0 называется процессом с независимыми приращения»
ми, если для любых значений аргумента t% < t2 < t3 < «»< < tk < tk+i < .»<
случайные величины приращения функции X (0
и±-Х (t2) - X ft); U2 = X ft,) - X ft)j .„« Uh = X {th+1) - X (tk) (9.0.5)
независимы.
247
Нормальный случайный процесс с независимыми приращениями называется
винеровским случайным процессом, если его математическое ожидание равно
нулю, а дисперсия приращения пропорциональна длине отрезка, на котором оно
достигается:
тх (0 =0; D Ш = а (th+l—tk), (9.0.6)
где а > 0 — постоянный коэффициент.
При прибавлении к случайной функции X (t) неслучайного слагаемого
Ф (0 к ее математическому ожиданию прибавляется то же неслучайное
слагаемое, а корреляционная функция не меняется.
При умножении случайной функции X (0 на неслучайный множитель ф {t)
ее математическое ожидание умножаемся на тот же множитель ф (*), а
корреляционная функция — на ф (t) ф (f).
Если случайную функцию X (0 подвергают некоторому преобразованию
Att то получается другая случайная функция Y (t) = At {X (t)}»
Преобразование Ц называется линейным однородным, если
U—1 J fe=n
(т. е. преобразование к сумме может применяться почленно);
2) L}°> {cX (ф - еЦ»> {X (t)}
(т. е» множитель с9 не зависящий от аргумента t9 по которому производится
преобразование, можно выносить 8а знак преобразования).
Преобразование Lt называется линейным неоднородным, если
£*{Х(0>-4в>{Х(0>+ф(0»
где ф (0 — не случайная функция.
Если случайная функция У (t) связана со случайной функцией X (t)
линейным преобразованием Y (t) = Lt {X (t)}9 то ее математическое ожидание ту (0
получается из тх (0 тем же линейным преобразованием:
ту (0 « U {X (0}, (9.0.7)
а для нахождения корреляционной функции Кх (t, t') нужно дважды
подвергнуть функцию Кх (U О соответствующему линейному однородному
преобразованию: один раз по t, другой раз по t'\
Kv (U П=Ц?> {Ц9> iKx(t9 *')>}. (9.0.8)
Взаимной корреляционной функцией Rxy (t9 t') двух случайных функций
X (0 и Y (0 называется функция
«^O-MlfcW* <*')!• (9.0.9)
Из определения взаимной корреляционной функции вытекает, что
Rxy(Ut')~RyX(t*,t).
Нормированной взаимной корреляционной функцией двух случайных функций
X (0, Y (0 называется функция
""•"'-»Лос,(о- уоттФ>- . ,9•0•'0,
Hxu(f,t') _ Rxv(t,t')
3x(t)°g(l') = VDX (0 Dy (t
Случайные функции X (t) и Y (t) называются некоррелированными, если
Rxeih О SO.
Если Z (0 =Х (0+К (0. то mz {t)=mx (t)+mv (<),
К2 (t, t*)~Kx(t. t*) +Ky 0, О+Яад (/, <')+#*»<<*. 0.
Если случайные функции X (f) я Y (f) некоррелированны, то
Kz (t, t') =*Kx(t, t') + Ky(t, t'). (9.0.11)
248
5
Если
п
Z(0=2 **<*)• (9.0.12)
где Х4 (0, Х2 (0, .,., Хп (0 — некоррелированные случайные функции, то
п п
mz (*) = 2 т*ь Ма ** <*. *') « 2 К- 0, #•).
При выполнении различных преобразований со случайными функциями
часто бывает удобно записывать их в комплексном виде* Комплексной случайной
функцией называется случайная функция вида
Z(0« X (t)+ iY (*), (9.0.13)
где X (0, Y (0 — действительные случайные функции, i — мнимая единица.
Математическое ожидание, корреляционная функция и дисперсия
комплексной случайной функции определяются следующим образом:
т2 (t)=>mx (t) + \my (t); Kz (t, О-МЙ (0 F(P)], (9.0.14)
где чертой вверху обозначена комплексная сопряженная величина, а
Dz (t) *=KZ (t. t) »M [I k (t) \% (9.0.15)
При переходе к комплексным случайным величинам и функциям необходимо
определять дисперсию как математическое ожидание квадрата модуля, а
корреляционный момент—как математическое ожидание произведения центрированной
одной случайной величины на комплексную сопряженную центрированной
другой**.
Каноническим разложением случайной функции X (Q называется ее
представление в виде
m
Х(0-«»(0+ 2 ^аФлЮ"1. (9-0.16)
ъ=1
где Vk (& = 1* 2, ,.«, т) — центрированные, некоррелированные случайные
величины, с дисперсиями D^ (fc = l, 2, ..., m); фь (t) (&=1, 2, .*., т) —
неслучайные функции. Случайные величины К&(6 = 1,'2, *»., т) называются
коэффициентами, а функции ф/i (/) (fc = l, 2, .*», m)—координатными функциями
канонического разложения*
Если случайная функция X (t) допускает каноническое разложение (9*0.16)
в действительной форме, то корреляционная функция Кх (t, t') выражается
суммой:
т
*«('.'*>=■ 2 D*9*w ф*('*ь <9-0-17)
которая называется каноническим разложением корреляционной функции*
Если случайная функция X (/) допускает каноническое разложение (9.0*16)
в комплексной форме, то каноническое разложение корреляционной функции
имеет вид
*> В дальнейшем мы каждый раз будем оговаривать комплексный характер
случайной функции! если он не оговорен, будем считать случайную функцию
действительной.
**> В частности, сумма может распространяться на бесконечное (счетное)
число слагаемых*
249
Кх(**П= S 0A<Pfc(O<Pk<<'>. (9.0.18)
где чертой вверху обозначена комплексная сопряженная величина.
Из возможности канонического разложения вида (9.0Л7) или (9.0Л8) кор-
реляционной функции вытекает представимость случайной функции X (/) в виде
канонического разложения (9*0Л6), где случайные величины Vk (k = l,
2, .*♦, т) имеют дисперсии Dk Ф = 1, 2, ..., т).
При линейном преобразовании случайной функции X (f), заданной
каноническим разложением (9.0.16), получается случайная функция Y (t) = Ц {X (t)}B
виде канонического разложения
т
Y (0« ту (0 + S ^*+А (0. (9.0.19)
*=1
где ту (0 = 1* {т* (*)» фА (0= ^0) (Фь (0). (9.0.20)
т5 е» при линейном преобразовании случайной функции, заданной каноническим
разложением, ее математическое ожидание подвергается тому же линейному
преобразованию, а координатные функции — соответствующему линейному
однородному преобразованию*
Стационарной случайной функцией X (t)*} называется случайная функция,
математическое ожидание которой постоянно, тх = const, а корреляционная
функция зависит только от разности между ее аргументами: Кх (t, t') = kx (т)
где т = V — L
Из симметричности корреляционной функции Кх (t, ?) следует, что kx (т)=
—&я(—*)» т- е* корреляционная функция стационарной случайной функции есть
четная функция аргумента т.
Дисперсия стационарной случайной функции постоянна:
Ох = Кх (t, f)^kx (0) « const. (9.0.21)
Корреляционная функция стационарной случайной функции обладает
свойством •-
\kx(v)\<Dx. (9.0.22)
Нормированная корреляционная функция стационарной случайной функции
равна
Рх (т) = kx (%)IDX « kx (%)/kx (0). (9.0.23)
Каноническое разложение стационарной случайной функции имеет вид
00
*(*)««*+ 2 (^ftCoso)ft^+Fftsino)feO, (9.0.24)
где Uk> Vk Ф = 0, 1, «.*) — центрированные, некоррелированные случайные
величины с попарно равными дисперсиями D [£/&] = D [Vu] = Oft.
Разложение (9.0.24) называется спектральным. Спектральному разложению
стационарной случайной функции соответствует разложение в ряд ее
корреляционной функции:
оо
M*)e S Dfecoso)ftx, (9.0.25)
откуда
ОО ^ '
Д*=2 Ofc. (9.0.26)
*=0
*> Точнее, стационарный в широком смысле,
250
Спектральное разложение (9.0.24) стационарной случайной функции
полагая о)0 = 0, можно переписать в комплексной форме:
X(t)-mx+ 2 Vh*"h\ (9.0.27)
Sx (ю) =— I kx (т) cos ©т<2т, kx (%) = I
n i i
kx (т) cos ayidx, kx {%) = I Sx (ю) cos cord©; (9.0.28)
где f
I
I
Спектральной плотностью стационарной случайной функции X (f) наз.ыва- i
ется предел отношения дисперсии, приходящейся на данный интервал частот- \
к длине этого интервала, когда последняя стремится к нулю. Спектральная плот, %
ность Sx (ю) и корреляционная функция kx (т) связаны преобразованиями Фурье. X
В действительной форме эта связь имеет вид \
из последнего соотношения вытекает, что \
ОО \
C>x=kx (0) = J Sx (©) d©. (9.0.29) |
о |
%
В комплексной форме преобразования Фурье, связывающие спектральную i
плотность Sx (ю) и корреляционную функцию kx (т), имеют вид |
оо оо |
SJ(o))=-^- f *«(••)e-lcwЛ, **(«)- rsJ(co)eiu)Xrfo). (9.0.30) j
—оо оо |
В приложении 7 дана таблица соответствий некоторых корреляционных \
функций и спектральных плотное гей. \
Как Sx (ю), так и S*(©) —действительные, неотрицательные функции; $
5^(0)) —четная ^функция, определенная на интервале (—оо. +оо); Sx (со) on- j
ределена на интервале (0,+ °°) и на этом интервале S* (©) =* 0,5 Sx (©). ]
Нормированной спектральной плотностью sx (©) [или в комплексной форме j
si (со)] называется спектральная плотность, деленная на дисперсию случайной |
функции X (0: |
sx((u)=*Sx(g>)/Dx< 5J (©)—SJ (od)/Dx. (9.0.31) J
i
Если взаимная корреляционная функция Rx, у (*» *') двух стационарных \
случайных функций X (t) и Y (/') есть функция только т =* f — *, то такие слу- *
чайные функции называются стационарно связанными* В этом случае между \
взаимной корреляционной функцией Rxy (т) и взаимной спектральной плот- \
ностью Sxy (ю) существуют соотношения: j
оо о» J
«*»W- f elOT^H* S^,(»)-■—- j е-1отЯад(«)*г. (9.0.32) j
_oo *—оо |
251 t
Если нормальные стационарные случайные функции X (t) и Y (0
стационарно связаны, то случайная функция Z (0 = X (О Y (i) будет стационарной
q характеристиками:
m2=mxmy+Rxy(b)> (9.0.33)
00
S* (со) = J S*x (co-i>) S* (v)dv+mx mp [S*xg (<o)+S*gx (со)] +
+ J" S^<«—o)S*,(D)&+m»S;(e»)+m«S;(<»). (9.0.34)
*-» oo
В чаетном случае, если Z (Q = X2 (Q, то
mz=mx+Dx=mx+kx(0), (9.0.35)
00
5г(со)«2 J SJ(w —o)S*(y)dt;+4m2 5*(ci)). (9.0.36)
moo
Белым шумом (или белым шумом в широком смысле) называется
случайная функция X (0, любые два различных (сколь угодно близких) сечения
которой некоррелированны и корреляционная функция которой пропорциональна
дельта-функции:
Kx(t, t') = G(t)6(t-t')< (9.0.37)
Величина G (/) называется интенсивностью белого шума» Определения и
свойства дельта-функции даны в приложении 6.
Стационарным белым шумом называется белый шум с постоянной
интенсивностью и (/) = G = const,
Корреляционная функция етационарного белого шума имеет вид
kx (т) = G 6 (т), (9,0.38)
откуда его спектральная плотность постоянна и равна
Si (ю) — G/2ji, (9.0.39)
Дисперсия стационарного белого шума Dx e G6 (0), т, е* бесконечна.
Если на вход стационарной линейной системы L поступает стационарная
случайная, функция X (/), то спустя некоторое время, достаточное для затухания
переходного процесса, влучайная функция Y (?) на выходе линейной системы
также будет стационарной. Спектральные плотности входного и выходного сир-
налов связаны соотношением
S* (ю) =SJ (ю) I Ф <!ю) |2, (9.0.40)
где Ф (ico) — амплитудно-частотная характеристика линейной системы»
Говорят, что етационарная функция X (f) обладает эргодическим свойством,
если ее характеристики [mXi kx (т)] морут быть определены как соответствующие
средние по времени для одной реализации достаточно большой
продолжительности. Достаточным условием эргодичности стационарной случайной функции
(по математическому ожиданию) является стремление к нулю ее корреляционной
функции при т ->- оо:
Пт^(т)=0. (9.0.41)
Т->оо
Для того чтобы случайная функция X (t) была эргодична по дисперсии Dx,
достаточно, чтобы случайная функция Y (f) = X2 (t) обладала аналогичным
свойством, т. е, при т -> oo lira kg (т)=0**.
*} Для того чтобы случайная функция была эргодична по корреляционной
функции, нужно, чтобы аналогичным свойством обладала функция Z (/, т) =
= Х(0Х(*+т),
252
4
Выбросом случайной функции X (f) за уровень а называется пересечение
реализацией этой,функции (снизу вверх) прямой, параллельной оси Ot и
отстоящей от нее на расстояние а (см. рис. 9.0.5, где выбросы отмечены, крестиками).
Число выбросов X за время Т есть дискретная случайная величина} если
выбросы редки, то ее можно считать распределенной по закону Пуассона.
Рис. 9.03
Для нормальной стационарной случайной функции X (/) среднее число
выбросов за уровень а в единицу времени равно
к
=J_expf_(£±^L)^L, (9.0.42)
2я v\ 2в» / <зх
где Од — среднее кв адратическое отклонение производной случайной функции
ПО=-£-*<<>• (9.0-43)
at
Таково же и среднее число пересечений заданного уровня сверху вниз»
ЗАДАЧИ И УПРАЖНЕНИЯ
9.1. Рассматривая неслучайную функцию времени ф (/) как
частный вид случайной функции X (t) =» q> (/), найти ее характеристики:
математическое ожидание пгх (/), дисперсию Dx (t) и корреляционную
функцию Кх (t, tl). Является ли случайная функция X (t)
стационарной?
О т в е т. mx (t) - <р (*); Dx (0 - 0; К* {U П - 0.
В общем случае случайная функция X (t) нестационарна, так как
при ф (t) ф const имеем mx (t) Ф const.
9.2. В условиях предыдущей задачи ф (t) «■ а = const, где а не
случайная величина : X (t) = а. Стационарна ли случайная функция
X (<)? Если стационарна, то обладает ли она эргодическим свойством?
Ответ. Случайная функция X (t) стационарна, так как mx (t) =
= а — const, Dx (t) — 0, Кх iff) =*kx ft) — 0, и обладает
эргодическим свойством.
9.3. Случайная функция X (t) в каждом сечении представляет
собой непрерывную случайную величину е одномерной плотностью
распределения / (х, /). Написать выражения для математического
ожидания mx (t) и дисперсии Dx (t) случайной функции X (t).
оо со
О т в е т. шх (0 = f xf (x, t) dx; Dx (/) - J lx—mx(f)]2f (x, t)dx.
—oo —со
9.4. Случайная функция X (t) представляет собой случайную
величину X (t) = V, где V — непрерывная случайная величина с плот-
253
новтью ф (v). 1) Написать выражение одномерного закона
(плотности) распределения f(x, f) случайной функции X (t); 2) найти
математическое ожидание тх {£) и дисперсию Dx (i) случайной функции X (/);
3) написать выражение двумерной функции распределения F (хъх29
tv t2) двух сечений X (tx), X (t2) случайной функции X (*); 4) найти
ее корреляционную функцию Кх (*, t'j) и спектральную плотность
SJ (©).
Решение. 1) / (х, t) =* ф (х)\
оо оо
2) mxit) = \ х ф (х) dx = mv; Dx (t) = J (x — mj2 ф (x) dx;
3) F (*b x2 Д, g = P {X ft) < *i, X (t2)< x2} =
= P {V<xx, Y<x2}.
Если хг < x2> то из F < хг следует V <.x2 и Р {V < x1} К <
г1
< хг) — ) <p (x) dx. Следовательно,
Г (Xi, X29 tl9 t2) —
{ q>(x)dx = F (хг) при xx < x%\
«-400
\ q>(x)dx = F (x2) при x2 < х1э
где F (x) = J ф (#) dx — функция распределения величины V;
—оо
4) /С* & **) - М [X (0 ^ 0*)1 = М IVV] « D0;
D* (0 = /(*(',**) = £>,,
Так как тх (f) = const и Кх (t, t*) = const, то случайная функция
X (0 стационарна. Так как среднее по времени для каждой реализации
равно значению, принятому случайной величиной V в этой реализации,
и различно для разных реализаций, то случайная функция X (t) не-
эргодична; ее спектральная плотность
о»
Si(co) = -~iL Г e-l^dco = D06(co),
где б (со) — дельта-функция. В этом можно непосредственно
убедиться, так как
оо оо
— оо —- оо
9.5. Случайная функция X (t) задана в виде X (t) = Vt + b9
где V — случайная величина, распределенная по нормальному
закону с параметрами mv, gv\ Ь — не случайная величина. Найти
одномерную плотность распределения f (x, t) сечения случайной функции X (t)
и ее характеристики: тх (t),Dx (t)t Kx (t, f).
254
О т в е т. / (х, t) — нормальный закон о параметрами m„t -f- Ь\
1*1 <V I
t% о-—у-= ыр-[х-?:\+Ь)]\ \
Н|а„У2л 2Яа» <
mx(t)=mBt + b; Dx(t) = i*ol; Kx(t, t') = aUtf. !
9.6. Показать, что любая функция двух аргументов вида •
S D«<M9<Pi(f). (9.6) ;
гдеО* — неотрицательные числа; q>$ (i) — любые действительные функ- \
ции (/ = 1,2,..., я), обладает всеми свойствами корреляционной функ- :
ции. s
Решение. Достаточно показать, что существует случайная \
функция X (/), имеющая корреляционную функцию (9.6). Рассмотрим ]
действительную случайную функцию X (/), заданных в виде канони- j
ческого разложения *
X(0«m«(0+2jv«4>t(0. !
где D [Vt] = Dt. Корреляционная функция этой случайной функции \
имеет вид \
что и требовалось доказать. \
9.7. Даны характеристики нормального случайного процесса J
X (/): m* (0; £>* (0; К* Ct **)• Известно, что в момент времени * слу- ::
чайный процесс находился в состоянии х (X (t) = #). Найти условную )
вероятность ра& того, что в момент времени t9 > t случайный процесс \
X (?) будет принадлежать некоторой области (а, Р); I
раЭ - Р {X <*') 6 («. Р) I X (0 - х). \
Решение. Обозначим X (f) = Xt, X (**) = Х2. Система слу- J
чайных величин Х19 Х2 имеет нормальное распределение / (хъ х2) I
с характеристиками \
mx% = mx(t)\ mXi = mx(tl); \
°2xt=Dx(t); ol2 = Dx{n rw-^L£i£L. |
Условный закон распределения з
/ (x2 \xj - f fa, *2) (ft fa))~l, где /^ (xt) = J / (*,, *2) dxz. ]
— OO J
Этот закон тоже будет нормальным с характеристиками:
о
mXi\Xl =Щ-\-ги2 ^(хх—т1)\ оХй, * = о,,К 1 —rf,2.
255
а*
Отсюда
а 2
(а— m2 + rlf2—— (х-> тг)
где Ф (х) — функция Лапласа.
9.8. Найти одно- и двумерный закон распределения и
характеристики случайной функции X (t), заданной своим каноническим
разложением
Х(0 = тя(*) + 2 Vt<Pi(0,
где Vt (i = 1,2,..., п) — взаимно-некоррелированные нормально
распределенные случайные величины с характеристиками т% = О, Df.
Решение. Одномерный закон распределения / (хг, t) —
нормальный с характеристиками
mXl (t) = тх (0; DXl(t) = 2 D* Ф* <'>•
/=. i
Корреляционная функция
u*-l /-1 J /=1
Двумерный закон распределения / (%, #2: t> P) — нормальный g
характеристиками mXi (t); mX2 (tl)\ DXl (/); Dx2 (tl)\ Kx (t9 f).
Случайная функция X (t) нормальна* поэтому двумерный закон
распределения является исчерпывающей характеристикой для любого числа
сечений этой функции.
9.9. Задана случайная функция
где ViH V2 — некоррелированные случайные величины g
характеристиками: mVt = mVi = 0; DVl> DV2. Найти характеристики случайной
функции X (f).
Решение. Случайная функция X (t) представлена каноническим
разложением без свободного члена, следовательно, тх (t) = 0;
Kx(t9 f'J^^e-^H-^ + D,, e-* <'+«■>;
Ac (t) = Dni e~a* 2< + DVi e«a* ».
9.10. Случайная функция X (t) задана своим каноническим
разложением
*(0=2 Vie-V + a,
256
где Vt — центрированные случайные величины о дисперсиями DDi
(i = 1, 2, ..., п)\ М [Vt, Vj\ = 0 при 1Ф\\ а — не случайная величина.
Найти характеристики случайной функции X (О-
Ответ.
mx(t) = a; *,(*,<•) = JJ Д. е"* <<+*•>;
*= i
*= i
9.11. Случайная функция X (t) задана каноническим разложением
X (t) = t + Vt cos <o t + V2 sin ©/,
где Vt и V2 — некоррелированные случайные величины с
математическими ожиданиями, равными нулю, и с дисперсиями D± = D2 =2.
Определить, является ли стационарной случайная функция X (t).
Решение, mji) = t\ Kx (t, f) = 2 (cos <ot cos <o*e + sin <ot x
X sin со/') = 2 cos со (/ — t').
Корреляционная функция случайной функции X (f) удовлетворяет
условию стационарности, однако математическое ожидание тх (t)
зависит от времени. Случайная функция X (t) нестационарна, но
центрированная случайная функция X (t) стационарна.
9.12. Заданы две случайные функции:
X (t) = Vx cos сох* + V2 sin corf; Y (t) = Ut cos cd2* + t/2 sin ®2t.
Математические ожидания всех случайных величин Vu V2, U\ и
U2 равны нулю, дисперсии D0t = DV2 = 1; DVt = D0, = 4;
нормированная корреляционная матрица системы (Vlt V%> Ul9 U2) имеет вид
111 0 0,5 ОН
1 0 —0,5
1 or
II Ml
Определить взаимную корреляционную функцию Rxy (t, f) и
найти значение этой функции при t = 0, t'j = 1.
Решение. Rxy(t9 tl) =M[X{t)f (t1)] = Ж[(угcoscox* +
+ V2 sin щ t) (Ut cos co2 VJ + U2 sin co2 t'J)] = cos cox t cos co2 /' MIVX Ux] +
+ coscoxt sin co2 tK M [V2 U2\ + sin cox t cos co2 tl M [V2 Ut] + sin cox / x
X sin co2 tl M |V2^2l = cos wi * cos co21*—sin щ t sin co2 tb = cos (cox t + co2 /')>
^(°; l) = cosco2; /?^(0; l) = coscox;
Дуя(*. О = £**('*» 0==COS(C0!^+C020.
9.13. Пуассоновский процесс. Рассматривается на оси 0t
простейший поток событий с интенсивностью % (точки на ogh 0t — см. рис.
9.13,а) и связанная с ним случайная функция X (t) — число событий,
появившихся за время (0, t). В момент появления очередного события
9 Зак. 1049 257
Рис. 9.13
случайная функция X(t) скачком увеличивается на единицу (рис.
9.13, а)*>. Случайная функция X (t) называется пуассоновским
процессом.
Найти одномерный закон распределения пуассоновского
процесса, его характеристики: тх (t), Dx (t), Кх (U?)> rx(tyf), а также
характеристики случайного процесса Z (t) = X (t) — It.
Решение. Закон распределения сечения X (t) есть закон
Пуассона с параметром а = М, значит, вероятность того, что случайная
величина X (t) примет значение т, выражается формулой Рт =
, =\(М)т (ml)"1 ег-л-' (т = 0,1,2,...). Математическое ожидание и
дисперсия случайной функции X (t): mx {t) =DX (t) = U.
Найдем корреляционную функцию Кх (t, ?). Пусть t' > t.
Рассмотрим интервал времени (0, t') (см. рие. 9.13, б). Разобьем этот интер-
Условимся считать функцию X (t) непрерывной слева.
258
\
вал на два участка: от 0 до t и от t до t'\ Число событий на всем
интервале (0, ?) равно сумме чисел событий на интервалах (0, t) и (*, <')*>:
X (С) = X (0 + Y (f — t),f где Y {f — t) — число событий,
наступивших на интервале (t, t')\ вследствие стационарности потока
случайная функция У (*'• — t) имеет то же распределение, что и X (t);
кроме того, согласно свойствам пуассоновского потока событий
случайные величины X (t) и Y (t' — t) некоррелированны.
Имеем
Кх (U П = М [X (t) X (t')] = М[* (t) (X (t) + Y (f - t))] =
= M(X(*))21 =#*(*)== W.
Аналогично при t > f получаем Kx (t9 О = Xf\ Таким образом,
Kx (t> t') = min {Xt, Xf} = X min {t, t'}9 где min {t,t'} —
минимальная из величин t, V (при t = f в качестве минимальной можно взять
любую из величин t, t).
Пользуясь символом единичной функции 1 (х) (см. приложение 6),
можно записать корреляционную функцию в виде
Кх {U t') = Xt\ (fi -t)+Xt'l (t-f).
На рис. 9.13, в показана поверхность Кх (*» ?). В квадранте t > О
и £ > 0 поверхность Кх (t> £) состоит из двух плоскостей,
проходящих соответственно через оси Ot и Of и пересекающихся по линии 0Dxf
аппликаты точек которой равны дисперсии Xt.
Нормированная корреляционная функция
rx(tJf)--rKx{t'n =i/^4<e-0+i/~ig-O-
-]/Dx(t)Dx(t') У Г у t
Поверхность rx (t, tf) показана на рис. 9.13, г.
Пуассоновский процесс является процессом с независимыми
приращениями, так как его приращение на любом участке есть число
событий, появившихся на этом участке, а для простейшего потока числа
событий, попадающие на неперекрывающиеся участки, независимы.
Процесс Z (t) = X (t) — Xt (см. рис. 9.13, д) есть неоднородное
линейное преобразование случайного процесса X (t).
Следовательно, тг (f) = тх (t) — Xt = 0; Dz (t) = Dx (t) = Xt\
Kt (t, П = Kx (t, П - X min (t, t%
так как соответствующее линейное однородное преобразование не
меняет корреляционной функции процесса X (t).
9.14. Случайный процесс X (t) возникает следующим образом. На
оси времени Ot имеется стационарный пуассоновский (простейший)
поток событий с интенсивностью X. Случайная функция X (t)
попеременно принимает значения + 1 и —1; при наступлении каждого события
она скачком меняет свое значение с + 1 на —1 или наоборот
(рис. 9.14, а). В начальный момент случайная функция X (t) с вероят-
*} Возможностью появления события в точности в момент t пренебрегаем,
так как вероятность этого равна нулю,
9* 259
ностью 1/2 равна + 1, а с вероятностью 1/2 равна — 1. Найти
характеристики тх (*), Dx (i) и Кх fo ?) случайной функции X (t).
Решение. Сечение случайной функции X (t) имеет закон
распределения, представленный рядом
Х(0 =
-1+1
0,5 | 0,5
Действительно, так как моменты перемен знака никак не связаны со
значением случайной функции, нет никаких оснований считать какое-
либо из значений +1,-1 вероятнее другого. Отсюда тх (/) =*
= _ 0,5 + 0,5 « 0; Dx (t) = (— 1) 2/2 + 12/2 = 1.
nx(t,tr)
Рис. 9.14
Чтобы найти корреляционную функцию Кх (U t'), рассмотрим
какие-то два сечения случайной функции: X (/) и X (t') (t,J > t) —
и найдем математическое ожидание их произведения:
Кх ft t') - М [X (t) X (Г)) = М [X (0 X (t%
Произведение X (0 X (f) равно — 1, если между точками t yl 1?
произошло нечетное число событий (перемен знака), и равно + 1,
если произошло четное число перемен знака (включая нуль).
Вероятность того, что за время т = tl — t произойдет четное число перемен
знака, равна
Рчет — 2л
(Хх)
2т
(2т)!
i—Кт _-. л—А.Т
еЯ,т^ е^Ьх
аналогично вероятность того, что за время т произойдет нечетное число
перемен знака, равна
Рнеч = е
-%х!
%х
,-Ад
260
Отсюда
где т = t,J — t. Аналогично при ? < t
Кх (/', t) = e-^c-^>, где т = t — *.
Объединяя эти формулы, получаем Кх (U О = kx (т) =* е~2Я-1r I .
График этой функции показан на рис. 9.14, б. Поверхность Кх (t, О =*
е-2Я | *<-*< I показана на рис. 9.14, в.
Случайная функция X (t) стационарна. Ее спектральная плотность
оо
SIM = 4- f *.We-'«MT = -L
2л J я
2Я,
(2Я,)2+о>2
*ю
i
х/У
н^
I [
1 I
LJ
Рис. 9.15
W
■Нг
9.15. На оси Ot имеется
простейший (стационарный пуассоновский)
поток событий с интенсивностью А,.
Случайный процесс X (t)
возникает следующим образом: в момент
появления /-го события в потоке (i =
= 1, 2,...) он принимает случайное
значение V% и сохраняет его до
следующего события в потоке (рис.
9.15). В начальный момент X (0) =
= V0- Случайные величины V0i Vx>
V2, ... >Vt, ... независимы и имеют
одно и то же распределение с плотностью q> (x). Найти характеристики
процесса тх (t), Dx (t), Kx (U t'). Является ли процесс стационарным?
Решение. Любое сечение случайной функции X (/)
распределено по закону ф (х); отсюда
тх (t) = М Wt\ = ] х<р.(х) dx =
тп
Dx (t) = Dv = J (* — mvf ф (х) dx.
— 00
Корреляционную функцию Кх (t, f) находим с помощью того же
приема, что и в задаче 9.14. Рассмотрим два сечения X (t) и X (t)
(t'J > t)9 разделенные интервалом т = Р — t. Имеем
Кх (*, t') = MIX (t) X (f%
Если между точками U t,J не появилось ни одного события, то X (f) =
= X (f) и Кх (t, f) = М [(X (0)21 =Dx(f) = D0. Если между точками
U ?' появилось хотя бы одно событие, то М [Я (t) X (f)\ == 0. Отсюда
Кх (*, О =■ е-** Dv + [1 — е~Ч * 0 =* D0q^\
Ah алогично, при tK < t
Kx(t,f)=Dver*-*\
261
откуда видно, что процесс стационарен. Его корреляционная
функция kx (т) =D0e-^ tт! не зависит от вида закона распределения ф (х)9
а зависит только от его дисперсии Dv.
9.16. Процесс с независимыми сечениями. Рассматривается
случайный процесс X (/), описанный в предыдущей задаче 9.15, в предельном
случае, когда интенсивность % потока событий неограниченно
увеличивается. Исследовать поведение характеристик этого процесса при
&-> оо.
ЬхМ
А,
кхМ
о
S)
Рис. 9.16
М*)
10
Решение. При увеличении X корреляционная функция kx (т) =
= Dv е-Л1т1 будет «стягиваться»*к началу координат (рис. 9.16,а).
В пределе получим корреляционную функцию вида
kx{%) =limfe,(x) -limDpe^l*! = D„lim е-*«Ч
т. е. функцию, равную нулю всюду, кроме т = 0, а при т = 0, равную
Dn (рис. 9.16, б). Записать это можно так:
при т = 0;
при т Ф 0.
Так KaKvno условию задачи 9.15 все сечения случайного процесса
X (t) независимы, мы получили модель случайного процесса, для
которого любые два сколь угодно близкие сечения независимы. Такой про-
цеее можно назвать «процессом с независимыми сечениями».
Получающийся в пределе при X ->■ оо случайный процесс а независимыми
сечениями X (t) не имеет ни одной точки непрерывности.
9.17. Белый шум. Рассмотреть предельный случай для случайного
процесса X (/), приведенного в задаче 9.15, при условии, что
интенсивность потока X неограниченно увеличивается (X ->■ оо) и одновременно
с этим стремится к бесконечности и дисперсия Dv каждого сечения
(Dv ->■ оо), причем DJX = с = const. Найти характеристики
случайного процесса Z (/), получаемого при таком предельном переходе, и
показать, что случайная функция Z (t) представляет собой
стационарный белый шум.
Решение. Поведение случайного процесса X (t) при X ->• оо
уже исследовано в задаче 9.16; теперь учтем еще условие DD ->■ оо,
DJX = с. Рассмотрим спектральную плотность Sx (0) для случайного
процесса X (t) задачи 9.15:
262
Из условия D0A = с имеем Dvl(nk) = с/л = a — const.
Корреляционная функция kx (т) = аяА, er*-j TI.
Для случайного процесса Z (f), который получится при А,-^оо,
£>„->- оо, D<A = с, получим
kz (X) = lim fcx (К) = lim ая^е-**т I = ая lim Ле^«т I =* акЬ (т),
Л-*оо Л,->оо Я->оо
где б (т) — дельта-функция (см. приложение 6);
(со) = hm = а.
Woo ^+0)а
Таким образом, мы убедились, что случайный процесс Z (t)
представляет собой стационарный белый шум, и построили модель
возникновения такого шума. Белый шум можно представить как предельный
случай последовательности коротких независимых одинаково
распределенных импульсов с большой дисперсией. Такие процессы встречаются на
практике при рассмотрении различных естественных помех, «теплового»
шума в электронных устройствах, «дробового» эффекта и т. п.
9.18. Рассматривается случайный процесс X (t), описанный в
задаче 9.15, при условии, что закон распределения каждой случайной
величины Vt (i = 0,1, 2,...) — нормальный с математическим ожиданием
т0 = 0 и дисперсией DD. Найти характеристики тх (t), Dx(t) и
Kx (t, t') случайного процесса X(t). Будет ли этот процесс
стационарным? Будет ли он нормальным?
Решение. Любое сечение случайной функции X (t)
распределено по нормальному закону с параметрами mv, а0 = Vdo. Как
следует из решения задачи 9.15, корреляционная функция kx (т) =
— DverK ix I. Процесс стационарен. Но является ли он нормальным?
Нет, несмотря на то, что одномерный закон распределения нормален.
Совместное распределение двух сечений случайного процесса X (/)
уже не является нормальным, так как эти сечения g отличной от нуля
вероятностью совпадают, чего не может быть для двух случайных
величин, совместное распределение которых нормально.
9.19. Модель электронного потока в радиолампе. Поток
электронов, направляющихся от катода к аноду радиолампы, представляет coN-
бой простейший поток g интенсивностью %. При поглощении электрона
анодом напряжение последнего возрастает скачком на единицу и
затем начинает убывать по экспоненциальному закону g параметром а,
зависящим от характеристик электронной схемы (рис. 9.19,а). Скачок
напряжения от прихода очередного электрона суммируется с
остаточным напряжением на аноде. Найти характеристики случайного
процесса X (t) — напряжения на аноде.
Решение. Электроны поступают на анод в случайные моменты
)времени Ти Т2, ..., Ти ... 9 образующие простейший поток событий.
Напряжение в момент t от воздействия t'-ro электрона» поступившего
в момент Ti9 будет
263
Wt(t)
4°-.* г.^^М-К'-^е-Р-Ч
где 1 (0 — единичная функция; Тг > О, * > 0. Рассмотрим
случайную величину Y — число электронов, поступивших на анод к моменту
t Эта величина имеет распределение Пуассона с параметром Ы.
Представим напряжение X (t) как сумму случайного числа случайных
слагаемых:
Х(0=2 e-*V~T*>l(t—Td. (9.19.1)
Ранее (см. задачу 8.80) было показано, что пуассоновский поток
событий на интервале (0, t) можно с достаточной точностью
представить как совокупность точек на этом интервале, координата каждой из
которых ®t £ (0, t) распределена равномерно на этом интервале (см.
8 £-Ь
ш
Х-7 2
01
4-НЙ]
<0
Рис. 9.19
xw=2e"a("
рис. 9.19, б) и не зависит от координат других точек. Следовательно,
выражение (9.19.1) можно переписать в виде
*_ ~'<~Ч (9.19.2)
где случайные величины @t независимы и распределены равномерно в
интервале (0, t).
Обозначим Xt (t) = е~" С" 0*> = e~at e«\ тогда
X(t)= 2 Х,(0=е-^ 2 е<*0*' <9Л93>
где Хг (/) представляют собой независимые одинаково распределенные
случайные величины, а случайная величина Y также не зависит от
случайных величин Xt (t). В соответствии с решением задачи 7.64
запишем выражение для mx (t) uDx (t):
264
mx (t) = щ (i) mXi (t); (9.19.4)
Dx (t) - mv (0 DKj (0 + Dy (0 mj, 0). (9.19.5)
Так как случайная величина Y имеет распределение Пуассона g
параметром %t, то triy (t) = Dv (t) = М. Найдем mx (t):
mH (t) = M [Xt (t)] = J- j e-« (' - *> dx = i^—.
0
Определим второй начальный момент случайной величины Xt(t):
М[Л7(*)] = -у- Г[е-а<<~*>]2^=-^е
— 2а*
2а*
Следовательно,
mx(t) = X l-e~ ; (9.19.6)
1 0«=*2<х*
Dx (0 = W [0Ж| (0 + mi4 (0] = ЯШ [Х<2 (t)} = X 4=|- . (9.19.7)
Заметим, что при *-> оо математическое ожидание и дисперсия
процесса X (t) не будут зависеть от времени: lim mx (t) = тх = Х/а;
HmDx (t) =DX = Щ2 а).
Чтобы найти закон распределения сечения случайного процесса
X (t) при тх = Я/а > 20, проведем следующие рассуждения. При
рассмотрении конечного, но достаточно большого интервала (0, f) и
гипотезе, что на этом интервале произошло достаточно большое число У
излучений электронов, процесс X (t) [см. формулу (9.19.2)] представляет
собой сумму независимых одинаково распределенных случайных
величин, которая будет распределена приблизительно нормально, так как
в этом случае практически выполняются условия центральной
предельной теоремы (см. гл. 8). Следовательно, сечение случайного процесса
будет распределено нормально с характеристиками: тх = Я/а; Dx =
= Я/(2а). Стационарный режим практически наступит через время
тс = 3/а.
Для нахождения корреляционной функции рассмотрим два сечения
исследуемого случайного процесса в моменты времени t и /' (/' > t). В
силу принятых допущений можно утверждать, что напряжение X (f)
на аноде лампы в момент времени f будет равно напряжению X (t)
в момент времени /, умноженному на экспоненту е-а(''~*>, плюс
напряжение У (tK — t)9 которое будет иметь место в результате
поступления на анод электронов в интервале времени (t, t'):
X (tl) = X (t) e-*«'~<> + У (** — 0. (9.19.8)
Очевидно, что случайные процессы X (t) и У (/* — t) независимы, так
как они порождены электронами, поступившими на анод в различные»
непересекающиеся интервалы времени (0 , /) и (tf tl) соответственно.
265
То же самое можно сказать и о центрированных случайных процессах
X (/) и Y (tl — t). Следовательно,
= М 1(Х (О)2] е-а («■'-« при V > t\
Kx(t, /0 = M[(X(O)2]e-a<<-<'> при t>V\
Объединяя последние два выражения, получаем
/С.М0 = Ac(min(/,*'))[!— e2amin<'- '')]e-<*M'-M.
Рассмотрим предельное поведение случайного процесса при t-+ oo,
Г ->• сх), но при конечном значении их разности т = f- — t. В этом
случае
kx(x) = Dxe-**x\ = JLe-«m.
*w * 2a
Таким образом, исследованный в этой задаче случайный процесс
X (0 при t-*- oo и Х/а > 20 является стационарным и практически
нормальным случайным процессом.
Рассмотренная задача является более общим случаем задачи 9.13.
Действительно, при a ->■ 0 напряжение на аноде лампы будет
представлять собой пуассоновскии процесс, так как с появлением каждого
нового электрона напряжение только возрастает на единицу и не
убывает с течением времени; Следовательно, для любых конечных tt t'
должны иметь место равенства:
lim/i^P) = Ппа-!—- = limDa(0 =ШпЬ -— = U\
а-*0 а-*0 а а-*0 а->0 2а
lim/Cx(*, f) = Hm— [1-е- aamin(t.<')je-«"''-4= Xminfc /'),
а-й) a-*0 2a
в справедливости которых предлагается читателю убедиться
самостоятельно.
9.20. Процесс функционирования линейного детектора. В
условиях задачи 9.19 положим, что электроны поступают на анод «пачками»,
моменты поступлений пачек образуют простейший поток с
интенсивностью Я. При этом число электронов в i'-й пачке представляет собой
случайную величину Wt) которая не зависит от того, какое число
электронов было в других пачках, и имеет закон распределения F (w) g
характеристиками mwy Dw. Эта задача эквивалентна задаче определения
напряжения на выходе линейного детектора, когда на его вход в
случайные моменты времени, определяемые пуассоновским потоком,
подаются положительные импульсы случайной величины (наибольшего
напряжения) Wi9 а в период между импульсами напряжение убывает
по экспоненциальному закону (рис. 9.20). Найти характеристики
процесса.
266
Решение. Исследуемый процесс можно представить формулой,
аналогичной (9.19.2):
Х(0= 2 ^е-а('~Ч (9.20)
где случайные величины У, Wiy ®г взаимно независимы.
Обозначим Xt (t) = W&~ut~e*\ тогда
М]ЗД]=т„
1-е
—а/
at
М[х;(0]=фю + лй)-
ft*-2a/
2а*
Рыс. 9.20
Следовательно,
При *-> оо
1— е
-at
; АЛО^МАи+яФ-
1-е
— 2a*
2a
*я(т) = Ояе—1*1.
Рассмотрим предельное поведение процесса X (/), когда
неограниченно возрастают: интенсивность пуассоновского потока,
порождающего импульсы (Я->оо); дисперсия амплитуды каждого импульса (Dw-*oo)
и параметр a (a->- оо). Неограниченное увеличение величины а
означает, что напряжение импульса очень быстро падает, т. е. в пределе при
a ->• оо площадь импульса будет стремиться к нулю. При этом
скорость возрастания величин % и Dw пропорциональна скорости возрас-
хания величины a:h = k±a\ Dw = &2a. Получаем (при t-*- oo):
lim mx=^ lim —mw = k1mw;
К a-*» K, a-»-ее a
|2\
lim Dx= lim
A,, a, Dw -* oo
X, a, Dyj -*• о©
2a
-*oo;
lim
&„ a, Dw-**>
kx{%)~ lim А^ае-«и1 = ^^б(т),
Л,, а, £),„-*«>
где б (т) — дельта-функция.
267
Таким образом, в пределе мы имеем белый шум, который
получается в результате бесконечно частой последовательности импульсов,
имеющих конечное математическое ожидание амплитуды импульса и
бесконечную дисперсию этой амплитуды, а также бесконечно малую
длительность самого импульса.
9.21. Дробовой Ьффект. Рассмотрим случайный процесс X (t),
порождаемый процессом Пуассона, как и в задаче 9.13. С появлением
г-го события пуассоновского потока в момент Tt в электрической цепи
возникает неотрицательный импульс напряжения Wt со случайным
значением (амплитудой), которое в дальнейшем изменяется по одному
и тому же закону ф (г)), где величина г) отсчитывается от момента Т]
(рис. 9.21) (ф(0)>ср(г))). Случайные величины Wt взаимно
независимы и имеют одну и ту же функцию распределения F (w).
Напряжение в электрической цепи представляет собой суммарное воздействие
всех импульсов с учётом их изменения во времени.
Рассматриваемый случайный процесс называется дробовым
эффектом. Исследованные в задачах 9.19 и 9.20 случайные процессы
являются частными случаями дробового эффекта. Требуется найти
характеристики дробового эффекта.
Рис. 9.21
Решение. В соответствии с решением задачи 9.20 дробовой
эффект на участке (0, t) можно представить аналогично (9.20) в виде
х(0=2^|ф('-в,),
/=1
(9.21)
где У, Wu ®t — взаимно независимые случайные величины, при этом,
как и в задаче 9.20, случайная величина Y подчинена закону Пуассона
с параметром %t, а случайная величина @t< распределена равномерно в
интервале (0, t).
Обозначим Xt (t)=Wi ф (* — 6,), тогда М IXt (*)] = mwfl Ф (/),
t
где mw *= М [Wih Ф (t) *= / ф (t — x) dx— площадь импульса (пло-
o
щадь, ограниченная кривой ф (г|) и осями координат);
М W (/)] *= (Dw + mi) Г1 Ф (/),
t t
rzeDw ■* D [Wt] « J (w — mw)2 dF (w); Ф (t) - J [<p (t — x))2 dx.
268
Следовательно, тх (t) « Jl mw Ф (f); Dx(t) = % (Dw + m%) Ф (/).
При t ->- ex) и существовании несобственных интегралов
О© оо
ПтФ(/) = \ <рЦ-х)с1х = Ф; ИтФ(0 = Г<р2#—х)йх = Ф\
/-*<» X /-►во J
о о
шх = ЧФ; О^ЦО^ + т^Ф.
Существование приведенных несобственных интегралов на практик
ке всегда имеет место, так как площадь импульса в начальной
амплитудой, равной единице, и площадь, определяемая квадратом
соответствующей функции, на практике — конечные величины.
Проводя рассуждения, аналогичные тем, которые были проведены
при выводе формулы (9.19.8), получаем при f > t9 чт® X (f) = X (t)X
X ф (tl — t) + Y (f — t). Следовательно,
" к It t') «P* W4>('£—0 при ?>t;
\Dx(t'')<p(t-t')npnt>t*.
Объединяя эти оба выражения, находим
Кх (U П = Dx (min <*, t')) q> (\t'< - *|).
При t9 f ->- оо получим kx (t) = Dx ф (| t|) (t = t'J — t). Таким
образом, мы видим, что при t, t' -»- оо дробовой эффект представляет
собой стационарный случайный процесс.
Рассмотрим предельный случай, когда интенсивность потока
импульсов X бесконечно возрастает, дисперсия импульса Dw тоже
бесконечно возрастает, а площадь импульса с единичной амплитудой Ф
стремится к нулю, так что величина Ф тоже стремится к нулю. При этом
выполняются условия:
lim ЛягшФ = т; lim X(Dw+m%,)Cb = D.
к -> оо %, D..
Ф->0 ф^.0
В этом случае дробовой эффект переходит в белый шум с
характеристиками тх = т\ kx{%) = Т> б (т), где б (т) — дельта-функция.
9.22. Импульсный дробовой эффект. Рассматривается дробовой
эффект, порождаемый импульсами, имеющими прямоугольную форму;
при этом амплитуда Wt и длительность xf импульса, поступающего в
момент Tt — независимые случайные величины с характеристиками
mw\ Dw; m* и DH соответственно (рис. 9.22). Найти математическое
ожидание и дисперсию такого случайного процесса X (t).
Решение. Рассматриваемый импульсный дробовой эффект на
участке (0* t) можно представить в виде
/=i /= 1
269.
где ф (t9 6ь Kt) — импульс, начало которого приходится на момент
времени Q*, высота равна единице, а длительность х$ (случайные
величины ®t и Kt — независимы): ф (/, 0Ь к£) = 1 (t — Qt) 1 (@ь + хг —
— t). Случайная величина ®t распределена равномерно внутри
интервала (О, t).
Найдем М [ф (t, в*, Xj)]. Введем гипотезу, состоящую в том, что
случайная величина тсг приняла значение х. В предположении, что эта
гипотеза имела место, найдем условное математическое ожидание при
достаточно больших значениях /:
М;
*[ф(*. ©ь х)] = -j- J1 (t-y) 1 (y + K—t)dy.
w
г tr t
Puc. 9.23
Подынтегральная функция представляет собой прямоугольный
импульс с высотой, равной единице, и длительностью, равной х, а
интеграл от этой функции будет равен площади этого импульса.
Следовательно,
Мк [ф (t, @i9 х)] = к/t,
откуда
М [ф (/, в,, щ)] = М ЫиЛ = mjt.
Аналогично
t
М„ [Ф(*. в„ Xif] =-i- j[l (*-*/) 1 (у + х-ОР
'*--*-;
М[ф(*,вг,хг)23 = -^-.
Следовательно,
М IXt (01 = М IIP, ф (*, вг> х,)] = /пшдак//; М Ш (01 =
= М [(1Р,ф if, в,, хг))23 = (Dw + да£) дан//; М [X (03 = тх =
= М[УЗ М[Хг (/)] = Urt^mjt = Яда^/я*; (4.22.1)
D [X (03 = Dx = М [УЗ М iXf (t)) = X(DW+ m*) да*. (4.22.2)
В пределе при неограниченном увеличении интенсивности
простейшего потока %, дисперсии амплитуды импульса Dw,
неограниченном уменьшении математического ожидания т*. и дисперсии D*
длительности импульса и сохранении постоянной величины Dy,=%(Dw+
270
+/Пш)тх== const импульсный дробовой эффект превращается в белый
шум с характеристиками тх\ kx (т) = Dx б (т).
9.23. Процесс изменения количества однородных элементов.
Рассматривается процесв X (t) — число функционирующих однородных
элементов в момент времени t. При этом предполагается, что каждый
элемент функционирует некоторое случайное время х, распределенное
по показательному закону с параметром \i9 одинаковому для всех
элементов, после чего выходит из строя («погибает»). Начало
функционирования (начало «жизни») каждого элемента является случайным
и определяется простейшим потоком с интенсивностью X. Например,
X (t) — число находящихся в эксплуатации ЭВМ, интенсивность к —
число производимых в единицу времени ЭВМ, х — случайное время
эксплуатации одной ЭВМ (среднее время эксплуатации ЭВМ равно
1/fx). Требуется найти характеристики случайного процесса X (/).
Решение. Случайный процесс X (t) представляет собой
импульсный дробовой эффект, рассмотренный в предыдущей задаче, о
той лишь разницей, что Wt = 1 для любых значений i (т^ = 1;
Dw = 0), а случайная величина х распределена по показательному
закону с параметром \i. Следовательно, при достаточно больших t [ем.
формулы (4.22.1), (4.22.2)] М [X (t)] = %mwmii = Wjr, D IX (t)] =
= % (Dw + mlt) mw = fyx.
Можно доказать, что одномерный закон распределения случайного
процесса X (t) является законом Пуассона g найденными
характеристиками.
При определении корреляционной функции рассматриваемого
случайного процесса X (t) используем свойство случайной величины х —
длительности импульса, распределенной по показательному закону,
состоящее в том, что «остаток» времени длительности импульса х
(рис. 9.23), отсчитываемый не от его начала 7\ а от некоторого момента
t± (Т < tx < Т + х), будет также распределен по показательному
закону с параметром \i (см. задачу 5.35).
Введем гипотезу, состоящую в том, что случайный процесс X (0=
= п (п = 0,1, 2,...). Вероятность этой гипотезы обозначим Рп (t)=
= Р (X (t) = ri). В предположении, что эта гипотеза имела место,
запишем выражение для случайной функции Хп (f) (f > t):
п
i= 0
где Vt — случайная величина, имеющая ряд распределения
V,:
0 1
1_е-м*'-о е_м*'_о
(^0);
V0 в 0; Y (f — t) — случайный процесс, порождаемый событиями,
наступившими в пуассоновском потоке в интервале времени (f, t').
п
Величина 2 Vt—есть число элементов, сохранившихся на момент вре-
мени tc9 если в момент времени t их было п.
271
Найдем условное математическое ожидание произведения X (t) х
XX (f) при условии, что X (*) в п:
где /Пк « 1/|д>- Следовательно, безусловное математическое ожидание
произведения X (*) X (f) будет
М[Х (О X (*')] = 2 М["Хп(О]Рп(0= 2 n«e-M''-opaW +
л=о
л=0
л=0
Отсюда
или
**<*. *«)-D«e-i'«,-«) при /*>*
*«(*. /c)-D.e-i4'-'*) при *>**.
Объединяя эти две формулы, получаем (т = р — /)
kx (%) = Dj-e-w iх i = — е-» i * i.
При Щ > 20 процеев накопления однородных элементов можно
считать практически нормальным в характеристиками /п„ = Я/ц и
Aj*(t) = Яц-*е-^"1. ^
-Я5г
^
ЛУГ,
а)
xs
ад
4
х'
МП
1 . *'
5|5
tfzy
i
, Я)
i 1
Хв
У
1
г
-
& 5 *
I
Рис. 9.24
9.24. Одномерное случайное блуждание частицы. Рассмотрим на оси
Ох частицу, которая акачками меняет свое положение (блуждает) под
действием случайных соударений с другими частицами (рис. 9.24 а)
В начальный момент частица находится в начале- координат, в
момент Тг первого соударения она перескакивает в точку Хг, в момент Т
второго соударения она скачком изменяет свою абсциссу на величину
Х2, в момент 78 — на величину Х3 и т. д. Случайные величины
Х1э А2,..., X*... независимы и имеют одно и то же распределение
272
0/71^= 0иОл-О. Моменты соударений Ти Г2, ..., Ти... образуют
простейший поток событий с интенсивностью А,.
Рассматривается случайный процесс X (t) — абсцисса блуждаю-
щей точки в функции времени (рис. 9.24, б). (Значения X (t) могут быть
как положительными, так и отрицательными.) Процесс X (i)
представляет собой упрощенную модель броуновского движения частицы.
Найти характеристики случайного процесса X (t).
Решение. Число событий на участке (0, t) представляет собой
случайную величину У, распределенную по закону Пуассона с
параметром \ t. Значение процесса X (t) в момент времени t определяется
формулой X (t) = 2 Хи т. е. представляет собой сумму случайного числа
случайных слагаемых;ч при этом все случайные величины X* и Y
независимы. Т^к же как в задаче 9.20, имеем
mx(t) = M[Y]MlXil = Ot так как MIH-W; M[Xj = m* = 0;
D.W-M[KlD[XfI+D тМ1Х*]2 = Ш, так как D[X*J=D.'
Аналогично решению, приведенному в задаче 9.20, при достаточна
большом / сечение случайной функции X (t) будет подчинено практи-.
чески нормальному закону с найденными параметрами.
Найдем корреляционную функцию процесса X (t), для чего
рассмотрим два его сечения: X (t) и X (f) (/' > t). Очевидно, что X \t') ==.
= X(t) + Y (t,j — t), здесь как и в задаче 9.20, случайный процесс
z
У (tl — /) = 2 Я*» где Z — число событий, наступавших в потоке на,
интервале времени f — t. Выше было показано, что случайные
процессы X (t), X (f) и У (t — t') имеют нулевое математическое ожидав
ние. Следовательно, при f > t
Кх (U П = М [X (О X (Щ = М[Х (0 {X (t) + Y(t' — t) }] =
= М [X2 (01 + М [X (t) Y (f — t)\ =» Dx (t) + M [X (0] M [Y (/' -.,
-t)]=Dx(t).
При t' < t получим Kx (t, t') = Dx (/')• Таким образом,
KxiU?) =Zra,min(f, /').
Рассмотренный случайный процесс X (t) является процессом с неза-вич
симыми приращениями.
Примечание. Процесс одномерного случайного блуждания частицы»
имеет те же характеристики, что и процесс Y (t) = X {t) — Xt, где X (f) —
процесс Пуассона, несмотря на то, что их реализации значительно отличаются (срав-.
ните рис. 9.13, д и рис. 9.24, 6"),
9.25. гВинеровский процесс. Рассматривается предельное поведе^
ние случайного процесса X (/) — одномерного случайного блуждания
частицы (см. задачу 9.24) при неограниченном увеличении
интенсивности Я, потока соударений и одновременном неограниченном уменьшении
дисперсии D перемещения частицы; при этом соблюдается условие
ID-a- const. Показать, что в этом предельном случае на достаточ-.
273
мо удаленных от начала участках времени процесс являетея винеров-
ским.
Решение. Условие тх (0 = 0 вытекает из условий
предыдущей задачи; независимость приращений и нормальность процесса при
t -»• оо показаны там же.
D [X (У — X (t2)\ = М ЦХ &) — X (t2))2l так как тх = 0;
М [(X ft) - X (t2))4 = M [X2 ft) + X2 (У - 2 X (« X (*2)1 =
= D [X (tt)) + D [X ft)] - 2 tf« ft Q.
В предыдущей задаче было показано, что D [X (t)] = %Dt\
Кх (h, Q = № min ft, t2). Отсюда при t2 > tt
D [X ft) — X ft)] = ^D/x + bD/2 — 2 ^D min ft, *2} =
= %Dtx + Wt2 — 2 Wtx = a ft — tx),
откуда следует, что процесс является винеровским.
Рис. 9.26
9.26. Случайная функция X (t) строится следующим образом.
В точке / = 0 она случайным образом и с одинаковой вероятностью 1/2
принимает одно из Значений + 1 или — 1 и остается постоянной^ до
t = 1. В точке t = 1 она снова, с одинаковой вероятностью 1/2 и
независимо от того, какое значение она имела на предыдущем участке,
принимает одно из значений +1 или —1 и сохраняет его до следующей
целочисленной точки / = 2, и так далее. Вообще, функция X (t)
постоянна на любом участке от п до п + 1, где п — натуральное число, а на
границе каждого нового участка независимо от предыдущих принимает
одно из значений +1 или — 1 а вероятностью 1/2 (одна из возможных
реализаций случайной функции X(t) показана на рис. 9.26, а). Найти
характеристики случайной функции X (t): математическое ожидание,
дисперсию и корреляционную функцию. Определить, является ли
случайная функция X (t) стационарной.
Решение. mx(0 = mx = (—l)-i-+ Ьу = 0; D*(0 =
= D* = (-l)2-l + l2-i-=l.
274
Найдем корреляционную функцию Кх (t, t'). Если точки t и ?
относятся к одному и тому же интервалу (/г, п + 1), где п — целое,
то Кх (ty О = Dx = 1, в противном случае Кх (/, t) = 0. Этот
результат можно записать в более компактной форме, если обозначить
через Ь (t) целую часть числа / (см. рис. 9.26, а). Тогда получаем (т =
= t< — t)
/Ся(МО==(1при|т|<1-
10при|т|>1 —
fc(min {/, Г»;
fc(min{/, /'}), где х = /'-
-/.
Эта функция зависит не только от т = /' — /, но также и от того,
где на оси Ot находится участок (t,t')\ следовательно, случайная
функция X (t) стационарной не является.
Поверхность Кх (t\ t') выглядит как ряд кубов с ребром, равным
единице, поставленных на плоскости tOt' вдоль биссектрисы первого
координатного угла, на которой t = t\ так что диагонали оснований
совпадают с биссектрисой (рис. 9.26, б).
9.27. Случайная функция X (t) формируется так же, как и в
предыдущей задаче, с той разницей, что точки, в которых происходит
«розыгрыш» нового значения случайной функции, не закреплены на оси
0/, а занимают на ней случайное положение, сохраняя между собой
постоянное расстояние, равное единице (рис. 9.27, а). Все положения
начала отсчета относительно последовательности моментов «розыгрыша»
одинаково вероятны. Найти характеристики случайной функции X (t):
математическое ожидание, дисперсию и корреляционную функцию;
определить, является ли случайная функция X (t) стационарной.
*rfr>
А
-/ о / т
Рис. 9.27
Решение. Как и в предыдущем случае, tnx (t) = тх = 0;
Dx(t)=Dx= 1.
Найдем корреляционную функцию. Зафиксируем момент / (рис.
9.27, а). Этот момент случаен относительно точек, в которых случайная
функция X (t) принимает новые значения. Обозначим Т промежуток
времени, отделяющий точку t от ближайшей точки, в которой будет
«разыгрываться» новое значение X (/). Случайная величина Т
будет распределена равномерно на участке от 0 до 1. Пусть t' > t;
% = tl — t > 0. Если т < Г, то Кх {U О = 1. если т > Г, то
Кх (t, О = 0. Поэтому при 0 < т < 1
Kx(t, ?) = Р(Т>т) • 1 +Р(Г<т) . 0 = Р(Г>т) = 1-х).
275
Аналогично при т < О
Кх (t,tl)=l+% при — 1< т < 0.
Отсюда
/ии')=мН'-|т|при>т!<;;
10 при |т|> 1.
График этой функции представлен на рис. 9.27, б. Так как КУ (tJ')~
— kx (т), то случайная функция X (t) стационарна.
Корреляционную функцию (9.27) можно записать в более
компактном виде с помощью единичной функции 1 (х):
kx (т) = (1 - |т|) 1 (1 - |т|).
[X(t) 9.28. Условия предыдущей зада-
I . чи 9.27 изменены в том отношении,
I i—I I что в каждый из случайных моментов
-н{н--9^ч{ь--нЦн!н—^—- Ти разделенных единичными интер-
^""L-J j *" валами, случайная функция X(t)
^" принимает (независимо от других)
Рис. 9.28 значение Uu являющееся
случайной величиной с математическим
ожиданием пги и дисперсией DU9 и сохраняет его до следующей
точки. Одна из реализаций такой случайной функции показана на
рис. 9.28. Найти характеристики этой случайной функции:
математическое ожидание, дисперсию и корреляционную функцию; определить,
являетея ли случайная функция стационарной, а если стационарна, то
какова ее спектральная плотн©сть.
Решение. Рассуждая точно так же, как и в предыдущей
задаче, находим
тх (0 - М IX (t)) = ти\ Dx (t) = D [X (t)] = Du\
10 при |т|>1 J
Случайная функция X (t) стационарна. Ее спектральная плотность
S*x (со) = Du (1 — cos a))/(jtft>2).
9.29. Случайная функция X (t) представляет собой ступенчатую
знакопеременную функцию (рис. 9.29, а), которая через единичные
интервалы принимает попеременно значения: + 1 и —1. Положение
ступенчатой функции относительно начала отсчета случайно;
случайная величина Т, характеризующая сдвиг первой точки перемены
знака относительно начала координат, есть случайная величина,
распределенная равномерно в интервале (0;1). Найти характеристики
случайной функции X (t)i математическое ожидание, дисперсию и
корреляционную функцию.
Решение. Рассмотрим сечение случайной функции X (/);
оно с равной вероятностью может попасть как на участок, где елучай-
ная функция равна + 1, так и на участок, где она равна'— 1.
Следовательно, ряд распределения любого сечения имеет вид
27fr
A(/)«
— 1
2
+ 1 1
1
2
откуда /иж=-Ь -i-+b-i-=P; D^-l^.-L-Kl)*-!^ 1.
Найдем корреляционную функцию (<с «= <е — *; 1* > Q:
/Сх (*, П = MIX (ОХ (* + т)1 - М [X (t) X(t + т)1.
Так как произведение X (t) X (t + т) может принимать только два
значения (+1 или —1), то М [X (t) X (t + т)1 = 1рх + (—1) х
Х(1 — Pi) — 2 Pi — 1» где рх—вероятность того, что точки t и t + г
попадут на участки, в которых X (0 и X (t + т) имеют один и тот
же знак.
X(t)
Н-Ы
! I
Рис. 9.29
1 h
1 2 3 U 5 6 t
о)
-31-г V/0
-7
hxM
i / i \ i
J/ 2 \J, Г
б;
В силу равномерности распределения сдвига Т на рис. 9.29, а
мы можем перенести начало отсчета в левый конец того участка, на
котором находится точка t, и считать, что точка t равномерно
распределена в интервале (0; 1) (рис. 9.29, б). При таком толковании рг есть
вероятность того, что точка (t + т) попадает в какой-либо из интервалов
вида (2п,2п + 1)э п = 0, ±1, ±2 ... (эти интервалы отмечены
жирными линиями на рио. 9.29, б); подсчитаем эту вероятность для разных
значений т.
Лри 0 < т < 1 точка (t + %) может попасть либо в интервал
(0, 1), либо в интервал (1; 2), поэтому
рх = Р {/ + т< 1} = Р {/< 1—<г} = 1—т.
При 1 < т < 2 точка X + * может попасть либо в интервал (1; 2),
либо в интервал (2; 3), поэтому
Рл = Р {/ + т>2} = Р {*>2 —т}= 1
(2-х) = т— 1.
Продолжая эти рассуждения, получаем
(1 —(т—2я) при 2п<т<2л+ 1;
ft 1(чс—2л)—1 при 2/г+1.<т<2я + 2.
277
/С«(*.< + т) = Мт) =
Отсюда видно, что ри а значит, H/(i(U + t)= 2 /^ — 1, зависит
только от х и является четной функцией т. Следовательно,
|4и+1 —2т при 2п<т<2п+1;
I2<t—(4л + 3) при 2п+1<т<2п + 2.
График корреляционной функции представлен на рис. 9.29, в.
9.30. Случайная функция X (/) представляет собой
последовательность равноотстоящих положительных импульсов напряжения,
имеющих одинаковую ширину у<1/2. Начало каждого импульса
отделено от начала каждого следующего единичным интервалом (рис. 9.30,а).
Последовательность импульсов занимает относительно оси 0t слу-
ш
1_
Щ-Г
В-
+U
щ
yj?u у(Ыт$
<М</>
а)
Рис, 9.30
чайное положение (см. условия предыдущей задачи). Напряжение I -го
импульса Ut случайно (i = 1,2, ...). Все случайные величины Ut
распределены по одному и тому же закону с математическим ожиданием
ти и дисперсией Du и независимы. Найти характеристики случайной
функции X it): математическое ожидание, дисперсию и
корреляционную функцию.
Решение. По формуле полного математического ожидания
тх = ти у + 0 (1 — у) = тиу. Дисперсию найдем через второй на-
г:.а2[Х (/)] = a2Wi]y ' ' " *
момент:
У + 0 (1 - у) = (D„ + ml) у.
чальный
откуда
Dx - а2 [X (01 - т* = (Du + ml)y-m2uy
+ v (1 — Y) rnl.
В данном случае случайная функция X (t) не центрирована.
Ее корреляционную функцию будем искать через второй смешанный
начальный момент:
Кх (t9 t + т) «= М [X (t) X(t + т)1 — т.
Найдем М [X (t) X (t + т)1. Будем его вычислять по формуле
полного математического ожидания. Как и в предыдущей задаче,
представим ось Ot покрытой перемежающимися участками: зачерненные
соответствуют импульсам, а светлые — промежуткам между ними.
Обозначим Т случайное значение левой границы участка (Т, Т + т).
Возможны три гипотезы:
278
Нг — обе точки ГиГ + т попали на участок одного и того же
импульса;
#2 — одна из точек Т9 Т+т попала на участок одного из импульсов,
а другая — другого;
Я3 — хотя бы одна из точек 7\Г + т попала вне участков каких-
либо импульсов.
При первой гипотезе величины X (Т) и X (Т + т) совпадают и
М [X (Т) X (Т + т)] = М [U2] = Dtt -f mS. При второй гипотезе
величины X (Т) и X (Т + т) представляют собой независимые случайные
величины с одинаковыми математическими ожиданиями ти\ по
теореме умножения математических ожиданий М IX (Т) X (Т + т)1 = ml.
При третьей гипотезе М [X (Т) X (Т + t)l = 0- Полное
математическое ожидание
М IX (t) X (t + т)] = Р {ЯЛ (Du + m2) + Р {Я2} /п2.
Вероятности Р {Нг} и Р {Н2}9 а значит, и корреляционная
функция зависят только от т:
1) при 0<\<v
Р№} = Т-т; Р{Я2} = 0; М[Х(ОХ(/ + т)] = (Т-т)х
X(DU +m2);
6* (т) = (т — т) (Dtt + m£) — т2 ^«;
2) при у < т < 1 — у
Р {Я^ - 0; Р {Я2} = 0; М [X (t) X (t + т)] = 0;
&* (т) = 0 — уЭД = — Y2 п&\
3) при 1 — у < т < 1
Р{Я1} = 0; Р{Я2}=Т-(1-т); М[Х(*)Х(* + т)] = [т-
- (1 - т)] ml; К (т) = (у - 1 + т - y2) mj.
Дальнейшие интервалы значений т исследуются аналогично.
График функции kx (т) представлен на рис. 9.30, б. При |т| > 1/2
кривая &я (т) периодически повторяется, достигая в , целых точках
местных" максимумов, равных у (1 — у) ml.
9.31*. Рассматривается стационарная случайная функция X (/),
представляющая собой пилообразное напряжение (рис. 9.31, а). Начало
отсчета занимает по отношению к зубцам случайное положение, как в
задаче 9.29. Найти математическое ожидание, дисперсию и
корреляционную функцию случайной функцци X (t).
Решение. Математическое ожидание тх легко найти, если
учесть, что распределение X(t) при любом t — равномерное на
интервале (0;1), отсюда тх = 1/2.
Для отыскания корреляционной функции поступим следующим
образом: свяжем последовательность зубцов жестко с осью 0t9 но зато
будем случайным образом бросать на эту ось начало t отрезка (/, t +т)
(рис. 9.31, б). Так как зубцы периодичны, достаточно случайным
образом бросать точку t на первый интервал (0; 1), распределяя ее с посто-
279
янной плотностью. При этом, как видно из рис 9.31, б, X (t) *= t, a
значение X (t + т) равно дробной части числа t + т, т. е. X (t + т) =*
в= t + t — £ (/ + т), где £ (/ + t) — целая часть числа (/ + т).
1
м
vx(t)
\1
к—>
1
<—>
-
««—*■
7
t
_. fl t1t+Z2 J
frit
a)
Ю
Рис. 9.31
Если целая часть числа т равна п (п < т < п + 1), то
U+ 1 при t+<z^n+ 1.
и, значит,
xit+%)=ltm*m%me~n при *<'г+1—т'>
U + T—(п+ 1)при *>л + 1—1?.
По формуле для математического ожидания функции от случайной
величины t имеем при п ^ т < п + 1
1 /l-fl^T
М[Х(0Х(^ + т)1=Гх(0Х(/ + т).Ь^= Г *(/+*— л)Л +
о v о
1
+ Г t(t + %— я-
«4- 1-х
l)d/ = -±-(/z+l-T)2 +
+ ±(Т_П)_± (/г = 0, ±1, ±2,...).
Отсюда следует, что корреляционная функция зависит только от
г и при п < т < п + 1 (п = 0; ± 1; ±2;...) имеет вид
Кх (t, f) «= £* (т) = М [X (0 X (f + %)] — тх=.
= 0,5 (п + 1 — т)2 + (т — л) / 2 — 5/12.
Это периодическая функция б периодом 1, график которой состоит из
периодически повторяющихся отрезков парабол, обращенных
выпуклостью вниз. В интервале 0 ^ т < 1 эта парабола имеет вид kx (т) =*
= (1 — т)2/2 + т/2 — 5/12 с вершиной в точке (1/2; — 1/24). Полагая
т = 0, получаем Dx = kx (0) = 1/12.
9.32. Рассматривается линейное преобразование п случайных
процессов Хх (t), Х2 (*)» .... ^п (0 вида
у(о=фо(о+2 <моад,
/= 1
280
где ф/ (0 (/ = О, 1, 2,..., п) — неслучайные функции времени.
Известны характеристики случайных процессов Хг {t): mt (t)y
Dt(f), Kt ft f) (i == 1, 2*..., n)y а также взаимные
корреляционные функции Ru ft t') = M iXt (t) Xj (t':)) ft / = 1, 2,...> n\ i ф /).
Найти характеристики случайного процесса Y (t).
п
Решение. ту (t) = 2 фг (t) m% (t);
кУ ft о=м [y (t)Y р)\=м Г 2 v>i (t) xt (t) 2 ф7.(*') Яj (**> 1 =
L*=i /-1 J
= 2 Ф* (О Ф1 ft') iCi ft *4) + 2 Ф| (О <Pi (*•) «w ft П +
+ 2ф|(*§)фИ0Я«('\0!
Df (0=#*Л о— s ^ wD* ^+2 2Ф1 (t)ф>(ол«ft о.
Если случайные процессы X* (/) (/=« 1, 2,. ♦..* /i) некоррелированны
(Ru ft tf) = 0; i, j = 1,2,..., n), то
^ЛО-Зф^Оф/^^СО;
9.33. Имеются две некоррелированные случайные функции X (f)
и Y (t) с характеристиками
my(0 = l; /Cy ft*1)-**■<«-''>■.
Найти характеристики случайной функции Z (0 =* X (t) +
+ tY (t) + t2. Решить ту же задачу, если случайные функции X (t)%
Y (t). коррелированны и их взаимная корреляционная функция
Решение. В случае, если Rxy ft tl) = 0,
mz « mx (t) + tmy (£) + t* = 2 t2 + t;
/<^'.Oe^*ftO + tt*^yft<e)ee^ <*+'') + «*е".<^'>\
В случае, когда Я^ ft *) = а ехр (—а | t — t'J\), m% (t) не меняется;
кг ft n - /с. ft V)+и* ку ft г *)+г* яЛ ft п+«„ «•, t)=
9.34. Найти математическое ожидание и корреляционную функцию
суммы двух некоррелированных случайных функций X (t) и Y (t)
с характеристиками
281
mx (О - t; Kx (t, f) = #*;
Ответ. тг(0 = та.(/) + т„(/) = 0;' Kz(t,t') =
= Kx(t,t') + Ky(t,t') = lt'ill+*<*«+''>}.
9.35. Имеется комплексная случайная функция Z (t) = X (t) +
-f- iV (Of гДе i — мнимая единица; X (t), Y (t) — некоррелированные
случайные функции о характеристиками
mx{i)^f; /Ся(/, <<) = е-*<«-*')";
<MQ=»1; *,(<,*') = ete» <«+''>.
Найти характеристики случайной функции Z (t):mz (f); /Cz (/,<')
и Dz (f).
Ответ. mz(f)=-p-\-i; K,(t, tl) = e-* «-<'>s+e-2«» «+<'>;
9.36. Комплексная случайная функция Z (0 задана в виде Z (0 =
= X (0 + i Y (0, где
И
з
2
Х(0= 2 Ч + П)е-а^; Г(0= S (*к + У»)е-р*'.
3
*=1
Математические ожидания всех случайных величин Kft и Uk{k~
= 1,2, 3)_ равны нулю, а корреляционная матрица системы
случайных величин (Vlt V2, V3y Ul9 (/2, U3) имеет вид
0 0
2 0
3
1
0 ■
0
1
0 0
-1 0
0 3
0 0
2 0
Найти характеристики случайной функции Z (t).
о о
Ответ. mz(t)= 2 айе"*аь'-Н 2 Ьке~*к*;
k=\ k=i
Kz(t, П = Kx(t, f) + Ky (t, t') + i [Rx„(/', 0-#*y(*. t%
где /UU')= 2 *e~°tft('"Ha'
282
9.37. Корреляционная функция произведения. Рассматриваются
две некоррелированные центрированные случайные функции X (О,
Y (t) и их произведение Z (t) = X (t) Y (t).
Доказать, что корреляционная функция произведения равна
произведению корреляционных функций сомножителей: Kz (t, t'J) =
= KAt,t4Ky{t,f).
Решение. Kz(t,f) = М [Z (t) t {t')\\ Z (t) = Z (t) — mz (t). Так
как случайные функции X (f) n Y (t) некоррелированны и центриро-
ванны, то mz (t) = тх (t) ту (t) = 0; отсюда
Z(t) = X(t))?(t) = X(f)Y(t);
Kz (U П = M IX (t) Y (t) X (f) t (*'<)] =
= M [X (t) X (<*)] M [Y (t) Y (t')\ = Kx (t9t*) Ky (t,f).
В частности, при t =* t'J
Dz{t)=Dx(t)Dy{t).
9.38. Доказать, что корреляционная функция произведения не-
п
зависимых центрированных случайных функций Z (t) = П Xt (t)
равна произведению корреляционных функций сомножителей:
Kz(tj')= йкхлип
Решение. Доказательство аналогично предыдущему, о той
разницей, что для применения теоремы умножения математических
ожиданий в этом случае недостаточно некоррелированности сомножителей,
а независимости — достаточно.
9.39. Случайная функция X (0 о характеристиками mx(f) = 0,
Кх (U t') подвергается линейному неоднородному преобразованию:
Y(t) = Ц" {X (t)} + Ф (0,
где ф (0 — неслучайная функция. Найти взаимную корреляционную
функцию Rxy (tt £).
Решение. Имеем Х(0=Х(0; ?(t) = Ф {X (t)} = Lt0) {X(t)}y
так как при центрировании случайной функции Y (t) не случайное
влагаемое ф (t) «уничтожается»; отсюда
Rxy (*, t') - М [X (t) t (Г)1 = М [к (0 Ь\9' {X (/')}] *
= LJ?> {М [к (0 X (*')]} = LP> {Kx V> *')}.
9.40. Характеристики производной случайного процесса. Имеется
случайный процесс X (t) о математическим ожиданием тх (t) и
корреляционной функцией Кх (U ?). Найти характеристики ту (t), Ky (t9 f)
и Dy (t) ее производной Y (t) = dX (f)/dt. Найти также взаимную кор:
реляционную функцию Rxy (t, t').
Решение. Случайная функция Y (0 связана с X (0 линейным
однородным преобразованием. Применяя общие правила (9.0.7),
(9.0.8), (9.0.9), получаем:
283
ej-^кфп_^. Rxy(/>n= M(jjrwj?(П] =
=м[1(^х<n]=-^- кх(t, f).
Заметим, что
dt
Rv*&t') = -±-JKx&n.
9.41. Случайная функция X (t) имеет характеристики тх (t) =* 1
и Кх {U О = еа<'+'г>. Найти характеристики случайной функции
Y (t) ~ tjj X (t) + I. Определить, являются ли стационарными
случайные функции X (t) и Y (t).
Решение. В силу линейности преобразования t J + 1
Ни одна из случайных функций X (t) и Y (t) не является
стационарной, так как их корреляционные функции зависят не только от т =*
= t$t — ty но от каждого из аргументов t, t'\
9.42. Случайная функция X (t) имеет характеристики
тх if) = fl— 1; Кх (/, П = 2е-« «' -<>\
Определить характеристики случайных функций
По = *Х(/ж2+1; 2(о = 2^Х(о+(1-/)2;
Решение. m^O^/MO + ^ + l ='3+*2—' + 1;
mz(t) = 2tJLmx (o + (l_02= 1 -2/ + 5<2;
Kz(i) = W.!-£p-Kx(t> *0 = 16а«'е-««-'')2[1-2а(/-^)2];
«»(0 = -—:«, (0 + 1=3;
tf« (*, /') = —*— к (t, t').
284
При вычислении Kz (*> t') мы уже нашли -щр Кх & t%
следовательно,
Ки 0, f) « ~(4ае~а('w')a [1 -2а(*-Г)2] =
= 8а2е-а^-^)2[3+4а2(Г—О4—12а(?—Г)2].
9.43. Случайная функция X (t) задана выражением X (t) «
ss I/ cos <ot, где V — случайная величина с характеристиками mv = 2;
оо = 3. Найти характеристики случайной функции X (t): тх (t)\
Kx(t9 ?■); Dx(t). Определить, является ли случайная функция X (t)
стационарной. Найти характеристики случайной функции Y (t) =
= X (t) + a jt X (t), где а — не случайная величина. Является ли
стационарной случайная функция Y (t)?
Решение. mx(t) = mv cos со/ = 2 cos со/;
Kx (ty t') = Dv cos (ot cos co/e = 9 cos со* cos <dt'J;
Dx(t) = 9 (cos at)2.
Случайную функцию Y (t) можно представить в виде
Y (t) = V cos (ot + a -jt V cos <ot =» V (cos со/ — aco sin ©0;
отсюда mj, (/> = m0 (cos со/ — a© sin со/) = 2 (cos со/ — aco sin a>/);
Ky (^ f) = 9 (cos со/ — aco sin со/) (cos со/' — aco sin со/'); Dy (/) =
= 9 (cos со/ — aco sin со/)2.
Случайные функции X (/) и Y (/) нестационарны.
9.44. На телефонную станцию поступает простейший поток заявок
g интенсивностью %. Случайная функция X (/) — число заявок,
поступившее за время / (см. задачу 9.13). Найти характеристики ее
производной У (/).
Решение. В обычном смысле разрывная случайная функция,
которая представляет собой процесс Пуассона, недифференцируема,
однако, пользуясь обобщенной дельта-функцией, можно записать
характеристики производной. Преобразование Y (/) =* dX (t)ldt%
связывающее случайную функцию Y (/) о X (/), является линейным одно*
родным. Поэтому на основе задачи 9.13
к*ь V)=w Kx(u 1!)^{^г1Ш «'-*>+*'1 «-<'>])-
at
но (t—t')b(l—Г)?зО, откуда
MU')=-|-(M (*-П)==лб(*-0=^(т).
285
Таким образом, корреляционная функция случайной функции
Y (t) пропорциональна дельта-функции, т. е. функция Y (t)
представляет собой стационарный белый шум с интенсивностью G = % и
средним уровнем ту=%. Спектральная плотность такого белого шума будет
оо
S*(co)=-— Г М(т)е-«^Л = — .
2л J 2л
— оо
9.45. Найти характеристики случайного процессе Y (t), равного
производной винеровского процесса X (t) [см. задачу (9.25)]: Y (t) =
Решение. Так как тх (t) = 0, то ту (t) = 0. Корреляционные
функции винеровского и пуассоновского процессов равны (с точностью
до постоянного множителя). Поэтому корреляционная функция
производной винеровского процесса (см. решение предыдущей задачи)
пропорциональна дельта-функции, сам процесс Y (t) представляет
собой стационарный белый шум.
9.46. Доказать, что производная процесса однородного
случайного блуждания (броуновского движения) частицы (см. задачу 9.24)
представляет собой стационарный белый шум.
Указание. Воспользоваться решением задачи 9.44.
9.47. Характеристики интеграла от случайного процесса. Имеется
случайный процесс X (t) и даны его характеристики: тх (t), Kx (t9 t').
Найти характеристики ту (t), Ку (t, f) интеграла этого случайного
процесса Y (t) = J* X (т) dx, а также взаимную корреляционную функ-
о
цию Rxy (t, t').
t
Решение. my (t) = f mx (t) dt\
о
t v
КЛ''0=НК*е*>т')^т';
о
Dy (0 = J J Kx (t, x') dxdx'; Rxy (t, f) = \ Kx (l, т') dx'.
0 0 0
Заметим, что
t
Ryx(t,t') = \Kx(r,t')dx.
0
Можно доказать, что не существует отличной от нуля случайной
функции X (t)y при которой Y (t) стационарна.
9.48. Случайная функция X (t) имеет характеристики: тх (t) = 0;
Kx (U f) = [ 1 — (/' — О2]""1- Найти характеристики случайной
функции Y (0 = J X (t) dt. Определить, стационарны ли случайные
функции X (t) и V (О-
286
Решение. В силу линейности преобразования J X (0 dt
о
my{t)=\mx{t)dt = Q\ КА*>0=Ы\ KAUt')dt' =
О 0 0
= JK [1+tf'—/)a]-^jd* = /arctg/ + *'arctg*' —
_(/_r)arctg(^-r)-^ln{(l +<")(1+г'")[1 +(/_П2]-1}.
Случайная функция X (0 стационарна: Кх (Л t') = Кх (t — tl);
случайная функция У (/) = J X (0 d* нестационарна, Действитель-
о
но, дисперсия случайной функции равна Dy(t) = /C^, (t, t) =*
=2/ arotg t — In (1 + t2), т. е. зависит от t.
9.49. Случайная функция X (t) с характеристиками тх (t) = /2 + 3;
К* (*> О = 5#'у подвергается линейному, преобразованию вида
t
Y(t)=$ тХ (т) dx + Л
о
Определить характеристики случайной функции Y (t): my (t)\ Ky (t, t'J).
t
Решение. my(t)= {-v(x2 + 3)d'v + ts=* —+— t2 + t\
J 4 2
Однородная часть рассматриваемого линейного преобразования^
t
Lj0){X(0}=fi?X(T)di7.
Следовательно,
t v
9.50. Счучайная функция X (0, имеющая характеристики /пх (*) =
= 0 и /Сзс & <*) =* Зе-('+**> подвергается линейному преобразованию
вида
t
Y®^—t^X(i)+{<vX(<v)d* + sin<ul
287
Найти корреляционный момент случайных величин X (0) и К (1) (т. е.
двух еечений случайных функций: X (t) при t = 0 и Y (?) при ? — 1).
Решение. На основании решения предыдущей задачи
RM(t.f)=U9>{KxV,t%
где bft} — однородная часть линейного преобразования, примененная
к аргументу ?\ В нашем случае
ЛЗД«.П-—«'-^-j; + 3|т'е-(Н-''>Л'«
о
«Зг'ег(*+«') + Зе-Че^'(—ir —1) + П = Зе^(1—е-<').
Полагая * «я 0, <• = 1, получаем
Кх (0), у (1) = Яху(<и> = 3(1 -е-1) «1,90,
9.51. Случайный входной сигнал X (/) преобразуется с помощью
реле в случайный выходной сигнал Y (t), связанный с X (t) нелинейной
зависимостью Y (t) = sign X (t)9 т. е.
f 1 при Х(0>0;
П0 = 0 при Х(/) = 0;
[ —1 при X(t)<0.
Входной сигнал представляет собой случайную функцию X (t),
рассмотренную в задаче 9.15. Найти закон распределения сечения
случайной функции У (t) и ее характеристики ту (t); Ку (t, ?).
Решение. Случайная функция Y (t) может принимать только
два значения: +1 и — 1; значением 0 можно пренебречь, так как
Р {X (0 « 0} = 0. Вероятность того, что X (t) > 0, равна р =
оо
= J ф W dx. Ряд распределения случайной величины Y (t) имеет вид |
о
Y(t)i
-1 +1
1-/7
Отсюда ту = 2р — 1; Dy = 1 — (2/7 — I)2 = 4/7 (1 — р).
Пусть т = ? — t и ? > t. Если за время.т? в пуассоновском потоке
не появилось ни одного события (а вероятность этого равна е-Ят), то
значения случайной функции Y (t) и Y (?) равны друр другу и
условная корреляционная функция Ку (t> f) = Dy = 4р (1 — р). Если же
за время т появилось хотя бы одно событие, то Y (t) и Y (?) между
собой не коррелированы и условная корреляционная функция Ку (t, ?)
равна нулю. Отсюда при ? > t
Ку (*, ?) - е-** 4р (1 - р),
а в общем случае (при любых t9 ?)
/Су<*. 0 = Мт)-ег*т 4р (1-р).
288
9.52. Случайный входной сигнал X (*), рассмотренный в задаче
9.15, преобразуется в случайный выходной сигнал Y (f) о помощью реле
о зоной нечувствительности:
Y{t)isignX(t)
при |Х(*)|>е;
при |Х(/)|<8,
где е — зона нечувствительности реле.
Найти закон распределения сечения случайной функции Y (/)
и ее характеристики: математическое ожидание и корреляционную
функцию.
Решение. Случайная величина Y (t) при любом t может
принимать одно из трех значений: — 1, 0, 1 и имеет ряд распределения
*(/)«
1 ~1
А
0
Рг
+ 1
Pa J
где
Pi-P{X(/)<-e}= J <p(x)dx;
р2 = Р{|Х(0|<е}= jj <p{x)dx; Pa = \—Pl—Pi.
Отсюда my = p8 — px\ Dy = pt + p9 — (p3 — pt)\
Рассуждая аналогично тому, как мы это делали в предыдущей
задаче, определяем корреляционную функцию
ку(т) = е^\*\.[Р1+Рэ-(Рз-РгП
9.53. Случайная функция X(t) преобразуется в случайную функцию
Y (t) g помощью нелинейного элемента, работа которого описывается
формулой
( —Ьг при Х(1)<—е;
ПОН bX(t) при |Х(*)|<е;
[ Ьг при Х(£)>е.
График зависимости у (х) показан на рио. 9.53, а.
На вход такого элемента поступает случайная функция X (*),
рассмотренная в задаче 9.15. Найти одномерный закон распределения
случайной функции Y (f) и ее характеристики: математическое
ожидание и корреляционную функцию.
Решение. Случайная величина Y (t) — сечение случайной
функции Y (t) — имеет непрерывное распределение в открытом интервале
(— Ьг, + Ьг) и, кроме того, дискретные возможные значения
—Ьг и +Ьг с отличной от нуля вероятностью; таким образом, сечение
Y (t) представляет собой смешанную случайную величину, функция
распределения которой, F (у) непрерывна на участке (— бе, + Ьг)>
10
Зак. 1040
289
а на концах участка (в точках Ьг и + Ьг) терпит разрыв. Скачки
F (у) в точках разрыва равны
—8
Р {Y (0 68} = Р {X (0 < в} - J Ф (х) dx = рх;
— оо
оо
Р {У (О = + И = Р {X (t) > 8} = ]' ф (X) dX = p2.
8
Найдем функцию распределения случайной величины Y (t) в
промежутке (— Ьг; + Ьг):
У1Ь
F(y) = P{X(t)<y} = Р|Х(0< JLj- J ф(х)^ =
ff/b
— Pi+ j ФМ^(-Ьг<у<Ьг).
График функции распределения Т7 (#) показан на рис. 9.53, б.
bs
1 >
\/
У
Г 1
0 Б
-bs
а)
X
1
-ьс
F(yj
Pi
0
б)
' ,
J
ЬС
У
Рис. 9.53
Плотность распределения смешанной случайной величины Y (t)
в интервале (— Ьг, + Ьг) равна производной от F {у) на этом
интервале:
/ (у) = F' (у) = т <р (*//&) при —Ьг<у< + Ьг.
Характеристики случайной функции У (t):
Ьг
туу) = ту=—Ьгр1 + Ьгр2 + — Г yq>f-J-W =
— Ь8
8
= &8 (p2—pi) + b f *ф (я) dx;
Dy(t) = a2[Y(t)]-m* = №f(Pl + p2) +
l
f>8
+i~ J ^(p(f)^-m?=D
у
Аналогично предыдущим задачам ky (т) = D^e-^l.
290
9.54. Рассматривается случайная функция X (/) — W cos (ю^—
— в), где W — центрированная случайная величина с дисперсией
Dw\ 0 — случайная величина, распределенная с постоянной
плотностью в интервале (0; 2я), а ^ — неслучайный параметр (©х > 0).
Случайные величины W и 0 независимы. Найти характеристики
случайной функции X (t): математическое ожидание, корреляционную
функцию. Определить, является ли случайная функция X (t)
стационарной и эргодической. Если она стационарна, то найти ее
спектральную плотность Sx (со).
Рис. 9.54
Решение. Представим случайную функцию X (t) в виде
X (/) = W cos (со^ — 0) = W cos 0 cos cox t + W sin 0 sin (ott.
Обозначим W cos 0 = (J; W sin 0 = V. Найдем сначала основные
характеристики системы случайных величин V и V:
М [U] = М [W cos 0] = М [W) M [cos 0] = 0;
М [V] = М [W sin 0] = М [W] M [sin 0] =0;
D W) = М [(W cos 0)2] = М [W4 М [cos2 0] = DWM [cos 20];
D М « М [(№ sin 0)2] = М [IF] M [sin2 0] = DwtA [sin2©];
/<uo = M IW cos 0№ sin 0] = DWIA [sin 0 cos 0].
Так как значение 0 распределено равномерно в интервале (0; 2я),
то
2л
M[sin2 0] = M [cos20]= f cos2* — dx = — ;
о
2л
М [sin 0 cos 0] = Г sin x cos x dx = 0.
о
Итак, М [V] = М IV] = 0; D [[/] = D [К] = DJ2\ Kuv = 0.
Следовательно, выражение
X (0 = W cos (©!* — 0) = U cos сохг + V sin %*
представляет собой спектральное разложение стационарной случайной
функции: тх = 0, а корреляционная функция имеет вид kx (т) =*
= (Dw cos со!т)/2. График этой функции показан на рис. 9.54.
Ю*
291
Эргодической случайная функция X (t) не является, так как
характеристики, найденные по одной реализаций, не совпадают с
характеристиками, определенными по множеству реализаций.
Действительно, каждая реализация случайной функции X (/) есть гармоническое
колебание, амплитуда которого представляет собой значение,
случайно принятое величиной W. Среднее по времени для каждой такой
реализации будет равно нулю и совпадает о математическим ожиданием
случайной функции X (f), но дисперсия и корреляционная функция,
найденные как средние по времени для одной реализации, уже не
будут совпадать в соответствующими характеристиками случайной
функции X (/). Например,
т т
lim-L f X»(/)tf=.limJL \ W*± [I+cos 2 (щ(-в)] dt =
—Г ~-Т
« — W2.
2
Найдем спектральную плотность случайной функции X (t).
Покажем, что она пропорциональна дельта-функции: Sx (со) = Dw8 (со —
— tojfe (О < со < оо). Действительно, при такой спектральной
плотности корреляционная функция
со во
л CD D
К (1?) = \ Sx (©) COS ООТЛО = I ^- б (ю—(Oj) COS СОтЛй = —^ COS % <С,
что совпадает с корреляционной функцией для X (t). А так как прямое
и обратное преобразования Фурье определяют спектральную
плотность и корреляционную функцию взаимно-однозначно, то написанное
выше выражение для Sx (со) дает спектральную плотность случайной
функции X (t).
Если воспользоваться не действительной, а комплексной формой
преобразований Фурье, получим спектральную плотность Sx (со) в виде
S* (ft)) » Dw [б ((О + (Ог) + б (СО — (0!)]/4 (— ОО < (О < ОО).
есхзг
Заметим, что аналогично можно было бы записать и S^co) =
8=8 Dw № (<*> + g>i) + б (со — <»i)]/2, но для положительных со (так
как щ > 0) б (со + сох) sa 0.
9,55. Показать, что сумма элементарных случайных функций вида
X (t) = mx+ 2 wi cos (®i '—ei).~
где U^i — центрированные случайные величины g дисперсией Dt (i ==
= 0, 1, 2, ...); @i —случайная величина, распределенная
равномерно на участке (0; 2я) (/ = 0, 1, 2, ...) (причем все случайные
величины Wi, @t независимы), представляет собой не что иное, как
спектральное разложение (9.0.24) случайной функции X (f).
Решение. В соответствии с решением предыдущей задачи
Wi cos (co^ — ®t) = Ut cos (ott + Vt sin со*/,
292
где Ui и Vi — некоррелированные случайные величины, имеющие
нулевые математические ожидания. Следовательно,
X (t) = mx+ 2 (ut cos «>t t + Vt sin (o, t),
что и требовалось показать.
n
9.56. Рассматривается случайный процесс У (/)= 2 а*Х* (/) + 6,
где X* (О— стационарные некоррелированные случайные процессы
с характеристиками: mt; kt (т); S! (со) (i = 1, 2, ..., п)\ аи
Ь—действительные числа. Найти характеристики случайного процесса У (/).
/г л
Ответ. s ту= 2 а* m>i + b; ky (т) = 2 fl^« (T)»
s»=2 rfs;(0).
Случайный процесс Y (t) стационарен»
n
9.57. Рассматривается случайный процесо У (t) «* П Х,(0, где
Xj (0 — независимые стационарные случайные процеосы с
характеристиками: тх = 0; &i (т); S? (<о) (/ — 1, 2, ..., л). Найти его
характеристики.
п п
Ответ. ту = П "V, ftv (т) = П kx (т);
/=1 *=i
S>)==~£T 1 П М*)е!«*Л.
Процесс У (/) стационарен.
9.58. Найти характеристики случайной функции X (t),
представленной своим спектральным разложением, приведенным в задаче 9.55.
Решение. Обозначим Wt (cos (ott — 0) = Xt (f)t тогда
X(/) = m*+2 Xi{t)'
*=i
В соответствии с решением задач 9.54 и 9.56 имеем
оо оо
М [X (/)] = тх\ kx (т) = ^ kx. (т) = -у 2 D*cos ю*т!
г=1 г=|
во
S; (©) = 2 — I6 (<о+«>*)+« (со—(0{)] ( — 00 < <o< 00).
Случайная функция Х (0 стационарна, но не эргодична.
9.59. Рассматривается произведение двух некоррелированных
стационарных случайных функций: Z (t) = X (t) У (t), причем случай-
293
2[thX(t)Y(t\
ная функция X (I) такая, как в
задаче 9.14 (случайное чередование
значений + 1 и — 1с простейшим
потоком перемен знаков), а
случайная функция Y (f) такая, как в
задаче 9.54. Найти
характеристики случайной функции Z (t).
Решение. Имеем тх (t) —
- ту (t) « 0; т2 (t) = 0; Кх (U О*
= е~2* I * I; Ки (*, t') = (D^cos©^)^
(x=stl—t). На основании
задачи 9.57
Kz (U П « Кх (t, П К у 0, П -
= (Dwe-**> 14 cos со1т)/2.
Рис. 9.59
На рис. 9*59 показана одна из
возможных реализаций случайной
функции Z (t), полученная перемножением соответствующих ординат
реализаций случайных функций X (0 и Y (t).
9.60*. Признак положительной определенности. Имеется функция
kx b)> обладающая свойствами:
1) kx (- т) - kx (т); 2) kx (0) > 0; 3) \kx (т) | < kx (0).
Требуется выяснить, может ли функция kx (т) быть
корреляционной функцией стационарной случайной функции, т. е. обладает ли она
свойством положительной определенности. Показать, что достаточным
условием положительной определенности является условие, чтобы
функция
Sx (со) = — l kx (т) cos corrft
п J
(9.60.1)
была неотрицательна при любом значении со:
Sx(<o)^0f (9.60.2)
т. е. чтобы, вычисляя спектральную плотность по формуле (9.60.1),
мы ни при каких со не получали отрицательных значений этой функции.
Решение. Предположим, что Sx (со) ^ 0, и докажем, что при
этом функция kx (т) = kx(t — t') будет положительно определенной.
Имеем
ОО 00
kx М = I Sx (ю) COS COTdCD = J Sx (О)) COS tot COS (dt'dCd +
+ J Sx (со) sin со/ sin cofdco.
(9.60.3)
Положительная определенность функции kx (t — t') состоит в том,
что для любой функции ф (/) и любой области интегрирования (В)
должно выполняться условие
294
J J kx (t — ?) ф (t) ф (?) dtd? > 0.
(В) <B)
Проверим это неравенство по отношению к функции (9.60.3):
j jM f S^ (со) cos Ы cos ©Г <р (t) ф в') dco +
(В) (В) [о
+ 5 Sx (со) sin со/ sin arf' ф (/) ф (/') d<o\ dtd? *•
= ^ s* (с°) \\ cos ®'<Р W Л f cos <о? ф (/') dtl +
О ((В) (В)
+ J sin <о/ф (t) dt J sin © /'ср^ДОЧ Ло.
(В) (В) J
Обозначая
J cos со/ер (/) d/ = ifo. (5, ©); J sin сойр (/) d/ = t|>2 (By ю),
<B) (B)
получаем
00
J I A* (t - О ф (/) ф (?) did? =*$Sx(<o) (Щ>г (В, (о))2 +
(В) (В) 0
+ bM*. ®)]2)d(o>0,
так как по условию S х (со) ^ 0.
Можно доказать, что условие (9.60.3) является не только
достаточным, но и необходимым для того, чтобы корреляционная функция была
положительно определенной.
9.61*. Определить, обладает ли функция
Mt) = e~am(chpT + — shp|x|] (a>0;P>0)
свойствами корреляционной функции.
Решение. Нужно проверить выполнение следующих ввойотв:
1) kx (0) > 0; 2) хх (-Т) = kx (т); 3) | kx (т) | < kx (0);
оо
4)S*(co) =— \ kx (т) е~*Шх dv ^ 0 при любом ш.
*— оо
Свойства «Ь и «2» очевидны. Проверим остальные.
3) Функция kx (т) — четная, поэтому достаточно исследовать ее
при т > 0:
295
Так как >kx (0) = 1, нужно, чтобы это выражение по модулю не
превосходило единицы. При а < Р это условие не выполняется, так
как прит-^оо выражение ег<в—0>т неограниченно возрастает. В
случае а = Р получаем kx (т) = 1; при а > р имеем — kx (т)< 1.
Таким образом, свойство «3» выполняется только при а ^ р.
4)S;((o) =
2л
оо
Г Ах(т)е-
2я
(C+f)
X
2л | а—p + io) "*" a+p+io) J 2лр [ (а—Р)*
-P + io) a+P+
1 . ^ а2—Р2
-Р)2+©2
- 1 а2—
(a+P)2+G)2J л [(а_р)2+0)2] [(a + P)2+a>2J
при а ^ р (Re — действительная часть). При a = р имеем S$ (со) =
« б (со).
Таким образом, функция kx (т) = е~а Iт' f ch Рт + у sh p |т| ) при
а ^ Р обладает всеми свойствами корреляционной функции. Графики
kx (т) и S*x (о) при a > р показаны на рис 9.61, а и б.
Рис. 9.61
9.62. Показать, что не существует никакой стационарной
случайной функции X (/), корреляционная функция которой kx (т) постоянна
в каком-то интервале (— т1э тх) и равна нулю вне его.
Решение. Предположим противное, т. е. что существует
случайная функция X (0, для которой корреляционная функция равна
Ь > 0при |т|< тг и равна 0при |т| > т1в Попробуем найти
спектральную плотность случайной функции X (/):
ь
Ь sin (OTf
Sx (со) = — I kx (т) cos cot di = — I
о о
b cos сот dt = -
Из этого выражения видно, что функция Sx (ю) для некоторых
значений со отрицательна, что противоречит свойствам спектральной плот-
296
ности, и, следовательно, корреляционной функции указанного вида
существовать не может.
9.63. Обладает ли функция kx (т) = Dofir*^! -Trsin p |т| свойст-
вами корреляционной функции?
Ответ. Нет, так как не выполняются два условия: kx (0) > 0
и А*(0)> |Мт)|.
9.64. Стационарная случайная функция X (/) имеет
характеристики тх и kx (т). Найти взаимную корреляционную функцию Rxy (t, f)
случайной функции X (t) и случайной функции Y (t) = 1 — X (i).
Решение./?^ (/, tf)«М[х (t) Y (/')] = М [—X(t) X 0')] =
9.65. Случайная функция X (t) имеет характеристики тх\ kx (т) =
= D3Ce-ctlTl. Найти ее спектральную плотность.
Решение.
00 ОО
S; (<о) = -1- Г 6* (т) е-»«* d т - -^ Re Г е-<в+' •> * dt,
«*.оо О
где Re — действительная часть. Имеем
ОО 00
• e-(a-f i ю) т ^т _ Г 1 е-<а-И (*)* d(a+i(0)T =
J а+i© v ^ '
(а + i <о)т = #
при т = 0; у = 0
при т = оо; # = оо
I'
а+i© J
1 rRe fe~<a+ifi»TdT = Re 1
a+i©
= Re
1
f
a—i©
a+ ico a—i©
Re
a+i©
a—i©
CG2 + ©2 ~~
\ a2+©2 a2+©2 / a2+©2
D*
Следовательно, S* (©) = -~—a2+u)2 "
9.66. Найти спектральную плотность случайной функции Х(0,
если ее корреляционная функция
Ax(T)»D„e-alTlcos рт.
Ответ. S!(a>)= ^^
a2+ft2+©2
я fa2+(£—©)2J fa2+(p+©)2]
Указание: представить cos ($т =* (eiPx + ег!0т)/2 и
воспользоваться решением задачи 9.65.
297
9.67. Найти спектральную плотность стационарной случайной
функции, у которой корреляционная функция
M*)-Ace-<xt>-.
Решение. Имеем
то оо
Пользуясь известной формулой
Г eAx*±2Bx-Cdx „ |/ -£- exp J АС~В* (Л > 0)
*— ОО
и имея в виду, что i2 = — 1, получаем
S;(co) = ^l/^expf-^l = -^=expf^-^l.
хК ' 2л V К I. 4Л^ J 4^Уя ]| 4X.2J
График этой функции подобен кривой нормального закона.
-0)1
(О/ О)
а)
Рис. 9.68
9.68. Спектральная плотность стационарной случайной функции
. X (0 на участке от — щ до + <ог постоянна, а вне его равна нулю,
т. е. имеет вид, показанный на рис. 9.68, а:
' S;(co) = IanPH|G>l<tt)l)=:alfl-^V
10 при | со | > (ux J V щ )
Найти корреляционную функцию kx (т) случайной функции X (/).
оо
Решение, кх(т) = Г S* (со) еШх dco =
е*00
(О,
= 2а f cos сот d(o = а sin щ т ; D* = kx (0) = 2я©1#
о
График корреляционной функции показан на рио. 9.68, б.
298
9.69. Производная стационарной случайной функции. Имеется
стационарная случайная функция с характеристиками тх (t) « тх;
Кх if у t') = kx W» где т.= t* — t. Найти характеристики ее
производной Y (t) = dX^{t)ldt и показать, что она также стационарна.
Решение. Так как Y (t) связана, в X (t) линейным однородным
преобразованием, то ;
mv (0 = -тг тх (0 = -тг т* = ° = const;
at at
ft U<' I dt \ di xK ' dt'J
Ho dr/d/? = 1 и dx/dt — — 1, поэтому
Так как правая часть равенства зависит только от т, то
K»(tJ') = ky(4)=-^kx(T)
и случайная функция Y (t) стационарна.
9.70. Стационарная случайная функция X (t) имеет
корреляционную функцию kx (т). Случайная функция Y (t) получается из нее
дифференцированием: Y (t) = dX (t)/dt. Найти корреляционную функцию
ky (т), если:
а)йх(х) = е-«^1;б)*яг(х) = е-«1*1(1 + а|г|);в)Ля(т) =
= e~a iтi /cospT+— sin р |т|] (а > 0, р > 0).
Решение. При решении задачи мы будем применять аппарат
обобщенных функций, правила пользования которыми приведены в
приложении 6.
»M4=-^.-'"=-i[-««-'^]=
= aГ_aе-aIт»/ALLLу+£f!±LLe-ai^i] = еее-«I^I [26 (т) —
—a (sign т)2].
Наличие слагаемого 26 (т) показывает, что в составе случайной
функции Y (t) есть белый шум. Далее запишем ответы, предоставив
читателю убедиться в их справедливости:
6)^(t) = a2e~alTl(l— a|x|);
B)^(T) = (a2 + p2)e-alTl/cospx —— sinpi x|].
9.71. Найти спектральную плотность стационарной случайной
функции с корреляционной функцией
299
ky (т) = ое-«1ч 126 (т)—a (sign %)*[.
оо
Решение. S*y{&)= —■ Г ky (т) е~1(втйт=
Э-ОО
оо оо
= — f ae"-a»TJ26(T)e-iwTdT—- f a2 (sign т)2е~а1*1 е*-1 **^т.
2nJ 2я J
Так как
, . ч2 г 1 при х Ф 0;
(signx)2=|o F r
при ts=0
и так как подынтегральная функция второго интеграла в точке т = 0
не имеет особенностей, то во втором интеграле можно пренебречь
точкой т = 0. Получим
a a2 2a
а юа
S* (©)= .
* v ' я 2л а2+ю2 я a2 4w2
График спектральной плотности S*y (со) представлен на рис 9.71.
Рас. 0.71
W
Спектральную плотность SJ (со) можно было получить проще
следующими рассуждениями. Представим случайную функцию Y (t) как
производную случайной функции X (t) из задачи 9.70 (п. «а»). Имеем
^) = e-^1;S>) = ±_|_;
амплитудно-частотная характеристика оператора дифференцирования
равна Ф (ia>) = ico, следовательно,
S* (©) = S; (со)|Ф (i со) |2 = - -— |ico |2 «-2 ?£_.
9.72. Имеется стационарная сдучайная функция X (t) с
корреляционной функцией kx (x) = (sin т)/т. Найти корреляционную
функцию, дисперсию и спектральную плотность ее производной: Y It) *=*
= dX(t)ldt.
Решение. Согласно решению задачи 9.40
М*) =
<Pkx(x)
d-r2
d2 / sin т? \
Разлагая (sin т)/т в ряд Маклорена, имеем
sing , т2 , т* г6 ,
y v ' dx* XK ' 3 21.5 ^ 4! 7 *
Отсюда Dy « ^ (0) « 1/3.
Спектральная плотность Si (©> « 2»1 (1 — |©|) (см. п. 14
приложения 6). Следовательно, S*y (<o) « SJ (со) о8 = 2<о21 (1 — |<о|).
9.73. Случайная функция X (/) имеет корреляционную функцию
^W = e^l^(chpT + yshp|TA (a>p>0).
Случайная функция К (/) = dX (t)ldt. Найти ее корреляционную
функцию ky (т) и спектральную плотность SJ (©).
Р е ш е н и е. При нахождении ky (т) Применяем свойства
обобщенных функций (см. [21):
«• М—£«.»- -^.[-^-1.1.^11 (<**+
+ у sh р |т|]+е-«'Ч(р sh рт+ach р |T|-^Jii)|-
*х я [(а-р)«+«Ч [(а+Р)2+о)Ч
Так как предел Ит Ау (т) существует (он равен ky (0) = a2 — р2),
то случайная функция X (t) дифференцируема.
9.74. Показать, что взаимная корреляционная функция Rxy (t, f)
стационарной случайной функции X (t) и ее производной Y (t) =
= dX (t)/dt удовлетворяет условию Rxy (t, t') = — Rxy (t\ t), т. е.
при перемене местами аргументов меняет знак.
Решение. Пусть Кх (t, t') *= kx (т), где х = f- — t.
Rxy (t, П = M [i «)-£- Я (О ] - JL M [X (tjX (/')] = ^ Л, (т).
Но т = *'- — tt следовательно,
С другой стороны,
4-Km(t. n=—к (т) 4L=—-
*»c. 0~£-к«е. о=-£-*« w -ir=—z-a«(t)=-r«(/, n.
что и требовалось показать.
Таким образом, взаимная корреляционная функция стационарной
случайной функции и ее производной зависит только от т = t'J — t:
^(т)^~1ГМт)'
т. е. функция X (0 и ее производная «стационарно коррелированы».
301
9.75» Доказать, что любая стационарная случайная функция X (t)
и значение ее производной Y (/) = йХ (t)ldt в той же точке t не корре-
лированы, а если случайная функция X (t) распределена нормально,
то и независимы.
Решение. В предыдущей задаче было показано, что Rxy (т) =*
= -Txk*W' ПРИ '' = '» т = 0
J-kx(0) = 1
дх дх
R*y (0) = —77 fe* (°) = -4" Ас = 0.
Таким образом, стационарная случайная функция в любой точке не
коррелирована со своей производной в той же точке.
Для нормально распределенных случайных функций из
некоррелированности X (t) и ее производной в той же точке вытекает и их
независимость.
9.76. Найти характеристики случайной функции Y (t) = X (t) X
X J у если нормальная случайная функция X (t) стационарна и
имеет характеристики
тх\ kx (т) = De-a ■т l (cos 0т + — sin рт] >
Решение. Y (t) = \ ^г** Обозначим X2 (t) = Z (t). В
соответствии е (9.0.35) и (9.0.36) имеем
mz = ml + kx (0) = ml + D;
oo
S*(<») = 2 J SjJ(co—t>)S*(y)dt»+4ml5:(co) =
= £2l (~2 \ m (D2(tD2+20a2+4p2) ■
я Н; [(G)2+4a2+4(52)2— 16P2o)2](©2+4a2)
+ 4m2 *L U2tm e Sj. (со).
Корреляционную функцию kz (т) можно найти из выражения
oo
М*)= I St (со) e'^co.
fc- OO
9.77. Квадратичное детектирование стационарной случайной
функции. Квадратичным детектированием случайной функции X (t)
называется нелинейное преобразование вида Z (t) = а2Х2 (t), где а —
постоянная; X (t) — случайная функция. Найти характеристики
случайной функции на выходе квадратичного детектора с параметром
а = 2, если на его вход подается нормальная стационарная случайная
функция с характеристиками тх = 3; kx (т) = 4е~3 *х I.
Решение. Обозначим Хх (t) = aX (t). Характеристики
случайной функции Хг (/): тХ1 =* яягж = 6; kXl (т) = a2kx (т) « 16е~3»* I.
302
Тогда Z (t) = X\ (t). Полагаем Dx = 16; щ = 3. По формуле (9.0.35)
находим mz — mXl + kx, (0) = 6 + 16 — 22. По формуле (9.0.36)
St (со) = 2 j SXl {(o-v) S*Xt (v) do+4mx, SXl (a>).
oo
«l ! 5д_1_Л+4^М- *
а2Н-(ю—у)2 я Jif+y2 Ж1 я af.+ a>2
~~. я (2об!)а+сй« я(а|+ю2)
Следовательно (см. п. 6 приложения 7),
где бг = 2D! ■= 2-162 « 512; аг = 2ах = 6; б2 -* 4D1m|1 = 4x
X 16-б2 « 2 304; а2 = 3.
Таким образом, сигнал на выходе квадратичного детектора можно
представить как сумму двух некоррелированных стационарных
случайных процессов Z (t) = Хг (t) + X2 (t) g указанными* выше
характеристиками. Особо обратим внимание на то, что случайный процесс
Z (t) не является нормальным.
9.78. Нормальная случайная функция X (t) имеет характеристики
/я*; kx (т) = D^"4*^'. Найти характеристики случайной функции
W(t) =Х(/)^,
Решение. W(t) = X(t)^ = ±-±-X*(f);
at 2 at
S*a,((o) = 0,5co2S^((o).
Так как операция дифференцирования является линейной, то
mw (t) = ~y Tt mx* (0- Но, в соответствии с решением предыдущей
задачи, тхг (I) = const, следовательно, mw (t) = 0. В предыдущей
задаче была найдена спектральная плотность Sx* (со), следовательно,
S*((o) = — o>2S^(tt))=— - .-4 ^-^
wK } 2 х У ' я ©2+(2а)2 ^ я(ю2+а2)
и в соответствии с п. 18 приложения 7 имеем
kw (т) = ^— е-2а I'" [26 (т)—2а (signт)2] +
Я
-| ^^ е~а Iх I [26 (т)—a (sign т)2].
По виду корреляционной функции kw (т) заключаем, что случайная
функция W (t) содержит белый шум.
9.79. Угол перемещения радиолокатора в горизонтальной
плоскости представляет собой нормальный случайный процесо X (t) с матема-
зоз
тическим ожиданием /йх=0 и корреляционной функцией kx (т) =
^D^e-^mcosPT, ГдеО*=4 град2; а = 10~8 1/с; Р = 0, 1 1/с.
В начальный момент t« 0 угол перемещения равен нулю: X (0) = 0.
Найти вероятность р того, что в момент tl = 0,2 с угол перемещения
будет меньше 1°.
Решение. Обозначим X (0) = Х0; X Цг) = J^. Условный
закон распределения случайной величины Хх при условии, что
случайная величина Х0 = х0, найдем из выражения / (хг \х0) = f (хъ x0)/f (хг)9
где / (хъ х0) — нормальный закон распределения системы двух
случайных величин с характеристиками: я^ = т0 = 0;
Dx = Dt = Dx = A град2; kXl,xo = kx(09.2) = Dxe~«\<>>z\cosp.0,2 =
= 3,68 град2; гХ1,Хо = кХи^УКЖ0 = №1"
Условный закон распределения / (ati|a:0 = 0) будет нормальным
с характеристиками
w*i l*о = 0; <**, |*о = Ъ VI— г\иХо = 0,776.
Тогда Р= f /(^1X01 = 0)^ = 0 f- 1_Л=о,81.
J \ 0,776 у 2 )
9.80. На вход Колебательного звена системы автоматического
регулирования, передаточная функция которой имеет вид
<b(p) = k/(Tp* + lp + k) (£>0),
подается белый шум со спектральной плотностью S$ (со) = N.
Определить дисперсию выходного сигнала (речь идет о достаточно
удаленных участках времени, после окончания переходных процессов).
Решение. S* (о>) = S* (а>)|Ф (ia>)|2 = Nkl(\T (ico)2 + gico +
«о
-f k\% откуда Dy= j" S*y(<o) da = nkN/%.
—-oo
Заметим, что дисперсия выходного сигнала не зависит от
постоянной времени колебательного звена 7\ а зависит лишь от коэффициента
усиления k9 коэффициента демпфирования £ и мощности сигнала N.
9.81. Передаточная функция системы, на которую подается сигнал
X (/), имеет вид
Ф (р) = (1 + TlP)l(T\p* + р + k)9
где k = 25 -~-; Тг = 0,05 с.
Спектральная плотность входного сигнала
SI (со) « 2T8JII + (7<о)2),
где Т = 1 с; ба = 4 градов2. Найти дисперсию выходного сигнала.
Решение.
SHcD) = SUco)|0(icD)|2~ **l-TUW+D
304
J * ' 2л J |a0(i©)3+ai(io))2+fl2io)+fi3p
0 — oo
—*?2 бр+вр ^i—Qq ai Ьч1аг
2a0(aQaB—ага2)
в нашем случае Ьй = 0; 6Х = — Г?; 62 = 1; а0 = TTY; a^Tl 7\;
а2 = 1 + &71; я3 = *• Тогда
D„-4яГбя *i-fliV*3 ^ o,0428 град2.
9.82. Выходной сигнал У (/) связан с входным сигналом X (t)
дифференциальным уравнением
a1^ + a0X(t)^b1^- + b0Y(t). (9.82)
at at
Стационарная случайная функция X (t) — нормальная с
характеристиками тх и kx (т) = Djsr^^K Найти характеристики выходного
сигнала У (/).
Решение. Так как случайная функция X (t) подвергается ста*
ционарному линейному преобразованию, то в установившемся режиме
случайная функция У (t) будет стационарной. Величину ту можно
найти из уравнения
dmx . , dtriy . *
at at
Так как тх = const и ту = const, то а0тх = Ь0ту, откуда ту =
= a0mjb0. Уравнение (9.82) можно записать в операторной форме:
(агр + а0) X (0 = (blP + Ь0) У (t),
откуда
Y{t) = ^£±?LX(t) = Q)(p)X(t),
где Ф (р) — передаточная функция.
sHco)=s:((o)io(Mi2=sn«)|^i?
\0110) + &о
_ Рха 1 Qg+Q?Q)2 __ Dxa> I flg + fl2Q>*
~~ я a2+w2 Ч+б2©2 3i6f а2+ю2 ag/af+w2 * .
Выражение для S$ (©) можно записать в виде
S*lQ)=D*a fl8+fliG)2 - D*a ( а I g
УК ' 9\Ь\ (а2+©2)^2/^|+(02) ^2 ^ &2 + G>2 ^+G>2
где
а2— ^g/6?
305
Обозначим Dx = D^xalb\ D2 = D^xcl(b\d). Тогда (см. п. 6
приложения 7) ky (т) = Dx е-*j TI + D2e~*IT'. Дисперсия выходного
сигнала Dy = йу (0) = Dx + D2.
9.83. Для уменьшения уровня шума X (t) применяется ЯС-фильтр
<рис. 9.83). На вход фильтра подается стационарный белый шум со
спектральной плотностью S£ (со) = 10~б В2-с. Определить наименьшую
постоянную времени фильтра Т == RC, при которой с вероятностью
/? = 0,05 сигнал на выходе фильтра не будет превосходить по модулю
100 мВ, если гпх = 0.
о
A(tl C± rftj X{t) RW m
Рис. 9.83 Рис. 9.84
Решение. Передаточная функция #С-фильтра имеет вид Ф (р)=
= 1/(1 + Тр). Следовательно,
где а = \1Т 1/с; Dy = яа-Ю"5 В2. Отсюда (см. п. 5 приложения 7)
Так как входной нормальный сигнал подвергается линейному
преобразованию, то и выходной сигнал будет нормальным с
характеристиками пгу — 0; Dy = (я/Т) Ю-6 В2. По условию задачи р = 1 —
— 2Ф(1(Ю/ау) = 0,05, где Ф (х) — функция Лапласа (приложение 5).
Имеем Ф (100/а„) = 0,475; 100/ау = 1,96; ау = 100/1,96 = 51,1 мВ;
al^Dy = 26,Ь10-* В2.
Искомая наименьшая постоянная времени фильтра Т = (n/Dy) X
X Ю^6 = 0,012 с.
9.84. На вход #С-фильтра, изображенного на рис. 9.84, подается
нормальная стационарная случайная- функция X (t) с
характеристиками mx\ kx (т) = Dy cos рт. Найти характеристики выходного
сигнала Y (t).
Решение. Передаточная функция фильтра имеет вид Ф (р) =
= Тр (1 + Тру1, где Т = RC. Следовательно, пгу = 0
(постоянная составляющая не проходит через конденсатор С). Спектральная
плотность выходного сигнала (см. п. 3 приложения 7) имеет вид
^^=|т^Г5'(ю)=г^^1б(<а+Р)+6((0-р)]-
Дисперсию выходного сигнала Dy найдем из выражения (см.
приложение 6)
00 ОО
306
Одномерный закон распределения выходного сигнала — нормальный
с параметрами ту = 0 и Dy.
9.85. На вход автоматического регулятора подается напряжение
X (0> которое представляет собой нормальный стационарный
случайный процесс с характеристиками тх = 220 В; kx (т) = Dxe^a\T I (1 +
+ <х|т|), где Dx = ol = 16 В2; а = 200 1/с. Регулятор напряжения
работает нормально, если напряжение X (t) не меньше 208 В и не
больше 232 В, в противном случае — он автоматически отключается и
включается вновь при возвращении входного напряжения X (t) в
указанный диапазон. Определить вероятность р того, что регулятор
будет работать в произвольно выбранный момент времени t9 закон
распределения длительности нормальной работы 7\ и среднюю
длительность отключения регулятора t2.
Решение. В соответствии с решением задачи 9.70 (пункт «б»)
ky(T)=--~r[Dxe~«\*\(l+a |*|)] =
= D:ca2e-«nl(l-a|T|), oy = *ox.
Среднее число выбросов за уровень а (вверх) будет
Хв = ^-(ехр[-^^11)^ = 10э3 1/с.
а 2л \ Н[ 2a« J/ ox
Следовательно, общее среднее число выбросов за допустимый уровень
в единицу времени будет 2ка = Х± = 20,6 1/с. С достаточной для
практики точностью закон распределения случайной величины 7\
можно считать показательным с математическим ожиданием t = 1/Ях =
= 0,0486 с. Вероятность того, что регулятор будет работать в
произвольно выбранный момент времени, равна
р = Р (208 < X (t) < 232) = Р (|Х (0 — тх\ < 12) = 2Ф (3) =
= 0,9973.
С другой стороны, вероятность р можно найти из выражения р =
= \1(к + 1,), откуда 72 = 1г (1 — р)1р = 1,31- Ю-4 с.
9.86. Радиоприбор может работать только в определенном
диапазоне температур t0 ± 30° С, где t0 — номинальная средняя
температура; при выходе температуры за эти границы прибор выходит из строя.
Температура окружающей среды X (/) есть стационарная случайная
функция с математическим ожиданием тх= 0 я средним квадрати-
ческим отклонением 0^=10° С, корреляционной функцией вида
kx (т) s= 100 (sin т)/т °С2; распределение нормальное. Найти среднее
число выбросов температуры за границы t0 ± 30 ° С в течение времени
Т = 50 с. Считая число выбросов распределенным но закону
Пуассона, найти вероятность того, что за время Т прибор выйдет из строя.
307
Решение. Согласно решению задачи 9.72
^w--^a--ioo{
+
3 2! 5 J
Полагая т *= 0t находим Dy = ky (0) = 33,3; оу =» 5,76° С. Среднее
число выбросов вверх за границу а = m* -f 30° С согласно формуле
<9.0.42) равно
Я,а = -!-е^г/20о^. = 0,00134 1/с.
2я ох
Таково же общее среднее число выбросов вниз, за границу тх — 30° С;
общее среднее число выбросов за допустимые границы будет 2Ха =
« 0,00269.
Для случайной величины Y — числа выбросов, имеющей пуассо-
новское распределение с математическим ожиданием 2%аТ = 0,00269 X
X 50 = 0,1345, вероятность того, что она примет значение, большее
нуля (произойдет хотя бы один выброс), равна 1 — е-°«1345 = 0,125.
глава ю
ПОТОКИ СОБЫТИИ. МАРКОВСКИЕ СЛУЧАЙНЫЕ
ПРОЦЕССЫ
10.0. Потоком событий называется последовательность однородных
событий, появляющихся одно за другим в случайные моменты времени. Примеры:
поток вызовов на телефонной станции; поток забитых шайб при игре в хоккей;
поток сбоев ЭВМ; поток заявок на проведение регламентных работ в
вычислительном центре и т. п.
Поток событий наглядно изображается рядом точек с абсциссами 0Ь 02,
.*., 0П, *». (рис. 10.0.1) с интервалами между ними: 7\ = 02 — 0Х, Т2 = 03 —
— 02, *»*, Тп = 0л+1 — ®п- При его вероятностном описании поток событий
может быть представлен как последовательность случайных величин: 0г, 0« =
= 0!+^; в, = вх + 71! + 7V ...
Заметим, что термин «событие» в понятии «поток событий» совершенно
отличен по смыслу от ранее введенного термина «случайное событие». В частности,
не имеет смысла говорить о вероятностях «событий», образующих поток
(например, о «вероятности вызова» на телефонной станции: ясно, что рано или поздно
вызов придет, и не один). С «потоком событий» можно связывать различные
случайные события, например:
А = {в течение времени от t0 до t0 + т придет хотя бы один вызов}
или
В = {в течение того же времени придут ровно два вызова}»
Вероятности таких событий можно вычислять*
Заметим также, что на рисунке в виде ряда точек мы можем изобразить не
сам поток событий (он случаен), а только какую-то его конкретную р е а л и з а-
цию,
В гл. 4 мы уже упоминали о потоках событий и некоторых их свойствах;
здесь мы осветим их более подробно* Поток событий называется стационарным,
если его вероятностные характеристики не зависят от выбора начала отсчета
или, более конкретно, если вероятность попадания того или другого числа
событий на любви интервал времени зависит толькот от д л и н ы т этого интервала
и не эависит от того, где именно на оси 0t он расположен.
Рис. 10.0.1
Поток событий называется ординарным, если вероятность попадания на
элементарный интервал времени Д* двух или более событий пренебрежимо мала
по сравнению с вероятностью попадания одного события. Практически
ординарность потока означает, что события в нем появляются «поодиночке», а не
группами по два, по три и т* д. (точное совпадение моментов появления двух событий
теоретически возможно, но имеет нулевую вероятность).
Ординарный поток событий можно интерпретировать как случайный
процесс X (t) — число событий, появившихся до момента / (рис* 10.0.2), Случайный
процесс X (0 скачкообразно возрастает на одну единицу в точках Biy в2,..., вп.
Поток событий называется потоком без последействия^ если число событий,
попадающих на любой интервал времени т, не зависит от того, сколько событий
попало на любой другой непересекающийся с ним интервал* Практически
отсутствие последействия в потоке означает, что события, образующие поток,
появляются в те или другие моменты времени независимо друг от друга.
Поток событий называется простейшим^ если он стационарен, ординарен и
не имеет последействия.
Интервал времени Т между двумя соседними событиями простейшего
потока имеет показательное распределение
/ (0 = hTu (при t > 0), (10.0.1)
где X = 1/М [Т] — величина, обратная среднему значению интервала Т.
Ординарный поток событий без последействия называется пуассоновским.
Простейший поток есть частный случай пуассоновского (а именно стационарный
пуассоновский поток).
Интенсивностью А, потока событий называется среднее число
(математическое ожидание числа) событий* приходящееся на единицу времени. Для
стационарного потока X = const; для нестационарного потока интенсивность в общем
случае зависит от времени: X = X (£)>
Мгновенная интенсивность потока X (t) определяется как предел отношения
среднего числа .событий, которые произошли за элементарный интервал времени
(*, tr\- Д0> к длине Д/ этого интервала, когда она стремится к нулю. Среднее
число событий, наступающих на интервале времени т, следующем
непосредственно-^
но за моментом /0 (см. рис. 10.0.1), равно a(t0, т)= J X (t) dt. Если поток событий
*б
стационарный, то a (t0> т) = а (т) = А,т,
Ординарный поток событий называется потоком Пальма (или
рекуррентным потоком, или потоком с ограниченным последействием), если интервалы
времени 7i, Г2, „. между последовательными событиями (см, рис, 10.0,1) представ-
t *
Рис. 10.0.2
309
\хт
в,
XI
вг Щ
-\ I
I 1
I i
-*—*-
ляют собой независимые, одинаково распределенные случайные величины. В
связи с одинаковостью распределений 7\, Т2, .». поток Пальма всегда
стационарен* Простейший поток является частным случаем потока Пальма; в нем
интервалы кежду событиями распределены по показательному закону (Ш.ОЛ), где
X — интенсивность потока*
Потоком Эрланга k-го порядка называется поток событий, получающийся
«прореживанием» простейшего потока, когда сохраняется каждая k-я точка
(событие) в потоке, а все промежуточные выбрасываются (см* рис. 10.0.3,$ где
показано получение потока Эрланга 4-го порядка из простейшего потока).
Интервал времени между двумя соседними событиями в потоке Эрланга fc-ro
порядка представляет собой сумму k независимых случайных величин Tlt T2, .♦»,
Ть, имеющих показательное распределение с параметром X:
k
Т=%Ти (10.0.2)
Закон распределения случайной величины Т называется законом Эрланга
k-го порядка (см. задачу 8*38) и имеет плотность
/fcW^V^m е~Х' (при/>0). (Ю.0.3)
(ft—1)!
Математическое ожидание, дисперсия и среднее квадратическое отклонение
случайной величины Т (10*0,2) соответственно равны:
mt=klX\ Dt=k/X*; ot = Yk/X. (Ю.0.4)
Коэффициент вариации случайной величины (10.0.2) равен
Vi^at/mt — \lVk\ (10.0.5)
Vf ->• 0 при k -*- оо, т* е. при увеличении порядка потока Эрланга «степень
случайности» интервала между событиями стремится к нулю.
Если одновременно с «прореживанием» простейшего потока изменять
масштаб по оси 0t (делением на /г), получится нормированный поток Эрланга &-п>
порядка, интенсивность которого не зависит от k. Интервал времени Т между
соседними событиями в нормированном потоке Эрланга £-го порядка имеет
плотность
^=*^-1*Г е"ш <при'>о)- (io-°-6>
Числовые характеристики случайной величины
1 *
равны:
M[f]=*lA; Drn = l/W; 6^=1/(^1/F)| vt = M~\/k. (10.0.7)
При увеличении k нормированный поток Эрланга неограниченно
приближается к регулярному потоку с постоянным интервалом / = 1/л между событиями*
310
Случайный процесс, протекающий в какой-либо физической системе S,
называется марковским (или процессом без последействия), если он обладает
следующим свойством: для любого момента времени t0 (рис. 10.0.4) вероятность
любого состояния системы в будущем (при t > /0) зависит только от ее состояния
в настоящем (при t = t0) и не зависит от того, когда и каким образом система S
пришла в это состояние (иначе: при фиксированном настоящем будущее не
зависит от предыстории процесса — от прошлого).
^(настоящее)
Рис. 10.0.4
В данной главе мы будем рассматривать толькр марковские процессы с
дискретными состояниями sb s2, ..., sn. Такие процессы удобно, иллюстрировать
с помощью графа состояний (рис. 10.0.5), где прямоугольниками (или кружками)
обозначены состояния sb s2, ... системы 5, а стрелками — возможные переходы
из состояния в состояние (на графе отмечаются только непосредственные
переходы, а не переходы через другие состояния). Иногда на графе состояний отмечают
не только возможные переходы из состояния в состояние, но и возможные
задержки в прежнем состоянии; это изображается стрелкой («петлей»),
направленной из данного состояния в него же (рис. 10.0.6), но можно обходиться и без
этого. Число состояний системы может быть как конечным, так и бесконечным (но
счетным).
Марковский случайный процесс с дискретными состояниями и дискретным
временем обычно называют марковской цепью. Для такого процесса моменты tlt
t2, ..., когда система 5 может менять свое состояние, удобно рассматривать как
последовательные шаги процесса, а в качестве аргумента, от
которого зависит процесс, рассматривать не время t, а номер шага: 1, 2, ..., k, ...
Случайный процесс в этом случае характеризуется последовательностью
состояний
S (0), S (1), S (2), ,.., S (*),
(10.0.8)
.где S (0) — начальное состояние системы (перед первым шагом); 5 (1) —
состояние системы непосредственно после первого шага; 4«.; S (k) — состояние
системы непосредственно после fc-ro шага ...
Событие {S (k) = St} = {сразу после fc-ro шага система находится в
состоянии Sf} (t = 1, 2, .j.) является случайным событием, поэтому последовательность
состояний (10.0.8) можно рассматривать как последовательность случайных
событий. Начальное состояние S (0) может быть как заданным заранее, так и слу-
«— Рис. 10.0.5
о
Si
Рис. 10.0.6
311
чайным. О событиях последовательности (10.0.8) говорят, что они
образуют марковскую цепь.
Рассмотрим процесс с л возможными состояниями s(, s2,..., %. Если
обозначить X (0 номер состояния, в котором находится-система S в момент I, то
процесс (марковская цепь) описывается целочисленной случайной функцией
X (0 > 0, возможные значения которой равны 1, 2, ..., л. Эта функция
совершает скачки от одного целочисленного значения к другому в заданные моменты
/lt t2, ... (рис. 10.0.7) и является непрерывной слева, что отмечено точками на
рис. 10.0.7.
BY
S
з[
2
]
X(t)
I
4.
I
Рис. 10.0.7
Рассмотрим одномерный вакон распределения случайной функции X (*)■
Обозначим Pi (k) вероятность того, что после &-го шага [и до (k + 1)-го]
система 5 будет в состоянии si (i = 1, 2, ••>, п). Вероятности р% (k) называются
вероятностями состояний цепи Маркова* Очевидно, для любого k
^Pi(k)-.
Л.
(10.0.9)
Распределение вероятностей состояний в начале процесса
Pi (0), р2 (0) Pi (0), ..., рп (0) (10.0.10)
называется начальным распределением вероятностей марковской цепи. В
частности, если начальное состояние 5 (0) системы S в точности известно, например
5 (0) = s^ начальная вероятность pi (0) = 1, а все остальные равны нулю.
Вероятностью перехода на &-м шаге из состояния $t в состояние s7-
называется условная вероятность того, что система 5 после &-го шага окажется в
состоянии s/, при условии, что непосредственно перед этим (после к — 1 шагов) она
находилась в состоянии Sf. Вероятности перехода иногда называются также
«переходными вероятностями»*
Марковская цепь называется однородной, если переходные вероятности не
зависят от номера шага, а зависят только от того, из какого состояния и в какое
осуществляется переход:
P{S(fc)=Si|S(fc—l)=Si}=P^. (10.0.11)
Переходные вероятности однородной марковской цепи Р$7* образуют
квадратную таблицу (матрицу) размера п X п:
Рц ^12 • • • Plj • • • Рщ
И^;11 =
Рп Р
12 •
2)
Ри —
nj<
Un
(10.0.12)
312
Сумма переходных вероятностей в любой строке матрицы равна единице:
л
2^0 = 1 (/«1.....П). (10.0.13)
/=1
Матрицу, обладающую таким свойством, называют стохастической. Вероятность
Рц есть не что иное, как вероятность того, что система, пришедшая к данному
шагу в состояние sj, в нем же и задержится на очередном шаге*
Если для однородной цепи Маркова заданы начальное распределение
вероятностей (10.0.10) и матрица переходных вероятностей (10.0.12), то вероятности
состояний системы р% (k) (i = 1, 2, *.., п) могут быть определены по
рекуррентной формуле
п
Pi{k)=^Pj{k-\)Pn (/«!,...,«; / = 1 я). (10.0.14)
/-ь
Для неоднородной цепи Маркова вероятности перехода в матрице (10.0.12)
и формуле (10.0.14) зависят от номера шага k. .^
При фактических вычислениях по формуле (10.0.14) надо в ней учитывать
не все состояния Sj, а только те, для которых переходные вероятности отличны от
нуля, т. е. те, из которых на графе состояний ведут стрелки в состояние s$.
Марковский случайный процесс с дискретными состояниями и непрерывным
временем иногда называют «непрерывной цепью Маркова». Для такого
процесса вероятность перехода из состояния s^b sj для любого момента времени равна
нулю. Вместо вероятности перехода Р^ рассматривают плотность вероятности
переходами, которая определяется как предел отношения вероятности перехода из
состояния sj в состояние Sj за малый промежуток времени А/, примыкающий к
моменту t, к длине этого промежутка, когда она стремится к нулю. Плотность
вероятности перехода может быть как постоянной (А,г-7- = const), так и зависящей
от времени [^ij = ^tf(0J« В первом случае марковский случайный процесс с
дискретными состояниями и непрерывным временем называется однородным»
Типичный пример такого процесса — случайный процесс X (/), представляющий
собой число появившихся до момента t событий в простейшем потоке (см.
рис. 10.0.2).
При рассмотрении случайных процессов с дискретными состояниями и
непрерывным временем удобно представлять себе переходы системы 5 из
состояния в состояние как происходящие под влиянием некоторых потоков
событий; при этом плотности вероятностей перехода получают смысл и н-
тенсивностей Хц соответствующих потоков событий (как только
происходит первое событие в потоке с интенсивностью А,^, система из состояния si
скачком переходит в sj). Если все эти потоки пуассбновские (т. е. ординарные
и без последействия, с постоянной или зависящей от времени интенсивностью),
то процесс, протекающий в системе S, будет марковским.
Рассматривая марковские случайные процессы с дискретными состояниями
и непрерывным временем, очень удобно пользоваться графом состояний, на
котором против каждой стрелки, ведущей из состояния si в sj, проставлена
интенсивность %ij потока событий, переводящего систему по данной стрелке
(рис. 10.0.8). Такой граф состояний называют размеченным*).
Вероятность того, что система S, находящаяся в состоянии s$, за
элементарный промежуток времени (/, /+ dt) перейдет в состояние sj (элемент вероятности
перехода из St в sj) есть вероятность того, что за^это время dt появится хотя бы
одно событие потока, переводящего S из s$ в s/. С точностью до бесконечно малых
высших порядков эта вероятность равна %tjdt.
Потоком вероятности перехода из состояния s% в s; называется величина
Ktj pf (t) (здесь интенсивность Хц может быть как зависящей, так и независящей
от времени),
*> На графе состояний системы с непрерывным временем мы не будем
проставлять петли, соответствующие задержке системы в данном состоянии, так как
такая задержка всегда возможна.
313
Рассмотрим случай, когда система S имеет конечное число состояний su
Sj, ...» sn. Для описания случайного процесса, протекающего в этой системе!
применяются вероятности состояний
Pi (0, Ра (0 Р»«. (10,0.15)
где pi (0 — вероятность того, что система 5 в момент t находится в состоянии
st:
Pi(*)=P {S(0 = s*}. (10.0.16)
Очевидно, для любого I
2>|«)-1. <10-0Л7>
*«i
Для нахождения вероятностей (10.0.15) нужно решить систему
дифференциальных уравнений (уравнений Колмогорова), имеющих вид
dpid)
dt
= 2 fc|jPj (*)<-**(') £ Ul (/ = 1,2,.;.. «)»
или, опуская аргумент t у переменных р%
dpi
. п п
-^Гв 2 hiPi-Pi S *« (*-1,2,...,л).
/-1 /-i
(10.0.18)
Напомним, что интенсивности потоков кц могут зависеть от времени I
(аргумент t для краткости написания опущен)*
^—\^;
1 г 1 Д/У -J о 1
о) 1 ■—^Н о^ L
1 с ^ 5*, к . Ц
— — 35\l\
1 sz 1 ^jl^
J ty [ ,: 1 SS\ \SB J И ^7 1
Рис. 10.0.8
Рис. 10.0.9
Уравнения (10.0.18) удобно составлять, пользуясь размеченным графом
состояний системы и следующим мнемоническим правилом: производная
вероятности каждого состояния равна сумме всех потоков вероятности, идущих из
других состояний в данное, минус сумма всех потоков вероятности, идущих из
данного состояния в другие. Например, для системы 5, размеченный граф
состояний которой дан на рис. 10.0.8, система уравнений Колмогорова имеет вид
dpf/dt ~ Х31Р3 + ^4iP4 — Ф12 + ^14) Pi'i
dpc/dt — ht2Pi — Я23р2;
dpjdt = %22p2 — (%m + Хы + Ц5) Pti (10.0.19)
dpjdt — \uPt + Яз4р3 + KlPb —■ ^4lP4j
dpjdt =» ^35Pi — К*Рь*
Так как для любого t выполняется условие (10.0.17), можно любую из
вероятностей (10.0.15) выразить через остальные и таким образом уменьшить число
уравнений на одно.
314
Чтобы решить систему дифференциальных уравнений (10.0.18) для
вероятностей состоянийрх (0» P%(t)> *•», Рп (0» нужно Задать начальное распределение
вероятностей
Pi (0), Рг (0)» •••> Pi (0) Рп (0), (10.0.20)
сумма которых равна единице:
2pj(0)=i.
/-I
Если, в частности, в начальный момент t =* 0 состояние системы S в точности
известно, например, 5 (0) -=- s$, то pi (0) = 1, а остальные вероятности (10.0.20)
равны нулю.
Во многих случаях, когда процесс, протекающий в системе, длится
достаточно долго, возникает вопрос о предельном поведении
вероятностей pt (t) при t-*oo. Если все потоки событий, переводящие систему из
состояния в состояние, являются простейшими (т, е* стационарными пуассонов-
скими с постоянными интенсивностями %н), в некоторых случаях существуют
финальные (или предельные) вероятности состояний
Pi = YimPi(t) (/ = !,..., я), (10.0.21)
не зависящие от того, в каком состоянии система S находилась в начальный
момент. Это означает, что с течением времени в системе S устанавливается
предельный стационарный режим, в ходе которого она переходит из состояния в
состояние, но вероятности состояний уже не меняются. В этом предельном режиме
каждая финальная вероятность может быть истолкована как среднее относительное
время пребывания системы в данном состоянии.
Система, для которой существуют финальные вероятности, называется эр-
годической и соответствующий случайный процесс — эргодическим.
Для существования финальных вероятностей состояний одного условия
%и = const недостаточно, требуется выполнение еще некоторых условий,
"проверить которые можно по графу состояний, выделив на нем «существенные»
и «несущественные» состояния. Состояние s$ называется существенным, если нет
другого состояния Sj такого, что, перейдя однажды каким-то способом из s$ в
Sj, система уже не может вернуться в s^ Все состояния, не обладающие таким
свойством, называются несущественными»
Например, для системы S, граф состояний которой дан на рис. 10.0.9,
состояния Si, s2 несущественны (из s^ можно уйти, например, в s2 и не
вернуться, а из % в Si или s5 и не вернуться), а состояния s4, s5, s8» se, s7 — существенны
(существенные состояния обведены жирными линиями).
При конечном числе состояний п для существования финальных
вероятностей необходимо и достаточно, чтобы из каждого существенного состояния
мооюно было (за какое-то число шагов) перейти в каждое другое существенное*
Граф, представленный на рис. 10.0.9, этому условию не удовлетворяет (например,
из существенного состояния s4 нельзя перейти в существенное состояние s6);
для графа, показанного на рис. 10.0.10, финальные вероятности существуют
(из каждого существенного состояния возможен переход в каждое другое
существенное).
Несущественные состояния потому так и называются, что из каждого
такого состояния система рано или поздно уйдет в какое-то из существенных и
больше не вернется. Естественно, финальные вероятности для несущественных
состояний равны нулю.
Если система S имеет конечное число состояний s%t s2> •»•> sn> то Для
существования финальных вероятностей достаточно, чтобы из любого состояния,
системы можно было (за какое-то число шагов) перейти в любое другое. Если число
состояний slt s2, ..., sn, *** бесконечно, то это условие перестает быть достаточным,
и существование финальных вероятностей зависит не только от графа состояний,
но и от интенсивностей Хц*
Финальные вероятности состояний (если они существуют) морут быть
получены решением системы линейных алгебраических уравнений* они получаются
315
из дифференциальных уравнений Колмогорова, если положить в них левые
части (производные) равными нулю. Однако удобнее составлять эти уравнения
непосредственно по графу состояний, пользуясь мнемоническим правилом:
для каждого состояния суммарный выходящий, поток вероятности равен
суммарному входящему. Например, для системы S, размеченный граф состояний
которой дан на рис.. 10.0.11, уравнения для финальных вероятностей состояний
имеют вид
(10.0.22)
(Xj2 + Kf3) Pi = k2lp2'i (^21 + ^2*) p2 = l^tfi + WV*
(^34 + ^$б) Рд в ^18W ^4204 — ^2«^2 "I" ^34Рз + ^мРб5 ^ЪфЬ — ^35Рз«
Таким образом, получается (для системы Sen состояниями) система п ли^.
нейных однородных алгебраических уравнений с п неизвестными plt р2, ..., р^в
Из этой системы можно найти неизвестные pi, р2,.«., рп с точностью до
произвольного множителя. Чтобы найти точные значения р±, ,*., рп, к уравнениям
добавляют нормировочное условие Pi + р2 + *•* + Рп =? 1, пользуясь которым можно
выразить любую из вероятностей pi через другие (и соответственно отбросить
одно из уравнений)*
1 si I h
Л-ХЗ-,
J fr |«с 1 ^U 1^1
Рис. 10.0.10
Рис. 10.0.11
На практике очень часто приходится встречаться с системами, граф
состояний которых имеет вид, показанный на рис. 10.0.12 (все состояния можно
вытянуть в цепь, причем каждое из них связано прямой и обратной связью с двумя
соседними, кроме двух крайних, каждое из которых связано только с одним
соседним)* Схема, изображенная на рис. 10.0.12, называется схемой гибели и раз-
мнооюения» Это название заимствовано из биологических задач, где состояние
популяции Sfe означает наличие в ней k единиц* Переход вправо связан с
«размножением» единиц, а влево — с их «гибелью», На рис. 10.0.12 «интенсивности
размножения» (А,0, %i, *.., Xn-f) проставлены у стрелок, ведущих слева направо,
«интенсивности гибели» (fij, |л2, ,*,, \in-i) — У стрелок, ведущих справа налево;
каждая из них отмечена индексом того состояния, из которого исходит
соответствующая стрелка *
Для схемы гибели и размножения финальные вероятности состояний
выражаются формулами:
А-о A.Q A,j
Pi=— Ро; рг = Ро; •..;
И-1 Vi Ц2
Рй =
Ро(6=0,..., п)\...\
316
Обратим внимание на правило вычисления любой вероятности состояния
(при k = 1, 2, ..., л)
pft=s ^
которое можно сформулировать так: вероятность любого состояния в схеме
гибели и размножения (см. рис. 10.0.12) равна дроби, в числителе которой стоит
произведение всех интенсивностей размножения, стоящих левее s&, а в
знаменателе — всех интенсивностей гибели, стоящих левее s&, умноженной на
вероятность крайнего левого состояния р0.
I \\\ 1^1 \Н~ _^J 1^*21 \XfL i Л-/
1—W—^W—Hi ^~
/<*
5n
• • •
Мы
^7-/
/**
Яд* /0.0.72
Если процесс описывается схемой гибели и размножения, то можно
записать дифференциальные уравнения для математического ожидания и дисперсии
случайной функции X (t) — числа единиц в системе в момент времени t:
dm<* (t) vi
|р—23 (*»-Wk)ftkWl (10.0.24)
/Г-« о
dD*t {П ■ S IX»+|ift+2*(ika|ifc)s2m,(0(X»si»^]plk(0. (10.0.25)
Jfe = 0
В этих формулах нужно полагать Кп = ji0 = 0» Интенсивности А,& (0 ^ k ^
^ я — 1) и ць (1 ^ & ^ я) могут быть любыми неотрицательными функциями
времени*
При достаточно больших значениях тх (t) (> 20) и выполнении условия
0 < тх (t) ± S1/dx (t) < n можно приближенно полагать,, что сечение
случайной функции X (0 представляет, собой нормальную случайную величину с пара
метрами тх {f)> ^/Dx (t)t полученными решением уравнений (10*0.24), (10.0*25'-
Формулы (10*0*24) и (10.0.25) остаются справедливыми при п -»• оо, если верх)
ний предел в суммах заменить на оо,
ЗАДАЧИ И УПРАЖНЕНИЯ
10.1. Производится наложение («суперпозиция») двух простейших
потоков: 1) потока I с интенсивностью Хг и 2) потока II с
интенсивностью %2 (Рис* 10.1). Будет ли поток III, получившийся в результате
суперпозиции, простейшим, и если да, то g какой интенсивностью?
Решение. Да, будет, так как свойства стационарности,
ординарности и отсутствия последействия сохраняются; интенсивность
потока III равна %1 + %2.
10.2. Производится случайное прореживание простейшего потока
событий с интенсивностью %; каждое событие, независимо от других,
с вероятностью р сохраняется в потоке, а о вероятностью 1 — р-
317
ш
0\
-т-t-
I I
! I
т—г
I I
I I
I I
х—а л 1—ю-l
Рис. /Л/
Т ft
Hi
ЛХ-U—*Л—«
выбрасывается (в дальнейшем такую операцию будем называть р-
преобразованием потока). Каким будет поток, получающийся в
результате р-преобразования простейшего потока?
Решение. Поток будет простейшим с интенсивностью \р.
Действительно, все свойства простейшего потока (стационарность,
ординарность, отсутствие последействия) при р-преобразовании
сохраняются, а интенсивность умножается на р.
10.3. Интервал времени Т между событиями в ординарном потоке
имеет плотность
/(0 =
Яе-М<-*.> при t>tQ\
0 при t<Ct<>.
(10.3)
Интервалы между событиями независимы. 1) Построить график
плотности / (/). 2) Является ли данный поток простейшим? 3) Является
ли он потоком Пальма? 4) Какова его интенсивность Я? 5) Каков
коэффициент вариации vt интервала между событиями?
Решение. 1) См. рис. 10.3; распределение такого вида назовем
«сдвинутым tfa t0 показательным». 2) Нет, не является, так как
распределение (10.3) не показательное. 3) Да, является в силу
ординарности потока, независимости интервалов и одинакового их
распределения.
4)1=1/М[Л; М[Г] = 1А+*о; ^=(lA+^0)-1=V(l+^o).
JL- a-—- v - Gt - IA - l
5) Dm —
1А+*о 1+Ц>
Рис. 10.3
318
|-48>-X-<§> # ©К© )(—© X <SH§) К © >< ©-—£
Рис. /0.4
10.4. На оси 0t имеется простейший поток событий о
интенсивностью %. Из этого потока формируется другой следующим образом;
интервал между каждыми двумя соседними событиями делится
пополам и в точку деления вставляется еще одно событие (см. рио. 10.4, где
кружками обозначены основные, крестиками — вставленные события).
Найти плотность распределения / (t) интервала Т между соседними
событиями в новом потоке. Будет ли этот поток простейшим? Будет ли
он потоком Пальма? Каков коэффициент вариации интервала Т
между событиями?
Решение. Г = Х/2, где X имеет показательное распределение
с параметром %: fx (х) = )&гХх (х>0). Пользуясь решением задачи
8.1 и полагая в формуле (8.1) а = 1/2, 6 = 0, получаем
/0-2**-**' (*>0). ' (10.4)
Это есть показательное распределение с коэффициентом вариации
vt = 1. Тем не менее новый поток не будет ни простейшим, ни даже
потоком Пальма. Докажем сначала, что он не будет потоком Пальма.
Хотя интервалы между событиями распределены одинаково по закону
(10.4), они не являются независимыми. Рассмотрим два соседних
интервала между событиями потока. С вероятностью 1/2 они независимы,
с вероятностью 1/2 равны друг другу, следовательно, зависимы.
Таким образом, новый поток событий — не пальмовский. Естественно,
он не будет и простейшим, так как простейший поток—частный случай
пальмовского.
Таким образом, показательное распределение интервала между
событиями — недостаточное условие для того, чтобы поток был
простейшим.
10.5. Условия те же, что и в предыдущей задаче, с той разницей,
что преобразованный поток состоит только из «крестиков» (середин
интервалов). Ответить на те же вопросы, что и в предыдущей задаче.
Решение. Очевидно, что интенсивность нового потока по
сравнению с интенсивностью исходного не изменится и останется равной
X. Интервал между двумя соседними крестиками (рис. 10.5) равен
Т=(Х£ + Х*+1)/2, (10.5)
где Хи Xi + i — Два соседних интервала исходного потока.
Величины X*, X|+i распределены обе по показательному закону с парамет-
Xi Хы
319
ром К, а их полуоумма (10.5) — по нормированному закону Эрланга
2-го порядка, так как интервал Т равен сумме двух независимых
показательно распределенных случайных величин, деленной на д в а.
Таким образом, интервал Т между двумя крестиками имеет плотность
/ (0 = 4Я2 е~2*< (t > 0).
В преобразованном потоке все соседние интервалы времени будут
зависимы, так как в состав этих интервалов входят одни и те же
случайные величины. Однако эта зависимость распространяется только на
соседние интервалы времени. Такие потоки иногда называют
потоками со слабым последействием.
Коэффициент вариации vt для случайной величины Т будет равен
1см. формулу (10.0.7)1 vt = 1/V2 < 1.
10.6. Поток машин, идущих по шоссе в одном направлении,
представляет собой простейший поток с интенсивностью А,. Человек
выходит на шоссе, чтобы остановить первую попавшуюся машину, идущую
в данном направлении. Найти закон распределения времени Г, которое
ему придется ждать; определить его математическое ожидание mt и
среднее квадратическое отклонение ot.
Решение. Так как простейший поток не обладает
последействием, то «будущее» не зависит от «прошлого», в частности, от того,
сколько времени тому назад прошла последняя машина. Распределение
времени Т точно такое же, как и распределение промежутка времени
между появлением соседних машин, т. е. показательное с параметром
%: f (t) = Лег** (t> 0); отсюда mt = 1/Jt; Dt■» 1/A,2; at =* 1/fc = mt\
vt = 1.
Примечание, Если поток машин, идущих по шоссе, является много-
рядным, то его можно рассматривать как суперпозицию нескольких потоков,
соответствующих каждому ряду, Если каждый поток — простейший, то
результат суперпозиции также является простейшим потоком, так как свойства
стационарности, ординарности и отсутствия последействия при суперпозиции
сохраняются (см* задачу 10.1),
10.7. Пассажир выходит на остановку автобуса в некоторый
момент времени, никак не связанный с расписанием движения. Автобусы
следуют друг за другом регулярно с интервалом времени длины /.
Найти закон распределения времени 7\ которое придется пассажиру
ждать автобуса, и выразить его характеристики mu at через
интенсивность потока автобусов X.
Решение. Момент прихода пассажира распределен о
постоянной плотностью на интервале длины / между двумя автобусами;
плотность распределения времени ожидания Т будет также постоянна
[равномерное распределение на интервале (0, /)]: f (t) = III (0 < t < /)
или, обозначая III = %, f (t) = %(0 < f < 1M). Для равномерного
распределения на участке длины Ш имеем mt = V(2X); Dt=* l/(12k2);
ot = 1/(21/3 X); о,- 1/1/3.
10.8*. На оси Ot имеется пальмовский поток событий,
интервалы между которыми распределены с плотностью f (t). На ось 0t
случайным образом бросается точка t* (например, прибывает «инспектор»,
наблюдающий за появлением событий, или же «пассажир» появляется
на остановке автобуса), причем момент t* никак не связан о моментами
320
появления событий потока (рис. 10.8). Найти плотность распределения
того интервала Г*, на который попала точка t*t его математическое
ожидание, дисперсию и среднее квадратическое отклонение.
Решение. С первого взгляда может показаться, что эта
плотность — такая же, как плотность распределения f (f) л ю б о г о
интервала Т между событиями, однако это не так. Тот факт, что на
участок Г* попала случайно брошенная точка **, меняет его
распределение; действительно, если на оси Ot есть разные участки (большие
и маленькие), tog большей вероятностью точка t* попадет на один из
больших участков.
Рис. 10.8
Найдем плотность распределения /* (t) того участка Г*, на
который попала точка <*. Для этого найдем элемент вероятности /* (/) dt,
равный вероятности того, что точка /* попадет на промежуток, длина
которого заключена в пределах (t> t + dt). Эта вероятность
приближенно равна отношению суммарной длины всех таких промежутков
на очень большом интервале времени Q к полной длине этого
интервала.
Пусть на очень большом интервале Q уложилось большое число N
промежутков между событиями. Среднее число промежутков, длина
которых лежит в пределах (t> t + dt), равна Nf (t) dt; средняя
суммарная длина всех таких промежутков приближенно равна- tNf (t) dt.
Средняя же общая продолжительность всех N промежутков Q будет
оо
(приближенно) равна Nmu где mt « М [71 = J tf (t) dt. Разделив
о
одно на другое, получим
Nrrif mt
Это равенство выполняется тем точнее, чем более длительный
интервал времени Q будет рассматриваться (чем больше N). В пределе
закон распределения случайной величины Г* будет
f*(t) = — f{t) (/>0). (10.8)
nit
оо
М[Г] = — U*fif)dt = — a20) = — (Dt + m?);
mi J m, ntt
D[T*]=;a2m —(М[Г*])2=:— Г t3f(t)dt—(МЩ)2.
m>t J
П Зак. 1040
321
10.9. В условиях задачи 10.8 поток Пальма представляет собой
простейший поток с интенсивностью К т. е. / (t) = ierM (t > 0).
Найти плотность /* (/) того интервала Г*, на который попадает точка /*.
Решение. С учетом того, что mt = 1A, формула (10.8) дает
/* (/) = X2te-kt (t > 0), что представляет собой не что иное, как за-
кон Эрланга 2-го порядка [см. формулу (10.0.3) при k = 2].
10.10*. На оси 0t имеется пальмовский поток событий с
плотностью / (t) интервала Т между соседними событиями. Случайная точка
t* («инспектор») попадает куда-то на интервал Т* (рис. 10.10). Она
делит его на два промежутка: Q — от ближайшего предыдущего события
до t* и Н — от t* до ближайшего последующего события. Найти
распределение, обоих этих промежутков.
/ '
•ч
Т*
>ч
**• „ *
Q t* H
Рис. 10.10
Рис. 10.12
4-
Z
0
а
5
а)
10
-t
j
7,5
О
Ш
1
%
5
б)
V-
10
Решение. Предположим, что случайная величина Г* приняла
значение s: Т*=5,и найдем условное распределение промежутка Q
при этом условии. Обозначим его плотность fa (t\s). Так как точка t*
бросается на ось Ot совершенно случайно (безотносительно к событиям
потока), очевидно, она будет иметь равномерное распределение в
пределах промежутка Т* = s: ^~
fa (t\s) — 1/s при 0< t<s. (10.10.1)
Чтобы найти безусловное распределение fa (t), надо осреднить
плотность (10.10.1) с «весом» /* (s). Пользуясь формулой (10.8),
получаем
00
/*(s)-—-?(5); /Q(/)= Г fa(t\s)r(s)ds.
Щ J
о
Учитывая, что fa (t\s) отлично от нуля только при s> U можно
написать
оо со
J smt rtif J nit
t t
где F (f) — функция распределения интервала Т между событиями
в потоке Пальма.
Итак,
h(t) = —[l-F(t)].
(10.10.2)
322
Очевидно, то же распределение будет иметь и промежуток времени
H=T* — Q:
/«(*)« — [I—Ftf)]. (ЮЛ 0.3)
10.11. Пользуясь результатами предыдущей задачи, проверить
решение задачи 10.6, полученное из других соображений.
Решение. Имеем / (t) = ter%t; F (t) = 1 — er* (t > 0); tnt =
= 1/Я. По формуле (10.10.3)
h (t) = Я [1 -1 + er**\ = Ье-** (t > 0);
т4 е. задача 10.6 решена верно.
10.12. Пассажир выходит на остановку автобуса в момент времени,
никак не связанный с расписанием. Поток автобусов представляет со*
бой поток Пальма о интервалами, имеющими равномерное
распределение в пределах от 5 до 10 мин. Найти: 1) плотность распределения
того интервала, на который попал пассажир; 2) плотность
распределения времени Я, которое ему придется ждать автобуса; 3) среднее
время ожидания автобуса.
Решение. Имеем'/ (t) = 1/5 при t £ (5, 10); mt = 7,5.
1) По формуле (10.8) /* (t) — #37,5 при t 6 (5, 10). График
плотности i* (t) показан на рис. 10.12, а.
при *<5;
2) F(i) = l (f_5)/5 при 5</<10;
Отсюда по формуле
h(t)
при *>10.
при *<0;
при 0<*<5;
при 5<*< 10;
при-* > 10.
График плотности /W (t) показан на рис. 10.12,6.
3) Среднее время ожидания
б 10
тн={ ^dt+ttl^dttt6,11 мин.
10.13. Рассматривается поток Эрланга fe-ro порядка с
плотностью распределения интервала Т между событиями: ^
ЪМ^^РтГ^ «>°>- (10.13.1)
Найти функцию распределения jFfc (t) этого интервала.
Решение. Можно было бы найти функцию распределения по
обычной формуле
о
И* 323
но проще найти ее исходя непосредственно из определения Fk (t) =
= Р {Т < t).
Перейдем к противоположному событию и найдем Р {Т > /}.
Свяжем начало отсчета 0 с одним из событий потока Эрланга и отложим
от него вправо два участка: Т (расстояние до следующего события
потока Эрланга) и t<T (рио. 10.13).
Для выполнения неравенства Т > t нужно, чтобы на участок t
попало меньше чем k событий простейшего потока g интенсивностью %
(либо 0, либо 1, ..., либо k — 1). Вероятность того, что на участок t
попадет rri событий, равна
По правилу сложения вероятностей
P{T>t}= S М-е-Ч
т=0 ШХ
откуда
M*) = l — S -^е-^=1-/?(&—1.М), (10.13.2)
где 1 — R (m, а) — табулированная функция (см. приложение 2).
10.14*. Поток отказов ЭВМ представляет собой поток Эрланга
&-го порядка с плотностью (10.13.1) интервала между отказами
(восстановление машины после отказа происходит мгновенно). «Инспектор»
прибывает в случайный момент времени t* и ожидает первого отказа.
Найти плотность распределения времени Я, в течение которого ему
придется ждать отказа, и его математическое ожидание m#. j
Решение, По формуле (10.10.3) |
fH(t)-—[\-Fh(t)]f Ь
щ w
\\
где Fk (f) дается формулой (10.13.2), a mt = klX. Отсюда \\
/я(0—T*S ^-e-*« = 4-*S -*^f-e-u (t>0). (10.14.1) !]
k ml k л ml
m=0 wi=0
Перепишем формулу (10.14.1) в виде
X(Xt)r-x
r=\
^W-TS-^jre-W C>0)- (ЮЛ4.2) -I
Из (10.14.2) видно, что случайная величина Н имеет распределение, Ц
«смешанное» из k эрланговских распределений разных порядков; с I
одинаковой вероятностью \lk она имеет эрланговское распределение *
324
1, 2, ..., fe-ro порядков. Математическое ожидание такой случайной
величины найдем по формуле полного математического ожидания:
m// = M[#] = -i- J M[#|r], (10.14.3)
k f~i
где М [Н | г] — условное математическое ожидание случайночй
величины Н при условии, что она распределена по закону Эрланга г-го
порядка.
Находим по первой формуле (10.0.4) Ж[Н\г\ — гА, откуда
"--S-2.-2^-i±!.. 00..4.4,
t
10.15*. Пальмовский поток событий о плотностью распределения
/ (t) интервала между событиями подвергается р-преобразованию
(см. задачу 10.2). Случайная величина V — интервал между
событиями в преобразованном потоке. Найти математическое ожидание и
дисперсию случайной величины V.
Решение. Случайная величина V представляет собой сумму
случайного числа независимых случайных величин (ем. задачу 8.63):
V 5= У, Тк, где Y — дискретная случайная величина, имеющая гео-
метрическое распределение Р {Y = пг} — pqm~*] (m = 1, 2, ...),
9=1 — р> а каждая из случайных величин Тк имеет
распределение / (t).
Тогда последовательные интервалы между событиями в р-преоб-
разованном потоке будут
Y Y
где случайные величины Vl9 V2, ... независимы, и преобразованный
поток есть' поток Пальма. В соответствии с задачей 8.63
р р р*
где mt=ytf (i) dl; Dt = J (I—mtf f (t)di.
Примечание. Можно доказать, что при многократном р-преобразо-
вании потока Пальма получается поток, близкий к простейшему.
10.16. Найти закон распределения интервала Т между событиями
в потоке Пальма, если случайная величина Т определяется из выра-
Y
жения Т ** У Tk, т. е. представляет собой сумму случайного числа
случайных слагаемых, где случайные величины Tk независимы и под-
325
чцнены показательному закону в параметром %, а случайная величина
Y не зависит от них и имеет геометрическое распределение,
начинающееся с единицы: рп » Р {У =* п} = pq*-1 (0 < р < 1; л « 1, 2,
3, ...).
Решение. В задаче 8.62 было показано, что случайная
величина Т подчинена показательному закону с параметром Хр,
следовательно, рассматриваемый поток Пальма является простейшим с
интенсивностью Яр, который получается путем р-преобразования простейшего
потока с интенсивнобтью К Это подтверждает правильность решения
задачи 10.2.
10.17. Поток автобусов, приходящих на остановку, представляет
собой поток Пальма; ицтервал Т между ними имеет плотность
распределения /г (/). Автобус находится на остановке в течение
неслучайного времени т. Пассажир, подойдя к остановке в случайный момент /*
(рис. 10.17, а), садится в автобув, если тот находится на остановке;
если же автобуса нет, то ждет его в течение времени те и, если за
это время автобус не подойдет, покидает остановку и идет пешком.
Закон распределения fT (t) таков, что случайная величина Т не может
быть меньше, чем т + т* (рис. 10.17, б). Найти вероятность того, что
пассажир сядет в автобус.
Решение. Переходим к противоположному событию Л~=
{пассажир не сядет в автобус}. Это означает, что пассажир прибудет на
остановку в момент t*9 когда на ней нет автобуса, и за время
ожидания следующий автобус не придет. Каждое событие «подход автобуса
к остановке» сопровождается «зоной захвата» пассажира; ширина
этой зоны т^_+т (рис. 10.17, в),
Событие А = {пассажир не сел в автобус} соответствует
попаданию точки t* вне пределов зоны захвата (рис. 10.17, г). Точка t*
распределена равномерно по всей длине интервала Т*. Вероятность того,
что она попадет на участок Т* — (т + т')> не вошедший в зону захвата,
равна (по интегральной формуле полной вероятности)
'Д- J
x+f
*-(*+*')
t
f*(t)dt:
oo
J
xH-t'
f-(T + T') t
f(t)dt =
326
щ
f if(t)dl-T-±f- f
/юл.
где m* — средний интервал между автобусами.
Вероятность того, что пассажир сядет в автобус, равна Р (А) =*
= 1_Р(1).
10.18. Происходит преобразование простейшего потока о
интенсивностью А-, состоящее в следующем. Если расстояние между соседними
событиями Tt оказывается меньше какого-то допустимого предела t0
(«интервала безопасности»), то событие отодвигается от предыдущего
о; о'и
Рис, 10.18
на интервал t0; если же Tt > t0> то событие остается на своем месте
(рис. 10.18). Является ли преобразованный поток, образованный
точками 0J, 6г,... на оси О'Р, простейшим? Является ли он потоком
Пальма?
Решение. Ни тем, ни другим преобразованный поток не
является, так как в нем имеется сколь угодно далеко идущее
последействие. Например, «теснящиеся» на ogh 0't'J точки в7, 08, 09, 01о
отодвигают каждую последующую точку на оси 04,J на отрезок времени,
зависящий от моментов прихода-событий и интервалов между ними в
прошлом. Если t0 много меньше среднего расстояния между событиями
в исходном потоке: t0 < Ш, то последействием в преобразованном
потоке можно пренебречь.
10.19. Происходит наложение (суперпозиция) двух независимых
потоков Пальма g плотностями распределения интервала между
событиями ft (t) и f2 (t). Будет ли результирующий поток — потоком
Пальма?
Решение. Суперпозиция двух потоков Пальма выглядит, как
показано на рис. 10.19. Ясно, что интервалы 7\, Г2, ...
результирующего потока III не будут независимыми, так как их размеры могут
быть обусловлены размерами одного и того же интервала на ogh I
или II. Например, 7\ и Т2 в сумме дают Тц и, значит, не являются
независимыми. Однако эта зависимость быстро затухает по мере
увеличения расстояния по времени между началами интервалов.
Примечание* Можно доказать, что при суперпозиции достаточно
большого числа независимых потоков Пальма со сравнимыми интенсивностями
получается поток, близкий н простейшему*
327
10.20. В процессе эксплуатации ЭВМ может рассматриваться как
физическая система S, которая'в результате проверки может
оказаться в одном из следующих состояний: sx — ЭВМ полностью исправна;
s2 — ЭВМ имеет незначительные неисправности в оперативной памяти,
при которых она может решать задачи; s3 — ЭВМ имеет существенные
неисправности и может решать ограниченный класс задач; s4 — ЭВМ
полностью вышла из строя.
Г*
S,
Г °-5 эр^
*У
0,6 ^
лА
Рис. 10.19
В начальный момент времени ЭВМ полностью исправна
(состояниеSi). Проверка ЭВМ производится в фиксированные моменты
времени tl9 t2, i3. Процесс, протекающий в системе S, может
рассматриваться как однородная марковская цепь с тремя шагами (первая,
вторая, третья проверки ЭВМ). Матрица переходных вероятностей
имеет вид
0,3 0,4
0 0,2
0 0
0 0
0,1
0,5
0,4
0
0,2
0,3
0,6
1,0
||Р|У||=
Определить вероятности состояний ЭРМ после трех проверок.
Решение. Граф состояний ЭВМ имеет вид, показанный на
рис: 10.20. Против каждой стрелки проставлена соответствующая
вероятность перехода. Начальные вероятности состояний рх (0) = 1;
Р2 (0) = Рг (0) = р4 (0) - 0.
По формуле (10.0.14), учитывая в сумме вероятностей только те
состояния, из которых возможен непосредственный переход в данное,
находим:
Pi О) = Pi (0) Pu = Ь0,3 - 0,3;
P2(l) = Pi (0)Р12 = 1-0,4 = 0,4;
Ps (1)= Pi (0) Pis = 1-0,1 =0,1;
P4 О) - Pi (0) Pu = 1-0,2 = 0,2;
Pi (2) = Pi (1) Pu = 0,3-0,3 = 0,09;
p2 (2) = Pl (1) P12 + p2 (1) P22 = 0,3-0,4 + 0,4 -0,2 = 0,20;
328
Рз (2) = Рг (1) Pi, + Р, (1) Р2з + Рз (1) ^зз = 0,27;
р4 (2) - Pl (1) Ри + р2 (1) Ры + р3 (1) ^34 + Р4 (1) Р44 - 0,44;
Рг (3) = р, (2) Ри = 0,09-0,3 « 0,027;
р2 (3) = Pi (2) Р12 + р2 (2) Р22 = 0,09-0,4 + 0,20-0,2 - 0,076;
р3 (3) - рг (2) Р13 + р2 (2) Р23 + р8 (2) Р88 = 0,217;
Р4 (3) = Рг (2) Ри + р2 (2) Ри + р8 (2) />з4 + Р4 (2) Р^ = 0,680.
Итак, вероятности состояний ЭВМ после трех проверок: рх (3) =
= 0,027- р2 (3) «= 0,076; р3 (3) = 0,217; р4 (3) = 0,680.
10.21. Точка S «блуждает» по оси абсцисс Ох (рис. 10.21, а) по
следующему закону: на каждом шаге она с вероятностью 0,5 остается
на месте, с вероятностью 0,3 перескакивает на единицу вправо и с
вероятностью 0,2 — влево. Состояние системы S после k шагов
определяется одной координатой (абсциссой) точки S. Начальное
положение точки — начало координат. Рассматривая последовательность
положений точки S как цепь Маркова, найти вероятность того, что она
после четырех шагов окажется от начала координат не дальше чем на
расстояний, равном единице.
s
1 1 » I 1 • L
-J
-2
-/
X
<L)
0,5 0,5 0,5 0,8 0,5
4J гД 0.3 XL U гД 0,5 SX 0.3 Д
0,2
S-i
0,2
0,2
0,2
О)
Рис. 10.21
0,2
"\
Решение. Обозначим состояние системы (точки S) через si9
где i — координата S на оси абсцисс. Размеченный граф состояний
показан на рис. 10.21, б. (Здесь для наглядности проставлены «петли»,
соответствующие задержке S в прежнем положении.)
Последовательность состояний образует цепь Маркова с
бесконечным числом состояний. Переходные вероятности Ptj отличны от
нуля только в случае / = /; / = i — 1; / = i + 1; Pitt = 0,5; Pti г+1=
= 0,3; Pit г-i = 0,2. Все остальные переходные вероятности равны
нулю. Искомая вероятность Р равна сумме вероятностей: р0 (4) +
+ Pi (4) + P-i*(4). Найдем их, пользуясь рекуррентными
соотношениями (10.0.14).
Имеем р0 (0) = 1; рх (0) = p_i (0) = ... = 0. Далее,
о0 (1) = Ро (0) Л>,о « 0,5; рг (1) = р0 (0) P0,i - 0,3; р_х (1) -
- Ро (1) Ро. -i - 0,2;
329
p0 (2) = p0 (1) Po.o + Pi (1) Pi.o + P-i (1) P-i, о = 0,5-0,5 + 0,2 X
X 0,3 + 0,3-0,2 = 0,37;
Pl (2) *= p0.(l) P0.i + Pi (1) Pw » 0,5-0,3 + 0,3-0,5 = 0,30;
Ps (2) - Pi (1) P12 = 0,3-0,3 = 0,09;
P-i (2) - Po (1) Л>,-1 +P-iO) P-i.-i = 0,5-0,2 + 0,2.0,5-0,20;
P-2 (2) = p.2 (1) P_x. _2 = 0,2-0,2 = 0,04;
Po (3) - Po (2) Po, о + Pi (2) Pi.o + P-i (2) P-x,o = 0,305;
Pi (3) = Po .(2) Po.fi + Pi (2) Pi. i + Pt (2) P2f i = 0,279;
P2 (3) = Pi (2) Р1в 2 + p2 (2) P2,2 == 0,135;
Рз(3) = р2(2)Р*.з = 0,027;
р-г (3) = P-2 (2) P^2, ^ + p.! (2) P_x, _x + p0 (2) P0, _x = 0,186;
- P-2 (3) = p_2 (2) P_2e _2 + p^j (2) P^l9 _2 = 0,060;
p_3 (3) = p_2 (2) P_2. _3 = 0,008;
Po (4) « Pi (3) Pl4 о + Po (3) P0, о + P-i (3) Alt0 » 0,264;
Pi (4) = p2 (3) P2, x + Px (3) Plt x + po (3) P0, x » 0,257;
P-i (4) - Po (3) P0, -i + P-i (3) P-i, -i + P-2 (3) P_2. «i » 0,172.
Искомая вероятность
P - Po (4) + Pi (4) + p_x (4) » 0,693.
Итак, вероятность события Л, состоящего в том, что за четыре шага
точка S окажется от начала координат на расстоянии., не большем
единицы, равна 0,693.
10.22. В условиях предыдущей задачи найти вероятности того, что
за четыре шага точка S ни разу не удалится от начала координат
дальше, чем на единицу.
Решение. Обозначим'р0 (&), pl9 k)\ р_х (&) вероятности
состояний s0, slt s_x при условии, что до &-го шага включительно точка S
ни разу не удалялась от начала координат больше, чем на единицу.
С первого взгляда здесь процесс не является цепью Маркова (так
как вероятности будущих состояний зависят от «предыстории» — была
ли точка S хотя бы один раз дальше, чем на одну единицу, от начала
координат), но его можно свести к цепи Маркова, если ввести еще одно
состояние s*—точка хотя бы один раз была от. начала координат на
расстоянии, большем, чем единица.
Граф состояний показан на рис. 10.22. Из состояния s* нет
перехода ни в какое другое; такое состояние называется в теории
марковских цепей «поглощающим». Вероятность события А — {точка S за
четыре шага ни разу не отойдет от начала координат на расстояние,
большее, чем единица} вычислится как сумма вероятностей р0 (4) +
+ P-i (4) + Pi (4) для системы с графом состояний,
соответствующие рис. 10.22. Предоставляем читателю вычислить эти вероятности
самостоятельно. , - .
зза
10.23. Система S — техническое устройство, состоящее из т
узлов и время от времени (в моменты tlf Lz, ..., tk) подвергающееся
профилактическому осмотру и ремонту. После каждого шага (момента
осмотра и ремонта) система может оказаться в одном из следующих
состояний: s0 — все узлы исправны (ни один не заменялся новым);
js± — один узел заменен новым, остальные исправны; s2 — два узла
заменены новыми, остальные исправны; ...; st — i узлов (i < m)
заменены новыми, остальные исправны; ...; $т — все т узлов заменены
новыми.
Л* 0,5 0,5
^KmSKmSK
0.2W 0JS 0,& 7
П I t Л1117 i* I , ППЯ Л I ■ ПИ t 1 Л
Рис. 10.22
Вероятность того, что в момент профилактики узел придется
заменить новым, равна р (независимо от состояния других узлов).
Рассматривая состояния системы S как марковскую цепь, найти переходные
вероятности и для т = 3, р = 0,4 вычислить вероятности состояний
системы.S после трех шагов (в начальный момент все узлы исправны).
Решение. Обозначая q = 1 — р, запишем переходные
вероятности цепи. Для любого состояния системы st вероятность Ptj равна
нулю при / < i\ вероятность Pti равна вероятности того, что на
данном шаге ни один узел не придется заменить новым, т. е. т — i еще
не замененных узлов остаются в составе устройства: Pti = qm—K
При i < / вероятность перехода Ри- равна вероятности того, что на
данном шаге из т — i еще не замененных узлов / — i придется
заменить новыми. Пользуясь биномиальным распределением, находим
Рц = Ckllip?—i(fnm-i+i. Состояние sm является поглощающим. Для
т = 3, р = 0,4 граф состояний системы имеет вид, показанной на
рис. 10.23:
1^11 =
Имеем р0 (0) « 1; р4 (0) = р2 (0) = р8 (0) = 0. Находим
вероятности состояний после одного, двух, трех шагов:
р0(1)«0а216; Pl (1)^0,432;
р2 (1)» 0.288; р , О) л 0,064;
0,216
0
0
0
0,432
0,36
0
0
0,288
0,48
0,6
0
0,064
0,16
0,4
1,0
Pi (2) = Pl (V Рц + Ро (1) Рп » 0,249;
Ра (2) = Р2 (1) Р2г + Ро (1) Рог + Pi (П /»ц » 0 442;
р3 (2) = р3 (1) Р33 + р2 (1) Р23 + Р, d)Pi/+Po (1) Роз » 0,262;
Ро (3) = Ро (2) Роо » 0,010;
Л (3) - рх (2)PU + р„ (2) Р01 « 0,110;
^ Рг (3) = р2 (2) Р22 + ро (2) Р02 + Pi (2) Pi2 » 0,398;
р8 (3) = р8 (2) /'зз + Ро (2) Роз + Pi (2) Рг8+Р2 (2) Р23 « 0,482.
10.24. В моменты времени tlt t2, t3 производится осмотр ЭВМ.
Возможные состояния ЭВМ: s0 — полностью исправна; ^ —
незначительные неисправности, которые позволяют эксплуатировать ЭВМ;
s8 — существенные неисправности, дающие возможность решать
ограниченное число задач; s8 — ЭВМ полностью вышла из строя.
Матрица переходных вероятностей имеет вид
0,5 0,3 0,2 0
0 0,4 0,4 0,2
0 0 0,3 0,7
0 0 0 1
Рц\\ =
Построить граф состояний. Найти вероятности состояний ЭВМ
после одного, двух, трех осмотров, если в начале (при / = 0) ЭВМ была
полностью исправна.
Решение. Граф состояний показан на рио. 10.24.
Ро (1) - Ро (0) Роо - Ь0,5 - 0,5;
Pi (1) = Ро (0) Poi - 1*0,3 = 0,3;
Р2 (1) - Ро (0) Р02 = Ь0,2 = 0,2;
Ро (2) = Ро (1) Роо = 0,25; р, (2) = р0 (1) Р01 + Л(1) Рп = 0,27;
Р2 (2) - Ро (1) Ро* + Рг (1) Ри + Pi 0) Р22 - 0,28; р3 (2) - р2 (1) х
X Р88 + Pi (1) Pis - 0,20; р0 (3) = р0 (2) Р00 - 0,125;
рх (3) = р0 (2) Р01 + Pl (2) Рц = 0,183;
Р2 (3) = Ро (2) Р02 + Pi (2) Ри + Рг (2) Р22 - 0,242;
Рг (3) = Pi (2) Р18 + р2 (2) Р28 + р8 (2) Р88 п 0,450.
10.25. Рассматривается процесс работы ЭВМ. Поток отказов
(сбоев) работающей ЭВМ — простейший с интенсивностью X. Если ЭВМ
дает сбой, то он немедленно обнаруживается, и обслуживающий
персонал приступает к устранению неисправности (ремонту). Закон
распределения времени ремонта — показательный с параметром р,: ф (f) =
= (ле-^ (t > 0). В начальный момент (t = 0) ЭВМ исправна. Найти:
1) вероятность того, что в момент t ЭВМ будет работать; 2)
вероятность того, что за время (0, t) ЭВМ даст хотя бы один сбойГ; 3)
финальные вероятности состояний ЭВМ.
Решение. 1) Состояния системы S (ЭВМ) следующие: s0 —
исправна, работает; sx — неисправна, ремонтируется. Размеченный
граф состояний дан на рис. 10.25, а.
*—
а)
Рис. 10.25
ю
\s[_
X
So
X
А.
■f
.JTpm
3
Рис, 10.26
Уравнения Колмогорова для вероятностей состояний р0 (/) и рг (t)
имеют вид
*£f- = m-XPo; -^- = ^о-№. (10.25.1)
ш_ at
Из этих уравнений одно (любое) может быть отброшено, так как для
любого момента t имеем р0 + рг — 1. Подставляя в первое из
уравнений (10.25.1) Pi = 1 — Роу получаем одно дифференциальное
уравнение относительно р0:
dpjdt = jjl — (А, Ч- |х) р0.
Решая 3JO уравнение при начальном условии р0 (0) = 1,
откуда
получаем
(10.25.2)
(10.25.3)
2) Для нахождения вероятности ~~р (t) того, что за время / ЭВМ
даст хотя бы один сбой, введем новые состояния системы S: s0— ЭВМ
ни разу не давала сбоя; sx — ЭВМ хотя бы один раз дала сбой.
Состояние 7j будет «поглощающим» (см. рис. 10.25, б).
Решая уравнение Колмогорова dpjdt = — %р0 при начальном
условии р0 (0) — 1, получаем р0 (t) = e~kt, откуда рг (t) = 1 — р0(/)=
е= 1 — e~Kt. Итак, вероятность того, что за время t ЭВМ даст
котя бы один сбой, равна рх (0 = 1 — егЧ Эту вероятность в данном
333
случае можно было бы вычислить и проще, как вероятность того, что
за время t появится хотя бы одно событие (сбой) в простейшем потоке
сбоев е интенсивностью %.
3) Из уравнений (10.25.2), (10.25.3) при t-+oo получим
финальные вероятности состояний: р0 = \л/(к + \i); рг = k/(k-\-\i), которые,
впрочем, можно было бы получить непосредственно из графа состояний,
пользуясь схемой гибели и размножения (представим читателю
сделать это самостоятельно).
10.26. В условиях предыдущей задачи 10.25 неисправность ЭВМ
обнаруживается не сразу, а по прошествии некоторого времени,
имеющего показательное распределение с параметром v. Написать и
решить уравнения Колмогорова для вероятностей состояний; Найти
финальные вероятности состояний (непосредственно по графу состояний).
Решение. Состояния системы: s0 — ЭВМ исправна, работает;
st — ЭВМ неисправна, но это не обнаружено; s2 — ЭВМ
ремонтируется. Граф состояний дан на рад. 10.26.
Уравнения Колмогорова для вероятностей состояний будут:
-%-==№-Ьр0; -^ = *A>-v/V, -%-=v/7t-w>2. (10.26.1)
at at at
Решать эту систему будем с помощью преобразования Лапласа. Тогда
уравнения (10.26.1) с учетом начальных условий для изображений nt
вероятностей р% примут вид:
sn0 = |ш2 — Лло + 1» OTi в ^яо — vni> sn2 ss= vni — И^г-
Решая эту систему алгебраических уравнений, получаем следующие^
уравнения для изображений:
s+v 0> а s+\x (s+v)(s+[i)
(s+v)(s+|i)
Обозначим
2 V 4
Тогда выражения для вероятностей примут вид:
/А aeat-bebt , , , ч е*'-е6< . , г 1 . beat-aebt 1
P»(t) = г— + (v+|i) — + № —-Ч г —- К
а—Ь а—Ь аЬ ab(a—b) J
л т . eat-ebt , л Г 1 , beat-aebt ] .
ат—Ь I аЬ аЬ(а—Ь) J
P2W [ аЬ ^ ab(a-b) J
, Для нахождения финальных вероятностей можно воспользоваться
как изображениями, так и самими вероятностями:
334
p0 = lim/?„(?) = ton sn0(s)= |*v—,
ft=I^T^; л-1-*-^-!^^- 00-26.2)
Финальные вероятности состояний можно найти и непосредственно
по графу рис. 10.26: ц,р2 = %р0; Хр0 = vpx; vpx «= цр2. Из этих
уравнений любое (например, последнее) можно отбросить. Выражая />а
через р0 и рг: р2 = 1 — р0 — р1г получаем два уравнения:
У 0 — Ро — Pi) = кРо', ^Ро = vpx.
Решение этих уравнений даст те же результаты (10.26.2).
ZX 1 , Л г-т-1 ,=—, ZA , , К '
/ \ г—-* ^У Уг
*—® • © >
Рнс. /0.27
10.27. Электронное техническое устройство (ЭТУ) состоит из двух
одинаковых узлов, которые могут заменять друг друга. Для работы
ЭТУ достаточно, чтобы работал хотя бы один узел. При выходе из
строя одного из узлов ЭТУ продолжает нормально функционировать
за счет работы другого узла. Поток отказов каждого узла —
простейший с параметром Я. При выходе из строя узла он сразу начинает
ремонтироваться. Время ремонта узла — показательное с
параметром (г. В начальный момент (при t = 0) оба узла работают. Найти
следующие характеристики работы ЭТУ:
1) Вероятности состояний: s0 — исправны оба узла; sx — исправен
один узел, другой ремонтируется; s2 — ремонтируются оба узла (ЭТУ
не работает) как функции времени.
2) Вероятность р (t) того, что за время *ЭТУ ни разу не прекратит
работу.
3) Финальные вероятности состояний ЭТУ.
4) Для предельного (стационарного) режима ЭТУ среднее
относительное время, в течение которого ЭТУ будет работать.
5) Для того же предельного режима среднее время tp
бесперебойной работы ЭТУ (от включения после восстановления до очередного
выхода из строя).
Решение. Граф состояний ЭТУ дан на рис. 10.27, а (у левой
верхней стрелки стоит 2Х, так как работают и могут выходить из строя
335
два узла; по аналогичной причине стоит 2jji у правой нижней стрелки,
так как оба узла ремонтируются).
1) Уравнения Колмогорова имеют вид:
-"Е^ = т-2Хр0; ^^Mpo + Zm^ib + Mfhi
at at
^_-,ЯЛ-2|1й. (10 27.1)
at
При этом должно выполняться условие р0 + рг + р2 — 1.
Решая эту систему уравнений при начальных условиях р0 (0) = 1;
Pi (0) *= р2 (0) = 0, получаем
ft(0» ; +&+т ' +2H-L+
, гдеа = —(^ + fi); &=— 2(X+\x);
ab(a—b) J
a—6 = X+[x,; afe = 2(^ + fi)2;
tf^^ye" , (М-Зц)(де*-6е") , 2|i(ert—e#Q , 2b ,A
\i(a— b) p,(a—ty a—6 ц
Из полученных выражений находим:
P2(0=l-Potf)-Pi(0; Р2(0) = 0.
2) Чтобы найти вероятность р (/), сделаем состояние s2 (ЭТУ
прекратило работу) поглощающим (Г2) (рис. 10.27, б). Уравнения
Колмогорова для вероятностей состояний ЭТУ будут
dpjdt = lift — 2Яр0; dpjdt = 2Xp0 — (к + \х) рг; dpjdt = Хрг.
Решая первые два уравнения при начальных условиях р0 (0) = 1,
р! (0) =в 0, получаем
Ро(0= д Ь (h + V>) —,
a—p a—Р
где
^-(з^+ц)+У^2+б^+м>2 _ —(за+11)—Ум+бХ|1+ц*
2
(величины аир отрицательны при любых положительных значениях
А и jx). Далее,
.1 /1 . ..ч ае0"—рер* Т , 2Х - /Л
+ (^+[л)— н М р0(0-
tt~P J ^
Искомая вероятность 7? (t) = р0 (f) + Pi О). Заметим, что функция
р (t) является монотонно убывающей, при этом р (0) = 1; р (оо) == 0.
3) Финальные вероятности состояний найдем по графу рис. 10.27, а
и общим формулам (10.0.23) для схемы гибели и размножения
Л = А>; Ръ = -гтРо = [— Poi Po + Pi + P2=l;
р0 = II + 2?^ + (Jt/ji)2]-1 = ^/(Х + ц)2,
4) Среднее относительное время, которое ЭТУ будет работать, равно
Л LJU+ц) U+nJ
5) Величина tv есть математическое ожидание времени Тр,
проходящего между моментом включения ЭТУ в работу и моментом ее
следующего выхода из строя.
Представим работу ЭТУ в стационарном режиме как состоящую из
ряда циклов: «работает» и «не работает» (см. рив. 10.27, в, где участки
работы показаны утолщенной линией). Среднее время *нр, в течение
которого ЭТУ не работает (математическое ожидание -длительности
нерабочего периода), очевидно равно l/(2|i) (так как на ЭТУ,
находящееся в состоянии «не работает», действует поток переходов в
«рабочее» состояние с интенсивностью 2[i).
Далее, отношение среднего времени бесперебойной работы Fp к
среднему времени «не работы» 7нр равно отношению финальной
вероятности 1 — р2 того, что ЭТУ работает, к вероятности р2 того, что
оно не работает: tJlnv = (1 — р2)/р2- Отсюда, учитывая, что Гнр =
= 1/(2*0,
7 —1 — 1"~/?2 _ 1- 1~-Р2
Р HP п ч-
10.28. Условия и вопросы те же, что и в задаче 10.27, с той
разницей, что пока один из узлов работает, другой находится в
«холодном резерве» и выходить из строя не может. При включении
резервного узла он немедленно начинает работать и подвергается потоку
отказов с интенсивностью X.
а) * *~. if)
Рис. 10.28
Решение. Граф состояний ЭТУ будет иметь вид, показанный
на рис. 10.28, ах граф g «поглощающим состоянием» — на рио. 10.28, б.
Ответы на вопросы:
337
i)Po(0-
aeat~, be*
+ (k+ 3[i) - — + 2fA2
[ a6
+
ab(fl —6) J ц(а—Ь) [>,(a—b)
2f»
« =
[e--e»'l+ — Po(0; Л(0=»1-Ро(0-Л(0;
-<2Н-Зц)+У4цХ+ц» . &__^ -(2Х+Зр) + У4|Д+р»
2 ' 2
2) /?„(*)
e^-PeP'
a—P
(* + !*)
a—P
Pi(0-1—A>(0—Pi(0;-«
a-p '
f (^ + Ц) £ + —Po(0;
a—P J Ц
-(Я2+Ю+ У4У+Ц2 .
-(k*+VL)-V4%li+vfi
-, P(t)=l-pAt);
3)Р1=АРо;йЧ(^й;л=[1+А+^(|уГ
4) l-p2; 5)?p = -
1 1-Р2
10.29. Условия задачи 10.27 изменены таким образом, что
неработающий узел находится в «облегченном резерве» и выходит из строя с
интенсивностью № < к. Л) Построить граф состояний ЭТУ, написать
уравнения Колмогорова для вероятностей состояний.* 2) Не решая
этих уравнений, найти финальные вероятности состояний; вычислить
их для А, = 1; X1 = 0,5, \l = 2. 3) Для этих же численных данных
найти среднее время Fp бесперебойной работы ЭТУ.
Рис. 10.29
QT
Д+У
/<
s,
X
К2/1{
~%]
Решение. 1) Граф состояний показан на рис. 10.29.
Уравнения Колмогорова:
dpo
dpi
dt =-ft+^)Po+W>i; ^ = -(b + \i)Pi + (b + V)p0 +
+ 2|лр2; A> + Pi + P2=l.
2) Финальные вероятности состояний найдем, пользуясь общими
формулами (10.0.23) для схемы гибели и размножения:
338
V 2|Л2 [ р 2Ц12 /
Подставляя сюда Я, = 1, № = 0,5, \ь = 2, получаем
Po = {l + -у- + -^Y1}"1» 0,516; ft « 0,387; ра« 0,097.
3) Fp = J--IlL££-^2,32.
10.30. В состав ЭВМ входят четыре накопителя на магнитных
дисках (НМД). Бригада в составе четырех человек обслуживающего
персонала проводит профилактический ремонт каждого диска.
Суммарный поток моментов окончания ремонтов для всей бригады — пуав-
I 1 МП
0
s,
рЩ
_%_
/ЛШ^
SJ
pwi
's7\
Рис. 10.30
соновский с интенсивностью X (t). После окончания ремонта диск
проверяется; с вероятностью р он оказывается работоспособным (время
проверки мало, и им можно пренебречь по сравнению со временем
профилактики). Если диск оказался неработоспособным, то вновь
проводится его профилактика (время, потребное на нее, не зависит от
того, проводилась ли ранее профилактика) и т. д. В начальный момент
все НМД нуждаются в профилактическом ремонте.
Построить граф состояний для системы S (четыре НМД),
написать дифференциальные уравнения для вероятностей состояний. Найти
Мх — математическое ожидание числа дисков, успешно прошедших
профилактику к моменту т.
Решение. s0 — все четыре НМД нуждаются в
профилактическом ремонте; s± — один НМД'успешно прошел профилактику, а три
НМД нуждаются в профилактическом ремонте; s2 — два НМД
успешно прошли профилактику, а два нуждаются в профилактическом
ремонте; s3 — три НМД успешно прошли профилактику, один
нуждается в профилактическом ремонте; s4 — все четыре НМД успешно прошли
профилактику.
То, что каждый профилактический ремонт заканчивается успешно
с вероятностью р, равносильно р-преобразованию потока окончаний
ремонтов, после которого он остается пуассоноввким, но в
интенсивностью рХ (t).
Граф состояний показан на рис. 10.30. Уравнения Колмогорова:
dpjdt = — рХ (t) p0; dpxldt = рХ (t) (p0 — Pi); dpjdt**
=pM0(Pi—Pi); dpjdt = рХ (0 (Pt-p3)\ dpJdt=pX (t) p3. (10.30.1)
Начальные условия р0 (0) =1; ft (0) = ... = p4 (0) = 0.
339
Математическое ожидание числа дисков, успешно прошедших
профилактику к моменту .т, равно
Мт= 2 iPi(x). (10.30.2)
При постоянной интенсивности к решениями уравнений (10.30.1) будут:.
р0 W = е-**; л (0 = Apte-**; р2 (0 = -^ е-**;
з
А(0 = -^е-^; Л(0- 1- S МО-
10.31. В условиях предыдущей задачи за каждым членом бригады
закрепляется свой НМД, который он ремонтирует." Поток окончаний
профилактики, приходящийся на одного члена бригады, имеет
интенсивность Я (/)/4. Ответить на вопросы предыдущей задачи. -
Ирщ |—| him—\Ьщ—\{&ю m
Рис. 10.31
Решение. Граф состояний дан на рио. 10.31. Уравнения
Колмогорова:
dpjdt = — р% (0 р0; dpjdt - p%it) (р0 — (3/4) рх); dp2/dt « pX{t) X
X ((3/4) рг - (1/2) р2); ф8/Л = рХ (0 ((1/2) р2 - (1/4) р3);
dp4/d/ = (1/4) рХ (i) p8.
Выражение (10.30.2) для-Л^ сохраняется.
10.32. Техническое устройство (ТУ) подвергается простейшему
потоку отказов.с интенсивностью Л.. Отказ обнаруживается не сразу,
а через случайное время, распределенное показательно с параметром v.
'Как только отказ обнаружен, производится осмотр ТУ, в
результате которого оно либо направляется в ремонт (вероятность этого р),
либо списывается и заменяется новым. Время осмотра —
показательное с параметром у> время ремонта — показательное с параметром \i9
время замены списанного ТУ новым — показательное с параметром х.
Найти финальные вероятности состояний ТУ. Определить: 1) какую
долю времени в среднем ТУ будет работать нормально; 2) какую долю
времени ТУ будет работать g необнаруженным отказом (давать брак);'
3) какова средняя стоимость ремонтов ТУ и его замен за единицу
времени, если средняя стоимость ремонта равна г, а нового ТУ равна с;
4) какова средняя величина потерь за единицу времени от ТУ,
работающего иногда с необнаруженным отказом, если такое ТУ
приносит в единицу времени убыток /.
Решение. Состояния ТУ: s0 — исправно, работает; s± —
неисправно, но отказ не обнаружен, дает брак; s2 — неисправность обна-
340
ружена, ведется осмотр; s8 — ремонтируется; s4 — заменяется новым.
Граф состояний дан на рис. 10.32.
Линейные алгебраические уравнения для финальных вероятностей
состояний:
%р0 = fi,p3 Ч- хр4; %р0 = vpx; vpx — ?ра; рур2 « (хРз;
(1 — р) ур2 « кр4.
формировочное условие р0 + Pi + Рг + Рз + Р4 = *• Решая эти
уравнения, получаем:
I v 7 М- к J
Я, X, рК (1—р)%
Pi=—Ро; р2=—Ро; р8=—ро; р*=-—— р<>.
v 7 ^ к
1) Доля времени нормальной работы ТУ равна р0; 2) pt; 3) ТУ
проводит в среднем долю времени р3 в состоянии ремонта; каждый
ремонт длится в среднем 1/jjl; поток отремонтированных ТУ,
выходящих из состояния s3, имеет интенсивность [гр3; средняя стоимость
ремонтов в единицу времени r\ip8. Аналогично средняя стоимость
новых ТУ, в единицу времени ехр4; общая средняя стоимость того и
другого равна Г[хр3 + схр4. 4) Средние потери от работы ТУ в
неисправном состоянии за единицу времени равны /vpx.
Рис. 10.32
10.33. Рассматривается процесс накопления информации в базах
данных, хранимых в ЭВМ. Интенсивность поступления единиц
информации в базы данных равна % (t) и не зависит от того, сколько их
накоплено. Каждая единица информации, поступившая в базы данных,
хранится в них бессрочно. Найти характеристики mx(t), Dx(t)
случайной функции X (t) — числа накопленных единиц информации в
базах данных в предположении, что поток поступлений единиц
информации пуассоновский е интенсивностью к (t) и в начальный момент
времени t « 0 случайная функция X (0) *= 0.
Решение. В этой задаче мы имеем дело о процессом «чистого
размножения» без ограничения числа состояний (п ->• оо). Все ин-
341
тенсивности «размножения» %h = % (t) (рис. 10.33) и интенсивности
«гибели» \Lk = \ik (t) = 0.
Дифферениальные уравнения (10.0.24) и (10.0.25) «для этого
случая примут вид
•^--2 МОр*(О=М0;
ш
k=Q
■^TL= S lb(t) + 2k%(i)-2mx(t)%(t)]pk(f) = Mt),
л *-о
так как
Ar=0 fe=0
Решая эти уравнения для начальных условий тх (0) = Dx (0) = 0,
получаем
о
Этот результат можно было ожидать; его можно найти
непосредственно из теории потоков. Можно доказать, что случайная величина X (t)
для любого момента времени t будет подчинена закону Пуабсона с
найденными характеристиками mx(t) = Dx(t).
Aft)
Aft)
Aft) Aft)
Aft)
Рис. 10.83
10.34. Условия те же, что и в предыдущей задаче, за исключением
того, что принятая на хранение в базах данных единица
информации хранится некоторое время, после чего по определенному
признаку исключается из баз данных. Поток исключений для каждой единицы
информации — пуассоновский g интенсивностью \i (t).
Решение. В этой задаче.имеет место процесс «гибели и
размножения» числа единиц информации, хранимых в базах данных ЭВМ.
Интенсивность гибели \ik (t) = k\i (t), так как в состоянии sk в базах
данных накоплено k единиц информации и на каждую из них
действует поток исключений с интенсивностью |д> (t).
Дифференциальные уравнения для функций пгх (f) и Dx(t) имеют
вид
dmx (0 __
dt
S (b(t)-kv(t))pk(t)~l(t)-u(t)mx(t); (10.34.1)
fe= 0
342
-^J®— S [X(t) + k\i(t) + 2kX(t)-2k*yL(t)-2mx(t)%(t) +
ft=0
+ 1mx (t) k\i (01 pft (0 = X (0 + ji (0 /ns (0- 2ц (0 Dx (t), (Ю.34.2)
так как -
S л(9» i; S *pfttf) = «*W; 2 &Рпц.)=Щхц)=
fc=0 £=0 ft= 0
= Dx(t) + m2x(t).
Для начальных условий m^ (0) = m0, Dx(0) = D0\ постоянных
интенсивностей пополнения и исключения единиц информации % (t) =
5= X; (л (t) = [х решения этих уравнений будут иметь вид
тхУ) = т0е-»< -f--L(l_e^<)= — + e-Wmo —Н,
— + - +(М-|*Д>+И1По)- £ +
И ц J ix
+ D0 (2e-2n<- e-i*0 = rnx (t) + (D0—mo) e~2^.
Для начальных условий m0 = D0 = 0 получим шх (t) = Dx (t) =
— —(i — e-^)- Можно доказать что для этих начальных условий про-
цесс накопления информации X (t) будет распределен по закону
Пуассона для любого момента времени t и для любого вида функции % (t)
(интенсивности поступления информации), но для этого интенсивность
исключения единиц информации \i должна быть постоянной.
При постоянных А,И(ги/-^оов системе будет устанавливаться
стационарный режим накопления информации, который, естественно,
не будет зависеть от начальных условий: тх = Dx = A/fi.
10.35. Рассматривается процесс производства ЭВМ определенного
вида. Интенсивность производства ЭВМ К (t) представлена на графике
рис. 10.35, а. Эта интенсивность линейно возрастает в течение
первого года производства от 0 до 1000 ЭВМ в год, затем три года
производство сохраняется на.уровне 1000 ЭВМ в год, после чего ЭВМ
снимается с производства. Средний срок эксплуатации ЭВМ 5 лет. Считая
все потоки событий простейшими, определить математическое
ожидание и дисперсию числа ЭВМ, находящихся в эксплуатации в любой
момент времени t.
Решение. Интенсивность производства ЭВМ
40 =
(0 при *<0;
kt при 0<*< 1;
к при 1<*<4;
0 при *>4,
где k = 1000 1/год2; Ь = 1000 1/год.
343
Найдем решения уравнений (10.34.1) и (10.34.2) для участка
времени 0</*<Г1 и при условии, что \i = 0,2 1/год для любых
участков />0. Уравнение (10.34.1) при этих условиях имеет вид
dt
• kt—iunx(t).
Решая это уравнение для начального условия тх (0) = 0, получаем
mx(t) = -£-(е^— 1 + ^) = 25000(е~"5— 1 Аг -^\
По истечении одного года в эксплуатации будет в среднем тх (1) =
= 25 000 (е~1/б — 1 + 0,2) = 468 машин. Заметим, что если бы ЭВМ
имели неограниченный срок службы, то их к концу года было бы в
эксплуатации 500 штук.
\*Ю
1000\
о)
ч t
Г I M3ft) pH(t) L^J /iMft)
6)
Рис. 10.35
Уравнение (10.34.2) при тех же условиях имеет вид
dDx {fildt = 1000* -Ь 0,2m * (t) — 0y4Dx (t).
Решая это уравнение для начального условия Dx (0) = 0, получаем
Dx (t) = tnx (t) — 25 000 (e**^6 — 1 + //5). По истечении одного года
дисперсия числа ЭВМ, находящихся в эксплуатации, будет равна
344
Dx = 468; ox =a 21,6. Число ЭВМ, находящихся в эксплуатации по
истечении года, будет приближенно подчинено нормальному, закону g
характеристиками тх = 468; ох = 21,6.
На участке времени 1 ^ t <; 4 соответствующие уравнения будут
иметь вид
Их нужно решать при начальных условиях: тх (1) = Dx (1) =* 468.
Решение этих уравнений было найдено в задаче 10.34, откуда
тхУ) = тх(1)е^»«~" Ч- —(1—е-*^ <<-1>) (1<*<4);
Dx(t) = mx(t).
Найдем, значение тх (f) для t = 4: /
тх(4)=*тх(1)е-**»+— (1—е~3*)^ 2513.
м-
Таким образом, среднее число ЭВМ, находящихся в эксплуатации
к концу четвертого года выпуска, будет равно 2513. Обратим
внимание на то обстоятельство, что к этому времени было выпущено в
среднем 3500 ЭВМ. Следовательно, в среднем за четыре года было ис*
ключено из эксплуатации 987 ЭВМ.
На участке времени / > 4 будет иметь место процесс «чистой
гибели», граф состояний которого имеет вид, показанный на рис; 10.35, б.
Дифференциальные уравнения для математического ожидания и
дисперсии процесса чистой гибели в общем случае имеют вид
%^=-2М0М0;
dt и л
оо
^*Г~ = 2 1*1** (0-2А»М*> + 2тх (0 £(xft (f)] pk(t).
Для нашего случая цй (/) = fey,, следовательно, получим уравнение
at
которое нужно решать при начальном условии тх (4) = 2513.
Решение этого уравнения будет иметь вид
"U0 = "U4)e~u«~4> (*>4).
Так как Dx (4) = тх (4) и \х » const, то Dx (t) = mx (/) на
участке времени t> 4.
На рис. 10.35, в показана зависимость тх (f) — среднего числа
ЭВМ, находящихся в эксплуатации от времени L На этом же графике
пунктирной линией показана зависимость от t среднего числа
выпущенных ЭВМ к моменту времени L
345
10.36. Рассматривается процесс накопления терминов в
динамическом словаре (тезаурусе) при функционировании автоматизированного
банка данных (АБД). Сущность процесса в том, что термины заносятся
в словарь по мере их появления в той информации, которая вводится
в АБД. Например, в АБД автоматизированной системы управления
производством (АСУП) могут в качестве терминов заноситься
наименования организаций, с которыми данное предприятие поддерживает
производственные отношения. Динамический словарь наименований
таких организаций будет накапливаться в АБД АСУП по мере
появления этих наименований в единицах информации, вводимых в АБД.
В каждой единице информации, поступающей в АБД, в среднем
встречается х терминов словаря, а интенсивность поступления единиц
информации в АБД X (/). Следовательно, интенсивность потока
терминов словаря в информации, поступающей в АБД, будет X (t) = кХ (f).
Предполагается, что поток терминов словаря является пуассоновским.
Число терминов словаря п является конечным и неслучайным, хотя,
возможно, и неизвестным нам заранее. Все термины словаря могут
находиться в единице информации с одинаковой вероятностью; а в
словарь заносятся естественно лишь те термины, которые до сих пор еще
не встречались в единицах информации. Требуется найти
математическое ожидание и дисперсию числа терминов, накопленных в
динамическом словаре.
Решение. Обозначим X (t) число терминов, накопленных в
динамическом словаре. Очевидно, что случайный процесс X (t) есть
процесс «чистого размножения» с конечным числом состояний я, граф
состояний которого представлен на рис. 10.36. Для нахождения
интенсивности lft (<) (4 = о, 1 я — 1) введем в рассмотрение
гипотезу о том, что процесс находится в состоянии sft; вероятность этой
гипотезы го» определению равна pk (t). В предположении, что эта гипотеза
имеет место, интенсивность потока новых (еще не занесенных в
динамический словарь) терминов будет
Дифференциальные уравнения (10.0.24) и (10.0.25) примут вид:
**&&-= s хф-±)Рк«)=т- "»(^« t (ю.36.1)
dt k=o \ n>
-2mx(t)X(t)(l-± )]Pk(t) = X(t)- X(t)^^L-2X{t) ^^L.
\ n J] n n
(10.36.2)
Найдем решение этих уравнений для простейшего случая, когда
X (t) = X = const; n = const; тх (0) = Dx (0) =* 0.
346
( —Л
mx(t) = n\\—е п к Пт тх (f) = п\
Оя(0 = л^1—е п )е п = mx(t)e «
HmDx(*) = 0.
(10.36.3)
(10.36.4)
Обратим внимание на то, что функция тх (t) монотонно
увеличивается, стремясь в пределе к я, в то время как функция Dx (t) равна нулю
при /=0и£->-оои достигает своего максимума при некотором
значении tm, которое можно найти из условия dD x (f)/dt =* 0 (t > 0).
Отсюда
0,5 = е
п ™>
<
0,7я А.
При этом значении tm максимальная дисперсия max Dx(t) & п X
t
X (1 — е-0»7) е-*°'7= п 0,25; ах (tm) = 0,5"|/7Г, а максимальное
значение коэффициента вариации ах (tm)/mx (tm) = 1/]/7Г.
н
Ш
Si
я,ю ЯмЮтШ
Щж
sn-1
1*2*>
Рис. 10.36
Если известна интенсивность А, потока терминов словаря в
единицах информации, поступающих в АБД, и общее число терминов п,
то можно с достаточной точностью определить среднее время ta,
потребное для накопления 95% объема динамического словаря:
_Л t
1_е » н = 0,95, откуда tH » Зп/%.
Если п неизвестно (что чаще всего на практике имеет место), то
можно найти оценку п величины п следующим образом. Для моментов
времени Ti, т2, т3, ..., тг (тг <Т|+1) определяют фактические
количества накопленных терминов в словаре тъ та, ..., т\. Полагаем эти
величины приближенно равными средним количествам накопленных
терминов: т% = п (1 — e^V") (г = 1, 2, ...»/). Решая это уравнение
относительно я, находим / значений nl9 n2, «.м щ для соответствующих
пар значений: (тъ тг); (т2, т2); ...; {ти tj). Оценку п находим по
формуле
Ч!"')/
10.37. Для условий предыдущей задачи найти время tH заполнения
словаря на 95% и вероятность того, что через два года после начала
накопления словаря он будет содержать не менее 90% всех терминов,
347
если общее число терминов п = 100 000, в год в АБД вводится 100 000
документов и каждый документ содержит в среднем 1,5 термина.
Решение. Найдем интенсивность потока терминов словаря в
единицах информации, вводимых в АБД:
91 = 100 000-1,5 = 150 000 1/год.
Величина tH определяется из выражения fH = Зп/К = 3*100 000 г
: 150 000 = 2 года. Для определения вероятности того, что через два
года после начала наполнения словарь будет содержать не менее 90%
всех терминов, нужно прежде всего найти пгх (2) и Dx (2) [см. формулы
(10.36.3) и (10.36.4)1: тх (2) - 100 000 (1 — е-ь5.2) ^ 0,95 х
X 100 000 = 95 000; Dx (2) = 95 000-0,05 = 4750; ах (2) = 68,9.
Заметим, что максимальная дисперсия Dx (tm) = 0,25/г =
« 25 000; ах (tm) = 158.
Число терминов в словаре в момент времени t = 2 года есть
случайная величина X (2), приближенно распределенная по нормальному
закону с найденными выше характеристиками; поэтому Р {X (2) >
> 0,9п} « 1, так как тх — Заа>0,9/г.
10.38. Рассматривается более общий случай функционирования
динамического словаря АБД. Первое усложнение по сравнению с
условиями задачи 10.36 gogtoht в том, что максимальное число терминов
словаря п не является постоянным, а зависит от времени t\ n (t) (в
случае g динамическим словарем названий организаций это означает, что
общее число организаций со временем изменяется: увеличивается или
уменьшается).
Кроме того, введенные в динамический словарь термины по
истечении некоторого случайного времени исключаются из словаря в связи
с тем, что сам термин устаревает. Предполагается, что поток
исключений термина в динамическом словаре — пуассоновский g
интенсивностью |х (f), одинаковой для всех терминов словаря.
В.этом случае интенсивности потоков «размножения» и «гибели»
будут иметь вид
Х* (i) - % (t) (l - -~^i; \xh (t) = p (t) k, (10.38.1)
а уравнения (10.0.24) и (10.0.25) примут вид (зависимости от времени
*функций пгх (t)> D х (0* п (f), X (f), у, (t), pk (t) для краткости опущены):
dmjdi. = %~mx (Xln + у)\
dD Jdt *=*% — mx QJn — |xj — 2 (к/п + ц) Dx. . (10,38.2)
Если величины А,, п, \i постоянны (не зависят от времени), то при
t -> оо существует стационарный режим работы, для которого dm Jdt =*
= dDjdt = 0, откуда
"••="('+^r';D-=m-(,+^r-
348
ГЛАВА 11
ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ
11.0. Системой массового обслуживания (СМО) называется любая систем»
предназначенная" для обслуживания каких-либо заявок (требований),
поступающих на нее в случайные моменты времени. Примеры СМО: телефонная
станция; бюро ремонта; билетная касса; парикмахерская; ЭВМ. Теория массового
обслуживания занимается изучением случайных процессов, протекающих в
системах массового обслуживания.
Любое устройство, непосредственно занимающееся обслуживанием заявок,
называется каналом обслуживания (или «прибором»). СМО бывают как одно->
так и многоканальными. Пример одноканальной СМО — билетная касса с
одним кассиром; пример многоканальной — та же касса с несколькими кассирами.
Различают СМО с отказами и СМО с очередью. В СМО с отказами заявка,
пришедшая в момент, когда все каналы заняты, получает отказ, покидает СМО и
в дальнейшем в процессе ее работы не участвует. В СМО с очередью заявка,
пришедшая в момент занятости всех каналов, не покидает СМО, а становится в
очередь и ждет, пока не освободится какой-нибудь канал* Число мест в очереди т
может быть как ограниченным, так и неограниченным..При т = 0 СМО с
очередью превращается в СМО с отказами. Очередь может иметь ограничения не
только по количеству стЪящих в ней заявок (длине очереди), но и по времени
ожидания (такие СМО называются «системами с. нетерпеливыми клиентами»).
СМО с очередью различаются не только по ограничениям очереди, но и по
дисциплине обслуживания: обслуживаются ли заявки в порядке поступления,
или в случайном порядке, или же некоторые заявки обслуживаются вне
очереди (так называемые «СМО с приоритетом»). Приоритет может иметь несколько
градаций или рангов.
Аналитическое исследование СМО. является наиболее простым, если все
потоки .событий, переводящие ее из состояния в состояние, — простейшие
(стационарные пуассоновские). Это значит, что интервалы времени между
событиями в потоках имеют показательное распределение с параметром, равным
интенсивности соответствующего потока. Для СМО это допущение означает, что как
поток заявок, так и поток обслуживании — простейшие. Под потоком
обслуживании понимается поток заявок, обслуживаемых одна за другой одним
непрерывно занятым каналом. Этот поток оказывается простейшим, только если врем»
обслуживания заявки Гобсл представляет собой случайную величину, имеющую
показательное распределение. Параметр этого распределения \х есть величина,
обратная среднему времени обслуживания: \х = 1Д)бсл» где *0бол = М[Г0бслЬ
Вместо «поток обслуживании — простейший» часто говорят «время
обслуживания — показательное». Условимся в дальнейшем для краткости всякую СМО,
в которой все потоки простейшие, называть простейшей СМО* В этой главе мы
будет рассматривать главным образом простейшие СМО.
Если все потоки событий простейшие, то процесс, протекающий в СМО,
представляет собой марковский случайный процесс с дискретными состояниями
и непрерывным временем. При выполнении некоторых условий для этого
процесса существует финальный стационарный режим, при котором как вероятности
состояний, так и другие характеристики процесса не зависят от времени.
Задачи теории массового обслуживания — нахождение вероятностей
различных состояний СМО, а также установление зависимости между заданным»
параметрами (числом каналов я, интенсивностью потока заявок X,
распределением времени обслуживания и т, д.) и характеристиками эффективности
работы СМО. В качестве таких характеристик могут рассматриваться, например,
следующие:
среднее число заявок Л, обслуживаемое СМО в единицу времени, или
абсолютная пропускная способность СМО;
вероятность обслуживания поступившей заявки Q или относительная
пропускная способность СМО; Q « А/Х;
вероятность отказа P0tki t* е« вероятность того, что поступившая заявка
не будет обслужена, получит отказ; Рош =1 — Q;
349
среднее число заявок в СМО (обслуживаемых или ожидающих в очереди) z
среднее число заявок в очереди г;
среднее время пребывания заявки в СМО (в очереди или под
обслуживанием) *СИСТ?" _
среднее время пребывания заявки_в очереди t04)
среднее число занятых .каналов к.
В общем случае все эти характеристики зависят от времени, Но многие СМ®
работают в неизменных условиях достаточно долгое время, и поэтому для них
успевает уетановиться режим, близкий к стационарному* Мы здесь повсюду, не
оговаривая этого каждый раз специально, будем вычислять финальные
вероятности состояний и финальные характеристики эффективности СМО, относящиеся
к предельному, стационарному режиму ее работы.
1—>/—W—*з /fr *М *л
Рис. 11.0.1
Для любой открытой СМО*) в предельном стационарном режиме среднее
время пребывания заявки в системе *сист выражается через среднее число
ваявон в системе с помощью формулы Литтла:
Wr=="2A, (11.0.1)
рде % — интенсивность потока заявок*
Аналогичная формула (называемая также формулой Литтла) связывает
среднее время пребывания заявки в очереди tQ4 и среднее число7 заявок в
очереди:
t~4=7/%. (11.0.2)
Формулы Литтла очень полезны, так как позволяют вычислять не обе
характеристики эффективности (среднее время пребывания и среднее число заявок),
а только какую-нибудь одну из них.
Специально подчеркнем, что формулы (11.0.1) и (1L0.2) справедливы для
любой открытой СМО (одноканальной, многоканальной, при любых видах
потоков заявок и обслуживании)! единственное требование к потокам заявок и
обслуживании — чтобы они были стационарными»
Аналогично универсальное значение для открытых СМО имеет формула,
выражающая вреднее число занятых каналов k через абсолютную пропускную
способность А:
X F=A/p,, . (11.0,3)
где fx = 1/^обол — интенсивность потока обслуживании* *
Очень многие задачи теории массового обслуживания, касающиеся
простейших СМО, решаются при помощи схемы гибели и размножения (см* гл. 10).
Если граф состояний СМО может быть представлен в виде, показанном на
рис. 11.0.1, то финальные вероятности состояний выражаются формуламй(10*0»23):
Ро
1 На № ^2 Mi М<2 • • -Mft "" "J Ш - - • №i J *
*) СМО называется открытой, если интенсивность поступающего на нее
потока заявок не зависит отчсостояния самой СМО,
350
X0 X0 Xt A,0 Xl...XkiSml
Pi = Po; P<l = Pol • • • 5 Pft= Po (0 < k < n)\ ... ;
• ••;
Pn —
Pfe=
h0 ^i • •
Ц1 l*2---l*fc
.*»-!
Po»
(1J.0.4>
Hi Иг--- И-п
При выводе формул для среднего числа заявок (в очереди или в системе)
широко применяется прием дифференцирования рядов, состоящий в следующем.
Если х < 1, то '
& &'dx dx & dx l-x l-*
и окончательно
oo
2***-тЬ- (11-°-5>
k—\
Ниже мы приведем без вывода ряд формул, выражающих финальные
вероятности состояний и характеристики эффективности для некоторых часто
встречающихся типов СМО. Другие примеры СМО будут разобраны далее в виде-
задач.
1. Простейшая СМО с отказами (задача Эрланга). На я-канальную СМО
с отказами поступает простейший поток заявок с интенсивностью X; время
обслуживания — показательное с параметром (л = 1/*обсл- Состояния СМО
нумеруются по числу заявок, находящихся в СМО (в силу отсутствия очереди, она
совпадает с числом занятых каналов):
s0 — СМО свободна;
s% — занят один канал, остальные свободны; ...
Sh — занято k каналов, остальные свободны (1 ^ k ^ я)} ,.,;
sn — заняты все п каналов. '
, Финальные вероятности состояний выражаются формулами Эрланга:
f Р , Р2 Р"]^1 Р*
РН1* и + 2Г + -*-+ыК 'iPkk\P* (*^«2* •••'*>> (И.0.6)
где р = A/jx.
Характеристики эффективности:
А=Х (1-рл);. Q = l—Рп, Ротк^Рп; F=p (1—рл). (11.0.7>
При больших значениях п вероятности состояний (11,0,6) удобно вычислять
через табулированные функции:
Р (т, а)=—— евв (распределение Пуассона) (11.0.8)
т\
R(m, a)=2 ife-a (Н.0.9)
(см. приложения I и 2), из которых первую можно выразить через вторую:
Р (т, а) = Я (т, а) — R (т — 1, а). (Н.0Л0)
Пользуясь этими функциями, формулы Эрланга (11.0.6) можно переписать в
виде
Pk = Р (Ь рУ# («, Р) {Ь = 0, 1, ,.,, n). U 1.0.11)
351
2» Простейшая одноканальная СМО с неограниченной очередью. На одно-
канальную СМО поступает простейший поток заявок с интенсивностью А.. Время
обслуживания — показательное с параметром р, = Ш0бсл. Длина очереди не
ограничена. Финальные вероятности существуют только при р = А/р, < 1 (при
>р !> 1 очередь растет неограниченно). Состояния СМО нумеруются по числу
заявок в СМО, находящихся в очереди или обслуживаемых:
s0 — СМО свободна;
ц — канал занят, очереди нет;
$2 — канал занят, одна заявка стоит в очереди; ..*;
Sfc — канал занят, k — 1 заявок стоят в очереди; ...
Финальные вероятности состояний выражаются формулами:
р.= 1 —р; ph = р* (1-р) №=1,2,...), (11.0.12)
•где р = А/р, < 1,
Характеристики эффективности СМО:
А = К; Q » 1; РОТк = 0; (11.0.13)
— О — Р2 — О — О2
1—р 1—р л. (1—р) л (1 —р)
среднее число занятых каналов (или вероятность того, что канал занят)
k^X/ц^р (11,0,15)
3. Простейшая одноканальная СМО с ограничением по длине очереди. На
одноканальную СМО поступает простейший поток заявок с интенсивностью X;
время обслуживания — показательное с параметром р, = 1/^бсл* В очереди т
мест. Если заявка приходит в момент, когда все эти места заняты, она получает
отказ и покидает СМО. Состояния СМО:
ь0 — СМО свободна;
Sf — канал занят, очереди нет;
s2 — канал занят, одна заявка стоит в очереди^ *.s$
Sft — канал занят, k — 1 заявок стоят в очереди; .«.§
Sm+j ~- канал занят, т заявок стоят в очереди.
Финальные вероятности состояний существуют при любом р = А/р и равны:
I—Р ь
00е": ZZI* ^вР*Ро<* = 1.... , -т + 1). (11.0.16)
1 —рш_1"z
Характеристики эффективности СМО:
4=V(l—pm+l); Q = l-pw+1 ;Я0тк==Рте+1 .
Среднее число занятых каналов (вероятность того, что канал занят)
1= 1 — р0< (11.0.17)
Среднее число заявок в очереди
-_ pMl—p^im + l -mp)J
0-Pm+2)(l-p) •
Среднее число, заявок в СМО
z=7+I. (1L0.19)
По формуле Литтла _ •
*сист=г/А,; Точ—г/Х. (11.0.20)
4. Простейшая многоканальная СМО с неограниченной очередью. На я-ка-
•кальную СМО поступает простейший поток заявок с интенсивностью А$ вре-
352
(11.0.18)
мя рбслуживания одной заявки — показательное с параметром р, =к 1//0б0л.
Финальные вероятности существуют только при р/д =» и < 1, где р = А/ц*
Состояния СМО нумеруются по числу заявок в СМ0:
s0 — СМО свободна;
Si — занят один канал; ,88; • • \
su — занято k каналов (1 < k < n); „,} I очереди нет
sn — заняты все п каналов; J
sn+i — заняты все п каналов," одна заявка стоит в очереди; .,*;
Sn+r — заняты все п каналов, г заявок стоят в очереди; ***;
Финальные вероятности состояний выражаются формулами:
ftJ1+JL+...+±L+P^._!_|-',
[ 1! п\ п*п\ 1—xj
р* s рл+г
Ри^-ггРо (1<^<л); Рп+г^—, Ро (г>1). (11.0.21)
Rl ^ п .л!
G помощью функций Р (ш, а) и R (т, а) формулы (11,0*21) могут быть приведены
к виду
Р (k, p) _
Рк~ R (я, 9)+Р (я. Р)/(1.-*) (*~°* "•" ' П); (11.0,22)
Рп+Р =хр рп (гв1,2, ...).
Характеристики эффективности СМО:
Г=рл+|р0/[Я'Л1 О— *)2] = >W(1— н)2) (11.0.23)
7==r+£W+p; (11.0.24)
7ewT=^;7o4-7Af (П.0.25)
5. Простейшая многоканальная СМО с ограничением по длине очереди.
Условия и нумерация состояний те же, что в п. 4, с. той разницей, что число т
мест в очереди ограничено* Финальные вероятности состояний существуют при
любых А и [I и выражаются формулами:
( Р 0п Pn+l 1—кт I"4*
р*
""+' =£Г^! Ро (1<г<от).« (Н.0.26)
где -л = р/я = Я/(«ц)(
Характеристики эффективности. СМО:
Л=Х(1-рп+т)5 Q = l-P„+m{/,oTK=P„+mt ^-РО-Рц+шУ (П.0.27)
1^7-fI, (11.0.29)
10^=7А; 7Сист ^гА (11.0.30)
12 Зак. Ю40 353
6* Многоканальная СМО с отказами при простейшем потоке заявок и
произвольном времени обслуживания. Формулы Эрланга (11.0.6) остаются
справедливыми и тогда, когда поток заявок —простейший, а4время обслуживания T0qcj1
имеет произвольное распределение с математическим ожиданием /обсл^/ц-
х7* Одноканальная СМО с неограниченной очередью при простейшем потоке
заявок и произвольном времени обслуживания. Если на одноканальную СМО
поступает простейший поток заявок с интенсивностью \, а время обслуживания
Т'обсл распределяется по произвольному закону с математическим ожиданием
1/р, и коэффициентом вариации t/^, то среднее число заявок в очереди
выражается формулой Полячека — Хинчина
Г=ф* (*+М2Л2 (1-9)Ъ (Ц.0.31)
где р = У\1, а среднее число заявок в СМО
Г={р2(1+^)2/|2(1-р)1}+р. (11.0.32)_
Из (11.0.31) и (11.0.32) по формуле Литтла получим
- Р>(1+"ц)а ,- р»(1+р£) , 1
2Ь(1-р) ;'сист~ 2М1-Р) + И
^оч = n; „ ,, ; ^сист = V/i ;., + — • (и.о.зз)
8. Одноканальная СМО при произвольном (пальмовском) потоке заявок
и произвольном времени обслуживания. Точных формул для этого случая не
существует, приближенная оценка длины очереди может быть произведена по
формуле
'г «Р2( v\+ vl)l\2 (1-р)], (11.0.34)
р-де v^ — коэффициент вариации интервала между событиями во входном потоке?
р = А/и.} А> — величина, обратная математическому ожиданию этого интервала}
\х = 1/^бсл — величина, обратная среднему времени обслуживания; оц —
коэффициент вариации времени обслуживания. Среднее число заявок, увязанных с
СМО,
2 * (р3 ( v2K+ »S)/P (1-PMJ4-P. (11.0.25)
а средние времена пребывания заявки в очереди и в СМО соответственно равны:
. Гоч » Ра ( v{+ v$l[2X (l-p)j; . (11.0.36)
Гост «{Р2 ( »х+ »Д)/12А. (1 —p>J> -Н 1/|г. (U.0.37)
9* Простейшая многофазовая СМО с очередью. Анализ многофазовых СМО
в общем случае затруднен, тем, что входящий поток каждой последующей фазы
является выходным потоком предыдущей и в общем случае имеет последействие»
Однако если на вход СМО с неограниченной очередью поступает простейший поток
заявок, а время обслуживания показательное^ то выходной поток этой СМО —
простейший, с той же интенсивностью А, что и входящий. Из этого следует, что
многофазовую СМО с неограниченной очередью перед каждой фазой, простейшим
входящим потоком заявок и показательным временем обслуживания на каждой
фазз можно анализировать как простую последовательность простейших СМО,
Если очередь к фазе ограничена, то выходной поток этой фазы перестает
быть простейшим и вышеуказанный прием может применяться только в качестве
приближенного.
Далее мы будем пользоваться обозначениями для характеристик
эффективности СМО, приведенными на с, 349. 350, и по мере необходимости вводить
некоторые другие обозначения.
В дальнейшем, задавая плотность / (х) разными формулами на разных<
участках оси 0*, мы также не будем указывать значения / (х) на границах
участков.
354
Если единица измерения времени не фиксирована, мы будем для краткости
обозначать интенсивности потоков событий просто буквами А,, ц, ... (беа указаний
размерностей). То же относится и ко времени tcaGT, /0ч- Если же единица
времени фиксирована (час, минута, год и т, д.), то мы будем указывать единицы
измерения.
В данной главе нам удобно будет записывать закон распределения смешанной
случайной величины Гнев форме функции распределения F (/), а в форме
«обобщенной» плотности / (0, которая определяется следующим образом:
f(t)=F'H(t) +2р|б('-'|).
где Fh (0 — производная функции распределения на участках ее непрерывнос-
ти: р. = р{Т = ti)\ 6 (х) — дельта-функция свойства которой даны в
приложении 6.
ЗАДАЧИ И УПРАЖНЕНИЯ
11.1. На вход одноканальной СМО о отказами поступает
простейший поток заявок с интенсивностью Х\ время обслуживания —
показательное с параметром ц,. В начальный момент времени t = О канал
свободен. Построить размеченный граф состояний СМО. Написать и
решить дифференциальные уравнения Колмогорова для вероятно-
J^l , Puc.lU
стей состояний СМО. Найти финальные вероятности состояний и (для
установившегося режима) характеристики эффективности СМО: Л,
Чс> * отк» R"
Решение. Состояния СМО: s0 — свободна; sx — канал занят.
Граф состояний показан на рис. 11.1. Уравнения Колмогорова:
dpjdt = — Хр0 + fipi*, dpjdt =» Хр0 — (хрх. (11.1.1)
Так как р0 + Pi = 1 для любого t, можно выразить рх через р0:
рг =s 1 — р0 и получить одно уравнение для р0:
dpjdt = — (Л + v) р0 + [i. (П.1.2)
Решая это уравнение, получаем р0 как функцию t:
'•<'>=пН1 + -Г"<1+""];
отсюда
p1(t) = l-Po(t)^T^'n-^^+Mtl
При * -»- оо получим финальные вероятности
Ро - № + У); Pi = */(Ь + |i), (И.1.3)
которые можно было бы найти и гораздо проще, решая линейные
алгебраические уравнения для финальных вероятностей состояний:
кро = WV> Ро + Pi = 1.
12*
355
Формулы (11.1:3) можно записать компактнее, если ввести
обозначение р => %1\х\
р0 = 1/(1 + р); рг = р /(1 + р).
Характеристики эффективности СМО:
л-м. - т^-яг-т^"--*- if-1 -a -rftr •
(11.1.4)
11.2. Одноканальная СМО в отказами представляет собой одну
телефонную линию, на вход которой поступает простейший поток
вызовов с интенсивностью X = 0,4 вызов/мин. Средняя
продолжительность разговора 7обсл = 3 мин; время разговора имеет показательное
распределение. Найти финальные вероятности состояний СМО: р0 и
р1э а также Л, Q, Ротк» *• Сравнить пропускную способность СМО с
номинальной, которая была бы, если бы разговор длился в точности
3 мин,^а заявки шли одна за другой регулярно, без перерывов.
Решение, ft =* 0,4; |* — Мобсл =* 1/3; р = Цг== 1, 2. По
формулам (11.1.3) Ро « 1/2,2 « 0,455; рг« 0,545; Q «0,455; Л = XQ «*
«0,182; k = ргъ 0,545. .
Таким образом, линия в среднем будет обслуживать 0,455
поступающих на нее заявок, т. е. 0,182 разговора в минуту.
Номинальная пропускная способность канала была бы (при регулярно
приходящих и регулярно обслуживаемых^заявках) Лном =* Ш0бсЛ в МЗ «
« 0,333 разг./мин, что почти вдвое больше, чем действительная
пропускная способность Л.
11.3. Имеется одноканальная СМО с отказами. Поток заявок —
простейший с ийтенбивн@стью X. Время обслуживания — не
случайное и в точности равно *обол = 1/[л. Найти относительную и
абсолютную пропускную способность СМО в предельном стационарном режиме.
h6cn
■i—® *-•-
Решение. Рассмотрим на оси 0t простейший поток заявок о
интенсивностью % (рис. 11.3). Будем отмечать кружками все заявки,
♦ которые приняты к обслуживанию. Пусть какая-то заявка,
пришедшая в момент tu принята к обслуживанию. Тогда все заявки,
пришедшие после нее за время 4бсл> получат отказ; следующей будет принята
к обслуживанию заявка, пришедшая в момент t2 такой, что /2 — tx >
> *обсл- Рассмотрим интервал Т между концом обслуживания первой
заявки и моментом /2 прихода ближайшей следующей, которая будет
принята к обслуживанию. Из-за отсутствия последействия в
простейшем потоке распределение интервала Т совершенно такое же, как и в
вообще интервала между заявками, т. е. показательное с параметром
%. Средняя длина интервала Т равна mt = 1А.
356
Гобсп
*обсп\
Рис. 11.3
Итак, на оси Ot будут чередоваться неслучайные интервалы
занятости канала длины *обол = 1/\ь и случайные свободные интервалы со
средней длиной 1/А». На первые попадет доля всех заявок» равная
1/jH _ к
1/ji + lA Ь-Ht '
а на вторые — доля, равная
Ц/(Ь + у) = 1/(1 -Ьд), где р = У(х.
Эта величина и есть относительная пропускная способность СМО
Q — 1/(1 + р)э (11.3.1)
откуда —
A=*%Q = V(l+p). (11.3.2)
Отметим, что формулы (11.3.1), (11.3.2) совпадают о (11.1.4),
соответствующими показательному распределению времени обслуживания
Это и естественно, так как формулы Эрланга остаются еправедливыми
при любом распределении времени обслуживания со средним
значением, равным 1/|л.
11.4. Доказать, пользуясь формулой (11.0.5), что для простейшей
одноканальной СМО q неограниченной очередью среднее число
заявок, находящихся в СМО, равно г = р/(1 — р), где р = X/\i, a
среднее число заявок в очереди г = р2/(1 — р).
Решен и.е. По формулам (11.0.12) р0 = 1 — р; pk = pfe (1 — р)
(k = 1, 2, ...).
Обозначим Z фактическое (случайное) число заявок в СМО:
. - F- м [Z] = J kPh = 2 *р* О -Р)=(1 -р) 2 *»* •
По формуле (11.0.5) для р < 1
**. (1-Р)2
f ^
откуда г = р/(1 — р). Среднее числозаявок в очереди равно г минус
среднее число занятых каналов k = Л/у> =* к/у, = р, т. е. 7 =
-1р/(1-р)1-р = Р2/(1-р).
11.5. Железнодорожная сортировочная горка, на которую
подается простейший поток составов с интенсивностью % = 2 состава в час,
представляет собой одноканальную СМО с неограниченной очередью.
Время обслуживания (роспуска) состава на горке имеет показательное
распределение со средним значением to6cjl ==.20 мин. Найти
финальные вероятности состояний СМО, среднее число г составов,
связанных в горкой,. среднее число г составов в очереди,- среднее время
*сист пребывания состава в СМО, среднее время t04 пребывания
состава в очереди.
Решение. А, = 2 состава/ч; /обсл = 1/3 ч; fx = 3 состава/ч;
р = Я/(л = 2/3. По формулам (11.0.12) р0 ** 1—2/3=1/3; pj = (2/3)x
357
X (1/3) - 2/9; p2 - (2/3)2 (1/3) = 4/27; ... pk = (2/3)fe (1/3); ... По
формулам (11.0.13), (11.0.14) z = p/(l — p) = 2 состава; r = 4/3
состава; *сист = 1 ч; t04 = 2/3 ч.
11.6. Условия предыдущей задачи усложняются тем, что в парке
прибытия железнодорожной сортировочной горки могут находиться
одновременно не более трех составов (включая обслуживаемый). Если
состав прибывает в момент, когда в парке прибытия уже находится три
состава, он вынужден ожидать своей очереди на внешних путях. За
один час пребывания состава на внешних путях станция платит штраф
а руб. Определить средний вуточный штраф, который придется
уплатить за ожидание составов на внешних путях.
ЕЕ
г Л
' ^
*<
*/
t Л.
t*
L"V
ъ
[ х
^
V
«ъ
X
&
1—12/$1—1
* 1
z ft. l
..> ....4
Рис. 11.7
Решение. Вычислим среднее число zB — составов,
находящихся на внешних путях:
2B=i^4+2p5+...= 21*лв 2 *p*Po=Pe 2 *р*;
£ = 4
* = 4
ft=4
Jr^t>'=pJ>'=piJ/
ф 1—Р (1—P)2 , A 1— P
fe==4
По формуле Литтла среднее время, проводимое одним составом на
внешних путях, tB « 1,18А = 1,18/2 = 0,59 ч. За сутки (24 ч) на
станцию приходит в среднем 24Х = 48 составов. Средний суточный штраф
доставляет 48*0,59*а « 28,3а.
11.7. Вычислить непосредственно по графу состояний, пользуясь
схемой гибели и размножения, финальные вероятности состояний для
простейшей двухканальной СМО (п = 2) с тремя местами в очереди
(т = 3) при A,j==J),6; (х =з.0»2; р = %l\i = 3. Найти для этой СМО
характеристики г, г, ^ист, *оч, не пользуясь формулами (11.0.26), а
непосредственно через финальные вероятности, и сравнить с теми,
которые получаются по формулам (11.0.26).
Решение. Граф состояний СМО показан на рис. 11.7. По схеме
гибели и размножения, обозначая %l\i = p, получаем:
Ро
= {l + P+f + -|+|- + ^r = (40.58)- «0,025;
358
Л-40ЖЖ0'074;Л-^Ж0'П1;Л-ЙЖ0Д6Б:Л-
10,15 л ncrrv 15» 18 л от1-
= —!— « 0,250; /?б = —■— « 0,375;
40,58 ' ™ 40,58
F= 1.0,074 + 2-0,111 + 3-0,165 + 4-0,250 + 5-0,375 « 3,67; 7 =
= 1-0,165 + 2-0,250_+ 3-0,375 « 1,79; 7СИСТ = г/0,6 » 6,11;
*оч = г/о,6 « 2,98.
11.8. Формула для г (11.0.28) справедлива для любого х < 1 или
х > 1. При х — 1 она перестает работать (дает неопределенность
вида 0/0). Пользуясь непосредственно схемой гибели и размножения,
вывести для этого случая вероятности состояний р0, ръ ...;рЛ+т и найти
характеристики эффективности СМО: Л, Q, Ротк, £, г, z, Точ, 7СИСТ.
^ дТЦ
Z/£
fyl .♦•
Рис, 11.8
пр
Jn+m\
nju пр
Решение. Граф состояний СМО имеет вид, показанный на
рис. 11.8. Пользуясь общими формулами для схемы гибели и
размножения и обозначая %1\л = р, имеем
Hl+i+f+...+^+£i+...+_^}-'=
={'+i+£+"-HHT+(i)'+~+(ir]P
ПрИ Х = р/А2= 1
ph = £-p0 (l<A<ft); pn+r =-Vp0 (l<r<m); (11.8.2)
^отк = Pn+m ', Q = 1 — A>+m =1 — A,*»
Ро
— vi vi Р Р V Р /и(т+П
г.- Е гри+,= s '-^гРв=^г/,° s r=;ir 2 Pn;
r=l
r=l
f=i
(11.8.3)
z s= r + А; *СИ(УГ = г/Я,; /оч = г/Л,.
359
11.9. Автозаправочная станция (АЗС) имеет две колонки (п =* 2);
площадка возле нее допускает одновременное ожидание не более
четырех автомашин (т = 4). Поток.автомашин, прибывающих на
станцию, простейший с интенсивностью X = 1 машина/мин. Время
обслуживания автомашины — показательное со средним значением 7d6cJT =
= 2 мин. Найти финальные_вероятности состояний АЗС и ее
характеристики: Л, Q, Ротк, ky z, г, 7СИСТ, t04.
Решение. X = 1, \i = 1/2 = 0,5; р = 2; и = р/п = 1.
По формулам (11.8.1)—(11.8.3) имеем:
Ро={1+2+|-+|--4Г=1Г; л-а-л-л-а-а--^;
Potk=s2/13;Q = 1— />отк = 11/13; Л = М2 = 11 /13 « 0,85 машины/мин;
& = Л/ц, = 22/13 ^ 1,69 колонки;
_ о2 4 Г4 -J- Ь 1 — — —
г = 1—L-L-» __ ^ 1,54 машины ; z = r + k « 3,23 машины.
11.10. Имеется двухканальная простейшая СМО с отказами. На
ее вход поступает поток заявок с интенсивностью % = 4 заявки/ч.
Среднее, время обслуживания одной заявки £обсл = 0,8 ч. Каждая
обслуженная заявка приносит доход с = 4 руб. Содержание
каждого канала обходится 2 руб./ч. Решить: выгодно или невыгодно в
экономическом отношении увеличить число каналов СМО до трех?
Решение. По формула^ Эрланга (11.0.6)
/70 = |l +3,2 +-^рР =(9,32)-* « 0,107; А « -|^-« 0,550;
Q = 1 _^2 « 0,450; Л = 4Q ^ 1,8 заявки/ч.
. Доход от заявок, приносимый СМО.в данном варианте, равен D =
N = A*c ж 7,2 руб./ч.
Подсчитаем те же характеристики для трехканальной СМО
(отмечая их штрихом^ вверху):
р'0 = {l +3,2 + i|l +"irP « °»0677; Р'з ^5.48- 0^677 « 0,371;
Q* = 1 — рз ^ 0,629; Л4 =* 4Q'- » 2,52; D'* - Л'-я ^ 10,08 руб./ч.
Увеличение дохода равно D*. — D = 2,88 руб./ч; увеличение
расхода равно 2 руб./ч; из этогб видно, что переход отп = 2к/г = 3
экономически выгоден.
11.11. Рассматривается простейшая СМО с практически
неограниченным числом каналов (п ->■ оо). На вход СМО поступает поток
заявок g интенсивностью А,; интенсивность потока обслуживании (для
одного канала) равна \l. Найти финальные вероятности состояний СМО
и среднее число занятых каналов Ъ.
360
Решение. Данная СМО не дает ни отказов, ни очередей; ее
можно рассматривать как предельный случай СМО и отказами при
п-^схэ. Формулы Эрланга (11.0.6) дают
s \\ = е~р'где р=7; Ph = "лГ*~Р = р{k>р)*
(см. приложение 1). При неограниченном числе каналов А = %\
11.12. Рассматривается одноканальная СМО с отказами; на ее
вход поступает простейший поток заявок с интенсивностью %. Время
обслуживания — показательное с параметром \х = 1//обСл1 Работаю-
-<§ъ
=-*-Ф 1 *-К ® *-#г
X — потоп обслуживании, /f
© -поток отказов )>
б)
Рис. 11.12
-*—®—<§>-*-
щий канал может время от времени выходить из строя (отказывать);
поток отказов канала — простейший с интенсивностью v.
Восстановление (ремонт) вышедшего из строя канала начинается мгновенно после
его отказа; время ремонта Гр — показательное с параметром у = 1/7р.
Заявка, которая обслуживалась в момент выхода канала из строя,
покидает СМО не обслуженной.
Найти финальные вероятности состояний СМО: s0 — канал
свободен; sx — канал занят, исправен; s2 — канал ремонтируется и
характеристики СМО: А и Q.
Решение. Граф состояний СМО дан на рис. 11.12, а.
Алгебраические уравнения для финальных вероятностей состояний:
Мо = M<Pi + УРъ\ (и + v) Pi = hPoi vPx = YP2; (ИЛ2.1)
к ним прибавляется нормировочное условие
Ро = Pi + Р2 = 1-
Выразим вероятности р19 р2 из (11.12.1) через р0г
X v _ Xv
(11.12.2)
Pv=
А>«
.361
Подставляя рг и р2 в (11.12.2), получаем
Ро = {1 + Я/(|* + v) +>/l? (|x + v)]}-1. (11.12.3)
Чтобы найти относительную пропускную способность Q, нужно
вероятность р0 того, что заявка будет принята к обслуживанию,
умножить на условную вероятность р' того, что заявка, принятая к
обслуживанию, фактически будет обслужена (канал не откажет за время
обслуживания заявки). Найдем эту условную вероятность по
интегральной формуле полной вероятности. Сделаем гипотезу, состоящую
в том, что время обслуживания заявки попало на участок от t до t + dt\
вероятность этой гипотезы приближенно равна / (/) dti где / (/) —
плотность распределения времени обслуживания: /(*)= ^е~^ (*> 0).
Условная вероятность того, что канал не выйдет из строя за время U
равна e-v'; отсюда
оо
р' = fy,e-^ e~vidt « I"|г е—<**+v)/^_
Гу,е-^г e~vidt « f |ге-
M. + V
Эту условную вероятность можно найти и проще: она равна
вероятности того, что начатое обслуживание закончится раньше, чем канал
выйдет из-строя. Представим на оси 0t (рис. 11.12, 6) совмещение
(суперпозицию) двух потоков: потока обслуживании с интенсивностью \i
(обозначен крестиками) и потока отказов, канала с интенсивностью v
(обозначен кружками). Зафиксируем любую точку t на оси Ot и найдем
вероятность того, что первый после нее крестик придет раньше,
чем кружок. Очевидно, она равна отношению интенсивности потока
крестиков к суммарной интенсивности потока крестиков и кружков;
[г/(|л + v). Таким образом,
о __ , __ / - \а \ j Л , X , Xv \ \х ф
Ч-РоР -(р + у)]{ + |i + v v(|i + v) J~ \i+v'+\(\+v/y) '
(11.12.4)
А = KQ.
11.13. Условия задачи 11.12 повторяются, но g той разницей, что
канал может выходить из строя и в неработающем состоянии (g
интенсивностью v- < v).
Решение. Граф состояний СМО дан на рис. 11.13. Из уравнений
(X + v') p0 « (xpi + YP2; (У + v) рх — %р0; ур2 = vpi + vfpQ;
Ро + Pi + Р2 = 1
найдем финальные вероятности
Ц+V Ц+V
362
11.14. Рассматривается простейшая одноканальная СМО с
ограниченной очередью т = 2; работающий канал может иногда выходить из
строя (отказывать). Заявка, которая обслуживается в момент отказа
канала, становится в очередь, если в ней еще есть свободные места;
если нет, она покидает СМО необсл уженной. Интенсивность потока
заявок X, потока обслуживании [i, потока отказов канала v, потока
восстановлений (ремонтов) у. Перечислить состояния СМО и найти
для них финальные вероятности, а также характеристики
эффективности СМО: Л, fe, 7,1, ^яст, ^ч при X = 2, ц,= 1, v = 0,5, у = 1-
Решение. Состояния СМО:
Soo — СМО свободна, канал исправен;
s10 — канал занят и исправен, очереди нет;
sn — канал вышел, из строя, ремонтируется; в СМО имеется
одна заявка, ждущая очереди;
s20 — канал занят и исправен; одна заявка обслуживается, другая
ждет очереди;
s21 — канал вышел из строя, ремонтируется; в очереди ждут две
заявки;
s30 — канал занят и исправен; две заявки ждут очереди, одна
обслуживается.
iK .
rj ^ ! 1 L_
%
л ,
9**
V
sw
IT
\*n
, Яг
p^
J M L
У *
1 Л I
ho
W
\ L
sz\
Л ,
г* ■
S30\
yf
Рис. 11.13
Рис. 11.14
Граф состояний СМО показан на рис. 11.14. Уравнения для
финальных вероятностей состояний:"
№ю = ^Роо; W>20 + VPu + ^Роо = (V> +> + v) Рю\
М-Р зо + YP2i + ^Рю = (и, + ^ + v) р20; Хр20 = (р + v) р30;
vp2o = (\*> + v) Рзо;
vPio = (Y + Ь) Pib ЬРхг + VP20 + vPso = ТРгь
Poo + Рю + Рп + P20 + P21 + Рзо = 1-
Решая эти уравнения при X = 2, у, = 1, v = 0,5, у = 1, получаем:
Роо = 3/61 «0,049; р10 = 6/61 « 0,098; р20 = 14/61 « 0,230;
Рзо « 56/183 « 0,306; рц = 1/61 « 0,016; р21 = 55/183 « 0,301.
Отсюда
г - 1>ю + Рп) + 2 (р20 + р21) + Зрзо = 383/183 « 2,09;
г ~ К Р20 + Рп) + 2 (р21 + рзо) = 89/61 « 1,46.
k = 1 (Рю + Р2о + Рзо) = П6/183 « 0,63.
363
Абсолютная пропускная способность А для СМО_с неотказываю-
щими каналами могла бы быть найдена умножением k на \i; в нашем
случае производительность одного канала (среднее число заявок,
фактически обслуживаемых в единицу времени) можно найти, умножая
на вероятность [хУ(р, + v) того, что начатое обслуживание будет
доведено до конца: А = k\L*\i/(ii + v) = fcfx2/(p, + v) « 0,42.
11.15. В зубоврачебном кабинете три кресла (п == 3), а в коридоре
имеются три стула (т = 3) для ожидания приема. Поток клиентов —
простейший с интенсивностью Я = 1,2 клиента/ч. Время обслуживания
(приема клиента) — показательное со средним значением *обсл =
= 20 мин. Если все три стула в коридоре заняты, клиент в очередь не
становится. Определить среднее число клиентов, обслуживаемых
кабинетом за час, среднюю долю обслуженных клиентов из числа
пришедших, среднее число занятых стульев в коридоре, среднее время 7СИСТ,
которое клиент проведет в коридоре ив кабинете; то же самое среднее
время при условии, что клиент-будет обслужен.
Решение. р = 12/3 = 4; х = р/3 = 4/3; п = 3; т = 3. По^
формулам (11.0.26)—(11.0.30) находим:
*-{'+V+f+Т+ й ■ ^^Г-0,012,8 «0,0,2..й-
= 4-0,01218 « 0,049; />,=8.0,01218 « 0,097; ра = —. 0,01218»
О
« 0,130; р3+, = -|L.0,01218 « 0,173; р3+2 = -j рз+i »
» 0,231; рз+з - 4" Рз+2 « 0,307.
Средняя доля обслуживаемых клиентов Q = 1 — Ротк = 1 —
—>з+з « 1 — 0,307 = 0,693.
Среднее число клиентов, обслуживаемых кабинетом за час, равно
A =%Q& 12.0,683^8,32.
Среднее число занятых каналов (кресел) [по формуле (11.0.27)1
k = 4 (1 — р8+8) « 2,78.
Среднее число клиентов в очереди [по формуле (11.0.28)1
-^ 44.0,01218 1-4.(4/3)3+3 (4/3)* _ j ^
3-6 (1—4/3)2 ~ ' '
F= 7+ k ъ 4,34; Гоч = г/% « 0,13 ч; Гсист = гА, ж 0,362 ч. -
Такие малые значения tCJICT и t04 связаны с тем, что некоторые
клиенты уходят, не становясь в очередь. Условное среднее время,
проведенное клиентом в системе, при условии, что он был обслужен, равно
^сист e \vaJQ ^ 0*52 ч» а условное среднее время пребывания в
очереди (при том же условии) 70ч =704/Q « 0,19 ч.
11.16. Формулы (11.0.26), (11.0.28) при х = 1 дают
неопределенность вида 0/0. Раскрыть эту. неопределенность и написать формулы,
справедливые при х = 1.
364
Решение. При правилу Лопиталя
1-х"
1-х
х^1
А>
,. 1-хш
lim—:—:— = = т;
1 " —X
= {' + 1+~+£+^г} . ■ омел,
Р
,*
Рй=~рРо (1 <£<"); (И.16.2)
Р/г+1 = Рл + 2 = ... =* Рп + т^—~ р0, (11.16.3)
Ш
т. е. все вероятности, начиная с рп и кончая pn+m, равны друг другу.
Формулыдля А у Q, P0TK, fe остаются прежними.
Раскрывая неопределенность в формуле (11.0.28), полунаем
1— (т + \)кт + ткт + 1 _ т(т+\) -_ Pn+! pQm(m+l)
к™ 0'—и)2 ~ 2 ; Г "" 2л.л!
(11.16.4)
Формулы (11.0.29), (11.0.30) остаются прежними.
Формулы (11.16.1)—(11.16.3) можно было бы вывести и не
раскрывая неопределенность, а непосредственно из схемы гибели и
размножения. V ^
11.17. О Подсчитать характеристики эффективности Л, Q, Ротк,
\ Л Я ^оч>"^сист Для простейшей одноканальной СМО_с тремя
местами в очереди (т= 3) при условиях: К = 4 заявки/ч; гобсл =1/^ = 0,5.
2) Выяснить, как эти характеристики изменятся, если увеличить
число мест в очереди до т = 4. '
Решение. fi = 2; р = k/\i = 2; по формулам (11.0.12)— .
(11.0.16) при т = 3 имеем: р0 = 1/31; р^== 16/31; Q « 0,484; Л =
»= kQ ^J,93 заявки/ч; * = pQ « 0,968; г « 2,19 заявки; z « 3,16
заявки; *оч « 0,55 ч; 7СИСТ « 0,79 ч.
2) При т = 4 имеем р0 = 1/63 « 0,0158; рб == 32/63 ^ 0,507;
Q ^ 0,493; А « 1,96 заявки/ч; г « 3,11 заявки; z = 4,09 заявки;
£ч«0,78 ч; 7СИСТ» 1,02 ч.
Таким образом, увеличение числа мест т с трех до четырех приводит
к незначительному увеличению абсолютной (и относительной)
пропускной способности, сопровождаясь при этом некоторым увеличением,
среднего числа заявок в очереди и в системе, а также соответствующих
средних времен. Это и естественно, так как некоторые заявки,
получающие отказ в первом варианте, все же становятся в очередь во втором.
11.18. Как изменятся характеристики эффективности СМО
предыдущей задачи, если Я и \i остаются прежними, m - 3, но число
каналов обслуживания увеличится до п = 2?
365
Р е ш е н и е. х = 1; по формулам (11.16.1), (11.16.2) имеем р0 =:
= 1/Ц; Рг = ... = Рь = 2/11; Q = 1 —-2/11 « 0,818-L Л « 3,27
заявки/ч; г == 12/11 « 1,09^ заявки; k = Л/ц « 1,64; г = г + ft « 2,73
заявки; *оч « 0,27 ч; ^сист ^ 0,68 ч.
11.19. Система массового обслуживания — билетная касса с
одним окошком (п = 1) и неограниченной очередью. Касса продает
билеты в пункты А и В\ пассажиров, желающих купить билет в пункт Л,
приходит в среднем трое за 20 мин, в пункт В — двое за 20 мин.
Поток пассажиров можно считать простейшим. Кассир в среднем
обслуживает трех пассажиров за 10 мин. Время обслуживания —
показательное. Установить, существуют ли финальные вероятности
состояний СМО и еели да — вычислить первые три_из них: р0, р1э р2.
Найти характеристики эффективности СМО: г, г, tCUCT и10ч.
Решение. %А = 3/20 = 0,15 заявки/мин; Хв = 2/20 = 0,10
заявки/мин. Общая интенсивность потока заявок % = %А + Хв —
= 0,25 заявки/мин; р = 3/10 = 0,3 заявки/мин; р = АУ|х л? 0,833 < 1,
финальные вероятности существуют. По формулам (11.0.12)—(11.0.14):
— 0 83*3
Ро « 0,167; Pi «0,139; р2« 0,116; z«~j^«4,99 заявки; fr =
= 0,8332/0,167» 4,16 заявки; 7СИСТ « 4,99/0,25 « 20,0 мин; Гоч ж
« 4,16/0,25 « 16,7 мин.
. 11.20. Одноканальная СМО — ЭВМ, на которую поступают
заявки (требования на расчеты). Поток заявок — простейший со средним
интервалом между заявками / = 10 мин. Время обслуживания Тобсл
распределено по закону Эрланга 3-го порядка с математическим
ожиданием £обсл = 8 мин. Определить среднее число z заявок в СМО и
среднее число г заявок в очереди, а также средние времена пребывания
заявки в системе 7СИС1 и в очереди 70ч.
Решение. Характеристики СМО могут быть найдены по формуле
Полячека—Хинчина (11.0.31), (11.0.32). Имеем: X = 0,1 заявки/мин;
fi = 0,125 заявки/мин^ р = Я/р, = 0,8.
Коэффициент вариации времени обслуживания для закона
Эрланга 3-го порядка равен 1/^3. По формуле (1L0.31)7 = 0,64 (1 + 1/3).:
: (2-0,2) « J2,13. По формуле (11.0.32) z = г + 0,8 ^ 2,93. По
формуле Литтла t04 « 21,3 мин, *сист ^ 29,3чмин.
11.21. Условия предыдущей задачи изменены: поток заявок уже
не простейший, а пальмовскии, причем интервал между событиями
в потоке распределен по обобщенному закону Эрланга 2-го порядка
(см. задачу 8.38) с параметрами %г = 1/2; %2 ==: 1/8. Найти
приближенно, по формулам (11.0.34)—(11.0.37), характеристики эффективности
СМО.
Решение. Случайная величина 7\ распределенная по
обобщенному закону Эрланга 2-го порядка, есть сумма двух случайных
величин 7\ и Т2, распределенных по показательным законам g
параметрами: Хх = 1/2; ?L2 = 1/8. Отсюда М [71 = 1/^ + Щ2 = 10 мин; D [71=
= D [TJ + D [Т2] = 22 + 82= 68; t* - 68/102 = 0,68;^= 1/3.
Следовательно,
зев
г= 1,62заявки; г = 2,42заявки; *оч = 16,2мин; tCBCT == 24,2мян.
11.22. Техническое устройство (ТУ) может время от времени
выводить из строя (отказывать). Поток отказов ТУ — простейший о
интенсивностью X = 1,6 отказа в сутки. Время Тъ восстановления
(ремонта) ТУ имеет равномерное распределение на участке от 0 до 1 су-,
ток. Найти (для предельного стационарного режима) среднюю долю R
времени, в течение которого ТУ работает.
Решение. Состояния ТУ: s0 — работает; Sj — ремонтируетея.
Граф состояний ТУ показан на рис. 11.22, где \i = 1/М [ТД,— 1/0,5 =
= 2. Этот граф в точности совпадает с графом состояний одноканалк-
ной СМО с отказами. Мы знаем, что если поток заявок, поступающих
на СМО, — простейший, а время обслуживания имеет произвольное
распределение, то справедливы формулы Эрланга (11.0.6); в данном
случае р = Я/(л = 0,8; р0 = {1 + р/Н}"1 = 1/1,8 ^ 0,556; рг = 1 —
— 0,556 « 0,444. Итак, R « 0,556, т. е. ТУ будет работать немногим
более половины всего времени, а остальное время ремонтироваться.
11.23. В условиях предыдущей задачи ТУ дублировано точно
таким же ТУ, которое может выходить из строя только в работающем
состоянии; X, (х — такие же, как в задаче 11.22. Найти величину R,
а также среднее число к неисправных ТУ.
Решение. Состояния системы S: s0 — оба ТУ исправны (одно
из них работает, другое нет); sx — одно ТУ работает, другое ремонта-,
руется; s2 — оба ТУ ремонтируются. Граф состояний дан на рис. 11.23.
Граф в точности совпадает с графом- состояний двухканальной СМО
с отказами. По формулам Эрланга (11.0.6)
Ро = {1 + "и" + 1гГ1 = {1 +0'8 + 0'64/2>~, «0.472;
рх » 0,8-0,472 = 0,378; R = р0 + рх « 0,850.
Очевидно, тот же прием (сведения к СМО с отказами) может быть
применен и в случае, когда число дублирующих ТУ, более одного.
11.24. Система массового обслуживания — обувной магазин, в
котором каждый покупатель проходит три фазы обслуживания: 1)
примерка и выбор обуви; 2) уплата денег в кассу и 3) получение покупки на
контроле. В магазин прибывает простейший поток покупателей с
интенсивностью X = 45 человек/ч.
В отделе примерки имеются четыре стула, занимая которые,
покупатели могут самостоятельно выбирать и примерять обувь. Среднее
время примерки и выбора обуви ^ == 5 мин. Выбравший обувь
покупатель направляется в кассу, где вторично становится в очередь
(касса в магазине одна). Среднее время оплаты товара в кассе 72 = 1 мин.
После оплаты покупатель идет на контроль, где становится в новую
очередь и получает покупку. -На контроле работают три продавца;
среднее время выдачи покупки ts = 2 мин. Все потоки событий —
простейшие.
Рассматривая магазин как трехфазовую СМО, найти
характеристики ее эффективности:
367
Ъ Л» гз) — среднее число покупателей в очереди к первой (второй,
третьей) фазе ©белужйвания;
zx (z2, z8) — среднее число покупателей, связанных с первой
(второй, третьей)_ фазой обслуживания;
йч* (&3\ №) — среднее время ожидания покупателя в' очереди
к первой_(второй, третьей) фазе;
йист (4иет» ^стст) — среднее время пребывания покупателя в
первой^ (второй, третьей) фазе обслуживания;
г — общее ереднее число покупателей во всех трех очередях;
г — общее среднее чиело покупателей в магазине;
70Ч — общее среднее время, проводимое покупателем в очередях;
*сист — общее вреднее время, затрачиваемое покупателем на
приобретение обуви в магазине.
Дополнительно ответить на следующие вопросы: 1) В каком звене
и как нужно улучшить обслуживание для *гого, чтобы сократить
затраты времени покупателей? 2) Как можно было бы учесть тот факт,
что не все покупатели находят себе подходящую обувь, и какая-то
доля а из них (0 < а < 1) уходит из магазина, не сделав покупки?
Решение. Так как все потоки событий — простейшие, то
выходные потоки всех трех фаз тоже будут простейшими, и можно рае-
сматривать три последовательные фазы как три отдельные СМО со
своими характеристками.
1. Первая фаза. Так как в отделе примерки четыре стула,
то число каналов пг = 4. Далее, имеем 1г = 1/цг = 5 мин — 1/12 ч;
Рх = 45/12 = 15/4 « 3,75; хх = рх/% = 15/16 < 1. По формулам
(11.0.21)—(11.0.25) находим:
pin-{1+3,75+ Г'75)2+ (3>75)2 + &'W +
Ип I 2 ^2*3 2»3-4
j (А>31 Л-* « (151,58)—^ » 0,0060; \ = 3,75;
2.3-4.4 (1 — 15/16)
гг= (3>75)6 Sll- » 13,01; 21= 16,76;
£i> t= Гг/Х ж 0,289 ч « 17,3мин; Йст *=гг/% « 0,372 ч » 22,3мин.
2. Вторая фаз a. ft, = 45; п2 = 1; р2 = 0,75 < 1. По
формулам (11.0.12)—(11.0.14) получаем:
. J, = Рр/(1 — р.) = 9/4 *= 2,25^ г2 = ра/(1 — р2) = 3;
<oi} e г2/[г = 0,05 ч==3 мин; tchlv = 1/15 ч = 4 мин.
3. Т р е т ь я ф а з a. ns = 3; % « 45; р8 = 3/2; х3 = 0,5 < 1.
По формулам (11.0.21)—(11.0.25) находим: р(03) « 0,210; Га» 0,237;
г8« 1,737; 1$ » 0,316 мин; 1JS,» 2,316 мин.
388
Складывая средние численности трех очередей, получаем общую
среднюю численность очереди:
7 = гх + F2 + г3« 15,5.
Аналогично находим среднее число покупателей в магазине z =
= ^+12,+z3« 21,5.
Среднее время пребывания покупателя в очереди
?оч = *#> + t£+l(oV «20,6мин.
Среднее время пребывания покупателя в магазине
+ *сист +^ист ^ 28,6 МИН.
*сист "~ *
■- сист
S?S
А
^
Рис. 11.22
Рис. 11.23
Рис. 11.25
I) Улучшить обслуживание можно, уменьшая время пребывания
покупателя в первой фазе, которая представляет собой наиболее
слабое звено СМО. Всего проще достигнуть этого, увеличив число пх
стульев в отделе примерки, т. е. число каналов обслуживания в
первой фазе. Например, простое увеличение числа стульев на единицу
(т. е. переход от пг = 4 к пг = 5) дает существенный выигрыш во
времени. Действительно, при пг = 5. для первой_фазы получим: рх =-
= 3,75; щ = 3,75/5 = 0,75; р<1} = {53J5}-1; гг & 1,38; гг « 5,13;
U)
1,84 мин; t&lT « 6,84 мин.
2) Учесть наличие доли покупателей а, уходящих из магазина беа
покупки, можно, умножив* интенсивность входного потока второй и
третьей фаз на (1 — а).
11.25. На железнодорожную сортировочную станцию поступает
эрланговский 10-го порядка поток составов с интенсивностью % = 1,2
состава/ч**. Время обслуживания состава Тобсл распределено в
интервале от 0 до 1 ч по закону с плотностью ф (<), показанной на
рис. 11.25. Оценить приближенно [по формулам (11.0.34)—(11.0.37)1
характеристики эффективности станции — среднее чиело z составов на
станции, в очереди г, ^среднее время *сиот пребывания состава на
станции, среднее время t04 ожидания составом очереди на
обслуживание.
^Подчеркнем, что эдесь X -- интенсивность именно эрланговского потока*
а не того простейшего потока, прореживанием которого получен эрланговский*
369
Решение. Для закона q> (t) имеем *обсл = 1/3; р = К/\х =
«= 0,8 < 1. Для потока Эрланга 10-го порядка vl = (l/jfk)2 = 0,1;
vl определяем, деля дисперсию DJTo6cjs] на квадрат математического
ожидания: v» = 1/2 = 0,57
Находим характеристики СМО:
г = Р2 (vl + vl)l[2 (1 — р)] « 0,82 (0,1 + 0,5)/(2.0,2) = 0,96;
^2 = г + р^_0,96 + 0,8= 1,76;
t04 = гА ^ 0,8 ч; *сист = 70ч +J/ji « 1,13 ч.
11.26. Показать, что для простейшей n-канальной СМО с
неограниченным числом мест, в очереди среднее число заявок, находящихся
в очереди, заключено в пределах
х**1 п - х'Н-1
1-х кп(п —1)+1 1-х
Решение. Запишем выражение для г в следующем виде [см.
формулы (11.0.23), (11.0.21)3:
г = -^—/1 ^ = "71 ГГ^> гдерп = -^г/?0.
/^л! (1-х)2 (1-х)2 я!
Следовательно,
п\ \. 2* /г! я! 1-х/
.(l + JL+JL£!=lI + ... + 4 + T2-r>
\ Р Р2 Р" 1—к у
>(i-l-J-+JL.+ ... +^l+TJL->)"1 = x»(i-x).
V Р Р2 Р" U-x/
С другой стороны,
• Рп<(\ + JL+JL + ... + -^- +—Z-Y1^ *n(]-*>n
А Р Р2 Рп 1-х У хл(л — 1)+Г
Так как [хп (1 —%) п]/[кп (п — 1) + 1] < рп<кп (1 — *), то
указанное в задаче неравенство также выполняется. Заметим, что
последнее неравенство может быть использовано для приближенного
определения всех характеристик рассматриваемой СМО.
11.27. Железнодорожная касса имеет два окошка, в каждом из
которых продаются билеты в два пункта: Ленинград и Киев. Потоки
пассажиров, приобретающих билеты в Ленинград и в Киев одинаковы
по интенсивности, которая равна к0 = 0,4& пасс/мин. Среднее время
обслуживания пассажира (продажи ему билета) *обсл = 2 мин.
Поступило рационализаторское предложение: для уменьшения
очередей (в интересах пассажиров) сделать обе кассы
специализированными: в первой продавать билеты только в Ленинград, а во
второй — только в Киев. Считая в первом приближении все потоки
событий простейшими, проверить разумность этого предложения.
370
Решение. 1) Вычислим характеристики очереди для двух-
канальной СМО (существующий вариант). Интенсивное™ потока
заявок % = 2А,0 = 0,9 пасс/мин; у, = 1/70бсл = 0,5 пасс/мин; р = Щ «
= 1,8; х = р/2 = 0,9 < 1, финальные вероятности существуют. По
формуле (11.0.21)
Ро={1 + 1,8 + -if- -тз^у}"1 * °>0575;
по формуле (11.0.23)
1,8».0,0575 0 л 1 8,4
- «8,4пасс: tnvi= ——
2-2.0,01 ' оч 0,9
г=== \ о 1м «8,4пасс; t04= -^ «9,3мин.
2) Во втором варианте (предлагаемом) имеем две одноканальные
СМО: р = Х0/|* = 0,45/0,5 = 0,9 < 1. ^
Средняя длина очереди у одной кассы (по формуле (11.0.13)] равна
г = р2/(1 — р) = 0,92/0,1 = 8,1 пасс. Суммарная длина очереди к
обеим кассам будет 2г = 16,2 пасс.
Время пребывания пассажира в очереди (11.0.14) Точ=7/Х =
= 8,1/4,5 = 18 мин, что почти вдвое превосходит время стояния в
очереди в существующем варианте: 9,3 мин.
Вывод: «рационализаторское» предложение нужно отвергнуть, как
резко снижающее эффективность СМО. Резкое ухудшение
характеристик СМО при переходе от двухканальной СМО (существующий
вариант) к двум одноканальным СМО (предлагаемый вариант)
объясняется тем, что, разделив кассу на две специализированные, мы лишили
кассиров возможности подменять друг друга.
11.28*. Простейшая многоканальная СМО с «нетерпеливыми»
заявками и с неограниченным числом мест в очереди. Имеется
простейшая д-канальная СМО с очередью; интенсивность потока заявок А,,
потока обслуживании [х, = М0бсл- Время пребывания заявки в
очереди ограничено некоторым случайным сроком 7\ распределенным по
показательному закону с параметром v (на каждую заявку,
стоящую в очереди, действует «поток уходов» с интенсивностью v).
Написать формулы для финальных вероятностей состояний, найти
относительную пропускную способность СМО Q, среднюю длину
очереди Ту среднее время Точ пребывания заявки в очереди, среднее число
Гзаявок в СМО и среднее время 7СИСТ пребывания заявки в СМО.
Решение. Состояния системы по-прежнему будем нумеровать
соответственно числу заявок, находящихся в СМО. Граф состояний
показан на рис. 11.28. Пользуясь общими формулами для схемы
гибели и размножения и вводя обозначения р = %/\i\ p = v/\i, получаем:
Ро
. [ "*" 1! ""*" 2! ~Г'" "Г п\ ~*~ п\ L" + P (« + Р)(/г + 2Р)
+ '~'+ (л+Р)(я+2Р)...(л+гР) + " JJ ' ■
371
Pi = -£-po; ■.■;Pk=-^rPo(i<k^n); ...; pn=-—-p0',
P»+i- «I ' „+p Po> -5^+r- nI * <я + р)(/1+2р)...(/1+гР) Х
Xpo(r>l); ... (11.28.1)
В первую формулу (11.28.1) входит бесконечная сумма, не
являющаяся геометрической прогрессией, но члены которой убывают
быстрее, чем члены геометрической прогрессии. Можно доказать, что
ошибка, возникающая от отбрасывания всех членов бесконечной суммы,
начиная с г-го, меньше, чем 2. l£iEL е—р/Р.
1 ~ V % Нр ^ "Я1 „м+* пр+П
Рис. 11.28
Предположим, что вероятности р0, р19 ..., рп, ..., рп+г, ...
вычислены, и.покажем, как можно найти характеристики данной СМО:
относительную пропускную способность Q, среднее число заявок в
очереди г и др. Найдем прежде всего Q. Обслужены будут все заявки,
кроме тех, которые уйдут из очереди досрочно. Подсчитаем, сколько
заявок в среднем уходит из очереди досрочно в единицу времени.
Интенсивность потока уходов, приходящаяся на одну заявку, стоящую в
очереди, равна v, а суммарная средняя интенсивность потока уходов,
приходящаяся на все заявки, стоящие в очереди, равна vr. Значит,
абсолютная пропускная способность СМО
А*=% — v7, (11.28.2)
а относительная
Q*= ЛА= 1— vr/X. (11.28.3)
Таким образом, для того чтобы найти Q, нужно прежде всего знать
7Г которую непосредственно можно было бы найти по формуле г =
e lPn+i + 2рп+2 + ... + грп+г + ... Но эта формула плоха тем,
что содержит бесконечное число слагаемых. Этого можно избежать,
если_восподьзоваться выражением для среднего числа занятых
каналов k через Ах k ~ A/\i или, учитывая (11.28.2),
1 « (X — vr)l[i «= р — р7. (11.28.4)
Из (11.28.4) получим
7=(р — k)l$, (11.28.5)
а среднее число занятых каналов k можно подсчитать как
математическое ожидание случайной величины К (число занятых каналов) с воз-
372
можными значениями 0, 1, 2, ..., п и соответствующими вероятностями
Ро> Ръ Р2У •••» Рп-1> П — (рО + Pi + ... + Pn-l)^
F = lpj + 2p2 + ... + (П — 1) pn_j + Л [1 — (p0 + рх + ... +
+ Pn-i)L (11.28.6)
Далее, по формуле (11.28.5) вычисляем г. Величину Точ находим по
формуле Литтла:
Гоч=7/Х. (11.28.7)
Среднее число заявок в СМО
г-F+fe, (11.28.8)
а среднее время пребывания заявки в СМО
W-гД. (11.28.9)
Примечание. Можно доказать, что для рассмотренной СМО с
«нетерпеливыми» заявками финальные вероятности существуют всегда, если только
Р > 0. Это подтверждается тем, что ряд в первой формуле (11.28.1) сходится
при любых положительных р и р. По существу это означает, что очередь не
может расти неограниченно: чем больше длина очереди, тем интенсивнее уходят
из нее заявки.
11.29. Рассматривается простейшая двухканальная .СМО с
«нетерпеливыми» заявками (см. задачу 11.28). Интенсивность потока
заявок % = 3 заявки/ч; среднее время обслуживания одной заявки
*обсл в ИV> ^ 1 ч> средний срок, в течение которого заявка
«терпеливо» стоит в очереди, равен 0,5 ч. Подсчитать финальные вероятности
состояний, ограничиваясь теми, которые не^еныпе 0,001. Найти
характеристики эффективности СМО: Q, Л, k, r, i04f tcaCT.
Решение. Имеем X == 3, \i =1, v = 2, р = 3, р = 2, п = 2.
По формулам задачи 11.28 получаем:
з2 , з2 Г з , з2 , з3 . з4
1 2 ^ 2 L 4 4-6 ^ 4.6-8
Ро
35 , Зб
4.6-8.10
1) *« 0,0692;
4.6.8-1С12-14.16 JJ
4.6.8*10.12 ' ^4.6.8.10.12.14
откуда
рх » Зр0 & 0,208; р2 - -~ рх & 0,311; р3 = -j- р2 » 0,234; р4 =
-YA»0lil7;pe-^p4»0,044;pe=-^-pe»0f013;ft«
--й-Ре» о,°оз; р8 - -£-р7жo,ooi.
Среднее число занятых каналов (11.28.6) k « lpi + 2 (1 —р0 —
•—Pi) ^1,654; средняя длина очереди (11.28.5) г* (р — £)/р—
s= (3 — l,654)/2 « 0,673; абсолютная пропускная способность
373
A sa £|л « 1,654 заявки/ч; относительная пропускная способность
Q « Л/Х « 0,551 и далее: 70ч = г/Л, « 0,224 ч; z = г + k « 2,327;
Тсист=гА~ 0,776 ч.
11.30. Простейшая СМО о «ошибками*. Имеется м-канальная
СМО в неограниченной очередью. На ее вход поступает простейший
поток заявок о интенсивностью %\ время обслуживания — показательное
в параметром у>. Обслуживание происходит без гарантии качества;
с вероятностью р оно удовлетворяет заявку, а с вероят&остью q =
-= 1 — р — не удовлетворяет, и заявка обращается в СМО вторично
либо сразу обслуживается, если нет очереди, либо становится в
очередь» если она есть. Ввести состояния СМО (нумеруя их по числу за-
— /Г—*гр нр—w nfi
Рис. 11.30
• «•
*л+г
• • ♦
явок в СМО); найти финальные вероятности состояний и
характеристики эффективности СМО. Найти среднее число рекламаций,
поданных в единицу времени, если каждая неудачно обслуженная заявка
подает рекламацию с вероятностью R.
Решение. Состояния" СМО:
s0 — СМО свободна;
Sj — занят один канал; ...;
sh — занято k каналов (1 < k < п)\ ...; \ очереди нет;
sn — заняты все п каналов
sn+r — заняты все п каналов, г заявок стоят в очереди (г = 1,2,...).
Граф состояний приведен на рис. 11.30, где \л = pp. Из этого графа
видно, что данная СМО эквивалентна другой СМО с полной гарантией
качества обслуживания, но б интенсивностью потока обслуживании,
равной уГ= pjr, для этой СМО р = Щ = Я/(р[х). Формулы (11.0.21)—
(11.0.25) остаются справедливыми, но при замене р на р, р на [г.
11.31. Простейшая одноканальная замкнутая СМО. Один рабочий
обслуживает т станков, которые время от времени отказывают
(требуют наладки). Интенсивность потока отказов одного станка равна X.
Если в момент отказа станка рабочий свободен, он немедленно
приступает к наладке; если нет — станок становится в очередь на наладку.
Поток отказов станка простейший, время наладки — показательное
с параметром р = Ш0бсл* Ввести состояния СМО, нумеруя их по
числу неисправных станков; найти финальные вероятности состояний СМО
и следующие характеристики ее эффективности: А — среднее
количество станков, ремонтируемое рабочим в единицу времени; w —
среднее число неисправных станков; г—среднее число станков, ожидаю"
374
щих ремонта в очереди; Р3ан — вероятность того, что рабочий будет
занят.
Решение. Состояния СМО:
s0 — все станки исправны (рабочий свободен);
sx — один станок неисправен (рабочий занят его наладкой); ...;
sfe — k станков неисправны, один налаживается, k — 1 ждут очереди
sm — все т станков неисправны, один налаживается, т—1
ждут очереди.
Граф состояний показан на рис. 11.31.
. тх (m-i)X (т-М)1 (т-Ш X
Рис. 11.31
По общим формуламГ схемы гибели и размножения^ обозначая
р = АУ|х, получаем
р0 = {1 + тр + т (т — 1) р2 + ... + .
+ т (т — 1) ... (ш — k + 1) pk + ... + mlp"}-1;
рг = mpp0; p2 = rn (m — l) p2p0; ...;
pk = т (т — 1) ... (т — k + I) pkp0 (1 < k <! n)\ ...;
pm = m\pmp0.
(11.31.1)
Чтобы определить абсолютную пропускную способность Л, найдем
сначала вероятность того, что рабочий занят:
Я,ан= 1-Ро. (11.31.2)
Если рабочий занят, он налаживает \i станков в единицу времени;
значит,
А = (1-Ро)н<- (11.31.3)
Среднее число неисправных станков w можноч выразить через А
с помощью следующих рассуждений. Каждый работающий станок
порождает поток отказов а интенсивностью^; в среднем работает т—w
станков; порождаемый ими поток отказов имеет интенсивность
(т — w) %; все эти неисправности ликвидируются рабочим, значит,
(1 — Ро) И* = (т — w) Ъ откуда
. ю = щ — (1 — р0)/р. (11.31.4)
Среднее число г станков в очереди найдем следующим путем:
w = T+k, (11.31.5)
где k — среднее число обслуживаемых станков (или, иначе, среднее
числе занятых каналов обслуживания). В нашем случае число занятых
375
каналов равно 0, если рабочий свободен, и 1, если он занят: k = О X
X р0 + 1 (1 — Ро) = 1 — Ро- Следовательно,
Г= m — (1 — р0)/р — (1 — Ро) или Г= m — (1 — р0) (1 + 1/р).
(11.31.6)
11.32*. В условиях задачи 11.31 найти среднее время 70Ч, которое
будет ожидать наладки произвольно выбранный вышедший из строя
станок.
Решение. Формула Литтла, которой мы пользовались ранее,
пригодна только для открытых СМО, где интенсивность потока заявок
не" зависит от состояния СМО. Для замкнутых .СМО она непригодна.
Время t04 найдем с помощью следующих рассуждений. Пусть какой-то
момент /появилась заявка (отказал станок). Найдем вероятность того,
что в этот момент СМО находилась в состоянии sh (k = 0, ..., т — 1)
(ясно, что в состоянии sm она находиться не могла). Рассмотрим т
гипотез:
Н0 — в момент появления заявки СМО находилась в состоянии s0;
Нг — в момент появления заявки СМО находилась в состоянии sx;
Hh — в момент появления заявки СМО находилась в состоянии
$к > • • • 9
Hm-i — в момент появления заявки СМО находилась в
состоянии sw_x.
Априорные вероятности этих гипотез равны р0, plf ..., pki ..., pm_i-
Теперь найдем апостериорные вероятности гипотез при условии,
что ниблюдено событие А = {на элементарном участке времени (/,
t + di) появился отказ станка}. Условные вероятности этого события
при гипотезах Н0, Нъ ..., #m_i равны:
Р (А \Н0) « mUt\ Р (А \НХ) = (т — 1) Ut\ ...;
Р (A \Hh) - (т - k) Ut\ ...; Р (А \Нт^) = ML
По формулам Бейеса найдем-апостериорные вероятности гипотез
(при условии, что событие А произошло). Обозначая эти вероятности
Ро, Pi» -.» Ри> •••> Рт-х> получаем:
~ _ / ^Ро . ~ _ (^—1) Pi . .
Ро — — > Pi""""!-i » •"»
2 (m—k)pk 2 (m—k)Pk
k= о fc= о
n — (m — k)Ph . . ~ Pm-1 ПГ39 1\
2 (m—k)pk 2 («—*)Pfc
Зная эти вероятности, найдем полное математическое ожидание
времени пребывания отказавшего станка в очереди. Если станок отказал
в момент, когда система находится в состоянии s0, он не будет стоять
в очереди; если в состоянии sl9 то будет находиться в ней в среднем
время 1/fi, если s2— время 2/jx и т. д. Умножая вероятности (11.32.1)
на эти числа и складывая, получаем ^
376
1 w«*l
^оч=— 2! *Л- (11.32.2)
11.33. Рабочий обслуживает четыре стайка (m ==* 4); каждый
станок отказывает с интенсивностью X = 0,5 отказаЛгг среднее время
ремонта /р = 1/fJt = 0,8 ч. Все потоки событий — простейшие.
Пользуясь формулами задач 11.31, 11.32, найти: 1) финальные
вероятности состояний; 2) пропускную способность Л; 3) среднее
относительное время простоя рабочего Рпр; 4) среднее число станков в очереди
7: 5) среднее число неисправных станков до; 6) среднее время
пребывания в очереди t04 одного отказавшего станка; 7) среднюю
производительность группы станков с учетом их неполной надежности, если в
работающем состоянии один станок дает / единиц продукции.
Решение. [г = 1/7р = 1,25; р = Х/рь = 0,4.
1) По формулам (11.31.1) имеем: р0 = {1 + 1,6 + 1,92 + 1,53 +
+ 0,61 У1 = 6.66-1 » 0,150; рг = 1,6р0 а? 0,240; р2 = 1,92р0 »
» 0,288; р8 = 1»53р0 « 0,230; р4 = 0,061 р0 » 0,092;
2) А — 0,850fJi « 1,06 станка в час; —
3) РПР = Ро = 0,150;
4) _г « 4 — 0,850 (1 + 2,5) » 1,03;
5) ai».l,03 + ft» 1,03^+0,85 = 1,88;
6) по формулам (11.32.1) и (11.32.2) Й"^^^^ ~
« 0,283; рх » 0,340; р2 = 0^70; р~ - 0,108; Гоч = 0,8 (р1( + 2р2 +
+ 3р3)^0,964 ч. '_
7) производительность группы станков равна (т — до) I « 2,12/.
11.34. Простейшая многоканальная замкнутая СМО. Бригада из
п рабочих обслуживает т станков (п <. т). Поток отказов каждого
станка имеет интенсивность X; среднее время наладки станка 7обол =
= 1/|д>. Все потоки событий — простейшие. Найти финальные
вероятности состояний СМО; абсолютную пропускную способность Л;
среднее число неисправных станков до.
Решение. Состояния СМО нумеруем по числу неисправных
станков:
So — все станки- исправны, рабочие не заняты;
$1 — один станок неисправен, один рабочий занят, остальные
свободны; ...;
sft — k станков неисправны, k рабочих заняты, остальные
свободны (k < m)\ ...;
sn — п станков неисправны, все рабочие заняты;
Sfi+l — п + I станков неисправны, из них п налаживаются, один
стоит в очереди; ../,
sn+r — п + г станков неисправны, из них п налаживаются, г в
очереди (п + г < яг); ...;
Sm — все т станков неисправны, из них п налаживаются, т — /г
ждут очереди.
-377
Предоставляя читателю самостоятельно построить граф состояний
СМО, приведем только окончательные формулы для вероятностей
состояний:
Роаа(1 + -2.р+те("-') рН,„+И»-1)...("-Н1)рЧ
{у . т .т (т—1) « , ,
V
i х rn{m—\) ... (m—n) ^n + x , t m(m-\) . . ^-(/i + r — l)j w
m mint—1) о
pi= —p/>o; p2=—^j—-p po\ •••;
m(m—1) ... (m—k4-\) ь ,. , ^ .
Pk= , Ml JL-LPkPo (l<k^n);
«I
m On— 1) ... (m — fi+l) „
л!
Pn+z = —s —J , l — P"+rPo (l<r<m— 1);
Pm= n(™L„ PfflPo, где p = V^. (11.34.1)
Через эти вероятности выражается среднее число занятых рабочих:
1 = 0.р0 + 1рх + 2р2 + ... + (п — 1) рп_г + п(рп+ рп+1 +
+ ... + рт) = рг + 2/?2 + ... + (л — 1) pft_! + /1 (1 — р0 —
-Pi-... -Рд-i). (11.34.2)
Абсолютная пропускная способность
А:«*|1э (11.34.3)
а среднее число неисправных станков
ш = m — ft|i/X = m — &/р. (11.34.4)
11.35. Два рабочих (л = 2) обслуживают шесть станков (т = 6).
Станок требует наладки в среднем через каждые полчаса. Наладка
занимает у рабочего в среднем 10 мин. Все потоки событий —
простейшие. 1) Определить характеристики СМО: среднее число занятых
рабочих Ъ\ абсолютную пропускную способность А; среднее число
неисправных станков до. 2) Установить, улучшатся ли характеристики СМО,
если рабочие будут налаживать станки совместно, тратя вдвоем на
наладку одного станка в среднем 5 минут.
Решение. 1) Решаем задачу в первом варианте (рабочие
налаживают станки порознь). Имеем т = 6; п — 2; % =* 2; |г = 6; р =
= Я/[х, = 1/3. По формулам (11,34.1)
(7 . 6 1,6-5 1 , 6-5.4 1 f 6*5*4*3 1 ,
1 1 3 Ь2 З2 1-2.2 33 ^ Ь2.22 ' 34 ^
378
6-5*4*3.2 1 . 6«5.4.3*2<1 1
^P~°'153;
J Ь2<23 35 t.2^24
Pl=s 6/Ы/Зр0« 0,306.
Среднее число занятых рабочих находим по формуле (11.34.2): Ъ =
= \-рх + 2J1 — Ро — Pi) ^ 1,235. Абсолютная пропускная^
способность А =а &|л л* 7,41. Среднее число неисправных станков о> = 6 —
— 7,41/2 « 2,30.
2) Если рабочие налаживают станки вместе, то СМО превращается
в одноканальную (т = 6; п = 1) при \i =; 12. Расчеты произведем для
р = X/\i = 1/6. По формулам (11.31 Л)
p0 = {l + l +
6*5 , 6-5*4 , 6*5*4*3 , 6'5«4.3«2
б2 63 б4 65 '
6«5»4.3*2*1 W *
<х
> 0,264; рх « 0,264; р2« 0,220; р8 ^ 0,147; р4
^0,076; р5« 0,024; р6« 0,004; ^=6 —^L^ 1,59.
1/6
Среднее число занятых каналов & = 1 — р0 = 0,736. Однако,
учитывая, что «канал» обслуживания состоит в данном случае из двух
рабочих, среднее число занятых рабочих будет
Р = 2-0,736 « 1,47; А - k\x = 0,736-12 « 8,8.
Таким образом, взаимопомощь между рабочими (каналами
обслуживания) в данном случае'повысила среднюю занятость с 1,23 до 1,47,
снизила среднее число неисправных станков ® 2,30 до 1,59 и повывила
пропускную способность о 7,4 до 8,8.
11.36. Имеется простейшая трехканальная СМО в отказами;"на нее
поступает поток заявок с интенсивностью А,— 4 заявки /мин; время
обслуживания заявки одним каналом *обсл = 1/jut = 0,5 мин.
Спрашивается, выгодно ли с точки зрения пропускной способности СМО
заставить все три канала обслуживать заявки сразу, причем среднее
время обслуживания уменьшается втрое? Как это скажется на среднем
времени пребывания заявки в СМО?
Решение. 1) Находим вероятности состояний СМО без
взаимопомощи между каналами по формулам Эрланга (11.0.6):
Po = {1 + "^ + ^+"l"r^0,158; Я««вЛ = -|-Ро^0,21;
Q = 1 — Ротк ^ 0,79;. А = XQ ^ 3,16.
Среднее время пребывания заявки в СМО вычислим как
вероятность Q того, что заявка будет принята к обслуживанию, умноженную
на среднее время обслуживания: 7СИСТ « 0,79*0,5 « 0,395 мин.
2) Объединяем BGe три канала в один с параметром у = 3»2 = 6;
получаем
379
Po=* (\+L)-L =°'6] Л-(2/3)0,6-0,4;
Pom e-Pi = 0>4'> Q = 1 — Л™ = 0,6; A =* JtQ - 4.0,6 - 2,4.
Сравнив эту пропускную способность g пропускной способностью
СМО в первоначальном варианте, видим, что она не увеличилась (как
это было в предыдущей задаче), а уменьшилась! Легко понять,
почему это произошло: благодаря объединению двух каналов в один
увеличилась .вероятность отказа (того, что пришедшая заявка застает оба
канала занятыми и уйдет яеобслуженной).
Среднее время пребывания заявки в СМО во втором варианте будет
меньше, чем в первом: *Сист— Q (1/6) = 0,1 мин. Однако это
уменьшение куплено «дорогой ценой» — тем, что ряд заявок вовсе не
обслуживаются и, значит, проводят в СМО нулевое время.
Почему же в предыдущей задаче объединение двух каналов в один
повысило эффективность обслуживания? Предлагаем читателю
подумать над этим вопросом и объяснить кажущееся-противоречие. Не
потому ли, что в СМО в отказами заявки не становятся в очередь?
11.37. Имеется проетейшая трехканальная СМО о
неограниченной очередью. Интенсивность потока заявок X = 4 заявки/ч; вреднее
время обслуживания 7обсл = 1/[* = 0,5 ч. Выгодно ли, имея в виду:
1) среднюю длину очереди, 2) среднее время пребывания.заявки в
очереди, 3) среднее время пребывания заявки в СМО, объединить все три
канала в один, с втрое меньшим средним временем обслуживания?
Решение. 1) В первоначальном варианте' (трехканальная СМО):
п = 3, % = 4, |л = 1/0,5 = 2; р =* Щ =* 2; и = р//г = 2/3 < 1.
Финальные вероятности существуют. Вычисляем р0 по формулам (11.0.21):
Ро
ft ■ 2 22 23 у.(2/3) у-*_ 1
\ 11 21 31 "^^ 3! (1—2/3) J 9 '
г = А:/,!,1 =4 *0,889; t04 - -f = -f *0,222ч; 7СЙСТ,
i^_J.« 0,889; F04 = -f~ 2
3*31(1/3)2 9 оч Л
==?оч+'об« 0,722.
р
2) При объединении трех каналов в один: п = 1; X = 4; (л = 6;
= 2/3. По формулам (11.0.12)—(11,6.14) имеем -
г - -^ « 1,333; 10Ч = y ^ °'333 Ч; ?сиот ~7" +'л =
= 1/3+1/6 = 0,500.
Таким образом, объединение трех каналов в один, несколько
снизив среднее время пребывания заявки в СМО (g 0,722 до.0,500),
повысило среднюю длину очереди и среднее время пребывания заявки в
ней. Это произошло потому, что, пока три канала совместно
обслуживают одну заявку, другим (вновь пришедшим) заявкам приходится
ждать в очереди.
380
Повышение эффективности обслуживания, наблюдаемое при
объединении каналов^ в замкнутой СМО, связан© о тем, что
интенсивность потока заявок при выходе из строя их ивточников (станков)
уменьшается.
11.38. Рассматривается система массового обслуживания —
стоянка такси, на которую поступают простейший поток пассажиров в
интенсивностью Я и простейший поток машин о интенсивностью у>.
Пассажиры образуют очередь, которая уменьшается на единицу, когда
к стоянке подходит машина (берется «идеальный» случай, когда
водитель безропотно везет каждого пассажира туда, куда ему требуется).
В~случае, если на стоянке нет пассажиров, в очередь становятся
машины. Число мест для машин на стоянке'ограничено (равно г); число
г Д Х\ А*.. . 1 )
\SltQ
SC,0
» 11»
Sf,0
-*—
fyo
—ji-
%
. •£, 1 . '.
« # • _
^ /Г1
S0,H
Г %1
st>A
Рис. 11.38
мест в очереди для пассажиров также ограничено (равно /). Все потоки
событий — простейшие. Посадка производится мгновенно. Построить
граф состояний СМО, найти финальные вероятности состояний,
среднюю длину 7П очереди пассажиров, среднюю длину 7М очереди машин,
среднее ^время t04bJ1 пребывания в очереди пассажира, среднее время
t04, м пребывания в очереди машины и-посмотреть, как эти
характеристики изменятся при т->оо; /->-оо.
Решение. Состояния СМО будем нумеровать соответственно
числу пассажиров и машин на стоянке двумя индексами: первый —
число пассажиров, второй — число машин. Состояние s0,o означает, что
на стоянке нет ни пассажиров, ни машин; состояние s0jft — нет машин,
k пассажиров достояние $с,р — <гмашин, ни одного пассажира. Граф
состояний СМО показан на рис. 11.38. Граф соответствует схеме
гибели и размножения. Применяя.общие формулы (11.0.4) для этой схемы
и обозначая %/\ь =* р, получаем:
Pi-i,o=p/>i,<>; Pi-2,o=p2p*,o; ...; pCfo=p^Pi,o;
P*,o = {l+P + P2 + ...+P/+w}-1 -
Pi.o,
(11.38.1)
или, суммируя геометрическую прогрессию со знаменателем р,
P*,o = 0-P)/(l-P/+m^). (11.38.2)
Вероятности (11.38.1) образуют геометрическую прогрессию с
первым членом pii0 и знаменателем р. Если р > 1, наивероятнейшее
состояние системы будет s0>m— машин нет, все места, в очереди
пассажиров заняты; если р < Г— наивероятнейшее состояние sii0 —
пассажиров нет, все места в очереди машин заняты.
381
При m->-oo, /->oo финальные вероятности не существуют; при
р > 1 очередь пассажиров, а при р < 1 очередь машин имеют
тенденцию возрастать неограниченно (эта тенденция сдерживается тем, что
как число пассажиров, так и число такси в городе бесконечными быть
не могут).
11.39*. В столовой самообслуживания имеется один раздаточный
пункт, на котором отпускаются как первые, так и вторые блюда.
Поток посетителей столовой — простейший с интенсивностью X; на
отпуск как первого, так и второго блюда идет случайное время,
распределенное по показательному закону с одним и тем же параметром |х.
Некоторые посетители берут и первое, и второе (доля таких
посетителей равна q), другие — только второе (доля 1 — q). Найти: 1)
условия, при которых существует устойчивый, стационарный режим
работы столовой; 2) среднюю длину очереди и среднее время пребывания
посетителей в столовой, если он съедает одно блюдо в среднем за
время т, а два блюда — за время 2т.
Решение/ Время, идущее на обслуживание одного посетителя,
представляет собой случайную величину Т, распределенную с
вероятностью q по закону Эрланга 2-го порядка, со средним значением
^обсл = 2/[х, а с вероятностью 1 — q — по показательному закону с
параметром fi. Найдем математическое ожидание случайной величины
7\ Для этого воспользуемся формулой полного математического
ожидания (4.0.20) с двумя гипотезами: Нг = {посетитель берет только
второе}; #2 =* {посетитель берет оба блюда}. Вероятности этих гипотез:
Р (//J = 1—^; P(H2) = q.
Полное математическое ожидание случайной величины Т равно
М [71 - Р (Нх) М [Т\ Нг] + Р (#2) М [Т\Н2] « (1 - q) (I /p) +
+ q (2/|i) - (q + lV|i;
значит, столовая может обслуживать в среднем \i/(q + 1)
посетителей в единицу времени; если к^ \i/(q + 1), то СМО перегружена, и
финальные вероятности не существуют, если же X < \i/(q + 1), то
они существуют. Предположим, что X<.\x/(q+l).
Для нахождения средней длины очереди г, средних времен
пребывания заявки в очереди 70ч и в системе (столовой) 7СИ0Т воспользуемся
формулой Полячека—Хинчина (11.0.31). Для этого надо знать
коэффициент вариации случайной величины Т — времени обслуживания,
Найдем сначала второй начальный момент этой величины М [ТЧ.
По формуле полного математического ожидания (с теми же
гипотезами Н1 и Н2) получим
М [ТЧ = (1 - q) М [Т2|#х] + qK [Т2\Н2]. (11.39.1)
При гипотезе Нг случайная величина Т распределена
показательно с параметром \i:
МЛТЦН,] = D [Т\Нг] + (М 1Т\Нг])2 = 1/fi2 + (1/jx)2 = 2/fx2.
При гипотезе Н2 вычислим второй начальный момент величины Т
по формуле
382
М [Т2|Я2] = D 1Т\Н21 + (М [Г|Я2])2.
Но М [Т\Н2] = 2/|*f (М[Г|Я21)2«4/|А2; дисперсия D 1Л#2)-вдвое
больше, чем D [r|#J> как дисперсия суммы двух независимых
одинаково распределенных случайных величин Тх и Тг% т. е. D [Т\Нг\ =*
= 2/fi2. Следовательно,
М 1Г2|Я2] = 2/jx2 + 4/jx2 - 6/ц\
откуда по (11.39.1)
М [Г] = (1 — q) 2/jji2 + <7б7[*2 в 2 (1 + 2<7)/^а.
Дисперсия случайной величины Г
D IT] = М [72] — (М [Г])2 - (1 + 2? — q2)/^;
отсюда коэффициен-г^вариации случайной величины Т
Vlx = Vl + 2q-q4(q+l).
Подставляя это выражение и р = % (q + 1)/у> в формулу Поляче-
ка—Хинчина (11.0.31), получаем
аз/ц*) (а+ l)2[l + 1+2<у~~^ }
2Ii-(Vji)to+l)[ 1-(^)(<? + l> •
Далее /"оч =* г/Я; £ист '=* £ч + (<7 + Wl* + (Я + 1) * в 'оч + (Q +
+ 1Х(т + 1/|х).
11.40. Пример простейшей СМО о отказами и о приоритетом.
Имеется двухканальная СМО с отказами, на которую поступают два
простейших потока заявок: I с интенсивностью ^ и II с интенсивностью
%2 (будем кратко называть их «заявки I» и «заявки И)». Заявки I
имеют перед заявками II приоритет, состоящий в следующем: если
заявка I приходит в момент, когда все каналы заняты и хотя бы один
из них обслуживает заявку II, то пришедшая заявка I «вытесняет»
из-под обслуживания заявку II, становится на ее место, а та покидает
СМО необслуженной. Если заявка I приходит в момент, корда все
каналы заняты обслуживанием заявок I, то она получает отказ и покидает
СМО. Заявка II получает отказ, если она приходит в момент, когда
заняты оба канала (безразлично какими заявками).
Построить размеченный граф состояний СМОииумеруя состояния
двумя индексами (/, /); первый указывает число заявок I, второй —
число заявок II, находящихся в СМО. Написать уравнения для
финальных вероятностей состояний. Решить их при ^ « %2 =' f.ix = щ «
« 1. Выразить через ptj (i + j < 2) следующие характеристики
эффективности СМО:
Ротк (Рстд — вероятность отказа в момент поступления для
заявки I (II);
At (А2) — среднее число заявок I (II), обслуживаемое СМО в
единицу^ времени;
k[ (£2) — среднее число каналов, занятых обслуживанием заявок
I 01);
383
Ротк, Л, k — те же характеристики для СМО в целом,
безотносительно к виду заявок.
Решение. Состояния СМО: s00 — в СМО нет заявок; s10 —
в СМО одна заявка I и ни одной заявки II; s01 — в СМО ни одной
заявки I и одна заявка II; % — в СМО две заявки I и ни одной заявки II;
sn — в СМО, по одной заявке 1 и Ц; s02 — в СМО ни одной заявки I
и две заявки II. Размеченный граф состояний СМО дан на рис. 11.40.
Уравнения для • финальных вероятностей состояний:
(%х + Jg р00 шв 1хгр10 + ji2p01; (кг + &2 + l*i)*Pio e ^iPoo + 2ft X
X Р20 + |Xt'Pu; 2fAiP2o e KPio + KPii> (K+K + 14) X
X P01 - ^Poo + H1P11 + 2|x2Po2; (*i + |*i + W) Pa = KPio +
+ ^iPoi + hPo2> (K + 2fx2) p02 = h2p01; Poo + P10 + P20 + P01 +
+ Pll+P02==s 1-
Решая их при ^ = V— Hi = jji2 = 1, получаем
poo = 0,20;. p10 = 0,25; p20 = 0,2D; p01 » 0,15;pu = 0,15; p02 = 0,05;
P& - Pzo = 0,2 /><*>" =- p20 + pu + p02 = 0,40; Лх = ^ (1 -
- ВД - 0,8.
Величину Л2 вычислим, учитывая то, что некоторые заявки П,
принятые к обслуживанию, вытесняются заявками I и покидают СМО
необслуженньши. Среднее число таких заявок в единицу времени
равно Лц (ри + р02)> следовательно,
Л2 = X, [1 — (p2J + Рц + Рог)! — fci (Рп + Роа) « 0,4;
Вероятность Ротк того, что произвольно выбранная заявка,
поступившая в СМО, получит отказ, найдем по формуле полной
вероятности с гипотезами: Н1 = {пришла заявка I}; Н2 « {пришла заявка
II}. Вероятности этих гипотез
Р (#i) = V(^i +'**); Р Ш%) - ЫК +}*).
Следовательно,
kj D(l) _|_ ^2 D(2) П^
отк — "7—ГТ~ ^отк "Т *"7—ГТ— *отк — U,0.
М "Г Л2 *П ~Г Л2
Заметим, что все характеристики для заявок! можно было бы
получить, совершенно игнорируя заявки li и рассматривая задачу так, как
если бы на двухканальную СМО с отказами поступали только
заявки 1. Предоставляем читателю убедиться в этом, подсчитав все
характеристики для двухканальной СМО с отказами, на которую поступает
только поток заявок I.
11.41. Условия предыдущей задачи изменены так, что количество
каналов СМО с отказами равно п = 3. Построить граф состояний СМО.
Написать уравнения для финальных вероятностей ptj (i + / < 3),
где i — число заявок I, / — число заявок II, находящихся в СМО.
384
Считая эти уравнения уже решенными, выразить через рц те же
характеристики эффективности, что и в предыдущей задаче.
л
2Д
ho
II
$01
XT
.Li
hi
i b г
■b/t, I
1 Л' r
V
XT
1 г
1 у
7Л'>1
i " ""^*
^"W
%
v;
44
PttC. //.40
Рис. 11.41 -♦
-1_А^г
1 Am 1 - П
J
Jl
T ^ l
1 Л»# 1 — - 1
J
r
t
u
f* L
'? |«- 1
t'v
Tl
I_L
*//
1 1
Li
^/2
1 Л;-[
-•"Wi
1 *»f
J*-^rj
szo
V 1
$21
i ^:,i
J^A/ '
%
j>^
zyd
J*£/%;
Ш
Решение. Граф состояний показан на рис. 11.41.
Уравнения для финальных вероятностей состояний:
(^ +'Я2) Роо =» 1ЛхРю + И2Р01; (*i + ^2 + l*i) Рю = КРоо +
+ ЗИ'Ло + М^Рш (К + К + З^Рго = Vio + Зуцрзо + (х2 ра;
(^i +Л* + ц2) р01 = ^гРоо + \hPn + 2(х2ро2;
(^ + К + ^ + ц>2) Рп e Xipoi + Х2р10 + 2у1р21 + 2р,2р12;
(Хх + [г2 + 2^) р21 = Ях (ри + р12) + Kpzol (^1 + Х2 + 2|х2) р02 «
^sPoi + W12 +'3fi2Po3; (Xi + fti + 2У>2) P12 -^ (p02 + p03) + It^;
(K '+ 3fJL2) роз e ^aPoa;
Poo + Pio + P20 + P30 + Poi+Pu + P2i + Po2 + Pi2 + Po3==l;
*отк = P30J * отк = Р30 + Р21 "ЬPl2 4" Роз»
^1 = ^(1—p30); Л2 = ^11 — (Р30 + Р21 + Р12 + Р03)]— МРоз + Ри + Роз);
^i == ^i/h*; ^2 =* ^2/fe; * = \+^2;
А»1+^2
^i"b^2
Р(2)
отя»
11.42. Пример СМО с очередью и о абсолютным приоритетом.
Имеется одноканальная СМО в двумя местами в очереди (т = 2). На
вход СМО поступают два простейших потока заявок I и II с интенсив-
ностями &!, Х2. Времена обслуживания — показательные с
параметрами ц,х, |л2. Заявка I, прибывшая в СМО, «вытесняет» заявку II, если она
обслуживается, и занимает место в очереди перед ней, если она стоит
в очереди. «Вытесненная» заявка IIJ покидает СМО необслуженной,
если в очереди уже нет мест, и становится в очередь, если места есть.
13 Зак. 1040
385
Нумеруя состояния СМО двумя индексами i9 j соответственно числу
заявок I и II, находящихся в СМО, построить размеченный граф
состояний СМО и написать уравнения для финальных вероятностей
состояний. Считая этим уравнения уже решенными, выразить через
Ри> (i + J ^ 3) следующие характеристики эффективности СМО:
^отк (Рот) — вероятность того, что заявка I (II) получит
отказ немедленно после прибытия;
л2
л>2
х2
S0D
FT
у 1
п
%
1 1'
у |
1 ЛЧ
J">/ L
1 Л'*\
i Mi L
Pz A2
1 I
FT
у j
FT
у j
$12
1 Лг>\
Mz h
ho
FT
1 1
\ 1
SZ1
1 л'~
**Mj
to/
ir^
jr1
Рис. 11.42
Qi (Q2) — вероятность того, что заявка I (II) будет обслужена;
£i fe) — среднее число заявок I (II), связанных с СМО;
гг fo) — среднее число заявок I (II), находящихся в очереди;
Йист» 4ист — среднее время пребывания в системе для заявки
i (H); _
J&V» (41) — среднее время пребывания в очереди для заявки I (II);
*сист — среднее время пребывания в системе для любой
(произвольной) заявки;
t04 — среднее время пребывания в очереди для любой заявки.
Решение. Состояние СМО: stj — в СМО находится / заявок
I и / заявок II (i + j ^ 3). Размеченный граф состояний показан на
рис. 11.42.
Уравнения для финальных вероятностей состояний:
(А* + Я,2) роо = HiPio + |^2Poi; (K + K+ Mi) Рю = *iPoo +
+ У1Р20 + \hPn\ (K + K + Mi) P20 = *iPio + M1P30 + U2P21;
MlP30 = ^L (P20 + P2l); (^1 + ^2 + ^2) P01 = ^2P00 + Ml Pi + 1*2 P02;
(K+K + t*>l + ^2) Pll = ^2PlO + ^lP01 + M1P2I + У2Р12; (K + ^2 +
386
+ |*a) /?02 = ^2Poi + M-iA.2 + VvPos* (Xi + Pi + P2) Pi2 = ^iPo2 +
+ W>ii + ^tPosJ (^1 + P2) Роз = ^гРо2»
Poo + Рю + P20 + Рзо + Poi + Pu + P21 + P02 + P12 + Роз = 1;
PSk=Рзо; 'P£n=Рзо+p2i+Pi2+Po3; Qi = i—?£* = i — Рзо-
Чтобы найти Q2% найдем сначала Л2 — среднее число обслуженных
заявок II в единицу времени:
Л2 = Х2 (1 - Р^) — К (Роз + Pi2 + Р21) = М* — (р30 + ра1 -Ь
+ Pl2 + Роз)1 — ^1 (РОЗ + Pl2 + P2l).
Деля это выражение на Х2> находим среднюю долю обслуживаемых
заявок II (вероятность того, что заявка II будет обслужена): Q2 = Л2А2.
Тогда
*i = Ь(Рю + Рп + Р12) + 2 (р20 + р21) + Зр80; Ч = Ь(Рох + Pii+
+ P2i) + 2(p02 + Pi2) + 3p03;r1 = b(p20 + p2i) + 2р80; r2 =* 1 (pn +
+ P2i)+2p12.
По формулам Литтла
taHGT — Zll^b *сист ==s 22/^2; *оч ==z ^ll^j *оч == ^2/^2 »
Г — ^i /d) | ^2 /(2) . J ^1 7(l> 1 ^2 7(2)
' 'сист ~~ л . n, ^еист-Г . >сист, *t>4 - —— *оч Т"—ГТ—*оч •
Все характеристики, относящиеся к заявкам I, можно вычислить
и не решая уравнений (11.42), а просто игнорируя наличие заявок II,
рассматривая СМО g ограниченным числом мест в очереди (т = 2)
и находя ее характеристики по формулам п. 3 раздела И.О.
11.43. Простейшая СМО без очереди и о «разогревом» каналов. На
вход я-канальной СМО поступает простейший поток заявок о
интенсивностью X. Время обслуживания — показательное о параметром
|л. Перед тем, как начать обслуживание заявки, канал должен
подготовиться («разогреться»). Время «разогрева» Тт& имеет
показательное распределение g параметром v и не зависит от того, как давно
канал прекратил работу. Заявка, заставшая канал свободным,
«занимает» его и ждет, пока он разогреется, после чего поступает на
обслуживание. Заявка, заставшая все каналы занятыми
(обслуживаемой или ожидающей заявкой), покидает СМО и остается необслужен-
ной. Найти финальные вероятности СМО и характеристики ее
эффективности: вероятность отказа Р0тк> относительную пропускную
способность Q, абсолютную пропускную способность Л, вреднее число
занятых каналов k.
Решение. Будем считать, что обслуживание заявки состоит
из двух фаз: ожидания разогрева и' самого обслуживания: Гобсл =
s ^раз + ^обсл- Случайная величина Гобсл распределена по
обобщенному закону Эрланга 2-го порядка (см. задачу 8.39) с
параметрами [г, v. Мы знаем, что формулы Эрланга (11.0.6) справедливы не
13*
387
только для показательного, но.и для любого распределения времени
обслуживания. Найдем величину fjb = 1/М [Тобсл\. Имеем
М [Тобсл1 - М [ГРаз1 + М [70&сл1 - 1/|* + 1/v - (|i + v)%v),
откуда у = (|xv)/(y, + v). Вычислив р = h/\i и подставив это
значение ~р в формулы Эрланга (11.0.6), получим:
л-{» + 4-+- + ^- + - + ^рА-^-л (!<*<«);
Р™=Рп=-^-Ро; Q=i—^-Po, A=w=k(i-lLp\
Чтобы найти среднее число занятых каналов k, нужно разделить
Л на у,:
'-К'-^Ь-'О
п\
1А>.
11.44. Простейшйя одноканальная СМО о очередью и «разогревом»
канала. На одноканальную СМО с неограниченной очередью
поступает простейший поток заявок в, интенсивностью X. Время
обслуживания — показательное о параметром у, (\х > А,). Перед тем как
приступить к обслуживанию заявки, свободный до того канал должен «разо-,
греться». Время «разогрева» — показательное g параметром v и не
зависит от того, как давно канал кончил работу. Если обслуживание
начинается сразу же после конца обслуживания предыдущей
заявки, «разогрева» не нужно. Составить граф состояний СМО и написать
уравнения для финальных вероятностей состояний; выразить через
эти вероятности характеристики эффективности СМО: средние числа
заявок в системе г и в очереди г, средние времена пребывания заявок
в системе /сист и в очереди t04.
Т*1 л '
&•-
Of
п
9
\
%
X \
, л' ,
р
г>'
?--
ч
1
и
9
г
%
Л
Г/i
<•
±_
Л
i /«
11 ♦
Рис. 11.44
Решение. Состояния СМО (рис. 11.44):
s0o — канал свободен, не разогрет;
5oi — пришла одна заявка и ждет, канал разогревается;
su — канал разогрет, одна заявка обслуживается, очереди нет;
s02 — канал разогревается, в очереди две заявки; ...;
38S
i
s0i — канал разогревается, в очереди / заявок;
Sn — канал обслуживает одну заявку, / — Г заявка стоит в
очереди; ....
Уравнения для финальных вероятностей:
ЬРоо = V>Pii> ft + v) Poi e ^Poo* ft + n) Pu «= vpoi + fip12;
ft + v) p02 = fy?oi; ft + ja) P12 = vPo2 + ^Pn + ша ...;
" ft + v)po,z = ^po.i-i;
(h + V)Pia = vPoa + xPi.i-i + m,i+i>---'>
2= 2J/(Pb,i+A,i); r== S '(au+a-m)-
По формуле Литтла
^сист == z A> ^оч ==s r A*
11.45*. Имеется одноканальная СМО g очередью, ограниченной
числом мест т = 2. На вход СМО поступает простейший поток заявок
с интенсивностью К. Время обслуживания распределено по
обобщенному закону Эрланга о параметрами (хх, \i2 (см. задачу 8.39).
Найти вероятности состояний СМО:
s0 — в СМО нет заявок;
sx — в СМО одна заявка (очереди нет);
s2 — в GMO две заявки (одна обслуживается, одна в очереди);
s3 — в СМО три заявки (одна обслуживается, две в очереди).
Найти характеристики эффективности СМО: Ротк, Q, Л,г, г,7сист,70Ч.
Вычислить их для значений К = 2, \ix = 6; |г2 =* 12. 2) Сравнить их
с теми, которые получились бы для простейшей СМО с таким же
значением X и значением \i, равным М0бсл> гДе £>бсл — среднее
время обслуживания заявки в данной СМО.
Решение. Поток обслуживании — не]| пуассоновский,
значит, система не марковская, и найти вероятности состояний СМО по
обычной методике, которую мы применяем для марковских
процессов с дискретными состояниями и непрерывным временем, нельзя.
Однако процесс, протекающий в СМО, можно искусственно свести к
Марковскому, применив так называемый «метод фаз».
Представим обслуживание состоящим из двух фаз (I и И),
продолжающихся соответственно время Тг и Т2; полное время обслуживания
Т'обсл — 7*1 + Т2) где Тг имеет показательное распределение с
параметром \1г; Т2 — показательное распределение с параметром (л2.
Тогда Гобсд будет иметь обобщенное распределение Эрланга с
параметрами \it и \i2 (см. задачу 8.39).
Введем следующие состояния СМО: -
s0 — СМО свободна;
sn — в СМО одна заявка, обслуживание в -первой фазе;
s12 — в СМО одна заявка, обслуживание во второй фазе;
s21 — в СМО две заявки (одна обслуживается и одна в очереди);
обслуживание в первой фазе;
389
s22 — в СМО две заявки, обслуживание во второй фазе;
s31 — в СМО три заявки, обслуживание в первой фазе;
Saa — в СМО три заявки, обслуживание во второй фазе.
Дальнейших состояний нет, так как (по условию т = 2) больше трех
заявок в СМО быть не может. Размеченный граф состояний СМО
показан на рис. 11.45. При таком подходе мы состояние sx расчленяем на
два: sn и s12 (или, короче, st = su + s12); аналогично s2 = s21 + s22,
s3 = s31 + s32. Уравнения для финальных вероятностей,
соответствующих графу рис. 11.45, будут:
ьро = v>tPi2\ (^ + i*i) Ри = ^Ро + ^2P22; (^ + ^2) Pi2 — HiPu;
(X + [ix) р2Х = fi2p32 + Ярхх; (X + \i2) р22 = ^!р21 + Яр12;
HlPsl = ^P2ll 1^32 в MlPsi + ^P22i
нормировочное условие р0 + Рп + Pi2 + Р21 + Р22 + Р31 + Рз2 = 1-
Решая эти уравнения, получаем:
Ро
и***! m-iIlaI
•г1-
P11 = Po> P12 — —- Po, Р21 — -7-7; Po»
^(Hl+li2±ALn. n . ^ft + El + l^+^mfl + fa) n.
P22 = ~ Po» P31 — T~Z Po»
Hil*i vlv\
Далее находим финальные вероятности состояний sx, s2, s3:
Pi = Pu + Pi2=: (b + fc + l4)W
p2 = P21+P22 = -77 [ft+Hi) ft+h<i -Ы*а) + ^ ft+M Po;
M-l ^2 -v
Рз = Рз1 + Р32=-Г^[(^2 + ^1 + (Х|)(^ + ^1 + (Х2)^
J*lM<2
+ h> №1 +14) ft +14)1 Po, (П .45.2)
где ро определяется первой из формул (11.45.1).
Характеристики эффективности СМО могут быть найдены через
вероятности р0, рх, р2, р3 по формулам:
Л>тк = Рз; _Q = 1 — Рз; А = Я (1 — рз); z == 1рх + 2р2 + Зр3;
г = 1р2 + 2р3; /сист = г/Я; /оч = г/1. (11.45.3)
390
Подставляя в формулы (11.45.1) численные данные X = 2, щ = 6, 1
|л2 = 12, получаем: р0 = 0,540; рХ1 « 0,182; р12 = 0,090; р21 = 0,087; |
р22 = 0,050; Psi = 0,029; р32 = 0,022. Отсюда, возвращаясь к
исходной (не марковской) СМО, имеем: р0 = 0,540; рх — 0,272; р2 = 0,137,
Рз = 0,051.
Далее, по формулам jl 1.45.3): Ротк = 0,051; Q = 0,949; А =* 1,89;
г = 0,705;- г = 0,243; /сист = 0,352; *оч = 0,122.
2) Подсчитаем те же характеристики для простейшей СМО с теми '
жеХ = 2, |л = (1/щ + l/fia)"1^ 4. Поформулам (11.0.12) — (11.0.15) \
имеем: р = 0,5; р0 « 0,533; k = 1 — р0 « 0,467; рх = рр0 « 0,267;
р2 = Р2Ро « 0,133; р3 = р3Ро « 0,067; Ротк = р8 « 0,067; Q == 1 — I
— р3 » 0,933; Л » 1,866; г"» 0,733; Г = 0,267; £ист« 0,367; t04 «
« 0,133.
Мы видим, что наша не марковская СМО имеет над простейшей
СМО некоторое преимущество по пропускной способности и очень мало
отличается от нее (в лучшую сторону) по времени пребывания заявки
в СМО и по длине очереди.
Рис. 11.45 Рис. 11.46
11.46*. Имеется одноканальная СМО о двумя местами в очереди.
На ее вход поступает пальмовский поток заявок с интервалом Г,
распределенным по обобщенному закону Эрланга с параметрами Хъ Xz;
время обслуживания — показательное g параметром р. 1) Применяя
метод фаз, написать уравнения для финальных вероятностей
состояний р0, Рх, р2, Рз^Выразить через эти вероятности характеристики СМО:
Л>тк> Q» ^э 2,7, £сист, /оч. 2) Вычислить финальные вероятности и ха
рактеристики эффективности для следующих исходных данных: Хг =
=- 3, Хг = 6; \х = 4 и сравнить их g теми, которые соответствуют
простейшей СМО в параметрами X — (1/?^ + 1А2)~Х = 2, (х = 4,
рассмотренной в задаче 11.45.
Решение. 1) Если рассматривать, как мы делаем обычно,
состояния СМО, нумеруя-их соответственно числу заявок в СМО: s0,
391
s±t s2, s3> т0 система не будет марковской. Чтобы ее марковизировать,
разделим на две фазы (I и II) не время обслуживания, а интервал Т
между заявками: Т = Тг + Г2, где случайные величины 7\ и Т2
имеют показательное распределение с параметрами Я^ и А,2 соответственно.
"Состояния СМО будем нумеровать по числу заявок в СМО и
номеру фазы между заявками:
s0i — заявок в СМО нет; интервал между заявками в первой фазе;
s02 — заявок в СМО нет; интервал между заявками во второй фазе;-
sii — в СМО одна заявка (обслуживается); интервал между
заявками в первой фазе;
s12 — в СМО одна заявка (обслуживается); интервал между
.заявками во второй фазе;
s21 — в СМО две заявки (одна обслуживается, другая в очереди);
интервал между заявками в первой фазе;
s22 — в СМО две заявки (одна обслуживается, другая в очереди),
интервал между заявками во второй фазе;
s31 — в СМО три заявки (одна обслуживается, две в очереди);
интервал между заявками в первой фазе;
s32 — в СМО три заявки (одна обслуживается, две в очереди),
интервал между заявками во второй фазе.
Граф состояний СМО дан на рис 11.46.
Уравнения для финальных вероятностей:
^iPoi = У>Рш КРо2 =* Voi + Wit* (К + V) Рп — b>iPoy+ H^2i!
(^2 + \>) Pi2 e Vu + УР22; (^1 + и) P21 — ^2Pi2 + tv>3i;
(К + v) P22 — KP21 + у>Рз2#> (K + u) Pn~ Кр%2 + ^гРзг;
(^2 + И) Рз2 « КРП-
Нормировочное условие р01 + р02 + ри + р12 + p2i + Р22 +
+ Psi + Рзг =* 1-
Э^и уравнения удобнее всего решать, выражая вероятности ptj
через последнюю, р82. Выражения для вероятностей ptj (i =3 0, 1, 2,
3; ] =* 1, 2) имеют вид:
Ps-fi 1 ^ + К 1 ^ + %* + **) 1 Р^' + ^М-З^Е + Ь» \
^ кщ "*"
. |*«ft*8+2** ft2 +Ы2 у?+Х1ц+2Х{Х2у,+3'к1 \1 + Ц) .
^ Ч Ц
**" ЧЦ
\i3(\i3+2Xi\i*+3%2\i2 + X\ii+2%i%2\x + 3\l\i-h'ki)
Рз1 — ""Г Рз2> Р22 -4 Г"7 Р32»
392
■г
—-.
._|i(|i'+Xni+2XlTi+Xl) , .
_ ^2(Ц2+2^Ц+2Я2ц+^+Х1Х2 + Ц) .
Pl2 ^2Ц ^82'
Pll J^j Р32>
H* (jji8+3>.i JX2+3X2 ц2+ "Xf \i+MiM\x +
■ _ , +3X»ti+xf+x;xa+x1x«+x} .
P02 —щ; Рз2,
P01 5^2 Л*
Переходя обратно к исходной (не марковской) СМО, получаем:
Ро = Р01 + Р02*» Pi = Pll + Pl2; Р2 — Р21 + P22J. ^3 = Р31 + Р32-
Далее, Р0Тв_= Рз'> Q =J — Р__3; Л = Ql\ z = 1р2 + 2р2 + Зр3;
' = 1р2 + 2р3; 4ист = ^Д; *оч = г/1.
Финальные вероятности состояний: р01 « 0,308; р02 « 0,208; рп &
« 0,231; р12 » 0,082; р21 « 0,091; р22 ^ 0,032; р31 « 0,037; р32 »
«0,011.
Для исходной (не марковской) СМО р0 = 0,616; рг = 0313; р2 =
& 0,123; рз « 0,048; Ротк& 0>048; Q « 0,952; А я* 1,904; 2 « 0,703;
г & 0,219; *сист « 0,352; /оч « 0,110.
Из сравнения этих данных с результатами предыдущей задачи
11.45 делаем вывод, что СМО задачи 11.46 имеет незначительное
преимущество перед СМО задачи 11.45 по всем характеристикам
эффективности и несколько большее преимущество перед простейшей СМО
с теми же X, \i.
11.47. Простейшая СМО без очереди с неограниченной
взаимопомощью между каналами. На л-канальную СМО с отказами поступает
простейший поток заявок с интенсивностью А,. Каналы работают со
«взаимопомощью» — если в момент обслуживания очередной заявки
в СМО есть свободные каналы, то все они подключаются к
обслуживанию данной заявки. Интенсивность простейшего потока обслуживании
заявки есть некоторая функция [i, = cp (k) числа k каналов,
одновременно обслуживающих ее. Построить граф состояний СМО и найти
финальные вероятности состояний. Выразить через них характеристики
эффективности СМО: вероятность отказа Р0тк» относительную
пропускную способность Q, среднее число занятых каналов k. Подсчитать эти
характеристики при п = 4Д = 1, р (k) = ftp, \l = 0,5 и сравнить их
с теми же характеристиками в случае отсутствия взаимопомощи между
каналами.
Решение. Так как в момент прихода первой же заявки все п
каналов подключаются к ее обслуживанию, то это означает, что все
каналы вместе всегда работают как один. СМО превращается в одно-
канальную СМО о отказами; ее состояния: s0 — ни один канал не
занят; sn — все п каналов заняты. Размеченный граф состояний показан .
393
на рис. 11.47. Пользуясь зтим графом, получаем финальные
вероятности состояний:
— fit- Х I*"1 — ф(/|) = — — 'К
Ро V Ф(я) J <р(л)+* ' Pl~ ф(я) Л"" ф(я)+Х '
При ф (я) = «(л имеем р0 = (л?jx)/(«jjl + Я); pj = k/(n\i + Я).
При п = 4Д = 1, и, = 0,5 имеем р0 = 2/3; pj = 1/3; Ротк = р3 =
= 1/3; Q = 1 - Pl = 2/3; Л = Щ *= 2/3 » 0,667.
Среднее число занятых каналов~k = 4-1/3 + 0-2/3 = 4/3 « 1,333.
Этот же результат получим, деля А на \х\ Ъ = (2/3)/0,5 = 4/3.
X
р»
>-
"S1
pw
Для сравнения рассчитаем те же характеристики эффективности
для четырехк-анальной СМО без взаимопомощи между каналами [см.
формулы Эрланга (11.0.6) и вытекающую из них (11.0.7)1; при р =
= Wjji = 2
Ро - (1 + Р + Р2/2 + р8/6 + PV24}-1 - 1/7;
Ротв = р4 == (2/3) (1/7) - 2/21; Л = Л (1 — 2/21) » 0,905; Q = А\
k « Л/|1» 1,81.
' Сравнивая эти характеристики с ранее полученными для СМО со
взаимопомощью между каналами, приходим к выводу, что в наших
условиях взаимопомощь невыгодна. Это на самом деле так — для СМО
с отказами неограниченная взаимопомощь (когда все каналы сразу
«набрасываются» на одну заявку, а тем временем вновь приходящие
заявки получают, отказ) всегда невыгодна.
11.48. Простейшая СМО без очереди с равномерной взаимопомощью
между каналами. Имеется простейшая л-канальная СМО с отказами,
на которую поступает поток заявок о интенсивностью Я,. Между
каналами осуществляется взаимопомощь, но не объединением всех
каналов в один, как в предыдущем примере, а так называемая «равномерная»
организованная следующим образом. Если заявка приходит в момент,
когда все п каналов сврбодны, то все каналы принимаются за ее
обслуживание; если в момент обслуживания заявки приходит еще одна,
часть каналов переключается на ее обслуживание; если, пока
обслуживаются эти две заявки, приходит еще заявка, часть каналов
переключаются на ее обслуживание и т. д., пока не окажутся занятыми все
п каналов; если они все заняты, вновь пришедшая заявка получает
отказ. Функция ф (k) = k\i, т. е. обслуживание k каналами в k раз
быстрее обслуживания одним Каналом.
Составить размеченный граф состояний СМО, определить
финальные вероятности состояний и характеристики эффективности: Q, Л,
394
k. Подсчитать их при п » 4, % = 1, ц = 0,5, т. е. в условиях задачи
11.47, и сравнить с тем, что получается без взаимопомощи*).
Решение. Состояния СМО нумеруются по числу заявок,
находящихся в СМО. Граф состояний дан на рис. 11.48. Этот граф *-
тот же, что для простейшей одноканальной СМО о
производительностью ji* = п\х и ограниченной очередью, имеющей п — 1 мест. Для
определения ее характеристик можно воспользоваться формулами
(11.0.16)—(11.0.19); полагая р = р* = У|л* « X/(n\i) = 0,5; имеем
при т =ь 3:
! —(Р*)5 1—0,55
' 0,032;
А = X (1 — р4) » 0,968; Q = 1 —р4 » 0,968; k = Л /fi* я* 1,936.
В тех же условиях (см. задачу 11.47) при отсутствии взаимопомощи
имеем: Л «0,905; Q^0,905; &« 1,81, т. е. «равномерная»
взаимопомощь несколько увеличивает пропускную способность СМО. В данном
случае это увеличение незначительно, так как СМО сравнительно
мало нагружена.
Г*
-fc
ъ)
п/с
пр.
Рис. 11.48
1.49. Для простейшей трехканальной СМО с отказами и
параметрами: X = 4 заявки/мин, среднее время обслуживания заявки одним
каналом 1/|х = 0,5 мин, интенсивность обслуживания заявки к
каналами ф (k) = k\L определить характеристики эффективности СМО
Q, Л, АГдля трех вариантов использования СМО: 1) при отсутствии
взаимопомощи; 2) при неограниченной взаимопомощи; 3) при
равномерной взаимопомощи между каналами.
Ответ: 1) Q » 0,79; Л « 3,16'Лг « 1,58; 2) Q = 0,6; Л = 2,4;
&~= 1,2; 3) Q « 0,887; Л « 3,51; ft « 1,76.
11.50. Простейшая СМО с неограниченной очередью и со
взаимопомощью между каналами. Имеется простейшая л-канальная СМО,
на которую поступает поток заявок с интенсивностью %\ время
обслуживания заявки одним каналом — показательное с параметром fi.
Интенсивность потока обслуживании заявки k каналами
пропорциональна их числу: ф (k) = k\i. Каналы распределяются по заявкам,
находящимся в СМО, произвольным образом, но при условии, что если
*)При нашей постановке задачи все равно, какая часть каналов
переключается на обслуживание вновь прибывшей заявки; важно, что все время работают
все п каналов и ни одна вновь пришедшая заявка не получает отказа, пока вСМ0
не окажется п ваявокГи все п каналов будут по одному их обслуживать*
395
в СМО находится хотя бы одна заявка, все п каналов заняты
обслуживанием.
Нумеруя состояния СМО по числу заявок, находящихся в ней,
построить размеченный граф состояний, найти финальные вероятности
состояний и вычислить характеристики эффективности СМО: &, \ 7,
*сиет> *оч»
Решение. Граф состояний этой СМО совпадает с графом
состояний простейшей одноканальной СМО g неограниченной очередью,
с интенсивностью потока заявок X и потопа обслуживании n\i (см. п. 2
раздела 11.0). Полагая в формулах (11.0.12)—(11.0.15) р = х == ?i/(/zjx),
получаем ро — 1 —и; pk — х* (1 — х) (k = 1, 2, ...); J= х/(1~х);
Г = х2/(1 — и);Лист = Х(1—н) ; *°ч = А,(1-к) '
Характеристики эффективности СМО в данном случае совершенно
не зависят от того, обслуживают ли каналы заявки «все как один»
или «равномерно», так как заявки не получают отказов (заметим, что не
меняются от этого только средние значения случайных величин Z,
/?, Тсист, Точ, а не их распределения).
11.51. Простейшая СМО с ограниченной очередью и равномерной
взаимопомощью между каналами. Рассматривается простейшая СМО
с п каналами и * равномерной взаимной помощью между каналами.
На СМО поступает простейший поток заявок с интенсивностью X;
поток обслуживании одного канала — простейший с интенсивностью
|i; k каналов, обслуживающих одну заявку, дают суммарный поток
обслуживании с интенсивностью уЩ = kp. Каналы распределяются
между заявками «равномерно» в том смысле, что каждая вновь
пришедшая заявка начинает обслуживаться, если только есть возможность
выделить для этого канал. Заявка, пришедшая в момент, когда все п
каналов заняты, становится в очередь. Число мест в очереди т\ если
они все заняты, заявка получает отказ.
Нумеруя состояния СМО по числу заявок, находящихся в ней,
составить размеченный граф состояний СМО и найти финальные
вероятности состояний. Найти характеристики эффективности СМО: Рогв, Q,
/1, С, Г, ^сИСТ» *ОЧ'
Решение. Состояния СМО:
s0 — система свободна;
sx — одна заявка обслуживается всеми п каналами; ...;
sft — k заявок обслуживаются всеми п каналами (1 < k < n)\ ...;
sn — п 'заявок обслуживаются п каналами, очереди нет;
sn+i — п заявок обслуживаются п каналами, одна заявка стоит
в очереди; ...;
sn+m — п заявок обслуживаются п каналами, т заявок стоят в
очереди.
Граф состояний СМО дан на рис. 11.51. Этот граф состояний СМО
совпадает чз графом состояний простейшей одноканальной СМО в
ограниченным числом т мест в очереди, интенсивностью потока
заявок К и интенсивностью потока обслуживании п\х (см. раздел
396
I 1 \\ 1 *4l 1 \. Jk. L?L. JL f
1 П/1 njt njl fi/4, Л/l Л/1
Рис. 11.51
11.0, п. 3). Подставляя в формулы (11.0.16)—(11.0.20) yt^k/(n\i) вместо
р и п + т вместо т, получаем:
ров(1_ху(1_х»+*+*); pft = x*p0 (£=1,...,я + т);
* отк ^ Pn +ml Q.— I —Pn+ml ^ == ^Q.
-_ х»[1^хя^(/1 + т+1-(я + т)х)] . -=- . ^
(1_к"+т+2)(1-х) ' '
^СИСТ = 2 А'» ^04 == Г А'
11.52. На вход автоматизированного банка данных (АБД)
подается в среднем к = 335 статей/ч. Первая операция по обработке
входного потока первичных информационных документов (ПИД) состоит
в отборе тех статей, которые должны вводиться в АБД. В отборе
участвует 6 человек (отборщиков); средняя производительность каждого
отборщика (х = 60 статей/ч. Известно, что в среднем из входного
потока отбирается для ввода в АБД 61,3% ПИД. Все потоки событий -—
простейшие. Рассматривая систему отбора ПИД для ввода в АБД
как шестиканальную (п = 6) СМО с неограниченной очередью,
определить ее характеристики эффективности: Л, Q, k, z, г, 7СИСТ, 70Ч.
Решение. Так как очередь неограниченна, Q = 1; А =%.
Интенсивность потока ПИД, отобранных для ввода в АБД, %0 = кр9
где р ж 0,613, т. е. %0 = 335-0,613 « 205 статей/ч.
Интенсивность потока ненужных для ввода в АБД ПИД будет
Ян = Я (1 — р) « 130 статей/ч.
Среднее число отборщиков, занятых отбором ПИД, Тг — У[л = р —
= 5,58 и не зависит от числа каналов (отборщиков). Стационарный
режим в СМО существует, если выполнено условие х = %1(п\х) < 1;
в нашем случае qho выполнено (х = 0,93).
Вероятность того, что в СМО будут заняты работой все п
отборщиков [см. формулу (11.0.22)], равна
Пользуясь таблицами, данными в приложениях 1, 2, получаем
р6 = 0,1584 /(0,67034-0,1584^LW0,0569.
Среднее число ПИД в очереди [см. (11.0.23)] 7 === pnx/(l — х)2 ^
«10,8. Среднее время пребывания ПИД в очереди t04=7/Xtt 1,87 мин.
Среднее число ПИД, находящихся в системе (в очереди и на обработ-
397
ке), z « г + р « 15,38. Среднее время пребывания ПИД в системе
'сист = *оч + V\*> « 2>87 МИН.
11.53. На вход СМО (рис. 11.53) подается простейший поток
заявок в интенсивностью X. Обслуживание состоит из двух
последовательных фаз, выполняемых в CMOi и СМ02. В СМОа проводится об-
loz
Поток заявок на повторное обслуживание
Aozf?-P) ecMOj
U/7-Д
Рис. 11.53
служивание заявки, а в СМ02 контролируется качество проведенного
в СМОх обслуживания. Если в СМ02 не обнаружено недостатков в
обслуживании, то заявка считается обслуженной в СМО; если в СМ02
обнаружены недостатки в обслуживании, то заявка возвращается на
повторное обслуживание в СМОх (см. рис. 11.53). Вероятность того,
что заявка, обработанная в СМОь будет в результате контроля в СМ02
возвращена на повторное обслуживание в CMOi, равна 1 — р и не
зависит от того, сколько раз она была обработана в СМОх.
СМОх и СМ02 представляют собой пг- й ^-канальные системы
с неограниченной очередью и интенсивностью потоков обслуживании
в каждом канале щ и ^ соответственно. Время повторного
обслуживания заявки в канале .в CMOj и повторного контроля качества
обслуживания заявки в канале в СМ02 распределено (так же, как и при
проведении этих операций впервые) по показательному закону с
параметрами у>! и |Х2 соответственно. Определить условия существования
стационарного режима работы рассмотренной СМО, считая, что
потоки заявок, поступающие в СМОх и СМ02, простейшие.
Решение. Обозначим %г интенсивность потока заявок,
подаваемых на вход CMOj. Очевидно, что %х > X, так как на вход СМОх
будет поступать поток заявок, направляемых на обслуживание в СМОх
впервые (интенсивность потока %), плюс поток заявок, направляемых
на повторное обслуживание (см. рис. 11.53). Если стационарный
режим существует, то интенсивность потока обслуженных в СМ02
заявок %01 будет равна интенсивности ^. Поток обслуженных в CMOi
заявок поступает в СМОг, следовательно, на вход СМ02 поступает
поток заявок с интенсивностью ^ = ^ = Я01. В силу наличия
стационарного режима в СМ02 интенсивность потока заявок на выходе
СМ02 (Х02) будет также равна i^. Таким образом,
^1 в ^01 *~ ^2 —"
(11.53.1)
398
Очевидно, что интенсивность потока обслуженных заявок к0 на
выходе СМО в стационарном режиме будет равна интенсивности
входного потока А,.
Интенсивность потока обслуженных в СМО заявок к0 будет равна
интенсивности потока заявок на выходе СМ02 (A,^), умноженной на
вероятность р того, что заявка не будет возвращена в СМОх на
повторное обслуживание:
KP = h = h (11.53.2)
откуда
%02=%!р. (11.53.3)
Таким образом [см. формулы (11.53.1)—(11.53.3)1,
Я1==^ = Мр. (11.53.4)
Для того чтобы существовал стационарный режим работы в СМО,
необходимо, чтобы как СМОх, так и СМ02 «справлялись» с потоком
поступающих на них заявок; следовательно, должны выполняться
два условия:
*i = V(ni|*i) = ^(рпгуьд < 1; (11.53.5)
Щ = Мл*Н*) = M(prh\h) < 1. (11.53.6)
Они вытекают из того, что как СМОц так и СМ02 представляют собой
пг- и я2-канальные системы с интенсивностью обслуживания в кана-
лак \i± и \i2 соответственно^ с неограниченными очередями (см. п. 4
начала этой главы).
11*54. Для условий предыдущей задачи определить среднее время
пребывания заявки в СМО и среднее число заявок, находящихся в СМО.
Решение. Среднее время однократного пребывания заявки в
СМОх \ (см. рис. 11.53) будет определяться из условия, что на вход
этой системы поступает простейший поток заявок с интенсивностью
%г = Я/р, число каналов обслуживания пъ интенсивность
обслуживания fx*, число мест в очереди неограниченно. Для этих условий в
соответствии с (11.0.21)—(11.0.25) имеем
^(Рх+йаг1^— + PT,tlp°\i - (1К54Л)
\ Of A X
Pi = ; *1 = -^-; Я1= — ;
где
Pi= . _ „ . _
Pai=[i+-£|_+^L+...+4+^4^1".
[ 1! 21 пг\ n^tijl 1— >ci J
Аналогично рассчитываем величину \ — среднее время
однократного пребывания заявки в СМ02 для условий Я^ = к/р; п%\ у^:
r2 = (p2+r^^1 = -i-+ Р",^'Р" , (И .54.2)
(л2 л2./г2!(1—Х2)2л2
399
где
Рог
-[
X
II "*" 21
п2
л2 =
1+4?-+-£?-+...+
Р2
1*2
я2!
1-х
Следовательно, ереднее время однократной обработки заявки
СМО! и СМ02 будет
*i2 = Fi+72. (11.54.3)
Из условия задачи 11.53 следует, что случайная величина X —
число циклов обработки одной заявки в СМОх и СМ02,будет иметь
геометрическое распределение, начинающееся с единицы, с параметром pi
X:
1
2 | 3
pq | pq*
РЯ[
fe-i
(11.54.4)
Обозначим 7\, Г2, ..., Tk, ... — время первого, второго, ..., ft-ro
цикла обработки заявки в СМОх и£М02. По условиям задачи
случайные величины 7\, ..., Tk, ... независимы, одинаково распределены
и имеют математическое ожидание т^.
. Время пребывания заявки в СМО (о учетом возможных возвратов
заявки на повторное обслуживание) можно записать в виде Т =*
х
= 2 Thi т. е. оно представляет собой сумму случайного числа слу-
чайных влагаемых, где число слагаемых X не зависит от случайных
величин Тц Т2, Т$, ... В еоответвтвии с решением задачи 7.64 находим
математическое ожидание величины Т:
7*= М IT] = М [Тк] М [X] *= т~/р. (11.54.5)
Для рассмотренной СМО формула Литтла также справедлива,
поэтому ереднее число заявок, находящихся в СМО, будет определяться
по формуле
г*= а. (11.54.6)
11.55. Условия задачи (11.53) изменены так, что в СМОх и СМ02
проводится только первичное обслуживание и его контроль; если
заявка не прошла контроль в СМ02, то она направляется на повторное
обслуживание в СМ03 и повторный контроль в СМ04 (рис. 11.55).
СМ03 и *СМ04 представляют собой п8- и /г4-канальные системы с
показательным распределением времени обслуживания заявок в каналах
с параметрами fi3 и |х4 соответственно. Вероятность того, что заявка»
обработанная в СМ03, будет в результате контроля в СМ04
возвращена на повторное обслуживание в СМ08, равна 1 — я. Определить
условия существования стационарного режима работы рассмотренной
в этой задаче СМО, считая, что потоки заявок, поступающие в СМОх,
СМ02, СМ03 и СМ04, являются простейшими.
400
Г'
я"
Лг
смо,
_смо_
М-р/ А.2
смог
Л(Т-р) Пото/е заявок, не прошедших контроля
\Лр\
в смо7
ШЦ
е-
\л0=л
—^-
|_.
Поток заявок на повторное обслуживание
Рис. 11.55
Решение. В рассматриваемой СМО в стационарном режиме
будет иметь место очевидное равенство (см. рис. 11.55)
л, — ^ — %01 = ^ = ^о;
(11.55.1)
Следовательно, интенсивность потока заявок, которые прошли
однократное обслуживание и контроль в СМО! и СМ02, будет %р. Поток
заявок, не прошедших контроля в СМ02 и направляемых на повторное
обслуживание в СМ03 и СМ04, будет иметь интенсивность X (1 — р).
Работа системы повторного обслуживания СМ03 и СМ04 (от точки I
до точки 2 на рис. 11.55) принципиально ничем не отличается от работы
системы, рассмотренной в задаче 11.53.
Из всего сказанного следует, что для стационарной работы
рассматриваемой в этой задаче СМО должны выполняться совместно
следующие условия:
fc ^i A, ^i Ml— Р)
к1 = <1; и2 = <1; и3= —-——
«1 |Я1 Л2 Щ ЛП3 ИЗ
<1;
ЯП JX4
•<1.
(11.55.2)
Кроме того, будут иметь место равенства (см. рис. 11.55)
%3 = Я03 - К = К, = * О - Р) я"1. (11.55.3)
11.56. Для условий предыдущей задачи определить среднее время
7 пребывания заявки в СМО и среднее число заявок г, находящихся
в СМО.
Решение. Среднее время пребывания заявки в СМОх будет
определяться из условия, что на вход этой системы поступает
простейший поток заявок с интенсивностью %г — % [см. рис. 11.55 и формулу
401
<11.55.1)1, число каналов обслуживания пг, интенсивность
обслуживания в канале \ilf числе меет в очереди неограниченно. Для этих
условий в соответствии е (11.0.21)—(11.0.25)
T1=(p1+F1)x»i=-L+ f)1'; (И.56.1)
где
I 1! 2 я*1 /ii»/if! 1—Xi J
Аналогично рассчитываем величину 4 Для СМ02 при %2~ К Ягэ Нз:
р,2 «2»Я21(1—Х2) *Л
где
ц2 п2
Среднее время пребывания заявки в СМОх и СМ02 равно
^i2 = ^i + 4. (11.56.3)
Среднее время t3 однократного пребывания заявки в СМ03 будет
определяться из следующих условий: на вход этой системы поступает
простейший поток заявок в интенсивностью %3 = к (1 — р)Ы [см.
рис. 11.55 и формулу (11.55.3)1, число каналов обслуживания п3>
интенсивность обслуживания в канале [х,3, число мест в очереди
неограниченно. Тогда в соответствии с (11.0.21)—(11.0.25)
еде
*з = (Рз + 'з) Ьз 1 = 1 /|Ц+ Р^*1 P<*/lnznsl (1 —*3)2U (11.56.4)
Po3=fi+^+-^+...+-^+^fri-ri.
I V 2I «з* «3Л31 1— Щ )
Аналогично рассчитываем величину ^ для СМ04 при ft4 «= Я (1—
— р)/я, п4, и^
74 «= (р4 + 74) V = 1/|х4 + рЧ*+1р0АПп**щ\(1 — *А)%}9 (11.56.5)
402
где
р4=—- =—г-^; **=—\
Следовательно, среднее время однократной обработки заявки в СМ05
и СМ04 будет
^4} = ^ + Г4. (11.56.6)
В соответствии с формулой (11.54.6) математическое ожидание
времени пребывания заявки в СМ03 и СМ04 (см. рис. 11.55) с учетом
возможной повторной обработки равно
?а4 = тЙ}/я. (11.56.7)
Для определения среднего времени пребывания заявки в СМО
рассмотрим две гипотезы: 1) Нг — заявка подвергалась только
однократной обработке; Р (Ях) = р; 2) Н2 — заявка подвергалась
многократной обработке; Р (Н2) = 1 — р.
При гипотезе Нг математическое ожидание времени пребывания
заявки в СМО будет определяться по формуле (11.56.3), при гипотезе
#2 — по формулам (11.56.7) и (11.56.3). Полное математическое
ожидание времени пребывания заявки в СМО будет
7 = т12 + xJV (1 — р)/я. (11.56.8)
Среднее число заявок, находящихся в СМО, определяется по
формуле Литтла:
г = к (11.56.9)
11.57. Рассмотрим условия задачи 11.53 применительно к
многократной обработке информации в двух фазах. С целью контроля
правильности перфорации она осуществляется дважды: на
перфораторе и на «контрольнике», с помощью которого обнаруживают
ошибку. Перфораторщица осуществляет в среднем одну ошибку на
1000 знаков (букв, цифр и т. п.). Каждая перфокарта содержит в
среднем 80 знаков. Если во время контроля на перфокарте обнаружена
хотя бы одна ошибка, то эта перфокарта возвращается снова на
перфорацию. За год необходимо обработать 50000 документов, каждый из
которых содержит в среднем 400 знаков.
Найти минимально необходимое число перфораторщиц,
работающих на перфораторах и контрольниках, если одна перфораторщица в
год перфорирует 4,2-106 знаков, и определить характеристики такой
системы.
Решение. Из условий задачи следует, что в год необходимо
в среднем отперфорировать и проконтролировать 50 000»400/80=
= 250 000 перфокарт. Следовательно, к = 250 000 перф./год = 125
перф./ч = 2^083 перф./мин. Производительность перфораторщицы, ра-
403
ботающей за перфоратором или на «контрольнике», составляет р* =в
=г,х2 = 4,2-106/80 = 52-5000перф./год = 26,25 перф./ч = 0,438 перф./
мин. Вероятность необнаружения ни одной ошибки на перфокарте
равна р = 0,99980 « 0,9. При этом мы пренебрегаем вероятностью того,
что и перфораторщица и контролер ошибутся одинаково в одном и
том же знаке. Эта вероятность намного меньше, чем (0,001)2 = 10~6,
так как клавиатура перфоратора и «контрольника» имеет около 50
различных знаков. Если считать, что ошибочно может быть нажат на
клавиатуре любой знак из 50, то получим вероятность одинаковой
ошибки, равную 10~6/2500. Если считать, что ошибочно может быть
нажат на клавиатуре только ближайший к нужному знак (а их от 5 до
8), то эта вероятность будет 10~6/25 — 10~6/64.
Условие стационарной работы перфораторщиц будет [см. формулы
(11.53.5), ^(11.53.6)1
ЩЧУ^Р) = хх < 1; %/(n2ii2p) = щ < 1,
откуда пг > У(ир) « 250 000/(52.500-0,9) « 5,29; щ > 5,29.
Таким образом, нужно иметь шесть перфораторщиц и шесть
контролеров.
Характеристики работы перфораторщиц: JiBXl = %/р = 250 000 :
: 0,9 = 278 000 перф./год; пг = 6; [1г = 52-500 перф./год; щ = % :
: (%р[х) = 0,882; рх = fc/(p|Ai) « 5,29.
По формуле (11.0.22) находим вероятность того, что вс£ шесть
перфораторщиц будут заняты и «очереди» документов, подлежащих
перфорации, нет:
рп>== ZUb-Jtt _= 2il* 0,107.
и 0 882
R (nlt 9i) + P(nlt Pl) j—^- 0,282 + 0,152 1JQ>882
Среднее число перфокарт, ожидающих в очередь на перфорацию,
~h - PW(1- *i)2 = 6,78.
Среднее время ожидания перфокарты в очереди: 70Ч = Т^рЪг1 =
= 2,92 мин; \ = ?оч1+ 1/^ — 5,21 мин. -
Общее число перфокарт в первой фазе z[ *= гг -f kx = rL + рг —
= 12,07.
Так как характеристики второй фазы (контроля) такие же, как и в
первой, то можно выписать общие характеристики работы еиетемы <э
учетом возврата перфокарт на новую обработку. Общее среднее число
перфокарт, находящихся в системе, г = 2гг — 24,14; из них в очереди
будет г = 2гх = 13,56. Общее среднее время обработки одной
перфокарты с учетом ее возможного возврата на повторную обработку равно
7= %l2/p ~ (tx + 72)/р = 2tx/p = 11,57 мин.
404
to to to to to *— «— -■— >—>—►— *- — .— и-
4^00Ю^-ОсО00^1СТ>СЛ^001О^-ОсО00^а>СЛ4^00Ю^-О
О О О О О ©О О
h-* СЛ ^ СО СО СО
СОС
© © © © © © © © о ©
©с
©©ООГОО>©©©©СЛ
toco^©»—to^^^aco
ЮОО"-МЮ-
) *-00 CO OO *^J *^00
. 1>-Ч /»4S /-»■ —- —~ —
О © © © © © © О-©-© © ©_©
>©©©<
5©©©<
:> © © >- ►- to to *- с
5ЮСЛ ©С£ tptO^ н
sgg§2sgi§g§2§
w© о о о о © о о © © © © ©j=> ©
ooooo^-^Vn-Vo
о©>—юслослсософ.'^*—
^-СЛСОСОСО^СЛСЛСЛ©0000
' ""-ЦОСО^^СЛСОСО
§8
© © _
•— tO G5 СО СО Ю00
© © © © о о о о о © © © о © © ©
о о© о о о ©io'^-^-'i-'"»-"—"©'©'©
©©©©©ь-соа>©4*^^34*ООСО©
©©•—СОООООСТ>СЛ^С75СЛСЛ©4^СО©
ЮСЛ004*.Ю>—СОС04*ЮСЛСЛ4*.Ю^^
©©©©©© ©©©©©©© © © © © ©
©©о©©©
©©©©©>—
©р©юсл to
>—СО СОЮ ЮС7>
©©©н-,— и->-*-©©©©
tO^©©COC75©COOOrf^^-©
Ю^-0000 *-J © © СО СО'*»- 4* Ю
слоооосо^©о5союа>сосл
© © © © ©©©©©©©© © © © © © © © ©
ОООООООО'
2Q2©o©>—to
оромсо ^аф^сл
•—' tOO> 4*. СО *— ЮСО
4*.^©ОЪ4ь>4*ЮсОСЛЮ©©
СЛ>—•—©COCO»-a»—' Ю ЮО> ©
Ю©45ь4ь.©©--ЛО>—004ь.сО
©\zr© © © © о©©©©©©©©©©©©© © ©
SQSQoooo'booo'^^^^oooooo
© © © © © © О >— Ю 4*. ^J СО'Ю СО СО Ю СО СЛ Ю >— © ©
© © © © to -4*. cooicoootoco^cp<oto»-'->ioo©to©
~ЬЭ4*-СО»-«СЛ©СОа> *-ЮСО>—05а>^-ОЭЮО)^^)00
© © о о © ©-© © ©©©©©©©©©©© © ©.© ©
S8S:
12
4*. СО 00 СО 4*.4*4*.00©б50000»-;>— -vJ^l©©»— >—
о © © © © ©©©*©© © © © © © © © о о © о ©о ©о
2 2Q 21=2^0 *©•© oooo"'-,'-,'n-moo © ©о'© ©о
© © © © © tO © •—<Ю СОСЛ»^Срн-ЮЮ>—СООСО ►-©©©©
© © © © >— со ^ to**— 4*ьэЮ4^сослслю©со^оо^1Ю©©
»— to 4*. coco *^»—oo *^«4j >— сооо^ь-н-о>>— ►— оосо© со ел ©
ОЭСЛ 4*. СО Ю *- ©
0#9048
0,0905
0,0045
0,0002
0,8187
0,1638
0,0164
0,0019
0,0001
0,7408
0,2222
0,0333
0,0033
0,0002
0,6703
0,2681
0,0536
0,0072
0,0007
0,0001
0,6065
0,3033
0,0758
0,0126
0,0016
0,0002
0,5488
0,3293
0,0988
0,0198
0.0030
0,0004
0.4966
0,3476
0,1217
0,0284
0,0050
0,0007
0,0001
0,4493
0,3595
0,1438
0,0383
0.Q077
0,0012
0,0002
0,4066
0,3659
0,1647
0,0494
0,0111
0,0020
0,0003
3^1
— 1
о 1
о 1
to 1
о 1
со
о
** 1
о
СЛ
0,6 ;
о
о
оо
о
45
S3
о
о
Я)
А
13
X
О
ф
X
X
о
х
ь
О
гп
I
X
Приложение 2. ЗНАЧЕНИЯ ВЕРОЯТНОСТИ*)
т ак
tf(m. а) = 1 — R(m а)=1- У\ — е~°
т
0
1
2
3
4
5
6
о=0.1
9,5163-2
4,6788-3
1.5465-4
3,8468-6
о=0.2
1,8127-1
1,7523-2
1,1485-3
5,6840-5
2,2592-6
о=0,3
2,5918-1
3,6936-2
3,5995-з
2,6581-4
1,5785-5
а=0 4
3,2968-1
6,1552-2
7,9263-3
7,7625-4
6,12*3-5
4,0427-*
а=0,5
8.9347-1.
9.0204-2
1.4388
1,7516-3
1,7212-4
1,4165-5
1,0024-6
гп
о
1
2
3
4
6
7
о=0.б
4,5119-1
1,2190
2,3115-2
3,3581-з
3,9449-4
3,8856-5
3,2931-6
а=0,7
5,0341-1
1,5580
3,4142-2
5,7535-з
7,8554-4
9,0026-5
8,8836-6
о=0,8
5,5067-1
1,9121
4.7423-2
9.0799-3
1,4113
1,8434-4
2,0747-5
2,0502-6
' а=0.9
5,9343-1
2,2752
6,2857-2
1,3459
2,3441-з
3,4349-4
4,3401-5
4,8172-6
** 1
т
0
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
а=1
6,3212-1
2,6424
8,0301-2
1,8988
3,6598-з
5,9418-4
8,3241-5
1,0219
1,1252-«
а=2
8,6466-1
5,9399
3,2332
.1,4288
5,2653-з
1,6564
4,5338-з
1,0967
2,3745-4
4,6498-5
8,3082-е
1,3646 .
о«3
9,5021-1
8,0085
5,7681
3,5277
1,8474
8,3918-3
3,3509
1,1905
3,8030-3
1,1025
2,9234-4
7,1387-5
1,6149
3,4019-в
oWi
9,8168-1
9,0842
7,6190
5,6653
3,7116
2,1487
1,1067
5,1134-2
2,1363
8,1322-з
2,8398
9,1523-4
2,7372
7,6328-5
1,9932
4,8926-6
lf1328
я=5
9,9326-!
9,5957
8,7535
7,3497
5,5951
3,8404
2,3782
1.3337
6.8094-2
3,1828
1,3695
5,4531-з
2,0189.
6,9799-4
2,2625
6,9008-5
1,9869
5,4163-°
1,4017
am __
*) Вероятность Р(т, а) —-jjjr е-""0 может быть найдена через вероятность R (т, а)
щнм образом? Р {т, а)=*И )m^\t a)^R (m, a) (m > 0), Р (0, а) = !*=-# (0, а).
1 m
о
1
1 2
3
1 4
5
1 6
1 7
8
9
10
и
12
13
14
15
v16
17
18
a=6
9,9752-1
9,8265
9,3803
8,4880
7,1494
5,5432
3,9370
2,5602
1,5276
8.3924-2
1 4,2621
2,0092 *
8,8275-3
3,6285
1,4004
5,0910-*
1,7488
5,6917-3
1,7597
a = 7
9,9909-»
9,9270
9,7036
9,1823
8,2701
6,9929
1 5,5029
4,0129
2,7091
1,6950-1
9,8521-*
5,3350
2,7000
1,2811
5.7172-3
2,4066
9,5818-*
3,6178
1.2985
a = 8
9,9966-1
9,9698
9,8625
9,5762
| 9,0037
8,0876
6,8663
5,4704
4,0745
2,8338-1
1,8411
1,1192
6,3797-2
3,4181
1,7257
8,2310-»
3,7180
1,5943
i 6,5037-*
a = U
9,9988-1
9,9877
9,9377
9,7877
9,4504
8,8431
7,9322
6,7610
5,4435
4,1259-1
2,9401
1,9699
1,2423
1 7,3851-2
4,1466
2,2036
1,1106
5,3196-3
2,4264
a=10 I
9,9995-1 I
9,9950 1
9,9723 1
9,8966
i 9,7075
9,3291
8,6985
7,7978
6,6718
5,4207-1
4.1696
3,0322
2,0844
1,3554
8,3458-2
4,8740
2,7042
1,4278
7,1865-3
1 m
19
20
21
22
?3
24
25
26
27
«»«
5,1802-*
1,4551
fl=;7
4,4402-*
1,4495
! 4,5263-*
1,3543
4-5
2,5294
9,39G8W*
3;3407
1,1385
3,7255^*
1,1722
Я*9
! 1,0560
| 4,3925-*
1,7495
6,6828-*
2,4519
8,6531-» ]
2,9414 ]
- ^
д=10
3,4543
1,5883
6,9965^*
2,9574
1,2012
1 4,6949-*
1,7680
6,4229-*
3,2535 J
Пример. Требуется, определить вероятность того, что событие А появится
не более двух раз, если а = 7.
Имеем
R (2,7) = 1 — R (2,7) « 1 — 9,7036-1 = 1 — 0,97036 « 0,02964.
При ме ч а н,и я: 1. Если у числа в таблице показатель степени
отсутствует, то им будет показатель степени ближайшего вышестоящего числа, у кото*
рого есть показатель степени. Например, £~(33j 19) = 1,2067 • Ю-3.
2. При а > 20 вероятность R (/и, а) можно рассчитывать по приближенной
формуле:
R, (m,
а)*фЛ
т+0,5—а \
Уа )
где Ф(х)—функция Лапласа (приложение 5).
407
+0,5
1 m
I 0
1 1
1 2
1 3
1 4
1 5
j 6
1 7
8
1 9
] 10
н
12
13
14 i
15 ;
16
17
18
19
20
21
22
23
24
25
26
27
l_sj
a^ii
9.9998-1
9,9980
! 9,9879
| 9,9508
9,8490
9,6248
9,2139
8,5681
7,6801
6,5949
5.4011
4,2073
3,1130
2,1871
1,4596
9,2604-* 1
5,5924
3,2191
1,7687
a,2895~»
4,6711
2,2519
1,0423
4,6386-*
1.9871
8,2050-*
3,2693
1,2584
4,6847--*
a=\2
9,9999-1
9.9992
9,9948
! 9,9771
9,9240
9,7966
9.5418
9.1050
8,4497
7,5761
6,5277
5,3840
4,2403
3,1846
2,2798
1,5558
1,0129
6,2966"»
3,7416
2,1280
1,1598
6,0651-»
3,0474
1,4729 |
6,8563-* !
3;0776 1
1,3335
5,5836-*
2,2616
a=13
9,9997-»
9,9978 ,
9,9895
9,9626
9,8927
9,7411
9,4597
9,0024
8,3419
7,4832
6,4684
5,3690
4,2695
3,2487
2,3639
1,6451
1,0954
6,9833-*
4,2669
2,5012
1,4081
7,6225-»
3,9718
1,9943
9,6603-*
4,5190
2,0435'
8.9416-»
fl=14
9,9999-»
9,9991
1 9,9953
9.9819
9,9447
9,8577
9,6838
9,3794
8,9060
8,2432
7,3996
6,4154
5,3555
4,2956
3,3064
2,4408
1.7280
1,1736
7,6505-*
4,7908
2.8844
1.6712
9,3276-»
5,0199
2,6076
1,3087
6,3513-*
2,9837
я=15
9,9996-1
9,9979
9,9914
9,9721
9,9237
9,8200
9,6255
9,3015
8,8154
8,1525
7,3239
6,3678
5,3435
4,3191
3,3588
2,5114
1,8053
1,2478
8,2972-»
5,3106
3,2744
1,9465
1,1165
6,1849-»
3,3119
1,7158
8,6072-*
1 m
29
30
31
32
33
34
35
36
. a^U
1,6882
a-12
8,8701-e
3,3716
1,2432
x л 1
0=13
3,7894
1,5568
6,2052-«
2,4017
e«14
• 1,3580
5,9928-5
2,5665
1,0675
4,3154-e
1,6963-
ii^lb
4,1843
1,9731
9,0312-5
4.0155
1,7356
7,2978"** .
2,9871
1,1910
408
m
о
1
2
3
4
5
6
7
8
9
10
"
12
13
14
1 15
16
17
18 ,
19
20
I 21
22
23
24
25
26
27
28
a=16
9,9998-1
9,9991
9,9960
9,9862
9,9599
9,9000
9,7801
9,5670
9,2260
8,7301
8,0688
7,2545
6,3247
5,3326
4,3404
3,4066
2,5765
1,8775
1,3183
8,9227-2
5,8241
3,6686
2,2315
1,3119
7,4589-»
4,1051
2,1886
a=l7
9,9999-*
9.9996
9.9982
9,9933
9,9794
9,9457
9,8740
9,7388
9,5088
9,1533
8,6498
7,9913
7,1917
6,2855
5,3226
4,3598
3,4504
2,6368
1,9452
1,3853
9,5272-2
6,3296
4,0646
! 2,5245
1,5174
8,8335-3
4,9838
a=l£
9,9998-1
9,9992
9,9968
9,9896
9,9711
9,9291
9,8462
, 9,6963
9,4511
1 9,0833
8,5740
1 7,9192
7,1335
6,2495
5,3135
4,3776
3,4908
2,6928
2,0088
1,4491
1,0111
6,8260-«
4,4608
2,8234
1,7318
1,0300
a=19
/
9,9999-1
9,9996
9/9985
9,9948
9,9849
9,9613
9,9114
9,8168
1 9,6533
9,3944
9,0160
8,5025
.7,8521 '
7,0797
6,2164
5,3052
4,3939
3,5283
2,7450
2,0687
1,5098
1,0675
7,3126-2
4,8557
3,1268
1,9536
a=20 1
9,9998-1 1
9,9993 1
9,9974 I
9^9922 I
9,9791 J
9,9500 1
9,8919 1
9,7861
9,6099 1
9,3337
8,9514
8,4349
7,7893 -
7,0297
6,1853
5,2974
4,4091
3,5630
2,7939
2,1251
1,5677
1,1218
7,7887-2
5,2481
3,4334
[Л """I
\ til
29
1 3®
31
32 1
I 3S 1
! 34
1 33
1 86-
1 37
1 dS. '
I -30
1 40
1 41
1 42
1 43
I 44
,**ia
1,1312
5,6726-4 !
2,7620 !
1,3067
6,0108~*
2,6903
; 3,1724
4,9772^•
\ 2,0599
к
•д«17
2,7272 1
1,4484 !
7,470&~*
3,7453
1 1,8260
, 8,6644w5
i 4,0035
i 1,8025
| 7,9123-^
3,3882
1,4162 *
л«18
5,9443-*
3,3308
1,8133
9,5975~*
14,9416 ■
! 2,4767
1,2090
5,7519~*
2,6684 .
1,2078
5,3365-c
2,3030
««19
1,1850
6,9819-3
3,9982 1
2,2267 j
, 1,2067 j
[ 0,8674-*
3,2732
1,6401
8,0154-»
3,8224
1,7797
8,0940-*
.3,5975
[1,6634
«sr2D I
2,1818 I
1,3475 I
8,0918-3 I
4,7274
l 2,6884
i 1,4890
I8,036S~*
4,2290
2,1708
1,0875
6,3202-*
2,5425
1,1877
5,4252~*
2,4243
1,0603
409
Приложение 3
ЗНАЧЕНИЯ ФУНКЦИИ е~*
- jr 1
0,00
0,01
02
03
04
05
Об
07
08
09
0,10
"
12
13
14
15
16
17
18
19
0,20
21
22
23
24
25
26
27
28
29
0,30
31
32
33
34
35
36
37
38
39
0,40
*~*
1.000
0.990
980
970
961
951
942
932
923
914
0,905
896
887
878
869
861
* 852 1
844
835
827
0.819
811
803
795
787
779
| 771
763
756
748
0.741
733
726
719
712
705
698.
691
684
677
0,670
д
10
10
10
9
10
9
10
9
9
9
9
9
9
9
8|
9
8
9
8
8
Л
8
в
8
8
8
8
7
8!
7
в
7
7
7
7
7
7
7
7
7
х 1
0.40
0,41
42
43
44
45
46
47
48
49
0,50
51
52
53
54
55
56
57
58
I 59
| 0.60
61
62
63
64
65
66
67
68
69
0.70
71
72
73
74
75
76
77
78
79
0,80
е~*
0,670
0.664
657
650
644
638
631
625
619
613
0,606
600
595
589
583
577
571
565
560
554
0.549
543
538
5.33
527
522
517
512
507
502
0,497
492
487
482
477
472
468
463
458
454
0,449
А
7
7
7
г>
г>
7
6
г>
г>
7
6
5
6
6
6-
6
6
5
6'
5
<>
5
5
61
5
5-
5
5
5
5
5
5
5
5
5
^
5
^
4>
5
X 1
0,80
0,81
82
• 83
84
85
Ы)
87
88
89
0,90
91
92
93
91
95
96
97
98
99
1,00
1,10
1,20
1,30
1,40
1,50
1,60
1,70
1,80
1,90
,2,00
2,10
2,20
2,30
2,40
1 2,^0
2,60
2,70
2,80
2,90
3,00
*"*
0.449
0.445
440
436
432
427
423
419
415
411
0.407
403
399
395
391
387
383
379
375
372
0.368
333
302
273
247
223
202
183
165
150
o,ia5
122
111
100
0.091
82
74
67
61
55
0.050
Д
4
5
4
4
5
4
4
4
4
4
4
4
4
.4
4
4
4
4
з
4
35
31
29
•26
24
'21
19
18
15
15
13
11
> И
9
9
8
7
6
6
5
1
X
3f00
3,10
3,20
3.30
3.40
3,50
3,60
1 3,70
3,80
3,90
4,00
4,10
4,20
4,30
4,40
4,50
4,60
4,70
4:80
i90
5,00
5,10
5,20
5,30
5,40
5,50
5,60
-5,70
5,80
5,90
6,00
6,10
$20
азо
6,40
6,50
660
S£2
f£2
6,90
J 7,00
г'*
0,050
0.045
41
37
33
ЛО
1>7
25
22
20
0.0183
166
150
136
123
111
101
0,0091
82
74
0,0067
61
55
50
45
41
37
33
30
27
0,0025
22
20
18
17
15
14
12
1 11
10
0,0009
*
5
4
4
4
з
3
2
5
2
2
17
16
14
13
12
10
10
9
8
7
6
6
5
5 1
4
4
4
3
3
2
3
2 1
2
1 I
2 1
1 1
2 1
1 1
1 1
1
410
Приложение 4
ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ НОРМАЛЬНОГО ЗАКОНА f(*) =
1 х
0,0
0,1 .
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
и
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
0
0,39.89.
3970
3910
3814
3683
3521
3332
3123
2897
2661
0,2420
2179
19Й2
1714
1497
1295
1109
0940
0790
0656
0,0540^
0440
0355
0283
0224
0175
0136
0104
0079
0060
0,0044
0033
0024
0017
0012
0009
0006
0004
0003
0002
1
3989
3965
3902
3802
3668
3503
3312
3101
2874
2637
2396
2155
1919
169L
1476
1276
1092
0925
1 0775
0644
0529
0431
0347
0277
0219
0171
0132
0101
0077
0058
0043
0032
0023
0017
0012
0008
0006
0004
0003
0002
*
3989
3961
3894
3790
3653
3485
3292
3079
2850 !
2613
2371
2131
1895
•1669
•1,456
1257
1074
0909
0761
0632
0519
0422
0339
0270
0213
0167
0129
0099
0075
0056
0042
0031
0022
0016
0012
оооа
0006
0004
0003
0002
3
3988
3956
3885
3778
3637
3467
3271
3056
2827
2589
2347
2107
1872
1647
1435.
1238
1057
0893
0748
| 0620
0508
0413
0332
0264
0208
0163
0126
0096
0073
0055
0040
0030
0022
0016
ООП
0008
0005
0004
0003
0002
4
3986
3951
387&
3765
3621
3448
3251
3034
2803
2565
2323
2083
1849
1626
1415-
1219
1040
0878
0734
0608
0498
0404
0325
0258
0203
0158
0122
0093
0071
0053
0039
0029
0021
0015
ООП
0008
0005
0004
0003
0002
5
3984
3945
3867
3752
3605
3429
.3230
#011
2780
'2541
2299
2059
1826
1604
1394
1200
"1023
0863
1 0721
0596
0488.
0396
0317
0252
0198
0154
0119
0091
0069
0051
0038
0028
0020
0015
0010
0007
0005
0004
0002
0002
6 1
3982
3939
3857
3739
3589
3410
3209
2989
2756
2516
2275
2036
1804
1582
1374
1182
1006
0848
0707
0584
0478
0387
0310
0246
0194
0151
0116
0088
0067
0050
0037
0027
0020
0014
0010
0007
0005
0003
0002
0002
7 |
3980
3932
3847
3726
3572
3391
3187
2966
2732
2492
2251
2012
1781
1561
1354
1163
0989
0833
0694
| 0573
0468
0379
0303
0241
0189
0147
0113
0086
0065
0048
0036
0026
0019
0014
L0010
0007
0005
0003
0002
0002
8 1
3977
3925
3836
3712
3555
3372
3166
2943
2709
2468
2227
1989
1758
1539
1334
1145
0973
1 0818
0681
0562
0459
0371
0297
0235
0184
0143
ОНО
0084
0063
0047
0035
0025
0018
0013
0009
0007
0005
0003
0002
0001
9 1
3973
3918
3825
3697
3538
3352
3144
2920
2685
2444
2203
1965
1736
1518
1315
1127
0957
0804
0669
0551
0449
0363
0290
0229
0180
0139
0107
0081
0061
0046
0034
0025
0018
0013
0009
0006
0004
0003
0002
0001
411
4*
to
•\
1 tn ►K4>spo со
ob о оГ©
0,49865
49977
499968
499997
49999997
,coco
49903
49984
I -*ito
49931
49989
' ,co,eo ,
coco
49952
49993
^coco
C©4s»
49966
49995
it ,-— i-Vn- и - -
cooo*gg>cn^.coto —о ~ <ooo«*jo>cnrf>coto*-*o ^Ъо^Ъ>с>£».'со10^-о
1 • S>
4s» 4s» 4s» 4s» 4:». 4s» 4s» 4s» 4s» »N 4s» >fc» >Js» 4s» 4s» Ф" 4s» CO CO CO U5N3Wb3w»-*MOOO
COCOCOCDCOCOOCCOOO~4 -Л CT> Ot 41-CO »— © GO О 4S» »—ООС^ЮСОСЛ»—<JcoO
OO-NJOiOtW^OOW^J »—*»СЛОтСОСОС045»4х>—» СЛОСОССЛ»—СЛ--1СОСО©
CO4s»CO4s»CO©00©4>Ot 00-^CO©C04>©COC04> ^^^OlQtO^OCOO
| 4s» 4s» 4b. 4s» 4*» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s*. 4s» CO CO CO CO tO N3 Ю *-*>-* н- О О О
COCOCCCCCDC©OOGOOO-«*4 -4 CD Ol 4s- СО Ю-О ОО О) 4X »—'CO 0>tOCOOU0 004s»©
•— OiQ^COOOi>UOt'"4 CO00CoCO4^*J'CO00Oi*4 СЛ©1—©CO*—-^1>—OOCO
COtO4s»-4C>tOO>0l-J00 С0СЛ-4О00С0О05ОСЛ COCOOi-»J-*l©tO-»J©CD
4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» ^ 4s» 4s» 4s» its* 4s» CO CO Co ' СО(ОЮЮь-м)-оОО
COCOCOCOCOCOCCOOOO-J <-^C?5 0*4s»C0lO©00O54S» tOCDC5COCOCT>tO004s»©
00«-JO>Ol4-tOCOO>COOC Ю O» ^1 —4 OUO О 00 ОС C5> >— CO4s-tO00tOOl-4«>J —1
МОЧСЛ^-ЮОСМОСО СЮ5ЮСОЧЮС»ЧО)^- tO00rOCO4s»««JCn©^4C©
СЛ©*»©С04*»СОСО©»— / »-JtO00004s»©00~44->4s» •— C04s»-»4-40>lOO>0>00
4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s-4s» 4s» 4s» .4u 4s» 4s» -4s» 4s» 4s» CO CO CO ССЮЮЮЮмн-оОО
COCOCOCPCOCOCOCCOO-^ Ч О O» •* C«5 top (O »J 4». Ю Ю О) СОч О Ct> Ю (D Ol ►-*
COCb00-4CO4s»»—*—4-00 IO CO •— *«• (О О Ivi Q 4 Ol OC**JCOO>COUs»COCO*4CO
►— МССССООЮСО»- Ю O.pO 00 Ol CO 4s» 4- Ol © © Ь-СООСЛЙ^ООСЛЮ^ u
4s»4s»4s»4s»'4s»4s»4s»4s»4s»4s» 4S»4s»Js-4s»4s»4s»4s»COCOCO COtOtOtOtO'—►—©©©
COCOCOCOCOCDCOOOOO-vI »УОСЯ*>С0ЮС©«0(Л IO CO.--J CO О -4 CO CO Ol >—
00-4©0»4s»tO©-*lCOC© CO~4COCOOOOlCCtOtO© ©CO©0OOl©CO4s»CnOl
CO -J CO ОС 4s» O>CO*»00CO OO •—О Ol tO О 00 OlOO 00 CO Ol CO CO 4s» О О OO ©CO
© 4s» CO Ol © © © Ol tO tO >— tO -»4 © tO -^ 00 »— ©Co СООЮ1н-©СО»^1СО-*1СЛ
4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» *fc» 4s» 4s» 4s» 4s» 4s» 4s» CO CO CO CO CO Ю tO tO »— »-» О О О
COCOCOCOCOCOCOOOOO-J -^1 © Ol О? Со ГО ►— CO *-J СЛ T0Q-»J4s»O-»lC0C0Cn>-*
00--J-*JOi4-IO©--14s»CO 4s»-lCOOCOO>»-4-4s»CO OO IO CO ГО 00 CO'© ОС СО СО
4s»00©CO©00©«^JIOOO 4-.OOCOOi44»4j»4-.COCO — СО СС СО »-ОС О) 00 Ч О) СО
•— »— Ю00«— © »- 00 Ю tO •— 4-.4*COCO»-4COC»C04s» >f* 4>t -J Ot 4*.4s» CO ►— W 4s»
4s»4s»4s»4s»4s»4^4s»4s»4s»4s» 4s»4s»4s»4s»4-.4fc.4s»CoCOCO COCOtOtOtO»--»—•—©©
COCOCOCOCOCOCDOOOOOO -4 © © Ol 4s» tO »— CO -^l СЛ CO©-44s»»—-»J4s»©©tO
00«-4-4©4-.CO©G04s»© О» ОС © —• © -4 CO.© © СЛ •—. Ol © Ol Ю -J О IO CO CO
»u oo »— очооооосо ослосслассо — со a** 4>»—cocototocnoioico
OOO»— CO ^JOi ©CO*—© OC504s»tOOCO-400CO «-4»—»»J»»i©4s»00-»4©tO
4s»4s»4s»4s»4s»4s»4s»4s»4i»4s» 4s»4s»Ju.4s-A-4s-4s»CCCoCO CoCOlOtOtO»-*»—»»— 00^\
COCOCOCOCOCOCOOOCOOO -vJ СЛ D О' ** I.O — CO — J Oi COO*^J4s»»—004s»OO^tO
OO-sl^Oi^CO — С»ОЮ OlCO—-Ю — C© 4- — ICO-4 CO--ICOOOOl©4s»©«^l-*J
OlCOtOt>SCOlO—'4s»0--4 OHOC5 0«4tOOCOQO) CD00COOl©00CO4s»4SwCP
ь-ОЮ — t0 4s» — OO^J OC©4-4s»CCtO©©©CO OOOlOX-JOtO — tOCOO
4b.4s»4s»4s»4s»4s»4s»4s»4s»4s» 4s»4s»4s»4s»4s»4s»4s»COCO'CO CCCCNJ.tOtO^^-^OO
COCOCOCOCOCOCOOOCOOO -4 © © СЛ 4- CO *— COOOOl Co »■*• 00 СЛ *— 00 4S» »— -4 CO
oooo^cncjicc-oooi^- ©союсою©©со»—с© °)P!S)'~:SS4>21:?2*r^
СЛОЮССОАСОЧСОЮ ►— CC4s^OiCOOltO-^OCO 4s»0*CO^©CO©t04s»00
Oi»—00t0 0iC04s»O^J4s» Ol Ol © IO Ol © — CO © Co © **J O'O» 4*. CO Co © tw 00
4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4s» 4*. 4s» 4s- 4s» 4s* 4s» CO Co CO CO tO tO tO •—► »— »-* О О
COCOCOCOCOCOCOOOCOOO --J ^J C75 СЛ 4S» CO — О OO Oi tO *— 00 Ot tO 00 Ot >—• «Ч чО
0000-vJO>OlCO»— OOOl*— ОЭОС04-.4*—«-vj»—tOtO OOCOOl4s»tO-^»—4s»OlO}
ООС04^ЮОСЛСО-ДО> -^ G> tO 4s» О OO -£l 4s» CO — ^^^Sfe^^S^^
►—■^OiCOO'—00CO4s»CO ©tO»^ICO00CO4s*-»J004s» »—»»44s»OOCOCOCOOlO>
> i ■■ m ■ ' ' ' ' '
"
О
**
*°
Ol
*.
Ol
en
*■*
CO
<o
■e.
ч:
I
e
<|
fr.
о
z
s
Ф
Приложение б
НЕКОТОРЫЕ СВОЙСТВА ОБОБЩЕННЫХ ФУНКЦИЙ
При решении задач, связанных со случайными функциями, часто бывает
удобно выполнять преобразования с помощью различных скачкообразных
функций, а также обобщенных функций типа дельта-функции.
Приводим определения и основные свойства таких функций от
действительного аргумента т.
1. |т| — модуль (абсолютная величина):
при,т>0;
при т<0.
2» 1 (т) — единичная функция (единичный скачок): .
1 при т>0;
'"-{.:
!(*) =
— при т=0;
О при т<0.
3. sign т — знак величины т (сигнум):
II при т>0;<
О при т=0;
— 1 при *<0.
4. б(т) — дельта-функция: . ..
в w-JL,W.
Дельта-функция — четная функция т. Основные свойства дельта-функции::
а) т6(т)==0 и вообще ф(г)б(т)езО, если ф(х) — нечетная функция,
непрерывная при т=0;
O-f-e
б) / ф(т)6(т)</т—ф(0),если функция $(/) непрерывна в точке т=0(е>0);.
0—8
0 04-е {
^ Ф(т)6(т)<*т= | ф(т)6(т)4т =— ф(0),
0—8 0
если функция ф(г) непрерывна з точке т=*0.
Из этих определений вытекают следующие свойства,. имеющие место для
любых действительных т и нечетной функции <р(т)>
1) |T|arsign v; 2) г =|т| sign Т7:
ч 3) ф(т)=ф( | г |) sign г; 4) ф (| т |) = ф (т?) sign щ
5) ф2(|Т|)=ф2(Т); б) s£gnv=52.1 (т?)—1;
7) t(T) = $ign2T + S 8) |«|—тГ2.1ч«) — Ц;
л ^И1 ,л d2|T| dsigni? _fi t ч
9) -^«signi?; 10) -—г1-—j—=2б(т);
ах ах2 ах
11) 1(<в) = f 8(т)Л=-£- f d(sigrrr).
в» 00 я>(Ю
413
Приложение 7
ТАБЛИЦА СООТВЕТСТВИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ^(т)
И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ Sx (ю)
1
1.
2.
3.
4.
5.
6,
1 7*
8.
9.
10.
П.
12.
13.
1 14#
15.
16.
17.
18.
kx(t)
D6(t), где 6(0—дельта-функция
D
D cos Рт 1
п
%DtcQsfoi
De*-a|x|
De^a^T| cos Pi
Deea 'T '(cos рт + — sin p | т |)
Detoa«T'(cosPT-—sinpixA
De""a,T,fchpT+YshPlTl)(a>P)
D(1Ht|)1(1-|t|),
где 1 (x)—единичная функция
De-alT|(1+a|T|)
De-aft|/1+a|T, + _La2T2^
De^,T,(l+a|T|—2a2т2 +
+-ya3lтl3)
2asin рт/т
2a2(2cospT-l)5MF
T
De~(aT)2
De""a 1 T • [26 (x)—a (sign t)2J
W
£/(2я)
D6(©)
(D/2)[6(© + P)+6(co-p)l
4" SDHS(o)+p£) + 6(o)~p£)|.
(Оа/я)(а2+ю2)-1
я j£ a?+©2
Da a2+P2 + co2
я [а« + (Р-ю)"|[а« +№+©)»]
Da 2(q2 + p2)
я (©2+а2—р2)2+4а2р2
Da 2©j>
я (©2 + a2 + P2)2—4p2©2
Da 2(a2—p2)
я f(a-.p)2+0)2J[(a+p)2 + a)2j
D_ 1 sin (©/2) \2
; 2я V ю/2 J
(Da/я) [2a3/(©2 + a2)2]
Da a»
я 3(©2 + а2)3
Da 16a3©4
Я (0)2_|_а2)4
a1(l—|©|/p)
(0 при 0<|©|<p,
I а2 при Р<|©|<2Р,
io при 2р<|©|
2^еХР["Ш1
1 (Оа.1п)[<а>Ч(а?+аР)] \
414
СПИСОК ЛИТЕРАТУРЫ
1. Вентцель Е. С. Теория вероятностей. — М.: Наука, 1964. — 564 с.
2. Вентцель Е. С, Овчаров Л. А. Теория вероятностей. — М.: Наука, 1973. —
366 с.
3. Гмурман В. Е.Руководство к решению вадач по теории вероятностей и
математической статистике. — М.: Высшая школа, 1979. — 477 с.
4. Гнеденко Б. В. Курс теории вероятностей. — М.: Физматгиз, 1961—406 с.
5. Гнеденко Б. В., Коваленко И. Н. Введение в теорию массового обслужива-
н/я. — М.: Наука, 1966. — 431 с.
6. Коваленко И. М., Филиппова А. А. Теория вероятностей и математическая
статистика. — М.: Высшая школа, 1973. — 368 с.
7. Кофман А., Крюон Р. Массовое обслуживание, теория и применение. —
М.: Мир, 1965. — 302 с.
8. Мешалкин Л.Д. Сборник задач по теории вероятностей — Изд. МГУ, 1963. —
131с.
9. Овчаров Л. А. Прикладные задачи теории массового обслуживания. — М.:
Машиностроение, 1969. — 324 с.
10. Пугачев В. С. Теория случайных функций, — М.: Физматгиз, 1962. — 659 с.
11. Пугачев В. С. Введение в теорию вероятностей. — М.: Наука, 1968. — 368 с.
12. Пугачев В. С. Теория вероятности и математическая статистика.—М,: Hay-
* ка, 1979.—495 с.
13. Сборник задач по теории вероятностей, математической статистике и теории
случайных функций/ Под ред. А. А. Свешникова. — Шл Наука, 1965. —
656 с.
14. Смирнов Н. В., Дунин-Барковский И. В. Теория вероятностей и
математическая статистика в механике. — М.: Физматгиз, 1965. — 554 с.
15. Тараканов К. В., Овчаров Л. А., Тырышкин А. Н. Аналитические методы
исследования систем. — М.: Сов. радио, 1975. — 240 с.
16. Феллер В. Введение в теорию вероятностей и ее применение в 2-х т. — М.:
Мир, 1964. — Т. 1 — 500 с, 1967. — Т. 2 — 752 с.
17. Хинчин А. Я. Работы по математической теории массового обслуживания. —
М: Физматгиз, 1963. — 127 с.
ОГЛАВЛЕНИЕ
Предисловие . 3
Глава 1. Основные понятия теории вероятностей. Непосредственный
подсчет вероятностей в схеме случаев 5
Глава 2. Алгебра событий. Правила сложения и умножения
вероятностей .- 23
Глава 3. Формула полной вероятности и формула Бейеса 56
Глава 4. Дискретные случайные величины 75
Глава 5. Непрерывные и смешанные случайные величины 100
. Глава 6. Системы случайных величин (случайные векторы) . . . .133
Глава 7. Числовые характеристики функций случайных величин . . * 154
Глава 8. Законы распределения функций случайных величин.
Предельные теоремы теории вероятностей 203
Глава 9. Случайные функции • 244
Глава 10. Потоки событий. Марковские случайные процессы • . * . 308
Глава 11. Теория массового обслуживания .349
Приложения 405
Список литературы , . 415
. ЕЛЕНА СЕРГЕЕВНА ВЕНТЦЕЛЬ
ЛЕВ АЛЕКСАНДРОВИЧ ОВЧАРОВ
ПРИКЛАДНЫЕ ЗАДАЧИ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Редактор./?. Г. Давыдова
Обложка художника П. П. Рогачева
Художественный редактор Л. Я. Силбянов
Технический редактор Т. Н. Зыкина
Корректор Л. Л. Жукова
ИБ № 157
Сдано в набор 21.06.82 г. Подписано в печать 22.11.82 г. Т-20367 Формат 60Х90т/ю.
Бумага тип. № 2. Гарнитура литературная. Печать высокая. Усл. п. л. 26.0. Усл. кр.-отт. 26,0
"Уч.-изд. л. 27,23. Тираж 30 000 экз. Изд. № 19639 Заказ № 1040 Цена 1 р. 60 к,
Издательство «Радио и связь», Москва, Главпочтамт, а/я 693
Московская типография № 4 Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговля,
129041, Москва, Б. Переяславская, 46