Text
ДЛЯ ВУЗОВ
МЕХАНИКА
КОСМИЧЕСКОГО
ПОЛЕТА
МАШИНОСТРОЕНИЕ
ДЛЯ ВУЗОВ
МЕХАНИКА
КОСМИЧЕСКОГО
ПОЛЕТА
Под редакцией академика В.П. Мишина
Допущено Министерством высшего и среднего специального
образования СССР в качестве учебника для студентов высших
технических, учебных заведений
МОСКВА
«МАШИНОСТРОЕНИЕ»
1989
ББК 39.6
/М55
УДК 629.78(075.8)
Авторы: М. С. Константинов, Е. Ф. Каменков, Б. П. Перелыгин,
В. К. Безвербый
Рецензент: д-р техн, наук А. М. Мхитарян
Механика космического полета: Учебник для втузов/
М55 М. С. Константинов, Е. Ф. Каменков, Б. П. Перелыгин,
В. К. Безвербый; Под ред. В. П. Мишина. — М.: Машино-
строение, 1989. — 408 с.: ил.
ISBN 5-217-00145-3
Изложены основы анализа и выбора траекторий космических ап-
паратов (КА), характеристик орбит искусственных спутников Земли
(ИСЗ). Проведен анализ маневрирования КА при сближении и сты-
ковке на орбите. Рассмотрена динамика орбитальных систем. Изложе-
ны вопросы спуска КА в атмосфере Земли и планет как при эл-
липтических, так и при гиперболических скоростях входа. Проанали-
зированы проектные баллистические характеристики межпланетных
траекторий.
„ 3500000000—411
м------------------
038(01)—89
КБ-13-91-89
ББК 39.6
ISBN 5-217-00145-3 © Издательство «Машиностроение», 1989
ПРЕДИСЛОВИЕ
Механика космического полета как один из разделов,
космонавтики занимает существенное место в практике проек-
тирования космических аппаратов различного назначения.
В настоящее время в развитии космической техники осуще-
ствляется качественно новый этап — создаются спутниковые
системы различного назначения, организуются космические
комплексы на околоземных орбитах.
Все это требует профессиональной подготовки инженеров в
области механики космического полета. Данный учебник дол-
жен способствовать повышению качества подготовки специа-
листов в области баллистики, динамики и управления движе-
нием КА.
Авторы не имели возможности охватить все аспекты косми-
ческой баллистики, однако ставили перед собой задачу позна-
комить читателя с рядом важнейших разделов теории движе-
ния КА, обучить читателя современным методам расчета тра-
екторий движения основных типов КА, проектно-баллистиче-
ским методам, которые используются на начальных этапах
проектирования КА. В учебнике представлены основы теории
движения 'искусственных спутников Земли и других планет,
особенности теории движения спутниковых систем, осно-
вы теории (перелетов между орбитами в окрестности небес-
ного тела и межпланетного перелета, основы теории движения
спускаемых аппаратов. В рамках рассматриваемых теорий ос-
новное внимание уделяется задаче проектирования траектории
КА, нахождению характеристик траектории, определяющих
энергетические и массовые параметры аппарата.
Читатель должен быть достаточно ознакомлен с соответст-
вующими разделами математики, теоретической механики,
аэродинамики. Табличные данные и графические материалы в
учебнике иллюстрируют результаты конкретных расчетов.
В списке литературы выделены работы, рекомендуемые для
более глубокого изучения (основная литература).
Введение и гл. 2, 3, 6, 7 написаны М. С. Константиновым;
гл. 1 — В. К. Безвербым и М. С. Константиновым, гл. 4, 5 —
Б. П. Перелыгиным; гл. 8—10 — Е. Ф. Каменковым.
Авторы приносят глубокую благодарность редактору учеб-
ника академику В. П. Мишину и проф. А. А. Дмитриевскому,
чьи советы во многом определили содержание учебника, его
методическую направленность.
Авторы выражают признательность рецензенту профессо-
ру А. М. Мхитаряну за ценные замечания, способствовавшие
существенному улучшению учебника.
3
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
а — большая полуось орбиты
b — малая полуось орбиты
с — фокальное расстояние
Cxyz — прямоугольная декартовая невращающаяся система коорди-
нат с началом в гравитационном центре
Сха — коэффициент лобового сопротивления
Суа — коэффициент аэродинамической подъемной силы
CZa — коэффициент аэродинамической боковой силы
Е — эксцентрическая аномалия
е — эксцентриситет орбиты спутника
FM — характерная площадь ИСЗ (площадь миделевого сечения)
f — гравитационная постоянная; реактивное ускорение
G — сила притяжения
g — гравитационное ускорение
go —ускорение свободного падения (go = 9,80665 м/с2)
Н — аналог эксцентрической аномалии Е для гиперболической тра-
ектории
h — высота; констапта энергии
I — тензор инерции
/у — удельный импульс тяги, /у= |Р|//и (эквивалентная величи-
на— эффективная скорость истечения W3)
i — наклонение орбиты ИСЗ
JD — юлианская дата
К — аэродинамическое качество GA
М —масса небесного тела; средняя аномалия, M = n(t—tn )
т — масса КА
mQ — начальная масса КА
тТ — масса топлива
Щц.н — масса полезного груза
tn — массовый расход рабочего тела
N — количество спутников в системе, число витков орбиты
п — среднее движение
it — перегрузка
лХа, пУа — составляющие перегрузки в скоростных осях
Onrb— орбитальная система координат (и — трансверсаль, г — ради-
аль, b — нормаль)
О£т|£ — перицентральная система координат
Р — тяга ракетного двигателя
р — фокальный параметр
q — скоростной напор, <7 = р V2/2
Ё — радиус гравитирующего тела
— средний радиус Земли (6371,1 км)
Ез.п — полярный радиус Земли
4
Яз.э— экваториальный радиус Земли
7?Сф.д — радиус сферы действия
г — радиус-вектор КА относительно гравитационного центра
S — площадь, заметаемая радиусом-вектором КА
Sa — площадь среза сопла
Sm — характерная площадь аппарата (для определения аэродина-
мических сил)
SK — конструктивный баллистический коэффициент, 5к = Сх^м/(2то)
Тег — дата старта
Тк — дата подлета к планете назначения
t — время
/п— время межпланетного полета
t— моторное время
t— момент прохождения перицентра орбиты КА
U — потенциал гравитационного поля
и — аргумент широ_ты спутника
V — скорость КА, V = drldt
Vi, Vn, Vih— первая, вторая и третья космические скорости
Vr — радиальная скорость КА, Vr = dr)dt
Vn — трансверсальная скорость КА, Vn=rdvldt
Voo — скорость КА относительно планеты в момент выхода КА
из грависферы планеты, гиперболический избыток скорости
Voo' — скорость КА относительно планеты в момент входа КА в
грависферу планеты
VK.c — гелиоцентрическая скорость КА в момент входа КА в гра-
висферу планеты
Vo.с — гелиоцентрическая скорость КА в момент выхода КА из
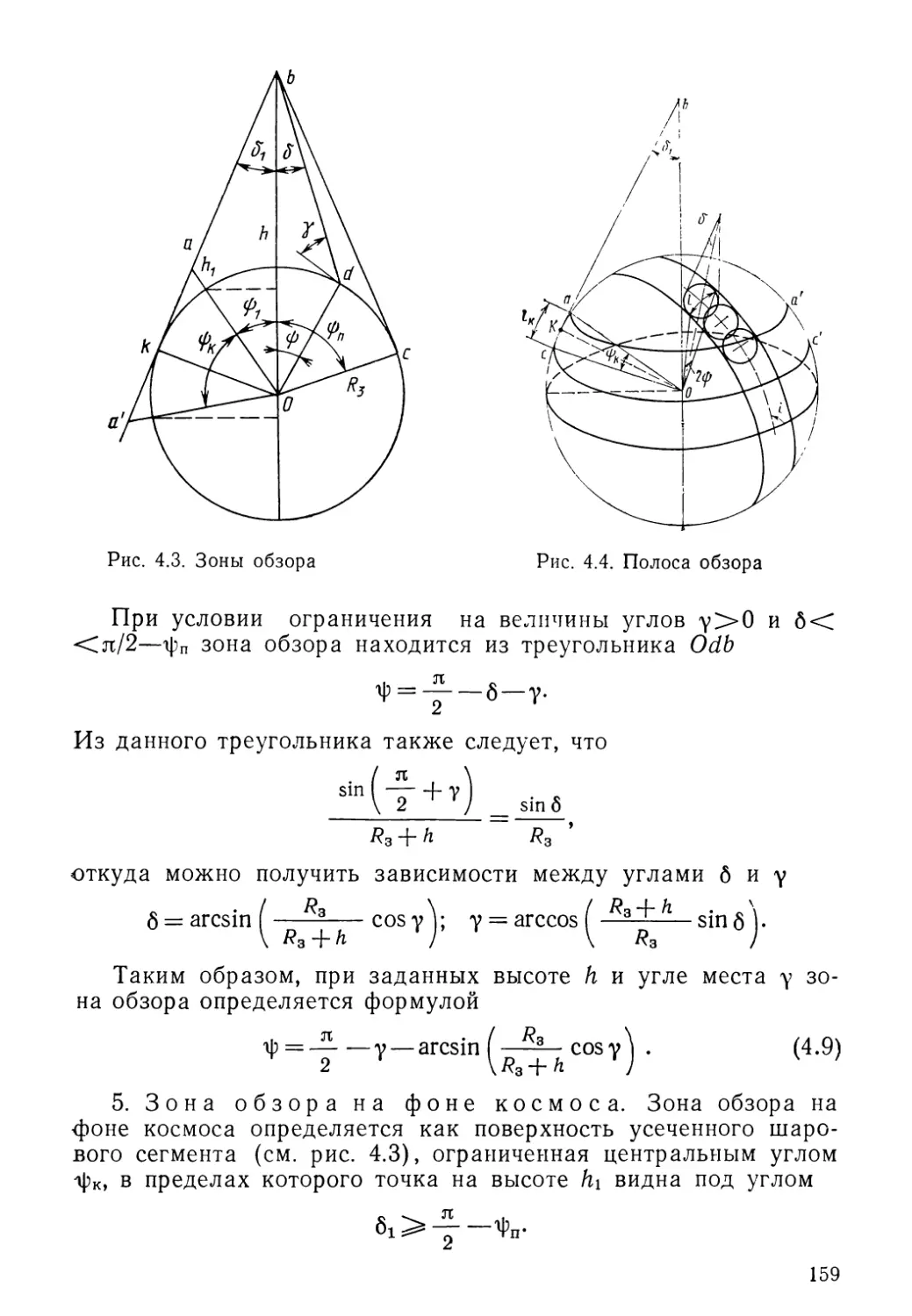
грависферы планеты
Vxap — характеристическая скорость
AV — импульс скорости
AV s— суммарный импульс скорости
AVrp, AVa, — потери в скорости гравитационные, аэродинамические, на
AVnp, AVynp противодавление, на управление соответственно
IV3 — эффективная скорость истечения (эквивалент удельного им-
пульса тяги)
Ха — сила лобового сопротивления
Ya — аэродинамическая подъемная сила
Za — аэродинамическая боковая сила
а — угол атаки, прямое восхождение
(Хбал — балансировочный угол атаки
Оп — пространственный угол атаки
а — коэффициент сжатия общего земного эллипсоида
(О,335589Х1О-2)
У — угол крена
6 — склонение
е — угол наклона земного экватора к плоскости эклиптики
0 — траекторный угол (угол наклона скорости к местному гори-
зонту)
О' — угол тангажа
% — долгота; средняя долгота X = QЧ-со4-М
К — вектор Лапласа
р. —гравитационный параметр небесного тела, jx = fM; безразмер-
ная масса КА, p, = m/m0; отношение масс гравитирующих тел
в ограниченной задаче трех тел, p = Mi/M2
Цт — относительный запас топлива
Р — плотность среды
— вектор площадей
5
о\ — баллистический параметр, ox=cXaSM/(mgQ)
Т — период обращения спутника
Ф_ — угловая дальность полета
Ф — возмущающее ускорение, Ф= [Фх, Фу, Фг] = [Г, S, W], где
Т, S, W — проекции возмущающего ускорения на оси орби-
__ тальной системы координат
Фа — аэродинамическое возмущающее ускорение
Фл — лунно-солнечные возмущающие ускорения
Фн — возмущающее ускорение от нецентральности гравитационно-
го поля Земли
ф — широта (геоцентрическая)
ф — угол рыскания
Q — долгота восходящего узла
со — угловая скорость; аргумент перицентра
Индексы,
вх — вход в атмосферу
з — Земля
к — конечное состояние
кр — круговая орбита
л — Луна
О — начальное состояние
пар — параболическая орбита
пл — планета
с— Солнце
а— апоцентр орбиты
п — перицентр орбиты
ВВЕДЕНИЕ
Механикой космического полета называется раздел механи-
ки, изучающий движение искусственных небесных тел — кос-
мических аппаратов. Другие названия этого раздела механи-
ки— теория движения КА, астродинамика, космическая балли-
стика. Многие авторы считают, что термин «Механика косми-
ческого полета» не совсем корректен, так как летают, строго
говоря, самолеты, вертолеты и другие атмосферные аппараты,
но не КА. Соглашаясь с этим в принципе, отметим, что в учеб-
нике в основном будет использоваться общее понятие движе-
ния КА, хотя в некоторых случаях допускаются также терми-
ны межорбитальный перелет, межпланетный перелет.
Теория движения КА тесно связана с классической небес-
ной механикой, использует ее постановки и методы. Небесная
механика — раздел астрономии, изучающий движение естест-
венных небесных тел (звезд, планет и их спутников, астерои-
дов, комет) на основе закона всемирного тяготения. В небес-
ной механике прежде всего анализируется траектория движе-
ния небесного тела. Под траекторией понимается непрерывная
линия, которую описывает центр масс тела при его перемеще-
нии в пространстве. Траектория, по которой движется вокруг
центрального тела центр масс планеты, спутника планеты, ис-
кусственного спутника и т. д., называется орбитой.
Описание и исследование траектории является очень важ-
ным элементом теории движения КА. Рассматривая КА как
динамический объект, важно выделить два типа его движения:
активное и пассивное. На активном участке полета на КА
включен ракетный двигатель, КА совершает управляемое дви-
жение, и характеристики этого движения во многом определя-
ются тягой ракетного двигателя. Активные участки полета для
традиционных КА, традиционных двигателей занимают отно-
сительно малое время и имеют малую протяженность. Пассив-
НЫе ^У?стки полета — это такие, на которых ракетный двига-
тель КА выключен. Пассивные участки полета занимают преоб-
ладающую часть всей траектории КА. Движение КА на пассив-
ных участках полета описывается теми же уравнениями, что и
движение естественных небесных тел.
Изучая движение КА, приходится анализировать большое
число различных траекторий и выбирать из них оптимальные,
удовлетворяющие определенным ограничениям и критериям.
Такое исследование с использованием численного интегрирова-
ния достаточно полных уравнений движения КА даже с исполь-
зованием современных быстродействующих ЭВМ требует боль-
ших затрат времени.
На начальном этапе проектирования КА особое значение
приобретает необходимость отыскания простых приближенных
зависимостей, позволяющих быстро анализировать большое чи-
сло возможных вариантов КА, наглядно представлять влияние
основных параметров КА на его траекторию. На основе таких
зависимостей выбирается небольшое число вариантов КА, удо-
влетворяющих поставленным требованиям. Эти варианты в
дальнейшем должны быть исследованы с применением более
точных методов.
Таким образом, в теории движения КА наряду с методами
точного исследования траекторий КА должны быть разработа-
ны и приближенные методы для оценки влияния различных
факторов на движение КА.
Начальные условия движения КА и их отклонение от рас-
четных значений определяют требования к характеристикам
транспортных аппаратов выведения КА, а также требования к
характеристикам корректирующих устройств, компенсирующих
отклонение конечных параметров движения КА от их расчет-
ных значений.
Развитие терии движения КА
Роль отечественных ученых в формировании меха-
ники космического полета как науки высока. Реальную возмож-
ность применения ракет для межпланетных сообщений теоре-
тически обосновал великий русский ученый Константин Эдуар-
дович Циолковский. В своей статье «Исследование мировых
пространств реактивными приборами» (1903 г.) и в дальней-
ших работах К- Э. Циолковский наметил основные проблемы
космонавтики и заложил теоретический фундамент принципи-
ального решения этих проблем. К- Э. Циолковским была сфор-
мулирована новая система понятий, таких как характеристи-
ческая или идеальная скорость КА, гравитационные, аэродина-
мические потери, оптимальная (рациональная) траектория и
т. д. Но это только начало перечня понятий, введенных
К. Э. Циолковским и положенных в основу современной тео-
рии проектирования траекторий КА.
Фридрих Артурович Цандер, выдающийся советский ученый
и изобретатель, начал заниматься проблемами реактивного
8
движения еще в 1908 г. Многие его идеи дали возможность раз-
работать современные методы для решения задач теории дви-
жения КА на начальных этапах проектирования. К таким иде-
ям можно отнести идею разбиения всего пространства на гра-
висферы влияния, идею импульсной аппроксимации активного
участка траектории разгонного блока, использование энерге-
тического критерия при анализе схем межпланетных полетов
и т. д.
Не менее важны предложения Ф. А. Цандера по схемам
движения КА. Очень интересные идеи по схемам полета и
конструкции КА высказывал Юрий Васильевич Кондратюк. В
частности, в рукописной работе «Тем, кто будет читать, чтобы
строить» (1918—1919 гг.) Юрий Васильевич рассматривал воз-
можность использования сопротивления атмосферы для тормо-
жения КА при его возвращении на Землю, предлагал при по-
летах к небесным телам использовать орбиту искусственного
спутника этих тел, а для, посадки на них человека — небольшой
взлетно-посадочный аппарат.
Большой вклад в развитие теории движения КА внесли Ни-
колай Егорович Жуковский и Ивап Всеволодович Мещерский.
Очень важны работы по космонавтике зарубежных ученых
Р. Эно-Пельтри, Р. Годдарда, Г. Оберта, В. Гомана, Е. Зен-
гера.
Первые практические результаты, предопределившие в
дальнейшем успехи советской космонавтики, были получены в
тридцатые годы и были связаны с работами групп энтузиастов
и пионеров ракетодинамики, возглавлявшихся С. П. Короле-
вым, М. К. Тихонравовым.
Послевоенное развитие ракетно-космической техники и вме-
сте с ней теории движения КА шло бурными темпами. В это
время развитие механики космического полета все более опре-
делялось проблемами, возникающими при проектировании ре-
альных ракетно-космических систем. Задачи механики все тес-
нее связывались с теорией и задачами проектирования КА.
Одной из основных задач проектирования КА, как и проек-
тирования любых транспортных аппаратов, является всесто-
ронне обоснованный выбор основных проектных параметров,
удовлетворяющих техническому заданию при наилучших пока-
зателях качества — критериях эффективности [8].
Удовлетворение требованиям технического задания невоз-
можно без нахождения необходимых энергетических, массовых
затрат на осуществление космических маневров проектируемо-
го космического аппарата. Получить оценки перечисленных ха-
рактеристик можно только после исследования движения ап-
парата, после анализа необходимого приращения скорости КА
и требуемых затрат топлива для такого приращения.
9
Баллистическое проектирование является важной частью
всей задачи проектирования КА. При баллистическом проекти-
ровании выделяются некоторые характерные проектные пара-
метры аппарата и связываются с выполняемой им транспорт-
ной операцией. Нахождение такой связи — одна из основных
задач теории движения КА. На основе решения этой задачи на
ранних этапах проектирования КА проводится массовый ана-
лиз КА, анализ его геометрических, стоимостных и других ха-
рактеристик, формируется облик аппарата.
С точки зрения теории движения характерной особенностью
ракет и КА в отличие от многих летательных аппаратов явля-
ется отсутствие установившегося режима движения. Существо-
вание установившегося режима во многом определяет подход
к расчету траектории самолета, кроме того, именно установив-
шийся режим, его характеристики прежде всего, определяют
проект самолета.
Для КА установившегося режима просто нет. Практически
на любом участке траектории КА их скорость и другие харак-
теристики движения существенно изменяются. Таким образом,
в этом классе аппаратов, пожалуй, впервые неустановившийся
режим движения во многом определяет облик аппарата.
В механику космического полета весомый вклад внесли со-
ветские ученые. Среди них можно отметить Д. Е. Охоцимско-
го, Т. М. Энеева, А. К- Платонова, Э. Л. Акима, работы кото-
рых, вышедшие в свет в 1950-х годах, создали теоретическую
базу для широких научных исследований. Очень велика роль
В. И. Левантовского, В. В. Белецкого, чьи блестящие работы
способствовали популяризации механики космического полета.
Авторы смогли раскрыть сущность и красоту задач механики
космического полета в простой и интересной форме.
Несмотря на большие успехи в становлении механики кос-
мического полета как науки, не следует считать, что все зада-
чи теории движения КА уже решены, что описать движение
любого КА не представляет творческого труда, а в эпоху со-
временных ЭВМ исследовать любую математическую модель —
«дело техники». В механике космического полета есть еще
очень много нерешенных задач. Например, решение проблем
выбора оптимальной траектории даже традиционных КА по-
рой наталкиваются на серьезные трудности. Еще сложнее об-
стоит дело с перспективными КА, движение которых трудно
исследовать традиционными методами. Больше того, развитие
механики космического полета порой поднимает нерешенные
проблемы «чистой» небесной механики.
ю
Задачи теории движения КА
На различных этапах проектирования, производства
и эксплуатации КА возникает большое число задач, решение
которых обеспечивает механика космического полета.
Из них можно выделить следующие задачи:
нахождение траектории КА по заданным его параметрам и
программе движения (основная задача);
проектирование траектории КА;
анализ влияния параметров КА на его траекторию;
анализ влияния возмущающих факторов на траекторию КА;
анализ управления движением КА.
Основная задача. Известны проектные параметры КА, из-
вестна программа движения КА. Требуется определить траек-
торию КА (программную траекторию КА), характеристики
движения КА (под характеристиками движения подразумевают-
ся кинематические характеристики, определяющие положение
КА относительно планет, Солнца, измерительных пунктов и
т. д.).
Решение основной задачи теории движения КА проводится
как на ранних этапах проектирования КА, так и на более позд-
них этапах (даже на этапе эксплуатации КА). Постановка та-
кой задачи на разных этапах существенно изменяется, преж-
де всего изменяется модель движения. Математическая мо-
дель движения (полная система, описывающая движение КА)
для решения основной задачи теории движения на этапе экс-
плуатации отличается существенно большей точностью, учетом
тех факторов, которые на ранних этапах проектирования КА
не рассматривались. Изменяется часто и понятие программы
движения.
Таким образом, решение основной задачи теории движения
отвечает на вопрос, какова траектория заданного КА с задан-
ной программой движения.
Второй задачей теории движения можно считать задачу вы-
бора программы движения КА, которая обеспечивает для за-
данного КА выполнение заданной транспортной задачи (задан-
ного космического маневра: попадания на заданную конечную
орбиту, в окрестность планеты-цели и т. д.). Для этапа про-
ектирования КА такую задачу целесообразно называть зада-
чей проектирования траектории КА.
При решении этой задачи возникает проблема выбора сре-
ди^ траекторий, обеспечивающих решение заданной транспорт-
ной задачи, такой траектории, которая удовлетворяет допол-
нительным требованиям. Среди этих требований важное место
отводится условиям оптимальности или рациональности траек-
тории. Поясним это. Выполнение поставленной перед КА транс-
фертной задачи часто возможно по многим траекториям, с ис-
11
пользованием ряда программ движения. В этом случае из тра-
екторий следует выбрать в определенном смысле лучшую, ра-
циональную. Критериев оптимальности (рациональности) весь-
ма много. Это, прежде всего, затраты топлива, характеристики
точности выполнения заданного космического маневра, точно-
сти удовлетворения конечных условий движения, характеристи-
ки потребных для выполнения движения навигационных-систем,
систем управления, систем ориентации и т. д.
В настоящей книге задача проектирования траектории бу-
дет рассматриваться с точки зрения обеспечения минималь-
ных затрат требуемого запаса топлива. При этом там, где это
возможно, будут приводиться характеристики точности, достиг-
нутые при использовании существующих навигационных си-
стем, систем управления движением КА.
Таким образом, задача проектирования траектории КА будет
рассматриваться как задача нахождения такой программы дви-
жения КА и соответствующей ей программной траектории, кото-
рая удовлетворяет конечным условиям движения, кинематичес-
ким, динамическим ограничениям, ограничениям по точности и
требует для сво-его осуществления минимальных энергетических
затрат. В условиях определенной точности модели -самого КА,
точности математической модели его движения постановка .
данной задачи в ряде случаев оказывается практически неце-
лесообразной. Поэтому требование минимальных энергетиче-
ских затрат заменяют требованием достаточного приближения
энергетических затрат к минимальным. При этом удается ис-
пользовать простые законы управления движением КА, кото-
рые в своей реализации не требуют переусложненных систем
навигации, ориентации и управления и дают возможность учи-
тывать большое число важных практических факторов, трудно
формализуемых в математической модели.
Третьей задачей теории движения КА можно считать зада-
чу анализа влияния параметров КА на его траекторию. Про-
ектные параметры КА в общем случае влияют па траекторию
аппарата. Начальная тяговооруженность КА будет влиять на
интенсивность набора им скорости, аэродинамические парамет-
ры КА (например, баллистический коэффициент) будут во
многом определять траекторию спуска КА в атмосфере и т. д.
Оценить это влияние, дать рекомендации по выбору программы
движения КА в зависимости от его параметров и является су-
ществом этой задачи.
Четвертая задача теории движения КА в приведенной клас-
сификации есть анализ влияния возмущающих факторов на
траекторию КА.
К возмущающим факторам относят те физические явления,
которые не были учтены в математической модели движения
КА. Это могут быть неучтенные силы в уравнении сил, различ-
12
хцые случайные факторы. Например, ошибки начальных усло-
вий движения КА, погрешности измерения характеристик дви-
жения, используемые при работе системы управления, отклоне-
ния параметров КА от номинальных значений и т. д. Важно
выявить, как эти возмущающие факторы влияют на траекто-
рию КА, к каким погрешностям в конечных характеристиках
движения они приводят.
Пятой задачей теории движения является задача ана-
лиза управления движением КА. Она не может быть реше-
на без рассмотрения теории навигационных измерений, теории
стохастичеких систем управления и анализа систем управления
движением КА. Такая задача не рассматривается в книге, в ря-
де случаев будут лишь обсуждены используемые в настоящее
время системы и приведены качественные и количественные
характеристики точности реализации рассмотренных траекто-
рий КА.
В дальнейшем основное внимание будет уделено двум пер-
вым задачам теории движения КА. Дадим им краткое матема-
тическое описание.
Основная задача теории движения КА
Решение основной задачи прежде всего предполага-
ет необходимость разработки математической модели, описыва-
ющей движение КА.
Пусть эта модель представлена в виде следующей системы
дифференциальных уравнений первого порядка:
=f(y, и, а), (В.1)
at
где у — вектор-столбец фазовых координат КА, для анализа
изменения которых математическая модель содержит диффе-
ренциальные уравнения (это, например, компоненты скорости
КА, его координаты); и — вектор функций управления движе-
нием КА (это, например, закон изменения тяги двигателя КА;
закон включения — выключения двигателя, закон ориентации
КА в пространстве и т. д.); а — вектор параметров КА; f —
вектор-столбец функций от у, а, и\ t — независимая переменная,
например время движения КА.
Форма математической модели (В.1) предполагает, что
дифференциальные уравнения, описывающие движение КА,
представлены в виде уравнений первого порядка, разрешенных
относительно производной.
Математически основная задача теории движения может
быть сформулирована следующим образом:
13
при заданном векторе параметров КА а\
при заданном векторе управления КА и (он может быть за-
дан в виде функции времени u(t) или функции фазовых коор-
динат космического аппарата и (у, /));
при заданных начальных условиях движения у(Л))=У° най-
ти решение системы дифференциальных уравнений (В.1).
Таким образом, математически построение траектории КА
с заданными параметрами а и программой движения и сводит-
ся к решению задачи Коши для системы обыкновенных диффе-
ренциальных уравнений. Понятно, что в общем случае при про-
извольно заданном управлении построенная траектория может
не удовлетворять условиям транспортной задачи — КА не вый-
дет на заданную конечную орбиту, к заданной планете назна-
чения и т. д. Задача выбора программы движения, при кото-
рой эти условия удовлетворяются, при классификации была
названа задачей проектирования траектории КА.
Теория движения КА и системы автоматизированного
проектирования КА
Создание системы автоматизированного проектиро-
вания КА, как и всякого технического объекта, является ос-
новным путем интенсификации процесса разработки и созда-’
ния аппаратов.
Одним из принципов построения систем автоматизирован-
ного проектирования является блочная структура создаваемых
систем. В соответствии с этим принципом при анализе проек-
та КА выделяется динамическая и массовые части. Динамиче-
ская часть разрабатывается на основе теории движения КА.
В нее входят характеристики затрат (массовых или энергети-
ческих) на выполнение тех маневров, для которых аппарат
предназначен, находятся зависимости, связывающие затраты с
проектными параметрами аппарата для каждого из маневров.
Эта часть задачи анализа проекта КА называется динамичес-
кой частью, так как ее решение предполагает произвольному
набору параметров аппарата поставить в соответствие рацио-
нальную траекторию выполнения каждого заданного маневра
и характеристики затрат при движении по этим траекториям.
Эта часть задачи может быть названа задачей проектирования
траекторий КА.
Решение динамической части может быть представлено в
виде функциональных зависимостей характеристик различных
затрат от параметров КА.
Такие зависимости существенно связаны с типом маневров,
которые аппарат должен выполнять. Учитывая, что КА проек-
тируется на диапазоны маневров, целесообразно ввести поня-
тие параметров космического маневра в вышеуказанные функ-
14
циональные зависимости. В таком случае решение динамичес-
кой части анализа проекта целесообразно представлять в виде
функциональной зависимости характеристик затрат от пара-
метров КА и параметров маневра.
При этом проектирование траекторий КА включает в себя:
решение задачи оптимального управления и поиска опти-
мальной траектории перелета для фиксированных проектных
параметров КА и параметров маневра;
выбор проектных параметров КА и параметров космическо-
го маневра из практически интересных диапазонов этих пара-
метров;
построение аппроксимационной зависимости характеристи-
ки затрат от проектных параметров КА и параметров космиче-
ского маневра.
Задача анализа проекта КА заключается в выборе рацио-
нальных проектных параметров аппарата по некоторым крите-
риям (например, массовым или экономическим), с использо-
ванием зависимостей, получаемых из баллистического анализа.
Таким образом, для разработки системы автоматизирован-
ного проектирования КА необходимо на основании методов
механики космического полета для каждого типа космической
операции (перелеты между орбитами, движения ИСЗ, межпла-
нетного перелета, спуск на поверхность планеты и т. д.) раз-
работать алгоритм расчета (и далее программу расчета), ко-
торый позволял бы по основным параметрам КА и параметрам
закона управления определить основные кинематические и ди-
намические характеристики траектории КА и затраты на транс-
портную операцию. Для проведения такой работы необходимо
рассмотреть основные транспортные операции КА, описать их
математически, получить качественные и количественные
оценки этих операций как функции выбираемых проектных
параметров КА и параметров закона управления им.
Настоящий учебник в основном посвящен выбору оптималь-
ных траекторий движения КА, нахождению характеристик дви-
жения КА для достижения цели, поставленной перед аппара-
том, стартующим с низкой орбиты. Вопросы, связанные с вы-
ведением КА с Земли на околоземные орбиты, не рассматри-
ваются.
ГЛАВА J. ОБЩАЯ ТЕОРИЯ ДВИЖЕНИЯ
Решение задач механики космического полета всегда связано с описа-
нием движения КА. Выбор математической модели, которая дает возможность
с определенной точностью получить решение той или иной задачи механики,
является важным начальным этапом исследования движения КА. Такая ма-
тематическая модель представляет в общем случае систему уравнений относи-
тельно переменных, характеризующих движение КА. Эти переменные в даль-
нейшем будут называться фазовыми координатами (переменными) КА. К ним
относят величины, характеризующие положение КА в пространстве, скорость
изменения этих величин и т. д. В общем случае уравнения, входящие в ма-
тематическую модель, могут быть алгебраическими, дифференциальными и бо-
лее сложной математической структуры.
Описать движение, разработать модель движения, т. е. записать полную
систему уравнений, описывающую движение КА, — это значит получить
замкнутую систему уравнений относительно фазовых координат КА.
Задача настоящей главы — показать, как можно описать движение КА,
как получить полную систему уравнений, описывающих движение КА, как
подойти к исследованию полученной модели.
1.1. ТРАЕКТОРИЯ ДВИЖЕНИЯ КА
Космический аппарат как объект движения — это
тело весьма сложной геометрии, часто внутри КА располага-
ются емкости с жидким наполнением, корпус КА не абсолютно
жесткий. Все это в общем случае нужно учитывать при опи-
сании движения КА, в частности колебания упругого корпу-
са — это тоже его движение. В таких условиях, если не конкре-
тизировать понятие движения КА, то подойти к его описанию
будет, по крайней мере, сложно.
Траекторией КА называется непрерывная линия, которую
описывает центр масс КА при своем движении в пространстве.
Будем считать, что основная задача в дальнейшем будет со-
стоять в исследовании и выборе траектории КА. При этом ос-
тальные степени свободы КА могут исследоваться только для
выявления их влияния на траекторию КА.
В некоторых случаях при исследовании траектории КА его
можно рассматривать как материальную точку, совпадающую
с центром массы КА. Материальная точка имеет три степени
16
^свободы (три координаты в пространстве, например %, у, z).
Для нахождения траектории требуется найти изменения этих
трех координат во времени:
x=x(t), y = y(t), z = z(t). (1.1)
Траектория КА в общем случае зависит от его углового по-
ложения в пространстве. Поэтому при исследовании траекто-
рии КА приходится рассматривать как твердое тело, у кото-
рого, кроме трех поступательных степеней 'свободы (1.1), суще-
ствуют три вращательные степени свободы. Обозначим их
О, у. Описание углового движения КА в пространстве долж-
но дать возможность исследовать изменение этих вращатель-
ных степеней свободы: *ф(/)» т(0-
Для исследования траектории движения КА в большинстве
задач, возникающих на ранних этапах проектирования КА,
к сложной модели движения (учитывающей упругость кор-
пуса, поведение жидкости в частично заполненных емкостях и
т. д.) прибегать не приходится. С достаточной для проектанта
точностью можно исследовать траекторию, рассматривая КА
как 'твердое тело. Важно подчеркнуть, что любая математичес-
кая модель, описывающая движение КА, не имеет абсолютной
точности. При разработке математической модели важно пони-
мать уровень требующейся точности и создавать достаточно
простую модель, удовлетворяющую этому уровню точности.
От простоты модели в ряде случаев зависит .возможность вы-
вода важнейших качественных зависимостей. Поэтому в тех
задачах, в которых можно обойтись без анализа враща-
тельных степеней свободы КА, математическая модель движе-
ния не должна включать уравнений, описывающих вращение
КА. В этих задачах нужно рассматривать КА как материаль-
ную точку, совпадающую с центром масс.
В некоторых случаях удается еще более упростить анализ
и вместо исследования изменения всех трех координат (1.1)
описывать изменение только двух из них (плоское движение)
или даже одной (одномерное движение).
Описание движения КА опирается на законы теоретичес-
кой механики. Среди этих законов основные теоремы динами-
ки: теорема о количестве движения, теорема о моменте количе-
ства движения. На этих законах останавливаться не будем и
отошлем читателя к курсам теоретической механики.
Напомним, что одним из основных законов динамики мате-
риальной точности является положение: ускорение материаль-
ной точки относительно инерциального пространства про-
порционально сумме векторов, действующих на нее сил
(S/ч), а коэффициентом пропорциональности является масса
i
материальной точки (mj):
Рассматривая КА как совокупность материальных точек пе-
ременного состава, удается вывести, что центр масс КА дви-
жется как материальная точка, масса которой равна массе
всего КА в данный момент времени и к которой приложены
равнодействующие всех внешних и реактивных сил и силы,
обусловленные относительным и кориолисовым ускорениями
центра масс:
т— + m rfVc0TH +2т[юХ^сотн], (1.2)
dt i dt
где V — скорость центра масс КА в инерциальном пространст-
ве; dV/dt — ускорение_центра масс КА в этом же пространст-
ве; т — масса КА; S/ч — сумма внешних сил, действующих
i _
на КА, включая реактивную силу; 1/СОТн — скорость центра
масс относительно корпуса КА; dVCQ1nldt — ускорение центра
масс относительно корпуса КА; — вектор угловой скорости
КА в инерциальном пространстве.
Уравнение (1.2) и его возможные упрощения часто будем
называть уравнением сил.
Два последних слагаемых в правой части (1.2) связаны с
перемещением центра масс КА относительно его корпуса. В
большинстве случаев такое перемещение и скорость перемеще-
ния весьма малы, поэтому этими слагаемыми можно прене-
бречь и вместо соотношений (1.2) использовать уравнение сил
в виде:
(1.3)
dt i
Обратим внимание на то, что равенство (1.2) или (1.3) опре-
деляет ускорение КА в инерциальном пространстве.
Для анализа движения КА вокруг центра масс (углового
движения) следует использовать уравнение моментов. Оно мо-
жет иметь вид
(1-4)
dt i
где I — тензор инерции (матрица, главная диагональ которой
состоит из значений осевых моментов инерции КА, остальные
элементы этой матрицы есть величины центробежных моментов
18
инерции, взятых со знаком минус)—вектор углового ус-
корения КА в инерциальном пространстве; SM;— сумма векто-
i
ров моментов, действующих на КА, включая момент реактив-
ной силы, момент кориолисовых сил, управляющий момент.
При нахождении и исследовании траектории КА основное
внимание уделяется уравнению сил (1.3), к уравнению момен-
тов (1.4) обращаются, если не удается разделить поступатель-
ное и вращательное движения КА.
Анализ уравнения сил (1.3) показывает, что для описания
движения КА необходимо:
ввести некоторую систему отсчета — систему координат;
проанализировать силы, действующие на КА, найти проек-
ции этих сил на оси введенных систем координат.
1.2. СИСТЕМЫ КООРДИНАТ ДЛЯ АНАЛИЗА
ДВИЖЕНИЯ КА
Абсолютное пространство, в котором справедливо
уравнение сил (1.3), есть некоторое гипотетическое простран-
ство. В механике космического полета абсолютной системой
координат считают прямоугольную декартову систему коорди-
нат с началом в центре Солнца. Оси этой системы координат
неподвижны относительно звезд.
Прямоугольная декартова система координат, начало кото-
рой помещено в некоторой точке пространства либо перемеща-
ется с постоянной скоростью, а направление осей относитель-
но звезд неизменно называется инерциальной. Инерциальную
систему координат можно определить как систему равномерно
и прямолинейно поступательно перемещающуюся относитель-
но абсолютной системы координат.
Всякие другие системы координат являются неинерциаль-
ными.
Описывать движение КА можно и в неинерциальных систе-
мах координат, но при этом придется учитывать то, что абсо-
лютное ускорение КА, входящее в левую часть равенств (1.2)
и (1.3), должно рассматриваться как сумма относительного
ускорения в неинерциальной системе координат /, переносного
ускорения системы координат je и кориолисова ускорения /с:
dV ~ _
dt 1 + 1е~\~ jc'
В настоящее время для описания движения КА использу-
ется большое число систем координат. Рассмотрим некоторые
из них.
19
Земные системы координат
К этой группе систем координат относятся правые
прямоугольные декартовы системы координат, начало и оси
которых фиксированы по отношению к Земле и выбираются в
соответствии с задачей. Среди этой группы систем координат
рассмотрим геоцентрическую экваториальную систему коорди-
нат, геоцентрическую эклиптическую и несколько позже — гео-
центрическую перицептральную системы координат.
Геоцентрическая экваториальная (невраща-
ющаяся) система координат. Начало этой системы
совпадает с центром Земли. Основная плоскость Сху совпада-
ет с плоскостью земного экватора, ось Cz направлена ло оси
Земли к Северному полюсу мира. Направление оси Сх выбра-
но постоянным в инерциальном пространстве. Ось Сх направ-
лена в точку весеннего равноденствия Y. Ось Сх перемещается
поступательно и параллельно радиусу-вектору Земля — Солн-
це в момент весеннего равноденствия. Отметим, что эта ось
принадлежит плоскости эклиптики (плоскости, в которой про-
исходит обращение вокруг Солнца центра масс системы Зем-
ля— Луна), так как в момент равноденствия Солнце нахо-
дится над земным экватором и радиус-вектор Земля — Солнце
принадлежит как плоскости земного экватора, так и плоскости
эклиптики.
Геоцентрическую экваториальную систему координат ис-
пользуют для анализа движения искусственных спутников Зем-
ли (ИСЗ), КА, осуществляющих перелеты между орбитами
ИСЗ, межпланетных КА в окрестности Земли. Эту систему для
большинства задач можно считать инерциальной, если прене-
бречь переносным ускорением, т. е. криволинейностью движе-
ния Земли относительно Солнца.
Положение КА в геоцентрической экваториальной системе
координат, кроме прямоугольных декартовых проекций х, у, г
(эти проекции являются компонентами радиуса-вектора КА г:
г=[х, У> г])» может характеризоваться сферическими коорди-
натами. На рис. 1.1 точка С — центр Земли, ось Сх направле-
на в точку весеннего равноденствия Y (астрономический сим-
вол созвездия Овен). Угол между радиусом-вектором КА
(СА = г) и экваториальной плоскостью называется склонением
и часто обозначается д(—л/2^6^л/2). Положительное скло-
нение соответствует положению КА в северном полушарии.
Угол между осью Сх и проекцией радиуса-вектора КА на
плоскость экватора Сху называется прямым восхождением и
обозначается а (—180°^а^ 180°). Положительные углы а со-
ответствуют углам, отсчитанным от оси Сх в сторону оси Су.
Таким образом, сферическими координатами КА в геоцен-
трической экваториальной системе координат являются г, д, а.
20
Рис. 1.2. Относительное положение геоцен-
трических экваториальной (Cxyz) и эклип-
тической (СхэГ/эИэ) систем координат
Рис. 1.1. Геоцентрическая эк-
ваториальная система коорди-
нат
Для очень небольшого круга задач механики космического
полета КА рассматривается и геоцентрическая гринвичская
экваториальная система координат, вращающаяся вместе с
Землей относительно ее оси. В этой системе координат хорошо
определять положение космодрома или пункта наблюдения на
земной поверхности. Плоскость CXqYq такой системы, как и
экваториальной невращающейся системы координат, совпада-
ет с плоскостью экватора. Ось СХ0 принадлежит плоскости
гринвичского (нулевого) меридиана. Сферические координаты
КА или земных объектов характеризуются геоцентрической
широтой, долготовой и длиной радиуса-вектора г. Геоцентриче-
ская широта — есть угол между радиусом-вектором КА и пло-
скостью экватора. Широту в дальнейшем будем обозначать ср
(—л/2^(р^л/2). Отметим, что геоцентрическая широта и скло-
нение равны между собой ср = 6. Долгота — есть двугранный
угол между меридиальной плоскостью, в которой находится
КА, и плоскостью гринвичского меридиана. Обозначается дол-
гота К (—180°<Х<С 180°).
Геоцентрическая эклиптическая система
координат. Эта система координат отличается от геоцент-
рической экваториальной расположением осей Су3 и Сзэ. Ее
начало находится в центре Земли, оси Схэ и Суэ принадлежат
плоскости эклиптики. Ось Схэ совпадает с осью Сх геоцентри-
ческой экваториальной системы координат. Оси Су3 и Cz3 по-
вернуты относительно осей Су и Cz геоцентрической экватори-
альной системы на угол е, равный углу между плоскостью эк-
ватора и плоскостью эклиптики. Этот угол равен 23°27'. На
Рис. 1.2 показано относительное положение геоцентрических
экваториальной Cxyz и эклиптической Схэуэгэ систем коорди-
нат. На нем показана часть орбиты Земли (центр которой обо-
значен С) относительно Солнца (центр Солнца обозначен бук-
вой О). Точка, в которой находится Земля в момент весенне-
21
го равноденствия, обозначена В. Точка, в которой находится
Земля в момент осеннего равноденствия, обозначена D. Ось
ВО проходит через точку D и направлена в созвездие Овен.
Именно это направление и выбрано для обеих рассмотренных
систем координат как направление оси Сх (т. е. Cx\\BD). Угол
наклона между плоскостью эклиптики и плоскостью экватора
на рисунке обозначен 8.
Связь компонентов произвольного вектора в геоцентриче-
ской экваториальной системе координат [х, у, г] с компонен-
тами этого вектора в геоцентрической эклиптической системе
координат [хэ, уэ, гэ] записывается следующим образом:
хэ = х;
уэ = у cos е + г sin е; (1.5)
гэ = —ysine+z cos е.
Матричная форма записи последней системы имеет вид
гэ=Аг, (1.6)
где
COS 8
—sin 8
— векторы-столбцы компонент векторов
в соответствующих системах координат;
0 \
sin 8 — матрица перехода от эквато-
cos 8 / р-иальной к эклиптической си-
стеме координат.
Обратим внимание на то, что обратный переход
г = А“1гэ
выполняется с помощью обратной матрицы А-1, которая в силу
ортогональности матрицы А равна транспонированной матри-
це: А-1 = АТ.
Таким свойством будут обладать все связи между система-
ми координат, которые в дальнейшем будут вводиться.
Гелиоцентрические системы координат
Наибольшее распространение имеет гелиоцентри-
ческая эклиптическая система координат. Ее начало распола-
гается в центре Солнца. Оси Ох и Оу находятся в плоскости
эклиптики, причем Ох направлена в точку весеннего равноден-
ствия (луч OD на рис. 1.2). Ось Оу перпендикулярна Ох и
получается ее поворотом на 90° в сторону вращения Земли.
Ось Oz дополняет систему координат Oxyz до правой.
В некоторых случаях оказывается целесообразным введе-
ние гелиоцентрической экваториальной системы координат. Та-
22
кая система отлична от гелиоцентрической эклиптической рас-
положением осей Оу и Oz.
Эти системы координат используются для анализа траекто-
рий межпланетных перелетов, анализа орбит небесных тел.
Связанная система координат
Эта система координат связана с корпусом КА. На-
чало связанной системы координат О располагается в центре
масс КА. Ось ОХ (продольная ось) этой системы направлена
от хвостовой к носовой части КА. Ось ОУ (нормальная ось)
перпендикулярна ОХ, находится» .в плоскости симметрии (про-
дольной плоскости) КА и направлена к верхней части КА или
части условно ей соответствующей. Ось OZ (поперечная ось)
дополняет систему OXYZ до правой. На рисунке 1.3 показано
возможное положение связанной системы координат. Плос-
кость OXY — продольная плоскость КА.
Фиксирование положения связанной системы координат в
пространстве определяет ориентацию корпуса КА в простран-
стве, т. е. угловые степени свободы КА. Именно в этих осях
часто описывается вращательное движение КА.
В связанных осях легко записываются некоторые силы и
моменты, действующие па КА (в частности, тяга ракетного
двигателя).
Орбитальная система координат
Рассмотрим движение КА относительно гравитиру-
ющего тела (например, Земли) с центром в точке С (рис. 1.4).
Пусть в какой-либо момент времени КА (его центр масс) на-
ходится в точке О. Будем говорить, что радиус-вектор КА в
этот момент времени есть вектор СО. Обозначим его г. Пусть
известна скорость КА относительно геоцентрической системы
координат V (естественно, V = drjdt). В том случае, если век-
тор V не коллинеарен вектору г, эти два вектора определяют
плоскость. Будем называть эту плоскость плоскостью траекто-
рии КА (мгновенной плоскостью траектории КА).
Орбитальная система координат имеет начало в центре
масс КА (точка О). Ось Or направлена по радиусу-вектору
КА, она называется радиальной или радиалью. Ось On перпен-
дикулярна Or, принадлежит плоскости траектории КА и на-
правлена в сторону движения аппарата. Эта ось называется
трансверсальной или трансверсалью. Третья ось ОЬ дополняет
систему Onrb до прямоугольной правой. Она называется нор-
малью. Плоскость ОпЬ называется плоскостью местного гори-
зонта.
23
7
Заметим, что последовательность осей орбитальной систе-
мы координат (какая из них есть первая, какая вторая и т. д.)
у ряда авторов оказывается различной. В дальнейшем орби-
тальной будем называть введенную систему координат Onrb,
в которой трансверсаль является первой осью, радиаль—вто-
рой и т. д. В литературе достаточно широко распространена
система координат, у которой первая ось — радиаль г, вто-
рая— трансверсаль п, третья — нормаль z. Обе системы — пра-
вые. Поэтому направление осей b и z в них противоположно. В
литературе орбитальной иногда называется геоцентрическая
система координат, оси которой связаны с характерной точкой
траектории КА и ее плоскостью. Эта система будет введена
позже, когда будут исследованы свойства траекторий КА. В от-
личие от введенной системы, ее будем называть перицентраль-
ной.
Перевод величин из одной системы координат
в другую
В этом разделе получим:
соотношения, которые позволяют найти компоненты произ-
вольного вектора в одной системе координат, если известны
компоненты этого вектора в другой системе координат;
выявим относительное взаимное положение некоторых си-
стем координат и введем угловые степени свободы КА (ориен-
тацию КА в пространстве).
Отметим, что связь геоцентрических экваториальной и эк-
липтической систем координат была рассмотрена недавно и
описана соотношением (1 6)
24
Обратим внимание на то, что проекции произвольного век-
тора на некоторую систему координат не зависят от положения
начала этой системы координат, а определяются только ориен-
тацией осей системы координат. Поэтому для перевода величин
из одной системы координат в другую можно параллельно пе-
реносить системы координат так, чтобы их начала совпадали.
Связь орбитальной и связанной систем координат
Рассмотрим произвольное угловое положение этих
систем координат (в произвольный момент времени). На рис.
1.5 начала орбитальной и связанной систем координат помеще-
ны в точку О. Оси орбитальной системы координат обозначе-
ны п, г, Ь. Оси связанной системы координат обозначены X, У,
Z. Осуществим переход от орбитальной к связанной системе ко-
ординат с помощью поворота орбитальной системы координат
на некоторые углы. Выберем следующую последовательность
трех поворотов, иллюстрируемых рис. 1.5:
1. Поворот орбитальной системы координат Onrb вокруг
оси Or на некоторый угол ф так, чтобы новое положение оси
On—Ох' принадлежало плоскости ОгХ (Ох'^ОгХ). Обозначим
полученную поворотом систему Ox'y'z' и назовем ее первой
промежуточной системой координат.
2. Поворот системы Ox'y'z' вокруг оси Oz', так чтобы новое
положение оси Ох' совпало с осью ОХ. Это можно сделать, так
как оси Ох' и ОХ принадлежат плоскости ОгХ (Оу'х'), перпен-
дикулярной оси Oz'. Угол поворота обозначим а систему ко-
ординат, полученную после этого поворота Ox"y"z", назовем
второй промежуточной.
3. Поворот системы Ox"y"z" вокруг оси Ох" = ОХ до совме-
щения системы со связанной. Это можно сделать, так как си-
стемы Ox"y"z" и OXYZ — прямоугольные декартовы и оси
Ох" и ОХ совпадают. Обозначим угол поворота — у.
Введенные углы поворота фиксируют относительное положе-
ние связанной и орбитальной систем координат. Они определя-
ют угловое положение КА в пространстве в произвольный мо-
мент времени.
Введем определения. Угол Ф — угол тангажа. Углом танга-
жа называется угол между продольной осью летательного ап-
парата и плоскостью местного горизонта.
Угол ф — угол рыскания. Углом рыскания называется угол
между трансверсалью On и проекцией продольной оси КА на
плоскость местного горизонта.
Угол у—угол крена, он характеризует поворот аппарата
относительно продольной оси. Углом крена называется угол
между нормальной осью OY связанной системы координат и
плоскостью ОгХ (плоскостью, проходящей через продольную ось
25
Рис. 1.5. Связь орбитальной (Onrb)
и связанной (OXYZ) систем коорди-
нат
летательного аппарата и ра-
диаль Or орбитальной си-
стемы координат).
Введенные три угла ха-
рактеризуют три угловые
степени свободы КА. В
случаях, когда КА на-
ходится вдали от планет
и его пространственную
ориентацию проще связать
с направлениями на на-
вигационные ориентиры
(Солнце, звезды, плане-
ты), углы тангажа и рыс-
кания могут вводиться с
учетом направлений на
эти ориентиры. Так, уг-
лы рыскания в этом слу-
не от плоскости траектории КА, а
чае могут отсчитываться
от плоскости, определяемой направлениями: КА — первый на-
вигационный ориентир, КА— второй навигационный ориен-
тир. При этом угол тангажа будет характеризовать положение
оси КА относительно плоскости, перпендикулярной направле-
нию КА — один из навигационных ориентиров. В дальнейшем
мы будем придерживаться определений углов тангажа, рыска-
ния и крена, проанализированных при помощи рис. 1.5.
Для получения соотношений, дающих возможность для век-
тора, компоненты которого известны в одной системе коорди-
нат, найти его компоненты в другой системе координат, необ-
ходимо математически описать проведенные переходы. Опи-
шем их последовательно.
1. Первый поворот проводится вокруг оси Or на угол гр
(см. рис. 1.5). При этом для нахождения компонент произволь-
ного вектора в промежуточной системе координат Ox'y'z' по
компонентам этого вектора в орбитальной системе координат
можно воспользоваться следующими соотношениями
x' = n-costp—b sin гр;
У' = г\
г' = п sin гр + b cos гр.
Л^атричная форма записи этого соотношения имеет вид
х' \ / п \
у' =AJ Г ,
z' ) \Ь /
(1.7)
26
где
(cos ip О
О 1
sin гр О
—sin гр
О
cos ф
(1-8)
Матрица Ai называется матрицей перехода от орбитальной
Onrb к первой промежуточной системе координат Ox'y'z'.
2. Второй поворот проводился вокруг оси Oz' на угол Об-
ратим внимание на то, что положительным поворотом всегда
считается такой поворот, при котором вращение происходит
против часовой стрелки, если смотреть со стороны оси, вокруг
которой вращение производится. Положительному повороту со-
ответствует положительный угол поворота.
Матричная форма записи второго поворота имеет вид
/ х" \ / х' \
Н/" =А2 Ь' , (1.9)
\ z" / \ z' /
где матрица перехода от системы Ox'y'z' к системе Ox"y"z"
находится следующим образом:
( cos'& sin б1 0 \
А2= —sintf cos’ft О I. (1-10)
\ О 0 1/
3. Третий поворот проводился вокруг оси ОХ на угол у.
Матричная форма записи этого поворота имеет вид
( X \ / х"\
у НАз у" > и-В * * 11)
\ Z J \z"J
где матрица перехода от системы Ox”y”z" к системе OXYZ
записывается так:
/ 1 0 0 \
А3 = I 0 cosy siny . (1.12)
\ 0 —sin у cosy /
Воспользовавшись равенствами (1.7), (1.9), (1.11), можно
выразить компоненты вектора в связанной системе координат
(X, У, Z) через компоненты этого же вектора в орбитальной
системе координат:
/ X \ ( п\ (п\
Y =A3A2A! г =А г . (1.13)
\Z / \ b) \bj
В последнем соотношении используются вектор-столбец
компонент вектора в связанной и орбитальной системах коор-
динат, а также произведение трех квадратных матриц. Такое
произведение есть квадратная матрица. Обозначим ее А и
27
назовем матрицей перехода от орбитальной к связанной систе-
ме координат:
cos # COS гр
sin гр sin 7—
—sin # cos гр cosy
этгрсозуЧ-
+ sin# cos гр sin у
sin ft
cos $ cos 7
—cos ft sin у
—cos # sin гр
cos гр sin у+
4- sin $ sin гр cosy
cos гр cos у—
—sin ft sin гр sin у
(1.14)
Во многих задачах теории движения КА оказывается, что
углы рыскания и крена в течение всего движения или на ка-
жом-либо участке движения очень малы. Это означает, что ось
КА практически принадлежит плоскости траектории КА, углы
поворота КА вокруг продольной оси малы. В таких условиях
пользуются упрощением модели движения КА и, в частности, в
соотношениях пренебрегают величинами второго порядка мало-
сти относительно гр и у. При этом матрица А принимает более
простой вид
/ cos ft sin О
А= —sin# cos#
\ у sin # +гр —ycos#
—гр cos#
у + ip sin #
1
(115)
Для осуществления обратного перехода (для нахождения
орбитальных компонент вектора, заданного в связанных осях)
из (1.13) получим
п \ ( Х\
Г = А-1 У .
bJ \ Z J
(1-16)
Так как матрица А является ортогональной матрицей, то об-
ратная для нее матрица А~] равна транспонированной матри-
це Ат: А-1 = АТ.
Приведем пример использования соотношения (1.16). Пусть
нам известны проекции тяги ракетного двигателя на оси свя-
занной системы координат: Р='[Р, 0, 0] (предполагается, что
тяга направлена по продольной оси КА). Найдем с помощью
(1.16) ее проекции на оси орбитальной системы координат:
Рп = Р cos#; Pr=P sin#; Рь = —Ар cos#.
Необходимо обратить внимание на то, что при положитель-
ном угле рыскания составляющая тяги, направленная по оси
ОЬ, меньше нуля. Это связано с положением оси ОЬ орбиталь-
ной системы координат и определением угла рыскания, при 'ко-
тором положительные углы рыскания соответствуют отклонению
оси КА за плоскость траектории, см. рис. 1.5.
Компоненты скорости в орбитальной системе координат.
Основная плоскость От орбитальной системы координат
28
Рис. 1.6. Связь экваториальной гео-
центрической (Cxyz) и орбитальной
(СпгЬ) систем координат:
€ — центр Земли; Сху — плоскость эквато-
ра; г = СО — текущий радиус-вектор КА от-
носительно центра Земли; V — скорость КА
относительно экваториальной системы ко-
ординат
определяет мгновенную плос-
кость траектории КА. В этой
плоскости находится вектор
скорости КА. Угол между
вектором скорости КА и транс-
версалью On называется
углом наклона траектории
(иногда траекторным углом) и обозначается 0. Диапазон
изменения этого угла — [—л/2; п/2]. Положительные траек-
торные углы соответствуют случаю, когда вектор скорос-
ти КА располагается над плоскостью местного горизонта
(угол между скоростью и радиалью меньше 90°). Радиаль-
ная Vr и трансверсальная Vn компоненты скорости находят-
ся из соотношений
Vr=Vsin0; l/n = Vcos0.
Связь экваториальной геоцентрической невращающейся си-
стемы координат с орбитальной системой. Рассмотрим рис. 1.6.
В нем С — центр Земли; плоскость Сху — плоскость эквато-
ра; г = СО — текущий радиус-вектор КА относительно центра
Земли; V — скорость КА относительно экваториальной систе-
мы координат. Радиус-вектор г и скорость V определяют плос-
кость (мгновенную) траектории КА. Эта плоскость в общем
случае пересекает плоскость экватора по некоторой прямой
DB, проходящей через гравитационный центр. Ниже для оси
DB обоснованно будет введено понятие линии узлов.
Обозначим угол между осью Сх экваториальной системы
координат и осью СВ — Q и назовем его долготой восходяще-
го узла.
Угол между плоскостью экватора и плоскостью траектории
КА назовем наклонением траектории КА и обозначим его I.
Угол между линией узлов СВ и текущим радиусом-вектором
назовем аргументом широты и обозначим и.
При помощи трех введенных углов Q, i и и определяют уг-
ловое относительное положение экваториальной и орбитальной
систем координат. Для осуществления перехода от экватори-
альной системы координат к орбитальной воспользуемся тремя
поворотами, иллюстрируемыми на рис. 1.6. На нем начало обе-
их систем координат помещено в точку С. Описывая элементар-
29
ные повороты системы Cxyz на углы Q + 270°, i +180° и 360° — и
можно получить матрицу перехода от Cxyz к Chrb\
—sin u eos Q— —cos и sin Q cos i —sin и sin Q + + 'COS и cos Qcos i cos usin i
А = cos r/ cos Q— cos и sin Q + sin и sin i
—sin и sin Q cos i H- sin и cos Qcos i
—sin Q sin i cos Q sin i —cos i
(Матричная форма перехода от геоцентрической системы ко-
ординат х, у, z к орбитальной п, г, b имеет вид
г \ / X \
п =А\ у .
b / \ z J
В разделе были введены наиболее употребительные в меха-
нике космического полета системы координат. Получены соот-
ношения, с помощью которых для вектора, заданного в одной
системе координат, можно получить его проекции в другой сис-
теме координат. Элементы матриц перехода между основными
системами координат сведены в табл. 1.1.
Таблица 1.1
Система координат Орбитальная система координат
п 1 T b
Связанная X cos ft cos яр sin -0* — cos -0* sin xp
Y sin ip sin у — — sin ф cos ip cos у cos -0* cos у cos xp sin у + + sin 4 sin xp cos у
Z sin хр cos у + -f- sin Ф cos xp sin у — cos ft sin у cos xp cos у — — sin ft sin xp sin у
Геоцентри- X — sin и cos Q — cos и cos Q — — sin Q sin i
ческая ор- — cos и sin Q cos i — sin и sin Q cos i
битальная У — sin и sin Q + + cos и cos Q cos i cos и sin Q + + sin и cos Q cos i cos Q sin i
2 cos и sin i sin и sin i — cos i
1.3. СИЛЫ, ДЕЙСТВУЮЩИЕ НА КА
Проанализируем силы, действующие на аппарат и
входящие в уравнение сил (1.3).
30
Реально на КА действуют: силы тяготения небесных тел,
тяга реактивного двигателя, аэродинамическая сила, электро-
магнитная сила, сила светового давления, сила, возникающая
из-за негерметичности емкостей, и т. д. Перечисленные и непе-
речисленные силы безусловно в разной степени влияют на дви-
жение КА. Эффект этого влияния зависит от типа КА и усло-
вий его движения. Можно выбрать такой тип КА, придумать
такие условия движения, что, наверное, любая из сил оказыва-
ла бы заметное влияние на движение аппарата. Ограничимся
распространенными типами КА, типовыми условиями их дви-
жения, теми задачами, которые стоят перед теорией движения
КА на ранних этапах их проектирования. При этом окажется,
что основными силами, действующими на аппарат, являются:
сила земного притяжения, тяга ракетного двигателя, сила при-
тяжения Луны, Солнца и других небесных тел. Описание имен-
но этих сил приведем в настоящем разделе.
Гравитационная сила
Рис. 1.7. Элементарная гра-
витационная сила
Одной из основных сил, действующих на КА, явля-
ется сила притяжения его Землей, Солнцем и другими небесны-
ми телами Вселенной. Сила притяжения КА любым телом яв-
ляется равнодействующей ньютоновских сил притяжения всех
составляющих элементарных масс КА dnii со стороны всех эле-
ментарных масс притягивающего (гравитирующего) тела dMj\
Gij=—f dMidmt ZiL, (1.17)
rH rH
где Gij—сила притяжения массы dmt массой dM^, f — грави-
тационная постоянная (6,6720±0,0041) • 10-11 (Н-м2)/кг2, й; —
радиус-вектор массы dnii относи-
тельно массы dMj (рис. 1.7. Здесь
С — центр масс гравптирующего
тела).
Суммирование элементарных сил
тяготения (1.17) по всем массам КА
и массам, например Земли, дает воз-
можность получить вектор силы
гравитационного поля Земли, дей-
ствующей на КА, или по-другому,
гравитационную силу. Эта сила в
общем случае не проходит через
Центр масс КА. Для КА, габарит-
ные размеры которого весьма ма-
лы (а чаще всего пренебрежимо
малы) по отношению к косми-
ческим расстояниям (например, к
31
радиусу Земли 7?3 = 6371 км), с большой точностью мож-
но считать, что вектор гравитационной силы проходит че-
рез центр масс КА, и определять величину этой силы, считая,
что КА есть материальная точка, помещенная в центре масс
аппарата. Такой подход может привести к определенным неточ-
ностям расчета траектории крупногабаритных космических кон-
струкций (с размерами порядка десятков километров). Отме-
тим, что в некоторых задачах анализа углового движения КА
необходимо учитывать гравитационный момент. Гравитацион-
ный момент обусловлен тем, что гравитационная сила в общем
случае не проходит через центр масс и создает момент относи-
тельно центра масс.
Для большого числа задач теории движения можно считать,
что Земля (или другое гравитирующее тело) есть шар со сфе-
рическим распределением плотности, т. е. плотность любой точ-
ки Земли является функцией только расстояния этой точки от
центра Земли, или по-другому: Земля состоит из однородных
по плотности сферических слоев. Оказывается, что сила тяготе-
ния от гравитирующего тела такой структуры равна силе тяго-
тения материальной точки с массой, равной массе Земли, по-
мещенной в ее центре:
где М — масса гравитирующего тела; г — радиус-вектор КА
относительно центра гравитирующего тела (относительно гра-
витирующего центра).
Именно таким выражением для гравитационной силы мы
будем в основном пользоваться. Более сложная форма Земли
будет рассматриваться при анализе движения ИСЗ. В этом
случае будем учитывать возмущающее гравитационное ускоре-
ние, связанное с «несферичностью» формы Земли.
Произведение гравитационной постоянной на массу гравити-
рующего тела М называется гравитационным параметром при-
тягивающего тела ц:
V = fM. (1.19)
Гравитационный параметр Земли равен ц3 = 398,6-103 km3i/c2.
Выражение для гравитационной силы при этом принимает
вид
Введение понятия гравитационного ускорения связано с та-
ким соотношением:
g=G/m= —\\./r2-rlr. (1.20)
32
Величина гравитационного ускорения g = p[r2 оказывается
обратно пропорциональной квадрату расстояния КА от гравити-
рующего центра. Гравитационное ускорение на удалении от
центра Земли, равном среднему радиусу Земли /?3 = 6371 км,
подсчитывается следующим образом: go = "Л = 9.820 м/с2.
Гравитационное ускорение, описываемое соотношением*
(1.20), называется ньютоновским.
Потенциал гравитационного поля
В каждой точке окрестности гравитирующего тела
есть свой вектор гравитационного ускорения. Таким образом,
перед нами векторное поле. Можно доказать, что векторное по-
ле гравитационного ускорения является потенциальным, а зна-
чит, имеет потенциальную функцию (гравитационный потенци-
ал). По физическому смыслу гравитационный потенциал (или
потенциал гравитационного поля) в некоторой точке равен
работе, которую необходимо совершить при перемещении то-
чечной единичной массы из данной точки в бесконечность от-
носительно гравитирующего тела. Гравитационный потенциал,,
взятый с обратным знаком, есть потенциальная энергия единич.-
ной массы, помещенной в рассматриваемую точку.
Векторное поле ньютоновского гравитационного ускорения1
(1.20) называется ньютоновским гравитационным полем.
Потенциальная функция ньютоновского гравитационного по-
ля зависит от длины радиуса-вектора точки и определяется по
соотношению:
U=p/r. (1.21}
В настоящее время разработан и рекомендован Междуна-
родным астрономическим союзом специальный математический
аппарат для описания гравитационного потенциала Земли и
других планет в виде разложения в ряде по сферическим функ-
циям Рп (sin ср) {61]:
Г °0 °° П / ГЛ . П
U = ~- 1+ S Jn(^) P„(sin<p)+ 3 з (^\ рм&ьч)*
Г L п=2 \ Г J п=2 Л=1 \ Г /
X (Xnftcos^ + BnftsinH)], (1.22)
где М3 — масса Земли; /?3.э — экваториальный радиус Земли;
л и ф — геоцентрические долгота и широта соответственно;
Ank и Bnh — безразмерные постоянные, характеризующие
индивидуальные особенности поля тяготения небесного тела.
Их значения для Земли определяются по данным гравиметри-
ческих измерений на ее поверхности и внешнетраекторных из-
мерений эволюций орбит искусственных спутников.
Наряду с влиянием нецентральности и аномалий поля тяго-
тения близкой планеты необходимо учитывать притяжение от-
носительно далеких, но больших планет и других небесных тел.
Учесть это притяжение можно с помощью рассмотрения грави-
тационного потенциала как суммы потенциалов небесных тел.
Воспользовавшись важным свойством потенциала векторного
поля (производная от потенциала по любому направлению
равна проекции гравитационного ускорения на это направле-
ние) и считая гравитационные поля п небесных тел ньютонов-
скими, можно получить:
_ dU n
gx =
дх J о J i=l ?!
dU n
gy = ду - t ^-(y yj) /=1 Гу
dU n
gz~ dz - 2 ±L(Z Z}), r3j
(1.23)
где ц; — гравитационный параметр /-го небесного тела (/VMJ;
Уь zi— координаты /-го небесного тела; г5= У (х—х3)2 +
+ (у—у3)2 + (г—г,)2— расстояние КА от /-го небесного тела.
В том случае, когда КА движется вблизи какого-либо небес-
ного тела, следует учитывать индивидуальные особенности поля
тяготения этого тела. При этом при нахождении производных в
равенствах (1.23) следует рассматривать потенциал этого тела
не ньютоновским, а имеющим вид (1.22). Отличие гравитацион-
ного ускорения от ньютоновского будем обозначать Ag.
Тяга ракетного двигателя
В большом числе случаев считается, что ракетный
двигатель устанавливается вдоль оси КА и вектор тяги Р на-
правлен по продольной оси аппарата:
Р=Р.Д (1.24)
где Х° — единичный орт продольной оси аппарата.
Величина тяги ракетного двигателя определяется по соотно-
шению
Р = /иГэ,
где W3 — эффективная скорость истечения.
Проекции вектора тяги ракетного двигателя на оси связан-
ной системы координат имеют вид:
Р = [/пГэ, 0, 0].
34
Проекции вектора тяги на оси других систем координат не-
сложно получить с помощью матриц перехода между система-
ми координат или анализом углов, характеризующих положе-
ние продольной оси КА относительно системы координат.
Так, проекции вектора тяги на оси орбитальной системы
координат (Qnrb) имеют вид
Р = [Р cos 'fl1 cos ф; Р sin —Р cos О'sin ф].
Участок траектории, на котором включен ракетный двига-
тель, называется активным. На пассивном участке двигатель
выключен.
1.4. ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ,
ОПИСЫВАЮЩАЯ ДВИЖЕНИЕ КА
Опишем движение произвольного КА. Движение ап-
парата будем рассматривать в геоцентрической системе коор-
динат. Приведем также уравнения движения центра масс КА а
орбитальной системе кооординат.
Уравнения сил
Запишем уравнения сил в проекциях на оси геоцент-
рической экваториальной невращающейся системы координат.
Строго говоря, рассматриваемая геоцентрическая система
координат неинерциальна, так как ее начало перемещается
вместе с центром Земли по некоторой траектории, близкой к.
эллиптической, вокруг Солнца, т. е. неравномерно и непрямоли-
нейно. Эта система координат не вращается относительно аб-
солютного (звездного) пространства. Кориолисово ускорение
КА в ней будет нулевым. Абсолютное ускорение КА будет рав-
но сумме относительного ускорения d2fldt2 (ускорения КА в1
геоцентрической системе координат) и переносного ускорения
d2p/dZ2 (ускорения центра масс Земли, обусловленного притя-
жением Земли небесными телами). При этом уравнение сил
имеет вид
тГ~ + ^) = б + Р + ^ + 6л + Сс + Ж.т, (1-25)
\ а га ага /
гДе С?л, Gc, SGh.t — силы протяжения КА Луной, Солнцем и
Другими небесными телами; Ra—аэродинамическая сила.
Одной из важных особенностей движения КА является его
длительность. Межпланетные перелеты могут достигать 10 и
более лет. В течение столь длительного времени даже неболь-
шие погрешности дифференциальных уравнений движения КА
могут привести к существенным отклонениям расчетной траек-
2* 35
Солнце - я/,
Меркурий -/77;
Венера -т^
Марс - т^
Фобос -m,t1
Дейнос-т
Юпитер -т, _
, Но - т5}
Европа -т5?
Ганимед-т55
Земля - т0
Луна -mt
*Т
Тцтан-т66 Титания - т„,
Сатурн - т6 Уран-т7
Минск - т61 Миранди-т,
Нептун-^
Тритон-т81
Нереида - твз
Рис. 1.8. Движение КА в гравитационном поле небесных тел
тории от действительной. Поэтому для ряда космических ма-
невров необходимо учитывать силы притяжения многих небес-
ных тел. При таком учете приходится определять не только ко-
ординаты КА г=’[х, г/, г]., но и координаты небесных тел g =
='[/г, #г, £г] (Солнца, планет, естественных спутников планет
(рис. 1.8)). При этом совместно интегрируется уравнение дви-
жения КА (1.25) и уравнения движения небесных тел. Распи-
сывая входящие в уравнение переносные ускорения, уравне-
ния движения КА и небесных тел удается записать в виде:
(1.26)
где Ag— приращение гравитационного ускорения, связанное с
- Р +
отличием поля тяготения Земли от ньютоновского; lzs = ——-----
кажущееся ускорение; p,j, Mj — гравитационный параметр и мас-
о*—г еМ3 + т —
са /-го небесного тела соответственно; ц7-—---, / —---- г —
1Ъ--7|3
ускорение притяжения КА /-м небесным телом и Землей соот-
36
П---n r Al3+^i “
ветственно; —, /--------r7-— ускорение притяже-
I >7—rj3. rt
ния i-ro небесного тела /-м небесным телом и Землей соответ-
ственно.
Обратим внимание на то, что использованные в (1.26) ра-
диусы-векторы небесных тел и КА имеют начало в центре
Земли.
Порядок системы дифференциальных уравнений возрастает
с увеличением числа небесных тел, которые необходимо учиты-
вать при анализе движения КА. Учитывая, что каждое из запи-
санных уравнений эквивалентно системе шести уравнений пер-
вого порядка, а число уравнений только с учетом больших пла-
нет Солнечной системы может достичь десяти, то порядок ин-
тегрируемой системы может быть в пределах 50—100.
В ряде задач механики космического полета к такой систе-
ме приходится прибегать при расчете пассивного участка тра-
екторий КА. При расчете активных участков траектории чаще
всего поступают иначе. Считают, что, например, в окрестности
Земли ускорение КА в инерциальном пространстве, вызываемое
воздействием Луны, Солнца и других небесных тел (Сл + Сс +
-!-SGh.t)/т, весьма близко к ускорению в том же пространстве
центра масс Земли d?pldt2\
g ^Сл + Сс+ SGh.t.
а г2
Поэтому возмущающим действием Луны, Солнца и других
небесных тел на движение КА относительно Земли в этих слу-
чаях можно пренебречь (так же, как и возмущающим воздей-
ствием аэродинамических сил), тогда уравнение сил (1.25)
примет вид
/n£L=G + p. (1.27)
d t
Отметим, что здесь пренебрегается не гравитационными си-
лами С?л, Gc и SGH.T, а разностью Сл + Сс + 2СН.Т—w 1 ха’
рактеризующей возмущающее воздействие Луны и Солнца на
движение КА относительно Земли. Уравнение сил (1.27) имеет
вид, эквивалентный уравнению, описывающему движение КА в
•инерциальном пространстве с учетом тяги ракетного двигателя
и гравитационной силы притяжения КА Землей.
Проекции уравнения сил (1.27) на оси геоцентрической сис-
темы координат имеют вид
т = —^.m2L + m№3cos(X, х);
37
m77 = --S-/raf+/ra^cos(X’^ (1.28>
m =--------— tn — 4- tnWa cos (X, z).
d t r2 r
Первые слагаемые в правой части системы (1.28)—проек-
ции вектора гравитационной силы на оси геоцентрической сис-
темы координат, вторые слагаемые—проекции вектора тяги на
эти же оси. В последних слагаемых cos(X, х) и т. д. — косину-
сы углов между продольной осью КА X и осями экваториаль-
ной системы координат. Чтобы получить такие направляющие
косинусы, можно воспользоваться матрицами перехода геоцент-
рической системы координат к орбитальной и от орбитальной
к связанной.
Выражения для направляющих косинусов, входящих в сис-
тему (1.28), удается получить, перемножая упомянутые мат-
рицы:
cos (X, х) = (— sin и cos Q—cos и sin Q cos i) cos O' cos гр 4-
+ (cos и cos Q—sin и sin Q cos i) sin 0 + sin Q sin i cos О sin гр;
cos (Y, y) = (—sin и sin Q + cos и cos Q cos i) cos 0 cos гр 4-
+ (cos и sin Q + sin и cos Q cos i) sin О—cos Q sin i cos О sin гр;
cos (Z, z) = cos и sin i cos О cos гр + sin и sin i sin О + cos i cos Osin гр.
(1.29)
Предположим, что параметры КА заданы, т. е. заданы его
начальная масса, массовый расход топлива, скорость истечения
газа из сопла ракетного двигателя и т. д.
Предположим, что нам известны начальные условия движе-
ния КА:
го=[*о» Уо» Vq = [Vx0, Vyo, lZzob
Пусть требуется найти траекторию движения аппарата.
Записанная система (1.28) не может рассматриваться как
замкнутая. Ее отдельно невозможно проинтегрировать и по-
строить зависимость компонент скорости КА от времени. Дей-
ствительно, в правые части (1.28) входят координаты КА х, у*
z, входят углы КА — О, гр и некоторые другие величины, опре-
делить которые, не записывая дополнительные уравнения, в об-
щем случае не представляется возможным.
Будем записывать новые группы уравнений для того, чтобы
получить замкнутую систему, описывающую движение КА.
38
Кинематические связи движения центра масс КА
Между проекциями скорости и координатами КА су-
ществуют кинематические связи, вытекающие из определения
понятия скорости:
— = VX; ^- = Vy\ — = Vz. (1.30)
dt ’ dt dt z ' ’
Здесь x, y, z — координаты KA в геоцентрической системе
координат, a Vx, Vy, Vz — скорость изменения этих координат,
то есть компоненты скорости КА в геоцентрической системе ко-
ординат.
Геометрические связи
В выписанные уравнения сил входит ряд углов. Сре-
ди них долгота восходящего узла траектории КА Q, наклоне-
ние траектории i, аргумент широты и. Из геометрических сооб-
ражений ясно, что эти углы определяются положением КА г
и его скоростью V. В разд. 2.10 будет показано, что Q, i и и мо-
гут быть найдены по радиусу-вектору КА г—[х, у, г] и его
скорости 7= [К, Vy, Vz] по следующим соотношениям:
i = arccos Vx-;
|[ r x v ]|
arccos • xVz , если yVz—zVy 0,
Q I |[rXV]|sini *
2л—arccos , если yVz—zVy<ZG\
|[rXV]|sini ц31)
arccos i — cosQ+—sinQ ], если sgn( — sinQ j =
\ r r ) \ r )
„I =sgn(z/Vz—zVy)-,
2л — arccos ( — cos Q + — sin Q ), если sgn [ — sin £2 । =
\ r r / \ r /
= -sgn(z/V2—zVy).
Программное движение KA
Совокупность уравнений (1.28), (1.30), (1.31), описы-
вающих движение КА, не является замкнутой системой уравне-
ний. Фазовых координат (переменных) КА в этих уравнениях
больше, чем число уравнений. Фазовыми координатами явля-
ются:
проекции скорости КА — Vx, Vy, Vz;
39
координаты КА — х, у, z\
угловые характеристики положения КА в пространстве —
ф, Q, г, и\
длина радиуса-вектора КА — г;
масса КА — т.
Перечисленных переменных—13, количество же уравнений
системы — 9. Система незамкнутая. Будем учитывать, что дли-
на радиуса-вектора КА определяется координатами КА:
r = Vx2+ y2 + z2. (1.32>
Будем считать, что масса КА есть известная функция вре-
мени —
m(t) = mQ—m (1.33}
(массовый расход топлива th считаем постоянным; t—to — вре-
мя активного полета КА).
При этом число уравнений, описывающих движение КА,,
окажется равным 11. Число перечисленных фазовых координат
КА превышает число уравнений на 2 единицы.
Именно это превышение дает необходимые степени свобо-
ды для выбора таких законов управления движением КА, ко-
торые обеспечивают выполнение транспортной задачи, постав-
ленной перед КА.
Для того чтобы система уравнений была замкнута, доста-
точно задать программу движения КА, записать уравнения сис-
темы управления. В наиболее простом случае это может быть
программа по угловым степеням свободы КА (по тангажу
и рысканию). Например, программа движения КА по этим уг-
лам может быть задана в виде
,&=^пр(0; ц 34*
=%₽ (0.
где #Пр(0, Фпр(0 —некоторые функции. Задание этих функций
фиксирует программу движения, делает систему уравнений,,
описывающих движение КА, замкнутой. Решение этой системы
при заданных начальных условиях движения (начального по-
ложения КА г0= [*о, Уо, ?о] и начальной скорости КА Го=
= [Кхо, Ууо, Vz0]) определяет некоторую конкретную траекто-
рию КА. Такую траекторию будем называть программной тра-
екторией КА. Программная траектория соответствует опреде-
ленной выбранной программе движения, например в виде
(1.34). Отметим, что реальная траектория КА всегда в большей
или меньшей степени не соответствует программной. Это несо-
ответствие определяется теми реальными возмущениями, кото-
рые не учитываются в модели движения КА, тем, что система,
управления КА работает неидеально, и выбранная программа
40
движения отрабатывается с определенными ошибками. С этой
точки зрения введенную программную траекторию КА в ряде
случаев называют опорной, невозмущенной, номинальной.
В дальнейшем в основном будет использован термин про-
граммная траектория КА, под которой подразумевается траек-
тория аппарата, соответствующая выбранной программе движе-
ния. Программная траектория может быть точно реализована
только в том гипотетическом случае, если на КА не будут дей-
ствовать возмущения, а система управления идеально «отрабо-
тает» программу движения КА.
Под программой движения часто понимается не только про-
грамма по угловым степеням его свободы, представленная, на-
пример в виде (1.34), а и законы включения и выключения ра-
кетного двигателя аппарата, в некоторых случаях закон изме-
нения величины тяги этого двигателя. Программа движения
КА — это совокупность законов изменения величин, влияющих
на траекторию аппарата, которые независимо могут быть вы-
браны и полностью определяют траекторию при конкретных ус-
ловиях его движения.
Запишем уравнение сил в проекциях на орбитальную систе-
му координат. Напомним, что приведенная ранее система урав-
нений (1.28) была проекцией уравнения сил на оси геоцентри-
ческой невращающейся системы координат. Последняя система
удобна для описания движения спутников планет и менее удоб-
на для описания активного движения КА из-за громоздкости
соотношений (1.29), определяющих положение продольной оси
КА относительно геоцентрических осей. Этого недостатка в
большой степени лишена орбитальная система координат.
Приведем уравнения движения КА в орбитальной системе
координат:
1/2п
[dVr
m\ —--
|_ dt
—mVn [ — cos «4
n I dt dt
(1.35)
dQ • • • VI Г"1
sin и sim
Из последнего уравнения системы (1.35) следует, что плос-
кое движение может быть реализовано в том случае, если сум-
ма проекций сил на нормаль к плоскости траектории равна
нулю.
Таким образом, в разделе была рассмотрена задача состав-
ления полной системы уравнений, описывающей движение КА,
было введено понятие программной траектории КА. Основой
Уравнений, описывающих движение КА, является уравнение
41
сил. Это векторное уравнение было спроектировано на оси гео-
центрической невращающейся системы координат и на оси ор-
битальной системы координат.
Напомним, что при исследовании пассивного участка траек-
тории КА может быть необходимым учет гравитационного воз-
действия на КА многих небесных тел. Так как такое воздейст-
вие определяется относительным положением КА и небесных
тел, то в полную систему, описывающую движение КА, входят
уравнения движения небесных тел, например в виде (1.26).
В этом случае определенную работу необходимо выполнить
для подготовки начальных условий для интегрирования систе-
мы (1.26). Используя данные Астрономического ежегодника
СССР или других публикаций, на определенные моменты вре-
мени (ближайшие к дате старта КА) получают численные зна-
чения координат (эфемерид) естественных небесных тел. После
этого можно численно интегрировать уравнения движения не-
бесных тел.
1.5. ОПРЕДЕЛЕНИЕ НАЧАЛЬНЫХ ДАННЫХ
ПРИ ИНТЕГРИРОВАНИИ УРАВНЕНИЙ ДВИЖЕНИЯ КА
Широкое использование ЭВМ позволило на многие
годы вперед получить таблицы численных значений координат
(эфемерид) естественных небесных тел на определенные мо-
менты времени, называемые эпохой. В Астрономическом еже-
годнике СССР приводятся данные на 0h Всемирного времени
предстоящего календарного года. В США опубликованы таб-
лицы координат пяти внешних планет — Юпитера, Сатурна,
Урана, Нептуна на период до 2060 г. Институт теоретической
астрономии АН СССР регулярно публикует эфемериды малых
планет.
Используя перечисленные и им подобные публикации, мож-
но для интегрирования уравнений относительного движения
(1.26) заимствовать координаты небесных тел на ближайший к
дате старта КА момент Всемирного времени. Однако неравно-
мерность шкалы Всемирного времени приводит к необходимо-
сти в качестве шкалы независимой переменной дифференци-
альных уравнений (1.26) использовать эфемеридное время, не
имеющего этого недостатка. Поэтому ниже поясняется ряд тер-
минов для обозначения различных по физическому смыслу сис-
тем измерения времени и рекомендации по переходу от одного
времени к другому.
В современной механике движения космических тел исполь-
зуются четыре системы измерения времени: всемирное,, звезд-
ное, эфемеридное и атомное.
42
Единица измерения времени — сутки. Продолжительность
солнечных суток — промежуток времени между двумя последо-
вательными нижними кульминациями Солнца. Продолжитель-
ность звездных суток — промежуток времени между двумя по-
следовательными верхними кульминациями точки весеннего
равноденствия — Y. Звездные сутки короче солнечных, по-
скольку Солнце за время суток в своем видимом движении пе-
ремещается на 360°/365 сут^Г/сут. Таким образом, за время
солнечных суток Земля поворачивается на 36Г, а за время
звездных — на 360°. Поэтому солнечные сутки содержат 86 400
среднесолнечных секунд, а звездные всего 86 163 с. Понятие
средней солнечной секунды, средних солнечных суток необхо-
димы в связи с периодическими изменениями интервала време-
ни между двумя кульминациями Солнца над местным меридиа-
ном вследствие обращения Земли вокруг Солнца по эллипсу.
Вот почему термин «Всемирное время» означает среднесолнеч-
ное время на меридиане Гринвича с началом суток в полночь
(гринвичское местное время).
Звездное время определяется часовым углом точки весенне-
го равноденствия Y на О71 всемирного времени. Звездное вре-
мя приводится в Астрономическом ежегоднике СССР на 0Л все-
мирного времени календарных суток и необходимо для вычис-
ления геоцентрических координат КА в момент окончания ак-
тивного участка полета ракеты-носителя, используемых как на-
чальные условия при интегрировании уравнений (1.26). Пояс-
ним это утверждение. Траектория активного участка выведения
КА в системе координат, связанной с Землей, например грин-
вичской экваториальной CxYyTzY, может быть рассчитана один
раз, а использоваться многократно с изменением московского
времени старта — ТмСт. При этом кинематические параметры
конца активного участка движения ракеты-носителя относи-
тельно гринвичской системы будут неизменными:
7г = [4, t/rK, ?“] ;
(1.36)
= Уг, Z?],
а относительно экваториальной невращающейся системы Cxyz
в зависимости от момента старта ГмСт — переменными, посколь-
ку Земля в своем вращательном движении меняет положение и
направление переносной скорости — ^соХгг] (со — угловая ско-
рость вращения Земли).
7К
7К
Начальные условия движения
= hK, z/K, zK] ;
= UK, yK, zK]
(1.37)
43
для интегрирования первого уравнения системы (1.26) опреде-
ляются зависимостями
г = гг ;
7к=в7? + [со х гк].
(1.38>
где матрица В зависит от угла S между системами Cxyz и
Схгуггг вокруг оси г;
= (oa s0 + (о (п • 86 400е + Тсмт — 10 800е + /а.у), (1.39>
где со3 = 7,2722052-10-5 1/с — угловая скорость Земли относи-
тельно звезд; со = 7,2921158«10”5 1/с — угловая скорость Земли
относительно Солнца; s^[c] — звездное время на базисную дату
(эпоху); и — количество полных суток с момента базисной да-
ты до календарных суток запуска КА; Тмст—10 800 с — всемир-
ное время старта в день старта; /а.у — продолжительность ак-
тивного участка выведения КА.
Матрица В равна
cos SK sin Ек 0
(1.40>
Равенства (1.38)в проекциях на оси координат
хк = Хг cos SK + у* sin S;
У* = — *r sin Зн + Уг cos S;
zK = zKr;
хк = Xr cos Ек + Уг sin SK—<луг ;
ук = — Хг sin 8К + Уг cos Зк4- сох* ;
zK = Zr-
При численном интегрировании уравнений (1.26) значение
независимого аргумента t (эфемеридного времени) отличается
от всемирного времени базисной даты заимствованных коорди-
нат небесных тел на величину поправки АТ. Поэтому эфеме-
ридное время в момент окончания активного участка выведе-
ния КА равно
= п 86 400е + Тст— 10 800е + /а.у + АТ. (1,42>
Физический смысл слагаемых в (1.42) тот же, что и в формуле
(1.39). Поправка при переходе от всемирного к эфемеридному
времени — АТ стабильна на протяжении довольно большого ин-
тервала лет, что видно из следующих цифр:
Год......................... 1960 1965 1970 1975 1980 1985
Поправка Д7\ с.............. 33,2 35,9 40,8 46,4 52,4 59,3
44
Однако изменение разности между всемирным и эфемерид- ным временами при очень про- должительных перелетах целе- сообразно учитывать, посколь- ку работа наземных командно- измерительных комплексов привязана к шкале московско- го или всемирного времени. Таблица 1.2
Небесное тело т°з а2 а3
Земля Венера Марс Юпитер Луна О ’'f ю ю 00 *— tF • сч coW ~ с? о 1111 1,30 0,09 2,8 0,015 2,7 0,19 2,39 —1,6 0 0 0,48 0,65 1,3J 0 0
В ходе интегрирования уравнений относительного движения
(1.26) необходимы начальные данные для использования нави-
гационных ориентиров. Для поиска и безошибочного захвата
навигационных ориентиров бортовыми приборами необходимо в
каждой точке траектории движения КА иметь возможность оп-
ределять видимую звездную величину — т3 (видимый блеск)
небесных тел. Звездная величина зависит от абсолютной звезд-
ной величины — т°з, расстояния от Солнца до предполагаемо-
го в качестве ориентира f-ro небесного тела (ri—й) и от рас-
стояния КА до небесного тела (г—г<), а также от условий ос-
вещенности
tn3i = т°з1 + 5 1g (rj — г) (г—п)+а2 ( i)2 +
(1.43)
где m3i и mQ3i — видимая и абсолютная звездные вели-
чины f-ro небесного тела; р — фазовый угол в градусах, опреде-
ляемый выражением
Р = arccos —2—2^ > (1 -44)
ki—rt\ k—rj
^2, аз— коэффициенты.
В табл. 1.2 для иллюстрации порядка величин приведены
начальные данные для вычисления характеристик блеска ряда
небесных тел при интегрировании уравнений (1.26).
При использовании в качестве ориентира звезды необходи-
мо в ходе интегрирования уравнений (1.26) определять направ-
ление ее визирования с КА — г°3, видимый блеск т3 постоя-
нен в пределах солнечной системы.
1.6. ПОГРЕШНОСТИ РАСЧЕТА ТРАЕКТОРИЙ
ДВИЖЕНИЯ КА
Точность расчета траектории движения КА с исполь-
зованием уравнений (1.26) зависит от:
одновременно учитываемых в правых частях уравнений не-
бесных тел;
45
погрешностей знания масс небесных тел, определяющих си-
ловую функцию поля тяготения, а также коэффициентов разло-
жения силовой функции для учета аномалий гравитации;
вычислительных погрешностей округления чисел в ЭВМ и
используемого метода численного интегрирования уравнений
движения.
Вычислительные погрешности в результате округления чи-
сел в ходе каждой операции на ЭВМ и приближенного характе-
ра формул численного интегрирования накапливаются по мере
увеличения количества шагов. Теоретический анализ позволяет
оценить увеличение вычислительных погрешностей при интег-
рировании уравнений движения в прямоугольных координатах
пропорционально количеству шагов в степени 3/2. Таким обра-
зом, через каждые 30 шагов вычислительные погрешности уве-
личиваются (Примерно в 10 раз, т. е. теряется одна значащая
цифра. Следовательно, в расчете траектории КА, требующем
большого количества шагов численного интегрирования, вы-
числительные погрешности могут быть неприемлемы даже при
использовании современных ЭВМ и контроль их накопления
желательно проводить хотя бы выборочно. Косвенный контроль
вычислительных погрешностей в решаемой задаче может осу-
ществляться повторным расчетом типичной траектории КА с
двойным количеством разрядов в мантиссе чисел, что предус-
матривается техническими возможностями ЭВМ.
Значения величин массы и размеров небесных тел, а также
расстояний между ними взаимосвязаны, поскольку они опреде-
ляются по результатам физических наблюдений и, следователь-
но, в совокупности наилучшим образом объясняют наблюдае-
мые в природе процессы. Поэтому в уравнениях (1.26) должна
использоваться совокупность согласованных постоянных для
массы, размеров планет и т. д. Такую совокупность еще имену-
ют системой фундаментальных астрономических постоянных.
В составе системы астрономических постоянных:
астрономическая единица расстояния 1 а. е.= 149,598-109 м;
экваториальный радиус Земли /?3.э = 6378,245 км;
скорость света с = 2,997925-105 км/с;
планетные массы (отношение массы Солнца к массе плане-
ты) для:
Меркурия — 6 000 000
Венеры — 408 000
Земли и Луны — 329 390
Юпитера — 1047,355
Сатурна — 3501,6
Урана — 22 869
Нептуна — 19 314
Плутона — 36 000.
Отношение массы Земли к массе Луны — 81,30.
По мере накопления физических наблюдений система астро-
номических постоянных может уточняться, но и при этом значе-
ния постоянных должны оставаться согласованными.
46
Среди методов численного интегрирования уравнений дви-
жения отметим метод Рунге — Кутта; он удобен при примене-
нии ЭВМ уже по двум соображениям:
для того чтобы начать вычисления, достаточно знать лишь
исходные значения искомых функций;
изменение шага численного интегрирования h не связано с
дополнительными вычислениями.
Четырехтактный метод Рунге—Кутта обеспечивает погреш-
ность порядка /г5 и наиболее широко используется на ЭВМ. Его
алгоритм:
Д//==_к(й1 + 2^ + 2^ + ^);
О
ki=hf(y0, /0);
k2 = hf(y0 + -^-k1, /0 + -^-Л); С-45)
k3 = hf(y0 + -j- k2, +
ki = hf(ya + k3, t0 + h),
где Az/ — прирост искомой функции на шаге интегрирования /г;
f(z/, 0 —правая часть уравнения y = f(yt t).
Обратим внимание на близость величин Az/ и k4 порядка /г4.
Эта особенность позволяет автоматизировать выбор шага ин-
тегрирования на ЭВМ с минимальными дополнительными вы-
числениями исходя из косвенной оценки вычислительной по-
грешности |Az/—&4|.
Для автоматизированного выбора шага экспериментально
подбирают предельно допустимую величину б. Интегрирование
уравнений (1.26) начинают с шагом Ло, и после первого шага
для всех искомых переменных выполняется анализ, в результа-
те которого при:
|Az/i—&4г| <б = 2_4 б(/=1, п) — интегрирование про-
должается с удвоенным шагом;
'6sC|Az/—й4г | ^6 — интегрирование продолжается с j, (1.46)
прежним шагом;
6<|Az/i—k4i| — интегрирование повторяется с ис-
ходными начальными условия и поло-винным шагом.
Эффективность использования автоматизированного выбо-
ра шага численного интегрирования для уравнений’ (1.26) воз-
растает по мере усложнения гравитационного поля вдоль тра-
ектории движения КА, например при последовательном пролете
вблизи нескольких планет. На участках движения КА с силь-
ным гравитационным полем кинематические параметры траек-
тории могут интенсивно меняться и дробление шага численного
интегрирования неизбежно, в то время как на остальных участ-
47
ках, составляющих основную часть общей протяженности тра-
ектории, шаг интегрирования может на порядок и более увели-
чиваться.
1.7. МЕТОДЫ ОЦЕНОК МАЛЫХ ВОЗМУЩЕНИЙ
КИНЕМАТИЧЕСКИХ ПАРАМЕТРОВ ДВИЖЕНИЯ КА
Действительная траектория движения КА отличается
от расчетной в силу многих физических причин, называемых
возмущениями. К числу возмущений относят ошибки системы
управления движением КА на активных участках траектории,
случайные отклонения условий движения (параметров атмосфе-
ры, ветра, характеристик поля тяготения, ... ) и неточности за-
писи дифференциальных уравнений движения.
Таким образом, отличия кинематических параметров движе-
ния КА от расчетных значений неизбежны, но важно, чтобы та-
кие отличия находились в допустимых пределах, при которых
задачи запуска КА надежно выполняются. В связи с изложен-
ным в механике движения КА разработаны методы оценок ма-
лых возмущений кинематических параметров движения. Мето-
ды оценок могут быть отнесены к двум группам: — аналитиче-
ские и статистические методы оценок возмущений.
Аналитические методы основаны на определении частных
производных от кинематических параметров движения КА по
возмущениям
_дг_. _дх_ ду_ (1.47)
dU ’ dU dU dU dU dU
Возмущения — U по физическому смыслу могут быть как
случайными отклонениями конструктивных параметров, усло-
вий движения или значений астрономических постоянных, так
и случайными функциями отклонений плотности и температуры
атмосферы по высоте, порывов ветра и т. д.
Методика получения частных производных по конструктив-
ным параметрам может использовать уравнения движения на
активном участке [3], [8] или численное интегрирование с ис-
пользованием ЭВМ траекторий с единичным отклонением одно-
го из возмущений — &U и последующим нахождением произ-
водных (1.59) по конечным разностям.
Важным этапом аналитических методов оценки малых воз-
мущений является определение корреляционной матрицы кине-
матических параметров движения [3]:
Кц (Ах, Ах), Ki2 (Ах, А у)... К16 (Ах, Аг)
К31(Ау, Дх), К22(Ау, Аг/). -. К26 (Аг/, Аг)
К61 (Дг, Дх), К62 (Дг, Ду).. . К66 (Дг, Дг)
(1.48)
48
Рис. 1.9. Область возможного выклю-
чения двигателя КА в фазовом про-
странстве кинематических параметров
движения xt=x; Х2 = у; ...; xQ = z
Элементы корреляционной
матрицы по существу являют-
ся вторыми моментами кине-
матических параметров как
случайных величин. Они ха-
рактеризуют возможные откло-
нения кинематических пара-
метров от расчетных. Их вычисление основано на теореме о сло-
жении дисперсий [3, 9]. Так, используя (1.47), можно записать
т дх
i
(1.49)
и
K“=s«)’D(^
K”=?(>X<W,; (1-50)
K6e = D&i),
i \ u*i J
где D(Zi) — дисперсия i-го независимого возмущающего фак-
тора.
Практическое использование корреляционной матрицы
(1.48) многообразно. Так, в фазовом пространстве шести кине-
матических параметров движения %, y,...z с использованием
обратной корреляционной матрицы К-1 можно определить об-
ласть возможного выключения двигателя КА в конце активно-
го участка (рис. 1.9). Введем обозначение для вектора откло-
нений кинематических параметров
Дх = [ Дхп Дх2, Дх3, .. ., Дхб ],
(1.51)
где ДХ1 = Дх, Дх2 = Ду... Дх6=Дг, матричное уравнение области
выключения двигателя КА записывается [9]
ДхК~гДхт= 1, (1.52)
49
где Дхт — транспонированная матрица. Матрица изохронных
производных в момент t\ дх\ дх2 3*2 дх2 дх*х дхв дх2 дх6 (1-53)
в = дх\ дхг дх2 дх±
3*6 ^хв
дхг дх2 дхв
Отклонения кинематических параметров движения в момент
t с учетом (1.51) и (1.53) выражаются матрицей-столбцом
Д^ = Вдхт. (1.54)
Соответственно матричное уравнение изохронной области
отклонений кинематических параметров
Дх? КГ1 Дх# = 1, (1.55)
где корреляционная матрица изохронной области возможных
отклонений
К/ = ВКВТ. (1.56)
Статистические методы оценок малых возмущений кинема-
тических параметров движения КА стали широко использовать-
ся благодаря возможностям современных ЭВМ. Суть подобных
методов сводится к заданию случайного возмущения (или сово-
купностей случайных возмущений) и оценке их влияния на от-
клонения кинематических параметров путем численного интег-
рирования уравнений движения (1.26).
Преимуществами статистических методов является относи-
тельно малое время подготовки к решению задачи оценки воз-
мущений кинематических параметров движения КА и весьма
точный учет нелинейных взаимосвязей.
Таким образом, (1.55), (1.56) определяют трубку возмож-
ных траекторий КА.
1.8. УПРОЩЕНИЯ УРАВНЕНИЙ ДВИЖЕНИЯ
ДЛЯ ВЫБОРА ТРАЕКТОРИИ КА
Воспользуемся записью уравнений относительного
движения в форме (1.26)
50
— = f У М} Г r}~r
dt* £ JLlT}—“I3
.3
^7+bi+V.
r3
(уравнение KA);
(1.57)
dt3
Ma+Mj -
,3 ri
3
(i= 1, n—уравнение небесных тел).
He все небесные тела и их естественные спутники одинако-
во влияют на движение КА. Влияние конкретного небесного те-
ла пропорционально его массе 7И;, которая для планет солнеч-
ной системы различается на несколько порядков, и обратно
пропорционально квадрату расстояния |гj—г|2.
Планеты Солнечной системы, обращаясь вокруг Солнца по
известным орбитам, не могут приблизиться друг к другу или к
Солнцу на расстояния, менее вполне определенного. При таких
ограничениях ускорение притяжения планет Солнцем намного
превышает ускорение притяжения между планетами. Восполь-
зуемся этими обстоятельствами и запишем уравнение движе-
ния Солнца (/=1) и i-й планеты с учетом только их взаимно-
го притяжения, т. е. пренебрегая влиянием остальных планет.
Из (1.57) следует:
уравнение движения Солнца
(1.58)
dt2 15--“113 4 ri
уравнение движения /-й планеты
dt3 х|т;—г>|3 ' Ч 1
В рассматриваемом случае Земля с массой Л43 не влияет
на относительное движение Солнца и /-й планеты, поэтому пе-
реносом начала системы координат в центр Солнца
= (1.59)
сведем запись (1.58) к одному дифференциальному уравнению
движения /-й планеты вокруг Солнца:
= -fM^ -fM^ -fM^ +
dt* dt* dt* rd ri rj
rl rc/ rj
ИЛИ
0 (1.60)
dt3 ft,-
51
Таким образом, каждая планета в первом приближении дви-
жется вокруг Солнца так, как будто бы остальных планет не
существует. Система уравнений движения (1.58) распалась с
учетом принятых допущений на отдельные уравнения (1.60)у
каждое из которых (см. гл. 2) может быть интегрировано от-
дельно, и, что важно, решение получается в квадратурах. Ко-
нечно, полученное при сделанных допущениях решение уравне-
ний относительного движения не соответствует действительной
орбите планеты; оно описывает фиктивное движение, но близ-
кое к действительному, и поэтому принято называть такое дви-
жение невозмущенным, а уравнение (1.60) —уравнением невоз-
мущенного движения больших планет.
Малые планеты и другие небесные тела солнечной системы
обладают пренебрежимо малыми массами Mj по сравнению с
массой Солнца, и уравнения невозмущенного движения для них
^Г-+/4£7си=° (Ь = ТЛ). (1.61)
а1 гск
К группе малых планет можно отнести и КА. Тогда урав-
нение невозмущенного движения по инерции для КА относи-
тельно Солнца
-^М-^-7с = 0- (1-62)
dt* rf
Однако в отличие от малых планет КА может оказаться
ь непосредственной близости у какой-либо планеты солнечной
системы и даже осуществить посадку на нее или взлет. В
такой ситуации ускорение притяжения КА планетой будет за-
ведомо превышать ускорение притяжением КА Солнцем, а не-
возмущенное движение КА определяется массой планеты —
МП и удалением от нее гп:
= (h63>
г я
Область межпланетного пространства, где превалирует при-
тяжение планеты и правомерно использование уравнения (1.63)\
называют грависферой планеты. В ряде задач механики дви-
жения КА целесообразно для приближенного описания траек-
тории КА использовать уравнение невозмущенного движения
(1.62) в грависфере планеты, согласовав их решения на гра-
нице упомянутых сфер. Эти вопросы подробно будут разоб-
раны в гл. 6.
На траекторию движения КА помимо гравитационных сил
влияют тяга и другие факторы, учитываемые кажущимся ус-
корением Vs. Поэтому уравнение первого приближения для
описания движения КА должно рассматриваться в записи
52
Гп =VS. (1.64}
d/2 Z f3 п S V /
За пределами атмосферы кажущиеся ускорение и скорость-
совпадают с характеристическими ускорениями и скоростью.
Характеристическая скорость КА
Возможности КА как транспортного средства опре-
деляются скоростью, которую он может набрать в идеальных
условиях движения при отсутствии атмосферы, гравитацион-
ных сил, когда вектор тяги направлен вдоль вектора скорости..
Уравнение сил в таких условиях
т^ = Р (1.65}
интегрируется в квадратурах
V„-Vo= ^K—dt= fdt =—^KWa — =—W3]n[iK, (1.66)
о т о 1 М-
р
где f — величина реактивного ускорения f=—; — эффек-
т
тивная скорость истечения.
Формулу (1.66) называют первой формулой К. Э. Циол-
ковского, она определяет характеристическую скорость КА
Ухар.
Отметим, что характеристическая скорость не зависит от
закона расхода топлива m(t) и определяется только относи-
тельной конечной массой КА 1Хк=тк/т0. Конечная скорость
КА отличается от характеристической на величину потерь из-
за влияния атмосферы и гравитации, а также из-за потерь на
управление. При заданной конечной скорости нахождение ра-
циональных схем движения КА сводится к минимизации ха-
рактеристической скорости и, таким образом, к увеличению ко-
нечной массы тк.
В настоящей главе сформулирован общий подход к пост-
роению математических моделей для расчета траекторий КА
и методов исследования этих моделей.
ГЛАВА 2. ДВИЖЕНИЕ КОСМИЧЕСКОГО АППАРАТА
В ЦЕНТРАЛЬНОМ ПОЛЕ ТЯГОТЕНИЯ
Для исследования траектории движения КА оказывается
целесообразным рассмотреть некоторую модельную задачу,
которая в небесной механике называется задачей двух тел. В
этой задаче изучается движение двух материальных точек с
массами М. и m под действием силы их взаимного притяжения.
Такая задача в определенных условиях может рассматривать-
ся как модельная для анализа движения в окрестности небес-
ного тела массой М (например Земли) космического аппара-
та (искусственного спутника Земли) с массой ш. Перечислим
основные допущения, которые нужно сделать при анализе дви-
жения КА относительно Земли, чтобы воспользоваться реше-
ниями задачи двух тел:
рассматривается пассивное движение КА;
гравитационная сила, с которой Земля притягивает спут-
ник, подсчитывается как ньютоновская сила взаимодействия
двух материальных точек с массами М и т, расположенных в
центрах масс Земли и КА;
притяжением других небесных тел Вселенной пренебрега-
-ется;
аэродинамическое воздействие среды на космический ап-
парат не учитывается;
предполагается, что на КА не действует никаких сил дру-
гой физической структуры (электромагнитными силами, сила-
ми светового давления, силами, свя-
занными с утечкой газа из емкостей
и т. д., — пренебрегают).
Все перечисленные допущения
вытекают из того, что в задаче двух
• тел учитывается единственная си-
ла — сила ньютоновского взаимо-
действия между двумя материаль-
ными точками. На рис. 2.1 эти ма-
териальные точки расположены в
Рис. 2.1. Задача двух тел геометрических точках С (центр
.54
масс Земли) и А (центр масс КА), а сила притяжения КА Зем-
лей обозначена G и направлена вдоль радиуса-вектора СА = г
к центру Земли.
Задача настоящей главы дать решение задачи двух тел,,
как некоторого приближения при исследовании траектории КА.
2.1. УРАВНЕНИЯ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ
В ЗАДАЧЕ ДВУХ ТЕЛ
Весьма просто можно описать абсолютное движение
в задаче двух тел. Для этого достаточно ввести некоторую
инерциальную систему отсчета ОИХИУИХИ (рис. 2.2,а). На этом
рисунке р1 = ОиС — радиус-вектор тела массой М; р2=ОиА —
радиус-вектор тела массой т. В инерциальной системе спра-
ведлив закон Ньютона и ускорения масс Мит пропорци-
ональны силам Gi и G, приложенным к этим массам. Отметим,
что Gi=—G, так как это силы взаимного притяжения масс.
Уравнения движения двух тел в инерциальной системе отсче-
та имеют вид
= m-^-=G. (2.1)
dt2 dt2
Легко охарактеризовать движения общего центра масс
системы двух тел. Учитывая, что Gi =—G, после сложения ле-
вых и правых частей двух векторных равенств из (2.1) получим
М = °- (2-2)'
at* at* '
Интегрируя равенство (2.2), имеем
M^ + m$_ = ^ = const; (2.3)
Мр1+ тр2 = Сг t + С2, (2.4):
где Ci, С2— некоторые константы интегрирования.
Выражение слева в (2.4) определяет радиус-вектор центра
масс системы двух тел (M+m)p4,M=Mpi+mp2. С учетом (2.4)
получаем
р - t+ -
Рц.м- м+т М+т ’
т. е. центр масс системы двух тел в задаче двух тел в инер-
циальном 'Пространстве движется равномерно, прямолинейно,,
с некоторой постоянной скоростью С\!(ТИф/п). Таким образом,
если рассматривать движение системы Земля — Луна в рам-
ках задачи двух тел, то можно утверждать, что центр масс
этой системы движется равномерно, прямолинейно. Ясно, что-
55
G
Рис. 2.2. Движение в задаче двух тел:
а — абсолютное; б — относительное
Р' = 0ИС' Р2=ОИЛ
такая модель могла бы пригодиться, если бы не Солнце, кото-
рое искривляет траекторию центра масс системы Земля — Лу-
на и ограничивает целесообразность рассмотрения абсолютно-
го движения такой системы.
Не будем останавливаться на описании абсолютного дви-
жения отдельных масс в задаче двух тел, так же как и абсо-
лютного движения центра масс системы, так как они имеют
очень ограниченное применение. Более важным является ис-
следование относительного движения. Расположим начало не-
вращающейся системы координат (Cxyz) в центре масс тела
М (точка С, рис. 2.2,6). На этом же рисунке оставим ранее
введенную инерциальную систему отсчета O^X^Y^Z^, Пусть г=
= СЛ— радиус-вектор, характеризующий относительное положе-
ние массы т относительно М. _ _
Из рис. 2.2,6 следует, что г=рг—рь Дифференцируя это
равенство дважды по времени, с учетом системы (2.1) полу-
чим следующее выражение для относительного ускорения
d?fldt2-.
(2.5)
dt2 т М 1 \ /
Так как _
Г2 г
1 г2 г
то уравнение (2.5) можно переписать в виде
d27 _ ,М+т ~
dt* ~ 'г* г
(2.6)
56
Последнее равенство и описывает относительное движение
в задаче двух тел. Входящее в это равенство произведение
универсальной гравитационной постоянной на сумму масс
Л1+т (тоже постоянную величину) называют гравитационным
параметром задачи двух тел и обозначают p=f (M-f-m). При
этом дифференциальное уравнение относительного движения
задачи двух тел принимает вид
Таким образом, получено уравнение относительного движения
в задаче двух тел. Это уравнение является дифференциаль-
ным уравнением шестого порядка (векторное уравнение вто-
рого порядка). При использовании введенной невращающейся
системы координат с началом в центре масс тела М—С, в ко-
торой координаты вектора г имеют проекции х, yt z, эквива-
лентная (2.7) скалярная запись будет иметь вид
d2 х ____d?y_____________И
dt2 г3 ’ dt* г8 оч
dt* г3
Напомним, что длина радиуса-вектора г связана с ее про-
екциями соотношением г = Ух2 + У2 -т?2 •
Итак, исследование относительного движения в задаче двух
тел сводится к интегрированию системы дифференциальных
уравнений шестого порядка (2.8). Естественно, что для полу-
чения конкретной траектории в задаче, описываемой дифферен-
циальной системой уравнений шестого порядка, нужны шесть
начальных условий движения. Естественней всего такими ус-
ловиями рассматривать начальное положение тела массы m
относительно М—rQ и начальную относительную скорость Vo=
_ г
dt о’
Для описания движения в рамках задачи двух тел не пот-
ребовалось исследовать их вращение относительно центра масс,
не потребовались геометрические связи углов, уравнения систе-
мы управления. Это все связано с допущениями задачи двух
тел, с тем, что единственная сила, учитываемая в задаче, не
зависит от углового положения КА в пространстве. Система
уравнений (2.8) замкнутая. При определенных начальных ус-
ловиях она имеет единственное решение, определяющее тра-
екторию относительного движения. Очень важно для механи-
ки космического полета, что эта система имеет аналитическое
решение. Для получения и исследования этого решения най-
дем первые интегралы системы (2.8).
57-
Прежде чем находить эти интегралы введем широко ис-
пользуемую модификацию задачи двух тел — ограниченную
задачу двух тел.
Для исследования движения КА (искусственного спутника)
относительно небесного тела можно полагать, что масса КА
пренебрежимо мала по отношению к массе небесного тела.
Использование этого дополнительного допущения приводит к
ограниченной задаче двух тел.
Уравнения движения в ограниченной задаче двух тел по
форме не отличаются от (2.7), единственное обстоятельство,
которое можно при этом учитывать, заключается в величине
гравитационного параметра задачи двух тел. Если в полной
задаче двух тел H = f (М-\-ш), то в ограниченной — р,=/М и
гравитационный параметр совпадает с гравитационным пара-
метром гравитирующего тела массой М.
Таким образом, сами уравнения относительного движения,
а значит, и решение в ограниченной задаче двух тел и полной
задаче двух тел по форме не отличаются. Принципиальная раз-
ница может быть отмечена при анализе абсолютного движения.
Дело в том, что если пренебрегать массой малого тела в зада-
че двух тел, то центр масс системы тел находится в гравити-
рующем теле. Но центр масс системы движется равномерно и
прямолинейно, поэтому движение КА относительно гравити-
рующего тела в ограниченной задаче двух тел совпадает с
движением в инерциальном пространстве. В этом случае урав-
нение (2.7) есть запись закона Ньютона. В нем слева записа-
но ускорение, которое имеет спутник, справа — гравитацион-
ная сила от притяжения спутника небесным телом, отнесенная
к массе спутника.
Таким образом, в разд. 2.1 записана математическая мо-
дель, описывающая относительное движение спутника в виде
уравнения (2.7). Следующие разделы посвящены исследованию
этой модели.
2.2. ИНТЕГРАЛ ПЛОЩАДЕЙ ЗАДАЧИ ДВУХ ТЕЛ
Переходим к нахождению первых интегралов сис-
темы дифференциальных уравнений, описывающих относитель-
ное движение в задаче двух тел (2.7).
Умножим левую и правую части равенства (2.7) векторно
слева на радиус-вектор КА относительно гравитирующего тела.
Получим
Правая часть последнего равенства равна нулю, так как
представляет векторное произведение коллинеарных векторов.
58
Таким образом,
[гхт] = °- <2-9>
Рассмотрим производную от векторного произведения ра-
диуса-вектора г на скорость КА относительно гравитирующего
тела V=dr[dt. По определению производной от произведения
с учетом (2.9) получим
— dr
г X —
dt
Таким образом, найден первый интеграл уравнений отно-
сительного движения в задаче двух тел. Из (2.10) следует, что
в течение всего движения векторное произведение радиуса-век-
тора КА на его относительную скорость есть константа. Обоз-
начим эту константу о (она векторная) и назовем константой
интеграла площадей задачи двух тел или вектором площадей:
= о = const. (2.11)
Само равенство (2.11) называют интегралом площадей или
векторным интегралом площадей.
Таким образом, если в какой-либо момент времени (напри-
мер, начальный) известен радиус-вектор КА г0 и его скорость
Го, то легко можно найти константу интеграла площадей:
[г0Х Ро]=о'» и утверждать, что для любого момента времени
векторное произведение радиуса-вектора КА на его скорость
будет равно найденной константе.
Из векторного равенства (2.11) следует система трех ска-
лярных равенств:
yVz—zVy = Gx-,
zVx—xVz = Gy\ (2.12)
xVy— yVx = oz.
Равенства системы (2.12) являются тремя первыми (ска-
лярными) интегралами дифференциальных уравнений относи-
тельного движения задачи двух тел. Таким образом, можно
утверждать, что получено три первых интеграла, уравнений
задачи двух тел. Можно показать, что эти интегралы незави-
симы между собой и поэтому отметить, что из 6-ти независи-
мых констант интегрирования системы (2.7) уже найдено три
константы ох, ov, oz.
Плоскость движения КА (спутника). Найден-
ный интеграл площадей дает возможность выявить очень важ-
ное свойство траектории спутника, позволяет доказать, чта
относительное движение спутника происходит в постоянной
59
(невращающейся) плоскости, проходящей через гравитацион-
ный центр (центр масс гравитирующего тела Л4).
Для доказательства отдельно следует рассмотреть два слу-
чая: (уУ=0 и о=0. Второй случай, когда константа площадей
равна нулю, следует рассматривать отдельно, как некий вы-
рожденный случай.
Обратимся сначала к более общему случаю. Пусть началь-
ные условия движения таковы, что [гоХЁо] = о’ и|о|=/=0. До-
скажем, что в любой момент текущий радиус-вектор спутника
f(t) будет перпендикулярен вектору о. Действительно, скаляр-
ное произведение г и о равно нулю:
(г, о) = (7, [гхИ) = 0. (2.13)
Но скалярное произведение равно нулю тогда, когда хотя бы
один из векторов равен нулю или когда векторы перпендику-
лярны. Вектор о в рассматриваемом случае ненулевой. Вектор г
также не может ни в одной точке траектории равняться нулю,
иначе из равенства (2.11) следовало бы, что о=0. Поэтому
остается единственная возможность для выполнения равенства
(2.13)—перпендикулярность вектора г вектору о. Таким об-
разом, в течение всего движения спутника его радиус-вектор
перпендикулярен постоянному в рассматриваемой невраща-
ющейся системе координат вектору о. Значит, в любой момент
^времени г принадлежит плоскости, перпендикулярной вектору
о. Эту плоскость назовем плоскостью траектории спутника. Она
проходит через гравитационный центр, постоянно расположена
в невращающейся системе координат и перпендикулярна по-
стоянному в этой же системе координат вектору о.
На рис. 2.3 заштрихована часть траектории спутника, ле-
жащая выше координатной плоскости ху, вектор площадей о
перпендикулярен плоскости траектории спутника и его начало
помещено в центр масс гравитирующего тела. _
Случай, когда константа площадей равна нулю |о|=0, яв-
ляется вырожденным. Без доказательства отметим, что этот слу-
чай соответствует прямолинейному движению спутника (ско-
рость и радиус-вектор спутника коллинеарны). Действительно,
при коллинеарности г и V их векторное произведение равно ну-
лю: I or I = I [rX7] I =0.
Замечание: Если исследовать ограниченную задачу двух
тел, при которой движение спутника относительно гравитиру-
ющего тела можно рассматривать как движение в инерци-
альном пространстве, то можно утверждать, что траектория
спутника принадлежит постоянной в инерциальном простран-
стве плоскости. Этой же плоскости принадлежит и гравита-
ционный центр тела массой М. Для того чтобы оставаться в
60
Рис. 2.3. Плоскость траектории спут-
ника
рамках более общей задачи, пришлось использовать понятие
плоскости траектории спутника в невращающейся системе ко-
ординат Слух с началом в гравитационном центре массы М.
В инерциальном пространстве эта система координат переме-
щается вместе со своим началом, вместе с массой М.
Скалярный интеграл площадей. Выберем специ-
альным образом систему координат. Ее ось Сх направим по
вектору а (предполагаем, что |сг| =#0). Из только что доказан-
ного свойства траектории спутника следует, что плоскость тра-
ектории спутника будет совпадать с плоскостью ху (специ-
альным образом выбранной системы координат). При этом
координата х спутника, так же как и компонента его скорости
Vz, тождественно по времени равняется нулю. Используя ска-
лярную форму записи интеграла площадей (2.12), можно по-
лучить
ах = °; а</ = °; (2.14)
xVv—yVx = o.
Рис. 2.4 является плоской картинкой. Ось Сх системы ко-
ординат направлена из начала координат на читателя, плос-
кость траектории спутника совпадает с плоскостью листа.
Последнее равенство из (2.14) называется скалярным ин-
тегралом площадей. Перейдем от прямоугольных декартовых
координат х, у к полярным г, р. Полярный угол р отсчитыва-
ется от оси Сх против часовой стрелки. Отметим, что на рис.
2.4 спутник в плоскости ху вращается против часовой стрелки.
Это следует из определения векторного произведения (о=
='[rXV]) и выбранного направления оси Сх (Сх направлена
по вектору о).
Скорость спутника можно разложить на два взаимно пер-
пендикулярных направления:
61
направление радиуса-вектора спутника, эта компонента
скорости называется радиальной (на рис. 2.4 она обозначе-
на Гг);
направление, перпендикулярное радиусу-вектору, эта компо-
нента скорости называется трансверсальной и будет обозна-
чаться Vn-
Радиальная компонента скорости или просто радиальная
скорость считается положительной, есл_и 7Г направлена по ра-
диусу-вектору, и отрицательной, если Vr направлена против г.
Радиальная скорость характеризует скорость изменения дли-
ны радиуса-вектора Vr=diidt. Обратим внимание на то, что
последнее равенство — скалярное в отличие от векторного 7=
= dr/dt.
Трансверсальная компонента скорости Уп чаще всего счи-
тается положительной, ее направление характеризует направ-
ление вращения радиуса-вектора спутника. Величина Vn есть
скорость конца радиуса-вектора спутника, обусловленная вра-
щением радиуса-вектора относительно гравитационного цен-
тра:
= (2.15)
at
где dtydt — угловая скорость радиуса-вектора.
Переход от декартовых координат в равенстве (2.14) к по-
лярным осуществим с помощью следующих соотношений:
х = г cos Р;
у = rsinP;
гл dx dr а б/р . D (2 16)
Vx=----- =-----cosp — г—— sinp;
х dt dt r dt r
= = “Jrsinp+r"f“cosP-
dt dt dt
Подставляя (2.16) в (2.14), получим:
Г2^_=ст (2.17)
dt
Равенство (2.17) представляет собой полярную форму ин-
теграла площадей. Анализ полярной формы скалярного интег-
рала площадей показывает, что при увеличении длины ради-
уса-вектора спутника угловая скорость радиуса-вектора умень-
шается: — = — <т. Естественно, при приближении спутника
dt г2
к гравитирующему телу угловая скорость его радиуса-векто-
ра увеличивается.
62
Если учесть (2.15) при анализе полярной формы интегра-
ла площадей (2.17), то можно записать следующую простую
форму скалярного интеграла площадей
г Vn = о = const.
(2.18)
Последнее равенство можно рассматривать как взаимоод-
нозначное соотношение между длиной радиуса-вектора спут-
ника и его трансверсальной скоростью. Для каждого спутни-
ка при его удалении от гравитационного центра трансверсаль-
ная составляющая скорости уменьшается и, наоборот, при приб-
лижении к гравитационному центру трансверсальная компонен-
та скорости растет.
У
В
Рис. 2.5. Площадь, заме-
таемая радиусом-векто-
ром спутника
Второй закон Кеплера. Г "
щадей дает возможность сформулировать закон,
отношению к планетам Солнечной систе-
мы (как спутникам Солнца) сформули-
ровал Кеплер. Он известен как второй за-
кон Кеплера. Методически нам оказалось
удобным объяснить второй закон Кепле-
ра, оставив вывод первого закона Кепле-
ра на будущее.
Введем понятие площади, заметаемой
радиусом-вектором спутника. На рис. 2.5
Л и г — радиусы-векторы спутника в два
произвольных момента времени ti и t
(для определенности За время
pi, Z] радиус-вектор спутника замел площадь фигуры САВ, за-
штрихованной на рис. 2.5 и обозначенной S.
Эта площадь естественно является функцией времени t при
фиксированном начале движения t\. Таким образом, S=S(t).
Можно показать, что S(t) — непрерывная, имеющая производ-
ную dSIdt, функция. Эта производная называется векториаль-
ной скоростью спутника и определяет скорость изменения
функции-площади, заметаемой радиусом-вектором спутника.
Найденный интеграл пло-
, который по
Можно доказать, что
dS _ 1
dt “ 2
(2.19)
Прежде всего обратим внимание читателя на то, что спра-
ва в равенстве (2.19) стоит постоянное число—константа ин-
теграла площадей. Именно это обстоятельство и является ос-
нованием для одной из возможных современных формулировок
второго закона Кеплера.
Секториальная скорость спутника остается постоянной в те-
чение всего времени его движения.
63
Несколько других формулировок второго закона Кеплера
связаны с интегрированием соотношения (2.19):
S(t)=-±-att-t,). (2.20)
Таким образом, площадь, заметаемая радиусом-вектором
спутника, пропорциональна времени. Это утверждение так же
часто рассматривается как формулировка второго закона Кеп-
лера. Распространена еще одна формулировка этого закона
как закона площадей: радиус-вектор спутника за равные про-
межутки времени заметает равные площади. Понятно, что во
втором законе Кеплера исследуются секториальная скорость
и заметаемые площади одного конкретного спутника, траекто-
рия которого имеет вполне определенную константу площадей
о. Разумеется, разные спутники даже одного гравитационного
центра могут иметь разные секториальные скорости.
Таким образом, в разд. 2.2 получен и проанализирован ин-
теграл площадей. Анализ дал большой объем информации о
свойствах траектории движения спутников и возможность
доказать, что траектория спутника — плоская. Связал просты-
ми соотношениями радиус-вектор и скорость спутника, рассто-
яние от гравитационного центра с угловой скоростью радиуса-
вектора, с трансверсальной скоростью спутника. Перейдем к
следующему первому интегралу дифференциальных уравнений,
описывающих относительное движение в задаче двух тел.
2.3. ИНТЕГРАЛ ЭНЕРГИИ ЗАДАЧИ ДВУХ ТЕЛ
Напомним, что исследуются уравнения относитель-
ного движения задачи двух тел (2.7). Умножим левую и пра-
вую части (2.7) скалярно на удвоенный вектор скорости 2У=
= 2-^-, получим, что в силу уравнений движения справедливо
di
равенство
) (2 21)
dt dt2 / г3 \ dt I
Рассмотрим отдельно левую и правую части равенства
(2.21).
Левая часть. Ее можно преобразовать следующим об-
разом,
2( dr d-LX =—(= F) = — (V2) (2 22)
I dt ’ dt2 dt \ dt ' dt I dt dt
64
Правая часть. Для ее преобразования отдельно рас-
смотрим входящее в нее произведение I г, . По определе-
нию скалярного произведения (Jr, P)=rVcosa, где угол a
есть угол между векторами г и Р, его обязательно следует на-
ходить как угол BAD (рис. 2.6, а не, например, CAD). Но»
Vcosa есть проекция скорости на радиус-вектор (радиаль-
ная скорость = поэтому
dt /
Г,
dr \ dr
dt J dt '
(2.23)
Обратите внимание, что слева в последнем равенстве стоит
скалярное произведение, справа — произведение двух скаляров.
Имея в виду это равенство, правую часть соотношения (2.21)
можно преобразовать к виду:
2|1 / — dr \_________ 2pt dr
г3 \ ’ dt ) г3 dt
d 2р,
dt г
(2.24)
С учетом отдельно рассмотренных выражений для левой и
правой частей равенства (2.21) в виде (2.22) и (2.24) получим.
dt 1 ’ dt\ г J
Из последнего соотношения находим еще один первый ин-
теграл:
V2—=Л = const, (2.25)
где h — некоторая константа интегрирования, которая называ-
ется константой (постоянной) энергии. Само соотношение
(2.25) называется интегралом энергии. Из него следует, что в
течение всего движения спутника величины скорости и ради-
уса-вектора находятся во взаимно однозначном соответствии.
Как всякую константу инте-
грирования, константу энергии
h можно найти по начальным
условиям движения. Отметим,
что для этого нужно знать
только длину радиуса-вектора и
величину скорости (и не нужно
знать направления этих век-
торов) : h — Vo--------— .
''о
Анализ интеграла энергии
позволяет утверждать, что чем
3—8
Рис. 2.6. Угол между радиусом-
вектором и вектором скорости КА
65
больше удаляется спутник от гравитационного центра, тем
меньше его скорость (!-Z2 = -?t h)y и, наоборот, при прибли-
жении спутника к гравитационному центру его скорость воз-
растает. Скорость спутника будет максимальной на наимень-
шем удалении от гравитационного центра.
На этом закончим анализ интеграла энергии задачи двух
тел. Найденные интегралы площадей и энергии являются не-
зависимыми, и можно утверждать, что система дифференци-
альных уравнений относительного движения задачи двух тел
проинтегрирована четыре раза. Найдены четыре независимых
первых интеграла (скалярных).
2.4. ИНТЕГРАЛ ЛАПЛАСА ЗАДАЧИ ДВУХ ТЕЛ
В разд. 2.2 и 2.3 были получены первые интегралы
системы дифференциальных уравнений задачи двух тел — ин-
тегралы площадей и энергии. Общая схема получения этих
интегралов была следующей: систему уравнений задачи двух
тел умножили слева и справа на некоторый вектор скалярно
или векторно и преобразовали равенство к виду, в котором
полная производная по времени оказывалась равна нулю. Для
вывода интеграла Лапласа можно умножить_уравнение зада--
чи двух тел векторно почленно на равенство: а=[7хР]. После
некоторых преобразований [4] удается получить еще один
векторный первый интеграл:
[о х V] + ц— = — % = const. (2.26)
г
Этот интеграл называется интегралом Лапласа. Константа
интегрирования этого интеграла X. Знак минус_используется
для определенного выбора направления вектора X, называемо-
го вектором Лапласа. Как всякая константа интегрирования
вектор Лапласа может быть найден по начальным условиям
движения.
Таким образом, найдено еще три скалярных интеграла (три
проекции векторного интеграла (2.26) Хх, Xz). В совокупно-
сти с ранее найденными четырьмя скалярными интегралами
(площадей — ох, оу, oz, энергии h) получилась система семи
первых интегралов. У системы шестого порядка независимых
первых интегралов шесть. Понятно, что между полученными
интегралами существует, по крайней мере, одна зависимость.
Можно показать, что таких зависимостей две и среди полу-
ченных первых интегралов можно считать независимыми любые
пять из семи. Покажем эти зависимости.
66
п сложение вектора Лапласа. Легко доказать, что
вектор Лапласа Л перпендикулярен вектору площадей о.
Скалярное произведение этих векторов имеет вид:
(X, о) = [ [ — [oxi7] — р— ], о | =— ([ох V], о)-— (г, а) — 0.
\ \ г / / г
(2.27)
Скалярное произведение равно нулю, если один из векто-
ров равен нулю или векторы перпендикулярны. Если какой-ли-
бо вектор % или о равен нулю, то и в этом случае можно счи-
тать, что условие перпендикулярности не нарушается. Поэто-
му доказано утверждение: вектор Лапласа X перпендикулярен
вектору площадей о. Так как вектор площадей перпендикуля-
рен плоскости траектории спутника, то вектор Лапласа при-
надлежит этой плоскости. Таким образом, получен вектор Z,
постоянный в рассматриваемой невращающейся системе коор-
динат и принадлежащий плоскости траектории спутника.
Указанное свойство вектора Лапласа дает возможность при
исследования движения спутника в его плоскости проводить
отсчет этого движения (положения радиуса-вектора) от по-
стоянного в этой плоскости вектора X.
Отметим, что равенство (2.27), записанное с использовани-
ем проекций на декартову прямоугольную систему координат,
имеет вид:
+ (2.28)
-Последнее соотношение и есть связь компонент векторов X
и о и доказывает зависимость найденных первых интегралов
(площадей и Лапласа).
Связь абсолютных величин векторов о, % и
константы энергии h. Равенство (2.28) дает связь ме-
жду найденными постоянными интегрирования. Существует
еще одна связь. Из выражения интеграла Лапласа (2.26), на-
ходя модуль вектора Лапласа, можно показать, что
Х = К |л2 + йо2.
(2.29)
Это и есть вторая зависимость между семью найденными
константами интегрирования. Таким образом, в данном раз-
деле найден интеграл Лапласа, доказано, что вектор Лапласа
принадлежит плоскости траектории спутника, установлено су-
ществование связей между семью полученными константами
интегрирования ох, ау, сг2, h, кх, Ку, kz, из которых в соответст-
вии с (2.28) и (2.29) только пять могут рассматриваться не-
з* 67
Рис. 2.7. Истинная аномалия
спутника
зависимыми. Можно доказать, что любые пять из перечислен-
ных семи можно считать независимыми и по соотношениям
(2.28) и (2.29) найти остальные две константы.
2.5. УРАВНЕНИЕ ОРБИТЫ ЗАДАЧИ ДВУХ ТЕЛ
Уравнением орбиты спутника задачи двух тел обыч-
но называется зависимость длины радиуса-вектора спутника
.как функции полярного угла радиуса-вектора спутника, под-
считанного в плоскости траектории
спутника. Такой угол удобно отсчи-
тывать от вектора Лапласа X, кото-
рый, как это доказано в предыду-
щем разделе, принадлежит плоско-
сти траектории спутника. Этот угол
(между вектором Лапласа и теку-
щим радиусом-вектором спутника)
называется истинной аномалией и
часто обозначается греческой бук-
вой ипсилон г. На рис. 2.7 стрелкой
показано направление движения
спутника, именно в этом направле-
нии и от вектора Лапласа А, отсчи-
тывается истинная аномалия г. Угол, отсчитанный в противопо-
ложном направлении, должен рассматриваться как отрицатель-
ный.
Итак, уравнение орбиты — это зависимость г=г(ъ). Такую
зависимость достаточно легко можно получить, используя вы-
ражение для интеграла Лапласа (2.26).
Умножим скалярно левую и правую части равенства (2.26)
на радиус-вектор г. Получим
(7 7)=-([БхЙ,7)—(л Ъ- (2-30)
По определению скалярного произведения
(X, г) = А г cos -и,
где v — угол между г и %.
Первое слагаемое правой части (2.30), используя цикли-
ческую перестановку в смешанном произведении и то, что
[УХг] =—о, преобразуем к следующему виду:
— ([охУ], г)= — ([Ухг], а) = (а, о) = о2.
Используя записанные соотношения, равенство (2.30) мож-
но переписать в виде
А г cos и == о2—цг.
68
Получить г (г) из последнего равенства не представляет
труда:
Справа в равенстве (2.31) а, Л, ц— константы (две кон-
станты интегрирования и гравитационный параметр). Для при-
ведения равенства к каноническому виду делят его числитель
и знаменатель на р и после введения обозначений
р = о2/|х; (2.32)
е = Z/p (2.33)
получают
Последнее равенство принято считать уравнением орбиты
спутника. Входящие в него постоянные р и е называются со-
ответственно фокальным параметром орбиты спутника и экс-
центриситетом этой орбиты, р и е — константы интегрирова-
ния, но зависимые от ранее найденных о и X.
Первый закон Кеплера. Спутник движется по траек-
тории, уравнение которой в плоскости этой траектории имеет
вид равенства (2.34). Последнее равенство есть полярная фор-
ма записи кривой второго порядка (эллипса, гиперболы или
параболы) с началом координат в фокусе этой кривой.
Таким образом, справедливость выведенного равенства до-
казывает первый закон Кеплера, современная формулировка
которого такова:
траектория спутника в задаче двух тел есть коническое се-
чение, в одном из фокусов которого расположен гравитацион-
ный центр.
Кеплер сформулировал свой закон по отношению к плане-
там, утверждая, что они движутся по эллипсам, в одном из
фокусов которых расположено Солнце. Таким образом, траек-
тория КА в задаче двух тел (траектория спутника, естествен-
ного и искусственного) относительно гравитирующего центра
является эллипсом, гиперболой или параболой. Такие траек-
тории часто называются орбитами. Поэтому в дальнейшем мы
чаще будем говорить об орбите планеты относительно Солн-
ца и т. д.
Таким образом, в данном разделе получено уравнение ор-
биты спутника (2.34) и сформулирован первый закон Кеплера.
Коротко рассмотрим возможные типы орбит КА в задаче
двух тел.
69
2.6. ТИПЫ ОРБИТ
Уравнение орбиты спутника (2.34) содержит две
константы: р, е. Эти константы определяют размер и форму
орбиты спутника. Можно утверждать, что размер орбиты оп-
ределяется значением фокального параметра р, форма орби-
ты— значением эксцентриситета е. Обычно тип орбиты спут-
ника связывают с формой орбиты и рассматривают следующие
основные типы:
эллиптическая орбита (0^е<1);
параболическая орбита (е=1);
гиперболическая орбита (е>1).
Определение «основные» при перечислении типов исполь-
зовано для того, чтобы подчеркнуть следующие два обстоя-
тельства.
1. Случай круговой орбиты является частным случаем эл-
липтической (при этом ^=0).
2. Возможен случай прямолинейного движения (при этом
р=о=0). Его следует рассматривать как вырожденный для
эллиптической, параболической и гиперболической орбит. При
этом эксцентриситет всегда равен единице (е=1) и тип ор-
биты доопределяется знаком константы энергии (Л). При h<.Q
это прямолинейное движение является вырождением эллипти-
ческого случая, при Л=0 — вырождением параболического слу-
чая, при А>0 — вырождением гиперболического случая.
Последнего замечания можно было не делать, если связы-
вать определение типа орбиты спутника не с величиной экс-
центриситета, а со знаком константы энергии h. Дело в том„
что эти две константы связаны между собой зависимостью
е= ]/ 1+Л-^-, (2.35}
которую легко получить, учитывая введенное обозначение
(2.33), а также связь констант интегрирования (2.29).
Из соотношения (2.35) следует, что величина эксцентриси-
тета во многом зависит от знака h. Обратим внимание на то,
что множитель при этой константе в выражении (2.35) неот-
рицателен.
В общем случае криволинейного движения спутника (а=/=0)
из (2.35) следует:
при А<0, е<1—орбита эллиптическая;
при Л=0, е=1 — орбита параболическая;
при Л>0, е>1 —орбита гиперболическая.
Отсюда становится понятнее, почему при описании обсто-
ятельства 2 мы связали классификацию прямолинейного дви-
жения со знаком константы энергии Л.
.70
Эллиптическая ор-
бита. На рис. 2.8 представ-
лена эллиптическая орбита
спутника. Точка С на рисун-
ке — центр гравитирующего
тела и совпадает с одним из
фокусов эллипса. От векто-
ра Лапласа X отсчитывается
истинная аномалия, опреде-
ляющая положение радиуса-
вектора спутника г.
Эллипс есть замкнутая
Рис. 2.8. Эллиптическая орбита спут-
ника
кривая. Таким образом, в задаче
двух тел относительное движение спутника происходит по зам-
кнутой постоянной кривой в невращающейся плоскости с фо-
кусом в гравитационном центре. При движении спутника ис-
тинная аномалия монотонно растет, становится равной 360°.
Дальнейшее изменение истинной аномалии при движении спут-
ника можно считать или монотонно увеличивающимся до зна-
чений 720° и далее, или увеличивающимся со значения нуль
опять до значения 360°.
Проанализируем зависимость г (у) в форме (2.34).
На одном витке эллиптической траектории спутника длина
радиуса-вектора спутника один раз достигает своего макси-
мального и один раз минимального значения. Эти значения со-
ответствуют минимуму и максимуму знаменателя правой ча-
сти равенства (2.34). При истинной аномалии -и, равной нулю,
знаменатель будет максимальным, а длина радиуса-вектора—
минимальной. Точка орбиты спутника с минимальным ради-
усом-вектором спутника называется перицентром орбиты. Она
обозначается л (см. рис. 2.8), радиус перицентра орбиты (или
перицентральный радиус) обозначается гя. Исходя из равен-
ства (2.34) следует
Итак, перицентр соответствует нулевой истинной аномалии,
а радиус-вектор перицентра направлен по вектору Лапласа.
Максимальное значение длины радиуса-вектора спутника до-
стигается при истинной аномалии, равной 180°. Эта точка ор-
биты называется апоцентром и обозначается а (см. рис. 2.8).
Апоцентральный радиус-вектор обозначается га. Из (2.34) лег-
ко получить
Р
1 — е ’
(2.37)
Перицентр и апоцентр орбиты лежит на прямой, проходя-
щей через гравитационный центр (угол между га и гп равен
71
180°). Обратим внимание, что эллиптическая орбита спутника
имеет один перицентр и один апоцентр. Это нужно иметь в ви-
ду, когда делается рисунок эллиптической орбиты: гравитаци-
онный центр (начало координат, фокус) нужно располагать
достаточно близко от перицентра, чтобы на рисунке ближай-
шая к гравитационному центру точка орбиты была действи-
тельно одна.
При рассмотрении орбит спутников (естественных и искус-
ственных) в рамках задачи двух тел Солнце — планета, Солн-
це— КА часто вводятся специальные термины для обозначения
«перицентров и апоцентров орбит. Так, для орбит спутников
Земли (в частности, для орбиты Луны) используются терми-
ны перигей, апогей. Гео — часть многих сложных слов (от гре-
ческого ge — Земля), означающая: относящийся к Земле. Для
искусственных спутников Луны используются термины пери-
селений, апоселений. Для планет, как спутников Солнца, ис-
пользуются термины перигелий, афелий (греческое helios —
Солнце).
Форма и размер орбиты могут быть определены не только
фокальным параметром р и эксцентриситетом е, но и любы-
ми другими двумя константами, по которым можно найти р, е9
Таких констант очень много. Среди них уже встречавшиеся
га, о, %, /г, а также большая а и малая b полуоси эллиптиче-
ской орбиты, фокальное расстояние с. Только два из перечис-
ленных параметров можно считать независимыми, остальные
можно найти по соотношениям. Приведем некоторые из них:
а= Р ; Ь = — р— ; с2 = а2— Ь2\
1-62 У l~e* _____________ (2.38)
е = с/а\ р= b2/a\ b = aY 1—е2.
Распространенным понятием для орбит спутников является
линия апсид. Это есть направленная прямая, совпадающая с
большой осью орбит и направленная по вектору Лапласа (т. е.
в перицентр орбиты). Перицентр и апоцентр орбиты объединя-
ются термином апсидалъные точки орбиты.
Параболическая орбита. На рис. 2.9, а представлена
параболическая орбита. Центр гравитирующего тела С нахо-
дится в фокусе параболы. Вектор Лапласа й, дает направле-
ние для отсчета истинной аномалии v текущего радиуса-векто-
ра г. На рисунке предполагается, что КА движется против ча-
совой стрелки (вектор площадей перпендикулярен плоскости
рисунка и направлен на читателя).
Парабола — это разомкнутая кривая. Если движение про-
исходит по параболе, то КА уйдет в бесконечность от грави-
72
д
Рис. 2.9. Траектория КА:
л — параболическая; б — гиперболическая;
тп, т\П\ — асимптоть. гиперболы; О — геометрический центр гиперболы; С — один из
фокусов гиперболы, в котором размещен гравитационный центр; BD — удвоенная боль-
шая полуось 2<з; BL — удвоенная малая полуось 2b; СА — текущий радиус-вектор КА г
тирующего центра. Бесконечность в таком случае следует по-
нимать как такое удаление от гравитирующего центра, при
котором рассмотрение траектории КА в рамках задачи двух
тел становится некорректным. Например, для двигающегося КА
в окрестности Земли это такое удаление от Земли, при кото-
ром нельзя не учитывать притяжение КА Солнцем. Точка л на
рис. 2.9,а — это перицентр параболы — ближайшая точка па-
раболы к гравитационному центру. Как для эллиптической ор-
биты (да и гиперболической орбиты) перицентр принадлежит
линии апсид — лучу, направленному из гравитационного цент-
ра по вектору Лапласа.
Минимальное значение длины радиуса-вектора спутника
(перицентральное расстояние гл) соответствует истинной ано-
малии, равной нулю. Само значение гл=р[(2.
Фокальный параметр на рис. 2.9,а отмечен отрезком
СВ (СВАЛ). Апоцентральной точки на параболической орбите
нет, можно считать, что она находится в бесконечности.
Параболическую орбиту часто рассматривают как гранич-
ный случай между эллиптической и гиперболической орбитами.
Гиперболическая орбита. На рис. 2.9,6 представ-
лена гиперболическая орбита КА. Сама гипербола имеет две
ветви. Орбита КА есть одна из ветвей гиперболы. Чаще всего
принято считать (хотя это и непринципиально), что орбита
является левой ветвью гиперболы, которая на рисунке нанесе-
на более жирно. Здесь направление движения спутника пред-
полагается против часовой стрелки. Вектор Лапласа X на ри-
сунке направлен по СО. Он определяет линию апсид гипербо-
лической орбиты.
Перицентр (ближайшая точка орбиты) достигается при v =
= 0 и лежит на линии апсид. На рис. 2.9,6 перицентром орби-
73
ты КА является точка л, а перицентральный радиус гя есть
С л (гп= .
\ 1+*/
Двигаясь по гиперболической орбите, КА уходит в беско-
нечность от гравитационного центра. Независимым парамет-
ром при анализе орбиты спутника часто рассматривают истин-
ную аномалию. Для гиперболической орбиты истинная анома-
лия не может беспредельно возрастать. На рис. 2.9,6 текущий
радиус-вектор СА соответствует истинной аномалии v (угол
ОСА). Предельное значение истинной аномалии определяется
направлениями асимптот гиперболы и равно углу GOB. Это
предельное значение истинной аномалии Vnp можно найти, при-
равнивая знаменатель правой части (2.34) нулю: l+ecosvnp=
= 0. Таким образом, cosT)np =— 1/е.
Оказывается, что соотношениями (2.38), записанными для
эллиптической орбиты, можно пользоваться и для гиперболи-
ческой орбиты, однако при этом следует считать, что большая
полуось гиперболической орбиты есть действительное отрица-
тельное число, по модулю равное OG; фокальное расстояние
с — действительное отрицательное число, по модулю равное
СО; малая полуось b — мнимое число, модуль которого ра-
вен DG.
Таким образом, в разд. 2.6 перечислены и коротко проана-
лизированы основные типы орбит КА в задаче двух тел.
2.7. АНАЛИЗ ИЗМЕНЕНИЯ СКОРОСТИ КА
ПО ОРБИТЕ. ЗАВИСИМОСТЬ ТИПА ОРБИТЫ
ОТ НАЧАЛЬНЫХ УСЛОВИЙ ДВИЖЕНИЯ
Рассмотрим изменение скорости КА при его движе-
нии по орбите. Для этого сначала рассмотрим законы измене-
ния радиальной и трансверсальной компонент скорости.
Величина радиальной скорости характеризует скорость из-
менения длины радиуса-вектора спутника. Используя уравне-
ние орбиты КА в задаче двух тел (2.34), получим
у _ dr dv _ ре sin и du
г dv dt (14-е cos и)2 dt
Но из полярной формы интеграла площадей (2.17) следу-
dv о
ет, что ---- = —, поэтому
dt г2
т, ре sin и о /1 . ч2 а
Vr = —-------------(1 4- е cos vr = — е sin и .
(14-е cost))2 р2 р
Правая часть последнего равенства включает в себя три
константы интегрирования, только две из которых можно счи-
74
тать независимыми. Легко с помощью соотношения (2.32) вы-
разить о через р:
О = /pi? (2.39)
и получить закон изменения радиальной скорости >по орби-
те КА:
Vr= esinu. (2.40)
Видно, что радиальная скорость изменяется синусоидально.
В перицентре орбиты и для эллиптической орбиты в апоцент-
ре она равна нулю. Амплитуда синусоидального закона про-
порциональна эксцентриситету. Максимальное значение ради-
альной скорости достигается тогда, когда истинная аномалия
равна 90°.
Величина трансверсальной компоненты скорости характери-
зует скорость конца радиуса-вектора спутника, обусловленную
его вращением относительно гравитационного центра, и опре-
деляется по равенству (2.15).
Используя уравнение орбиты и только что анализируемое
выражение для dv>!dt, получим
Vn = r — = — =— (1 +ecosu).
г2 г р
Учитывая (2.39), окончательно получим закон изменения
трансверсальной компоненты скорости по орбите:
= +ecosv). (2.41)
Максимальная трансверсальная компонента скорости дости-
гается в перицентре орбиты и равна:
max V п = К„я= (1 + е). (2.42)
Для случая эллиптической орбиты минимальное значение
трансверсальной скорости достигается в апоцентре орбиты и
определяется по формуле
min Vn = Vna = (1-e). (2.43)
С помощью геометрического суммирования компонентов
скорости получим закон изменения полной скорости КА
V = /1/2 + у г = j/jL У 1 + е2 + 2е cos и. (2.44)
Анализ последнего соотношения позволяет утверждать, что
максимальную скорость КА имеет в перицентре своей орбиты.
75
Эта скорость перпендикулярна радиусу-вектору, т. е. равна
своей трансверсальной компоненте:
шах1/ = 1/я = ]/±-(1 + 4 (2.45)
Минимальную скорость (что четко соответствует интегра-
лу энергии) спутник имеет в наиболее отдаленной точке ор-
биты. Для эллиптической орбиты такой точкой является апо-
центр. Вектор скорости в апоцентре перпендикулярен апоцент-
ральному радиусу-вектору, и значение скорости рассчитыва-
ется так:
minV=ya = Vna=]/±-(l-e). (2.46)
Отметим, что вектор скорости перпендикулярен радиусу-
вектору только в перицентре и апоцентре орбиты, т. е. там, где
радиальная компонента скорости равна нулю.
Значения скоростей спутника в перицентре и апоцентре ор-
биты связаны простым соотношением, называемым правилом
рычага:
raVa — rnVn. (2.47)
Для случаев параболической и гиперболической орбит ми-
нимальная скорость достигается в бесконечности. Для пара-
болы эта скорость равна нулю.
Для случая гиперболической орбиты минимальное значение
скорости будет в бесконечности и ее можно найти по констан-
те энергии 1/00=]/ h.
Связь константы энергии с величиной боль-
шой полуоси орбиты спутника. Оказывается, что в
задаче двух тел между константой энергии и большой полу-
осью орбиты спутника существует простая однозначная связь.
Значение постоянной интегрирования h можно определять по
начальным условиям или по условиям движения в любой точ-
ке траектории. Определим константу по условиям движения
в перицентральной точке траектории (заметим, что такая точ-
ка есть у траектории любого типа):
h=V2„----(2.48)
гп
Используя (2.36) и (2.45), из равенства (2.48) получим
7г=±Ч1 + е)2----— (1 + <Э = — (1 +e)U + 2)=----У-(1-е2).
р р р р
Используя первое равенство из соотношений (2.38), полу-
чим, что для эллиптической орбиты справедливо
h=—p,/a. (2.49)
76
Можно считать, что (2.49) справедливо для гиперболиче-
ской и параболической орбит, но для этого большую полуось
гиперболы считают отрицательной, а большую полуось пара-
болы полагают равной бесконечности.
Таким образом, получена взаимно однозначная связь боль-
шой полуоси и константы энергии. Имея в виду эту связь,
очень просто решать следующий тип задач. Если в задаче двух
тел заданы величина скорости К и длина радиуса-вектора Г1
в какой-либо точке траектории, то однозначно определяется
большая полуось орбиты КА а =---------— = — ---------.
h
Г1
Обращаем внимание на то, что величина константы энергии
не зависит от направления скорости КА, поэтому тип орбиты
КА, ее большая полуось могут быть определены по значениям
Л, Vi, и они не зависят от направления скорости.
Таким образом, было проанализировано изменение скоро-
сти спутника по орбите; показано, как по начальным услови-
ям движения (или условиям движения в текущей точке тра-
ектории) определить тип орбиты спутника, связанный со зна-
ком константы энергии h.
2.8. КОСМИЧЕСКИЕ СКОРОСТИ
Круговая скорость. Найдем скорость космического
аппарата, двигающегося по круговой орбите. Уравнение такой
орбиты получается из общего уравнения орбиты (2.34) подста-
новкой в него нулевого значения эксцентриситета, т. е. по-
лучим
r~ р = const. (2.50)
Так как длина радиуса-вектора на круговой орбите не из-
меняется, то радиальная скорость КА будет нулевой. Это мож-
но получить из выражения для радиальной компоненты ско-
рости (2.40). Таким образом, величина скорости равна транс-
версальной компоненте, т. е.
V = V„ = |/ -у(1 + е cos г)|е=,0 = Р у- (2-51)
Используя равенства (2.51) и (2.50), можно утверждать,
что скорость на круговой орбите спутника связана с радиусом
этой орбиты соотношением
(2-52)
Последнее соотношение и определяет понятие круговой ско-
рости. Как видно из соотношения, эта скорость зависит от гра-
77
витационного параметра р, и расстояния до притягивающего
центра г.
Когда говорят, что скорость КА равна местной круговой, то
полагают, что V= ]/ \^г в этой точке траектории. При этом
не обязательно орбита КА будет круговой. Для того чтобы ор-
бита была круговой, достаточно, чтобы скорость была равна
местной круговой и вектор скорости был направлен перпенди-
кулярно радиусу-вектору КА.
На рис. 2.10 показана зависимость круговой скорости спут-
ника от расстояния спутника до гравитационного центра. Чем
больше расстояние г, тем меньше значение круговой скорости.
Если рассмотреть спутник, двигающийся по низкой круговой
орбите (например, высотой Л=200 км) около Земли (полага-
ем радиус Земли 6371 км), то скорость такого спутника бу-
дет равна:
у — 1Z_Ез_ — 1Z1398 600 км3/с2 _ у
V~ I г “ V (6371 + 200) км КМ/С’
Если увеличить радиус кругового спутника, то скорость, до-
статочная для движения по этой орбите, будет уменьшаться.
Если рассматривать орбиту кругового спутника Земли с ради-
орбиты Луны г=ал = 384-103 км,
то . скорость такого спутника
будет V= 1,02 км/с. Эту скорость
можно принять как среднюю ско-
рость Луны. То, что скорость на
более высокой круговой орбите
меньше, чем скорость на низкой
орбите, разумеется, никак не оз-
начает, что вывести спутник на
высокую орбиту энергетически
легче, чем на низкую. Наоборот,
энергетические затраты выведе-
ния на высокую орбиту превышают энергетические затраты вы-
ведения на низкую орбиту. Дело здесь в потенциальной энергии
спутника, в разнице потерь при выведении этих спутников, в
частности, гравитационных потерь.
Определение. Первой космической скоростью называ-
ется круговая скорость на нулевой высоте относительно гра-
витирующего тела.
Понятие первой космической скорости связывается с грави-
тирующим телом (а не гравитирующим центром), и для полу-
чения величины 'первой космической скорости важен размер
тела. Чаще всего считают, что гравитирующее тело есть шар,
размер которого определяется радиусом. На рис. 2.10 R — ра-
диус гравитирующего тела, первая космическая скорость обоз-
начена Vi.
78
усом, равным большой полуоси
Рис. 2.10. Зависимость круговой
скорости от расстояния до грави-
тационного центра
Первая космическая скорость для Земли или просто первая
космическая скорость определяется так:
Vi=|/K=|/«|«l^ = 7,91 и/с.
Эта величина определяет минимальные энергетические за-
траты, потребные для выведения спутника Земли. Характери-
стическая скорость ракеты-носителя превышает Vi на величи-
ну потерь и может составлять при выведении на низкую ор-
биту 9,5 ... 10 км/с.
Приведем примеры значения первой космической скорости
других небесных тел.
Первые космические скорости Луны, Венеры и Марса со-
ответственно равны 1,68 км/с; 7,31 км/с; 3,60 км/с.
Параболическая скорость. Рассмотрим вопрос о том, како-
ва должна быть скорость КА, чтобы он двигался по параболи-
ческой орбите. Тип орбиты определяется знаком константы
энергии h. При h = 0 орбита параболическая. При этом вели-
чина скорости и длина радиуса-вектора на параболической ор-
бите связана соотношением V2—2ц/г=0. Таким образом, для
того чтобы КА двигался по параболической траектории отно-
сительно гравитирующего центра, достаточно, чтобы V=
= ]/r2pJ/r. Эта скорость называется параболической
= (2.53)
Итак, если КА имеет скорость, равную УПар, то независимо
от ее направления траектория КА будет параболической. Само
направление вектора скорости будет влиять на ориентацию
параболы, на ее размер (фокальный параметр).
Если скорость КА меньше параболической (такая скорость
называется эллиптической) , то траектория КА эллиптическая,
КА будет двигаться по замкнутой траектории и никогда не по-
кинет окрестность гравитирующего тела. Если скорость КА
больше параболической (такая скорость называется гипербо-
лической), то траектория КА будет гиперболической и он, как и
в случае параболической траектории, не сделав оборота вокруг
гравитационного центра, покинет окрестность гравитирующего
тела.
Параболическая скорость (2.53) очень простым соотноше-
нием связана с круговой (2.52) Vnap=VKpl/<2. Характер зависи-
мости параболической скорости от расстояния до гравитацион-
ного центра тот же, что и у круговой скорости.
Определение. Вторая космическая скорость 1/ц есть
параболическая скорость на нулевой высоте относительно гра-
витирующего тела.
79
Таким образом,
Уг1=У2^Я. (2.54)
Вторая космическая скорость характеризует минимальную
скорость, которую нужно сообщить КА для того, чтобы он,
стартуя с небесного тела, покинул его окрестность. Реальная
потребная энергетика для такого космического маневра отли-
чается от второй космической скорости на величину потерь
(гравитационных, аэродинамических и т. д.).
Вторая космическая скорость в 1/2 раз превышает первую
космическую. Приведем соответственно ее значения для Земли,
Луны, Венеры, Ма-рса: 11,19 км/с; 2,37 км/с; 10,31 км/с; 5,09
км/с соответственно
Введены понятия круговой и параболической скорости, пер-
вой и второй космических скоростей, которые являются важны-
ми понятиями для механики космического полета.
2.9. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ КА
ПО ОРБИТЕ
В предыдущих разделах при исследовании орбиты в
задаче двух тел независимым переменным считался полярный
угол радиуса-вектора КА и многие величины (радиус, скорость,
компоненты скорости) считались функциями этого угла (чаще
всего истинной аномалии), связь величин со временем пока не
была рассмотрена. Настоящий раздел и посвящен этому во-
просу.
Для решения вопроса о временном движении спутника по
орбите нужно получить зависимость характеристик движения
как функции времени. Наиболее естественно выглядит подход,
при котором со временем связывается истинная аномалия спут-
ника v. Это определяется тем, что ранее истинная аномалия
считалась независимой переменной и, в частности, уравнение
орбиты спутника записывалось как функция истинной анома-
лии. Итак, поставим задачу нахождения зависимости £ = f(v).
Получение этой зависимости связано с еще одним (послед-
ним) интегрированием уравнений задачи двух тел. Напомним,
что эти уравнения (2.7) представляют собой дифференциаль-
ную систему шестого порядка и пять независимых первых ин-
тегралов были нами получены ранее. Получение искомой зави-
симости легче всего связать с интегрированием полярной фор-
мы интеграла площадей (2.17):
г2 — = G. 2.55)
dt
Обратим внимание, что отличие (2.55) от (2.17) состоит
только в различных осях отсчета полярного угла радиуса-век-
80
тора спутника. В равенстве (2.17) отсчет ведется от произволь-
ного инерциального направления в плоскости траектории, этот
угол обозначался (3. В равенстве (2.55) отсчет ведется от век-
тора Лапласа % (от линии апсид)—это одно из возможных
инерциальных направлений в плоскости траектории.
Учитывая, что уравнение орбиты г(-и) (см. (2.34)) нами по-
лучено, в дифференциальном уравнении (2.55) легко разделить
переменные:
Напомним, р, е, о — постоянные, причем о= Урр.
Интегрируя левую и правую части (2.56) в соответствующих
пределах, можно получить
(2.57)
где — время прохождения перицентра орбиты (v= 0);
t, к — текущие значения времени и истинной аномалии.
Именно это соотношение и дает связь положения г» со вре-
менем t. Для его записи необходимо взять квадратуру в правой
части равенства (2.57). Затруднение при этом состоит в том,
что квадратура имеет разные формы записи в зависимости от
значения эксцентриситета. Случаи е<1, е=19 е>\ нужно рас-
сматривать отдельно. Подробно рассмотрим случаи эллиптиче-
ской орбиты, а для остальных случаев в основном ограничимся
лишь результатами.
Связь положения со временем для эллиптической
орбиты
Рассмотрим случай эллиптической орбиты спутника
(е<С1). При этом квадратура, входящая в (2.57), берется, но
получающееся выражение оказывается весьма громоздким.
Время t оказывается сложной по записи функцией истинной ано-
малии -и. Однако можно ввести другую угловую характеристику
положения спутника: вместо истинной аномалии -и рассмотреть
эксцентрическую аномалию Е (разумеется, однозначно связан-
ную с истинной Е(у>)) так, чтобы зависимость t\E) была до-
статочно простой. Пойдем по этому пути.
Уравнение орбиты спутника как функции экс-
центрической аномалии. Введем эксцентрическую ано-
малию (только для случая эллиптической орбиты) следующим
образом. Известна параметрическая форма записи эллипса:
Н' = a cos Е\
т]' = fesin £,
(2.58)
81
Рис. 2.11. Эллиптическая орбита в
прямоугольных координатах с нача-
лом в геометрическом центре эл-
липса
где a, b — большая и малая по-
луоси эллипса; Е— параметр
—rf— координа-
ты точек эллипса в прямо-
угольной системе с началом в
геометрическом центре эллип-
са О и осью Og', направленной
по большой полуоси (рис. 2.11).
В фокусе эллипса С распо-
ложен гравитационный центр.
Если рассмотреть произ-
вольное положение КА на рас-
сматриваемой эллиптической
орбите (точка А на рисунке),
то это положение может характеризоваться ранее рассматривае-
мыми полярными координатами г, и или прямоугольными декар-
товыми gz, rf, которые соответствуют некоторому значению экс-
центрической аномалии Е. Можно показать, что есть однознач-
ное соответствие между Е и v
‘б4 = ‘8т]'/т11- <2М>
В частности, зная эксцентриситет е, по v однозначно на-
ходим Е
£ = 2arctg[tg (2.60)
Причем однозначное соответствие можно с координатного
круга (—л^иСл, —л^Е<л) распространять и на многообо-
ротное движение спутника.
Для пояснения геометрического смысла эксцентрической
аномалии на рис. 2.11 проведено дополнительное построение.
Из точки А (текущее положение спутника) проведен перпенди-
куляр тп к большой полуоси эллипса. Построена полуокруж-
ность EGK радиусом, равным большой полуоси а с центром в
О. Точка пересечения перпендикуляра тп и полуокружности
(она обозначена В) соединена с точкой О. Можно показать,
что эксцентрическая аномалия есть угол ВОС\ Е= Z.BOC.
Ранее было найдено уравнение орбиты как функции истин-
ной аномалии и (2.34). Можно получить уравнение орбиты
спутника как функции эксцентрической аномалии [4]
г=. а(1—ecosE). (2.61
Оно имеет такую же силу, как и уравнение орбиты в виде
функции истинной аномалии (2.34).
Уравнение Кеплера. Уравнение Кеплера, которому
посвящен настоящий раздел, связывает эксцентрическую ано-
82
малию (характеристику положения спутника) со временем.
Для вывода этого уравнения получают дифференциальную за-
висимость Е и t и затем ее интегрируют [4, с. 108]:
Е—e sin E = n(t—tn), (2.62)
где п= ц/а3 — константа, называемая средним движением
спутника.
M = n(t—tn) называется средней аномалией спутника.
Уравнение Кеплера (2.62) дает возможность связать поло-
жение спутника на орбите со временем, прошедшим после про-
хождения спутником перицентра. При этом возможно два типа
задач. В первом типе задается некоторая точка орбиты (экс-
центрическая аномалия Е) и нужно найти время, когда спут-
ник попадает в эту точку. Во втором типе задач, напротив, за-
дается время, прошедшее после прохождения перицентра, и
требуется определить положение спутника. Оба типа задач
связаны с решением уравнения Кеплера, только в первом слу-
чае неизвестным является время /, во втором — эксцентриче-
ская аномалия Е. Решение первого типа задач проводится ана-
литически— уравнение Кеплера линейно по t и легко разре-
шается относительно t. Решение второго типа задач сводится к
решению трансцендентного уравнения.
Третий закон Кеплера. В рассматриваемом случае
эллиптической орбиты орбита КА замкнутая и КА (спутник)
многократно проходит один и тот же эллиптический путь. Вре-
мя между двумя последовательными прохождениями одной и
той же точки эллиптической орбиты называется периодом об-
ращения спутника и часто обозначается Т.
С помощью уравнения Кеплера легко можно найти период
обращения спутника как функцию большой полуоси его орби-
ты. Рассмотрим начальное положение спутника в перицентре
его орбиты. В этот момент эксцентрическая аномалия спутника
равна нулю (Е = 0). Через период (/—/Л = Т) спутник опять
придет в перицентр и его эксцентрическая аномалия будет рав-
на 2л. Из уравнения (2.62) следует
2л—esin 2л = пТ;
т = — = аз/2. (2.63)
Таким образом, период обращения спутника зависит от
большой полуоси его орбиты и гравитационного параметра за-
дачи двух тел. Если гравитационную константу задачи двух тел
можно рассматривать одной и той же для разных спутников
(это вполне можно делать при анализе орбит ИС одного грави-
тирующего тела, например Земли), то период оказывается
функцией только большой полуоси орбиты спутника. Чем боль-
83
ше большая полуось орбиты, тем больше период обращения.
Если рассмотреть орбиты двух спутников с большими полуося-
ми ах и а2, то, исходя из (2.63), можно утверждать, что перио-
ды обращения этих спутников Ti и Т2 находятся в соотноше-
нии
Tf/T2 = a3/a3. (2.64)
Равенство (2.64) является математической формулировкой
третьего закона Кеплера: квадраты периодов обращения спут-
ников относятся как кубы их больших полуосей.
Обратим внимание на то, что при формулировке этого за-
кона:
рассматривают спутники одного гравитирующего тела (на-
пример, два спутника Земли);
движение каждого спутника рассматривают в рамках огра-
ниченной задачи двух тел.
Третий закон Кеплера дает возможность получить периоды
обращения спутника по его большой полуоси, если известен пе-
риод одного спутника. Действительно, из (2.64) вытекает
Т^Т^/аУ72. (2.65)
Зная период обращения, например, кругового спутника ну-
левой высоты относительно гравитирующего тела, с которым
мы сталкиваемся при введении понятия первой космической
скорости ( Т2 = ^з/2 = 84,3 мин\ можно подсчитать перио-
\ V Из /
ды обращения спутников Земли по формуле
Т = 84,3 ( -— У/2 ,
\ 6371 /
где а — в километрах; Т — в минутах.
После получения соотношений для периода обращения спут-
ника легко указать физический смысл среднего движения п и
средней аномалии спутника М.
Физический смысл п — средняя угловая скорость движения
спутника. Действительно, период обращения спутника по орби-
те (Т) находится с помощью (2.63). За период радиус-вектор
спутника поворачивается на 2л радиана вокруг гравитацион-
ного центра. Поэтому средняя угловая скорость находится с
2л -и /~ и
помощью следующих равенств: -----= I/ _Е_ =
Т г а3
Физический смысл средней аномалии М — радиальная ме-
ра дуги, которую описал бы в промежутке времени [/я, /] во-
ображаемый спутник, двигающийся по круговой орбите с ра-
диусом, равным большой полуоси исследуемой орбиты.
Для контроля усвоения материала предложим читателю за-
дачу. В окрестности Земли находится некоторая небольшая
84
масса т(т<^М3). В какой-то момент времени она разорвалась
на две части так, что скорости каждой из частей относитель-
но невращающейся системы координат с началом в центре'
Земли оказались эллиптическими, равными по величине. На-
правление этих скоростей различно. Вопрос заключается в том,,
встретятся ли эти части (спутники) в своем движении вокруг
Земли. Предполагается, что орбиту каждого из спутников мож-
но рассматривать в рамках ограниченной задачи двух тел.
Решая эту задачу, можно нарисовать эллиптические орбиты
каждой из масс. Эти эллиптические орбиты имеют хотя бы од-
ну общую точку, совпадающую с начальной (в которой масса
разорвалась). Для того чтобы спутники через один оборот
встретились в этой точке, достаточно, чтобы их периоды совпа-
дали. Осталось доказать, что периоды спутников совпадают.
Для этого необходимо воспользоваться соотношениями (2.64) и.
(2.49). Последнее соотношение нужно для того, чтобы дока-
зать, что большие полуоси рассматриваемых спутников равны.
Связь положения со временем для гиперболической
орбиты
Полученное в предыдущем разделе уравнение Кеп-
лера справедливо только для случая эллиптической орбиты
спутника. Укажем итоговые соотношения для случая гипербо-
лической орбиты:
уравнение орбиты КА
r= |а| (echtf— 1); (2.66)
среднее движение
1-1 = (2.67)
уравнение Кеплера
— Н + eshH= |n| (/— tn). (2.68)
Величина большой полуоси и среднего движения стоят со зна-
ком модуля для того, чтобы подчеркнуть, что иногда эти значе-
ния считаются отрицательными и мнимыми. В соотношениях
(2.66) — (2.68) |а|, |п| —положительные действительные чис-
ла. Величина Н — аналог эксцентрической аномалии Е для
случая гиперболического движения.
Связь Н и истинной аномалии г описывается соотношением
и 1 / е + 1 ., Н
(2.69}'
85-
Связь положения со временем для параболической
орбиты
В случае параболической орбиты связь истинной
.аномалии со временем получается достаточно простой. Ника-
кой эксцентрической аномалии или ее аналога для параболиче-
ской орбиты не вводится. В соотношении (2.57) осуществляет-
ся подстановка е=1 и берется входящая в него квадратура.
Результат оказывается следующим:
/4Й-и=-И‘8т+т'Е’тУ (2-70’
Равенство (2.70) дает возможность получить время движе-
ния спутника по параболической орбите от перицентра орбиты
до произвольной точки, характеризуемой истинной аномалией
v. При решении второго типа задач (когда ищется положение)
равенство (2.70) следует рассматривать как алгебраическое
уравнение относительно tgu/2.
Перелет между произвольными точками орбиты
До сих пор, связывая время с положением КА на
орбите, мы опирались на характерную точку орбиты (пери-
центр) и отсчитывали время от момента прохождения пери-
центра. Для более общего случая, когда нужно измерить вре-
мя движения КА от одной произвольной точки орбиты до дру-
гой, поступают следующим образом.
Пусть t\ и t2 — два произвольных момента времени. Поло-
жения КА в эти моменты времени характеризуются истинными
аномалиями щ и v2. Для получения зависимости, связывающей
Л, ^2, щ, v2, дважды запишем уравнение Кеплера. Пусть для
определенности орбита эллиптическая, тогда
д(/х— tn) = Е± — esinff,
(^2 ^Jl) ^2 & Sin £2*
Вычитая эти равенства почленно, получим
п (/2—1±) = Е2— Е±—е (sin Е2—sin £х). (2.71)
Последнее равенство и связывает время движения между
двумя точками с расположением этих точек.
При нахождении связи времени с положением можно вос-
пользоваться разработанными вычислительными процедурами
современных ЭВМ. Внутри процедуры проводится диагностика
типа орбиты спутника. Использование такой процедуры не та-
ит в себе возможность аварийного останова или других вычис-
лительных неприятностей.
£6
Таким образом, в данном разделе проанализирована связь
положения КА со временем в задаче двух тел, для трех основ-
ных типов орбит КА исследована зависимость времени от ха-
рактеристики положения (эксцентрической аномалии, истинной
аномалии).
2.10. ЭЛЕМЕНТЫ ОРБИТЫ СПУТНИКА
Вернемся к рассмотрению пространственного движе-
ния спутника в задаче двух тел. Как было доказано выше,
траектория спутника относительно гравитационного центра
располагается в невращающейся плоскости, проходящей через
гравитирующий центр. Рассмотрим движение спутника в пря-
моугольной декартовой системе -координат с началом в гра-
витирующем центре. Чаще всего будем полагать, что эта сис-
тема координат планетоцентрическая экваториальная.
Плоскость орбиты спутника в общем случае пересекает
плоскость ху системы координат (возможен частный случай
совпадения этих плоскостей). Для определенности будем рас-
сматривать эллиптическую орбиту спутника. На рис. 2.12 пря-
мая пересечения отмеченных плоскостей обозначена DB. В од-
ной из точек этой прямой спутник пересекает плоскость ху и
меняет свои отрицательные координаты z (аппликаты) на по-
ложительные. Эта точка (на рис. 2.12 она обозначена В) назы-
вается восходящим узлом орбиты. Для случая эллиптической
орбиты обязательно есть и вторая точка, в которой спутник,
пересекая плоскость ху, переходит в область отрицательных
аппликат z. Эта точка называется нисходящим узлом орбиты
(на рис. 2.12 она обозначена D). Прямая DB, соединяющая уз-
лы орбиты, и есть прямая пересечения плоскости орбиты спут-
ника и плоскости ху системы координат. Разумеется, этой пря-
мой принадлежит и гравитационный центр (он принадлежит и
плоскости орбиты — находится в фокусе орбиты и экваториаль-
ной плоскости ху). Эту прямую
под линией узлов понимают
ось, направленную из нисходя-
щего узла орбиты в восходя-
щий (из гравитационного цен-
тра в восходящий узел).
Положение линии узлов ха-
рактеризуется углом между
осью х и линией узлов. Этот
угол обозначается Q (на рис.
2.12 угол хСВ) и называется
долготой восходящего узла.
Долготу восходящего узла ча-
называют линией узлов. Часто
Рис. 2.12. Элементы орбиты спут-
ника
87'
ще всего отсчитывают в диапазоне 0^Q<360°. Впрочем, это
не мешает использовать отрицательную долготу восходящего уз-
ла, например —30°. При этом совершенно ясно, что восходящий
узел орбиты находится в четвертой координатной четверти пло-
скости ху, и это значение эквивалентно значению 330°.
Для фиксации любой плоскости, проходящей через начало
координат (и плоскости орбиты спутника), нужно два парамет-
ра. Одним из таких параметров может быть введенная долгота
восходящего узла. Она фиксирует линию узлов орбиты. Второй
параметр должен зафиксировать угловое положение плоскости
орбиты относительно линии узлов. Таким параметром чаще все-
го принимают наклонение орбиты. Этот угол характеризует на-
клон плоскости орбиты КА к плоскости ху системы координат.
Строго наклонение орбиты вводится следующим образом. Стро-
ится внешняя нормаль к плоскости орбиты. Ее начало берут
в гравитационном центре и направляют перпендикулярно плос-
кости орбиты спутника в ту сторону, с которой движение спут-
ника видно против часовой стрелки (именно поэтому она на-
зывается внешней). Внешней нормалью к плоскости можно счи-
тать вектор площадей or. С конца вектора or={rXV] видно, что
спутник вращается против часовой стрелки. Угол между осью
z и внешней нормалью к плоскости орбиты называется накло-
нением орбиты спутника. На рис. 2.12 этот угол равен zCo. На-
клонение обозначается I.
Наклонение орбиты как угол между двумя осями изменяет-
ся от 0 до 180°. Оно не может быть больше 180°. Легко убе-
диться, что наклонение i равно углу между плоскостью ху и
плоскостью орбиты спутника. Разберемся в этом на примерах.
Рассмотрим случай, когда наклонение орбиты равно нулю: i=
= 0. Это значит, что орбита спутника принадлежит плоскости
ху и сам спутник движется в этой плоскости так, что со сторо-
ны оси Cz радиус-вектор спутника вращается против часовой
стрелки. Орбита такого спутника называется экваториальной.
Пусть наклонение орбиты i = 90°. Это означает, что вектор
о перпендикулярен оси Cz (т. е. принадлежит плоскости ху).
При этом плоскость орбиты спутника перпендикулярна плоско-
сти ху. Такая орбита называется полярной. Двигаясь по та-
кой орбите, спутник на каждом витке оказывается над полю-
сами.
Рассмотрим еще один частный случай. Пусть наклонение
орбиты— 180°. Орбита такого спутника принадлежит плоскости
ху, но внешняя нормаль к такой орбите противоположна на-
правлению оси Cz. Орбита такого спутника называется обрат-
ной экваториальной. Направление его вращения в плоскости ху
обратное: со стороны оси z вращение радиуса-вектора спутника
происходит по часовой стрелке (с востока на запад).
• 88
Можно утверждать, что два параметра й и i определяют
положение плоскости орбиты в пространстве. Отметим, что ес-
ли 1 = 0 или /--=180°, то теряется понятие линии узлов, теряет
смысл и долгота восходящего узла, но в этом случае положе-
ние плоскости орбиты полностью определено одним значе-
нием L
Отметим, что хотя пояснения при введении й и i проводи-
лись для случая эллиптической орбиты спутника, принципиаль-
но ничего не меняется и для случая параболической и гипербо-
лической орбит КА. Отличие состоит в том, что орбита может
пересекать плоскость ху только в одной точке. Например, мо-
жет существовать только нисходящий узел орбиты. В этом слу-
чае понятие линии узлов не теряется, считается, что восходя-
щий узел находится в бесконечности оси: нисходящий узел —
гравитационный центр.
Итак, положение плоскости орбиты определяется двумя па-
раметрами й и I. Форму и размер орбиты определяют, напри-
мер, фокальным параметром р и эксцентриситетом е. Остается
зафиксировать положение орбиты в плоскости, определяемой с
помощью параметров й и i. Положение орбиты в ее плоскости
чаще всего фиксируется с помощью понятия аргумента пери-
центра. Аргументом перицентра называется угол со между ли-
нией узлов (на рис. 2.12 ось СВ) и линией апсид (Сл). Аргу-
мент перицентра характеризует положение перицентра орбиты
КА относительно линии узлов. Аргумент перицентра обычно
измеряется в диапазоне [0, 360°].
Пять параметров р, е, й, /, со полностью определяют орбиту
спутника. Первые два параметра определяют форму и размер,
й и i— положение плоскости орбиты, со — положение орбиты
в ее плоскости. Для временной увязки движения спутника по
орбите нужно рассмотреть еще один параметр. Чаще всего та-
ким параметром считают уже введенное ранее время прохож-
дения спутником перицентра орбиты tn. Таким образом, для
полного определения орбиты спутника и его движения по ней
достаточно задать 6 параметров: р, е, й, i, со, tn. Это число
равно порядку системы дифференциальных уравнений, описы-
вающих относительное движение в задаче двух тел. Эти пара-
метры можно рассматривать как постоянные интегрирования
задачи. Перечисленные шесть параметров — не единственный
набор параметров, полностью определяющий орбиту. Так, вмес-
то р и е можно использовать параметры a, b, с, гп, га и т. д.
Вместо параметров й и i — отношение компонентов вектора
площадей о=-'[сгх, оу, оД. Например, если oz^0, то два числа
определяют положение плоскости орбиты спутника в
пространстве, при этом уравнение этой плоскости имеет вид:
x+-^ly +z = 0.
Oz oz f
8&
Любой набор шести параметров, полностью характеризую-
щий орбиту спутника в задаче двух тел и движение спутника
по орбите, называется элементами орбиты спутника. Введенные
нами элементы орбиты спутника р, е, Q, Z, со, пожалуй, са-
мые распространенные. Исключение чаще всего делается для
элемента, определяющего размер орбиты: вместо фокального
параметра р может использоваться большая полуось а.
Определение элементов орбиты КА по его положению
и скорости в один момент времени
Пусть в некоторый момент времени t\ известно поло-
жение rj и скорость Vi спутника. Этот момент может быть на-
чальным (после выведения спутника ракетой-носителем на ор-
биту) или произвольным.
Число скалярных начальных условий (хь у\, Zi), (Vix, Viy,
Viz) равно шести, что совпадает с порядком системы дифферен-
циальных уравнений относительного движения в задаче двух
тел. Задача двух тел, в рамках которой рассматривается дви-
жение спутника, при фиксированных начальных условиях име-
ет единственное решение. Это решение и описывает орбиту
спутника. У орбиты есть однозначные элементы, которые мож-
но определить по этим начальным условиям.
Дано: ц, Г1, Vi, ti.
Требуется определить: р, е, Q, f, со, tn.
Рассмотрим возможную последовательность операций:
1. Определяем вектор площадей
а = [Г1 х VJ
и единичный вектор внешней нормали
а° = —-—= Г о0, а0, о°1.
| —I L х> yf гГ
|а I
2. Так как проекции орта внешней нормали о0 через долго-
ту восходящего узла и наклонение орбиты выражаются в виде
(см. рис. 2.12)
о0 = [sin Qsirn, —cos Q sin г, cos г], (2.72)
то, учитывая найденный а0 в п. 1, получим: sin Q sin t=o°x;
—cos Q sin i = a%; cos i = o°z.
Последние равенства дают возможность определить Q и I:
i = arccos о0 = arccos -*1 2 ; (2.73)
2 |[Г1ХИ1]|
90
.0
arccos (---— , если cf° 0;
_ \ sin i /
Q = ( - a° \
2л — arccos I---— , если o° < 0.
\ sin i /
3. Определяем фокальный параметр орбиты
Р= |о|2/Н-
4. Определяем эксцентриситет орбиты
(2.74)
(2.75)
(2.76)
5. Определяем истинную аномалию ui КА в заданный мо-
мент ti.
Из уравнения орбиты, записанного для заданного момен-
та t\,
1 е cos uj
определяем
cosvissf-^- — 1^ —. (2.77)
\ Л / е
Чтобы из последнего соотношения однозначно определить щ,
можно определить знак радиальной скорости Vr в заданной
точке траектории. Если радиальная скорость положительная,
‘то КА находится на восходящей ветви траектории и Di принад-
лежит промежутку (0... 180°). Если радиальная скорость отри-
цательная, то КА находится на нисходящей ветви траектории и
ui принадлежит промежутку (180 ... 360°).
Определить знак радиальной скорости можно по знаку
скалярного произведения (л, Pi). Если (л, Vi)>0, то угол
между векторами л и 71 меньше 90° и, значит, 7г>0.
Если (л, Pi) <0, то 7г>0.
Имея это в виду, решение уравнения (2.77) относительно
Di можно записать в виде
^i =
arccos Г ( —---1 —1, если (л, 7J 0;
L \ Л / е J
—arccos Ц—----1^—J, если (г1»
(2.78)
6. Определяем аргумент широты орбиты спутника и\ для
заданного момента t\. Напомним, что под аргументом широты
понимается угол между линией узлов и текущим радиусом-век-
тором КА. На рис. 2.12 аргумент широты — угол ВСА,
91
Напишем единичный орт линии узлов: 0='[cosQ, sin Q, 0].
Единичный вектор, направленный по п, есть п/п. Скаляр-
ное произведение единичных векторов равно косинусу угла
между векторами. Отсюда
cosr/^^p, = (x1cosQ 4-(/х sin Q)-у-. (2.79)
Для однозначного нахождения щ нужна информация о зна-
ке sin и\. Для получения такой информации можно рассмотреть
векторное произведение тех же единичных векторов р и п/п. В
.результате математических преобразований получим
arccos ( — cos Q + — sin Q ), если sqn ( — sin Q ) =
\ ri J \ ri /
U1 = = sqn (У1 viz-21 Vly); (2.80)
— arccos ( — cos Q + — sin Q ), если sqn ( — sin Q | =
\ 4 ''i / \ ''i /
= — sqn^l^ — ггУ1у).
7. Определяем аргумент перицентра
со = иг—(2.81)
Эта простая геометрическая связь следует из определения •
.фигурирующих в ней углов (см. рис. 2.12).
8. Определяем эксцентрическую аномалию заданного поло-
жения.
Эксцентрическая аномалия орбиты спутника для момента
-Л равна
E1 = 2arCtg[/4H|tgA].
С помощью уравнения Кеплера определяем момент прохож-
дения перицентра
"]/" (1_е2)з е sin Ех).
Последние два соотношения записаны для эллиптической ор-
биты. Аналогично эти соотношения можно записать для гипер-
болической орбиты. Для параболической вместо них можно
использовать равенство, вытекающее из (2.70)
Таким образом, найдены все шесть элементов орбиты по ус-
ловиям движения в одной точке орбиты (по начальным усло-
виям движения).
32
Прогнозирование положения спутника в задаче двух
тел
Рассмотрим задачу определения положения спутника
в любой заданный момент времени если известны элементы
орбиты. Если заданы элементы орбиты спутника (все шесть),
то движение спутника в рамках задачи двух тел полностью оп-
ределено и поставленная задача об определении положения
спутника в любой момент времени однозначно решается. Ко-
ротко сформулируем задачу.
Дано: ц, р, е, Q, г, со,
Найти: r(Zi).
Для решения такой задачи, кроме прямоугольной декарто-
вой системы координат Cxyz, которая чаще всего предполага-
ется экваториальной, рассмотрим перицентральную систему ко-
ординат Cgr]g. Ее начало пусть совпадает с гравитационным
центром. Ось Ct> перпендикулярна плоскости орбиты и направ-
лена в сторону, с которой вращение радиуса-вектора спутника
видно проходящим против часовой стрелки (по внешней нор-
мали к плоскости орбиты). Ось Cg направлена в перицентр ор-
биты спутника. Ось Ст] дополняет систему Cgr]g до правой.
Рис. 2.13 иллюстрирует взаимное положение рассматриваемых
систем координат. Это положение фиксировано с помощью
трех углов Q, i, со.
Для нахождения положения спутника в экваториальной сис-
теме координат можно поступить следующим образом: найти
координаты спутника в перицентральной системе; пересчитать
эти координаты в экваториальную систему.
1. Нахождение перицентральных координат
спутника. Обратимся к рис. 2.14. На нем нарисована плос-
кость орбиты спутника, перицентральные оси Cg и СТ]. Теку-
щее положение спутника в момент h отмечено радиусом-векто-
Рис. 2.13. Связь экваториальной и пе-
рицентральной систем координат
Рис. 2.14. Перицентральные коорди-
наты КА
93
ром СА = г. Параметрическое уравнение эллиптической орби-
ты в этой системе координат может быть записано с учетом
равенств (2.58) и использованием того, что система координат
Cgr] смещена относительно геометрического центра эллипса на
фокальное расстояние с = ае в виде
£ = acosE—ae = a(cosE—е);
т] = b sin Е\
£ = 0.
(2.82)
Значение эксцентрической аномалии в заданный момент
времени следует найти с помощью уравнения Кеплера
5,-esinE^ (2.83)
Таким образом, нахождение перицентральных координат g,
ц, g сводится к решению трансцендентного уравнения Кеплера
(2.83) относительно Е\ и подстановке найденного Е\ в равенст-
ва (2.82).
2. Нахождение экваториальных координат
спутника. Обратим внимание на то, что переход от эквато-
риальной системы координат к перицентральной аналогичен пе-
реходу от экваториальной системы к орбитальной, описанному
в разд. 1.2. Орбитальная система фиксировалась относительно
экваториальной углами £2 + 270° ((поворот вокруг оси Cz), i+
+ 180° (поворот вокруг оси Су'У 360°—и (поворот вокруг оси
Cz"). Перицентральная система фиксируется относительно эк-
ваториальной углами £2, i, со. Переход от геоцентрической не-
вращающейся системы к перицентральной осуществляется по-
воротами: на угол £2 вокруг оси Cz, на угол i вокруг оси Сх\
на угол со ©округ оси Cz" (рис. 2.14). Описав повороты так, как
это проводилось в разд. 1.2, перемножив матрицы этих поворо-
тов, получим матрицу перехода от геоцентрической системы ко-
ординат к перицентральной. Тогда получение координат КА в
экваториальной системе сводится к следующей операции:
(х\
У =в п >
\z ) Ч /
(2.84)
где
cos £2 cos со —
I —sin £2 sin со cos i
В = I sin £2 cos co +
I + cos £2 sin co cos i
x sin i sin co
— cos £2 sin co —
— sin £2 Cosco cos i
— sin £2 sin co +
+ cos £2 cos co cos i
sin i cos co
sin £2 sin i
— cos £2 sin i
cos i
94
Таким образом, задача прогнозирования движения спутни-
ка в рамках задачи двух тел сводится к решению уравнения
Кеплера (2.83), вычислению g, т], £ по (2.82) и проведению
матричной операции (2.84).
В данном разделе были введены элементы орбиты спутника,
показано, как эти элементы находятся по условиям движения
в какой-либо (например, начальной) точке орбиты. Рассмотре-
на задача определения положения спутника в произвольный
момент времени, если известны элементы его орбиты.
В настоящей главе достаточно подробно проанализировано
движение КА относительно гравитирующего тела в рамках за-
дачи двух тел. Полученные решения будут использованы при
исследовании траекторий КА различных классов. Это прежде
всего траектории ИСЗ и других небесных тел, которые в пер-
вом приближении можно рассматривать в рамках задачи двух
тел. Это и участки траектории межпланетных КА, и участки
траекторий КА, маневрирующих в окрестности планет и т. д.
Таким образом, материал настоящей главы является основой
исследования траектории многих классов КА, рассматриваемых
далее.
ГЛАВА 3. ДВИЖЕНИЕ ИСКУССТВЕННЫХ
СПУТНИКОВ ЗЕМЛИ
Искусственным спутником Земли (ИСЗ) называется КА,
выведенный на орбиту вокруг Земли для решения научных и
прикладных задач.
В рамках задачи двух тел можно в ряде случаев достаточно
точно исследовать движение ИСЗ относительно Земли. Но, бе-
зусловно, полученная при этом траектория (орбита) должна
рассматриваться как некоторое приближение реальной траек-
тории спутника.
При исследовании траектории спутника нужно учитывать
большое число возмущающих факторов. К этим возмущающим
факторам (возмущающим силам) следует отнести:
гравитационные силы, связанные с «неправильностью» фигу-
ры Земли (нецентральность гравитационного поля Земли);
аэродинамические силы, которые могут быть весьма сущест-
венны, если исследуется движение низких спутников Земли;
силы тяготения Луны, Солнца и других небесных тел.
Кроме перечисленных факторов, которые чаще всего счита-
ются основными возмущениями, в некоторых случаях приходит-
ся учитывать и силы более сложной структуры: электромагнит-
ные, реактивные, связанные с сублимацией материала, силу
светового давления и т. д.
Движение КА с учетом перечисленных возмущающих фак-
торов будем называть возмущенным. В этом смысле движение
в задаче двух тел назовем невозмущенным.
3.1. ВОЗМУЩАЮЩИЕ УСКОРЕНИЯ ПРИ АНАЛИЗЕ
ДВИЖЕНИЯ СПУТНИКА
Для описания движения в задаче двух тел использо-
валась дифференциальная система шестого порядка (2.7). Гра-
витационное ускорение, входящее в правую часть (2.7), будем
называть основным ускорением при исследовании возмущенно-
го движения КА и обозначим а=------— г. Таким образом, не-
г3
возмущенное движение описывается системой:
d2r!dt2 = a. (3.1)
96
В возмущенном движении учитываются эффекты от возму-
щающих факторов. Если обозначить Ф вектор суммарного
возмущающего ускорения, то дифференциальная система, опи-
сывающая возмущенное движение, примет вид
d27/dt2 = a+& (3.2)
В настоящей главе исследуются такие траектории КА, на
которых возмущающее ускорение существенно меньше основ-
ного: | Ф | «С | а |. При этом решение задачи двух тел (невозму-
щенное движение) действительно может являться первым при-
ближением возмущенного движения.
Для создания полной модели возмущенного движения не-
обходимо обратиться к описанию возмущающих ускорений*
входящих в Ф.
Нецентральность гравитационного поля Земли
Если во всех точках шара, равноудаленных от его
центра, плотность равна, то говорят, что шар имеет сфериче-
ское распределение плотности. Если бы Земля была шаром со
сферическим распределением плотности, то можно было бы по-
казать, что гравитационная сила такой Земли была бы равна
ньютоновской гравитационной силе точечной массы, равной
массе Земли, помещенной в ее центр, т. е., если бы Земля была
такой «правильной», то гравитационная сила, действующая на
спутник, была бы та же, что и в задаче двух тел. Реальная
Земля существенно сложнее. Прежде всего на гравитационное
ускорение влияет полюсное сжатие Земли. С определенной
степенью точности можно считать, что сечение Земли плос-
костью, проходящей через ее ось, имеет форму эллипса с боль-
шой полуосью, равной экваториальному радиусу /?3.э=
= 6378,245 км, и малой полуосью, равной полярному радиусу
Яз.п = 6356,863 км. Коэффициент сжатия Земли подсчитывается
так:
а=3-э~*3-"- ~ = 0,0033523.
/?а9 298,3
Для того чтобы найти гравитационный потенциал произ-
вольного тела, необходимо каждую элементарную массу тела
рассматривать как притягивающую материальную точку и сум-
мировать (проинтегрировать) элементарные ньютоновские по-
тенциалы материальных точек тела по всему его объему. Обыч-
но такой интеграл вычисляют, раскладывая подынтегральную*
Функцию в ряд по сферическим функциям [4]. Для модели
4—8 97
Земли как сжатого сфероида получают следующее приближен-
ное равенство:
и = -^-----^6(3sin2<p-l), (3.3)
Г оГ
где ц3 — гравитационный параметр Земли; г — расстояние от
центра Земли до точки, потенциал в которой рассматривается;
<р — широта точки;
/ со2 R х
б = 7?2 8-----~ 1 ,6242.10-3 /?2 = 66,07 • 103 км2;
33 \ 2£э / 3-э
£э— ускорение свободного падения на экваторе; со3 — угловая
скорость собственного вращения Земли.
В литературе [4] встречается и эквивалентное (3.3) выра-
жение для потенциала Земли в виде
U = -7" [1 + А (ФУ (3sin* Ф-1)],
где /2 = —1098,08-10-6.
Первое слагаемое справа в равенстве (3.3) есть ньютонов-
ский потенциал. Второе слагаемое учитывает сжатие Земли по
полюсам.
Многочисленные исследования показали, что в громадном
большинстве задач проектирования орбит ИСЗ оказывается
достаточным рассматривать гравитационный потенциал Земли
в виде (3.3). Такой потенциал часто называют нормальным. С
другой стороны, понятно, что задача точного прогнозирования
траектории спутника на длительный интервал времени требу-
ет более сложных моделей земного потенциала, учитывающего
аномалии. Существуют и оценки вклада возмущения каждой
гармоники в общее возмущение [43; 57; 9]. По результатам
этих исследований можно сделать вывод о том, что учет гар-
моник, не входящих в нормальный потенциал, очень слабо (на
проценты) изменяет характер возмущения орбиты ИСЗ, а ос-
новное возмущение орбиты связано со сжатием Земли. Имея
это в виду, рассмотрим возмущения, обусловленные сжатием
Земли.
В гл. 1 был приведен (1.22) общий вид используемого в
настоящее время потенциала гравитационного поля Земли, со-
держащий большое число членов разложения, называемых зо-
/ 7? \«
нальными jn I _А? 1 рп (sin ф) (п = 3, 4...), тессеральными —
(о \
j (sin <р) (Лпй cos k X + Bnk sin kh)
(k= I,-, n; n = 2,...).
98
Для того чтобы получить проекцию гравитационного ускоре-
ния на какое-либо направление, достаточно найти производную
потенциала по этому направлению. Так, проекцию гравитацион-
ного ускорения для Земли как сжатого сфероида на радиаль-
ное направление с учетом (3.3) можно записать как
gr = (3 Sin2 ф- 1). (3.4)
д г г2 г4
Первое слагаемое в правой части последнего равенства
представляет собой проекцию гравитационного ускорения в за-
даче двух тел (аг). Второе слагаемое в той же правой части
есть проекции возмущающего ускорения (Фг).
Для получения меридиональной (Проекции гравитационного
ускорения gm (рис. 3.1) найдем предел отношения приращения
потенциала к приращению широты:
gm = lim =-----Li_fiSin2<p. (3.5)
Д ф—>0 Г Дф Г О ф г4
Знак «минус» (6>0) свидетельствует о том, что меридио-
нальное гравитационное ускорение направлено в сторону
уменьшения широты, т. е. к экватору (на рис. 3.1 нанесено поло-
жительное направление меридионального ускорения).
Для получения третьей проекции гравитационного ускорения
(широтного gh см. рис. 3.1) нужно было бы исследовать прира-
щение потенциала, получающегося из-за приращения долготы
при фиксированных г и ф. Так как долгота X не входит в вы-
Рис. 3.1. Компоненты гравитационного ускорения
4*
99
ражение потенциала сжатого сфероида, то широтная составля-
ющая гравитационного ускорения равна нулю.
Таким образом, нами найдены проекции гравитационного
ускорения от Земли как сжатого сфероида на три взаимно
перпендикулярных направления (радиальное, меридиональное
и широтное). Если нужно получить проекции этого ускорения
на другие направления, то можно воспользоваться определени-
ем потенциальной функции (т. е. находить ее производную по
направлению) или же проецировать уже найденные проекции.
В заключение приведем выражение для возмущающего ус-
корения от нецентральности гравитационного поля Земли как
сжатого сфероида
ф7. = (3 sin2 ср— 1);
Фт=—^sin2<p; (3.6)
Фх = 0.
Аэродинамические воздействия на ИСЗ
Строение земной атмосферы таково, что плотность
среды р, в которой движется спутник, мала. При этом сами
аэродинамические силы по отношению к гравитационным так-
же малы и их можно отнести к категории возмущающих.
Пусть вектор аэродинамической силы, действующей на спут-
ник, в проекциях на оси скоростной системы координат запи-
сывается в виде ^А=|[^а, Уа, Za], где Ха~ сила лобового со-
противления спутника, направленная против скорости КА отно-
сительно среды, в которой он движется, Ya и Za — подъемная и
^боковая составляющие аэродинамической силы. Последние две
компоненты аэродинамической силы очень редко учитываются
при анализе поступательного движения спутника (при анализе
движения его центра масс). Основным возмущающим аэроди-
намическим фактором считается сила лобового сопротивления.
Ее вектор направлен против вектора скорости спутника и ве-
личина аэродинамического ускорения может быть вычислена
как
= CXaqFM
а т > ’ 4 7
р V2
где сХа— коэффициент лобового сопротивления; ^ = —-------
скоростной напор; — характерная площадь спутника (на-
пример, площадь его миделевого сечения); т — масса спут-
ника.
100
Для того чтобы оценить величину возмущающего аэродина-
мического ускорения, как следует из (3.7), нужно задаться
определенными аэродинамическими характеристиками спутни-
ка (его формой, размером и связанным с ними сХд), нужно за-
даться определенной массовой характеристикой аппарата (такой
характеристикой может быть нагрузка на мидель или отноше-
ние пг1Рм, входящее в (3.7)). Если взять некоторые средние
значения перечисленных величин для некоторого «типичного»
спутника, то для оценки Фа достаточно будет получить инфор-
мацию о плотности среды р и о скорости спутника V. Для оцен-
ки возможного значения (порядка) аэродинамического возму-
щающего ускорения можно считать, что плотность среды явля-
ется функцией только высоты полета спутника (стандартная
атмосфера в ее статическом варианте [22]). Для оценки скоро-
сти спутника можно обратиться к круговым орбитам и считать,
что скорость спутника равна местной круговой, которая опре-
деляется высотой полета спутника над Землей или, точнее, уда-
лением спутника от центра Земли.
При таких допущениях возмущающее аэродинамическое ус-
корение Фа становится функцией только высоты орбиты h спут-
ника над поверхностью Земли и их оценки могут быть представ-
лены в следующем виде:
А, км....................... 100 200 400 800
Фа, см/с2 .................. 30 2,2-10-2 3,1 -10“4 2,6-10-8
Анализ приведенных данных позволяет сделать следующие
выводы. На низких высотах ~ 100 км возмущающее аэродина-
мическое ускорение столь значительно, что спутник на них не
сможет существовать — не сможет сделать и одного витка вок-
руг Земли.
С подъемом на высоту аэродинамическое ускорение быстро
убывает: с увеличением высоты в 2 раза с 200 до 400 км возму-
щающее ускорение убывает на два порядка. На высоте 800 км
и выше возмущающее аэродинамическое ускорение очень мало,
поэтому при проектировании орбит спутников, учитывая точ-
ность проектных расчетов, им можно пренебрегать.
Итак, выражение для вектора возмущающего аэродинамиче-
ского ускорения имеет вид:
Ф-------СМГм. уо (3.8)
d т 4 7
где V0 — единичный вектор скорости спутника.
Для нахождения (проекций вектора Фа нужно знать проек-
ции вектора скорости спутника в соответствующих осях.
101
Возмущающее воздействие на ИСЗ со стороны Луны
и Солнца
Рассмотрим возможный подход к анализу гравита-
ционного возмущения Луны, Солнца или любого другого не-
бесного тела. На рис. 3.2 точка
Рис. 3.2. Движение КА в гравитаци-
онном поле двух тел
С центр Земли, масса которой
для общности обозначена Ми
В точке В расположена другая
гравитирующая масса (Лу-
на, Солнце и т. д.) ТИ2. В
окрестности Земли в точке
А расположен КА (спутник),
его масса — т. Заранее пред-
полагаем, что m<^Mi и т<^
<^М2. О соотношении масс
Mi и М2 никаких предположе-
ний не делаем.
Гравитационную силу Г2, действующую на спутник со сто-
роны массы М2, можно определить по закону всемирного тя-
готения
f т -
— I —~
г2
(3.9)
где г2 — радиус-вектор спутника относительно массы М2 (ВА);
F2 — реальная сила, с которой М2 притягивает спутник.
Неправильно получать выражение для ускорения, возму-
щающего движение спутника относительно Земли, из (3.9) в
виде
ф= (3.10)
/п Г2
Поясним сказанное. Для анализа движения спутника в
инерциальном пространстве 0иХиУи2и (см. рис. 3.2) совер-
шенно справедливо анализировать ускорение (3.10) совместно
с ускорением от притяжения спутника Землей, т. е.
Р __ Ml ~ f М2 -
6#2 Г? 1 Г32 2’
(З.П)
где p — радиус-вектор спутника в инерциальной системе ко-
ординат; ri — радиус-вектор спутника относительно Mi (можно
было для этого радиуса оставить обозначение г).
Мы же рассматриваем движение спутника относительно
Земли (тела Mi) и уравнение для анализа такого движения
представляем в виде
= 7 + Ф
d/2 ' г3 1
102
f Ml -
Г1 основное ускорение в задаче двух тел (Земля —
спутник). В уравнении (3.2) это ускорение обозначено а; Ф —
возмущающее ускорение, которое появляется из-за существо-
вания возмущающего гравитирующего тела М2. Оно не может
определяться выражением (3.10), так как гравитирующее тело
притягивает не только спутник (массу т), но и тело массой
Mi. Поэтому в выражении возмущающего ускорения от массы
М2 при анализе движения спутника относительно Mi безуслов-
но должна учитываться сила .притяжения массой М2 массы Mi.
Ограниченная задача трех тел
Рассматриваемая в настоящем разделе задача о
движении малой (негравитирующей) массы т в системе двух
гравитирующих масс Mi и М2 называется ограниченной зада-
чей трех тел. Результаты анализа этой задачи понадобятся
при рассмотрении межпланетных перелетов, поэтому остано-
вимся на ней достаточно подробно.
Описание движения массы т относительно гравитирующей
массы Mi сводится к составлению дифференциальных уравне-
ний относительно радиуса-вектора CA = fi. Из рис. 3.2 следует
П= Р —Рр (3.12)
где р = ОиД; pi = O„C — радиус-вектор центра масс гравити-
рующего тела Mi в инерциальной системе координат 0иХиУи2и.
Дифференцируя дважды левую и правую части равенства
(3.12), получим
d2rl = d2 р _ d2 ft (з 13ч
dt2 dt2 dt2 ' v ’
Выражение ускорения спутника в инерциальном простран-
стве d2p!dt2 описывается (3.11). Ускорение гравитирующей
массы Mi в этом же пространстве получим из уравнения, опи-
сывающего движение массы Mi в инерциальном пространстве:
м = f М2М1 - (3. U)
1 d/2 1 г32 12’ 1 >
где ri2 — радиус-вектор, характеризующий положение тела М2
относительно М\, на рис. 3.2 он равен СВ.
Используя (3.13), (3.14) и (3.11), получим
Ш Г1 г2 г12
103
Последнее уравнение и описывает движение спутника от-
носительно гравитирующей массы Afi в ограниченной задаче
трех тел.
Первое слагаемое в правой части (3.15) — ускорение спут-
ника в задаче двух тел (Afi, m). Это ускорение при анализе
возмущенного движения спутника нами называлось основным
и обозначалось а. В дальнейшем иногда будет уместным за-
писать а в виде а,\. Индекс 1 подчеркивает, что это основное
ускорение в задаче двух тел ЛЛ — т, а не тел М2— т (задача
двух тел ТИ2— т тоже может рассматриваться).
Два последних слагаемых справа в (3.15) определяют воз-
мущающее ускорение Ф1 в задаче двух тел ЛЬ— т. Это воз-
мущающее ускорение можно рассматривать как разность двух
ускорений
— с19 (3.16)
где Ьг = —f —- г2— ускорение, которое имеет спутник в ограни-
г2
ченной задаче двух тел М2— т (ускорение от притяжения
массой М2 спутника в предположении отсутствия массы ЛЛ);
__ £ -^2
ci — l — ri2—ускорение, которое имеет масса М{ в ОГраНИЧеН-
^З
ной задаче двух тел Af2—ЛЬ, если массу ЛЛ считать неграви-
тирующей.
Таким образом, возмущающее ускорение, действующее на
спутник, двигающийся в окрестности Земли, от Луны, Солнца
или любого другого небесного тела равно разности влияний на
спутник и Землю со стороны возмущающего тела. С учетом
сделанных обозначений уравнение, описывающее движение
спутника относительно тела Afi в ограниченной задаче трех
тел, имеет вид
^1=^+0,. (3.17)
Возмущающее ускорение, действующее на ИСЗ
от Луны
Воспользуемся выведенным выражением возмущаю-
щего ускорения в ограниченной задаче трех тел для оценки
возмущающего ускорения, действующего на ИСЗ со стороны
Луны. На рис. 3.3 представлена траектория ИСЗ А1А2А3А4А$
и Луна, расположенная в точке В. Рассмотрен частный слу-
чай, когда Луна находится в плоскости орбиты спутника (при
таком положении Луны возмущающие ускорения достигают
104
Рис. 3.3. Возмущающее ускорение от Луны
максимальных значений). Дополнительно предположим, что
орбита спутника с точностью до -возмущений круговая. Оце-
ним возмущающее ускорение Луны в нескольких точках орби-
ты спутника. Начнем с точки Ai (см. рис. 3.3). Векторы b и с,
входящие в выражение возмущающего ускорения, коллинеар-
ны и направлены по прямой CAi в сторону В. Величина возму-
щающего ускорения при этом будет равна
где гл — расстояние Земля — Луна (среднее расстояние Зем-
ля— Луна 384,4-103 км); гисз —радиус орбиты спутника;
/Л4л = Цл = 4890 км3/с2 — гравитационный параметр Луны.
Некоторые числовые оценки величины возмущающего лун-
ного ускорения для точки Л1 представлены в следующем виде:
Радиус орбиты ИСЗ, км . . 6600 7000 8000 100 000
ФА1, см/с2 ........... 1,17-10-4 1,24-10—4 1,42-10-4 2,75-10"3
Из приведенных данных видно, что величина возмущающе-
го ускорения от Луны для низких спутников мала (она суще-
ственно меньше ускорения от нецентральности гравитационно-
го поля Земли и аэродинамического ускорения). На больших
высотах значения ускорения становятся значительными.
Для того чтобы получить возмущающее ускорение во всех
остальных точках орбиты спутника, нужно провести вычисле-
ния векторов
Ф = b—с.
Вектор с является вектором, не зависящим от точки, в ко-
торой находится спутник. Вектор b зависит от положения спут-
105
Рис. 3.4. Возмущающее ускорение от Лу-
ны для случая, когда плоскость орбит
______________________е ИСЗ перпендикулярна направлению Зем-
/ул ля — Луна
ника на орбите. Вычитание векторов проиллюстрировано в
нижней части рис. 3.3.
В точке А5 вектор возмущающего ускорения направлен от
Земли (и от Луны). В том, что в этой точке вектор возмущаю-
щего ускорения направлен от Луны, никакого противоречия
нет. Конечно, Луна притягивает и спутник, и Землю. Эффект
от притяжения Земли оказывается большим (Земля ближе к
Луне, чем к КА, расположенному в точке А5), и Луна как бы
«отрывает» спутник от Земли.
На второй половине траектории спутника картина симмет-
рична относительно направления Земля — Луна. Отметим, что
максимальная величина возмущающего ускорения, как это сле-
дует из (3.16) или рис. 3.3, достигается в точке Аь Именно по-
этому даны числовые оценки для этой точки.
Если направление Земля — Луна перпендикулярно плоскос-
ти орбиты спутника (рис. 3.4), то возмущающее ускорение Ф
не «изменяется по величине и равно ускорению в уже рассмот-
ренном случае (см. рис. 3.3, точка А3).
Возмущающее ускорение, действующее на ИСЗ
от Солнца
Оценку возмущающего солнечного ускорения также
следует проводить с помощью (3.16). Но при этом можно учи-
тывать, что, так как Солнце находится далеко от Земли, ради-
ус-вектор Земля — Солнце (ri2) и радиус-вектор Солнце —
спутник (г2) направлены по одной прямой в противоположные
стороны. При этом слагаемые ускорения b и с будут коллинеар-
ны во всех точках орбиты спутника. На рис. 3.5 представлена
эпюра возмущающего солнечного ускорения по орбите спутни-
ка в случае, если Солнце находится в плоскости орбиты спут-
ника. Максимальное возмущающее ускорение действует на
спутник, находящийся в точке Аь Вектор этого ускорения на-
правлен от Земли радиально вверх. В точках А2 и А4 возму-
ф Д/
щающее ускорение отсутству-
ет. В точке Аз возмущающее
корения в точке Ai и направле-
но также радиально.
Если плоскость орбиты
Рис. 3.5. Возмущающее Солнечное спутника перпендикулярна на-
ускорение, действующее на ИСЗ
105
правлению Земля — Солнце,
то несложно увидеть из (3.16), что возмущающее солнечное ус-
корение не будет действовать на спутник ни в одной точке ор-
биты.
Для оценки эффектов от возмущающего воздействия Луны
и Солнца придется учитывать кинематику Солнечной системы.
Так, если в какой-либо момент времени Солнце находится в
плоскости орбиты спутника, перпендикулярной плоскости эк-
липтики, и если положение этой плоскости неизменно в инер-
циальном пространстве, то че^рез три месяца направление Зем-
ля — Солнце будет перпендикулярно плоскости орбиты спут-
ника.
Численные оценки величин возмущающих солнечных уско-
рений показывают, что они меньше лунных примерно в 2,2 ра-
за. Так, для орбиты радиусом 100 000 км для случая, когда
Солнце находится в плоскости орбиты спутника, возмущающее
ускорение в точке Xi (см. рис. 3.5) равно 8,3-10—4 см/с2, что
составляет 0,024% от местного гравитационного ускорения.
Сравнение величин возмущающих ускорений
от различных факторов
Оценки возмущающих ускорений, проводимые в раз-
личных случаях, зависят от большого числа факторов. К ним
можно отнести характеристики орбиты спутника, включая раз-
мер и форму орбиты, положение плоскости орбиты в простран-
стве, положение Луны и Солнца по отношению к орбите и т. д.
Никаких рекомендаций по сравнительной оценке в общем слу-
чае дать практически невозможно. Для частной оценки обычно
поступают так: рассматривают только круговые орбиты (ско-
рость спутника при этом четко связана с высотой орбиты, не
усложняет картину положение перицентра орбиты и т. д.). При
этом удается сделать следующие выводы. На совсем малых вы-
сотах до 150 км определяющим возмущением является аэро-
динамическое возмущение. На высотах 150 ...400 км необходи-
мо учитывать аэродинамические возмущения и возмущения,
связанные с нецентральностью формы Земли. На высотах
400... 20 000 км нужно прежде всего учитывать возмущения от
нецентральное™ гравитационного поля Земли. На высотах
20 000... 50 000 км наряду с возмущениями от нецентральное™
гравитационного поля Земли нужно учитывать лунно-солнечные
возмущения. На высотах более 50 000 км, лунно-солнечные
возмущения являются превалирующими.
107
3.2. МОДЕЛЬ ВОЗМУЩЕННОГО ДВИЖЕНИЯ ИСЗ
Проведенный анализ -возмущающих ускорений, влия-
ющих на движение ИСЗ, позволяет получить модель возму-
щенного движения спутника (3.2)
=я+ Фн+Фа+Фл, (3.18)
где а — вектор основного ускорения спутника в задаче двух
тел Земля—спутник ( — 7 j ; фд_вектор возмущающего
ускорения от нецентральное™ гравитационного поля Земли (в
случае учета только сжатия Земли, компоненты этого вектора
записаны в (3.6));
Фа — вектор аэродинамических ускорений (3.8);
Фл — вектор лунно-солнечных возмущающих ускорений
(вычисляется как сумма ускорений, подсчитанных с помощью
равенства (3.1'6)).
Если бы возмущающие ускорения отсутствовали (Фн = Фа =
= Фл = 0), то траектория спутника становилась бы невозмущен-
ной, ее анализ мог бы проводиться в рамках задачи двух тел.
Такая задача аналитически интегрируется и ее подробное ист
следование было проведено выше. Анализ уравнений возму-
щенного движения существенно сложнее. Практически можно
утверждать, что такой анализ без допущений и приближений
аналитически не выполним. В общем случае для анализа воз-
мущенного движения приходится прибегать к численному ин-
тегрированию. При этом для заданных (конкретных) началь-
ных условий движения с помощью какого-либо метода числен-
ного интегрирования (метода Рунге — Кутта определенного по-
рядка, Адамса и т. д.) решают задачу Коши и численно строят
траекторию КА. При этом возникают определенные трудности,
связанные с выбором шага интегрирования, оценкой точности
расчета траектории, трудоемкостью вычислений (большим ма-
шинным временем, необходи-
мостью использования двойной
точности при расчетах) и т. д.
Такие трудоемкие расчеты
практически невозможно (да-
же с учетом современного раз-
вития вычислительной техни-
ки) широко проводить на эта-
пе проектных изысканий, при
проектировании космических
объектов, при проектировании
орбит КА. В таких случаях
должны помогать приближен-
los
Рис. 3.6. Оскулирующие элементы ор-
биты:
С — центр масс Земли; г — радиус-вектор
КА относительно центра Земли
но-аналитические исследования или другие подходы к анализу
возмущенного движения ИСЗ. Одним из таких подходов, нашед-
ших широкое применение в механике космических полетов, яв-
ляется метод оскулирующих элементов орбиты. Суть его заклю-
чается в следующем.
Пусть траектория возмущенного движения спутника есть
дуга АВ (ряс. 3.6). В какой-либо момент Л спутник 'находится
в точке Л1 (радиус-вектор Г\) и имеет скорость Pi. Если пред-
положить, что в этот момент Л спутник начал двигаться в рам-
ках задачи двух тел (возмущающие ускорения на него перес-
тали действовать), то его траектория (орбита) будет кривой
второго порядка, один из фокусов которой будет расположен в
точке С. Элементы такой орбиты ,(р^ elf Qi, coi, /Я1) будут
определяться начальными условиями и, Vi, t\. Если бы возму-
щений не существовало, траектория полностью определялась,
бы этими элементами. Такая траектория на рис. 3.6 обозначе-
на дугой Л1В1. Л1В1 касается реальной траектории КА АХВ в
точке А1 (вектор Рь как скорость на реальной возмущенной
траектории, начинающейся в Аь касается этих траекторий).
Если возмущающее ускорение мало по отношению к основно-
му, то реальную траекторию в окрестности точки Ai можно
приближенно заменить частью дуги AiBj.
Рассмотрим момент времени t2. Пусть КА в этот момент
находится в точке А2 возмущенной траектории. Аналогично
уже построенной дуге AiBi построим коническое сечение А2В2,
соответствующее невозмущенному движению с начальными усло-
виями r2, V2, t2. Элементы такого конического сечения обозна-
чим р2, е2, ...» /Я2. Дуга A2B2i так же как и AiBi, касается воз-
мущенной траектории АВ и может служить приближением тра-
ектории КА. Рассматривая последующие моменты времени
t4 ит. д., можно было бы построить дуги невозмущенного дви-
жения A3B3i AtBt, ... с элементами р3, е3, ..., tn3-f р4, е4, ...,
и т. д. Таким образом, исследование возмущенной траектории
КА может быть сведено к анализу совокупности невозмущен-
ных траекторий, соответствующих каждому моменту времени..
Другими словами, при анализе возмущенного движения мы мо-
жем считать, что в любой момент времени КА находится на
дуге конического сечения с определенными значениями элемен-
тов орбиты, и коническое сечение по движению КА изменяет-
ся. При этом изменяются элементы орбиты КА, т. е.
р = р (/), Q = Q (/), со = со (/),
e-e(0, i = /я=/я(0. (3.19)
Форма и размер орбиты, положение орбиты в пространстве
изменяются. Орбита как бы «разбухает», «поворачивается» и
т. д. Причем, если возмущающие факторы малы, эти измене-
ния протекают медленно.
юз
Элементы орбиты, рассматрив.аемые как функции времени,
через которые координаты и составляющие скорости в -возму-
щенном движении выражаются теми же формулами, что и в
невозмущенном движении, называются оскулирующими эле-
ментами орбиты. Реальная возмущенная траектория есть оги-
бающая оскулирующих конических сечений Л1Вг, А2В2; А3В3
и т. д. Понятно, что -совокупность оскулирующих элементов в
виде (3.19) — не единственная совокупность. Как и при опре-
делении элементов орбиты невозмущенного движения, можно
пользоваться любыми независимыми шестью постоянными ин-
тегриров1ания задачи двух тел. Так, вместо фокального пара-
метра как оскулирующего элемента орбиты р(/) часто рас-
сматривается большая полуось a(Z).
Если для какого-либо момента времени t* известны оскули-
рующие элементы орбиты ИСЗ (р*, е*, /*я), то однозначно
можно найти координаты спутника, скажем, в экваториальной
системе координат (см. разд. «Прогнозирование положения
спутника в задаче двух тел»). По элементам орбиты легко на-
ходится и скорость спутника.
Таким образом, исследование траектории возмущенного
движения КА, описываемого уравнением (3.18) или проекция-
ми этого уравнения на геоцентрическую невращающуюся сис-
тему координат
Л2 г
— =ат+Фнх+Фах + Флх;
=^+Фвд + ФаУ + ФЛУ; (3-20)
---- “ “Ь Фцг 1“ ^az “Ь
^2---с tijC 1 d-c 1
можно свести к анализу изменения оскулирующих элементов
орбиты КА. Такое преобразование можно трактовать как заме-
ну переменных в системе дифференциальных уравнений (3.20).
От переменных этой системы (она шестого порядка)
(з.21)
можно перейти к оскулирующим элементам
р (/), е (/), Q (0, i (/), о) (/), tn (t). (3.22)
Прежде чем осуществить переход, выявим возможные преи-
мущества такой замены переменных.
Совершенно ясно, что надеяться на аналитическое решение
системы дифференциальных уравнений в новых переменных не
приходится. Какие же преимущества имеет система с оскули-
рующими переменными? Пожалуй, все эти преимущества вы-
текают из единственного факта: в невозмущенном движении
НО
эти переменные являются постоянными интегрирования, конс-
тантами. Поэтому, так как возмущения малы, то оскулирую-
щие элементы изменяются медленно. При использовании чис-
ленных методов интегрирования это дает надежды на доста-
точно большой шаг интегрирования при достижении высокой
точности. Но основные преимущества оскулирующих элементов
проявляются при проведении приближенно-аналитических ис-
следований. Идея их может заключаться в том, что прираще-
ние оскулирующих элементов орбиты определяется на интер-
вале траектории КА, на котором оскулирующие элементы пред-
полагаются неизменными.
После того, как некоторые идеи анализа уравнений для ос-
кулирующих элементов изложены (они должны были пояснить
целесообразность перехода в уравнениях (3.20) от прямоуголь-
ных координат (3.21) к оекулирующим элементам (3.22)), осу-
ществим вывод уравнений в оскулирующих элементах.
Вывод уравнений в оскулирующих элементах
Возможных подходов вывода уравнений в оскули-
рующих элементах много, однако во всех случаях по существу
проводится переход от переменных, в которых записана диф-
ференциальная система возмущенного движения, к другим пе-
ременным — оекулирующим элементам. Будем использовать
подход, основной идеей которого является метод вариации про-
извольных постоянных при решении систем дифференциальных
уравнений.
Идея вывода уравнений. Пусть известна запись
уравнений возмущенного движения в прямоугольной декарто-
вой системе координат
=ах + Фх-,^- =аг+Фг; ^-=Vy-,
dt х dt z z dt y'
d^L =ау+Фу ; — = ’/x; — =VZ.
dt y y dt x dt z
(3.23)
Система состоит из шести скалярных дифференциальных
уравнений первого порядка. Первые три — уравнения сил (ди-
намические уравнения, описывающие возмущенное движение
спутника). Последние три — кинематические связи. Отметим,
что в дальнейшем будут использованы два свойства системы
(3.23):
правые части уравнений сил должны представлять сумму
двух слагаемых (первое слагаемое определяется основным ус-
корением, второе — возмущающим);
111
правые части кинематических связей «не содержат никаких
возмущений, в общем случае являются функцией координат и
•скоростей. Это замечание дает возможность рассматривать
.дифференциальную систему возмущенного движения не толь-
ко в прямоугольной декартовой системе координат (3.23), но и
относительно многих других систем координат, в других пере-
менных.
Невозмущенное движение спутника может быть исследовано
с помощью системы (3.23), если положить нулевыми возму-
щающие ускорения:
dVx
dt
dx
= ar ; — = VX ;
x dt x
=v- (3'24>
Пусть общий интеграл системы (3.24), описывающей невоз-
мущенное движение, представлен следующим образом:
Wi (*> У» ^z> ^1» ^2» Сз, С4,
С5, С6) = 0 (i=l, ... ,6), (3.25)
где Ci, ..., С6 — постоянные интегрирования.
Из (3.25) следует, что в невозмущенном движении выпол-
няется следующая система равенств:
дер г dx дх dt dtp, dy d<pj ду dt дг dz dg>i dVx dt dVx dt ‘t’
+ d<Pi dVy дф/_ dvy dt dVz dVz , _q dt ’r dt (3.26)
(i=l. ... ,6).
Или, используя (3.24), получим
Vx + — ]/ + ^21 V2+ ах +
дх ду у дг dVx '
+ =°- <3-27>
Будем искать решение системы (3.23), описывающей возму-
щенное движение спутника, в виде (3.25), полагая, что Сь ...
112
С6 являются функциями времени (идея метода вариации
постоянных). Тогда из (3.25) следует
дуг dx_ дфг- dy
дх dt ду dt
дщ dz
dz dt
д ф; dVx д Ф; dVy d щ dVz
dVx dt dVy dt dVz dt
dt dC±
dC± дф; dC2 . . д фг dC6
dt Ф dC2 dt Ф “ Ф дСв dt
= 0
(1 = 1,... ,6).
Используя (3.23), из (3.28) получим
7Я+ Vv+ Vz+ (ах+Фя) +
дх х ду у дг 2 dVx х х’
+ (^+ФУ)+ («г+Фг)+ +
дУу о У2 dt
д фг d Сх дфг dC2 дфг dCQ = Q
"г дС± dt дС2 dt dCQ dt
G=l, ,6).
(3.28)
(3.29)
Учитывая (3.27), последнюю систему равенств можно пере-
писать в виде
д Фе d С± д фг d С2 . . д Ф/ d С6 _
дС± dt дС2 dt' дС* dt
= _ ф _ ^££ ф _ ф
dVx х dVy у dVz
(1=1,... ,6).
(3.30)
Систему равенств (3.30) можно рассматривать как алге-
браическую относительно dC^ldt, dC^ldt? ...» dCeldt. Тогда (3.30)
есть линейная неоднородная система относительно dC^dt,
dC2/dt, ..., dCeldt. Разрешимость этой системы относительно не-
известных (dC\!dt, dC2jdt, ..., dCeldt) следует из предполагае-
мой независимости первых интегралов уравнений возмущенно-
го движения, константами которых являются Сь С2, С6. Та-
ким образом, из системы шести линейных алгебраических урав-
нений (3.30) можно определить dC^dt, dC2jdt, ..., dCeldt. Но
Ci, С2, ..., Св есть один из возможных наборов оскулирующих
элементов. Под системой Сь С2, ..., С6 мы можем рассматри-
вать элементы р, е, ..., /л.
Замечание 1. Если имеется возможность пользоваться од-
ним из равенств (3.25) в виде первого интеграла невозмущен-
ного движения
ФДх, y.z, Vx,Vy, V2,t) = C}, (3.31)
113
то в соответствии с приведенным выводом можно утверждать,
что дифференциальное уравнение для оскулирующего элемента
Cj имеет вид
dCj
di
= ЭЫ ф + djv ф d_w
dVx dVy dVz
(3.32)
Замечание 2. Понятно, что если удается разбить систему
(3.25) на независимые по константам интегрирования подсис-
темы, то и система алгебраических уравнений (3.30) относи-
тельно dCxIdt, dCzIdt, ..., dCtddt разбивается на подсистемы.
Этим целесообразно пользоваться для уменьшения трудоем-
кости вывода уравнений для оскулирующих элементов.
Уравнения для оскулирующих переменных р, Й, i
Проекции вектора площадей о на оси экваториаль-
ной системы координат (см. (2.72)) имеют следующий вид
ox = osin Qsini;
Gy = —о cos Q sin i; (3.33)
gz = a cos i.
С другой стороны, ox, Gy, gz как постоянные интегрирования
невозмущенного движения определяются из равенства
i j k
o = [ax, Оу, oJ = [rxV]= * у z. (3.34)
Vx Vy vz
Используя (3.33) и (3.34), получим
—yVz + zVy + о sin Q sin i = 0;
—zVx + xVz—ocosQsinz = 0; (3.35)
— xVy + yVx + о cos i = 0.
Систему трех равенств (3.35) можно рассматривать как не-
зависимую подсистему системы (3.25) относительно трех кон-
стант интегрирования о, й, i.
Уравнения (3.30) для подсистемы имеют вид
. . . d a , . . d Q , . .di
sin Й sin I--h O COS Й sin I--h G sin Й COS I-=
dt dt dt
гФДуФ,;
— cosQsinf-^- + osinQsinf —ocosQ cosf-^-= (3.36)
dt dt dt v '
= ?ФХ—хФг;
.do . .?di
cost-----asm I-= —уф.. +x Ф„.
dt dt y x y
114
Решение этих линейных алгебраических уравнений относи-
ла d Q di
тельно —, , — дает возможность получить
sin i + о cos i = —z (Фу sin Q + Фж cos Q) +
+ (ysinQ+xcos Й)Ф2; (3.37)
о — = Ф>. (уsin i—z cos г cos Q) + Фу(— xsin i—zcosi sinQ) +
dt
+ Ф2 cos i(ysinQ + xcos Q); (3.38)
о sin i = Фхг sin Q — Фу z cos Q +Ф2 (у cos Q—xsin Q). (3.39)
dt
Равенства (3.38) и (3.39) можно рассматривать как диф-
ференциальные уравнения для оскулирующих элементов i и Q.
Чтобы получить аналогичное уравнение для фокального пара-
метра р, вспомним, что р = <у2/ц.
Из последнего равенства следует, что dp!dt =------. По-
p. dt
этому
= 2 1Z — {Фх (— У cos i—z sin i cos Q) +
dt V p,
+ Ф^ (x cos i — z sin i sin Q) -j- Ф2 sin i (y sin Q + x cos Q)}. (3.40)
Равенства (3.38) ... (3.40) — дифференциальные уравнения
для рассмотренных оскулирующих элементов орбиты р, Q, i.
Отметим, что полученная форма уравнений мало распростране-
на. Значительно чаще в проводимых в литературе уравнениях
используют не проекции возмущающего ускорения на эквато-
риальную систему координат Фх, Фу, Ф2, а проекции этого ус-
корения на орбитальные оси.
Пусть Т — проекция вектора воз-
мущающего ускорения на трансвер-
саль; S — проекция вектора возму-
щающего ускорения на радиальное
направление в точке, в которой на-
ходится КА (рис. 3.7); W — проек-
ция возмущающего ускорения на
нормаль к плоскости орбиты (поло-
жительное направление W противо-
положно направлению вектора пло-
щадей и составляет правую тройку
векторов Т, S, U7). Отметим, что в
Рис. 3.7. Компоненты возму-
щающего ускорения
литературе распространены проек-
ции векторов ускорений, отличаю-
115
щиеся от введенных направлением нормальной проекции IF, т. е.
W направляется по вектору кинетического момента. При этом
правая тройка векторов имеет вид S, Т, W.
На рис. 3.7 точка А — положение КА (характеризуется ра-
диусом-вектором г), мгновенная плоскость орбиты обозна-
чена EAF и характеризуется долготой восходящего узла Q и
наклонением I. Положение спутника в этой плоскости характе-
ризуется аргументом широты и (угол между линией узлов и
текущим радиусом-вектором). Компоненты возмущающего ус-
корения в экваториальной системе координат Фх, Фу, Фг можно
найти по орбитальным компонентам Т, S, IF, используя матри-
цу перехода между системами (см. табл. 1.1) по соотношениям
Фх = Т (— sin и cos Q — cos и sin Q cos i) +
+ S (cos и cos Q—sin и sin Q cos i) — IF sin i sin Q;
ФУ = Т (— sin r/sinQ+ cos и cos Q cos i)+ (3.41)
+ S (cos и sin Q + sin и cos Q cos i) + IF sin i cos Q;
Фг = T cost/sin t’ + Ssint/sint—IF cost.
Подстановка (3.41) в полученные уравнения для оскули-
рующих элементов орбиты с учетом зависимостей координат
от элементов орбиты и широты (см. рис. 3.7)
х — г (cos и cos Q — sin и sin Q cos t);
y = r (cos и sin Q + sin и cos Q cos t); (3.42)
z = r sin t/sin i
после алгебраических преобразований дает
-^ = 2r V~^T-
dt У р ’
d г sin и
dt "]/u р sin i
d i _ r cos и
dt Д/р- P
Уравнения для оскулирующих переменных е, со, tn
Уравнения для остальных оскулирующих элементов
орбиты можно получить, анализируя другие первые интегралы
невозмущенного движения.
Для возможности дальнейшей ссылки на систему для оску-
лирующих элементов запишем их совместно с ранее получен-
ными уравнениями:
*_ = 2rj/ir; (3.44)
116
(3.43)
{[(1+y;c°s^+^]T+sinuS};
d& __ r sin и
dt ~]/^P sin i ’
Л _reg«. (3.44)
dt у p p *
4^= l/Z /( 1 + 21^ T-c-^S+ —ctgisinulV'};
dt r p I \ p } e e p ° J *
.?n = / — N T+ (esinuW—cos») Si,
dt e p I r )
A7 2p2 P cos и du
где N=z-t— f--------.
r2 £ (1 + e cos u)3
Система уравнений в оскулирующих элементах (3.44) явля-
ется замкнутой системой, если учитывать следующее обстоя-
тельство.
При заданных в произвольный момент времени t о-скули-
рующих элементах можно определить:
по уравнению Кеплера или по уравнению, из которого выво-
дится уравнение Кеплера (оно универсально и не зависит от
типа орбиты), истинную аномалию г спутника в момент t
Р3/2 У ^и .
Л 1/р J (l + ^cosu)2’
длину радиуса-вектора спутника
Г =-------р------;
1 + е cos и
(3.45)
(3.46)
аргумент широты спутника в мгновенной плоскости орбиты
и = (о + и. (3.47)
Таким образом, при известных элементах орбиты и извест-
ных возмущающих ускорениях правые части системы (3.44) оп-
ределены. В этих условиях исследование возмущенного движе-
ния КА с помощью этой системы может сводиться к ее числен-
ному интегрированию.
Если входящие в правые части (3.44) возмущающие уско-
рения являются функциями координат и скоростей КА, то на
каждом шаге интегрирования приходится по оскулирующим
элементам находить положение и скорость КА по соотношени-
ям раздела «Прогнозирование положения спутника в задаче
двух тел».
117
Анализ особенностей уравнений для оскулирующих
элементов
Записанная система (3.44) есть система обыкновен-
ных дифференциальных уравнений шестого порядка, разрешен-
ная относительно производных. Правые части этой системы
есть линейные однородные функции компонент возмущающих
ускорений. Если возмущения отсутствуют T=S = W = 0, то пра-
вые части (3.44) обращаются в нуль и элементы орбиты не
изменяются по времени, как им и положено в задаче двух тел.
Обращают на себя внимание особенности правых частей
(3.44), которые в ряде случаев усложняют ее использование.
При е = 0 теряются понятия аргумента перицентра со и мо-
мента прохождения перицентра tn. При этом в уравнениях для
d^dt, dtn/dt появляются особенности.
При i = 0 становятся неопределенными долгота восходящего
узла Q и аргумент перицентра со. При этом в уравнениях для
dQldt и d^ldt появляются особенности.
При р = 0 (оскулирующая орбита прямолинейна) становит-
ся неопределенной плоскость оскулирующей орбиты, что про-
является в особенностях уравнений для dQldt и dildt.
Что касается случая р = 0, то из-за того, что на реальных
траекториях КА и спутников этот случай практически не встре-
чается, он не является важным (на эту особенность дифферен-
циальной системы (3.44) (часто не обращают внимания).
Для того чтобы в процессе исследования не натолкнуться
на особенность, связанную с обращением наклонения в ноль,
есть возможность за основную плоскость ху системы коорди-
нат, в которой рассматривается движение, выбирать не эква-
ториальную плоскость, а плоскость, которая в процессе всего
движения КА не может быть плоскостью оскулирующей орби-
ты. При этом возможны и другие подходы.
Рис. 3.8. Угловая скорость радиуса-вектора спутника в возмущенном состоянии
118
Случай околокруговых орбит весьма интересен для <п/рак-
тами, поэтому особенность дифференциальной системы (3.44)
при е = 0 существенна. Для того чтобы исключить особенность,
распространен следующий прием. Вместо оскулирующих эле-
ментов е и со рассматривают такие функции этих переменных
= е cos со;
А2 = esin со.
(3.48)
При этом е=
Г А
arctg—— , если > 0;
^•1
А
arctg —— + л, если А,г < 0;
Ai
(0 — , если А1 = 0, А,2 > 0;
---— , если Ат = 0, Х2<0;
2 1 2
(3.49)
^неопределенно, если А.1 = А,2 = О.
Величины Ai и А, 2 как функции констант интегрирования не-
возмущенного движения также являются постоянными невоз-
мущенного движения. Использование их в качестве оскулирую-
щих элементов приводит к следующим уравнениям:
=1Z— Г Т (1 + — cos u + S sin и +
dt г р l \ р )
+ — (Т Х2 — W ctg i sin u)l;
P J
== Гт (1 + — ^ sin и—S cos u +
dt V p L \ p j
+ y(T A, + W X2 ctg i sin «)].
Последние уравнения не содержат особенностей при е = 0,
ими можно заменить второе и пятое уравнения системы (3.44),
оскулирующие значения е и со при этом подсчитываются по
(3.49).
Что касается последнего уравнения из (3.44) (оно харак-
теризует tn — момент прохождения перицентра), существуют
несколько приемов избавиться от сложностей этого уравнения.
Остановимся на одном из приемов, идея которого взята из
[62]. При этом дадим информацию, представляющую само-
стоятельный интерес. Угловая скорость радиуса-вектора спутни-
ка в возмущенном движении в каждый момент времени есть
119
вектор, перпендикулярный мгновенной плоскости орбиты. Обоз-
начим ее dv\ldt. Величина угловой скорости радиуса-вектора
может быть найдена из значения трансверсальной скорости
спутника
Vn = г = У (1 + е cos «). (3.50)
Направление радиуса-вектора спутника в пространстве оп-
ределяется тремя углами й, Z, и. Введем векторы угловых ско-
ростей й, z, и. Вектор й направлен по оси z невращающейся
системы координат. Он характеризует угловую скорость линии
узлов (рис. 3.8). Вектор i направлен по линии узлов и харак-
теризует скорость изменения угла наклона плоскости оскули-
рующей орбиты. Вектор и направлен перпендикулярно плос-
кости орбиты (по вектору интеграла площадей) и характери-
зует скорость изменения аргумента широты. Рассмотрим сумму
введенных векторов
<о = й +z + и. (3.51)
Разложим ее на три взаимно перпендикулярных компонен-
ты. Одну компоненту возьмем вдоль линии узлов t]i = z. Вто-
рую компоненту рассмотрим в плоскости мгновенной орбиты
перпендикулярно линии узлов Y]2 = Qsinf. Третья компонента
направлена вдоль нормали к плоскости t]3==u + £2cos f.
Докажем, что сумма двух компонент T]i + rj2 направлена
по радиусу-вектору спутника. Для этого достаточно показать,
что
Л2/Л1 = tgu.
Действительно, с помощью второго и третьего равенств из
(3.43) получим
т]2 Q sin i sin и sin iW »
— =-------=-----------= tg U.
4i I sin i cos uW
Таким образом, векторная сумма (3.51) может быть разло-
жена на две составляющие. Первая составляющая (zz + й cos i)
перпендикулярна плоскости орбиты и характеризует угловую
скорость вращения радиуса-вектора спутника
—u+^cosz. (3.52)
Вторая составляющая ] z2 + £22sin2z направлена по ради-
усу-вектору спутника. Так как эта составляющая угловой ско-
120
роста направлена по радиусу-вектору, то она никак не влияет
на его угловую скорость.
Таким образом, нами доказано, что угловая скорость ра-
диуса-вектора спутника в возмущенном движении определяет-
ся соотношением (3.52). С другой стороны, эта же угловая
скорость удовлетворяет равенству, полученному с помощью
(3.50):
г2 -^1 = р = а.
dt
Из последнего соотношения следует, что константа площа-
дей в возмущенном движении выражается через полную угло-
вую скорость радиуса-вектора спутника (а не через dvldt, как
в невозмущенном движении).
Используя последние два равенства, получим
и — Л/ — — Q cos i .
V Г2
Именно этим равенством можно заменить имеющее особен-
ности уравнение для оскулирующей переменной tn. Действи-
тельно, система уравнений
— [Т ( 1 + — cos и +Ssinu+ —(ТК2 —
Н \ Р / Р
— ctg i sin и)];
— [T ( 1 + — sinu—S cos и + — (TK1 +
M- \ P / P
+ №X2ctg/snra)]; (3.53)
dQ __ r sin и
dt Vm-P sin t
di _ r cos и
dt Д/ jip
---— _|-r_— sjn u ctg Z W
dt г*
не имеет существенных особенностей. Используя ее, не прихо-
дится решать уравнение Кеплера, брать квадратуру Af, входя-
щую в (3.44). В случае круговой орбиты (Zi = Z2 = 0) истинная
аномалия не определяется, здесь г = р. Сделаем два замечания.
1. Обратим внимание на то, что последнее уравнение в сис-
теме (3.53) не есть уравнение для оскулирующего переменного.
121
Правая часть этого уравнения не обращается в нуль при от-
сутствии возмущений. Действительно, аргумент широты моно-
тонно изменяется и в невозмущенном движении со скоростью
цр/r2 (целесообразно не ограничивать и диапазоном 0 ...2л,
а рассматривать монотонной переменной). Авторы [62] пред-
лагают рассматривать не аргумент широты, а отклонение ар-
гумента широты от невозмущенного движения.
2. Дифференцируя равенство, следующее из уравнения ор-
биты r(l+ecosu) =р, и используя выражения для оскулирую-
щих переменных deldt, dpldt, можно получить дифференциаль-
ное уравнение для истинной аномалии в возмущенном движе-
нии
Это равенство может быть использовано при анализе воз-
мущенного движения.
Таким образом, в данном разделе введено понятие оскули-
рующих элементов орбиты, записаны дифференциальные урав-
нения, характеризующие изменение оскулирующих элементов в
возмущенном движении, проанализирован вид и особенности
этих уравнений.
3.3. ПЕРИОДИЧЕСКИЕ И ВЕКОВЫЕ ВОЗМУЩЕНИЯ
ОРБИТЫ СПУТНИКА
Системы дифференциальных уравнений для оскули-
рующих элементов (3.44) или (3.53) являются точной моделью
возмущенного движения КА. Таким образом, исследование
возмущенного движения может заключаться в нахождении ком-
понент возмущающих ускорений Ф=[Т, S, 117] и численного интег-
рирования системы (3.44) или (3.53). Трудоемкость такого интег-
рирования несмотря на определенные преимущества, которые
существуют при интегрировании этих систем по отношению к
системам, описывающим изменения, например, прямоугольных
декартовых координат спутника типа (3.23), велика. Нужно
отметить, что чаще всего правые части дифференциальных
уравнений для оскулирующих переменных вычисляются значи-
тельно сложнее правых частей системы (3.23). Основным преи-
муществом уравнений для оскулирующих элементов является
возможность их приближенного исследования. Дадим одну из
возможных трактовок такого исследования. При этом будем
рассматривать движение спутника, предполагая, что его траек-
тория многовитковая и оскулирующий эксцентриситет в каж-
дой точке орбиты меньше единицы (оскулирующая траекто-
122
рия — эллипс). Все возмущения орбиты спутника можно раз-
делить на две большие группы: периодические и вековые.
Периодическими называются возмущения элементов орби-
ты, появляющиеся в течение одного оборота спутника и не на-
капливающиеся от оборота к обороту. Поскольку время одного
оборота невелико (ограничено), а возмущающие факторы (ус-
корения) малы, то и периодические возмущения (отклонения
элементов орбиты от элементов в невозмущенном движении)
будут малы.
Вековыми называются возмущения элементов орбиты, кото-
рые, возникая на витке орбиты, накапливаются от витка к
витку. Эти возмущения могут быть весьма значительны, так
как являются результатом воздействия малых возмущающих
ускорений на больших интервалах времени.
В дальнейшем в качестве примера приведены некоторые
цифры, дающие оценку периодических и вековых возмущений.
Здесь же отметим, что периодические возмущения от нецент-
ральное™ гравитационного поля Земли в координатах спутни-
ка могут иметь порядок десятка километров. Вековые же воз-
мущения орбиты спутника при значительном времени сущест-
вования могут достигать тысяч километров и более. Понятно,
что неучет периодических возмущений может быть допустим на
определенных этапах проектирования спутника и его орбиты.
С другой стороны, вековые возмущения чаще всего приходит-
ся учитывать. Остановимся на анализе лишь вековых возмуще-
ний орбиты ИСЗ.
Общий подход к анализу вековых возмущений
орбиты спутника
Общую идею используемого в разделе подхода мож-
но назвать идеей конечных разностей. Рассмотрим один из эле-
ментов оскулирующей орбиты £j. Уравнение для этого элемен-
та, полученное в предыдущем разделе, имеет вид
^ = ^,...,^,/,7,5, Г). (3.55)
at
Найдем приращение этого элемента орбиты за виток траек-
тории
ЛЧ-Т dEi G+T
J J t,T,S,W)dt, (3.56)
ц ц
где fi — начальный момент времени; Т — время, в течение ко-
торого спутник сделал полный оборот вокруг Земли.
Причем £i, ..., £6, входящие в подынтегральное выражение,
можно считать постоянными, соответствующими начальному мо-
менту t\. Интеграл в (3.56) может быть вычислен, если возму-
123
щающие ускорения выражены через время и через элементы
орбиты. В ряде случаев для определенной структуры возмуще-
ний удается аналитически вычислить квадратуру (3.56) и по-
лучить аналитическую запись приращения элемента орбиты за
виток траектории (получить вековое возмущение элемента ор-
биты)
(3.57)
Таким образом, (3.57) определяет приращение элемента
орбиты за виток траектории. Считая, что это приращение от
витка к витку траектории изменяется слабо и достаточно мало,
то его можно рассматривать как производную от элемента ор-
биты по числу оборотов спутника Af, т. е. рассматривать диф-
ференциальное уравнение
^ = Si(Ei....£в)- (3.58)
Если такую операцию провести для всех оскулирующих эле-
ментов орбиты, то можно получить полную систему для анали-
за вековых возмущений спутника
................................. (3.59)
d-^ = ge(Ei, -.£6).
dN
Система (3.59) дает возможность анализировать только ве-
ковые уходы элементов орбиты, шаг ее интегрирования может
быть равен оборотам спутника, трудоемкость ее исследования
несоизмеримо меньше трудоемкости исследования (3.44). Сис-
тема (3.59) иногда называется осредненной (по виткам) сис-
темой для оскулирующих элементов.
Замечания. 1. Чтобы не возникло дополнительных труд-
ностей с нахождением времени полного оборота спутника Т,
входящего в (3.56), обычно в уравнениях для оскулирующих
элементов предварительно переходят от времени, как незави-
симого переменного, к аргументу широты и.
Для этого можно воспользоваться связью t и и (последнее
уравнение из (3.53))
__ Урр
dt — j г* '
где
j = Г 1 + — W ctg i sin и] .
L pp J
(3.60)
(3.61)
124
Уравнения (3.44) для оскулирующих элементов р, е, Q, f, со
при этом можно переписать в виде
dp__
du р,
— = — Г( 1 + — Т coso+ Ssin о + е— Т1 ;
du р, L \ р j р J
— = — rU- W; (3.62)
du [ip sin i
di г3 j rV7
— =------- cos uw;
du pp
— = — [( 1+ — Tsino—Seos u+ e — I^ctgisinul.
du pe L \ p ) p J
2. Обратим внимание на то, что правые части уравнений
(3.44), (3.53) есть линейные функции от возмущающих ускоре-
ний. Сами возмущающие ускорения составляются как сумма
ускорений от отдельных возмущающих факторов:
т = т1+т2+т3;
S = Sx S2 И- S3; (3.63)
w=w1+w2 + w3i
где индексы 1, 2, 3 используются для обозначения групп воз-
мущающих факторов.
Выделение при этом вековых возмущений приводит к неза-
висимому приращению оскулирующих элементов орбиты спут-
ника на витке траектории от отдельных возмущающих ускоре-
ний:
з Z1+T
f fj(E11...fEGttlfTi1Si,Wi)dt, (3.64)
i=l ц
Если допустить, что возмущения элементов орбиты от каж-
дого возмущающего фактора малы, то можно не учитывать
интерференционного воздействия возмущающих факторов меж-
ду собой на больших отрезках времени. Таким образом, оказы-
вается допустимым рассматривать в отдельности каждый из
возмущающих факторов, а общее возмущающее воздействие
определять как сумму отдельных возмущающих воздействий.
Таким образом, рассмотрен подход к анализу вековых воз-
мущений ИСЗ. Предложен приближенный аналитический ме-
тод нахождения вековых возмущений орбиты ИСЗ.
125
3.4. ВОЗМУЩЕНИЯ ОРБИТЫ ИСЗ, ВЫЗЫВАЕМЫЕ
НЕЦЕНТРАЛЬНОСТЬЮ ГРАВИТАЦИОННОГО ПОЛЯ
ЗЕМЛИ
При анализе возмущений орбиты ИСЗ, вызываемых
нецентральностью гравитационного поля Земли, будем исследо-
вать вековые возмущения элементов оскулирующей орбиты спут-
Рис. 3.9. Проекции возмущающих ус-
корений в орбитальной системе коор-
динат
ника, считая гравитационный
потенциал Земли потенциалом
сжатого сфероида (3.3).
Возмущающее ускорение в
проекциях на радиаль, мест-
ный меридиан и местную па-
раллель определяется системой
(3.6). Для записи проекций
этого возмущающего ускоре-
ния на оси орбитальной систе-
мы координат воспользуемся
соотношениями, вытекающими
из рис. 3.9. На этом рисунке
положение спутника характе-
ризуется точкой А; плоскость
орбиты спутника есть EAF\ ме-
ридиональная плоскость, про-
ходящая через точку А,— BCD. Угол между местным меридиа-
ном и трансверсальным направлением в точке А обозначен ф,
угол ЕСА — и (аргумент широты), ZАВС — ср. Легко получить
7 = — A- (sin 2ср cos ф) =--------------sin 2и sin2 i\
3 = Цз^(351П2ф_1)=М2А(351п2и51п2г-_1); (3.65)
U7 р-з6, s-n2„ sjn.ф_ Изб sjnи sjn 2i
г* г*
При выводе последних равенств были использованы следую-
щие формулы сферической тригонометрии:
[sin <р = sin и sin i, cos ф = ctg и tg <р.
Эти же соотношения можно было бы получить, если запи-
сать гравитационный потенциал сжатого сфероида (3.3) через
аргумент широты и наклонение орбиты спутника
U = -^-----tM-(3sin2usin2z — 1)
г Зг3
и продифференцировать его по направлениям орбитальной
тройки векторов (Т, S, №).
126
Уравнения в оскулирующих переменных (3.62) при возму-
щающем ускорении (3.65) принимают вид
dp 26 / . п . 9 .
—- = — —- Sin 2 U Sin2 I ;
du г
— = — /sin v (3sin2 и sin2 i —
du r2 I
— L 1 + — j cos и + e — j sin 2 и si
dQ 2 6/ . 2
— =----------— sin2 и cos i ;
du pr
di 6/ . o . o .
— =----------— sin 2 и sin 2 i ;
du 2 pr
da di f cos и /o . 2 • о • i
— = — {--------------(3 Sin2 U Sin“ i— 1
du r2 I e
(3.66)
/ 1 । r \ sin U . q . 2 • I 2 7* . л o*
— 1 + — ----------sin 2 и sin21H----sin2 u cos21
\ P ) e P
. Til 2 6 . 2 о • 1 I
где j = 1 + — sin2 и cos21 J
Переходим к анализу вековых возмущений (уходов) от-
дельных оскулирующих элементов орбиты.
Возмущение фокального параметра орбиты ИСЗ
С помощью первого уравнения системы (3.66) оцен-
ка приращения фокального параметра на витке траектории
спутника представляется в виде:
Др = — f sin 2 и sin2 i du. (3.67)
о r
В соответствии с общим подходом к анализу вековых воз-
мущений считаем, что внутри витка орбиты в связи с ограни-
ченным временем движения на нем и малым возмущающим
ускорением элементы орбиты не изменяются, т. е. i = const; р =
= const; е = const. Кроме того, анализ множителя /, введенного
с помощью (3.66), показывает, что максимальное его отклоне-
ние от единицы составляет ~ 0,003. Такого порядка ошибки
соизмеримы с ошибками использующегося метода осреднения.
Поэтому чаще всего j полагают равным 1. При этом вычисле-
ние интегралов существенно упрощается, а точность их вычис-
ления практически не страдает.’ Такое допущение будем вво-
127
дить для всех элементов орбиты спутника. Равенство (3.67)
при этом принимает вид
2 6 2л
Др =------sin2 i f (1 -|- e. cos v) sin 2 udu.
P о
Но v = u—co, a co = const на витке. Поэтому du = dv
и
Др = — — sin2 i /— — cos2u-------— Feos (Щ-co)+
P l 2 2 L
4—~ cos (3 и — co) j}2" = 0.
Таким образом, фокальный параметр орбиты спутника не
имеет вековых возмущений из-за нецентральное™ гравитаци-
онного поля Земли, принимаемой сжатым сфероидом. Анализ
выражения для первообразной функции в последнем равенстве
дает оценку периодическим возмущениям фокального парамет-
ра. С точностью до эксцентриситета е периодические возмуще-
ния фокального параметра имеют вид косинусоиды
------ cos 2 и с амплитудой б sin2 ii/p. Максимальные значения
Р
этой амплитуды соответствуют полярным / = л/2 предельно низ-
ким p = pmin орбитам. Численная оценка такой амплитуды —
10 км. Таким образом, периодические возмущения фокального
параметра орбиты ИСЗ из-за сжатия Земли не превышают
10 км.
Возмущение эксцентриситета орбиты спутника
Проанализируем аналогично второе уравнение из
системы (3.66)
А С (1 + е C0S и)2 f • /О • 2 • 2 • 1 \
Д е = б — --------- j sin и (3 sin2 и sin2i — 1) —
о Р2 I
— Г f 1 Н-----5----cos и + е------!-----1 sin 2ц sin2 i) du, (3.68)
L \ 1 -f- е cos и ) 1 + е cos и J J
Первообразная подынтегрального выражения оказывается
тригонометрической функцией и с периодом 2л. Это дает воз-
можность утверждать, что векового ухода эксцентриситета ор-
биты спутника из-за нецентральности гравитационного поля
Земли (сжатия Земли) нет.
Возмущение долготы восходящего узла
Для долготы восходящего узла анализ векового
ухода сводится к следующим операциям:
128
2 6 2я
ДЙ =-------cos i f sin2 и (1 + e cos u) du =
P2 о
9 8 2л t e
=-----—vosi f 12 sin2 и 4----[2cos(u — <o) — cos(u +
P2 0 I 4
+ co) — cos (3u—co) J | du = — cos i.
Таким образом, приращение Q за виток траектории равно
ДЙ= — cosz (3.69)
и восходящий узел имеет вековой уход. За один виток траек-
тории долгота восходящего узла уменьшается на величину
2л6
--- cos I.
Р2
Коротко проанализируем результат. Прежде всего вековой
уход восходящего узла оказался линейной функцией б-числа,
которое характеризует сжатие Земли (см. (3.3)). Вековой
уход оказался обратно пропорционален квадрату фокального
параметра, т. е. чем больше размер орбиты (больше р), тем
меньше орбита возмущается «нецентральностью» сжатой Зем-
ли (Землю все с большей точностью можно заменить матери-
альной точкой).
Наконец, вековой уход долготы восходящего узла оказался
пропорционален cos i. Видно, что максимальные уходы Q соот-
ветствуют орбитам, близким к экваториальным (r^O;
Для полярной орбиты долгота восходящего узла не имеет ве-
ковых возмущений. При 0<д<л/2 долгота восходящего узла
уменьшается AQ<0. Это значит, что восходящий узел сдвига-
ется по виткам траектории в экваториальной плоскости в сто-
рону, обратную направлению вращения спутника. Этот вывод
не меняется, если рассмотреть ИСЗ с л/2<д<л.
Геометрическое представление такого ухода дадим после
анализа вековых возмущений наклонения орбиты спутника.
Возмущение наклонения орбиты спутника
Из четвертого уравнения системы (3.66) следует,
что приращение наклонения орбиты за виток траектории
6 2л
Д/ =--------sin 2/ f sin 2и (1 + ecos и) du =
2р^ J
§ 2л [ е 1
= —------sin 2r j J sin 2u-|--— [sin (u + o>) + sin (3u—co)] =
2 P2 о I 2 J
(3.70)
129
5-8
Таким образом, векового ухода наклонения орбиты из-за
сжатия Земли нет. Анализ первообразной функции для ин-
теграла, записанного в последней строке (3.70), дает возмож-
ность проводить оценку периодических возмущений наклонения
орбиты. Видно, что с точностью до эксцентриситета периодиче-
ские возмущения наклонения орбиты изменяются на витке по
закону cos 2и, и амплитуда этой косинусоиды б sin 2i/4p2. Мак-
симальное значение этой амплитуды достигается при f = n/4 и
/ = 3/4л и равно б/4р2. Даже для самых низких орбит это число
не превышает 0,00037. Последнее значение соответствует мак-
симальному отклонению спутника в боковом направлении, рав-
ному 0,00037-6600 = 2,4 км (здесь 6600 км — фокальный пара-
метр низкой орбиты ИСЗ).
Долгота восходящего узла Q и наклонение орбиты i опре-
деляет положение плоскости орбиты в пространстве. Проведен-
ный анализ показал, что вековой уход имеет лишь Q, вековой
уход наклонения орбиты отсутствует. Геометрически это мож-
но представить следующим образом. Построим вектор площа-
дей о, который перпендикулярен плоскости орбиты спутника.
Если рассматривать орбиту спутника в рамках задачи двух
тел (Земля — спутник), то вектор о был бы постоянен в про-
странстве и определял постоянную плоскость движения спутни-
ка. В возмущенном движении, когда Земля рассматривается
как сжатый сфероид, вектор площадей о и плоскость орбиты
спутника вращаются вокруг оси Земли. При этом вектор пло-
щадей о описывает круговой конус вокруг Земли. Угол между
с и осью Земли постоянен и равен наклонению орбиты спутни-
ка, которое не имеет вековых уходов. Поворот плоскости орби-
ты вокруг оси Земли называется прецессией узла орбиты (прос-
то прецессией орбиты). Прецессия орбиты иллюстрируется на
Рис. 3.10. Прецессия линии:
а — узлов орбиты ИСЗ; б — апсид орбиты ИСЗ
130
рис. 3.10,а. При этом восходящий узел вращается в плоскости
экватора вокруг той же оси Oz.
Дадим числовую оценку для максимального приращения
долготы восходящего узла за виток траектории:
max |ДЙ| = = .2л-66,07И0^к1^ ~ 001 рад
Pm in 66002 км2
При этом уход восходящего узла за одни сутки может дос-
тигать 0,18 рад ^10°. Для примера укажем, что суточная пре-
цессия спутника «Восток» примерно составляла 4°.
Возмущение аргумента перицентра орбиты ИСЗ
Из анализа последнего уравнения системы (3.66)
получают приращение аргумента перицентра орбиты спутника
за виток возмущенной траектории
А 6 f COSU • 9 . 9 . ,
Дсо = — I---------(3 sin2 и sin2 i — I) +
о f2 I е
+ ( I Н—— sin 2и sin2 i + — sin2 и cos2 i\ du (^.71)
X P ) e P J
He останавливаясь на процессе вычисления определенного
интеграла, входящего в (3.71), запишем результат вычисления
Д® = 51 (4 — 5sin2i). (3.72)
р2
Таким образом, за виток траектории аргумент перицентра
изменяется. Это значит, что изменяется положение линии ап-
сид, траектория вращается в своей плоскости вокруг гравита-
ционного центра. Это явление иллюстрируется на рис. 3.10,6.
На нем показано положение последовательных витков траек-
тории спутника в плоскости его орбиты. Векторами Xi, Л2, Хз
обозначены положения вектора Лапласа (линии апсид) на этих
трех витках траектории.
Вековые уходы аргумента перицентра, как это следует из
(3.72), зависят от фокального параметра р и от наклонения ор-
биты L
Видно, что при увеличении р (увеличении удаления орбиты
от Земли) вековой уход со уменьшается, что находится в соот-
ветствии с законом изменения величины возмущающего уско-
рения. Действительно, чем дальше от Земли, тем менее замет-
на неправильность ее формы.
Более сложна зависимость Д(о(1). Оказывается, что есть
такое наклонение орбиты ИСЗ, при котором векового ухода ар-
5* 131
гумента перицентра, связанного со сжатием Земли, нет. Это
возможно при выполнении равенства
4 — 5 sin2 i = 0.
Последнее равенство выполняется при г‘ = 63;4°. Этим об-
стоятельством активно пользуются проектанты космических
систем. В частности, орбита спутников серии «Молния» имеет
наклонение порядка 63°, что позволяет этим спутникам иметь
апоцентр орбиты постоянно в Северном полушарии.
Знак приращения Асо зависит от L Действительно, если
<63О26Л или i> 116°34/, то Асо>0. Это значит, что линия ап-
сид вращается в ту же сторону, в которую вращается спутник.
Если 63°26'<л< 116°34/, то Асо<0. Это значит, что линия
апсид вращается в сторону, противоположную вращению спут-
ника.
Проведем числовую оценку возможного ухода аргумента
перицентра. За виток траектории максимальное смещение ли-
нии апсид равно:
А 4л6 4л-66,07-103 км2 ппо
max Дсо = ---- =---------------- « 0,02 рад.
А 6600 км2 1
Это соответствует почти 20° суточного возмущения линии
апсид.
Запишем итоговые равенства для вековых уходов элементов
орбиты ИСЗ
dp _ de _ di _ g.
dN ~ dN ~ dN ~ ’
d(a 6 л (л * 9 *\
— = — (4 —5sin2 t).
dN p* 1
Система уравнений (3.73) дает возможность исследовать
вековые уходы оскулирующих элементов орбиты ИСЗ по вит-
кам траектории. Так как правые части этой системы не зависят
от элементов, имеющих вековые уходы Q и со, то для получе-
ния полного возмущения элемента орбиты достаточно умно-
жить правую часть (не изменяющуюся от витка к витку тра-
ектории) на количество витков.
Остается неисследованным вопрос о связи траектории и
времени полета.
Расчет времени полета
Расчет времени полета нужно вести на основе соот-
ношений, полученных из (3.60).
132
Время одного оборота спутника вокруг Земли, за которое
аргумент широты изменяется от 0... 360°, называется дракони-
ческим периодом обращения спутника Тд. По-другому, драко-
нический период обращения спутника есть время между двумя
последовательными прохождениями спутника экваториальной
плоскости. Нахождение драконического периода с помощью
(3.60) сводится к нахождению следующего интеграла:
2Л
ТД = J v-
О Ун
/72
я Р3/2
du= ——
2Л
_ du.
У|ЛР 0 (l + ecosu)2
(3.74)
Если положить /=1, как это делалось при анализе вековых
уходов оскулирующих элементов, то драконический период бу-
дет равен периоду обращения спутника в невозмущенном дви-
жении:
а3/2
Тд « 2л —---- . (3.75)
УГ
Нами доказано выше, что векового ухода не имеют фокаль-
ный параметр и эксцентриситет орбиты. Но эти элементы оп-
ределяют большую полуось а, входящую в (3.75). Таким обра-
зом, большая полуось оскулирующей орбиты не имеет вековых
уходов, и с точностью /«1 можно утверждать, что дракониче-
ский период спутника для случая возмущения от сжатия Зем-
ли постоянен. Расчет времени движения спутника может вес-
тись следующим образом:
а3/2
= 2л . (3.76)
d. N Д/р.
Иногда не удовлетворяются точностью такого подхода, и при
нахождении интеграла в (3.74) учитывают, что /=/=1. При
этом упомянутый интеграл чаще всего находится приближен-
но. В [62] приведены несколько аналитических соотношений
для расчета приращений драконического периода. Приращение
драконического периода прямо пропорционально б и обратно
пропорционально и Iх р. Подсчет возмущения драконичес-
кого периода на витке круговой орбиты малой высоты г =
= 6600 км малого наклонения i^O приводит к следующему ре-
зультату:
6ТД= ( -4cos2i+ 1)=—24,36 с. (3.77)
Урр
Напомним, что период невозмущенной орбиты такого спут-
ника равен почти 90 мин, точнее 5333,4 с. Таким образом, воз-
мущение драконического периода составляет 0,45% от периода.
На больших временных интервалах такое маленькое возмуще-
ние приходится учитывать.
133
Таким образом, в разд. 4.4 рассмотрены характеристики
возмущения элементов орбиты ИСЗ, вызванные нецентраль-
ностью гравитационного поля Земли, проанализированы веко-
вые уходы элементов орбиты от этого возмущающего фактора.
3.5. ВОЗМУЩЕНИЯ ОРБИТЫ ИСЗ, ВЫЗЫВАЕМЫЕ
ДЕЙСТВИЕМ АТМОСФЕРЫ. ОПРЕДЕЛЕНИЕ ВРЕМЕНИ
СУЩЕСТВОВАНИЯ СПУТНИКА
В соответствии с рассмотренной в (3.8) моделью
возмущающего ускорения, вызванного аэродинамическими си-
лами, действующими на спутник, проекции возмущающего аэро-
динамического ускорения Фа можно записать в виде
Т= — Ф 1 + g COS и
а V1 + e24-2ecos и ’ (3.78)
S = -Фа -gsinu...== ;
Д/1 -J- g2 + 2 е cos и
тг = о,
Q F..
где Фа= (см. (3.7)).
Множители при Фа в выражении для Т_и S есть косинусы
угла между скоростью КА V (направление Фа противоположно
У) и трансверсальным и радиальным направлением.
При этом уравнения возмущенного движения (3.62) имеют
вид
dp_ =___L гз ф 1 + g cos u .
du p a Д/1 + e2 -j- 2 e cos и
de ____r*Фа (
du p 1 4- g2 4" 2 e cos и I
14- — (1 4- e cos u) cos v-j- e —
P / Pa
d Й q dt q
du du ’
г2 Фа ( .
— - z--- —e sin v cos и 4-
p e у 1 4- g2 4“ 2e cos и I
(1 + е cos -и) j ; (3.79)
dco
du
Прежде всего бросается в глаза отсутствие возмущений (да-
же периодических) по долготе восходящего узла и наклонению
орбиты. Это определяется тем, что возмущающее аэродинами-
ческое ускорение находится в плоскости орбиты и поэтому не
меняет ее положение в пространстве.
134
Для нахождения вековых уходов остальных элементов ор-
биты после алгебраических преобразований (3.79) в рамках
общего подхода к анализу вековых возмущений легко получить
9п3 2л (Т)
Д Р = “ — ------------ а------- d V, (3.80)
Р- о (1 + е COS и)2 Д/1 + е2 + 2е cos и
Д е = — 2f"---------фа (e + cosu) j v; (3.81)
И о (1 + e cos и)2 Д/1 Д- e2 + 2e cos и
дсо = — Г--------------9.a_sinu..— -----d u. (3.82)
И о (1 + £ cos и)2 Д/l + e2 + 2e cos и
В записанных квадратурах независимой переменной выбра-
на истинная аномалия. Это допустимо, так как из и = (о+т>, ес-
ли считать, что приращение аргумента перигея внутри витка
траектории мало, следует du = dv.
Оценка квадратур, входящих в (3.80) ... (3.82), существенно
зависит от принимаемой модели аэродинамического ускорения
Фа. Методика расчета аэродинамических коэффициентов ИСЗ
С F
приведена в [24]. Комбинация = которая входит в
выражение для ускорения Фа, называется конструктивным бал-
листическим коэффициентом (под баллистическим параметром
полагают или -------------— . Баллистический коэффициент ха-
m mgQ J
рактеризует КА, его геометрию. С учетом обозначения выр?же-
ние для Фа примет вид
<Da = SKpP. (3.83)
Учитывая зависимость скорости на витке орбиты ИСЗ
(2.44), равенство (3.83) можно переписать так:
Фа = SH — (1 + 2е cos и + е2) р. (3.84)
Р
Из (3.80) ... (3.82) с учетом (3.84) можно получить
. о 2 с "|/1 2^ COS О 4“ j i о
Д р = —2р2 SK f ^-f+ecosJ2 р d и; (3.85)
Д е= —2рМ Т1 + 2еcosu + (е + cosu) • рdи; (3.86)
0J (1-f-ecosu)2
Дсо = - 2f" Vl + 2е cos о + casino . (3 87)
e J (14-ecosu)2
Остается ввести зависимость для плотности атмосферы. Нас
интересует верхняя атмосфера, характерная для движения
спутников. В настоящее время существует несколько моделей
135
атмосферы Земли [21, 22, 23]. Среди них есть модели, которые
учитывают большое количество факторов, таких как время дня,
время года, период солнечной активности, географическую ши-
роту и многое другое. Но все известные модели все же явля-
ются приближенными, они содержат параметры, значения ко-
торых известны с погрешностями, да и сам характер используе-
мых функциональных зависимостей также приближенный. Су-
ществуют и вероятностные модели атмосферы. Основная вели-
чина, характеризующая атмосферу с точки зрения теории по-
лета, это ее плотность. Приведем зависимость плотности от
геометрической высоты над поверхностью Земли [22]
р = аоехр[ах—a2(h—а3)|/2 ], (3.88)
где а0, ..., а3 — коэффициенты модели, которые являются
функциями индекса солнечной активности и геометрической
высоты Л, измеряемой от поверхности земного эллипсоида.
Отметим, что подсчет h как высоты над поверхностью сфе-
рической Земли может привести для низких спутников к очень
существенным ошибкам. В [23] предлагается более, сложная
модель плотности, отличная от зависимости (3.88) несколькими
множителями, являющимися функциями звездного времени,
гринвичских координат, прямого восхождения и склонения-
Солнца. Существуют и другие аппроксимационные зависимости
плотности верхних слоев атмосферы.
В [62] показано, что если модель плотности принять в виде
Р = Рое-кТ/л-\ (3.89)
где ро, х, йо — некоторые постоянные, то, используя (3.87),
можно доказать: векового ухода аргумента перицентра от аэро-
динамических возмущений нет. Соотношения для оценки веко-
вого ухода фокального параметра и эксцентриситета, исполь-
зующие разложение по степеням эксцентриситета, представле-
ны в [12, 9, 62].
Выражения для оценки вековых уходов существенно упро-
щаются, если рассматривать уходы оскулирующих элементов
на круговой орбите
Др = -^- = — 4л5кр2ря; Де=~=0,
dN dN
где рл — плотность в перигее оскулирующей орбиты.
Простой вид имеет при этом и вековое возмущение периода
оскулирующей орбиты:
ДТ=—^5КР5/2РЯ. (3.90)
136
Очень важным в связи с аэродинамическими возмущениями
представляется вопрос о времени существования спутника.
Аэродинамическое сопротивление, совершая работу, умень-
шает энергию ИСЗ. Спутник переходит на все более низкие
орбиты. Это строго следует из анализа Др в выражении, на-
пример (3.85).
Вековые приращения эксцентриситета тоже имеют отрица-
тельные значения (3.86). Объясним физику этого явления.
Пусть ИСЗ движется по сильно вытянутой эллиптической ор-
бите. При этом самое большое лобовое сопротивление будет в
перицентре орбиты (см. с. 101). Действительно, ведь аэроди-
намическое торможение на высоте 400 км на два порядка ни-
же, чем на высоте 200 км. Отсюда следует, что в первом при-
ближении можно считать, что спутник испытывает импульсное
торможение в районе перигея орбиты, а на остальной части ор-
биты сопротивление сравнительно мало. Но если воспользо-
ваться такой моделью аэродинамического воздействия, то при-
ходим к следующему эффекту. Перигей орбиты ИСЗ практи-
чески не будет изменяться, и в нем спутник, тормозя, будет
переходить на орбиту с меньшей большой полуосью и меньшим
апогеем. Последовательность таких оскулирующих орбит ил-
люстрирована на рис. 3.11. На нем качественно показаны три
последовательных оскулирующих витка траектории ИСЗ (I, II,
III). Перигей орбиты не изменяется. Апогей существенно пони-
жается. Разумеется, эксцентриситет такой орбиты уменьшает-
ся. С некоторой неточностью можно утверждать, что эксцент-
риситет ИСЗ вследствие аэродинамического торможения стре-
мится к нулю. При этом размер орбиты уменьшается до вели-
чины, при которой спутник не может выполнить ни одного
оборота вокруг Земли, входит в плотные слои атмосферы и
прекращает свое существование как спутник (это соответству-
ет высотам порядка 135 км).
Вопрос о времени существования спутника решается с по-
мощью численного интегрирования дифференциальных уравне-
ний его движения, при этом ис-
пользуются самые современные мо-
дели атмосферы [23]. К такой до-
статочно трудоемкой операции ста-
раются не прибегать на ранних
этапах проектирования. Очень по-
могают приближенные аналитиче-
ские зависимости, а также за-
висимости, построенные на основа-
нии многочисленных исследований
рке. 3.11. Влияние аэродинами-
ческих возмущений на положе-
ния апогея орбиты спутника
и расчетов, представленных в виде
диаграмм. Использование таких за-
висимостей часто позволяет прове-
137
сти качественный анализ. С зависимостями можно познакомить-
ся в [9; 12; 62].
Таким образом, в разделе был рассмотрен характер веко-
вых уходов оскулирующих элементов орбиты ИСЗ, вызывае-
мых аэродинамическими возмущениями, проанализирован воп-
рос о времени существования спутника.
3.6. ВОЗМУЩЕНИЯ ОРБИТЫ ИСЗ, ВЫЗЫВАЕМЫЕ
ВЛИЯНИЕМ ЛУНЫ И СОЛНЦА
Возмущающее ускорение, вызванное влиянием Луны
и Солнца, достаточно строго описано в разд. 3.1. Для того
чтобы воспользоваться общим подходом к анализу вековых
возмущений с помощью системы для оскулирующих элементов,
например в виде (3.62), необходимо получить проекции возму-
щающего ускорения (Т, S, W) на орбитальные оси. Такие про-
екции найдем для каждого возмущающего тела (отдельно от
Луны, отдельно от Солнца), получим возмущающее воздейст-
вие на ИСЗ этих тел, а общий эффект возмущения найдем
как сумму отдельных возмущений.
Для простоты описания возмущенного движения выберем
основную координатную плоскость, совпадающую с плоскостью'
движения возмущающего тела относительно Земли. При иссле-
довании возмущения от Луны такой плоскостью является плос-
кость орбиты Луны. Именно от этой плоскости (а не от эквато-
риальной плоскости) в этом разделе будем измерять наклоне-
ние орбиты спутника и другие элементы его орбиты. Для по-
лучения возмущений элементов орбиты в экваториальной сис-
теме координат придется прибегать к тригонометрическим пре-
образованиям (рис. 3.12).
Положение возмущающего тела относительно восходящего
узла орбиты ИСЗ зафиксируем углом BCD, обозначим его т].
Относительное угловое положение ИСЗ и возмущающего тела
характеризуем углом DCA. Обозначим его ср.
Рис. 3.12. Положение радиуса-вектора
возмущающего тела относительно плос-
кости траектории спутника:
С — центр Земли; ху — плоскость движения
возмущающего тела относительно Земли;
CD — единичный вектор, характеризующий по-
ложение возмущающего тела в некоторый
момент времени t; BAE — плоскость движе-
ния ИСЗ; точка А — проекция положения
спутника в момент t на сферу единичного
размера; ZxCB = Q — долгота восходящего уз-
ла орбиты спутника относительно плоскости
орбиты возмущающего тела; ZDBA = i — на-
клонение орбиты ИСЗ по отношению к той
же плоскости
138
Отметим дополнительно, что сферический треугольник ABD
в общем случае не прямоугольный. Положение плоскости ACD
определяется положением ИСЗ и возмущающего тела.
Возмущающее ускорение принадлежит плоскости DCA
(плоскости, которой в этот момент времени принадлежит и
ИСЗ, и возмущающее тело). Это_следует, например, из выра-
жения возмущающего ускорения Ф в виде b—с (3.16). Дейст-
вительно, вектор b направлен по радиусу-вектору возмущаю-
щее тело — ИСЗ, вектор с направлен по направлению CD.
Оба эти направления принадлежат плоскости DCA.
Можно показать, что проекции возмущающего ускорения Ф
на оси орбитальной системы координат [62] будут следующи-
ми:
Т = — Зр,7- — cos ср; (cos т]; sin щ — cos tij sin т]j cos ij)-f
S = Hj—!— (3 cos2 cp;— 1); (3.91)
4
IF = 3pj — sin ij sin cos cpj,
где индекс j характеризует возмущающее тело, например j =
= 1 — возмущения от Луны, / = 2 — возмущения от Солнца (в
общем случае можно было рассматривать возмущения от дру-
гих небесных тел); — гравитационный параметр возмущаю-
щего тела; г — длина радиуса-вектора ИСЗ (относительно Зем-
ли); rj — длина радиуса-вектора возмущающего тела относи-
тельно Земли; ц?- — аргумент широты спутника относительно
плоскости орбиты возмущающего тела (угол ВС А на рис. 3.12).
Для нахождения приращений оскулирующих элементов за
виток траектории ИСЗ допустимо считать, что положение воз-
мущающего тела (угол т]) за виток траектории изменяется сла-
бо. Действительно, простые расчеты показывают, что для кру-
говой орбиты с радиусом, меньшим 8000 км, за один оборот
спутника угол т] для Луны изменяется на Aqi<lo, а для Солн-
ца на Дт]2<0,1°. Для высоких орбит эти значения существен-
нее. Так, при г = 40000 км Дт]1«12°, Аг]2~10. Но и эти значе-
ния таковы, что для оценки возмущений за виток траектории
ИСЗ можно положить т] =т]Ср = const.
Осреднение по витку траектории ИСЗ, проводимое в соот-
ветствии с общим подходом к анализу вековых возмущений
(см. разд. 3.3), приводит к следующим результатам [62].
Общий вид приращений за виток оскулирующих элементов
орбиты из-за влияния Луны, Солнца и других небесных тел
следующий:
139
,ка
ке
AQ
A i
\Ды
/ 0
I f2(e, т], ю, г)
= q fa (?, Т]> ®- О
I ft (е, л, ®, z)
\/5(е, т], to, i)
(3.92)
В последней системе использовано приращение большой
полуоси а вместо чаще всего нами рассматриваемого оскули-
рующего элемента — фокального параметра. Это сделано из-за
того, что векового возмущения большой полуоси орбиты спут-
ника (из-за лунно-солнечных возмущений) нет.
Параметр £ в этих отношениях определяется массами цент-
рального М3 и возмущающего Mj тел, большой полуосью орби-
ты спутника а, удалением возмущающего тела от центрально-
го г у.
t Mj
м0
(3.93)
Отметим, что чаще всего полагают, что Гу не изменяется по
времени, при этом для Луны принимают, что
5«0,56-10-7 ( £1^11 У
\ 6378 )
для Солнца
1Е « 0,26-10-7 ( LWy.
l' \ 6378 )
Входящая в правые части системы (3.92) угол г| характе-
ризует положение возмущающего тела (см. рис. 3.12). На вит-
ке траектории спутника он считается неизменным. При иссле-
довании орбиты спутника на больших временных интервалах
появляется целесообразность оценки возмущения орбиты спут-
ника за время полного оборота возмущающего тела относитель-
но центрального Ту. За это время угол г| изменится от т|0 до
г|о + 2л:. Имея это в виду, приращения оскулирующих элемен-
тов орбиты спутника за период обращения ИСЗ Тсп, представ-
ленные равенствами (3.92), можно рассматривать длиннопе-
риодическими, а вековыми считать возмущения орбиты за ви-
ток траектории возмущающего тела. Чтобы получить такие
вековые уходы, нужно просуммировать приращения из (3.92)
за время Ту. Такое суммирование можно провести следующим
образом.
Пусть &g — приращение произвольного элемента. Тогда
вековой уход этого элемента за время Ту будет
Д£в
1 Ту
2тс Тсп
Т]о+2Л
j А £<*?]•
Ло
(3.94)
140
Множитель —— равен числу оборотов спутника за время
Тсп
полного оборота возмущающего тела относительно централь-
ного.
Осуществляя интегрирование в соответствии с (3.94) для
приращений элементов орбиты, описанных равенствами
(3.92), можно получить [62] выражения для вековых уходов
элементов за время полного оборота возмущающего тела:
Дав = °;
Дев = е Y1 — е sin2 i sin 2со;
4 Тсп
ДЙВ =----I -7 n (1 — e2 + 5e2 sin2 co) cos i- (3.95)
2 у 1 e2 Ten
Д iB =---— В 7ne sin 2i sin 2co;
8 yi^T2 Tcn
Д(0в = ——Tj Г (cos2/ — 1 -F (?2) sin2 G) + —(1—e2)l.
2 Vl-e2 Ten L 5 J
Численный анализ возмущений, подсчитанных по (3.92) и
(3.95), дают следующие результаты [62]. Для орбиты ИСЗ с
большой полуосью а = 7350 км и эксцентриситетом е = 0,1 при-
ращение угловых элементов орбиты за один виток орбиты спут-
ника не превышает 0,29". Приращение за это время эксцентри-
ситета меньше 2-Ю-7.
Такому малому приращению эксцентриситета соответствует
возмущение перигея орбиты порядка 1,5 м.
При численной оценке возмущений за один оборот возму-
щающего тела максимальное приращение среди угловых эле-
ментов имеет аргумент перигея, который за счет возмущающе-
го влияния Солнца за год изменяется на Дсовс~ 11,3х. Отме-
тим, что за это время наклонение орбиты очень мало возму-
щается Д/в.с~2,4". Аналогичное влияние Луны из-за меньшего
периода ее обращения относительно Земли существенно мень-
ше солнечного:
ДЙВ л < 34"; Д(ОВ Л<2'; Д/в>л«0,43".
Оценка векового ухода эксцентриситета орбиты спутника
следующая:
Девс^2,ЗЬ10-4 ; Д ев л 0,41 • 10~4 .
Такие приращения эксцентриситета соответствуют годово-
му приращению перигея рассматриваемой орбиты ИСЗ поряд-
ка 5,1 км.
Если рассматривать очень высокие орбиты ИСЗ, то возму-
щающее воздействие Луны и Солнца будет значительней.
141
Итак, рассмотрены вековые уходы оскулирующих элементов
орбиты ИСЗ, вызываемые гравитирующим воздействием Лу-
ны и Солнца, приведена численная оценка таких возмущений.
Таким образом, нами рассмотрены основные возмущающие
факторы, влияющие на движение ИСЗ и возмущенное воздей-
ствие их на элементы орбиты спутников.
3.7. ТРАССА СПУТНИКА. ВЫБОР ОРБИТЫ ИСЗ
В настоящем разделе будет введено понятие трассы
спутника, проведен анализ трасс ИСЗ и их зависимости от
элементов орбиты спутника, а также охарактеризованы орбиты
спутников различного назначения.
Проекция положения спутника Земли на ее поверхность на-
зывается подспутниковой точкой. Совокупность подспутниковых
точек есть трасса спутника.
Положим, что Земля есть шар. Тогда подспутниковая точка
есть точка, в которой радиус-вектор спутника пересекает по-
верхность Земли. Если считать траекторию спутника невозму-
щенной, то его орбита принадлежит невращающейся плоскос-
ти, проходящей через центр Земли. В этих условиях, если бы
Земля не вращалась вокруг своей оси, делая один оборот в
сутки, то трассой спутника был бы большой круг, по которому
плоскость орбиты спутника пересекала бы поверхность Земли.
Вращение Земли приводит к существенной деформации трас-
сы спутника. Чтобы выявить закономерности трассы спутника,
рассмотрим ту меридиональную плоскость, которая перпенди-
кулярна плоскости орбиты ИСЗ (рис. 3.13).
Спутник, двигаясь по орбите, проходит восходящий узел,
при этом его географическая широта (так же как и широта
подспутниковой точки) равна нулю. Затем географическая и
геоцентрическая широта спутника и подспутниковой точки уве-
личиваются, достигая максимального значения в точке макси-
мального возвышения спутника над плоскостью экватора. В
этой точке аргумент широты равен 90°, а геоцентрическая ши-
рота спутника равна наклонению орбиты спутника. На рис.
3.13 точка В — положение спутника в момент максимального
возвышения. Геоцентрическая широта спутника есть ВСЕ.
Рис. 3.13. След плоскости траектории
спутника при анализе его трассы:
Зкватор
С — центр Земли; АВ — след плоскости орби-
ты ИСЗ (сама плоскость орбиты перпендику-
лярна плоскости рисунка); точка В—точка
наибольшего возвышения спутника относи-
тельно плоскости экватора, след которой есть
СЕ; n и S -- географические полюсы Земли.
Наклонение нарисованной орбиты пусть ха-
рактеризуется углом BCE = i (i<90°)
142
Этот угол равен наклонению орбиты спутника Л На этом же
рисунке BCi — перпендикуляр к поверхности Земли в точке
Pi, а угол ВС\Е есть географическая широта спутника в точ-
ке В. Если рассматривать Землю как шар, то нет разницы
между геоцентрической и географической широтами. В даль-
нейшем будем пользоваться понятием геоцентрической широты,
а подспутниковой точкой будем считать точку D на радиусе-
векторе спутника СВ. Геоцентрическая широта спутника ср и
геоцентрическая широта подспутниковой точки <рТр при этом
будут совпадать, т. е. в любой момент времени
Фтр(0=ф(0- (3.96)
После того, как спутник достиг максимального возвышения
над плоскостью экватора и его геоцентрическая широта стала
равна наклонению орбиты г, геоцентрическая широта начнет
уменьшаться. Таким образом, максимальной широтой спутника
и подспутниковой точки оказывается значение I. Когда спут-
ник, пройдя нисходящий узел орбиты, окажется в южном по-
лушарии, аналогично можно будет показать, что максимальная
южная широта спутника и его подспутниковой точки есть
опять i.
Таким образом, трасса спутника оказывается некоторой
кривой на поверхности Земли, лежащей в широтном поясе [—г,
-Н’], если г<л/2. Спутник не может появиться над точками по-
верхности Земли с широтой, большей г, т. е. при г<л/2 суще-
ствуют полярные области, ни одна точка которых никогда не
может быть подспутниковой. Эти зоны на рис. 3.13 заштрихо-
ваны. Незаштрихованный на рисунке широтный пояс состоит
из точек, которые могут быть подспутниковыми и могут войти
в состав трассы, если временное движение спутника по орбите
и суточное вращение Земли приведут к этому.
Отметим, что если />л/2, то также существуют аналогич-
ные полярные зоны, над которыми спутник не может проле-
теть, а подспутниковые точки принадлежат широтному поясу
[г—л, л—г].
Зависимость (ртр(^тр), определяющая трассу спутника, час-
то имеет синусоидальный вид на развертке поверхности Земли.
Рассмотрим качественный характер зависимости. Для опреде-
ленности проанализируем трассу низкого кругового спутника
с периодом обращения спутника по орбите, существенно мень-
шим 24 ч. (Напомним, что возможное значение периода орби-
ты спутника больше 86 1/3 мин.) Наклонение орбиты i для оп-
ределенности будем полагать меньшим л/2.
В какой-то момент времени t1 спутник находится в восхо-
дящем узле орбиты и координаты его подспутниковой точки
будут
Фгр (^i) — Хтр — X*.
143
Через четверть оборота спутник окажется в точке с макси-
мальным возвышением над плоскостью экватора. Геоцентриче-
ская широта спутника в этот момент будет равна I. После про-
хождения этой точки спутник начнет приближаться к плоскос-
ти экватора и еще через четверть витка попадет в нисходящий
узел орбиты. В момент Л4-Т/2 геоцентрическая широта спут-
ника и его подспутниковой точки окажется нулевой.
На следующей половине витка траектории спутник достиг-
нет максимальных южных широт (в этот момент фтр = —0 и
затем, закончив виток траектории, попадет в восходящий узел.
Если пренебречь возмущением долготы восходящего узла, ко-
торое может иметь место из-за нецентральное™ гравитацион-
ного поля Земли и влияния Луны и Солнца, то положение
восходящего узла в инерциальном пространстве не изменится.
Но положение подспутниковой точки изменится в общем слу-
чае весьма существенно. Это произойдет из-за суточного вра-
щения Земли. Спутник, сделав виток траектории с точностью
до возмущений, попадает в ту же точку в инерциальном прост-
ранстве, а Земля за это время повернулась и «подставила» под
спутник другую свою точку. Таким образом, через виток тра-
ектории (в момент Л + Т) координаты подспутниковой точки
окажутся следующими:
Фтр (^i + Т) = 0; Хтр (/х + Т) = X* — (о3 Т.
На рис. 3.14 на развертке поверхности Земли качественно
представлена трасса спутника на двух витках траектории. Это
кривые, смещенные одна относительно другой на величину о)3Т
(на тот угол, на который поворачивается Земля за время од-
ного оборота спутника).
Если рассмотреть трассу спутника, двигающегося по некру-
говой орбите, картина несколько изменится. В районе апогея
орбиты угловая скорость радиуса-вектора спутника уменьша-
ется, что приводит к искажению синусоидальной зависимости,
представленной на рис. 3.14. Чтобы пояснить картину таких ис-
Рис. 3.14. Трасса спутника на двух
витках траектории на развертке по-
верхности Земли
Рис. 3.15. Часть трассы спутника, ор-
бита которого имеет большой эксцен-
триситет, а аргумент перигея равен
270°
144
кажений, можно рассмотреть сильно вытянутую орбиту с
очень большими значениями апогея (га). Угловая скорость ра-
диуса-вектора спутника в апогее может оказаться меньше уг-
ловой скорости суточного вращения Земли. При этом Земля в
своем вращении будет обгонять спутник, на трассе появятся
так называемые «петли». На рис. 3.15 представлена качествен-
ная картина трассы на одном витке траектории спутника с
большим эксцентриситетом орбиты, апогей которой находится
в северном полушарии и совпадает с точкой максимального
возвышения над плоскостью экватора (в этой точке аргумент
широты равен 90°). Аргумент перицентра орбиты равен 270°.
Если спутник запущен на экваториальную орбиту, то под-
спутниковыми точками такого спутника могут быть только
точки экватора. В общем случае трассой экваториального
спутника является весь экватор. Действительно, спутник, нахо-
дясь на низкой экваториальной орбите, проходит над всеми
точками экватора, так как угловая скорость его радиуса-векто-
ра больше угловой скорости Земли. Так, спутник, имеющий пе-
риод вращения 90 мин, шестнадцать раз успевает обогнуть
Землю по экватору, в то время как Земля сделает всего один
оборот. Если спутник находится на круговой экваториальной
орбите, то подспутниковая точка равномерно движется по эк-
ватору. Если орбита эллиптическая, то подспутниковая точка
движется неравномерно.
Очень интересной для практики оказалась так называемая
геостационарная (или просто стационарная) орбита. Это эква-
ториальная круговая орбита, период обращения которой равен
периоду обращения Земли вокруг своей оси. Найдем радиус
такой орбиты. Приравнивая выражение для периода обращения
спутника периоду вращения Земли (Т=1 звездные сутки =
= 86 164 с = 23ч 56 мин 4 с), получим
/>3/2 __ Т*
УТ ~ ’
откуда
ГУТ гг*'|2/3 3/“398602 км3/с2861642 с2
а = Уг- т =1/ ----------------й“2---------= 42164 км.
I- 2л J г 4л2
Таким образом, спутник, находясь на круговой экватори-
альной орбите с радиусом 42 164 км (высотой над поверхностью
Земли ~35 786 км), будет «висеть» над одной точкой эквато-
ра, так как угловые скорости радиуса-вектора спутника и Зем-
ли совпадают. Понятно, что если запустить спутник на обрат-
ную экваториальную орбиту (f= 180°), то подспутниковая точ-
ка будет облетать весь земной экватор независимо от радиуса
орбиты. В этом случае направления вращения спутника и Зем-
ли противоположны.
145
Весьма интересны формы трасс спутников, орбиты которых
имеют большую полуось 42 164 км, но не круговые.
Так, если такой спутник экваториальный, то его трассой яв-
ляется отрезок экватора. Это происходит из-за того, что дви-
жение спутника неравномерно: на части витка угловая скорость
его радиуса-вектора превышает угловую скорость Земли ш3, на
другой части витка — меньше со3. Поэтому в определенный мо-
мент спутник «обгоняет» Землю, а затем Земля «догоняет»
спутник. Так как периоды обращений совпадают, то это при-
водит к повторению цикла на одном отрезке экватора.
Если рассмотреть трассы суточных спутников (спутников,
период которых равен суткам) с наклонением, несколько от-
личным от нуля, то окажется, что трасса их имеет форму вось-
мерки, перекрестие которой расположено в некоторой точке
экватора. При этом максимальная широта подспутниковой точ-
ки (высота восьмерки) равна наклонению плоскости орбиты
спутника.
Выбор орбиты ИСЗ
Выбор орбит запускаемых ИСЗ осуществляется с
учетом большого числа факторов. К этим факторам относятся
условия старта и прежде всего географические координаты
космодромов, которые могут быть использованы для старта
ракет-носителей, возможные азимуты старта, положение на
земной поверхности пунктов контроля и наблюдения и т. д. Но
основным фактором, во многом определяющим выбор орбиты
ИСЗ, является назначение спутника. При классификации спут-
ников по назначению нужно иметь в виду, что большое коли-
чество спутников неспециализированы и выполняют широкий
спектр работ. К таким спутникам чаще всего относятся науч-
но-исследовательские спутники, например спутники серии «Кос-
мос». Остановимся на нескольких широко используемых систе-
мах спутников, имеющих специализированное назначение.
Спутники связи в настоящее время очень широко эк-
сплуатируются в мире. Их задача — ретранслировать информа-
цию от передающего пункта, находящегося на поверхности Зем-
ли, к пунктам ее приема на поверхности Земли. При наиболее
простой схеме такой ретрансляции спутник в течение всей пе-
редачи должен находиться в зоне видимости (радиовидимос-
ти) передающего и приемных пунктов. Поэтому при выборе
орбиты спутника связи должен быть прежде всего решен воп-
рос о достаточной радиовидимости спутника или лучше систе-
мы спутников. В нашей стране система спутниковой связи в
течение длительного времени опиралась на спутники «Мол-
ния», которые до сих пор используются, в частности для пере-
дачи телевизионных программ в системе «Орбита» и обеспече-
146
ния эксплуатации дальней телефонно-телеграфной радио-
связи.
Орбита спутника «Молния-1» является сильно вытянутой
эллиптической орбитой с периодом, равным половине суток
(~12 ч). Высота перигея спутника выбирается малой, но обес-
печивающей малые аэродинамические возмущения, — 500 км.
Высота апогея при этом составляет порядка 40 000 км. Такие
значения высот апогея и перигея обеспечивают период 12 ч.
Наклонение орбиты спутника «Молния-1» выбирается 63,5°.
Такое положение обеспечивает отсутствие векового ухода ли-
нии апсид (положения перигея орбиты относительно экватори-
альной плоскости), связанное с нецентральностью гравитаци-
онного поля Земли, точнее, связанное со сжатием Земли. Спут-
ник запускается так, чтобы аргумент перицентра его орбиты
был равен 270°, при этом перигей орбиты оказывается в юж-
ном полушарии, а апогей — в северном полушарии. То, что
апогей находится в северном полушарии и не имеет векового
ухода, обеспечивает длительное нахождение спутника в север-
ном полушарии. Из 12 ч своего периода 11 ч он находится в
районе своего апогея (свойство сильно вытянутой орбиты),
при этом он смещается по долготе не более чем на 10°. Имен-
но это свойство и используется. Положение орбиты в прост-
ранстве (долгота восходящего узла) выбирается так, чтобы в
районе апогея спутник находился в зоне радиовидимости пе-
редающего пункта и приемных пунктов на территории СССР.
Большая высота апоцентра обеспечивает при этом радиовиди-
мость спутника с очень значительной части земной поверхнос-
ти, включая полярные районы. Продолжительность сеансов
связи между пунктами зоны видимости для одного спутника за
сутки может достигать 8 ч. Дело в том, что если на первом
витке траектории спутник находится в апогее над восточным
полушарием и обеспечивает устойчивую связь между точками
территории СССР, то на втором витке траектории в апогее
своей орбиты спутник находится над западным полушарием.
Действительно, за 12 ч спутник делает полный оборот и при-
ходит в ту же апогейную точку, но Земля за это время делает
половину оборота и «подставляет» под спутник точку западно-
го полушария. Так что из двух оборотов спутника только один
оборот (вернее его часть) рабочий. Отсюда становится понят-
ным, почему период обращения спутника «Молния» выбран
12 ч. Через два витка траектории спутник оказывается над
той же точкой поверхности Земли, над которой находился 24 ч
назад. Это дает возможность использовать конкретный спут-
ник в конкретное время суток, например, с 12 ч дня до 8 ч
вечера по московскому времени. Если создать систему спутни-
ков, то возможно обеспечивать постоянную в течение суток
связь на значительной части территории СССР.
147
В настоящее время в нашей стране запущено более 70
спутников «Молния-1» (26 декабря 1986 г. запущен 71-й спут-
ник), более 30 спутников «Молния-3» (22 января 1987 г. запу-
щен 31-й спутник). Система «Орбита» была введена в дейст-
вие в 1967 г. Отметим, что система «Орбита» оказалась очень
рациональной для нашей северной страны. Развитие спутнико-
вой техники позволило в 1976 г. ввести в СССР новую систему
спутниковой связи на базе спутников, находящихся на стацио-
нарных орбитах. В настоящее время в СССР на стационарную
орбиту запускаются спутники серии «Радуга» (22 октября
1986 года запущен 18-й спутник серии), «Экран» (22 марта
1985 года запущен 14-й спутник), «Горизонт» (13 ноября 1986
года запущен 13-й спутник). Эти спутники широко применяют-
ся для передачи телевизионных программ на сеть станций «Ор-
бита», «Москва», «Интерспутник», кроме того, служат для свя-
зи с судами и самолетами при помощи дополнительных ретран-
сляторов. Введением таких систем, включающих мощные бор-
товые ретрансляторы, использованием остронаправленных пе-
редающих антенн удалось существенно упростить и удешевить
приемные установки коллективного пользования и значительно
увеличить площадь территории СССР, на которой можно вести
устойчивый прием нескольких телевизионных программ. Спут-
никовый ретранслятор, расположенный на большой высоте над
Землей, способен одновременно обслуживать до 1/3 поверхнос-
ти Земли. При этом для создания почти глобальной спутнико-
вой системы связи достаточно поместить три спутника на ста-
ционарную орбиту со смещением один относительно другого на
120° (рис. 3.16). Потребности в каналах связи приводят к
очень плотному «заселению» стационарной орбиты. В настоя-
щее время на стационарной орбите находятся спутники мно-
гих стран. С помощью собственной ракеты-носителя запуск
спутников на стационарную орбиту проводят США, СССР,
Японии, КНР, а также западно-европейская организация ЕСА.
Чтобы охарактеризовать размах использования систем спутни-
ковой связи, можно отметить, что 8 февраля 1985 г. с помощью
ракеты «Ариан-3» выведен на стационарную орбиту спутник
«Арабсат» для системы спутниковой связи 21 арабской страны,
а также спутник «Бразилсат». При этом Бразилия стала 17-й
страной, обладающей собственным ИСЗ. Надо отметить, что
разработка и изготовление последнего спутника выполнялись
канадской фирмой.
Отметим также, что возмущающие факторы приводят к
сдвигу геостационарного ИСЗ по долготе, а также к изменению
наклонения орбиты на 0,9° в год. Изменение наклонения орби-
ты приводит к появлению трассы спутника в виде восьмерки,,
размах которой с севера на юг равен наклонению орбиты. В
том случае, когда период активного существования спутника
148
большой, приходится периодически вклю-
чать двигатели коррекции. При этом кор-
рекция наклонения орбиты требует боль-
шего расхода топлива, чем коррекция
долготы точки стояния. Стационарная
орбита становится в настоящее время
самой «населенной», поэтому в даль-
нейшем, возможно, придется исполь-
зовать орбиты с периодом обращения
12, 8 и 6 ч. Орбиты с таким перио-
дом обращения называются синхрон-
ными, так как через несколько виткоё
(через 24 ч) спутник оказывается над
той же точкой поверхности Земли, и его
трасса — замкнутая кривая. Использо-
Рис. 3.16. Схема возмож-
ной глобальной космиче-
ской связи с помощью
трех стационарных спут-
ников
вание синхронных экваториальных ор-
бит менее удобно не только из-за того, что спутник не висит
над одной точкой экватора, но и из-за меньшего охвата терри-
тории Земли вследствие меньшей высоты их полета. Практи-
ческого применения такие орбиты еще не нашли, а количество
спутников, выводимых на стационарную орбиту, все возраста-
ет и составляет очень значительный процент от всех выводи-
мых в настоящее время спутников.
Метеорологические спутники в настоящее вре-
мя используются очень широко. Все мы привыкли к тому, что
в телевизионной информационной программе «Время» нам по-
казывают снимки облачного покрова Земли, переданные со
спутников серии «Метеор». Именно спутник в настоящее вре-
мя дают возможность получать информацию об атмосфере и
всей поверхности Земли, анализировать и прогнозировать ус-
ловия погоды над Мировым океаном и районами стран с ред-
кой сетью наземных метеорологических станций. Существую-
щие в настоящее время на земном шаре около 10 000 метеоро-
логических станций не позволяют решить задачу глобального
анализа погодных условий по всей поверхности Земли, что дос-
таточно уверенно делают спутниковые системы.
При выборе орбит метеорологических спутников учитывает-
ся положение районов Земли, с которых необходимо снять ин-
формацию, потребная широта полосы обзора, разрешающая
способность всех видов бортовой научной аппаратуры. Можно
указать несколько условий, которым должны удовлетворять ор-
биты метеорологических спутников. Эти спутники или значи-
тельная часть спутников из всей системы должны иметь воз-
можность обозревать всю Землю, включая полярные области
Земли. Такому условию удовлетворяют только полярные и при-
полярные орбиты.
149
Достаточно важным представляется условие одномасштаб-
ности тех снимков, которые передаются с метеоспутника. Оди-
наковый масштаб снимков упрощает их обработку, увеличива-
ет оперативность анализа. Для того чтобы выполнить это тре-
бование, достаточно орбиту метеоспутника сделать круговой
или околокруговой. При этом, в какой бы точке орбиты спут-
ник не находился, его высота над поверхностью Земли и ее
облачным покровом одинакова, и масштабность получаемой
метеоинформации постоянна.
И, наконец, последнее условие, которое нужно учитывать
при выборе орбит метеоспутников. Высота полета ИСЗ важна
для получения метеоинформации. С одной стороны, чем боль-
ше высота, тем больше полоса обзора поверхности Земли, но,
с другой стороны, меньше разрешающая способность бортовой
аппаратуры. При этом выбор высоты полета каждый раз дол-
жен решаться совместно с техническими трудностями, возни-
кающими при совершенствовании аппаратуры для увеличения
ее разрешающей способности.
Отработка отдельных устройств для метеорологических
ИСЗ проводилась в нашей стране еще в период 1963... 1964 гг.
на ИСЗ «Космос-14» и «Космос-23». Первая метеорологическая
информация была получена с ИСЗ «Космос-122», орбита кото-
рого была околокруговой с высотой 650 км и наклонением 65°.
В дальнейшем использовалась орбита с наклонением около
81,2°. Указанная высота дала возможность проводить покадро-
вую съемку (освещенной облачности и земной поверхности) по-
лосы шириной около 1100 км. Для ночной (неосвещенной) сторо-
ны Земли при получении метеоинформации используется инф-
ракрасный диапазон. Разрешающая способность инфракрасной
аппаратуры была в шестидесятых годах существенно хуже те-
левизионных камер и поэтому «просматриваемая» ночная по-
лоса была существенно уже.
Начало советской метеосистемы «Метеор» положили запу-
щенные в 1967 году спутники «Космос-144» и «Космос-156». Их
орбиты имели наклонение 4 = 81,2°, высоту 630 км и период об-
ращения 97 мин. С 1969 г. эта система стала пополняться
спутниками, имеющими названия «Метеор», с 1971 г. изменена
высоты полета запускаемых спутников этой системы (h= 900 км).
Восполнение системы спутников «Метеор» проводилось
так, чтобы в ее составе постоянно находились два-три рабо-
тающих ИСЗ, передающих информацию на сеть наземных
пунктов приема, обработки и распространения информации по
всей территории СССР. С 1975 г. в СССР стали запускаться
усовершенствованные спутники «Метеор-2». 5 января 1987 г.
осуществлен запуск очередного (15-го) оперативного ИСЗ «Ме-
теор-2». Аппаратура такого спутника обеспечивает получение
глобальных изображений облачности и поверхности Земли в
150
видимом и инфракрасном диапазонах, а также наблюдение за
потоками проникающих излучений в околоземном пространст-
ве. Аппаратура ИСЗ может работать как в режиме запомина-
ния, так и в режиме передачи информации на Землю.
Метеоспутник при высоте полета 900 км имеет период обра-
щения 102,5 мин. За это время Земля поворачивается вокруг
своей оси на угол (о3Т = 25,6°, что соответствует линейному сме-
щению на экваторе 2800 км и 1500 км на широте Москвы. В
то же время используемая в настоящее время телевизионная
аппаратура дает полосу обзора всего 2100 ...2200 км (кстати,
инфракрасная аппаратура, используемая сейчас, имеет ширину
полосы 2600 км). Это меньше межвиткового смещения трассы.
Следовательно, с помощью одного ИСЗ «Метеор-2» нельзя ос-
матривать всю поверхность Земли без пропусков в экватори-
альной зоне. Такой трудности не возникает, если использовать
систему двух или трех спутников, разнесенных по долготе вос-
ходящего узла.
Управление системой спутников является непростой зада-
чей. Если мы вспомним о вековых возмущениях орбиты, то ряд
причин (например, разная высота орбит) могут привести к де-
формации построенной системы спутников. Последнее может
привести к тому, что один спутник не будет дополнять инфор-
мацию другого, будет снимать те же области. Чтобы этого не
происходило, проводят коррекцию орбит спутников. Например,
на спутнике «Метеор», запущенном в 1971 году, коррекцией
орбиты с помощью ионно-ллазменного двигателя была увеличе-
на высота его полета на 16,5 км. Это позволило довести коли-
чество витков, совершаемых им в течение суток, до 14. Пос-
леднее дало возможность осуществлять съем метеоинформации
с одних и тех же районов Земли почти в одно и то же время
суток, что очень удобно для прогноза погоды и организации
работ по обслуживанию системы.
С аппаратурой спутников серии «Метеор», организацией
приема с них информации, процессом обработки информации
можно познакомиться в [58]. Там же представлена сводная
таблица характеристик запусков ИСЗ метеорологической сис-
темы «Метеор». При анализе этой таблицы обращает на себя
внимание то, что с 1977 г. в этой системе появились спутники,
имеющие наклонение около 98°. Орбита, на которую выводятся
эти спутники («Метеоры-28,-29,-30»), называется солнечно-син-
хронной (иногда гелиостационарной). Наклонение орбиты этих
спутников выбрано так, чтобы угловая скорость векового ухо-
да восходящего узла орбиты была равна угловой скорости ра-
диуса-вектора Земли относительно Солнца, т. е. была равна од-
ному обороту за год. Если это условие выполняется, то относи-
тельно направления Солнца — Земля плоскость орбиты спут-
ника оказывается примерно в одном положении. Это обстоя-
151
тельство иллюстрируется на рис. 3.17. На нем представлена ор-
бита Земли, в точке С находится Солнце, и для нескольких
положений Земли отмечен след плоскости орбиты гелиостацио-
нарного спутника. Выбран один из частных случаев такой ор-
биты, когда Солнце всегда принадлежит плоскости орбиты
ИСЗ. Ясно, что на рассмотренной орбите условия освещеннос-
ти от витка к витку строго повторяются, что дает возможность
четкого планирования метеорологической информации и наб-
людения в одно и то же местное время.
Прецессия орбиты таких ИСЗ в основном связана со сжа-
тием Земли по полюсам и зависит (3.69) от высоты орбиты и
ее наклонения. Таким
но-синхронной орбиты
Рис. 3.17. Схема процес-
сии орбиты гелиостацио-
нарного спутника
образом, величина наклонения солнеч-
выбирается в строгой зависимости от
высоты полета ИСЗ. Наклонение тем
больше, чем выше его орбита. Для
«Метеоров» высота орбиты 630—
650 км, наклон должен быть около 98°.
Для американских метеорологических
спутников НОАА, имеющих высоты ор-
бит около 1500 км, угол наклона со-
ставляет 115—116°.
Таким образом, в главе рассмотре-
на теория движения ИСЗ, проанализи-
рованы основные возмущающие фак-
торы, действующие на спутник, описа-
ны орбиты спутников различного на-
значения.
ГЛАВА 4# ДИНАМИКА И МЕТОДЫ РАСЧЕТА
ОРБИТАЛЬНЫХ СИСТЕМ
КОСМИЧЕСКИХ АППАРАТОВ
Изучение методов анализа невозмущенного движения (за-
дача двух тел, см. гл. 2) и движения искусственных спутников
Земли с учетом основных возмущающих сил (см. гл. 3) позво-
ляет перейти к рассмотрению прикладных задач расчета сис-
тем космических аппаратов. Освоение околоземного космичес-
кого пространства в научных и народнохозяйственных целях
последовательно проходило через этапы запуска и получения
информации от единичных спутников до создания систем спут-
ников — связных, метеорологических, навигационных и др. Не-
которые вопросы выбора параметров орбит единичных спутни-
ков и уже созданных и эксплуатируемых систем спутников
различного назначения кратко были рассмотрены в разделе
«Выбор орбиты ИСЗ» гл. 3.
В данной главе рассматриваются вопросы динамики и мето-
дов расчета систем спутников, которые в зависимости от кон-
кретного назначения должны иметь определенное геометриче-
ское построение как между отдельными объектами, так и отно-
сительно некоторых опорных точек земной поверхности.
4.1. КИНЕМАТИЧЕСКИЕ ЭЛЕМЕНТЫ СИСТЕМЫ
СПУТНИКОВ
Под орбитальной космической системой будем пони-
мать группу (два и более) аппаратов, взаимодействующих ме-
жду собой и наземными станциями. В соответствии с данным
определением это могут быть системы метеорологических, связ-
ных, навигационных, обслуживающих (инспектирующих, транс-
портных) спутников. В качестве -конкретных примеров (реализа-
ции спутниковых систем можно указать навигационное обеспе-
чение авиационного, морского и наземного транспорта спутни-
ковыми радионавигационными системами. Спутниковая систе-
ма позволяет за короткий интервал времени определить коор-
динаты транспортного средства с точностью нескольких десят-
ков метров. Дальнейшее развитие идей глобальной непрерыв-
ной и одномоментной навигации с помощью спутниковой систе-
мы связано с определением трех координат и трех составляю-
153
Рис. 4.1. Угловые параметры орбиты
в геоцентрической системе координат
щих скоростей, что требует
обеспечение одновременной ви-
димости в любой точке земной
поверхности 3—4 спутников
под углами над местным гори-
зонтом превышающими 7... 10°.
При этом накладываются
ограничения на условия на-
хождения спутников в раз-
ных плоскостях и на взаим-
ные углы визирования, боль-
шие 15... 20°. Примером такой
системы является сеть из 24
спутников, координированно
движущихся по круговым орби-
там, высотой 20 000 км, лежащих в трех пересекающихся пло-
скостях (по 8 спутников в каждой) с наклонением 63° [59].
Поэтому проблемами создания любой орбитальной системы,
кроме приборной реализации, являются как само орбитальное
построение системы, так и обеспечение определенной «геомет-
рии» системы и устойчивости этой системы в процессе эксплу-
атации. Более подробно с вопросами динамики и принципом
построения орбитальных систем можно ознакомиться в [5, 59].
В зависимости от конкретных задач, выполняемых данной
системой, она характеризуется определенными параметрами,
некоторые из которых в процессе функционирования изменяют-
ся. Это, в свою очередь, характеризует орбитальную -систему
как динамическую, поведению которой присущи определенные
закономерности.
Система из 7V спутников как динамическая система харак-
теризуется 7V орбитами; движение каждого спутника, в свою
очередь, определяется параметрами своей орбиты. В процессе
функционирования относительное положение аппаратов будет
зависеть от параметров орбит, начальных условий и действую-
щих сил. В качестве параметров орбит будем рассматривать
введенные в гл. 2 элементы р, е, i, Й, со, tn как функции неза-
висимой переменной времени t или аргумента широты и (рис.
4.1). Система дифференциальных уравнений, описывающих из-
менение элементов орбиты, приведена в гл. 3 [(3.44) или
(3.53)].
При наличии в орбитальной системе N спутников их коор-
динаты и составляющие скорости относительно друг друга и от-
носительно геоцентрической системы координат определяются
в общем случае совокупностью 6М функций времени:
it {t), coJZ).
Ui(t) (t= 1, 2,..., N).
154
Число функций 6N является максимальным и может быть
уменьшено, если на все или часть параметров системы накла-
дываются дополнительные кинематические ограничения (оди-
наковые взаимные угловые расстояния в плоскости орбиты,
одинаковые наклонения орбит и т. д.).
Под кинематическими элементами орбитальной системы
спутников будем понимать определенные соотношения, завися-
щие от элементов орбит спутников. Эти соотношения различны
в зависимости от конкретных задач, решаемых данной орби-
тальной системой. Ниже рассматриваются эти соотношения
для некоторых характеристик кинематических элементов.
1. Высота полета. Определим высоту полета спутника
над земным эллипсоидом в направлении геоцентрического ра-
диуса (см. рис. 4.1)
h = -Р-— ----Я3.э(1 —asin2<p), (4.1)
1 -|- е cos v
где геоцентрическая широта <р определяется по теореме си-
нусов из сферического треугольника abc
sin ф — sin и sin i,
и постоянные для референц-эллипсоида Ф. Н. Красовского рав-
ны [9]
Язэ = 6378245 м, а = —.
3 298,3
Формула (4.1) дает погрешность по высоте не более 0,1 км.
Для модели сферической Земли со средним радиусом Т?4 =
= 6371 км эта погрешность достигает 14 км.
2. Подспутниковая точка. Подспутниковая точка
(см. рис. 4.1) определяется долготой X, геоцентрической широ-
той ф или геодезической широтой фг. Названные широты связа-
ны соотношением
tg Ф = (1 —а)21§фг,
которое, с учетом малости а, может быть записано* в виде
Фг—ф = азш 2ф,
что приводит для модели сферической Земли к наибольшей
ошибке в определении координат при ф = 45° для низких орбит
порядка 2 ... 3 км.
3. Трасса спутника. Каждому моменту времени соот-
ветствует своя подспутниковая точка, а геометрическое место
этих точек образует трассу движения спутника на земной по-
верхности. Трассу можно рассчитать либо непосредственным
численным интегрированием уравнений движения в сферичес-
155
кой системе координат г, ср, К, либо преобразованием по фор-
мулам (3.42) элементов орбиты из системы (3.44).
Трасса начинается в какой-то начальный момент времени
/о, но для простоты построения и анализа трассы удобно в ка-
честве начального момента времени взять время прохождения
восходящего узла орбиты tQ. Промежуток времени между дву-
мя последовательными прохождениями плоскости эква-
тора в восходящих узлах называется драконическим пе-
риодом обращения TQ, который может быть вычислен при ин-
тегрировании системы дифференциальных уравнений (3.44),
когда аргумент широты меняется от 0 до 360°.
В общем случае алгоритм расчета трассы спутника, движу-
щегося по эллиптической орбите, приводится в разд. 3.7. Ниже
для анализа таких понятий как межвитковый сдвиг, суточный
сдвиг трассы, квазисинхронность орбит рассматриваются кру-
говые орбиты невозмущенного движения, тем более, что для
определения этих понятий в певозмущенном движении главным
является период орбиты. За независимую переменную в этом
случае естественно принять аргумент широты, линейно завися-
щий от времени. Из сферического треугольника abc следует
(см. рис. 4.1):
геоцентрическая широта sin <p = sin и sin i\
sin ab = tg cp/tg t. (4.2)
Тогда долгота подспутниковой точки в геоцентрической вра-
щающейся системе координат для произвольного момента вре-
мени равна
Х = —/д), (4.3)
где — долгота в момент прохождения восходящего узла;
(Оз — угловая скорость вращения Земли, равная 2jn/T3B; Тзв —
звездные сутки.
Разность времени можно выразить через аргумент широты
где Т — период обращения спутника по круговой орбите ра-
диуса Го
Т = 2л/^Г
Таким образом, при расчете трассы на интервале 0^и^2л
с учетом (4.2, 4.3) следует пользоваться соотношениями
ф = arcsin (sin и sin i);
— т
X = ZQ+ ab-----щ
Тзв
156
tg (p n Л
arcsin к при ;
tgi 2
tg ср л . 3
ab = J л — arcsin —— при — «< и — л;
tgi 2 2
2л—arcsin-^-2- при — л<и<2л.
tg i 2
(4-4)
Из (4.4) следует
Фтах = arcsin (sin i) при u = -^-;
Фт1п= —arcsin (sin i) при и=-|-л,
и видно, что для орбит с наклонением 0<г< —
трасса про-
ходит в широтном поясе —(рис. 4.2), а для орбит с
наклонением — <7<л—в широтном поясе
— (л — i) ф л— i.
Как следует из второй формулы (4.4), при изменении аргу-
мента широты на 360° начало трассы каждого последующего
витка смещено относительно начала предыдущего на величину
ДХВ =-----—2л,
Т3в
(4.5)
«откуда также следует, что любая точка трассы на последую-
щем витке смещена по долготе в западном направлении на од-
ну и ту же величину (см. рис. 4.2). Это смещение называется
межвитковым сдвигом и зависит только от периода обращения
орбиты. Например, для высоты круговой орбиты 284 км пери-
межвиткового сдвига составляет
Земли (звездные сутки) витки
будут каким-то образом распола-
од равен 1,о ч, и величина
22,55°.
После полного поворота
трассы последующих суток
гаться относительно витков
предыдущих суток. Если в
звездных сутках укладыва-
ется целое число периодов
обращения орбиты, то трас-
са, начиная с некоторого
витка, повторяется. В про-
тивном случае наблюдается
сдвиг по долготе, который
затем сохраняется для всех
о
О 60 120 100 240 300 Х°
Рис. 4.2. Трассы двух смежных витков
157
последующих витков предыдущих суток и называется суточным
сдвигом.
Пусть отношение звездных суток к периоду представляется
числом Тзв/Т = п, п', где п — целая часть; п' — дробная часть
числа.
Если условиться считать суточный сдвиг в западном напра-
влении, то его величина определяется формулой
Д^Сд = (1—п')ДАв. (4.6)
В каждых из последующих суток суточный сдвиг укладыва-
ется в межвитковое расстояние и может происходить таким об-
разом, что в р межвитковых расстояний укладывается q суточ-
ных сдвигов [р и q целые) и трасса повторяется через q звезд-
ных суток. Такие орбиты называются квазисинхронными. Из
них можно выделить класс орбит, для которых отношение
Тзв/Т является целым числом п. Высота этих орбит вычисляет-
ся по формуле
/1 = (Дзв_у/3 и1/з_/?з) (4.7)
\ 2п jt /
примеры расчета по которой показывают, что для количества
витков /г=16, 12, 10, 1 высоты круговых орбит составляют со-
ответственно Л = 269, 1673, 2713, 35 793 км.
Отметим еще раз, что соотношения (4.2—4.7) и числовые
данные справедливы только для невозмущенного движения.
Эффекты от возмущений вследствие нецентральности поля тя-
готения Земли рассматриваются ниже.
Проведенный анализ для круговых орбит с точки зрения
свойств трассы по межвитковому и суточному сдвигу справед-
лив и для эллиптических орбит, так как единственным парамет-
ром, определяющим рассмотренные эффекты, является период
обращения.
4. Зона обзора на поверхности. Зона обзора ф
может определяться как максимальной величиной телесного
угла обзора аппаратуры спутника 6, так и минимальной вели-
чиной угла места над горизонтом у (рис. 4.3). Зона обзора
представляет собой сферический круг, граница (окружность)
которого видна со спутника под углом 6 или спутник виден из
каждой точки границы под углом места у.
Предельный угол обзора, соответствующий у = 0, находится
из прямоугольного треугольника ОсЬ
4’“ = arc“s(' (4-8)
а для отношения в расчетах может использоваться бо-
лее простая формула
^n^V2h/Ra.
158
Рис. 4.3. Зоны обзора Рис. 4.4. Полоса обзора
При условии ограничения на величины углов у>0 и б<
<л/2—фп зона обзора находится из треугольника Odb
Из данного треугольника также следует, что
/?3 + Я3
откуда можно получить зависимости между углами б и у
/ D X / D t X
б = arcsin ----5 cos у I; у = arccos ——---------sin б V
\ Кз + h ) \ Яз )
Таким образом, при заданных высоте h и угле места у зо-
на обзора определяется формулой
ф = ——у — arcsin f cosy^ . (4.9)
2 \ /?3 + ft J
5. Зона обзора на фоне космоса. Зона обзора на
фоне космоса определяется как поверхность усеченного шаро-
вого сегмента (см. рис. 4.3), ограниченная центральным углом
фк, в пределах которого точка на высоте hi видна под углом
159
Угол 4>к находится из (Прямоугольного треугольника Oka
% = 2arccos ———, (4.10)
Ъ+Ь
а угол от направления аО на подспутниковую точку состав-
ляет
р о
гр! = arccos--5-----arccos----5—.
Rz+h Яэ + Zii
Для малых по сравнению с радиусом 7?3 величин h и hx
можно использовать приближенные формулы
' A3 г А3 Г Г<з
6. Полоса обзора. Полоса обзора на земной поверхно-
сти определяется как геометрическое место мгновенных зон об-
зора на некотором интервале времени. Ширина полосы обзо-
ра— это расстояние между огибающими мгновенных зон об-
зора в плоскости большого круга (рис. 4.4). Для зоны обзора
земной поверхности, задаваемой соотношением (4.9), ширина
полосы обзора будет
I = 27?э гр = 2R3 [ у—у — arcsin ( cos у. (4.11)
Полоса обзора определяется шириной и средней линией (трас-
сой) и, как следствие этого, она повторяет основные свойства
трассы: наклонение, межвитковый и суточный сдвиг, условия
синхронности.
Полоса обзора на фоне космоса — это геометрическое место
точек мгновенных зон обзора в форме усеченных шаровых сег-
ментов с центральным углом фк:
ZK = 2R arccos ——— .
Яз+^i
Эту полосу обзора можно представить как последователь-
ность покрытий усеченных шаровым сегментом аса'с' при его
«обкатывании» поверхности Земли.
Полученные соотношения для расчета кинематических эле-
ментов будут использованы ниже при рассмотрении методов
расчета орбитальных систем космических аппаратов различно-
го назначения.
4.2. МЕТОДЫ РАСЧЕТА СПУТНИКОВЫХ СИСТЕМ
Выше уже указывалось, что среди общих проблем
при выборе орбитального построения спутниковых систем явля-
ется обеспечение стабильности взаимного положения или, в
160
более общем смысле, такое изменение «геометрии» системы,
при котором ее функциональные свойства находятся в задан-
ных пределах. Основным критерием при выборе пара-
метров системы является критерий минимальных затрат
на создание системы и ее эксплуатацию. Этот критерий зави-
сит от многих факторов, таких как характеристики аппарату-
ры, потоков процессов управления на интервале функциониро-
вания системы (прогнозирование орбит, сеансы связи, коррек-
ция траекторий), количества спутников и т. д. Так, например,
для системы с однотипными спутниками при решении пробле-
мы минимальных затрат следует стремиться к построению си-
стемы с минимальным количеством объектов. Но это не озна-
чает, что эти спутники должны выводиться на одинаковые ор-
биты (по наклонению, большой полуоси, эксцентриситету). Это
также не означает, что система спутников с различными ха-
рактеристиками аппаратуры не может быть более дешевой.
В данном разделе в краткой и упрощенной постановке рас-
сматриваются примеры построения систем и анализ минималь-
ного количества объектов в системах наблюдения, связных и
навигационных системах. Для более глубокого изучения вопро-
са рекомендуется [5].
Система глобального обзора земной поверхности
Требуется определить такое количество спутников и
их взаимное размещение в пространстве, чтобы обеспечить ус-
ловия глобальности и непрерывности обзора земной поверх-
ности. Задачу решаем в предположении:
орбиты спутников полярные и круговые;
спутники имеют равномерное угловое распределение в каж-
дой из плоскостей орбит;
ширина полосы обзора для всех спутников одинакова.
В этом случае следует найти число плоскостей орбит m и
число спутников в каждой плоскости п, при которых выполня-
ются условия глобальности и непрерывности обзора.
Рассмотрим два предельных, с точки зрения количества
спутников, случая: точки непрерывного обзора находятся на
полюсе и на экваторе. Для первого случая (рис. 4.5,а) условие
непрерывности обзора полюса Р выполняется при отсутствии
разрывов между соседними зонами обзора в одной плоскости
полярной орбиты. Из условия покрытия всей окружности зона-
ми обзора п спутников
In = 2Rq фи = 2л 7?а,
где I определяется соотношением (4.11), следует
п = л/ф,
6—8
161
Рис. 4.5. Линии и полосы непрерывного обзора
откуда найдем потребное число аппаратов в одной плоскости
n = El'— W1, (4.12)
\ /
где Е (зт/гр) — наибольшее целое число, не превышающее л/ф.
На рис. 4.5, а показан случай, когда зоны обзора только со-
прикасаются, и в этом случае полоса непрерывного обзора вы-
рождается в линию. При увеличении числа спутников в одной
плоскости полоса непрерывного обзора начинает увеличивать-
ся и стремится к 2гр при zw-oo. При некотором перекрытии зон
обзора условие непрерывности выполняется не только для точ-
ки на полюсе, но и для некоторого диапазона широт в окрест-
ности полюса (рис. 4.5, б)
90°>ф>90°—&,
где 2Ь — угловое перекрытие двух соседних зон обзора (шири-
на полосы непрерывного обзора).
Для второго случая условием непрерывности обзора точек
экватора является, по крайней мере, соприкасание полос спло-
шного обзора для т плоскостей орбит
2л = 2т2Ь,
откуда находится потребное число плоскостей
/п = е(А)+1. (4.13)
Если выполняется условие непрерывности обзора на эквато-
ре, то, значит, выполняется условие непрерывного глобально-
го обзора. Общее число спутников находится как произ-
162
Рис. 4.6. Зона непрерывного об-
зора между смежными плоско-
стями
ведение числа плоскостей на число аппаратов в одной плоскости
N = mn. (4.14)
Ширина полосы непрерывного обзора и число плоскостей
орбит зависит от числа спутников в плоскости орбиты п, сле-
довательно, общее число спутников М является функцией толь-
7<о п, которое может принимать значения на интервале
со.
Когда /г = л/ф (зона непрерывного обзора вырождается в
линию), то число плоскостей орбит обращается в бесконеч-
ность, а при зоне непрерывного обзора, равной ф, число плос-
костей орбит минимально, но число спутников в одной плос-
кости стремится к бесконечности. Между этими предельными
случаями существует множество
значений N, удовлетворяющих усло-
виям непрерывного глобального об-
зора. Это определяет возможность
выполнения некоторых ограничений
или удовлетворение дополнитель-
ным условиям. Естественным явля-
ется постановка задачи нахождения
минимума функции N=N(m, ri).
На рис. 4.6 показано расположе-
ние зон обзора с угловой величиной
ф, обеспечивающее непрерывное на-
блюдение между двумя смежными
плоскостями полосы шириной Ь.
Ширина полосы обзора b зависит от
величины перекрытия смежных зон
обзора в одной плоскости, т. е. от
числа спутников в одной плоскости. Если половина углового рас-
стояния между двумя спутниками в одной плоскости равна а, то
число спутников в плоскости находится из соотношения
2п = 2ап,
Из сферического прямоугольного треугольника АВС
а = arcsin (sin ф sin Д);
& = arcsin f \
\ tg4 )
Используя (4.13, 4.15), выразим величины т и
угол А\
л
т =-------------------------------------------;
г tg [arcsin (sin sin Л)] )
2arcsin <-------—------->
I tg A )
л
n =------------------•
arcsin (sin sinj4)
(4.15)
получим
и через
(4.16)
(4.17)
6*
163
Напомним, что в (4.16, 4.17) угол зоны обзора зависит от
высоты полета h, минимального значения угла места наблюде-
ния у или максимального значения угла обзора б, например
в соответствии с соотношением (4.9)
, л . / 7?з \
ф =------у — arcsin ---5— cos у .
2 k R3 + h U
На основании (4.14) общее количество аппаратов представ-
ляется формулой
Лт2
N = тп. =-------------------2-------------------. (4.18)
....... . (tg [arcsin (sin sin Л)] -i
2arcsin (sin гр sin A) arcsin |-------j
Каждому значению угла А соответствует определенное ко-
личество орбит (4.16) и количество аппаратов в одной плоско-
сти орбиты (4.17). Приравнивая производную по А от (4.18)
нулю и решая данное уравнение, получим оптимальное значе-
ние угла А, при котором общее количество аппаратов в систе-
ме минимально
А = arcsin —7=. 1 (4.19)
Vl+cosip 47
Функции (4.16, 4.17) по определениям (4.12, 4.13) целочис-
ленные, поэтому в общем случае решение (4.19) может не сов-
падать со значением оптимального угла для целочисленной оп-
тимизации, но оно будет находиться в близкой окрестности.
Поэтому в этой окрестности следует варьировать угол, вычис-
ляя значения функции N (А) (4.18) и выбирая наименьшее.
В нижеследующем примере не проводилось варьирование
угла, полученные величины т и п достаточно близки к целым
величинам. Пусть дано: высота круговой орбиты h= 1000 км,
минимальный угол места обзора у=10°. По формуле (4.9) на-
ходим, что угол зоны обзора составляет ф = 21,6°, а оптималь-
ная величина угла (4.19) равна Л = 46с. Величины тип, вычи-
сляемые по (4.16, 4.17), достаточно близки к целям т = 6; п=12.
Таким образом, для заданных высот и угла места непрерывный
глобальный обзор земной поверхности для орбитальной системы
на полярных орбитах реализуется 72 спутниками.
Как видно из приведенного примера, количество аппаратов
для непрерывного глобального обзора земной поверхности до-
статочно велико. Потребности практики не требуют непрерыв-
ного обзора и могут ограничивать время разрыва наблюдений
для определенных регионов земного шара. Это будет приво-
дить к уменьшению потребного количества спутников, так же
как и переход на орбиты с наклонением f<90°. Эти и близкие
к ним вопросы рассматриваются в [5].
164
Система спутников связи
Системы связных космических аппаратов служат для
создания устойчивой радиосвязи на больших расстояниях меж-
ду наземными пунктами. Выбор орбит системы спутников ра-
дио- и телевизионного вещания определяется многими факто-
рами, главными из которых являются протяженность обслужи-
ваемой территории (регион), величина интервала связи каж-
дые сутки в заданное время суток, дублирование каналов свя-
зи, условия энергопитания от солнечных батарей, характерис-
тики радиоаппаратуры, количество и место расположения на-
земных приемных и передающих станций.
Сами аппараты могут быть использованы в качестве актив-
ных и пассивных ретрансляторов. Активные ретрансляторы в
процессе функционирования могут работать в двух режимах:
ретрансляция с задержкой сигнала по времени, ретрансляция в
реальном масштабе времени. По функциональному назначению
системы это может быть глобальная или региональная системы
связи.
Достаточно общие рекомендации по выбору системы мож-
но сформулировать так: для создания связи на больших рас-
стояниях с большим количеством станций используются круго-
вые (в частности геостационарные) орбиты, а для обеспечения
региональной связи в пределах определенного географического
района целесообразным становится использование высоких эл-
липтических орбит с угловым расположением апогея над гео-
центрической широтой центра рассматриваемого района. Воз-
можный вариант орбитального построения системы спутников
радиовещания и телевидения показан на рис. 4.7.
Достоинством геостационарных орбит 3 является стабиль-
ность их географических координат и возможность круглосу-
точной связи в некотором регионе с использованием неподвиж-
ных наземных антенн. К недостаткам этих орбит следует от-
нести сравнительно большие энергетические затраты при выве-
Рис. 4.7. Схема построения системы
спутников связи:
/ -- рабочий участок одной из эллиптических
орбит солнечно-синхронного спутника с на-
клонением г = 117,50; 2 — рабочий участок од-
ной из эллиптических орбит спутника с на-
клонением г=63,4о; 3 — орбита стационарного
спутника; 4 — зона видимости стационарного
спутника; 5 — направление на Солнце; 6 —
терминатор
165
дении на них, увеличение требуемой мощности аппаратуры и
отсутствие радиовидимости в полярных районах Земли.
Для связных спутников на высоких эллиптических орбитах
2 благодаря высокому апогею (порядка 40 000 км для периода
12 ч) более 80% времени обращения спутник виден из полу-
сферы Земли, обращенной к апогею орбиты. Энергетические
затраты выведения на эту орбиту существенно меньше по срав-
нению со стационарной орбитой: масса выводимого полезного
груза в 3...4 раз больше. Однако как для стационарной ор-
биты, так и для высокоэллиптических орбит произвольного на-
клонения в процессе функционирования свойственно пересе-
кать зоны затенения от Земли, что нарушает непрерывное
энергопитание -солнечных батарей. Этого недостатка не имеет
солнечно-синхронная орбита /, но у этой орбиты вследствие
возмущений от несферичности Земли происходит угловой уход
апогея, что требует или коррекции орбиты, или выведения до-
полнительных аппаратов на аналогичные орбиты.
С позиции минимальных затрат на разработку и производ-
ство аппаратуры, выведения аппаратов и эксплуатацию систе-
166
ма может состоять из спутников не только на геостационарных
и высокоэллиптических орбитах, но и на иных орбитах, особен-
но в тех случаях, когда задачи радио- и телевещания решают-
ся комплексно с другими задачами.
Стационарный спутник на экватор ной орбите (/г = 35 800 км)
обеспечивает предельную зону обзора (4.8) фп = 81,3°. Это рав-
но и величине предельных зон радиовидимости по геоцентриче-
ским широтам <рп = ±81,3°. Для минимально возможного угла
места работы приемо-передающих наземных станций у=10°
зона обзора (4.9) составляет <р = 71,5°. Три спутника, располо-
женных на равных углах, образуют непрерывную зону обзора
ф3 по экваториальному поясу. Но между этой зоной обзора и
широтами, меньшими по модулю ф = 71,5°, существуют зоны,
связь с которыми невозможна (рис. 4.8, а, б).
Определим наименьшее необходимое число спутников, осу-
ществляющих непрерывную радиосвязь в некотором экватори-
альном поясе ±фв. Из прямоугольного сферического треуголь-
ника abc для заданных значений фв и ф определяется угловое
расстояние между двумя спутниками
— 2arcens ( \
Z(XC — dl CCUo I - 1 ,
\ COS фв /
откуда получаются значения углов ас в зависимости от величи-
ны фв экваториального пояса непрерывной связи
фв, °.............................. ±50 ±60 ±65 ±68 ±71 ±71,5
<хс, °........................... 60,4 50,6 41,3 32,1 12,9 0
Число аппаратов, реализующих непрерывную связь в диа-
пазоне широт ±фв, находится по формуле
лг=е( — \ + 1
\ ас /
и приведено ниже,
фв, °......................... ±50 ±60 ±65 ±68 ±71
N............................. 3 4 5 6 15
Отсюда становится ясным, что для создания глобальной
связи наименьшее число спутников равно шести: три из них на
экваториальных орбитах реализуют связь в экваториальной
зоне, а для покрытия полярных зон служит цепочка из трех
спутников на полярных орбитах.
Для расчета необходимого числа спутников связи для дан-
ного региона требуется определять интервалы времени одно-
временной радиовидимости с территории региона. Космический
аппарат наблюдаем с некоторой территории, если он наблюда-
ется из каждой точки этой территории. Практически имеет
смысл характеризовать радиовидимость данной территории для
конечного числа точек (например двух). Тогда разность вре-
167
мен самого позднего радиозахода и самого раннего радиовос-
хода является сеансом связи для граничных точек и считается
сеансом радиовидимости для всей территории.
В общем случае задача формулируется следующим образом;
для территории с заданными координатами граничных точек
требуется определить минимальное число спутников системы и
параметры их орбит, обеспечивающих круглосуточную связь
или связь с временными интервалами разрывов не больше за-
данных. Выбор параметров орбит зависит от географических
координат граничных точек. При выборе наклонений эллипти-
ческих орбит большого эксцентриситета следует учитывать ус-
ловие стабильности углового положения линии апсид, поэтому
наклонение f = 63,4° считается наиболее целесообразным для
орбитальных систем длительного функционирования. Зависи-
мости изменения долготы восходящего узла и аргумента широ-
ты перицентра за один виток, вызываемые нецентральностью
гравитационного поля Земли, определяются соотношениями
AQr = ЗиЛ, ( -5^-V cos z; (4.20)
\ Р /
Асо = —-^-Г(1 —5cos2z), (4.21)
2 \ Р /
где экваториальный радиус земного эллипсоида /?3.э =
= 6378,245 км, коэффициент в представлении потенциала гра-
витационного поля Земли J2=—0,109808-10“2.
Данные формулы аналогичны ранее полученным (3.69) и
(3.72), в которых следует принять б=66,07-103 км2.
Для повторяемости сеансов (или сеанса) связи в каждые
последующие сутки должно выполняться условие совпадения
трасс полета в каждых смежных сутках. Это получается в том
случае, когда за время th спутник сделает целое число оборо-
тов в сутки
t _ ____Тзв
t AQtfec ’
2л
где AQi — уход долготы восходящего узла за один оборот;
kc — количество витков в сутки.
Рассмотрим кратко последовательность определения количе-
ства спутников с целым числом оборотов в сутки, равномерно
распределенных по долготам восходящих узлов для обеспече-
ния непрерывной связи в течение суток для заданной террито-
рии. Для этого нужно построить зависимость сеансов радиови-
димости от долготы восходящего узла орбиты Лв. На рис. 4.9
приведен приближенный график зависимости времени радио-
восхода и радиозахода от восходящего узла орбиты для терри-
168
Рис. 4.9. Зависимость времени радиовосхода и радиозахода от долготы восхо-
дящего узла орбиты:
1 — радиовосход для граничных точек; 2 — радиозаход для граничных точек; 3 — радио-
видимость для обеих граничных точек
Рис. 4.10. Зависимость времени сеансов связи для граничных точек от дол-
готы восходящего узла орбиты
тории с граничными точками (pi = 45°, Xi = 15°, ф2 = 45°, Л2 = Ю5°.
Приняты орбиты с наклонением I = 63,4°, угловым положением
перигея со = 270°, низким перигеем Ля=500 км и числом обо-
ротов за время tk (4.22), равным трем (апогей орбиты пример-
но равен 27 000 км). Продолжительность сеансов связи (зашт-
рихованная область 3 на рис. 4.9) перенесем на другой график
и получим зависимость продолжительности сеансов связи от
долготы восходящего узла орбиты Хв (рис. 4.10). Из графика
видно, что существует долгота восходящего узла, при которой
реализуется максимальный интервал сеанса связи /р = 6 ч при
Ав = 260°.
Определим число спутников, потребное для осуществления
непрерывной связи в течение суток. Систему можно строить
Рис. 4.11. Сеансы связи на суточном интервале
169
так, что в момент радиозахода одного спутника другой в это
время входит в сеанс связи. Построим схемы покрытия сеанса-
ми связи суточного интервала для двух случаев (рис. 4.10):
I — долготы восходящих узлов равны %в —30°; 150°; 270°;
II — долготы восходящих узлов равны ^в = 60°; 180°; 300°.
Как видно из схемы покрытия суточного интервала (рис.
4.11), для случая I существует разрыв в радиосвязи продол-
жительностью 1 ч, а для случая II — три спутника обеспечива-
ют непрерывную радиовидимость на суточном интервале.
В общем случае для других высот орбит, а значит и для
другого числа оборотов в сутки kc, следует искать такое со-
четание суточных сеансов связи, которое дает минимальное чи-
сло аппаратов в системе.
Сетевые спутниковые радионавигационные системы
Спутниковой радионавигационной системой принято
называть такую систему, в которой роль навигационных точек
выполняют искусственные спутники Земли, несущие навигаци-
онную аппаратуру. Навигационные системы космических ап-
паратов могут создать радионавигационное покрытие всей по-
верхности земного шара и обеспечить навигационное обслужи-
вание самолетов, кораблей и других подвижных объектов.
Спутниковая радионавигационная система содержит следую-
щие элементы:
собственно орбитальную систему аппаратов на определен-
ных орбитах;
наземный измерительный комплекс и вычислительный
центр, олределяющий точные параметры орбит;
средства для передачи параметров орбит каждому аппа-
рату;
средства передачи собственных координат аппарата пользо-
вателям системы.
Наиболее целесообразными орбитами для навигационной
системы (Представляются полярные или близкие к ним. Высоты
орбит находятся в диапазоне 600 ... 1000 км, а для системы
«Навстар» [59] — 20 000 км, что диктуется следующими сооб-
ражениями:
орбиты с меньшей высотой подвержены влиянию сопротив-
ления атмосферы, вариации плотности которой недостаточно
известны, и поэтому приходится часто определять параметры
орбиты и передавать их на борт аппарата;
дальнейшее увеличение высоты требует увеличения мощ-
ности сигнала трансляции навигационной информации.
Для навигационных систем определение местоположения
наземного объекта возможно только в случае, когда определя-
ющийся объект находится в зоне радиовидимости нескольких
170
аппаратов. Пусть п аппаратов
находятся в плоскости орбиты
на одинаковых угловых рас-
стояниях между собой и каждый
имеет зону обзора ф. Кратность
перекрытия зависит от углово-
го расстояния между двумя
смежными аппаратами и зоны об-
зора ф. Обозначим угловое рас-
стояние 2а
2а = 2л/п, (4.23)
где п — число аппаратов в одной
плоскости (рис. 4.12).
Максимальная кратность пе-
рекрытия зоны обзора, как это
видно из рисунка, равна
maxfew = Е Г—1 + 1. (4.24)
L 2а J
Если ф/2а — целое число, то в
плоскости орбиты будет п точек
Рис. 4.12. Кратность перекры-
тия зоны
между смежными парами аппаратов с кратностью перекрытия
kN (например, подспутниковая точка 3'). В сферическом
прямоугольном треугольнике kac угол b — геоцентрический угол
зоны перекрытия с кратностью kN. Угол са от середины зоны
перекрытия до подспутниковой точки крайнего аппарата, зона
обзора которого накрывает зону перекрытия, равен akN. Тогда
ширина зоны перекрытия кратности kN находится по формуле
, cos ib
b = arccos---------J—
cos akN
или в конечном виде
1 cos ф
b = arccos----------— ,
COS---
П
(4.25)
где
nk^
n
Рассмотренную на рис. 4.12 цепочку п спутников можно
считать находящейся на полярной орбите. Тогда для условия
непрерывности перекрытия экватора зонами непрерывного об-
зора потребное число плоскостей орбит находится по соотно-
шению (4.13)
т=Еш+'’
171
а потребная кратность перекрытия зон обзора kN в такое же
количество раз увеличивает число плоскостей.
В этом случае необходимое количество космических аппара-
тов в навигационной системе при известной зависимости шири-
ны полосы обзора (4.9) в функции от кратности перекрытия и
числа аппаратов в плоскости орбиты с использованием соот-
ношений (4.13) и (4.25) определяется по формуле
N=nmkN. (4.26)
Определение требуемого количества аппаратов в навигаци-
онной системе с заданным интервалом по времени перекрытия
приводится в [5].
Таким образом, в этом разделе рассмотрены геометриче-
ские схемы построения орбитальных систем космических аппа-
ратов различного назначения. Для функционирования системы
требуется сохранение в определенных пределах «геометрии»
системы, что относится к вопросам динамики и рассматривает-
ся в следующем разделе.
4.3. ДИНАМИКА ОРБИТАЛЬНЫХ СИСТЕМ
В процессе функционирования орбитальной системы
относительное положение аппаратов будет зависеть от парамет-
ров орбит, начальных условий и действующих сил. Выбор ор-
бит системы определяется многими факторами, но при этом
всегда одним из основных является фактор создания устойчи-
вости в процессе функционирования системы.
Согласованное функционирование нескольких космических
аппаратов определенного назначения осуществляется в их сов-
местном полете. Два и более аппарата в процессе согласован-
ного функционирования представляют динамическую систему,
создание и управление которой является более сложной зада-
чей, чем выведение одиночного аппарата и управление его
функционированием. Среди проблем и методов, традиционных
при анализе динамики движения одиночного аппарата, здесь
появляется ряд дополнительных проблем, связанных с созда-
нием орбитального комплекса, анализом устойчивости орби-
тальной системы под действием возмущающих сил и вследст-
вие отклонений в начальных параметрах движения, синтезом
алгоритмов управления при создании определенной геометрии
системы.
С точки зрения традиционно общих методов исследования
относительного движения аппаратов, как для задач сближения
на орбите, так и для исследования вышеуказанных задач ниже
при рассмотрении динамических вопросов относительного дви-
жения не делается различие между этими задачами.
172
Уравнения относительного движения на околокруго-
вых орбитах во вращающейся системе координат
Рис. 4.13. Система координат:
1 — невозмущенная круговая орбита;
2 — возмущенная орбита
Введем системы координат (рис. 4.13):
xyz — геоцентрическая неподвижная, плоскость хСу кото-
рой совпадает с орбитальной плоскостью невозмущенной круго-
вой орбиты;
Х\У12х — геоцентрическая,
вращающаяся с постоянной
угловой скоростью со, ось у\
которой связана с аппара-
том в его невозмущенном
движении, а ось Xi направ-
лена в сторону, противопо-
ложную направлению движе-
ния;
— система координат,
начало которой связано с аппа-
ратом, а направление осей сов-
падает с вращающейся геоцен-
трической системой координат.
Уравнения движения в не-
подвижной геоцентрической си-
стеме координат для случая движения в центральном поле силы
тяготения записываются в виде
Х=и'х-, у-Vy, 2 = и’г,
(4-27)
где правые части — частные производные от потенциала
U = . и =
ух2 + У2 + z2
по соответствующим координатам.
Запишем уравнения перехода между системами xyz и xxy\Z\
х = хг cos со/—у± sin со/;
у = xr sin со/ + уг cos со/; (4.28)
г = гь
Последовательное дифференцирование (4.28) по времени
приводит к следующим соотношениям:
х = хг cos со/ — уг sin со/— 2со (jq sin со/ +
+ у г cos со/) — со2 (хг cosco/ — у± sin со/);
у = Х1 sin со/ + у± cos со/ — 2со (хх cos со/ —
— у± sin со/) — со2 (%! sin со/ — у± cos со/),
г = гх.
173
Умножая последовательно первые два уравнения соответствен-
но на cos со/ и sin со/, а затем на —sin со/ и cosco/ и складывая,
с учетом (4.27) получим следующую систему дифференциаль-
ных уравнений во вращающейся геоцентрической системе ко-
ординат
хг—2со уг—со2 %! = Ux cos со/ + U'y sin со/,
/^+2(0%!—co2z/1= —Ux sin + U'y cos co/, (4.29)
Правые части (4.29), как это следует из уравнений перехо-
да между системами (4.28), тождественно равны частным про-
изводным потенциала
и = - ц-----------
V *Si+A+z2!
по соответствующим координатам вращающейся системы Xif/iZi.
На основании этого уравнения движения записываются в виде
xt—2co«/1—<агх1 = и’Х1 ;
у + 2со xL—ы2 Уi = Uyi ; (4.30)
z = ^i •
Чтобы рассматривать отклонение от кругового движения,
определим координаты (см. рис. 4.13) соотношениями
хх=г0^ г/i=''о(14-п); гх = г0?. (4.31)
Замена (4.31) в системе (4.30) приводит к следующей си-
стеме дифференциальных уравнений:
|-_2Ц-=
Г8
т] + 2со?— со2 (1 + т|) =-у (1 + п);
Г3
£= - С. (4.32)
rs = rg [^+(1 + п)2+И3/2-
Проведем линеаризацию правых частей (4.32), считая от-
клонения от круговой орбиты при возмущенном движении ма-
лыми. Функция
9 __з ___з
4 = ^2+(1 + п)2+:2] 2-(1+2г]+б2) 2.
где б2 = £2 + Ц2 + £2,
174
разлагается в ряд
4 ~ 1-Зп+6т12~4 a2 + n2 + m-. (4.33)
г3 2
Сохраняя в (4.33) и после подстановки в правые части
(4.32) только линейные члены, получим1 систему линейных диф-
ференциальных уравнений относительного движения на около-
круговой орбите во вращающейся системе координат. При
наличии возмущающих ускорений их проекции на оси вращаю-
щейся системы координат входят в правые части системы:
т]+2®£—3<о2г| = аТ|; (4.34)
£ + со2 £ = .
Получим решение однородной системы (4.34). Из первого
уравнения следует первый интеграл системы
I—2®т] = С1, (4.35)
после подстановки которого во второе уравнение (4.34), по-
лучим
Л + <о2т) = —2а>С1.
Этому уравнению удовлетворяет решение
т) = — + b cos (со t + <р0). (4.36)
СО I.
Последний интеграл найдем, проведя подстановку (4.36) в
(4.35),
|=—ЗСХ/ + 2 b sin (со t + <Ро)+ ^а» (4-37)
и, дифференцируя (4.37), получим
| = —3 С\ + 2 b со cos (со t + <р0). (4.38)
Произвольные постоянные Ci, С2, b, <ро найдем из началь-
ных условий
/ = 0; g = ?0, i = |0; т] = !)о>П = !1о.
которые связаны с постоянными в уравнениях (4.35—4.38) ал-
гебраической системой уравнений
По = — — + b cos Фо!
СО
Т)о = —6 со sin Фо ;
С 1 = 2 сот)о ;
С2 = ?0 — 2 6 sin Фо-
175
Окончательно решение системы (4.34) имеет вид I
Е (0 = U (0+2ftsin М+ Фо);
Л (0 Лоо + b cos (® t + Фо) ;
£ (0 = Со cos © t + sin © t;
U(O = ?o+ ^-°+ -f-Поо®/;
Лоо = 4 По—2 ;
b=Y(Яо-Лоо)2+(^У ; (4-39)
sin Фо=-^-;
cos<p0= 4-(Ло—Лоо)-
ь
Как видно из системы дифференциальных уравнений (4.34)
и ее решения (4.39), движение разделяется на движение в пло-
скости невозмущенной орбиты и движение по нормали к этой
плоскости. Движение по нормали к плоскости орбиты
£ (0 = £о cos t + -7“ sin со t (4.40)
представляет собой гармонические колебания вдоль оси £
с периодом, равным периоду круговой орбиты, с амплитудой
(4-41>
и фазой
Фо = arctg •
ьо
Рис. 4.14. Относительное движение в
плоскости орбиты
Движение в плоскости бо-
лее сложное, но также допу-
скает достаточно простую фи-
зическую интерпретацию: пер-
вые два уравнения (4.39) пред-
ставляют собой параметриче-
ское описание эллипса с коор-
динатами центра goo(^) и
т]оо, большой полуосью 2Ь
и малой полуосью b (рис.
4.14). Период движения точ-
176
ки по этому эллипсу равен периоду обращения по опорной
круговой орбите. Центр эллипса движется с постоянной гори-
зонтальной скоростью, пропорциональной т]Оо — высоте центра
эллипса над осью g. Если высота т]оо равна нулю, то это зна-
чит, что период обращения равен периоду опорной
центр эллипса неподвижен по отношению к началу
При т]ооУ=О центр эллипса уходит по оси § со
3
— ^Лоо- Угловое положение точки на эллипсе
орбиты и
координат,
скоростью
произволь-
ДЛЯ
ного момента времени равно
Ф = Ф0 + ®/.
Рассмотрим частные случаи относительного движения. Эти
частные случаи рассматривают движение при отклонениях по
начальным составляющим скорости. С точки зрения приклад-
ных задач их краткий анализ применим при изучении движения
отделяемых от космического аппарата объектов, динамики от-
носительного движения при обслуживании и инспектировании
аппаратов, методов сближения и совместного движения в опре-
деленной геометрической конфигурации.
1. Начальный импульс прикладывается по нормали к плос-
кости орбиты. Движение в соответствии с (4.40) описывается
уравнением
?(/) = sin со t.
Траектория относительного движения лежит в плоскости тр£
(см. рис. 4.13) и представляет собой гармонические колебания
с периодом, равным периоду круговой орбиты, и с амплитудой
а= ]/~(£0/со)2. Объект перемещается от плоскости орбиты на
расстояние а, а затем возвращается в эту плоскость через ин-
тервал времени, равный половине периода.
2. Начальный импульс прикладывается в вертикальном на-
правлении. В этом случае, как это следует из решения (4.39),
т]оо = О и центр эллипса (см. рис. 4.14) не перемещается вдоль
оси Параметрические уравнения эллипса представляются в
виде ______
U0 = тт2- + 2 V(По/®)2 sin (® t + Фо) ;
“ _______ (4.42)
Т) (0 = 1^(Ло/®)2 COS (со t + Фо)»
где фазы соответственно равны
• а 3
при По > °- Фо = — л;
при Т)о < 0, ф0 = -у ,
177
а центр эллипса находится на расстоянии £оо = 2ц0/со (рис. 4.15).
Объект в своем относительном движении удаляется от нача-
ла координат на расстояние 2Ь по оси %,
и через период возвращается снова.
3. Импульс (или отклонение) скорости имеет составляющие
по нормали к плоскости и в вертикальном направлении. Этот
случай представляет собой комбинацию первых двух.
Запишем уравнения движения в системе координат gir)i£i,
повернутой относительно оси £ системы на угол ао. Тогда в
новых координатах уравнение движения можно представить
матричным соотношением
П1
cos а0
— sin а0
которое для
3
ср0= — л принимает вид
условия т]о>О и
1
О
О
о
178
\ Из условия движения в плоскости giOrp
2
— sin а0
+ — cos а0 = О
СО
получим величину угла поворота
а0 = arctg -
со
to_________
~2
Записывая уравнение движения в системе
11(0 = -^----2
СО
cos со/;
2 По 2
со
2
cos со/ cos а0 +
2
I sin со/sin а0;
Cl (0 = 0,
можно видеть, что движение происходит по эллипсу, наклонен-
ному к орбитальной плоскости невозмущенного движения
угол ао, отношение полуосей эллипса уже не равняется 2,
центр
оси i
на
но
эллипса так же, как и в случае 2, не перемещается по
Уравнения относительного движения на околокруговых
орбитах в цилиндрической системе координат
Начало координат находится в центре Земли (рис.
опорная плоскость, перпендикулярная Cz, совпадает с
плоскостью невозмущенной круговой орбиты, a CQ — инер-
циальное базисное направление, от которого отсчитывается
угловая координата и. Возмущенное движение определяется
координатами г, и, z, которые можно получить из решения сис-
темы дифференциальных уравнений:
dt г* г ’
dVn _ УтУп . т.
dt г
— =-----— zГ;
dt Р3
dr _у du _Уп dz _ у
~dt ~ т' ~di~ г ’ ~dt~
4.16),
(4.43)
П1 (0 =
179
Рис. 4.16. Цилиндрическая си-
стема координат:
/ — невозмущенная круговая орби-
та; 2 — возмущенная орбита
где S, Т, W — составляющие ускорений ло радиусу-вектору,,
трансверсали и нормали к плоскости орбиты от нецентрально-
сти гравитационного поля, сопротивления атмосферы, возму-
щений Луны, Солнца или других возмущающих факторов.
При анализе динамики относительного движения использу-
ется линейная теория возмущенного движения. В этом случае
параметры возмущенного движения представляются в виде
сумм
Vr = Vro + Д Vr, Г = г0 + Дг;
Vn ~ Vjiq + Д Vn, и Hq 4~ Ди;
Vz = Vz0+AVz, 2 = г0+Дг,
вторые члены которых получаются из решения линеаризован-
ной системы дифференциальных уравнений (4.43)
=4д г+д1/* - 4Ar+S;
dt г3 г г2
= —-^ДУП—^Д7г+^^ДГ+Т; (4.44>
dt г г г2
--t-M+W;
dt г3
d&r Аг/ dku AVп vп ^Az_______ . Т/
17 = аГ'; ~а=-—
Для случая круговой опорной орбиты уравнения (4.44) уп-
рощаются:
-^ = й>гдг + 2®дУп+5;
dt
= — иду, + Т; (4.45>
dt
dt
d±=WT-t ^? = ДУГ,
dt dt r0 r0 dt
где (l> — угловая скорость движения по круговой орбите.
180
Найдем решение однородной системы (4.45). Из второго
уравнения системы следует первый интеграл
ДУП = — соДг+ (4.46)
который после подстановки в первое уравнение приводит к
дифференциальному уравнению второго порядка относитель-
но Дг:
с решением
Дг = С2 sin ©/ + С3 cos ©/ + — . (4.47)
©
Подставляя (4.46 и 4.47) в пятое уравнение системы (4.45) и
интегрируя, получим полное решение системы. После опреде-
ления произвольных постоянных через начальные условия
/ = 0; Дг = Дг0, ДУГ = ДУГО,
Д^ = Дг/q, ДУ п = Д V ng,
Д^—Д?о, ДУх — ДУzo
запишем решение однородной системы дифференциальных
уравнений (4.45) в конечном виде
Дг Д'о A,, 0
= M ; M = П A
ДК Д^о 0 A2
2—cos со/— sin ©/
со
© sin ©/ cos ©/
О — (1 — cos©/)
СО
О 2 sin ©/
2 1
2 sin ©/—3©/ — (cos©/— 1) 1 — (4sin©/—3©/)
co co
©(cos©/—1) —sin©/ 0 2 cos©/—1
(4.48)
, 1 . .
cos ©/ — sin©/
(0
—©sin©/ cos©/
181
Если возмущающие ускорения в (4.45) постоянны S=S0,
Т=То, W=Wo, то влияние этих ускорений представляется сле-
дующими зависимостями [12]:
Дг = a2 [So (1 —cos со/) + 2Т0 (со/—sin со/)];
Д7Г = a [So sin со/ + 2Т0 (1 —cos со/)]; (4.49)
г0Ди = —а2{2S0(со/—sin со/)+Т0 |^-|-(со/2)—4(1 — cosco/)Jj ;
ДУП = —a{S0 (1 — cos со/) + То (со/—2 sin со/)};
Дг = а21Г0 (1 — cos со/);
Дкг = aW0 sin со/,
где а = Го/2//Й’.
Из рассмотрения (4.48, 4.49) можно сделать следующие вы-
воды:
вековые (изменяющиеся пропорционально времени) возму-
щения по углу Azz реализуются только при отклонениях в на-
чальных условиях Дг0 (высоте) и Д1/п0 (трансверсальной ско-
рости) ;
для случая выполнения условия соДг0—ДУпо=О- вековое
возмущение по углу отсутствует;
все остальные отклонения в начальных условиях приводят
только к периодическим возмущениям;
при действии постоянного возмущающего ускорения по
трансверсали То спутник сначала смещается в направлении
действия ускорения, а затем его радиус увеличивается или
уменьшается пропорционально времени в зависимости от зна-
ка Го;
постоянное ускорение по нормали к плоскости орбиты Wo
не приводит к вековым возмущениям по высоте орбиты;
постоянное ускорение в радиальном направлении So не при-
водит к вековым возмущениям по высоте орбиты.
Заметим, что эти выводы сделаны из анализа движения в
окрестности круговой орбиты в линейном приближении (4.45)
и предполагают при использовании в расчетах ограниченной
области изменения как по начальным условиям движения, так
и по величине возмущающих ускорений. Для приближенных
расчетов пользоваться соотношениями (4.48, 4.49) можно для
практически широкого диапазона:
при возмущениях Дг/г0<0,5 погрешность по скорости не
превосходит 5%;
опорная орбита может быть эллиптической с эксцентриси-
тетом 0<0,1, в этом случае вместо Го следует брать большую
полуось а, а отклонения в параметрах движения следует рас-
сматривать относительно параметров невозмущенного движе-
ния на эллиптической орбите.
182
Возмущения параметров относительного движения
двух аппаратов
Взаимное положение аппаратов можно получить в
общем случае интегрированием системы дифференциальных
уравнений (4.43). Для более наглядного анализа закономер-
ностей относительного движения на околокруговых орбитах
следует пользоваться решениями (4.48, 4.49). Проведем крат-
кий анализ относительного движения двух аппаратов, орбиты
которых отличаются вследствие отклонений в начальных ус-
ловиях движения.
Относительное положение двух аппаратов (г, /) в цилинд-
рической системе координат (см. рис. 4.16) характеризуется
дальностью Л1ц в плоскости опорной орбиты и боковым откло-
нением Azij:
Mij = V(r0 + Дгг)2 + (r0 + Ao)2—2 (r0 + \Г(У/г0 + Дг;) cos Дио ;
Дио — \Uj — Ди;; (4.50)
Дггу = ~№f.
Тогда дальность Дг/ij между двумя аппаратами находится по
формуле
= V(Д/г>)2 + (Дг,7)2 . (4.51)
Для возмущенного движения в линейном приближении, как
это следует из уравнений (4.48), составляющие в (4.51) неза-
висимы и могут рассматриваться отдельно.
Рассмотрим боковую составляющую Дг^-. Используя урав-
нения (4.48), запишем
Д?/7- = Azof ,• cos со/ + AVzo*7 sin (о/;
со
= Д^О/ Д^Ог» (4.52)
Д^хог j = Д^го/ Д^хо / •
Из (4.52) видно, что вековых возмущений в относитель-
ном положении (расстоянии) двух аппаратов по направлению,
нормальному плоскости орбиты, не существует и изменение
этого расстояния происходит по зависимостям, аналогичным
возмущенному движению одиночного аппарата по оси г. От-
носительное положение описывается гармоническими колеба-
ниями
Дго- = asin (о)/+ ср0)
с периодом, равным периоду опорной орбиты, с амплитудой
и фазой соответственно
а= 1/(Дz0o)2 + ; <р0 = arctg .
183
Максимальное взаимное отклонение двух аппаратов не пре-
восходит величины амплитуды а, отклонение зависит только
от начальных условий и периода опорной орбиты
Т = 2 л/(о.
Рассмотрим теперь вторую составляющую (4.51) — отно-
сительное расстояние в плоскости орбиты AZ$j. Считая в (4.50)
Дгг, Аг, малыми, с точностью до квадратов и произведений
этих величин запишем
~ 1Л(1+ + (1-са5Дио). (4.53)
f0 V \ го го /
На основании (4.48) получим выражение для первого сом-
ножителя. Он изменяется в соответствии с зависимостью
Дг ДУГО . , / Дг0 . 2 Д Vno \ , .
— = —— sin со t— — Ч--— cos со t +
rQ WTq \ Г0 /
2 (—4-(4.54)
\ о /
что представляет собой гармонические колебания относитель-
но средней величины
/Дг_\* = 2 /Дго. + Д^по\ (4.55)
\ rQ ) \ r0 wro /
с амплитудой
а = + (4.56)
У \ <0 <oro ) \ <ог0 /
и фазой
Таким образом, первый сомножитель не имеет вековых воз-
мущений и его максимальная величина не превосходит единицы
плюс удвоенной суммы среднего значения (4.55) и амплиту-
ды (4.56).
Для анализа величины второго сомножителя подкоренно-
го выражения (4.53) следует рассмотреть изменение углового
положения аппаратов AUij. Из уравнений (4.48) получаем
Д«и = Д«0О-3 (^+ С0< +
\ ro wro /
+ 2 ( AL1LL + 2 sinco^—2 А VroiJ' (1—cos at), <4-57)
\ Го .сого / сого
где A А Цо./“"А , А Д Gu* А ^ог > A ^noo* A l^noj
A Vnoi , A Vroij A V^rOJ AVr0|,
184
откуда видно, что колебания происходят относительно
(ДМ* = Д«оО— 2^-^— — (4.58)
со^о \ 'о о /
с амплитудой
а = 2
A roij । 2 & п°И \2 । / & Vroij \2
г0 сого / \ wro /
(4.59)
и фазой
Фо = arctg
ДУгоО-
соД r0ij + 2 Д Vnoij
Как видно из уравнения (4.56) и (4.59) амплитуда колеба-
ний по углу в два раза превосходит амплитуду колебаний по
радиусу, а фаза отличается на 90°. Это свойство возмущенно-
го движения отмечалось ранее при физической интерпретации
уравнений возмущенного движения аппарата во вращающейся
системе координат (4.39) (см. рис. 4.14).
Таким образом, относительно величины, определяемой фор-
мулой (4.58), отклонения не превосходят амплитуды (4.59) г
а вековое возмущение характеризуется линейной функцией
(А«м)»= -3(^-+ ai,
\ го СО
Изменение этой функции будет приводить к долгопериоди-
ческим колебаниям относительной дальности между двумя ап-
паратами. Если в (4.53) учитывать только долгопериодические
члены, то можно записать
« 1/2/1 —cos Гдио0— ^£olL_3 (AZoU +
rQ у I L СОГО \ г0
<4М>
Период долгопериодических колебаний Тк находится из соот-
ношения
3 А г oil + го A VnOf J coro ©Тк = 2л, (4-61)
в котором 3 (г°и + \ ния аппаратов А УпоО \ СО г0 / равна разнице периодов обраще-
ATt7 = T,-Tf
То То
185.
Это следует из непосредственного вычисления изменения
периода опорной круговой орбиты То:
гр _ 2ла3/2 т/9 2р. _ ц
Д/р, го а
В результате дифференцирования получим
т',т; =з -Ь-,
и Г0 ПО (1) г0
откуда следует
__ g / А гоИ । А Упои \ (4 g2)
То \ го О)го /
Из (4.61) и (4.62) получим, что период долгопериодических
колебаний равняется
т = 2яТ0 _ —( (4 63)
со|ДТг>| |ДТг/| '
а взаимное отклонение по дальности двух аппаратов в плос-
кости орбиты определяется выражением
A hj
Го
1 —cos( &uQij—2--ГОг-- —2л t
\ w го То
(4.64)
Как следует из (4.57), вековое возмущение по угловому по-
ложению двух аппаратов будет отсутствовать в двух случаях:
1) Д f^oij= 0 ; Д^по1./ = О>
2) ^roti । АУп0/у __ q (4.65)
r0 cor0
В этих случаях на основании (4.53, 4.54, 4.57) характер ко-
лебаний будет описываться следующими уравнениями:
в первом случае
AVro? + AVrOj sin (1 — cosAufj) ;
0)Г0 /
во втором случае
A/fj 1 Г о I 1 । A VrOt + A VrOj . , A VnQi + A Vnoj
— ” -— 1 / ^<11 -Г" O111 ш ь
Го У \ (0 го (1)Г0
X COS (dt) (1—COS Д иц) .
Во всех других случаях, не соответствующих условиям
(4.65), будут иметь место долгопериодические колебания с
периодом
186
2л
За)
r^ij
''о
А Уnoij
coro
и через интервалы времени, равные половине этого периода,,
относительная угловая дальность будет изменяться на величи-
ну 180°, т. е. аппараты расходятся по антиподным точкам на
орбите с относительным расстоянием, как это следует из
(4.64), равным
Л 1ц — 2 г0.
Заметим, что при малых значениях (Шц для определения
относительной дальности между аппаратами следует пользо-
ваться формулой
А/у = /(Arj7)2+(r0A«ij)2. (4-66)
которая получается из (4.50) при представлении
а 1 (д uij)2
cos Д щ j ~ 1 — -—
и отбрасывании квадратов и произведений величин Дгй Arj..
Итак, проведен анализ закономерностей изменения относи-
тельного расстояния между двумя аппаратами. Используя ре-
шение уравнений возмущенного движения (4.48), можно про-
вести анализ изменения любого другого кинематического па-
раметра. В качестве примера рассмотрим определение предель-
ной дальности между двумя аппаратами, при которой возмож-
на их взаимная радиовидимость. Как следует из рис. 4.17, от-
носительная дальность, при которой реализуется связь между
двумя аппаратами, должна удовлетворять условию
А/о<2/ Го — (Яэ+/гп)2,
где hn— предельная минимальная высота радиовидимости над
горизонтом.
Для определения времени существования связи следует ис-
пользовать ранее полученные зависимости, например (4.60).
Таким образом, проведен анализ
динамики относительного движения
двух аппаратов при отклонениях в
начальных параметрах движения
от своих номинальных значений
каждого из них. При рассмот-
рении большого количества объек-
тов (орбитальные системы космиче-
Рис. 4.17. Предельная даль-
ность взаимной радиовидимо-
сти
ских аппаратов различного назна-
чения) задача значительно ослож-
няется, так как количество па-
187
раметров относительного движения будет определяться вели-
чиной 6^—1), где Л/’ — количество аппаратов. Принимая во
внимание вероятностный характер отклонений по начальным
условиям движения, естественно приходим к выводу о необ-
ходимости представления «геометрии» системы в вероятност-
ных величинах (например, математическое ожидание и диспер-
сия времени отсутствия радиовидимости и т. д.).
За пределами материала данной главы остаются вопросы
создания и обслуживания орбитальных систем космических
аппаратов. Близкие к этим вопросы рассмотрены ниже в разд.
5.4 «Монтажные орбиты», однако более подробно с ними мож-
но ознакомиться в указываемой ранее монографии [5].
ГЛАВА 5, МАНЕВРИРОВАНИЕ И СБЛИЖЕНИЕ
КОСМИЧЕСКИХ АППАРАТОВ
При изучении маневров перехода между орбитами и сбли-
жения космических аппаратов теоретической основой являют-
ся рассмотренные ранее в гл. 2 методы анализа невозмущен-
ного движения (задача двух тел) и в гл. 4 вопросы возмущен-
ного движения в окрестности круговой орбиты.
Задача перехода между орбитами в ее частном случае, ког-
да фиксированы моменты времени начала /0 и конца /к пере-
хода, является классической задачей небесной механики — за-
дачей Ламберта, рассматриваемой в разд. 6.4. При нефикси-
рованных моментах времени /0 и /к переход представляет со-
бой задачу выбора орбиты с подвижными концами, поскольку
траектория перехода может начинаться из любой точки неко-
торого участка начальной орбиты, соответствующего возмож-
ному диапазону изменения /0, и заканчиваться в любой точке
некоторого участка конечной орбиты, соответствующего воз-
можному диапазону изменения времени tK. В этом случае за-
дача имеет бесконечное множество решений и выделение сре-
ди них единственного возможно из дополнительных условий
обеспечения экстремальных значений некоторых величин, на-
пример затрат топлива на переход, или ограничений на пара-
метры орбиты перехода. Естественно, что задача может иметь
модификации в части фиксированного начального момента
времени перехода to или интервала перехода tK—tQ, обеспече-
ния минимального времени перехода при ограничении на ве-
личину располагаемого запаса топлива и т. д.
Заметим, что в классической небесной механике задача
межорбитального перехода с подвижными концами не рассма-
тривалась. Однако большинство задач космических полетов
связано именно с такими задачами. Отметим также следую-
щий важный момент, который должен пояснить читателю ме-
тодическую направленность раздела о межорбитальных пере-
ходах.
Задачи межорбитальных переходов являются одними из
первых в области теоретической космонавтики. Однако для по-
лучения программы перехода (точки изменения величин и на-
189
правлений скорости, количество этих точек) даже в достаточ-
но простых случаях нужно находить решение сложной системы
нелинейных уравнений. Возможно, например, сформулировать
и математически записать задачу перехода между двумя точ-
ками произвольных орбит при условии изменения скорости
только в начальной и конечной точках и свободном времени
перехода. В результате получается система нелинейных урав-
нений 16-го порядка с 17-ю неизвестными [55]. Для решения
задачи 17-е уравнение можно получить, например из условия
минимума затрат топлива на переход, однако невозможность
получить решение в достаточно удобном виде для проведения
практических расчетов, кроме общности постановки задачи, в
данном случае ничего не дает.
Поэтому практически важный интерес представляют слу-
чаи решения или их даже качественные исследования при раз-
личных упрощающих предположениях. Эти положения лежат
в основе методической направленности разделов о межорби-
тальных переходах данной главы. В разд. 5.1, 5.2 в порядке ус-
ложнения и в некотором смысле в рецептурном плане рассмат-
риваются межорбитальные переходы, некоторые из которых
используются в баллистических схемах реальных космических
полетов. В разд. 5.3 в объеме, который представляется целесо-
образным для учебника, рассматриваются более сложные схе-
мы межорбитальных переходов и проблемный вопрос — о ко-
личестве импульсов.
5.1. КОМПЛАНАРНЫЕ МЕЖОРБИТАЛЬНЫЕ ПЕРЕХОДЫ
Маневром межорбиталъного перехода будем называть
управляемое движение, в результате которого космический ап-
парат переходит с начальной орбиты на конечную. Орбиту,
проходящую через точки начальной и конечной орбит, будем
называть переходной орбитой. Переход является компланар-
ным, если он осуществляется между орбитами, находящимися
в одной плоскости, и переходная орбита лежит в этой плос-
кости.
Для определения затрат топлива на межорбитальные пере-
ходы используется импульсная аппроксимация активных уча-
стков [27]. Это широко используемое в практике проектных
расчетов упрощение основано на том, что при использовании
термохимических двигателей (жидкостные или твердотоплив-
ные реактивные двигатели) время их работы на активных уча-
стках значительно меньше продолжительности пассивных уча-
стков переходных орбит. Это обстоятельство позволяет для
проектных расчетов считать, что к космическому аппарату
прикладывается импульс, изменяющий мгновенно величину и
направление скорости и неизменяющий координаты. При оцен-
190
ке массы топлива, потребного на маневр, к величине импульс-
ной скорости V следует прибавлять гравитационные потери и
потери скорости на управление (формирование траектории ак-
тивного участка). Полученная величина скорости по известной
формуле Циолковского пересчитывается в массу топлива для
реализации маневра (1.66):
Г1 / V + AVX-i /с
mT = т0 1 —ехр ------j—) J , (5.1)
где т0 — начальная масса космического аппарата; /у — удель-
ный импульс тяги; V — импульсная скорость реализации манев-
ра; ДУ—гравитационные потери скорости и потери скорости
на формирование траектории активного участка.
Чтобы не зависеть от характеристик конкретной двигатель-
ной установки и программы управления на активном участке,
ниже в качестве меры расхода топлива будет использоваться
импульсная скорость.
Сформулируем одно положение для компланарных межор-
битальных переходов без ограничения времени на переход.
Как будет следовать из рассматриваемых ниже частных слу-
чаев, требование экономичности (как правило, одного из кри-
териев оптимальности) реализуется в этом случае приложени-
ем импульсов скорости в апсидальных точках, и импульсы ско-
рости направлены по вектору скорости при увеличении полной
энергии переходной орбиты (2.25) и против вектора скорости
при уменьшении этой энергии. Такое управление при форми-
ровании переходных орбит обеспечивает наибольшее увеличе-
ние (уменьшение) интеграла энергии (разд. 2.3)
у2_?И_=Лф (5.2)
Переходим к рассмотрению частных случаев компланарных
межорбитальных переходов без ограничения времени на пе-
реход.
Импульсный переход между круговыми
компланарными орбитами
Условия компланарности и наиболее простые формы
начальной и конечной орбит казалось бы предполагают простое
и однозначное решение данной задачи. Однако даже в этой
задаче мы обнаруживаем зависимости затрат топлива от от-
ношения радиусов орбит и количества импульсов при межор-
битальном переходе.
Круговые орбиты (компланарные) не могут пересекаться,
поэтому минимальное количество импульсов для перехода рав-
но двум. Естественным вариантом переходной орбиты является
191
Рис. 5.1. Переходы меж-
ду круговыми компла-
нарными орбитами:
а — двухимпульсный; б —
трехимпульсный
эллипс минимальной энергии, касающийся в апогее и перигее
круговых орбит (переход Цандера — Гомана [45, 64]*, рис.
5.1,а). Для вычисления требуемой скорости на переход по эл-
липсу минимальной энергии будем пользоваться интегралом
энергии (5.2), из которого для переходной орбиты следует
179 _ .
л1 2 r I г ’
Г1 Г1“ГГ2
т/2 ___ 2jx _ __ 2ll
где 1/Л12, Га12— скорости в перицентре и апоцентре переход-
ного эллипса.
После некоторых преобразований получим следующие за-
висимости, которыми будем пользоваться в дальнейшем
Vn.8 = Vm(r,)
Va,! = VKP(r,) •
(5-3)
(5-4)
где Гкр(г) —скорость на круговой орбите радиуса г.
Суммарная требуемая скорость на переход вычисляется
по формуле
+ v«p(rj(^l- Кутт,) <5-5)
* Впервые такой переход был рассмотрен в трудах Ф. А. Цандера и про-
анализирована его оптимальность. Независимо от Ф. А. Цандера такой пе-
реход был предложен В. Гоманом и в литературе часто называется его
именем.
192
Разделив (5.5) на УКР(Г1) и обозначив r2lr\ = r, получим-
|АБ)' (5-6)
Анализ данного уравнения показывает, что
Нт др2 = /2—1 ~ 0,414.
Г —> оо
Эта величина в сумме с круговой скоростью соответствует
параболической скорости для точки с радиусом г\. Из необхо-
димого условия экстремума (5.6) (APs)/r=0 получаем куби-
ческое уравнение
г3— 15 г2 — 9г— 1 =0,
положительный корень которого 15,58 соответствует мак-
симальному значению (5.6) шах 0,536.
На рис. 5.2 показана зависимость требуемой скорости для
двухимпульсного гомановского перехода между круговыми ком-
планарными орбитами от относительного радиуса г. Как вид-
но из рисунка, величина перво-
во импульса ограничена значе-
нием параболической скорости
ухода в бесконечность
~0,414 и в этом случае второй
импульс стремится к нулю. Это
и объясняет поведение суммар-
ных затрат топлива с точкой
максимума при гк~ 15,58.
Если величина г становится
больше некоторого предельно-
го значения, то оптимальным
по суммарной скорости стано-
вится трехимпульсный переход
(см. рис. 5.1,6), предложенный
в [64]. Этот переход называют
также биэллиптическим, по-
Рис. 5.2. Зависимость скорости пере-
хода между круговыми компланар-
ными орбитами от относительного
скольку он состоит из двух эл- радиуса
липсов перехода. Отношение суммарной скорости к круговой на
начальной орбите радиусом Г\ получается при использовании со-
отношений (5.3), (5.4):
A V2 = (Д + A V2 4- Д Vs)=
193
где гС6 = гсс/Г1—отношение радиуса апоцентра переходной ор-
биты к радиусу начальной круговой орбиты.
Проведение сравнения двух- и трехимпульсных маневров
приводит к следующим выводам [55]:
если ri/ra<ri/r2, то трехимпульсная программа более эко-
номична, чем оптимальная двухимпульсная, при ri/r2<0,064
(г^ 15,56) и менее экономична при Г1/(г2>0,084 (rc^'l 1,94);
если 0,064^Г1|/1Г2^0,084(11,94^г^15,56), в зависимости
от величины отношения ri/ra экономичным может быть двух-
или трехимпульсный маневр.
Импульсный переход между эллиптическими
компланарными орбитами
В отличие от перехода между круговыми орбитами,
где угловое положение точки схода с начальной орбиты было
произвольным, в данном случае потребности практики могут
ограничивать как область начала переходной орбиты, так и
область выхода на конечную орбиту. В частном случае требу-
ется определить траекторию перехода с минимальными затра-
тами топлива при условии произвольности выбора начальной
и конечной точек.
В отличие от круговых эллиптические орбиты могут иметь
точки пересечения или точку касания. В этих случаях возмо-
жен одноимпульсный переход, который в общем случае не бу-
дет оптимальным по затратам скорости. В практической ре-
ализации переходов, как правило, рассматриваются двух- и
трехимпульсные переходы. Наиболее просто находятся опти-
мальные орбиты для двухимпульсного перехода.
В этом случае первый импульс определяется из условия,
что переходная орбита будет иметь хотя бы одну общую точку
с конечной орбитой. В точке пересечения (касания) переходной
и конечной орбит прикладывается второй импульс, выравнива-
ющий скорости.
Рассмотрим переходы между эллиптическими орбитами при
следующих условиях:
направления вращения одинаковы;
угловые положения граничных точек переходной орбиты
произвольные;
орбиты не пересекаются и не имеют точки касания;
угол между линиями апсид по аргументу перицентра не
превосходит 90°.
Для указанных условий установлено [45], что минимум
скорости при двухимпульсном маневре достигается при пере-
ходе из перицентра внутренней орбиты в апоцентр внешней. В
194
Рис. 5.3. Двухимпульсный переход между соосными
компланарными эллиптическими орбитами
силу обратимости движения оптимальный пе-
реход с внешней орбиты на внутреннюю дол-
жен осуществляться из апоцентра внешней ор-
биты в перицентр внутренней.
При пересечении орбит может реализовать-
ся одноимпульсный переход. Для случая кру-
говой орбиты, если одна из апсидальных то-
чек эллипса касается круговой орбиты, то оп-
тимальным становится одноимпульсный ма-
невр. При условии пересечения круговой и эл-
липтической орбит оптимальным является
двухимпульсный маневр.
Минимальная суммарная скорость на переход достигается
при совпадении линий апсид эллиптических орбит (рис. 5.3).
Используя (5.3, 5.4), получим
Некоторые трех- и четырехимпульсные схемы межорби-
тальных компланарных переходов рассматриваются в разд. 5.3.
5.2. НЕКОМПЛАНАРНЫЕ МЕЖОРБИТАЛЬНЫЕ ПЕРЕХОДЫ
Маневр поворота плоскости орбит
Некомпланарные (пространственные) переходы ре-
ализуются в случае, когда начальная и конечная орбиты ле-
жат в разных плоскостях. Поворот плоскости орбиты обычно
требует значительных затрат скорости. Вектор импульса ско-
рости осуществления маневра с поворотом плоскости орбиты
находится по формуле
дГ=72-7г,
где р2, Vi — векторы скорости в точке маневра.
Величина импульса скорости составляет
Д V = l/V2+V2-2V2V1CosAf, (5.10)
где Д/— угол поворота плоскости орбиты (угол некомпланар-
ности).
Так, например, для случая одноимпульсного перехода ме-
жду круговыми орбитами в точках их пересечения имеем
AV = 2yKpsinAL,
откуда видно, что при угле поворота плоскости орбиты Af=
= 60° характеристическая скорость перехода равна круговой,
а при Д/=90° эта скорость равна параболической.
Задача оптимального импульсного некомпланарного перехо-
да между произвольными орбитами не решена, однако при ис-
следовании практических задач рекомендуется пользоваться
следующим правилом: изменение плоскости орбиты следует
проводить в точке, где скорость минимальна. В этом смысле
становится ясной оптимальность трехим|Пульсных переходов.
Например, если угол Ai>38,94°, то оптимальным трехимпульс-
ным переходом между круговыми орбитами одного радиуса
будет такая схема [39, 55]:
первый импульс реализует переход на эллипс, лежащий в
плоскости круговой орбиты;
в апогее эллипса происходит поворот плоскости, орбиты на
требуемый угол;
в перигее повернутого эллипса производится переход на
круговую орбиту.
Двухимпульсный переход между некомпланарными
круговыми орбитами разных радиусов
Рассмотрим возможные схемы двухимпульсных пе-
реходов с орбиты радиуса и на орбиту радиуса r2
Схема 1 (рис. 5.4, а). Первый импульс одновременно
поворачивает плоскость переходной орбиты на угол некомпла-
нарности Ai и увеличивает скорость до такой величины, чтобы
апоцентр переходной орбиты равнялся г2. Второй импульс ско-
рости осуществляет переход на круговую орбиту.
Схема 2 (рис. 5.4,6). Первый импульс увеличивает ско-
рость до такой величины, чтобы апоцентр переходной орбиты
равнялся г2, но угол некопланарности при этом не изменяет-
ся. В апогее переходной орбиты второй импульс скорости из-
меняет угол некомпланарности и увеличивает скорость до кру-
говой.
Схема 3 (рис. 5.4, в).. Первый импульс одновременно
увеличивает скорость до достижения в апогее переходной ор-
биты расстояния г2 и поворачивает плоскость переходной ор-
биты на угол Ди (Ди<Аг). Второй импульс поворачивает пло-
196
Рис. 5.4. Двухимпульсный переход
между некомпланарными круговыми
орбитами разных радиусов
скость на угол Дг2 = Д1—ДА и увеличивает скорость до кру-
говой.
Как уже отмечалось в практических рекомендациях по оп-
тимизации при некомпланарных переходах, первая схема яв-
ляется заведомо неоптимальной — поворот плоскости переход-
ной орбиты производится на орбите меньшего радиуса, где ско-
рость наибольшая.
При переходе по третьей схеме с использованием зависимо-
стей (5.3, 5.4) и (5.10) отношение суммарного импульса ско-
рости к круговой скорости на орбите радиуса Г\ определяется
формулой
дУ2 = (дУ1 + ДУ2)/Укр(г1) =
(5.11)
Если положить ДА = 0, то (5.11) определяет затраты скоро-
сти по второй схеме перехода.
Простого выражения для нахождения угла ДА, доставля-
ющего минимум затрат скорости (5.11), получить не удается.
Уравнение для необходимого условия экстремума приходится
решать численно. Однако угол первого поворота не превышает
197
Двухимпульсный
спутника Земли
Рис. 5.5. Относительная скорость двухим-
пульсного перехода между некомпланарны-
ми круговыми орбитами с поворотом плос-
кости в апогее переходной орбиты
5,5° и, рассчитывая (5.11) в преде-
лах Afi = O... 5,5°, можно получить
минимум ДР2^
На рис. 5.5 [10, 55] показано от-
ношение суммарного импульса к
величине круговой скорости на внут-
ренней орбите при двухимпульсном
переходе с Дь = 0 (поворот плоско-
сти переходной орбиты только в апо-
гее, рис. 5.4,6).
переход на стационарную орбиту
Стационарным называется спутник на круговой ор-
бите, скорость движения которого в направлении запад — во-
сток совпадает с плоскостью земного экватора, а период ра-
вен звездным суткам (7,3 = 86164 с). Эта круговая орбита име-
ет радиус порядка 42164 км и круговую скорость 3075 м/с.
Спутник с разгонным космическим блоком выводится ра-
кетой-носителем на низкую орбиту (высота порядка 200 км).
Из условия уменьшения требуемой скорости при переходе спут-
ника на стационарную орбиту наклонение низкой орбиты дол-
жно быть минимально возможным. Для спутников, запуска-
емых с территории СССР, это наклонение составляет величи-
ну порядка 51°. Примем радиус низкой круговой орбиты выведе-
ния ri = 6570 км, что дает г=г2/г1 = 6,42, и определим требу-
емые скорости при переходе для трех ранее рассмотренных
схем, используя формулу (5.11).
При повороте плоскости орбиты на угол 51° в перигее пере-
ходной орбиты при первом импульсе (схема 1) суммарная ско-
рость составляет
ДУх = Д71+Д1/2 = 8075 м/с+1478 м/с=9553 м/с.
Для схемы 2, когда поворот плоскости переходной орбиты
осуществляется в апогее,
Д1/2=ДУ1+Д1/2 = 2457 м/с+2413 м/с = 4870 м/с.
Для схемы 3, когда при первом импульсе реализуется пово-
рот плоскости переходного эллипса на 3°, а при втором — пло-
198
скость орбиты поворачивается на угол 48°, затраты скорости
составляют
д1/х = дУ1+дУ2 = 2501 м/с+2329 м/с=4830 м/с.
Таким образом, схема выведения 3 по сравнению со схе-
мой 2 дает выигрыш в скорости порядка 40 м/с. Схема выведе-
ния 1 является самой невыгодной, что еще раз на численном
примере подтверждает ранее приведенную рекомендацию по
оптимизации некомпланарных переходов — изменение пло-
скости орбиты следует производить там, где скорость мини-
мальна.
Дальнейшее уменьшение затрат скорости при выведении на
стационарную орбиту связано с изменением схем перелета, а
именно [10]:
использование трехимпульсных схем выведения с тремя по-
воротами плоскости орбиты и высотой апоцентра переходной
орбиты порядка 400 000 км, что приводит к уменьшению ско-
рости на величину порядка 300 м/с при соответствующем уве-
личении времени перехода до 11 сут;
использование гравитационного поля Луны при достаточ-
но близком пролете ( — 5000 км) в окрестности узла ее орбиты
относительно плоскости земного экватора, что приводит к
уменьшению скорости по сравнению с двухимпульсным переле-
том на —500 м/с (без учета корректирующих маневров).
Трехимпульсныи переход между некомпланарными
круговыми орбитами
Дальнейшим развитием методов оптимизации неком-
планарных переходов является
переходов. В трехимпульсных
переходах заложена основная
идея получения высокой пере-
ходной орбиты, в апогее кото-
рой при минимальной скорости
вторым импульсом АУг (рис.
5.6) осуществляется поворот
плоскости переходной орбиты
на основную величину угла не-
компланарности. Наиболее
простым маневром является
переход с одним поворотом
плоскости переходной орбиты,
причем линии апсид переход-
ных полуэллипсов совпадают
с линией пересечения плоско-
стей начальной (радиус и) и
конечной (радиус г2) орбит
(линия узлов). В общем слу-
рассмотрение трехимпульсных
Рис. 5.6. Трехимпульсный переход
между некомпланарными круговыми
орбитами одинакового радиуса
199
чае различных радиусов круговых орбит переход с одним пово-
ротом плоскости переходной орбиты реализуется по следующей
схеме:
после первого импульса скорости получается переходная
орбита, компланарная начальной, с перицентром, равным и, и
апоцентром га>Г2;
второй импульс, который дается в апоцентре переходной
орбиты, поворачивает ее плоскость на угол некомпланарности
Дг, причем радиус апоцентра остается прежним, а радиус пе-
рицентра увеличивается до г2;
третий импульс прикладывается в перицентре переходной
орбиты, компланарной конечной, и реализует переход на кру-
говую орбиту радиусом г2.
Отношение суммарной импульсной скорости к скорости на
начальной круговой орбите определяется формулой [55]
А Ух = Д Ух/Укр (G) = (д У1 + ДУ2 + А Жр (г1) =
где f=f2lrl, fa^ralri.
Как следует из приведенной формулы, величина относитель-
ной суммарной скорости зависит от относительного радиуса г,
угла некомпланарности орбит Дг и относительного радиуса апо-
центра переходной орбиты, который может выбираться. В за-
висимости от указанных параметров оптимальными могут быть
двух- или трехимпульсные переходы.
Наиболее общей постановкой задачи с точки зрения нахож-
дения оптимальных переходов в классе трехимпульсных пере-
ходов являются переходы с тремя поворотами плоскости пере-
ходных орбит. Отношение суммарной импульсной скорости к
скорости на начальной круговой орбите для такого перехода
определяется формулой [55]
cos Д +
200
++~^~------------4 V —~—cos д I>2 +
Г 1+r« r + ra Г 0+га)(г+га)
cos (Д i — Д ir—Д i2),
(5.13)
где Ar*i, Ai2— углы поворота переходных орбит при первом и
втором импульсе соответственно.
Сравнение затрат скорости для двух- и трехимпульсных не-
компланарных переходов показывает, что выигрыш по суммар-
ной скорости порядка 10% для трехимпульсных переходов реа-
лизуется в области углов некомпланарности 45° и более.
5.3. О ЧИСЛЕ ИМПУЛЬСОВ
ПРИ МЕЖОРБИТАЛЬНЫХ ПЕРЕХОДАХ
Литература, посвященная оптимизации импульсных
межорбитальных переходов, достаточно обширна. И частные
задачи оптимальных переходов, рассмотренные нами в разд.
5.1, 5.2, далеко не исчерпывают того количества задач, для ко-
торых получены решения. Тем более, что в этих разделах мы
ограничились только трехимпульсными переходами между кру-
говыми некомпланарными орбитами. Однако известны и дру-
гие случаи, когда приложение дополнительных импульсов в бо-
лее общей постановке задачи позволяет уменьшить требуемую
скорость [71]. В некоторых случаях здесь будут использовать-
ся результаты, полученные ранее в разд. 5.1, 5.2. Они повторя-
ются в методическом плане для пояснения логики развития за-
дач оптимизации межорбитальных переходов.
Задача об оптимальном по расходу топлива межорбиталь-
ном переходе в ньютоновском поле является одной из старых
задач в области космонавтики. Перелет между любыми орби-
тами можно осуществить двумя импульсами тяги. Импульсы
представляют собой удобную, а с учетом гравитационных по-
терь скорости и достаточно точную аппроксимацию сравни-
тельно кратковременных активных участков движения при ис-
пользовании термохимических двигателей. В некоторых случа-
ях двухимпульсный маневр является оптимальным по величи-
не требуемой скорости. Однако известны случаи использования
Дополнительных импульсов, позволяющих уменьшить величину
этой скорости.
Несмотря на многочисленные исследования, проведенные в
этой области, вопрос об оптимальном числе импульсов для пе-
201
рехода между произвольными орбитами (общий случай) до на-
стоящего времени остается нерешенным. Достаточно важным
в постановке задачи является условие ограниченного или не-
ограниченного времени перехода.
Число импульсов при незакрепленном времени
перехода
По-видимому, первый важный результат в теории
межорбитальных переходов между круговыми компланарными
орбитами получил Гоман [45, 64]. Он предположил, что опти-
мальный по затратам скорости переход должен происходить по
эллипсу, касательному к обеим граничным орбитам (рис.
5.7,а).
Советский ученый Штернфельд [64] обнаружил, что при
высоте конечной орбиты, много большей высоты начальной»
оптимальный переход следует выполнять по эллипсу, апоцентр
которого больше радиуса конечной орбиты, а затем по эллип-
су, касательному к конечной орбите в своем перицентре (рис.
5.7,6). Этот переход получил название «биэллиптический пере-
лет». Оптимальный биэллиптический перелет (рис. 5.7,в) вклю-
чает «перелет через бесконечность», который реализуется по
схеме:
первый импульс — уход по параболической траектории «в
бесконечность»;
второй импульс — бесконечно малый импульс «в бесконеч-
ности» для возвращения на конечную орбиту;
третий импульс — переход на конечную круговую орбиту.
Если радиус конечной орбиты более чем в 15,56 раз превы-
шает радиус начальной, то -суммарная скорость перехода умень-
шается ino сравнению с гомановским при любом биэллиптичес-
ком перелете, если апоцентр переходного эллипса находится
выше -конечной орбиты. Заметим, что перелет через «бесконеч-
ность» обеспечивает абсолютный минимум. Для величин отно-
шений радиусов в пределах 11,94... 15,56 условия оптимальности
двух- и трехимпульсных переходов были указаны в разд. 5.1.
Рис. 5.7. Схемы перехо-
дов между круговыми
орбитами
202
Еще один способ многоимпульсного перехода рассматривал
Оберт 1[71]. Он показал, что при разгоне с круговой орбиты до
определенной гиперболической скорости может оказаться оп-
тимальным: первым импульсом перейти на переходную эллип-
тическую орбиту с низким перицентром, а вторым импульсом
разогнаться в перицентре до заданной энергии, соответствую-
щей гиперболической скорости (двухимпульсный переход). Од-
ноимпульсный переход показан на рис. 5.8,а, а двухимпульс-
ный (переход Оберта) — на рис. 5.8,6.
Рис. 5.8. Схемы переходов с круговой орбиты на гиперболическую
Одним из интереснейших свойств рассматриваемого двухим-
пульсного перехода является следующее: если скорость в бес-
конечности точно равна начальной скорости освобождения (до-
бавочной скорости для получения параболической скорости), то
требуемые скорости не зависят от высоты перицентра переход-
ного эллипса, где дается второй импульс. В случае большей ги-
перболической скорости оптимальная точка приложения второ-
го импульса должна располагаться наиболее близко к притя-
гивающему центру.
Переход Оберта может иметь практическое применение.
При полете в сфере действия планеты с гиперболической ско-
ростью для выхода на околопланетную орбиту может оказаться
оптимальным по суммарным затратам топлива двухимпульсный
переход:
первый тормозной импульс дается в перицентре пролетной
гиперболы, величина которого ограничена радиусом планеты
или высотой ее «плотной» атмосферы;
второй разгонный импульс дается- в апоцентре переходного
эллипса для получения околопланетной орбиты с заданными
параметрами.
Автор '[71] нашел переход, более оптимальный, чем двухим-
пульсный переход Оберта, и всегда более выгодный, чем одно-
203
импульсный переход. Это уже трехимпульсный переход, кото-
рый показан на рис. 5.8,в. На рис. 5.8,г показан вариант пере-
хода с абсолютным минимумом по затратам скорости. Этот
переход состоит из ухода «в бесконечность», а затем возвраще-
ния оттуда по прямолинейной траектории к притягивающему
центру и, наконец, в приложении бесконечно малого импульса
для обеспечения выполнения конечных условий. Приближаясь
по возможно максимальным интервалам времени на реали-
зацию маневра и возможно минимальным расстояниям пролета
притягивающих центров к этому идеализированному случаю,
можно получать орбиты довольно большой энергии при скоро-
сти, которая ненамного превышает скорость на освобождение
(на достижение отлетной параболической скорости с началь-
ной орбиты).
Трехимпульсный перелет с двумя переходными эллипсами
(см. рис. 5.8,в) в зависимости от высот апоцентра переходных
эллипсов обеспечивает некоторый локальный минимум по ско-
рости. Если есть ограничение по переходам ниже начальной
круговой орбиты, то для компланарного случая оптимальным
будет одноимпульсный переход на гиперболическую орбиту.
Для некомпланарного случая применение многоимпульсных пе-
реходов может обеспечить меньшие скорости.
В рассматриваемых выше случаях глобальные минимумы по
требуемой скорости достигались приложением промежуточных
импульсов «в бесконечности» или они совпадали с притягиваю-
щим центром («нулевая» высота относительно центра). Пер-
вое требует бесконечно большого времени для выполнения ма-
невра, второе приводит к ограничениям, связанным с конечны-
ми величинами радиусов планет и высот их атмосфер.
Но существует пример перелета с приложением промежуточ-
ного импульса на конечном радиусе, который представляет ре-
шение с абсолютным минимумом. Это переход между двумя
неком1планарными круговыми орбитами одинакового радиуса.
Первый импульс превращает круговую орбиту в эллиптическую
и одновременно поворачивает плоскость орбиты на небольшой
угол. Второй импульс поворачивает плоскость орбиты на основ-
ную величину угла некомпланарности, а третий тормозной им-
пульс переводит КА на конечную круговую орбиту с заданным
углом наклона.
Небольшие повороты, выполненные с помощью первого и
третьего импульсов, дают меньшие требуемые скорости по срав-
нению с одноимпульсными и обычным (с одним поворотом
плоскости) трехимпульсным перелетом даже при малых углах
некомпланарности. В случае одного поворота плоскости пере-
ходного эллипса трехимпульсный переход выгоднее при Д/>
>38,94°. Для этого случая оптимальные значения относитель-
204
ного радиуса ^апоцентра и относительной скорости определяются
формулами
7 _ sin (At/2)
а— 1 - 2 sin (Д i/2) ’
— sin
На рис. 5.9 приведены зависимости относительных скоро-
стей для одноимпульсных и трехимпульсных переходов в зави-
симости от угла некомпланарности исходных орбит. Здесь по-
казаны также оптимальные значения относительных радиусов
апоцентров переходных эллипсов. Для угла некомпланарности,
равного 60,19°, возможны два маневра, которые приводят к оди-
наковым затратам скорости:
для первого относительный радиус апоцентра переходного
эллипса равен примерно 10;
для второго переход осуществляется через «бесконечность».
Как видно из графика рис. 5.9, дальнейшее увеличение угла
некомпланарности исходных орбит при переходе через «беско-
нечность» не увеличивает скорость.
Для некомпланарных соосных эллиптических орбит класс
оптимальных переходов содержит:
Рис. 5.9. Относительная скорость одноимпульсного и трехимпульсного пере-
ходов между круговыми орбитами одинаковых радиусов:
1 — один импульс; 2 — три импульса
Рис. 5.10. Схемы переходов между эллиптическими орбитами
205
двухимпульсные переходы;
трехимпульсные переходы с апоцентром промежуточного
эллипса выше апоцентра наибольшей из начальных орбит, и
его высота конечна;
трехимпульсные переходы с маневром через «бесконеч-
ность»;
четырехимпульсные переходы с маневром через «бесконеч-
ность».
Получены также результаты в классе четырехимпульсных
перелетов между компланарными эллиптическими орбитами,
когда два импульса прикладываются «в бесконечности». На
рис. 5.10,6 показан вариант четырехимпульсного перехода с ко-
нечным промежуточным радиусом. Первый импульс 1 даётся
в перицентре первой орбиты, второй 2—на достаточно боль-
шом расстоянии, после чего орбита проходит над обоими эллип-
сами; третий импульс 3 формирует орбиту, перицентр которой
совпадает с перицентром конечной орбиты; четвертый импульс
4 осуществляет переход на эту орбиту. Если радиусы апоцент-
ров трех промежуточных эллипсов удалить «в бесконечность»,
то суммарная требуемая скорость перехода будет равна сумме
разностей скоростей освобождения (параболических скоростей)
и скоростей в перицентрах соответствующих эллипсов. На рис.
5.10,а для сравнения показан двухимпульсный переход 1—2:
Одной из решенных задач в области перехода с незакреп-
ленным временем является задача перехода между гиперболи-
ческими орбитами. Такой переход может быть выполнен с ми-
нимальными затратами топлива, если шесть бесконечно малых
импульсов прикладываются или в бесконечности, или в притя-
гивающем центре (на «нулевом» расстоянии).
Шестиимпульсный переход осуществляется по следующей
схеме (рис. 5.11,6) :
Рис. 5.11. Схемы переходов между гиперболическими орбитами:
а — одноимпульсный переход; б — шестиимпульсный переход
206
первый импульс 1 прикладывается на достаточно большом
расстоянии и\формирует перелетную орбиту так, что ее пери-
центр становится близким к притягивающему центру;
второй (тормозной) 2 импульс прикладывается в перицент-
ре, и орбита становится близкой к параболической;
’третий импульс 3 прикладывается на большом .расстоянии и
переводит аппарат в новое положение 4\
четвертый импульс 4 снова обеспечивает возвращение к при-
тягивающему центру;
пятый импульс \(разгонный) 5 увеличивает энергию до ве-
личины, близкой к Заданной;
шестой импульс\6 опять прикладывается на достаточно
большом расстояний и формирует конечную гиперболическую
орбиту. '
В {71] отмечается, что если первый, третий, четвертый и
шестой импульсы прикладываются в бесконечности, а второй и
пятый — в притягивающем центре, то переход между произ-
вольными гиперболическими орбитами будет реализовываться
с бесконечно малой суммарной скоростью при бесконечно боль-
шом времени. Практическое использование такой схемы (с ог-
раничением высот приложения импульсов) возможно, например,
в такой космической операции, когда требуется, чтобы косми-
ческий аппарат находился некоторое время в окрестности пла-
неты и затраты топлива при этом должны быть гораздо мень-
ше варианта выхода на околопланетную орбиту с малым пе-
риодом.
Число импульсов при закрепленном времени перехода
Ограничение на время перехода позволяет получать
решения, удовлетворяющие практические потребности выбора
баллистических схем полета при осуществлении конкретных
космических полетов. Это объясняется тем, что в отличие от
случая незакрепленного времени перехода, когда абсолютные
минимумы затрат топлива достигаются при переходных орби-
тах через «бесконечность», в данном случае такие переходы уже
ограничены максимальными удалениями переходных орбит. По-
этому часто (и это не более как удобный прием исследования)^
задачу перехода с закрепленным временем заменяют за-
дачей перехода с ограничениями на максимальный и мини-
мальный радиусы переходных орбит. Отметим, что в этом слу-
чае также исключаются переходы с импульсами в «нулевой»
окрестности гравитационного центра.
^Следует отметить, что объем результатов в решении дан-
кои задачи пока еще невелик. К наиболее простым результа-
там, имеющим сравнительно нетрудоемкие численные решения,
а Для космических перелетов Земля — орбиты некоторых пла-
207
нет Солнечной системы, затабулированные на достаточно дли-
тельный интервал, относятся задачи двухимпульсных переходов
с заданным временем ‘[11].
5.4. МОНТАЖНЫЕ ОРБИТЫ
Операцию сборки космических аппаратов на орбите
можно условно рассматривать состоящей из следующих эта-
пов: /
выведение на монтажную орбиту и операции маневрирова-
ния на ней для обеспечения условий сближения;
сближение — маневры уменьшения рассогласований кинема-
тических параметров движения центров мабс КА;
причаливание — маневры уменьшения рассогласований как
кинематических параметров движения центров масс космиче-
ских аппаратов, так и угловых параметров взаимной ориента-
ции;
стыковка — механическое соединение стыковочных узлов
космических аппаратов.
Следует отметить, что для операций инспекции или сов-
местного полета двух или более космических аппаратов в оп-
ределенном геометрическом положении операция стыковки от-
сутствует. Тогда вместо нее должны проводиться операции уп-
равления относительным положением космических аппаратов в
режиме «зависания» или периодических движений с ограниче-
ниями по угловому положению и расстоянию одного аппарата
относительно другого.
Часто монтажной орбитой называют орбиту космического
аппарата, выполняющего пассивную роль на этапе сближения.
Однако если на этапе сближения коррекции орбит проводят
оба аппарата, то за монтажную орбиту следует принимать ор-
биту, на которой заканчивается этап причаливания.
Монтажная орбита должна удовлетворять следующим тре-
бованиям:
достаточное время существования для проведения сборки и
дальнейших операций в совместном полете;
минимум суммарных затрат топлива на проведение всех
этапов сборки;
удовлетворение условиям работы командно-измерительного
комплекса и др.
Рассмотрим выбор монтажной орбиты пассивного аппарата
и определение условий старта (азимута и времени) активного
аппарата с точки зрения минимальных энергетических затрат
на проведение этапов сборки. Будем рассматривать случай
сборки аппаратов при выведении их с одной стартовой площад-
208
ки. Исходя из требований минимума затраттоплива 'следует со-
гласовать\параметры обеих орбит аппаратов с учетом ряда дру-
гих ограничений (например, когда по условиям старта не до-
пускается изменение азимута старта, что практически выполня-
ется всегда )\
Идеальным случаем с точки зрения минимума энергетиче-
ских затрат и времени осуществления сборки, когда не допус-
кается изменения азимута старта и параметры конца активных
участков выводимых аппаратов одинаковы, является соблюде-
ние условий кратности прохождения восходящим узлом орбиты
одной и той же'точки земной поверхности.
Условие кратности
Выполнение условия кратности обеспечивает равен-
ство нулю отклонений между аппаратами по координатам и
составляющим скорости. Условие кратности прохождения за-
писывается в виде
/еТэ = рТа, (5.14)
где k, р — целые величины эффективных суток и количества
витков соответственно;
эффективные сутки определяются соотношением
<5Л5)
с использованием зависимостей разд. 3.4, в частности соот-
ношения (3.69), угловая скорость изменения долготы восходя-
щего узла находится по формуле
209
величина драконического периода с использованием зависи-
мости (3.74) определяется соотношением
2 л с q /' R \2 i
Та = г™ {1 - А ) (1 + 5 cos2 i-6 sin2 и0 sin2 i)}. (5.17>
Задаваясь в (5.14) различными значениями А, для принятых
наклонений i следует определять г0, при которых р — целые
числа. По результатам расчетов может быть построена номо-
грамма для определения высот кратных орбит (рис. 5.12 |[9]).
Изменение времени старта при выведении
Соблюдение условий кратности прохождения, обеспе-
чивающее равенство нулю отклонений между аппаратами по
координатам и скоростям (главным образом по продольному
положению, нормали к плоскости орбиты и боковой составляю-
щей скорости), в практических случаях затруднительно по ряду
.причин. Главная из них заключается в том, что для проведения
ряда коррекций траектории аппарата, находящегося на орбите
(при этом для уменьшения ошибок последние коррекции долж-
ны проводиться как можно ближе ко времени старта второго
аппарата), требуется увеличение затрат топлива.
Поэтому в общем случае, учитывая такие факторы как за- •
траты топлива и время сближения, можно рассматривать вы-
ведение второго аппарата в плоскость, некомпланарную плоско-
сти орбиты первого. Это можно осуществить как изменением
азимута старта, так и изменением времени старта. Изменение
азимута старта связано с изменением зон падения отработав-
ших ступеней и в практике решения задач сближения не ис-
пользуется. Однако этот свободный параметр, влияющий на
изменение угла некомпланарности орбит, принципиально можно
использовать при операциях сборки на орбитах других планет.
При соответствующем выборе времени старта второй аппа-
рат может выйти в плоскость орбиты первого аппарата (рис.
5.13). Но в этом случае в момент выхода между аппаратами
существует угловое рассогласование. Изменив время старта
Рис. 5.13. Трассы орбит при
изменении времени старта:
1 — трасса аппарата, находяще-
гося на орбите; 2 — трасса ап-
парата, выводимого на орбиту;
3 — плоскость экватора
210
(на рис. 5.13 — это положительная задержка) на Д/с, можно
уменьшить рассогласование по углу в плоскости орбиты, полу-
чив при этом какое-то отклонение по нормали.
Будем считать западное смещение по долготе восходящего
узла орбиты второго аппарата положительным. Тогда
Дйг = (о)а+АЙ)А/С, (5.18)
где AQ находится по формулам (5.16, 5.17).
Из сферического треугольника ADB следует
sin i ctg (180° — i) = ctg DB sin AQf — cos i cos Д Qt,
откуда находим
ctg pB = cos 1 (cos ~ 1)
® sin A Qj
Из теоремы синусов
sin AQf sin DB
sinAtH ~~ sin (180° — i)
найдем, что угол некомпланарности плоскостей орбит
sin Д iH = sin i V(cos Дйг— l)a cos2Z + sin2 AQt (5.19)
и для малых AQ/ достаточно точна формула
sin Д ~ AQf sin i. (5.20)
Широта узла В находится из сферического треугольника
АВС, в котором, как видно из рисунка 5.13, угол АС равен
90° —AQ//2:
(pu = arctg ^cos tg г у (5.21)
Обозначим широту выведения <рв и будем отсчитывать бо-
ковое смещение первого аппарата относительно второго по дуге
большого круга FE. Тогда из сферического треугольника EFB
имеем
FE-— = arcsin (sin Д и sin Д Q, (5.22)
го
где z — линейное боковое отклонение; г0 — радиус условно при-
нятой круговой орбиты; Au — угловое расстояние от точки вы-
ведения Е до узла В.
Если точка окончания активного участка Е находится до
точки орбиты с максимальной широтой, то
Д и = arcsin —— arcsin ——, (5.23)
sin i sin i
211
иначе, если точка окончания активного участка Е находится7
после точки орбиты с максимальной широтой, то
. • SID G)/j • Sin (Dr .• л л а
Д и = л—arcsin ———arcsin ——. (5.24)<
sin i sin i
Для случая малых Дй/ и срв~г можно использовать более
простые формулы:
из (5.19) получим:
Д iH ~ д£\ sin i\ (5.25)j
из (5.22, 5.23) последовательно имеем
г . • * • а • • / sin фи . sin <рв \
— ~ sin Д u sin Д iH ~ Д tn sin arcsin-— — arcsin —— ~
r0 \ sin i sin i )
. . • Г • , Гл / sin фв \2
~AiHsin arcsin 1/ 1— —— ।
J/ \ sin l j
и окончательно
— ~ Д1в-1/1 —(^Рв_у . (5.26)
r0 у \ sin / j
Для малых углов некомпланарности в этом случае в ок-
рестности точки выведения боковая скорость относительного
движения аппарата 1 относительно аппарата 2 составляет
г~УД1ц. (5.27)
Из полученных формул можно определить, что отклонение
взаимного положения по составляющей относительного рассто-
яния в плоскости орбиты очень эффективно корректировать из-
менением времени старта, получая при этом существенно мень-
шую боковую составляющую по координате и незначительную
составляющую по боковой скорости. Например, для круговой
орбиты с наклонением i = 45° и высотой /г = 200 км задержка по
времени старта на Д/с = 10 с приводит к изменению продольной
составляющей в плоскости орбиты
ДI V Д tc
порядка 80 км, при этом составляющая боковой скорости (5.27)
будет примерно равна 4 м/с.
Ниже приводится иллюстрирующий пример расчета по со-
отношениям (5.18 ... 5.23). Исходные данные:
смещение долготы восходящего узла орбиты выведения второго аппарата
в западном направлении Q* = 30°;
наклонение орбит /=45с;
широта точки выведения фв = 40°.
Рассмотрим случай, когда точка выведения находится до точки орбиты
с максимальной широтой. Широта узла пересечения орбит В (5.21) составляет
фи ~ 44,01°;
212
угол некомпланарности (5.19)
А 21,09°;
угловое расстояние (5.23)
Awe- 13,92°;
боковое отклонение по углу (5.22)
г/г0~4,97°.
Для случая, когда точка выведения находится за точкой орбиты с мак-
симальной широтой, расчеты по указанным формулам дают
A we- 35,34°, г/г0 ~ 12,01°.
Такая разница объясняется условием отсчета бокового смещения первого
аппарата относительно второго, на основании которого получилось соотно-
шение (5.22), и другим значением величины Au, вычисляемой по формуле
(5.24).
Изменение азимута старта
При выведении второго аппарата в плоскость, не
компланарную первому, соответствующим изменением азимута
старта можно уменьшить угол некомпланарности орбит. Пара-
метры орбиты второго ..
аппарата, главным об-
разом наклонение i2 и
долгота восходящего уз-
ла Е', определяются гео-
графическим положени-
ем точки старта (широ-
той фс), временем запу-
ска и азимутом старта
(рис. 5.14). Азимут стар-
та с точностью до попра- т *
/а н о рис 5 14 Трассы орбит при изменении вре
л *1 к». • • 1 • X М d V» V. О1 \_7 U V/ *1 1 11 Lz *1 *1 01V1 vilvll xl 1Т ГЭ С
ВОК, связанных С угловой Мени и азимута старта
скоростью (Оз, определяет
наклонение орбиты и долготу восходящего узла. Из сферическо-
го треугольника EKF следует
cos = sin А! cos фс,
где Al — азимут старта; фс — широта точки старта.
Можно показать, что для минимизации угла некомпланарно-
сти Д/н угловая дальность от точки старта D до точки В долж-
на составлять 90°. Из сферического треугольника DBC следует
sin Д /н = sin DC/sin DB.
В общепринятых обозначениях для сферических треугольников
sin Д fH = sin ft/sinc.
(5.28)
213
Оптимальный угол перехода с можно найти из необходимо-
го условия экстремума (5.28)
d (sin Д ZH) _ sin b cos c g
de sin2 c
отсюда следует copt = 90°.
Тогда из (5.28) получаем
sin Д iH = sin by
т. e. минимальный угол некомпланарности Дгн равен угловому
расстоянию от точки старта при выведении второго аппарата
до плоскости орбиты первого аппарата
Mn = b = DC. (5.29)
Угловое смещение точки старта FP зависит от изменения
^времени старта (5.18), а азимут старта Л2 выбирается из усло-
вия равенства
c = DB = 90°.
В этом случае наклонение плоскости орбиты второго аппа-
рата f2 отличается от наклонения 'плоскости орбиты первого
Однако следует заметить, что условие минимума в общем
случае может не соответствовать минимальным энергетическим
затратам на операцию сближения.
Приведенные оценочные формулы по определению началь-
ных условий по относительному положению аппаратов при из-
менении времени и азимута старта используются для выбора
монтажных орбит в качестве начального приближения при ре-
шении краевой задачи при уточнении параметров монтажной
орбиты и времени старта. При этом могут изменяться в не-
больших пределах азимут старта, параметры программы угла
тангажа (программа выведения) и время старта. Следует учи-
тывать также ряд ограничений и требований к монтажной ор-
бите и принятым условиям по взаимному положению аппара-
тов на участке причаливания (например, освещенность Солн-
цем).
Фазирование. Для уменьшения затрат при маневрах
сближения возникает потребность получения определенной ве-
личины фазового угла между орбитами. При выполнении усло-
вия по фазовому углу может реализоваться переход с мини-
мальными энергетическими затратами (например типа гома-
новского, см. разд. 5.1). Для получения требуемого фазового
угла выведение осуществляется на специальные орбиты, кото-
рые называются фазирующими. Время ожидания оптимальной
величины фазового угла называется временем фазирования.
Это время зависит от начала угловой фазы uQ и разницы угло-
вых скоростей coi и о)2 орбит первого и второго аппаратов.
£14
Рис. 5.15. Схемы сбли-
жения по полуэллипсам
Гомана
Рассмотрим наиболее простой случай фазирования и пере-
хода по эллипсу минимальной энергии между круговыми комп-
ланарными орбитами (рис. 5.15). Время движения по полови-
не эллипса между орбитами 1 и 2 составляет
. (S-30)
ИЦ \ 2 /
а за это время второй аппарат пройдет угловое расстояние
и = ш2/12, (5.31)
где (0 = 1/р/г23/2.
Используя полученные соотношения, найдем начальный фа-
зовый угол, удовлетворяющий условию встречи двух аппаратов
в точке приложения второго импульса (выравнивание скоро-
стей) :
для случая перехода на внешнюю орбиту (рис. 5.15,а)
для случая перехода на внутреннюю орбиту (рис. 5.15,6)
где г=Г1/г2-
Время фазирования зависит от начальной угловой фазы и0 и
разницы угловых скоростей a>i и со2. Период времени реализа-
ции фазового угла перехода ui2 находится по формуле
2л г3/2
ттах=—<5-32>
Уй|1-^3/2|
Если в начальный момент времени рассогласование по фа-
зовому углу составляет
Ди — Uq Uj2,
21S
где 0^Ды<2л, то время фазирования определяется (см. рис.
5.15):
для случая а
//2
Т,, =------!-----Д и;
Уй(1-Г3/2)
для случая б
Из формулы (5.32) следует, что
(5.33)
отношение периода повторения фазового угла перехода к пе-
риоду орбиты активного аппарата зависит от отношения ради-
усов или разницы в периодах орбит. Чем меньше разница в пе-
риодах, тем больше время фазирования для данного начально-
го фазового угла. Поэтому при малых разницах в периодах для
уменьшения времени фазирования следует использовать биэл-
липтические переходы. В этом случае первым импульсом фор-
мируется эллиптическая орбита, для которой время ожидания'
фазового угла для гомановского или близкого к нему перехода
уменьшается. В общем случае при ограничении времени пере-
хода, как отмечено в разд. 5.3, оптимальными могут быть и че-
тырехимпульсные переходы {71].
5.5. СБЛИЖЕНИЕ КОСМИЧЕСКИХ АППАРАТОВ
Уравнения относительного движения
Для анализа закономерностей относительного движе-
ния на этапе сближения космических аппаратов используются
различные системы координат, начало которых совмещается с
пассивным аппаратом. Таким образом, предполагается, что
движение пассивного аппарата известно, и для заданных на-
чальных условий движения активного аппарата следует опреде-
лить программу управления для осуществления сближения ап-
паратов.
В гл. 4 были получены уравнения относительного движе-
ния в окрестности круговых орбит во вращающейся системе
координат и в цилиндрической системе координат. Для даль-
нейшего анализа будем пользоваться уравнениями относитель-
ного движения во вращающейся системе координат xyz (рис.
5.16). Эта система координат с точностью до обозначений соот-
216
Рис. 5.16. Орбитальная система координат и
схема двухимпульсного сближения (ось z пер-
пендикулярна плоскости рисунка)
ветствует ранее рассматриваемой и по-
ясняемой в 4.3 (см. рис. 4.13).
В принятых обозначениях для осей
системы координат xyz (см. рис. 5.16)
система линейных дифференциальных
уравнений относительного движения
на круговой орбите запишется (соот-
ношения (4.34)) в виде
х—2сог/ = 0; у + 2сох—Зсо2 r/ = 0; z+co2z = 0 (5.34)^
с начальными условиями
/ = 0; х = х0, У = 2 = z0;
* = У = Уо, z = z0-
(5.35)
Используя ранее полученные решения (4.39), с учетом на-
чальных условий (5.35) запишем решение (5.34) в матричной
форме __
г
V
где г и V — матрицы-столбцы;
(5.36)
и М — матрица размерности 6x6
1 6 (со t—sin со t) 0 — sin (dt — 3t co — (1—cosco/) co 0
0 4—3 cos со t 0 — (COS (dt— 1) CO — sin co t co 0
м= 0 0 COSCO t 0 0 — co - sin co / •
0 бсо(1—COSCO t) 0 4 cosco t—3 2 sin co/ 0
0 Зсо sin co t 0 —2 sin co t cosco/ 0
0 0 —co sin со/ 0 0 cos co/
(5.37)
Для линейной системы дифференциальных уравнений (5.34)
движение разделяется на движение в плоскости орбиты и пер-
217
пендикулярное плоскости орбиты. Решение (5.36) можно запи-
сать в таком виде
х = 2 ( 2 —-3 у0 sin tot — 2 — cosоН +
+ (б!/0-3-^) + + ; (5.3
«/ = (2 — Зу0) costo/+ Sincoi +
+ (4».-2А);
z = zQ cos tot + sin tot,
x = 2 (2x0—3coy0) cos tot + 2y0 sin tot + (6coyo— 3x0);
у = (3 toy0—2 x0) sin co t + y0 cos tot; (5.39)
z = z0 cos tot—zQ to sin co t
и проводить анализ управления при сближении отдельно для
указанных движений.
Импульсные программы управления при сближении
(метод свободных траекторий)
Сближение может рассматриваться как маневр пере-
хода с одной орбиты на другую при дополнительном условии
согласования времени движения двух космических аппаратов.
Могут накладываться также другие ограничения, например на
угол подхода на участке причаливания одного аппарата отно-
сительно другого в заданной полусфере, но общим будет яв-
ляться приведение аппаратов в малую окрестность. Будем при-
нимать расчетные рассогласования по координатам равными
нулю, что означает при рассмотрении движения в относитель-
ной системе координат (см. рис. 5.16) выход маневрирующего
аппарата в начало координат.
На энергетические затраты при сближении влияют многие
факторы (точностные характеристики системы навигации, на-
званные выше ограничения и т. д.), но наиболее весомыми иг
них являются условия по времени сближения. Можно указать
три типа начальных и конечных условий по времени сближения:
моменты начала /н и конца tK сближения заданы;
задан момент начала /н, а время окончания tK произвольно;
произвольными являются времена начала и конца /к сбли-
жения.
218
Проводя аналогию между задачами сближения и перехода
между орбитами (см. разд. 5.1—5.3), отметим особенности за-
дания начальных и конечных условий по времени сближения с
точки зрения рассматриваемых ранее задач перехода между ор-
битами. Наиболее полные результаты в задачах перехода полу-
чены для случая незакрепленного (свободного) времени пере-
хода, чему отвечает третий тип указанных условий по времени
сближения. Естественно, что в практических задачах реализа-
ции сближения космических аппаратов этот случай не имеет
места, хотя здесь сближение может осуществляться с мини-
мальными энергетическими затратами.
Первый тип задания условий по времени сближения опреде-
ляет точки орбит начала и конца сближения. В этом случае
при двухимпульсном переходе энергетические затраты при оп-
ределенном положении точек могут быть неприемлемо больши-
ми. Для уменьшения этих затрат следует переходить на трех-
импульсные или четырехимпульсные схемы перехода.
В практических задачах сближения общее время на фазиро-
вание, а также непосредственно на сближение ограничивается,
но в пределах некоторого диапазона время конца сближения
произвольно. Таким образом, можно сказать, что в практиче-
ских задачах в некотором смысле реализуется второй тип ука-
занных выше условий по времени сближения с ограничением
верхнего предела по времени конца сближения.
Рассмотрим сближение космических аппаратов, используя
уравнения относительного движения в окрестности круговой ор-
биты (5.38, 5.39). Сближение будет осуществляться приложени-
ем импульсов (одного или нескольких) скорости с пассивными
участками движения в дальнейшем. Такое сближение получило
название — метод свободных траекторий.
Пусть в начальный момент времени /н = 0 активный аппарат
имеет параметры движения (начальные условия) относительно
пассивного, заданные по (5.35).
Определим составляющие импульса скорости в данный мо-
мент времени при условии, что в момент времени t = tK коорди-
наты активного аппарата равны нулю. Для этого, приравнивая
левые части (5.38) нулю, получим начальные составляющие
скорости
х0 sin со 4- ул [6 со sin со — 14 (1 — cos со /к)1
хи = со —-------------------------------------;
3 со sin со 8 (1 — cos со /к)
• 2 х0 (1 — cos со/к) + Уо [4 sin со — 3 соcos со/н] . (5.40)
3 со sin со — 8 (1 — cos со/к)
219
а также приращения составляющих скорости и величину пер-
вого импульса для осуществления сближения
Дхн хн , Дун t/ц Уо, AzH = ^о» (5.41)
И = К(ДХН)2 + (АУн)2 + (AZH)2. (5.42)
Импульс (5.42) является функцией начальных условий дви-
жения (5.35) и времени осуществления сближения или угловой
дальности Uk = (dtK. Из последнего уравнения (5.40) видно, что
при го=Н=О переход через углы uK = (&tKf близкие к ш (f=l,2,...
... , м), требует больших значений скоростей.
Составляющие второго импульса скорости в точке встречи
определим из соотношений для скоростей (5.39), подставив ту-
да значения скоростей после первого импульса
Хк = (4 х„—6 tt>y0) cos <£>tK + 2 уа sin © tK + 6 соу0—3 хн ;
Ук = Ун c°s <о/к—(2 хв—3 ©у,) sin <о/н ; (5.43)
ZK = ZH COS — (i)Zn sin (dtK.
к н ли Л
Запишем выражение для величины второго импульса ско-
рости
Vz — ]/" ^к+Ук+ Zk • (5.44),
Решая совместно последние уравнения из (5.40) и (5.43), полу-
чим
cozo
zK =--------— ,
sin со tK
откуда также видно, что переход через углы, близкие к крат-
ным 180° (половине периода по времени), требует больших ве-
личин скорости. В дальнейшем при анализе примеров зависимо-
сти требуемых скоростей от начальных условий (5.35) и углов
перехода будем различать пространственное движение и движе-
ние в плоскости опорной орбиты.
В случае сближения без ограничения скорости встречи тре-
буемая скорость находится из соотношений (5.40, 5.41, 5.42).
Для заданных величин начальных параметров движения (5.35)
величина скорости I/*i зависит только от времени сближения
или угловой дальности uK = &tK. Оптимальная величина угловой
дальности может быть определена из уравнения
=°>
решение которого в явном виде относительно <о/к получить не
удается. Выписывать выражение для условия оптимальности
не имеет смысла, так как вместо численного решения его отно-
сительно ик opt представляется более наглядным просчитать ве-
220
личины потребных скоростей (5.42) в интересующем диапазоне
Бремени с какой-то величиной шага по времени.
Приближенное решение (5.45) можно получить, если вос-
пользоваться разложением sinco/к и coso>/K в ряд. Как показано
в |[55], уравнение (5.45) в линейном приближении записывает-
ся в виде
хо + Уо + го + “ (хохо+Уо Уо+22о) ю/к = о.
Из этого уравнения находится оптимальная величина угла пе-
рехода
Цк opt — ® ^к opt — G)
*о + У о + 2о
хх0 + УУо + 2*0
ИЛИ
wKoPt = — со, (5.46)
'о
поскольку го-7о = грго, где гр — проекция относительной скоро-
сти Vo на линию визирования. Формулой (5.46) рекомендуется
пользоваться при углах перехода, не превышающих 45... 50°.
На рис. 5.17 для определенных начальных условий показана
общая зависимость потребной скорости от угла перехода. Пер-
вый (абсолютный) минимум соответствует времени перехода,
который меньше периода обращения. Увеличение требуемой
скорости при уменьшении времени перехода понятно, так как из
(5.40) в пределе можно получить при /к~>0 —(х0/М и у^-
—>(—ydt*). Увеличение скорости после минимума (правая ветвь
кривой на рис. 5.17) происходит при приближении угла перехо-
Рис. 5.17. Зависимость
импульса скорости при
•сближении от угла пере-
хода
Рис. 5.18. Зависимость суммарной скорости для
двухимпульсного перехода от времени сближения
для различных начальных условий движения:
орбита круговая высотой 464 км; 1 — х0 = 36,8 км; 2 — х0=
= 5,2 км
221
n.
да к «к = 2л;. В этом случае знаменатели в соотношениях (5.40)
стремятся к нулю, и если z/o=#O или zo=^=O, то скорость стремится
к бесконечности. Если z/o=0 и zo = O, то с увеличением угла пе-
рехода до нескольких оборотов, раскрывая неопределенности в
первых двух уравнениях (5.40), получим
хя=^-,уя = 0; 1 = 1,2,.
о (2 зт )
Этот переход своего рода маневр фазирования, когда орбиты
имеют одну общую точку (точку касания).
При сближении с выравниванием скоростей в точке встречи
(двухимпульсный маневр) скорость находится по формуле
Г*= ]/’(г[)2+(^)2. (5.47)
Используя соотношения (5.40—5.43), можем находить вели-
чины скорости двухимпульсного перехода для заданных началь-
ных условий движения и времени сближения. Оптимальное зна-
чение угла (времени) перехода может быть определено числен-
ным решением уравнения
Пик =°
рис. 5.18 [55] доказана зависимость
перехода от времени сближения для
относительно uK = (&tK. На
скорости двухимпульсного
различных начальных условий движения.
Как видно из графика, минимум реализуется в пределах вре-
мени до одного периода обращения, а минимум для кривой 2 со-
Рис. 5.19. Траектория движения активного космического аппарата при сбли-
жении для различных начальных условий движения:
a — tK=1000 с; б — tK=2000 с; 1—8 — траектории сближения
222
ответствует примерно половине периода (романовскому пере-
ходу) .
На рис. 5.19,а, б показаны траектории сближения в относи-
тельной системе координат Оху, вращение которой в отличие от
системы координат Оху (см. рис. 5.16) происходит по часовой
стрелке. Опорная круговая орбита (орбита пассивного аппара-
та) имеет высоту 464 км, начальные условия характеризуются
равенством
х0 + уо = 32 км ,
а время сближения равно соответственно 1000 и 2000 с. За-
метим, что такое движение активного космического аппарата
видел бы наблюдатель, находящийся в начале системы коорди-
нат. Траектория движения для внешнего наблюдателя показана
на рис. 5.16.
На рис. 5.20 показаны зависимости требуемой скорости при
сближении с выравниванием относительных скоростей в точке
встречи (двухимпульсный переход) от времени сближения для
начальных условий и траекторий, изображенных на рис.
5.19,а, б. Как видно из рис. 5.20, величины скорости равны для
точек активного аппарата, расположенных симметрично на
прямой, проходящей через начало координат. При ограничении
времени сближения до 3000 с наименьшие требуемые скорости
реализуются для положений 3 и 7. Это положение следует учи-
тывать при формировании программы выведения на орбиту и
выборе времени старта. Выбором точки выведения в соответст-
вующем квадранте можно уменьшить затраты топлива на сбли-
жение и гарантировать условие подхода *
к пассивному аппарату в заданной полу-
сфере, что требуется иногда из условий
освещенности на участке причаливания.
Таким образом, время сближения 120
можно выбирать таким, чтобы свести к
минимуму характеристическую скорость
двух импульсов (5.47) или чтобы еде-
лать минимальной скорость сближения
(5.44) после первого импульса. В послед-
нем случае в зависимости от начальных
условий скорость сближения может быть 60
достаточно малой и без выравнивания
скоростей корректирующей двигательной
установкой можно переходить к участку зо
Рис. 5.20. Зависимость суммарной скорости для
двухимпульсного перехода от продолжительности
сближения для траекторий, показанных на рис. д
5.19, 5.20
223
причаливания, используя другие исполнительные органы (реак-
тивные двигатели).
Практически вследствие ошибок определения параметров
траекторий аппаратов, ошибок прогноза их движения и реализа-
ции расчетных величин корректирующих импульсов, методиче-
ских ошибок, связанных с линеаризацией уравнений относитель-
ного движения, не удается свести к требуемой малой окрестно-
сти координаты в точке встречи после первого импульса скоро-
сти. Это приводит к необходимости введения дополнительных
включений корректирующей двигательной установки. Оптималь-
ное время сближения, число корректирующих импульсов и рас-
пределение их по величине и времени исполнения зависят от на-
чальных условий движения и аппаратурных погрешностей систе-
мы управления [37].
Моменты исполнения коррекций и величины корректирующих
импульсов могут определяться наземными средствами или для
космических аппаратов, обладающих достаточными аппаратур-
ными и вычислительными средствами, определяться по упрощен-
ным алгоритмам на борту. В случае автономных измерений сле-
дует учитывать возрастание с увеличением дальности ошибок
измерения тангенциальных составляющих скоростей и коорди-
нат, поэтому в этом случае используется следующий метод сбли-
жения 1[9].
Рассмотрим сближение через время, кратное периоду обра-
щения пассивного аппарата. За начало сближения принимается
момент минимальной разности высот космических аппаратов. Из
первого уравнения (5.40), раскрывая неопределенность, при
(oZk = 2ju (f= 1, 2,..., п) получим выражение для величины пер-
вого корректирующего импульса
= +2ю^о—^о; t = 2’: (5-48)
3 (2 л I)
Дг/1 = 0; Дх1 = 0,
где Хо — расстояние между аппаратами по координате х (ду-
ге орбиты) при минимальной разности высот; yQ — минималь-
ная разность высот; Xq — измеренная скорость изменения ко-
ординаты х в данный момент; i — число оборотов, отсчитывае-
мое от момента времени, при котором реализуется минималь-
ная относительная высота и начинаются операции по сближе-
нию.
Этот корректирующий импульс называют предварительным
дальним сближением при автономном управлении и это своего
рода — фазирование, при котором отклонение по дуге орбиты
можно уменьшить с минимальными затратами топлива. Второй
импульс дается в момент равенства нулю отклонения активно-
224
го аппарата от плоскости орбиты пассивного (в узле орбиты)
Д?2 = — г0.
После проведения этих коррекций остаются разности по вы-
соте и относительной скорости. Если эти величины меньше по
модулю предельных, то можно переходить на другой метод уп-
равления, обеспечивающий малые относительные составляю-
щие скорости в конце сближения. Если перед первым коррек-
тирующим импульсом прогнозируемая величина минимальной
высоты больше предельной, то нужно перед первым корректи-
рующим импульсом за половину периода до прогнозируемой
точки встречи выполнить импульс, обеспечивающий разность
высот, меньшую погрешности ее измерения.
Для уменьшения относительной высоты за половину перио-
да на величину Д/г, как это следует из второго уравнения (5.38) ь
следует дать импульс скорости
Дх0= -4- A h sign (у0).
4
Отмечая еще раз, что в зависимости от минимальной высо-
ты этот импульс может и не реализовываться, обозначим его с
индексом «о».
Теперь условия в момент начального прохождения мини-
мальной относительной высоты изменяются. Используя соотно-
шения (5.38, 5.39), определим изменения начальных условий
движения на интервале половины оборота, и (5.48) запишется
в виде
со Г*° — — лД h sign (yQ) 1
Д*1 = ------777—7—77----------h 2(0 [уо—A h sign (t/0)] —
О [ZJt — IJJ
— ---J- «оД/isign (z/0)j ;
4 = 2, 3, ... , n.
Отметим, что вследствие погрешностей определения и прог-
ноза траекторий движения аппаратов, а также погрешностей
формирования корректирующих импульсов скорости практиче-
ская реализация двухимпульсной схемы сближения маловероят-
на. Кроме рассмотренных существуют и другие методы сбли-
жения, например «затухающего перехвата», предполагающего
реализацию большего, чем два или три числа импульсов.
Таким образом, мы рассмотрели основные схемы межорби-
тальных переходов, некоторые из которых используются в бал-
листических схемах реальных космических полетов, и в краткой
форме представили методы сближения космических аппаратов.
Читателю, желающему ознакомиться с этими вопросами более
подробно, рекомендуются монографии [37, 39].
8—8 225
ГЛАВА 6. РАСЧЕТ ТРАЕКТОРИЙ МЕЖПЛАНЕТНЫХ
АППАРАТОВ
Траектория межпланетного космического аппарата, в отли-
чие от траектории спутника Земли, не ограничена окрестностью
Земли, значительная ее часть проходит вдали от Земли. В та-
ких условиях очень приближенно исследовать траекторию
межпланетного космического аппарата в рамках задачи двух
тел, Земля — КА, даже с учетом возмущений невозможно. При
удалении от Земли КА попадает в область преобладающего
гравитационного воздействия Солнца, планеты назначения, а
возможно и других планет Солнечной системы. Для составле-
ния математической модели движения межпланетного КА при-
дется воспользоваться общими уравнениями, описывающими
движение аппарата весьма широкого класса. Основой этой мо-
дели являются динамические уравнения, описывающие движе-
ние центра масс КА, ставящие в соответствие силам, действу-
ющим на КА, его ускорение. Среди сил, действующих на КА, и
тяга ракетного двигателя, и гравитационные поля Земли, Солн-
ца, Луны и т. д. Полная математическая модель, описывающая
движение такого КА, окажется сложной, мало отличной от об-
щей модели, рассмотренной в гл. 1. Использовать такую модель
при анализе проекта КА, при выборе (проектировании) траек-
тории межпланетного КА невозможно, даже если учесть совре-
менную вычислительную технику.
При решении проектных задач для выбора программы поле-
та КА используют подходы, которые опираются на ряд допу-
щений, существенно упрощающих математическую модель, опи-
сывающую движение межпланетного КА. Такой подход дает
возможность приближенно рассчитать траекторию межпланет-
ного КА, выявить закономерности этих траекторий, найти про-
грамму полета аппарата, при которой удовлетворяются много-
численные ограничения, оценить потребные энергетические за-
траты на межпланетный перелет. Такой анализ удается про-
вести, не прибегая к численному интегрированию.
Схема исследования выглядит так:
на основании свойств используемых рациональных схем по-
лета межпланетных КА необходимо сформулировать допуще-
226
ния, вводимые на этапах проектных проработок, и описать идеи
приближенного метода расчета траекторий межпланетных ап-
паратов;
ввести понятие грависферы небесных тел как основы при-
ближенного метода расчета межпланетных аппаратов;
показать возможность использования приближенного мето-
да расчета межпланетных КА при нахождении третьей косми-
ческой скорости — важной характеристики в механике косми-
ческого полета;
описать метод расчета траектории межпланетных КА, сво-
дящийся к анализу гелиоцентрического, геоцентрического и
планетоцентрического участков траектории межпланетного КА.
Глава заканчивается анализом выбора оптимальной схемы
межпланетных перелетов, оптимальных дат старта и времени
полета к планете назначения; гравитационного маневра у про-
межуточной планеты, который расширяет возможности реше-
ния задач межпланетного перелета; вопросами коррекции тра-
екторий межпланетного перелета.
6.1. СХЕМА ПОЛЕТА МЕЖПЛАНЕТНОГО КА.
ИДЕИ ПРИБЛИЖЕННОГО МЕТОДА РАСЧЕТА
ТРАЕКТОРИЙ МЕЖПЛАНЕТНЫХ АППАРАТОВ
В разделе описывается используемая в настоящее
время схема полета межпланетных КА, и на основании анали-
за этой схемы формулируются основные допущения и идеи при-
ближенного метода расчета траекторий межпланетного пере-
лета.
Промежуточная орбита ИСЗ
При реализации траекторий межпланетного перелета
в настоящее время используется промежуточная орбита ИСЗ,
т. е. ракета-носитель выводит КА с разгонным блоком на низ-
кую околоземную орбиту. С этой орбиты стартует межпланет-
ный аппарат. Более того, даже для КА более «близкого» на-
значения используется низкая промежуточная орбита. Так
только для первых трех лунных советских аппаратов («Лу-
на-1»— «Луна-3») использовалась прямая схема полета без
выведения КА на орбиту ИСЗ. Для остальных «Лун» исполь-
зовалась промежуточная орбита ИСЗ. Для выведения ИСЗ на
высокие орбиты также используется низкая промежуточная ор-
бита спутника Земли.
Использование промежуточной орбиты ИСЗ во многих кос-
мических маневрах выгодно по ряду обстоятельств. Это и чисто
технические обстоятельства. Такие как возможность контроля
8* 227
систем космического аппарата, систем разгонного блока КА по-
сле его выведения на низкую околоземную орбиту. Кроме того,
есть и «баллистические» преимущества такой схемы полета. К
ним следует отнести:
возможность оценить ошибки выведения на орбиту при за-
дании программы работы разгонного блока межпланетного КА;
возможность использовать выбор момента старта с земного
космодрома для получения определенного положения в про-
странстве плоскости промежуточной орбиты ИСЗ и затем плос-
кости геоцентрической траектории КА (значения долготы выхо-
дящего узла), не учитывая ограничений на ориентацию геоцент-
рической траектории в ее плоскости. При использовании проме-
жуточной орбиты ИСЗ есть возможность за счет выбора момен-
та включения двигателей разгонного блока добиться различной
ориентации траектории iKA в плоскости этой траектории;
возможность получения энергетического выигрыша (умень-
шения требуемой характеристической скорости). Использование
промежуточной орбиты ИСЗ разбивает весь активный участок
на два участка: выведение на промежуточную орбиту и старт с
этой орбиты. При этом один крутой участок разгона заменяет-
ся двумя пологими разгонами (по крайней мере, второй разгон
можно осуществить так, что угол между скоростью и местным
горизонтом был бы близок к нулю). При пологих разгонах гра-
витационные потери в скорости оказываются весьма малыми. В
этом заключается важное преимущество маневров с использо-
ванием промежуточной орбиты ИСЗ.
Объективности ради отметим, что использование промежу-
точной орбиты заставляет преодолевать и определенные техни-
ческие трудности. Так приходится запускать двигатель разгон-
ного блока в невесомости, обеспечивать радиовидимость КА в
момент старта его с промежуточной орбиты с наземных или
других пунктов слежения и т. д. Но эти трудности не являются
определяющими при выборе схемы полета КА. Именно эту схе-
му мы и будем обсуждать.
При выборе высоты промежуточной орбиты следует рас-
сматривать следующие обстоятельства:
увеличение высоты промежуточной орбиты приводит к увели-
чению энергетических затрат (характеристической скорости) ра-
кеты-носителя, но к уменьшению энергетических затрат разгон-
ного блока. Увеличение требующейся характеристической скоро-
сти ракеты-носителя оказывается более существенным, опреде-
ляющим. Поэтому высоту промежуточной орбиты целесообразно
брать минимальной.
Уменьшение высоты промежуточной орбиты может привести
к большим аэродинамическим возмущениям. Высота этой орби-
ты должна выбираться так, чтобы сделать достаточно малым
аэродинамическое сопротивление ИСЗ, обеспечить достаточное
228
время существования спутника на этой высоте. Для автоматиче-
ской межпланетной станции Венера-1, запущенной 12 февраля
1961 года, промежуточная орбита была близка к круговой: пери-
гейное и апогейное расстояния были равны соответственно
6601 км и 6658 км (средняя высота 230 км). Для американского
лунного корабля Аполлон использовалась промежуточная орбита
высотой 188 км.
Таким образом, межпланетный КА стартует с промежуточной
орбиты ИСЗ. Высота этой орбиты такова, что аэродинамически-
ми силами на участке схода с орбиты, как и в дальнейшем по-
лете, можно пренебречь.
Импульсная аппроксимация активного участка полета
КА при старте с промежуточной орбиты
Предполагаем, что разгонный блок КА оснащен хи-
мическим ракетным двигателем. Время работы такого двигате-
ля равно нескольким минутам, что составляет малую часть от
всего времени полета КА. Это обстоятельство дает возможность
использовать импульсную аппроксимацию активного участка
траектории КА при его старте с промежуточной орбиты ИСЗ.
При реализации траектории межпланетного перелета раз-
гонный блок (кстати, он может быть и многоступенчатым) со-
общает КА гиперболическую относительно Земли скорость Vi.
После этого КА движется относительно Земли по определенной
гиперболической орбите до тех пор, пока не удалится от Земли
на такое большое расстояние, что его траектория не может
быть с достаточной точностью рассмотрена в рамках задачи
двух тел (Земля — КА). И здесь мы подошли к важной идее
приближенного расчета траектории межпланетных аппаратов.
Идея грависфер влияния
Задача двух тел, которая описывает пассивное дви-
жение КА относительно гравитирующего центра в предположе-
нии, что никаких сил, кроме силы ньютоновского притяжения,
на КА не действует, имеет простое аналитическое решение.
Траектория КА оказывается коническим сечением (эллипсом,
параболой или гиперболой), в одном из фокусов которого нахо-
дится гравитационный центр. Все характеристики траектории
Достаточно легко связываются с начальными условиями (поло-
жением и скоростью КА), с условиями движения в любой точке
траектории.
Это обстоятельство натолкнуло исследователей на мысль о
Целесообразности разбиения всего космического пространства
на области — грависферы с преобладающим влиянием на траек-
торию космического аппарата только одного гравитирующего
229
тела (Земли или Солнца, или другой планеты Солнечной систе-
мы) с тем, чтобы в каждой области воспользоваться решением
задачи двух тел—получить «куски» траекторий КА в грави-
сферах, а затем провести «сшивку» этих «кусков» на границах
грависфер. Такая идея оказалась исключительно плодотворной.
Оказалось, что можно указать такие правила разбиения про-
странства на грависферы, при которых траектория, «собран-
ная» из «кусков» конических сечений, окажется весьма близкой
к истинной траектории КА.
В настоящее время есть несколько правил выделения грави-
сфер. Во всех этих правилах планеты окружаются некоторыми
замкнутыми поверхностями, внутренность которых считается
грависферами планет. Остальное пространство считается грави-
сферой Солнца. Впрочем, понятие грависферы Солнца иногда
формально не вводят, а считают, что если КА не находится в
грависфере планет, то расчет его траектории проводится в рам-
ках задачи двух тел Солнце — КА.
Задача исследования траектории КА, предназначенного, на-
пример, для полета к Венере, в рамках метода грависфер раз-
бивается на следующие этапы (рис. 6.1).
1. Этап движения КА в грависфере Земли. На этом этапе
траектория КА (AAi) исследуется в рамках задачи двух тел
Земля — КА. Этап заканчивается получением характеристик
движения КА в момент выхода из грависферы Земли (в точке
А1). Этот участок траектории часто называется геоцентриче-
ским. Другое его название — первый внутренний участок.
2. Этап движения КА относительно Солнца (вне грависфер
планет). Этот участок траектории называется гелиоцентриче-
ским. На участке траектория КА исследуется в рамках задачи
двух тел Солнце—КА. Этап начинается с получения гелио-
центрических характеристик (характеристик относительно
Солнца) траектории КА в момент выхода из грависферы Земли.
При этом для получения вектора гелиоцентрической скорости
(скорости относительно Солнца) КА 7о.с необходимо векторно
относительно Солнца в момент выхода
КА из грависферы Земли
V3 (переносную скорость)
и скорость КА относи-
тельно Земли (геоцентри-
ческую скорость) в этот
же момент К», получен-
ную на предыдущем эта-
пе: й0.с=Рз+Роо.
По начальным харак-
теристикам для гелиоцен-
трического участка дви-
жения КА строится сама
о.с
сложить скорость Земли
Кг. с
Уз
грависфер
Рис. 6.1. Идея
метода
мв
в®
230
гелиоцентрическая траектория AM2 как коническое сечение, в
одном из фокусов которого расположено Солнце. Исследуется,
попадает ли КА в грависферу Венеры, и если да, то осуществля-
ется переход к рассмотрению второго внутреннего венероцентри-
ческого участка траектории. Сам же расчет гелиоцентрического
участка траектории называется внешней задачей.
3. Этап движения КА в грависфере Венеры. На этом участ-
ке траектория КА исследуется в рамках задачи двух тел Вене-
ра — КА. Этап начинается получением венероцентрических ха-
рактеристик траектории КА в момент входа в грависферу Вене-
ры. Для этого находится скорость КА относительно Венеры (ве-
нероцентрическая скорость) в момент входа в ее грависферу
V'oo как разность гелиоцентрических скорости КА VK.C и Венеры
VB в этот момент времени V/Oo= 7К.с—VB.
Венероцентрическая траектория КА оказывается гиперболи-
ческой. Если не предусматривать программного включения дви-
гательной установки и торможения КА, то он, двигаясь по ги-
перболе относительно Венеры, или войдет в плотные слои ее
атмосферы, или пролетит мимо Венеры и удалится от нее в бес-
конечность.
Расчеты показали, что описанный метод исследования тра-
екторий КА, часто называемый методом грависфер, дает доста-
точно высокую точность при проектных исследованиях, очень
высокую точность оценки требуемой на перелет энергетики
(требуемых скоростей для межпланетного перелета).
Таким образом, в данном разделе проанализирована схема
движения межпланетного КА, введены основные допущения и
идеи приближенного метода расчета траекторий межпланетных
КА —идея импульсной аппроксимации активного участка раз-
гонного блока КА и идея грависфер планет.
6.2. ГРАВИСФЕРЫ НЕБЕСНЫХ ТЕЛ
СОЛНЕЧНОЙ СИСТЕМЫ
Понятие грависферы, введенное выше, дает возмож-
ность приближенно рассчитать траекторию межпланетного КА.
Свободу в выборе размера и формы грависферы следует ис-
пользовать для повышения точности расчета траектории. Рас-
смотрим несколько возможных правил введения грависферы.
Но прежде всего напомним общую структуру Солнечной систе-
мы, которая, безусловно, определяет эффективность того или
иного метода расчета межпланетных траекторий. Основная мас-
са Солнечной системы сосредоточена -в Солнце (почти 99,87%).
На значительном расстоянии друг от друга и от Солнца дви-
гаются девять больших планет. Их основные характеристики
приведены в табл. 6.1.
231
Таблица 6.1
Планета Большая полуось, а. е. Эксцен- триситет Наклоне- ние, ° Синодиче- ский пе- риод средний, сут Сидерический период
г. сут
Меркурий 0,387 0,206 7,0 115,88 0 87,97
Венера 0,723 0,007 3,4 583,92 0 224,70
Земля 1 0,017 0 — 1 —.
Марс 1,524 0,093 1,9 779,94 1 321,73
Юпитер 5,203 0,048 1,3 398,88 11 314,84
Сатурн 9,539 0,056 2,5 378,09 29 116,98
Уран 19,182 0,047 0,8 369,66 84 —.
Нептун 30,058 0,009 1,8 367,48 164 280,30'
Плутон 39,439 0,250 17,2 366,72 247 255,1
Большие расстояния между планетами и между планетами
и Солнцем, малые массы планет относительно Солнца приво-
дят к тому, что движение КА на большой части траектории
можно рассматривать в рамках ограниченной задачи трех тел.
Гравитирующими массами в этой задаче является Солнце и
планета, в окрестности которой движется КА. Учет при этом
возмущающего влияния других планет может быть целесообра-
зен только при поверочных расчетах траекторий КА. На этапах
проектных проработок, при проектировании траектории КА та-
кой учет не проводится. Рассмотрим ограниченную задачу трех
тел как основу для введения грависферы планеты.
На рис. 6.2 в точке С расположена гравитирующая точечная
масса Л41, в точке В — масса ТИ2, в точке А — КА массой т.
Для определенности предположим, что Afi<Af2, т. е. Mi — мас-
са планеты, М2— масса Солнца. Будем учитывать, что
Для использования метода грависфер при исследовании тра-
Рис. 6.2. Ограниченная задача трех тел.
Сфера притяжения
ектории КА в рамках ог-
рениченной задачи трех
тел нужно найти принци-
пы выделения некоторой
области пространства во-
круг тела Mi, чтобы счи-
тать ее грависферой тела
массой Mi, а все осталь-
ное пространство считать
грависферой тела массой
М2.
Сфера притяжения
Одним из принципов разбиения пространства может
служить сравнение сил притяжения КА массами Mi и М2,
(Массы Mi и М2 в каждой точке пространства притягивают КА
232
с определенными силами (скажем G{ и G2). Можно найти гео-
метрическое место точек в пространстве, в которых величины
этих сил равны: Gi = G2. Это геометрическое место представля-
ет собой замкнутую поверхность вокруг меньшего из гравити-
рующих тел — Л4ь Введем некоторую систему координат с
центром в точке С (см. рис. 6.2) и осью Сх, направленной по
прямой, соединяющей гравитирующие тела (от меньшего тела
к большему). Оси Су и Cz произвольно дополняют систему до
прямоугольной декартовой.
Можно показать, что во введенной системе координат урав-
нение поверхности Gi = G2 имеет вид:
/ и \ 2
(х+Г12 ) + у2 + г2 =
\ 1 -н/
Н г 2
(1—|Х)а 12 ’
(6.1)
где п2 — расстояние между М1 и М2: |x=Mi/M2.
Несложно видеть, что равенство
уравнение сферы радиусом
1 — ц 12’
(6.1) представляет собой
геометрический центр ко-
торой имеет координаты ( —г12 —— , 0, 0 ) . На рис. 6.2 сме-
\ 1 -и )
щение геометрического центра сферы относительно С обозначе-
но d, при этом d = г12 р>-
1 -и
Обратим внимание на то, что центр
сферы смещен по прямой, соединяющей гравитирующие тела в
сторону, противоположную радиусу-вектору большего гравитиру-
ющего тела относительно меньшего (d<0). Таким образом, в
ограниченной задаче трех тел все пространство разделяется
сферой (6.1) на две части. Внутри сферы сила притяжения от
массы Mi больше силы притяжения от массы М2, вне сферы
сила притяжения от массы М\ меньше силы притяжения от
массы М2.
Сферой притяжения меньшего гравитирующего тела относи-
тельно большего тела называется область пространства, в кото-
ром сила притяжения тела меньшей гравитарующей массы
больше силы притяжения тела большей гравитирующей массы.
Таким образом, сфера притяжения меньшего гравитирующего
тела относительно большого тела есть внутренность геометриче-
ской сферы, уравнение которой имеет вид (6.1).
Сфера действия
При рассмотрении возмущенного движения спутника
(см. гл. 3), анализировалось влияние Луны и Солнца на траек-
торию ИСЗ. В процессе анализа были записаны точные урав-
нения движения КА относительно Земли (массы Мi) в ограни-
233
ченной задаче трех тел (см. рис. 3.2 и соотношения 3.15, 3.17).
Они имеют следующую структуру:
d2 г~ — —
-^^аг + Ф,. (6.2)
где ах=—f ~ ri.— ускорение КА от притяжения его массой
'i
Mi (оно называлось основным); Фг = — f— —f— г12 — уоко-
гз 3
г2 '12
рение КА относительно Земли, появляющееся из-за возмущаю-
щего воздействия тела массы М2 (оно называлось возмущаю-
щим).
Еще раз отметим, что (6.2) —точное уравнение, описываю-
щее движение КА относительно массы Ali в рамках ограничен-
ной задачи трех тел.
Совершенно аналогично можно точно описать движение КА
относительно массы М2 в рамках той же ограниченной задачи
трех тел:
^р=а2+Ф2, (6.3)
где а2= —f — — ускорение КА в ограниченной задаче двух
г2
тел М2—tn ; Ф2 = — fML ( Д- — возмущающее ускоре-
\ Ч Г12/
ние, которое имеет КА при движении относительно тела М2 из-
за существования тела массой Mi.
Идея метода грависфер состоит в том, что в некоторой ок-
рестности тела массой Mi рассматриваем движение КА относи-
тельно этого тела в рамках задачи двух тел Mi~т, при этом
пренебрегаем в уравнении (6.2) возмущающим ускорением Ф1
(т. е. пренебрегаем Ф1 по отношению к di). В остальной части
пространства рассматриваем движение КА относительно грави-
тирующего тела большей массы М2 и пренебрегаем в уравнении
(6.3) возмущающим ускорением Ф2 (т. е. пренебрегаем Ф2 по
отношению к а2). Таким образом, точность метода зависит от
того, насколько возмущающие ускорения Ф1 и Ф2 пренебрежи-
мо малы по отношению к а\ и а2 соответственно. Важно так
выделить грависферы, чтобы возмущающее ускорение было как
можно меньше основного. Эта идея введения грависферы на ос-
нове сравнения Ф и а находит отражение в следующем подходе.
Рассмотрим геометрическое место точек пространства в ог-
раниченной задаче трех тел, для которых выполняется условие
Ф1/Я1 = Ф2/а2. (6.4)
234
При введении понятия сферы действия уравнение поверхно-
сти, где выполняется равенство (6.4), играет ту же роль, что и
условие равенства гравитационных сил Gi = G2 при введении
понятия сферы притяжения, т. е. эта поверхность и разграничи-
вает все пространство на области. Та область пространства,
где
Ф1/а1<Ф2/а2 (6.5)
и где естественней пренебрегать Ф1 по отношению к аь рас-
сматривая движение КА в рамках задачи двух тел Mi—т, на-
зывается сферой действия меньшего гравитирующего тела М\
по отношению к большему гравитирующему телу. В остальном
пространстве, где неравенство (6.5) не выполняется, целесооб-
разно рассматривать движение КА относительно большего гра-
витирующего тела (в рамках ограниченной задачи двух тел
М2—w), пренебрегая Ф2 по отношению к а2.
Сферой действия меньшего тела относительно большего на-
зывается область пространства, в котором выполняется нера-
венство (6.5).
Можно показать, что граница области, уравнение которой
есть (6.4), представляет собой замкнутую поверхность, охваты-
вающую гравитирующее тело меньшей массы. Для случая, ин-
тересного для -практики, когда массовый параметр jx=Afi/Af2
очень мал (для ограниченной задачи трех тел Земля — Солн-
це— КА ц = 0,3008 • 10-5), граница сферы действия очень близ-
ка к слегка приплюснутой сфере с центром в точке С (масса
MJ. Сжатие сферы проводится по прямой, соединяющей грави-
тационные центры (по СВ рис. 6.3). Коэффициент сжатия, под-
считанный как отношение диаметра сжатого сфероида FE, пер-
пендикулярного ВС (см. рис. 6.3), к диаметру Z)G, направлен-
ному по ВС, равен 1,15.
Очень часто считают, что граница сферы действия есть гео-
метрическая сфера с центром в малом гравитирующем теле
(MJ радиуса
Ясф.д=1Г12Н2/5. (6.6)
Рис. 6.3. Сфера действия в ограниченной задаче трех тел
235
Радиус сферы действия Земли (по отношению к Солнцу) ра-
вен 925-103 км. Обратим внимание на то, что сфера действия
Марса, масса которого существенно меньше Венеры и Земли,
оказывается достаточно большой из-за большого расстояния
Солнце—Марс (л2 в соотношении (6.6)) по отношению к рас-
стоянию Солнце — Венера, Солнце — Земля.
Самая маленькая сфера действия из планет у Меркурия —
112-103 км. Небезынтересно отметить, что радиус сферы дейст-
вия Луны относительно Земли равен 66-Ю3 км.
В![11] отмечается, что некритическое использование сферы
действия или, по терминологии автора, грависферы Лапласа в
практике баллистических расчетов может привести к нежела-
тельным методическим ошибкам. Авторы |[60] предлагают в ка-
честве грависферы рассматривать «грависферу минимальных
отклонений». Границу грависферы минимальных отклонений
они определяют как геометрическую сферу с центром в планете
и радиусом, равным /?сф min = ri2*H1/3.
Грависфера минимальных отклонений существенно больше
сферы действия. Так, для Земли /?Сф min = 2,16-106 км (|/?Сф.д=
= 0,925-106 км), для Венеры */?Сф min= 1,46-106 км (/?Сф.д=
= 0,6161-106 км). Расчеты и других авторов показывают, что
точность исследования траектории при использовании сферы
действия планеты в качестве грависферы может быть повышена
увеличением размеров грависфер. Так, Д. Е. Охоцимский пред-
ложил радиус грависферы Земли считать равным 3...4-106 км
[50], М. Д. Кислик на основании энергетических расчетов пред-
ложил использовать сферу влияния [29], радиус которой
7?сф.в = 1,15Г12|Х1/3-
Для Земли радиус сферы влияния 2,48-106 км.
В. И. Левантовский, анализируя в [42] используемые в на-
стоящее время грависферы, называет их динамическими, а сфе-
ру притяжения, которая по словам автора «не играет никакой
роли в космодинамике», — статической грависферой. Он подчер-
кивает, что использование сферы притяжения имело бы смысл
только в задачах перелета между неподвижными небесными те-
лами. Это замечание безусловно верно. Отметим, что нами рас-
смотрено понятие сферы притяжения прежде всего из методиче-
ских соображений.
Существует разновидность метода грависфер, в которой кон-
кретных границ грависфер не вводится. Он называется методом
грависфер нулевой протяженности.
Метод грависфер нулевой протяженности
Сущность метода сводится к следующим трем допол-
нительным допущениям метода грависфер.
236
\ 1. Основное допущение. При исследовании гелиоцентричес-
кой траектории КА пренебрегается протяженность грависфер
планет. Считается, что после выхода из грависферы, напри-
мер Земли, КА находится в точке, в которой располагается
центр Земли (а самой Земли и ее грависферы нет). При под-
лете к планете назначения ее грависфера также имеет нуле-
вую протяженность и транспортная задача гелиоцентрического
участка траектории заключается в попадании в точку, в кото-
рой располагается планета назначения.
2. Время начала гелиоцентрического участка траектории
считается равным времени старта КА с промежуточной орби-
ты ИСЗ. Аналогичное допущение делается при анализе време-
ни подлета КА к планете цели.
3. При анализе планетоцентрического участка траектории
планетоцентрическая скорость КА в момент его выхода из гра-
виоферы планеты считается равной гиперболическому избытку
скорости Voo. Это та скорость, которую КА, двигаясь по гипер-
болической траектории относительно гравитирующего центра
в задаче двух тел, имеет при удалении от гравитационного
центра в бесконечность.
Отметим, что первое из перечисленных допущений является
основным и определяющим сущность метода грависфер нуле-
вой протяженности. Остальные допущения могут не вводиться
и в их использовании наблюдается некоторый произвол.
Отметим, что метод грависфер имеет хорошую точность,
когда КА пересекает границы -грависфер не очень много раз,
когда он находится в окрестности границ сравнительно неболь-
шое время.
Таким образом, в данном разделе были рассмотрены нес-
колько типов грависфер планет, использующихся при расчете
траекторий межпланетных КА (сфера действия, грависфера
минимальных отклонений, сфера влияния). Введена модифика-
ция метода грависфер — метод грависфер нулевой протяжен-
ности, нашедшая применение в практике проектно-баллистиче-
ских расчетов.
6.3. ТРЕТЬЯ КОСМИЧЕСКАЯ СКОРОСТЬ
Третьей космической скоростью называется мини-
мальная скорость, которую нужно сообщить КА в непосредст-
венной окрестности Земли (не учитывая существования атмос-
феры Земли и потерь, связанных с ней), чтобы КА в своем
дальнейшем движении покинул Солнечную систему. Хотя эта
задача имеет самостоятельный интерес, в настоящей главе она
рассматривается для раскрытия сущности метода грависфер,
точнее метода грависфер нулевой протяженности. Таким обра-
зом, задача раздела прежде всего методическая. При расчете
237
этой скорости предполагают, что орбита Земли круговая с ра-
диусом, равным большей полуоси орбиты Земли — одной аст-
рономической единице (а. е.).
Пусть КА в окрестности Земли в результате работы раз-
гонного блока сообщили некоторую эллиптическую скорость.
Двигаясь в грависфере Земли по эллиптической (относительно
Земли) траектории, КА скорее всего не покинет окрестность
Земли. Даже если скорость КА — большая эллиптическая
(приближается к параболической) и КА достигает границы
грависферы Земли, то после недолгого пребывания вне грави-
сферы Земли скорее всего он в нее вернется. Этот вывод од-
нозначен при использовании метода грависфер нулевой протя-
женности, точнее, использования третьего его допущения. В
рамках этого допущения скорость выхода из грависферы Зем-
ли считается равной скорости КА на бесконечности относитель-
но Земли. Но так как в рассматриваемом случае КА относи-
тельно Земли движется по эллиптической траектории, то в
бесконечность от Земли он не уходит.
Пусть КА в окрестности Земли сообщили параболическую
скорость. При этом КА обязательно (если не столкнется с
Землей или не попадет в окрестность Луны) выйдет из грави-
сферы Земли (он уйдет в бесконечность). В бесконечности от-
носительно Земли у КА скорость будет нулевая (1Лю = 0). Эту
скорость можно рассматривать как скорость КА относительно
Земли в момент выхода из грависферы Земли. В тот же мо-
мент времени гелиоцентрическая скорость КА будет равна
Го.С=7з + Уоо= Рз.
Таким образом, в начальной точке гелиоцентрического уча-
стка гелиоцентрическая скорость КА оказалась равна перенос-
ной скорости Земли. Если рассматривать гелиоцентрическую
траекторию КА в рамках метода грависфер нулевой протяжен-
ности, то эта траектория будет совпадать с траекторией Зем-
ли относительно Солнца. Более точное рассмотрение траекто-
рии без использования допущения метода грависфер нулевой
протяженности дает возможность построить гелиоцентрическую
траекторию КА, которая оказывается очень близкой к орбите
Земли относительно Солнца.
Если КА в окрестности Земли сообщить гиперболическую
скорость, то в бесконечности относительно Земли на гипербо-
лической орбите будет некоторая скорость V™. Эту скорость в
рамках метода грависфер нулевой протяженности можно рас-
сматривать как скорость выхода из грависферы Земли. Век-
торно складывая ее с переносной скоростью Земли, можно по-
лучить начальную гелиоцентрическую скорость КА 7О.С
Уо.с=Уз+ Voo.
(6.7)
238
Х^Если эта скорость окажется эллиптической относительно
СоЛяца У0.с<]^2|1с/Гз (где г3 — расстояние Земля — Солнце),
то траектория КА будет траекторией искусственной планеты
(спутника Солнца). Если 7о.с — параболическая или гипербо-
лическая Р0.с>]/ 2|1с/г3, то траектория КА относительно Солн-
ца будет параболической или гиперболической. При этом, если
КА не встретится с какой-либо планетой (грависферой плане-
ты) или Солнцем, то он уйдет из Солнечной системы в беско-
нечность.
Задача по определению третьей космической скорости свя-
зана с нахождением такой скорости в окрестности Земли, ко-
торая обеспечивала бы выход КА из грависферы Земли и
дальнейшее движение по гелиоцентрической траектории, ухо-
дящей в бесконечность. Таким образом, гелиоцентрическая
траектория должна быть параболической или гиперболической.
Скорость движения Земли относительно Солнца близка к кру-
говой скорости. Средняя скорость Земли относительно Солнца
равна V3 = }^1*с/г3 = 29,78 км/с.
Несложно подсчитать параболическую скорость на расстоя-
нии, соответствующем среднему расстоянию Земли от Солнца:
Vn=V3 ]/2 = 42,12 км/с.
Таким образом, для того чтобы КА покинул пределы Сол-
нечной системы, его гелиоцентрическая скорость в момент вы-
хода из грависферы Земли должна быть больше или равна
42,12 км/с.
Обратим внимание на то, что мы закончили анализ гелио-
центрического участка траектории. Более подробный анализ
этого участка в рассматриваемой задаче не требуется. Одно-
временно отметим, что очень часто при расчетах межпланет-
ных перелетов приходится рассматривать сначала именно ге-
лиоцентрический участок траектории, а лишь затем переходить
к геоцентрическому (последовательность расчета не соответст-
вует хронологии полета).
Перейдем к анализу геоцентрического участка траектории
в задаче нахождения третьей космической скорости. Нам из-
вестна оценка снизу гелиоцентрической скорости КА в момент
выхода из грависферы Земли 1/0.с = 42,12 км/с. Связь этой ско-
рости с геоцентрической в тот же момент времени осуществ-
ляется с помощью векторного равенства (6.7).
Геоцентрический участок траектории представляет собой
гиперболу, скорость на которой в бесконечности относительно
Земли есть Роо. Величина этой скорости определяет константу
энергии гиперболы h и связана с условиями движения в лю-
бой точке гиперболы следующим образом:
V2_ =/l = V2 . (6.8)
239
Так как в определение третьей космической скорости вхо-
дит скорость, которую нужно сообщить КА в непосредственной
окрестности Земли, то рассмотрим условия движения в на-
чальной точке траектории гиперболы, соответствующей нулевой
высоте КА относительно поверхности Земли. В этой точке г =
= R3i а скорость обозначим Кн. Тогда из (6.8) следует:
у2_ = ]/2^ . (6.9)
Наша задача найти минимальную скорость относительно
Земли Кн, которая дает возможность КА уйти в бесконечность
относительно Солнца. Из соотношения (6.9) следует, что
min VH соответствует min Коо, т. е. чем меньше требуемая Коо,
тем меньше Кн. Таким образом, траекторию КА при определе-
нии третьей космической скорости следует реализовать так,
чтобы скорость выхода из грависферы Земли была бы мини-
мальной.
Обратимся к равенству (6.7) для определения требуемого
минимального значения Коо. В этом векторном равенстве нам
известен вектор К3: направление этой скорости перпендикуляр-
но радиусу-вектору Земли относительно Солнца, величина
скорости равна 29,78 км/с. Известна и минимальная величина
| Ко.с|, она равна 42,12 км/с. Требуется найти минимальную
величину вектора Коо. Легко увидеть, что минимальная вели-
чина Коо соответствует коллинеарному расположению векторов
Ко.с, Кз, Коо. Скорость выхода из грависферы Земли Коо долж-
на быть направлена по скорости Земли К3 для того, чтобы при
минимальных энергетических затратах можно было набрать
параболическую относительно Солнца скорость. При таком
расположении векторов из (6.7) следует скалярное равенство
Ко.с=К3 + Кто.
Таким образом, минимальное значение потребной Коо ока-
зывается равно Koomin=K0.c—К3= 12,34 км/с.
Подставляя это значение в соотношение (6.9), получим ве-
личину третьей космической скорости:
Таким образом, в непосредственной окрестности Земли до-
статочно сообщить КА скорость 16,65 км/с, чтобы он полетел
по гиперболической траектории относительно Земли, вышел из
ее грависферы, имея относительно Земли скорость 12,34 км/с.
Если направление этой скорости будет совпадать с направле-
нием переносной скорости Земли, то гелиоцентрическая ско-
рость КА окажется параболической. КА по параболической от-
носительно Солнца траектории удалится от Солнца в беско-
240
не*Ьгость. Отметим, что начальная точка гелиоцентрического
участка траектории будет перицентральной (в ней скорость
Fo.c церпендикулярна радиусу-вектору). На рис. 6.4 представ-
лена гелиоцентрическая часть траектории КА — Ат, пункти-
ром показана орбита Земли, начальная гелиоцентрическая ско-
рость Го.с получена как сумма коллинеарных векторов У3 и
Foo, А — перигелий параболы Ат (одновременно — это точка,
в которой находится Земля), С А — радиус-вектор КА относи-
тельно Солнца в момент начала гелиоцентрического участка
полета.
Сделаем три замечания.
1. Первое замечание касается вопроса о выборе такой схе-
мы траектории геоцентрического участка, чтобы скорость на
выходе из грависферы Земли К» была коллинеарна скорости
Земли F3. Коротко ответить на этот вопрос можно так: усло-
вие коллинеарности выполняется за счет ориентации гипербо-
лической геоцентрической траектории. На рис. 6.5 (в точке С
его находится центр Земли) рассмотрена плоскость, в которой
расположен вектор скорости Земли относительно Солнца 73 и
начальный при старте из окрестности Земли радиус-вектор
СА=гн. Начальная скорость Рн= 16,65 км/с, которую нужно
сообщить КА, должна принадлежать рассмотренной плоскости.
Варьируя направление этой скорости в той же плоскости, бу-
дем получать разные гиперболические траектории с одним и
тем же значением константы энергии h и, значит, одной и той
же величиной скорости на бесконечности. На рис. 6.5 показа-
ны три дуги таких гипербол АВ, AD, АЕ. Они отличаются на-
правлением скорости на бесконечности Уоо. Видно, что за счет
выбора направления начальной скорости Ун можно сделать
так, чтобы скорость на бесконечности относительно Земли Уоо
(асимптота гиперболы) была направлена по вектору скорости
Земли V3.
Рис. 6.4. Начальные условия гелиоцентри- Рис. 6.5. Ориентация гипербо-
ческого участка траектории при получении лической геоцентрической тра-
третьей космической скорости ектории КА
241
Впрочем варьировать можно было не направление скорос-
ти, а положение начального радиуса вектора гн. При фиксиро-
ванном направлении скорости (например, перпендикулярном
радиусу-вектору) за счет выбора положения начальной точки
можно геоцентрическую гиперболу сориентировать так, что
скорость Voo была бы параллельна скорости Земли К3-
2. Второе замечание касается понятия четвертой космичес-
кой скорости. Четвертой космической скоростью называется ми-
нимальная скорость, которую следует сообщить КА в непосред-
ственной окрестности Земли так, чтобы КА достиг Солнца
(«упал» на Солнце).
Чтобы КА «упал» на Солнце, гелиоцентрическая траектория
КА должна быть прямолинейной (через гравитационный центр
в задаче двух тел Солнце — КА проходят только такие траек-
тории). Таким образом, гелиоцентрическая скорость КА в мо-
мент его выхода из грависферы Земли К0.с должна быть на-
правлена по или против радиуса-вектора КА относительно
Солнца. Минимальные энергетические затраты будут соответ-
ствовать нулевой начальной гелиоцентрической скорости К0.с =
= 0. В этом случае КА из точки покоя в гелиоцентрическом
движении начнет под действием притяжения Солнца «падать»
на него по прямолинейной траектории. Для того чтобы выпол-
нялось условие Ко.с = 0, геоцентрическая скорость КА в момент
его выхода из грависферы Земли должна быть по величине
равна скорости Земли и_направлена против скорости Земли.
Действительно, из V0.c = Уз + Уоо = 0 следует, что Уоо =—V3.
Требуемая минимальная скорость в окрестности Земли мо-
жет быть найдена с помощью выражения, вытекающего из ин-
теграла энергии геоцентрического участка траектории
V1V = 1/ + Vi = 1/ ^3- + V2 = 31,82 км/с.
Достижение КА Солнца оказывается энергетически сущест-
венно более сложной операцией по сравнению с уходом из
Солнечной системы Viv = 31,82 км/с> Vni= 16,65 км/с.
3. Последнее замечание раздела касается сравнительного
анализа по энергетике (по требуемому приращению скорости)
двух схем полета КА, который по параболической гелиоцентри-
ческой траектории должен «уйти» из Солнечной системы. Одна
схема полета нами была проанализирована при выводе третьей
космической скорости. В этой схеме КА в окрестности Земли
сообщалась гиперболическая (относительно Земли) скорость
(16,65 км/с), которая позволяла уйти из грависферы Земли с
некоторой скоростью Коо =12,32 км/с, так, чтобы гелиоцентри-
ческая траектория была параболической и в дальнейшем дви-
жении КА покинул Солнечную систему.
242
Рассмотрим другую возможную схему полета. Считаем, что
ракеткый двигатель, которым оснащен разгонный блок нашего
космического аппарата, будет включаться дважды. В первый
раз в непосредственной окрестности Земли, при этом КА полу-
чит параболическую относительно Земли скорость (эта ско-
рость равна второй космической 11,19 км/с). После этого гео-
центрическая траектория КА окажется параболической и КА
покинет грависферу Земли с нулевой скоростью (скорость в
бесконечности от Земли на параболической траектории нуле-
вая). Гелиоцентрическая скорость КА при этом окажется рав-
ной скорости Земли. После выхода КА из грависферы Земли
еще раз включим ракетный двигатель разгонного блока так,
чтобы гелиоцентрическая скорость КА оказалась параболиче-
ской. При этом КА придется сообщить импульс скорости, рав-
ный А1/2= 12,36 км/с, и направить его по скорости Земли. Дей-
ствительно, гелиоцентрическая скорость КА после отработки
разгонного импульса будет равна V3 + AV2 =42,12 км/с. Полу-
ченная скорость и есть параболическая скорость относительно
Солнца на расстоянии одной астрономической единицы.
Таким образом, во второй схеме полета разгонный блок,
включаясь дважды, должен сообщать космическому аппарату
следующее суммарное приращение скорости A = 11,19 +
+ 12,34 = 23,53 км/с.
Вторая схема двухимпульсного полета по энергетическим
затратам сильно проигрывает схеме полета, рассмотренной при
выводе третьей космической скорости (23,53 км/с>16,65 км/с).
С точки зрения энергетических затрат выгодно весь требуемый
импульс скорости сообщить в непосредственной окрестности
Земли. Такой вывод оказывается справедливым не только для
маневра ухода из Солнечной системы, но и при межпланетных
перелетах. Поэтому схемы межпланетных перелетов, которые
в дальнейшем будут рассмотрены, не будут иметь активных
участков на гелиоцентрических траекториях КА. Скорость,
достаточная для полета, например к Вейере, будет вся сооб-
щаться КА вблизи Земли. Включение двигателя на гелиоцент-
рических участках траектории используется в настоящее вре-
мя только для коррекции орбиты.
Таким образом, здесь была рассмотрена задача определе-
ния третьей космической скорости. Основная цель раздела —
методическая: показать возможность использования метода
грависфер в задачах межпланетного перелета. Одновременно в
разделе получено значение третьей космической скорости, вы-
явлена нерациональность схем полета с включением ракетного
Двигателя на гелиоцентрическом участке траектории.
243
6.4. РАСЧЕТ ГЕЛИОЦЕНТРИЧЕСКОГО УЧАСТКА
ДВИЖЕНИЯ КА
Разд. 6.4... 6.6 посвящены анализу отдельных участ-
ков траектории межпланетного перелета в рамках приближен-
ного: метода исследования траекторий межпланетных аппара-
тов.
При проектировании траекторий межпланетных КА чаще
всего сначала обращаются к анализу гелиоцентрического уча-
стка полета. Больше того, в рамках анализа только этого уча-
стка часто удается выбрать рациональную схему полета, опти-
мальную дату старта, целесообразное время полета и т. д. Это
связано с рядом обстоятельств.
Прежде всего гелиоцентрический участок траектории по
продолжительности, протяженности является определяющим во
всем перелете. Время планетоцентрических участков траекто-
рии КА составляет во всем времени полета, измеряемом меся-
цами, а то и годами, очень малую часть. Для КА рассматри-
ваемыми в этой главе химическими двигателями (двигателями
большой тяги) это время измеряется несколькими сутками.
При этом часто допустимо пренебрегать продолжительностью
припланетных участков, особенно, если расчет проводится на
основе метода грависфер нулевой протяженности.
При исследовании гелиоцентрической траектории полета ес-
тественно и просто удается выбрать траекторию КА, выпол-
няющую поставленную транспортную задачу — попасть в ок-
рестность планеты назначения. Если начинать расчет с анализа
геоцентрического участка, весьма непросто выбрать элементы
промежуточной орбиты ИСЗ, с которой будет стартовать КА,
точку схода с этой орбиты, требуемую характеристическую ско-
рость разгонного блока, чтобы в дальнейшем движении КА по-
пал в окрестность планеты назначения. Гелиоцентрический
участок траектории содержит (в случае использования схемы
полета, при которой на гелиоцентрическом участке полета
включение ракетного двигателя проводится только для коррек-
ции траектории, и метода грависфер нулевой протяженности)
очень мало выбираемых параметров. Чаще всего независимых
выбираемых параметров для гелиоцентрического участка поле-
та оказывается два. Это время начала гелиоцентрического по-
лета (время старта Тс) и время перелета tn (или время подле-
та к планете цели Тк).
Задавая эти два значения Тс и /п, однозначно определяем
положение Земли в момент старта и планеты-цели в момент
подлета КА к ней. Таким образом, с помощью астрономичес-
кого справочника можно однозначно определить радусы-векто-
ры КА в начальный и конечный моменты гелиоцентрического
полета. Еще раз обратим внимание на то, что межпланетный
244
перелет исследуется с помощью метода грависфер нулевой
протяженности, поэтому полученный из астрономического спра-
вочника радиус-вектор Земли (например, в эклиптической сис-
теме координат) и будет начальным радиусом-вектором КА го.
Аналогично радиус-вектор планеты цели будет равен конечно-
му радиусу-вектору гк (рис. 6.6).
Рис. 6.6. Гелиоцентрический участок
траектории межпланетного КА:
1 — орбита Земли; 2 — орбита планеты
назначения; 3 — траектория перелета
Рис. 6.7. Эллиптическая орбита пере-
лета между начальным и конечным
положениями КА, заданными радиу-
сами-векторами Го и Гк
Отметим, что определение положения планет Солнечной
системы проводится чаще всего с помощью соотношений для
элементов орбит планет как функций времени (справедливых
в определенную эпоху). Такие соотношения можно получить
из [61].
После этого нахождение координат планеты может прово-
диться на основе соотношений (2.83), (2.82), (2.84), получен-
ных при прогнозировании положения спутника в задаче двух
тел. На основе решения задачи двух тел может быть найдена
и скорость планеты.
Таким образом, находится положение и скорость Земли в
момент старта КА (r0, Гз) и положение и скорость планеты-
цели в момент подлета КА к этой планете (rK, Гк).
Возвращаемся к задаче расчета гелиоцентрического участка
траектории. Еще раз, так как двигатель КА на участке гелио-
центрического перелета не включается и никаких сил, кроме
силы притяжения Солнца, на КА не действует, то его траекто-
рия может рассчитываться в рамках ограниченной задачи двух
тел Солнце — КА. При этом траектория КА есть коническое
сечение (эллипс, гипербола или парабола), в одном из фоку-
сов которого расположено Солнце. Нужно выбрать такое ко-
ническое сечение, которое проходит через г0 и гк так, чтобы
время перелета между г0 и гк было равно tn. Сформулирован-
ная задача сводится к решению так называемого уравнения
Ламберта.
245
Уравнение Ламберта задачи двух тел
Немецкий математик И. Ламберт во второй поло-
вине XVIII века предложил метод определения орбиты небес-
ного тела по двум его положениям в некоторые моменты вре-
мени. Этот метод оказался очень интересным для исследова-
ния траекторий межпланетных аппаратов.
Метод Ламберта предполагает, что даны г0 и гк, а также
время перелета между г о и гк — tn- Метод основан на фор-
муле (уравнении), которая носит имя Ламберта. По этой
формуле можно определить время полета между точками ко-
нического сечения /п, если известны длины начального и ко-
нечного радусов-векторов г0, Гк, угловая дальность полета Ф
(угол между начальным и конечным радиусами-векторами,
подсчитанный в направлении движения КА) и большая полу-
ось орбиты перелета а. На рис. 6.7 рассмотрена эллиптическая
орбита КА относительно гравитационного центра С. Началь-
ный и конечный радиусы-векторы есть СА = г0 и СВ = гк. Уг-
ловая дальность полета есть угол АСВ(Ф). По г0, гк, Ф опре-
деляется расстояние между начальной и конечной точками
полета, которое на рисунке обозначено s= |АВ| =Х72о+
-|-г2к—2гоГкСОзФ. Оно входит в формулу Ламберта.
Не останавливаясь на доказательстве формулы, приведем
ее в достаточно полном виде. Для случая эллиптической орби-
ты формула Ламберта имеет вид
а3/2
7П= — [л + sign (tm — /п) (е—sins —л)—sign (sin Ф) (6—sin 6)],
1/р
(6.10)
где
tm = (Г|, + Гк + 5) ' [л—sign (sin Ф) (6m—sin 6J],
8У(х
( 1 при sinO>0 (случай а, рис. 6.8),
sign (sin Ф) = { 0 при sinO=0,
(— 1 при sinOcO (случай б, рис. 6.8)
6т = 2 arcsin У 7 + + s ’ 0 < л;
f Г0Т S
6 = 2 arcsin У-Г1 +/2'~$ , 0 < 6 < л;
е = 2 arcsin У-1 + 5 , 0 е .
246
Для случая гиперболической орбиты формула Ламберта име-
ет вид
/п= 1Л [sha—a—sign (sin <D)(shP—P)], (6.11}
где
sh4=/r,t|a|~S' »>₽>»
В случае перелета между заданными радиусами-вектора-
ми Го и гк по параболической орбите время перелета опреде-
ляется следующим образом
= 1(^0 +>-и+$)3/2—(г0+ rK-s)3/2sign [sin Ф]]. (6.12)
Таким образом, для того чтобы найти траекторию перелета
между начальным г0 и конечным гк радиусами-векторами за
заданное время /п, следует рассматривать формулу Ламберта
как уравнение относительной большой полуоси. При этом сна-
чала следует определить тип орбиты перелета, для чего по
формуле (6.12) находится время перелета между заданными
векторами по параболической орбите. Полученное время
(^п)пар сравнивается с заданным временем tn.
Если окажется, что /п<(^п)пар, то перелет между задан-
ными радиусами-векторами возможен только по гиперболи-
ческой орбите.
Если tn> (tn) пар, то перелет может быть реализован только
по эллиптической орбите.
Если же окажется, что ^п=(^п)пар, то перелет между за-
данными векторами должен проводиться по параболической
траектории.
Таким образом, если /п>(/п)пар, равенство (6.10) следует
рассматривать как уравнение относительно а. Решение ука-
Рис. 6.8. Различные типы перелета, связанные с величиной угловой дально-
сти Ф:
а — угловая дальность меньше 180°; б — угловая дальность больше 180°
247
занного трансцендентного уравнения относительно а (обра-
тите внимание на то, что г есть функция а) является непрос-
той задачей. Для решения уравнения используются современ-
ные вычислительные итерационные процедуры. Эти процеду-
ры часто основываются на стандартном обеспечении и не всег-
да их эффективность высока.
Если ^п<(/п)пар, то большую полуось орбиты перелета а
находят из решения трансцендентного уравнения (6.11).
После нахождения большой полуоси перелетной орбиты
нужно определить фокальный параметр, эксцентриситет и дру-
гие элементы перелетной орбиты.
Нахождение фокального параметра, эксцентриситета, а
также истинной аномалии в начальной точке перелета орбиты
может быть проведено следующим образом. Из уравнения ор-
биты, записанного для начальной и конечной точки траекто-
рии, можно получить соотношения:
1 + е CQs и0 ’
к 1 -|- е cos (и0 + Ф)
Добавляя к этим двум равенствам очевидное р=а(1—е2),
получим три уравнения относительно трех неизвестных р, е,
гзо (большая полуось а нами найдена). В литературе исполь-
зуются различные выражения для р, е. Вот некоторые из них.
Для эллиптической орбиты
а лг г Qin2 ф е|п2 а 4-Sign (sin Ф) sign .
Р — s2 2 ,
Для параболической орбиты
P = sin2 -у- [ ]/ r0 + rK + s + sign (sin Ф)]/г0 + rH—s];
e= 1.
Для гиперболической орбиты
p = 14 4r rK sin2 sh *+*8п (sin Ф)?
r s2 2 2
Для нахождения остальных элементов орбиты в [И] пред-
лагается последовательность вычислений, общая для всех ти-
пов орбит.
248
Находится скорость в начальной точке орбиты перелета
К.с:
7о.е = _ 14? Гi_2k(i_coso)1f0), (6.13>
fi^sinO I L J J
затем по начальным условиям движения определяются эле-
менты орбиты (используя равенства (2.73), (2.74) и т. д.).
Укажем соотношение, по которому, не определяя элемен-
тов орбиты, можно найти вектор гелиоцентрической скорости
КА в любой точке гелиоцентрической траектории:
7Т=( di?’ К°.с) (1—С05фт)---Ll/jLsinO 17 +
prQ rQr p ]
+ |l-Zo [1_С05фт]р
I p J
где Фт — текущая угловая дальность полета КА (полярный
угол между начальным и текущим радиусом-вектором КА.
Если требуется вычислить гелиоцентрическую скорость КА
в момент подлета к планете назначения, то проще воспользо-
ваться равенством, эквивалентным (6.13):
Voc = ~ <! —Го + [1—— (1—созФ)] гк}.
°'с rxr2smO 1 0 L Р J к'
В заключение отметим, что в данном разделе был прове-
ден анализ гелиоцентрического участка траектории КА, алго-
ритм которого сводится к следующему. По двум парамет-
рам — времени старта от Земли и времени полета к задан-
ной планете назначения определяются гелиоцентрические ра-
диусы-векторы Земли и планеты назначения, а также их ско-
рость в эти моменты. Исследуется уравнение Ламберта, нахо-
дится большая полуось перелетной гелиоцентрической орбиты.
Определяются фокальный параметр, эксцентриситет и, по не-
обходимости, другие элементы гелиоцентрической траектории.
Определяется гелиоцентрическая скорость КА в момент выхо-
да из грависферы Земли и в момент подлета к планете назна-
чения.
6.5. АНАЛИЗ ГЕОЦЕНТРИЧЕСКОГО УЧАСТКА
ТРАЕКТОРИИ МЕЖПЛАНЕТНОГО ПЕРЕЛЕТА
Из анализа гелиоцентрического участка межпла-
нетной траектории получен вектор гелиоцентрической скорости
КА в момент выхода из грависферы Земли Vo.с- Для нахожде-
ния геоцентрической скорости КА Уоо в тот же момент времени
249*
нужно из вектора V0.c вычесть вектор переносной скорости
Земли (относительно Солнца) У3
Уоо=Уо.С— Уз.
Так как векторы V0.c и У3 часто задаются в эклиптической
системе координат (основная плоскость ху которой есть плос-
кость эклиптики), то и полученный вектор геоцентрической
скорости Гоо чаще всего получается в этой системе координат:
Voo = [VooX3, ^oozj-
Зная эклиптические проекции геоцентрической скорости вы-
хода из грависферы Земли, легко получить .экваториальные
проекции этой скорости по соотношениям
ооХ ~ УооХэ',
Ужу = Ужуэ cos е — Voo^sin 8; (6.14
Vooz = Ужуэ sin 8 + 1/0О2э COS 8,
где е — угол наклона плоскости земного экватора к плоскости
эклиптики (23°27/).
Таким образом, вектор геоцентрической скорости выхода из
грависферы Земли (или в рамках метода грависфер нулевой
протяженности — вектор геоцентрической скорости в бесконеч-
ности относительно Земли) найден. Задача состоит в том, что-
бы подобрать удовлетворяющую определенным условиям про-
межуточную орбиту ИСЗ, с которой должен стартовать КА,
подобрать момент старта с этой орбиты, требуемое прираще-
ние скорости для того, чтобы геоцентрическая траектория КА
представляла собой гиперболу с величиной и направлением
скорости в бесконечности, соответствующей найденной по
(6.14) скорости Voo.
Наиболее естественными условиями, которые всегда долж-
ны учитываться при выборе геоцентрического участка, явля-
ются следующие. Для промежуточной орбиты ИСЗ чаще всего
считается заданным ее размер и форма. С точки зрения энер-
гетических затрат целесообразно выбрать достаточно низкие
орбиты, близкие к круговым. О том, что такая орбита должна
быть достаточно низкой, говорилось при обсуждении схемы по-
лета межпланетного КА. Что касается малой эллиптичности
орбиты, отметим следующее. Если промежуточная орбита ИСЗ
будет иметь значительную эллиптичность, то выбор точки стар-
та с этой орбиты будет ограничен определенной частью дуги
орбиты. Действительно, при выборе точки старта с орбиты, в
которой велика радиальная скорость, гравитационные потери
в скорости при работе разгонного блока могут стать значитель-
ными, характеристическая скорость разгонного блока должна
250
будет неоправданно возрасти. Это проиллюстрировано на рис.
6.9. На нем точка старта с орбиты ИСЗ обозначена А. Угол
между скоростью ИСЗ в этот момент времени /н и местным го-
ризонтом (траекторный угол) — 0Н. Гравитационные потери
скорости АГгр за время работы разгонного блока ta (активный
участок полета — дуга АВ) подсчитываются по формуле:
ДГгр = J gsinQdt.
Видно, что гравитационные потери зависят от траекторного
угла и чем больше 0, тем, в общем случае, больше гравитаци-
онные потери.
На рис. 6.9 Го — скорость на промежуточной орбите ИСЗ,
Vi — скорость КА в момент окончания активного участка по-
лета. Дуга BD — геоцентрическая траектория КА после окон-
чания работы разгонного блока.
Для примера укажем, что промежуточная орбита ИСЗ, ко-
торая была использована для первого полета автоматической
межпланетной станции к Венере (старт 12 февраля 1961 г.),
была близка к окружности. Перигейное расстояние орбиты бы-
ло равно 6601 км, апогейное — 6658 км.
При выборе промежуточной орбиты ИСЗ часто считают за-
данным наклонение орбиты. Это связано с определенным по-
ложением космодрома, фиксированной его широтой, фиксиро-
ванными допустимыми азимутами запуска с космодрома. Пояс-
няя последнее, нужно учитывать следующее. С точки зрения
энергетических затрат ракеты-носителя ее траекторию целесо-
образно иметь плоской (при этом не нужно расходовать энер-
гию (топливо) на искривление траектории КА); целесообразно
Рис. 6.9. Схема старта с околоземной проме-
жуточной орбиты ИСЗ:
Го — скорость на промежуточной орбите ИСЗ; 0Н —
угол наклона Vo к плоскости местного горизонта:
АВ — активный участок траектории; BD — пассивный
участок геоцентрической траектории; 16 — скорость
КА в момент окончания активного участка полета
Рис. 6.10. Схема запуска ра-
кеты-носителя с азимутом,
равным 90°:
С — центр Земли; ECO — мери-
диальная плоскость, проходя-
щая через космодром, располо-
женный в точке О
251
азимут запуска (угол между северным направлением меридиа-
на и плоскостью стрельбы) выбрать близким 90°. Если вы-
полнить это условие, скорость космодрома относительно невра-
щающейся системы координат, связанная с вращением Земли,
будет арифметически складываться со скоростью аппарата,
которую он набирает относительно Земли. В этом случае полу-
чается максимальный эффект использования скорости враще-
ния Земли при наборе скорости КА. Понятно, что при таком
запуске орбита спутника будет иметь наклонение, равное гео-
центрической широте космодрома. Это обстоятельство схема-
тично проиллюстрировано на рис. 6.10. На нем нанесена мери-
диальная плоскость Земли (О — ось Земли), в которой на-
ходится космодром (точка О). Угол <р — геоцентрическая ши-
рота космодрома. Проекция траектории запуска с азимутом
90° показана отрезком ОА, точка А — положение КА в момент
выведения спутника на орбиту. Скорость КА в точке А перпен-
дикулярна нанесенной меридиальной плоскости и направлена
от читателя (она обозначена Ф). Переносная скорость старто-
вой системы координат, связанная с суточным вращением Зем-
ли, равна созГк cos <р (гк — радиус-вектор КА — СА) и направ-
лена по скорости КА в точке А. При этом О А будет отрезком
следа плоскости орбиты ИСЗ, а наклонение орбиты будет рав-
но углу АСЕ, т. е. широте космодрома <р.
Каждый космодром имеет определенные допустимые азиму-
ты запуска, при этом наклонение орбиты ИСЗ при использо-
вании плоского выведения ИСЗ не меньше широты космодрома
и часто его следует рассматривать заданным.
Долготу восходящего узла промежуточной орбиты ИСЗ
можно получать практически любой за счет выбора момента
старта с космодрома. Космодром (вместе с Землей) относи-
тельно инерциального пространства вращается со скоростью
один оборот за сутки. Поэтому, выбирая внутри суток момент
старта с космодрома, можно обеспечить любую долготу восхо-
дящего узла орбиты спутника. Возможные моменты запуска с
космодрома для получения определенного значения долготы
восходящего узла повторяются через сутки.
Определенные ограничения на выбор геоцентрического участ-
ка траектории оказываются связанными с радиовидимостью
КА с наземных пунктов для определенных критических точек
траектории КА. Возможны и некоторые другие ограничения.
Покажем, как решается задача выбора геоцентрического
участка траектории КА, если получен вектор геоцентрической
скорости Гоо (6.14) в момент выхода из грависферы Земли и
заданы фокальный параметр ро, эксцентриситет е0 и наклоне-
ние iQ промежуточной орбиты ИСЗ. Считаем, что другие эле-
менты орбиты не фиксированы и мы имеем право их выбирать.
252
3 частности, выбираемыми считаются долгота восходящего
узла и аргумент перицентра этой орбиты.
Ограничиваем себя рассмотрением такой рациональной схе-
мы полета КА, при котором старт с промежуточной орбиты
происходит в перигее этой орбиты, причем приращение скорос-
ти КА за счет работы разгонного блока направлено по ско-
рости КА на орбите ИСЗ. Это самый целесообразный с точки
прения энергетических затрат случай. Более выгодно изменять
константу энергии КА:
там, где скорость КА самая большая (это условие выпол-
няется в перигее орбиты);
таким образом, чтобы не тратить топливо на искривление
траектории, а только на набор КА скорости.
Последнее обстоятельство приводит к тому, что направле-
ние скорости КА после того, как ему сообщен импульс скорос-
ти АГ, остается таким же, как направление скорости на про-
межуточной орбите ИСЗ. При этом положение плоскости ор-
биты ИСЗ и КА, стартующего с нее, не изменяется. Начальная
точка геоцентрической траектории КА оказывается перицент-
ральной (в ней скорость перпендикулярна радиусу-вектору
КА).
Определим положение плоскости орбиты ИСЗ и КА. Этой
плоскости должен принадлежать полученный вектор геоцентри-
ческой скорости Гоо. Второе условие, которому должна удовлет-
ворять выбираемая плоскость, — ее наклонение должно быть
равно г0.
Орт внешней нормали к плоскости промежуточной орбиты
ИСЗ в геоцентрической экваториальной системе координат мо-
жет быть записан в виде (2.72):
о° = [pin Qo sin г0; —cos Qo sin r0; cos r0].
При этом уравнение плоскости, проходящей через начало
координат, перпендикулярно орту о0, может иметь вид:
sin Qo sin iox—cos Qo sin roy + cos IqZ = 0. (6.15)
Для того чтобы вектор Гоо принадлежал плоскости орбиты
(6.15), должно выполняться условие:
sin Qo sin io VooX—cos Qo sin r0 Гооу + cos r0 Vooz —0. (6.16)
Последнее равенство следует рассматривать как уравнение
относительно неизвестного Qo. Прежде чем представить его ре-
шение, рассмотрим два частных случая.
1. Если промежуточная орбита ИСЗ экваториальная (г’о =
= 0), то равенство (6.16) эквивалентно равенству: Vooz = 0.
Таким образом, очевидно, что равенство (6.16) в этом слу-
чае не может удовлетворяться за счет выбора долготы восхо-
дящего узла Qo. Если при этом скорость КА в момент выхода
253
из грависферы не принадлежит экваториальной плоскости, то
исследуемую схему полета реализовать не удается.
2. Если скорость КА в момент выхода из грависферы Зем-
ли перпендикулярна экваториальной плоскости (т. е. VooX =
= Vooy = 0), то равенство (6.16) выполняется только при усло-
вии /0 = я/2. При этом долгота восходящего узла может иметь
произвольное значение.
Рассмотрим общий случай, т. е. г’оУ=О и V2ooX+Е2ооУ=^0.
При этом равенство (6.16) тождественно равенству
V V V
• °°х Г\ °°У ooZ I
sin Qo--------------cos Qo — y — = — — ctg- r0.
V vix+viy V V2„x + vly V + vly
(6.17)
Решаем это уравнение относительно Qo. Введем вспомога-
тельный угол т]. Пусть
V V
оо х • оо и
COS Т] = — — ; Sin Т] = — —,
1/ у2 , у 2 1/ у2 I у2
' ооХ 1 ' оо X ~ Г оо у
тогда уравнение (6.17) перепишется в виде
у
sin (й0—п) =-----. ctg i0. (6.18)
Это уравнение имеет решение при условии
—|У°°г1 (6.19)
У у2 д-j/2
В том случае, когда неравенство (6.19) не удовлетворяется,
уравнение (6.16) не имеет решения. Это значит, что в рамках
рассматриваемой схемы полета (когда во время старта с про-
межуточной орбиты ИСЗ разгонный блок КА не изменяет
плоскость движения аппарата) реализовать траекторию КА с
полученным из анализа гелиоцентрической траектории векто-
ром скорости 7оо невозможно. Выход при этом может быть та-
ким: нужно вернуться к исследованию гелиоцентрического уча-
стка полета, изменяя дату старта Тст или время полета tn та-
I ^0О2|
ким образом, чтобы уменьшить — 002 —. Предполагая
Vv2 4-V2
такой выход, мы утверждаем, что исследованные ранее даты
старта и время полета были назначены (выбраны) неудачно,
реализация траектории с этими временами наталкивается на
энергетические трудности (нужно проводить пространственный
маневр).
254
Пусть ограничения (6.19) удовлетворяются, тогда уравне-
ние (6.18) имеет два решения QOi, Q02:
йо> = т)+U —/М +(—1)' arcsin —У“г Ctg'° +-£- (1— 5,), (6.20)
]/ HL+V2 2
r оо X 1 оо у
где
г) = 62 arccos
6i = sign [cos i0]; 62 = sign [V„y];
j — номер решения (принимает значения 1 и 2).
V
Полученные два решения совпадают, если —.. 002 — = tg /0.
]/ V2 4- V2
r v оох “ v СО у
Таким образом, положение плоскости промежуточной орби-
ты ИСЗ и совпадающей с ней плоскости геоцентрического
участка траектории межпланетного КА найдено (знаем i0 и в
общем случае два значения Qo).
Определим энергетические затраты и элементы, характери-
зующие форму и размер геоцентрической траектории КА.
Скорость в начальной точке орбиты ИСЗ (до включения
двигателя разгонного блока) есть скорость в перигее и нахо-
дится из соотношения ун = 1/Из_(1 + е0). Расстояние КА в этот
* Ро
момент времени от центра Земли есть перицентральное рас-
__________________________________________ р0
стояние на промежуточной орбите ИСЗ гн~~
Из интеграла энергии получим значение скорости КА после
того, как разгонный блок сообщил КА импульс скорости
у2__2нз_ = h = vi- v0 = Vvi +
и гн ' гн
Величину требуемого приращения скорости (импульса ско-
рости) получаем с помощью соотношения: AV=V0—Ун-
Характеристическую скорость разгонного блока с точностью
до гравитационных потерь можно считать равной полученному
значению приращения скорости VXap = AV+AVrp~AV.
Элементы геоцентрического участка траектории КА опре-
деляются по соотношениям
г2 V2 Г----------
р = e=-|/i + V2 Р.
Первое соотношение следует из (2.32) с учетом того, что ско-
рость в начальной точке перпендикулярна радиусу-вектору
гн±Уо. Второе соотношение следует из (2.35).
Отметим, что из последнего соотношения видно, что е>1,
т. е. геоцентрический участок траектории гиперболический.
255
Для ответа на некоторые вопросы целесообразно найти
большую полуось а и среднее движение п геоцентрического
участка траектории а = -^е <0; |n| = jZ-^-3.
Эта информация нужна для определения временных харак-
теристик движения на геоцентрическом участке траектории.
Если используется метод грависфер конечной размерности (не
метод грависфер нулевой протяженности), интересно знать вре-
мя движения внутри грависферы Земли. Приведем соотноше-
ния для определения этого времени Л, причем для определен-
ности предположим, что за границу грависферы Земли прини-
мается геометрическая сфера радиуса /?Сф.д-
Из уравнения Кеплера для гиперболической орбиты (2.68)
с учетом того, что начальная точка геоцентрической орбиты
является перицентром траектории, получим
*i = — ( — H+eshH). (6.21)
1«1
Значение Н находится с помощью равенства (2.66):
ch Н = (
\ |а| 1 е
/7 = In (ch// + ]Zch2//—1).
Для полной информации о геоцентрическом участке КА по-
кажем, как могут быть определены:
аргумент перигея этого участка траектории со (он равен
аргументу перигея промежуточной орбиты ИСЗ);
склонение начальной точки траектории (соответствующей
моменту схода с орбиты ИСЗ);
координаты КА на грависфере Земли (конечной точки гео-
центрического участка);
склонение конечной точки.
Аргумент перигея геоцентрического участка траектории на-
ходится из соотношения
со = ф1—Гоо, (6.22)
. ч VooX cos Q + Voojt sin Q
где ф! = sign (Иоо2) arccos— -----*---- — угол между ли-
нией узлов Ст (рис. 6.11) и скоростью КА в момент выхода из
грависферы Земли (угол тЕп на рис. 6.11); Гоо =
/ 1 \
== arccos (---— угол между линиеи апсид и асимптотой ги-
перболы (угол пО1 на рис. 6.11).
Так как в общем случае мы получили два решения для дол-
готы восходящего узла (6.20), то естественно получим соответ-
ствующие два решения для угла <pi и аргумента перигея со.
256
Рис. 6.11. Схема геоцентрического участка траектории межпланетного КА:
А — точка старта КА с промежуточной орбиты ИСЗ; CD — линия узлов промежуточной
орбиты ИСЗ и геоцентрической траектории КА; Еп — асимптота гиперболической гео-
центрической траектории КА
Отметим, что найденные нами значения долготы восходя-
щего узла, так же как и аргумента перигея, позволяют реали-
зовать рациональную схему плоского разгона из перигея про-
межуточной орбиты ИСЗ. Ясно, что найденные решения нужно
обеспечивать за счет выбора промежуточной орбиты ИСЗ. Мы
отмечали, что за счет выбора момента старта ракеты-носителя
удается получить любое значение долготы восходящего узла.
Отметим, что получить определенное значение аргумента пе-
ригея можно за счет подбора величины и направления векто-
ра скорости ракеты-носителя в момент конца активного поле-
та (в момент выведения на орбиту). Эта операция, в общем
случае, требует дополнительных энергетических затрат ракеты-
носителя. Не останавливаясь подробно на этом вопросе, отме-
тим, что проблема пропадает, если используется круговая про-
межуточная орбита ИСЗ. С точ-
ки зрения радиовидимости с зем-
ных пунктов наблюдения небезын-
тересна информация о положении
точки старта с промежуточной
орбиты и о положении точки вы-
хода КА на границу грависферы
Земли.
Экваториальные координаты
КА в момент старта с промежу-
точной орбиты находятся с помо-
щью тригонометрических соотно-
шений, следующих из рис. 6.12.
На рис. 6.12 Z£'CA = g), ZxCA =
= Qo, ZAEB = i0.
Склонение точки старта с
промежуточной орбиты д есть
9—8
Рис. 6.12. Склонение и прямое вос-
хождение точки старта КА с про-
межуточной орбиты ИСЗ:
А — точка старта КА с промежуточной'
орбиты ИСЗ; СЕ — линия узлов про-
межуточной орбиты ИСЗ; плоскость
zCB — меридиальная плоскость
257
угол АСВ. Прямое восхождение точки старта с промежуточной
орбиты а есть угол хСВ. Из сферического прямоугольного
треугольника ЕАВ легко получить
6 = arcsin[sin со sin f0],
(6.23)
arcsin
sin со cos i0
1 — sin2 co sin2 z0 _
если —
2
3
или — n<;co<c2n
2
(6.24)
л—arcsin
s i n co cos iq
— sin2 co sin2
~ если — <co<
о J 2
1л.
2
Полученное значение прямого восхождения а может не по-
пасть в нормативный диапазон 0^а<360°. Вычитая или при-
бавляя к полученному значению 360°, получаем значение этого
угла в диапазоне 0г^а<360о.
Таким образом, найдено склонение и прямое восхождение
точки старта с промежуточной орбиты. Определение прямо-
угольных координат этой точки проводится по соотношениям
= cos 6 cos а;
Уа = Го cos 6 sin а;
2А = Го sin 6.
Положение радиуса-вектора КА после старта с промежу-
точной орбиты в любой момент времени можно характеризо-
вать аргументом широты ^ = со + т>. Поэтому определить положе-
ние КА в любой момент времени можно с помощью того же
рис. 6.12, но вместо угла со рассматривать угол и.
Положение радиуса-вектора КА в момент его попадания на
границу грависферы Земли получим следующим образом.
Используя уравнение геоцентрической траектории в виде
(2.34), истинную аномалию КА в момент попадания на грани-
цу грависферы находим из соотношения
ип> = arccos (' 1 ")^ , 0 < »гр < л.
Аргумент широты КА в момент попадания на границу гра-
висферы равен: wrp = (o+t>rp.
Подставляя игр вместо со в соотношения (6.23), (6.24), на-
ходим склонение 6К и прямое восхождение сск КА в момент
его попадания на границу грависферы и по значениям 6К,
ак — прямоугольные координаты этой точки траектории.
Напомним, что в общем случае нами получено два допус-
тимых значения долготы восходящего узла, им соответствует
два решения и для всех других характеристик геоцентрической
траектории, т. е. получены две геоцентрические траектории,
258
имеющие заданное значение и направление вектора скорости в
момент выхода из грависферы Земли, заданное значение на-
клонения орбиты и т. д. Выбор траектории из этих двух дол-
жен проводиться на основе выполнения дополнительных огра-
ничений, таких как радиовидимость. Энергетические затраты
двух полученных решений (требуемый импульс скорости) одни
и те же. 1 . ; >
Таким образом, был проанализирован метод исследования
геоцентрического участка траектории* межпланетного перелета.
Представлен алгоритм расчета, позволяющий по геоцентричес-
кой скорости КА в момент выхода из грависферы Земли, по-
лученной из анализа гелиоцентрического участка траектории
(см. разд. 6.4), определить кинематические характеристики
геоцентрического участка, потребленные энергетические затра-
ты разгонного блока КА.
6.6. АНАЛИЗ ДВИЖЕНИЯ КА В ГРАВИСФЕРЕ
ПЛАНЕТЫ НАЗНАЧЕНИЯ
Характер анализа движения КА в грависфере пла-
неты назначения существенно зависит от транспортной задачи,
поставленной перед КА. Среди таких задач могут быть рас-
смотрены:
задача пролета вблизи планеты;
задача выведения спутника на орбиту планеты;
задача прямого попадания в атмосферу планеты;
комбинированные задачи, при которых одна часть КА осу-
ществляет вход в атмосферу планеты назначения, а другая за
счет импульса скорости выводится на пролетную траекторию
или на траекторию ИС планеты.
В рамках объема учебника трудно остановиться на анализе
всех этих задач. Рассмотрим общий подход к анализу движе-
ния КА в грависфере планеты назначения. При этом от-
метим общность идей расчета всех припланетных участков,,
включая и геоцентрический, уже нами рассмотренный в
разд. 6.5.
Считаем, что из анализа гелиоцентрического участка траек-
тории нам известен вектор гелиоцентрической скорости в мо-
мент входа КА в грависферу планеты назначения 7к.с Плане-
тоцентрическая скорость (скорость относительно планеты) КА
в момент входа в грависферу планеты назначения находится с
помощью соотношения
V OO=Vk.C Упл,
где Упл — гелиоцентрическая скорость планеты назначения.,
Если считать, что Ук.с и Упл нам известны в эклиптической
системе координат, то вектор V'<x> будет получен в эклиптичес-
9* 259/
ких координатах. Для решения многих задач требуется пере-
вести его в экваториальную, для планеты назначения, систему
координат. Такой переход не описывается простой зависимостью,
аналогичной (6.14), использующейся для связи эклиптической
и экваториальной геоцентрической системы координат. Дело в
том, что плоскость орбиты планеты назначения не совпадает с
плоскостью эклиптики, а положение плоскости экватора зада-
ется по отношению к плоскости орбиты планеты.
Рассмотрим задачу нахождения такой планетоцентрической
траектории КА в окрестности планеты назначения, которая
обеспечивает определенное значение величины радиуса-векто-
ра перицентра пролетной орбиты. Предполагаем, что ограниче-
ний на положение этой перицентральной точки относительно
поверхности планеты не наложено. В таком случае можно не
переводить вектор Р'оо в экваториальную систему координат.
Пусть [V'oox, V'ooy, V'ooz] — компоненты планетоцентрической
скорости в рассматриваемой системе координат. Найдем такую
точку входа КА в грависферу планеты назначения, чтобы пла-
нетоцентрическая траектория аппарата имела заданное значе-
ние перицентрального радиуса-вектора. Для решения такой за-
дачи необходимо рассматривать грависферу планеты назначе-
ния, имеющую конечные размеры. Пусть граница грависферы
есть геометрическая сфера радиуса Лсф.д. На рис. 6.13 пред-
ставлена плоскость сечения грависферы планеты назначения,
проходящая через центр планеты С и параллельная вектору
V'oo. Есть возможность выбирать любую точку входа КА в гра-
Рис. 6.13. Схема возможных гиперболических планетоцентрических траекто-
рий КА для различных точек входа в грависферу планеты назначения:
С — центр планеты значения; — вектор скорости входа в грависферу планеты на-
значения; Hi — различные точки входа в грависферу планеты назначения
Рис. 6.14. Семейство гиперболических планетоцентрических траекторий
260
яисферу планеты. Если КА попадет в точки границы грави-
сферы на «тыловой» ее части (дуга окружности EGF), то на-
правление планетоцентрической скорости V'oo не дает возмож-
ности войти КА в грависферу планеты. Таким образом, точки
этой части грависферы должны исключаться из области воз-
можных точек входа. Только вход в точки «лобовой», относи-
тельно вектора V'oo, части грависферы планеты обеспечивает
дальнейшее движение в грависфере планеты. На рис. 6.13 на-
несено семейство таких траекторий, соответствующих одному
вектору У'оо и разным точкам входа в грависферу (точкам ду-
ги окружности EDF). .При входе КА в грависферу в точке D
планетоцентрическая траектория будет прямой DC. При входе
КА в грависферу в точках дуги DF КА будет по гиперболам
огибать планету назначения по часовой стрелке. Каждая из
этих гиперболических траекторий будет иметь свое значение
перицентрального радиуса-вектора. При использовании точек
входа, принадлежащих окрестности лобовой точки грависферы
(дуга DH3), КА, двигаясь по гиперболической орбите, попадает
в планету назначения или в атмосферу планеты назначения.
Эта часть семейства гиперболических орбит на рис. 6.13 при-
надлежит заштрихованной области.
При входе КА в точки дуги DE планетоцентрические траек-
тории аппарата окажутся гиперболическими, симметричными
относительно CD (направления Уоо), рассмотренным ранее тра-
екториям с точками входа, лежащими на дуге DF. Семейство
гиперболических планетоцентрических траекторий, соответст-
вующих точкам входа в грависферу, лежащих на дуге DE, на
рис. 6.13 нанесено пунктирной линией.
Понятно, что две симметричные относительно CD гипербо-
лические траектории из нанесенного семейства имеют заданное
значение перицентрального расстояния (одна гипербола из
группы траекторий, нанесенных на рис. 6.13 сплошной линией
и одна — пунктирной). Нами исследована только одна плос-
кость сечения грависферы, параллельная V'*,. Остальные ана-
логичные плоскости можно получить поворотом рассмотренной
Плоскости вокруг V'oo(CD). Таким образом, гиперболические
планетоцентрические траектории КА с заданным значением пе-
рицентра представляют сечения поверхности вращения вокруг
CD. Такая поверхность -вращения проиллюстрирована на
рис. 6.14. На нем точка С есть центр ^планеты. Ось тела враще-
ния проходит через С параллельно V'<x>. Геометрическое место
точек -входа в грависферу планеты обозначено окружностью
DmEnD; геометрическое место перицентров гипербол — окруж-
ностью с точками А, В; в точке F все семейство траекторий
пересекается (эта точка принадлежит оси симметрии фигуры).
Выбор из нанесенного семейства планетоцентрической тра-
ектории (и выбор точки входа в грависферу) может быть про-
261
веден из условия наблюдаемости из перицентра траектории
определенной области планеты, из условия радиовидимости
и т. д.
Несколько слов скажем о задаче выведения искусственного
спутника планеты назначения. Такая задача в принципе реша-
ется с помощью рассмотренного семейства гиперболических ор-
бит. Пусть величина и форма орбиты спутника задана в виде
значений фокального параметра рк и эксцентриситета ек и нет
ограничений на положение этой орбиты в пространстве.
С точки зрения энергетических затрат схему планетоцент-
рической траектории целесообразно выбрать следующей. Точ-
ку входа в грависферу планеты выбираем такой, чтобы пери-
центральное расстояние на гиперболе было равно перицент-
ральному расстоянию орбиты ИС планеты гл=рк/(1+ек). Это-
му условию удовлетворяет семейство гиперболических орбит,
нанесенных на рис. 6.14, если расстояние СВ на этом рисунке
Рк/(1+ек).
В тот момент, когда КА, двигаясь по гиперболической тра-
ектории, попадает в ее перицентр, можно включить ракетный
двигатель КА и затормозить аппарат до эллиптической скорос-
ти на конечной орбите ИСЗ. Приращение скорости, которое в
рамках импульсной аппроксимации должен сообщить разгон-
но-тормозной блок КА, подсчитать несложно.
Скорость КА в перицентре гиперболической орбиты
найдем с помощью интеграла энергии:
д/ v: = •«/ ?нпл (1+ек)+V-
ул у Рк
Эта скорость перпендикулярна радиусу-вектору.
Скорость КА на орбите ИС планеты в перицентре этой ор-
биты Ул тоже перпендикулярна радиусу-вектору и может быть
определена по соотношению (2.45). Минимальный импульс ско-
рости, потребный для перехода с гиперболической пролетной
траектории на эллиптическую орбиту ИС планеты, найдется
как арифметическая разность скоростей Улг и Ул:
ДУ= ] /2Епл-(1 + <,к)+У:_ 1/Епл (1 + бк).
у Рк у Рк
Этот импульс скорости должен быть направлен против ско-
рости (должен затормозить КА, не изменяя направление
скорости). Плоскость эллиптической орбиты спутника при этом
будет совпадать с плоскостью гиперболической планетоцентри-
ческой траектории.
Нами ранее было получено целое семейство гиперболичес-
ких траекторий с заданным значением перицентра орбит
(см. рис. 6.14), с различным положением плоскости орбиты.
Таким образом, из этого семейства можно выбрать такую ги*
262
перболу, плоскость которой удовлетворяет каким-либо допол-
нительным ограничениям, в частности ограничениям, связан-
ным с выполнением задач, которые поставлены перед ИС пла-
неты.
Нужно отметить, что очень малые дополнительные иссле-
дования нужно проделать для рассмотрения задачи о выборе
планетоцентрической траектории КА, обеспечивающей вход КА
в атмосферу планеты с заданным значением угла входа в ат-
мосферу (ввх). Предполагаем, что ракетный двигатель КА при
движении в грависфере планеты не включается. Тогда величи-
на скорости входа КА в атмосферу планеты может быть най-
дена из интеграла энергии:
VBX
2 Нпл у'2
Я + ^атм °°
где 7? — радиус планеты; haTM — высота ее условной атмос-
феры.
Угол входа КА в атмосферу планеты можно изменять за
счет выбора точки входа КА в грависферу планеты. Если об-
ратиться к рис. 6.13, то чем дальше от «лобовой» точки D гра-
ницы грависферы выбирается точка входа в грависферу, то тем
меньше величина угла входа КА в атмосферу. Если точкой вхо-
да выбрана точка D, то угол входа <в атмосферу равен —90°.
Если точкой входа выбрана точка Яь то угол входа в атмосфе-
ру (на рис. 6.13 она заштрихована) по величине будет меньше
90°. Если точкой входа в грависферу является точка /73, то ги-
перболическая траектория лишь коснется атмосферы (угол вхо-
да при этом равен нулю '9вх = 0).
Если задано значение угла входа 9*вх, то среди точек дуги
DH3 можно найти соответствующую точку входа в грависферу
планеты. Заданному значению угла входа будет удовлетворять
целое множество точек входа и соответствующих им гипербо-
лических планетоцентрических траекторий. Семейство таких
траекторий имеет вид, иллюстрируемый на рис. 6.14. На этом
рисунке окружность CL характеризует геометрическое место
точек с одним значением направления скорости относительно
местного горизонта. Среди траекторий этого семейства можно
выбрать траекторию, которая удовлетворяет дополнительным
условиям, например по району посадки на поверхность пла-
неты.
Таким образом, в разделе был рассмотрен метод исследо-
вания участка траектории КА в окрестности планеты назначе-
ния. Рассмотрены алгоритмы исследования этого участка тра-
ектории в задаче пролета на заданном расстоянии от планеты
Назначения, входа в атмосферу, выведения ИС планеты. Разд.
6.6 заканчивает описание метода исследования межпланетных
траекторий, являющегося содержанием разд. 6.4 ...6.6.
263
6.7. ОПТИМИЗАЦИЯ ПЕРЕЛЕТОВ КА
К ПЛАНЕТЕ НАЗНАЧЕНИЯ
Пусть транспортная задача состоит в доставке не-
которой исследовательской аппаратуры (полезного груза) в
окрестность планеты назначения. Не будем исследовать манев-
ры КА в окрестности планеты назначения, считая, что не су-
ществует ограничений на кинематические характеристики это-
го участка траектории. В таком случае главным критерием
оценки и выбора траектории КА является величина характерис-
тической скорости разгонного блока, который обеспечивает
старт с промежуточной орбиты ИСЗ и движение к планете на-
значения. Минимизация характеристической скорости разгон-
ного блока соответствует максимизации массы полезного гру-
за КА при фиксированной начальной его массе. Под начальной
массой мы подразумеваем массу, которую ракета-носитель вы-
вела на промежуточную орбиту ИСЗ.
Характеристическая скорость разгонного блока отличается
от приращения скорости на величину потерь Vxap = AV+SAVi.
Здесь A Vi — потери в скорости (гравитационные и на управле-
ние).
Потери в скорости на управление появляются тогда, когда
вектор тяги двигателя направлен не по вектору скорости ле-
тательного аппарата. Потери на управление при работе раз-
гонного блока можно сделать строго нулевыми, если програм-
му вектора тяги выбрать так, чтобы угол атаки на ак-
тивном участке полета был тождественно равен нулю. Та-
Рис. 6.15. Схема тангенциального
(Pi) и трансверсального (Рг) разго-
на КА:
DA|3— траектория разгона КА; Da — про-
межуточная орбита ИСЗ; С — центр Земли
кой разгон называется танген-
циальным.
Кроме тангенциального раз-
гона может использоваться и
трансверсальный, т. е. когда
на протяжении всего активного
участка вектор тяги ориентиру-
ется по местному горизонту в
плоскости траектории КА. На
рис. 6.15 Da — дуга промежу-
точной орбиты ИСЗ, траекто-
рия КА на участке старта с
промежуточной орбиты обозна-
чена Dp. Точка А — положение
КА в текущей точке траекто-
рии активного полета. Ско-
рость в этой точке траектории
обозначена V. В случае танген-
циального разгона вектор тяги
Л направлен по скорости. В
264
случае трансверсального разгона вектор тяги Р2 направлен пер-
пендикулярно радиусу-вектору.
В случае трансверсальной тяги потери тяги на управление
в общем случае не нулевые, так как угол атаки КА а, равный
в этом случае траекторному углу 0, не равен нулю («=0^=0).
Для того чтобы потери на управление при трансверсальном
разгоне были незначительны или, по крайней мере, малы, дос-
таточно, чтобы траекторный угол в процессе активного полета
был небольшой.
Для того чтобы траекторный угол в процессе активного по-
лета был мал, достаточно, чтобы старт с промежуточной ор-
биты ИСЗ проводился из перицентра орбиты и активный учас-
ток был не очень продолжителен. При старте с круговой орби-
ты или почти круговой начальное значение траекторного угла
всегда небольшое. Что касается условия, чтобы активный уча-
сток полета был не очень продолжителен, используемые в
настоящее время тяговооруженности разгонного блока этому
условию удовлетворяют. При уменьшении тяговооруженности
КА становятся рациональными схемы полета КА с нескольки-
ми включениями двигателя в районе перицентра орбиты. При
такой схеме полета после сообщения КА некоторой эллипти-
ческой относительно Земли скорости ракетный двигатель раз-
гонного блока выключается. КА делает виток вокруг Земли,
двигаясь по эллиптической орбите. Затем, когда КА попадает
в окрестность перигея этой орбиты, еще раз включается ра-
кетный двигатель. При этом потери на управление при транс-
версальном разгоне удается сделать очень малыми.
Интересно то, что эта же схема полета оказывается целе-
сообразной и с точки зрения гравитационных потерь (ДУГр =
= J g'sin'Od/). Если в течение активного участка полета тра-
^0
екторный угол будет небольшим, то гравитационные потери
будут тоже небольшими. Если организовать траекторию ак-
тивного полета так, чтобы угол 0 оказался тождественно нуле-
вым, то и гравитационные потери будут нулевыми. Для стар-
та, скажем, с круговой промежуточной орбиты ИСЗ такой по-
лет можно реализовать. Для этого необходимо, чтобы КА в
процессе набора скорости продолжал двигаться по круговой
орбите. На траектории разгона скорость в текущей точке тра-
ектории будет больше круговой. При этом для того чтобы
«удержать» КА на круговой орбите (не дать ему постепенно
Удаляться от Земли), придется вектор тяги направить внутрь
орбиты ИСЗ, обеспечивая определенный отрицательный угол
атаки а. Угол атаки и связанное с ним радиальное реактив-
Р
ное ускорение—sin а нужно выбрать так, чтобы радиальное
m
ускорение КА оказалось нулевым:
265
Если в течение всего активного участка за счет выбора а
удовлетворять последнее равенство, то радиальная скорость
КА на этом участке окажется постоянной. Если, к тому же, на-
чальная радиальная скорость нулевая, то КА будет двигаться
по круговой орбите.
Описанная схема полета не используется, так как она со-
ответствует большим потерям скорости на управление. На
практике при разгоне КА с орбиты ИСЗ используются линей-
ные законы управления углом тангажа $ = -©о + 'tK Гравитаци-
онные потери в скорости при использовании этих законов не-
нулевые. При больших протяженностях активных участков они
достигают десятков метров в секунду и более. Эти потери в
скорости целесообразно учитывать при выборе проектных па-
раметров разгонного блока, прежде всего, его тяговооружен-
ности. Для анализа траектории межпланетного перелета мож-
но считать целесообразной такую схему перелета, которая тре-
бует минимального импульса скорости ДГ при сходе с проме-
жуточной орбиты ИСЗ. При этом считается, что чем меньше
Д1/, тем меньше характеристическая скорость разгонного блока.
Чем же можно варьировать в рамках рассматриваемых ра-
циональных схем межпланетных перелетов? Конечно же вре-
менем старта Тсг и временем полета tn к планете цели. Имен-
но эти две величины при заданно?! планете назначения одно-
значно определяют гелиоцентрическую траекторию КА, гелио-
центрическую скорость выхода из сферы действия Земли Го.с>
геоцентрическую скорость КА в этот же момент времени Voo.
Требуемое приращение скорости при старте с орбиты ИСЗ из
перицентра промежуточной орбиты с элементами р0, е0 нахо-
дится следующим образом:
дУ== ^^(l + ^+P- |/Шь(1 + ео).
У Ро V Ро
Из последнего равенства видно, что минимальное значение
приращения скорости ДГ соответствует минимальному значе-
нию скорости КА относительно Земли в момент выхода из гра-
висферы Земли. Поэтому выбор времени старта Тст и времени
полета tn к планете цели можно проводить, не анализируя при-
планетные участки траектории. Поставим задачу исследования
зависимости скорости КА относительно Земли в момент выхо-
да из грависферы Земли (гиперболического избытка скорости) >
от даты старта Тсг и времени полета tn:
Гоо=Ко(Гст, (6.25)
Алгоритм нахождения по значениям Тст и tn величины Г»
уже описан в разд. 6.4, посвященном исследованию гелиоцент-
266
рической траектории. Дополнительно к соотношениям этого
раздела следует рассмотреть равенство Voo=V0,c—Г3, которое
дает возможность найти V<x> по гелиоцентрической скорости
КА в момент выхода из грависферы Земли Го.с и гелиоцентри-
ческой скорости Земли.
Зависимость (6.25) исследуется численно. Результаты чис-
ленных расчетов анализируются чаще всего с помощью линий
одного значения гиперболического избытка скорости V<x> на
плоскости Тст, tn (изолиний гиперболических избытков ско-
рости) .
На рис. 6.16 представлена качественная картина этих изо-
линий для полета к Марсу в 1966—1970 гг. По оси абсцисс
диаграммы отложена дата старта, римские цифры вдоль оси
абсцисс характеризуют номер месяца в соответствующем году.
По оси ординат отложено время полета к Марсу в сутках.
Числа у изолиний означают величину гиперболического избыт-
ка скорости (в км/с), соответствующую точкам изолиний.
Прежде всего, обратим внимание на то, что изолинии обра-
зуют семейства, отстоящие друг от друга по оси абсцисс, при-
чем характер, структура семейств повторяются. Это связано с
тем, что через определенный промежуток времени (называе-
мый синодическим периодом планеты) положение планеты на-
значения относительно Земли повторяется. Действительно,
Земля и планета назначения (в данном случае Марс) движут-
ся относительно Солнца по своим орбитам с определенными
Рис. 6.16. Зависимость гиперболического избытка скорости от времени старта
7СТ и времени полета ta к Марсу в 1966—1969 гг. Цифры у изолиний озна-
чают величину гиперболического избытка скорости Voo в км/с
267
роста разные, то радиус-вектор Земли будет «догонять» ради-
ус-вектор Марса. Минимальное время между одинаковыми от-
носительными положениями рассматриваемых радиусов-векто-
ров называется синодическим периодом. Он может быть под-
считан как время между последовательными противостояния-
ми. Если обозначить угловую скорость радиуса-вектора Земли
относительно Солнца — Q3, угловую скорость радиуса-вектора
Марса — QM, то синодический период Марса Тм.с (относитель-
но Земли) находится из соотношения TM.c = 2ni/(Q3—QM).
Синодический период Марса равен 2,14 г. Отметим, что это
самый большой из синодических периодов всех планет. Вели-
чины синодических периодов планет приведены в табл. 6.1.
Из таблицы видно, что для планет юпитерианской группы
(Юпитер, Сатурн и др.), чем более удалена планета от Солн-
ца, тем меньше ее синодический период, тем ближе он прибли-
жается к одному году. Это происходит из-за того, что радиус-
вектор более удаленной планеты медленнее вращается относи-
тельно Солнца, поэтому Земля за время, немного большее го-
да, успевает, сделав полный оборот вокруг Солнца, «догнать»
планету. Синодический период Меркурия мал, что объясняется
тем, что его радиус-вектор очень быстро вращается относитель-
но Солнца и быстро «догоняет» радиус-вектор Земли.
В той же таблице для справки приведены сидерические
(звездные) периоды обращения планет.
Если бы орбиты были круговыми и плоскость орбиты пла-
неты назначения совпадала с плоскостью эклиптики, то через
синодический период абсолютно точно повторялось бы относи-
тельное положение планеты назначения и Земли. При этом се-
мейство изолиний на плоскости Тст, tn строго повторялось бы
через синодический период. Из-за эллиптичности и пространст-
венности орбит семейства изолиний неточно повторяют друг
друга через синодический период. При этом все же общий ха-
рактер семейства сохраняется.
Второе обстоятельство, которое бросается в глаза при рас-
смотрении изолиний на рис. 6.16, это то, что линия уровня од-
ного значения К» из семейства, соответствующего одному сино-
дическому периоду, имеет ветви (состоит из двух кривых).
Эти ветви разделены областью с очень частым расположением
изолиний. Эта область называется энергетическим хребтом.
Объясним физическую сущность этого хребта. Рассмотрим за-
висимость гиперболического избытка скорости от времени по-
лета при фиксированной дате старта. Такую зависимость
Voo(/n) можно рассматривать как сечение семейства анализи-
руемых изолиний плоскостью, проходящей через фиксирован-
ную дату старта Тст-
На рис. 6.17 для фиксированной даты старта показано по-
ложение радиуса-вектора Земли относительно Солнца го»
268
Cxyz — гелиоцентрическая эклиптическая система координат.
Радиус-вектор г0 принадлежит плоскости эклиптики Сху. Ли-
ния узлов орбиты планеты назначения обозначена СЕ.
Изменяя время полета к планете цели /п, тем самым мы
изменяем дату подлета КА к ней. Дата подлета КА к планете
фиксирует положение этой планеты. Таким образом, рассмат-
ривая различные /п, мы изменяем положение КА в момент его
подлета к планете назначения. На рис. 6.17 нанесено несколько
возможных векторов гк, соответствующих разным rKi, rK2,
гк3. В соответствии с анализом, проводимым на этапе исследо-
вания гелиоцентрической траектории перелета, строится такое
коническое сечение (эллипс, гипербола или парабола), прохо-
дящее через го и гк, что время полета между г0 и гк оказыва-
ется равным заданному /п. Обратим внимание на то, что плос-
кость гелиоцентрического участка траектории проходит через
векторы го и гк-
Пусть малому времени полета Zni соответствует радиус-век-
тор гК1 = СВ1 (см. рис. 6.17) положения планеты назначения в
момент подлета к ней КА. Плоскость орбиты перелета для слу-
чая, показанного на рисунке, имеет малый наклон к плоскос-
ти эклиптики. Малый наклон к плоскости эклиптики — благо-
приятный факт с точки зрения энергетических затрат. Так как
для того чтобы гелиоцентрическая скорость после выхода КА
из грависферы Земли была сильно наклонена к плоскости эк-
липтики, нужны большие значения гиперболического избытка
скорости. Таким образом, с точки зрения энергетических зат-
рат на исправление пространственности рассматриваемое поло-
жение гк благоприятно.
С другой стороны, для рассматриваемого положения rKi не-
благоприятным для энергетических затрат является очень ма-
Рис. 6.17. Схемы гелиоцентрического участка пе-
релета при различных временах перелета:
СА=тп— радиус-вектор Земли в момент отлета КА от
Земли; CBi=rKi— радиусы-векторы планеты назначения
в момент подлета КА к планете назначения, соответ-
ствующие разным временам полета tn
Рис. 6.18. Схема гелио-
центрического перелета
между начальным г0 и
конечным гк радиусами-
векторами
269
лая угловая дальность полета Ф на гелиоцентрическом участ-
ке (Z4CBi = O! — мал, допустим, он меньше 90°).
На рис. 6.18 в плоскости траектории перелета показаны на-
чальный го и конечный гк радиусы-векторы перелетной гелио-
центрической траектории. Малая угловая дальность перелета
может привести к траекториям, близким к прямолинейным,
или, по крайней мере, таким, начальная скорость на которых
Го.с имеет значительную радиальную составляющую. Это долж-
но привести к большим значениям требующихся величин Voo.
Таким образом, малые времена перелета приводят к малым
угловым дальностям полета, что, в свою очередь, вызывает
большие начальные скорости (большие радиальные компонен-
ты начальной скорости) и, как правило, большие К».
Увеличивая время полета до значения /п, соответствующего
радиусу-вектору г2 = СВ2 (см. рис. 6.17), можно, не очень ус-
ложняя «проблему пространственности» (плоскость АСВ2 хотя
и сильнее наклонена к плоскости эклиптики, чем АСВ^ но это
может не приводить к очень большому росту затрат на прост-
ранственность), существенно облегчить «проблему угловой
дальности». Увеличение угловой дальности перелета до значе-
ния ~ 150° уменьшает энергетические затраты в плоскости пе-
релета, и Уоо при этом может уменьшаться.
Дальнейшее увеличение времени перелета /п приведет к то-
му, что плоскость гелиоцентрической орбиты перелета будет
иметь большой наклон к плоскости эклиптики. Так, на рис.
6.17 показано, что для времени перелета, соответствующего ко-
нечному радиусу-вектору г3 = СВ3, плоскость перелетной орби-
ты (она заштрихована) почти перпендикулярна плоскости эк-
липтики. Ясно, что для перелета по такой траектории потребу-
ются очень большие энергетические затраты. «Проблема про-
странственности» проявляется при угловых дальностях, близ-
ких к 180°, причем зависимость энергетических затрат (Voo)
от положения гк (от времени /п) в этом диапазоне времени пе-
релета очень существенная.
При дальнейшем увеличении времени перелета угловая
дальность будет продолжать увеличиваться, «проблема прост-
ранственности» достаточно быстро перестает быть определяю-
щей, плоскость перелета все менее будет наклонена к плоскос-
ти эклиптики. В этом диапазоне времени перелета зависимость
Уоо(/П) убывающая.
Дальнейшее увеличение времени полета приведет к такому
росту угловой дальности полета (в конце концов, к Ф—кВ60°),
что энергетические затраты увеличатся. При угловой дальнос-
ти Ф, стремящейся к 360°, перелетная траектория будет вы-
рождаться в прямолинейную, с очень «тяжелой энергетикой».
На рис. 6.19 нанесена качественная зависимость гиперболи-
270
Рис. 6.19. Зависимость гиперболиче-
ского избытка скорости от вре-
мени полета /п (угловой дальности
полета Ф)
ческого избытка скорости от-
носительно Земли Voo от време-
ни полета Zn при фиксирован-
ной дате старта. По оси абс-
цисс на этом графике дополни-
тельно нанесена угловая даль-
ность полета, соответствующая
времени tn. Характер этой кри-
вой определяется двумя проти-
воположными тенденциями. С
точки зрения затрат на прост-
ранственность «плохими» явля-
ются траектории с угловой
дальностью, близкой к 180°. С
точки зрения затрат на кру-
тизну траектории полета не-
удачными являются траектории с угловыми дальностями, близ-
кими к нулю и к 360°.
Дополнительно отметим, что кривая Коо(^п) в районе време-
ни перелета, соответствующего угловой дальности, близкой к
180°, очень крутая. Именно эта крутизна и образует «энергети-
ческий хребет» между двумя типами перелета. Первый тип
траектории перелета соответствует угловой дальности переле-
та, меньшей 180°, и называется траекториями первого полувит-
ка. Второй тип траектории перелета соответствует угловой
дальности, большей 180°, и называется траекториями второго
полувитка. На рис. 6.16 изолинии траекторий второго полувит-
ка лежат выше изолиний траекторий первого полувитка. Каж-
дый из типов траекторий имеет свой локальный минимум. На
рис. 6.19 минимум Коо среди траекторий первого полувитка,
обозначенный Poomin, меньше минимума Коо среди траекторий
второго полувитка K2oomin. В общем случае это совсем необя-
зательно. Для случая полета к Марсу в период 1966—1967 гг.,
иллюстрируемого рис. 6.16, дело обстоит наоборот. Из анализа
ИЗОЛИНИЙ ЭТОГО рисунка ВИДНО, ЧТО K2oomin< K^min ДЛЯ многих
дат старта. Таким образом, в рассмотренную эпоху выгодней
было использовать траектории перелета второго полувитка. Из
анализа семейств изолиний удается найти самое целесообраз-
ное время старта и время полета с точки зрения энергетичес-
ких характеристик (минимума Коо). Из рис. 6.1'6 видно, что
минимальные значения гиперболического избытка скорости
составляют ~3 км/с и соответствуют времени старта январь
1967 г. и времени полета 330 сут.
Более подробное рассмотрение примеров изолиний можно
провести с помощью рис. 6.20, взятого из ’[И]. На нем в более
крупном масштабе представлены гиперболические избытки ско-
рости относительно Земли для полета -к Венере в 1983 г.
271
a
5
Рис. 6.20. Зависимость гиперболического избытка скорости от времени старта
Тст и времени полета /п к Венере в 1983 г.:
.а — при полете по первому полувитку; б — при полете по второму витку
Сплошные линии — изолинии гиперболического избытка скорости Vx относительно Зем-
ли. Пунктирные линии — изолинии гиперболического избытка скорости V'ж относи-
тельно Венеры. Цифры у изолиний — величины гиперболических избытков скоростей
Л км/с
272
Часть а анализирует полеты по первому полувитку, часть б
рисунка — полеты по второму полувитку. Каждой точке плос-
кости Тст—tn соответствует определенное значение гиперболи-
ческого избытка скорости. Из рис. 6.20 видно, что при старте
6.6.1983 г. и времени полета к Венере 119 суток гиперболичес-
кий избыток скорости у Земли равен ~3,2 км/с.
Поле изолиний дает возможность находить гиперболичес-
кий избыток скорости у Земли по заданным дате старта и вре-
мени полета, дает возможность выбирать целесообразные даты
старта и время полета, соответствующие минимальным или
близким к минимальным Энергетическим затратам.
Так, из рис. 6.20 видно, что для рассмотренной эпохи
(1983 г.) целесообразные даты старта и времени полета могут
выбираться близкими к следующим значениям:
при полете по траектории первого полувитка Тст= 12.VI.1983,
/п=140 сут; при этом 1/00 = 2,66 км/с;
при полете по траектории второго полувитка TCt = 27.V.1983,
/п=156 сут; при этом Уоо = 2,42 км/с.
Таким образом, анализируя диаграммы гиперболических из-
бытков скорости, можно выбрать целесообразные даты стартов
и время полета КА к планетам назначения с точки зрения ми-
нимальной характеристической скорости разгонного блока меж-
планетного КА (минимального значения гиперболического из-
бытка скорости относительно планеты назначения).
Заметим, что с помощью аналогичной диаграммы легко
анализировать планетоцентрическую скорость КА при входе
его в грависферу планеты назначения (гиперболический из-
быток скорости у планеты назначения У'оо). Анализ этой ско-
рости интересен для исследования энергетических затрат ак-
тивных маневров в окрестности планеты назначения (если они
предусмотрены схемой полета). Если рассматривается пролет
КА мимо планеты назначения или прямой вход спускаемого
аппарата в атмосферу планеты, то величина У'оо определяет
скорость пролета, скорость входа в атмосферу и другие важ-
ные кинематические характеристики планетоцентрического
движения.
Так как гелиоцентрическая скорость определяется по Тст и
tn в результате анализа гелиоцентрического перелета, то изо-
линии гиперболических избытков скоростей относительно пла-
неты назначения можно нанести на ту же плоскость Тст—tn,
что и изолинии гиперболических избытков скорости относитель-
но Земли. При этом с помощью диаграммы можно не только
определять V'oo, но и выбирать Тст, tn из условия удовлетворе-
ния определенных ограничений на
Анализ и выбор времени старта Тст и времени полета к
планете назначения tn ведется с учетом многих ограничений.
Укажем несколько обстоятельств, которые приходится учиты-
273
вать при выборе схемы перелета. Для определенности, пусть
планета назначения — Венера.
При сближении КА с Венерой на первом полувитке (Ф<
<180°) подлет КА к Венере осуществляется с затененной сто-
роны Венеры (со стороны, противоположной Солнцу). Пояс-
ним утверждение. На рис. 6.21 (он взят из ’[36]) траектория
полета к Венере на первом полувитке представлена дугой
АВ. В момент подлета КА на первом полувитке положение
Земли на ее орбите обозначено точкой D. Точка В есть первое
пересечение траекторией КА орбиты Венеры; радиальная ге-
лиоцентрическая скорость КА в момент подлета к Венере от-
рицательная. Характерные направления при подлете КА к Ве-
нере в точке В вынесены отдельно под номером 1. Направле-
ние КА — Венера в момент подлета к ней определяется на-
правлением подлетной скорости (направлением планетоцентри-
ческой скорости КА в момент входа в грависферу Венеры).
Эта скорость получается как геометрическая разность гелио-
центрической скорости КА в момент его подлета к Венере Ук.с
и скоростью планеты VB. На рис. 6.21 эта разность найдена
(см. треугольник скоростей). Из рис. 6.21 (/) видно, что при
сближении с Венерой на первом полувитке подлет к планете
осуществляется с теневой стороны. Сама планета (освещенная
Солнцем часть планеты) видна в виде узкого серпа. Это мо-
жет вызвать определенные трудности системы ориентации и на-
вигации КА.
Рис. 6.21. Геометрические характеристики подлета КА к Венере на первом
(/) и втором (2) полувитках:
VK. с — гелиоцентрическая скорость КА в момент подлета к грависфере Венеры; VB —
гелиоцентрическая скорость Венеры в этот же момент времени; V' ж — гиперболический
избыток скорости при подлете к Венере
274
Подлет
7
Направление
на Солнце
Направление
Венера
Сближение с Венерой на втором полувитке происходит с
освещенной стороны (см. траекторию АЕ рис. 6.21 и выноску 2
этого рисунка, точка F рисунка есть положение Земли при
подлете КА к Венере на втором полувитке траектории).
При полете к внешним (относительно Земли) планетам
(Марсу, Юпитеру и т. д.) картина освещенности изменяется.
При полете к Марсу на первом полувитке сближение с Мар-
сом происходит с солнечной стороны, на втором — с затенен-
ной. Отметим, что рассмотренная кинематика влияет на выбор
компоновочных схем КА, выдвигает определенные требования
на взаимное расположение звездных, солнечных и планетных
датчиков и т. д.
Чтобы оценить такие ограничения, в ряде случаев целесо-
образно на той же плоскости Гст, tn нанести семейство изоли-
ний_указанных угловых характеристик (например, угла меж-
ду V'oo и направлением на Солнце в момент подлета к Венере).
В некоторых случаях на плоскости анализируемых времен
Тст, tn строится семейство изолиний кинематических и динами-
ческих характеристик, которые определяются после анализа
геоцентрического движения КА (как отмечалось, такой анализ
проводится после исследования гелиоцентрического участка
траектории). Как примеры таких характеристик можно наз-
вать: требующееся приращение скорости, сообщаемое КА раз-
гонным блоком (или даже массовую отдачу разгонного блока,
например массу полезного груза разгонного блока), склонение
точки старта с промежуточной орбиты ИСЗ, склонение точки
выхода из грависферы Земли и т. д. Отметим, что анализ скло-
нения должен учитываться, например при рассмотрении усло-
вия радиовидимости КА с наземных пунктов в критические
моменты его полета.
Аналогично геоцентрическим возможно исследовать плане-
тоцентрические характеристики движения КА в окрестности
планеты назначения.
Окна запуска
Анализ всех ограничений на характеристики КА,
анализ критерия или критериев выбора схемы полета КА при-
водит к нахождению целесообразных дат старта и времени по-
лета и, следовательно, рациональной схемы полета КА в эту
эпоху. Мы уже отмечали, что целесообразные даты старта
повторяются через, примерно, синодический период. Они соот-
ветствуют, например минимальным энергетическим затратам
разгонного блока Vxapmin. Если мы создадим разгонный блок
с такой характеристической скоростью, то этот блок обеспе-
чит перелет к планете назначения только в том случае, если
точно будут выдержаны дата старта и другие параметры, ха-
275
Рис. 6.22. Понятие окна запуска
рактеризующие схему полета.
Если по техническим или
другим причинам КА в этот
момент времени запустить не
удалось, то придется ждать
следующей хорошей даты за-
пуска (для Марса нужно
будет ждать более двух лет).
Понятно, что предлагаемая
ситуация не удовлетворяет
конструктора. Характеристи-
ческая скорость разгонного
блока должна быть боль-
ше Vxapmin на какую-либо величину. Предположим, что она
больше Vxapmin на 10%. Тогда появляется возможность варьи-
ровать, сдвигать момент старта КА с промежуточной орбиты
ИСЗ. Энергетический запас позволяет отойти от даты старта,
соответствующей минимальным энергетическим затратам. До-
пустимый диапазон дат старта называется окном запуска.
«Ширина» окна запуска зависит от планеты назначения и
от энергетического запаса разгонного блока. Ширина окна за-
пуска с помощью изолиний потребного приращения скорости в
плоскости Гст—tn определяется следующим образом. Из изве-
стного значения характеристической скорости разгонного бло-
ка Vxap вычитает оценку потерь в скорости при работе разгон-
ного блока XAVi и получаем приращение скорости, которое
i
разгонный блок может сообщить КА — AV*. В ряде случаев
потерями можно пренебречь и считать, что AV*=Vxap. Нахо-
дим для рассматриваемой эпохи запуска изолинию, соответст-
вующую AV*. Если такой нет, т. е. AVmin>AV*, то полет к
планете с располагаемой энергетикой невозможен.
Пусть изолиния существует и состоит из двух ветвей. На
рис. 6.22 показаны две такие ветви. Верхняя ветвь соот-
ветствует полету по второму полувитку, нижняя — по первому
полувитку. [Жттш, Т(2)ст max] — ВОЗМОЖНЫЙ ДИаПЗЗОН ДЗТ
старта при полете ко второму полувитку. Это значит, что для
любой даты старта, лежащей внутри диапазона, можно подо-
брать время полета такое, что энергетические затраты полета
AV будут меньше располагаемых AV*. Действительно, каждая
точка (Тст, лежащая внутри изолинии, представляющей со-
бой замкнутую кривую, соответствует энергетическим затратам,
меньшим AV*.
Аналогичный допустимый диапазон времени перелета
(Т<Ост min, Т(1)СТтах] есть и для полета по первому полувитку.
Допустимые даты старта (с точки зрения энергетических зат-
276
рат) принадлежат объединению диапазонов [Г(1)ст min,.
У^ст max]U [^^ст min, ст max] •
На рис. 6.22 допустимые даты старта находятся в диапазо-
не [ТЧ^стппп, Г^сттах]. Этот диапазон и может быть рассмот-
рен как окно запуска КА к планете назначения.
В том случае, когда учитываются дополнительные ограни-
чения, приходится из полученного допустимого по энергетиче-
ским затратам диапазона дат старта исключить те даты, при
которых ограничения не удовлетворяются.
Таким образом, в этом разделе рассмотрены оптимальные
схемы межпланетных перелетов. Основным критерием опти-
мальности проектируемых траекторий межпланетного переле-
та считается минимум характеристической скорости разгонного
блока, который, при старте с промежуточной орбиты ИСЗ, со-
общает КА скорость, достаточную для достижения планеты на-
значения. Показано, что минимум характеристической скорос-
ти разгонного блока соответствует минимуму гиперболического
избытка скорости относительно Земли.
Показано, как определяются целесообразные даты старта
к планете, которые повторяются примерно через синодический
период планеты. Введено понятие окна запуска как диапазона
дат старта, допустимого с точки зрения энергетики разгонного
блока.
Рассмотрены дополнительные критерии при выборе схемы
межпланетного перелета: величина гиперболического избытка
скорости относительно планеты назначения, освещенность пла-
неты назначения в момент подлета к ней.
6.8. ГРАВИТАЦИОННЫЙ МАНЕВР В МЕЖПЛАНЕТНЫХ
ПЕРЕЛЕТАХ
Одной из красивейших идей механики космического
полета является гравитационный маневр. Сущность его заклю-
чается в следующем. Для расширения окон запуска, для умень-
шения потребных энергетических затрат на перелет к планете
назначения в ряде случаев оказывается целесообразным на
участке гелиоцентрического движения межпланетного КА вой-
ти в грависферу «промежуточной» планеты. За счет энергии
этой планеты изменить величину и направление скорости КА.
В настоящем разделе будет обсуждена принципиальная воз-
можность изменения гелиоцентрической траектории за счет
гравитационного маневра, описан гравитационный маневр и
приведены примеры его использования в практике космических
полетов.
Пусть на гелиоцентрическом участке межпланетного пере-
лета КА попадает в окрестность некоторой промежуточной
планеты. Термин «промежуточная» не предполагает, что боль-
277
шая полуось этой планеты по величине — средняя между боль-
шими полуосями орбиты планеты старта и планеты назначе-
ния. Промежуточной может быть любая планета Солнечной
системы (в том числе и планета старта, т. е. при старте с Зем-
ли может оказаться целесообразным встретиться с ней на уча-
стке гелиоцентрического движения для гравитационного ма-
невра).
Гелиоцентрическая скорость КА в_момент попадания КА в
грависферу промежуточной планеты У-П.с определяет плането-
центрическую скорость входа КА в грависферу этой планеты
У'оо
V 00—1/ п.с Упл, (6.26)
где Упл — гелиоцентрическая скорость планеты. Скорость У'оо
является гиперболической, и планетоцентрическая траектория
КА оказывается гиперболой. Если точка входа КА в грави-
сферу планеты выбрана так, что КА не входит в атмосферу
(если она существует) планеты и не падает в планету, то, об-
летев планету по гиперболе, КА покинет грависферу промежу-
точной планеты. Планетоцентрическая скорость выхода КА из
грависферы планеты Уоо по величине будет равна планетоцент-
рической скорости входа в атмосферу | Уоо| = | У'оо!, но у нее
будет новое направление (гравитация планеты искривила пла-
нетоцентрическую траекторию). Поэтому гелиоцентрическая
скорость КА в момент выхода из грависферы планеты У+П.с
будет отличной от гелиоцентрической скорости входа КАвгра-
виоферу планеты У-П.с:
У+п.с =Упл + Уоо. (6.27)
Таким образом, встречая на своем пути промежуточную
планету, за счет гравитационного маневра КА как бы получа-
ет определенный импульс скорости. Выясним, от чего зависит
величина этого импульса и его направление.
Гелиоцентрическая скорость подлета к грависфере проме-
жуточной планеты У“п.с определяется гелиоцентрическим уча-
стком траектории КА Земля — промежуточная планета. Этот
участок может рассчитываться так же, как и гелиоцентричес-
кий участок траектории Земля — планета назначения, рассмот-
ренный в разд. 6.4. Для заданной даты старта от Земли Тст и
времени полета к промежуточной планете tn, решая уравнение
Ламберта, удается получить все характеристики этого участка
траектории, включая гелиоцентрическую скорость КА в момент
входа в грависферу промежуточной планеты У“п.с. Подсчет
планетоцентрической скорости входа в грависферу промежу-
точной планеты проводится с помощью (6.26). Выбор точки
входа КА в грависферу планеты полностью определяет пролет-
-278
ную гиперболическую орбиту, ее элементы, перицентральное
расстояние.
Для того чтобы оценить возможный эффект от пролета про-
межуточной планеты при расчете межпланетной траектории в-
рамках метода грависфер нулевой протяженности, найдем
угол между векторами планетоцентрических скоростей входа
в грависферу планеты и выхода из нее. На рис. 6.23 представ-
лена пролетная гиперболическая орбита. Планетоцентрическая
скорость входа в грависферу планеты (подлетная планетоцен-
трическая скорость) с точностью до допущений метода грави-
сфер нулевой протяженности направлена по асимптоте гипер-
болы Ют. Планетоцентрическая скорость КА в момент выхода,
из грависферы — по асимптоте Ор. Центр облетаемой планеты
на рис. 6.23 расположен в точке С. За счет гравитационного
маневра произошел поворот вектора подлетной планетоцентри-
ческой скорости на угол тОр (угол между асимптотами гипер-
болы). Обозначим его (3. Подсчитать этот угол несложно. Дей-
ствительно, из (2.49) и соотношения h=V2oo следует
а = — ц/1/2то.
(6.28)
Но гл=а (1—е), поэтому из последних двух равенств
г V2
1 , 'л V оо
е = 1 4- ----------------------- •
И
Предельное значение истинной аномалии г)Пр (см. рис. 6.23)
связано с эксцентриситетом е простым соотношением
COSDnp = — 1/е.
получим
г V2 ”1— *
1+
И _
показывает, что угол
Отсюда, после преобразований,
р = 180° — 2 arccos
(6.29)
Анализ зависимости (6.29)
вектора планетоцентрической скорости увеличивается
поворота
с умень-
Рис. 6.23. Схема гиперболической
пролетной траектории
Рис. 6.24. Изменение гелиоцентриче-
ской скорости КА при гравитацион-
ном маневре
279
шением перицентрального расстояния гл (более близким про-
летом окрестности планеты), с уменьшением планетоцентриче-
ской скорости входа КА (меньшая скорость легче подвержена
гравитационному воздействию планеты), с увеличением грави-
тационного параметра планеты (более мощная планета сильнее
воздействует на траекторию). Таким образом, максимальный
угол поворота вектора подлетной планетоцентрической скорос-
ти соответствует минимальному перицентральному расстоянию,
который в пределе равен радиусу промежуточной планеты /?
Ртах — 180° — 2 arccos
J
(6.30)
На рис. 6.24 СА = Упл, СВ = V~n.c — векторы гелиоцентриче-
ской скорости промежуточной планеты и гелиоцентрической
скорости КА в момент входа КА в грависферу планеты. АВ =
= Fzoo — вектор планетоцентрической скорости. Максимальный
угол поворота этой скорости может быть найден по (6.30).
Варьируя точками входа в грависферу планеты, соответст-
вующие перицентральному расстоянию /?, можно в различных
плоскостях искривлять планетоцентрическую траекторию. При
этом векторы планетоцентрической скорости выхода из грави7
сферы планеты назначения будут описывать коническую по-
верхность С ОСЬЮ AB(V'oo) И УГЛОМ ПОЛураСТВОра КОНуса Ртах-
На рис. 6.24 эти возможные положения отмечены лучами, про-
веденными из точки А.
В том случае, если перицентральное расстояние пролетной
гиперболы больше радиуса планеты /?, угол поворота скорости
меньше и вектор планетоцентрической скорости выхода из гра-
висферы планеты Уоо, начинаясь в точке А, принадлежит ша-
ровому сектору, ось которого есть АВ, а угол полураствора ра-
вен ртах. Таким образом, вектор Уоо, начинаясь в точке А, кон-
чается на сферической поверхности шарового сектора радиуса
| У'оо| = | Уоо|, угол полураствора которого равен ртах. При этом
вектор гелиоцентрической скорости выхода из грависферы пла-
неты У+п.с на рис. 6.24 начинается в точке С, а его конец при-
надлежит описанной сферической поверхности шарового сек-
тора. На рис. 6.24 рассмотрена точка D этой поверхности, угол
DAB равен углу р поворота вектора планетоцентрической ско-
рости, А/)=Уоо, СП = У+п.с.
Для» получения максимального изменения модуля гелиоцен-
трической скорости нужно искать такую точку D поверхности
.шарового сектора, которая дает максимальное значение разни-
цы
.280
Анализ позволяет утверждать, что от гравитационного ма-
невра можно получить значительные эффекты изменения гелио-
центрической траектории. Облет Юпитера позволяет изменить
гелиоцентрическую скорость на десятки километров в секун-
ду, весьма большие эффекты удается получить от облета Са-
турна, Нептуна, Плутона. Значительные эффекты — от облета
Земли и Венеры. При реализации некоторых схем полетов
можно использовать и гравитационные маневры около Луны и
других естественных спутников.
Использование гравитационных маневров требует увязки
гелиоцентрических участков траектории до пролета промежу-
точной планеты и после его. Совсем необязательно при этом,
чтобы эффект пролета с точки зрения какого-либо критерия
был очень большим. Важно, чтобы после пролета условия ге-
лиоцентрического движения привели к встрече КА с планетой
назначения. Один из возможных подходов к анализу таких ус-
ловий может быть следующим. Фиксируется дата старта от
Земли, дата подлета к планете назначения (например, Марсу).
Варьируя дату пролета промежуточной планеты (например,
Венеры), строят два независимых гелиоцентрических участка
траектории КА: Земля — Венера, Венера — Марс. Из анализа
первого участка получают венероцентрическую скорость входа
в грависферу Венеры, из анализа второго участка — венеро-
центрическую скорость выхода из грависферы Венеры. В об-
щем случае их модули не равны. Варьируем дату пролета Ве-
неры для уравнивания этих модулей. Если это удалось сде-
лать, то, обращаясь к анализу траектории в окрестности Вене-
ры, с помощью соотношения (6.30) можно выяснить, осущест-
вим ли гравитационный маневр (не проходит ли гиперболиче-
ская орбита через Венеру или ее атмосферу). В том случае,
когда маневр неосуществим, следует варьировать дату подлета
к планете цели или дату отлета от Земли.
Гравитационные маневры требуют высокой точности реали-
зации траектории движения КА (точных навигационных изме-
рений, высокой точности коррекции орбиты). В современных
космических программах достаточно широко используют грави-
тационные маневры. Приведем несколько примеров.
3 марта 1972 г. в США был запущен КА «Пионер-10». В
декабре 1973 г. КА попал в грависферу Юпитера. В этот мо-
мент гелиоцентрическая скорость КА была 10,6 км/с. Пери-
центр гиперболической относительно Юпитера траектории нахо-
дился на минимальном расстоянии 130 000 км от края атмос-
феры Юпитера. Гелиоцентрическая скорость КА в момент вы-
хода из грависферы Юпитера была равна 22,1 км/с. Таким об-
разом, гелиоцентрическая скорость КА увеличилась более чем
в два раза. «Пионер-10» не должен в дальнейшем движении
сближаться с какой-либо планетой, он должен уйти из Солнеч-
281-
ной системы. В 1979 г. его траектория пересекла орбиту Ура-
на (не встретив планету). Интересные программы полета у
КА «Пионер-11», «Вояджер-1», «Вояджер-2». Во всех про-
граммах используется гравитационный маневр. В программе
«Вояджер» предусматривается так называемый «Гранд Тур»,
при котором после пролета окрестности Юпитера с исследова-
нием его спутников (близкие пролеты около спутников) и са-
мого Юпитера последовало изучение Сатурна и его спутников,
Урана и в дальнейшем Нептуна.
Триумфом Советской космонавтики было недавнее осуще-
ствление проекта «Вега». Осуществляя программу исследова-
ний, два КА «Вега-1» и «Вега-2», стартовав в декабре 1984 г.
с промежуточной орбиты ИСЗ, в июне 1985 г. попали в грави-
сферу Венеры. При входе в грависферу произошло отделение
орбитального аппарата от аппарата, входящего в атмосферу
Венеры. Аппараты, вошедшие в атмосферу Венеры, в своем со-
ставе имели аэростатные зонды, аппаратура которых получила
уникальные научные результаты. Орбитальные аппараты, осуще-
ствив гравитационный пролет около Венеры, после определен-
ных коррекций орбиты вышли на гелиоцентрические траекто-
рии, проходящие вблизи кометы Галлея. Телевизионные каме-
ры передали на Землю изображения кометы, ее ядра, научная
аппаратура проанализировала большое число физических яв-
лений кометы Галлея.
Упоминая успех программы «Вега» в разделе о гравитаци-
онном маневре, необходимо обратить внимание на важную осо-
бенность выполненного на КА «Вега» гравитационного манев-
ра. Приведенный маневр можно рассматривать как активный
гравитационный маневр. Активным гравитационным маневром
называется гравитационный маневр, в процессе которого вклю-
чается реактивный двигатель КА с целью изменения скорости
и условий гравитационного облета. Активный гравитационный
маневр существенно раздвигает возможность использования
маневра облета промежуточной планеты. Если обычный (пас-
сивный) гравитационный маневр можно использовать только в
том случае, если величины планетоцентрических скоростей вхо-
да КА в грависферу планеты и выхода из нее равны, то такого
ограничения нет при активном гравитационном маневре. Вклю-
чая реактивный двигатель, например в окрестности перицент-
ра пролетной гиперболы, можно за счет небольшого импульса
скорости существенно деформировать траекторию КА, сильно
изменить величины планетоцентрической скорости выхода из
грависферы промежуточной планеты [33].
В этом разделе была рассмотрена возможность использо-
вания пролета промежуточной планеты (гравитационного ма-
невра) при реализации схем движения межпланетных КА. Вы-
явлено, что эффект гравитационного маневра зависит от харак-
282
теристик планеты (ее массы, размера, гелиоцентрической ско-
рости), от скорости подлета КА к планете, от точки входа КА
в грависферу планеты, определяющую гиперболическую про-
летную траекторию и ее перицентральное расстояние.
6.9. КОРРЕКЦИЯ ТРАЕКТОРИЙ МЕЖПЛАНЕТНЫХ КА
При реализации траекторий КА из-за большого ряда
факторов, которые принято называть возмущениями, реальная
траектория КА отличается от программной. К таким возмуща-
ющим факторам относятся:
несоответствие расчетной математической модели реальным
условиям движения (неточность знания гравитационных по-
стоянных, положения и скорости небесных тел; неучет в моде-
ле возмущающих физических воздействий: от какого-либо гра-
витирующего тела, аэродинамических сил, светового давления
и т. д.);
ошибки начальных условий старта КА с промежуточной ор-
биты ИСЗ;
неточность оценки положения и скорости КА навигацион-
ными системами, связанная с неточностью навигационных дат-
чиков и несовершенством обработки измерений (навигацион-
ные ошибки);
неточность реализации управляющих воздействий (разбросы
величины тяги ракетного двигателя, моментов включения и
выключения двигателя, неточность угловой ориентации КА в
процессе активного полета и т. д.).
В условиях действия возмущений, реальных возможностей
системы навигации и управления для того чтобы КА выполнил
поставленную перед ним транспортную задачу, не удается
обойтись ‘совершенствованием системы управления движением:
КА на участке разгона от Земли, необходимо, чтобы в процес-
се межпланетного перелета имелись средства, корректирующие
движение КА.
Коррекция траектории КА
Это целенаправленное изменение характеристик дви-
жения аппарата, обеспечивающее движение КА к планете на-
значения и реализацию требуемой траектории движения отно-
сительно этой планеты.
Коррекция траектории полета межпланетного КА осуществ-
ляется включением корректирующей двигательной установки
(КДУ) на участке межпланетного перелета. В том случае, ког-
да эта же двигательная установка используется для маневров
283;
в окрестности планеты назначения, она называется корректи-
рующей тормозной двигательной установкой. КДУ обычно ра-
ботает на жидких высококипящих компонентах и допускает
многократное включение на небольших интервалах времени.
Эти интервалы несоизмеримо малы по отношению ко времени
межпланетного перелета. Поэтому активные участки работы
КДУ можно импульсно аппроксимировать и использовать по-
нятие корректирующих импульсов скорости. Выбор стратегии
коррекции (количества предполагаемых коррекций, моментов
коррекций) является сложной задачей. Решение этой задачи
должно учитывать вероятностную картину всех возмущающих
факторов. Постановка задачи может быть следующей: для за-
данных вероятностных характеристик возмущений, для выбран-
ной структуры навигационной системы найти такую стратегию
коррекции, которая обеспечивает определенную точность вы-
полнения транспортной задачи (определенную точность реали-
зации входа спускаемого аппарата в атмосферу планеты назна-
чения, определенную точность выхода КА на орбиту ИС пла-
неты назначения и т. д.) с минимальным потребным запасом
характеристической скорости (топлива). Так как потребный за-
пас характеристической скорости в указанном вероятностном
подходе является величиной вероятностной, то можно миними-
зировать какую-либо вероятностную оценку характеристичес-
кой скорости. Такой оценкой может быть математическое ожи-
дание потребной характеристической скорости КДУ АГ[1/Хар]
или, лучше, величина характеристической скорости, которой с
заданной вероятностью хватит для коррекции траектории. Ес-
ли вероятность выбрана равной 0,997, то это значение равно
А1[Ухар] Ч-Зс^Ухар], где ^[Ухар] —среднеквадратичное откло-
нение требуемой характеристической скорости.
Сформулированная задача называется стохастической зада-
чей оптимального управления. Полное решение задачи стоха-
стического оптимального управления получено в ограниченном
числе модельных задач. Численные алгоритмы, которые стро-
ятся даже для приближенных моделей, трудоемки, для ранних
этапов проектирования КА их использование затруднительно.
Их роль существенна при проектировании систем навигации и
управления.
(Решение задачи выбора стратегии коррекции на ранних
этапах проектирования должно заканчиваться рекомендация-
ми по требуемой характеристической скорости КДУ. Такие ре-
комендации, имея в виду то, что вероятностные характеристики
возмущающих факторов известны недостаточно, а модели, опи-
сывающие движение КА, являются приближенными, целесооб-
разно получать приближенными методами. Основные допуще-
ния этих методов следующие:
284
предполагается, что реальная траектория КА не очень от-
лична от программной невозмущенной траектории;
рассматривается линейная математическая модель (счита-
ется, что отклонение реальной траектории от программной есть
линейная функция возмущающих факторов). Например, ошиб-
ка координаты точки входа в грависферу планеты назначения
есть линейная функция ошибки в величине импульса корректи-
рующей скорости, ошибки начального положения КА и т. д.;
считается, что возмущающие факторы есть случайные величи-
ны с простыми законами распределения (чаще всего нормаль-
ными). От возмущающих факторов, являющихся случайными
функциями, с помощью дополнительных уравнений (формиру-
ющих фильтров) искусственно освобождаются.
Коротко остановимся на важном моменте подхода к реше-
нию задачи нахождения стратегии коррекции межпланетной тра-
ектории. Введем понятие картинной плоскости. Картинной пло-
скостью называется плоскость, проходящая через центр плане-
ты назначения и перпендикулярная вектору гелиоцентрической
скорости подлета КА к грависфере планеты назначения. В
этой плоскости можно указать точку «прицеливания» КА. Это
такая точка (пусть ее координаты в которую в невоз-
мущенном гелиоцентрическом движении должен попасть КА в
определенный момент времени th. Характер транспортной зада-
чи определяет область допустимых координат картинной плос-
кости, она характеризуется допустимой неточностью yh, th-
Проводимые коррекции должны обеспечить «попадание» КА в
область допустимых координат в картинной плоскости.
Рассмотрим промежуток времени и интервал траектории
между последней коррекцией и попаданием КА в картинную
плоскость. Координаты КА в картинной плоскости и время по-
падания КА в эту плоскость есть функция его положения и
скорости перед последней коррекцией r(th-\), V(4-i) направ-
ления и величины корректирующего импульса скорости (ком-
понентов импульса скорости ДКХ, ДКУ, ДУ?) и самого момента
коррекции th-\'.
xk — fi (x ttk—i), У (6t—i)> z (fk—i)* Vx (6t—1)> Vy (^—i),
Vz (^.J, hVx)bVy, ДУ2, ^);
Uh = fz (X (^fe-1), У (6i-l)> Z (61-1), Vx
Vy Vz Д Vx, Д Vyi Д Vz, th-,) ;
zk U <th-i)> У z (^1), Vx О Vy
Vz{th-1Y AVX, Д^, ДУ2, tk-,).
В соответствии с приведенными ранее допущениями послед-
ние соотношения линеаризируют в окрестности невозмущенной
Траектории;
285
8xh = T7T~T 6^(^-i)+ —
dx dy (^-i)
... + (К (/й_х) + Д Vz) + 6;
dVz dtk-i
6 уh = ——— 6 X (Zft_x) + —6 у (tk) + ...
dx(ik-i) v dy(tk-i) yKM
- + -J (Vz (^_x) + A Vz) + 6 Zft-x ;
dV z d^k—i
^k= = // ft ч bx (tk-l) + . 5 ft 6 У (th) + •
... + (Vz (t^) + Д Vz) + 6 t^ .
dVz dtjl—1
Входящие в последние равенства производные называют
изохронными производными. Если известны допустимые веро-
ятностные характеристики отклонений 6xk, Mh, то из этих
соотношений можно получить рекомендации на допустимые по-
грешности навигационных измерений координат и скоростей
КА в момент проведения последней коррекции, на допустимые
погрешности проведения корректирующего импульса, получить
оценку затрат на корректирующий импульс как функцию этих
погрешностей.
Коррекции могут быть однокомпонентными, двухкомпонент-
ными и трехкомпонентными. При однокомпонентной коррекции
используется одна степень свободы корректирующего импуль-
са— его величина; направление корректирующего импульса
при этом фиксировано. Пример — солнечная коррекция, при ко-
торой с помощью солнечного датчика ось камеры сгорания
КДУ выставляется по прямой Солнце — КА. При двухкомпо-
нентной коррекции используются две -степени свободы корректи-
рующего импульса. Одной степенью свободы может служить
величина импульса скорости, второй — направление этой ско-
рости в фиксированной плоскости. При этом кроме датчика
Солнца обычно используется и звездный датчик. При трехком-
понентной коррекции используются все три степени свободы
корректирующего импульса скорости (AVX, AV?/, AVz). При
этом работает трехосная система ориентации КА.
Трехкомпонентная коррекция может одновременно коррек-
тировать обе координаты КА в картинной плоскости и время
попадания в нее. Двухкомпонентные и однокомпонентные кор-
рекции, влияя на все три перечисленные характеристики, не
могут их одновременно корректировать. При использовании од-
нокомпонентной коррекции нужны в общем случае три коррек-
ции, чтобы добиться удовлетворения всех трех характеристик
картинной плоскости.
286
Приведем несколько рекомендаций, которые получены в ре-
зультате исследования рассматриваемой задачи стохастическо-
го управления и использовались в реальных космических про-
ектах.
Рациональное количество коррекций при полетах к ближай-
шим к Земле планетам (Венере и Мар-су) не превышает трех.
С учетом технических ограничений используются две коррек-
ции. Первая коррекция проводится в начале гелиоцентричес-
кой перелетной траектории, вторая за 10... 15 сут до подлета к
планете. Допустимый промах в картинной плоскости Венеры
для многих космических операций -считается равным ЗООтыс. км.
Первая -коррекция не может обеспечить допустимый про-
мах в картинной плоскости из-за ошибок ее проведения (нави-
гационных ошибок, которые приводят к неправильно вычислен-
ным корректирующим импульсам, и ошибок реализации им-
пульса корректирующей -скорости). Целесообразность ее прове-
дения объясняется тем, что траектория КА в окрестности пла-
неты назначения очень «чувствительна» к коррекции на на-
чальном участке траектории — небольшой импульс скорости в
начале траектории сильно меняет траекторию в окрестности
планеты назначения. Первая коррекция исправляет большую
часть погрешности выведения КА, в частности работы разгон-
ного блока.
На КА «Венера-5» и «Венера-6» использовалась коррекция
с ориентацией по Солнцу и Сириусу. Величина первого кор-
ректирующего импульса у них была 9,2 м/с и 37,4 м/с соот-
ветственно.
На КА «Венера-9» и «Венера-10» также были проведены
две коррекции. Первая коррекция (11,93 м/с и 14,42 м/с) сдела-
ли траектории КА попадающими, вторые (последние) коррек-
ции (13,44 м/с и 9,68 м/с) уточнили места посадок и время
входа спускаемых аппаратов в атмосферу Венеры.
КА «Венера-15» и «Венера-16» стартовали от Земли в на-
чале июня 1983 г., 10 и 15 июня 1983 г. были проведены пер-
вые коррекции траектории этих КА. Вторая коррекция прово-
дилась за 10 сут до встречи с Венерой, для «Венеры-15»—1
октября, «Венеры-16» — 5 октября. Эти аппараты вышли на
эллиптические орбиты относительно Венеры. Выход на эти орби-
ты и, в дальнейшем, коррекция самих орбит проводились той
же корректирующей тормозной двигательной установкой.
Требуемый запас характеристической скорости на коррек-
цию полета к близким планетам при располагаемых навигаци-
онных системах и системах управления КА, включая его уг-
ловую ориентацию, не превышает 70 ... 150 м/с.
Для уже упоминавшихся КА «Вега-1» и «Вега-2» предпо-
лагалась возможность проведения пяти коррекций. Две коррек-
ции на траектории перелета Земля — Венера -и три коррекции
287
на участке полета к комете Галлея после гравитационного ма-
невра у Венеры. Выбор трех коррекций объяснялся прежде
всего не сложностью и точностью исполнения гравитационного
маневра, а плохим знанием орбиты кометы Галлея, по край-
ней мере, в момент старта КА от Земли. За время полета КА
эфимириды кометы подвергались уточнению. Реализация про-
екта «Вега» подтвердила хорошую точность расчета и реали-
зации траектории. Точность реализации пролета кометы была
исключительно высокой. На каждом из аппаратов еще остался
запас топлива для корректирующей двигательной установки.
Используемая для навигации и коррекции траектории меж-
планетных КА аппаратура включает солнечные, планетные и
звездные датчики, астровизиры и космические секстанты (опти-
ческие угломерные приборы), гироскопические устройства. Ра-
бота аппаратуры координируется бортовой вычислительной ма-
шиной. В ряде случаев удается определенные ключевые функ-
ции возложить на мощные наземные комплексы. Дальнейшее
развитие космических исследований, совершенствование борто-
вых систем управления должно привести к увеличению роли
автономных систем КА.
В этом разделе в общем плане рассмотрена задача коррек-
ции траектории межпланетных КА. Введено понятие картинной
плоскости. Поставлена задача поиска оптимальной структуры
коррекции, решение которой дает оценку энергетических за-
трат на реализацию межпланетной траектории. Приведены ха-
рактеристики используемых в настоящее время систем, коррек-
тирующих траекторию межпланетных КА.
Таким образом, в настоящей главе проведено исследование
траекторий межпланетных перелетов. Основой приближенного
метода расчета траектории являются идеи грависфер и им-
пульсной аппроксимации активных участков движения КА.
Нахождения рациональных схем полета межпланетных КА в
рамках существующих ограничений сводится к выбору дат
старта и времени движения КА к планете назначения. Грави-
тационный маневр может существенно уменьшить энергетиче-
ские затраты на межпланетный перелет, расширить возмож-
ности КА. Выбор траекторий межпланетного перелета должен
проводиться с учетом требований к системам коррекции и на-
вигации.
ГЛАВА 7, ИССЛЕДОВАНИЕ ДВИЖЕНИЯ КА
С ДВИГАТЕЛЕМ МАЛОЙ ТЯГИ
Развитие космической техники в рамках использования тра-
диционных химических ракетных двигателей наталкивается на
серьезные трудности, связанные с ограниченностью скоростей
истечения газов из сопла таких двигателей. Для энергонапря-
женных космических маневров КА, которым соответствуют боль-
шие значения требующейся характеристической скорости КА,
массовая отдача аппарата становится очень малой и целесооб-
разно перейти к использованию двигателей с более высокими
значениями удельного импульса тяги.
Среди таких двигателей большой интерес представляет
электрореактивные двигатели (ЭРД), удельный импульс тяги
некоторых типов которых достигает 105 м/с и принципиально
может быть увеличен. В настоящей главе будут исследованы
траектории КА с ЭРД.
7.1. ОСОБЕННОСТИ ТРАЕКТОРИЙ КА С ЭРД
Для КА с ЭРД используют следующие названия:
КА с двигателем ограниченной мощности, КА с двигателем ма-
лой тяги.
Первое из этих названий связано с тем, что на КА с ЭРД
существует принципиальное ограничение по мощности, имею-
щейся на борту энергетической установки, энергия которой ис-
пользуется для создания реактивного ускорения. Утвердивше-
еся за таким двигателем название — двигатели малой тяги
или, иногда, малого ускорения — связано с тем, что реактив-
ное ускорение КА с ЭРД мало и находится в пределах 10-2—
Ю~5 м/с2 и на несколько порядков меньше ускорения свобод-
ного падения на поверхности Земли.
Те небольшие величины реактивного ускорения, которыми
располагает КА с ЭРД, не дают возможности использовать та-
кие аппараты для старта с Земли или с поверхности любого
сколько-нибудь значительного небесного тела. Запуск такого
аппарата должен проводиться с орбиты спутника небесного
тела, а конечной целью полета может служить либо другая ор-
Ю—8
289
бита вокруг того же небесного тела, либо орбита спутника дру-
гого небесного тела. Возможность непрерывной работы в тече-
ние длительного времени предполагает целесообразность ис-
пользования КА с ЭРД в качестве космических «буксиров»
для грузовых перевозок, для удержания на заданной траек-
тории, коррекции орбиты, управления ориентацией спутников
и КА.
Использование ЭРД для КА, осуществляющих переходы с
одной орбиты на другую в окрестности Земли, приводит к мно-
говитковым траекториям, спиралевидным движениям. Реактив-
ное ускорение на таких аппаратах медленно изменяет оскули-
рующие элементы орбиты КА. Время активного полета таких
аппаратов в ряде случаев может совпадать с временем полета
(т. е. пассивных участков траектории может не быть).
При движении КА с ЭРД на гелиоцентрическом участке
траектории, а также в окрестности малых гравитирующих тел
(астероидов, естественных спутников) реактивное ускорение
может оказаться сравнимым с гравитационным ускорением. В
этом случае активный участок траектории КА может быть не
многовитковым. Так, на гелиоцентрическом участке полета
межпланетного КА включение ЭРД на время, соответствующее
угловой дальности полета 50°, может обеспечить полет КА к
Венере, Марсу, Юпитеру и т. д.
При использовании ЭРД для коррекции и поддержании ор-
биты спутника участки активного полета могут быть относи-
тельно небольшими.
При использовании массовых критериев оценки проекта КА
подход к анализу проекта КА с ЭРД существенно отличается
от. анализа проекта КА с химическими двигателями. Для КА
с химическим двигателем в первом приближении допустимо
пренебрежение массой двигательной системы и задача мини-
мизации массового критерия сводится прежде всего к отыска-
нию условий наименьшей затраты топлива на совершение за-
данного космического маневра. Это связано с тем, что при до-
статочно энергоемких маневрах масса двигательной установки
у таких аппаратов существенно меньше затрат топлива (масса
топлива может составлять две трети и более всей массы аппа-
рата). На основании формулы Циолковского условие миними-
зации топлива сводится к минимизации характеристической
скорости (1.66). Для ряда космических маневров КА с двига-
телем большой тяги потери скорости малы, характеристическая
скорость при этом не сильно отличается от того приращения
скорости, которое должен получить КА на активных участках
полета. Таким образом, анализ массового критерия КА с хими-
ческим двигателем часто легко сводится к анализу характери-
стической скорости КА или просто к приращению скорости ап-
парата.
290
Иначе обстоит дело для КА с ЭРД. В этом случае силы тя-
готения часто превышают ракетную тягу. При этом, по край-
ней мере, гравитационными потерями скорости пренебрегать
нельзя, а приращение скорости имеет очень мало общего с ха-
рактеристической скоростью. Таким образом, хотя характери-
стическая скорость для КА с двигателем малой тяги опреде-
ляет затраты топлива на маневр, но сама характеристическая
скорость существенно зависит от параметров аппарата и его
двигательной установки. С общей постановкой анализа проек-
тов КА с двигателем малой тяги можно ознакомиться в [20].
В дальнейшем, при нахождении рациональных схем полета
КА с ЭРД с заданными параметрами, будет минимизироваться
характеристическая скорость или для случая нерегулируемого
двигателя полное моторное время полета Тц (время полета
на активных участках траектории). В случае нерегулируемо-
го однорежимного двигателя минимум моторного времени соот-
ветствует минимальным затратам топлива и минимальной ха-
рактеристической скорости. Действительно, однорежимность
двигателя предполагает постоянство массового расхода рабо-
чего тела пг и постоянство скорости истечения W. При этом
закон изменения реактивного ускорения оказывается следу-
ющим:
f=------------ = , (7.1)
W Н
где Гц — текущее моторное время (текущее время активного
полета).
Выражение для характеристической скорости принимает
вид
Кхар = ? —k— dt= -rin ( 1- А т|Л . (7.2)
о о 1 10, \ ™ /
W "
Из последнего соотношения видно, что минимум полного мо-
торного времени Тц соответствует минимуму характеристиче-
ской скорости. Затраты топлива при этом будут тоже мини-
мальными, так как тт = тТ^.
Таким образом, реактивное ускорение КА с ЭРД не превы-
шает 10-2 м/с2. Траектория такого КА в окрестности Земли и
Других больших планет чаще всего многовитковая и может
представлять медленно раскручивающуюся спираль. Хотя ра-
циональная траектория КА с ЭРД соответствует минимуму ха-
рактеристической скорости (для нерегулируемого двигателя
Моторного времени), но сама характеристическая скорость яв-
Ю* 291
ляется существенной функцией проектных параметров КА, что
необходимо учитывать при анализе проектных решений КА и
выборе его проектных параметров.
7.2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЛЯ ИССЛЕДОВАНИЯ
ДВИЖЕНИЯ КА С ДВИГАТЕЛЕМ МАЛОЙ ТЯГИ
КА с двигателем малой тяги могут иметь весьма
большую протяженность активных участков, измеряемых сут-
ками, месяцами и даже годами (при реализации межпланетных
перелетов). При этом допущение об импульсной аппроксима-
ции активных участков безусловно не проходит. Анализ актив-
ного участка полета аппаратов с ЭРД должен проводиться на
основе исследования весьма полной математической модели,
часто с учетом ускорений, которые для аппаратов с большой
тягой рассматривались как возмущающие. Последнее связано
с малостью реактивного ускорения, с тем, что ускорение, на-
пример связанное с нецентральностью гравитационного поля
Земли, может иметь тот же порядок малости, что и реактивное
ускорение. Эти обстоятельства приводят к тому, что для кос-
мических маневров оказывается целесообразным рассматри-
вать тягу как возмущающую силу и описывать движение КА
так, как это было сделано для анализа возмущенного движе-
ния ИСЗ. Такое описание часто целесообразно проводить с-
использованием оскулирующих элементов, например в виде
системы (3.44).
Используя (3.44), можно получить (
=2о 1/^_________5_____f •
dt г у р 1 + е cos и п ’
de , ecos2u + 2 cos и 4- e f \.
-гг = I/ — Sill V fr H------r-y------—— / n >
dt V p \ 'r 1 + e cos и )
d®
dt ~
di
dt
COS V fr +
COS U f 9
1 + e cos и '& ’
sin и cosec i r
1 + e cos d ' b ’
sin и (2 + e cos и) c
1 4- e cos и 'n
e sin и ctg i <. -i
+ —----------- / ъ ;
1 + e cos и J
dt p2 г
df = L<eNsin”-C0S”> !' +
+ — q.
1 + e cos и J
(7.3)
292
где fn, fr, fb — соответственно трансверсальная, радиальная и
нормальная проекции реактивного ускорения;
fn = f cos ft cos гр;
fr= f sin ft; (7.4)
fb = —f cos ft sin г|),
ф, гр — углы, характеризующие направление вектора тяги в
орбитальной системе координат. Если вектор тяги направлен
по оси КА, то это — углы тангажа и рыскания (см. рис. 1.5).
В ряде случаев целесообразно перейти к полярному углу
как независимой переменной. Этим углом может быть аргу-
мент широты и. Воспользовавшись равенством (3.60), получим
du = Урр , (7,д)
dt jr2
где
/ = Г1 + — fb ctg i Sin и 1 1 . (7.6)
l HP J
Принципиальное отличие соотношений (7.3) ... (7.6) главы
от соотношений (3.44), (3.60) и т. д. состоит в следующем. В
гл. 3 предполагалась известной природа возмущающих уско-
рений. Ускорения связывались с характеристиками движения
КА (положением, направлением скорости и т. д.) и получались
вполне однозначные возмущающие эффекты, которые учитыва-
лись при проектировании орбит спутников и прогнозировании
их движения на значительных интервалах времени. В настоя-
щей главе возмущающее ускорение — это реактивное ускоре-
ние, выбор направления (а иногда и величины) которого нахо-
дится в распоряжении проектанта. Задача ставится так, чтобы
выбрать законы изменения вектора реактивного ускорения, при
котором, возмущая траекторию наиболее рациональным спо-
собом, можно было выполнить заданный космический маневр,
решить транспортную задачу, т. е. задача состоит в выборе
fn(0, fb(t) (или $(t), г|)(0).
В некоторых случаях не следует прибегать к уравнениям
в оскулирующих элементах (7.3), а использовать орбитальную
систему координат, планетоцентрическую или гелиоцентричес-
кую невращающиеся системы координат.
Рассмотрим законы управления вектором реактивного ус-
корения, которые позволяют максимально быстро изменять
элементы оскулирующей орбиты КА. Закон управления векто-
ром реактивного ускорения, который максимально быстро из-
меняет фокальный параметр (размер орбиты), мы сможем най-
ти из анализа правой части первого уравнения системы (7.3).
Чтобы dpldt в какой-то момент времени было максимально
большим, необходимо, чтобы fn в этот момент достигало своего
293
максимального значения. Если полная величина реактивного
ускорения ограничена, то при этом следует выбрать fr = fb = O.
Таким образом, локально оптимальное реактивное ускорение
для увеличения размера орбиты направлено по трансверсали
(трансверсальное ускорение)'. fn = f', fr=fb = O-
С другой стороны, для того чтобы фокальный параметр ос-
кулирующей орбиты в течение всего движения с включенным
двигателем оставался постоянным, достаточно сделать fn=®.
Из уравнений системы (7.3) следует, что положение плос-
кости орбиты в пространстве, определяемое долготой восходя-
щего узла и наклонением орбиты, изменяется только под влия-
нием перпендикулярной к мгновенной плоскости орбиты состав-
ляющей ускорения fb- Для наискорейшего изменения долготы
восходящего узла величина fb должна быть максимальной. Для
увеличения долготы восходящего узла нужно, чтобы fb = fmaxX
Xsignfsinu]. Записанный закон обеспечивает монотонное из-
менение Q и соответствует переключению нормальной компо-
ненты реактивного ускорения в узлах оскулирующей орбиты
КА.
Для изменения наклонения орбиты КА можно предложить
закон, основанный на анализе уравнения для i из (7.3): fb =
= f max sign [cos и]. Наклонение орбиты KA монотонно изменя-
ется, если переключение нормальной компоненты реактивного
ускорения происходит в точках максимального возвышения КА’
над плоскостью экватора.
Рассмотрим несколько законов реактивного ускорения для
изменения плоских оскулирующих элементов орбиты КА. При
этом нормальную компоненту реактивного ускорения будем
считать нулевой fb = O. Тогда fn = fcosf&; fr=fsin4 и дифферен-
циальные соотношения для плоских оскулирующих элементов
могут быть с помощью (7.3) записаны в виде
dp_ 1/Т" cQsfr .
dt I н у 1 е cos и ’
de р 1 /~ р Г • - di 6 cos2 и + 2 cos и е « п
-п- =f I/ — sinusin vH--------т-р------—— cos v ; (7.7)
dt 1 V p. L 1 + e cos и J ’ v 7
do f 1/ P Г • о. । sinu (2-f- e cosu) a “I
dt e r p, L 1 1 + e cos и J
Все правые части (7.7) являются линейными однородными
функциями sin-ft и cos-ft.
Приравнивая поочередно эти функции нулю, можно полу-
чить законы управления, при которых соответствующий оску-
лирующий элемент не имеет возмущений.
Для нахождения законов управления вектором реактивного
ускорения, обеспечивающих максимальную скорость изменения
элементов орбиты, нужно найти такой закон -О*(и), при котором
294
достигается максимум правой части одного из равенств систе-
мы (7.7).
Такие законы можно использовать при коррекции орбит
спутников, в более ограниченном виде для синтеза законов,
обеспечивающих перелет между орбитами.
В данном разделе была введена широко используемая мо-
дель для анализа траектории КА с двигателем малой тяги и
показано, как анализ уравнений этой модели дает возможность
выделить некоторые рациональные законы направления реак-
тивного ускорения, максимально быстро изменяющие (коррек-
тирующие) отдельные элементы орбиты КА или не изменяю-
щие их.
7.3. ИССЛЕДОВАНИЕ ДВИЖЕНИЯ КА ПРИ ПРОСТЫХ
ЗАКОНАХ УПРАВЛЕНИЯ ВЕКТОРОМ ТЯГИ
Рассмотрим основную задачу теории движения КА с
двигателем малой тяги. Пусть известны начальные условия
движения. Задается программа управления движением КА
(будет задаваться некоторый простой закон изменения вели-
чины и направления реактивного ускорения). Требуется рассчи-
тать траекторию КА, выявить, как изменяется его положение и
скорость.
Исследование траектории КА с двигателем малой тяги в
ряде случаев целесообразно вести, анализируя изменение ос-
кулирующих элементов траектории КА. Таким образом, будем
фиксировать определенный простой закон управления векто-
ром тяги Р (вектором реактивного ускорения f = Plm) и иссле-
довать изменение элементов траектории КА.
Рассмотрим движение КА >с малой невыключаемой тягой.
Трансверсальная тяга
Трансверсальная тяга (т. е. тяга, направленная по
трансверсали) привлекает при проектировании траекторий КА
(не только траекторий КА с малой тягой) относительной прос-
тотой реализации, целесообразностью такого закона для ряда
космических маневров.
Уравнения для оскулирующих элементов в случае транс-
версальной тяги (/& = 0, ф = 0) запишутся в виде
%- = 2р ]/— ; (7.8)
dt r V р, 1 + е cos и ’ ' 7
de ____е 1 Г р е cos2 и 4“ 2 cos и + е .
dt * V р, 1 -f- е cos и ’ * • /
295
(7.12)
- _L 1/JL sin d (2 +cos eu) . (7 m
dt e V ik 1 + ecosu ’
dQ/dt = O, dildt = Q. (7.11)
Первые три уравнения при использовании полярного угла
как независимой переменной могут быть записаны в виде
dp _ 2р3/ 1.
du ц (1 + е cos и)3
de _ fp2 е cos2 и -f- 2 cos и -f~ е .
du p (1 + ^cosd)3 *
do) _ fp2 sin d (2 -f- e cos u)
du ep (14"£cosd)5
С помощью системы (7.12) при заданных начальных значе-
ниях оскулирующих элементов возможно численным интегриро-
ванием найти траекторию КА с трансверсальной тягой.
Рассматривая реактивное ускорение как возмущающее уско-
рение, выделим вековые уходы от его действия. При этом пред-
полагается, что:
реактивное ускорение мало (по отношению к гравитацион-
ному ньютоновскому ускорению);
движение КА — многовитковое;
реактивное ускорение на одном витке траектории изменя-
ется пренебрежимо мало и на каждом витке траектории его
можно считать постоянным (fj — const).
Воспользуемся методом осреднения. Для нахождения возму-
щений на произвольном витке траектории интегрируют на
этом витке уравнения системы (7.12), пренебрегая изменения-
ми оскулирующих элементов внутри витка траектории (считая,
что на этом витке элементы постоянны). Таким образом, при-
ращения оскулирующих элементов р, е, со на /-м витке траекто-
рии можно записать в виде
—1
м-
= P2jfi 2ГЯ ej cos2 и -f- 2 cos и + еу
J* |i о (1 + eicos и)3 *
А М
А СО; = -L
ejp
При записи последних
дующие обстоятельства:
подынтегральные функции в (7.12) периодические с периодом
2л (это дало возможность пределы интегрирования взять равны-
ми 0 ... 2л),
при со = const из соотношения u = v + (o следует du = dv.
1 du;
о (l + ejcosu)3
(1 + ej cos и)3
sin и (2 + ej c°s и) j
(1 -f- ej cos d)3
2л
О
соотношений были использованы сле-
(7.13)
296
Квадратуры, входящие в правые части равенства (7.13), мо-
гут быть взяты. Приращения оскулирующих элементов
рии КА за виток траектории оказываются равными
И
Злру fj
------
ej
LI
траекто-
(7.14)
(7.15
(7.16)
А(0; = 0.
Последние равенства можно использовать для анализа траек-
тории КА под действием трансверсального ускорения.
Из равенства (7.15) следует, что если начальная орбита
КА — круговая, то эксцентриситет оскулирующей траектории
не будет иметь вековых уходов. Вся траектория КА в этом слу-
чае представляется совокупностью оскулирующих круговых ор-
бит Ае; = 0, е7 = 0 (/ = 0, 1, 2, ...). При этом фокальный параметр
(радиус) этих орбит будет изменяться в соответствии с равен-
ством
4nr3.f j
O+i = O + ——
и
Рассмотрим этот интересный для практики случай.
(7.17)
Перелет с помощью нерегулируемой трансверсальной
тяги между круговыми орбитами
Пусть начальная орбита КА—круговая. Для пере-
лета используем трансверсальный закон направления тяги. В
соответствии с равенством (7.17) такой разгон с помощью ме-
тода осреднения может быть описан одним из следующих со-
отношений:
dr _ 2 г3 f
du pi
dr __ 4 nr3 f
dN ~
где W— номер витка траектории КА.
Для того чтобы исследовать решения последних уравнений,
необходимо задать закон изменения величины реактивного ус-
корения f(u). Считаем, что двигатель КА — нерегулируемый, по-
стоянно включенный, тогда ускорение f(t) можно записать в
виде
(7.18)
P
f (о = —
т (0 — — /0)
fo
1 - — (/-/„)
U7
(7.19)
297
Свяжем угловую дальность полета (аргумент широты) со
временем. В рамках метода осреднения, когда траектория КА
представляется совокупностью оскулирующих круговых орбит,
аа которых угловая скорость КА постоянна, связь времени с
угловой характеристикой с или и имеет вид
du — ndt= dt.
r3/2
(7.20)
Используя (7.19) и (7.20), из равенства (7.18) получим
2/0 г3/2 dt
Z/Q ' aL_
М'-’Н
Разделяя переменные в последнем дифференциальном урав-
нении и интегрируя его, придем к равенству
Последнее соотношение дает возможность подсчитать ради-
ус конечной орбиты, которую КА может достичь с помощью
трансверсальной тяги за определенное моторное время. Для
нахождения времени достижения заданного конечного радиуса
г к воспользуемся соотношением, следующим из (7.21),
tK = у- (1 — exp
(7.22)
/о I
Соотношение (7.22) полностью характеризует энергетичес-
кие затраты на переход между круговыми орбитами с транс-
версальной тягой. Так как такие затраты часто представляют-
ся в виде характеристической скорости, то приведем выражения
для ее определения
(7.23)
Нормальная тяга
Рассмотрим влияние на траекторию КА реактивного
ускорения, направление которого перпендикулярно плоскости
оскулирующей орбиты КА. Такое ускорение называют нор-
мальным. Итак, f=fb, a fr=fn = O (ф =—л/2, '&=0 (7.4)). При
таком направлении возмущенного ускорения элементы орбиты,
характеризующие форму и размер оскулирующей орбиты КА,
изменяться не будут (7.3): = 0.
298
Изменение остальных элементов описывается следующими
соотношениями
d& __ ? р2 sin и cosec i
du ц (1 -|- e cos u)3
di __ e p2 cos и
du p, (1e cos u)3 ’ (7-24)
d& ___i p2 sin и ctg i
du p, (1 -f- e cos u)3
В соотношениях (7.24) величиной второго порядка малости
относительно f пренебрегаем и считаем, что величина / (см.
(7.6)) равна единице.
Изменение оскулирующих элементов по виткам траектории
в рамках метода осреднения движения КА можно получить из
следующих соотношений
dQ _ 3 л/р2 е sin со
dN pi sin Z (1 — e2)5/2
di _ ~dN ~ d& ~dN ” 3 JT fp^1 & OC\ = Г/T cos (7-25) р,(1_е2)5/2 > 3nfp2e sin (D ’ц(1-е2)5/2 tgi *
Интересно то, что если эксцентриситет начальной орбиты
равен нулю, то из (7.25) следует, что плоскость оскулирующей
орбиты и положение линии апсид в среднем не возмущаются:
dQ I _____ di
d N |e=o d N e=0
day
dN e=0
= 0.
Рассмотрим возможность однократного переключения нор-
мального реактивного ускорения на каждом витке траектории.
Для сокращения объема выкладок рассмотрим случай круго-
вой начальной орбиты КА. Как уже отмечалось, при нормаль-
ном законе реактивного ускорения — = —=0. Поэтому ос-
кулирующая орбита КА в рассматриваемом случае всегда ос-
тается круговой постоянного радиуса.
Для того чтобы максимально быстро изменить наклонение
круговой орбиты КА, следует воспользоваться следующим за-
коном переключения нормального реактивного ускорения:
==—I f I sign [cos и]. В этом случае с использованием системы
(7.24) получим
ДЙ, = 0 ; Д i} = .
299
При таком законе реактивного ускорения только наклоне-
ние круговой орбиты КА будет иметь вековой уход. Соотно-
шения, характеризующие этот процесс, имеют вид
di W ,
dt р
М= —Дх; (7.26)
4 1/1 р2
2|/|
Аналогично можно исследовать другие фиксированные за-
коны направления реактивного ускорения. Среди проанализи-
рованных в настоящее время — тангенциальный радиальный за-
коны. В некоторых случаях предусматривается изменение на-
правления реактивного ускорения на противоположное в неко-
торых точках витка траектории КА. В том случае, когда суще-
ствует техническая возможность многократного включения дви-
гателя, рассматривают траекторию КА с участками пассивно-
го полета. И в этом случае удается [67] выработать рекомен-
дации по количеству активных участков на витке траектории,
по расположению и длительности этих участков, по направлег
нию тяги на них.
Таким образом, в данном разделе рассмотрен подход к ана-
лизу многовитковых траекторий КА с фиксированными зако-
нами направления реактивного ускорения. Показано, что ис-
пользование метода осреднения может позволить получить
аналитические соотношения для оценки временных и энергети-
ческих характеристик в задачах коррекции орбиты ИСЗ и в
задачах перелета между орбитами.
7.4. МНОГОВИТКОВЫЙ ПЕРЕЛЕТ МЕЖДУ
НЕКОМПЛАНАРНЫМИ КРУГОВЫМИ ОРБИТАМИ
В ньютоновском гравитационном поле заданы на-
чальная и конечная круговые орбиты. Рассматривается КА с
нерегулируемым двигателем. Выключение двигателя на траек-
тории перелета не предполагается. Ставится задача о нахож-
дении (проектировании) траектории перелета между заданны-
ми орбитами и соответствующей ей программы управления
движением. Критерием оптимальности выбираемого закона уп-
равления движением считается минимум времени полета КА
или, что то же самое в рассматриваемой постановке, — мини-
мум моторного времени КА,
Сузим класс допустимых управлений. Будем считать, что
рациональное направление реактивного ускорения перпенди-
зоо
кулярно радиусу-вектору КА (т. е. вектор реактивного уско-
рения состоит из трансверсальной и нормальной составляющих,
а радиальная составляющая равна нулю). В этих условиях вы-
бор закона направления вектора реактивного ускорения сво-
дится к нахождению угла между вектором реактивного уско-
рения и мгновенной плоскостью оскулирующей орбиты, угла ф
(см. (7.2), #=0).
Рассмотрение задачи будем вести в рамках осреднения
движения КА по виткам, т. е. предполагая многовитковость
траектории, малость реактивного ускорения.
Первое решение этой задачи получим при следующем пред-
положении о структуре управления на витке траектории. Пусть
в течение всего витка траектории трансверсальная компонен-
та реактивного ускорения постоянна по величине. Нормальная
составляющая реактивного ускорения постоянна по величине
и имеет одну «перекладку» на витке траектории, т. е. на поло-
вине витка траектории (на участке восходящего движения,
когда-----нормальная компонента реактивного
ускорения, например, положительная. На другой половине вит-
ка траектории эта компонента отрицательная. Такой закон из-
менения нормального ускорения рассматривался в разд. 7.3.
Компоненты реактивного ускорения при таком законе за-
писываются в виде fn = fcosip; /7=0; fb =—f sign (cos fz) sin | |.
где реактивное ускорение f для рассматриваемого нерегулиру-
емого двигателя меняется так:
_ Vxap
f= ---------- = foe w • (7.27)
1 — — t,
w
Поясним, почему выбран такой закон изменения вектора
реактивного ускорения, почему он может быть рационален при
перелете между орбитами, особенно круговыми. Выбранный за-
кон для нормальной компоненты реактивного ускорения обес-
печивает наискорейшее изменение наклонения круговой орби-
ты без изменения остальных ее элементов. С другой стороны,
трансверсальная тяга обеспечивает максимальное изменение
размера орбиты (ее фокального параметра). Таким образом,
комбинация законов может одновременно изменять и положе-
ние орбиты, и ее размер.
Для того чтобы оценить вековые уходы элементов орбиты
КА под действием такого реактивного ускорения, можно вос-
пользоваться результатами разд. 7.3. В нем рассмотрены веко-
вые уходы элементов орбиты под действием трансверсального
закона реактивного ускорения и отдельно нормального закона
реактивного ускорения. В рамках метода осреднения, в рамках
301
неучета интерференции одного вида возмущения на другое
(который допустим на ограниченных временных интервалах при
небольших возмущающих ускорениях) вековой уход под дейст-
вием комбинации трансверсальной и нормальной составляю-
щих реактивного ускорения можно рассматривать как сумму
вековых уходов от отдельных возмущений.
При этом большое число элементов орбиты не будут иметь
приращения на произвольном /-м витке траектории.
Так, эксцентриситет орбиты не будет иметь вековых уходов.
Действительно, эксцентриситет оскулирующей орбиты из-за
трансверсальной составляющей реактивного ускорения в об-
щем случае имеет приращение (7.15). Но так как начальная
орбита — круговая, то из (7.15) следует Де; = 0 и всю траек-
торию перелета можно рассматривать как совокупность оску-
лирующих окружностей ( — = 0 .
Аналогично можно показать, что для рассматриваемого за-
dQ п
кона управления ----=0.
Из оскулирующих элементов орбиты только фокальный па-
раметр (для круговой орбиты ее радиус) и наклонение имеют
вековые уходы. Используя (7.17) и (7.26), можно получить
— = ,W cosj|> . JL = ±!7sini|,. (7.28)
dN р dN р
Напомним, что соотношения (7.28) выведены для случая,
постоянного на витке реактивного ускорения, т. е. они справед-
ливы, если можно считать, что f=const, |ф| =const. Допуще-
ние f=const является естественным условием при использова-
нии метода осреднения. Постоянство модуля угла рыскания на
витке траектории следует рассматривать как один из возмож-
ных законов управления, и оно может быть заменено более ра-
циональным законом управления КА.
Используя то, что период на круговой орбите радиуса
2Л
равен Tj = —=г*./2, приращение времени по виткам траек-
Ун 1
dt 2тс g i -i—г
тории оценивается с помощью----- = —7= г К Поэтому из соот-
dN у [i
ношений (7.28) легко получить
А. = 2-^3-/C0S1P; -%- = <fsinДО. (7.29)
dt у р dt тс у р
Последняя система дает возможность исследовать вековые
уходы фокального параметра (радиуса) и наклонения оскули-
рующей орбиты, подставляя в нее закон изменения величины
реактивного ускорения (7.27) и угла рыскания ф(0- Напом-
302
ним, что (7.29) описывает осредненное движение. При выводе
1(7.29) предполагалось, что | ip |= const на витке траектории.
Но это, безусловно, не значит, что |гр| не изменяется от витка
к витку. Фиксирование |яр|, безусловно, сужает возможность
управления. Но для исследования это самый простой закон.
Рассмотрим его. Итак, пусть радиус начальной орбиты равен
Го, радиус конечной орбиты — гк, наклонение начальной орби-
ты равно нулю, наклонение конечной орбиты — fK. Найдем та-
кое постоянное значение | ip |, чтобы КА осуществил перелет ме-
жду заданными орбитами. Никаких возможностей оптимиза-
ции перелета в таком узком классе управлений нет. Единствен-
ный выбираемый параметр гр можно использовать, чтобы в
какой-либо момент попасть на конечную орбиту. Исследуем та-
кой перелет.
Из (7.29) следует
— г л ctg гр.
Разделяя переменные и проводя интегрирование выражений
слева и справа, получим:
In — = л iK ctg гр. (7.30)
Из (7.30) легко получить необходимый для перелета между
орбитами угол, характеризующий направление реактивного ус-
корения,
1п-^
ф = arctg—— . (7.31)
л
При этом время, требующееся на перелет между орбитами,
найдется из любого равенства системы (7.29). Например, из
первого соотношения следует
dr 2 /0 cos гр dt
г3/г VfT
Г
/к= — (1-ехрГ—(—----------------— )11. (7.32)
/о I L И7005* \ V~«
Учитывая (7.31), равенство (7.32) перепишется в виде
303
Соотношения (7.31) и (7.33) в безразмерных переменных (ког-
да за единицу расстояния выбирается г0, а за единицу скоро-
сти— j/" —j имеют вид:
ф = arctg .
Безразмерная характеристическая скорость КА, соверша-
ющего маневр перелета между заданными некомпланарными
круговыми орбитами с рассматриваемым законом управления,
найденная с помощью (7.2), будет равна
1— 57г ("1—т7г /« +л2 %
у ___ V "к _ \________к_{к/_____________
Полученный закон управления движением можно улучшить
с точки зрения уменьшения времени перелета, характеристи-
ческой скорости, рассматривая величину угла -ф, меняющейся-
от витка к витку траектории. Рассмотрим такую возможность.
Как и раньше, считаем, что на каждом витке траектории |ф| =
= const, но в отличие от предыдущего |ф| пусть является мед-
ленно меняющейся функцией времени (изменяется от витка к
витку траектории).
Ставится задача о нахождении такой функции ф(/), кото-
рая обеспечивает перелет между орбитами за минимальное
время.
Используя принцип максимума, такую задачу оптимально-
го управления удается решить аналитически [41]. Оптималь-
ный закон управления в безразмерных переменных оказывает-
ся следующим:
Минимальная характеристическая скорость КА для такого
маневра определяется из соотношения
304
. -JL
“ fo
Минимальное время полета при этом равно
1 — exp
Оказывается, что зависимость r(t) может быть немонотон-
ной [41]. Это случается тогда, когда параметры конечной ор-
биты удовлетворяют неравенству cos^^-<—. При этом
2 гк
радиус растет, достигая максимума
а затем уменьшается до заданного значения гк.
Максимальное значение радиуса растет с ростом наклоне-
ния конечной орбиты. При гк->2 Гтах-^оо. Последнее обознача-
ет, что рассматриваемую схему оптимального перелета нельзя
использовать при больших iK (fK>2). Это происходит из-за
того, что в процессе движения оскулирующая орбита, уходя в
бесконечность от гравитирующего тела, перестает быть эллип-
тической и использованный метод осреднения по виткам «не
работает».
Таким образом, в настоящем разделе построены раци-
ональные траектории многовиткового перелета между круго-
выми некомпланарными орбитами для КА с нерегулируемым
невыключаемым двигателем, получены соотношения для на-
хождения потребной характеристической скорости и времени
движения.
7.5. МЕЖПЛАНЕТНЫЕ ПЕРЕЛЕТЫ КА С ДВИГАТЕЛЕМ
МАЛОЙ ТЯГИ
В основе метода исследования траектории межпла-
нетных КА с двигателями большой тяги, рассмотренного в гл. 6,
лежали две идеи: идея импульсной аппроксимации активных
участков и идея грависфер влияния. Обращаясь к анализу
межпланетных аппаратов с двигателями малой тяги, приходит-
ся распрощаться с идеей импульсной аппроксимации активных
участков. В отличие от нее идея грависфер очень активно ис-
пользуется при анализе межпланетных траекторий с малой тя-
гой. Остановимся на одном подходе при использовании метода
грависфер для анализа межпланетных перелетов КА с малой
тягой.
305
Метод исследования межпланетных траекторий КА
с двигателем малой тяги
КА с двигателем малой тяги, стартуя с промежуточ-
ной орбиты ИСЗ, будет достаточно медленно набирать энергию,
двигаясь на некоторой спиралевидной относительно Земли тра-
екторий. Этот участок траектории КА можно рассматривать в
рамках возмущенной реактивным ускорением задачи двух тел
Земля — КА. К^к всякую константу интегрирования задачи
двух тел, константу энергии Л = 1/2— можно рассматри-
г
вать как оскулирующий элемент траектории возмущенного
движения. Эта константа будет медленно (ускорение мало)
увеличиваться. В некоторой точке траектории она станет рав-
ной нулю. В этой точке скорость КА окажется равной местной
параболической скорости. Если в этот момент времени th=o вы-
ключить ракетный двигатель КА, то КА будет двигаться по
параболической относительно Земли траектории и уйдет в бес-
конечность от Земли (покинет грависферу Земли). С опреде-
ленной неточностью метода грависфер траектория КА относи-
тельно Солнца после выхода из грависферы Земли очень близ-
ка к орбите Земли относительно Солнца. Ясно, что никакую
окрестность планеты назначения КА не достигнет, если на тра-
ектории гелиоцентрического перелета не будет активных участ-
ков. Картина перелета принципиально не изменится, если в мо-
мент набора параболической скорости th=o не выключить ра-
кетный двигатель КА. Независимо от того, в какой точке гра-
висферы Земли КА наберет параболическую скорость, время
его дальнейшего движения в грависфере Земли относительно
небольшое (ну, скажем, сутки, пусть двое). За ограниченное
время, двигаясь в грависфере Земли, КА с двигателем малой
тяги не сможет набрать гиперболический избыток скорости,
достаточный для полета к планете назначения.
Таким образом, КА с двигателем малой тяги выходит из
грависферы Земли с небольшой величиной гиперболического
избытка скорости. Поэтому на участке гелиоцентрического пе-
релета необходимо предусматривать активные участки полета.
Исследования показали, что рациональная схема траектории
межпланетного КА с нерегулируемым двигателем малой тяги
содержит несколько активных участков. Первый активный уча-
сток начинается на промежуточной орбите ИСЗ, на которую
КА с его двигательной установкой малой тяги выводится ра-
кетой-носителем. На этом участке КА, набирая энергию, вы-
ходит из грависферы Земли и продолжает движение по неко-
торой гелиоцентрической траектории. Затем ракетный двига-
тель КА выключается и КА по отношению к Солнцу движется
по некоторой эллиптической орбите. В наиболее простом случае
306
при реализации пролетной относительно планеты назначения
траектории больше включения двигателя можно не предусма-
тривать. Чаще всего рассматривают, по крайней мере, еще один
активный участок движения. Задача второго активного участ-
ка состоит в обеспечении входа в грависферу планеты назна-
чения с определенными кинематическими характеристиками и
торможения КА на планетоцентрическом участке движения в
окрестности планеты назначения для выхода на некоторую ор-
биту относительно этой планеты.
Наиболее распространенный метод исследования межпла-
нетных траекторий КА с двигателем малой тяги базируется на
следующих положениях и допущениях:
1) траектория перелета КА состоит из планетоцентри-
ческих (внутренних) и гелиоцентрических (внешних) уча-
стков;
2) задача геоцентрического (первого внутреннего) участка
заключается в наборе параболической относительно Земли ско-
рости. Именно в момент набора параболической скорости и за-
канчивается геоцентрический участок;
3) гелиоцентрический (внешний) участок траектории КА с
двигателем малой тяги начинается в фиксированной точке ге-
лиоцентрической орбиты, совпадающей с радиусом-вектором
Земли относительно Солнца. Начальная гелиоцентрическая ско-
рость КА считается равной скорости Земли в этот момент вре-
мени. Заканчивается гелиоцентрический участок межпланет-
ного перелета в точке, совпадающей с радиусом-вектором пла-
неты назначения.
Сделаем несколько замечаний по сформулированным допу-
щениям.
Метод предполагает так называемую нулевую стыковку
внутреннего и внешнего участков. Начальная скорость гелио-
центрического участка траектории У0.с считается равной ге-
лиоцентрической скорости Земли У3. Считается, что гипербо-
лический избыток скорости КА в момент выхода из грависфе-
ры Земли Voo равен нулю.
Пренебрежение протяженностью грависфер Земли и планет
при исследовании траектории гелиоцентрического перелета эк-
вивалентно основному допущению метода грависфер нулевой
протяженности. Естественно, и для КА с малой тягой возмож-
ны более общие подходы метода грависфер.
Траектория КА в окрестности планеты назначения в рас-
сматриваемом методе часто анализируется аналогично геоцен-
трической траектории. Эта некоторая скручивающая спираль,
в начальной точке которой скорость равна местной параболи-
ческой. Спиральная траектория заканчивается выходом, напри-
мер, на круговую орбиту ИС планеты назначения.
307
Таким образом, в рамках описанной схемы полета и метода
ее исследования траектория КА с малой тягой включает:
участок набора параболической скорости относительно пла-
неты старта (участок раскрутки — другое название этого уча-
стка) ;
участок межорбитального перелета;
участок скрутки у планеты назначения.
Сформулированный метод решения дает возможность рас-
сматривать эти три участка независимо.
Набор параболической скорости у планеты
Пусть промежуточная орбита ИСЗ — круговая. Для
КА с двигателем малой тяги эта орбита является начальной.
Предполагаем двигатель малой тяги нерегулируемым, тогда
траектория полета КА полностью определяется законом изме-
нения направления реактивного ускорения, т. е. углами # и 1р.
Наименьшие затраты на разгон соответствуют случаю, когда
i|)=0. При этом тяга не будет тратиться на изменение, положе-
ния плоскости оскулирующей орбиты. Для случая движения в
Рис. 7.1. Траектория набора КА па-
раболической скорости при старте с
круговой орбиты
центральном поле • траектория
такого КА будет плоской, а са-
ма плоскость орбиты будет сов-
падать с плоскостью промежу-
точной орбиты ИСЗ.
Критерием оптимизации
участка раскрутки чаще все-
го считают минимальное вре-
мя набора параболической
скорости. Расчеты показали,
что трансверсальный и тан-
генциальный законы управле-
ния движением КА весьма
близки к оптимальному за-
кону управления, обеспечивающему минимальное время на-
бора параболической скорости. Такие траектории пред-
ставляют собой медленно раскручивающуюся спираль, каче-
ственно представленную на рис. 7.1. На нем за единицу рас-
стояния принят радиус начальной круговой орбиты г0. Началь-
ное реактивное ускорение /0 взято равным ц/г20 • 10-3. Началь-
ные витки спирали имеют очень небольшой шаг и на рисунке
не показаны. Цифры у раскручивающейся спирали соответст-
вуют текущему безразмерному времени раскрутки НУ р!г\.
Начальные витки спирали имеют очень небольшой шаг (рас-
стояние КА от гравитационного центра очень медленно растет).
В дальнейшем шаг спирали увеличивается и в точке, в которой
308
КА набирает параболическую скорость, скорость КА имеет
большой наклон к трансверсали.
Современные ЭВМ позволяют достаточно быстро рассчи-
тать траекторию разгона КА с любым законом управления, в
том числе тангенциальным и трансверсальным. Впрочем, при
проектировании траектории КА, которое проводится на ранних
этапах проектирования КА, такой подход к анализу траекто-
рии неприемлем.
Приведем широко используемую для оценки времени на-
бора параболической скорости /к аппроксимационную зависи-
мость:
tK = — [ 1 — с Vf0 — (1~с ^о)21, (7.34)
К и 2 W J V
где константа с=0,8082— для тангенциальной постоянной тя-
ги; с=0,7555 — для трансверсальной постоянной тяги.
Отметим, что время набора скорости с трансверсальной тя-
гой несколько больше времени набора скорости с тангенциаль-
ной тягой. Впрочем, разница мала.
При использовании более сложного закона управления, при
котором угол между реактивным ускорением и трансверсалью
& является некоторой колебательной функцией, удается умень-
шить потребное время набора параболической скорости. Оцен-
ка этого времени может быть получена с помощью уже
записанного равенства (7.34), если константу с в нем взять
равной 0,8209.
Важным вопросом является точность аппроксимационных
соотношений для подсчета потребного времени перелета. В
[20] утверждается, что точность записанных в разделе соотно-
шений не хуже 1% в диапазоне 0</0<Ю-2. С увеличением
W и уменьшением fo точность возрастает. Если начальное
ускорение меньше 10-3, то можно считать, что погрешность вы-
числения времени набора скорости меньше 0,5%.
Значение характеристической скорости (7.2), соответствую-
щее tKl подсчитанному по (7.34), оказывается равным
Из последнего соотношения получается предельное значе-
ние (при бесконечно малых ускорениях) безразмерной харак-
теристической скорости маневра выхода из грависферы притя-
гивающего центра, равное единице. При этом значение грави-
тационных потерь оказывается равным 2.
Если допустить многократное выключение двигателя на
траектории набора параболической скорости, то можно добить-
ся того, чтобы гравитационные потери были малы или даже
бесконечно малы. Для этого двигатель следует включать в рай-
309
оне перицентра витков траектории, а направление вектора тя-
ги выбирать трансверсальным. При этом сама траектория бу-
дет представлять набор эллиптических орбит с одним перицен-
тром и увеличивающимся апоцентральным расстоянием.
Значение безразмерной характеристической скорости манев-
ра будет минимальным V2—1^0,41 (К2 — безразмерная
местная параболическая скорость на начальной орбите). Мо-
торное время полета при этом может быть вычислено по соот-
ношению
'Г [ 1
inf = — { 1 —exp
/о I
"1/2—Г
W
(7.35)
В случае возможного выключения двигателя важно иметь
зависимость моторного времени выполнения маневра. Мотор-
ное время набора параболической скорости для аппарата с
двигателем постоянной тяги можно оценить с помощью следу-
ющего соотношения
т» (Т)=inf+(Tinf inf) ,
где Гц inf вычисляется по (7.35); Tmf вычисляется по (7.34)
(константа с в этом выражении берется равной 0,8209); и —
эмпирический коэффициент (в [20] он равен 1,103).
Замечание. Анализ затрат на скрутку (маневр выхода
КА на круговую орбиту спутника радиуса г0 вокруг планеты
назначения) для аппарата, входящего в грависферу планеты
с параболической скоростью, может проводиться по записан-
ному соотношению (7.34). При этом начальное ускорение fQ
КА может вычисляться по массе аппарата в начальный момент
(когда скорость КА параболическая), а единицей расстояния
следует выбрать радиус конечной орбиты г0.
Межорбитальный перелет
Задачу о нахождении оптимальной траектории межорби-
тального перелета как участка траектории межпланетного по-
лета КА с нерегулируемым двигателем малой тяги можно ста-
вить следующим образом.
Параметры КА: начальное реактивное ускорение f0 и ско-
рость истечения W заданы.
Характеристиками траектории межпланетного перелета яв-
ляются время перелета Г, угловая дальность полета Ф, время
работы двигателя на межорбитальном перелете (моторное
время) Тц.
Критерием оптимальности траектории межорбитального пе-
релета часто рассматривают моторное время или время пе-
релета Т. Задачу ставят, например, так. Найти такую прог-
310
рамму движения (такой закон включения — выключения ра-
кетного двигателя, такой закон изменения направления векто-
ра реактивного ускорения на активных участках движения),
чтобы для заданных времени перелета Т и угловой дальности
перелета Ф, для заданных параметров КА f0 и W моторное
время полета оказалось минимальным.
Такая постановка не является единственно возможной. На-
пример, может быть не фиксировано Ф и нужно будет нахо-
дить оптимальную траекторию и оптимальное значение угловой
дальности полета Форь которое обеспечивает min 7Ц. Может
быть не фиксировано Т или одновременно Т и Ф. Возможных
постановок очень много и в рамках настоящего раздела с ни-
ми познакомиться невозможно. Пожалуй, лучше всего это сде-
лать можно с помощью фундаментального труда [20].
Для того чтобы было понятным, почему в ряде случаев це-
лесообразно фиксировать характеристики траектории Т и Ф,
отметим, что при рассмотрении гелиоцентрической траектории
перелета КА с двигателем большой тяги также приходилось
фиксировать, а затем анализировать две характеристики —
время полета tn и время старта ГСт. Что касается времени по-
лета, произошло лишь изменение обозначения, что связано с
тем, что время полета tn в гл. 6 есть не только время межорби-
тального перелета, но и время всего перелета от промежуточ-
ной орбиты ИСЗ к планете назначения. Обозначение Т, ис-
пользованное в настоящем разделе, предполагает, что в это
время не входит время движения на внутренних участках тра-
ектории.
Что касается времени старта (важного параметра при оцен-
ке межпланетных траекторий), то от его рассмотрения удается
отказаться и ценой дополнительного допущения перейти к бо-
лее универсальной характеристике — угловой дальности полета.
Предполагают, что межорбитальный
перелет происходит между компланар-
ными круговыми орбитами Земли и
планеты назначения. Такие две орби-
ты показаны на рис. 7.2. Внутренняя
круговая орбита — орбита Земли. Вне-
шняя орбита — орбита планеты назна-
чения. В точке С находится Солнце.
Положение Земли в момент начала ге-
лиоцентрического участка обозначено
буквой А. Положение планеты назна-
чения в момент окончания межорби-
тального перелета — буквой В. Угло-
вая дальность перелета Ф есть угол
АСВ. Сама траектория межорбиталь-
ного перелета есть дуга АВ.
Рис. 7.2. Схема гелиоцентри-
ческой траектории перелета
КА с двигателями малой
скорости
311
Фиксирование Ф для заданного времени межорбитального
перелета эквивалентно в рассмотренной схеме фиксированию
даты старта. Именно подбирая дату старта, можно обеспечить
встречу КА с плането?! назначения в точке В при фиксирован-
ных Т и Ф.
Допущения, которые нами перечислены, дали возможность
получить некоторые аналитические результаты по оптималь-
ным траекториям межорбитального перелета. Основной вклад
в это исследование внесен авторами [20]. Используя принцип
максимума, авторы [14] свели задачу поиска оптимальных
траекторий межорбитального перелета к краевой задаче и про-
вели массовые расчеты краевых задач для полета к орбите
Марса и орбите Венеры и траекторий возвращения от этих
планет. Результаты обработок этих массовых расчетов авторам
[20, 14] удалось аппроксимировать в виде соотношений, кото-
рые можно использовать для проектирования межорбиталь-
ных перелетов КА с малой тягой. Приведем некоторые из этих
аппроксимационных соотношений.
Минимальное время межорбитального перелета орбита Зем-
ли— орбита Марса или обратного перелета при оптимально
выбираемой угловой дальности перелета может быть подсчита-
но по соотношению
T’min [сут] = Т min [сут] = - 1,725 + 17 (1 — ---40 Y
./fo [м/с2] \ IT [км/с] /
V 9,8
При этом угловая дальность перелета Ф оказывается равна
Oopt [градус]
= 1,245 -+ 15Н
l//о [м/с2] \
V 9,8
d
W [км/с]
Константа d в последнем равенстве для случая полета орбита
Земли — орбита Марса равна 31,2; для обратного переле-
та — 43,5.
Минимальное моторное время рассматриваемого перелета
при оптимально выбираемых угловых дальности и времени пе-
релета
/ _ 5-59 \
= 18-10-
fo [м/с2]
9,8
7oPt[сут] =259+0,4857^ mln [сут];
Ф0Р1 [градус] = 180+0,3677'и mln [сут].
Результаты численного решения более общих задач межор-
битального перелета можно взять из графиков, приведенных
в [20].
312
Т. А. Гуриной и М. С. Константиновым исследована задача
перелета КА с нерегулируемым двигателем малой тяги при по-
лете орбита Земли — орбита Сатурна. Нахождение оптималь-
ной траектории перелета для перебираемых параметров КА
(fo и W) проведено для оптимально выбираемой угловой даль-
ности перелета, оптимально выбираемого времени перелета.
Схема перелета была фиксированной: два активных участка,
разделенных одним пассивным. Критерием оптимизации траек-
тории был минимум моторного времени перелета. Аппроксима-
ционная зависимость, определяющая энергетические затраты,
имеет вид
У\ар [км/с] = 0 45 0,016
29,78 ’ /4^
5,9293
Перелет с начальной круговой орбиты ИСЗ на орбиту
спутника планеты назначения
В заключение раздела, посвященного межпланетным
перелетам КА с двигателем малой тяги, приведем результаты
анализа траекторий перелета с начальной круговой орбиты
ИСЗ на орбиту вокруг Марса и Венеры, полученные описанным
в разделе методом.
Результаты расчетов авторами [20] сведены в следующие
соотношения:
Тmln (fo> Тц) 1СУТ] —
Г, если
Тц sup, если
оо, если
Гц > Гц sup
Гц < Гц inf,
где
Г — ГSUp (Гsup Гц sup) X
X I 1 t(7\t sup Гц)/(Гц sup Гц inf)]2 ] е
I 1 8 [(Гц sup Гц)/(Тц8ир Тц inf)]2 J
Гц sup [сут] = сх— - /а + (с3 — с4 W [км/с]-*) X
W [км/с]
х I .0-98
\/о {мм/с2]
Гц inf [сут] =
0,98
/о [мм/с®] ’
31
7\up [сут] — c12 + (c13 + 14 - Тц inf;
\ Ц7 [км/с] )
е=С15+йб^[км/с].
Значения постоянных коэффициентов для случая перелета
с орбиты ИСЗ высотой 200 км на орбиты ИС Марса и Венеры
высотой 300 км приведены в табл. 7.1.
Таблица 7.1
Планета Ci с2 Сз с4 С5 с6 С? с8 с9 Сю
Марс Венера 33 39 730 580 277 286 1440 1210 1 0,81 0,75 0,9 0 2,53 0 —37,12 187 264,25 657 912,15
Планета Си С12 С13 С.4 С15 С16 С17
Марс Венера 0,8 0,7 259 147,1 0,815 0,864 0,54 0 0,181 —1,23 —8,36 0,455 —0,9 0,176
Таким образом, в настоящей главе исследованы методы
расчета траекторий КА с двигателем малой тяги. Проанализи-
рованы особенности траекторий КА с малой тягой и особен-
ности постановки задачи о нахождении рациональных траекто-
рий таких КА. Представлена математическая модель, которая,
может быть использована для расчета траекторий КА с малой
тягой. Рассмотрено несколько простых законов управления при
полете КА с двигателем малой тяги и построены соответству-
ющие траектории КА. Рассмотрено два космических маневра
(перелет между некомпланарными круговыми орбитами, меж-
планетный перелет) и проанализирован ряд результатов по
проектированию траекторий КА, выполняющих эти маневры.
ГЛАВА 8, СПУСК КОСМИЧЕСКОГО АППАРАТА
С ОРБИТЫ СПУТНИКА ПЛАНЕТЫ
Спуск КА на поверхность Земли или другой планеты явля-
ется заключительным этапом космического полета. При спу-
ске КА с экипажем решающее значение приобретает необхо-
димость получения приемлемых перегрузочных и тепловых ре-
жимов в процессе спуска, а также обеспечение посадки с вы-
сокой точностью.
Спуск космического аппарата на поверхность планеты мо-
жет быть проведен как с межпланетной траектории движения
КА, так и с орбиты спутника планеты, причем при спуске с
межпланетной траектории аппарат или осуществляет прямой
спуск, или предварительно переводится на орбиту спутника
планеты. При спуске аппарата на планету с атмосферой ис-
пользуется тормозящее влияние атмосферы для гашения скоро-
сти аппарата. Возможно использование также двигательной
установки в процессе спуска, особенно при спуске аппарата в
разреженной атмосфере (например, в атмосфере Марса).
8.1. КЛАССИФИКАЦИЯ РЕЖИМОВ СПУСКА
По характеру формирования траектории все режи-
мы спуска можно разделить на три большие группы.
1. Баллистический спуск.
2. Спуск с постоянным аэродинамическим качеством.
3. Управляемый спуск.
Управляемый спуск предполагает изменение аэродинамиче-
ского качества аппарата в процессе полета. Возможно исполь-
зование комбинированного спуска, объединяющего указанные
выше режимы.
По характеру управления все режимы спуска можно раз-
делить на следующие группы:
1) управление в процессе спуска углом атаки аппарата
а-управление);
2) управление в процессе спуска углом крена (у-управле-
ние);
3) комбинированное управление (а—у-управление).
315
Наиболее простым с точки зрения организации управления
является управление углом крена, так называемое управление
эффективным аэродинамическим качеством. При этом спуска-
емый аппарат (СА) сбалансирован на некотором угле атаки
(абал) и при развороте по углу крена меняется вертикальная
составляющая подъемной силы аппарата. Характер обтекания
СА в процессе спуска не изменяется, что облегчает его тепло-
защиту. В связи со статической нейтральностью такого рода
аппаратов по углу крена затраты рабочего тела на управление,
как правило, невелики. Однако у-управление имеет ряд суще-
ственных недостатков, в частности, наличие бокового ухода и
Рис. 8.1. Схемы возможных вариантов спуска
316
необходимость его компенсации путем изменения знака угла
крена, невозможность одновременного управления продольной
и боковой дальностью и т. д. В связи с этим более перспектив-
ными следует считать двухканальные системы управления, ос-
нованные на изменении угла атаки и угла крена СА.
В процессе спуска ограничиваются как управляющие пара-
метры, так и параметры траектории СА. В качестве ограниче-
ний могут быть приняты ограничения по температуре, скорост-
ному напору, времени спуска, перегрузке, вертикальной скоро-
сти снижения и т. д.
Схемы возможных вариантов спуска приведены на рис. 8.1.
На рис. 8.2 показаны приближенные значения гиперзвуко-
вого аэродинамического качества некоторых эксперименталь-
ных и штатных КА и скорости их входа в атмосферу. Из рис.
8.2 видно, что в дальнейшем исследование проблемы спуска бу-
дет в основном развиваться в направлении анализа больших
скоростей входа и в создании КА, обладающих сравнительно
высоким аэродинамическим качеством. Диапазон скоростей от
круговой до параболической будут иметь аппараты, соверша-
ющие полеты в пределах Земля — Луна. У КА, возвращающих-
ся из полетов к планетам Солнечной системы, скорости входа
в атмосферу Земли превышают параболическую.
Баллистический спуск в атмосфере, при котором после по-
дачи тормозного импульса и схода с орбиты управление тра-
екторией не ведется, является
технической реализации, одна-
ко разброс точек посадки-отно-
сительно расчетной может до-
стигать нескольких сотен кило-
метров в зависимости от раз-
броса начальных параметров
входа и параметров атмосферы.
Совершенствование техники
входа в атмосферу будет заклю-
чаться в использовании КА, об-
ладающих аэродинамическим
качеством и позволяющих в
процессе спуска осуществлять
управление траекторией и
дальностью спуска.
При спуске с начальной
сверхорбитальной скоростью
накладывается дополнительное ограничение на рикошетирование
аппарата из атмосферы. Вход КА со сверхорбитальной скоро-
стью должен быть произведен в определенном входном коридо-
ре по высоте или по углу входа. Ширина коридора определя-
ется разностью высот условных перигеев верхних и нижних
317
самым простым с точки зрения
Рис. 8.2. Значения гиперзвукового
аэродинамического качества СА
граничных траекторий спуска. Использование подъемной силы
КА в процессе спуска при двухканальном управлении по углам
атаки и крена позволяет расширить входной коридор как по
сравнению с баллистическим спуском, так и со случаем одно-
канального управления по углу крена и улучшить динамику
движения аппарата в процессе полета. Наличие даже неболь-
шой подъемной силы позволяет значительно снизить перегруз-
ки в процессе спуска. Таким образом, перспективными СА яв-
ляются аппараты, обладающие аэродинамическим качеством и
располагающие системой управления спуском (СУС), основан-
ной на управлении по углам атаки и крена.
8.2. ВНЕАТМОСФЕРНЫЙ УЧАСТОК СПУСКА КА
С ОРБИТЫ СПУТНИКА ПЛАНЕТЫ
Возвращение КА с низких орбит спутника Земли и
планет принципиально можно организовать двумя способами:
аэродинамическим, используя тормозящее влияние атмосферы
планеты, и газодинамическим, путем приложения тормозного
импульса. Аэродинамический метод торможения заключается
в целенаправленном регулировании силы торможения в апо-
центре и перицентре орбиты. Путем увеличения силы тормо-
жения в апоцентре орбиты и уменьшения ее в перицентре мо-
жно сохранить в течение длительного времени требуемую эл-
липтичность орбиты. Управление полетом и перевод аппарата
на траекторию спуска можно осуществить за счет изменения
подъемной силы Уа и силы лобового сопротивления Ха. Изме-
нение силы лобового сопротивления осуществляется либо по-
воротом КА вокруг центра масс, либо путем раскрытия специ-
альных поверхностей. В том и в другом случае меняется бал-
листический параметр а (а = -.Ха причем эффектив-
х \ х mg0 Г
ность торможения зависит от возможного диапазона изменения
параметра ох.
Наиболее широко распространенным в настоящее время
способом перевода КА на траекторию спуска является способ
приложения тормозного импульса. Последовательность прове-
дения операций на орбите заключается в следующем. Снача-
ла проводится ориентация КА на орбите, т. е. связанные оси
КА занимают определенное направление в пространстве. За-
тем в заранее заданный момент времени включается тормоз-
ная двигательная установка, время работы которой определя-
ется из условия перевода КА на заданную переходную траек-
торию спуска и обеспечения расчетных условий входа КА в ат-
мосферу. Как правило, при проведении проектировочных рас-
четов временем работы тормозной двигательной установки
(ТДУ) можно пренебречь и считать изменение скорости КА им-
318
пульсным, т. е. считать, что тормозной импульс прикладывает-
ся мгновенно (рис. 8.3).
При проведении проектировочных расчетов могут решаться
задачи двух типов:
1. Дано: величина вектора тормозной скорости Д17, направ-
ление вектора тормозной скорости со (угол между местным го-
ризонтом и вектором Д17), время
теля Ti (отсчитывается от момен-
та прохождения перицентра).
Известны также параметры дви-
жения КА в момент включения
ТДУ — скорость КА Pop, угол
наклона вектора скорости к мест-
ному горизонту 0ор, радиус из
центра планеты /?Ор, аргумент
широты (sin г/i = sin ф/sin Z, где
<р — географическая широта
включения ТДУ, i — угол накло-
на исходной орбиты).
Определить: Условия входа
КА в атмосферу — скорость VBX,
угол между вектором скорости
и местным горизонтом 0ВХ, вре-
мя полета от подачи тормозно-
го импульса до входа КА в ат-
мосферу ZCn, дальность спуска по
поверхности планеты при по-
лете по переходному эллипсу
Lcn, аргумент широты точки вхо-
да WBX.
За условную границу атмосферы принимается высота h=
= 100 км, т. е.
включения тормозного двига-
Рис. 8.3. Спуск аппарата с орбиты
спутника планеты:
1 — точка схода КА с орбиты; 2 — мест-
ный горизонт; 3 — точка входа КА в ат-
мосферу
Явх=Япл+100,
где Rnn — средний радиус планеты (для Земли 7?3 = 6371 км).
2. Дано: Увх, 0вх> Явх» ^вх-
Эти величины целиком определяют параметры переходно-
го эллипса.
Известны также: радиус апоцентра га исходной орбиты, ра-
диус перицентра гп, аргумент широты перицентра ип.
Точка пересечения исходной орбиты с переходным эллипсом
определяет точку схода КА с орбиты и параметры тормозного
импульса.
Определить: ДУ, со, п, ZCn, Lcn.
Задача первого типа может быть решена следующим об-
разом.
319
Скорость КА и угол наклона вектора скорости после пода-
чи тормозного импульса можно определить из соотношений
Vi = V V2p + AV2-21/ор Д V cos (со—0ор). (8.1)
Если принять, что
AV/Vop^l,
то приближенно получим
Vi = Кор—Д Vcos (со —0ор); (8.2)
угол наклона:
91 = еор—arctg —д Vsin (со-Оор)-- (8 3
р Гор - Д V cos (со - 0ор) v '
или приближенно
01 = 0op-VLsin((O-eop)- <8-4)
V ор
Используя интегралы энергии и площадей, получим значения
параметров движения КА в момент входа в атмосферу
|72 __ у2 2[1 .
* *ОР ’ ' /о
VR cos 0= Vi-Rop cos 0i, ' ' '
где р, — произведение массы притягивающего тела на посто-
янную тяготения (для Земли ji=3,986-1014 м3/с2); V, R, 0 —
текущие значения параметров движения КА.
Из уравнений (8.1), (8.4) и (8.5) нетрудно получить пара-
метры движения КА при входе в атмосферу, если положить
R=Rbx- Имеем
п _ Vi #ор cos 01
^вх
(8-6)
(8-7)
Определим го эллипса фокальный параметр и эксцентриситет переходно- (8.8) (8-9)
где а= PjSBS ; (8.10) 2р, — /?вх С
а — большая полуось переходного эллипса.
320
Текущее время спуска от момента подачи тормозного им-
пульса (/) и дальность спуска по поверхности планеты (L)
можно определить из соотношений
fiop dR
I V sin 0 *
А
RnjI
2 Rtg0
(8.Н)
(8.12)
Вычисляя интегралы (8.11) и (8.12) и используя (8.5), получим
формулы для определения tcn и £сп
- [т ( Т-атаГТг + arcsin )] ; (8.13)
£оп = «плдв=[«пл arcsin д (8-14)
где a = V2_21L; Ь = 2р.;
^ор
С = — (/?вх Vbx COS 0bx) 2 = —цр.
Следует иметь в виду, что коэффициенты а,Ь и с необходи-
мо вычислять с достаточно высокой точностью во избежа-
ние появления отрицательных чисел под квадратным корнем
в уравнениях (8.13) и (8.14).
Аргумент широты точки входа определяется следующим
образом [9]:
Ubx = Щ—Vi+Vbx, (8.15)
где vi и vbx — углы истинных аномалий точек 1 и 3, Ui — аргу-
мент широты точки 1
Яор Vop cos2 °1 - И Р — Рвх
cos V, =-----; cos vBX = —-------------.
М вх еЯвх
Необходимые формулы для решения задачи второго типа
приведены в [9]. Формулы получены из уравнений невозму-
щенного кеплеровского движения КА.
Большое значение имеет выбор оптимального направления
тормозного импульса. Сформулируем задачу следующим об-
разом: определить оптимальную ориентацию тормозного им-
пульса ДУ из условия получения максимального по модулю уг-
ла входа в атмосферу. Величина тормозного импульса счита-
ется заданной. Задача в такой постановке эквивалентна зада-
че определения оптимальной ориентации минимального по ве-
личине тормозного импульса для получения заданного угла
входа в атмосферу.
П—8 321
Для определения необходимого условия оптимальности уг-
ла нужно продифференцировать угол 0ВХ (8.7) по со и прирав-
нять полученное выражение к нулю. Решение данной задачи
достаточно подробно рассмотрено в [10].
Для случая спуска с круговой орбиты или приложения тор-
мозного импульса в апоцентре (или перицентре) орбиты 0ор =
= 0. Получим
(Vop—AV cos со) Vop sin co— (VOp—2Д VTOp cos co+
+Д V2+&)sin co = 0,
где k = — 1) .
-^op \^BX /
Отсюда находим два значения угла со, удовлетворяющих не-
обходимому условию оптимальности
n aV2 + * /о
сох = 0, со2 = arccos-1, (8.16)
AV
4 Г; Д V Г k
где ДУ - — , k = — .
V°P Vop
Внутри некоторой области Г в плоскости начальных пара-
метров ДР и к величина со2=^=0. Граница области Г определя-
ется из условия (02=0, т. е.
ДР2—Д Р+&=0.
(8.17)
Уравнение (8.17) определяет параболу в плоскости (ДР, 6)
(рис. 8.4). Анализ второй производной угла 0вх по со показы-
вает следующее: если начальные -параметры ДР и £ находятся
внутри области Г, то для получения минимального по величи-
не тормозного импульса при заданном угле входа его необхо-
димо прикладывать под углом со = со2. Если же начальные па-
раметры ДР и 6 лежат на границе или вне области Г, то оп-
тимальным направлением будет co = coi = 0.
Скорость и угол входа можно определить из следующих со-
отношений (для случая, когда начальные параметры находят-
ся внутри области Г):
*ZBX = VOP 1/3—2 —(ДУ)2;
F ^вх
cos0BX= 1/3—2 —(ДУ)2 .
Явх V Явх
(8.18)
(8.19)
Величина тормозного импульса при заданном угле входа в ат-
мосферу 0*вх равна
ду = 1 Г3—2 cos 0* У . (8.20)
I / D \ D вх /
V аВх \ ^ор /
322
Существует предельная высота
точки торможения, при которой
(Оопт>0- Она определяется по
следующей формуле [10]:
/ /?ОР \ = ( 1 У°Р
\ ^вх /пр ' 8 р, /
(8.21)
Для круговой начальной орби-
ты (-/?орД?вх) пр = 1,125. При им-
пульсном оптимальном торможе-
нии при спуске с круговой орби-
ты, когда параметры движения
находятся на границе или вне об-
ласти Г, параметры движения КА
Рис. 8.4. Граница области опти-
мального направления тормозного
импульса
при входе в атмосферу можно определить из следующих соотно-
шений:
Vbx = Vop 1/(1-ДГ)2 + 2(^₽ -1) ; (8.22)
cos 0ВХ = (7?op//?w) О-АУ). . (8.23)
вх VBX/Vop
д V = 1 — -1 /Г—2KW^bx)-11— (8.24)
V [(Rop/Rax) sece*x]2 — 1
Расчетные формулы при спуске с произвольной эллиптиче-
ской орбиты приведены в [10].
При проведении приближенных баллистических расчетов
на начальных этапах проектирования КА величину шОпт для
начальной круговой орбиты можно определить из следующих
соотношений:
coscoODT= — 2 при ) >7; (8.25)
,/ / &Rop V ' Rop-Rbx /
У \ ^ор — ^вх /
1 I ВХ хор I Т
Z<ys> (0ОПТ = 1 при I —----— I < 7.
\ °ор — Авх /
Заданный угол входа 0*вх в (8.25) берется в радианах. Из
(8.25) следует, что при малых по абсолютной величине углах
входа КА в атмосферу направление тормозного импульса дол-
жно быть противоположно направлению вектора орбитальной
скорости КА. При йопт=0° угол входа в атмосферу можно вы-
числить по формуле (8.23).
323
Требуемое значение AV можно определить по формуле
(8.24) или приближенно из соотношения
(Др)тщ«-^ .
Разброс по дальности на атмосферном участке может быть
уменьшен путем увеличения точности определения параметров
исходной орбиты, а также выбора оптимальной величины и
направления тормозного импульса. Производные рассеивания
существенно возрастают по абсолютной величине при умень-
шении 10вХ |. С этой точки зрения слишком малые по абсолют-
ной величине углы входа являются неприемлемыми.
Пример расчета траектории движения КА
на внеатмосферном участке спуска
Провести расчет тормозного импульса и параметров
движения КА на внеатмосферном участке при следующих на-
чальных условиях (спуск на поверхность Земли): спуск с кру-
говой орбиты высотой /тор = 200 км, угол входа в атмосферу
0вх=—2,2°, масса КА на орбите mQ = 6fi т, удельный импульс
тяги тормозной двигательной установки /у = 3924 м/с.
Расчет начнем с определения параметров тормозного им:
пульса. Предварительно найдем орбитальную скорость КА
Vop= = У =V (earl’9!6200°НО~= 7789 М/С-
Уравнения (8.5) содержат следующие неизвестные величины:
VBX, 0вх, AV и со. Нам известен только угол входа 0ВХ. Чтобы
воспользоваться системой (8.5), необходимо определить еще
один какой-либо параметр. Из уравнения (8.25) определим оп-
тимальное направление тормозного импульса, при котором ве-
личина тормозного импульса минимальна. Предварительно вы-
числим параметр
0Bg ^ор \а
flop — Авх /
— 2,2-6571 у =6 4<7
57,3-(6571 —6471) J
Следовательно, cos со0пт= 1, со0пт = 0. Теперь из системы (8.5)
можно определить VBX и AV, положив А = /?вх=6471 км. Ве-
личину AV можно приближенно определить из уравнения
(АЮтш =0,019.
min 2 57,3-2
Тогда AV=AP-Vop=0,019-7789= 148 м/с (для более точных
расчетов необходимо использовать формулу (8.24)).
324
В связи с тем, что формула (8.25) приближенная, требует-
ся провести проверку нахождения начальных параметров дви-
жения КА в области Г (см. рис. 8.4). Имеем
Д7 = 0,019 ; k = 1 \ =
*ор \ /
=- £13'986-1014 / 6571 _ j \ = Jgg 83. 104 М2/С2
6571-103 \ 6471 )
k = k/V2 = 186’83-101
ор (7789)2
= 0,31.
Таким образом, параметры движения КА лежат вне обла-
сти Г, т. е., действительно, соопт = 0. Если бы начальные пара-
метры движения КА лежали внутри области Г или на ее гра-
нице, то ©отп>0 ((8.16) для о2), а величину ДР необходимо бы-
ло бы определять по формуле (8.20).
Величину скорости входа КЛА в атмосферу определим по
формуле (8.22). Имеем
VBX = VOP 1/ (1 —Др)2 + 2 (^-1) =
У \ ^вх /
= 7789 -1/(1 —0,019)2+ 2 (— — = 7763 м/с .
V \6471 /
Определим большую полуось, фокальный параметр и эксцен-
триситет переходного эллипса, используя формулы (8.10), (8.8)
и (8.9). Имеем
а = ^вх =
2(л — 7?вх
3,986-105-6471
2-3,986-10* — 6471-7,7632
= 6333 КМ ;
__ ^вх ^вх cos2 ввх _ 6471а-7,763а(0.9993)2 _
Р Ц 3,986-10*
= 6325 км; е= 1/1- /- = 1/1-=0,04.
Т а Г ODDO
Время спуска (fCn), дальность спуска (Lcn) на внеатмос-
ферном участке, а также аргумент широты точки входа опре-
делим по (8.13), (8.14), (8.15).
Для определения количества топлива, необходимого для
подачи тормозного импульса, используем формулу
АУ
mT —т0(1—е у ).
325
Получим
_ 148
mT = 6,0(1 —е 3924) = 0,35 т.
На этом приближенный расчет параметров траектории на
внеатмосферном участке спуска можно считать законченным.
8.3. УРАВНЕНИЯ ДВИЖЕНИЯ СА
НА АТМОСФЕРНОМ УЧАСТКЕ СПУСКА
В связи с необходимостью расчета траекторий дви-
жения СА с помощью наземных вычислительных комплексов и
широким применением вычислительной техники в бортовых
системах управления рассмотрим уравнения движения С А, ко-
торые могут быть использованы в наземных и бортовых ЭЦВМ.
Спускаемый космический аппарат в общем случае следует
считать телом переменного состава, состоящим из точек пере-
менного состава, движение каждой из которых в инерциальной
системе координат описывается основным уравнением И. В. Ме-
щерского [47]. В процессе движения спускаемого аппарата в
результате изменения с течением времени его состава могут
изменяться его масса, положение центра масс внутри аппара-
та, моменты инерции и т. д. В процессе спуска вследствие де-
формации конструкции аппарата, абляции и сублимации теп-
лозащитного покрытия изменяется внешняя конфигурация СА,
меняются его аэродинамические коэффициенты.
Таким образом, спускаемый аппарат следует рассматривать
как сложную систему с большим числом степеней свободы.
При общей оценке динамических свойств СА допустимо при-
нять упрощенную схему твердого тела переменного состава
постоянной конфигурации и при определении внешних сил учи-
тывать лишь силы инерции переносного движения и кориолисо-
вы силы. При исследовании устойчивости движения СА необ-
ходимо учитывать деформацию конструкции, колебание жид-
ких наполнителей, изменение аэродинамических коэффициен-
тов в результате изменения внешней конфигурации аппарата
и т. д.
Движение СА, отождествляемого с твердым телом, описы-
вается системой шести дифференциальных уравнений равнове-
сия сил и моментов. При исследовании траекторий движения
СА воспользуемся гипотезой стационарности, в соответствии с
которой при определении внешних сил, действующих на СА
при спуске, неустановившийся характер движения не учитыва-
ется и считается, что движение является установившимся с
постоянными значениями кинематических параметров, равны-
ми их мгновенным значениям. Таким образом, траектории дви-
жения СА можно определить, исследуя только три уравнения
326
равновесия сил в проекции на координатные оси, что значи-
тельно упрощает решение задачи. При исследовании вопросов
устойчивости и управляемости необходимо рассматривать урав-
нения сил и моментов совместно.
Рассмотрим подход к составлению уравнений движения СА
в общем случае. Абсолютное движение СА удобно рассматри-
вать состоящим из двух движений: из абсолютного движения
центра масс (ц. м) и вращательного движения аппарата отно-
сительно поступательно движущейся системы осей координат,
начало которой находится в центре масс СА.
Спускаемые аппараты, управляемые с использованием аэро-
динамического качества, обычно имеют плоскость массовой
симметрии, проходящую через продольную ось геометрической
симметрии и ц. м СА. В качестве спускаемого аппарата рас-
смотрим аппарат в виде полуконуса с плоской верхней частью.
Оси связанной системы координат OXYZ направим параллель-
но осям симметрии СА так, чтобы плоскость OXY совпала с
плоскостью массовой симметрии СА, а ось ОХ была параллель-
на продольной оси аппарата (рис. 8.5). Управляющие моменты,
создаваемые двигателями стабилизации и реактивными сопла-
ми, необходимыми для изменения угла атаки, направлены по
осям системы координат Oxyz, повернутым относительно свя-
занных осей аппарата на угол ао.
Аэродинамические силы, действующие на СА, будем опре-
делять в системе координат Oxcyczc, начало которой находится
в ц. м. СА, ось Охе направлена_по вектору скорости и, ось 0г/с—
по векторному произведению Яор-Гвх, а ось Ozc образует пра-
Рис. 8.5. Схема отсчета углов атаки и крена
Ус
Плоскость отсчета угла крена у
Плоскость угла
атаки осп
Плоскость маисовой
симметрии С А
327
вую систему. За угол атаки ап принимается угол между векто-
ром скорости V и осью ОХ. Плоскость угла атаки при поступа-
тельном движении СА является мгновенной плоскостью аэро-
динамической симметрии и содержит главный вектор аэроди-
намической силы 7?а. Угол крена у есть угол между плоскостью
ХсУс И плоскостью угла атаки. Угол р определяет поворот
плоскости OXY относительно плоскости угла атаки.
Результирующий момент определяется соотношением
л-а+л,
Л1а = ГдХ7?а + Л1в + Мд,
где Мл — полный аэродинамический момент; A1B —_возмущаю-
щий аэродинамический момент (из-за уноса ТЗП); Мл — демп-
фирующий аэродинамический момент; гд — радиус-вектор цент-
ра давления СА; Мт — момент от реактивных сил.
Аэродинамический момент будем определять в предположе-
нии стационарности обтекания СА набегающим потоком воз-
духа. На балансировочном угле атаки ап=абал момент силы 7?а
относительно ЦМ равен нулю, а производная момента по углу
атаки отрицательна в соответствии с наличием статической ус-
тойчивости.
Для определения производных по времени от углов ап, Р» у
имеем
ап сох sin р sin ао + <ау sin р cos ао + cos Р;
у = —-— (—©х cos р sin а0—ау cos Р cos а0 + <лг sin Р); (8.27)
sinan
Р = ©х (ctg ап cos р sin ао + cos ао) + ©v (ctg ап X
X cos р cos ао—sin ао) —©z sin р ctg ап.
Компоненты полного аэродинамического момента в системе
координат Oxyz определяются следующим образом:
Мах = [—сп (а) (уд cos а0—хд sin а0) sin р +
+ тх\ Я I + Л1Дх ;
Мау = [сп («) (*д c°s ао + УЛ sin а0) sin р + my] qSMl + МДу; (8 2g)
Maz = [ст (а) уд + сп (а) хд cos р + tnz} qSMb + МДг,
где тх, ту, mz — коэффициенты возмущающего аэродинами-
ческого момента; Sm, I — характерные площадь и размер СА;
Хд., Уд, 2Д — безразмерные коэффициенты центра давления в
системе координат OXYZ (хл = и т.д. j.
328
В работе [63] рассмотрено управление углом атаки СА по-
средством изменения центровки (при наступательном и враща-
тельном перемещении подвижной массы). Указывается, что
«...наиболее рациональной для управления углом атаки (с точ-
ки зрения эффективности управляющего органа, весовых зат-
рат и мощности) представляется комбинированная система,
состоящая из механизма изменения статической моментной ха-
рактеристики и реактивных органов». В такой системе управ-
ление углом крена и демпфирование колебаний осуществляет-
ся реактивными органами, а отработка навигационного сигна-
ла — посредством перемещения подвижного элемента.
Уравнения движения СА в векторной форме можно запи-
сать следующим образом:
та = R + Р + та0ТВ + такор ; (8 -2)
d (я/dt = J""1 — со х J со, (8.30)
где a = dV]dt\ aor}i = dW\/dtf аКор = 2(оХ№ — соответственно аб^
солютное, относительное и кориолисово ускорения ЦМ СА, R
и Р — равнодействующие внешних активных и реактивных
сил; со — вектор угловой скорости СА; W — скорость ЦМ по
отношению к границам аппарата; J1 — обратная матрица тен-
зора инерции; М —вектор обобщенного момента; Mr—глав-
ный момент внешних сил.
Движение ЦМ СА практически удобно рассматривать в
инерциальной геоцентрической системе осей координат Cxyz.
Ось Сх лежит в плоскости экватора и направлена в точку ве-
сеннего равноденствия. Ось Cz направлена к северному полю-
су, ось Су образует правую систему координат. Уравнения
движения имеют следующий вид:
т/ Xax + Yax+Zax .
vx = —-—------------ + gx<x = vx;
Vy = -\-gy, y — Vy', (8.31)
у = + 4 + у
v z m 4 gz» c v Z-
Уравнения движения СА относительно ЦМ будем рассмат-
ривать в системе координат Oxyz. Имеем
гм
юх = ---1* Jy _
Jx Jу — ^ху
х wz+
х
—— co„coz— — сох X
г У & г •*-
X J X
X
X
My __ jx — J;
Jy
(0 = ---Ldv----
T J [2
Jx Jy — Jxy
-Г- °>yaz
x-Jz
—T--* ^x^z-T
Jy
Jy
'My_
Jy
329
+ (ОУ(О2+ (М* —
Jy Jу \ ^х
- ау«>- (О, ®уЧ ; (8.32)
JX / .1
Jz Jz Jz
Интегрирование систем уравнений (8.31) и (8.32) с учетом
(8.27) и (8.28) при заданных начальных условиях полностью
определит движение ЦМ СА и движение СА относительно ЦМ.
Определим проекции ускорения свободного падения с уче-
том нецентриальности поля тяготения:
Здесь
/ (Д? 7?э
Э \ 2£э
Для Земли ^3.3 = 6378,245 км; ц = 398620 км3/с2; §’3.э = 9,7830Х
ХЮ-3 км/с2; ~^= 1/298,3; со3 = 7,2921 • 10-5 1/с.
Масса СА в процессе спуска из-за уноса ТЗП и расхода
рабочего тела на управление и стабилизацию является сугубо
переменной величиной. Определим проекции аэродинамических
сил на оси инерциальной системы координат Cxyz.
Известно
= сха (а) SM, Уа = сУа (а) SM, Za = cZa
где и — вектор скорости аппарата относительно атмосферы,
v = V—созХг; г — радиус-вектор центра масс аппарата,
r = Vx2 + y2+z2, р = р(й), h = r—R3, R3 = R3(1 — а-^Л
При управлении СА изменением угла крена у, т. е. при раз-
вороте аппарата относительно вектора текущей скорости, про-
екции аэродинамических сил на оси скоростной системы ко-
ординат запишем следующим образом:
A'o = cXa(a)-^SM, Ya = cVa(a)-^-SKcosy,
Za = cZa-^-SMsm у.
330
Проекции аэродинамических сил на оси инерциальной сис-
темы осей координат
^ах Ха 1х^ ^ах = а ^ах ~
*ау ' lyi Yay = Yа ГПу, Zay = Za П,у\
^az= Xalz> Yaz=Y atTlzi Za^ — Zatlz^
здесь
/x==^xl/^, fT^'X=='^Z^/y lytlzi
ly=^Vy!'U у 1Yly^lxtLz lztlx\
/z=^z/^, ^Z = lyftx lxtly>
где
n. = ёУ Vz —SzvV
V(gy VZ - gz v,j)2 + (gz vx - gx vz)2 + (gx Vy—gy vx)2
n _ gz^x — gX Vz .
V ’V(gyV2 — gzVy)2-^(gzVz—gxvz)i+(gxVy—gyV^i
П = gxVy— gy Vx
~V(gy Vz — gz Vy)2 + (gz Vx - gx VZ)2 + (gx Vy—gy Vx)2
Проекции текущей скорости СА на оси инерциальной сис-
темы координат соответственно равны
^x=Vx + (p3f/, Vy=Vy—i(D3X, VZ=VZ.
Зная координаты и составляющие скорости аппарата в
инерциальной системе осей координат Cxyz, нетрудно полу-
чить текущие географические координаты и кинематические
параметры траектории в процессе спуска:
широту
Ф = ф+ азт2ф, ф = arcsin—;
г
долготу
X = а* — а>, t, a* — arcsin , у ;
У^ + </2
угол наклона траектории к местному горизонту
fl _ arrcin 8х Vx + §У иУ + gz Vz .
gv
угловую дальность полета без учета вращения атмосферы
_ х0 х + у0 у + г0 г
Ф = arccos _О—J_20_O_0— .
''о''
Дальность по поверхности Земли Л = Ф/?3.
331
Текущий азимут спускаемого аппарата
л vz и X г cos ф
cos А =------л----; sin А =---------
V COS 6 COS ф V cosj)
где
i __ XVy — yvx
!*2 + y2
Иногда необходимо определить плоскость орбиты спускае-
мого аппарата на внеатмосферном участке и некоторые кине-
матические параметры траектории спуска относительно этой
плоскости. Плоскость орбиты определяется двумя векторами
fo и Ро, -где fo и Ро — соответственно радиус-вектор аппарата и
его инерциальная скорость в некоторой точке на внеатмосфер-
ном участке траектории. Уравнение плоскости орбиты СА в
системе Cxyz
АоХ 4- В$у + CqZ = О,
где
Д __ УО Ур2 — 20 Ур У . Q = 2Р Ур X — ХР Ур Z ,
° Го Vo ’° Го Vo
Q Х0 VОУ — УР УР X
°“ r0V0
Угол между вектором относительной скорости аппарата и
плоскостью орбиты можно найти из уравнения
о — оух A~B0Vy + Cov2
oil! С/у /____________•
vV A2+ B2 +С2
Точно также
ния угла между
ки посадки
нетрудно записать уравнение для определе-
плоскостью орбиты и радиусом-вектором точ-
sjn ф _ Aoxk + Bq Ук. +C0Zfe
Для получения дальности полета с учетом вращения плане-
ты необходимо пересчитать координаты аппарата во вращаю-
щуюся планетоцентрическую систему координат СоХоУо2о:
Xq = x cos (Ло + (Оз^) А-у sin (Хо + (ОзО
Уо = —х sin (Хо + сМ) + у cos (Хо + со3/);
Zo = z,
где Хо — угол между осями Ох и СоХо в момент времени t = 0.
Тогда
Ф= arccos xoxh + VoFh + ZoZh
го гн
332
где Ан, Ун, Zh — начальные координаты аппарата и соответст-
венно Л=ЛСрФ.
При записи уравнений движения СА в планетоцентрической
экваториальной вращающейся системе осей координат CqXqYqZo
считая, что в момент t = t0 она совпадает с инерциальной сис-
темой, необходимо к правым частям системы (8.31) добавить
ускорение переносного движения и кориолисово ускорение.
Уравнения движения будут иметь вид
Vx„ = Xax + Ya^+Zax + gx + ©2 Хо + 2(0а Uy,;
fr. = + gv +fi)*y0-2<W (8.33)
X. — vXq ; Y о — Vy0; Zo — vZo •
Величины, входящие в данную систему, определяются по
формулам, приведенным выше.
Приведенные уравнения движения СА могут быть исполь-
зованы в наземных вычислительных комплексах для расчета
траекторий движения СА на атмосферном участке спуска.
Для расчета траекторий движения СА с помощью борто-
вых ЭВМ могут быть использованы уравнения, полученные в
работах [49, 54], которые были опробированы расчетами и
показали приемлемую точность при проведении расчетов тра-
екторий СА с прогнозированием точки посадки.
Наиболее рациональными методами численного интегриро-
вания уравнений движения на борту являются модифицирован-
ный метод Эйлера и метод Адамса третьего порядка с шагом
интегрирования 10 с [49, 53].
В инерциальной планетоцентрической системе осей коорди-
нат уравнения движения СА запишутся следующим образом
(в обозначениях работы [49]):
— = — а[6(1— 2а)—2с^г], а = -Н-;
d ф rv2
d 0 1 . с. v г
---=1 —а + хс£г, 1 = е ;
d ф
г = У х2 + у2 + z2;
* - = гЪ, ^ = -^(
d ф v
- *l = v|r9, п=—. (8-34)
d ф г
333
qi, n . (и, г) .
- — — V, 0 = arcsin
а ф vr
х= г cos ср; (8.34)
dip . с.
-7х = —ат]+с^г%2, t/ = rsinq>;
а ф
Xz = К sin у,
где v — скорость СА; 0 — угол вектора скорости с горизонтом;
Ф — угловая дальность; с — баллистический коэффициент СА;
v — отношение логарифма плотности атмосферы к высоте; z —
боковое отклонение; ц — произведение массы Земли на пос-
тоянную тяготения; % — аэродинамическое качество СА в вер-
тикальной плоскости; у — угол крена СА; К — аэродинамиче-
ское качество СА. i
В этой системе tg0 заменен на 0, cosO«l, отброшены чле-
ны вида zQ и vzd.
В работе [49] приведены также уравнения движения СА с
учетом нецентральное™ поля тяготения и вращения Земли. В
[53] проанализированы потребные ресурсы БЦВМ при исполь-
зовании одного из алгоритмов работы системы управления
спуском.
8.4. МЕТОДЫ ИССЛЕДОВАНИЯ УРАВНЕНИЙ ДВИЖЕНИЯ
СПУСКАЕМЫХ АППАРАТОВ
Уравнения движения спускаемых аппаратов в плане-
тоцентрической экваториальной вращающейся системе коорди-
нат (8.33) являются сугубо нелинейными дифференциальными
уравнениями. Оценим характер величин, входящих в правые
части системы (8.33). Анализ уравнений показывает, что цент-
ростремительное ускорение, обусловленное суточным вращени-
ем планеты, мало по сравнению с ускорением свободного паде-
ния и ускорением, вызванным аэродинамическими силами
(при 100 км). Центростремительное ускорение на экваторе
на высоте й=100 км (для Земли) составляет порядка 0,35%
от ускорения свободного падения на этой высоте, так что с
достаточной степенью точности центробежной силой можно
пренебречь. Кориолисовы силы инерции при спуске с первой
космической скоростью составляют порядка 10%, а при спус-
ке со второй космической скоростью — порядка 14% от силы
тяжести. При точных навигационных расчетах их необходимо
учитывать. При приближенных количественных и качествен-
ных исследованиях с целью выявления основных закономер-
ностей целесообразно пользоваться системой упрощенных
уравнений движения СА, полученных при ряде допущений. К
этим допущениям относятся:
334
1) планета — сфера с радиусом (/?пл;
2) поле тяготения — центральное, т. е. g = go (ЯплД?)2;
3) рассматривается плоское движение. Движение относи-
тельно центра масс не учитывается.
При данных допущениях уравнения движения СА в скоро-
стной системе координат запишутся следующим образом:
dv pv2 . гп
2----85,П'в;
°! Кcos У + |/ ;'------| < О'. О
dt Аё0 2 Y \ 7? V )
= v sin 6; (8.35
dL_ _ v #пл cos g.
dt g
Перегрузки в скоростных осях:
о v2
ла Мг
2G
р v2
„______ид м г_____jz ~ п
Пуа ~~ 2G ~
Полная перегрузка равна
/2%
а
стх<?;
В настоящее время для общего случая нет точных анали-
тических решений системы (8.33). Однако можно найти неко-
торые приближенные решения. В работе Чепмена [66] дается
приближенное аналитическое решение уравнений движения
спускаемого аппарата применительно к атмосфере любой пла-
неты для баллистических и планирующих КА при различных
углах входа. Аналогичные результаты получены в работе
В. А. Ярошевского [68].
Поскольку при рассмотрении задачи в первом приближении
некоторыми членами пренебрегали, полученные приближенные
решения ограничиваются относительно узкими рамками при-
менения к задачам спуска в атмосфере.
Спуск КА с постоянным качеством требует переменных уг-
лов наклона траектории. Большие по модулю углы наклона
приводят к большим тепловым потокам, но к меньшему сум-
марному количеству подведенного тепла за счет уменьшения
времени спуска. Малые углы наклона дают обратный эффект.
Траектории при переменном аэродинамическом качестве могут
быть построены таким образом, что максимальные перегрузки
аппарата, его нагрев и т. д. поддерживаются в допустимых пре-
делах. Управление качеством спускаемого аппарата может
335
быть введено для обеспечения следующих режимов спуска:
1) полет с постоянным торможением или постоянным ско-
ростным напором (изоперегрузочные траектории спуска);
2) полет с постоянным углом наклона траектории;
3) полет с постоянным тепловым потоком в критической
точке или полет с постоянной средней температурой в крити-
ческой точке теплоизолированной стенки;
4) полет с постоянной скоростью спуска.
Математические методы исследования уравнений движения
спускаемого аппарата, позволяющие получить основные термо-
баллистические параметры траектории КА в процессе спуска,
заключаются в следующем:
1) уравнения движения можно свести к одному уравнению,
пренебречь некоторыми членами этого уравнения и затем про-
вести его интегрирование, получив тем самым приближенные
аналитические решения;
2) можно получить точное решение уравнений движения для
некоторых частных режимов спуска;
3) уравнения, описывающие планирующее движение воз-
вращающегося в атмосферу КА с произвольно меняющимися
подъемной силой и лобовым сопротивлением, можно привести
к безразмерному виду, что позволяет использовать метод раз-
ложения в ряд по степеням малого параметра;
4) выводится закон подобия, по которому целый класс тра-
екторий спускаемого аппарата может быть представлен одной
кривой, называемой относительной траекторией. Фазовые ко-
ординаты КА в процессе спуска могут быть представлены как
произведения масштабных величин на безразмерную функцию
подобия;
5) можно провести численное интегрирование уравнений
движения на ЭВМ и составить эмпирические формулы, поз-
воляющие производить быстрые инженерные расчеты основных
параметров движения аппарата в процессе спуска.
Рассмотрим различные режимы спуска КА, которые реали-
зуются при спуске как с постоянным, так и с переменным аэро-
динамическим качеством.
8.5. АНАЛИЗ ТИПОВЫХ РЕЖИМОВ СПУСКА
АППАРАТА В АТМОСФЕРЕ
Из системы (8.35) следует, что только два парамет-
ра — аэродинамическое качество и баллистический параметр
сгх — могут влиять на параметры траектории в процессе спус-
ка. Как правило, в качестве управляющего параметра выби-
рается аэродинамическое качество спускаемого аппарата. Для
расчета траекторий управляемого спуска необходимо к системе
336
(8.3Й) добавить так называемое уравнение управления и ин-
тегрировать систему (8.35) совместно с уравнением управле-
ния, которое представляет собой закон изменения аэродинами-
ческого качества КА или его баллистического параметра
по траектории спуска. Если аэродинамическое качество равно
нулю, то такой спуск называется баллистическим, а аппараты,
на которых реализуется такой спуск, — аппаратами баллисти-
ческого спуска. Примером подобного типа аппаратов являются
«Восток», «Восход», «Джемини». Если аэродинамическое каче-
ство в процессе спуска не равно нулю, то спуск называется
планирующим, а аппараты, на которых реализуется такой
спуск, называются аппаратами планирующего спуска. Приме-
ром такого аппарата является орбитальная ступень многора-
зовой транспортной системы США «Спейс Шаттл». Особым
видом спуска является так называемый скользящий спуск. Ап-
параты, осуществляющие скользящий спуск, имеют аэродина-
мическое качество в пределах 0</С<0,7. Примером такого
типа аппаратов являются аппараты затупленных форм (типа
«Фара») — «Союз», «Аполлон». Потребность в разработке по-
добного типа аппаратов была связана с необходимостью сни-
жения перегрузок при спуске с орбиты по сравнению с бал-
листическим спуском.
Реальные траектории спуска часто могут быть представле-
ны в виде сочетания отдельных модельных участков, на каж-
дом из которых управление либо отсутствует, либо осуществ-
ляется таким образом, чтобы выдержать неизменными какие-
либо параметры движения аппарата в процессе спуска.
Рассмотрим следующие модельные участки:
1) баллистический спуск; 2) спуск с постоянным значени-
ем аэродинамического качества; 3) равновесное планирование;
4) изовысотный участок спуска; 5) изоперегрузочный участок
спуска.
Баллистический спуск
Для случая баллистического спуска КА.с^ = 0 (а в
общем случае и коэффициент аэродинамической боковой силы
% = 0).Примем следующие допущения:
а) планета — правильная сфера, атмосфера планеты не
вращается;
б) атмосфера планеты изотермическая;
в) высота спуска мала по сравнению с радиусом планеты;
г) проекция ускорения свободного падения на касательную
к траектории мала по сравнению с ускорением от силы лобо-
вого сопротивления.
337
Тогда первое уравнение системы (8.35) можно записать
приближенно в виде:
dv р v2 о
m----= —сх —— 5М.
dt а 2 М
(8.36)
При сравнительно больших по модулю углах входа (|0ВХ|^
^5°) до достижения пика перегрузки изменение угла наклона
вектора текущей скорости КА к местному горизонту можно
считать достаточно малым, т. е.
0Bx~0 = const. (8.37)
С учетом (8.37) третье уравнение системы (8.35) можно за-
писать в виде
dh
~dt
v sin 0ВХ.
(8.38)
Используя (8.36), (8.38), получим
dv _ SM роехр[ —₽/i]
dh Сха 2т sin 0ВХ
(8.39)
или
dv __ SM роехр[ -p/z]
v ха 2т sin 0ВХ
(8.40)
Интегрируя (8.40), получим
v = vBX exp
СХд •$№ (Р ~ Рвх) I
2т р sin 0ВХ J
(8.41)
где рвх = роехр[—рЛвх].
Величину перегрузки при баллистическом спуске можно
найти из следующего соотношения *
П^п
а
а следовательно, максимум
муме скоростного напора
pt)2 1
— =^-РУвх
Су
Хд М 2
- п Р ,
перегрузки достигается при макси-
(8.42)
PYA [ 0X0 (Р ~ РИ) I
А‘ I т р sin 6ВХ ] ’
(8.43)
что имеет место при
р = - mPsineBX . (844)
Сха 6М
Это условие нетрудно получить, продифференцировав частным
образом (8.43) по р.
* Здесь и в дальнейшем имеется в виду модуль продольной перегрузки,
которая в процессе спуска в атмосфере является отрицательной величиной.
338
Подставив (8.44) в (8.41), получим значение текущей ско-
рости КА в момент достижения максимального значения пере-
грузки аппарата
и*-ивхе*р ( 2 + 2mPskieBX )] (8‘45)
и, использовав (8.42) и (8.45), — величину самой максималь-
ной перегрузки
Psin0Bx Г / сх5мрвх \1
птй =-------«----exp — 14------------»-— . (8.46)
ах 2g0 вх 1 [ \ /npsin0B3: /] 4 7
Если принять, что рвх<Ср* (где р* — значение плотности ат-
мосферы в точке максимума перегрузки), то формулы (8.41),
(8.45) и (8.46) сводятся к выражениям, приведенным в [46], а
именно:
у = увхехр
С~ <5.. О 1
ха М r I.
2т Р sin 0ВХ ]’
v* = vBxe~I/2~0,61 авх;
Пх
a max
Р sin 0ВХ 2
2^о е вх‘
(8.47)
(8.48)
(8.49)
Рис. 8.6. Максимальная перегрузка
при спуске в атмосферах Земли и
Марса
Из полученного выражения следует, что в первом прибли-
жении значение максимальной перегрузки зависит от парамет-
ров входа и параметров атмосферы и не зависит от величины
баллистического параметра. На рис. 8.6 приведена прибли-
женная зависимость максимальной перегрузки от угла входа
при баллистическом спуске в атмосферах Земли и Марса с на-
чальной скоростью, равной
первой космической скорости
для каждой из планет, на вы-
соте /г=100 км. Для расчета
теплового потока и общего ко-
личества поглощенного в про-
цессе баллистического спуска
тепла воспользуемся прибли-
женными соотношениями, при-
веденными в [9], [46].
Тепловой поток (q), в об-
щем случае, является суммой
конвективного теплового пото-
ка и теплового потока от излу-
чения. Тепловой поток от излу-
чения при спуске с орбиты
спутника не превышает 10%
от конвективного и во мно-
гих приближенных вычисле-
339
ниях им можно пренебречь. При увеличении начальной ско-
рости входа КА в атмосферу доля теплового потока из из-
лучения начинает резко увеличиваться [9]. Так, например, для
аппаратов с сильно затупленной носовой частью при ивх =
= 11 км/с тепловой поток от излучения составит ~60%, а при
ивх=13... 14 км/с порядка 90 ...95% от общего теплового пото-
ка. Учитывая только конвективный тепловой поток и считая
обтекание ламинарным, тепловой поток в критической точке
может быть определен по следующей приближенной формуле:
с ( р \п( v \т
^нр = i/р— \ \ ~~К
V ^кр \ Ро / \ I /
где с, т, п —-некоторые постоянные, зависящие от типа тече-
ния в пограничном слое и от кинетических свойств газа; /?Кр —
радиус кривизны носка КА, Vi — значение первой космической
скорости на поверхности планеты.
Обозначив —---------= k,
1/Якр Р”о^
перепишем (8.50) в виде
qK? = kpnvm. (8.51)
Для ламинарного обтекания приближенно можно принять
п= 1|/2. Если считать, что вязкость газа связана с его темпе-
ратурой по закону Т1/2, то значение т можно принять равным
3. Величина с для воздуха меняется в пределах
~(38 . 45)10- (tg»4) .
Выражение для среднего теплового потока имеет вид [44]:
<7ср = ^-4Ру3> (8-52)
где c'F — эквивалентный коэффициент поверхностного трения.
Полное количество поглощенного в процессе спуска тепла
равно
Q = —4S (8.53)
4 t
где S — площадь поверхности КА.
И, наконец, температура в критической точке в соответст-
вии с законом Стефана — Больцмана может быть определена
как
340
где а — постоянная Стефана — Больцмана, а е — коэффици-
ент черноты обшивки КА (берется, обычно, равной 0,9).
Из (8.51) следует, что максимальное значение теплового
потока в критической точке достигается при максимуме произ-
ведения p1/2v3. Подставив в это произведение выражение для
v из (8.41) и продифференцировав его частным образом по р,
получим условие экстремума дКр:
_ т Р sin евх rrx
р о (о. 55)
6С*а
Подставив (8.55) в (8.41), получим значение скорости, при ко-
торой тепловой поток в критической точке достигает своего
максимального значения
у* = v ехр Г — ( -F- + 'j 1 (8.56
вх г l \ 6 2/п р sin 6ВХ / J v
или, считая рВх<Ср*,
v* = 0Bxe-1/6~O,85tiBx. (8.57)
Максимальное значение теплового потока в критической
точке получим, подставив (8.55) и (8.56) в (8.51):
_Г.,з , /~ т 0 sin 0ВХ Г ( 1 , Зсха SM рвх \ 1
?кр max - Ьвх у-------еХР [ ~ + 2«psin0BX ) ] (8-58)
или, использовав приближенное соотношение (8.57),
= (8.59)
j М
Из (8.59) следует, что с увеличением баллистического па-
раметра ох и уменьшением угла входа (по абсолютной вели-
чине) максимальный тепловой поток в критической точке
уменьшается.
Аналогично можно достаточно просто определить средний
тепловой поток по поверхности аппарата и полное количество
поглощенного тепла. Значение Q получим, подставив (8.41) в
(8.53) и проинтегрировав полученное выражение:
О ! fl cxrf \~| /8 60х
Q~ 4 F cXaS^ f1 еХЦ m₽sineBX J]1
Как видно из (8.60), с увеличением баллистического парамет-
ра и угла входа (по абсолютной величине) полное количество
поглощенного тепла уменьшается.
Плотность теплового потока от излучения может быть при-
ближенно оценена по формуле [2]
=7'5-10,1 (—П У*«.»(Вт/мч.
\ Ро / \ 1и. /
341
Таким образом, наряду с тяжелым перегрузочным режимом
баллистический спуск характеризуется и тяжелым тепловым
режимом. Так, при спуске с орбиты ИСЗ максимальная темпе-
ратура на поверхности аппарата составляет порядка 2500...
3000 °C. С увеличением скорости входа максимальные тепло-
вые потоки и температуры значительно увеличиваются.
Все приведенные выше соотношения применимы при доста-
точно больших по абсолютной величине углах входа |0ВХ| ^5°
при входе с первой космической скоростью и |0ВХ| ^9... 10°
при входе со второй космической скоростью.
Для получения приближенных соотношений при достаточно
малых (но не равных нулю) углах входа (при принятых выше
допущениях, кроме (8.37)) сведем первые два уравнения сис-
темы (8.35) к одному уравнению вида
^ + 2_(l-e-3) = 0, (8.61)
j_ Р / т \
^ПЛ \ ^хй *^М Ро /
В работе [35] дано приближенное решение уравнения (8.61)
в виде (считая зт'0Вх~9вх)
f______ / 1 k' \
\ 2 )'
где
k' = —!—.
Р ^пл 0вх
В этом случае перегрузка аппарата будет выражаться фор-
мулой
пХа = — 9вх Z ( 1 — г) ег. (8.62)
Максимальное значение перегрузки равно
На рис. 8.7 приведена зависимость максимальной перегруз-
ки от угла входа при достаточно широком диапазоне измене-
ния баллистического параметра и при различной скорости
входа аппарата в атмосферу, полученная путем численного ин-
тегрирования уравнений движения спускаемого аппарата [9].
Если считать, что при пилотируемом спуске максимально до-
пустимая перегрузка равна 10, то, как видно из рис. 8.7, до-
342
Рис. 8.7. Зависимость максимальной перегрузки от угла входа в атмосферу
Рис. 8.8. Зависимость времени переносимости перегрузки от ее величины и на-
правления:
------нормальные уровни переносимости перегрузки;-----предельный уровень пе-
реносимости перегрузки
пустимый диапазон углов входа составляет от 0 до —(2 ... 2,5)°.
Увеличение по абсолютной величине угла входа приводит к
резкому возрастанию перегрузки. Величина баллистического
параметра определяет высоту точек достижения максимальной
перегрузки. Следует отметить, что при спуске КА с экипажем
необходимо принимать во внимание не только величину пере-
грузки, но и время ее действия. На рис. 8.8 приведены экспе-
риментальные графики зависимости времени (Г) переносимос-
ти перегрузки от величины перегрузки и ее направления ср по
отношению к продольной оси человеческого тела [13].
dt
Величина D — j называется дозой перегрузки. Считает-
ся, что при траектория спуска «комфортна», так как
указанное выше ограничение по перегрузке будет выполняться
в каждой точке траектории.
В заключение настоящего раздела необходимо отметить,
что максимальная перегрузка при баллистическом спуске мо-
жет быть уменьшена, если изменять конфигурацию аппарата
(а тем самым и его аэродинамическое сопротивление) в про-
цессе спуска. Величину аэродинамического сопротивления мож-
но менять с помощью управляемых тормозных щитков, вы-
343
движных игл и т. д. Если потребовать, чтобы в процессе бал-
листического спуска величина перегрузки не превосходила не-
которого заданного значения пхтгх^.пх зад, то на перегрузоч-
ном участке траектории из уравнения (8.36) нетрудно опреде-
лить закон изменения коэффициента лобового сопротивления в
функции высоты и скорости полета. Характер изменения пара-
метров траектории КА с изменяемой конфигурацией будет нес-
колько иным, чем при обычном баллистическом спуске. Поми-
мо регулирования перегрузки в процессе спуска изменяемая
конфигурация КА может быть использована для регулирова-
ния дальности спуска при малых начальных углах входа в ат-
мосферу планеты.
Спуск КА с постоянным значением
аэродинамического качества
Основными недостатками баллистического спуска
КА является наличие больших перегрузок в процессе спуска,
резкое возрастание максимального значения перегрузки при
увеличении углов входа в атмосферу, а также большой раз-
брос точки посадки. Это, в свою очередь, накладывает жесткие
требования к точности начальных параметров входа и пара-
метров системы управления (для баллистических аппаратов с
изменяемой конфигурацией). Ограниченные маневренные воз-
можности КА приводят к усложнению службы обнаружения и
спасения из-за значительных разбросов точки посадки, обус-
ловленных разбросом характеристик аппарата, атмосферы и
ошибок системы управления.
Использование спускаемых аппаратов, обладающих аэроди-
намическим качеством, т. е. способных создавать подъемную
силу в процессе спуска, позволяет снять многие ограничения,
присущие баллистическим спускаемым аппаратам, и значи-
тельно расширить диапазон их применения. Наличие даже не-
большой подъемной силы позволяет значительно снизить пере-
грузки в процессе спуска, а управление подъемной силой —
значительно расширить допустимый коридор входа в атмосфе-
ру. Это, с одной стороны, позволит избежать необходимости
специальной ориентации членов экипажа относительно вектора
перегрузки и приведет к снижению аэродинамического нагрева
аппарата, а с другой стороны, позволит уменьшить требования
к точности начальных параметров входа. Использование подъ-
емной силы в процессе спуска позволит значительно увеличить
маневренные возможности спускаемых аппаратов, что сущест-
венно облегчает выбор места посадки как в продольном, так и
в боковом направлениях.
Рассмотрим некоторые приближенные решения уравнений
движения спускаемого аппарата при наличии подъемной силы.
344
Как показывают результаты численного интегрирования
уравнений движения, при использовании подъемной силы ско-
рость КА вплоть до достижения максимального значения пе-
регрузки меняется незначительно (при спуске с орбиты спут-
ника). В связи с этим в дополнение к допущениям предыдуще-
го раздела примем, что разность между центробежной силой и
силой тяжести мала по сравнению с подъемной силой, т. е.
----G cos0«O. (8.63)
\ ^пл + h /
В этом случае из (8.35) с учетом (8.63) и считая |0 ] малым
(101 ^5°), получим
m 4г = Сиа^1А Роехр $(8-64)
Интегрируя (8.64), будем иметь
Р = Рвх— -7^— (б2—бвх). (8.65)
сУа дМ \ /
Для того чтобы получить формулу для текущей скорости
КА разделим первое уравнение системы (8.35) на второе и
проинтегрируем получаемое выражение:
v = ехр Г — 9~--1, (8.66)
L Д -I
где K = cUalcXa-
Из (8.66)
8 = 9вх + Я1п^- (8.67)
Выражение для суммарной перегрузки в процессе спуска
можно записать следующим образом:
п = ъа3мРУ2 1/1 -1-7(2 = £« р 1)2/1 +7(2. (8.68)
2G 2
Из (8.68) следует, что максимум п соответствует максиму-
му ро2. Определим значение 0, при котором ро2 достигает мак-
симального значения. Для этого продифференцируем частным
образом выражение для ро2, полученное из (8.65) и (8.66), по
углу 0. Условие экстремума имеет вид
02 — 7(0 — 02 = 0. (8.69)
Откуда
0’- Т±1^“Г+0“-
(8.70)
345
Тогда
* Pzn/^_l_l/'^C2|n2 \ ,
Р Рвх “7 ё I ~Т~ 1/ ~ H“0BX 0BX I X
с»а6М \ 2 V 4 /
x(f ± V +eB2x+0BJ
\ 2 F 4 /
и
(8.71)
Если считать |0ВХ| достаточно малым, а аэродинамическое
качество аппарата достаточно большим, то (8.69) можно при-
ближенно записать в виде
0(0_7<)^О.
(8.73)
Из (8.73) следует, что приближенными условиями экстремума
п можно считать
0* = О; (8.74)
0* = К. (8.75)
Проанализируем полученные условия.
Условие 0* = О может быть выполнено только при сУа > 0,
что следует из второго уравнения системы (8.35). В этом слу-
чае траектория спускаемого аппарата имеет точку, в которой
вектор скорости КА направлен по местному горизонту. При
дальнейшем движении КА угол 0 становится положительным
и аппарат начинает увеличивать высоту полета (рикошетирую-
щий спуск аппарата). Подставив (8.74) в (8.65), получим ус-
ловие рикошетирования аппарата
СУд ____ ^вх Р
™ р* — рвх
(8.76)
где р* значение р при 0 = 0.
Используя условие (8.74) и формулы (8.65) и (8.66), вы-
ражение для максимальной суммарной перегрузки можно за-
писать следующим образом:
«max = ^^/Т+^(рвх+ /т 0вх ) еХР Г 1 ’ (8<77)
2 к иу g / L л J
где о = Сха . о - CVa Sm .
где их » иу —
Если в (8.77) положить рвх ~0, то формула примет вид
»iA2, />+ А <*Р [*>]• (8-78)
346
Анализ (8.78) показывает, что при достаточно больших К
(К>2||0ВХ|) с увеличением аэродинамического качества КА
его максимальная суммарная перегрузка уменьшается.
Условие 0* = К выполняется при сУа<.0. Отрицательная ве-
личина подъемной силы приводит к росту крутизны траекто-
рии. В этом случае 0 всегда отрицательна. Выражение для пШах
запишется в виде
п^„=- i у (№-еу exp [- А (Л^в„) ].
(8.79)
Для случая |0вх|СЛ
Птах = - -Ц ^вх К /Т+Т2 • (8.80)
2 g е2 вх
Из (8.80) следует, что увеличение абсолютной величины
аэродинамического качества (при^д<; приводит к уве-
личению максимального значения суммарной перегрузки.
До сих пор рассматривались случаи спуска с малыми на-
чальными углами входа.
Рассмотрим случаи, когда начальные углы входа достаточно
велики (5°^ 10вх | г^90°). Как показывают результаты числен-
ного интегрирования, п хорошо совпадает с точным решением
от нуля до первого максимума при 2 и |0ВХ| J>4,5... 5°.
В этом случае первый максимум перегрузки характеризует аб-
солютный максимум.
Очевидно,
^р ^Р dh di , q oi\
~dQ~ ~ ~dh ~dt~ d& ' \ )
HO
^-=-рРое-рА =-0p. (8.82)
an
Используя (8.82) и (8.35), получим:
dp =-----2?pSin6 dQ (8.83)
Д Cxu '->M
Интегрируя (8.83), будем иметь (считая рвх«0)
Р = кгЧг <cos 0bx-cos 0) (8.84)
ДСзса 15 И
или после подстановки (8.67)
Р = [cos 0BI—cos (бВ1 + К In )] . (8.85)
347
Продифференцируем (8.68) по скорости и приравняем нулю
2р + о-^- =0. (8.86)
dv
Из (8.86) нетрудно получить значение скорости КА и*, при
которой полная перегрузка аппарата достигает своего макси-
мального значения. Подставив полученное значение и* в (8.85),
получим значение р* и далее выражение для максимальной
полной перегрузки.
Следует отметить, что при больших начальных углах входа
(|0вх|^20°) увеличение качества аппарата приводит к увели-
чению Птах. Это объясняется сильным возрастанием боковой
составляющей полной перегрузки.
Таким образом, для снижения максимального значения пол-
ной перегрузки увеличение аэродинамического качества аппа-
рата при спуске с орбиты спутника можно использовать только
при малых углах входа в атмосферу, причем наибольший эф-
фект дает увеличение аэродинамического качества в пределах
до А—1,0. Дальнейшее увеличение аэродинамического качества
аппарата с этой точки зрения малоэффективно.
Влияние аэродинамического качества аппарата на макси-
мальную полную перегрузку при спуске с орбиты спутника по-
казано на рис. 8.9.
Особенностью траекторий спуска КА при постоянном каче-
стве является их колебательный характер (рис. 8.10). Траек-
тории проходят около траектории равновесного планирования,
на которой аэродинамическая подъемная сила уравновешивает
центробежную силу и силу тяжести.
Рис. 8.9. Зависимость максимальной
перегрузки от угла входа при спуске
аппарата с постоянным аэродинами-
ческим качеством в атмосфере Земли
Рис. 8.10. Зависимость основных па-
раметров движения СА от времени
при спуске с орбиты ИСЗ с постоян-
ным аэродинамическим качеством
348
Частота и амплитуда колебаний зависят от параметров вхо-
да и величины аэродинамического качества аппарата.
Приближенные выражения для дальности спуска, угла на-
клона вектора скорости к местному горизонту и высоты поле-
та при спуеке в плоскости большого круга с малыми углами
наклона могут быть записаны следующим образом [46]:
L = К In
2
-
ёо ^ПЛ
6 = arcsin
2 §0 ^пл \ .
РЯплЯ /
/ \
. 2^0 1 — ——
* _____\_____So °пл /
₽ К CXaSM t,2po
т
(8.87)
(8.88)
(8.89)
Использование аппаратов с
аэродинамическим качеством
позволяет значительно увели-
чить дальность спуска в атмо-
сфере по сравнению с балли-
стическим спуском. На рис.
8.11 приведена зависимость
дальности спуска в атмосфере
Земли от качества аппарата
при различных начальных уг-
лах входа, полученная числен-
ным интегрированием уравне-
ний движения [9]. Из рис.
8.11 следует, что даже малое
аэродинамическое качество ап-
парата позволяет в несколько
раз увеличить дальность спу-
ска по сравнению с дальностью
баллистического снижения.
Значение теплового потока в
Рис. 8.11. Зависимость дальности спу-
ска от точки входа до точки посадки
от аэродинамического качества аппа-
рата и угла входа
критической точке при малых
начальных углах входа найдем, подставив (8.65) и (8.66) в
(8.51)
-8.4 ]',г ехР [- . <8.90
349
Тепловой поток достигает максимального значения в момент
достижения максимума выражения p1/2w3. Продифференциро^
вав частным образом это выражение по 0, получим условие
экстремума
02-V-0B2x = O ^-91)
о
или, считая 10вх | малым,
0 = 0; (8.92)
0= -у . (8.93)
Условие (8.92) соответствует условию полета с сУа > 0,
(8.93) — условию полета с ^а<0.
Подставив (8.92) в (8.90) (и считая рвх~0), получим мак-
симальное значение теплового потока при полете по рикошети-
рующей траектории
<7кр max = k v3x 10ВХI (V/2 еХр . (8.94)
Таким образом, при спуске по рикошетирующей траектории
максимум теплового потока имеет место в момент максимума
перегрузки, т. е. в нижней точке рикошета.
Аналогично можно получить выражение для максимального
значения теплового потока в критической точке для случая
спуска с сУа < 0
(8.95)
При достаточно большом значении качества аппарата и
малом угле входа в атмосферу выражение (8.95) можно при-
ближенно записать следующим образом:
дНртах^Ьзх (_^_у/2е->. (8.96)
Из уравнения (8.96) следует, что в случае спуска с отри-
цательным значением качества максимальный тепловой поток
в критической точке в первом приближении не зависит от уг-
ла входа и увеличивается с увеличением по абсолютной вели-
чине аэродинамического качества аппарата. Общее количество
поглощенного тепла больше, чем при баллистическом спуске,
из-за увеличения общего времени спуска.
Спуск КА с переменным аэродинамическим качеством
Аэродинамическое качество космического аппарата
в процессе спуска может быть изменено непрерывно или ре-
лейно и для этого существует несколько способов:
350
1) изменение угла атаки КА. При этом меняется (в соот-
ветствии с полярой аппарата) как коэффициент подъемной си-
лы, так и коэффициент лобового сопротивления;
2) разворот аппарата по крену. Аппарат, сбалансированный
на некотором угле атаки, разворачивается по крену вокруг
вектора скорости с помощью аэродинамических или реактив-
ных сил, что приводит к изменению вертикальной составляю-
щей подъемной силы. При этом коэффициент лобового сопро-
тивления не изменяется;
3) изменение коэффициента лобового сопротивления при
постоянном коэффициенте подъемной силы (щитки, выдвиж-
ные иглы и т. д.);
4) комбинация вышеизложенных способов.
Регулирование качества в процессе спуска позволяет обес-
печить спуск с приемлемыми аэродинамическими и тепловыми
нагрузками, еще более снизить максимальные значения пере-
грузок и расширить коридор входа по сравнению со спуском
с постоянным аэродинамическим качеством.
Для того чтобы оценить преимущества, связанные с регули-
рованием качества, рассмотрим случай ступенчатого регулиро-
вания качества аппарата. Особый интерес представляет отноше-
ние п*2М*ь где n*i является максимальной величиной суммарной
перегрузки в случае, когда качество аппарата в процессе спуска
не изменяется.
Используя приближенные соотношения, полученные выше,
для параметров движения аппарата при спуске с постоянным
качеством можно записать
где 0*1— угол наклона траектории в точке, где перегрузка до-
стигает максимального значения, если бы качество аппарата в
процессе спуска не изменялось; 0*2— угол наклона траектории
в точке максимальной перегрузки после изменения качества ап-
парата; 01 — угол наклона траектории в момент изменения ка-
чества аппарата.
Значение 01 можно однозначно определить из уравнения
(8.98), если предположить, что максимальная перегрузка пос-
ле изменения аэродинамического качества аппарата равна пе-
регрузке в момент изменения качества.
Имеем
351
Если допустить, что
то
’ 4 02
VBX
К1Ка
4 — к3) ef
о?
и (8.97) примет вид
п2
*
"1
(8.99)
(8.100)
(8.101)
*1 :
< 1,
В качестве примера рассмотрим следующий случай:
0вх = —5°, Ki = 2,0, /<2 = 0,5. Тогда из (8.99) 0*1 ~—0,22° и из
(8.100) 0*2 ^ — (0,0038+1,5 00.
Величину 01 можно определить из (8.98). Получим 0i~
2,26°. Окончательно из (8.101) находим п*2//г*1~ 0,825.
Можно ожидать, что двукратное изменение аэродинамиче-
ского качества КА будет уменьшать максимальную перегрузку
еще в большей степени, а при непрерывном регулировании ве-
личины качества уменьшение величины максимальной перегруз-
ки будет максимальным.
На рис. 8.12 приведен график эффективности использования
регулируемой переменной подъемной силы аппарата в функ-
ции его располагаемого аэродинамического качества, получен-
ный по результатам работы ([46].
Таким образом, при использовании непрерывного изменения
качества аппарата в процессе спуска допустимое значение угла
входа при заданной величине максимальной перегрузки по аб-
солютной величине увеличи-
вается или, наоборот, макси-
мальная перегрузка при за-
данном угле входа уменьша-
ется. В общем случае при
спуске в атмосфере планеты
с переменным качеством до
настоящего времени не полу-
чены в общем случае точные
аналитические решения, по-
зволяющие определить пара-
метры движения аппарата в
процессе спуска. Однако
имеется целый ряд работ, в
Рис. 8.12. Эффективность регулирования
аэродинамического качества спускаемо-
го аппарата
352
которых приведены приближенные аналитические решения и да-
ны оценки этим решениям по сравнению с численным интегри-
рованием уравнений движения с произвольным законом измене-
ния качества аппарата [1, 68].
Рассмотрим некоторые типовые режимы движения спускае-
мых аппаратов, требующие для их реализации изменения аэро-
динамического качества в процессе спуска.
Равновесное планирование
Рассмотрим спуск космического аппарата в режиме
равновесного планирования. В этом случае в каждый момент
времени выполняется условие:
— SM + f —----------g') cos e = 0, (8.102)
Уа 2 m K \ Rnjl + h *}
что соответствует полету с постоянным углом наклона траекто-
рии 9.
Из (8.102) нетрудно определить программное значение ко-
эффициента подъемной силы, при котором существует баланс
между подъемной, центробежной и силой тяжести спускаемого
аппарата
б: / г 9
2т 1 .
Су Q /П . «V I COS 1
Спуск космического аппарата в режиме равновесного плани-
рования предложен впервые Ю. В. Кондратюком {31] и доста-
точно подробно исследован в работах [35, 46].
Выражения для текущих значений скорости, плотности, мак-
симальной перегрузки и теплового потока в критической точке
можно записать следующим образом ;[35]:
v = vBX ехр (Р ~ Рвх) ~] 2 tn р sin 0 J ’ (8.104)
Р = Рвх Н- 2 tn Р sin 0 ! v с s 1п ; ха увх (8.105)
^тах г « —174 sin 0вх; (8.106)
9„=г(2-^в|п^У'%-. \ с*а г'вх / (8.107)
Изоперегрузочные траектории спуска
Подобного типа траектории дают возможность наи-
более рационально избавиться от того запаса кинетической
энергии, которым обладал космический аппарат при входе в
12—8 353
атмосферу. При рассмотрении изоперегрузочных траекторий бу-
дем считать, что полет происходит с регулированием аэродина-
мического качества аппарата при неизменном коэффициенте
лобового сопротивления (т. е. вх = const). Будем рассматривать
только малые по модулю углы наклона вектора скорости к
местному горизонту. Тогда можно принять:
пХа sin в; sin 9 — 0; cos i0~l.
Кроме того, будем считать атмосферу планеты — изотерми-
ческой и + — /?пл.
Дифференцируя уравнение для плотности изотермической
атмосферы по высоте, получим
dp/dft = Pp. ' (8.108)
Из первого уравнения системы (8.35) с учетом вышеуказан-
ных допущений будем иметь
,. 2 G dv
dt — п о •
gp«2^asM
Используя (8.108), получим
(8.109)
Продифференцируем (8.109) по скорости аппарата и подста-
вим полученное выражение во второе уравнение системы (8.35).
Используя первое уравнение системы (8.35), можно найти
Vй Ох g Р / d2 р , d р \ р v2 , V2
---------- и —- Н------------ J = g — а„ Н----------------
4? \ dva dv 2 у R„n
Из первого уравнения системы (8.35) имеем
2 пх
Р = Т-5' , = const.
r V2 ох Ха
Дифференцируя (8.111) дважды по v и подставив
ные выражения в (8.110), получим
(8.110)
(8.111)
получен-
к _ 1 „ &
А--------g---------
пха § \ ^пл
4g2 <
ла
(8.112)
Таким образом, для полета по изоперегрузочной траектории
необходимо регулировать качество аппарата в соответствии с
(8.112). При этом интересно отметить, что потребное качество
КА не зависит прямо от а связано с ох через скорость аппа-
рата.
Определим максимальное требуемое качество КА, необходи-
мое для полета по изоперегрузочной траектории. Условие экст-
ремума качества
dK!dv = Q.
354
Рис. 8.13. Зависимость, требуемого
аэродинамического качества КА от
скорости спуска:
4, 6, 10 — величины перегрузок
Из этого условия нетрудно
получить
1 f 4 пха S2 Япл
max |/ о
(8.113)
Подставив (8.113) в (8.112),
получим
^тр шах — ~ ~|/р"" ft ’ (8-114)
Пха V /?пл Р
На рис. 8.13 приведена зависимость требуемого качества КА
от скорости спуска при различных ограниченных значениях про-
дольной перегрузки (спуск в атмосфере Земли). Как видно из
графика, при скорости, большей первой космической, с увели-
чением ограничения по перегрузке требуемое качество КА
уменьшается по абсолютной величине, причем требуемое каче-
ство отрицательно. Этот же вывод вытекает из работ [30, 55].
Участок траектории с ограничивается двумя положитель-
ными корнями уравнения
1
пха§
Рис. 8.14. Зависимость макси-
мального требуемого аэродина-
мического качества КЛА от
максимальной перегрузки
12°*
S *пл 7
Решая это уравнение, получим
1/ D а \/ #пл£2 4«МЛЛ
vK=o=V ± |/ --------------- • (8.115)
При пХа> ]/р/?пл подкоренное выражение второго корня
получается отрицательным, т. е. полет происходит с отрицатель-
ным качеством. При спуске в атмосферах Земли и Венеры это
значение пХа равно 6 ... 7,5, для Марса ~ 1,35.
На рис. 8.14 приведена зависимость максимального требуе-
мого аэродинамического качества аппарата от перегрузки (для
Земли) при спуске в атмосферах Земли, Венеры, Марса и Юпи-
тера. Как видно из графика, при посадке аппарата на поверх-
ность Земли и Венеры с перегрузками, не превышающими 4—5,
необходимо иметь максимальное аэродинамическое качество
КА порядка 0,1... 0,15, для Юпитера — 0,5 ... 0,6. Посадка на
Марс может быть произведена аппаратом с довольно малым
качеством
ГЛАВА у. СПУСК КОСМИЧЕСКОГО АППАРАТА
С МЕЖПЛАНЕТНОЙ ОРБИТЫ
В настоящее время проблему возвращения СА с орбиты спутника Земли
для аппаратов однбразбвого использования можно считать, в основном, ре-
шенной. Многочисленные теоретические исследования советских и зарубеж-
ных ученых, а также целый ряд экспериментальных данных показывают, что
спуск с орбиты ИСЗ может быть произведен в широком диапазоне начальных
условий с приемлемыми перегрузочными и тепловыми нагрузками в процессе
спуска как при баллистическом спуске, так и при спуске с использованием
аэродинамического качества аппарата.
9.1. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ
При возвращении от Луны скорость входа СА в ат-
мосферу Земли близка ко второй космической скорости. При
этом приходится сталкиваться с теми же проблемами и трудно-
стями, что и при спуске с орбиты спутника. Однако эти пробле-
мы значительно усложняются как с точки зрения обеспечения
приемлемых перегрузочных и тепловых режимов спуска, так и,
особенно, с точки зрения точности наведения аппарата. Неточ-
ное определение параметров движения аппарата на внеатмо-
сферном участке, а следовательно, неточное корректирование
его траектории, может привести к появлению чрезмерно боль-
ших перегрузок и тепловых потоков в процессе спуска или к не-
захвату аппарата атмосферой. Именно эти условия определяют
границы коридора входа аппарата в атмосферу.
Исследованию коридоров входа КА в атмосферу посвящено
значительное количество работ, так как ширина коридора вхо-
да является одной из важнейших характеристик космического
комплекса. Границы рабочего коридора зависят как от аэро-
динамических характеристик аппарата, так и от способа ис-
пользования располагаемого аэродинамического качества СА
на начальном участке погружения. В работе [6] достаточно по-
дробно исследованы коридоры входа КА в атмосферу Земли при
использовании численного интегрирования уравнений движе-
ния аппарата. В [69] приведены приближенные аналитические
зависимости для расчета ширины коридора входа. Величина ра-
бочего коридора входа определяется в основном допустимой пе-
13—8 357
регрузкой и резко уменьшается с увеличением скорости входа
Уменьшение величины подлетного коридора входа приводит к
необходимости увеличения точности работы систем навигации и
коррекции на подлетном участке траектории. При скоростях
входа более 17 км/с управление только по углу крена (у-управ-
ление) при подлетных коридорах входа порядка ±6... ±8 км
практически невозможно [9] (более подробно коридоры входа
анализируются в разд. 9.3).
Возвращение к Земле со скоростями, значительно превы-
шающими вторую космическую скорость, будет представлять
заключительный этап полета к планетам IMapc и Венера. На-
пример, при перелете Земля — Марс — Земля при общей про-
должительности полета 400 ... 500 сут скорость входа СА в ат-
мосферу Земли составляет порядка 20 км/с 1[60]. Если осущест-
влять перелет к Марсу по траектории, близкой к эллипсу Хома-
на — Цандера, то продолжительность полета составляет около
250 сут, при этом время ожидания у Марса составляет около
450 сут, т. е. общее время перелета составит порядка 950 сут.
Уменьшить общую продолжительность перелета можно путем
использования перелета по так называемым быстрым эллипсам.
При этом общая продолжительность полета составит около 500
земных суток. Скорость входа в атмосферу в этом случае будет
больше, так как вектор скорости КА и вектор орбитальной ско-
рости Земли не коллинеарны в момент встречи.
На рис. 9.1 приведена скорость входа КА в атмосферу Зем-
ли для рассмотренных типов перелетов. Минимальная скорость
входа (~12,5 км/с) соответствует продолжительности полета
по траектории, близкой к эллипсу Хомана — Цандера. Имеется
локальный минимум скорости входа при продолжительности по-
лета около 350 сут. Приведенные выше цифровые результаты
Рис. 9.1. Зависимость скорости входа
КА в атмосферу Земли от суммарной
продолжительности полета к Марсу
применимы только для КА с
ограниченными возможностями
силовых установок. Если же
силовая установка имеет боль-
шие энергетические возможно-
сти, то скорость входа можно
значительно уменьшить, ис-
пользуя торможение КА при
подходе к Земле.
Необходимо заметить, что
нынешнее поколение космиче-
ских кораблей и спускаемых
аппаратов обладает ограничен-
ными возможностями, явно не-
достаточными для решения
этой более сложной задачи.
Системы управления, основан-
358
ные на использовании у-управления, не могут обеспечить спуск
в пределах очень узкого* коридора, соответствующего большим
гиперболическим скоростям входа.
Одной из характерных особенностей возвращения СА с ги-
перболическими скоростями является необходимость высокой на-
дежности технической реализации узкого диапазона условий вхо-
да в атмосферу, обеспечивающих безопасное возвращение аппа-
рата на Землю. Кроме того, значительная протяженность участ-
ка полета в атмосфере вызывает длительное воздействие на эки-
паж корабля значительной перегрузки, ограничиваемое предела-
ми физиологической переносимости.
Исследованию динамики движения СА и его системы управ-
ления спуском (СУС) при гиперболических скоростях входа по-
священо гораздо меньшее количество работ. Из наиболее сущест-
венных необходимо отметить ^6, 15, 16, 17, 18, 25, 30 и др.]. В
настоящее время нет еще полной ясности в вопросе о наиболее
вероятном диапазоне скоростей входа при возвращении от пла-
нет Солнечной системы; о схеме спуска (спуск по «коротким»
или «протяженным» траекториям); о форме СА и количестве уп-
равляющих параметров; о перегрузочных режимах траекторий
спуска и т. д. Однако можно утверждать, что трудности, имею-
щие место при спуске с параболической скоростью, при спуске с
гиперболическими скоростями значительно усугубляются: значи-
тельно увеличивается унос теплозащитного покрытия (ТЗП), что
приводит к изменению аэродинамических характеристик СА и
ухудшению динамических режимов спуска; резко увеличивается
влияние возмущающих факторов (в частности, атмосферных воз-
мущений) на траектории спуска, увеличивается влияние движе-
ния СА относительно центра масс на продольное движение аппа-
рата; резко возрастают перегрузки в процессе спуска, что приво-
дит к невозможности использования в аварийной ситуации ре-
жима баллистического спуска; в значительной степени возраста-
ет необходимость обеспечения «комфортности» траекторий с точ-
ки зрения минимизации дозы перегрузки в процессе спуска; уве-
личиваются требования к точности работы СУС и т. д.
Эти особенности определяют содержание технических трудно-
стей, которые необходимо преодолеть при разработке СА, вхо-
дящих в атмосферу с гиперболическими скоростями.
Существует несколько способов разрешения этих трудностей,
позволяющих существенно упростить задачу обеспечения входа
СА в атмосферу Земли. Рассмотрим некоторые из них.
1. Уменьшение начальной скорости входа СА в атмосферу пу-
тем торможения аппарата двигателем на внеатмосферном участ-
ке до скоростей порядка первой космической.
С одной стороны, этот способ позволяет значительно расши-
рить коридор входа, однако, с другой, — приводит к увеличению
продолжительности полета, которое при реально возможных в
13* 359
обозримом будущем сравнительно небольших тяговооруженно-
стях космических кораблей будет довольно значительным. Кро-
ме того, этот способ для существующих двигательных устано-
вок приводит к необходимости больших затрат топлива на тор-
можение. Сколько-нибудь реальным этот способ может считать-
ся, по-видимому, лишь при использовании новых источников
энергии (например, ядерных). Возможно использование для
торможения КА атмосферы планеты.
2. Увеличение располагаемого аэродинамического качества
СА для расширения коридора входа. Однако увеличение каче-
ства СА свыше 1,0... 1,2 с точки зрения расширения рабочего
коридора входа становится малоэффективным ;[2] и, кроме то-
го, может привести к существенному увеличению массы его теп-
лозащитного покрытия.
3. Разработка систем управления движением СА, наиболее
рационально использующих его аэродинамические характерис-
тики при сравнительно небольших значениях располагаемого
аэродинамического качества аппарата.
Перспективным, по-видимому, является использование всех
перечисленных выше способов при их рациональном сочетании.
В зависимости от дальности полета по поверхности Земли
от точки входа до точки посадки (Асп) различают два типа тра-
екторий спуска: 1) короткие траектории с дальностью полета в
пределах ~4000 км; 2) протяженные траектории с дальностью
полета более 4000 км.
Короткие траектории реализуются при прямом спуске, ког-
да аппарат, погрузившись в атмосферу, не покидает ее вплоть
до точки посадки.
Протяженные траектории, особенно для аппаратов с малым
располагаемым аэродинамическим качеством, реализуются при
спуске с однократным или многократным прохождением атмо-
сферы планеты. При однократном прохождении атмосферы
(рис. 9.2) КА после кратковременного погружения в атмосферу,
погасив скорость до круговой,
Условная граница. атмосфера * \ \\ \ / / / X \\ \/ 5 ( выходит из плотных слоев, движется по эллиптической траектории вне атмосферы, за- 1 тем опять погружается в ат- 1 мосферу и совершает посадку ' (типичный спуск по протяжен- ной траектории при возвра- Рис. 9.2. Траектория спуска с одно- кратным прохождением атмосферы планеты
360
щении от Луны). В этом случае на траектории различают три
участка спуска:
а) участок первого погружения (/—2— первый участок);
б) участок полета вне атмосферы или в сильно разрежен-
ных слоях (2—3 — второй участок);.
в) участок второго погружения в атмосферу и посадка в за-
данном районе (3—4— третий участок).
Дальность полета и рассеивание в точке посадки зависит в
основном от первого участка, так как параметры движения КА
на втором и третьем участках зависят от параметров движения
КА в точке 2 на выходе из атмосферы (уВых, 0Вых). Даже ма-
лые погрешности в уВЬ1х и 0ВЫх приводят к большому промаху по
дальности (ошибки Д^Вых=1 м/с и А0Вых=1/ дают промах в не-
сколько десятков километров).
На третьем участке спуска можно скомпенсировать ошибки,
накопившиеся на первых двух участках, однако основное уп-
равление спуском должно производиться на первом участке.
9.2. ВЫХОД АППАРАТА НА ОРБИТУ
СПУТНИКА ПЛАНЕТЫ
В общем случае выход КА на орбиту спутника плане-
ты при подходе к планете с начальной сверхорбитальной ско-
ростью может быть обеспечен следующими способами:
1) уменьшением скорости КА до орбитальной с помощью
тормозных ракетных двигателей;
2) использованием для торможения КА атмосферы планеты;
3) комбинированным методом.
Основными преимуществами первого способа являются воз-
можность осуществить не только выход на орбиту спутника
планеты, но и посадку на планету, не обладающую плотной ат-
мосферой, а также возможность достаточно точного регулиро-
вания текущей скорости КА при подходе к планете. Основным
(и пожалуй самым крупным) недостатком является необходи-
мость затрат большого количества топлива для торможения.
Это количество топлива может быть приближенно определено
по формуле К. Э. Циолковского. На рис. 9.3 приведена зависи-
мость относительной массы топлива от декремента скорости КА
при различных значениях скорости истечения (£РУД). Как вид-
но из графика, для того чтобы снизить скорость КА со второй
до первой космической скорости,х необходимо затратить такое
количество топлива, которое составляет по массе 60 ...80% от
начальной массы КА. ’В связи с этим большой практический ин-
терес представляет использование для торможения КА атмо-
сферы планеты. Торможение КА в атмосфере при подходе к
планете с начальной сверхорбитальной скоростью довольно
сложно, однако позволяет добиться значительного увеличения
361
Рис. 9.3. Зависимости относительной
массы топлива для торможения КА от
декремента скорости
Условная
~ граница
атмосферы
Рис. 9.4. Схема спуска КА с мно-
гократным торможением в атмо
сфере планеты
^Подлетная
траектория КА
^Заданная ордиьт
спутника
массы полезного груза КА, так как отпадает необходимость за-
траты топлива на торможение. Основным недостатком этого
способа является большое время торможения, а тем са-
мым и длительное время пребывания в возможных радиацион-
ных поясах около планеты, что требует принятия соответствую-
щих мер для радиационной защиты экипажа КА.
Схему многократного торможения КА в атмосфере можно
представить следующим образом (рис. 9.4): КА входит в ат-
мосферу планеты с начальной сверхорбитальной скоростью и с
начальным углом входа, меньшим по абсолютной величине
верхней границы коридора входа, многократно тормо-
зится в атмосфере, двигаясь по тормозным эллипсам, после че-
го либо выходит на орбиту спутника планеты, либо осуществля-
ет прямой спуск в атмосферу. При переходе на заданную орби-
ту спутника необходим дополнительный импульс скорости. В
{26] показано, что минимум импульса скорости, требуемого для
перехода, получается в момент касания тормозным эллипсом
заданной круговой орбиты в апоастре. Ниже приведены некото-
рые результаты данной работы. Вводятся следующие допуще-
ния:
1. Гравитационное поле планеты центральное и движение
КА происходит в плоскости заданной круговой орбиты высо-
той /г0.
2. Считается, что атмосферный участок значительно меньше
длины одного витка, поэтому траектория КА на каждом витке
принимается эллиптической.
362
В соответствии с рис. 9.4 за ДУ обозначим импульс скоро-
сти, необходимый для перехода с эллиптической орбиты на
круговую высотой h0, т. е.
ДУ=У— Уор (9.1)
или
Д V= И2 + У2ор—2УУор cos 0. (9.2)
На основании интегралов энергии и момента количества
движения можно записать:
ДУ2 = 1/2 [3—2 ]//------(1--.е2) ^р] , (9.3)
°р L > яор р J ' 1
. , Ц£пл Rпл
где Уоо ~ ; е— эксцентриситет эллиптической ор-
1 / 1 г
V 1 "Г О
Апл
биты; р — параметр эллиптической орбиты; £Пл — ускорение си-
лы тяжести на поверхности планеты с радиусом /?Пл.
Обозначим
Р
Яор(1 + 0 ’
тогда
1 — е
дР = 1/2р 3-2У^п(\ + е)
(9-4)
R
л
Так как и мало меняется в процессе торможения,
то можно считать, что R*n = const. Из (9.4) получим
д (А V2) = г Д_
де opU;
(9-5)
Из (9.5) следует, что минимум ДУ2 достигается при макси-
мально допустимом е, а так как /?я; = а(1—е), то при минималь-
но допустимом значении большой полуоси эллиптической орби-
ты а. Это имеет место в момент касания эллиптической орби-
ты в апоцентре заданной круговой орбиты спутника планеты
Минимальное значение ДУ можно определить по следующей
формуле:
(9-6)
363
где hn — высоты перицентров эллиптических орбит над поверх-
ностью планеты.
/i
Так как 1, то
^пл
(9-7)
Уравнение (9.7) можно переписать следующим образом:
"И^пл ^пл
(9.8)
A ^mln
мый для выхода на круговую орби-
ту высотой h0
На рис. 9.5 приведена зави-
симость AVmin от ВЫСОТЫ КругО-
вой орбиты ho для Венеры,
Земли, Марса и Юпитера.
Таким образом,практически
для всех орбит искусственных
спутников указанных планет
величина импульса скорости,
потребного для выхода на кру-
говую орбиту, в несколько раз
меньше величины характери-
стических скоростей, потребных
для торможения КА с помощью
двигательной установки. Это
объясняется тем, что часть ки-
нетической энергии КА рассеи-
вается в момент его прохожде-
ния через атмосферу планеты.
9.3. КОРИДОРЫ ВХОДА
При входе космического аппарата в атмосферу пла-
неты с начальной сверхорбитальной скоростью приходится
сталкиваться с теми же проблемами, что и при спуске с орбиты
спутника, однако эти проблемы значительно усложняются как
с точки зрения обеспечения приемлемых перегрузочных и теп-
ловых режимов спуска, так и, особенно, с точки зрения точно-
сти наведения аппарата. Как уже указывалось ранее, неточное
определение параметров движения аппарата на внеатмос-
ферном участке, а тем самым и неточное корректирование его
траектории может привести к появлению чрезмерно больших
перегрузок в процессе спуска (большие углы входа) или к вы-
364
ходу аппарата из атмо-
сферы планеты (слишком
малые углы входа). Та-
ким образом, возникает
задача об определении
возможного диапазона
изменения начальных па-
раметров движения аппа-
рата при входе в атмосфе-
ру, при которых осущест-
вляется захват аппарата рис gg Фиктивная кеплерова траектория
атмосферой и перегруз- аппарата
ки (или тепловые потоки)
в процессе спуска не превосходят некоторой допустимой ве-
личины.
При спуске аппарата с орбиты спутника за начальные пара-
метры входа обычно принимаются значения угла входа и ско-
рости входа на некоторой высоте, которую считают «условной
границей атмосферы» (обычно это высота порядка 100... 120 км
для Земли). В случае очень пологой траектории входа понятие
угла входа становится довольно неопределенным. В связи с
этим, как показано в [9], угол входа удобнее задавать через па-
раметр, зависящий от высоты расположения перигея фиктив-
ной кеплеровой траектории, по которой двигался бы аппарат,
если бы планета была лишена атмосферы (рис. 9.6). Параметр
перигея определяется через параметры аппарата и значение
плотности в точке фиктивного перигея следующим образом:
. _ Рр Сха$М ~| / Rp
р 2т У Р
(9-9)
Высота условного перигея (йл) связана с начальными па-
раметрами входа следующим приближенным соотношением
[9]:
^вх —At _ Ах евх , (9.10)
^пл + ^вх 1)
где, как обычно,
у =_____Ив*.
Т/^пл ^пл
Понятие о «фиктивном перигее» удобно использовать для
определения границ коридора входа. Шириной коридора входа
называется разность фиктивных перигеев двух граничных тра-
екторий входа, из которых нижняя определяется допустимой
величиной максимальной перегрузки (или теплового потока), а
верхняя условием захвата аппарата атмосферой, т. е. условием
365
получения на выходе из атмосферы скорости аппарата, не пре-
вышающей круговой на данной высоте-.
Л ^ЛН' (9-11)
Придерживаясь терминологии работы «[9], будем разли-
чать следующие характерные типы коридоров входа:
Подлетный коридор входа, определяемый точностью работы
систем навигации и коррекции на подлетном участке траекто-
рии, что позволяет сформулировать требования к проектно-бал-
листическим характеристикам СА.
Теоретический коридор входа, определяемый максимальным
значением располагаемого аэродинамического качества аппара-
та (Ашах). Верхняя граница такого коридора соответствует по-
лету СА с —/Стах, а НИЖНЯЯ с “И/Стах-
Предельный коридор входа, соответствующий выбранной
системе управления СА при идеальной работе и отсутствии
внешних возмущений, действующих на СА в процессе спуска.
Для СА с малым значением располагаемого аэродинамическо-
го качества и скоростях входа, близких к параболической, пре-
дельный коридор входа совпадает с теоретическим.
Рабочий коридор входа, соответствующий реальной работе
системы управления, при учете всех ограничений и наличии
возмущающих факторов, действующих на СА в полете. Рабочий
коридор входа составляет часть предельного коридора.
Указанные коридоры входа в зависимости от располагаемо-
го качества аппарата при различных значениях максимально
допустимой перегрузки приведены в работе ![6].
В [69] приводится следующее выражение для определения
ширины коридора входа
Р (Fp пг/сХа 5М)В
(9.12)
или при одинаковом значении величины mlcxS для граничных
траекторий
дЛя 1 In^s-. (9.13)
Р FPB
В табл. 9.1 приведены значения коридоров входа в атмо-
сферы планет при баллистическом спуске космического аппара-
та (Увх= 1,4; /С=0).
Если в процессе баллистического спуска аппарата имеется
возможность регулировать величину его лобового сопротивле-
ния, то ширина коридора входа увеличивается. Величину рас-
ширения коридора входа можно приближенно определить по
следующей формуле:
Р (Сха 5м)т1п
366
Таблица 9.1
Ширина коридора входа
т. км
Планета П v ашах
5 1 0 20 40
Земля 0 11,3 32,2 113
Венера 0 12,9 37 129
Марс 310 645 2000 3540
Юпитер 0 0 0 16,1
Как видно из табл. 9.1, осу-
ществление баллистического
спуска космического аппарата
в атмосфере Земли и Венеры
требует высокой точности наве-
дения, так как ширина коридо-
ра входа составляет всего не-
сколько километров. Одним из
возможных путей расширения
коридора входа является при-
менение подъемной силы в про-
цессе спуска. Использование
максимальной отрицательной подъемной силы при спуске по
верхней границе коридора и максимальной положительной —
при спуске по нижней границе (для уменьшения величины мак-
симальной перегрузки) позволяет соответственно поднять верх-
нюю и опустить нижнюю границу коридора.
В табл. 9.2 приведены значения ширины коридора входа в
атмосферу различных планет при постоянном значении коэф-
фициента лобового сопротивления спускаемого аппарата (VBX=
= 1,4; сХа == const).
Приведенные значения ширины коридора входа имеют мес-
то при управлении КА в процессе спуска по углу крена. Если
управление производится по углу атаки, то при расчете шири-
ны коридора входа необходимо учитывать поляру конкретного
аппарата. Как указывается в |[6] учет зависимости сХа(сУа)
приводит к расширению коридора входа при больших значениях
качества, однако регулирование качества (при больших его
значениях) связано с ухудшением теплового режима аппарата
в процессе спуска.
Таблица 9.2
Ширина коридора входа км
пх а max
5 1 ю | 20
Планета К
4 <з ' о < <з
и? ' - 551 и 1 551
(V та '° та <и та
Q. И 0 1 ° 2 о. и 0 1 о Б о. и _ 0 1 °
О О- Si и 1 О о. си и 1 о Q. си
s к Я S S S
- л ~ к; я —। ^ К
Земля 0 43,5 55 11,3 82 105 32,2 161 210
Венера 0 43,5 58 12,9 84 113 37 169 226
Марс 340 483 595 645 885 1160 2000 1900 2800
Юпитер 0 55 67,6 0 84 113 0 145 193
367
Рис. 9.7. Ширина коридора входа при
спуске в атмосфере Земли с постоянным
аэродинамическим качеством
На рис. 9.7 приведена
зависимость ширины ко-
ридора входа от скорости
входа в атмосферу Земли
и гиперзвукового качест-
ва аппарата. Здесь значе-
ние качества принима-
лось постоянным и отри-
цательным при полете
вдоль верхней границы
коридора до достижения
круговой скорости и по-
стоянным положительным
при полете вдоль нижней
границы до момента до-
стижения нулевого угла
наклона траектории. Не-
трудно видеть, что шири-
на коридора входа может
быть значительно увели-
чена при увеличении качества аппарата, особенно в интервале
от 0 до 0,5. При больших значениях постоянного качества интен-
сивность расширения коридора уменьшается за счет увеличения
поперечной составляющей полной перегрузки. Коридор быстро
сужается с увеличением скорости входа. Следовательно, при
большой скорости входа нужно найти методы управления, обе-
спечивающие приемлемую величину коридора входа.
Ширину коридора входа можно рассчитать аналитически. В
[69] приведены приближенные выражения для ширины коридо-
ра входа при условии постоянства коэффициента лобового со-
противления аппарата в процессе спуска. При этом пренебрега-
ем сплюснутостью планеты, нецентральностью поля тяготения
и вращением планет. Атмосфера планеты считается изотермиче-
ской. Для не слишком малых значений качества аппарата ши-
рину коридора входа можно получить из следующего прибли-
женного соотношения:
А/г" р
[1 + In |Л +
(1 +H)v
(9.15)
1 +/2л
где и (Пх-оуг+^
__________^тах__________
йвх VvL- 1 У^ТРугрг®'
368
При Л>3 выражение (9.15) можно свести к более просто-
му виду
Д hn
nmax _|_ ^max
V2 — 1 V2 _ 1
вх * v вх 1
(9.16)
С увеличением скорости входа параметр ц уменьшается и
коридор входа постепенно сужается, а при достижении значе-
ния ц, близкого к единице, практически исчезает, поскольку
должно быть ц^1. Таким образом, минимальная ширина кори-
дор а входа будет равна 2/р~ 14 км 'при скорости входа Ёвх<
</l+nmax, а при Увх >]/’1 + итах коридор полностью исче-
зает. При спуске космического аппарата по траектории, лежа-
щей выше верхней граничной траектории коридора входа, про-
исходит выход аппарата из атмосферы со скоростями, превы-
шающими круговую на данной высоте. В этом случае траекто-
рия спуска будет представлять собой траекторию с многократ-
ным погружением в атмосферу планеты. Достоинством такой
траектории является экономия стартовой массы космического
аппарата, так как использование двигательной установки для
гашения скорости при подлете к планете связано с большими
затратами топлива. Кроме того, регулирование величины лобо-
вого сопротивления аппарата в перигее позволяет ускорить
превращение эллиптической орбиты в круговую. Недостатком
траекторий подобного типа являются значительные трудно-
сти в осуществлении посадки в заданном районе и возможность
многократного прохождения пояса радиации, что потребует до-
полнительных затрат массы для радиационной защиты экипа-
жа космического корабля.
Ширина коридора входа является исходной величиной для
определения требований, предъявляемых к точности наведения
космического аппарата. Зная ширину коридора входа (Д/гл),
нетрудно определить диапазон допустимых отклонений в фазо-
вых координатах аппарата в любой момент времени при под-
ходе к планете. Пусть в некоторый момент времени to фазовые
координаты аппарата есть Vo, Rq и 0о. Тогда в соответствии с
(9.10)
Rp —
2(Й02-1) ’
(9-17)
где Rp — расстояние от центра планеты до перигея фиктивной
траектории; Rq — расстояние от центра планеты до ЦМ аппа-
рата в момент времени /0-
Если приращения начальных значений фазовых координат
аппарата обозначить через Д/?о, ДЁо и Д0О, то полное прираще-
24—8 369
ние величины Rp можно определить из 'соотношения
Д^ = ^Д/?о + ^дГо+^Д0о (9Л8)
dR0 dV0 д 0О
или, после подстановки значений частных производных,
Д Rj> = 1 —
Фо2
2(Й~-1)
vffiRo 4г/
----------А V о--------
(V2-i)2 il-1
Д0о-
(9.19)
А +
В случае входа в атмосферу планеты с начальной парабо-
лической скоростью в'[56] приведено более простое выражение,
связывающее ширину коридора входа с погрешностями фазо-
вых координат аппарата в некоторый момент времени /0
^L = 2 2 ,/А| 1-(2А \ +
Ro v0 V Rv L \ Ro JJ Ro
(9.20)
На рис. 9.8 приведена зависимость допустимой погрешности
в направлении вектора скорости аппарата в момент времени
/0 от относительного расстояния до планеты при спуске на Зем-
лю, Венеру, Марс и Юпитер при прямом спуске с перегрузка-
ми, не превышающими итах=10. Из графика следует, что до-
пустимая погрешность в величине Во уменьшается с увеличени-
ем расстояния до аппарата. Опорное направление вектора ско-
рости выбирается таким образом, чтобы траектория аппарата
проходила посредине входного
коридора. Требования, предъ-
являемые к точности выдер-
живания величины скорости,
оказываются менее жесткими,
чем требования к точности вы-
держивания направления век-
тора скорости аппарата [56].
Ниже приведены допусти-
мые значения погрешности в
величине скорости аппарата
при спуске с начальной
параболической скоростью
(А/?о = О, Л9о = О, Рвх =1,4,
^max =10).
Рис. 9.8. Зависимость допустимо:! по-
грешности в направлении вектора
скорости аппарата от ра^ссокния до
планеты: _
/?max=10’ А^о = О; ЛГо = О
370
Планета .
дТо
* Йо
Земля Венера Марс Юпитер
-0,003 -0,003 -0,03 -0,0003
При выборе траекторий спуска внутри коридора необходи-
мо вопросы управления движением аппарата рассматривать
совместно с вопросами его теплозащиты. При входе аппарата
в атмосферу с большими начальными углами (т. е. при спуске
вблизи нижней границы коридора) тепловые потоки достигают
больших значений, в связи с чем использовать излучение в ка-
честве средства теплозащиты не представляется практически
возможным. Однако общее количество поглощенного тепла не-
велико, так что возможно использование теплозащиты путем
уноса материала. При спуске вблизи верхней границы коридо-
ра возможно, наоборот, использование теплозащиты путем из-
лучения, т. к. тепловые потоки оказываются сравнительно ма-
лыми.
Таким образом, при входе в атмосферу Земли с начальной
скоростью, близкой к параболической, необходимо, чтобы ап-
парат обладал некоторым (довольно незначительным) качест-
вом, причем методы управления движением спускаемого аппа-
рата могут быть достаточно простыми. При входе в атмосферу
с начальной скоростью, значительно превышающей параболиче-
скую, необходимо использовать такие методы управления, ко-
торые давали бы приемлемую ширину коридора входа. При
спуске в атмосферах других планет имеет место ряд особенно-
стей, которые могут либо усложнить, либо облегчить процесс
спуска. В частности, при спуске на поверхность Марса очень
малая плотность атмосферы у поверхности может потребовать
или большого аэродинамического качества аппарата, или ис-
пользования в процессе спуска силовой установки.
9.4. РАСЧЕТ КОРИДОРОВ ВХОДА
ПРИ а—у-УПРАВЛ ЕН И И
Современная космическая техника для осуществления
спуска в плотных слоях атмосферы с последующей посадкой в
заранее заданный район поверхности планеты располагает ап
пиратами баллистического спуска, аппаратами, обладающими
малым (до 0,3 ... 0,4) аэродинамическим качеством и аппарата-
ми многоразового использования со сравнительно высоким ги-
перзвуковым аэродинамическим качеством (до 2,0).
В полетах с экипажем используются такие аппараты, кото-
рые в диапазоне от первой до второй космической скорости
входа позволяют реализовать траектории спуска на Земле с не-
большими максимальными перегрузками (от 3 до 8) и имеют
возможность управления дальностью полета.
371
Перспектива космических исследований предполагает в бу-
дущем организацию экспедиций к планетам солнечной системы,
в первую очередь, к планете Марс. Предшествующие этим экс-
педициям исследования планет с помощью автоматических ап-
паратов проводятся в настоящее время.
Разработку технического решения задач посадки на Землю
при возвращении от планет Солнечной системы следует счи-
тать одной из важных и актуальных перспективных работ. Как
уже указывалось выше, возвращение из полета к Марсу харак-
терно скоростью входа, существенно превышающей вторую кос-
мическую. В зависимости от вида траектории возвращения ско-
рость входа КА может составлять от 12 до 13 км/с (продолжи-
тельность экспедиции около трех лет), а в некоторых случаях
превышать 18 км/с (при продолжительности экспедиции около
двух лет) [60].
Так как на аппаратах для этих экспедиций, по-видимому,
будут применены двигатели, использующие ядерную энергию,
то можно рассчитывать на уменьшение указанных величин ско-
ростей входа (например, до второй космической) посредством
торможения возвращающегося корабля с помощью этих дви-
гателей, однако при ожидаемых характеристиках этих двигате-
лей использование их неизбежно приведет к существенному
увеличению длительности полета при возвращении. Поэтому
вход в атмосферу без предварительного торможения (или с не-
большим торможением), после которого скорость входа остает-
ся .порядка 16—17 км/с, представляет в настоящее время прак-
тический интерес.
Имеющиеся расчетные материалы [1, 9] показывают, что
аппараты типа «Союз» (К^0,3) могут иметь в зависимости от
скорости входа следующие максимальные величины теоретиче-
ского коридора входа Д/гл при максимальной перегрузке 6 и 8
(табл. 9.3).
Д/гл=20 км может считаться достаточной для скорости вхо-
да 11 км/с и более, так как она уверенно обеспечивается сред-
ствами прогнозирования с учетом возмущений на внеатмосфер-
ном участке траектории возвращения.
Таблица 9.3
nmax Гвх, км/с
1 1 1_3 1_5 1 7
6 34 22 0 0
8 44 (20)* 28 17 0
* = км — эксплуатационная величина коридора при км/',
в которой обеспечивается управляемый полет на дальность L ^о 9000 км
и дублирование управляемого спуска баллистическим.
372
Таблица 9.4
^max Гвх, км/с
13 15 17
6 0,28 0,7 1,6
8 0,25 0,45 0,9
Условие обеспечения коридора входа A/zJX = 20 км требует
значений аэродинамического качества в зависимости от скоро-
сти входа согласно табл. 9.4.
Приведенные в табл. 9.3 и 9.4 данные имеют место при уп-
равлении только углом крена аппарата и предполагают вход на
верхней границе коридора с К=—Ктах(у= 180°), а на нижней
с + Ктах (у = 0°). При этом не учитывается влияние отклоне-
ний параметров атмосферы на
высотах более 50 км, погреш-
ностей процесса управления
и т. д.
Из рассмотрения приведен-
ных данных следует, что для
обеспечения возвращения эки-
пажей космических кораблей
при VBX> 13 км/с необходимы
спускаемые аппараты, обладающие большим аэродинамическим
качеством, нежели аппараты типа «Союз» и «Аполлон». Из дан-
ных таблицы следует также, что при скорости входа более 16,5...
17 км/с даже аппараты, обладающие аэродинамическим каче-
ством К=1 ... 1,5 при управлении только углом крена не смогут
обеспечить спуск с nmax^6 в коридоре входа Д/?л^20 км.
Как показывают результаты ряда отечественных и зарубеж-
ных исследований [1, 2, 7, 38, 44, 66 и др.], надежное решение
задачи спуска в этих случаях достигается путем управления, ис-
пользующего изменение угла атаки аппарата. При таком управ-
лении вход в атмосферу осуществляется следующим образом.
При движении вдоль нижней границы коридора вначале вы-
держивается максимальное положительное значение коэффици-
ента подъемной силы (сУа = сУатах), а затем, после достижения
максимальной допустимой перегрузки (п = птах = пл) угол
атаки изменяется таким образом, чтобы перегрузка со-
храняла постоянное значение вплоть до достижения точки, в
которой Суа = 0 и сХа = cX(i min- При движении вдоль верхней гра-
ницы необходимо выдерживать постоянный угол атаки, соответ-
ствующий максимальному отрицательному коэффициенту подъ-
емной силы. В этом случае приближенная формула для опреде-
ления ширины коридора входа примет вид [1]:
* ь 1
р
, . / иП1ах суа max
+ ln —------------. =
\(Гувх- ') Г СХ '(а*)
4 х ' а
nmax /__________________________
v вх — 1 \ У с1 (а*) + с2 (а*)
'а а
СУаЫЖ
К Сха + С1,
373
Рис. 9.9. Зависимость ширины
коридора входа:
а — от максимального аэродинами-
ческого качества и максимальной
перегрузки; б — от максимального
аэродинамического качества СА и
максимального допустимого угла
атаки (а*)
Формула (9.21) дает
приближенную оценку
ширины коридора входа,
заниженную в среднем
на 20%.
Для получения более
точного значения ширины
коридора необходимо ин-
тегрировать численно
уравнения движения СА
при выбранном алгорит-
ме управления углом
атаки.
При значениях аэро-
динамического качества,
меньших 0,5, регулирова-
ние угла атаки не позво-
ляет получить заметного
увеличения ширины кори-
дора входа.
способ регулирования угла
атаки а вблизи нижней границы коридора имеет недостаток:
достижение максимальной перегрузки реализуется путем
уменьшения коэффициента cr = Vc2 +с2 ,
ха У а
при этом аппарат
выходит на меньшие высоты, что приводит к увеличению тепло-
вых потоков в процессе спуска.
Эффект регулирования угла атаки приведен на рис. 9.9.
Наиболее эффективным и гибким является сочетание уп-
равления углами атаки и крена, причем управление углом ата-
ки и а—у-управление наиболее целесообразны при использова-
нии соответствующей ветви поляры аппарата.
Возможности управления углом атаки для нескольких ти-
пов СА иллюстрируются табл. 9.5, в которой приведены вели-
чины коридоров входа при таком управлении (nmax = 6) *.
Из сравнения данных табл. 9.3—9.5 следует, что использо-
вание управления углом атаки (а также а—у-управления) эф-
* Величина /гтах = 6 может считаться приемлемой при воздействии на эки-
паж во время спуска.
374
Таблица 9.5
Форма СЛ Аэродинами- ческое каче- ство VBX' км/с
13 15 17
«Фара» (типа «Союз») 0,3 26 0 0
«Фара» (типа «Аполлон») 0,4 33 16 0
«Диск» 0,5 43 28 19
«Полуконус» 1,0 55 38 24
фективно для аппаратов, имеющих форму «полуконус» и мало-
эффективно для аппаратов, имеющих формы «фара» и «диск».
Очевидно, свойства поляры аппарата формы «полуконус» мо-
гут быть обеспечены также в гипотетической схеме аппарата,
представляющего собой продолговатый конус, снабженный
крылом. Крылатые аппараты позволяют получить величину
аэродинамического качества порядка 2... 3 при гиперзвуковых
скоростях. Однако при больших скоростях входа и условии ог-
раничения максимальной перегрузки увеличение значения К
при гиперзвуковых скоростях более 1,2... 1,5 имеет смысл толь-
ко с целью осуществления бокового маневра, а эта задача при-
менительно к траекториям со второй космической и большими
скоростями входа может быть решена проще, с помощью ком-
бинированного аэрогазодинамического маневра [9].
С другой стороны, при больших скоростях входа для кры-
латых аппаратов существенно возрастают трудности обеспе-
чения защиты конструкции от аэродинамического нагрева при
спуске в атмосфере. Поэтому крылатые аппараты в обозри-
мом будущем вряд ли могут рассматриваться как реально осу-
ществимое средство при больших скоростях входа.
Наиболее реальным и перспективным для скоростей входа,
превышающих вторую космическую скорость, следует считать
использование бескрылых аппаратов, имеющих поляру, анало-
гичную поляре аппарата формы «полуконус», благоприятную
для управления углом атаки и углом крена. Такие аппараты,
аналогичны аппаратам типа «Союз» и «Аполлон», удобны для
сочленения с современными типами носителей, схемами аварий-
ного спасения и обладают преемственностью по отношению к
этим апппаратам в смысле принципов управления, компонов-
ки, оснащения и теплозащиты.
Рассмотрим влияние управляющих параметров на ширину
коридора входа для подобного рода аппаратов.
В качестве примера возьмем СА в виде «полуконуса» с
плоской верхней частью (масса аппарата т = 8800 кг, характер-
ная площадь SM = 23,2 м2). Максимальное аэродинамическое
качество 7<=1,5 реализуется при а = 0. ^flmax ~ 0,5 при
а = 30°.
375
Оценим, насколько расширяется коридор входа в атмосферу
невращающейся Земли такого аппарата при использовании уп-
равления углом атаки и углом крена по сравнению со случаем
управления только углом крена.
Для обеспечения затененности верхней плоскости части СА
будем считать, что балансировочный угол атаки (абал) может
лежать в диапазоне от максимального значения а(сУатах) =
= 30° до минимального значения amin = 7o. Для обеспечения
запаса на управление значения с были уменьшены на 10%
при неизменных значениях сх •
а
На основании [1] по приближенным формулам оценим эф-
фект регулирования угла атаки с точки зрения расширения ко-
ридора входа. Имеем
A hn (a — var)
A hn (a — const)
1 + In
^max
vbx “ *
Р
СУа <ao)] «max f сУа . . r ve dcVa
c^(a*) V2BK— Й c(a.) CK J
' У CL '
(9.22)
Начальный угол атаки a0 близок к углу атаки, соответству-
ющему c!ZflTndX, а минимально допустимый угол атаки а* соот-
ветствует сят1п- При спуске с постоянным углом атаки
(а0, а* или некоторым промежуточным значением) нижняя гра-
ница коридора определяется из условия получения максимума
перегрузки, не превышающего допустимого значения, и даль-
нейшего поддержания перегрузки с помощью изменения угла
крена. Верхняя граница определяется условием захвата аппа-
рата атмосферой при полете с у=180°.
При спуске с переменным углом атаки ширина коридора
входа может быть значительно увеличена за счет уменьшения
высоты нижней границы вследствие возможности осуществле-
ния изоперегрузочного режима полета путем изменения угла
атаки СА. Чем больше возможный диапазон регулирования а,
тем больше расширяется коридор входа.
Рассмотрим два варианта: а* = 7° и а* = 0. Для обоих ва-
риантов ao = a(Cyamax) =30°. Принимая в качестве предель-
но допустимой «перегрузки лтах —6, получим (при 1/0 = 7,17 км)
на основании приведенной формулы следующие приближенные
значения для ширины коридора входа Д/гя, выраженной в ки-
лометрах.
376
Таблица 9.6
а, ° VBX, км/с
13 16
ao=7=const 33 20,4
ao = 30 = const 23,7 14
30-*7 45 28,6
зо-*о 57,1 36,7
Рис. 9.10. Зависимость ширины
коридора входа от скорости входа
Учитывая, что формула дает несколько заниженное значе-
ние выигрыша за счет регулирования угла атаки (особенно
при больших птах/и2о—1), можно предположить, что коридор
входа расширяется на 40... 50% при регулировании угла ата-
ки в пределах от 30° до 7° и на 80... 100% при регулировании
угла атаки от 30° до 0. Более значительного расширения кори-
дора входа можно достичь при регулировании угла атаки в
пределах от 30° до а(снт1 ), причем для данного аппарата
В связи с тем, что ширина коридора входа СА является
очень важной характеристикой космического комплекса и в
связи с необходимостью более точного определения ширины
коридора входа при регулировании угла атаки необходимо
проводить расчеты на ЭВМ. граничных траекторий спуска при
различных значениях начального угла атаки.
При расчетах в качестве нижней границы принималась та-
кая минимальная высота условного перигея йян, при которой
на траектории входа с у = 0 величина суммарной перегрузки
не превосходит допустимого значения пд = 6. На траекторию,
соответствующую верхней границе коридора входа с высотой!
и с у=180о, накладывалось следующее требование: в мо-
мент достижения осевой перегрузкой значения, обеспечиваю-
щего захват СА атмосферой, траекторный угол 0 по модулю
достигает первого минимума и близок по величине к нулю, что
Делает возможным непрерывный переход на заданный режим
полета (например, изоперегрузочный с управлением по углу
крена). Как показывают расчеты, при входе СА в атмосферу с
различными значениями углов атаки a = const (при постоян-
ном аэродинамическом качестве) наименьшая высота нижней
границы может быть получена при ao = amin = 7°, а наибольшая
!4—8 377
высота верхней границы — при aQ = ac max = 30°, при этом
Vam
максимальный коридор составит при VBX=13 км/с Дйя =
= 45,4 км, при Увх=16 км/с Д/гл = 28,1 км и при VBX= 18 км/с
Д/гл = 21,7 км.
Если на верхней границе в известной мере исчерпаны воз-
можности для обеспечения условий захвата, то нижняя грани-
ца представляет определенный резерв в смысле расширения ко-
ридора, так как ее высота может быть существенно уменьше-
на, что обуславливается выбором оптимальной программы из-
менения угла атаки на начальном участке входа. В момент вхо-
да угол атаки а0 = ас тах=30° и поддерживается постоян-
на111
ным вплоть до момента достижения перегрузкой допустимого
значения (п = пд), после чего угол атаки уменьшается до amin
для поддержания перегрузки СА на допустимом уровне п =
= пл = const. Такой алгоритм входа позволяет сместить ниж-
нюю границу по сравнению с ее положением при a = 7° = const
на 11 км (VBX=13 км/с), на 6 км (VBX = 16 км/с) и на 4,2 км
(Увх=18 км/с). Результаты расчетов на ЭВМ приведены на
рис. 9.10.
ГЛАВА 10. МЕТОДЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ
’ СПУСКАЕМЫХ АППАРАТОВ
Система управления спуском — это комплекс устройств»
предназначенных для организации управления аппаратом в
процессе спуска. Задача управления СА в атмосфере состоит в
том, чтобы перевести аппарат из заданной точки пространства,
лежащей на условной границе атмосферы и имеющей опреде-
ленные фазовые координаты, в заданную точку на поверхнос-
ти планеты или в какую-либо другую точку при наличии огра-
ничений на параметры движения СА в процессе спуска.
10.1. КЛАССИФИКАЦИЯ СИСТЕМ УПРАВЛЕНИЯ
СПУСКОМ (СУС)
Задачу приведения СА в заданную точку посадки
можно разделить на три функционально связанных друг с
другом алгоритма.
1. Навигационный алгоритм, предназначенный для опреде-
ления текущих значений кинематических параметров движения
аппарата на основе априорной информации и показаний изме-
рительных устройств.
2. Алгоритм управления, осуществляющий процесс форми-
рования углового движения СА для получения необходимого
изменения (или ориентации) вектора подъемной силы СА.
3. Алгоритм стабилизации, реализующий управление движе-
нием СА относительно центра масс и обеспечивающий откло-
нение в допустимых пределах фактического углового движе-
ния аппарата от движения, формируемого алгоритмом управ-
ления.
Структурная схема СУС приведена на рис. 10.1.
Общая задача управления спуском, как правило, разбива-
ется на две самостоятельные задачи.
1. Выбор номинальной траектории и соответствующей ей
программы управления.
Под номинальной траекторией понимается траектория, удо-
влетворяющая всем поставленным требованиям и ограниче-
ниям.
!4« 379
Рис. 10.1. Структурная схема системы управления спуском
2. Анализ возмущенного движения СА.
К основным возмущениям, действующим на СА в процес-
се спуска, относятся [9]:
1) возмущения по начальным условиям входа: ошибки по
углу и скорости входа, а также по координатам точки входа;
2) возмущения, вызванные неточным знанием массовых, ге-
ометрических и аэродинамических характеристик СА;
3) возмущения, вызванные неточным знанием характери-
стик атмо-сферы (изменение плотности по высоте), а также
турбулентностью атмосферы и т. д.;
4) приборные погрешности СУС (ошибки чувствительных
элементов, средств обработки информации, исполнительных ор-
ганов и т. д.).
Вследствие значительного различия времени длинно- и ко-
роткопериодических колебаний СА при спуске в атмосфере
влиянием последних на первые при проведении приближенных
расчетов можно пренебречь и при анализе траекторий СА рас-
сматривать как материальную точку.
В настоящее время СУС современных аппаратов в основном
построены на использовании управления эффективным аэро-
динамическим качеством путем разворотов аппарата по углу
крена (у-управление) при постоянном балансировочном угле
атаки (абал). Поворот продольной оси СА вокруг вектора ско-
рости на угол крена у приводит к изменению вертикальной со-
ставляющей полного аэродинамического качества СА — К, т. е.
Аэфф = A cos у,
и вертикальной составляющей подъемной силы аппарата, что
позволяет управлять продольной дальностью полета СА.
При однопараметрическом управлении по углу крена упра-
вление продольной и боковой дальностями спуска осуществля-
ется путем использования модуля и знака угла крена, причем,
как правило, модуль угла крена используется для управления
продольной дальностью спуска, а знак — для ликвидации отно-
сительно небольших боковых отклонений.
Классификацию СУС можно провести по некоторым общим
признакам. В работе [9] приведена классификация СУС, на
наш взгляд, наиболее полно отражающая ее характерные при-
знаки.
1. По структуре используемых алгоритмов управления и
принципу синтеза можно рассматривать СУС:
с использованием заранее рассчитанных программных зави-
симостей (управление относительно опорной траектории);
с прогнозированием точки посадки;
смешанного типа, когда по результатам прогноза точки по-
садки выбирается опорная траектория.
2. По использованию информации:
381
автономные;
командного наведения с Земли или спутника;
полуавтономные или комбинированные;
с использованием высокоточных методов наведения СА в
точку посадки на конечном участке (самонаведение, по опор-
ному направлению и т. д.).
3. По способу управления:
с непрерывным управлением;
с дискретным корректированием траектории в некоторых
характерных точках.
4. По роли человека в управлении полетом:
автоматические;
ручные;
смешанного типа.
5. По характеру обработки информации:
с простейшей обработкой;
с использованием специализированных вычислителей или
бортовых вычислительных комплексов.
6. По типу расположения чувствительных элементов:
с использованием гиростабилизированных платформ;
с чувствительными элементами, жестко связанными с кор-
пусом СА.
Каждая СУС имеет свои преимущества и недостатки с точ-
ки зрения обеспечения требуемой точности, надежности рабо-
ты, массовых характеристик, информационного обеспечения,
простоты тактической реализации и т. д. Наиболее распростра-
ненными в настоящее время являются автономные СУС с ис-
пользованием командного наведения с Земли на конечном
участке.
Для аппаратов многоразового использования широкое при-
менение получили СУС, основанные на использовании борто-
вых цифровых вычислительных комплексов (БЦВК). Структу-
ра управления спуском при использовании БЦВК очень гибка
и позволяет в процессе полета получить значительный объем
информации на борту и сформировать многошаговые адаптив-
ные алгоритмы управления спуском. Всю траекторию спуска,
как правило, разбивают на несколько характерных участков,
на каждом из которых СУС решает специфические задачи.
Первым участком является участок от точки входа СА в атмо-
сферу до точки достижения максимального значения ограничи-
ваемого параметра (теплового потока, перегрузки и т. д.). На
втором участке выдерживаются заданные ограничения на па-
раметры движения СА. На основном участке спуска произво-
дится управление по продольной дальности и в боковом на-
правлении. На последнем участке обеспечивается выход на за-
данные условия по высоте, скорости, углу наклона и траекто-
рии, дальности до точки посадки и т. д. Такой метод управле-
382
ния позволяет упростить решения сложной технической зада-
чи и обеспечить посадку- СА в заданную точку с приемлемыми
аэродинамическими и тепловыми нагрузками в процессе спу-
ска.
10.2. АНАЛИЗ АВТОНОМНЫХ СИСТЕМ УПРАВЛЕНИЯ
СПУСКОМ
Самым простым с точки зрения практической реали-
зации является неуправляемый (баллистический) спуск, одна-
ко его основным недостатком является большой разброс то-
чек посадки (до нескольких сотен километров) особенно при
спуске в атмосфере, параметры которой могут колебаться от-
носительно номинального значения в широких пределах.
При управлении СА с использованием номинальной (опор-
ной) траектории параметры движения аппарата по опорной
траектории вычисляются заранее и хранятся в бортовом вычи-
слительном устройстве. Отклонения измеренных значений па-
раметров движения от номинальных используются для форми-
рования управляющего воздействия либо для выбора новой
траектории. В бортовом вычислительном устройстве заложены
или параметры опорной траектории, или некоторые коэффици-
енты влияния в функции независимой переменной, в качестве
которой может быть время, перегрузка, скорость СА или вы-
сота полета.
Если систему нелинейных дифференциальных уравнений
движения СА, задающих опорную траекторию, записать в виде
^- = Fm(xn,up,Ti), (10.1)
(где хп(1^п^.т)—переменные величины системы; Fm — за-
данные функции; ир — управляющие функции; -q — независи-
мые переменные), то уравнение, связывающее конечное значе-
ние отклонения bxq регулируемой величины от опорного значе-
ния с отклонениями фазовых координат СА Ъхт в текущий мо-
мент времени и изменением управляющего воздействия 6ир от
текущего момента до конца траектории, запишется следующим
образом:
6 xq (T]ft) = 2 Ч С7!)6 хт (л) + 2 Ju4 (я)S «Р- (10.2)
м т Р
При этом, приняв управляющее воздействие кусочно-посто-
янным и положив конечное отклонение регулируемой величи-
ны равным нулю, получим
«р(^1)=«ро(п)+ 3 6xm(n). (10.3)
М \ ахт /0
где индекс «0» соответствует опорной траектории.
383
Системы управления спуском с отслеживанием номиналь-
ной траектории применимы при малых отклонениях фактиче-
ской траектории от номинальной. В подобного рода СУС в ка-
честве простой, наиболее доступной для измерения информа-
цией является информация от измерения перегрузок, интегра-
лов от перегрузок и времени полета.
Одним из возможных вариантов такой системы является
СУС, в которой закон изменения аэродинамического качества
СА К имеет следующий вид [73]:
ДК= — KibVy—Kz\tiXa-K^L, (10.4)
где ДК= К Ко; VyOr Апха = Пха ^ха0
причем все номинальные значения фазовых координат СА за-
даны в функции горизонтальной составляющей скорости Vx.
Номинальное аэродинамическое качество определяется зако-
ном Ко = —KiVyQ] /<1, /С2, Кз— постоянные коэффициенты уси-
ления системы (передаточные коэффициенты).
Использование переменных коэффициентов позволяет более
эффективно влиять на процесс управления и, как правило,
улучшает характеристики системы [72].
Большое развитие получили системы, в которых отслежива-
ние опорной траектории производится на основе линейного
прогноза отклонений конечной дальности (Лк) [1, 2, 9] и др’.
Отклонения точки посадки в продольной плоскости при усло-
вии, что с момента времени возмущения не будут действо-
вать, можно записать в виде [9]
д£Л(^)=^Ахг + (10.5)
dXi dyt dvxi dvyi
дЬъ дЬъ
где —...» •— -----частные производные конечной дальности
dxi dvyi
полета по координатам и скоростям в момент времени ti\
&x,i, ..., \Vyi — отклонения координат и составляющих скорости
СА в момент времени от расчетных значений.
Если в качестве управляющего параметра использовать
угол крена у, то соответствующее управляющее воздействие оп-
ределяется следующим образом:
ДМ,Н-~ЛМ- (Ю.6)
оу
Коэффициент £^0 вводится для улучшения динамики про-
цесса управления.
Методы построения СУС с переменными передаточными ко-
эффициентами системы (функциями влияния) являются проме-
жуточными между методом отслеживания номинальной траек-
тории и методом прогнозирования точки посадки ([25], [28] и
др-)-
384
Пусть уравнения движения СА в векторной форме имеют
вид:
и, П), (10.7)
где и — скалярное управляющее воздействие; х — вектор фа-
зовых координат СА; Г—вектор-функция фазовых координат
и управляющего воздействия.
Используя метод сопряженных уравнений Блисса [1], зна-
чения для вариации составляющей вектора х в конечный мо-
мент времени Т можно записать следующим образом:
6х1(Т)= [ pv~(,)7'(7’, T)J(T)]6«(r)dT + X-(1)r(r, t0)8x(t0),
t о
(Ю.8)
где /о)—вектор функций влияния, определяемых при
решении системы сопряженных уравнений; вектор b(t) состав-
dF' —
лен из производных —- [х0 (£), м0(/)]. Если при известном на-
ди
чальном отклонении вектора бхо(^) считать, что бц(/) на ос-
тавшемся интервале времени постоянно, то его можно опреде-
лить из предыдущего уравнения, положив бХ1(Г)=0:
6 »(/)= — (Ю.9)
j[X-(1)r(T, т)Г(т)]б/т
io
Если иметь в виду, что вектор фазовых координат СА л?(£)
определяется непрерывно, то управление осуществляется по
закону
= (10.10)
Составляющие вектора h~T(t) вычисляются* предваритель-
но. В ряде случаев они могут быть определены аналитически [ 1 ].
Данный алгоритм не может обеспечить высокой точности по-
садки, так как не учитывает неточность определения парамет-
ров траектории, погрешности в аэродинамических коэффициен-
тах СА, отклонения плотности атмосферы и т. д. В связи с
этим делались попытки улучшить данный закон управления
путем введения коэффициентов перекомпенсации. В ряде ра-
бот (например, [28]) переменные коэффициенты перекомпенса-
ции подбирались эмпирическим путем, причем они оказывались
различными для различных сигналов управления.
Разновидностью управления относительно опорной траекто-
рии является метод Z-матричного управления, предложенный в
[70]. Х-матричное управление заключается в минимизации ин-
теграла от квадрата отклонения управляющего воздействия
385
при наличии ограничений на фазовые координаты СА. Пусть
число фазовых переменных равно п и число связей на кон-
це— р. Тогда Хг-матрица содержит р строк и п столбцов, т. е.
для каждого заданного момента времени запоминается пхр
чисел. Если число заданных управлений равно т, то запомина-
ется матрица состоящая из т строк и р столбцов. Схему X-
матричного управления можно применить на начальном участ-
ке погружения СА в атмосферу до выхода на стационарную
траекторию спуска. В этом случае за управляющую перемен-
ную можно принять угол атаки а (или угол крена у), а за уп-
равление — высоту и угол наклона траектории в конечной точ-
ке, определяемой моментом достижения круговой скорости.
Тогда п=4, т=\ и р = 2.
В заданные моменты времени четыре фазовые координаты
СА (две компоненты скорости и положения) сравниваются с
номинальными и составляется матрица ошибок
Sx(/o) =х(/о)—Хном(/о). (10.11)
Отклонение управляющей переменной равно
ба(0=—М0ММб*(М (10.12)
и управляющий сигнал вычисляется по формуле
а(/)=аНом(0+ба(0. (10.13)
Элементы матриц Xi и определяются номинальной траек-
торией, граничными условиями и условием минимума интегра-
t
ла J W (бсс) 2dt, W—весовой коэффициент.
^0
Схема Х-матричного управления приведена на рис. 10.2.
Все рассмотренные алгоритмы управления, построенные на
отслеживании номинальной траектории, обладают двумя суще-
ственными недостатками: во-первых, они обладают методичес-
кими ошибками, заключающимися в невозможности полностью
скомпенсировать влияние ряда возмущающих факторов, дей-
Рис. 10.2. Схема Х-матричного управления
386
ствующих на СА на траектории спуска,, и, во-вторых, при ре-
шении задачи попадания в заданную точку нет необходимости
компенсировать возмущение в каждой точке траектории. При-
вязка к одной опорной траектории приводит к перегрузке в ра-
боте СУС и нерациональному расходу рабочего тела. Рацио-
нально сводить к нулю не текущие отклонения параметров дви-
жения от номинальных, а конечное отклонение регулируемого
параметра (обеспечение минимума рассеивания точки по-
садки) .
Как показали расчеты [1, 9], подобные СУС позволяют осу-
ществить посадку СА с разбросом точек приземления от не-
скольких десятков до сотен километров (аВх= 11 км/с, Лп>
>,8000 км).
От указанных недостатков в значительной степени свобод-
на СУС, построенная на основе метода попадающих траекто-
рий [9]. Принцип действия данной автономной системы дис-
кретного управления заключается в следующем. В момент до-
стижения СА фиксированного значения аргумента системы р
на основе получаемой на борту информации определяется зна-
чение угла крена у0, обеспечивающее попадание СА в задан-
ную точку посадки, т. е. определяется расчетная траектория
первого приближения. В момент достижения аргументом зна-
чения p = pi по результатам сравнения величины функционала,
вычисленного по данным бортовых измерений, и некоторым из-
вестным значениям проводится коррекция первоначального
значения угла крена у1=уо + Ауь В дальнейшем при Р = р2,
Рз, ...» рт аналогично проводится коррекция значений уь Y2, ...
..., Ут, Т. е. на каждом этапе осуществляется переход на бли-
жайшую попадающую траекторию, при этом выполняется ус-
ловие минимизации расстояния между конечными точками воз-
мущенной и номинальной траекторий
ALK = L—Ло—нит.
Реализация данного алгоритма управления возможна при
использовании достаточно простых специализированных борто-
вых вычислителей. Если в качестве информации используется
время (Z), перегрузка (пХа ) по скоростной оси СА и кажущая-
ся скорость (us), то данный алгоритм управления обеспечивает
точность посадки порядка нескольких сотен километров при
возвращении корабля от Луны по «протяженным» траектори-
ям и нескольких десятков километров при спуске с ОСЗ [9].
Дальнейшим развитием методов управления СА на участке
спуска с использованием опорных траекторий является метод,
разработанный коллективом авторов под руководством чл.-кор.
АН СССР Д. Е. Охоцимского [51, 52, 53]. В основу алгоритма
решения задачи управления положен метод параметризации
опорной зависимости угла крена у с помощью модулирующих
387
функций. Наиболее простой вариант этого метода выражается
соотношением:
Y = Vo(m)(I+₽). (Ю.14)
Изменение параметра 0 вызывает вариацию функции
аналогичную амплитудной модуляции, а изменение 8 — фазо-
вой. Опорная зависимость у0(/) —задается.
При варьировании каждого из параметров 0 или 8 от их
опорных значений, кроме опорной, возникают еще две допол-
нительные точки, несущие информацию о характере влияния
0 и 8 на величину конечного промаха. После того, как такие
точки получены, вычисляются поправки Д0 и Де, обеспечиваю-
щие нулевой промах по продольной дальности и в боковом
направлении.
Как показало математическое моделирование процесса уп-
равления с помощью алгоритма, основанного на этом методе
(и на его модификациях), угол крена в процессе управления
меняется достаточно плавно, а точность приведения СА при
спуске с начальной параболической скоростью составляет по-
рядка 1 ... 2 км при наличии вариаций плотности атмосферы
[16, 51]. В [18] рассмотрен аналогичный метод управления
при спуске с гиперболическими скоростями.
Использование бортовых цифровых вычислительных машин
(БЦВМ) раскрывает широкие возможности в построении СУСГ
обладающих большой гибкостью, и позволяет в процессе спус-
ка получить значительный объем информации о движении СА,
на основе которой можно формировать алгоритмы управления.
В настоящее время имеется достаточно большое количество
работ по построению СУС при полном прогнозировании пара-
метров движения [1, 9, 16, 51] и др. Основной принцип таких
систем заключается в том, что полные (или приближенные
[49, 53]) дифференциальные уравнения движения СА в уско-
ренном масштабе времени (с опережением) интегрируются на
борту СА вплоть до точки посадки или же на борту заложены
приближенные аналитические решения [54, 68], определяющие
все или часть возможных траекторий спуска. Информация, не-
обходимая для прогнозирования дальности спуска, является
результатом измерения координат и составляющих скорости
СА с помощью навигационного блока. Задаются начальные
значения угла крена или угла атаки, и с помощью БЦВМ про-
водится расчет траектории до точки посадки. Разность между
прогнозируемой и заданной точками посадки подается в авто-
пилот, где формируется так называемый «попадающий» угол
крена или угол атаки. При последующих сеансах измерений
эти значения управляющих параметров корректируются.
Основной частью системы является БЦВМ. Она работает
совместно с инерциальной гироплатформой (навигационным
388
блоком) и системой управления спуском. Если на траекторию
спуска наложены ограничения на фазовые координаты и в про-
цессе спуска эти координаты достигают своих предельных зна-
чений, то процесс прогноза точки посадки останавливается, и
происходит спуск по границе. Пусть 6L — ошибка по дальности,
равная разности между заданной дальностью до точки посадки
и ее предсказанным значением, т. е. ЬЬ = Ьзал—Ln. Тогда алго-
ритм управления можно представить в виде
д я т
(Кcos у); = (Кcosv)i_, + -- , (10.15)
^зад
где К — аэродинамическое качество СА; А — коэффициент
усиления системы.
Для точного прогнозирования необходимо знать параметры
движения СА. С помощью инерциальной системы навигации
можно получить значение координат и скорости аппарата, а
используя высоту полета, — значение плотности атмосферы в
каждой точке траектории. Ошибки в определении плотности
приводят к большим ошибкам по дальности. Для компенсации
ошибки по дальности необходимо измерять в момент прогноза
действительное значение лобового сопротивления СА. Для кор-
рекции возможно использование коэффициента, полученного из
уравнения
Q= __________\ /Д___________
2 \ пг Г
где (—) — действительное отношение силы лобового сопро-
\ /д
тивления к массе СА; v — воздушная скорость СА.
Зависимость коэффициента лобового сопротивления СА от
скорости и угла атаки, а также зависимость плотности атмос-
феры от высоты заложены на борту СА в виде таблиц. Коман-
ды управления дальностью перед подачей на автопилот опти-
мизируются. Под оптимизацией подразумевается получение
максимальных маневренных возможностей аппарата для пари-
рования ветровых возмущений, колебаний плотности атмосфе-
ры и ошибок СУС. На рис. 10.3 приведена схема СУС при дан-
ном методе наведения СА в точку посадки.
Большим преимуществом методов управления движением СА
с прогнозированием точки посадки (что особенно важно для
аппаратов многоразового использования) является возмож-
ность определения в процессе спуска максимальной перегруз-
ки, максимальных тепловых потоков, высоты полета и т. д., что
делает их гибкими методами, работоспособными в любых ре-
альных условиях полета. При данных методах управления кос-
389
Рис. 10.3. Схема системы управления с прогнозированием точки посадки
монавт получает достаточное количество информации для ус-
пешного осуществления ручного управления. Основным недо-
статком таких систем является необходимость иметь на борту
БЦВМ с достаточно высоким быстродействием и большим объ-
емом памяти. Однако в настоящее время имеются определен-
ные успехи в создании малогабаритных БЦВМ, которые могут
быть использованы в СУС СА [19]. При применении БЦВМ в
контуре СУС СА одним из важных вопросов является выбор
системы дифференцированных уравнений прогноза и методов
их численного интегрирования, так как именно это определя-
ет требования к быстродействию БЦВМ и объему оперативной
памяти.
В работе [49] разработан вариант системы уравнений про-
гноза, описывающий пространственное движение СА при вхо-
де в атмосферу. В [53] рассмотрена задача о прогнозировании
параметров движения, используемых в алгоритме управления
при входе СА в атмосферу с параболической скоростью. При-
ведены две системы упрощенных уравнений движения СА. Рас-
смотрены два метода интегрирования: модифицированный ме-
тод Эйлера и модифицированный метод Адамса третьего по-
рядка. Указывается на предпочтительность метода Адамса.
390
Еа участке первого погружения шаг интегрирования можно вы-
бирать в пределах ~9 с, а на внеатмосферном участке его
можно увеличить до 200 с. Ошибка приведения СА в точку по-
садки с учетом возмущений плотности атмосферы лежит в пре-
делах 1 ... 2 км.
Требования к БЦВМ можно значительно уменьшить, если
вместо интегрирования уравнений движения использовать их
приближенное решение. Траекторию спускаемого аппарата мож-
но составить из отдельных «модельных» участков, на каждом
из которых имеется решение в замкнутой форме (изоперегру-
зочные, изовысотные участки, участки равновесного планиро-
вания и т. д.). Практический выбор того или иного типа траек-
тории СА зависит от большого количества иногда противоре-
чивых факторов, однако наибольшее значение имеет простота
системы управления и возможность осуществления безопасно-
го спуска в аварийной ситуации.
В связи с тем, что точность аналитических решений может
оказаться недостаточно высокой, ошибки приведения СА в точ-
ку посадки будут несколько больше, чем при прямом интегри-
ровании уравнений движения на борту СА.
При проектировании СУС с прогнозированием точки по-
садки необходимо стремиться к тому, чтобы ошибка прогнози-
рования, обусловленная неточным расчетом траектории, не пре-
вышала среднеквадратичного отклонения прогнозируемого мес-
та посадки вследствие действия на СА в процессе спуска слу-
чайных возмущающих факторов. Суммарная ошибка приведе-
ния СА складывается из динамической ошибки управления,
которая остается нескомпенсированной к концу процесса уп-
равления, и навигационной ошибки, обусловленной неточно-
стью определения фазовых координат СА.
Таким образом, анализ автономных СУС СА показывает,
что в лучшем случае суммарную ошибку приведения СА в точ-
ку посадки не удается получить меньше 1 ... 2 км. При прямом
спуске СА с гиперболическими скоростями входа суммарная
ошибка приведения СА в точку посадки может оказаться зна-
чительно больше. Стремление уменьшить конечный промах при-
водит к необходимости усложнения алгоритма управления, уве-
личения быстродействия БЦВМ. и объема оперативной памяти,
усложнения бортового навигационного оборудования СА.
В связи с этим, особенно для многоразовых систем, необ-
ходимы СУС, обладающие на порядок меньшими динамичес-
кими и навигационными ошибками и обеспечивающие приве-
дение СА непосредственно на космодром. К числу таких систем
могут быть отнесены комбинированные системы, с использова-
нием алгоритмов наведения СА в точку посадки на конечном
участке спуска.
391
10.3. УПРАВЛЕНИЕ ДВИЖЕНИЕМ СА
НА КОНЕЧНОМ УЧАСТКЕ СПУСКА
В связи со значительным расширением в ближайшем
будущем класса задач, которые будут решаться космическими
аппаратами в околоземном и окололунном пространстве, во-
просы повышения точности посадки возвращаемых ракетно-
космических объектов становятся весьма актуальными. Суще-
ствующие системы управления спуском (СУС), основанные на
использовании только автономных методов управления, не поз-
воляют решить эти вопросы.
Имеющиеся в настоящее время автономные СУС не обес-
печивают требуемой точности посадки порядка сотен метров,
и получение такой точности наведения СА в заданную точку с
использованием только автономных средств управления весьма
затруднительно из-за наличия ошибок в определении началь-
ных параметров входа, инструментальных погрешностей нави-
гационных систем, действия различного рода возмущающих
факторов и т. д.
Ведущиеся в последнее время интенсивные исследования
автономных СУС с использованием бортовой вычислительной
техники позволяют значительно повысить точность посадки СА.
Однако, как показывает анализ работы подобных СУС (см.
10.2), обеспечение точного приведения СА на космодром связа-
но с рядом технических трудностей, так как прогнозирование
траектории спуска на конечном участке будет довольно неточ-
ным из-за существенной переменности аэродинамических ко-
эффициентов на околозвуковых скоростях полета.
При значительном увеличении в будущем грузопотока на
орбиты ИСЗ и увеличении интенсивности полетов в околозем-
ном и окололунном пространстве необходимо решать задачу
об обеспечении посадки СА непосредственно на космодром с
ошибками в точке посадки, не превышающими нескольких со-
тен метров. В связи с этим возникает необходимость разработ-
ки СУС, обеспечивающих такие точности посадки. Одним из
возможных путей решения данной задачи является создание
комбинированных (полуавтономных) СУС, использующих на
конечном участке спуска внешнюю информацию с целью уточ-
нения взаимного положения СА и точки посадки.
Такую информацию можно получить при использовании на-
земной радиолокационной станции (РЛС) или всенаправленно-
го радиомаяка. Подобного рода СУС могут быть применены
для точного приведения на космодром современных орбиталь-
ных космических аппаратов многоразового использования, об-
ладающих сравнительно высоким аэродинамическим качест-
вом, а также космических аппаратов, входящих в атмосферу
Земли и других планет с гиперболическими скоростями.
392
Одной из основных проблем при проектировании данных
СУС является обеспечение радиосвязи СА с Землей на конеч-
ном участке спуска. Так как в настоящее время радиосвязь не
может быть обеспечена на всем атмосферном участке спуска,
то на начальном участке входа могут быть использованы доста-
точно отработанные в настоящее время автономные СУС, а ра-
дионаведение используется с момента восстановления радио-
связи.
При использовании командного наведения СА в точку по-
садки положение СА в геоцентрической системе координат оп-
ределяется с помощью наземной РЛС. Путем обработки ре-
зультатов измерений определяется вектор фазового состояния
СА. В наземном вычислительном комплексе проводится интег-
рирование полных уравнений движения СА в ускоренном мас-
штабе времени и определяется требуемая величина управляю-
щего параметра, обеспечивающая приведение СА в заданную
точку посадки. В связи с большими возможностями по быстро-
действию и объему памяти наземной ЭЦВМ частота коррекций
управляющего параметра определяется возможностями испол-
нительных органов СА. При управлении по одному параметру
(углу крена у) для отработки бокового отклонения необходимы
перекладки по углу крена, так как для управления продольной
дальностью спуска используется эффективное аэродинамиче-
ское качество СА. С этой точки зрения более рациональным
является управление СА по двум параметрам (а—у-управле-
ние), причем угол крена может быть использован для стаби-
лизации плоскости наведения, а угол атаки а для обеспечения
полета на заданную дальность.
Для уменьшения требований к быстродействию ЭЦВМ воз-
можен режим работы ЭЦВМ, основанный на сравнении реаль-
ной траектории полета СА с серией опорных траекторий, зало-
женных в память ЭЦВМ, и выбор опорной траектории, удовле-
творяющей фактическому фазовому состоянию СА.
Сигналы коррекции высоты, дальности, азимута передают-
ся на борт аппарата по радиолинии с предварительным разде-
лением их по каналам автопилота. В запоминающем устройст-
ве наземной ЭЦВМ содержатся несколько опорных траекторий,
которые позволяют осуществлять более гибкое управление СА
и производить посадку в любую из наперед заданных точек
при значительных ошибках в начальных условиях входа в ат-
мосферу или, например, в случае аварийной посадки.
Число наземных РЛС определяется из условия обеспечения
непрерывного сопровождения СА от момента входа в атмосфе-
ру до момента посадки. Вследствие кривизны поверхности Зем-
ли сопровождение СА при некоторой заданной максимальной
дальности действия РЛС и некотором минимальном угле воз-
вышения РЛС может быть осуществлено в том случае, когда
393
высота полета СА больше некоторого минимального значения.
Для средних дальностей спуска при непрерывном сопровожде-
нии СА достаточно двух РЛС, одна из которых должна быть
установлена в районе расчетной точки посадки. Одним из важ-
нейших вопросов, который должен учитываться при проектиро-
вании данной системы управления, является вопрос о прохож-
дении радиосигналов через ионизированный слой газа, окружа-
ющий СА при спуске с большими скоростями в атмосфере.
Оболочка из плазмы и связанные с ней явления электромаг-
нитного поглощения, отражения, рефракции и т. д. в значи-
тельной степени затрудняют связь с СА в процессе спуска.
Данный метод управления СА на конечном участке требу-
ет минимума бортовой аппаратуры СА. Метод обеспечивает
гибкое управление движением СА при наличии аварийной си-
туации.
На конечном участке спуска возможно также использова-
ние различных методов самонаведения СА на маяк. В связи с
тем, что скорость полета СА значительно превышает окружную-
скорость маяка в геоцентрической системе осей координат, с
кинематической точки зрения все известные методы самонаве-
дения в данном случае приблизительно равноценны. Сравни-
тельный анализ в данном случае различных методов самонаве-
дения в существующих системах проводится на основании ана-
лиза закона поворота руля, соответствующего каждому из ме-
тодов самонаведения. При самонаведении СА на радиомаяк
закон поворота руля вблизи точки посадки не играет сущест-
венной роли, так как допустимая точность приведения состав-
ляет несколько сотен метров. Поэтому выбор того или иного
метода самонаведения диктуется, в первую очередь, составом
бортового оборудования, плавностью изменения кинематиче-
ских параметров траектории, возможностью ограничения этих
параметров, возможностью выполнения задачи в аварийных си-
туациях. С этой точки зрения заслуживает внимания метод
пропорциональной навигации, при котором угловая скорость
вектора скорости СА пропорциональна угловой скорости линии
визирования точки посадки. Соответствующим выбором коэф-
фициента пропорциональности (или его программированием по
траектории) возможно воздействие на параметры движения
СА в процессе спуска [28].
При использовании в качестве управляющего параметра
утла крена (у) самонаведение СА на маяк может быть органи-
зовано в плоскости наведения, проходящей через вектор теку-
щей скорости СА и линию визирования, причем в качестве
управляющей силы используется проекция вектора подъемной
силы на эту плоскость. При соответствующем усложнении за-
кона самонаведения возможна стабилизация плоскости наведе-
ния вблизи ее первоначального положения в момент начала са-
394
монаведения. Косинус угла крена СА в' первом приближении
пропорционален сигналу рассогласования между требуемой и
фактической угловой скоростью поворота вектора скорости
СА. Для осуществления самонаведения СА в точку посадки на
борту необходимо иметь пассивную радиолокационную головку
самонаведения и аппаратуру канала управления, а на Земле —
радиомаяк с всенаправленным излучением.
Таким образом, использование на конечном участке спуска
внешней информации о точке посадки является одним из не-
обходимых условий повышения точности посадки современных
космических аппаратов.
СПИСОК ЛИТЕРАТУРЫ
Основная литература
1. Алексеев К. Б., Бебенин Г. Г., Ярошевский В. А. Маневрирование кос-
мических аппаратов. М.: Машиностроение, 1970. 416 с.
2. Андреевский В. В. Динамика спуска космических аппаратов на Зем-
лю. М.: Машиностроение, 1970. 232 с.
3. Аппазов Р. Ф., Лавров С. С., Мишин В. П. Баллистика управляемых
ракет дальнего действия. М.: Наука, 4966. 308 с.
4. Балк М. Б. Элементы динамики космического полета. М.: Наука, 1965.
339 с.
5. Баринов Н. К., Бурдаев М. Н., Мамон А. А. Динамика и принципы^
построения орбитальных систем космических аппаратов. М.: Машинострое-
ние, 1975. 230 с.
6. Иванов Н. М.. Дмитриевский А. А., Лысенко Л. Н. Баллистика и на-
вигация космических аппаратов. М.: Машиностроение, 1986. 296 с.
7. Механика оптимального пространственного движения летательных ал-
па|ратов в атмосфере (Л. М. Шкадов, Р. С. Буханова, В. Ф. Илларионов,.
В. П. Плохих).—М.: Машиностроение, 1972. 240 с.
8. Мишин В. П., Безвербый В. К., Панкратов Б. М., Щеверов Д. hL
Основы проектирования летательных аппаратов. М.: Машиностроение, 1985.
360 с.
9. Основы теории полета космических аппаратов/Под ред. Г. С. Нарима-
нова, М. К. Тихонравова. М.: Машиностроение. 1972. 608 с.
10. Сихарулидзе Ю. Г. Баллистика летательных аппаратов. М.: Наука,
1982. 352 с.
11. Тарасов Е. В. Космонавтика. М.: Машиностроение, 1977. 216 с.
12. Эльясберг П. Е. Введение в теорию полета искусственных спутников
Земли. М.: Наука, 1965. 540 с.
Дополнительная литература
13. Барер А. С. Проблемы ускорений в космической физиологии//Кос-
мическая физиология и медицина. 1967. № 1. С. 57—64.
14. Безменов В. М., Овсянников Р. Н., Токарев В. В. Построение опти-
мальных управлений и траекторий межпланетных перелетов с нерегулируе-
мыми двигателями ограниченной мощности//Труды ЦАГИ. 1974. Вып. 1558.
С. 73.
15. Бочаров Л. А., Иванов Н. М., Голуб И. Б. Алгоритмы управления
спуском аппаратов, входящих в атмосферу Земли с гиперболическими скоро-
стями//Космические исследования. 1971. Т. IX. Вып. 5. С. 662—668.
46. Бухаркина А. П. Управление в широком диапазоне дальностей при
входе в атмосферу с параболической скоростью//ИПМ АН СССР. Препринт.
1974. № 8. С. 38.
17. Геловани В. А. Исследование диапазона дальностей участка посадки
при гиперболических скоростях входа в атмосферу Земли//Космические ис-
следования. 1972. Т. X. Вып. 3. С. 338—344.
396
18. Голубев Ю. Ф., Филиппович И. В. Алгоритмы управления входом в
атмосферу с гиперболическими скоростями//Космические исследования. 1974.
Т. XII. Вып. 2. С. 190—199.
19. Горелик А. А., Бутко Г. И., Белоусов К). А. Бортовые цифровые
вычислительные машины. М.: Машиностроение, 1975. 204 с.
20. Гродзовский Г. Л., Иванов Ю. Н., Токарев В. В. Механика косми-
ческого полета проблемы оптимизации. М.: Наука, 1975. 704 с.
21. ГОСТ 4401—81. Атмосфера стандартная. Параметры.
22. ГОСТ 25645.101—83. Атмосфера Земли верхняя. Модель плотности
для проектных баллистических расчетов ИСЗ.
23. ГОСТ 25645.115—84. Атмосфера Земли верхняя. Модель плотности
для баллистического обеспечения полетов ИСЗ.
24. ГОСТ 25645.301—83. Расчеты баллистические ИСЗ. Методика расче-
та затрат топлива на маневрирование.
25. Иванов Н. М., Мартынов А. И. Управление движением космического
аппарата в атмосфере Марса. М.: Наука, 1977. 416 с.
26. Ильин В. А. Переход на орбиту ИСЗ за счет торможения в атмо-
сфере//Инженерный журнал. 1963. Т. III. Вып. 2. С. 203—206.
27. Ильин В. А., Кузмак Г. Е. Оптимальные перелеты космических ап-
паратов. М.: Наука, (1976. 744 с.
28. Каменков Е. Ф. Маневрирование опускаемых аппаратов. М.: Машино-
строение, 1983. 184 с.
29. Кислик М. Д. Сферы влияния больших планет и Луны//Космичес-
кие исследования. 1964. Т. 2. Вып. 6. С. 853—858.
30. Климин А. В. Торможение в атмосфере аппарата с экипажем после
межпланетного перелета//Космические исследования. 1973. Т. XI. Вып. 1.
С. 31—37.
31. Кондратюк Ю. В. Завоевание межпланетных пространств. М.: Обо-
ронгиз, 1947. 90 с.
32. Константинов М. С. Методы математического программирования в
проектировании летательных аппаратов. М.: Машиностроение, 1975. 164 с.
33. Константинов М. С., Елизаров О. А. Активный гравитационный ма-
невр— естественное развитие одной из интереснейших идей Ф. А. Цандера.//
Тр. восьмых Цандеровских чтений. Секция «Астродинамика». М.: 1986.
с. 95—102.
34. Королев С. ГТ. Основы проектирования баллистических ракет даль-
него действия//Творческое наследие академика Сергея Павловича Королева.
М.: Наука, 4980. С. 208—290.
35. Космическая техника/Под ред. Г. Сейферта. М.: Наука, 1964. 727 с.
36. Кубасов В. Н., Дашков А. А. Межпланетные полеты. М.: Машино-
строение, 1979. 271 с.
37. Кубасов В. Н., Дашков Г. Ю., Яблонько Ю. ГТ. Методы сближения
на орбите. М.: Машиностроение, 1985. 183 с.
38. Лебедев А. А., Красильщиков М. Н., Малышев В. В. Оптимальное
управление движением космических аппаратов. М.: Машиностроение, 1974.
199 с.
39. Лебедев А. А., Соколов В. Б. Встреча на орбите. М.: Машинострое-
ние, 1969. 366 с.
40. Лебедев А. А., Чернобровкин Л. С. Динамика полета беспилотных
летательных аппаратов. М.: Машиностроение, 1973. 616 с.
41. Лебедев В. Н. Расчет движения космического аппарата с малой тя-
гой. М.: ВЦ АН СССР, 1968. 408 с.
42. Левантовский В. И. Механика космического полета в элементарном
изложении. М.: Наука, 1980. 511 с.
43. Лидов М. Л. О приближенном анализе эволюции орбит искусствен-
ных спутников//Проблемы движения искусственных небесных тел. М.: Изд-во
АН СССР. 1963. С. 119—134.
397
44. Лис Л., Хартвинг Ф., Кохен К. Использование аэродинамической
подъемной силы при входе летательного аппарата в плотные слои атмо-
сферы Земли//БНТИ ЦАГИ. 1960. Техн, перевод. № 9984. 36 с.
45. Лоуден Д. Ф. Оптимальные траектории для космической навига-
ции/Пер. с англ. М.: Мир, 1966. 152 с.
46. Лох У. Динамика и термодинамика спуска в атмосферах планег/
Пер. с англ. М.: Мир, 1966. 276 с.
47. Мещерский И. В. Работы по механике тел переменной массы. М..
ГИТТЛ, 1952. 280 с.
48. Назаренко А. И., Скребушевский Б. С. Эволюция и устойчивость
спутниковых систем. М.: Машиностроение, 1981. 284 с.
49. О применении прямых методов в алгоритмах управления спуском
аппарата в атмосфере/В. П. Чарный, А. П. Бирзгал, В. И. Борисенко,
А. Г. Свищев//Космические исследования. 1969. Т. VII. Вып. 6. С. 814—818.
50. Охоцимский Д. Е. Исследование движения в центральном поле под
действием постоянного касательного ускорения//Космические исследования.
1964. Т. 2. Вып. 6. С. 817—842.
51. Охоцимский Д. Е., Бухаркина А. П., Голубев Ю. Ф. Алгоритмы авто-
номного управления приведением космического аппарата в заданную точку
посадки//Космические исследования. 1970. Т. VIII. Вып. 2. С. 169—189.
52. Охоцимский Д. Е.. Бухаркина А. П., Голубев Ю. Ф. Управление дви-
жением при входе в атмосферу//Космические исследования. 1969. Т. VII.
Вып. 2. С. 171 — 178.
53. Охоцимский Д. Е., Голубев Ю. Ф., Сихарулидзе Ю. Г. Алгоритмы
управления космическим аппаратом при входе в атмосферу. М.: Наука, 1975.
399 с.
54. Парышева Г. В., Ярошевский В. А. Приближенный расчет траекто-
рий квазистационарного планирования//Космические исследования. 1981.
Т. XIX. Вып. 2. С. 101 — 199.
55. Пономарев В. И. Теория управления движением космических аппа-
ратов. М.: Наука, 1965. 455 с.
56. Проблемы входа летательных аппаратов в атмосферу//БНТИ ЦАГИ.
1961. Обзор № 42. 171 с.
57. Проскурин В. Ф., Кочина Н. Г. Влияние гравитационных аномалий
Земли на движение искусственных спутников//Проблемы движения искус-
ственных небесных тел. М.: Изд-во АН СССР, 1963. С. 144—149.
58. Румянцев П. А. Космическая система «Метеор». М.: Знание//Сер.
Космонавтика, астрономия. 1983. № 10. 60 с.
59. Сетевые спутниковые системы/Под ред. П. П. Дмитриева и
В. С. Шебашаевича. М.: Радио и связь, 1982. 263 с.
60. Соловьев Ц. В., Тарасов Е. В. Прогнозирование межпланетных по-
летов. М.: Машиностроение, 1973. 400 с.
61. Справочное руководство по небесной механике и астродинамике/
Под ред. Г. Н. Дубошина. М.: Наука, 1'976. 863 с.
62. Тихонравов М. К., Яцунский Н. М., Максимов Г. Ю., Бажинов И. К.,
Гурко О. В. Основы теории полета и элементы проектирования ИСЗ. М.:
Машиностроение, 1967. 295 с.
63. Управление углом атаки космического аппарата посредством изме-
нения центровки/Б. Н. Петров, Ж. С. Агеев, Б. В. Викторов, И. С. Уколов//
Космические исследования. 1970. Т. VIII. Вып. 6. С. 855—86'1.
64. Штернфельд А. А. Введение в космонавтику. 2-е издание. М.: Наука,
1974. 240 с.
65. Хединг Д. Введение в метод фазовых интегралов (метод ВКБ)/Пер.
с англ. М.: Мир, 1965. 238 с.
66. Чепмен Д. Приближенный аналитический метод исследования входа
тел в атмосферу планет/Пер. с англ. М.: ИЛ, 1962. 114 с.
67. Юрин В. В. Оптимальная коррекция параметров орбиты космического
аппарата с двигателем малой тяги//Космические исследования. 1983. Т. XXI.
Вып. 5. С. 666—674.
398
68. Ярошевский В. А. Приближенный расчет траектории входа в атмо-
сферу//Космические исследования. 1964. Т. II. Вып. 4. С. 507—531.
69. Ярошевский В. А. Аналитический метод расчета коридора входа в
атмосферу//БНТИ ЦАГИ. Вып. 94. 21 с.
70. Bryson А. Е., Denham W. F. Guidance scheme for supercircular re-ent-
ry of a lifting vehicle//ARSJ, 1962.32. P. 894—898.
71. Edelbaum T. N. How many impulses? Astronaut and Aeronaut, 1967.
No 5. P. 64—69.
72. Foudriat E. C., Wingrove R. C. Guidance and control during direct-
descent parabolic re-entry. NASA TN 1961. D-979.
73. Windgrove R. C., Coate R. E. Lift-control during atmosphere entry
from super-circular velocity//Proceedings of the National Meeting on Manned
Space Flight. 1961. P. 15-24.
СПИСОК ЛИТЕРАТУРЫ ДЛЯ ФАКУЛЬТАТИВНОГО
ИЗУЧЕНИЯ
Аксенов Е. П. Теория движения искусственных спутников Земли. М.:
Наука, 1977. 360 с.
Аппазов Р. Ф., Сытин О. Г. Методы проектирования траекторий носите-
лей и спутников Земли. М.: Наука, 1987. 440 с.
Белецкий В. В. Очерки о движении космических тел. М.: Наука, 1972.
360 с.
Брандин В. И., Васильев А. А., Худяков С. Т. Экспериментальная косми-
ческая баллистика/Под ред. Д. А. Погорелова. М.: Машиностроение, .1974.
340 с.
Демин В. Г. Движение искусственного спутника в нецентральном поле
тяготения. М.: Наука. 1968. 352 с.
Дмитриевский А. А. Внешняя баллистика. М.: Машиностроение, 1979,
479 с.
Дмитриевский А. А., Иванов Н. М., Лысенко Л. Н., Богодистов С. С.
Баллистика и навигация ракет. М.: Машиностроение, 1985. 312 с.
Дмитриевский А. А., Лысенко Л. Н. Прикладные задачи теории опти-
мального управления движением беспилотных летательных аппаратов. М.:
Машиностроение, 1978. 328 с.
Дубошин Г. Н. Небесная механика. Основные задачи и методы. М.:
Наука, 1975. 800 с.
Егоров В. А., Гусев Л. И. Динамика перелетов между Землей и Луной.
М.: Наука, 1980. 544 с.
Захаров Ю. А. Проектирование межорбитальных космических аппаратов.
М.: Машиностроение, 1984. 176 с.
Ивашкин В. В. Оптимизация космических маневров при ограничениях на
расстояния до планет. М.: Наука, 1975. 392 с.
Инженерный справочник по космической технике./Под ред. А. В. Со-
лодов.а. М.: Воениздат, 1977. 430 с.
Основы теории полета и элементы проектирования искусственных спут-
ников Земли./Под ред. М. К. Тихонравова. М.: Машиностроение, 1974. 331 с.
Салмин В. В. Оптимизация космических перелетов с малой тягой. М.:
Машиностроение. 1987. 208 с.
Эрике К. Космический полет. Т. П (Динамика). Ч. I. М.: Наука. 1969.
572 с.
Эрике К. Космический полет. Т. П (Динамика). Ч. II. М.: Наука, 1970.
744 с.
Эскобал П. Методы астродинамики. М.: 1971. 341 с.
Эскобал П. Методы определения орбит. М.: 1970. 471 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автономные системы управления
спуском 383
Аномалия истинная 68
—и средняя 83, 84
— эксцентрическая 81
Апогей орбиты 72
Апоцентр орбиты 71
Апоцентр а л ьный радиус 71
Аргумент -перицентра 89
— широты 91, 293
Атмосферный участок спуска 326
Афелий 72
Аэродинамические силы 96, 100, 330
Аэродинамическое качество 317
Баллистический параметр 318
Бортовые цифровые вычислительные
машины 333, 388
Вековой уход элементов орбиты 124,
141, 168, 209, 297
Вектор Лапласа задачи двух тел 66
—• площадей задачи двух тел 59
Внеатмосферный участок спуска 318
Возмущение траектории СА при спус-
ке 381
Возмущения орбиты спутника веко-
вые 123, 128, 129, 182
--------периодические 123, 128,
182
— параметров относительного дви-
жения спутников 183
Возмущенное движение 52, 96
Время моторное 291, 300, 312
—• перелета 207, 244
— прохождение перицентра орби-
ты 81, 89
— спуска 321
— старта 244
— существования спутника 137
— фазирования 214
Гиперболические скорости входа СА
в атмосферу 358
Гиперболический избыток скорости
237, 266, 273
Грависфера 229, 231, 277
— миним;альных отклонений 236
Гравитационный маневр 277
----активный 282
— параметр небесного тела 32
---- задачи двух тел 57
Дальность спуска 321, 384
Двигатель малой тяги 289
Движение возмущенное 52
— невозмущенное 52
— относительное 173, 179, 183
Долгота 21
— восходящего узла 87, 168
Доза перегрузки 343
Задача двух тел 54
------- ограничения 58
— теории движения КА основная
11, 13
—• трех тел ограниченная 103
Задачи теории движения 11
Закон Кеплера второй 63, 64
----первый 69
---- третий 83
Зона обзора на поверхности 158
---- на фоне космоса 159
Изоперегрузочные траектории спуска
353
Импульс скорости 191, 194, 196, 198,
199, 218, 255
Импульсная аппроксимация активно-
го участка траектории 190, 201, 229
Интеграл Лапласа задачи двух тел
66
— площадей задачи двух тел 58, 59
—• площадей скалярный 61
—• энергии задачи двух тел 64, 65,
191
Интервал радиовидимости 168
Кинематические элементы орбиталь-
ной системы 153, 155
Командное наведение СА в точку по-
садки 393
Константа интеграла площадей 59
— энергии 65
Координаты фазовые 16, 39
Коридоры входа 364, 372
401
—• классификация 366
-----методы расчета 368, 371
— — методы расширения 374, 375
Коррекция траектории 224, 283
Космический аппарат (КА) 7
Коэффициент баллистический конст-
руктивный 135
— сжатия Земли 97
Линия апсид 72
— узлов 87
Лямбда — матричное управление 385
Матрица перехода между системами
координат 22, 27, 28, 30, 94
Межвитковый сдвиг трассы 157
Межорбитальный переход 190, 195,
201
Метод грависфер 231, 307
-----нулевой протяженности 236
— попадающих траекторий 387
— свободных траекторий 219
Многократное торможение КА в ат-
мосфере 361
Модулирующие функции 387
Наклонение орбиты спутника 88
Начальные условия входа 319
Начальный участок погружения СА
в атмосферу 346
Нецентральность гравитационного по-
ля Земли 97
Нормаль (к плоскости траектории) 23
Область начальных параметров 319
Окно запуска 276
Орбита гелиоцентрическая 151
— гиперболическая 73
— ИСЗ промежуточная 227, 229,
250
— • квазистационарная 158
— • круговая 70, 77
• — монтажная
— • обратная экваториальная 88
— параболическая 72
— полярная 88
— солнечносинхронная 151
— стационарная 145, 148, 165, 167,
198
— эллиптическая 71
— • экваториальная 88
Орбитальная система спутников 153
Орбитальный переход двухимпульс-
ный 191, 194, 198
— . — компланарный 190
—• — некомпланарный 195
-----трехимпульсный 199
Параметры входа в атмосферу 319,
321
— переходного эллипса 320, 325
Перегрузка 335
Перигелий орбиты 72
402
Перигей орбиты 72
Период обращения спутника 83
------- драконический 133, 156
— сидерический 232, 268
— синодический 232, 268
Перицентр орбиты 71
Перицентральный радиус 71
Плоскость горизонта • (местного) 23
— движения КА (спутника) 59
— картинная 285
— траектории 23, 60
— эклиптики 20, 21
Площадь, заметаемая радиусом-век-
тором спутника 63
Поле гравитационное ньютоновское 33
Полоса обзора 160
Полуавтономные СУС 391
Полуось орбиты большая 72, 73, 76
--- малая 72
Полярная форма интеграла площа-
дей 62
Постоянная гравитационная (универ-
сальная) 31
Потенциал гравитационного поля 33,
98
—------Земли 98
-------сжатого сфероида 98
— нормальный 98
—• ньютоновского гравитационного
поля 33
Потери в скорости 53, 164, 191
—• —• гравитационные 251, 264, 265
--- на управление 264, 266
Правило рычага 76
Прецессия орбиты 130
Прогнозирование параметров движе-
ния СА 388
Программа движения КА 41, 218
Проектирование траектории КА 11,
14
Прямее восхождение 20, 257
Равновесное планирование СА 353
Радиаль 23
Радиус-вектор КА 20, 23, 32
Разгон тангенциальный 264
— трансверсальный 264
Разгонный блок 227, 229, 243
Ракета-носитель 227
Расчет внеатмосферного участка
спуска 318
Режимы спуска 336
— — анализ 337
---расчет 337, 344, 350
Рикошетирующий спуск 361
Сближение КА 216
Сила аэродинамическая боковая 100
---подъемная 31, 100
— гравитационная 31
— лобового сопротивления 100
— притяжения ньютоновская 46
Система координат абсолютная 19 .
----- гелиоцентрическая эклипти-
ческая 22
—• — геоцентрическая экватори-
альная невращающаяся 19
-----гринвичская 21
----- эклиптическая 21
----- инерциальная 19
----- орбитальная 23
----- перицентральная 93
-----• связанная 23
Системы управления спуском 379
--------алгоритмы 379
-------- анализ 383
----------классификация 381
Системы спутников навигационных
170
----- обзора 161
----- связи 165
Склонение 20
Скоростей напор 100
Скорость гелиоцентрическая 230, 239
— геоцентрическая 230, 249, 252
— гиперболическая 79, 239
— истечения эффективная 34, 53
—• космическая вторая 79
------ первая 78
------ третья 237
— круговая 77
— параболическая 79
— плапетоцентрическая 259, 273
— радиальная 62, 74
— секториальная 63
— трансверсальная 62, 75
— характеристическая 53, 266, 273,
291, 304
— эллиптическая 79, 239
Спуск 315
— баллистический 337
— с постоянным аэродинамичес-
ким качеством 344
— управляемый 350
Спускаемый аппарат (СА) 316
Среднее движение спутника 83, 84,
85
Сутки звездные 156
— эффективные 279, 209
Суточный сдвиг трассы 158, 220
Сфера влияния (сфера Кислика) 236
—• действия (грависфера Лапласа)
235, 236
—• притяжения 233
Температура в критической точке
СА 340
Тензор инерции 18
Тепловой поток 340
— конвективный 340
---- от излучения 341
Тип орбиты гиперболический 70, 73 *
----параболический 70, 72
----эллиптический 70, 71
Типы траекторий спуска 337
Тормозной импульс 319
—--- оптимизация 323
---- расчет 322
Точки орбиты апсидальные 72
Траектория движения КА 7, 16
— программная 40, 41
— сближения 219
Трансверсаль 23
Трасса спутника 142, 144, 145
Тяга нормальная 298
— тангенциальная 264
— трансверсальная 264, 265, 295,
297
Угол атаки 264, 265
— крена 25
— • рыскания 25, 293
— тангажа 25, 293
—• траекторный 29, 251, 265
Угловая дальность полета 246, 311
Удельный импульс тяги 191, 289
Узел орбиты восходящий 87
----нисходящий 87
Управление движением СА 315, 379
---------- комбинированное 315, 371
------- —• скоростным углом крена
315
— •---углом атаки 315
— • сближением 216
Уравнение Ламберта 246
— • Кеплера 82, 85
— • моментов 18
— • орбиты спутника 68, 69, 85
— сил 18, 35
Ускорение 18, 19
— возмущающее 97, 107, 108
------- аэродинамическое 101, 108
—• — лунно-солнечное 104, 105,
106, 108
------- от пецентралы-юсти гравита-
ционного поля Земли 100
—• гравитационное 33
•---• ньютоновское 33
— нормальное 293
— радиальное 293
— реактивное 53
— трансверсальное 294
Условие кратности 209
Условная граница атмосферы 319
Участок активный 7, 35, 251
—• движения КА гелиоцентричес-
кий (гелиоцентрический участок
траектории) 230, 239, 241, 243, 244
403
— — — геоцентрический (геоцент-
рический участок траектории) 230,
239, 241, 249, 252
------- планетоцентрический (пла-
нетоцентрический участок траекто-
рии) 259, 260
—• пассивный 7, 35
—• раскрутки (набора параболичес-
кой скорости) 308
Фазирование 214
Фазовый угол 214
Фокальный параметр орбиты 69
Фокальное расстояние орбиты 72
Формула Циолковского 53
Ширина коридора входа 365
Широта геодезическая 155
— геоцентрическая 21, 155
Эксцентриситет орбиты спутника 69
Электрический ракетный двигатель
(ЭРД) 289
Элементы орбиты спутника 90, 154
--------оскулирующие НО
Эллипс минимальной энергии 192
Эффективное аэродинамическое ка-
чество С А 381
ОГЛАВЛЕНИЕ
Предисловие....................................................... 3
Основные обозначения.............................................. 4
Введение.......................................................... 7
Глава 1. Общая теория движения . . ... 16
1.1. Траектория движения КА.............................16
1.2. Системы координат для анализа движения КА . 19
1.3. Силы, действующие на КА............................30
1.4. Полная система уравнений, описывающая движение КА 35
1.5. Определение начальных данных при интегрировании
уравнений движения КА...................................42
1.6. Погрешности расчета траекторий движения КА . . 45
1.7. Методы оценок малых возмущений кинематических
параметров движения КА..................................48
1.8. Упрощения уравнений движения для выбора траекто-
рии КА .................................................50
Глава 2. Движение космического аппарата в центральном поле тя-
готения ............................................................54
2.1. Уравнения относительного движения в задаче двух
тел....................................................55
2.2. Интеграл площадей задачи двух тел..................58
2.3. Интеграл энергии задачи двух тел..................64
2.4. Интеграл Лапласа задачи двух тел..................66
2.5. Уравнение орбиты задачи двух тел..................68
2.6. Типы орбит.........................................70
2.7. Анализ изменения скорости КА по орбите. Зависи-
мость типа орбиты от начальных условий движения 74
2.8. Космические скорости...............................77
2.9. Временные характеристики движения КА по орбите . 80
2.10. Элементы орбиты спутника..........................87
Глава 3. Движение искусственных спутников Земли .... 96
3.1. Возмущающие ускорения при анализе движения спут-
ника ...................................................96
3.2. Модель возмущения движения ИСЗ....................108
3.3. Периодические и вековые возмущения орбиты спут-
ника ..................................................122
3.4. Возмущения орбиты ИСЗ, вызываемые нецентраль-
ностью гравитационного поля Земли......................126
3.5. Возмущения орбиты ИСЗ, вызываемые действием ат-
мосферы. Определение времени существования спут-
ника ..................................................134
405
3.6. Возмущения орбиты ИСЗ, вызываемые влиянием Лу-
ны и Солнца............................................138
3.7. Трасса спутника. Выбор орбиты ИСЗ................142
Глава 4. Динамика и методы расчета орбитальных систем космичес-
ких аппаратов.....................................................153
4.1. Кинематические элементы системы спутников . .153
4.2. Методы расчета спутниковых систем ... .160
4.3. Динамика орбитальных систем.................... .172
Глава 5. Маневрирование и сближение космических аппаратов . 189
5.1. Компланарные межорбитальные переходы ... 190
5.2. Некомпланарные межорбитальные переходы . . 195
5.3. О числе импульсов при межорбитальных переходах 201
5.4. Монтажные орбиты................................ 208
5.5. Сближение космических аппаратов................. 216
Глава 6. Расчет траекторий межпланетных аппаратов . 226
6.1. Схема полета межпланетного КА. Идея приближенно-
го метода расчета траекторий межпланетных аппаратов 227
6.2. Грависферы небесных тел Солнечной системы
6.3. Третья космическая скорость......................237
6.4. Расчет гелиоцентрического участка движения КА . 244
6.5. Анализ геоцентрического участка траектории межпла-
нетного перелета......................................24*9
6.6. Анализ движения КА в грависфере планеты назначения 259
6.7. Оптимизация перелетов КА к планете назначения . 264
6.8. Гравитационный маневр в межпланетных перелетах . 277
6.9. Коррекция траекторий межпланетных КА .... 283
Глава 7. Исследование движения КА с двигателем малой тяги 289
7.1. Особенности траекторий КА с ЭРД..................289
7.2. Математическая модель для исследования движения
КА с двигателем малой тяги.............................292
7.3. Исследование движения КА при простых законах уп-
равления вектором тяги.................................295
7.4. Многовитковый перелет между некомпланарными кру-
говыми орбитами........................................300
7.5. Межпланетные перелеты КА с двигателем малой тяги 305
Глава 8. Спуск космического аппарата с орбиты спутника планеты 315
8.1. Классификация режимов спуска....................315
8.2. Внеатмосферный участок спуска КА с орбиты спутни-
ка планеты.............................................318
8.3. Уравнения движения СА на атмосферном участке
спуска.................................................326
8.4. Методы исследования уравнений движения спускаемых
аппаратов .............................................334
8J5. Анализ типовых режимов спуска аппарата в атмос-
фере ..................................................336
Глава 9е Спуск космического аппарата с межпланетной орбиты . 357
9.1. Предварительный анализ....................... . 357
9.2. Выход аппарата на орбиту спутника планеты . 361
9.3. Коридоры входа............................... . 364
9.4. Расчет коридоров входа при а—у-управлении . 371
406
Глава 10. Методы управления движением спускаемых аппаратов 379
10.1. Классификация систем управления спуском (СУС) 379
10.2. Анализ автономных систем управления спуском 383
10.3. Управление движением СА на конечном участке спуска 392
Список литературы................................................396
Предметный указатель.............................................401
УЧЕБНОЕ ИЗДАНИЕ
Константинов Михаил Сергеевич, Каменков Евгений Федорович,
Перелыгин Борис Павлович, Безвербый Виталий Константинович
МЕХАНИКА КОСМИЧЕСКОГО ПОЛЕТА
Редактор Г. П. Филипповская
Художественный редактор В. В. Лебедев
Технический редактор Н. М. Харитонова
Корректоры Л. Е. Сонюшкина и Л. А. Ягупьева
ИБ № 5300
Сдано в набор 29.12.87. Подписано в печать 15.08.89.
Т-04928. Формат 60X88’/l6. Бумага типогр. № 2. Гарнитура литературная.
Печать офсетная. Усл. печ. л. 24,99. Усл. кр.-отт. 24,99. Уч.-изд. л. 25,0.
Тираж 2970 экз. Заказ № 8. Цена 1 р. 20 к.
Ордена Трудового Красного Знамени издательство «Машиностроение».
107076, Москва, Стромынский пер., 4
Типография издательства «Радио и связь». 101000 Москва, ул. Кирова, д. 40.