Л.Э. Генденштейн, А.П. Ершова, А.С. Ершова
НАГЛЯДНЫЙ
СПРАВОЧНИК
для абитуриентов,
школьников,
учителей
ИЛЕКСА
Москва
2009

Рецензент
Ю.В. Гандель, доктор физико-математических наук,
профессор Харьковского государственного университета
Генденштейн Л.Э., Ершова А.П., Ершова А.С.
Наглядный справочник по математике с
примерами. Для абитуриентов, школьников, учителей.—
М.: Илекса, 2009,— 192 с.
ISBN 978-5-89237-108-7
Справочник отличается максимальной наглядностью:
каждая тема школьного курса математики иллюстрируется
«говорящими» графиками и рисунками.
Книга поможет учащимся школ, лицеев и гимназий,
независимо от того, по каким учебникам и по какой
программе изучается курс математики, наглядно
представить изучаемый материал и быстро найти необходимые
сведения. Такой справочник на столах учеников позволит
учителю освободить время урока для решения задач.
Выпускникам и абитуриентам справочник даст
возможность увидеть предмет в целом и систематизировать свои
знания.
© Генденштейн Л.Э.,
Ершова А.П.,
Ершова А.С., 2003
ISBN 978-5-89237-108-7 © ИЛЕКСА, 2003

3
СОДЕРЖАНИЕ
АЛГЕБРА И НАЧАЛА АНАЛИЗА
функции 10
Основные свойства функций 11
Четность и нечетность 11
Периодичность 12
Нули функции 12
Монотонность (возрастание, убывание) 13
Экстремумы (максимумы и минимумы) 13
Асимптоты 14
Обратные функции 15
Нахождение формулы для функции, обратной данной 15
Преобразования графиков функций 16
Преобразование симметрии относительно оси х 16
Преобразование симметрии относительно оси у 17
Параллельный перенос вдоль оси х 18
Параллельный перенос вдоль оси у 19
Сжатие и растяжение вдоль оси х 20
Сжатие и растяжение вдоль оси у 21
Построение графика функции у = |f(x)| 22
Построение графика функции у = f(|x|) 22
Построение графика обратной функции 23
Построение графиков сложных функций с помощью
последовательных преобразований графиков
элементарных функций 24
Линейная функция 26
Частные случаи линейной функции (прямая
пропорциональность и постоянная функция) 26
Взаимное расположение графиков линейных функций 26
Свойства линейной функции 27
Построение графика линейной функции по двум точкам 28
Построение графика линейной функции у = kx + b
с помощью элементарных преобразований графика
функции у = х 29
Квадратичная функция 30
Различные представления квадратичной функции 30
Выделение полного квадрата 30
Разложение на линейные множители 30
Свойства квадратичной функции и ее графика 31
Направление ветвей, характерные точки и ось симметрии
параболы 32

4
Построение графика квадратичной функции
по направлению ветвей, характерным точкам
и оси симметрии параболы (примеры) 33
Построение графика квадратичной функции
с помощью элементарных преобразований
графика функции у = х^2 34
Степенные функции с натуральными показателями степени 36
Степенные функции с целыми отрицательными
показателями степени 37
Функции у = x^(1/n) 38
Степенные функции с действительными
показателями степени 39
Показательная функция 40
Логарифмическая функция 41
Тригонометрические функции 42
Обратные тригонометрические функции 46
уравнения 48
Линейные уравнения 49
Квадратные уравнения 50
Неполные квадратные уравнения 51
Теоремы Виета 52
Формулы Виета для корней приведенного квадратного
уравнения 52
Уравнения, сводящиеся к квадратным 53
Иррациональные уравнения 54
Простейшие показательные уравнения 55
Простейшие логарифмические уравнения 55
Простейшие тригонометрические уравнения 56
Уравнение с двумя переменными и его график 59
неравенства 61
Линейные неравенства 62
Квадратные неравенства 63
Метод интервалов для неравенств вида
(x-al)^k1(x-a2)^k2...(x-an)^kn >0 64
Применение метода интервалов для решения дробно-
рациональных неравенств 65
Иррациональные неравенства 66
Показательные неравенства 67
Логарифмические неравенства 67
Простейшие тригонометрические неравенства 68

5
системы двух уравнений с двумя
неизвестными 71
Основные методы решения систем уравнений 72
Метод подстановки 72
Метод сложения 73
Графический метод решения системы двух уравнений
с двумя неизвестными 74
Системы двух линейных уравнений с двумя неизвестными 75
производная и ее применения 76
Производная 76
Геометрический смысл производной 76
Уравнение касательной 76
Вторая производная 77
Физический смысл производной 77
Правила дифференцирования 77
Производная сложной функции 77
Применение производной к исследованию функций 78
Монотонность 78
Экстремумы 79
Схема применения производной для нахождения
интервалов монотонности и экстремумов 80
Наибольшее и наименьшее значения функции,
непрерывной на отрезке 81
Схема нахождения наибольшего и наименьшего значений
функции, непрерывной на отрезке 81
первообразная и интеграл 82
Первообразная 82
Основное свойство первообразных 82
Неопределенный интеграл 82
Правила интегрирования 82
Определенный интеграл 83
Связь между определенным интегралом и первообразной
(формула Ньютона-Лейбница) 83
Основные свойства определенного интеграла 83
Геометрический смысл определенного интеграла 84
Физический смысл определенного интеграла 84
Вычисление площадей и объемов с помощью определенного
интеграла 85

6
ГЕОМЕТРИЯ
планиметрия 86
Прямые и углы на плоскости 86
Виды углов 86
Углы с соответственно параллельными сторонами 86
Углы с соответственно перпендикулярными сторонами 86
Параллельные прямые 87
Признаки и свойства параллельных прямых 87
Перпендикуляр и наклонные 88
Треугольники 89
Произвольный треугольник 89
Соотношения между сторонами и углами 89
Признаки равенства треугольников 90
Признаки подобия треугольников 90
Свойство прямой, параллельной стороне треугольника 90
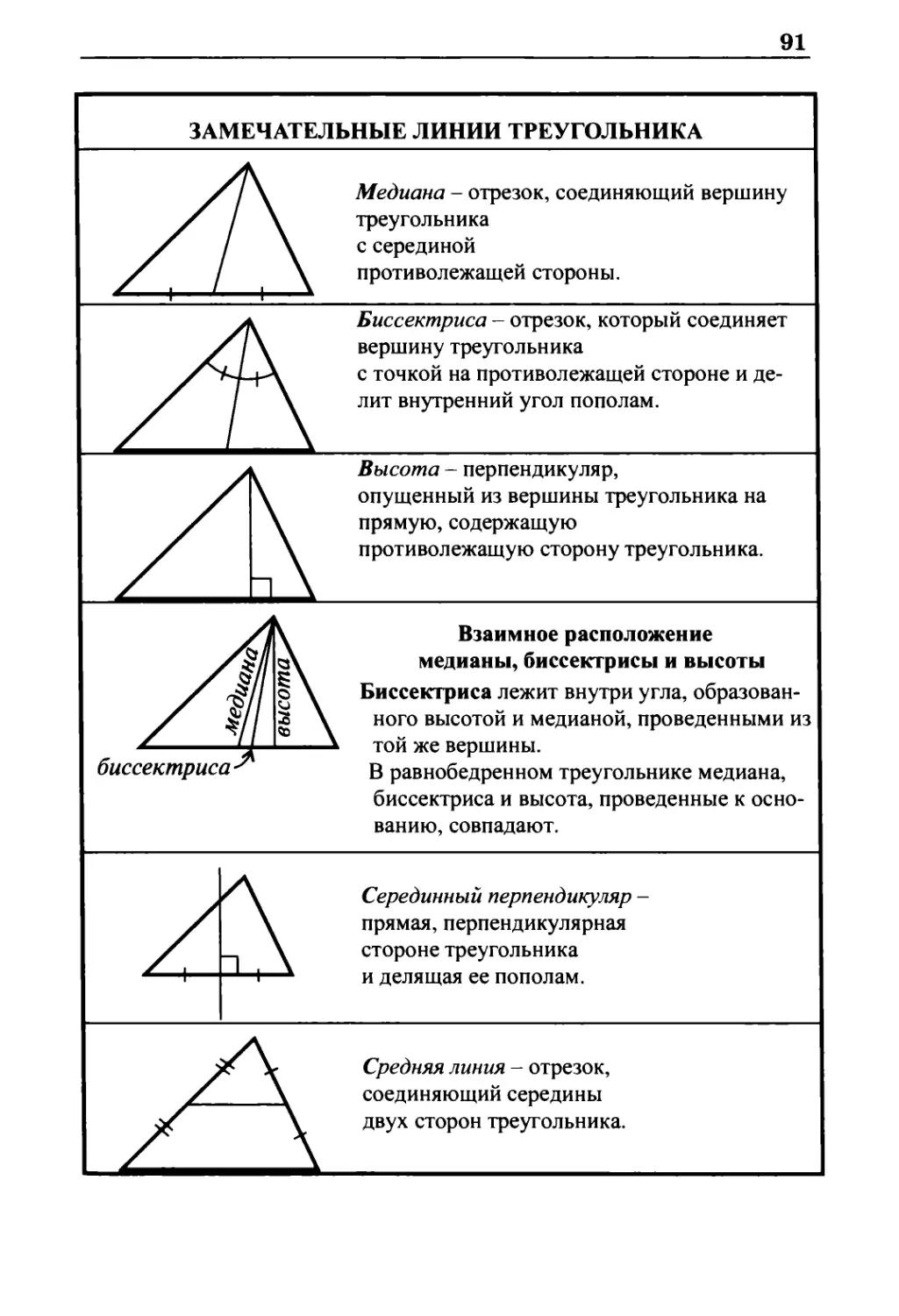
Замечательные линии треугольника 91
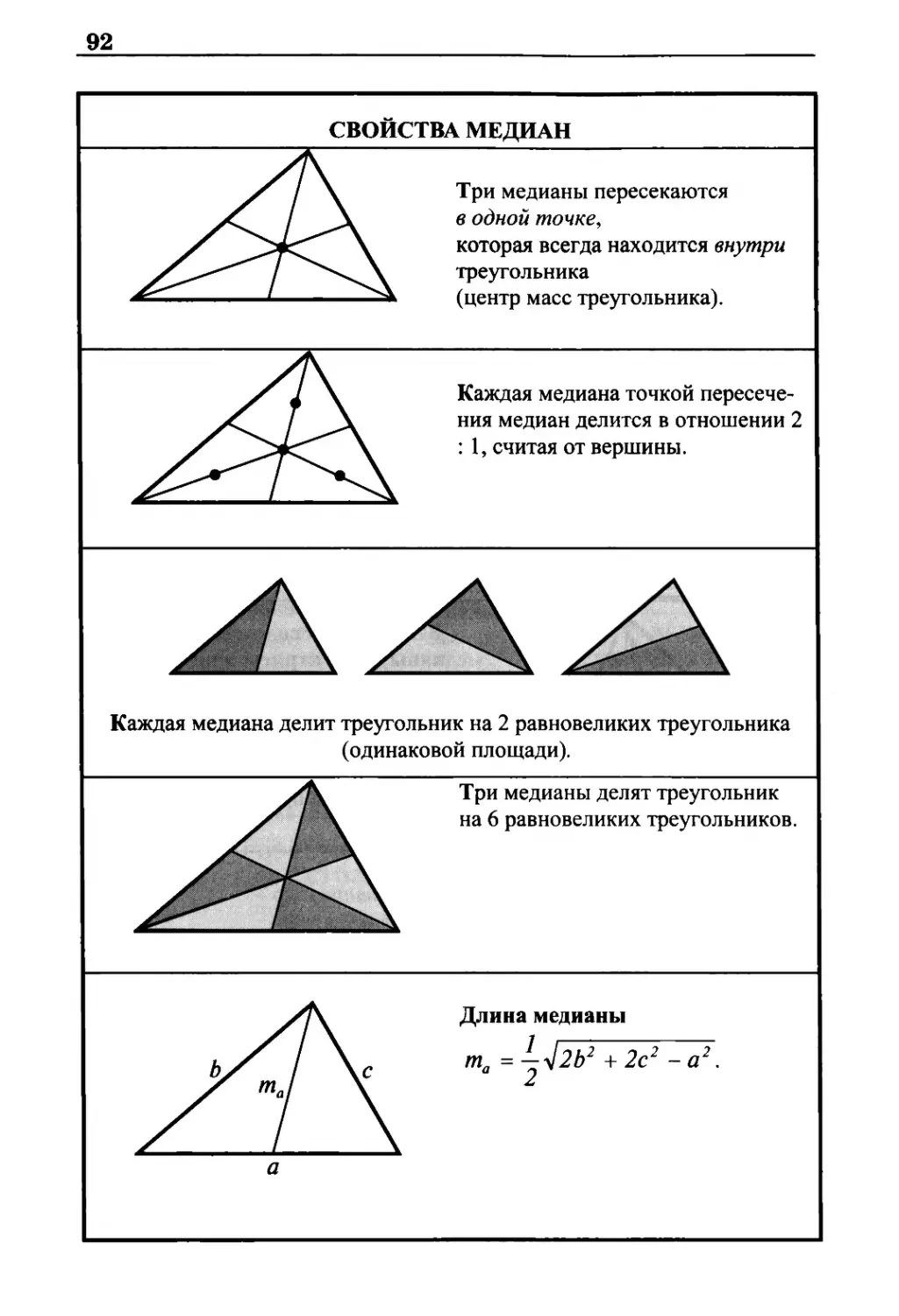
Свойства медиан 92
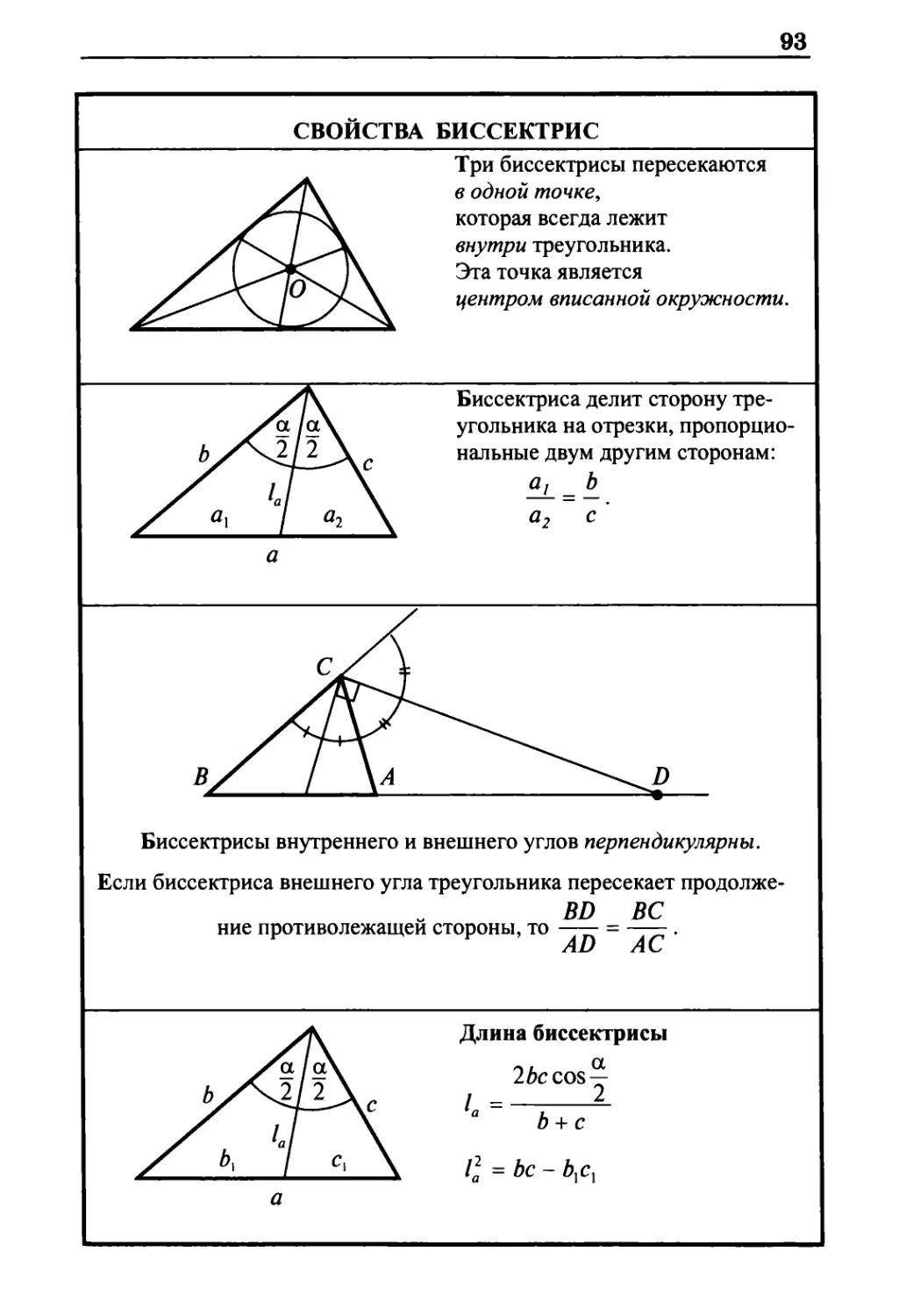
Свойства биссектрис 93
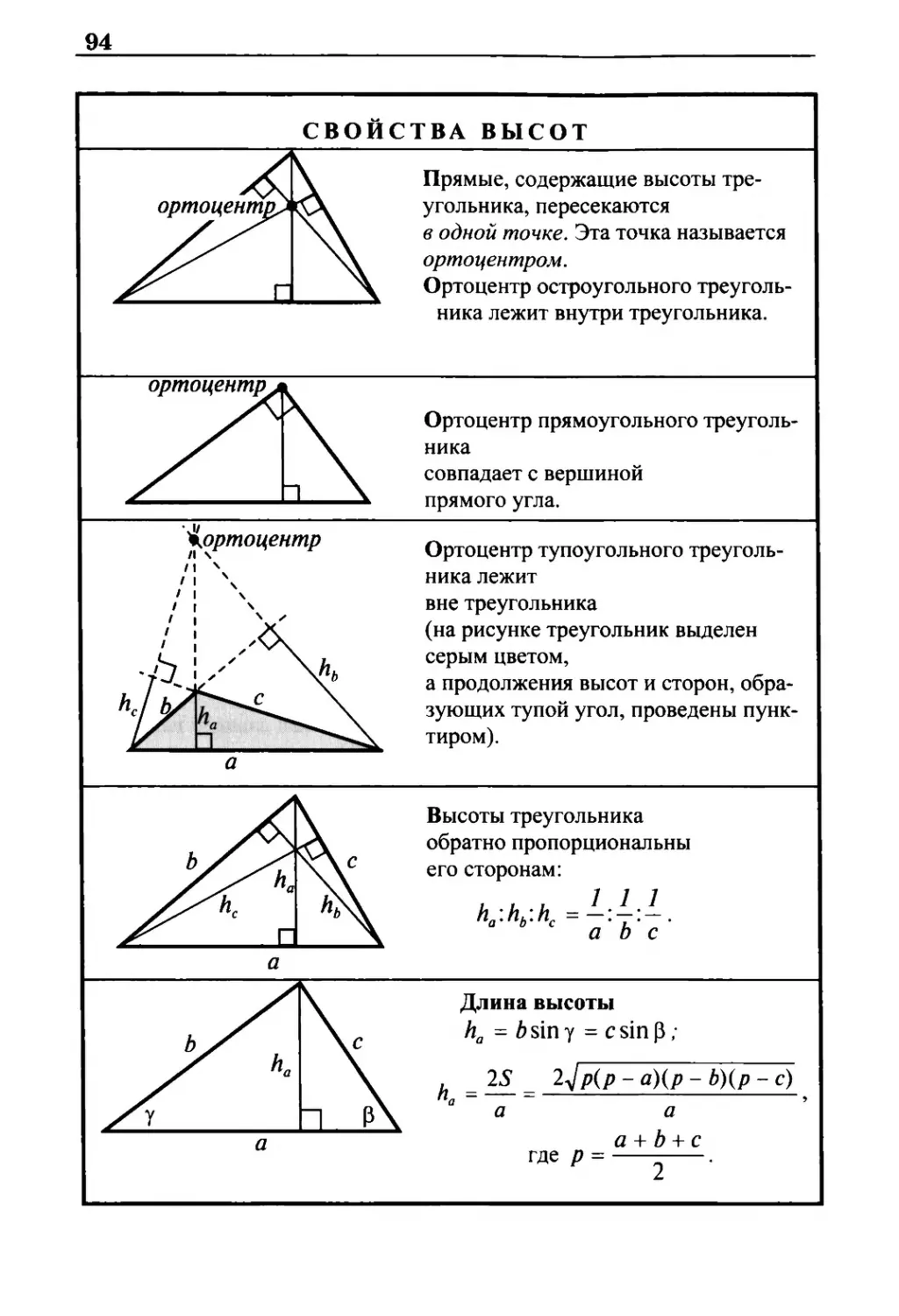
Свойства высот 94
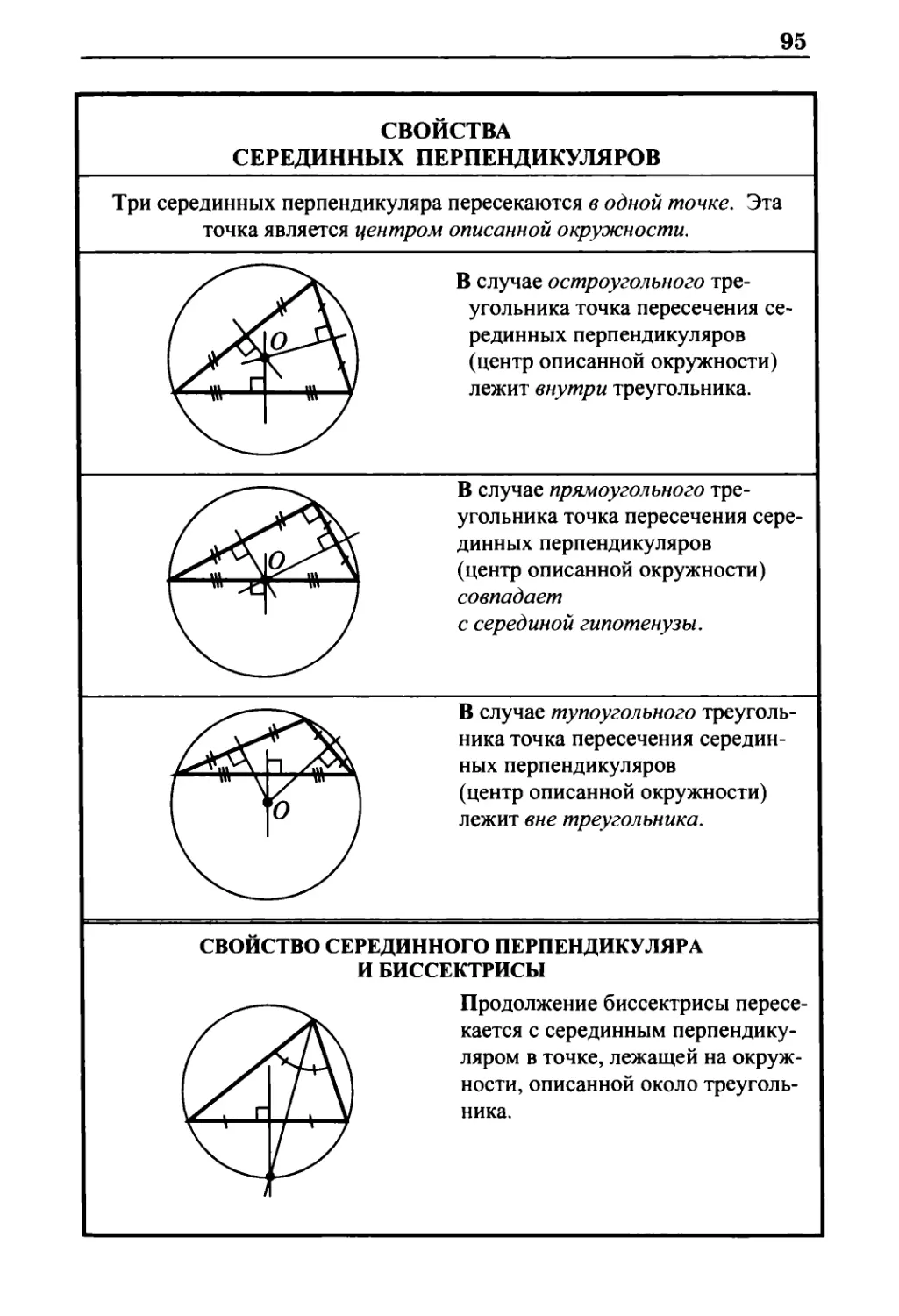
Свойства серединных перпендикуляров 95
Свойства средней линии 96
Вписанная и описанная окружности 96
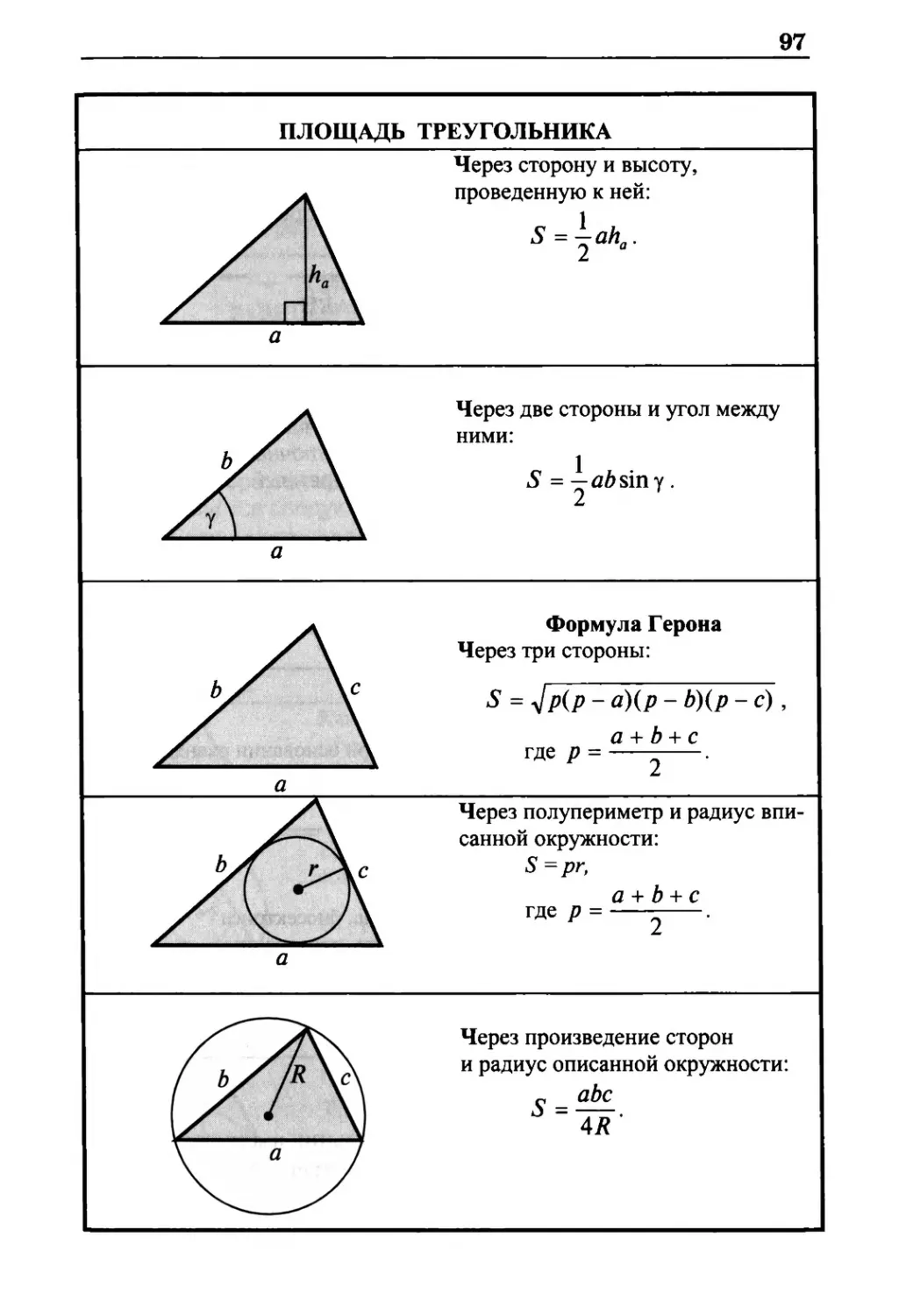
Площадь треугольника 97
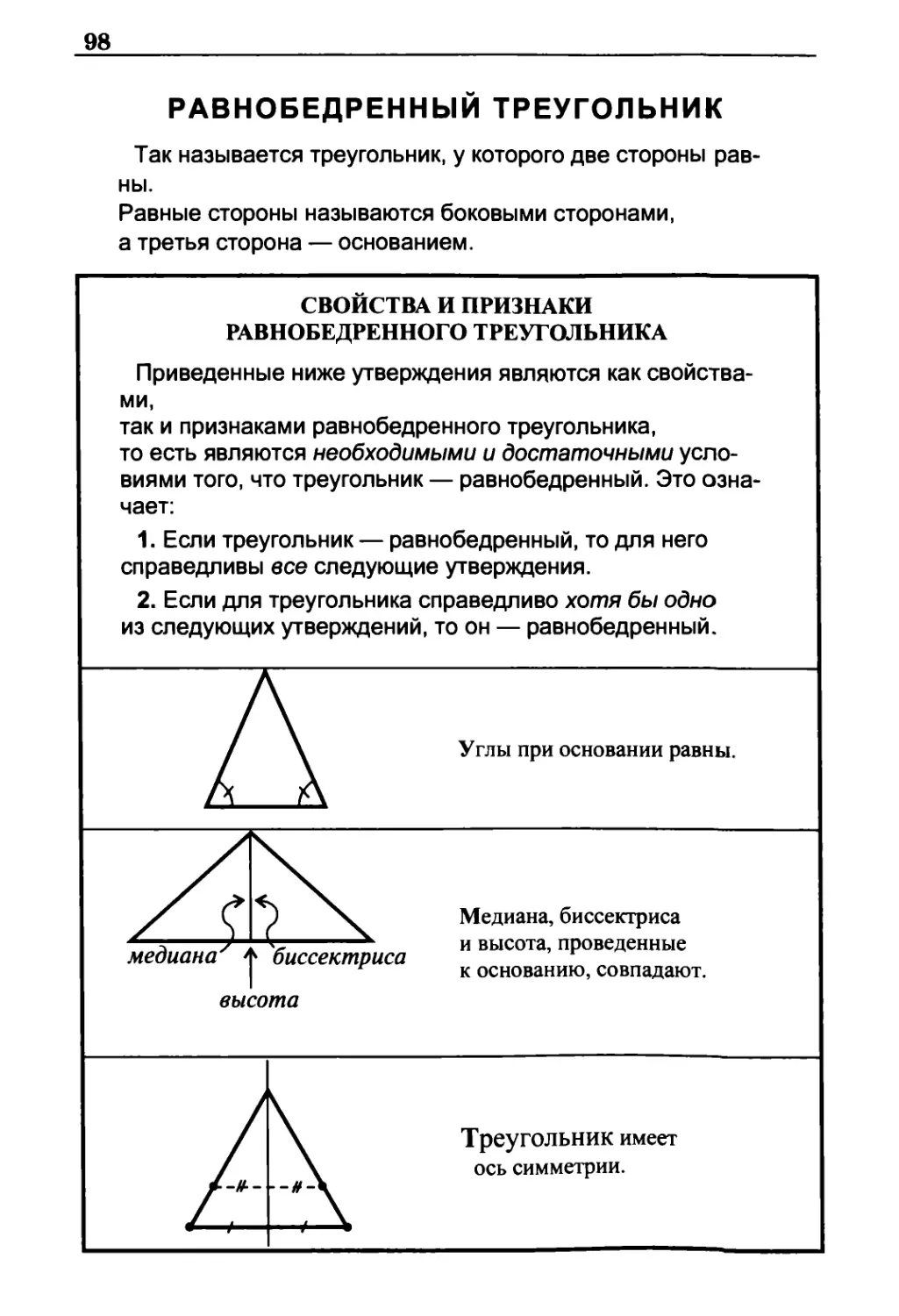
Равнобедренный треугольник 98
Свойства и признаки равнобедренного треугольника 98
Равносторонний треугольник 99
Свойства и признаки равностороннего треугольника 99
Высота и площадь равностороннего треугольника 99
Прямоугольный треугольник 100
Признаки равенства прямоугольных треугольников 100
Признаки подобия прямоугольных треугольников 101
Теорема Пифагора 101
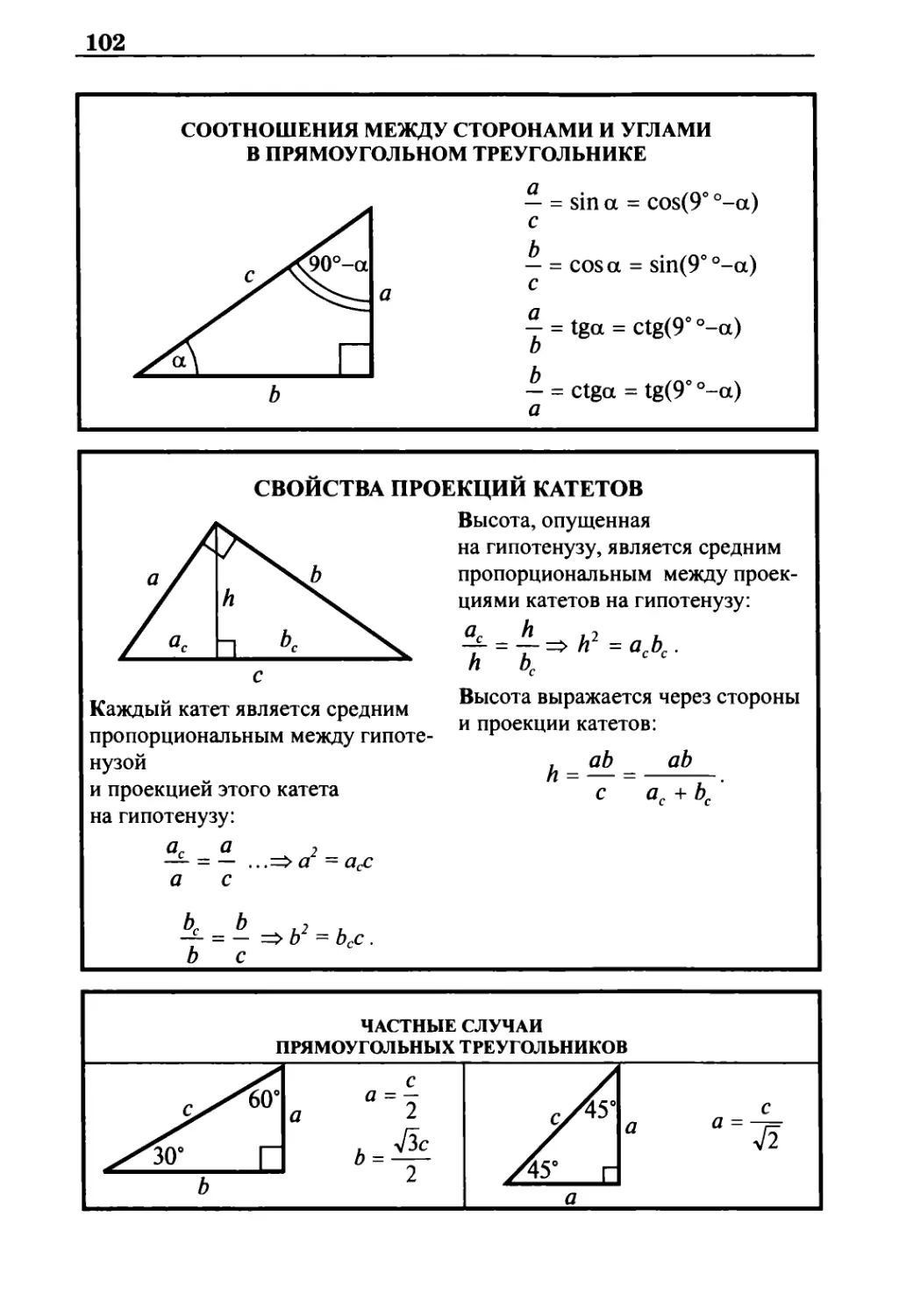
Соотношения между сторонами и углами в прямоугольном
треугольнике 102
Свойства проекций катетов 102
Частные случаи прямоугольных треугольников 102
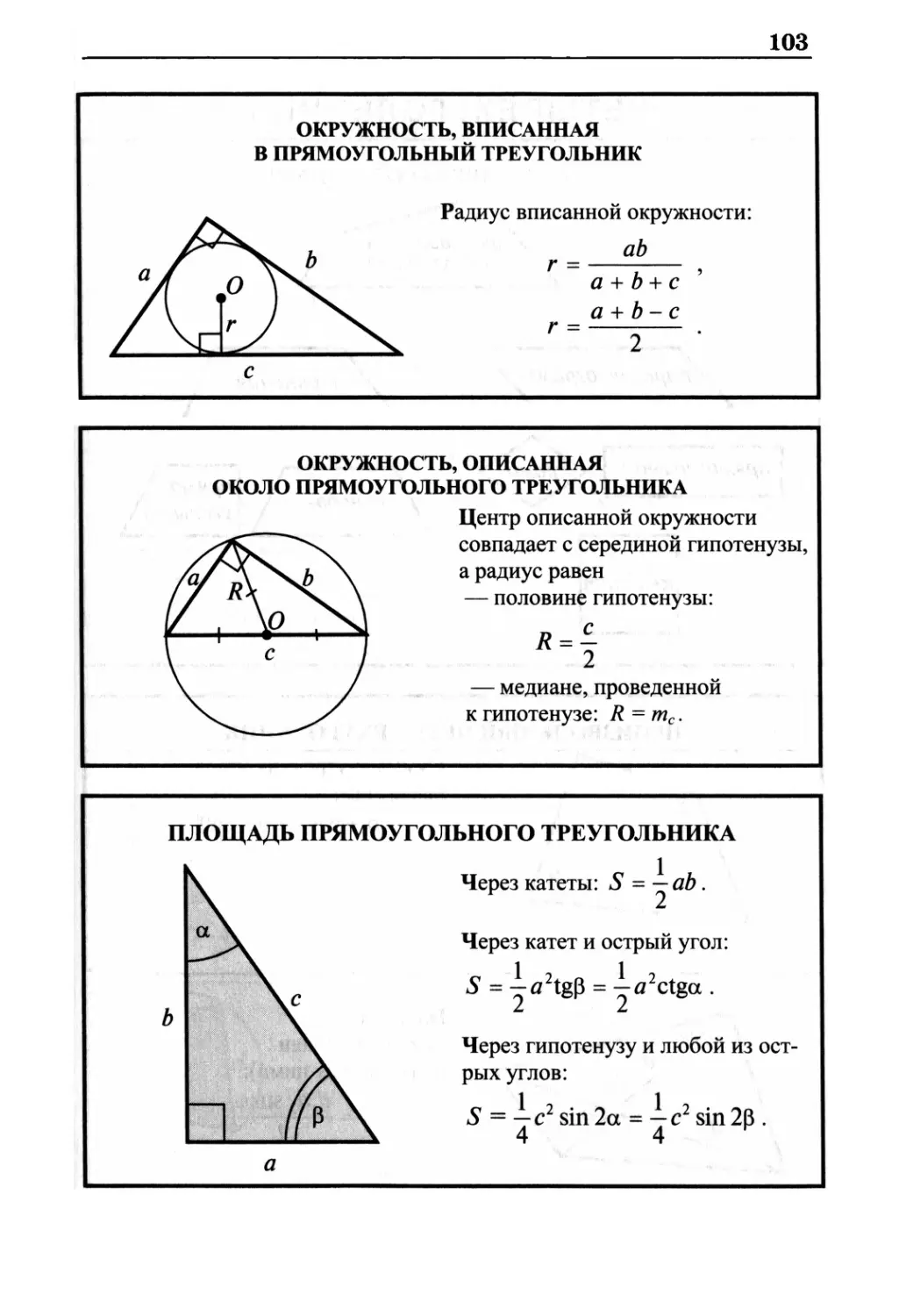
Окружность, вписанная в прямоугольный треугольник 103
Окружность, описанная около прямоугольного треугольника 103
Площадь прямоугольного треугольника 103
Четырехугольники 104
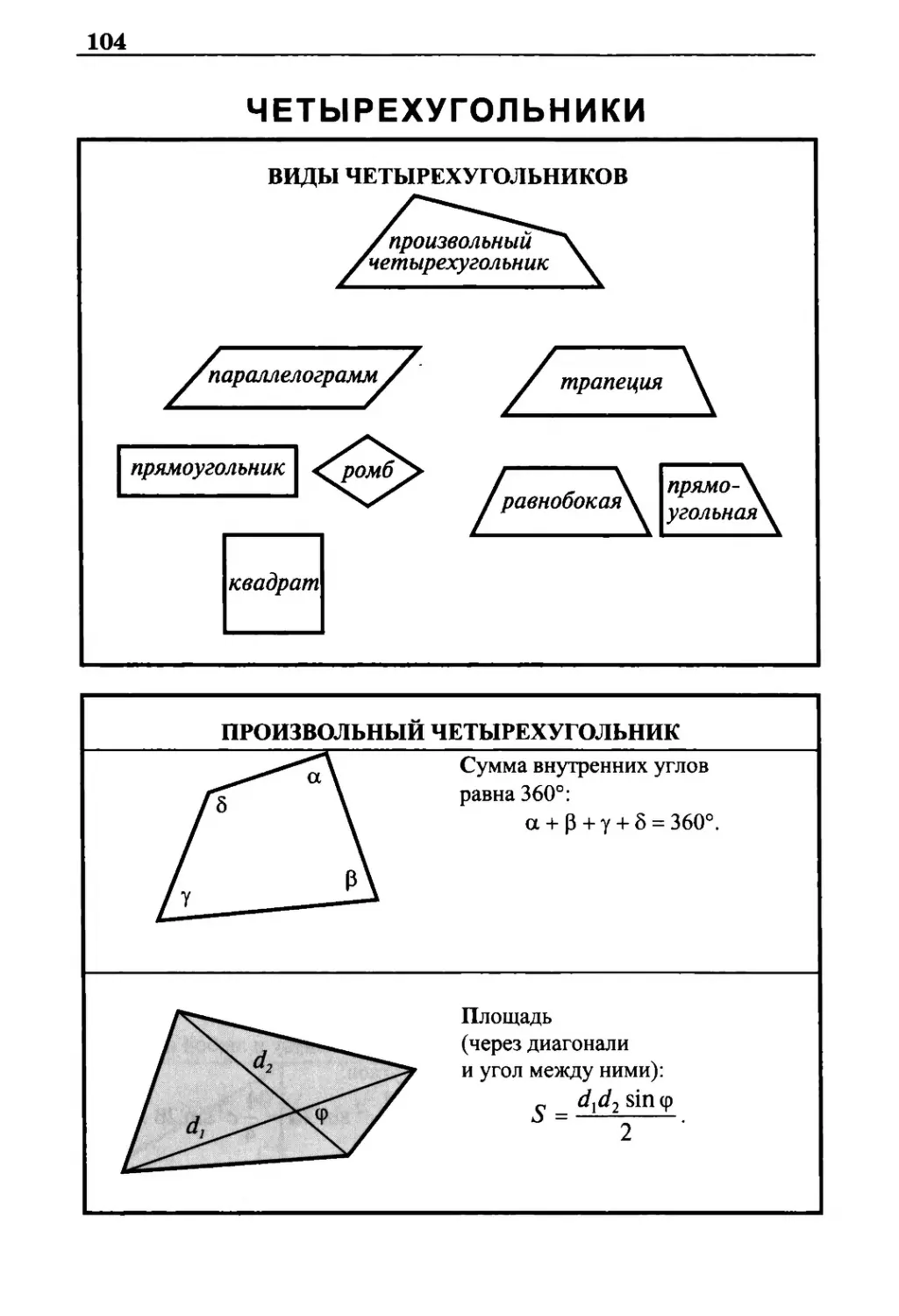
Виды четырехугольников 104

7
Произвольный четырехугольник 104
Четырехугольник, описанный около окружности 105
Четырехугольник, вписанный в окружность 105
Параллелограмм 106
Свойства и признаки параллелограмма 106
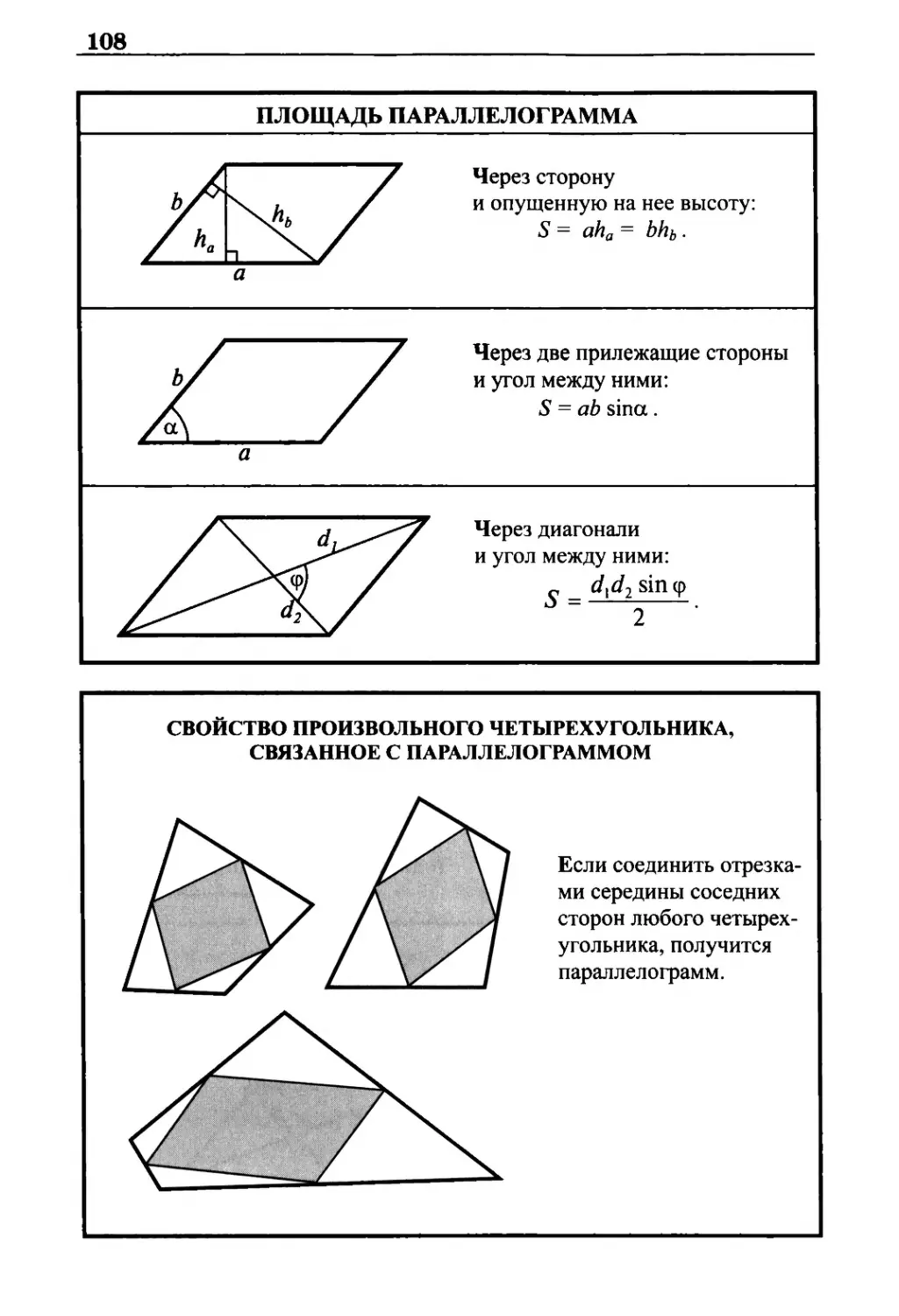
Площадь параллелограмма 108
Свойство произвольного четырехугольника, связанное с
параллелограммом 108
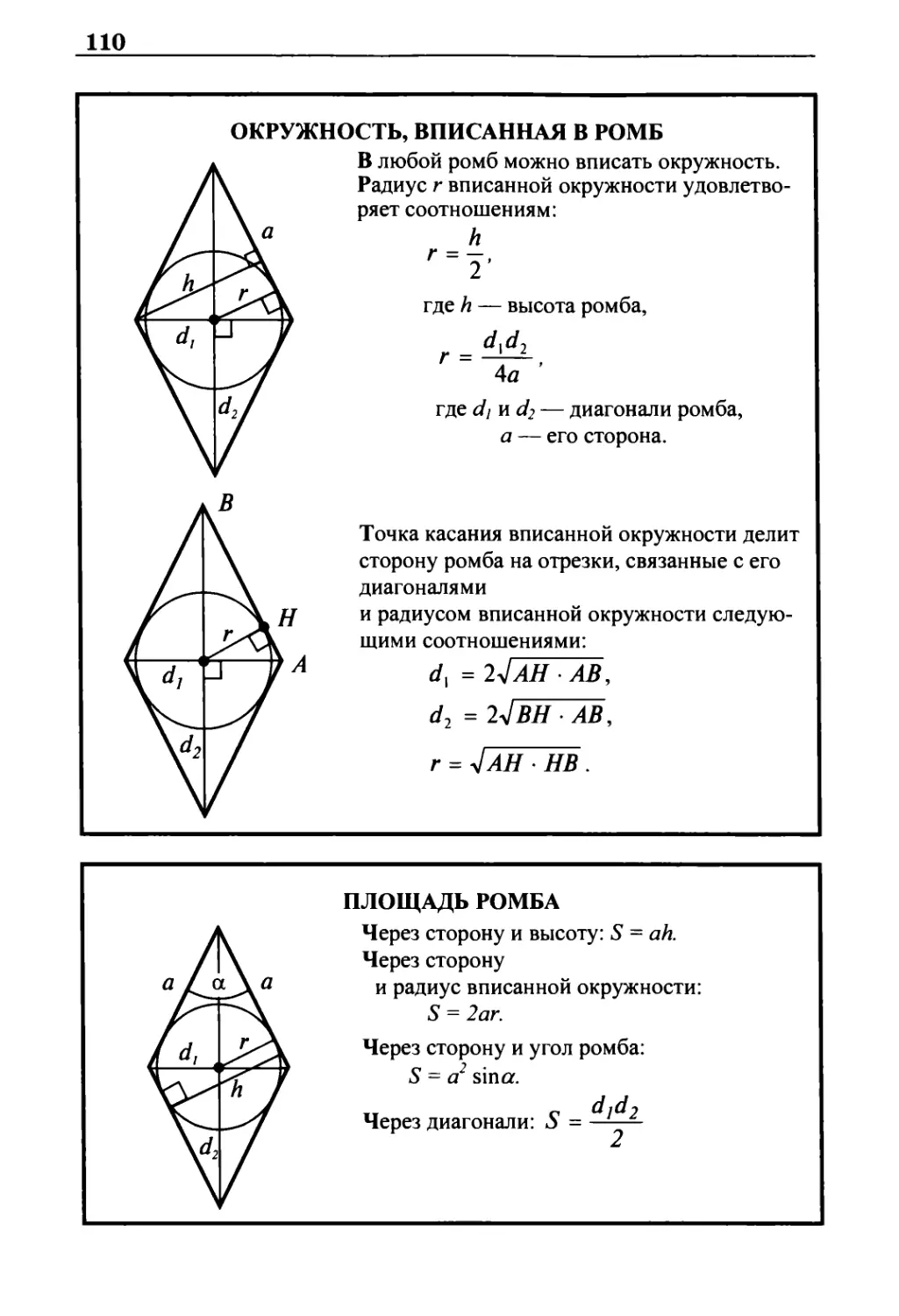
Ромб 109
Свойства и признаки ромба 109
Окружность, вписанная в ромб 110
Площадь ромба 110
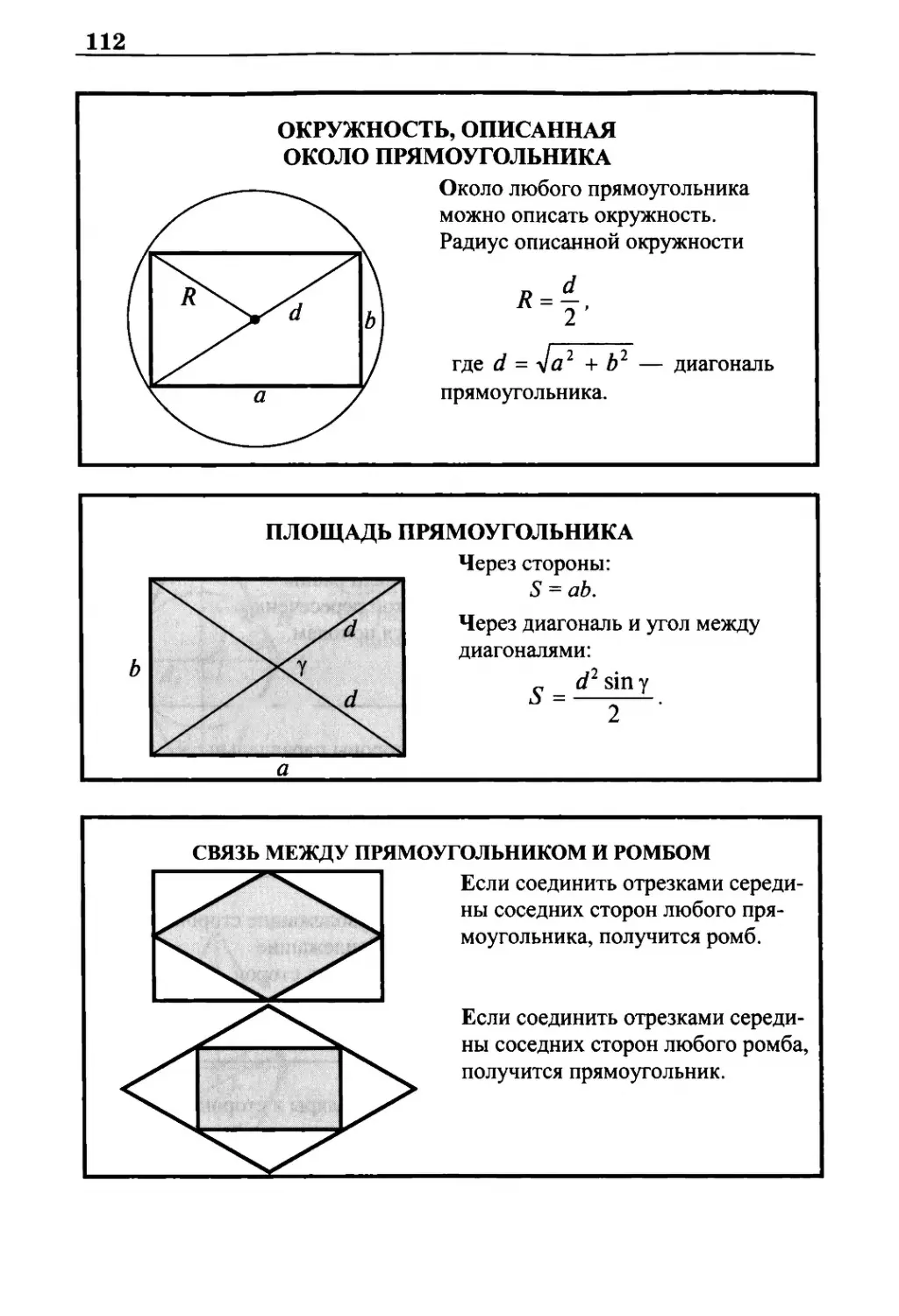
Прямоугольник 111
Свойства и признаки прямоугольника 111
Окружность, описанная около прямоугольника 112
Площадь прямоугольника 112
Связь между прямоугольником и ромбом 112
Квадрат 113
Свойства и признаки квадрата 113
Окружность, описанная около квадрата 114
Окружность, вписанная в квадрат 114
Площадь квадрата 114
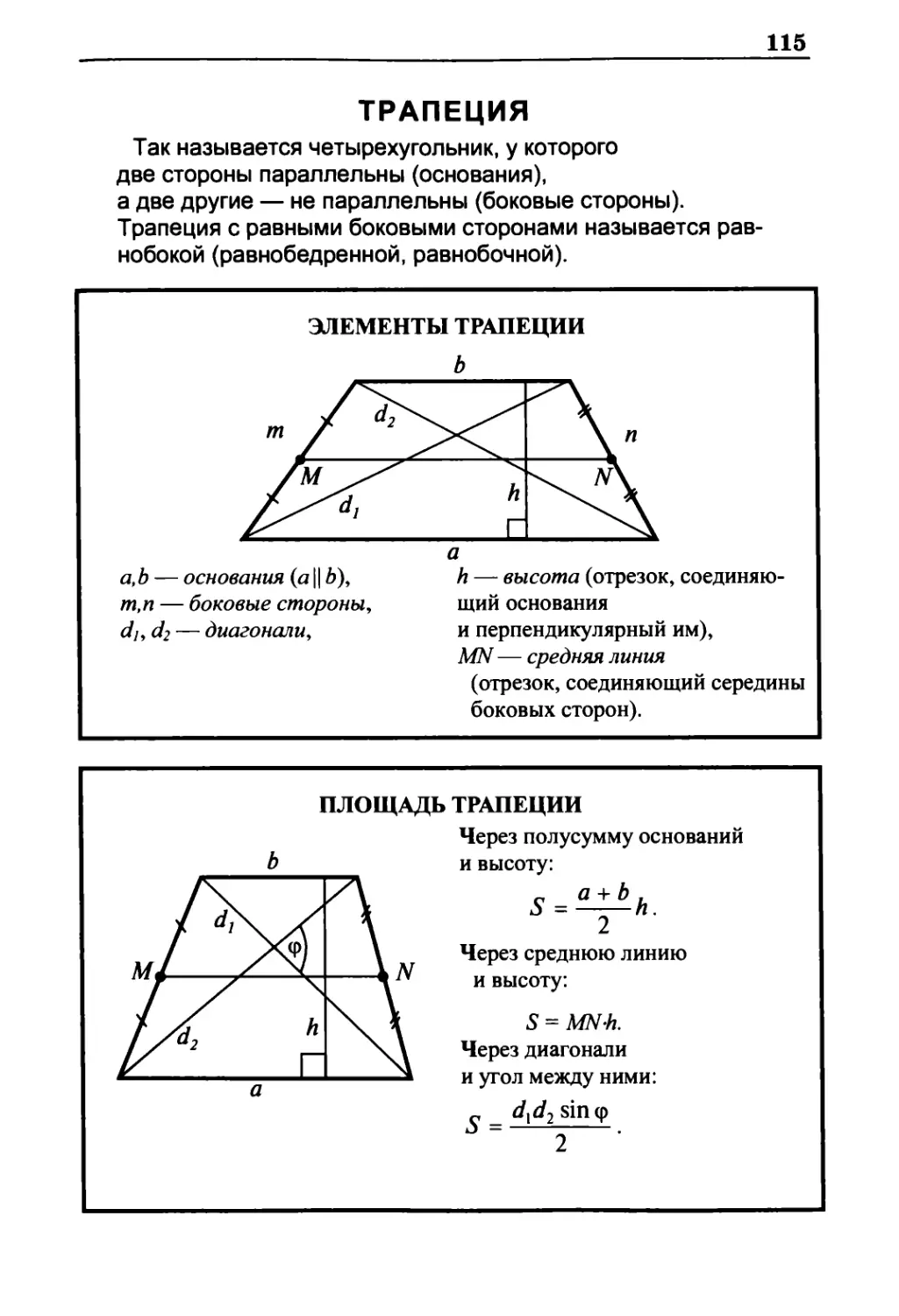
Трапеция 115
Элементы трапеции 115
Площадь трапеции 115
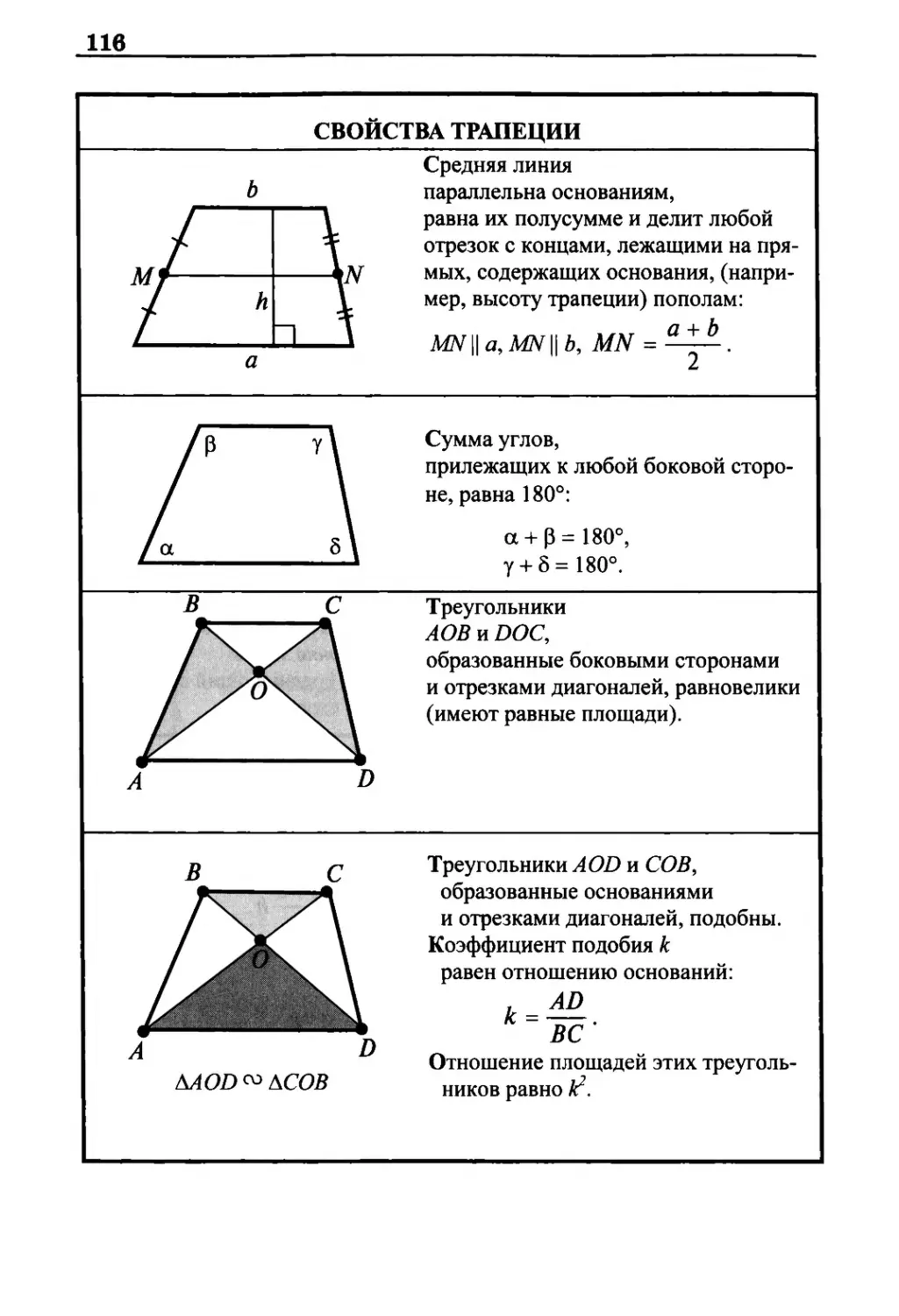
Свойства трапеции 116
Окружность 118
Прямые и отрезки, связанные с окружностью 118
Углы, связанные с окружностью. Угловая мера дуги
окружности 118
Радианная мера угла 118
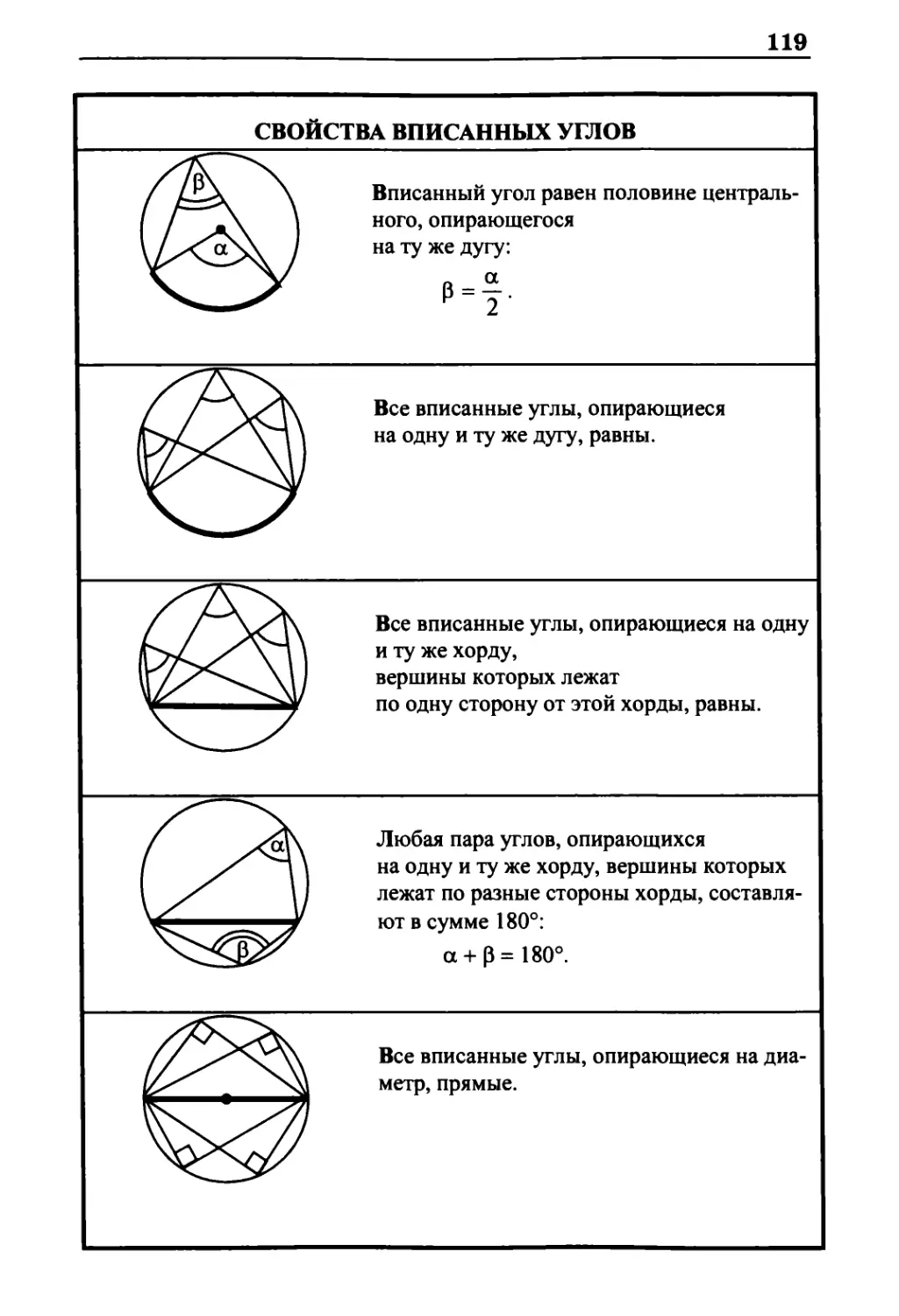
Свойства вписанных углов 119
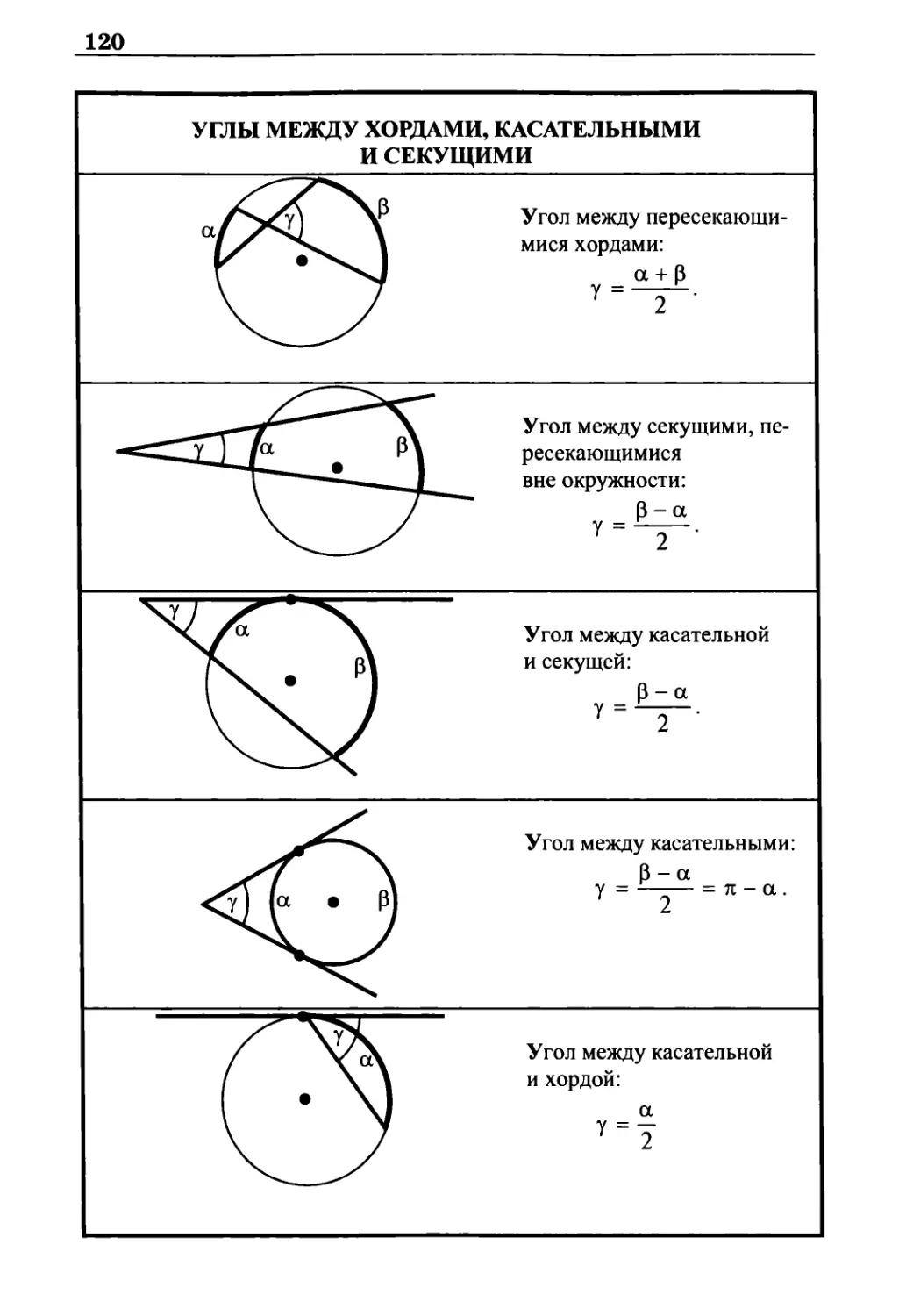
Углы между хордами, касательными и секущими 120
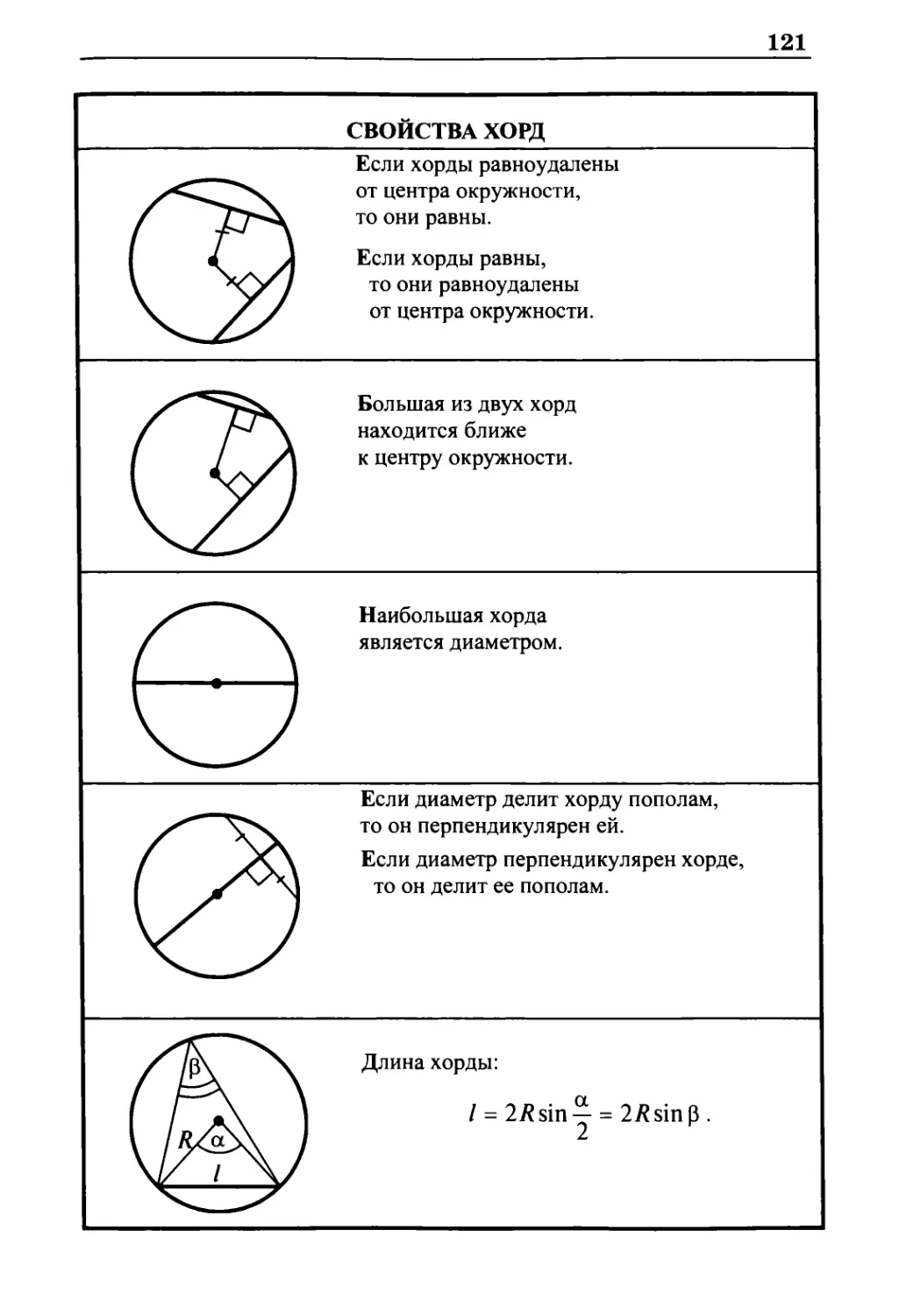
Свойства хорд 121
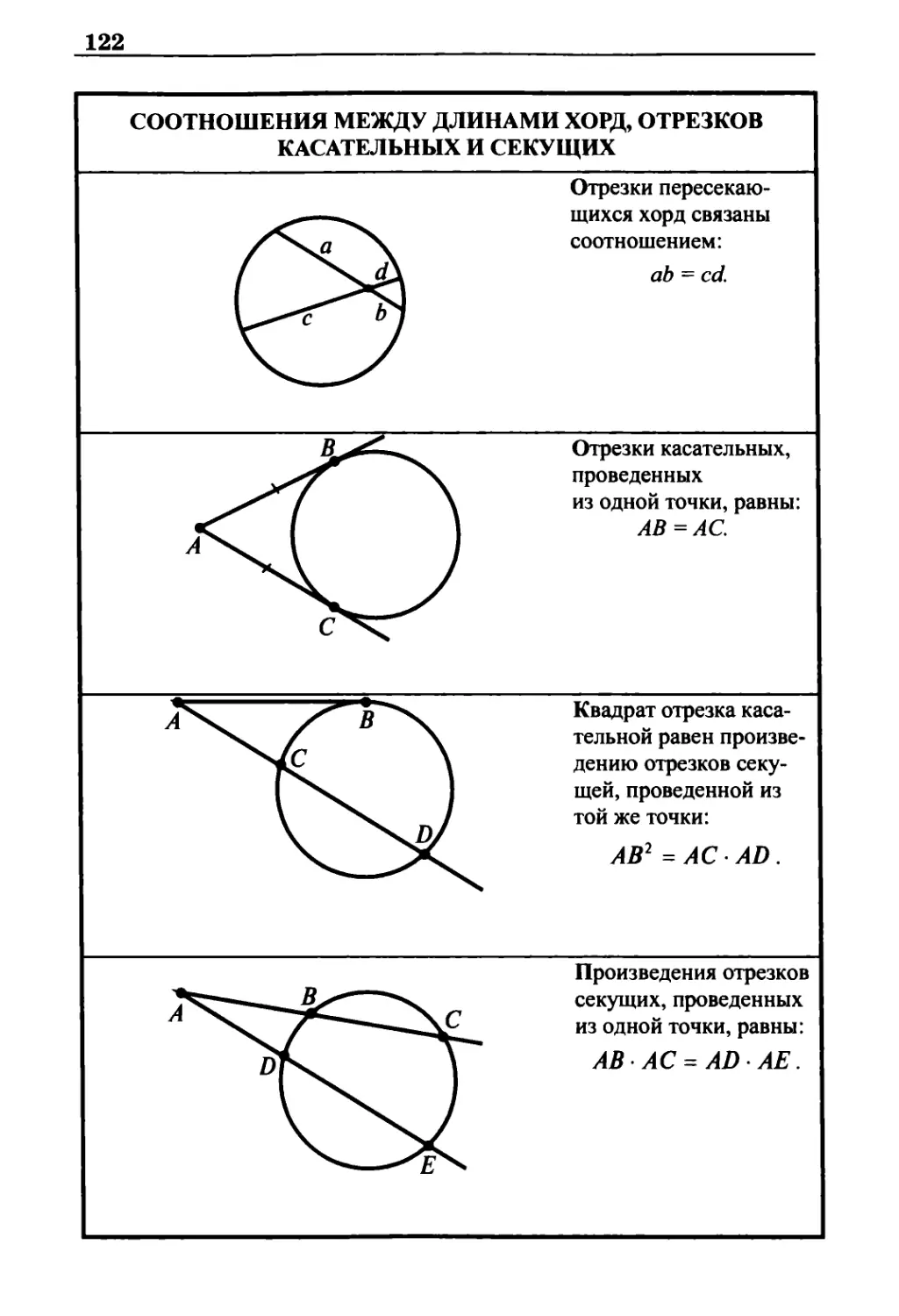
Соотношения между длинами хорд, отрезков касательных и
секущих 122
Свойства дуг и хорд 123
Длина дуги и окружности 123
Площадь круга и его частей 123
Взаимное расположение двух окружностей.
Общие касательные 124
Многоугольники 126
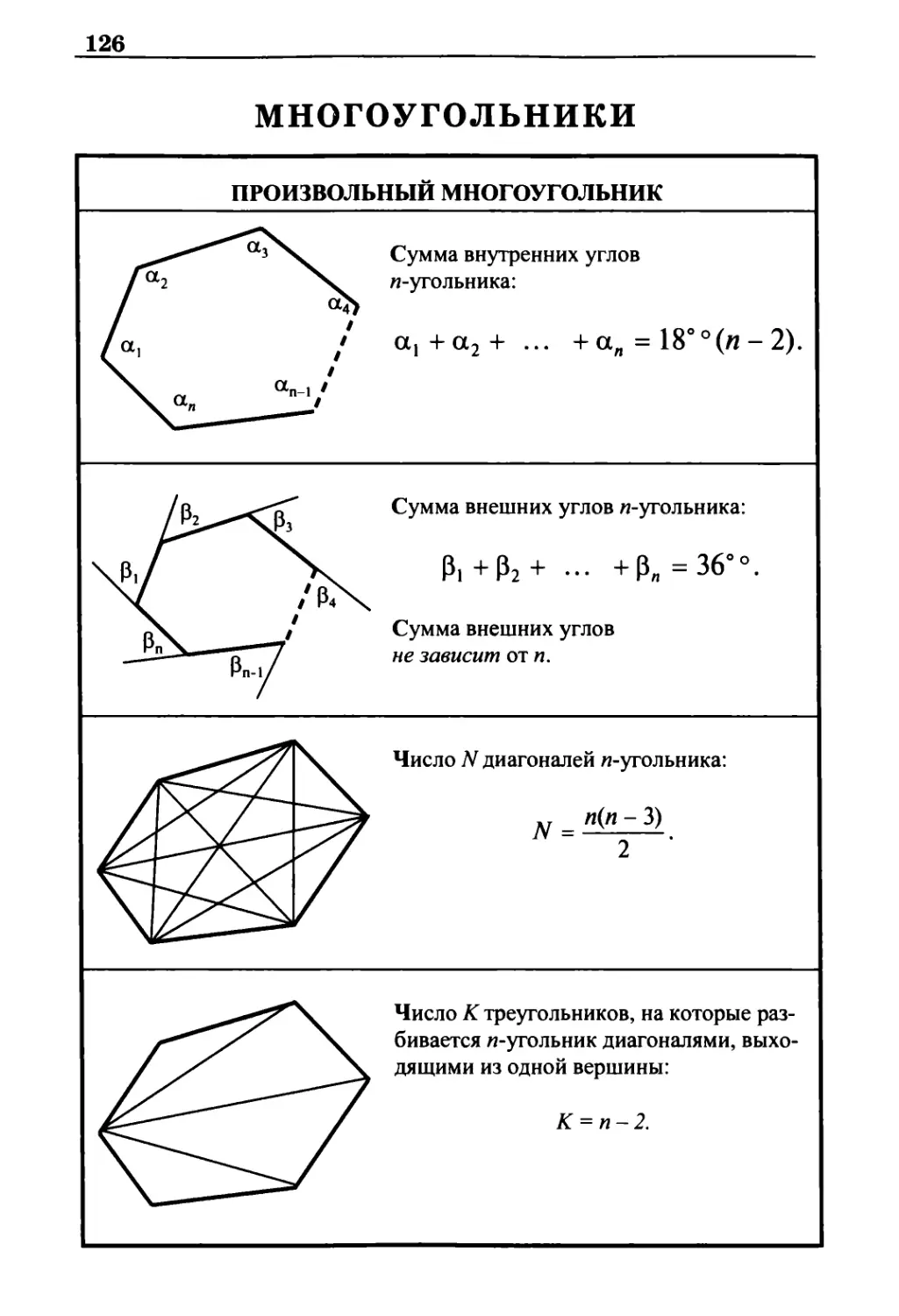
Произвольный многоугольник 126
Правильные многоугольники 127

8
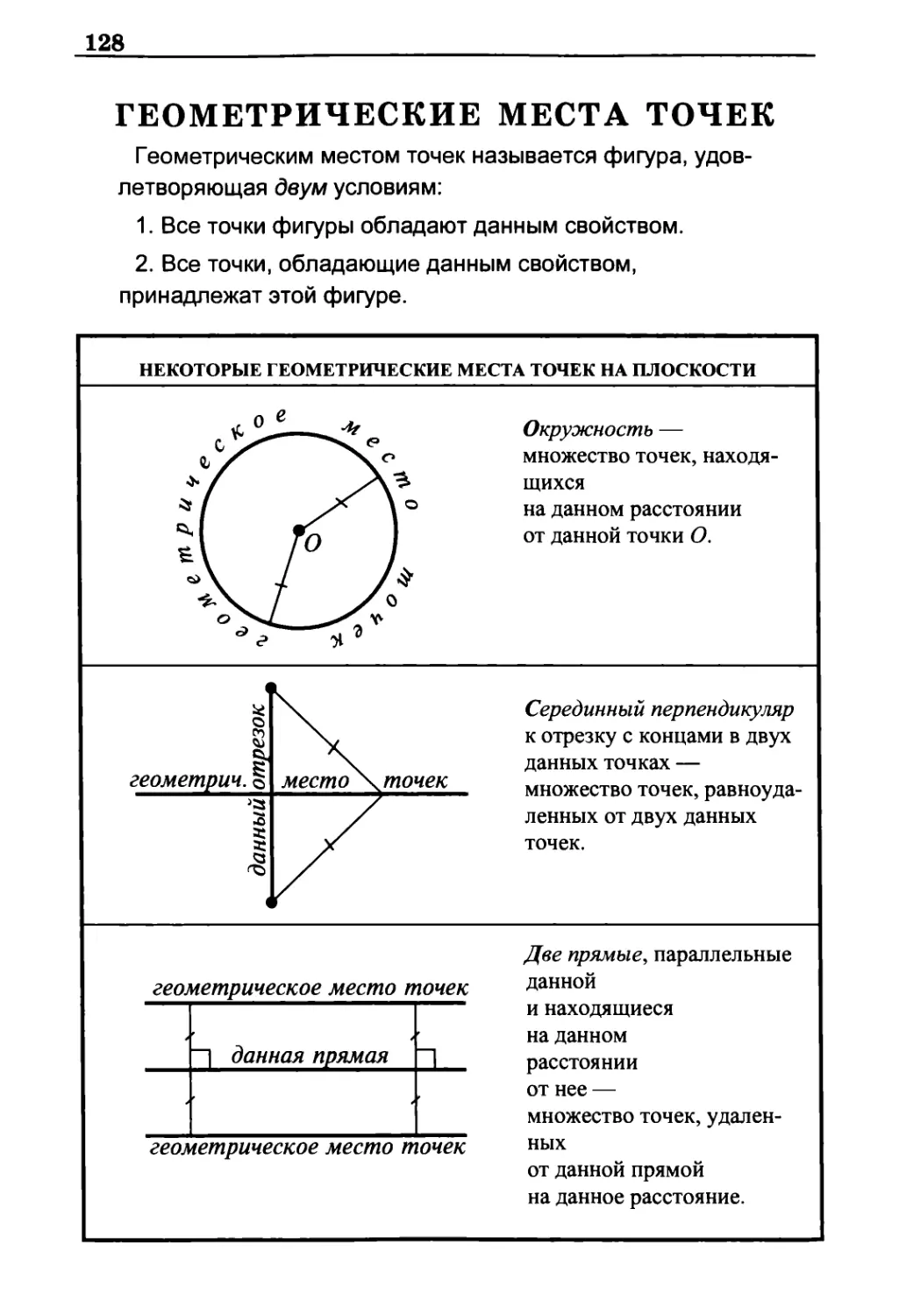
Геометрические места точек 128
Некоторые геометрические места точек на плоскости 128
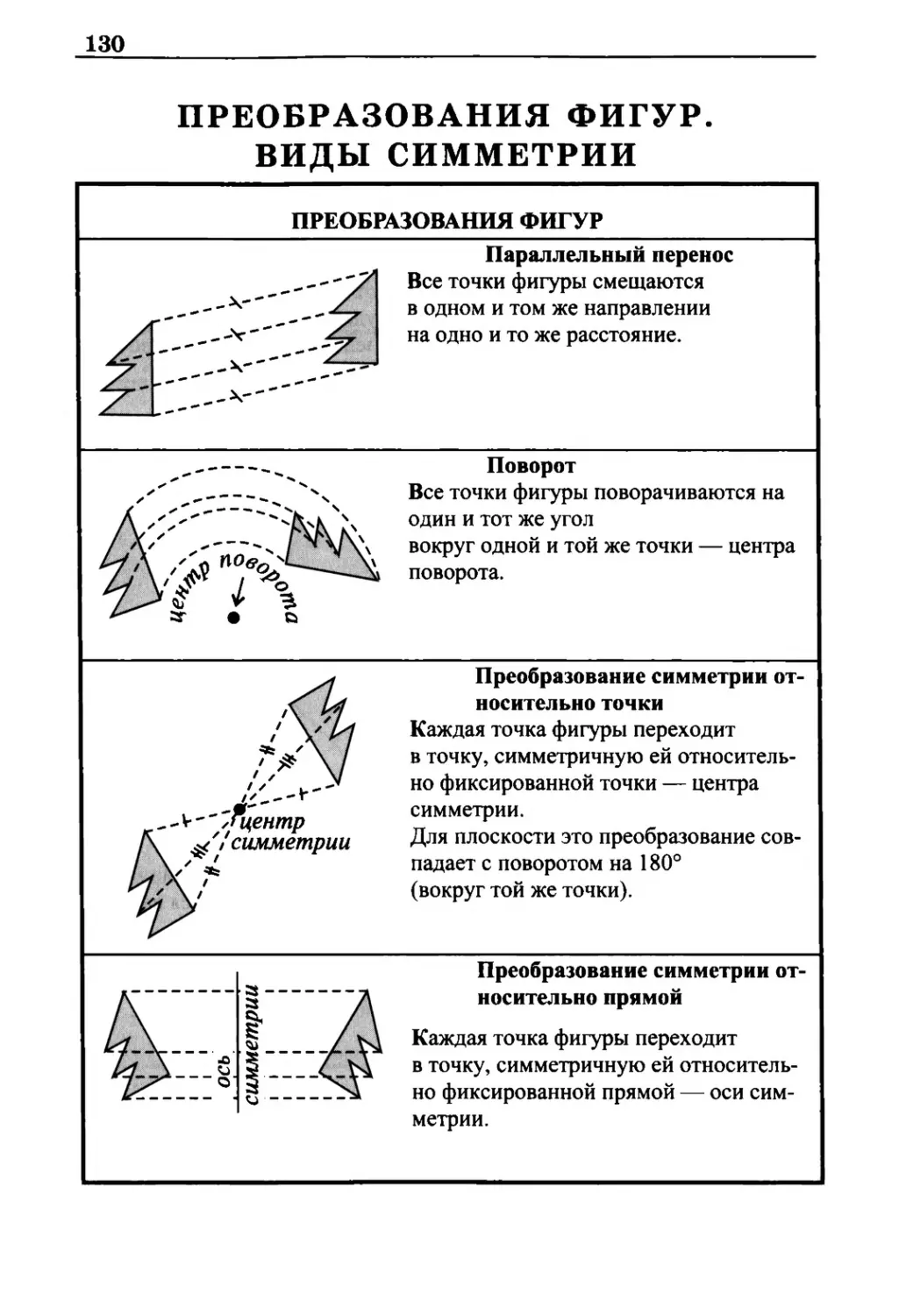
Преобразования фигур. Виды симметрии 130
Преобразования фигур 130
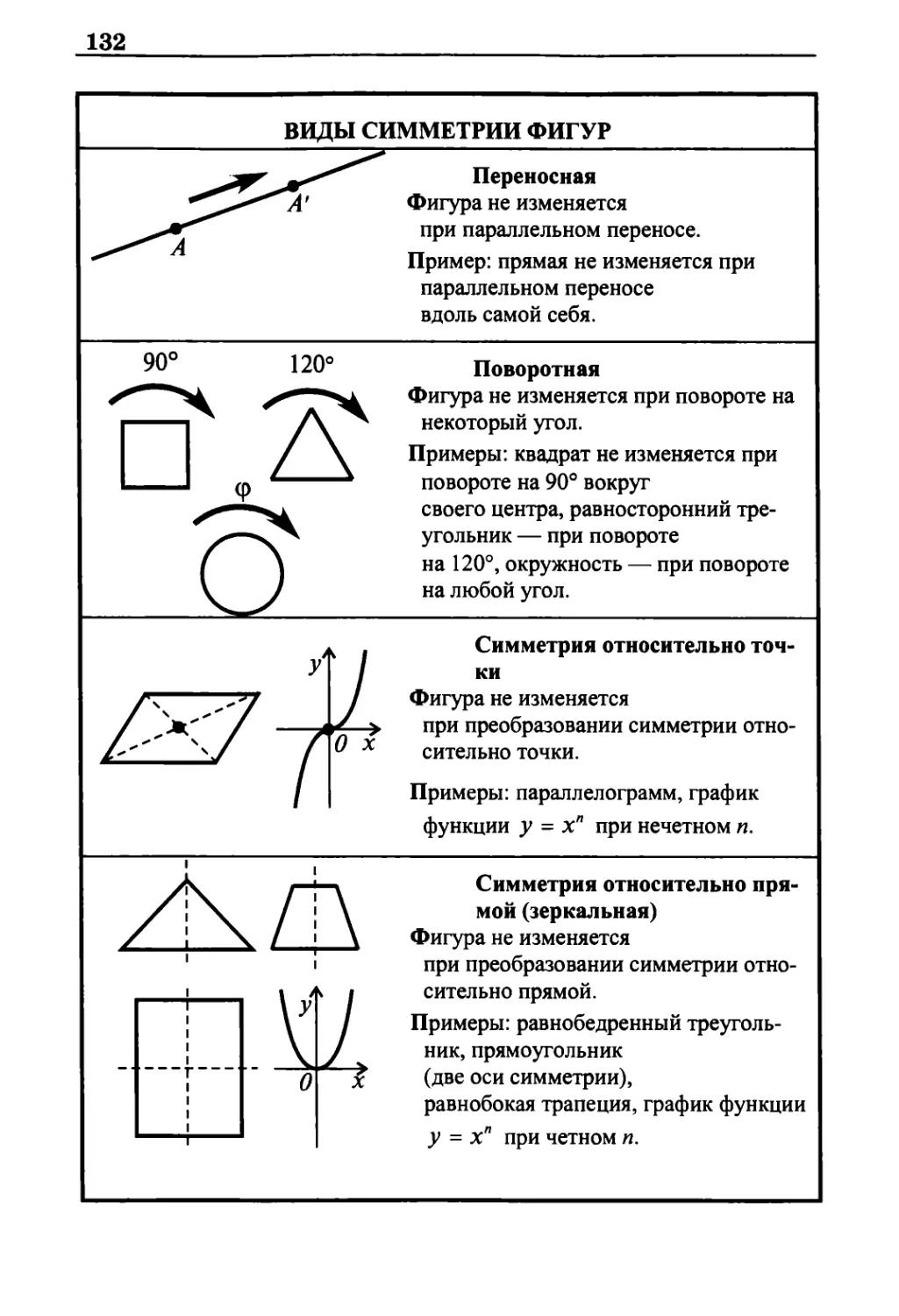
Виды симметрии фигур 132
Декартовы координаты 133
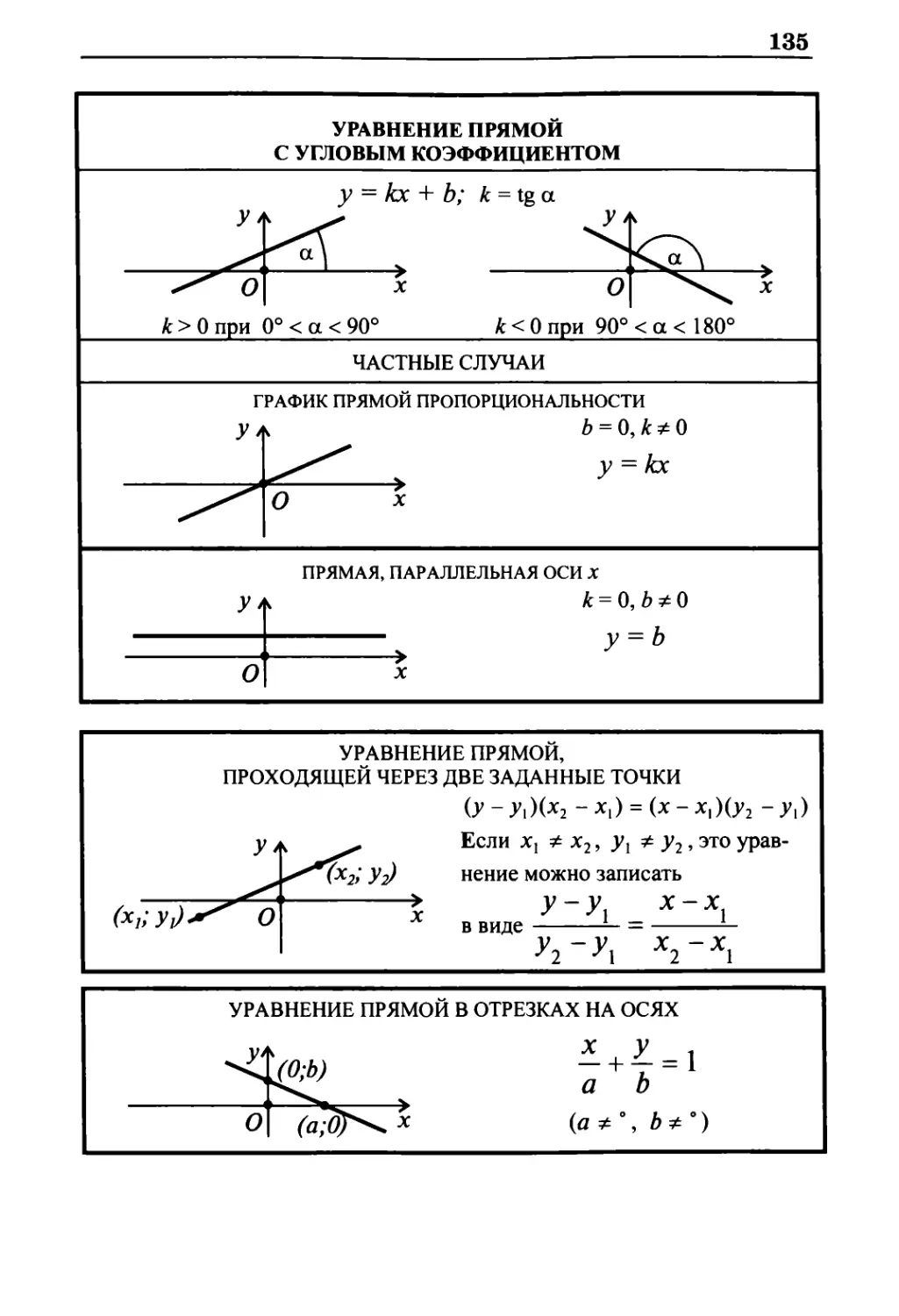
Уравнение прямой 134
Общее уравнение прямой 134
Уравнение прямой с угловым коэффициентом 135
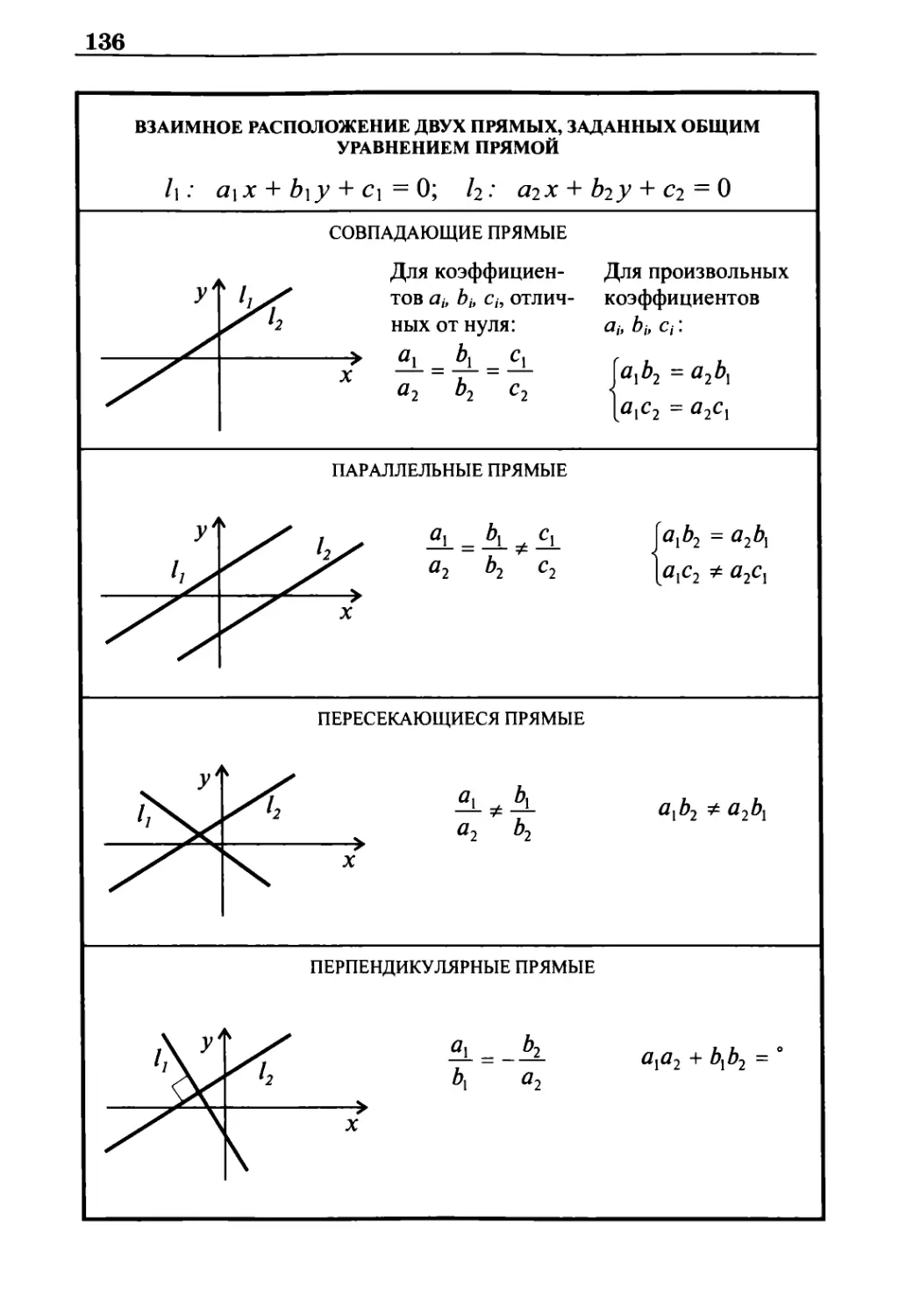
Взаимное расположение двух прямых, заданных общим
уравнением прямой 136
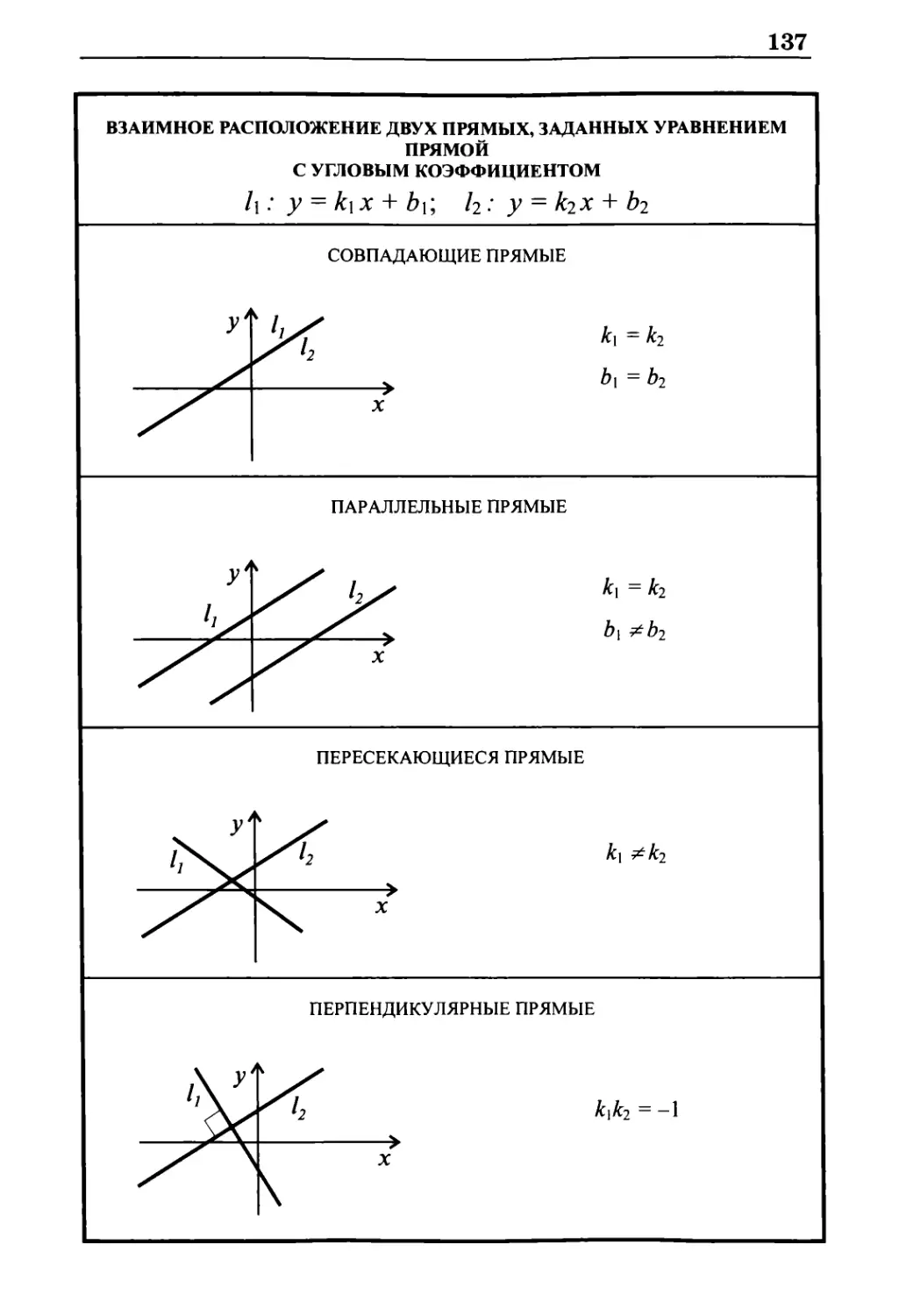
Взаимное расположение двух прямых, заданных уравнением
прямой с угловым коэффициентом 137
Уравнение окружности 138
векторы 139
Обозначения векторов 139
Нулевой вектор 139
Коллинеарные векторы 139
Виды коллинеарных векторов 139
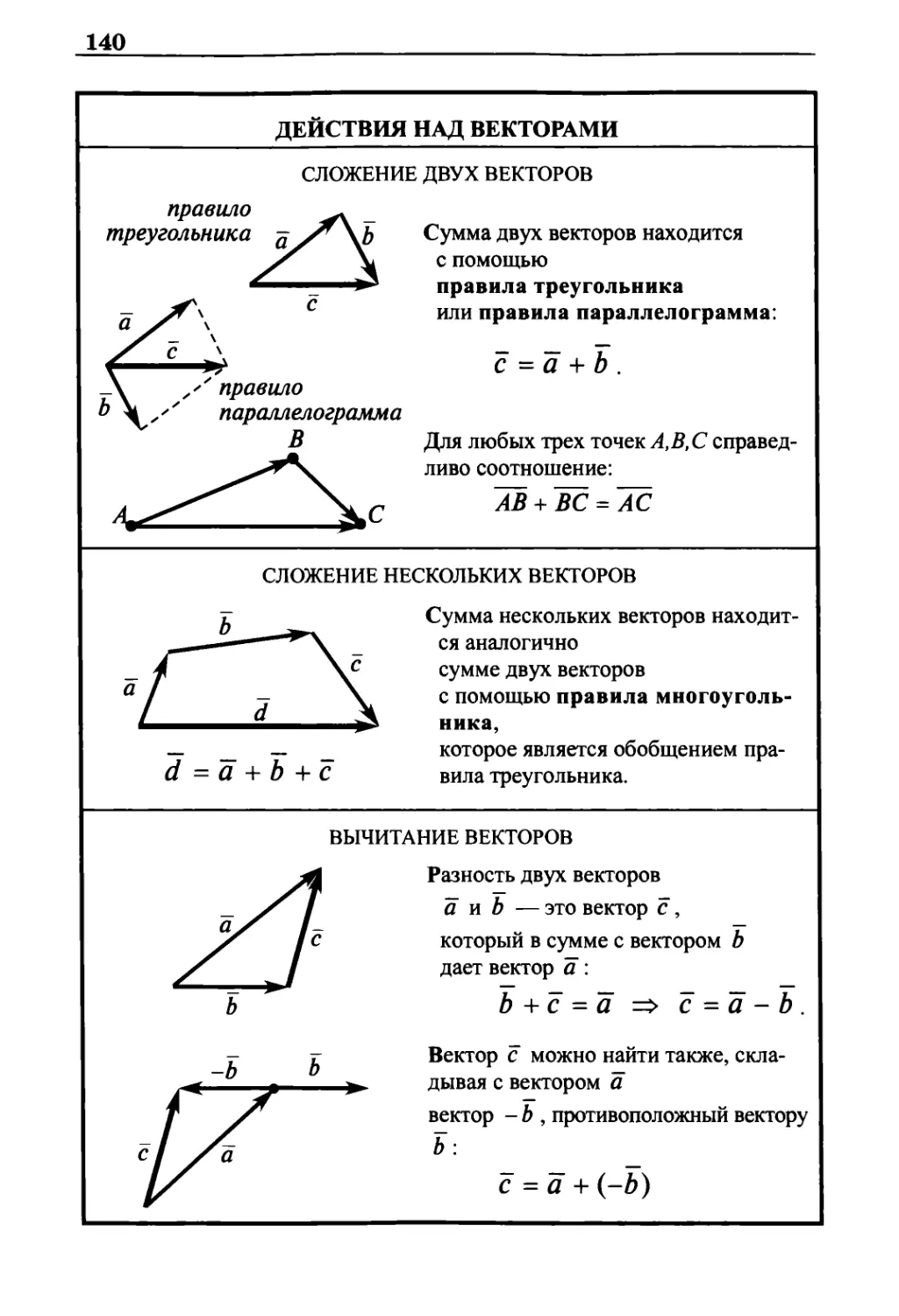
Действия над векторами 140
Сложение двух векторов 140
Сложение нескольких векторов 140
Вычитание векторов 140
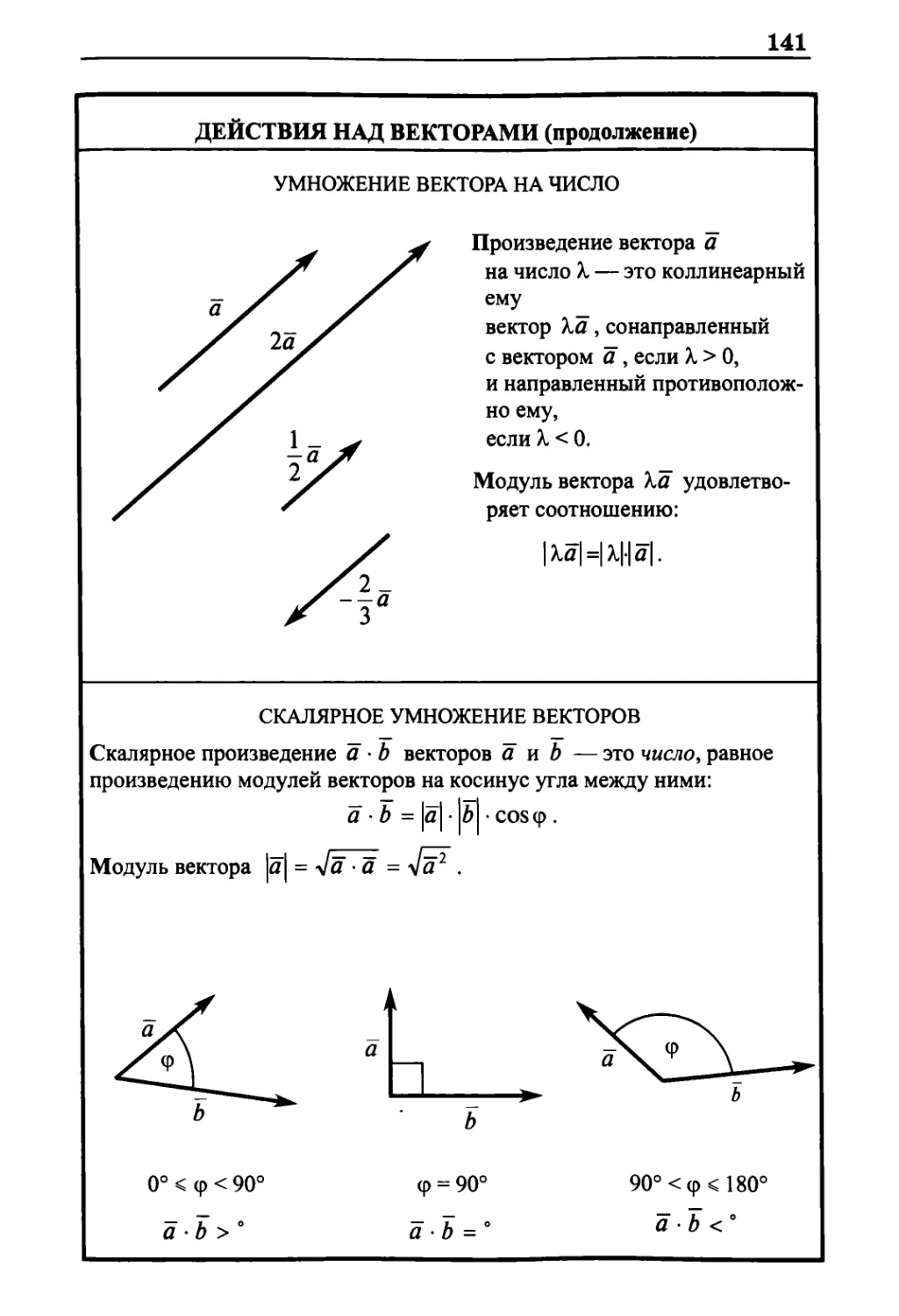
Умножение вектора на число 141
Скалярное умножение векторов 141
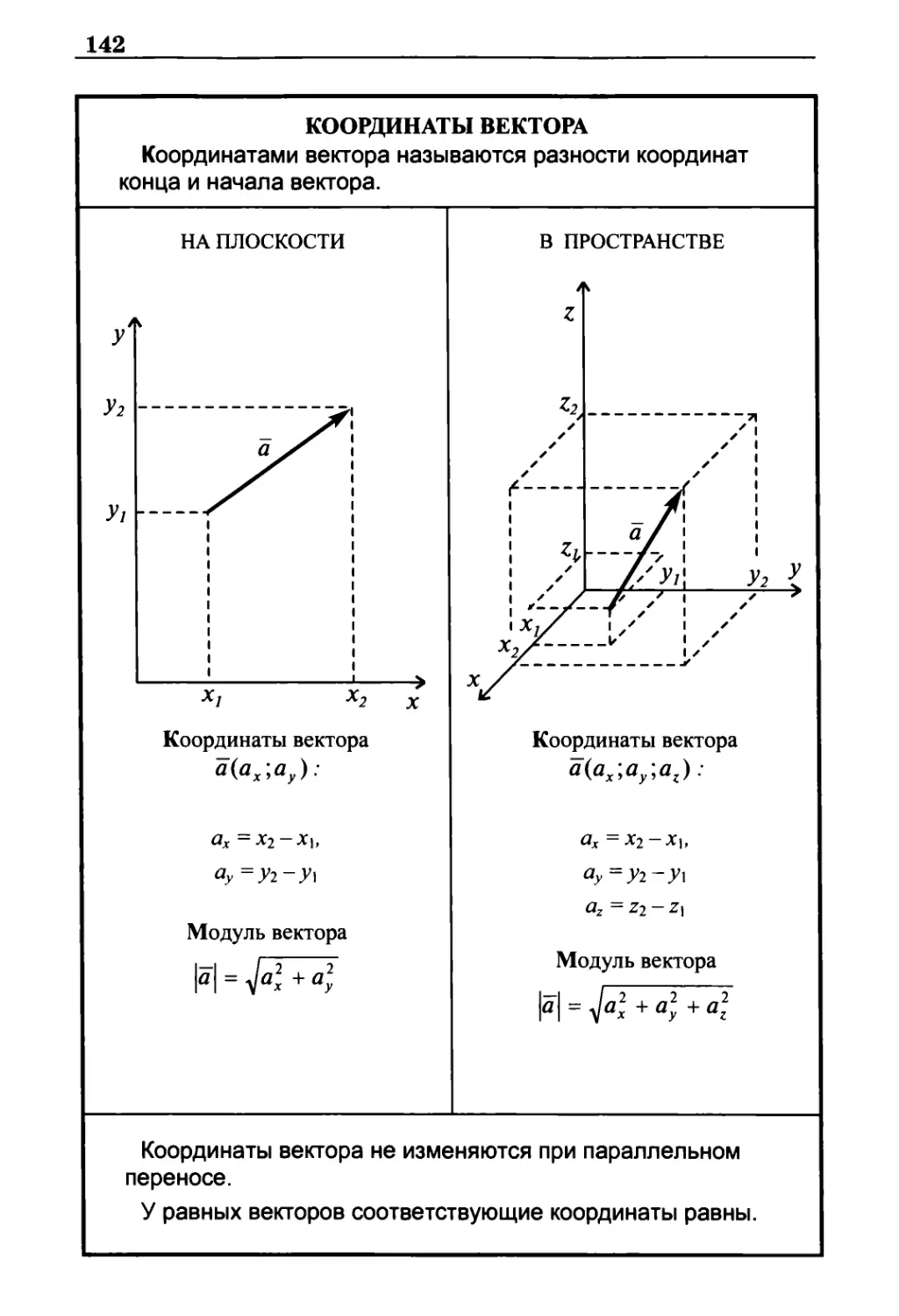
Координаты вектора на плоскости и в пространстве 142
Действия над векторами в координатном представлении 143
Взаимное расположение векторов 144
Разложение вектора на плоскости по двум неколлинеарным
векторам 145
Разложение вектора в пространстве по трем некомпланарным
векторам 145
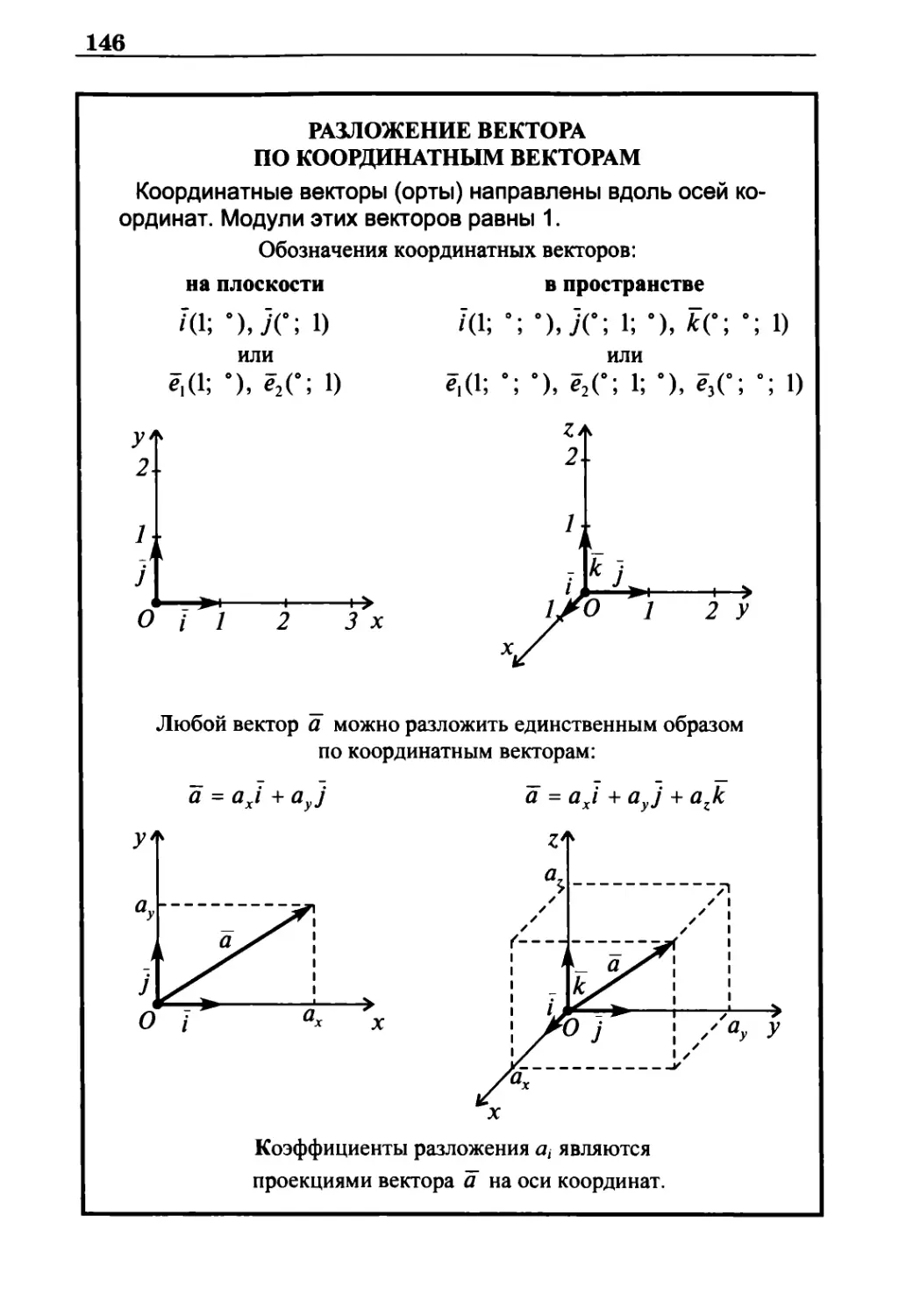
Разложение вектора по координатным векторам 146
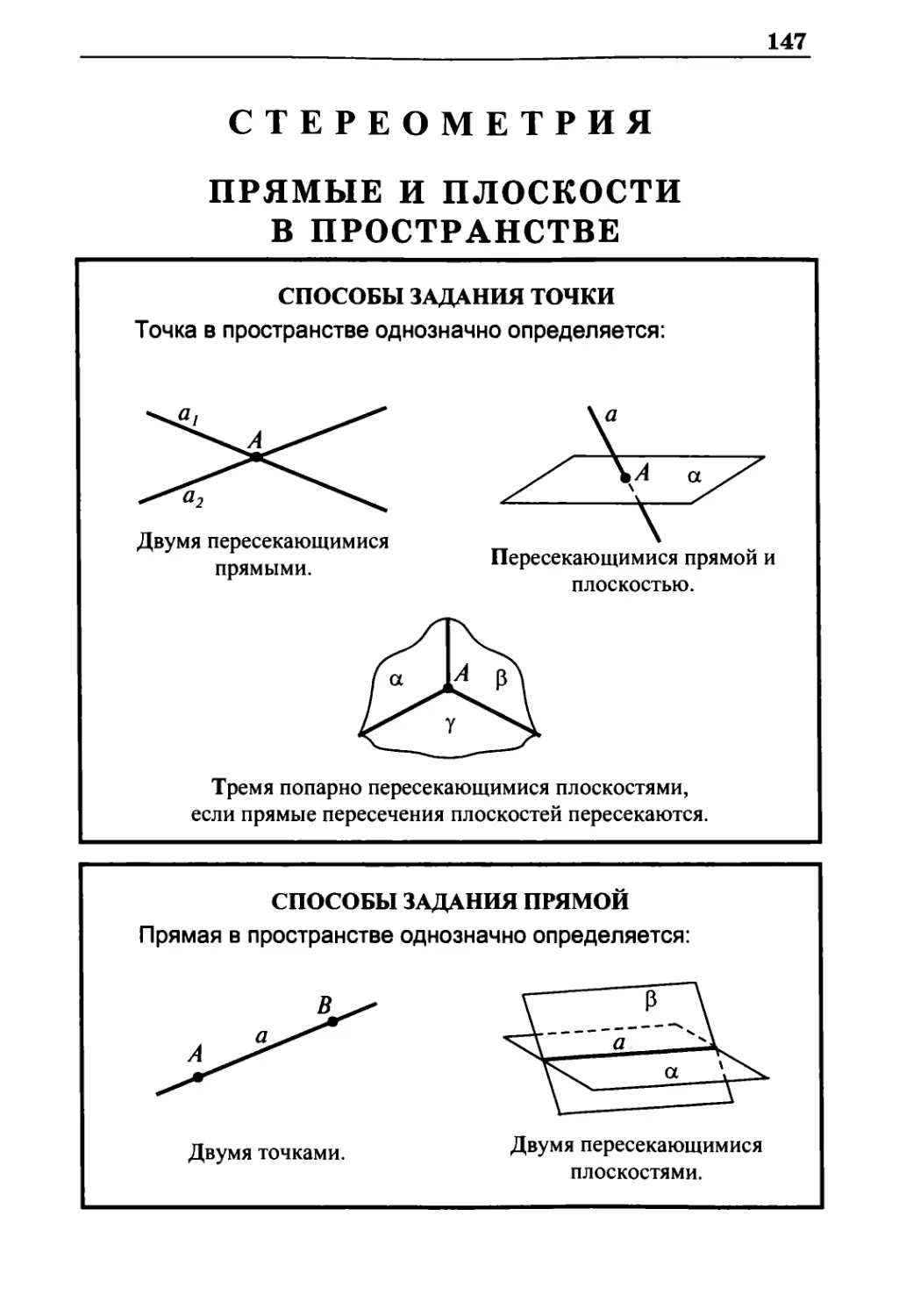
стереометрия 147
Прямые и плоскости в пространстве 147
Способы задания точки 147
Способы задания прямой 147
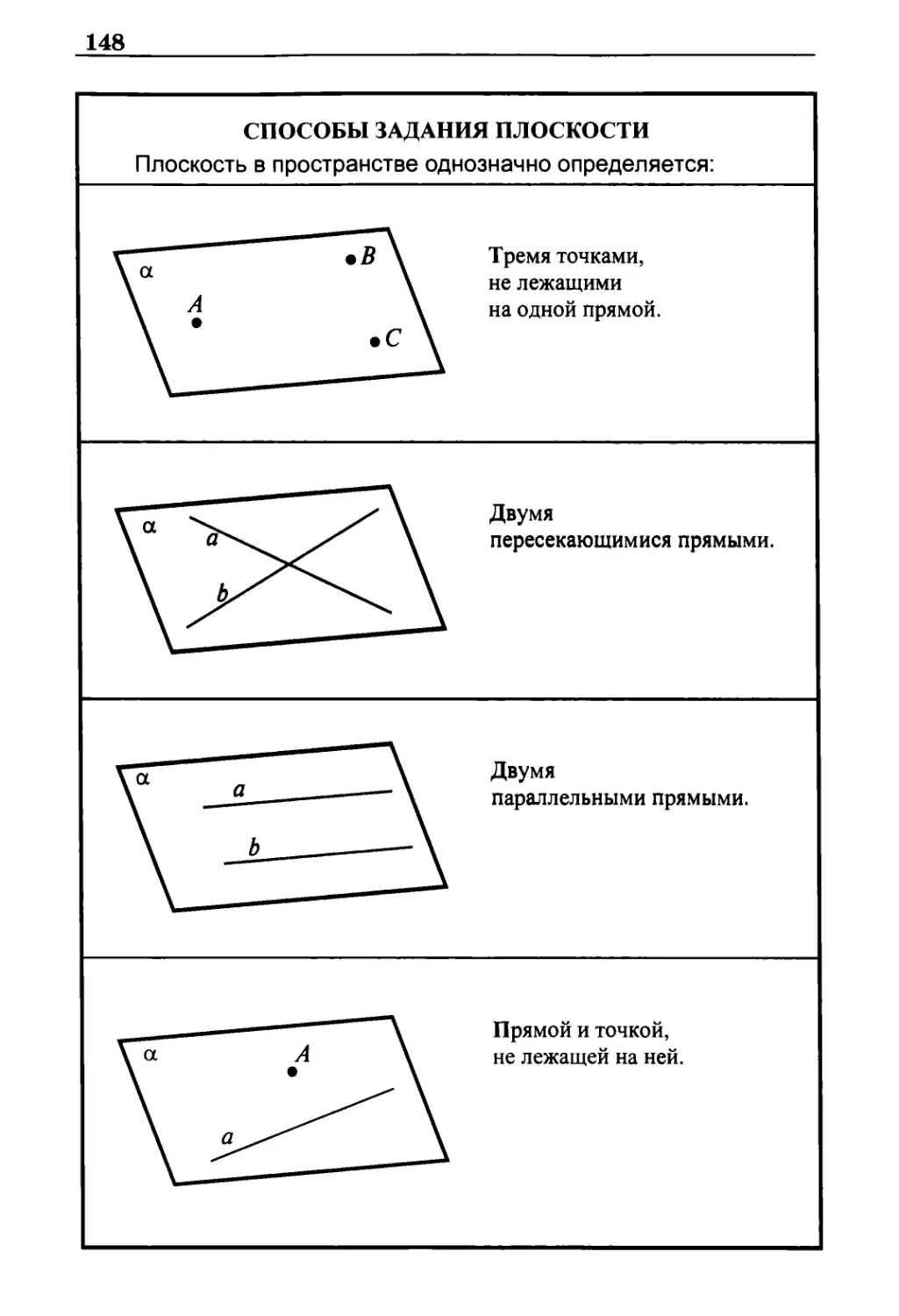
Способы задания плоскости 148
Параллельность прямых и плоскостей 149
Параллельные прямые 149
Параллельные прямая и плоскость 149
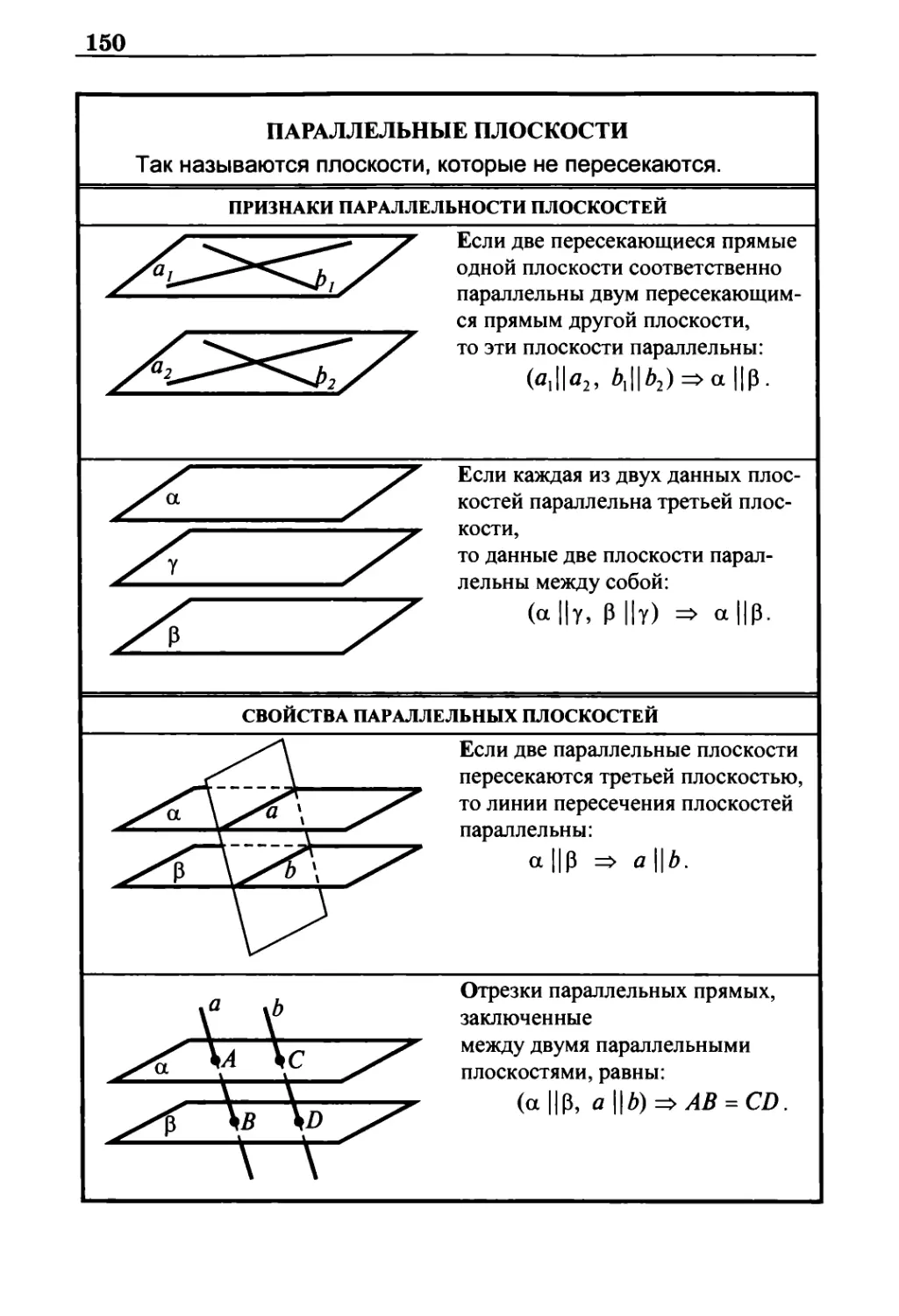
Параллельные плоскости 150
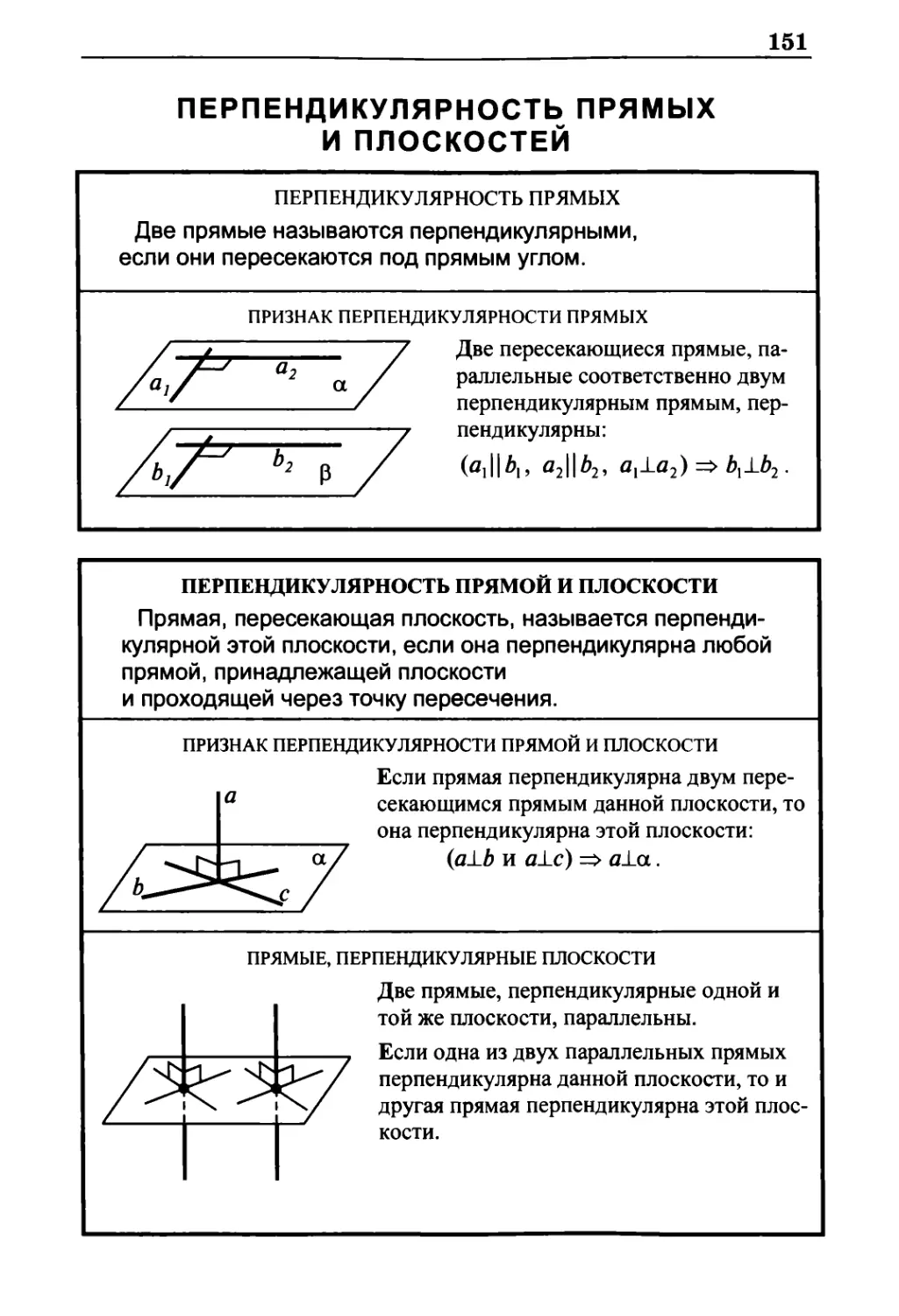
Перпендикулярность прямых и плоскостей 151
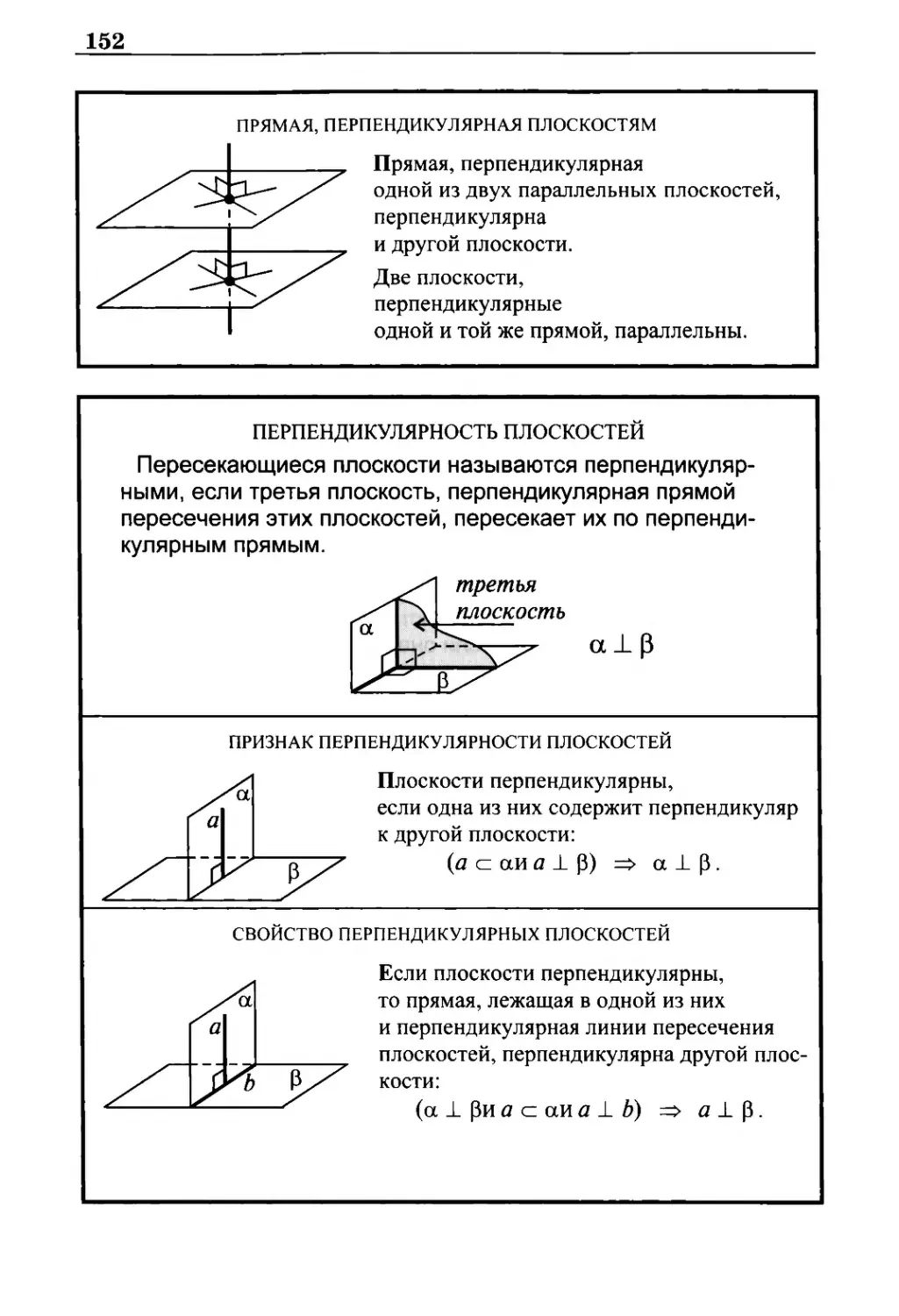
Перпендикулярность плоскостей 152

9
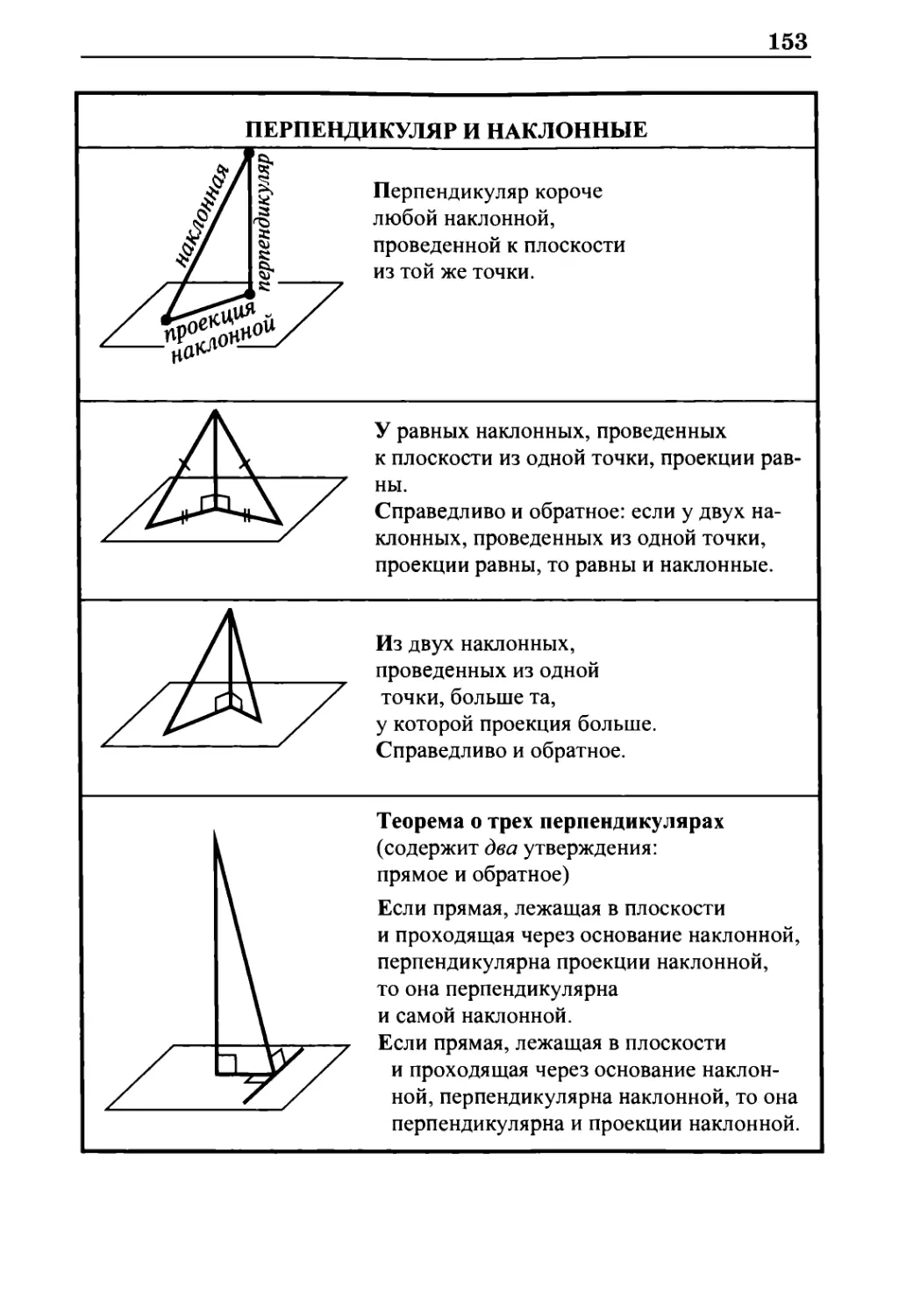
Перпендикуляр и наклонные 153
Скрещивающиеся прямые 154
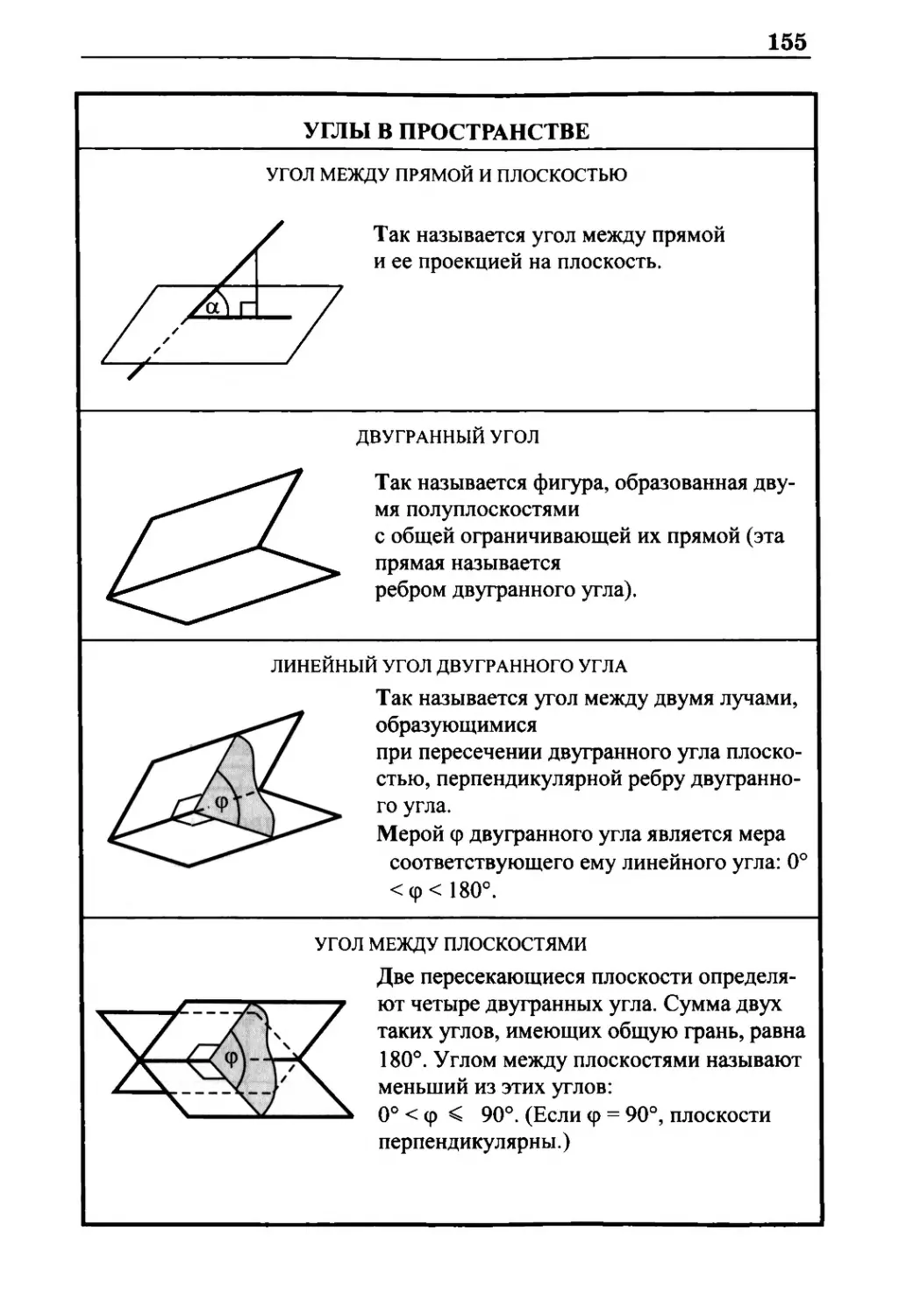
Углы в пространстве 155
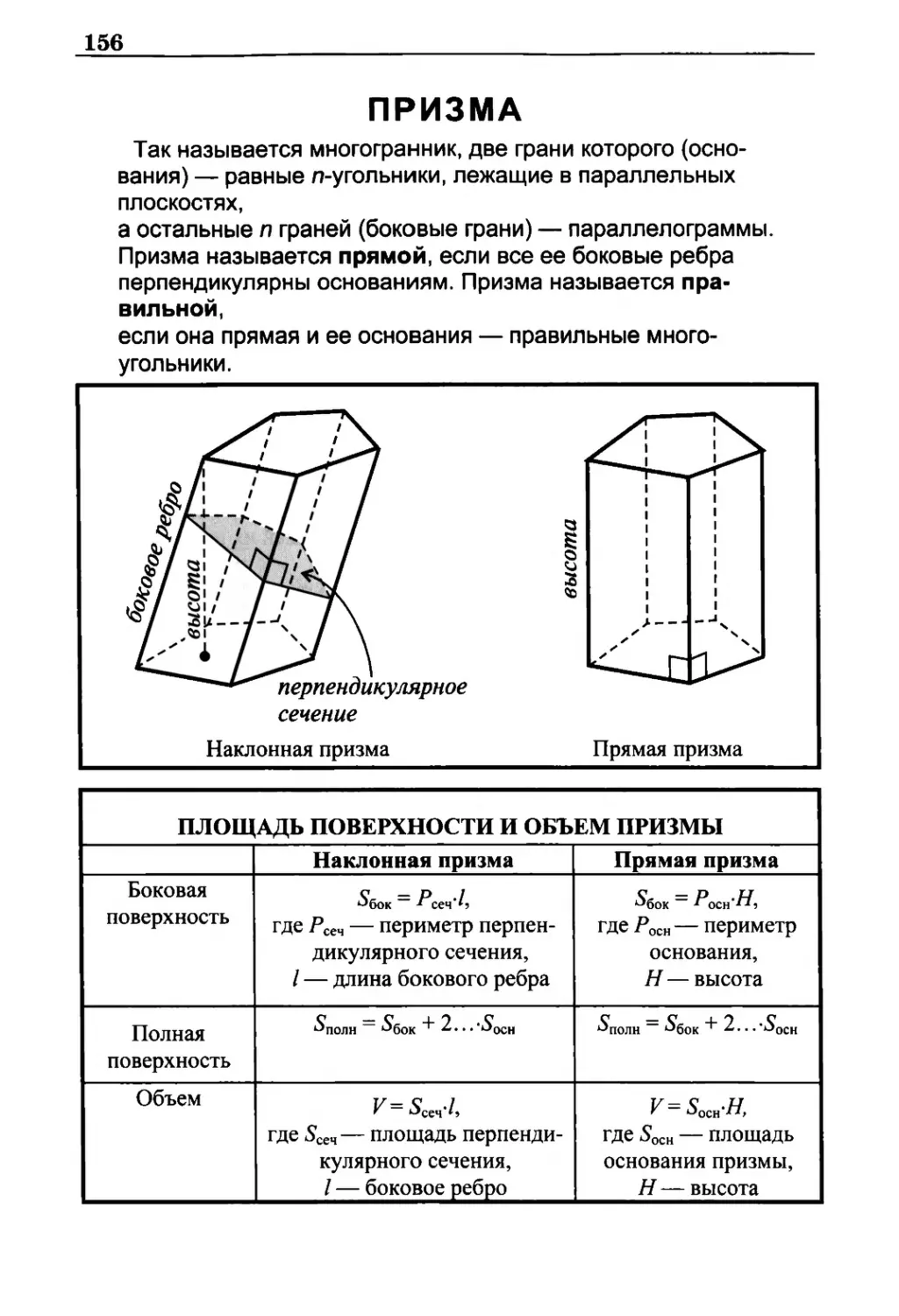
Призма 156
Площадь поверхности и объем призмы 156
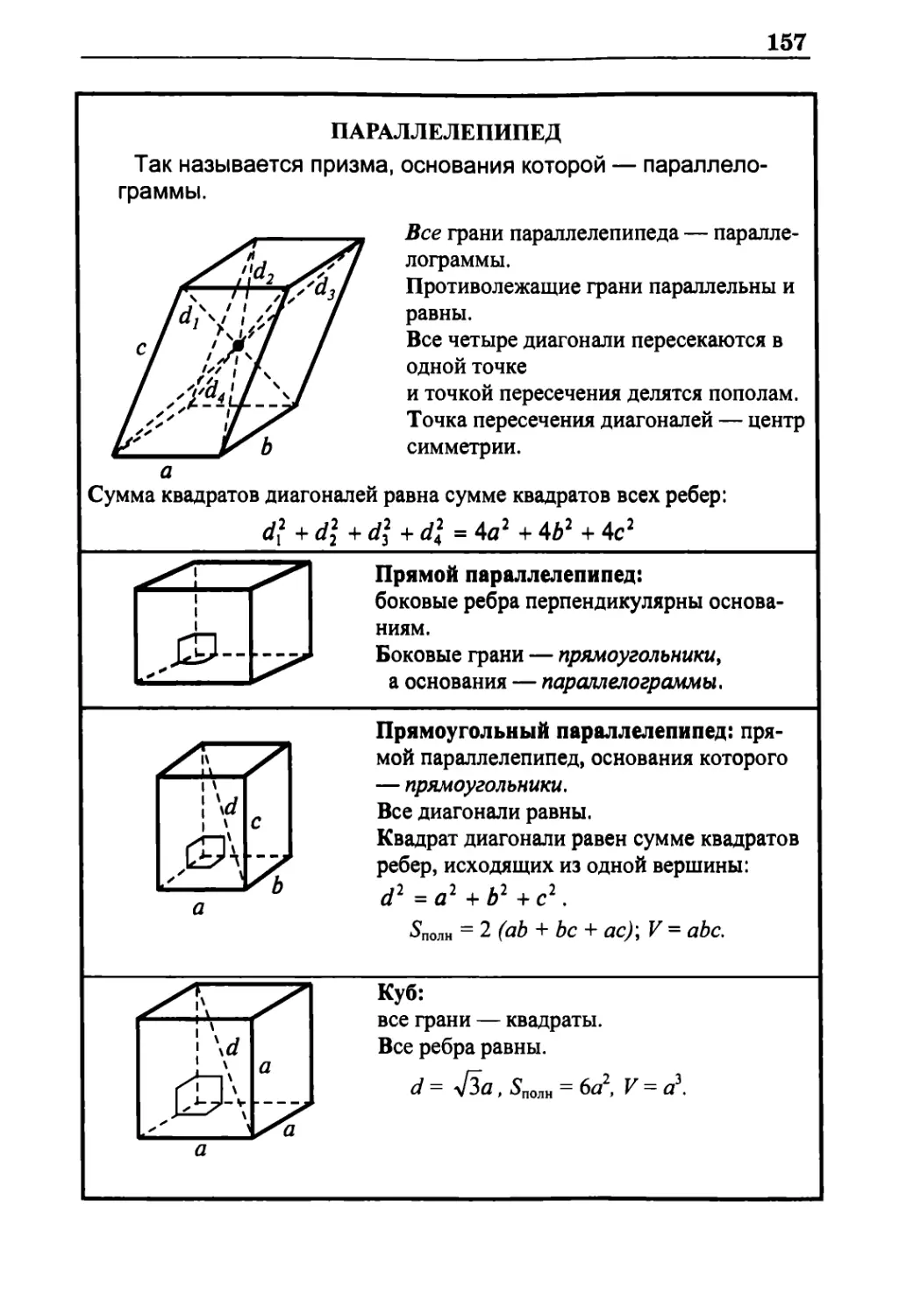
Параллелепипед 157
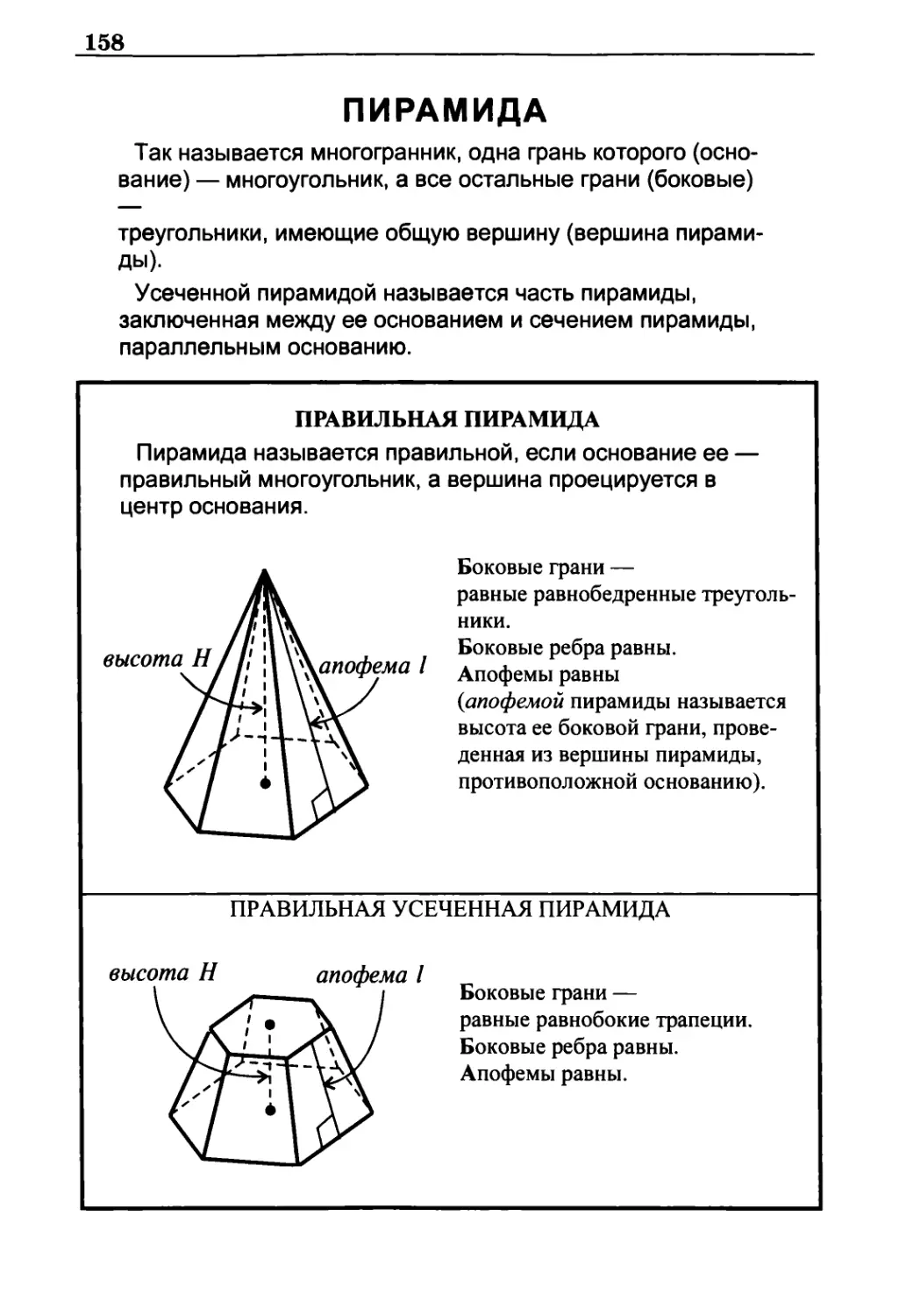
Пирамида 158
Правильная пирамида 158
Площадь поверхности и объем произвольной пирамиды 159
Площадь поверхности и объем правильной пирамиды 159
Тела вращения 160
Цилиндр 160
Конус 160
Площадь поверхности и объем цилиндра 160
Площадь поверхности и объем конуса 160
Сфера. Шар 161
Вписанные и описанные тела 162
Цилиндр, описанный около призмы 162
Цилиндр, вписанный в призму 162
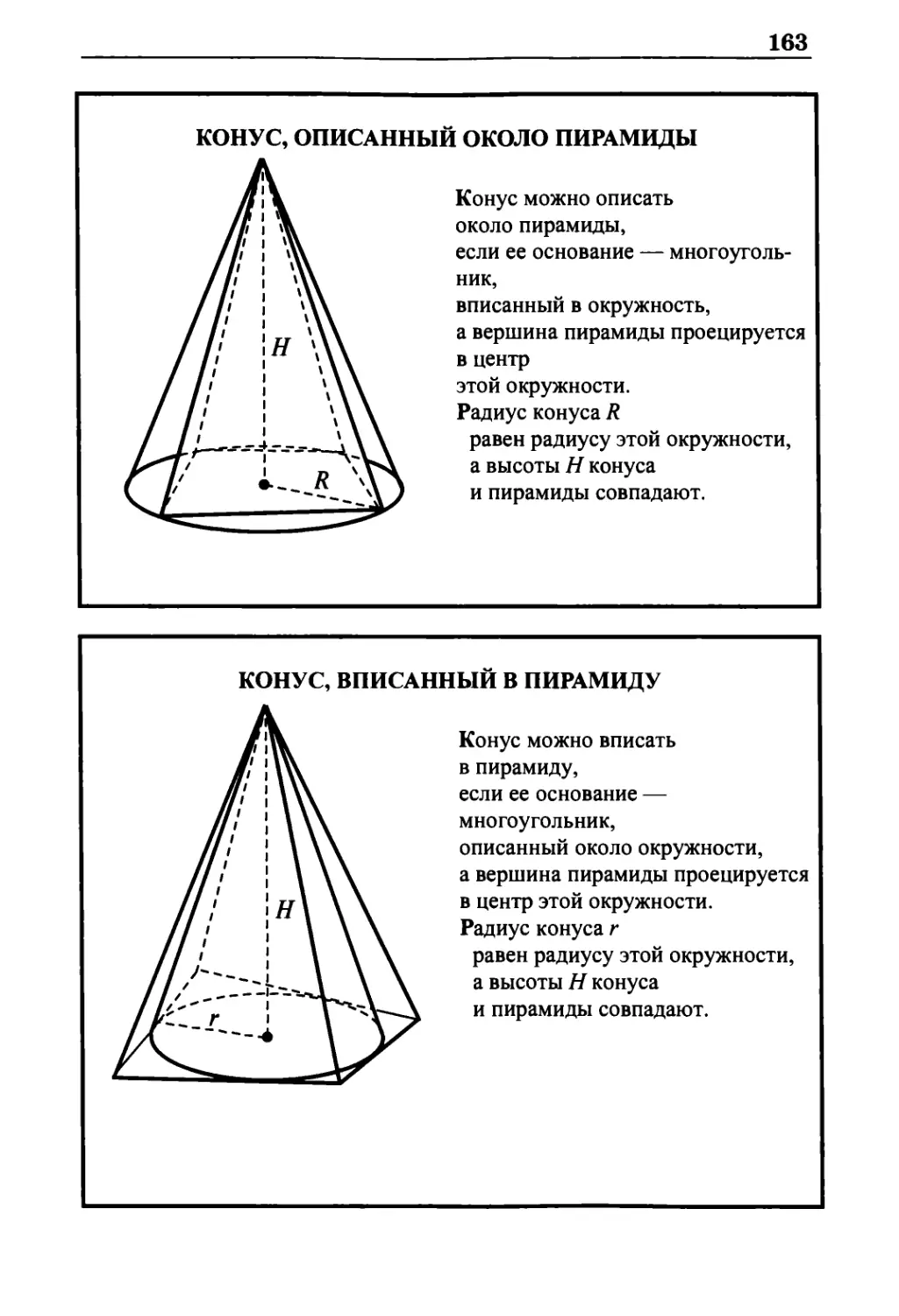
Конус, описанный около пирамиды 163
Конус, вписанный в пирамиду 163
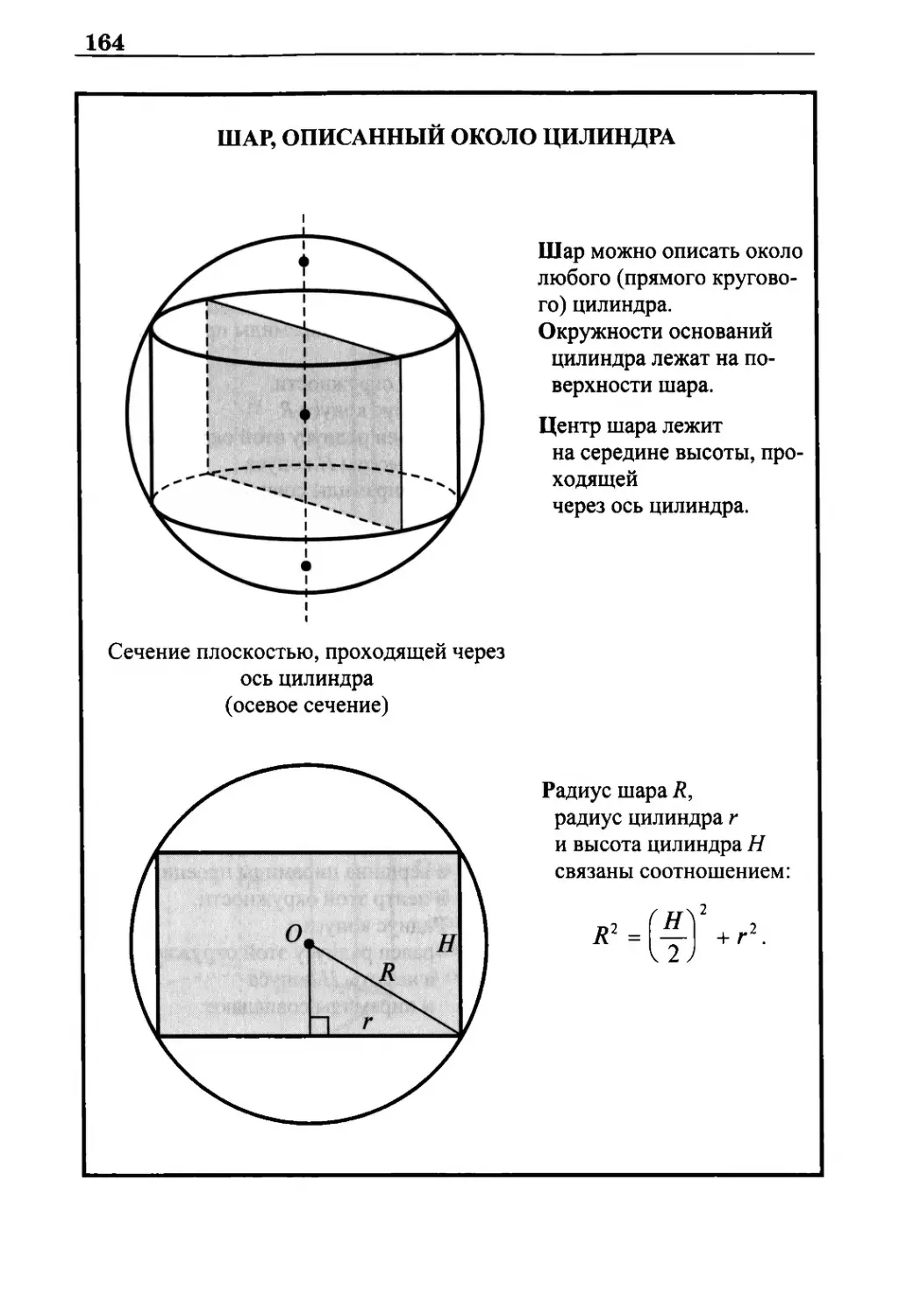
Шар, описанный около цилиндра 164
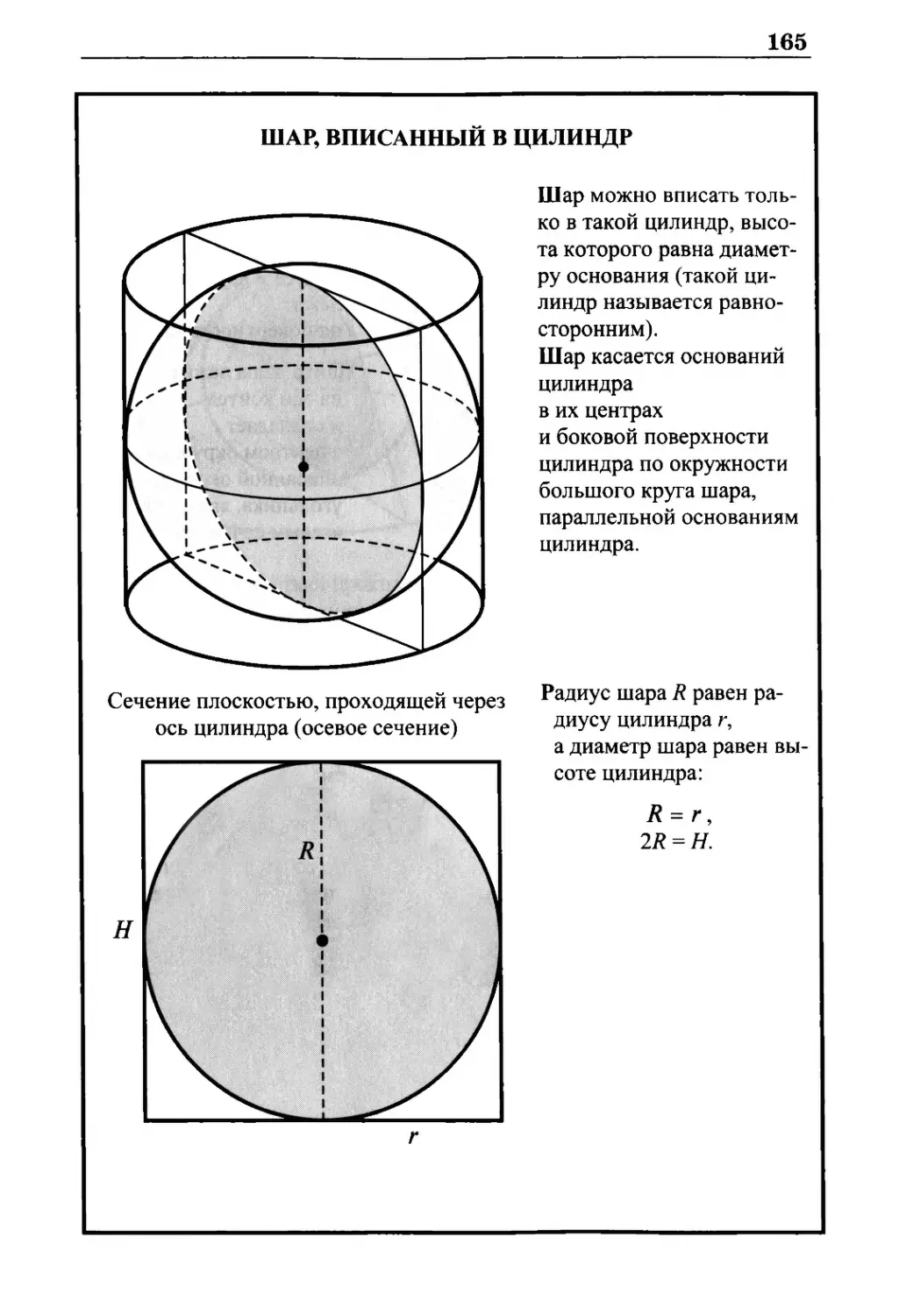
Шар, вписанный в цилиндр 165
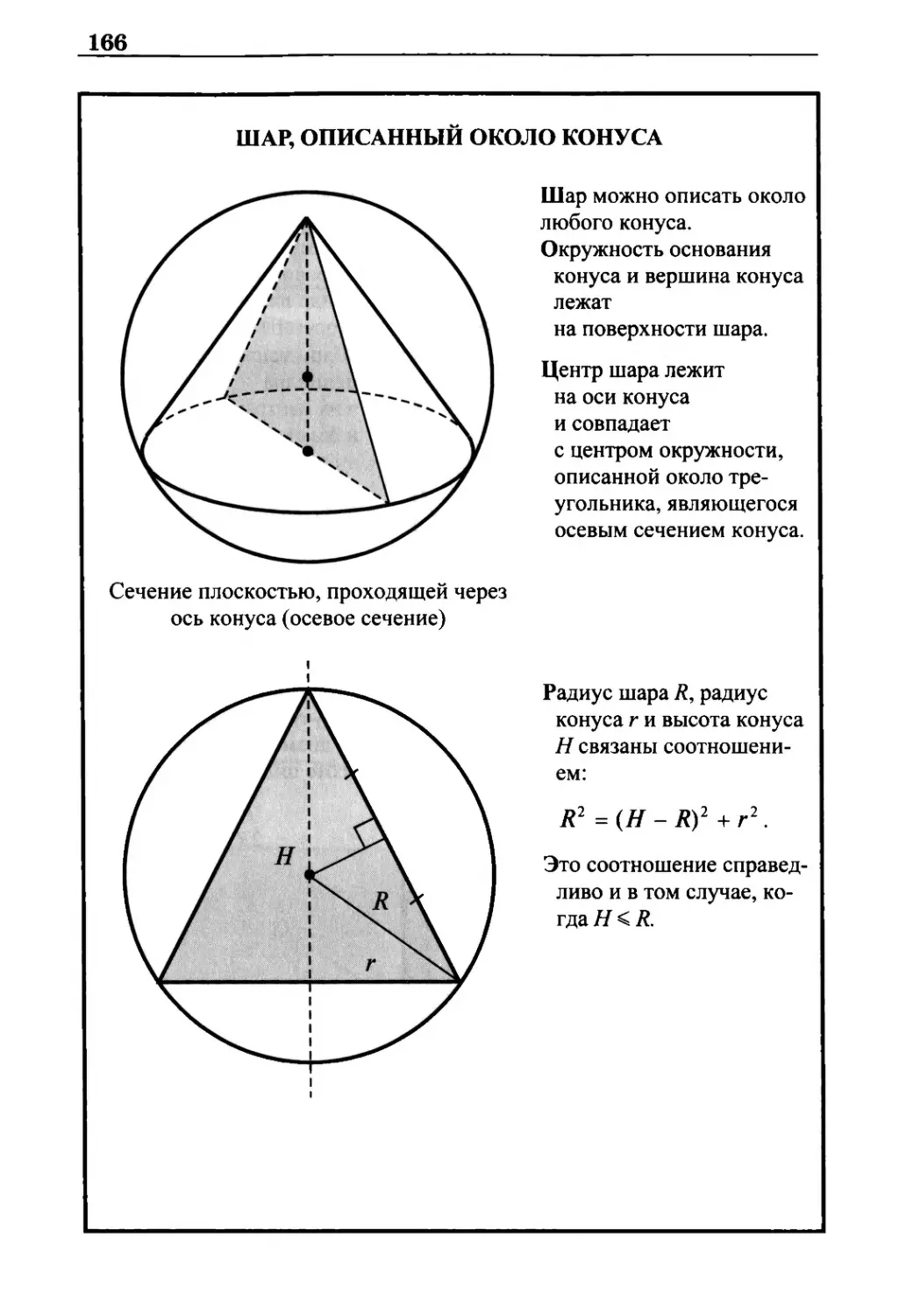
Шар, описанный около конуса 166
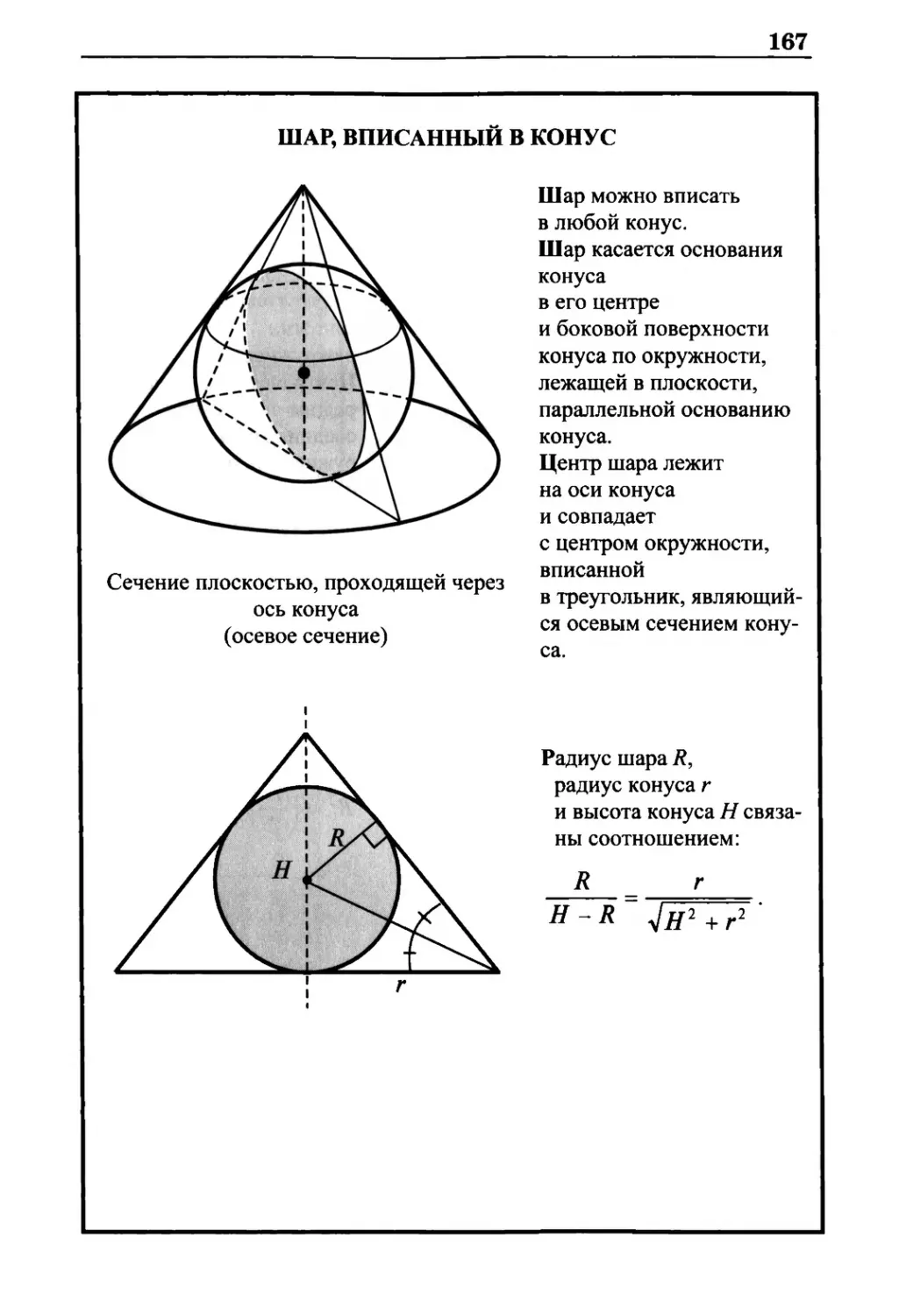
Шар, вписанный в конус 167
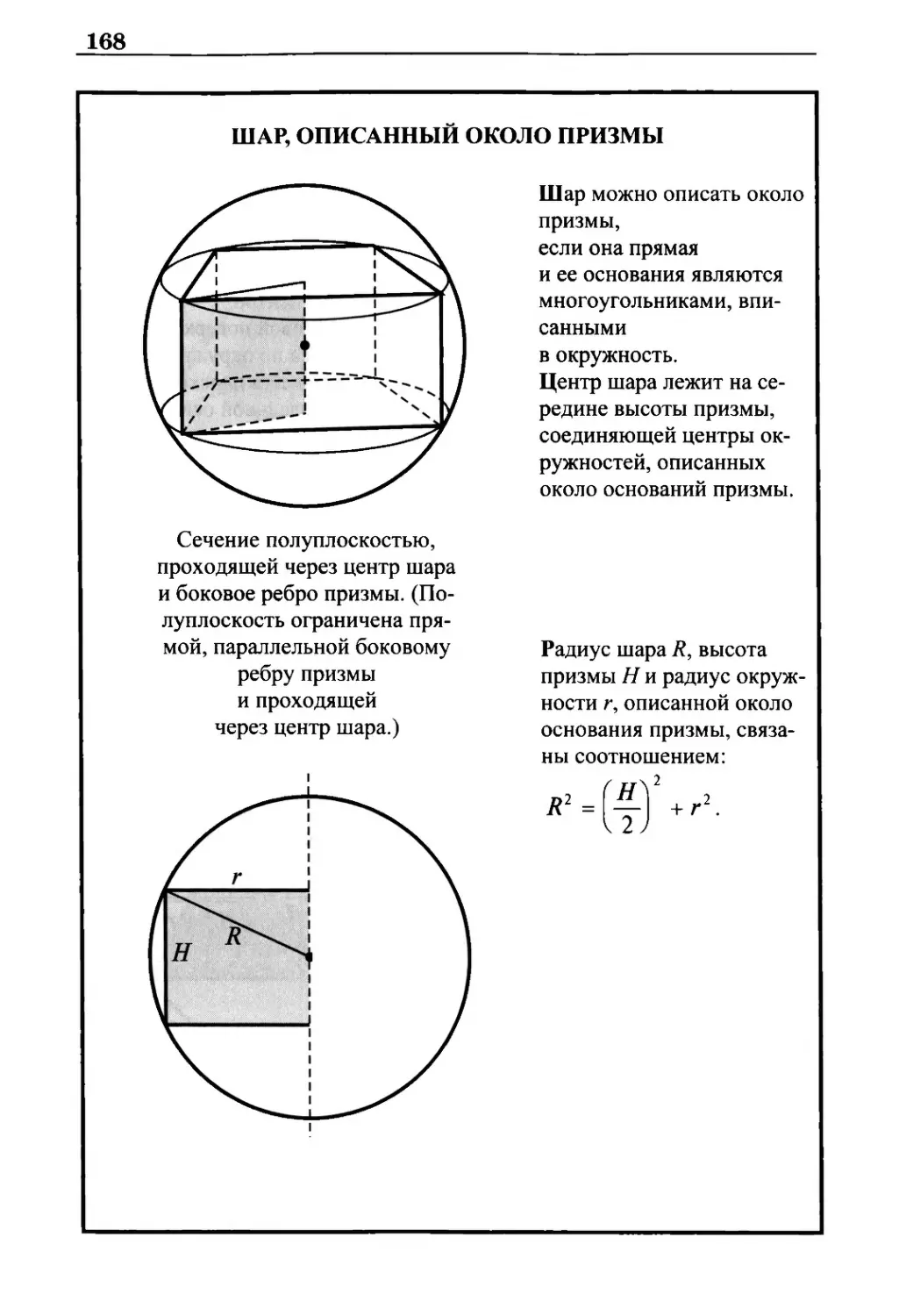
Шар, описанный около призмы 168
Шар, вписанный в прямую призму 169
Шар, описанный около правильной пирамиды 170
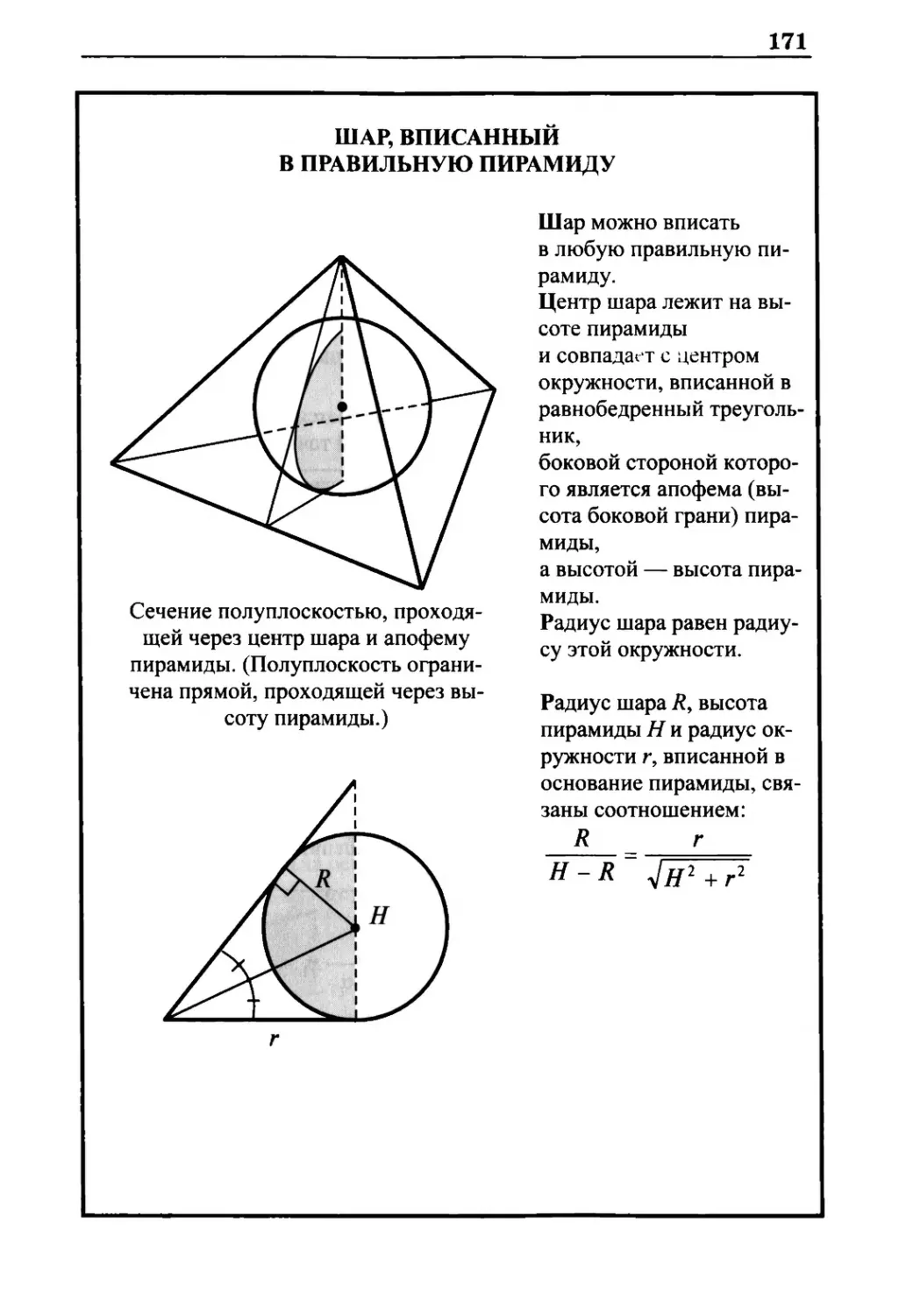
Шар, вписанный в правильную пирамиду 171
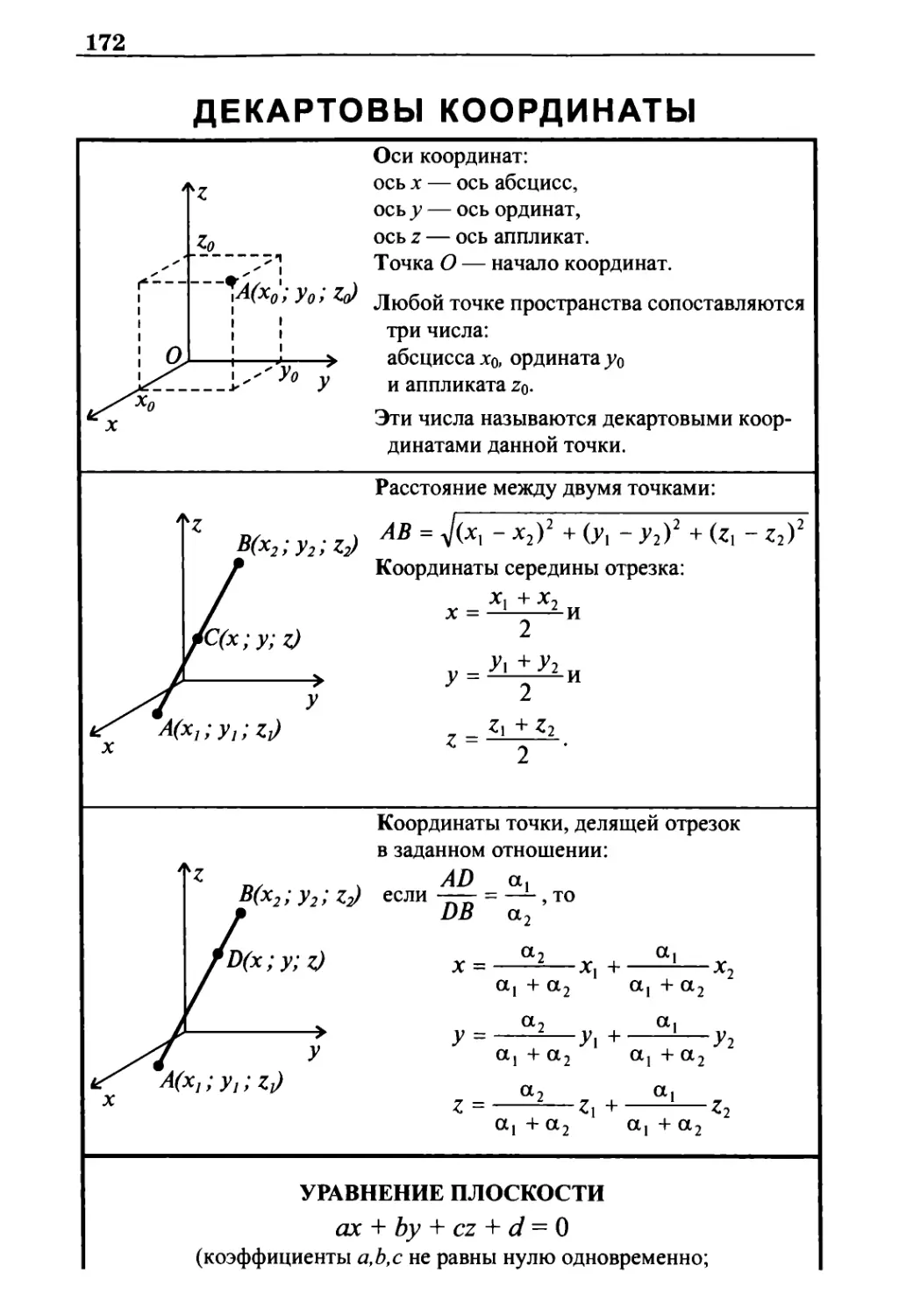
Декартовы координаты 172
Уравнение плоскости 173
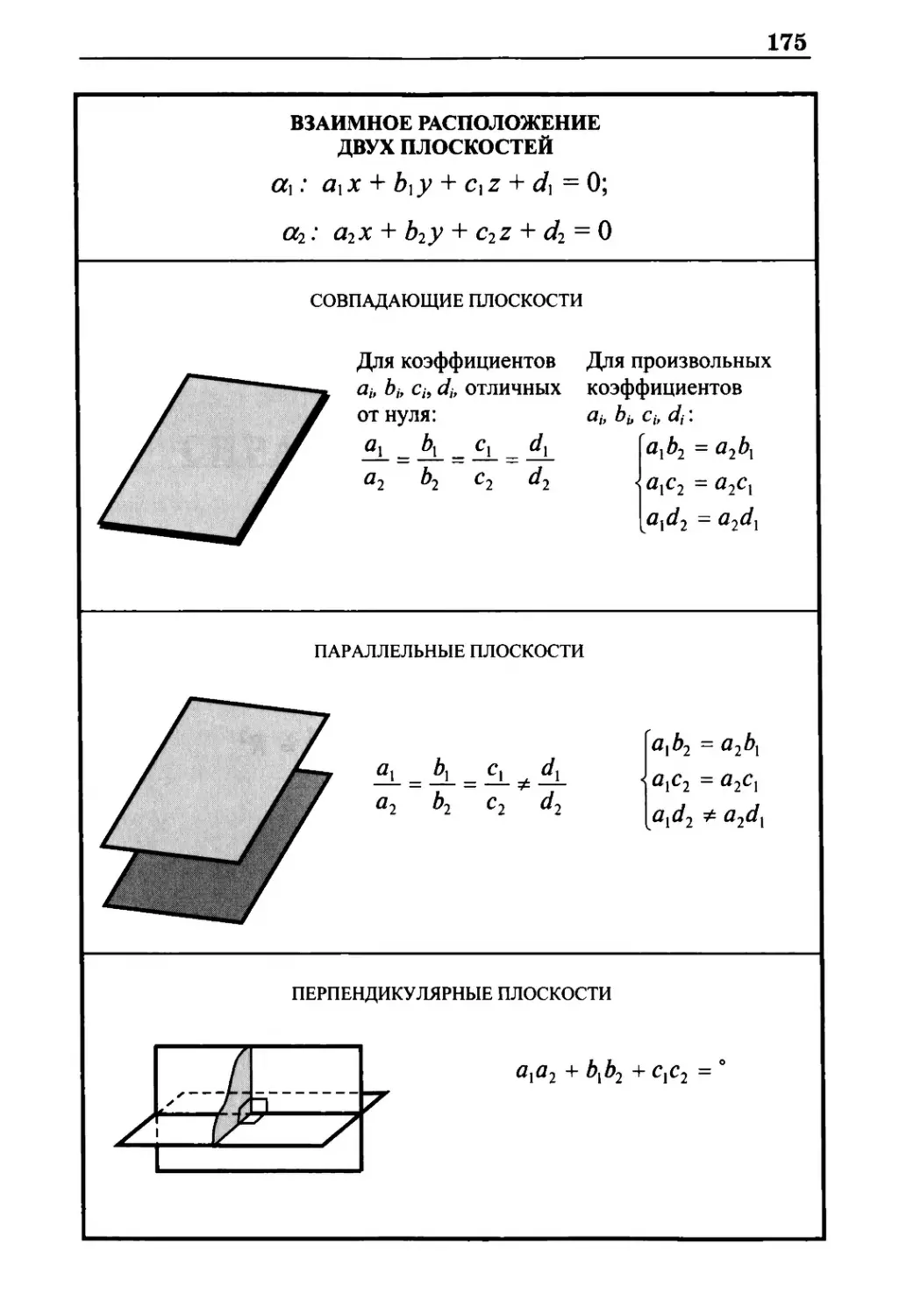
Взаимное расположение двух плоскостей 175
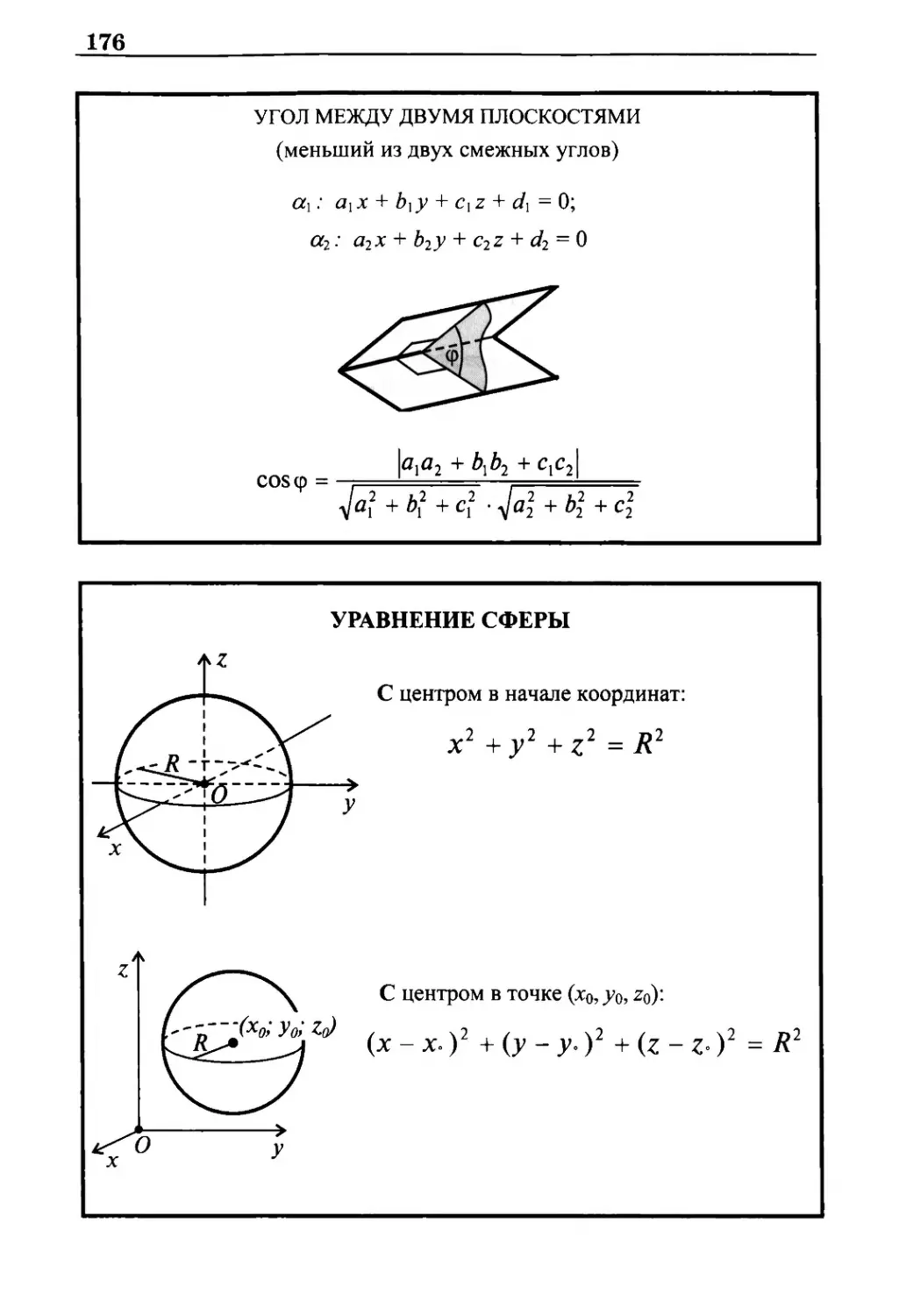
Уравнение сферы 176
СПРАВОЧНЫЕ ТАБЛИЦЫ 177

10
АЛГЕБРА И НАЧАЛА АНАЛИЗА
ФУНКЦИИ*)
Числовой функцией называется соответствие, которое
каждому числу х из некоторого заданного множества
сопоставляет единственное число у.
Обозначение: у = f (х), где х — независимая
переменная (аргумент функции), у — зависимая переменная
(функция).
Множество значений х называется областью
определения функции (обычно обозначается D).
Множество значений у называется областью значений
функции (обычно обозначается Е).
Графиком функции
называется множество точек
плоскости с координатами
(х, f(x)).
способы задания функций
• Аналитический способ: функция задается с помощью
математической формулы.
Примеры: у = х2, у = ln х
• Табличный способ: функция задается с помощью таблицы.
Пример.
X
1
2
3
4
5
У
2
4
6
8
10
• Описательный способ: функция задается словесным
описанием.
( 1 для рациональных х,
Пример: функция Дирихле f (х) = \
(0 для иррациональных х.
• Графический способ: функция задается с помощью
графика.
*)Все параметры функций, в том числе коэффициенты многочленов,
считаются действительными.

11
основные свойства функции
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ
Функция называется
четной, если:
область определения
функции симметрична
относительно нуля,
для любого х из
области определения
f(-x)= f(x).
График четной функции
симметричен относительно
оси у.
Функция называется
нечетной, если:
область определения
функции симметрична
относительно нуля,
для любого х из
области определения
f(-х) = -f(x).
График нечетной функции
симметричен относительно
начала координат.
Многие функции не являются ни четными, ни нечетными.
Пример графика функции, не являющейся ни четной, ни нечетной:
У
Примеры четных функций: у = x2n, п е Z; у = cos х
Примеры нечетных функций: у = x2n+1, п е Z; у = sin х
Примеры функций, не являющихся ни четными, ни нечетными:
у = ех, у = ln х, у = х - 2, у = (х + 1)2

12
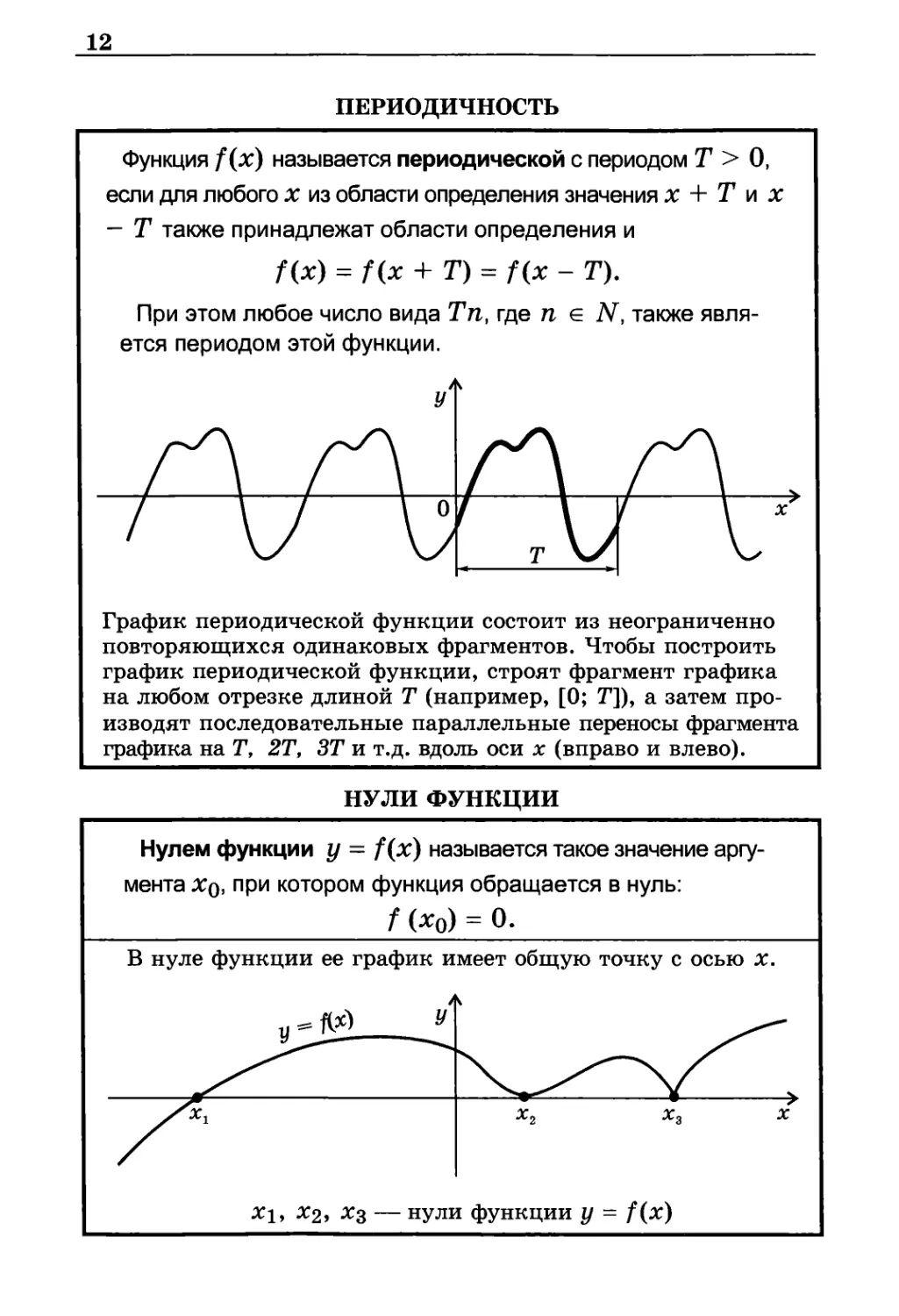
ПЕРИОДИЧНОСТЬ
Функция f(x) называется периодической с периодом Т > О,
если для любого х из области определения значения х + Т и х
— Т также принадлежат области определения и
f(x) = f(x + Т) = f(x - Т).
При этом любое число вида Тп, где п е N, также
является периодом этой функции.
График периодической функции состоит из неограниченно
повторяющихся одинаковых фрагментов. Чтобы построить
график периодической функции, строят фрагмент графика
на любом отрезке длиной Т (например, [0; T]), а затем
производят последовательные параллельные переносы фрагмента
графика на Т, 2Т, ЗТ и т.д. вдоль оси х (вправо и влево).
НУЛИ ФУНКЦИИ
Нулем функции у = f(x) называется такое значение
аргумента X0, при котором функция обращается в нуль:
f(x0) = 0.
В нуле функции ее график и
меет общую точку с осью х.
x1, x2, x3 - нули
функции у = f(x)

13
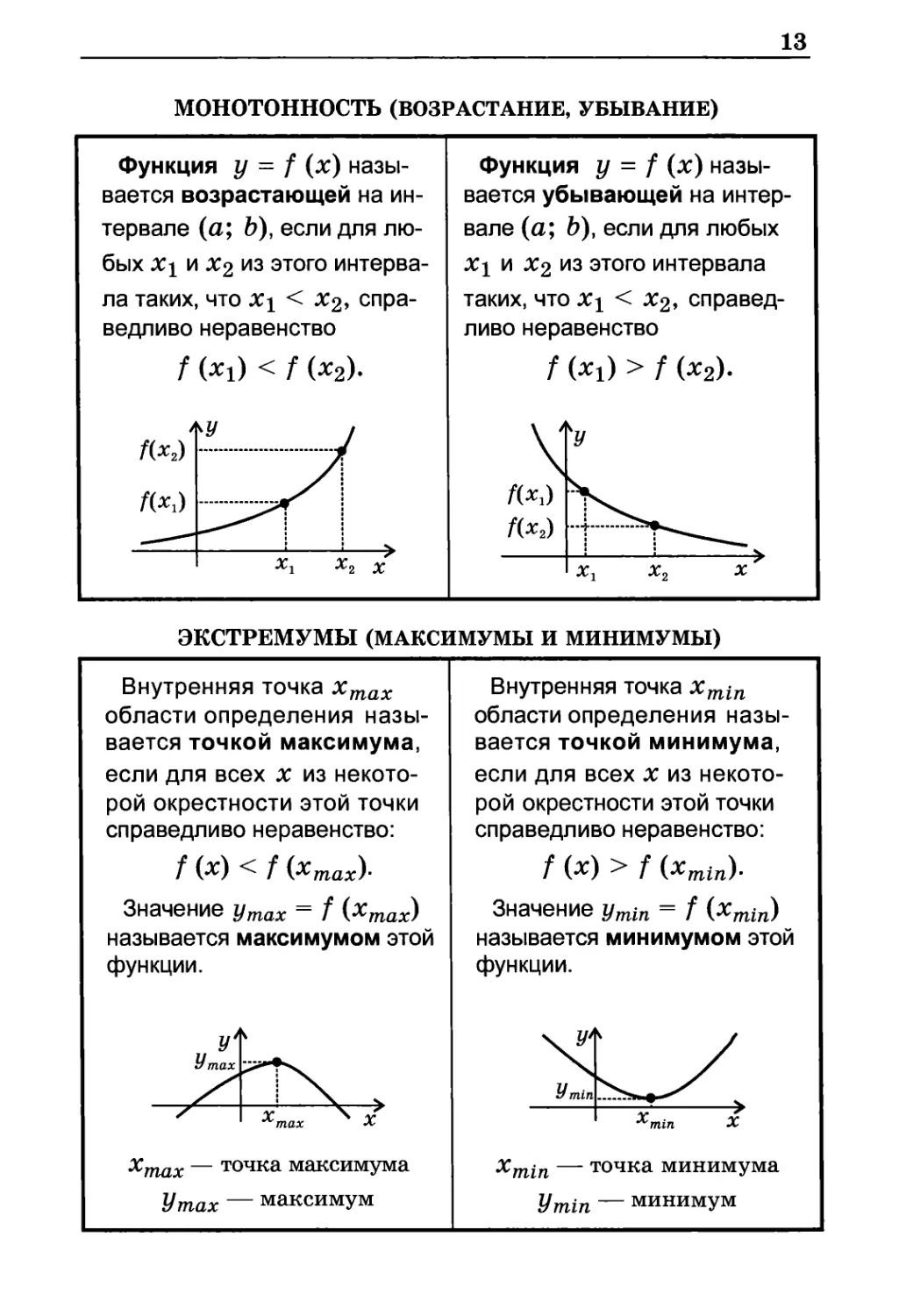
МОНОТОННОСТЬ (ВОЗРАСТАНИЕ, УБЫВАНИЕ)
Функция у = f (х)
называется возрастающей на
интервале (а; b), если для
любых Х1 и x2 из этого
интервала таких, что x1 <
x2справедливо неравенство
f(x1)<f(x2)
Функция у = f (х)
называется убывающей на
интервале (а; b), если для любых
Х1 и x2 из этого интервала
таких, что x1 < x2,
справедливо неравенство
f(x1)>f(x2).
\ У
'У
f(x2)
■■•]
Хп
X
ЭКСТРЕМУМЫ (МАКСИМУМЫ И МИНИМУМЫ)
Внутренняя точка хmax
области определения
называется точкой максимума,
если для всех х из
некоторой окрестности этой точки
справедливо неравенство:
f(x)<f (хmax).
Значение уmax = f (хmax)
называется максимумом этой
функции.
Хmax — точка максимума
Уmax — максимум
Внутренняя точка xmin
области определения
называется точкой минимума,
если для всех х из
некоторой окрестности этой точки
справедливо неравенство:
f(x)>f (xmin).
Значение ymin = f (xmin)
называется минимумом этой
функции.
Xmin — точка минимума
Уmin — минимум

14
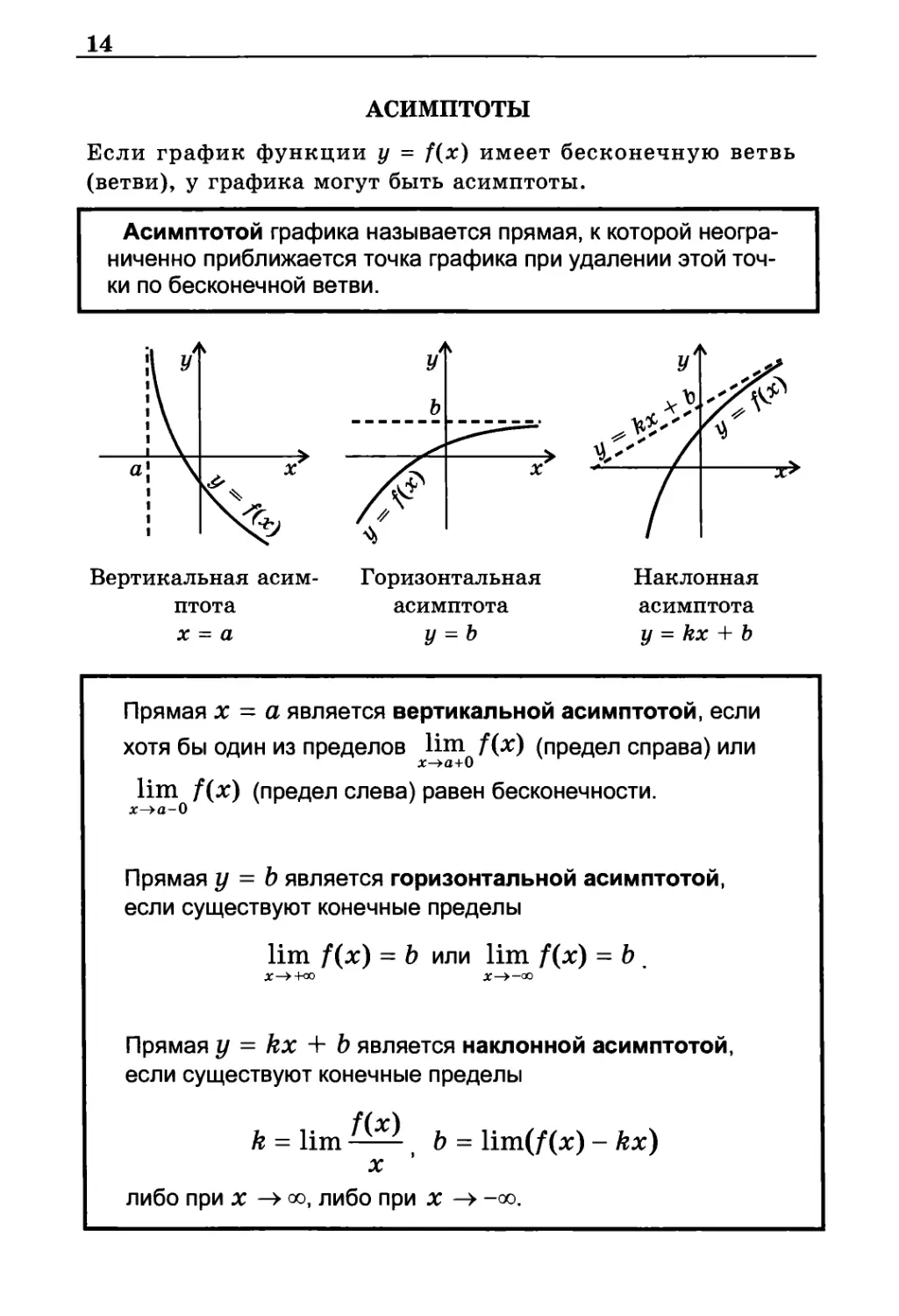
АСИМПТОТЫ
Если график функции у = f(x) имеет бесконечную ветвь
(ветви), у графика могут быть асимптоты.
Асимптотой графика называется прямая, к которой
неограниченно приближается точка графика при удалении этой
точки по бесконечной ветви.
Вертикальная асим- Горизонтальная Наклонная
птота асимптота асимптота
х = а у = b у = kx + b
Прямая х — а является вертикальной асимптотой, если
хотя бы один из пределов lim f(x) (предел справа) или
x->а+0
lim f(x) (предел слева) равен бесконечности.
x->а-0
Прямая у = b является горизонтальной асимптотой,
если существуют конечные пределы
lim f(x) = b или lim f(x) = b .
Прямая у = kx + b является наклонной асимптотой,
если существуют конечные пределы
k = lim f(x) b = lim(f(x) - kx)
x
либо при х —> ∞, либо при х —> -∞.

15
ОБРАТНЫЕ ФУНКЦИИ
Понятие обратной функции применимо к функциям,
обладающим следующим свойством: каждому значению у из
области значений функции соответствует единственное значение х
из области определения этой функции.
Замечание. Для многих функций это свойство выполняется лишь на
части области определения, в частности, на любом промежутке
монотонности (для функции у = х2 таким промежутком является,
например, луч [0; ∞), для функции у = sin х — отрезок [-π/2; π/2]).
Функция g называется обратной для функции f, если
каждому у из области значений функции f функция g ставит в
соответствие такое х из области определения функции f, что
у = f(x). Таким образом, если у = f(x), то х = g(y).
Функции f и g являются взаимно обратными.
• Область определения функции f является областью
значений функции g, а область значений функции f
является областью определения функции g.
• Графики взаимно обратных функций симметричны друг
другу относительно прямой у = х (построение графика
обратной функции см. на стр. 23).
Примеры взаимно обратных функций:
у = х3 и у - , у = 2х и у = log2x
нахождение формулы для функции, обратной данной
• Пользуясь формулой у = f(x), следует выразить х через у,
а в полученной формуле х = g(y) заменить х на у, а у на
х.
Пример. Найти формулу для функции, обратной
функции
1 ,
у = — X + 1 .
2
Выражение х через у: х = 2у - 2.
Замена х на у, у на х дает: у = 2х - 2.
Результат: функция у=2х-2 является
обратной для функции у = 1/2х +1.

16
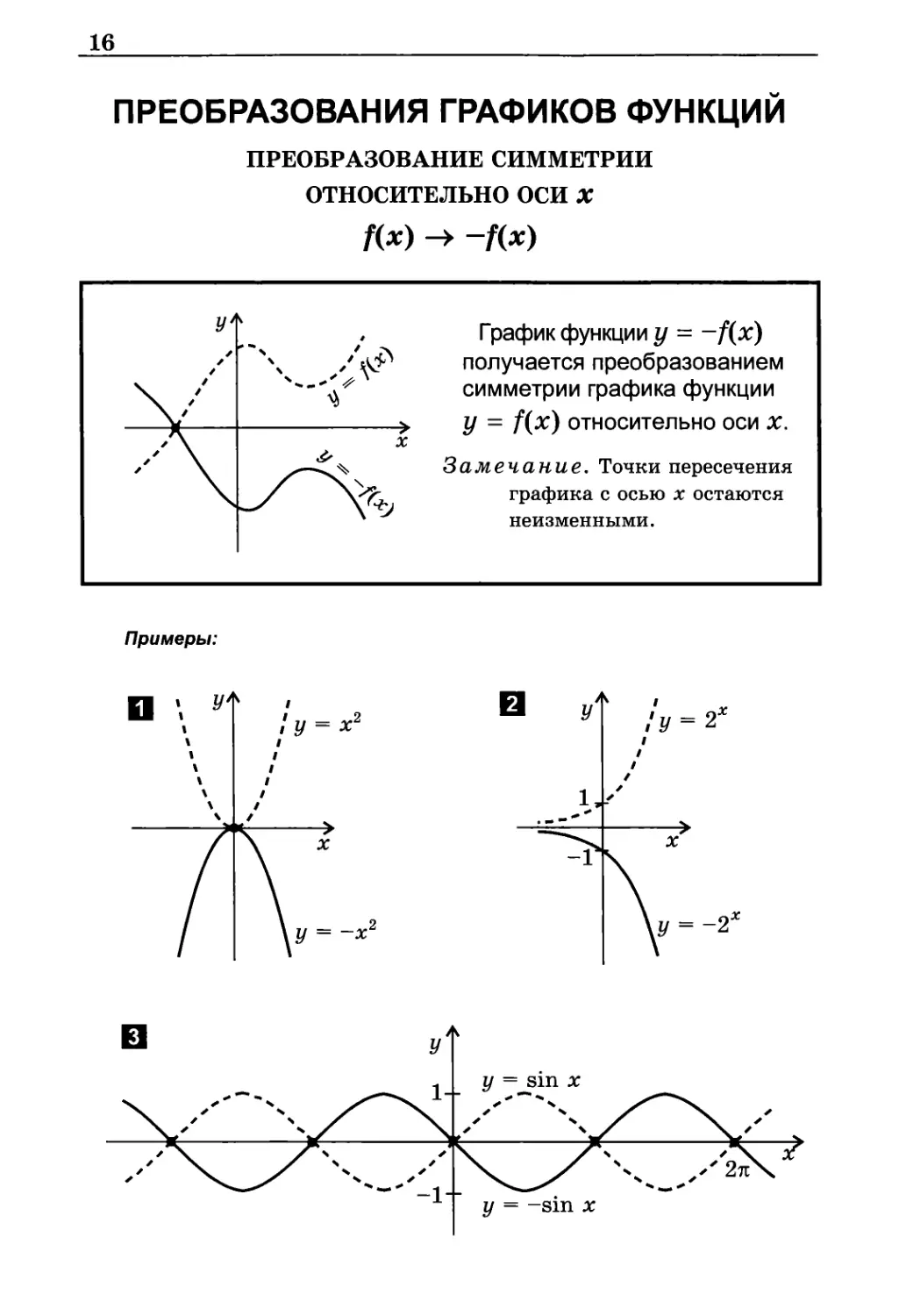
ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИИ
ПРЕОБРАЗОВАНИЕ СИММЕТРИИ
ОТНОСИТЕЛЬНО ОСИ X
f(x) -> -f(x)
График функции у = -f(x)
получается преобразованием
симметрии графика функции
у = f(x) относительно оси х.
Замечание. Точки пересечения
графика с осью х остаются
неизменными.
Примеры:
/У = 2x
3

17
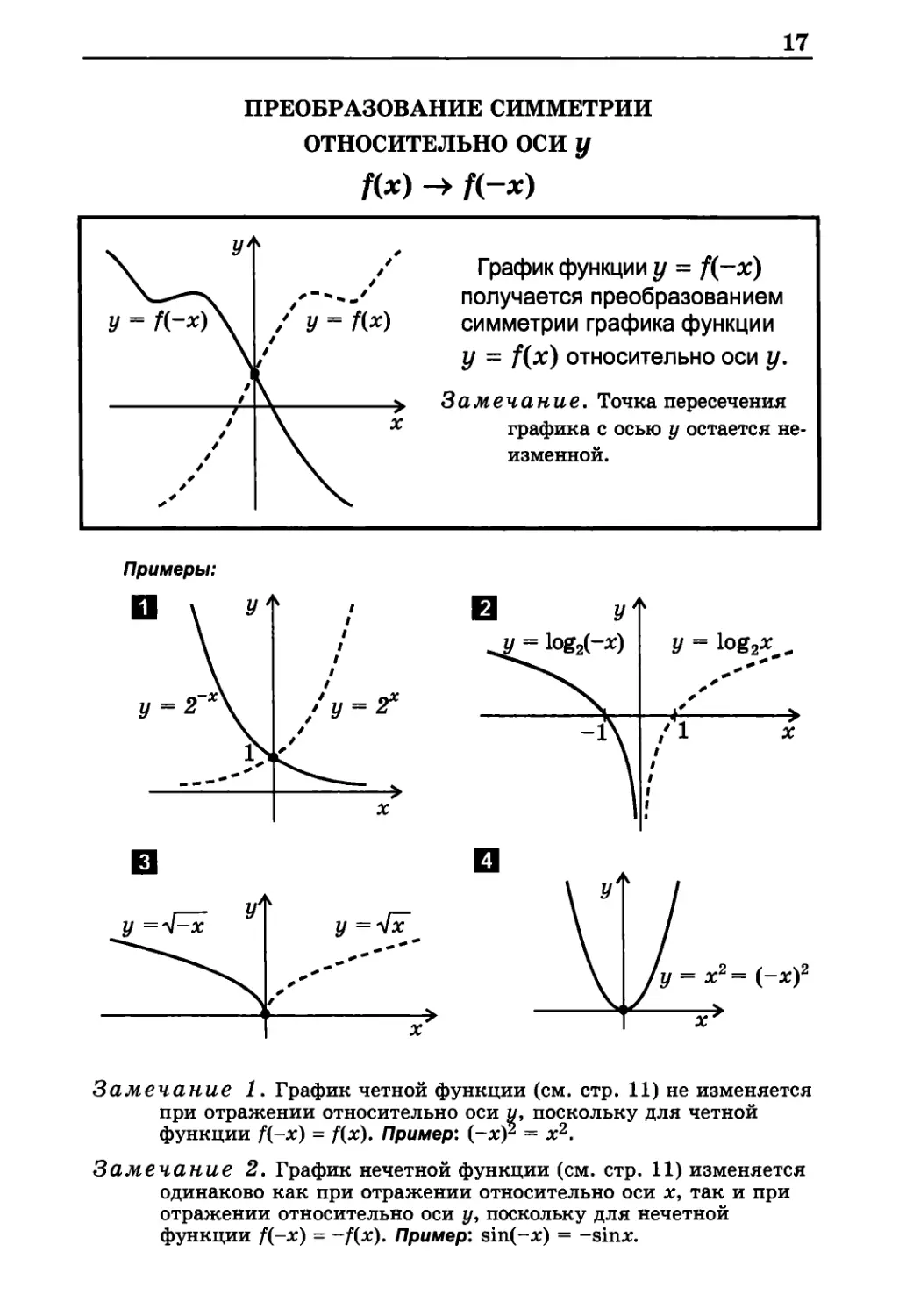
ПРЕОБРАЗОВАНИЕ СИММЕТРИИ
ОТНОСИТЕЛЬНО ОСИ у
График функции у = f(-x)
получается преобразованием
симметрии графика функции
у = f(x) относительно оси у.
Замечание. Точка пересечения
графика с осью у остается
неизменной.
Примеры:
Замечание 1. График четной функции (см. стр. 11) не изменяется
при отражении относительно оси у, поскольку для четной
функции f(-x) = f(x). Пример: (-х)2 = х2.
Замечание 2. График нечетной функции (см. стр. 11) изменяется
одинаково как при отражении относительно оси х, так и при
отражении относительно оси у, поскольку для нечетной
функции f(-x) = -f(x). Пример: sin(-x) = -sinx.

18
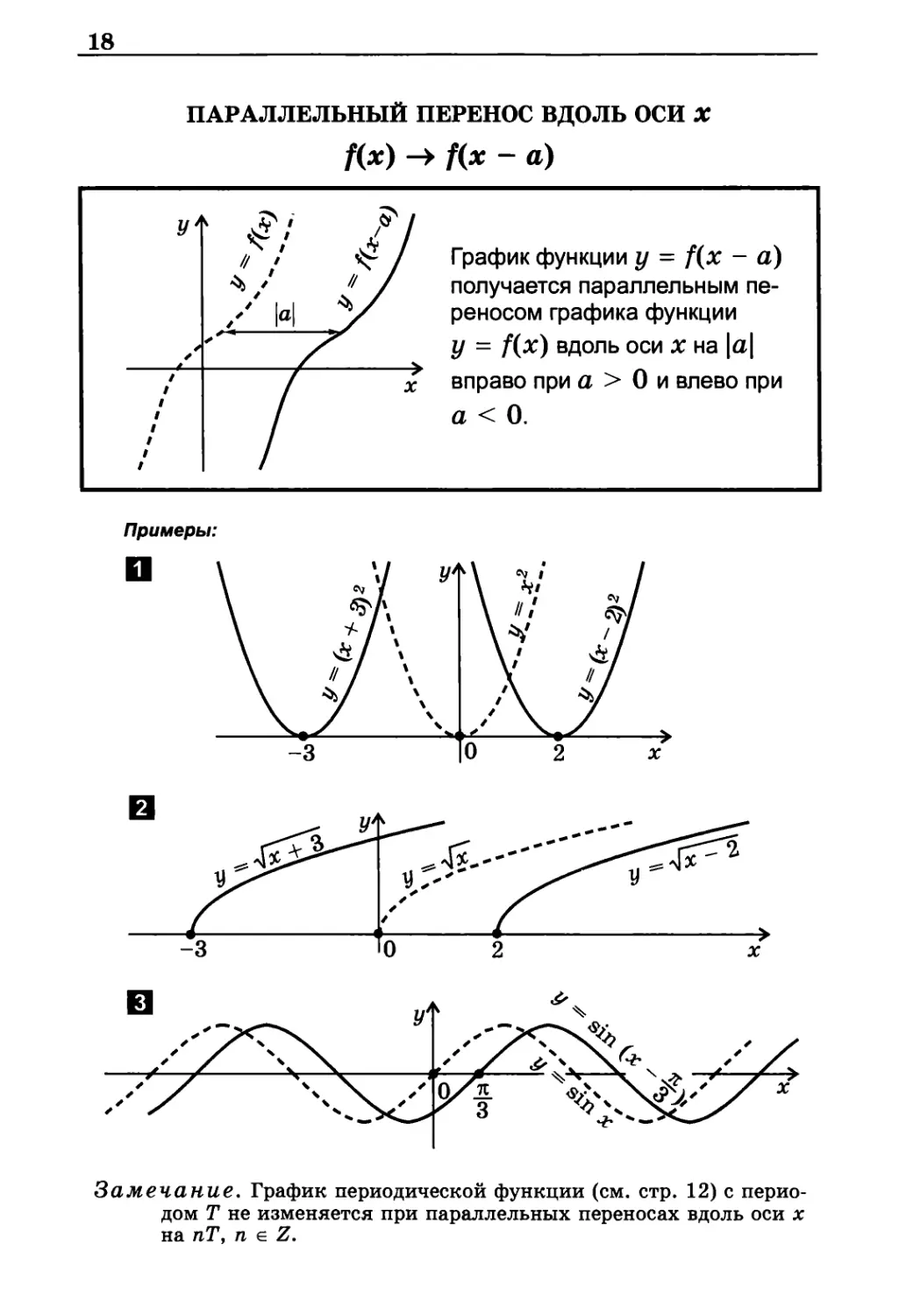
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ ОСИ X
f(x) -> f(x - а)
График функции у = f(x - а)
получается параллельным
переносом графика функции
у = f(x) вдоль оси х на \а\
вправо при а > 0 и влево при
а < 0.
Замечание. График периодической функции (см. стр. 12) с
периодом Т не изменяется при параллельных переносах вдоль оси х
на пТ, п g Z.

19
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ ОСИ у
f(x) f(x) + b
График функции у = f(x) +b
получается параллельным
переносом графика функции
у = f(x) вдоль оси у на |b|
вверх при b > 0 и вниз при
Ь < 0.
Примеры:

20
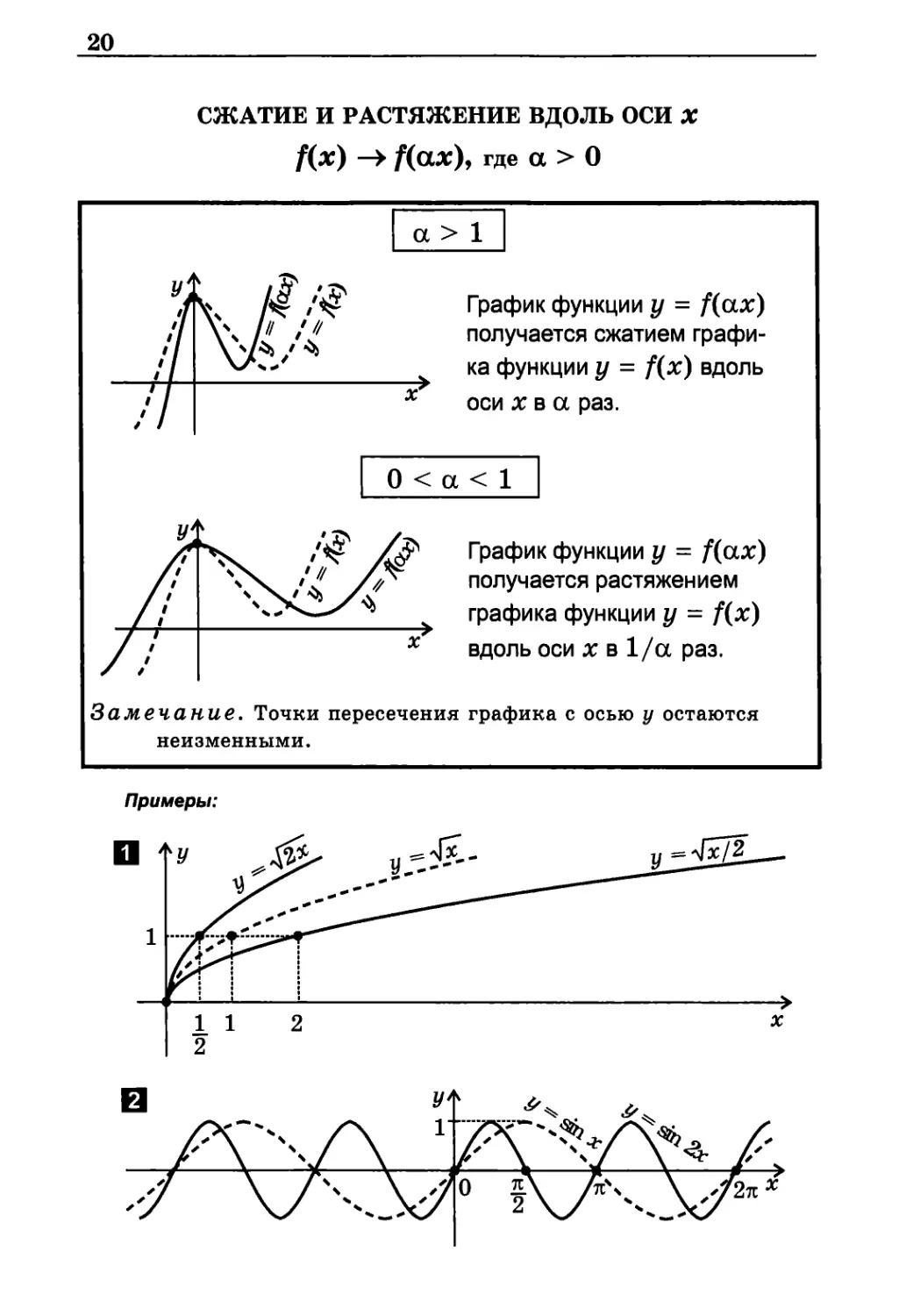
СЖАТИЕ И РАСТЯЖЕНИЕ ВДОЛЬ ОСИ X
f(x) -> f(ax), где а > 0
а > 1
График функции у = f(ax)
получается сжатием
графика функции у = f(x) вдоль
оси х в а раз.
О < а < 1
График функции у = f(ax)
получается растяжением
графика функции у = f(x)
х вдоль оси х в 1/а раз.
Замечание. Точки пересечения графика с осью y остаются
неизменными.
Примеры:

21
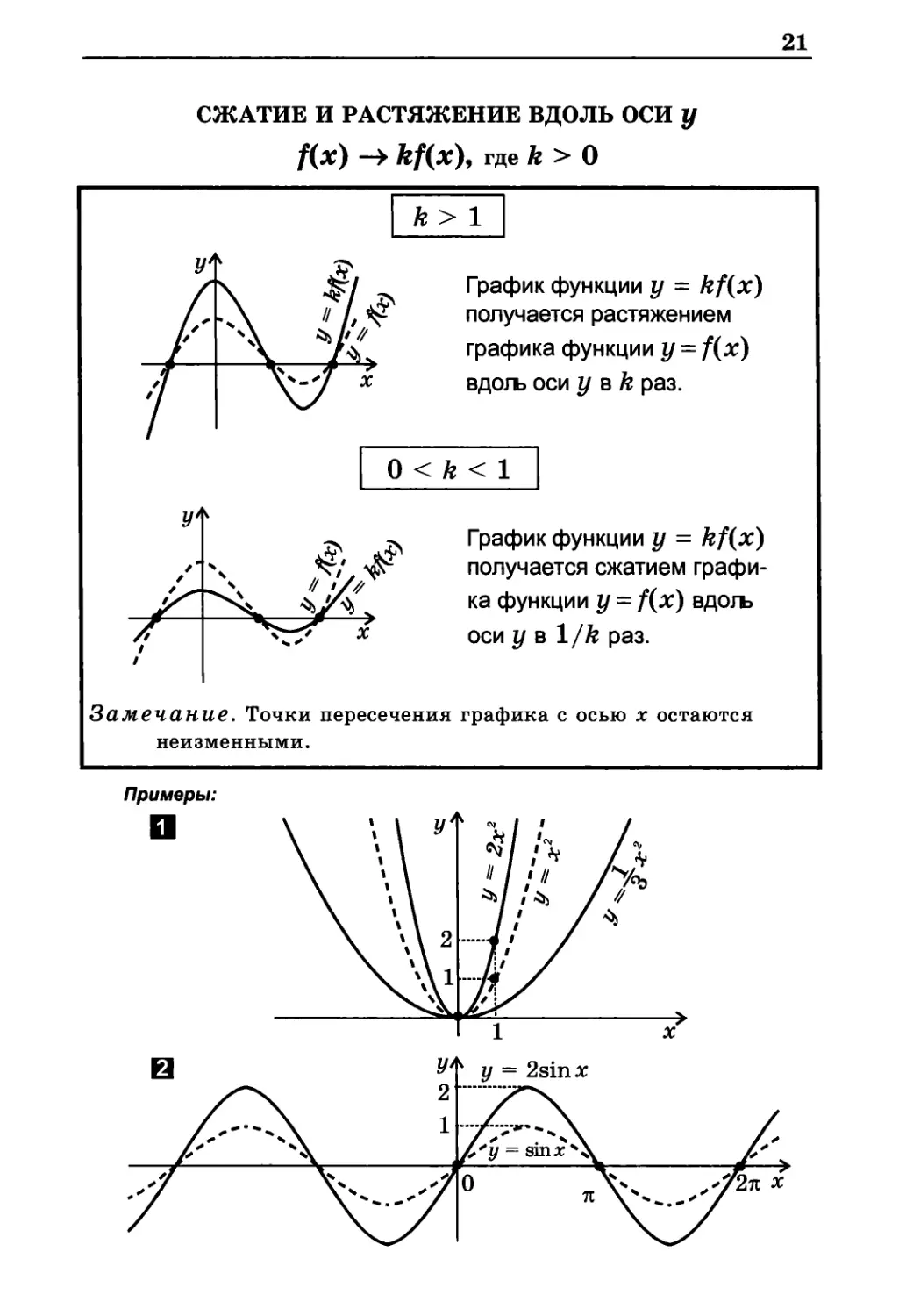
СЖАТИЕ И РАСТЯЖЕНИЕ ВДОЛЬ ОСИ у
f(x) -> kf(x), где k > О
к > 1
График функции y= kf(x)
получается растяжением
графика функции у = f(x)
вдоль оси у в k раз.
О < k < 1
Замечание. Точки пересечения графика с осью х остаются
неизменными.
Примеры:
График функции у = kf(x)
получается сжатием
графика функции у = f(x) вдоль
оси у в 1 /k раз.

22
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ у = |f(x)|
Части графика функции у = f(x), лежащие выше оси х и на
оси х, остаются без изменения, а лежащие ниже оси х —
симметрично отражаются относительно этой оси (вверх).
Замечание. Функция у = |f(x)| неотрицательна (ее график
расположен в верхней полуплоскости).
Примеры:
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ у = f(|х|)
Часть графика функции у = f(x), лежащая левее оси у,
удаляется, а часть, лежащая правее оси у — остается без изменения и,
кроме того, симметрично отражается относительно оси у (влево).
Точка графика, лежащая на оси у, остается неизменной.
Замечание. Функция у = f(|x|) четная (ее график симметричен
относительно оси у).
Примеры:

23
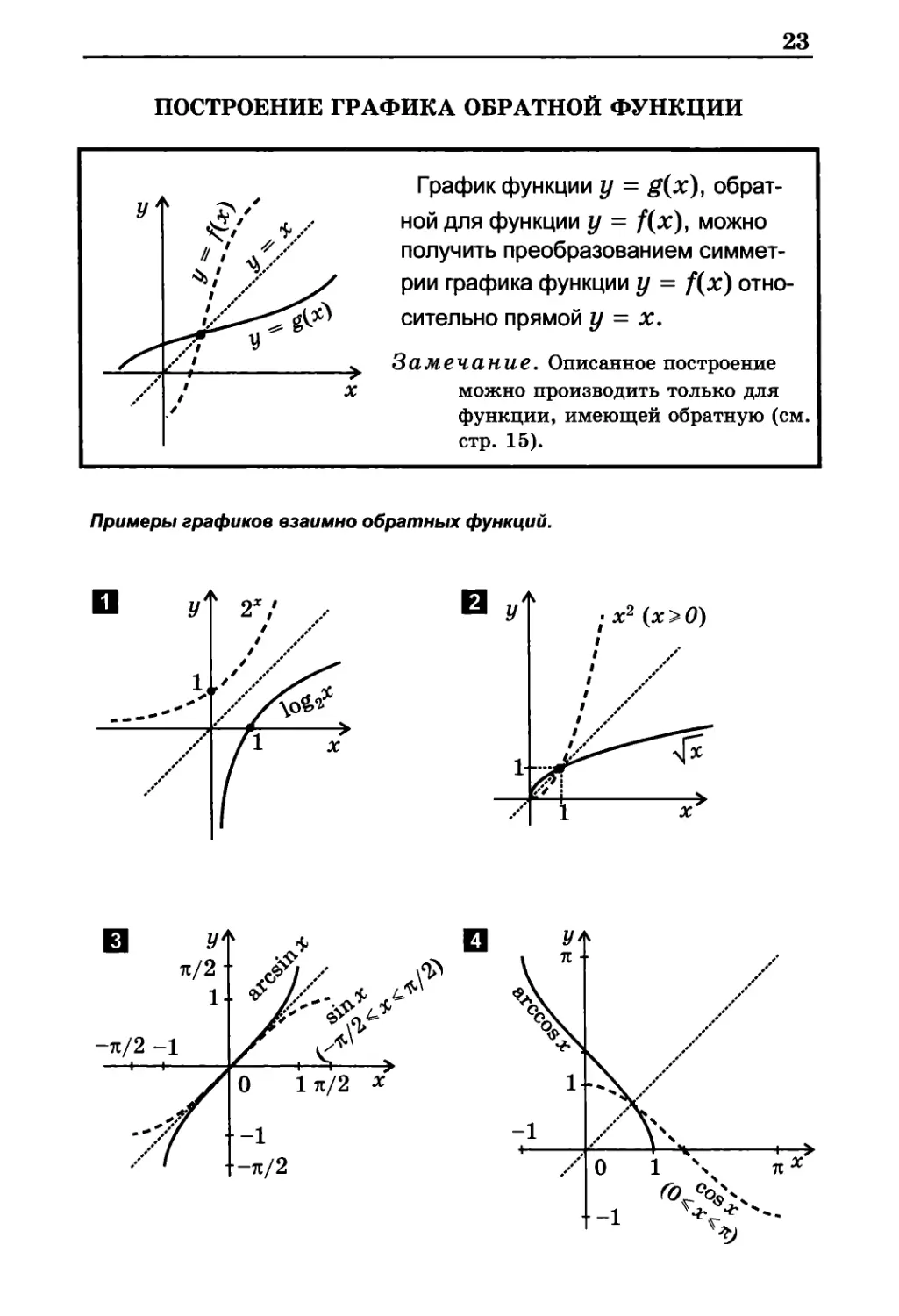
ПОСТРОЕНИЕ ГРАФИКА ОБРАТНОЙ ФУНКЦИИ
График функции у = g(x),
обратной для функции у = f(x), можно
получить преобразованием
симметрии графика функции у = f(x)
относительно прямой у = х.
Замечание. Описанное построение
можно производить только для
функции, имеющей обратную (см
стр. 15).
Примеры графиков взаимно обратных функций.

24
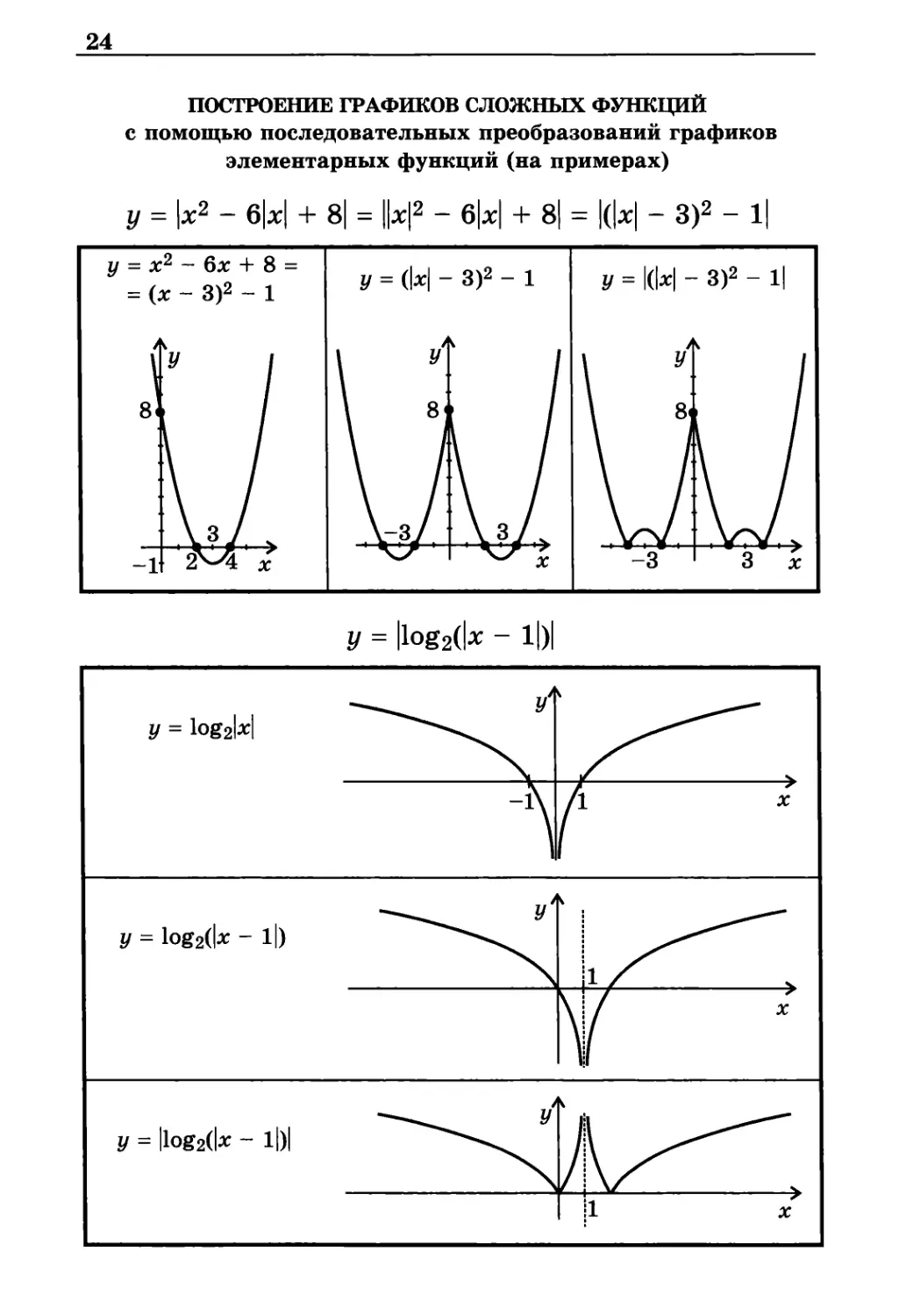
ПОСТРОЕНИЕ ГРАФИКОВ СЛОЖНЫХ ФУНКЦИЙ
с помощью последовательных преобразований графиков
элементарных функций (на примерах)
у = |х2- 6|x| + 8| = ||х|2 - 6|x| + 8| = |(|x -3)2-1

у = |3sin2x| - 1
25

26
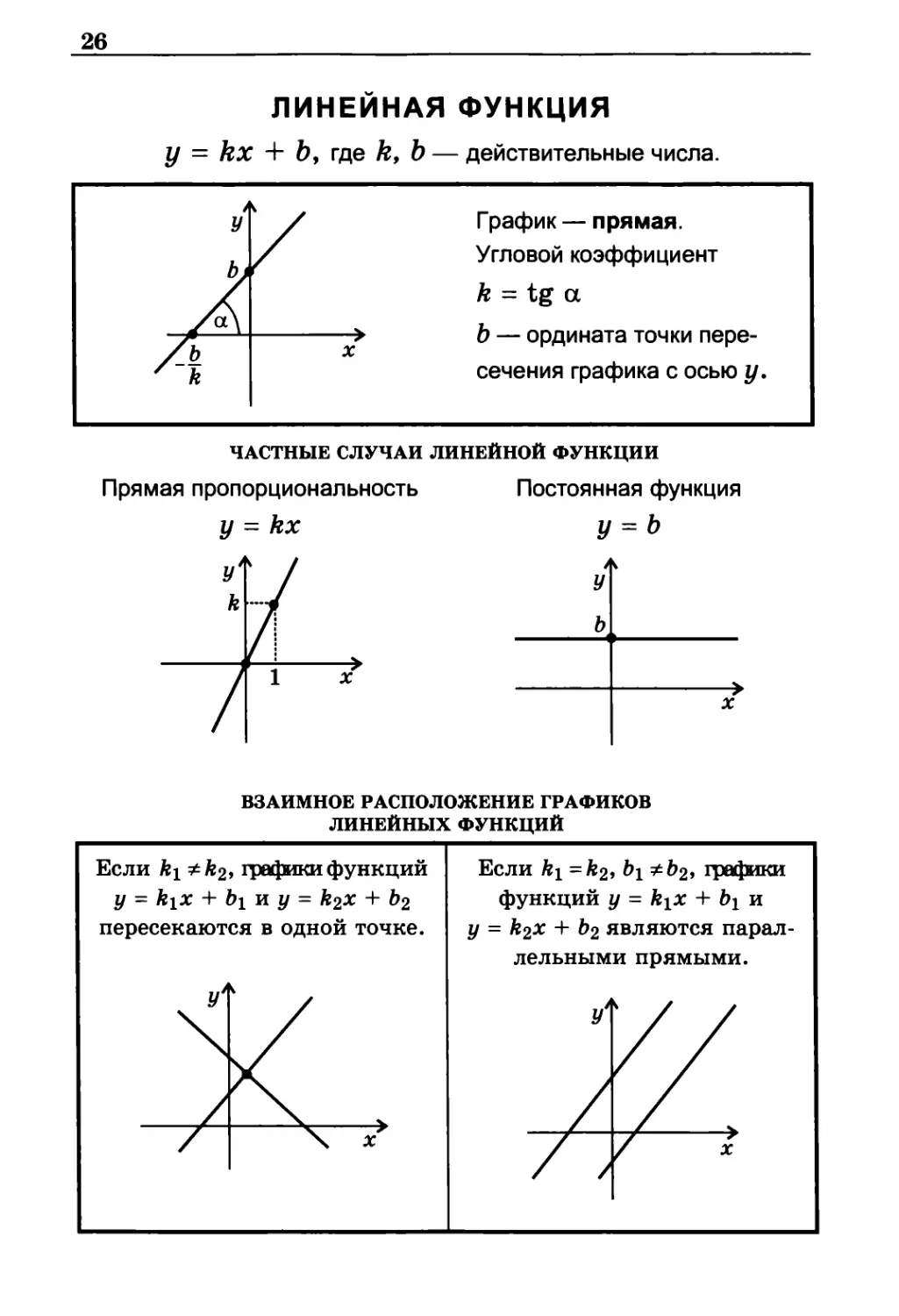
линейная функция
у = kx + bу где k, b — действительные числа.
График — прямая.
Угловой коэффициент
k = tg а
b — ордината точки
пересечения графика с осью у.
частные случаи линейной функции
Прямая пропорциональность Постоянная функция
у = kx У = b
взаимное расположение графиков
линейных функций

27
свойства линейной функции у = kx + b
Область определения: R
Область значений:
при k ≠ 0 R
при к =0 {b}
• Четность, нечетность:
если k ≠0, b≠0, то функция не является ни четной,
ни нечетной
если k ≠0, b = 0, то функция нечетная
если к = 0, b≠0, то функция четная
если k=0, b = 0, то функция тождественно равна нулю,
то есть является одновременно четной и нечетной
Нули:
если k≠0, то у = 0 при x = -b/k
если к = 0, b ≠ 0, то нулей нет
если к = 0, b = 0, то y = 0 при х е R
Промежутки знакопостоянства:
- „ при х е (~b/k; оо)
если k > 0, то < _ . ....
при х е (-оо; -bk)
у>о
у<о
у > 0 при x е (-00; -b/k)
y<0
если k < 0, то » _ . ,
при x е (-b/k; об)
если k = 0, b > 0, то y > 0 при хеR
если k = 0, b < 0, то у < 0 при хеR
если k = 0, b = 0, то y = 0 при х е R
Промежутки монотонности:
если k > 0, то функция возрастает при х е R
если /г < 0, то функция убывает при х е R
если /г = 0, то функция постоянна при х е R
Экстремумов нет

28
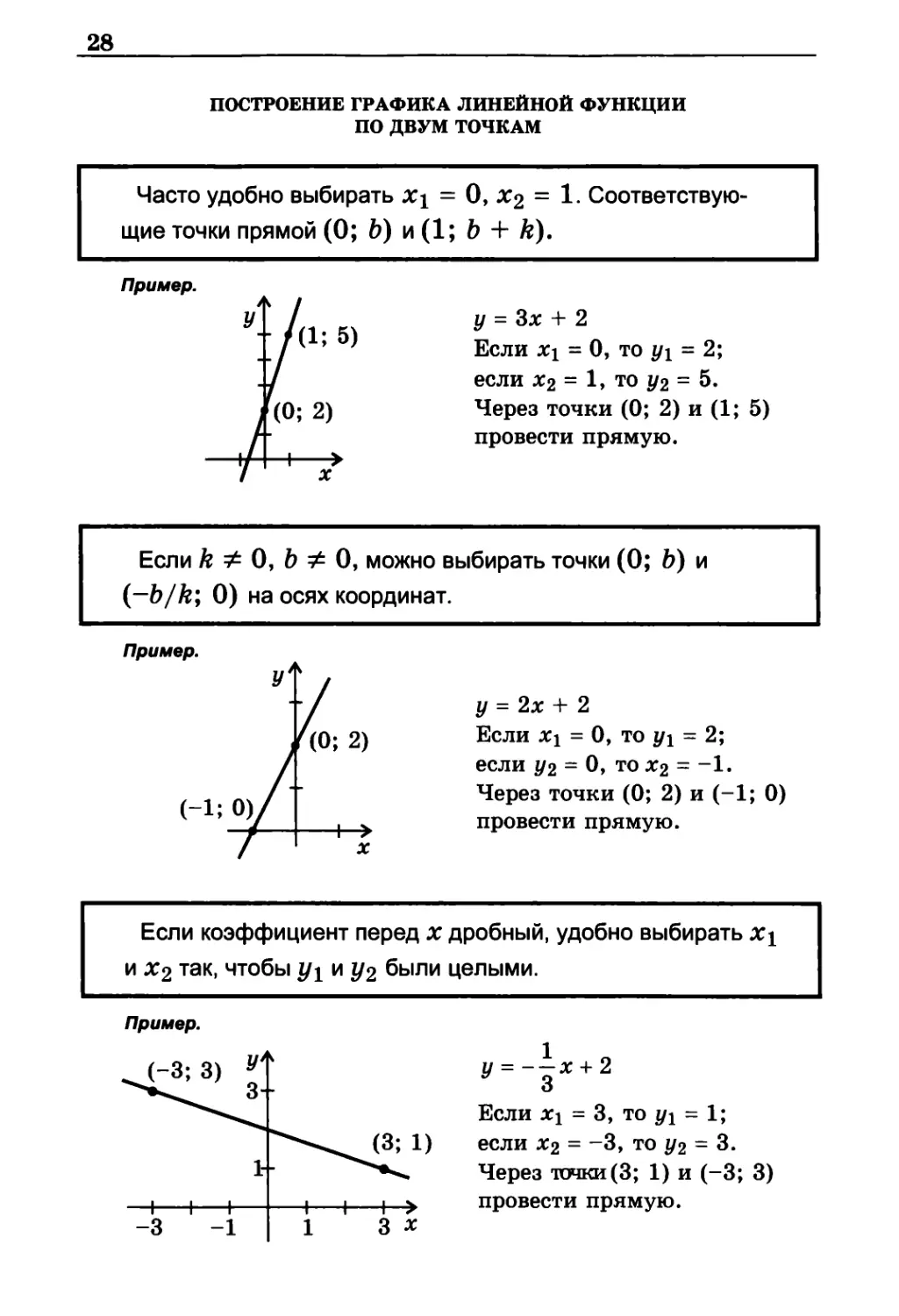
построение графика линейной функции
по двум точкам
Часто удобно выбирать X1 = 0, х2 = 1.
Соответствующие точки прямой (0; b) и (1; Ь + k).
Пример.
у = Зх + 2
Если х1 = 0, то у1 = 2;
если x2 = 1, то у2 = 5.
Через точки (0; 2) и (1; 5)
провести прямую.
Если k ≠ 0, b ≠ 0, можно выбирать точки (0; b) и
(—b/k; 0) на осях координат.
Пример.
у = 2x + 2
Если ;x1 = 0, то у1 = 2;
если у2 = 0, то x2 = -1.
Через точки (0; 2) и (-1; 0)
провести прямую.
Если коэффициент перед х дробный, удобно выбирать х1
и х2 так, чтобы y1 и у2 были целыми.
Пример.
y = —1/3 х + 2
Если х1 = 3, то у1 = 1;
если x2 = - 3, то у2 = 3.
Через точки (3; 1) и (-3; 3)
провести прямую.

29
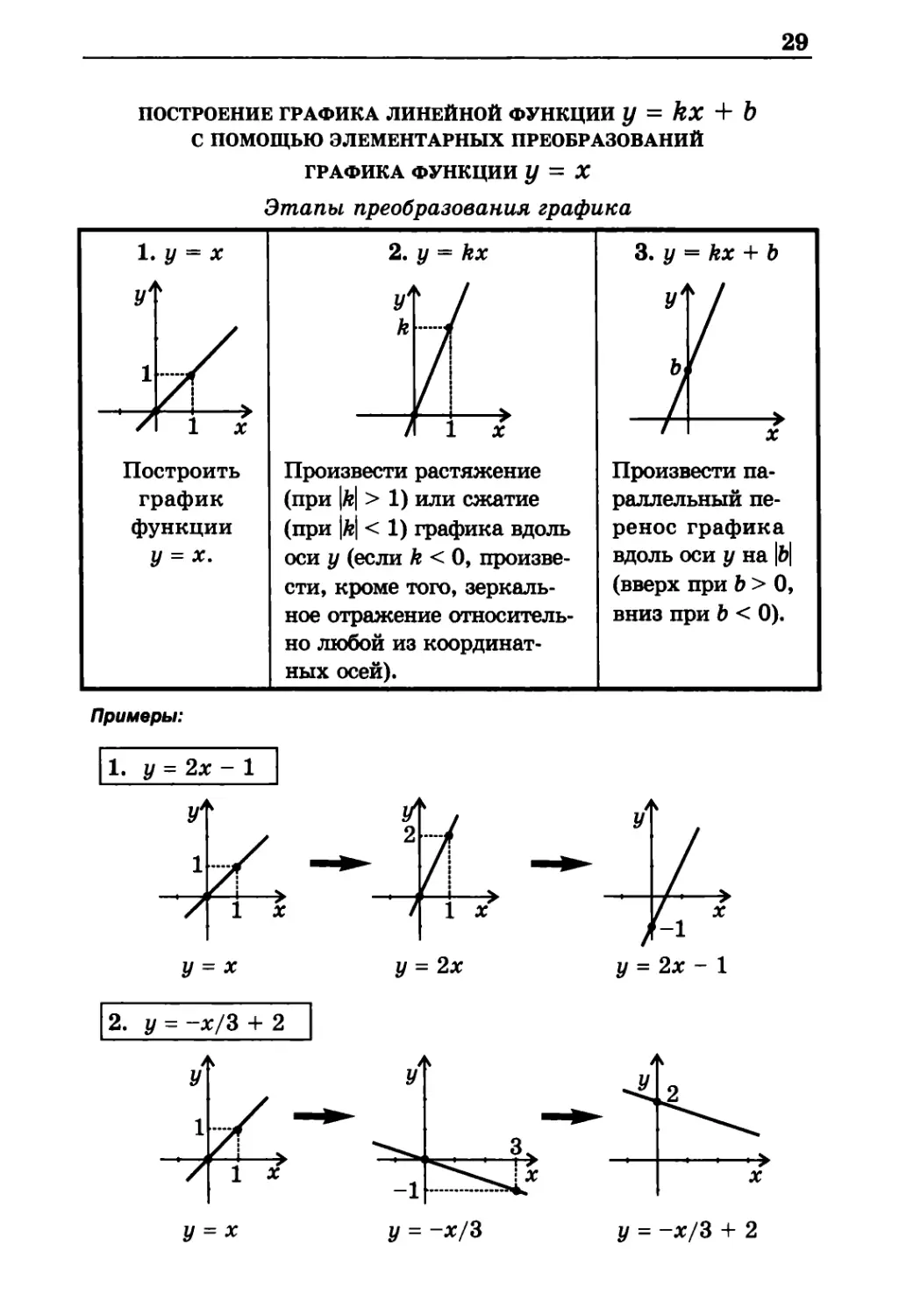
ПОСТРОЕНИЕ ГРАФИКА ЛИНЕЙНОЙ ФУНКЦИИ y = kx + b
С ПОМОЩЬЮ ЭЛЕМЕНТАРНЫХ ПРЕОБРАЗОВАНИЙ
ГРАФИКА ФУНКЦИИ у = X
Этапы преобразования графика
Построить Произвести растяжение Произвести па-
график (при |k| > 1) или сжатие раллельный пе-
функции (при |k| < 1) графика вдоль ренос графика
У = х. оси у (если k < 0, произве- вдоль оси у на |b|
сти, кроме того, зеркаль- (вверх при b > 0,
ное отражение относитель- вниз при b < 0).
но любой из
координатных осей).
Примеры:

30
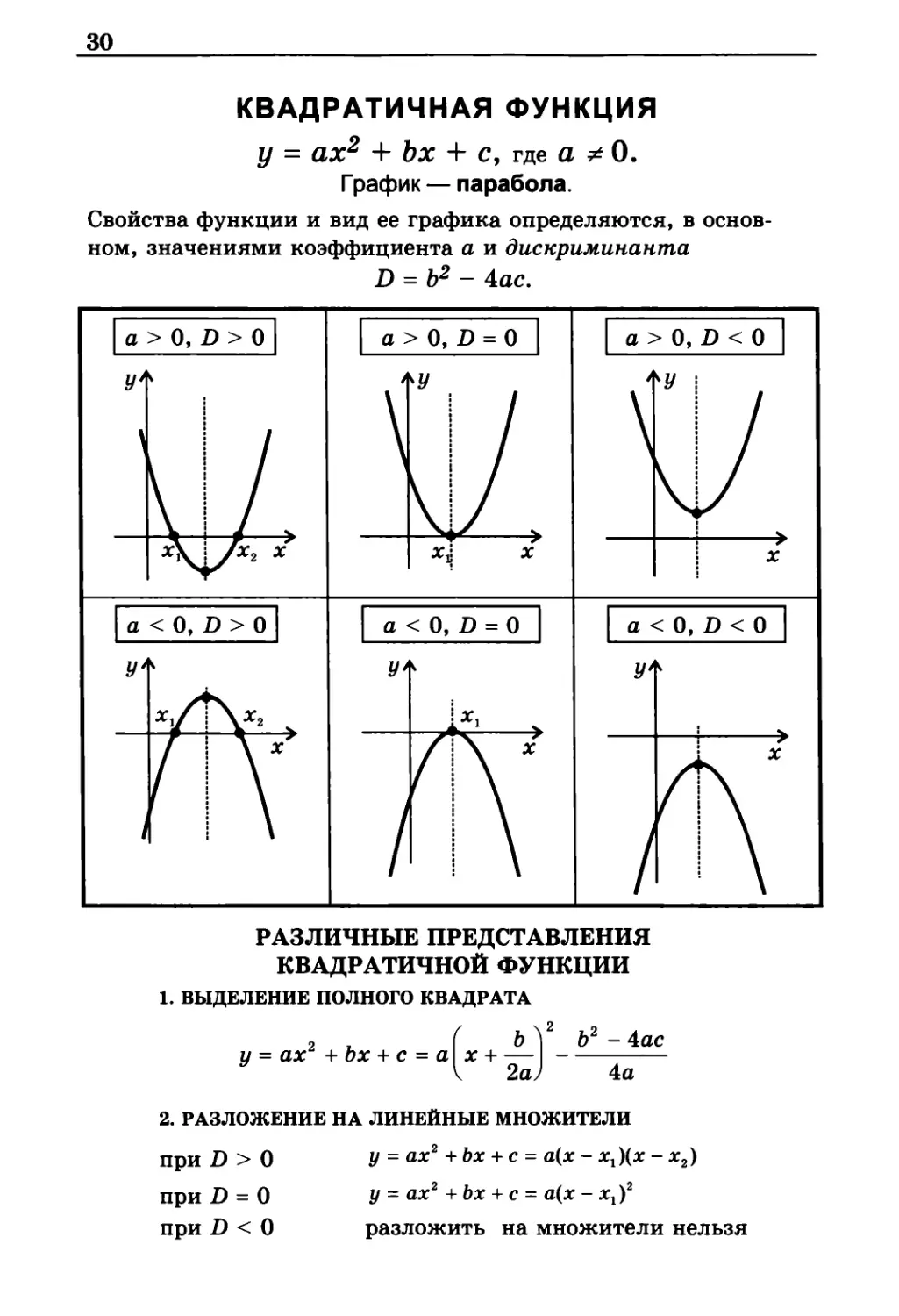
квадратичная функция
у = ах2 + bх + с, где а ≠ 0.
График — парабола.
Свойства функции и вид ее графика определяются, в
основном, значениями коэффициента а и дискриминанта
D = b2 - 4ас.
РАЗЛИЧНЫЕ ПРЕДСТАВЛЕНИЯ
КВАДРАТИЧНОЙ ФУНКЦИИ
1. выделение полного квадрата
2 t f bV Ь2-4ас
и = ал: +м + с = о х + —
I 2а) 4а
2. разложение на линейные множители
при D > 0 1/ = а*2+Ь* + с = а(*-дг1)(дг-*2)
при D = 0 i/ = a*2 + Ь* + с = а(х-х1 f
при D < 0 разложить на множители нельзя

31
свойства квадратичной функции у = ах2 + bх + с
Область определения: R
Область значений:
при а > 0 [-D/(4a); оо)
при a < 0 (-оо; -D/(4a)]
Четность, нечетность:
при b = 0 функция четная
при b ≠ 0 функция не является ни четной, ни нечетной
Нули:
-Ъ-4Ъ -Ъ + 4Ъ
при D > О два нуля: = — , х2 =
2а 2а
при D = О один нуль: Х\ = -Ъ/{2а)
при D < 0 нулей нет
Промежутки знакопостоянства:
\у > 0 при jc е (-оо; x^)\j(x2\ оо)
если a > О, D = 0, то i/ > 0 при jc е (-оо; jci)U(*i; °°)
если a > О, D < 0, то i/ > 0 при х е R
{у > 0 при jc е (-оо; jc
у < 0 при X е (Xl; х2
{у > 0 при х е (хг; х2)
у < 0 при х е (-oo;Xl)[j(x2; оо)
если а < О, D = 0, то i/ < 0 при х е (-оо; jci)U(*i; °°)
если а < О, D < 0, то i/ < 0 при х е R
Промежутки монотонности:
{функция возрастает при х е [-Ь/(2а); оо)
функция убывает при х е (-оо; -Ь/(2а)]
{функция возрастает при х е (-оо; -Ь/(2а)]
функция убывает при х е [-Ь/(2а); оо)
Экстремумы:
при а > 0 xmin = - b/(2а); ymin = - D/(4a)
при а < 0 хтах = - b/(2а); утах = - D/(4a)

32
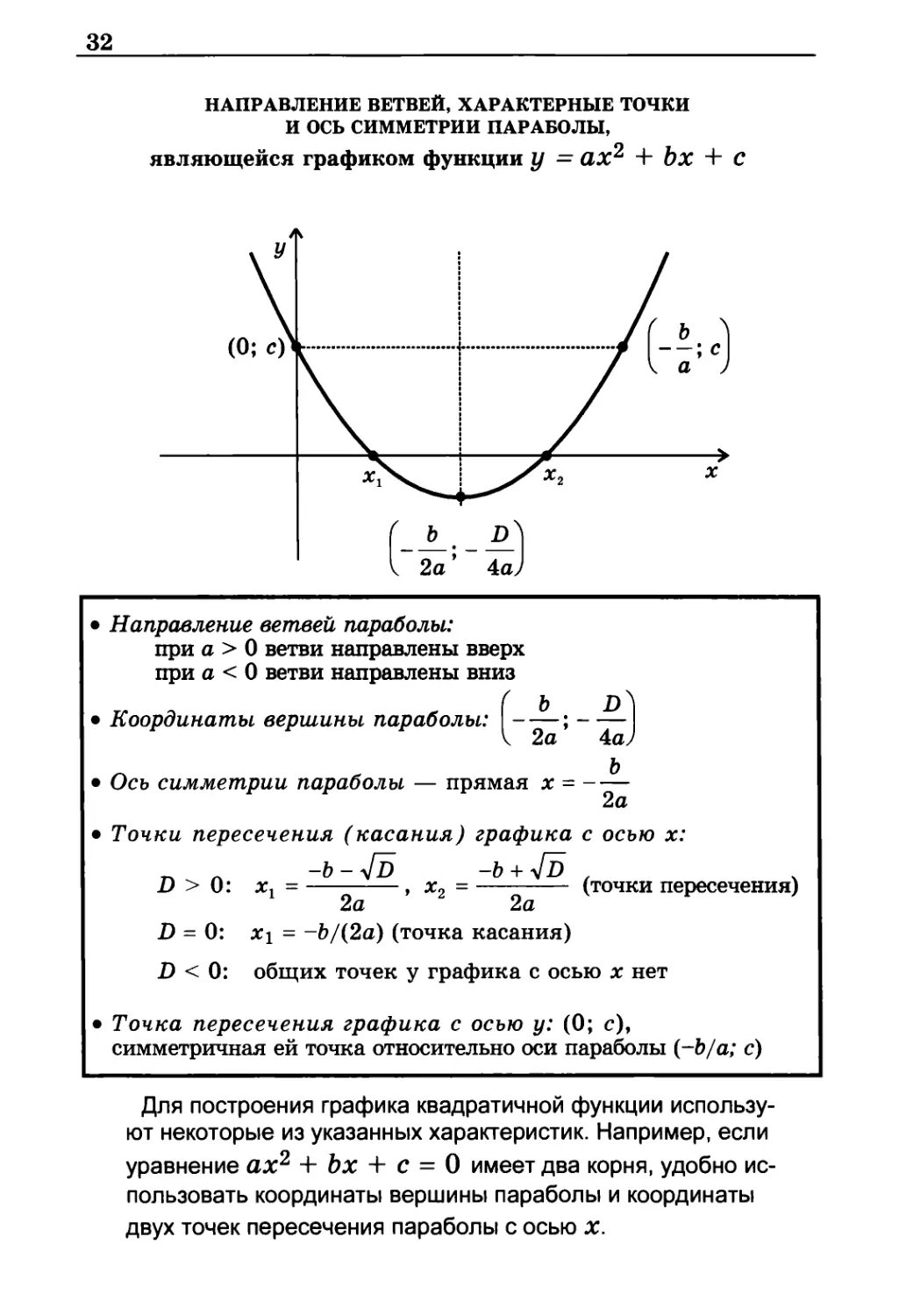
направление ветвей, характерные точки
и ось симметрии параболы,
являющейся графиком функции у = ах2 + bх + С
Направление ветвей параболы:
при а > 0 ветви направлены вверх
при а < 0 ветви направлены вниз
Координаты вершины параболы: (- —; - —
v 2а 4а.
Ось симметрии параболы — прямая х =
2а
Точки пересечения (касания) графика с осью х
л л -ъ-4Ъ -ъ + 4Ъ
D > 0: хх =
2а
, х2 —
2а
(точки пересечения)
D = 0: Х\ — -Ъ/(2а) (точка касания)
D < 0: общих точек у графика с осью х нет
Точка пересечения графика с осью у: (0; с),
симметричная ей точка относительно оси параболы (-b/а; с)
Для построения графика квадратичной функции
используют некоторые из указанных характеристик. Например, если
уравнение ах2 + bх + с = 0 имеет два корня, удобно
использовать координаты вершины параболы и координаты
двух точек пересечения параболы с осью х.

33
построение графика квадратичной функции
по направлению ветвей, характерным точкам
и оси симметрии параболы
Примеры:
у = х2 - 4х + 3
1. Ветви направлены вверх, т.к. а = 1 > 0.
2. Координаты вершины (2; -1), т.к.
2а 2
1/(2) = 22 - 4- 2 + 3 = -1.
3. Ось симметрии параболы
* = -А = 2.
2а
4. Координаты точек пересечения с осью х:
0) = (1; 0) и (х2; 0) = (3; 0).
5. Координаты точки пересечения с осью у:
(0; с) = (0; 3);
симметричная ей точка относительно
оси параболы: | —; с \ = (4; 3).
у = - х2 - 6* - 9
1. Ветви направлены вниз, т.к. а = -1 < 0.
2. Координаты вершины (-3; 0), т.к.
2а -2
!,(3) = -(-3)'-6-(-3)-9 = 0.
3. Ось симметрии параболы х = = -3 .
2а
4. Координаты точки касания с осью х:
(xt; 0) = (-3; 0).
5. Координаты точки пересечения с осью у:
(0; с) = (0; -9);
симметричная ей точка относительно
оси параболы: \ —; с \ = (-6; -9).

34
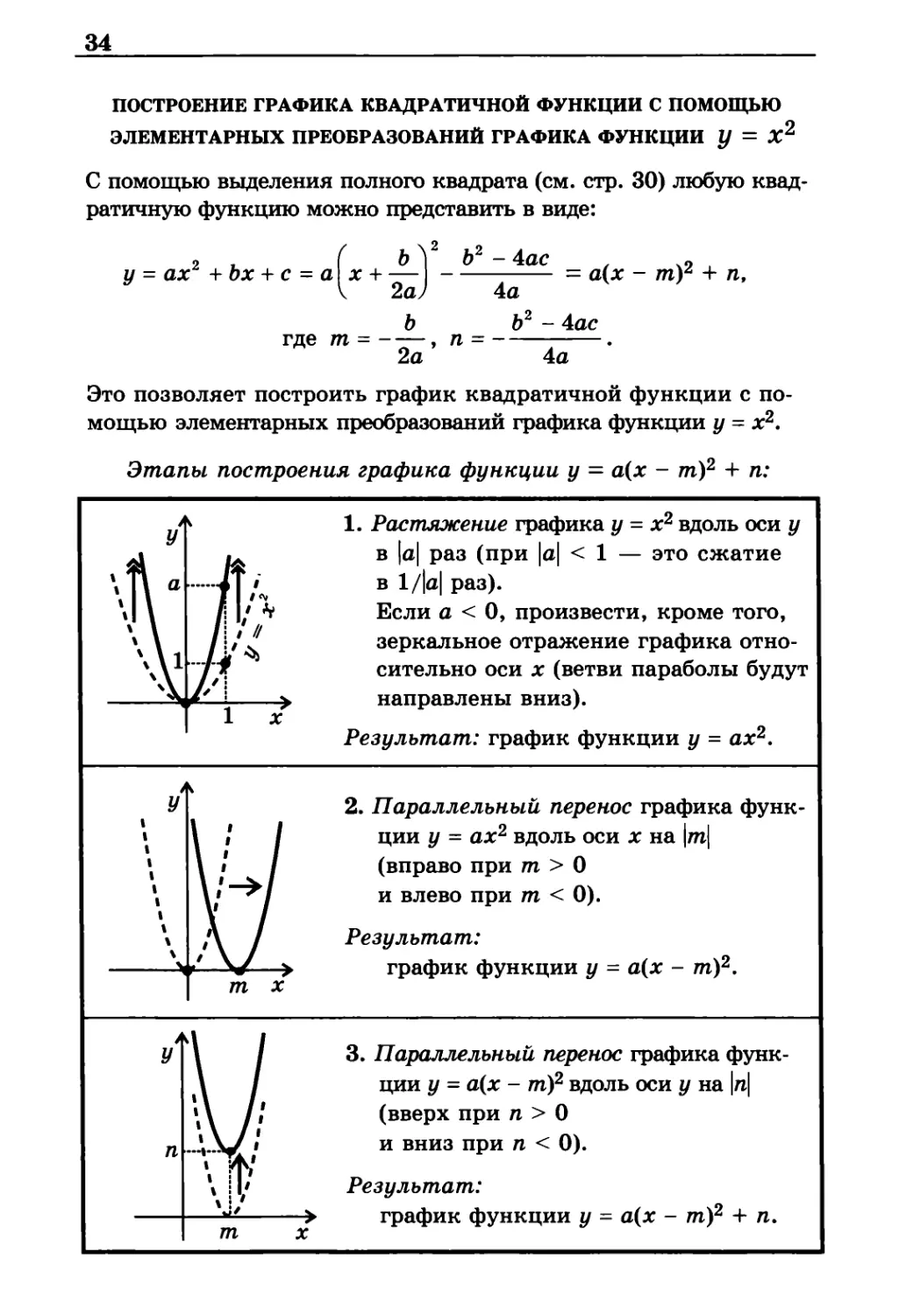
построение графика квадратичной функции с помощью
элементарных преобразований графика функции У = X2
С помощью выделения полного квадрата (см. стр. 30) любую
квадратичную функцию можно представить в виде:
у = ах + Ьх + с = а \ х + — | -
Ь2 - 4ас
4а
Ь2 - 4ас
= а(х - т)2 + п,
где т = , 71 = -
2а
4а
Это позволяет построить график квадратичной функции с
помощью элементарных преобразований графика функции у = х2.
Этапы построения графика функции у = а(х - т)2 + п:
1. Растяжение графика у = х2 вдоль оси у
в |а| раз (при |а| < 1 — это сжатие
в 1/|а| раз).
Если а < 0, произвести, кроме того,
зеркальное отражение графика
относительно оси х (ветви параболы будут
направлены вниз).
Результат: график функции у = ах2.
2. Параллельный перенос графика
функции у = ах2 вдоль оси х на \т\
(вправо при m > 0
и влево при m < 0).
Результат:
график функции у = а(х - т)2.
3. Параллельный перенос графика
функции у - а{х - т)2 вдоль оси у на \п\
(вверх при n > 0
и вниз при n < 0).
Результат:
график функции у = а(х - т)2 + п.

35
Примеры:
у = 2х2 - 12* + 19 = 2(х - З)2 + 1
V
у = 2(х-3)2
3 х
у - 2(*-3)2
■у = 2(x-Sf+l
1. Растяжение
графика
функции
у - х2 вдоль
оси y в 2 раза.
2. Параллельный
перенос графика
функции
у = 2х2 вдоль оси х
на 3 вправо.
3. Параллельный
перенос графика
функции
у = 2(х - З)2 вдоль
оси у на 1 вверх.
х2 1
у = 2*-3 = —(* + 2)2 -1
2 2
7Ж
---у = х2
у = х2/2
у = -х2/2
1. Сжатие графика
функции
у = х2 вдоль оси у
в 2 раза и
преобразование
симметрии относительно
оси х.
---у = -х2/2 —У = ~(х+2)2/2
— у = -(х+2)2/2 у = -(х+2)2/2 - 1
2. Параллельный
перенос графика
функции
у = -х2/2 вдоль
оси х на. 2 влево.
3. Параллельный
перенос графика функции
у = -(х + 2)2/2 вдоль
оси у на 1 вниз.

36
СТЕПЕННЫЕ ФУНКЦИИ
с натуральными показателями степени
у = Хп, где п е N
Примеры графиков
п нечетное
п четное
свойства функций
Область определения: R
Область значений:
при п нечетном R
при п четном [0; оо)
Четность, нечетность:
при п нечетном функция нечетная
при п четном функция четная
Нули: у = 0 при х = 0
Промежутки знакопостоянства:
при х g (0; оо)
при х g (-оо; 0)
если п четное, то у > 0 при х е (-оо; 0) U (0; оо)
Промежутки монотонности:
если п нечетное, то функция возрастает при х е R
(функция возрастает при х е [0; оо)
функция убывает при х е (-оо; 0]
если п нечетное, то
1у>о
\у<о
если п четное, то
Экстремумы:
если п нечетное,
если п четное,
экстремумов нет
Уmin = 0 при xmin = 0
Графики функций проходят через точки:
при п нечетном (-1; -1), (0; 0), (1; 1)
при п четном (-1; 1), (0; 0), (1; 1)
Замечание. При п = 0 функция у = хп определяется так:
х° = 1 при х ≠ 0; при х = 0 функция не определена.

37
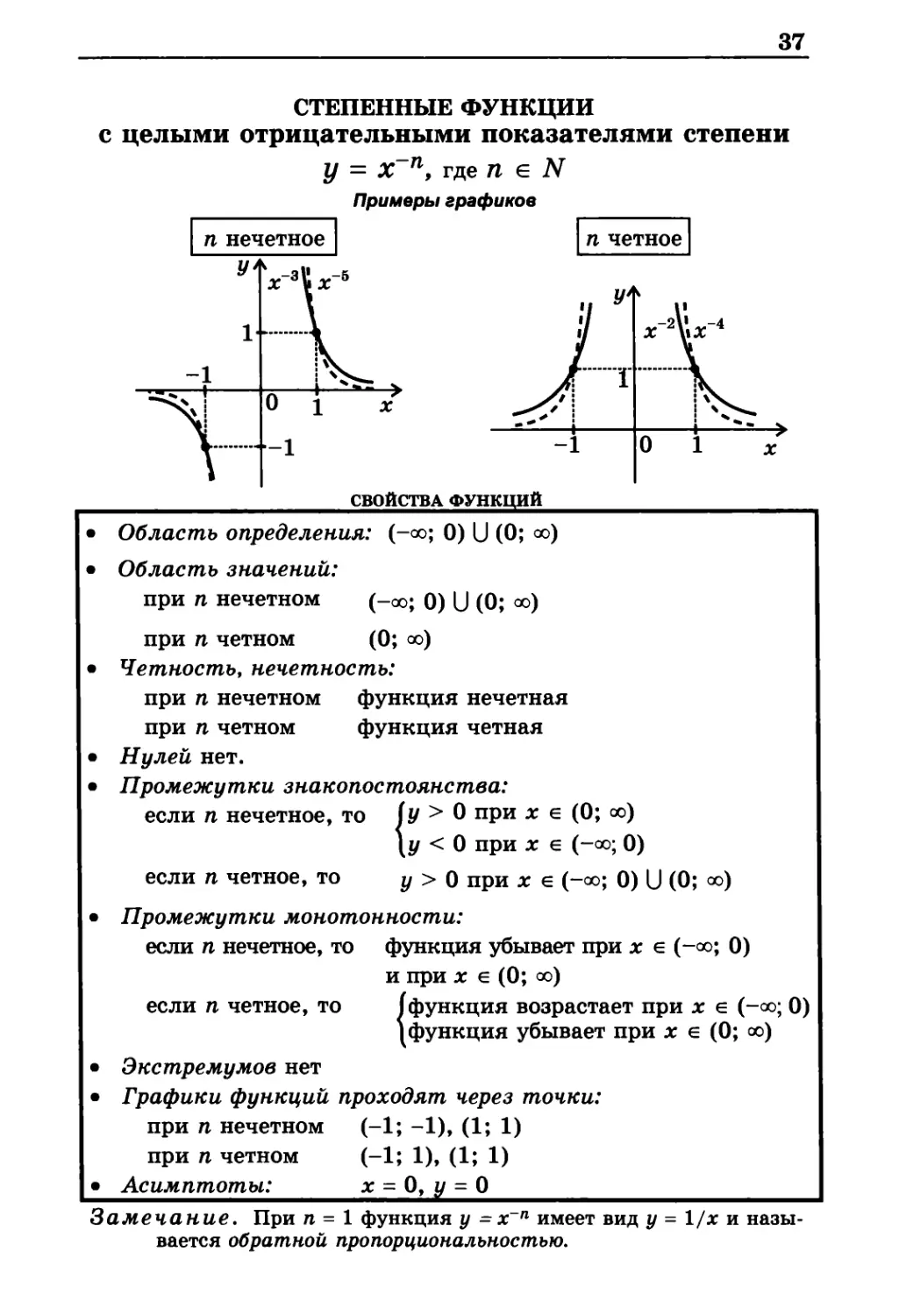
СТЕПЕННЫЕ ФУНКЦИИ
с целыми отрицательными показателями степени
у = Х-п, где п е N
Примеры графиков
п нечетное
п четное
У4
-21' -4
X ZyX 4
Л
-1
о i /
СВОЙСТВА ФУНКЦИЙ
Область определения: (-оо; 0) U (0; оо)
Область значений:
при n нечетном (-оо; 0) U (0; оо)
при n четном (0; оо)
Четность, нечетность:
при тг нечетном функция нечетная
при тг четном функция четная
Нулей нет.
Промежутки знакопостоянства:
если n нечетное, то [у > 0 при х е (0; оо)
\у < 0 при х е (-оо; 0)
если n четное, то у > 0 при х е (-оо; 0) U (0; оо)
Промежутки монотонности:
если n нечетное, то функция убывает при х е (-оо; 0)
и при х е (0; оо)
если n четное, то (функция возрастает при х е (-оо; 0)
^функция убывает при х е (0; оо)
Экстремумов нет
Графики функций проходят через точки:
при n нечетном (-1; -1), (1; 1)
при тг четном (-1; 1), (1; 1)
Асимптоты: х = 0, у = 0
Замечание. При n = 1 функция у = х п имеет вид у - 1/х и
называется обратной пропорциональностью.

38
свойства функций
• Область определения:
при п нечетном R
при п четном [0; оо)
• Область значений:
при п нечетном R
при п четном [0; оо)
• Четность, нечетность:
при п нечетном функция нечетная
при п четном функция не является
ни четной, ни нечетной
• Нули: у = 0 при х = 0
• Промежутки знакопостоянства:
при х е (0; оо)
\у<о
если п нечетное, то , ^ Л / пч
при jc е (-оо; 0)
если п четное, то у > 0 при х е (0; оо)
Промежутки монотонности:
функция возрастает при всех х из области определения
Экстремумов нет
Графики функций проходят через точки:
при п нечетном (-1; -1), (0; 0), (1; 1)
при п четном (0; 0), (1; 1)

39
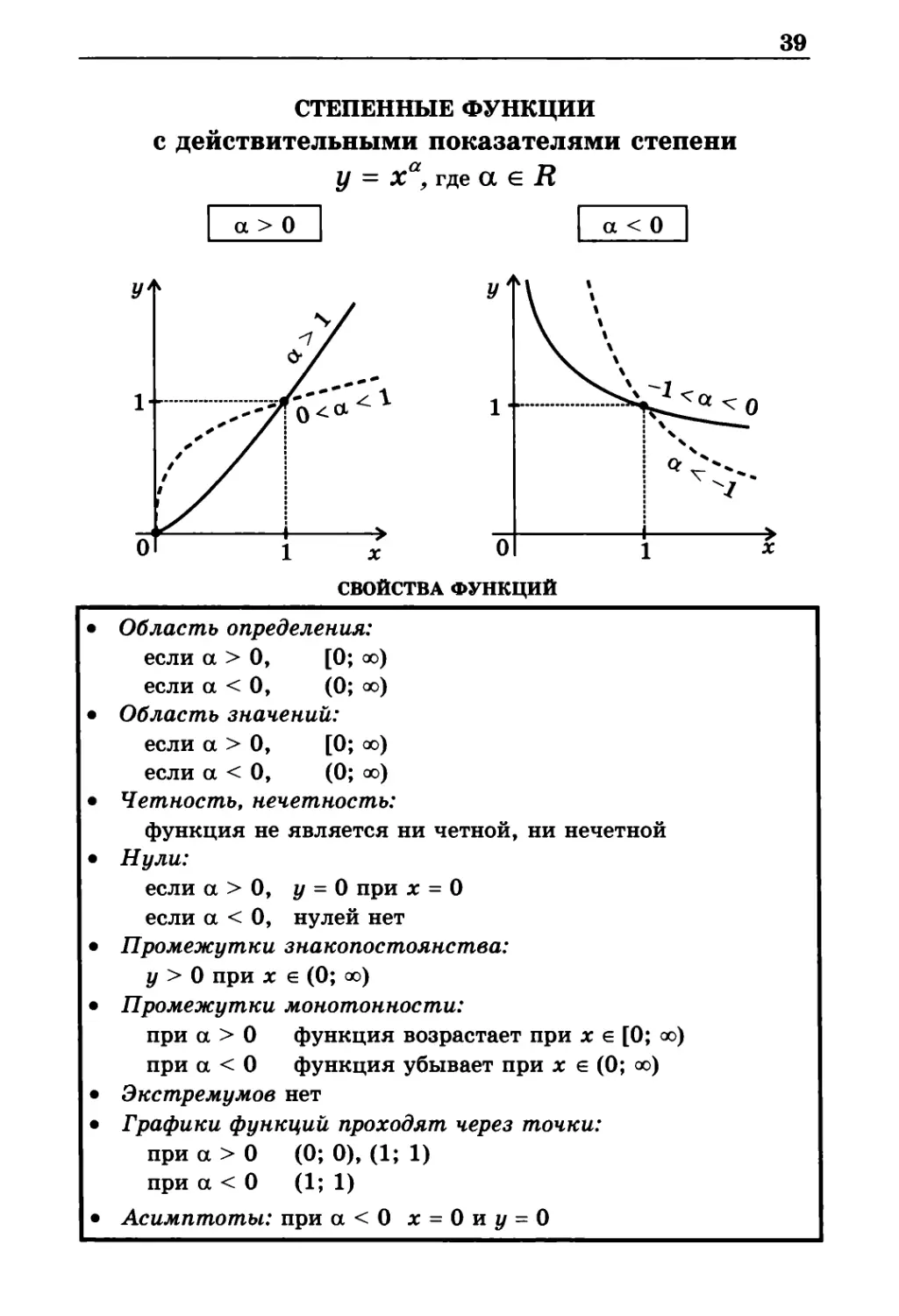
СТЕПЕННЫЕ ФУНКЦИИ
с действительными показателями степени
У = Ха, где a G R
а > О
а < О
свойства функций
Область определения:
если а > 0, [0; оо)
если а < 0, (0; оо)
Область значений:
если а > 0, [0; оо)
если а < 0, (0; оо)
Четность, нечетность:
функция не является ни четной, ни нечетной
Нули:
если а > 0, у = 0 при х = 0
если а < 0, нулей нет
Промежутки знакопостоянства:
у > 0 при х g (0; оо)
Промежутки монотонности:
при а > 0 функция возрастает при х e [0; оо)
при а < 0 функция убывает при х g (0; оо)
Экстремумов нет
Графики функций проходят через точки:
при а > 0 (0; 0), (1; 1)
при а < 0 (1; 1)
Асимптоты: при а<0 х = 0 и у = О

40
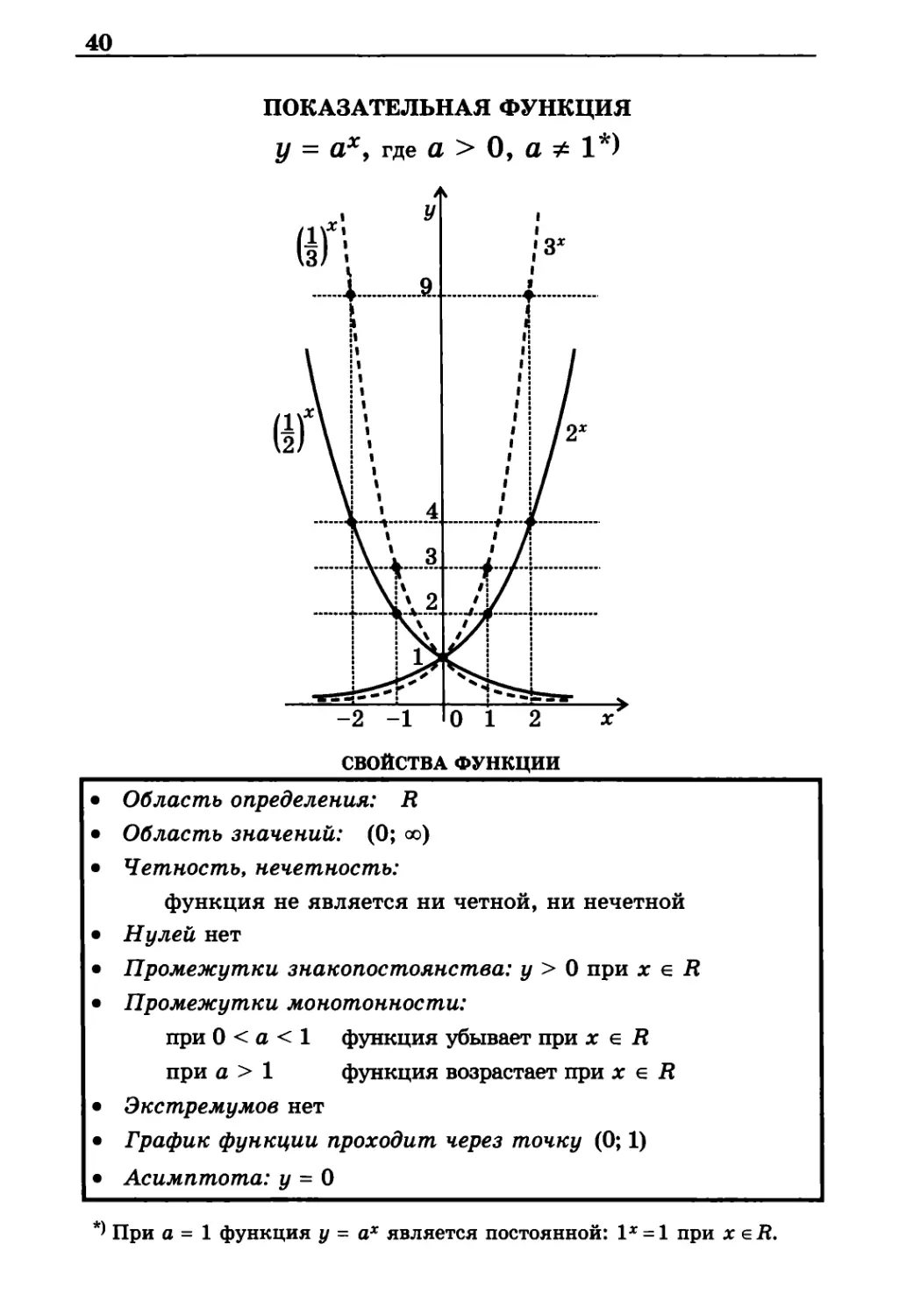
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
у = ах, где а > О, а ≠ 1*)
свойства функции
• Область определения: R
• Область значений: (0; оо)
• Четность, нечетность:
функция не является ни четной, ни нечетной
• Нулей нет
• Промежутки знакопостоянства: у > 0 при х е R
• Промежутки монотонности:
при 0 < а < 1 функция убывает при х е R
при а > 1 функция возрастает при х е R
• Экстремумов нет
• График функции проходит через точку (0; 1)
• Асимптота: у = 0
*) При а = 1 функция у = ах является постоянной: 1x = 1при х eR.

41
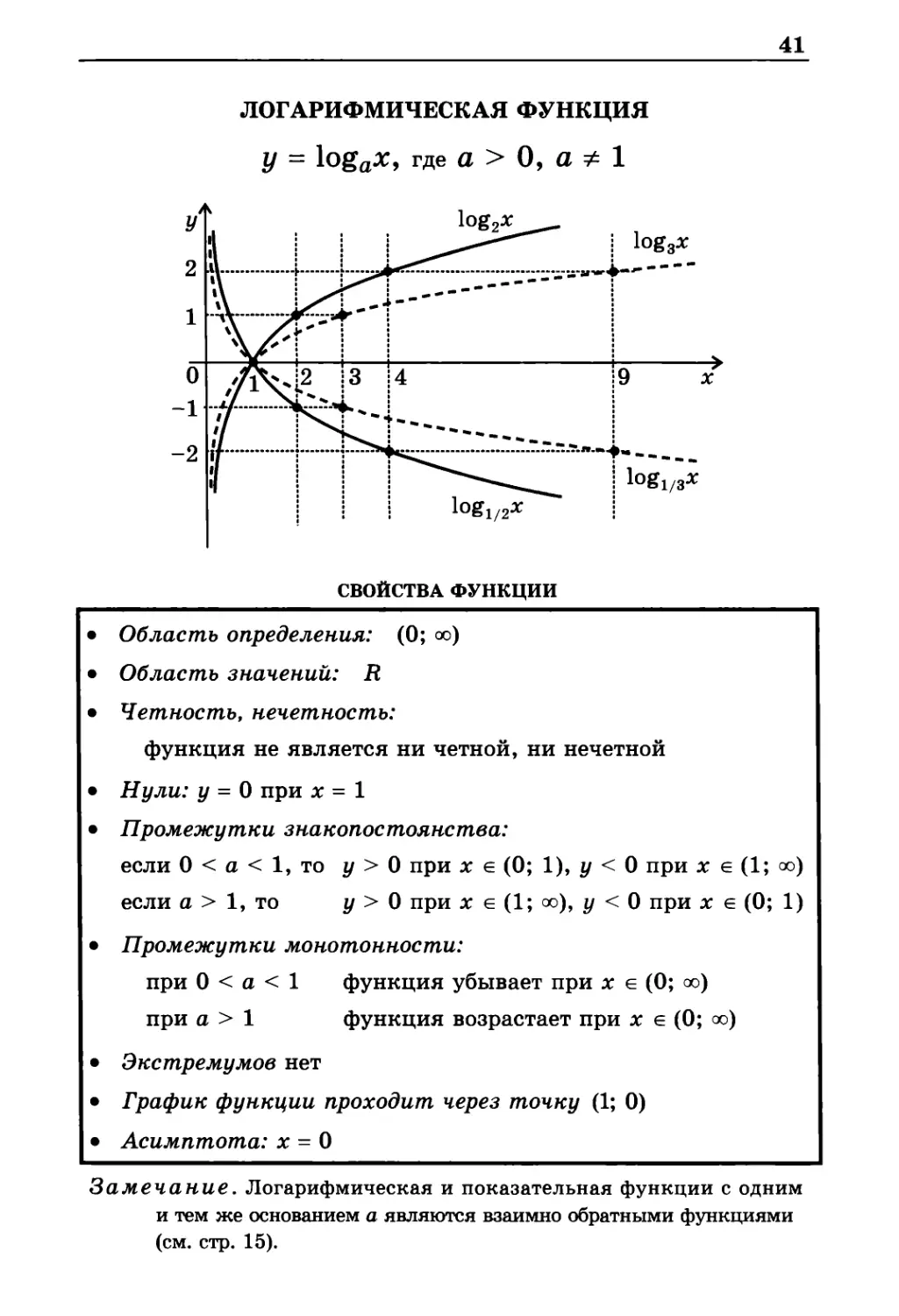
ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
у = logax, где а > 0, а ≠ 1
СВОЙСТВА ФУНКЦИИ
• Область определения: (0; оо)
• Область значений: R
• Четность, нечетность:
функция не является ни четной, ни нечетной
• Нули: у = 0 при х = 1
• Промежутки знакопостоянства:
если 0 < а < 1, то у > 0 при х е (0; 1), у < 0 при л: е (1; оо)
если а > 1, то у > 0 при л: е (1; оо), у < 0 при x; е (0; 1)
• Промежутки монотонности:
при 0 < а < 1 функция убывает при х е (0; оо)
при а > 1 функция возрастает при x: е (0; оо)
• Экстремумов нет
• График функции проходит через точку (1; 0)
• Асимптота: х = 0
Замечание. Логарифмическая и показательная функции с одним
и тем же основанием а являются взаимно обратными функциями
(см. стр. 15).

42
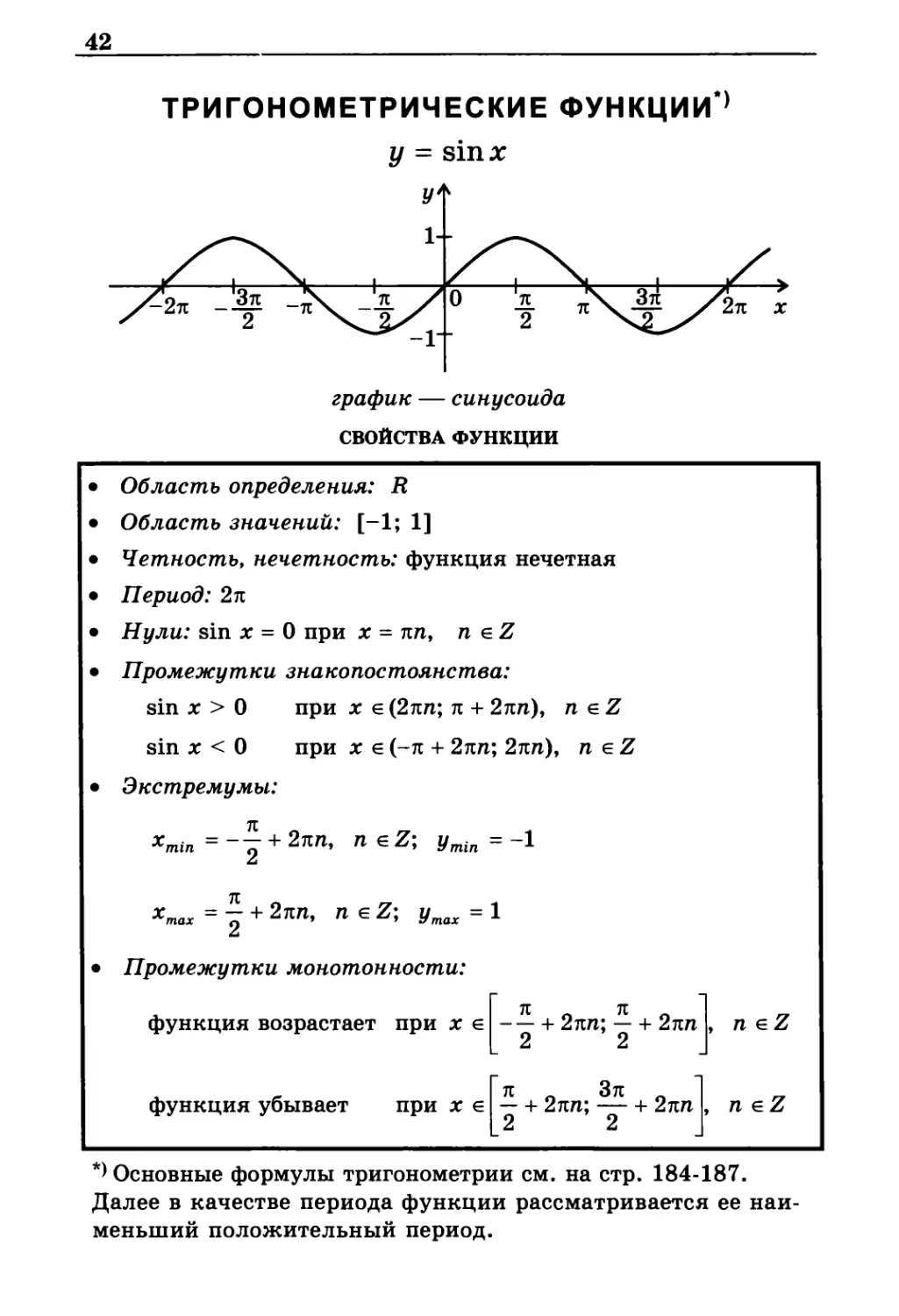
график — синусоида
свойства функции
Область определения: R
Область значений: [-1; 1]
Четность, нечетность: функция нечетная
Период: 2 π
Нули: sin х = 0 при х = πn, n е Z
Промежутки знакопостоянства:
sin х > О при х е (2πn; π + 2πn), п е Z
sin х < 0 при х е (-π + 2πn; 2πn), neZ
Промежутки монотонности:
функция возрастает при х е
функция убывает при х е
я я
— + 2ял; — + 2ял
2 2
я Зя
— + 2ял; — + 2ял
2 2
, л е Z
, л е Z
*) Основные формулы тригонометрии см. на стр. 184-187.
Далее в качестве периода функции рассматривается ее
наименьший положительный период.

43
график — косинусоида
свойства функции
• Область определения: R
• Область значений: [-1; 1]
• Четность, нечетность: функция четная
• Период: 2π
я
• Нули: у = 0 при х = —h ял, п & Z
2
• Промежутки знакопостоянства:
[я я
- — + 2ял; — + 2ял |, л е Z
[я Зя
— + 2ял; — + 2ял|, neZ
• Экстремумы:
xmin = π + 2πn, n eZ; ymin = -1
xmax = 2πn, neZ; ymax =1
• Промежутки монотонности:
функция возрастает при х е [-я + 2ял; 2ял], л е Z
функция убывает при х е [2ял; я + 2ял], л е Z
Замечание. Графики функций у = sin х и у = cos л: получаются
друг из друга с помощью параллельных переносов вдоль оси х
на я/2 : cos л: = sinl х + — I» smx = cos\x - —

44
У = tgx
-2%у
-71 у
У
0
2я/
/ Зя
/ 2
/ 2
я
2
/ Зя
/ 2
/ х
график — тангенсоида
свойства функции
• Область определения: объединение интервалов
я я ^
+ ял; — + ял , nez
2 2 /
Область значений: R
Четность, нечетность: функция нечетная
Период: я
Нули: у = 0 при х = πn, п е Z
Промежутки знакопостоянства:
tg х > О при х е[ ял; — + ял|, л е Z
tg х < 0 при х е + ял; тт|, л е Z
Экстремумов нет
Промежутки монотонности:
функция возрастает на каждом интервале
области определения
Асимптоты: х = — + ял, п eZ
2

45
У = Ctg*
1
1
1
1
\ Зя
я
я
\ Зя
\ 5я
V 2
V 2
Ч, 2
4.2
\|2
V >
-2я \
-я \
0 "\
Я >i
2я "\ х
график — котангенсоида
свойства функции
• Область определения: объединение интервалов
(πn; π + πn), п е Z
• Область значений: R
• Четность, нечетность: функция нечетная
• Период: я
я
• Нули: у = 0 при х = — + я/г, /г е Z
2
• Промежутки знакопостоянства:
ctg x> 0 при х е^я/г; + nnj, п eZ
ctg x < 0 при х е + я/г; я/г|, /г е Z
• Экстремумов нет
• Промежутки монотонности:
функция убывает на каждом интервале
области определения
• Асимптоты: х = πп, п eZ
Замечание. График функции у = ctgx получается из графика функции
у = tgx отражением относительно любой из координатных осей
и последующим параллельным переносом вдоль оси х на я/2.

46
обратные тригонометрические
функции
у = arcsinx
функция, обратная функции
у = sin х, -л/2 < х < л/2
у = arccosx
функция, обратная функции
у = cos x, 0 < х < л
свойства функций*)
arcsin х + arccos х = п/2
См. также стр. 187.

47
у = arctg* у = arcctg*
функция, обратная функции функция, обратная функции
у = tg х, -л/2 < х < л/2 у = ctg jc, 0 < х < л
свойства функций
arctg x + arcctg x = π/2

48
УРАВНЕНИЯ*)
Уравнением называется равенство, содержащее одно
или несколько неизвестных.
Общий вид уравнения
с одним неизвестным:
с п неизвестными:
f1(x1,...,xn) = f2(xlt...,xn).
Часто все функции переносят в одну часть уравнения, и тогда
уравнения принимают вид:
f(x) = 0;
f(x1,...,xn) = 0.
Областью допустимых значений уравнения называется
область определения функций f(x) или f(x1,...,xn).
Пример. Областью допустимых значений уравнения
yJx-2 = >/3 - х является х е [2; 3].
Решением уравнения с одним неизвестным (корнем
уравнения) называется такое значение неизвестного, при подстановке
которого уравнение обращается в верное числовое равенство.
Решить уравнение — значит найти все его корни или
доказать, что корней нет.
Примеры. Решить уравнение х2 - 4 = 0 — значит найти его
корни Х\ — —2; х2 — 2; решить уравнение х2 + 4 = 0 —
значит доказать, что корней нет.
Равносильными называются уравнения, множества
корней которых совпадают.
В частности, равносильны все уравнения, не имеющие корней.
Примеры равносильных уравнений:
1. х - 2 = 0 и 2х = 4,
2. sin л: = 2 и у[х = -1.
*) Решения всех уравнений, неравенств и систем рассматриваются только
на множестве действительных чисел.

49
ЛИНЕЙНЫЕ УРАВНЕНИЯ
ах + b = О,
где О, и b —действительные числа
Наличие корней и их число зависит от значений а и Ь.
а ≠ О, b — любое число
Уравнение ах + b = О
имеет один корень:
Ъ
х = .
а
Прямая у = ах + b пересекает
ось х в одной точке.
Пример: 2х + 3 = 0 х = -1,5
а = О, b ≠ О
Уравнение 0 х + b = 0 не
имеет корней.
Прямая y = 0 х + b не пересекает
ось х.
У*
у = Ъ
X
Пример: 0-х + 2 = 0 — уравнение не имеет корней.
а = 0, Ь = 0
Уравнение Ox + 0 = 0
имеет бесконечно много
корней: корнем является любое
число.
У*
у = о
Прямая у = 0х + 0 совпадает
с осью X.
X
Пример: 0-x-l-2 = 2<=>0-x = 0 — корнем является любое
число.

50
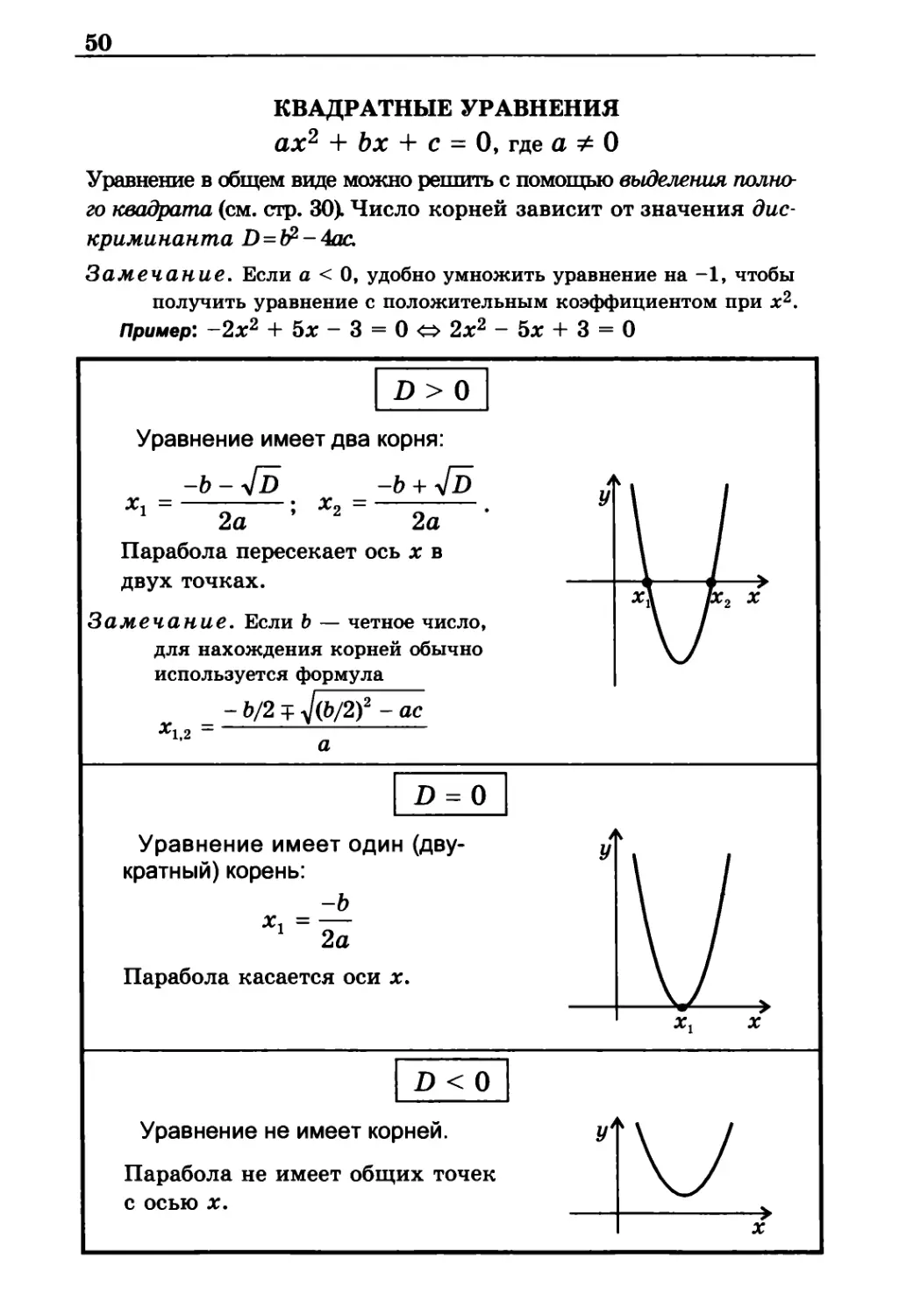
КВАДРАТНЫЕ УРАВНЕНИЯ
ах2 + bх + с = О, где а Ф О
Уравнение в общем виде можно решить с помощью выделения
полного квадрата (см. стр. 30). Число корней зависит от значения
дискриминанта D = b2- 4ас
Замечание. Если а < О, удобно умножить уравнение на -1, чтобы
получить уравнение с положительным коэффициентом при х2.
Пример: -2х2 + 5х - 3 = 0 о 2х2 - 5х + 3 = О
D > О
Уравнение имеет два корня:
хЛ =
-ь-лГБ
Хо =
-ь + 4Ъ
2а * 2а
Парабола пересекает ось х в
двух точках.
Замечание. Если b — четное число,
для нахождения корней обычно
используется формула
_ - Ь/2 + У(Ь/2)2 - ас
Х1,2 *
D = О
Уравнение имеет один
(двукратный) корень:
-Ь
1 2а
Парабола касается оси х.
ХЛ X
D<0
Уравнение не имеет корней.
Парабола не имеет общих точек
с осью х.

51
неполные квадратные уравнения
ах2 + bх = О, ах2 + с = О, ах2 = О
Такие уравнения решают обычно без применения общей
формулы для корней квадратного уравнения.
ах2 + bх = О, b ≠ О
Уравнение всегда имеет два корня.
Решается с помощью разложения
левой части уравнения на множители:
х (ах + b) = О
Ь
Х\ — Oj *2 —
а
Парабола пересекает ось х в двух точках, одна из
которых является началом координат.
h \УХ2 X
Пример: х2 - 2х = О <=> х (х - 2) = 0 <=> = 0; х2 = 2
ах2 + с = О, с ≠ О
Уравнение не имеет корней, если
знаки а и с совпадают; уравнение имеет
два корня, если знаки а и с различны:
X
X
Парабола или не пересекает ось х, или пересекает ее в двух
точках, симметричных относительно начала координат.
Примеры: х2 + 1 = 0 — нет решений
х2 - 1 = 0 <=> xi = -1; х2 = 1
ах2 = О
Уравнение имеет один (двукратный)
корень: X1 = 0.
Парабола касается оси х в начале
координат.

52
теоремы виета
1. Если Х\ и JC2 — корни квадратного уравнения
ах2 + bх + с = 0, то Xi + лг2 = _Ь/а; • лг2 = с/а.
2. Если и таковы, что Х\ + = -b/a, #i • #2 = с/а,
то Х\ и являются корнями квадратного уравнения
ах2 + Ьдс + с = 0.
приведенные квадратные уравнения
Приведенным квадратным уравнением называется
уравнение вида х2 + рх + g = 0
Замечание. Любое квадратное уравнение ах2 + Ьх + с - 0 можно
привести к такому виду с помощью деления уравнения на а.
формулы виета для корней
приведенного квадратного уравнения
*1 + х2 = -р; Xi • х2 = q
Теоремы Виета часто используются для:
• Подбора корней без решения уравнения
• Определения знаков корней без решения уравнения (при
условии D > 0) по следующим правилам:
р > 0
р < 0
q > 0
Оба корня
отрицательны
Оба корня
положительны
q < 0
Корни имеют противоположные знаки
Примеры подбора корней с использованием теорем Виета:
1. х2 - 7х + 6 = 0. Нетрудно подобрать пару чисел, сумма
которых равна 7, а произведение равно 6 — это 1 и 6.
Согласно теоремам Виета корнями квадратного
уравнения х2 - 7х + 6 = 0 являются 1 и 6.
2. х2 - 4х - 5 = 0. Нетрудно подобрать пару чисел, сумма
которых равна 4, а произведение равно -5 — это -1 и 5
Согласно теоремам Виета корнями квадратного
уравнения х2 - 4х - 5 = 0 являются -1 и 5.

53
уравнения, сводящиеся к квадратным
af2(x) + bf(x) + с = О
СХЕМА РЕШЕНИЯ
1. С помощью введения новой переменной t = f(x) уравнение
приводят к виду
at2 + Ы + с = О
2. Если это уравнение имеет корни t\ и t2 (или один корень ti),
решения исходного уравнения ищут как решения совокупности
f(x) = t1
уравнений \ _ + (или одного уравнения f(x)=ti).
Частный случай уравнений, сводящихся к квадратным —
биквадратные уравнения (уравнения вида ах4 + Ьх2 + с = 0). В этом
случае вводят переменную t = х2.
Примеры:
Биквадратное уравнение
х4 - х2 - 2 = 0; замена t - х2
х2 = -1 корней нет
t2 - t - 2 = 0 о
t = -1
t = 2
х2 = 2 хх= ±^2
Иррациональное уравнение
х2 + V*2 -2 = 4 <=> (*2 — 2) + V*2 -2 -2 = 0;
замена £ = -Jx*--^
t2 + t- 2 = 0<^
t = -2
t = l
V*2 - 2 = -2 корней нет
V*2 - 2 = 1 *12= ±V3~
Тригонометрическое уравнение
sin2* - cosx + 1 = 0 <=> cos2* -I- cos* -2 = 0; замена t = cos*
"* = -2
(2 + (- 2 = 0o
* = 1
cos* = -2 корней нет
cos* = 1 * = 27m, n e Z
Показательное уравнение
32x - 12 • 3*-1 + 3 = 0 о З2* - 4 • 3* + 3 = 0;
замена £ = 3*
*2 - 4t + 3 = 0 о
= 1
3х
= 1
* = 0
= 3
_3*
= 3
* = 1

54
ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Как правило, иррациональное уравнение сводится к
равносильной системе, содержащей уравнения и неравенства.
Г7Т ]«*) = *<*) //<*) = *(*)
1. vft*) = v£(*) <=> l - * - - или
т > о
*(*) > О
Замечание. Из двух систем выбирают ту, которая решается
проще.
[z П—" Г 3 - jc = х2 -Ъх-2
Пример: V3 - jc = V* - Ъх - 2 о <^
3-х >0
\х - 4х - 5 = О
U <з
jc = 5
X — —1 <=> jc = -1
jc <3
2. -y/rt^) = а
Если а < 0, уравнение не имеет корней.
Если а > 0, уравнение равносильно уравнению /(jc) = а2.
Замечание. Иногда иррациональное уравнение можно свести к
приведенному виду с помощью введения новой переменной.
Пример: х - yjx + 1 = 5 <=> (jc + 1) - yjx + 1 -6 = 0
VjcTT = -2
= Vjc + 1 , z2-z-6 = 0<=>
z = -2
z = 3
V* + i = з
Первое уравнение совокупности не имеет корней, корень
второго уравнения х = 8.
3. y[f{x~) = g(x)
*(*) > о
Д*) = £2(*)
/ х - 1 >0
Пример: ы7-х=х-1<5>< „ <=>
[7-х = (х-1)2
х>1
х2 - х - 6 = 0
х>1
х — —2 о х = 3
jc =3

55
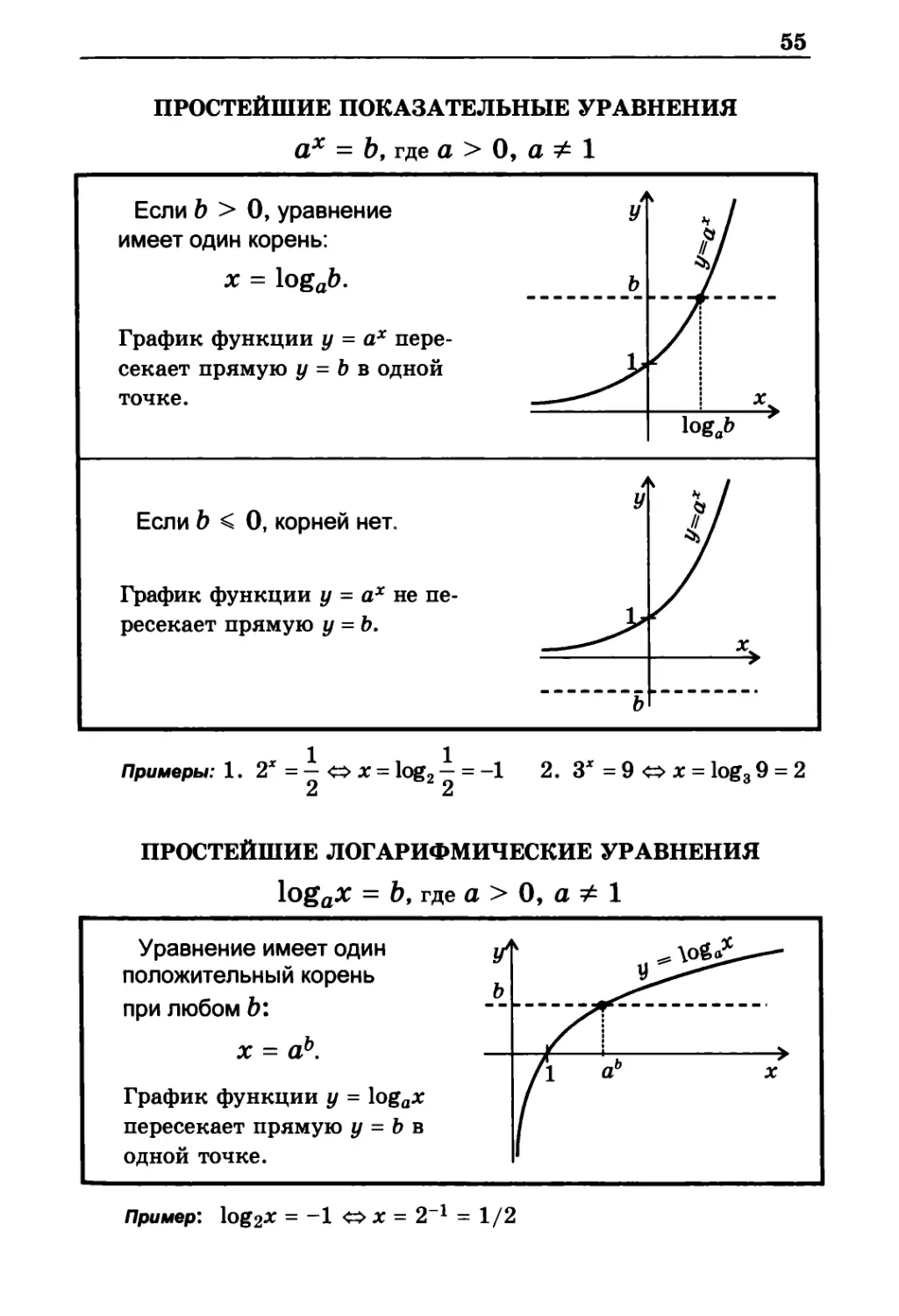
ПРОСТЕЙШИЕ ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
ах = b, где а > 0, а ≠ 1
Если b > 0, уравнение у
имеет один корень:
х = logab. ь
** /
7
График функции у = ах
пересекает прямую у = b в ОДНОЙ
точке. —
logeb
Если b < 0, корней нет.
График функции y = ах не
пересекает прямую у = b.
** /
7
л
Ь
Примеры: 1. 2* = - <^ л: = log2 - = -1 2. 3* = 9 «• jc = log3 9 = 2
2 2
ПРОСТЕЙШИЕ ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
logax = b, где a > 0, а ≠ 1
Уравнение имеет один
положительный корень
при любом b:
х = аb.
График функции у = logax
пересекает прямую у = b в
одной точке.
Пример: log2x = —1 <=> x = 2 -1 = 1/2

56
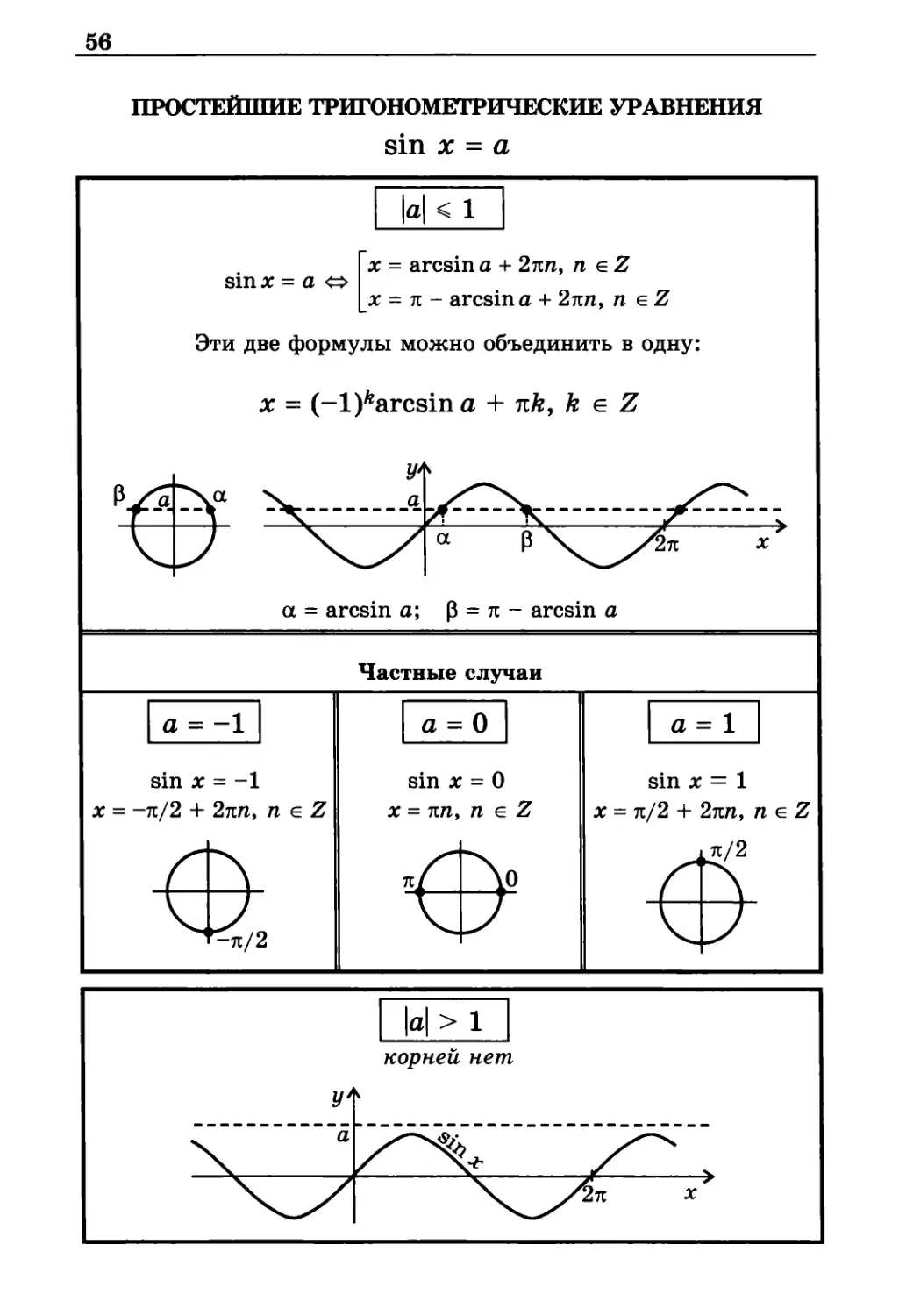
ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
sin х = а
а
< 1
sin х = а <=>
х = arcsin а + 2πп, п e Z
х = тс - arcsin а + 2πn, п e Z
Эти две формулы можно объединить в одну:
х = (-1)^arcsina + πk, k е Z
a = arcsin a; b = πn - arcsin a

57
cos x = a
a < 1
cos x = a <=>
x = arccosa + 2πn, n eZ
x = - arccos a + 2πn, n eZ
Эти две формулы можно объединить в одну:
х = ±arccos а + 2πп, п е Z
N. Уа
"Чу
TNv У 1 n.
N. у' а
у/ in х'
а = -arccos а; р = arccos а
Частные случаи
а = -1
cos х = -1
х - п + 2пп, п & Z
а = О
cos л: = О
л: = я/2 + я я, п & Z
а = 1
cos # = 1
л: = 2кп, п е Z
а > 1
корней нет
У*
а
У2я
У
л:

58
tg x = a
ctg x = a
x = arctg a + πn, n e Z
1! V
Oaj /
a = arctg a
x = arcctg a + πn, n e Z
a-7i\0
a = arcctg a
a sin x + b cos x = с (a, b ≠ 0)

59
уравнение с двумя переменными
и его график
Общий вид:
Решением уравнения с двумя переменными называется
пара чисел (x0, y0), при подстановке которых вместо
соответствующих переменных х, у уравнение обращается в
верное числовое равенство.
Решить уравнение с двумя неизвестными — значит найти
все его решения или доказать, что решений нет.
Примеры:
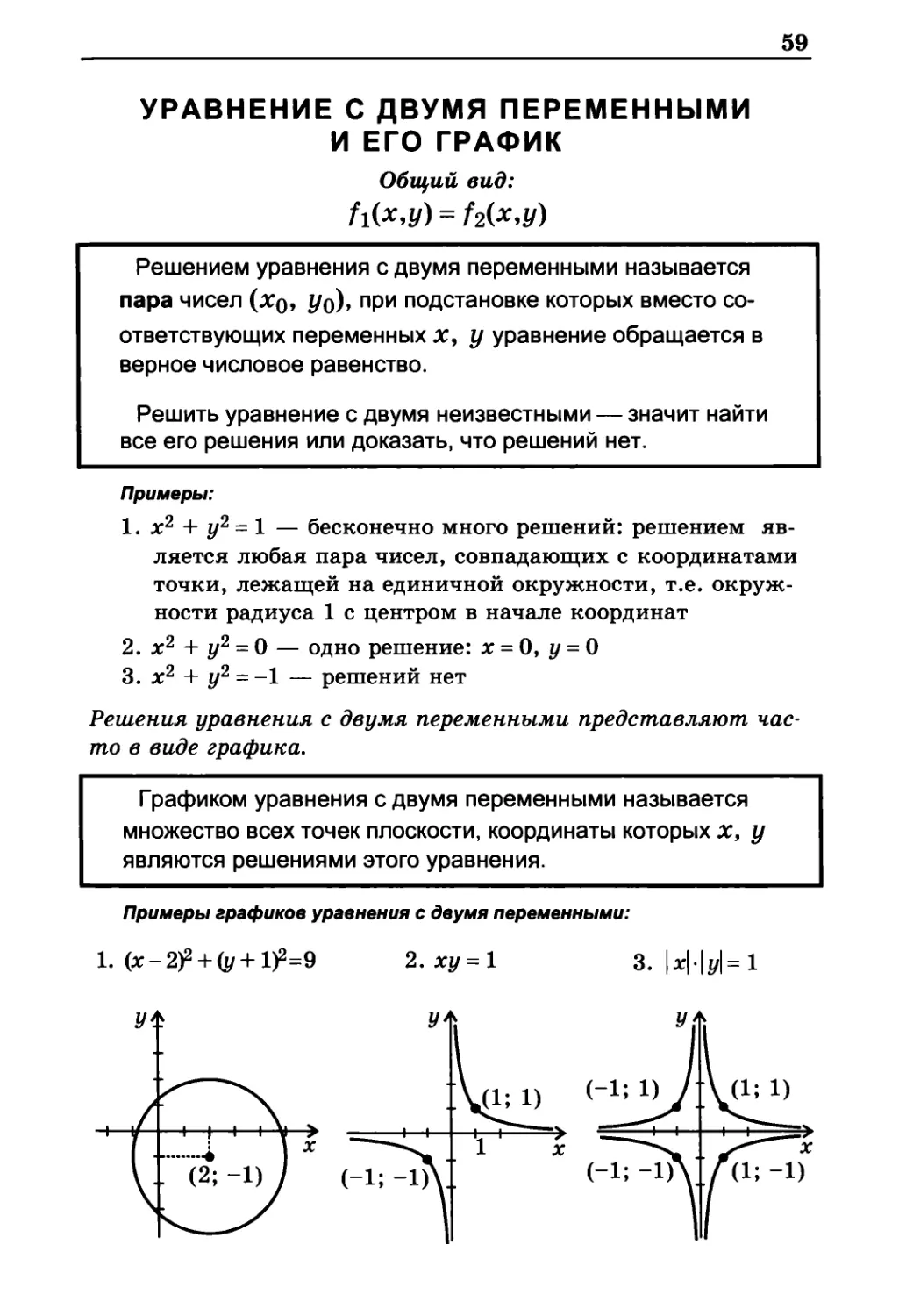
1. х2 + у2 = 1 — бесконечно много решений: решением
является любая пара чисел, совпадающих с координатами
точки, лежащей на единичной окружности, т.е.
окружности радиуса 1 с центром в начале координат
2. х2 + у2 = 0 — одно решение: х = 0, у = О
3. х2 + у2 = -1 — решений нет
Решения уравнения с двумя переменными представляют
часто в виде графика.
Графиком уравнения с двумя переменными называется
множество всех точек плоскости, координаты которых х, у
являются решениями этого уравнения.
Примеры графиков уравнения с двумя переменными:
1. (х-2)2 + (y + 1)2=9 2.ху = 1 3. |х|*|y|=1

61
НЕРАВЕНСТВА
Неравенствами называются выражения вида а <b,
а <b, а > b, а > b, где а и b могут быть числами
(числовыми выражениями) или функциями. Неравенства,
содержащие знаки < или >, называются строгими, а содержащие
знаки < или > — нестрогими.
Различают два вида неравенств: числовые и неравенства с
переменными.
Примеры:
1. 5 < 10 — числовое неравенство
2. 2х > 3 — неравенство с одной переменной
3. 2х < 5у — неравенство с двумя переменными
Решением неравенства с одной переменной называется
такое значение переменной, при подстановке которого
неравенство обращается в верное числовое неравенство.
Решить неравенство — значит найти все его решения
или доказать, что решений нет.
Примеры:
1 x2 + 5>0оx e R
2x-4<0охе (-оо; 4]
3. х2 < 0 — решений нет
Равносильными называются неравенства, множества
решений которых совпадают.
В частности, равносильны все неравенства, не имеющие решений.
Примеры равносильных неравенств:
1. х > 2 к х3 > &
2. sinx > 2 и
Из неравенств так же, как из уравнений, составляют системы
и совокупности (примеры см. на стр. 66). Кроме того, часто
рассматриваются системы и совокупности, содержащие
одновременно уравнения и неравенства (примеры см. на стр. 54).

62
линейные неравенства
ах + Ъ > О, ах + Ъ > О, ах + Ъ < О, ах + Ъ < О
Замечание. Если неравенство нестрогое (ах + b > О, ах + b < 0),
его решением является объединение решений
соответствующего строгого неравенства и уравнения ах + b - 0. Например,
x + 2 > 0 о х е [-2; оо); 0x;<0оxеR.

63
квадратные неравенства
ах2 + bх + с > О ах2 + bх + с < О
ах2 + bх + с > О ах2 + + с < О
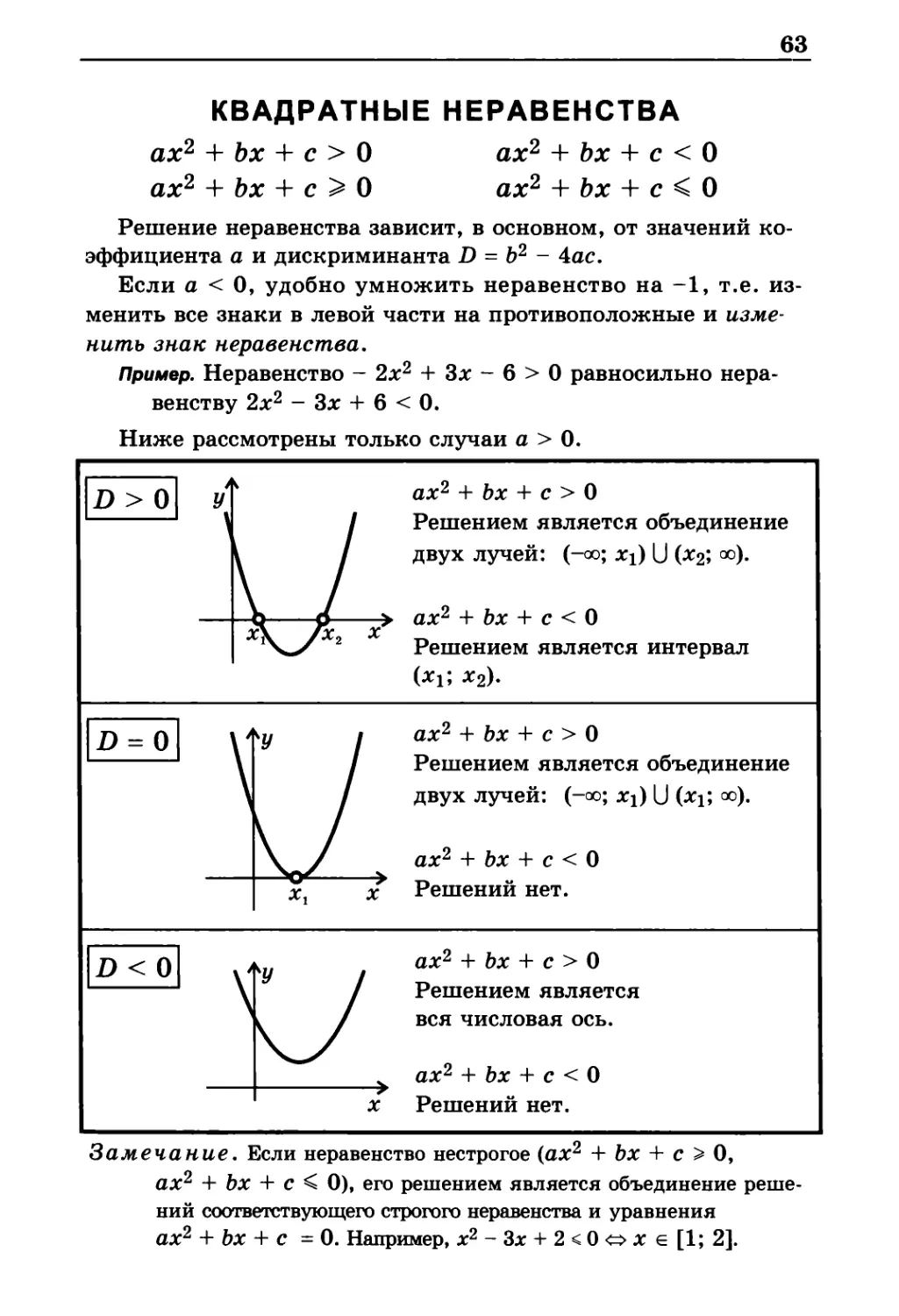
Решение неравенства зависит, в основном, от значений
коэффициента а и дискриминанта D = b2 - 4ас.
Если а < О, удобно умножить неравенство на -1, т.е.
изменить все знаки в левой части на противоположные и
изменить знак неравенства.
Пример. Неравенство - 2х2 + Зх - 6 > 0 равносильно
неравенству 2х2 - Зх + 6 < 0.
Ниже рассмотрены только случаи а > 0.
Замечание. Если неравенство нестрогое (ах2 + bх + с > 0,
ах2 + bх + с < 0), его решением является объединение
решений соответствующего строгого неравенства и уравнения
ах2 + bх + с = 0. Например, х2 - Зх + 2 < 0 о х е [1; 2].

64
метод интервалов
для неравенств вида
(х - ax)kx(x - a2)h2...(x - ап)К > О (> 0; < 0; < 0), где kt е N
схема решения
1. Найти нули функции, стоящей в левой части неравенства.
2. Отметить положение нулей на числовой оси и определить
их кратность (если kt четное, то нуль четной кратности,
если kt нечетное — то нечетной).
3. Найти знаки функции в промежутках между ее нулями,
начиная с крайнего правого промежутка: в этом промежутке
функция в левой части неравенства всегда положительна
для приведенного вида неравенств. При переходе справа
налево через нуль функции от одного промежутка к
соседнему следует учитывать:
• если нуль нечетной кратности, знак функции изменяется;
• если нуль четной кратности, знак функции сохраняется.
4. Записать ответ.
Пример: (х - 2)(х - 3)2(х - 4)3 > 0
1. нули: х = 2, х = 3, х = А
4. х е ( -оо; 2] U {3} U [4; оо)
Замечание. Если функция, стоящая в левой части неравенства,
содержит множители вида (at — x)ki , следует заменить их
соответствующими множителями (х — at)kl с учетом четности kt.
Примеры:
1. (2 - х)2 = (х- 2)2; 2. (2 - х)3 = -(х - 2)3

65
применение метода интервалов
для решения дробно-рациональных неравенств
СТРОГИЕ НЕРАВЕНСТВА
(х-а^ ■ ... (x-an)k»
< О (или > 0), где ki, Pj е N
(х-Ь)" ■ ... {х-Ът)р™
равносильно неравенству
(x-axt ■ ...(x-a^ix-bX ■ ... ■ (х - Ът)р" <0 (или > 0)
Схему решения таких неравенств см. на стр. 64.
Пример:(* ~ 2){<Х~ 3) < 0 о (х - 2)(х - 3)2(* - 1) < 0
х-1
1^^^2 3
НЕСТРОГИЕ НЕРАВЕНСТВА
U;2)
(х ax)h...(x an)kn < 0 (или > 0) k е N
равносильно системе
\(х -a,t- ...-(х- an)k" {x-bX—ix- Ът)р™ < 0 (или > 0)
{х*Ьх,Ь2,...,Ьт
Схему решения первого неравенства системы см. на стр. 64.
(х - 2)(х - З)2 ^ ft _ \(х - IX* - 2)(* - З)2 < 0
Примеры: 1. О
х-1 |х*1
±» x€(l;2]U{3}
2. (jC-3^-2)>0^
х-З
3
(х-3)2(х-2)> 0
л: * 3
xe[2;3)U(3;oo)
Замечание. Сокращение числителя и знаменателя на (х - 3) во
втором примере привело бы к неравенству х - 2 > 0, решение
которого [2;оо) содержит значение х = 3, которое не является
решением исходного неравенства.

66
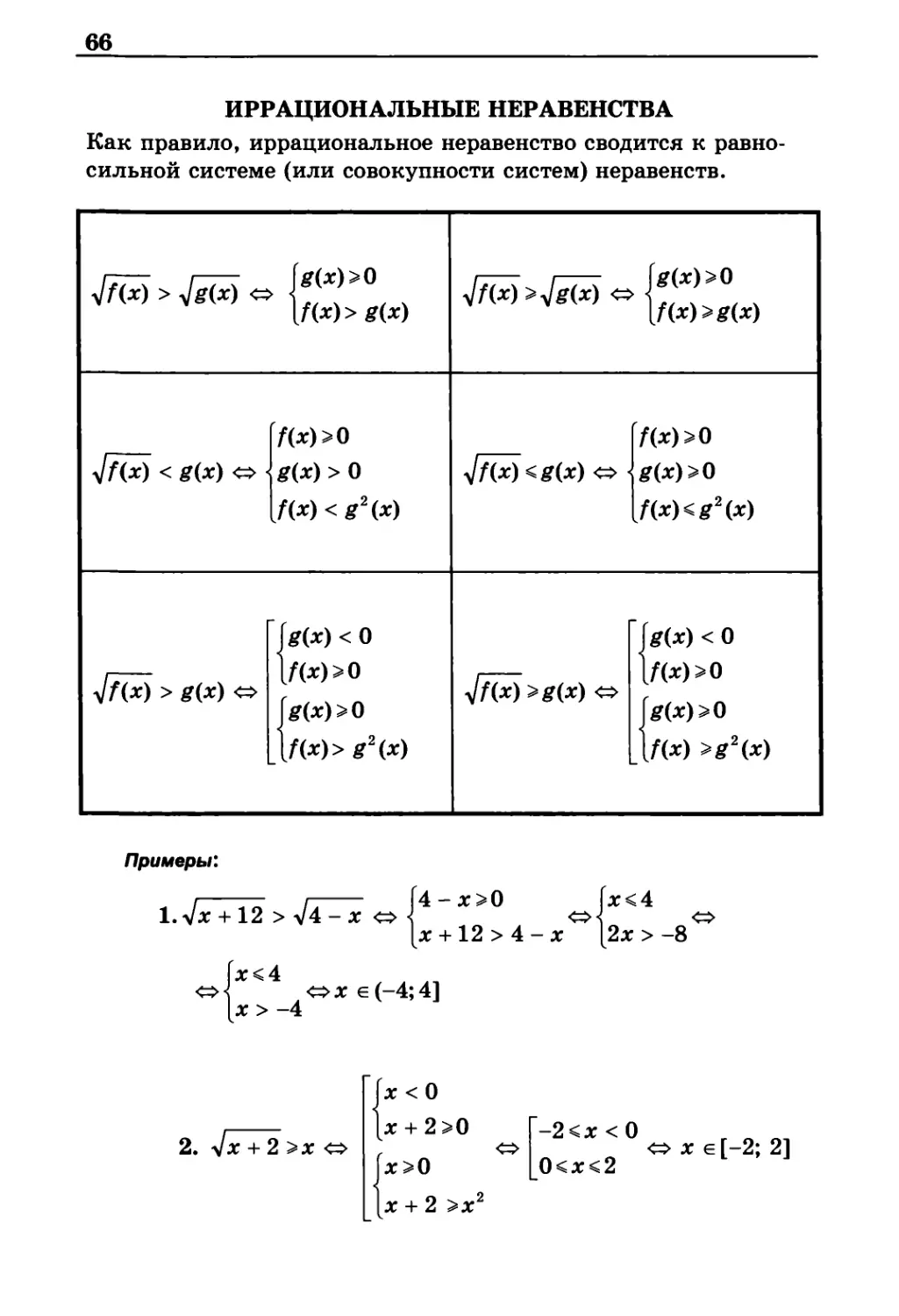
ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
Как правило, иррациональное неравенство сводится к
равносильной системе (или совокупности систем) неравенств.

67
ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
Замечание. В случае нестрогих неравенств знаки > и < в решениях
заменяются соответственно на > и < .
ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
logaf(x) > logag(x), где a > О, 0 ≠ 1
Примеры:
1. log2(x + 8) > log2(2x + 4) о
2л: + 4 > О
x + 8 > 2x + 4 jc<4
jc > -2
о * e (-2; 4)
\x - 2 > 0
2. 1о&1(х-2)>1о&1(^-Зх + 1) о о
д:-2<д:2-Зд: + 1
x-2>0
U -4jc + 3 > О
д: > 2
х < 1 о д: е [3; со)
д: > 3
Замечание. Следует обратить внимание на область определения
функции у = loga х: решения нестрогих неравенств не всегда
получаются из решений соответствующих строгих неравенств
просто заменой знаков > и < на знаки > и < .

68
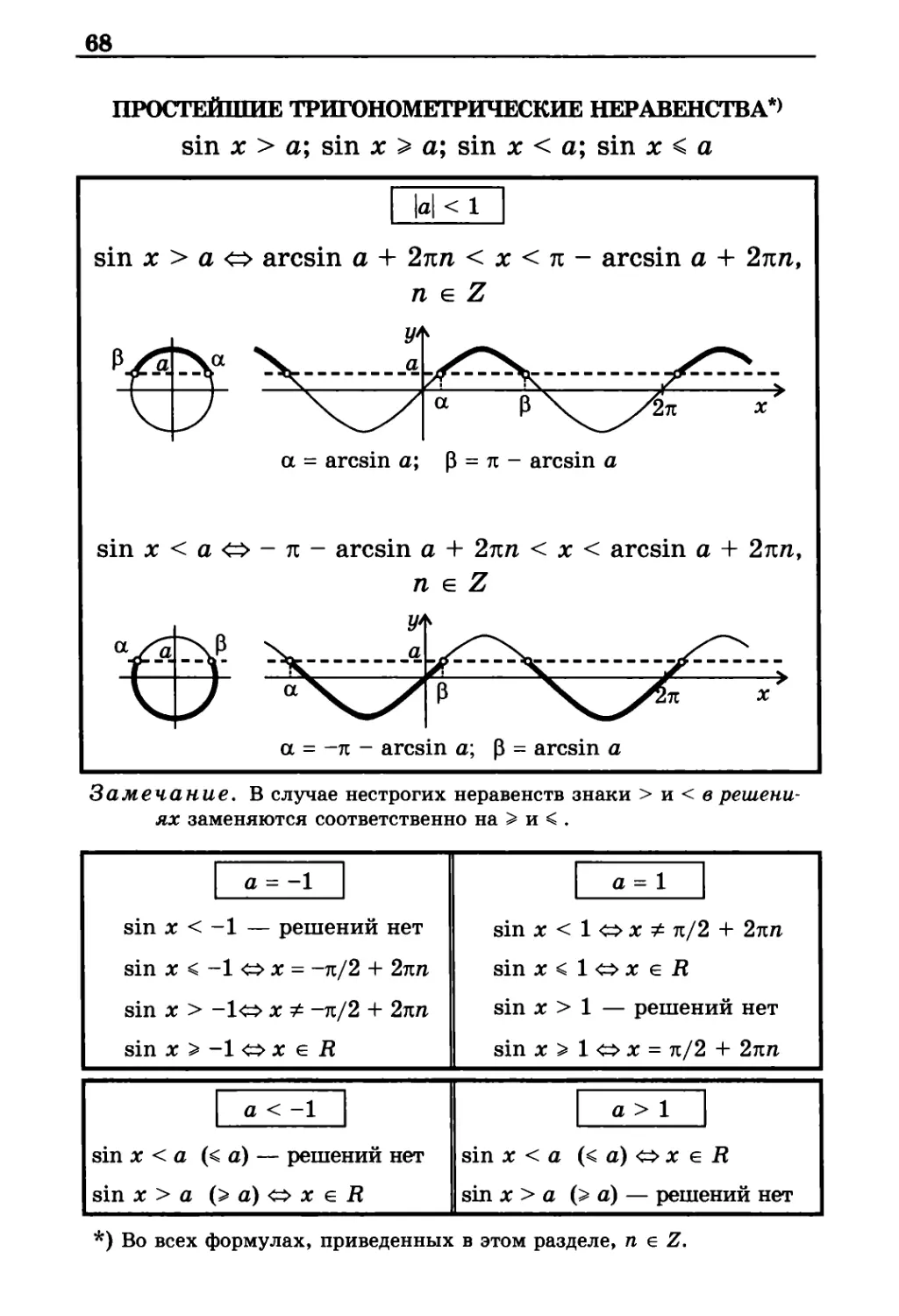
ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА*)
sin х > a; sin х > a; sin х < a; sin х < а
а = arcsin а; р = л - arcsin а
sin х < а <^> - п - arcsin а + 2пп < х < arcsin а + 2пп,
п е Z
У*
а = -л - arcsin а; р = arcsin а
Замечание. В случае нестрогих неравенств знаки > и < в
решениях заменяются соответственно на > и < .
*) Во всех формулах, приведенных в этом разделе, п е Z.

69
cos x > a; cos x > a; cos x < a; cos x < a
\a < 1
cos x > a <=> - arccos a + 2nn < x < arccos a + 2nn,
n e Z
В
2n x
a = - arccos a; p = arccos a
cos x < a <=> arccos a + 27m < л; < 2ти - arccos a + 2nn,
n e Z
a = arccos a ; В = 2тс - arccos a
Замечание. В случае нестрогих неравенств знаки > и < в решениях
заменяются соответственно на > и < .
a = -1
a = 1
cos х < -1 — решений нет
cos x<-lojc = 7t + 2тт
cos х>-1охФп + 2пп
cos л: > -1 о л: 6 Я
cos х < I <z> х Ф 2nn
cos x < 1 О X 6 Я
cos л: > 1 — решений нет
cos л: > 1 о л: = 2кп
а < -1
а > 1
cos л: < a (< a) — решений нет
cos x>a(>a)oxeR
cos ж<о(< o)o^6i?
cos х > а (> а) — решений нет

70
tg x > a; tg x > a; tg x < a; tg x < a
tg x > a
arctg a + nn < x < я/2 + nn,
n eZ
tg x > a
arctg a + пп < x < я/2 + пп,
n eZ
tg x < a
-я/2 + пп < x < arctg a + nn,
n eZ
tg x < a
-я/2 + ял < x < arctg a + nn,
n eZ
ctg x > a; ctg x > a; ctg x < a; ctg x < a
Замечание. Следует обратить внимание на область определения
функций y = tg х и y = ctg x: решения нестрогих неравенств не
всегда получаются из решений соответствующих строгих
неравенств просто заменой знаков > и < на знаки > и < .

71
СИСТЕМЫ ДВУХ УРАВНЕНИЙ
С ДВУМЯ НЕИЗВЕСТНЫМИ
Общий вид:
Решением системы двух уравнений с двумя
неизвестными называется пара чисел (x0, y0), при подстановке
которых вместо соответствующих переменных х, у оба
уравнения системы обращаются в верные числовые равенства.
Примеры:
{2 2у j
Решение системы: (3; 1)
2х + Зу = 9
\ У = х2
2. < Решения системы: (-1; 1) и (2; 4)
\у = х + 2
Решить систему уравнений — значит найти все ее
решения или доказать, что решений нет.
Равносильными называются системы, множества
решений которых совпадают.
В частности, равносильны все системы, не имеющие решений.
Система, не имеющая решений, называется несовместной.
Пример несовместной системы:
{х + 2у = 2
[Зх + 6у = 5
Замечание. Наряду с системами уравнений часто рассматриваются
совокупности уравнений. Решением совокупности является
объединение решений всех уравнений совокупности.
Для обозначения совокупности уравнений используют
квадратную скобку.

72
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ
метод подстановки
Этапы решения
Примеры
1. С помощью какого-
либо из уравнений
выразить одно
неизвестное через другое.
{2х-у = 4
\х + 3у = 9
из первого
уравнения
у = 2х - 4
\х2 + ху - у2 = 1
\х + у = 2
из второго
уравнения
У = 2-х
2. Подставить найденное
выражение в другое
уравнение системы: в
результате получится
одно уравнение с
одним неизвестным.
х + 3 (2х - 4) = 9;
7х = 21
х2 + х{2 - х) -
-(2-х)2 = 1;
х2 - 6х + 5 = 0
3. Найти корень
(корни) этого уравнения,
то есть найти
значение (значения)
одного из неизвестных
системы.
х = 3
*i = 1;
х2 = 5
4. Использовать
найденное выражение одного
неизвестного через
другое (подстановку),
то есть найти
значение
(соответствующие значения)
второго неизвестного.
у = 2х - 4 =
=2-3-4=2
У\ = 2 - *i =
= 2-1 = 1;
у2 = 2 - х2 =
= 2 - 5 = -3
5. Записать ответ.
(3; 2)
(1; 1), (5; -3)

73
метод сложения
Этапы решения
Примеры
1. Сложить почленно
уравнения системы,
умножив
предварительно каждое из
уравнений на
подходящее число так,
чтобы в результате
сложения получилось
одно уравнение с одним
неизвестным.
|4jc + by = 19 х4
\1х - 4у = -5 х5
(lQx + 20у = 76
\35х - 20у = -25
(2ху + х2 = 2 хЗ
\3ху - 4х = 5 х(-2)
( Qxy + Зх2 = 6
\-Qxy + 8х = -10
51* = 51
Зх2+ 8х = -4
2. Найти корень
(корни) этого уравнения,
то есть найти
значение (значения)
одного из неизвестных
системы.
х = 1
xi = -2;
х2 = -2/3
3. Подставить найденное
значение (значения)
одного из
неизвестных в любое из
уравнений системы: в
результате снова
получится уравнение
(уравнения) с одним
неизвестным.
Подстановка в
первое
уравнение дает:
4 • 1 + Ьу = 19;
5i/ = 15
Подстановка
во второе
уравнение дает:
при х = xi = -2
6у = 3;
при х — х2 = -2/3
2у = -7/3
4. Найти решение
(решения) этого уравнения
(этих уравнений), то
есть найти
значение
(соответствующие значения)
второго неизвестного.
*/ = з
У1 = 1/2;
У2 = -7/6
5. Записать ответ.
(1; 3)
(-2; 1/2),
(-2/3; -7/6)

74
графический метод решения
системы двух уравнений с двумя неизвестными
Надо построить графики обоих уравнений и найти координаты
общих точек этих графиков — эти координаты являются
решениями системы.
Примеры:
г \х2+у2=2
' \х*-у = 0
График первого уравнения —
окружность радиуса 42 с
центром в начале координат,
график второго уравнения —
кубическая парабола у = х3. Эти два
графика пересекаются в двух
точках с координатами
(-1; -1) и (1; 1).
у
У
/ 1
0
1 ) х
я-1; -1)
-1
2 \х2+у2=25
' \ху= 12
График первого уравнения —
окружность радиуса 5 с центром
в начале координат, график
второго уравнения — гипербола
12
у = — . Эти два графика пере-
х
секаются в четырех точках с
координатами (-4; -3),
(-3; -4), (4; 3) и (3; 4).
Замечание. Хотя графический метод не всегда позволяет найти
точные решения системы уравнений, он помогает обнаружить
решения, которые часто упускаются из виду при
аналитическом решении (например, отрицательные значения
неизвестных в приведенных примерах).

75
СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ
С ДВУМЯ НЕИЗВЕСТНЫМИ*)
\ахх + b1у = с1
\а2х + b2у = с2
Возможные случаи
Графическая
интерпретация
1. Коэффициенты при неизвестных в
уравнениях не пропорциональны, т.е.
а\Ь2 ф а2Ъ\.
Система имеет единственное решение:
х =
У =
-с2Ъх
- а2ъ\
а1С2
- а2сх
ахЪ2
- а2Ьх
Прямые — графики
уравнений системы
пересекаются в одной
точке, координаты
которой являются
решением системы:
2. Коэффициенты при неизвестных в
уравнениях пропорциональны, т.е.
аф2 = a2&i,
но они не пропорциональны свободным
членам, т.е. а\с2 ф а2с\ или Ь\с2 ф Ь2с\.
Система не имеет решений.
Прямые — графики
уравнений системы
параллельны:
•а
3. Коэффициенты при неизвестных и
свободные члены в уравнениях
пропорциональны, т.е.
аф2 = а2Ъъ а,\с2 = а2с\, Ъ\с2 = Ъ2с\.
Система имеет бесконечно много
решений: решениями является любая
пара (л:; у), удовлетворяющая одному
(любому) уравнению системы.
Прямые — графики
уравнений системы
совпадают:
*) Предполагается, что в каждом уравнении системы хотя бы один из
коэффициентов при неизвестных отличен от нуля, т.е. графиком
каждого уравнения системы является прямая.

76
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ*)
ПРОИЗВОДНАЯ
Производной функции f(x) в точке Xq называется предел
отношения приращения функции А/ = f(xQ + Ад:) - /(#o) к
приращению аргумента Ад: при Ад: -»0, если этот предел
существует:
Г(Хо) = lim А*, + А*)-/(*0)
Дх->0 Д#
Пример: (х2)' = lim + ?_ = lim(2* + Д*) = 2х .
Ах->0 АХ Ах->0
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Производная в точке Xq равна угловому коэффициенту
касательной к графику функции у = f(x) в этой точке:
У
У у
N.
! ^
—г >
х° x
f'(x0) = tg а > 0 Д*о) = tg а = 0 f(xQ) = tg а < 0
УРАВНЕНИЕ КАСАТЕЛЬНОЙ
к графику функции I/ = Дд:) в точке х§\
y = f(x0) + f'(x0)(x-x0)
Пример. Нахождение уравнения касательной к графику
функции f(x) - в точке xq = l:
1. я*о) = Я1) = 1
2. Г(*и4=^
3. Пх0) = Г0) = -
4. у = 1 н— (дс — 1) = — х л—
2 2 2
*)Таблицу производных см. на стр. 188.

77
ВТОРАЯ ПРОИЗВОДНАЯ
Второй производной функции у = f(x) называется
производная от производной f'(x) (обозначается f'(x)).
ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Если точка движется вдоль оси х и ее координата
изменяется по закону x(t), то мгновенная скорость точки:
,+. x(t + At)-x(t)
v(t) = lim — — — = x'(t),
At-*0 At
а ускорение:
At->0 д£
gt2
Пример. При свободном падении x(t) = —— , v(t) = x'(t) = gt,
ait) = v'(t) = g .
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Если у функций и(х) и v(x) существуют производные, то
(u±V)'=u'±v' , ч'
[ и } u'v - uv'
(си)' = си', где с — const — = р (v Ф- u)
(uv)' - u'v + uv
производная сложной функции
Если у = f(g(x)) и существуют производные /у и g'x, то
Ух fg & X >
где индексы g и х указывают, по какому аргументу
вычисляются производные.
/ I \ 1 ' COS X
Примеры: 1. Nsinx\ =—. (sin*) =—. (sin л; > 0)
^ ' 2vsinx 2vsinx
' 1 ' COS X
2. (In sin x) = (sin x) = = ctg x (sin x > 0)
sin x sin x
3. (xx) =(exlnx) = exlnx(x\nx) = xx(\nx +1) (x > 0)

78
применение производной
к исследованию функций
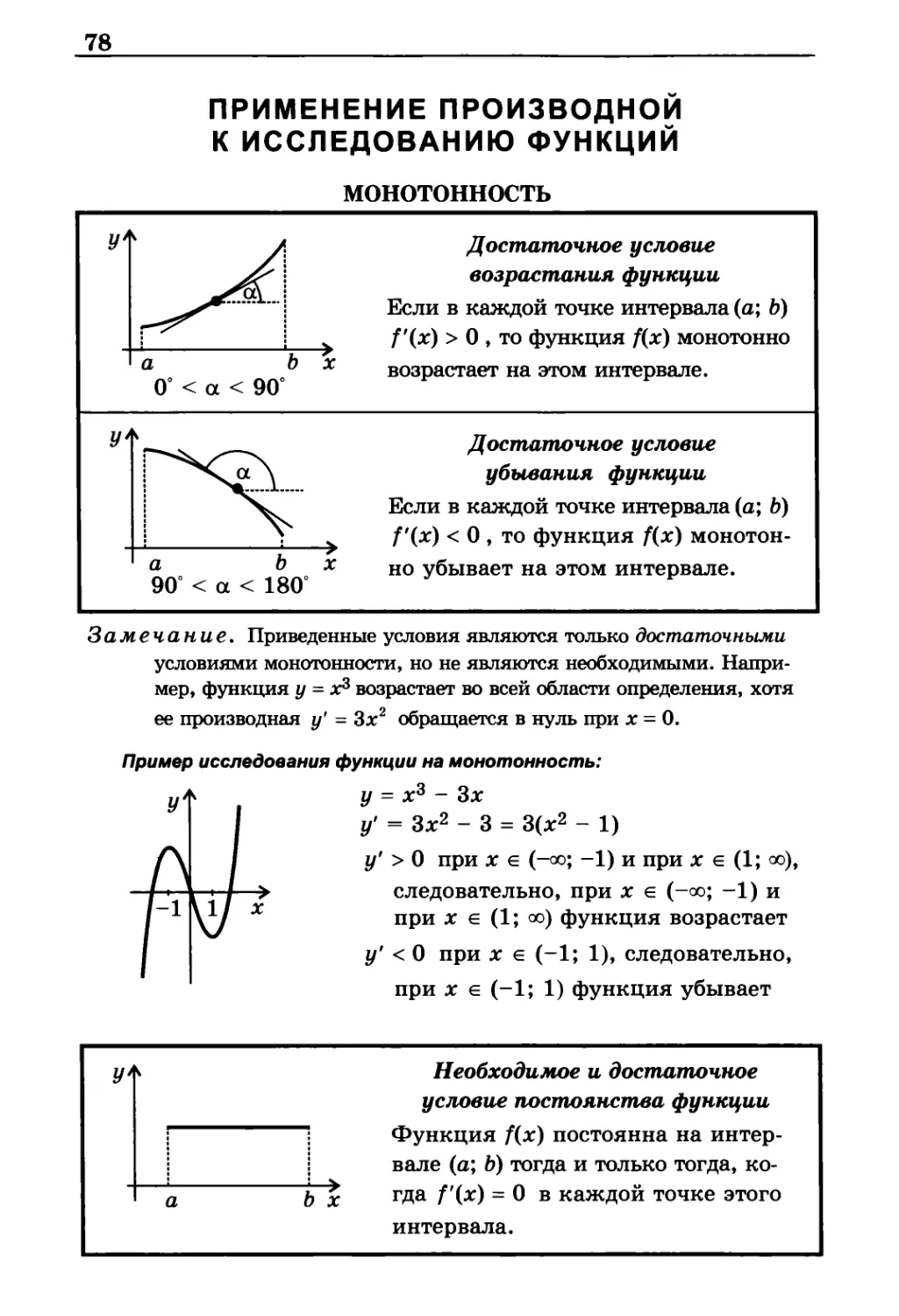
МОНОТОННОСТЬ
Достаточное условие
возрастания функции
Если в каждой точке интервала (а; b)
f(x) > 0 , то функция f(x) монотонно
возрастает на этом интервале.
Достаточное условие
убывания функции
Если в каждой точке интервала (а; b)
f(x) < 0 , то функция f(x)
монотонно убывает на этом интервале.
Замечание. Приведенные условия являются только достаточными
условиями монотонности, но не являются необходимыми.
Например, функция у = X3 возрастает во всей области определения, хотя
ее производная у' = Зх2 обращается в нуль при х = 0.
Пример исследования функции на монотонность:
у = х3 - Зх
у' = Зх2 - 3 = 3(x2 - 1)
у' > 0 при х е (-оо; -1) и при х е (1; оо),
> следовательно, при х е (-оо; -1) и
* при х е (1; оо) функция возрастает
у' < 0 при х е (-1; 1), следовательно,
при х е (-1; 1) функция убывает
Необходимое и достаточное
условие постоянства функции
Функция fix) постоянна на
интервале (а; Ъ) тогда и только тогда,
коa
Ъ х
гда f'{x) = 0 в каждой точке этого
интервала.

79
ЭКСТРЕМУМЫ
необходимое условие экстремума
Если Xq — точка экстремума функции у = f(x), то эта
точка является критической точкой данной функции, т.е. в этой
точке производная либо равна нулю, либо она не существует.
Замечание. Приведенное условие является только необходимым
условием экстремума, но не является достаточным:
критическая точка не обязательно является точкой экстремума.
Примеры отсутствия экстремума в критической точке х = 0:
у = X3
У
0 = |x|- 2х
f' не существует
х х
достаточное условие экстремума
Если функция у = f(x) непрерывна в точке Xq и
производная f '(х) меняет знак в этой точке, то Xq — точка
экстремума функции у = f(x).
Если f '(х) > 0 при х < xq>
f '(х) < 0 при х > Хо,
то Xq— точка максимума.
Если f '(х) < 0 при х < лго»
f'(х) > 0 при х > Хо,
то Xq— точка минимума.
Замечание. В самой точке x0 производной у функции у = f(x)
может не существовать.
Примеры экстремумов:
г--
V
= 0 У
1
" не существует
\ Xmin ^
/ X >v
max >
\ xmnv -А
• ^^>^ max \
f не с
X
уществует

80
схема применения производной для нахождения
интервалов монотонности и экстремумов
Этапы
Пример
для функции
у = 2х3 - Зх2 - З6х + 5
1. Найти область определения
функции и интервалы, на
которых функция непрерывна.
Обл. определения: R
Функция непрерывна во
всей обл. определения
2. Найти производную f'(x).
f'(x) = 6х2 - 6х - 36
Найти критические точки,
т.е. точки, в которых
производная функции равна нулю
или не существует.
/'(*) = о
при х = -2, х = 3
4. В каждом из интервалов, на
которые область определения
разбивается критическими
точками, определить знак
производной и характер
изменения функции (с
помощью достаточных условий
монотонности).
знак f
+
—
+
■ s
характер
изменения
функции
-2
/
\
3
/
5. Относительно каждой
критической точки определить,
является ли она точкой
максимума, минимума или не
является точкой экстремума.
х = -2
точка максимума;
х = 3
точка минимума
6. Записать результат
исследования функции: промежутки
монотонности и экстремумы.
f(x) возрастает при
х е (-оо; -2) и при
х е (3; оо);
f(x) убывает при
х е (-2; 3);
Хтах = ~~ 2»
Утах = Я-2) = 49;
Xmin = 3,
У тш = A3) = -76

81
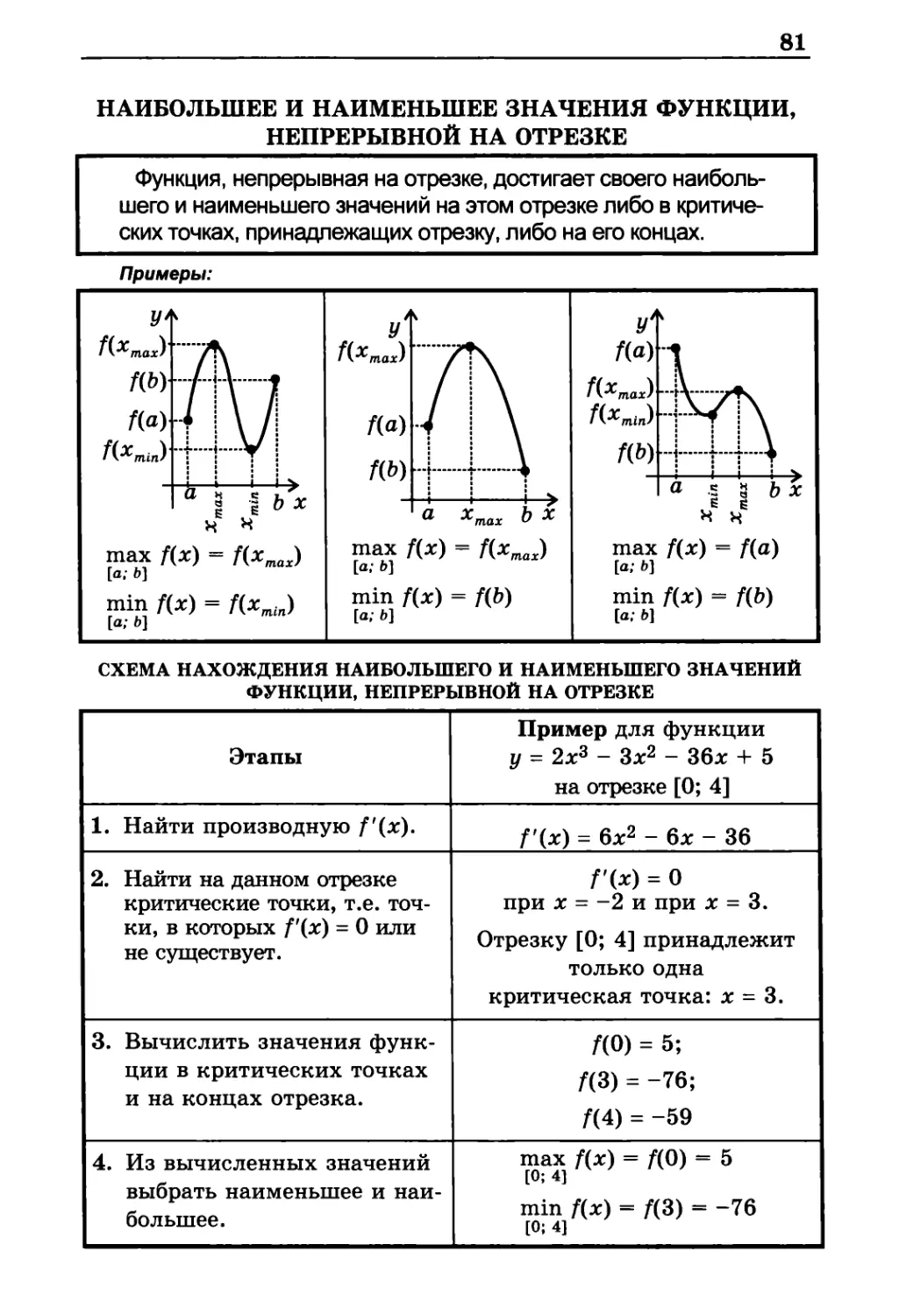
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ,
НЕПРЕРЫВНОЙ НА ОТРЕЗКЕ
Функция, непрерывная на отрезке, достигает своего
наибольшего и наименьшего значений на этом отрезке либо в
критических точках, принадлежащих отрезку, либо на его концах.
Примеры:
max f(x) = f(xmax)
[a; b]
min f(x) = f(xmin)
[a; b]
max f(x) = f(xmax)
[a; b]
min f(x) = №
[a; b]
max f(x) = f(a)
[a; b]
min f(x) = №
[a; b]
схема нахождения наибольшего и наименьшего значений
функции, непрерывной на отрезке
Этапы
Пример для функции
у = 2х3 - Зх2 - 36* + 5
на отрезке [0; 4]
1. Найти производную f'(x).
f'(x) = 6х2 - 6х - 36
2. Найти на данном отрезке
критические точки, т.е.
точки, в которых f'(x) = 0 или
не существует.
f'(x) = 0
при х = -2 и при х = 3.
Отрезку [0; 4] принадлежит
только одна
критическая точка: х = 3.
3. Вычислить значения
функции в критических точках
и на концах отрезка.
/(0) = 5;
ЯЗ) = -76;
/(4) = -59
4. Из вычисленных значений
выбрать наименьшее и
наибольшее.
max f(x) = ДО) = 5
[0; 4]
min f(x) = /(3) = -76
[0; 4]

82
ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ*)
ПЕРВООБРАЗНАЯ
Функция F(x) называется первообразной для функции
f(x) на данном промежутке, если для любого х из этого
промежутка F (х) = f(x).
Пример. Первообразной для функции f(x) = х на всей
числовой оси является F(x) = х2/2, поскольку (х2/2)' = х.
основное свойство первообразных
Если F(x) — первообразная функции f(x), то и функция
F(x) + С, где С — произвольная постоянная, также
является первообразной функции f(x).
геометрическая интерпретация
У*
k . Графики всех первообразных данной
у функции f(x) получаются из графи-
^ У. у ка какой-либо одной первообразной
"^■^—/я параллельными переносами вдоль
оси у.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Совокупность всех первообразных данной функции f(x)
называется ее неопределенным интегралом и
обозначается jf(x)dx:
| f{x)dx = F(x) + С, где С — произвольная постоянная.
ПРАВИЛА ИНТЕГРИРОВАНИЯ
^cf(x)dx = с jf(x)dx, где с — const
\(f(x) ± g(x))dx = \f(x)dx ± \g(x)dx
[f(ax + b)dx = — F(ax + b) + С , а Ф 0
J a
*)Таблицу интегралов см. на стр. 189.

83
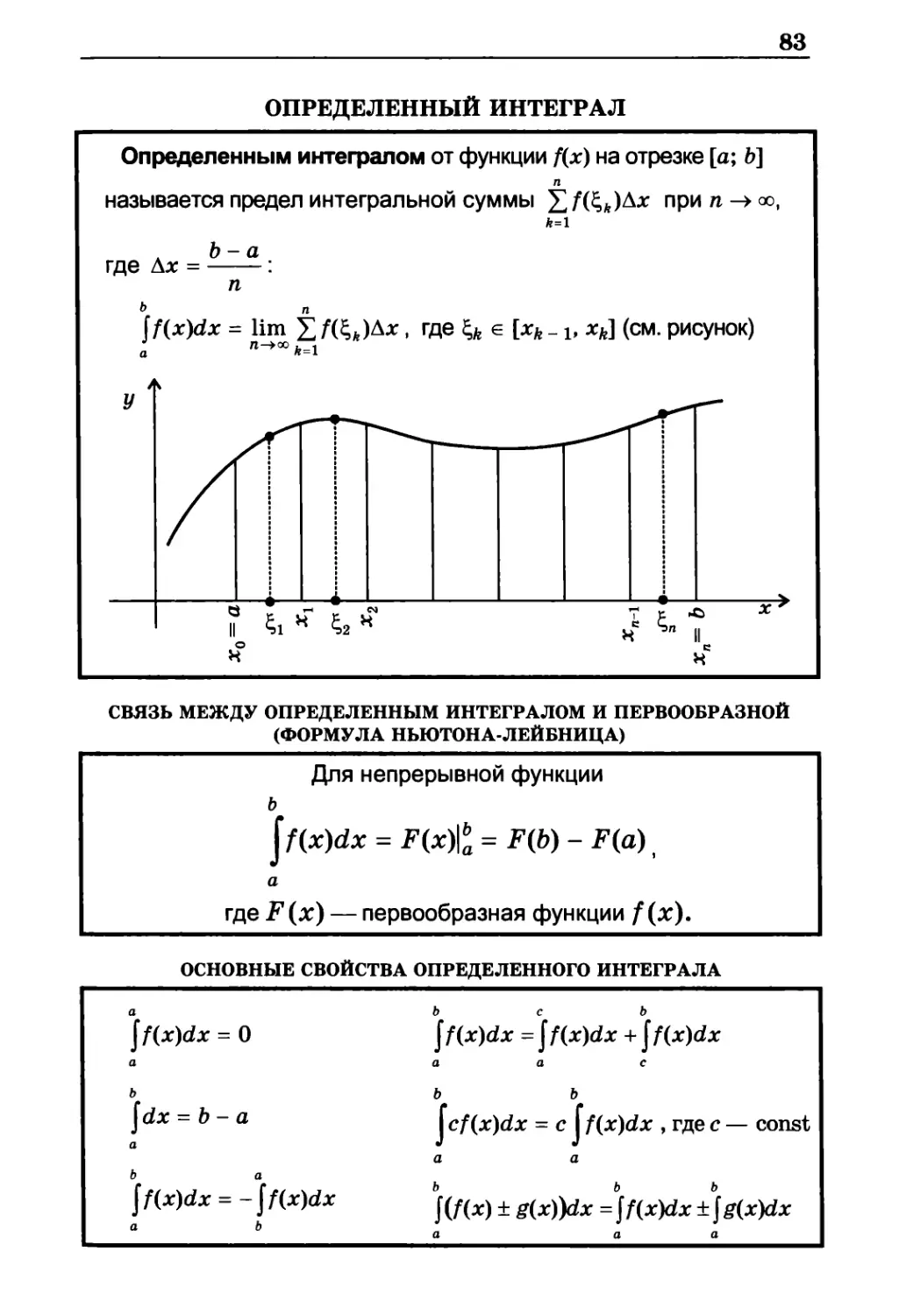
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определенным интегралом от функции fix) на отрезке [а; Ь]
п
называется предел интегральной суммы Х/(£л)Дх при л-> со,
h=\
где Ах =
СВЯЗЬ МЕЖДУ ОПРЕДЕЛЕННЫМ ИНТЕГРАЛОМ И ПЕРВООБРАЗНОЙ
(ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА)
Для непрерывной функции
ь
jf(x)dx = F(x)\ba = F(b) - F(a) t
a
гдеF(x) —
-первообразная функции f(x).
ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
а
\f(x)dx = 0
а
Ь с Ь
\f(x)dx=\f(x)dx+\f(x)dx
а а с
Ь
jdx = b - а
а
ь ъ
^cf(x)dx = с jf(x)dx , где с — const
Ь а
\f(x)dx = -\f(x)dx
а Ь
f (f(x) ± gix))dx =)fix)dx ±)gix)dx
a a a

84
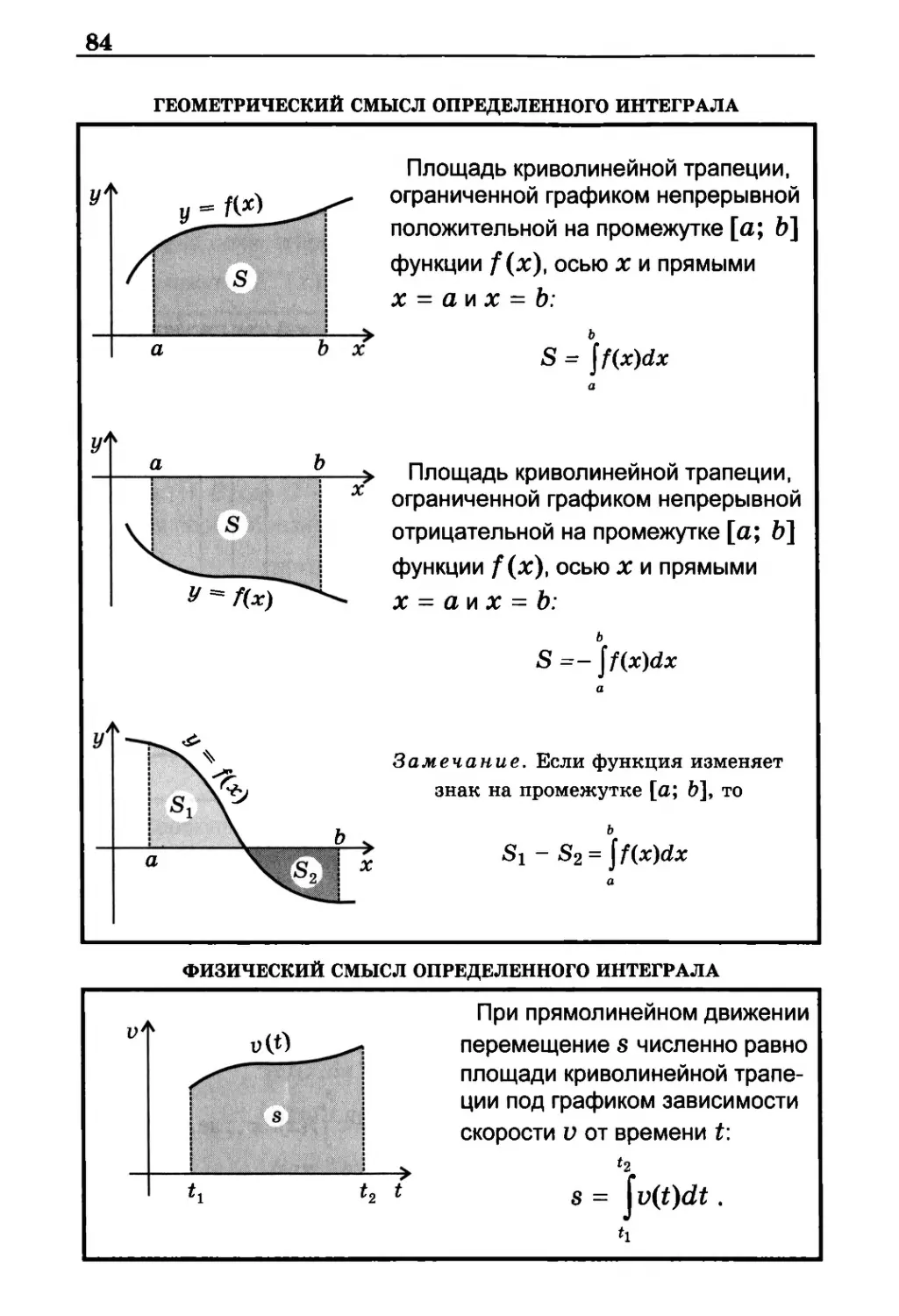
геометрический смысл определенного интеграла
Ъ х
Площадь криволинейной трапеции,
ограниченной графиком непрерывной
положительной на промежутке [а; b]
функции f(x), осью х и прямыми
х = а и х = b:
ь
S = \f(x)dx
Площадь криволинейной трапеции,
ограниченной графиком непрерывной
отрицательной на промежутке [а; b]
функции f(x), осью х и прямыми
х = а и х = b:
S =-\f(x)dx
Замечание. Если функция изменяет
знак на промежутке [а; b], то
Si-S2 = \f(x)dx
физический смысл определенного интеграла
t0 t
При прямолинейном движении
перемещение s численно равно
площади криволинейной
трапеции под графиком зависимости
скорости v от времени t:
н
s = jv(t)dt.
h

85
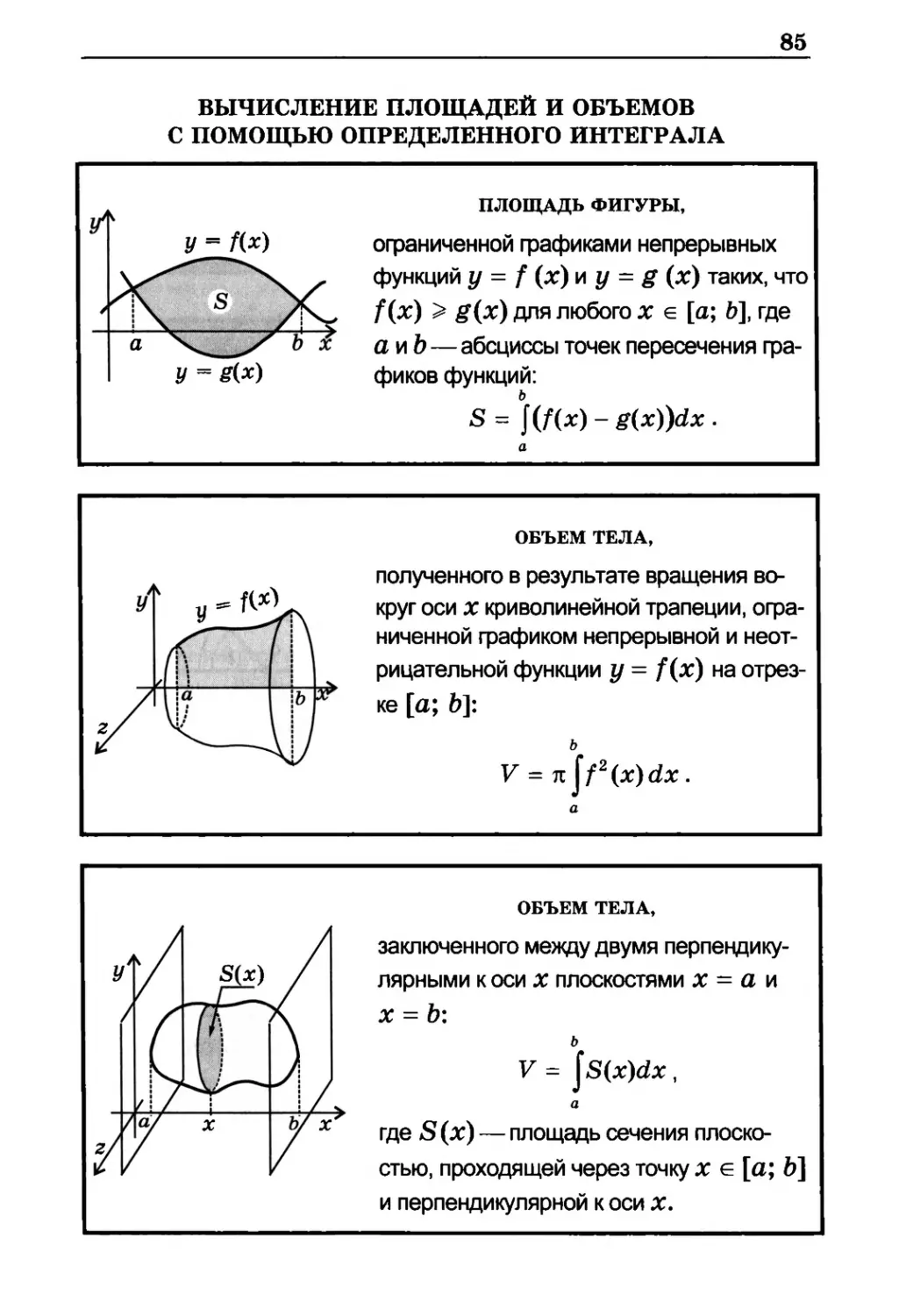
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
С ПОМОЩЬЮ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
У = g(x)
площадь фигуры,
ограниченной графиками непрерывных
функций у = f (x) \л у = g (x) таких, что
f(x) > g(x) для любого х е [а; b], где
а и b — абсциссы точек пересечения
графиков функций:
S = )(f(x) - g(x))dx .
объем тела,
полученного в результате вращения
вокруг оси jc криволинейной трапеции,
ограниченной графиком непрерывной и
неотрицательной функции у = f(x) на
отрезке [а; Ь]:
и
V = njf2(x)dx
объем тела,
заключенного между двумя
перпендикулярными к оси jc плоскостями jc = а и
х = Ь:
и
V = jS(x)dx,
где S (jc) — площадь сечения
плоскостью, проходящей через точку х е [а; Ь]
и перпендикулярной к оси jc.

86
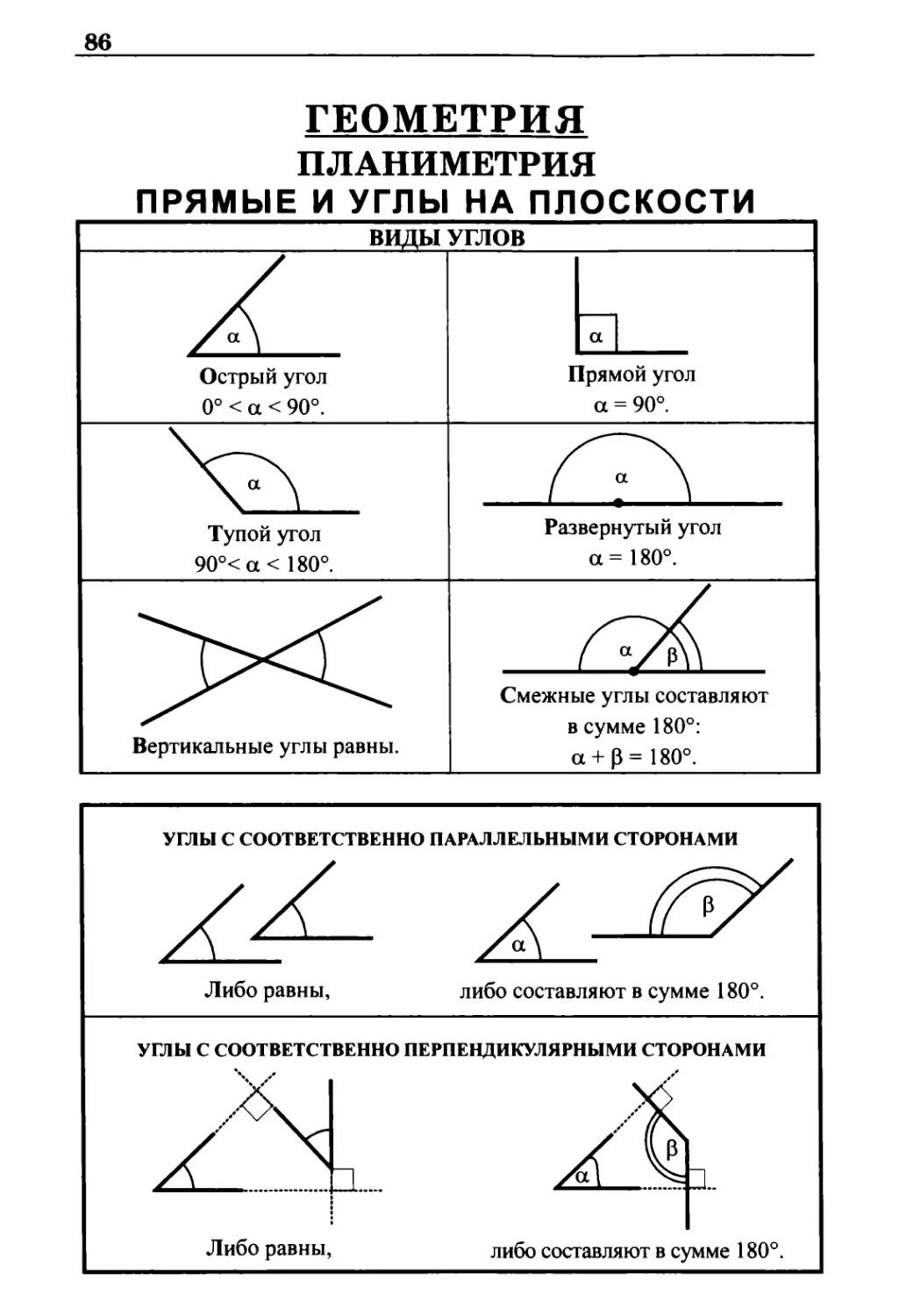
ГЕОМЕТРИЯ
ПЛАНИМЕТРИЯ
ПРЯМЫЕ И УГЛЫ НА ПЛОСКОСТИ
углы с соответственно параллельными сторонами
а
Либо равны,
либо составляют в сумме 180°.
углы с соответственно перпендикулярными сторонами
А.
Либо равны,
51
либо составляют в сумме 180е

87
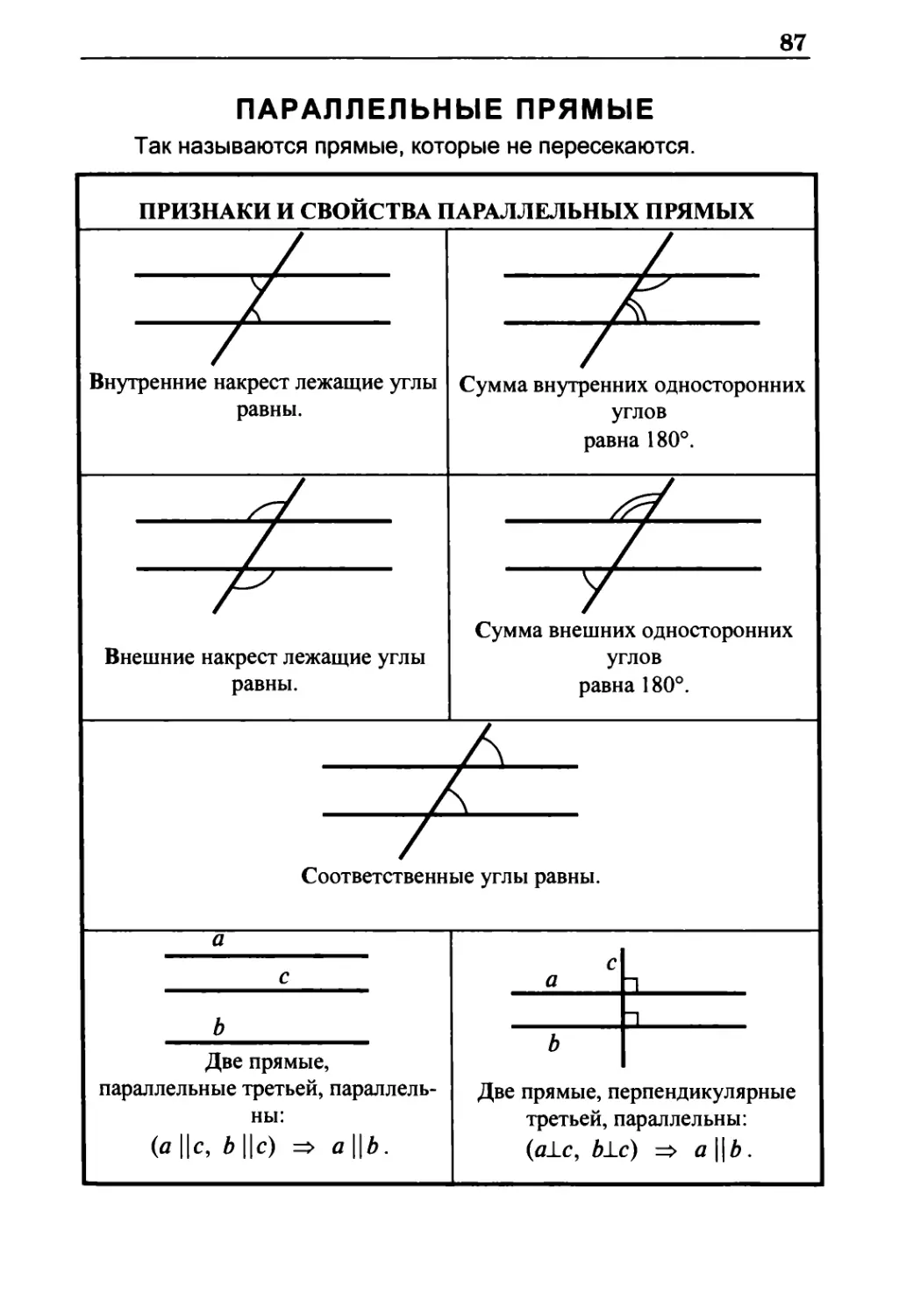
параллельные прямые
Так называются прямые, которые не пересекаются.
ПРИЗНАКИ И СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
/
/
/
/
Внутренние накрест лежащие углы
равны.
/
Сумма внутренних односторонних
углов
равна 180°.
/
/
Внешние накрест лежащие углы
равны.
У
Сумма внешних односторонних
углов
равна 180°.
Соответственные углы равны.
Две прямые,
параллельные третьей,
параллельны:
(а ||с, b||c) => а||b.
с
а
-1
п
Ь
Две прямые, перпендикулярные
третьей, параллельны:
(alb, alс) => а||b.

88
ПРИЗНАКИ И СВОЙСТВА
ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ (продолжение)
Теорема Фалеса
Если параллельные прямые, пересекающие
стороны угла,
отсекают на одной стороне угла равные
отрезки,
то они отсекают равные отрезки
и на другой стороне угла.
Верно и обратное: если некоторые прямые, не пересекающиеся внутри
угла, отсекают на одной стороне угла равные между собой отрезки и
на другой стороне тоже равные между собой отрезки, то такие прямые
параллельны.
Параллельные прямые, пересекающие
стороны угла, отсекают на сторонах угла
пропорциональные отрезки:
а_ = _6
с ~ d '
ПЕРПЕНДИКУЛЯР И НАКЛОННЫЕ
икуля
«и
У
перп
проекция
наклонной
Перпендикуляр короче
любой наклонной,
проведенной
к прямой
из той же точки.
У равных
наклонных, проведенных из
одной и той же
точки, проекции равны.
Верно и обратное:
если проекции равны,
то равны и
наклонные.
Из двух наклонных,
проведенных из
одной и той же точки,
больше та, у которой
проекция больше.
Верно
и обратное.

89
ТРЕУГОЛЬНИКИ
произвольный треугольник
СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ
и УГЛАМИ
ч ь
Неравенство треугольника
Любая сторона треугольника
меньше суммы
двух других сторон,
но больше модуля
их разности:
\a-b\<c<a + b.
Сумма углов треугольника равна
180°: а + р + у = 180°.
Против большей стороны
в треугольнике лежит больший
угол: b > а о р > а
Внешний угол треугольника равен
сумме двух внутренних углов, не
смежных с ним:
8 = а + р.
Теорема косинусов:
с2 = а2 + bz - 2ab cosy.
Теорема синусов:
a b с
sin a sin р sin у
Это отношение равно 2R,
где R - радиус
описанной окружности.

90
СВОЙСТВО ПРЯМОЙ, ПАРАЛЛЕЛЬНОЙ
СТОРОНЕ ТРЕУГОЛЬНИКА
Прямая, параллельная
одной из сторон треугольника
и пересекающая две другие
стороны треугольника, отсекает
треугольник, подобный данному.

91
ЗАМЕЧАТЕЛЬНЫЕ ЛИНИИ ТРЕУГОЛЬНИКА
Медиана - отрезок, соединяющий вершину
треугольника
с серединой
противолежащей стороны.
Биссектриса - отрезок, который соединяет
вершину треугольника
с точкой на противолежащей стороне и
делит внутренний угол пополам.
Высота - перпендикуляр,
опущенный из вершины треугольника на
прямую, содержащую
противолежащую сторону треугольника.
Взаимное расположение
медианы, биссектрисы и высоты
Биссектриса лежит внутри угла,
образованного высотой и медианой, проведенными из
той же вершины.
В равнобедренном треугольнике медиана,
биссектриса и высота, проведенные к
основанию, совпадают.
Серединный перпендикуляр -
прямая, перпендикулярная
стороне треугольника
и делящая ее пополам.
Я£ V Средняя линия - отрезок,
/ \ соединяющий середины

92
СВОЙСТВА МЕДИАН
Три медианы пересекаются
в одной точке,
которая всегда находится внутри
треугольника
(центр масс треугольника).
Каждая медиана точкой
пересечения медиан делится в отношении 2
: 1, считая от вершины.
Каждая медиана делит треугольник на 2 равновеликих треугольника
(одинаковой площади).

93
СВОЙСТВА БИССЕКТРИС
Три биссектрисы пересекаются
в одной точке,
которая всегда лежит
внутри треугольника.
Эта точка является
центром вписанной окружности.
Биссектриса делит сторону
треугольника на отрезки,
пропорциональные двум другим сторонам:
а, _ Ь
а2 с
Биссектрисы внутреннего и внешнего углов перпендикулярны.
Если биссектриса внешнего угла треугольника пересекает
продолжеBD ВС
ние противолежащей стороны, то —— = —— .

94
СВОЙСТВА ВЫСОТ
Прямые, содержащие высоты
треугольника, пересекаются
в одной точке. Эта точка называется
ортоцентром.
Ортоцентр остроугольного
треугольника лежит внутри треугольника.
ортоцентр
Ортоцентр прямоугольного
треугольника
совпадает с вершиной
прямого угла.
^ортоцентр
Ортоцентр тупоугольного
треугольника лежит
вне треугольника
(на рисунке треугольник выделен
серым цветом,
а продолжения высот и сторон,
образующих тупой угол, проведены
пунктиром).
Длина высоты
ha = Ъ sin у = с sin р;
2S 24р(р-а){р-Ь){р-с)
где р =
а
а + Ь + с
Высоты треугольника
обратно пропорциональны
его сторонам:
а о с

95
СВОЙСТВА
СЕРЕДИННЫХ ПЕРПЕНДИКУЛЯРОВ
Три серединных перпендикуляра пересекаются в одной точке. Эта
точка является центром описанной окружности.
^Н»—С
В случае остроугольного
тре\\ угольника точка пересечения
се(T^J-VA рединных перпендикуляров
<Г \ 1 (центр описанной окружности)
—В случае прямоугольного
треугольника точка пересечения
сере<VT динных перпендикуляров
\ (центо описанной окружности)
\ J совпадает
1 с серединой гипотенузы.
—В случае тупоугольного треуголь-
хч ника точка пересечения середин-
"1 ных перпендикуляров
f \ (центр описанной окружности)
^ 1 лежит вне треугольника.
СВОЙС
1
:тво СЕРЕДИННОГО ПЕРПЕНДИКУЛЯРА
И БИССЕКТРИСЫ
Продолжение биссектрисы
пересе>7^\ кается с серединным
перпендику'xjA \ ляром в точке, лежащей на
окруж/ \ J ности, описанной около
треуголь/ ^ у ника.

96
СВОЙСТВА СРЕДНЕЙ ЛИНИИ
Средняя линия параллельна
одной из сторон треугольника
и равна ее половине:
MN\\AC; MN = -AC.
2
Она отсекает треугольник,
подобный данному,
с коэффициентом подобия 1/2.
Три средние линии треугольника делят
его на 4 равных треугольника,
подобных данному,
с коэффициентом подобия 1/2.
ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ
В любой треугольник
можно вписать окружность.
Центр вписанной окружности —
точка пересечения биссектрис.
Радиус вписанной окружности
г = S/p, где S — площадь треугольника,
а + Ь + с
Р = ^ •
Около любого треугольника
можно описать окружность.
Центр описанной окружности —
точка пересечения серединных
перпендикуляров.
Радиус описанной окружности
abc
R =
4S
где S - площадь треугольника.

97
ПЛОЩАДЬ ТРЕУГОЛЬНИКА
/1
к
/ п
\
Через сторону и высоту,
проведенную к ней:
S = \aK.
Через две стороны и угол между
ними:
S = — absiny.
2
Формула Герона
Через три стороны:
S =-JР(Р - а)(Р - Ь)(р - с),
а + Ь + с
где р = .
Через полупериметр и радиус
вписанной окружности:
S=pr,
а + b + c
где р = .
Через произведение сторон
и радиус описанной окружности:
abc
S =
4R

98
равнобедренный треугольник
Так называется треугольник, у которого две стороны
равны.
Равные стороны называются боковыми сторонами,
а третья сторона — основанием.
СВОЙСТВА И ПРИЗНАКИ
РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА
Приведенные ниже утверждения являются как
свойствами,
так и признаками равнобедренного треугольника,
то есть являются необходимыми и достаточными
условиями того, что треугольник — равнобедренный. Это
означает:
1. Если треугольник — равнобедренный, то для него
справедливы все следующие утверждения.
2. Если для треугольника справедливо хотя бы одно
из следующих утверждений, то он — равнобедренный.
Углы при основании равны.
Медиана, биссектриса
и высота, проведенные
к основанию, совпадают.
высота
Треугольник имеет
ось симметрии.

99
равносторонний треугольник
Так называется треугольник, у которого три стороны
равны.
Равносторонний треугольник называется также
правильным треугольником.
СВОЙСТВА И ПРИЗНАКИ
РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА
Приведенные ниже утверждения являются как
свойствами, так и признаками равностороннего треугольника,
то есть являются необходимыми и достаточными
условиями того, что треугольник — равносторонний. Это
означает:
1. Если треугольник — равносторонний, то для него
справедливы все следующие утверждения.
2. Если для треугольника справедливо хотя бы одно
из следующих утверждений, то он — равносторонний.
Все углы равны.
Каждая медиана совпадает
с биссектрисой и высотой,
проведенными из той же вершины.
Центры вписанной и описанной окружностей
совпадают.
a n a
(Их радиусы: г = —j= ; К - —f= ; R = 2г.)
2V3 V3
Треугольник обладает поворотной симметрией:
он не изменяется
при повороте на 120°.
Треугольник имеет три оси симметрии.
. Ля с Ля2 , гг 2 зЛя2
высота и площадь: п = ; S -= 3V3r =
2 4 4

100
прямоугольный треугольник
Так называется треугольник, у которого один угол прямой.
Стороны, прилежащие к прямому углу, называются
катетами,
а сторона, противолежащая прямому углу — гипотенузой.
ПРИЗНАКИ РАВЕНСТВА
ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
По двум катетам.
По одному катету
и гипотенузе.
По катету
и прилежащему острому
углу.
По катету
и противолежащему
острому углу.
По гипотенузе
и острому углу.

101
ПРИЗНАКИ ПОДОБИЯ
ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
По одному острому углу.
По пропорциональности двух
катетов.
По пропорциональности
катета и гипотенузы.
ТЕОРЕМА ПИФАГОРА
Сумма квадратов катетов
равна квадрату гипотенузы:
а2 + b2=с2.
Справедливо и обратное
утверждение: если для сторон а, b, с
треугольника выполняется
соотношение
а2 + b2 = с2,
то треугольник является
прямоугольным,
причем стороны а и b —
его катеты,
а сторона с — гипотенуза.

102
СВОЙСТВА ПРОЕКЦИЙ КАТЕТОВ
Высота, опущенная
на гипотенузу, является средним
a /
пропорциональным между
проекh X.
циями катетов на гипотенузу:
/ oc
a, h |2 ,
— = — => п = a b .
h bc сс
с
Каждый катет является средним
Высота выражается через стороны
и проекции катетов:
^ °ь °ь
пропорциональным между
гипотенузой
и проекцией этого катета
с ас + Ьс'
на гипотенузу:
а^ =
а
0 2
— ...=> а = асс
с
К .
ъ
Ь 1.2 L
= — ^>b - bcc.
с
частные случаи
прямоугольных треугольников
^30° г
ъ
с
а а = г
Л° г
а
СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ
В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ

103
ОКРУЖНОСТЬ, ВПИСАННАЯ
В ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Радиус вписанной окружности:
а /
>v Ь
ab
г = ,
р \\
а + b + с
У
а + Ь-с
с
ОКРУЖНОСТЬ, ОПИСАННАЯ
ОКОЛО ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
Центр описанной окружности
совпадает с серединой гипотенузы,
а радиус равен
— половине гипотенузы:
R=C-
2
— медиане, проведенной
к гипотенузе: R = тс.
ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
Через катеты: S = — ab.
2
Через катет и острый угол:
S = ifl2tgp = ifl2ctga
Через гипотенузу и любой из
острых углов:
S = — с2 sin 2a = — с2 sin 2В .
4 4

104
ЧЕТЫРЕХУГОЛЬНИКИ
ВИДЫ ЧЕТЫРЕХУГОЛЬНИКОВ
квадрат
ПРОИЗВОЛЬНЫЙ ЧЕТЫРЕХУГОЛЬНИК
Сумма внутренних углов
равна 360°:
а + р+ у + 6 = 360о.
L д
Площадь
(через диагонали
f и угол между ними):
Ь~ 2 •

105
ЧЕТЫРЕХУГОЛЬНИК, ОПИСАННЫЙ ОКОЛО ОКРУЖНОСТИ
Четырехугольник можно описать около
окружности, если суммы противолежащих
*/v к
сторон равны:
w а + с = b + d.
Если четырехугольник описан около
окружности, то суммы противолежащих сторон
равны.
а + b + с + d ,
Площадь: 5 :
= рг, где р --- (полупериметр),
г
— радиус вписанной окружности.
Формула S - рг справедлива для любого многоугольника, описанного
около окружности.
ЧЕТЫРЕХУГОЛЬНИК, ВПИСАННЫЙ В ОКРУЖНОСТЬ
Четырехугольник можно вписать в окружность, если
l/v
сумма противолежащих углов равна 180°: а + у = (3 +
6= 180°.
Если четырехугольник вписан в окружность, то
суммы противолежащих углов равны 180°.
Теорема Птолемея
Сумма произведений противолежащих сторон
равна произведению диагоналей:
ас + bd = d1d2 .
/7\
(КК2
d 1
Площадь
и
S = J(p-a)(p-b)(p-c)(p-d),
а + b + с + d .
где р = (полупериметр).

106
параллелограмм
Так называется четырехугольник,
у которого противолежащие стороны параллельны.
СВОЙСТВА И ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
Приведенные ниже утверждения являются как
свойствами,
так и признаками параллелограмма, то есть являются
необходимыми и достаточными условиями того,
что четырехугольник — параллелограмм. Это означает:
1. Если четырехугольник — параллелограмм, то для него
справедливы все следующие утверждения.
2. Если для четырехугольника справедливо хотя бы одно
из следующих утверждений, то он — параллелограмм.
Противолежащие стороны
попарно равны.
Противолежащие стороны
равны и параллельны.
Противолежащие углы
попарно равны.
Сумма углов, прилежащих к
любой стороне, равна 180°:
а + р= 180°.
Диагонали точкой
пересечения
делятся пополам.

107
СВОЙСТВА И ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
(продолжение)
Сумма квадратов диагоналей равна
сумме квадратов
всех сторон:
d2 + d\ = а2 + b2 + с1 + d2.
Каждая диагональ делит
четырехугольник
на два равных треугольника.
Обе диагонали делят
четырехугольник
на четыре равновеликих
треугольника
(одинаковой площади).
а
Точка пересечения
диагоналей является
центром симметрии.

108
ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА
СВОЙСТВО ПРОИЗВОЛЬНОГО ЧЕТЫРЕХУГОЛЬНИКА,
СВЯЗАННОЕ С ПАРАЛЛЕЛОГРАММОМ
Если соединить
отрезками середины соседних
сторон любого
четырехугольника, получится
параллелограмм.

109
ромб
Так называется параллелограмм, у которого все стороны равны.
СВОЙСТВА И ПРИЗНАКИ РОМБА
Приведенные ниже утверждения являются как
свойствами,
так и признаками ромба, то есть являются необходимыми и
достаточными условиями того, что четырехугольник —
ромб. Это означает:
1. Если четырехугольник — ромб, то для него
справедливы все следующие утверждения.
2. Если для четырехугольника справедливо хотя бы одно
из следующих утверждений, то он — ромб.
Все стороны равны.
Диагонали перпендикулярны
и точкой пересечения делятся
пополам.
Обе диагонали являются
биссектрисами
внутренних углов.
Прямые, содержащие
диагонали,
являются осями симметрии.

110
ОКРУЖНОСТЬ, ВПИСАННАЯ В РОМБ
В любой ромб можно вписать окружность.
Радиус г вписанной окружности
удовлетворяет соотношениям:
И
г = г
где h — высота ромба,
г =
d\d2
4а
где d}\\d2 — диагонали ромба,
а — его сторона.
Точка касания вписанной окружности делит
сторону ромба на отрезки, связанные с его
диагоналями
и радиусом вписанной окружности
следующими соотношениями:
dx = UАН АВ,
d2 = 2V ВН АВ,
г = 4АН НВ .
ПЛОЩАДЬ РОМБА
Через сторону и высоту: S = ah.
Через сторону
и радиус вписанной окружности:
S = 2аг.
Через сторону и угол ромба:
S - a2 sin а.
лл с d}d2
Через диагонали: о =

Ill
прямоугольник
Так называется параллелограмм, у которого все углы
прямые.
СВОЙСТВА И ПРИЗНАКИ ПРЯМОУГОЛЬНИКА
Приведенные ниже утверждения являются как
свойствами,
так и признаками прямоугольника, то есть являются
необходимыми и достаточными условиями того,
что четырехугольник — прямоугольник. Это означает:
1. Если четырехугольник — прямоугольник, то для него
справедливы все следующие утверждения.
2. Если для четырехугольника справедливо хотя бы одно
из следующих утверждений, то он — прямоугольник.
Диагонали равны
и точкой пересечения
делятся пополам.
П.
Две стороны параллельны
и углы, прилежащие
к одной из этих сторон, прямые.
Две противолежащие стороны равны
и углы, прилежащие
к одной из этих сторон, прямые.
Перпендикуляры к сторонам,
проходящие через их середины,
являются осями симметрии.

112
ОКРУЖНОСТЬ, ОПИСАННАЯ
ОКОЛО ПРЯМОУГОЛЬНИКА
Около любого прямоугольника
можно описать окружность.
Радиус описанной окружности
«4
где d = л[а2 + Ь1 — диагональ
прямоугольника.
ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА
Через стороны:
S = ab.
\ yd
Через диагональ и угол между
ъ
У
диагоналями:
с d2 sin у
а
СВЯЗЬ МЕЖДУ ПРЯМОУГОЛЬНИКОМ И РОМБОМ
Если соединить отрезками
середины соседних сторон любого
прямоугольника, получится ромб.
Если соединить отрезками
середины соседних сторон любого ромба,
получится прямоугольник.
<_>

113
квадрат
Так называется прямоугольник, у которого все стороны
равны.
СВОЙСТВА И ПРИЗНАКИ КВАДРАТА
Приведенные ниже утверждения являются как
свойствами,
так и признаками квадрата, то есть являются
необходимыми и достаточными условиями того,
что четырехугольник — квадрат. Это означает:
1. Если четырехугольник — квадрат, то для него
справедливы все следующие утверждения.
2. Если для четырехугольника справедливо хотя бы одно
из следующих утверждений, то он — квадрат.
i_—
Все стороны равны
и среди внутренних углов
есть прямой угол.
X
Диагонали равны,
перпендикулярны
и, пересекаясь,
делятся пополам.
\
^ Четырехугольник имеет четыре оси
симметрии:
прммыс, перпендикулярные ^lUpUHaM и
проходящие
^ через их середины;
— прямые, содержащие диагонали.
90°
^ Четырехугольник обладает поворотной
Л симметрией:
он не изменяется
при повороте на 90°.

114
ОКРУЖНОСТЬ, ОПИСАННАЯ
ОКОЛО КВАДРАТА
Около квадрата можно описать
окружность. J
\ R/
\ Радиус описанной окружности
\ выражается через сторону а
а
квадрата и его диагональ d сле-
/ дующим образом:
/ R = 4= = ~-
Л 2
ОКРУЖНОСТЬ, ВПИСАННАЯ
В КВАДРАТ
Г \
. г
В квадрат можно
вписать окружность.
Радиус вписанной окружности
равен
половине стороны:
а
а
ПЛОЩАДЬ КВАДРАТА
Через сторону:
S = a2.
Через диагональ:
-Г
а

115
трапеция
Так называется четырехугольник, у которого
две стороны параллельны (основания),
а две другие — не параллельны (боковые стороны).
Трапеция с равными боковыми сторонами называется
равнобокой (равнобедренной, равнобочной).
ЭЛЕМЕНТЫ ТРАПЕЦИИ
ь
л.
h
Г
а, Ь — основания (а || Ь),
т,п — боковые стороны,
di,d2 — диагонали,
И — высота (отрезок,
соединяющий основания
и перпендикулярный им),
MN— средняя линия
(отрезок, соединяющий середины
боковых сторон).
ПЛОЩАДЬ ТРАПЕЦИИ
Через полусумму оснований
и высоту:
Через среднюю линию
и высоту:
S = MN-h.
Через диагонали
и угол между ними:
_ J,J2sincp
о — .

lie
свойства трапеции
LL
Средняя линия
параллельна основаниям,
равна их полусумме и делит любой
отрезок с концами, лежащими на
прямых, содержащих основания,
(например, высоту трапеции) пополам:
MN\\a,MN\\b, MN = Oil.
Сумма углов,
прилежащих к любой боковой
стороне, равна 180°:
а + р= 180°,
у + 8= 180°.
Треугольники
АОВ и DOC,
образованные боковыми сторонами
и отрезками диагоналей, равновелики
(имеют равные площади).
AAOD ™ АСОВ
Треугольники AOD и СОВ,
образованные основаниями
и отрезками диагоналей, подобны.
Коэффициент подобия к
равен отношению оснований:
. AD
к-~вс'
Отношение площадей этих
треугольников равно к2.

117
СВОЙСТВА ТРАПЕЦИИ (продолжение)
Любой отрезок, соединяющий
основания и проходящий
через точку пересечения диагоналей
трапеции,
делится этой точкой
в отношении
ОХ ВС
OY ~ AD
Это справедливо, в том числе, для
самих диагоналей
и высоты.
Любую равнобокую трапецию можно
вписать в окружность.
Вписать в окружность можно
только равнобокую трапецию.
Если трапеция ABCD
описана около окружности,
то треугольники АОВ и DOC
прямоугольные
(точка О — центр вписанной
окружности).
Высоты этих треугольников,
опущенные на гипотенузы, равны
радиусу вписанной окружности,
а высота трапеции равна диаметру
вписанной окружности.

118
ОКРУЖНОСТЬ
ПРЯМЫЕ И ОТРЕЗКИ,
СВЯЗАННЫЕ С ОКРУЖНОСТЬЮ
УГЛЫ, СВЯЗАННЫЕ С ОКРУЖНОСТЬЮ
УГЛОВАЯ МЕРА ДУГИ ОКРУЖНОСТИ
Угловой мерой дуги окружности является центральный угол, который
опирается на эту дугу.
РАДИАННАЯ МЕРА УГЛА
Угол в один радиан равен центральному углу,
опирающемуся
на дугу, длина которой равна радиусу окружности.
/ У
1 радиан* 57°17'45",
10= у|г радиан
я радиан = 180°,
— радиан = 90°.

119
СВОЙСТВА ВПИСАННЫХ УГЛОВ
Вписанный угол равен половине
центрального, опирающегося
на ту же дугу:
Р 2
Все вписанные углы, опирающиеся
на одну и ту же дугу, равны.
Все вписанные углы, опирающиеся на одну
и ту же хорду,
вершины которых лежат
по одну сторону от этой хорды, равны.
Любая пара углов, опирающихся
на одну и ту же хорду, вершины которых
лежат по разные стороны хорды,
составляют в сумме 180°:
а + р= 180°.
Все вписанные углы, опирающиеся на
диаметр, прямые.

120
УГЛЫ МЕЖДУ ХОРДАМИ, КАСАТЕЛЬНЫМИ
И СЕКУЩИМИ
Угол между
пересекающимися хордами:
а + р
Угол между секущими,
пересекающимися
вне окружности:
р-а
Угол между касательной
и секущей:
Р-а
У = —Г"-
Угол между касательными:
р-а
У = —~— = л - а .
Угол между касательной
и хордой:
а
У=2

121
СВОЙСТВА ХОРД
Если хорды равноудалены
от центра окружности,
то они равны.
Если хорды равны,
то они равноудалены
от центра окружности.
Большая из двух хорд
находится ближе
к центру окружности.
©Наибольшая хорда
является диаметром.
Если диаметр делит хорду пополам,
то он перпендикулярен ей.
Если диаметр перпендикулярен хорде,
то он делит ее пополам.
Длина хорды:
/ = 2/?sin^ = 2/?sinp\

122
СООТНОШЕНИЯ МЕЖДУ ДЛИНАМИ ХОРД, ОТРЕЗКОВ
КАСАТЕЛЬНЫХ И СЕКУЩИХ
Отрезки
пересекающихся хорд связаны
соотношением:
ab = cd.
Отрезки касательных,
проведенных
из одной точки, равны:
АВ = АС.
Квадрат отрезка
касательной равен
произведению отрезков
секущей, проведенной из
той же точки:
АВ2 = АС • AD .
Произведения отрезков
секущих, проведенных
из одной точки, равны:
АВ AC = AD АЕ.

123
СВОЙСТВА ДУГ И ХОРД
Равные дуги стягиваются равными Дуги, заключенные между парал-
хордами. дельными хордами, равны.
ДЛИНА ДУГИ И ОКРУЖНОСТИ
(у )
Длина дуги: / = а г
Длина окружности:
(угол а в радианах).
L = 2пг.
ПЛОЩАДЬ КРУГА И ЕГО ЧАСТЕЙ
0
Площадь круга: S = пг2.
Площадь сектора: S = ^"а/*2
(угол а в радианах).
Площадь сегмента: S = у (а - sin а)г2
' (угол а в радианах).

124
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ДВУХ ОКРУЖНОСТЕЙ.
ОБЩИЕ КАСАТЕЛЬНЫЕ
Общей касательной к двум окружностям называется
прямая,
касающаяся обеих окружностей.
/^^Оч Одна окружность лежит внутри другой
/ (02JrS \ — общих касательных нет.
1 ^^!л^У 1 Расстояние между центрами окружностей
V R,/ J меньше разности
\У у их радиусов: 0\02 <R\- R2.
М Одна окружность касается другой
изнута ри — окружности имеют одну общую
02 J точку М, лежащую
^ \ на прямой 0]02.
0, ] Одна общая касательная а проходит че-
J рез эту точку и перпендикулярна
пря/ мой 0/02.
^/ Расстояние между центрами окружностей
равно разности
их радиусов: 0\02 = R\ - R2.
Же
Д *N
Окружности пересекаются —
имеют две общих точки MnN.
-*\ Есть две общих касательных а и Ъ. Если
q \ , радиусы окружностей равны, то каса-
-«^J\ тельные параллельны,
^ а если радиусы не равны, то касатель-
X ные пересекаются в точке,
\ лежащей на прямой 0/02.
' 1 \ Общая хорда MN перпендикулярна
пря/ мой 0/02 и делится ею пополам: MN±
J 0,02; МК = KN.
Расстояние между центрами окружностей
больше разности их радиусов, но меньше
суммы:
R]-R2<0]02<R\ + R2.

126
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ДВУХ ОКРУЖНОСТЕЙ
(продолжение)
Одна окружность касается другой
снаружи — окружности имеют одну общую
точку М,
лежащую на прямой О1О2.
Есть три общих касательных.
Одна из них (а) проходит через
точку касания окружностей
и перпендикулярна прямой O1O2.
Если радиусы окружностей равны, то
две другие общие касательные (Ь и с)
параллельны, а если радиусы не равны,
то эти общие касательные пересекаются
в точке,
лежащей на прямой 0102.
Расстояние между центрами окружностей
равно сумме их радиусов: Oi02 = R1 + R2
Одна окружность лежит вне другой.
Есть четыре общих касательных: две из
них (а и b) называются внутренними
и всегда пересекаются в точке, лежащей
на отрезке 0102.
Две другие общие касательные
(с и d) называются внешними. Если
радиусы окружностей равны, то внешние
касательные параллельны, а если
радиусы не равны, то внешние касательные
пересекаются в точке, лежащей на
прямой О 1О 2.
Расстояние между центрами окружностей
больше суммы их радиусов: 0102 > R\ +
Rt.

126
МНОГОУГОЛЬНИКИ
ПРОИЗВОЛЬНЫЙ МНОГОУГОЛЬНИК
Сумма внутренних углов
и-угольника:
а, +а2+ ... + а„ = 18°°(я - 2).
Сумма внешних углов и-угольника:
р,+р2+ ... + р„ =360°.
Сумма внешних углов
не зависит от п.
Число N диагоналей и-угольника:
N п(п - 3)
Число К треугольников, на которые
разбивается n-угольник диагоналями,
выходящими из одной вершины:

127
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
Так называются многоугольники, у которых все стороны
равны
и все углы равны. Любой правильный многоугольник можно
вписать в окружность и описать около окружности.
СООТНОШЕНИЯ МЕЖДУ СТОРОНОЙ ПРАВИЛЬНОГО
МНОГОУГОЛЬНИКА
И РАДИУСАМИ ВПИСАННОЙ И ОПИСАННОЙ
ОКРУЖНОСТЕЙ
(обозначения: а — сторона, г — радиус вписанной окружности, R —
радиус описанной окружности)
г через а
R через а
а через г
д через /?
треугольник
а
Г~ 2 Л
a = 24br
a = SR
квадрат
а
V2
а = 2г
а = 42R
шестиугольник
г =
2
R = а
2г
V3
a = R
n-угольник
а
Г~ 18°°
2tg
п
R~ . 18-
2 sin
п
о . 18°°
л
то • 18°°
a = 2R sin
п
ПЛОЩАДЬ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ
через а
через г
через /?
треугольник
« Sa2
*~ 4
S = Зл/Зг2
с Зл/ЗЯ2
Л - 4
квадрат
S = a2
5 = 4г2
5 = 2/г2
шестиугольник
е 343а2
*~ 2
S = 2л/3г2
s - 3y^R2
2
n-угольник
с 02П
л. 18°°
4tg
п
S = r2n tg18°°
п
с 1 о2 • 36°°
л = — R л sin
2 «

128
ГЕОМЕТРИЧЕСКИЕ МЕСТА ТОЧЕК
Геометрическим местом точек называется фигура,
удовлетворяющая двум условиям:
1. Все точки фигуры обладают данным свойством.
2. Все точки, обладающие данным свойством,
принадлежат этой фигуре.
НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ МЕСТА ТОЧЕК НА ПЛОСКОСТИ
Окружность —
множество точек,
находящихся
на данном расстоянии
от данной точки О.
Серединный перпендикуляр
к отрезку с концами в двух
данных точках —
множество точек,
равноудаленных от двух данных
точек.
геометрическое место точек
*
•
~~| данная прямая
1
•
■
геометрическое место точек
Две прямые, параллельные
данной
и находящиеся
на данном
расстоянии
от нее —
множество точек,
удаленных
от данной прямой
на данное расстояние.

129
некоторые геометрические места точек на плоскости
(продолжение)
одна из двух данных прямых
| геометрическое место точек
одна из двух данных прямых
Прямая, параллельная двум
данным прямым
и находящаяся
на одинаковом расстоянии
от них — множество точек,
удаленных от двух
параллельных прямых на одно и
то же расстояние.
<о ^ €>
Две дуги окружности
равных радиусов
(за исключением крайних
точек), опирающиеся на
данный отрезок —
множество точек,
из которых данный отрезок
виден под данным углом.

130
ПРЕОБРАЗОВАНИЯ ФИГУР.
ВИДЫ СИММЕТРИИ
ПРЕОБРАЗОВАНИЯ ФИГУР
Параллельный перенос
Все точки фигуры смещаются
в одном и том же направлении
на одно и то же расстояние.
аг • с*
Поворот
Все точки фигуры поворачиваются на
один и тот же угол
вокруг одной и той же точки — центра
поворота.
,i центр
^'/симметрии
Преобразование симметрии
относительно точки
Каждая точка фигуры переходит
в точку, симметричную ей
относительно фиксированной точки — центра
симметрии.
Для плоскости это преобразование
совпадает с поворотом на 180°
(вокруг той же точки).
Преобразование симметрии
относительно прямой
Каждая точка фигуры переходит
в точку, симметричную ей
относительно фиксированной прямой — оси
симметрии.

131
ПРЕОБРАЗОВАНИЯ ФИГУР (продолжение)
Движение
Преобразование фигуры,
при котором расстояния между любыми
соответственными точками фигуры
сохраняются.
Примерами движений являются
параллельный перенос, поворот,
преобразования симметрии относительно точки
и прямой.
Гомотетия
Все точки фигуры смещаются вдоль
прямых, проходящих
через одну и ту же точку
(центр гомотетии) так, что
ОА2 = к ■ ОАх,
ОВ2=к- ОВх и т. д.
Величина к называется коэффициентом
гомотетии.
При к = -\ гомотетия совпадает с
преобразованием симметрии
относительно точки.
Подобие
Преобразование фигуры,
при котором расстояния между
любыми соответственными точками
изменяются в одно
и то же число раз. Пример подобия —
преобразование гомотетии.
Площади подобных фигур относятся как квадраты их линейных
размеров (например, соответствующих сторон, высот, периметров, радиусов
и т.п.).

132
ВИДЫ СИММЕТРИИ ФИГУР
j^>^^ Переносная
^^t^^A Фигура не изменяется
^^**г^ при параллельном переносе.
Пример: прямая не изменяется при
параллельном переносе
вдоль самой себя.
90° 120° Поворотная
^^т**^ Фигура не изменяется при повороте на
1 /Ч ^ некоторый угол.
/ \ Примеры: квадрат не изменяется при
ф * * повороте на 90° вокруг
Х*""""11'^ своего центра, равносторонний
треугольник — при повороте
( Л на 120°, окружность — при повороте
V J на любой угол.
А:/ у
* . Симметрия относительно
точ/ ки
/ Фигура не изменяется
t У > при преобразовании симметрии отно-
0 х сительно точки.
Примеры: параллелограмм, график
функции у = х" при нечетном п.
X 1 X
/ 1 \
1
1
1
1
1
1
1
1
К
-1 Симметрия относительно пря-
\ мой (зеркальная)
\ Фигура не изменяется
при преобразовании симметрии
отно1 сительно прямой.
/ Примеры: равнобедренный
треуголь/ ник, прямоугольник
Г ~
1
1
1
0
£ (две оси симметрии),
равнобокая трапеция, график функции
у = хn при четном п.

133
ДЕКАРТОВЫ КООРДИНАТЫ
У4
Уо
Оси координат:
к ось л: — ось абсцисс,
ось у — ось ординат.
1Л'хо> У (у Точка О — начало координат.
! Любой точке плоскости сопостав-
; ляются два числа: абсцисса д;0 и
О
х0 х ордината ^о-
Эти числа называются
декартовыми координатами данной точки.
У'
Расстояние между двумя точками:
'^*В(х2;У2) АВ = ^(х{-х2)2 +(у1 -у2)2 .
О
А
X
У*
Координаты
* ^»В(х2; у J середины отрезка:
^сос;у) х=х'+*2,
О'
у=У1+У2
У 2 '
У'
Координаты точки, делящей
отрезок в заданном отношении: если
к AD а,
^В(х2;У2) — =— ,то
DB а2
**х;у) ,
0
х а, + а2 а{ + а2
а2 а,
У = У\+ У 2
а{ + а2 а, + а2

134
уравнение прямой
ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ
ах + by + с = 0
(коэффициенты а,Ъ не равны нулю одновременно;
они являются координатами вектора (а; Ь), перпендикулярного данной
прямой).
ЧАСТНЫЕ СЛУЧАИ
ПРЯМАЯ, ПРОХОДЯЩАЯ ЧЕРЕЗ НАЧАЛО КООРДИНАТ
ПОД УГЛОМ К КООРДИНАТНЫМ ОСЯМ
(ГРАФИК ПРЯМОЙ ПРОПОРЦИОНАЛЬНОСТИ)
у А
(а*°,Ь*°,с = 0) => ах + by = "
^> а
*^ > V — — т
О х у b
ПРЯМАЯ, ПАРАЛЛЕЛЬНАЯ ОСИ*
У*
* (a = °,b*0,c±°)^>by + c = 0
1 % о
О
A L
1 х у = -ь
ПРЯМАЯ, ПАРАЛЛЕЛЬНАЯ ОСИ у
У
* (а*°,Ь = °,с*°)=>ах + с = °
О
х X =
а
УРАВНЕНИЕ ОСИ*
у А
(а = °, b ±°, с = °) => by = °
о
У =
О
X
УРАВНЕНИЕ ОСИ у
У
< (а*°,Ь = °,с = °) => ах = °
х = °
О
X

135
УРАВНЕНИЕ ПРЯМОЙ
С УГЛОВЫМ КОЭФФИЦИЕНТОМ
У*
у = кх + Ь; к = tg а
У*
а
£ > 0 при 0°<а<90с
О
к<0 при 90°<а< 180е
ЧАСТНЫЕ СЛУЧАИ
ГРАФИК ПРЯМОЙ ПРОПОРЦИОНАЛЬНОСТИ
У*
Ь = 0,к*0
у = кх
о
ПРЯМАЯ, ПАРАЛЛЕЛЬНАЯ ОСИ X
У*
о
к = 0,Ь*0
у = Ь
УРАВНЕНИЕ ПРЯМОЙ,
ПРОХОДЯЩЕЙ ЧЕРЕЗ ДВЕ ЗАДАННЫЕ ТОЧКИ
(У ~ Ух)(х2 - х,) = (х - х,)()>2 - у{)
Если х1 ф х2, ух ф у2, это
уравнение можно записать
(х» Уг)
в виде
У'У\ _ х~х\
у2-у1
х2-х,
УРАВНЕНИЕ ПРЯМОЙ В ОТРЕЗКАХ НА ОСЯХ
а Ъ
О

136
взаимное расположение двух прямых, заданных общим
уравнением прямой
1\: а\Х + Ъ
\у + с\=0; h: <22X + b2y + C2 = 0
СОВПАДАЮЩИЕ ПРЯМЫЕ
У*
X
Для
коэффициентов ait bit с,,
отличДля произвольных
коэффициентов
ных от нуля:
% п ПС
а» Ьи ct:
А "1 и\ ^1
х — - т~ - —
а2 о2 с2
\axb2 = a2bx
\axc2 = a2cx
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
У'
^^^^ CL2 Ь2 ^2
\axb2 - a2bx
[alc2 ф a2cx
л
X
ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ
и
£l± А.
а2 b2
axb2 ф a2bx
\
А
X
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ
Ik ^
щ_ = Ь^
Ьх а2
axa2 + bxb2 = °
X

137
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ, ЗАДАННЫХ УРАВНЕНИЕМ
ПРЯМОЙ
С УГЛОВЫМ КОЭФФИЦИЕНТОМ
l1: у = к1 х + b1; l2: у = к2х + bг
СОВПАДАЮЩИЕ ПРЯМЫЕ
У*
' h/f *i = к2
^ b\=b7
X
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
У'
ъ bi *ъ.
ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ
у'
у/12 к\ *к2
>
>w X
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ
\?
Ы2 = -1
\ х

138
КООРДИНАТЫ ТОЧКИ ПЕРЕСЕЧЕНИЯ ДВУХ ПРЯМЫХ
1\: а\х + Ь\у + с\ = 0; h: а^х + Ъгу + сг = 0
или
1\: у = к\ х + b\; h: у = кгх + Ьг
являются решением системы уравнений:
У*
Уо
' Ч7 У
\ахх + Ьху + сх = 0
\а2х + Ь2у + с2 = °
откуда
х _ Ь\С2 ~ Ь2с\
axb2 - a2bx
\y = kxx + bx
\y = k2x + b2
откуда
x - bx~bl
у _ ^1^2 _ ^2^1
хо \ х
axb2 - a2bx
Jc^ /^2
УРАВНЕНИЕ ОКРУЖНОСТИ
(
У
,—
С центром в начале координат:
р.
>
У
V
С центром в точке (х0; уо):
Уо
\
Jp\ (JC-JC.)2 +(у-у.)2 = R2,
1 J
о]

139
ВЕКТОРЫ
Так называются величины, которые характеризуются
численным значением и направлением. На чертежах векторы
изображаются в виде направленных отрезков. Длина
отрезка называется модулем (абсолютной величиной) вектора.
ОБОЗНАЧЕНИЯ ВЕКТОРОВ
а или АВ,
где А — начало вектора,
В —конец вектора.
Обозначение модуля: | а | или| АВ \.
НУЛЕВОЙ ВЕКТОР
Так называется вектор, конец которого совпадает с началом.
На чертежах такой вектор изображается точкой и обозначается
О. Модуль нулевого вектора равен нулю,
а его направление не определено.
КОЛЛИНЕАРНЫЕ ВЕКТОРЫ
Так называются векторы, лежащие на одной прямой
или на параллельных прямых.
(Нулевой вектор считается коллинеарным любому вектору.)
ВИДЫ КОЛЛИНЕАРНЫХ ВЕКТОРОВ
сонаправленные
противоположно направленные
равные
противоположные

140
ДЕЙСТВИЯ НАД ВЕКТОРАМИ
СЛОЖЕНИЕ ДВУХ ВЕКТОРОВ
правило
треугольника
правило
параллелограмма
В
Сумма двух векторов находится
с помощью
правила треугольника
или правила параллелограмма:
с = а + b .
Для любых трех точек А.В.С
справедливо соотношение:
АВ + ВС = АС
СЛОЖЕНИЕ НЕСКОЛЬКИХ ВЕКТОРОВ
d = а + Ъ + с
Сумма нескольких векторов
находится аналогично
сумме двух векторов
с помощью правила
многоугольника,
которое является обобщением
правила треугольника.
ВЫЧИТАНИЕ ВЕКТОРОВ
Разность двух векторов
а и b — это вектор с ,
который в сумме с вектором b
дает вектор а :
b + с =а => с - а - b
Вектор с можно найти также,
складывая с вектором а
вектор - b , противоположный вектору
b:
С = а + (-b)

141
ДЕЙСТВИЯ НАД ВЕКТОРАМИ (продолжение)
УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
а / /
f Произведение вектора а
на число X — это коллинеарный
ему
вектор Ха, сонаправленный
с вектором а , если X > 0,
и направленный
противоположно ему,
если X < 0.
Модуль вектора Ха
удовлетворяет соотношению:
Л
\Ха\=\Х\\а\.
СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ
Скалярное произведение а • Ь векторов а и Ь — это число, равное
произведению модулей векторов на косинус угла между ними:
а Ь = \а\ ■ |z>| • coscp.
Модуль вектора \а\ = 4й • а ■■
а1 .
ъ "**
Ь
0° < ф < 90°
Ф = 90° 90°<ф<180°
а-Ь >'
а
• b = " а•b <°

142
КООРДИНАТЫ ВЕКТОРА
Координатами вектора называются разности координат
конца и начала вектора.
на плоскости
У2
У]
l2 X
Координаты вектора
а(ах\ау):
ах = х2 - x),
ау =Уг~У\
Модуль вектора
\а\ = ^а2х + а
в пространстве
Координаты вектора
а(ах\ау\аг) :
ах =x2-xh
ау=Уг~У\
az=z2- Z|
Модуль вектора
\а | = yjaj + а2у + а
Координаты вектора не изменяются при параллельном
переносе.
У равных векторов соответствующие координаты равны.

143
ДЕЙСТВИЯ НАД ВЕКТОРАМИ
В КООРДИНАТНОМ ПРЕДСТАВЛЕНИИ
НА ПЛОСКОСТИ
В ПРОСТРАНСТВЕ
СЛОЖЕНИЕ ВЕКТОРОВ:
с = а + b
сх = ах + bх
су = ау + by
сх = ах + bх
су = ау + by
cz = az + bz
ВЫЧИТАНИЕ ВЕКТОРОВ:
с = а - b
сх = ах- bх
су = ау- by
cx-ax- bx
cy = ay- by
cz = az- bz
УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО:
b = Ха
Ьх = Хах
by = Хау
bx - Xax
by - "kay
bz = "kaz
СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ:
s = а • b
s = ахЬх + ауЬу
s = axbx + ayby +azbz

144
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ВЕКТОРОВ
УГОЛ МЕЖДУ ВЕКТОРАМИ
В координатном представлении:
Косинус угла между
векторами находится
из соотношения
ab
coscp =
на плоскости:
coscp =
ахЬх + ауЬу
yja2x+a2y -^b2x +b2y
в пространстве:
COSCp =
axbx+ayby+azbz
\а\
Ja2x+a2y+a2 .Jb2x+b2y+bl
ПЕРПЕНДИКУЛЯРНЫЕ (ОРТОГОНАЛЬНЫЕ) ВЕКТОРЫ
Скалярное произведение
равно нулю:
а Ъ = ° .
В координатном представлении:
на плоскости:
axbx + ауЬу = О,
в пространстве:
axbx + Qyby + azbz = 0.
КОЛЛИНЕАРНЫЕ ВЕКТОРЫ
В координатном представлении:
координаты векторов пропорциональны,
то есть удовлетворяют соотношениям:
на плоскости: axby = ауЬх,
а й
(если ab bi ф 0, то = -f-),
0. Ь„
Модуль скалярного
произведения векторов равен
произведению
их модулей:
\а ■ b\ = \а\■ \Ь\.
в пространстве:
\ахЪу = ауЬх
а, ау _ az
(если ab bi ф 0, то -f- = -f- = ).
or b„ 0,

145
РАЗЛОЖЕНИЕ ВЕКТОРА НА ПЛОСКОСТИ
ПО ДВУМ НЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ
На плоскости любой вектор с
может быть представлен
1 ~~уР
в виде суммы двух векторов,
соотХа /
ветственно коллинеарных двум
/ '''
заданным неколлинеарным
векторам а и b :
—» —
с = Ха + [ib ,
Ь lib
где X и (j. — числа.
Х>0, ц>0
Такое представление называется
_ J
разложением вектора по двум
заданным векторам.
Разложить вектор
на плоскости по двум заданным
неколлинеарным векторам можно
Х<0, ц>0
единственным образом.
РАЗЛОЖЕНИЕ ВЕКТОРА В ПРОСТРАНСТВЕ ПО ТРЕМ
НЕКОМПЛАНАРНЫМ ВЕКТОРАМ
(Компланарными называются векторы,
параллельные одной и той же плоскости)
В пространстве любой вектор d может быть представлен в виде суммы
трех векторов, соответственно коллинеарных трем заданным
некомпланарным векторам а , b и с:
d = Ха + \ib + vc ,
где X, [i и v — числа.
Такое представление называется разложением вектора
по трем заданным векторам.
Разложить вектор в пространстве по трем заданным некомпланарным
векторам можно единственным образом.

146
РАЗЛОЖЕНИЕ ВЕКТОРА
ПО КООРДИНАТНЫМ ВЕКТОРАМ
Координатные векторы (орты) направлены вдоль осей
координат. Модули этих векторов равны 1.
Обозначения координатных векторов:
на плоскости
/(1; °),Д°; 1)
или
ад •), ад 1)
О i 1
в пространстве
/(1; •),;<•; 1; °), *("; °; 1)
или
°; в), ё2(°; 1; °), e3(e; °; 1)
2
3 х
1*0
2 У
Любой вектор а можно разложить единственным образом
по координатным векторам:
а = axi + ayj
а = aj + a j + а к
Коэффициенты разложения ах являются
проекциями вектора а на оси координат.

147
СТЕРЕОМЕТРИЯ
ПРЯМЫЕ И ПЛОСКОСТИ
В ПРОСТРАНСТВЕ
СПОСОБЫ ЗАДАНИЯ ТОЧКИ
Точка в пространстве однозначно определяется:
Тремя попарно пересекающимися плоскостями,
если прямые пересечения плоскостей пересекаются.
СПОСОБЫ ЗАДАНИЯ ПРЯМОЙ
Прямая в пространстве однозначно определяется:
Двумя пересекающимися
прямыми.
Пересекающимися прямой и
плоскостью.
Двумя точками.
Двумя пересекающимися
плоскостями.

148
СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ
Плоскость в пространстве однозначно определяется:
Тремя точками,
не лежащими
на одной прямой.
Двумя
пересекающимися прямыми.
Двумя
параллельными прямыми.
а
А
Прямой и точкой,
не лежащей на ней.

149
параллельность прямых
и плоскостей
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Так называются прямые, которые лежат в одной
плоскости
и не пересекаются.
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ
Две прямые, параллельные
треть—\
ей,
/? \
параллельны между собой:
/а\- - ~ ~ ~ ~ \
(а 11 с , Ь 11 с) => а 11Ь
ПАРАЛЛЕЛЬНЫЕ ПРЯМАЯ И ПЛОСКОСТЬ
Прямая и плоскость называются параллельными,
если они не пересекаются.
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
Если прямая, не принадлежащая данной
плоскости, параллельна одной из
прямых этой плоскости,
то она параллельна
этой плоскости:
(b\\а, beta, ааа) =>0||а.
СВОЙСТВО ПРЯМОЙ, ПАРАЛЛЕЛЬНОЙ ДАННОЙ ПЛОСКОСТИ
/ Л^—-— ~7 Любая плоскость, проходящая через
х ***"^*^ прямую параллельную данной
плоскости, либо параллельна этой плоскости,
либо пересекает ее по прямой,
параллельной данной прямой:
(Ь с р\ о||а) => (311ot или а\\Ь .

150
ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
Так называются плоскости, которые не пересекаются.
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПЛОСКОСТЕЙ
Если две пересекающиеся прямые
одной плоскости соответственно
параллельны двум
пересекающимся прямым другой плоскости,
то эти плоскости параллельны:
(я,||я2, Z>1||Z>2)^a||p.
Если каждая из двух данных
плоскостей параллельна третьей
плоскости,
то данные две плоскости
параллельны между собой:
(a||y, Р ||у) ^ а||р.
Если две параллельные плоскости
пересекаются третьей плоскостью,
то линии пересечения плоскостей
параллельны:
а ||р => a\\b.
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ
Отрезки параллельных прямых,
заключенные
между двумя параллельными
плоскостями, равны:
(а ||р, a\\b)^AB = CD.

151
перпендикулярность прямых
и плоскостей
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ
Две прямые называются перпендикулярными,
если они пересекаются под прямым углом.
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМЫХ
Две пересекающиеся прямые,
параллельные соответственно двум
перпендикулярным прямым,
перпендикулярны:
(e,||A,, a2\\b2, ах±.а2) => bxLb2.
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Прямая, пересекающая плоскость, называется
перпендикулярной этой плоскости, если она перпендикулярна любой
прямой, принадлежащей плоскости
и проходящей через точку пересечения.
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ и плоскости
Если прямая перпендикулярна двум
переа секающимся прямым данной плоскости, то
она перпендикулярна этой плоскости:
(а±Ь и а±с) => da.
ПРЯМЫЕ, ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ
Две прямые, перпендикулярные одной и
той же плоскости, параллельны.
Если одна из двух параллельных прямых
перпендикулярна данной плоскости, то и
другая прямая перпендикулярна этой
плоскости.

152
ПРЯМАЯ, ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТЯМ
Прямая, перпендикулярная
одной из двух параллельных плоскостей,
перпендикулярна
и другой плоскости.
Две плоскости,
перпендикулярные
одной и той же прямой, параллельны.
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
Пересекающиеся плоскости называются
перпендикулярными, если третья плоскость, перпендикулярная прямой
пересечения этих плоскостей, пересекает их по
перпендикулярным прямым.
а
третья
плоскость
Ту
a_Lp
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ
Плоскости перпендикулярны,
если одна из них содержит перпендикуляр
к другой плоскости:
(а с аи а 1 р) a _L р.
СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПЛОСКОСТЕЙ
Если плоскости перпендикулярны,
то прямая, лежащая в одной из них
и перпендикулярная линии пересечения
плоскостей, перпендикулярна другой
плоскости:
(a 1 ри а с аи а 1 b) => а 1 р.

153
ПЕРПЕНДИКУЛЯР И НАКЛОННЫЕ
i/
i/
'в,
^ Перпендикуляр короче
г|> любой наклонной,
ц проведенной к плоскости
из той же точки.
Iе ~7
ХфуУ
A
Ч У равных наклонных, проведенных
\ к плоскости из одной точки, проекции
рав•Цц^ У Справедливо и обратное: если у двух
на/ клонных, проведенных из одной точки,
проекции равны, то равны и наклонные.
\ Из двух наклонных,
\ проведенных из одной
\ У точки, больше та,
^ У у которой проекция больше.
Справедливо и обратное.
Теорема о трех перпендикулярах
(содержит два утверждения:
{ прямое и обратное)
\ Если прямая, лежащая в плоскости
\ и проходящая через основание наклонной,
\ перпендикулярна проекции наклонной,
\ то она перпендикулярна
\ и самой наклонной.
V.y—у Если прямая, лежащая в плоскости
' , \У У и проходящая через основание наклон-
S У ной, перпендикулярна наклонной, то она
перпендикулярна и проекции наклонной.

154
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ
Так называются прямые, которые не лежат в одной
плоскости
(то есть не параллельны и не пересекаются).
ПРИЗНАК СКРЕЩИВАЮЩИХСЯ ПРЯМЫХ
Если одна из двух данных прямых
пересекает плоскость, в которой лежит другая
прямая, и точка пересечения прямой и
плоскости
не принадлежит другой прямой,
то данные прямые скрещиваются.
РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Через две скрещивающиеся прямые можно
провести две параллельные плоскости
(единственным образом).
Расстоянием между скрещивающимися
прямыми называется расстояние
между этими плоскостями.
ОБЩИЙ ПЕРПЕНДИКУЛЯР К ДВУМ СКРЕЩИВАЮЩИМСЯ ПРЯМЫМ
Так называется отрезок,
перпендикулярный каждой из двух скрещивающихся
прямых, концы которого лежат на этих
прямых.
Длина общего перпендикуляра равна
расстоянию между скрещивающимися
прямыми.
УГОЛ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Так называется угол между
пересекающимися прямыми, соответственно
параллельными
двум данным скрещивающимся прямым.
(Одна из упомянутых пересекающихся
прямых
может совпадать
с одной из скрещивающихся.)
общий
перпендикуляр

155
УГЛЫ В ПРОСТРАНСТВЕ
УГОЛ МЕЖДУ ПРЯМОЙ и плоскостью
Так называется угол между прямой
и ее проекцией на плоскость.
ДВУГРАННЫЙ УГОЛ
Так называется фигура, образованная
двумя полуплоскостями
с общей ограничивающей их прямой (эта
прямая называется
ребром двугранного угла).
ЛИНЕЙНЫЙ УГОЛ ДВУГРАННОГО УГЛА
Так называется угол между двумя лучами,
образующимися
при пересечении двугранного угла
плоскостью, перпендикулярной ребру
двугранного угла.
Мерой ф двугранного угла является мера
соответствующего ему линейного угла: 0°
<Ф<180°.
УГОЛ МЕЖДУ плоскостями
Две пересекающиеся плоскости
определяют четыре двугранных угла. Сумма двух
таких углов, имеющих общую грань, равна
180°. Углом между плоскостями называют
меньший из этих углов:
0° < ф < 90°. (Если ф = 90°, плоскости
перпендикулярны.)

156
ПРИЗМА
Так называется многогранник, две грани которого
(основания) — равные n-угольники, лежащие в параллельных
плоскостях,
а остальные п граней (боковые грани) — параллелограммы.
Призма называется прямой, если все ее боковые ребра
перпендикулярны основаниям. Призма называется
правильной,
если она прямая и ее основания — правильные
многоугольники.
сечение
Наклонная призма Прямая призма
ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЕМ ПРИЗМЫ
Наклонная призма
Прямая призма
Боковая
поверхность
*^бок — -^сеч'А
где Рсеч — периметр
перпендикулярного сечения,
/ — длина бокового ребра
^бок — Росн'Н)
где Pqch — периметр
основания,
Н — высота
Полная
поверхность
■^полн — $бок "t" 2... "iSoch
^полн — "$бок 2... 'S0CH
Объем
V= S -l
' '-'сеч '»
где Sce4 — площадь
перпендикулярного сечения,
/ — боковое ребро
где 50СН — площадь
основания призмы,
Н — высота

157
ПАРАЛЛЕЛЕПИПЕД
Так называется призма, основания которой —
параллелограммы.
Все грани параллелепипеда —
параллелограммы.
Противолежащие грани параллельны и
равны.
Все четыре диагонали пересекаются в
одной точке
и точкой пересечения делятся пополам.
Точка пересечения диагоналей — центр
симметрии.
Сумма квадратов диагоналей равна сумме квадратов всех ребер:
d\ + d\ + d\ + d\ = 4o2 + 4Z>2 + 4c2
Прямой параллелепипед:
боковые ребра перпендикулярны
основаниям.
Боковые грани — прямоугольники,
а основания — параллелограммы.
Прямоугольный параллелепипед:
прямой параллелепипед, основания которого
— прямоугольники.
Все диагонали равны.
Квадрат диагонали равен сумме квадратов
ребер, исходящих из одной вершины:
d2=a2+b2+c2.
Snom = 2 (ab + be + ас); V = abc.
Куб:
все грани — квадраты
Все ребра равны.
d= 4Ъа, S,
= 6а2, V = а\

158
ПИРАМИДА
Так называется многогранник, одна грань которого
(основание) — многоугольник, а все остальные грани (боковые)
треугольники, имеющие общую вершину (вершина
пирамиды).
Усеченной пирамидой называется часть пирамиды,
заключенная между ее основанием и сечением пирамиды,
параллельным основанию.
ПРАВИЛЬНАЯ ПИРАМИДА
Пирамида называется правильной, если основание ее —
правильный многоугольник, а вершина проецируется в
центр основания.
Боковые грани —
равные равнобедренные
треугольники.
Боковые ребра равны.
Апофемы равны
(апофемой пирамиды называется
высота ее боковой грани,
проведенная из вершины пирамиды,
противоположной основанию).
ПРАВИЛЬНАЯ УСЕЧЕННАЯ ПИРАМИДА
высота Н
апофема I
Боковые грани —
равные равнобокие трапеции.
Боковые ребра равны.
Апофемы равны.

159
ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЕМ ПРОИЗВОЛЬНОЙ
ПИРАМИДЫ
Пирамида
Усеченная пирамида
Боковая
поверхность
п
^бок = S t ,
1=1
где Sj — площадь одной
боковой грани
п
"$б0К = SJ ,
/=1
где Sj — площадь одной
боковой грани
Полная
поверхность
^полн — ^бок Soch
^полн — ^бок S + S,
где S — площадь нижнего
основания,
s — площадь верхнего
основания
Объем
V = — Н... • 5"осн
V = — H...-(S + s+JSs)
3
ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЕМ
ПРАВИЛЬНОЙ ПИРАМИДЫ
Пирамида
Усеченная пирамида
Боковая
поверхность
"$бок — "2 Р ' I '
где Р — периметр
основания,
/ — апофема
SeoK=^(P + Р)1,
где Р — периметр нижнего
основания,
р — периметр верхнего
основания,
/ — апофема
Полная
поверхность
^полн — "^бок $осн
^полн — "$бок + 5 + 5,
где 5 — площадь нижнего
основания,
s — площадь верхнего
основания
Объем
V = — Н... • S0CH
V = | H...(S + s+y[Ss)

160
ТЕЛА ВРАЩЕНИЯ
ЦИЛИНДР
Прямым
круговым
цилинКОНУС
Прямым
круговым конусом
УСЕЧЕННЫЙ
КОНУС
Так
называется часть
конуса,
ограниченная его
основанием и

сечением,параллельным
основанию.
дром
называется фигура,
называется
фигура,
полуполученная
ченная при
при вращении
вращении


прямоугольнока вокруг оси,
содержащей
го
треугольника вокруг оси,
одну из его
содержащей
сторон.
его катет.
образующая
^— 1
i!
§1 ^ \
С 4-О
ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЕМ ЦИЛИНДРА
Боковая поверхность
Полная поверхность
Объем
^бок ~ 2nRH
5П0ЛН = 2nR(R + Н)
V=nR2H
ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЕМ КОНУСА
Конус
Усеченный конус
Боковая
поверхность
•$бок= kRL
5бок = n(R + r)L
Полная
поверхность
Snom = nR(R + L)
Sno/IH=n(R + r)L + n(R2 +r2)
Объем
V = \nR2H
3
V = |лЯ(Я2 +Rr + r2)

161
СФЕРА. ШАР
Сферой называется множество всех точек пространства,
находящихся на данном расстоянии R от данной точки О.
Шаром называется множество всех точек пространства,
находящихся от данной точки О на расстоянии,
не большем данного расстояния R.
Сфера является поверхностью шара.
Площадь сферы S = 4nR
4
Объем шара V = — я/?3
ЧАСТИ ШАРА
V *
Шаровой сегмент
k Объем V = -яЯ2(ЗД- Я)
1 3
О
Площадь сегментной поверхности
5бок= 2 я/?Я
С *
Шаровой сектор
, Объем V = — nR2H
> 3
О
Площадь полной поверхности
Snom = nR(2H + J2RH - Н2)
Шаровой слой
^ Объем
A V = ^nH'+^n(r2 + r2)H
^^у/ Площадь боковой поверхности
>$бок= 2 nRH

162
ВПИСАННЫЕ И ОПИСАННЫЕ ТЕЛА1
ЦИЛИНДР, ОПИСАННЫЙ ОКОЛО ПРИЗМЫ
Цилиндр можно описать около
прямой призмы, если ее основание —
многоугольник,
вписанный в окружность.
Радиус цилиндра R равен радиусу
этой окружности.
Ось цилиндра лежит
на одной прямой
с высотой Н призмы, соединяющей
центры окружностей, описанных
около
оснований призмы.
ЦИЛИНДР, вписанный в призму
Цилиндр можно вписать
в прямую призму, если
ее основание — многоугольник,
описанный около окружности.
Радиус цилиндра r равен радиусу этой
окружности.
Ось цилиндра лежит
на одной прямой
с высотой Н призмы, соединяющей
центры окружностей, вписанных
в основания призмы.
* На рисунках этого раздела описанное тело изображено как
прозрачное. Рассмотрены наиболее часто встречающиеся комбинации тел.

163
КОНУС, ОПИСАННЫЙ ОКОЛО ПИРАМИДЫ
Конус можно описать
около пирамиды,
если ее основание —
многоугольник,
вписанный в окружность,
а вершина пирамиды проецируется
в центр
этой окружности.
Радиус конуса R
равен радиусу этой окружности,
а высоты Н конуса
и пирамиды совпадают.
конус, вписанный в пирамиду
Конус можно вписать
в пирамиду,
если ее основание —
многоугольник,
описанный около окружности,
а вершина пирамиды проецируется
в центр этой окружности.
Радиус конуса r
равен радиусу этой окружности,
а высоты Н конуса
и пирамиды совпадают.

164
ШАР, ОПИСАННЫЙ ОКОЛО ЦИЛИНДРА
Шар можно описать около
любого (прямого
кругового) цилиндра.
Окружности оснований
цилиндра лежат на
поверхности шара.
Центр шара лежит
на середине высоты,
проходящей
через ось цилиндра.
Сечение плоскостью, проходящей через
ось цилиндра
(осевое сечение)
О
К н
И г \
Радиус шара R,
радиус цилиндра r
и высота цилиндра Н
связаны соотношением:
R2 =
+ г

165
ШАР, ВПИСАННЫЙ В ЦИЛИНДР
Сечение плоскостью, проходящей через
ось цилиндра (осевое сечение)
Н
R
Шар можно вписать
только в такой цилиндр,
высота которого равна
диаметру основания (такой
цилиндр называется
равносторонним).
Шар касается оснований
цилиндра
в их центрах
и боковой поверхности
цилиндра по окружности
большого круга шара,
параллельной основаниям
цилиндра.
Радиус шара R равен
радиусу цилиндра г,
а диаметр шара равен
высоте цилиндра:
R = r,
2R = H.

166
ШАР, ОПИСАННЫЙ ОКОЛО КОНУСА
Шар можно описать около
любого конуса.
Окружность основания
конуса и вершина конуса
лежат
на поверхности шара.
Центр шара лежит
на оси конуса
и совпадает
с центром окружности,
описанной около
треугольника, являющегося
осевым сечением конуса.
Сечение плоскостью, проходящей через
ось конуса (осевое сечение)

167
ШАР, ВПИСАННЫЙ В КОНУС
Шар можно вписать
в любой конус.
Шар касается основания
конуса
в его центре
и боковой поверхности
конуса по окружности,
лежащей в плоскости,
параллельной основанию
конуса.
Центр шара лежит
на оси конуса
и совпадает
с центром окружности,
вписанной
в треугольник,
являющийся осевым сечением
конуса.
Сечение плоскостью, проходящей через
ось конуса
(осевое сечение)

168
ШАР, ОПИСАННЫЙ ОКОЛО ПРИЗМЫ
Шар можно описать около
призмы,
если она прямая
и ее основания являются
многоугольниками,
вписанными
в окружность.
Центр шара лежит на
середине высоты призмы,
соединяющей центры
окружностей, описанных
около оснований призмы.
Сечение полуплоскостью,
проходящей через центр шара
и боковое ребро призмы.
(Полуплоскость ограничена
прямой, параллельной боковому
ребру призмы
и проходящей
через центр шара.)
Радиус шара R, высота
призмы Н и радиус
окружности г, описанной около
основания призмы,
связаны соотношением:

169
ШАР, ВПИСАННЫЙ В ПРЯМУЮ ПРИЗМУ
Сечение полуплоскостью,
перпендикулярной боковой
грани призмы
и проходящей через высоту
призмы, соединяющую
центры окружностей,
вписанных в основания.
I
Шар можно вписать
в прямую призму, если ее
основания являются
многоугольниками,
описанными около окружности,
а высота призмы равна
диаметру
этой окружности.
Радиус вписанного шара
равен радиусу этой
окружности.
Центр шара лежит
на середине высоты
призмы, соединяющей
центры окружностей,
вписанных
в основания призмы.
Радиус шара R,
высота призмы Н и радиус
окружности r, вписанной
в основание призмы,
связаны соотношениями:
D Н
К - Г = .
2

170
ШАР, ОПИСАННЫЙ
ОКОЛО ПРАВИЛЬНОЙ ПИРАМИДЫ
1 Шар можно описать около
любой правильной
пирамиды.
Центр шара лежит на
прямой, содержащей высоту
пирамиды
и совпадает с центром
окружности, описанной
около равнобедренного
треугольника,
боковой стороной
которого является боковое ребро
пирамиды,
а высотой — высота
пирамиды.
Радиус шара равен
радиусу этой окружности.
Сечение полуплоскостью,
проходящей через центр шара
и боковое ребро пирамиды.
(Полуплоскость ограничена прямой,
проходящей
через высоту пирамиды.)
i
Радиус шара R, высота
пирамиды Н и радиус
окружности г, описанной
около основания
пирамиды, связаны
соотношением:
R2 = (H-R)2 +г2.
Это соотношение
справедливо и в том случае, когда
H<R.

ШАР, ВПИСАННЫЙ
В ПРАВИЛЬНУЮ ПИРАМИДУ
Сечение полуплоскостью,
проходящей через центр шара и апофему
пирамиды. (Полуплоскость
ограничена прямой, проходящей через
высоту пирамиды.)
Шар можно вписать
в любую правильную
пирамиду.
Центр шара лежит на
высоте пирамиды
и совпадает с центром
окружности, вписанной в
равнобедренный
треугольник,
боковой стороной
которого является апофема
(высота боковой грани)
пирамиды,
а высотой — высота
пирамиды.
Радиус шара равен
радиусу этой окружности.
Радиус шара R, высота
пирамиды Н и радиус
окружности r, вписанной в
основание пирамиды,
связаны соотношением:
R г

172
ДЕКАРТОВЫ КООРДИНАТЫ
а
Оси координат:
ось х — ось абсцисс,
ось у — ось ординат,
ось z — ось аппликат.
"""""] Точка О — начало координат.
*А(х '• v ■ 7 )
I \ о> so> чу Любой точке пространства сопоставляются
три числа:
абсциссах$, ордината^
и аппликата zq.
Эти числа называются декартовыми
координатами данной точки.
Уо
Расстояние между двумя точками:
B(x2;y2;Z2) ^B = 4(xx-x2f-v(yx-y2Y^(zx-z2)2
Координаты середины отрезка:
A(xj;yj;zj)
+ х2
2
Ух
+ У2
2
Z\
+ z2
2
и
Координаты точки, делящей отрезок
в заданном отношении:
AD а,
В(х2; у2; Z2) если = —L, то
DB а2
]D(x;y;z)
х =
Л(х,; у,; Zj)
а2
а
+ а2
а2
а
+ а2
а2
а,
+ а2
X, +
У\ +
Z, +
а,
а
+ а2
а,
а
+ а2
а,
а,
+ а2
У2
УРАВНЕНИЕ ПЛОСКОСТИ
ax + by + cz + d = 0
(коэффициенты а,Ъ,с не равны нулю одновременно;

173
они являются координатами вектора (a и b и c), перпендикулярного
данной плоскости)
ЧАСТНЫЕ СЛУЧАИ УРАВНЕНИЯ ПЛОСКОСТИ
d =0 => ах + by + cz = 0
Плоскость проходит через начало
координат.
а = ° => by + cz + d =
Плоскость параллельна оси х.
(а = ° и d = 0) => by + CZ =
Плоскость проходит через ось х.
гл.
ху
Ь =0 => ax + cz + d =
Плоскость параллельна оси у.
(Ь = ° и d = 0) => ах + CZ =
Плоскость проходит через ось у.
с = ° => ах + by + d =
Плоскость параллельна оси z.
(с = ° и d = 0) => ax + by =
Плоскость проходит через ось z.
ЧАСТНЫЕ СЛУЧАИ УРАВНЕНИЯ ПЛОСКОСТИ
ax + by + cz + d = 0
(продолжение)

174
(а = °иЬ = °) => CZ + d = °
Плоскость параллельна плоскости
ху.
(a = °Hb = °Hd = ') => CZ =
Плоскость совпадает
с плоскостью ху.
It
(а = ° и с = °)
Плоскость параллельна плоскости
XZ.
(a = °HC = 0vid = o)
Плоскость совпадает
с плоскостью XZ.
(Ь = "ис = °) => ax + d = °
Плоскость параллельна плоскости
yz.
(b = °Hc = °vid = 0) => ах =
Плоскость совпадает
с плоскостью yz.
УРАВНЕНИЕ ПЛОСКОСТИ В ОТРЕЗКАХ НА ОСЯХ
a b с
(а±0иЬ*0исФ0)

175
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ДВУХ ПЛОСКОСТЕЙ
«1: а\ х + bx у + С\ z + d\ = 0;
а2: а2х + Ъ2у + c2z + d2 = 0
СОВПАДАЮЩИЕ ПЛОСКОСТИ
Для коэффициентов Для произвольных
ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
— ф
с, d.
ахЬ2 = a-,h
ахс2 = а-^с
24
axd2 ф a2dx
ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ
аха2 + ЪХЬ2 + схс2 =

176
УГОЛ МЕЖДУ ДВУМЯ ПЛОСКОСТЯМИ
(меньший из двух смежных углов)
а,: ахх + bxy + cxz + dx = 0;
а2: а2х + Ъ2у + c2z + d2 = 0

177
СПРАВОЧНЫЕ ТАБЛИЦЫ

178
ПРИЗНАКИ ДЕЛИМОСТИ
на 2
последняя цифра числа четная
на 3
сумма цифр числа делится на 3
на 4
две последние цифры числа нули или образуют число,
делящееся на 4
на 5
последняя цифра числа 0 или 5
на 6
число должно делиться на 2 и на 3 (см.
соответствующие признаки делимости)
на 8
три последние цифры числа нули или образуют число,
делящееся на 8
на 9
сумма цифр числа делится на 9
на 11
сумма цифр, стоящих на четных местах, отличается
от суммы цифр, стоящих на нечетных местах, на
число, кратное 11
на 25
две последние цифры числа 00, 25, 50 или 75
ТАБЛИЦА ПРОСТЫХ ЧИСЕЛ (до 997)
2
79
191
311
439
577
709
857
3
83
193
313
443
587
719
859
5
89
197
317
449
593
727
863
7
97
199
331
457
599
733
877
11
101
211
337
461
601
739
881
13
103
223
347
463
607
743
883
17
107
227
349
467
613
751
887
19
109
229
353
479
617
757
907
23
113
233
359
487
619
761
911
29
127
239
367
491
631
769
919
31
131
241
373
499
641
773
929
37
137
251
379
503
643
787
937
41
139
257
383
509
647
797
941
43
149
263
389
521
653
809
947
47
151
269
397
523
659
811
953
53
157
271
401
541
661
821
967
59
163
277
409
547
673
823
971
61
167
281
419
557
677
827
977
67
173
283
421
563
683
829
983
71
179
293
431
569
691
839
991
73
181
307
433
571
701
853
997

179
ТАБЛИЦА КВАДРАТОВ ДВУЗНАЧНЫХ ЧИСЕЛ
ДЕСЯТКИ
ЕДИНИЦЫ
0
1
2
3
4
5
6
7
8
9
1
100
121
144
169
196
225
256
289
324
361
2
400
441
484
529
576
625
676
729
784
841
3
900
961
1024
1089
1156
1225
1296
1369
1444
1521
4
1600
1681
1764
1849
1936
2025
2116
2209
2304
2401
5
2500
2601
2704
2809
2916
3025
3136
3249
3364
3481
6
3600
3721
3844
3969
4096
4225
4356
4489
4624
4761
7
4900
5041
5184
5329
5476
5625
5776
5929
6084
6241
8
6400
6561
6724
6889
7056
7225
7396
7569
7744
7921
9
8100
8281
8464
8649
8836
9025
9216
9409
9604
9801
ПРОПОРЦИИ*)
СВОЙСТВА ПРОПОРЦИЙ
1.
Произведение крайних членов равно произведению средних,
т.е. если
а С J ¥
— , то аа - ос .
Ъ d
2.
В пропорции, все члены которой отличны от нуля, можно
менять местами средние и крайние члены пропорции, т.е. если
а с
а Ь d с d Ь
то — = — , — = — , — = — .
с d Ъ а с а
ПРОИЗВОДНЫЕ ПРОПОРЦИИ,
а с
полученные из пропорции — = — :
Ъ d
а±Ь с ±d a + b с + d
а с а - b с - d
a±b с ± d а±с а с
~b~~d'
b d b±d b d
anii
+ bnx cm1 + dnx amx + cnx bm1 + dnx
ат2
+ bn2 cn%2 + dn2 an%2 + cn2 bm2 + dn2
где mi, 7П2, пъ n2 — произвольные числа.
*) Во всех приведенных формулах знаменатели не должны
равняться нулю.

180
МНОГОЧЛЕНЫ
а2 - Ь2 = (а - b)(a + Ь)
(а + Ь)2 = а2 + 2аЬ + Ь2
(а - Ъ)2 = а2 - 2аЪ + Ъ2
(а + Ъ + с)2 = а2 + Ъ2 + с2 + 2аЪ + 2Ъс + 2ас
a3 + b3 = (a + Ь)(а2 - ab + b2)
а3 - Ь3 = (а - b)(a2 + ab + b2)
(а + b)3 = а3 + Sa2b + Sab2 + b3 = а3 + b3 + Sab(a + b)
(a - b)3 = a3 - Sa2b + dab2 - b3 = a3 - b3 - Sab(a - b)
Для n e N
an-bn = (a- b)(an~l + an~2b + an~3b2 + ... +abn~2 + b""1)
Если n — четное,
an - bn = (a + b)(an~l - an~2b + an~3b2 - ... + abn~2 - bn~l)
Если n — нечетное,
an + bn = (a + b)(an~l - an~2b + an~3b2 - ... - abn~2 + b""1)
бином ньютона
(а + Ь)п = £cy-V =
= С°а" + Cla^b1 + C2nan~2b2 +... + C^aV-1 + Cnnbn
где C*n =
k\(n-k)\
число сочетаний из n no k.
МОДУЛЬ ЧИСЛА
а, а > О .i Г~Г
\а\ = i , \а\ = yja
[ -а, а < О
\а\ > 0;
\а\ = 0 о а = О
|а-&| = |a|-|b|
= тт, Ь*0
Ы
\а + Ь\< \а\ + \Ъ\
\а - b\ > \\а\ - \Ь\\

181
ПРОГРЕССИИ
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
ап + 1 = ап + d>
Ъп + 1 = Ъп ■ q,
где d - разность прогрессии
где q * 0 - знаменатель прогрессии
Формулы п-го члена
ап = а1 + (п ~ 1)^
ап = аь + (п - k)d
_ an_k + an+k
2
bn = K-k • bn+k
Формулы суммы первых п членов
0 2ах + (л - l)d _
о_ — • П —
2
1-g g-1
а, + а„
= — *--71
2
<Sn = h ■ 7i, <? = 1
Формула для разности
Формула для знаменателя
d = an + i~ ап
q =
Если 71 + т = к + р, то
ал + <*т = а* + Яр
bn ■ bm = bk- bp
Сумма последовательных
Сумма бесконечно убывающей
натуральных чисел от 1 до л:
геометрической прогресии:
s _ 71(71 + 1)
2
s = -^-, И<1
1-9
ПРОСТЕЙШИЕ НЕРАВЕНСТВА*)
а2 + Ь2 > 2аЪ; - + ->2,аЬ>0
b а
а + b г— Л , Л
> ыаЬ , а>0,Ь>0
2
(Среднее арифметическое не меньше среднего геометрического)
*) Равенства в приведенных неравенствах достигаются тогда и
только тогда, когда а = Ь.

182
АРИФМЕТИЧЕСКИЙ КОРЕНЬ
Арифметическим корнем n-ой степени из неотрицательного числа
а называется такое неотрицательное число b, п-ая степень которого
равна а, т.е. у[а = Ъ , если Ъп - а (а > О, Ь > 0).
СВОЙСТВА КОРНЕЙ
Основное свойство корня
п4ат = пу1атк ,а>0
Умножение корней
^a-^b=^ab,a>0,b>0
Деление корней
>/а [а
-V = * - , а > 0, Ь >0
Возведение корня в степень
(я[а)т = tfa™ ,а>0
Извлечение корня из корня
?Щ = пУа~, а > 0
Вынесение множителя
из-под знака корня
2^а2пЪ = \а\ ■ 24b , Ъ > 0
в частности, yla2b = \a\y[b
2nia2n+lb = а ■ 2п+Уь
Внесение множителя
под знак корня
а-2Ф>- \ ^а2пь>(а>0, Ъ>0)
\-2yla2nb,(a<0, b>0)
а ■ 2n+)[b = 2nia2n+1b
СТЕПЕНИ
С натуральным показателем
ап = а • а а» а1 = а
п раз
С положительным
дробным показателем
ап = т[а™ , гдеа> 0, m,n^N
С нулевым показателем
а° = 1, где а Ф 0
С отрицательным
рациональным показателем
а~г = — , где а > 0
аг
Умножение степеней
ар • а9 = ap+q ; apbp=(ab)p
Деление степеней
aq bp \b)
Возведение степени в степень
(ap)q = apq

183
ЛОГАРИФМЫ
Логарифмом положительного числа b по основанию а
(а > 0, а ≠ 1) называется такой показатель степени с, в
которую надо возвести число а, чтобы получить число b:
\ogab = с <=> ас = Ь.
СВОЙСТВА ЛОГАРИФМОВ*)
Основное логарифмическое тождество: а1ов"ь = Ь, Ь > О
loga а = 1
loga 1 = О
Логарифм произведения: loga лгу = loga|х\+ \oga\y\, ху > О
Логарифм частного: loga — = \oga\х\-loga|у\, - > О
У У
• Логарифм степени:
loga хр = p\oga\x\, хр > О
loga, хр = — loga|*|, хр > О
9
• Логарифм корня: loga л/* = -loga дс, дс > О
• Формула перехода к другому основанию:
log. Ь ,
logo & = » гДе & > О, с > О, с * 1
log, a
loga b = ——— , где Ъ > 0, b * 1
logba
*) Во всех приведенных формулах a > 0, a * 1

184
ОСНОВНЫЕ ФОРМУЛЫ
ТРИГОНОМЕТРИИ*)
СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
ОДНОГО И ТОГО ЖЕ АРГУМЕНТА
sin2 х + cos2 х = 1 tg х ■ ctg x = 1
sin x
te* = i + tff2* = —i
cos X ° * 2
cos jc
cos jc 0 1
ctgx = — l + ctg2* =
sin л: sin2x
ФОРМУЛЫ СЛОЖЕНИЯ
sin(x + y) =
sin дс cos i/ + cos x sin z/
sin(x -y) =
sin x cos i/ - cos x sin z/
cos(x + y) =
cos x cos i/ - sin x sin z/
cos(* -y) =
cos л: cos у + sin дс sin у
tg(x + y) =
tg x + tg у
1 - tg*tgz/
. , ч ctg x ctg у - 1
Ctg(* + y) = —= ^
ctg л: + ctg у
tg(* -y) =
tg x - tg 1/
1 + tg л: tg у
Ctg*Ctgl/ + l
ctg(x y)= 9
ctg x-ctgy
ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО УГЛА
2tg- 2tg-
2 2
sin х = — tg x = —
1 + tg — 1 - tg —
e 2 e 2
1-tg 2 t 1-tg 2
cos л: = — ctg л: = —
l + tg*§ 2tgf
*)Bo всех формулах, приведенных в этом разделе, следует
учитывать область допустимых значений левой и правой частей
формул.

185
ФОРМУЛЫ ДВОЙНОГО АРГУМЕНТА
sin 2х = 2 sin х cos х
cos 2х - cos2 х - sin2 х - 1 - 2 sin2 х = 2 cos2 jc - 1
tg2* =
ctg 2jc =
2tgjc _ 2
1 - tg2 x ctg л: - tg x
ctg2 jc - 1 _ ctg x -tgx
2ctgjc ~ 2
ФОРМУЛЫ ПОЛОВИННОГО АРГУМЕНТА
• 2 *
sin — =
2
1 - cos X
2
6 2
1 - cos X
1 + cos д;
2 X
cos — =
2
1 + cos X
2
, 2 *
ctg v
1 + cos д;
1 - cos X
4. X
tg" =
6 2
sin jc
1 - cos д;
1 + cos jc
sin x
ctg- =
sin д;
1 + cos X
1 - cos X
sin*
ФОРМУЛЫ ТРОЙНОГО АРГУМЕНТА
sin Зд; = 3 sin x - 4 sin3 x
cos Зд; = 4 cos3 x - 3 cos jc
3 tg jc — tg3 x
tg3x
l-3tg2 jc
, _ ctg ^-3ctgx
ctg3* = 5—
3ctg2jc-l

186
ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ СУММЫ В ПРОИЗВЕДЕНИЕ
sin х + sin у =
_ . JC + у JC - w
2 sin -cos -
2 2
sin x - sin у =
_ . * - у x + у
2 sin -cos -
2 2
cos x + cos у =
_ x + у x - у
2 cos 2- cos -
2 2
cos x - cos у =
_ . x + у . x - у
-2 sin sin
2 2
tgx + tgy
sin(* + y)
cos X cos i/
ctg * + ctg у =
tgx-tgy
sin(* - y)
cos * cos у
ctgx - ctgy =
sinjx + y)
sin x sin i/
sin(* - y)
sin * sin i/
cos(x - y)
tgx + ctgy = ,
cos x sin у
cos(jc + i/)
tg * - ctg i/ = -
tg * + ctg x = —
cos x sin у
1 2
sin * cos x sin 2*
„ cos 2x „ , „
tg * - ctg л = -2 = -2 ctg 2x
sin 2*
cos я + sin x = V2 008(45°-*) = V2 sin(45°+x)
cos* - sin* = V2 sin(45°-jc) = V2 cos(45°+*)
a sin x + b cos * = Va2 + b2 sin(* + cp)»
ft a
где sin ф = . , cos ф = .
Va2 + Va2 + ft2
ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ ПРОИЗВЕДЕНИЯ В СУММУ
sin х sin у =
i[cos(* - y) - cos(* + y)]
cos х cos 1/ =
i[cos(* - I/) + cos(* + y)]
sin x cos 1/ =
-[sin(x-y) + sin(x + y)]

187
ФОРМУЛЫ ПРИВЕДЕНИЯ
угол
функция^^^
3 = -±a
2
3 = я ± a
n Зя
3 = — ±a
2
3 = 2я ± a
sin 3
cos a
+ sin a
-cos a
±sin a
cos 3
+ sin a
- cos a
±sin a
cos a
tg3
+ ctg a
±tga
+ ctg a
±tga
ctg3
+ tga
±ctga
+ tga
±ctga
ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ НЕКОТОРЫХ УГЛОВ
Угол в
градусах
0°
30°
45°
60°
90°
180°
270°
360°
Угол в
радианах
0
я
6
я
4
я
3
я
2
я
Зя
2
2я
sin a
0
1
2
1
V2"
V3
2
1
0
-1
0
cos a
1
Я
2
1
1
2
0
-1
0
1
tga
0
1
Я
1
не
сущ.
0
не
сущ.
0
ctg a
не
сущ.
1
1
0
не
сущ.
0
не
сущ.
СВОЙСТВА ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
arcsin (-а) = - arcsin а,
|а| < 1
arccos (-а) = я - arccos а,
|а| < 1
arctg (-а) = - arctg а,
а е R
arcctg (-а) = я - arcctg а,
а g R
я
arcsin а + arccos а = — ,
2
\а\ < 1
arctg а + arcctg а = — ,
2
а g R

188
НЕКОТОРЫЕ ПРЕДЕЛЫ
.. sin х
lim = 1
*->о х
limtg*=l
ех -1
lim =1
*->0 X
1. a*~l 1
lim = In a, a > 0
*->o X
lim(l + х)1/х = е
*->0
limln(1 + *> = l
x->0 x
ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Функция
Производная
fix) = с
с' = 0, где с — const
fix) = ха
(ха)' = ax0-1
fix) = ех
ie'Y = ex
fix) = а*
iax)' = ax\na
fix) = lnx
OnxY = -
X
fix) = \ogax
(loga X)' =
xma
fix) = sinx
(sinx)' = cosx
fix) = cosx
(cos x)' = -sin x
fix) = tgx
(tgx)' =
COS X
fix) = ctgx
(ctgx)' = —ri-
sin X
fix) = arcsinx
/ • v 1
(arcsin x) = ,
VI-x2
fix) = arccos x
(arccos x)' = —, *
yll-x2
fix) = arctg x
(arctg x)' =
1 + x2
fix) = arcctg x
(arcctg x)' = —-
1 + x2

189
ТАБЛИЦА ИНТЕГРАЛОВ
0 • dx = С
1 • dx = х + С
а+1
xadx = - + С, (а*-1)
а + 1
— dx = lnljcl + С
х 1 1
1 , f arcsin х + С
. dx = <
JI _ x2 [- arccos x + С
1 , f arctg x + С
7&X = <
1 + x I - arcctg x + С
axdx =
+ C
In а
sin xdx = — cos x + С
cos xdx = sin x + С
tg x dx = — ln| cos x\ + С
ctg xdx = ln| sin x\ + С
f—\—dx = tg* + C
J cos X
f—\— dx = - ctg x + С
J sin x
f—-— dx = In
J sin jc
■ л;
tg—
+ C
cosjc
f-_i
dx = In
+ C
Va2 - jc2
djc =
arcsin — + С
а
x
-arccos — + С
а
Ь4
djc =
г 1 1 а + дс
H = "^~ln
Ja -x 2a a-x
1 j. x гу
— arctg — + С
а а
- — arcctg — + С
а а
+ С
ПРОСТЕЙШИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Уравнение радиоактивного распада: у' = -ау
у = Се~ах, где С — произвольная постоянная.
Уравнение гармонических колебаний: у" = -со2у
у = A cos(cojc + ф), где Аиф — произвольные постоянные.

190
КОМПЛЕКСНЫЕ ЧИСЛА
Комплексное число имеет вид z = а+ bi,
где а и b — действительные числа, i — мнимая единица, i2 = -1.
Число а называется действительной частью комплексного
числа, а число b — его мнимой частью;
они обозначаются соответственно Rez и Imz.
Числа а + bi и а - bi, которые отличаются только знаком мнимой
части, называются сопряженными.
ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ
Сложение
(а + Ы) + (с + di) = (а + с) + (Ь + d)i
Вычитание
(а + Ы) - (с + di) = (а - с) + (b - d)i
Умножение
(а + Ы)(с + di) = (ас - bd) + (ad + bc)i
Деление
а + Ы ac + bd be-ad , ,
= — Г + — 7l> c2+d2#0
c + di с +d2 с + d~
Возведение
в степень числа i
i4m=l, i4m+1=i, i4m+2=-l, i4m+3=-i.
ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНЫХ ЧИСЕЛ
Модуль
r = yla2+b2
Аргумент
Число а такое, что tga = — .
a
Тригонометрическая
форма комплексного
z = r(cosa-Hsina)
числа
Умножение
zxz2 = r,r2 (cos (a, +a2) + isin(a, +a2))
Деление
— = — (cos(a,-a2) + isin(a,-a2))
Возведение в степень
z" = r"(cosna + / sin на)
* ормула Муава
(cos a + /sin a)" =cosna + isinna
Извлечение корня:
Г г a + 2kn a + 2kn
V z = v r (cos + i sin ),
n n
k = \,2,...,n -1.

191
с* - п|
п • (п -1) • (п - 2) •... • (n - k + 1)
п k\(n-k)\'
1-2-3- ... k
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Вероятность
случайного
события
РуА) = —, где т — количество
элеменп
тарных событий, благоприятствующих
событию А,
п — общее количество равновозможных
и несовместных событий, образующих
полную группу.
Теорема сложения
вероятностей
несовместных событий
Р(А + В) = Р(А) + Р(В)
Теорема умножения
вероятностей
несовместных событий
Р(АВ) = Р(А)Р(В)
Вероятность
осуществления хотя бы ОДНОГО
из независимых
событий
Д^) = 1-(1-ДД)).(1-/>(Л))-и
•0-Д4))
Аъ А2,... Ап — взаимно независимые
события.
Формула Бернулли
р" = р*. - вер°-
т\{п - ту.
ятность того, что событие А наступит в п
испытаниях т раз.
ОСНОВНЫЕ ФОРМУЛЫ КОМБИНАТОРИКИ
Число перестановок из п элементов:
Рп = п! = 1-2-3- ... п
Число размещений из п элементов по k элементов:
Ап = Г-^ТТ7 = * ■ (п - 1) • (п - 2) • ... • (п - * + 1)
Число сочетаний из п элементов по k элементов:

Лев Элевич Генденштейн
Алла Петровна Ершова
Анна Сергеевна Ершова
Наглядный справочник по математике
с примерами
Для абитуриентов, школьников, учителей
Ответственный за выпуск ЛЛ. Кирик
Художник-оформитель АЛ. Андреев
Подписано в печать 28.08.2009. Формат 60x88/16.
Усл.-печ. л. 11,73. Тираж 15 ООО экз. Заказ 1575.
ООО «Илекса», 105187, г. Москва, Измайловское шоссе, 48а,
сайт: www.ilexa.ru, E-mail: real@ilexa.ru,
факс 8(495) 365-30-55, телефон 8(495) 984-70-83
Отпечатано в ОАО ордена Трудового Красного Знамени
«Чеховский полиграфический комбинат»
142300, г. Чехов Московской области,
сайт: www.chpk.ru, E-mail: marketing@chpk.ru,
факс 8(49672) 6-25-36, факс 8(499) 270-73-00,
отдел продаж услуг многоканальный: 8(499) 270-73-59

ДЛЯ ШКОЛЬНИКОВ И АБИТУРИЕНТОВ
Л.Э. Генденштейн
А.П. Ершова
А.С. Ершова
МАТЕМАТИКА
0-1аглядный справочник
с примерами

МАТЕМАТИКА