Н. В. БУТЕНИН
ВВЕДЕНИЕ
В АНАЛИТИЧЕСКУЮ
МЕХАНИКУ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для студентов высших учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1971

531
Б 93
УДК 531.0И
Введение в аналитическую механику. Б у т е н и н Н. В., Главная
редакция физико-математической литературы изд-ва «Наука»,
1971, 264 стр.
В книге дано систематическое и достаточно доступное изложение
основ аналитической механики. В нее включены разделы: уравнения
Лагранжа, уравнения Гамильтона, теория Якоби, неголономные
системы, вариационные принципы и теория возмущений. Приводятся
многочисленные примеры, иллюстрирующие применение рассмат-
рассматриваемых методов.
Книга предназначена для студентов втузов, аспирантов и инже-
инженеров различных отраслей промышленности. Она является дополне-
дополнением к «Курсу теоретической механики» (авт.; Бутенин Н. В.
и др.).
Илл. 61. Библ. 12 назв.
Николай Васильевич Бутенин
Введение в аналитическую механику
М., 1971 г. 264 стр. с илл.
Редактор Л. Г. Наумова
Техн. редактор А. П. Колесникова Корректоры Т. С. Плетнева, А. Л. Ипатова
Сдано в набор 23/VIII 1971 г. Подписано к печати 16/XI 1971 г#
Бумага 84Х1081/*?. Физ. печ. л. 8,25. Условн. печ. л. 13,86. Уч.-иэд. л. 13,11.
Тираж 25 000 экз. Т-16862. Цена книги 56 коп. Заказ № 1231.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени
Ленинградская типография № 2 имени Евгении Соколовой Главполиграфпрома
Комитета по печати при Совете Министров СССР. Измайловский проспект, 29,

ОГЛАВЛЕНИЕ
Предисловие <»,*«.*.•»«.• 6
Глава 1. Основные понятия аналитической механики ¦ . . 7
§ 1.1. Свободные и несвободные материальные системы.
Связи и их классификация 7
§ 1.2. Виртуальные скорости. Виртуальные перемещения . . 12
§ 1.3. Виртуальная работа. Признак идеальности связей ¦ . 18
§ 1.4. Обобщенные координаты. Обобщенные силы .... 22
Глава 2. Принцип виртуальных перемещений ..¦,.... 29
§ 2.1. Принцип виртуальных перемещений * 29
§ 2.2. Принцип виртуальных перемещений в обобщенных ко-
координатах , , 35
§ 2.3. Случай консервативных сил ...» 38
§ 2.4. Устойчивость состояния равновесия « t ¦ » . . . 41
Глава 3. Уравнения движения # ...... , ¦ • . . 48
§ 3.1. Уравнения Лагранжа первого рода . 48
§ 3.2. Общее уравнение динамики . 51
§ 3.3. Уравнения движения в обобщенных координатах
(уравнения Лагранжа второго рода) 56
§ 3.4. Примеры на составление уравнений Лагранжа второ-
второго рода 60
§ 3.5. Учет дополнительных связей 66
§ 3.6. Обобщенные реакции отброшенных связей .... 70
§ 3.7. Выражение кинетической энергии через обобщенные
координаты и обобщенные скорости. Гироскопические
и диссипативные силы 74
§ 3.8. Уравнения Лагранжа в квазикоординатах 80
Глава 4. Уравнения движения в потенциальном поле ... 94
§ 4.1. Уравнения Лагранжа второго рода в случае потенци-
потенциальных сил ; 94
§ 4.2. Обобщенный интеграл энергии 100

4 ОГЛАВЛЕНИЕ
§ 4.3. Метод Уиттекера 103
§ 4.4. Циклические координаты. Уравнения Рауса ¦ . . .110
§ 4.5. Обобщенный потенциал 115
Глава 5. Канонические уравнения Гамильтона 119
§ 5.1. Переменные Гамильтона. Функция Гамильтона . . .119
§ 5.2. Канонические уравнения Гамильтона 122
§ 5.3. Канонические уравнения при наличии циклических ко-
координат . 128
§ 5.4. Скобки Пуассона. Теорема Якоби — Пуассона . . . 132
§ 5.5. Канонические преобразования 137
Глава 6. Теория Якоби 153
§ 6.1. Уравнение Гамильтона — Якоби 153
§ 6.2. Метод разделения переменных 158
§ 6.3. Примеры 162
§ 6.4. Теорема Лиувилля . 166
§ 6.5. Переменные действие — угол . 170
Глава 7. Неголономные системы 177
§ 7.1. Число степеней свободы неголономной системы. При-
Примеры неголономных систем 177
§ 7.2. Уравнения движения для неголономных систем с
множителями Лагранжа 180
§ 7.3. Уравнения движения в квазикоординатах 184
§ 7.4. Уравнения Аппеля 188
§ 7.5. Вывод уравнений движения неголономной системы
из общего уравнения динамики. Уравнения С. А. Чап-
Чаплыгина 196
Глава 8. Вариационные принципы механики 213
§ 8.1. Пути прямой и окольный. Действие по Гамильтону . 213
§ 8.2. Принцип Гамильтона — Остроградского 215
§ 8.3. Неизохронное варьирование 224
§ 8.4. Принцип стационарного действия Лагранжа .... 226
§ 8.5. Принцип стационарного действия в форме Якоби . . 231

ОГЛАВЛЕНИЕ 5
Глава 9. Некоторые методы теории возмущений 237
§ 9.1. Явный вид уравнений Лагранжа второго рода . . . 237
§ 9.2. Метод вариации постоянных . 238
§ 9.3. Метод вариации постоянных при использовании урав-
уравнений Гамильтона. Канонические уравнения возму-
возмущенного движения 250
§ 9.4. Уравнения в вариациях 259

ПРЕДИСЛОВИЕ
Предлагаемая читателю книга входит в серию учеб-
учебных пособий, дополняющую курс теоретической механики
Н. В. Бутенина, Я. Л. Лунца и Д. Р. Меркина (М., 1970—
1971 г.). Издание этих дополнений связано с тем, что
учащиеся некоторых втузов нуждаются в более подроб-
подробном ознакомлении с рядом важнейших разделов, кроме
изложенных в основном курсе. Книги, входящие в на-
названную серию, посвящены аналитической механике, тео-
теории устойчивости, теории механических колебаний, тео-
теории гироскопов. В дальнейшем серию предполагается
продолжить.
Эта книга предназначена для ознакомления учащих-
учащихся с рядом разделов аналитической механики и ее мето-
методов, которые находят или могут найти приложение при
решении инженерно-технических задач.
Цель настоящей книги — изложение методов анали-
аналитической механики и иллюстрация применения их к ре-
решению конкретных задач. Поэтому некоторые теоретиче-
теоретические положения приводятся без доказательств, со ссыл-
ссылкой на источники, где эти доказательства приведены.
Автор благодарен профессорам Ю. И. Неймарку,
Н. Н. Поляхову, Н. А. Фуфаеву и доценту Л. Г. Наумо-
Наумовой за ценные советы, которые позволили значительно
улучшить содержание книги.
Автор
Ленинград,
апрель 1971 г.

ГЛАВА 1
ОСНОВНЫЕ ПОНЯТИЯ АНАЛИТИЧЕСКОЙ
МЕХАНИКИ
§ 1.1. Свободные и несвободные материальные
системы. Связи и их классификация
Совокупность материальных точек называется систе*
мой материальных точек или материальной системой,
если движение каждой из них в отдельности зависит от
движения и положения остальных точек Это значит, что
между точками материальной системы существуют1 силы
взаимодействия *).
Материальная система, для которой расстояния меж-
между двумя любыми ее точками не изменяются, называется
твердым телом.
В данном курсе будет рассмотрено движение мате-
материальной системы в инерциальной системе отсчета.
Если каждая точка материальной системы может за-
занять любое положение в пространстве и иметь любую
скорость, то такую материальную систему называют
свободной. Классическим примером свободной матери-
материальной системы может служить солнечная планетная си*
стема. Между всеми планетами и Солнцем существуют
силы ньютоновского тяготения, положения же и скоро-
скорости самих планет и Солнца ничем не ограничены.
Если вследствие каких-либо ограничений (условий)
точки и тела, составляющие материальную систему, не
мотут занять произвольного положения в пространстве и
иметь произвольные скорости, то такая материальная
система называется несвободной.
*) Напомним, что силы взаимодействия между точками мате-
материальной системы называются внутренними силами. Силы, действую-
действующие на точки материальной системы со стороны точек и тел, не при-
принадлежащих данной системе, называются внешними*

8 основные понятия аналитической механики {гл. i
Ограничения (условия), которые не позволяют точ-
точкам материальной системы занимать произвольное поло-
положение в пространстве и иметь произвольные скорости,
называются связями. Связь налагает ограничения на из-
изменение координат и скоростей точек. Аналитически эти
ограничения записываются в виде уравнений или нера-
неравенств.
Пусть материальная система состоит из п точек, а де-
декартовыми координатами i-й точки будут Х\, у и z% (i = I,
2, ...,л). Если на материальную систему будет нало-
наложена одйа связь, то в общем случае аналитически это
можно записать в виде*)
1\х\у Уъ ZU Х2> #2» Z2> • • •» Хп> Уп> %п> Х\> У\* ^Ь • • •
...» *п>йп> *п> 0<0, A.1)
где ?и У и U (i = 1,2,..., п) — проекции скорости йй
точки на оси декартовой системы координат, a t — время.
В случае знака равенства в выражении A.1) связь на-
называется удерживающей; если стоит знак неравенства, то
связь называется неудерживающей.
Пусть две материальные точки, положение которых
определяется соответственно координатами хи #ь z{ и
#2, #2, ^2, связаны между собой жестким стержнем дли-
длиной /. В этом случае связь является удерживающей и ее
уравнение имеет вид
(х2 - xxf + (у2 - УхУ + (г2 - z{f - Р = О,
т. е. расстояние между этими точками все время остается
неизменным.
Если же стержень заменить гибкой нерастяжимой
нитью, то точки получат возможность сближаться, но,
как и прежде, удалиться друг от друга на расстояние,
большее /, не смогут. В этом случае связь будет неудер-
неудерживающей и ограничения на координаты запишутся
в виде неравенства
*) Будем предполагать здесь и в дальнейшем^ что функция f
непрерывна н имеет непрерывные тфоизяоднш тго вшд аргументам*

§ 4.11 СВОБОДНЫЕ И НЕСВОБОДНЫЕ СИСТЕМЫ #
В дальнейшем будут рассматриваться только удер-
удерживающие связи *).
Если уравнение удерживающей связи
f(xt> Уь zh xh уц zh 0 = 0 A.2)
содержит явно время t, то связь называется реономной
или нестационарной.
Примером такой связи может служить негибкий стер-
стержень, соединяющий две материальные точки и изменяю-
изменяющий свою длину / заданным образом, например, / =
= U + /о sin t. Уравнение связи в этом случае содержит
время t и имеет вид
(*2 - *iJ + {У2 - Уд2 + (*2 - ZiJ - 0i + k sin tf = 0,
где Xi, у и Zi и л;2, уг, z% — координаты точек.
Если же уравнение связи не содержит времени ty т. е.
уравнение связи имеет вид
f(*tf У и zi9 xi9 уь Zi)=*0,
то связь называется склерономной или стационарной.
Связь, накладывающая ограничения только на коор-
координаты точек системы, т. е. связь, уравнение которой не
содержит производных от координат:
f(xt, yi,zhf) = 09 A.3)
называется геометрической или голономной. Связь же,
уравнение которой имеет вид A.2), называется кинема-
кинематической.
Если уравнение A.2) кинематической связи путем ин-
интегрирования нельзя привести к виду {1.3), не содержа-
содержащему производных, то эта связь называется неголоном-
ной или неинтегрируемой. Если же уравнение кинемати-
кинематической связи A.2) может быть путем интегрирования
приведено к виду A.3), то связь, по существу, будет го*
лономной.
*) При наличии неудерживающих связей движение материаль-
материальной системы можно разбить на участки Свободного и несвободного
движения. Несвободного, когда в выражении A.1) имеется знак
равенства, и свободного, когда стоит знак неравенства.

10
ОСНОВНЫЕ ПОНЯТИЯ АНАЛИТИЧЕСКОЙ МЕХАНИКИ [ГЛ. I
Пусть, например, уравнением связи, наложенной на
материальную систему, будет
После его ивтегрировалия получим
п
(с — произвольная постоянная интегрирования). Следо-
Следовательно, данная связь является геометрической.
Если на материальную систему наложено k связей, то
будет k уравнений связи следующего вида:
Ун
(/=1, 2, ¦.., k).
Если эта система уравнений интегрируема, то связи
будут голономными, в
противном случае — не-
голономными.
Материальная си-
система, на которую на-
наложены голономные
связи, называется го-
лономной, 2l материаль-
материальная система с неголо-
номными связями — не-
голономной.
В настоящей книге
основное внимание уде-
лвно голономньш системам, т. е. рассматриваются мате-
материальные системы, на которые наложены связи, уравне-
уравнения которых могут быть записаны в форме
рис. 1Л.
Уи *и 0 = 0 (/= 1, 2,
k),
A.4)
где k — число связей.
Рассмотрим несколько примеров голономных связей.
Пример 1. Точка Mi, к которой присоединена на нерастяжимом
стержне длиной: / точка M2t движется по дуге окружности радиуса R
(рис. 1.1), расположенной в вертикальной плоскости. Обозначим
координаты точки Mi через xh yu ги а координаты точки Мг через

§1.11 СВОБОДНЫЕ И НЕСВОБОДНЫЕ СИСТЕМЫ
*2, У2* *2, тогда уравнениями связей будут
II
Пример 2. Для точек Mi и Мг кривошипно-шатунного механиз-
механизма, изображенного на рис. 1.2, уравнения связей дмеют вид
Z0 г0 # 0
S-ZlJ-/2 = 0,
где хи уи г\ и х2, у% г% — соотеетствен-но координаты точек
Z
и М2.
Рис. 1.2.
Рис. 1.3.
Пример 3. Стержень вращается вокруг вертикальной оси с по-
постоянной угловой скоростью со. На стержне могут свободно дви-
двигаться две материальные точки Afi и М2, соединенные между собой
пружиной (рис. 1.3).
В этом случае для системы точек Мх и М2 связь уже будет
реономной (нестационарной), так как в уравнения связей
Х\ sin Ш - у\ cos со* = 0,
х2 sin ©/ — у2 cos Ш = О,
2, = 0, 22 = О
входит время L
Числом степеней свободы голономной материальной
системы называется число независимых параметров, пол-*
ностью определяющих ее положение (конфигурацию),
т. е. определяющих положение каждой точки системы.
Пусть на материальную систему, состоящую из п то*
чек, наложено k связей вида A.4). Это значит, что не все
декартовы координаты точек системы независимы друг
от друга. В самом деле, на Ъп координат наложено k
независимых уравнений связей. Решая эти уравнения
связей относительно k каких-либо координат, мы выра-
выразим эти k координат через остальные Зп—k. Эти 3/г — k

32
ОСНОВНЫЕ ПОНЯТИЯ АНАЛИТИЧЕСКОЙ МЕХАНИКИ [ГЛ4 1
координат, которые могут принимать произвольные
значения, и определяют положение точек системы. Та-
Таким образом, число степеней свободы будет равно
s = 3л-ft. A.5)
Заметим, что решить систему A.4) можно лишь относительно
тех координат, для которых функциональный определитель
Ml Ma M
D-
Ml JIl. Ml
dfi df2 dfk
A.6)
не равен нулю. В определителе A.6) через Pi, P2, ..., Р& обозна-
обозначены те декартовы координаты, для которых этот определитель не
равен нулю.
§ 1.2. Виртуальные скорости. Виртуальные
перемещения
Понятия о виртуальных скоростях и виртуальных пе-
перемещениях точек материальной системы являются од-
одним из фундаментальных понятий аналитической меха-
механики. Введем сначала эти понятия на примере одной
материальной точки.
Предположим, что материальная точка подчинена
связи, уравнение которой имеет вид
I \Лг у у , <С, *• j —— V/. у Д • I j
Пусть закон движения точки, обусловленный дей-
действующими на точку силами, будет
х _. х /Л у -_ у /Л 2 = 2 @- A -8)
Подставляя закон A.8) в уравнение связи A.7), по-
получим тождество
f[x(t), y(t), z(t), f]-0. A.9)
После дифференцирования этого тождества по времени
будем иметь
¦Л- Z | ;\j V»
A.10)

§141 ВИРТУАЛЬНЫЕ СКОРОСТИ И ПЕРЕМЕЩЕНИЯ ГЗ
Предположим, что в какой-либо фиксированный мо-
момент времени t = t0 материальная точка имеет коорди-
координаты дсо, yoy Zq. Для этого момента времени условие A.10)
примет вид
где индекс 0 означает, что все четыре производные вы-
вычислены для значений Хо, уОу Zq и to. Производные х> у и
z, входящие в условие A.11), также соответствуют мо-
моменту времени t = U. Выражение A.11) представляет
собой условие, которому должны удовлетворять в данный
момент времени t = U проекции х = vXy у = vy, z = vt
скорости точки
v = jci + yj + zk.
Эту скорость называют действительной скоростью.
Если связь стационарная, то ее уравнение имеет вид
f(x, y,z) = 0 A.12)
и условие A.11) упрощается:
Наряду с действительной скоростью точки введем
в рассмотрение скорости
, A.14)
проекции которых в данный фиксированный момент вре-
времени удовлетворяют условию A.13), т. е. тому же усло-
условию, которому удовлетворяют проекции действительной
скорости при стационарной связи. Следовательно, если
связь нестационарная, то введенные нами скорости v*
представляют собой в данный момент времени кинема-
кинематически возможные скорости точки при мгновенно оста-
остановленной связи, т. е. v* — это скорости, совместимые со
связью, но не имеющие составляющих, обусловленных
деформацией связи.
Такие скорости v* будем называть виртуальными ско-
скоростями.
Поясним сказанное на простом примере.

14 ОСНОВНЫЕ ПОНЯТИЯ АНАЛИТИЧЕСКОЙ МЕХАНИКИ [ГЯ. I
Пусть материальная точка движется по тсакой-либо
поверхности, которая в свою очередь перемещается в про-
пространстве. Действительная скорость точки будет суммой
двух составляющих: составляющей г>*, расположенной
в касательной плоскости, проведенной к точке поверхно-
поверхности, где находится в данный момент времени матери-
материальная точка, и определяемой уравнением A.14), и со-
составляющей, обусловленной перемещением поверхности.
Виртуальные же скорости будут расположены только
в касательной плоскости.
Из сравнений условий A.11) и A.13) вытекает, что
в случае нестационарной связи действительная скорость
не совпадает с виртуальными скоростями. В случае же
стационарной связи действительная скорость совпадает
с одной из виртуальных скоростей.
Рассмотрим систему материальных точек, подчинен-
подчиненную k голономным нестационарным связям, описываю-
описывающимся уравнениями
Ы*1> УU Zl> Х2> У2> *2> • • •» Хп> Уп> *tv 0=0
(/=1, 2, ..., k). A.15)
Виртуальными скоростями такой системы называют ско-
скорости, проекции которых в данный момент времени удов-
удовлетворяют системе уравнений *)
Проекции же действительных скоростей точек системы
удовлетворяют следующей системе уравнений:
|#-0 0-1,2 „.
0.17)
Это значит, что в случае нестационарных связей дей-
действительные скорости в общем случае не совпадают
с виртуальными скоростями.
*) Для упрощения записи здесь и в дальнейшем индекс 0
опущен.

§ i.2| ВИРТУАЛЬНЫЕ СКОРОСТИ И ПЕРЕМЕЩЕНИЯ 1$
В случае стационарной связи уравнения A.17) при-
нимают вид
), 0.18)
совпадающий с уравнениями A.16), т. е. в этом случае
действительные скорости совпадают с одной из систем
виртуальных скоростей.
Для материальной системы, состоящей из двух точек, соединен-
соединенных между собой жестким стержнем длины /, уравнением связи
будет
(*2 - *iJ + (У2 - УхJ + (*2 -*,)»-/*- 0.
Условие A.16) при этом запишется в виде
или в векторной форме:
('*-'i)-(«'2-«'i)-0. CI9)
где Г\ и гч — радиусы-векторы, определяющие положения точек. Ра-
Равенство A.19) выражает условие того, что разность виртуальных
скоростей двух точек твердого тела всегда перпендикулярна к пря-
прямой, соединяющей эти точки. Для действительных скоростей этот
факт известен из кинематики.
Действительным перемещением материальной точки
называется вектор
dr^vdt A.20)
Проекции этого вектора dx = ?dt, dy — у dt и dz = zdt
удовлетворяют уравнению
&** + %-*!' + '&¦**+§*-О, A.21)
которое получается из уравнения A.10) путем умноже-
умножения его на dt
Действительными перемещениями точек материальной
системы называются векторы
(/=1, 2 ..., п).
A.22)

16 ОСНОВНЫЕ рОНЯШЯ АНАЛИТИЧЕСКОЙ МЕХАНИКИ (ГЛ. 1
Очевидно, что проекции этих векторов должны удовлет-
удовлетворять системе k уравнений
(/=1, 2, ..., k). A.23)
Перейдем к определению понятия виртуального пере-
перемещения. Предположим, что точка находится на поверх-
поверхности f (х, у, г, t) = 0. Радиус-вектор r = xi + yj + zk
в фиксированный момент времени t определяет положе-
положение точки. Рассмотрим теперь множество бесконечно
близких положений точки, допускаемых связью в этот
фиксированный момент времени. Пусть эти бесконечно
близкие положения определяются радиусом-вектором
где бх, 8у, 6z — проекции вектора бг. Вектор
представляет собой бесконечно малое приращение радиу-
радиуса-вектора r(t) при мысленном перемещении точки из по-
положения, определяемого радиусом-вектором r(t), в поло-
положение, определяемое радиусом-вектором r'(t). Этот век-
вектор называется вектором виртуального перемещения.
Таким образом, вектор виртуального перемещения пред-
представляет собой бесконечно малый вектор, который позво-
позволяет мысленно, не нарущая связи, перевести точку из
одного ее положения в бесконечно близкое, относящееся
к тому же моменту времени. Вектор 6г иначе называют
вариацией вектора г, а его проекции б#, 8у, 8z— вариа-
вариациями координат.
Проекции х + бх, у + 8у, z + 8z векторов r*(t) долж-
должны удовлетворять уравнению связи A.7), т. е.
, у + бу, z + &z, /) = 0.
Разлагая это выражение в ряд по степеням бх, бу, 6-г,
учитывая, что f(x, у, z, t) = 0, и пренебрегая членами по-
порядка малости выше первого, получаем условие, накла-
накладывающее ограничение на вариации координат;
¦?** + ¦? **+ •&<*-о- О-24)

§ U] ВИРТУАЛЬНЫЕ СКОРОСТИ И ПЕРЕМЕЩЕНИЯ If
Поскольку при получении выражения A.24) время счи-
считается фиксированным, то вариации 8х, 8у, дг называют-
называются изохронными. Пусть т— коэффициент, имеющий раз-
размерность времени; тогда, умножая почленно уравнение
A.13) на этот коэффициент т и вводя обозначения
6а: = х*х, Ьу — у*х, bz = z*x,
получим
Следовательно, проекции вектора
Ьг = bxi + byj + 6zk = v*x
удовлетворяют условию A.24). Если теперь выбрать ко-
коэффициент х таким, чтобы перемещения Ьг были совме-
совместимы со связью (х дол- f(xu,zt)=0
жно иметь порядок мало- 2 у ^ '
сти не меньше порядка
малости величин 6л;, 8у,
б«г), то, поскольку вели-
величины б*, Ьу, bz удовлет-
удовлетворяют условию A.24), ,
векторы Ьг будут пред-
представлять собой виртуаль-
виртуальные перемещения, т. е. " Рис ,4
Ьг = 8г. Из соотношения
йг = г>*т следует, что векторы виртуальных перемеще-
перемещений имеют направления виртуальных скоростей.
Если связь, которой подчинено движение материаль-
материальной точки, стационарная, то проекции (dx, dy, dz) дейст-
действительного перемещения dr удовлетворяют, в соответст-
соответствии с A.21), уравнению
т. е. в этом случае вектор действительного перемещения
совпадает с одним из виртуальных перемещений.
Условию A.24) можно дать геометрическую интер-
интерпретацию. Уравнение связи f(x, y,z,t) = 0 в фиксирован-
фиксированный момент времени можно рассматривать как уравне-
уравнение поверхности. Тогда из условия A.24) вытекает, что

18 ОСНОВНЫЕ ПОНЯТИЯ АНАЛИТИЧЕСКОЙ МЕХАНИКИ [ГЛ. I
виртуальные перемещения точки 8г представляют собой
векторы, расположенные в касательной плоскости, прове-
проведенной в той точке поверхности, в которой в данный
(фиксированный) момент времени находится материаль-
материальная точка (рис. 1.4).
Виртуальными перемещениями точек материальной
системы, подчиненной k связям вида A.15), называют со-
совокупность бесконечно малых векторов
brt« bxti + tyi i + bztk, A.25)
проекции которых удовлетворяют системе уравнений
Отметим, что при стационарных связях в соответ-
соответствии с условием A.23), проекции действительных пере-
перемещений удовлетворяют следующей системе уравнений:
(/«1,2,..., ft). A.27)
Это значит, что для стационарных связей действительные
перемещения совпадают с одним из виртуальных переме-
перемещений. Материальная система, состоящая из п точек,
имеет Зп вариаций координат. Однако в силу уравнений
A.26) эти вариации координат не являются независимы-
независимыми друг от друга. Решая уравнения A.26) относительной
вариаций координат, для которых это решение возможно,
мы их выразим через остальные Зп — k. Следовательно*
независимых вариаций координат будет Зп — k, т. е. чис-
число независимых вариаций координат равно числу степе-
степеней свободы материальной системы.
§ 1.3. Виртуальная работа. Признак идеальности
связей
Если на точки материальной системы в данном поло-
положении и в фиксированный момент времени действует си-
система сил Fi, F2, ^з, ..., Fn, а виртуальные перемещения
точек системы равны б/ч, бг2,,.., бгп, то виртуальной ра-

$ L3] ВИРТУАЛЬНАЯ РАБОТА 19
ботой называется работа этих сил на виртуальных пере-
перемещениях системы, т. е.
бЛ=2*<-«г<, A.28)
или
б А = %(Xfixt + Yfiyi + Zttet). A.29)
Определим лонятие идеальных связей. Идеальными
связями называются такие связи, для которых виртуаль-
виртуальная работа реакций связей на любим виртуальном пере-
перемещении системы равна нулю, т. е.
2 Яг 6^ = 0, (ЬЗО)
где Ri — реакция связи, приложенная к i-й точке.
Определение идеальной связи, известное из курса
теоретической механики, как связи, реакция которой не
содержит составляющей обусловленной трением, являет-
является частным случаем приведенного выше определения.
Воспользуемся условием A.30) для выражения реак-
реакций связей, используя неопределенные множители Лаг-
ранжа.
Записав условие A.30) в виде
2 {Rixbxi + RtybVi + Riztei) = 0, A.31)
вспомним, что вариации координат 6**, Ьуи 62* (в соот-
соответствии с A.26)) подчинены уравнениям
(^ Sr^ ^) </-Ь2. ....*М1.32)
Каждое из этих k уравнений умножим соответственно на
неопределенные множители Лагранжа Xi, Яг,* ..., кн, ко-
которые могут быть функциями координат и времени:
(/-1,2,..., А).

20 ОСНОВНЫЕ ПОНЯТИЯ АНАЛИТИЧЕСКОЙ МЕХАНИКИ [ГЛ.
Полученные выражения сложим:
Вычтя теперь из соотношения A.31) выражение A.33),
получим
= 0. A.34)
Так как в силу уравнений A.32) независимых вариаций
координат будет Зп— k, то выберем множители Лагран-
жа К\, ta, Я3,..., Ял таким образом, чтобы коэффициенты
при k вариациях координат обращались в нуль. Остав-
Оставшиеся в выражении A.34) Зп — k вариации координат
будут независимы, и поэтому множители при них также
должны быть равны нулю*). Таким образом,
A.3Б)
Приведем примеры идеальных связей.
Пример 4. Связь между двумя материальными точками Mi и М%
осуществлена в виде абсолютно жесткого стержня (рис. 1.5).
Пусть R\ и /?2 — соответственно реакции связей, приложенных
к точкам М\ и М2. Если v\ и v*2— виртуальные скорости соответ-
*) Обоснование возможности такого подбора %j дано, например,
в книге: Г. К. Суслов, Теоретическая механика, Гостехиздат, 1944,
стр. 295.

§ K31
ВИРТУАЛЬНАЯ РАБОТА
21
етвенно точек Mi и М%, то виртуальные перемещения этих точек
будут равны
бг; = v, т и бг9 = v9t.
II ? ?
Работа реакций на виртуальных перемещениях точек
Rx • Ьтх + R2 • бг2 = 1?! • (бг, - бг2) = flj • (у] - 1$ т = О,
так как /?2 = —R\; реакция R\ направлена вдоль стержня, а разность
vi ~" и2 перпендикулярна к направле-
направлению стержня [см. формулу A.13)].
Пример 5. Точка движется по
внутренней стороне абсолютно глад-
гладкой поверхности параболоида вра-
вращения
/ (дг, уу z) = х2 + у2 — az = 0.
По условию поверхность абсолютно
гладкая, следовательно, реакция на-
направлена по нормали к поверхности,
но виртуальные перемещения распо-
расположены в касательной плоскости.
Значит, реакция R перпендикулярна
к бг и R • бг = 0. Приведем другое доказательство, с использова-
использованием множителя Лагранжа. Так как реакция направлена по нор-
нормали к поверхности, то можно записать
Рис. 1.5.
или
дх ду
Ъ Ry Rz
дг
2х
= Я.
Отсюда имеем Rx = Я2х, Ry = Х2уу Rz = — Ха. Тогда
R • бг = Rx 6х + Ry by + Rz bz = Я {2х 6х + 2уду-а бг) = 0,
так как на основании уравнения связи вариации координат дх, 6у
и бг удовлетворяют уравнению
дх
ду
К
которое в рассматриваемом случае имеет вид
0.
В дальнейшем будут рассматриваться только идеаль-
идеальные связи.

22 ОСНОВНЫЕ ПОНЯТИЯ АНАЛИТИЧЕСКОЙ МЕХАНИКИ {ГЛ. f
§ 1.4. Обобщенные координаты. Обобщенные силы
В § 1.1 было установлено, что положение материаль-
материальной системы, подчиненной k голономным связям, опреде-
определяется s = 3/г — k независимыми декартовыми координа-
координатами. Однако во многих случаях использование декар-
декартовых координат приводит к громоздким выкладкам.
Поэтому для определения положения материальной
системы можно использовать другие независимые друг
от друга параметры qu q2, ••«> Я*- Эти параметры могут
иметь различную размерность — это могут быть углы,
длины дуг, площади и т. п. Все 3/г декартовых коорди-
координат можно выразить через введенные параметры
Яи Яъ • • •, qs'.
Hi =>УЛЯиЯ2> •••> Яз> 0> (/=1, 2, ,.., п). A.36)
zi = гг(Я\> Я* •• •> Яз> О
Эти функции обращают в тождество уравнения связей
fl(Xi,yi,Zi,t) = O (/=1,2, ..., k).
Будем предполагать, что любое положение материальной
системы, совместимое со связями, однозначно определя-
определяется при помощи функций A.36) некоторыми значениями
параметров qu 92, ..., qs. Эти независимые между собой
параметры qif 92, ..., q* (s — число степеней свободы)
называются обобщенными координатами.
Уравнения A.36) могут быть записаны в векторной
форме:
ti = Xii + на + ztk = rt {qu q2y ..., qs> t). A.37)
При наличии стационарных связей функции A.36) мож-
можно выбрать так, чтобы они не содержали явно времени tf
т. е. имели вид
У1~УАЯ\> ?2> ...> Я,), ('«1» 2, ..., п). A.38)
Zl^ZiiQl* Я2> •••> Яз)

§ 1.4}
ОБОБЩЕННЫЕ КООРДИНАТЫ. ОБОБЩЕННЫЕ СИЛЫ
При этом радиусы-векторы точек системы также будут
функциями только обобщенных координат:
П = П (<7i, <fe. • - • > <fc) (/=1,2,..., п). A.39)
Пример 6. Положение сферического маятника длины / можно
определить двумя углами qx = 9, q2 = Ф (рис. 1.6).
Уравнения A.38) в этом случае имеют вид
х = / sin 9 cos ф =» / sin qx cos цъ
у = / sin 9 sin ф = / sin qx sin q2>
z~ /cos 9 =
Дифференциалы от функций A.36), вычисленные в
предположении, что время
фиксировано, имеют вид
т = \
s
Рис. 1.6.
Найдем дифференциалы при фиксированном / от тож-
тождеств, которые получаются из уравнений связей после
подстановки в них функций A.36):
yt,zh 0 = 0 (/=1,2, ..., k),
1=1
Полученные уравнения совпадают с уравнениями A.26).
Следовательно, дифференциалы %хи Зуи Szi совпадают
с вариациями координат 8хи §Уи б^.
Таким образом, мы установили «рецептуру» вычисле-
вычисления вариаций координат. Как для стационарной связи,

2* ОСНОВНЫЕ ПОНЯТИЯ АНАЛИТИЧЕСКОЙ МЕХАНИКИ [ГЛ. Г
так и для нестационарной вариации координат будем вы-
вычислять по формулам
Здесь
= 1, 2,
A.40)
называются вариациями обобщенных координат.
В соответствии с выражениями A.37) и A.40) для
виртуальных перемещений будем иметь
A.41)
Подставляя соотношение A.41) в выражение для вир-
виртуальной работы
6А = 2 F, • 6rh
получим
m=l
Внося Fi под знак второй суммы и меняя порядок сум-
суммирования, будем иметь
М

I f.41 ОБОБЩЁННЫЕ КООРДИНАТЫ. ОБОБЩЕННЫЕ СИЛЫ 25-
Суммы
называются обобщенными силами. Каждой обобщенной
координате qm соо!ветствует своя об-
обобщенная сила Qm*). Итак
A.43)
Выражение A.43) позволяет дать сле-
следующее определение обобщенных сил:
обобщенными силами называются ко-
коэффициенты при вйриациях обобщен-
обобщенных координат в выражении для вир-
виртуальной работы.
Пример 7. Однородный стержень ОЛ, вес которого Р, может
вращаться вокруг перпендикулярной к нему горизонтальной оси Ог
без трения (рис. 1.7). К концу А стержня прикреплена пружина
О\А = /. Точка О\ крепления пружины находится от точки О по
вертикали вверх на расстоянии, причем О\О = О А — г. Длина пру-
пружины в ненапряженном состоянии равна /о. Найти обобщенную
силу.
За обобщенную координату примем угол ф. Тогда будем иметь
xA = r cosф, УД~Г sin Ф>
iHC>
где хс, ус — координаты центра тяжести стержня. Сила, действую-
действующая на конец стержня А со стороны пружины, равна
*) Отметим, что размерность обобщенной силы равна размер-
размерности работы, деленной на размерность обобщенной координаты.

26 ©сновньш понятая аналитической механики
где
-~.
Проекциями этой силы на оси координат будут
Хг - -с \2rcos-|. - /oj cos -|> Yx - -с \2r cos-|- - /0) sin-|.
Проекциями силы Р, приложенной в центре тяжести С стержня,
будут
В нашем случае
&ХА дуА дхс дус
QX + Y + x + Y
В силу того, что
дхА дуА дхс г
, = —г sincp, а «г /- cos ф, . =—jr-
^Ф ^ ^Ф Y дф 2
получим
Q = ^г \2r ces^-- /0) sin-~ —^~ sinФ-
Пример 8« Найтц обобщенные силы для сферического маятника
(рис. 1.6). В данном случае п » I, s — 2. Обобщенные координаты;
?i e 0, <7г в Ф- Обобщенные силы определяются формулами A.42):
Так как X - У - О, Z - Я, а
* = / sin 9 cos ф, у ^ Ism В sin ф, z « / cos О
и
ТО
Определим теперь обобщенные силы через виртуальную работу
6А - F • бг - J &х + F бу + Z 6г - Р 62.
Так как
d2= -/sin 9 69,
то

§1.41
ОБОБЩЕННЫЕ КООРДИНАТЫ. ОБОБЩЕННЫЕ СИЛЫ
27
и, следовательно,
?! = -/>/sinG, Q2=*0.
Пример 9. Найти обобщенные силы для материальной системы,
схема которой представлена на рис. 1.8. Веса грузов /4, В и С
соответственно равны Р\у Рг и Р3. Грузы Л, В перемещаются по
гладкой горизонтальной поверхности. Стержни невесомы и соеди-
соединены с грузами Л, В и между собой идеальными цилиндрическими
шарнирами. Жесткости пружин с\ и с%
У
Рис. 1.8.
Выберем начало координат О в положении равновесия груза А.
Для определения числа степеней свободы рассматриваемой ме-
механической системы применим формулу s = Зп — k. Пусть коорди*.
наты точек Л, В и С соответственно будут Хи Уи zu #2, #2, Z2, х& у&
г$. Напишем уравнения связей:
Х\ =0, х2 в 0, #i » 0, г2 в 0, г3 =» 0,
Их* -Р)-Х1]> + (у3 - ^/,J 4- (г3 - ^iJ - /2 - 0,
f(*, - р) - *2]2 + (у, - у2J + (гз - *2J - /2 - 0.
Число точек в системе п = 3, число связей Л = 7, следовательно,
число степеней свободы s = 2. За обобщенные координаты примем
qx -> s, #2 ~ Ф (см- Рис. 1.8). Координатами грузов А, В и С будут
#1 =0, #! - S,
#2 = 0, #2 = s + 21 sin ф,
лг3 = / cos ф + р, уз~ s + l sin ф.
Проекции активных сил Pi, P2, Рз, ^i, ^2» действующих на грузы^
равны
2> У2
- 5 — ^i ~ 2/ cos ф),
где Ki и Я2 — статические удлинения пружин*

28 ОСНОВНЫЕ ПОНЯТИЯ АНАЛИТИЧЕСКОЙ МЕХАНИКИ [ГЛ. \
Найдем виртуальную работу
ЬА =» Хг 6л:, + Fi 6*/, + Х2 Ьх2 + Y2 Ьу2 + Xz 6*3 + Y 6уъ.
Так как
6л: j = 0, Ьух = 6s, 6лг2 = 0, 6у2 = 6s + 2/ cos ф 6ф,
6#з = — / sin ф 6ф, 6#з = 6s + / cos ф 6ф,
то
дЛ = — сх (s + Xi) ds + с2 (а — s — Xi — 21 sin ф) Fs + 21 cos ф 6ф) —
- /У'sin ф 6ф = ] - ci (s + Ki) -Ь с2 (а - s - Я2 - 2/ sin ф)] 6s +
+ [°2 (« — 5 — %\ — 2/ sin ф) 2/ cos ф — P3/ sin ф] 6ф.
Следовательно,
Qx « — C\ (s + Я^ -f c2 (^ — s ~ ^i — 2/ sin ф),
Q2 ~ c2 (a — s — hi — 21 sin ф) 21 cos ф — P3/ sin ф.

ГЛАВА 2
ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ
§ 2.1. Принцип виртуальных перемещений
Принцип виртуальных перемещений является принци-
принципом механики, устанавливающим необходимые и доста-
достаточные условия равновесия (покоя) материальной си-
системы.
Пусть материальная система подчинена k голоном-
ным стационарным связям
// = (*ь У» *и *2> У2, *2> • • • > хп> Уп> гп) = О
(/=1,2, ..., к).
Дифференциальные уравнения движения этой несво-
несвободной системы имеют вид
m,w, = F,+JR, (/=1, 2, ..., л), B.1)
где / — номер точки, Wi — ее ускорение, т\ — масса, ?\ и
Ri — соответственно равнодействующие всех активных
сил и реакций связей, приложенных к t-й точке.
Под равновесием (покоем) материальной системы бу-
будем понимать такое ее положение, в котором система бу-
будет находиться все время, если она в начальный момент
времени, имея скорости, равные нулю, находилась в этом
положении. Отсюда следует, что в положении равновесия
материальной системы скорости и ускорения всех ее то-
точек равны нулю, т. е.
г;, = 0, г^ = 0 (/=1, 2, ..., п)
или, в соответствии с уравнениями B.1),
O (/«1,2,...,*). B.2)

30 ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ [ГЛ. 2
Сформулируем теперь принцип виртуальных переме-
перемещений.
Необходимым и достаточным условием равновесия го-
лономной материальной системы, подчиненной только
идеальным связям, является равенство нулю работы
всех активных сил на любом виртуальном перемещении
точек материальной системы, т. е.
2!Л-бг,«0. B.3)
Кроме того, в соответствии с определением равновесий
Vi(to) = 0 (I = 1, 2,..., /г), где U — начальный момент
времени.
Докажем необходимость этого условия. Пусть систе-
система находится в положении равновесия. Это значит, что
выполняются условия B.2). Умножим скалярно второе
выражение этого условия на вектор виртуального пере-
перемещения i-й точки:
Это выражение справедливо для любой точки материаль-
материальной системы. Складывая все эти выражения, получим
или
Так как по предположению связи, наложенные на систе-
п
му, идеальные, то 2 Rt * &ri в0и, следовательно,
Скорости же всех точек равны нулю по предположению*
Докажем, что условие B.3) будет и достаточным ус-
условием равновесия системы.
Очевидно, для этого достаточно показать, что уравне-
уравнения B.2) являются следствием условия B.3), Запишем

f2.ll ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИИ 31
условие B.3) в виде
Д z,)- 0, B.4)
где Х{, Y{, Zi — проекции силы F» на оси координат. Ва-
Вариации координат бхи буи 6Zi подчинены k уравнениям
A.26):
Умножая эти уравнения соответственно на неопределен-
неопределенные множители Лагранжа А*, Аг, ...» А,* и складывая за-
затем полученные выражения, будем иметь
или
п
B.5)
Складывая соотношения B.4) и B.5), получим
Выбираем теперь Xj так, чтобы коэффициенты при k
вариациях координат обратились в нуль; тогда обратят-
обратятся в нуль и коэффициенты при остальных Зп — k вариа*
циях в силу независимости этих последних. Следователь-
Следовательно, мы получим уравнения

82 ЛРИНВДП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИИ |ГЛ.
или, с учетом формул A.35),
*, + /?„ = (), У,+ /?„ = <>, Zi + Rt^O (/=1,2 л)
Умножая каждое из этих уравнений соответственно
на единичные векторы /, / и k координатных осей х, у и z
и складывая полученные выражения между собой, будем
иметь
Ft+Hi-0 (/=1,2, ..., п\
т. е. уравнения B.2). Начальные же скорости равны нулю
по условию B.3)*).
Принцип виртуальных перемещений позволяет опре-
определить положение равновесия несвободной материаль-
материальной системы, не вводя в рассмотрение неизвестных ре-
реакций идеальных связей, так как в формулировку этого
принципа эти реакции не входят.
Однако принцип виртуальных перемещений может
быть применен и для нахождения реакций идеальных
связей. Для этого, в соответствии с принципом освобож-
освобождаемое™, следует отбросить связь и заменить ее дейст-
действие реакцией, а затем включить эту реакцию в число
активных сил. При этом следует помнить, что при отбра-
отбрасывании связи увеличивается число степеней свободы си-
системы.
Если наложенные на систему связи не идеальные, то
непосредственно принцип виртуальных перемещений к та-
таким системам неприменим. Однако в этом случае, напри-
например при движении точек по негладким поверхностям, сле-
следует реакции разложить на нормальные составляющие и
силы трения. Далее принять, что связи идеальные, а силы
трения отнести к активным силам. Конечно, при этом сле-
*) Рассмотрение различных доказательств достаточности усло-
условия B.3) приведено в книге Г. К. Суслова «Теоретическая механи-
механика», Гостехиздат, 1944, стр. 377—384.

ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ
33
дует учитывать условия равновесия при наличии тре-
трения *).
Пример 10. Тяжелый однородный стержень длины 21 опирается
промежуточной точкой на выступ В. Другой конец стержня удер-
удерживается невесомой нитью длины /, прикрепленной к точке О
(рис. 2.1). Дано: О А = О В = /. Найти угол ф, образуемый стержнем
с горизонтальной линией при равновесии. Стержень считать глад-
гладким, точки О и В находятся на
одной горизонтали.
Активная сила здесь одна —
вес стержня Р, приложенный в
центре тяжести стержня С. Со-
Согласно формуле B.3) условием
равновесия стержня будет
Р • Ьгп ~ Р Ьхп =* 0 или Ъх~ — 0.
Так как
хс =* / sin 2ф — / sin ф,
то
Рис. 2.1,
6хс
*с —• / B cos 2 ф — cos ф) бф = 0.
Поскольку бф выбирается произвольно, можно считать бф ф 0, и,
следовательно,
2 cos 2ф — cos ф == 0,
или
4 cos2 ф — cos ф — 2 = 0,
откуда
COS ф =
8
0,842.
Пример 11. Определить реакцию опоры С трехпролетной раз-
разрезной балки (рис. 2.2, а).
Заменим действие опоры С реакцией Re- На рис. 2.2,6 показано
одно из виртуальных перемещений системы. Согласно принципу вир-
виртуальных перемещений
где бп, бгг, бгз, 6>с — виртуальные перемещения точек балки, к ко-
которым приложены силы Pi, P2, Рз и реакция Re. Поскольку мы
отбросили опору С, балка получила одну степень свободы. Положе-
Положение балки теперь можно определить углом ф поворота левой части
балки вокруг точки Л (в положении равновесия ф = 0). При сооб-
сообщении балке, находящейся в равновесии, выбранного виртуального
*) Н. В. Бутенин, Я. Л. Лунц, Д. Р. Меркин, Курс
теоретической механики, т. 1, «Наука», 1970, стр. 82—90.
2 Н. В. Бутенин

34
ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИИ
[гл.
перемещения величины | 6г{ |, 1 $г2I, 16г31 и | Ьгс I можно заменить
через вариацию 6<р угла ф по следующим соотношениям (см.
рис. 2.2,6):
3 /
так как в соответствии с рисунком у / бф = — 6q>i и, следовательно,
бф! = 3 6ф.
Рис. 2.2.
Подставляя полученные соотношения в уравнение B.6), имеем
Так как бф выбирается произвольно, то можно принять бф ф 0.
Тогда
Пример 12. При каком соотношении между весами Рь Р2, Р3 и
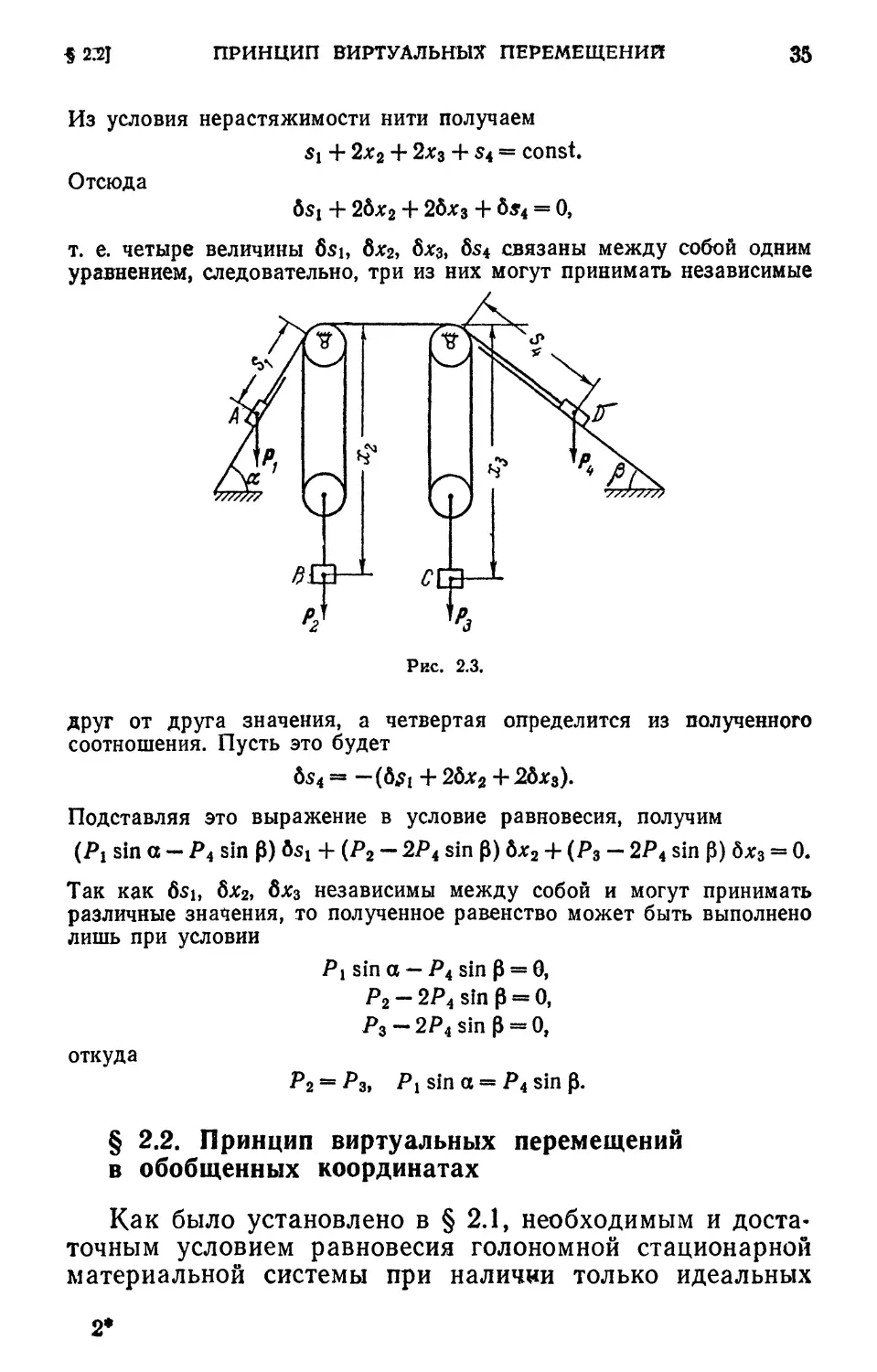
Ра грузов А, В, С и D система, изображенная на рис. 2.3, будет
находиться в равновесии? Нить невесома и нерастяжима. Трением
пренебречь.
Пусть величины si, *2, *з, s4 определяют положение грузов Л, В,
С, D. На основании принципа виртуальных перемещений можно на-
написать условие равновесия
Pi sin a 6s, + Р2 6*2 + Pz 6*3 + Р4 sin ? 6s4 = 0.

2I2J
ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ
35
Из условия нерастяжимости нити получаем
Si + 2л:2 + 2*з + s4 = const.
Отсюда
6$i + 26jc2 + 2б*з + 6s4 = О,
т. е. четыре величины б$ь 6*2, 6*3, 6s4 связаны между собой одним
уравнением, следовательно, три из них могут принимать независимые
1>2
Рис. 2.3.
друг от друга значения, а четвертая определится из полученного
соотношения. Пусть это будет
Подставляя это выражение в условие равновесия, получим
(Рх sin a - Р4 sin Р) 6st + (Р2 - 2Р4 sin Р) 6*2 + (Р3 - 2Р4 sin р) 6*3 - 0.
Так как 6sb 6*2, б*3 независимы между собой и могут принимать
различные значения, то полученное равенство может быть выполнено
лишь при условии
/>lsina-/>4sinP = 8,
откуда
Р3 - 2Р4 sin р - О,
= Р3, Pi sin о = Р4 sin p.
§ 2.2. Принцип виртуальных перемещений
в обобщенных координатах
Как было установлено в § 2.1, необходимым и доста-
достаточным условием равновесия голономной стационарной
материальной системы при наличии только идеальных
2*

36 ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИИ {ГЛ. 2
связей является условие B.3):
*<«>)-0 (/=1,2, ..., /г), 6Л= j]F^6r< = 0,
где Fi — активные силы.
В обобщенных координатах второе выражение усло-
условия B.3), в соответствии с равенством A.43), имеет вид
Так как 8qu б?2, . ¦., 6q8 могут принимать любые значе-
значения независимо друг от друга, то полученное соотноше-
соотношение может быть выполнено, если все обобщенные силы
одновременно будут равны нулю, т. е.
или
Qm = 0 (m = 1,2, ..., s). B.7)
Следовательно, необходимым и достаточным условием
существования положения равновесия голономной ста-
стационарной системы, подчиненной идеальным связям, яв-
является равенство нулю скоростей всех точек системы и
равенство нулю всех обобщенных сил.
Пример 13. В рассмотренном в § 1.4 примере 7 (рис. 1.7) обоб-
обобщенная сила имела выражение
Q » cr ( 2r cos -2- -
или
r[cBr cos I -/о)-Я cos f] sin f
выражение нулю, найдем значение уг
жет находиться в равновесии:
r[CBrcosf-/0)-/>cosf-]sinf =0.
Приравнивая это выражение нулю, найдем значение угла <р, при ко-
котором система может находиться в равновесии:
Отсюда
sin^^O, т. е. q>i«0,
или, если sin~
с i 2rcos y — /0) — Р cos y * 0t

§2.2]
ПРИНЦИП ВИРТУАЛЬНЫХ ЛЕРЗМЕЩЕНИЙ
37
и окончательно
CD o dn
cos—= 27^гр-
Однако это состояние равновесия будет существовать, если
с10
\2гс-Р\
<U
т. e. при P < cBr — l0) или P > cBr -f /0) будет еще состояние рав-
равновесия (кроме ф1 «= 0)
Пример 14. В примере 9
для рассмотренной материаль-
материальной системы обобщенные силы
равны
+ с2(а — s — Я] — 2/ sin ф),
— 2/ sin ф) 2/ cos ф — P$l sin ф.
При равновесии s = 0, ф = ф0
и, следовательно,
— Xi— 21 sin ф0) 21 cos (р0 —
— Р3 / sin ф0 = 0.
Рис- 2Л-
гч ,, c2{a — 2lcos ф0)
Отсюда следует, что ах = —^ ?^-, а так как
С\ + С2
a==Xi + %2 + 2/ sin ф0,
то
2
Уравнение для определения ф0 имеет вид
2ciC2 cos ф0 (а— 21 sin ф0) — (сх 4- с2) Ръ s
Представив это выражение в виде
а-21 sin ф0 =* Рэ ^ С2 tg ф0>
построим на плоскости фог/ две кривые (рис. 2.4):
и г/ Я ^ ^
0.
фо>

8S ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ [ГЛ. 2
Точки пересечения этих кривых и дают искомые значения ф^. Оче-
Очевидно, при 0 < фо < я/2 будет только одна точка пересечения, соот-
соответствующая единственному положению равновесия системы. Если
р3 = о, то уравнением для определения фо будет
cos фо(а - 2/ sin ф0) =» 0.
Отсюда cos фо = 0, т. е. ф0»-^ • Это значит, что существует поло-
положение равновесия, когда стержни горизонтальны. Но если а < 2tt то
может быть
а —21 sin ф0 *= 0,
т. е.
Следовательно, при а > 2/ возможно (при Рз = 0) ©дно положение
равновесия ф0 = -*г • При, а < 2/ — два: ф0 — -^ и фа = arcsin ^~.
§ 2.3. Случай консервативных сил
Если силы, действующие на точки голономной стацио-
стационарной системы, консервативные, то выполняются соот-
соотношения
у _ ап у _ an _ дп @ Av
z<--iV у^-^т» Z^~li7f ( '
где n = n(A:L, уи гь хъ уъ z2> ..., ^ уя, ^-потен-
^-потенциальная энергия.
Подставляя B.8) в формулу для обобщенной силы
A.42) и приняв во внимание A.36), получим
(т=1,2, ..., s). B.9)
Таким образом, если силы консервативны, то обобщен-
обобщенная сила, соответствующая обобщенной координате qm,
равна взяткой с обратным знаком производной от потен-
потенциальной энергии по обобщенной координате.
Условие B.7) в этом случае запишется в виде
1^0 (т-1,2. ..., s). B.10)

СЛУЧАЙ КОНСЕРВАТИВНЫХ СИЛ
39
Отсюда следует, что в положении равновесия потенци-
потенциальная энергия системы имеет экстремальное значение.
Пример 15, Найти обобщенную силу и положение равновесия
материальной системы, схема которой представлена на рис. 2.5.
В точках О, Л и В имеются шарниры. Стержни ОА и АВ однород-
однородные и имеют одинаковую длину а и массу т. Поршень М имеет
массу mi. Середины стержней О А и АВ соединены
пружиной жесткости с. Длина пружины в ненапря-
ненапряженном состоянии /о < а. Трением и массой пру жи-
жилы пренебречь. Механизм расположен в вертикаль-
вертикальной плоскости.
Система имеет одну степень свободы. За обоб-
обобщенную координату примем q « ф.
Потенциальная энергия будет
где
xCi
П - -mgxCi - mgxCi - mxgxM + у
а 3
у cos ф, хСг - j a cos ф, хв « 2а cos ф,
и. С2 —
а % « CiCa—/о —^ удлинение пружины (С\
точки крепления пружины). Так как С1С2 =
то X = a cos ф — /о. Следовательно,
П = —2 (т + mi) ga cos ф + -г- с (a cos ф — /0)
Дифференцируя по ф, получим
~т— « 2 (mi + m) gfa sin ф — ас (a cos ф — /0) sin ф
иф
и обобщенная сила будет
Q == —-г- « — 2 (т + mi)?a sin ф -Ь ас (a cos ф - /0) sin ф.
При равновесии системы Q = 0, т. е.
[—2 (m + mi) ^fa + ас (a cos ф - /0I sin ф = 0.
Отсюда следует, что в положении равновесия
sin ф = 0.
Значит, ф1 = 0 является одним из равновесных состояний системы.
Но может быть и
-2 (т + mi) g + с (a cos ф — /0)^ 0,
откуда
ca

40 ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ [ГЛ.2
Согевндае равн©#есия, определяемое этим выражением, может су-
существовать» если
Таким образом, если
2(tn + ml)g>c{a-l0),
то существует одно состояние равновесия
ф|=0.
При 2(т + mi)g < с(а — /0) существуют два состояния равновесия:
Ф,=0, Фг
Пример 16» Две материальные точки Mi и M?t соедиленные
между собой жестким стержнем длины /, притягиваются к непо-
неподвижной точке О по закону всемирного тяготения. Пренебрегая мас-
массой стержня, найти обобщенные силы, при-
принимая, что движение происходит в одной
плоскости.
При движении точек в одной плоско-
плоскости положение каждой из них определяется
двумя координатами. По условию расстоя-
расстояние между точками не изменяется, сле-
следовательно, независимых координат будет
три, т. е. рассматриваемая материальная
система имеет три степени свободы. За
*6' обобщенные координаты примем qi = г,
Я2 = ф, Цъ = ф (рис. 2.6).
Потенциальная энергия системы равна
где аир — постоянные величины. Но так как
г*
то
Отсюда
дф [г
3-ф fr2 + /2-f 2г/соь(ф-
г
[г2
,2 + /2 + 2г/ СО:
1
Vr2 + /2 + 2i
а р[г
г2 [г2 + /2
!-H2-b2rfcos
s(q
г 1 с
+ i
(Ф
? ¦)
оэ(ф-
? cos (<
2г/ cos
))
-¦)]
*
-«
.(¦-¦И*

§141 УСТОЙЧИВОСТЬ СОСТОЯНИЯ РАВНОВЕСИЯ 41
§ 2.4. Устойчивость состояния равновесия
Принцип виртуальных перемещений, рассмотренный
в предыдущих параграфах, устанавливает необходимые
и достаточные условия равновесия материальной систе-
системы. Но не каждое состояние равновесия можно реализо-
реализовать практически. В самом деле, для сферического маят-
маятника, рассмотренного в примере 8 (§ 1.4, рис. 1.6), обоб-
обобщенные силы равны
QlS« ~ />/sin9, Q2 = 0.
Условием равновесия будет
Р/sin 9 = О,
откуда 6«ля (/г = 0, ±1, ±2, ...).
Практически этому условию соответствуют два положе-
положения равновесия: нижнее при 9 = 0 и верхнее при 9 = п.
Для положения равновесия при 9 = 0 характерно то, что
при сообщении маятнику достаточно малого отклонения
от этого положения равновесия и достаточно малой Ско-
Скорости он будет совершать движения вблизи состояния
равновесия. Для состояния же равновесия при 9=я при
сколь угодно малых отклонениях маятника от него и при
сколь угодно малой начальной скорости маятник будет
удаляться от этого положения равновесия.
Положения равновесия материальной системы, для
которых небольшие отклонения от этих положений раз-
новесия и небольшие начальные скорости точек системы
не приводят к выходу материальной системы из доста-
достаточно малой окрестности положения равновесия, назы-
называются устойчивыми.
Если же сколь угодно малые отклонения системы от
положения равновесия и сколь угодно малые начальные
скорости приводят к возрастающему отклонению мате-
материальной системы от положения равновесия, то этб по-
положение равновесия называется неустойчивым.
Может существовать еще и так называемое безраз-
безразличное положение равновесия, характерное тем, что при
выводе системы из этого положения она окажется в но-
новом положении равновесия и не будет стремиться при-
приблизиться к прежнему положению равновесия или уда-
удалиться от него. Примером такого положения равновесия

42 ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ [ГЛ. 2
может служить положение равновесия тяжелого шара на
горизонтальной плоскости.
А. М. Ляпунов дал строгое определение устойчивости
состояния положения равновесия:
Устойчивым положением равновесия системы назы-
называется такое ее положение, когда при достаточно малом
начальном отклонении от него и при достаточно малых
начальных скоростях все точки системы, имея сколь
угодно малые скорости, будут двигаться так, что все
они не уйдут от своего равновесного положения далее
наперед заданного расстояния, как бы оно мало ни было.
Приведем теперь достаточный признак устойчивости
положения равновесия материальной системы в консер-
консервативном силовом поле, даваемый теоремой Лагранжа —
Дирихле.
В теореме Лагранжа — Дирихле дается строгое дока-
доказательство того, что для любой материальной системы
(в консервативном силовом поле) минимум потенциаль-
потенциальной энергии является признаком устойчивого состояния
равновесия. Приведем формулировку теоремы Лагран-
Лагранжа—Дирихле: если для материальной системы, находя-
находящейся в консервативном силовом поле и подчиненной
голономным идеальным стационарным связям, потенци-
потенциальная энергия в положении равновесия системы имеет
минимум, то это положение равновесия устойчиво*).
Отметим, что минимум потенциальной энергии обес-
обеспечивает выполнение условий равновесия B.10), так как
в положении равновесия потенциальная энергия имеет
экстремальное значение.
Если заданными силами, действующими на систему
с идеальными связями, будут только силы тяжести, то из
теоремы Лагранжа — Дирихле следует: если центр тяже-
тяжести системы занимает наинизшее положение, то это по-
положение будет устойчивым положением равновесия
(принцип Торичелли).
Если в положении равновесия потенциальная энер-
энергия не имеет минимума, то исследование устойчивости
*) Эта теорема представляет собой частный случай теоремы
А. М. Ляпунова (А, М. Ляпунов, Общая задача об устойчиво-
устойчивости движения, ОНТИ, 1935; Н. Г. Четаев, Устойчивость движения,
Гостехиздат, 1946; Д. Р. М е р к и н, Введение в теорию устойчиво-
устойчивости движения, «Наука», 1971),

§2.41 УСТОЙЧИВОСТЬ СОСТОЯНИЯ РАВНОВЕСИЯ 43
состояния равновесия становится очень сложной за*
дачей.
Приведем формулировку одной из теорем Ляпунова:
если отсутствие минимума потенциальной энергии П
в исследуемом положении равновесия обнаруживается
уже по членам второго порядка (или вообще по членам
наименьшего порядка) в разложении функции H(
92,..., <7«) в ряд Тейлора, то равновесие неустойчиво.
Пример 17. Для механической системы, рассмотренной в при-
примере 7, потенциальная энергия может быть выражена формулой
где Хсо — значение координаты Хс при недеформированной пружи-
пружине, X = |/ — /о|—растяжение пружины. В соответствии с приведен-
приведенными в примере 7 расчетами
хг = — cos ф, xCQ = — cos фо, Я = 2r cos-~ — 2 г cos -~-
Следовательно,
П = -—¦ Рг (cos фо — cos ф) + 2cr2 (cos— — cos-|M ,
где
cos-^=^ (/0<2г).
Так как
то отсюда получаем условие равновесия
Bсг - Р) cos -— — cto\ sin —- == О,
что, естественно, совпадает с условием равновесия для данной си-
системы, полученным в примере 13 из условия Q = 0. Там же было
установлено, что всегда существует состояние равновесия при ф1 = 0,
а при
P<cBr-tQ)
или
Р>сBг + 10)
существует еще одно состояние равновесия:
Выясним характер этих состояний равновесия. Вторая производ-
производная от П по ф равна
Т [(Р ~ 2cr) cos ф + cl° cos "f]'

44 ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ [ГЛ. й
При ф = 0
d2U
Значит, при Р>сBг — /0) -ут^0 и это состояние равновесия
устойчиво, а при Р < сBг +/0)-—неустойчиво. Для состояния рав-
равновесия
ф2 - 2arc cos
- />) (Я -
2 Р - 2cr
Если Р < 2сг — ck> то " *2* > 0, т. е. состояние равновесия устой-
d2ll
чиво. Если Р > 2сг + с/0, то , 2 < 0 и, следовательно, состояние
равновесия неустойчиво. Итак, при Р <.2cr — cl0 существуют два со-
состояния равновесия: ф! = 0 — неустойчивое и ф2 = 2 arccos ¦=—~gr —
устойчивое. При Р > 2сг + cl0 существуют также два состояния рав-
равновесия: ф1 =* 0 — устойчивое и ф =* ф2 — неустойчивое. При
сBг — /0) < Р < сBг + /0) существует одно устойчивое состояние рав-
равновесия ф! == 0.
Пример 18. Определить устойчивость положений равновесия в
примере, схема которого изображена на рис. 2.5 (§ 2.2).
Дифференцируя
-1— = 2 (т + mi) ga sin ф — ас (a cos ф — /0) sin ф
по ф, получим
-т-у -= 2 (т + mi) ga cos ф + са2 sin2 ф — ас (a cos ф - /0) cos ф =
= а [2 (т + тх) g + с/0] cos ф + са2 A — 2 cos2 ф).
При ф = 0 будет
^- = а [2 (mi + m) g - с (а - /<>)].
При
2(m + ml)g>c(a — /0)
будет

УСТОЙЧИВОСТЬ СОСТОЯНИЯ РАВНОВЕСИЯ
45
т. е. потенциальная энергия имеет минимум и состояние равновесия
Ф = 0 устойчиво. При
2(m + ml)g<c(a-l0)
и, следовательно, состояние равновесия неустойчиво. При
ф = ф2 = arccos -
са
Если
dm
то , 2">0 и состояние равновесия ф = ф2 устойчиво. Значит, при
2(m + tnl)g>c(a-l0)
существует одно устойчивое состояние рав-
равновесия ф = 0. При
(а — /о)
существуют два состояния равновесия: не-
неустойчивое ф = 0 и устойчивое ф = ф2.
Пример 19. Невесомый стержень О А
длины а может свободно вращаться
вокруг точки О. К концу А стержня шар-
нирно прикреплен невесомый стержень АБ
длины а, на другом конце которого
закреплен груз В массы т. Точка О и р«с. 2.7.
точка В соединены между собой пружиной
жесткости с. Масса пружины пренебрежимо мала, длина пружи-
пружины в ненапряженном состоянии равна а. Найти положения равнове-
равновесия (рис. 2.7), считая, что система расположена в плоскости ху.
Пусть обобщенными координатами будут
Ях - ф» <7г = *•
Выражение для потенциальной энергии имеет вид
Здесь
xR~a (cos ф -Ь cos t|>),
А. =» 2а cos т г — а;

46 ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ {ГЛ. 2
значит, потенциальная энергия
П = — mga (cos q> + cos ф) + -г- са2 |2cos -ЗЦ—2- - 1) •
Далее вычисляем
дЛ п I ф — ш \ ib — ф
-^-- - mga sin ф -f са212 cos у ^ - 11 sin Y ^ ,
щ- - m^a sin ф - са2 \2 cos -^-^- - 1J sin -^-y^.
Углы ф и ф в положении равновесия определяются из уравнений
/ ф-ф \ ф-ф
— ca Bcos' y — 1) sin g «О.
Очевидно, что в положении равновесия
Ф1 = 0, -ф! = О
и
Фг — зт, фг5== л.
Складывая между собой оба уравнения B.11), получим положение
равновесия, для которого
sin ф + sin ф = О,
т. е. когда
<ф=-ф.
Вычислим теперь вторые производные от П:
Л = д 2 ^ ш^а cos Ф + са2 sifl2 о ""
—rl2cos
\|)-<р ,\ ф-ф
2 "Г08 2 '
В положении равновесия (рг =0, ф! == 0,
са
2
и
А - ЛС - В2 = f m^a - -^Y* - -^- - m^a (mga - са2).
При m^f > са А > 0, а так как при этом Л > 0, то потенциальная
энергия имеет минимум и положение равновесия устойчиво. При

I2.4J
УСТОЙЧИВОСТЬ СОСТОЯНИЯ РАВНОВЕСИЯ
47
А < 0, т. е. при mg<ca, потенциальная энергия экстремума не
имеет.
В положении равновесия фг = я, фг = я,
а2 са2 са2
са2
са2
са2
B \ о 2 4
wga + -g-J 4~ - mga (mga + c2a2) >0.
Поскольку Л < 0, то состояние равновесия фг = я, фг = я неустой-
неустойчиво.
Рассмотрим теперь случай, когда фз = —Фз Ф 0. Уравнения для
определения фз и фз получим из уравнений
B.11): 0\
[mg — са B cos ф3 — 1)] sin ф3 = 0, Л
[mgf — ca B cos ф3 — 1)] sin ф3 « 0.
Считая, что sin фз^Ои sin фзФ0, имеем
т^ — са B cos фз — 1) = 0,
откуда
tng + са
cos фз « cos фз2сд
Это положение равновесия существует, если
mg + са< 2са>
т. е.
mg < са.
Далее находим
(са2\
mga + -^-J cos фз + с а2 A — 2 cos2 ф3),
са^
В = — са2 A—2 cos2 фз) «г- cos фз>
(са2 \
я*?я Н—j—J cos фз + са2 A—2 cos2 ф3),
Л = АС - В2 - 2mgca* cos ф3 A — cos2 ф3).
Так как решение ф = ф3 существует при са > mg, то А > 0, но так
как при этом
^р cos фз + са2 A - cos2 ф3) > 0,
то положение равновесия ф = нн фз, ф = ±фз при са > mg устой-
устойчиво. На рис. 2.8 показаны эти состояния равновесия.

ГЛАВА 3
УРАВНЕНИЯ ДВИЖЕНИЯ
§ 3.1. Уравнения Лагранжа первого рода
Рассмотрим систему п материальных точек, подчинен-
подчиненную k голономным идеальным связям. Дифференциаль-
Дифференциальные уравнения движения точек материальной системы
в координатной форме, в проекциях на оси декартовой
системы координат имеют вид
ntiXi^Xi + Rxi, )
miffi-Yi + Ryi, \ (/=1,2, ...,«), (ЗЛ)
ntiZi = Zi + R2i )
где rrii — масса i-й точки, Хи Yi, Z% — проекции равнодей-
равнодействующей активных сил, приложенных к i-й точке, /?х;,
Ryu Rzi — проекции равнодействующей реакций связей,
действующих на i-ю точку.
Если активные силы заданы, то система уравнений
C.1) представляет собой систему Зп уравнений с 6я не-
неизвестными: 3/г координат (хг-, уи z%) и 3/г проекций реак-
реакций связей (Rxu Ryu Rzi). Присоединяя к этим уравне-
уравнениям k уравнений связи
// (*/, yi9zhi) = 0 (/=1,2,..., *), C.2)
будем иметь уже Зп + k уравнений. Для получения ос-
остальных Зп — k уравнений следует учесть характер
связей.
Так как связи идеальные, то проекции реакций свя-
связей, в соответствии с формулами A.35), запишутся в

УРАВНЕНИЯ ЛАГРАНЖА ПЕРВОГО РОДА
49
виде
/-1
k
(/=1,2, ...,n). C.3)
Подставляя эти выражения в уравнения C.1), получим
(/=1,2, ...,n). C.4)
Присоединяя к этим 3/г уравнениям k уравнений связей
C.2), будем иметь 3/г -\- k уравнений относительно 3/г + k
неизвестных координат (х^ Уи %д
и множителей Лагранжа (К\, Ая, ...
..., %и)- После решения этой си-
системы уравнений проекции реакций
могут быть найдены по формулам
C.3).
Уравнения C.4) называются
уравнениями Лагранжа первого ро-
рода. Следует отметить, что практиче-
практическое использование уравнений C.4)
в системах с большим количеством
точек весьма затруднительно из-за рис. зл.
большого числа уравнений.
Покажем применение этих уравнений на примере системы с одной
степенью свободы. Пусть математический маятник совершает движе-
движение в вертикальной плоскости ху (рис. 3.1). Уравнения связей имеют

50 УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ.
в этом случае вид
Мх,у.г)-г-0.
На основании C.4) уравнениями движения будут
ту = кх2у, \ C.6)
0 = Я2, i
так как 2 = 0. Следовательно,
^ = 0, *i--|?. C.7)
После умножения первого уравнения системы C.6) на # и вычита-
вычитания из него второго уравнения, умноженного на х, получим
m(xy~yx)~tngy. C.8)
Введем замену
х »/ cos ф, # == / sin ф. C.9)
Отсюда
Jc — — / sin ф • ф, у = / cos ф • ф, "I
?= - /сО8ф»ф2 — /85Пф»фг [ (ЗЛО)
у = — / sin ф • ф2 + / cos ф • ф, /
и уравнение C.8) примет известную форму дифференциального урав*
нения колебания математического маятника:
ф + -у sin ф « 0.
Проинтегрируем это уравнение при начальных условиях: t =• 0»
ф = о, ф = фо. Тогда первый интеграл будет равен
ф2 = ф2 - 2-J-0- cos ф). C.11)
Найдем теперь реакцию нити. В соответствии с формулами C.3)
и, следовательно,

§32] ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ 51
ИЛИ
Так как
— -у- Sin ф,
а ф2 определяется формулой C.11), то
R « ml Uq - 2 у A - cos ф) + у cos ф « ml I ф§ - у B - 3 cos (p)
Из этого уравнения следует, что связь в виде нити будет удержи-
удерживающей, если при ф = я R ^ 0. Это будет, если начальная угловая
скорость фо удовлетворит неравенству
§ 3.2. Общее уравнение динамики
В курсе теоретической механики при рассмотрении
несвободного движения материальной точки иногда при-
применяется принцип Даламбера (метод кинетостатики).
Если в дифференциальном уравнении движения мате-
материальной точки
mw=F + R, C.12)
где w — ускорение точки, т — ее масса, a F и R — соот-
соответственно активная сила и реакция связи, ввести обо-
обозначение
/«-/ют, C.13)
то уравнение C.12) можно записать в форме
0, C.14)
которое и выражает принцип Даламбера. Вектор / =
= —mw называется силой инерции.
Уравнение C.14) представляет собой уравнение дви-
движения, записанное в форме уравнения статики. Принцип
Даламбера можно сформулировать следующим образом:
в любой момент движения сумма активной силы, реакции
связи и силы инерции равна нулю.
Рассмотрим теперь систему материальных точек, под-
подчиненную идеальным связям. Для каждой точки системы
согласно C.14) можно написать
F, + Jf, + /, = 0 (/=1,2, ..., /г), C.15)

52
УРАВНЕНИЯ ДВИЖЕНИЯ
{гл. а
где Fi и Кг — равнодействующие активных сил и реакций
связей, действующих на i-ю точку, а /* = —miWi — сила
инерции, соответствующая f-й точке. Умножая каждое из
выражений C.15) на соответствующее рассматриваемой
точке виртуальное перемещение fir* и складывая затем
полученные соотношения между со-
собой, получим
У
!<'<
= 0. C.16)
Так как связи, наложенные на ма-
материальную систему, идеальные, то
п
и, следовательно,
п
w
Рис. 3.2.
= 2 (Ft -
i
дг( == 0. C.17)
Полученный результат можно сформулировать так:
в каждый момент движения материальной системы, под-
подчиненной идеальным связям, виртуальная работа всех
активных сил и сил инерции на виртуальных перемеще-
перемещениях точек материальной системы равна нулю.
Уравнение C.17) и представляет собой общее уравне*
ние динамики, или уравнение Даламбера — Лагранжа.
Если Хи У и Zi — проекции силы Fi на оси декартовой си-
системы координат, а я*, у и и — проекции ускорения /-й
точки на эти же оси, то уравнение C.17) можно записать
в виде
РЗ
(Z< - mfid 6z{] = 0.
C.18)
Пример 20. Неоднородный блок массы m и радиуса R может
вращаться без трения вокруг горизонтальной оси, проходящей через
его геометрический центр. Центр тяжести С блока находится на
расстоянии а от оси вращения. Через блок перекинута нерастяжимая
нить, массой которой можно пренебречь. Нить по блоку не про*

ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
скальзывает. Массы грузов А и Bt подвешенных к концам нити, р#в-
ны т\ и т2 (rti2 > mi). Определить ускорение груза В.
Предположим, что груз В имеет ускорение w, направленное
вниз (рис. 3.2). В соответствии с условием C.18) имеем
(m2g - m2wNx2 + Д1 [{mfi + Jix) bx
где последняя сумма относится к точкам диска, а
— сила инерции t-й точки диска. Так как ускорение /-й точки диска
равно *)
где е — угловое ускорение, со — угловая скорость диска, г* — радиус-
вектор 1-й точки диска, то
где 8 «= | ег |, и, следовательно,
Таким образом, имеем
+ 2 [(miS "
+ (m^e + т^У^2) &yt] = 0.
Координаты f-й точки диска равны (рис. 3.3) х{ = r{ cos (ф 4- аХ
yt = r^ sin (ф + а^), где щ — постоянный угол между ради усом-векто-
усом-вектором *-й точки и направлением отрезка ОС. Значит,
Тогда
(^i^ + nt\w) Ьхх
« — /\ sin (ф + at.) 6ф = — у
/ ~ ri cos (Ф + a^) 6ф =а ^ бф.
S
*) Н. В. Б у т е н и н, Я. Л. Л у н ц, Д. Р. М е р к и н, Курс тео-
теоретической механики, т. 1, «Наука», 1970.

54 УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. 3
ИЛИ
(tnxg + тхт) Ьх{ + {m2g - m2w) 6х2 + (- mycg + zIQ) бф - О,
где /о — момент инерции блока относительно центра О. Так как
нить нерастяжима и не проскальзывает, то
и, следовательно,
myr el
(
-
mxg - mxw + m2g - m2w
Принимая 6*2 Ф 0, получим
/ yr\ eln
\m2 - mi + m -±-jg - (m, + m2) w - -^ - 0.
Учитывая, что
найдем
m2 — mi + m -^- sin <p
Движение грузов будет колебательным, если
так как при выполнении этого условия и при sin ф > 0 ускорение
w < 0, при sin ф < 0 ускорение w > 0, ибо по условию задачи
т2 > mi. Если блок будет однородным, то а = 0 и
2(/n2--m1)
так как /^ = —т>— - В этом случае до > 0.
Пример 21. Через блок А массы т и радиуса R перекинута не-
невесомая нерастяжимая нить. На одном конце этой нити привязан
груз массы ти к другому концу прикреплен блок В радиуса г и
массы /П2. Через блок В также перекинута невесомая и нерастяжи-
нерастяжимая нить, на концах которой прикреплены грузы массой тг и т^
(рис. 3.4). Ось блока А неподвижна. Нити по блокам не проскаль-
проскальзывают. Определить ускорение грузов, считая блоки Л и В одно-
однородными.

t 3.2]
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
55
Рассматриваемая система имеет две степени свободы. В соот-
соответствии с выражением C.18) можно записать
{m2g~m2wzx)bx2 +
+ {m4g - tnAwAx) 6*4 - /0е2 6ф - Ioe2z 6q>x - О,
где /0 и /Oi —моменты инерции блоков А и В относительно их
осей вращения, а е* и г2г их угловые ускорения. Составим уравне-
уравнения связей: ,л
где 1\ и /г —длины нитей. Из этих,
уравнений следует, что
6*1+6*2 = 0,
6*з+ 6*4-2 6*2 = 0
и
*1 + *2 = 0, *з + *4 ~ 2*2 » 0,
т. е.
Из этих выражений можно найти
6*2 — — 6*1э
6*4 = — 6*з — 26*1,
Кроме того, имеем
= Ем.
R '
Следовательно,
I (/TZj — Ш2 — 2/724) g —
2 '
6*,
m2r2
2 #
-~Ч ^1лг -
Рис. 34.
6*з
Ф1- —
I (m3 - т4) g - 2т4ш^ - fm3 + m4 + -^-j шЗЛГ1 6*3 = 0,
откуда
[ + m2 + 4m4 + -ir Wix + 2tn wZx = (шл — nio-i
Шэ + nii + ~q~ J ®)зх — (ntz — nti) g.

УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. $
Решая эти уравнения, получим
\Ш\ — тп% — Zmi) I /723.-Г tri\ Л—TjT) "~"
+ т2 + 4ет4 + —-J (т3 + т4 + -~^-j - 4mf
4- m* +
-yJ (m3 — m4) —
" i ¦
Так как w2x— — u>ix и wix=* — wbx — 2wlXt to окончательно
— m* — 2m4) f m3 + m4 + -~-J — 2m4 (m3 - ntt)
( + 4 +j ^+ m4
-m4) (m, + m2 + ~j + 2(тх-т2- 2ttii) fm8 + -~M
Если числитель в выражении wix равен нулю, т. е.
(mi — т2 — 2m4) (m3 + т4 + —А — 2т4 (/и3 — т4) = 0f
то это значит, что масса пц или движется с постоянной скоростью,
или находятся в покое. Величина п%\ при этом равна
§ 3.3. Уравнения движения в обобщенных
координатах (уравнения Лагранжа второго рода)
Уравнения движения несвободной голономной систе-
системы в обобщенных координатах мы получим из общего
уравнения динамики C.17). Приступая к выводу,следует
прежде всего определить число степеней свободы, затем
выбрать обобщенные координаты. Они должны удовлет-
удовлетворять условиям — однозначно определять положение си-
системы и быть между собой независимыми. В остальном
выбор обобщенных координат вообще произволен. Од-
Однако весьма важен «удачный» выбор этих координат.
Термин «удачный» нужно понимать в том смысле, что

$3.3! УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА 57
уравнения движения при таком выборе получают наибо-
наиболее компактный вид. Например, для математического
маятника (рис. 3.1) наиболее удачной обобщенной коор-
координатой является угол ср. Для сферического маятника
(рис. 1.6) такими координатами будут 8 и ф.
Выбрав обобщенные координаты qu q& ...» q& (s —
число степеней свободы), следует далее выразить декар-
декартовы координаты точек системы через эти обобщенные
координаты, т. е. получить функций
?2> • • • > Qs> О»
(/=1, 2, ..., п). C.19)
Отсюда получается эквивалентная им зависимость
ri-r{(qiy q2, ..., qs, t) (/-1, 2, ..., n) C.20)
(r< — радиус-вектор i-й точки).
В соответствии с A.41) можно записать
Подставляя это выражение для 6г» в общее уравнение
динамики C.17), получим
или, меняя порядок суммирования,
Так как вариации обобщенных координат могут выби-
выбираться независимо друг от друга, то полученное равен-
равенство будет выполняться только тогда, когда коэффи-
коэффициенты при 6#ь 6#2, ..., bqs будут равны нулю, т. е.
t - m,w,) • ^- = 0 (m - 1, 2 s). C.21)
m

68 УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. 3
Вспомнив, что обобщенные силы выражаются формулой
A.42):
п
2 = 1 M
перепишем выражения C.21) в виде
= Qnt (m-1, 2, ..., s). C.22)
/«i
Выражение, стоящее под знаком суммы, преобразуем
следующим образом:
дг, dv? дг.
На основании C.20) имеем
dr* дг, дг. дг,
—*+*+ +
•••+-fe-^+-?r- C-24)
Так как частные производные
drt dri drt drt
17 !u "^7 "^Г
являются функциями обобщенных координат и времени,
то, дифференцируя C.24) по gm, найдем, что
5«ёг О»-».*,....*). C-25)
Продифференцировав выражение C.24) по qm, получим
dvt d2rt . d2rt

§ 3.3} УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА 59
С другой стороны,
d I drt\
Следовательно,
dt
Подставляя соотношения C.25) и C.26) в выражение
C.23), будем иметь*)
дг, d I dv, \ dv.
Используя полученное выражение C.27), перепишем со-
соотношения C.22) в виде
2 J dqn
но так как
C.28)
есть кинетическая энергия материальной системы, то
?(?)-•&-<*« («-1.2..-.S). C.29)
Полученные уравнения называются уравнениями Ла~
гранжа второго рода. Производные от обобщенных коор-
координат qu <?2, ..., ?s называются обобщенными скоро-
скоростями. Уравнения Лагранжа второго рода не содержат
реакций идеальных связей, что делает их удобными для
практического использования. Таким образом, в об-
общем случае каких угодно активных сил и при наличии
идеальных связей движение материальной системы опре-
определяется s уравнениями Лагранжа второго рода C.29).
*) Здесь используется равенство v #-^—¦* °~л~"* вытекающее
из соотношения v • v = v2.

60 УРАВНЕНИЯ ДВИЖЕНИЯ [ГД. 3
Для доставления левых частей этих уравнений сле-
следует выразить кинетическую энергию через обобщенные
координаты и обобщенные скорости. Обобщенные силы,
стоящие в правых частях этих уравнений, могут быть най-
найдены или непосредственно по формулам A.42), или как
коэффициенты при вариациях обобщенных координат
в выражении Для возможной работы A.43).
Система уравнений Лагранжа второго рода представ-
представляет собой систему s обыкновенных дифференциальных:
уравнений второго порядка относительно обобщенных ко-
координат. Интегрирование этих ураэнений дает нам обоб-
обобщенные координаты <7ь <7г, ..., Qs как функции времени
и 2s произвольных постоянных интегрирования. Далее
на основании формул C.19) можно получить декартовы
координаты в зависимости от времени / и 2s произволь-
произвольных постоянных интегрирования.
Если бы рассматриваемая материальная система была свобод-
свободной, решение дифференциальных уравнений ее движения содержало
бы 2 • Ъп = бп произвольных постоянных. Следовательно, решение
уравнений несвободной системы не досчитывает 6я — 2s*=
= 2Cи — s)=2& постоянных интегрирования. Это произошло по-
потому, что задача решалась при наперед заданных 2k интегральных
формулах, именно k уравнениях связей и k тех соотношениях, кото-
которые можно получить путем однократного дифференцирования этих
уравнений связи; соответственно с этим и понизилось число необ-
необходимых актов интегрирования на 2k. Поэтому для задачи о движе-
движении несвободной системы полученное решение, содержащее 2s про-
произвольных постоянных, является окончательным, исчерпывающим все
варианты в задании начальных условий.
Замечание. При применении уравнений Лагранжа
второго рода к задачам на относительное движение,
а также к задачам с нестационарными связями кинети-
кинетическую энергию материальной системы следует вычис-
вычислять в ее абсолютном движении; при нахождении обоб-
обобщенных сил нужно исходить из того, что связи считаются
мгновенно остановленными.
§ 3.4. Примеры на составление уравнений Лагранжа
второго рода
Пример 22. Составить уравнение движения физического маят-
маятника, представляющего собой однородный диск массы М и радиу-
радиуса г, жестко прикрепленный к концу А стержня длины /. Другой
конец О стержня является точкой подвеса (рис. 3.5). Массой стерж-
стержня пренебречь»

f *<
ПРИМЕРЫ
61
Рассматриваемая система имеет одну степень свободы. За об-
обобщенную координату примем угол q •=» <р.
Координатами центра тяжести диска к с и у с будут
хс = (/ + г) cos ф, ус « (/ + г) sin ф.
Кинетическая энергия равна
Г~1/Оф*, где /o»/c + Af(/ + rJ
есть момент инерции маятника относительно точки подвеса
Рис. 3.5.
Рис, 3.6.
Aс — момент инерции диска относительно его центра). Так как
то '0=
Согласно формуле A.42) обобщенная сила
. _ дх,
Имея в виду, что
от
С Mg A+ г) sin ф.
. дТ „
получим
или
Приведенная длина такого маятника равна
Пример 23. Составить уравнение движения математического
маятника, точка О\ подвеса которого совершает гармоническое дви-
движение в вертикальной плоскости вдоль прямой, наклоненной пол
углом а к горизонту (рис. 3.6).

62 УРАВНЕНИЯ ДВИЖЕНИЯ [ТЛ. 3
Пусть 00\ = a sin at. За обобщенную координату возьмем угол
^ф. Координаты точки М зависят от <р следующим образом:
х в / cos ф — 001 sin а = / cos <p — a sin cotf sin а,
у = / sin ф + ООХ cos а = / sin ф + а sin Ш cos а.
Так как
х ~ — / sin ф • ф — а@ cos ®t sin a,
г/ = / cos ф • ф + а© cos Ы cos а,
то скорость точки М олределяетея из условия
v2-x2-hy2~ /2ф2 + 2/фя<о cos ©/ cos (ф — а) 4- а2а>2 cos2 ©/.
Следовательно, кинетическая энергия будет равна
Т «-~ m [/2ф2 + 2/фаа> cos ©/ cos (ф - а) + а2ю2 cos2 ©/].
Отсюда
-— в ш/2ф + m/aco cos ш/ cos (ф — а),
-_ = — т/фа<о cos ©/ sin (ф — а).
Виртуальная работа равна
ЬА = mg Ьх » — mg/ sin ф бф.
Следовательно, обобщенная сила
Q = — mg/ sin ф.
Составим теперь уравнение Лагранжа второго рода:
-тг [т/2ф + mlaco cos ©/ cos (ф — а)] =
» mlyaiu cos co^ sin (ф — <z) ^= — mg/ sin ф,
откуда
т/2ф — mla®2 sin 0/ cos (ф — a) + mg/ sin ф ~ 0,
или
ф ~ у ©2 sin со/ cos (ф — a) + -y- sin ф = 0.
Для малых ф это уравнение имеет вид
ф 4- (-у- — -у ю2 sin a sin ©/1 ф »-у ©2 cos a sin ®t.
рр 24. Составить уравнения движения центробежного регу-
регулятора, схема которого представлена на рис. 3.7, Точечные грузы

§3.41
ПРИМЕРЫ
63
Cs>
Mi и Мъ имеют массы, равные т. Масса муфты А равна М. Мас-
Массой стержней, длина которых /, пренебречь. Угловая скорость
вращения регулятора постоянна и равна о>. Трением пренебречь.
Рассматриваемая система состоит
из трех тел: точек М\ и М2 и муфты
А. Число степеней свободы равно еди*
нице. За обобщенную координату при*
мем угол ф.
В неподвижной системе коорди-
координат Охуг координатами точек М\ и
М2 и муфты А будут соответственно
Х\ = / COS ф,
ух = / sin ф cos (со/ -Ь а),
Z\ = / sin ф sin (со/ + а),
х2 ¦* / cos ф,
у2 = — / sin ф cos (со* + а),
г2 =» — / sin ф sin (со/ + а).
л:3 = 2/ cos ф,
Рис. 3.7-
где а — угол, который образует плоскость регулятора с неподвиж-
неподвижной плоскостью ху в начальный момент времени. Скорости точек Mi
и М2 и муфты А соответственно определяются соотношениями
Кинетическая энергия системы будет равна
Т = 12(т + 2М sin2 ф) ф* + ml2®? sin5 ф.
Отсюда
Л7
-^— в 4Л1/2ф2 sin ф cos ф + 2tnPa>2 sin ф cos ф.
Виртуальная работа равна
6А = mg Ьхх + m^r Ьх
e (— mgl sin ф — mgt sin Ф —

64
УРАВНЕНИЯ ДВИЖЕНИЯ
(ГЛ. 3
и, следовательно,
Q = - 2gl (m + М) sin ф.
Составим уравнение Лагранжа:
(m+2Af sin2 ф) ф Н-2Мф2 sin ф cos ф-тоэ2 sin ф cos ф= — -у- (т + М) sin ф.
Регулятор будет в положении равновесия, если ф =» 0, ф = 0. Это
будет при *)
СОЗфо
mJ
" Введем в рассмотрение новую координа-
координату ф, определяемую равенством
Ф = Фо + ф.
Тогда
sin (ф0 + -ф) = sin фо cos -ф + cos ф0 sin ф,
cos (фо + *ф) ~ cos фо cos ф — sin фо sin -ф.
Для малых ф
sin (фо + ф) » sin фо + ф cos ф0,
Рис- 3-8< cos (фо + *ф) «* cos фо — *ф sin ф0.
Подставляя эти выражения в уравнения движения и сохраняя
только линейные члены относительно г|?, "ф, будем иметь
m©2
где
sin2 фо:
Г (т + М) g
- [ ^^-s J
Пример 25. Составить уравнения движения для системы, состоя-
состоящей из груза Л массы М, движущегося без трения по наклонной
плоскости, образующей с горизонтом угол а, и прикрепленного к
нему математического маятника. Масса груза маятника равна т,
нить невесома и имеет длину /. К грузу А прикреплена пружина
(рис. 3.8) жесткостью с, другой конец которой закреплен в непод-
неподвижной точке.
Рассматриваемая система имеет две степени свободы. За обоб-
обобщенные координаты выберем расстояние | вдоль плоскости от гру-
груза А до точки статического равновесия пружины и угол ф, образуе-
образуемый маятником с вертикалью.
*) Это значит, что равновесное положение возможно, если

f 3 4} ПРИМЕРЫ 66
Координатами центра масс груза А и координатами точки В
соответственно будут (начало координат помещено в точку статиче-
статического равновесия)
хх = I sin а, ух« % cos а,
#2 == #i 4- / cos ф = ? sin а 4- / cos <p,
У 2 — У\ +1 sin Ф — % c°s а 4- / sin ф.
Кинетическая энергия системы равна
= 4- Лф + i- m li2 + /2<ps + 2|/ф cos (ф + а )
Отсюда
—г- = (М + т) 4 + тЩ cos (ф 4- а),
-^- = 0, — = т/2ф -Ь т|/ cos (ф 4- а),
¦^— = - т|/ф sin (ф + а).
Найдем обобщенные силы. Сила, действующая на груз А со
стороны пружины, равна F = с [? + X |,« где Я — статическое удлине-
удлинение пружины, равное
. (М -f m) gsina
с
Следовательно,
6Л = — с Ц + К) sin a 6*! - с (I + X) cos a 6r/! -f M? 6xx + mg блг2«
e f — с (g + a) + (M + m) g sin a] 6* - mgl sin ф 6ф.
Отсюда
Qi = - с (| + Л) + (M + т) g sin a = - c^,
Q2 ~ — ^^ sin ф.
Уравнениями Лагранжа будут
~-jj [{M + m)i + тЩ cos (ф + a)] = - с\9
--г- [т/2ф -Ь m\l cos (ф + а)] + т\Щ sin (ф + а) = — mgl sin ф
или
(М + т) 1 + т/ф cos (ф + а) — т/ф2 sm (ф + а) « — с|,
/л/2ф -f- т%1 cos (ф 4- а) = — mgl sin ф.
3 н. в. Бутенш*

66
УРАВНЕНИЯ ДВИЖЕНИЯ
ггл. а
§ 3.5. Учет дополнительных связей
Рассмотрим теперь вопрос об учете дополнительных
связей, которые могут быть наложены на точки матери-
материальной системы.
Пусть на систему, подчиненную k связям, дополниг
тельно налагается еще г связей. В этом случае число ра-
ранее выбранных обобщенных координат Ъп — k будет пре-
превосходить число степеней свободы Ъп — k — г, которые
теперь имеет рассматриваемая система. Дополнительные
связи мы будем учитывать путем введения реакций этих
связей в число активных сил. Обозначим эти реакции че-
через /?/. Виртуальная работа при этом вычисляется по
формуле
где Qm—обобщенные силы, обусловленные реакциями
Я». Следовательно, обобщенные силы в уравнениях Лаг-
ранжа будут состоять из двух частей, соответствующих
активным силам и реакциям новых связей, т. е.
ж -Q-+Q* <* -1. * • • •. *>• <3-зо>
Если новые связи идеальные, то в соответствии с фор-
формулами A.35)
dtp
дх:
дуГ
(/=1, 2, ..., n), C.31)
где Хр — множители Лагранжа, а
/Р (*i> Уь г1% t) = 0 (р = 1, 2 г) C.32)
— уравнения дополнительных связей.

УЧЕТ ДОПОЛНИТЕЛЬНЫХ СВЯЗЕЙ
67
Согласно формуле A.42) имеем
v dxi , n/ *Уг
или, учитывая выражения C.31), получим
т
у(дх'
а/р I дУ!
1*Г **
Ух а/
dfp I аг Ух а/р
^Р dxt I a/p ^f I dU dzi\_
h л dh
(т=1, 2, .... s). C.33)
Таким образом, уравнения C.30) могут быть записаны
в виде
d ( дТ \ дТ Л , Л dh , л dh , . 1 д/г
C.34)
Для фактического решения этой задачи к уравнениям
C.34) (их число Зп — k) следует присоединить еще г
уравнений новых связей C.32).
Тогда мы получим систему °
Ы — k + г уравнений с тем же
числом неизвестных: Зп — k об-
обобщенных координат и г лагран-
жевых множителей.
Пример 26. Найти реакции, обуслов-
обусловленные введением дополнительной свя-
связи, для двойного математического маят-
маятника. Массы грузов Мх и М2 равны
соответственно тх и т2, а длины —
h и /2.
Составим сначала уравнения движе-
движения двойного маятника без дополни-
дополнительных связей (рис. 3.9). Число степе- рис. 3.9.
ней свободы равно двум. Пусть q\ — ф,
q2 = -ф. Координаты грузов М\ и М2 выражаются через ф и
мула*ми
хх = U cos ф, у\ = / sin ф,
х2 = 1Х cos ф + /2 cos ф, у2 = h sin ф + h sin ф.
фор-

фор68 УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. 3
Кинетическая энергия системы равна
—j («1 + т2) 'У + \ «2 ['I*2 + 2/^гФФ cos (Ф -
и, следовательно,
* cos (<p - ф),
дф ~~ "•^i^yV sin (ф ~ *Ф)>
cos (ф — ф),
(Ф-Ф).
Виртуальная работа
ЬЛ — triig 6*1 + m2g Ьх2 =
= (— m\gl\ sin ф — m2g/i sin ф) бф — tn2l2g sin ф бф,
откуда
Qj = _ (tn\ + т2) gl\ sin ф,
Q2 =sx — m2g72 sin ф.
Уравнениями движения системы будут
(in j + т^ /|ф + m2l\l2 cos (ф — ф) ф + ^2/1/2ф sin (ф ~ Ф) —
=» — (mi + т2) gl\ sin ф:
т2/2ф + A^/j/g cos (ф — ф) ф — /Пз/^зф2 sin (ф — ф) =
= — m2gl2 sin ф.
Рассмотрим два случая введения дополнительной связи.
1) Пусть f(xi, 0ь 2i, х2, 02, z2) e 0i ™ 0 (рис. ЗЛО). Для этого
случая уравнения C.34) имеют вид
(/Wj -f- т2} /|ф Н- m2/j/2 cos (ф — ф) ф + т2/^/2ф sin (ф —• ф) =*
== — (пгх + т2) gt\ sin ф + %l\ cos ф,
т2/|ф + m2/j/2 cos (ф — ф) ф — т2/!/2ф2 sin (ф — ф) = — m2g/2 sin ф.
Присоединим к этим двум дифференциальным уравнениям движе-
движения уравнение связи
0! «¦ 1Х sin ф = 0.
Из этого уравнения связи следует, что ф яв 0, и, следовательно
ф — 0, ф= 0 (т. е. точка Mi неподвижна). Второе дифференциальное
^ '

§3.5]
УЧЕТ ДОПОЛНИТЕЛЬНЫХ СВЯЗЕЙ
69
уравнение вырождается в уравнение колебаний простого математи-
математического маятника
ф + -— sin ф = 0.
h
Из первого дифференциального уравнения находим Я:
Я = m2h cos фф — т2/гф2 sin ф.
Так как
ф = —f- sin ф,
h
ТО
Я = — sin ф [m2/2^o "" т2? B — 3 cos
В соответствии с C.31) имеем
Д? « Я = - sin -ф [т2/2ф^ - m2g B-3 cos ф)],
т. е. дополнительная сила реакции равна проекции реакции, дей-
действующей на точку М2, на направление оси у (см. стр. 51).
Ряс. 3.11.
2) Пусть теперь дополнительная связь принуждает, груз М2 дви«
гаться только вдоль оси х (рис. 3.11). Уравнением этой связи будет
ь У и
sin q> + /2 §in ф = 0.
*) Начальные условия: при / = 0, ф = 0i ф==фо (см.
стр. 50).

70 УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. 3
Для того чтобы получить уравнения C.34), следует к правой части
первого дифференциального уравнения движения прибавить член
X -_L — hl\ cos Ф,
аф
а к правой части второго дифференциального уравнения — член
C.36)
Для упрощения выкладок в дальнейшем положим l\ = k
В этом случае из уравнения связи следует:
sin ф = — sin ф,
откуда
Подставив этот результат в уравнения движения, получим
(тх + m2) /2ф - m2/2 cos 2фф + т2/2ф2 sin 2ф =
= — (тх + tn2) gt sin ф + Я/ cos ф,
— т2/2ф + m2/2 cos 2ф ф — щ212у2 Ып 2ф ==
= m2ql sin ф + XI cos ф.
Вычитая из первого уравнения второе, будем иметь
(пгх + 4m2 sin2 ф) ф 4- 2ш2ф2 sin 2ф » - (тх + 2т2) -у sin ф.
Это уравнение служит для определения закона движения получен-
полученной системы.
Складывая теперь между собой уравнения C.36), найдем урав-
уравнение для определения Я:
Дальнейшее решение задачи заключается в определении из урав-
уравнения движения угла ф; после этого по формулам
находится реакция дополнительной связи.
§ 3.6. Обобщенные реакции отброшенных связей *)
Рассмотрим голономную систему с s степенями свобо-
свободы. Пусть <7ь 92, ..., Qs — обобщенные координаты, опре-
определяющие положение системы. Отбросим г связей. Тогда
*) А. И. Лурье, Аналитическая механика, Физматгиз, 1961»
стр. 327—331.

§ З.е] ОБОБЩЕННЫЕ РЕАКЦИИ ОТБРОШЕННЫХ СВЯЗЕЙ 71
число степеней свободы увеличится до s + r. К старым
обобщенным координатам <7ь Чь <7з, ..., из прибавим г
новых qs+u 9s+2, ..., qs+r и будем иметь в виду, что при
qs+lx = О (ц=1, 2, ..., г) новая материальная система
совпадает с исходной системой. Мы можем представить
переход от новой системы к исходной как наложение на
новую систему г новых связей вида
0 (|i=l, 2, ..., Г).
Тогда, в соответствии с уравнениями C.34), имеем
ц=1
но так как
д/5+й f 0, s + цФт (m= I, 2, ..., s + r),
d<tm ""( 1, s + ^ = m (fx = l, 2, ..., r),
то
Эти уравнения следует рассматривать совместно о
уравнениями связей
/s+ц = fls+ц = 0 (\i = 1,2, . . ., Г).
Следовательно, после составления полученных уравнений
в них. следует положить
0 (м= 1, 2, ..., г).
Итак, для получения обобщенных реакций отброшен-
отброшенных связей служат уравнения
^-^ <*-*+!,....* + г). C-37)
в которых после их составления следует положить
0> <7s+n = 0, ^s+J1 = 0 (ji=l, 2, ..., г).
Пример 27. Тело Л массы mi, подвешенное на пружине жест*
костью с, может совершать движение по вертикали. С помощью
шарнира к телу А прикреплен невесомый стержень длиной /, на

72
УРАВНЕНИЯ ДВИЖЕНИЯ
[ГЛ. Э
другом конце которого прикреплено тело В массы т2. Тело В дви-
движется по горизонтальной направляющей (рис 3.12). Пренебрегая
трением, определить реакцию направляющей.
Начало координат возьмем в положении тела А при ненапря-
ненапряженной пружине. Рассматриваемая система имеет одну степень сво-
свободы. За обобщенную координату примем отклонение тела А от его
положения при ненапряженной пружине (^i = Xi). Рассмотрим те-
теперь новую систему, когда отсутствует направляющая. Эта система
У/У/Л
г*
?» :
s Aft
к
X
Рис. 3.12.
Рис. 3.13.
имеет уже две степени свободы. За обобщенные координаты примем
q\ = xi, q* = % (рис. 3.13). Координатами тела А и В соответственно
будут
где а — расстояние от начала координат до направляющей.
Кинетическая энергия системы выразится формулой
где
Найдем теперь
дТ
x\ — m2
dK .
d (дТ\ dK 5
dt \дЦ dt

§ 3.61
ОБОБЩЕННЫЕ РЕАКЦИИ ОТБРОШЕННЫХ СВЯЗЕЙ
73
где
дК
dK
dt
Xlh
В соответствии с выражением C.37) получаем реакцию направляю-
направляющей, полагая ? = 0, | = 0, f = 0:
- m
2 /2 - (а - ххJ
2 [/2 _ (а _ J
но так как
то
и, следовательно,
Я2 =
Q, - - схх + m^, Q2
2 /2 (п — Y
Уравнение для определения
г 1„ _ v \2
имеет вид (см. стр. 71)
"*~"У/
Это уравнение Лагранжа, составленное для координаты *ь в кото-
котором положено g = | = | = 0.
Пример 28. Тело А массы М мо-
жет двигаться по гладкой горизон-
тальной направляющей. К нему на не-
невесомом стержне длины / шарнирно
прикреплено тело В массы т (рис.
3,14, а). Найти реакцию направляю-
направляющей, принимая тела Л и В за мате-
материальные точки.
Примем за обобщенные коорди-
координаты расстояние у\ точки А от нача-
начала координат и угол q> отклонения
стержня от вертикали:
а)
Отбросим теперь связь, нало-
наложенную на тело Л, т. е. освободим
тело А от направляющей. Новая
система имеет три степени свобо-
свободы, и новая обобщенная координата
<7з = *1 (рис. 3.14,6). При *, ss 0
новая система совпадает с исход-
исходной. Пусть координаты точки А — ^
х2 = х{ -f / cos ф, Уг
б)
Рис. 3.14.
а точки В — х2, У2\ тогда

74 УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. 3
Кинетическая энергия определяется выражением
4)(ii^i)+{7n (/2ф2"" 2*№sin ф+2^/ф cos ф)
Отсюда имеем
-^j- = (М + m) ij - m/ф sin ф, -^- = О,
-тг \~]Г~\
+ m) Jcj — т/ф sinф — т/ф2 cosф.
В соответствии с выражением C.37) получим
Я3 = — тЩ sin ф — m/ф2 cos ф — Q3.
Найдем обобщенные силы. Так как
ЬА = Mg Ьхх + mg 6дг2 = (М + т) g 6хх — т2^/ sin ф 6ф,
Го
Qi=0, Q2~-mglsin ф, Q3 = (Af-f-m)?
и, следовательно,
Я3 = — m/ф sin ф — т/ф2 cos ф — (М + т) ^.
Значения ф, ф и ф, которые следует подставить в это выраже-
выражение, находятся из уравнений Лагранжа второго рода, составленных
для координат у\ и ф, в которых учтено, что х\ = х\ = л?1 = 0:
— [(М + т) ^*! + т/ф cos ф] = 0,
ф + -у- cos ф + -~ sin ф == 0.
§ 3.7. Выражение кинетической энергии через
обобщенные координаты и обобщенные скорости.
Гироскопические и диссипативные силы
При составлении уравнений Лагранжа второго рода
кинетическая энергия системы должна быть выражена
через обобщенные координаты и обобщенные скорости.
В рассмотренных примерах предыдущего параграфа бы-
было показано, как это сделать в частных случаях.
Выразим кинетическую энергию через обобщенные
координаты и обобщенные скорости в общем случае. Для
этого сначала нужно радиусы-векторы Г\ точек матери-

§ 3.7] ГИРОСКОПИЧЕСКИЕ И ДИССИПАТИВНЫЕ СИЛЫ 75
альной системы определить как функции обобщенных ко-
координат, т. е. получить зависимости C.20):
*i = *i (Яи Яъ • • • у Яз> t) (/=1,2,..., п).
Затем скорости точек материальной системы определяют-
определяются по формулам
»< = 1Г=2|^ + 1Г 0-1.2,....»). C.38)
Подставляя эти скорости C.38) в выражение для кине-
кинетической энергии, получим
п п
1.ХJ. = ~
S 5 &
где
п
(очевидно, что
C.42)
Таким образом, кинетическая энергия нестационарной
(реономной) голономной материальной системы может

76 УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. 3
быть представлена как сумма трех частей: Г2, Ti и Го, т. е.
Т « Т2 + Тх + Го, C.43)
где
S S
ЬтрЯтЯр C.44)
является однородным многочленом второй степени от
обобщенных скоростей.
8
1 ^ 2j "mQm (о.45)
m=l
— Многочлен первой степени от обобщенных скоростей;
от обобщенных скоростей не зависит.
Для стационарных (склерономных) связей, т. е. свя-
связей, для которых
П = гг{дь q2, ..., qs)
и, следовательно,
кинетическая энергия будет однородной функцией второй
степени относительно обобщенных скоростей, т. е.
C.46)
Пример 29. Определить кинетическую энергию сферического
маятника (рис. 1.6). Груз имеет массу, равную т, длина маятника /.
Рассматриваемая система стационарная. За обобщенные коорди-
координаты примем q\ = 0, #2 = Ф- Тогда декартовыми координатами, опре-
определяющими положение маятника, будут
х ~ / cos 0, у == / sin 0 cos ф, г = / sin 0 sin ф.
Для определения кинетической энергии по формуле C.46) следует
сначала найти коэффициенты Атр. В соответствии с формулой

§ 37) ГИРОСКОПИЧЕСКИЕ И ДИССИПАТИВНЫЕ СИЛЫ 77
C.40) имеем
*¦-[(#)
Следовательно,
Выяснив, что кинетическая энергия нестационарной
материальной системы выражается формулой C.43), оп-
определим, как связано изменение кинетической энергии
с характером сил, действующих на систему.
Так как кинетическая энергия является функцией об-
обобщенных координат, обобщенных скоростей и времени,
т. е. Т = T(qmyqmy /), то
dT yi дт . у» вт d
2 9+ i
Lk Ydqm dt \dqj\4m ^ dt Zi dqm 4m ^ dt '
Чт
но так как согласно формуле C.43) Т == Т2 + Т{ + Го, то
По теореме Эйлера об однородных функциях им^е
следовательно,

УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. 3
AT
Если теперь учесть выражения C.29), то для -тг полу-
получим
где Qm — обобщенные силы. На основании формулы
C.43) можем записать
ОТ _i_ Т — ОТ IT _1_ ОТ \«
zi 2 -г 11 — Zi — \i i -г л 0;,
тогда
~Ж ^ ~~ ZA ЧтЧт "Г -j
т=1
ИЛИ
Полученная формула определяет изменение кинетической
энергии материальной системы при любом ее движении.
Рассмотрим случай стационарных связей. Для них
Т= Т2 и
dT =
dt
m—\
Рассмотрим частные случаи сил, являющихся линей-
линейными и однородными функциями обобщенных координат,
т. е.
Если Bmix = ymix, где
Ymn=-Ynm И Уцд = 0 ("*, У = 1, 2, . . ., s),
ТО
5
1

§ 3.7] ГИРОСКОПИЧЕСКИЕ И ДИССИПАТИВНЫЕ СИЛЫ 79
называются гироскопическими силами. Покажем, что эти
силы не вызывают изменения кинетической энергии*).
Так как
S S S
2 ^^
т~\ т = \ (л=»1
то можно записать
S 5-1 S
ЧГ= ЪУттЯ1г+ Ц Ц (Y«.i + Yum) &n<7,i»
т==1 т=1 (А=т + 1
и, следовательно, в силу условий, наложенных на коэф-
коэффициенты ут[х (утт = 0, ут1Х = —Yjxm),
Это значит, что работа гироскопических сил равна нулю.
Пусть теперь
где
Pmp, = Рц.т*
s
Тогда Qm = - 2 Ртц<7и и
1 а -л
тцЧтЧу,'
Если квадратичная форма 2 2 Pmu<7m4u > 0> то
m=l |x=l
dt
т. е. кинетическая энергия убывает. Силы
называются диссипативньши.
*) Подробнее о гироскопических силах см. в монографии
Д. Р. Меркина, Гироскопические системы, Гостехиздат, 1956.

80 Сравнения движения {гл. з
§ 3.8. Уравнения Лагранжа в квазикоординатах
Введем в рассмотрение величины й&ь (А,= 1,2, ..., s),
которыми обозначим линейные комбинации дифферен-
дифференциалов обобщенных координат:
йкк = akl dqx + a^2dq2 + ... + aKs dqs = 2 аш dqmy C.47)
где ахт могут быть функциями обобщенных координат.
Для того чтобы dttxB выражении C.47) были полными
дифференциалами достаточно выполнения условий
^^1 = 0 fc«,v-l,2,....,), C.48)
В этом случае я*, могут быть приняты за обычные обоб-
обобщенные координаты.
Мы будем рассматривать случаи, когда
^L-^L^O, C.49)
т. е. когда выражения C.47) не являются полными диф-
дифференциалами. Если бы обобщенные координаты <7ь
92, •.., qs нам были известны как функции времени, го
величины ях можно было бы определить по формулам
t
%= J
0 т=\
Эти величины уже не являются функциями положения
материальной системы и не могут быть приняты за обоб-
обобщенные координаты. Поясним это на примере. Как из-
известно*), проекции угловой скорости твердого тела,
имеющего одну неподвижную точку, на оси, жестко свя-
связанные с телом, выражаются формулами Эйлера:
а>х = oj) sin 9 sin ф + 8 cos <p,
со^ = -ф sin 9 cos ф — 8 sin ф,
<о2 = ф cos 9 + tj>.
*) Н. В. Б утенин, Я. Л. Лунц, Д. Р. Меркин, Курс тео-
теоретической механики, т. 1, «Наука», 1970.

§3.8]
УРАВНЕНИЯ ЛАГРАНЖА В КВАЗИКООРДИНАТАХ
81
Введем величины
dn{ = d-ф sin 8 sin ф + dQ cos q> = со* dt,
dn2 = di|) sin 8 cos <p — dQ sin ф = ®у dt,
dn3 = dif> cos 8 + dcp = <ог d/.
Предположим, что углы Эйлера 8, \|) и ф нам известны
как функции времени. Тогда величины щ9 зтг, яз можно
было бы определить по формулам
t
= J
dt, щ
т. е. величины яь яг, яз представляли бы собой углы по-
поворота тела соответственно относительно осей х9 у и г.
Однако эти углы не определяют однозначно положения
тела, так как, поворачивая тело на эти углы в разной по-
последовательности, мы придем к различным положениям
тела*). Несмотря на это, мы примем п% за обобщенные
координаты и будем их называть квазикоординатами
(псевдокоординатами). Величины
C.50)
dt
т=\
называются квазискоростями.
В соответствии с выражением C.50) определим ва-
вариации квазикоординат с помощью выражений
т=1
C.51)
Предполагая, что определитель
«11 «12 • • • «is
«21 «22
«si «52
«2s
?=0,
*) Ю. И. Неймарк, Н. А. Фуфаев, Динамика неголономных
систем § 8, «Наука», 1967,

82 УРАВНЕНИЯ ДВИЖЕНИЯ [ГД. 3
из соотношений C.50) можем получить
s
Ят = 2 РтЛ (/И = 1, 2, .... S) C.52)
К=* 1
и
б<7т = 2 IW К (/» = 1, 2, . . ., S). C.53)
Подставляя Л*,, определяемое формулой C.50), в выра-
выражение C.52), имеем
Ят = 2 2 РтЛц?ц (^ = 1, 2, . . ., 5).
Отсюда следует, что
V
Перейдем к выводу уравнений Лагранжа в квазикоор-
квазикоординатах. Каждое из уравнений Лагранжа
умножим на соответствующий коэффициент рт*, и про-
просуммируем по т:
C.55)
Виртуальная работа равна
6Л= 2 Qm6<7m.
В соответствии с выражением C.53)
s
bqm = 2 PmA,*% (m = 1, 2, ..., 5);
л= 1
следовательно,
6Л= 2 2
m=*l Л=1

§ ЗД УРАВНЕНИЯ ЛАГРАНЖА В КВАЗИКООРДИНАТАХ 83
где
/\= 2fWQ* (*-L 2, ...,*). (з.бб)
Величины Рх называются квазиобобщенными силами.
Итак,
Заменяя в выражении для кинетической энергии обоб-
обобщенные скорости qm с помощью формулы C.52) на Лл,
получим
( s \
Т[qm, qm«2! Pm^%j = Г (?m, ftj (m = 1, 2, ..., s). C.58)
Далее имеем
дТ "\Л дТ <7Jtn m"i дТ
C.59)
"dq^~~'dq^
так как в силу C.50)
~</v (\i, m= 1, 2, ..., 5).
Подставим выражения C.59) и C.60) в уравнения
C.55):
m=l
Г / s / \1 s
L \^=1 /J m»

УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. 3
Имея в виду, что
d (EL ) d (дТ'\ ¦ дГ
d /дг\ er i
-^Г^ О».
перепишем C.61) в виде
m=l jut=l v=i
2^ 2 р
m=-l |i=-l v=l
или, в соответствии с условием C.54) и формулой C.52),
л ( дй J
дГ
(Я-1, 2, .... s).
Обозначая
SS(^^) C.62)
(Л, (i, /=1, 2, .... 5),
получим
5 S S
il^1 C>63)
(Л-1, 2, ...,s).
Вводя чисто условное обозначение

§3.8] УРАВНЕНИЯ ЛАГРАНЖА В КВАЗИКООРДИНАТАХ 85
найдем, что
+ 1 2Ля'вР* C.65)
(Л=1, 2, ..., 5).
Эти уравнения носят название уравнений Эйлера — Лаг-
ранжа. Отметим, что коэффициенты yjw не зависят от
структуры и движения механической системы, а их зна-
значение зависит только от определения величин п% через
обобщенные скорости qu g2, ..., qs-
Из формулы C.62) следует, что
v/цх
(/, ц, Я=1, 2, ..., s).
Сравнив формулы C.62) и C,66), получим, что
УШ = - Y/цх (Л, |i, У = 1, 2, ..., s). C.67)
Отсюда
0 (Я, и.— 1. 2, ..., s). C.68)
Рассмотрим способ нахождения трехиндексных коэф-
коэффициентов Ybui при помощи перестановочных соотноше-
соотношений. Для этого используем зависимости C.47) и C.51 > г
dnk = JS аш dqm (Я = 1, 2, ..., s), C.69)
5
Ьлк = 2 Ukmfym (Я = 1, 2, . . ., 5). C.70)
Из формулы C.69) следует, что
dqm = 2 Pmv^v (m = 1, 2, ..., s) C.71)

86 УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ.
Ьдт = S PmvStv (от = I, 2, ..., s). C.72)
Применим операцию нахождения дифференциала
к соотношению C.70):
d F%) = 2 ^md Fqm) + 22 T
(Л-1, 2, ..., s).
Используя равенства C.71) и C.72), получим
5 5 S
2 S S ^
m=»l m=l /«=1 v=l ц=1 '
(Я-J, 2,,.., s).
Применим теперь операцию варьирования к соотно-
соотношению C.71):
о о
m=J
S S S
j + 2 2 ~w- 2 p^6«v 2
m=l m=l /-1 ' v=l
m=l
s s s
V V V1 V ft о akm & л /1—10
Zl Zj Zj 2j P/vPmjA лЛ "rtv йПр \K-~ I, Z, ...>
4Ш ^Hl ЛШШ 4ШЯЛ l"f /

§ 3.8] УРАВНЕНИЯ ЯАГРАНЖА В КВАЗИКООРДИНАТАХ 87
Меняя во второй сумме этого выражения индексы v
и \х, j и т местами, получим
) +
Чт
т=1
C.74)
<ям ^— ^~ ¦ vijtn
(Я = 1 2 5).
Найдем разность выражений C.73) и C.74):
— Zj аш Ы {bqm) ~
m=l
(Я = 1 2 ... s).
Согласно выражению C.62)
m=l
и, следовательно,
- V V а а (дЧт duKi \
m=l /=l Ч J m '
но,
d F%) - б (dnO = 2 aXm [d Fqm) - 6 (dqm)} +
l
22 YliXv ix v A, 2, ..., S).
v=l jx=l ^
Полученное соотношения называются перестановочными*
Так как dFqm) -*b(dqm) - 0*), то
S S
d Fпк) - б {й%ч) = 22 Ynxv б^ц ^я;у (А, = 1, 2, ..., 5).
V=I(i=1 C.75)
*) Пусть <7j (/) — обобщенные координаты, определяющие поло*
жение материальной системы в момент времени /. При сообщении
системе виртуального перемещения ее положение в тот же момент
времени / определяется координатами

8а УРАВНЕНИЯ ДВИЖЕНИЯ [ГЛ. 3
Применим уравнения Эйлера — Лагранжа C.65) к выводу урав-
уравнений движения твердого тела, имеющего одну неподвижную точку.
Положение тела будем определять углами Эйлера*). Примем
Кинетическая энергия твердого тела при условии, что оси х, у и z
жестко связаны с телом и являются главными осями инерции для
неподвижной точки тела, равна
Г=1(/Х + У^ + /2«$( C.76)
где 1Ху !у, 1г — осевые моменты инерции тела, а со*, ®у и со* — про-
проекции угловой скорости тела соответственно на оси х, у и г. Проек-
Проекции угловой скорости связаны с углами Эйлера и их производными
кинематическими формулами Эйлера:
со^ — ф sin 9 sin ф + 9 cos <p,
Фу ss ф sin 9 cos ф — 9 sin ф,
юг — ф cos 9 -f ф.
Примем за квазискоростй проекции угловой скорости, т. е.
3Xi = qv cos qn + qz sin qx sin q2, ]
^2 = — q\ sin ^2 + ^3 sin q\ co?q2, \ CJ7
зхз = Цч + (\ъ cos qx. J
где
— вариации координат.
Аналогично вариации обобщенных скоростей можно предста-
представить в виде
но
Следовательно,
Доказательство этого свойства в случае неголономных связей
подробно рассмотрено в книге Ю. И. Неймарка и Н. А. Фуфаева,
Динамика неголономных систем, «Наука», 1967.
*) Н. В. Бутенин, Я. Л. Лунц, Д. R Меркин, Курс тео*
ретической механики, т. 1, «Наука», 1969.

§ 3.81 УРАВНЕНИЯ ЛАГРАИЖА В КВАЗИКООРДИНАТАХ 89
Отсюда следует, что
cti2 ~ 0, cti3 = sin qx sin q2%
a2! = - sin qti a22 - 0, a23 = sin qx cos q2,
a3i — 0, аз2= 1, a33 = cos?i.
Из соотношений C.77) получим
<fi = cos q2 hx — sin q2 эт2»
cos qx sin q2 . cos qx cos q2 . , .
Cj2 = : Я1 : 3X2 + fta,
sin <7i sin qx
. ^ sin q2 . cos ^2 .
sin qf| ! sin qx ъ
откуда
pu = cos^2, P^^-sin^, Pis
Q COS ^i Sin ^2 л COS ^i COS ^2 л «
Psi= iii^—' pM iiir^—• p23=l>
Очевидно, что
Г^^^' + ^ + ^з).
Формулы для подсчета у^«/ имеют вид
Уш - (Р.лР2/ - JW»i/) ("Ж- ^) +
Отсюда
Y231 = —
Y312= ~ 1, Y321= 1.
Все остальные у равны нулю.
Уравнения Эйлера — Лагранжа будут иметь вид

90
УРАВНЕНИЯ ДВИЖЕНИЯ
[ГЛ.З
ИЛИ
MX>
где Мх, My, Mz — моменты сил соответственно относительно осей
х, У, z.
Пример 30. Вывод уравнений движения гироскопа в кардановом
подвесе с учетом массы кардановых колец.
Схема гироскопа представлена на рис. 3.15. Начало координат
выберем в точке пересечения осей карданова подвеса. Подвижную
систему координат свяжем с внутренним кольцом, направив ось Ох
ft,
oJ^T-1
Рис. 3.15.
Рис. 3.16.
по оси вращения ротора, ось Оу — по оси вращения внутреннего
кольца. Ось O-2i неподвижной системы координат направлена по оси
вращения наружного кольца. Тогда положение подвижной системы
координат Охуг по отношению к неподвижной Ox\y\Z\ определится
двумя углами \j) и #. Угол вращения ротора вокруг оси Ох обозна-
обозначим через ф (рис. 3.16). Проекции угловой скорости наружного коль-
кольца равны
= 0, сон
= 0, сон
¦4».
Проекции угловой скорости внутреннего кольца и ротора соответ-
соответственно равны
°Ыг = — ф sin Ф, (йВу — О, (Овг = Ф cos Ф
со^. = ф — ф sin "ft, о>у — О, o&z — Ф c°s Ф«
Кинетическая энергия рассматриваемой системы равна
•9 I/» 9 * 9 » 9
2 ^ » *
1
1

3.8]
УРАВНЕНИЯ ЛАГРАНЖА В КВАЗИКООРДИНАТАХ
91
где /нг — момент инерции наружного кольца относительно оси Оги
/вх, hy, /bz — моменты инерции внутреннего кольца, Ix, Iy, Iz — мо-
моменты инерции ротора. В силу симметрии имеем 1ВХ = hy и 1У = /г.
За обобщенные координаты примем
а за квазискорости
^i = со^г = ф — ф sin Ф = — q{ smq 2 + #з> }
п2 = юу = О - ^2, |
зх3 == со2 == ф cos О = ^1 cos q* >
Из соотношений C.78) получаем
1 . . . . . sin #2 •
где
Таким образом, имеем
Г' Mr -2 | г «2 t г /л \ iJt
2 1*1 ?, ?. Q \1 ?./ «.
3 (^2)
Так как для рассматриваемой системы
dnx = — sin q2dqi+ dq3, bnt == — sin q2
dn2 = dq2i 6n2 = 6^2»
dnz == cos q2dq и 6я3 = cos q2bqu
cos q2
6^!
cos ^2
bq2 = 6%,
то в соответствии с формулой C.75)
з з
— 6 (dnx) =2 2
v=l ц=1
з з
V=l Ц=
0,
з з
— 6 (dnz)
C.73)
C.79)
C.80)
^in^
cos q2 cos ^2

92 УРАВНЕНИЯ ДВИЖЕНИЯ {ГЛ. 3
Отсюда
Остальные y равны нулю. Найдем теперь производные от V по
яь я2, я3:
дГ -. дГ . . дГ
Далее находим
з
дГ
дГ
m=l
3
1x2 dqm dq2 2 3 dq2
m=I
Уравнениями движения в квазикоординатах будут
~~"
COS С]2
Переходя к обобщенным координатам, получим
/(фф8тд)ЛГ
| - Ix (ф - ф sin Ф) О - sin d/3
Так как
db

§ 3.8] УРАВНЕНИЯ ЛАГРАПЖА В КВАЗИКООРДИНАТАХ $3
то окончательно будем иметь
Овх + h) Ь + 1Х (ф~ф sin Ь) <ф cos Ъ + {1ъг+1г-1ъх) Ф2 sin Ь cos Ф=Му
['в* + Кг + !г + Gв* - 'в* " 'z) sin2 Ь] ф - /, (ф - ф sin О) * COS <> -
- 2 (/B* + Az ~ hx) Ф# sin # cos ft - Л!2 cos d.
Так как 6А =» М^. 6ф + М^ 6^ + M2i 6ф, где /VfZj — момент всех
сил относительно неподвижной оси Оги а
• » & sin Ь .
Оф = О^з ~ 0Я1 Н ^- 0Я3,
то
С другой стороны,
6Л = Мх Ьях + Му 6я2 + Mz 6я3,
следов ательно».
2 г« cos О * cos Ф
или
Afz cos Ф * W2i + M^ sin О.
В гироскопических приборах обычно Мх~0. Тогда
ф — ф sin # = Q = const
и уравнения движения гироскопа в кардановом подвесе будут
иметь вид
Овх + /г) * + /*8+ COS Ф + (/Вг + /2 - /в^) Ф2 sin # COS ^ == Муу
Umt + ^в, + /, + (/в* ~ Лк - М si Щ ¦ - ^* «* * -
- 2 (/м + /г - /вх) ф^ sin О cos ^ = Afг|.
В современных гироскопических приборах угловая скорость соб-
собственного вращения ротора ф много больше угловых скоростей ф
и Ф. Принимая это во внимание и считая угол # малым, получим
(Ли + h) ^ + W - My, (/нв| + /В2 + 7г) * - 7xQ^ = Мг>
Эти уравнения называются «техническими» уравнениями движения
гироскопа в кардановом подвесе.

ГЛАВА 4
УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ
ПОЛЕ
§ 4.1. Уравнения Лагранжа второго рода
в случае потенциальных сил
Обобщенные силы называются потенциальными, если
существует функция
П = П(<71, q2t .... qSi О, D.1)
частными производными от которой по обобщенным ко-
координатам, взятыми с обратным знаком, являются эти
силы, т. е.
Qm=~~&b (w=I> 2> •••'s)- D-2)
Функция D.1) называется потенциальной энергией.
В § 2.3 нами был рассмотрен частный случай потенци-
потенциальных сил — консервативные силы — и была установле-
установлена формула B.9), аналогичная формуле D.2).
Используя формулу D.2), перепишем уравнения
C.29) в виде
d_ I дТ \ _
dt \ dqm)
дТ
dqm dqm '
Введем в рассмотрение функцию
L = r-II, D.3)
которая называется функцией Лагранжа или кинетиче-
кинетическим потенциалом. Так как потенциальная энергия от об-
обобщенных скоростей не зависит, то

УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
95
и, следовательно, уравнения Лагранжа могут быть запи-
записаны в виде
А. ( дЬ \ _ dL
dt \ dqm I dqm
О
(m=l, 2, ..., s). D.4)
Из структуры уравнений D.4) видно, что если вместо
функции L выбрать другую функцию Li = L+ /(')» где
f(t)—любая функция времени, то функция Li тоже бу-
будет удовлетворять уравнениям D.4). То же самое будет,
если вместо L взять Li = с?, где с — любое постоянное
число, кроме нуля. Существуют и другие преобразова-
преобразования, относительно которых уравнения Лагранжа инва-
инвариантны *).
Пример 31. Составить уравнения D.4) для материальной систе-
системы, схема которой представлена на рис. 4.1. Прямая, по которой
1 с, Д сг J!* с, Д
''//// У/VVx! VVVVx. VVVVVVV
Рис. 4.1.
движутся грузы Mi, Af2 и Мз, абсолютно гладкая. Массы грузов
соответственно равны mi, я*2 и т3, а жесткости пружин сь сг и с3.
За обобщенные координаты примем расстояния грузов от поло-
положения, при котором все пружины находятся в ненапряженном со-
состоянии. Пусть <7i — *ь #2 = *2, Яъ = Хз. Кинетическая и потенциаль-
потенциальная энергии соответственно равны
П = 
~2

Составим функцию Лагранжа L = Г—П и найдем
dL dL dL
dL
*) Подробнее об инвариантности уравнений Лагранжа можно
прочесть в книге И. М. Беленького, Введение в аналитическую меха-
механику, «Высшая школа», 1964.

96
УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ ПОЛБ [ГЛ. 4
Следовательно, уравнения D.4) для рассматриваемого случая будут
иметь вид
тхх\ + аххх — с2 (х2 — хх) = О,
тх2 + с2 (х2 - ^i) - съ (хг - хх) « О,
тхг + сг (хг — х2) = 0.
Пример 32. Составить уравнения движения материальной си-
системы, состоящей из двух тяжелых однородных стержней равной
длины /, шарнирно соединенных между собой в точке А (рис. 4.2).
X
Рис. 4.2.
Конец одного стержня шарнирно укреплен в неподвижной точке О;
конец другого стержня шарнирно укреплен в центре однородного
диска радиуса г и массы М. Диск катится без скольжения. Центр
диска соединен с неподвижной точкой D пружиной жесткости с.
Пружцна находится в ненапряженном состоянии при вертикальном
положении стержней. Масса каждого из стержней — т.
Рассматриваемая система имеет одну степень свободы. За об-
обобщенную координату примем угол ф (угол между осью х и стерж-
стержнем О А), т. е. q = ф. Запишем координаты центра масс стержня О А:
I
стержня АВ:
х2 = у cos ф, у2 = / sin ф + y sin ф = у / sin ф,
диска (точки В):
Хъ = 0, уг = 2/ sin ф
(так как ОА = АВ = /).
Кинетическая энергия системы равна *)
*) При нахождении кинетической энергии стержня АВ и диска
применяем теорему Кёнига,

§ 4.1] УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА 97
где /о — момент инерции стержня О А относительно точки О, / — мо-
момент инерции стержня АВ относительно его центра масс, 1В — мо-
момент инерции диска относительно его центра, си —- угловая скорость
диска. Найдем теперь v% v2B и угловую скорость со диска. Очевидно,
что
v,
X)гв » 4/ ф cos ф и со — —~ = —
Таким образом,
где
° 4 3
N = 2m/2 + 6M12
. Mr2 . ml2 . m/2
так как ^^— 2 » /о"~ з ' 12 *
Потенциальная энергия равна
П = — m^jCj — mgx2 + -о* с^з ~ — m^/ cos ф + 2с/2 sin2 ф.
Составим функцию Лагранжа:
L = r-n«-i(/C + ^ cos2 ф) ф2 + mgl cos ф - 2с/2 sin2 ф.
Далее находим
-_ == — N cos ф sin ф • ф2 — mgl sin ф — 4с/2 sin ф cos ф.
Напишем теперь уравнение движения:
-тт [(К + N cos2 ф) ф] + Л^ф2 cos ф sin ф + mgl sin ф + 4с/2 sin ф cos ф =» О,
или
(К + N cos2 ф) ф — #ф2 cos ф sin ф + 4с/2 sin ф cos ф + mgl sin ф =* 0.
Если угол ф мал, т. е. если можно пренебречь членами, содержа-
щим» ф и ф в степени выше первой, то
(/С + Л0 ф-ЪDс/2 + mg/) ф == (^
4 Н. В. Бутенин

УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ ПОЛЕ [ГЛ. 4
т. е. система будет совершать гармонические колебания, период ко-
которых равен
Г=!
K + N
4с/2 + mgl
Пример 33. Составим уравнения движения материальной точки
относительно Земли, происходящего под действием ньютоновской
силы притяжения. Землю будем
считать однородным шаром.
Введем в рассмотрение систе-
систему координат Oxyz, имеющую на-
начало в центре Земли, причем ось г
направим по оси вращения Зем-
Земли. Считаем, что эта система не
участвует во вращательном дви-
движении Земли. Движение по отно-
отношению к этой системе координат
будем называть абсолютным.
За обобщенные координаты
примем q\ = г, q2 = a, q$ = Р,
где г —- расстояние точки М от
центра Земли, а — долгота в аб-
абсолютном движении, р — геоцен-
геоцентрическая широта (рис. 4.3). Де-
Декартовы координаты материальной точки связаны со сферическими
при помощи формул
х = г cos p cos а, у « г cos P sin а, г « г sin p.
Кинетическая энергия выражается формулой
z
4.3.
Потенциальная энергия равна *)
П — тИ>2
""" г
Таким образом, функция Лагранжа
Y (г2 + г2р2 + г2&2 cos2 p) (т- масса точки).
где ц2 =
1
Вычислим производные от L:
jmr ^
+ r2d2 cos21
IF-1"*
dL
— wr2d2 cos P sin p,
*) H. В. Б у те нин, Я. Л. Лунц, Д. Р. Меркин, Курс тео-
теоретической механики, т. I, «Наука», 1970.

УРАВНЕНИЯ ЛАГГАНЖА ВТОРОГО РОДА
99
и составим уравнения D.4):
mr2 а cos2 р
D.5)
D.6)
D.7)
(а — постоянная интегрирования).
Так как движение происходит под действием центральной силы,
то момент количества движения
точки является постоянной величи-
величиной. Найдем проекции момента ко-
количества движения на оси х> y,z:
= tnr2 (р sin a — а cos а sin р cos Р),
Ky — tn (zx — xz) =
*= — tnr2 (P cos а 4- а sin а sin p cos P),
Kz = пг (ху - ух) = tnr2 & cos2 p.
Отсюда видно, что уравнение D.6)
выражает постоянство момента
количества движения точки отно-
относительно оси Oz. Модуль момента количества движения равен
Рис. 4.4.
К
mr2
a2 cos2 р = с2 = const. D.8)
Как известно*), движение точки под действием центральной
силы происходит в плоскости, перпендикулярной к вектору момента
количества движения. Это движение происходит в плоскости, прохо-
проходящей через центр шара. Линию О К пересечения этой плоскости с
экваториальной плоскостью называют линией узлов (рис. 4.4). Обо-
Обозначим через Q угол между линией узлов и осью х, через i — угол
между экваториальной плоскостью и плоскостью движения точки.
В плоскости движения положение точки определяется радиусом г и
углом ф. В полярныхкоординатах г и <р момент количества движения
точки выражается формулой
JC«mr*q>»<?2. D.9)
Следовательно, в соответствии с формулой D.8)
р2* &2cos2p = cp2. D.10)
Уравнение D.5) движения точки при этом будет
r-rq>2 = --§-. D.11)
*) Н. В. Бутенин, Я. Л. Лунц, Д. Р. Меркин, Курс тео-
ретической механики, т, 1, «Наука», 1970.

f90 УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ ПОЛЕ [ГЛ. 4
С помощью замены
« = ~г DЛ2)
и соотношения
г2ф-с DЛЗ)
(интеграл площадей) это уравнение преобразуется к виду
где
Решая это уравнение, получим
« » a cos (ф + е) -J , D.16)
где а и е — постоянные интегрирования. Так как и =¦ —, то
DЛ7)
^-аА>. D.18)
Полученная зависимость представляет собой уравнение кониче-
конического сечения *).
§ 4.2. Обобщенный интеграл энергии
Предположим, что функция Лагранжа (кинетический
потенциал) голономной системы является функцией об-
обобщенных координат, обобщенных скоростей и времени,
т. е.
L = L{qmt 1)m t) (iii-l, 2, ..., s). D.19)
Дифференцируя по времени функцию D.19), будем иметь
dL %Г\ ( dL . . dL „ \ . dL
*) Дальнейшее решение этой задачи, т. е. нахождение зависи-
зависимости между величинами а, р, Q, if ф, читатель найдет в khhw
Л. Н. Л а х т и н, Свободное движение в поле земного сфероида,
Физматгиз, 1963.

§ 4?] ОБОБЩЕННЫЙ ИНТЕГРАЛ ШЖРГИИ
Из уравнений D.4) следует, что
Тогда
dL . 6L .. _ d ( dL \ . dL , __ d ( dL
dqm Ят + ^4m qm~~ dt\ dqm ) ^ + dqm 4» dt \ dqm
(m-1, 2, ..., 5).
Значит, выражение D.20) можно переписать в виде
dL d 4л dL . dL
2 Ч +
ИЛИ
dt " dt 2j dqm
m=I
±(yjk
dt \Zk dqm
Если -^j- = 0, т. е. если функция Лагранжа явно от
времени не зависит, то
\
,-L =0
D.22)
Это выражение называется обобщенным интегралом энер-
энергии (интеграломЯкоби).Вспоминая, что-^р— qm =-^—qmt
можем записать
тп—\ тп—\
реономной системы кинетическая энергия выра-
выражается формулой C.43), т. е.

102 УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ ПОЛЕ [ГЛ. 4
Подставляя это в формулу D.23), получим
У dL * _/_VJZi,v л.Л±.л т т т
2udqm4™ L~ Zl dqm Чп^-Щ^Чт-и-и-'о
т =1 m = l
По теореме Эйлера об однородных функциях имеем
m—\
Следовательно,
s
im-L = T2-T0 + u. D.24)
m—\
Заметим, что это выражение не совпадает с полной
энергией системы
Е = Т + II = Т2 + Г, + Го + П.
Используя формулу D.24), перепишем обобщенный ин-
теграл энергии D.22) в виде
T2-T0 + n = h. D.25)
Итак, обобщенный интеграл
энергии существует, если силы
потенциальны, а функция Ла-
гранжа явно от времени / не
зависит.
Для склерономных консер-
Рис. 4.5. вативных систем, когда L явно
не зависит от времени, Т =Т2
и обобщенный интеграл будет обычным интегралом
энергии:
Г + П = Г2 + П = А. D.26)
Пример 34. Шарик массы m находится внутри прямолинейной
горизонтальной трубки АВ (рис. 4,5), которая равномерно вращается
с угловой скоростью о вокруг вертикальной оси, проходящей через
точку А. Шарик соединен с неподвижной точкой Л пружиной же-
жесткости с. Пренебрегая трением, составить обобщенный интеграл
энергии.
Примем за обобщенную координату расстояние х шарика от
точки Л, т. е. q = х. Так как х\ = х cos (dt, y\ = х sin ©/, то ско-

$ 4.3] МЕТОД УИТТЕКЕРА ЮЗ
рость шарика равна
Следовательно, если пренебречь массой пружины, кинетическая энер-
энергия шарика будет равна
Т «~т(*2 + *2©2).
Если лг0 — длина пружины в ненапряженном состоянии, то потен-
потенциальная энергия
П-| <*-*,)»
(#о — длина пружины в ненапряженном состоянии).
Составим функцию Лагранжа
найдем -^г-«гпх, и обобщенный интеграл энергии будет равен
Напишем теперь уравнение движения. Учитывая, что
-г— = moo2* — с (х — х0),
получим уравнение движения:
4г (ж) - ж - т* ~ тф2х+с {х -Хй)=°-
Перепишем это уравнение в виде
тх -= т®2х + с (х — х0) = 0.
После его интегрирования получим
11 <?
у mi2 - у /поо2*2 + у (* - *оJ = К
т. е. вычисленный выше обобщенный интеграл энергии.
§ 4.3. Метод Уиттекера
Метод Уиттекера позволяет с помощью обобщенного интеграла
энергии понизить порядок системы D.4) на две единицы. Пусть рас-
рассматриваемая голономная система будет консервативной. Это зна-
значит, что функция Лагранжа не зависит явно от времени, т. е.
L = L(qm,qm) (m-1, 2, ..., s). D.27)

1(М УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ ПОЛЕ [ГЛ. I
Идея метода Уиттекера заключается в использовании интеграла
энергии для замены аргумента t в уравнениях Лагранжа D.4) но-
новым аргументом — какой-либо обобщенной координатой, например q{.
Пусть q\ будет новым аргументом, тогда
йЦп dQp йЦ\ ,
*'--аг-з»г"зг "**'•*' (р=1>2 s)> D>28)
где
/_f*l-.J*_. D.29)
Заменяя в функции Лагранжа D.27) q9 на qfp , получим
L {qm, qm) = L (qm, qv qp s qlt q'p)<
Введем обозначение
L{qm,qvqp^(ivq'p) = u{qm,qvqp) (p-2, 3, .... s). D.30)
В соответствии с выражениями D. 30) и D. 29) имеем
dL dQ Л дп dqp дп
dL 3Q dq' [ dQ
w/-к-?Р"< ("=2>3 s)> D32)
Из выражения D.31) следует, что
dQ dL
Принимая во внимание соотношение D.32), получим
_ dqp qx
откуда
Следовательно, обобщенный интеграл энергии D.22) можно запи-
записать в виде

§ 4 S| МЕТОД УИТТЕКЕРА 105
или, в силу D,3G),
Решая соотношение D.35), найдем $\ как функцию qmt Яр(т=*
vss 1, 2, . .¦, s; р=*2, 3, ...» $). Подставив затем найденное выра-
dQ
жение для <ji в производную -гр—, получим функцию
которую будем называть функцией Уиттекера. Найдя q% из соотно-
соотношения. D.35) и подставив это q\ в то же соотношение, получим тож-
тождество. После дифференцирования этого тождества по q'p и qm бу-
будем иметь соответственно
d Q дй\ | Г dQ uQ d(j\
Я о dqi dQn j I dq o dq* dqo
dqi I __
Г dQ t dQ dq
. Г д2п
qi[dd dq\
D.38)
Из выражения D.37) следует:
dQ . Г ^2О
— a ^, ~- + ¦
Из соотношения D.36) получим
dLr __ d2Q d2Q dqx
dqp dq{dqp dq\ 6qp*
Следовательно,
—Г~Яутт (Р-%*..... 9). D.39)
В соответствии с D.38) имеем
d2Q d2Q dq% ,
так как

106 УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ ПОЛЕ [ГЛ. 4
1, 2, .... *). D.40)
Сравнивая теперь соотношения D.32) и D.33) с соотношениями D.39)
и D.40), получим
§ 0»-**....* D.4,)
Используя соотношения D.40) и D.41), перепишем уравнения D.4)
в виде
dQ\
Так как Я1~~~ы~> то
A:—==0 (р = 2, з,..., s).
Уравнения D.43) называются уравнениями Уиттекера.
На основании соотношения D.34) функцию Уиттекера D.36)
можно определить по формуле
где в правой части qx выражено с помощью формулы D.35) через
Яш и V
Таким образом, метод Уиттекера дает возможность использо-
использовать обобщенный интеграл энергии для исключения времени / из
системы уравнений Лагранжа и приведения ее к новой системен— I
уравнений Уиттекера D.43), имеющих вид уравнений Лагранжа, в
которых роль аргумента играет переменная q\ (вместо времени /)
и в которые вместо производных qP по аргументу t входят произ-
производные q'p по аргументу q\. Для построения уравнений Уиттеке-
Уиттекера D.43) следует предварительно построить функцию Уиттекера L'.
Для этого составляется выражение D.44), в которое вместо (j\ под-
подставляется его выражение, полученное из обобщенного интеграла
энергии D.35).
Заметим, что описанная операция выполнима только при усло-
условии, что число степеней свободы материальной системы больше
одной, так как иначе задача решается самим обобщенным интегра-
интегралом энергии. Следует также иметь в виду, что если координа-
координата #i не будет входить явно в выражение функции L\ то метод Уит-
гекера можно было бы применить вторично, взяв в качестве но-

$ 4.3] МЕТОД УИТТЕКЕРА ИO
вого аргумента обобщенную координату q2 вместо прежнего ар-
аргумента q\.
Пример 35. Движение материальной точки под действием цен-
центральной силы.
За обобщенные координаты примем полярные координаты q\ =
= ф, q2 = г. Так как в этом случае
х — г cos ф, у = г sin ф,
то
r lB + ^)(
В случае центральных сил потенциальная энергия является функ-
функцией г, т. е. П = П(г), и функция Лагранжа имеет вид
1»1
За новый аргумент примем координату ф, тогда
Г dt dq> ^ Г ^'
В соответствии с обозначением D.30) имеем
Следовательно, выражение D.35) в рассматриваемом случае примет
вид
~тф2(,
Отсюда получим
2 [ft--П(/-)]
Найдем теперь функцию Уиттекера. Согласно формуле D.44) и соот«
ношению г ф'
Подставляя в это выражение полученное выше ф, найдем функцию
Уиттекера
*> Полученное выражение есть интеграл энергии, т. е. Г+П==А.

J08 УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ. ПОЛЕ [ГЛ. 4
Составим теперь уравнение Уиттекера
<*ф \ дг
Так как
то уравнением Уиттекера будет
~р г2 (г2 + г'2) + 2г (/г - П) (гг" - 2г'2 - г2) - 0. D.45)
Полученное уравнение является дифференциальным уравнением тра-
траектории точки при ее движении в центральном поле. Общее реше-
решение этого уравнения зависит от постоянной h и постоянных интегри-
интегрирования с\ и С2, т. е.
г = г(ф, А, сь с2\
При изучении движения точки под действием центральной силы ча-
часто пользуются заменой г — — . Тогда
дг ди дг ~~ ди '
Подставляя полученные соотношения в уравнения D.45), получим
Мы не будем заниматься интегрированием этого уравнения, а
найдем уравнение траектории путем составления «нового» обобщен-
обобщенного интеграла энергии, используя то обстоятельство, что коорди-
координата ф в функцию Уиттекера не входит. В соответствии с выраже-
выражением D.22) имеем

§ 4.31 МЕТОД УИТТЕКЕРА |09
Так как
ТО
ИЛИ
- r2V2tn(h-U) - К У г2 4-г'2- D.4в)
Выясним смысл нового обобщенного интеграла энергии. В силу
того, что h —• П = Г, а
Т -1 m (г2 + г*ф*). 1 тф^ (г'2 + г>),
выражение D.46) примет вид
— я*г2ф = Н^
т. е. выражение D.46) представляет собой интеграл площадей.
Вводя обозначение с« —х- и возводя выражение D.46) в квадрат,
получим
получим
Если ввести замену г = —, то
Дифференцируя это уравнение по ф, имеем
Это уравнение называется уравнением Бинэ.
Пусть действующая на точку сила будет ньютоновской силой
притяжения, тогда
?2
П » ——- = — k2u (k2 — постоянная)
и, следовательно,
*) Это уравнение первого порядка сводится к квадратурам.

НО УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ ПОЛЕ [ГЛ. 4
Ас2
Вводя обозначение р = —р-, получим
Р
Решение этого уравнения рассмотрено в § 4.1.
§ 4.4. Циклические координаты. Уравнения Рауса
Те обобщенные координаты, которые не входят явно
в функцию Лагранжа, называются циклическими коор-
координатами. Те же, которые входят в функцию Лагранжа,
называются позиционными координатами.
Метод Рауса заключается в одновременном исклю-
исключении циклических координат из уравнений Лагранжа
второго рода, при этом число уравнений движения в не-
независимых координатах понижается на число исключен-
исключенных циклических координат. Предположим сначала, что
все обобщенные координаты позиционные. Тогда функ-
функция Лагранжа будет функцией всех обобщенных коор-
координат, обобщенных скоростей и времени ty т. е.
L = L{qu ..., qs, qu ..., qSi t)\ D.47)
в этом случае мы будем иметь s уравнений Лагранжа
D.4):
Mfc)ih О»"».*-.*)- D-48)
Для производных от L по первым r(r^.s) обобщенным
скоростям qif q<i, ..., qr введем обозначение
jr^ = Pm (m=l, 2, ..., г), D.49)
где рт называются обобщенными импульсами. Тогда на
основании уравнений D.48) имеем
j^~pm (m=l, 2, .... г). D.50)
Найдем полный дифференциал от функции D.47):

5 4,4] ЦИКЛИЧЕСКИЕ КООРДИНАТЫ, УРАВНЕНИЯ РАУСА Ц[
Принимая во внимание формулы D.49) и D.50), по*
лучим
S Г
dct+
m=r+l
+l
Так как
то будет
1 2j p"
\т=\
г
2 Рт<*
т-1
Л
г
г
т-1
г
т=1
Рт
5
?т
т
г
- 2 qmdpm,
s
т=г+1
т = 1 т«г+1-
Введенную Раусом функцию
/?= 2 РтЯт-L D*52)
т=1
называют функцией Рауса.
Полный дифференциал от функции Рауса имеет вид
Г S Г
m=r+l m=l
Сравнивая между собой выражения D.51) и D.53)
с учетом обозначения D.52), получим
^--А-'ТО-0'^-*» (т==1'2 г) D'54)
И
?^ ? ^ ,). D.55)

112 УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ ПОЛЕ |ГЛ. 4
Кроме того,
dR _ dL
dt ~~ dt *
Из условия
^-0 (т=1, 2, ..., г)
вытекает, что функция Рауса от первых г обобщенных
скоростей не зависит. Подставляя теперь результаты
D.54) и D.55) в уравнения Лагранжа D.48), будем
иметь
it)^ («-'+!.....«) D-56)
Рт=-э^- D-57)
Пусть теперь первые г обобщенных координат
..., qr) будут циклическими, тогда
следовательно, в соответствии с D.50) рт=0 (т==1,
2,..., г) и
P («-Ь 2, .... г)
будут постоянными величинами. Из уравнений D.57)
в связи с этим получим
Это значит, что циклические координаты не входят в со-
состав функции Рауса. Уравнения же D.56), которые на-
называются уравнениями Рауса, своего вида не изменят.
Итак, нами установлено, что функция Рауса не содер-
содержит циклических координат и их производных по ере-
мени.
Для отыскания позиционных координат служат s—r
уравнений Рауса D.56). Циклические же координаты,
в соответствии с D.58), определяются по формулам
t (m=l, 2, ..., г). D.59)

§ 1.4} ЦИКЛИЧЕСКИЕ КООРДИНАТЫ. УРАВНЕНИЯ РАУСА ЦЗ
Пример 36. Рассмотрим движение материальной точки, притяги-
притягиваемой к неподвижному центру по закону всемирного тяготения.
Воспользуемся полярными координатами. Пусть q\ = <р, q2 = г.
Так как
Т -. 1 m (г2 + г2ф2) и n=~ii
(&2— постоянная величина), то
Координата <р является циклической. Значит,
—- ев шг2ф = р « const
с/ф
Это выражение является интегралом площадей.
Составим функцию Рауса:
k2
Поскольку
Г2 •
Отсюда
Составим
дг
уравнение
г р2
Л ~ 2тг2
Рауса:
1
2
дг
тг2
k2
г #
тг3 1
ИЛИ
""¦—Й&- + 7Г-0-
Это уравнение служит для определения г как функции времени*).
Так как
dR р__
dp mr2 f
*) Введя замену г = — и учитывая, что ф ~ 2 , уравне-
уравнение D.60) можно привести к дифференциальному уравнению траек-
траектории
|^ + « = с (с = const).

П4 УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ ПОЛЕ [ГЛ.4
ТО
куда вместо г нужно вставить решение уравнения D.60). Используя
то, что f = -тг == f -г-, перепишем уравнение D.60) в виде
к тг6 гг
или, после интегрирования,
-— + А. D.62)
Это выражение представляет собой интеграл энергии*).
Рассмотрим движения, не уходящие в бесконечность. Для таких
движений, в соответствии с формулой D.62), А < 0. Введем обо-
обозначение
Из выражения D.62) теперь следует, что
dr 1/ 2 / р» *»
dt~V т\ 2тг2 + г
dr
— dt*
Таким образом,
~" " rdr
2 . 1 Г
Г Р2
2mP2
Введя обозначения
р
*) Так как система консервативная, то Г + П = А, т. е.
Введя замену ф=—^", получим
2mr2 г

§4.5] ОБОБЩЕННЫЙ ПОТЕНЦИАЛ И5
получим
У Ъ — (а - гJ
Заменяя _
а - г « }/" 6 cos ?,
будем иметь
й('-'о)- J A-еcos?)</?,
где е « . Пусть ? = ?0 при / — *0> тогда
где ? — arccos
ц (f - t0)« ? - ?0 - «(sin ? - sin ?<>), D.63)
—г
Уравнение D.63) называется уравнением Кеплера,
§ 4.5. Обобщенный потенциал *)
До сих пор мы рассматривали только такие силы,
для которых потенциальная энергия была функцией
обобщенных координат и времени (§ 4.1), т. е.
П = П(?1, q2, ..., q8, t). D.64)
Введем в рассмотрение функцию
У = V (qu q2y ..., qs, cju Чъ • • •, Ь> 0 D.65)
и потребуем, чтобы уравнения Лагранжа
имели вид
^(ж)~~&Ь=0 (т==1'2> •¦••s)> D-66)
где
L = Т - V. D.67)
Очевидно, что если функция V такова, что
--Ё- (т;=1> 2» •••» s)> D-68)
*)Ф. Р. Гантмахер, Лекции по аналитической механике,
Физматгиз, 1960.

Цб УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ ПОЛЕ [ГЛ.4
то уравнения Лагранжа будут иметь вид уравнений
D.66). Функция D.65), с помощью которой можно по-
получить обобщенные силы по формуле D.68), называется
обобщенным потенциалом.
Выясним структуру зависимости функции V от обоб-
обобщенных скоростей. На основании формулы D.68) имеем
dV
(m=l, 2, ..., s).
Так как обобщенные силы явно от обобщенных ускоре-
ускорений не зависят, то
т. е. обобщенный потенциал V может быть только ли-
линейной функцией от обобщенных скоростей:
1/ = 11 (qm, t) + S П^ (qm, 0 ?я (т = 1, 2, ..., s). D.69)
Используя формулу D.69), определим вид обобщенных
сил с помощью соотношения D.68):
dt dqm
Введем обозначения
Очевидно, что
Утц.=

$4,5] ОБОБЩЕННЫЙ ПОТЕНЦИАЛ Ц7
Следовательно,
+ T (/n-1.2, .... s). D.71)
Если функции Пт не зависят от времени, то д™ = 0 и
m<Jli (m-l, 2 5). D.72)
Таким образом, если функции Пт не зависят явно от
времени, то обобщенные силы складываются из по-
тенциальных сил I—^-—J и гироскопических сил
B УтМ-
Пример 37. Примером силы, имеющей обобщенный потенциал,
является сила Лоренца, действующая на точечный заряд в электро-
электромагнитном поле *):
[ ] D.73)
где е —заряд, v — скорость точки, Е и Я —напряженности электрк:
ческого и магнитного полей соответственно, с — скорость света. Если
координаты заряда х, у п г, то проекциями силы F на оси х, у и z
будут
Рж-еЪ+
Так как
р . 1 дА __
? = —grad ср ^—, Я==
где ф — скалярный .потенциал, А — векторный потенциал, то в силу
того, что
/ дА2
ГО1 А в I -
V ду дгГ^\ дг дх Г^\дГ ду )*'
*) Л. Д. Ландау, Е. М. Л и ф ш и ц, Теория поля, Фнзматгиз,
1962.

118 УРАВНЕНИЯ ДВИЖЕНИЯ В ПОТЕНЦИАЛЬНОМ ПОЛЕ [ГЛ.4
имеем
» дЛ*\ -1дА* дА
)
дЛ*\ -1
ду~)~ \
дх с dt + с[У\~дх ду~)~ \~Ы
d(f e (дАх дАх _ дА^ \ el дАу dAz
с\ dt + ду
е I дАх дАу dAz \
+ Т[-дГ* + -дГ* + -дГ*)- D-74)
Введем функцию
V = eq>~vA = eq>-~(xAx + yAy + zAz) D.75)
и составим выражение
А^, &АХ дАх дАх .\
±ldV\_dV_ .д^.
dt\dx) дх ~ едх + с
dt +дГх + -ду~У
е I дАх _ дАу dAz
Сравнивая между собой равенства D.74) и D.76), получаем
F d (дУ\ дУ
r*~~ dt\dx) дх;
аналогично можно доказать, что
d IdV\ dV
F =. d (dV\ dV
z dt\dz) dz'
Следовательно, обобщенный потенциал для силы Лоренца опреде-
определяется формулой D.75).

ГЛАВА 5
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
§ 5.1. Переменные Гамильтона.
Функция Гамильтона
Дифференциальные уравнения движения в обобщен-
обобщенных координатах qu q%, ..., qs для голономной системы
в случае потенциального силового поля имеют вид
где Ь = Т — П, представляют собой систему $ обыкновен-
обыкновенных дифференциальных уравнений второго порядка.
Вводя s новых переменных Zi, z2, ..., zs как функ-
функции t, qu qi, ..., qs и qu q2, ..., qs, т. е.
Zm^Zmity q\> q* •••» 4s, Qu <3l2> •••, Qs)
(m=l, 2, ..., 5), E.2)
и предполагая, что эти зависимости могут быть разре-
разрешены относительно qu ..., qm> мы можем привести
систему уравнений E.1) к системе 2s уравнений первого
порядка.
Особый интерес представляют предложенные Га-
Гамильтоном переменные
Рт = -щ^- = Рт (t, qu #>> • • •» Qs> Qu Q2> • • •» Qs)
(m=l, 2, ..., s), E.3)
так как они дают возможность получить систему уравне-
уравнений движения в симметричной форме, обладающую ря-
рядом свойств, позволяющих плодотворно применять эти
уравнения к решению задач на определение движения

120
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
[ГЛ. 6
материальной системы. В дальнейшем переменные
Яи Яь • • •» Яв, Ри Р2> ..., рз будем называть переменны-
переменными Гамильтона в отличие от переменных Лагранжа
Яи Я2у ..., 9s, Я\> ?2> •••> Яэ- Система E.3) может быть
разрешена относительно qm. В самом деле, как было
установлено в § 3.6, кинетическую энергию можно пред-
представить в виде
Т = Т2 + Г, + Го, E.4)
где
2
трЯ
/ dri V*
В соответствии с выражением E.3) имеем
Рпг = 2 АщрЯр + Вт-
Так как определитель этой системы*)
E.5)
... А,
ЛАтр\
дрп
то она разрешима относительно qu q2t ..., qs- Гамиль-
Гамильтон ввел в рассмотрение функцию
Я^Г? ^ • г /г; Л1
=» ^ РтЯт — **9 \D.Oj
которая называется функцией Гамильтона. Сумму
21 Pm<7m на основании E.3) и E.4) можно записать
*) Доказательство этого утверждения можно найти, например,
в книгах: Ф. Р. Гантмахер, Лекции по аналитической механике,
Физматгиз, 1960; А. И. Лурье, Аналитическая механика, Физматгиз,
1961.

§ 5.1) ПЕРЕМЕННЫЕ ГАМИЛЬТОНА. ФУНКЦИЯ ГАМИЛЬТОНА
следующим образом:
m=>l m=l m=l m=l
По теореме Эйлера об однородных функциях
дд„
V
и, следовательно,
12!
2 рт^2 Р
Таким образом,
Я-2Гг + Г1-(Г2 + Г, + Го-11)=72-71о + П. E.7)
Если рассматриваемая материальная система стацио-
стационарная, то Т—Тг и
Я = Г2 + П = Г + П, E.8)
т. е. функция Гамильтона равна
полной механической энергии си-
системы.
Переменные Гамильтона рт
называются обобщенными им-
импульсами*).
Пример 38. Найти функцию Гамиль-
Гамильтона для математического маятника
длины /, точка подвеса которого совер-
совершает движение по вертикальной окруж-
окружности радиуса г с постоянной скоростью
vо (рис. 5.1).
За обобщенную координату примем q — ср. Так как
Г cos~ t + * cos Ф'
У а
= г sin— t + / sin ф,
*) Для свободной материальной точки
и
Pi = mi, p2 * m^, р3 = tni
представляют собой проекции количества движения точки на оси
координат.

122 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА [ГЛ. 5
При нахождении обобщенных сил связи считаются мгновенно оста-
остановленными (§ 3.3), поэтому за потенциальную энергию мы можем
принять *)
П *• — mgl cos ф.
Функцией Лагранжа будет
L=-r~n = -i-m Г/2ф2 + 2do/<P cos L> - -у- t) + t>|jl + mg/ cos <p,
и, следовательно,
/п/2ф + mt)/ cos (ф — t\,
откуда
Составим функцию Гамильтона
Я = -^г- ф — L — ~ /п/2ф2 — v\ — /ng/ cos ф. E.10)
Если v0 ~ 0, то
Я = -гг- т/2ф2 — т^/ cos ф = Г + П = /г,
т. е. Я является интегралом энергии, так как в этом случае связи
будут стационарными и L не зависит от t явно. Подставляя выра-
выражение E.9) в функцию E.10), получим
, E.11)
§ 5.2. Канонические уравнения Гамильтона
Функция
m=l
*) Поскольку в уравнения Лагранжа входит dYlldqm, то П, взя-
взятое в виде П = — mg I/ cos ф + 2cos-~- t\f ничего в выкладках не
изменит.

§ 5.2] КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА 123
является функцией t, qu q2i ..., qSi qu q& ..., q8, Pu Рг, < *.
..., ps, пока в ней не произведена замена всех qiy <?2, •»•
,.., qs через pi, р2> ..., Ps- Следовательно,
S 5 5
бя= У(б * + 6* )— У -^-6 У aL б *
m = l m—I m=l
Так как в силу E.3)
ТО
s
Определив из выражений E.3) обобщение скорости qm
через рт и подставив их затем в функцию E.6), полу-
получим, что Я будет уже функцией только t, qiy q2t ..., q8t
pu p2, ..., Ps, т. e.
H = H(t, qu q2i ..., qs, pu p2, ..., ps). E.13)
Тогда можно записать, что
m=l
Сравнивая выражения E.12) и E.14), имеем
s s
dL fi VI дН
24 ^ ^
m=l m==l т=1 т=1
ИЛИ
В силу независимости вариаций bqm и Ьрт получим
. U it л U Li i (/// /\ / | Л \

124 КА1ЮНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА [ГЛ. 5
Поскольку рт = -^-> Т0 из уравнений E.1) следует, что
dL _ dpm _.
dqm~ dt -P"-
Таким образом, имеем
? ^ (»-1.2....,в). E.15)
Полученная система 25 уравнений первого порядка на-
называется системой канонических уравнений Гамильтона,
Если действующие на материальную систему силы не консер-
консервативны, то уравнения Лагранжа имеют вид
d ( дТ \ дТ (w=l 2 s)
Так как
Составив функцию
и проиаведя выкладки, аналогичные проведенным при выводе
уравнений E.15), получим канонические уравнения в виде
1.2. ...,*). E.16)
Если силы консервативны, то Qm =» —^— и
^(/С + П) . (9(/С+П)
Рт д?Г' Чт ?ЙГ"»
ибо
Однако так как
то
дН . дН
-^т,—* чт e ~az— (m =* 1, 2, •»., s).
uQm орт

§5 21 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА 125
Дифференцируя функцию E.13) по времени /, получим
dH
dt
Учитывая, что
Ят
найдем
dH
dH
dPm
dH
dH
dt
»
s
V
+ 2
m—\
Pm =
Л dH
dH
дЯт(
dH
дЯт
дН
(w= 1, 2, ..., 5),
^. ^ dH dH
dt dt JjL dqm dpm *A dqm dpm dt '
Если
CLtl A Oil
И
H = const.
Для стационарных связей Т = Г2, следовательно,
Я = Г + П = А, E.17)
т. е. функция Гамильтона для стационарных связей и консерва-
консервативных сил является постоянной величиной, равной полной механи-
механической энергии системы.
Пример 39. Составить канонические уравнения Гамильтона для
примера, рассмотренного в предыдущем, параграфе.
Так как функция Гамильтона имеет вид E.11), то
дН р v0 ( v0 \
—г— — —^75" ~ COS f ф t]
dp ml2 I \r r I
,
p = -mlv0 j^-^j ~ -7-cos (<P ~ -7- *) J sin (ф - ~ 4 ~
и, следовательно,
Пример 40. Точка М массы щ притягивается к двум неподвиж-
неподвижным центрам М\ и Мг силами, пропорциональными расстоянию

126
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
[ГЛ. 5
точки от этих центров (рис. 5.2). Найти траекторию точки для на-
начальных условий: при t = О х = О, х «= щ, у = Ь > a, (/ = О,
г = Л, 2 = 0. Расстояние между центрами Л^Мг = 2а.
Начало координат поместим в середине отрезка М1М2, ось у на-
направим по направлению отрезка М1М2 от М\ к Мг. За обобщенные
Рис. 5.2.
Рис. 5.3.
координаты примем декартовы координаты точки, т. е. q\ = x, qi «=
= 1/, <?з ==,2. Выражения для кинетической и потенциальной энергии
соответственно имеют вид
где
и ^2 —коэффициенты пропорциональности,
р2
Так как
2 - *2 + (у + аJ + г2, р2 = х2 + (у - аJ + 22.
= mi, р2 ~ ту, р% — mi, то
Следовательно,
i = ~ -щ- = -сх {у + а)- с2 (у - а),
Отсюда имеем
х-
где
— « у — —— ^ — ——
mm m
/n
m

§5.2] КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА 127
Общими решениями этих уравнений будут
N
у = А2 eos kt + В2 sin kt -f - 2-f
z = Аг cos kt + B3 sin &/.
Используя начальные условия, получим
и, следовательно,
х « -^-sin &/, ^/ = f 6 — -р-] cos Aj/ + -p-, 2 = A cos R
Если Л = 0, то 2 = 0 и движение будет происходить в плоскости ху.
Траекторией движения будет кривая второго порядка — эллипс
18
*~
Пример 41. Составить канонические уравнения Гамильтона для
плоского движения материальной точки М массы т, притягиваемой
к двум неподвижным центрам силами, обратно пропорциональными
расстояниям от точки до притягивающих центров Mi и Мг*).
Начало координат возьмем в середине отрезка М1М2 и напра-
направим ось х по отрезку MiAf2 от Mi к М2 (рис. 5.3). Длина отрез-
отрезка М\М2 = 2а. Выражения для кинетической и потенциальной энер-
энергии соответственно имеют вид
где с\ и с2 — коэффициенты пропорциональности,
За обобщенные координаты примем
Х в Ц (Г + р)> й в ~2а (Г"" Р)*
Так как г + р > 2а и | г — р | < 2а, то координаты % и ja, которые
называются эллиптическими координатами, могут принимать только
те значения, которые удовлетворяют неравенствам
Из выражений для р, г, Я, и [х следует, что
*) Г. Н. Дубошин, Небесная механика, «Наука», 1964.

128 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА [ГЛ. 5
Находя теперь
получим выражения для кинетической и потенциальной энергий:
1
Вычислив
и подставив полученные значения в выражение для кинетичес-
кинетической энергии, получим
Следовательно,
- С2) Jl].
Каноническими уравнения будут
т
таг (А* - ц*у а (Хг - \
Р2\\ т
а (Я2 -
§ 5.3. Канонические уравнения при наличии
циклических координат
В общем случае функция Гамильтона Н является
функцией времени, 5 обобщенных координат и 5 обоб-
обобщенных импульсов, т. е.
Н = Я (/, qu q2> ..., qs, pu P2> * • • > Р5)«

$5.3] СЛУЧАЙ ЦИКЛИЧЕСКИХ КООРДИНАТ 129
Циклическими координатами мы ранее назвали обоб-
обобщенные координаты, не входящие в явном виде в функ-
функцию Лагранжа. В § 5.2 было установлено, что
т: е., если частная производная от L по qm равна нулю,
то будет равна нулю и частная производная от Н по qm.
Следовательно, циклические координаты не входят и
в функцию Гамильтона.
Предположим, что первые k обобщенных координат
являются циклическими, тогда, согласно уравнениям
E.15), будем иметь
Р/=-|^- = 0' Ь-Щ (/ = 1,2,..., ft). E.18)
Отсюда следует, что
Pi = ci и Ь-Тй]- (/=1>2, ..., ft), E.19)
где Cj — постоянные интегрирования,
Функция Гамильтона теперь будет зависеть от вре-
времени t, s—k обобщенных координат, s—k обобщенных
импульсов и k постоянных интегрирования су.
• ->Ps> с\> С2, • • •> скУ
E.20)
Используя E.15), получим
Ь--Ж' Ь'Ж (* = * + !. * + 2---.s).
E.21)
Это система 2s—2k дифференциальных уравнений пер-
первого порядка относительно р% и q^ Решения этих ура в-
нений будут содержать 2^=2(s—k) произвольных по-
постоянных интегрирования сх и с'к, а также постоянные
интегрирования Cj, т. е.
(,.4+,,...,,, E.22)
С» cl ci) I
5 Н. В. Бутепин

130
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
[ГЛ. 5.
Подставляя эти решения в функцию Н E.20) и затем
пользуясь выражениями EЛ9):
найдем
9/= ^77
(/=1,2, ..., k), E.23)
где Cf — новые постоянные интегрирования.
Следовательно, при наличии k циклических коорди-
координат решение задачи сводится к решению системы урав-
уравнений E.21), порядок которой уменьшен по сравнению
с первоначальной на 2k единиц.
Пример 42. Составить канонические уравнения Гамильтона для
гироскопического маятника (рис. 5.4). Груз В имеет массу n%2 и
7.
Рис. 5.5.
расположен от неподвижной точки О на расстоянии U. Ротор имеет
массу ти а его центр тяжести находится на расстоянии 1\ от непод-
неподвижной точки О. Массой стержня и кольца пренебречь.
Ось у' подвижной системы координат Ox'y'z' направим по стер-
стержню, а ось х' — горизонтально, перпендикулярно к стержню. Си-

§ 5.3} СЛУЧАЙ ЦИКЛИЧЕСКИХ КООРДИНАТ 131
стема координат Axyz имеет оси, параллельные осям системы коор«
динат Ox'y'z' (рис. 5.5). За обобщенные координаты примем
где ф — угол вращения ротора вокруг оси у. Координаты центра
тяжести ротора и груза соответственно определяются формулвами
д:1Л = —/л sin0 sin if», y[A — l{ sin 9 cos if», г{Д = l{ sin 9;
XIB ~ 4 Slfl ^ Sin *' У\В ^ ~"*2 SIn ® C0S *' ^lS ^ ~~l2 C0S ®"
Проекциями угловой скорости ротора на оси системы координат
Axyz будут
<йх = 9, со^ = *ф cos 9 + ф, (о2 — ф sin 9.
Составим выражение для кинетической энергии
+1 (/X + /X + /«) + 1
т=-1 «,«? +1
Так как
и Ix~h> то
Г -1 [m,/f + m2/| + Ix) (92 + гр2 sin2 9) + Iy « cos 9 + фJ],
Выражение для потенциальной энергии имеет вид
П - tn{gzlA + m2gz{B = (Wj/j - m2/2) ^f cos 9.
Найдем теперь обобщенные импульсы:
р! = —,- « Ля|) sin2 9 + /»(I? cos 0 + ф) cos 0,
Рз - дг- = 1У (Ч> cos 0 + ф),
где Л = /и1/2 + т2/2 + /х. Решая эти уравнения относительно •$,
и ф, получим
: Pi —
sin2 0

132 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА [ГЛ. 5
Функция Гамильтона будет выражаться формулой
1 Г о (Р\-Р\cos GJ
Н Т + П И +
sin» 9
1 р\
\ +-7^
Обобщенные координаты г|э и ср являются циклическими. Значит,
. в__<^ . дН
То есть
и, следовательно,
1 [ 2, (c,-c3cose):
Составляем теперь канонические уравнения:
<Э# (W|/i-m2?2) fi (ci - с3 cos 6) (с3 - С| cos 6)
Р>--Ж~ A
д дН p2 ¦ ci - c3 cos 8 c3 ci - c3 cos 6 fi
Отметим, что данная система имеет интеграл
(интеграл энергии).
§ 5.4. Скобки Пуассона, Теорема Якоби — Пуассона
Если для всех значений qm и рт, являющихся реше-
решением канонических уравнений Гамильтона
р = дН л — дн (m=l,2 s), E.24)
какая-либо функция /(/, <7i,?2, ..., ^s, PuP2> ..., Ps) cox«
раняет постоянное значение, то
называется интегралом канонических уравнений Гамиль-
Гамильтона.
Например, при стационарных связях и консервативных
силах функция Гамильтона является постоянной величи-
величиной, следовательно,
Н(йи Чъ •••> <7s> Pu Р2> •••» Psi — h
есть интеграл канонических уравнений.

§5.4] СКОБКИ ПУАССОНА. ТЕОРЕМА ЯКОБИ — ПУАССОНА 133
Если обобщенная координата qu является цикличе-
циклической, то
pk = const
— интеграл уравнений E.24).
Предположим, что нам известны 2s интегралов урав-
уравнений E.24), т. е.
fk С <7i, <Ь • • м Яз> Р\> р2, ..., Ps) = ck (k = 1, 2, .. , 25),
E.25)
где ch<—постоянные величины*). Разрешая систему
уравнений E.25) относительно qm и рШу получим
Яш = Чш (', си с2,..., c2s) J {тяя1929в9Л98)9 E<26)
т. е. решение уравнений E.24). Если же число интегра-
интегралов меньше 25, то с их помощью можно судить лишь
о некоторых свойствах движения. Отсюда вытекает есте-
естественное желание получить возможно большее число
независимых интегралов.
Прежде чем перейдем к доказательству теоремы
Якоби — Пуассона, которая в некоторых случаях позво-
позволяет по двум имеющимся интегралам получить третий,
рассмотрим некоторые свойства так называемых скобок
Пуассона. Пусть функции <р и г|) являются функциями t
и 9т, Рт (т = 1, 2, ..., 5). Для операций над этими
функциями вида
dq> дер I
s
\ ( д(
2л \dq
Пуассон вве,д
p <Э<ф д<р
m дрт dpm
обозначение
w V1 ( di
dip )
dqm)
P dy\
тбр,
s
dqm
dqm
), т. е.
? д<р аф
n dpr
ndqm
E.27)
*) Предполагаем, что рее интегралы являются независимыми,
т. е. в число рассматриваемых интегралов не включаются произволь-
произвольные функции от этих интегралов.

134 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА [ГЛ. 5
Это специальное преобразование называется скобками
Пуассона. Из рассмотрения выражения E.27) следует:
1) (Ф, г|))=-(г|),Ф),
2) (сф, г|)) = с (ф, ф),
(с — постоянная величина).
Если кроме функций ф и г|) рассмотреть еще какую-
либо функцию %(t, qmi /7m), то в соответствии с выраже-
выражением E.27) можно записать:
4) (Ф + Ф, х) = (Ф, X) + 0Ф, х)«
Кроме того, можно получить путем непосредственных
вычислений тождество Пуассона:
5) ((Ф, Ф), %) + ((Ф, х), Ф) + ((X, Ф), г|)) = 0, E.28)
которое, однако, можно доказать и несколько проще.
Каждый из членов этого тождества в силу E.27) дол-
должен содержать вторые производные от функций, входя-
входящих во внутренние скобки Пуассона, причем каждая
вторая производная какой-либо функции будет умно-
умножаться на первые производные от двух других функций.
Значит, если доказать, что рассматриваемое выражение
E.28) не содержит вторых производных от функций ф,
ty и х, то тождество будет доказано. Рассмотрим сумму
', х), ф) + ((х> ф), Ф) = ((Ф> х), ф) - ( (ф, х)> Ф) =
= (Ф, (ф, х)) - (ф, (Ф, х))
и докажем, что она не содержит членов с вторыми про-
производными от функции х- На основании E.27) можно
записать
(Ф, (ф, X)) ~ (ф> (Ф, X)) =
s
(ф'х) - -ък ~к

§5.4] СКОБКИ ПУАССОНА, ТЕОРЕМА ЯКОБИ - ПУАССОНА 135
ИЛИ
(Ф, (ф> х)) - (ф> (Ф, х)) =
5
"VI Г д\|) д дг|? д  VI / дф д% дф д% \
д^ J АЛ \ dqm дрт дрт dqm;
s s
^^ ( дф д дф д \ VI / di|) д% дг|5 д% \
^к \ dqk dpk дрь dqk ) тЛ \ dqm дрт дрт dqm)
/г=1
s 5
Li Lk\\dqu dqm dqu dqm) дрьдрщ*
fel l
^Pm ^ <^Pm/ dpkdqm*
/дф Eг|) аф дф \ д2х . / д\|) дф дф дг|? \
\др.% dqm dpk dqm) dqudpm *\дрь дрт dpk дрт)
X q—j—1 + члены, не содержащие вторых производных
от %.
Если в полученном выражении заменить т на k, a k
на т, то выражение под знаком двойной суммы изменит
знак на обратный. Следовательно, двойная сумма равна
нулю и исходное выражение
не содержит членов со вторыми производными от %.
Аналогично можно показать, что выражения
((Ф, Ф), X) + ((Ф, X), Ф) и ((ф, ф), х) + ((Х> Ф), Ф)
не содержат соответственно членов со вторыми произ-
производными от г|? и ф. Тем самым доказывается тождество
Пуассона.
Предположим теперь, что функция
f(t, qu Яг, ¦*.., qs, pu рг, .... Ps)
такова, что для <7ь 9г, ..., qSi являющихся решениями
канонических уравнений E.24), справедливо равенство
/ (*, Чь Яъ • • • > Я & Pi> Р2> • • • > Ps) = с»

136 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА [ГЛ. б
выполняющееся для заданного с при определенных на-
начальных условиях*). Отсюда получаем
qm
т-=1
или, используя уравнения E.24),
К л. V (
1
JLML-M
\ 7т рт дрт dqm
т=1
т. е.
iL + tf,tf)-0. E.29)
При помощи этого тождества можно доказать, что (f\|>)
будет интегралом канонических уравнений, если / и ф
являются интегралами этих уравнений (теорема Яко-
би — Пуассона). Действительно, так как / и я|) — интег-
интегралы уравнений E.24), то в соответствии с тождеством
E.29) имеем
-g- + (ff Я)-0, -^+(г|),Я) = 0. E.30)
С другой стороны, на основании свойства скобок Пуас-
ссна
¦*№«-(#.»)+('.$)¦
Значит, выражение
•5Г &*) + ((/,*), #)
с учетом E.30) может быть переписано в виде
- ((f, Я), ф) - (/, (ф, Я)) + ((/, я|>), Я),
или
((/,¦), Я)+ ((ф, Я), /) + ((Я,/), ¦),
а это тождественно равно нулю в силу E.28).
Таким образом, доказано, что
&¦) + «/, Ф), Я)-0,
*) То есть f (/, #1, #2» .. •. <?si Рь Рг, ..., Р») = с является инте-
интегралом канонических уравнений E.24)»

%5.Щ КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 137
т. е. (/, ф) является интегралом канонических уравнений
E.24). При нахождении нового интеграла при помощи
теоремы Якоби — Пуассона следует иметь в виду, что
он может оказаться тождественно равным нулю или
быть функцией от ранее известных интегралов (т. е. не
будет независимым).
Пример 43. Для свободной изолированной материальной точки
выполняются интегралы количества движения
и момента количества движения
Кх = УРг - zPy e 0и Ку = zpx - хрг = с6, К2 = хру - урх = с6.
Покажем, что
(Кх> Ку) = Кг = с8,
В самом деле,
дКх дКу дКх дКу дКх дКу дКх дКу
х' у'~~ дх др др дх
дх дрх дрх -дх ду дру дру ду
дКх дКу дКх &КУ
+ дг дРг --^-^Г = (
§ 5.5. Канонические преобразования
При составлении уравнений Лагранжа или канони-
канонических уравнений Гамильтона выбор обобщенных коор-
координат был произволен в том смысле, что за такие ко-
координаты можно было выбрать любые s независимых
между собой величин, однозначно определяющих поло-
положение рассматриваемой динамической системы. Фор-
Формальный вид этих уравнений не зависит от той системы
обобщенных координат, которая выбирается. Это зна-
значит, что если от каких-либо обобщенных координат
Яи Qz, - • •, Qs перейти к новым обобщенным координа-
координатам q\f qf2y ..., q's по формулам
q'm = q'm(qi, ?2, ..., qs, t) (m = 1, 2, ..., s), E.3i)
то вид уравнений Лагранжа и Гамильтона останется
прежним. Преобразование кородинат E.31) называется
точечным.
Если же в канонических уравнениях E.15), содержа-
содержащих 25+1 переменных qu Чг> .-., ?*, Ри Р*> ...» Ps, t,

138 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА [ГЛ. 5
перейти к новым переменным^, #2, .. •> q's, р'и Рь • • • > Ps>
t по формулам *)
Ят = q'm (t,
r
Pm
(m=l,2, ..., s),
т = q'm (t, qu Й2> ..., qs, Pi, рг, • • •, Ps), \
Pm = Pm (<, ^b <72, • • •, ?5, Pi, P2, • • •, p5) J
то в общем случае канонические уравнения своей формы
E.15) не сохранят. Однако существуют такие преобра-
преобразования переменных, при которых канонические уравне-
уравнения сохраняют свою форму. Такие преобразования на-
называются каноническими.
Прежде чем рассмотреть канонические преобразова-
преобразования, познакомимся с преобразованием Лежандра, имею-
имеющим в теории канонических преобразований существен-
существенное значение. Пусть дана какая-либо функция -ф от п=
=2s-f-l переменных хи х2, ..., хп:
Ф = Ф(*1, х29 ..., хп), E.33)
которую будем называть производящей по отношению
к переменным Хи #2, •.., хп. Введем новые переменные,
определяемые из соотношений
Ui = W; 0'= 1.2,3 л-1). E.34)
Тогда дифференциал от функции ф будет иметь вид
-§;;dxn. E.35)
Разрешая уравнения E.34) относительно старых пере-
переменных Хи #2, ...., хп-и получим **)
Xi = xt (ylf y2, ..., уп-и хп) (i = 1, 2, ..., п - 1).
Эти формулы обратного преобразования от новых пе-
переменных к старым можно записать в форме E.34). Для
*) Предполагается, что уравнения E.32) разрешимы относи-
относительно q\, #2, ..., qs, pu P2, ..., ps.
**) Мы предполагаем, что функция "ф обладает для этого всеми
необходимыми свойствами.

§ 5.5} КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 139
этого выберем функцию Ч? от переменных у и у2> ¦,*
. • • , Уп-U Хп'-
* == * \У\> У2> • • •! Уп—U Хп/9
так, чтобы
*-!? (/-1,2,..., п-1). E.36)
Полный дифференциал от функции vp равен
i dyi + -л— ^*л« E.37)
Функцию W называют производящей по отношению к пе-
переменным у и У2у ..., #n-i. Переход от переменных
*i, *2, ..., ^n~i к переменным уи уг, ..., Уп-i и от функ^
ции г|г- к функции УР называется преобразованием Ле«
жандра.
Это преобразование можно осуществить с помощью
преобразования
2J ¦• E.38)
В самом деле, так как
п-1 п-1
a dij; выражается формулой E.35), то
Сравнивая это выражение с выражением E.37) и при-
приняв во внимание соотношения E.36), получим
<5-39>

140 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА {ГЛ. б
Таким образом, соотношения E.34), E.36) и E.39)
определяют прямое и обратное преобразования (преоб-
(преобразования Лежандра).
Пусть теперь требуется перейти от старых перемен-
переменных хи х2, ..., а:п_1, хп к новым переменным хи #2, ...
..., Xs, #s+1, r/s+2, ..., Уп-U Хп И ОТ фуНКЦИИ \|) (Хи Х%, . . .
• .., Хп) К ФУНКЦИИ 4я (*Ь Х2, ..., Х8, ±)s+U •.•> Уп-U Хп).
В этом случае преобразование можно осуществить с по-
помощью формулы
^= S х1У,-Ъ. E.40)
? = 5 + 1
Так как
п-\ п-\
2 xt dyi + 21
TO
С другой стороны,
/==1 i-sfl
Сравнивая правые части этих выражений, получим фор-
формулы преобразования
I, ..., л-1),
E.41)
В качестве примера преобразования Лежандра рас-
рассмотрим переход от переменных Лагранжа /, qm, qm
к переменным Гамильтона /, qm, рш. Напомним, что

§ 5.5J КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 141
pm=dL/dqm [ см. равенство E.3)]. Из уравнений Ла-
гранжа
d ( dL\ dL п , , о ч
-тг -^-г— —-^— = 0 (га = 1, 2, ..., s)
dt \dqm) дцт ч > » » /
следует, что
Рт = -Щ^ (т== 1, 2, ..., s).
В качестве производящей функции от переменных Ла-
гранжа возьмем функцию Лагранжа
L = L{qm, qm, t).
В соответствии с формулой E.40) производящей функ-
функцией W будет
m=l
т. е. функция *? совпадает с функцией Гамильтона E.6):
S
Я^\1 • г
===: / I QmPm Li»
На основании формул E.41) теперь имеем
dqm '
dL
. _
Чт~~
ко -^—
дН
dH
dqm'
dH
dt
следовательно,
dH
dqm>
dH
dt
dL
dt
(m =
dL
dt
(m =
1,
1,
2,
2,
дрт>
S).
Эти последние уравнения представляют собой уравне-
уравнения Гамильтона.
Перейдем к рассмотрению канонических преобразо-
преобразований. В общем случае канонических преобразований
при переходе от переменных qm, pm, t к переменным
q'm% р'тУ t канонические уравнения
dH . dH / t r\ \

142 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА [ГЛ. 5
переходят в уравнения вида
рт=—-т-г, qm = -r-r~ (m= 1, 2, ..., S),
дЯт дРт
где функция Я' уже не является прежней функцией Га-
Гамильтона Я, преобразованной к новым переменным
q\, q2> -•-, q's, pi, Ph ..., ps-Если функция Гамильтона
при каноническом преобразовании не меняется, т. е.
Н'=Н, то такое преобразование называется вполне ка-
каноническим.
Рассмотрим это преобразование несколько подроб-
подробнее. Пусть H(qu q2, ..., qs, Pu p2, ..., ps) — старая
функция Гамильтона, а Н'{q'u 42, ..., q's,, Pu p'2, ...
..-, Ps) —новая функция Гамильтона. Рассмотрим вы-
выражение
5 5
7П= 1 Ш=\
где \|) — произвольная функция от старых и новых обоб-
обобщенных координат (qu ..., qs> q'u •••» q's)- Это выра-
выражение можно переписать в виде
S
__ }т^1т — ^ = 2^ ртС/т — Я' + -^р E.43)
т—\ т=1
ИЛИ
Отсюда следует:
Это выражение будет тождественно выполняться, если
о, p^+Jl—о, н-н> = о
(т=1, 2, ..., s).

§ 5.5] КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 143
Отсюда и получаем формулы нужных преобразований
т = dqm 9 m dqm 9 — »»•••»;•
Докажем, что рассмотренное преобразование являет-
является вполне каноническим. Так как Н' = Я, то на основа-
основании выражения E.43) можно записать
или
S 5
т—\ т=\
Так как
Pmbqm = 2и Р*Ь \ЧГ) =2iP>nW F^) =
tn== 1 Tt%—\ tJi — \
S i
m *4m == Iff 2j Pm *4m — La Pm *Чт9
m=l
d
TO
s s s s
m=\ m=l m=l m = l
г s 5
m=l

Щ КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА [ГЛ. о
Соотношение E.42) при #' = # может быть записано
в виде
m«=l
и, следовательно,
E.430
Для переменных qm и рт канонические уравнения
имеют вид
дН . дН , 1 о ч
^=~^' ^=^Г (т = 1. 2 s).
Значит, левую часть полученного выражения E.43')
можно запирать в виде
S S
m=l
Таким образом,
ЬН = ±q'mbp'm- ±/mbq'm. E.44)
m=l m = 1
В силу того, что Hf = Я,
6Я=:6Я',
и, следовательно, выражение E.44) утверждает, что
Ж> = ± q>mbp'm - ±P'mbq'm. E.45)
m=*l m=l
С другой стороны,

§о,5} КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЙ 145
Значит,
5
В силу независимости Ьр'т и bq'm получим
Следовательно, рассмотренное преобразование является
вполне каноническим.
Таким образом, если задаться какой-либо произво-
производящей функцией it)(<7P ..., qs, q'v •••, q's)> т0> в соот-
соответствии с соотношениями E.41), из уравнений
5& («-». 2. ¦•¦.»)
определим все
Я'т = <4 (<?i> Я2> • • - Я*> Рр Р2. • • м Р,)- E-47>
Из уравнений
P'm = -JZ («-1,2,..., 5)
после подстановки в них всех <?', q'2, ..., ^, определен-
определенных по E.47), найдем все
Рт = Рт0/1»<72> •'•> 9,. РрР2. •••» Р,)-
Новая же функция Гамильтона равна
В более общем случае, когда функция Гамильтона
будет зависеть от времени, т. е. если Я(<7ь Яь •••> Я**
Ри р2г ..., Ps, 0» можно доказать*), что обратимое пре-
преобразование E.32) будет каноническим, если дифферен-
дифференциальной формой будет
2 Ртdqm - ± р'т dq'm + Hodt + dV, F.48)
*) Доказательство будет дано в главе 8.

146 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА [ГЛ. 5
где #0 и V — произвольные функции от /, старых и но-
новых переменных, удовлетворяются тождественно. Если
ввести обозначение
Н' = Но — Я,
где Н — старая функция Гамильтона, то выражение
E.48) можно переписать в виде
т=\
Рассмотрим некоторые типы канонических преобра-
преобразований.
1. Пусть К = ф(<7Р<72> ..., q8, q'v q'2, ..., <& t). Тогда
соотношение E.49) будет иметь вид
т=\ т=\
ИЛИ
5 S
Это условие будет тождественно удовлетворено, если
р = , рт = — —у , ii = /i -j (o.oU)
(т= 1, 2, ..., 5).
Теперь из формул E.50) можно получить искомое пре-
преобразование E.32) и новую функцию Гамильтона #'.
2. Пусть производящая функция г|) будет функцией
,.., qs, p[, p'v ..., p's, t)\ тогда, выбирая

§ 5.5] КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 147
перепишем выражение E.49) в виде
m=l m=l m = \
Отсюда
Полученное условие будет удовлетворено, если
(т=1, 2, ..., 5),
откуда и находится искомое преобразование.
3. Пусть производящая функция ф будет функцией
Ч'и Я'г> •••• 9s' Pv Pp -•> Ps и *> т-е- * = *(^» 9г» •••
..., ^, рр р2, ..., /?s, /). Примем, что
v = ^Du42, •¦¦> q's> Pi' Pi pS' 0+ 2 <7mpm,
m— 1
и подставим это V в соотношение E.49):
2 ^^
m=l m=l Чт
s s s

148 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИДЬТОНА [ГЛ. 5
Отсюда получаем
Это соотношение удовлетворяется, если
П—Ц. «.~?. *'-* + ? E.52)
(т=1,2, ..., s).
Из уравнений E.52) определяется искомое преобразо-
преобразование.
4. Пусть производящая функция \|) есть функция t,
старых и hob^ix импульсов, т. е. г|г='Ф(/?1, р2, ..., ps, р[>
р'2, • • •, />J, t). Выберем
У = *(РР Р2» • • • > Р*> Pv Pv • • •» Pi» 0 -
m=l m=l
Соотношение E.49) будет иметь вид
/71= 1 /71= I
S S
^j РтЯту
m = \ m=»l
ИЛИ

$ 5.5] КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЕ \ 49
Это соотношение будет удовлетворено, если
E.53)
дрт дрт dt
(m=l, 2, .... s).
Очевидно, что, задавшись какой-либо функцией
¦(Ля' Pm' О' И3 УРавНеНИЙ
можно найти р^ как функции /, <7т> /V Далее, в урав-
уравнения
подставляются найденные р'т как функции i, qm, pm, и,
таким образом, находится искомое преобразование
E.32).
Пример 44. Пусть производящая функция имеет вид
На оснозании зависимостей E.51) имеем
m=l
^m e fm (^1» <72» • • " ^ 0 <m - 1, 2, . .., s),
т. е. при таком каноническом преобразовании обобщенные коорди-
координаты <7j, ^2» •••» ^5 и <7i» ^2» •••» ^s преобразуются только между
собой. Такие преобразования называются точечными.
Пример 45. Для цилиндрических координат г,фиг введем обо-
обозначения <7i = Г» #2 = Ф, ^з = z. Рассмотрим свободную материаль-
материальную точку, находящуюся в поле силы тяжести. Для такой точки
Т = 1 пг D? +$7? + $, П

150 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА [ГЛ. 5
Поэтому
Рассмотрим каноническое преобразование, получающееся при
производящей функции вида
ф « p\qx cos q2 + p2q{ sin q2 + p^3.
На основании E.51) имеем
P\ = ~Ъ === Pi COS 02 "*"* P2 Sin 02»
<5ф / . /
/?2 — -^ =г — Pl01 sin 02 "^" P201 COS 02»
I COS ^2»
sin q2>
,_ аф e
d/>3
Из первых трех уравнений находим
р\ — т [q{ cosq2 — 1
Р2 = т @1 s*n 02 + 0102 cos <72) :
Новая функция Н' будет иметь вид
Очевидно, что новые координаты q^ q2, q% являются декарто-
декартовыми координатами точки.
Пример 46. Рассмотрим прямолинейное движение точки под дей-
действием восстанавливающей силы F = с | х |, где х — расстояние точ-
точки от притягивающего центра.

§ 5.5) КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 15i
Приняв за обобщенную координату координату х, т. е. поло-
положив q = хг найдем выражения для кинетической и потенциальной
энергий:
Так как L = Т — П = --- (mq2 — cq2), то
dL
p = — = mq.
Напишем выражение для функции Гамильтона:
где k2 =—. Составим канонические уравнения:
^ dq ч dp m
Так как рассматриваемая система консервативная, то функция
Гамильтона равна полной энергии системы, т. е. Н = h. Найдем та-
такое каноническое преобразование, при котором бы новая функция
Гамильтона не содержала новой координаты q\ а новый импульс
входил бы в первой степени, т. е.
Я'= Jfep'.
Воспользуемся вторым типом канонических преобразований, когда
ф = i|?(<7> РО- В соответствии с формулами E.51) Н = #', т. е.
Отсюда
|* VFi^ E.54)
о
Так как
Г
<7
о
7
то
o V2mkp'-k2m2q '
^=arcsin|/ -^-rq

152 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА [ГЛ. б
Из формулы E.54) получаем
р - V2mkff - k2m2q2
Новая координата q' является циклической, так как она не входит
в функцию Гамильтона. Следовательно, новый импульс является по-
постоянной величиной
- h
Координату q' определим из канонического уравнения
4 др'
Следовательно, q' = Ы + е, и, значит,
р - V2mh cos (kt + e), q - у -~ sin (ki + е).

ГЛАВАб
ТЕОРИЯ ЯКОБИ
§ 6.1. Уравнение Гамильтона — Якоби
Пусть движение голономной системы описывается
каноническими уравнениями Гамильтона
Ь pm==--?t (m=l'2* ••••s)- FЛ)
В § 5.3 было выяснено, что наличие k цикличееких
обобщенных координат у рассматриваемой системы по-
позволяет получить для этих координат решение E.23).
В связи с этим естественно поставить вопрос о возмож-
возможности нахождения такого канонического преобразова-
преобразования, при котором в преобразованных уравнениях Гамиль-
Гамильтона функция #' не будет содержать обобщенных коор-
координат, т. е. все новые обобщенные координаты будут
циклическими. Предположим, что, пользуясь вторым ти-
типом (см. стр. 146) канонических преобразований, где
<Ф = 1Ф(?1, <72> •••> ?s> P'\> Pv •••> Ps> 9» F*2)
Pm-J^-' *«-т?- ("-I, 2, ..., S), F.3)
мы найдем новую функцию Гамильтона вида
H'-ftf, P'2,..., К), F.4)
где / — любая функция. Тогда для новых переменных
будет
р'т=-Щ- = 0 (т= 1, 2, .... s), F.5)
#¦=-^1 (т-1, 2, .... s) F.6)

154 ТЕОРИЯ ЯКОБИ [ГЛ. 6
И
Я/ гт • di|) /п 7\
Из уравнений F.5) следует:
где ат — постоянные интегрирования. Подставляя те-
теперь выражения F.8) в уравнения F.6), получим
<,« « («-1, 2, .... s), F.9)
где сот = ( д , ) — постоянные величины, а рт~ по-
стоянные интегрирования. Выражения F.8) и F.9)
представляют собой систему интегралов уравнений F.5)
и F.6). Используя теперь преобразование F.3), мы
могли бы получить старые переменные qm и рш, т. е.
решить задачу о движении системы*). Однако мы не
можем этого сделать, так как нам неизвестна функция
г|). Рассмотрим соотношение F.7) с учетом выражения
F.4):
H(qv q2> ..., q8, Pv P2> .-•> Ps) + -jf = f'{p\> p'v ..-, p's\
Заменяя в этом соотношении в соответствии с форму-
формулами F.3) и F.8) переменные рт на -т-^- и рт на ат,
будем иметь
= /(«!, а2, ..., а8). F.Ю)
Это дифференциальное уравнение в частных производ-
производных называется уравнением Гамильтона — Якоби. Та-
Таким образом, мы получили дифференциальное уравнение
первого порядка в частных производных, которому
должна удовлетворять производящая функция
(i, 92, ••-, Vs, at, яг, ..., as, t) с основными перемен-
*) Мы предполагаем, что функции / и г|? обладают свойствами,
необходимыми для такого преобразования.

§6.1] УРАВНЕНИЕ ГАМИЛЬТОНА - ЯКОБИ 155
ными #ь #2, ..., qSy t. Так как в выражении F.4) функ-
функция f произвольная, то мы можем принять
f(au а2, ..., as) = 0. F.11)
Тогда уравнение F.10) примет вид
*(*•
*
Решение дифференциального уравнения в частных про-
производных, содержащее столько произвольных постоян-
постоянных, сколько имеется независимых переменных, назы-
называется полным интегралом этого уравнения. Функция ty
в уравнение F.12) входит только через свои производ-
производные. Это значит, что одна произвольная постоянная
будет входить в полный интеграл в виде слагаемого,
т. е. полный интеграл уравнения Гамильтона — Якоби
имеет вид
s==(*M<7i> Чъ •••> Qs> Щ> «2» •¦•> Q*s, O + <*o, F.13)
где ао — произвольная постоянная. В самом деле, если
^(<7ь <7г, ...» qs> он, а2, ..., as, t) является решением
уравнения F.12), то в силу того, что
^~~dq^ (m~l> 2> •••» 5), dt ~ dt * №.14)
функция S является решением уравнения F.12), содер-
содержащим 5+1 произвольных постоянных, т. е. является
его полным интегралом.
Итак, если известен полный интеграл F 13) уравне-
уравнения Гамильтона — Якоби, то для получения решения ис-
исходной системы уравнений F.1) следует за производя-
производящую функцию взять функцию
затем в формулах канонического преобразования F.3)
заменить р'ш на ат и q'm, в соответствии с выражением
F.9), на рт. Тогда будем иметь
ж-

156 ТЕОРИЯ ЯКОБИ [ГЛ. б
1=ак как при /=0
от-Ав0 (т=1, 2, ..., 5). F.17)
Уравнения F.16) дают возможность выразить обобщен-
обобщенные координаты <7ь #2, ..., qs через время * и 2s про-
произвольных ПОСТОЯННЫХ <Хт И рт (/72=1, 2, ..., S).
Таким образом, мы показали, что если известен пол-
полный интеграл уравнения Гамильтона — Якоби, то нет
необходимости интегрировать систему обыкновенных
дифференциальных уравнений F.1), т. е. задача инте-
интегрирования системы F.1) заменяется задачей нахожде-
нахождения полного интеграла уравнения F.12).
Пример 47. Составим уравнение Гамильтона — Якоби для точки,
движущейся в однородном поле силы тяжести.
За обобщенные координаты примем q\ = х и q<i = у —- декарто-
декартовы координаты точки.
Запишем выражения для кинетической и потенциальной энергий:
Так как px = mq\ и P2 = m^2. H=T + Tl, то функция Гамильтона
и, следовательно, уравнение Гамильтона — Якоби будет иметь вид
dq{ } 2tn \ dq2 )
Предположим, что рассматриваемая механическая
система подчинена стационарным связям. В этом слу-
случае функция Гамильтона от времени явно не зависит
и уравнение F.12) имеет вид
,*,-$¦ &) + #-<>. F-20)
Вместо этого уравнения можно рассматривать более
простое, приняв
ф(<7„ .. ., qs, аь . .,, as, 0 =
Г(|71э ..., ^s, Л, а2, .,., а,), F.21)

$?П УРАВНЕНИЕ ГАМИЛЬТОНА - ЯКОБИ 157
где 1г = оси аг, ..., as — произвольные постоянные. Так
как при этом
W=~h> ?—§Г (w=I'2 s)' F'22)
ot oqm иЦт
то вместо уравнения F.20) будем иметь
H(qit q2, .... q» -щ^. -ЩТ"'- ^7J = Л> F*23)
где h — полная механическая энергия [см. равенство
E.8)]. Это уравнение называется укороченным уравне-
уравнением Гамильтона — Якоби. Проинтегрировав его, найдем
W = W (ft, q2, • • • > qs> ht а2, а3, ..., as)
и, следовательно,
$= -ht+W(qlt ..., qst ht a2t ..., as).
Отсюда имеем
45
а--'+
5-
На основании F.16)
Положив pi =—/о, окончательно получим
^ = '-'()> F^26)
Ш =Pm (m = 2, 3, ..., s), F.27)
а также
xxvr
Из формул F.26) и F.27) теперь можно найти обоб-
обобщенные координаты qu <7г, ..., 9s. Заметим, что время f
входит только в уравнение F.26), уравнения же F.27)

158 ТЕОРИЯ ЯКОБИ [ГЛ. 6
времени не содержат и представляют собой уравнения
связи между обобщенными координатами.
Итак, показано, что интегрирование канонических
уравнений Гамильтона можно заменить нахождением
полного интеграла уравнения Гамильтона — Якоби.
В общем случае обе эти задачи обладают одинаковой
трудностью, однако имеются динамические задачи, для
которых нахождение полного интеграла уравнения Га-
Гамильтона— Якоби оказывается более простым, чем ин-
интегрирование канонических уравнений Гамильтона.
В следующем параграфе мы рассмотрим метод раз-
разделения переменных, позволяющий в ряде важных слу-
случаев получить полный интеграл уравнения Гамильтона —«
Якоби.
§ 6.2. Метод разделения переменных
Предположим, что часть обобщенных координат, на-
например qu #2, ..., cjh (&<s), и соответствующие им
обобщенные импульсы ри рг, ..., ри входят в функцию
Гамильтона в виде функций q>i(qu Pi), Ф2(?2, рг), ...
..., q>k(qk, pk), причем каждая из этих функций не за-
зависит от времени t и обобщенных координат и обобщен-
обобщенных импульсов, не имеющих индекса функции.
Функция Гамильтона будет при этом иметь вид
Я = #[ф1(<7ь р,), ф2(<72, р2), ..., Фа(<7*, pk)>
• • •» Qs, Pk+u
Напишем соответствующее этой функции уравнение Га-
Гамильтона — Якоби:
^-¦¦¦- ¦%¦¦
Будем искать решение этого уравнения в виде
^*(я/,+1* • • •» Яз> О-
F.29)

§ &2] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 159
После подстановки этого выражения в уравнение F.28)
получим
л
Предположим теперь, что выражение F.29) является
решением уравнения F.28), тогда уравнение F.30)
представляет собой тождество. Это тождество должно
сохраняться при любых значениях qu <7г, ..., <7л. Так как
эти координаты между собой независимы, то это может
быть только в том случае, если функции срь ср2, ..., ф.ч
при изменении координат qu Яг, ..., Ци останутся по-
постоянными. Это значит, что уравнение F.30) распадается
на k+l уравнений
F.31)
til dV д<$* Л i dV л
Hlau а2, ..., ак9 qk+i, ..., q$9 ^- ,..., ^—, Ч + -^ = 0,
\ 4k + l 4s I
F.32)
где ai, 062, *.., аи — произвольные постоянные. Первые
k уравнений F.31) являются обыкновенными дифферен-
дифференциальными уравнениями. Уравнение F.32) остается
уравнением в частных производных, но переменных
в этом уравнении меньше, чем в исходном.
Рассмотрим случай наличия циклических координат.
Если обобщенные координаты qu #2, ..., qu (&<s) бу-
будут циклическими, то соответствующие им обобщенные
импульсы ри /?2, ..., ри будут постоянными величинами,
т. е.

160 ТЕОРИЯ ЯКОБИ ДО*. «
Следовательно, уравнение Гамильтона — Якобд в этом
случае имеет вид
••> Я** «j, а2, ..., аь ^-, ..., ^-, ^
F.33)
Так как -~- = ац, функцию г|э запишем в виде
k
"Ф = 2 %q» + 'Ф* (qk+u • • • > ^э О-
Тогда получим
dob* dob*
F.34)
В этом уравнении Гамильтона — Якоби функция ф* яв-
ляетдя уже функцией s—k неизвестных.
Для консервативной динамической системы в случае,
если функция Гамильтона имеет структуру вида
Я = Я[ф1(^1, р,), ф2(?2, р2), ..., <ps(qs, ps)l
где функции (рт(Ят, Рт) не зависят от времени, обоб*
щенных координат и обобщенных импульсов, имеющих
индекс, отличный от индекса функции, уравнение F.23)
принимает вид
ы\ ( 0W\ ( dW\\ u ,аок\
Если искать решение этого уравнения в виде
W = Wl (</,) + 1^2 (q2) + ... +W. (qs) =S^ (9m), F.36)
m==l
то получим
Если вырал<ение F.36) будет решением этого уравнения,
то в силу независимости обобщенных координат каждая

§ 6.2] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 161
ИЗ фуНКЦИЙ фт(<7т, Рт) (W=l, 2, ..., S) будет ПОСТОЯН-
на, т. е.
Фт (<7т> ^) = <*т (т - 1, 2, ..., s), F.38)
где aw — произвольные постоянные.
Следовательно, решение задачи сводится к интегри-
интегрированию обыкновенных уравнений F.38). Постоянная А
в силу зависимостей F.37) и F.38) будет функцией
ось QC2, ... > а*, т. е.
Для функции г|> имеем
^ =» - М + S lFm (^m, am). F.39)
В соответствии с преобразованием F.16) окончательное
решение задачи получим из формул
4^ = Рт + -??-' (Ю=1, 2, ..., 5), F.40)
где pi, Рг, ¦ • •, Ps — произвольные постоянные.
Рассмотрим случай, когда консервативная система
имеет циклические координаты. Пусть циклическими ко-
координатами будут qu #2, •••, Qk(k<is)y тогда укорочен-
укороченное уравнение Гамильтона — Якоби F.23) примет вид
dW dW
Решение этого уравнения можно искать в виде
Тогда уравнение Гамильтона— Якоби
dw* dW*
а
s> а1> а2»
служит для определения функции 1^* от s—ft перемен-
переменных <7fc-H, • • •» 9s- Предположим, что мы нашли полный
6 Н. В. Бутенин

162
ТЕОРИЯ ЯКОБИ
[ГЛ. в
интеграл этого уравнения (с точностью до аддитивной
постоянной)
W* = W* (qk+l, qk+2> • ••> qs>
Тогда, приняв h=ah+i на основании F.26) и F.27), по-
получим
dW*
dW*
dW*
dav
= t-t0,
= 1, 2, .... k),
= k + 2, ..., s).
F.41)
Из рассмотрения метода разделения переменных сле-
следует, что для его применения существен удачный выбор
обобщенных координат, так как при одной системе обоб-
обобщенных координат переменные могут быть разделены,
а при другой нет.
§ 6.3. Примеры
Пример 48. Применить метод разделения переменных для урав-
уравнения F.19). Координата q\ является циклической, поэтому примем
и тогда
а? 1 /dWo
+ (
Отсюда следует:
Так как
o=-- <6-42)
--i-'+ffl-pl.
да2
то
<3a2 da 2
dW2
da2
da2
F.43)

§ 6.31 ПРИМЕРЫ 163
Найдем теперь решение уравнения F.42). Для этого перепишем
его в следующем виде:
dq2
Отсюда
(a2 - mgq2).
W2=* J dq2 V2m (a2 - mgq2) + с
dW2 _ С mdq2
da2 J У 2m (a2 — mgq2) mg
Таким образом, имеем
m(a2->mgq2).
^ ^ (a2 -
или
<7i= — / + Pi, ^ g + —.
Кроме того,
Пусть начальными условиями будут: при t = 0 ^i = 0,
Я\ — Уо» ^2 = 0- Тогда
о» «2 = w^A, pi = 0, р2 = О
и, следовательно,
Пример 49. Рассмотрим плоское движение материальной точки,
притягиваемой к неподвижному центру силой, пропорциональной рас-
расстоянию точки от притягивающего центра. Начало системы коорди-
координат поместим в притягивающем центре.
Примем за обобщенные координаты декартовы координаты q\ =
= х, q2 = у. Кинетическая и потенциальная энергии выразятся при
помощи формул
где т — масса точки, с — коэффициент пропорциональности. Так как
рх = mqi, p2 = тс/2, то функция Гамильтона будет

164 ТЕОРИЯ ЯКОБИ {ГЛ. 6
и уравнение Гамильтона — Якоби примет вид уравнения F.35):
1 tdW\* с 2 1 (dWy с о_
2т \ dqt ) + 2 9l + 2т \ дд2 ) + 2 9а
Приняв для W выражение F.36)
в соответствии с условиями F.38), получим для определения №» и
W2 обыкновенные дифференциальные уравнения:
, с 2
причем Л = ai + a2. Отсюда
^ = J ymBax-cq\)dqif
Г2-| VmBa2~cq%)dq2.
В соответствии с выражениями F.40) имеем
Но
i т /"m* . q{ dW2 -. /~m" . q2
-i- = 1/ — arcsm ~==rt -r-1- = 1/ — arcsin ;2
и, следовательно,
arcsin -^ = /Z (/ + Pl), arcsin
Отсюда
Так как
dWx
dW2
/ 71
V m B<X2 ""

§6 3} ПРИМЕРЫ 165
то, введя начальные условия, можно определить постоянные аь а2,
р! и р2. Пусть, например, при / = 0 q\=a, q2*=*0, ^=0, q2 = v0.
Уравнениями для определения аь а2, Pi и р2 будут
с У т ' г с
Vm Bа! - са2) - 0, V2a2m = t и
Отсюда имеем
и, значит,
a cos
TsmV mL
Таким образом, решение этой задачи свелось к операциям диф-
дифференцирования и вычисления квадратур.
Пример 50. Применим теорию Якоби к гироскопическому маят-
маятнику.
Для этой задачи функция Гамильтона имеет вид (см. пример 42)
fp, — Ро cos аЛ2
+ X
.X
1 По
Напишем уравнение Гамильтона — Якоби:
1 / dW \2
Координаты q\ и #з циклические, поэтому,- если решение искать в
виде
то получим
= А. F.44)
Это уравнение является обыкновенным дифференциальным урав-
уравнением первого порядка. Приняв h = аг, на основании выражений
F.41) имеем
ТЕГ"'-'* <М5)

166 ТЕОРИЯ ЯКОБИ [ГЛ.
И
dW2 _
- <7з + Ре.
да3
Перепишем уравнение F.44) в виде
sin q2
dW2
dq2
л/* Г f аП 1
= I/ 2Л (w2/2-/ni/i)^sin2^2COs^2H-la2~27-lsin2^2 -(ai-
или
-J/i
j Ddq2
где
/
fa, —a.
1 3
В соответствии с формулами F.45) и F.46) получим
Adq2 __±_± _Г («1 — аз cos q2) dq2 __ __
И2Ла3 __ 2 (gt — аз cos q2) cos q2 1 ^2 ^ _
/^ sin2 <72 J D ^
Таким образом, задача свелась к квадратурам.
§ 6.4. Теорема Лиувилля
Как было показано в предыдущих параграфах, при-
применение метода разделения переменных позволяет по-
получить полный интеграл уравнения Гамильтона — Яко-
би. Однако этот метод не всегда применим. Поэтому
естественно заранее выяснить, при каком виде гамиль-
тоновой функции (или отдельно кинетической и потен-
потенциальной Энергий) возможно применение метода разде-

§0.4]
ТЕОРЕМА ЛИУВИЛЛЯ
ления переменных. Исследованию этого вопроса были
посвящены работы Лиувилля, Штеккеля, Гурса и др.*).
Остановимся лишь на рассмотрении практически важ-
важного случая Лиувилля. Если в голономной системе с s
степенями свободы кинетическая и потенциальная энер-
энергии имеют вид
F.47)
5
П = у 2 Пш (<7m),
m=l
где f = 2 Fm (qm)y то интегрирование уравнения Га-
Гатя =1
мильтона — Якоби приводит к квадратурам (теорема
Лиувилля).
Для доказательства этой теоремы составим функцию
Гамильтона. В соответствии с выражениями F.47)
имеем
Рт-
дТ
dqm
= fAm (qm) qm (m - 1, 2, ..., 5). F.48)
Составим функцию Гамильтона:
или, учитывая соотношение F.48),
m=l
Вводя замену
_
6W
dqm
*) Изложение результатов этих работ можно найти в книгах:
Ф. Р. Мультон, Введение в небесную механику, ОНТИ, 1936;
А. И. Лурье, Аналитическая механика, Физматгиз, 1961.

J68 ТЕОРИЯ ЯКОБИ ГГЛ. б
получим уравнение Гамильтона — .Якоби
Будем искать полный интеграл этого уравнения в виде
W = Wx (Я1) + W2 (q2) + ... +WS (gs).
Уравнение F.49) при этом примет вид
- <6-50>
Каждое слагаемое левой части этого уравнения зависит
только от одной обобщенной координаты qm, поэтому
можно применить метод разделения переменных. Урав-
Уравнению F.49) можно удовлетворить, если каждое из сла-
слагаемых приравнять постоянной величине, т. е.
1 (dwm\* ¦ „ ,_ ^-hFm(qm) = amt F.51)
2Am(qm) \ dqt
причем должно выполняться условие
щ-jr о>2 ~\- ... + cis =й 0. F.52)
Каждое из уравнений F.51) является дифферен-
дифференциальным уравнением первого порядка, интегрирование
которого сводится к квадратуре
Wm = J V2Am (qm) [am + hFm (qm) - Пм [qj] dqm. F.53)
Следовательно, полный интеграл уравнения Гамильто-
Гамильтона — Якоби
(qm) [am + hFm (qm) - Um (qm)] dqm. F.54)
Этот интеграл содержит s произвольных постоянных
A, ab C&2, ..., cts^,

I 6.4] ТЕОРЕМА ЛИУВИЛЛЯ 169
и постоянную as, которая, в соответствии с формулой
F.52), равна
as=— (a! + a2+ ... +as_j). F.55)
Таким образом, теорема Лиувилля доказана.
Пример 51. Для обобщенных координат q\ = %, q<i = \i в при-
примере 41 (§ 5.2) кинетическая и потенциальная энергии имеют вид,
соответствующий выражениям F.47). Поэтому можно применить ме-
метод разделения переменных.
Функция Гамильтона в этом случае будет
/ Г 2\ - (<м - c2) q2]>
и, следовательно,
Принимая, что
получим
- 0 - 2«2« (с< + С2) ь - а» Arf+
- 4) + ^а (с, - с2) д2 + 2ma4q\ - 0.
Это уравнение будет удовлетворено, если
"J 0 "
Отсюда имеем
J I

170 ТЕОРИЯ ЯКОБИ [ГЛ. 0
Полный интеграл уравнения Гамильтона — Якоби
W = Wx + W2
содержит две произвольные постоянные ai и h. Конечные интегралы
уравнений движения найдем, применяя формулы F.26) и F.27):
^ dqx +
Уq\ - 1 Уа{ + 2т2а (cl + c2) qx + 2ma2hq\
та q2 dq2
J
a (Cj - c2)
a{ + 2m2a (c{ + c2) q2 + 2ma2hq\
f
т. е. задача сводится к вычислению квадратур.
§ 6.5* Переменные действие — угол *)
В этом параграфе рассматривается метод примене-
применения уравнения Гамильтона — Якоби к материальным си-
системам, совершающим периодические движения. Исполь-
Использование этого метода целесообразно в тех случаях, когда
не требуется полного исследования поведения матери-
материальной системы, а требуется определить только частоты
периодических движений.
Мы рассмотрим только такие материальные системы,
для которых возможен выбор канонических переменных,
допускающих полную разделимость переменных, т. е. та-
такие системы, для которых функция W определяется из
уравнений F.35):
В этом случае W может быть представлена в виде
W = S Wm(qm, о„ ог, ..., а,). F.57)
m=I
*) Более полное рассмотрение этого вопроса можно найти в кни-
книге: Г. Г о л ь д с т е й н, Классическая механика, пер. с англ., Гостех-
издат, 1957.

§€.5) ПЕРЕМЕННЫЕ ДЕЙСТВИЕ — УГОЛ 171
В соответствии с выражением F.38) уравнение F.56)
примет вид
Н(аь а2, ..., а5) —А.
Так как
'"в!?-т5г (m=I' 2'---'s)> F-58)
то
Рт = Рт((!т> «Ь СС2, . . ., as). F.59)
Пусть 9т и рт — координатные оси прямоугольной
декартовой системы координат. Плоскость этих перемен-
переменных называют фазовой плоскостью. Точка на этой пло-
плоскости с координатами (qm, рт) называется «изобра-
«изображающей» точкой. При движении системы координаты qm
и рт изменяются и изображающая точка на плоскости
cjmpm описывает кривую, которую называют фазовой
кривой.
В дальнейшем мы будем предполагать, что на фазо-
фазовых плоскостях Цтрт фазовые кривые F.59) будут или
замкнуты, или рт будет периодической функцией отно-
относительно qm.
Введем в рассмотрение новые переменные /ь h, .. f
..., /s, которые называются действиями и определяются
формулами
Jm=§Pmdqm {т = 1, 2, ..., s), F.60)
где символ ф означает, что интеграл берется за полный
период изменения qm. В соответствии с выражением
F.58) имеем
Лп=Ф^^т («=1. 2, .... S). F.61)
Переменные Jm являются функциями независимых вели-
величин cci, CC2, ... as; так как изменение каждой пары qm,
рт (по предположению) независимо, то переменные Jm
также независимы. Эти переменные Jm примем за новые
обобщенные импульсы.
Выразим теперь величины аь аг, ..., as с помо-
помощью соотношений F.61) через /ь /г, ..., Js и внесем

172 ТЕОРИЯ ЯКОБИ 1ГЛ. 6
полученные значения в выражения для IF и Я. В ре-
результате этого получим
W = W(ql9 </2, .... qs, Ji9 /2> ..., /,) F.62)
Я(/„ /2, ..., /,) = *. F.63)
За обобщенные координаты, соответствующие обобщен-
обобщенным импульсам, примем величины
wm = -^ (т=1, 2, ..., s). F.64)
Величины wm называются угловыми переменными. В со-
соответствии с выражениями F.6)
*« = 5^—*« (m=l, 2, ..., s), F.65)
тде vw — постоянные величины, являющиеся функциями
Л, h, ..., /s. Из соотношений F.65) следует:
Wm = Vmt + $m, F.66)
где рт — постоянные интегрирования. Пусть хт — период
изменения функции wm. Тогда
Wm (t + TW) = VW (/ + Tj + pm. F.67)
Вычитая из выражения F.67) выражение F.66), полу-
получим изменение wm за период:
kwm = vmTm. F.68)
С другой стороны, изменение Awm можно получить сле-
следующим образом. Согласно выражению F.64)
_ dW
Пусть теперь координаты qu Цг, .. *, q%-u Qi+u • • •, qs
сохраняют постоянные значения, а координата q\ совер-
совершает полный цикл своего изменения. Тогда функция wm
изменится на величину
Дш_ = л) d'w~,. f6 69^
где

ПЕРЕМЕННЫЕ ДЕЙСТВИЕ - УГОЛ
173
— изменение wm вследствие изменения q\. Таким обра-
зсм,
d2W
¦dqh
F.70)
или
dW
в соответствии с формулами F.58) и F.60) имеем
Отсюда следует, что если i—m, то
F.71)
если же хфт^ то Awm—0. Сравнивая выражения F.68)
И F.71), ПОЛуЧИМ ГтТт=1 Й
v« = t- (m=U29...,s). F.72)
Следовательно, величины vm представляют собой ча-
частоты периодических изменений qm.
Пример 52. Найти частоты главных колебаний механической си-
системы, состоящей из двух физических маятников, представляющий
собой однородные стержни оди-
наковых поперечных размеров
и сделанных из одного и того
же материала. Маятники под-
подвешены на одной горизонтали
при помощи шарниров Оь 0%,
и соединены между собой пру-
пружиной, жестквсть которой
равна с. Длина пружины в
ненапряженном состоянии рав-
равна расстоянию между точками
подвеса маятников. Осталь-
Остальные размеры указаны на
рис. 6.!.
Положение маятников бу- Рис- 6Л-
дем определять углами их от-
отклонения от вертикали, т. е. углами <р и -ф. Выражение для кинети-
кинетической энергии в этом случае имеет вид:

174 ТЕОРИЯ ЯКОБИ [ГЛ. 6
где h и /2 — моменты инерции маятников относительно их осей вра^
щения. Потенциальная энергия выражается формулой
где т\ и А?22 — массы маятников, К — удлинение пружины. Для ма*
лых отклонений
ф2 <ф2
со$ф«1——-, cos Ф « 1—^—9 Я = аф — аф,
следовательно,
Для упрощения выкладок рассмотрим частный случай, когда
h = /2 = /, mi = m2*= т, /2 = /3 =* /.
В этом случае
Г = 4/(ф2 + 1И' F.73)
П - -j [а, (Ф2 + ф2) - 2са*уМ, F.74)
где fl! ~mg~+ ca2.
Если теперь составить уравнение Гамильтона — Якоби, то обна-
обнаружится, что переменные не разделяются. Поэтому мы перейдем
к другим координатам q\ и <7г, которые связаны с координатами ф
и г|з формулами *)
Кинетическая и потенциальная энергии соответственно равны
где а2 = ^~-. Так как pi = 2/^i, ?2 = 2/<72, то уравнение F.56)
примет вид
*) Вводимые координаты q\ и q* представляют собой нормаль-
нормальные координаты, т. е. координаты, для которых выражения для ки-
кинетической и потенциальной энергий н$ содержат членов с Произве-
Произведениями обобщенных координат й обобщенных скоростей.

§6.5],
ПЕРЕМЕННЫЕ ДЕЙСТВИЯ - УГОЛ
Учитывая, что функция W имеет вид соотношения F.57), получим
В соответствии с зависимостями F.38)
» it
т. е.
Теперь найдем
iP2~ dq2 dq2 *Vl{
Используя формулы F.61), получим
Введя в эти выражения замену
получим
Аналогично
F.76)
2Я
— a! cos2Y^Y = 2
#2 J
О
F.78)
Из выражений F.78) и F.79) следует:
а1==2Й"У "Г' °2^2^У 7 '

176 ТЕОРИЯ ЯКОБИ [ГЛ. в
Равенство F.76) теперь принимает вид
Следовательно.
\ 1 1
2я К / в 2я Г 2/
так как
гг-,

ГЛАВА 7
НЕГОЛОНОМНЫЕ СИСТЕМЫ
§ 7.1. Число степеней свободы неголономной
системы. Примеры неголономных систем
Наиболее существенные успехи в развитии механики
неголономных систем связаны с именами С. А. Чаплыги-
Чаплыгина, В. Вольтерра, П. В. Воронца и П. Аппеля. В этой
главе будут рассмотрены лишь некоторые методы со-
составления дифференциальных уравнений движения не-
неголономных систем. Достаточно полное изложение меха-
механики неголономных систем содержится в монографиях
А. И. Лурье*) и Ю. И. Неймарка и Н. А. Фуфаева**).
В этой главе будут рассмотрены системы с линей-
линейными неголономными связями, т. е. со связями, в урав-
уравнения которых проекции скоростей входят линейно.
Уравнения таких связей имеют вид
2 (A** + Bviyt -r Cvizt) + Dv = 0 (v = 1, 2, ..., d) G.1)
или
n
.2 {Avi dxt + Bvi dyt + Cvi dzt) + Dvdt = O G.2)
(v=l, 2, ..., d),
где d — число неголономных связей, Avii BV2-, CV2, Dv —
функции координат, а в случае нестационарных связей
и времени. Если Z)v==0, то указанные связи называются
однородными линейными неголономными.
*) А. И. Лурье, Аналитическая механика, Физматгиз, 1961.
**) Ю. И. Н е й м а р к и Н. А. Ф у ф а е в, Динамика неголоном-
неголономных систем, «Наука», 1967.

178
НЕГОЛОНОМНЫЕ СИСТЕМЫ
[ГЛ. 7
Пусть на материальную систему наложено k голо-
номных связей
//(*/, У и *ь 0 = 0 G.3)
и d неголономных связей вида G.2). Тогда вариации ко-
координат должны удовлетворять следующим уравнениям:
^' + ^ + S,**')-0 CeI-2 *), G.4)
= 0 (v=l,2, ..., d). G.5)
?
Рис. 7.1.
Следовательно, если эти k-\-d уравнений независимы,
то число независимых вариаций координат равно Зп—
— k — d. Это число независи-
независимых вариаций координат на-
называется числом степеней сво-
свободы неголономной системы.
Остановимся на одном свой-
свойстве неголономных связей, не
отмеченном нами ранее. Вся-
Всякая геометрическая связь яв*
_ ляется также и кинематиче-
х свой связью, т. е. ограничения,
накладываемые на координаты
точек, накладывают ограниче-
ограничения и на скорости точек. Но оказывается, что наличие
неинтегрируемых кинематических связей может не вли-
влиять на независимость координат. Это будет показано
в приводимых ниже примерах.
Приведем примеры неголономных систем.
Пример 53. Пусть тело А перемещается по неподвижной пло-
плоскости, касаясь ее в трех точках (рис. 7.1). Предположим, что одна
из точек касания М является точкой касания острого конька по-
поверхности плоскости и может перемещаться только вдоль плоскости
конька, движение же двух других точек по плоскости пусть будет
свободным (так как расположение этих точек несущественно, то на
рисунке они не показаны).
Поскольку тело А совершает плоское движение, его положение
может быть определено координатами х и у точки М и углом ф,
образуемым плоскостью конька с осью х. Условие отсутствия про-
проскальзывания конька может быть записано в виде vy/vx = tg ф или,
что то же,
у - х tg ф =» 0. G.6)

§ 7.J].
ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
179
Итак, из-за наличия связи G.6) изменения координат х, у и ф не
могут быть произвольными; однако в силу неинтегрируемости урав-
уравнения связи G.6) эти координаты остаются независимыми.
Пример 54. Рассмотрим качение без скольжения шара по гори-
горизонтальной плоскости (рис. 7.2). Положение шара будет определено,
если задать координаты хс и ус его центра и три угла Эйлера г|?, 0
и ф. Условием качения без скольжения будет равенство
*Л-«С + ©ХР-О, G.7)
где ю—мгновенная угловая скорость шара, р—радиус-вектор, оп-
Рис. 7.2.
ределяющий положение точки касания М относительно центра шара.
Следовательно, в соответствии с условием G.7) имеем
G.8)
где а — радиус шара, о* и озу — проекции угловой скорости соот-
соответственно на ось х и ось у. Так как *)
($х = ф sin 9 sin i|? + 9 cos ф,
toy = — ф sin 9 cos \|з + 0 sin ф,
то два выражения G.8) перепишутся в виде
хс — а (9 sin ф — ф sin 0 cos i|)) = О,
yc + a @ cos ф + ф sin 9 sin г|>) = 0.
G.9)
Эти уравнения неинтегрируемы, следовательно, связь неголономная.
Отметим, что в данном примере есть еще и голономная связь гс = й<
*) Н. В. Б у те нин, Я. Л. Лунц, Д. Р. Меркин, Курс теоре-
теоретической механики, т. 1, «Наука», 1970.

180 НЕГОЛОНОМНЫЕ СИСТЕМЫ [ГЛ. 7
показывающая, что центр шара находится все время на расстоя-
расстоянии а от плоскости качения шара.
Таким образом, и в этом примере видно, что координаты Хс, ус>
<р, ф, D независимы, но изменения их в силу условий G,9) не могут
быть произвольными.
§ 7.2. Уравнения движения для неголономных
систем с множителями Лагранжа
Пусть <7ь #2, . •«> q& будут обобщенными коордцд^-
тами механической системы. Пусть на систему наложе-
наложено d неголономных связей вида,
S<W7m + av = 0 (v=l. 2, ..., d). G.10)
7И=1
В § 3.5 был рассмотрен прием составления уравне-
уравнений Лагранжа второго рода, если на материальную си-
систему наложены дополнительные связи. Этот прием за-
заключался во введении реакций дополнительных связей
в число активных сил.
Воспользуемся этим приемом для учета вводимых не-
неголономных связей GЛ0). Так как вводимые связи
идеальные, то
п $
2 % Ьг{ = 2 Q'm bqm = 0, G. И)
где Ri — реакции неголономных связей, Q'm — обобщенные
силы, соответствующие этим реакциям. Из уравнений
связей G.10) следует, что
Умножим каждое из этих соотношений на соответствую-
соответствующий множитель Лагранжа Xv и сложим полученные вы-
выражения между собой:
s d
2 bqm 2 v*vm = o. G.i2>
Вычитая из выражения G.11) соотношение G.12), по-
получим

§ 7.2] УРАВНЕНИЯ ДВИЖЕНИЯ С МНОЖИТЕЛЯМИ ЛАГРАНЖА 181
Независимых вариаций обобщенных координат $—d.
Выберем Яь Хг, ..., hi так, чтобы множители у осталь-
остальных d вариаций обращались в нуль; тогда
Q; = 21 4e»m (т = 1, 2, ..., s), G.13)
и, следовательно, уравнения движения при наличии d
неголономных связей будут иметь вид
d
d I дТ \ дТ л
Уравнения G.14) вместе с уравнениями связей G.10)
образуют систему 5 4- d уравнений относительно неиз-
неизвестных (<7ь q2, -.., q8, Ьи ^2, ..., Ла).
Пример 55. Пусть в примере 53 проекция центра тяжести тела А
совпадает с точкой касания конька. Рассмотрим движение этого тела
по инерции.
Кинетическая энергия теда равна
где М — масса тела, /с — момент инерции тела относительно верти-
вертикальной оси, проходящей через центр масс тела. Так как активные
силы отсутствуют, то Qm = 0. В силу уравнения G.6) имеем
Следовательно, уравнения G.14) примут вид
Мхс - - Я, ig ф, Myl = Kv /сф-0. G.15)
Присоединяя к этим уравнениям уравнение связи G.6):
*/с-*с18Ф = 0, G.16)
получим систему четырех уравнений с четырьмя неизвестными. Из
третьего уравнения системы G.15) следует, что
ф — ю = const,
и, следовательно,
Ф«0/ + Фо G.17)
(фо — начальное значение угла ф). Исключая Xi whs первых двух
уравнений системы G.15), получим
0. G.18)

182 НЕГОЛОНОМНЫЕ СИСТЕМЫ [ГЛ. 7
Переписав уравнения G.16) и G.18) в виде
— yr cos <p + xr sin ф = 0,1
> G 19)
#с sin ф + хс cos ф = О J
и сложив, получим
z/c sin ф + хс cos ф - ус cos ф + i0 sin ф = О,
или
Отсюда
r/c sin ф -Ь *с cos ф = с G.20)
(с — произвольная постоянная). Из уравнений G.19) и G.20) сле-
следует, что
хс = с cos ф, Ус^ с sm Ф*
Отсюда имеем
*с = "S" (sin ф "sln фо)+ хо> ус = "--^ (cos V -cos Фо)+ %
где х0 и #о — начальные значения координат хс и у с, ф = ш? + ф0.
Пример 56. Составим уравнения G.14) для однородного шара,
катящегося без скольжения по шероховатой горизонтальной плоско-
плоскости по инерции (§ 7.1, пример 54).
За обобщенные координаты примем
Уравнения неголономных связей имеют вид G.9), т. е.
Xq + аф sin 6 cos я|э — aQ sin ф = 0,
г/с + аф sin 6 sin г|) + аб cos -ф = 0
или
sin qs cos ^4 — ад5 sin ^4 = 0,
Я2 + Щъ sin q5 sin ^4 + ^^5 cos q± = 0.
Сравнивая эти выражения с формулами G.10), получим
#п = 1, #12 = 0, #13 = я sin ^5 cos ^4 == a sin 0 cos-ф, )
#н = 0, aI5= - а sin ^4= - # sin ф, а2Х = 0, а22=1> ! ,? .,
а2з = a- sin ^5 sin q4 = а sin 0 sin -ф, «21 — 0, j
а25 — a cos q* = a cos ф. )
Кинетическая энергия выражается формулой

§7.2] УРАВНЕНИЯ ДВИЖЕНИЯ С МНОЖИТЕЛЯМИ ЛАГРАНЖА 183
так как шар однородный, то Ix = Iv = h = / и, следовательно,
Подставляя сюда выражения
0^. = ф sin 0 sin *ф + 0 cos г|?,
®у ~ "" Ф sin 6 cos ф + 0 sin ф,
со2 — *ф + ф cos 0,
будем иметь
Найдя производные
дГ ... дТ
!? зе), Ц—о.
^Г. = / (^ + ф cos 0), — = 0,
Д- = /0, — -= — /ф-ф sin в,
дО ^0 ^ •
составим уравнения G.14), приняв во внимание соотношения G.21):
Мхс = Я,, Мус = Л2,
/ (ф + *Ф cos 0 — ijH sin 0) « Яь a sin 0 cos ф + Я2а sin 0 sin г|),
/ (ф + ф cos 0 ~ ф0 sin 0) = 0,
/ @ + ф-ф sin 0) = -Хха sin -ф + Х2а cos -ф.
К этим уравнениям следует присоединить два уравнения неголоном*
ных связей:
хс + аф sin 0 cos -ф — aQ sin -ф = 0,
z/c + аф sin 0 sin ф + а0 cos -ф = 0.
Исключая из полученных уравнений Xi и ta, найдем:
У (ф + -ф - ф0 sin 0) = Ma sin 0 (xQ cos ф + yc sin -ф),
/ (ф + ф cos 0 - ф0 sin 0) - 0,
/ @ + ф*Ф sin 0) = Ma (t/c cos ф — J?c sin ф),

184 неголономньш системы [гл. ?
хс + Щ sin & cos ф — tt9 sin i|? = 0,
#c + аф sin 8 sin ф + аВ cos 1)>=* 0.
Полученные уравнения являются достаточно сложными. В сле-
следующем параграфе эта же задала будет рассмотрена другим мето-
методом и будут найдены первые интегралы составленной системы диф-
дифференциальных уравнений.
§ 7.3. Уравнения движения в квазикоординатах
& случае голономщдх стационарных связей уравне-
уравнения движения в квазикоординатах были получены в § 3.8
(уравнения C.65)).
Пусть теперь на рассматриваемую систему будет на-
наложено d неголояомных связей вида
(v-1, 2, ..,, rf)# G.22)
где avrm #v зависят только от обобщенных координат.
Как было показано в § 7.2, уравнения Лагранжа при
учете новых связей имеют вид G.14), т. е.
ilS^^. G.23)
Произведя с этими уравнениями те же операции, кото-
которые были проведены в § 3.8, получим
У v дГ
о о
- Л. + 5J 2 (W4»»* (х - 1. 2, ..., s). G.24)
где Г' определяется формулой C.58), Рк — формулой
C.56), YxW — формулой C.62), а квазискорости выра-
выражаются через обобщенные скорости при помощи соот-
соотношений
-v ^ п A /v — 1 9 <Л И 9^

5 7.31 УРАВНЕНИЯ ДВИЖЕНИЯ В КВАЗИКООРДИНАТАХ 185
Выберем теперь в последних d соотношениях G.25) ко-
коэффициенты ахт следующим образом:
где x==s—rf-j-v(v=l, 2, ..., d). Правые части уравне-
уравнений G.24) при этом примут вид
или
d s
Px + 2 К 2 ftnx<*s-rf+v, hi (K = 1, 2, . . ., S). G.26)
На основании свойства
s
делаем заключение о том, что
v — 19 с И
/V ~"~ X, Arfy • • » J О t*. .
Следовательно, уравнения Эйлера — Лагранжа при на-
наличии неголономных связей будут иметь вид
(х=1, 2, ..., s-rf),
Присоединяя к этим уравнениям d уравнений связей
G.22), получаем систему s—d уравнений второго по-
порядка и d уравнений первого порядка для определения
неизвестных Щи Цъ, - - •, У* и яь зх2, ..., ns-d- Оставшиеся
последние d уравнений G.24) могут служить для опре-
определения Xv, т. е. для определения реакций связей.
Пример 57. Составим уравнения Эйлера — Лагранжа для сво-
свободного движения однородного щара по горизонтальной шерохова-
шероховатой плоскости.
Как и в § 7.2, при рассмотрении этой задачи примем q\ = #с,
Я2 = Ус Яг = ф, Я а = ф, Яъ = 0- Неголономные связи имеют вид

186 ИЕГОЛОНОМНЫЕ СИСТЕМЫ
Кинетическая энергия без учета этих связей
[ГЛ. 7
За квазискорости примем *)
&\ — ®х = Ф Sln Э sin -ф + 0 cos а|?,
зх2 = (иу = — ф sin 9 cos г|) + 0 sin a]?,
я3 = со2 = Ф cos 9 + 'Ф,
я4 = а0 sin г|) — аф sin 0 cos -ф — хс,
я5 = а0 cos г|) + аф sin 0 sin -ф + ус*
Из этих уравнений найдем обобщенные скорости;
ф= ft,
sin
cos *
sin0
; sin ab
W = — jx i —;——
sin 0
0 = Я! cos г|) + я2 sin -ф.
Запишем теперь выражение для Г':
T' = -jM [(ая2 - я4J + (- aft,
Отсюда следует:
. = — Ма (— ак\+ я5)
дТ
cos -ф
1ше
1 /(Л?
дл2
= (/ + Ма2) Л, -
= Ма (ая2 — я4) + /я2 = (/ + Ма2) к2 — Majt$,
G.28)
G.29)
Поскольку обобщенные координаты в выражение для кинетической
энергии не входят, то в соответствии с формулой C.64)
•!?¦-" О D=1,2,3).
Перейдем к нахождению трехиндексных коэффициентов Укд/-
(см. стр. 87). Для этого воспользуемся формулой C.75);
=2 S Yukv бя^ dnv (к = 1, 2, ..., s). G.30)
l1
*) Заметим, что в силу неголономности связей h\ = 0, fts = 0.

§ 7.3] УРАВНЕНИЯ ДВИЖЕНИЯ В КВАЗИКООРДИНАТАХ
Пользуясь соотношениями G.28) и G.29), получим
dfti — dq> sin 9 sin \|) + dQ cos \|),
dn2 = — dy sin 9 cos \|) + dQ sin \|),
dn3 — dcp cos 9 + dty,
dnA = — a d<p sin 9 cos \|) + a d9 cos i|? — d#c,
dftg — a dq> sin 9 sin \|) + a db cos \|) + dyc,
6я;3 = 6ф sin 9 sin ф + 69 cos ф,
6я2 = ~ бф sin 9 cos ф 4- 69 sin я|),
6я3 — 6ф cos 9 + 6ф,
6я4 = — a 6ф sin 9 cos \[) + a 69 sin ф — bxc,
6я5 == а 6ф sin 9 sin a|? + a 69 cos ф
с?л:с = a dn2 — cfrt4, с?г/с =* — a dn{
j sin \b . cos ф ,
d& = cos г|) dnx -f sin
лгс = a бя2 — 6я4, 6г/с = — а 6я1
. sin гЬ . cos г|? «
6ф = . I бях г—к- 6я2,
Y sin 9 х sin0 ^'
cos9 6ях + ^q cos 9 6я2 + 6я3,
69 = cos ф бя, + sin ф 6я2.
В соответствии с формулой G.30) получим
d (бяО — б (dnx) = — 6я2 dn3 + 6я3 dn2,
d Fя2) — б (dn2) — бях dn3 — 6я3 сТя^
d Fя3) — 6 (б/Яз) = — бях dn2 + бя2 diti,
d Fя}) — 6 (dnA) = а бя! с?я3 — а 6я3 rfrtJf
d Fя5) — 6 (с?я5) = — а 6я2 б/яз + а 6я3 с?я2.
Отсюда следует, что
Y2I3 = ~Y3I2 = - 1, Y123 = - Y321 = 1,
Yi32 = - Y231 = - 1, Y143 = - Van = а, у25г = - уззг«- — Л
Остальные утц р^вны нулю.

188 НЕГОЛОНОМНЫЕ СИСТЕМЫ [ГЛ. 7
Подсчитаем теперь суммы:
5 5
2л 2j а
= (/ + Ma2) я2зт3 - Mak47t3 — Ma (an2 — зх4) я3 — /зт3я2 = О,
5 5
2^«
==-(/ + Ма2) Л^з + Мап5пд + 1я3щ - Ma (- ajtj + я5) зт3 « О,
5 5
Л2 — эт4) ^i + Ala (— апх + fc5) n2 = 0.
Следовательно, уравнения Эйлера ^~ Лагранжа G.27) будут иметь
вид
4(-?Ц = о, -&.[?-)-(>, ^-D^)-а G.30
d/ \^J ^/ \ ^л2 ) dt \дпъ ) х '
Так как в силу неголономных связей 3X4 = 0» ^5=» 0, то из уравне-
уравнений G.31) получаем
71\= (йх~ cl> 3t2 = 0^==C2, ЗХ3 = (пг = С3,
где сь с2, сз — постоянные интегрирования. Учитывая значения лх
зт2, я3, получим
ф sin 9 sin ф + 6 cos \|) = ci,
— ф sin 8 cos -ф + 6 sin г|э =» с2,
фсо8б + 'ф= сг.
Из уравнений неголономных связей следует, что хс = ас^ У^— ~~ ^^j.
Таким образом, первые интегралы уравнений движения известны.
§ 7.4. Уравнения Аппеля *)
Пусть на материальную систему, состоящую из п
точек, наложено k голономных и d неголономных свя-
связей. Если <7ь <7г, .«., Qs, где 5=3я — к, — независимые
*) Ф. Р. Г а н т м а х е р, Лекции по аналитической механике,
Физматгиз, 1960.

§7.41
УРАВНЕНИЯ АППЕЛЯ
189
обобщенные координаты, то формулы
rt = П (*, ?„ q2, ..., qs) (* = Ь 2, ..., п) G.32)
устанавливают связь между декартовыми и обобщенны-
обобщенными координатами. Из формул G.32) следует, что
~Ж 0-L2, .... п) G.33)
m-l
(/=1,2,..., л). G.34)
Пусть уравнения неголономных связей имеют вид
S о^ + «v =0 (v =. 1, 2, ..., rf), G.35)
Выберем за 5—d независимых квазискоростей (по числу
степеней свободы) s—d независимых линейных комбина-
комбинаций обобщенных скоростей
1, 2, ..., 5 -
G.36)
Из уравнений G.35) и G.36) определим зависимость
обобщенных скоростей от квазискоростей пк. Очевидно,
что это можно сделать в том случае, если определитель
системы уравнений G.35) и G.36) отличен от нуля:
=7^0.
Пусть найденная зависимость имеет вид
s-d
qm = S 6/пЛ + bm (m = 1, 2, ,..,
<7.37)

190 НЕГОЛОНОМНЫЕ СИСТЕМЫ [ГЛ. 7
где bmix и Ьш — функции времени и обобщенных координат.
Величины яи могут принимать произвольные значения,
так как по формулам G.37) всегда можно подобрать
соответствующие им значения qm. Подставляя теперь
значения qm, определяемые формулами G.37), в фор-
формулу G.33), получим
'<-2-&B'**.+».)+-&-
s-d s s
dr. л vi drt dr{
[х=1 т=1
Введя обозначения
т = 1 т=1
будем иметь
ri = 2 е^Лц + ^ (/ == 1,2, ..., п), G.38)
откуда
brt = 2 е/|А бя^ (/ = 1,2, ..., п). G.39)
Вычислим производную по времени от выражения
G.38):
s—d s—d
S
• d
Отсюда видно, что частная производная от ускорения
Wi=ri i-й точки по Яц равна е^, т. е.
§^ = е11Х (/=1,2, ...,/г, |* = 1,2 s-d). G.40)
В общее уравнение динамики [см. § 3.2, C.17)]

§ 7.4] УРАВНЕНИЯ АППЕЛЯ 191
подставим 8ги определяемое формулой G.39):
S (ты-Ft) 2*^6^ = 0.
Отсюда имеем
s-d / п \
S 2 m,»^ - П^ 6яц = 0, G.41)
где обобщенные силы*), соответствующие квазикоорди-
квазикоординатами Яр,, равны
п s п
G.42)
Так как величины бя^ взаимно независимы, то из выра-
выражения G.41) следует:
п
2 rmwieiv, = Пй {\i = 1, 2, ..., 5 - d). G.43)
Используя зависимость G.40), получим
или**)
Функция
*) То есть возможная работа определяется формулой
s-d

192 ИЕГОЛОНОМНЫЕ СИСТЕМЫ [ГЛ. 7
называется энергией ускорений (по аналогии с кинети-
кинетической энергией). Таким образом, получаем s—d урав-
уравнений
-1^ = 1^ (ц«1,2, ..., s-d), G.46)
которые называются уравнениями Аппеля.
Система уравнений G.46) совместно с соотношения-
соотношениями G.35) доставляет полную систему уравнений для
определения декартовых координат хи Уи %и х% Уг, *%
..., хп, уп, zn и квазискоростей пи я2, ..., hs-d как
функций времени t.
Возьмем теперь в качестве квазискоростей s—d не-
независимых обобщенных скоростей gi, q%, ..., qs-d й вУ-
разим через них с помощью соотношений G.35) осталь-
d обобщенных скоростей;
qs-d+v = Zi hs-d+v, ^ (v = 1, 2, ..., d).
i
Отсюда
s~d
^s-d+v= 2 hs-d+v,^».' G.47)
i
Заменяя теперь в выражении для возможной работы
s
ЪА = 2 Q/ в<7/
/-J
вариации dqs-d+\ (v=l, 2, ..., d) с помощью формулы
G.47), получим
где
d
— обобщенные силы, соответствующие независимым ва-
вариациям 6<7|х(ц=1, 2, ц,, 5—dL

§7.4} УРАВНЕНИЯ АППЕЛЯ 193
Уравнения Аппеля теперь примут вид*)
dS в 0~ (=12 s — d)
Для голономной системы уравнениями Аппеля будут
-?--Qm («-1,2...., .).
При вычислении функции 5 бывает целесообразно ис-
использовать теорему, аналогичную теореме Кёнига.
Пусть подвижная система координат имеет начало
в центре масс материальной системы и движется посту-
поступательно. Тогда положение i-й точки системы в непо-
неподвижной системе координат определяется радиусом-век-
радиусом-вектором
г,=гс + р„ G.48)
где гс — радиус-вектор центра масс в неподвижной си-
системе координат, а р/—радиус-вектор точки I в подвиж-
подвижной системе координат. Из выражения G.48) следует,
что
Wt ~wc + wrh G.49)
где wri — относительное ускорение 1-й точки. Подставим
соотношение G.49) в выражение для функции S:
i ¦= 1 i == I
n
где M = 2 Щ — масса всей системы. Далее имеем
*) Функция S будет функцией времени /, s обобщенных коорди-
координат (<7ь ^2, ...,</s), s — d обобщенных скоростей (</i q2i ..., Я^ч)
и s — d обобщенных ускорений (д\} Цч> •••>^e-d)«
7 Н. В, Б>темин

194 НЕГОЛОНОМНЫЕ СИСТЕМЫ
так как Рсв0. Следовательно,
где
[ГЛ. 7
G.50)
— ускорение системы в относительном движении.
Пример 58. Составить уравнение Аппеля для тяжелого однород-
однородного шара, катящегося без скольжения по наклонной плоскости,
образующей угол а с горизонталь-
горизонтальной плоскостью (рис. 7.3).
За независимые обобщенные
координаты примем q\=xc, о2 =
—Ус #з=ф> <74=Ф> #5 —6> гдеяс,
ус — координаты центра тяжести
шара, ф, ф, 9 — углы Эйлера.
Уравнение голономной связи:
zc = а (а — радиус шара).
Уравнения неголономных свя-
связей:
хс — аса = О,
Рис. 7.3. #с + асо^ = 0.
Проекции угловой скорости шара на оси х, уу z:
®х = Ф sin 9 sin ф + 9 cos ф,
со^ == — ф sin 9 cos -ф + 9 sin ф,
caz = ф cos 9 + ф.
Примем за независимые квазискорости следующие выражения:
3^1 = сож = ф sin 9 sin г|> + 9 cos -ф, \
п2 = ®у =» — ф sin 9 cos -ф + 9 sin -ф, > G.53)
зх3 = со2 = ф cos 9 + ij). j
Из уравнений G.51) и G.53) определим обобщенные скорости через
независимые квазискорости:
хп = ал,
G.51)
G.52)
— ая,
Ф:
2» if С u-ji-j,
sin ф . созф
sin 9 Щ sin 9
>= —пх sin
\ ctg 9+зх2 cos ф ctg'O'-b зх3,
9 — hi cos ф -f зх2 sin ф.
G.54)

§7 4] УРАВНЕНИЯ АППНЛЯ 195
Найдем теперь энергию ускорений. Используя формулу G.50),
получим
или
s -1 м D + уЪ) + у / К + й« + **)-
где М —масса шара, / — осевой момент инерции шара. Используя
формулы G.53) и G.54), будем иметь
S -1 (/ + Л*а2) п\ +1 (/ + Ма2) Л2 + у /4 G.55)
Вычислим возможную работу:
Но 1 = 0, У = Mg sin a, Z = ~М^ cos а, a согласно формулам
G.54)
бд:с = а 6я2, Ьус = —
Кроме того, bzc = 0 (так как zc = а). Следовательно,
6Л == — Л1^а sin а дли
откуда
Уравнения Аппеля
dS dS OS n
-.. = IIi, -гт- = По, -... = Из
в рассматриваемом случае будут иметь вид
(/ + Ма2) П\ = — Mga sin a,
(/ + Ма2) я2 = О,
(/ + Ма2) я3 = 0.
Отсюда
. _ Mga sin a .
1 / + Ala2 l'

19& НЕГОЛОНОМНЫЕ СИСТЕМЫ [ГЛ. 7.
где си с2, с3 — постоянные интегрирования. Для обобщенных скоро-
скоростей имеем
Mga2 sin а .
sin ф Mga sin а sin \|? созф
~ sine i + ма2 1 + С{ sine ^ТпТе"
sin -ф ctg 9 /1^дг" ' ~* ri sin "Ф ctg 9 + c2 cos -ф ctg 9 + c3,
a . Alga sin a , , . , . ,
9 - - cos t|) /^Afg2 ^ + ??! cos ф + c2 sin ф.
Дальнейшее интегрирование первых из этих уравнений дает
sin a
Это значит, что в общем случае центр масс шара движется по
параболе, расположенной в плоскости, параллельной наклонной пло-
плоскости.
§ 7.5. Вывод уравнений движения неголономной
системы из общего уравнения динамики.
Уравнения С. А. Чаплыгина
В § 3.3 из общего уравнения динамики было полу-
получено соотношение
m=l * = 1 Ш
Там же показано, что
(m=l,2, ..., s).
Введем в рассмотрение оператор
т =* — ( дТ \ _ дТ

$ 7.5] УРАВНЕНИЯ С. А, ЧАПЛЫГИНА 497
Тогда выражение G.56) примет вид
2 6?m(Qm--7?w)=0. G.57)
Пусть на систему наложено d неголономных связей
2 avmqM + av = 0 (v = 1,2, ..., d). G.58)
Примем первые s—d обобщенных координат за незави-
независимые и выразим обобщенные скорости qs-d+u qs-d+2, ...
..., qs с помощью уравнения неголономных связей через
s-d
ft=SU, + Ai (ft = s-rf+l, ..., 5), G.59)
откуда следует, что
s-d
&7*= 2 ^m6^m (k = s~d+ 1, s-rf + 2, ..., 5).
m—l
Подставляя эти выражения в соотношение G.57), по-
получим
S (Tqn - Qm) 6(?m + 2 (Tqk - Q,) #S hkm bqm = 0,
m = l k=s-d+l m=\
ИЛИ
2d f Tqm - Qm + 2 (Г* - Q^) A J S?m = 0.
В силу независимости dqly dq2, ..., bqs-d >имеем
Tqm-Qm+ S (Гл-<г*)ААя, = 0 G.60)
(m=l,2, ..., s-d).
Это и есть искомые уравнения движения. Присоединяя
к ним уравнения неголономных связей G.58), получим
полную систему уравнений для определения всех обоб-
обобщенных координат.

198 НЕГОЛОНОМНЫЕ СИСТЕМЫ [ГЛ. 7
Если коэффициенты hum, кинетическая энергия Т и по-
потенциальная энергия П не зависят от qs-d+u <7s-d+2, . ¦ •» ?*»
то уравнения G.60) примут вид
s
d (дТ \ дТ | ^С^ / d [ дТ \ дП
~dt Щ^) " lq^+ 2а ^ Hkm ~df \д^1 ~~"ды
(т= 1,2, ..., s — d).
Пусть 71* будет кинетической энергией системы после
исключения скоростей qs-d+u qs-d+2, ..., qs\ тогда
дТ dq.
дТ dqk
Из выражения G.59) следует, что
dqm
Следовательно,
дТ . \\ JT_ \\ dhkr
Теперь можно написать
? dt
k^s-d+l
h дТ dhkm

§ 7.5] УРАВНЕНИЯ С. As ЧАПЛЫГИНА 199
Замечая, что
s-d
dhkm _ V dhkm h
Z 4
dt U dqT Чг>
r«=l
перепишем уравнения движения в виде
d I ОТ* \ ОТ* | ^Г1 ОТ V4* / dhkr dhkm \ * дП
(т-1,2, ..., s-d).
Эти уравнения получил С. А. Чаплыгин*), и они носят
его имя. Исключая в полученных уравнениях с помощью
зависимостей G.59) скорости gs-d+i, gs-d+2, ..., #s, вхо-
входящие в выражения dT/dqk, получим систему s—а урав-
уравнений с 5—d неизвестными qu #2, . •., #s-d, которая ин-
интегрируется независимо от уравнений неголономных свя-
связей. Остальные координаты можно затем определить из
уравнений G.59).
Пример 59. Составить уравнения движения велосипеда, пренеб-
пренебрегая движением ног велосипедиста, движением педального механиз-
механизма и считая колеса велосипеда абсолютно жесткими тонкими ди-
дисками **).
Будем считать велосипедиста твердым телом, жестко скреплен-
скрепленным с рамой. Исходя из условий задачи и рассмотрения рис. 7.4 и
7.5, велосипед можно считать системой, состоящей из четырех кине-
кинематически связанных между собой твердых тел: рамы с седоком, пе-
переднего и заднего колес и вилки переднего колеса.
На рис. 7.5 представлена схема велосипеда в вертикальном по-
положении и при совпадении плоскости переднего колеса и рамы. Цент-
Центры заднего и переднего колес соответственно обозначены буквами М\
и Мг, точка Мо — точка пересечения рулевой оси с перпендикуляром,
опущенным на эту ось из центра Л1г. Точками Мз и М^ обозначены
соответственно положения центров масс задней части велосипеда
(рама, велосипедист, заднее колесо) и передней части (вилка перед-
переднего колеса, переднее колесо). Величина с\ = &2&3COsA,, где kokz на-
называется выносом, величина с = a cos ф + Ь cos \ называется базой
велосипеда, угол X — угол между вертикалью и рулевой осью,
*) Об этих уравнениях С. А. Чаплыгин доложил на заседании
физического отделения Общества любителей естествознания 25 октя-
октября 1895 г. (С. А. Ч а п л ы г и н, Исследования по динамике него-
неголономных систем, Гостехиздат, 1949).
**) Наиболее подробное изложение теории велосипеда имеется
в книге Ю. И. Неймарка и Н. А. Фуфаева «Динамика неголономных
систем», «Наука»; 1967, и в их статье «Устойчивость неуправляемого
и управляемого велосипеда и мотоцикла», Механика твердого тела,
№ 2, 1967.

200
1ШГОЛОНОМНЫЕ СИСТЕМЫ
[ГЛ. 7
отрезок МЩ = R sin К. В обычных конструкциях велосипеда точ-
точка Мо лежит внутри отрезка ЛШ2, поэтому с{ > 0; угол X обычно
положительная величина.
Рис. 7.4
Рис. 7.5.
Предполагая, что велосипед движется по горизонтальной пло*
скости, примем за обобщенные координаты следующие переменные:
<у1 зв= гр — угол поворота руля, q% = % — угол поворота рамы, отсчи-
отсчитываемый от вертикали, <7з = xt qA = у — декартовы координаты
точки к\ соприкосновения заднего колеса с дорогой, q5 = 0 — угол
между следом заднего колеса и осью у, q$ = 9i, qi = 02 — углы соб*

§7.5]
УРАВНЕНИЯ С. А, ЧАПЛЫГИНА
201
ственных поворотов соответственно заднего и переднего колес.
Введем вспомогательные переменные х', у', 0', %', определяющие
положение переднего колеса, и найдем их связь с обобщенными
координатами. В соответствии с рис. 7.6 координатами центра Mi
заднего колеса будут
G.61)
где R — радиус колес велосипеда.
Найдем координаты точки Мо, являющейся точкой пересечения
рулевой оси с перпендикуляром, опущенным на эту ось из центра Мг
i — у + R sin % sin 0,
Рис. 7.6.
переднего колеса (рис. 7.5). Пусть система координат Atfi?ii]iCi имеет
начало в центре заднего колеса. Ось г\\ направим от точки М\ к точ-
точке Мо, ось ?i — ей перпендикулярно в плоскости рамы, ось |i — пер-
перпендикулярно к плоскости рамы. Расположение этих осей по отно-
отношению к осям неподвижной системы координат Охуг показано на
рис. 7.7. Обозначим через i, /, k единичные векторы осей систе-
системы Oxyz, через 1ь *ь, gi— единичные векторы осей системы
MigiTii?b а через iu /ь &i — единичные векторы вспомогательной си-
системы координат MjgjTj^. Очевидно, что
i, « cos 0«-f-sin 0/,
/,-- sin9*-fcos9/,
fct — sin % cos 0* + sin x
sin 0/ -f cos %k.
G.62)

202
Так как
НЕГОЛОНОМНЫЕ СИСТЕМЫ
1ГЛ. 7
v\x — cos Ф /i — sin ф ku
то в соответствии с формулами G.62) имеем
li = cos x cos 9 i + cos % sin 6 / — sin x &,
Ч1=»(- cos ф sin G — sin ф sin % cos 9) s +
+ (cos ф cos 9 — sin ф sin % sin 9) / — sin ф cos % k,
Si = (cos ф sin % cos 9 — sin ф sin 9) i +
+ (cos ф sin % sin 9 + sin ф cos 9) / + cos ф cos % k.
В системе координат AiigiTjiSi точка Мо расположена на оси rj2 на
z
G.63)
Рис. 7.7,
расстояния а от точки М\. Следовательно, ее координатами в си-
системе Охуг будут
х0 = Xi — a (cos ф sin 9 + sin ф sin % cos 9),
Уо — l/i + a (cos ф cos 9 — sin ф sin % sin 9),
zQ — ^i — a sin ф cos x>
G.64)
где #i, #i, 2i определяются формулами G.61).
Для нахождения координат центра М2 переднего колеса введем
систему координат ЛЫгт^Ь- Ось & направим от точки Мо к точ-

§7.5]
УРАВНЕНИЯ С. А. ЧАПЛЫГИНА
203
ке М2, ось г}2 — по оси вращения вилки, ось ?г — им перпендикуляр-
перпендикулярно (рис. 7.8). Из рассмотрения рис. 7.8 следует, что единичные
Рис. 7.8.
векторы §2t %, 62 системы Мг^гЬ могут быть определены в виде
|2 e cos г|> li + sin t|) cos а г), + sin -ф sin a gb 1
fb^sinorcii-cosaCi, > G.65)
?2 — ~ sin ф ij + cos ф cos a tli + cos г|з sin a?i. '
Косинусы углов между осями системы Oxyz и Мо^ЛгСг равны
cos (*,?,)=-*.?,-
« cos <ф (i|,) + sin \|з cos a (t • t|i) + sin ф sin a (i • g^ =
«=cos ф cos % cos 8—sin ф cos a (cos q> sin 9 + sin <p sin % cos 0) +
+ sin t|> sin a (— sin ф sin 9 + cos ф sin % cos 0) =
= ~81*п'ф[со5(ф—а)81п9 + 81'пхсо89зт(ф—a)]+cosa|)cos%cos9,
cos (x, r\2) = i • r}2 = sin (ф — a) sin 9 — cos (ф — a) sin % cos 9,
G.66)
—cost)) [соз(ф~-a) sin 0+sin x cos0 sin (ф—a)]—sin ф cos %cos9,
= sin ф [cos (ф—a) cos9~sinx sin^ sin (ф-а)] +cost])cosxsin9,
cos (y, t|2) = / • ц2 == — sin (ф — a) cos 9 — cos (ф — a) sin % sin 9,
= соз\|)[со8(ф—a) cos 9—sin % sin 9 sin (ф — а)] — sin i|) cos %sin 0,
cos (zy g2) = k • I2 = - sin ф cos x sin (ф — a) — cos -ф sin %,
cos B, tj2) «it • ri2 =» — cos (ф - a) cos %y
cos B, g2) — k • g2 e ~ cos ф sin (ф - a) cos % + sin ф sin %•

204 НЕГОЛОНОМНЫЕ СИСТЕМЫ [ГЛ. 7
Точка М2 в системе координат МобгЛгЬ имеет координаты |2 = О,
П2 = 0, & = Ь (рис. 7.8); следовательно, в соответствии с форму-
формулами G.66) имеем
*2 == *о — Ь {cos ф [cos (ф — a) sin 6 + sin % cos 8 sin (ф - а)] +
+ sin ф cos % cos 0},
У2'=аУо + Ь{cos ф [cos(ф — a)cos6 — sin % sin 9 sin (ф — а)] —
— sin ф cos % sin 9}$
z2 — Zq — b [cos ф cos x sin (ф — a) — sin ф sin %],
G.67)
где #o, Уо, zo определяются формулами G.64). Определим теперь ко-
координаты точки Мч через вспомогательные переменные 8', х'> я7» #'•
Пусть система координат К2%'ц%' имеет начало в точке касания Кч
переднего колеса с плоскостью дороги, ось г\' направлена по следу
переднего колеса, ось ?' направлена к центру переднего колеса. От-
Отметим, что ось J' будет параллельной оси |2 (рис. 7.9). Единичные
векторы осей системы /Сгб'л'Е' представим в виде
V = cos %'cos 0' i + cos x' sin 8' / — sin %' k>
П' - - sin 0' i + cos 0' /,
?' = sin %' cos 8' i + sin x' sin 0' / + cos x b>
и, следовательно,
x2 ~ x' + /? sin x' cos 8',
i G.68)
Для нахождения связи между обобщенными координатами и
вспомогательными переменными *', у\ 0', х' приравняем х2, У2* *ь
найденные по формулам G.67) и G.68), и, кроме того, учтем, что
оси \' и ?2 параллельны:
х' + R sin x' cos 0' =
= х0 — b {cos ф [cos (ф — a) sin 8 + sin x cos 8 sin (ф — a)] +
-f sin ф cos x cos 8},
y( + R sin x' sin 0'«
¦" Уо + b {cos ф [cos (ф — a) cos 0 — sin x sin 0 sin (ф — a)] —
— sin ф cos x sin 0},
R cos x'e z0 — 6 [cos ф sin (ф — a) cos x — sin ф sin x],
cos xf sin 0/« sin ф [cos (ф — a) cos 0 — sin x sin 0 sin (ф — о)] +
-f cos ф cos x sin 0,
— sin x ~ ~ sin ф cos x sin (ф — cr) — cos ф sin %.
G.69)

7 5]
УРАВНЕНИЯ С. А. ЧАПЛЫГИНА
205
В дальнейшем будем рассматривать лишь малые отклонения от
движения велосипеда вдоль оси у.
Линеаризуя *) выражения G.69) относительно малых величин 9,
0'» Х> X'» Ф» получим
х' = х — 6 [a cos ф + Ь cos (<р - <>)] — ф \b + R sin (ф — а)],
у' = У + a cos ф + Ь cos (ф — а),
л sin ф + Ь sin (ф — а) =¦ 0, 8'« 9 -f ф cos (ф — а), %' =
Отсюда вытекает, что ф = const. Вводя обозначения X =* а — <
с = a cos ф -f ^ cos Я, с\ = z
«= /? sin X — 6, окончательно по- у
лучим //
G.70)
9' - 9 + ф cos Л,
Рассмотрим рис. 7.5.
Запишем условия качения
колес велосипеда без про-
проскальзывания. По условию за-
задачи колеса представляют со-
бой абсолютно жесткие тонкие
диски; тогда для заднего колеса
л: =-/?#! sin 9,
// = /?<*! cos 9 G.71)
и для переднего колеса
jp « - #fr2 sin 9',
Рис. 7Д
,cos9'.
G.72)
Если заднее колесо вращается с постоянной угловой скоростью
v
(о = -7J- > где у — скорость велосипеда, то
^>, - at - 0.
Используя выражения G.70), перепишем зависимости G.71) и
G.72) для малых 0 и 0':
л: +
0, с9 - cnj> -
0.
G.74)
Уравнения G.73) являются интегрируемыми связями, а уравнения
G.74) — уравнениями неголономных связей. Таким образом, рассмат-
рассматриваемая система имеет две степени свободы.
*) То есть сохраняя в выражениях G.69) члены, содержащие
6> 9'» X» X'» Ф только в первой степени.

206
НЕГОЛОНОЛШЫЕ СИСТЕМЫ
Составим уравнения движения велосипеда, воспользовавшись
уравнениями G.60). Кинетическая энергия системы состоит из кине-
кинетической энергии Т\ рамы с седоком и заднего колеса и кинетиче-
кинетической энергии Т2 вилки и переднего колеса. Кинетическая энергия
рамы с седоком и заднего колеса равна
тде 77 е "тт w 1^з"~ кинетическая энергия поступательного движе-
движения задней части велосипеда, т\ — масса задней части велосипеда,
Рис. 7.10.
Vz — скорость центра масс М$ задней части велосипеда, Гвр —кине-
—кинетическая энергия вращательного движения задней части относитель-
относительно мгновенной оси, проходящей через центр масс велосипеда. В со-
соответствии с рис. 7.5 и 7.10 координатами центра масс М3 будут
х3 = х — /j sin 9 + hx sin % cos 9,
Уз — У + h cos 9 + hi sin % sin 9,
z$~h\ cos/.
После дифференцирования получим
хъ = х — /i9 cos 9 + h\% cos % cos 9 — hxQ sin % sin 9,
Уг ~ v — /i9 sin 9 + hx% cos % sin 9 + hxQ sin % cos 9,
*з = ~ ^iX sin x.
Отбрасывая постоянный член и сохраняя члены не выше второго
порядка малости, имеем

§ 7.5] УРАВНЕНИЯ С. А. ЧАПЛЫГИНА 207
Следовательно,
Пусть оси M^xiyiZi жестко связаны с рамой велосипеда и при
9 = % = 0 параллельны осям х, у, г. Проекции мгновенной угловой
скорости задней части велосипеда на эти оси равны соответственно
— 0 sin %, х, 9 cos %. Для заднего колеса wjci = —v/r — О sin %. Тогда
с точностью до малых второго порядка и без постоянного члена
где Iyi, IZi, IyxZx— соответственно момент инерции относительно
оси уи момент инерции относительно оси zi, центробежный момент
инерции задней части велосипеда, 1\ — момент инерции заднего ко-
леса относительно собственной оси вращения. Таким образом,
у m, l(x - /jG + hiY - 2v (Ifi -
-J ex.
Кинетическая энергия передней части велосипеда (рулевая вил-
вилка и переднее колесо) вычисляется по формуле
где тг — масса передней части велосипеда, v4 — скорость центра
масс передней части (точка М4), Г^—кинетическая энергия враща-
вращательного движения передней части. Координаты точки М4 в систе-
системе Мо?2Т]2?2 равны ^2 = 0, т]2 = —d\, ?>2 = d (рис. 7.5). Используя
формулы G.66), получим
#4 ~ #о — d sin -ф cos % cos 9 + d cos ф (sin % cos 9 sin X — sin 0 cos X) +
+ c?i sin Я sin 0 + cfi cos X sin % cos 0,
y\ — y<> + d cos ф (cos X cos 0 + sin X sin % sin 0) —
— d sin \|) cos % sin 0 — dx sin Я cos 0 + di cos X sin % sin 0,
24 = Zo + ^i cos Я cos % + d sin ф sin % + d cos ф sin X cos %.
После дифференцирования и сохранения членов не выше второго
порядка малости получим
У а - у + (/г2х ~ ^20 ~ Ф<*) 0 + Л20Х ~ d @ Н- ф cos
«4 е- /?2ХХ + d ОС ~ Ф sin X) ф + хФ^,

208 НЕГОЛОНОМНЫЕ СИСТЕМЫ {ГЛ. 7
где
А2 =* R - я «»п ф +d sin Я + я?! cos Я,
/2 = a cos ф + d cos Я — dx sin Я.
Смысл величин h* и /2 виден из рис. 7.5*). Кроме того, из рассмот-
рассмотрения этого же рисунка видно, что между параметрами велосипеда
существует зависимость
d ~ h2 sin Я — С\ — (с — /2) cos Я.
При сделанных ранее предположениях о малости переменных имеем
+ m2vh2d% — tn2v d @ + ф cos Я) ф.
Мгновенная угловая скорость передней части велосипеда без
учета собственного вращения переднего колеса складывается из угло-
угловой скорости вращения вместе с рамой и угловой скорости враще-
вращения вокруг рулевой оси. Пусть оси у2 и z2 лежат в плоскости пе-
переднего колеса, причем ось у2 горизонтальна. Отметим, что угловая
скорость вращения вокруг рулевой оси (ф) перпендикулярна к
оси х2. Очевидно, что во введенной системе координат, имеющей
начало в точке М$, ось х2 параллельна оси |г, а ось у2 повернута
по отношению к оси ц2 на угол Я. Следовательно, проекциями абсо-
абсолютной мгновенной угловой скорости передней части велосипеда на
оси системы M\X2y2z2 будут
<ду2« ©^ sin Я + ©^ cos Я, } G.75)
©2г = — ©% cos Я + ©?а sin Я.
Проекции мгновенной скорости задней части велосипеда (без
учета вращения заднего колеса) на оси системы -Migir|i?i равны
(рис. 7.7)
©^ =» — в sinx»
(о^ =а — G cos х sin ф + X cos Ф»
<д^ == в cos х cos ф + х sin ф.
Переходя теперь к нахождению проекций мгновенной угловой
скорости передней части велосипеда (без учета вращения переднего
колеса) на оси системы Мо^гЦгЁг, воспользуемся формулами G.65) и
*) При вертикальном положении велосипеда величина h2 есть
расстояние от дороги до центра масс М4 передней части велосипеду
/2 — расстояние по горизонтали от центра заднего колеса М\ до пер"
пендикуляра, опущенного из точки Af4 на дорогу.

§ 7.5] УРАВНЕНИЯ С. А. ЧАПЛЫГИНА 209
учтем угловую скорость ty (рис. 7.8). Тогда
<0g2 = - 9 sin % cos -ф + ( - 0 cos % sin ф + % cos ф) sin i|) cos % +
-Ь @ cos % cos ф + % sin ф) sin ф sin <J.
Линеаризуя это выражение, получим
®h =* ХФ c°s ^ ~ (X ~ *Ф S1'n ^) в.
Аналогично найдем
сэ^ — — -ф — 0 cos Я + % sin Я,
со* = 0 sin Я + % cos Я.
Используя теперь формулы G.75), окончательно будем иметь
(дХ2 = хг|) cos Я — (х — ф sin Я) 0,
®у* = * - 'Ф sin A"
сог2 = 0 4- ij) cos Я.
Для переднего колеса
Обозначив через 1уг и /2а моменты инерции передней части
велосипеда относительно осей #2 и гг, через ly%Zi — центробежный
момент инерции, через h — момент инерции переднего колеса отно-
относительно собственной оси вращения, можем записать
Т1Р - Y Uy, (* " + sin Я>2 ~ 2/y!Z! (* - 4 sin Я> F + * cos *) +
+ /Zj (9 + г!> cos ЯJ] - /2 у хф cos Я + /2-| в (Х - -ф sin Л).
Итак, кинетическая энергия системы равна
t [(* /ё + А/J + 2о (/,9 - А,х)
-j m2 (X + А8Х - /28 - йф
+ т2чй28х — triivd (9 + if cos Я) ф +
Т [7у: <* ~ * sin Я>2 ~ 2/№ <* ~ + sin Я> F + Ф cos Я) +
+ IZ2 (в + ф cos ЯJ] - /2 -^ хФ cos Я + /, ±. ё (х - ф sin Я). G.76)
1/27 Н. В. Бутенин

210
НЕГОЛОНОМНЫЕ СИСТЕМЫ
[ГЛ. 7
Потенциальная энергия велосипеда
П =* m\gzz + m2gZi * mighi cos % + m2g [(R — a cos ф) cos % +
+ rfi cos Я cos x + d sin ф sin x + d cos i|) sin Я cos %]
"" "К ё
in
2 - 2m2
Предположим, что рассеивание энергии происходит только из-за
вязкого трения в рулевой колонке, и, следовательно, обобщенная
сила, соответствующая этому трению, будет (см. § 3.7)
Найдем обобщенные силы:
Q
m2gd sin я<*"~
+ m2h2) g% -
GJ7>
Для рассматриваемого случая уравнения G.60) принимают вид
Т^ - Q^ + (Г^ - Q,) Л41 + (Ге - Qe) h5l = 0,
Гх - Qx + (fjf - Qx) h42 + (TQ - Qe) h52 - 0.
На основании уравнений неголономных связей G.74) имеем
и уравнениями движения будут
Вычислим операторы Ту, Т% и Ге:
1* + ^»»S -
¦ I2 — cos Я-ф — 1$,
G.79)

§7 5] УРАВНЕНИЯ С А. ЧАПЛЫГИНА 211
где
h = rtiihi + m2h2,
+ m2h\ + Iyx + 1уг, /22 = m/j + tn2l\
/3 = m2h2d + /^ sin Я + Iy2Z2 cos Я,
/4 = т2/2сГ + /^22а sin Я + IZ2 cos Я,
G.80)
yf sin2 Я + Iyat sin 2Я + lz% cos2 Я.
Используя выражения G.77) и G.79), составим теперь уравне-
уравнения G.78) движения велосипеда:
— (m2cd + cxl) х + (cl4 4- сх122) 8 - (с1ъ + сх1Х2) % +
+ (Cl + СХ14) ф + 4" tc/2 COS ^ + С\ G1 + ^)] X +
к
+ cl2 -5"sm № — ^2/2 -5- sin Xty — cm2gd sin Яф + c/n2g" c?x + cnty = 0,
V
т
XJ • V •
Л? — /i29 я" (^i + ^2) 9 + /их — hty — h~KcosЯф—Л^х +я*2#^"Ф — О»
А *\
К этим уравнениям следует присоединить уравнения неголономных
связей G.74):
jc+u8 = 0, cQ — Cjij) + у\|) cos Я.
После исключения х и 0 при помощи уравнений неголономных свя-
связей получим
где
.», ¦ <ш>
а4 = cm2gd, а5 = f Л + -~ + -^-J cos Я,
/ /22 \ с?/
j = /4 cos Я + c6i + Ci m2i + cos Я I + —=-,
\ с I с
i + ~¦sinЯ^—^-)со8Я, 63 = cm2^sin^,
а с )
62=

212 НЕГОЛОНОМНЫЕ СИСТЕМЫ [ГЛ. 7
Ь± ~ cl$ + С\1±, Ь5 = с-Q- cos Я Н—g- (/i + /г)> ^е e CM2§d*
Система уравнений G.81) представляет собой линеаризованные урав-
уравнения движения неуправляемого велосипеда с жесткими колесами.
Рассмотрим простейшую модель велосипеда, которая получает-
получается при условии, что ось руля вертикальна, проходит через центр
переднего колеса и является главной осью инерции передней части
велосипеда.
В этом случае
Следовательно, в соответствии с формулами G.80)
/3 = 0, /4 = IZt, I = /Z|> /12 = mjVi + IVl2l
Уравнения G.81) при этом примут вид
Пусть /о и Ло — координаты центра масс всего велосипеда. По-
Положим, что /j = m/iQ, /12=^0^0» h = mh0, т—т1 + т2, и прене-
пренебрежем моментами инерции 1\ и /г колес по сравнению с величи-
величиной mhoR; тогда первое уравнение
описывает движение велосипеда и соответствует элементарной тео-
теории велосипеда*). Из этого уравнения вытекает, что если велосипед
начинает падать вправо, то для остановки падения нужно создать
% < 0, а для этого нужно, чтобы tj> < 0, т. е. руль следует повер-
повернуть в сторону падения. Так как -ф < 0, то это приведет к возникно-
возникновению г|) < 0, что увеличит абсолютное значение %,
Исследование устойчивости велосипеда в более общем случае
изложено в работах Ю. И. Неймарка и Н. А. Фуфаева, указанных
на стр. 199.
*) Л. Г. Лойцянский и А. И. Лурье, Теоретическая меха-
механика, ч. III, ГТТИ, 1934, стр. 188.

ГЛАВА 8
ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
§ 8.1. Пути прямой и окольный.
Действие по Гамильтону
Предположим, что рассматриваемая консервативная
материальная система подчинена голономным идеаль-
идеальным связям. Пусть действительное движение системы
описывается обобщенными координатами
<7i@. <72(О> ..., q8(t). (8Л)
Для наглядности введем в рассмотрение понятие «изо-
«изображающей» точки. Пусть система имеет две степени
свободы, a qi(t) и <7г@ суть обобщенные координаты,
описывающие ее движение. Очевидно, что каждому по-
положению системы, определяемому координатами <7i и Цг,
на плоскости q^qi будет соответствовать точка с коор-
координатами qu q% При изменении q± и q2 точка на плоско-
плоскости ?i?2 будет менять свое положение. Эту точку назы-
называют изображающей точкой. При рассмотрении системы
с s степенями свободы под изображающей точкой будем
понимать точку в 5-мерном пространстве с координата-
координатами <7ь 92, ..., qs>
Под прямым путем изображающей точки понимается
геометрическое место ее действительных положений в ее
s-мерном пространстве. Окольным путем называется
геометрическое место воображаемых смещенных поло-
положений прямого пути, причем смещения в начальный и
конечный моменты должны равняться нулю. В соответ-
соответствии с условиями (8.1) прямой путь параметрически
изображается уравнениями
qm = qm{t) (m=l, 2, ..., s). (8.2)

214 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ТЛ 8
Окольные пути параметрически изображаются уравне-
уравнениями
?(<Н?тЮ + Ч, (m=l, 2,..., s),
где вариации обобщенных координат 8qm, вследствие не-
независимости обобщенных координат qm, представляют
собой любые бесконечно малые дифференцируемые
функции, не нарушающие связей, подчиненные условиям:
где ti и h — фиксированные, но произвольно выбирае-
выбираемые моменты времени. Условия (8.3) называются усло-
условиями закрепленности концов окольных путей. Из вы-
выражений
<7;ю=<7»ю+ч, («-1.2,..., 5)
следует, что
т. е. вариации обобщенных координат представляют со-
собой изменения обобщенных координат при фиксирован-
фиксированном времени t. Такие вариации называются «изохрон-
«изохронными».
Действием по Гамильтону за промежуток времени
(tu t2) называется величина S, определяемая выраже-
выражением
и
S= | Ldt, (8.4)
где L = T—П — функция Лагранжа. Таким образом, дей-
действие по Гамильтону представляет собой функционал.
Значение 5 определяется выбором 5 функций времени
Qu <7г, <7з, ..., <7s, так как L является функцией qu Цг, ...
..., <7s, qu ?2, • • •, g8, t. На прямом пути, когда qu q2, ...
• • •, 9s» Qu Цг, • • •, ^s соответствуют действительному
движению, действие S имеет определенное числовое зна-
значение.

§8.2] ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО 215
§ 8.2. Принцип Гамильтона — Остроградского *)
Принцип Гамильтона — Остроградского утверждает,
что вариация действия по Гамильтону
и
65 = б J Ldt
и
(конечного «импульса лагранжевой функции»), на пря-
прямом пути по сравнению с любым окольным путем равна
нулю, т. е.
6S = 0. (8.5)
При этом действие 5 имеет стационарное значение на
прямом пути **).
Покажем, как исходя из принципа Гамильтона —
Остроградского, получить уравнения Лагранжа второго
ррда. Пусть qt(t), <7г@> •••> 4s(t)—обобщенные коор-
координаты, соответствующие прямому пути консервативной
голономной механической системы. Рассмотрим околь-
окольный путь, определяемый функциями <7i+6<7i, ?2+б?2, ...
..., <7s+6?s. Тогда, с точностью до членов первого по-
порядка малости по сравнению с bqm и 8qm, будем иметь
6L = L (qm + 6qm, qm + bqm, t)-L (qm, qm, t) =
m
Следовательно,
и и n
- J (L + 6L) dt = J Ldt + J Ы dt,
*) Этот принцип сформулирован Гамильтоном в 1835 г. для ста-
стационарных связей. Независимо от него для общего случая неста-
нестационарных связей этот принцип был сформулирован и обоснован
М В. Осгроградским в 1848 г.
**) Говорят, что функционал вида
Х2
J f[y
)9 у'2(х), ..., у'п(х), x]dx
имеет стационарное значение при функциях ут(х) (т = 1, 2, ..
..., п), если вариация этого функционала, обусловленная заданием
вариаций бут с точностью до величин первого порядка малости
относительно дут, равна нулю.

216 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 8
где
и
5= J L(qm,qmit)dt.
и
Отсюда следует:
Используя свойство операторов б -—- = -^-hq (стр. 87),
перепишем последнее выражение в виде
ИЛИ
В силу условия закрепленности концов (8.3) второй ин-
интеграл в последнем выражении равен нулю. В самом
деле,
•ул(.
J -J dt \
s т2
/n=l t\
s
dL
и
m-i Цт
Таким образом,
f' S
= J 2j\"d^ dt~d^)bqmdt'
= 0.

§8 21 ПРИНЦИП ГАМИЛЬТОНА—ОСТРОГРАДСКОГО 217
Согласно принципу Гамильтона — Остроградского 65 =
=0. Значит,
j
tx m=l
Вследствие произвольности интервала интегрирования
/ dL d
m=\
Так как вариации координат независимы, то получаем
уравнения Лагранжа второго рода:
-t-0 <"¦=¦•2 * <">
Покажем теперь, как исходя из уравнений Лагранжа
второго рода, можно прийти к принципу Гамильтона —
Остроградского. Умножая каждое из уравнений (8.8) на
соответствующую вариацию 8qm и складывая между со-
собой полученные выражения, найдем, что
dL dL
или
т=\
Так как
d / dL \ д = rf / ^L д \ ^L ^
dL
то выражение (8.9) можно переписать в виде

218 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. В
В соответствии с соотношением (8.6)
Следовательно,
т=\
Умножая это выражение на dt и интегрируя в пределах
от ti до h (/i, h—фиксированные, но произвольные мо-
моменты времени), будем иметь
г'
J
t
так как Fqm)t=t = 0 и {(>qm)t=st2 = 0, а время не варьи-
варьируется. Таким образом,
Итак, показано, что из принципа Гамильтона —
Остроградского можно получить уравнения движения,
а из уравнений движения — принцип Гамильтона —
Остроградского. Из этого следует, что этот принцип мо-
может быть положен в основу механики голономных кон-
консервативных систем*).
Из принципа Гамильтона — Остроградского можно
получить и канонические уравнения Гамильтона. Дей-
Действительно, из выражения E.6) для функции Гамильтона
*) Распространение принципа Гамильтона — Остроградского на
неголономные системы рассмотрено, например, в монографиях
А. И. Лурье «Аналитическая механика», Физматгиз, 1961, и
Ю. И. Неймарка и Н. А. Фуфаева, Динамика неголономных систем,
«Наука», 1967.

ПРИНЦИП ГАМИЛЬТОНА-ОСТРОГРАДСКОГО
219
определяем
где H=H(qmy pm). Из условия (8.5) следует:
и i s \
Так как
•-2-
т=1
(8.10)
m-1
m==l
/n=l
т-1
^РтТГб9т:
Кт^ dt
то соотношение (8.10) примет вид
ибо
J
dt
4i
= 0
в силу закрепленности концов окольных путей. Несмотря
на то, что qm и рт входят в функцию Н как независи-
независимые переменные, при вычислении интеграла (8.11) нель-
нельзя считать 8qm и Ьрт независимыми, так как они свя-
связаны временной зависимостью. Если взять частную

220 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ {ГЛ. 3
производную по рт от функции Гамильтона
S
то получим
дН = . (т = 1 2 5)
Следовательно, первая круглая скобка в выражении
(8.11) тождественно равна нулю*). Вследствие произ-
произвольности интервала интегрирования и независимости
bqm имеем, что и
Pm+^-0 (m = l, 2,..., s).
Итак, получаем
дН дН
Принцип Гамильтона — Остроградского дает только
необходимое условие стационарности действия по Га-
Гамильтону на прямом пути. Для решения вопроса о ха-
характере экстремума следует определить знак второй
вариации 62S. Значение действия по Гамильтону на пря-
прямом пути по сравнению с окольными будет минималь-
минимальным, если 62S>0. Если промежуток времени 1г—ti вы-
выбрать достаточно малым, то условие 62S>0 будет
выполнено и действие по Гамильтону на прямом пути
будет минимальным по сравнению с окольными путя-
путями**).
Докажем теперь, что обратимое преобразование
E.32) будет каноническим, если выражение E.49)
*) А. Зоммерфельд, Механика, ИЛ, 1947.
**) Г. К. Якоби, Лекции по аналитической механике, ОНТИ,
J936. Д. К. Бобылев, О начале Гамильтона или Остроградского
и о начале наименьшего действия. Приложение к XI тому Записок
Российской Академии наук, 1889.
Определение характера экстремума пояснено в примере 60.

§8.2] ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО 221
будет тождественно удовлетворяться. Перепишем выра-
выражение (8.10) в виде
Из этого выражения, как только что было показано,
получаются уравнения Гамильтона для переменных qm
и рт. Для того чтобы обратимое преобразование E.32)
было каноническим, т. е. чтобы новые переменные
q'm, p'm удовлетворяли уравнениям Гамильтона, должно
выполняться условие
Оба последних равенства должны удовлетворяться од-
одновременно. Следовательно, их подынтегральные выра-
выражения могут отличаться друг от друга не более чем на
дифференциал от какой-либо функции V, так как
и
б f dV = d[V(t2) — V(t{)]*=*0.
Следовательно, должно выполняться условие
2j Pm dqm — Н dt« ^j p'm dq'm — Hf dt -f- dV *
/71= 1 tn*** 1
Рассмотрим теперь неконсервативную голономную
систему. Уравнения Лагранжа второго рода для такой
системы имеют вид (см. § 3.3, C.29))
dt\dqm) ддт -у™ ^m-l> 2'
Умножая каждое из этих уравнений на соответствующую
вариацию обобщенной координаты bqm и складывая ме-
между собой полученные соотношения, будем иметь

222 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 8
Проведя вычисление
d [ дТ \ . d I дТ . \ дТ ..
dt \ dqm ) m dt \ dqm Чт) dqm
и принимая во внимание, что
S 5
дТ , .
dqm
перепишем соотношение (8Л2) в виде
(^4
Умножая это выражение на dt и интегрируя в пределах
от ti до /г, получим
J ЛГ+Е^Лй»)*-0' (8.13)
так как в силу закрепленности концов окольных путей
Результат (8.13) также называют принципом Гамильто-
Гамильтона— Остроградского, однако следует иметь в виду, что
это уже не вариационная формулировка, а лишь утвер-
утверждение, что этот интеграл равен нулю. В самом деле,
выделяя в обобщенных силах консервативные силы
^ (m=I>2 s)'
где П — потенциальная энергия, a Qrm — обобщенная
сила, происходящая от неконсервативных сил, и вспоми-
вспоминая, что
ап _0
qm '
можем выражение (8.13) переписать в виде

§8.2]
ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО
223
где
m=l
dcjm
Но так как L = T—П и время не варьируется, то
U s U
Ь [ Ldt+У, [ Q' 6о dt = O. (8.14)
(8.15)
Введя теперь величину 6S', можем записать
т=1 /|
Результат (8.15) утверждает только то, что величина
6S' на прямом пути по сравнению с окольными равна
нулю. Самого же функ-
функционала S' не существует.
Пример 60. Рассмотрим
движение по инерции матери-
материальной точки по гладкой по-
поверхности.
Принимая П = 0, имеем
9
L —
const. Действие по
Гамильтону имеет вид
5 =
У
2 х * и' Рис. 8.1.
Согласно принципу Гамильтона при движении точки по прямому
пути между начальным и конечным положениями точки действие
по Гамильтону имеет стационарное значение по сравнению с околь-
окольными путями при условии, что сравниваемые движения происходят
за один и тот же промежуток времени t2 —1\. Следовательно, для
действительного движения
о
6 (v2) = 0.

224 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ {ГЛ. 8
Для выяснения характера экстремума рассмотрим частный слу-
случай— движение точки по гладкой сфере радиуса R (рис. 8.1). При-
Приняв за обобщенные координаты q\ = 9, q$ = ф, найдем
l^T^ILm @2 + 8|п29ф2).
Для прямого пути выполняются уравнения Лагранжа
0> М
dt\dQ/ dQ dt
Отсюда 9—sin 0 cos Эф2 = 0, sin*0<p = с (с — постоянная).
Пусть в начальный момент 9 = 90, ф == 0. Тогда ф = const и
9 — 9о, т. е. движение будет происходить по меридиану (например,
по меридиану Af0M0) (рис. 8.1). Скорость материальной точки равна
о2 — /?29q. Из этого следует, что движение по прямому пути
представляет собой равномерное движение по дуге большего круга.
Если расстояние между начальной точкой Мо и конечной точ»
кой ЬАг (рис. 8.1) будет меньше nR, то любой окольный путь между
этими точками будет больше, чем дуга большого круга MqM2. А так
как движение по окольному пути происходит за тот же промежуток
времени, что и по прямому, то скорость движения по прямому пути
будет минимальной. Если же дуга MqM2 будет больше nR, то наи-
наименьшее значение действия по Гамильтону будет достигаться по до-
дополнительной кратчайшей дуге М^М^-
Таким образом, скорость точки М2 будет минимальной до тех
пор, пока она не достигнет точки Ми# диаметрально противополож-
противоположной точке Мо. Точка MQ называется сопряженным кинематическим
фокусом точки Мо*).
§ 8.3. Неизохронное варьирование
При сравнении прямого пути и окольных мы сопо-
сопоставляли функции qm(t) и q*m{t)"=qm(t)Jirbqm для од-
одного и того же момента времени /. Геометрически это
представлено на рис. 8.2. На этом рисунке изображены
функции qm(t) и q*m (/). Точки Mi и М2, лежащие на
одной вертикали, сопоставляются друг с другом в один
и тот же момент времени.
*) Можно доказать, что и в общем случае действие по прямому
пути имеет наименьшее значение по сравнению с окольными путями,
если на прямом пути нет сопряженного для начальной точки кинема-
кинематического фокуса.

НЕИЗОХРОННОЕ ВАРЬИРОВАНИЕ
225
Рассмотрим теперь момент времени /+Д/. Точка Ms
получается из точки Mi благодаря действительному дви-
движению в промежутке времени от t до t-\-At. Соответ-
Соответствующее этой точке значение функции qm(t+At) сопо-
сопоставляется со значением функции в точке М4 q*m(t + Ы)=*
= qm{t + ДО + &qm (t -ЬА/)» Сопоставление опять-таки
происходит для одного момента времени /+Д/. Отметим,
что с точностью до ма- д %ма
лых первого
малости
порядка
Рис. 8.2.
(8.16)
Приведем теперь в
соответствие точки кри-
кривых qm{t) и q*m(t) не
в момент времени /,
а в моменты / и / + At, т. е. приведем* в соответствие
точки Mi и М4. В этом случае варьируется не только
координата, но и время. Эту операцию называют не-
изохронной вариацией и обозначают символом Д. Для
точки М^ теперь можно написать
?;(/+д/Н?;@+д<7т. (8.17)
Сравнивая между собой выражения (8.16) и (8.17),
имеем
Aqm^bqm + qmMt (8.18)
где Д/ — бесконечно малая дифференцируемая по вре-
времени функция. Операция (8.18) может быть применена
к любой функции времени. Например,
bqm~bqm + qmAt. (8.19)
Продифференцируем выражение (8.18) по времени:

226 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. «
и, приняв во внимание соотношение (8Л9), получим
^? (8.20)
Отсюда следует, что перестановка операций А и диффе-
дифференцирования по времени d/dt не имеет места. Для опе-
операции же б, как было ранее выяснено, аналогичная пе-
перестановка существует:
§ 8.4. Принцип стационарного действия Лагранжа
Рассмотрим консервативную голономную систему,
подчиненную стационарным связям. В такой системе
справедлив закон сохранения энергии
П-Л. (8.21)
Пусть qm(ti) и qm(t2) (m=l, 2, ..., s) — фиксиро-
фиксированные точки на прямом пути. Рассмотрим только та-
такие окольные пути, на которых выполняется условие
(8.21) и которые соединяются в фиксированных точках
qm(ti) и qm(t2) (m=l, 2, ..., s) на прямом пути. Усло-
Условие (8.21) не дает возможности сопоставлять точки
прямого пути с точками окольных путей в один и тот
же момент времени, так как накладывает определенные
ограничения на скорости точек на окольных путях
(скорости должны быть такими, чтобы все время удов-
удовлетворялось соотношение (8.21)). Например, промежу-
промежуток времени движения системы из фиксированного по-
положения qm(ti) до фиксированного положения qm(^2)
(m=l, 2, ..., 5) по окольному пути может быть не ра-
равен промежутку времени /2—ti движения системы по
прямому пути*). Таким образом, при условии (8.21)
следует применять операцию асинхронного варьирова-
*) Так, при прямолинейном движении точки при отсутствии сил
mv2l2 = h. Отсюда v = dx/dt «* V2h/m и x2 «¦ УЩт (t2 - /1) + x\.
Значит, по любому окольному пути при одном и том же h нельзя
за промежуток t% —1\ пройти тот же путь х% — х\.

*§8*] ПРИНЦИП СТАЦИОНАРНОГО ДЕЙСТВИЯ ЛАГРАНЖА 227
ния. Отметим, что в силу закрепленности концов околь-
окольных путей
Для рассматриваемой механической системы справед-
справедливы уравнения Лагранжа
где L = T—П. Так как
S S
m=\
m=l m=l
то в силу уравнений (8.23)
где рт = -^— (см. § 5.1). Но 8? = 8Г —611 и, кроме того,
в соответствии с условием (8.21) 8Г + 8П = 0. Значит,
(8.25)
Согласно формуле
это в соотношение
d VI
~dt 2л^т
Далее имеем
s
т=\
(8.18)
(8.25),
-S-
получим
s
Hi 2jpml
dL .
, — 4т Д'- Подставляя
jmM = 26T. (8.26)
S
у дТ .
*) Здесь использовано то условие, что bqm — — 6qm.

228 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 8
dL дТ ~
так как -р—==-^—. Рассматриваемая механическая
система подчинена стационарным связям, следовательно
(§ 3.7, формула C.46)),
Учитывая выражение (8.27), перепишем соотношение
(8.26) в виде
ИЛИ
=2
На основании формулы (8.18)
и, следовательно,
Умножая это выражение на dtf интегрируя в пределах
от t{ до t2 и используя условия (8.22), получим
и
J [А BГ) + 2Г -^- (A/)] dt = 0. (8.28)
Докажем, что
A J 2Tdt= | [дBГ) + 2Г-~-(А/)]^. (8.29)

§ 8.43 ПРИНЦИП СТАЦИОНАРНОГО ДЕЙСТВИЯ ЛАГРАНЖА 229
Так как
А BТ) = 6 BГ) + ~- BТ) М = бBГ) + ? BТ At) - 2Г -^ (АО,
то
и
J [А B7) (И + 2Т-^ (АО] Л = J б B7*) Л + 2ГА/
. (8.30)
Применим теперь операцию А к интегралу | 2Г А/:
0 0 0
Отсюда следует, что
A J 2ГЛ« J бBГ) rf/ + Bf A/)/eft (8.31)
A J 2Г rf/ = J 6 BГ) rf/ + BГ M)tmtti. (8.32)
о о
Вычитая из выражения (8.31) выражение (8.32), по-
получим
и и t
A f 2Tdt= f 6BГ)^ + 2ГАП\ (8,33)
Из равенства правых частей формул (8.30) и (8.33)
следует равенство левых, т. е. справедливость соотноше-
соотношения (8.29). Таким образом, из (8.28) и (8.29) следует:
и
А |2Г<# = 0. (8.34)
Величина
и
А= $2Tdt (8.35)

230 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 8
называется действием по Лагранжу. Формула (8.34) вы-
выражает принцип стационарного действия Лагранжа*):
действие по Лагранжу между двумя фиксированными
положениями системы имеет стационарное значение на
прямом пути, если на окольных путях сохраняется
одно и то же постоянное значение полной механической
энергии.
Если взять только одну материальную точку, то согласно фор-
формуле (8.35)
U U st
А » Г mv2 dt - j mv-jfdt=\ mv ds. (8.36)
Отметим, что условие (8.34) является условием ста-
стационарности величины Л. Вопрос о том, будет ли при
этом А иметь минимальное значение, требует дальней-
дальнейшего исследования. Можно доказать, что для достаточ-
достаточно близких t\ и t<i действие по Лагранжу А будет мини-
минимумом. В этом случае этот принцип можно назвать
принципом наименьшего действия.
Формула (8.34) была получена на базе уравнений
Лагранжа второго рода. Но можно сделать и наоборот —
принять эту формулу за исходное положение механики
консервативных голономных систем со стационарными
связями и получить из нее уравнения движения мате-
материальной системы**).
Рассмотрим в качестве примера движение точки по инерции по
гладкой поверхности.
Так как П = 0, то Т =*—-—« const. Действие по Лагранжу
равно
U и
2Т dt = f mv2 dt« mv2 (t2 - tx).
J
*) Этот принцип иногда называют принципом Мопертюи, кото-
который высказал его первым, но в весьма неясной форме. Своим уста-
установлением этот принцип обязан Эйлеру и особенно Лагранжу (сбор-
(сборник Вариационные принципы механики, Физматгиз, 1959).
*"*) См., например, А. И. Лурье, Аналитическая механика, Физ-
Физматгиз, 1961, стр. 711.

§ 8.53 ПРИНЦИП СТАЦИОНАР. ДЕЙСТВИЯ В ФОРМЕ ЯКОБИ 231
Для действительного движения
дл = о,
т. е.
mv2At = 0.
Так как mv2j2 = h, то v является постоянной величиной и, следо-
следовательно, Д/ = 0.
По всем окольным путям движение точки происходит с постоян-
постоянной скоростью, так как h = const. Значит, при движении по прямому
пути время движения будет минимальным.
§ 8.5. Принцип стационарного действия
в форме Якоб и
Исключим теперь из выражения принципа стационар-
стационарного действия (8.34) время t, используя интеграл энергии
Г + П = Л. (8.37)
Поскольку кинетическая энергия
у __
a Vi = ds
2Т (dtf =
Отсюда
п
1 VI
ildt,
п
S
m V2 я 1 \
ТО МОЖНО
/л
s
записать
»..* *»ы«
, используя (8.37), что
dqm dqk = 2 (А — П) (dtf.
Подставляя это значение dt в формулу (8.35), будем
иметь
U B) г ;
А = J 27 Л = J 1/ 2 (Л - П) 2 я»« (fifsj2 (8.39)
или
А = J 27" rf/ = f 1/ 2 (А -
*. (О ^
/ П) S 2 ^mft d?m rf?ft. (8.40)

232 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ рЛ. 8
Формулы (8.39) и (8.40) представляют собой выраже-
выражения для действия по Лагранжу. Пределы интегрирова-
интегрирования соответствуют начальному и конечному положению
системы.
Следуя Якоби, примем обобщенную координату дч
за независимую переменную; тогда
5 5 S S
41 У Amk dqm dqk = У У Amk
2 Amk dqm dqk = J J Amk ^L l
л 4. V и f*2L + V л rf<?ft 4- V V A dU d% _
Вводя обозначение
m=? m=2 /:-2 7
(8.41)
перепишем выражение (8.40) в виде
К) _
Л= J 1//?^,, (8.42)
(•1)
где */| — значение координаты #i B начальном положе-
положении системы, </2 —ее значение в конечном положении си-
системы. Формула (8.42) представляет собой действие по
Лагранжу в форме Якоби. Заметим, что поскольку функ-
функция УR не зависит от времени t> то в принципе ста-
стационарного действия в форме Якоби рассматривается
уже не закон движения изображающей точки по траек-
траектории, а сахма фазовая траектория. Это следует из того,
что равенство (8.42) имеет вид формулы (8.4), только
вместо функции L стоит функция VR, а роль времени t
играет координаты q^ Поэтому аналогично тому, как из
формулы (8.4) получаются уравнения Лагранжа второго

§ 8.5] ПРИНЦИП СТАЦИОНАР. ДЕЙСТВИЯ В ФОРМЕ ЯКОБИ 233
рода, так из формулы (8.42) получаются уравнения,
определяющие траекторию изображающей точки, так
как их решение дает зависимость обобщенных коорди-
координат qm (m=2, 3, ..., s) от обобщенной координаты qx:
= 0 (А = 2, 3, ..., 5). (8.43)
Используя формулы (8.38) и (8.41), получим время
движения простой квадратурой:
J
1)
(8.44)
Общее решение задачи будет содержать 25 произ-
вольных постоянных — /о, h и 25—2 постоянных интегри-
интегрирования, получаемых при решении уравнений (8.43)
(число этих уравнений равно s—1).
Пример 61. Определение траектории материальной точки в одно-
однородном поле силы тяжести.
Рассматривая движение только в вертикальной плоскости, най-
найдем траекторию, проходящую через две фиксированные точки с ко-
координатами (хо, уо) и (хи У\)- Направим ось у по вертикали вверх,
а ось х — по горизонтали. За обобщенные координаты примем q\=x%
q2 = у. Закон сохранения энергии имеет вид
Так как
2Т-т{х2 + у*),
то в соответствии с выражением (8.41) имеем
R~2{h-mgy){tn+ my'\
и, следовательно,
VJ- V2m(h-mgy)(\+y'2).
Вычислим производные
dV~R ^ V2m(h~mgy) , dVJ ^ m*g(\+y'2)
ду' VTT7 ' ду V2m(h(
8 Н. В. Бутелвя

234 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 8
Используя уравнения (8.43), найдем дифференциальное уравнение
траектории
d dVJ dV~R Q
dx ду' ду
Подставляя сюда производные от Y~R, получим
2 (h - mgy) y'r + mg (l + у'2) - 0. (8.45)
Продифференцировав это уравнение по х, имеем
или у'" = 0, так как h — mgy Ф 0. Следовательно,
у=*ах2 + Ьх + с. (8.46)
Для нахождения связи между постоянными a, b и с подставим
найденное у в уравнение (8.45)
4а [h- mg (ax2 + Ьх + с)] + mg [I + b2 + 4abx + 4а2*] - 0.
Отсюда
c=JL + l+>i. (M7)
mg 4a v '
Семейство траекторий (8.46) представляет собой семейство парабол
с вертикальной осью. Для нахождения искомой траектории следует
определить а и b из уравнений
у0 = ах\ + 6*0 + су ух** ах] + ^ + с,
где с определяется формулой (8.47). Пусть Xq = 0, уо = 0, тогда
с = 0. Из формулы (8.47) следует
«=«<0. (8.48)
Уравнение для определения b имеет вид
. 1&0. (8.49)
Отметим, что выбор точки (#i, г/i) не может быть произвольным при
заданном h. Из уравнения (8.49) следует, что b будет иметь дей-
действительные значения при
4h (h - mgyx) > m2g2x% (8.50)
т. е. во всяком случае должно быть h > mgy\. При выполнении
условия (8.50) a vi b имеют по два значения, что соответствует факту

8>5] ПРИНЦИП СТАЦИОНАР. ДЕЙСТВИЯ В ФОРМЕ ЯКОБИ
235
пересечения в точках @,0) и (х\уу\) двух парабол (рис. 8.3).
Наименьшему действию соответствует парабола 1, так как время
движения по этой параболе от точки @, 0) к точке (х\у у{) меньше,
чем по другой параболе.
X
Рис. 8.3.
Рис. 8.4.
Пример 62. Задача о брахистохроне. В 1696 г. И. Бернулли по-
поставил и решил следующую задачу: материальная точка, имеющая
начальную скорость, равную нулю, движется под действием силы
тяжести по некоторой кривой, соединяющей две заданные точки.
Найти такую кривую, при движении по которой время движения бу-
будет наименьшим. Эта задача получи-
получила название, задачи о брахистохроне
и положила начало вариационному
исчислению.
Пусть начальная точка будет
началом координат, а вторая точка
имеет координаты х\у у\ (рис. 8.4).
Время движения по кривой (при по-
сточнном К) определяется формулой
(8.44):
_^
О
х
J
2(/г-П)
Рис. 8.5.
Пусть в рассматриваемой задаче q\ = ху цч = у. Кинетическая
и потенциальная энергии выражаются формулами
Г = 1/
П = - mgy.
В силу начальных условий из интеграла энергии Т 4" П = h следует,
что Л = 0 и функция

236 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ {ГЛ. S
Принимая to = 0, перепишем выражение (8.44) в виде
--—~^—dx. (8.51)
Vy
Таким образом, поставленная задача сводится к нахождению ми-
минимума интеграла (8.51), т. е. к нахождению функции у(х), при ко-
которой этот интеграл имеет наименьшее значение. Уравнение кри-
кривой у = у (х) определяется из уравнения (см. (8.43)):
д (УТГу
ду \ Vy
Производя необходимые вычисления, получим
Вводя замену и~у\ имеем
2и du __ dy
I + «2 V
Отсюда
In A + u2)= \nci — In у
и
_?i_
TT7"*
где Ci — постоянная интегрирования. Так как
?(8.52)
где 6 — угол наклона касательной к кривой у~у(х) (рис. 8.5), то
У - l4_Ctg2Q e ^i cos2 0 - ^ (I + cos 29). (8.53)
Из соотношения (8.52) находим dx*—ctgQdyt а из формулы (8.53)
Значит,
^л;= -2c1cos29cf9== ~c, (i + cos
Отсюда
х - - -^- B9 + sin 20) + (?,» (8.54)
где С2 — постоянная интегрирования. Кривая, определяемая уравне-
уравнениями (8.53) и (8.54), представляет собой дугу циклоиды.

ГЛАВА 9
НЕКОТОРЫЕ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ
§ 9.1. Явный вид уравнений Лагранжа второго рода
Пусть рассматриваемая материальная система под-
подчинена голономным связям. Тогда кинетическая энергия
системы выражается формулой C.43):
^^ *
Т = Т S
т*=1 /?¦=!
где То и коэффициенты Атр, Вр — функции обобщенных
координат и времени. Находя
S
дТ
dqm
s s -¦ s дв„
1^Г~ 2
и подставляя полученные выражения в уравнения Ла-
Лагранжа второго рода
J
dq
получим
p=l / Ц-1 p-1
p-1

238 НЕКОТОРЫЕ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ [ГЛ. 9
Отсюда
р=1 Ц=1 р=1
двт двр\
дАтр
(т=1, 2, .... 5),
или
l
Р=1
где (стр. 79) Г^ = 2 Ymp<7p называется обобщенной
гироскопической силой, а
Vmp \ptn ~~~ дпщ. "~ до
(т=1, 2, ..., 5; р= 1, 2, ..., 5)
-— гироскопическими коэффициентами.
Для стационарных связей получим
[dAmD 1 дЛи
р = 1 ц=1 Р=1
(т=1, 2, ..., 5).
§ 9.2. Метод вариации постоянных
Предположим, что рассматриваемая механическая
система описывается дифференциальными уравнениями
=-1 р=1

§ ?2] МЕТОД ВАРИАЦИИ ПОСТОЯННЫХ 239
Предположим, что система уравнений (9.3) при
От =0 (т=1, 2, ..., 5) имеет решение
Чт — Чт \1> СЬ C2i • • • > C2s) \т ~~ м А • • •» •*/• \у«^/
Метод вариации постоянных, предложенный Лагран-
жем*), заключается в следующем: пусть найдено реше-
решение системы (9.3) при Qm = 0 (т == 1, 2, ..., s), т. е.
определено движение системы под действием основных
сил Qm', предполагая теперь, что дополнительные силы
Q*m, которые называются «возмущающими», достаточно
малы по сравнению с основными, решение системы урав-
уравнений (9.3) ищут в форме (9.4), причем величины
Си С2, ..., c2s считаются уже не постоянными, а медлен-
медленно меняющимися функциями времени.
Итак, будем искать решение системы уравнений (9.3)
в виде решений (9.4), считая величины С\> с^, ..., c2s
функциями времени. Дифференцируя решение (9.4) по
времени, получим
2s
"m dt • ^ dck k% \ • )
Так как обобщенных координат qm столько же, сколь-
сколько степеней свободы, т. е. 5, а число функций сь. равно
25, то ck можно связать по собственному выбору. Выбе-
Выберем эти функции си такими, чтобы первые производные
от qm имели бы такой же вид, как при постоянных Ck,
т. е.
Чт — qi \ш — 1, I, .¦., S) W'W
и, следовательно,
2s
v = О (т — 1 9 <Л /О7^
*) Ж. Л а г р а н ж, Аналитическая механика, пер. с франц., Гоо
техиздат, 1950, стр. 412—437.

240 НЕКОТОРЫЙ МЕТОДЫ ТЕОРИИ -ВОЗМУЩЕНИИ (ГЛ. 9
Далее находим
"т /] Л/Дл б& ^ — i, z, ..., б;. \У.о;
#2
д/дС
Подставляя теперь выражения (9.6) и (9.8) в урав-
уравнения (9.3) и принимая во внимание, что при постоян-
постоянных си обобщенные координаты qm являются решениями
уравнений (9.3) при Q* =0, имеем
2s
НтР dt дси
(9.9)
ИЛИ
2s
d2qx
I A
I 4-/1
ms dt dck
¦)*»-«:•
(9.10)
Соотношения (9.7) и (9.10) представляют собой систему
2s уравнений относительно производных dfc. Вводя обо-
обозначения
л
d/ dck
dt dck %
%
(m=l, 2,..., s; *«lf 2, ..., 2$), (9.12)
перепишем соотношения (9.7) и (9.10) в виде
2s
(m-1, 2 s). (9.13)
Решая эти уравнения относительно cfc, получим
F=1, 2, .... 2s), (9.14)

МЕТОД ВАРИАЦИИ ПОСТОЯННЫХ
241
где
«1!
«21
«si
fcl
hi
«12
«22
«S2
Pl2
ft»
•• • «1.2s
• • • «2, 2s
• • • «s, 2s
• • • Pi, 2s
• • • P2, 2s
Psl Ps2
Ps.
2S
(9.15)
рис. 9.l
a Amk — минор определителя (9.15), соответствующий
m-й строке и k-ыу столбцу. Соотношения (9.14) яв-
являются уравнениями для
определения функций ск и
называются уравнениями
возмущенного движения.
Уравнения (9.14) представ-
представляют собой уравнения (9.3),
преобразованные к новым
переменным с&, и их решение, вообще говоря, не менее
трудно, чем решение уравнений (9.3). Но если возму-
возмущающие силы Qm достаточно малы, то функции Ck мож-
можно считать медленно меняющимися функциями времени
и применять к отысканию решений уравнений (9.14) раз-
различные приближенные методы.
Пример 63. Тело массы т, прикрепленное к неподвижной пре-
преграде пружиной жесткости с (рис. 9.1), может перемещаться по го-
горизонтальным прямолинейным направляющим. Возмущающая
сила, действующая на тело, имеет вид: F = е/(дг, jc), где е — малый
параметр.
Поместив начало координат в точке, соответствующей положе-
положению тела при ненапряженной пружине, примем за обобщенную ко-
координату q = х — отклонение тела от начала координат. Кинетиче-
Кинетическая энергия и основная обобщенная сила выражаются формулами
1 - -¦ -«.
и, следовательно, Ли = т. Уравнение движения тела имеет вид
xt x).
При е = 0 решением уравнения будет
х = сх cos kt Л- cz sin kt.

242 НЕКОТОРЫЕ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ [ГЛ. 9
где k = Vclm. Так как
то
—mk sin kt mk cos kt
cos /г/ sin &/
и уравнения (9.14) примут вид
с\«- - -^- / (*, *) sin A;/,
где
х = с\ cos kt + с2 sin kt,
x~ — C\k sin &/ + с2/г cos /г/.
Вводя замену
C\ = a cos Ф, c2 — a sin *,
получим
a cos d — aO sin Ф = ~ f[e cos (&/ - 'б1), —ak sin F/ — #)] sin kt,
a sin О + aO cos d = —-r f [a cos (kt — Ф), — a/г sin (kt - ft)] cos kt.
Отсюда
a = - _L- / [a cos (kt - d), -ak sin F/ - #)] sin (kt - #),
ad « —г- / [a cos (kt — Ф), ~a^ sin (kt — Ф)] cos (kt — Ф).
Если е достаточно мало, то а и Ф будут медленно меняющимися
функциями времени, т. е. такими, изменением которых за время
Т = —-¦ можно пренебречь. Поэтому вместо полученных уравнений
можно взять «укороченные», т. е. уравнения с осредненными пра-
правыми частями *):
2njk
8
2nm
о
Г / [a cos (kt - ^), - aA: sin (kt - #)] sin (kt - 0) rf/,
2n/k
f [a cos (kt - #), -ak sin (^/ - #)] cos (fe/ - Ф) ff/.
*) H. H. Боголюбов, Ю, А. Митропольский, Асимпто-
Асимптотические методы в теории нелинейных колебаний, гл. У, Физматгиз,
1953.

§ 0.2] МЕТОД ВАРИАЦИИ ПОСТОЯННЫХ 243
После замены % = kt — Ь имеем
2л
f ас08*. -«*sing)sin
о
2л
f
2
J
о
J f (a cos |, -ak sin ?) cos g d%.
о
Предположим теперь, что возмущающая сила складывается из
малого сопротивления движению, пропорционального скорости, и ма-
малой подталкивающей силы, действующей только по направлению
движения, т. е.
F = -&* + #'sign*,
где Ь и #' — постоянные величины. Введем малый безразмерный па-
параметр
е=я—_..
mk
тогда
где
Укороченные уравнения теперь будут иметь вид
? Г Г . . - , И . ,
2Л J L ^л5
аД; sin g)j sin
fl^ — __ a^sin^H — sign ( — ak sin |)| cos
0
Отсюда после интегрирования получим
2 ят&) mk 2m'
Следовательно,
4#' /4Я'
где ao и Фо — начальные значения а и б1. Таким образом, имеем
f4#' /4Я'

244 НЕКОТОРЫЕ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ ЦЛ. 9
Это знацит, что при t~*oo при любых начальных условиях движе-
движение будет происходить по закону
АИ'
X - -jjr- COS (kt - do)>
т. ё. тело будет совершать незатухающие колебания с амплитудой,
не зависящей от начальных условий. Такое движение называете*!
автоколебательным *).
Пример 64. Рассмотрим влияние сопротивления атмосферы на
движение свободной тяжелой точки в однородном гравитационном
поле Земли, пренебрегая вращением Земли**). Движение точки про-
происходит в вертикальной плоскости. Направим ось у вертикально
вверх, ось х — горизонтально.
Если <7i = х и <72 = У — координаты точки, то выражение для
кинетической энергии имеет вид
и, следовательно,
Ац~т, Л^^ 0, А22 — т.
Основные обобщенные силы равны
Qi=0, Q,e_mg.
Будем считать, что сопротивление атмосферы мало и является функ-
функцией скорости точки. Сила сопротивления направлена по касатель-
касательной к траектории в сторону, противоположную скорости, и выра-
выражается формулой
Fв/(о)
где е — малый параметр. Отсюда следует, что возмущающие силы
будут
где v ~ Yx2 + у2. Уравнения движения точки имеют вид
X
*) Подробнее об автоколебаниях см. А.. А. Андронов,
Л. А. В и т т, С. Э. X а й к и н, Теория колебаний, Физматгиз, 1959?
Н. В. Б у т е н и н, Элементы теории нелинейных колебаний, Судпром-
гиз, 1962; Я. Г. Пацовко, Введение в теорию механических коле-
колебаний, «Наука», 1971.
**) G. Hamel, Theoretische Mechanik, Berlin, 1949, стр. 310;
А. И. Лурье, Аналитическая механика, Физматгиз, 1961, стр. 572,

§9.2
МЕТОД ВАРИАЦИИ ПОСТОЯННЫЕ
245
При е = 0 эта система уравнений имеет решение
х = cxt -f с*
Составим теперь уравнения возмущенного движения (9.14). Так
как
дх
= 0,
ду ду ду ду
дс\ ' дс2 * дс$ * dCi
дЧ • д*х _П д*к п '
' dtdct
.-о д2у -о
dtdc3
д2у
= 0,
c/f t/6| ^/ dc2
то определитель (9.15) равен
m О О О
О 0 т О
' д/дс4
Д =
* I О О
О 0 * I
-т1.
Далее вычисляем
и в соответствии с уравнениями (9.14) находим
где
Интегрируя последние выражения, найдем
t

246
НЕКОТОРЫЕ МЕТОДЫ ТЕОРИЙ ВОЗМУЩЕНИЙ
t
[ГЛ 9
-h f (Сг~к
т J v
где сю, С20у с3о, с4о — постоянные.
Для достаточно малых е можно лри интегрировании пренебречь
изменениями с\ и с3 и считать их равными соответственно Сщ и ?20.
Тогда получим
t
С\
е
т
Г JlSLd*
-^-*io J 1^-
где v
Подставляя эти значения ci, сг, с3 и й в формулы для х и #,
получим закон возмущенного движения точки.
Пример 65. Возмущенное дви-
Ht жение спутника вблизи круговой
орбиты.
Пусть инерциальная система
координат Ox\y\Z\ имеет начало в
центре планеты. Введем подвиж-
подвижную систему координат Cxyz (ор-
(орбитальная система), начало кото-
которой движется по круговой орбите
радиуса л>; ось х направлена по
радиусу Го, ось у — по касатель-
касательной к круговой орбите в сторону
движения (рис. 9.2).
Положение спутника М в воз-
возмущенном движении по отноше-
отношению к круговой орбите будем
определять радиусом-вектором
Р - х1 + yl + zk,
где x,ynz — координаты спутника в орбитальной системе координат.
Кинетическая энергия спутника (принимаемого нами за матери-
материальную точку) определяется формулой
Рис. 9.2.

§ 9.23 МЕТОД ВАРИАЦИИ ПОСТОЯННЫХ 247
где
Х\ — г0 cos ф + х cos ф — у sin ф.
Ух = г0 sin ф + х sin ф + у cos ф,
Z\ = 2, ф = CD/.
Так как круговая скорость спутника vKp — У[л2/г0 *), где fx2 — по-
постоянная притяжения центрального поля планеты, то со (угловая
скорость орбитальной системы координат) равна
_ °КР
^"""гГ"
и, следовательно,
Вычислив
.*! = —г0со sin ф + (х — ^со) cos ф - (jcco + у) sin ф,
t/l = Г0СОо cos Ф + (* — 0е0) sin Ф + С*® + ^/) cos Ф»ч
г, = 2,
найдем кинетическую энергию
Г = -i-m (л:2 + ^2 + z2-2yx® + 2л#со + (/V + д:2©2 +
Отсюда следует, что
Ац — т, A22~tnt Лзз^/п, А12 = А^ = Л2з = 0.
Центральная сила, обеспечивающая движение по круговой орбите,
равна
где г = Го + Р, а г « ^(го + хJ + y2 + z2. Считая х, у и г, координа-
координаты спутника в орбитальной системе, малыми по сравнению с Го, мо-
можем приближенно принять
_ ц2т , 2jn2m
*) Н. В. Б у те нин, Я. Л. Лунц, Д. Р. Меркин, Курс тео-
теоретической механики, т. 2, «Наука», 1971.

248 НЕКОТОРЫЕ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ [ГЛ. О
Пусть дополнительная возмущающая сила будет
Составим теперь уравнения движения:
х — 2щ — Зсо2х =* Ф^,
у + 2coi = Ф^,
z + со2* « Фг,
К фи Фг
^ Ф П Ф Фф 0 эта си-
сиК фи Фг
где Ф^«—, Ф^«-^-, Фг« —. При Фг = Ф^«ф
стема уравнений имеет решение:
2
х = — Ci + c2 cos со/ + Сз sin cf>/,
^ = ~ Serf — 2с2 sin со/ + 2с3 cos со/ + с4,
г — съ cos со/ + сб sin ®/.
Далее находим
дх 2 дх дх . дх дх дх
._—=-— __—«cosсо/, -=—«sin со/, -=——-^—«-г—«О,
дс\ со ас2 (^Сз ^с4 дс5 дсв
(?Ci a^2 дсг дс^ дсъ
dz dz dz dz л dz A dz
~r— = -r = -= e-r-eO, -=— = COS CO/, -r «S1J1 CO/,
ac, <^c2 <^c3 a^4 ^5 dc6
д2х д2х д2х д2х д2х
0
dtdcx dtdcA dtdc5 dt dc6 ' dt dc2
d2x
dtdcz
d2y
- CO COS 0/,
- 2co cos со/, -^r~- ¦= — 2co sin со/,
-=rr-3 = CO COS CO/.

§ 9.2] МЕТОД ВАРИАЦИИ ПОСТОЯННЫХ 249
Следовательно,
ап = О, (*i2 = — m© sin ©/, а13 = /n© cos ©/, ап=а!5 = а1б = О,
а21 = — Зш, а22 ~ — 2m© cos ©/, а2з = — 2m© sin ©/, а2* = а25 =» а2в — О,
а31 = 0, а32 в 0, а33 = 0, а34 в 0, а35=» — т© sin ©/, азб = т© cos ©/,
2
Рпв —f Pw'-coso/, pi3 = sin©*, Эм = Pis = Pie^O,
p21 « — 3/, p22 = - 2 sin ©/, р2з = 2 cos ©/, P24 e Ь Р25 =» P26 e 0,
р31 в Р32 = РзЗ в Р34 в 0, р35 e COS ©/, Рзб == Sin ©/.
Вычисляя определитель (9.15), получим Д——/п3©2.
Тогда согласно выражениям (9.14) будем иметь
Отсюда
— Фх sin ©/ — 2ФУ cos ©/,
Ф^ cos ©/ - 2ФУ sin ©/,
с5 = — ф2 sin
сб = фг cos ©/.
+ ©
о
t
о
С2 а ^20 - I (Фл- sin ©/ -|- 2ФУ cos ©/) flf/,
о
I (Ф^ cos ©/ — 2Фу sin ©/) rf/,
о
о
Сь ~ ^50 — Фг sin ©/ fif/,
J
Ф2 COS ©/
где сю, C20, C30, ^40, C50, ceo — постоянные величины. С помощью по-
полученных формул при конкретно заданной силе можно определить
возмущенное движение точки.

250 НЕКОТОРЫЕ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ [ГЛ. 9
§ 9.3. Метод вариации постоянных
при использовании уравнений Гамильтона
Канонические уравнения возмущенного движения
Предположим, что движение рассматриваемой дина-
динамической системы описывается каноническими уравне-
уравнениями
Ят~ дРт > Р*- дЯт (УЛЬ>
(т= 1, 2, ..., 5),
где Н — функция Гамильтона, составленная для системы
при ее движении под действием основных сил, а функ-
функция Я* учитывает дополнительные (возмущающие) си-
силы. Считая, что решения
Ят = Ят С. alf a2, ..., a5, р1э р2, • • • > Ps)> )
Г (9-17)
Pm = Pm (*> а1э а2, ..., а5, рь р2, ..., ps) J
(m= 1, 2, ..., s),
где ai, аг, ..., as, Pi, P2, ..., Ps — независимые постоян-
постоянные, системы уравнений Гамильтона
|Ь Ш <»-».2,...,s) (9Л8)
известны, будем искать решение системы уравнений
(9.16) в форме (9.17), считая, что величины ai, ct2, ...
..., as, pi, P2, ..., Ps — функции времени. Предполагая,
что уравнения (9.17) можно разрешить относительно ве-
величин оы, аг, ..., ae, pi, рг, ..., ps, получим
am = am(r, <7ь 9г> • • •» 9s» Pi* Pi> * • •> Ps)* \
I (9-19)
Pm = Pm {t, Яи ?2. • • •. <7s> Pb P2 Ps) J

§ 9.3) МЕТОД ВАРИАЦИИ ПОСТОЯННЫХ
Найдем производные от ат и рт по времени:
дат . VI [ дат . да
—
-1,2,....,).
Учитывая уравнения (9.16), перепишем эти выражения
в виде
s
дат i V^ Г дат д (Я + Я*) дап
W
. _ дат .
(m=l, 2, ..., 5).
Вспоминая определения и свойства скобок Пуассона
E.27), можем записать
< = ^Г + (*т> # + #*) = ^ + (am, #) + (am, Я*),
(т=1, 2,..., 5).
Поскольку функции (9.19) при постоянных ат и рт
является интегралами системы уравнений (9.18), то
в силу условий E.29) имеем
•3|р- + (ат, Я) = 0 (m-lf 2, ,,,,s),

252 НЕКОТОРЫЕ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ [ГЛ 9
и, следовательно,
дН' дпт дН'
P
gk др др dq
(т=1, 2,..., s).
(9.20)
Уравнения (9.20) являются уравнениями возмущенного
движения.
В § 6.1 было показано, что если можно найти ре-
шение
¦ = ¦(', Яи Яъ • • •» </s, «i, «2, ..., as)
(где ai, аг, •••, as — произвольные постоянные) уравне-
уравнения Гамильтона — Якоби
то решением системы (9.18) будет
Л--ЙГ' Pm = ^J- («-1.2,....5), (9.22)
в которых pi, p2, ..., р« — произвольные постоянные. Ре-
Решая эти уравнения относительно qm и рт, мы и получим
выражения (9.17).
Поскольку решение системы (9.16) ищется в форме
(9.17), то, считая оы, <х2, ..., а8, рь р2, ..., ps функция-
функциями времени, выражения (9.17) можно рассматривать как
преобразование переменных qm и рт системы (9.16)
к новым переменным рт и ат. Покажем, что такое пре-
преобразование будет каноническим. Для этого нужно по-
показать, что выражение E.49), т. е.
S S
РшЯт~(Н + /Г)- JJ ajm~Н' + ~} (9.23)
при выполнении условий (9.21) удовлетворяется тожде-
тождественно. Выбрав функцию V в виде
У-¦(', Яи Я** ¦¦• Яп «1, «2 a*)" ^J «mftn.

МЕТОД ВАРИАЦИИ ПОСТОЯННЫХ
253
найдем
l m1 1
m=l
Подставляя эту производную в выражение (9.23) и учи-
учитывая условия (9.22), получим
т. е. преобразование будет каноническим, если новая
функция Гамильтона равна
Н' = Н* + Н + -^.
Но в силу уравнения (9.21)
# + -^- = 0
п + dt u>
и, следовательно, Н'=Н*.
Таким образом, новые переменные будут удовлетво-
удовлетворять каноническим урав-
нениям вида
. дН*
а
М
(т=1, 2, ...,s). (9.24)
Пример 66. Движение ма-
материальной точки относительно
вращающейся Земли*).
Будем считать Землю од-
однородным шаром радиуса R.
Пусть точка А на земной
поверхности определяется по-
полюсным углом #о (рис. &3) и
долготой Хо. Исследование дви-
движения точки проведем относи-
относительно системы координат
Axyz, у которой ось х направ-
направлена по касательной к мери-
меридиану на север, ось у — по касательной к параллели на запад и
ось z — по направлению радиуса Земли от центра Земли.
Рис. 9.3.
*) Этот пример в более общей постановке рассмотрен в книге
А. И. Лурье, Аналитическая механика, Физматгиз, 1961, стр. 565.

254 НЕКОТОРЫЕ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ [ГЛ. 9
Скорость точки по отношению к инерциальной системе коорди-
координат О?г)?, имеющей начало в центре Земли, равна
где vA = © X Ra — скорость точки Л, © — угловая скорость Земли,
р — радиус-вектор материальной точки, определяющий ее положение
по отношению к точке Л, vr — скорость материальной точки по от-
отношению к системе координат Axyz. Если *\ / и & —единичные век-
векторы системы координат Axyz, то
©> = ica sin d0 + k(u cos d0,
sin dQ, RA = Rk,
и, следовательно,
Vx ~ x — щ cos do,
vy = y + <u (x cos d0 — z sin d0) — <aR sin d0,
t;2 = z + щ sin d0.
Принимая, что w=l, получим следующее выражение для ки-
кинетической энергии:
+ 2@ [(z sin d0 - x cos d0) у +«/ (jf cos d0 — z sin d0 - R sin d0)] +
+ a2 [^/2 + (a: cos d0 - z sin d0 - R sin d0J]}.
Отсюда имеем
Pi = -TT- = х — щ cos d0,
p2 = -^r- = у + 0) (x cos d0 — z sin d0) — со/? sin d0,
Pz = -0-T- = z + cot/ cos d0.
Составим выражение для функции Гамильтона
Я- 2 Ря»*«-(Г-П),
т=1
где ^i = х, q2 = у, ^з = г, П — потенциальная энергия силы тяго-
тяготения Земли. В нашем случае это будет
Я = -1 (х2 + у2 + z2) - -~ ©2 [t/2 + (х cos d0 ~ z sin d0 - R sin d0J] + П,

0.3] МЕТОД ВАРИАЦИИ ПОСТОЯННЫХ 255
или
у Up* + щ cos ^
+ [pi + ®^ sin #о — со (* cos d0 - z sin O0)]2 + (p3 — co# sin Ф0J} -
-|ю2 [#2 + (x cos #0-2 sin %-Rsin #0J] + П.
Если точка падает в пустоте без начальной скорости, то время
ее падения измеряется несколькими секундами. Так, например, если
высота Л= 1000 м, то h—y —** 14 сек. Поэтому примем за
малый параметр безразмерную величину \i = (otu где со — угловая
скорость вращения Земли, равная © » 24 - 60 - 60 ~ ТзТТз" *^' Слев
довательно,
14
р 13713 1000*
Функцию Я теперь можно записать в виде
+ [Р2 + у- Л sin do ~ у- (^ cos #0-2: sin do)! + (рз - j~ У sin #0) -
1 u2
-^- [у2 + (x cos #o~zsin %-R sin #0J] + П.
2 ^
Введем преобразование
x = x, y^y, z=*z,
Pi e Pi» P2 = P2 ~ 0^ C0S ^0» P* в Рз*
Это преобразование является каноничесюш **). Произведя замену
*) Такой малый параметр использован А. Н. Крыловым (Со-
(Собрание трудов академика, т. VIII, Изд-во АН СССР, 1950, стр. 330).
**) Рассмотрим преобразование
ЯЯ РР+ (m=I> 2> •••• s>-
Покажем, что если в качестве функции V взять любую функцию
от старых координат и времени, т. е.

256 НЕКОТОРЫ€ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЯ (ГД. 9
переменных и пренебрегая членами, содержащими множители ц2,
получим
+ © \(р[ cos % - рз sin %) У - Pi (х cos #о ~ z sin %
Потенциальная энергия выражается формулой
Поскольку
то получим *)
R
"^"—з?—)
Следовательно,
то условие E.49)
будет выполнено тождественно. Используя рассматриваемое преоб-
преобразование, получим
6V.
1йгг
т — \ т—\
Это выражение выполняется тождественно, если
Выбирая в рассматриваемой задаче за функцию
V = - toRy sin Фо,
имеем: -тт- ~ 0 и Н'*=Н.
иг
*) Мы ограничиваемся приведенными членами, считая, что точка
движется вблизи поверхности Земли и, следовательно» г достаточно
мало.

§ 9,31 МЕТОД ВАРИАЦИИ ПОСТОЯННЫХ 257
Итак, выражение для функции Гамильтона Я принимает вид
+ © [(р{ cos % - р'з sin Фо) у - р., (х cos %-z sin %)] +
где
Я* » (й f(p{ cos d0 — Рз s*n ^о) У ~~ р'г (х cos ^о"~ ^ S1 n d0)] +
g x2 + y2-2z2
Решение уравнений Гамильтона
имеет вид
где ai, a2, a3, рь Рг> Рз — постоянные интегрирования.
Подставим теперь это решение в выражение функции Я*:
#• • © | ах (a2t 4- р2) cos О0 - («з - gt) (a2t + р2) sin ^0 -
- a2 j\a,f 4- р,) cos O0 - (a8* + Рз - ~j sin O0j 1
Составим уравнения (9.24):
Pi - ©Pi cos d0+ -^ (a,/+ Pi),
p2 - a>p3 sin d0 - <Dpt cos d0 + у cd^/2 sin d0 4- -^- (a2^ + p2),
a, - ©a2<:os d0 --|- (o,/ -f Pi),

258 НЕКОТОРЫЕ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ [ГЛ. 9
а2 = — coai cos Фо + ©аз sin Оо —С- (а2/ + р2) — ©g* sin фо>
а3 - - ©а2 sin Фо + Щ- (а3* + Рз - у g*2).
Решение этих уравнений проведем приближенным путем; заме-
заменяя в правых частях уравнений величины всех а и р их начальными
значениями ао и ро и интегрируя, получим
Pi = Рю + ©*Рго cos О0 + -|- (а10 -у + Рю -у),
Рг = Рго + ®Фзо sin Фо — ®Рю^ cos д0 + -^- 0^3 sin
2й { t2 I
аз = азо ~ ©а20/ sin Фо + -^- I а3о у + рзо - у
и, следовательно,
х = рп + а10/ + ю (р20/ + а20/2) cos д0 - -|- (а10 -j- + Рю у],
~ © (Рю* + аю*2) cos Oq + ш (Рзо* + а30*2) sin O0 —
- "f (а2о Т + Р20 т)"" Т °^3 sin °0>
- © (Рго* + а2о*2) sin O0 +
После дифференцирования по времени получим
х = a1Q + © (Р20 + 2a20*) cos д0 - -|- (а10у- + Рю*],
U = а2о ~ о (Рю + 2а10*) cos Фо + © (Рзо + 2а3о*) sin d0 —
- ¦*- (а20 у-
i: = а30 ~ © (Р20 + 2a20*) Sin d0 + Ц- ^а30 у + Рзо* - ^)
Пусть начальными условиями движения материальной точки будут:
при t = 0 х = хо,у=*уо, г=* г0, * - х0, у - ^0» * - ^о- Тогда величины

§ 9.4] УРАВНЕНИЯ В ВАРИАЦИЯХ 259
сцо, а20, а3о» Pio, Р2Э, Рзо определятся из уравнений
#о — Рю» Уо^Рго» ^о = Рзо»
хо =» аю + ©р2о cos #0>
#0 — а20 - G>p10 cos d0 + соРзо sin Фо>
io = «зо ~ ©Р20 sin ft0.
Если *e = O, ^о = 0, zo = h, ^o = O, ^e0. ?о = О, то Рю = 0, Pao^O,
Рзо — К «io = 0, а2о = — ©A sin do, а3о = 0 и, с точностью до ц,2, имеем
х « 0, у= — -^
о
Формула для у дает восточное отклонение падающей без начальной
скорости точки.
§ 9.4. Уравнения в вариациях
Рассматриваемый в этом параграфе метод позволяет
изучать малые отклонения материальной системы от ее
известного движения, которое называется невозмущен-
невозмущенным движением. Эти отклонения (возмущения) могут
быть вызваны, например, изменением начальных усло-
условий. Метод основан на составлении дифференциальных
уравнений для возмущений, которые считаются малы-
малыми*).
Пусть рассматриваемая материальная система под-
подчинена голономным стационарным связям, a qu Ц% ...
..., q8 — обобщенные координаты. Дифференциальные
уравнения движения системы имеют вид
Q'» («-I.2.....S). (9.25)
Пусть для невозмущенного движения решение известно:
qm = fm(f) (m=l,2, ...,s); (9.26)
тогда для возмущенного движения
(t) (/if-1, 2, ..., s), (9.27)
где xm(t)—малые отклонения (возмущения) от невоз-
невозмущенного движения. Так как кинетическая энергия
*) Этот метод развит Пуанкаре.

260 НЕКОТОРЫЕ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИИ [ГЛ. 9
системы равна
то
1 у ?/*••) О/*
Подставляя в это выражение решение (9.27) и ограничи-
ограничиваясь в разложении по степеням хт и хт (т = \, 2, ...
..., s) членами, содержащими хт и хт в степени не
выше цервой, получим
S
дТ
S S
S S (^) ^'/fe («=1.2 s). (9.29)
ft=l/=l V / /0
Индекс О означает, что в Ати и производных от Amk вме-
вместо fw+^m (ап=1, 2, .,,, s) подставлено /т. Далее
имеем
d ( дТ
i
(А \? . V
at—fk +
S S
ft-1 ft=l ^=l/=lv
0
В соответствии с выражением (9.28)
дт i 4- s

§ 9.4] УРАВНЕНИЯ В ВАРИАЦИЯХ 261
После замены <?/ и qk их выражениями (9.27) и разло-
разложения по степеням Х} и xk (/, & = 1, 2, ..., s) будем
иметь
дТ
(с точностью до членов с х\ и jc% в первой степени).
Для обобщенных сил разложение по степеням хт и хт
(т=1, 2, ..., 5) с точностью до членов с хт и хт в пер-
первой степени имеет вид
Qm (?l, Й2> • • •» ?s> 9b ?2» • • •» </s> 0 =
(m-1, 2,..., s).
Так как qm=fm(t) являются решениями уравнений
(9.25), то справедливо равенство
(Amk)o fk + Zj Ht fk """*
.f — /^ (m 10 «Л /Q QQ^
Подставляя теперь выражения (9.30), (9.31) и (9.32)
в уравнения (9.25) и учитывая тождество (9.33), по-
лучим
s s s s
2 аткхк + 2 ***** + 2 cmkxk + 2 dmA*ft = 0, (9.34)
Л1 k\ kl fcI

262
НЕКОТОРЫЕ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ
1ГД. 9
где
amk e (^mfe)o» bmk —
(dQm\
\ да I '
_ivv(d*A» \it (dQm\
2 ft&\dqbdq>»)o Vе»Jo*
dA
(9.35)
(m=l, 2,..., s; k=\, 2,..., s).
Система из s линейных уравнений (9.34) называется
уравнениями возмущенного движения или уравнениями
в вариациях. Если невозмущенное движение таково, что
коэффициенты уравнений (9.34) постоянны, то это дви-
движение называется стационарным. Для стационарного
движения справедливо
атк = akm> t>mk == ~" I jja ) »
(m = 1, 2, ..., s; &= 1, 2, ..., s).
Из последнего равенства следует:
/ dAjk \ у
(9.36)
(/п== 1» 2, ,.., 5; Л= 1,2,..., 5).

§9.4] УРАВНЕНИЯ В ВАРИАЦИЯХ 263
5
Слагаемые 2 dmkxk в уравнении (9.34) являются ги-
гироскопическими членами, так как коэффициенты dmu об-
обладают следующими свойствами:
dmm = 0> dmk = - dkm (m = 1, 2, ..., s; k = 1, 2, ..., s).
Полученные нами уравнения возмущенного движения
обычно используются для суждений об устойчивости не-
невозмущенного движения *).
Пример 67. В примере 30, § 3.8, было получено выражение для
кинетической энергии свободного гироскопа в кардановом подвесе:
Учитывая, что
cuBjf = — ф sin ft, coB^ = v, (uRZ ^ Ф cos O,
Юг5=в ф ~ "ф sin tr, ©« = v, ©я a=s tb COS V|
а также что IBX = hy и /^ — /г, получим
1
2
где
^11 = Jazx + ^bz + Л/ + (^bjc "" ^B2 ~~ Iy) sin2 ^ + Jx sin2 ^»
Уравнения движения в случае отсутствия внешних сил имеют вид
[/HZi + /BZ +1y + (IBX — 1вг — /^) sin2 О] "ф — /Л (ф — ij> sin О) d cos ft —
- 2 (/В2 + Iy - Лит) ^ sin ft cos ft = 0,
*2<* + /д: (Ф - 4 sin ft) -ф cos ft + (/bz + /у ~ Лиг) Ф2 sin ft cos ft - 0,
-gf [МФ-Ф sin <>)]-0.
За частное решение этих уравнений (невозмущенное движение)
может быть взято я|) = i|H, ft = fto, Ф = со/, где со = const. Таким
образом, fi = ofo, f2 = fto, h == со/. Согласно формулам (9.35) имеем
a,, - /H2l + /вг + /y + (/„ - /B2 - /y) sin2 ft0 + Ix sin2 ft0 - /1§
^22 == Лг> ^зз S=B ^дг» ^13=s ~~ ^jf sin fto,
Л12 =* — CO/jp COS fto, ^21 а ®^jf COS fto.
*) Л. Г. Лойцянский, А. И. Лурье, Теоретическая меха-
механика, ч. III, ГТТИ, 1934, стр. 550.

264 НЕКОТОРЫЕ МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ [ГЛ. 9
Остальные коэффициенты равны нулю. Так как qx = г|?0 + хъ q2 —
= #о + *2> Яъв <*>* + *з> то уравнения возмущенного движения (9.34)
представятся в виде
1ххх - lx®x2 cos О0 = 0,
/я*2 + /*<djcj cos 'б'ов 0,
Хг — Х\ sin do = c,
где с — постоянная. Решение этих уравнений имеет вид:
хх = с, + с2 cos /г/ + с3 sin kt,
у -j- (c2 sin Ы — с3 cos ^0»
х3 = с/ -h (r2 cos Atf + ^з sin kt) sin fr0 + c',
где сь с2, ^з, с4, с' — постоянные интегрирования, а
При начальных условиях: при t = 0 ^ = 0, лг2 = 0, х3 = 0, к\ = 0,
х2 = i20, х3 = 0, т. е. при ударе по внутренней рамке,- получим,
1
лг3 - 4^- % ^о cos Л/.
Из этих выражений видно, что возмущенное движение по каж-
каждой координате представляет собой гармоническое колебание (ну-
(нутационные колебания) *). Если со достаточно велико, то амплитуды
этих колебаний малы.
*) Если рассматривать нелинейную задачу,- учитывая члены с
xk и хи в степени выше первой, то можно обнаружить систематиче-
систематические уходы гироскопа, т. е. появление в решении членов, пропорцио-
пропорциональных времени. Эта неустойчивость гироскопа была впервые обна-
обнаружена Е. Я. Николаи. Подробности исследования этого вопроса
можно найти в книге: Я. Л. Лун ц, Ошибки гироскопических при-
приборов, Судостроение, 1968.