В. В. БОЛОТИН
НЕКОНСЕРВАТИВНЫЕ ЗАДАЧИ
ТЕОРИИ
УПРУГОЙ УСТОЙЧИВОСТИ
т
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1961

ОГЛАВЛЕНИЕ
Предисловие • 7
Введение . . . • 9
§ 1. Эволюция постановки задачи об упругой
устойчивости • . 9
§ 2. Продольный изгиб центрально сжатого стержня ... 14
§ 3. Случай стержня, нагруженного «следящей» силой.
Метод Эйлера 15
§ 4. Устойчивость по отношению к малым возмущениям 18
§ 5. Критическое значение «следящей» силы 19
§ 6. Истолкование результатов. Роль потенциала внешних
сил . . . . • 21
§ 7. Круг вопросов, рассматриваемых в настоящей книге 24
Глава первая. Общие принципы 29
§ 1.1. Предварительные замечания 29
§ 1.2. Конечные деформации 32
§ 1.3. Уравнения равновесия и граничные условия ... 34
§ 1.4. Геометрическое истолкование уравнений 37
§ 1.5. Связь между напряжениями и деформациями ... 40
§ 1.6. Криволинейные координаты 41
§ 1.7. Уравнения нелинейной теории упругости в
произвольной криволинейной системе координат .... 46
§ 1.8. Постановка задачи об устойчивости. Уравнения
в вариациях 48
§ 1.9. Различные случаи поведения нагрузки 52
§ 1.10. Статическая краевая задача 54
§ 1.11. Исследование колебаний около положения
равновесия и метод Эйлера 61
§ 1.12. Сведение к системам обыкновенных
дифференциальных уравнений ••.... 64
§ 1.13. Вычисление коэффициентов для некоторых
конкретных систем 69

4
ОГЛАВЛЕНИЕ
§ 1.14. Исследование устойчивости 77
§ 1.15. Пример. Система второго порядка 81
§ 1.16. Влияние диссипативных сил на устойчивость ... 86
Глава вторая. Устойчивость равновесия упругих систем
при наличии следящих сил 93
§ 2.1. Исторические сведения 93
§ 2.2. Задача об устойчивости стержня, сжатого
тангенциальной силой 97
§ 2.3. Влияние способов распределения массы «. 101
§ 2.4. Приближенное решение задачи 104
§ 2.5. Влияние затухания на устойчивость 108
§ 2.6. Задача об устойчивости стержня, сжатого силой
с фиксированной линией действия НО
§ 2.7. Устойчивость плоской формы изгиба (вывод
уравнений) 114
§ 2.8. Некоторые числовые результаты 122
§ 2.9. Некоторые другие задачи 126
§ 2.10. Уравнения равновесия сжатого и скрученного
стержня ; . . . 130
§ 2.11. Устойчивость прямолинейной формы сжатого и
скрученного стержня (метод Эйлера).
Классификация граничных условий * 135
§ 2.12. Стержень с сосредоточенной массой на конце.
Метод малых колебаний 142
§ 2.13. Учет распределенной массы стержня и затухания 145
Глава третья. Устойчивость гибких валов с
регулируемым числом оборотов 150
§ 3.1. Предварительные замечания 150
§ 3.2. Уравнения движения гибкого вала 154
§ 3.3. Вязкое внутреннее трение. Неустойчивость,
вызванная действием внутреннего трения 157
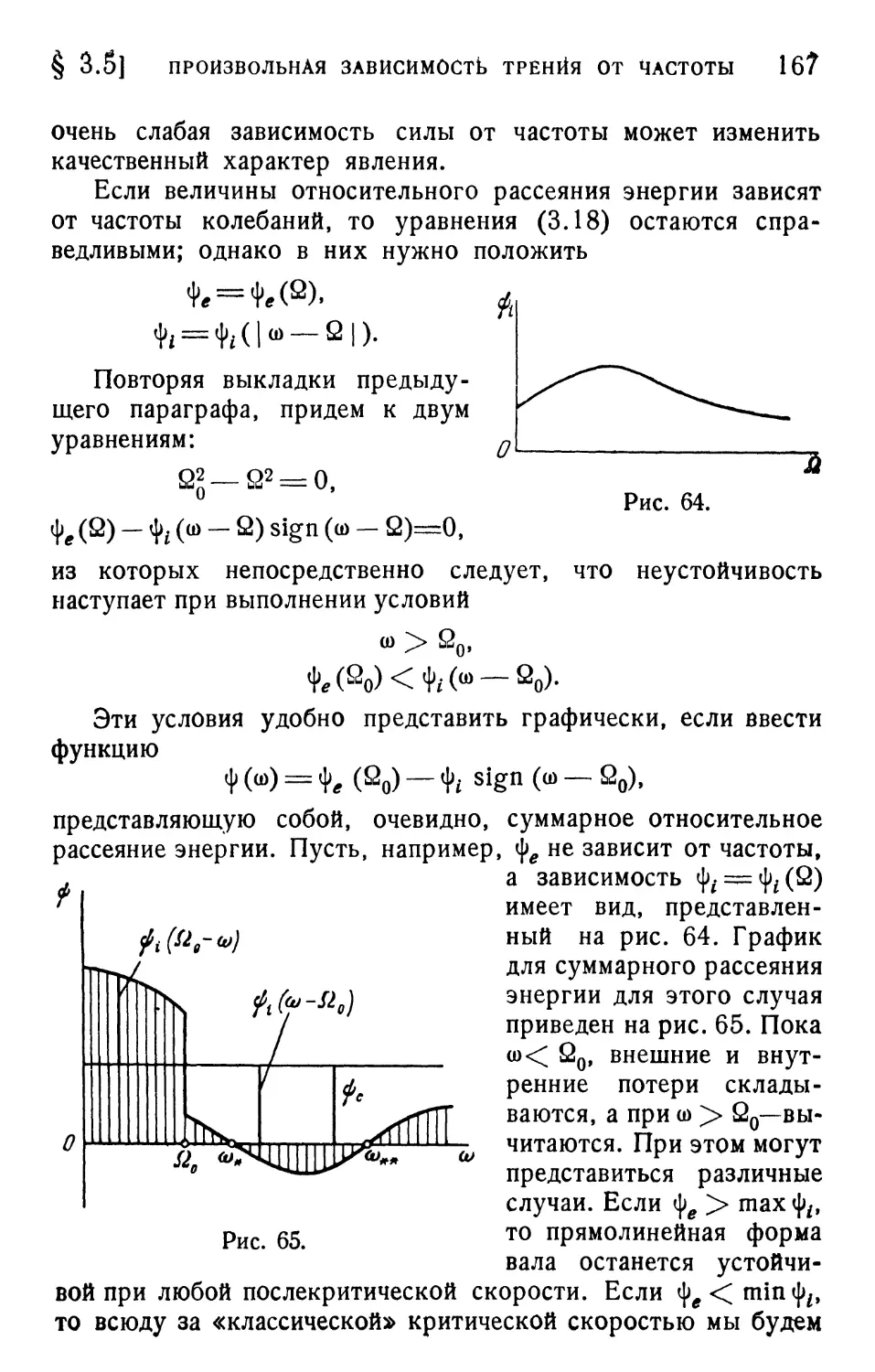
§ 3.4. Трение, не зависящее от скорости 162
§ 3.5. Случай произвольной зависимости трения от
частоты 166
§ 3.6. Обобщение на случай неодинаковых главных
жесткостей и на случай бесконечного числа
степеней свободы 168
§ 3.7. Нелинейная задача 173
§ 3.8. Установившаяся асинхронная прецессия 179
§ 3.9. Примеры амплитудных зависимостей 183

ОГЛАВЛЕНИЕ
5
§ 3.10. Трение, обусловленное макроскопической тепловой
диффузией 189
§ 3.11. Влияние сил трения при тугой посадке деталей
на вал 197
§ 3.12. Неустойчивость роторов, связанная с влиянием
масляной пленки в подшипниках 200
§ 3.13. Явления неустойчивости в центрифугах при
неполном наливе жидкости 204
§ 3.14. Неустойчивость роторов в магнитном поле .... 208
Глава четвертая. Устойчивость упругих тел в потоке
газа 212
§ 4.1. Краткие исторические сведения 212
§ 4.2. Флаттер крыла как неконсервативная задача
упругой устойчивости .... • 216
§ 4.3. Общая постановка задач об устойчивости упругих
тел в потенциальном потоке газа 222
§ 4.4, Устойчивость упругой цилиндрической оболочки
в потоке сжимаемого газа 228
§ 4.5. Случай бесконечно длинной оболочки. Различные
случаи обтекания 231
§ 4.6. Определение критических скоростей флаттера и
дивергенции 237
§ 4.7. Устойчивость упругих пластинок в потенциальном
потоке • . . 245
§ 4.8. Определение аэродинамических сил в случае
больших сверхзвуковых скоростей. Закон плоских
сечений 250
§ 4.9. Устойчивость упругих пластинок при больших
сверхзвуковых скоростях 257
§ 4.10. Применение вариационного метода Галеркина.
Влияние демпфирования и усилий в срединной
поверхности 262
§ 4.11. Границы применения метода Галеркина.
Разъяснение парадокса в задаче о флаттере мембраны . . . 272
§ 4.12. Постановка нелинейных задач в теории
аэроупругости. Роль геометрической и аэродинамической
нелинейностей 280
§ 4.13. Вывод уравнений нелинейного флаттера пологой
оболочки при больших сверхзвуковых скоростях . . 289
§ 4.14. Приближенный метод решения уравнений 296

6
ОГЛАВЛЕНИЕ
§ 4.15. Панель, опертая по всему контуру . . • 302
§ 4.16. Нелинейный флаттер плоской панели. Решение
в тригонометрических рядах 306
§ 4.17. Метод малого параметра для исследования
нелинейного флаттера 316
§ 4.18. Анализ результатов 324
Заключительные замечания. Предполагаемые направления
дальнейших исследований 331
Именной указатель • . . 336
Предметный указатель 338

ПРЕДИСЛОВИЕ
Книга посвящена изучению устойчивости упругих систем,
находящихся под действием неконсервативных сил. Как
известно, для таких систем обычные методы теории упругой
устойчивости, основанные на рассмотрении форм равновесия,
смежных с невозмущенной формой, вообще говоря,
оказываются неприменимыми. Здесь необходимы более общие
методы и более сложные средства исследования.
Книга состоит из введения и четырех глав. Первая глава
посвящена общим вопросам, постановке задачи и методам
решения. Ее содержание было изложено в докладе автора
на Третьем всесоюзном математическом съезде (Москва, 1956).
Остальные главы посвящены приложениям. Во второй главе
рассматривается устойчивость упругих систем, находящихся
под действием неконсервативных сил, которые в процессе
потери устойчивости ведут себя некоторым заранее
предписанным образом (так называемые «следящие» силы). В третьей
главе рассматривается устойчивость быстро вращающихся
упругих роторов, находящихся под влиянием различных
возмущающих сил, например сил внутреннего трения,
гидродинамических и электромагнитных сил и т. п. Четвертая глава
посвящена задачам устойчивости упругих систем, обтекаемых
высокоскоростным потоком газа; при этом основное
внимание обращено на задачи сверхзвукового флаттера упругих
пластин и оболочек. Ряд задач рассматривается в нелинейной
постановке, что позволяет исследовать поведение системы
после потери устойчивости. Уже на основании этого
перечисления можно сделать заключение, что рассматриваемые
задачи представляют интерес для современного
машиностроения, авиации и ракетной техники.
Значительная часть книги основана на результатах,
полученных автором. Там, где используются результаты других

8
ПРЕДИСЛОВИЕ
авторов, в подстрочных примечаниях даны соответствующие
ссылки. Э. Л. Позняк, Л. В. Епишев, Б. П. Макаров,
Ю. Ю. Швейко, Г. В. Мишенков и Ю. В. Гаврилов
выполнили для книги или проверили некоторые вычисления,
а также предоставили некоторые не опубликованные
ранее экспериментальные результаты. Перечисленным лицам
автор выражает искреннюю признательность. Автор
выражает благодарность А. И. Лурье за сделанные им ценные
замечания по программе книги.
Автор

ВВЕДЕНИЕ
§ 1. Эволюция постановки задачи
об упругой устойчивости
Теория упругой устойчивости, начало которой было
положено еще в работах Леонарда Эйлера, в настоящее время
является весьма подробно разработанным разделом
прикладной механики, располагающим рядом эффективных методов,
большим количеством решенных задач и обширной
литературой. Благоприятным фактором, предопределившим быстрое
накопление материала в теории упругой устойчивости,
несомненно, явилась весьма удачная концепция устойчивости и
критической силы. В теории упругой устойчивости
предполагается, что при достаточно малых нагрузках
равновесие упругой системы устойчиво и что оно остается таковым
вплоть до первой точки разветвления форм равновесия, за
которой исходная форма равновесия становится
неустойчивой. Критическая сила (или, в более общем случае, параметр
группы сил) определяется при этом как наименьшее значение
силы, при котором наряду с исходной формой равновесия
имеют место смежные, весьма близкие к ней другие формы
равновесия. Эту концепцию мы находим еще у Эйлера,
который определял критическую силу как «силу, требующуюся для
самого малого наклонения колонны» 1). Такой подход, или, как
мы его будем в дальнейшем называть, метод Эйлера, позволил
свести вопрос об устойчивости формы равновесия к более
1) Э й л е р Л., Метод нахождения кривых линий, обладающих
свойствами либо максимума, либо минимума, или решение изопе-
риметрической задачи, взятой в самом широком смысле, Гостехиз-
дат, 1934, стр. 491.

10
ВВЕДЕНИЕ
простому вопросу об отыскании минимальных собственных
значений некоторых краевых задач.
Плодотворность метода Эйлера в теории упругой
устойчивости является бесспорной. Этот метод был распространен
также и на задачи неупругой устойчивости, что нашло
выражение в концепции «приведенного модуля». Вместе с тем
метод Эйлера не является универсальным; он имеет вполне
определенную область применения, выход за пределы
которой уже не раз служил источником ошибок и
недоразумений. Три обстоятельства должны быть отмечены в связи
с критикой метода Эйлера в теории устойчивости.
Одно из .них связано в первую очередь с развитием
нелинейной теории тонких упругих оболочек. Уже в
тридцатых годах нашего столетия было установлено
систематическое и весьма существенное расхождение между значениями
критических сил, которые дает для оболочек классическая
теория, и опытными результатами. Оказалось, что для
тонких оболочек важное значение приобретают начальные
неправильности и нелинейные эффекты и что критические силы,
соответствующие точкам разветвления, являются на самом
деле лишь «верхними» критическими силами, с трудом
реализуемыми даже при самых идеальных условиях
эксперимента ]).
Другое обстоятельство связано с развитием теории
пластической устойчивости. В 1946 г. Шенли 2) обратил
внимание на то, что концепция «приведенного модуля»
соответствует лишь некоторому частному предположению о
поведении нагрузки и что для пластической стадии следует ввести
определение критической силы, отличное от того, которое
используется для упругой стадии. Исследования,
проведенные в последнее время, выявили существенную роль
поведения нагрузки в процессе потери устойчивости и, вообще,
роль фактора времени, который в классической теории
упругой устойчивости попросту не учитывался.
Третье обстоятельство, серьезно ограничившее область
применения метода Эйлера, состоит в следующем. Еще
') Вольмир А. С, Тонкие пластинки и оболочки, Гостехиз-
дат, 1956.
2) Шенли Ф., Теория неупругой колонны. Сб. перев.
«Механика», № 2, ИЛ, 1951.

§ 1] ЭВОЛЮЦИЯ ПОСТАНОВКИ ЗАДАЧИ И
в 1928—1929 гг. Е. Л. Николаи1), исследуя одну из
задач об упругой устойчивости скрученного стержня,
обнаружил, что метод Эйлера приводит к парадоксальному
результату. В рассмотренной им задаче вообще не существует
форм равновесия, смежных с невозмущенной
(прямолинейной) формой и, казалось бы, прямолинейная форма стержня
остается устойчивой при всех значениях скручивающего
момента. Этот результат был, однако, правильно истолкован
как признак того, что метод Эйлера к данной задаче
неприменим и должен быть заменен более общим методом
исследования устойчивости — «методом малых колебаний». В
дальнейшем было установлено, что здесь имеет
существенное значение наличие потенциала у внешних сил 2). Метод
Эйлера применим, если внешние силы обладают потенциалом
(т. е. если они являются консервативными силами), и
становится, вообще говоря, непригодным, если потенциал у
внешних сил отсутствует.
Основным методом исследования неконсервативных задач
теории упругой устойчивости является динамический метод,
основанный на рассмотрении колебаний системы вблизи
положения равновесия. Это сближает теорию упругой
устойчивости с общей теорией устойчивости движения, а также
с ее приложениями в теории автоматического регулирования,
в гидромеханике вязкой жидкости и других областях
механики и техники. Метод Эйлера, сводящий задачу к анализу
разветвлений форм равновесия системы, может
рассматриваться как частный случай динамического метода.
Настоящая книга целиком посвящена неконсервативным
задачам теории упругой устойчивости. Аэродинамические и
гидродинамические нагрузки, силы, действующие на элементы
турбомашин и электрических машин, нагрузки, возникающие
в объектах и промежуточных звеньях систем автоматического
!) Николаи Е. Л., Об устойчивости прямолинейной формы
равновесия сжатого и скрученного стержня, Изв. Ленингр.
политехи, ин-та 31 (1928); К вопросу об устойчивости скрученного
стержня, Вестн. прикл. матем. мех. 1 (1929). См. также:
Николаи Е. Л., Труды по механике, Гостехиздат, 1955.
2) Среди последних работ по этому вопросу необходимо указать
на исследования Циглера: Ziegler H., Die Stabilitatskriterien der
Elastomechanik, Ing.-Arch. 20, № 1 (1952); Циглер Г., Об
устойчивости упругих систем, Сб. «Проблемы механики» под ред.
X. Драйдена и Т. Кармана, вып. 2, ИЛ, 1959.

12
ВВЕДЕНИЕ
регулирования, в большинстве случаев представляют собой
неконсервативные силы. Классическая теория упругой
устойчивости развивалась главным образом в связи с
потребностями промышленного, транспортного и гражданского
строительства. Традиционные нагрузки классической теории упругой
устойчивости — это потенциальные силы, обычно
гравитационного происхождения («мертвые» нагрузки). Что касается
неконсервативных задач упругой устойчивости, то они
представляют интерес в первую очередь в связи с
развитием современного машиностроения, авиации и ракетной
техники.
Общие вопросы устойчивости упругих систем,
нагруженных неконсервативными силами, обсуждались в работах Ци-
глера !) и автора 2). Представляет некоторый интерес
полемика, имевшая место в более ранних статьях В. И. Реута
и Б. Л. Николаи 3). Среди работ, посвященных частным
задачам, помимо указанных выше статей Е. Л. Николаи 4),
должны быть упомянуты работы Г. Ю. Джанелидзе,
И. Е. Шашкова, К. С. Дейнеко и М. Я. Леонова,
Морриса, Циглера, Треша, Бека и Пфлюгера5).
К этому вопросу примыкает обширная литература по устойчи-
1) Ziegler H., цит. на стр. 11.
2) Болотин В. В., Вопросы общей теории упругой
устойчивости, Прикл. матем. мех. 20, № 4 (1956); Некоторые проблемы
теории упругой устойчивости, Тр. Третьего всесоюзн. матем. съезда,
т. 1, Изд-во АН СССР, 1956; Динамическая устойчивость упругих
систем, Гостехиздат, 1956; О колебаниях и устойчивости стержней,
находящихся под действием неконсервативных сил, Сб. «Колебания
в турбомашинах», Изд-во АН СССР, 1959.
3) Р е у т В. И., О теории упругой устойчивости, Тр. Одесск.
ин-та инж. гражд. и комм, стр-ва, вып. 1 (1939); Николаи Б. Л.,
О критерии устойчивости упругих систем, там же. К современной
точке зрения примыкает точка зрения Б. Л. Николаи.
4) Николаи Е. Л. , цит. на стр. 11.
5) Джанелидзе Г. Ю., Об устойчивости стержня при
действии следящей силы, Тр. Ленингр. политехи, ин-та, № 192 (1958);
Ш а ш к о в И. Е., Об устойчивости прямолинейной формы
равновесия борштанги, Инж. сборн. 1, № 1 (1941); Шашков И. Е., Об
устойчивости сжатого и скрученного призматического стержня
с произвольной формой поперечного сечения, Инж. сборн. 7 (1950);
Дейнеко К. С. и Леонов М. Я., Динамический метод
исследования устойчивости сжатого стержня, Прикл. матем. мех. 19,
№ 6 (1955); Morris J., Torque and flexural stability of a cantile-

§ 1] ЭВОЛЮЦИЯ ПОСТАНОВКИ ЗАДАЧИ 13
вости быстро вращающихся валов 1). Большое количество
работ посвящено важным задачам об устойчивости упругих
элементов, находящихся в потоке газа 2), среди которых в
последнее время наибольшее внимание привлекают задачи
устойчивости пластин и оболочек в сверхзвуковом потоке3). Ряд
родственных задач, трактуемых, однако, с точки зрения
механики систем с конечным числом степеней свободы,
рассмотрен в книге Р о к а р а 4). Вопросы устойчивости конструкций
при отсутствии потенциала внешних и внутренних сил
обсуждались в книге Хоффа 5).
Дальнейшие параграфы будут посвящены элементарному
введению в существо изучаемого вопроса.
ver, Aircraft Engng. 23, № 274 (1951); Ziegler H.,
Stabilitatsprobleme bei geraden Staben und Wellen, Zeitschr. angew. Math. Phys.,
№ 4 (1951); Troesch A., Stabilitatsprobleme bei tordierten Staben
und Wellen, Ing.-Arch. 20, № 4 (1952); Beck M., Die Knicklast
der einseitig eingespannten, tangential gedruckten Stabes, Zeitschr.
angew. Math. Phys. 3, № 3 (1952); Pfluger A., Zur Stabilitat
des tangential gedruckten Stabes, Zeitschr. angew. Math. Mech. 35,
№ 5 (1955).
*) Капица П. Л., Устойчивость и переход через критические
обороты быстро вращающихся роторов при наличии трения, Журн.
техн. физ. 9, № 2 (1939); Диментберг Ф. М., Изгибные
колебания вращающихся валов, Изд-во АН СССР, 1959; Болотин В. В.,
Исследование автоколебаний гибкого вала, вызванных действием
внутреннего трения и родственных факторов, Научн. докл. высш.
школы, сер. <Машиностроение и приборостроение», №4, 1958;
Болотин В. В., Нелинейные колебания валов за критическими
скоростями вращения, Сб. «Проблемы прочности в машиностроении»,
вып. 1, Изд-во АН СССР, 1958.
2) См., например, книгу: Бисплингоф Р. Л., Эшли X. и
X а л ф м э н Р. X., Аэроупругость, ИЛ, 1958.
3) Болотин В. В., Колебания и устойчивость упругой
цилиндрической оболочки в потоке сжимаемой жидкости, Инж. сборн. 24,
(1956); Hedgepeth J., On the flutter of panels at high Mach
numbers, Journ. Aeron. Sci.23,№ 6 (1956); Мовчан А. А., Об
устойчивости панели, движущейся в газе, Прикл. матем. мех. 21, № 2 (1957);
Болотин В. В., О критических скоростях в нелинейной теории
аэроупругости, Научн. докл. высш. школы, сер. «Машиностроение
и приборостроение», № 3, 1958; Болотин В. В., Г а в р и л о в Ю. В.,
Макаров Б. П. иШвейкоЮ. Ю., Нелинейные задачи
устойчивости плоских панелей при больших сверхзвуковых скоростях,
Изв. АН СССР, ОТН, № 3, 1959; Болотин В. В., Нелинейный
флаттер пластин и оболочек, Инж. сборн. 28 (1960).
4) Рок ар Н., Неустойчивость в механике, ИЛ, 1959.
5) Хофф Н., Продольный изгиб и устойчивость, ИЛ, 1955.

14
ВВЕДЕНИЕ
§ 2. Продольный изгиб центрально
сжатого стержня
Для того чтобы разъяснить причины, приводящие в ряде
случаев к постановке задачи устойчивости, отличной от
классической постановки Эйлера, мы рассмотрим вначале
известную из элементарного курса сопротивления материалов
задачу о продольном изгибе сжатой стойки (рис. 1).
Найдем минимальное значение сжимающей силы Я, при
котором наряду с прямолинейной формой равновесия
впервые становится возможной слегка искривленная форма.
Выбрав оси координат, как показано
I на рис. 1, составим
дифференциальное уравнение упругой линии для
слегка искривленного стержня:
EJ^=P(f-v). (1)
Здесь EJ — жесткость сечения при
изгибе, / — прогиб на конце стержня.
Вводя, как обычно, обозначение
Я
EJ
= k2
(2)
запишем уравнение (1) в виде
Его общий интеграл, очевидно, будет:
v = Сх sin kz -f- C2 cos kz -f- /. (3)
Рис. 1. Для нахождения трех постоянных
Cj, C2 и / имеем три граничных
условия: г>(0) = 0, <?/(0) = 0 и <и (/) = /. Подставляя
выражение (3) в граничные условия, получим три соотношения:
C2+f = 0, |
кСг = 0, (4)
Cl sin kl -\- C2 cos kl = Ot )
представляющих систему трех линейных алгебраических
уравнений относительно трех постоянных Cv C2 и /. Тривиальное
решение этой системы Сг = С2 = f = 0 соответствует прямо-

§ 3] СЛУЧАЙ СТЕРЖНЯ, НАГРУЖЕННОГО «СЛЕДЯЩЕЙ» СИЛОЙ 15
линейной форме равновесия сжатого стержня. Следуя пути,
впервые намеченному Эйлером, выясним условия, при
которых наряду с прямолинейной формой равновесия возможны
близкие к ней слегка искривленные формы. Чтобы
однородная система (4) имела решения, отличные от тривиального,
необходимо, чтобы был равен нулю определитель,
составленный из ее коэффициентов:
О 1 1
у^ 0 0
sin kl cos kl 0
= 0.
Отсюда следует, что cos kl = 0, и минимальное значение
силы, удовлетворяющее этому условию, будет:
ъ2Е1
71 hJ (5)
* 4/2 '
т. е. будет равно эйлерову значению сжимающей силы.
То, что минимальное значение силы Р, при котором
наряду с невозмущенной (прямолинейной) формой стержня
становятся возможными близкие к ней искривленные формы,
является вместе с тем и критическим значением, в
классической теории упругой устойчивости считается
самоочевидным. Это определение критической силы лежит не только в
основе методов, оперирующих непосредственно с
дифференциальными уравнениями равновесия, но и в основе ряда
других методов.
§ 3. Случай стержня, нагруженного «следящей» силой.
Метод Эйлера
Попробуем распространить метод Эйлера на задачу
об устойчивости стойки, загруженной сжимающей силой,
которая поворачивается при изгибе вместе с торцовым
сечением, будучи все время направленной по касательной к
искривленной оси (рис. 2). Вопрос о способах осуществления такой
«следящей» силы пока оставим открытым.
Ввиду предполагаемой малости прогибов РХ^Р, Ру^Ру,
где ср — угол поворота торцового сечения, причем ср^ ?/(/).

16
ВВЕДЕНИЕ
Уравнение упругой линии для слегка искривленного стержня
имеет вид
d2v
EJ
dz2
= P(f — v) — P<f(l—z),
(6)
а его общий интеграл, с учетом обозначения (2), записывается
в виде
v = Сх sin kz -f- C2 cos kz + / -f- <p (/ — z)- (J)
Число граничных условий в данном случае равно
четырем: г;(0) = 0, i/(0) = 0, v(l) = f, <i/(/) = cp. Подстановка
в них выражения (7) приводит
к четырем соотношениям:
С2 + /-ср/ = 0,
Cj sin kl -\- C2 cos kl = 0,
Сг cos &/ — C2 sin ?/ = 0,
определитель которых равен
0 1 1 —/
k 0 Q 1
I sin kl cos kl 0 0
cos kl — sin kl 0 0
= -1,
т. е. отличен от нуля при всех
значениях силы Я. Следовательно, ни при
каких значениях силы Р не
существует криволинейных форм равновесия
Рис. 2. стержня, близких к невозмущенной
(прямолинейной) форме.
А. Пфлюгер и В. И. Феодосьев1), впервые
рассмотрев эту задачу, получили приведенный выше результат
и сделали вывод, что стержень, сжатый «следящей» силой,
вообще не может потерять устойчивости. Чтобы выяснить,
является ли такое истолкование результата правильным, нужно
l) Pfluger A., Stabilitatsprobleme der Elastostatik, Springer-
Verlag, Berlin, 1950, стр. 217; Феодосьев В. И., Избранные
задачи и вопросы по сопротивлению материалов, Гостехиздат, 1953,
стр. 165.

§ 3] СЛУЧАЙ СТЕРЖНЯ, НАГРУЖЕННОГО «СЛЕДЯЩЕЙ» СИЛОЙ 17
проанализировать содержание метода Эйлера, установив его
связь с общепринятыми понятиями устойчивости равновесия
(движения).
Выраженное в технических терминах условие
устойчивости состоит в следующем. Форма равновесия называется
устойчивой, если малые возмущающие воздействия вызывают
малые отклонения системы от рассматриваемой формы
равновесия, причем, уменьшая возмущающие воздействия, можно
сделать эти отклонения сколь угодно малыми. Форма
равновесия называется неустойчивой, если даже сколь угодно
малые возмущения вызывают конечные отклонения системы
от рассматриваемой формы равновесия.
Легко видеть, что метод Эйлера в теории упругой
устойчивости не включает в себе, по существу, понятия
устойчивости. Конечно, при наличии формы равновесия, смежной
с исходной (невозмущенной) формой, последняя может стать
неустойчивой, сменившись на другую форму равновесия.
Однако наличие точки разветвления не является ни
необходимым, ни достаточным условием смены устойчивости.
Исходная форма равновесия может перестать быть устойчивой не
только в точках разветвления, но и в так называемых
предельных точках *). С другой стороны, известны случаи, когда
наличие точек разветвления не приводит к неустойчивости
исходной формы равновесия2). Самое главное соображение
состоит все же в следующем. Применяя статический метод
Эйлера, т. е. рассматривая лишь совокупность форм
равновесия, мы тем самым полностью исключаем из анализа
возможные формы движения. Исходная форма равновесия может
стать неустойчивой, сменившись некоторой формой движения;
между тем при помощи метода Эйлера мы рассматриваем
лишь возможные формы равновесия, близкие к начальной
форме.
Полное решение задачи мы получим, предполагая
возмущения зависящими от времени и составляя уравнения,
!) Болотин В. В., Нелинейная теория упругости и
устойчивость «в большом». Расчеты на прочность, вып. 3, Машгиз,
1958.
2)Ишлинский А. Ю., Малашенко С. В. и Тем-
ч е и к о М. Е., О разветвлении устойчивых положений
динамического равновесия одной механической системы, Изв. АН СССР,
ОТН, № 8, 1958.

18
ВВЕДЕНИЕ
позволяющие проследить поведение возмущений во времени.
Грубо говоря, исследуемая форма равновесия будет
устойчивой, если все возмущения будут ограничены во
времени.
§ 4. Устойчивость по отношению к малым возмущениям
Возвратимся к простейшей задаче об устойчивости стержня,
сжатого силой неизменного направления. Составим уравнение
малых колебаний стержня около прямолинейного положения,
принимая в целях упрощения, что распределенная масса
стержня пренебрежимо мала по сравнению с массой М,
сосредоточенной на конце (рис. 1), и что силами
сопротивления можно пренебречь.
Уравнение малых колебаний имеет вид
EJ^=P(f-v)-M(l-z)^r, (8)
где v(z, t) — динамический прогиб в каждой точке, f (t) —
прогиб на конце. Уравнению (8) можно удовлетворить при
помощи выражений
v (z, t) = V О) е<2', / (0 = FelQe, (9)
где Q — некоторая константа, подлежащая определению. Если
эта константа действительна, то это означает, что стержень
совершает гармонические колебания с частотой 2 около
прямолинейного положения. В этом случае можно считать
(хотя ниже мы увидим, что это не совсем так), что
прямолинейная форма стержня устойчива. Если же окажется, что
2 является комплексным числом, причем его мнимая часть
отрицательна, то это будет соответствовать возмущениям,
неограниченно (вследствие линеаризации задачи)
нарастающим со временем. Действительно, если 2 = а-т-ф, то
V(z, t) = V{z)e^~^)ti
и при р<0 в выражении для v(z, t) появляется
экспоненциально возрастающий множитель.
Перейдем к вычислениям. Подставляя (9) в (8) и
используя обозначение (2), получим:

§ 5] КРИТИЧЕСКОЕ ЗНАЧЕНИЕ «СЛЕДЯЩЕЙ» СИЛЫ 19
Общий интеграл этого уравнения будет:
V(z) = Cldnkz + C2coskz + F + -j^(l — z)F9
граничные же условия остаются прежними: 1/(0)=0, V//(0)=0,
V(l) = F. Используя граничные условия, получим систему
трех линейных алгебраических уравнений относительно Сг,
С2 и F, приравнивание нулю определителя которой дает
«уравнение частот»:
Отсюда
О
k
sin kl
1
О
cos kl
/¦
1
k2EJ
MQ2
k2EJ
0
= 0.
cos kl
Ml sin kl
(10)
kl
cos kl
Пока выражение под радикалом положительно, обе
частоты действительны, т. е. прямолинейная форма стержня
устойчива (в смысле, указанном выше). Частоты обращаются
в нуль при cos kl = 0 и при дальнейшем увеличении силы Р
становятся чисто мнимыми, причем одна из них имеет
отрицательную мнимую часть. Условие cos&/ = 0 соответствует
переходу от устойчивой прямолинейной формы к
неустойчивой форме, а критическое значение силы Р, очевидно,
совпадает с эйлеровым значением (5).
Итак, в задаче об устойчивости стержня, сжатого силой
неизменного направления, метод Эйлера и динамический метод
дают один и тот же результат.
§ б. Критическое значение «следящей» силы
Применим динамический метод к задаче об устойчивости
стержня, сжатого «следящей» силой (см. рис. 2). Уравнение
малых колебаний стержня около положения равновесия имеет
вид
EJ
d2v
dz2
••P(f-v)-PV(l-z)-M^(l-z). (И)

20
ВВЕДЕНИЕ
Подстановкой
:V(z)eiQt, f(t) = FeiQt, ср(0 = Ф^/а/
приведем уравнение (11) к виду
*^_|_ k2V = k2F _ ?2ф (/ _ г) +
Его интеграл
у (2) = Cj sin ?z + C2 cos kz + F — Ф (/ — z)-
MQ2F
EJ
(l-z).
MQ2F
(/-*)
k2EJ
должен удовлетворять граничным условиям: У(0) = 0,
y'(0) = (0), VQ) = F, У'(/) = Ф. Отсюда получаем
«уравнение частот»
MQ4
0
k
sin kl
1
0
coskl
1
k cos &/ — k sin &/ —
&2?/
MQ2
?2?/
0
AfQ2
?2?/
= 0,
решение которого приводит к формуле
Q= ±
V
р
Ml
sin kl
kl
(12)
- cos kl
С увеличением силы Р от нуля собственные частоты растут
по модулю, при
igkl = kl (13)
обращаются в бесконечность, а при дальнейшем увеличении
силы Р становятся чисто мнимыми, оставаясь
противоположными по знаку. Наименьший корень уравнения (13)
соответствует переходу от устойчивой прямолинейной формы к
неустойчивой. Этот корень равен Ы = 4,493, откуда,
учитывая (2), находим, что критическое значение «следящей» силы
составляет:
20,19?/
I2
(14)
Итак, в случае стержня, нагруженного «следящей» силой,
метод Эйлера приводит к ошибочным результатам: прямоли-

§ 6]
ИСТОЛКОВАНИЕ РЕЗУЛЬТАТОВ
21
нейная форма стержня при достаточно больших значениях
силы Р оказывается неустойчивой, хотя в данной задаче и
не существует каких-либо криволинейных форм равновесия
стержня, близких к первоначальной прямолинейной форме.
§ 6. Истолкование результатов.
Роль потенциала внешних сил
В связи с рассмотренными задачами естественно
возникают следующие вопросы. Почему в одном случае метод
Эйлера оказался пригодным, а в другом — нет? Каков
физический смысл явления неустойчивости, обнаруженного во
второй задаче?
Чтобы ответить на эти вопросы, проследим еще раз за
поведением малых отклонений от прямолинейной формы
в обеих задачах. Вместо частот Q введем характеристические
показатели s, связанные с частотами простой зависимостью
5 = /2. Тогда выражение для динамического прогиба стержня
примет вид
v(z, t) = V{z)est. (15)
Прямолинейная форма стержня становится неустойчивой, если
среди характеристических показателей окажется хотя бы один,
обладающий положительной действительной частью.
Поведение характеристических показателей удобно
представить графически, откладывая по оси абсцисс их
действительную часть, по оси ординат — мнимую часть и соединяя
в непрерывные кривые точки, соответствующие различным
значениям силы Р.
На рис. 3, а показана зависимость характеристических
показателей для первого случая (сила неизменного
направления). Когда Р = 0, мы имеем s=±/20, где 20— частота
собственных колебаний незагруженного стержня. С
увеличением силы Р характеристические показатели, оставаясь чисто
мнимыми, уменьшаются по модулю, пока при Р = Р^ не
становятся равными нулю. Обращение в нуль характеристических
показателей как раз соответствует «безразличному»
равновесию— наличию, помимо первоначальной формы равновесия,
других, бесконечно близких к ней форм равновесия. При Р > Р^
один из характеристических показателей оказывается действи-

22
ВВЕДЕНИЕ
тельным и положительным, что соответствует неустойчивости
прямолинейной формы равновесия стержня.
Если в случае силы неизменного направления
характеристический показатель переходит на правую полуплоскость
комплексного переменного, проходя через значение $ = О,
то в случае «следящей» силы (рис. 3, б) он переходит на
правую полуплоскость, минуя это значение. В первом случае
Л, 9
i
Р=Р. \
-* 1
Р>Р,
k
S20l
| Ims
^~
\0 Re
Si,*>
Р>Р*
i -*-
V ~*ц
^X^J
Ims
^^¦/¦.
, Л
Р>Р« Re
о) б)
Рис. 3.
метод Эйлера позволяет обнаружить переход от устойчивости
к неустойчивости, во втором случае он оказывается
непригодным.
Метод Эйлера применим в тех случаях, когда
действующие на тело внешние силы являются
консервативными, т. е. обладают потенциалом (поскольку всюду
в настоящей книге мы рассматриваем идеально упругие тела,
то потенциал внутренних сил во всех задачах существует).
Легко показать, и это будет сделано в соответствующем
месте книги, что в том случае, когда имеется потенциал
внешних сил, переход от устойчивости к неустойчивости
будет происходить только через значение 5 = 0, т. е. в этом
случае метод Эйлера приводит к правильным результатам.
Если же внешние силы не являются консервативными, то
метод Эйлера, хотя и дающий в ряде задач правильное
решение, должен быть заменен более общим динамическим

§ 6]
ИСТОЛКОВАНИЕ РЕЗУЛЬТАТОВ
23
методом, основанным на рассмотрении колебаний системы
около исследуемого положения равновесия.
Нетрудно видеть, что в рассмотренной здесь задаче
«следящая» сила не обладает потенциалом. Признаком
существования потенциала внешних сил является независимость работы,
совершаемой силами, от пути, которым система приводится
в окончательное состояние. На рис. 4 показаны три способа
перемещения стержня в состояние, характеризуемое
поперечным прогибом / и углом поворота торцового сечения ср.
В случае а (поворот на угол ср с последующим смещением)
работа силы Р, очевидно, отрицательна, в случае б
(смещение с последующим поворотом) она равна нулю, а в случае в
(поворот на угол —ср, смещение и окончательный поворот
на угол 2ср) работа положительна.
Из этих рассуждений видна одна особенность, присущая
всем неконсервативным задачам, рассматриваемым в
настоящей книге. В отличие от широко известных и подробно
изученных автоколебательных систем, неконсервативный
характер которых обусловлен «отрицательным трением», в
рассматриваемых здесь задачах определяющую роль играет
парное взаимодействие степеней свободы. Приток энергии
к нагруженному «следящей» силой стержню (рис. 4) возможен
лишь при определенном изменении во времени угла поворота ср
и линейного смещения /. Чтобы это парное взаимодействие
было более очевидным, следовало бы рассмотреть малые

24
ВВЕДЕНИЕ
колебания стержня как системы с двумя степенями свободы
(т. е. в предположении, что масса на его конце не является
точечной). Тогда неустойчивость системы носила бы
колебательный характер с определенным фазовым соотношением
между ср и /, соответствующим поглощению энергии извне.
Рассмотренный выше случай точечной массы следует
трактовать как предельный случай такой системы с двумя степенями
свободы, у которой вторая парциальная частота стремится
к бесконечности.
§ 7. Круг вопросов, рассматриваемых в настоящей книге
Прогресс теории упругой устойчивости в прошлом был
связан главным образом с потребностями промышленного,
гражданского и транспортного строительства. Сила веса и
различного рода силы, также имеющие гравитационное
происхождение, — таковы типичные нагрузки в классической
теории упругой устойчивости.
Развитие современного машиностроения, авиации и
ракетной техники существенно расширило класс нагрузок,
подлежащих изучению. Аэродинамические силы, действующие на
крыло самолета или на обшивку корпуса ракеты, не являются
консервативными силами. То же следует сказать о силах,
действующих на ротор электрической машины или на ротор
газовой турбины. По существу, все системы автоматического
регулирования являются неконсервативными системами.
Поэтому в тех случаях, когда рассматривается упругая
устойчивость звеньев или объектов автоматического регулирования,
воздействие остальных звеньев системы заменяется силами,
которые также являются неконсервативными. Отсюда видно,
что изучение условий устойчивости упругих систем,
нагруженных неконсервативными силами, представляет
значительный интерес для современной техники.
В настоящей книге, помимо общих вопросов, будут
рассмотрены три круга задач. В первую очередь это — задачи
об устойчивости упругих тел, нагруженных «следящими»
силами, т. е. силами, ведущими себя в процессе потери
устойчивости по некоторому закону, отличному от закона
для сил веса. Рассмотренная выше задача об устойчивости
сжатой стойки под действием силы, сохраняющей
направление по касательной к изогнутой оси стержня, была простей-

§ 7] КРУГ ВОПРОСОВ, РАССМАТРИВАЕМЫХ В КНИГЕ 25
шей задачей этого рода (рис. 5, а). Такую силу можно
осуществить, например, используя реакцию струи от
реактивной установки, закрепленной на конце стержня (при
условии, что можно пренебречь инерционной и демпфирующей
составляющими). Другой неконсервативной задачей является
задача об устойчивости стержня, который сжат силой, всегда
направленной вдоль первоначально прямой его оси (рис. 5, б).
Очевидно, что нечто подобное такой силе можно создать при
помощи давления струи, которая направлена вдоль оси
стержня. То, что в обоих случаях потенциал у внешних сил
4 Л |
Г 'I
ч
отсутствует, видно из самого способа их осуществления.
Еще один пример неконсервативных задач упругой
устойчивости получим, рассматривая вал, скручиваемый моментом,
вектор которого в процессе потери устойчивости остается
направленным по касательной к оси вала (рис. 5, в).
Интересно, что случай, когда вектор скручивающего момента
сохраняет свое направление в пространстве (рис. 5, г), также
является неконсервативным. Условий нагружения, близких
к двум последним, можно ожидать в некоторых типах
турбомашин.
Второй круг задач — это задачи об упругой устойчивости
звеньев и объектов систем автоматического регулирования.
Важнейшими среди них являются задачи об устойчивости
гибких валов с регулируемым числом оборотов. Известно,
что даже идеально сбалансированные валы, работая за
критическими числами оборотов, нередко обнаруживают склонность
Рис. 5.

26
ВВЕДЕНИЕ
к опасным изгибным вибрациям. Внешним поводом для
этого могут служить различные факторы: внутреннее трение
в материале вала, трение диска об окружающую среду,
влияние масляной пленки в подшипниках и т. п. Основная же
причина состоит в неконсервативности системы. Если привод
поддерживает постоянную угловую скорость независимо от
поведения вала, то при определенных условиях часть энергии
передается поперечным колебаниям; при этом внутреннее
трение и аналогичные факторы играют роль лишь
передатчиков энергии (рис. 6, а). Похожие явления наблюдаются также
а) б) б)
Рис. 6.
у центрифуг при частичном заполнении жидкостью (рис. 6,(5),
а также у ферромагнитных или токонесущих роторов,
помещенных в магнитном поле (рис. б, в).
Третий круг задач связан с потребностями авиации.
В первую очередь это — широко известная и хорошо
изученная задача о флаттере крыла самолета (рис. 7, а), которая
является типичной неконсервативной задачей упругой
устойчивости. Применяя к задаче об устойчивости крыла метод
Эйлера, мы можем найти лишь критическую скорость
дивергенции (скорость, при которой происходит статическое
перекручивание крыла). Чтобы определить критическую
скорость флаттера, необходимо рассмотреть малые
колебания, совершаемые крылом около положения
равновесия.
В последнее время большое внимание привлекли задачи
устойчивости пластин (рис. 7, б) и оболочек (рис. 7, в), обте-

§ 7] КРУГ ВОПРОСОВ, РАССМАТРИВАЕМЫХ В КНИГЕ 27
каемых потоком газа (так называемые задачи «панельного
флаттера»). Эти задачи, особенно в случае больших
сверхзвуковых скоростей, имеют немало общего с первым классом
задач. Разница между ними состоит скорее в степени
схематизации действующих на упругое тело сил, чем в каких-либо
других особенностях.
Все перечисленные задачи при всем их физическом
различии обладают глубокой математической аналогией, поскольку
все они приводят к несамосопряженным краевым задачам.
В этом состоит существенное отличие рассматриваемого здесь
круга проблем от решаемых в классической теории упругой
устойчивости, все задачи которой ввиду наличия потенциала
внешних сил являются самосопряженными.
Методы исследования неконсервативных задач упругой
устойчивости могут быть разбиты на две группы. К первой
группе принадлежат методы, основанные на непосредственном
анализе дифференциальных уравнений, описывающих
движение упругого тела. Эти методы мы будем условно называть
«точными». Последовательное осуществление этих методов
приводит обычно к большим вычислительным трудностям, и
поэтому до сих пор точно решены лишь некоторые самые
простые задачи. К тому же, теория несамосопряженных
операторов не принадлежит к числу достаточно разработанных
разделов математики, обладающих эффективными методами
фактического построения решений. К другой группе
относятся приближенные методы, суть которых сводится к замене
упругого тела некоторой эквивалентной системой с конечным
числом степеней свободы с последующим анализом этой
эквивалентной системы. Хотя в большинстве прикладных

28
ВВЕДЕНИЕ
задач эквивалентность такой замены не вызывает сомнений,
ее математически строгое обоснование в настоящее время
отсутствует. Некоторые общие закономерности можно
подметить, сопоставляя известные точные результаты с
результатами приближенного решения. Ниже будут использованы
методы, принадлежащие как к первой, так и ко второй
группе. Там, где имеется точное решение, будет дано
сопоставление точных и приближенных решений. В нелинейных
задачах приходится опираться исключительно на
приближенные методы.

ГЛАВА ПЕРВАЯ
ОБЩИЕ ПРИНЦИПЫ
§ 1.1. Предварительные замечания
Основные объекты, которые рассматриваются в теории
упругой устойчивости и для которых самая постановка задачи
устойчивости имеет практический смысл, — это стержни и
стержневые системы, пластины и оболочки. Тем не менее
при изложении общих вопросов теории упругой
устойчивости целесообразно исходить из общих уравнений для
упругого тела. Уравнения для более частных объектов всегда
можно получить из общих уравнений теории упругости, вводя
соответствующие кинематические и статические гипотезы и
применяя вариационные принципы. Следовательно, исходя
из общих уравнений теории упругости, мы выигрываем
в двух отношениях. Во-первых, мы можем рассматривать
проблему упругой устойчивости в целом, не расчленяя ее на
отдельные части (устойчивость стержней и стержневых систем,
устойчивость пластин, устойчивость оболочек). Во-вторых,
мы получаем возможность выводить уравнения для
конкретных объектов единым путем из более общих соотношений
вместо того, чтобы в каждом случае использовать какие-либо
частные (хотя, может быть, и более привычные) приемы.
В силу сказанного при рассмотрении общих вопросов мы
будем всюду исходить из уравнений теории упругости для
произвольного упругого тела.
Исследование устойчивости равновесия упругого тела по
отношению к малым возмущениям (т. е. устойчивости «в малом»)
приводит, как известно, к линейным дифференциальным
уравнениям. Эти уравнения отличаются, однако, от уравнений
классической теории упругости наличием дополнительных
членов, содержащих параметры, с точностью до которых.

30
ОБЩИЕ ПРИНЦИПЫ
[гл. 1
задана внешняя нагрузка. Чтобы получить эти члены,
приходится делать различие между геометрией начального,
невозмущенного состояния, устойчивость которого исследуется,
и геометрией других, близких к нему состояний. В
классической теории упругости это различие, как известно, не
учитывается. Чтобы получить уравнения, описывающие поведение
малых возмущений для заданной формы равновесия,
приходится исходить из уравнений нелинейной теории упругости.
К сказанному необходимо добавить следующее. Если
в основу положить уравнения классической теории упругости,
то в силу теоремы единственности Кирхгофа мы придем
к выводу, что при заданных нагрузках и заданных граничных
условиях возможна лишь единственная форма равновесия.
Между тем сама постановка задачи упругой устойчивости
предполагает возможность существования форм равновесия
(или движения), отличных от невозмущенной. Так, исследуя
устойчивость равновесия в смысле Эйлера, мы ищем те
значения параметра нагрузки, при которых наряду с
невозмущенной формой равновесия существуют смежные с ней
другие формы равновесия.
Нелинейность уравнений теории упругости может быть
как геометрического, так и физического происхождения.
Геометрическая нелинейность связана с необходимостью
различать координаты начального и конечного состояний, а также
с необходимостью пользоваться полными выражениями для
компонентов тензора деформаций. Физическая нелинейность
проистекает от нелинейной связи между компонентами
напряженного и деформированного состояний, с которой в ряде
случаев следует считаться.
В применении к задачам упругой устойчивости
представляется возможным воспользоваться упрощенным вариантом
уравнений нелинейной теории упругости. Вопрос о
возможности таких упрощений подробно разбирался в книге
В. В. Новожилова1). Здесь же мы отметим следующее.
Поскольку речь идет о проблеме упругой устойчивости, то
можно ограничиться случаем малых деформаций, но больших
перемещений. Точнее, при составлении уравнений
устойчивости можно не принимать во внимание различия между
1) Новожилов В. В., Основы нелинейной теории упругости.
Гостехиздат, 1948.

§ 1.1] ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 31
длинами, площадями и объемами до и после деформации.
Это допущение не выходит, очевидно, за рамки прикладных
теорий. Так, в задаче о продольном изгибе сжатого стержня
не имеет практического смысла учитывать изменение длины
стержня или размеров его сечения в процессе нагружения,
так как связанная с этим поправка чрезвычайно мала.
Сказанное не относится к случаю резины и резиноподоб-
ных материалов; но такие материалы мы рассматривать не
будем.
Изучение проблемы упругой устойчивости мы начнем
с краткого изложения нелинейной теории упругости. Хотя
тензорный аппарат и
является здесь весьма
естественным, мы, по
существу, почти не будем им
пользоваться.
Единственное, что будет
заимствовано из тензорного
анализа, — это некоторые
обозначения,
соединяющие свойства
чрезвычайной краткости и
наглядности. За исключением
нескольких мест, мы всюду
будем пользоваться
прямоугольной декартовой
системой координат,
обозначая координаты через хг,
х2, х3 (вместо обычных х, у, г). Напряжения, действующие по
граням прямоугольного параллелепипеда (рис. 8), будем
обозначать оп, о12, ..., а33, не делая различия между
обозначениями для нормальных и касательных напряжений. Тогда
известные уравнения равновесия запишутся в виде (Xv Х2,
Х3— компоненты объемных сил):
Рис. 8.
дхх
dq2i
дхх
dg3i
дхх
dqi2
дх2
д<з22
дх2
д<?32
дх2
<fol3
дх3
да23
дх3
д<?зз
дхг
•Хг = 0,
•Хо
•х*
О,
:0.
(1.1)

32
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
Наконец, будем пользоваться правилом суммирования
по «немым» индексам. Это правило состоит в следующем.
Если в произведение двух или большего числа сомножителей
какой-либо индекс входит дважды (такой индекс называется
«немым»), то это значит, что здесь подразумевается
суммирование по этому индексу, но знак суммы для сокращения
опущен. Так, уравнения (1.1) запишутся теперь в виде
¦S* + *i = 0. (1.2)
причем наличие «свободного» индекса i говорит о том, что
имеется в виду не одно, а три уравнения при /=1, 2, 3.
§ 1.2. Конечные деформации
Изложение нелинейной теории упругости (или, как ее
называют также, теории конечных деформаций) можно найти
в ряде книг1). Здесь будут изложены лишь сведения,
необходимые для понимания дальнейшего текста.
Первое, что отличает теорию конечных деформаций
от классической теории упругости,—-это необходимость делать
различие между геометрией недеформированного и
деформированного состояний. Деформированное состояние может быть
описано несколькими способами. Можно, например,
пользоваться неподвижной системой координат, не связанной с тел^'
(рис. 9, а). Тогда положение какой-либо точки М до
деформации будет характеризоваться тремя координатами xk,
а положение после деформации — тремя координатами
xk = xk-\-uk, где uk — компоненты вектора смещения. (Здесь
и в дальнейшем знак ~ относится к деформированному
состоянию.) Можно поступить и иначе, введя систему
координат, увлекаемую вместе с телом, В недеформированном
состоянии эта система является декартовой, а в
деформированном состоянии она, вообще говоря, становится
криволинейной (рис. 9, б). При этом координаты какой-либо
точки М до и после деформации совпадают, т. е. xk = xk.
Первый способ описания широко применяется в гидроь»еха-
1) Новожилов В. В., цит. выше; Mournaghan F., Finite
deformation of an elastic solid, New York, 1951; Гольденблат И. И.,
Некоторые вопросы механики деформируемых сред, Гостехиздат,
1955.

§ 1.2] КОНЕЧНЫЕ ДЕФОРМАЦИЙ 33
нике и называется способом Эйлера. Второй способ,
называемый способом Лагранжа, по ряду причин
предпочтительнее в теории упругости. В дальнейшем мы будем
пользоваться переменными Лагранжа.
Второе различие между классической и нелинейной
теориями упругости состоит в выборе компонентов
деформированного состояния. В классической теории упругости
компоненты тензора деформаций определяются соотношениями
•» = *(&+&) <'-3>
и имеют смысл относительных удлинений (при I = k) и
половины углов сдвига (при i Ф k). В случае конечных
деформаций это истолкование утрачивается. Казалось бы, что
за характеристики деформации в этом случае следовало бы
Z\m'
м
хг\
ь
\ \
I п
Mill I
Till
0 W~s
И-i 1
Гггп 1
И
III
>|Щ
J м
< *Н
О)
Рис. 9.
^яять точные выражения для удлинений и углов сдвига. Однако
^ги выражения не удовлетворяют условию тензорной
инвариантности и поэтому крайне неудобны для построения общей
теории. Роль характеристик деформации в нелинейной теории
упругости играют компоненты тензора конечных
деформаций
l*~ 2\dxk~t' dxi ^ dxt dxk )' u'^;
механический смысл которых вытекает из следующих
соображений.
6)

34
ОБЩИЕ ПРИНЦИПЫ
[гл. 1
Вычислим разность между квадратом длины произвольно
направленного элемента ds после деформации и до
деформации:
ds2 — ds2 = dx2. — dx2
Здесь
~ dut
dxj = dxJ-+-j^-dxi;
в соответствии с правилом суммирования dx2,
расшифровывается как
dXj dx, = dx2 -\- dx2 -\- dx2.
После вычислений получаем:
ds2 — ds2 = 2eik dxt dxk,
где eik определяется по формуле (1.4). Выражение (1.4)
отличается от (1.3) наличием нелинейных членов.
§ 1.3. Уравнения равновесия и граничные условия
Переходя к уравнениям равновесия и граничным условиям,
заметим, что в случае конечных деформаций само определение
напряжений становится неоднозначным. Помимо того, что
можно пользоваться различными системами координат, можно
по-разному определять компоненты напряжений: относить их
к площадям после деформации или до деформации,
раскладывать по разным направлениям и т. д. По этой причине
уравнения нелинейной теории упругости могут иметь
различный вид, причем переход от одного вида к другому далеко
не всегда легок1). Мы будем здесь пользоваться уравнениями
равновесия в форме, которая обсуждалась еще в классических
исследованиях Кирхгофа и Буссинеска, но
окончательно утвердилась благодаря работам Треффца в области
теории упругой устойчивости2).
1) Анализ различных форм записи уравнений и граничных
условий можно найти в статье: Г а л и м о в К. 3., Уравнения
равновесия теории упругости при конечных перемещениях и их
применение к теории оболочек, Изв. Казанск. фил. АН СССР, сер. физ.-
мат. и техн. наук, № 1, 1948.
2) Trefftz Е., Ober die Ableitung der Stabilitatskriterien des
elastischen Gleichgewichts aus Elastizitatstheorie der endlichen Defor-
mationen, Verhandl. Ill Intern. Kongr. techn. Mech. 3 (1930).

§ 1.3] УРАВНЕНИЯ РАВНОВЕСИЯ И ГРАНИЧНЫЕ УСЛОВИЯ 35
Вначале выведем эти уравнения, исходя из принципа
возможных перемещений. Пусть Ф — внутренняя энергия,
отнесенная к единице объема в недеформированном состоянии.
По смыслу Ф есть функция состояния, причем, если отвлечься
от тепловых явлений, то она зависит только от компонентов
тензора деформаций:
Ф = Ф(еп, е12, ..., е33). (1.5)
Полная энергия, накопленная в теле, очевидно, будет:
U = j<b(xl9 х2, x3)dV, (1.6)
v
где интегрирование производится по объему V недеформи-
рованного тела.
Применение принципа возможных перемещений приводит
к соотношению
W
— f X^dV— f f PlbaldS = 09 (1.7)
где Ьиь — кинематически допустимые вариации смещений,
рь — поверхностные силы, действующие на внешнюю
поверхность тела S. Силы Хь и pt отнесены соответственно к
единице объема и площади, взятых до деформации!).
Займемся вычислением вариации bU. Заметив, что
e*ft = -2(*/* + *« + fyV' (L8)
где для сокращения обозначено
~дхк
запишем вместо (1.5):
Ф = Ф(г/п, vl2f ..., v3Z).
1) Здесь предполагается, что
XldV=XidV, ptdS^pidS,
хотя вследствие допущения о малости изменения площадей и
объемов эта оговорка не имеет существенного значения.

36 ОБЩИЕ ПРИНЦИПЫ [ ГЛ. 1
Тогда, произведя преобразования, аналогичные
преобразованиям при выводе вариационных уравнений Эйлера —
Остроградского ]), найдем:
J dvij dxj
V V
Но согласно формуле Гаусса — Остроградского
!д-шйу-П Ain'ds (1ло)
V S
(здесь rij — компоненты единичного вектора внешней нормали
к поверхности S; известные условия, налагаемые на
компоненты Ал и поверхность 5, в данном случае выполняются).
Отсюда
s J v
Теперь уравнение (1.7) принимает вид
Л47(&)+*ЬД'-Я(?''--»ЬЛ=0-
V S
Приравнивая, в силу произвольности вариаций, множители
при Ьи( нулю, получим уравнения равновесия и граничные
условия на 5:
дФ
Уравнения и граничные условия (1.11) внешне совпадают
с соответствующими соотношениями классической теории
упругости
(1.П)
Л. J
1) См., например, книгу: Курант Р. и Гильберт Д.,
Методы математической физики, т. 1, Гостехиздат, 1951.

§ 1.4] ГЕОМЕТРИЧЕСКОЕ ИСТОЛКОВАНИЕ УРАВНЕНИЙ 37
если в них произвести замену
дФ
дФ
Однако тензор -^— лишь в линейном приближении совпадает
с тензором напряжений в обычном смысле. Вообще же он
даже не является симметричным.
Уравнения (1.11) можно несколько преобразовать, заменив
дФ дФ дв^
и заметив, что вследствие (1.8) и (1.9)
Здесь 8у— символ Кронеккера, т. е.
ft..— 1, если i = /, )
JJ (1.12)
8.j == 0, если i ф j. J
Окончательно уравнения равновесия принимают вид
а граничные условия на загруженной поверхности 5 —
?М-&Ь = Л. СИ)
§ 1.4. Геометрическое истолкование уравнений
Для выяснения физического смысла величин -=— (они
имеют размерность напряжений и в линейном приближении
обращаются в напряжения в обычном смысле) поступим
следующим образом1). Рассмотрим деформированное состояние
бесконечно малого элемента, имевшего до деформации вид
прямоугольного параллелепипеда с ребрами dxv dx2, dx3
1) К a p p u s R., Zur Elastizitatstheorie endlicher Verschiebungen,
Zeitschr. angew. Math, Mech. 19 (1939); Новожилов В. В., цит?
на стр. 32,

38
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
(рис. 10). Внутренние силы, действующие по его граням,
представим в виде векторов аг dx2dxz, <72dxldxZl asdxldx2.
Очевидно, что компоненты векторов «jj, j2» аз представляют
собой напряжения, отнесенные к площадям элемента в его
недеформированном состоянии.
Уравнения равновесия и граничные условия на загруженной
поверхности, будучи записанными в векторной форме, как
обычно, имеют вид
d<3j
dxj
-r-*=0,
ajnj=p.
(1.15)
Рис. 10.
Перепишем эти
соотношения в проекциях на оси
xv х2, хъ, т. е. в лагранже-
вых переменных для неде-
формированного тела. Тогда
вместо (1.15) получим:
ajkliknjl
(1.16)
где Xt и pt имеют такой же смысл, как и раньше,
Ojk — проекции вектора <Уу на координатные направления для
деформированного элемента, lik — косинусы углов между
направлениями оси xt и координатного вектора rk для
деформированного элемента (для плоского случая lik = cosaik, см.
рис. И).
Из геометрических соображений (рис. 12) следует, что
ди.
hk=-
°ik-
dxk
1+^
(1.17)
где Ek — относительное удлинение волокна, которое в
недеформированном состоянии было направлено вдоль оси xk,
по-прежнему символ Кронеккера (1.12). Вводя (1.17)
*»

§ 1.4] ГЕОМЕТРИЧЕСКОЕ ИСТОЛКОВАНИЕ УРАВНЕНИЙ 39
в (1.16), получим:
дщ \
+ *, = <>.
nj = ph
откуда, сравнивая с (1.13) и (1.14), находим, что
дФ aJk
де
jk
l + Ek
(1.18)
Формула (1.18) позволяет дать следующее толкование
тензору дФ/де*к: с точностью до приближенного соотношения
1 -{-Ektt 1 величины дФ/де]к представляют собой компоненты
тензора напряжений в лагранжевых переменных, отнесенные
Рис. И.
не к действительным площадям, а к площадям, взятым
до деформации. Как уже указывалось, при рассмотрении
вопросов упругой устойчивости вполне допустимо считать
перемещения (включая углы поворота) конечными, а
изменения площадей и линейных размеров—пренебрежимо малыми.

40
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
В таком случае разница между дФ/dej^ и Ojk исчезает, а также
исчезает разница между напряжениями а;7е, отнесенными
к первоначальным площадям, и «истинными» напряжениями
в лагранжевых переменных. Уравнения
и граничные условия
диЛ1
будут положены в основу дальнейшего анализа. Как уже
*г
/
( /
1
0
дх.
дх,
*i
Рис. 12.
указывалось, точность уравнений (1.19) и (1.20) не меньше,
чем точность соответствующих прикладных теорий стержней,
пластин и оболочек.
§ 1.5. Связь между напряжениями и деформациями
Свойства материала характеризуются выражением для
плотности внутренней энергии
Ф = Ф(еп, е12, .... egg).
Как и в классической теории упругости, может быть
предложена зависимость
<&=-jW*a?; (i-2i)
дсесь \щ — тензор упругих постоянных, симметричный отно-
знтельно перестановки индексов ink, аир, а также их

§ 1.6] КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 41
пар. Для изотропного тела тензор \1Ы^ выражается через
две постоянные Ляме X и [г.
^? = >ЛЛз + 21*8/Л?. (1.22)
Используя приближенную зависимость
дФ
получим из (1.21) обычное соотношение между напряжениями
и деформациями:
§ 1.6. Криволинейные координаты
Предыдущее изложение строилось для простейшего случая
прямоугольной декартовой системы координат. Во многих
разделах теории упругости и, особенно, в теории упругих
оболочек переход к криволинейным координатам становится
совершенно необходимым.
Для того чтобы представить уравнения нелинейной теории
упругости в форме, пригодной для любой криволинейной
системы координат, воспользуемся методами тензорного
анализа !). Собственно, основной задачей тензорного анализа и
является исследование таких величин и математических
операций над ними, которые сохраняли бы один и тот же вид
для возможно более широкого класса систем координат.
Применение тензорного анализа крайне облегчает
преобразование уравнений, записанных для прямоугольной декартовой
системы координат, к произвольным криволинейным
координатам, сводя это к чисто формальной операции.
Положение точки в пространстве может быть задано тремя
криволинейными координатами qv q2, qz. При этом функции
4i = 4i(xv x2, х3) (1.24)
мы будем предполагать однозначными, непрерывными и
имеющими непрерывные производные стольких порядков, сколько
нам в дальнейшем потребуется. Кроме того, будем
предполагать, что якобиан преобразования (1.24) во всех точках
отличен от нуля.
1) Кочин Н. Е., Векторное исчисление и начала тензорного
исчисления, Изд-во АН СССР, 1951.

42
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
Важнейшим свойством криволинейной системы координат
является ее метрика, характеризуемая квадратом расстояния
между двумя бесконечно близкими точками пространства.
Для прямоугольной декартовой системы это расстояние дается
формулой
ds2 = dx\ -\- dx\ -f- dx\,
в общем же случае криволинейных координат
ds2 = glkdqtdqk. (1.25)
Здесь gik— так называемый метрический тензор,
причем gik = gki. В случае декартовой системы координат,
очевидно, gik = bik, где bik — символ Кронеккера. Для
цилиндрических координат г, ср, z имеем:
ds2 = dr2 -)- г2 df2 -|~ dz2
т. е. метрический тензор будет:
8ik =
110 0
' 0 г2 0
0 0 11
Рассмотрим теперь способы задания вектора в
произвольной системе координат. Вектор А будет задан, если известны
его ортогональные проекции на направления касательных
к координатным линиям. В элементарной механике имеют
дело именно с этими составляющими, называемыми в
тензорном анализе физическими составляющими. Для построения
общей теории эти составляющие оказываются неудобными.
По существу, они являются лишь составляющими вектора для
местной декартовой (в общем случае — косоугольной) системы
кооординат, т. е. не являются «истинными» составляющими
для криволинейной системы координат.
Поясним сказанное на примере цилиндрических
координат г, ср, z. Физические составляющие дифференциала радиуса-
вектора будут, очевидно, равны dr, rdy, dz, однако было
бы формально проще и с математической точки зрения
естественнее определить их как dr, dy, dz. При этом их
физическая размерность становится неодинаковой, однако они
приобретают общую размерность в более широком смысле —
общую тензорную размерность. Аналогично для произволь-

§ 1.6] КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 43
ного вектора А наряду с физическими составляющими Лг,
Лг Az можно ввести составляющие
аг = АГ, а? = —— , az = Az.
г г z
Их размерность теперь соответствует размерности dr, dy, dz,
и, более того, при переходе от одной системы координат
к другой они преобразуются по тем же законам, что и
дифференциалы координат dr, д?ср, dz. Такие составляющие
называются контравариантными.
Для обозначения контравариантных составляющих принято
пользоваться верхними индексами (которые, конечно, не
являются показателями степени). Поскольку дифференциалы
координат являются контравариантными векторами, то сами
координаты также принято снабжать верхними индексами:
q1 = xli q2 = x2, q3 = x3. При переходе от одной системы
координат к другой, т. е. при преобразовании
xi=-xi(xl1 х2, х3),
контравариантные составляющие преобразуются по формулам
al = —~ak.
dxk
Наряду с контравариантными составляющими вектора
вводят также ковариантные составляющие аь = gikak. Так,
в рассмотренном выше случае цилиндрической системы
координат ковариантные составляющие вектора будут равны
аг=Ап a<9 = rAy, az = Az. Закон преобразования для
ковариантных составляющих имеет вид
- dxk
-^=^-а
дх1 k'
Связь между этими составляющими и физическими
составляющими дается формулами
А=тА=- (1.26)
V gu
(здесь по индексу / суммирование не производится!).
Для прямоугольной декартовой системы координат
gik = ^ik и> следовательно, ak = ak = Ak. Различие между
всеми этими составляющими здесь полностью исчезает.

44
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
Вектор можно рассматривать как тензор первого ранга
(а скаляр — как тензор нулевого ранга). Тензор второго
ранга может быть определен при помощи ковариантных
составляющих bik, контравариантных составляющих blk и
смешанных составляющих blk или btk (если тензор является
симметричным, то смешанные составляющие можно
обозначить просто через Ь1Л. При переходе от одной системы
координат к другой компоненты преобразуются по некоторым
правилам, которые, собственно, и являются признаком того,
что данные числа характеризуют тензор второго ранга.
Например, для ковариантных составляющих закон
преобразования имеет вид
— дх* дх$
гКа-
дх1 дх1
Переход от одних составляющих к другим сводится к
операциям «поднятия» или «опускания» индекса при помощи
умножения на метрический тензор. Так,
Смешанные компоненты метрического тензора представляют
собой символ Кронеккера, т. е. р1 = Ъ
Переходим к самой важной операции тензорного анализа —
к операции тензорного дифференцирования. Для ее
пояснения рассмотрим вначале простейший случай, сопоставив
А+ДА
м
м'
'^
А
+АА
'А
*)
Рис. 13.
прямоугольную декартову систему координат и полярную
систему координат на плоскости (рис. 13). Производная от
вектора характеризует изменение вектора при переходе от

§ 1.6) криволинейные координаты 45
одной точки поля к другой, бесконечно близкой к первой.
Возникает вопрос, в какой мере это изменение может быть
описано при помощи производных от компонентов вектора.
В случае прямоугольных декартовых координат частные
производные
дЛх дЛу дЛх дЛу
дх ' ду ' ду ' дх
составляют тензор — первую производную от вектора А,
называемую также дивергенцией вектора. В случае полярных
координат частные производные
дАг дА9 дЛг дЛ9
~дГ' ~д^~' ~Щ~' ~дГ>
взятые сами по себе, не могут еще охарактеризовать
изменение вектора А. Объясняется это тем, что при параллельном
переносе вектора А из точки М в смежную точку М,' (рис. 13)
меняется метрика пространства, и это изменение метрики
должно быть учтено при вычислении производных от вектора.
Указанное обстоятельство хорошо знакомо читателю вне всякой
связи с тензорной трактовкой. Например, в классической
теории упругости относительные удлинения выражаются через
перемещения и и v в направлении координатных осей по-
разному в различных системах координат: если в
прямоугольной декартовой системе
да dv
ехх -fa > eyy -jy >
то в полярной системе координат
да 1 dv , a
второй член в формуле для е^ учитывает как раз
изменение метрики (формулы записаны в «физических»
составляющих).
Тензорная производная от вектора равна соответствующей
частной производной, к которой добавляются некоторые
слагаемые, учитывающие изменение метрики при переходе к
смежной, бесконечно близкой точке. Так, ковариантная производная
от ковариантных составляющих at вычисляется по формуле
^ а1=Щг — Т)ьа,9

46
ОБЩИЕ ПРИНЦИПЫ
[гл. 1
где Yik — так называемые символы Кристоффеля, которые
выражаются через компоненты метрического тензора
следующим образом:
1*=р?Г Г _ * / d^k dgtVk dgik \
ik 8 ¦*./*• *.tb — 2 [ dxi -Г dxk -Г dxV. J •
Производные Vkat образуют ковариантный тензор второго
ранга, однако символы Кристоффеля (равно как и частные
производные от вектора) не являются тензорами.
Аналогично ковариантная производная от контравариантных
составляющих вектора определяется по формуле
В некоторых случаях удобно введение контравариантных
производных:
Vfy = gkxVxat\ lkal = gkxVxal.
Приведем также правила дифференцирования тензора
второго ранга:
dbij х х
Чфц = —?- — Tikhj — Tjkba,
(аналогичные правила для контравариантных производных и
производных от смешанных составляющих не выписываем).
§ 1.7. Уравнения нелинейной теории упругости
в произвольной криволинейной системе координат
Если величины, входящие в некоторое уравнение, имеют
тензорный характер, то переход от уравнения, записанного
для прямоугольной декартовой системы координат, к
уравнению, которое пригодно для любой криволинейной системы
координат, осуществляется весьма просто. Частные
производные должны быть заменены соответствующими тензорными
производными, а «физические» составляющие векторов и
тензоров — их ковариантными и контравариантными
составляющими. При этом тип составляющих выбирается таким образом,
чтобы соблюдались требования тензорной размерности, т. е.

§ 1.7] УРАВНЕНИЯ НЕЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ 47
чтобы каждое слагаемое, входящее в уравнение, имело
одинаковый тензорный ранг и чтобы «свободные» индексы, по
которым суммирование не производится, были одинаковы во
всех слагаемых. Например, вместо формул для компонентов
тензора деформаций в декартовых координатах (1.4)
получается формула для ковариантных составляющих в
произвольной криволинейной системе координат:
»/* = \ (V*V, + Vi4 + V,«yV4«>). (1.27)
Уравнения равновесия (1.13) и граничные условия (1.14)
могут быть записаны в виде
M^i + V'JJ+^O. (1.28)
°Jk(gik + Vk*t)nJ = Pl- (1.29)
Здесь X1 и р1 — контравариантные составляющие вектора
объемных сил и вектора поверхностной нагрузки,
где Ф— по-прежнему плотность упругой энергии тела
(скаляр).
Все слагаемые в формуле (1.27) имеют размерность ко-
вариантного тензора второго ранга со свободными
индексами / и k\ все слагаемые в формулах (1.28) и (1.29) —
размерность контравариантного вектора со свободным
индексом /. Там же, где производится симмирование по «немым»
индексам, эти индексы встречаются дважды: один раз в
верхнем положении, другой раз обязательно в нижнем положении.
Умножая почленно каждое из соотношений на компоненты
метрического тензора, мы получим те же физические
соотношения, но представленные в иной тензорной размерности.
Чтобы перейти к конкретной криволинейной системе
координат, необходимо вычислить символы Кристоффеля для этой
системы и выразить тензорные производные через обычные
частные производные. Далее, если это целесообразно, можно
перейти к «физическим» составляющим по формулам типа (1.26).
В дальнейшем мы будем прибегать к криволинейным
координатам лишь в некоторых необходимых случаях.

48
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
§ 1.8. Постановка задачи об устойчивости.
Уравнения в вариациях
Перейдем непосредственно к проблеме упругой устойчивости.
Само по себе понятие «устойчивости» или «неустойчивости»
является довольно трудным и допускает различные толкования,
что не раз служило источником недоразумений ]). Крупнейшей
заслугой А. М. Ляпунова является введение такого
определения устойчивости равновесия (в общем случае — движения),
которое, будучи математически строгим, вполне соответствует
нашим интуитивным, почерпнутым из повседневного опыта
представлениям об этом понятии, а также большинству
технических приложений. Определение устойчивости по
Ляпунову, выраженное в математических терминах, можно найти
в любом учебнике по теории устойчивости движения или
в достаточно полном курсе теории колебаний2).
В дальнейшем мы будем всюду говорить об устойчивости
(неустойчивости) некоторой формы равновесия. Эту форму
равновесия мы будем называть невозмущенной. Наряду с
невозмущенной формой равновесия будем рассматривать
некоторые достаточно близкие к ней возмущенные формы
движения.
Равновесие называется устойчивым, если малые «причины»
вызывают малые отклонения от положения равновесия, и,
более того, делая эти «причины» сколь угодно малыми, мы
получаем сколь угодно малые отклонения от невозмущенного
равновесия. Если отклонения от положения равновесия, будучи
малыми, асимптотически стремятся к нулю при времени
t—>oo, то равновесие называется асимптотически
устойчивым. Это, очевидно, более сильный случай устойчивости,
чем первый. Наконец, если даже сколь угодно малые
«причины» вызывают конечные отклонения от невозмущенного
равновесия, то оно называется неустойчивым.
Данные выше формулировки не являются строгими. Так,
остается неопределенность в отношении того, что понимать
1) Р. Беллман назвал понятие устойчивости «сильно
перегруженным термином с неустановившимся определением»
(Беллман Р., Теория устойчивости решений дифференциальных
уравнений, ИЛ, 1954).
2) См., например, Ч е т а е в Н. Г., Устойчивость движения,
Гостехиздат, 1956,

§ 1.8] ПОСТАНОВКА ЗАДАЧИ OB УСТОЙЧИВОСТИ 49
под «причинами», вызывающими отклонения от
невозмущенного равновесия, и под самими отклонениями. Если речь
идет об устойчивости равновесия некоторого упругого тела
(стержня, стержневой системы, пластины или оболочки), то
роль возмущающего воздействия могут играть различные
малые импульсы, малые дополнительные нагрузки, не
учтенные в расчете, малые дефекты и отступления от проектных
размеров и т. п. Мерой же отклонения от невозмущенного
равновесия могут служить как перемещения и деформации,
так и дополнительные напряжения или другие силовые
характеристики.
Во многих случаях для суждения об устойчивости
(неустойчивости) равновесия можно предположить возмущения
достаточно малыми и исследовать их характер, исходя из
линеаризированных дифференциальных уравнений. Эти
уравнения, следуя Пуанкаре, называют уравнениями в вариациях.
Покажем порядок их составления применительно к задаче
об устойчивости форм равновесия упругого тела.
Рассмотрим некоторое невозмущенное равновесие упругого
тела, характеризуемое вектором перемещений ut, тензором
напряжений aik, векторами объемных и поверхностных сил X-t
и рь. Характеристики невозмущенного равновесия подчиняются
уравнениям (1.19) и граничным условиям на
поверхности (1.20):
щЫь+-Ш+*=°-1
/ да-\ (1-30>
<Ц8«+*?)», = л- ]
Дадим телу некоторые малые отклонения от невозмущенного
равновесия и проследим за тем, как эти возмущения
изменяются со временем. Компоненты характеристик
возмущенного движения (мы будем снабжать их значком —, а
возмущения обозначать черточкой наверху) будут иметь вид
xi = X{ + Xt — p -~ ,

50
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
Здесь Xi и pt — возмущения объемных и поверхностных сил,
которые в общем случае зависят от времени t. Силы инерции
также, по существу, являются возмущениями объемных сил,
однако для удобства дальнейших рассуждений они выделены;
р — плотность материала тела.
Компоненты возмущенного движения также должны
удовлетворять уравнениям и граничным условиям типа (1.30):
(8*+¦&)"' = л-
Подставляя сюда (1.31) и учитывая (1.30), получим
уравнения возмущенного движения
(1.32)
и граничные условия
Теперь используем условия малости возмущений. Это по-
— диг
зволяет опустить в уравнениях слагаемые Ojk -~-, поскольку
они начинаются с членов второго порядка малости. Что
касается тензора aik, то его легко выразить через вектор ui%
используя формулы (1.4) и (1.23). С точностью до членов,
линейных относительно ut, имеем:
aik — 2 a/*«pUjcp + дха ) ~ ik^ дхр
(здесь использованы условия симметрии тензора \-йар).
Последнее упрощение, которое мы сейчас введем, носит
более специальный характер. В подавляющем большинстве
технических задач, с которыми приходится встречаться,
невозмущенное состояние сравнительно мало отличается от
первоначального недеформированного состояния и лишь переход
от устойчивости к неустойчивости характеризуется быстрым
нарастанием перемещений. Поэтому при решении прикладных

§ 1.8] ПОСТАНОВКА ЗАДАЧИ ОБ УСТОЙЧИВОСТИ 51
задач упругой устойчивости геометрия невозмущенного
равновесия, устойчивость которого исследуется, обычно
отождествляется с геометрией недеформированного состояния.
Количество задач, в которых влияние перемещений,
предшествующих потере устойчивости, было подвергнуто исследованию,
весьма невелико. В качестве примера укажем на задачу об
устойчивости плоской формы изгиба полосы, которая была
рассмотрена Пфлюгером1) с учетом ее начального прогиба
в плоскости наибольшей жесткости.
Влияние перемещений перед потерей устойчивости
учитывается в уравнениях (1.32) и граничных условиях (1.33)
членами, содержащими dujdxk. Опуская эти члены, мы получаем
дальнейшее упрощение уравнений. Вместе с тем следует
отметить, что исследование эффекта, вызванного этими
членами, является совершенно самостоятельным аспектом теории
упругой устойчивости.
После всех упрощений уравнения в вариациях и
соответствующие граничные условия принимают вид
aafii + a,-fr -т-^ #» = Pi-
x нужно рассматривать совместно с соотношениями
п — 1 д"«
(1.34)
(1.35)
(1.36)
Невозмущенное равновесие будет устойчивым или
неустойчивым в зависимости от поведения возмущений при t-^oo.
Если все решения системы (1.34) с краевыми условиями (1.35)
затухают со временем, то равновесие является устойчивым.
Часто встречающийся случай, когда система (1.34) с краевыми
условиями (1.35) имеет только периодические решения, мы
также будем условно квалифицировать как устойчивость. Если
среди решений найдется хотя бы одно, неограниченно
возрастающее во времени, то равновесие является неустойчивым.
Здесь мы полагаем, что аналогично классическим теоремам
в теории устойчивости движения могут быть доказаны
l) P f 1 u g е г A., Stabilitatsprobleme der Elastostatik, Springer-
Verlag, 1950.

52
ОБЩИЕ ПРИНЦИПЫ
[гл. 1
теоремы, позволяющие судить об устойчивости нелинейной
континуальной системы по линеаризированным уравнениям ее
движения.
Допустим, что действующие на систему силы заданы
с точностью до некоторого параметра (3. Задача состоит в том,
чтобы найти критическое значение параметра р, начиная с
которого невозмущенная форма равновесия перестает быть
устойчивой.
§ 1.9. Различные случаи поведения нагрузки
Известно, что характер поведения нагрузки при малых
отклонениях тела от невозмущенного равновесия может
оказать существенное влияние на устойчивость (неустойчивость).
Рассмотрим теперь этот вопрос более подробно.
Наиболее распространенный вид нагрузки — это «мертвая»
нагрузка, которая остается неизменной как по величине, так
о) 6)
Рис. 14.
и по направлению и при малых отклонениях тела от
начального положения перемещается вместе с соответствующей
точкой тела (рис. 14, а). В проекциях на неподвижные оси
компоненты такой нагрузки, очевидно, остаются неизменными,
т. е. Х. = р. = 0.
Рассмотрим теперь случай «следящей» нагрузки, которая,
оставаясь постоянной по величине и перемещаясь вместе с телом,
поворачивается таким образом, что углы, составляемые
вектором нагрузки с координатными векторами лагранжевого
базиса, остаются неизменными (рис. 14, б).

§ 1.9] РАЗЛИЧНЫЕ СЛУЧАИ ПОВЕДЕНИЯ НАГРУЗКИ 53
Направляющие косинусы координатных векторов после
деформации определяются согласно формуле (1.17):
» . да*
lJ l+Ej "^ dxj
откуда возмущенные значения нагрузки
Xt — Xjly :
¦¦*'+*,%¦ 1
(1.37)
Pi = Pjhi^Pi + Pl-g?-
Следовательно, в случае «следящей» нагрузки
^ = Х,-Щ, -Р1 = Р,Щ. (1-38)
Предположим, что объемные и поверхностные силы
составляют поле, зависящее от эйлеровых координат точки.
В этом случае
Xt(xv Х2, *з) = */(*1 + «1. *2 + ^ь *3 + "з) =
pt(xv x2t хг) = Р1(х1 + и1у х2 + и2, х3 + %):
dpi
dxk
<Pi + &«u+-.
откуда
*i = |?".. Л = #-»»• (Ь39)
Более специальный пример дает случай воздействия
аэродинамических сил на тело, находящееся в потоке жидкости
или газа. Наиболее просто эти силы вычисляются в случае
обтекания тела невязким сжимаемым газом со скоростью U,
значительно превышающей скорость звука с^ (рис. 15).
В этом случае давление газа на возмущенную поверхность
складывается из невозмущенного значения р и избыточного

54 общие принципы (гл. i
давления, которое определяется по приближенной формуле1)
(1.40)
хРоо /ди3
р = — I-
Соо \ dt
даъ\
дх\ / '
Здесь х — отношение удельных теплоемкостей газа. Таким
образом, для плоской
пластины вектор
возмущений поверхностной
нагрузки будет:
—>-
/?оо-»-/7
Pi
Рис. 15.
0
0
*Рао 1 ди
Соэ
( ди3 ди3 \
Рассмотренные выше случаи укладываются в общую
зависимость вида
dut
ди*
dt
•d,
— r — r duj i j
pt = atjuj -f bijk -щ + си -g;- + dtjk
d2uf
duj
V* dxkdt
d2uj
dxk dt
(1.41)
Здесь dij, bij^ •••, d'k — некоторые коэффициенты, не
зависящие от вектора uk и его производных, но меняющиеся,
вообще говоря, от точки к точке.
§ 1.10. Статическая краевая задача
Рассмотрим статическую задачу, соответствующую системе
(1.34) с краевыми условиями (1.35). Допустим, что все
внешние силы заданы с точностью до параметра (3. Тогда можно
записать, что
ву* = Р°5г ^ = К- /», = Ptf.
) Подробности см. в четвертой главе настоящей книги.

§ 1.10] СТАТИЧЕСКАЯ КРАЕВАЯ ЗАДАЧА 55
где а* , X* и р* не зависят от [3, но линейно зависят от иь.
Мы приходим, таким образом, к однородной линейной
системе
?(чн1!г)+р4К-&)+|Я!-0 (,-42)
с граничными условиями на поверхности 5:
Звездочки у с* , ЛГ* и /?* в дальнейшем опускаем.
Классическая постановка задачи об упругой устойчивости сводится
к отысканию минимальных по модулю действительных
собственных значений линейной краевой задачи. В связи с этим
возникает вопрос об условиях, которые должны быть
наложены на внешнюю нагрузку для того, чтобы поставленная
таким образом задача имела решение. Общего ответа на
поставленный вопрос не существует. Однако могут быть легко
получены достаточные условия того, чтобы краевая задача
имела только действительные собственные значения.
Как известно 1), если линейная краевая задача является
самосопряженной, то все ее собственные значения
действительны. Пусть иь и vt — два вектора с дважды
дифференцируемыми компонентами, удовлетворяющие граничным
условиям (1.43) на поверхности 5 и условиям ui = 0i vt = 0
на остальной части поверхности тела. Краевая задача является
самосопряженной, если в силу граничных условий
обращается в нуль выражение
A=/^i(«i. "2, u3)dV- fHfo(vv v2, v3)dV = 0(\A4)
V V
при любом выборе векторов ut и vit удовлетворяющих этим
условиям. Здесь 2/ — левые части уравнений (1.42).
Покажем, что условие (1.44) выполняется в случае, когда
Xt = Pi = 0. Применяя формулу Гаусса — Остроградского,
1) См., например, Н а й м а р к М. А., Линейные
дифференциальные операторы, Гостехиздат, 1954; М и х л и н С. Г., Проблема
минимума квадратичного функционала, Гостехиздат, 1952, и др.

56 ОБЩИЕ ПРИНЦИПЫ [ГЛ. 1
найдем, что
= //°<V«TtnidS~n"Л« ТГГ, "IdS-
S ? S ?
V V
=11 "ъ* ? nidS -11 »ъ* Ц nJdS-
s s
Отсюда
J vfii («i, «2. «3)rfV— J ufit(vv v2, v3)dV =
V V'
S l
s H
Но подынтегральные выражения в правой части обращаются
в нуль вследствие условий (1.43), откуда вытекает, что при
Xt = Pi = 0 («мертвая» нагрузка) статическая краевая задача
является самосопряженной. Этот результат не является
неожиданным. Нетрудно показать, что уравнения (1.42) и
граничные условия (1.43) играют соответственно роль уравнений
Остроградского — Эйлера и естественных граничных условий
для вариационной задачи об отыскании стационарных
значений функционала:
'=тЛ«ц #+u°«f kdv- <l45)
V Р V
Первый член в правой части представляет собой приращение
энергии деформации при отклонении системы от исследуемого
положения равновесия, второй член — приращение работы
внешних сил, выраженное через компоненты тензора о^.

§ 1.10] СТАТИЧЕСКАЯ КРАЕВАЯ ЗАДАЧА 5?
Заметим, что функционал / с точностью до множителя г/2
равен второй вариации Д2<9 полной энергии системы Э. (Эта
вариация вычисляется в предположении, что вариации
перемещений равны возмущениям uj).
Допустим теперь, что Xt Ф О, рьФ 0. Левая часть
условия (1.44) принимает для этого случая вид:
A:= fv^t(uv «2, u3)dV — f u^t{vv v2, v3)dV =
I" J* fljAi (alf «2, u^dV + jf vtpt(uv u2, иг) ds]-+-
s J
j utX{ (vlt v2t v3) dV^-jjuipi (vv v2, t>3) dS
_v
+
У S
Чтобы краевая задача была самосопряженной, необходимо и
достаточно, чтобы выполнялось условие
/ ^Д («1. %, U3) dV + ff Vi Pi (Ul> U2> Цъ) dS =
V S
= j "ЛЦ. ^2» vz)dV-jrjj^iPi(^v v2> v^dS, (1.46)
v s
имеющее очевидный механический смысл: оно требует, чтобы
для совокупности всех внешних нагрузок, приложенных
к телу, выполнялась теорема о взаимности работ.
Условие (1.46) эквивалентно условию существования
потенциала внешних сил П. Если потенциал существует, то
виртуальная работа внешних сил при переводе системы из
состояния, характеризуемого векторным полем #., в смежное
состояние Uj -\- buj является функцией состояния и может быть
выражена через вариацию потенциала II:
f(Xi + Xi)buidV + ff(pi-+-pi)buidS = bIL. (1.47)
v s
Для обозначения вариации здесь используется обозначение Ш
в отличие от вариации АП, связанной с переходом из
состояния Uj в состояние Uj-{-Uj. Эквивалентность условий (1.46) и
(1.47) легко может быть доказана аналогично тому, как в
теории упругости и строительной механике доказывают теорему

58
ОБЩИЕ ПРИНЦИПЫ
(гл. 1
Бетти, исходя из факта существования потенциала внешних
и внутренних сил.
Если потенциал внешних сил существует, то будем
называть силы консервативными. Заметим, что здесь используется
более общее понятие о консервативных силах, чем это
принято в теоретической механике. Каждая из внешних сил
может и не обладать потенциалом. Важно лишь, чтобы
совокупность всех внешних сил, приложенных к телу, обладала
потенциалом, или, иначе, чтобы система сил в целом являлась
консервативной. Такое определение более соответствует
техническим приложениям, в которых представление о
консервативном (неконсервативном) характере внешних сил
связывается с отсутствием (наличием) внешних источников или
потребителей энергии.
Если условия (1.46) или (1.47) выполняются, то задача
об устойчивости в смысле Эйлера соответствует вариационной
задаче о минимуме функционала
V р V
Здесь А2П — вторая вариация потенциала внешних сил. В
случае «мертвой» нагрузки потенциал, очевидно, существует, и
он равен
П0 = j Xflt dV + ff P^i dS + const.
V S
Если силы составляют поле, зависящее от эйлеровых
переменных, то
п=по+4 /If «^+y f/U~u^dS-
v s
В случае «следящих» сил потенциала, вообще говоря, не
существует. Остановимся на некоторых исключениях. При
v
или, иначе, при
f X^dV + f f pibaldS = 0
7 S
I

§ 1.10] СТАТИЧЕСКАЯ КРАЕВАЯ ЗАДАЧА 59
потенциал «следящих» сил будет равен П0. Условие (1.48)
выполняется, например, если все точки, в которых приложены
внешние силы, закреплены либо от перемещений, либо от
поворотов. Тогда дополнительные составляющие «следящих»
сил, которыми последние отличаются от «мертвой» нагрузки,
не совершают работы на совместимых со связями
перемещениях (рис. 16).
Случай равномерно распределенной по какой-либо части
внешней поверхности тела нагрузки, остающейся нормальной
к деформированной поверхности, пред-
р ставляет особый интерес. Такая нагрузка
называется обычно гидростатической. Если
эта нагрузка действительно создана
Рис, 16.
Рис. 17.
давлением покоящейся жидкости, то она, очевидно, является
консервативной. Однако нередко так схематизируются нагрузки,
которые по своему характеру не относятся к
консервативным силам 1).
Рассмотрим оболочку, отнесенную к некоторым
криволинейным координатам срединной поверхности л:1 и л:2;
хг — координата, отсчитываемая по внешней нормали к
срединной поверхности (рис. 17). Пусть dS — площадь элемента
срединной поверхности до деформации. Тогда после
деформации
dS = dS{\ +Vatfa),
*) Дальнейшее содержание настоящего параграфа предполагает
знакомство с элементами тензорного анализа хотя бы в объеме
§§ 1.6 и 1.7 настоящей книги.

60
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
где индекс а пробегает значения 1 и 2. Допустим, что
оболочка загружена равномерным давлением р, направленным по
нормали к срединной поверхности. Вектор поверхностной
нагрузки после деформации с точностью до линейных членов
будет равен
-pvy
Р =
pV3u*
— Р
Отсюда виртуальная работа внешних сил на совместимых со
связями перемещениях Ьиа(а= 1, 2) с точностью до
линейных членов оказывается равной
bA = -pf f{(\+Vau«)bu, + V3u«bua]dS. (1.49)
Используем теперь гипотезу Кирхгофа— Лява: V3#a:=—Va#3.
Применяя формулу Гаусса — Остроградского
j j Vatf3 К dS= j u3 bua dT* — J j и3Ь (Vatfa) dS
s г s
и полагая, что интеграл по контуру Г, ограничивающему
загруженную часть 5, будет
f u3buadTfl = 0, (1.50)
г
запишем выражение (1.49) в виде
ЬЛ = - р f f [(1 + Va««) Ьиг + и3Ь (Vaa«)] dS.
s
Легко видеть, что виртуальная работа ЬЛ может быть
теперь выражена через потенциал
Jl = — p f f(\+Vau*)u3dS.
Здесь существенную роль играет обращение в нуль
интеграла (1.50). Он будет равен нулю, например, если всюду
на границе Г обращается в нуль либо нормальное
перемещение я3» либо тангенциальное перемещение u0LdYa, При за-

§ 1.11]
МЕТОД ЭЙЛЕРА
61
гружении части поверхности со свободно смещающейся
границей так называемая «гидростатическая» нагрузка оказывается,
вообще говоря, неконсервативной. Разумеется, в этом случае
она не может быть реализована лишь за счет давления
покоящейся жидкости ]).
§ 1.11. Исследование колебаний около положения
равновесия и метод Эйлера
Рассмотрим уравнения
описывающие малые колебания тела около положения
равновесия, и краевые условия на загруженной поверхности 5
^^»/+К^»/=Рл- с1-52)
Для случая малых колебаний возьмем решение в виде
ui(x1, х2, хг, t)= Ui(xli х2у х3) е12 , (1.53)
где Ul— компоненты вектора, который характеризует
форму колебаний, ?2 — вообще говоря, комплексная частота
колебаний. Подстановка выражения (1.53) в уравнения (1.51)
и граничные условия (1.52) приводит к новой краевой задаче:
д (\ диЛ _l r д I dui\\
dxj VAW Щ) "Г" Р Щ \а1* дГк) "+"
ХУ.р^яУ + РвУ*5§лУ = Рл(^1. ^ ?/3. &)•
Исследованию подлежит поведение собственных значений этой
краевой задачи 2 при изменении параметра нагрузки [3. Если
все собственные значения й ((3) имеют положительные мнимые
части или в крайнем случае действительны (мы условились
ранее и этот случай квалифицировать как устойчивость,
1) Часть результатов этого параграфа была другим путем
получена в работе: Болотин В. В., Некоторые вопросы теории
упругой устойчивости, Прикл, матем. мех. 20, № 4 (1956).

62
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
см. § 1.8), то невозмущенное движение устойчиво. Если хотя бы
одно собственное значение имеет отрицательную мнимую часть,
то это, как видно из (1.53), будет означать возрастание
возмущений во времени, т. е. неустойчивость. При р = 0, как
хорошо известно, все собственные значения краевой задачи
(1.54) — чисто действительные (собственные частоты ненагру-
женного упругого тела). Допустим, что параметр (3 возрастает
по модулю, оставаясь, скажем, положительным. Может
найтись такое значение фт, при сколь угодно малом превышении
которого одна или несколько частот 2 впервые перейдут
на нижнюю полуплоскость комплексного переменного. Это
значение соответствует переходу от устойчивости исследуемого
равновесия к неустойчивости и является, таким образом,
критическим значением. Аналогично можно ввести
критическое значение в области отрицательных р.
Вместо частот Й удобно рассматривать
характеристические показатели s = iQ. Пока все показатели лежат в левой
полуплоскости, исследуемое равновесие устойчиво.
Наименьшие по модулю значения параметра р, соответствующие
переходу хотя бы одного показателя на правую полуплоскость,
являются критическими.
N. Ъч
?1?
| Ims
^г
\f=h
1
SI л
1 Ims
fi-P*
О Res 0 Res
а) б)
Рис. 18.
Необходимо различать два типа перехода от устойчивости
к неустойчивости. Первый тип характеризуется тем, что один
показатель 5 переходит на правую полуплоскость через начало
координат и остается, по крайней мере при значениях р,
достаточно близких к критическому, чисто действительным
(рис. 18, а, где показана лишь верхняя полуплоскость). Соот-

§ 1.11]
МЕТОД ЭЙЛЕРА
63
ветствующий график для действительных частей частот ?2
показан на рис. 19, а. Такой тип неустойчивости будем
называть статической неустойчивостью. Если
характеристический показатель 5 впервые попадает на правую полуплоскость
в точке, отличной от начала координат (рис. 18 и 19), то
такой тип неустойчивости будем называть колебательной
¦я. а
неустойчивостью1). Эти виды неустойчивости отличаются
поведением возмущений вблизи границы устойчивости: в
первом случае возмущения монотонно возрастают во времени,
во втором случае нарастание возмущений носит
колебательный характер.
Рассмотрим краевую задачу (1.54) в предположении, что
внешние силы обладают потенциалом. Выражения для Xi
и pt в уравнениях (1.54) оказываются не зависящими от 2,
и мы приходим к краевой задаче с собственными значениями
&2 = 22ф). При этом, поскольку при 2 = 0 краевая задача
является самосопряженной, то и краевая задача
(1.55)
1) Правда, статическая неустойчивость возможна еще и при
переходе через бесконечно удаленную точку (ср. рис. 3, б).

64
ОБЩИЕ ПРИНЦИПЫ
(гл. 1
является самосопряженной и, следовательно, все значения Q2
действительны. Переходу от устойчивости к неустойчивости
соответствует переход от положительных 0>2 к
отрицательным &2. Ввиду непрерывной зависимости &2([3) этот переход
возможен лишь через значение Q2 = 0. Таким образом, если
внешние силы обладают потенциалом, то потеря
устойчивости может происходить лишь по типу статической
неустойчивости.
Для нахождения критических значений параметра (3
положим в уравнениях (1.55) 22 = 0. Тогда мы придем к задаче
о собственных значениях (1.42), соответствующей методу
Эйлера в теории упругой устойчивости. Если внешние силы
являются консервативными, то метод Эйлера позволяет
получить правильное решение задачи об устойчивости, не прибегая
к рассмотрению малых колебаний около положения
равновесия.
В случае неконсервативных сил выяснение типа потери
устойчивости для каждой задачи требует специального
исследования. Здесь возможны оба типа неустойчивости. В ряде
задач в зависимости от соотношения параметров минимальным
критическим нагрузкам может соответствовать как статическая,
так и колебательная формы потери устойчивости.
§ 1.12. Сведение к системам обыкновенных
дифференциальных уравнений
Непосредственный анализ собственных значений
несамосопряженной краевой задачи (1.54) удается провести до конца
лишь в самых простейших случаях. Поэтому возникает вопрос
о приближенных методах решения задачи. Наиболее
эффективный приближенный метод основан на представлении
компонентов вектора смещения в виде рядов по системе
координатных функций, удовлетворяющих всем или части граничных
условий. Применяя метод Галеркина, можно свести задачу
к исследованию системы обыкновенных дифференциальных
уравнений относительно коэффициентов ряда — функций
времени, а в дальнейшем даже к чисто алгебраической задаче.
В связи с применением метода Галеркина к
несамосопряженным задачам, естественно, возникает вопрос о сходимости. Этот
вопрос исследовался до сих пор лишь по отношению к
некоторым простейшим несамосопряженным задачам. Широкое при-

§ 1.12] ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 65
менение метода Галеркина для задач, где сходимость не является
строго доказанной, основано на сопоставлении имеющихся
точных результатов с результатами, получаемыми по методу
Галеркина. Существенную роль здесь играет также глубокое
и ни разу не поколебленное ни опытом, ни точными
расчетами убеждение в том, что интересующие нас формы потери
устойчивости могут быть удачно аппроксимированы при помощи
линейной комбинации небольшого числа первых форм
собственных колебаний. Так оказалось, во всяком случае, во всех
рассмотренных до сих пор задачах г).
Рассмотрим систему уравнений
да
Тх
?+hM*?)+«-'?=° <ь56>
с граничными условиями
РЛ - ву«у - Р«у* ^ «у = 0- (1-57)
Будем искать ее решение в виде ряда
сю
Ui(Xv X2, Х3, 0= 2/л(0<Р*л(*1. *2. ХъУ С1-58)
я = 1
Здесь fn(t) — некоторые функции времени, ?in(xlf x2, х3) —
координатные векторы (тройки координатных функций),
обязательно удовлетворяющие всем геометрическим граничным
условиям, но, вообще говоря, не удовлетворяющие
естественным граничным условиям (1.57). Система функций <р/я (хг, х2, х3)
предполагается полной.
Поставленным условиям удовлетворяет, например, система
форм собственных колебаний незагруженного упругого тела.
Уравнения собственных колебаний
J Л диа\ ^ д*щ
\KWdxJ'
= 0
dxj \ <w дх$ ) v dt2
с граничными условиями на поверхности 5
\ ди« „ _ о
l) Причины известного противоречия между точным и
приближенным решениями в задаче о флаттере мембраны в сверхзвуковом
потоке разъясняются в § 4.11.

66
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
подстановкой
ut(xv х2, xs, t) = yi(xl, х2, Xz)elQt
приводятся к уравнениям
щ(\м^У^Ъ = 0 (1.59)
с граничными условиями на поверхности
Все собственные частоты 2 действительны и образуют для
ограниченного тела дискретный спектр Qx <; й2 <; 23 ^С • • •
Соответствующие собственные векторы ^ц(х1% х2, х3),
(?i2(xv x2> xz)> ?iz(xv x2> хг)> ••• образуют полную систему
функций, удовлетворяющих условию ортогональности
fpbmbndV = bmn. (1.61)
V
Здесь Ьтп — символ Кронеккера, равный единице при т = п
и нулю в остальных случаях.
Применим к уравнениям (1.56) и граничным условиям (1.57)
принцип виртуальных перемещений. Вводя виртуальные
перемещения Ъии, bui2, Ъи1г, . . ., совместимые с
геометрическими связями, и трактуя левые части уравнений (1.56) как
компоненты объемных сил, а левые части соотношений (1.57)
как компоненты поверхностных нагрузок, получим:
V
(т=19 2, 3, ...).
Выберем виртуальные перемещения Ьа1т следующим образом:
buim = bfm(?lm(Xl> Х2> *з)« (1-63)
Подставляя выражения (1.63) в (1.62) и приравнивая нулю
коэффициенты при произвольных вариациях 8/ш, получим

§ 1.12] ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 67
уравнения метода Галеркина:
Г Г дЪи л д I даЛ - д2~иь 1
+ / / [ Р-Р* — °*УЯУ — Р°У*-^ «/] «Pi« rf-S = 0 (1.64)
(т=1, 2, 3, ...).
Заметим, что уравнения (1.64) могут быть переписаны в
другом виде, если учесть, что
= -fa р.**1ау.
J >k dxk dxj
Следовательно,
- f f (°ij>ij — W<?imdS = <> (^ = 1. 2> 3, ...)-
' s
Вместо otj сюда следует подставить выражения (1.36), а вместо
ui — ряды (1.58), удовлетворяющие уравнениям (1.59) и
граничным условиям (1.60). Принимая во внимание, что в силу
уравнений (1.59), граничных условий (1.60) и условия (1.61)
-f4r Ы? 1%г) ?/» dV = S« f ПшЪп dV = Q2mbmn,
v ' ¦ v
ff^M^f^mdS = 0,
s ?
получим систему уравнений:
П
(т= 1, 2, 3, . . .).

68
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
Здесь
h — 1
f'»&i?"-f*M"-
dxj дхь
Ly J V
If
P№m)9imdS
(1.66)
Мы пришли, таким образом, к системе обыкновенных
линейных дифференциальных уравнений относительно обобщенных
координат fn(t), каждая из которых характеризует вклад
я-й формы колебаний в движение системы около
невозмущенного равновесия.
Остановимся кратко на структуре коэффициентов (1.66).
Для «мертвой» нагрузки Xt = pt = 0; обозначая для этого
случая Ьтп = атп, получим:
'^wf'j^&w- О-67)
Заметим, что матрица с элементами атгр^т оказывается здесь
симметричной.
В случае «следящих» сил
Pi =
dui
и, следовательно,
I Г Г daJk dyin
bm = am„-^J——bmdV-
ff
dyin
"jk-^-bmnjdS
k
Принимая во внимание уравнения равновесия и граничные
условия, которым удовлетворяют невозмущенные
компоненты aiJt Xt и pt\
TxJ + Xi = °> °iJnJ = Pi>

§ 1.13] ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ ДЛЯ НЕКОТОРЫХ СИСТЕМ 69
после преобразований найдем
Ь*г,п =
j~ j v^
d2ffa
dV.
(1.68)
Матрица &2тЬтп симметричной, вообще говоря, не является,
что указывает на несамосопряженный характер задачи.
§ 1.13. Вычисление коэффициентов
для некоторых конкретных систем
Пользуясь формулами (1.67) и (1.68) и вводя
дополнительные геометрические гипотезы, можно получить выражения
для коэффициентов атп и Ьтп в различных случаях стержней,
пластин и оболочек. Рассмотрим в качестве простейшего
примера тонкий упругий стержень
с нерастяжимой осью,
нагруженный осевой нагрузкой и могущий
потерять устойчивость, изгибаясь
в плоскости zOy (рис. 20). Для
такого стержня в рамках
элементарной теории изгиба тензор
напряжений для невозмущенного
состояния и вектор смещения от
невозмущенного состояния будут
иметь вид
0 0 0
a, t =
и,=
0
0
о
N(z)
— у
F
0
v(z)
dv(z)
dz
Рис. 20.
Здесь N {г) — продольная сила, положительная в случае
растяжения, F — площадь поперечного сечения, v(z) — прогиб
оси стержня, Подставляя эти выражения в формулу (1.67),

70
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
найдем:
е:
/n(z)
dv dv
т п_
dz dz
dz,
(1.69)
У-**
где / — длина стержня, vm(z) — формы собственных
колебаний стержня. Заметим, что формула (1.61) приводит здесь
к условию
i
J pFVmVndz-lr
0
(1.70)
:/ где Jx — момент
инерции сечения относительно
оси Ох. Второй член,
очевидно, соответствует
учету инерции вращения.
Для тонких стержней его влияние весьма невелико, и мы
в дальнейшем будем им пренебрегать. Мы будем
пренебрегать также аналогичными членами для пластин и оболочек.
Формула (1.68) дает1):
bmn = -~fN(z)vm^-dz. (1.71)
Рис. 21.
В случае пластинки с постоянной толщиной А,
нагруженной в своей срединной плоскости хОу (рис.21), имеем:
°у* =
Nx
h
N.
ух
h
0
N
ху
h
_Ny
h
0
Uj =
dw (x,
дх
dw (x,
" dy
w(x, y)
У)
У)
l) Формулы (1.69) и (1.71) другим путем были получены в книге:
Болотин В. В., Динамическая устойчивость упругих систем,
Гостехиздат, 1956,

§ 1.13] ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ ДЛЯ НЕКОТОРЫХ СИСТЕМ 71
где w(x, у)— прогиб срединной поверхности. Применяя
формулы (1.67), получим:
т с
dwn j_ dwm dwn\ . N dwm dwn
+ NXA^
]dS,
'ХУ\ dx dy ! dy dx ) T iyy ду ду
где dS — элемент площади срединной поверхности S. В случае
«следящих» сил аналогично получаем:
>„ = —?-//«.(".
Условие ортогональности и нормировки (1.61) при этом
записывается в виде
J J phwmwndS-\-
, Г Г р/г3 / dwm dwn .
"«J J 12 V дх дх "г
Рис. 22.
^ ду ду ;ад —°тл-
Второй интеграл
учитывает инерцию вращения
и для тонких пластин
должен быть отброшен.
Если используются
криволинейные
координаты, то соответствующие формулы получим, заменяя обычное
дифференцирование тензорным:
amn=-^~f f N*? Vawm V„«e dS,
m s
bmn = --±rf fN*wm Va VpW„ dS.
m sf
Остановимся кратко на вычислении матричных элементов
атп и Ьтп для тонких оболочек. Пусть л;а(а—1, 2) —
криволинейные координаты срединной поверхности,
л;3—координата, отсчитываемая по нормали к срединной поверхности

72
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
(рис. 22). Безмоментное состояние оболочки описывается
тензором тангенциальных усилий TV , смещения же срединной
поверхности при отклонении от безмоментного состояния
равновесия — вектором смещений vt (i = 1, 2, 3). Используя
гипотезы теории тонких оболочек, получим для вектора
смещения произвольных точек оболочки и1 выражения:
[ — zVlvz\
и{ =
Отсюда
v2 — z V2i>3
amn = ^f /М****Ш* ftn*S.
h-f f^toWfiJS
a, p= 1. 2
?= 1. 2. 3
Здесь vlm — компоненты вектора смещения срединной
поверхности для m-ft формы собственных колебаний, dS — элемент
площади срединной поверхности 5. Условие (1.61), если
пренебречь инерционными силами вращения, имеет вид
j j №imvindS = bmn.
В качестве последнего примера рассмотрим задачу об
устойчивости плоской формы изгиба стержня, нагруженного
поперечной нагрузкой в плоскости наибольшей жесткости.
Чтобы не усложнять выкладок, ограничимся случаем стержня
сплошного поперечного сечения с двумя осями симметрии
(рис. 23). Предположим, что в каждом сечении внешняя
поверхностная нагрузка сводится к результирующей, лежащей
в одной из плоскостей симметрии (плоскости наибольшей
жесткости) и направленной перпендикулярно к оси балки.
Тогда исходное напряженное состояние, устойчивость которого
исследуется, представляется в виде
°у*-
0 0 0
0
УУ
yz

§ 1.13] ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ ДЛЯ НЕКОТОРЫХ СИСТЕМ 73
где согласно элементарной теории изгиба
Л
У.
QA
у^х
У*
гу ¦
Jxb
(здесь, как и в дальнейшем, используются общепринятые
обозначения, кроме обозначения Lx для изгибающего момента
в сечениях стержня). Распределение напряжений оуу зависит
от конкретного характера приложения внешней нагрузки, но,
&ъ-2,
Рис. 23.
как будет показано ниже, знание этого распределения в
данном случае не обязательно.
Определим вначале матричные элементы атп для случая,
когда внешняя нагрузка не меняет своего направления. По
формуле (1.67)
?•/*/(•
dy/m дуь
душ душ
& J J \ уу ду ду ] zz dz dz '
т О F
+ V^^ + ^%^K (1-72)
Здесь производится суммирование по индексу t=lt 2, 3.

74
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
Вектор смещений для любой точки балки
W-
и — уд
v + xd
du dv
- X-z V -7-
dz * dz
(1.73)
где u(z), v(z), w(z) — перемещения точек, лежащих на
оси стержня, вдоль координатных осей Ox, Oy, Oz;
б (z) — угол закручивания,
положительное направление
которого показано на рис. 24.
Эффектом депланации здесь
пренебрегаем.
Учитывая, что потеря
устойчивости плоской формы
изгиба описывается
перемещениями u(z) и Q(z),
составим выражения для векто-
Р°в <?1т- ПУСТЬ «яй и
дт (z) — /ft-e формы
собственных колебаний
незагруженного стержня, Qxm
и 20т — соответствующие
собственные частоты (если
сечение имеет две оси сим-
Рис. 24. метрии, то собственные из-
гибные и крутильные
колебания происходят независимо друг от друга). Для удобства
дальнейших записей положим:
0»=1. 2,
лихт "2/71-1»
з, ...)•
Тогда в соответствии с (1.73) векторы yim представятся
в виде
тг/,2т-1 :
Ът-\
О
у d(?2m-l
у dz
5 Ъ,2т =
— УЪт
О
(1.74)

§ 1.13] ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ ДЛЯ НЕКОТОРЫХ СИСТЕМ 75
Как следует из формулы (1.61), функции ср2/7г_1 и ср2т должны
удовлетворять условиям нормировки:
/рр$п-1<*г=1. /р-Ы» <**=!. (1-75)
О О
где Jz — полярный момент инерции сечения.
Подставим выражения (1.74) в формулы (1.72). Легко
получим:
i
1
атп =
„I 0 р
_т u{dVm d24<* l d^rn d4n\\dp
ЪгУ\ dz dz* ~т~ dz2 dz /J '
если т и n — нечетные числа;
i
?- / dz f [a2Z (*» + &*?*? + ayyMn -
— *угУ(?п
^llL-Ucn dV™
4n dz
rm dz
если т и n — четные числа;
ж
./V/V^^+v^.
dym dyn
dy„
)dF.
0 F
если m — нечетное, n — четное число;
i
q2 J az J у**У dz dz ^ VP* dz )ar'
m 0 F
если m — четное, n — нечетное число.
Но согласно элементарной теории изгиба
fa„dF=0, fezzydF = Lx, fxy,dF = Qy
F F F
и, кроме того, из соображений симметрии
/ W dF = О, / а„х* dF=f ozzfdF = 0.
dLx
dz '

76
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
Осталось выразить через внешние силы интеграл
f'yydF.
F
Для этого воспользуемся известной формулой 1) для средних
значений компонентов тензора напряжений, согласно которой
f°ikW = ffPixkdS.
V S
Рассматривая элемент стержня единичной длины, найдем:
fcyydF = fpyydT,
F Г
где ру — составляющая поверхностных сил вдоль оси Оуу
Г — контур, ограничивающий поперечное сечение. Введем
результирующую поверхностных сил, отнесенную к единице
длины стержня, и ее превышение над осью Oz
f РуУЛТ
г
-q. e = —r •
J
PydV--
(1.76)
Тогда
foyydF = -qe =
Г
d2Lx
Таким образом,
dz2
если т и п —
нечетные числа;
если т и п — четные
числа;
т 0
I
2~ / ~~^ — (А*?л) dz> если т — нечетное,
Qm о dz dz n — четное число;
«- / —— {Lr4m)dz, если т — четное
Q* J dz dz xTm' „ „_ .
n — нечетное число.
(1-77)
^Ландау Л. Д. и Л и ф ш и ц Е. М., Механика сплошных
сред, Гостехиздат, 1954.

§ 1.14]
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ
77
Переходим к случаю следящей нагрузки. Формулу (1.66)
для рассматриваемого случая представим в виде
i
Ьтп = ^mn+f d* / Ру ^г ?*» dT-
о г
Подстановка сюда выражений (1.74) и (1.77) с
использованием (1.76) дает *):
О,
если т и п — числа одинаковой четности;
г i i
*-|
dz dz
Л
Qi
!• I-
-О """ """ О
если т — нечетное число, п — четное число;
i
(1.78)
-аг/З?-^"-
если т — четное, п — нечетное число.
Заметим, что матрица Ьтп имеет для рассматриваемой задачи
своеобразную структуру:
О Ью О Ь
'12
ь21 о ь,
23
О ^2 0 ^4 •
ЬАХ О й43 0 .,
§ 1.14. Исследование устойчивости
Допустим, что система нагружена консервативными
силами, заданными с точностью до параметра а, и, кроме того,
заданными с точностью до параметра (3 силами, которые
1) Формулы (1.77) и (1.78) были получены впервые из уравнений
теории тонкостенных стержней в работе: Болотин В. В., О
колебаниях и устойчивости стержней, находящихся под действием
неконсервативных сил, Сб. «Колебания в турбомашинах», Изд-во АН
СССР, 1959.

78 ОБЩИЕ ПРИНЦИПЫ [ГЛ. 1
потенциалом не обладают (например, «следящими» силами).
Соответствующие матрицы коэффициентов будем, как и ранее,
обозначать через ajk и bjk. Кроме того, примем, что на
систему действуют диссипативные силы, пропорциональные
обобщенным скоростям dfj/dt. При этом будем считать, что
диссипативная связь между различными формами колебаний
отсутствует. Тогда диссипативные силы будут
характеризоваться диагональной матрицей с элементами Sy. Система
уравнений, описывающая малые колебания около положения
равновесия, имеет вид
d'fi . df* _i_
(1.79)
Здесь n — число форм колебаний, достаточных для
удовлетворительного представления движений упругой системы
вблизи невозмущенной формы равновесия.
Разумеется, уравнения (1.79) можно трактовать как
частный случай уравнений движения механической системы с п
степенями свободы вблизи положения равновесия:
d2fj vi dfk Л
Представление матрицы Bjk в виде суммы симметричной и
антисимметричной матриц
&jk — § ' 2
соответствует при этом разделению сил, зависящих от
положения, на потенциальные и существенно непотенциальные
силы 1). Однако такое разбиение, вообще говоря, отличается
1) Последние называются по-разному: циркуляционные силы
(Ц и г л е р Г., Об устойчивости упругих систем, Сб. «Проблемы
механики», вып. 2, ИЛ, 1959), псевдогироскопические силы
(О б м о р ш е в Н. А., Колебания и устойчивость движения в
машиностроении, МВТУ, 1952), силы радиальной коррекции (М е р-
к и н Д. Р., Гироскопические системы, Гостехиздат, 1956).

§ 1.14] ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ 79
от разбиения
Bjk = atijajb-+-$Q2jbjk.
Так, в случае «следящих» нагрузок матрица Q)bjk не
обязательно является антисимметричной. Поскольку основной
задачей теории упругой устойчивости является исследование
условий устойчивости (неустойчивости) в зависимости от
параметров нагрузок, то представление уравнений в форме (1.79)
более предпочтительно.
Для нахождения параметров, соответствующих
разветвлению форм равновесия, имеем уравнение
1*у* + ««у* + Р*у*| = 0. (1.80)
которое получается приравниванием нулю определителя,
составленного из коэффициентов однородной алгебраической
системы
/y+«Sfyk/* + PSV* = 0 U=L 2, .... п).
Поскольку матрица а*к симметризуема при умножении слева
на матрицу Qftjk, то все ее собственные значения,
определяемые из уравнения
являются действительными. Это утверждение, вообще говоря,
несправедливо для матрицы bjk. Допустим, что значение
параметра а фиксировано, причем оно меньше минимального
собственного значения а^. Тогда при [3 = 0 равновесие
системы является устойчивым. Задача о поведении системы при
возрастании параметра (3 от нуля до некоторого значения
не может быть разрешена в общем виде, поскольку здесь
существенную роль играет структура матриц а^к и bjk.
Рассмотрим теперь малые колебания системы около
положения равновесия, полагая вначале затухание равным нулю.
Уравнения (1.79) удовлетворяются подстановкой
/, = />»'.
где Fj — некоторые константы. Для определения частот
колебаний Q имеем уравнение
Q2
l-%r)bJk + **j* + №j*
= 0. (1.82)

80
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
Если а =(3 = 0, то частоты действительны и равны &у. Они
остаются действительными и при а Ф 0, (3 Ф 0, если только
эти параметры достаточно малы и среди частот Q, нет
кратных частот. Это значит, что все характеристические
показатели s — iQ при достаточно малых значениях параметров
нагрузки находятся на мнимой оси. При (3 = 0 все Q2
действительны и, следовательно, переход характеристических
показателей на правую полуплоскость возможен лишь через
значение s = 2 = 0. Это соответствует статическому типу
потери устойчивости. Если (3 Ф 0, то возможен как
статический, так и динамический (колебательный) тип
неустойчивости. Реализация того или иного типа зависит как от
структуры матриц ajk, bjk и Q)bjkt так и от соотношения между
а и р. В каждом частном случае необходимо специальное
исследование. Практически оно сводится к вычислению
действительных корней Q уравнения (1.82) в функции от
параметров а и (3 и отысканию таких соотношений
параметров, при которых действительные корни становятся
кратными и при дальнейшем изменении параметров делаются
комплексными.
При наличии затухания решение уравнения (1,74) будем
искать в виде
/, = V' (/=1. 2 я)-
Если все Bj > 0, что соответствует системе с полной
диссипацией, то при а = (3 = 0 все корни характеристического
уравнения
| (s2 + ejs + Qj) bjk + QJ (aa}k + pfy) | = 0 (1.83)
лежат в левой полуплоскости. Задача состоит в отыскании
области устойчивости на плоскости параметров а, (3 или
в каком-либо другом пространстве параметров. Эта задача
при небольших п решается при помощи алгебраических
критериев устойчивости, например критерия Гурвица. В более
сложных случаях могут быть использованы другие способы,
подробно разработанные главным образом в связи с задачами
теории автоматического регулирования.
Представляет большой интерес ответ на следующий
вопрос. Допустим, что область устойчивости найдена в двух
предположениях — без учета затухания и с его учетом, В пер-

§ 1.15] ПРИМЕР. СИСТЕМА ВТОРОГО ПОРЯДКА 81
вом случае под устойчивостью подразумевается нахождение
всех характеристических показателей на мнимой оси, а во
втором случае — нахождение всех показателей в левой
полуплоскости комплексного переменного. Спрашивается, будет ли
область устойчивости для первого случая включать в себя
как часть область устойчивости для второго случая? Иначе,
будет ли добавление диссипативных сил стабилизировать
невозмущенное равновесие или нет? Для равновесия системы,
находящейся под действием потенциальных сил, ответ на этот
вопрос является положительным. Ответ дается известной
теоремой Кельвина, согласно которой добавление диссипативных
сил с полной диссипацией обеспечивает асимптотическую
устойчивость невозмущенного равновесия. В случае
неконсервативных систем это, вообще говоря, не имеет места: здесь
добавление диссипативных сил может в некоторых
случаях оказывать дестабилизирующее влияние.
С этим связан и другой весьма интересный вопрос.
Допустим, что найдена граница устойчивости при наличии
затухания, после чего все коэффициенты Sj устремлены к нулю.
Будет ли граница устойчивости, соответствующая исчезающе
малому затуханию, совпадать в пределе с границей
устойчивости, найденной в предположении, что затухание
тождественно равно нулю? В случае консервативных сил ответ
на этот вопрос является положительным. Если силы не
обладают потенциалом, то границы устойчивости,
установленные для системы с исчезающе малым затуханием и для
системы без затухания, вообще говоря, не совпадают.
§ 1.15. Пример. Система второго порядка
Все основные особенности неконсервативных систем могут
быть проиллюстрированы на простейшем примере системы
второго порядка с матрицами
II 0 а12
К такой системе приводит в первом приближении задача
об устойчивости плоской формы изгиба стержня,
нагруженного следящими силами. Аналогичную систему получим при
приближенном рассмотрении задач об устойчивости прямо-
V
°
1 *21

82 ОБЩИЕ ПРИНЦИПЫ [ГЛ. 1
линейной формы скрученного стержня, об устойчивости
пластины, обтекаемой сверхзвуковым потоком газа, а также
об устойчивости прямолинейной формы вала, вращающегося
с постоянным числом оборотов при наличии внутреннего
трения.
Заметим, прежде всего, что критические в смысле Эйлера
значения параметров аи^ будут равны
- 1 р. = + -=!=. (1.84)
У'а12а21 ' * Уbl2b2
Поскольку нас больше интересует случай, когда под
действием нагрузок с параметром р статическая форма потери
устойчивости невозможна, то будем полагать, что b12^i < 0.
Напротив, а12а21 > 0.
Рассмотрим задачу без учета затухания. Пусть вначале
сс = 0. Уравнение (1.82) принимает вид
2? — Q2 Щ\Ъ12
= 0.
Вводя обозначения
Qj Q 1
— = шу, — = о), ft12&2i = —тг» О-85)
где 20 — характерная частота (например 22), придем к
уравнению
Его корни
,=± h 1A1+-2 ± /н-^)2-4
2 2 Р*
2Ро
действительны, пока выражение под внутренним радикалом
положительно. Отсюда критическое значение параметра р
будет:
2 2
п п ^ — ^1
Г* ^0 20X0,
1Ш2
(1.86)

§ 1.15] ПРИМЕР. СИСТЕМА ВТОРОГО ПОРЯДКА 83
Зависимость безразмерных частот w от отношения р/ро
показана на рис. 25. С возрастанием (3 частоты w
приближаются друг к другу и при (3 = {3# становятся кратными и
равными
—2—-
При дальнейшем увеличении (3 два характеристических
показателя а = ш из четырех переходят на правую полуплоскость
А
Рис. 25.
(см. рис. 26, где показана лишь верхняя полуплоскость).
Заметим, что если парциальные частоты незагруженной
системы равны между собой (ы1 = ю2), то, как видно из
формулы (1.86), равновесие системы будет неустойчиво даже

84
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
при сколь угодно малых значениях р. Этот парадоксальный
результат является следствием того, что затухание не
принималось во внимание.
Предположим теперь, что оба параметра, аир, отличны
/тО
Rg6
от нуля. Уравнение (1.82)
примет вид
Q?-22 аа12 + р&12
= 0.
Обозначая
придем к уравнению
О)4
Иначе,
О)
\ а* Ро а*Р0 /
4_Ш2(Ш2 + Ш2) + Ш2Ш2[1 +^+^(ф2_2Лф— 1)] = 0.
(1.87)
Здесь
а Р . v
^Т' v = l^ * = *¦•
(1.88)
т. е. параметр ja характеризует консервативную
составляющую нагрузки, параметр v — неконсервативную
составляющую, параметр ф — соотношение между ними.
Корни уравнения (1.87) определяются из формулы
<°2 =4 [•»?+wi±/"(»s-°>?),-4<»Xxttf' (f _2^~1}] •
(1.89)
Два корня уравнения (1.87) обратятся в нуль при
Отсюда критическое в смысле Эйлера значение параметра
[х —]— v будет:

§ 1.15]
ПРИМЕР. СИСТЕМА ВТОРОГО ПОРЯДКА
85
Колебательный тип неустойчивости будет иметь место,
если в формуле (1.89) выражение под радикалом станет
отрицательным. Отсюда
" п 1 + Ф
<P + v),=
2 2
0)2 —COj
(1.91)
2(0^2 |/"ф2—2Лф — 1
Переход от одного типа неустойчивости к другому будет
иметь место при
ф = ф0 = Л + /Л2+1.
(1.92)
График, иллюстрирующий зависимости (1.90) и (1.91),
показан на рис. 27. При этом принято, что Л= 1,07, (о2^=2у00(ог.
Я
Ю
15
W
0,5
/
'/
V
г
С5
II
^
Оо
^=?
Рис. 27.
Пока ф не слишком велико, добавление неконсервативных
сил способствует стабилизации невозмущенного равновесия*).
*) В гироскопических приборах неконсервативные силы,
создаваемые, например, давлением струи, используются для придания
большей устойчивости («силы радиальной коррекции», см. М е р-
к и н Д. Р., цит. на стр. 78).

:0.
86 ОБЩИЕ ПРИНЦИПЫ [ГЛ. 1
§ 1.16. Влияние диссипативных сил на устойчивость
Чтобы проиллюстрировать своеобразное влияние
диссипативных сил в присутствии неконсервативных сил, зависящих
от положения, рассмотрим систему уравнений
iS-+e> ж+д? (fi+t 2 *у*/Л=° и=и 2).
\ ft = l,2 /
Вводя обозначения
где Q0 — некоторый параметр частоты, запишем
характеристическое уравнение в виде
Рю2*21 с2 + 5Г2° + а
Раскрывая определитель и используя обозначение (1.85)
для р2» получим:
«4 + °3 (^ + g2) + о2 (»? + «)22 + * ,* 2) +
Мы получили алгебраическое уравнение четвертой степени
а0о4 -\- агсг -\- а2о2 + а3а -\- а4 = О,
все корни которого лежат в левой полуплоскости, если все
его коэффициенты
aQ > О, ах > 0, а2 > О, а3 > 0, а4 > О
и, кроме того, выполняется условие
(а1а2 — аоаг)аг — а1а4>°- О-95)
При положительных g1 и g2 все коэффициенты
уравнения (1.94) положительны. Остается последнее условие,
которое принимает вид
Р2 < Ро X
,j[(gl + g2)(ml + *2 + glg2W^ Л

§ 1.16] ВЛИЯНИЕ ДИССИПАТИВНЫХ СИЛ НА УСТОЙЧИВОСТЬ 87
Отсюда критическое значение параметра [) будет:
(1.96)
Исследуем формулу (1.96). Если обозначить
,— #2 —
?1
= +> Si = B
(1.97)
и учесть формулу (1.86) для критического параметра (3*,
найденного без учета затухания, то получим:
р~=р,
2/ч
1 + 1
1+0
2\2
| (4-0)2)
При малом затухании и при не слишком близких
парциальных частотах можно положить:
%
Р* 1 + т) •
(1.98)
Рассматривая правую часть как функцию параметра т\,
приходим к выводу, что она достигает максимального значения,
равного (Зф, при т] = 1. Это соответствует, как видно из
J7
w
0,5,
Г
/
—
Рис. 28.
обозначения (1.97), равенству коэффициентов затухания ег = е2.
Если Sj Ф е2, то критическое значение ^, найденное при
наличии исчезающе малого затухания, оказывается меньше,
чем критическое значение (3#, найденное без учета затухания
(рис. 28). При достаточно больших g влияние затухания

88
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
может стать вновь стабилизирующим (рис. 29). На простом
примере двойного маятника, нагруженного «следящей» силой,
явление дестабилизации вследствие трения было обнаружено
впервые Г. Ци г л ер ом1). Приведенный здесь результат,
относящийся к влиянию
Меустойчидость
Л
А
Устойчибость
соотношений между
коэффициентами затухания,
был получен автором2).
Явление
дестабилизации проиллюстрировано
на рис. 30, где показано
поведение
характеристических показателей при
отсутствии затухания и
при наличии затухания
с неравными ег и е2. Если
затухание невелико, то
"Т при Sj Ф е2 один из пока-
" зателей покидает левую
полуплоскость при
значении р^ меньшем, чем р#.
Рассмотрим случай близких парциальных частот.
Формулу (1.96) представим в виде
(1.99)
Здесь даже малое затухание может оказаться
стабилизирующим фактором. Так, в случае кратных частот
Рис. 29.
P- = Po«r^ = PoV"ft«r2.
(1.100)
между тем как без учета затухания мы получили бы
парадоксальный результат Р* = 0.
Покажем, что обнаруженные особенности сохраняются
и в более общем случае системы с двумя степенями сво-
1) Ziegler H., Die Stabilitatskriterien der Elastomechanik,
Ing.-Arch. 20, № 1 (1952).
2) Болотин В. В., Некоторые проблемы теории упругой
устойчивости, Тр. Третьего Всесоюзного матем. съезда, т. 1, Изд-во
АН СССР, 1956,

§ 1.16] ВЛИЯНИЕ ДИССИПАТИВНЫХ СИЛ НА УСТОЙЧИВОСТЬ 89
боды при довольно широких предположениях относительно
матрицы bjk. Рассмотрим случай, когда Ьп > О, Ь22 > О,
*i2*2i < 0. Тогда уравнение
очевидно, не имеет действительных корней. Сопоставим для
этого случая критические значения, найденные при исчезающе
I \тО
О Re6
Рис. 30.
малом затухании, и соответствующие значения, найденные
в предположении, что затухание с самого начала отсутствует.
Характеристическое уравнение
la' + o^ + aJ+Pcofti ^\bn I
приводится к виду
a0o4 -f- axQ% -\- a2a2 -f- я3о -f- a4 = 0,
где
Оо=1,
el=fir(l+1).
«2 = <¦>?+^+чв3 + P («>?*„ H- «>%„,).
e3 = g- [rtm\ + 0)2 + p (7)(D^n + a>^22)],
a4 = «ft [ 1 + p (ft„ + *22) + P2 (*, A, - V21)] •

90
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
Вследствие предположения о свойствах матрицы bjk все
коэффициенты ak положительны. Следовательно, остается лишь
одно нетривиальное условие Гурвица (1.95), которое
запишем в виде
Здесь
Ф(р) = лр2+яр+с>о.
А = ч (^ _ ^2 _ (1 + ч)2 *yj,l2b2V
В = 7]0)^22 [2 (0)2 - 0)2) + ?2 (1 + ^ _
- 7]0)2?п [2 (0)2 - 0)2) -^2(1+ ,)]§
С = Ч [(0)2 _ 0)2)2 + ^2 ^Ш2 + 0)2) (1 + 7])].
Устремим теперь затухание к нулю, оставляя т\ отличным
от нуля. Последнее условие примет вид
где
Ф1(р) = Л,р» + Д1р+С1>0.
\ = (»?*„ - ^22)2 - (уъ + /^)2 «А. |
(1.101)
(1.102)
Рассмотрим теперь систему с затуханием, тождественно
равным нулю. Характеристическое уравнение имеет вид
или
Р»&1 °2+ ">! + №*
= 0
где
а4 = ш*ш§ [1 + р (*„ + *22) + р (^ _ *lAl)]. }
(1.103)

§ 1.16] ВЛИЯНИЕ ДИССИПАТИВНЫХ СИЛ НА УСТОЙЧИВОСТЬ 91
Все корни этого уравнения лежат на мнимой оси, если а2 > О,
аА > 0 и, кроме того, а\ — 4#4 > 0. Первые два условия
удовлетворяются тождественно вследствие предположения
о свойствах матрицы b:k. Последнее условие можно записать
в виде
Ф2(р)-Л# + ?2р + С2>0, (1.104)
где
В2 — Вх, C2 — Cv
Составим разность
фх (р) - ф2 (р)=- р«у2ь12ь2х [4 - (yii+^L)2 J.
Нетрудно видеть, что максимальное значение квадратной
скобки, рассматриваемой как функция т/, достигается при
т] = 1 и равно нулю. Отсюда получаем, что при всех у\ и (3
Ф,(р)-Ф2(Р)<0, (1.105)
если только b12b2i < 0. При (3 = 0 имеем Ф1 (0) = Сг > 0,
10
Рис. 31.
Ф2 (0) = С2 > 0. Пусть р меняется от нуля в сторону
положительных значений. Тогда из неравенства (1.105)

92
ОБЩИЕ ПРИНЦИПЫ
[ГЛ. 1
вытекает, что корни уравнений Фг (Р) = 0 и Ф2 ф) = 0,
обозначаемые Рз* и р# соответственно, удовлетворяют соотношению
Р** ^С Р*« Аналогичное соотношение мы имеем и при р < 0;
здесь |pJ<|P.| (рис. 31).
Таким образом, если Ьп > 0, Ь22 > 0, bnb2i < 0, то
критический параметр р^, найденный в предположении, что
затухание исчезающе мало, по модулю меньше или равен
(при ?]=1) критическому параметру р# для системы без
затухания.

ГЛАВА ВТОРАЯ
УСТОЙЧИВОСТЬ РАВНОВЕСИЯ УПРУГИХ СИСТЕМ
ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ
§ 2.1. Исторические сведения
Е. Л. Николаи был, по всей вероятности, первым, кто
рассмотрел задачу об устойчивости упругой системы,
нагруженной следящими силами. В одной из его работ,
опубликованной впервые в 1928 г. !), исследуется устойчивость
прямолинейной формы гибкого стержня, один конец которого
защемлен, а другой (свободный) — нагружен сжимающей
силой и скручивающим моментом. Было установлено, что
в случае, когда вектор момента является «тангенциальным»
(т. е. остается направленным по касательной к изогнутой
оси стержня), не существует никаких иных форм равновесия,
кроме прямолинейной. Отсюда Е. Л. Николаи сделал вывод,
что обычный метод определения критической силы в данной
задаче неприменим. Составив уравнение малых колебаний
стержня около прямолинейной формы равновесия, Е. Л.
Николаи установил, что это равновесие неустойчиво при любых
значениях скручивающего момента (если не учитывать
затухание и рассматривать стержень круглого сечения). В
следующей работе 2) было показано, что при наличии неравных
изгибных жесткостей прямолинейная форма стержня является
устойчивой при достаточно малой величине крутящего момента.
^Николаи Е. Л., Об устойчивости прямолинейной формы
равновесия сжатого и скрученного стержня, Изв. Ленингр.
политехи, ин-та 31 (1928); см. также Николаи Е. Л., Труды по
механике, Гостехиздат, 1955.
2) Николаи Е. Л., К вопросу об устойчивости скрученного
стержня, Вестн. прикл. матем. мех. 1 (1929).

94 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
При этом существует критическая величина момента, начиная
с которой прямолинейная форма перестает быть устойчивой.
В 1930 г. на Международном конгрессе по прикладной
механике Е. Л. Николаи прочел доклад по вопросу
об устойчивости гибких валов 1). В этом докладе он
подытожил результаты своих исследований по устойчивости сжатых
и скрученных стержней, распространив их на случай
вращающихся валов. В последующие годы результаты Е. Л.
Николаи были расширены в работе Г. Ю. Джанелидзе2),
который, анализируя точные уравнения изгиба стержня,
показал, что в рассмотренной Е. Л. Николаи задаче
действительно не существует иных форм равновесия, кроме
прямолинейной. Различные формы опорных закреплений были
рассмотрены И. Е. Шашковым3).
До недавнего времени многое в задаче Е. Л. Николаи
все же оставалось неясным, и это давало основание говорить
о «парадоксе Николаи». В последние годы интерес к задачам
об устойчивости скручиваемых валов значительно возрос.
В 1951 г. Моррис4) вновь рассмотрел задачу об
устойчивости консольного стержня круглого сечения под действием
осевой силы и тангенциального момента, имея в виду
приложения к валам авиационных газовых турбин. Начиная
с того же 1951 г., был опубликован ряд исследований
Циглера5), в которых он рассмотрел задачи устойчивости
гибкого стержня при различном поведении скручивающего
2) N i k о 1 a i E L., Uber den Einfluss der Torsion auf die
Stability rotierenden Wellen, Proc. of the 3d Congr. Appl. Mech.,
Stockholm, 1930.
2) Джанелидзе Г. Ю., К вопросу о форме равновесия
сжатого и скрученного стержня, Тр. Ленингр. индустр. ин-та, № 3,
вып. 1 (1939).
3) Ш а ш к о в И. Е., Об устойчивости прямолинейной формы
равновесия борштанги, Инж. сборн. 1, № 1 (1941); Об устойчивости
сжатого и скрученного призматического стержня с произвольной
формой поперечного сечения, Инж. сборн. 7 (1950).
4) М о г г i s J., Torque and the flexural stability of a cantilever,
Aircraft Engng. 23, № 274 (1951).
5) Ziegler H., Ein nichtkonservatives Stabilitatsproblem,
Zeitschr. angew. Math. Mech. 31, № 8/9 (1951); Stabilitatsprobleme
bei geraden Staben und Wellen, Zeitschr. angew. Math. Phys. 2, № 4
(1951); Knickung gerader Stabe unter Torsion, Zeitschr. angew. Math.
Phys. 3, № 2 (1952); Kritische Drehzahlen unter Torsion und Druck,
Ing.-Arch. 20, № 6 (1952),

§2.1] ИСТОРИЧЕСКИЕ СВЕДЕНИЯ 95
момента. При этом были повторены многие результаты,
принадлежащие Е. Л. Николаи. Циглер дал классификацию
случаев поведения момента, выделив среди них те, которые
соответствуют наличию потенциала внешних сил. В частности,
он показал, что момент, вектор которого делит пополам
угол между касательными к неискривленной и
деформированной осям стержня, является консервативным (заметим, что то
обстоятельство, что в данном случае задача устойчивости
в смысле Эйлера имеет решение, было обнаружено еще
Е. Л. Николаи в 1928 г.). Дальнейшее рассмотрение этих
вопросов было сделано Трешем !). Некоторые
дополнительные сведения можно получить из обзоров Г. Ц и г л е р а 2).
В 1939 г. В. И. Реутом3) была поставлена другая
неконсервативная задача упругой устойчивости. В. И. Реут
рассматривал стержень, заделанный одним концом и
нагруженный на другом конце сжимающей силой, линия действия
которой при деформации стержня остается неизменной. Такая
нагрузка может быть реализована, например, за счет
давления струи жидкости или газа, отклонением которой при
деформации стержня можно пренебречь. Как и в задаче
Е. Л. Николаи, здесь оказалось, что форм равновесия,
отличных от прямолинейной, не существует. Б. Л. Николаи4)
исследовал малые колебания стержня около неискривленного
положения и нашел таким путем критическое значение
сжимающей силы.
Следующий цикл работ связан с задачей об устойчивости
гибкого стержня, заделанного одним концом и нагруженного
на другом конце тангенциальной сжимающей силой.
Отсутствие в этой задаче форм равновесия, смежных с
неискривленной формой, было установлено В. И. Феодосьевым5)
^Troesch A., Stabilitatsprobleme bei tordierten Staben und
Wellen, Ing.-Arch. 20, № 4 (1952).
2) Ziegler H., Linear elastic stability, Zeitschr. angew. Math.
Phys. 4, № 2—3 (1953); см. также Advances in applied mechanics,
vol. 4, Academic Press, N. Y., 1956 (недавно вышел русский
перевод в сб. «Проблемы механики», т. 2, ИЛ, 1959).
3) Реут В. И., О теории упругой устойчивости, Тр. Одесск.
ин-та инж. гражд. и комм, стр-ва, вып. 1 (1939).
4) Николаи Б. Л., О критерии устойчивости упругих систем,
Тр. Одесск. ин-та инж. гражд. и комм, стр-ва, вып. 1 (1939).
5) Ф е о д о с ь е в В. И., Избранные задачи и вопросы по
сопротивлению материалов, Гостехиздат, 1953, стр. 38 и 165.

96 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
и А. Пфлюгером1). Критическая сила для этой задачи
была вычислена Беком2), а также К. С. Дейнекои
М. Я. Леоновым3). В последней работе было дано также
приближенное решение для стержня с двумя
сосредоточенными массами. Случай массы, сосредоточенной на конце
стержня, был проанализирован Г. Ю. Джанелидзе4),
который учел одновременное действие тангенциальной силы
и силы неизменного направления. Одновременный учет
распределенной и сосредоточенной массы был проведен
Пфлюгером5). К данному циклу работ примыкает также статья
Ю. Д. Копейкина и М. Я. Леонова6).
В. И. Феодосьев7) указал еще на одну задачу,
в которой отсутствуют формы равновесия, смежные с
невозмущенной. Такова задача об устойчивости плоской формы
изгиба узкой полосы, нагруженной моментом неизменной
величины и неизменного направления. Критическое значение
момента для этого случая до сих пор не было вычислено 8).
В. В. Болотин9) рассмотрел другую задачу об устойчивости
плоской формы изгиба. Эта задача оказалась весьма удобной
моделью для демонстрации различных закономерностей, присущих
неконсервативным задачам теории динамической устойчивости.
!) Р f 1 u g е г A., Stabilitatsprobleme der Elastostatik, Springer-
Verlag, Berlin, 1950, S. 217.
2) Beck M., Die Knicklast des einseitig eingespannten
tangential gedruckten Stabes, Zeitschr. angew. Math. Phys. 3, № 3 (1952).
3) Д е й н е к о К. С. и Л е о н о в М. Я., Динамический метод
исследования устойчивости сжатого стержня, Прикл. матем. мех.
19, № б (1955).
4) Джанелидзе Г. Ю., Об устойчивости стержня при
действии следящей силы, Тр. Ленингр. политехи, ин-та, № 192 (1958).
5) Pfluger A., Zur Stabilitat des tangential gedruckten Stabes,
Zeitschr. angew. Math. Mech. 35, № 5 (1955).
6) Копейкин Ю. Д. и Леонов М. Я., Об одном особом
случае потери устойчивости равновесия сжатого стержня, Прикл.
матем. мех. 19, №• б (1955). По поводу этой статьи см. реф. журн.
«Механика», 1958, № 4, реф. № 4535.
7) См. ссылку 5) на стр. 95.
8) Вычисления для весьма сходной задачи были недавно
проделаны в статье: Гопак К. Н. и Кривошеева С. Г., Изгибно-
крутильные колебания и устойчивость плоской формы изгиба
консольной балки — полосы, Изв. АН СССР, ОТН, «Механика и
машиностроение», № 4, 1959.
9) Болотин В. В., Динамическая устойчивость упругих
систем, Гостехиздат, 1956.

§ 2.2] СТЕРЖЕНЬ, СЖАТЫЙ ТАНГЕНЦИАЛЬНОЙ СИЛОЙ 97
Это было широко использовано в другой работе В. В.
Болотина !).
Упомянем еще о двух задачах упругой устойчивости при
наличии следящих сил. В работе В. В. Болотина2)
рассмотрена задача об устойчивости симметричной формы изгиба
круговой арки, которая нагружена сосредоточенной силой,
поворачивающейся при деформации вместе с соответствующим
сечением. Оказалось, что в этом случае потеря упругой
устойчивости происходит по типу разветвления форм
равновесия, хотя нагрузка и не является консервативной. В своей
работе, посвященной анализу статического критерия
устойчивости, Г. Циглер 3) использовал в качестве модели задачу
о колебаниях двойного маятника, сочлененного упругими
звеньями и нагруженного тангенциальной силой.
В дальнейшем мы приведем результаты, относящиеся
к некоторым из перечисленных выше задач, а также
рассмотрим некоторые новые вопросы.
§ 2.2. Задача об устойчивости стержня,
сжатого тангенциальной силой
Рассмотрим задачу о поведении гибкого упругого стержня
постоянного сечения, нагруженного тангенциальной силой и
совершающего малые колебания около невозмущенной
(прямолинейной) формы равновесия. При этом ограничимся случаем
колебаний, происходящих в одной из главных плоскостей
инерции (рис. 32).
Пусть v(z, t) — малый прогиб в любой точке стержня,
f(t) — прогиб его свободного конца, ср(^) — угол поворота
торцового сечения, EJ—жесткость сечения при изгибе.
В рамках обычных предположений элементарной теории изгиба
уравнение малых колебаний стержня принимает вид
Ej2? = P(f-v)-P9(l-z) + Lj,
') Болотин В. В., О колебаниях и устойчивости стержней,
находящихся под действием неконсервативных сил, Сб. «Колебания
в турбомашинах», Изд-во АН СССР, 1959.
2) Болотин В. В., О параметрически возбуждаемых
колебаниях упругих арок, Докл. АН СССР 88, № 4 (1952).
3) Ziegler H., Die Stabilitatskriterien der Elastomechanik,
Ing.-Arch. 20, № 1 (1952).

98 устойчивость при наличии следящих сил [!\л. й
где Lj—изгибающий момент, вызываемый действием
инерционных (в смысле принципа Даламбера) сил. Дифференцируя
это уравнение дважды и замечая, что
d2L,
dz2
т
d2v
где т
погонная масса стержня, получим
d2v
EJ^L + Pd2v
¦т
= 0.
(2.1)
dz2 ' "' dt2
Уравнение (2.1) ничем не отличается от соответствующего
уравнения при наличии консервативной силы неизменного
а направления. Сохраняются также и
о^ условия на защемленном конце:
v(0, t)
dv (0, t)
dz
:0. (2.2)
Условия на свободном конце
записываются в виде
d2v (/, t) _ d*v (/, t) _
dz2 ~ dz*
вместо условий
d2v (/, t)
0 (2.3)
dz2
0,
d*v (/, t) _
dz* ~'
Р dv(l,t)
EJ dz
(2.4)
ГоШ
Рис. 32.
в консервативном случае.
Уравнение (2.1) будет
удовлетворено, если положить
v(Zt t) = V(z)emt (2.5)
где V(z) — неизвестная функция, Q — неизвестная, вообще
говоря, комплексная постоянная. Подстановка в уравнение (2.1)
дает:
*iV ..р*?_ш1у = 0, (2.6)
dV
d&
где введены безразмерные параметры:

§ 2.2] СТЕРЖЕНЬ, СЖАТЫЙ ТАНГЕНЦИАЛЬНОЙ СИЛОЙ 99
Общее решение уравнения (2.6) имеет вид
V (С) = Сх sin rjC + С2 cos r? + С3 sh г2С -f- С4 ch r2C,
где
' \ (2-8)
i=-!+/(f)'+»J-1
Удовлетворяя граничным условиям (2.2) и (2.3), получим
следующие уравнения для определения постоянных
интегрирования:
С2 + С4=:0, Г1Сг-\-г2Сг = 0.
С1 (r\ sin rx + rx r2 sh г2) + С2 ( r i cos гх + r2 ch г2) — °»
— Cj (rf cos rx + Tj r* ch r2) + C2 ( r^ sin rx — r\ sh r3) = 0.
Отсюда, приравнивая определитель нулю, получим
характеристическое уравнение:
I rx sin rx -f- r2sh г2 г\ cos Tj+r^ ch r21
— г2 cos rx — г2 ch /*2 а-з sin /^ — r\ sh r2
или
A(ri' r2)=r\+rl + rir2{r\— i)sinrlShr2 +
-f- 2r2 г2 cos f-jCh r2 = 0.
Возвращаясь к обозначениям (2.7), получим:
А (со, р) = рз _|_ 2а)2 _+_ ^о) Sin rx sh r2 + 2u>2 cos rx ch r2 = 0. (2.9)
Если внешняя сила отсутствует, то р = 0 и корни
уравнения (2.9) являются действительными. Они соответствуют
частотам собственных колебаний незагруженного стержня.
С возрастанием параметра р два наименьших корня
сближаются между собой и при некотором значении р = р#
становятся кратными (рис. 33). При дальнейшем увеличении р
корни становятся комплексными, причем один из них имеет
отрицательную мнимую часть. Следовательно, как видно из
формулы (2.5), значение р$ соответствует критической силеРг

100 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
По вычислениям Бека, это значение равно (3^ = 20,05,
а по вычислениям К. С. Дейнеко и М. Я. Леонова
10
20
/5\
Рис. 33.
<^
N
i
Г
pf
0 5 Ю 15 20 J3=jj-
Рис. 34.
Р# = 2,0028тс2= 19,77. Приближенно можно положить, что
Р*~Ц^~- (2-10)
График изменения частот со в области их действительных
значений показан на рис. 34.

§ 2.3] ВЛИЯНИЕ СПОСОБОВ РАСПРЕДЕЛЕНИЯ МАССЫ 101
§ 2.3. Влияние способов распределения массы
А. Пфлюгер 1) рассмотрел задачу в предположении,
что помимо распределенной массы на конце стержня имеется
сосредоточенная масса М (рис. 35). Уравнение (2.1),
граничные условия (2.2) и первое из условий (2.3) остаются без
изменения. Вместо четвертого
условия следует записать:
d2v (/, t) _ M d2v (/, t)
dz2
EJ
dt2
(2.11)
Повторяя выкладки предыдущего
параграфа и используя граничное
условие (2.11), придем к уравнению,
которое является обобщением
уравнения (2.9):
Д (а), р) = р2 _|_ 2(1)2 _|_ pa) sin rx sh r2+
+ 2си2 cos/^ chr2 —
М
ml
2ш
/(«¦+¦
1 (r2sin rx chr2—
rx cos rx sh r2).
Рис. 35.
же собственная масса
Результаты численного решения этого
уравнения представлены на рис. 36.
Если Ж = 0, то р#« 20,05. Если
стержня пренебрежимо мала по сравнению с
сосредоточенной на конце массой М, то р оказывается равным
наименьшему корню уравнения tg ]/"р = Ур » т- е- Р*=20,19.
Случай двух сосредоточенных масс, значения которых
велики по сравнению с массой стержня, был рассмотрен
К. С- Дейнеко и М. Я. Леоновым2), Уравнения малых
колебаний стержня около невозмущенной формы равновесия
запишем в виде
5 лл d2Vi * %я d2v2
*1 = —MV
¦M*i
dt2
d2v{
¦ §12^2
dt2
Ь22М2
dt2
d2v2
dt2
1) См. сноску 5) на стр. 96.
2) Цит. на стр. 96.

102 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
Г'1Г
20
15
ю У
Ш05
20,19 \
О 0,5 10 0,5 0
ml M
Рис. 36.
У/0'Ш У
Рис. 37.

§ 2.3] ВЛИЯНИЕ СПОСОБОВ РАСПРЕДЕЛЕНИЯ МАССЫ ЮЗ
где vx(t) и v2(t) — перемещения точек, в которых
сосредоточены массы Мх и М2 (рис.37), 8П(Р), 842(Р), 821(Р) и
822 (P) — соответствующие перемещения от единичных
поперечных сил, приложенных к стержню, определяемые с учетом
силы Р.
Единичные перемещения нетрудно найти из элементарных
соображений. Для этого воспользуемся уравнением статичен
ского изгиба
dzK ' dz2
которое имеет общий интеграл
v (z) = Сх sin kz + С2 cos kz + C3z + C4,
где k2 = P/EJ. Рассматривая последовательно случай действия
единичной силы, приложенной к массам Мх и М2, и подчиняя
решение граничным условиям, получим:
8П — ¦—— (sin ka — ka cos ka),
812 = -jp- [sin kl—kacos kl — sin k (/—a)],
821 = —гр- [sin kl—kl cos ka -\- sin k (/—a)],
822 = —rp- (sin kl — kl cos kl).
Принцип взаимности перемещений здесь, очевидно, не имеет
места.
Полагая
Vi(t) = VleiQt, v2(t) = V2elQt,
получим характеристическое уравнение
[Af^nQ2—1 M2812Q2
IM&fi* M2b22Q2-l
= 0.
Отсюда
og Mfin + М2Ъ22 ± Y(Mxbn — M2b22f + 4МХМ2Ь12Ь2
~~ 2М1М2(ЪпЬ22 — Ъ12Ъ21)

104 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
Критическое значение силы Р найдем, приравнивая нулю
выражение, стоящее под радикалом. На рис. 38 показаны
результаты вычислений для случая а = 1/2. Когда Мх = 0,
Р U
80
60
40
го
20,19
1&кл
80,76 \
О 0,5 t 0,5 О
Рис. 38.
мы получаем, как и ранее, (^^20,19. При М2 = 0
критическое значение, как и следовало ожидать, оказывается ровно
в четыре раза больше.
§ 2.4. Приближенное решение задачи
Точное исследование устойчивости стержней, загруженных
неконсервативными силами, представляет большие
вычислительные трудности, которые связаны с изучением поведения
корней трансцендентных уравнений на плоскости комплексного
переменного. Эти трудности резко возрастают при
усложнении постановки задачи (переменные сечения, сложные нагрузки,
учет затухания и т. п.). В таких случаях приближенный
метод, изложенный в § 1.14, будет иметь несомненные
преимущества.

§ 2.4] ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ
105
В случае стержня, нагруженного тангенциальными силами,
уравнения (1.79) принимают вид
оо
^-+еУ1Г + 2^ + д^2 *;*/* = ° U=i. 2,...).
k = l
(2.12)
где fj (t) — коэффициенты разложения прогиба v(z, t) в ряд
по формам собственных малых колебаний стержня Vj(z),
Qj — частоты этих колебаний, е;. — коэффициенты затухания,
р — параметр, с точностью до которого заданы значения
продольной силы N (z) в каждом сечении стержня, bjk —
коэффициенты, вычисляемые по формуле (1.71):
/
J о
Формула (2.13) дана для случая, когда функции Vj(z)
удовлетворяют условию нормировки
с.= Гт(z) vjdz = 1.
о
Если же это условие не выполнено, то вместо формулы (2.13)
получаем:
b,k = 9 1 fN^vt^-dz. (2.14)
jk &Ус,с J v ' j dz2 K
J J 0
Формула (2.13) была получена в первой гл^ве из общих
уравнений теории упругой устойчивости; здесь мы покажем
кратко, каким путем ее можно получить непосредственно из
уравнения изгибных колебаний стержня. Если все продольные
силы, действующие на стержень,—тангенциальные, то
уравнение, как нетрудно показать, имеет вид
%<p) = ^[EJ{z)^]+m^-$N(z)^ = Q. (2.15)
Граничные условия будут меняться в зависимости от способа
опорных закреплений; существенно, однако, что
тангенциальные силы не будут входить в динамические граничные условия.

106 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
Представим решение уравнения (2.15) в виде ряда
оо
/=i J J
и применим вариационный метод Галеркина. Учитывая, что
на основании только что сделанного замечания о граничных
условиях уравнения метода Галеркина для этой задачи не
будут содержать внеинтегральных членов, т. е. будут
иметь вид
i
fi(v)vjdz = 0 (y=l, 2, ...),
о
легко придем к уравнениям (2.12).
Применим уравнения (2.12) для приближенного решения
задачи из § 2.2. Для этой задачи N(z) = — Я,
Vj (С) = sin ХуС — sh ХуС — fy (cos If — ch \fi),
Здесь \j и [Ay — некоторые константы. Например, \х— 1,875,
Х2 = 4,694, ji1= 1,3622, [х2 = 0,98187. В качестве
параметра р, характеризующего внешнюю нагрузку, по-прежнему
удобно взять величину
Р/2
$ = -ir- (2-16)
Тогда матричные элементы bjk оказываются безразмерными.
Полагая
fj = F/2i, (2.17)
приведем задачу к исследованию корней характеристического
уравнения типа (1.82)
К-?—*) VHP*,» | = 0. (2-18)
где оъ = 2у/2х, со = QfQv
При малых значениях р все безразмерные частоты ш
действительны; этот случай мы будем, как и ранее,
квалифицировать как устойчивость невозмущенного (прямолинейного)
достояния стержня. Приближенный анализ устойчивости сво-

§ 2.4] ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ 107
дится к определению условий, при которых усеченные
уравнения, получающиеся из бесконечного определителя (2.18),
не имеют корней, лежащих в правой полуплоскости
комплексного переменного.
В качестве первого приближения возьмем определитель
второго порядка. При этом могут быть использованы
результаты § 1.16. В рассматриваемом случае о)2=:6,250,6П = 0,0666,
bl2=—0,954, *21=0,00387, Ь22=—0,0274. Условия а2(Р) > 0,
'CU-
1
и
1
1 Imo
¦fi'fi.
A.W
у ш
Рис. 39.
а4(Р)>^» гд-е а2 и а4 определяются согласно (1.103), в
данной задаче выполняются при всех значениях р. Условие (1.104)
после подстановки в него выражений для а2(Р) и а4(Р) и
числовых значений принимает вид
Р2 — 120,5р + 2020>0.
Отсюда критическое значение параметра р будет равно
Р^ = 20,15 и, следовательно, критическая сила
Р, = 20.15^-.
Это значение примерно на 0,5 % отличается от значения,
найденного Беком.
Нетрудно проследить за поведением характеристических
показателей a = lw на плоскости комплексного переменного
при постепенном увеличении внешней нагрузки (рис. 39).
Пока р < р# = 20,15, все показатели остаются на мнимой оси.
При Р = Р# характеристические показатели становятся попарно
кратными, а при дальнейшем увеличении р мы имеем типичную

108 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
колебательную неустойчивость. Это имеет место, пока
р < р* = 100,35. В дальнейшем характеристические показатели
становятся чисто действительными, и поскольку два из них
положительны, то мы имеем здесь неустойчивость с
экспоненциально возрастающими возмущениями.
Учет затухания, как это, впрочем, следует и из общей
теории, йносит некоторые коррективы в эти результаты.
§ 2.5. Влияние затухания на устойчивость.
Рассмотрим теперь уравнения (2.19), содержащие первые
производные от обобщенных координат /у по времени.
Коэффициенты затухания, вообще говоря, различны для
каждой формы колебаний и, кроме того, могут зависеть от
частот рассматриваемого движения. Используя результаты
§ 1.16 и полагая затухание малым, придем к услбвию
устойчивости (1.101) с коэффициентами (1.102):
Аг (т|) р + Вх (т|) р + Сх (т]) > 0, (2.19)
где т] — отношение парциальных характеристик затухания:
Явные выражения для коэффициентов уравнения (2.19) не
выписываем. Корни уравнения, которые получаются путем
приравнивания левой части соотношения (2.19) нулю,
представляют собой критические параметры р^, найденные с
учетом затухания1). График для параметра р^ при различных
соотношениях между парциальными коэффициентами затухания
представлен на рис. 40. Лишь в том случае, когда ег = е2,
имеет место равенство р^ = р^. Во всех остальных
случаях р„ < р„.
Наиболее естественной мерой затухания является
относительное рассеяние энергии за один цикл колебаний
(подробнее об этом см. § 3.4):
) Точнее, с учетом исчезающе малого затухания.

§ 2.5] ВЛИЯНИЕ ЗАТУХАНИЯ НА УСТОЙЧИВОСТЬ 10§
Здесь Q — действительная частота колебаний для
периодического процесса, который будет иметь место на границе
области устойчивости. Таким образом,
Рассмотрим, например, случай, когда ^г = ^29 что
соответствует вполне правдоподобному предположению о
независимости относительного рассеяния энергии от частоты.
Тогда т] = о)2 = 39,06 и критический параметр р , найденный
/**
А
#7
&5]
/
/
¦^-^
0 / г з 4 ~ _&
7 9t
Рис. 40.
с учетом исчезающе малого затухания, оказывается значительно
меньше, чем параметр ^ (рис. 40).
Вопрос о характере влияния диссипативных сил на
устойчивость неконсервативных систем уже обсуждался ранее (§ 1.16).
Здесь мы встречаемся с эффектом,- который противоречит
интуитивным представлениям о диссипативных силах как
о стабилизирующих факторах. Они действительно являются
таковыми, если внешние силы, действующие на систему,
обладают потенциалом (об этом гласит одна из теорем
Кельвина). Тангенциальные же силы потенциалом не обладают.
Следует еще раз подчеркнуть различное толкование
понятия устойчивости, которое использовалось в двух последних

110 устойчивость при наличии следящих сил [гл. 2
параграфах. В предыдущем параграфе невозмущенное
равновесие считалось устойчивым, если все характеристические
показатели находятся на мнимой оси. В данном параграфе
мы полагаем, что устойчивость имеет место, когда все
характеристические показатели лежат левее мнимой оси. Поскольку
рассматриваемая физическая задача является нелинейной,
а случай чисто мнимых показателей относится, по Ляпунову,
к сомнительным случаям (когда линейное приближение
\1тб
О Re6
Рис. 41.
оказывается недостаточным для суждения об устойчивости),
то имеется больше оснований доверять решениям,
полученным при учете затухания. Вообще же этот вопрос требует
дальнейшего изучения, основанного, в частности, на
нелинейных уравнениях.
На рис. 41 показано поведение характеристических
показателей при постепенном увеличении параметра (3, найденное
при помощи уравнения типа (1.83). При достаточно
больших р влияние затухания становится почти неощутимым.
§ 2.6. Задача об устойчивости стержня, сжатого силой
с фиксированной линией действия
Остановимся кратко на случае силы с фиксированной
линией действия, следуя вначале постановке Б.Л.Николаи.
Будем пренебрегать распределенной массой стержня, полагая,
что вся масса сосредоточена на свободном конце в одной
точке (рис. 42). Пусть М — величина этой массы, f (t) — про-

§ 2.6] СЖАТИЕ СИЛОЙ С ФИКСИРОВАННОЙ ЛИНИЕЙ ДЕЙСТВИЯ 111
гиб на свободном конце. Уравнение малых изгибных
колебаний запишется в виде
d2v
v d2f
'Z) dt2
Как обычно, полагаем:
v (z, t) = V (z) eiQi, f (t) = Fem.
Подстановка в (2.20) приводит к уравнению
d2V
dz2
(2.20)
(2.21)
+ #V
M92F
EJ
(l-г).
решение которого будет:
V (z) = Сг sin kz +
, n . , MQ2F n ч
+ C2 cos kz + -?2?j- (I — z)
(здесь, как и ранее, k2 =
=P/EJ). Подчиняя это
решение граничным условиям
dV(0)
V(0)
dz
0t
легко получим формулу для
частоты 2:
Q=±
/¦
1
Ml sin kl
kl
- cos kl
(2.22)
Рис. 42.
Частоты, определяемые по формуле (2.22), остаются
вещественными, пока выражение, стоящее в знаменателе,
больше нуля. Из условия tgkl = kl найдем, что критическая
сила для этой задачи
Это значение, как, собственно, и формула (2.22), полностью
совпадает с соответствующими результатами для задачи об

112
УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
устойчивости стержня при действии тангенциальной силы
(§ 5 введения).
Аналогия сохраняется и для случая распределенной массы!).
Уравнение (2.1) и граничные условия на заделанном конце (2.2)
остаются неизменными, а вместо условий (2.3) имеем:
EJPv(l,t) _ pv(l ty F,d*v(lJ) _ pdv(l,t)
Применяя к поставленной краевой задаче метод,
описанный в § 2.2, придем к характеристическому уравнению
Л + Л + г/2 (г\ — r22) sin гх sh г2 +
-(- 2r\r\ cos rx ch r2 = О,
где
:=-4±/(4У
mQ2/
?/
mQH
EJ *
Это уравнение ничем не отличается
от характеристического уравнения
(2.9).
В работе Б. Л. Николаи был
также рассмотрен случай
одновременного действия неконсервативной
силы и силы, которая, оставаясь
постоянной по величине,
перемещается вместе со свободным концом
стержня (рис. 43). Вторая сила,
очевидно, является обычной потенциальной силой,
рассматриваемой в теории упругой устойчивости.
Уравнение малых колебаний для этого случая имеет вид
^ж
Рис. 43.
EJ^ = Pv-Q(f-v)-M(l-
Z) dt2
Подставляя сюда выражения (2.21) и используя обозначение
>_P + Q
EJ '
ft2:
2) Это было показано Э. Л. Позняком (неопубликованная
работа).

§ 2.6] СЖАТИЕ СИЛОЙ С ФИКСИРОВАННОЙ ЛИНИЕЙ ДЕЙСТВИЯ 113
получим:
После обычной процедуры найдем, что
/¦
^=±1/ f + Qcoskl (2.23)
17 Ml (^L-coskl)
Рассмотрим некоторые частные случаи.
1) Если Р — 0, то частота 2 станет чисто мнимой, пройдя
через значение 2 = 0 при kl = к/2. Это соответствует
обычной потере устойчивости в смысле Эйлера при критическом
значении сжимающей силы
2) Если 0 < Р < Q, то потеря устойчивости также
происходит по типу разветвления форм равновесия, причем
критическое значение параметра kl определяется из условия
ut Р
cos kl = — -q .
Весьма существенно, что с увеличением неконсервативной
составляющей Р критическое значение суммарной нагрузки
1 2
возрастает. Например, при P = -^Q имеем &/ = -^7и» т- е»
(я+<г).=ияг-.
Таким образом, добавление неконсервативной составляющей,
не превышающей некоторого значения, оказывает
стабилизирующее влияние. Аналогичный эффект имеет место при
стабилизации гироскопических систем путем введения «сил
радиальной коррекции».
3) Если Р > Q, то переход от вещественных
собственных частот к чисто мнимым через значение Q = 0
становится невозможным. Суммарная критическая сила оказывается
равной
где k# — корень уравнения tg kl = kl.

114 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
График изменения параметра kl в зависимости от
отношения нагрузок P/Q показан на рис. 44. Любопытным
обстоятельством является наличие
М разрыва в величине крити-
1 ' ] ' ' ческой силы
к\
N.
\
\
0,5
1,0
Рис. 44.
1,5
2,0
?_
Q
Рис. 45.
Г. Ю. Джанелидзе1) показал, что задача об
устойчивости стержня под действием тангенциальной силы Р и
консервативной силы Q (рис. 45) также приводит к формуле (2.23),
т. е. к тем же результатам.
§ 2.7. Устойчивость плоской формы изгиба
(вывод уравнений)
В дальнейшем, следуя в основном работе В. В.
Болотина2), рассмотрим задачу об устойчивости плоской формы
изгиба стержней, нагруженных следящими силами. Допустим,
*) Джанелидзе Г. Ю., Об устойчивости стержня при
действии следящей силы, Тр. Ленингр. политехи, ин-та, № 192 (1958).
2) Болотин В. В., О колебаниях и устойчивости стержней,
находящихся под действием неконсервативных сил, Сб. «Колебания
в турбомашинах», Изд-во АН СССР, 1959,

§ 2.7] УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА 115
что имеется стержень с прямолинейной осью, нагруженный
силами, перпендикулярными к этой оси и лежащими в одной
плоскости. Не стремясь к чрезмерной общности,
предположим, что плоскость действия сил является плоскостью
симметрии стержня и вместе с тем плоскостью наибольшей
жесткости (рис. 23). Пусть внешняя нагрузка q(z)t
приложенная на расстоянии e(z) от оси Oz, вызывает в сечениях
стержня изгибающий момент Lx{z). Установим условия
устойчивости плоской деформации стержня, считая, что внешние
силы являются следящими.
Уравнения, описывающие равновесие стержня в
положении, смежном с исходным, для случая нагрузки неизменного
направления были получены В. 3. Власовым1):
EL
d4u
d2
EL
dz*
•01
У dz*
d4
f^-(M) = o.
dz2
d dz2
<*,ML'?)+
d2u
+ q(e-ay)Q+Lx^ = 0
x dz2
(2.24)
Здесь u(z) — перемещения оси стержня из плоскости
наибольшей жесткости, 6 (г)— угол закручивания (его
положительное направление было показано на рис. 24), EJy, EJ^,
GJd — изгибная, секториальная и крутильная жесткости
сечения, F — его площадь, ау — координата центра изгиба,
Ру — геометрическая характеристика:
Перечислим наиболее часто встречающиеся граничные
условия, на которые придется ссылаться ниже.
I. Шарнирное опирание. Здесь прогиб и угол поворота,
а также изгибающий момент и изгибно-крутящий бимомент
обращаются в нуль:
d2u d4
dz2 dz2
:0.
Ч Власов В. 3., Тонкостенные упругие стержни, Физматгиз,
1959.

116 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ (ГЛ. U
II. Полная заделка. В этом случае
о du dft ~
dz dz
III. Свободный конец (без нагрузки). Здесь
d^u _dh^ __^!_п if!!_ 2 db — Q
где
G/rf
.Cj,,.
IV. Свободный конец при наличии сосредоточенной
силы Р. В этом случае должны выполняться «естественные»
(в смысле вариационного исчисления) граничные условия:
d2u _ d4 _
dz2 ~~~ tfz2 — U'
«,?-«=-ч.(?—'?)-"<—•л>=°-
Переходя к случаю следящей нагрузки, будем отклонения
от невозмущенного равновесия считать функциями времени:
и = u(z, t), 6 = 6(2, ?). Соответствующие уравнения получим,
если введем в уравнения (2.24) дополнительные компоненты
нагрузки, появляющиеся при изгибно-крутильной деформации,
а также инерционные члены:
EJy-^ + ~ {Lxb) + т -^ (и + ау6) = bqx%
Здесь т — погонная масса, г — радиус инерции сечения,
отнесенный к центру изгиба, r2 — a2y-\-(Jx-\-Jy)IF. Силами
инерции вращения и депланации, существенными лишь в
случае коротких стержней типа оболочек, пренебрегаем.
В правых частях уравнений (2.25) представлены
дополнительная поперечная нагрузка kqx и дополнительный
распределенный крутящий момент А^. В случае сил неизменной

§ 2.71
УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА
117
величины и направления hqx — A|x2 = 0; если же силы
являются следящими, то, как видно из рис. 46,
hqx = — <7sin9~ — qd, \
^z=q(e — ay)sm0^q(e — ay)d. J
После подстановки (2.26) в (2.25) получаем систему уравнений:
(2.26)
fiJ-^+-^(M) + ^ + m-?-(ii+M) = Oi
У dz*
а4о
dz2
дЧ
dt*
EJ<» dz* GJd dz2
dz
64
2^ML^)+
M\
d2
+ Lx^*+mJ§P (вув+г2в)=0.
(2.27)
При переходе к следящим нагрузкам граничные условия
У
Рис. 46.
для случаев I—III не изменяются. В случае IV граничные
условия примут вид

118 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ- СЛЕДЯЩИХ СИЛ [ГЛ. 2
Попробуем свести систему уравнений в частных
производных (2.27) к системе обыкновенных дифференциальных
уравнений. Для этого наряду с уравнениями (2.27) рассмотрим
уравнения
г-,г д4и , д2и п
п, дЧ п, дЧ 2 дЧ „
EJ»1F -GJt-M ~ mr ~dF = °'
которые, очевидно, описывают собственные колебания
некоторого стержня с сечением, имеющим две оси симметрии.
Положив и — иj (z) cos Qjt, б = б;- (z) cos Qjt, получим:
dAUj 2
у dz<
d4j
ZJy-7f^r-^J»J=0>
d*tij d4f « n
(2.28)
Допустим, что найдены решения уравнений (2.28),
удовлетворяющие граничным условиям для первоначально
поставленной задачи. Это будут формы собственных изгибных
колебаний ul(z)t u2(z), ..., Uj(z), ... и собственных
крутильных колебаний bx{z), 62(г), •••» ®j(z) которые,
как известно, обладают свойством ортогональности. Мы будем,
кроме того, предполагать их нормированными:
j mujuk dz = bJk, j /иг28Д dz = bJk (2.29)
(bjk — символ Кронеккера).
Ищем решение системы (2.27) в виде
и (г, 0 = 2 Uk (0 ик (z), 0 (z, 0 = S в* (0 9ft (*). (2.30)
применяя вариационный метод Галеркина. Сходимость рядов
(2.30) вытекает из того, что системы функций uk(z) и bk(z)

§ 2.7]
УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА
119
являются полными. В дальнейшем, однако, будем считать,
что число членов каждого из рядов конечно и равно п.
Заметим, что в случае следящих сил, в отличие от случая
сил неизменного направления, уравнения метода Галеркина
не будут содержать членов, учитывающих «естественные»
граничные условия. Подставив ряды (2.30) в уравнения (2.27),
умножив первое из них на Uj(z), второе — на Qj(z) и
проинтегрировав по всей длине стержня, получим систему
уравнений:
d2Uj 2 ^ d2Sk Г
k=\ о
+ 2 в* / а1 [ш <LA) + ?9 J dz = °'
ft=l 0
dWj о Л Л d2Uk Г
-^Г + &Ы% + 2d ~W~ J mayb)uk dz —
k = l 0
p
A=l 0
(2.31)
k=l 0
(7=1, 2, ...).
В этих уравнениях 2^ и Qy — парциальные частоты
собственных изгибных и крутильных колебаний, определяемые как
собственные значения, соответствующие уравнениям (2.28) и
краевым условиям для данного стержня.
Введем, как в § 1.13, сплошную нумерацию обобщенных
координат: Uj = /2y_i, в/ = /«
V
Тогда
&xj — &2J-V
2,
8/:
:2
27»
[j=z(f2,_v Оу = ср2у. Система (2.31) может бьщ?
и,=

120 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
представлена в виде
"Ж + 2 ejufk + $ l/j + p J bjkfk) = 0 (2.32)
(/=1. 2. ¦••).
где
ejk
Ь,
jk
\ mayyftkdzt если jiik— нечетное число,
о
О, если jiik —четное число,
О, если j и k —
нечетные числа,
1 Г Г d2 ,, л . I , если j—нечетное,
-&Jb[-dF{L^k) + №J rf*' k — четное число,
-/ о
. /• ,2 если у — четное,
7?" / Ь L* -dbF dz> k — нечетное
"у о число,
— -i / 2Ру?у -J~z (L* Чг) dz' еСЛИ J И А ~~ чеТНЫе
Ч/ о числа.
Предполагается, что следящая нагрузка задана с точностью
до параметра [3.
Допустим, что сечение стержня имеет две оси симметрии.
Тогде ау = ру = 0 и, следовательно, все в]к = 0. Производя
интегрирование по частям:
Г Г d2 1 d \l Г d<?j d
J ЬЫ^Щdz = Ьlu^ъ)|0-ilulu (Z^}**•
о о
J bL* ~d^dz=-dF L#* I-J 4FHF (^T*)dz-

§ 2.7] УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА
придем к формулам
О,
121
»,» =
если j и k—числа
одинаковой четности,
1
°5
Ту^-(^*)
/
d4t d
о
+ J W/Pft ^
если у—нечетное, k—
четное число,
(2.33)
¦LJfk\ —
4^1
aj L dz
С d9, d I
если у—четное,
А—нечетное число.
Сопоставим формулы (2.33) с формулами (1.78),
полученными из общих уравнений теории упругости. Легко видеть,
что они совпадают в случае граничных условий I—III.
Если же на свободном конце стержня имеется
сосредоточенная сила, то некоторое внешнее расхождение между
формулами сохраняется. Оно объясняется тем, что в формулах (1.78)
сосредоточенная сила на конце учитывается как особенность
у распределенной нагрузки q в формулах (2.33) — во внеин-
тегральных членах.
В более общем случае совместного действия
консервативных сил с параметром а и следящих сил с параметром (3
получим систему уравнений:
^ + 2 ejkfk + Q) \fj + S (««,* + pfy) Д
*=1
k = \
= 0. (2.34)
Здесь коэффициенты djk определяются по формулам (1.77).

122 устойчивость при наличии следящих Сил (гл. i
§ 2.8. Некоторые числовые результаты
Рассмотрим случай сечения с двумя осями симметрии.
В этом случае ау = ру = ejk — 0. Тогда, как видно из
формул (2.33), все элементы матрицы ajk и bjk с индексами
разной четности обращаются в нуль. Некоторые результаты,
относящиеся к системам, матрицы коэффициентов которых
имеют такую структуру, были приведены в первой главе.
Здесь мы ограничимся числовой оценкой критических сил
1
Л
°ц
1
г \
1 1
л
«с 1 >!
< 2 >
ь
I
1
г
Рис. 47.
применительно к задаче об устойчивости плоской формы
изгиба балки, опертой по концам и нагруженной в середине
пролета (рис. 47). Силу Q примем в качестве параметра
консервативной нагрузки, силу Р — в качестве параметра
следящей нагрузки.
Для нормированных форм собственных колебаний имеем
выражения
-т=- sin ±—,
%/-i:
?2/:
n
sin
JKZ
(2.35)
YmrH I
а для соответствующих собственных частот
2,
V-i
2,
;%» xfEJy
rl f m \ c
I2
El
")•)
(2.36)

§ 2.8] НЕКОТОРЫЕ ЧИСЛОВЫЕ РЕЗУЛЬТАТЫ 123
В первом приближении ограничимся учетом основных
форм колебаний. Подставляя в формулы (1.77) выражения
(2.35) и (2.36) и учитывая, что Lx = z/2 (0<*<//2),
получим:
/
1 о у
i
1 Г d<o2 d ,r ч , 2/rC
fl2i= — "5Г / -dT'fc(L**fJdz = 7 i? V
Q2 ? ^(o/rf+^-f^)
где
1/2
~ 27Z Г TlZ / . UZ . TZZ 1ZZ \ , 1 / л , 7t2 \
C== —j cos-r(sin-r+-rcos-r)rf2; = T^+x).
0
Отсюда, используя формулу (1.84), найдем критическое
значение параметра Q:
(это значение лишь на 5% отличается от точного значения;
заметим, что тс3/2С= 17,9).
Вычислим элементы матрицы bjk. Представляя
сосредоточенную силу при помощи дельта-функции, найдем:
i
1 Г 2/3
*в = «М + -?Г1/ ЯЪЪйг = -?щг$-С).
1 О У
В то же время Ь2г = а12. Для дальнейшего удобно ввести
параметр
Р0 = -7=4= = г-^-= — \fEJv (GJd+4- EJo>),
0 f~bl2b2l 2YC(\ — С) Р * y\ d т р <»)>
(2.38)
имеющий размерность силы. Этот параметр связан с
критической силой Q# соотношением

124 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
Критическое значение следящей нагрузки без учета
затухания определяется по формуле (1.86):
4-1
'* —'о 2<о2 •
Здесь и>2— отношение парциальных частот:
Ш2=2
GJd + -jr EJ*
EJV
Для узкой полосы высотой h
(2.40)
(2.41)
где |х—коэффициент Пуассона. Пусть, например, h — l/5,
I* = 0,3. Тогда по формулам (2.38) и (2.40) Р„ = 3,35Р0 =
= 8.б7<?..
Как видно из формулы (2.40), с приближением
парциальных частот друг к другу критическое значение параметра /\
6
т^Т
Рис. 48.
убывает. При безразмерной частоте о>2,
близкой к единице, формула (2.40)
становится непригодной. Типичный
случай такой ситуации получим,
рассматривая устойчивость плоской
формы изгиба балки, сечение
которой является двутавром (рис. 48).
Пусть Ъ — ширина полок, 8— их
толщина, h — расстояние между
центрами тяжести полок; толщину стенки
считаем пренебрежимо малой. Тогда
Jy « *38/6, Jdж^ЬЪ\ ^=ЬШ/24,
r2 = h2/4-\-b2/l2, откуда по формуле (2.41)
1 +
8
*»(i + ri
Ш'Ш'
1 +
Ь2
3h2
(2.42)
Пусть / = 400 см, h = 60 см, Ь = 20 см, 8=1 см,
|х = 0,3. Тогда по формуле (2.42) о>2= 1,047. Учет членов,
содержащих квадраты коэффициентов затухания, становится

§ 2.8] НЕКОТОРЫЕ ЧИСЛОВЫЕ РЕЗУЛЬТАТЫ 125
здесь совершенно необходимым. Действительно, по
формуле (2.40) мы нашли бы в этом случае, что Р# = 0,045Р0.
Между тем по формуле (1.99)
^=(i^-/(o,i-1)2+«r8[li2+iiH+1)+<i]- (2-43)
Если т)=1, ? = 0,05, то Р^ = 0,0735Р0, т. е. критическая
сила оказывается примерно в 1,6 раза больше значения,
вычисленного без учета
затухания.
Влияние
неконсервативных сил может
оказаться стабилизирующим,
если они действуют
совместно с
консервативными силами.
Проиллюстрируем это на примере
задачи об устойчивости
плоской формы изгиба,
используя результаты § 1.15.
Введем параметр А
согласно формуле
^=^^(*12e21+*12*2l)«
Подставляя сюда формулы
(2.40) и (2.41), найдем, что
Л= 2С~1 .(9 4Д) Рис-49-
2|/С(С—1) V '
Вычисления по формуле (2.44) дают А =1,07. Далее,
аналогично (1.88) введем параметр
^ Р, Q '
Добавление следящей силы будет способствовать
стабилизации при потере устойчивости по типу разветвления форм
равновесия, которая будет иметь место, пока ф_ < <]>„, где
Фо-л+Ул^ТТ^г.бз.

126 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
р Q
Если ф > ф0, т. е. если -^-> 2,53-^г-, то потеря устой-
чивости носит колебательный характер.
То обстоятельство, что в случае, когда потеря
устойчивости происходит по типу разветвления форм равновесия,
следящая составляющая способствует стабилизации
невозмущенного равновесия, вытекает и из физических соображений
(рис. 49). При отклонении балки от положения
невозмущенного равновесия составляющая следящей силы Рх стремится
возвратить балку к этому положению.
§ 2.9# Некоторые другие задачи
Рассмотрим некоторые другие задачи, допускающие
сравнительно простое исследование. Рассмотрим узкую полосу
Рис. 50.
прямоугольного сечения, нагруженную на конце
сосредоточенным моментом L (рис. 50). Наряду с неподвижной
системой координат xQyQZq введем систему xyz, поворачивающуюся

§ 2.9] НЕКОТОРЫЕ ДРУГИЕ ЗАДАЧИ 127
вместе с сечениями полосы. Пусть L — вектор момента до
деформации и Lx — после деформации. Предположим, что
вектор ?j остается лежать в плоскости поперечного сечения,
но с направлением L он составляет угол Х6,
пропорциональный углу поворота 6 торцового сечения вокруг оси Oz0.
Тогда, проектируя вектор Lx на неподвижные оси координат»
получим с точностью до величин первого порядка
LXo = L, 1Уо = Ш(0, LZo = -L^-.
Для подвижной системы координат соответственно найдем:
LX = L, Ly = -LHz) + L\Hl)t
г , du(z) r du(l)
Рассматривая положения равновесия, смежные с
невозмущенным, получим систему уравнений
п , db , da r du (I)
UJd-d^—L~dF~L~dT-'
Она эквивалентна уравнению
d20
dz2 f ?20==?2Х0(/),
в котором обозначено
*=. Lt
EJyGJa
Его интеграл имеет вид
0 = Сх sin kz + С2 cos kz + Х0 (/).
Подчиняя интеграл краевым условиям
8(0) = ^ = О,
придем к характеристическому уравнению
cos kl = TZTT'

128 устойчивость при наличии следящих сил [гл. 2
Это уравнение имеет действительные корни, пока Х<; 0,5.
Если это условие выполнено, то потеря устойчивости
происходит по типу разветвления форм равновесия. При X > 0,5
ни при каких значениях момента L не существует форм
равновесия, смежных с невозмущенной. В этом случае потеря
устойчивости может происходить лишь по типу
колебательной неустойчивости !).
В дальнейшем ограничимся случаем X = 1, вычисления
для которого были недавно сделаны К. Н. Гопак и
С. Г. Кр и в о шеев о й 2). Уравнения малых колебаний
являются частным случаем уравнений (2.27):
„, д4и , , д26 . д2и л
EJy-M+LJ*r + m-W = Q'
п, д2Ь . , д2и . 2 <Э26 .
- GJa -g? + L S* + ш Ж = °-
Краевые условия имеют вид
«(0) = -^- = 0(0) -о,
д2и (I) __ д3и (I) _ дб (I) _
dz2 ~ dz* ~~ dz ~U>
(2.45)
(2.46)
Решение системы (2.45) ищем, как обычно, в виде
и (z, t)=U (г) ет, 0 (z, t) = Q (г) еш.
Для функций ?/(С) и в (С) (С = -г//) получаем выражения
U (С) = См ch |а1С + C2Tl sh [xxC + С3т2 cos ц2С +
+ С4Т2sin \h?> + сзЪcos ft? + сеТзsin fc?-
0(C) = Dx ch (AjC -f- D2 sh [XjC + 03 cos |x2C + D4 sin jx2C -f-
+ D5cos(x3C + D6sin1x3C.
*) Сходная задача была рассмотрена В. И. Феодосьевым
(Избранные задачи и вопросы по сопротивлению материалов, Гос-
техиздат, 1953). Различие состоит в том, что в задаче В. И. Фео-
досьева вектор момента остается лежать в плоскости,
параллельной Оху.
2) Цит. на стр. 96.

(2.47)
§ 2.9] НЕКОТОРЫЕ ДРУГИЕ ЗАДАЧИ 129
Здесь
1*1,2=1/ +Y + V Т+")2' ^З^^.
Удовлетворяя краевым условиям (2.46), получим
характеристическое уравнение
Д (о>2, р) = f^tb — Тз) l*i (l*i + HD (1*з sin (*3 + V-x sh \xx) X
X sh j*t cos (x2 — f2 (^ Sin [a2 -}- [ij sh |»j) cos ji8 [^ (f j — Тз) X
X (Т31*з — TiHO sin \b H-1*, (Tj — Тз) (Тз!*1 + Ti!*i) sh j»J +
+ T1T3 (Ti — Тз) 1*2 (t*i +1*2) (l*3 sin t*3 —1*2 sin 1*2) sin ^ ch ^ —
— [Tit*! (Ti — Тз) cos (J-2 + f^ (Ti — Тз) ch (*,] X
X [Ti (Ti(*j-Тз1*з) c°s 1*2 cos J», +1 j (^ + T^) ch |», cos jia—
— T1T3 (l*i +11!) ch l*icos 1*з] = °-
Для достаточно узкой и длинной полосы уравнение можно
упростить. Если 8/Л<1/10, А//<1/20, то

130 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
и, следовательно, Тз<СЛ1- Вычисления были сделаны для
случая ? = 2,1 • 106 кг/см2, 0 = 8,1 • 105 кг/см2. Результаты
представлены на рис. 51, из которого видно, что критическое
4{*>Щ 1 1 1 1
Рис. 51.
значение параметра р равно примерно 1,43. Вспоминая
обозначение (2.47), найдем:
§ 2.10. Уравнения равновесия сжатого
и скрученного стержня
Остальные параграфы настоящей главы мы посвятим
задаче об устойчивости прямолинейной формы скрученного
стержня при различном поведении скручивающего момента.

§ 2.10] РАВНОВЕСИЕ СЖАТОГО И СКРУЧЕННОГО СТЕРЖНЯ 131
Вначале, следуя классическим работам Е. Л. Николаи !),
составим уравнения равновесия сжатого и скрученного
стержня, находящегося в состоянии, близком к неискри-
вленному.
Рассмотрим тонкий упругий стержень произвольного
сечения и с произвольным очертанием его оси (рис. 52).
Введем подвижную систему координат x0y0z0, начало которой
будем помещать в точках недеформированной оси AQt ось z0
направлять по касательной к этой
оси, а оси х0 и у0 — по главным
осям инерции сечения. Положение
точки А0 можно охарактеризовать
длиной дуги s0, отсчитываемой от
некоторой начальной точки.
Кривизны и кручение
недеформированной оси стержня обозначим
через р0, д0 и г0.
Допустим, что под действием
некоторых нагрузок ось стержня
перешла в новое положение.
Точка А0 переместилась при этом
в положение А; компоненты
вектора смещения этой точки в
системе координат xQy0z0 обозначим Рис. 52.
через и, v и w. Система
координат, увлекаемая вместе со стержнем, приняла новое
положение xyz. Углы, составляемые новыми осями координат с
одноименными исходными осями, обозначим через ср, ф и ^. Новые
значения кривизн и кручения будут равны
Р = Ро + ЬР>
Девять кинематических величин—три смещения и, v и wt
три угла поворота ср, ф и х и три приращения кривизн и
кручения Ър, bq и 8г~ связаны между собой при малых
1) Цит. на стр. 93. См. также книгу: Пономарев С. Д.,
Бидерман В. Л., Лихарев К. К., Макушин В. М.,
М а л и н и н Н. Н., Ф е о д о с ь е в В. И., Расчеты на прочность
в машиностроении, т. III, Машгиз, 1959.

132 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
деформациях шестью соотношениями:
8р =
Ьд =
8г =
Ф =
-<? =
0 =
чг+г&~
-аг+'оф-
da ,
dv ,
day ,
rfF + W-
-гоФ.
-PoX-
-9oT.
-'o^.
-Pow-
-?o«-
(2.48)
Последнее из них выражает условие нерастяжимости оси
стержня ds = dsQ.
Составляющие главного вектора внутренних сил в
поперечном сечении стержня вдоль осей х, у и z обозначим
через Vx, Vy и Vz, а составляющие главного момента — через
Lx, Ly и Lz. Предполагая, что стержень нагружен внешними
силами с интенсивностями fx и /у, и составляя уравнения
равновесия элемента стержня, получим шесть уравнений
Кирхгофа:
dVr
ds
dV*
ds
dV7.
ds
dLr
ds
dLv
ds
dU
ds
\-qVz-rVy + f,
rVx-pVz + fy = 0
PVy-qVx =0
qL*-
pLz+Vx = Q
qLx =0
\
rLy-Vy = 0,
¦rL,
pLy
(2.49)
Замкнутую систему уравнений получим, дополняя
уравнения (2.49) и кинематические соотношения (2.48)
соотношениями упругости:
Lx = EJxbp, Ly = EJybq, Lz
¦ GJdbr.
(2.50)

§ 2.10] РАВНОВЕСИЕ СЖАТОГО И СКРУЧЕННОГО СТЕРЖНЯ 133
Здесь EJX и EJy — изгибные жесткости, OJd — жесткость
при кручении.
Пользуясь приведенными выше уравнениями, нетрудно
составить уравнение, которому подчиняются отклонения
сжатого и скрученного стержня от прямолинейной формы
равновесия (рис. 53). Допустим, что естественное
закручивание стержня отсутствует. В то же время кручение
прямолинейного стержня под действием внешнего момента L может
быть достаточно велико, чтобы оно существенно влияло на
поведение стержня при изгибе
(это влияние, очевидно, тем
заметнее, чем больше
отличаются между собой изгибные
жесткости сечения). Чтобы
учесть это конечное
закручивание, следует в соотношения
(2.48) вместо г0 подставить
выражение
L
GJd ¦
(2.51)
Рис. 53.
полагая в то же время, что
pQ — q0 = 0. Это соответствует
тому, что система координат
xQy0z0 связывается со
скрученным стержнем в его прямо- ?
линейном состоянии.
Рассматривая малые
отклонения от прямолинейного
состояния, будем считать перемещения и и vy углы ср и ф и
кривизны р и q малыми величинами первого порядка,
пренебрегая их квадратами и степенями более высоких порядков.
Тогда третье и шестое уравнения Кирхгофа можно
приближенно представить в виде
dV,
ds ds
т. е. продольную силу V'z и крутящий момент Lz можно
считать постоянными по длине. Следовательно, в
уравнениях (2.49) можно произвести замену Vz = — Pt LZ = L.
Отбрасывая в этих уравнениях величины второго порядка,

134 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
получим упрощенную систему уравнений
dVx
ds
dV„
r0Vy
ds
dLy
ds
dLv
ds
pP + r0Vx + fy = 0,
r0Ly+qL-Vy = 0,
pL+rQLx + Vx = 0.
и V„
(2.52)
Исключая из этих уравнений Vx и V у и используя
соотношения Клебша (2.48), нетрудно получить систему уравнений,
связывающих либо углы ср и ф, либо перемещения и и v.
Последние уравнения удобны для рассмотрения малых изгиб-
ных колебаний около положения равновесия. Тогда в
уравнения следует ввести инерционные силы:
, д2и
Остановимся подробнее на случае равных изгибных
жесткостей EJx = EJy = EJ. В этом случае все центральные
оси сечения являются главными, и поэтому возможен
широкий произвол в выборе систем координат x0yQz0 и xyz.
В частности, можно выбрать такие системы, в которых
кручение отсутствует. Тогда в соотношениях Клебша (2.48) и
уравнениях Кирхгофа (2.49) можно положить г0 = 0:
/у = "
d2v
(2.53)
р =
ф=
dVx
ds
dVy
ds
dLx
ds
dLy
ds
Lx
dy
ds
du
"ds
1
1
-4-
. <7^
. <? =
-яР+f,
pP+fy
-qL-Vy
PL + VX
EJp, Ly
di/
ds '
dv
ds
= 0,
— 0
= 0,
= 0,
= EJ
dv I
~ds~' J
(2.54)
(2.55)
(2.56)

§ 2.11] УСТОЙЧИВОСТЬ ПРЯМОЛИНЕЙНОЙ ФОРМЫ СТЕРЖНЯ 135
§ 2.11. Устойчивость прямолинейной формы
сжатого и скрученного стержня (метод Эйлера).
Классификация граничных условий
Рассмотрим задачу об устойчивости прямолинейной формы
сжатого и скрученного стержня при EJx = EJy = EJ.
Применим к этой задаче вначале метод Эйлера. Полагая в
уравнениях (2.55) fx = fy = 0 и исключая из них усилия VX и V ,
получим:
d2Lv dp
4^'^L + ^P = °-
Используя соотношения (2.54) и (2.56), придем к системе
уравнений
EJu™ + Lv'"-\-Pu"=Ot
Ejvw _ Lur" + Рч?' = 0.
(2.57)
Здесь штрихами обозначено дифференцирование по дуге s,
которое ввиду малости перемещений совпадает с
дифференцированием по z.
Задача состоит в отыскании таких сочетаний
параметров L и Р, при которых краевая задача, описываемая
уравнениями (2.57) и соответствующими граничными условиями,
имеет решения, отличные от тривиального и = v = 0. Можно
говорить о собственных значениях краевой задачи L(P),
зависящих от Р как от параметра. Если краевая задача
является самосопряженной (что соответствует наличию
потенциала внешних сил), то все ее собственные значения
действительны, и, следовательно, применяя метод Эйлера, мы найдем
такие пары значений L и Р, при которых имеет место
разветвление форм равновесия. При этом условии переход от
устойчивости прямолинейной формы равновесия к
неустойчивости наступает при некоторых минимальных по модулю
значениях L = L(P).
Установим класс граничных условий, для которых
исследование упругой устойчивости в постановке Эйлера приводит
к самосопряженной краевой задаче. Как известно, краевая
задача, описываемая дифференциальным уравнением 2(#) = 0t

136 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
является самосопряженной, если выражение
Д = f [и2% (их) — axZ (u2)] dz (2.58)
6
обращается в нуль для любых двух функций иг(г) и u2(z),
удовлетворяющих граничным условиям задачи. Обращение
в нуль величины А соответствует выполнению теоремы о
взаимности работ.
Вычислим аналогичное выражение для системы
уравнений (2.57). В этом случае вместо формулы (2.58) имеем:
i
Д = f [u2 {EJu™+Lv'['+Puf[) — их (EJuW+Щ' +Я<)] dz+
о
+ f[v2 (EJv™ - Ы>; + Pv'[) - vx (EJv™ - Lu'Z + Pvl)] dz.
о
После четырехкратного интегрирования по частям найдем:
Д = [(?/«;" + Ьо\ + Ра[) а2 + (ЕЩ' - Luf[ + Pv\) v2 —
- \EJu\ + Lv[ + Раг) и'2 - {EJv\ - Lu\ - Pvx) v'2 +
+ {EJu[ + Lvl) ul + iE^-L^) vl-EJu^-EJvtf^.
(2.59)
Равенству Д = 0 можно удовлетворить бесчисленным
количеством способов, выбирая различные комбинации восьми
граничных условий для и и v. Для заделанного одним
концом стержня u(0) = v (0) = и' (0) = vr (0) = 0; мы
предположим, что эти условия выполняются. Кроме того, предположим,
что на свободном конце z = l выполняются условия
EJu"'-\-Lv" + Pu' = 0t \
EJv"' — Lu" + Pv' = 0. J (2,60)
Чтобы установить смысл этих условий, рассмотрим
уравнения Кирхгофа (2.55):
V'x — Pu" = 0t
L'M + Lu"-Vy = 0t
ii + Lv" + Vx = 0.

§ 2.11] УСТОЙЧИВОСТЬ ПРЯМОЛИНЕЙНОЙ ФОРМЫ СТЕРЖНЯ 137
Интегрируя первые два уравнения, получим:
Vx = Pu' + bPlt
причем постоянные интегрирования ЬР1 и ЬР2 имеют смысл
внешних поперечных сил, приложенных к концу стержня.
Подставляя эти выражения в два других уравнения, получим:
EJa'" •+•№ + Ри' = — ЪР2, \
EJv"' — Lu" + Pvf = — lPv } (2'61)
Отсюда видно, что при 8Р1 = 8Р2 = 0 условия (2.60)
выполняются.
Формула (2.58) с учетом условий (2.60) запишется в виде
Д = [— Ehi\u'2 — EJv\v'2 + EJur2u\-\-
+ EJv;v[ — Lv[u'2-{-Lu[v'2]2=i = 0. (2.62)
Это условие будет удовлетворено, если положить:
EJu" (/) = L [Alt' (/) + kv' (/)],
— EJv" (I) = L [(1 + k) ur (/) -f-Bv' (/)],
где Л, Б и к — некоторые константы. В этом можно
убедиться непосредственной подстановкой.
Условия (2.63) имеют весьма простой механический смысл.
В их левых частях находятся изгибающие моменты Ly(l)
и Lx(l)t равные проекциям момента L на оси х и у в
торцовом сечении. Следовательно, соотношения (2.63)
предписывают некоторый способ поведения внешнего момента L при
изгибных деформациях стержня.
Рассмотрим некоторые частные случаи. Пусть А = В =
= /5 = 0; тогда Lx (/) = Lit' (/), Ly (I) = 0. Этому случаю
соответствует загружение стержня парой сил L = 2Pat
приложенных к жесткому диску на линии у = 0 (рис. 54, а).
Предполагается, что в закрученном состоянии,
непосредственно предшествующем потере устойчивости, силы
направлены по касательной к диску, а при потере устойчивости
сохраняют это направление и точки приложения.
Допустим теперь, что А = В = 0, но k = — lj2. В этом
случае Lx{l) = -^-Lur(/), Ly{l) — — -^-Lvr(l)t т. е. вектор
(2.63)

138 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ ['ГЛ. 2
L — 2Ра делит пополам угол между направлениями осей z
и zQ. Такой момент можно осуществить при помощи трех^
или большего числа равных и равноотстоящих сил,
приложенных к окружности диска и ведущих себя подобно силам
в предыдущем случае (рис. 54, б).
Еще один вариант граничных условий получим, полагая
Л = й = 0, B = tgd. Тогда Lx = L(u'-\-igbv'), Ly = 0. Этот
случай может быть реализован путем приложения пары сил Р,
Рис. 54.
направленных по касательной к диску в незагруженном
состоянии и сохраняющих это направление в дальнейшем. При
этом б — угол закручивания перед потерей устойчивости,
L = 2PacosQ (рис. 54, в). Если 6 = 0, то мы получаем
первый из рассмотренных случаев.
Перечисленные типы скручивающих моментов были
классифицированы Г. Циглером, который назвал первый из них
квазитангенциальным, второй — полутангенциальным и
третий — псевдотангенциальным моментами !).
Консервативный характер моментов в этих задачах очевиден, поскольку
моменты создаются консервативными же силами.
*) См. работы, цитированные на стр. 94. В русском переводе
статьи Г. Циглера (Сб. «Проблемы механики», т. 2, ИЛ, 1959)
моменты названы соответственно квазиследящими, полуследящими
и псевдоследящими,

§ 2.11] УСТОЙЧИВОСТЬ ПРЯМОЛИНЕЙНОЙ ФОРМЫ СТЕРЖНЯ 139
Консервативные задачи устойчивости для скрученных
стержней рассматривались Е. Л. Николаи1), И. Е. Шашко-
вым2), В. М. Макушиным3), Циглером4), Беком5)
и др. авторами. Не останавливаясь на них, перейдем
непосредственно к изучению неконсервативных задач.
Момент, вектор которого остается направленным вдоль
искривленной оси стержня, может быть создан при помощи
Рис. 55.
пары тангенциальных сил (рис. 55, а). Назовем этот момент
тангенциальным. Для этого момента Lx(l) = Ly(l) — О и,
следовательно,
b = -Lv[(l)u'2(l) + Lu[(l)v'2(l).
1) Николаи Е. Л., Труды по механике, Гостехиздат, 1955.
2) Шашков И. Е., Об устойчивости сжатого и скрученного
стержня с произвольной формой поперечного сечения, Инж. сборн.
7 (1950).
3) Макушин В. М., Исследование устойчивости скрученного
стержня с равными главными жесткостями при изгибе, Сб. «Расчеты
на прочность», вып. 2, Машгиз, 1958; см. также в книге:
Пономарев С. Д., Бидерман В. Л., Лихарев К. К., Макушин В. М.,
М а л и н и н Н. Н., Ф е о д о с ь е в В. И., Расчеты на прочность
в машиностроении, т. III, Машгиз, 1959.
4) Z i e g 1 е г Н., Knickung gerader Stabe unter Torsion. Zeitschr.
angew. Math. Phys., 3, № 2 (1952).
5) В е с k M., Knickung gerader Stabe durch Druck und kon-
servative Torsion, Ing.-Arch. 23, № 4 (1955).

140 устойчивость при наличии следящих сил [гл. 2
Если торцовое сечение может поворачиваться, то при
произвольном выборе функций uv uv vx и v2 имеем, что А Ф 0.
Краевая задача оказывается несамосопряженной.
Рассмотрим момент, вектор которого сохраняет
направление, параллельное недеформированной оси. Такой момент
может быть создан силами с фиксированными в пространстве
линиями действия {аксиальный момент, рис. 55, б). В этом
случае Lx(l) = Lu'(/), Ly(l) = — Lv'(I) и, следовательно,
величина
А = EJulttx + EJv;v[ = Lu[ (/) v'2 (/) — Lv\ (I) u'2 (I)
имеет то же значение, что и для тангенциального момента.
Неконсервативный характер тангенциального и
аксиального моментов виден также из следующих элементарных
соображений (рис. 56). Переведем твердое тело, к
которому приложен тангенциальный или аксиальный момент Z,,
в новое состояние, повернув
его на угол 2тс относительно
оси Oz. Работа момента при
этом будет равна 2тг/,. В то
же состояние можно прийти,
поворачивая тело
последовательно на угол тс
относительно оси Ох и на угол тс
относительно оси Оу. Работа
оказывается равной нулю как
у в случае тангенциального,
так и в случае аксиального
момента. Таким образом,
величина работы, совершенной
моментом при переходе из
одного состояния в другое,
зависит от пути, что указы-
Рис. 56. вает на отсутствие
потенциала внешних сил.
Покажем теперь, что при наличии тангенциального момента
не существует изогнутых форм равновесия стержня,
близких к прямолинейной. Следуя Е. Л. Николаи, рассмотрим
систему уравнений
ЕЫШ — Lv" -f /V = — 8Р2,
EJv'" + Lit" + PV' = — ЬРХ.

§ 2.11] устойчивость прямолинейной формы стержня 141
Найдем вначале общее решение этих уравнений при ЬРХ Ф О,
ЬР2 Ф 0. Используя своеобразную симметрию системы, введем
комплексный прогиб w = u-\-iv и комплексное усилие ЪР—
= bPl-\~ibP2. Тогда получим уравнение
где
wr" — i$w" -\-ciwf = — 8/?,
PI2 0 LI a ЪР1*
'=f
(2.64)
(2.65)
EJ ' * EJ ' ' EJ
Соответствующее характеристическое уравнение
r3 — /pr24-<w = 0,
помимо корня г = 0, имеет два чисто мнимых корня: г = /гг
и г = ir2. Здесь
г1.2— 2 -
/(!)'+«.
(2.66)
Общее решение уравнения (2.64) имеет вид
Ьр-Ц
w = С^ + С2е*г« + ^з
(2.67)
Краевые условия для стержня, заделанного одним концом
и нагруженного на другом конце тангенциальным моментом
и сжимающей силой, имеют вид
/m dw (0)
d2w(l)
dX2
:ЬР = 0.
Отсюда находим, что
С1 + С2 + С3 = 0; 1ггСг + 1г2С2 = 0;
:0.
**?/
г\С2е»>:
(2.68)
(2.69)
Чтобы эта система уравнений имела отличные от нуля
решения, необходимо и достаточно, чтобы ее определитель был
равен нулю:
Д =
1
irx
гуи
1
ir2
r^elT'
1
0
0
:0.
По определению гг и г2 действительны. Раскрывая
определитель, отделяя действительную и мнимую части и беря модуль

142 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
комплексного выражения, легко найдем:
\^\ = rir2[r\ + rl~ 2r1r2cos(r1 — r2)].
Имеются две возможности удовлетворить условию | Д | = 0.
Первая возможность — это принять, что rl = r2. Тогда, как
это следует из формулы (2.66),
Таким образом, поставленная краевая задача имеет
действительные значения в области растягивающих сил Р. Этот
результат оставался до сих пор незамеченным, хотя он легко
вытекает из соотношений, полученных Е. Л. Николаи.
Условие | Д | = 0 будет также удовлетворено при гг= — г2,
cos 2^ =—1. Это соответствует предположению, что р = 0,
а а = п2)к2/4 (п=\, 2, 3, . . .). Отсюда
%2EJ
Р* = -
4/2
т. е. мы приходим к хорошо известному результату. Если же
Р Ф 0, а > 0, то краевая задача не имеет действительных
собственных значений.
Аналогичные результаты нетрудно получить и для
аксиального момента; в этом случае третье граничное условие из
числа условий (2.68) следует заменить на w" (\) = ifywf (\).
Поскольку рассматриваемые задачи являются
неконсервативными, то из факта наличия или отсутствия точек
разветвления статических решений еще нельзя делать выводов
об устойчивости (неустойчивости) прямолинейной формы
равновесия. Поэтому в дальнейшем мы рассмотрим малые
колебания стержня около положения равновесия.
§ 2.12. Стержень с сосредоточенной массой на конце.
Метод малых колебаний
Допустим, что на конце стержня имеется
сосредоточенная масса М (рис. 57). Пренебрегая инерцией вращения
этой массы, запишем приближенные уравнения малых
колебаний массы:
^21^+Ж822§- + ^ = 0.
) (2.70)

§ 2.12] СТЕРЖЕНЬ С СОСРЕДОТОЧЕННОЙ МАССОЙ НА КОНЦЕ 143
Здесь 8И и 812— перемещения конца стержня в направлении
осей Ох и Оу под действием единичной сосредоточенной
силы, направленной в сторону оси Ох; 821 и 822—
аналогичные перемещения от единичной силы, направленной в
сторону оси Оу. Указанные перемещения вычисляются, разумеется,
с учетом силы Р и момента L.
Чтобы избежать громоздких
выкладок, ограничимся случаем
тангенциального момента,
причем положим, что Р = 0.
Уравнение (2.64) принимает вид
wm — $w" = — bp%
где сохраняются
обозначения (2.65). Характеристическое
уравнение
-^г2
О
имеет чисто мнимый корень
г = /р и двойной нулевой
корень. Отсюда общий интеграл
уравнения (2.64) будет:
w
:С,^+С2С + С3-
Удовлетворяя граничным условиям w(Q)
получим:
™(1)=^[1+^-(1+^)«-'р]
Рис. 57.
w'(0) = ww(l) = 0.
(2.71)
Чтобы найти единичные перемещения 8И и 812, в
формулу (2.71) нужно подставить значение Ьр = — l3/EJ и
разделить действительные и мнимые части. Легко получим:
8n = Re^(l)=^(l+|-cosp-psinp),
812 = Im w(\)= —^^^(sinp —pcosp).
^EJ
'21
Перемещения a
Отсюда
821 = Re w (1):
822=rlm^(l):
u22
найдем, полагая Ьр = — iP/EJ.
P
ЩХ~ (sin p — p cos p),
/3
р2Я/
{'+!¦
-cos
sin
*)¦

1 — МЪпОР — Ж81222
— M821Q2 l — М82222
144 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
Заметим, что 8П^=822 (это вытекает и из соображений
симметрии), но 812 = — 821. Это обстоятельство весьма
существенно для вопроса об устойчивости прямолинейной формы
равновесия !).
Подставляя в уравнения (2.70) выражения
u(t)=UeiQi, v(t) = VeiQt,
получим уравнение для собственных частот
- жо21ъб* 1 — /kjo22w |
Среди его корней
Q +1 / Ell + S22 ± У(^11—^22)2 + 4о12521
~ - У 2М(ЪиЬ22-Ъ12Ь21)
вследствие отмеченных свойств единичных перемещений, при
Р Ф 0 всегда найдутся два корня, имеющих отрицательную
мнимую часть. Таким образом, прямолинейная форма стержня
оказывается неустойчивой при любом отличном от нуля
значении момента L. Этот парадоксальный результат был впервые
получен Е. Л. Николаи. Очевидно, это является следствием
того, что система обладает кратными парциальными частотами
(при р = 0), и того, что не учитывается затухание. Если
учесть затухание, то для критического момента получается
конечное значение. Оно получается также конечным, если
сечение стержня имеет различные главные жесткости. В этом
случае парциальные частоты оказываются различными, что
дает отличное от нуля значение критического момента.
Несомненно, что неконсервативное кручение всегда в той
или иной мере имеет место в турбомашинах. То, что
специфические явления неустойчивости, порождаемые
неконсервативным кручением, в турбомашинах не обнаруживаются, сле-
х) Чтобы привести уравнения (2.70) к виду, аналогичному виду
уравнений, которые рассматривались в первой главе, достаточно
ввести матрицу Ь^ ((*), обратную матрице Mbjk (р). Тогда уравнения
примут вид
5+2 *У*<Р)«; = 0.
k = l, 2
Поскольку Ь12 = — Ь21, то Ь12 = — Ь2

§ 2.13] УЧЕТ РАСПРЕДЕЛЕННОЙ МАССЫ СТЕРЖНЯ И ЗАТУХАНИЯ 145
дует объяснить не столько влиянием диссипативных сил и
слабой эллиптичности вала, сколько влиянием консервативной
составляющей момента. Если следящий момент представляет
собой достаточно малую добавку к консервативной
составляющей, то он способствует стабилизации невозмущенной формы
равновесия (движения). Это явление, отмечавшееся в задачах
устойчивости сжатых стержней (§ 2.5) и устойчивости
плоской формы изгиба (§ 2.8), будет иметь место и в
рассматриваемом случае.
§ 2.13. Учет распределенной массы стержня
и затухания
Уравнения малых изгибных колебаний сжатого и
скрученного стержня получим, вводя в уравнения (2.57)
инерционные члены:
г.,д4и , r d3v , г>д2и . д2и А
^rdAv , д3и . nd2v . d2v A
dz4 dz3 ' dz2 ' dt2
(2.72)
Введя комплексный прогиб w — u-\-iv, запишем систему
(2.72) в виде
Граничные условия для стержня, один конец которого
заделан, а другой — нагружен сжимающей силой и аксиальным
моментом, имеют вид
^ = -р = 0 при z = О,
^rd2w .r dw А , А
Ei-=-2 —jL-^- = 0 при / = 0,
T2Tdzw .j d2w . ndw A , л
EJ^-lLw+p-di=0 при z=°-
Последнее условие можно истолковать как требование
равенства нулю реактивных сил ЬРг и ЬР2, приложенных к концу
стержня 1).
1) См. уравнения (2.61).

146 УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ СЛЕДЯЩИХ СИЛ [ГЛ. 2
Подстановкой
w(z, t) = W(z)sln(?t + yQ)
приведем уравнение (2.73) к виду
d*W ,Qd*W , d2W 2W/ n ,0 7АЛ
l^-l^ + *~d?-i»W=0> (2-74)
где сохранены обозначения для безразмерных величин (2.65)
и, кроме того, введено обозначение
EJ
Граничные условия будут следующие:
Характеристическое уравнение имеет вид
г4 — /рг8 + аг2 — со2 = 0.
Его корни обозначим через г1% г2, г3, г4. Подчиняя интеграл
краевым условиям (2.75), получим уравнение для нахождения
безразмерных частот о>:
(2.75)
=0.
1111
Г\ г2 гг га
{r\ — l$r^er* (rl — i$r2)e'* (r\-i^e^ (r\ — l$rA)er-
1 г 1 г 1 г 1 г
— ?гх — #г* — еГз — eTi
Г\ г2 г3 г4
Вычисления, связанные с раскрытием определителя и
отделением его корней, сложны; поэтому ограничимся
случаем а = 0. Ожидая, что критические значения параметра (3
будут достаточно малы, положим, что р<^о)2. Тогда
приближенно 1)
i 'P i
1) Мы следуем здесь изложению Треща (цит. на стр. 95).

§ 2.13] УЧЁТ РАСПРЕДЕЛЁННОЙ МА^СЫ СТЕРЖНЯ И ЗАТУХАНИЯ iif
где г0 — один из корней уравнения г4 — u)2 = 0. Общее
решение уравнения (2.74) примет вид
w 4
W{^) = e* 2 С^оС+ ....
; = i
Учитывая граничные условия (2.75), получим
приближенное уравнение (Х^^^ш):
1 +cos X ch X —|-
2 У со
(cosXshX + sinXchX) = 0. (2.76)
Его наименьший корень будет У со = 1,875 -f- 0,144/(3-f- •••
Таким образом, при любом отличном от нуля {$ частота
колебаний Q будет содержать мнимую часть и прямолинейная
форма равновесия стержня будет неустойчивой.
Аналогичный результат получим для случая краевых
условий // (рис. 58). В случае краевых условий /// и IV потеря
I
и ш
Рис. 58.
устойчивости происходит по типу разветвления форм
равновесия (хотя в случае /// кручение является
неконсервативным).
Остановимся кратко на учете затухания при Р = 0. Вводя
в уравнение (2.73) член, содержащий первую производную
от комплексного прогиба по времени, придем к уравнению
*?¦
., d3w , d2w
' dz*
dt2
dw A
¦rmw = 0.

148 устойчивость при наличии следящих сил [гл. 2
Подставим сюда выражение
w(z, t) = W(z)est.
Задача исследования устойчивости невозмущенной формы
стержня сводится к изучению комплексных собственных
значений со краевой задачи
d*W
dV
d*W . d2W
1 rfC3 ~^"a rfC2 "
afiW = 0
с условиями на концах (2.75). При этом
со
где
2 = _(в2+ ?(,),
___!_ „_ е Q _ 1 fTj
(2.77)
(2.78)
(2.79)
Равновесие устойчиво, если все характеристические
показатели а лежат в левой полуплоскости комплексного
переменного. Левая полуплоскость отображается при помощи
формулы (2.79) во
внутреннюю часть параболы,
уравнение которой имеет
вид
)_
Im со2 = g (Re со2)2.
к™ (2.80)
Пока Im со2 < g (Re co2)Va,
прямолинейная форма
стержня устойчива. Выход
за пределы параболы
означает неустойчивость
прямолинейной формы
стержня (рис. 59).
Точный анализ комплексных собственных значений
краевой задачи требует весьма кропотливых вычислений.
Ограничимся приближенным решением, считая затухание малым и
исходя из условия устойчивости в форме Re a < 0, где
Рис. 59.

§ 2.13] УЧЕТ РАСПРЕДЕЛЁННОЙ МАССЫ СТЕРЖНИ И ЗАТУХАНИЯ 149
Из формулы (2.81) видно, что при малом затухании,
точнее, при
г_
?<C(Re№)2,
на границе параболы устойчивости имеет место неравенство
Im(D2<CReco2.
Отсюда по формуле (2.81)
.*_4±,*.(,+,&).
Условие устойчивости принимает вид
g">2Imo). (2.82)
Для со выше была дана оценка (2.76), пригодная при
малых параметрах момента (3. Используя ее, получим,
что Imo)^0,54p, откуда критическое значение параметра
P**~0,93g". Как и в случае системы с двумя степенями
свободы (§ 1.16), мы установили, что при кратных
парциальных частотах критический параметр пропорционален мере
затухания.
Вычисления были проделаны для случая аксиального
момента. Аналогичные результаты получим, рассматривая
тангенциальный момент, для которого третье из краевых
условий (2.75) заменяется условием W" (\) = 0.

ГЛАВА ТРЕТЬЯ
УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ
С РЕГУЛИРУЕМЫМ ЧИСЛОМ ОБОРОТОВ
§ 3.1. Предварительные замечания
Среди элементов машин, назначение которых состоит
в передаче мощности, важнейшее место занимают валы.
В связи с вопросом об устойчивости валов необходимо
обратить внимание на следующее обстоятельство. При
стационарном режиме числа оборотов вала с той или иной точностью
поддерживаются постоянными. В простейших случаях, когда
изменения потребляемой мощности невелики и когда они
происходят около некоторой средней величины, роль
регулятора чисел оборотов может выполнять маховик с достаточно
большим моментом инерции; в других случаях вал становится
звеном некоторой системы автоматического регулирования.
Одна из задач проектировщика состоит в том, чтобы не
допустить опасных поперечных вибраций вала,
поддерживаемых за счет некоторой части мощности вращательного
движения. Вал с регулируемым числом оборотов является
типичной неконсервативной системой, а задача об
устойчивости прямолинейной (чисто вращательной) формы
вала—типичной неконсервативной задачей упругой устойчивости.
Простейшей моделью этой задачи может служить
невесомый вал круглого сечения с одним сосредоточенным диском
при отсутствии перекоса диска (рис. 60). Элементарная теория
для этого случая была дана еще Ренкиным, Лавалем
и Стодолой на первых этапах развития паровых турбин
и сводится вкратце к следующему.
1) Существует некоторая критическая скорость
вращения вала, при которой имеют место наибольшие амплитуды
поперечных колебаний, обусловленных дисбалансом; эта кри-

§3.1] ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 151
тическая скорость совпадает с частотой собственных
колебаний невращающегося вала
(М — масса диска, с — коэффициент жесткости, который
равен силе, необходимой для получения прогиба, равного
единице).
2) С дальнейшим ростом угловой скорости после перехода
через критическое значение амплитуды колебаний убывают,
т. е. диск стремится к самоцентрированию. В реальных
роторах, имеющих не одну, а целый спектр критических
Рис. 60.
скоростей, это самоцентрирование будет происходить,
разумеется, до тех пор, пока угловая скорость не приблизится
к следующему критическому значению. Здесь мы имеем
полную аналогию с задачей о колебаниях обычной упругой
системы под действием внешних периодических сил.
Опыт показывает, однако, что гибкие валы часто
обнаруживают тенденцию к самовозбуждающимся поперечным
колебаниям при скоростях, отличных от критических. Эти
колебания непосредственно не связаны с наличием дисбаланса или
других возмущающих воздействий. Первое истолкование
самовозбуждающихся колебаний, происходящих за
критическими числами оборотов, было дано Кимбаллом*), который
выяснил роль внутреннего трения.
^Kimball A. L., Internal friction theory 'of shaft whirling,
Gen. Electric Rev. 27, № 4 (1924); Internal friction as a cause of shaft
Whirling, Phil. Mag., ser. 6, 54 (1925).

152 устойчивость гибких валов [гл. 3
Силы внутреннего трения в материале вала способствуют
затуханию колебаний, если он вращается со скоростью,
меньшей, чем первая критическая скорость. При скоростях,
превышающих критическую, силы внутреннего трения
оказываются направленными не против вращательного движения,
а по направлению движения. Если эти силы достаточно
велики по сравнению с силами внешнего сопротивления, то
они могут привести к возбуждению незатухающих колебаний.
Причина самовозбуждения становится понятной, если
учесть, что вал, вращающийся с постоянной угловой
скоростью независимо от его состояния, является
неконсервативной системой. Действительно, в рассматриваемой задаче
имеется внешний источник энергии — двигатель, который дает
постоянное число оборотов и сообщает валу дополнительную
мощность, идущую на поддержание вибраций. Внутреннее же
трение является передатчиком энергии от невозмущенного
(чисто вращательного) движения к возмущенному движению.
Здесь уместно провести аналогию с задачей об устойчивости
ламинарных течений вязкой жидкости, где силы вязкости
также способствуют передаче энергии от невозмущенного
(ламинарного) движения к возмущенному (турбулентному)
движению и являются, таким образом, косвенной причиной
неустойчивости.
Теоретическая сторона задачи после Кимбалла
рассматривалась Робертсоном1), Смитом2), Е. Л.
Николаи3), М. Я. К у ш у л е м 4), М. Я. Леоновым,
М. И. Чаевским и Л. А. Беспалько5) и другими
авторами. Наиболее обстоятельные исследования принадлежат
^Robertson D., The vibrations of revolving shafts, Phil.
Mag., ser. 7, 13, № 8 (1932); Hysteretic influences on the whirling of
rotors, Proc. Inst. Mech. Engrs. 131 (1935).
2) Smith D. M., Motion of a rotor carried by a flexible shaft
in flexible bearings, Proc. Roy. Soc. 142, № 846 A (1935).
3) Николаи Е. Л., К теории гибкого вала, Тр. Ленингр.
индустр. ин-та, разд. физ.-мат. наук, № 6, вып. 3 (1937); см. также
Николаи Е. Л., Труды по механике, Гостехиздат, 1955.
4) К у ш у л ь М. Я., Поперечные колебания вращающихся валов
при наличии внутреннего и внешнего трения, Изв. АН СССР, ОТН,
№ 10, 1954.
5) Леонов М. Я. и Ч а е в с к и й М. И., Экспериментальная
проверка устойчивости вращения валов за критической скоростью,
Сб. «Вопросы машиноведения и прочности в машиностроении»,
вып. 3, Изд-во АН УССР, 1955; Леонов М, Я. и Бес-

§3.1] ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 153
Ф. М. Диментбергу1). Критический обзор литературы
по этому вопросу, доведенный до 1956 г., был составлен
Э. Л. П оз н я ком2).
Перечисленные работы были посвящены исследованию
устойчивости вращательного движения по отношению к малым
возмущениям и определению условий, при которых
становится возможным самовозбуждение колебаний. Новое
направление связано с исследованием амплитуд автоколебаний за
критическими скоростями вращения и требует анализа
нелинейных уравнений3).
Помимо сил внутреннего трения, причиной неустойчивости
вращающегося вала могут служить различные другие силы
аэродинамического, гидродинамического и электромагнитного
происхождения. П. Л. Капица4) исследовал явления
неустойчивости, обусловленные трением в опорах скольжения
и аэродинамическим трением о среду, окружающую ротор.
Широко известны явления неустойчивости, вызванные
влиянием гидродинамического трения в масляной пленке
подшипников, Этот вопрос играет весьма существенную роль для
современных быстроходных турбомашин, и ему посвящена
п а л ь к о Л. А., К исследованию устойчивости вала, вращающегося
со сверхкритической скоростью (там же); Ч а е в с к и й М. И.,
Исследование устойчивости вращения гибких валов за критической
скоростью, Изв. АН СССР, ОТН, № 9, 1955.
1) Диментберг Ф. М., Поперечные колебания вращающегося
вала с дисками при наличии сопротивления трения, Сб.
«Поперечные колебания и критические скорости», вып. 1, Изд-во АН СССР,
1951; Об устойчивости гибкого вала с неуравновешенным диском
при действии внутреннего и внешнего трений, Изв. АН СССР,
ОТН, № Ю, 1954; Изгибные колебания вращающихся валов,
Изд-во АН СССР, 1959.
2) П о з н я к Э. Л., Влияние сопротивления на устойчивость
вращающихся валов, Сб. «Проблемы прочности в машиностроении»,
вып. 1, Изд-во АН СССР, 1958.
3) Болотин В. В., Исследование автоколебаний гибкого вала,
вызванных влиянием внутреннего трения и родственных факторов,
Научн. докл. высш. школы, сер. «Машиностроение и
приборостроение», JSfe 4, 1958; Нелинейные колебания валов за критическими
скоростями вращения, Сб. «Проблемы прочности в
машиностроении», вып. 1, Изд-во АН СССР, 1958.
4) Капица П. Л., Устойчивость и переходы через критические
обороты быстро вращающихся роторов при наличии трения, Журн.
техн. физ. 9, № 2 (1939).

154
УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ
[гл. 3
обширная литература*). Сходные явления обнаруживаются
в случае роторов, несущих ферромагнитный сердечник и
помещенных в магнитное поле, а также роторов,
содержащих жидкость со свободной поверхностью. Исследование
этих явлений было выполнено Э. Л. Позняком и
Л. В. Епишевым2).
В настоящей главе задачи о явлениях неустойчивости
роторов, обусловленных перечисленными выше факторами,
будут рассмотрены с общей точки зрения; при этом будет
подчеркнута тесная связь этих задач с другими
неконсервативными задачами упругой устойчивости. Большое внимание
будет уделено нелинейной трактовке. Будут частично
использованы впервые публикуемые экспериментальные результаты,
полученные Э. Л. Позняком и Л. В. Епишевым.
§ 3.2. Уравнения движения гибкого вала
Составим уравнение движения для случая гибкого вала
с одним сосредоточенным диском (рис. 60). Вал будем
считать симметричным, а диск — посаженным посредине и
совершающим колебания только в вертикальной плоскости, т. е.
гироскопический эффект диска учитывать не будем. Далее,
вал будем считать невесомым и обладающим бесконечно
большой жесткостью на кручение; это равносильно
предположению, что основная частота собственных поперечных
») N е w k i г к В. L. and T а у 1 о г N. D., Shaft whirling due to
oil action in journal bearings, Gen. Electric Rev. 28, № 8 (1925);
H a g g A. C, The influence of oil-film journal bearings on the
stability of rotating machins, Journ. Appl. Mech. 13, № 3 (1946);
P о r i t s к у Н., Contribution to the theory of oil whip, Trans. Amer.
Soc. Mech. Engrs. 75, № б (1953); N e w к i г к В. L. and Lewis J. F.,
Oil-film whirl — an investigation of disturbances due to oil-films in
journal bearings, Trans. Amer. Soc. Mech. Engrs. 78, № 1 (1956);
В о с к е г G. F. and Sternlicht В., Investigation of translatory
fluid whirl in vertical machines, там же.
2) П о з н я к Э. Л., Некоторые вопросы устойчивости стального
сердечника в магнитном поле, Научн. докл. высш. школы, сер.
«Электромеханика и автоматика», № 2, 1958; Об устойчивости
железного сердечника в магнитном поле, Изв. АН СССР, ОТН,
№ 10, 1958; Устойчивость вращающегося железного сердечника
в магнитном поле, Изв. АН СССР, ОТН, сер. «Энергетика и
автоматика», № 3, 1959; Епишев Л. В., О динамической
неустойчивости вращающегося ротора при неполном наливе жидкости, Научн.
докл. высш. школы, сер. «Машиностроение и приборостроение»,
№ 2, 1959.

§ 3.2] УРАВНЕНИЯ ДВИЖЕНИЯ ГИБКОГО ВАЛА 155
колебаний вала значительно ниже, чем его высшие частоты,
а также чем частота его собственных крутильных колебаний.
Силу веса диска учитывать не будем, что либо соответствует
случаю вертикального вала, либо случаю достаточно больших
чисел оборотов, при которых эффекты, связанные с наличием
силы веса, становятся пренебрежимо малыми.
Пусть Ох — точка прикрепления диска к валу, С — центр
массы диска. Расстояние е = ОхС> называемое
эксцентриситетом или дисбалансом, будем считать достаточно малым. При
сделанных допущениях деформированное состояние вала будет
полностью определено, если известны координаты точки
прикрепления диска и и v (т. е. составляющие прогиба вала
посредине пролета) и угол ср, который отрезок ОхС
составляет с осью Ох (рис. 60).
Для получения уравнений движения диска воспользуемся
Принципом Даламбера. Проекции силы инерции на оси Ох
и Оу будут:
P^ = --M[^-4Fesin^-(^fec0^]'
p>=~M[w*+i?ecosv-{-wfesin4
где М — масса диска. Первый член в скобках соответствует
линейному ускорению, второй — угловому и третий —
центростремительному ускорению.
Для вычисления момента сил инерции относительно оси Oz
имеем формулу
^— М\ dt* Vc^ dt* Uc^r dt*)'
где г — радиус инерции диска относительно оси, проходящей
через точку С перпендикулярно к его плоскости, ис и
vc — координаты точки С,
ис = u-\-ecosyt
vc=zv-\-e sin ср.
Уравнения движения диска принимают вид
M4W + cu = Me[^s{n^ + {^zos^\ I
жw+™=м~scos?+(J&)2sin<p], )
Mr^ = M(^vc-«^-uc) + Lk-LT. (3.3)

156 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
Здесь La —¦ активный (вращающий) момент, передаваемый на
вал от двигателя, Z,T — тормозящий момент, с -^ коэффициент
жесткости вала.
Рассмотрим уравнение вращательного движения (3.3).
Из него следует, что вращение с постоянной угловой
скоростью
-—|-== со = const (3.4)
становится возможным, если
т. е. если активный момент изменяется соответствующим
образом. Условие (3.4) выполняется с той или иной
точностью во всех установках с регулируемым числом оборотов.
Даже если равномерность вращения поддерживается при
помощи маховика, то условие (3.4) выполняется приближенно,
по крайней мере на протяжении не слишком больших
интервалов времени1).
Пусть активный момент в точности уравновешивается
моментом нагрузки (La = LT)- Обозначив через а характерное
значение амплитуды поперечных колебаний, заметим, что
.,/—асо2, —п?- — аы2. Отсюда из уравнения (3.4) получим
оценку
d2<p ea 9
Но —щ- = —~ и, следовательно, для изменения угловой
скорости в течение одного оборота До> находим:
Aw 0 ea /Q р-ч
— ~^-рт- (3-5)
По данным Бицено и Граммеля2), для паровых
турбин эксцентриситеты не превышают, самое большее, несколь-
1) Системы с ограниченным источником мощности и падающей
характеристикой являются предметом специального рассмотрения.
См., например, Кононенко В. О., О прохождении через
резонанс механической системы, содержащей двигатель, Сб. «Проблемы
прочности в машиностроении», вып. 5, Изд-во АН СССР, 1959.
2) Бицено К. Б. и Граммель Р., Техническая динамика,
т. II, Гостехиздат, 1952, стр. 225.

§ 3.3] ВЯЗКОЕ ВНУТРЕННЕЕ ТРЕНИЕ 157
ких тысячных долей от радиуса инерции диска г. Поэтому
приме
дает:
примем?~10 Зг. Пусть, далее, а—10#~10 V. Оценка (3.5)
-^~1(Г4,
О)
т. е. в течение одного оборота угловая скорость вращения
вала изменится не более чем на 0,01%.
С учетом (3.4) уравнения (3.2) существенно упрощаются:
d2u
М —7Щ- -\-си = Мею2 cos at,
d2v
М —n^r-\-cv == Мею2 sin atf,
at1 '
или, после введения обозначения для частоты собственных
колебаний Q0:
d2u , ^2 2 А
li0u = ею cos wr,
dt2
d2V . n2 2 . .
1 • y0t/ = ею sin Ы.
dt2
(3.6)
Вывод о самоцентрировании диска после перехода через
критическое число оборотов вытекает непосредственно из
рассмотрения частного решения уравнений (3.6).
§ 3.3. Вязкое внутреннее трение.
Неустойчивость, вызванная действием внутреннего
трения
Еще Кимбалл1) указал, что при рассмотрении
вопросов, связанных с устойчивостью вращающихся валов,
необходимо различать две группы сил трения. К первой группе
принадлежат силы, развиваемые при контакте вращающегося
вала с неподвижными деталями, к нему примыкающими,
а также силы трения об окружающую среду, если последнюю
можно считать неподвижной. Ко второй группе относятся
силы трения, возникающие вследствие гистерезиса в
материале вала, а также некоторые другие силы (например, сила
1) Цит. на стр. 151.

158 устойчивость гибких валов [гл. 3
трения между валом и диском, плотно на него насаженным).
Отличительной особенностью второй группы сил является то,
что они зависят от относительных смещений и относительных
скоростей вращающихся частей вала и, следовательно, должны
вводиться во вращающейся системе координат. Сходными
свойствами обладают силы трения в подшипниках при наличии
масляной пленки, частично увлекаемой валом, а также силы,
действующие между ротором и частично увлекаемой вслед
за ним средой. Как это уже утвердилось в литературе, силы,
принадлежащие к первой
группе, будем условно
называть силами
внешнего трения, а силы,
принадлежащие ко
второй группе, — силами
внутреннего трения.
Если силы внешнего
трения всегда
способствуют демпфированию
колебаний, то силы
внутреннего трения при
определенных условиях могут
вызвать явление
неустойчивости, обусловленное,
в конечном счете,
перекачкой части энергии вращательного движения в энергию
поперечных колебаний. Важнейшие особенности этого
явления выясняются на простейшем примере, когда силы
внешнего и внутреннего трения пропорциональны соответствующим
скоростям движения диска.
Рассмотрим случай слегка возмущенного движения идеально
сбалансированного вала, для которого в уравнениях (З.б)
следует положить е = 0. Чтобы ввести силы внутреннего
трения, пропорциональные скоростям, которые измеряются
относительно вращающегося вала, введем систему координат,
вращающуюся с угловой скоростью о) (рис. 61). Переход
от новых переменных ?, у\ к старым переменным ut v
осуществляется формулами
Рис. 61.
и = ? cos Ы — т] sin Ы,
у = ? sin Ы -\- т] cos Ы.
(3.7)

§ 3.3] ВЯЗКОЕ ВНУТРЕННЕЕ ТРЕНИЕ 159
Применяя преобразование (3.7) к уравнениям (3.6), легко
получим:
dt2 dt
(3.8)
Введем в эти уравнения члены s^ и s/ —?, которые
учитывают силы внутреннего трения (е^— коэффициент
внутреннего трения). Тогда после возвращения к неподвижной
системе координат приходим к уравнениям
d2u , du , 02 , а
~Ж+8<^Г + д°*+сог/г;==()'
d2v dv i
Последнее, что следует сделать, это ввести силы внешнего
da dv
трения ее —тт- и ее —ц-, пропорциональные скоростям
движения диска в неподвижной системе координат (ее —
коэффициент внешнего трения). Уравнения возмущенного движения
принимают вид
^ + ^ + ?/)4г + аой + а)^==0^
d2v dv J ^3*9^
-dt2- + (ee + ei)^f+Qlv — <oe,tf = 0.
Весьма существенным с точки зрения устойчивости является
наличие в уравнениях (3.9) псевдогироскопических членов,
составляющих антисимметричную матрицу
О 0)8^ II
— 0)8^ О (I *
В этом смысле уравнения (3.9) аналогичны уравнениям малых
колебаний стержня, подвергнутого неконсервативному
кручению, или, например, уравнениям, описывающим колебания
полосы, нагруженной «следящей» силой. Роль параметра,
с точностью до которого псевдогироскопические члены
определяются, играет угловая скорость вращения вала.
Из сказанного вытекает, что задачу об устойчивости
прямолинейной формы вращающегося вала при наличии

160 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
внутреннего трения можно трактовать как частный случай
неконсервативных задач, рассмотренных в первой главе.
Данная задача имеет две отличительные особенности.
Во-первых, псевдогироскопические члены и диссипативные
члены содержат здесь один и тот же параметр. Таким образом,
внутреннее трение порождает здесь две противоположные
тенденции — демпфирование и дестабилизацию, из которых
при достаточно малых скоростях со доминирует первая, а при
больших — вторая тенденция. Следует заметить, что этой
особенностью обладают и некоторые другие неконсервативные
задачи упругой устойчивости. Например, на тело,
помещенное в поток газа, помимо сил, вызывающих неустойчивость
типа флаттера, действуют также и силы аэродинамического
демпфирования. При достаточно больших скоростях потока
начинают доминировать дестабилизирующие силы.
Во-вторых, в случае вала круглого сечения имеется пара
кратных собственных частот 20 и, вообще, весь спектр
состоит из попарно равных частот. Таким образом, то, что
в общей теории трактовалось как исключение, в данной
задаче становится правилом. Разумеется, задача останется
неконсервативной, если главные изгибные жесткости сечения
неодинаковы. Этот случай будет затронут кратко в § 4.3.
Поскольку в данной задаче обе координаты (х и у)
полностью равноценны, то весьма целесообразен переход к
комплексному представлению перемещений. Вводя комплексное
перемещение
получим вместо (3.9) одно уравнение
-^ + (e.-l-ei)-^-hQ§a>-toe,W = 0. (3.10)
Это уравнение имеет решение
w = aem, (3.11)
где 2 — комплексная частота.
Прямолинейная форма вала устойчива, если Im 2 > 0.
Подставляя (3.11) в (3.10) и принимая во внимание, что на
границе области устойчивости Im 2 = 0, получим два
уравнения:
22 _ Q2 = о, (ее + 8/) 2 — ше, = 0.

§ 3.3] бЯЗкОЕ ВНУТРЕННЕЕ ТРЁНЙЕ 161
Q0, т. е. что
Из первого уравнения вытекает, что Q
на границе области неустойчивости колебания происходят
с собственной частотой. Из второго уравнения находим
выражение для критической скорости1)
М1+Ъ)-
(3.12)
Заметим, что формулу (3.12) можно получить из более
общих соотношений, приведенных в первой главе. Учитывая,
что в обозначениях § 1.16 при
р = о)/20
О), = 0)2 = 1 ,
у21 '
as
g\ = g<>-
*0
ч '
?g + Ч
со=0
tt
Ims
Res
co=0
<tt
co=co»
Рис. 62.
и используя формулу (1.96),
легко придем к формуле (3.12). —
График изменения
характеристических показателей s=iQ,
аналогичный рис. 3, 18 и др.,
показан на рис. 62.
Согласно формуле (3.12), прямолинейная форма идеально
сбалансированного вала становится неустойчивой при скорости
вращения, которая тем больше превышает «классическую»
критическую скорость 20, чем больше внешнее трение по
сравнению с внутренним трением. Качественно эта формула
правильно отражает стабилизирующую роль сил внешнего
трения. Однако количественно эта формула не подтверждается
опытом из-за чрезмерной схематизации сил трения.
1) Эту формулу можно найти в работах: Smith D. M., The
motion of a rotor carried by a flexible shaft in flexible bearing, Proc.
Roy. Soc, ser. A 142, 92 (1933); Диментберг Ф. М., Поперечные
колебания вращающегося вала с дисками при наличии
сопротивления трения, Сб. «Поперечные колебания и критические скорости»,
вып. 1, Изд-во АН СССР, 1951.

162 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
§ 3.4, Трение, не зависящее от скорости
Широко известные опытные факты указывают на то, что
силы внутреннего трения в материале по крайней мере в
некотором достаточно широком диапазоне частот практически
не зависят от частоты колебаний. Другими словами, площадь
петли гистерезиса практически не зависит от скорости
деформирования. Поэтому случай, когда силы трения не зависят
от скоростей, представляет значительный интерес.
Детали изменения сил трения в течение периода
колебаний весьма слабо влияют на процесс в целом, а решающее
значение имеет суммарный эффект сил трения, измеряемый
величиной энергии, рассеиваемой за период. В терминах
явления гистерезиса это означает, что затухание колебаний
зависит главным образом от площади, ограниченной петлей
гистерезиса; форма же петли имеет третьестепенное значение.
Поэтому при рассмотрении колебаний валов при наличии сил
трения представляется целесообразным ввести интегральные
характеристики — величины относительного рассеяния энергии
за период колебаний, обусловленного внешним и внутренним
трением:
¦.-^. *-¦?¦ <з-'з>
Здесь bWe и bWt — абсолютное рассеяние энергии за период,
W — полная энергия цикла, равная, например, потенциальной
энергии упругой деформации при наибольшем смещении от
положения равновесия. В настоящем параграфе мы рассмотрим
случай tye = const, ф; = const.
Можно предложить несколько способов введения
характеристик (3.13) в уравнения колебательного движения. Один
из них, пожалуй, наиболее простой, состоит в следующем]).
Пусть по-прежнему диссипативные члены будут содержать
первые производные от перемещений по времени, умноженные
на некоторые коэффициенты. Однако для того чтобы эти
члены не зависели от частоты колебаний (точнее, чтобы эта
1) П а н о в к о Я. Г., Об учете гистерезисных потерь в задачах
прикладной теории упругих колебаний, Журн. техн. физ. 23, № 3
(1953); Сорокин Е. С, Метод учета неупругого сопротивления
материала в расчетах конструкций на колебания, Сб.
«Исследования по динамике сооружений», Стройиздат, 1951, и др.

§ 3.4] ТРЕНИЕ, НЕ ЗАВИСЯЩЕЕ ОТ СКОРОСТИ 163
(3.15)
зависимость, если она имеет место, входила исключительно
в выражения для tye и ф^), нужно эти члены разделить на
частоту. Например, в случае вынужденных колебаний системы
с одной степенью свободы под действием гармонической
силы, описываемых уравнением
M^ + s^ + ca = Pcos(Qt-<i), (3.14)
коэффициент е необходимо взять в виде
сф
где ф— относительное рассеяние энергии.
Действительно, уравнение (3.14) имеет решение
u = acos{Qt — v).
Отсюда относительное рассеяние энергии за цикл
о
в то время как полная энергия цикла равна
W = 1 са2.
Следовательно, -=- = ф, т. е. уравнение (3.14) с
коэффициентом (3.15) действительно описывает колебания,
происходящие с относительным рассеянием энергии ф.
Заметим, что в случае, когда коэффициенты при
инерционных членах в уравнениях движения равны единице, вместо
(3.15) нужно взять выражение
e = 5f. (ЗЛ6)
Составим уравнения возмущенного движения идеально
сбалансированного вала при силах внешнего и внутреннего
трения, не зависящих от скорости. Будем исходить из
уравнений во вращающейся системе координат:
¦§+2.§ + (<>»о-«*)Ч = <>.
} (3.17)

164 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
Введем сюда члены, учитывающие внутреннее трение.
Пусть 2 — комплексная частота колебаний в неподвижной
системе координат, входящая в выражения для решений
и,е
т
v = vae
I2t
Поскольку в системе координат, вращающейся вместе с валом,
частота колебаний равна со — Q, то согласно формуле (3.16)
диссипативные члены должны быть представлены в виде
^o+i
dt
*lh
drt
2tl I со — Q | dt ' 2n I co — Q | dt '
Если добавить эти выражения соответственно в первое
и второе уравнения (3.17), возвратиться к неподвижной
системе координат и после этого подставить члены с
внешним трением,
Qptye dll Qptye dv
2icQ dt ' 2tcQ dt '
то придем к уравнениям
d2u
dt2 '
^;
d2v
U0 / Ф* ¦ Ф/ \
2те V Q ""l со — Q\)
du
dt
dv
2tc
(3.18)
dt* ' 2те VQ"" |co — Q\) dt 2%\a — Q\~r~0
И здесь возможность явления неустойчивости видна из
наличия псевдогироскопических членов с антисимметричной
матрицей
О
2те|
-й|
2ти | со — У |
О
Строго говоря, формула (3.16) справедлива лишь для
случая установившихся колебаний, когда частота 2 —
действительная величина. В том случае, когда Q — комплексная
величина, но Im&<^ReQ, т. е. движение мало отличается
от замкнутого цикла, она может трактоваться как
приближенная формула, а уравнения (3.18), на ней основанные,—
как приближенные уравнения. В дальнейшем, однако, урав-

§ 3.4] ТРЕНИЕ, НЕ ЗАВИСЯЩЕЕ ОТ СКОРОСТИ 165
нения (3.18) будут применяться лишь для нахождения границ
областей неустойчивости. На этих границах мы имеем
условие Im2 = 0, и, следовательно, уравнения (3.18) полностью
соответствуют предпосылкам, положенным в основу
формулы (3.16).
Переходя к комплексной форме записи, получаем вместо
(3.18) одно уравнение:
d^w ^ _Jn_\dw КФ| W + WW==0 (319)
Его решение ищем в виде
w = wQe1*'. (3.20)
Прямолинейная форма вала устойчива, если Im Й > 0, и
неустойчива, если Im & < 0. На границе области устойчивости
имеем Im2 = 0, ReQ = Q. Подставляя (3.20) в (3.19) и
приравнивая нулю порознь действительную и мнимую части
результата подстановки, получим два уравнения:
Из первого уравнения, как и в случае вязкого трения,
находим, что частота колебаний 2 = 20. Второе уравнение
можно переписать в виде
Ф,—<Wsign(a> —Q) = 0, (3.21)
где sign — функция перемены знака:
1, если х >*0,
signx = ^ 0, если jc = 0, (3.22)
¦—1, если х < 0.
Уравнение (3.21) может быть удовлетворено лишь при
одновременном выполнении двух условий: 1) угловая
скорость со должна быть больше, чем «классическая» критическая
скорость 20; 2) величины относительного рассеяния энергии
вследствие внешнего и внутреннего трения должны быть
равны между собой.
Таким образом, если со < 20, то прямолинейная форма
идеально сбалансированного вала всегда устойчива. Если же
'о > 20, то, как нетрудно показать, могут представиться

166 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
два случая. При ф/ < tye прямолинейная форма устойчива,
а при ф; > tye она становится неустойчивой.
Уравнение (3.21) может быть истолковано как
энергетическое соотношение между силами внешнего и внутреннего
трения, причем наличие функции sign* указывает на
различную роль силы внутреннего трения при докритических
и послекритических скоростях. Если со < 20, то сила
внутреннего трения складывается с силой внешнего трения, т. е.
направлена против движения (рис. 63, а). В этом случае она
оказывает стабилизирующее воздействие. При со > 20 силы
внешнего и внутреннего трения направлены в
противоположные стороны и, следовательно, возможно самовозбуждение
колебаний (рис. 63, б). Переходный случай, когда со = 20,
соответствует так называемой синхронной прецессии. В этом
случае изогнутый вал вращается вокруг продольной оси, не
испытывая дополнительных деформаций, зависящих от времени,
и, следовательно, сила внутреннего трения отсутствует.
§ 3.5. Случай произвольной зависимости трения
от частоты!)
Случай, когда силы внешнего и внутреннего трения
произвольно зависят от частоты колебаний, представляет
значительный интерес, поскольку, как легко показать, даже
1) П о з н я к Э. Л., цит. на стр. 153.

§ 3.5] ПРОИЗВОЛЬНАЯ ЗАВИСИМОСТЬ ТРЕНИЯ ОТ ЧАСТОТЫ 16?
очень слабая зависимость силы от частоты может изменить
качественный характер явления.
Если величины относительного рассеяния энергии зависят
от частоты колебаний, то уравнения (3.18) остаются
справедливыми; однако в них нужно положить
Ч»« = Ф* < I«° — QI >-
Повторяя выкладки
предыдущего параграфа, придем к двум
уравнениям:
22 = 0,
54
О
ч-
¦2)=0,
Рис. 64.
что неустойчивость
ФД2) ~ Ф/ (<* ~ 2) siSn (®
из которых непосредственно следует,
наступает при выполнении условий
ш> 20,
t,(2o)<t/(w-2o)-
Эти условия удобно представить графически, если ввести
функцию
Ф («О = Ф* (2о) — Ь siSn (ш — 2о)«
представляющую собой, очевидно, суммарное относительное
рассеяние энергии. Пусть, например, фв не зависит от частоты,
а зависимость <j^ = ^(2)
* I имеет вид,
представленный на рис. 64. График
для суммарного рассеяния
энергии для этого случая
приведен на рис. 65. Пока
<о< 20, внешние и
внутренние потери
складываются, а при а) >
20—вычитаются. При этом могут
представиться различные
случаи. Если tye > max ф/э
то прямолинейная форма
вала останется
устойчивой при любой послекритической скорости. Если фв < min ф/э
то всюду за «классической» критической скоростью мы будем
!Ыиш11И^
Рис. 65.

168 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
иметь неустойчивость. Если ттф; < фе < тахф^, то при
некоторой угловой скорости о^ > Й0 мы получим
неустойчивость, но после прохождения скорости о)^ снова получим
стабилизацию (рис. 65). Этот последний случай нередко
наблюдался при натурных испытаниях или в опытах над
моделями.
Рис. 66.
Рассмотренный в § 3.3 случай сил вязкого трения легко
может быть получен из общих соотношений. Выражая
относительное рассеяние энергии через коэффициенты et и ее,
получим:
_2ти?0_ 2тг?/1 со —Q |
™ О2 ' ™~ q2
График для функции ф = ф(со) построен на рис. 66.
§ 3.6. Обобщение на случай неодинаковых главных
жесткостей и на случай бесконечного числа
степеней свободы
В предыдущих параграфах рассматривался вал круглого
сечения. Если главные жесткости неодинаковы, то задача,
разумеется, остается неконсервативной. Остановимся кратко
на этой задаче, ограничившись случаем внешнего и
внутреннего вязкого трения1).
Чтобы получить уравнения с постоянными
коэффициентами, будем пользоваться системой координат, вращающейся
1) Д и м е н т б е р г Ф. М., цит. на стр. 153.

§ 3.6] СЛУЧАЙ НЕОДИНАКОВЫХ ГЛАВНЫХ ЖЕСТКОСТЕЙ 169
вместе с валом. Пренебрегая анизотропией коэффициентов
трения, вместо уравнений (3.9) получим:
l? + (". + «,)-3- + 2»§ + (^-» 2h + V^0.
Здесь Qj и й2— парциальные частоты невращающегося вала
(вычисленные, разумеется, без учета трения).
Соответствующее характеристическое уравнение имеет вид
s* + 2 (se + в,) *з + [Q\ + 91 + 2о)2 + (ее + е^] s2 +
+ [(ве + е,) (2? - 922 - 2а)2) + 4еХ] s +
_|_ (Q2 _ о)2) (2| _ о)2) _|_ ?2о)2 = 0.
Среди условий Рауса — Гурвица нетривиальными при
ее > 0, et > 0 оказываются два. Первое из них
(й2 — a)2) (al _ со2)+s2o)2 > о
позволяет найти границы области неустойчивости, которая
располагается в интервале между парциальными частотами.
Этот вид неустойчивости обусловлен неодинаковыми
главными жесткостями; он подробно изучен, и мы на нем
останавливаться не будем !).
Второе нетривиальное условие
- 2 (s, + e^(Q? + ?22) + (ее + ?/)2 ($ - &V? +
+ 4о)2(г, + ^)2[2(2? + 222)-+-4] —1б82а)4>0 (3.23)
соответствует специфической неустойчивости, порождаемой
внутренним трением. Если 21 = 22 = 20, то условие (3.23)
приводит к критической скорости, определяемой по формуле
(3.12). Если Qx Ф 22, но внешнее и внутреннее трение
1) См., например, книгу: Болотин В. В., Динамическая
устойчивость упругих систем, Гостехиздат, 1956, в которой
рассмотрена соответствующая нелинейная задача.

170 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
достаточно мало, то может быть предложена простая
формула:
До сих пор мы рассматривали невесомый вал с одним
сосредоточенным диском, трактуя его как систему с двумя
степенями свободы. Обобщение на случай многих степеней
свободы и даже бесконечного числа степеней свободы не
представляет принципиальных затруднений, если известны
аналитические выражения для членов, учитывающих
внутреннее и внешнее трение.
В качестве примера рассмотрим вал постоянного сечения,
полагая, что материал вала можно трактовать как упруго-
вязкий. Тем самым будет задан закон для сил внутреннего
трения. Итак, полагаем, что напряжение о связано с
относительной деформацией волокон е зависимостью
а = ?(е + *^). (3-24)
где х — некоторая константа, характеризующая величину
внутреннего трения.
Рассмотрим вначале случай невращающегося вала. Пусть
и (z, t)t v (z, t) — проекции перемещений произвольной точки
оси вала на неподвижные оси координат. Тогда в рамках
гипотезы плоских сечений получаем формулу для продольной
деформации произвольного волокна:
д2и d2v
Учитывая (3.24), легко получим формулы для изгибающих
моментов в сечениях вала
Lx — ~~CJ\dz* "+ч dz*dt )'
I -EJJ^ + y. д3и )
Ly — CJ\dz* ^ dz2dt )
3.

4 3.6J СЛУЧАЙ НЕОДИНАКОВЫХ ГЛАВНЫХ ЖЕСТКОСТЕЙ 171
Уравнения собственных колебаний невращающегося вала
принимают вид
nJ4a , т?г д5и . д2и л
EJ -л~т + *EJ з-гзг + m -315- = О,
dzA ' dzAdt ' ctf2
где m — масса вала, отнесенная к единице длины. Таким
образом, учет внутреннего трения сводится к введению
в уравнения колебаний дополнительных членов
йг4 ^ ' " йг4 ^ #
Перейдем теперь к случаю вращающегося вала. В этом
случае силы внутреннего трения должны, очевидно, вводиться
во вращающейся системе координат и должны выражаться
через проекции перемещений ?(z, t) и y\(z, t) именно на эти
оси координат (см. рис. 66). Преобразуем уравнения
РГ д4и , ^ д2и п
dz* ' dt2
с, , dAv , d2v ~
к вращающейся системе координат. Подставляя сюда
ti = \ cos Ы — т] sin atf,
-у = \ sin atf -)- 7] cos atf,
получим:
»^-«-* + -(5—Л)-в;
Введем в эти уравнения дополнительные члены
хШ dz*dt ' X/:J &r4d*
и возвратимся к неподвижной системе координат, после чего
добавим члены
ди dv

172 устойчивость гибких валов [гл. 3
которые учитывают вязкое внешнее трение. Окончательные
уравнения принимают вид1)
о т д4и , „ т d4v , с,, д5и , ди . д2и л
EJ1F + wtEJ-W +%EJ^di + Be St + m SF = °'
с г d4t> г-, д4и . j? r d5v , dv , d2tJ A
?J -3-1 coxz:J 3-r -4- х? J -f- e -37- -f- m -375- = 0.
(3.25)
В случае вала, свободно опертого по концам, система
(3.25) допускает особенно простое решение. Полагая
и (z, t) = Uj (t) sin Л^- ,
v (z, t) = Vj (t) sin ^-
(7 = 1, 2, ...),
мы, очевидно, удовлетворим граничным условиям.
Подстановка в (3.25) дает:
* % + (х25 + е,) ^f + Qfo + coxQ^y = 0,
dt2 ' ч y ' e} dt
42Vj /9 ч dVi о «
_l+(x25+Se) _l+<ф, _ о^.й,=о
C/=l. 2, ...),
где
' I2 V m '
Если опустить индекс / и произвести замену xQ^ = s?,
то мы получим систему, целиком совпадающую с (3.9).
Отсюда, применяя формулу (3.12) и возвращаясь к
прежним обозначениям, найдем, что критические скорости будут:
ЛЛ.
М1+^) С/=1.2,...).
Как видно из предыдущего, в данной задаче связь между
различными формами колебаний полностью отсутствует и
1) Уравнения такого типа были впервые даны Ф. М. Д и м е н т-
б е р г о м (см., например, книгу: Изгибные колебания вращающихся
валов, Изд-во АН СССР, 1959).

§ 3.7]
НЕЛИНЕЙНАЯ ЗАДАЧА
173
явление неустойчивости для какой-либо формы происходит
независимо от других форм колебаний. Для наступления
неустойчивости требуется, чтобы угловая скорость вращения
превышала соответствующую «классическую» критическую
скорость (равную частоте собственных колебаний невращаю-
щегося вала) на некоторую величину, тем большую, чем
больше силы внешнего сопротивления.
Полученный результат является следствием принятой
схематизации для сил внешнего и внутреннего трения. Нетрудно
обобщить этот результат на случай произвольной
зависимости сил трения от частоты так, как это сделано в § 3.5
для вала с одним сосредоточенным диском. Пусть Q —
частота колебаний. Тогда для напряжений можно взять
следующее выражение:
где ф; — некоторая произвольная функция частоты во
вращающейся системе координат ш — 2. При таком выборе
закона для внз^треннего трения относительное рассеяние
энергии оказывается одинаковым для всех форм колебаний и
равным ф;. На дальнейших деталях останавливаться не будем.
§ 3.7. Нелинейная задача
До сих пор исследовалась устойчивость невозмущенного
(т. е. чисто вращательного) движения по отношению к малым
возмущениям. Исследование нелинейной задачи представляет
двоякий интерес. Во-первых, оно позволит найти амплитуды
автоколебаний, возбуждаемых вследствие внутреннего трения,
и, таким образом, даст возможность ответить на вопрос,
насколько опасными являются эти колебания и какими мерами
их можно снизить до допустимых величин. Во-вторых,
исследование нелинейной задачи позволит ответить на вопрос
об устойчивости по отношению к конечным возмущениям,
т. е. об устойчивости в «большом». То, что вопрос
устойчивости «в большом» имеет не только теоретический интерес,
видно из следующего. Еще Ньюкирком1) было замечено,
1) N е w k i г к В. L., Shaft whipping, Gen. Electric Rev. 27, № 3
(1924).

174 устойчивость гивких валой [гл. 3
что вал, сохраняющий прямолинейную форму за критической
скоростью вращения, начинает испытывать значительные
вибрации, если ему сообщить небольшой толчок. Таким образом,
движение, устойчивое «в малом», оказывается неустойчивым
«в большом». При этом для перехода к неустойчивости
требуется возмущение, хотя и конечное, но достаточно малое
с практической точки зрения. Здесь мы имеем случай, когда
трактовка устойчивости по отношению к малым
возмущениям оказывается недостаточной для практических
приложений.
В ближайших параграфах задача о вибрации гибкого вала
круглого сечения за критической скоростью вращения
рассматривается в нелинейной постановке *)• Поскольку нашей
целью является установление общих закономерностей,
связанных с учетом внутреннего трения при послекритических
числах оборотов, то мы максимально упростим задачу
в остальной ее части. Как и при анализе линейной задачи,
будем рассматривать невесомый вал с одним диском,
ограничившись лишь той формой колебаний, при которой не
происходит перекашивания диска и, следовательно, не возникает
гироскопических моментов. Удобной моделью такого вала
по-прежнему является свободно опертый по концам вал
с диском посредине (см. рис. 60). Диск будем вначале
считать идеально сбалансированным, а влиянием его
собственного веса будем вообще пренебрегать.
Рассмотрим колебания вращающегося вала с конечными
амплитудами, трактуя его вначале как систему с бесконечным
числом степеней свободы (рис. 67). В отличие от
элементарной постановки этой задачи будем пользоваться точным
(нелинейным) выражением для кривизны упругой линии, а
также будем учитывать силы инерции, упругости и
сопротивления, возникающие вследствие осевых смещений точек
вала. Как нетрудно установить, учет этих сил эквивалентен
учету нелинейных членов в соответствующих компонентах
тензора конечных деформаций (1.4).
^Болотин В. В., Исследование автоколебаний гибкого
вала, вызванных влиянием внутреннего трения и родственных
факторов, Научн. докл. высш. школы, сер. «Машиностроение и
приборостроение», № 4, 1958; Нелинейные колебания валов за
критическими скоростями вращения, Сб. «Проблемы прочности в
машиностроении», вып. 1, Изд-во АН СССР, 1958.

§ 3.7]
НЕЛИНЕЙНАЯ ЗАДАЧА
175
Пусть и и v — проекции смещения точек вала на
неподвижные оси координат Ох и Оу, 1/рх и !/ру — проекции
вектора кривизны на те же оси, EJ—жесткость сечения вала
при изгибе, т — масса, отнесенная к единице длины его,
Рис. 67.
N — продольная сила. Тогда уравнения колебаний вала
в неподвижной системе координат примут вид
?(#)+?«)+« ?-0-1 <3'26)
Здесь 5 — дуга, отсчитываемая вдоль деформированной оси
вала (которая считается нерастяжимой); члены, которые
учитывают внешнее и внутреннее трение, будут введены позднее.
Для случая, когда изогнутая ось вала — плоская кривая,
получим:
д2г
1 ds2

176 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
где r2 = u2-{-v2. Отсюда, учитывая, что
1 _ 1 ы
?Х ~~ Р Г '
найдем:
1 _
Р* ,/
1 _ 1 v
д2и
ds2
т (дг\2 '
д2г
ds2 ~
1 _
д2и г d2v r
ds2 и ds2 v
d2v
ds2
,/ 1 ldr\2 '
Продольная сила /V слагается из сил инерции,
-возникающих на осевых смещениях диска w(l/2), а также силы
трения в подвижной опоре и реакции упругой связи (рис. 68).
Рис. 68.
Пусть М — масса диска, k — коэффициент сопротивления,
с — коэффициент жесткости связи. Тогда, считая ось вала
нерастяжимой, получим:
N(s, ty.
d2w
¦М
(4.<)
dt2
dw (/, t)
dt
cw{ly t)
(o<*<4).
Здесь w(s, t) — осевое перемещение точек вала, т. е.
*Ф
со—//.-(#)¦
ds.

§ 3.7] НЕЛИНЕЙНАЯ ЗАДАЧА 177
С точностью до величин второго порядка
W[
Чтобы перейти от уравнений (3.26) к обыкновенным
дифференциальным уравнениям, положим:
%s
и (s, t) = ux (t) sin — ,
TtS
r (s, t) = rx (t) sin -j-
и применим вариационный метод Галеркина. Заменяя в
уравнениях (3.26) m(s) = Mb (1/2, s)t где 8 — дельта-функция,
получим:
d*V -о -о ./ Нг Н2Г\ I (0.27)
~dF
.+<*+(*,/(,. *.*.)=<>. |
Здесь &0— приближенное (в смысле метода Галеркина)
значение частоты собственных малых колебаний
2Л№ '
/ — нелинейная функция, которая с точностью до величин
второго порядка имеет вид1)
f{ 1*L d*r\_/ n2 , cl \ 2 ,
7V' -dt * dt* j- U/2 ~T~4Ej)r "+"
Индексы при и1э ^ и гх опущены.
l) Нелинейная функция типа (3.28) применительно к задаче
о колебаниях вала с неодинаковыми главными жесткостями при
изгибе была введена в работах: Болотин В. В., Об изгибных
колебаниях валов, сечения которых имеют неодинаковые главные
жесткости, Инж. сборн. 19, Изд-во АН СССР, 1954; Динамическая
устойчивость упругих систем, Гостехиздат, 1956.

178
УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ
[гл. 3
Первый член в правой части (3.28) учитывает нелинейное
выражение для кривизны и влияние продольной упругой
связи, второй — силу инерции диска, возникающую при его
осевых смещениях, третий член — силу трения в продольной
связи. Будем в дальнейшем говорить о нелинейной
упругости, нелинейной инерционности и нелинейном затухании
соответственно, записывая нелинейную функцию в виде
При этом
7Ь .
Т Я/2 I
cl
4EJ'
Ml
kl
4EJ
AEJ
(3.30)
Введем в уравнения (3.27) члены, учитывающие
внутреннее и внешнее трение. Преобразуя уравнения (3.27) к системе
координат, вращающейся вместе с валом, и подставляя
в преобразованные уравнения члены
Q2^
<Я
*lh
df\
2тс|
-Q\ dt
2те|
dt
а затем, уже возвратившись к неподвижной системе
координат, подставляя члены
Ql<\>e du Ql<\>e dv
2nQ dt ' 2rcQ dt '
получим:
d2u
dt2
d2v
7i \ Q ' I Ш —Q| / dt "*" 2те | <o — Q | ' |
+ 2^ + 0^/(r, ¦?.,?) = <>.
dt2
Wti ¦ Ь \ dv шоЬ „ ,
:n\Q ' | со — Q\ ) dt 2тс | со — У | '
(3.31)
Здесь ф,. и фе — произвольные функции амплитуды и частоты,
т. е.

§ 3.8) УСТАНОВИВШАЯСЯ АСИНХРОННАЯ ПРЕЦЕССИЯ 17§
§ 3.8. Установившаяся асинхронная прецессия
Среди решений системы (3.31) рассмотрим определенный
класс, представляющий для достаточно хорошо
сбалансированного вала наибольший практический интерес. Это будут
решения, соответствующие установившейся асинхронной
прецессии, т. е. круговому движению центра диска с
постоянной амплитудой и угловой скоростью, которая, вообще
говоря, не совпадает со скоростью вращения вала (в противном
случае прецессию
называют синхронной). Именно
этот вид автоколебаний
наблюдал, по-видимому,
Ньюкирк в своих
известных опытах по
устойчивости гибкого вала.
Пусть г — амплитуда,
Q — частота колебаний
(рис. 69). Тогда решения,
о которых говорилось
выше, запишутся в виде
: Г COS Ш,
(3.32)
v = r sin Qt.
Рис. 69.
Подставляя (3.32) в первое из уравнений (3.31), получим:
(Qo — Q2)r+2or/(r, 0, 0) = 0, (3.33)
Фе — Ф/ siSn (о) — 2) = 0. (3.34)
Подстановка во второе уравнение дает те же результаты;
это становится понятным, если учесть, что уравнения (3.31)
симметричны относительно и и v (точнее, перемена их
местами соответствует изменению направления вращения вала
на противоположное) и что искомое решение (3.32) не
зависит от начальных условий.
К тем же результатам придем, вводя комплексное
представление для перемещений w = и -f- iv и записывая
искомое решение в виде
w = rei2t.

180 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
Подставляя это выражение в уравнение
d2w Qg / ф ф; \dw Ш?0 ф.
dt2 + 2ти \У ~+~ | со — Q\ ) dt 2тс | со — У| ^ '
+ !*. + <*/(,. *,?)_0.
легко придем к соотношениям (3.32) и (3.33).
Весьма важно подчеркнуть, что соотношения (3.32) и
(3.33) дают точное решение нелинейной системы (3.31). Это
оказывается возможным благодаря тому, что нелинейность
входит в уравнения (3.31) через полный прогиб
который для случая установившейся прецессии не зависит
от времени.
Рассмотрим внимательнее уравнения (3.33) и (3.34).
Первое из них представляет собой соотношение между силами
инерции и силами упругости, второе — между силами
внешнего и внутреннего трения. Пусть tye > 0, ф^ > 0, /(г)>0
(это соответствует предположению о том, что диссипация
энергии вследствие внешнего и внутреннего трения
положительна, а нелинейность системы — «жесткая»). При
сделанных весьма несущественных оговорках уравнение (3.33)
может быть удовлетворено лишь при Q > 20 (если только
г Ф 0), а уравнение (3.34) — лишь при 2 < со. Отсюда
вытекает, что система имеет отличные от нуля решения, если
только о) > й0.
Итак, самовозбуждение вследствие внутреннего
трения возможно лишь при со > 20, причем частота уста-
повившейся асинхронной прецессии лежит в пределах
20 < Q < о).
Этот вывод становится несправедливым в случае «мягкой»
нелинейности, ибо, как видно из (3.33), если /(г)<0, то
решения возможны и при ш < 20. Это, однако, не
противоречит общему выводу о том, что неустойчивость вследствие
внутреннего трения возможна лишь в закритической области.
Дело в том, что при «мягкой» нелинейности собственная
частота колебаний с конечными амплитудами оказывается
ниже, чем частота собственных малых колебаний 20,
которой обычно приписывается смысл критической скорости.

§ 3.8] УСТАНОВИВШАЯСЯ АСИНХРОННАЯ ПРЕЦЕССИЯ 181
Уравнения (3.33) и (3.34) позволяют также найти
верхнюю границу для амплитуд вибраций при установившейся
асинхронной прецессии. Действительно, поскольку для
установившейся асинхронной прецессии всегда 2 < со, то /*</?,
где R определяется из уравнения
&1—о)2+д^/(/?, о, о) = о. (3.35)
Так, если /(r) = fr2, то
*~77]/ГЦ
1 . (3.36)
Зависимость (3.36) нанесена на рис. 71, 73, 76, 82 и др.
штриховой линией.
Оценим порядок возможных амплитуд; предположим
вначале, что подвижная опора вала допускает свободное осевое
смещение (с = 0). Тогда по первой из формул (3.30)
_ к2
т ~~ 8/2
и, следовательно,
/? = ^2/_1/^__1> (337)
v\
Рассмотрим противоположный случай, когда обе опоры
являются несмещающимися, т. е. изгиб вала возможен только
за счет удлинения его оси. В этом случае вместо с в
формулу нужно подставить
_ EF
где с0 — жесткость вала при растяжении. Отсюда по
формуле (3.37) находим:
«=т/
"2
(здесь d — диаметр сечения вала).
Итак, верхняя граница для амплитуд вибраций вала при
неустойчивости вследствие внутреннего трения меняется от
величин порядка диаметра {если концы вала закреплены от
осевых смещений) до величин порядка длины вала (если
осевым смещениям ничто не препятствует). При этом, правда,
следует иметь в виду, что формула (3.37) получена при

182 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
удержании нелинейных членов не выше третьего порядка и,
следовательно, в случае больших прогибов дает
преувеличенные значения»
Полученные решения соответствуют лишь одному из
возможных режимов автоколебаний. Если при всех значениях
2 и г имеет место неравенство ф/ > фв, то уравнение (3.34)
удовлетворено быть не может и, следовательно, режим
установившейся асинхронной прецессии неосуществим. В статье
автора]) было показано, что в этом случае колебания будут
носить характер биений. В той же статье была исследована
устойчивость установившихся решений.
Строгое исследование устойчивости может быть до
некоторой степени заменено весьма простыми «бифуркационными»
соображениями. Еще Пуанкаре2), исследуя устойчивость
форм равновесия вращающейся жидкости, создал изящную
теорию, позволяющую судить об устойчивости лишь на
основании вида кривой «перемещение — параметр» (в
рассматриваемой задаче роль перемещения может играть прогиб г,
а роль параметра — угловая скорость со). Пуанкаре показал,
что если две ветви кривой в какой-либо точке пересекаются,
М>
М,
а)
*)
Рис. 70.
то в ней происходит бифуркация (разветвление) форм
равновесия', решение, устойчивое до этой точки, после нее
становится неустойчивым, и наоборот (см. рис. 70, а, где устой-
1) Болотин В. В., Нелинейные колебания валов за
критическими скоростями вращения, Сб. «Проблемы прочности в
машиностроении», вып. 1, Изд-во АН СССР, 1959.
2) А п п е л ь П., Фигуры равновесия вращающейся однородной
жидкости, ОНТИ, 1936.

§ 3.9] ПРИМЕРЫ АМПЛИТУДНЫХ ЗАВИСИМОСТЕЙ 183
чивые ветви обозначены жирными линиями, а неустойчивые—
тонкими линиями). Другой точкой, в которой также
происходит смена устойчивости на неустойчивость, является
предельная точка, где касательная становится вертикальной (точки
Мх и М2 на рис. 70, б). Рассмотрение бифуркационных
кривых позволяет также судить и об устойчивости «в большом»:
неустойчивые ветви играют роль «водораздела», отделяющего
области тяготения двух соседних устойчивых решений.
Отсюда легко находится величина возмущения, необходимого
для того, чтобы перебросить систему с одной устойчивой
ветви на другую.
Теория Пуанкаре была дана впервые для исследования
равновесия систем, находящихся под действием
консервативных сил. А. А. Андронов1) развил ее для случая
автоколебательной системы с одной степенью свободы,
зависящей от параметра и обладающей малой нелинейностью. Он
показал, что все основные положения теории Пуанкаре могут
быть перефразированы для этой задачи, если под
характерным перемещением понимать амплитуду предельного цикла.
Эти результаты были недавно обобщены Ю. И. Неймар-
к о м2). Мы будем в дальнейшем пользоваться для
выделения устойчивых и неустойчивых ветвей бифуркационными
соображениями, которые обладают большой интуитивной
убедительностью.
§ 3.9. Примеры амплитудных зависимостей
Переходя к детальному анализу зависимости амплитуд
колебаний от угловой скорости после потери устойчивости,
рассмотрим вначале случай линейного трения:
27сЙе,, , 2тс I со — Q I е/
¦•=-щ- ь—щ—
Уравнение (3.32) принимает вид
в? °8
^Андронов А. А., Применение теории Пуанкаре о
«точках бифуркации» и «смене устойчивости» к простейшим
автоколебательным системам, Собр. трудов, Изд-во АН СССР, 1956.
2) Н е й м а р к Ю. И., Метод точечных отображений в теории
нелинейных колебаний. Изв. высш. учебн. завед., сер.
«Радиофизика» 1, Ж№ 1, 2, 5, б (1958),

184 устойчивость гибких валов [гл. 3
откуда частота автоколебаний
Q = —-—. (3.38)
1 + i*-
?/
Из уравнения (3.33) находим:
1 fW
Подставляя сюда (3.38) и учитывая, что согласно формуле
(3.12)
Q.(i+*) = ...
получим:
1
У Л
kV
1
(3.39)
Зависимость (3.39) представлена на рис. 71. Чем больше
внешнее трение, тем далее отодвигается область
неустойчивости прямолинейной формы и тем меньше становятся ампли-
*(*е=0)
Рис. 71.
туды автоколебаний. Здесь же штриховой линией нанесено
решение г = /?, определяемое по формуле (3.36).
До сих пор предполагалось, что коэффициенты трения ei
и ее ни от амплитуды колебаний, ни от частоты не зависят.

§ 3.9]
ПРИМЕРЫ АМПЛИТУДНЫХ ЗАВИСИМОСТЕЙ
185
Теперь мы дадим некоторое обобщение теории для случая,
когда
et = kt+Kt(r),
se = ke + Ke{r),
где kt и ke — константы, а /Сг (0) = /Св (0) == 0.
Формула (3.38) для этого случая принимает вид
(О
2 = -
1-f
ke + Keif) '
(3.40)
ki + Ki(r)
а из уравнения (3.33) находим:
а = со01Л+/(/•). (3.41)
При этом функция /(г) может иметь вид, отличный от
(3.29).
Амплитудная кривая проще всего строится графическим
путем. Для этого достаточно найти точки пересечения
кривых, определяемых формулами (3.40) и (3.41). На рис. 72
Рис. 72.
представлено такое построение для случая /(г) = ^г2,
Ki = (iir29 Ke — oLer2 {аь > 0, ае > 0). Пока угловая скорость
достаточно мала, не существует действительных корней,

186 устойчивость гибки* валов [гл. 3
отличных от нуля. При а) = о)^ > 20 появляется пара
кратных корней г = г^. С дальнейшим увеличением угловой
скорости один из корней возрастает, а другой убывает, пока
при со = о)^ не становится равным нулю. При а) > о)#
существует лишь один действительный корень.
Зависимость амплитуд вибраций от угловой скорости
приведена на рис. 73. Точка N является точкой бифуркации
(для этой точки (0 = 0)^, где o> = u>*— критическая скорость,
определяемая по линейной теории). Точка М является
предельной точкой: при переходе через эту точку неустойчивое
г
г*
V*
,-*
<<у
<^^
^у^
^^^
s^ZS^
^^^
У\>г
sZs^
R-^^y^
У^*г
s\S^
<Ss^
^r.
/уГ
А
т^
1
1
(м
N
Sim Ы*
Рис. 73.
решение NM становится устойчивым (здесь, как и ниже,
устойчивые решения обозначены жирными линиями).
Если постепенно увеличивать от нуля угловую скорость,
то можно наблюдать следующую картину. Прямолинейная
форма вала останется устойчивой, пока со < со^. При со = ш^
будет иметь место «жесткое» возбуждение колебаний с
конечной установившейся амплитудой rt. С дальнейшим
увеличением скорости амплитуда возрастает (рис. 74, а). При
снижении чисел оборотов режим колебаний сохраняется вплоть
до a> = a>W8, где колебания «сорвутся» и вновь восстановится
первоначальная неискривленная форма вала (рис. 74, б). Здесь
мы имеем явление «затягивания», типичное для многих задач
нелинейных колебаний.
Сказанное относилось к случаю, когда возмущения,
действующие на вал, достаточно малы. Если же возмущения не

§ 3.9] ПРИМЕРЫ АМПЛИТУДНЫХ ЗАВИСИМОСТЕЙ 187
являются малыми, то необходимо считаться с возможностью
потери устойчивости «в большом». Например, если
прямолинейному валу, работающему в интервале со^ < о> < со^,
дать достаточно большой боковой толчок, то вал может не
вернуться к первоначальному положению, хотя оно и является
устойчивым. С другой стороны, вал, совершающий
колебания в интервале а)^ < со < а^, можно «успокоить», если дать
ему достаточно большое возмущение, возвращающее его
к прямолинейной форме. Порядок возмущения, нужного для
перебрасывания с одной устойчивой ветви на другую,
определяется положением неустойчивой ветви, играющей, как уже
' ##
со*
а)
Рис. 74.
00*
б)
со
было сказано, роль водораздела. Грубо говоря, нужно
систему «перебросить» через неустойчивую ветвь1).
Анализ нелинейной задачи заставляет по-новому подойти
к вопросу об устойчивости прямолинейной формы вала.
Оказывается, что рассмотрения «уравнений в вариациях» для
нулевого решения еще не достаточно для того, чтобы судить
об устойчивости. Вал, устойчивый по отношению к весьма
малым возмущениям, может оказаться неустойчивым по
отношению к конечным, хотя и достаточно малым с практической
точки зрения возмущениям.
Особенно ярко это видно из следующего примера. Пусть
линейная часть внутреннего трения отсутствует, т. е. kt = О,
а /Q (г) = с^г2. Этот случай близок к тому, что мы имеем
1) Здесь речь идет о возмущениях одного определенного типа
(амплитудные возмущения). Для того чтобы дать полный ответ на
этот вопрос, следовало бы рассмотреть фазовые траектории системы
в пространстве четырех измерений, что едва ли практически
осуществимо.

188 устойчивость гибких валов [гл. 3
— сихо+н
на практике (площадь петли гистерезиса при исчезающе
малых напряжениях стремится к нулю). Тогда, вычисляя
критическую скорость по
формуле (3.12), найдем,
что <о#—>оо, т. е. вал
остается устойчивым при
любой угловой скорости.
Графическое
построение для этого случая
показано на рис. 75, а
результаты приведены на
рис. 76. Прямолинейная
форма вала, устойчивая
по отношению к малым
возмущениям при всех
угловых скоростях,
начиная с (0 = 0)^, может
оказаться неустойчивой
«в большом». При этом
величина возмущения,
необходимая для перехода
к вибрациям, будет тем
меньше, чем выше число
оборотов.
Скорость о) = а)^, при которой прямолинейная форма
вала перестает быть единственной устойчивой формой, имеет
Рис. 75.
S20 k>**
Рис. 76.
смысл «нижней» критической скорости (в отличие от
«верхней» критической скорости coj. Здесь мы имеем близкую

§ 3.10] МАКРОСКОПИЧЕСКАЯ ТЕПЛОВАЯ ДИФФУЗИЯ 189
аналогию с известным положением в теории гибких
оболочек, где «нижняя» критическая нагрузка приобретает важное
практическое значение, а «верхняя» критическая нагрузка,
определяемая по линейной теории, в значительной мере
утрачивает свой смысл.
§ ЗЛО. Трение, обусловленное макроскопической
тепловой диффузией
В дальнейшем мы не будем рассматривать различные
законы изменения внешнего и внутреннего трения, а выберем
среди них те, которые наиболее соответствуют наблюдаемым
на опыте закономерностям.
Одной из важнейших составляющих внутренних потерь
являются необратимые процессы, связанные с
макроскопической тепловой диффузией. Остановимся на этом вопросе
подробнее.
Широко известно, что при растяжении стержня из
материала с положительным коэффициентом температурного
расширения он несколько охлаждается, а при сжатии — несколько
нагревается (это можно установить из чисто
термодинамических соображений). Поэтому, если стержень испытывает
изгибные колебания, то его волокна попеременно то
нагреваются, то охлаждаются. При этом от нагретых (сжатых)
волокон к охлажденным (растянутым) волокнам устремляется
тепловой поток, который вследствие периодичности
изменения температуры также оказывается периодическим.
Процесс передачи тепла от более холодной части к нагретой
не является обратимым. Колебания сопровождаются некоторым
рассеянием энергии: часть механической энергии упругих
колебаний превращается в тепло и рассеивается.
3 и н е р 1) рассмотрел процесс рассеяния тепла при изгиб-
ных колебаниях и установил формулу
Ег — ЕТ со Q
Здесь Е$ и Ет — адиабатический и изотермический модули
упругости, сог — релаксационная частота, равная для стержня
1) 3 и н е р К., Упругость и неупругость металлов, Сб. статей
кУпругость и неупругость металлов», ИЛ, 1954.

190 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
круглого сечения
d2
(3.43)
(D — коэффициент макроскопической тепловой диффузии).
Зависимость (3.42) представлена на рис. 77. При очень
малых частотах (Q <^ а)г) процесс происходит почти
адиабатически. Напротив, при
2^>сог температура почти
не успевает измениться,
т. е. мы имеем здесь почти
изотермический процесс.
В обоих случаях потери
энергии вследствие
тепловой диффузии весьма
малы, что видно из рис. 77.
Наибольшие потери имеют
ft место при 2 = сог и со-
Рис. 77. ставляют:
max ф/ = тсД/г,
где А? — так называемая степень релаксации
(3.44)
у ESET Es
Из термодинамических соображений следует, что
D =
bE = EsT^-t
где Т—абсолютная температура, с — объемная теплоемкость,
X — коэффициент теплопроводности, а — коэффициент
линейного расширения, р — плотность.
Вычисления по формулам дают для стали (при
комнатной температуре)
Д? = 0,0024, D = 0,20 см2/сек.
Найденные отсюда значения ф; удовлетворительно
совпадают с опытными результатами Беневитца и Ретгера 1).
Подставляя эти значения в формулы (3.43) и (3.44), получим
(при d = 20 мм) max fy« 0,0075, а)г = 0,05 1/сек.
1) См. сноску на стр. 189.

§ $.10] МАКРОСКОПИЧЕСКАЯ ТЕПЛОВАЯ ДИФФУЗИЯ 191
Из того, что релаксационная частота крайне мала, можно,
казалось бы, сделать вывод, что отмеченные эффекты не
могут оказать существенного влияния на устойчивость вала.
Это, однако, не так. Поскольку внутреннее трение связано с
деформациями вала, т. е. зависит от его поведения во
вращающейся системе координат, то в формулу (3.42) вместо Q
должна входить частота | со — Q |. Другими словами,
релаксационную частоту сог следует сравнивать не с 2, а с | со — Q |.
Из уравнения (3.33) вытекает, что 2 = (d0]/^1-|-/(г). Но
при малых колебаниях / (г) <^ 1, Q ^ 20^ со. Отсюда видно,
что по крайней мере на границе области неустойчивости
| со — Q | *-— шг.
Макроскопическая тепловая диффузия лишь частично
объясняет рассеяние энергии при вибрациях. Если
напряжения достаточно велики, то важную роль начинают играть
потери энергии вследствие необратимых пластических
деформаций и упругого гистерезиса. Эти потери, не зависящие от
частоты вибраций, зависят от амплитудного значения
напряжений, т. е. в конечном счете от амплитуды вибраций г.
Поэтому полное выражение для внутренного рассеяния энергии
можно записать в виде
fr = Cr« + 2«A, ^'trf1,. (3-45)
(со — Qy -f- со*
Здесь С и п — некоторые константы, определяемые из опыта.
По ряду данных, показатель степени п для стали имеет
значения от двух до трех.
Задача определения амплитуд и частот для установившейся
асинхронной прецессии сводится к решению уравнений (3.33)
и (3.34) при предположении (3.45). Обозначив для
сокращения
(a)_2)2-f-c02==F, (3.46)
запишем уравнение (3.34) в виде
со* у г — сог
Решая это уравнение относительно F, найдем:
Р_ 2*4«? Г, + л/. Ме-СгГ]

192 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
откуда, после использования (3.46),
Q = o) — (
У (>-# v ^~
Здесь введены обозначения
теД,
(3.47)
¦а, (3.48)
Г-
^ = г0. (3.49)
Формула (3.47) справедлива лишь для случая 2 < о), т. е.
только за критической скоростью вращения вала.
Переходя к исследованию формулы (3.47), попробуем,
прежде всего, найти границы области неустойчивости. На
этих границах г—>0, откуда частота вибраций
Q = (o-»f|/'2*2(1 ±|Л _-?-)_ 1.
С другой стороны, из уравнения (3.33) следует, что при
г->0 имеем 2->20. Отсюда критические частоты
оказываются равными
A + «vjAa2(l ±jA--L)_i. (3.50)
Формула (3.50) дает, вообще говоря, две критические
частоты со* и а)11, причем вследствие неравенства шг<^20
обе они имеют порядок «классической» критической
скорости 20. В интервале между этими скоростями
невозмущенное движение вала неустойчиво, а вне их — устойчиво. Таким
образом, имеется область неустойчивости, целиком лежащая
за скоростью 20 (рис. 78).
Если <х< 1, т. е. 7гД?<фв, то формула (3.50) не дает
для о)^ действительных значений, т. е. область
неустойчивости исчезает. Этот случай соответствует, очевидно,
достаточно большому внешнему трению. Если же а2^>>1, то
формула (3.50) заменяется более простыми соотношениями:
со.

§ 3.10] МАКРОСКОПИЧЕСКАЯ ТЕПЛОВАЯ ДИФФУЗИЯ 193
Два возможных случая показаны на рис. 79, где по
вертикальной оси отложено полное рассеяние энергии
* = <k + <hsign(a> — QQ)
при /*->0. Эти случаи иллюстрируются также на рис. 80,
где изображено поведение характеристических показателей 5
в зависимости от угловой скорости со.
Займемся теперь определением амплитуд вибраций.
Установим, прежде всего, смысл постоянной г0, введенной
согласно (3.49). Пусть со — й0^>сог, что соответствует очень
большим закритическим скоростям; тогда вместо (3.45)
получим:
Отсюда, используя уравнение (3.32), найдем:
пГ1Г
Г = У ТГ = Г<>' <3-51)
т. е. г0 имеет смысл амплитуды вибраций при весьма
больших закритических скоростях.
Формула (3.47) дает действительные значения для 2, пока

194
Амплитуда
УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ
[гл. 3
, = г01Л+«
имеет смысл максимально возможной амплитуды вибраций
(разумеется, при установившейся асинхронной прецессии,
которой соответствует рассматриваемое решение).
Чтобы установить зависимость амплитуды от угловой
скорости со, нужно найти совместное решение уравнений (3.33)
и (3.34). Это проще всего сделать графически, отыскивая
точки пересечения кривых

§ 3.10] МАКРОСКОПИЧЕСКАЯ ТЕПЛОВАЯ ДИФФУЗИЯ 195
Для случая а>1 построение приведено на рис. 81.
Система уравнений может иметь до пяти действительных
корней. При этом угловые скорости о)^, со^ и со^
соответствуют изменению числа корней, т. е. изменению характера
вибраций.
Амплитудная кривая представлена на рис. 82. Как и
ранее, устойчивые ветви обозначены жирными линиями
(разделение решений на устойчивые и неустойчивые произведено
S2-CU
Рис. 81.
здесь без строгого анализа, на основании бифуркационных
соображений).
В зависимости от направления изменения угловой
скорости (разгон или выбег), а также величины и характера
возмущений возможны различные экспериментальные кривые,
показанные на рис. 83. При всем их разнообразии ясно
одно: при малых закритических скоростях мы имеем
зависимости типа (3.39), а при больших закритических скоростях

196 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
амплитуды установившихся вибраций примерно постоянны и
близки к значению (3.51).
Если а< 1, то невозмущенное движение остается
устойчивым «в малом» при любых скоростях вращения. Чтобы
Ma*»1* «>S
Рис. 82.
R „
/у'*'^—Г
^JL L
а,** <° 0 (oi
ш о
¦<r-lJ-
&»** и
R
1--
~А
. А..
ш?й>»» <о 0 со;
Рис. 83.
вызвать установившиеся вибрации, нужно дать системе
достаточно большое возмущение. Для этого случая также можно
представить себе несколько типов экспериментальных
диаграмм.

§ 3.11] ВЛИЯНИЕ СИЛ ТРЕНИЯ ПРИ ТУГОЙ ПОСАДКЕ ДЕТАЛЕЙ 197
§ 3.11. Влияние сил трения при тугой посадке
деталей на вал
До сих пор рассматривался случай, когда внутреннее
трение зависит от амплитуды по простейшему степенному
закону. Можно рассмотреть более общий случай,
предполагая произвольную зависимость от амплитуды как
внутренних, так и внешних потерь. Вид резонансных кривых
изменяется в зависимости от принятого закона для сил трения.
В частности, может измениться число устойчивых решений
типа решения АВ на рис. 82 (если силы внешнего трения
растут с амплитудой быстрее сил внутреннего трения, то
такие решения вообще отсутствуют).
Известно, что наиболее ярко явления неустойчивости
обнаруживаются в случае тугой посадки диска на вал и,
особенно, в случае крепления диска при помощи цангового
зажима. Силы трения, возникающие на контактной
поверхности втулки и вала, играют ту же роль, что и силы
внутреннего трения в материале, однако здесь они более
значительны.
Силы трения зивисят от состояния контактной
поверхности, и при изгибе вала они, вообще говоря, возрастают.
Однако более существенной является, по-видимому,
зависимость сил трения от скорости относительного движения
втулки и вала, т. е. в конечном счете от частоты вибраций
во вращающейся системе координат. Наличие этой
зависимости подтверждается опытами, произведенными в МЭИ
Э. Л. Позняком. На рис. 84 показана экспериментальная
зависимость кажущегося декремента (инкремента) затухания
от угловой скорости, полученная для двухопорного валика
с диском, закрепленным при помощи двух цанговых
зажимов. До критического числа оборотов, равного примерно
900 об/мин, силы внешнего трения и «вращающегося»
трения в зажимах складываются, а после критического числа
оборотов — вычитаются. Предполагаемая зависимость следует
кривым а и б на рис. 85, хотя принципиально возможна и
зависимость типа кривой е. Для ниспадающего участка любой
кривой примем выражение

198 устойчивость гибких валов [гл. 3
где mz и п — константы, Л (г) — некоторая функция
перемещения.
Из уравнения (3.32)
легко получим:
ф,(г. |ш-9|) = ф,(г)
0 "А Л (г) л
2 = со — (0.1/ , ) ; —1
(3.53)
Далее, предположим, что трение в зажиме быстро растет
при малых амплитудах, но его рост замедляется, когда
амплитуды становятся достаточно велики. Напротив, рост внешних
д
0,5
-Q51
1000 2000 3000 4000 5000,., об/
Рис. 84.
сопротивлений становится существенным лишь при больших
амплитудах. На рис. 86 показана амплитудная кривая для
этого случая. Неустойчивость прямолинейной формы вала
наступает сразу же после классической критической
скорости 2, причем в этой области устанавливаются
автоколебания малой амплитуды, которые накладываются на
синхронную прецессию с амплитудой г = R. При дальнейшем
увеличении угловой скорости происходит срыв на другую ветвь,

§ 3.11] ВЛИЯНИЕ СИЛ ТРЕНИЯ ПРИ ТУГОЙ ПОСАДКЕ ДЕТАЛЕЙ 199
соответствующую установившейся асинхронной прецессии.
За скоростью оз^* прямолинейная форма вала оказывается
устойчивой как «в малом», так и «в большом». В интервале
ш* < ю < ю** прямолинейная ,
форма, будучи устойчивой «в / i I
малом», все же неустойчива по
отношению к достаточно
большим возмущениям.
Несомненно, нужны
дальнейшие теоретические и,
особенно, экспериментальные
исследования поведения валов за
критическими числами
оборотов. Приведенные здесь
результаты должны способствовать
более правильному пониманию
явлений, происходящих в за-
критической стадии, а также О \co-S2\
более разумной постановке Рис. 85.
и истолкованию эксперимента.
Кроме того, целесообразна дальнейшая теоретическая
разработка вопроса по части исследования различных законов для
Рис. 86.
^
сил трения, рассмотрения многодисковых и гироскопических
систем, изучения квазипериодических режимов и их
устойчивости и т. п.

200 устойчивость гибких валов [гл. 3
§ 3.12. Неустойчивость роторов, связанная с влиянием
масляной пленки в подшипниках
Явления, весьма сходные с автоколебаниями,
обусловленными внутренним трением в материале вала, вызываются
влиянием сил трения в масляном слое подшипников. По
указанному вопросу имеется обширная литература, количество
которой в последние годы быстро растет в связи с
важностью этих явлений для
современных
быстроходных машин !).
Рассмотрим жесткий
ротор диаметром 2/?,
вращающийся с постоянной
скоростью со в
подшипнике с начальным зазо-
- ром А <^ /?, заполненным
маслом (рис. 87).
Колебательные свойства
такого ротора
обеспечиваются благодаря
упругости масляной пленки.
Пока ротор вращался
коаксиально с
подшипником, силы трения в
Рис. 87. подшипнике сводились
к паре сил,
направленной в сторону, противоположную движению. Предположим
теперь, что центр ротора Ох сместился относительно
центра подшипника О на расстояние г = y~u2-{-v2 < А и
совершает прецессионное движение с угловой скоростью 2.
При смещении центра ротора трение становится
неодинаковым по окружности; оно будет больше с той стороны, где
зазоры уменьшились, и меньше — где зазоры увеличились
(рис. 88). Таким образом, возникает сила трения, направленная
перпендикулярно к смещению а* и в линейном приближении
пропорциональная этому смещению. При определенных условиях
сила трения может стать причиной возбуждения
автоколебаний, аналогичных колебаниям валов вследствие гистерезиса.
1) См. сноску на стр. 154.

§ 3.12] ВЛИЯНИЕ МАСЛЯНОЙ ПЛЕНКИ В ПОДШИПНИКАХ 201
Автоколебания допускают формальное описание, если
исходить из концепции «вращающегося» трения.
Распределение скоростей в пленке, которое с большой точностью
можно считать линейным, заменим равномерным
распределением со средней скоростью и>/?/2. Преобразуем уравнения
колебаний ротора
¦ <20и = 0у
dt2
dt* ^ °
0
к системе координат,
вращающейся со средней
скоростью о>/2:
d2% dt\ .
d2f]
dfi
+ (Qj_4)1 = 0.
Рис.
Вводя в эти уравнения члены k^d\\dt и k^dr^jdt, которые
учитывают вязкое трение в пленке, возвращаясь к
неподвижной системе координат и добавляя члены, учитывающие
внешние («невращающиеся») сопротивления, получим:
dt2
d>v
It2
+
+
du о
1 Qi/j
dt 1 U{)U
dv 2
?до>
2
?дО>
<tt
¦ + Q<fa
<у = 0,
(3.54)
Решение этой системы уравнений ищем в виде (3.20), где
по-прежнему w = и -\- iv. На границе области неустой*-
чивости
Qa
о,
2тс
К
¦(;-»)¦
0.
(3.55)

202 устойчивость гибких валов [гл. 3
Следовательно, критическая скорость вращения ротора
:220(1
Я?л
(3.56)
При малом внешнем сопротивлении а>ф^220.
Несмотря на большую условность рассмотренной схемы,
она приводит к результатам, удовлетворительно
согласующимся с опытом. На рис. 89 сведены вместе опытные
данные из работы Ньюкирка и Льюиса1), показывающие
до
4vs^ х
Ч^*
ЕИХ^
—-*
о J
1
-- -|
/0 15 10 25 30 35 40 45
Рис. 89.
55
изменение безразмерной критической скорости в зависимости
от коэффициента вязкости масла |х, выраженного в санти-
пуазах. Результаты относятся к валам с различным
отношением диаметра к длине подшипника и к различным
значениям давления на подшипники. Как видно из графика,
критическая скорость «)# не превышает удвоенной величины
«классической» скорости и приближается к ней, когда
вязкость пленки уменьшается. Это вполне согласуется с
мулой (3.56), которую можно представить также в виде
220(l+^!L).
1) См. сноску на стр. 154.

§ 3.12] ВЛИЯНИЕ МАСЛЯНОЙ ПЛЕНКИ В ПОДШИПНИКАХ 203
На рис. 90 представлены результаты из другой, недавно
опубликованной работы ]). Первый максимум амплитуд
соответствует вынужденным колебаниям, вызванным дисбалансом.
Частота этих колебаний совпадает с угловой скоростью
вращения. Начиная примерно с а) = 220, возникают вибрации,
обусловленные влиянием масляной пленки. Частота этих
вибраций остается в широком диапазоне примерно
постоянной и равной частоте собственных колебаний ротора. Это
п\
j
v
А
J20 2000 2Sl0
Рис. 90.
4000
Об/
б/
7"
'мин
указывает на автоколебательный характер явления и
согласуется с теоретическими результатами.
Более строгая теория, объясняющая явления
неустойчивости вследствие трения в масляной пленке, основана на
рассмотрении гидродинамических явлений в масляном слое.
При этом используются обычные предположения
гидродинамической теории смазки: толщина пленки считается достаточно
малой, чтобы влиянием кривизны и изменением давления
по толщине можно было пренебречь, силы инерции жидкости
полагаются пренебрежимо малыми по сравнению с силами
вязкости, течение в подшипнике считается плоским. В
случае, когда жидкость целиком заполняет зазор между цапфой
и подшипником, радиальная и тангенциальная составляющие
0 Н о г i Y., A theory of oil whip, Journ. Appl. Mech. 26, № 2
(1УЭУ).

204 устойчивость гибких валов [гл. 3
силы трения определяются по формулам
р = \2ку.ф уг
т А3 (1 —с2)'^ '
P^^^L с /U_2RV\
А2 (2 + с2)(1 — с2)'* \ г 7
Здесь U = со/? — скорость вращательного движения ротора,
V§ = rQ — скорость прецессионного движения, Vr = drjdt,
b — ширина подшипника, с = г/Л — относительный
эксцентриситет. Если с <^ 1, то формулы могут быть записаны
в виде
Pr«-/C-g-f Pe^/c(-J-S)r, (3.57)
где
„ 12тг[х^з
К= ДЗ •
Из второй формулы (3.57) видно, что тангенциальная
составляющая Яе действует по направлению движения, если только
со/2 — Q > 0. Отсюда приходим к выводу о том, что
критическая угловая скорость не может быть меньше, чем
удвоенная частота собственных колебаний.
Вполне вероятно, что автоколебания ротора
сопровождаются разрывом пленки. Устойчивость вращательного
движения при условии, что пленка лишь частично заполняет
зазор и что имеется начальный эксцентриситет г0,
рассматривалась в упоминавшейся уже работе Хори. Следует
отметить, однако, что теоретические исследования приводят
к отличным друг от друга и даже противоречивым
результатам 1). Уточнение гидродинамического описания явления
весьма существенно для успешного решения задачи об
автоколебаниях роторов, обусловленных влиянием масляной пленки.
§ 3.13. Явления неустойчивости в центрифугах
при неполном наливе жидкости
Известно 2), что центрифуги, содержащие небольшое
количество жидкости, могут испытывать опасные колебания,
1) Коул Дж. Е., Протяженность масляной пленки и вибрации
вала в неразъемном подшипнике, Сб. «Машиностроение», № 3,
ИЛ, 1958.
2) См. работу Епишева Л. В., цит. на стр. 154.

§ 3.13] ЯВЛЕНИЯ НЕУСТОЙЧИВОСТИ В ЦЕНТРИФУГАХ 205
амплитуды которых значительно превосходят амплитуды
колебаний пустой или полностью загруженной центрифуги.
Эти колебания происходят с частотами, близкими к частоте
собственных колебаний центрифуги, и носят ярко
выраженный автоколебательный характер. Энергия, идущая на
поддержание колебаний, сообщается двигателем; роль
передатчика энергии играют силы трения в слое жидкости,
помещенной в центрифугу. Здесь имеет место полная аналогия
с влиянием внутреннего трения
в материале или трения в
масляной пленке подшипников.
Рис. 91.
Рис. 92.
Концепция «вращающегося» трения успешно может быть
применена и в этом случае. Предположим, что длина ротора
центрифуги, вращающегося с постоянной скоростью со, мала
по сравнению с расстоянием от неподвижной опоры (рис. 91).
При этом задача может быть сведена к исследованию плоских
движений ротора с упругими связями. Будем считать, что
масса жидкости пренебрежимо мала по сравнению с массой
ротора, а толщина слоя жидкости Л<^/? (рис. 92).
Приближенно можно принять, что в невозмущенном движении
вся жидкость, заполняющая ротор, вращается с угловой
скоростью оу. При малых возмущениях с компонентами и и v
на ротор будут действовать силы трения, зависящие от ско-

206 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
ростей движения ротора относительно вращающейся жидкости.
Эти силы должны вводиться в системе координат,
вращающейся с угловой скоростью со. Уравнения возмущенного
движения примут вид
d2u I Ql ф<, \ da о )
d4 ( Q20 Ь \dv „ (3'58)
чё + Ыъ+Ч-ж-***+<&>=*• )
Отсюда находим, что критическая скорость равна
». = Qo(1+^)' (3-59>
т. е. явления неустойчивости, обусловленные наличием слоя
жидкости, могут наступить лишь за «классической»
критической скоростью 20.
На рис. 93 приведены данные, полученные для модели
центрифуги с ротором емкостью около 1600 смъ. Кривая /
г, мм
2,5
1,875
1,25
0,625
О 1000 1500 2000 2500
(О06/мин
Рис, 93.
соответствует пустому ротору, а ее максимум — колебаниям
от дисбаланса вблизи со = 20. Кривая 2 соответствует
добавлению в ротор 50 см3 жидкости, а кривая 3 — добавле-
Я
г
з 1
Чч<^
~^ч
4
у-2

§ 3.13] ЯВЛЕНИЯ НЕУСТОЙЧИВОСТИ В ЦЕНТРИФУГАХ 207
нию 600 см3 жидкости. Колебания начинаются сразу же
после перехода через скорость &0 и удерживаются в
широком диапазоне угловых скоростей. Частота колебаний близка
при этом к собственной частоте. При заполнении ротора
(кривая 4) колебания успокаиваются.
Исходя из теоретических соображений, следует ожидать,
что устройство в роторе перегородок, препятствующих
перетеканию жидкости, будет способствовать более спокойной
работе центрифуг. Это было подтверждено экспериментом.
Устройство четырех сплошных радиальных перегородок
полностью устраняет автоколебания. Если даже эти перегородки
имеют малую высоту и не доходят до свободной
поверхности, то это тоже способствует более спокойной работе
центрифуги.
Автоколебания не возникают в рбторах сепараторов,
пакет тарелок которых погружен в жидкость. Благодаря
этому обстоятельству и оказывается возможной работа на
современных сепараторах. Однако, если заполнение
сепаратора происходит при его вращении за критическим числом
оборотов, то в начальный момент, когда жидкость еще не
доходит до тарелок, создаются условия для возбуждения
опасных колебаний.
Заметим, что устойчивость вращающихся (в частности,
гироскопических) систем, содержащих жидкость со
свободной поверхностью, представляет интерес с точки зрения и
некоторых других приложений. В этом направлении сделан
ряд исследований 1). Обычный подход основан на
предположении, что жидкость является невязкой, а возмущения —
малыми. Исходя из этого предположения и разлагая вектор
смещений частиц жидкости в ряды по полной системе
функций, можно получить бесконечную систему обыкновенных
дифференциальных уравнений, содержащих
псевдогироскопические члены (т. е. члены с обобщенными координатами,
матрица которых антисимметрична). Наличие этих членов
сближает данную задачу с другими задачами,
рассматриваемыми в настоящей книге.
1) См., например, Нариманов Г. С, О движении
симметричного гироскопа, полость которого частично заполнена
жидкостью, Прикл. матем. и мех. 21, №5 (1957); Stewartson К.,
On the stability of a spinning top containing liquid, Journ. Fluid Mech.
5, № 4 (1959), и др.

208 устойчивость гибких валов [гл. 3
§ 3.14. Неустойчивость роторов в магнитном поле
Еще один класс неконсервативных задач упругой
устойчивости связан с действием на вращающиеся роторы
магнитных и электродинамических сил !). В качестве простейшего
примера рассмотрим движение гибкого вала, несущего
ферромагнитный сердечник, который помещен в постоянном
магнитном поле (рис. 94). Помимо сил магнитного
притяжения, на сердечник действуют силы, обусловленные движением
Н— 2R *Н
[* 2(R+b) Н
Рис. 94.
сердечника относительно поля. Эти силы связаны в первую
очередь с потерями на магнитный гистерезис и токи Фуко.
Если ротор и магнитное поле не вращаются, то эти силы
способствуют затуханию собственных колебаний ротора.
Если же ротор вращается относительно поля с некоторой
постоянной скоростью, то при определенных условиях эти
силы могут вызвать перекачку энергии поля или двигателя
из чисто вращательной формы движения в колебательную и
вызвать, таким образом, автоколебания ротора.
1) См. работы Позняка Э. Л., цит. на стр. 154.

§ 3.14] НЕУСТОЙЧИВОСТЬ РОТОРОВ В МАГНИТНОМ ПОЛЕ 209
Для описания этого явления воспользуемся, как и ранее,
концепцией «вращающегося» трения. Пусть со — скорость
вращения ротора, соп — скорость вращения поля. Подобно
тому как силы внутреннего трения вводились в системе
координат, вращающейся со скоростью со, силы магнитного
трения введем в системе координат, вращающейся со
скоростью соп. После обычных преобразований приходим к
системе уравнений, аналогичной (3.18):
#» , 12о (Ь , Ф/ Фм \du
dt2
, Ц> (Ь | Ь i Фм \ da 2 ,
, Q0 ( Ь" , U \ _n
^ , Qo /Ф. , «W , Фм \ ^
Ф/*> , Ф:
, Q0 /Ф* , Ф/ , Фм \ *" , Q2„
°5
П-2|Г U'
(3.60)
2ti \ I <o — Q I
Здесь ф^, ф,- и фм— относительное рассеяние энергии,
вызванное внешним, внутренним и магнитным трением
соответственно, 2— частота прецессии. Отсюда приходим к условию
устойчивости типа (3.21):
Ф* — ф; sign (со — 20) — <]>Msign(con — 20)>0. (3.61)
Рассмотрим условие (3.61) подробнее. Если со < 20, соп < 20,
то и внутреннее, и магнитное трение способствуют
стабилизации установившегося вращения и прямолинейная форма вала
устойчива. Если со < 20, соп > 20, то неустойчивость может
быть вызвана силами магнитного трения при фм>Фг-г~Ф/-
При со>20, соп<20 неустойчивость будет, если ф;>фм-г~Фе-
Наконец, если со > 20, соп > 20, то неустойчивость наступает
ПРИ Фм + Ф/>Фе-
Некоторые экспериментальные результаты, относящиеся
к поведению гибкого валика с железным ротором,
помещенным в двухполюсном магнитном поле, приведены на рис. 95.
По горизонтали отложена величина максимальной индукции
в зазоре В (в гс), а по вертикали — декремент (инкремент)
малых изгибных колебаний. Валик был закреплен от
вращения (со = 0), а магнитное поле вращалось с угловой
скоростью соп = 3000 об/мин. Частота собственных колебаний

210 УСТОЙЧИВОСТЬ ГИБКИХ ВАЛОВ [ГЛ. 3
ротора в отсутствие поля была 1460 кол/'мин и несколько
снижалась с увеличением индукции г). Колебания сердечника,
6
0Л
0,1
-0}f
500
I*
/000
JnA
/Ж
х
\
\
к
\
2500
N
Вес
Рис. 95.
возбужденные поперечным толчком, затухают, пока индукция
в зазоре невелика. Это
значит, что условие
устойчивости фм < фв —|— ф^
выполняется. При В tt
я^2000 гс возникают
автоколебания типа прецессии
в направлении вращения
поля; их частота равна
примерно 1330 кол/мин
(т. е. собственной частоте
при наличии
неподвижного поля).
Аналогичные явления
будут наблюдаться не
только в случае роторов,
несущих ферромагнитный
сердечник, но и в случае
ротора с
электрообмоткой. Рассмотрим силы,
действующие на вращающийся виток в магнитном поле ста-
Рис. 96.
1) Вследствие влияния магнитного притяжения.

§ 3.14] НЕУСТОЙЧИВОСТЬ РОТОРОВ В МАГНИТНОМ ПОЛЕ 211
тора (рис. 96). Пусть В — индукция в зазоре. Тогда,
учитывая, что амперова сила пропорциональна скорости
пересечения силовых линий поля и квадрату индукции, получим,
что на проводник витка действует сила
P=T(u)-0)n)S2,
где f — некоторый коэффициент пропорциональности. При
центральном расположении ротора силы, действующие на
виток, создают пару сил, которая вносит определенный вклад
во вращающий (или тормозящий) момент. Однако, если виток
смещен, то силы оказываются неодинаковыми и, таким
образом, появляется составляющая, направленная перпендикулярно
к плоскости рассматриваемого витка.
Полагая, что индукция обратно пропорциональна величине
воздушного зазора Л, найдем, что
Vt7 од — и cos у — г; sin ^
Отсюда для малых перемещений
Я(?)«т(а) —a)n)fl§(l+2-j-cos(p + 2^sin(p).
Проекцию равнодействующей сил, приложенных к ротору,
на неподвижные оси координат найдем по формулам:
2%
Рх= Г Р(<р) sinср с(ср)^/ср,
о
2те
Ру -= JP(cp)C0Scp c(cp)Jcp.
О
Здесь с (ср) — плотность витков (количество витков,
приходящихся в среднем на один радиан). В частности, если
с = const, В0 = const, то
Рх = — Т*с (о) — о)п) B\v = — Ti (^ — шп) **.
Ру = ^кс (a) — соп) В\и = fг (о) — о)п) и.
Введение этих сил в уравнения возмущенного движения
ротора будет также приводить (при определенных условиях)
к неустойчивости чисто вращательного движения.

ГЛАВА ЧЕТВЕРТАЯ
УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА
§ 4.1. Краткие исторические сведения
Среди неконсервативных задач упругой устойчивости особо
важное место занимают задачи устойчивости упругих тел,
находящихся в потоке газа или жидкости. Силы, действующие
на тело со стороны потока, зависят от упругих деформаций
тела, и поэтому решение этих задач требует совместного
рассмотрения уравнений теории упругости и
аэрогидромеханики. На стыке двух областей образовался новый раздел
механики — теория аэроупругости, — имеющий
разработанные аналитические и численные методы и весьма обширную
и с каждым годом все более разрастающуюся литературу.
Задачи аэроупругости представляют исключительный
интерес для авиации и реактивной техники, а также, в меньшей
мере, и для других областей (энергетика, строительство и т.п.).
Естественно, что первые задачи такого рода были
поставлены именно в связи с потребностями авиационной техники.
Аэроупругие явления (дивергенция крыла, флаттер крыла и
хвостового оперения), по-видимому, были причиной ряда
неудач и катастроф уже на самой заре авиации; однако
правильное понимание и теоретическое объяснение этих явлений
пришло значительно позже. Теория дивергенции крыла (т. е.
-крутильной формы потери статической устойчивости) была
дана впервые Рейснером1). Анализ явления флаттера
крыла в потоке несжимаемой жидкости на основе так
называемой «квазистационарной» теории был произведен Ф р е й з е -
OReissner H., Neuere Probleme aus der Flugzeugstatik,
Zeitschr. fur Flugtechnik und Motorluftschiffahrt., Bd. 17, № 7 (1926).

§4.1] КРАТКИЕ ИСТОРИЧЕСКИЕ СВЕДЕНИЯ 213
ром и Данкеном1), Раушером2) и Е. П.
Гроссманом3). Другой подход, основанный на более точном
определении аэродинамических сил и положивший начало
«нестационарной» теории флаттера, был предложен Кюсне-
ром4), М. В. Келдышем и М. А. Лаврентьевым5)
и Теодор сеном6).
Развитие авиации в период второй мировой войны и,
особенно, в послевоенный период дало резкий толчок к
развитию теории аэроупругости. Основное направление работ
состояло в учете сжимаемости и исследовании флаттера и
дивергенции при околозвуковых и сверхзвуковых скоростях.
Это прежде всего отразилось на методах определения
аэродинамических сил. Из-за изменения конструктивных форм
самолетов изменилась и «упругая» сторона задачи (учет
стреловидности, учет влияния изгиба хорды и т. п.). В настоящее
время литература по приложению теории аэроупругости
к расчету крыльев и оперения самолета почти необозрима;
представление о ней дают некоторые книги и учебные
руководства, посвященные практически лишь этому вопросу7).
В последние годы большое внимание уделяется задачам
устойчивости пластин и оболочек, обтекаемых с большими
сверхзвуковыми скоростями. Эти задачи представляют
интерес в связи с вибрацией обшивки современных летательных
аппаратов («панельный флаттер»). Ряд работ был посвящен
исследованию флаттера плоских панелей, обтекаемых
потенциальным сверхзвуковым потоком8). Устойчивость бесконечно
1) F г a z е г R. A. and Dunkan W. J., The flutter of airplane
wings, Britisch Aeron. Res. Couns. Rep. and Mem., № 1155 (1928).
2) Rauscher M., Ober die Schwingungen freitragender Flugel,
Luftfahrtforschung, Bd.4, № 3 (1929).
3) Гроссман Е. П., Флаттер, Труды ЦАГИ, № 284, 1937.
4) К u s s n е г Н. G., Schwingungen von Flugzeugflugeln,
Luftfahrtforschung, Bd. 4. № з (1929).
5) Келдыш М. В. и Лаврентьев М. А., К теории
колеблющегося крыла, Техн. заметки ЦАГИ, № 45, 1935.
6) Theodorsen Т., General theory of aerodynamic instability
and the mechanism of flutter, NACA Rep. № 496, 1935.
7) Бисплингофф Р. Л., Эшли Х. иХалфмэнР. Л.,
Аэроупругость, ИЛ, 1958; Фын Я. Ц., Введение в теорию
аэроупругости, Физматгиз, 1959.
8) G о 1 a n d M. and L u k e Y. L., An exact solution for two-
dimensional linear panel flutter at supersonic speeds, Journ. Aeronaut.
Sci. 21, № 4 (1954); HedgepethJ. M., Budiansky B. and

214 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
длинной круговой цилиндрической оболочки, обтекаемой
газом, невозмущенная скорость которого направлена вдоль
образующих, рассматривалась автором 2). Течение предполагалось
при этом потенциальным (как дозвуковым, так и
сверхзвуковым), а возмущения — малыми. В несколько иной
постановке та же задача позднее рассматривалась Майлсом2).
Специфические трудности флаттерных задач вызваны тем,
что аэродинамические силы, вообще говоря, не могут быть
достаточно просто выражены через возмущения обтекаемой
поверхности. Однако в области больших сверхзвуковых
скоростей возможны существенные упрощения, основанные на
асимптотических свойствах сверхзвукового потока. Начиная
с работы Хейса3), сформулировавшего условия подобия
гиперзвукового потока при обтекании тонких тел, был
предложен ряд приближенных методов для определения
аэродинамических сил. Наиболее простой вариант известен под
названием «закона плоских сечений»4) или «поршневой
теории» 5); он приводит к формуле, связывающей местное давление
на тело с нормальной компонентой скорости поверхности
в рассматриваемой точке. Полагая возмущения малыми, можно
эту формулу линеаризировать. Тогда многие задачи
панельного флаттера можно свести к исследованию собственных
значений некоторых обыкновенных линейных
дифференциальных уравнений с постоянными коэффициентами 6). Наряду с этим
Leonard R. W., Analysis of flutter at supersonic speed, Journ.
Aeronaut. Sci. 21, № 7 (1954); N e 1 s о n H. С and
Cunningham H. J., Theoretical investigation of flutter of two-dimensional flat
panels with one surface exposed to supersonic potential flow, NACA
Rep. № 1280 (1956).
1) Болотин В. В., Колебания и устойчивость упругой
цилиндрической оболочки в потоке сжимаемого газа, Инж. сборн. 24 (1956).
2) Miles J. W., Supersonic flutter of a cylindrical shell, Journ.
Aeronaut. Sci. 24, № 2 (1957); 25, № 5 (1958).
3) Hayes W. D., On the hypersonic similitude, Quart. Appl.
Math. 5, № 1 (1947).
4) Ильюшин А. А., Закон плоских сечений при больших
сверхзвуковых скоростях, Прикл. матем. и мех. 20, № 6 (1956).
5) L i g h t h i 11 M. J., Oscillating airfoils at high Mach number,
Journ. Aeronaut. Sci. 20, №6(1953); Ashley H. and Zarta-
r i a n C, Piston theory — a new aerodynamic tool for the aeroela-
stician, Journ. Aeronaut. Sci. 23, № 6 (1956).
6) H e d g e p e t h J. M., On the flutter of panels at high Mach
numbers, Journ. Aeronaut. Sci. 23, № 6 (1956); Мовчан А. А.,
О колебаниях пластинки, движущейся в газе, Прикл. матем. и мех.

§4.1] КРАТКИЕ ИСТОРИЧЕСКИЕ СВЕДЕНИЯ 215
были применены приближенные методы, основанные на
сведении упругой системы к некоторой конечномерной системе1).
Вопрос о границах применения этих методов, тесно
связанный с известным парадоксом о флаттере мембраны,
обсуждался в работе автора2). Имеются некоторые
экспериментальные результаты 3).
Перечисленные работы были посвящены линейной трактовке
флаттера. Нелинейная трактовка представляет интерес в двух
отношениях. Во-первых, она позволяет оценить амплитуды
прогибов и напряжений при превышении критической
скорости флаттера и, таким образом, ответить на вопрос, в
какой мере это превышение является опасным. Во-вторых,
следует ожидать, что в некоторых задачах (особенно при
гиперзвуковом обтекании) нелинейность аэродинамических сил
может вызвать новые аэроупругие эффекты, не наблюдавшиеся
при умеренных скоростях. Внимание на эти аспекты было
обращено в работе автора4). В этой работе, в частности,
были приведены примеры задач, в которых аэродинамические
силы способны поддерживать незатухающие движения при
скоростях, меньших, чем критические скорости,
определяемые из линейной теории. В дальнейших работах5) флаттер
20, № 2 (1956); Об устойчивости панели, движущейся в газе, Прикл.
матем. и мех. 21, № 2 (1957); Устойчивость лопатки, движущейся
в газе, 21, № 5 (1957); Махортых Ж. К., Устойчивость
многопролетной панели, движущейся в газе, Изв. АН СССР, ОТН,
«Механика и машиностроение», № 2, 1959.
!) Болотин В. В., К вопросу об устойчивости пластинки
в потоке сжимаемого газа, Сб. «Вопросы прочности материалов
и конструкций», Изд-во АН СССР, 1959; Хеджепет Д., Флаттер
прямоугольных свободно опертых панелей при больших
сверхзвуковых скоростях, Сб. «Механика», ИЛ, 1959, № 2.
2) Болотин В. В., О применении вариационного метода Га-
леркина к задачам флаттера упругих панелей, Изв. высш. школы,
сер. «Машиностроение», № 11, 1959.
3) М и к и ш е в Г. Н., Экспериментальное исследование
автоколебаний квадратной пластины в сверхзвуковом потоке, Изв.
АН СССР, ОТН, «Механика и машиностроение», № 1, 1959.
4) Болотин В. В., О критических скоростях в нелинейной
теории аэроупругости, Научн. докл. высш. школы, сер.
«Машиностроение и приборостроение», № 3, 1958.
5) Болотин В. В., Г а ври лов Ю. В., Макаров Б. П. и
Ш в е й к о Ю. Ю., Нелинейные задачи устойчивости плоских панелей
при больших сверхзвуковых скоростях, Изв. АН СССР, ОТН,
«Механика и машиностроение», № 3, 1959; Болотин В. В.,
Нелинейный флаттер пластин и оболочек, Инж. сборн. 29 (1960).

216 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
плоских и криволинейных панелей рассматривался с учетом
геометрической и аэродинамической нелинейностей,
аэродинамического нагрева и взаимодействия панели с
подкрепляющей конструкцией. Было показано, что благодаря
значительной геометрической нелинейности установившийся флаттер
панелей, взаимодействующих с подкрепляющей конструкцией,
характеризуется умеренными амплитудами. В других случаях
(например, при цилиндрическом изгибе плоской панели со
свободно сближающимися кромками) может иметь место
«жесткое» возбуждение флаттера на границе области устойчивости.
Нелинейные задачи флаттера плоских панелей при учете
одной лишь геометрической нелинейности рассматривались также
Фыном1) и Шеном2).
§ 4.2. Флаттер крыла как неконсервативная задача
упругой устойчивости
Для того чтобы показать тесную связь между задачами
флаттера упругих элементов в потоке газа и
рассмотренными ранее неконсервативными задачами упругой
устойчивости, рассмотрим простейшую
задачу об изгибно-крутиль-
ном флаттере
консольного крыла. Эта задача весьма
подробно изучена и
излагается в специальных
руководствах 3). Поэтому, не
углубляясь в чисто
технические детали или
подробности вычислений,
ограничимся наиболее простой ее
постановкой.
Будем рассматривать
крыло с прямой осью центров
изгиба, направленной
перпендикулярно к потоку (рис. 97).
Рис. 97.
1) Fung Y. С, On two-dimensional panel flutter, Journ.
Aeronaut. Sci. 25, № 3 (1958).
2) Ш е н С, Приближенное исследование нелинейных флаттер-
ных задач, Сб. «Механика», № 4, ИЛ, 1959.
3) См., например, сноску7) на стр. 213.

§ 4.2]
ФЛАТТЕР КРЫЛА
217
Крыло будем трактовать как упругий стержень, жесткость
которого в направлении потока максимальна и весьма
велика по сравнению с другой изгибной жесткостью, а также
с крутильной жесткостью. При этом условии
деформированное состояние крыла может быть охарактеризовано смещениями
U
Рис. 98.
центров изгиба v (z, t) и углами поворота поперечных
сечений b(z,t). Эти смещения показаны на рис. 98. Уравнения
малых колебаний крыла имеют вид
д2 /pr d2v\ . d2v дЪ , ,ч
dz2
д2
dz2
'EL
дЧ\ _
dz2)
KS
тх
d2v
™ dt2
+
•тг'
d20
dt2
••V.(z,t).
(4.1)
Здесь EJ, GJd и EJa— соответственно изгибная,
крутильная и секториальная жесткости, т — масса крыла на
единицу длины (вдоль размаха), хт — расстояние от центра
изгиба до центра масс, г — радиус инерции сечения
относительно центра изгиба, q и \i — соответственно
аэродинамическая сила и аэродинамический момент, отнесенные к
единице длины крыла.
Некоторая трудность заключается в определении
аэродинамических сил, действующих на колеблющееся крыло.
Одно из упрощений, которое обычно вводится, состоит в том,

218 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
что аэродинамические силы вычисляются для случая
плоского течения. Если крыло достаточно длинное и если его
параметр вдоль размаха меняется медленно, то это
предположение может быть оправдано. Тогда в линейном приближении
p(z,t) = A21v + Л228 + Вп -2L + S22 -|
(4.2)
Здесь Aik и Bik — некоторые коэффициенты, которые зависят
от скорости набегающего потока U и, вообще говоря, от
координаты z. Кроме того, в ряде случаев они зависят и от
характера изучаемого движения. Например, если движение —
периодическое с частотой 2, то коэффициенты в
выражениях (4.2) могут зависеть и от безразмерного параметра —
приведенной частоты QbjU (здесь Ъ — длина хорды).
Явные выражения для коэффициентов Ajk и Bik мы
выписывать не будем. Заметим лишь, что они имеют простейший
вид в двух случаях: если они вычисляются по
«квазистационарной теории», а также если рассматриваются большие
сверхзвуковые скорости и применяется «поршневая теория».
Рассмотрим, прежде всего, стационарные решения
системы (4.1). Тогда v = 0 и второе уравнение запишется
в виде
d2 / d4\ d ( d6 \ dc„ pU2b2
Здесь коэффициент А22 выражен через эмпирическое значение
производной от коэффициента аэродинамического момента с^у
р — плотность набегающего потока. Для консольного крыла
краевые условия принимают вид
е(0)=^=^)==^)=0. (4.4)
При U —0 краевая задача не имеет никаких других
решений, кроме тривиального решения 6 = 0. Минимальное
значение скорости Ut при котором краевая задача имеет
решения, отличные от тривиального, соответствует
разветвлению форм равновесия: наряду с тривиальной (незакрученной)
формой появляется смежная с ней форма равновесия, которая
сопровождается закручиванием крыла. Исследование
соответствующей неоднородной задачи показывает, что прибли-

§ 4.21
ФЛАТТЕР КРЫЛА
219
жение к указанной скорости ведет к резкому нарастанию
углов закручивания — к дивергенции (перекручиванию) крыла.
Дивергенция крыла является полным аналогом обычной
статической неустойчивости в упругих системах, а метод
определения критической скорости дивергенции — полным аналогом
метода Эйлера в теории упругой устойчивости.
В случае крыла постоянного сечения с равной нулю
секториальной жесткостью задача весьма упрощается:
-g. + A.e = 0. О(0) = 4^ = 0.
где
9U2b2 дс^
&2 =
2GJd дЬ '
Нетривиальные решения имеют место при cos&/ = 0; отсюда
критическая скорость дивергенции
or: r
(4.5)
Рассмотрим теперь задачу о флаттере крыла, для чего
возвратимся к системе (4.1), положив в ней
v(z, t) = V(z)est,
0 (z, t) = в (z) est,
где V (z) и в (г) — некоторые функции (формы колебаний),
s — характеристический показатель. Подстановка приводит
к уравнениям
~d* [EJ4^) + ms2V ~ mxms<2® =
= Al2Q + BnsV + B12s9,
?(".?)-?(<ч.?)-«* ^+»v»-
- (A2l + B2ls) V + (A22 + B22s) в;
и к краевым условиям типа (4.4).
Задача состоит в исследовании поведения показателей 5
в зависимости от скорости U. Равновесие крыла в потоке
газа устойчиво, пока все показатели 5 лежат в левой
(4-6)

220 устойчивость упругих тел в потоке газа [гл. 4
полуплоскости комплексного переменного. Наименьшее значение
скорости ?/, начиная с которого хотя бы один из
показателей переходит на правую полуплоскость, является
критической скоростью. Выход на правую полуплоскость означает
колебательную форму неустойчивости (флаттер). Исключение
составляет случай, когда переход осуществляется через
точку 5 = 0; этот случай, очевидно, соответствует дивергенции.
Ггп 5 /мин
-*--"""*
г \._
350
304,0
30Р~^А
276,0
250
200
103,5
юо —
50
-60
-40
-20
Рис. 99.
го Ыв'/шн
Таким образом, мы имеем здесь полную аналогию с
рассмотренными выше неконсервативными задачами упругой
устойчивости. Как в последних, при изгибно-крутильном
флаттере существенное значение имеет парное взаимодействие
различных степеней свободы. Эта сторона становится особенно
ясной, если от системы с бесконечным числом степеней
свободы перейти к конечномерной системе. Наиболее
распространенный подход предполагает задание движения крыла
в следующем виде:
v(z,t) = Jigk(t)9k(z); Hz,t)=^J,fk(t)^(z). (4.7)

§ 4.2]
ФЛАТТЕР КРЫЛА
221
Здесь gk и fk — обобщенные координаты, первая из которых
соответствует изгибу, вторая кручению, yk(z) и
tyk(z)—функции, удовлетворяющие краевым условиям (например,
«балочные» функции). Подставляя выражения (4.7) в уравнения (4.6)
и применяя вариационный метод Галеркина, придем к системе
двух обыкновенных дифференциальных уравнений относительно
?й(0 и fk (0- Эти уравнения имеют такую же структуру,
1У^
О 0,2 0,4 0,6 0,8 1,0 Ц ttjL
я.
Рис. 100.
что и уравнения (1.79); однако роль параметра нагрузки
в них играет скорость U.
Сравнение показывает, что, удерживая в рядах (4.7) по
одному первому члену, мы получаем вполне
удовлетворительные результаты. Изгибно-крутильный флаттер поддерживается,
таким образом, благодаря взаимодействию основных форм
изгибных и крутильных колебаний. Соотношение между
парциальной собственной частотой изгибных колебаний й и
парциальнной собственной частотой крутильных колебаний &0
оказывает существенное влияние на критическую скорость
флаттера, чего и следовало ожидать, исходя из общих
соображений. На рис, 99 показано поведение характеристических

222 устойчивость упругих тел в потоке газа [гл. 4
показателей, рассчитанное для двух различных
соотношений парциальных частот1). С увеличением отношения 2/2^
от 0,34 до 0,91 параметр критической скорости уменьшается
от 740 до 250. На рис. 100 показана рассчитанная для
одного примера зависимость критической скорости флаттера от
отношений хт\Ъ и 2y/2G. Здесь же отложена величина
критической скорости дивергенции. В зависимости от
соотношения параметров критическая скорость флаттера может
оказаться как меньше, так и больше критической скорости
дивергенции.
§ 4.3. Общая постановка задач об устойчивости
упругих тел в потенциальном потоке газа
Задачи аэроупругости допускают общую постановку при
самых широких предположениях о свойствах упругого тела
и о характере взаимодействия тела с потоком. Ниже мы
рассмотрим случай, когда течение газа является потенциальным
и непрерывным всюду, кроме, может быть, конечного числа
поверхностей разрыва, а возмущения являются малыми.
Допустим, что упругое тело объемом V имеет
поверхность 5, обтекаемую установившимся потенциальным потоком
газа. Это установившееся состояние мы примем за
невозмущенное движение, выбрав декартову систему координат хг,
х2, хг, связанную с телом2). Будем считать, что
невозмущенная скорость имеет потенциал у(хг, х2, хг), т. е.
компоненты скорости vv v2, v3 выражаются через ср следующим
образом:
v ~^-
Vk ~ dxk '
Возмущенное состояние характеризуется вектором
смещений точек тела uk и потенциалом возмущений ср:
** = ^ + -г?-'
иь = иь
1) Golan d M. and Luke Y. L., A study of the bending-
torsion aeroelastic modes for airplane wing, Journ. Aeronaut. Sci. 16,
№ 7 (1949).
2) В дальнейшем мы придерживаемся обычного соглашения
о суммировании по «немым» индексам (стр. 32).

§ 4.3] устойчивость в потенциальном потоке газа 223
(знак ~ относится к возмущенным параметрам). Возмущения,
порождаемые деформацией тела, будем считать достаточно
малыми, чтобы их квадратами и более высокими степенями
можно было пренебречь. Тогда для потенциала возмущенных
скоростей, исходя из уравнения для потенциального течения
сжимаемой жидкости !)
д2у 2vi д2у урь д2у 1 д2ср
О,
д4 <4 dxidt CL dxi dxk clo dt<1
получим линеаризированное уравнение:
00 дх\ ' dxt dt ' к дхг дхк
—ь(^+^)^"#=«- <*¦*>
Здесь с0о = уГдр/др—скорость звука для невозмущенного
потока, р — давление, р — плотность. Например, если
невозмущенная скорость направлена вдоль оси xv т. е. если
vx = U, vy = vz = О, то, вводя обозначение для числа Маха
невозмущенного потока
лл U
м= — 9
*"оо
запишем уравнение (4.8) в виде
V ' дх2 ^ ду2 с^ dxdz с2^ dt2 V '
Для упругих смещений иь имеем систему уравнений
-2'««*-ft)-SL = 0. (4Л0)
где р0 — плотность материала тела. Например, в случае
изотропного тела
^*=^+(х+.)^-,
где X и (1 — коэффициенты Ляме, Ъ1к — символ Кронеккера*
1) См., например, Франкль Ф. И. и Карпович Е. А.,
Газодинамика тонких тел, Гостехиздат, 1948.

224 устойчивость упругих тел в потоке газа [гл. 4
Переходим к граничным условиям. Будем различать два
типа граничных условий — общие и специальные. Общие —
это те, которые выполняются в любой точке поверхности 5
контакта тела и газа. Специальные граничные условия
учитывают способ закрепления тела, условия на бесконечности
и т. п. и меняются от задачи к задаче. Здесь, очевидно,
достаточно рассмотреть общие граничные условия.
Составим условие непроницаемости поверхности тела. Пусть
F (av а2, #3) — уравнение поверхности тела в лагранжевых
координатах, хг, х2, хг — эйлеровы координаты. Тогда для
возмущенной поверхности получим уравнение
F(хг — uv х2 — #2» -^з — uz) = F\(xv х2> хз> 0 = 0-
Субстанциональная производная от функции Fx должна быть
равна нулю (поток газа через возмущенную поверхность
отсутствует):
Отсюда на всей поверхности 5 должно выполняться условие
дп —\dt + *' dxjn*'
где nk — компоненты вектора внешней нормали к
поверхности тела. После линеаризации получаем:
Динамическое условие на поверхности 5 имеет вид oiknk = pv
где aik — компоненты тензора напряжений в теле, pt = pnt —
компоненты давления р. Составляя интеграл Коши для
возмущенного движения
где F (t) — некоторая функция времени, получим после
линеаризации:
P = -r(lH+v>-3%;)- (4.12)
Следовательно,
ад = -Р"/(-^+^^) на S. (4.13)

§ 4.3] УСТОЙЧИВОСТЬ В ПОТЕНЦИАЛЬНОМ ПОТОКЕ ГАЗА 225
Дополняя граничные условия (4.11) и (4.13) специальными
граничными условиями, получим полную постановку задачи.
Потенциал возмущений ср всегда может быть выражен через
нормальную составляющую dyjdn скорости на поверхности
тела:
f(A) = f/K(A,B)^P-dSB. (4.14)
Здесь К (А, В) — некоторое ядро, зависящее от координат
xv х2, х3 и Ei» ?2, ?3 Двух произвольных точек А и В, взятых
на поверхности тела. В случае несжимаемой жидкости К (А, В)
является функцией Грина для задачи Неймана (фактическое
построение этого ядра требует исключения условий на
поверхностях разрыва). В случае двумерного сверхзвукового
обтекания плоской пластины, направленной вдоль
невозмущенного потока и колеблющейся с частотой Q, ядро К (А В)
принимает вид ])
fM*-l 4 Соэ(М*-1)} ° Lcoo (VW2 — 1) J
при 0<$<х,
О при \ > л:,
(4.15)
где /0 — функция Бесселя нулевого порядка.
Используя соотношения (4.11) и (4.14), потенциал ср
можно исключить:
9-(Л) = //к(А,В)[*Ц^-+ vt **?*-]ЧdSB.
s
Тогда задача будет описываться обычными уравнениями (4.10)
динамической теории упругости с краевым условием ^ikrtu==Pni-
При этом
К (А, В) =
p = -?(w+4<k)ffK(A>B)l
duk(B,t)
dt
+V]{B)<^ML]4dsE
l) См. § 4.7.

226 устойчивость упругих тел в потоке газа [гл. 4
Представим вектор смещений ui в виде разложения по
формам собственных колебаний упругого тела в вакууме:
ut(xv х2, х3. *) = 2/л(0<Ы*1. х* *з)«
Уравнения вариационного метода Галеркина запишем в виде
(1.64):
/ (-fe~Ро П&) bmdV-f f (РиПь-рп)bmdS - 0 (4.16)
V S
(т=\% 2, ...)•
Преобразуем интеграл:
duk(B,t)
—>f/&+*¦&){/!*«¦*>[¦
+ vj(В) dUk{d*J)] nk dSB J n$im(A)
dt '
dS a
Здесь
•s L s J
S l 5

§ 4.3] устойчивость в потенциальном потоке газа 227
Уравнения (4.16) принимают вид
оо
2(
/2=1
[3™+-^я„
+2(
Qm^mn U
/г = 1
л=1
,)/я = 0 (/и=1, 2, ...). (4.17)
2^
Ро
Здесь под р, р0 и U следует понимать некоторые
характеристические значения плотности газа, упругого тела и
невозмущенной скорости потока соответственно, Qm — частоты
собственных колебаний в вакууме. В уравнения (4.17) введены
члены с матрицей ?тЪтп, учитывающие конструкционное
демпфирование.
Из уравнений (4.17) вытекает постановка основных задач,
относящихся к малым деформациям упругого тела в
потенциальном потоке газа. Уравнение собственных частот в
покоящемся газе имеет вид
Qlbmn-{bma+j-amn)Q?
О,
(4.18)
откуда видно, что матрица атп характеризует
присоединенные массы среды. Разветвление форм равновесия
(дивергенция) будет иметь место при скорости U, которая является
минимальным корнем уравнения
&tr$ri
Ро °"
= 0.
(4.19)
Наконец, для определения критической скорости флаттера
подставим в уравнения (4.17) выражения fm = Fmest и
рассмотрим определитель
\{Kn~3rj~ami)s^ + (Bmbmn + 2U j-bmn)s +
+ (Q?mlmn-U2j-cmn)\ = 0. (4.20)
Невозмущенная форма равновесия остается устойчивой, пока
все показатели s лежат в левой полуплоскости комплексного
переменного. Наименьшее значение скорости U, при котором
один из показателей 5 переходит на правую полуплоскость,
оставаясь при этом комплексным, является критической
скоростью флаттера. Фактическое отыскание этой скорости может

228 устойчивость упругих тел в потоке газа [гл. 4
быть затруднено вследствие того, что коэффициенты атп,
Ътп и стп могут зависеть от безразмерных комбинаций,
содержащих скорость U и частоту колебаний тела 2 на
границе области флаттера.
§ 4.4. Устойчивость упругой цилиндрической оболочки
в потоке сжимаемого газа
Приведенные выше общие соображения проиллюстрируем
на примере задачи об устойчивости круговой цилиндрич.еской
оболочки в потоке газа (рис. 101). При этом мы будем
в основном придерживаться работы автора *). Течение будем
считать потенциальным со
*х скоростью невозмущенного
потока U\ внутри оболочки
и Ue—во внешней области
(U^ Ue) Относительно
оболочки с радиусом срединной
поверхности R и толщиной h
предполагаем, что к ней
применимы уравнения моментной
теории.
Будем пользоваться
цилиндрическими
координатами (х, г, 6), совместив
полярную ось х с осью
оболочки. Отклонения
срединной поверхности от без-
моментного состояния
описываются тангенциальными перемещениями и(х, б) и v(x, 6)
и нормальным перемещением w(x, 6). Положительные
направления перемещений показаны на рис. 101.
Уравнения движения оболочки имеют вид
Рис. 101.
-2V + -2V + ^i3^
^21^ + ^22^ + ^23^
^31^ + ^32^ + ^33^
1 —(х2
~~ Eh
1— fx*
— 1 г
Eh q
__ 1— (X2
Eh
Чн.
Яп
(4.21)
l) Болотин В. В., Колебания и устойчивость упругой
цилиндрической оболочки в потоке сжимаемого газа, Инж, сборн. 24 (1956),

§ 4.4] устойчивость упругой цилиндрической оболочки 229
где J2?in — дифференциальные операторы
2 ds2 '
1 + f* д2
-^п — дх2 ~^ 2 ds2 ' °^22 ~ 2 d*2 ~r ds2
<2?Yl — -2*21 — 2 UK (?S '
1 д 3 —а 0Г| д3
-З^З — J?32 — D "лГ о а R
23 — -Z 32 — # ^ 2 ^ d*2 <?S '
-^13 — ~^3i — r дх а К\дх* 2 dxds2)'
^зз = -2(^^ + 2^ + ^) + ^,
#*> <7о> <7г — компоненты нагрузки, отнесенные к единице
площади срединной поверхности, \к — коэффициент Пуассона и,
кроме того,
s = M, «2==^. ?2=^ + ^г- (4-22)
Пусть pt — внутреннее, ре— наружное давление на
оболочку. Тогда, очевидно,
Чх = — Ро^^Т» ?0 = — Ро^-^Г' Яг = — hh -tfT + Pi— Pe-
(4.23)
Для форм колебаний с достаточно большим показателем
изменяемости влияние тангенциальных составляющих сил инерции,
как известно, становится пренебрежимо малым. Можно
показать, что наименьшим критическим скоростям потока
соответствуют движения с длиной полуволн X, имеющей порядок
j_
X— (Rh)2. Таким образом, если оболочка тонкая (/г//?<^1),
то наиболее интересными будут именно те движения,
которые характеризуются большим показателем изменяемости и
для которых, следовательно, тангенциальными силами
инерции можно пренебречь. В этом случае, введя функцию
Ф(х, б, t), связанную с перемещением w соотношением
^ = #472у2фэ (4.24)
приведем систему (4.21) к одному уравнению:
v v w ^ a2R* dx* R*D * ( 'Z0)

230 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
Здесь D = Eh3/\2(l—ц2) — цилиндрическая жесткость; при
переходе к уравнению (4.25) были опущены члены, влияние
которых для состояний с большим показателем изменяемости
также пренебрежимо мало. С учетом (4.23) и (4.24) получим:
qr = -PohR4W**- + pt-pt. (4.26)
Переходим к уравнениям движения жидкости. Поле
скоростей возмущенного движения может быть представлено
в виде
^ дх ' V*~ r дв ' Vr~ дг '
" ' ОХ ' ' Г СО
- } (4.27)
Vx—Ue-r дх > Vi— r ^0 > Vr— or
где срДдг, г, G, t) и cpe(x, г, 0, t) — потенциалы возмущений
для внутренней и внешней областей соответственно. (Значок /
в дальнейшем обозначает принадлежность к внутренней области,
значок е — к внешней области; там, где это не может
привести к недоразумениям, значки будут опущены).
Если деформации оболочки достаточно малы, то
вызванное ими возмущенное движение будет достаточно мало
отличаться от заданного течения с постоянными скоростями Ui
и Ue. При сделанной оговорке о малости возмущения
потенциалы cpj и ®е удовлетворяют линеаризованному
уравнению (4.9)!):
к т } дх2^ дг* ^ г дг^
+ J-*SL-M.J!2 L^L = 0 (4 28)
г2 д№ соо дх dt с^ д?
В это уравнение вместо Соо подставляются скорости звука
сь и се в невозмущенном потоке, Мь = UJciy Me = UJce.
Решения уравнений (4.21) и (4.28), помимо специальных
граничных условий, должны удовлетворять общим граничным
1) Уравнение (4.9) записано для прямоугольных декартовых
координат, а уравнение (4.28) — для цилиндрических координат
% = U, vr = v^ 0.

§ 4.5] СЛУЧАЙ БЕСКОНЕЧНО ДЛИННОЙ ОБОЛОЧКИ 231
условиям на колеблющейся стенке. Условие непроницаемости
(4.11) для рассматриваемого случая принимает вид
(4.29)
Кроме того, потенциал сре должен удовлетворять условию
затухания возмущений на бесконечности
Ve->°> i)F~*0 (при г->о°)-
Если потенциал уе описывает волновой процесс, то этих
условий недостаточно для полного определения решения; они
должны быть заменены условиями излучения. Эти условия
требуют, чтобы потенциал сре удовлетворял условию
Р.= 0 ('"*).
т. е. чтобы он описывал распространение волн, интенсивность
_^
которых убывает по мере удаления от источника, как г 2.
Кроме того, и это наиболее существенный элемент условий
излучения, потенциал должен описывать расходящиеся волны,
если оболочка излучает энергию, и, наоборот, сходящиеся
волны, если оболочка поглощает энергию потока.
Динамическое условие на колеблющейся стенке следует
из общего условия (4.12):
-р,= Р,(<Й-+"#). *__,,(?+«,?). «4.30,
§ 4.5. Случай бесконечно длинной оболочки.
Различные случаи обтекания
Рассмотрим случай бесконечно длинной оболочки и будем
искать решение задачи в классе волн, распространяющихся
вдоль оболочки. Уравнения (4.21) будут удовлетворены, если
положить
tf = 7]**(a'-ft*)sin/*9, I (4.31)
w = W(2t"kx) cos nb. )

232 устойчивость упругих тел в потоке газа [гл. 4
Здесь Е, т], С — некоторые, вообще говоря, комплексные
коэффициенты, волновое число & = тс/Х, где X — длина полуволны
в направлении образующих, /г = 0, 1, 2, 3, ... Для
потенциала ср имеем соответственно выражение
f = /(г) *' <fi'-**) cos яв, (4.32)
где /(г) — функция, подлежащая определению. Подстановка
в уравнение (4.28) дает:
dr2 * г dr'
Введем обозначение V = Q/k для фазовой скорости
распространения упругой волны в оболочке и обозначение
для числа Маха в относительном движении газа и упругой
волны. Если Ж1< 1, то, обозначив r0 = vrt где
v=*V"|jWi — 1|. (4.35)
получим вместо (4.33) уравнение
Это уравнение интегрируется в функциях Бесселя чисто
мнимого аргумента порядка п:
Если Мг > 1, то аналогично получаем уравнение
d2f . 1 df - ' - "2
dr\
ro dro \ ro)
интеграл которого выражается либо через функции Бесселя
действительного аргумента порядка п\
/(г0) = С^п(г0) + С2Мп(г0),
либо через соответствующие функции Ганкеля первого и
второго рода:
/(г0) = С1^1)(г0) + С2//112)(г0).

§ 4.5] СЛУЧАЙ БЕСКОНЕЧНО ДЛИННОЙ ОБОЛОЧКИ 233
Если Ж = 1, имеет место вырождение в степенные функции:
Вообще, f(r0) = CZn(r0), где Zn(r0) — некоторая
цилиндрическая функция порядка п. Следовательно,
y = CZn(vr)el W-kx)cosnB. (4.36)
Для определения постоянной С используем условия (4.29).
Подставляя сюда (4.31) и (4.36), находим:
с= i{? — kU)t
где
аГ0 lro = v/?
Возвращаясь к (4.36), получим:
~=_Zn(yR) цр_ш^1 w-*x) cos nQ.
vZ„ (v#)
Теперь по формуле (4.32) можно определить давление на
внутреннюю и внешнюю поверхности оболочки. Обозначим
„.- z«№ ¦ ае = *nJeRl , (4.37)
где v^ и v^ получаются из (4.35) подстановкой ct, Mt и се, Ме
соответственно. Легко находим:
[аются из (4.35) подстановкой с
Легко находим:
р. = р #а, (2 — kUt)2 W №-**) cos пв,
_ l \ (4.38)
ре= — PeRae(Q — kUe)KelW-kx)cosn§. '
Формулы (4.38) могут быть также представлены в виде
р= ±PoRa(Jr+U-H7fw(x, б, t), (4.39)
где верхний знак относится к внутреннему, нижний знак —
к внешнему давлению.
Вид функции Zn(r0) устанавливается с учетом граничных
условий для ср. Хорошо известно, что функции Кп (г0) и Nn (г0)

234 устойчивость упругих тел в потоке газа [гл. 4
имеют особенности в начале координат. Поэтому для
внутренней области следует положить С2 = 0 или, точнее:
2>Н J.<yr) (Af, > 1). (4-40)
Для внешней области функция выбирается из условия
затухания возмущений на бесконечности или из условия
излучения. Если Mj <С 1, то условию затухания на бесконечности
можно удовлетворить, полагая Сг = 0. Сложнее обстоит
дело при Мх > 1. Из асимптотических представлений для
функций Бесселя
Jn (г0) = V— cos (г0 - 8„) + О (г~ 2),
"п (го) = j/"-^ sin (г0 - 8Я) + О (г0" » )
(bn = rnzl2 — тс/4) видно, что обе функции убывают как /-"'^
при г0->оо. Поэтому условия затухания возмущений на
бесконечности в данном случае недостаточно для однозначного
определения решений.
Условие излучения нетрудно получить, исходя из
физических соображений. Если V > U, то это значит, что
колеблющаяся оболочка излучает энергию в окружающее
пространство. Напротив, движения, происходящие при V^U
(этот случай как раз и представляет интерес с точки зрения
флаттера), могут поддерживаться лишь за счет поглощения
энергии потока оболочкой. Рассмотрим асимптотические
представления
//? (го)«/^*-'<'•-•-) +О (г0^).
Легко видеть, что при V > U условиям излучения
удовлетворяет только вторая функция, т. е. что Сх = 0. В самом
деле, при временнбм множителе еш первая функция дает
решения типа f (г0-{-Ш), т. е. сходящиеся волны, вторая
функция — решения типа / (r0 — Qt). Аналогичные
соображения для случая V < U приводят к выводу, что С2 = 0.

§ 4.5]
СЛУЧАЙ БЕСКОНЕЧНО ДЛИННОЙ ОБОЛОЧКИ
235
Итак, для внешней области
[ Кя(уг) (А*1<1).
Zn(yr) = { H{?(yr) (Мг>1, V>U), (4.41)
{ нР(уг) (Mx>l9V<U).
Необходимо заметить, что в статье автора !) был
рассмотрен лишь случай, когда оболочка излучает энергию
в пространство; поэтому последний случай (Мг > 1, V< U)
остался неидентифицированным.
Используя известные формулы дифференцирования
цилиндрических функций, получим:
_1_
V/?-
vfl
Jn-\
(Л*! < 1).
<Л*1 > 1).
(4.42)
Соответственно для внешнего обтекания получим:
ОИ, < 1),
я<2>,
11п-\
Ал
-v/г-
V/?
Я<2)
(Ж1>1,У<^/)> (4.43)
(М,>1, V>?/).
В формулах (4.42) и (4.43) (а также и ниже) цилиндрические
функции вычисляются при г0 = vR.
Коэффициенты ае при Mj > 1 оказываются комплексными.
Можно записать также
( 1 Jn-Mn
,R j'n-iN'n
(V < U),
(V > ?/).
Отделяя вещественные и мнимые части, представим
коэффициент ае в виде
*, = *• — Ф sign (К— ?/),
') Цит. на стр, 228.

236 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
где
v»-"X
J Ж.
•вд
v* W + W
ЮЧ«)2
Коэффициент а# > 0 характеризует приведенную массу газа,
а р > 0 — коэффициент демпфирования !). В самом деле,
в рассматриваемом классе движений при временнбм
множителе exp(/2tf)
-{32 sign(V-
« Я2
= а.
дг2
где второй член учитывает затухание (положительное при
V > U и отрицательное при V < {/ в полном соответствии
с введенным нами принципом излучения).
W
0,8
0,6
пл
02
¦/
-3
W
0,8
0,6
Pi
o,z
-п-0
//7=/
\\^Л
-2
^п-3
О Z 4 6
Рис. 102.
vR
Z 4 6
Рис. 103.
10
vR
Коэффициенты a/f ae, а# и (3 вычислялись в работе автора 2).
На рис. 102 и 103 приведены графики для наиболее важных
коэффициентов.
*) Неравенство р > 0 вытекает из того, что числитель формулы"
для р представляет собой вронскиан бесселевых функций
JnNu-N„j'„=^>0.
2) Цит. на стр. 228.

§ 4.6] ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ СКОРОСТЕЙ ФЛАТТЕРА 237
§ 4.6. Определение критических скоростей флаттера
и дивергенции
Возвратимся к уравнениям колебаний оболочки (4.21).
Подставляя в них (4.23) и (4.39), получим:
Ро*(1 —ца) &и
Eh dt2
Ро*<1 —Е2) d*v
Eh
dt2
-h -2n« + &\& + J? if» = 0.
¦h ^21« + -2ю* + ^23^ = 0,
¦«¦^[o-aS+^lfc+^S]
(4.44)
(4.45)
• dt dx ^^ w л <Элс2 J ""•""
+ ^31^ + ^32^ + ^33^ = 0, j
где введено обозначение
_ (?iai + pggg) #
Л Рой
Подставляя в уравнения (4.44) выражения (4.31), получим
систему алгебраических уравнений
з
&=1
в которой обозначено
= w2.
а,, = w
1~У n2
О " э
-*22"
±=^m2-\-n\
a33 = a2 [(даа + „2)2 _ 2да2 + *. J ,
a„ = a,
21 ¦
mn,
, = a31 = [J. + a2m (m2
1-ii
/t2),
a23 — a32 — m ¦
3 — u. о 9
azmznt
2l также введены обозначения m^= kR = тс/?/Х, «i = (?, tj, С)
Sy3 = (0, 0, 1). Следовательно, уравнение (4.20) принимает
для нашего случая вид
I Ро/^%) - Q2hk -1 (2 - W 5уз | = 0. (4.46)

238 устойчивость упругих тел в потоке газа [гл. 4
При U = 0 уравнение (4.46) позволяет найти частоты
собственных колебаний в неподвижной акустической среде.
Зафиксируем значения тип. Тогда уравнение
Е
-^aJk — Q4j^
О
|ро#2(1
будет иметь три корня Qv Q2, Q3> соответствующих частотам
собственных колебаний в вакууме с заданными волновыми
числами. Допустим, что матрица, составленная из
коэффициентов ?, т] и С, для форм собственных колебаний в влкууме
имеет вид
*i *4i *
Ъ ъ 1
Тогда матрица
<v*=
где
kУъ ъ Уъ
%Уъ ъУъ
1
У1
Уъ_
Уъ
7«:
будет ортонормированной матрицей и будет приводить
матрицу ajk к диагональному виду
Vafyk^k :
п2*
: маоая
Замечая, далее, что
получим вместо (4.46) уравнение
| (Ql - 22) 8ар - х (Q - kUf Vt^I I = 0.
Это уравнение может быть также представлено в виде
з
V Та _ 1
Q2
¦ Q? t(u — kUf
(я Ф 0).
(4.47)
Если п = 0, то число членов в левой части сокращается
до двух.

§ 4.6] ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ СКОРОСТЕЙ ФЛАТТЕРА 239
При достаточно больших волновых числах п одна из
собственных частот (а именно та, которая соответствует
преимущественно изгибным колебаниям) оказывается значительно
меньше двух других частот. Пусть 2?<^2г. Q? <^С й§»
7з^>1- Тогда уравнение (4.47) можно представить в виде
q\ — а2 — х(2 — kUf = 0. (4.48)
Уравнение (4.48) можно получить, исходя из уравнения (4.30)
для пологой оболочки, вводя в его правую часть вместо
(4.26) выражение
и полагая, что
Подстановка приводит к уравнению типа (4.48):
(m2 + „2)4 + lZ-ii2 m4__Poft ("*2 + "2)2 ^4 [a2 + x(Q_6?/)2] = 0.
(4.49)
Частота преимущественно изгибных собственных колебаний
в вакууме определяется по формуле
а1=жУЛ5Г/?<Я|',1>- (4-50)
При этом
F(m, п) = }/~{т*+пУ+1-* (|Я, + ^Г- (4-51)
Для нахождених критической скорости дивергенции
положим в уравнениях (4.47) 2 = 0. Тогда получим формулу
Если исходить из упрощенного уравнения, то
^~^- (4-52)

240 устойчивость упругих тел в потоке газа [гл. 4
Здесь Vx — фазовая скорость распространения
преимущественно изгибных волн при собственных колебаниях в вакууме:
".=?=-*/?¦ f'^-^
fl(„,„) = /-Mi+!^
т2
Ж~ \т2 + /г2)2
(4.53)
Поскольку параметр х также зависит от скорости U, то
вычисления должны вестись последовательными
приближениями. Возможен также графический способ решения 1).
Очевидно, что критическая скорость дивергенции
существует только в том случае, если параметр % является
действительным. При внешнем обтекании сверхзвуковым потоком
(М = Мг > 1) дивергенция оказывается невозможной, как это
следует из формул (4.43). Если ограничиться формами потери
устойчивости преимущественно изгибного характера, которые,
собственно, и представляют наибольший интерес, то
накладывается дополнительное условие % > 0.
Расчеты показывают, что минимальная скорость
распространения изгибных волн в вакууме для оболочки толщиной
/z ~ 0,01/? имеет порядок скорости звука в газе и даже может
превышать ее. В самом деле, минимум функции Fx (mt n)
достигается при
4
тп* + п2 Vl — fx2 l
(4.54)
m Ya 1
и составляет (рис. 104)
mI„fl«(!f.
Пусть m2^>n2. Тогда соотношение (4.54) примет вид
m^l/a2, откуда получим оценку для длины полуволн,
соответствующих минимальной фазовой скорости:
Х^1,68(/?/г)2. (4.55)
]) Болотин В. В., Некоторые новые задачи динамики
оболочек, Сб. «Расчеты на прочность», вып. 4, Машгиз, 1959.

§ 4.6] ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ СКОРОСТЕЙ ФЛАТТЕРА 241
Для самой скорости получим оценку
V^'-07{^W' (4-56)
Соответствующая частота 22 будет составлять примерно
Ч1)1
(4.57)
2l = ^i^l,99l(-J
Пусть, например, Е = 2- 1°6 kzjcm2, р0 = 8- 10"6 кгсек2/см4
(сталь), h = 0,01/?. Тогда по формуле (4.56) Vx =
= 5,4- 104 см/cetc, что близко к скорости звука в воздухе
(Соо = 3,3 • 104 см/сек).
Займемся теперь определением критической скорости
флаттера, ограничившись наиболее интересным случаем обтекания
при Мг>1. Наряду F(mo)
с аэродинамическим демп- 40 г
фированием будем
учитывать конструкционное
демпфирование с
коэффициентом е. Вместо
уравнения (4.48) получим:
—22-X(Q—A(/)2 = 0.
(4.58)
При U = 0 все значения
частоты 2 лежат в верхней
полуплоскости
комплексного переменного, что
соответствует затуханию
возмущений типа (4.31). Рис. 104.
Скорость флаттера
определяется здесь как минимальная скорость, при которой
появляются бегущие волны с прогрессирующей амплитудой.
При этом среди частот 2 появляются частоты, имеющие
отрицательную мнимую часть, т. е. у соответствующих
характеристических показателей 5 ==/2 появляются
положительные вещественные части.
Параметр % является сложной трансцендентной функцией
скорости U и частоты 2. Тем не менее критическая скорость

242 устойчивость упругих тел в потоке газа [гл. 4
может быть найдена, если применить к уравнению (4.58)
известные критерии Коши — Найквиста и т. д. При
достаточно больших числах Мх выражение для х может быть
заменено более простым асимптотическим представлением,
ввиду чего становится возможным применение алгебраических
критериев устойчивости и получение оценки для критической
скорости в явном виде.
Рассмотрим случай, когда
м\^>1, v/? = kR Ум\ -1>/г. (4.59)
Первое условие требует, чтобы числа М1 в относительном
движении газа и упругой волны в оболочке были достаточно
велики. Второе условие требует, чтобы показатель
изменяемости поперек потока не был чрезмерно велик.
Будем исходить из последней формулы (4.43):
<** = Тп (4-6°)
n — vR——
(случай V < U нас не интересует, так как при этом
колеблющаяся оболочка не поглощает, а, наоборот, излучает энергию
в окружающую среду). С учетом асимптотических формул
(4.43) получим:
/ (л —1) тс
е 2
Отсюда по формуле (4.60) придем к асимптотическому
выражению
1
а«- л Г—
n — ikRV M\ — \
или, с учетом неравенств (4.59) и формул (4.34) и (4.45),
i р# i
*е ~ kRM{ ' X~^h kU — il '
Уравнение (4.58) принимает вид
Q2 _ iQ (e _|_ т) _ 22 _|_ цк U==0t (4.61)
где
?Соо
(4.62)

§ 4.6] ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ СКОРОСТЕЙ ФЛАТТЕРА 243
Уравнение (4.61) представляет собой алгебраическое
относительно Q уравнение с комплексными коэффициентами.
Условия отсутствия у этого уравнения корней с отрицательными
мнимыми частями могут быть представлены в форме,
аналогичной общеизвестным критериям Рауса — Гурвица *).
Все корни уравнения
F{Q) = a0Q? + alQn-1+. ••+«„ +
+ /(*0S» + *1Q»-1 + ...+O = 0.
где aQ, av ..., ап, bQ, bv ..., bn — действительные числа,
имеют положительные мнимые части, если все главные миноры
четного порядка матрицы
а0
bo
ai
h
а0
bo
ап
Ьп
ьп
а0
bo
а, .
h ¦
¦ ап
.. Ъп
положительны. Матрица Н для рассматриваемого случая
имеет вид
| 1 О —Q\ О II
0 -(е + Т) ^kU О
О 1 О —QA
I 0 0 — (e + T) *\kU I
Условия устойчивости записываются в виде
е_|-т>0, (2в + 7)^2 — (Т^)2>0.
Первое условие, требующее положительности затухания
(внутреннего и аэродинамического), выполняется во всех случаях.
1) Чеботарев Н. Г. и МейманН. С, Проблема Рауса —
Гурвица для полиномов и целых функций, Изд-во АН СССР, 1949.

244 устойчивость упругих тел в потоке газа [гл. 4
Второе условие дает:
-<V-<V1(m,n), (4.63)
где Vx — фазовая скорость распространения упругих волн
в оболочке, определяемая по формуле (4.54). Отсюда с учетом
обозначения (4.62) находим, что критическая скорость 1)
U, = Vl(m.n)fl-\-^t^j. (4.64)
Заметим, что в любом случае скорость движения волн на
границе области устойчивости совпадает со скоростью Vv
Действительно, подставляя в уравнение (4.61) согласно (4.63)
легко найдем, что Q == Qx и, следовательно, V = VV
Влияние конструкционного демпфирования в данной задаче
весьма существенно. В самом деле, второй член в скобках
формулы (4.64) можно представить в виде
р а 2ъ р с^ '
где ф — относительное рассеяние энергии вследствие
конструкционного демпфирования. Подставляя сюда частоту Qx согласно
формуле (4.57) и скорость звука в газе
,=/~^
(4.65)
Р
(Роо — давление, х— показатель политропы), получим:
G-AI^fA^i (4.66)
Пусть Е — 2 • 106 кг/см2, р0 = 8 • 10~6 кг сек2/см4 (сталь),
p00=l кг/см2, p=l,3- 10"9 кг сек2/см4, х=1,4 (воздух
при нормальных условиях), h = 0,01/?, ф = 0,02 (сравни-
1) Эта формула была получена при использовании для
аэродинамических сил «закона плоских сечений» в работе: Б о л о-
т и н В. В., Некоторые новые задачи динамики оболочек, Сб.
«Расчеты на прочность», вып, 4, Машгиз, 1959. Границы ее
применения (4.59) даются впервые.

§ 4.7] устойчивость упругих пластинок 245
тельно малое конструкционное затухание). Тогда по
формуле (4.66) получим, что G = 2,99.
Из приведенного примера видно, что критическая скорость
газа обычно должна в несколько раз превосходить
минимальную скорость распространения изгибных волн в оболочке,
чтобы возбуждение волновых движений стало возможным.
При этом число Маха Мх в относительном движении для не
слишком тонких оболочек будет значительно больше единицы
и первое из условий (4.59) окажется выполненным. В самом
деле,
м Ц.-Уг ^Xlq,
причем с учетом формул (4.57) и (4.65)
Coo WooPq^/
Если использовать данные предыдущего примера, то получим,
что VJCoo^lM и Жи^4,89.
Необходимо заметить, что приведенные выше результаты
относились к случаю бесконечно длинной оболочки. Если
оболочка имеет конечные размеры, то благодаря отражению
упругих волн от ее концов мы получаем более сложную
картину. Поэтому выведенные здесь формулы для критических
скоростей, естественно, могут и не совпадать с
соответствующими формулами для конечной, хотя и весьма длинной оболочки.
§ 4.7. Устойчивость упругих пластинок
в потенциальном потоке
Допустим, что упругая пластинка, обтекаемая с одной
стороны газом, совершает малые колебания. Пусть w (x, у, t)—
прогиб, D — цилиндрическая жесткость, Nx и N—
растягивающие силы в срединной поверхности, р0 — плотность
материала, г — коэффициент затухания, р (х, у, t) — составляющая
аэродинамического давления, обусловленная отклонением
пластинки от невозмущенного состояния. Уравнение малых
колебаний пластинки имеет вид
DV^-(A^ + A^) +
+ Ро>*5? + Ро^ + Р(*. У, 0 = 0. (4.67)

246 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
Следуя в основном работе Нельсона и Каннинг-
хэма1), рассмотрим устойчивость плоской пластинки,
бесконечно простирающейся в направлении, перпендикулярном
к потоку, вмонтированной в абсолютно жесткую диафрагму
и испытывающей цилиндрический изгиб (рис. 105). Течение
Рис. 105.
газа будем считать плоским и потенциальным. Потенциал
возмущений ср должен удовлетворять уравнению (4.9)
дх2 V J-T dz2 ^ dxdt ? dt2 V
и условию
JL = v(x, t) при z = 0.
Допустим, что пластинка совершает гармонические колебания
с частотой ?2:
w(x, t) = W(x)eiQt, }
l dW\ \ (4.69)
v (х, t) = V (x) ет = liQW +U^j ei2t- J
l) Nelson H. C. and Cunningham H. J., Theoretical
investigation of flutter of two-dimensional flat panels with one surface
exposed to supersonic potential flow. NACA Rep. № 1280 (1956).

§ 4.7] устойчивость упругих пластинок 247
Тогда для потенциала ср(х, z, t) также должно быть взято
выражение
у(х, z, t) = f(x, z)ei2ty
а уравнение (4.68) примет вид
^(l-^) + ^-^f + ^/ = 0. (4.70)
При х < 0 можно положить / = df/dz — 0, что делает весьма
удобным преобразование Лапласа. Полагая
оо
f*(q9 z)= f e~*xf(x, z)dxy
о
приведем уравнение (4.70) к виду
^ = V?f*t р= 1 / ^(М2— 1) + 2? -д-.
Его решение, затухающее при z->oo и удовлетворяющее
преобразованному граничному условию, имеет вид
где V*(q) — преобразование Лапласа для функции V (х).
Правая часть представляет собой произведение двух функций
от q\ поэтому для обращения можно применить теорему
о свертывании. Произведя вычисления, получим:
X
у 6xD Г-ша<*-6> 1 J Г а(*~^ ] <*
ХёхР[ Coo(A«»-l)JJo[eoo(Aia_1)J^.
где У0 — функция Бесселя нулевого порядка. Отсюда по
формуле (4.12) легко найдем давление на колеблющуюся
пластинку:
р = -ре'« [iQf(x, 0)+t/d/?,0)].
Таким образом, анализ устойчивости плоской формы
панели в потенциальном сверхзвуковом потоке сводится

248 устойчивость упругих тел в потоке газа [гл. 4
к исследованию интегро-дифференциального уравнения
т(<2+^)/[^)+^]х
^ fM2-
с соответствующими краевыми условиями для W (х).
Например, в случае опертых кромок
*(0) = *(«) = ^=^ = 0. (4.72)
Частоты Q, при которых однородная краевая задача,
описываемая уравнением (4.71) и граничными условиями (4.72),
имеет решения, отличные от тривиальных, вообще говоря,
являются комплексными. На границе области устойчивости
они, однако, принимают действительные значения. Исходя из
этого, можно найти критическую скорость флаттера.
Представим решение уравнения (4.71) в виде разложения
по функциям, удовлетворяющим условиям (4.72):
оо
^W = 2/*sin^. (4.73)
Вводя (4.73) в уравнение (4.71) и применяя метод Галеркина,
получим систему алгебраических уравнений
с»
(«>2,-<о2 +Ы/у+2 */»(«>. М) = 0 (/=1. 2, ...)-(4.74)
k=i
Здесь
^y q
Qj — частоты собственных колебаний пластинки в вакууме,

§ 4.7] устойчивость упругих пластинок 249
ftyft(o), M) — безразмерные коэффициенты, вычисляемые по
формуле
Вместо pk в формулу следует подставлять последний член
уравнения (4.71) для случая
W(x) = sln^.
Уравнение для нахождения 2 получим, приравнивая нулю
определитель бесконечной системы (4.74)1):
|(т8_и2 + /?Ш)8ям + *уй(ш, М) | = 0. (4.76)
Коэффициенты bjk не могут быть выражены явно через со
и М] поэтому для определения критической скорости
приходится прибегать к весьма кропотливым вычислениям.
Нельсон и Каннингхэм произвели эти вычисления в
интервале от М= 1,3 до Ж = 2,0 для случая опертой пластины,
а также для пластины, защемленной по концам. В последнем
случае в качестве аппроксимирующих функций были взяты
«балочные» функции. При этом вместо бесконечного
определителя (4.76) рассматривался определитель второго или
четвертого порядка. На рис. 106 показаны результаты
вычислений в виде графической зависимости отношения /г/а,
необходимого для предотвращения флаттера при различных
числах М. График составлен для панели из алюминиевого
сплава и условий на высоте 25 000$/я (7,62 км). Следует
отметить, что наименьшая толщина соответствует числам М,
близким к У 2. Здесь же нанесены экспериментальные точки,
1) Майлс показал (Miles J., On a reciprocity condition for
supersonic flutter, Journ. Aeronaut. Sci. 24, № 2 (1957)), что в
случае квазистационарной аппроксимации аэродинамических сил
коэффициенты bjk удовлетворяют «соотношениям взаимности»:
bJk = (-l)J+kbkj, (4-75)
типичным и для других неконсервативных задач упругой
устойчивости. Аналогичный результат был получен Хеджпетом
(Флаттер прямоугольных свободно опертых панелей при больших
сверхзвуковых скоростях, Сб. «Механика», № 2, ИЛ, 1958), также
исходившим из квазистационарных (хотя и трехмерных) представлений.

250 устойчивость упругих тел в потоке газа [гл. 4
относящиеся к плоским панелям (кружки) и к выпученным
панелям (квадратики).
Точные решения уравнения (4.71) могут быть получены
при помощи преобразования Лапласа. Голанд и Лак1)
рассмотрели случай мембраны (D = 0). Они ограничились
предельным случаем М -> со, показав, что при достаточно
больших сверхзвуковых скоростях плоская форма мембраны
Л
а
0,08
0,06
ОМ
0,02
О
/ 1,25 1,50 1.75 2.00 2,25
м
Рис. 106.
будет устойчивой. Задача об устойчивости пластинки
представляет гораздо большие трудности. Нельсон и К а н -
нингхэм2) получили весьма громоздкое уравнение для
нахождения критической скорости флаттера, однако не
выполнили никаких вычислений.
§ 4.8. Определение аэродинамических сил
в случае больших сверхзвуковых скоростей.
Закон плоских сечений
Как было видно из предыдущего, решение задач
устойчивости упругих тел в потоке газа затрудняется из-за
сложного характера выражений, описывающих нестационарные
1) G о 1 a n d M. and Luke Y. L., An exact solution for
two-dimensional linear flutter at supersonic speeds, Journ. Aeronaut. Sci.
21, № 2 (1954).
2) Цит. на стр. 246.

§ 4.8] ОПРЕДЕЛЕНИЕ АЭРОДИНАМИЧЕСКИХ СИЛ 251
¦
Pt>4
*Y/ P
щ,
аэродинамические силы в возмущенном потоке. К счастью,
при достаточно больших сверхзвуковых скоростях,
представляющих в настоящее время наибольший интерес,
аэродинамическая сторона существенно упрощается (если,
разумеется, не принимать во внимание эффектов, связанных с
вязкостью, диссоциацией, фазовыми превращениями на границе
тела и потока и т. д.). В данном параграфе мы познакомимся
с некоторыми упрощенными подходами.
Рассмотрим вначале установившееся движение тонкого
профиля со сверхзвуковой скоростью U (рис. 107). В
отличие от дозвукового случая, в котором поле скоростей в каждой
точке оказывается
зависящим от нормальной
составляющей скорости v
во всех точках
поверхности тела, здесь
возмущения сносятся лишь вниз
по потоку. С увеличением
скорости U влияние
возмущений носит все
более локальный
характер. В предельном
случае весьма больших
сверхзвуковых скоростей
каждая частица газа движется
практически лишь в направлении, перпендикулярном к
скорости U. Профиль как бы врезается в толщу газа, частицы
которого движутся в узких областях, ограниченных весьма
близкими вертикальными плоскостями. Чем больше скорость
движения U', тем точнее выполняется этот «закон плоских
сечений».
Следуя изложенной физической картине, приходим к
выводу, что давление на поверхности тела р можно вычислить
как давление газа на поршень, который движется в
одномерном канале 1):
г-'^+^ЬГ- <4'77)
Рис. 107.
!) Отсюда происходит название поршневая теория,
распространяемое на различные приближенные подходы, которые
связывают давление с локальным скосом потока,

252 устойчивость упругих тел в потоке газа [гл. 4
Здесь х — показатель политропы, р^ и с —давление и
скорость в невозмущенном газе. Если определяется давление на
часть профиля, лежащую за ударной волной, то вместо р^
и с^, вообще говоря, берутся параметры рх и сг газа,
находящегося за ударной волной.
Формула (4.77) и ее модификации вводились рядом
авторов из различных соображений 1) и оказались весьма
удобным средством для исследования задач аэроупругости. Их
можно рассматривать также как следствие законов подобия
при больших сверхзвуковых скоростях 2). Отложив
обсуждение вопроса о границах применимости формул типа (4.77),
рассмотрим некоторые частные случаи.
Разлагая двучлен в формуле (4.77) в ряд, получим
формулу
'-'-[1+^^(?),+*те)*+-]-
(4.78)
Линейное приближение соответствует известной формуле
Аккерета 3) для стационарного давления на тонкий профиль,
находящийся в сверхзвуковом потоке:
р — р =—===•
Усо Vm2 — 1
(tj — угол наклона профиля). Если формулу Аккерета
толковать более широко, понимая под т\ характеристику
местного «скоса» потока, который может меняться по длине про-
') Ильюшин А. А., Закон плоских сечений при больших
сверхзвуковых скоростях, Прикл. матем. мех. 20. № 6 (1956); Ligh-
thill M. J., Oscillating airfoil at high Mach number, Journ.
Aeronaut. Sci. 20, № 6 (1953); Ashley H. and Zartarian C, Piston
theory — a new aerodynamic tool for the aeroelastician, Journ.
Aeronaut. Sci. 23, № 6 (1956).
2) Hayes W. D., On hypersonic similitude, Quart. Appl. Math. 5,
№ 1 (1947); Бам-Зеликович Г. М., Бунимович А. И. и
Михайлова М. П., Движения тонких тел с большими
сверхзвуковыми скоростями, Изв. АН СССР, ОТН, «Механика и
машиностроение», № 1, 1960; Черный Г. Г., Течения газа с большой
сверхзвуковой скоростью, Физматгиз, 1959.
3) См., например, Ф е р р и А., Аэродинамика сверхзвуковых
течений, Госгехиздат, 1952,

§ 4.8] ОПРЕДЕЛЕНИЕ АЭРОДИНАМИЧЕСКИХ СИЛ 253
филя, то получим формулу
'-'«=У*гГ (4'79)
которая при М2 ^> 1 переходит в линейное приближение
формулы (4.78). Аналогично квадратичное приближение
соответствует известной формуле Буземана при Ж2^>1.
Остановимся более подробно на приближении третьего
порядка. Это необходимо потому, что изменение энтропии
при переходе через ударную волну начинается именно с
членов третьего порядка. Поэтому именно с этих членов
появится разница между формулой (4.77) и формулой
Р = л(1+-т^^р. (4-80)
предложенной А. А. Ильюшиным1) (vQ — скос потока
на носике профиля).
Для сопоставления формул (4.77) и (4.80) весьма удобен
случай слегка наклоненной к потоку плоской пластины (рис. 108).
Рос, С
Рис. 108.
Если v = v0, то давление во всех точках пластины за
ударной волной будет постоянно и согласно формуле (4.80)
равно рг, где рх определяется как
л=М'+^ (?)"+'?/'+№]"}•
Разлагая правую часть в ряд, найдем:
!) Цит, на стр. 252,

254 устойчивость упругих тел в потоке газа [гл. 4
Первые три члена в квадратных скобках совпадают с (4.78);
разница между последними выписанными членами оценивается
сопоставлением величины (5 — Зх)/8 с единицей. При х=1,4
расхождение между кубическими членами составляет 10%.
Если учесть, что вклад этих членов в полное давление сам
0.25 0,5 0,75 W
Рис. 109.
по себе невелик, приходим к выводу о том, что более
простая формула (4.77) может широко использоваться вместо
уточненной формулы (4.80).
На рис. 109 показано изменение избыточного давления,
вычисленное по формуле (4.78) с различным числом членов
ряда (х=1,4). При этом использовано обозначение
•ч = ?- (4-81>
Влияние членов выше третьего порядка в диапазоне 0 ^ Мг\ <
<Л,0 оказывается весьма незначительным.

§ 4.8] ОПРЕДЕЛЕНИЕ АЭРОДИНАМИЧЕСКИХ СИЛ 255
Вопрос о границах применения «закона плоских сечений»
рассматривался рядом авторов. Помимо требования М2^> 1,
должно выполняться условие малости возмущений ч\. Это
условие формулируется по-разному: Мч\ < 1, т]2 <<^ 1 и т. д.
По А. А. Ильюшину ошибка приближенных формул
оценивается величиной порядка
И^+ж)-
Наряду с ограничениями, выражаемыми через М и т), должны
быть наложены дополнительные ограничения, которые
учитывали бы эффекты нестационарности и трехмерный характер
течения. То, что эти ограничения существуют, видно, если
сопоставить формулы для давления, получаемые из (4.77), и
формулы, полученные путем предельного перехода из точных
соотношений.
Рассмотрим линеаризированное течение газа вдоль оболочки,
по которой распространяются упругие волны. В этом случае
dw , rrdw ,. ооч
ю^Ж+иЖ' <4'82>
и, следовательно, по формуле (4.78) избыточное давление
- %Р™ I dw dw\
Подставляя сюда выражение (4.31) для w:
w = Ul №-**) cos nb, (4.84)
получим:
р = рсоо* (2 — kU) Ul W-^ cos nb. (4.85)
Возьмем теперь точную формулу (4.39)
Вводя сюда выражение (4.84), найдем:
р = — pRa (Q — kUf W (2/-^> cos пв. (4.86)
Для рассматриваемого случая
а= ГЖ^'
П — чИ тгт

256 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА (гл- 4
где
Чтобы от формулы (4.86) перейти к формуле (4.85),
недостаточно положить М2^> 1 • Необходимо, чтобы М\^>\,
kRM-i ^> п. Только в этом случае можно положить
kRMx ~ R{kU — Q) '
что обеспечивает переход к формуле (4.85).
Происхождение первого требования М\^> 1 очевидно: газ
должен перемещаться достаточно быстро относительно волн,
о
распространяющихся по оболочке. Требование М\ ^>1 можно
записать в виде
Ж2(1 — ~^>")2:> 1. (4.87)
где
— V Q
Поскольку 1/А является характерным линейным размером
возмущения, то параметр со можно толковать как
приведенную частоту. Условие (4.87) не совпадает с условием
Лайтхилла
М{ч\ + ^)< 1,
однако оно удовлетворяется, если наряду с условием
Лайтхилла выполняется условие М2 ^> 1.
Условие kRMx ^> n не содержится ни в одном из
перечисленных выше условий. Оно связывает показатели
изменяемости возмущений вдоль потока и поперек потока. Следует
предположить, что аналогичные требования должны
выполняться и в других случаях.
Сопоставление результатов, которые дают простые
формулы типа (4.77), с результатами более точных
аэродинамических теорий1) указывает на хорошее совпадение, начиная
с М = 4 и даже с М = 2. С поправками, зависящими от
М2 — 1, область применения формул может быть несколько
1) См., например, Morgan H. G., RuniyanH. L. and Hu-
с k e 1 V., Theoretical considerations of flutter at high Mach numbers,
Journ. Aeronaut. Sci. 26, № 6 (1958).

§ 4.9] устойчивость упругих пластинок 257
расширена в сторону меньших чисел М (примерно до М=У 2)-
Верхняя граница применения формул в настоящее время не
установлена. При весьма больших сверхзвуковых скоростях
необходимо, очевидно, принимать во внимание эффекты,
связанные с вязкостью, диссоциацией, ионизацией, фазовыми
превращениями на границе газа и тела и другими эффектами.
Однако локальный характер связи между возмущениями р
и скосом потока v должен, разумеется, сохраниться. В
частности, формула (4.83) для малых возмущений останется
в силе, хотя коэффициент перед скобкой окажется функцией
расстояния, измеряемого по потоку, и будет зависеть от
физических явлений, происходящих в пограничном слое
невозмущенного течения.
§ 4»9. Устойчивость упругих пластинок
при больших сверхзвуковых скоростях
Рассмотрим малые колебания плоской прямоугольной
в плане панели (рис. 110), вводя аэродинамические члены
Рис. ПО.
согласно линеаризированной формуле «закона плоских
сечений» (4.83). Вместо уравнения (4.67) получим значительно
более простое уравнение
DV2V2^— N
d2w
х дх2
-лл
д2т
) + Ро^
d2w
dt2
-\-pQhe
dw %/> / dw dw\
Здесь сохранены все обозначения из § 4.7.

258 устойчивость упругих тел в потоке газа [гл. 4
Имеются два простейших случая, когда число независимых
переменных в уравнении (4.88) может быть сведено до двух
(х и t): случай цилиндрического изгиба и случай пластинки,
которая свободно оперта по двум кромкам, параллельным
потоку. В последнем случае подстановкой
w (х, у, t) = wx (xt t) sin ~y~- (n = 1, 2, . . .)
уравнение (4.88) приводится к виду
r^/d^Wi 2п2к2 d2w{ . n%4 \ /., d2wl AT n2n2 \ .
d2Wi dwi хл / dw\ dw{ \
Jrhh-W- + ?^-w + ^-{-w^rU4r) = 0. (4.89)
Случай цилиндрического изгиба может быть получен из (4.89)
путем предельного перехода b -> оо.
Решение уравнения (4.89) ищем в форме
Wl(x, t) = W(x)esf, (4.90)
где W (х)— некоторая функция, которая должна
удовлетворять уравнению
^-2k,?^- + kWW+V^[-+\W = 0. (4.91)
Здесь 1)
_ a2Nx — a2Nv ър^иа*
n*D ' "У~ K2D ' r— Dcoo '
d=\Nl+n2f{Nx--Ny)
и, кроме того,
ш2 = _(а2 + ^о)> (4-92)
' = ?• *=i(e + l*r)' 2o = i|/"^"- (4-93)
l) Целесообразность разбиения члена, содержащего W, на два
слагаемых будет видна из последующего.

§ 4.9] устойчивость упругих пластинок 259
Плоская форма равновесия пластинки устойчива, если все
показатели s лежат в левой полуплоскости комплексного
переменного. Сравнивая уравнения (4.91) и (4.92) с
уравнениями (2.77) и (2.79), видим, что рассматриваемая
задача весьма сходна с задачей об устойчивости прямолинейной
формы стержня в условиях неконсервативного кручения.
Устойчивость невозмущенной формы пластинки имеет место
при условии, что все собственные значения со2 краевой
задачи, описываемой уравнением (4.91) и соответствующими
краевыми условиями, лежат внутри «параболы устойчивости»,
т. е. при условии, что
Imo)2<?(Rea^- (4*94)
Задача, таким образом, сводится к исследованию комплексных
собственных значений со и применению критерия (4.94).
Трудоемкие вычисления могут быть сокращены, если
условие устойчивости (4.94) заменить приближенным
условием (2.82) или достаточным условием Im a)2 < 0. Последнее
условие соответствует решениям, не учитывающим ни
аэродинамического, ни конструкционного демпфирования, когда
«парабола устойчивости» вырождается в узкую полосу,
охватывающую действительную положительную полуось (рис. 59).
Вопрос о возможности пренебрежения затуханием в
неконсервативных задачах упругой устойчивости уже обсуждался
в первой главе; в § 4.12 мы вновь вернемся к этому вопросу,
рассматривая его применительно к задаче о флаттере панелей.
Краевая задача, описываемая уравнением (4.91) и
соответствующими граничными условиями, рассматривалась рядом
авторов1). Подставляя в уравнение (4.91)
W (х) = егх,
получим характеристическое уравнение
(г2 — k2v?f -f- рг — X = 0, (4.95)
где X = о)2 ~j- TC4flf. Пусть гг = [х + h и г2 = |х — h — два
комплексно сопряженных корня этого уравнения. Тогда два других
1) См. сноску6) на стр. 214. Дальнейшее изложение данного
параграфа следует публикациям А. А. Мовчана.

260
УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА
ГЛ.
корня, а также параметры (3 и X выражаются через |л и v
следующим образом:
р = — 4jx(v2 — р2 _|_ ftic2)f у (4.9б)
X _, ?2-4 + ({Х2 _|_ v2) (v2 _ 3[Х2 _|_ 2kv?). ]
Рассмотрим теперь краевую задачу, которой соответствуют
условия W(0) = W"(0) = W(\) = W"(\) = 0. Подчиняя
решение краевым условиям, получим уравнение
" 1 1 1 1
Д(*. К Р) =
' 1
r^e-r,
'3
е~Гз
г\е-п
'4
г\е~т*
= 0,
которое весьма громоздко для исследования. Однако, выразив
показатели rk через переменные [х и v согласно (4.96),
приведем уравнение к более простому виду:
Д (&, |х, v) = [х2 (ch 2р. — ch ]Л2 — 2[x2-f-2^2 cos v) +
(v2 _ p.2 __ ^2)2 _L 2{x2 (p.2 _ kTZ2) Sinv
|/"v2 __ 2{X2 + 2krf
2v
sh /v2-2{x2-f-2Ы = 0.
Аналогично для защемленных передней и задней кромок,
т. е. для случая W(jS) = W'(Q) = W (\) = W'{\) = Ql),
получим уравнение
А (А, X, р) =
которое после пр
Д(&, |i, v) = ch2[j
1 '
1 У^
1111
г\ г2 Г3 Г4
е-Тх е-Г2 е-Га 0-Тк
rxe-^ r2e~Ti г3е~Га r4e~Ti
еобразования приводится к виду
l — ch V v2 — 2|х2 + 2?u2 cos v +
№*-Зц» S111V у 2_ 2 ,
_____ —..ь м -|* ^
= 0,
•2Ы
1) Напомним, что кромки, параллельные невозмущенному
потоку, полагаются опертыми.

§ 4.9] устойчивость упругих пластинок 261
Вычисления выполняются следующим образом. Методом
последовательных приближений находятся корни |х, v
уравнения Д(&, [х, v) = 0. Затем по формулам (4.96) подсчитываются
соответствующие значения (3 и X. Если Р = О, то краевая
задача является самосопряженной и все собственные
значения X действительны. При некотором р одна из пар
собственных значений сливается и далее становится комплексно
сопряженной (рис. 111). Поскольку Х = со24-^4^, a d —
действительное число, то значение р^
соответствует нарушению
достаточного условия
устойчивости Im со2 < 0.
Соответствующую скорость можно назвать
условно критической скоростью
флаттера, хотя, как видно,
например, из (4.92), для
наступления флаттера
необходимо, чтобы величина Im со2
превышала по модулю некоторую
величину, зависящую от меры
затухания. Дивергентной
неустойчивости соответствуют
отрицательные значения о)2.
Критическая скорость дивергенции,
следовательно, может быть
найдена из условия Х = тЛ/.
Исследуя уравнение Д(&, ja, v) = 0, можно получить ряд
качественных и количественных выводов о влиянии
различных факторов на устойчивость плоской формы панели.
В частности, оказывается, что на плоскости X, р имеются
точки, для которых можно найти точное решение
уравнения (4.91). Эти точки соответствуют параметру скорости
P=*?l (»» + „»).
Для опертой пластинки решение уравнения (4.91) имеет вид
W (0 = sin rrnzl • sin (шс? -f-у) е~т^,
где т и п — положительные целые числа, а число т1 и
фаза % определяются по формуле
т.
= уГ1/Г2«2+»?+-^. г
¦¦ arctg'
1

262 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
Для пластинки, защемленной по двум кромкам, аналогично
получаем:
W (?) = sin2 тъ\е-т<&.
Эти точные решения удобны для контроля результатов,
получаемых приближенными методами.
В отличие от пластинок в случае оболочек мы приходим
к дифференциальным уравнениям восьмого порядка и к
необходимости удовлетворения четырех краевых условий на
каждой стороне. В некоторых работах *), посвященных флаттеру
оболочек в постановке, весьма близкой к изложенной в
настоящем параграфе, доминировало стремление свести задачу
к уравнению четвертого порядка. Эти работы мы не
рассматриваем.
§ 4. 10. Применение вариационного метода Галеркина.
Влияние демпфирования и усилий
в срединной поверхности
Введение аэродинамических членов согласно «закону
плоских сечений» существенно упрощает исследование и
в ряде случаев, как мы видели, дает возможность получить
точное решение задачи. Однако в случае сложных краевых
условий при учете реальных законов конструкционного
демпфирования и, особенно, при исследовании нелинейных задач
приходится искать приближенные решения. Обычный путь
состоит в том, что искомое решение представляется в виде
разложения по функциям, удовлетворяющим граничным
условиям, и далее применяется вариационный метод Галеркина.
В результате задача сводится к исследованию некоторого
уравнения, получаемого путем приравнивания нулю
соответствующей системы линейных однородных алгебраических
уравнений2). Данный параграф будет посвящен не столько
1) Степанов Р. Д., О флаттере цилиндрических оболочек и
панелей, движущихся в потоке газа, Прикл. матем. и мех. 21, №5
(1957); Мовчан А. А., О влиянии аэродинамического
демпфирования на сверхзвуковой флаттер обшивки, Изв. АН СССР, ОТН,
«Механика и машиностроение», № 1, 1960.
2) X е д ж п е т Д., Флаттер прямоугольных свободно опертых
панелей при больших сверхзвуковых скоростях, Сб. «Механика»,
№ 2, 1958; Fung Y. С, On the two-dimensional panel flutter, Journ.
Aeronaut. Sci. 25, № 3 (1958); Болотин В. В., К вопросу об

§ 4.10] ПРИМЕНЕНИЕ ВАРИАЦИОННОГО МЕТОДА ГАЛЕРКИНА 263
вычислительной стороне вопроса, сколько выяснению
некоторых интересных свойств флаттерных задач, которые
становятся весьма прозрачными, если перейти к конечномерной
системе.
Ищем решение уравнения (4.88) в виде ряда
оо
w (х, у, о = 2 fk (0 wk (*. у)
по функциям wk(x, у), удовлетворяющим краевым условиям
для w(x, у, t). Применяя метод Галеркина, получим систему
уравнений
'(7=1.2....).
где
а Ь
f f [dv*.> -(",-??-+ N> *$)} WJdx «у
aib =
о о
*jk a b
pQhWjWkdxdy
о о
и и
Г Г дть
J J-d9'
dxdy
, 0 0 %Poo PooCo
jk a ь ' Po^oo ?0h
/ / ^hwjWkdxdy
о о
Если в качестве функций wk(x, у) выбрать формы
собственных колебаний пластины в вакууме, то
устойчивости пластинки в потоке сжимаемого газа, Сб. «Вопросы
прочности материалов и конструкций», Изд-во АН СССР, 1959;
Ливанов К. И. Устойчивость защемленной панели в
сверхзвуковом потоке, Инж. сборн. 25 (1959) и др.

264 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
где &у — соответствующие собственные частоты. После
введения безразмерных параметров
*s0
fap^M - ?Qha
^2-. b)k = —TUJb
?0haQ0
(20 — характерная частота, например Qq^Qj) система
уравнений примет вид
оо
*=i
(У=1. 2, ...).
Плоская форма пластинки устойчива, если все корни
уравнения
|(»5+^ + ^)8/*+Р*)*| = 0 (4.98)
лежат в левой полуплоскости. Если влияние затухания не
учитывается, то условие устойчивости сводится к требованию,
чтобы все частоты со = iat определяемые из уравнения
1Н-»2)^+^*1=°- с4-")
оставались лежать на действительной оси. Параметр (3,
соответствующий дивергентным режимам, найдется из уравнения
\*Ф»+&»\=°- <4Л00>
Рассмотрим простейший случай опертой панели ]). В этом
случае, фиксируя число полуволн в поперечном направлении,
примем, что
. Нх . лтсу
w, = sin sin -——
VJ 01" a b '
*) = (P + nY? + PNx + nyNr (4.101)
где сохранены обозначения § 4.9. Вычисления дают:
т а и2 » если J — k — четное число, I
bjk={ f-» \ \ (4.102)
[ 0, если j±k — нечетное число. J
1) Эта задача без учета затухания рассматривалась в ряде
работ. См., например, Johns В. J., Some flutter studies using
piston theory, Journ. Aeronaut. Sci. 25, № 11 (1958).

^ 4.10] ПРИМЕНЕНИЕ ВАРИАЦИОННОГО МЕТОДА ГАЛЕРКИНА
Заметим, что условие взаимности (4.75), указывающее на
неконсервативный характер задачи, здесь также выполняется.
Для определения критического параметра (3# можно
использовать готовые результаты из §§ 1.14—1.16. Беря в
качестве первого приближения определитель второго порядка,
получим формулу
Р« - 4 V(">1 - wi)2+2s2 №+ш1)> (4Л03>
полностью аналогичную формуле (1.96). Если парциальные
собственные частоты &г и 22 достаточно удалены друг
от друга, то поправка
на затухание,
учитываемая вторым членом
под радикалом, является
пренебрежимо малой. В
этом случае имеет место
приближенная
зависимость
750
р,=!(ю2-°?и4-104>
500\
1 \ '
-J*S
~Л±
о
&
50
75
100
125
Ш
Формулы (4 Л 03) и
(4.104) правильно оцени- ^
вают порядок
критического параметра. Так,
для пластинки
бесконечного размаха, не
нагруженной осевыми силами
(Nx = 0, uj = j2), вычи- Рис- 112-
сления по формуле (4.104)
дают р#= 11,25, в то время как точное решение
составляет ^=13,9 (вычисление с четырьмя членами ряда дает
^=13,6). При своей простоте формулы (4.103) и (4.104)
учитывают все основные особенности задачи о панельном
флаттере.
Как уже указывалось, роль затухания становится
существенной, когда парциальные частоты приближаются друг
к другу. Для удлиненных вдоль потока нагретых панелей
случай кратных частот является вполне возможным. На
рис. 112 показана зависимость квадрата безразмерной
частоты от безразмерного сжимающего усилия для панели

266 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
с отношением сторон ср = а/д = 3,0, Ny = Q. Примерная
зависимость критического параметра р# от величины \NX\
AI
значений
о Щ
Рис. 113.
представлена на рис. 113. Минимумы р# лежат вблизи
\NX\, соответствующих кратным частотам, и
составляют величину
порядка g. Заметим, что
критическое значение параметра не
обязательно соответствует
паре наименьших частот: здесь
играет роль не столько
величина частот, сколько
интервалы между соседними
частотами (рис. 114).
До сих пор
предполагалось, что парциальные
коэффициенты затухания являются
одинаковыми. Однако, как уже
было указано (§ 2.5), нет
никаких оснований считать рав-
ными коэффициенты конструк-
J3 ционного демпфирования
(аэродинамическое демпфирование
оказывается для всех степеней
и
О Д
Рис. 114.
свободы одинаковым). Вместо (4.98) рассмотрим уравнение
1(»}+<*+*/о^+р*;*|=о.
В КОТОрОМ е- + Т

§ 4.10] ПРИМЕНЕНИЕ ВАРИАЦИОННОГО МЕТОДА ГАЛЕРКИНА U6?
или, иначе,
Здесь аналогично (4.66) обозначено
7 2тссо р Cqo '
ф;- — относительное рассеяние энергии вследствие
конструкционного демпфирования, соответствующее у'-й форме
колебаний; формула справедлива для периодических процессов
с безразмерной частотой а>. Производя замену
тс* TD n_ Eh* _1/^oo
v J ' ^ 19 Л _ г,2\ ' Г°° |/
получим для G;. формулу
Ф--о)*;- тс I h \2 / Е рл чу
o, = 0oJ^. o0 = i7=f==r(^)
Для стальной пластинки и воздуха при нормальных условиях
О0^12,6-10"(^)2.
Для ненагруженной квадратной пластинки о)х = 2, со2 = 5,
а безразмерная частота на границе флаттера
V'-
2_i_ ,,2
'1+ "
-«3,81.
Если й/а = 0,01, то даже при ф = 0,10 (сравнительно малое
конструкционное демпфирование) получаем, что Ga = 1,32,
G2 = 8,25. Таким образом, роль конструкционного
демпфирования не менее существенна, чем роль аэродинамического
демпфирования.
В § 1.16 было показано, что если парциальные
коэффициенты затухания е;. (или gj) различны, то критическое
значение параметра неконсервативных сил (3^, найденное с учетом
затухания, может оказаться ниже, чем значение р^, найденное
для системы без затухания. Это остается полностью
справедливым и для флаттерных задач. Нетрудно видеть, что

268 устойчивость упругих тел в потоке газа [гл. 4
условие (4.94) справедливо лишь для случая, когда
коэффициенты демпфирования совпадают; поэтому достаточное
условие устойчивости Im а)2 < 0 и вытекающее из него условие
Р** ^- Р* справедливы лишь для этого случая.
Коэффициенты конструкционного демпфирования являются,
вообще говоря, различными для разных форм колебаний.
Это может явиться причиной снижения параметра р^ по
сравнению с р#. Указанное влияние несколько сглаживается из-за
того, что коэффициенты аэродинамического демпфирования
равны между собой.
Вводя правдоподобное предположение о том, что
относительное рассеяние энергии вследствие конструкционного
демпфирования для всех
форм одинаково, получим:
1 + Со
фа)2
1 + Сс
фсо2
Здесь т] = g<ljgl —
параметр, входящий в
приближенную формулу (1.98):
1+7)
Рис. 115. Возьмем для примера
ненагруженную
квадратную пластинку (о)1 = 2,00, о)2 = 5,00). Изменяя параметр G0<|)
в пределах от нуля до 5,00, найдем, что (^/(3* меняется от
1,00 до 0,73. Последний случай соответствует при/г/а = 0,01
декременту затухания в вакууме, равному примерно 0,2.
Основываясь на общей теории (§ 1.15), можно ожидать,
что добавление аэродинамических сил при определенных
условиях способствует стабилизации пластинки, сжатой
осевыми силами. На рис. 115 представлена область
устойчивости на плоскости р, \NX\ для случая ср=1, Ny = 0. Если
в уравнении (4.100) сохранить определитель второго порядка,
то получим следующую формулу для параметра дивергенции:

§ 4.10) ПРИМЕНЕНИЕ ВАРИАЦИОННОГО МЕТОДА ГАЛЕРКИНА 2б9
В то же время параметр флаттера определяется по
формуле (4.104). Нижняя ветвь кривой ЛВС соответствует
границе выпучивания, прямая BE— границе флаттера. С
увеличением параметра скорости потока от нуля в некотором
интервале аэродинамические силы несколько повышают
устойчивость пластинки против выпучивания.
В заключение остановимся кратко на задаче об
устойчивости пластинки, защемленной по одной кромке, свободной
на другой кромке и
неограниченно
простирающейся в направлении,
перпендикулярном к
потоку (рис. 116). Эта
задача представляет
некоторый интерес: в случае,
когда поток направлен от
заделанной кромки к
свободной, возможен
флаттер, а в противоположном
случае — дивергенция.
Рассмотрим эту задачу в предположении цилиндрического
изгиба и без учета осевых сил и затухания. Беря в качестве
аппроксимирующих функций балочные функции
ch \j + cos \j
Рис. 116.
W: (?) = ch \Л — cos \Л . / , . / (sh \Л —
(o, = X2, \= 1,875, \ = 4,694, ...
sin Xjl),
и замечая,
что
/
cv>4
w.w'k d\ = \
21)
при j = k,
\
*r
при j ф k,
j WjWktK = ±w)(0)bjk,
найдем, что bn = 2,000, b22 = 2,000, bv
3,450,
621 = 1,055. Таким образом,
bnhx < °>
хотя bx2 Ф — b,
21-

270 устойчивость упругих тел в потоке газа [гл. 4
Если ограничиться определителем второго порядка, то
получим простое уравнение относительно безразмерной частоты ш
в функции параметра скорости р 1). Результаты вычислений
показаны на рис. 117. Если р < 0, т. е. если поток
направлен от свободной кромки к заделанной, то с увеличением
скорости вначале наступит дивергенция (при Р* =— 6,33).
Если р > 0, то дивергенция невозможна, а флаттер
наступает при значениях р^ = 122,7. Заметим, что точное решение
(О2
г—! 1 1 \800 1 1 1
для этой задачи2) дает значение параметра дивергенции,
практически совпадающее с указанным выше. На рис. 117
нанесены еще две точки, относящиеся к точному решению.
Если вместо формулы (4.83) пользоваться формулой
"" _ 9ooU (dw , ц dw \
1) Здесь принято, что
цо - yi - а2 у роА •
2) М о в ч а н А. А., О колебаниях пластинки, движущейся
в газе, Прикл. матем. и мех. 20, № 2 (1956).

§ 4.10] ПРИМЕНЕНИЕ ВАРИАЦИОННОГО МЕТОДА ГАЛЕРКИНА 271
то можно несколько расширить область применения
результатов. На рис. 118 показана зависимость критического числа
iMaxa для дивергенции от параметра
™ — Е U/ '
Штриховой линией нанесены результаты, вытекающие из
обычной формулы для давления (4.83). Наименьшая
относительная толщина, необходимая для обеспечения устойчивости,
м
4,5
3,5
3,0
2,5
2,0
15
V2
W
О 2 4 66,33 8 Ю
Е [hi
Рис. 118.
имеет место вблизи М = V'2, что качественно согласуется
с результатом, полученным для другого случая закрепления
пластинки при потенциальном обтекании (рис. 106). В
околозвуковой области решение становится непригодным.
К/, -
ХУ
Устойчибость
х%—
^
HeycmoL
\
У/у \
X// N
у.
1чи6ость
S

272 устойчивость упругих тел в потоке газа [гл. 4
§ 4.11. Границы применения метода Галеркина.
Разъяснение парадокса в задаче о флаттере мембраны
Задачи флаттера панелей относятся к классу
несамосопряженных краевых задач, общие свойства которых в
настоящее время еще не изучены. В связи с этим не раз
высказывались сомнения в возможности применения метода
Галеркина к задачам такого рода. Для этих сомнений имелись
следующие основания.
Линейная задача об устойчивости прямоугольной мембраны
в потоке газа решается несложно, и это решение показывает,
что для закрепленной по контуру мембраны критической
скорости флаттера не существует, т. е. плоская форма
натянутой мембраны остается устойчивой при всех достаточно
больших сверхзвуковых скоростях. Применение к той же задаче
метода Галеркина обнаруживает, казалось бы, критическую
скорость флаттера, величина которой с увеличением числа
взятых членов приближается к некоторому пределу. На этом
основании даже высказывались предположения !), что не
только в случае мембраны, но и в случае пластины
вариационный метод Галеркина не дает правильного ответа на
вопрос о критической скорости флаттера и что
наблюдавшиеся до сих пор случаи разрушения панелей следует
объяснить другими причинами.
С другой стороны, для пластин имеет место
удовлетворительное совпадение результатов точных расчетов и
расчетов, основанных на применении метода Галеркина, если
в последнем случае удержать четыре члена ряда. В связи
с этим возникает вопрос, чем объяснить существенную
разницу в результатах, которые дает метод Галеркина в
применении к пластинам и к мембранам (т. е. к пластинам,
цилиндрическая жесткость которых стремится к нулю). Этот
вопрос имеет не только теоретическое, но и большое
практическое значение. Большинство задач панельного флаттера и,
особенно, нелинейные задачи приходится решать, прибегая
О Ashley H. and Zartarian С, Piston theory —a new
aerodynamic tool for the aeroelastician, Journ. Aeronaut. Sci. 23, № 6
(1956); Bisplinghoff R. L., Some structural and aeroelastic
considerations of high-speed flight, Journ. Aeronaut. Sci. 23, № 4 (1956);
см. также в книге: Бисплингхофф Р. Л., Эшли X. и
X а л ф м з н Р. Л., Аэроупругость, ИЛ, 1958, стр. 762 и 779.

§ 4.1 IJ ГРАНИЦЫ ПРИМЕНЕНИЯ МЕТОДА ГАЛЕРКИНА 273
к вариационному методу Галеркина. Поэтому крайне важно
знать границы применения метода к этому классу задач.
Парадоксальное расхождение результатов для мембраны до
сих пор оставалось неразъясненным, и этому разъяснению
в основном посвящен настоящий параграф !).
Вновь рассмотрим прямоугольную в плане плоскую
панель со сторонами а и Ь, обтекаемую односторонним
сверхзвуковым потоком с невозмущенной скоростью U (см.
рис. ПО). Будем пренебрегать демпфированием и
ограничимся плоской задачей, для которой уравнение (4.88) после
подстановки
w(x, t) = W{x)em
примет вид
Нетрудно показать, что для мембраны (D = 0) все
частоты оказываются действительными независимо от числа Ж,
т. е. плоская форма мембраны остается устойчивой при всех
достаточно больших сверхзвуковых скоростях. А именно,
вычисления приводят к формуле
где m — любое положительное целое число.
Если теперь применить к этой задаче метод Галеркина,
представляя решение в виде ряда
сю
W(*) = V/ftSin^( (4.107)
то для пластинки уже в первом приближении (два члена ряда)
мы получим результаты, довольно близкие к точному. Для
мембраны же (D = 0) в том же приближении получим р^ = 2,25.
В то же время, как это следует из точного решения,
флаттер для мембраны вообще исключен.
*) Болотин В. В., О применении вариационного метода
Галеркина к задачам флаттера упругих панелей, Изв. высш. школы,
сер. «Машиностроение», № 11, 1959.

274 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
Чтобы выяснить характер поведения (3# при возрастании
числа членов ряда (4.107) и причину качественного
расхождения точного и приближенного решений, были
предприняты вычисления частот со при различном числе членов. На
рис. 119—122 показаны кривые для пластины при Nx = 0.
Замыкание «петли» соответствует появлению двух комплексно
сопряженных частот, и минимальное значение параметра (3^,
при котором имеет место замыкание «петли», является
критическим. Из графика видно, что критическое значение р#
мало меняется с увеличением числа членов ряда (при двух,
трех, четырех и пяти членах мы получим соответственно
(3^=11,2; 14,3; 13,6 и 13,8). Характерно, что для
нечетного числа членов ряда имеет место размыкание одной из
петель из-за отсутствия для одной из обобщенных координат
«парной» координаты. Вообще, приближение с четным числом
членов ряда (4.107) является более естественным для данной
задачи, в которой неустойчивость связана с «парным»
взаимодействием обобщенных координат.
На рис. 123—126 приведены кривые для мембраны.
Заслуживает внимания то обстоятельство, что основная «петля»,
соответствующая двум первым членам ряда (4.107), с
увеличением числа членов изменяет свой характер, причем при
нечетном числе членов размыкается. В то же время «петля»,
соответствующая двум последним членам, остается почти без
изменений и замыкается примерно при одном и том же
значении (3^ — 2,3. По-видимому, все авторы, применявшие до
сих пор метод Галеркина к задаче о мембране, вычисляли
именно это минимальное значение, истолковывая его как
критическое значение. Между тем на последние из взятых
членов ряда следовало бы смотреть лишь как на поправки
к основному решению и не принимать в расчет тех
результатов, которые возникают главным образом за счет
этих членов. Если же следить за поведением первой «петли»,
то окажется, что, по существу, нет противоречия между
точным решением и решением по методу Галеркина. Два
члена ряда дают (^ = 2,25, три члена приводят к
результату р~>со (размыкание первой «петли»), при четырех членах
получаем, что (^ = 3,22, при пяти снова получаем, что ^->оо.
Мы имеем здесь типичный расходящийся процесс при
определении (3:;:. Заметим, что в то же время для частот со, по крайней
мере при достаточно малых р, процесс последовательных

§ 4.11] ГРАНИЦЫ ПРИМЕНЕНИЯ МЕТОДА ГАЛЕРКЙНА 275
Ю
[си2
п=2 1
i 1
10
Рис. 119.
Ю
<ч?
\b>2
|с«^ ^*
1
п = 3
со-*~ 4,45
W 20
Рис. 120.
30
fi

276 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [гл. 4
приближений сходится. Это видно, например, из рис. 126,
где штриховыми линиями нанесены зависимости
^V~m2+i$2
(т=1, 2, ...),
вытекающие из точной формулы (4.106).
70 90 100
Рис. 122.
110
Рассмотрим теперь сходимость бесконечного
определителя (4.99). Если у'-ю строку разделить на о)у, a k-Pi
столбец— на а>?, то этот определитель можно представить в виде
bjk + C]k\>
(4.108)

§ 4.11] границы применения метода гаЛеркйна 277
к>
\со,
Р*=2,25
п-2
о 1 г
Рис. 123.
к*
\сиг
\(о,
'
3
п=3
со-~!,70 |
\jB„=2.27
3 О
р
/ 2 3
Рис. 124.
/

2?8 устойчивость упругих тел в потоке газа [гл. 4
где b-k — символ Кронеккера,
С;
+-^
)Ь a>ju>k ' a>j(uk f — k2
вуо)Л
(jitk— нечетное число),
(jiik— четное число).
^5
СО л.
Щ
О)2
\cot _
^00^^^. -—
«^^
_—-*-
______- —
<^*^ -»-"
;::^:::-
/7=5
__^-Н
^^\
со-*2,25\
2 3
Рис. 126.
4
5
/
(4.109)
Как известно1), бесконечный определитель (4.108)
сходится, если сходится двойной ряд
оо оо
2 2Ы-
(4.110)
Определитель, удовлетворяющий этому условию, называется
нормальным.
') Канторович Л. В. и Крылов В. И., Приближенные
методы высшего анализа, Гостехиздат, 1952.

§ 4.11] ГРАНИЦЫ ПРИМЕНЕНИЯ МЕТОДА ГАЛЕРКИНА 279
По соответствующей формуле (4.101) при п = 0у Nx =
= Му = 0 имеем, что wk — k2. Поскольку | у2— &2|^>У +
+ k > 2 VJk, то
\cjk\<-j\ ^Yf^rr
Двойные ряды, составленные из стоящих в правой части
элементов, сходятся, откуда вытекает сходимость ряда (4.110).
Следовательно, определитель (4.108) для пластины относится
к классу сходящихся (нормальных) определителей.
Аналогичное утверждение может быть доказано и для других
типов закрепления пластины по контуру.
Перейдем теперь к случаю мембраны (со^ = k). В этом
случае сходимость ряда (4.110) зависит от сходимости ряда
сю сю сю сю
у v \ _у у __^_
jU -и \f — k2\ ~ jU —i j2 — k2
j k 7 = 1 k<j
(у и k—числа различной четности). Замечая, что при k < у
p — k2 ^ p
и что число отличных от нуля членов в у-й строке равно
либо у/2, либо (у—1)/2, но во всяком случае не меньше,
чем у/3, получим:
оо оо оо
V V 1 - v —
Zaau \f — k2\ > Zd зу •
У k j = i
В правой части стоит заведомо расходящийся ряд, откуда
следует, что ряд (4.110) для мембраны расходится.
Следовательно, определитель (4.108) в случае мембраны не
принадлежит к классу нормальных определителей.
В общем случае прямоугольной пластины
Ш2 = (Д.2 + „2^2)2 f _?L (&NX + tl2fNy)>
где y = a/b. Очевидно, что при цилиндрической жесткости D,
отличной от нуля, и при фиксированном п всегда можно
выбрать такое конечное число k, чтобы выполнялось нера-

280 устойчивость упругих тел в потоке газа [гл. 4
венство (1)# > Ctz!\ где С — некоторая постоянная. Тогда
при достаточно больших j и к имеет место неравенство
1*7* К с/Л "+" cfW*\f-tf\ < С//' + 2С//*В>«
и, следовательно, ряд (4.110) сходится, если только D Ф 0.
Сходимость будет тем медленнее, чем меньше D, т. е. чем
больше пластина приближается к мембране.
Из приведенного анализа вытекает, что применение метода
Галеркина к задаче о флаттере пластины приводит к
бесконечным определителям, относящимся к классу нормальных
(сходящихся) определителей. В случае мембраны (пластины
с равной нулю изгибной жесткостью) определитель не
относится к классу нормальных определителей и его
использование приводит к кажущемуся противоречию между точным
решением и решением по методу Галеркина. Это
противоречие может быть устранено, если проанализировать
поведение решения при последовательном возрастании числа членов
ряда. Неэффективность метода Галеркина в случае мембраны
не связана непосредственно с тем, что задача панельного
флаттера является несамосопряженной; аналогичное явление
мы имели бы и в некоторых соответствующим образом
построенных самосопряженных краевых задачах. Хотя из
доказательства сходимости определителей и не вытекает со всей
строгостью сходимость метода Галеркина для данного класса
задач, тем не менее проведенное исследование показывает,
что в применении к пластинам с отличной от нуля изгибной
жесткостью этот метод дает весьма надежные результаты.
§ 4.12. Постановка нелинейных задач
в теории аэроупругости. Роль геометрической
и аэродинамической нелинейностей
Устойчивость пластин и оболочек в потоке газа
рассматривалась до сих пор в линейной постановке. Пользуясь
линейной теорией, можно найти наименьшее значение скорости
(критическую скорость флаттера или дивергенции), при
которой невозмушенная форма плоской или криволинейной
панели перестает быть устойчивой. Анализ нелинейных задач
представляет интерес по двум причинам. Во-первых, во
многих случаях превышение критической скорости флаттера не

§ 4.12] НЕЛИНЕЙНЫЕ ЗАДАЧИ В ТЕОРИИ АЭРОУПРУГОСТИ 281
означает немедленного разрушения панели, а разрушение
наступает лишь спустя определенный период и носит
усталостный характер. Для того чтобы найти ожидаемый срок службы
панели, необходимо определить амплитуды ее колебаний в
области флаттера, а это можно сделать лишь на основе
нелинейной теории. Во-вторых, с ростом чисел М возрастает роль
аэродинамических нелинейностей. Характер влияния этих не-
линейностей в некоторых случаях таков, что их учет
позволяет обнаружить возможность возбуждения незатухающих
колебаний или поддержания дивергентных форм равновесия
при скоростях, меньших критической скорости флаттера (или
дивергенции), если только системе дать достаточно большое
возмущение. В таких случаях критическая скорость,
определяемая методами линейной теории аэроупругости,
оказывается лишь верхней границей критических скоростей для
реальных конструкций.
Важнейшим нелинейным фактором, лимитирующим
амплитуды при флаттере пластин и оболочек и их прогибы при
статической неустойчивости, являются нелинейности
геометрического происхождения, связанные главным образом с
возникновением растягивающих усилий в срединной поверхности.
Эти усилия существенно зависят от краевых условий, т. е.
от совместной работы пластины или оболочки со стержневым
набором и с конструкцией в целом. Кроме указанных
факторов, в некоторых задачах следует учитывать нелинейные
неупругие эффекты и влияние конструктивных нелинейностей
(люфтов, ограничителей и т. п.).
Рассмотрим подробнее влияние аэродинамической
нелинейности *). Формулу (4.77) запишем в виде
где т) — безразмерный параметр возмущений (угол атаки,
безразмерная амплитуда и т. д.). Одно из условий применимости
формулы требует, чтобы Мг\ < 1. Однако для возможности
^Болотин В. В., О критических скоростях в нелинейных
задачах теории аэроупругости, Научн. докл. высш. школы,
«Машиностроение и приборостроение», № 3, 1958.

282 устойчивость упругих тел в потоке газа [гл. 4
использования различных приближений в формуле
(4.111)
ставятся более жесткие требования. Так, линейное
приближение дает удовлетворительные результаты, если только
(Мт])2<^1. Чем больше число /И, тем уже интервал
значений — tjj < т] < 7]j, при которых допустим переход к
линейному приближению.
Поскольку исследуется устойчивость «в малом»,
уравнения могут быть линеаризированы относительно упругих
перемещений тела. Однако лишь в том случае, когда
возмущения, вносимые жестким телом, удовлетворяют условию
— ^i < ^ < ^i (например, в случае движения тела нулевой
толщины с нулевым углом атаки), результат линеаризации
совпадает с формулой (4.83)
Итак, при больших сверхзвуковых скоростях
аэродинамические силы становятся преимущественно нелинейными. Из
формулы (4.111) видно, что во многих случаях при М ^>> 1
аэродинамические силы обладают жесткой нелинейностью
в том смысле, что знак нелинейной добавки совпадает со
знаком т]. Например, если плоский профиль обтекается
установившимся потоком (рис. 127), то при вычислении
подъемной силы и аэродинамического момента члены второго
порядка в формуле (4.111) уничтожаются и, следовательно,
нелинейная добавка начинается с членов порядка т]3 (рис. 128).
Если панель обтекается с одной стороны, то квадратичные
члены, разумеется, сохраняются. Однако при движениях
панели, близких к гармоническим колебаниям с частотой
Q (т] —^ т]0 sin Qt), квадратичные члены не содержат
составляющих с этой частотой, между тем как кубические члены
эти составляющие содержат (7]3~3/4 ^ sin Qt -f- . . Л Поэтому
и здесь существенная нелинейная добавка начинается с членов
порядка т]3.
Там, где аэродинамические силы имеют жесткую
нелинейность, их влияние на поведение упругой системы будет
по своему характеру противоположно влиянию
геометрической нелинейности. Увеличение геометрической нелинейности

§ 4.12] НЕЛИНЕЙНЫЕ ЗАДАЧИ В ТЕОРИИ АЭРОУПРУГОСТИ 283
(например, увеличение нелинейных составляющих усилий
в срединной поверхности, вызванное стеснением перемещений
кромок пластин или оболочек) вызывает уменьшение
амплитуд при установившемся флаттере. Напротив, увеличение
аэродинамической нелинейности вызовет увеличение этих
амплитуд. При достаточно большой геометрической
нелинейности возбуждение флаттера или дивергентное
выпучивание на границе области неустойчивости будет «мягким»
в том смысле, что малое
превышение критической скорости
соответствует малым амплитудам
установившегося флаттера или малым
Рис, 127. Рис. 128.
дивергентным деформациям. Другими словами, граница
устойчивости будет «безопасной» в смысле Н. Н. Б а у-
тина1): Напротив, в случае, когда превалирует
аэродинамическая нелинейность, возбуждение колебаний на границе
области неустойчивости может стать «жестким», а граница
области устойчивости — «опасной». В этом случае
аэродинамические силы могут поддерживать состояния движения,
отличные от невозмущенного, даже в том случае, когда
невозмущенное движение устойчиво «в малом». При
уменьшении скорости U выход из области неустойчивости будет
1) Б а ути н Н. Н., Поведение динамических систем вблизи
границ области устойчивости, Гостехиздат, 1949.

284 устойчивость упругих тел в потоке газа [гл. 4
сопровождаться «затягиванием». Если это действительно имеет
место, критические скорости, определяемые из
линеаризированных уравнений, играют роль верхних критических
скоростей. Наряду с этими скоростями приобретают смысл
нижние критические скорости, т. е. наименьшие скорости,
при которых впервые становится возможным возбуждение
установившихся флаттерных движений или дивергентных
форм равновесия. Истинная критическая скорость для
реальной конструкции находится в этих случаях в достаточно
сильной зависимости от различного рода возмущений
{начальные неправильности, начальный угол атаки, атмосферная
турбулентность и т. п.), причем при достижении этой скорости
переход к неустойчивости происходит скачкообразно.
Например, состояние дивергенции осуществляется по типу прощел-
кивания, подобно тому как это происходит при статическом
нагружении тонких упругих оболочек. Вообще, здесь
обнаруживается ситуация, весьма близкая к той, которую мы
имеем в теории устойчивости тонких оболочек.
Возможность описанных явлений должна устанавливаться для
каждой конкретной системы и для каждого конкретного
диапазона чисел М. Следует иметь в виду, что благодаря вязкости,
развитию и отрыву пограничного слоя и т. п. перечисленные
эффекты сглаживаются, а при определенных условиях
аэродинамическая нелинейность вновь становится мягкой (см. рис. 128).
Вышесказанное проиллюстрируем на двух простейших
примерах. Рассмотрим задачу о кручении тонкого
прямоугольного в плане крыла, установленного под нулевым углом
атаки. Для упрощения будем считать крыло плоским,
принимая, что смещение линии аэродинамических фокусов
относительно оси жесткости достигается за счет наличия
предкрылка, не принадлежащего к несущей конструкции крыла
(см. рис. 127). Примем, что явление флаттера для этого
крыла исключено и что изменением энтропии при переходе
через ударную волну можно пренебречь. Уравнение кручения
крыла запишем в виде
2х
О J #*_ _L_ Poo (Ь + Хо)Х0 '
ddz2
2* T
= 0, (4.112)

§ 4.12] НЕЛИНЕЙНЫЕ ЗАДАЧИ В ТЕОРИИ АЭРОУПРУГОСТИ 285
где 6 — угол закручивания, GJd — крутильная жесткость.
Критическое значение числа Маха, определяемое из
линеаризированного уравнения
GL 4^ + *рт (Ь + *0) ЧМЪ = О
d dz2
и краевых условий
db (/)
как нетрудно показать, равно
= 0,
М=~:
GJd
Приближенное решение нелинейного уравнения (4.112)
будем искать в виде ряда по собственным функциям
соответствующей линейной $
задачи о,ЗОг
=S//
sin
(27-1)**
J=i
2/
(4.113)
Результаты
вычислений для частного случая
с одним членом ряда
(4.113) приведены на
рис. 129. Ветви, которым
соответствует dd/dM < 0,
очевидно, неустойчивы.
При достижении
критического значения М^ =
=9,15 происходит
скачкообразное закручивание
крыла до некоторого
значения bk, величина
которого лежит уже в области
срывных углов атаки (см.
найдена быть не может.
Для оценки влияния начальных неправильностей
предположим, что крыло имеет начальное закручивание по закону
0 = ео sin 5 *
Рис. 129.
рис. 128) и из уравнения (4.112)

286 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
Соответствующее уравнение получается из (4.112), если
внутри квадратных скобок 6 заменить на 0о + 6. Результаты
вычислений представлены также на рис. 129. Обратим
внимание на значительное снижение критического числа М^ при
наличии начальных эффектов; при 60 = 0,01/?#д критическое
число составляет М# = 8,2, т. е. на 10,5% ниже верхнего
критического значения. Для закрученного крыла при 0о =
= 0,02 рад снижение составляет уже около 21%.
Рассмотренный пример характерен тем, что
геометрическая нелинейность здесь отсутствует (точнее, она
.пренебрежимо мала). Такую же ситуацию мы будем иметь и для
Рис. 130.
других элементов консольного типа в потоке газа, для
которых граница области устойчивости является «опасной».
Для реальных конструкций такого типа явление
неустойчивости может наступить при скорости, меньшей, чем
найденная на основе линеаризованной теории критическая скорость
для идеализированной конструкции. Напротив, для обшивки,
тангенциальные деформации которой стеснены вследствие
взаимодействия с подкрепляющими элементами, типичным
является преобладание геометрической нелинейности.
В качестве простейшей модели обшивки рассмотрим
бесконечную пластину, лежащую на упругом основании и
обтекаемую потоком газа (рис. 130). Вопрос о перенесении
результатов на пластину конечных размеров оставим открытым.
Уравнение возмущенного движения пластины имеет вид
4-
/>оо[
1 4-
1 (dw , *jdw\~\
~ "7)7" i u лТ"
2соо \ dt
дх /J
-А=0, (4.114)

§ 4.12] НЕЛИНЕЙНЫЕ ЗАДАЧИ В ТЕОРИИ АЭРОУПРУГОСТИ 287
где k — жесткость основания, Nx — осевая сила в пластине,
равная х
N^ = No + W;f [/^Wf-l]dx, (4.115)
о
Хх— некоторая характерная длина (в дальнейшем — длина
полуволны), с — некоторый коэффициент жесткости,
характеризующий сопротивление уменьшению длины пластины. Он
изменяется в пределах
А . ^ Eh
и позволяет оценить влияние геометрической нелинейности
на поведение пластины.
Из рассмотрения линеаризованной задачи легко найдем,
что критическая скорость равна
"•-^v['+5 *&&?]• <4"6'
где V (кх, Ху) и &0(кх, \у) — фазовая скорость
распространения упругих волн и собственная частота пластины,
зависящие от длин полуволн Хх и X как от параметров,
o0(X^, Xy) — декремент затухания собственных колебаний
пластины в вакууме. Существуют некоторые пары значений \х
и Ху, соответствующие минимуму выражения (4.116).
Заметим, что линеаризованное уравнение допускает частные
решения вида
w(x, у, t) = Asin^s\n(Qt — ™). (4.117)
Это решение остается точным также и в том случае, когда
учитывается одна лишь геометрическая нелинейность, а
аэродинамические силы линеаризуются. Ограничимся учетом
нелинейных членов третьего порядка. Разлагая радикал в
формуле (4.115) в ряд, удерживая члены не выше второго
порядка и подставляя результат в уравнение (4.114),
получим:
DV2V2^
\
д2т .
О
, , , d2w , dw %p^/dw dw\

288 устойчивость упругих тел в потоке газа [гл. 4
Поскольку с учетом (4.117)
Г /dwV , теМ2
J Ы dx = nrx>
о
то для нахождения амплитуды А и частоты Q получим
уравнения:
(4.118)
Требуя, чтобы А Ф О, из второго уравнения найдем:
JL=JL
где &0(\г, Ху)— частота собственных колебаний пластины
в вакууме, U^(kx, Xy) — критическая скорость (4.116). Отсюда
из первого уравнения
*=l/Wh^ (4Л,9)
где
2\ХШ0 У р0 '
Вычисления по формуле (4.119) показывают, что если
коэффициент жесткости с имеет максимальное значение (это
означает, что длина проекции изогнутой пластины на
направление оси Ох остается неизменной), то амплитуда А имеет
порядок h даже при двукратном превышении критической
скорости U^.
При учете аэродинамической нелинейности решение (4.117)
перестает быть точным. Однако приближенное решение можно
найти, если отбросить члены, содержащие тригонометрические
функции дуг, кратных по отношению к Ш— тгдг/Х^.
Например,
(т?+"?)Г»Иа-?Мв<-?)+-"

§ 4.13] НЕЛИНЕЙНЫЙ ФЛАТТЕР ПОЛОГОЙ ОБОЛОЧКИ 289
Первое уравнение (4.118) остается без изменения, а второе
запишется в виде
тг)х
Ройе2 +
%
tiU\ 3
X
X J
х/?оо(Х+1)
12с*
:0.
Результат решения уравнений для некоторых частных
данных показан на рис. 131. Характер решения зависит от
h
(О
ом
0,5
ш
У
s-o^
\S = 4,05
\\
и
и
^-S=5,70
- S=8,Q5
0,5
Рис.
W
131.
1,5
2,0
LL
"*
параметра жесткости 5. Если 5 = 8,05 (при выбранных
данных это соответствует верхнему пределу для с), то мы имеем
«мягкое» возбуждение бегущих волн. При снижении 5 имеет
место переход к жесткому возбуждению.
§ 4.13. Вывод уравнений нелинейного флаттера пологой
оболочки при больших сверхзвуковых скоростях
Рассмотрим вначале равновесие упругой оболочки,
опирающейся на прямоугольный в плане контур и обтекаемой
с одной стороны сверхзвуковым потоком газа с
невозмущенной скоростью Ut которая направлена параллельно оси Ох0

290 устойчивость упругих тел в потоке газа [гл. 4
(рис. 132). Оболочку будем считать достаточно пологой,
чтобы метрику ее срединной поверхности можно было
приближенно отождествлять с евклидовой метрикой. Будем
пользоваться обычными гипотезами нелинейной теории
упругих оболочек1), считая справедливой гипотезу Кирхгофа —
Лява и полагая прогибы оболочки сопоставимыми с ее
толщиной /г, но малыми по сравнению со сторонами контура а
Рис. 132.
и Ь. Предположим, что для оболочки задано распределение
температуры Г, которое можно представить в виде двух
слагаемых:
T=TQ(x,y) + zQ(x,y). (4.120)
Здесь 7^ (л;, у)— температура на срединной поверхности,
®(*» У) — градиент температуры в нормальном направлении2),
х и у— криволинейные координаты, отсчитываемые вдоль
линий кривизны недеформированной срединной поверхности,
z — координата, отсчитываемая по нормали к срединной
поверхности во внешнюю сторону (к обтекаемой стороне).
Допустим, наконец, что механические свойства материала
оболочек зависят от температуры Т, однако они
незначительно меняются при переходе от одной точки оболочки
!) В оль мир А. С, Гибкие пластинки и оболочки, Гостехиз-
дат, 1956; М у ш т а р и X. М., Г а л и м о в К. 3., Нелинейная теория
упругих оболочек, Таткнигоиздат, 1957.
2) Определению функций Т0 и О посвящена работа:
Болотин В. В., Уравнения нестационарных температурных полей
в тонких оболочках при наличии источников тепла, Прикл. матем.
и мех. 24, № 2 (1960).

§ 4.13] НЕЛИНЕЙНЫЙ ФЛАТТЕР ПОЛОГОЙ ОБОЛОЧКИ
291
к другой. Это допущение оправдано, если неоднородность
температурного поля в пределах оболочки невелика, и может
быть снято путем очевидного обобщения предлагаемых
в дальнейшем уравнений.
Компоненты тензора деформаций в каждой точке оболочки
ех, еу и еху связаны с компонентами тензора напряжений
ох, о и а зависимостями:
р-К — FO + a^ ]
~х ? \~х г~у
~ху
Е а*У'
(4.121)
где a — коэффициент температурного расширения. Обратные
зависимости имеют вид
СХ = Г=Г?2 1ВХ + PSy — С1 + Р) а7Ь
0-„ =
ху~1 + р**У'
(4.122)
Наряду с компонентами е^, еу и exv введем также осред-
ненные по толщине h компоненты гх> еу и еху. Их можно
рассматривать как компоненты деформации срединной
поверхности:
Л/2
~ху
1
"~ h
1
~~ h
1
— h
I
-hfl
Л/2
/
-Л/2
Л/2
exdz =
еу dz —
exydz =
1
= Eh
1
= Eh
_ 1-
{Nt — rNJ + aT»
(Ny-pNx) + oiT0,
¦N
xy
-Л/2
(4.123)

292 устойчивость упругих тел в потоке газа [гл. 4
Здесь Nx, Ny и Nxy
сечения оболочки
усилия, отнесенные к единице длины
т. е.
Л/2
Л/2 /г/2
Nx = f cxdz, Ny = f aydz, Nxy= f
axydz.
-Л/2 -Л/2 -4/2
С другой стороны, для компонентов тензора деформаций
ех, е и е имеют место чисто геометрические соотношения:
— да
dv
kxw
дх I
и I I tdw\2
~ху
1 (да . dt/\ ,
1 дш дге>
2"d7d7
(4.124)
При этом и(х, у), v(x, у) и w(x, у) — тангенциальные
и нормальные смещения точек срединной поверхности, kx
и ky — главные кривизны недеформированной срединной
поверхности, которые мы будем считать положительными, если
центр кривизны лежит с внешней (обтекаемой) стороны.
Исключая из формул (4.124) смещения и и v, получим
условие совместности деформаций:
дЧл
д2^
дЧ
ху
ду2
дх2
_( d2w У
— \ дх ду )
дх ду
d2w \2 d2w d2w
дх2 ду2
, d2w
, d2w
, дх ду i
Подстановка формул (4.123) в условие (4.125) дает:
1 /d2Nx „d2Nxv . d2Nv
(4.125)
Eh \ ду2
d2Nxv
дх ду '
fi /d2Nr
дх2
¦)-
d2N
xy
d2N,
Eh \ ду2
\ дх ду
дх ду
ду'
'-)+*
d2w \2
г
Ч*Т0 =
d2w
d2w d2w ,
~дхт 'ду2 — x ~ду2
, d2w
У ~дхт'
Выразим, как обычно, усилия в срединной поверхности через
функцию Ф (х, у):
д2Ф ЛГ д2Ф хт д2Ф
Nv
ду2
N..
дх2
*У дхду '
(4.126)

§ 4.13] НЕЛИНЕЙНЫЙ ФЛАТТЕР ПОЛОГОЙ ОБОЛОЧКИ 293
Тогда уравнения равновесия
dNr
dN
ху
дх
ду
= 0,
дМ
ух
дх
L = o N =N
ду U' У* 1У/ху
будут автоматически удовлетворены, и мы получим первое
уравнение, связывающее функцию прогиба w(x, у) и
функцию Ф(х, у):
^V2V2O + aV270 =
Eh
_( d2w V
~~\дхду)
d2w
d2w d2w b
~dxT'dy2'~flk~dy2~
d2w
v,-^. (4Л27)
Чтобы получить второе уравнение, необходимо рассмотреть
^*х
Рис. 133.
уравнения равновесия, связывающие поперечные силы Qx
и Qy с нормальной нагрузкой q (рис. 133):
dQx t dQy ( ат [и ( d2w\
дх2 )~т~
d2w \ , 0хт д2^
dx
^
дл: ду
0,
а также уравнения, связывающие поперечные силы с
изгибающими моментами пгх и пгу и с крутящими моментами
/я
*у ¦
/я
ух*
Q* =
dm»
dm
ху
дх
ду
Qy =
dm
ух
dmv
дх
ду '

294
УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
Исключая отсюда поперечные силы, получим:
№тх
д2т
ху
d2mv
дх2 ' дхду ' ду2
+
+Nx(l
^2) + ^(V
ду2 j^^xy дхду
-q = 0.
(4.128)
Выразим теперь моменты mxt ту и тху через функцию
прогиба w(x, у). Заметим, прежде всего, что
Л/2 Л/2 Л/2
Шг= Гoxzdz, ту = )Gyzdz, mxy= iaxyzdz. (4.129)
-Л/2
-Л/2
-Л/2
Сюда нужно подставить выражения (4.122). Замечая, что
в силу гипотезы Кирхгофа — Лява и формулы (4.121)
d2w
дх2
d2w
*ху *ху
ду2
д2т
дхду '
-агв,
¦olzQ,
и используя соотношения (4.123), подстановкой в формулы
(4.129) найдем:
[д21ю d2iso /-% "I ^
тху = — D(l — ц)
d2w
дх ду
(4.130)
(здесь D — цилиндрическая жесткость). Введем теперь
выражения (4.130) и (4.126) в уравнение (4.128):
DV2 V2w + а (1 + ц) DV26 =
д2Ф / г I d2w \ , д2Ф
_ д2Ф /, , д2?еЛ
~~ ay2 р*~Г" d*2/
д*2
^У +" ду2 J дхду дхду "i~?'
(4.131)

§ 4.13] НЕЛИНЕЙНЫЙ ФЛАТТЕР ПОЛОГОЙ ОБОЛОЧКИ 295
Уравнения колебаний получим, вводя в уравнения (4.131)
члены, учитывающие силы инерции, диссипативные силы и
давление газа:
' — "~ n h ~дГ2 ;"°"& ~~di
, d2w , dw .
(p0 — внутреннее давление). Влиянием же тангенциальных сил
инерции будем пренебрегать. Это может быть сделано
практически всегда, так как собственные частоты тангенциальных
колебаний тонкой пологой оболочки всегда достаточно высоки
по сравнению, по крайней мере, с несколькими низшими
собственными частотами нормальных колебаний. Что касается
давления газа, то мы его будем вводить по формуле (4.78),
удерживая в разложении три членах). В результате придем
к системе уравнений:
DV2V^ + a(l+lx)DV29 + p0^ + Po^^ =
— (ь . d2w\ д2ф i (и . d2w\ д2Ф 0 д2т д2Ф .
— р*"+" дх2 I ду2 "Т"\Лу "Г" ду2 ) дх2 дхду дхду ~+~
/dw TTdwi\ r.(%+l)Poo/dw rTdv>i\2
+ р-р~-*рА-эг+и-дъ) 4—Ы+иж-0) -
( dw dwx \3
12
g^V2V^+aV270 =
/ d2w \2 __
''[дхду)
d2w d2w , d2w b d2w (> . o9\
dx2 ^~**~df'~~IZy~dxT' (*A6Z)
где wl = wQ-\-wt w0 = w0(xQ, у)— уравнение недеформиро-
ванной срединной поверхности.
Заметим, что если средняя температура Т0(х, у) и
градиент в(х, у) постоянны по всей оболочке или являются
линейными функциями координат срединной поверхности х,
у, то температурные члены в уравнениях (4.132) исчезают.
1) Уравнения (4.127) и (4.131) также соответствуют учету
нелинейных членов не выше третьей степени по отношению к w.

296 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
При этом, однако, температурные члены остаются в
граничных условиях. Вопрос о граничных условиях будет рассмотрен
несколько ниже, в связи с обсуждением принятого метода
решения.
§ 4.14. Приближенный метод решения уравнений
Сложность системы уравнений (4.132) побуждает искать
пути приближенного ее решения. Ниже будет изложен один
из приближенных методов!). Его преимущество состоит,
в частности, в том, что он позволяет учесть нелинейные
граничные условия для тангенциальной деформации.
Представим функцию w(x, у, t) в виде разложения
по функциям Wj(x, у), удовлетворяющим всем граничным
условиям для нормального прогиба,
п
™ (х, у, t) = 2 fj (t) wj (x% у). (4.133)
/ = i
Граничные условия для нормального прогиба
формулируются, как обычно. Если край л; = 0 полностью заделан, то
Ч =4т| = °- (4Л34>
\х=0 их Це = 0
Если край х = О свободно опирается на абсолютно жесткий
в нормальном направлении контур, то, кроме прогиба,
обращается в нуль также изгибающий момент тх. Учитывая
соотношения (4.130), получим:
w
d2w , d2w , /i . \nl a
= -^ + ^^ + а(1+^)в =°-
Наиболее общий случай представляет опирание края
на стержневой элемент (стрингер или шпангоут), обладающий
изгибной жесткостью в нормальном направлении, равной В,
и крутильной жесткостью С. Для этого случая условия
]) Болотин В. В., Нелинейный флаттер пластин и оболочек,
Инж. сборн. 28 (I960). В менее общей форме он был использован
в работе: Болотин В. В., Г а в р и л о в Ю. В., Макаров Б. П.,
Ш в е й к о Ю. Ю., Нелинейные задачи устойчивости плоских
панелей при больших сверхзвуковых скоростях, Изв. АН СССР ОТН,
«Механика и машиностроение», № 3, 1959.

§ 4.14] ПРИБЛИЖЕННЫЙ МЕТОД РЕШЕНИЯ УРАВНЕНИЙ 297
на краю х = О принимают вид
d4w I / дтху \ I
BwLo~\Q*+-*r)l.o'
п д3х I |
Подстановка сюда выражений для пгх, тху и Q^. дает:
При опирании на один элемент двух соседних панелей
краевые условия должны быть обобщены. Заметим, что при
градиенте температуры в, отличном от нуля, краевые
условия, кроме условия (4.134), оказываются неоднородными.
Это затрудняет подбор функций wAx, у), удовлетворяющих
необходимым условиям.
Допустим, что система функций Wj(xt у) построена.
Тогда, подставляя ряд (4.133) в правую часть второго
уравнения (4.132), получим уравнение, линейное относительно
функции усилий Ф(х, у, t) (время рассматривается при этом
как параметр). Его общее решение, как обычно, содержит
произвольные функции, распоряжаясь которыми можно
удовлетворить граничным условиям для функции Ф(л:, у, t). Однако
условия работы оболочки совместно с подкрепляющими
элементами обычно настолько сложны, что точная формулировка
граничных условий для Ф(х, у, /) лишена практического
смысла. Достаточно сформулировать эти условия «в среднем»,
характеризуя взаимодействие оболочки с окружающей
конструкцией некоторыми осредненными параметрами.
Представим приближенно функцию усилий в виде
Ф(*. у, t) = <bl(x, у, t) + ±(Nxy* + Nyx*-2Nxyxy). (4.135)
Здесь Ф1(х, у, t) — какое-либо частное решение второго
из уравнений (4.132), Nx, Ny и Nxy — некоторые параметры,
которые выбираются таким образом, чтобы условия для
функции Ф(лг, у, /) были удовлетворены «в среднем». Весьма
удобно в качестве функции Фг (х, у, t) взять выражение,

298 устойчивость упругих тел в потоке газа [гл. 4
удовлетворяющее условиям:
ь ъ
fw-Ldy==f
д2Ф,
и.
f
д2Ф{
дх2
dx
у = 0
и,
I
ду2
д2Ф{
дх2
dy = 0,
dx = 0,
у = Ь
J дхду \XsQ У J
= f дЩ
J дх д
} (4.136)
дхдУ \х=а
dy.
и
д2Ф{
dx=0.
у=Ь
дх ду
о - v - 0
Тогда параметры Nx, Ny и Nxy приобретают смысл осреднен-
ных вдоль кромок усилий:
ъ
Ь J ду2
о
а
а ./
О
а
a J
ду2
д2Ф
дх2
д2Ф
л:=0
dy=Nx
dx = N„
(4.137)
у = 0
дх ду
dx = N
у = 0
ху
В дальнейшем будем полагать, что условия (4.136)
выполняются и, следовательно, соотношения (4.137) имеют место.
Наряду с осредненными усилиями введем осредненные
относительные сближения кромок и относительный сдвиг:
а Ь
О О
а Ь
A*=-i/f^dxdy<
о о
а Ь
dv
'ху
mff(i?+iE)dxd>-
о о
(4.138)

§ 4.14] ПРИБЛИЖЕННЫЙ МЕТОД РЕШЕНИЯ УРАВНЕНИЙ 299
Краевые условия для функции Ф(х, у, t) могут быть теперь
представлены в виде
N.
¦с А'
N„
СА-
^у-^Лг (4Л39>
где сх, с и с —некоторые коэффициенты,
характеризующие сопротивление подкрепляющей конструкции сближению
кромок и искажению углов у контура, на который опирается
оболочка. Этих условий достаточно для отыскания трех
параметров ЛЛ^., Ny и Nxy.
Чтобы использовать условия (4.139), нужно выразить
производные от перемещений а и v, входящие в
формулы (4.138), через функции Ф и w. Из соотношений (4.122)
и (4.124) найдем:
Eh K у
1 (dw\2
ду
_L / df | ди \
2\дх~1 ду)'
-^,) + аГ0 + ^-4(^)2
1+fX
1 dw dw
2~дх~ду
Nxy-4r^r^r
(4.140)
После того как параметры Nx, Ny и Nxy найдены,
выражение (4.135) и ряд (4.133) подставляются в первое
из уравнений (4.132). Записав это уравнение коротко в виде
%(w) = 0, потребуем, чтобы оно удовлетворялось
приближенно в смысле метода Галеркина:
J* f%(w)wj(x, y)dxdy = 0 (y = l, 2,
п).
о о
Отсюда получим систему обыкновенных дифференциальных
уравнений относительно коэффициентов ряда (4.133). Если
в качестве функций Wj(x, у) взять формы малых
собственных колебаний панели с собственными частотами 2у, то
система уравнений принимает вид
^ -H^r + 2/// + /Wi. /2 /«• М) = 0 (4.141)
dt*
(7=1. 2,
")•

300 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
Здесь Fj — некоторые, вообще говоря, нелинейные
функции fv /2, ..., /я, зависящие от параметров панели и
от числа М. Полученная система уравнений допускает более
легкое аналитическое исследование, чем исходная система
уравнений (4.132).
В дальнейшем целесообразно расчленить решение задачи
на два этапа, на первом из которых решается задача о
температурном выпучивании панели, на втором — задача о флаттере
выпученной панели. Рассмотрим вначале первый этап. Пусть
w = wT(x, у), Ф = Фг(л:, у). Тогда вместо (4.132) получим:
DV>V2wT + а (1 + jx) D V28
d2wT\ д2Ф
— 2
д2тт
дх2 J ду2
?+('
d2wT\ д2Фт
~ду2)~дхт'
д2Фг
-Ро-
хрооМ
д (wQ + wT)
дхду дхду ' ^ усо ~yaj"x дх0
х(х+1) рооМ2 [d(w0 + wT) |2
rd(W0 + WT)\2
I дх0 J
х(х+1)РсоМ3
12
\d(w0 + wT)
y2V2<Dr4-aV270
gg-v-v^r-r-av^o-
/ d2wT \2 d2wT d2w7
=(
дхду )
дх2 ду2
— k.
d2w7
ду2
дх0
k
d2wT
У дх2
(4.142)
Если известно поле температур 7(х, у), то, представляя
нормальный прогиб в виде ряда
wT(x, у)
: *Ef*Wj(X, У)
(4.143)
и применяя метод, описанный выше, найдем приближенные
выражения для функции Фт(х, у) и прогиба wT(x, у).
Заметим, что решение задачи о температурном выпучивании
упрощается, если предположить, что по толщине панели
температура остается неизменной и что температура Т0(х, у)
является линейной функцией координат. В этом случае
температурные члены из уравнений (4.142) вообще исчезают,
остаются лишь в краевых условиях для Фг.

§ 4.14] ПРИБЛИЖЕННЫЙ МЕТОД РЕШЕНИЯ УРАВНЕНИЙ 301
Возвратимся к уравнениям (4.132). Полагая в первом из
них w = wt-\-Wp% Ф = Фт-\-ФР и учитывая, что Wt и Ф^
удовлетворяют уравнениям (4.142), получим:
2
ду2 дх2 ^ дх2 ду2
д2Фт d2wp д2Фр Г д2 (wT + wp)
дхду дхду ' ду-
1Л^ ЗР J +
a2*F
Л*2
d2 (t»,. + wp) 1 д2ФР <?2 (wr + wP)
d2^ / x/?^ \ dwF dwF
0 WF I *-P5o \ owF
: - Po* -gr - K8+^rj "5Г - *^ dXo
x (x + 1) pcoAl2 Гоаю^ d 0*0 + WT) _l |^/A21
^o J
4
da^ d (w0 + wT) (dwF\2l
дхп дх* ' \ длгп
2
+
% (% + 1) pooMз L <^ Г d (^o + «у)'
12 1 dx0 L dx0
(из членов, учитывающих аэродинамическое демпфирование,
мы сохранили лишь наиболее существенный линейный член).
Второе уравнение принимает вид
1 / d2wF\2 d2wFd2wF
^2ф— (a^f)-
Eh v v r~~ \дх ду I дх2 ду2
d2wr\ d2wp l . d2wT\ d2wF _ d2wr d2wF
Г/ d2wT\d2wF I d2wT\d2wF d2wr
[\k*Jr~dxir) Tty*"^~\ky Jr~dy2~) ~dx~2 2dx~fry
дх ду дх ду
(4.146)
Рассмотрим теперь условия на контуре:
Nx = схЪ?, 7v; = c$% NFxy = cxyKFxy. (4.147)
Средние значения усилий и смещений определяются по
формулам (4.137) и (4.138) с заменой Nx на NFx, Ny на NF
и т. д. При этом и? —и — иг, vp^=v — vT. В результате
краевые условия (4.147) оказываются выраженными через
Wf(x, У, 0 и Фр(х, у, t).

302 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
§4.15. Панель, опертая по всему контуру
Допустим, что первая часть задачи — исследование
температурного выпучивания панели —решена, т. е. wT(x, у) и
Фг(#. У) известны. Займемся второй, более трудной частьк>
задачи. Если температурный прогиб задан в виде ряда (4.133),
то динамический прогиб при флаттере также целесообразна
искать в виде
п
wF(x, у. 0= S fFj(t)wj(x, у). (4.148)
У = 1 J J
Подставляя этот ряд в правую часть уравнения (4.146), мы
найдем его интеграл типа (4.135), содержащий три
постоянных Nx, Nyi Nxy, значения которых определим из условий
на контуре (4.147). После этого ряд (4.148) и найденное
выражение для Фр(х, у, t) подставляются в уравнение (4.144),
которое удовлетворяется приближенно, в смысле метода
Галеркина. Результатом этих преобразований должна явиться
система обыкновенных дифференциальных уравнений типа
(4.141).
В качестве примера рассмотрим случай опертой по кон-
туру панели, приняв форму выпучивания панели в виде
v>t(x, y) = /rsin-^sin-^-. (4.149)
Для динамического прогиба возьмем представление в виде
двух членов ряда
wF (х% у, t) = fx (t) sin — sin -y-+ /2 (0 sin ~T sin b #
(4.150)
Судя по результатам, которые приближение (4.150) дает для
линейной задачи (§ 4.10), его можно использовать и для
предварительного количественного анализа нелинейной задачи.
Подставив выражение (4.150) в правую часть уравнения (4.146),
получим:
фг (х, у, t) = Фг (*, у, t) + ~ (Nxy2 +~Nyx^ - 2Nxyxy)t
(4.151)

§ 4.15] ПАНЕЛЬ, ОПЕРТАЯ ПО ВСЕМУ КОНТУРУ 303
где
+ (2/r+/')/'cos^ + (/r+o/l)/2cos^+4cos —
1 8 а ' 9 а ' 32 а
. ^(/r + /1)/2 их 2т:у (fr + fi)f2 Зтсд: 2*у
-1- — XJ—±cos — cos —г^ — ' , /,чо2cos — cos —г1-¦
(i + V)2
(9 + V)2
(2/r+/i)/i + 4/2 2*у , Wifkx + ky)^ и %х 9 пу
8<?2
-cos
*2(1+?2)2
sin —sin -Г- +
/7 А '
4*2(?2^ + 4*у)/2 . 2« .
¦ sin sin
т2 (4 4- <р2)2
*У 1
Здесь, как и ранее, используется обозначение у = а\Ь.
Выразим теперь NFX, Ny и Nxy через Ф/? и подставим их
наряду с выражением для wF в формулы (4.138):
Д* = -
i;=.
(Nx —plfy) 4A(fkx+ky)(9*-ix)
Eh
71* (1 + ?2)2
4*,/i
-+g2?[<2/r+/i>/i + 4/21.
Wy-pNx) 4A(<(*kx + ky)(\-w*)
Eh
*2(1 + <P2)2
4^y/l Я2
[(2/r+/i)/i+/n.
TF
Выражение для сдвига Дху не вычисляем, ибо в дальнейшем
пренебрегаем сопротивлениями подкрепляющих элементов
перекосу контура оболочки в плане, полагая сху = 0.
Используя краевые условия (4.147), получим:
N.
п-к а Л(2/г + /1)/1 + 4/1-^/1 +
8«2(1-ц2Р,Ру>
+ рРу?* [(2/r + /1)/,+/22 + 5yA/i]}.
^У = 8^(1-t^y) {^ [(2/r+/1)/1+/i+5/A]+
1(4.162)

304 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
Для сокращения введены следующие обозначения:
1
1 _l_ ^ * 1 | Eh
h
cyb
а также
Я.
32a Г ? (<P%* + *y) (<P2 — I1)
32a Г
ти4Д L
(l + 'f2)2
У ~~ ^h [ (1 + ?2)2 ХУ
*r = ^a» xy = Vе
]•
(4.153)
Теперь перейдем к уравнению (4.144) с правой частью
(4.145). Будем искать его приближенное решение по методу
Галеркина, для чего подставим в него выражения (4.149),
(4.150), (4.151) и (4.152) и, кроме того, выражение для
известной функции температурных усилий Фг(х, у). Потребовав,
как обычно, чтобы результат подстановки был ортогонален
к каждой из выбранных «координатных» функций, получим
систему двух обыкновенных дифференциальных уравнений
второго порядка, роль аргумента в которых играет время t.
Поскольку объем последующих выкладок быстро
увеличивается, введем на этом этапе некоторые разумные ограничения.
Ограничимся случаем цилиндрической панели, полагая:
X Xq ,
dwQ
дх
:0, kx = Q,
ky = const.
Далее, примем, что температурные сжимающие усилия
равномерно распределены вдоль кромок, а сдвигающие усилия
отсутствуют:
Nl = — Px = const, Л/у = — Ру = const,
Уравнение (4.144) принимает вид
d2Wr
п п d2wF l %p^ \ dwF
+р.
d2wF
х дх2
d2wf
y~Jf
--27i(^)=0,

§ 4.15] ПАНЕЛЬ, ОПЕРТАЯ ПО ВСЕМУ КОНТУРУ 305
где через Jg'iiwp) обозначена совокупность членов:
^,(w) = — Щку
_[Nr^p^+Nfl^^+w^J^!l>]+
dwF *(*+l)/>00Af2r dwTdwF (dwrfl
+ *РсоМж+ 5 [2жт^+Ьл~)\ +
, *(*+!)/W^3 Г JdwT^dwF ~dwT (dwF\2 , /dwF\3]
|_ \ (JJC I (JЛ UJC \ (JJC I \ (JJC l J
12
Уравнения метода Галеркина получаем в следующем виде:
а Ь
d2/, , „4?
dt
d<.-f-»^r+Q?/i-
ab^h
/ / J?!Сяу) sin — sin^dJt^Ty^O,
о о
^~ + 8^ + У2/2~+~^
/ / J^iC^sin-^ sin^djtflTy = 0.
о о
Здесь Sj и Q2 — соответствующие парциальные частоты
собственных малых колебаний плоской панели, т. е.
На подробностях дальнейших вычислений, хотя, по существу,
и элементарных, но весьма громоздких, мы не имеем
возможности останавливаться. Приведем окончательные результаты.
Если ввести безразмерные перемещения и безразмерное время
/:
/i
/г
<i = T' ^ = f- b = i. x = Q^
и безразмерные параметры
— г—- m .*
Qj ! / i *М О ^ лГ D )
Ж— =v,
а
4*д
?oh2Q20
' 16Ро^20 '
(4.154)

306 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
то уравнения принимают вид1)
dz2 ] * dz
-*§+«*.+
+ /cf-4vC2 + |v2(/+l)(C1+Cr)C1 +
+
56.
45
'¦ (x + 1) C22 + v3?n (C, + Cr)2 C2 + v^l2q] +
16cp;
я. КЗ+<121)+4^ 5f(rfn+,ncr+,1^)C1+
(4.155)
rf2i.
rfT2
¦g-
dl2
dz
4+
+ K [1 V^ + 1 v2 <* + * > в + W + vft2iq +
+ ^'%2 (s+v) 1]+^ (C]2q + c^+
§ 4.16. Нелинейный флаттер плоской панели.
Решение в тригонометрических рядах
Если панель является плоской (х = 0) и температурное
выпучивание отсутствует (Сг-=0), то все члены в
уравнениях (4.155), которые содержат dik и eik, исчезают, а члены,
содержащие blk, упрощаются:
|^+^+ч+^[-4^+|^+1)ч+ '
+ f v» с/. + i)c?+^2 (*„Ч+*,&»)]+
+sc1(cnq + c12q) = o> [(4Л56)
16
ИХ2
-g'(§ + ^2 + ^[4vC1 + ^v2(x+i)C1!;2 +
+var, (*2lq+^)]+sc2 (Slq + c22q) = 0.
l) Явные выражения для коэффициентов этих уравнений можно
найти в работе: Болотин В. В., Нелинейный флаттер пластин и
оболочек, Инж. сборн. 28 (1960).

§ 4.16) НЕЛИНЕЙНЫЙ ФЛАТТЕР ПЛОСКОЙ ПАНЕЛИ 307
Здесь
bn = b2l--
~(*+1), ft12 = _^-(x+l).
Птг2
j22-
-12"
70
l+?4 +
2(Эх + 2?2^?у + ?4?у)
c21 = 4(l+'f4)-+
1 — №х?у
Cny '¦
[6 + cp4 +
1 - i*2My
2(16^ + 8^ЭЛ + Т4^)
1 — f^My
(4.157)
J
При обтекании пластины с двух сторон с равными
скоростями система (4.156) принимает более простой вид, поскольку
все квадратичные члены исчезают:
dz2 -t-g dz
-to^i-
4-v/c [-|-c2+v3(6„i:i+*,2C2)]+
H- SCi (спЙ -|- c12Ci) = 0.
+ v/C [-| Ci + v3 (?21Ci + &22C22)] +
(4.158)
Параметр /С принимает здесь значение, в два раза большее,
чем. ранее!). Критическое значение параметра v определяется
по приближенной формуле
-47cH-*i)>
(4.159)
1) Можно ожидать, что при одностороннем обтекании влияние
членов второго порядка будет мало по сравнению с влиянием
членов третьего порядка и, следовательно, уравнения (4.158) могут
рассматриваться как приближенное уравнение и для этого случая.
Это подтверждается анализом с применением метода малого
параметра (§ 4.17).

308 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
вытекающей из формулы (4.104), если учесть, что v/C=(3
в обозначениях § 4.10.
Будем искать приближенное решение системы (4.158)
в классе периодических движений с конечными амплитудами !)
Cj = Ах cos сот -\- Вг sin сот -f- . . ., С2 = А2 cos tox ~Ь • • • (4.1 60)
Здесь Аг, В1у А2, со— неизвестные постоянные; точками
обозначены члены, содержащие гармоники. Рассматривается
установившийся автоколебательный режим, и поэтому
начальная фаза несущественна. Подставляя (4.160) в
уравнение (4.158) и пренебрегая членами, содержащими гармоники,
получим систему уравнений:
(со 1 — со2) А1 -+- guBi — -j ЖА2 +
+ |"5Л1[с11(Л? + В?)-Ьс12л1] = 0.
(со? _ со2) Вг — ?чоЛ! +1 vS/C&n^HaBi +
+ ^SBl[cn(A\ + E§+^^41 = 0. J
о > (4.161)
((022_C02)^2 + |-v/C41 +
+1 v3/C^г [*21 (Л? + B?) + ?22Л22] + I
+ 45^2[c21(^ + j5i) + C22^1] = 0,
- ?чоA2 +1 v/Cft + ~ v3/C^i [ft21 (A\ + B\) +
+ -g- *22Л1] + ~ Sc2iA1A2Bl = 0. I
Приближенное решение этой системы может быть получено,
если предположить, что затухание достаточно мало. Тогда
!) Болотин В. В., Г а ври лов Ю. В., Макаров Б. П.
и Швейко Ю. Ю., Нелинейные задачи устойчивости плоских
панелей при больших сверхзвуковых скоростях, Изв. АН СССР,
ОТН, «Механика и машиностроение», № 3, 1959.

§ 4.16] НЕЛИНЕЙНЫЙ ФЛАТТЕР ПЛОСКОЙ ПАНЕЛИ 309
2 2
В\<^А\У A2~Ai, gBi<^A\. Пользуясь первыми двумя и
последним уравнением, можно выразить Av Bx и со через Л2,
после чего, подставляя найденные значения в третье
уравнение, получим разрешающее уравнение А(Л2) = 0, корни
которого находятся графически. На рис. 134 представлено
поведение функции Д(-тМ для панели бесконечного размаха при
Рис. 134.
v = v#. Для вычисления были взяты значения: К = 30,2,
?• = 0,05, х=1,4. При этих значениях vsH = 0,372.
Результаты вычислений для тех же данных приведены
на рис. 135 и 136. Наиболее интересным результатом этих
вычислений является то, что при достаточно малых [3 (в
рассматриваемом примере это имело место уже при ^ = 0,4)
периодические движения возможны при v < v#. Это видно
уже из рис. 134, где ветви кривой Д = д(-^-) уходят

310 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [гл. 4
& 5
м
j?t
0,ак
u=
№
hy
0 0,25 0,5 0,75 1,0 1,25
v
Рис. 135.
4
Ю
-ю
\ 0,i
W*
}5 О,.
h=0 /
\BX=0J25
5^
fix-0.125
г0,1
|А=«
>5
fix = 1.0
25
V
К
Рис. 136.

§ 4.16] НЕЛИНЕЙНЫЙ ФЛАТТЕР ПЛОСКОЙ ПАНЕЛИ 311
в верхнюю полуплоскость при значениях фх ^ 0,4. Вопрос об
устойчивости найденных решений не рассматривался; однако
из вида кривых при $х <; 0,4 по аналогии с результатами
для нелинейной системы с одной степенью свободы можно
заключить, что эти решения неустойчивы (на том же
основании можно сказать, что ветви, идущие от точки v = v^
вправо, соответствуют устойчивым решениям). Этот вывод
был полностью подтвержден анализом соответствующих
уравнений на электронных моделирующих устройствах (об этом
см. ниже). Несомненно, что в области v < v^ физическая
система имеет устойчивые предельные циклы, обусловленные
всякого рода нелинейностями, появляющимися при больших
перемещениях (явлением срыва потока, резким возрастанием
диссипации энергии при выходе из упругой стадии
конструкции и пр.). Эти движения из используемых здесь
уравнений типа (4.158) не могут быть получены. Полученные
неустойчивые решения все же имеют ценность, поскольку
они указывают порядок возмущений, необходимых для того,
чтобы вызвать незатухающие колебания панели при докрити-
ческих скоростях. Наиболее чувствительными к начальным
возмущениям оказываются панели со свободно смещающимися
кромками ((3^ = 0). Поскольку наибольший прогиб пластины
имеет порядок Axhy то из рис. 136 видно, что для
возникновения опасных колебаний при v = 0,^ достаточно
возмущения порядка 0,5/г. Если v = 0,8vs{:, порядок необходимого
начального возмущения возрастет до h. npnv^^O^v^
необходимо начальное возмущение 2,5/г. С возрастанием жесткости
продольных связей чувствительность панели к возбуждению
флаттера при докритических скоростях быстро убывает, и,
начиная с некоторого значения, «жесткое» возбуждение
перестает быть возможным. Таким образом, совместная работа
панели как элемента конструкции оказывается весьма
благоприятным фактором. Для панелей, кромки которых
закреплены от осевых смещений, будет иметь место «мягкое»
возбуждение с медленным увеличением амплитуд в закрити-
ческой области. При этом установившиеся амплитуды будут
иметь порядок толщины панели (см. кривую на рис. 136,
соответствующую случаю $х=\).
Если ввести некоторые дальнейшие упрощения, то можно
получить конечную формулу для амплитуд Аг и А2.
Из четырех уравнений (4.161) выпишем первое и третье,

312
УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА
[гл. 4
(4.162)
опуская в них малые члены, содержащие gB\ и В\\
(а)1 _ ^ А1 _ | „КА2 + -f- v3/C^2 (bnfi + ^пИ2) +
+ |-5Л1(с1И? + с12Л1)=0,
(0)2 _ о)2) Л2 +1Ж А! + -i J К A, (b2lA\ + ?22Л22) +
+ ^SA2(c21A21 + C22aD = 0.
Два оставшихся уравнения учитывают эффект демпфирования.
Линеаризируя эти уравнения, получим:
(со2 — а)2) Вх — gu>Ai = О,
2
огкуда
Л2 =
2 v/C
Q 2 ,2
О О) COj
А-
На границе области устойчивости v = v^ и to = со^, где
2 , 2
2 «!+^2
Следовательно, А2^,— Av Можно ожидать, что это
соотношение сохранится и при v > v#, если разность v — v^
достаточно мала. Это предположение подтверждается также и
более точными расчетами (см., например, рис. 136).
Полагая в уравнениях (4.162) А2 = — Ах и исключая
частоту со, придем к формуле
где
Если обозначить
А\*
16 ^-Т('°2~1Й1)
~ 9 Sc0 — 43Kb0
~-h\ + b12 — bU—b\2'
- с2\ ~Г с22 С11 С12-
(4.163)

§ 4.16] НЕЛИНЕЙНЫЙ ФЛАТТЕР ПЛОСКОЙ ПАНЕЛИ
313
то формула примет весьма простой вид:
А = А(
/
¦Ш
(4.165)
В случае «мягкого» возбуждения на границе устойчивости
Vqo > v^; в случае «жесткого» возбуждения v^ < v#. На рис. 137
дано сравнение результатов, которые дает формула (4.165),
и результатов, полученных из уравнения Д(Л2/Л1) = 0, для
двух крайних значений коэффициента фх.
Л
15\
Z5
Г-
\
\л
•о
^А
л-
с
/ J
> /
0.2 0,3
Рис. 137.
ол
0,5
0,6
0.1
Для проверки полученных приближенных решений, а также
для выяснения характера их устойчивости система
уравнений (4.158) решалась на электронной математической машине
непрерывного действия1). Решение проводилось для панели
бесконечного размаха со свободно сближающимися кромками.
Задача состояла в том, чтобы выяснить характер
возмущенных решений при различных начальных условиях. Для всех
случаев принималось С! (0) = Сг (0) = 0, а значения Ci (0) и Сг (0)
изменялись таким образом, чтобы при заданных v и р,
установить границу между затухающими и неограниченно
возрастающими решениями.
1) См. работу, цит. на стр. 308.

314 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
На рис. 138 показаны границы областей устойчивости
для примера, рассмотренного выше. Область притяжения
тривиального решения располагается вблизи начала
координат; границы области в трех других квадрантах плоскости
^(0), С2(0) не определялись. Из графика видно, что с
приближением к критическому значению v^^ 0,372 размеры
области притяжения тривиального решения уменьшаются и
С, (о)
-Сг(о)
Рис. 138.
в предельном случае она исчезает. На том же графике
нанесены точки С1(0) = Л1, С2(0) = 42, соответствующие
значениям приближенного решения (4.160) при х = 0.
На рис. 139 и 140 приведены типичные решения вблизи
границы области устойчивости. Рис. 139 соответствует
случаю v = 0,3. При d(0) = — С2(0)= 1,15 начальное
возмущение, хотя и медленно, но затухает со временем. Небольшое
увеличение начального возмущения до ^(0) = — С2(0)= 1,22
приводит к резкому изменению характера колебаний: мы
имеем флаттерное движение с быстро нарастающими
амплитудами. Аналогичное поведение системы мы имеем при v = 0,15
(рис. 140). Переход от устойчивости к неустойчивости здесь
имеет место при увеличении начального возмущения со
значений Cj(0)=—^(0) = 4,3 до значений СХ (0) =—С2(0) = 4,4.

§ 4.16] НЕЛИНЕЙНЫЙ ФЛАТТЕР ПЛОСКОЙ ПАНЕЛИ 315
В заключение еще раз подчеркнем, что эти данные
относятся к цилиндрическому изгибу пластины со свободно
сближающимися кромками, т. е. к случаю, когда геометрическая
4
2
О
-2
-4
Рис. 139.
C,(t)
4
2
О
-2
-4
-6
Рис. 140.
нелинейность, обусловленная действием усилий в срединной
поверхности, отсутствует. Реальные панели обшивок
обладают значительной геометрической нелинейностью, и для них
характерно «мягкое» возбуждение флаттера.
* 1 1
III
С,(0)=-С2(0) = /,22
C,(oj = -C2(0) = fJ5
к/ '
? \
!?/ го

316 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
§ 4.17. Метод малого параметра для исследования
нелинейного флаттера
До сих пор для определения установившихся
периодических решений систем типа (4.141) использовались
упрощенные нестрогие приемы. Наибольший интерес представляет
поведение системы вблизи границы области флаттера. Теория
для этого случая может быть построена на основе метода
малого параметра. Запишем систему уравнений (4.141)*в виде
dKj . rfC
dx2
8^ + "%+*К^Ь,к(у)!.к =
= Vj&i. C2, ..., Ся. v) (7=1, 2 я). (4.166)
Здесь bjk — аналитические функции параметра v, Wj —
аналитические (нелинейные) функции обобщенных координат ?ft
и параметра v. Соответствующая линейная система
dKj dtj 2
п
+ v^S*y*WC* = 0 C/=l. 2> •••• п) (4.167)
допускает решение в виде С;- = Z еах. При достаточно малых v
все характеристические показатели а лежат в левой
полуплоскости комплексного переменного и тривиальное решение
системы (4.166)Сх := С2^ . . . =СЛ = 0 асимптотически
устойчиво по отношению к малым возмущениям. Значение
параметра v = v^, при котором два характеристических показателя
становятся чисто мнимыми, а остальные по-прежнему лежат
в левой полуплоскости, является критическим и соответствует
критической скорости панельного флаттера в обычной
(линейной) постановке этой задачи.
Будем искать периодические решения системы (4.166)
в окрестности критического значения. Положим, что v = v^-j-tjvj,
где Vj имеет тот же порядок, что и v, а т\ — малый
параметр. Принимая за порождающую систему уравнений (4.167)
ри v = v^ и вводя малый множитель ц при нелинейных

§ 4.17]
МЕТОД МАЛОГО ПАРАМЕТРА
317
функциях, получим:
п
= — V\K 2 *У*(v* + WJ С* —
k=l
п
- *Л Ц \b]k (v. + ijv,) - ?уй (vj] Cft 4"
+-nWj (^,r2 Cn v, + Vl) (y = 1.2 я). (4.168)
Учитывая, что при v = v^ порождающая система (4.167) имеет
два периодических линейно независимых решения
Су = ?*(*). ^ = <р^(т) (4.169)
с простыми характеристическими показателями а==±ш#
//7?0 I 7/770
(ш# — безразмерная частота флаттера, см. рис. 141, а), вводим
преобразование времени
и ищем решение нелинейной системы (1.168) в виде
<i W=^.iW+i(11,(t1)+^)(t.)+ • • •
^ Ы=^«1 W+W W+^ N + ¦ ¦ ¦

318 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
Здесь Л — амплитуда первого приближения, рг, р2, ...—
поправки к частоте колебаний 1).
Подставим эти выражения в уравнения (4.168) и приравняем
коэффициенты при одинаковых степенях малого параметра tj:
п ч
ш* -&+gw* -*Г+^+^К S *;* (v*) v» = °-
d2t<P d&
= - *Pi<A ~ПГ ~ PiS^A -^i - v,* J */Jk W cpftl -
1 * k=l
n
-V^S-^+^(^u. A<hi A%v \)
(/=1, 2 и)
(4.170)
и т. д. Первое уравнение удовлетворяется в силу
выбранного порождающего решения (4.169), второе и последующие
уравнения имеют вид
,d4f dtp 2{s) A is)
= чУ{а% #>. tf>..... сГ1},kpl P2t.... /v vlf tO
(y = l, 2, ..., n; 5=1, 2, ...)• (4.171)
Постоянные Л, /?lf /?2, . . ., ps должны быть выбраны таким
образом, чтобы уравнения (4.171) имели периодические
решения с периодом 2iu.
Пусть фу! (tj) и фу2 (тг) — периодические линейно
независимые решения системы, сопряженные по отношению к
системе (4.167) и соответствующие характеристическим
показателям ± т^ Условия периодичности системы (4.171) при
1) Введение малого параметра означает в данном случае, что
рассматривается поведение системы в достаточной близости от
границы области флаттера и что амплитуды нелинейных колебаний
считаются достаточно малыми. Параметр ч\ указывает на малость
соответствующих членов; после выполнения выкладок можно
вернуться к исходным уравнениям, положив т]=1, vj = v — v;...

§ 4.17] МЕТОД МАЛОГО ПАРАМЕТРА 319
5 = 1 имеют вид
п 2тс
2/^)(Д л, vlf т^^Л^О,
У = Ю
л 2тс
; = ю
Отсюда найдем постоянные Ли /?lf и решением системы будет
^0) = Axykl (тх) -f- !¦?) (тД где Лх — новая постоянная
(поправка к амплитуде порождающего решения), ^ (т2) —
какой-либо частный интеграл системы (4.171) при 5=1 и
найденных А и pv Подставляя эти выражения в уравнения
следующего приближения и используя условия периодичности,
придем к уравнениям для нахождения Ах и р2:
п 2%
2/ 4f(Al% A,, vle т^^А^О,
У = Ю
п 2тс
2/ ^(А. ft. vlf ^^2(^)^ = 0.
/=ю
Этот процесс может быть продолжен. При этом всегда
может быть выбрано такое достаточно малое значение
параметра т], при котором процесс будет сходящимся.
Для фактического построения условий периодичности
воспользуемся следующим приемом. Рассмотрим
определитель системы линейных уравнений, получающихся в
результате подстановки выражений сру2 = Zjx exp (пг) в
порождающие уравнения (4.170):
Д = | W - < + *".) *J* + \Kbjk (v.) |. (4.172)
Здесь bjk — символ Кронеккера. Ранг определителя (4.172)
равен, очевидно, п—1, поскольку система (4.170) допускает
единственное периодическое решение с простым
характеристическим показателем, равным I. Представим правые части
уравнений (4.171) в виде
У (А. С(Л tf> (Г4, А. А. ••-. Р„ vlt т,) =
- /$V + Я$е~'* + ... (4.173)
(/=1. 2 я; s=l, 2, 3, ...)

320 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
(точками обозначены члены, содержащие высшие гармоники).
Заменяя один из столбцов определителя (4.172) столбцом из
коэффициентов Фурье R{f}(j=\, 2, ..., п) и приравнивая
полученный определитель нулю:
(4.174)
(4.175)
Заметим, что если подставить в уравнения (4.171) другое
периодическое решение: ср^.2 = Zy2 ехр (—1ъг), то в силу того,
что коэффициенты R$ и R$ в формулах (4.173) являются
комплексно сопряженными, придем к определителю,
комплексно сопряженному по отношению к (4.174), т. е. к тем же
условиям периодичности (4.175).
Сделаем замечание о выборе порождающей системы.
Поскольку в практических задачах мера затухания g
оказывается обычно малой величиной, то может возникнуть мысль
принять за порождающую систему уравнений систему,
которая описывает поведение соответствующей недиссипативной
системы:
получим
условия
л<? = д</>
+/дГ
= 0,
после разделения действительной и
периодичности:
ReW = W(As.
\m&bs) = $\As.
0=1, 2
-1. Ps<
-1. Ps-
...)¦
v,) = 0, 1
v,) = 0
,
dKj
(4.176)
(y=l, 2, ..., n).
Если значение v достаточно мало, то все характеристические
показатели такой системы остаются чисто мнимыми. При
некотором значении v0 появляются две пары кратных
характеристических показателей, равных /со0 и —/со0 (см. рис. 141, б,
где показана лишь верхняя полуплоскость). Дальнейшее
увеличение параметра v связано с появлением характеристических
показателей с положительной действительной частью. В
большинстве работ по флаттеру упругих панелей при больших
сверхзвуковых скоростях влияние диссипативных членов не
учитывается; за критическое значение параметра (и соответственно
за критическую скорость флаттера) принимается то значение,

§ 4.17] МЕТОД МАЛОГО ПАРАМЕТРА 321
при котором впервые появляются кратные
характеристические показатели. Если попытаться, однако, приняв за
порождающую систему (4.176) при v = v0, искать периодическое
решение соответствующей нелинейной системы вблизи v = v0
в виде ряда по степеням малого параметра, то встретятся
серьезные трудности, характерные, по-видимому, и для
других флаттерных задач. При v = v0 порождающая
система (4.176) имеет двукратные характеристические
показатели ш0 и —ia)0, причем соответствующие им элементарные
делители являются нелинейными. Поэтому функциональный
определитель Пуанкаре при таком выборе порождающей
системы обращается в нуль.
Трудности будут преодолены, если, как это было сделано
выше, принять за порождающую систему (4.167).
Действительно, в этом случае при v = v* мы имеем простые
характеристические показатели (рис. 141, а). Если затухание мало,
то целесообразно сохранить в решении лишь те члены, которые
содержат g в степени не выше, например, первой. В
некоторых случаях возможно построение решений с «исчезающе
малым затуханием»: затухание учитывается при построении
порождающего решения и условия периодичности, после чего
вследствие малости оно выпадает из окончательного решения.
Своеобразная роль затухания и различие в поведении двух
систем, одна из которых рассматривается без учета
затухания, а другая — с исчезающе малым затуханием, отмечались
уже выше (§ 1.16).
Порядок вычислений поясним на примере системы
уравнений
(4.177)
описывающей колебания плоской невыпученной панели.
Исследуя характеристическое уравнение соответствующей линейной
системы
в4 + 2гв8 + (Ш2 + »2+^)02 + ^(ш2 + а)2)о4-
+ О)2ц)2_|-^2/С2 = 0)

322 устойчивость упругих тел в потоке газа [гл. 4
нетрудно установить, что эта система имеет периодические
решения с частотой (о^ = (а0 при v^^ v0-f~O(^2), где
о 2 2
6 0)2 — ^l
Vn=-: 7? , (0П
Эти решения имеют вид
cp„ = cosT1 + 0(g-2),
/¦
2 i 2
<йг + а>2
где
?21 = — C0S Tl — ЯС Sin Т1 + ° (?2)>
<Р 12 = Sin Т1 + ° (^2)'
?22 = — Sin Tl + ?X C°S ^l + O (g2),
V2.V
C02 + Q)l
(4.178)
В дальнейшем члены, содержащие g в степени выше первой,
вообще выписывать не будем !). В частности, будем считать,
что v*
Составим определитель (4.172) для системы (4.177):
Д =
•igb
Л
,К
i+^%
Отсюда условие периодичности (4.174) примет вид
(со2 - (og 4- tg%) /?Й> - 4 VCflff = 0, (4.179)
где /?2i и Rn ~~ коэффициенты Фурье для функций 4?i
и Wy при ехр(/тх). Если функции ч7р и Ч725) записаны
в действительной форме, то
W[S) = P[S) COS T! + Q^ Sin T! + . . . ,
^) = P^cosT1 + Q^)sinT1+...,
причем
RfS-
pl»)-iQ[*)
^21
MJ>-/(??>
(4.180)
]) При этом предполагается, что парциальные собственные
частоты достаточно удалены друг от друга. В случае кратных или
очень близких собственных частот роль затухания, как видно из
формулы для v$, становится весьма существенной.

§ 4.17] МЕТОД МАЛОГО ПАРАМЕТРА 323
Подставляя (4.180) в уравнение (4.179) и разделяя
действительную и мнимую части, получим:
оР+^ + яс/^-о. ( (4' >
Это и есть искомые условия периодичности.
Переходя к вычислениям, возьмем нелинейные функции чТх
и ч72 для случая плоской невыпученной панели:
+ vC2 (ftnC? + *12Й)] + -SCi (сцС? + c12®. I
^2 (C,. Cj. V) = vW [i| (x + 1) C,C2 + VC, (*2,C? + Ь22Щ +
+ 5C2 (c2iC? + с22ф. J
(4.182)
С учетом соотношений (4.178) ищем периодическое решение
в виде
Сх = A cos т, + ift1) + ч]2С<2> + ..., )
С2 = - Л (cos х, + gX sin тг) + ¦$?) + f ф) + ... J (4'183)
После подстановки выражений (4.183) в формулы (4.182)
получим:
Рх = 2р1ШМ-| v^X+ 4 vJ/СЛЗ (ftu+*u)-|- 5ЛЗ (Сп + cn)t
р2 = - 2/^ М -1 \КА -1 v3/C ЛЗ (ft21 + Ь22) +
+ |-SA»(c2I + Cj4).
Q2 = — 2р,?ха>2Л _ р^ Л — -^ ^KA^gb^x •+-
+ ^5Л8гх(Си + Зся).

324 устойчивость упругих тел в потоке газа [гл. 4
Первое из условий периодичности (4.181) для случая
g2 <^ 1 примет вид
-± v,tf Л + |^Л» (Ьп + Ьа - Ь21 - Ь22) +
~~г~ "4" SA (^21 I ^22 ^11 — ^12) == О-
Отсюда амплитуда первого приближения
Л = !|/ЕЖ", (4.184)
где использованы обозначения (4.163). Первая поправка
к частоте рх определяется из второго условия
периодичности (4.181).
Необходимо отметить, что коэффициенты при
квадратичных членах не вошли в формулу (4.184). Это значит, что
в первом приближении они не влияют на амплитуду
установившегося флаттера вблизи границы устойчивости.
§ 4.18. Анализ результатов
Проанализируем формулу (4.184) с точки зрения
поведения системы вблизи границы флаттера. Если dA/dv > 0 при
v ^ v*> т0 эт0 значит, что имеет место «мягкое»
возбуждение. Если же при v > v^ действительные значения А
отсутствуют, а при v ^ v^ выполняется неравенство dA/dv < 0, то
это соответствует «жесткому» возбуждению флаттера.
Решение, для которого dA/dv < 0, является, по-видимому,
неустойчивым: оно имеет смысл лишь как своего рода
«водораздел», отделяющий область притяжения устойчивости
тривиального решения (А = 0).
Используя обозначения (4.164), можно формулу (4.184)
записать в виде, аналогичном (4.165):
*=**у ^щ ¦ (4Л85)
Формулы дают результаты, тем более близкие, чем ближе v
к v^. Хотя формула (4.165) дана без строгого обоснования,

§ 4.18]
АНАЛИЗ РЕЗУЛЬТАТОВ
325
но границы ее применения, по-видимому, шире. Другая
редакция формулы (4.185) имеет вид
А=Ао у ^-iky • (4Л86)
где
и и, о ш1
м = - - м
* 4 h К '
_дУ Sc0
~~ьУ KbQ
Ло~ 3V Sc0 T '
(4.187)
Возбуждение флаттера, очевидно, будет «мягким», если
М^ > М^ и жестким, если М^ < Ж^.
Произведем вычисления для квадратной плоской панели
при у-= 0,25, х=1,4, Рх — Ру = 0 и двух крайних
предположениях относительно жесткости подкрепляющей
конструкции. Если со стороны конструкции не оказывается никакого
сопротивления сближению кромок, то это соответствует
случаю, когда сх = су = 0, т. е., как вытекает из формул (4.153),
$x=$yz=0. Другое крайнее предположение—это случай
абсолютно жесткой подкрепляющей конструкции. Если сх->оо,
су -> оо, то, как видно из формул (4.153), фх = (Зу = 1. Этими
двумя случаями мы и ограничимся, называя первый из них
условно случаем абсолютно податливого стержневого набора,
второй — случаем абсолютно жесткого стержневого набора*).
Для абсолютно податливого стержневого набора
вычисление по формулам (4.157) дает сп = 2,00, с12 — с21 = 11,24,
с22— 17,00 и, следовательно, с0— 15,00. Для абсолютно
жесткого набора по формулам (4.157) находим, что си = 7,34,
с12 = с21 = 24,44, ?22 = 57,50, откуда с0 = 50,16. Далее,
учитывая, что bn — b21 = 0,59, b12=—3,04, ft22 = 3,72,
получим, что #0 = 6,76.
*) Упругие реакции могут возникать, разумеется, не только со
стороны стержневого набора, но и со стороны других стесняющих
деформацию панели элементов. Кроме того, здесь идет речь лишь
о жесткости подкрепляющей конструкции в тангенциальном
направлении; ее жесткость в нормальном направлении полагается все
время достаточно большой, чтобы панель можно было считать
опирающейся на жесткий контур.

326 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА [ГЛ. 4
Используя формулы (4.154), найдем, что
48(1-(х2) %р„/а\* . 3
К-
(х)4. *-!(¦-•).
Отсюда для стальной панели (? = 2 • 106 кг/см2, jj- = 0,3) при
р = 1 кг/см2, х— 1,4 получим:
/С = 32.7 (-^)4 , 5 = 0,
682
и, следовательно, по формулам
(4.187)
Af.=
mL =
ж^
^J=
= 0,48- 108
= 168
= 251
1.63.
(4)т
(If
А« =
(if-
>
»
= 0.89
(4.188)
(индекс I относится к случаю
свободно смещающихся
кромок, а индекс II — к случаю
несмещающихся кромок).
Числа Маха М„ ML и м"
в функции от /г/а отложены
Рис. 142. на рис. 142. «Жесткое»
возбуждение флаттера даже в
случае смещающихся кромок здесь возможно лишь при весьма
больших числах Маха. Напомним, что здесь, в отличие от
§ 4.16, рассматривается квадратная в плане панель,
испытывающая изгиб в двух направлениях, т. е. система,
обладающая достаточно большой геометрической нелинейностью.
На рис. 143 представлен график зависимости амплитуды
от превышения критического числа М^ для различных
отношений a/h. Он построен по формуле (4.165), имеющей более
широкие пределы применения, чем формула (4.185), которая
соответствует первому приближению по методу малого
параметра. Если мы переходим от абсолютно жесткого стержне-

§ 4.18] АНАЛИЗ РЕЗУЛЬТАТОВ 327
вого набора к абсолютно податливому, то это вызывает
увеличение амплитуд колебаний примерно в два раза. Реальные
краевые условия будут соответствовать некоторому
промежуточному случаю.
В заключение оценим порядок напряжений, возникающих
в панели при превышении критической скорости флаттера.
Вычислим величину
Eh
d2w
х~ 2{\ — ^2)\дх2
вдоль, прямой у = Ь/2. Замечая, что
Ь
, d2w\ . Nx
w
( о \ f • ъ* I f • %кх
__ n*Ehf* Г
~~ Д2 [
9/,/2
fif»
tzx
\\~+ Ц2)2 C0S ~~а ~ (9 + 4ср2)2
cos •
+" 8ср4
Й%ТТ[/? + 4/1 + иРу(/? + ^)]
8а«(1-^Р-гРу)

328 устойчивость упругих тел в потоке газа [гл. 4
и принимая во внимание формулы (4.183), получим:
тах^-^^^ + лад], (4.189)
где
2пх
ъх
Gx (х) = - (4 + W2) sin ^f- + (1 + !J?2) sin -f-,
5 ^ (5 + 2fxpy)
2W~ 8 + 8(l-fx^py)
9cp2 tijc , y4 Зкх
(l+4cp2)2 C0S^ Г-(9 + 4?2)2 C0S-^-
График функций Gj и G2 для случая cp=l, jx = 0,25
представлен на рис. 144. Максимальное значение функции,
0JS 0,75 W а
Рис. 144.
стоящей в квадратных скобках формулы (4.189), при не
слишком больших А, например при А ^ 3, мало отличается

§ 4.18] АНАЛИЗ РЕЗУЛЬТАТОВ 329
от ее значения при х = -т-а. Отсюда получаем весьма
простые формулы:
max ах^^~ (2,74Л + 0,99Л2),
max о" « ^- (2,74Л + 1,62Л2).
Зависимость напряжения от числа М при различных
отношениях h/a представлена на рис. 145. Сплошными линиями,
как и на предыдущих чертежах, показано изменение
напряжений в случае абсолютно податливого набора, штриховыми
линиями — в случае абсолютно жесткого набора. Как видно
Рис. 145.
и» рис. 145, даже довольно значительное превышение
критического числа М, определяемого методами линейной теории,
не приводит к чрезмерно большим напряжениям. Для панели
с отношением длины стороны к толщине, равным 250,
критическое число
Ж,^3,14.

330 УСТОЙЧИВОСТЬ УПРУГИХ ТЕЛ В ПОТОКЕ ГАЗА {ГЛ. 4
При М = 5 максимальные напряжения не превышают
2000 кг/см2 даже в самом неблагоприятном случае абсолютно
податливого набора.
В связи с этим возникает вопрос о возможности
кратковременного нахождения системы в области панельного флаттера
при условии, что усталостные повреждения не развиваются
в опасные трещины. Необходимо отметить, что кривые на
рис. 142 — 145 построены для частных данных, которые
приведены в тексте. При их построении не учитывалось
термическое выпучивание и температурные напряжения, которые
могут ухудшить условия работы панели.

ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ.
ПРЕДПОЛАГАЕМЫЕ НАПРАВЛЕНИЯ
ДАЛЬНЕЙШИХ ИССЛЕДОВАНИЙ
В книге был рассмотрен широкий класс
неконсервативных задач теории упругой устойчивости. Их
неконсервативный характер обусловлен специфической зависимостью сил,
действующих на упругую систему, от перемещений. Анализ
устойчивости приводит к необходимости исследовать
собственные значения несамосопряженных краевых задач;
конечномерным аналогом этих задач являются системы уравнений, матрицы
коэффициентов которых при обобщенных координатах содержат
антисимметричные составляющие. В этом заключается отличие
рассматриваемых задач от других задач, в которых силы
оказываются явно зависящими от времени, либо
автоколебательный характер которых обусловлен «отрицательным трением».
Исследование неконсервативных задач упругой
устойчивости тесно связано с теорией линейных несамосопряженных
дифференциальных операторов. Эта теория находится еще
в начальной стадии разработки. Необходимы эффективные
методы нахождения комплексных собственных значений
операторов, не уступающие существующим методам для
самосопряженных краевых задач, где решение облегчается благодаря
наличию соответствующих вариационных принципов. Нужны
методы исследования зависимости собственных значений от
одного или большего числа параметров; нужны методы,
позволяющие установить для несамосопряженного оператора с
действительными коэффициентами число собственных значений,
лежащих в некоторой заданной части комплексной плоскости
(например, в правой полуплоскости). Для задач упругой
устойчивости интерес представляют операторы четвертого и более
высокого порядков; существующее состояние теории пока еще
не дает оснований для оптимизма.

332
ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Наиболее эффективным методом решения неконсерватив-
ных задач упругой устойчивости является сведение к
системам с конечным числом степеней свободы путем представления
искомых функций в виде рядов, удовлетворяющих некоторым
условиям, и применения метода Галеркина. Для неоднократно
высказывавшихся сомнений в возможности применения метода
Галеркина к несамосопряженным задачам, по-видимому, не
было оснований. В частности, как было показано в настоящей
книге, известный парадокс в задаче о флаттере мембраны не
связан непосредственно с тем, что эта задача является
несамосопряженной. Тем не менее исследование условий
сходимости метода Галеркина для различных классов
несамосопряженных краевых задач представляет интерес.
Конечномерный аналог несамосопряженных краевых задач —
системы обыкновенных дифференциальных или алгебраических
уравнений, которые содержат циркуляционные или
псевдогироскопические члены (члены с обобщенными координатами,
матрицы которых антисимметричны), допускают элементарное
исследование. Однако общие свойства этих систем еще не
изучены исчерпывающе. Достаточно указать, что в классических
результатах Кельвина, относящихся к малым колебаниям
конечномерных систем около положения равновесия,
циркуляционные силы не нашли отражения. Некоторые результаты
были сформулированы недавно применительно к
гироскопическим системам, где малые циркуляционные добавки играют
роль корректирующих факторов.
Наибольший теоретический интерес представляет,
по-видимому, своеобразное влияние демпфирования в присутствии
псевдогироскопических сил и, особенно, расхождение между
результатами, относящимися к системам с исчезающе малым
затуханием и к системам, затухание в которых с самого
начала положено равным нулю. Здесь мы имеем ситуацию,
весьма близкую к ситуации в теории устойчивости
ламинарных течений (парадоксальное расхождение между параметрами
«вязкой» и «невязкой» неустойчивости). В настоящей книге была
обнаружена зависимость устойчивости при исчезающе малом
затухании от соотношения между парциальными коэффициентами
затухания и исследованы экстремальные свойства задачи при
отсутствии затухания. Эти интересные особенности нуждаются
в дальнейшем изучении и могут послужить эвристическим
основанием для получения других, более сильных результатов.

ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
333
В нелинейных задачах наиболее важным является
исследование ненулевых решений вблизи критических значений
параметров, соответствующих пересечению собственными
значениями мнимой оси. Метод малого параметра, как было
показано, служит вполне эффективным средством для решения
этой задачи. Характер решений (в физических терминах —
«мягкое» или «жесткое» возбуждение) существенно зависит
от свойств нелинейной составляющей оператора. Представляет
интерес получение результатов, аналогичных известным
результатам, относящимся к поведению собственных функций
нелинейного самосопряженного оператора вблизи точки бифуркации.
До сих пор говорилось о теоретических аспектах,
связанных с изучением неконсервативных задач упругой
устойчивости. Переходя к практическим аспектам, начнем с задач
об устойчивости равновесия упругих систем при наличии
«следящих» сил.
Следует отметить, что появление большинства работ,
посвященных этим задачам, не было связано с какими-либо
практическими целями. Именно поэтому неконсервативный
характер «следящих» сил оказался в некоторых работах
нераскрытым, что явилось источником недоразумений. Среди
сил, встречающихся в технических приложениях, силы,
которые создаются давлением или реакцией струи, ближе всего по
характеру к «следящим» силам (если, разумеется, движение
упругой системы является достаточно медленным по сравнению
с течением газа, чтобы инерционной и демпфирующей
составляющими струи можно было пренебречь). Условия, близкие
к загружению стержня тангенциальной силой или
тангенциальным моментом, можно осуществить, например, располагая
на нем соответствующим образом сопла. Нет сомнения, что
«следящие» силы могут играть определенную роль в
реактивных и ракетных установках, турбомашинах и т. п.
Основное направление исследования в этой области должно, на наш
взгляд, состоять не в увеличении числа решенных чисто
академических задач, а в выяснении вопроса, насколько
удовлетворительно «следящие» силы схематизируют силы,
действующие в реальных установках. Здесь необходимы в первую
очередь экспериментальные исследования.
В задачах об устойчивости прямолинейной формы гибкого
ротора с учетом внутреннего трения, гидродинамического
трения в масляном слое и других родственных факторов

334
ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
неконсервативный характер обусловлен наличием
регулируемого двигателя, поддерживающего постоянное число
оборотов. При малых смещениях ротора указанные выше
факторы порождают силы, которые направлены по нормали
к смещению. В уравнениях возмущенного движения эти силы
учитываются при помощи членов с обобщенными
перемещениями и антисимметричной матрицей коэффициентов.
Аналогия с другими неконсервативными задачами упругой
устойчивости сохраняется и в том случае, когда сечения вала
имеют неодинаковые главные изгибные жесткости.
В первую очередь необходимо уточнить выражение для
сил, обусловливающих передачу энергии в задачах такого
типа. Это относится не только к гистерезису в материале
вала или к трению в зажимах, но в большей степени к
гидродинамическим силам, возникающим в слоях жидкости,
которая частично увлекается ротором. Исследование явлений
неустойчивости, обусловленных трением в масляном слое
подшипников, представляет собой едва ли не самую важную
задачу из числа задач рассматриваемого типа. Наряду с
экспериментальными исследованиями в этой задаче необходимо
также построение безупречной гидродинамической картины
явления. В данной книге было показано, что различные
предположения о характере нелинейных составляющих сил
приводят к большому разнообразию результатов. Поскольку
явления неустойчивости не всегда могут быть полностью
подавлены, то представляет большой интерес дальнейшее
исследование нелинейной задачи.
Задачи устойчивости упругих пластин и оболочек в потоке
газа были рассмотрены в настоящей книге наиболее подробно.
Большой практический интерес представляет исследование
устойчивости термически выпученных панелей, а также
исследование устойчивости с учетом реальных законов для
конструкционного демпфирования. Как известно, учет
демпфирования совершенно необходим в задачах с кратными или
достаточно близкими парциальными частотами. Такую
ситуацию мы имеем в удлиненных вдоль потока плоских панелях
при наличии сжимающих сил, в замкнутых цилиндрических
оболочках, где спектр парциальных частот довольно густ,
и в ряде других задач.
Благодаря подкупающей простоте выражения для
аэродинамических сил, которые дает «поршневая теория», коли-

ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
335
чество публикаций, основанных на ее использовании, быстро
растет. Нижняя и верхняя границы для применения
«поршневой теории» должны быть установлены более надежно.
Поэтому нужны дальнейшие исследования аэроупругих задач
в области умеренных сверхзвуковых скоростей с
использованием более точных аэродинамических зависимостей. Наряду
с числовым сопоставлением результатов должны быть
предприняты попытки получения решений, соответствующих
«поршневой теории», путем предельного перехода из более
точных решений. В данной книге на примере точного
решения задачи об устойчивости цилиндрической оболочки в
потенциальном потоке газа было показано, что такой предельный
переход позволяет обнаружить некоторые дополнительные
условия применения «поршневой теории». Наряду с этим
необходимы исследования аэроупругих задач в области
высоких сверхзвуковых скоростей с учетом явлений,
происходящих в пограничном слое.
Как было показано в настоящей книге, возбуждение
флаттера панелей из-за преобладающей геометрической
нелинейности носит преимущественно «мягкий» характер. Это
означает, что попадание системы в область флаттера не
означает немедленного разрушения обшивки: оно наступает спустя
некоторое количество циклов и носит усталостный характер.
Поэтому в отличие от классической задачи о флаттере крыла,
где возбуждение является «жестким», здесь исследование
нелинейной задачи приобретает практический смысл. В этом
направлении нужны дальнейшие исследования. В частности,
большой интерес представляет изучение нестационарных
явлений, связанных с прохождением через флаттерную область.
Этот вопрос должен рассматриваться совместно с проблемой
накопления повреждений в конструкции.

ИМЕННОЙ УКАЗАТЕЛЬ
Андронов А. А 183
Бам-Зеликович Г. М. 252
Баутин Н. Н. 283
Бек (Beck M) 13, 96, 100, 13S
Беллман (Bellman R ) 48
Беспалько Л. А. 152
Бидерман В. Л. 131
Бисплингофф Р. Л. (Bisplinghoff R. L )
13 213 272
Бицено К.' Б. (Biezeno С В ) 156
Боккер (Bocker G F.) 154
Болотин В. В. 12, 13, 61, 70, 77, 88,
96, 97, 114, 153, 169, 174, 177, 182,
214, 215, 228, 240, 244, 262, 273. 281,
306, 308
Будянский (Budiansky В ) 213
Бунимович А. И 252
Власов В 3 115
Вольмир А. С. 10
Гаврилов Ю. В. 8, 13, 215, 308
Галимов К. 3. 34
Голанд (Goland M ) 213, 222, 250
Гольденблат И. И 32
Гопак К. Н 96, 128
Граммель Р (Grammel R ) 156
Гроссман Е. П. 213
Данкен (Dunkan W J ) 213
Дейнеко К. С. 12, 96, 100, 101
Джанелидзе Г. Ю 12, 94, 96, 114
Джонс (Johns В J ) 264
Диментберг Ф М 13, 153, 161, 168, 172
Епишев Л. В. 8, 154, 204
Зартарьян (Zartarian С ) 214, 252,
272
Зинер (Zener С ) 189
Ильюшин А А 214, 252, 255
Ишлинский А Ю. 17
Каннингхэм (Cunningham H J ) 214,
246, 250
Канторович Л. В 278
Капица П. Л. 13, 153
Каппус P. (Kappus R ) 37
Карпович Е. А. 223
Келдыш М. В. 213
Кимбалл (Kimball A L ) 151, 157
Кононенко В. О. 156
Копейкин Ю. Д. 96
Кочин Н. Е. 41
Кривошеева С. Г. 96, 128
Крылов В. И 278
Кушуль М. Я. 152
Кюснер (Kussner H. J.) 213
Лаврентьев М. А. 213
Лайтхилл (Lighthill M. J ) 214, 252,
256
Ландау Л Д. 76
Леонард (Leonard R W) 214
Леонов М Я 12, 96, 100, 101, 152
Ливанов К. И. 263
Лившиц И М 76
Лихарев К К 131
Лурье А И 8
Льюис (Lewis J F ) 154, 202
Люк (Luke Y L ) 213, 222, 250
Ляпунов А М 48
Майлс (Miles J W ) 214, 249
Макаров Б П 8, 13, 215, 308
Макушин В. М 131, 139
Малашенко С. В 17
Малинин Н Н 131
Махортых Ж. К. 215
Мейман Н. С. 243
Меркин Д Р. 78, 83
Микишев Г Н. 215
Михайлова М П. 252
Михлин С Г 55
Мишенков Г. В 8
Мовчан А А 13, 214, 259, 262, 270
Морган (Morgan H J ) 256
Моррис Дж (Morris J ) 12, 94
Мурнаган (Mournaghan F ) 32
Наймарк М. А. 55
Наймарк Ю. И. 183
Нариманов Г. С. 207
Нельсон (Nelson H С.) 214, 246, 250
Николаи Б. Л. 12, 95, ПО, 112
Николаи Е. Л. 11, 12, 93, 94, 139, 140,
152
Новожилов В В 30, 37
Ньюкирк (Newkirk В. L ) 154, 173,
202

ИМЕННОЙ УКАЗАТЕЛЬ
337
Обморшев Н. А. 78
Пановко Я. Г. 162
Позняк Э. Л. 8, 112, 153, 154, 166, 197,
208
Пономарев С. Д. 131
Порицкий (Poritsky H ) 154
Пуанкаре (Poincare H ) 49
Пфлюгер (Pfluger A ) 13, 16, 51, 96, 101
Раньян (Runiyan H. L ) 256
Раушер (Rauscher M.) 213
Рейсснер (Reissner H.) 212
Реут В. И. 12, 95
Робертсон (Robertson D.) 152
Рокар (Rocard N ) 13
Смит (Smith D М.) 152, 161
Сорокин Е С. 162
Степанов Р. Д. 262
Стьюартсон (Stewartson К) 207
Темченко М. Е. 17
Теодорсен (Theodorsen T ) 213
Треффц (Trefftz E.) 34
Треш (Troesch A.) 13, 95, 147
Тэйлор (Taylor N. D ) 154
Феодосьев В. И. 16, 95, 96, 128, 131
Ферри (Ferri A ) 252
Франкль Ф. И. 223
Фрейзер (Frazer R. А) 213
Фын (Fung Y. С.) 213, 216, 262
Хаккель (Huckel V.) 256
Халфмэн (Halfman R.) 13, 213, 272
Хеджпет (Hedgepeth J. M) 13, 213,
214, 215, 249, 262
Хейс (Hayes W. D ) 214, 252
Хори (Hori Y) 203
Хофф (Hoff N ) 13
Хэгг (Hagg А. С ) 154
Циглер (Ziegler H) 11, 12, 13, 78,
88, 94, 95, 97, 138, 139
Чаевский М. И 152, 153
Чеботарев Н Г. 243
Черный Г. Г. 252
Четаев Н. Г. 48
Шашков И Е 12, 94, 139
Швейко Ю. Ю. 8, 13, 215, 308
Шен (Shen S ) 216
Шенли (Shanley F.) 10
Штернлихт (Sternlicht В ) 154
Эйлер Л. 9
Эшли (Ashley H ) 13, 213, 214, 252,
272

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоколебания гибкого вала 153
Амплитуды установившегося
панельного флаттера 326
— установившейся асинхронной
прецессии 181
Аэроупругости теория 212
Валы гибкие 25, 150
Векторы координатные 65
Взаимодействие степеней свободы
парное 23, 274
Возбуждение «мягкое» 283, 313
— «жесткое» 283, 313
Возмущения малые 49
Дивергенция крыла 212
Задача нелинейная о колебаниях
гибкого вала 173
Задачи краевые несамосопряженные
27
самосопряженные 55
— нелинейные в теории
аэроупругости 280
«Закон плоских сечений» в
аэродинамике 214, 251
Затухание исчезающе малое 81
—, влияние на устойчивость
пластинок в потоке газа 265
Значения критические 62
— собственные 61
Индексы «немые» 32
Критерий Рауса — Гурвица 243
Координаты криволинейные 41
Маятник двойной 88
Метод динамический 11, 17, 22, 61
— Галеркина 64
— малого параметра 317
— малых колебаний 11, 142
— Эйлера 9, 17, 22, 61
Момент аксиальный 140
— квазитангенциальный 138
— полутангенциальный 138
— псевдотангенциальный 138
— тангенциальный 93, 139
Нагрузка гидростатическая 59
— «мертвая» 52
— «следящая» 52
Нелинейность аэродинамическая 281
Неустойчивость гибкого вала,
вызванная внутренним трением 157
— колебательная 63
— статическая 63
Оболочка пологая 289
— тонкая 59, 70
— упругая цилиндрическая 228
Парабола устойчивости 148, 259
Парадокс в задаче о флаттере
мембраны 272
— Николаи 94
Пластинка тонкая 70
—, устойчивость в потенциальном
потоке 245
— при больших сверхзвуковых
скоростях 257
Пленка масляная, ее влияние на
устойчивость валов 200
Плоская форма изгиба 114, 126
Показатели характеристические 62
Поле магнитное, его влияние на
устойчивость роторов 208
Потенциал внешних сил 22, 57, 64
Прецессия асинхронная 179
— синхронная 166
Принцип возможных перемещений 35
Размерность тензорная 42
Сила критическая 9
— с фиксированной линией действия
ПО
Силы диссипативные, их влияние на
устойчивость 81, 86, 108
— консервативные в целом 58
, их влияние на устойчивость 85,
112
Силы потенциальные 78
— псевдогироскопические 78
— радиальной коррекции 78
— следящие 65
— существенно непотенциальные 78
Система с двумя степенями свободы
81
Скорость критическая верхняя 284
гибкого вала 150
дивергенции 26
для оболочки 237
— *- нижняя 284

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
339
Скорость критическая флаттера 26
для оболочки 237
Скорость фазовая распространения
упругих волн в оболочке 232
Составляющие тензора физические
42
Способ описания Лагранжа 33
Эйлера 32
Стержень сжатый 69
и скрученный 130
тангенциальной силой 97
, влияние способа
распределения массы 101
Тензор конечных деформаций 33
— метрический 42
Теория «поршневая» 214
Точки предельные 17, 183
— разветвления 17, 182
Трение внешнее 158
—¦ вязкое внутреннее 158
—, не зависящее от скорости 162
—, обусловленное макроскопической
тепловой диффузией 189
— при тугой посадке деталей на вал
197
Уравнения в вариациях 49
— равновесия в теории упругости 31,
34, 46
Условия излучения 231
Устойчивость «в большом» 173, 187
— плоской формы изгиба 72
— по Ляпунову 48
— упругих тел в потоке газа 222
— упругой цилиндрической оболочки
в потоке газа 228
Флаттер крыла 212, 216
— нелинейный 215
плоской панели 306
— панельный 26, 213
— пологой оболочки 289
Форма равновесия асимптотически
устойчивая 48
неустойчивая 17, 48
устойчивая 17, 48
Функции координатные 65
Центрифуги, их устойчивость 204
Эйлера метод 9, 61
Энергия внутренняя 35

Болотин Владимир Васильевич
Неконсервативные задачи
теории упругой устойчивости
Редактор И. К. Снитко
Техн. редактор Е. А. Ермакова
Корректор О. А. Бутусова
Сдано в набор 30/Ш 1961 г. Подписано к
печати 11/VIII 1961 г. Бумага 84х108/3?. Физ.
печ. л. 10,625. Условн. печ. л. 17.43. Уч.-изд.
л. 16,84. Тираж 7 000 экз. Т-09Э39. Цена
книги 1 р. 04 к. Заказ № 2390.
Государственное издательство
физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Типография № 2 им. Евг Соколовой УПЛ
Ленсовнархоза. Ленинград,
Измайловский пр., 29.